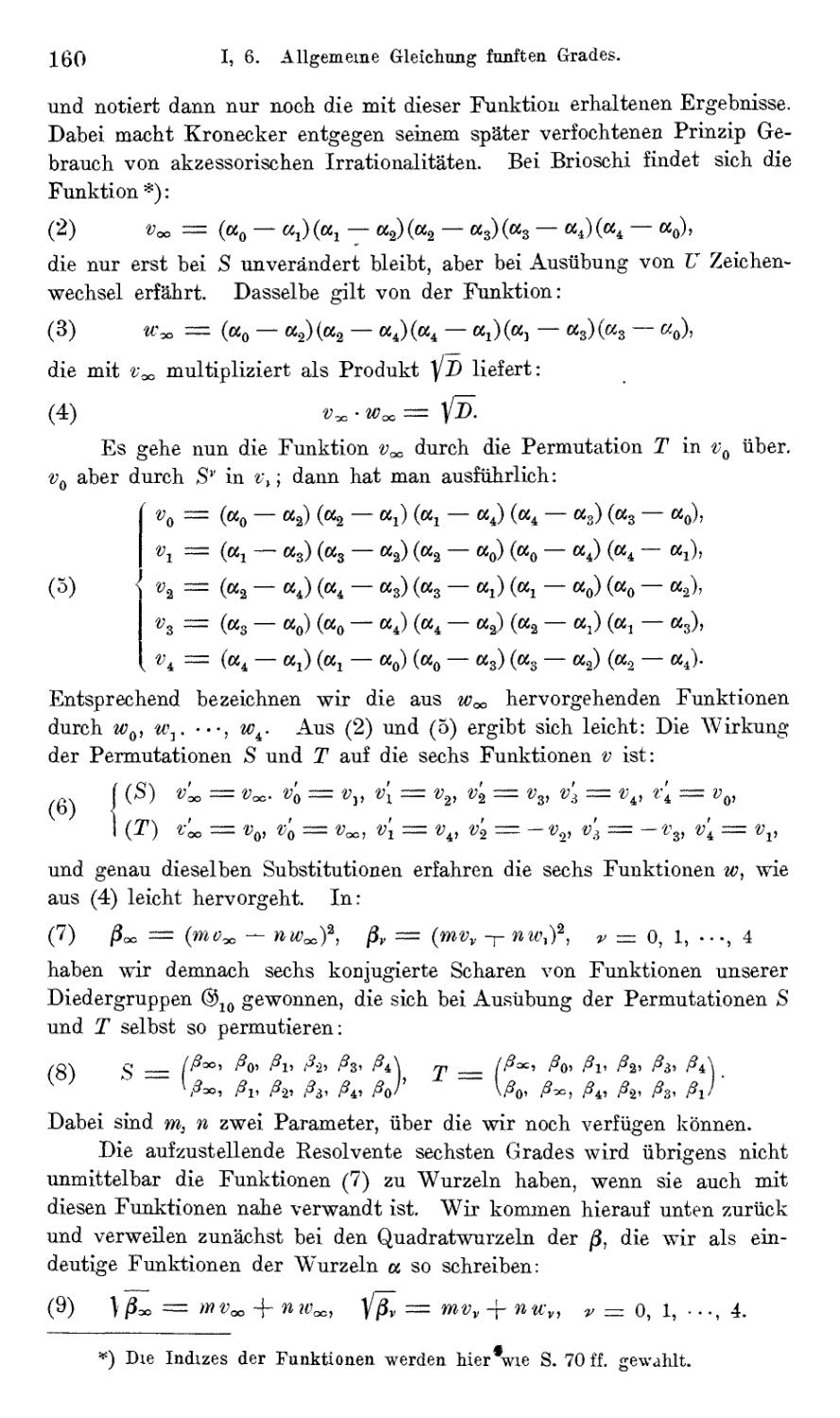Текст
Robert Fricke
Lehrbuch der Algebra
verfaßt mit Benytzung
von Heinrich Webers glei<?hnamigem Buche
Zweiter Band:
Ausführungen über Gleichungen niederen Grades
Mit 33 in den Text gedruckten Figuren
Braunschweig
Druck und Verlag von Friedr. Vieweg & Sphn Akt.*Ges.
1926
/^BTT^LIOTHBCA^
IKEGIA ACADEIV
GEOEGIAE
AUG.
c
Alle Rechte vorbehalten
^
Vorwort.
Einige kurze Angaben über den Gesa^itplaa meines
Algebrawerkes findet man im Vorwort 2ram ersteji vor zwei Jahren
erschienenen Bande. Diesem Plane entsprechend behandelt der zweite
nun zur Ausgabe gelangende Band die niedersten nicht mehr
metazyklischen und also nicht mehr algebraisch lösbaren Gleichungen.
Es handelt sich um die in den letzten sieben Jahrzehnten entstandenen
Theorien der Gleichungen fünften, secl^sten und siebenter^ Grades.
Die hier gebotene Darstellung ist wesentlicji durch den Grundsatz
beherrscht, die das Gebiet der Algebra übersteigenden, also
transzendenten Hüfsmittel der Gleichui^gslösung klar von dem
algebraischen Teile der einzelnen Theorie ziu sondern und die Notwendigkeit
des transzendenten Teiles darzutun. Es ist nicht so, daß das
Eingreifen der elliptischen Modulfunktioneu in den Lösungsprozeß der
allgemeinen Gleichung fünften Grades als eine der Aigebrs-
fremdartige, vereinzelt dastehende Entwicklung anzusehen ist. Vielmehr
hat man allemal die „algebraische" ]Pntwicklu3ig biß zur Formuliening
des einfachsten jeweils zugrunde liegenden „Normalproblem's" zu
treiben, dieses letztere dann aber durch die naturgemäß dem
Normalproblem als verwandt zugehörigen automoi-phen Funktionen auf
„transzendentem" Wege zu lösen. Darüber hinaus Jiabe ich der
transzendenten Theorie auch schon hei der „ßegründung" der
algebraischen Entwicklungen eine Rolle zugewiesen. Kein anderer Weg
eröffnet uns so schnell und tief den Eingang in die algebraische
Seite der einzelnen Theorie; das Beispiel der Valentinergruppe dürfte
in dieser Hiosicht überzeugend wirken.
Auch beim vorliegenden zwßiten Bande ha]be ich Webers Namen
mit in den Titel des Buches aufgenommen- Ich darf zuy Begründung
dieses Vorgehens darauf hinweisen, da,ß der Gedankengang des letzten,
zum Teil auch des vorletzten Kapitels, die beide freilich mit den übrigen
Teilen des Bandes nur in losereni Zusammenhang stehen,
entsprechend dem Vorbilde des Weber gehen Werkes gestaltet ist. Auch
bei eänigeaa Erörterungen im Kapitel über die allgemeine Gleichung
fünften Grades habe ich das Webersche Werk benutzen können. In
den beiden ersten Abschnitten aber habe ich in ausgedehntestem
Maße die Grundgedanken der algebraischen Forschungen meines
verewigten Lehrers und lieben Freundes Felix Klein zur Geltung
gebracht. Ich habe ihm während der Entstehung des vorliegenden
Bandes noch über die vielfältig neuen und überraschenden Wendungen,
die die Entwicklung annahm, regelmäßig Bericht erstatten können.
Stets unvergessen wird mir mein letztes Zusammensein mit ihm
bleiben. Bei der Rückkehr von der Darmstädter Hochschultagung
im Januar 1925 durfte ich eine Stunde an seinem Krankenbette
weilen und konnte ihm über den Abschluß meiner Untersuchung
über die allgemeine Gleichung sechsten Grades berichten. Voll
Freude und mit dem lebhaftesten Interesse nahm er meinen Bericht
entgegen, und sein lebendiger Geist ließ das Siechtum des Kö^^pers
fast vöUig vergessen. Es war eine glückliche Fügung meines Lebens,
daß ich in jungen Jahren in Feüx Klein den begeisternden Führer
fand, und daß ich alle die Jahrzehnte lang ihm wissenschaftlich und
persönlich so nahe treten durfte. Er ist mir stets ein leuchtendes
Vorbild gewesen, und ich schließe mit dem Wunsche, daß auch
dieses Buch Zeugnis von der Dankbarkeit ablegen möge, die ich
stets für ihn empfunden habe.
Bad Harzburg, den 25. April 1926.
Robert Fricke.
Inhaltsverzeichnis.
Seit^
Einleitung L
Erster Ätfsclii^itt.
Endliche Gruppen binärer Substitutionein und Gleichungen
fünften tirades.
Erstes Kapitel. Einleitende ^ätze über Gruppen
linearer Substitutionen.
§ 1. Erklärung und Zusammensetzung linearer Subst;itutionen
§ 2. Pole und charakteristische Grleichung einer Substitution
§ 3. Normalgestalt einer linearen Substitution
§ 4. Endliche Gruppen linearer Substitutionen
§ 5. Invarianten endlicher Gruppen @^
§ 6. Existenz und Darstellung der Invarianten einer @^
§ 7. Pormenproblem einer endlichen Gruppe @^
Zweites Kapitel. Polyedergruppen.
5 1. Einteilung der linearen Substitutionen eiper Variablen '34
5 2. Veranschaulichung der linearen Substitutionen einer Variablen .... 26
5 3. Projektion der 2-Ebene auf eipe Kn.gelfläche 29
5 4. Diophantische Gleichung fur die Grupper^ @^ 32
5 5. Existenz der endlichen Gruppen @ 35
j 6. Normalgestalt der Ikosaedergruppe 41
j 7. Erweiterte Polyedergruppen ^3
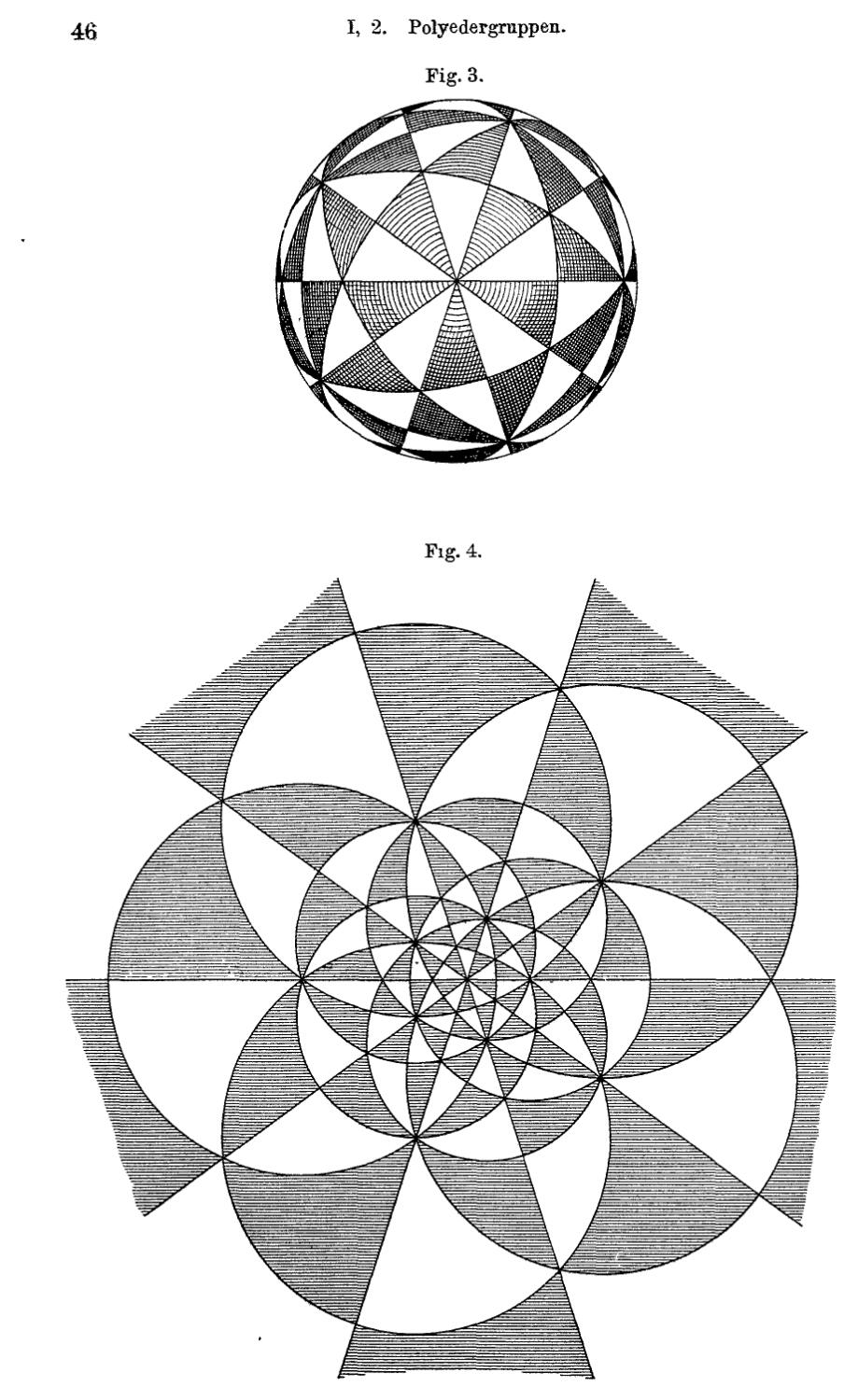
j 8. Diskontinuitatsbereich einer Gruppe 47
j 9. Homogene Polyedergruppen 50
Drittes Kapitel. IkosaedergHeichi^ng ufld ihre Reisolveflten.
5 1. Invarianten der Ikosaedergruppe 52
5 2. Pormenproblem der Ikosaedergruppe 55
5 3. Eesolvente fünften Grades der Ikosaedergleichpng 58
5 4. Weitere Gestalten der Eesolvente fünftei^i Grades 62
5 5. Diskriminanten der Eesolventen fünften Grades 66
5 6. Eesolvente sechsten Grades der Ikosaedergleichung 69
17. Diskriminante der Eesolvente sechsten Grades 72
j 8. Beziehung zwischen den beiden Eesolventen fü^iften und sechsten Grades 74
fl Inhaltsverzeichnis.
Seite
Viertes Kapitel. Transzendente Lösung der Ikosaedergleichung.
\ 1. EiHführang der Modulgruppe ® 76
; 2. Dreiecksnetz und DB der Modulgruppe 79
; 3. ModHlfunktiou J(eo) 84
( 4. ifodulformen g^, g^ und ^ 85
) 5. Formenproblem der Modulgruppe 89
f 6. HauptkoHgruenzgruppe fünfter Stufe 91
( 7. Modulfunktionen fünfter Stufe 94
; 8. Transzendente Lösung der Ikosaedergleichung und ihrer Eesolventen 98
Fünftes Kapitel. Bring sehe Gleichung fünften Grades.
\ 1. Einführung einer neuen unendlichen Gruppe 100
\ 2. Funktionen der Gruppe @<^^^ 103
5 3, Hauptkongruenzgruppe fünfter Stufe 107
\ 4. DB der Hauptkongruenzgruppe fünfter Stufe 109
} 5. Bringsche Gleichung fünften Grades 113
; 6. Transzendente Lösung der Bringschen Gleichung 116
} 7. Galois scher Körper der Bringschen Gleichung 119
; 8. Bringsehe Kurve in Tetraederkoordinaten 122
5 9. Parameterdarstellung der Bringschen Kurve 124
5 10. Eesolvente sechsten Grades der Bringschen Gleichung 127
5 11. Beziehung der Eesolvente sechsten Grad«s zur Bringschen Kurve . . 129
5 12. Beziehung der Bringschen Gleichung zur Eesolvente fünften Grades
der Ikosaedergleichung 132
5 13. Beziehung zwischen den beiden Eesolventen sechsten Grades .... 135
Sechstes Kapitel. Allgemeine Gleichung fünften Grades.
5 1. Allgemeine Gleichting und Hauptgleichnng fünften Grades 138
5 2. Zwei Scharen von Hauptgleichungen als Eesolventen 141
5 3. Bringsche Gleichung als Eesolvente der allgemeinen Gleichung fünften
Grades ^ 146
5 4. Diagonalgleichnng fünften Grades mit einem Parameter 148
g 5. Allgemeine Gleichung fünften Grades und PartiaJresolventen der
Ikosaedergleichung 152
§ 6. Ikosaedergleichung als Eesolvente der allgemeinen Gleichung fünften
Grades 153
§ 7. Schar der Hauptresolventen 156
I 8. Zweiter Weg von der allgemeinen Gleichung zum Ikosaeder .... 159
§ 9. Pormensystem der temäien Ikosaedergruppe 164
I 10. Jacobische Gleichung sechsten Grades 169
§ 11. Aufstellung einiger Hilfssätze 171
§ 12. Eesolventen mit einem Parameter 176
§ 13. Satz von Kronecker 179
Zweiter Abschnitt,
Endliche Gruppen ternärer Substitutionen und zugehörige
Gleichungen.
Erstes Kapitel. Klein sehe Gruppe und zugehörige invariante Formen.
§ 1, Kongruenzgruppen siebenter Stufe in der Modulgruppe 182
§ 2. Erklärung der Kleiuschen Gruppe 188
§ 3, Darstellung der Kleiuschen Gruppe in oktaedrischen Koordinaten, . 189
lahalt^verz^iehnis. VII
Seite
4. Geometrische Sätze über die Kollineation^gruppe ©igg 194
5. Darstellung der Klein sehen Gruppe in Wendedjfeieckpkoordinatep . . 196
6. Zwei Systeme von quadratischen Oktaedeyfonn«n 201
7. System der Invarianten der Klein sehen Qruppe . . ' 203
8. Invarianten der Klein sehen Gruppe in oktaedrischen Koordinaten . . 208
9. System der acht Wendedreiecke 210
Zweites Kapitel. Formenprolflem der Kleins^hen Gruppe
und Gleichungen siebenten Grades.
1. Ansatz des Formenproblems nnd Resolvente siebenten Grades .... 211
2. Spezielle Resolventen siebenteii Grawes 212
3. Eesolvente achten Grades 218
4. Allgemeine Gleichung siebenten Grades mit Galoisscjier Gruppe ©^gs ^22
5. Zurückführung der Gleichung siebenten Grades £),uJ d^s Formenproblem
der Kleiaschen Gruppe 226
6. Lösung der speziellen Formenprobleme der Kleyi sehen Gruppe . . . 231
7. Lösung des allgemeinen Forme^probl^ems der Klein sehen Qmppe . . 235
Drittes Kapitel. Valentinergruppe un(d zugehörige invariante Formen.
j 1. Einführung einer neuen unendlichen Substitutionsgruppe 241
j 2. Dreiecksnetz und DB der Gruppe @ 243
\ 3. Hauptkongruenzgruppe dritter Stufe in der Gruppe @ 246
j 4. Zyklische und verwandte Teiler der Gruppe ©ggo 249
\ 5. Tetraeder-, Oktaeder- und Ikosaedergruppen in der ©ggo 253
\ 6. Kongruenzgruppen vom Index 6 und zugejiörige Gleichungen sechsten
Grades 255
j 7. Galois scher Körper der Gleichungen sechsten Grades 258
\ 8. Herstellung der Valentinergruppe 263
\ 9. Invariante sechsten Grades. Erweiterung der ©ggo 268
\ 10. Zwei Systeme von je sechs Ika^aederformen 271
\ 11. Zwei Systeme von je 15 Oktaederiormen 276
} 12. Formensystem der Valentinergruppe 279
} 13. Neue Auswahl des Formensystems der Valentinergruppe 284
\ 14. Gebrauch der ikosaedrischen Koordin3,ten 286
\ 15. Gebrauch der kanonischen Koordinaten 289
Viertes Kapitel. Formenproblem der Valentinergruppe und
allgemeine Gleichung sechs^ten Grades,
§ 1. Formen problem der Valentinergruppe und Eesolvente sechsten Gifades 295
§ 2. Spezielle Eesolventen sechsten Grades 298
§ 3. Notizen über die allgemeine Gleichung sechsten Grades 299
§ 4. Herstellung »einer Klein sehen Bilinearform 302
§ 5. Zurückführung der allgemeineii Gleichung secjisten Grades auf das
Formenproblem der Valentinergruppe 308
§ 6. Lösung des Foxmenproblems der Valentinergruppe 311
§ 7. Theorem von. Wiman 314
§ 8. Quatemäre Kollineationsgruppe für di^ allgemeine Gleichung siebenten
Grades 321
§ 9. Bericht über weitere Untersuchungen 326
ITIJI Inhaltsv^rzeiclmis.
Dritter Abschnitt.
aeometrische Anwendungeii der Gnippentheorie.
Erstes Kapitel. Wendepunkte ebener Kurven dritten Grades. Seite
§ 1. Kovarianten der ternären kubischen Form 330
§ 2. Wendepunkte der ebenen Kurve dritten Grades 333
§ 3. Das singulare Koordinatensystem der Kurve dritten Grades 335
§ 4. Kollineationsgruppen bei der ebenen Kurve dritten Grades 337
§ 5. Das kanonische Koordinatensystem bei der Kurve dritten Grades . . 340
§ 6. Berechnung der Wendepunkte in kanonischen Koordinaten „ . . . . 343
§ 7. Beziehung zu den elliptischen Funktionen 344
§ 8. Begriff einer Tripelgleichung neunten Grades 347
§ 9. Galoissehe Gruppe einer Tripelgleichung neunten Grades 349
§ 10. Ordnung und Struktur der Galois sehen Gruppe einer Tripelgleichung
neunten Grades 353
§ 11. Notizen über reelle Tripelgleichungen 355
Zweites Kapitel. Doppelfangenten ebener Kurven vierten Grades.
§ 1. Anzahl der Doppeltangenten einer ebenen Kurve vierten Grades . . 357
§ 2. Steiner sehe Komplexe von Doppeltangenten 363
§ 3, Tripel und Quadrupel von Doppeltangenten 367
§ 4. Paare und Tripel von Steiner sehen Komplexen 370
§ 5. Aronholdsche Siebensysteme 373
§ 6, Neue Bezeichnungen der Doppeltangenten nebst Folgerungen .... 375
§ 7. Sätze von Aronhold 382
§ 8, Galoissehe Gruppe der Doppeltangentengleichung 388
§ 9. Erzeugung der Galois sehen Gruppe der Doppeltangentengleichung . . 392
§ 10. Einfachheit der Gruppe der Doppeltangentengleichung 396
§ 11. Transitivität der Gruppe der Doppeltangentengleichung 400
§ 12. Eeaütät der Doppeltangenten bei reellen Kurven vierten Grades . . 4QI
§ 13. Existenzbeweis der vier Fälle reeller Doppeltangenten 409
Register 415
Einleitung.
Zufolge der Gralois sehen Gleichungstljeorie besitzt eine algebra,isclie
Gleichung mit einer Unbekannten in der Galdisschm Gruppe, die ihr
bei Zugrundelegung eines bestit^mten Zaijen- oder Fui^ktionenkörperS
zukommt, ein für den Auflösungsprozeß der Grleichung wichtiges Attribut
[vgl. I, 372ff.*)]. Will man den|.nach ein Einteilungsprinzip für die mit
der Auflösung der Grieichungen im Zusammenhang stehenden Probleme
aufstellen, so erscheint es richtiger, statt nach dem Grrade n der (jrleichung,
vielmehr nach der Ordnung m de;- Galois sehen Gruppe @^ anzuordnen.
Unter dem ersten Hundert der Ordnimgen m findet sich nun nach
I, 310 nur eine eiuzige Gruppe &^, 4ie nieht-metazyklisch ist, nä^nlich
die Gruppe ©g^, die durch die 60 geraden Vertauschuagen von fünf
Diagen gegeben ist. Diese „alternierende Permutationsgruppe fünften
Grades", aixf die sich die Galoissche Gruppe der „allgemeinen Gleichung
fünften Grades" nach AdjunktioijL der Quadratwurzel aus der Diskrimi-
nante reduziert, ist nach I, 308 n^it der „Ikosaedergruppe" @gj, isomorph.
Dieser Umstand liefert die Grundlage für die Behandjung der Gruppe @ ^
und der allgemeinen Gleichung vom fünften Grade, die im ersten
Abschnitt gegeben werde. Die Darstellung wird sich nach einem ersten
Kapitel über endliche Gruppen Hnearer Substitutionen insbesondere zvi den
endlichen Gruppen binärer Substitutionen wenden, wobei dann eben die
Ikosaedergruppe das Hauptinteresse in Anspruch nehmen wird.
Die beiden weiter folgenden einfachen nicW^metazyklischeu Gruppen
sind nach I, 310 eine @jgg und eine ©^gp, deren letztere als die ^.Iter-
nierende Permutationsgruppe secbsten Grades erklärt werden kann und
also zur Theorie der allgemeinen Gleichung secbsten Grades in derselben
Beziehung steht, wie die Ikosaedergruppe zu derjenigen der allgemeinen
Gleichung vom fünften Grade, ßeide Gruppen sind als solche teraärer
linearer Substitutionen darstellbar, ein Umstand, den wir im zweiten
Abschnitt wieder zur Grundlage für die Behaiidlung der algebraischen
Theorie der Gruppen @jgg und ©ggo benutzen werden.
Der dritte Abschnitt des vorliegenden zweiten Bandes wird einigen
algebraischen Problemen gewidmet sein, die der analytischen Geometrie
entstammen.
=") I, 372 bedeutet Bd. I, S. 37^.
Friclce, Algebra. II.
Erster Abschnitt.
Endliche Gruppen binärer Substitutionen
und Gleichungen S**'' Grades.
Erstes Kapitel.
Einleitende Sätze über Gruppen linearer
Substitutionen.
§ 1. Erklärung und Zusammensetzung linearer Substitutionen,
Die n koniplexen Variablen z^, z^, ■-•, s^ sollen einer durch S zu
bezeichnenden 'homogenen linearen Substitution:
unterworfen werden. Die Anzahl n der Variablen heißt die
„Dimension- der Substitution S. In den niedersten Fällen w =: 1, 2, S
und 4 spricht man von unären, Mnärcn, ternären und qiiaternären
Substitutionen. Die Koeffizienten unc sind beliebige komplexe Zahlen, ihre durch
a zu bezeichnende Matrix heißt die „Matrix'' der Substitution S und
deren Determinante D die „Determinante^ von S. Ist I> = 0, so heißt
S „Singular^, anderenfaüs „nicM-singulär''. Ist nichts weiter gesagt, so
gilt die Substitution als nicht-singulär*).
Sind nur die in der einen Diagonale der Matrix a stehenden
Elemente «n, «23, ••-, Unn von 0 verschieden, hat also S die Gestalt:
(2) z[ = «ij^i, 4 =^2-^3' •••' 4 = C!inn^n^
SO spricht man, von einer „miätiplikutiven Substitution^ und nennt Wj^j,
<^3ä» * • •? ^nn die „MultipKJcatoren'' von yS. Sind dabei insbesondere alle
Multiplikatoren einander gleich, so hat man eine „ÄhnlieMeitssuhstitution^:
(3) ^^ = a^j, ^jf^ = «■2^2> •"> 4 = a^n-
*) Ist jD = 0, so sind nach I, 72 die z'i, 4» • *' > .^^ linear abhängig.
Zusammensetzung linearer Substitutionen. 3
Ist hier endlich noch « = 1, so lieg^. die „identische Substitution- vor,
die mit Rücksicht auf ihr Verhalten bei Zusammensetzung der
Substitutionen durch das Symbol 1 bezeichnet wir^.
Man übe jetzt auf die in (1) berechneten /^, z'^^ ■■•, z'j^ eine zweite
Substitution 8' der Koeffizienten a[jc aus:
(4) 4-' =: «;-i/^ + c^-s^ + i- Ckn^'n, i = 1, 2, • • •, »
Dabei findet maa durch Eintragen der Aiisdröcke (1) der z'^, daJ3 auch
die neuen Variablen z'^, z'^^ •••, z'^ mit den ursprüngliche^i s^, s^, •••, s^
durch eine lineare Substitution S'':
(5) s'i = a'/i^i -f w'/o^2 -}-••■ -r %'«'^«> i = 1, 2, ..., 11
zusammenhängen, und zwar gilt dabei:
(6) a'i'ic == Uii Uu + «»-2 Ciük~\ + taln Unk, i, k = 1, 2, ■■■, n
Man sagt, die Substitution S" eatstejie aus S und S' durch „Zu-
bammensetzung^ y und bezeichnet S" symbolisch als „ProduM-^ B' • S von
S und S\ wobei wir bei Produkten von Gruppenelementen (s. I, 267)
die Anordnung der Faktoren von rechts nach links zu lesen haben. Für
die Matrizen a, a' und a" der drei Substitutionen S, S' und S" gilt das
in I, 61 aufgestellte Multiplikationsgesetz des Pi'oduktes a" = a' -a. Die
Determinante D" von S" = S' • S ist nach I, 63 gleich dem Pr(>duU
D" = jD' -J) der Determinanten J)' und D von S' und 8. Danach, ist
S" stets und nur daim nicht-singulär, wenn 8 mxi S' nicht-singulär sind.
Da nach I, 62 für die Prodi^kte von Matrizen d^s kommutative
Gesetz nicht gilt, so gilt dieses Gesetz auch für Produkte von Substitutionen
nicht, d. h. die Substitutionen 8' • 8 und S • 8' t,ind m allgemßmen
verschieden. Dies schließt nicht aus, daß in besonderen Fällert. 8' ■ 8 ^= 8 • 8'
gelten kann. Die Substitutionen S im.d S" heißen dann „vertauscJtttar-
oder „kommutatip". So ist z. B- jede Substitution (1) mit einer
Ähnlichkeitssubstitution (3) vertauschbar, da man bei beiden Anordnxmgen
der Substitutionen a^'i- = a-a^k als Koeffizienten eihält. Übrigens
bezeichnet man alle Substitutionen, die aus ejner beliebigen Substitution 8
durch Zusammensetzang mit Ähnlichkeitssubstitutionen hervorgehen, als
mit S „ähnliche Substitviionen^.
Die Zusammensetzung der Substitutionen ist bereits in I, liSff.
behandelt*). Insbesondere ist daselbsb unter (6) für mehyglie4rige sym-
bolis(5he Produkte von Substitutionen das „assoziative Gesetz^:
(7) 8"-{S'-S} = {8"-S')-S
bewiesen.
=«=) Die einzelne Substitution S ist daselbst jn derjenigen Gestalt geschrieben,
die aus der hier vorgelegten Gestallt (1) durch Auflösung naßh ^j, z-i^ • ■ ■■> z^^
hervorgeht.
4 I, 1- Sätze über Gruppen linearer Substitutionen.
Ist die durch (1) gegebene Substitution S nicht singular, so sind
die Gleichungen (1) nach ^j, z^, •••, 2^ lösbar und liefern:
^g) I ^2 = ßxi^'x + ß^2^'i + ••• + /3„2%,
1^1 = ßn^\ +/32i^; -1 + /3^:
^7. = /5l24 + /5224 + • • • +
^n = ßm^'i -\- ßin^'i H \- ßnn^'n:
wo:
(9) ft'=^
gilt und Ä^j; das Komplement des Elements ccijc der Matrix a ist (vgl. I,
77). Die Substitution (8) heißt zu S „invers" und wird durch S~^
bezeichnet; auch diese Substitution S~^ ist nicht-singulär, da nach I, 66
ihre Determinante den Wert D~^ hat. Zu S~-' ist die ursprüngliche
Substitution S wieder invers. Je zwei einander inverse Substitutionen
geben, in jeder der beiden Anordnungen zusammengesetzt, stets die
identische Substitution:
s-s-i = 1, s-^-s = 1.
Zu einer aus zwei nicht-singulären Substitutionen S, S'
zusammengesetzten Substitution S' • S invers ist die Substitution S~ ^ • S'~ ^:
(10) (S'.S)-i = S-i.S'-i.
Xach dem assoziativen Gesetz gilt nämlich:
(S'.S).(S-i.S'-i) = S'.(S.S-i).S'-i = S'-S'-' = 1.
§ 2. Pole und charakteristische Gleichung einer Substitution.
Zur Erleichterung der Darstellung bedienen wir uns einer
geometrischen Sprechweise, indem wir die ^^ z^, •••, % als homogene
Koordinaten eines Raumes Bn—i von (n — 1) Dimensionen deuten*). Dem
einzelnen System endlicher, nicht durchweg verschwindender Werte 2
gehört dann ein bestimmter „Punkt"* des Raumes Jin-i zu, den wir
symbolisch durch (<^,, z^, •••, z^) bezeichnen. Die Koordinaten z des
Punktes dürfen dabei noch mit einem beliebigen von 0 verschiedenen
gemeinsamen Faktor ^ versehen werden, ohne daß sie aufhören, den
gleichen Pimkt darzustellen. Alle Wertsysteme /,, ^g, •••, ^^, die aus
einem ersten 2^, z^, •••, % durch Ähnlichkeitssubstitutionen hervorgehen,
stellen demnach den gleichen Punkt im R^-i dar.
Eine nicht-singuläre Substitution S ordnet einem beliebigen Punkte
(^j, z^y ' ■ •, ^„) des Rn-\ umkehrbar eindeutig einen Punkt (/,, z'^^ • • •. z'j,)
zu oder transformiert (^j, z^, •••, z^) in (/,, z'^, •••, z'^). Dabei werden
*) Einen anschaulichen Sinn besitzt diese Sprechweise natürlich nur für die
niedersten Fälle » < 4 und auch da nur für reelle Werte z.
Pole und charakteristische Crleichung einer Substitution. 5
entsprechend der eben gegebenen Ausfiihnpig alle mit iS ähnlichen
Substitutionen die gleiche Zuordnung der Punkte zu Paaren darstellen.
Ein Punkt (^j, s^, •••, z^, der durch die Substitution S in sich
transformiert wird, heißt ein „FixpunM" oder „Pol" von S. Pie
Koordinaten -^j, -^3, ••-, ^n des Poles werden also drp-ch S in v- Werte z[, z'^^
• ", z'^ transformiert, die den z^^ ifg, .. , % abgesehen von eiuem
gemeinsamen Faktor ft gleich sind:
Trägt man diese Werte der z\, z^, ••-, z'^ in den Ausdrucl^ (1), S. 2
der Substitution S ein, so folgeii für die JCoordinaten z^, z^, • • •, e,j des
Poles die n linearen homogenen Gleichungen;
(«11 — t^)~i + «la^ä ^ + «i«^n = ^>
... f «äl^j -f («32 — ll)Z^ ^ -f Uin^n = 0»
^ ^ I
i a,a ^1 + a»2 ^2 4- • • • H- (««« ~ ft) ^» = 0.
Umgekehrt liefert jede Lösung dieses Gleichungssystems in n nicht
durchweg verschwindenden z^, z^, •••, z^ eipen Pol fijr S.
Nach I, 79 ff. gibt es stets und nur dann mindestens eiu solches
Lösungssystem, wenn der Rang der Determinante der n Gfleichungen (1)
kleiner als n ist. Dann verschwindet diese Determinante
m
Die mit (— 1)'^ multiplizierte linke Seite dieser Gleichung soll mit G- (jt)
bezeichnet werden und liefere, nach abfallenden Potenzen von {i
entwickelt, an Stelle von (2) die Gleichu:|ig:
(3) aiti) = ii- + Ä,ii^^-' + A,ii^-' + ■■• ^ A^ =0.
Sie heißt die „charaMeristisehe Gleichung'^ der Substitution S. Lidern
wir auch weiter S als nicht-singulär vora,ussebzen, ist Ä^ dz 0. Die
Gleichung (3) hat dann n von 0 verßchiedene Lösungen, die natürlich
nicht alle verschieden zu sein braucheif. Hfit für eine einzelne Lösung ^u
die Determinante (2) den Rang r, so haben die Gleichungen (1) nach I,
81 ff. im ganzen (n — r) Hnear-unabhängige Lösungen, in denen alle
Lösungen nach den daselbst angegebenen Regein darstellbar sind. Im
einfachsten Falle r = n — 1 hat S einen einzigen der fraglichen Losung ft
entsprechenden Pol.
Es soll jetzt die Wirkung eir^er Koordinatentransform^^tion im JR„_i
auf die Gestalt der Substitutionen S festgestellt werden. Die neuen
5«11 — /^'
^21' «22
y^l, «»2
«12'
) ■ • •?
•••,
«,l
«— /* i
6 . I, 1. Sätze über Gruppen linearer Snbstitutionen.
Koordinaten mögen ^, F^, •••, ^ beißen und sollen aus den alten durch
die nicht-singuläre Substitution:
^ == Tai ^, 4- Tää ^2 H + ^2« ^n,
hervorgehen. Diese Substitution werde mit T bezeichnet, ihre
Determinante habe den Wert ^. Reclmet maoQ nun eine beliebige Substitution
S auf die neuen Koordinaten um, so gelangt man zur Substitution:
(5) S = T-S-T-\
von der man sagt, sie gehe aus 8 durch Transformation mit der
Substitution T hervor. Umgekehrt wird- 8 durch Transformation mit T- ^ wieder
in S übergeführt. Da T-^ die Determinante ^-^ hat, so haben ewei
ineinander transformierbare Substitutionen S und S stets gleiche Determinanten.
Sie sind demnach immer zugleich nicht-singulär.
Weiter stellen wir die Wirkung einer Transformation von S durch
eine Substitution T auf die charakteristische Gleichung von S fest. Die
Koeffizienten von S seien mit öj^fc bezeichnet. Ihre Matrix berechnet
man, indem man die Matrizen von T, S und T~^ unter Zugrundelegung
des Gesetzes (6) S. 3 für Substitutionenprodukte miteinander
multipliziert. Eben dieselben Koeffizienten Uik stellen sich dann auch bei
folgender Rechnung ein: Wir multiplizieren erstlich die Determinante zl
von T mit der auf der linken Seite von (2) stehenden, durch D (ft) zi;
bezeichnenden Determinante, in der wir ^ als unabhängige Variable
fassen. Das Ergebnis ist:
(6) ^•D(li)=i ^21~f''^2l' C«22 — ;iT22, • • •; «2« — /^ ^2^ [
unter ä^^ die Koeffizienten der Substitution T • S verstanden. Die Matrix
von T-^ ist:
J t,.-^-\ t,.'ZJ-\ ..., t^^.J-\
(7)
wobei t^j. das Komplement von r^j^ in der Determinante zf ist. Setzt
man als dritten Faktor in (6) die zugehörige Determinante ^~^ hinzu,
so ergibt sich immer bei Benutzung der Multiplikationsregel (6) S. 3 und
lavariaaten und Koltiplikatoren einer Snbstitutioii. 7
Heranziehuag der Formeln (2) und (4) in I, 54, angewandt auf die
Determinante A:
(8) ^•D(^)-^-^ =
H; W»2! *• "^ OLnn — ft) (
WO in den ^^ die Koeffizienten der transformierten Substitution B>
erreicht sind. Diese bei variablem ^ gültige Gleichung hat rechts
(— 1)* Gr (ft), wenn (r (ji) = 0 die charakteristische (xleichung der
transformierten Substitution ist. Links aber steht nach Forthebung von /J
gegen ^-^ einfach (— Vf-Gr {^. Es gilt demnach die Crleichung:
G(^) = a{^)
in ^ identisch. Hiermit ist der folgende wichtige Satz bewiesen: Die
Koeffizienten ^j, A^^ • • •, A^ der charal^eri&ti&chen G-lepchtmg (3) sind
n ,Jnvarianten'- der Substitution S, die ihren Wert unverändert erhalten
gegenüber einer Transformation von S durch irgend eine nich(;-singulare
Substitution T. Für das Absoli^tglied, das von der Determinante der
Substitution geliefert wird, war die Invarianz oben schon festgestellt.
Die n von 0 verschiedenen Wurzeln ^l der charakteristischen
Gleichung unserer nicht-singulären Substitution S heißen die „Multi2'>liJcatoren"
von S (wegen ihrer in § 3 hervortretenden Bedep.tung). Sie sind n
„irrationale Invarianten" von jS, denen gegenüber die A gls die n ,^rationahn
Invarianten" der Substitution bezeichnet werden.
§ 3. Normalgestalt einer linei^ren Substitution.
Es sei fij eine erste Wurzel der charakteristischen Gleicliung einer
vorgelegten nicht-singulären Substitution S. ]V][an setze ^^ für ^ in (1)
S. 5 ein und kann dann ein System nicht durchgängig verschwindender
Lösungen dieser Gleichungen angeben, die wir z^ '-= öj^^, ^^ = 6^^, - ■-,
2n = öin nennen. Diese Zahlen sollen zu Elementen der ersten Spalte
der Matrix einer durch T""^ zu bezeichnenden Substitution gesetzt werden,
deren übrige Elemente wir so wählen^ daß T"^ und dan^.it auch die
zugehörige inverse Substitution T nicht-singulär ausfallen. Die Matrix
von jS • T~ ^ hat dann zufolge (1) S. 5 in der ersten Spalte die Eleraente
/ijöii, /iiöj2, •••, J^i^m- Andererseits hi^t die Substitution J' in ihrer
ersten Zeile als Elemente die dui'ch die Determinante von T~^ geteilten
Komplemente der Elemente öj^, 6-^^, •••, 6jn '^^V erst-en Spalte von T~^.
Rechnen wir also die Matrix von T'(S-T~^) wie immer nach der
Regel (6) S. 3 aus, so wird das erste Element nach (2) in I, 54 gleich [i^
Die weiteren Zeilen von T aber liefern nach Formel (4) in I, 55 fiir die
übrigen Elemente der ersten Spalte der Matrix von T-(S-T~^) durch-
8 I, 1. ^aa« »be» ^Sms^^^ Jfeeacer Sabsfcitali«ttea.
weg den Wert 0. Die äbrigen Etemente der traoisformierten Substitution
nennen wir wieder Oij. und haben also lür die Matrix dieser Substitution
die Gestalt:
[ /^i> «12' f>hs> •••' ^in>
I 0, «23, Was' •■•' «2«'
(1) {
[ 0, an2> «J13J •'•> f^nw
Die {n — 1) übrigen Multiplikatoren \l<^, /ig, •••, (in der.
ursprünglichen Substitution S werden wegen der Invarianz der charakteristischen
Gleichung von der Gleichung (n— 1)*^» Grades:
I «22 —/i, «23' •••' «2«
(2) 1 «32' Ciss — (l, ■■-, CCsn
: 0
I «Ji2, dns, '•', Cinn — tl
geliefert. Wir wollen dann für eine zweite Transformation eine neue
nicht-singuläre Substitution T heranziehen, welche sich nur noch auf die
Veränderlichen 2^, z^, • • •, % bezieht und also insbesondere ^^ unverändert
räßt Es wird somit T eine Matrix:
( 1, 0, 0, '■-, 0,
/3\ ) 0> "^22' ''^23' '*■' '''^m
[ 0, Xn2, tns, ■•', T^nn
und demnach zufolge (7) S. 6 die inverse Substitution T"^ eine solche
der Gestalt:
!1, 0, 0, ..., 0,
0, *22-^~'' •••' tn2'^~',
haben. Heißt die durch die erste Transformation erreichte Substitution
der Matrix (1) gleich wieder S, so erzielt man die Matrix der
Substitution T-S-T-^ durch Multiplikation der Matrizen (4), (1) und (3). Die
Matrix von T • S hat die erste Zeile und die erste Spalte mit (1) gemein,
und die übrigen Elemente ergeben sich durch Multiplikation der beiden
(n— l)-reihigen Matrizen:
"•» t2n, «32' «23' •••' «2w:
(o)
Der Zusatz des Faktors (4) ergibt für (T-S).T-i eine Mafeix, die mit
(1) in der ersten Spalte übereinstimmt, während die außerhalb der
'Srss^otmaM.&B. eiaer SabstitaticBi aM eine Normalgestalt. Q
ersten-^ieile und der ersten Spalte stehenden Elemente durch
Multiplikation von: f
kn-^~
■zl-^
laait dem Produkt der Matrizen (o) erhalten werden. Die neue
Substitution hat also, abgesehen von ihrer ersten Gleichung, die nur noch auf
die ^3, ig, •••, z^ bezogene Gestalt:
die aus der von ihrer ersten Gleichung befreiten ursprünglichen
Substitution S einfach durch Transformg^tion mittels der Substitution, der
Dimension (w — 1) und der ersten Matrix (5) entsteht.
Diese Transformation kann nun unter Bevorzugung eines zweiten
Multiplikators fig genau so vollzogen werden, wie die am Anfang des
Paragraphen für ^, ausgeführte Transformation. "W^ir gelangen dabei
zu einer transformierten Substitution, deren. Matrix die Gestalt:
(6)
f*,,
0,
0,
0,
«12'
f*2'
0,
0,
«13' ••
«23' ••
«33' ••
<^z^ ■■
, div
, C^2n
, Cisn
' Cinn
hat, wobei die et natürlich in neuer Bedeutung gebraucht ßind.
Diese Betrachtung ist entsprechei|d foi-tsetzbar. Wir transformieren
drittens durch eine Substitution der Matrix:
1, 0, 0,
0, 1, 0,
0, 0, rs3,
0, 0, Vns,
'-, 0,
■; 0,
••, r^n
• •? T^nn
und finden leicht, daß in der transformierten Substitution wieder die-
selhen beiden ersten Spalten wie in (6) vorliegen, wäiirend sich die
außerhalb der beiden ersten Zeilen und beiden ersten Spalten stehenden
Elemente genau so berechnen, als handelte es sich um Transformation
IQ I, X. Satze über Crrappen linearer Substitutionen.
einer.Snbstitution der Dimension {n — 2). Insbesondere kann man also
zu einer transformierten Substitution der folgenden Matrix gelangen:
f^l'
0,
0,
0,
0,
«12'
f^S'
0,
0,
0,
«13'
«23'
^3'
0,
0,
«14' •
«24' •
«34' •
«44' •
dm, '
•) «IW)
•) «2wj
•, dön,
; din,
•j «M71-
Transformiert man nacheinander mittels der Substitutionen T, T',
T", •", so laßt sieb das Ergebnis auch durch eine einzige Transformation
mittels ... T"-T'-T erzielen. Sind aber aKe T, T', T", -•■ nicht-
singulär, so gilt dasselbe von •.• T"-T''T. Durch Zusammenfassung
gewisser (n — 1) Transformationen gelangen wir zu dem Satze: Die
vorgelegte nicht-singtüäre Substitution S kann mittels einer nicht-singulären
Substitution in eine neue Gestalt der Matrix:
(7)
f^l' «12'
0, ii„
0, 0,
0,
0,
0,
Km,
transformiert werden, wo die fi^, (i^, • • •, (in ^^^ Multiplikatoren von S in
irgend einer Melhenfolge sind, und wo auf der eineti Seite der Diagonale
lauter Nullen stehen.
Kommen unter den Multiplikatoren einander gleiche vor, so wollen
wir die Bestimmung treffen, daß gleiche Multiplikatoren in der Diagonale
der Matrix (7) stets unmittelbar hintereinander angeordnet werden sollen.
Sind nicht alle Multiplikatoren gleich, so läßt sich eine weitere
Vereinfachung der Substitution durch Transformation erzielen. Man
transformiere mittels einer Substitution T der folgenden Gestalt:
(8)
i i- -r%,
wobei k ^ i gelte. Es soll also nur die i^^ Variable eine Änderung
erfahren. Die zu T inverse Substitution T~^ ist:
(9)
= ^i+ij
Man stellt mittels dieser Formeln leicht direkt die Matrix der
transformierten Substitution T-S-T~^ her, unter S die Substitution der
Matrix (7) verstanden. Es zeigt sich, daß sich gegenüber (7) nur die
Normalgestalt einer lineare];^ Substitution. IJ
Elemente der i*«" Zeile vom ¥^^ bis zum letzten und d|e Element^e def
¥^^ Spalte vom ersten bis zum ^*^e" ändern. Die neuen Elemente sind:
(10)
«2i ~T«22,
dik — T (^* — [ii). (^i,}:^i-\-tak,k^l- •••• Oiirt -fr f^kn
Falls nun ft^ z^ fi;. gilt, können wir (\\e nqch verfügbare ^^ahl r aus
der Gleichung:
«*/: —T(fl» —/i/3 = 0
als endliche Zahl berechnen. Die Transformation durch die Substitution (8)
führt zu einer neuen Gestalt unserer Substitution S, in der an Stelle des,
bisherigen Elementes u^^ der Wert 0 getreten ist. Dabei bleiben alle
Elemente einer späteren als i^^ Zeile und alle Eieipente einer früheren
als Zj*^** Spalte unverändert. Man nehme nun an, daß die llultiplikatoren
fin, fin — i? "'i ^i+i einander gleich seien, -Vt^ährend von ^i an neue
Werte auftreten. Wir können danp huitereinander Transformai ion en
ausführen, die nach und nach die Elemente uijj^i, ß^t + aj "-j «/,» der
P^^ Zeile durch 0 ersetzen. Gilt dann etwa weiter (ii = fii^i = fi;_.>
=::•..=: ^ff^j^i, während mit u^ wieder ein neuer Wert einsetzt, so
können wir in gleicher Weise so transformieren, daß <Zj_i_ ;4-i? •••, «/_i,«,
sodann «;—s, z + d "••, «z—2, •» us^., endlich a^^^i^ij^i, •••, «m + Lw durch
0 ersetzt werden, d. h. es sind immer die letzten (u — 7) Elemente dieser
Zeilen durch 0 ersetzt. Da aber {i„i von allen folgenden Multiplikatoren
verschieden ist, so können wir in der w^^" und in den voranfgehenden
Zeilen sogar die letzten (n — m) Elemente auf 0 transformieren. Purch
Fortsetzung dieses Verfahrens gel9,ngen wir zu der aufzustellenden Xormal-
gestalt unserer Substitution S. Da alle zur Transformation benutzten
Substitutionen T nicht-singulär sind, ßo ergibt sich der Satz: Eine nicht
singulare Bubstitution S ist durch Trßnbformation )Mtteh einer gJeiclifälh
nicM-singulären Substitution auf eine NormalgedaU von der Matru (7)
überfuhrhar, in der die Multiplihatoren ^ in irgeti^d einer -Aft so angeordnet
sind, daß gleiche Multiplikatoren stets um}%ittelhar hintereinander t^tehen,
und in der auch oberhalb der Diagonale jedes Element «j /; verschwindet, so
oft ^j dr fi^ gilt. In der Matrix (7) geigen also die nicht
verschwindenden Elemente eine treppenförmige Anordnung.
In dem gewonnenen Ergebnis ist als Spezialfall dec folgende Satz
enthalten: Eine nieht-singuJäre Substitution S mit lauter vefschiedenen
(nicM-verschwindenden) Multiplikatoren, ^^, ^.^j •••, ii« ist wi die Gestalt:
(11) 4=^«j^^, 4 == ^2^2, ■•', s'^ — ^ri^n,
d. h. in eine „inultiplihative Suhstitution^' tran»formierbar.
J 2 I, 1- Sätze über Gruppen linearer Substitutionen.
§ 4. Endliche Gruppen linearer Substitutionen.
In I, 268 sind drei charakteristische Kennzeichen dafür angegeben,
daß m Elemente eine „Gruppe" der endlichen Ordnung m bilden. Sind
die Elemente insbesondere nicht-singuläre Substitutionen S der Dimension n,
so ist bereits das erste Kennzeichen hinreichend: Ein System von m
verschiedenen nicht-singular en Substitutionen der Dimension n bildet eine
Gruppe @^ der Ordnung m, falls irgend zwei Substitutionen des Systems
zusammengesetzt stets meder eine Substitution des Systems liefern. Das
Gruppenkennzeichen II, das assoziative Gesetz betreffend, ist nach S. 3
bei den linearen Substitutionen stets vorhanden. Aber auch das
Kennzeichen III trifft hier immer zu. Besteht nämlich z. B. für drei
Substitutionen S, S' und S" des Systems die Gleichung S- S' = S- S", so folgt
durch Zusatz des Faktors S~^, mag diese zu S inverse Substitution dem
System angehören oder nicht, wegen des assoziativen Gesetzes:
S~'''(S-S') = S~''-{S-S"), {S~^-S)'S' = iS~^-S)-S", S'=S".
Die Substitutionen einer vorgelegten Gruppe @^ bezeichnen wir nun
mit Sq = 1, Sj, Sg, ••-, S^-i, unter S^ die in der @^ sicher auftretende
identische Substitution verstanden. Weiter aber tritt nach I, 271 mit der
einzelnen Substitution stets auch ihre inverse Substitution in der @^ auf.
Transformieren wir die m Substitutionen der @^ zugleich durch eine und
dieselbe Substitution T, so bilden die m transformierten Substitutionen
eine mit @^ isomorphe Gruppe, die wir durch T-@^-T~^ bezeichnen
und auch wohl einfach als eine neue Gestalt der @^ auffassen.
Wir transformieren nun so, daß eine beliebig aus der @^
herausgegriffene Substitution S die am Schluß von § 3 beschriebene
Normalgestalt annimmt. Dabei mag ••• = fi^-_2 = ft^-i = (H gelten, wäiirend
von fi^ + i an neue Multiplikatoren auftreten. Dann hat die Substitution S
die Gestalt:
•-•, z'i^j^ = fi^t-i -j-azi, z'i = (iZi, ••■,
wo zur Abkürzung ^ für fi^^j z= ^- und u für cci-^i^i gesetzt ist. Die
v^e Potenz S" von S wird also, wie man durch Induktion leicht zeigt, die
Gleichungen enthalten:
4-1 = ^^^i~i -\- V fi"-^ aZi. s[ = fi* Zi.
Xun ist die Periode von S nach I, 272 ein Teiler der Gruppenordnung m.
Versteht man unter v die Periode, so gilt in den letzten Gleichungen:
Somit verschwindet a, und ^ ist eine m*« Wurzel der Einheit. Nehi
wir noch die (* — 2)*^ Gleichung von S hinzu, so ist:
•^z-2 = li'^i-'i + cc2i^i -f- a ^i, zi_i = iiZi_i, z'i == ^Zi
Endliche Gruppen linearer Substitutionen. 13
ein Aussclmitt aus S, wo u und cf,' statt cci_^i_.j^ und Ui-^^j gesetzt ist,
S" enthält somit die Gleichungen:
Wie soeben ziehen wir den Sclüuß, daß a =^ 0, of' = 0 gelten muß.
Durch Fortsetzung der Überlegung in gleicher Art gelangt man zu dem
Ergebnis: In einer endlichen Q-ru^e @^ Uneßrer Suhstitutianen treten
nur Substitutionen S auf, die auf die Normalgestali geh facht „muftipU-
Jcativ" sind:
(1) 2[ = fij ^j, 4 = fi2^2' '' •) 4 = ^%;
die Multiplikatoren aber sind durchweg W« Wurzeln der Einheit.
In der @^ mögen im ganzen X Älmlichkeitssubstitutioneii enthalten sein,
unter ihnen die identische Substitution. Da eine Ähnliclik.eitsspbstitution
nach S. 3 mit jeder Substitution vertauschbar ist, so Mlden jene X Ahn-
Uchkeitssuhstitutionen einen Normalteiler @;i voti @^. Die eipzelne
zugehörige Xebengruppe besteht jeweils aus den X Substiti(.tionen der ®m?
die mit einer unter ihnen ähnlich siad. JDie Gruppe ©„,, reduziert sich
demnach auf das Komplement @^ des Normalteüers %i, falls man je die X
miteinander ähnlichen Substitutionen der ®m. als nicht voneinander ver-
schieden ansieht. Ist ^ = e «* ein in der @;. auftretender Multiplikator,
so ist dessen A*^ Potenz gleich 1, so daß ßX ein Vielfaches }cm von m
ist. Es folgt also:
^ = p ^- ,
und da wir X verschiedene Multiplikatoren dieser Ait haben, so kommen
aUe Zahlen Je = 0, 1, 2, "-, X — 1 zur Geltung. Der Teiler @;i ist
somit zyMisch und aus der Substitution erzeugbar:
^^,
(2) z\ = e ^ z^, 4 =
Im Falle n = 1 hat jede in der @^ enthaltene Substitution die
Gestalt:
(3) z == e '» z,
und da wir m verschiedene Substitutionen dieser Art haben müssen, sq
müssen alle Zahlen ä; = 0, 1, 2, • •-, w— 1 zur Geltung kommen Es
existiert also für jede natürliche Zahl m eine imd nur eine Gruppe @^,
die die zyklische Bauart besitzt. Diese Gruppen ßind also noch sehr
einfach; sie spielen in den folgenden Entvjdcklungen nur eine beiläufige
Rolle.
14 I, 1. Satze über Gruppen linearer Substitutianen.
§5. Invarianten endlicher Gruppen @^.
Eine Form f {z^, ^g, •••, ^„)) ^- ^- ^^^ rationale ganze homogene
Funktion mindestens ersten Grades*) der n unabhängigen Variablen
^j, ^2' ■") ^ni die bei Ausübung der Substitutionen S^ = 1, Sj, Sg, •••,
S^-i einer vorgelegten Gruppe ®^, abgesehen von konstanten Faktoren,
in sich selbst übergeht, heißt eine „Invariante"' der Gruppe ®^. Sind die
m konstanten Faktoren alle gleich 1, so heißt f eine „absolute" Invariante,
anderenfalls eine ^relative-. Wir bezeichnen die den m Substitutionen
Sq=1, S„ Sg, •••, S«j_i entsprechenden Faktoren durch ö^ = 1.
öj, ög, •••, 6^,-1 uöd nennen ihre Zusammenstellung das „FaUoren-
system'- der Invariante f. Ist S^-S« = S^ so gilt für die zugehörigen
Faktoren ö^. ö« = öc, eine Regel, die sich sofort auf mehrgUedrige
Produkte überträgt. Hieraus folgt, da der identischen Substitution der
Faktor 1 entspricht, leicht der Satz: Der zu einer Substitution S gehörende
FaMor 6 einer Invariante f ist eine i/* Wurzel der Einheit, unter v die
Periode von S verstanden. Alle Faktoren ö sind demnach m^^ Einheits-
2l7l
wurzeln und als solche Potenzen der primitiven Einheitswurzel s = e '^
dieses Grades.
Weiter besteht der Satz: Alle Stibditutionen der @^, die für eine
Invariante f den FaUor 1 liefern, bilden einen Normalteiler ®i, dessen
Komplement zyklisch ist. Es mögen im ganzen die ? Substitutionen Tq=1.
Tj, T^, ..., T;_i den Faktor 1 liefern. Mit T« und T^ ergibt auch
T^-Ta den Faktor 1, so daß die ? Substitutionen T einen Teiler ®i der
@«, büden. Mit T liefert auch S'T'S~^ bei beliebigem der @^
entnommenen S den Faktor 1, so daß @; ein Normalteiler ist. Sind S und
S' beliebige Substitutionen der @^, so gehört zu S~^ • S'~''- • S • S' der
Faktor 1, so daß (3i die Kommutatorgruppe von ®^ als Teiler enthält.
Xach I, 290 ist also das Komplement von ®i kommutativ. Die zyklische
Struktur dieses Komplementes ergibt sich so: Man setze m-l~^ = t
und bilde die zu @; gehörenden ]S[ebengruppen @;, Fj • @;, Fg • @;, • • •,
Vt~i'(S>i, denen, wie man leicht zeigt, t verschiedene bei der vorliegenden
Invariante f überhaupt auftretende Faktoren:
(1) öq =1, Öj =r £^-1, ög ■= £^-2, ..., ö^_i = Eh~i
entsprechen. Die Faktoren (und damit die Xebengruppen) seien so ge
ordnet, daß die Zahlen A", die dem Intervall 0 <^Jo<^m angehören mögen,
nach steigender Größe aufeinander folgen. Da inverse Substitutionen
reziproke Multiplikatoren liefern, so kommt mit dem einzelnen Je auch
(m — Ic) vor. Die Faktoren (1) reproduzieren sich gegenüber
Multiplikation und geben dabei eine Darstellung des Komplementes @^ von @;.
Die t Exponenten /.-^ == 0, 7.-^, Jc^, •••, 7^^_i reproduzieren sich also
mod m genommen gegenüber Addition und wegen des Auftretens von
*) Formen nullten Grades, d. h. von 0 verschiedene Konstante, sollen also
ausgeschlossen sein.
Invarianten einer @^ und ihre Taktprensysteine io
(m — k) mit Je auch gegenüber Subtraktion. Es kommen somit jedepfalls
auch, die Vielfachen fcj, 2 fcj, 3>fcj, 4^;^, ••• des kleinsten positiven
Exponenten Äj vor. Träte aber zwischen zwei aufeinander folgenden unter
diesen Vielfachen noch ein weiterer Exponent Je auf, so gäbe es zufolge
der voraufgehenden Ausführungen auch nqch einen zwischen 0 und 7.;^
gelegenen, so daß Zr^ nicht der kleinste positive Exponent wäre. Also
sind die Je einfach die Vielfachea vop. Je^, womit die zyklisclie Bauart
von ®i deutlich ist. Das System (1) der Faktoren aber lautet:
(2) öo =1, 6, = s\ Ö2 = 8'\ ■■■, 6t-i = £^'~'^'-
Ist andererseits ®i ein beliebiger Xormalteiler vop ^^ mit zyklischem
Komplemente @^ = ®^, so ist nach I, 290 in ®i die Konimutatorgruppe
T
von @^ enthalten. Das System der t Einheitswurzeln des Grades t, wie
es ja auch in (2) vorliegt, heiße dann ein ^ÜieordücJi mögjlclies FaJdoren-
system^. Auf die Frage, inwie^^z-eit zu irgend eineip solchen Faktoren-
system Invarianten wirklich vorkommen, gehen wir (inten ein.
Entsprechend der Erklärung in I, 129 fassen wir den Begriff einer
Kovariante bei n Variablen. Eine J'orm K{2^, z^, •-■, z^ heißt eine
Kovariante irgend einer gegebeneii Form /'(s'j, z^, • • -, z^^, wenn K in den
Koeffizienten von f rational, ganz und homogen aufgebaut ist, und wenn
K bei Ausübung irgend einer nicht-singulären Substitutiop *), abgesehen
von einer ganzzahligen Potenz der Substitittionsdeterminapte als Faktor,
in den gleichgebauten Ausdruck .S''(^i, z'^, •••, :«) der transformierten z
und der Koeffizienten der transformierten Form /"(^i, z'2^ •••, z'^i)
übergeht. Ist nun f wieder eine Invariante unserer @^, und werden zur
Transformation nur noch Substitutionen S der (^^ zugelassen, so sipd in
jedem Falle die Koeffizienten der transformierten Form/''(^i, z'21 •••, -'n)
bis auf einen gemeinsamen Faktor fi gleich den ursprünglichen
Koeffizienten. Also hat auch K'(z'i, z'o, •••, z'„) nach Absonderung einer in
allen Gliedern als gemeinsamer Faktor auftretenden Poten^j vo^. fi wieder
die Koeffizienten von K(z^, z^, -r-, z„). Durch Bildung von Kocarlauten
für irgend eine schon gewönnest; J[nvanaute f vor^ (3^^ findet man demnach
neue Invarianten dieser Gruppe.
§ 6. Existenz und Darstellung der Invarianten einer (^m«
Zur Herstellung von Invarianten für eine vorgelegte Gruppe C^),^,
linearer Substitutionen der n unabhängigen Variablen z^, z^, .. , z^ bilde
man irgend eine lineare Form:
(1) Cp {Z) =z C^Z^-^C^Z^A r C,,Zn
^) Von der Gruppe @^ ist hier zunaphst r^cht die Rede.
Iß I, 1. Sätze über Gruppen linearer Substitutionen.
und übe auf die z die m Substitutionen S^j = 1, S^, Sg, •••, S^_i der
®^ aus. Si möge die z^^ ^g, • • • in ^(^'), ^(g*), • • • überführen, wobei also
die ^^), ^^2^), • • • einfach die z^^ z^^ • • • sind. Die m Ausdrücke:
(2) 9? (^(0) 3= Cj ^(0 + C2^(f) + ... + c^^Jf), i = 0, 1, 2, ..., m - 1
sind dann vermöge der Substitutionen S der ®^ [vgl. (1) S. 2] ebenso
viele lineare Formen der ^^, z^^ • • •, und es werden sich diese m Formen
bei Ausübung irgend einer Substitution der Gruppe @^ nur
untereinander permutieren. Ihr Produkt ist also eine Invariante der @^, und
zwar vom m'^" Grade in den z.
Diese Invariante ist absolut. Jedoch kann eine Erweiterung des
Ansatzes gelegentlich auch zu relativen Invarianten führen. Es sei S
die erzeugende Substitution eines zyklischen Teilers @y der Ordnung v
von @^. Dann kann man durch Einführung geeigneter neuer
Koordinaten ^^, ig? '"i ^n di^ Substitution S in die Gestalt (11) S. 11
transformieren, wo die Multiplikatoren ^ Einheits würz ein v^^^ Grades sind.
Nimmt man einen der n Ausdrücke dieser neuen Koordinaten in den z^,
z^, '" r Zn als Form q)(z), so ist diese Form (p(z) eine (relative)
Invariante des Teilers ©,,, und die m Ausdrücke (2) werden, abgesehen von
konstanten Faktoren, zu je v einander gleich. Somit ist das Produkt der
m Formen (2) in diesem Falle die v^^ Potenz einer Form des Grades
m v~ ^, die eine Invariante der @^ ist, Sie bleibt nämlich gegenüber
den Substitutionen der @^ entweder unverändert oder nimmt als Faktor
eine r*® Wurzel der Einheit an. Eine relative Invariante kann natürlich
nur dann vorliegen, wenn @^ einen Normalteiler mit zyklischem
Komplement einer in v aufgehenden Ordnung hat.
Jedenfalls ist hiemach infolge der willkürlich wählbaren
Koeffizienten c in (1) die Existenz unendlich ■ vieler absoluter Invarianten der
Gruppe ®^ sichergestellt. Auch kann man aus bereits erhaltenen
Invarianten durch Bildung rationaler ganzer Funktionen derselben, die in
den z^^ ^g, ..., 0n homogen sind, neue absolute Invarianten herstellen.
Hierbei besteht der wichtige Satz: Die gesamten absoluten Invarianten
der Gruppe @^ sind in einer endlichen Anzahl unter ihnen als rationale
ganze Funktionen darstellbar. Diese Aussage wird als der „Satz von
der Endlichkeit des Invariantensystems" einer Gruppe @^ bezeichnet,
womit also nicht etwa gemeint ist, daß die @|„ überhaupt nur endlich
viele Invarianten besäße. Der erste Beweis des Satzes ist von Hilbert
im Jahre 1890 gegeben*). Einen elementaren Beweis, der zugleich eine
Vertiefung des Satzes brachte, fand Frln. E. Noether im Jahre 1915**).
Dieser Beweis arbeitet mit der folgenden Überlegung.
*) „Ober die Theorie der algebraischen Fornipn", Math. Ann. Bd. 41, S. 473 ff.
Vgl. hierzu auch Weber, Lehrb. d. Algebr. ^2. Aufl.) Bd. 2, S. 231 ff.
*♦) „Der Endlichkeitösatz der Invarianten endlicher Gruppen", Math. Ann.
Bd. 77, S. 89 ff.
Endlichkeitssatz bei den Invarianten einer (5_. 17
Es sei eine beliebige absolute Invariante der Gruppe ®^:
(3) f{^,, ^2, ..., ^n) = 2 C^«,/?,...^?4'--' « + /? + ... = r
cc,ß, ...
vorgelegt, deren Grad mit r bezeichnet wird. Durch die Substitution
Sf der ®m mögen die ^1,^2' *' *> ^n ^^ ^^\ ^^fj '' *> ^^^^ übergeführt werden.
Übt man auf die Gleichung (3) die (m — 1) Substitutionen S^, S^, • • •,
Sjn—i aus und addiert die Ergebnisse zur Gleichung (3), so ergibt die
Teilung der Summe durch m für die Invariante f die Darstellung:
(4)
Der rechts in der Klammer stehende Ausdruck bleibt für sich genommen
bei allen Substitutionen der @^ unverändert. Schreiben wir somit:
(5) Ja,ß,... = '^4---+4''4?---+4"-^2l'--- + --;
so haben wir in diesem Ausdruck eine absolute Invariante des Grades r.
und man kann f als lineare homogene Funktion solcher Invarianten (5):
(6) f= ^ ^C«,^,...^.,^,...
darstellen*). Wenn wir also für alle Invarianten Ja,ß,.., den
„Endlichkeitssatz" zeigen können, so ist dieser Satz damit allgemein bewiesen.
Man setze nun mit n unbestimmten Größen w,, ti^, • • •, u^ die
Summe:
an. die durch die m Substitutionen 1, S^, Sg, • • •, S^ —1 in die ftt Summen
^1^1 +^2^2 H \-^n^n,
^i^i' + ^2^2 H h^^nC^
(7)
übergeführt wird. Die r*^ Potenzsumme Pr der m Größen (7):
(8) i^r = K^l + ^2^2 H f- '^n^nY + K ^i + ^2^2 H h ^n4X + ' '
entwickle man dadurch, daß man rechts auf die einzelne r*^ Potenz den
polynomischen Lehrsatz (5) in I, 27 anwendet und allemal die in den u
gleichgebauten Glieder zusammenfaßt. Es ergibt sich so für j?^ die
Darstellung :
(9) p,= SL/ )ja,(i,...u-y-', r = « + /?+...,
*) Die Frage des etwaigen identischen Verschwindens eines Ausdrucks (5)
braucht nicht erörtert zu werden. Da nämlich f als nicht identisch verschwindend
angenommen ist, so treten in (6) rechts sicher Glieder mit nicht identisch
verschwindenden J„ f. auf.
a, p, ...
Fricke, Alaebra.. II. o
X8 I, 1. Sätze über Grruppen lineacer Substitutionen.
wo sich die Summe auf alle Zerlegungen der Zahl r in Summen
nichtnegativer ganzer Zahlen a, ß, • • • bezieht, die Klammersymbole die
ganzzahligen Polynomialkoeffizienten sind und die J"«^ ^^... unsere Invarianten (5)
bedeuten. Dabei treten die gesamten nicht identisch verschwindenden
Invarianten (5) des Grades r als Koeffizienten der Entwicklung (9)
wirklich auf.
Nun sind die Potenzsummen j)^ + i, Pm + 2i ••• ^^ symmetrische
Funktionen der m Größen.(7) rationale ganze Funktionen mit rationalen
Zahlenkoeffizienten in den m symmetrischen Grundfunktionen dieser
m Größen, also wegen (13) in I, 103 auch in den m ersten
Potenzsummen i>j, i>2, '•', Pm, <56r m Größen (7):
(10) Pr = (^r(Pv Pi, '' ; Pm), r = m + 1, m + 2, • ■ ■
Diese Gleichung ist in den Größen (7) und also auch in den 2 und u
eine identische. Der rechts stehende Ausdruck ist demnach in den u
homogen vom Grade r imd ergebe, in bezug auf die u geordnet:
(11) Pr= ^ ^a,ß,...iJ,J','-')-1*1^2"'' « + i^^ = r,
a,ß,...
WO die Koeffizienten 0 ganze Funktionen der Invarianten (5) der m ersten
Grade sind, deren Anzahl endlich ist. Wegen des identischen Bestehens
dieser Gleichung in den u ergibt der Vergleich von (9) und (11) die
Gleichimg;
(12) {^^^[„)ja,ß,... = ^a,ß,...i'^,'^',-")-
Damit ist der Endlichkeitssatz bewiesen und in folgender Art
vertieft: Jede absolute Invariante f der Gruppe ®^ ist als rationale ganze
FunJdion der endlich vielen Invarianten (5) der ersten m Grade darstellbar,
ioobei insbesondere in den Darstellungen (12)^ nur- rationale ZulüenTcoef-
fizienten auftreten.
Für die Darstellung re lativer Invarianten f{z-^, z^, • • •, z,^) der @^ ist
der zweite Satz von § 5, S. 14 zugrunde zu legen. Es gehöre f als
absolute Invariante zum Normalteiler @; des Index t = 'm-l~\ und es
seien ®i, Fj • ®i, V^ ®i, • • • die t zugehörigen Nebengruppen, denen die
Multiplikatoren 1, s\ s^\ ••• wie S. 15 zugehören. Setzt man f wieder
in der Gestalt (3) an und übt auf diese Gleichung die m Substitutionen
der ®^ aus, so bleibt die linke Seite bei den l Substitutionen der ®i
unverändert, bei den l Substitutionen von F, • ®i nimmt sie den Faktor £',
bei denen von V^'®i den Faktor £^' usw. an. Hieraus folgt eine
Darstellung :
(13) f = l^^ ^«,ft...(i«,ft... + f-%ft... + £-^'i;>,...+ •••),
'^0 ja,ß,... die Summe der Glieder ist, die aus z^-z^^--- durch die
Substitutionen von ®i hervorgehen, und die j^ ft,.., i«,« ..., • • • aus ja- a^... durch
Herstellung relativer Invarianten einer Grfippe. 19
die Substitutionen Fj, Fg, ••• entstehen. Da die ®j ei)i Nonnalteüer
der @^ ist, so folgt der Satz: Die u,ß,...> j'a,ß,..., ••• sind äbsolutß
Invarianten der ®i und als solche rational tmd ganz darstellbar in einer
endliehen Anzahl solcher Invarianten, deren Grade ^Z sind; in den
ja,ß,..j j'a,ß,..., j'ä,ß,...t •••> <^^ß ö^^ß a«*s der ersten unter ihnen durcfi die
Substitutionen 1, Vp V^, • • • hervorgehen, ist jede relative Invariante des in
Rede stehenden FaMorensystems in der Gestalt (13) darstellbar. Auf der
anderen Seite kann man in der Gestalt:
(14) h,ß,... -f £-%ft... + £-'%ft... + •• ■
aus einer beliebigen absoluten Invariante j^^^^... von ®i einen Ausdruck
herstellen, der, sofern er nicht i(3entisch verschwindet, eipe relative
Invariante des Faktorensystems e'^ == l, e^ s^\ ••• darstellt. Aus den
Entwicklungen des nächsten Pai'agraphen wird[ hervorgehen, daß für
jedes theoretisch mögliche FaJctorensystem ßuf diese Weise relative
Invarianten gebildet werden Jcönnen.
§ 7. Formenproblem einer endlichen Gruppe ®^.
Unter den Invarianten (5) S 17 der ®^ mit Grader^ <w decken
wir uns ein System:
(1) J, J', J", -■■, J^P-^)
derart ausgesucht, daß alle übrigen Invarianten rational und ganz in
diesen Invarianten (1) darstellbar sind, daß aber in dieser Weise l^ehxe
unter den p Invarianten (1) durch die übrigen dargestellt werden
kann. Drücken wir alle GHeder der einzelnen Summe (5) S. 17 durch
die ursprünglichen z^ z^, •••, z^ mittels der Substitutionen der ©^ aus,
so erhalten wir für die J^Darstelluagen in z^ z^, •• •, z^ mit Koeffizienten
eines Körpers, der aus dem rationalen Körper durch Adjunktion der in
den Substitutionen auftretenden Koeffi^ientea hervorgeht. Dabei ist aber
sehr wohl möglich, daß die Koeffizienten in ^en Darstellungen der /
bereits in einem echten Teuer (Jieses Körpers, ja vielleicht sogar im
rationalen Körper enthalten sind.
Ist j)^ n, so bestehen zwischen den Invarianten (1) (p — n)
algebraische Relationen:
[ W^(J, r, J", ..., J(i'-i)) = Ü,
(2) I W^(J, J', J", ..., J(i>-i)) = 0,
die man durch Elimination der n unabhängigen Variablen z^^, z^, • • •, z^
aus den Darstellungen der jo absoluten Inv&rianten in iipien gewinnen
kanu; und deren Koeffizienten demselben Körper angehören wie die
2*
20 I^ 1- Sätze über Gruppea linearer Sabstitutionen.
Koeffizienten dieser DarsteUungen. Übrigen? denken wir diese Dar-
steUun^en in. der Gestalt:
wirklich gegeben, wo also die il) rationale ganze Funktionen mit Graden
^m in den z sind.
Hieran schließt sich das folgende von Klein*) aufgestellte und für
seine algebraischen Schöpfungen grundlegende „Formenproblem der
Gruppe @«i": Es seien p die Melationen (2) 'befriedigende Werte der
Invarianten (1) irgendwie gegeben; es soUen durch Zösmig der Gleichungen (3)
die gesamten zugehörigen Wert&ysteme z^, z^j •••, ^„ gefunden werden.
Mit einem Wertsystem gehören natürlich immer gleich m solche, die aus
jenem ersten durch die Substitutionen der @^ hervorgehen, zu den
gegebenen J, J\ •••, J"(^~^); denn gegenüber diesen Substitutionen sind
ja die J-^J'-, •••, J^'^~^) invariant. Denkt man die absoluten Invarianten
variabel, so ist das Problem so zu charakterisieren: Zu dem Zahlkörper ^,
der durch die Koeffizienten in den Ausdrücken (3) rechts gegeben ist,
adjungiere man die an die Relationen (2) gebundenen komplexen
Variablen J, J', •••, J(P~^). Dann sollen die s^, z^, •••, z^ aus (3) als in
hesug auf den Körper (Ä, J, J', •••, J(-P~^)) algebraische FunUionen
berechnet werden.
Zur Charakterisierung dieses Formenproblems diene zunächst seine
ümformxmg in ein gewöhnliches Problem der Auflösung einer Gleichung.
Wie S. 17 setzen wir mit zunächst unbestimmten Koeffizienten u die
lineare Form an:
(4) W = U^Z^ -^ U^Z^ -\ + U^^n-
Durch Ausübung eiaer in (1) S. 2 gegebenen Substitution S von (^^
geht w über in:
w' = U^z[ -{- U^z'^ -\- [- Unz'n
oder wieder nach ^j, z^, ••-, z^ geordnet in:
W = u[z^-\-u'^Z^-\ -f u'n 2n,
*) Man vergleiche die Abhandlungen „Über die Auflösung gewisser
Gleichungen vom siebenten und achten Grade", Math. Ann., Bd. 15 oder Ges. matb.
Abb., Bd. 2, S. 390 und „Zur Theorie der allgemeinen Gleichungen sechsten und
siebenten Grades", Math. Ann., Bd. 28 oder Ges. math. Abb., Bd. 2, S. 439. Siehe
auch Kleins „Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen
vom fünften Grade„ (Leipzig 1884), 'S. 126,
Formenproblem einer endlicfien Gruppe. 21
WO die u\, u^, ■'-, Un sieh in den u^, u^, *••, u^ durch die zn S
gehörende „transponierte Substitution" 'S:
( u[=: «11 Wj 4- «2j M^ + i- Kni%r
darstellen. Nun gut von vornherein als selbstverständli^ch, daß ieine
zwei Substitutionen der @„j, also auch keine :?wei der transponierten
Substitutionen identisch sind. Geht demr^ach die Form (4) durch die
Substitutionen S« = 1, S,, S„ ••• in die m Formten:
r w = u^z^ + %^2 + •■
W = U\Z^ -\- M'ä^'ä-f •■
•• -T t^n^n,
■■+<^n,
(6)
L,(m-i) __ ^^(m-l)^-^ ^ j^ ^^(»'-l)^„
über, so wird die Differenz keiner zwei dieser m Formen lauter in den
u identisch verschwindende Koeffizienten erhalten. Xaph dem Satze
in I, 96 können wir demnach für die u ein System vpn n ganzen Zahlen
in der Art eintragen, daß keine zwei der m Formen (6) ia den s
identisch werden.
Aus den so gewonnenen durchweg vei schiedenen m formen bilden
wir mittels einer Variablen Z die ganze Funktion m^'^^ Grades von Z:
(7) ® (Z) = (Z — w){Z — w') {Z, — w") ■■ (Z — «;(^«-^)),
die entwickelt und gleich 0 gesetzt die Gleichung m^^^ Grades mit den
Lösungen w, w', w", ■ • • liefert:
(8) @(Z) = Z»» + C.Z'«-^ 4- C^Z^'-^ + ... + C^, = 0.
Bei Ausübung der Substitutionen der (3^ pe^'mutieren sich die
m Formen (6), so daß ihre symmetrischen Fu^ktio^en und damit die
Koeffizienten der Gleichung (8) g,bsoli(.te Invarianten sind und sich als
solche rational und ganz ia den p Invarianten (1) darstellen. Pie
Koeffizienten der linearen Formen (6) gehören dem Zahllcörper an, der aus
dem rationalen Körper durch Adjunkiion der Substjtutioaskoeffizienten
hervorgeht. Demnach werden auch die Koeffizienten in den Ausdrücken
der G^, C^, •■• durch die /, /'. • • • diesem Körper angehören, köpnen
aber auch schon in einem echtep Teiler dieses Körpers enthalten sein.
Wir bezeichnen den durch die fraglichen Koeffizienten gegebenen Körper
mit ^' und haben damit der Gleichung (8) den Körper:
(9) (^', J, J", ■-., J(P~''^)
zugrunde zu legen.
Es besteht der Satz: Die Gleichung (8) ist im FtmUmienl^rj^er (9)
irreduzihd und hJeiU auch dann irreduzibel, we^^n mun zum JS^Örper (9)
22 I, 1- Sätze über Gnippen linearer Substitutionen.
irgendwelche „numerische" Irrationalitäten adjungiert. Würde nämlicli
dieser Satz nickt gelten, so würde eine Gleiclmng:
(10) g{Z) =^ D,Z^ -f D,Zi-' + ... -f D^ =;. 0
eiaes Grades l <I in mit Koeffizienten, die irgendwelche absolute
Invarianten der @^ sind, angebbar sein, die durch die Form w der n
unabhängigen Variablen z^, z-^, •••, % erfüllt würde. Die Darstellung der
J} durch die ^j, z^^ .••, % und die Eintragung von w für Z würde zu
einer in den z identischen Gleichung führen. Sie würde also auch gelten,
wenn wir für ^j, z^., •.., z^ irgend eines der m Systeme z\, z'^, •••;
z'[, z'^, ..•; •" einführten. Hierbei würden sich die Koeffizienten!)
nicht ändern, während w in w', w", ••• überginge. Die Gleichung (10)
müßte also durch die m „verschiedenen'* Formen w, w\ w\ ••• erfüllt
werden, d. h. es wäre l~^m. Damit ist der Trreduzibüitätssatz bewiesen.
Man verstehe wie in (l) S. 15 untex q> eine beliebige lineare Form
etwa mit rationalen Koeffizienten. Durch die Substitutionen der @^
gehe 9) in g), g)', ••., g)^"*"^) über, wo alsdann in den Koeffizienten
dieser linearen Formen auch die Substitutionskoeffizienten auftreten. Wie
in I, 362 ff. wiederholt ausgeführt wurde, schließe man hieran den
Amsatz:
und hat in H{Z) eine Funktion {m — l)*^'* Grades, deren Koeffizienten
absolute Invarianten und als solche rationale ganze Funktionen der
J, J', ... sind. Diese Koeffizienten gehören also dem
Funktionenkörper (9) an, zu dem nur nötigenfalls noch numerische Irrationalitäten
zu adjungieren sind, die indessen dem Körper der Substitutionskoeffizienten
angehören. Setzt man in (11) insbesondere Z = «;, so folgt:
so daß die Form (p rational in einer ersten Lösung w der Grleichung (8)
darstellbar ist. Für (p können wir insbesondere eine einzelne Variable ß^
wählen. Wir gelangen so zu dem Ergebnis: Jede der Variablen z^,
z^, '•', % und damit jede der Formen (6) sowie überhaupt jede rationale
FunMion der z ist nach AdjunJction einer einzigen beliebig wählbaren
Lösung w der Gleichung (8) zum FunUionenWrper (9) rational beJcannt.
Es sind dabei freilich nötigenfalls noch numerische Irrationalitäten zu
adjungieren; für die Berechnung der z einzeln und der Formen (6)
genügt jedenfalls die Adjunktion der Substitutionskoeffizienten.
Aus diesen Darlegungen ergibt sich mit Benutzung der in I, 368
entwickelten Grundsätze: Die im Körper (9) irreduzibele Gleichung (8)
ist eine „Norm^gleiehung" mit einer Qaloisschen Gruppe, die mit unserer
Substitutionsgruppe @^ isomorph ist. In der Tat ist ja nach den nötigen
Algebraischer Ghaxalkter eines ipormenproblems. 2B
numerischen Adjunktionen in dem durch Zusatz einer Lösung der
Gleichung (8) zu (9) gewonnenen Körper bereits der Galois sehe Körper
jener Gleichung gewonnen. Die m Transformationen dieses Körpeys in
sich, bei denen etwa w der Reihe pach in w^ w', fv", ■ • • übergeht, werden
aber gerade durch unsere m Substitutionen der @^ geliefert.
Fassen wir die ©^ in ihrer eigentlichen Gestalt als die Galoi^sche
Gruppe von (8), d. h. als Permutationsgruppe der «^, w', • • •, und weaden
die in I, 378 entwickelten Prinzipien ß,n, so können wir z. B. für einen
beliebigen Normalteiler (S>i mit zj^klischem Komplement (^j eine
gegenüber der @; invariante Fimktion der w, w', ■■■ und also der ^j, z^, •■•
bilden, die im eigentlichen Sinne der @; zugehört, d. h. gegenüber der
gesamten @^ in t durchweg verschiedene Funktionen übergeht. Von
hieraus erkennt man ohne Mühe die ßxistens von relativeM Iiß,varia/nten
unserer Qnippe @^ für jedes theoretisch mögliche FaJdorenstfstem (vgl. S. 19).
Die vorstehenden allgemeinen Entwipklungen finden später ihre
Einzeldurchführung an wichtigen und friichtbaren Beispielen. Hier
mögen vorerst nur noch folgende allgemeine Bemerkimgen über die
Bedeutung der*^ Formenprobleme folgen. Ist bei der eben beendeten
Überlegung das Formenproblem der Sphstitutior^sgruppe @^ umgewandelt in
die Aufgabe der Lösung der Gleichung (8) mit einer zur @^ isomorphen
Galoi&sch.en Gruppe, so kann man umgekehit versuchen, die Lösung einer
Gleich.ung durch ein äquivalentes Formenproblem einer Substitutjons-
gruppe @^ zu ersetzen, die mit der Galoisschep Gruppe der Gleichung
isomorph, ist.
In dieser Hinsicht mag zunächst erwähnt werden, d3,ß die Lösung
der „allgemeinen" Gleichung n^^ Grades (vgl. t, 389):
(13) ^ + a^0^~'' + a^z^~'' -] ^«^=0
unmittelbar als ein Formenproblem der Dimension n aufgefaßt werden
kann, wobei die „Dimension des Formenproblems" natürlich die der
Substitutionen <ist. Schreiben wir die Permutationen der symmetrischen
Gruppe der n Lösungen ^^, z^, •••, z^.
z\ = ^,^, z\ = Zi^, ..., 4 == Zi^,
wo ij, ig, ••-, i„ die » Indizes 1, 2, •••, n in irgend einer Anordnung
sind, so hat jene @„j die Gestalt einer Substitutionsgruppe. Ein System
voneinander unabhängiger Invarianten, in denen alle Invg-rianten dieser
Gruppe (d. h. alle rationalen ganzen symmetrischen Fnnktipnen der
n Wurzeln z^^ z^, •••, z^) rational und gan:? darstellbar sind, ha|,t man in
den n symmetri«eh.en Grundfunktionen der z^, z^, •••, z^, die gleich den
— a^, «3, —«3, ••• sind. Die Vorlage der Gleichung (13) konnnt also
auf die Angabe der n Werte jener.-InV9,rianten hinaus. Ifan sieM, daß
das zugehörige Formenproblem unipittelbar die Auffiadnng der
Gleichungswurzeln verlangt.
Ist es möglich, die Lösung einer Gleichung ^uf verschiedene Formen-
probleme zurückzuführen, so hat man dem mit der niedrigsten Dirnen-
24 I? 2. Polyedergrappenu
sionenanzabl n den Vorzug zu geben. Dieser Auffassung entsprecbend
sind die Gleicbungen als die einfaebsten anzuseben, die auf
eindimensionale Formenprobleme oder auf solche mit tmärer Gruppe zurtickfübrbar
siad. Nach S. 13 haben wir für jede Anzahl m eine und nur eine unäre
Gruppe @^, die aus den m Substitutionen:
z' = e'^ z, A; = 0, 1, 2, .. •, m — 1
besteht. Relative Invariante ist jede Potenz der einen Variablen z \ eine
absolute Invariante ist ^, und jede absolute Invariante ist als Potenz
von ^ darstellbar. Das Formenproblem fordert die Bestimmung von z
bei gegebenem Werte von z"^ ==■ c. Die eindimensionalen FormenproUeme
Jcommen demnach einfach auf die Aufgabe der Lösung der reinen
Gleichungen z^ = c zurüek. Hieran schließen sich als nächste Fälle die
Formenprobleme der endlichen Gruppen binärer Substitutionen, zu deren
Untersuchimg wir uns jetzt wenden.
Zweites Kapitel.
Polyedergruppen *)•
§ 1. Einteilung der linearen Substitutionen einer Variablen.
Die binären nicht - singulären Substitutionen schreiben wir fortan in
der Gestalt: *
(1) 4 = az^ + ßz^, z\ = yz^ + 8z^.
In einer vorgelegten @^ solcher Substitutionen mögen X
Ähnlichkeitssubstitutionen enthalten sein, die nach S. 13 einen Kormal teuer ®x bilden.
Die @^ reduziert sich auf das zugehörige Komplement @^, falls man in
ihr jeweils die X miteinander ähnlichen Substitutionen als nicht
verschieden ansieht. Diese Auffassung läßt sich in der Art sehr einfach
*) Die folgende Darstellung bezieht sich zwecks näherer Begründung und
Weiterführung vielfach auf die Veröffentlichungen von P. Klein und diejenigen
des Verfassers. Es handelt sich um folgende Werke: Klein, „Vorlesungen über
das Ikosaeder und die Auflösung der Gleichungeoi vom fünften Grade" (Leipzig
1884), zitiert durch „Ikos."; Klein und Pricke, „Vorlesungen über die Theorie
der elliptischen Modulfunktionen", 2 Bde. (Leipzig 1890 und 1892), zitiert durch
„Modulfunkt."; Pricke und Klein, „Vorlesungen über die Theorie der
automorphen Funktionen", 2 Bde. (Leipzig 1897 und 1912), zitiert durch „Autom. Funkt.";
Fr icke, „Die eUiptischen Punktionen und ihre Anwendungen", bisher 2 Bde.
(Leipzig 1916 und 1922), zitiert durch „Ellipt. Punkt."; Klein, „Gesammelte
mathematische Abhandlungen", 3 Bde. (Berlin 1921, 1922 und 1923), zitiert durch
„Ges. Abh.", stets unter Angabe der Band- und Seitenzahl. Die Entstehungszeit
der Abhandlungen Kleins ist aus dem letzten Werke zu ersehen.
Invarianten und Pole linearer Substitutionen einer Variablen. 25
verwirkliclien, daß mau von den beiden Jwrnogey^n Variablen" ,e,, ^^ zu
ihrem Quotienten z = s^: z^ übergeht und ^ di^ Stelle der homogenen
binären Substitution (2) die gebrochene lineare Substitution der einen
Variablen z treten läßt:
(2)
r^ + 5
Man sagt auch, die Substitution (1) sei hier in die „wicht - homogene
Gestalt" gesetzt. In der Tat kann man in (2) die vier Koeffizienten um
einen beliebigen, von 0 verschiedenen gemeinsamen Faktor ändern, ohne
damit die „nicht-homogene Substitution" (2) selbst wesentlich z\\ ändern.
Allen einander ähnlichen Substitutionen entspricht dernnach dieselbe
Substitution (2).
Die Unbestimmtheit der Koeffizienten der einzelnen Substitution (2)
hebt man wenigstens teilweise dadurch fort, daß man:
(3) ccd-ßy=l
vorschreibt und damit, wie man sagt, die Substitution (2) „unimodular^
schreibt. Aber auch dann ist noch ein gemeinsamer Zeichenwechsel der
Koeffizienten ohne wesentliche Änderung de^ Substitution möglich.
Sehen wir von der Substitutionsdeterminante (B) des konstanten
Wertes 1 ab, so hat die unimodulare Substitution (2) nur noch eine
rationale Invariante (vgl. S. 7), die fortan di^reh j bezeichnet werden soll
und gegeben ist durch:
(4) j = oc-r8.
Die charakteristische Gleichung (3) S. o hat die Gestalt:
(5) ^2-j^4-l=0
und ergibt für die beiden Multiplikatoren die zueinander reziproken
Werte:
(6) fi=|(i±V?~4).
Deutet man die komplexen Werte von z and z' in der gleichen
Ebene, so wird diese durch eine einzelne Substitution (2) umkehrbar
eindeutig und winkeltreu auf sich selbst bezogen. Dabe^. treten zwet sich
selbst zugeordnete Pimkte oder „Pole" (,Fixpunkte") der Substitution
auf (vgl. S. 5), die durch die Lösungen der (quadratischen Gleichang:
(7) yz'-^(d~a)z~ß = 0
geliefert werden. Für y^O liegen dje Pole an den endlichen Stellen:
(8) z===~(cc~dxiF^,
für y = 0, cczjzd ist nur ein Pol im Ekidlichen, und ^iwar bei:
(9) - =- Y^-
26 I, 2. Polyeder^raj^en.
gelegen, während der andere im Punkte ^ = oc liegt, imd endlich
für y = 0, cc = d, ß =t^-^ fallen ' beide Pole im' Punkte ^ = oo zu-
Eine Klasseneinteilung der Substitutionen (2), deren
Zweckmäßigkeit aus den folgenden Entwicklungen hervorgehen wird, hat J&lein*)
durchgeführt. Die unimodulare Substitution heißt „loxodromisch^, falls
ihre Invariante j nicht reell ist; die Substitutionen mit reellen Invarianten
aber werden in die drei Klassen der „eTliptisehen^, der „parabolischen"
und 4er „hyperbolischen Substitutionen" eingeteilt, je nachdem für die reelle
Invaxiaate j die Bedänguag }i j <C 2, | j| = 2 oder j j j > 2 zutrifft. Die
identische Substitution, die jj| = 2 und natürlich reelles j hat, soll
jedoch für sich stehen, d. h. nidit etwa den paraboKschen Substitutionen
zugerechnet werden. Aus den vorstehenden Angaben, insbesondere der
Gleichung (8) folgt: Eine parabolische Substitution hat zusammenfallende
Pole, bei einer Substitution der drei anderen Arten liegen die beiden Pole
getrennt.
Wir nehmen für die Substitutionen (2) die symbolischen
Bezeichnungen S, T, -•' wieder auf Wd geben die einzelne Substitution durch
bloße Nennung ihrer Koeffizienten etwa in- der Gestalt S = [st]' '^^'
folge (6) sind, abgesehen von der identischen Substitution, nur bei einer
parabolischen Substitution die beiden Multiplikatoren einander gleich, bei
einer Substitution der übrigen Arten sind sie verschieden und einander
reziprok. Aus dem Satze von S. 11 über die Normalgestalten der
Substitutionen ergibt sich: Jede unserer unimodularen Substitutionen (2)
Jcann durch Transformation mittels einer Substitution T in die erste oder
sweite der nachfolgenden Gestalten:
(10) s = (J;0.
/^, 0
lo, fi-
ubergeführt werden, je nachdem sie parabolisch ist oder nicht. Die beiden
Pole einer paraboKschen Substitution (10) fallen im Punkte ^ = oo
zusammen, diejenigen einßx nicht-parabolischen Substitution {10) Kegen bei
z =z ö und z = oo.
§ 2. Veranschaulichung der linearen Substitutionen einer Variablen.
Die durch eine Kneare Substitution S gegebene Abbildung der
^-Ebene auf sich selbst ist dadurch ausgezeichnet, daß Kreise der s-Ebene
stets wieder in Kreise übergeführt werden. Dabei sind die Geraden der
S-Ebene den Kreisen zuzurechnen, nämKch als solche des Radius oo.
Die fragHche konforme Abbildung wird deshalb auch als eine „Kreis-
*) Vgl. „Ges. Abb." III, 25 und 661 und etwa „Äutom. Punkt." I, 7 ff.
Elliptische, parabolisehe osw. Substitationen. 27
vermandischaft' > bezeichnet *). Man bestätigt dies unmittelbar an den
beiden,eben unter (10) gewonnenen Substitutionen**):
(1) z'==:2-\-ß, / =- {l^Z,
deren zweite man unter Benutzung der Pqlard^rsteliung re**' für den
Koeffizienten fi^ aus den beiden Substitutionen:
(2) / = e^iz, z == TZ
zusammensetzen kann. Die durch die-paraboKsche Substitution (1) yer-
mittelte Abbildung wird durch eine Translation der ^-Ebene heygestellt,
bei der der Nullpunkt in den Punkt ß rückt; die erste Substitution (2)
bedeutet eine Drehtmg der ^-Ebene urp den Nullpunkt und die zweite
eine ÄhnJicJikeitstransfor motion. Alle drei Transformationen erkennt man
unmittelbar als Kreisverwandtschaften. Der gleiche Chaiakter kommt
demnach auch der aus ihnen zusammensetzbaren beliebigen ganzen
linearen Substitution zu:
(3) z' = az^ß.
Die zunächst wieder unimodular geschriebene beKebige Substitution (2)
S. 25 mit 7^0 lä£t sich in die Gestalt:
z' == ——1_ + «
umrechnen und also aus folgender^ vier Substitutionen zusammensetzen:
z =• Y^z. z = z -f- yO, z = , ^ = z A •
' ' * ' z y
Drei von ihnen sind ganze Substitutionen, die dritte liefert unter
Benutzung der Schreibweise z :=. x -^-iy für die rechtwinkligen
Koordinaten a;, y\
(4) a;' = , y= -^—^,
x^ + y^ a;2 -f 2/
woraus der Charakter dieser Substitution als einer Kreisverwandtschaft
leicht folgt.
Kleinf) veranschaulicht eine Substitution S durch eine stetige
Umformung der ^-Ebene in sich, was hier für die weiterhin allein in
Betracht kommenden nicht-loxodromischen Substitutionen ai^sgefiihrt
werden soU. Es kommen also i^ur reelle Invarianten j ■= a,-{- 8 in
Betracht. Die Substitution S liege zunächst in der Xormalgestalt (10)
*) Vgl. Moebius, „Die Theorie der Kjeisverwandtschaft ^n rein
geometrischer Darstellong", Abh. der Leipz. Ges. der Wiss., Bd. 2 (1855) oder Moebius,
Ges. Werke, Bd. 2. Man vgl. auch „ülQdulfuukt.'- I, 82 und „Ellipt. Funkt." I, 66.
**) An der unimodularen Gestalt der Substitutip^en ist bei den nächsten
Rechnungen nicht durchweg festgehalten.
t) Vgl. „Modnlfunkt." I, 165 ff.
28 I) 2. Polyedergruppen.
S. 26 vor. 1st |ij<C'-^ THid also S elliptisch, so ist ^ eine komplexe
Zahl des absoluten Betrages 1. Xan schreibe:
(5) ^ =-{jJrif~4:) = cos- + ism~= e^
und gelangt zur ersten Substitution (2). Die Veranschauüchung von S
ist einfach mittels einer Drehung der ^-Ebene um den Nullpunkt durch
den Winkel %• gegeben. Die konzentrischen Kreise um den XuUpunkt,
längs deren die einzelnen Punkte .der ^-Ebene laufen, heißen die
„Bahnlinien'' von S, die zu ümen senkrecht verlaufenden Geraden durch den
Nullpunkt werden ihre „Niveaulinien^ genannt. Ist |j|>.2 und also S
hyperbolisch, so ist ^ reell und ^^ = r positiv, und man gelangt :^ur
zweiten Substitution (2). Sie wird, der Ähnlichkeitstransformation ent-
Fig. 1.
sprechend, durch eine stetige Dehnung {V^ 1) oder Zusammenziehung
(r << 1) der -3;-Ebene versinnlicht, bei der der einzelne Punkt z auf der
durch den Nullpunkt ziehenden Geraden nach dem Punkte z = rz
hinläuft. Die vom Nullpunkt ausstrahlenden Geraden sind jetzt die „Bahn-
Imien" und die sie senkrecht schneidenden konzentrischen Kreise um
den Nullpunkt die „Niveaulinien-'. Ist \j\ = 2, so haben wir die
parabolische Substitution (1). Sie wird versinnlicht durch die Parallei-
verschiebung der ^-Ebene, welche den Nullpunkt nach dem Punkte z = ß
führt. „Bahnlinien- sind jetzt die Geraden, die die
Verschiebungsrichtung haben, „Niveaulinien'' die zu ihnen senkrecht verlaufenden
Geraden.
Eine beliebige Substitution S mit reeller Invariante j wird durch
Transformation mittels einer geeignet gewaMten Substituüon T in eine
Bahn- und Niveaulinien einer Substitution. 29
der drei besprochenen Xormalgestalten übergeführt. Indem man von der
zu dieser Kormalgestalt gehörenden Bewegung der ^--Pbene in sich das
durch die Substitution T~^ gegebene kreisver^andte Abbüd ninimt,
gelangt man zur Veranschanlichung der Substitution S. Die im Falle
|j]z^2 soeben bei z = 0 und z =z co gelegenen Pole werden dr^rch
T~^ an die beiden durch (8) S. 25 gelegenen Stellen ^j, z^ verlegt.
Die Bahn- und die Niveaulinien werden dann von der Schar der Kreise
durch die Pole z^, z^ und der zugehörigen orthogonßlen Kreis$char geliefert.
Fig. 1 versinnlicht den Fall einer hyperbolischen Substitution, wo die
mit Pfeüen versehenen Kreise die Bahnlinien sind. Im elliptischen Falle
sind sie die ISTiveaulinien, während die andere Kreisscjiar die Bahnlitiien
darstellt. Die Versinnlichung einer parabolischen Substitution ([j| = 2)
kann als Grenzfall der Fig. 1 für den Zusammepfall von z-^ und z^
angesehen werden: lAegt der Fol z^ der parabolischen Substitution S im
Endlichen, so werden die Bahnlinien von einer gewissen Schar einander
im PunMe z^ berührender Kreise geliefert, die Niveaulinien aber von der
lörigen orthogonalen Kreisschar.
§ 3. Projektion der ^-Eben^ auf eine Kugelfläche.
Neben der ^-Ebene benutzen wir eine Kugelfläche als Trägerin der
Werte der komplexen Variablen z = x -\- iy. Pi« ^-Ebei^e denken wir
horizontal und legen um ihren Xullpunkt eine Kugel d,es B^adius 1.
Rechtwinklige Raumkoordinaten |, rj, t, i^ögen so eingeführt werden,
daß die ^-Ebene die |, ij-Ebene wird und in ihr die positive reelle
^-Achse die positive |-Achse liefert. Die positive ^■-Achse weise n^ch oben.
Die ^-Ebene wird nun stereographisch auf die Kugelfläche projiziert,
wie dies Fig. 2 in irgend einer durch die ^-Achse laufenden, also vertikal
Fig. 2.
gedachten Diametralebene
der Kugel darstellt. Das
Projektionszentrum soll also
der tiefste Punkt der Kugel
sein. Der einzelne Punkt P
der Ebene gehe in den
Punkt P' der Kugel über.
Insbesondere geht der Punkt
^ = 0 in den höchsten
Punkt der Kugelfläche über,
der Punkt oo aber in den
tiefsten. Ist P der Bildpunkt von z = x -{-iy und hat P' die
Koordinaten ^, ti, t„ so gilt erstKch:
(1) r + V' + r = i-
und die |, ?;, t, berechnen sich aus den x, y durch die Gleichungen:
/ox 2 0^ _ 22/ _ . __ 1-^^-/
^-^ ^-rr^MV' "^"i + ^^^ + f ^-l + o^M-/'
go I, 2. Polyedergruppen.
Während umgekehrt:
^«> -ril' -i^' ^ = ^ + .-. = |±^
ist (vgl. Fig. 2).
Es besteht der Satz: Die stereographische FrojeMion $teTlt eine
winheHreue AhNldung der z-E'bene auf die EugelfläcJie dar, hei der die
Kreise der Ebene (unter Einschluß der Geraden) die Kreise der Kugd-
fläche liefern. Zum Beweis lege man die Tangentialebene im Punkte P'
an die Kugel, die die Ebene der Fig. 2 in der Geraden P' Q schneidet.
Dann gilt PQ = P^. Die Schenkel der Winkel des Scheitelpunktes P
werden auf die Kugeloberfläche und damit auf die Tangentialebene
mittels des Ebenenbüschels der Achse PP' projiziert. Wegen PQ=zP' Q
ist die Projektion auf die Tangentialebene und damit auf die
Kugeloberflache winkeltreu. Andererseits wird der Kreis der ^-Ebene von der
Grleichung;
a(x^+ f)-{-hx-\-cif-\r d — 0
zufolge (3) auf den Schnitt der Kugelfläche mit der durch:
fe| + C7j + ((l-a)^ + (^ + a) = 0
gegebenen Ebene, d. i. also wieder auf einen Kreis abgebildet.
Besonders anschaulich wird die Versinnlichung der nicht-loxodro-
mischen Substitutionen 8. Ist j j [ z^ 2, so liegen die beiden Pole auf der
Kugelfläche getrennt. Durch die sie verbindende Sehne imd ihre
konjugierte Polare lege man die beiden Ebenenbüschel, die auf der
Kugelfläche die Bahn- und Niveaulinien ausschneiden. Im paraboKschen Falle
treten an Stelle der Sehne und ihrer Polare zwei einander senkrecht
kreuzende Kugeltangenten. Sind die beiden Pole ^j, z^ insbesondere
diametral auf der Kugel, und ist jjj < 2, d.h. ist S elliptisch, so sind
die Niveaulinien die zu diesen beiden Polen gehörenden Meridiauhalb-
kreise, imd die Bahnlinien werden von den Parallelkreisen geKefert. In
diesem Falle wird S durch eine gewöhnliche Drehung der Kugel um
einen Durchmesser versinnlicht: Die gesamten Drehungen der Kugd-
oberfläche in sieh um Durchmesser stellen gerade die gesamten elliptischen
Substitutionen S dar, deren Pole auf der Kugel fläche jeweils diametral
liegen *).
XJm diese besonderen elliptischen Substitutionen durch Formeln
darzustellen, berechnen wir für irgend zwei diametrale Punkte (|, ri, ^) und
(— I? — if}r — Dj ^i® ^^ 8ls Pole nehmen wollen, die Werte:
(4.) z -^'+^'^ z ~ ^ + ^'?- 1+S
1-fg 1—§ l~%ifl
*) Einer „loxodromisclien'' Substitution z' = re^^z entspricht eine stetige
Umformung der Kugel in sich, bei der die „Bahnlinien" sogenannte „Loxo-
dromen" sind.
Darstellung der Kugeldrehimgen d^rcli lineare Substitutipnen. 31
von denen jeder gleich dem negativ und reziprok genommenen konjugiert
komplexen Werte des anderen ist. Die zugehörige Substitution habe
die Invariante;
(5) i = 2cös-,
drehe also die Kugel um den Winkel Q: Durch Transformation mittels
der Substitution :
die die Pole 0^, z^ nach 'z^ = 0, <^a = oc» verlegt, gelangt pian zur
Normalgestalt F = e^^^. Die Substitution kann also, in z geschrieben,
in die Gestalt gesetzt werden:
„. Z Z.. c^ Z—Z^
Trägt man für ^j, z^ die Werte (4) ein und löst nach z^ auf, so
gelangt man bei-unimodularer Schreibweise ?:ur Substitution:
n\ z' = (-4 + ^-^)^ + (C + ^i))
^ ^ (—C + iByz + iÄ — iB)'
wo Ä, B, C, JD die folgenden vier reellen Größen sind:
(8) Ä = cos-, B = ^sin-, C = risin^, P = —^sin-,
die in der Tat die Gleichung:
(9) A^ + B^ + C'^ D^ = 1
befriedigen. Die Bauart der unimodularen eTlipUschen Substitution (7) ist
also die, daß der erste und vierte Koeffi^ent ijconjugiert komjplex sind, und
ebenso der zweite und der negativ genommene dritte.
Ist umgekehrt eine beliebige von der identischen Substitution yer-
schiedene unimodulare Substitution (7) gegeben, so berechne man d; sowie
I, rj, t, aus:
(10)
bei beliebiger Auswahl des Vorzeichens der Quadratwurzel. Die beiden
I*iiJikte (I, Yi, l) und (— I, — VI, — l) liegen auf der Kugelfläche, und
zwar diametral. Erklären wir 2wei zugehörige Werte z^, z^ durch (4),
so läßt sich die Substitution auf die Gestalt (6) umrechnen: Die
gesamten Drehungen der Kugel um ifire Durchpiesser werden gerade genau
von allen unim^duJaren elliptischen Substitutionen (7) geliefert. Die
identische Substitution (7), die ^ = + 1, B = C ^ D = 0 h^t, wird
32 I> 2. Polyedergrappen.
früherer Festsetzung entsprechend nicht zu den elliptischen Substitutionen
gerechnet.
Es besteht der Satz: Die unimodularen elliptischen Substitutionen (7)
im Verein mit der identischen Substitution, d. h. alle unimodularen
Substitutionen (7) mit reellen Ä, B, C, J) bilden eine Gruppe unendlicher
Ordnung. Irgend zwei Substitutionen:
nn Q — ( A + iB, C + iD \ ^, __ [ A' + iB', C' + iB' \
(11) S- (_c + iD^ A-iJßJ' ^ -[-C' + iD\A'--iB')
liefern nämKch zusammengesetzt;
(1^) ^ —^^—[-C" + iD",A"-iB"}'
wo sich die A", B", C", D" wieder als reelle Größen durch:
(A" = ÄA — B'B — G'G — D'D,
B" = A'B + B'A-r- CD — D' C,
C" = A'C-B'D-i- CA + D'B,
[D" = ÄD-^B'C — CB ~\-D'A
berechnen. Außerdem ist S" unimodular, da dies von S und S' gilt.
Der aufgestellte Satz entspricht der Tatsache, daß die Verschiebungen
der Kugelfläche iu sich in ihrer Gesamtheit eine Gruppe bilden. Jede
solche Verschiebung ist nämlich eine Drehung um einen Kugel durch-
messer *).
§ 4. Diophantische Gleichung für die Gruppen ®m'
Entsprechend den Entwicklungen von S. 25ff. suchen wir jetzt
zunächst alle endlichen Gruppen ®^ von unimodularen Substitutionen:
« ^■ = ^' ««-^^ = '
zu bestimmen, für die wir die Bezeichnung z' = S{z) beibehalten. Der
kleinste positive Exponent v, für den S" = l ist, heißt die „Periode^
von S (vgl. I. 272). Aus den Normalgestalten (10) S. 26 und (2) S. 27
folgt, daß eine paraboKsche, hyperbolische oder loxodromische Substitution
keine endliche Periode hat **). In der @^ finden sich neben der
identischen Siibstitutimi 8^=1 ausschließlich elliptische Substitutionen, deren
Perioden v in der Gruppenordnung m aufgehen j).
Zweitens gilt der Satz: Zwei elliptische Substitutionen S und S' der
endlichen Gruppe @^ haben entweder beide Pole gemein oder keinen.
Auch diese Eigenschaft ist von einer Transformation der Gruppe unab-
*) Weitere Ausführungen über die letzten Eflitwicklungen findet man in
„Ikos.". S. 36.
**) Zwei ineinander transformierbare Substitutionen 8 und T- 8- T—i haben
offenbar stets die gleiche Periode.
t) Vgl. den an (1) S. 13 angeschlossenen Satz.
Formeln für die Zusammensetzung zweier Kugeldrehungen. 33
Mngig. Man nelime demnacli etwa an, daß S und S' den Pol oo gemein
Laben, und da£ der zweite Pol ^on S bei ^ = 0 gelegen ist. Dann
hat man:
und berechnet für den Kommutator dieser Substitutionen (vgl. I, 289):
s-.s'-.s.s'=(J; ('-*;>''■*').
Da parabolische Substitutionen in der (Srruppe nipht vorkommen, so gilt
<1 —d^)ß'ö' = 0. Xun aber gjlt ^4=+ 1, ö'^zO, so da£ ß' = 0
folgt. S' hat also auch den zweiten Pol mit S gemein, woraus die
Behauptung hervorgeht.
Hieran reiht sich der weitere Satz: Alle S'ahstitutimien der @^ mit
dem gemeinsamen Polpaare z = e, ^ = e bilden im Verein mit S^ =^ 1
ein&ii zyklischen Teiler @„. Haben S und S' die Pole e, e', so werden
diese Punkte auch durch S' • S in sich transformiert, woraus die (rruppen-
eigenschaft des fraglichen Systemgi von Substitutionen einleuchtend ist.
Handelt es sich um einen Teiler (§„ der Ordnung ^, sp geht die Periode
jeder zugehörigen Substitution in ^ auf. Bei Benutzung der
Schreibweise (6) S. 31 kann man also die Substitutionen von @„ ßo schreiben:
/ — e ' z — e '
wo J: auf die Zahlen des Intervalls 0 ^ /^ <C f* beschränkt werden
kann und für k = 0 die identische Substitution vorKegt. Da sich ^
verschiedene Substitutionen ergeben müssen, so kommen alU Zahlen
k = 0, 1, 2, •••, fi— 1 zur Geltung. Also ist dip ©„ aus der zu
Je = 1 gehörenden Substitution erzeugbar, womit sie als zyklisch
erkannt ist. Die Gruppe ®a heißt ein „größter- z-yUischer Teiler von ®„^,
da sie nicht in einem noch umfassenderen zykKschen Teiler der Ö)^^
enthalten sein kann. Zwei verschiedene grüßte .zyklische Teiler ®a und 03«'
haben, abgesehen von S^ = 1, keine gemßin&a^ne Substitution. Z"v\^ei
elliptische Substitutionen S, S' aus @,f und ®a' haben näinlich verschiedene
Zwei Punkte der ^-Ebene, die durch Substitutionen der ©^
ineinander überführbar sind, heißen „bezüglich der Gruppe @^ äquivalent".
Miteinander äquivalent sind also allemal die Punkte:
(3) ^0, ^^ — Sj(^^), ^2=Sa(^o)' '■•' ^w-i = ^»-i(^o)-
Die m äquivalenten Punkte (3) Kegen getrennt, so oft z^ nicht Pol einer
elliptischen Substitution der ®^ ist. Ist indessen z,^ einer der beiden
Pole eiaes größten zykKschen Teilers ®u des Index t = m- ^~^, so
rücken die m Punkte (3) zu je fi ^ ^ verscl^iedene Stellen. Jede dieser
Stellen ist dann'Pol für (fi— 1) elliptische Substitutio|ien, die ii^i Verein
Fricke, Algebra H. 3
34 I» ^- Polyedergruppen.
mit So = 1 einen mit @^ konjugierten Teiler bilden. Stellt man. nämlich
die Nebengruppen:
her, so transformieren die Substitutionen der einzelnen Nebengruppe 0^^
in einen und denselben Punkt. Vi und Fj; mit i zj:z Je liefern aber
verschiedene Punkte Vi (2^) und Vjc{0q), weil sonst ^^ durch V^^ • Fj; in sich
transformiert würde, während doch diese Substitution nicht dem Teiler
@^ angehört. Wenn wir demnach sagen, daß die (m — 1) elliptischen
Substitutionen der @^ im ganzen (2 m — 2) Pole liefern, so ist der
einzelne Pol, falls er zu einem größten zyklischen Teiler (Ba gehört, dabei
(fi—l)-fach gezählt, und die ^ eben betrachteten äquivalenten Pole
erschöpfen von der Gesamtzahl aller (2 w — 2) Pole im ganzen:
(4) t(ii—l) = mf-^{^ —l)^m\l \
Pole.
Sind durch dieses System äquivalenter Pole noch nicht alle {2 m — 2)
Pole erschöpft, so schreiben wir ^^ statt der eben mit /i bezeichneten
Zahl und mögen durch ein zweites System äquivalenter Pole weitere
mfi~i(fi2— 1) -^^^^ erschöpfen. Lassen sich alle (2 m— 2) Pole ia Je
solche Systeme zerlegen, so gilt offenbar:
2 w — 2 = w« ft-i (^j — 1) -j- mfi-i (ftg — 1) -] \- m ^^^ Qi}. — 1)
oder nach Division durch m:
Hiermit haben wir eine diophantische (xleichung für die Anzahlen m, ^^,
ftg' '"' f*Jk gewoimen.
Da die Zahlen w = 1 und fx = l nicht in Betracht kommen, so gilt:
(6) 1 < 2 - - < 2, 1 < 1 _ i < 1.
^ m 2 " ft
Hieraus folgt für die rechte Seite der Gleichung (5):
woraus sich wegen (5) und der ersten Formel (6):
l<2l-?-<fc, |-<2-l<2
— m 2 = m ■
Diophantische Grleichong fur eine en4hclie Gruppe ®^^. 35
ergibt. Es bleiben also nur die beiden Möglichkeiten Jf = '2 un4 Jo =. 3.
Man gelangt leicht zu folgendem Ergebnis: Es gibt im ganzen nitr die
folgenden fünf Lösungen der diophßwtiscfien Gleiehimg (o):
I.
n.
III.
IV.
V.
fc =: 2,
k = 3,
}c = 3,
h = 3,
k = S,
Uj = m,
ii,r=%
(ll == 2,
^^^2,
11, = 2,
fig, = m,
11^ = %
11^ = 3,
^^ = 3,
."ä = ^:
;*3 = 1*^'
(h = 3'
^3 = 4,
^3 = S'
m := 12,
w» == 24,
m := 60,
«jo&e'* im Falle I ^ie Za^Z w» > 3 isi ^<wä! übrigens helieUg wählbar ist,
während im Falle II die Zahl m gerade und > 4 «s^. Im Falle k =- 2
folgt nämlich aus (o):
(7) !?l + !^..2, .
und da ^u^ und fig Teiler von m sind, so stehen hier links in beiden
Gliedern ganze positive Zahlen, die demnach nui" gleich 1 sein können.
Daraus ergibt sich I als einzige Lösung mit k = 2 Ist k = 3, so
nimmt die diophantische Gleichung (5) die Gestallt an:
(8) l^i + i=l+i.
fi, ftg fig m
Wären alle Zahlen /i > 3, so ware die linke Seite < 1, während die
rechte ^ 1 ist. Also ist mindestens ein fi = 2, und wir setzen etwa
fij = 2. Gleichung (8) ergibt dann weiter:
('> ^-,;^ = ¥ + |-
Also können nicht beide Zahlen fig '^^.d ^^ größer ^Is 3 sein. Wir setzen
demnach fi^ zuerst gleich 2 und d^nn gleich 3. Für fig = 2 gelangen
wir zur Lösung II, in der m als gerade Zahl oberhalb 2 willkürlich
wählbar bleibt. Für ^ = ^ folgt aus (9):
1=14-1,
fig b m
so daß nur noch die drei Werte ftg = 3, 4 und ^ brauchbar bleiben •==)-
Wir gelangen zu den drei Lösunge^fi III; IV und V.
§ 5. Existenz der endlichen Gruppen (S»i.
Es ist jetzt die Frage, ob den^ einzelnen der eben aufgestellten fünf
Zahlensysteme I bis V eine Gruppe @„j voi| linearen Substitutionen S
entspricht, und wie viele verschiedene Gruppen ihm etwa zugehöipen
*) fi^ zz: 2 wurde zum Falle II mit pi z=z & und umgestellten fahlen fi
zurückfuhren.
3ß I, 2. Polyedergruppen.
mögen. Zwei Gruppen, die ineinander transformierbar sind, werden wir
dabei nicht als wesentKch verschieden ansehen. Von vornherein ist
einleuchtend, daß wir hier zu den in I, 266, 307, 335 und 344 wiederholt
betrachteten Gruppen der Drehungen der regulären Polyeder in sich
zurückgeführt werden müssen,- denn z. B. ein mit der ^-Kugel
konzentrisches Ikosaeder liefert in seinen sechzig Drehungen in sich sechzig eine
Gruppe @g(, bildende Substitutionen der Gestalt (7) S. 31. Es läßt sich nun
aber zeigen, daß jeder der fünf Zahlenzusammenstellungen eine und im
wesentlichen, d. h. von Transformation abgesehen, auch nm eine Gruppe @^
von Substitutionen S zugehört, wobei die letzten drei Fälle die Gruppen des
Tetraeders, des OMaeders und des Ikosaeders liefern. Dies ist im einzelnen
darzulegen und jedesmal eine zweckmäßige Normalgestalt der betreffenden
Gruppe anzugeben. Wir halten dabei wenigstens nicht stets an der
unimodularen Schreibweise der Substitutionen fest*).
Im ersten Falle fi^ = m, fi^ = m haben wir nur zwei miteinander
nicht äquivalente Pole, deren jeder bei der ganzen ©^^ festbleibt. Wir
gelangen zur zyklischen Gruppe ®^, als deren Normalgestalt wir:
(1) z' = e "^ z, 1 = 0, 1, 2, •-•, w—1
benutzen.
Im Falle II ist m gerade und werde gleich 2 n gesetzt. Hier liefert
fig = » zwei miteinander äquivalente Pole, deren jeder bei einer größten
zyklischen @^ erhalten bleibt. Da wegen ^^ = 2, ^^ = 2 alle weiteren
Pole zu größten zyklischen ®^ gehören, so sind jene beiden ersten Pole
diejenigen eines zyklischen Teilers ©j^. Wir nehmen für die @,j die Noxmal-
gestalt (1) in Anspruch. Alle n noch fehlenden Substitutionen der @2«
sind wegen ^^ = 2, ^^=12 von der Periode 2. Eine einzelne von
ihnen, S, tauscht die Pole 0 und oo der @^ aus, so daß S = ( '^] gilt.
Da man noch mit einer beliebigen Substitution z = az transformieren
kann, ohne die Pole 0 und oo von @„ zu ändern, so ist erreichbar, daß
der eine Pol von S in den Punkt z = i rückt. S hat dann, unimodular
geschrieben, die Gestalt | ' ^ ), so daß wir zu der aus den Substitutionen:
(2) / = e « z, z ^ , l ^ 0, 1, 2, - •., n— 1
bestehenden ©2« gelangen.
Um die der @2w entsprechenden Kugeldrehungen zu versinnlichen,
denken wir die Kugel in der Anordnung von S. 29 mit den Werten z
belegt. Der höchste und der tiefste Punkt liefern die Pole von @„, und
der zugehörige , Äquator "^ trägt die z vom absoluten Betrage 1. Man
beschreibe in den Äquator ein reguläres Polygon von n Seiten ein,
dessen erste Ecke bei ^ = i liegt, und denke ^ie Fläche dieses Polygons
*) Vgl. hier überall „Ikos.", Äbschn. I, Kap. 1 und 2.
Zyklische Gruppen und Diedergruppen. 37
doppelseitig, so daß man die Vorstellung eineß „ Zweiüäclmers" oder
„Dieders" gewinnt. Die ©2« besteht q,us ajlen Drehiyagen der Kugel in
sich, bei denen das Dieder in sich übergeführt wird: Die gewonnene
Gruppe heißt dieserhalb „Diedergruppß"' @2w Sie enthält die @„ der
n Drehungen um die Kugelachse als Normalteiler. Weiter ist zu
unterscheiden, ob n ungerade oder gerade ist. ßei ifngeradem n hat man n
konjugierte ©g, den Umklappungep des Polygons um geine fi äquivalepten
Symmetrielinien entsprechend. Bei geradem n hat das Polygon zwei
Systeme zu je | n äquivalenten Symmetrielinien, nämlich die | n
Diagonalen und die ^n Mittellinien. Entsprechepd enthält hier die ®2n zwei
Systeme zu je | » konjugierten ©g*).
Für n = 2 erhält man die als „ Vierergruppe" bezeichnete Dieder-
gruppe @4, die bei der gewähltea Normaldarstellung aus den
Substitutionen :
besteht**). Jede der drei letzten Substitutionen erzeugt einen Xormal-
teiler %^\ in der Tat erweisen sich je zwei dieser Substitutionen als
kommutativ.
Das Zahlensystem III liefert wegen jw,i = 2, m == 12 zunächst
sechs äquivalente Pole für größte zyklische ©g, und da alle weiteren
Pole zu zyklischen ©3 gehören, so ergeben diese ßechs Pole die drei
Polpaare für drei konjugierte ©g. Nach I, 289 hat die einzelr^e ©g als eine
unter drei konjugierten Gruppen als Nprmajisator eine ©^, die auch die
beiden anderen ©3 enthalten muß, da alle weiteren Substitutionen der
©j2 wegen ^i^ == 3, fig == 3 die Periode 3 haben. Aus dem gleichen
Grunde ist die ©^ ein Normalteilef der ®^^ und stellt als nicht-zyklisch
notwendig eine Vierergruppe dar. Wir nehnien die Gestalt (3) für diese
Gruppe in Anspruch und schreibep ihre von S^, = 1 verscbiedepen
Substitutionen unimodular:
Die übrigen acht Permutationen, die sämtlich die Periode 3 haben, sind
mit den Substitutionen (4) nicht komnmtativ. ßei Transformation mit
einer unter ihnen, die T heiße, werden demnach die Substitutionen (4)
zyklisch permutiert, etwa in der Anordnung:
(5) T.S,.T-i = S3, T-Sa-y-i^S^, T-Sg-T-i^S^.
T^ wird dann die inverse zyklische Permutation der S hervorbringen.
Vier unter den acht Substitutionen de^ Periode 3 werden demnach die
zyklische Permutation (5) der S bewirken. Übrigens ist wegen der
Beziehungen Sj- Sj = S3, Sg • S3 =3 Si die dritte Gleichung (5) eiifie Folge
*) Vgl. das Näkere in „Ikos.", S. 11.
**) Vgl. „Ikos.", S. 12.
38 I, ^. Polyedergruppen.
der beiden ersten. Diese beiden Gleichungen nehmen, wenn wir T
nnimodular mit beKebigen Koeffizienten a, ß, y, ö ansetzen, die Ge-
^(a8 + ^y)i, -2aßi\ __ (0,-l\ ray + ß 8, - <.^-ß^\ ^ (0, i\
[2y8i, -(a8-\-ßy)il — [l, Op [y^ J^ S^, ~ ay—ßS) \i, O)
Hieraus gewinnt man hinreichend viele Gleichungen zur Bestimmung der
a, ß, y, ö. Es findet sich, daß es überhaupt nur die folgenden vier
Substitutionen gibt, die die Bedingung (5) erfüllen:
^^^ (1^ i-jl' \_isil Izzif \i±i ÜJ/' \_i±i l±i
Sie stellen die Drehungen der Kugel durch den Winkel ^ n um die vier
Achsen der zum Koordinatenkreuz |, ij, t, gehörenden Raumoktanten dar.
Man gewinnt im Falle III nur dine Gruppe ©jg, nämlich die Tetraeder-
gruppe, für die wir in den Substitutionen (4) und (6) und den vier
Quadraten der letzteren eine Xormaldarstellung besitzen.
Im Falle IV hat man wegen ^3 ==: 4, m == 24 sechs äquivalente
Pole für zyklische ®^, die, da sonst nur zyklische ©^ ^"^^ ®z aultreten,
zu Paaren vereinigt, die Polpaare für drei konjugierte größte zyklische
Teiler @^ liefern. Nach I, 289 hat die einzelne @^ als Kormalisator
eine @g, die den Diedertypus haben muß. Die erste ®g bestehe aus den
Substitutionen:
f 1, S, S^ = T, S^
(7)
wobei in der zweiten Zeile vier Substitutionen der Periode 2 stehen. Für
die beiden mit @g konjugierten ®'g, ©§ benutzen wir die Bezeichnungen
1, S', ••• und 1, S" der Substitutionen. In der ®^^ kommen neben den
drei konjugierten Substitutionen T, T' und T" der Periode 2 wegen
/ij = 2, fi^ = B nur noch sechs weitere konjugierte Substitutionen der
Periode 2 vor. Tritt weder T' noch T" in der zweiten Zeile (7) auf,
setzen sich also die zweiten Zeilen der Gruppen @g, ®'s, ®8 nur aus den
letzten sechs Substitutionen zusammen, so gibt es zwei dieser
Substitutionen, die sowohl in der Reihe Z7, S • U, S^- U, S^-U als auch in U',
S' • ü", S"^ • TJ', S'^ ■ ü" auftreten. Nun können wir unter II irgend eine
der vier nicht in der zyklischen ®^ enthaltene Substitution der ^g
verstehen. Im fraglichen Falle dürfen wir also U' =^ U setzen, worauf
eine der Substitutionen S-U, S^ ■ U, S^-U auch in der Reihe S' ■ U, S'^ ■ U,
S'^' TJ enthalten ist Dies ist aber nicht möglich, da sonst eine der
Substitutionen S', S'^, S'^ zuwider einem S. 33 aufgestellten Satze in der ®^
enthalten wäre. Es findet sich also mindestens eine der Substitutionen T'
und T", etwa T', in der zweiten Zeile (7). Somit ist T' im NormaJisator
der ®^ enthalten, so daß T und T' konamutativ sind. Mit T und T' ist
Tetraedergrappe ©^g ^°<i Oktaedergruppe (5^- 39
auch T'T' = T'-T von der Periode 2, und da diese SubstitutioQ in
der @24 ^^^ i^ <ii^ 'l^^i Substitutionen
rp rpr rpf ^ rn rpf ^ rptf rpff rr\f rpff rp rp ^ rpf^
transformierbar ist, so haben wir hier notwendig wieder die drei
Substitutionen T", T, T' vor uns: Pie drei konjugierteifi Substitutionea T,
T\ T" der Periode 2 bilden in der ©24 einen Normaiteiler @^^ der den
Vierertypus besitzen muß.
Für diese ®^ nehmen wir dje Darstellung (3) in Anspruch- Dann
erledigen sich zunächst sofort die deif Anzaiil ^2 = 3 entsprechenden
acht Substitutionen der Periode 3. Eß sind die eben im Falle III
berechneten Substitutionen (6) und ihre zweiten Poten?:en; die
Tetraedergruppe in der oben festgestellten Normalgestalt fiaden wjj als Normal-
teuer @j2 d^^ ®u-
Die einzelne der noch fehlenden zwölf Substitutionea wiipd immer
eine der drei Substitutionen:
^ = ß,_"J. r=(»;-).."=(».^)
in sich transformieren und die beiden anderen permutieren. Um ?:. B.
die in (7) dargestellte @g in allgemeinster Weise zu bilden, haben wir
die unimodulare Substitution S mit den Polen 0 und 00, also in der
Gestalt S = t ' _j I so zu bilden, daß:
'"'«'=(o::-^)=(i-.)
wird. Man findet nur die beiden einander inverßcn Substitutiopen *):
V " ' TT/ \ " ■ IT
Also gibt es nur eine einzige solche @g. Auch im Falle IV gelangen
wir nur zu einer einzigen Gruppe ®^^, die demnach die sich hier
einstellende OUaedergruppe ist; ihre Kormaldarstellung aber gewinnen wir
durch Zusammensetzung der Tetr9,edergruppe (4), (6) mit der in (8)
angegebenen Substitution S der Periode 4.
In einer zu dem Zahlensysteme fi, = 2, 11^ = 3, fig := 5, m =■- 60
gehörenden Gruppe ®^^ findet man eben diesen Zahlen ^ entsprechend
15 konjugierte größte zyklische Teiler ©g, 10 ebensolche ©3 und 6
Teuer ®^. Nach I, 306 ist die ®^^^ einfach md i^ach 1, 308 mit der Iko-
saedergrappe ®^^ isomorph. Eine einzelne der sechs l^onjugierten ®^ hat
als Normalisator eine ®^^ vom Diedertypus. Für eine dieser ®^^ nehmen
=*) Man vergesse nicht, daß gleichzeitiger Zeichgnwechsel der vier
Koeffizienten einer Substitution statthaft ist.
40 I> 2. Polyedex^i^ppen.
wir die Gestalt (2) der Diedergruppe in Anspruch und können diese ®^^
demnach aus den beiden nnimodular geschriebenen Substitutionen:
erzeugen. Es sei nun T = i ' j irgend eine unimodular geschriebene
Substitution der Periode 2 aus ©g^. Dann gehören auch die Substitutionen
S'T, T'TJ und S-T-U der ©g^ an; ihre Invarianten, die sich zu:
(10) j:^ui6'-6% j'=ß-y, j"=s'ß-E'y
berechnen, sind demnach reell. Aus der Realität von j und j' folgt, daß
a rein imaginär ist, und daß die imaginären Bestandteile von ß und y
übereinstimmen:
a — iB, ß=C-^iD, y = C + il).
Aus der Gleichung:
^ 1^2 — ßy = B^ — C C + D^ — (C + C')i D = 1
folgt weiter, daß entweder D = 0 oder C + C =r 0 gilt. Ist D =^ 0,
so benutze man die Realität von:
j" = Cs^-C's^= (C- C)cos~ + i(C+ C) sin ~
und findet C + C = 0. Die Substitution T hat also die Gestalt (7>
S. 31 einer Drehung der ^-Kugel um einen Durchmesser.
Die Substitution U, deren Drehungsachse die ij-Achse des
Koordinatensystems ist, hat als ISTormalisator eine Vierergruppe @^, die neben
1 und U die Substitutionen T und U • T enthalte. Die Drehungsachsen
von TJ, T und TJ' T bilden ein rechtwinkliges Achsenkreuz, so daß
insbesondere die Achsen von TJ-T und T in der |, ^-Ebene liegen und im
Nullpunkt zueinander senkrecht stehen. In jedem der vier Quadranten
des Achsenkreuzes der |, ^ - Ebene liegt demnach eine Halbachse, und in
einem der beiden längs der positiven ^-Achse benachbarten Quadranten
bildet die betreffende Halbachse mit der positiven ^-Achse einen Winkel
< — • Sollte dies der auf Seiten der negativen |-Achse liegende Quadrant
sein, so transformiere man noch durch ^ = — z, eine Substitution, die
sowohl S als auch U in sich transformiert. Dann bildet die Halbachse
mit der positiven ^-Achse auf Seiten der positiven |-Achse einen Winkel
< — • Die dieser Halbachse zugehörige Substitution der Periode 2 sei
T; sie hat zufolge elementarer Betrachtung die Gestalt:
(11) T = (\^ *^J, -!.<£< 1, i) == _yrir^^.
\tD,—tBJ 1/2
Ikosaedefgrappe ®qq. 41
Die Invariante j von S • T ist nun,
(12) i = iBie^-s') = 2Bsin^=ßy^^~^—.
o 1 2
Aber als von 0 verschiedene, positiv genommene Inv^xianten treten in
der @g(, nur die drei auf:
j = 1, j = 2cos~^ = ir^—, y = —2008--- = -^-.
o 2 5 2
y^5 — Vö"
i—
bzw. gleich l/ -=^- Keiner dieser beiden Werte gehört dem in (11)
für B angegebenen Intervalle an. Also ist j = 1 urjid man findet mit
Benutzung der Beziehung:
(13) £ _ £2 _ ^3 _|_ ^4 ^ y^
für i B und i D leicht die Darstell^ngen:
iB = '-^, iD=~^'-''
Vo V5
Es gibt hiernach nur eine einzige brauchbare Substitution T und, da die
@gQ aus S, T, TJ erzeugbar ist*), auch nur eine eiazige ©g^, nämlich die
Ihosaedergru'ppe.
Der am Anfang von § 5 aufgestellte Satz über die Existenz der
Gruppen @^ ist hiermit im vollen Umfang bewiesen. Die gewönne pen
Gruppen unter Einschluß der zyklischen und der Diedergnippeii mögen
hinfort die ^Polyedergrappen- genannt werden.
§ 6. Normalgestalt der Ikos^edergruppe.
Die Ikosaedergruppe möge ihrer größeren Bedeutung halber noch
etwas genauer betrachtet werden. Die Festlegung der ersten soeben
in (9) gegebenen Substitution S läuft darauf hinaus, das Ikosaeder der
^-Kugel so einzuschreiben, daß die beiden diametralen Punkte z =■- 0
und ^ :z3: oo, d. h. bei der S. 29 vereinbarten Lage der Kugel der höchste
und der tiefste Kugelpunkt zwei liosaederecken tragen. Der horizontale
größte Kugelkreis halbiert dann gerade 10 Ikosaederkanten**) und liefert
in diesen 10 Kantenmitten die 5 Polpaare für die 5 Teiler ®^, die in
der aus S und TJ zu erzeugenden Diedergruppe ©^g enthaltea sind- Das
Ikosaeder ist um die Vertikalachse so gedreht, daß eines dieser fünf Pol-
*) T und JJ erzeugen die Vierergruppe ®^, 8 isf von der Perio4e 5 und
8 • T von der Periode 3, so daß die aus S, T, U zu erzeugende Gruppe eine
durch 3 • 4 • 5 teilbare Ordnung hat. Sie ist also die ©g^.
*=") Man veranschauliche sich diese Angaben an einem Modell des Ikosaeders.
42 I, 2' Polyedergruppen.
paare (zur Substitution U gehörig) von der ly-Achse ausgeschnitten wird.
Diese Anordnung bleibt aber auch dann noch bestehen, wenn wir das
Ikosaeder um seine Vertikalachse durch 180° drehen. Von den beiden
so noch möglichen Lagen ist in § 5 diejenige bevorzugt, bei der sich am
Punkte ^ = 0 (höchsten Punkte der Kugel) in Richtung der positiven
reellen ^-Achse unmittelbar eine Ikosaederkante anreiht. Die Mitte dieser
Kante ist der eine Pol der Substitution T.
Es besteht nun der Satz: Die Ikosaedergruppe ©g^ ist bereits aus den
leiden Substitutionen:
(1) S = I
V^ ' 1^
\ß ' 1/5
er^eiighar, so daß sich insbesondere TJ in S und T darstellen lassen muß.
Da nämHch S, T und S-T die Perioden 5, 2 und 3 haben, so erzeugen
S und T einen Teiler einer durch 30 teilbaren Ordnung. Der einzige
solche Teuer ist die ©g^, selbst, da nach I, 308 kein Teuer ©^^ auftritt.
Um U ia S und T darzustellen, berechne man unter Benutzung der
Schreibweise (11) S. 40 für T die Substitutionen:
I.b^l-b — (5J)(i_,3), 52_|_X>2,2J' L-b-l—{^ iBsMDs4
Trägt man die inzwischen berechneten Werte von B und D ein, so
erweisen sich diese beiden Substitutionen als gleich. Hieraus folgt als
Darstellung von f7 in S und T:
(2) U = T-S^'T-S'-T-SK
Durch Zusammensetzung der Substitutionen S, T und U findet man
die folgende NormaldarsteUung der IJcosaedergruppe, wie sie der oben
bezeichneten Anordnung des Ikosaeders in der ^-Kugel entspricht:
. 0, s^'
S^-T'S^-
V^^^ 0/'
\ -3(^+2) ^-g^ oy + 2X^^~^^j
\ ]/^ IT/
wo X und A unabhängig voneinander die Zahlen 0, 1, 2, 3, 4 durchlaufen
sollen. Es liegen hier in der Tat 60 verschiedene Substitutionen vor, die
die Gruppe ®g^ erschöpfen. Man müßte also neben der identischen
Substitution S" = 1 noch 15 Substitutionen der Periode 2, 20 solche der
Periode 3 und 24 der Periode o nachweisen können. Die Substitutionen
S, S^, S^, S* haben die Periode 5 und alle fünf Substitutionen U-S" die
Normalgestalt und Teiler der Ikosaedergruppe. 43
Periode 2. Von den 50 Substitutionen S^-T-S\ UtS^-T-S'- müssen
also 20 die Periode o, ebenso viele die Periode 3 und 10 die Periode 2
haben. In der Tat haben die Invariant^ j ~- 0 und also die Periode 2
die 10 Substitutionen:
S^'T-S-'; LT- S-'.T' S", ^ =.= 0, 1, 2, 3, 4,
weiter liegt die Invariante j = + 1 und also die Periode 3 bei den
20 Substitutionen;
S'T- S~''-\ U- S'' -T-B'-^-, >^ = 0, 1, u>, 3, 4
vor, während 10 von den 20 Substitutionen:
S^ . T- S-'^-^, (7. S^'T.S'--\ y. ^ 0, 1, 2, 3, i
die Invariante + (f + £*) und die 10 übrigen ~ (£" -^ £^) als Invariante,
also alle 20 die Periode o haben.
Neben den schon in I, 306 aufgezählte^ zyklischen Teilern der %^^
mögen hier auch die nicht-zyklischen Teiler der Ikosaedergr^ppe
angegeben werden. Teiler ©g^ treten nach I, 3Q8 nicht auf. Ein Teiler %^^
würde nach dem Sylow sehen Satze (I, 294) nxys: eitjien z^^^küschen Teiler @g
enthalten (da er nicht alle sechs ©^ entjialten ka^n) und müßte übrigens
sein eigener J^ormalisator sein (da er sonst ein Xonnalieiler wäre). Also
gäbe es drei konjugierte @2o ^^^ d£f,mit :(iur drei konjugierte (5)^, während
es doch deren sechs gibt. Also kommt kein Teuer %^^ vor. In einem
Teiler @j. wäre nach dem Satze von Frobenius (I, 295) ein ynd pur
ein Teiler @g enthalten, was auf Grund der eben schon vollzogenen
Überlegung zu einem Widerspruch fühi't. Ein Teiler @,2 kann weder
zyklisch noch diedrisch sein, da ipi der ®g^ zyklische ©^^ und ©g nicht
auftreten. Ein Teuer ©^^ stellt also notwendig eine Teiraedergruppe
dar, und solcher Gruppen gibt es in der ©g^ nach \ 307 fünf konjugiei^e,
aber auch nicht mehr; denn in der ©g^ sind aur fünf konjugierte
Vierergruppen ©^ enthalten, zu denen die ©^g als Kormalisatoren gehören.
Teiler @j^ und @g sind notwendig diedrisch. l[an stellt sofoft sechs
konjugierte ©j^, und zehn konjugierte ©g fest, die die Xormaüsatoren der
zyklischen ©5 und ©3 sind. Xehmen wir noch die fünf konjugierten
Vierergruppen ©^ hinzu, so sind damit alle nicht-zykKschen Teiler der
©go aufgezählt. Wegen der späteren Verwendung merken wir noch den
Satz an; Die Teuer der Ikosaedergru]^e vwi lieinstem Index, nämlich dem
Index 5, sind die fünf "konjugierten Tetraedergruj}pen ®^^; darafi reihen
sieh mit dem nächst höheren Index 6 die sechs TconjugieHen Dieder-
gruppen ©j^,
§ 7. Erweiterte Polyedergruppen.
Die unendliche Gruppe © aller Difehungen der ^-Xugel mpii ih|:en
Mittelpunkt besteht nach S. 31ff. aus allen linearen Substitutionen:
44 Ti 2. Polyedergruppen.
mit irgendwelchen reellen Zahlen A, B, C, D, die die unter (1)
beigefügte Gleichung erMlen. Diese Gruppe ist einer wichtigen
Erweiterung fähig, die zunächst ohne Bezugnahme auf die Polyedergruppen
besprochen werden soll. Versteht man unter i fortan den zu z konjugiert
komplexen Wert, so wird durch die weiterhin mit S^ zu bezeichnende
Transformation des einzelnen Kugelpunktes z in den Punkt:
(2) ^' = =i
jeder Kugelpunkt in seinen diametralen übergeführt*). Die
Transformation heiße deshalb kurz „Diameträlsymmetrie^. Durch eine einfache
Rechnung zeigt man, daß die Biameträlsymmetrie mit jeder im Ansatz (1)
enthaltenen Suhsiitution S vertauschhar ist. Die Gruppe ® wird demnach
durch Zusatz von S^ zu einer Gruppe:
(3) ® = ® + So . ®
erweitert, in der ® ein Normalteiler des Index 2 ist. Neu hinzu kommen
die Substitutionen:
, _ (C + iD)z—(A~\^iB)
(4)
' {A~iB)z-\-{G — iD)
oder, wie wir zum besseren Anschluß an (1) unter Ersatz von A, B, C^
D durch — C, — D, A, B schreiben:
Sie werden als „Substitutionen zweiter Art-' und ihnen gegenüber die
Substitutionen (1) als solche der „ersten Art" bezeichnet. Als Symbole
für die Substitutionen (5) benutzen wir S, T, •••.
Soll S = Sß-S die Periode 2 haben, so muß:
(6) S^ = {S,. S)2 = S^ S^ = S2 = 1
gelten, also S entweder die identische Substitution sein, was zu S = S^
führt, oder die Periode 2 besitzen, was in (4) das Verschwinden von A
und also in (5) das von C fordert. Im letzteren Falle gelangt man zur
Substitution:
(7) ^,^iA+iB)z~l^iI) ^.^^._^^._1
^^ iDz + {A~iBy ^i-^i-^— -i.
die die Eigenschaft besitzt, daß sie jeden Punkt des Kreises:
(8) D{x^ + i/)~2Bx-\-2Ay — D = 0
*) Die Transformation lauft auf einen gleichzeitigen Zeichenwechsel der drei
Koordinaten |, jj, g hinaus, woraus mit Hilfe der Gleichungen (1) und (3) S. 29 ff.
leicht die Darstellung durch die Substitution (2) gewonnen wird.
Erweiterte Polyedergruppen. 45
in sich selbst transformiert. Nach S. 30 wird dieser Kreis auf der
Kugel durch die Ebene:
(9) Bt-An+Dt = 0
ausgeschnitten und stellt also einen größiten I^ugeljireis dar. Map kann
auch durch geeignete Auswahl von A, B, D zu jedem gewünschten
größten Kugelkreis gelangen. Die Substitution (7) stellt einfach eine
Spiegelung (im elementaren Sinne) der ^-E.ugel an der Djametralebeue (9)
oder an dem von ihr ausgeschnittenen größten Kugelkreis (8) dar. Es
ist dies aus der Zusammensetzung der Substitution (7) aus einer
Substitution S der Periode 2 mit der Diametralsymmetrie S^ einleuchtend;
der Kreis (8) ist der „Äquator-' zu den beidep Polen der Substitution S.
In der ^-Ebene tauscht die Transfonpation (7) das Innere des Kreises (8)
mit dem Äußeren aus; es handelt sich um die als „Inversion" oder
„Transformation durch reziproke JRadie^i" oder kurz „Spiegelung" apa
Kreise (8) bezeichnete Umformung der ^-I^bene in sich, und der Kreis (8)
heißt der „Invsrsionskreis~ oder auch der „Symmetriekreis" der
Spiegelung*). Die Substitutionen zweiter Art (5) der Periode 2 sind außer der
Diametralsymmetrie S^ die Spiegelungen (7) an größten Kptgellcreisen.
Da die Diametralsymmetrie S^ mit jeder Substitution (1)
vertauschbar ist, so entsteht aus jeder Polyedergruppe @^ durcl^ Zusatz von S,,
eine „ erweiterte Polyedergruppe" @2 m = ®m, "f" -^o ' ®m > ^ <ier die
ursprüngliche Gruppe ®^ ein Normalteiler des Index 2 ist;. Die
Erweiterungsfähigkeit der @^ ist auch anschaulich eitjileuchtend. Das Oktaeder
und Ikosaeder werden durch die Diametralsympietrie in sich übergeführt,
und in den erweiterten Gruppen @^g und ©^g^ siq.d demnach, wie wir
sogleich am Beispiel des Ikosaeders ausfüjiren, die Spiegßlungen an allen
Symmetrieebenen des Polyeders enthalte^. Anders liegen die
Verhältnisse beim Tetraeder, das durch S,, in das Gfegenfcetraeder übergeführt
wird; das letztere wird auch durch die Drehungen der ursprünglichen ®^^
in sich übergeführt. In der. erweiterten Tetraedergrappe ®^^ ifcreten deni.-
nach an Spiegelungen nur diejenigen drei auf, die das Tetraeder mit dem
Gegentetraeder austauschen**).
Zur Erläuterung diene das für uns wichtigste Beispiel der Iko^aeder-
gruppe. Die 15 Substitutionen der Periode 2 in der ®^^ ergeben nac|i
der obigen Darlegung die 15 Spiegelungen der erweiterten Iko^aedei-
grappe an den Symmetrieebenen des Ikosaeders. Die to zugehörigen größtem
*) Man hat in (8) mit allen Kreisei^ der z-Ebe^ie zu tun, die den
„Einheitskreis", d. h. den Kreis des Radius 1 upi den Nullpunkt, jeweils in zwei
diametralen Punkten schneiden. Vgl. übrigens wegen weiterer Ausführungen
„Modulfunkt.« I, 85 oder „Ellipt. Funkt." I, 73. __
**) Es gibt eine zweite erweiterte Tetraedergruppe ©34' ^^ der die sechs
Spiegelungen an den sechs Symmetrieebenen dßs Tei,raeders _eni^halteifi smd; vgl.
darüber „Modulfunkt." I, 104. Beide Grruppen ©.^^ und ©34 sind in der
erweiterten Oktaedergruppe @^ enthalten.
46
I, 2. Polyedergruppen.
Fig. 3.
Flg. 4.
Ikosaedrisclie Kugelteilung. 47
Kugelkreise liefern dann, eine Zerlegung der Kugel fläcfie in 120 abwechselnd
symmetrische und kongruente sphärische Dfeieche der Winkel --, —, -, die
cäs die „ikosaedrische Kugelteilung" hegeiehnet wird und in Fig. 3
dargestellt ist. Man denke hier die ^-Kugel von qben angesehen, so daß der
Mittelpunkt der Figur der Nullpunkt 2 = 0 ist. Die Ecken der
Einteilung sind die Pole der Substitutionen der (S>^^. Den 10 um. ^ == 0
herumliegenden Dreiecken entspricht eine Fläche des Dodekaeders, 6 um einen
Pol einer Substitution der Periode 3 herumliegende Dreiecke aber liefern
eine Ikosaederüäche.
In Fig. 4 ist die stereographische Projektion der ikosaedrischen
Kugelteiiung auf die if-Ebene dargestellt*). In Fig. 3 und 4 si|id die
Dreiecke, um sie als solche noch besser hervortreten zu lassen,
abwechselnd schraffiert und frei gelassen. Eine Substitution erster Art der
®i2o transformiert dann ein schraffiertes Dreieck stets wieder in ein
solches und ebenso ein freies Dreieck wieder in ein freies. Die
Substitutionen zweiter Art dagegen tauschen die Dreiecke der beiden Arten
aus. Man mache sich deutKch, daß pian zu der gesamten ikosaedrischen
Kugelteiiung gelangt, wenn man an ein einzebies der 120 Dreiecke
anknüpft, dies längs seiner Seiten spiegelt und den Spiegelungsprozßß mit
den so neu zu gewinnenden Dreieckep weiter und weiter fortsetzt**).
§ 8. Diskontinuitätsbereich einer Gruppe.
Es sei ® eine der ursprünglichep oder erweiterten Polyedergruppen.
Unter Aufnahme einer S. 33 eingeführten Bezeichnung iiennen wir zw^ei
Punkte z und z' bezüglich @ „äquivalent", falls es in @ eine Substitution
gibt, die ^ in ^' überführt. Hieran reiht sich die Erklärung eines von
Klein eingeführten grundlegenden Begriffes: Man bezeichnet; als „Dis-
kontinuitäisbereich^ der Gruppe @ [abgekürzt „PB*" geschrieben j)] eirw(v
Bereich der 2-Ebene oder s-Kugel, der für jeden Pmnkt z einen und nur
einen bezüglich ® äquivalenten FunM aufweist ff). Zur Erläuterung diene
zunächst die erweiterte Ikosaedergnippe ©^go- ^^^ einzeLaßs ai^s der
ikosaedrischen Kugelteilung beliebig herausgegriffenes Dreieck, z- B. das
*) Entsprechend der vorletzten Note wird Mer der Einlieitskre;s je m zwei
diaxaetralen Punkten vom einzelnen der 15 Symmetriekreise geschnitten. Map
suche in Fig. 4 insbesondere die auf depi Eiiiheits}ireis gelegenen 10 Pole der
Substitutionen U • S"" auf.
**) Siehe wegen aller weiteren Ausführungen ai^ch fur die übrigen Polyedei-
gruppen „Modulfunkt." I, 75, 104 und 197 ff.
t) Bereiche werden wie in I, 87 ff. durch Pettsclirift gekennzeichnet.
tt) Klein bediente sich ursprünglich der Benennung „Fupdameifitalpolygon-
einer Gruppe, vgl. „Ges. Abh." III, 35. per Begriff „Fundamentalbeieich'- wurde
später in etwas allgemeinerer Bedeutung gebraucht, vgl. ,.Ges. Abh.'- III, 637
und „Ant. Punkt." 11, 4.
48 I, 2. Polyedergruppen.
schraffierte Dreieck, das am Nullpunkt ^ = 0 zunächst sich an die
positive reelle ^-Achse anlagert, und das die hei:.
0)
.= 0,
i + Vö
2
fs+Vs
+ I/54VI,
i/isTsW
gelegenen Pole der Substitutionen S, T und T • S zu Ecken hat, ist ein
DB der ©jgo- ^ ^^^ "^^^ ^^^ keine zwei verschiedene Punkte dieses
Dreiecks äquivalent, während andererseits irgend ein Punkt eines freien
oder'schraffierten Dreiecks mit dem homologen Punkte des ausgewählten
Dreiecks äquivalent ist.
Einen DB für die ursprüngKche Ikosaedergruppe @g(, kann man
dadurch bilden, daß man dem eben herausgegriffenen Dreieck sein
Spiegelbild längs der reellen .sr-Achse anfügt. Als ein DB der ®^q entsteht so
das Breieck&paar der ikosaedrischen Kugelteilung, das neben den Ecken (1)
noch die zu 2^ konjugierte, den einen Pol der Substitution S • T bildende
Ecke:
(2) ,, = ,3(H^_|/iM_iV5)
besitzt. Hierbei ist indessen ein Vorbehalt zu machen. Es sind n'ämlich
je zwei homologe Randpunkte auf den Seiten z^^z^ und z^~z^ des
Dreieckspaares äquivalent, indem der eine durch S m den anderen transformiert
wird, und ebenso sind je zwei homologe Randpunkte auf den Seiten z^ z^
und .sr^ig äquivalent, indem sie durch T ineinander transformiert werden.
Man begegnet diesem Hindernis dadurch, daß man etwa nur die auf den
beiden Seiten z^z^ und z^z^ gelegenen Randpunkte, nicht jedoch die
übrigen, als dem Dreieckspaar angehörig ansieht. Dann ist in der Tat
jeder Punkt z mit einem und nur einem Punkte des Dreieckspaares
bezüglich der Gruppe ©g^ äquivalent.
Schneidet man von dem DB einer Gruppe @ ein beliebiges Stück
ab und ersetzt dies durch ein äquivalentes Stück, so ist auch der in
dieser Art abgeänderte Bereich noch ein DB der Gruppe. Man spricht
in diesem Sinne von einer „erlaubten Abänderung^ eines DB. Bei einer
unserer Polyedergruppen erster Art, d. h. einer solchen, die noch nicht
durch Substitutionen zweiter Art erweitert ist, kann man insbesondere
eine erlaubte Abänderung stets in der Art vornehmen, daß der DB ein
zusammenhängender, d. h. aus einem Stücke bestehender Bereich bleibt.
Mit Rücksicht auf die späteren Anwendungen möge dies erstlich am DB
der Tetraedergruppe ®^^ -erläutert werden, die wir in der
Normalgestalt (4), (6) S. 37ff. gegeben annehmen.
Erweitem wir die ®^^ durch die Diametralsymmetrie zur ®^^, so
finden sich in der ®^^ drei den Substitutionen (4) S. 37 entsprechende
Diskontinuitätsbereiche bei l'olye^ergruppen. 49
Spiegelungen, deren Symmetriekreise auf der Kugel durch die drei Ko-
ordinatenebenen ^ = 0, rj = 0, ^ = 0 außgeschnitten werden. Es
entsteht die Einteilung der Kugelfläche in acht Oktanten, die zu der
durch die Diametralsymmetrie erweiterten Vierergruppe @g gehört. Fig. 5
zeigt die Projektion auf die ^-Ebene, ^o die Oktanten abwechselnd
schraffiert und frei gelassen sind. Verbindet man den Mittelpunkt jedes
Oktanten mit den drei Ecken durch die größte^ Kugelkreise*), so zerfällt
jeder Oktant in drei bezüglich der ®^^ äquivalente Dreiecke Ein
einzelnes dieser Dreiecke, z. B. das in Fig. 5 mit AJß G bezeichnete,
ist ein DB der ©g^, und als einen DB der ®^^ kann man z. ]B. das
Dreieckspaar AB CD benutzen. Dabei sind freilich die Jiandpunkte
wieder zu Paaren äquivalent; es gehen nämlich die Seiten AB und Ap
hx CB bzw. CD über durch die ia der ©^g enthaltenen Substitutionen:
(3)
l-r^• Ij-
2 ' i
2 ' 2 /
Fig. 5.
Fig. 6.
Fig. 6 zeigt nun einen DB der (3^^, der durch eine erlaubte Ä.bänderung
aus dem eben konstruierten DB hervorgeht, wobei der Deutlichkeit halber
der Maßstab etwas größer gewählt wurde. Die Stücke AA'B und AA'B
sind durch die äquivalenten Stücke C CB und GC"D ersetzt. Der DB
der @j2 ist nun das Fünfeck Ä B C C" D, wobei die Seiten A' B ui^d
A' JD wieder durch die Substitutionen (3) in C B bzw. C" I» übergehen
und die beiden Hälften CG' und CG" de^ fünften Seite durch die erste
Substitution (4) S. 37 ineinander transformiert werden.
*) In Fig. 5 stark ausgezogen,
ricke, Algebra. II.
50 I, 2. Polyedergrappen.
§ 9. Homogene Polyedergruppen.
Wir gehen jetzt von den nicht - homogenen Substitutionen zu den
homogenen:
(1) ^; =3 a^i + /3^ä, 4 =: y^^-fd^a, a8 — ßy=l
zurück, die wir nach wie vor unimodular schreiben, und für die wir die
symboKsche Bezeichnung S = /"' ^\ beibehalten. Von der einzelnen
Substitution S = ("' J gilt also jetzt die etwa durch — S zu
bezeichnende Substitution [~"' ~'; j als verschieden. S geht in — S durch
Zusammensetzung mit der abgekürzt durch — 1 zu bezeichnenden
Substitution ["" ' ) über. Auf Grund des Gesetzes (6) S. 3 der
Zusammensetzung zweier Substitutionen oder auch durch Rückgang auf die
Normalgestalt (11) S. 11 beweist man leicht den Satz: Die Periode 2
hat aUän die Substitution — 1, und weiter liegt die Periode 3, 4, 5, 6, 8,
10 vor, je nachdem die Invariante der Substitution bzw. den Wert hat:
(2) i = -i,o, nl±VI,i,±y2,i±V5.
Ist nun @^ [irgend eine unserer Polyedergruppen, so ordnen wir
ihrer einzelnen (nicht-homogenen) Substitution S die beiden homogenen
Substitutionen S und — S zu. Da die Substitution — 1 mit jeder
Substitution S vertauschbar ist, so bilden die so zu geimnnenden homogenen
Substitutionen eine im Sinne von I, 277 der @^ l-2-dezäig hom-omorphe
Giruppe ®2rn ^^^ doppelten Ordnung 2 m, die als eine „homogene Polyeder-
gruppe" bezeichnet werden soll. In der ©3^ liefern die beiden
Substitutionen 1 und — 1 einen Normalteiler ©^t dessen Komplement natürlich
wieder die „nicht-homogene Polyedergruppe" @^ ist.
Was die Struktur dieser homogenen Polyedergruppen angeht, so
stellen sie, abgesehen von den zyTdischen Grruppen, lauter neue Typen dar.
Die homogene zyklische Gruppe ©ä^^, die bei der Normaldarstellung aus
der Substitution:
(3) z't^ z= e"^z^, z'^ = e "^z^
erzeugbar ist, ist wieder zyklisch.
Die homogene Diedergruppe ©4^, die entsprechend der
Normaldarstellung (2) S. 36 aus den beiden Substitutionen:
(4) 1 4= e»^^,, 4 = e -^z^,
yz[= — ^2, 4 = ^x
erzeugbar ist, enthält einen zyklischen Normalteiler, der aus der ersten
Substitution (4) erzeugt wird, und n Teiler ®^. Diese n ®^ sind bei
Homogene Polyedergruppen. 51
ungeradem n alle konjugiert, bei geradem n ergeben sie zwei Systeme zu
je I w konjugierten Teilern. Für » = 2 gelangt man zuf homogenen
Vierergruppe @g, die aus den beiden Substitutionen:
erzeugbar ist. Diese @g enthält, ol^le kommutativ zu sein *), nur N'orn^al-
teiler, nämlich drei @^ und ihnen gemeinsam einen Teiler ®^. Die @g
wird wegen ihrer Beziehung zur Hapülton sehen Quateniionenrechnung**)
als „ Quaternionengruppe^ bezeichnet. Sie ist das niederste Beispiel eipier
„Hamiltonsehen G-ruppe"; so bezeichnet Dedekindf) jede Gruppe, die,
ohne kommutativ zu sein, nur Normalteiler besitzt.
Die homogene Tetraedergruppe ®^^ enthält als imifa,ssendste zyklische
Teiler vier konjugierte @g und drei konjugierte @^, die als homogene
Gruppen den umfassendsten zyklischen Teilern der nicht - ho]:pogenen
Tetraedergruppe zugehören. Entsprechendes gilt bei den horp.ogenen
Gruppen des Oktaeders und Ikosaeders.
Allgemein hat man zwei Artexf. von Teilern bei den homogeaen
Polyedergruppen zu unterscheiden, näifdich solche, die die Substitution — 1
enthalten und also 1-2-deutig homomorph auf entsprechende Teiler der
nicht-homogenen Gruppen bezogen sind, und solci^e, dje — 1 nicht
enthalten und also isomorph mit den entsprechenden nicht-homogenen Teilern
sind. Gruppen der zweiten Art, die also keine iVhnlichkeitstraiisforma-
tionen (natürlich von 1 abgesehen) enthalten, werden als „reine" Gruppen
bezeichnet. Jeder Teiler @^ einer unserer Gruppen von gerader Ordnung ^
enthält nach dem Sylow sehen Sat2e (vgl, I, 291) einen Teiler ©g, und
der einzige solche Teiler, den es gibt, besteht aus den Sybstitutionen
— 1 und 1. Andererseits hat jeder Teuer ©„, der diese ®^ enthalt,
gerade Ordnung fi. Also gehören zur ersten Art ^.Ue Teiler @^ gerader
Ordnung fi, zur zweiten Art also zu <ien reinen Gruppen alle Teurer
ungerader Ordnung (i.
Die einzigen Teiler ungerader Ordnung, die bei den nicht-homogenen
Polyedergruppen, auftreten, sind nmi die zyUisdie^ Tejler ®^ ungerader
Ordnung fi. Die zugehörige homogene Gruppe ©a^^ ist entsprechend (3)
aus der Substitution: ^. ^^
(6) z[ = ei^ z^, z'^ -j= e " z,^
erzeugbar. In dieser @2u weist man nun vß. der Tat sofort einen mit
der nicht-homogenen ®^ isomorphen Teiler nacl^, deip einfach als
erzeugende Substitution: ^. ^^.
(7) z[ =:z —ei^ z^, Zo_ = ~ e ^'< z^
*) Es ist nämlich z. B. Ä'- T ^ T-S.
**) Man vergleiche die Regeln der JZiisanvmensetzung der drei Substitutionen
S, T, Z7 = Ä' • r mit den Regeln der Multipl^katiop der drei :p:inlieiten *', 3, Tc in
der Quatemionenrechnung.
t) „Über Gruppen, deren sämtliche Teiler Jformalteilersindt, Math. Ann. Bd. 48.
4*
52 I, 3. Ikosaedergleichung und ihre ßesoiventen.
hat. Die in den homogenen Polpedergruppen @2w enthaltenen Teiler sind
1 - 2 - deutig homomorph auf die entsprechenden Teiler der nicht-homogenen
Gruppen @m bezogen, mit alleiniger Ausnahme der gyMisehen Teiler tm-
gerader Ordnung der @2«i- ^i^ den entspreeilenden zyMisehen Teilern der
Qby^ isomorph sind.
Um zu dem ursprünglichen Ansatz am Eingang dieses Kapitels
(S. 24) zurückzukehren, würde jetzt noch übrigbleiben, die gewonnenen
homogenen Gruppen mit zyklischen Crruppen @;. von
Ähnlichkeitstransformationen :
•2 i n •2 z 7g
(8) z\ = e '"■ z^, z'i = e^ z^, Ä = 0, 1, 2, • •., X-1
zusammenzusetzen. Doch haben die so entstehenden Gruppen weiterhin
kein besonderes Interesse.
Drittes Kapitel.
Ikosaedergleichung und ihre Resolventen.
§ 1. Invarianten der Ikosaedergruppe.
Die Invarianten der homogenen Polyedergruppen ©^^ und die
zugehörigen Formenprobleme sind leicht nach den allgemeinen Regeln von
S. 15 ff. aufzustellen. Diese Formenprobleme sind aber für uns
keineswegs alle von gleicher Bedeutung. Man erkannte nämlich leicht in den
Polyedergruppen mit alleiniger Ausnahme der Ikosaedergruppe
„metazyklische Gruppen-' (vgl. I, 284). Die nicht-homogene Ikosaedergruppe
@gQ aber liefert uns gerade die erste derjenigen einfachen
nicht-metazyklischen Gruppen, deren nähere algebraische Erforschung zufolge der
Einleitung (S. 1) Gegenstaad unserer neuen Entwicklungen sein sollte. Wir
wenden uns demnach sogleich zur Ikosaedergruppe*).
Setzt man nach Vorschrift von S. 16 absolute Invarianten der
Ikosaedergruppe @gQ als Produkte „äquivalenter" linearer Formen an, d. h.
solcher Formen, die aus einer unter ihnen durch die Substitutionen der
Gruppe hervorgehen, so gelangt man zu Formen <6Q^^^^ Grades, deren
Xullpunkte 60 äquivalente Punkte z der ikosaedrischen Kugelteilung
sind. Entsprechend den Ausführungen von S. 16 haben wir dabei drei
besondere Fälle zu nennen. Rücken die 60 äquivalenten Punkte zu je
dreien in die Mittelpunkte der 20 Ikosaederflächen zusammen, so ist die
Form die dritte Potenz einer Form 20sten Grades, die (p{z^, z^ heiße
und vielleicht erst eine relative Invariante darstellt. Entsprechend
gelangen wir zu einer Invariante SO^ten (grades i^(^j, z^, deren Kulipunkte
die 30 Kantenmitten des Ikosaeders sind, und endlich zu einer Form
*) Siehe wegen der übrigen Gruppen ^Ikos.", S. 62ff.
Grundformen der Ikos^edergruppe. 53
12*«'^ Grades ^i^i, ^2), deren Kulipunkte die 12 Ikoßaederecken sipid.
Diese drei Invarianten sollen als die „ Orzmäformen"- des Il^osaeders
bezeichnet werden.
Um zu prüfen, ob die Grundformen relß-tive oder absplute
Invarianten sind, und um die Grundformen wdrklich aufzustellen, denken wir
die Ikosaedergruppe in der Xormalgestalt von ß. 42 gegeben und behalten
die Bezeichnung S, T und TJ für die daselbst so beaannten Substitutionen
bei. Da T als homogene Substitution die Periode 4 hat, aber T^ = — 1
ist, so wird z. B. die Form ^^ {z^, z^ als solche geraden Grades
gegenüber T höchstens Zeichenwechsel erfal^rea können. Indessen ist die
fünfte Potenz von x{z^, z^ absolut invariant, so daß ti^v -i selbst
gegenüber irgend einer Substitution der Gruppe höchstens eine fünfte
Einheitswurzel als Faktor annehmen kana. Also bleibt %{ß^i 2^ gßg*'-^-
über T absolut invariant. Ebenso findet maa, daß %{z^, z^) gegenüber
S • T unverändert bleibt. Dann aber ist 4iese J'orm aucl^ invariant
gegenüber S = (S • T) • T~ 1 und damit gegenüber allen Substitutionen d^ev
Gruppe, die ja aus S und T erzeugbar ist. Ebenso verfährt man bei den
beiden anderen Formen: Die drei Grundforrßen tp, (p, ^ des Ikosaeders
bind absolute Invarianten der Ikosaedergn^ppe.
Nach S. 15 ist jede Kovariante einer Grundform selbst wieder eine
Invariante der ©g^. Zufolge I, 131 haben wir eine solche Kovariante in
der Hesseschen Determinante der Grundform 12*^'* Gradps xi^^, 22)-
Diese Hessesche Determinante ist \om 20^^^^*^ Grade und muß demnach
zur Grundform (p (^^, z^) führen; denn diese ist die einzige Invariante
2 Osten Grades bis auf einen konstant;en Faktor, der hier zunächst überall
bei unseren Formen noch zugesetzt werden mag. Wir haben ferner
nach (11) in I, 131 eine Invariante 30^^^^* (lirades in der
Funktionaldeterminante von (p (z^, ^2) ^"d X (^1 j '^2)- I^ißse muß dann zur
Grundform i^i^i, ^.j) führen, die als einzige Invariante des Qrades 30 wieder
bis auf einen konstanten Faktor eindeutig bestimmt ist. Indem ^ir den
Zusatz geeigneter Faktoren vorbehalten, merken wir den Satz an: i'^e
Grundform op {z^, z^ ist die Hesse sehe Determinante von x {^i, z^, tvahrefiä
die Grundform ti^i' ^2) ^*^ FunMionäldeternimante von (p{z^, 2^ u(id
X{s^,z^)i§t.
Zur wirkKchen Gewinnung der Form x {^i • ^2) beachte man, daß die
„lineare Form'" z^ ihren Nullpunkt in einer Ikoßaederecke hat.
Entsprechend geht sie, abgesehen von konstanten Faktoren, dufch die
Substitutionen der homogenen Ikosaedergruppe in nur 12 verschiedene lineare
Formen:
z^, z^, {e—e^)s^-''z,--{e^ — e^)s'-''-z^, {s^ — E^)ß^'2,-^{a — s')s'''z^
mit X = 0, 1, 2, 3, 4 über, wie die S. 42 angegebene Normalgestalt der
Ikosaedergruppe lehrt. Das Produkt dieser zwölf Formen kür2;en wir
noch um den Faktor — 25 V^ nnd gewiimen damit die Grundform:
54 I, 3. Ikosaedergleichung und ihre Eesolventen.
Zufolge des letzten Satzes stellen wir dann weiter die Formen (p (^^, 2^)
und i^izj, 2^) so dar:
\d (p d (p
■dh ^"X
(2) cp{z„z,)--
-1 j dzf dz^dz
ti^„^.2) =
20
d z^ d s^
dz^ Oz^
und gewinnen damit aus (1) leicht folgende Gestalten der beiden
Grundformen (p und ip:
(6) q> {z,, ^,) = (40 + 4«) - 228 {zf z\ -
15) -j- 4944040,
(4)
ti^i, ^2) '-
r (40 + 40)+ 522(454-
- 10005(4040 + 4040).
Mittels zweier nicht zugleich verschwindender Parameter a, h stelle
man aus (p und ^l; die Schar von Formen 60^*^^* Grades:
(5)
acpiz^, ^2)^ -^hi;{z^, z^y
her. Man kann dann über das Verhältnis a: h der Parameter a, & in
einer und nur einer Weise so verfügen, daß die Form (5) an einer
beliebig vorgeschriebenen Stelle des DB der Ikosaedergruppe (vgl. S. 48)
verschwindet, da diese Forderung für a, h eine Gleichung ersten Grades
mit nicht zugleich verschwindenden Koeffizienten liefert. Die Form (5)
als solche vom 60^*^^* Grade hat nun im ganzen 60 Nullpunkte auf der
i^-Kugel, die, insofern wir in (5) eine Invariante vor uns haben, 60
bezüglich der @go äquivalente Punkte darstellen. Diese 60 Punkte, fallen
für & = 0 zu je drei in die 20 Flächenmitten des Ikosaeders und für
a =: 0 zu je zwei in die 30 Kantenmitten. Weiter ist dann zunächst
festzustellen, wie wir a und h zu wählen haben, damit die 60 Nullpunkte
zu je fünf in die 12 Ikosaederecken fallen. In diesem Falle liefert die
Form (5) bis auf einen konstanten Faktor c die fünfte Potenz von ^ (z^, z^,
so daß die Gleichung:
identisch besteht. Da a z^ 0 ist, so darf a = 1 gesetzt werden. Dann
gut weiter h = — 1, da ;^ mit ^ verschwindet und also der links
stehende Ausdruck kein von z^ unabhängiges Glied aufweisen darf. Wir
tragen endKch z^ = 1, z^ = l und also (p = 4:- 124, i^ =: — 8-2501,
;U = 11 ein, woraus sich c = — 12^ ergibt: Die eine nach S. 19 zwischen
den drei Invarianten rp, i^ und ^ bestehende identische Belation ist somit
gegeben durch:
(6) (p'— t^ + 12^ x' = ^-
Formensystem der Ikosaedergruppe. 55
In Übereinstimmung mit den Ausfülirungen von S. 18 besteht femer
der Satz: Jede Invariante J(z^, z^ der Ikosaedergruppe isi mittels der
drei Grundformen cp, ip-, % in der Gestalt:
(7) J{z„ z,) = ccp>''4,' yj^ f I (ö, g,3 ^ ^^ ^3)
l' = l
darstellbar. Die Invariante ist näinlich durch ihre Kullpunkte bis auf
einen konstanten Faktor c bestimmt. D^s System dieser Kullpuntte geht
aber bei allen Drehungen der Ikosaedergruppe in sich über. Der
Darstellung (7) liegt die Annahme zugrunde, daß in den J'lächenmitten des
Ikosaeders je ein fc-fach er Nullpunkt liegt, in den Kanten;nitte|i je ein
Z-facher und in den Ecken je ein m-facl^er, während darüber hinaus im
DB der ^^^ noch n einfache NuUpupkte p,uftreten, die aber auch zu
Nullpunkten höherer Ordnung zusammenrücken dürfen.
§ 2. Formenproblemi der Ikosaedergruppe.
Nach den Regeln von S. 20 ff. ist das Formenproblem der
Ikosaedergruppe ®f^Q in folgender Art anzusetzen: Es werden drei an die
Bedingung :
(1) u^ — v^ + 12^w^ = 0
gebundene, im übrigen aber frei wählbare komplexe Zahlen (i, v, w
vorgeschrieben, und es sollen dann die drei Gleichungen:
(2) . (p(z^,z^) = u, ti^v^i) — ^, Xi^v ^i) = ^
nach z^, z^ gelöst werden. Der algebraische Charakter dieses Problepis
ist bereits durch die allgemeinen Darlegungen von S. 21 ff. erschöpf end
hezeichnet. Da die Koeffizienten der Grundformen rationale gar^ze
Zahlen sind, so ist der zunächst zugrunde zu legende] Funktionenkörper:
(3) {U, u, V, w),
wo 9t der rationale Zahlkörper ist. Es besteht dann der Sat?: Das
Formenproblem der Ikosaedergruppe ©j^o ^^^ ^^^ Lösungen z^, z^, die
nach den nötigen AdjunMionen numeriscJißr Irrationalitäten aus einer unier
ihnen rational, nämlich mittels der X20 Substitutionen der ©^g^^,
berechenbar sind. Aus der Normalgestalt der (^^^^ geht hervor, daß bei
Darstellung aller Lösungen durch eine die Adjunktion der primitiven fünften
Wurzel der Einheit s als numerischer Irrationalität erforderlich und hin-'
reichend isi.
Im Funktionenkörper (dt, s, u, v, w) ist das ]Formenproblem
gleichwertig mit der Aufgabe der Lösung einer Nomialgleichmig 120^*«'! Grades,
deren Galoissche Gruppe mit der l^omogenen Ikosaedergruppe ®^^q
isomorph ist. Die Kompositionsreihe dieser ®^^q ist nun durch ©jgo' ®v
®i gegeben, wo ®^ der aus den beiden Substitutionen 1 und — 1
bestehende Normalteiler ist. Irgend einem Nomialteiler der ©^go ^^^
5g I, 3. Ikosaedergleichung und Uire Eesolventen.
nämlich bei der 1-2-deutigen Beziehung der ©jao ^^ ^^^ nicht-homogene
@g^ wieder ein Normalteiler der ©g^ zugeordnet. Die ©g^ hat aber nur
die Kormalteiler ©g^ und @j, von denen der letztere die genannte Gruppe
@2 liefert. Das zugehörige Komplement ©g^ = ®i2o/®2 ^^^ ^^ ^^^
nicht-homogenen Ikosaedergruppe isomorph*).
Nach den Grundsätzen der Galois sehen Theorie (I, 383 ff.) ist
somit die Lösung des Formenproblems der Ikosaedergruppe oder die
Lösung der gleichwertigen Xormalgleichung 120^*60 Grades in zwei
Schritte zerlegbar: Nach Lösung einer Normal gleichung 60^^'^ Grades
mit der einfachen Gcäois sehen Gruppe ©g^ hat man nur noch der ®^
entsprechend eine Quadratwurzel zu ziehen.
Zur Herstellung der Gleichung ßO^ten Grades bilde man aus z^, z^
den Quotienten z :=z z^\ z^, der gegenüber der ®^ invariant ist. Man
wird hierdurch zur nicht-homogenen ©g^ zurückgeführt. Entsprechend
stelle man aus den Grundformen der Ikosaedergruppe die gebrochene
Funktion:
U\ Z = ^ = 1 — —^
W ^ j23;^5 12^;^^
nullter Dimension in den z^, z^ her, die demnach von z allein abhängt.
In entwickelter Gestalt kann man die beiden in (4) gegebenen
Darstellungen von Z in der Proportion zusammenfassen:
'(5) Z: (Z — 1): 1 = ((^2ö + 1) — 228 (^^^ — z^) ■\- 494 z^'J
: ((^sö + 1) + 522 (^25 _ ^5) _ 10005(^^0 + ^i"))2
: —12S(^(^"-f- 11 ^= — 1))^
Hier haben wir die „I}Mi,aedergleichung- vor uns, die im
Mittelpunkte von Kleins Theorie des Ikosaeders steht**). Sie ist im FunJc-
tionenJcörper (dt, s, Z) irredu,zibel und bleibt auch bei Adjunktion weiterer
„numerischer" Irrationalitäten irreduzibel (vgl. S. 21 ff.). Sie ist eine
Normalgleichung mit einer zur Ikosaeder-^g^ isomorphen Galois sehen
Gruppe, und ihre sämtlichen Wurzeln berechnen sich aus einer ersten
unter ihnen mittels der sechzig Substitutionen der nicht-homogenen Iko-
Xach Lösung der Ikosaedergleichung (5) erfordert die Erledigung
des Formenproblems nur noch das Ausziehen einer Quadratwurzel. Man
kann zu diesem Zwecke an die Gleichung:
*) Wahrend die ©gQ isomorph ist mit der alternierenden Permutationsgruppe
fünften Grades, hat die ©130 niit der symmetrischen Permutationsgruppe dieses
Grades, wie man sieht, nichts zu tun.
**) Vgl. „Ikos.^ S. 60 ff.
Ikosaedergleich|ing.
anknüpfen. Die fragliche Quadratw^rzel ist also:
''^ ^ ^.-.„.. ,y
wo man für z eine Lösung der Ikosaedergleichung einzusetzen hat.
Entsprechend den rationalen Koeffizienten der Ikosaedergleichung (5)
hat man der algebraischen Behandlung dieser Gleichung zunächst den
Funktionenkörper (9?, Z) zugrunde zu legen. Der GaLoissche ^örppr
der Ikosaedergleichung enthält mit den beiden Wurzeln z und £^ dieser
Gleichung auch ihren Quotienten £, 00 dß^ diß primitive fünfte
Einheitswurzel E eine „natürliche- Irrationalität der Ikosaedergleichung id. Dßr
Galois sehe Körper der Ikosaedergleichung ist dann einfach der Körper
($R, E, ä); denn dieser Körper enthält (9?, Z) als echten Teiler, and in
ihm sind alle sechzig Lösungen der Ikosaedergleichung enthaltep. In
hezug auf (9t, Z) id nun C^, e, 2) ein Körper deb Grades 4-60, und
entsprechend hat die Ilco&aedergleichmig (o) vqt AdjunUion von e eine
Galoissche Gruppe ©340 ^^*" Ordnung 240, in der die (^g^ ^^'^ JS(ormal-
teiler des Index 4 ist. Man gewinnt die ©j^^, aus der als
Permutationsgruppe hergestellten ®^^^ durch Zusatz der zyklischen Gruppe (^\, die
man durch wiederholten Ersatz von e durch £^ erzeugt. Bei diesem
Ersatz gehen die Ikosaedersubstitutionen (vgl. S. 42) ineinander über,
öO daß in der Tat die ©g^ einen Xormalteiler darstellt.
In diesem Zusammenhang kann man eine wichtige funktionen-
th-eoretische Erklärung für die Gruppe ©^^ geben. Durch (5) ist Z als
eine Funktion I^O^*^^ Grades von z gegeben in der Art, daß eiußm
beliebig vorgeschriebenen komplexen Werte Z ein System von 60 bezüglich
der ©g^ äquivalenten Punkten z der «--Kugel zugehört, in denen die
fragliche rationale Funktion den vorgeschriebene]^ Wert Z annirpimt. Diese
60 Punkte sind im allgemeinen durchweg verschieden. Xur für Z =: 0
fallen die 60 äquivalenten Punkte 3 zu je B in die 20 Flächenmitten des
Ikosaeders (Nullpunkte der Grundform (p), im Z = 1 fallen sie zu je 2 in
die 30 Kantenhalbierungspunkte und für Z = 00 zu je o in die 12 Iko^a-
ederecken. Bildet man demnach die -5-Kvigel mittels der Funktion Z auf
die Z-Ebene ab, so gelangt man zu eiper öO-hlcittrigen Biemannsch.'u
Fläche nher der Z-Ebene, deren einzelnes Blatt einem Dreieckspai^re der
ikosaedrischen Kugelteilung entspricht, piese Fläche ist nur bei Z = 0.
1 und 00 verzweigt, und zwar finden sich bei Z = 0 zwanzig
dreiblättrige Verzweignngspunkte, bei ^' = 1 dreißig zweijblättiige und hei
Z = 00 zwölf fünf blättrige =*).
Auf dieser Fläche ist nun die 60-deatige algebraische Funktion z
von Z eine eindeutige Funktion des Ortes. Dabei stellen sich alle
60 Zweige in einem ersten, der z heiße, durch die 60 Substitutionen der
*) Über derartige „regulär verzweigte Eiemami sehe Flachen"-vergleiche man
Klein, „Ges. Äbh." Ill, 656 und 121 ff. sowie „M(?dulfu|xkt.- 1, 319 und 333.
58 I, 3. Ikösaedergleiclumg und ihre Eesolventen.
nichit-Iiomogenen (S>^^ dar. Da die Fläche zusammenhängend ist, so ist
es möglich, von einem ersten, den Zweig g tragenden Blatte durch
Umläufe um die Verzweigungspunkte zu allen übrigen Blättern zu gelangen
und damit auch z stetig in alle übrigen Zweige unserer algebraischen
Funktion überzuführen. Man kann das Sachverhältnis auch so auffassen,
daß man nur mit der einfachen ^-Ebene arbeitet und die 60 Wurzeln
<0, ^', z", ' • - der Ikosaedergleichung in irgend einer Anordnung
nebeneinander stellt. Bei irgend einem geschlossenen Umlauf von Z in seiner
Ebene von eiaer Anfangsstelle Z aus- zu dieser Stelle zurück
reproduzieren sich die Wurzeln in einer gewissen Reihenfolge d^, ^W^ d^, • • •.
Damit die Wurzeln eindeutig fortsetzbar sind, wolle man bei den
geschlossenen Umläufen nur die Verzweigungspunkte Z =: 0, 1 und oo
vermeiden. Die auf diese Weise zu gewinnenden Permutationen der
60 Wurzeln der Ikosaedergleichung bilden dann gerade die mit der
Ikosaeder-@ß(, isomorphe, einfach transitive Penmitationsgruppe (5)^^^, die
die Galois sehe Gruppe der Ikosaedergleichung bei Zugrundelegung des
Körpers (9t, s, Z) ist. Entsprechend ihrer Herstellung mittels der
geschlossenen Umläufe des einen in der Ikosaedergleichung auftretenden
„Parameters" Z in seiner Ebene heißt die fragliche Permutationsgruppe
die „Monodromiegruppe^ der Gleichung (5)*).
Wir haben also hier sowie weiterhin bei der Betrachtung von
Gleichungen mit einem Parameter, d. h. bei der Untersuchung von
algebraischen Funktionen eines Argumentes, zwischen der „Galoissehen
Gruppe" und der „Monodromiegruppe" zu unterscheiden. Für unsere
Ikosaedergleichung ist die Galoissche Gruppe bezüglich des Körpers
(9i, Z) die oben bezeichnete ©g^o, und erst nach Adjunktion von s
reduziert sich die Graloissche Gruppe auf die Monodromiegruppe ©g^^.
§ 3. Resolvente fünften Grades der Ikosaedergleichung.
Nach I, 381 ff. entspricht den umfassendsten echten Teilern der
Ikosaeder-@go, nämlich den fünf konjugierten Tetraeder-@j2 ^^^
Resolvente niedersten, nämlich fünften Grades der Ikosaedergleichung. Zur
AufsteRung dieser Resolvente benutzen wir eine von Klein erdachte
funktionentheoretisch - geometrische Methode, die er mit großem Erfolg
insbesondere bei der Untersuchung der Modulargleichungen der
elliptischen Funktionen angewandt hat**).
Die S. 42 mit T und U bezeichneten Substitutionen der ®^^ liefern
in T, U, T'IT, 1 eine der fünf Vierergruppen @^. Die durch die
Diametralsymmetrie erweiterte @g enthält drei Spiegelungen, deren
Symmetriekreise die reeUe ^-Achse und die beiden aus Fig. 4 (S. 46) leicht
herausfindbaren, zu dieser Achse senkrecht verlaufenden Symmetriekreise
*) Die Monodromiegruppe ist von Hermite eingeführt; vgl. die Pariser
Compt. ßend., Bd. 32, S. 458 (1851).
**) Ygl. „Ges. Abh." HI, 35 ff. und insbesondere III, 81 ff.
Monodromiegnippe 4er Ikosaedergleichung. 59
der ikosaedrischen Teilung sind. Sie zerlegen die E^ugeloberfläche in
acht bezüglich der &q äquivalente Oktanten. In z^ei benachbarten unter
diesen acht Oktanten grenzen wir nun genau nach Vorschriift vop Fig. 6
(S. 49) einen DB für den KormaKsator der @^, Fig. 7,
d. h. für die zugehörige Tetraeder-®^, in Gestalt
eines Fünfecks ein. Das hiemeben in Fig. 7
gezeichnete Fünfeck trägt dieselben ]Eckenbezeich-
nungen wie das Fünfeck der Fig. 6 *). Wie damals
sind bezüglich der ©^^ die Seiten Ä' B imd C B
äquivalent, ebenso die Seiten Ä'D wßd CD, sowie
CG' und CG". Die jeweils zuerst genannten Seiten
dieser drei Paare gehen in die äquivalenten bzw.
durch die Substitutionen S-T-S^ S^-^-S^ T
der @j2 über. Der gewonnene DB der ©^g ^^'
steht aus fünf Dreieckspaaren der ikosaedrischen
Kugelteilung, die sich rings um den NuUpaakt
^ = 0 heramlagern, und die aus dem oben
(S. 48) ausgewählten DB der Ikosaeder-®^^ durch die fünf
Substitutionen 1, S, S^, S^, S^ entstehen. Dei^ entspricht die Zerlegung:
(1) ®,, =3®,, + ®,,.S + @,,.S2^®,,.3^ + @,,.S^
der ®gQ in fünf znr ©^^ gehörende Nebeagruppen.
Bei der Tetraeder-®^^ kann man genau so, wie es oben bei der
Ikosaedergruppe ausgeführt wurde, aus den Invarianten eine rationale
Funktion ^ zwölften Grades von ^ herstellen, die einen beliebig
vorgeschriebenen komplexen Wert in einem und nur einem Punkte des DB
der ®j2 annimmt. Dabei wolle man beachten, daß diese Furiktioq ^ noch
nicht eindeutig bestimmt ist; in der Tat hat auch jede lineare Funktion:
(2) r = ^^^^
von ^ die eben von t, genannte Eigenschaft. Man kann von diespm
Umstände in der Art Gebrauch machen, daß man für ^' an irgend drei
verschiedenen Punkten des DB drei willkürlich gewählte verschiedene
Werte vorschreibt**). Wir lassen den Index bei t,' gleich wieder fallen
und schreiben etwa vor, daß t, iin Mittelpunkt £• == 0 des PB
unendlich wird, im Punkte C versch\^?inde1: und in den drei äquivalenten
Ecken A, C, C" des DB den Wert 3 annimmt.
Der Ordnung 12 der ausgewähltea ®j2 entsprechend ist ^ eiae
rationale Funktion lä*^'' Grades vop 2, and zwar wird sich zeigen, daß
*) Der DB der Tetraeder-©!^ wir4 also von einer Flache des Dodekaeders
geliefert.
**) Daraus ergeben sich namlich drei lineare |iomo^ene Qleichungen für die
vier Koeffizienten a, h, c, d.
ßf) I, 3. Ikosaedergleichung und ihre Eesolventen.
diese Funktion dem Körper (^, 2) angehört. Sie ist eine unt-er fünf
konjugierten Funktionen:
(3) U^), ^(£*^), Us'^), U^'^), t{e^),
die im Sinne der allgemeinen Grundsätze der Galois sehen Theorie (\gl
I, 378 und 389ff.) zu den fünf Tetraedergruppen ©^g, S-'^-®^^-S,
S~'^'(§>^^' S^, ■•■ gehören. Diese fünf Funktionen (3) sind, nun die
Wurzeln der aufzustellenden Resolvente fünften Grades der
Ikosaedergleichung. Man würde diese Resolvente gewinnen können, indem man
aus dem Ausdruck von ^ als rationale Funktion von z und der
Ikosaedergleichung 2 eliminiert. Hier setzt nun aber die Methode von Klein
zur Herstellung der Resolvente ein, die uns gestattet, diese Gleichung
mit einem Mindestmaß von Rechnung herzustellen.
Die algebraische Beziehung zwischen ^ und Z ist so, daß dem
Einzelwert ^ (zwölf äquivalenten Stellen g) stets nur ein Wert Z
zugehört, umgekehrt dem Einzelwert Z aber (fünf Systemen zu je zwölf
bezügKch der ©^3 äquivalenten 2) immer fünf Werte (3). Somit ist
einfach Z eine rationale Funktion fünften Grades von ^, und insbesondere
eine ganze rationale Funktion, da Z nur mit ^ unendlich wird. Um
diese Funktion anzusetzen, denke man den in Fig. 7 dargestellten DB
der Tetraeder-@j2 durch die Funktion Z auf eine fünfblättrige geschlossene
Riemannsche Fläche über der Z-Ebene abgebildet, wobei die Abbilder
der durch die ®^^ aufeinander bezogenen Seiten Ä'B und C'B usw. zum
Zusammenschluß zu bringen sind. Die Fläche ist wieder nur bei Z = 0,
1 und oc verzweigt, und zwar entnimmt man aus der Zuordnung der
Seiten des DB leicht folgende Angaben: Bei Z = 0 laufen zwei
Blätter isoliert (den Ecken B und D entsprechend), die übrigen bilden
einen dreiblättrigen Verzweigungspunkt (den Ecken Ä', C\ C"
entsprechend) ; bei Z = 1 verläuft ein Blatt isoliert (dem Punkte G
entsprechend), und weiter liegen hier zwei zweiblättrige Verzweigungspunkte
(den Mitten der Seiten Ä'B, C'B und A'D, C" D entsprechend); beiZ = cxs
hat man (dem Punkte ^ === 0 entsprechend) einen fünfblättrigen
Verzweigungspunkt.
Diesen Angaben entsprechen die beiden Ansätze:
(4) cZ=(^'-\-a^^b)(^- 3)^ ciZ--l) = ^(^^ + dt + ey
für die zu gewinnende Funktion Z von ^. Man hat nur zu beachten,
daß im dreiblättrigen Verzweigungspunkt bei Z = 0 vorschriftsgemäß
^ = 3 ist, und daß bei Z rrz 1 in dem hier isoKert verlaufenden Blatte
^ = 0 zutreffen sollte.
Aus (4) folgt die in ^ identisch bestehende Gleichung:
(5) (^'^a^ + h)(^-3y-c = ^(^2 -^ J^ + ef,
die durch Differentiation nach ^ zu der weiteren identischen Gleichung:
(5^2 ^ (4«_ 6)5 + 3(fc- 0)) (5-3)^ = (6t^^Bdt + e)(t' + d^^e)
Eesolvente faulten Grades der Ikosaedergleichung.
hinführt. Da (f + d^-\-e) nicht durch (^ — 3) teüfear ist,
sich diese Gleichung in die beiden:
5^ + 3^^ + . = o(r--6^T9),
5f -^ (4a - 6)^ + 3(6 - a) = 5(f + ^^ -f e).
Der Vergleich der Koeffizienten ergibt:
' 3d = —30, e = 45, 4:ß — (} = od, 3(6—a) = 5e
und damit
a = — 11, 6 = 64, d—--m, e = 46.
Trägt man diese "Werte in (5) ein imd setzt g = 3, so folgt:
— c = 3 (9 — 10 . 3 + 45)2 ^ 3 .242 ^ 12^ = 1728.
Die Besolvente fünften Grades der IkosaedergMchufig nimmt für die
ausgewählte FunUion t, eine Gesteint an, die tcir wie die IkosaedergleicJpung (0)
S. 56 seihst al$ Proportion schreiben:
(6) Z:(Z-1):1 = (^2-11^4 64)(^-3)3
: —1728.
Die Funktion g nimmt demnach in den Eckpunkten B und D des DB
der ®,2 die Werte |(11 + 3iflE) an, in den Mittelpqnkten der Seiten
Ä'B usw. aber die Werte (5 4:2*1/5).
Die Darstellung von ^ als ,, na,türliche Lprationalität "^ dßr
Ikosaedergleichung, d. h. als Funktion des Körpers (% s, z), gewinnt man so: Die
zwölf Pole dieser rationalen Funktion sind die Ikosaed[erecken und also
die Nullpunkte der Fimktion z{z^^ -f- 11 ^° — 1) uad der Punkt ^ == oc.
Die zwölf Nullpunkte von t, sind die bezüglich der Tetraeder-®^^ mit
der Stelle G der Fig. 7 äquivalenten Puiikte, d. h sie fallen zu Paaren
in die sechs Schnittpunkte der Symmetriekreise der oben geaannten
erweiterten Vierergruppe @g. Diese drei Kreise haben die Gleichungen:
«/ = 0, {x^ + 2/^ — 1) cos -^ + a; = 0,
{x^ + 2/^—1) cos— -Vx = 0,
wo wie oben (S. 29 ff.) z =: x -{-iy gesetzt ist. Es handelt sich also
um die vier reellen Nullpunkte der Funktion:
{{z' - 1) + (1 ^ VS)^) {{z' _!) + (]- V5) ,)
= ^* + 2^^ —6^2__2^+ 1
62 I, 3. Ikosaedergleichung und ihre Resolventen.
und außerdem um die Pole ^ = +i der Substitution Z7. Von hieraus
gewinnt man leicht den Satz: Die swr ausgeswMen Tdrwäer-%^^ ge-
Mrende FtmUion.t, ist im Körper (9t, 2) enthalten und gegeben durch:
^'^^ ^~ ^(^lö-f 11^^—1)
Xach den bisherigen Angaben ist ^ das Produkt einer Konstanten c und
der hier rechts stehenden Funktion. Für Um 2 = 00 findet man dann
unter Zuziehung von (6):
^ = C2, — 122Z=r f = C5^^
SO daß der Vergleich mit der Ikosaedergleichung (5) S. 56 die Folgerung
c^ = 1 gestattet. Da nun für reelles z auch ^ reell sein muß, so gilt
in der Tat c = 1. Die Eintragung des Ausdrucks (7) für ^ in (6)
führt zur Ikosaedergleichung (5) S. 56 zurück.
§ 4. Weitere Gestalten der Resolyente fünften Grades.
Die Einfachheit der eben gewonnenen Resolvente (6) gründet sich
auf die günstige Auswahl der zur Tetraeder-@j2 gebörenden Funktion ^.
Sie wird noch überboten, falls wir die homogenen Variablen z.^, z^ wieder
einführen und damit auch „Formen" der Tetraedergruppe als Unbekannte
von Resolventen zulassen. Wir verstehen erstlich unter f{z^, z^ die
Form sechsten Grades:
(1) f (^„ z^ = {z\ -f 4) + 2 ^1 ^, {z{ - 4) -oz\z\ (4 -f 4),
deren Nullpunkte die sechs Schnittpunkte der drei Symmetriekreise der
durch die Diametralsymmetrie erweiterten %^^ sind. Da f{z^^ z^
gegenüber der Substitution — 1 invariant ist, so werden die 16 Substitutionen
der homogenen Tetraedergruppe, die den Perioden 3 und 6 angehören,
die Form /"(^j, &^ bis auf multiplikative dritte Einheitswurzeln
reproduzieren. Indessen ist nach der aus (7) § 3 folgenden Gleichung:
(2) f{^r.^^^iliß)l{?,.^^
das Quadrat von f{z^^ z^ gegenüber jenen 16 Substitutionen absolut
invariant, so daß die dritten Eiaheitswurzeln durchweg gleich 1 sind.
Somit ist /*(^j, z^ gegenüber den 16 Substitutionen und also gegenüber
allen 24 Substitutionen der homogenen Tetraedergruppe absolut invariant.
Hiemach gewinnt man durch die Substitutionen der Ikosaeder-®j2o
aus der Form (1) im ganzen fünf konjugierte Formen, die wir durch
Ausübung der Substitutionen 1, S, S^ S^ S^ herstellen und:
nennen, wo v = 0, 1, 2, 3, 4 zu setzen ist. Diese fünf Formen sind
nun die WurzeLo einer Gleichung fünften Grades, deren Koeffizienten
Weitere Gestalten der Resolvente funftep Grades. 63
Invarianten der Ikosaeder-^^gjj und als solche durch die Grundformen
cp, il}, X darstellbar sind. Diese Gleichung ergibt sicli aber sofort [aus
der Resolvente (6) § 3 und der Ikpsaedergleichung. Man hat pämlich,
falls man die Ikosaedergleichung in die abgekürzte Gestalt:
(4) Z:(Z—1): 1 = cp^-.tj;^:—1728 x""
setzt, zunächst die Gleichung:
r' e (^' - 10 ^ + 45)2 = - 1728 f (Z - 1) = f.
Nach Einführung von f auf Grund von (2) und Ausziehen der
Quadratwurzel folgt:
f{r-iQxf-f^^i') = ±^-
In dieser für z-^, z^ identischen Gleichung muß rechts das obere Zeichen
gelten, wie man durch Eintragung vor^ z^ r=i 1, ^^ = 0 leicht zeigt.
Die jResolvente fünften Grades in homogener Gestßlt alß solcher mit den
fünf Lösungen (3) hat die Gestalt:
(5) fö_io^f^ + zi,ox'f-t = 0.
Man gelangt zu einer Gleichung fiinfte^ Grg,des, in der die vierte und
die zweite Potenz der Unbekannten f ausfallen. Gleichungen fünft.en
Grades dieser Gestalt bezeichnet Klein als „DiagonalgleicMmgen" *).
Will man von (5) zu einer nicht-homogenen Resolvente, ohne zu
quadrieren, zurückgelangen, so kann man die vom Quotienten z = Z-^:Zc^
allein abhängende Funktion:
als Unbekannte einer Gleichung fünften Grades einführen. Für diese
Gleichung berechnet man aus (5) leicht die Gestalt:
(7) 4:8(Z—iyF^ + 40(Z—l)^^+ 16 F—A = 0.
Als rationale Funktion von ^ ist F, wie man leicht feststellt, durch:
(^^ ^ - F^"1Ö^ + 45
gegeben.
Auch die Hessesche Determinante von f{Zj^, z^) ist eine Invariar^te
der Tetraeder-®Jg. Sie ist vom achten Grade in den z-^^ £^, und m&n
findet, wenn man:
g'Y g2^
)zl ' dz^ dz^
d^f d^f
: —A00h(z^, z^
'bzJbz, ' d^
*) Vgl. wegen der Begründung dieser Bßnenn(ing „Ikos.", S. 166.
^4 I, 3. Ikosaedergleicliung und ihre Resolventen,
setzt, für Ä(-^i, ^^ den Ausdruck:
^^^ i +7 44(4-4)-
Ihirch die Substitutionen der Ikosaedergruppe geht die Form 'h{s^,g^ im
ganzen in die fünf konjugierten Formen:
über, die die Wurzeln einer weiteren Gestalt der Resolvente fünften
Grades sind. Man könnte diese Resolvente gleichfalls leicht aus (6)
S. 61 ableiten. Doch möge an diesem Beispiel eine andere Schlußweise
erläutert werden.
Die Koeffizienten der fraglichen Gleichung sind Invarianten der
Ikosaeder-@j2Q der durch 8 teilbaren Grade 8, 16, 24, 32 und 40. Xaeh
(7) S. 55 gibt es aber für diese Grade an nicht verschwindenden
Invarianten der @j2(j bis auf konstante Faktoren nur die drei Invarianten
y^, cpi und (p^ der Grade 24, 32 und 40. Für die Resolvente gilt somit
der Ansatz:
h^ -\-afh'' -l-h(pxh + c(p^ = 0,
wo a, h, c konstante Faktoren sind. Kun muß diese Gleichung in ^^
und ^2 identisch bestehen. Ordnen wir aber unter Eintragung der
Ausdrücke von h, (p und y i^ den ^j, z^ die linke Seite dieser Gleichung
nach abfallenden Potenzen von ^j, so liefern die drei ersten Glieder die
Gleichung:
(^c + 1)4" + (p — o) ^f ^2 + (a — 6 + 45)^f 4 -^ = 0.
Diese Gleichung soll also identisch bestehen, und also ist c = — 1,
h = 5 und a = — 40. Die homogene jResoIvente fünften Grades mil
den fünf Jionjugierten Formen (10) als Wurzdn ist:
(11) }v> — Aöx'h^ + ocpx'h — cp^ = 0.
Wir sind hier zu einer sogenannten „Hauptgleichung- fünften Grades im
Sinne Kleins geführt, d. h. zu einer Gleichung, in der die vierte und
die dritte Potenz der Unbekannten nicht auftreten*).
WiU man die Gleichung (11) so umschreiben, daß sie nur vom
Quotienten z der homogenen Variablen 0^, z^ abhängt, so führe man etwa
die von z allein abhängende Funktion:
(12^ TI{z\ = l^^C^i' ^2)z(^i' ^2)
ein. Man findet dann unter Benutzung der Ikosaedergleichung (4):
(13) ZJ?^ + 40irä—^60B^+144 = 0
*) Vgl. „Ikos.", S. 160.
Verschiedene Gestalten der ßesolvente fünften Grades. 65
als Gestalt der Resolvente fünften Grades. Die Darstellung von E als
rationale Funktion von ^ erhält man d[urch folgende Überlegung: Die
acht KuUpunkte von h{z^, z^ bilden ein |bezüg;lich der Tetr^eder-@iä
invariantes Punktsystem. Hierbei kann es sich nur h^jideln um die vier
Tetraederecken, je doppelt gezählt, oder um die vier doppelt gezählten
Flächenmitten oder um das aus den Ecken und Flächenmittßn
zusammengesetzte Punktsystem. Der letzte Fall trifft zu, da h nicht das Quadrat
einer Form vierten Grades ist. Also sind die Nullpunkte von h die
Punkte B und D des DB der Fig. 7 S. 59 und die mit ihjien bezüglich
der @j2 äquivalenten Punkte. Somit ist h Teiler def Ikosaederform (p,
und in der Tat bestätigt dies die Rechnung; man findet:
(p{z^, z^) = g(z^, ^2)-Ä(^i, ^2^
wo die Form 12*^^* Grades g gegeben ist durch:
(14) ] — 20 ^f 4 {4 — -^1) + 15 ^* 4 {z\ 4 4) — 24 4 z\ {z\ - 4)
i +1144-
Die rechte Seite der Gleichung (12) kürzt sich demnach so:
(15) H(.) = l?li^^i>,
so da£ E als Quotient zweier Tetrapderformen zwölften Grades eine
lineare Funktion von ^ ist. Der Xullpunkt von E liegt iin Mittelpunkt
^ = 0 des DB (Fig. 7, S. 59), vo ^ = cxd ist, wäJirend der Pol von
E sich in den äquivalenten Ecken A', C, C" findet, wo ^ = 3 ist. Die
Darstellung von E als rationale Funktion von ^ ist hiemach:
(16) E{z) := -i^,
wobei man den im Zähler zugesetzten ]Faktor 12 leicht bestätigt. Für
den auf der reellen ^-Achse gelegenen Punkt G des DB der Fig. 7, wo
^ = 0 und Z = 1 zutrifft, ist nämlich H reell. Die Gleich (ing (13)
aber wird für Z = 1 reduzibel und liefert:
{E+4:)(E^ — 2E+ ^y = 0,
so daß nur der reeUe Wert B^=—4für^ = 0in Betracht kommt.
Zur Bestätigung trage man den Wert (16) -von E in (13) ein:
^9^ 12^ 12
tt-3)'^ (5-3)» t
woraus man sofort:
- 12^Z = (^_ 3)^((g-3)ä- o(^ - 3) + 40)^
d. h. die Resolvente (6) S. 61 wieder gewinnt.
Fricke, Algebra. H. £
(56 I, 3. Ikosaedergleiclmng und ihre ßesolventen.
§ 5. Diskriminanten der Resolventen fünften Grades.
Die fünf Wurzeln einer einzelnen der aufgestellten Resolventen
fünften Grades sind bei Ausübung der Substitution — 1 invariant; denn
sie sind entweder nur von z abhängig oder Formen geraden Grades der
^j, z^. Die Substitution S permutiert die fünf Wurzeln zyklisch; diese
Permutation ist gerade. Die Substitution T ist nur in einer
Tetraedergruppe enthalten, so daß sie eine Wurzel unverändert läßt und die vier
anderen paarweise austauscht; auch diese Permutation ist gerade. Aus
S und T ist die ganze Ikosaedergruppe erzeugbar. Da die fünf
Tetraedergruppen "nur die Substitution 1 gemeinsam enthalten, so liefert nur
diese die identische Permutation der Wurzeln. Es besteht also der Satz:
Die fünf Wurzeln der einzelnen JResolvente fünften G-rades erfahren hei
Ausübung der Tkosaedersuhstituüonen die sechzig geraden Vertauschungen,
so daß ihr DifferenzenproduM stets eine Invariante der Ikosaedergruppe
darstellt.
SoU die Resolvente (5) S. 63 eine Doppelwurzel f haben, so muß
für diese Wurzel auch die durch Differentiation nach f entstehende
Gleichung gelten:
5(r- 6;^/"' + 9f) = oif'-SxY = 0-
Trägt man den hieraus folgenden Wert /" = i VS ;^ in die Resolvente
ein, so ergibt sich:
so daß wegen (6) S. 54 eine Doppelwurzel f nur für (p = 0 eintreten
kann. Das Differenzenprodukt der fünf Wurzeln (3) S. 62:
(1) Pfi^^,^,) = il(^-^')
v<v'
als Ikosaederform 60^*^^* Grades mit dem Faktor (p ist zufolge (7) S. 55,
abgesehen von einem konstanten Faktor, notwendig die dritte Potenz
von (p. Diesen Faktor bestimmt man durch Eintragen der Werte
^1 = 1, ^2 = 0, wobei das Differenzenprodukt die Gestalt annimmt:
Pfih 0) =n («"'-'''') = 25 vs,
v<v'
wie man mit Hilfe der Gleichung (13) S. 41 leicht ausrechnet. Da
(p(l, 0) = 1 ist, so folgt: Das DifferenzenproduM (1) der Besolvente
fünften Grades (5) S. 63 ist:
(2) Pf {z^. ^o) = n (^^ - f^) = 25 V5 9 {z^, ^,)^
r<r'
woraus man mit Hilfe der Ikmaedergleichung (4) S. 56 für die Besolvente
(7) S. 63 als DifferenzenproduM berechnet:
(3) P.(.)=n(^.-^.0 = ^*1^,
Differenzen Produkte fur die ßesolveuten fünften Gra4es. 67
Das Differenzenprodukt der fünf Wurzeln (10) der Resolvente (11)
S. 64 ist eine Invariante SO^ten Grades, die jedejifalls den Teiler cp hat,
da die Resolvente für 9) = 0 die Doppelwurzel h = 0 h^t. Man kann
die Resolvente nach Zusatz des Faktors 12^;^^ ir^i die Gestalt kleiden:
(12h2y — 4:0-125 ^5 (j 2 h xf + 60-12^ f (p (12 h x)
— 14A -12^ 2^ cp'^ == 0.
Gilt 1^ = 0, so kann man hier zufolge (6) S. 54 für 12^;^° den Wert
— (p^ eintragen und findet:
(12 h yf + 40 9^ (12 /i yf — 60 ^* (12 h i)-\-\^^ 9=^ = 0,
eine Gleichung, die reduzibel ist und zufolge ihrer Gestalt:
(i2;i;K + 49)((i2^z)'-2(i2;ix)9-f 6g'T = o
zwei Doppelwurzeln hat. Das gesuchte Differenzenprodukt J^hiß^^ ^2)
muß also auch mit 7^ verschwinden und hat somit den Teiler (p ^. Der
noch übrig bleibende Faktor ist vo|n 30^*^'^ Grade und muß demiiach, von
einem konstanten Faktor abgesehen, notwendig wieder gleich -^ sein.
Der konstante Faktor bestimmt sich gerade wie oben durch Einträgen
der Werte ^^ = 1, ^^ = 0 zu 25 V5. Das BifferenzßnproduU der
Besolvente (11) S. 64 gestattet als Invariante ßer Ikosaedergruppe die
Darstellung:
(4) Pa (^,, ^,) = n (^^ - ^'^') = 25 y5'^ (^„ ^2). ^ {z,, z,)\
woraus man mit Hilfe der IJcosaedergleichung (4) S. p6 f^r das Diffe-
renzmproduM der fünf Wurzeln der Gleichung (13) S. 64 erhält:
(5) Pj,iz) = n (^^ - ^^^') == si^^oo ys ^^^ •
v<v'
Endlich ergibt sich aus (16) S. 65:
Das Produkt der fünf Funktionen H^ berechnet sich aber aus (18)
S. 64 zu — 12^-Z—^ Auf Grund von (5) gelangt man demnach zu (^em
Satze: Bas BifferemenproduU dßr fi^nf Wurzeln t, der Besolvente (6)
S. 61 stellt sich in Z wie folgt dar:
(6) P,^{z,, ^2) = n (^^ - ^^') == 12« • -S V5 Z (Z - 1).
Wie es sein muß, ist die Diskri^iinante stets im Körper (9?, Z)
bzw. (Ö?, cp, tl;, x) enthalten. Dagegen tritt in den jpi-fferenzenprod^ikten die
numerische Irrationalität ys auf, die somit in jedem Fßlle eine natürliche
Irrationalität der Besolvente fünften Grades ist. Der algebraische
68 • I, 3. Ikosaedergleicliung und ihre Eesolventen.
Charakter der einzelnen Resolvente fünften Grades liegt hiemach am
Tage. Sie ist im Körper (9t, Z) bzw. (^, (p, tj;, %) eine irreducible und
aifeUlose Gleichung fünften Grades, indem ihre Galois sehe Gruppe die
symmetrische Permutationsgruppe ©jgo ^^^- Entsprechend den Sätzen
in I, 391 ff. reduziert sich die Galois sehe Gruppe nach Adjimktion der
Wurzel der Diskriminante, d. h. hier der natürlichen Irrationalität \ 5
auf die alternierende ©g^? ^^^ zufolge des ersten Satzes im vorliegenden
Paragraphen die Monodromiegrupjpe der Resolvente ist (vgl. S. 58). Im
Sinne von I, 382 ist die Gleichung fünften Grades bei Zugrundelegung
des Körpers (5R, Z) bzw. (9?, (p, ip, y) eine Partiairesolvente der Ikosaeder-
gleichung. Die Galois sehe ©^go ^^^ Resolvente ist das Komplement
eines Xormalteüers ©g ^^^ Galois sehen Gruppe ©^^^^ der Ikosaeder-
gleichung. Dieser Xormalteiler ©^ ist leicht angebbar. Der Ersatz
von B durch £^ liefere die Permutation F, die von den Wurzeln der
Resolvente eine unverändert läßt (nämlich ^q, /"q, • • •) und die anderen
vier zyklisch permutiert. F^ bewirkt dann dieselbe Permutation wie
die Ikosaedersubstitution TJ, so daß die Operationen 1, V'^-TJ den
fraglichen Teuer ©g bilden. Auch nach Adjunktion von yS bleibt die
Gleichung fünften Grades eine Partialresolvente, dagegen wird sie nach
Adjunktion von e eine Totalre&olvente der Ikosaedergleichung; denn jetzt
sind die beiderseitigen Galois sehen Gruppen isomorphe ©g^. Auch die
homogenen Gleichungen (o) S. 63 und (11) S. 64 sind für das Formen-
prohlem der Ikosaedergruppe nur Fartialresolventen; denn die symmetrische
@J2Q fünften Grades ist keineswegs mit der homogenen Ikosaeder-®^^^
isomorph. Xach Adjunktion von s muß zwar die Lösung z der
Ikosaedergleichung nach Lösung einer Resolvente fünften Grades rational
bekannt sein. Aber durch diese Lösung kann die letzte Quadratwurzel
(S. 57) bei Lösung des Formenproblems, die zur Kenntnis von ^j, ^^
einzeln führt, noch nicht mit erledigt sein. Dies geht auch unmittelbar
aus der Überlegung am Anfang des vorliegenden Paragraphen hervor.
Die Rechnung bestätigt die hier gezogenen Schlüsse. Besonders
einfach gestaltet sich die Berechnung von z nach Adjunktion von s aus
den Wurzeln der Resolvente (11) S. 64. Aus der Gestalt (10) S. 64
der /«, (^j, ^2) findet man leicht die vier Gleichungen:
l' = 0
2 s^'K (^1, ^2) = — 5 ^f ^2 (4 — 7 4),
i = 0
2 «'^^'v (^1, ^2) = oz, s\ (7 £\ + 4),
2 £*''/^(^i, ^2) = 54(7^^ + 4),
(7)
Algebraischer Charakter 4er ßesolventen fünften Grades. t)9
aus denen man für s die beiden Ausdrücke folgej-t:
Die eine der beiden in (8) vereintep Gleichtuigen für z geht in die andere
über, indem man die vorhin mit F^ • JJ bezeichnete Operation ausübt.
Die Iriy bleiben dabei unverändert, £ ist durch £* zu ersetzeii und z dflrch
— ^-1, da die Permutation F^ dey 60 Wurzeln der Ikosaedergleichuag z
an seiner Stelle läßt.
§ 6. Resolvente sechsten Grades der Ikosaederglejchuiig.
Weit leichter ist die Resolvente sechsten Grp^des zugänglich, die den
sechs konjugierten Teüem ©^^ ^^^ Ikosaeder-@gp vom Diedertypus
entspricht. Eine dieser ©^^ ist die aps den Ikpsaedersubstitutionen S ui^d V
zu erzeugende Gruppe, der als Pimktion z. B. der Ausdruck {f-"—^~5)
zugehört. Um besseren Anschluß an die Ikosaedergleichung zu
gewinnen, wollen wir jedoch statt dieses Ausdrucks seine lineare Funktion:
als Wurzel für eine zunächst aufzustellepde Gestalt der Resolvente
sechsten Grades benutzen. Dann gilt umgekehrt,:
Die Ikosaedergleichung (5) S. 56 lä£t sich in die Gestalt setzen:
Z:(Z-\):\ = ((^3-^-5)2-228(5° = 5-5)^ 49(5)3
: {{f^ - z- 5)2 + 4) ((^5 - z~ 5)2 + 622 {f - ^- 5) _ 10 004)^
:-12^ ((^^-^-5) ^11)5
Trägt man für {z^ — zr^^ den Ausdruck (2) in | ein, so führt die
Umrechnung der entstehenden Gleichung zu folgei^.dem Satze: Die
Hesolvente sechsten Grades der Ikoßaedergleicftung, deren erste Wurzel die
durch (1) erklärte Funktion | ist, kann in die Gestalt geklei^ä werden:
rZ:(Z-1):1 = (f-10| + 5)^
(3) ..(|2_22| + 125)(f-4|-l)2
I :-l2^|.
Eine zweite Gestalt der Resolvente sechsten Grades, die leicht aus
(3) entnommen werden könnte, die aber auch auf anderem Wege
herstellbar ist und damit einen neuen Beweis der Gleichung (3) liefert,
gewinnt man in'folgender Art: Das Produkt z-^-z^ ist gegenüber
der homogenen Substitution S (vgl. ß. 42) inxiariant und erfährt bei
70 I, 3. Ikosaedergleicliang und ihre ßesolventen.
Ausübung von TI Zeichenwechsel. Somit geh9rt die biquadratische
Form zl zl zur homogenen Diedergruppe ®2 - lo > ^^^ ^^s S und TJ erzeugt
wird. Für die Rechnung ist es zweckmäßiger, ^z\zl einzuführen, eine
Form der @2 • lo > die wir durch:
(4) gooiß^, ^ä) = S^f4
bezeichnen *). Durch die fünf Substitutionen T, S ■ T, S^ -T, S^-T, S^-T
geht die Form (4) zufolge (1) S. 42 über in die fünf untereinander und
von g^ verschiedenen Formen:
(5) g,(0^, 0^) = (s^^l + ^1^2 — £*''4)^ *' = 0, 1, 2, 3, 4,
die demnach mit g^ sechs konjugierte Formen der Diedergruppen liefern.
Setzen wir nun die Gleichung an, deren Lösungen diese Formen
sind, so sind deren Koeffizienten Invarianten der Ikosaedergruppe, und
da die Invarianten niedersten Grades, von konstanten Faktoren abgesehen,
%' 9' X^ d^^ Grade 12, 20 und 24 sind, so hat man den Ansatz:
(6) g^ + axg^ + hcpg + cx" = 0
für die Resolvente. Das Produkt c;^^ ist zufolge (4) und (5) gleich 5;^^,
so daß c = 5 ist. Trägt man weiter:
ein und hebt durch oz^zl, so folgt:
55^10^10 ^ a'IözUtx +icp + {z\'' + 11 zUl—ziy = 0
als eine in den r^, z^ identische Gleichung. Für z-^ = 1, z^ = 0 folgt
0+1=0, so daß h = — 1 ist. Weiter ergibt sich für ^^ = 1,
z^ = 1:
5^ +11-25« —496 + 121 = 0, a = — 10.
JDle Besolvente bechden Gradeb der IJcosaedergleichung, deren Lösmigen die
sechs Formen g sind, hat die Gestalt:
(7) g^-io^g^-cpg + 6x' = 0.
Um hieraus eine nur vom Quotienten 0 = 0^^:z^ abhängende Resolvente
herzustellen, setze man etwa:
(8) a (A — g'(^i'^ä)y(gi>^2)
Die Gleichung (7) geht dann in folgende Gleichung für Cr über:
(9) (J« +lOZG-2 —12Z2(J +5Z2 = 0.
Der Zusammenhang der Form g (z^, z^) mit der Funktion | (s) ist
durch:
(IQ) • 9(~^. ^,f = H^)% {^^, ^2)
'') Die Wahl des Index 00 und weiterhin der Indizes 0, 1, 2, 3, 4 bei den
biquadratischen Formen g rührt von der Bedeutung dieser Formen in der Theorie
der elliptischen Modulfunktionen her.
ßesolvente sechsten Grades der Ikosae4ergleicliung. 7]
hergestellt. Die Gleichung (7) liefert dabei:
(r-10|-|-5);K' = ^fe
woraus man durch Erheben zur dritten Potenz unter Benutzung der
Ikosa'edergleichung (4) S. 56 die Resolvente (3) wiedergewinnt
Zufolge (4) und (5) sind auch noch die Qu^drat^vurzeln der Formen
g rational in den z^, z^\
(11) y^ = y5^,^,, ig.^^^z\^2^z^-E^^z\, ^ = 0,1,..., 4;
sie gehören zu den fünf konjugierten zyklisphen Teilern ©2-5 der
homogenen Ikosaedergruppe. In den drei quadratischen Verbir^dungen:
(12) u^^z^s^, u^ = z\. u^ = —4,
die an die Beziehung:
(13) UI + U,U,:=0
gebunden sind, stellen sich die Quadratwurzeln der Formen g so dar:
(14) ig^ = VöWo, idv = % + £"«1 + £*"%•
Die durch (11) eindeutig erklärten Quadratwurzeln der Formen g sind
hiernach durch die folgenden Beziehungen aneinander gehunden:
r - y5 v^ + v^, + y^, + ij, + ij, + n = o,
(15) y^o + £' ii, + e' yj, -i- e y^3 +«' v^. = o,
I v^o + ^'ü + £ v^2 + ^* v^3 + ^'il = 0-
Gegenüber den binären lipearea Si;bstitq.tionpn der homogenen
Ikosaedergruppe müssen sich die w^, u^, m, te:pnär linea:p substituieren.
Da sie bei der Substitution — 1 einzeln unverändert bleiben, so gelangen
wir nur zu einer ©g^ von sechzig ternären Substitutionen der ip, die mit
der nicht-homogenen IJcosaeder-®^^^ isomorph ist und erzeugt wenden kann
aus den heiden wieder mit S und T zu hesetchne^den Suhstitutio'mn:
(S) u'q = U(^, ^[ =■ BU^, % = ^*%)
( ] ou'q = a^-\- u^~ u^,
(T) y 5 2*; = 2 u, -^ (£2 + e') a^ + {8 -V £*) u,,
( ys % = 2 u, + (£ + £*) u, + (£' -f e') «2-
Die Substitutionen dieser ternären ©g^ sind ummodular, und sie trans
formieren die quadratische Form (Uq -f- u^ u^) in sich =*).
Die Resolvente (7) wird als eine „JacoUsche Gleichung^ bezeichnet.
Jacobi**) fand in den „Multiplikatorgleichungen-, die er für die Trans-
*) Über die Theorie der temareii ©g^ bei unabhängig variablen u, ube^- ihre
Invarianten und ihr Formenproblem vergleiche ^l^an „Ikos.", S. 211 ff.
"'*) Vgl. dessen „Notices sur les foi\ctions elliptiques'- im Journ. f. >Iath.,
Bd. 3, S. 308 oder Jacobis Werke, Bd. 1, S. 261.
72 I, 3. Ikosaedergleichung und ihre Resolventen,
formation der elliptischen Funktionen bei primzahligem Grade n
aufstellte, Gleichungen (n -f- 1)*«" Grades, bei denen die Quadratwurzeln der
(n + 1) Lösungen sich mittels der Einheitswurzeln »*^° Grades genau so
in l(^ _j_ 1) Größen w^' ^i» %>•••) %—i darstellen lassen, wie dies für
» = 5 in (14) vorliegt. Auch die Relationen (15) verallgemeinem sich
dabei*).
§ 7. Diskriminante der Resolvente sechsten Grades.
Die Form g^o wird durch die Substitution S in sich transformiert,
die übrigen fünf Formen g^ aber werden durch S zyklisch permutiert,
so daß alle sechs Formen g durch S eine gerade Permutation erfahren.
Die Substitution T ist in zweien unter den sechs konjugierten
Diedergruppen @2-io enthalten**). Es werden also zwei Formen g durch T in
sich transformiert, und die übrigen vier werden, da alle g hei T^ = — 1
in sich selbst übergehen, durch Ausübung von T zu Paaren ausgetauscht.
Damit ist wieder eine gerade Permutation aller sechs g gegeben. Wir
notieren sogleich den Satz: Die Monodromiegruppe der Besolvente sechsten
Grades hesteht aus 60, den IJcosaedersubstitutionen entsprechenden „geraden^
Permutationen der sechs Wurzeln.
Hiernach ist das Differenzenprodukt:
(1) P,(^„ z,) = n iß^-ga)- n i-9r-9.')
u = 0 r<r'
der sechs Wurzeln (4) und (5) S. 70 der Resolvente (7) S. 70 eine
Invariante der Ikosaedergruppe, und zwar eine solche 60^^^^* Grades. Diese
Invariante hat den Faktor i^(^j, ^2)) ^^^ ^^ nach Abtrennung desselben
ein invarianter Faktor SO^*^"^ Grades übrig bleibt, so ist sie, abgesehen
von einem konstanten Faktor, gleich dem Quadrat der Grundform ^.
Es hat nämlich die Resolvente für i^ = 0 zwei Doppelwurzeln, was man
am leichtesten an der Gleichung (9) S. 70 sieht, die für Z = 1 die
Gestalt:
(a^^ G —1)2 ((j2 _ 2 (j + 0) = 0
annimmt j). Den konstanten Faktor bestimmt man wie üblich durch
Eintragung der Werte z^= 1, 3^==: 0. Das DifferensenproduU der sechs
*) Über den allgemeinen Begriff der „Jacobischen Gleichungen" und
insbesondere über diejenigen vom sechsten Grade vgl. „Ikos.", S. 148ff. und 223ff.
**) In der nicht-homogenen Ikosaeder-@60 sind 15 konjugierte Substitutionen
der Periode 2 enthalten, die sechs Dieder-@io enthalten aber im ganzen 30
solche Substitutionen, so daß jede derselben in der Tat in zwei Diedergruppen
auftritt.
t) Wegen der Beziehung (8) S. 70 hat dann auch die Gleichung (7) daselbst
fur 1^ =: 0 zwei Boppelwurzeln.
Differenzenprodukte fur die Resolventen sechsten Grades. 73
Wurzeln der Besolvente (7) S. 70 ist dt= Invßriante der IJcQsaedergruppe
', durch:
(2) Pg{z,,z,)== -2oV5^^(5„..,)^
woraus man mit Hilfe der IJcosaedergleichun9 (4) S. 06 als Differemen-
produJd der Wurzeln der Besolvente (9) S. 70 herechnd:
(3) Po {z) = - 12^. 25 VS'Z^ (Z - 1).
Sind g und g zwei verschiedene Wurzeln dey Gleichung (7) S. 70,
so besteht zufolge dieser Gleichung in den z^, z^ 4ie Gleichung:
9'-9"-l(i%i9' -9") = <p(9-9')
identisch. Da g' nicht mit g identisch ist, so besteht auch:
(g' + g' - 10x) (9' + 99 + 9") = g>
identisch. Die Form achten Grades (ß^-\-99'-\-9"^) verschwindet also
nur in Mittelpunkten von Ikosaederflächen. Xun Jiat man:
9^ — 9'^ = (9- 9) (9^ + 99 ^ 9'^)
und findet hieraus für das Differ enzenprodukt der sechs Kuben der
Formen g:
n i9'^-9td n i9i - 9i) = -p, • n ^"+99 + 9'%
WO rechts das dem links stehenden Produkt gleich gebildete Produlfvt
der 1 o Faktoren {ff^ -\- 99 -\- 9^) gepieint ist. ^JsTach der vorg-ufgesandten
Überlegung ist dies Produkt, abgesehen von einem konstanten Faktor,
gleich der sechsten Potenz der Forn^ (p. Setzt man noch für Fg seinen
Wert (2) ein, so hat man den Ansatz:
(4) n (^- - 9'u) Yi {gl - 91') --=■ <^ cp' t',
u = 0 v<v'
wobei man c durch Eintragen der Werte z^ z=.-- 1, z^ = Q zu:
c = - n ^"- n (a'^-fO^'-^sys
berechnet. Die Gleichung (4) liefert nun zufolge (10) S. 70:
p.(^).^i5 ^ 25 V5"y«y.
Mit Benutzung der Ikosaedergleichu^g (4) S. 56 folgt: Das Differenzen-
produM P^ (z) der sechs Wurzeln | der Besolvente sechsten Grawes (3)
S. 69 stellt sich als rationale FunUimi von Z so dar:
(5) • P| (z) = — 12^». 25 i&Z^ (Z - 1).
Die Diskriminanten für die verschiedenen Gestalten der Resolvente
sechsten Grades sind durch die FormeLi (2), (3) und (5) unmittelbar
74 I, 3. Ikosaedergleicliung und ihre ßesolventen.
mitgegeben. Sie gehören, wie es sein muß, dem durch die Koeffizienten
der Resolvente festgelegten Körper Qit, (p, i^, i) bzw. (9^, Z) an. Die
AdjunJction der Quadratwurzel der Dishriminante läuft auch hier auf die
AdjunJction von ^6 hinam, worin wieder eins natürliche Irrationalität der
Besolvente gewonnen ist. Auch die übrigen algebraischen Folgerungen
schließen sich denen bei der Resolvente fünften Grades genau an. Die
Gäloibsche Gruppe der JResolvente sechsten Grades ist tvie die der jResol-
vente fünften Grades das Komplement des aus den Operationen 1 und V^ • U
hsstelienden Normalteüers ®^ der Galois sehen Gru/ppe ©^.eo ö!er Ikosaeder-
glekhung. In der Tat bleiben zufolge (4) und (5) S. 70 die g einzeln bei
Ausübung der Operation Y^ • TJ unverändert. Betreffs des Charakters
unserer Gleichungen sechsten Grades als Partial- bzw. Totalresolventen
der Ikosaedergleichung gelten unverändert die bei der Resolvente fünften
Grades gemachten Angaben. Erst nach Adjunktion von e haben wir in
den Gleichungen sechsten Grades Totalresolventen der Ikosaedergleichung.
Entsprechend ist die Lösung z der Ikosaedergleichung nach Adjunktion
von £ rational in den Wurzeln einer Resolvente sechsten Grades
darstellbar. Aus (5) S. 70 leitet man z. B. leicht die Gleichungen ab:
(6) ^B^^g. = 2zg^, 2^^^v= -2^-^^^,
^ = 0 v — o
die wieder durch die Operation F^ • TJ ineinander überführbar sind.
§ 8. Beziehung zwischen den beiden Resolventen fünften
und sechsten Grades.
Die untersuchten Gleichungen fünften und sechsten Grades gehören
als Partialresolventen der Ikosaedergleichung zu dem gleichen Xormal-
teiler ©g ^^^ Galois sehen Gruppe ©^.go der Ikosaedergleichung. Hieraus
ergibt sich, daß sich die einzelne Wurzel der einen unserer 'beiden jResol-
venten stets als eine rationale FunJdion der Wurzeln der anderen Besolvente
darstellen lassen muß, wobei in den Koeffizienten als einzige Irrationalität
Vo auftreten darf, die ja fur beide Besolventen eine „natürliche'- ist.
Die fragliche Darstellung z. B. der ersten Lösung | der Resolvente
sechsten Grades in den fünf Wurzeln der Resolvente fünften Grades (5)
S. 63 ist leicht angebbar. Wir entnehmen aus (3) S. 62 :
2 fVv = ~26z^zi, 2 «*V. = -25^*4,
und folgern hieraus durch Multiplikation und Benutzung von (4) und
(10) S.70:
(2^V,)-(2^*Y.) = 625.M = 6|x{^^, ^,),
wobei sich hier und in den nächsten Formeln die Summation stets auf die
Zahlen v = 0. 1, 2, 3, 4 bezieht. Durch Entwicklung der linken Seite
Zusammenhang der ßesolventen fünften und sechsten Grades. 75
der letzten Gleichung gelangt man mit Benutzung des Umstandes, daß
die beiden ersten Potenzsummen der f^ verschwindea, leicht zu dem Satze:
Die erste WurM | der Besolvente sechsten Grades stellt sich in den
Lösungen der BesoVoente fünften Grades (5) S. 63 so ßar:
wo die Indizes der Lösungen f nötigenfalls mod 5 0U reduzieren sind. Die
den Substitutionen T, S-T, S^-T, S^-T, S*-T entsprecheüden
Permutationen der f^ führen zur Darstellung der übrigen Wurzeln der
Resolvente (3) S. 69*).
Um die umgekehrte Aufgabe zu lösen, knli-pfen wir an das
Differenzenprodukt Pg der Resolvente sechsten Grades (7) S. 70 a|i. Aus der
Darstellung (2) S. 73 von Fg geht hervor, daß die viey Nullpunkte der
einzelnen der 15 konjugierten Formen (g — g') vierte^ Grades in vier
Kantenhalbierungspunkten des Ikogaeders liegen. Insbesondere liegen
die vier XuUpunkte von {g^ — ^q) auf de|- reellen ^-Achse an den Stellen:
also in den vier auf diesem Symmetriejvreis der Ikosaederfceilung (vgl.
Fig. 4, S. 46) gelegenen Kantenlialbierungspunkten. Die Form (g^o — g^)
wird dementsprechend, vom Vorzeichen abgesehen, durch die Substitutionen
T und T • U, also auch durch U in sich transformiert. Der Form {ß^ - g^)
gehört hiernach eindeutig ein Symmetriekreis, nämlich die reelle i?-Achse,
und gleichfalls eindeutig eine der 15 Substitutionen der Periode 2 an,
nämlich U, deren Drehungsachse zur Diametralebene des
Symmetriekreises senkrecht steht.
Kun gehört zu der in (7) S. 62 gegebenen ersten Wurzßl ^ der
Besolvente fünften Grades gerade die aus 1, T, U, T-TJ bestehende
Vierergruppe @^. Durch Ausübung einer in der zugehörigen Tetraeder-(§>^2
enthaltenen Substitution der Periode 3 fiifidet man von (g^ — g^ aus ^%
Formen, die den beiden anderen Sjn^imetriekreisen der Viereygruppe
entsprechen, (^r^ — g^ und (^2 — g^. Das Produkt aller drei Formen hat
demnach in den sechs Schnittpunkteii jÄier drei Sjnnmetriekreise je einen
XuUpunkt zweiter Ordnung. Genaij diege Punkte, einfach gezählt, sind
nun aber die Nullpunkte der in (1) S. 62 gegebenen Foym sechsten
Grades /(^j, ^g). Also gilt der Ansatz:
i9o. - g^) i9i - g^) {92 — 9s) == cfi^i, ^2^»''
w^o c eine Konstante ist. Indem man ^^ = 1, z^ = 0 einsetzt, folgt
c = y 5. Dieses Ergebnis kann auch durch direkte Rechnung bestätigt
werden, wenn man für die g ihre Ausdriicke (4) und (5) S. 70 einträgt.
=<)-M-an vergleiche hiermit die EntM'icklungen pon Kronecker, über die j
„Ikos.", S. 153ff. berichtet ist.
76 I, 4. Transzendente Lösnng der Ikosaedergleichnng.
Mt Benutzung von (2) S. 62 gelangt man zu dem Ergebnis: Die erste
Wurzel ^ der Besölvente fünften Grades (6) S. 61 siellt sich in den Wurzeln
der Besolvente sechsten Grades (7) S. 70 so dar:
(2) Vs" ^ Z = (^» - ^o) (^1 - 9d (^3 - 9z)-
Zur Darstellung der übrigen Wurzeln t, hat man bei unverändertem g^
die fünf Größen g^^, g^, g^, g^, g^ zyklisch zu permutieren*).
Viertes Kapitel.
Transzendente Lösung der Ikosaedergleichung.
§ 1. Einführung der Modulgruppe @.
Die bei der Teilung und Transformation der elliptischen Funktionen
auftretenden algebraischen Gleichungen haben verschiedentlich fördernd
in die Entwicklung der Algebra des vorigen Jahrhunderts eingegriffen.
Die sogenannten allgemeinen Teilungsgleichungen und der Prozeß ihrer
Lösung haben für Abel das Vorbild abgegeben bei der Entwicklung der
Lösung der späterhin nach ihm benannten Gleichungen. Die Modular-
gleichungen für Transformation eines Primzahlgrades waren für Galois
führend bei der Ausbildung seiner gruppentheoretischen Grundsätze. Die
Auflösungsmethoden der Gleichung fünften Grades durch elliptische
Funktionen, die Ende der fünfziger Jahre des vorigen Jahrhunderts durch
Hermite, Kronecker und Brioschi entwickelt wurden, knüpfen an
die Modular- und Multiplikatorgleichungen an, die bei Transformation
fünften Grades der elliptischen Funktionen auftreten, und stehen in
engstem Zusammenhang mit den Entwicklungen des vorigen Kapitels
über die Resolventen der Ikosaedergleichung. Die eigentliche Grundlage
zum Verständnis dieser Gegenstände gewinnt man in der transzendenten
Lösung der Ikosaedergleichung durch elliptische Modulfunktionen. Um
sie darzulegen, müssen wir uns uciit einigen Hauptsätzen über elliptische
Modulfimktionen bekannt machen, die wir auch für andere spätere
Untersuchungen zur Verfügung haben müssen. Wegen aller weiteren
Ausführungen ist auf die Spezialwerke (vgl. die Xote S. 24) zu verweisen '^*).
=") Mittels einer Transformation der Gestalt (2) hat bereits Hermite ans
der Modnlargleichnng sechsten Grades für die Transformation der elliptischen
Funktionen des Primzahlgrades 5 die in diesem Falle existierende Eesolvente
fünften Grades hergestellt. Vergleiche die Abhandlung „Sur la resolution de
l'eqnation dn cmqniöme degre", Compt. Eend., Bd. 46 (1859).
=•*) Vergleiche hierzu die Vorbemerkungen, die Klein in Bd. 3, S. 3 der „Ges.
Abh.** dem Wiederabdruck seiner Arbeiten über elliptische Modulfunktionen vorans-
gesandt hat.
Einführung 4er Modnlgruppe. 77
Unter o = | -f * ^ wird eine komplexe Variable verstanden*), die
einer ganssaMigen unimodularen Substitution:
(1) -■=^^. aS-ßy=l
unterworfen werden soll. Wir stellen die Sabstitutio^en (J(.) wipder
abkürzend durch das Symbol /'"' A dar uifid bedienen uns füf sie der
Bezeichnungen S, T usw. Wie S. 25 bei den damaligen nicht-hopiogepen
Substitutionen kann man auch hier eir^en gleichzeitigen Zeichenwechsel
der vier ganzzahligen Koeffizienten ohne Änderung der Substitution
vornehmen. Durch Zusammensetzung z^veier Substitutionen:
(2) s = f;;^,), s' = (;;;^;i
nach der Regel (6) S. 3 gelangt m£^n zur Substitution:
, ^a'a^-ß'y, a'ß ^ ß'd\
^•^ — [y'a^S'y, y'ß + S'SJ'
die wieder ganzzahlig und, wie man leicht feststellt, unimodular ist: pie
Gesamtheit der ganzsiahligen unimodularen Suhstitutim^en (1) Mldet eine
Gruppe @; die die Grundlage der Theoriß der elliptische^ MoßulfunUionen
Mldet und als „Modulgruppe'- heeeichnet wird.
Zwei durch eine Substitution (1) der Modulgruppe @) verbundene
Punkte ö und o' heißen bezüglich @ „ äquivalent "•. A(is (1) folgt, wenn
man co = ^ -{- i rj, co' = ^' -{- i rj' schreibt:
.o. ,, _ ocrir^ + v')-^(oc8~\'ßr)^^ßö , n
Ist demnach r} =j=: 0, so haben stets fj' und rj das gleiche Vorzeichen.
Den durch ij ^ 0 charakterisierter^ Teil der o-J^bene nennen wir die
positive (o-HaTbebene, den Bereich mit « <i 0 aber die negßtive co-Halb-
ebene. Die mit einem Punkte der einzelnen Halbebene äquivalenten
Punkte gehören dann zufolge (3) stets der gleichen B[albebene an, und
ein Punkt der reellen o-Achse kann bezüglich @ stetß nu:p wieder piit
einem reellen Punkte o äquivalent seir^. Dabei ist der Punkt oo den
reellen Punkten zuzurechnen.
Da die Invariante j = a -{- 8 von S eine g^nze Zahl ist, so ergibt
sich aus S. 26ff.: Alle Substitutionen der Modmlgrupfe (§) sind nieU-
loxodromisch, und zwar hat man für a ~\- 8 = 0 elliptische
Substitutionen der Periode 2, für j a ~f «5 =1 ßben solche der Periode 3,
fur a -\- 8\ = 2 neben der identischen Stibstitution parabolische Spob-
stitutionen und endlich für | a + d I > 2 hyperbolische. Zufolge (8) S, 25
liegen die beiden Pole einer elliptischen Substitution in zwei zur reellen
=") In der Theorie der elliptischen Punktionen ist (a der Quotient der Perioden
des elliptischen Integrals erster Gattung. Z\^ecks leichterer Bezugnahme auf die
SpezialWerke wird die Bezeichnung co hier bßibeha|,lten.
78 I, 4. Transzendente Lösung der Ikosaedergleictung.
Achse symmetrischen Punkten der o-Halbebenen, während die Pole der
parabolischen und hyperbolischen Substitutionen auf der reellen o-Achse
liegen, und zwar diejenigen der parabolischen in rationalen Punkten.
Wie die Polyedergruppen (S. 50), so kann man auch die Modul-
gnippe @ zu einer homogenen Gruppe ausgestalten. Man spaltet o in
den Quotienten a^: ög zweier homogener Variablen ca^, a^ *) und läßt
der nicht-homogenen Substitution (1) die beiden homogenen:
iöi = -f a «1 -f- /3 öo, 0.2 = ~f 7 «1 ~f ^ ß^s'
öi = — a «1 — /3 «2, 0-2 = — 7 «1 — 8 a.2
entsprechen, von denen die eine aus der anderen durch Zusammensetzung
mit der symbolisch durch — 1 zu bezeichnenden Substitution ca\ = — ca^,
0.2 = — «2 hervorgeht/ Wenn wir hier auch mit Gruppen unendlicher
Ordnung zu tun haben, so wird doch sofort folgender Satz verständlich
sein: Die beiden Substitutionen 1 und — 1 bilden einen Normälteiler der
homogenen Modulgruppe, und das zugehörige Komplement ist mit der
nichthomogenen Modulgruppe isomorph.
Während die Polyedergruppe (S. 43 ff.) mittels der
Diametralsymmetrie der ^-Kugel durch Hinzunahme von , Substitutionen zweiter
Art- erweitert wurde, ist bei der Modulgruppe @ eine andere Art der
Erweiterung am Platze. Ist cö = | — irj der zu co konjugiert komplexe
Wert, so hat der Übergang von co zu o' = — cö die Bedeutung einer
Spiegelung der «-Ebene an der imaginären Achse, wobei wieder jede der
beiden Halbebenen in sich selbst übergeführt wird. Diese Spiegelung
transformiert die einzelne Substitution
/«:
S' =
^-\y,s) v-7,
und also die nicht-homogene Modulgruppe ® in sich. Wenn wir
demnach jene Spiegelung durch U bezeichnen, so gewinnen wir durch
Zusammensetzung aller Substitutionen „erster'' Art (1) mit U ebenso viele
gam zahlige unimodulare Substitutionen ,, zweiter- Art:
(5) «' = -"^, a8-ßr^l,
fca — 0 ^'
die zusammen mit den Substitutionen (1) die „erweiterte- Modulgruppe ®
bilden:
(6) @ = @ -f ®. r.
Wie bei den erweiterten Polyedergruppen sind auch hier die
Spiegelungen unter den Substitutionen (5) wichtig. Die zweite Potenz der
Substitution (5) ist:
,^{a' — ßy)co—ß{a — d)
"^ Y(<^-S)co + {d'-ßy)'
*) Es sind in der Theorie der elliptischen Funktionen die to^,
einfach die beiden Perioden des elliptischen Integrals erster Gattung.
Homogene und erweiterte Modulgri^ppe. 79
Soll sie die identische Substitution sein, so ist hierzu die Bedingung
d = a, hinreichend und notwendig. Die in der erweiterten Modulgruppe
® enthaltenen Substitutionen zweiter Art der Periode 2 sind die folgenden:
(7)
y CO — a
die einzelne Substitution (7) steüt eine „Sjpiegelung'- von der S. 44 ff. näher
charaUerisietien Art dar und hat als „Symmefirie-'' oder „InpersiansJcreis"
den die reelle ca-Achse senkrecht schneidenden Kreis:
(8) y(|3_|_^2)_2a|-f/3 = 0, a'-ßy=l.
§ 2. Dreiecksnetz und DB der Modulgrtfppe.
Indem man in der einzelnen, etwa der positiven o-Ifalbebene die
Symmetriehalbkreise (8) aller in @ enthaltenen Spiegelungen gezeichnet
denkt, entsteht eine eigentümliche Figfir \j\ dieser B albebene, die zu
einem äußerst wertvollen Hilfsmittel für die Entwicklung der Theorie
der elliptischen Modulfunktionen geworden ist. Man kann diese Kreise
leicht in eine übersichtliche Anordnung loringen. Zimächst hat jnan fur
y = 0 unendlich viele gerade Linien:
(1) 21 = ^, ^ = 0, + 1, ± -i, X 3, • • •,
die zur reellen o-Achse senkrecht verlaufen und mit der imaginären
Achse beginnend je im Abstand -| aufeinander folgen. Ist y r^ 0, so
mag man, da ein gemeinsamer Zeichen^^echsel von a, /3, y statthaft ist,
7 >> 0 setzen. Aus (8) § 1 folgt dann als Gleichung des Synmietrie-
kreises:
und zwar haben wir hier alle positiven ganzen Zahlen y = 1, 2, 3, • ••
zuzulassen, und für das einzelne y hat p; alle positiven und negativen,
der Kongruenz:
a- = 1 (mod y)
genügenden ganzen Zahlen zu durchlaufen. Ifan hat also die Kreise des
Radius 1 um die ganzzahligen Punkte o = 0, + 1, +2, • • •, sodann iie
Kreise des Radius \ um die Punkte o == ±_\, +|, +|, •••, weiter die
Kreise des Radius | um die Punkte o = 4:|, zi 3) 2:1' ZI §> "'■> ^'^^*^
Kreise des Radius \ um die Punkte o = 4:|, 2l|) ±f) ••' ^s"^"-
Eine eingehende Untersuchung der durch die gesamten Synimetrie-
kreise der in @ enthaltenen Spiegelungen entstehende Einteilung der
positiven o-Halbebene findet man z. B. in „Ellipt. Funkt.'- I, 285 ff. Es
80 I» 4. Transzendente Losung der Ikosaedergleichung.
entsteht eine lückenlose Überspannung der gesamten co-Hdlhehene durch ein
Netz von unendlich vielen Kreisbogendreiecken mit den Win'keln -^y ~^y ^•
Die nebenstehende Fig. 8, in welcher, einige Dreiecke dieses Netzes
gezeichnet und zur Erleichterung der Anschauung abwechselnd schraffiert
Fig. 8,
sind, möge eine anschauliche Vorstellung dieses Ketzes vermitteln. Es
sind einige Werte co eingetragen, wobei q die dritte Wurzel der Einheit
^^^^^——^^ bedeutet.
Der Schlüssel zum Verständais dieser Figur ist durch den Satz
gegeben, daß die einzelne Spiegelung (7) § 1 durch irgend eine Substitution
der Gruppe @ wieder in eine Spiegelung transformiert wird, und daß
demnach das System aller Halbkreise (8) § 1 durch jede Substitution der
erweiterten Modulgruppe in sich übergeführt wird. Insbesondere wird
also durch Spiegelung oder Transformation durch reziproke Radien an
einem einzelnen der Halbkreise (8) die ganze Halbkreisfigur in sich
übergeführt. Man betrachte speziell die drei Symmetriekreise:
(3)
1 = 0, 2|+1 =0, r-f 12^ =
1,
von denen zwei parallele Gerade sind, und deren Spiegelungen durch IT,
T, S bezeichnet werden mögen:
(4) cj' = S(cj) :
5,' = T(ö) = -CJ-1,
: U{a)=-co.
Sie grenzen das in der Fig. 8 schraffierte Dreieck mit den Ecken ca = q, i
und i oo ein, das wir als das „erste Dreieck-' des ganzen Ketzes be-
Dreiecksnetz und Diskontinuitatsbereich der Modulgruppe. 81
zeichnen wollen*). Durch die Spiegelungen (4) geht das erste Dreieck
in die drei benachbarten, in Fig. 8 frei gelassenen Dreiecke über. Wir
wollen diesen Dreiecken, den Spiegelungen (4) entsprechend, die X^men
S, T und U erteilen und belegen entspi-eche^d dg,s erste Dreieck mit dem
Symbol 1 der identischen Substitution als N'amen. Pas Dreieck S, das
mit seiner Ecke des Winkels 0 an den ]?unki o == 0 der reellen o-Achse
heranreicht, geht durch die Spiegelungen an seinen drei Seiten wieder
in drei benachbarte Dreiecke über, von denen eiaes das erste Dreieck 1
ist. Die beiden anderen würde man aus dem Dreieck 1 mittels der
Substitutionen S • f7 und S-T herstellen könnea; sie mögen wieder diese
Substitutionen als Xamen bekommen. Man kann nun das ganze
Dreiecksnetz durch Fortsetzung des eingeleiteten Spiegelungsprozesses vom Dreieck 1
aus herstellen, wobei nach und nach die ganze co - Halhehene einfach und
ohne Lücke von Kreishogendreiecken überspannt wird, die sich mß ihre im
Innern der Halhehene gdegenen Ecken zu sechs hzw. vier glßU
aneinanderreihen. Der Prozeß kommt nicht zum Abschluß, vielmehr folgen gegen
die reelle «-Achse hin immer neue Dreiecke, die kleiner imd kleiner
werden.
Es besteht nun der leicht beweisbare Sat:?:: Für den Bereich der
positiven co-Halhehene ist das Dreieck 1 ein DB der erweiterten
Modulgruppe @**). Da nämlich die ganze c)-Hp,lbebene einfach und lückenlos von
Dreiecken des Xetzes überspannt ist, ^o findet jeder Punkt dieser B
albebene, als einem bestimmten Dre:|-eck angehörig, im homologen Pupkte
des Dreiecks 1 einen äquivalenten. Es können aber im Dreieck 1 keine
zwei verschiedene miteinander äquivalente punkte auftreten. JEs müßte
nämlich sonst eine von 1 verschiedene Substitution in @ geben, die das
Dreieck 1 in sich überführt. Aber diese Substitution, als eine „konforme''
Abbildung des Dreiecks 1 auf sich selbst darstellend, müßte jede der
Ecken q, i und i oo einzeln in sich transforipieren. D^s tut indessen nur
die identische Substitution 1, wie man leicht ausrechnet.
Wir haben oben die ersten beim Spiegelungsprozeß \om Dreieck 1
aus hergestellten Dreiecke desXet2;es mit denjenigen Si^bstitiitionen, durch
die sie aus dem Dreieck 1 hergestellt werden, als Xamen versehen. Dabei
war das Dreieck 1 zunächst ^'on den Dreiecke^ S, T, U umgeben, das
Dreieck S entsprechend von den Dreiecken S • S = 1, S-T, S-U. Ist
man beim Spiegelungsprozeß bis zu e|nem Dreieck des Xetzes gelangt,
das durch die Substitution erster oder zweiter Art F aus 1 entsteht, so
sind die drei mit Funmittelbar benachbarteA Dreiecke durch V-S, V-T,
F- f7 zu benennen, soweit sie nicht schon ihre Benennung gefunden haben.
*) Ein eigentliches Dreieck liegt erst bei Projektion der Figur auf die
^fü-Kugel'' vor.
**) Es wird leicht verstandlich sein, wenn hier der Begriff des DB nur auf
einen Teil der ßj-Ebene, nämlich die positne ßj-Halbebene angewandt wird.
Fr icke, Algebra. IL G
82 I, 4, Transzendente Lösung der Ikosaedergleichnng.
d. h. dem bereits hergestellten Netze angehören. Der Fortschritt zu
benachbarten Dreiecken läuft also immer nur darauf hinaus, den sym-
boKschen Produkten, die bis dahin als Namen der Dreiecke Verwendung
fanden, einen weiteren Faktor S oder T oder TJ vorzusetzen*). Alle
Dreiecke des Netzes erhalten als Namen symboKsche Produkte der
Faktoren S, T, TJ. Damit ist der Satz gewonnen: Aüe Substitutionen der
erweiterten Modulgruppe sind als symbolische ProduMe der FaJctoren S, T,
TJ darstellbar, d. h. die Modulgruppe @ ist aus den Substitutionen S, T, TJ
erzeugbar. Da hierbei die Relationen:
(5) S^ = 1, T^ = 1, fj^ = 1
zu beachten sind, so hat man nur solche symboKschen Produkte
zuzulassen, in denen niemals zwei aufeinander folgende Faktoren gleich sind.
Man wird nun bei den eben betrachteten Produkten zu einer
Substitution erster oder zweiter Art geführt, je nachdem die Anzahl der
Faktoren gerade oder ungerade ist. Fassen wir in einem Produkt mit
gerader Faktorenanzahl, das also eine Substitution V der ursprünglichen
Modulgruppe @ darstellt, die Faktoren zu Paaren zusammen, so läßt sich
V als ein symbolisches Produkt von Faktoren fj- T, ^-TJ, T • S, T- TJ,
TJ-S, S'T darstellen. Die drei ersten Substitutionen mögen durch S,
T, TJ bezeichnet werden; die drei letzten sind zu ihnen invers:
S=U-T, T=S-U, U=T-S,
(6) - - - _ - -
(S~^ = T-U, T-^=U-S, f7-i = S-T.
Aus (4) folgt:
(^) «=(J:1). ^=(roO. ^=(-::J).
so daß S parabolisch mit dem Pole oo ist, T elliptisch, von der Periode 2
mit den Polen +« und TJ elliptisch von der Periode 3 mit den Polen q
und Q^ ist:
(8) T^ = 1, U^ = 1.
Aus den drei letzten Gleichungen (6) folgt noch wegen (5):
(9) S-i.T-i-f7-i =z 1, U=S~^-T-\ U-^=U^ = T-S.
Da auch U~^ die Periode 3 hat, so besteht zwischen S und T die
Beziehung :
(10) T-S-T-S-T-S= 1.
Für die letzten vier Substitutionen (6) findet man hiernach die Dar-
(11) U=T-S-T'S, S-^= T-S'T-S-T, T-^ = T, U~-' = T'S
*) Man beachte, daß die Faktoren der symbolischen Produkte von rechts
nach links zu lesen sind.
Erzeugung und Diskontirfuitat^bereicli der Modulgruppe. 83
in S und T. Damit hat sich der Satz ergeben: Jede Substitution V der
ursprünglichen Modulgruppe @ ist als symbolisches Produkt:
(12) F = S»»!. T• Sf^r. T-S^^ ■'• T■ S"h
darstellbar, wo die m ganze positive ZaJßen sind, von dene^ die erste und
letzte auch verschwinden Tiann*); S und T sind fbiemach erzeugende Sub-
btitutionen der ursprünglichen Modulgruppe. Zufolge (7) entspricht der
Darstellung (12) die ,.KettenbruchentwicMung" der Substitution F:
(13) a)' = m^ — - --
Durch die gesamten Substitutiopen F der ursprüngliche a Modul-
gnippe @ wird das Dreieck 1 in alle schraffierten Dreiecke des Xetzes
übergeführt, das zur rechten Seite der imaginären Achse liegepde
Dreieck U aber in alle freien Dreiecke dieses ^N'etzes. Es möge nun das
Dreieck 1 mit dem benachbarten Dreieck U, wie in Fjg. 9 angegeben ist,
zu einem „ersten Dreieckspaar" zusammengefügt
werden und entsprechend jedes weitere schraffierte
Dreieck F mit seinem benachbarten Dreieck F- U,
das nicht schraffiext ist, zu einem weiteren
Dreieckspaare, dem wir den Kamen F verleihen. Das erste
Dreieckspaar, mit dem Namen 1 der identischen
Substitution belegt, geht dann di^rch die gesamten
Substitutionen der Modulgruppe @ in alle
Dreieckspaare über, die die o-Halbebene lückenlos und
einfach mit einem Xetze von Dreieckspaa:fen bedecten.
Diese Betrachtung führt uns zu deii^ Satze: Bei
Beschränkung auf die positive co - Halbebene ist ßas
in Fig. 9 dargestellte erste Dreieckspaar i ei» DB der
ursprünglichen Modulgruppe @. Jeder Pi^nkt im
Innern eines Dreieckspaares findet nämlich im homologen Punkte des
Paares 1 einen äquivalenten. Zwei Ijanenpunkte des Paares 1, die vcipschieden
sind, können aber nicht äquivalent sein, da der eine durch eine von 1
verschiedene Substitution F in einen In^enpunkt des Paares F übergeführt
wird. Allein die Raadpunkte des Paares 1 erweisen sich zu Paaren als
äquivalent. In der Tat ist der einzelne Punkt o des linken geradlinigen
Randes des Bereiches der Fig. 9 mit depi homologen Punkte c)' == ö -f 1
der rechts liegenden Randgeraden äquivalent, und ebenso ist ein Puntt o
=*) Wäre auch m^ = 0, so könnten wir die beiden aufeinanderfolgenden
Faktoren T zu T^ =:: l zusammen ziehen.
34 I, 4. Transzendente Lösung der Ikosaedergleichung.
des die Punkte q und i verbindenden Kreissegments mit dem
symmetrisch liegenden Punkte ca' = des Kreissegments zwischen*—jO^
found i äquivalent. Man woUe demnach die Randpunkte des ersten
Dreieckspaares nur insoweit dem Paare als angehörig ansehen, als sie dem in
Fig. 9 stark ausgezogenen Randstücke angehören. Dann g-enügt das
Dreieckspaar allen Anforderungen eines ©B der Modulgruppe <^ für die
positive ö-Halbebene *).
§ 3. Modulfunktion J(g>).
Wie bei einer endlichen Gruppe linearer Substitutionen können wir
auch bei der homogenen Modulgruppe @ den Begriff einer zugehörigen
Invariante bilden. Wir verstehen danmter eine homogene Funktion der
beiden Argumente e?j, Og, die unverändert bleibt, wenn wir auf co^, co^
irgend eine Substitution der homogenen Modulgruppe ausüben. Wir
nennen eine solche Invariante eine „Modulform^, falls ihre Dimension
in den Oj, ög eine von 0 verschiedene ganze Zahl ist, und insbesondere
eine ^ModtilfunMion^, wenn sie in Oj, Og von. der Dimension 0 ist und
also nur vom Quotienten a der Oj, ca^ abhängt.
Der wichtigste Zugang zur Theorie dieser Modulfunktionen und
Modulformen ist die Theorie der doppeltperiodischen oder elliptischen
Fimktionen in der von Weierstrass gegebenen Gestalt**). Man lernt
hierbei nicht nur von vornherein die Bedeutung der Modulfunktionen für
die elliptischen Funktionen kennen, sondern entnimmt umgekehrt aus der
Theorie der letzteren Funktionen wichtige analytische Darstellungen der
Modulfunktionen. Für den Zweck des vorliegenden Exkurses über
Modulfunktionen ist ein anderer Weg vorteilhafter, d«r zuerst von
Dedekind^-) eingeschlagen ist, und der späterhin von Klein ganz
allgemein für den Existenz beweis automorpher Funktionen entwickelt
wurde.
Xach den Riemann sehen Grundsätzen über die Abbildung einfach
zusammenhängender Bereiche aufeinander gibt es eine Funktion /(«), die
die Flache des ersten Dreiecks der Teilung der o-Halbebene auf die
oberhalb der reellen /-Achse gelegene positive /-Halbebene abbildet.
Eine beliebige gebrochene lineare Funktion von / mit reellen Koeffizienten
leistet die gleiche Abbildung des Dreiecks 1. Unter den cc^ so zur
Verfügung stehenden Funktionen J(co) wählen wir eine bestimmte
dadurch aus, daß wir die Festsetzung treffen:
(1) , J{q) = 0, J(i) = 1, J{i oo) == oc.
*) Entsprechend ist der bezuglich der reellen «-Achse zum ersten
Dreieckspaar symmetrische Bereich ein DB der Gnfppe @ fur die negative «w-HaWebeüe.
**) Vgl. hierzu die Darstellung in „Ellipt. Funkt." I, insbesondere S. 279 ff.
t) In dem „Schreiben an Herrn Borcbardt über die Theorie der elliptischen
Modulfunktionen-, Journ. f. Math., Bd. 83, S. 265 (1877).
Einführung der ModiilfunLtion J{ta). 85
Der Rand des Dreiecks 1 wird also in der Arit auf die reellp J-Achse
abgebildet, daß die Ecken des Dreiepks die Punkte / =:= 0, 1 und oo
liefern. An diesen Stellen hört die Abbildung auf, lvonfo|-m zu seiij,
insofern sich die Dreieckswinkel —, —. 0 auf Winkel der Größe % in der
J-Ebene übertragen.
Setzt man nun die Funktiop J {(o) über den Rand des Dreiecks 1
hinaus in eines der drei benachbarten Dreiecke fort, so gelangt m^^n zu
einem äußerst einfachen „Gesetze der Symmetrie-, das der Dedekindsehen
Betrachtung implizite zugrunde liegt, mit aller Ausführlichkeit aber in
den Arbeiten von H. A. Schwarz*) znr Benutzung kommt: Bildet eine
analytische Funktion w = f(z) eitlen Kreisbogen der s-Ebene auf ein Stück
der reellen w-Ächse ab, so tragen bei der Fortsetzung der Funldion zwei
Punkte z, die durch Inversion oder Spiegelung am Kfeisbogen ineinander
übergehen, konjugiert komplexe FunUionswerte w. Bieraus folgt sofort,
daß die in eines der mit 1 benachbarten Dreiecke fortgesetzte Funktion
/(ö) dieses Dreieck auf die negative J-Halbebene in der Art abbildet,
daß in zwei bezügKch ® äquivalenten Punkten dieser beiden Dreiecke
stets konjugiert komplexe Werte / stattfinden. Gehen wir aufs neue
über den Rand des zweiten Dreiecks in ein weiteres schraffiertes Dreieck,
so wird dieses durch /(«) wieder auf die positive /-Halbebene in der
Art abgebildet, daß äquivalente Punkte des ersten und d|-itten Dreiecks
gleiche Werte / tragen. Dieser Prozeß ist über das ganze Dreiecksnetz
hin fortsetzbar und führt zu dem für die Theorie der Modulfanktionen
grundlegenden Satze: Die Funktion J(ca) id eine im ganzen Bereich der
positiven a-Halbebene existierende eindeutige Funfäion von co, (Me in den
bezüglich @ äquivalenten PunUen gleiche Werte hßt:
(2) j-(^^) = j,<„),
\yco~rO/
und die einen einzelnen komplexen Wert im DB der Modulgrupjpe @ und
damit überhaupt im einzelnen DreiecJcspaar des Netzes nur einmal
annimmt **).
§ 4. Modulformen g^y g^ und ^»
Die Modulfunktion /(«) nimmt gegenüber der Modulgruppe ®
dieselbe Stellung ein wie die durch die Ikpsaedergleichung (5) S. 5b erklärte
Funktion Z {z) gegenüber der Ikosaedergruppe ©g^. Z war eine eindeutige
Funktion von z, die bei den 60 Substitutionen der ©g^ unverändert bleibt
und im DB der ©g^ jeden vorgeschriebenen komplexefi Wert nur eiimial
annimmt. Wie wir nun oben (S. 33 ff.) neben Z{z) die drei Grundformen
=^) Vgl. die Abhandlung „Über einige Äbbüdungsaufgaben"', Joum. f. :\iath.,
Bd. 70, S. 105 (1869). Siehe auch „IVfodulfiinkt." I, 88 ff.
*=*) Vgl. .Modulfunkt.'■ I, 113 ff. oder „EUipt- Funkt.'- [, 301 ff.
86 I, 4. Transzendente Losung der Ikosaedergleichung.
(pi^i! ^2)' ti^i! ^2); X(.^i' ■^s) ^^^ Ikosaedergruppe hatten, deren
Nullpunkte in den Ecken der bei der Ikosaederteilung der Kugel
auftretenden Dreiecke liegen, so reihen sich an /(«) drei „Modulformen-:
(1) ^2(01,03), g^ico^, co^), zl{(o^,G)^),
welche die entsprechende Stellung bei der homogenen Modulgruppe @
einnehmen.
Die natürlichste Einführung dieser Größen ist wieder die Theorie
der elliptischen Funktionen, wo g^, g^ die Invarianten und zi die JDis-
hriminante der biquadratischen „Verzweigungsform-' sind, die ein
elliptisches Gebilde algebraisch begründet, und wo insbesondere g^ und g^ als
Koeffizienten in der Weierstrass sehen Xormalgestalt des Integrals erster
Gattung auftreten ='). Indessen ist es ein für den vorliegenden Zweck
gangbarer Weg, die Modulformen (1) durch einen „Differentiationsprozeß"
direkt aus /(«) herzustellen ='*).
Ist eine beliebige Substitution von (^ durch:
(■2) '»•=^^
gegeben, so findet man durch Differentiation nach co der Gleichung:
Vy ö -+-0/
dJ(a') da' _ 1 dJ{(o') _ dJ{a)
da' da (y o -j- d)^ da da
und hieraus durch Division mit Og bei Einführung der zu (2) gehörenden
homogenen Substitution:
(3) «i = a «1 i" /3 ög, 0.2 =: 7 «1 4- d öo,
dJ{a') dj{a)
(4)
öo^ • d a
Für die hier auftretenden Nenner gilt folgende Rechnung. Aus (3) ergibt
sich zunächst durch Differentiation:
(5) da'i =z a da^-\- ß da^. da'^ = y da^-^ 8 da^-
Aus (3) und (5) folgt, daß der symbolisch durch (o, da) zu bezeichnende
zweigliedrige Differentialausdruck :
(6) (ö, da) = «1 da^ — a^ da-^ = —alda
gegenüber den Substitutionen der homogenen Gruppe ® invariant ist;
(«', da) = (o), da).
Der Gleichung (4) geben wir nach Zusatz des Faktors — 1 die Gestalt:
dj(a') dj(a)
O)
(«', da) (a, da)
*) Vgl. „EUipt. Funkt." I, 118.
*) Vgl. die ausführliche Darstellung in „EUipt. Funkt.'- I, 313ff.
Herstellung der Modulformen g^, g^, z/. g7
und haben demnach in dem hier rechts stehenden Ausdruck eine erste
Modulform der Dimension —J2 in den Oj, Og gewonnen.
Es sollen nun die Kullpunkte und Pole dieser Modulform festgestellt
werden, wobei man sich auf den DB der Gruppe @ beschränken kann.
Wegen der Winkeltreue der Abbildung können Nullpunkte oder Pole nur
in den Punkten q, i und i oo de^ DB auftreten. An dei^ beiden ersten
Stellen der o-Halbebene haben / bzw. (/— 1) Nullpunkte der Ordnung 3
und 2, also die Form (7) solche der Ordnung 2 und 1. Um das
Verhalten im Zipfel bei o = i oo des Dß festzustellen, bemerken wir, daß
dieser Zipfel des DB durch das Quadrat der Exponentialfunktion:
(8) q = e'^»"' = e~^
auf die einfach bedeckte geschlossene Urfigebifng des X^lp^iJiktes der
g^-Ebene abgebildet wird. Wir haben hier die EntwickluQgsgröße g, die
seit Jacobi in der Theorie der elliptische^ Fui^tionen apfs vielfältigste
gebraucht ist und auch weiterhin oft Verwen4ung finden wird. Da J
im Nullpunkt der g^-Ebene einen Pol erster Ordnung hat, so gilt eine
Entwicklung der Gestalt:
(9) J(Gy) = c_,q-'-^ c, + c, q^ + c, g* -f- . •..
Wir bringen die Sachlage dadurch zum Ausdri^ck, daß \^ir sagen, /(«)
habe im Zipfel des DB feei o = f oo einen Pol erster Ordnung.
Aus (9) ergibt sich nun leicht;
.-./^x dJ(co) 2%i^ ^ 9 0 1 N
(ö, dco) coi ^
Man berücksichtigt hier nur die in der Klammer stehende Entwicklung,
indem man sagt, die Modulform (7) habe im Zipfpl des DB bei fo = i oo
einen Pol erster Ordnung.
Man kann nun aus Potenzen der Modi^lforni (7) durch Division mit
geeigneten Potenzen von / und (/— 1) drei „gan^e-', d. h. polfrde
Modulformen der Dimensionen —4, — 6 tmd — 12 herstellen, von denetp die
erste einfache NuTlpunUe nur an den mit a = q, äquivalenten Stellen hat,
die zweite ebensolche nur an den mt o = i äquivalenten Stellen, wäJi/rend
die dritte je einen einfachen NuUpunM im Zipfel des DB bei ^ = i oo
und in den Spitzen der übrigen DreiecJcspaare hat In der Tat stellt man
diese Art des Verschwindens leicht an den folgenden drei Aasdrücken fest:
g,{co„ CO,) -= - sT^TZTi) [-(c^^Ta,)) '
(11)
jtH /dJ(G})\
g,ia>,, CO,) == -r 27J M^r^D ((^^j
^K, CO,) -= - ^fjT^j:.- 1)3 ^(«, dco))
88 I) 4. Transzendente Lösung der Ikosaedergleichung.
in denen wir die drei bereits unter (1) genannten Modulformen gewonnen
haben. Die numerischen Faktoren sind hinzugesetzt, damit g^, g^ und ^
unmittelbar auf die oben schon genannten, aus den algebraischen
Grundlagen der elliptischen Funktionen entspringenden Invarianten
hinauskommen. Aus (11) ergibt sich:
(12) ^ = gl-21 gl
als ein Ausdruck für zJ in g^ und g^. Andererseits folgt als Darstellung
der Modulfunktion / in den Modulformen:
(13) /:(/-!):! =^|:27^|:^,
die in dieser Gestalt genau der Ikosaedergleichung (4) S. 63 entspricht.
Faßt man die g^, g^, zJ als Formen der Argumente o^, (o^, so hat man
hier die Gleichung, die in „Modulfunkt." I, 125 als „ModulgJeichung^
eingeführt wurde. ■
Wir sind damit zu [den Formeln (12) und (14) in I, 141
zurückgeführt, wo man übrigens -ausführlich die algebraische Begründung der
g^, g^ als der rationalen Invarianten der in I, 138 unter (1) gegebenen
biquadratischen binären Form f(x, y) dargestellt findet. Jetzt ist die
Abhängigkeit der g^, g^ und ^ von den Perioden o^, Og des elliptischen
Integrals erster Gattung:
C X dy — y dx
hervorgekehrt, und es ist für unsere Zwecke vor allem wünschenswert,
daß wir wenigstens eine analj^ische Darstellung der g^, g^ und zl in
dieser Abhängigkeit von «^ und Og kennenlernen. Wir bevorzugen
hierbei Potenzreihen nach der Jacobischen Entwicklungsgröße q, wie man
sie z. B. in „Ellipt. Funkt." I, 271 ff. ausführlich behandelt findet. Für
g^ und ^3 hat man die Reihen:
f g, («„ «,) =: (^y (^ -f 20 2] Zs W 2-').
(14)
wo ;Kfc(w) die ganzzahlige Summe der k^^ Potenzen aller Teiler von n
(unter Einschluß von 1 und n) ist. Die Anfangsglieder sind:
(15)
(g, (co„G)^)=(^j(^ + 203^ + 180g* + 560g« + 1460 q^+ --X
L / ^ /2^\V 1 ^ 2 ^'- 4 l'^OS « '^399 , \
Analytische Darstellungen der Mod|ilformen. 80
Die Reihen sind konvergent für j g | << 1, eine Bedingung, die für den
ganzen Bereich der positiven o-ü^albebene und nur für diesea zutrifft.
Für ^(öj, ög) ist am bekanntesten die Produktdarstellung:
(16) ^ (CO,, CO,) = (~j' a'(U{i-a'")
über die man „Ellipt. Funkt." I, 313 vergleichen wplle.
glieder der Potenzreihe sind:
(17)
^ (ö,, cjg) =: [~^\ {(f — 24 cf + 252 g« — L472 g« -[- • • •).
Die Anfangsglieder der Potenzreihe für /(cp) siq.d:
(18) ^(.)=;4,-.+|+!|?,.+...,
Die von H. Weber mit j (o) bezeichnete Funktion 12^-/(o) hat eine
Potenzreihe mit durchweg ganzzahligen Koeffizienten. Die ersten.
Glieder sind:
(19) j (ö) =: g-2 ^ 744 -t 19Ö 884 öV • • •-
Die Konvergenzbedingung aller dieser Reilien ist | g <C 1"^)-
Daß die g,, g^, J, J gegenüber allen Substitutionen der llodul-
gruppe @ unveränderlich sind, geht freilich aus diesen Reihendarstellu|igen
nicht unmittelbar hervor. Kur ihre Invarianz bei Ausübung der unter (7)
S. 82 gegebenen Substitution S ist sofort einleuchtend, da bereits q-
selbst diese Invarianz hat.
§ 5. Formenproblem der Alodulgruppe.
Das S. 19 ff. für irgend eine endliche Gruppe linearer Substitutionen
und S. 55 ff. insbesondere für die Ekosaedergruppp besprochene „Formen-
problem^ kann auch auf die Modulgrappe @ übert^-agen werden. Es
handelt sich dabei um die Aufgabe, aus drei heliehigen an die Bedingung (12)
S. 88 gebundenen Jcomplexen Werten g,, g^, A die zuyeMrigen ca^, co, so,
bestimmen. Man soll also einfach für ein durch seine rationalen Inyari-
anten g,, g^ gegebenes elliptisches Integral erster Gattung die Perioden
CO,, cOq bestimmen.
Die Lösung der Aufgabe setzt sich aus einem transzendenten und
einem algebraischen Teile zusammen. Der transzendente Teil besteht in
*) Betreffs der Abbildung der ßj-Halbebene auf die g^.^bene vergleiche man
Flg. 63 in „Ellipt. Funkt." I, 300. 4.us der Eigenari|; dieser Abbildung ergibt
sich eine Folgerung über die Schnelfligkeit der Konvergenz der Potenzreihen
nach q, falls to dem DB der Gruppe @ angehört, worüber d^s Nähere a. a. 0. m
der ersten Xote S. 299 gesagt ist.
90 I, 4. Transzendente Lösung der Ikosaedergleichung.
der Berechnung des Periodenquotienten a aus gegebenem Werte /*). Hierauf
kommen wir sogleich zurück. Mit o gelten dann als bekannt auch:
S,,(<i,, 1) = (2^)'(^+20 ä'+•••),
,,(«, l) = (2.)«(4-|ä>—•)•
Die Berechnung von ca^ und ca^ einzeln ist dann nur noch durch eine
I zu leisten [vgl. (6) S. 57]:
(1) . _.,^
Die Berechnung von co aus gegebenem / stützt sich auf die Tat-
12
Sache, daß die mit dem Faktor y^ multiplizierten Perioden als
Funktionen von / der hypergeometrischen Differentiälgleichimg:
d^£i /7 2\dSl i
(2) /(/-l)^ + (-/--)_ + _ß = 0
genügen *=*). Die hypergeometrische Differentialgleichung ist allgemein
integrierbar durch die „hypergeometrische Reihe'":
und die mit ihr nahe verwandte Reihe j):
F, (a, ß, z) _ ^^(- + J-Ty + 1727172
Unter den verschiedenen Darstellungen, welche sich aus dieser
Theorie für den Periodenquotienten o ergeben, notieren wir die folgende:
^.(^■-'-)
(ö) 2!jrra = —Inj-—31ttl2+ '^ ''^'
<rrrr-'7)
=") Man kann sagen, es handele sich um die Lösung der .,Modulgleichung'-,
in der wir J als gegeben und co als Unbekannte ansehen.
**) Vgl. hierzu die ausfuhrliche Darstellung in „Ellipt. Funkt." I, 323 ff.
f) Vgl. hierüber die aUgemeineu Erörterungen über die hypergeometnsche
Differentialgleichung in „Ellipt. Funkt." I, 105 ff.
Hauptkongruenzgruppe n^ei Stufe. 91
Die benutzten Reiben konvergieren für J "^ 1. Nifmnt man den
„Hauptwert" des natürKcben Logarithmus In/, so gebort die gewonnene
Lösung CO dem DB der Modulgruppe @ an. Die übrigen Lösungen geben
aus diesem co durcb die Substitutionen der Gruppe @ bervor*).
§ 6. Hauptkongrtjienzgruppe fünfter Stufe.
Zwei nicbt-bomogene Substitutionen V = [^' ^j und V = l"^,^,)
beißen modulo n kongruent, V' ^ V (mod n), fajls die Kongruenzen :
(1) a =±a, ß' ^±ß, y' ^ ±y, 8' = ±8 (mod n)
gelten, wo entweder nur die oberen oder nur die unteren Vorzpicben
zutreffen. Aus dem S. 77 angegebenen Gesetz der Zusammensetzung
zweier Substitutionen ergeben sieb leicbt die Folgerangen-. Ist Vi = F^
und Fa = Fg (mod n), so ist aucb Vi-V2^ F^ • V^ (mpd n). Ist eine der
beiden Substitutionen F, F' mit dpr identischen Substitution 1 kongruent,
so ist F' • F mit der anderen kongruent. Ist eine der Substitutionen F,
F' mit der inversen Substitution der anderen kongruent, so gilt V -V ^ 1
(mod n). Hieran schließt sich der Satz: ^lle Substitutionen 4ef nicM-
homogenen Modulgru^^e @, die mQd n mit 1 kongruent sind:
(2) a^8^±l, ß = Y~(} (mod n),
bilden einen Normalteiler der G-ruppe @. Daß sie einen Teiler bilden,
geht aus den beiden ersten der di-ei vorausgesandten Sätze heryor. Daß
dieser Teiler ein normaler ist, folgt aus den beiden letzten Sätzen. Der
Teiler wird „Haux^tJcongruenzgru^pe n*^^ Stufe- genannt und soll durch
^n bezeichnet werden**).
Die Substitutionen der einzelnen zu §„ gehörenden Xebengr^ippe
sind mod n kongruent, zwei aus verschiedenen Xebeng^-uppen entnommene
Substitutionen aber inkongruent. Reduziert man in den Substitutionen
der einzelnen Xebengruppe die Koeffizienten n^od n auf ihre kleitjisten
nicht-negativen Reste, so liefert die Xebengruppe ein Zahlenqu^druppl a,
ß, y, 8, das die Kongruenz:
(3) a8— ßf=l (mpd n)
befriedigt. Andererseits gibt es zu jeder Lösung dieser Kongruenz in
ganzen Zahlen a, ß, y, 8 aucb sicher mod n kongruente Substitutionen
in der Modulgruppe @f). Da sich die Entwicklungen in I, 275 ff. über
*) Darstellungen von co durch die ßeil^e i^(a, ß, y; z) allein, falls ' J < 1
oder jj—li<l gilt, findet man in den Formell^ (7) und (8) m „Ellipt.
Funkt.« I, 334.
="*) Vgl. hier und weiterhin „Mpdulfuiikt.'- I, 387 ff. und „Ellipt. Fupkt.«
II, 218 ff.
t) Einen Beweis hierfür findet man in „Ellipt. Funkt." II, 223. In den
weiterhin in Betracht kommenden Fallßn wird die Behauptung leicht nachträglich
eingelost werden können.
'«(/-i)-i, ^
r/if~l), Sif--
;(J2_l)^
-^)~.P
92 I, 4. Transzendente Lösung der Ikosaedergleichung.
die Komplemente der Normalteüer endKcher Gruppen ohne wesentliche
Änderung auf unendliche Gruppen übertragen, so ergibt sich der Satz:
Der Index der Haupfkongruenzgrupj^e n*^"" Stufe ah Normalteiler der
Modiügruppe und damit die Ordnung des zugehörigen Komplements ist
gleich der Anzahl inkongruenter Lösungen der Kongruenz (3), wobei zwei
Lösungen, die durch gleichzeitigen Zeichenwechsel der a, ß, y, 8 der einen
Lösung einander kongruent werden, als nicht verschieden gelten *).
Man trägt den bei der fraglichen komplementären Gruppe
vorliegenden Verhältnissen dadurch Rechnung, daß man F= ( ' ^j(mod n)
schreibt und bei der Zusammensetzung der Substitutionen die Koeffizienten
der erzeugten Substitution stets wieder mod n reduziert. Man kann auch
so verfahren, daß man mod n kongruente Substitutionen als nicht verschieden
ansieht, wobei sich die unendliche Gruppe ®, mod n reduziert, auf das
Komplement von ^^ zusammenzieht*^).
Im Falle n = 6 knüpfen wir, unter j = a -^ 8 wie S. 77 die
Invariante der einzelnen Substitution verstanden, an die Kongruenzen:
zunächst den Satz: Im Komplement der Hauptkongruenzgruppe ^^
fünfter Stufe haben die Substitutionen V die Perioden 2, 3 oder 5, je
nachdem j = 0, j = + 1 [oder j = + 2 (mod 5) ist, abgesehen davon, daß
bei j = -±^2 au^h noch die identische Substitution hinzukommt. Die Fälle
j = 0 und j = + 1 erledigen sich aus (5) sofort. Im dritten Falle zieht
man aus a -p ^ = HZ 2 leicht die Folgerung, daß F^ mit der inversen
Substitution von Y^ kongruent ist, woraus F^ = 1 folgt.
Für j =0 ist nun die Anzahl wesentlich verschiedener, d. h. durch
Zeichenwechsel der a, ß, y nicht ineinander überführbarer Lösungen
der Kongruenz:
ßy = — a^ — 1 (mod 5)
abzuzählen. Ist a = 0, so darf man ß auf die „beiden- Werte 1, 2
beschränken, wobei in beiden Fällen y = — ß~~'^ (mod 5) eindeutig
mitbestimmt ist. Ist a = 1, so ist ß auf die „vier-' Werte 1, 2, 3, 4
beschränkt und in jedem dieser vier Fälle y = — 2 ß-^ (mod 5) eindeutig
mitbestimmt. Ist endlich a = 2, so gilt ßy=ö (mod 5), so daß eine
der beiden Zahlen ß, y durch 5 teilbar ist und dann die andere
willkürlich bleibt. Dies gibt „neun-' inkongruente Zahlen paare ß, y. Da
*) Die fragliche Anzahl ist:
wo ^j, _po, _P3, ••• die .,verschiedenen'- in n aufgebenden Primzahlen sind.
="*) Weber bezeichnet die so erklärte endliche Gruppe als eine „Kongruenz-
gruppe-', eine Sprechweise, der wir m einem späteren Kapitel gelegentlich folgen
werden.
Hauptkongruenzgruppe fiipfter ßtufe. 93
die Fälle a = 3 und 4 durch Zeichenweclisel auf die scl^on abgez^hltei^
Lösungen mit a = 2 und 1 zurückkompien, so haben wir 15 inkongruente
Substitutionen mit j = 0 (mod 5). Da wir wegen des wiederholt
genannten Zeichenwechsels nur noch die beiden Möglichkeiten j = 1 unci
j = 2 (mod 5) zu verfolgen brai^chen, so gilt es npch, die Aiizahl der
Lösungen der Kongruenzen:
j=l, 8=1 — oc, —ßy^a^ — a 4-1 (mod 5)
so\\äe weiter der Kongruenzen:
j=2, 8 = 2—Di. —ßy=ia—lf (mod 5)
abzuzählen. Die Zahl a hat beide Male alle Reste 0, 1, 2, 3, 4 zu
durchlaufen. Da stets a^ — a -\- 1 ^E 0 gilt, so ist im Falle j = 1 für
jedes a die Zahl ß auf die Reste 1, 2, 3, 4 zu besch^-änken, worauf dann
y eindeutig aus:
f = — ß~~'^{a? — « -f- 1) (mod 5)
zu bestimmen ist. Also liefert j = 1 im gq,nzen 20 Lösungen. Bei j = 2
ergibt a= 1 wieder ßy=Q, also 9 Lösungen. Bei den übriger), vier
Resten a ist /3^0 und y = —/3"K«—l)^ was im ganzen 16
Lösungen liefert. Unter diesen 25 Substitutionen ist die identische
enthalten. Hiermit ist folgender Satz bewiesen: Das Kompfement det
Hauptkongruen^grußpe fünfter Stufe ^»^ ist eine Gruppe (Sg^ mit 15
Substitutionen der Periode 2, 20 Substitutionen der Periode 3, 24 Substitutionen
■der Periode 5 und der identischen Substitution.
Als Substitution der Periode 2 ist insbesondere T = ( ' j in der
<SgQ enthalten. Eine Substitution F" = ( ' 'I j, die T in sich trapsfonniert,
muß die Kongruenz befriedigen:
C:'s)■Cd)-Cd)-CA) (-^«'-
Man stellt leicht fest, daß dem im ganzen die folgenden vier Substitutionen:
- ^' U, OJ' 1-2, OJ' lo, 3J
genügen. T hat somit als Xormalisator eine ®^ vom Vierertypus, &o
daß alle 15 Substitutionen der Periode 2 konjugiert sind. Dq,bei reihen
sie sich zu fünf konjugierten Vierergrupper). zusammen. Damit steht der
Satz fest: Das Komplement der Eaupfkongruenzgruppe fünfte^ Stufe ^^
ist isomorph mit der Ihobaedergruppa ©„^ *). Es ist jet?:t aucih eii^leucl^tend.
daß man bei Reduktion der Hkfodulgruppe @ mod 5 alle 60 den 60
inkongruenten Lösungen der Kongruenz (3) S. 91 entsprechenden Sub-
*) Hieran scMieJ3en sich die Satze: Die Modulgruppe reduziert sich mod 4
auf eine mit der Oktaedergruppe isomorphe ©gl' ^^^ '^ ^^^ ^^^^ ^^^^ ^^^ Tetr3,eder-
.gruppe isomorphe ©^g ^^^ endlich mod 2 auf ßine rfiit der Dietier-©^ isomorphe
Gruppe. Vgl. darüber „"Modulfunkt.'- I, 353 ff.
94 I, 4. Transzendente Lösung der Ikosaedergleichung.
stitutionen erhält. Anderenfalls würde sich die Modulgruppe ® mod 5
auf eine Gruppe reduzieren, die mit einem echten Teiler der Ikosaeder-
Gßo isomorph wäre. Aber dieser Teiler enthielte, den Substitutionen S,
T und U von @ entsprechend, zyklische Teiler ®^, ©^ und ©g, hätte also
die Ordnung 30. Indessen gibt es in der Ikosaeder-@g(, keinen Teiler ©g^.
Durch "Übertragung der Betrachtung von I, 277 ff. finden wir einen
l-oo-deutigen Homomorphismus zwischen dem Komplement ©g^ der ^.
und der Modulgruppe ®. Dabei entspricht jedem Teiler @„ der
Ordnung fi und des Index 60-fi-^ der ©g^ ein „größter" Teiler der
Modulgruppe @ des gleichen Index 60 • fi~ ^ Dieser Teiler besteht aus allen
jenen Nebengruppen der ^^, die als Elemente der ©g^ den Teiler @„
bilden. Alle so zu gewinnenden Teiler der Modulgruppe ®, die offenbar
die Hauptkongruenzgruppe ^^ als gemeinsamen Teiler enthalten, heißen
gleichfalls „Kongruenzgruppen fünfter Stufe-'; sie sind ja sämtlich durch
Angabe von Kongruenzen, denen die Substitutionskoeffizienten genügen
sollen, erklärbar. So entspricht den fünf konjugierten Teilern ©^^ der
@gQ ein System von fünf konjugierten Kongruenzgruppen fünfter Stufe
vom Index 5, ebenso den sechs konjugierten Teilern ®^^ sechs
Kongruenzgruppen fünfter Stufe des Index 6 usw. ==).
§ 7. Modulfunktionen fünfter Stufe.
In der eben betrachteten ©g^, dem Komplement der §., ist ein
zyklischer Teiler ©^ enthalten, der aus der Substitution S= ( ' )
erzeugt wird. Ihm entspricht eine etwa durch @(i2) zu bezeichnende
Kongruenzgruppe fünfter Stufe vom Index 12, die durch die Kongruenzen:
a=d = + l; y = 0 (modo)
zu erklären ist**}. Die Überlegung von S. 78 zeigt, daß ®(i2) durch
Zusatz der Spiegelung U zu einem Teiler des Index 12:
®(12) = ®(l2)~f®(l2}-C^
der Modulgruppe ® erweiterungsfähig ist. Dieser ©(^g) gehören alle
Spiegelungen (7) S. 79 mit y = 0 (mod 5) an; denn aus (8) S. 79 folgt:
(1) a^ = 1 (mod y),
so daß u mod 5 auf die Zahlklassen ^ 1, wie zu fordern ist, beschränkt
erscheint. Unter diesen Spiegelungen treten zunächst für y = 0 alle
==) Allgemeine Angaben über das von Klein aufgestellte „Prinzip der
Stufenteilung" findet man in „Ellipt. Funkt." I, 374; es ist für die gesamte
Theorie der elliptischen Funktionen im höchsten Grade aufklärend und fordernd
gewesen. Das Werk „EUipt. Punkt." ist ganz auf dem Stufenprinzip aufgebaut
und entwickelt ausfuhrlich die Theorie der elliptischen Punktionen erster Stufe
(Weierstrass) sowie der zweiten Stufe (Jacobi).
**) Damit der Index 12 nicht als Gruppenordnung gelesen wird, ist er an
der Bezeichnung @(i2) in Klammem gesetzt.
Diskontinuitätsbereich der Hauptkcaigri;enzgruppe fünfter Stufe.
95
Geraden (1) S. 79 der Dreiecksteüung der «-Halbebene auf. Weiter hat
man y = 6, 10, 15, 20, >• • zu setzen, die der Kongruenz (1) genügendei^
ganzen Zahlen a zu bestimmen*) und für jedes Paar a, y den Halbkreis
zu zeichnen, der die reelle o-Acl^se in den beiden
Punkten unter rechtem Winkel erreicht
y
Man zeichne nun insbesondere die beiden
Halbkreise, die den Zahlenpaaren a == 1, y = 5 und
a = 9, y = 20 zugehören. Sie sind in Fig. 10
gezeichnet und bilden mit zwei Geraden des
Dreiecksnetzes den Rand eines Kreisboger|.vierecks der
Ecken 0, |, -|, i oo, in das, wie man leicht zeigt,
keiner der übrigen Symmetriehalbkreise der ®(i2)
eindringt**). Wie bei der Ges^mtgjnippe @
gelangt man demnach hier zu dem Satze: Das
Viereck der Fig. 10 stellt einen DB der @(i2) <^ß^
und säzt sich dem Index 12 entsprechend, wie die
Figur zeigt, aus zwölf Dreiecken der
ursprünglichen Teilung zusammen. Nun gilt:
)+®(
'(12)
l^,
®(12) = ®(12) -
Man wolle demnach das Viereck dei- Fig. 10 durch Anfügung seines
Spiegelbildes an der itnaginären Achse 2;u einem Doppelviereck
ausgestalten und dem letzten die vier durch die Substitiitionen S-^, S--^ zu
erzielenden äquivalenten Doppelyierecke anfügen. So entsteht der 120
DreiecJce des ursprünglichen Netzes umspannende Ißereicfi der Fig. 11 (S. 96),
in dem man einen DB der Hauptkongruenzgruppe fünfter Stufe ^^ erkennt.
Die Randkurven dieses DB sind zu Paaren bezüglich der Gruppe ^^
äquivalent. Es geht nämlich die Koke gerade Seite durch die
Substitution S^ in die rechte über. Im übrigen aber ist die 21usammen-
ordnung der Seiten durch Pfeije angedeutet; es kommen dabei die
fünf parabolischen Substitutionen der fole 0, 3; !> i 2-
/l, 0^ / 4, If 5\ / 9, + 20A
U, 1/' l±o, — 6/' l±5, — 11/
zur Geltung, femer die vier parabolischen Substitutionen der Pole -}z\r
±|--
/ 9, + q\ / 29, If 45\
l±20, —11/' l±20, —31/
*) Vgl. wegen der Anzahl inkongruenter Losungen dieser Kongruenis die
Angaben bei „DiricUet-Dedekind" (s. die Jfote ip I, 266) S. 87.
**) Man braucht natürlich nur die ^em Viereck angehörenden ßymmetrie-
kreise des gesamten Dreiecksnetzes daraufhin zu prüfen, ob sie der @(is) zu-
gehören.
96 '^I, 4. Transzendente Lösung der Ikosaedergleichung.
endlich die hyperbolische Substitution (t^' ^'^A. In der Tat gehören
alle diese Substitutionen der Hauptkongnienzgruppe fünfter Stufe ^^ an.
Wir haben nun auf folgende wichtige Eigenschaft des DB der ^^
aufmerksam zu machen: Denkt man sich diesen in Fig. 11 dargestellten
Bereich aus der to-Halbebene herausgeschnitten und sodann die aufeinander
bezogenen Randkurven durch Zusammenbiegen um die Spitzen herum bis
Fig. 11.
zum Zusammenfall gebracht, so erhält man einen geschlossenen „einfach
zusammenhängenden-' Bereich, d. h. einen Bereich vom Zusammenhang
der Kugel. Man bilde nun den DB der ^^ mittels der Funktion J(ci)
auf die J-Ebene ab. Die 60 Dreieckspaare des DB ergeben 60
übereinander liegende und miteinander verzweigte Blätter über der J-Ebene.
Denken wir dabei die Bilder je zweier einander zugeordneter Randkurven,
die Stücke der Ufer der positiven und der negativen J-Halbebene werden,
wie vorhin miteinander verklebt, so entsteht eine 60-Uättrige geschlossene
Biemann sehe Fläche über der J-Ebene, die wieder einen einfach
zusammenhängenden Bereich darstellt, also im Sinne Biemann^ das Geschlecht p = 0
hat. Diese Fläche heiße kurz Fg^.
Die mit dem DB der ^^ bezüglich dieser Gruppe äquivalenten
Bereiche von je 60 Dreieckspaaren des Netzes bedecken nun, dem
Betriff des DB entsprechend, die to-Halbebene lückenlos und einfach. Jeder
^eser Bereiche wird durch J{c3) auf die gleiche Fgo abgebildet. Es be-
steU also zwischen der Biemann sehen Mäche Fg^ und der a-Ralbebene eine
l-oo-deutige Beziehung, wobei einem PunJcte der a-Halbebene ein PunU
Herstellung von Modulfuiiktionen fünfter Stufe. 97
der Flache zugeordnet ist, einem Punlie der Fläche ßher ein System
unendlich vieler bezüglich der ^5 äquivalenter Punkte der a-Halbebene.
Auf dieser Grundlage fülirt Klein*) den Existenzbßweis der
„ModulfunUionen fünfter Stufe'-, d. h. solcher eindeutiger Funktionell
von CO, die bei den Substitutionen der §. miveräadert bleiben und im DB
der ^5 frei von wesentlich singulären P]inkten sind**), Eine solche
Funktion wird, ia Abhängigkeit von / aufgefaßt, zu einer Funktion, die
auf der Fg^ eindeutig und frei von wesentlich singulären Punkteii ist,
also eine „algebraische Funktion der Fg^" darstellt; denn sie ist ia allen
bezüglich der ^^ äquivalenten Punkten co vo^q glejcheni Weite. Umgekehrt
liefert jede algebraische Funktion der Fg^, in Abhängigkeit von co
aufgefaßt, eine eindeutige Modulfunktion fünfter Stufe; denn die
„übereinander- liegenden Blatter der Fg^, die den verschiedenen Zweigen der
Funktion entsprechen, liefern „aebeneinander'- liegende Dreieckspaare
der to-Halbebene, und dem einzelnen Pwikte der Fg^ entsprechen
bezüglich der ^5 äquivalente Punkte a. Et, werden hiernach gerade die
gesamten ModulfunMionen fünfter Stufe von allen algebraischen FanMionen
der Fgo geliefert.
Xun aber hatte die Fg^ das Greschlechi j) = 0. Auf einer solchen
Fläche gibt es 00^ sogenannte einwertige Funktionen, d. h. Funktionen,
die einen beliebig vorgeschriebenen komplexen Wert nur einmal auf der
Fläche annehmen, und sie sind ^lle linear-gebrochene Funktionen piner
einzelnen unter ihnen j). In Abhängigkeit von co bezeichnen wir eine
solche einwertige Funktion als eip-e „Maiqjtfunliion fünfter Stufe'-. Wir
wählen sogleich eine geeignete HauptfunL tion aus, die s (co) gekannt
werde, und in der alsdann jede weitere Hauptfunktion / (co) in der
Gestalt :
, a^ -r- Z>
darstellbar ist.
Es seien nun 1, F^, V.^, ••• F.g die 60 Substitutionen der
Modulgruppe @, die das Dreieckspaar l in alle 60 Paare des DB der Fig. 11
iiberführen, und die also den 60 Xebengruppen von ^^ ziigehören. Ist
V eine beliebige unter jenen Substitutionen, so gehört s' (co) = z (V(co))
als Modulfunktion zur Gruppe ^'^ = F~ ^ • §5 • V- Aber die ^^ ist ein
Xormalteiler, so daß auch s'(co) eine Mod]ilfunktion fünfter Stufe, und
zwar eine „Hauptfunktion'- ist: Also ist / in der Gestalt (2) durch ^
darstellbar: Die SauptfunTdion s (eo) erfahrt gegeri,über allen Substitutionen
von @ im ganzen nur 60, von dm 1, V^, V^, ••-, F^g bereitb gelieferte
lineare Substitutionen, die nach S 35 ff. eine Ikosaeder-®^^ bilden. Wir
*) Vgl. hierzu „Modulfunkt.'- I, 574 ff.
**) Siehe die allgemeine Begriffsbestipimung einer automorphen Funktion
„Äutom. Funkt." II, 5.
t) Vgl. hierzu auch „Ellipt. Funkt." ], 94.
Fncke, Algebra. IL 7
98 I, 4. Transzendente Lösung der Ikosaedergleicliung.
wählen die Hauptfunktion g {ci) so aus, daJ3 wir hier unmittelbar die
Normalgestalt der Ikosaeder-@g(, von S. 42 wiedergewinnen, und daß
insbesondere den beiden erzeugenden Substitutionen S und T der
Modulgruppe (S. 82) die unter (1) S. 42 genannten erzeugenden Substitutionen
der Ikosaeder-®gQ entsprechen *). bn übrigen mag dann noch der Satz
genannt werden, daß jede Modulfunktion fünfter Stufe als rationale
Funktion von z darstellbar ist, und daß umgekehrt jede solche rationale
Funktion eine Modulfunktion fünfter Stufe liefert.
Transzendente Lösung der Ikosaedergleichung und ihrer Resolventen.
Bildet man in der Hauptfunktion z{Gi) die rationale Funktion Z
ßQsten (Jrades (5) S. 56, so entsteht eine einwertige Modulfunktion erster
Stufe, d. h. eine solche, die im DB der Gruppe ® einen vorgeschriebenen
Wert nur einmal annimmt. Da Z in den Ecken des DB bei p, * und
i oo die Werte 0, 1 und oo annimmt, so ist unmittelbar Z = J(g)), so
daß zwischen J{g)) und z(c}) die Ikosaedergleichung:
(1) J:(J~1):1 = cp (z, ly : t (^, 1)^ ■- - 1728 ;k (^> ^f
besteht. Die gegebene Variable Z der IJcosaedergJeichung und ihre Wurzel z
sich also als eindeutige ModulfunJctionen von co darstellen oder es
wie man nagt, co eine ,,uniformislerende Variable^ der Ikosaeder-
Eine uniformisierende Variable der Ikosaedergleichung ist natürlich
bereits 0 selbst. Dujch die Einführung von oj als unabhängiger Variablen
gewinnt indessen die Behandlung der Ikosaedergleichung sowie weiterhin
auch ihrer Resolventen Anschluß an die ausgedehnten und bekannten
Entwicklungen der Theorie der elliptischen Funktionen und ihrer
Modulfunktionen, und es Jcönnen insbesondere die anal^ischen Darstellungen dieser
FunUionen für eine transzendente Lösung der Ikosaedergleichung und ihrer
Jßesolventen verwertet werden.
Um dies zunächst für die Ikosaedergleichung selbst näher darzulegen,
so wird man erstlich aus dem gegebenen Werte Z = J((jo) durch
hypergeometrische Reihen [vgl. die Formel (5) S. 90] das zugehörige co des
DB der Modulgruppe ® bestimmen. Damit ist dann zugleich die durch (8)
S.87 erklärte Jacobische Entwicklungsgröße ihrem Werte nach festgelegt.
Zur Lösung der Ikosaedergleichung gut es dann, eine geeignete
Darstellung von z (co) in q der Theorie der Modulfunktionen zu entnehmen.
Am nächsten liegt eine Darstellung durch die Jacobische ^^-Funktionr
19^ 25
(2) d-i{v,q) = 2 gi sin n: ^ — 2qismB xv -\- 2 qi sino^v .
*) Die Abbildung des DB der ^5 mittels dieser Hauptfunktion z (<») auf die
z-Ebene liefert dann unmittelbar die ikosaedrische Teilung der Fig. 4, S. 46.
Lösung der Ikosaedergleichung durch elliptische Funktionen. 99
Nach Klein*) gilt nämlich für s die Da:fStellung:
(3)
' ^1 (2 CJ, ö')"
2 (-l)-r»^-^'^
2 i-iYr^'^-
Aus der ersten damit gewonnenen Lösung z der Ilcosaedergleichung
ergeben sich die übrigen 59 Lösungen durch die Ikosaedersubstitutioneii.
Die Resolventen der Ikosaedergleichung sind m:|t der letzteren
natürlich zugleich als gelöst anzusehen, ijasofe:fn die Wurzeln der
Resolventen bekannte rationale Funktionen von z sind. Bemerkenswert ist
in dieser Hinsicht nur, daß K^lei^ für die Wurzel | der Resolvente
sechsten Grades (3) S. 69 auch unjuittelbar einen besonders eiijifachen
Ausdruck durch die Diskriminante zJ (fOj, a^ aufstellte *"•==) JEs gut nämUeh
(4)
wo im Zähler de^ BadiJcanden diß durch „'J'rani,formation fünften Grades-'
am ^ (öj, «a) entstehende Modulforn} fünfter Stufe steht. M^-n hs^i also
in der Resolvente eine beim fünften Grade auftretende .,
Transformationsgleichung" vor sichf).
Für die numerische Durchfiihrung der Lösung unserer Crleichungep
mittels ModuHunktionen ist die außerordentlich schnelle Konvergenz der
Potenzreüien in q, sobald o dem DB der Modulgruppe angehört, wertvoll.
Dagegen sind die hypergeometrischen Reihen, die der Berechnung von co
dienen, keineswegs schnell konvergent. Man kann überhaupt der
Heranziehung von CO als „uniformisierender Vaiiableii" den Vorwurf machen,
daß sie einen weiten Umweg bedeute. In der Tat ist ja schon z selbst
als „uniformisierende Variable-' der Ikosaedergleicliung brauchbar, und
wenn man schon analytische Hilfsmittel zulassen ^ill, so kann man z
direkt in Z mittels der hypergeometrischen Reit.e odpr def Riepiann sehen
P-Funktion darstellen ff). Gleichwojil ist der Wert der transzendenten
Entwicklungen für die Algebra sehr hoch einzusehätzen. Es kommt
ihnen eine wichtige heuristische Bedeutung zu, indem sie uns ip be-
*) Vgl. „Ges. Äbh." III, 186 oder „Modulfunkt.- II, 383.
**) Vgl. hierzu „Ges. Äbh." III, 49 und „Ellipt. Funkt.'- II, 390ff.
t) Vgl. allgemein über die bei Transformation der elliptischen Funktionen
auftretenden Gleichungen (Modular- und Multip] ikatorgleichungen) „Ellipt.
Funkt.'- n, 335ff.
tt) Vgl. „Ikos.«, S.78ff.
IQO I, 5. Bringsclie Gleichung fünften Grades.
sonders zugänglicher Weise neue und wertvolle algebraische
Entwicklungen aufdecken werden. Schon das nächste Kapitel liefert hierzu
ein interessantes Beispiel.
Fünftes Kapitel.
Bring sehe Gleiehung fünften Grades.
§ 1. Einführung einer neuen unendlichen Gruppe.
Man bilde für eine komplexe Variable ^ die unimodularen
Substitutionen der beiden Typen:
mit ganzen Zahlen a, ß, y, d, die bzw. den Gleichungen genügen:
(2) 2ad — ßy=l, a8 — 2ßy=l.
Die Rechnung lehrt dann, daß zwei Substitutionen gleicher Typen zu-
sarDmengesetzt eine Substitution des zweiten Typus liefern, zwei
Substitutionen ungleicher Typen aber eine solche des ersten. Daraus ergibt
sich der Satz: Die gesamten Suhstitiitionen (1) bilden eine Gruppe
unendlicher Ordnung, in der die SuhsÜtutimien des zweiten Typus einen
Normdlteiler des Index 2 liefern. Die G-ruppe werde wieder durch ®
bezeichnet; liegt eine Verwechslung mit der Modulgruppe nahe, so werde
sie durch ®(^) und die Modulgruppe ihr gegenüber durch ©(">) bezeichnet.
Soll eine Substitution (1) elliptisch sein, so muß ihre Invariante
j = (a -j- ö) \2 bzw. j = a -\- 8 absolut <[ 2 sein. Substitutionen mit
j = 0 kommen bei beiden Typen (1) vor. Soll \j\ = 1 sein, so würde
der zweite Typus vorliegen, und es müßte eine der Zahlen u, 8 gerade
sein, was der zweiten Gleichung (2) widerstreitet. Dagegen treten
Substitutionen mit I j { = \2 beim ersten Typus wirklich auf: Die Gruppe
® enthält elliptische Substitutionen der Perioden 2 und 4, sowie weiter nur
parabolische tmd hyperbolische Substitutionen.
Wir verstehen unter t, die zu ^ konjugiert komplexe Zahl und
stellen fest, daß die Gruppe @ durch die Spiegelung ^' = — ^ an der
imaginären ^-Achse zu einer Gruppe @ erweitert werden kann, in der @
ein Iformalteiler des Index 2 ist*). Die in dieser Gruppe @ enthaltenen
Spiegelungen:
(3) t = ^^iLlI r ^ dul^
yt-ui2' yf2l~a
*) Man vergleiche die entsprechende Überlegung bei der ilodulgruppe S. 78.
Xetz der Dreiecke mit den Winkehi jr/4, 7r/2, 0. 1()1
haben die Symmetriekreise der Gleichungen;
(4) rCr +f)-2V2c«| + ^ = 0, 2a'-ßy=l,
(5) y(t'+n')- i2a^-rß = 0, a'^-2ßy=l.
Xur im Falle (5) treten Gerade auf, nämlich für a = 1, y ■.= 0
(6) y2|=-^, ß = 0, ±1, ±2, .-..
Im übrigen haben wir nur eigentliche Kreise:
Wir entnehmen nun den Ansätzen (6) \ir\.d (7) die beiden Geraden
und den Kreis:
(9) I = 0, V21 -1 == 0, r - >j^- = 1,
l ^
die das in Fig. 12 mit den Ecken t = = , i und ioo verseherfie
V2
schraffierte Dreieck eingrenzen. De;- Kreis (8) mit a -= — 1. y = 1
läuft gerade noch durch die Epke =.— dieses
Dreiecks hindurch, ebenso der zua= — 1. y = 1
gehörende Kreis (7). Aber keinem de^ übrigen
Kreise (7), (8) hat einen Punit mit dem Dreieck
gemein. Übt man nun auf dies Kreisbogendreieck
der Winkel —, —, 0 als „erstes Dreieck- ienT^xozeQ \/
4 2 \J
fortgesetzter Spiegelung aus, der ^ns pben zum
Dreiecksnetz der Modulgruppe ®H führte, so ergibt
sich eine lückenlose und einfache Ißedeckung der
^-Halbebene mit Kreisbogendreiecken de;- Winkel
—, —, 0. Es gilt dann wieder der Satz: E^n einzelnes DreiecJ:, z. B-
das m Ficr. 12 diirch die EcJcen f=^, i, l oo bestimmte, ist ei\i DB
V2
der Gruppe ®(^),- das aus diesem Dräech und seinem Spiegelbild be-
Miglioh der imaginären Achse bestehende Breiedcspaar aber liefert ein&t
DB der ursprünglichen Gruppe @>(-), i4;obä etwa wieder die auf der i echten
Seite der imaginären Achse gelegenen BandpunUe alt, nicht dev^i
Breieckspaar angehörig angesehen werden sollen.
Der Beweis gestaltet sich genau so wie bei der Modiilgruppe. Jeder
Punkt der positiven ^-Halbebene, auf die wir uns hier wieder beschränken.
102
I, 5. Bring sehe Gleichung fünften Grades.
hat einen homologen im ersten Dreieck der Fig. 12, der also bezüglich
der ® mit ihm äquivalent ist. Gäbe es innerhalb dieses Dreiecks aber
zwei verschiedene bezüglich ® äquivalente Punkte, so würde die diese
Äquivalenz vermittelnde Substitution, die doch das von den Kreisen (6),
(7) und (8) gelieferte Dreiecksnetz in sich transformiert, insbesondere
das erste Dreieck der Fig. 12 in sich transformieren. Sie hätte also die
drei Ecken zu Polen und wäre also die Substitution 1. Der Übergang
zum DB der ursprünglichen Gruppe @(Ö vollzieht sich gleichfalls wie bei
der Modulgruppe. Wir notieren noch den Satz: Die Gruppe @(^) ist er-
zeughar aus den leiden Substitutionen:
(10) r = ^ + y2. ^' = ^-
Transformiert man die Substitutionen (1) der Gruppe @(^) auf die
Variable:
(11) « = ^y2,
so nehmen sie die Gestalt an:
(12)
V2
-8f2
J^CJ + (
Die Substitutionen (1) des zweiten Typus, die in @(^ einen Xormal-
teiler des Index 2 bilden, gehören in der neuen Gestalt zugleich der
Modulgruppe ©H an, wo sie, wenn wir zur Schreibweise (1) S. 77 der
®^'") zurückgehen, die durch /3 = 0 (mod 2) erklärte Kongruenzgruppe
zweiter Stufe vom Index 3 bilden. Haben zwei
unendliche Substitutionsgruppen einen
gemeinsamen Teiler, der in jeder der beiden Gruppen
endKchen Index hat, so heißen jene beiden
Gruppen miteinander „Jcommensurahel'-. Es
besteht somit der Satz: Die mittels der Glei-
clmng (11) auf co transformierte Gruppe ©(^^ ist
mit der Modulgruppe @H kommensurabel; der
gemeinsame Teiler hat in der ©(^^ den Index 2
__ und in der ©('") den Index 3. Der DB des
gemeinsamen Teilers ist in Fig. 13 dargestellt:
er besteht aus vier Dreiecken der Gruppe @Ö, die in der Figur stark
umrandet sind, und aus sechs durch Schraffierung hervorgehobenen
Dreiecken der ©('"). Die Randkurven dieses Bereiches sind zu Paaren äqui
valent; die bezügKchen Substitutionen sind:
(13)
■- CO -\- 2, CO
-CJ+ 1'
aus denen der gemeinsame Teiler der beiden Gruppen erzeugbar ist. Wir
halten für die Gruppe @(^) an dieser Bezeichnung fest, auch wenn sie
Kommensurabihtat der beiden Gruppei\ ®^'^ und ®^'"\ 103
auf OJ transformiert ist. Den in co da^-gestellten Durchschnitt beider
Gruppen @0 und ©('") nennen wir T> (@(^), ©M) ode|- kufz S). Aus
dem Normalteiler S) von @^^) eitsteht diese letztere Gruppe wieder durch
Zusatz der ersten Substitution (12) rpit a = 8 = Q, ß = — 1, y = 1-
§ 2. Funktionen der Gruppe @^-->.
Zur Bildung von Funktionen der Gruppe @^^ knüpfen wir an dje
Modulform erster Stufe — 12*«' Dimension ^ (co-^, co^) an, die im Innern
der ö-Halbebene überall endlich und von 0 verschieden ist, ur|.d schreiben
zur Abkürzung:
(1) ^ K, CO,) = zi, zl (^, CO, Vä) = J'.
Die zweite dieser beiden Funktionen bleibt zwar nicht bei der gesamten
Modulgruppe ©('") invariant, wohl aber gegenüber den Substitutionen des
Durchschnitts 3), d. h. der durqh ß = 0 (mod 2) erklä?:ten
Kongruenzgruppe zweiter Stufe, wie aus:
= ^("^ + f-»V2, ■2,^-...,V2) = 4(^, .J2)
hervorgeht. Somit ist der Quotient:
eine Funktion von co allein, die zur Gruppe 3) gehört und im DB der
Fig. 13 abgesehen von den beiden Spitzen bei o = * cx5 und co rrz 0
allenthalben endlich und von 0 verschieden ist. Aus (17) S. 89 folgt »un:
^' = ^ {^y {a - 24 g^ -r 252 g^ - • • •).
so daß man für 64 Q (o) als Anfangsglied der Reihenentwicklung:
64^(a») = T'^---
findet. Q {co) hat demnach in der Spitze a» = « c« des Dß der Gruppe X
einen Pol erster Ordnung und m^ß bei et) = 0 einen XuUpunkt dieser
Ordnung im DB aufweisen, so daß in Q (to) eine einwertige Funktion der
Gruppe S) vorliegt.
Durch die Substitution:
<3) «;=-V2«„ «^ = :^'
104 I' 5. BriAgsclie Gleichung fünften Grades.
die den Durchschnitt D zur Gesamtgruppe ®(f> ergänzt, wird die
Funktion Q (ca) zufolge (2) in ihren reziproken Wert transformiert. Somit ist:
eine einwertige Funktion der ©(-), die ihren Pol erster Ordnung im
Zipfel ö = ^ oo des DB hat. Im Pole co =^ i \2 der nicht-homogen
geschriebenen Substitution (3) kann man Oj = ^ V2, Og = 1 setzen und
findet ■ aus (2) mit Rücksicht auf die Dimension — 12 der Modulform
erster Stufe ^(«i, ca^) leicht Q{i'^2) = 1. Durch diese Substitution
werden auch die beiden Eckpunkte:
+ 1 + ^
(5) a> = :rl + l, ^ = =Sf=--
des DB der ©(^^ ineinander transformiert, die aber auch bezügKch D
äquivalent sind. Somit liegt in diesen Ecken ein und derselbe Wert
Q (co) vor, der zugleich seinem reziproken Werte gleich ist. Da ^ = 1
nicht mehr in Betracht kommt, so gilt:
Q{l-^i) = Q{~l + i)= -1.
Wir setzen demnach:
und merken den Satz an: Die FimUion K(ca) nimmt in den Eclcen
(+; 1-{-^), i\2 und ioo des in der co-JSälhehene gezeichneten DB der
Gruppe @^ö die Werte 0, 1 und oo an und Mdet diesen DB in der Art
eindeutig auf die K-Ebene ab, daß das in Fig. 12 schraffierte Dreiedc der
— 1+i
Ecken ——, i, i oo die positive K-Halhehene liefert und das- nicht-
schraffierte die negative. Die Anfangsglieder der Reihenentwicklung dieser
Funktion K (o) sind gegeben durch:
(7) 256Jr(c)) = g-i + 104 + 4372 3 + 96 256^2 ^ .
Mittels des oben (S. 86 ff.) bei der Modulgruppe @H angewandten
Differentiationsprozesses gelingt es, auch für die Gruppe (S(^) drei
„Formen^ herzustellen, die den Grundformen (p, i^, ^ der Ikosaedergruppe
und den drei Modulformen g^, g^, zl entsprechen und wie diese Formen
je nur in einem System äquivalenter Punkte einfache Nullpunkte
aufweisen. Diese „Grundformeu" der Gruppe @(-) sind, in Abhängigkeit von
öj, «2 geschrieben:
}^K(K—l)\{(o,d(o)
(8)
yJK {K — 1) V(cj,
T. r \ , ^* { dK \^
Funktionen und Formen der Gruppe @^-^-
und sie hesit^en die folgenden JR^henentwicklungen:
(9)
h, K, «,) = (^)\l + 24g ^ 24g^ 4- 96 9^ + ■■'),
- 2240 q^ + .
h^ K, CJg) = (—) (1 — 80 q — 400 q^
\ K, CO,) = (^y (2- 82^ + 12,f + 64ä* + •.-)■
Das Symbol (o, ö!«) bedeutet den durch (6) S. 86 gegebenen zweigliedrigen
dK
Differentialausdnick. Der Differentialquotient hat nä,mlich einen
(co, dco)
Nullpunkt dritter Ordnung im Punkte (— 1 + «) und einen solchen
erster Ordnung im Punkte co = i\2. Der Zusatz des Xenners ^ K(I\: — 1)
hat zur Folge, daß \ (Oj, a^) einen Xullpiinkt erster Ordnung im Punkte
CO = — 1 -f- * ^^^ damit in allen äquivalenten Punkten hat, während die^e
Form im Punkte co = i^2 endlich und von 0 verschieden ist. Ebenso
findet man, daß h^icOj^, co^) je einen Xullpunit erster Ordnung in dea
mit CO = i\2 äquivalenten Punkten hat, wäh^-end h^(co^, co^) im Zipfel
des DB bei a = i oo einen XuUpunkt erster Ordnun» hat. Als l)arstellung
von JST in den Formen (8) findet man:
(10 JT: (Ä" — 1) : 1 = J4 : hl : 256 \,
eine Gleichung, die sich der „Mo4ulgleichung- (13) S 88 genau anscjiließl.
Gegenüber der Substitution o' = o + 2 sind die drei Forpien h
zufolge (9) invariant. Bei Ausübung de^^ Substitution (3) ist zwar h^
invariant, dagegen erfahren h^ und \ eptweder beide ZeicJienwechseL
oder beide sind gleichfalls invariant, da bei ihrer Definition die Qu^,drat-
wurzel \ K(K— 1) verwendet wurde. Um hierüber zu entscheiden, setze
man in:
(—12 «2, ^j = ± \ (to, . Qs)
y2
öj = « y 2, «2 = 1 ein, für welches Argupaentj^aar h^ nicht verschwindet:
\ (— y"2, i) = 2Z \ (« V^, !)•
Da \ die Dimension — 2 in co^, co^ hat, so folgt:
\ (— y2, i) = ±\ (i Y2, — i ■ 0 == - (—«T h (- V^,«).
so daß das untere Zeichen gilt: G-egenüher der Substitution o' = c? -f 2
sind alle drei Formen h invariant; gegenüber der Substitution (3) erfahren h^
und h^ Zeichenwechsel, während h^ invariant ist.
Zur Hauptkongruenzgruppe zweiter Stufe gehört als ., Hauptfunktion ^
der Legendre-Jacobische Integralmodul h-{co), worüber man etwa
„Ellipt. Funkt.-' I, 433 vergleichen wolle. Bei Ausübung der zweiten
Substitution (13) S. 102 wird F {co) in seinen reziprokeifi Wert transformiert,
106 I, 5. Bringsche Gleichung fünften Grades.
so daß (Jc^ (ö) + Ä-2 (ö)) als einwertige Funktion zu der oben mit 3)
bezeichneten Gruppe gehört und also mit der oben bereits ausgewählten
einwertigen Funktion Q (o) linear zusammenhängt. Nun hat man als
zusammengehörige Werte *):
Q{i oo) = oo, P(ioo) = 0,
^ (- 1 + i) = - 1, ^2 (- 1 + i) = - 1,
^(0) = 0, JcHO)=l.
Hieraus folgt für die lineare Beziehung zwischen Q und (k^-{-k~^):
wo Ä;'^ = 1 — F der „komplementäre Integralmodul" ist. Mit Benutzung
von (6) findet man den Satz: Die HauptfunUion K(a) der Gruppe @(^
hängt mit dem Integralmodul h^(ca) durch die Gleichung zusammen:
Der Kommensurabilität der Gruppen @(^) und ©('") entspricht eine
algebraische Beziehung zwischen Kia) und /(«), die leicht aufstellbar ist.
Wir setzen die Gleichung (6) zunächst in die Gestalt:
(13) ^:(^—1):1 = (^ + 1)2:(^_1)2.4^.
Sie bringt zum Ausdruck, daß im DB der Fig. 13 die beiden Stellen mit
JST = 0 bei Q = — 1 zusammenfallen, ebenso die beiden Stellen mit
JST = 1 bei ^ = 1, während die beiden Pole von JST in den Zipfeln
o = i oo und 0=0 des DB liegen, wo ^ = oo und ^ = 0 gilt.
Die Funktion / ihrerseits ist als rationale Funktion dritten Grades von
Q darstellbar, und aus der Werteverteilung von /in den durch Schraffierung
hervorgehobenen Dreiecken der Fig. 13 liest man den Ansatz ab:
(14) /:(/-l):l = {Q + af:{Q + 1){Q -^yf -.cQ.
Im Zipfel a = i oo gilt demnach angenähert cJ= Q^, und da:
12^J=q~^-] , 43 ^ = ^-1^
die Anfangsglieder der Reihenentwicklungen sind, so folgt 64c = 27.
Man wird demnach den Ansatz (14) besser in die Gestalt kleiden:
/:(/__ 1):1 ^ (4:Q-^d)^:{Q-^l)(8QJref:2lQ,
wobei d und e reell sein müssen, da Q auf dem Rande des DB und auf
der imaginären «-Achse reell ist. Es muß nun die Gleichung:
(4Q + d)^-27Q = (Q+1)(8Q + ef
*) Vgl. hier und weiterhin „EUipt. Funkt." I, 440 ff. und II, 516 ff. Die
Funktion ¥^{01) trägt dort auch die Bezeichnung X{to), und statt K{o}) ist L{ta)
geschrieben.
Algebraische Beziehung zwischen den Ffinktipnen J'{co) und K{co), 107
in Q identisch bestehen. Man trage Q = — 1 ein und findet:
{d — 4)3 = — 33 und also d == 1,
woraus dann weiter sofort e = — 1 folgt. Die Darstellung von / in""^
ist somit:
(15) /:(/-l):l = {AQ -^ ly -.{Q -\- 1){S Q -Vf -.2,1 Q.
Zu einem gegebenen Werte ^gehören nun zwei Werte Q ]ind Q' =: Q''^,
und also zwei Werte / und /', die zfifolge (15) durch:
ri6^ j = (^ ^ + ^)' r ^ ('^Q' + ^y ^ iQ±_^
^ ^ 27 Q ' 27 Q' 27 Q'^
gegeben sind. Die beiden symmetrischen Funktionell (J -{-J') und J-J'
rechnet man mit Hilfe der Gleichung:
Q -^-[ = 4:K -2
leicht in rationale Funktionen von K um. Die Relq,tion zwischen / und
K ist die in J quadratische Gleiphung mit den beiden in (16) gegebenen
Wurzeln / und /'. Daraus ergibt sich leicht der Satz: Die zwischen J
und K bestehende algebraische Beziehung ist:
(17) 729 /2 _ 54/(512 K^ — 414 K -f 27) -f (16 K -f- 9)^ = 0.
§ 3. Hauptkongruenzgruppe fünfter Stuf^.
Zwei Substitutionen (1) S. 100 von gleichem Typus heißen rpiod 5
einander kongruent, wenn ihre Zahlen a, ß, y, d and a, ß', y', 8' die
Kongruenzen:
a=2ia, ß' = ±ß, y' = z:y^ 8'-=:^^ (modo)
befriedigen, wo entweder nur dje oberen oder nur die (interen Zeichen
gelten sollen. Heißen die Substitutionen V ]ind V. so soll ihre Kongruenz
wieder durch V = V (mod 5) bezeichnet werden. Wie S. 91 bei der
Modulgruppe @('"^, so folgert man auch für die QK^) ajis dem Gesetz
der Zusammensetzung der Substitutionen die Sätze: Ist Vi = V, und
F2 = Fg (mod 5), so gilt auch Vi -V^^V^-V^ (mod 5). Ist eine der beide^
Substitutionen V, V mit der identischen Substitution 1 kongruent, sq
ist V. V mit der anderen kongruent. Ist eine der Substitutionen V, V^
mit der inversen Substitution der anderen kongruent, so gilt F'. F= 1
(mod 5). Genau wie S. 91 entnimmt man hieraus den Satz: Alle Substitutionen
der ®^^K die mod 5 mit der identischen Substitution 1 kongruent sind und
also dem zweiten Typus (1) S. 106 angehören, bilden einen Normalteüer der
@(S), der „Hüuptkongruen0gruppe fünfter Stufe- genannt und durch ^O
oder kurz ^^ bezeichnet werden soll.
Zu der zugehörigen komplementären Gruppe gelangen wir, wenn
wir einander mod 5 kongruente Substitut:|onen der ®(') als nicht ver-
IQQ I, 5. Bring sehe Gleichung fünften Grades.
schieden ansehen. Für die Substitutionen dieses Komplements bedienen
wir uns dann wieder der Schreibweise durch Kongruenzen:
wo 2u8 — ßy =^ bzw. Cid — 2 ßy = 1 (mod 5) gilt. Im Komplement
bilden die Substitutionen des zweiten Typus für sich einen Teiler, der
zunächst näher betrachtet werden soll. Für die niedersten Potenzen einer
einzelnen solchen Substitution findet man:
(2\v^h^^ ^2^/«i-i,,^iy2\ -p.3^A(/-i)-i'^(/-i)V2\
unter j z=z a -\- 8 die Invariante von V verstanden. Man darf sich auf
die Betrachtung der Fälle j = 0, 1 und 2 (mod 5) beschränken, da ein
gleichzeitiger Zeichenwechsel der vier Koeffizienten statthaft ist. Aus (2)
liest man nun ohne Mühe ab, daß V die Periode 2, 3 oder 5 hat, je
nachdem j = 0, 1 oder 2 ist; nur gehört natürlich auch hier zu j = 2 die
identische Substitution. Insbesondere zeigt man für j = 2 leicht V^ = V"^,
woraus F° = 1 folgt. Die Anzahl der Lösungen der Kongruenz:
(3) a8—2ßy=l (mod 5)
zählt man in den drei Fällen j = 0, 1 und 2 leicht ab. Indem wir
2 ß = ß' schreiben, kommen wir sofort auf die 60 inkongruenten Lösungen
der Kongruenz (3) S. 91 zurück, die wir S. 92ff. abzählten. Der aus den
Substitutionen des zweiten Typus bestehende Teiler des Komplements
der Gruppe ^W ist also wieder mit der Ikosaeder-^g^ isomorph*).
Für eine Substitution des ersten Typus (1) S. 100 notieren wdr, unter
j = (a -|- d) \2 die Invariante verstanden:
Dabei können wir j auf die drei Werte 0, ]^2 und 2 ^2 beschranken. Man
findet: V hat die Periode 2, 4 oder 6, je nachdem j = 0, ]'2 oder 2 \'2
zutrifft. Im ersten Falle ist nämlich V^ = 1, im zw^eiten und dritten
Falle hat die Substitution des zweiten Typus F^ die Invariante:
j' = (ci^8)]l2j-2=f--2,
so daß j' = 0 bzw. = 1 (mod 5) gilt. V^ hat also die Periode 2 bzw. 3,
so daß V die Periode -i bzw. 6 hat, da eine ungerade Periode bei V aus-
*) Dem Zweifel, ob sich der aus den Substitutionen des zweiten Typus
bestehende Teiler der &(.-) modo nicht vielleicht auf einen .lechten" Teiler der
Ikosaeder-@60 reduziert, begegnet man durch Angabe der drei Substitutionen
/ 1, V2 \ /3, 2 \l2\ /l, ]l2\
\_\f^ W' I9 1/^ qj' In )' ^^^ ^^ ^^^ ®^"^ auftreten und mod 5 reduziert
Substitutionen der Perioden 2, 3 und 5 liefern. Jener Teiler hatte also eine durch
30 teilbare Ordnung und ist demnach die ©g^ selbst.
Hauptkongruenzgruppe fünfter Stufe in (ier Gruppe @^'\ 109
geschlossen ist. Um die Anzahlen dieser Substitutionen der Perioden 3,
4 und 6 abzuzahlen, hat man die Anzahlen der zugehörigen Lösungen
der Kongruenz :
(5) 2a8 — ßy=l (mod 5)
festzustellen. Ist erstlich j = 0 und also § = — a, so hat ma^ •
— ßy = 2a^ ^ 1 (mod 5)
zu lösen. Für a = 0 hat man zwei, für p« = 1 und a = 2 je vier verschiedene
Lösungen, so daß man zehn Substitutionen der Periode 2 findet. Für
j -=:r y2 und also 8=1 — a ist die Kong|?uenz:
— ßy^2a^ — 2a-^l (mä 5)
zu lösen. Für a = 2 und a = 4 findet man je neun, für die übrigep. drei
Zahlen a je vier wesentlich verschiedene Lösungen: also ergeben sich
30 Substitutionen der Periode 4. Endlich führt j = 2 \2, also 8 = 2 — a
zur Kongruenz:
— ßy =2a- — 4ta -\- l (mod 5).
Da rechts für kein, a eine durch 5 teilb£(.re Zahl steht, hat man beim
einzelnen a je vier Zahlenpaare ß, y, so daß 20 Substitutionen der
Periode 6 vorliegen.
Diese Anzahlen stimmen genau überein mit den in I, 344 ff.
festgestellten Anzahlen ungerader Permutationen der Perioden 2, 4 und 6 vor|.
fünf Dingen. In der Tat besteht der Satz: Das Komplement der Haupt-
Tiongruenzgruppe fünfter Stufe ^^p id eine G-rujjpe (§^20 ^^^ Ordnung 120,
die isomorph mit der bymmetrischen Permuta(;lonsgnippe det, fünften Gtradcb
ist. Die bereits im Kormalteiler (Sg^ enthaltenen Teiler ©^g vom
Tetraedertypus bilden nämlich auch in der (§^20 ^^ System von fünf konjugierten
Teilern ®^^, deren Durchschnitt nur aus der identischen Substitution 1
besteht. Daraus folgt die Behauptung nach einem bekannten in I, 38q
aufgestellten Satze.
§ 4. DB der Hauptkongruenzgifuppe fünfter Stufe,
Zur Gewinnung eines DB der Gruppe ^(-) \ erfahren y^n wie S. 94ff.
bei der Gruppe ^C"*), indem \^dr zunächst die aus der Substitution
^' = ^ -j- V2 zu erzeugende zyklische ®- innerhalb dpr @^2o heranziehen.
Ilir entspricht als Teiler der ®^^) eine Kongruenzgruppe fünfter Stufe ®(^i)
des Index 24, deren Substitutionen dem zweiten Typus angeiiören und
die Kongruenzen:
a = 8 = ^l. j^=0 (mod 5)
erfüllen. Die ®{^i) ist durch die Spiegelung D" an der imaginären ^-Achse
zu einer Gruppe (^(24) erweiterungsfähig, der insbesondere als Spiegelungen
IIQ I, 5. Bringsche Gleichung fünften Grades.
alle Substitutionen des zweiten Typus (3) S. 100 angehören, bei denen
j; = 0 (mod 5) gilt. Die der zweiten Gleichung (5) S. 101 entspringende
Kongruenz:
(1) u^=l (mod 2 /)
liefert nämlich für y = 0 (mod 5) nur Zahlen a, die = + 1 (mod 10) sind.
Man stellt nun leicht die folgenden niedersten Lösungen dieser Kongruenz
fest: u = 1 für j; =z 5, w = 9 für j; = 20, a =z 11 für j; == 20,
a = 19 für j; =3 30, « = 11 für j; = 15 und endlich w = 9 für
y = 10. Die zugehörigen Symmetriehalbkreise der betreffenden
Spiegelungen in der positiven ^-RaXhehene bezeichnen wir durch
Zusammenstellung je ihrer beiden Fnßpunkte auf der reellen ^-A.chse:
lo V!\ lil Jl\ / J_ _^\ IJ- Vi\ /VI 2V2 \ /2V2 n
\ ' 5/'\5'2y2M2V2'5V2M5V2' 3/' \ 3 ' 5 /' \ 5 '^2]'
die Spiegelungen selbst sind gegeben durch:
,,^ J dl--2p__ IU-3V2
. 5V2e-l' 20V2^-9' 20V2^-ll'
,^ 19^--6V2 .,^ lll-4y2 ^,_ 9^_4V2
'30y2i;—19' 15y2^—11' 10V2^—9"
Fügt man noch die beiden Spiegelungen ^' = — ^ und ^' = — ^ -j- y 2
mit den Symmetriegeraden der Gleichungen | = 0 und y2 | =z 1 hinzu,
so bilden diese mit den sechs genannten Halbkreisen das in Fig. 14
gezeichnete Kreisbogenachteck, in dem wir den DB der ©(24) gewoimen
haben; in der Tat stellt die Fläche dieses Achtecks, wie Fig. 14 zeigt,
einen Komplex von 24 Dreiecken des zur @(?) gehörenden Netzes dar.
Fügt man diesem Achteck sein Spiegelbild bezüglich der imaginären
^-Achse an, so entsteht ein DB der Gruppe ©(24). Dabei geht der linke
gerade Rand in den rechten durch die Substitution ^' = ^ + y2 über,
während der einzelne zur Linken von der imaginären Achse gelegene
untere Halbkreis in den ihm symmetrisch rechts gelegenen Halbkreis
durch eine Substitution der ©(2^) übergeht. Die betreffenden aus den
Spiegelungen (2) sofort zu gewinnenden Substitutionen sind:
^, ^ 9^ + 2y2 ^, _ lU + 3y2
(3)
5y2^+l' 20y2^ + 9' 20y2^ + ll'
^ 19^4-6y2 lU_+4y2 9^ + 4y2
30y2^ + 19' 15y2^+ll' 10y2^ + 9'
von denen die erste parabolisch ist, während die übrigen fünf hyperbolisch
sind. Diese Substitutionen mögen durch die Symbole F^,, Fj,---, F5
bezeichnet werden, während die Substitution ^' •= ^ -\- '^2 kurz S heiße.
Diskontmuitatsbereich der Hauptkongruenzgruppe fünfter Sipufe.
Man übe nun auf den DB der (
) die vißr Substitutionen S-^
aus und füge ihm die vier entstehenden Bereiche ß.n. Von diesen
S±2
füpf
zusammengefügten
Bereichen sind keine zwei
bezüglich der ^^p äquivalent.
Zusammengenommen liefern
sie demnach einen DB
der Hauptkongruenzgruppe
fünfter Stufe Ajö. Dabei geht
der linke gerade Rand ia den
rechten durch die
Substitution ^' — ^ + 5 "^2" über.
Aus den sechs ia (3)
gegebenen Substitutionen F^,
Fj, • • •, Fg stellt man weiter
durch Zusammensetzung mit
geeigneten Potenzen von S
die folgenden sechs ia der
Gruppe ^p enthaltenen
Substitutionen her, die, wie
zugleich mit angegeben ist,
die zwischen ^ = 0 und
t = ;^ gelegenen sechs
V2
Randkreise ia die
bezüglich ^p äquivalenten
überführen :
Fig. 14.
(4)
S2.
_ /89, 20 M / _
^~ \20y2,9/' \
S^ • F,
S-F =
/91, 25^2'
1^20^2, 11^
79, 25 1/2'
30^2, 19
41, 15^2
15 V2, 11
11, 5|/2
-lOl/^,-
U2 I) 5. Bring sehe Gleichung fünften Grades.
Die erste und letzte dieser Substitutionen sind parabolisch, die übrigen
hyperbolisch. Da die Substitution S den „Xormalteiler" ipp in sich
transformiert, so ist die Randkurvenzuordnung gegenüber S invariant.
Aus den vorstehenden Angaben ergänzt man demnach leicht die Zuordnung
der noch nicht genannten Randkurven des DB der Hauptkongruenzgruppe
fünfter Stufe.
Schon aus diesen Angaben folgen einige vorläufige Sätze über die
Funktionen der Hauptkongruenzgruppe ^p. Denken wir den DB der
§p durch die Funktion K(^y'2) auf die JST-Ebene abgebildet*) und dabei
die Bilder je zweier einander entsprechender Randkurven
zusammengeschlossen, so entsteht eine 120-hJättrige Biemannsche Fläche F^g^) ^*e
30 vlerUättrige VersweigungspunUe hei K = 0 hat, 60 sweihlättrige hei
K = l und 24 ftinfhldttrige hei K = oo und uhrigens unverzweigt ist.
Das Geschlecht dieser Fläche ist p = 4t. Die letzte Angabe folgt aus
der bekannten Gleichung *"*) :
^ V —1
(o) p= ^,n+i^ ^ ^__,
mittels der man das Geschlecht einer m-blättrigen geschlossenen Riemann-
schen Fläche mit Z Verzweigungspunkten bestimmt, in denen bzw. v^,
•j/g, • • •, Vi Blätter zusammenhängen.
Bei einer Riemann sehen Fläche eines Geschlechtes p'^'2 tritt als erste
Frage die auf, ob sie hyperelliptisch ist oder nicht. Im ersteren Falle
gestattet die Fläche eine eindeutig bestinmite Transformation der Periode 2
in sich mit {2 p -^ 2), also in unserem Falle mit zehn sich selbst
entsprechenden Punkten. Diese zehn Punkte müßten bei allen sonstigen
Transformationen der Fläche in sich nur untereinander permutiert werden.
Aber bei unserer ©^go bilden die 24 Punkte mit K = <x> das kleinste
System äquivalenter Punkte. Also id unsere Biemannsche Fläche F^oo
mcht hypereUiptisch. Nach bekannten Sätzen aus der Theorie der
algebraischen Funktionen j) hat man demnach bei Benutzung einer
geometrischen Sprechweise den folgenden Satz: Es ist möglich, unsere
Biemann sehen Flache F^go eindeutig auf eine irreduzihele Bamnkurve
sechsten Grades ahsuhilden, die der ©^go entsprechend durch 120 Eollineationen
in sich üherfuhrhar ist. Wir machen uns diese Verhältnisse dadurch
zugänglich, daß wir mit der Untersuchung der niedersten Resolventen
des „Formenproblems der ©jjo'" beginnen.
=*) Die Funktion K wnrde dnrch (6) S. 104 als solche des Arguments (o
mit der Bezeichnung K(o)) eingeführt und ist also als Funktion von ^ durch
K(^\2) zu bezeichnen.
=^*) Man vergleiche z. B. „Ellipt. Funkt.'- I, 88.
t) Vgl. hierzu die Sätze über die Kormalkurve der Funktionen y einer
Eiemannschen Flache des Geschlechtes p, wie man sie z. B. in „Modulfunkt.-' I,
545 ff. entwickelt findet.
ßiemannsche Flache F120 der Hauptkongruei^grnppe fünfter Stnfe. 113
§ 5. Bringsche Gleichung fünften Grades.
Die 15 Substitutionen der Periode 2 innerhalb des Normalteilers ©g^
•der ®j3Q ordnen sich zu je drei zusanmien und bilden so je im Verein
mit der Substitution 1 auch innerhalb der ©j^^ fünf konjugierte Vierer-
j^ruppen @^. Diese haben als Xormalisatoren fünf konjugierte ©„^ vom
Oktaedertypus =*). Den ©24 entsprechen fünf konjugierte Kongraenzgfuppen
fünfter Stufe ©(5) des Index 5 innerhalb der @(^T.
Eine der Vierergruppen besteht aus den Substitutiopen:
<^> ''--(o;:> ^-e/o> ^-r^:f)
Diese @^ wird durch folgende vier Substitutionen:
l 3 \i, _y2y' ' \i,-2]/2j
in sich transformiert. Es genügt, um dies e:|.nzusehen, die vier Kongruenzen
festzustellen: a
(3) 1' 2 1 2 3'
Irgend zwei unter den fünf Vierergruppen ©^ haben nämlich n^r die
Substitution 1 gemein. Eine @^, die eine der Substitutionen F^, Fg, Fg
enthält, ist also stets wieder die ®, der Substitutionen (1), so d^ß die
Behauptung aus den Gleichungen (3) folgt.
Ist S wie S. 110ff. die Substitution ^' = ^ -f- V^, so sind von den fünf,
den Substitutionen 1, S-^, S-^ entsprechenden Dreieckspaarep. dos
Dreiecksnetzes der ^-Halbebene keine zv^ei bezüglich der zur eben
betrachteten @^ bzw. zum ]S[ormalisator ©34 gehörenden K^ongruenzgruppe ©(5)
äquivalent, da die aus S zu erzeugende zyklische Gruppe ©^ keip.
Teiler der zur ®^ gehörenden Oktaedergruppe @24 ^^^- Einep DB
der Kongruenzgruppe ©(5) kann man entsprechend aus den füi^f Dreiecks-
paaren des Netzes, die den Substitutionen 1, S-^, S-^ zugehören, aufjbauei^..
Dieser DB ist in Fig. 15 (S. 114) dargestellt, wobei die Zuordnung der
Eandkurven sogleich in der Figur angedeutpt ist. Es handelt; sich
zunächst um die drei elliptischen Substitutionen T^, T^, T^ def Periode 2
mit den Polen ^ = «', 4; V'S -j- l, die ausführlich unter (2) gegeben sind.
*) Bei diesen ©g^ handelt es sich einfacl^ nm die funf konjugierten
Permuta tionsgruppen ©4! vierten Grades, die in der symmetrischen Grnppe @5!
auttreten (vgl. I, 336).
Fricke, Algebra. II. S
114
Bringsche Gleichung fünften Grades.
sodann um die hyperbolische Substitution T^, die unter (2) sich an letzter
Stelle findet. Endlich ist noch die in Fig. 15 nicht weiter berücksichtigte
Substitution ^' = ^ -f 5 y2 zu nennen, die den linken geradlinigen Rand
des DB in den rechten überführt. Aus Fig. 15 folgert man nun sofort
den wichtigen Satz: Der DB der ausgetvoMtm Kongruensgruppe ®(5) ergibt,
mittels der FunUion K (^ '^2) ahgeUldet, eine fünfhlätterige Biemann sehe
Fläche F5 über der K-Fhene, die hei K = 0 einen vierhlätterigen Ver-
zmeigungbpunM hedtd, hei K = 1 einen sweihlätterigen, hei K = cx> einen
fünfhlätterigen, ührigens unverzweigt id und also dab GrebChleoht j5 == Q
hesitst. Zur Bestätigung aller dieser Angaben beachte man nur, daß, wie
oben gezeigt wurde, die Tj, T^, T^, T^ die Vierergruppe @^ in sich
transformieren und also als unimodulare Substitutionen der
Kongruenzgruppe ®(5) angehören.
Eine Hauptfunktion (einwertige Funl^tion) der Gruppe i^i^) werde
durch ö (^) bezeichnet und durch die Festsetzung eindeutig bestimmt,
:i + i ±3 + .-
daß ö in den vier bezüglich (^^5) äquivalenten Punkten ~
gleich 0 werden soll, in den beiden äquivalentes
V2 f2
Punkten =^
gleich 5 und im Zipfel t, = i 00 gleich 00. Dann gilt, da 0 =r 0 im
vierblätterigen Verzweigungspunkt bei Z" = 0 stattfindet, ö = 5 bei
^ = 0 in dem daselbst isoliert verlaufenden Blatte und 0 = 00 im
fünfblätterigen Verzweigungspunkte bei JST = 00, für K als rationale
Funktion fünften Grades von 6 der Ansatz:
ö*(ö —5) = cK,
wo c eine nichtverschwindende Konstante ist. Bei JST = 1 liegt noch
ein zweiblätteriger Verzweigungspunkt. Also hat die Gleichung:
eine von 0 verschiedene Doppelwurzel, die sich aus der durch
Differentiation der letzten Gleichung folgenden Gleichung 5 ö^ (ö — 4) = 0
Hauptfunktion der Kqngruenzgruppe fünfter Stufe ©(5). 115
zu ö = 4 berechnet. Zusammenfassend haben wir also die
Werteverteilung :
(4) ' ^ '
Ö (^—-^—j := 5, ö (i OC) = OC.
Indem man K = 1 und ö = 4 in die zwischen ö upd Z" angesetzte
Gleichung einträgt, folgt c = — 256, und man gelangt :^u dem wichtigen
Ergebnis: Die algebraische Beziehung zwischen der erldärten HauptfunUion
6(t,) der Eo7igruenzgruppe ©(5) und der FanMion K laßt ■pich in die
Gredalt Meiden:
(5) Ä':(Ä"-1):1 = ö*(ö-5):(ö-4)2(öM-3ö^-i-8ö^ 16):-256.
Bei gegebenem Werte K ist somit 6 die Lösang der besonders einfach
gebauten Gleichung fünften Grades:
(6) ö° — 5 <5* -f 256 K = 0.
Xennen wir die besondere zum DB der Fig. 15 gehörende Funktion 6 (t)
speziell ö^, so sind die fünf Wurzeln der Gleichung (6) gegeben durch:
[ Öo = ö (D. Ö, = ö a + V2), 6, = 6 it T 2 ]%•
1 03 = 0(^ + 3^2), ö, = ö(e-r412).
Aus (5) folgt bei Benutzung von (10) S. 105:
256 ^ == ^ = ö* (5 - ö).
Demnach hat man in;
(8) cp (oji, ojo) = — = V(5 — ö) h^
eine Form (—2)^^'' Dimension xß den ajj, co^, die gegenüber den
Substitutionen der in den oji, a^ homogen geschriebenen Gnippe (^(5), vom
Vorzeichen abgesehen (vgl. S. 105), invariant ist. Aus (6) aber ergibt
sich: Die Form cp der Kongru£n0grußpe fünfter Stufe @(o) ist die Lösimg
der Gleichung fünften Grrades:
(9) (p^ — o h^ (p i- \ h^ == 0,
deren fünf Lösungen aus einer erden unter ihnen entsprechend den
Grleichungen (7) in den Gestalten:
(10) [ ^0 = ^ ("^1' ^^2). ^1 = y («1 + 2 a>2, öo),
i ^2 "= y («1 + 4 ^2' ^'2)' • • •' ^4 = y («1 -r 8 0^2' «2)
gewonnen werden. Will man lieber den Gebrauch homogener Variablen
OJi, ÜJ.2 vermeiden, so mag man die Funktion:
5 5 op
116 I, 5. Bringsche Gleichung fünften Grades,
einführen, die zufolge (6) die Gleichung fünften Grades befriedigt:
(12) ^^-2?^(/+l) = 0-
Xahe mit diesen Gleichungen verwandt ist auch die von Hermite*)
eingeführte Resolvente fünften Grades der Modulargleichung sechsten
Grades, die bei Transformation fünften Grades der elliptischen Funktion
auftritt. Man gelangt von (6) aus zu ihr, indem man in Übereinstimmung
mit (12) S. 106:
(13) ^^-4V5(1+^ K=^1^:J^
^ ^ 6 16 äH-'^
setzt. In der Tat hat die Hermitesche Gleichung fünften Grades die
Gestalt:
(14) i,t — 2* • 53 }^ k'^ w — 2'- 52 VS Jc^ Jc'^ (1 + h^) = 0.
Sie ist indessen weniger einfach als die vorstehenden Gleichungen, da
ihre Wurzel erst eine Funktion derjenigen Gruppe ist, die der Durchschnitt
unserer hier zugrunde gelegten Kongruenzgruppe fünfter Stufe mit der
Hauptkongruenzgruppe zweiter Stufe innerhalb der Modulgruppe ist.
Die Gleichungen, zu denen wir gelangt sind, stehen im Mittelpunkt
des vorliegenden Kapitels. Legen wir die Gestalten (9) und (12)
zugrunde, so handelt es sich hierbei um Grleichungen fünften Grades, in
denen die vierte, dritte und zweite Potenz der Unbekannten nicht auftreten.
Mit Klein bezeichnen wir eine Gleichung fünften Grades dieser besonderen
Gestalt als eine „Bringsche Gleichung'- und verweisen wegen der Begründung
dieser Benennung auf die ausführliche Darstellung in „Ikos*-, S. 143. Eine
Bring sehe Gleichung kann immer in eine Gleichung fünften Grades mit nur
einem „Parameter'- transformiert werden. Hat die Gleichung die Gestalt:
(15) z^ + a^z + a^ z= 0,
so liegt, falls einer der Koeffizienten a^, a^ verschwindet, eine Gleichung
fünften Grades mit nur einem „Parameter'" a- bzw. a^ vor. Sind aber
beide Koeffizienten a,, a. von 0 verschieden, so setze man z :=: -^ v
und fiadet die Gleichung:
(16) ^-5 J^l{v-^1) = 0, & = 4-
mit nur noch einem einzigen Parameter &.
§ 6. Transzendente Lösung der Bringschen Gleichung.
Die bei Hermite vorliegende Darstellung der Wurzel w der
Gleichung (14) in den transformierten Werten des Legendre-Jacobi sehen
Integralmoduls 1^ findet man auch in „EUipt. Funkt *• 11, 518 ff. dar-
*) „Sur la resolution de l'equation du cinquieme degre-, Pariser Compt. Rend.,
Bd. 46 (1859).
Hermitesche Resolvente fünften Grades. 117
gestellt. Mittelbar sind dadurch auch die üjbrigeii Gleichungen fünften
Grades von § 5 durch elliptische Modulfuiiktionen gelöst. Der Wert dieser
transzendenten Lösungen der Gleichupgen liegt in den Reihenentwicklungen
nach Potenzen der Entwicklungsgröße q, die wir jenen Lösfingeii entnehmen.
Diese Potenzreihen ermöglichen die Durchführuiig algebraischer
Entwicklungen. Andererseits gestatten sie apgen'^herte nur^erische Lösungen
der Gleichungen. Man hat dabei aus den „Parametern- der Gleichungen,
d. h. aus K bzw. h^ und h^, den Wert ca bzw. ^ zu berechnen, was
entweder ähnlich wie die Berechnung von co aus /durch hypergeometrische
Reihen (vgl. S. 90) oder direkt duroh Vermittlung von / bei Lösung der
für / quadratischen Gleichung (17) S. 107 gescjiehen kann. Aus co
oder ^ ist dann der Wert der Entwicklungsgröße:
herzustellen.
Wir können übrigens eine ausreichepde Anzahl vori Anfangsgliedem
der Potenzreihen für die Wurzeln unserer Gleichlingen fünften Grades
auch ohne weitergehende Entwicklungen iiber Mod^lfunlvtionen auf
folgendem Wege gewinnen. Die polfreie Form (— 2)*^'' Dirpension (p (cOj, o?.^)
ist,entwicklungsfähig in eine Pptenzreihe der Gestalt:
(1) (p («1, «2) = (^^ ) («1 g-" ~f a.^(f ~f «8 (f -I ),
\02/
wie aus der Erklärung (8) S. 115 von tp und dem Verhalten voq 6 im
DB der Gruppe ©(5) hervorgeht. Da (p polfrei ist, so ist die Reihe im
ganzen DB der Hauptkongruen:?gruppe ^j'"^ kpnveigent'='). Man trage
diese Entwicklung in die Gleichung (9) S. 115 für (p eip. und ersetze hi
und \ durch ihre Potenzreihen (9) S. 105. Ent\yicke]t m^n dann die
linke Seite der Gleichung nach ansteigenden Potenzen vpn q, so muß der
Koeffizient jedes Gliedes verschwinden, da in ^ eine identische Gleichung
vorliegt. Hieraus bestimmt sich a, bis auf eine mulriplikp^tive fünfte
Einheitswurzel, während nach deren ßestimmuriig a^, a^, 1 • • sich eindeutig
berechnen. Eine der Reihen hat reelle Koeffizienten. Sie liefert die
Form cpQ {eo-^, (o^), da die Funktion ö^ zufolge ihrer ErJdäruQg upd der
Symmetrie des DB der Fig. 15 bezüglich der imaginären o)-Achse auf
dieser Achse reelle Werte besitzt. Man gelangt zu dem Ergebnis: jDfe
transzendente Lösung der Bring sehen (xleichmig (9) S. 115 i,bt gegeben durck:
{ g), («1, ö,) = (-^ (— S^(f — E^-^'q-' + £^' (f — £*'3'
(2) ' ^"^^'
*") In den bis zur reellen Achse l^eranrßichenden Spitzen dieses DB
verschwindet f {co^, «2).
118 I, 5. Bringsche Grleichung fünften Grades.
WO die Sterne andeuten, daß alle Glieder mü gamsahligen Poten^exponenten
ausfällen*). Für die Lösungen der Gleichungen (6) und (12) § 5 leitet
man hieraus leicht auch transzendente Darstellungen ab. Wir merken
etwa für die Funktionen 6 die Potenzreihen an:
j...
[ — 12 £*^ f/-H*— 4£'g=~f 13£2rg5_ 12£3^g5 ^ ^
WO wieder alle Glieder mit ganzzahligen Exponenten, abgesehen vom
Absolutgliede, ausfallen **).
Eine erste Verwendung mögen die vorstehenden Reihenentwicklungen
bei der Berechnung der Differenzenprodukte der Gleichungen fünften Grades
finden. Die Diskriminante Dg der Gleichung (6) S. 115 berechnet man
am einfachsten auf Grund der Regel (15) in I, 111, die:
-öo=n(5ö;(ö,-4)) = -5^(nö.)'n(4-ö.)
1=0 11
liefert. Zufolge (6) S. 115 aber ist:
JJ ö, = — 256 K. n (^ ~ ^'') = -5^ (^ — ^) ■'
man findet also als Dibkriminarde Do der genannten Gleichung:
(4) Da= h^-2^^K\K—V).
Das Differenzenprodukt P„ der 6 sei gegeben durch:
und entsprechend seien die Differenzenprodukte P^ und Vf für die
Gleichungen (9) und (12) S. 115 ff. erklärt. Dann gilt zufolge (8) S. 115:
11(0. -M
^'f = ^'\' "^ ^^ = ?i-Pa-
und da man aus (4) mit Benutzung von (10) S. 105.-
P. = ±25V5^
findet, so gilt für P^^i
P^ =:^25V5'/*3/i|.
*) Dies ist selbstverständlich, da die Summe aller fünf Formen f identisch
verschwindet.
=•*) Vgl. die Gleichung (9) in ,.Ellipt. Funkt.'- II, 524.
Diskriminanten und Differenzenprodukte der Bring Sßhen Gleichungen. 119
Zur Bestimmung des Vorzeichens berechne man auf Grund von (2) das
Anfangsglied der Reihenentwicldung für P^, ^obei die Gleichung:
(5) 2l (£" — £'') =—25]'^
zur Benutzung gelangt. Als Differensenpraduli P^p der )\^urzeln der
Bring sehen Gleichung (9) S. 1 15 findet sich:
(6) P,p = Jl(cp,- 9v) == - 25 V5/., hl
Wir notieren endlich noch für die Gleichung (12) S. 116:
§ 7. Galoisscher Köyper der Bringßcheri Gleichung.
Die S. 113 mit S und Tj bezeichneten Substitutionen mögen jetzt
S und T genannt werden und als homogene Substitutiopen in den
Variablen co^, co^ geschrieben werden:
(S) a'i = o»! ~f 2 CO,, coo = «a! (^) '^'i = — V'^'t^'a) «2 '-= ^-•
Aus diesen beiden Substitutionen läßt sich die Gruppe ®^3 erzeugen.
Bei Ausübung von S erfahren die füaf Funktion (J die zyklische Permutation:
(1) Öo = öl, öl = Ö2, Ö2 == Ö3, Ö3' = ö^, ö'i = öo,
und ebenso permutieren sich die fünf Wurzeln f der Gleichung (12)
S. 116 und die fünf Wurzeln (p von (9) S. 115. Aadererseits gehört die
Substitution T den drei Gruppen von ö^, öi, ö^, nicht aber den Gruppen
von ög und Ö3 an. Bei Ausübung dpr Substitution T erfahren die ö die
Transposition:
(2) öo = Öq, öl = öl, 02 = Ö3, öi = Ög, öl = Ö4,
und die gleiche Permutation erfahre^ die f^, während dje tp^ infolge des
in der Erklärung (8) S. 115 auftretenden Faktors \ das Verhalten zeigen:
(3) 9o =-9o. 9^1 = -9i. 92 ==-^3. ^i =-^2' 9i =-94-
Aus den beiden Permutationen (1) und (2) läßt sich die gesamte
symmetrische Permutationsgruppe ©ig^ erzeugen ="). Bei den fünf Formen <p
handelt es sich, wie man sieht, um eine ©120> <iie ^i^ 60 gera,den
Permutationen enthält, während die 60 ungeraden Permutationpn je mit
gleichzeitigem Zeichenwechsel aller fünf <p verbundep sind.
*) Die aus den Permutationen (1) und (2) zu erzeugende Gruppe ist trfinsitiv,
da sie die zyklische Permutation (1) enthalt, und kann n:|cht imprimitiv sein, da
sie die Primzahl 5 zum Grade hat (vgl. I, 337). Sie ist also nach I, 345 die
symmetrische ©1201 da sie die Transposition (2) enthalt.
120 Ii ^- Brmgsche Gleichung fünften Grades.
In der S. 112 eingeführten 120-blätterigenRiemann sehen Fläche F^go»
auf weiche der DB der Hauptkongruenzgruppe ^- durch die Funktion K
abgebildet wird, entspricht der Substitution S ein Umlauf um den Punkt
K = oo und der Substitution T ein solcher um den Punkt K = 1.
Indem wir den S. 58 eingeführten Begriff der „Monodromiegruppe'- wieder
aufnehmen, werden wir zu dem Satze geführt; Für die Gleichung (6)
S. 115 und die Bring sehe Gleichung (12) S. 116 mit dem Parameter K
ist die Monodromiegruppe die symmetrische Permutationsgruppe ©jgo- ^^
dieser Hinsicht unterscheiden sich also diese Gleichungen wesentlich von
den im vorigen Kapitel gefundenen Gleichungen fünften Grades mit
einem Parameter.
Der Betrachtung des „Galoissehen Körpers'- unserer Gleichung legt
man zweckmäßig die fünf Formen (pr((o^, co^) zugrunde. Sie sind,
linearabhängig, da die Gleichung:
(4) 2 9>K. «2) = 0
1 =0
identisch besteht. Aber es besieht keine wettere lineare homogene
Begehung zwisclien ihnen, da sonst auch bereits zwischen den vier Größen
9i' 9^2' 93' 9^4 ^^^ Gleichung:
«1 9l + «2 92 + «3 93 i- «4 94 = 0.
mit nicht durchweg verschwindenden a bestände. Kach Eintragung der
Reihen (2) S. 117 würde man zu den vier Gleichungen:
«1 E^ -^ «2 ^^^ + '^3 ^^^ + «4 f*'^ = 0, ^ r= 1, 2, 3, 4,
gelangen, aus denen indessen nach I, 79 ff. das Verschwinden aller a folgt.
Man führe nun das Differential:
(5) (co, dcö) = cOj dco^ — co^ da^ = — cof dco
ein und setze:
(6) 2Ö^ J ^' ^"'' "2^ ' ^"' da}) = w, (a).
Dann fiadet man aus (2) S. 117 für v = 0, 1, 2, 3, 4;
!J 2 _3 £ 0
w,((o) = s'qo 4-|£2rg5_l£3v^5 ~f| 5*^35 -f*—-ef'a^
Es besteht dann wieder die Relation:
(8) •^w,{co) = 0,
jedoch sind die vier Funktionen w^ (co), • • •, w^ia) linear-unabhängig.
Wie die 9?^ (cjj, C3^ sind auch w^ (co) im DB der Hauptkongruenzgruppe §-
tiberall endlich, ändern sich jedoch gegenüber den Substitutionen dieser
Gruppe als Integrale um additive Konstante. Xun hat die dem DB
Br^ngsche Kurve. 121
entsprechende Riemann sehe Fläche F^go über der X-Eber^e das Geschlecht
p = 4 und ist nicht hyperelliptisch. Wir gelangen zu dem Sat?e: Bie
Wy (co) sind, in Abhängigkeit vor^ w aufgefaßt, Integrale erster Gattung der
Biemann sehen Fläche Y^^^ des Geschlechtes p == 4, und insbesondere sipd
IV ^, w^, u\, w^ vier linear-unabhängige Integrale, in denen ßlle weiteren
linear darstellbar sind.
Damit haben wir Anschluß gewopnen an bekaimte Sätze über
algebraische Funktionen*). Wir füjiren die vier Größep (p^, (p^, (p^, <p^
als homogene Koordinaten im Räume ein oder behalten sogar, wie es
Klein in „Ikos.-', S. 162ff. tufc, alle fünf durch die Relation:
(9) 9o + 9i T 92 -f 93 -f 9* = 0
verbundenen Größen bei, die dann sogenannte „PentaedßrJcoofdinat:en'- im
Räume B^ von drei Dimensionen liefern. Die Riemanri, sehe Fläche F^g^
wird dann durch die Formen (pr(fx}^, to^ auf eipe Baumkarve oechstßn
Grades des Geschlechtes p = 4 abgebildet, die in der Theoiie der
algebraischen Funktionen als die „Xormalkurve der Fori^en cp" bezeichnet
wird. Im hier vorliegenden 2usai|imenhang nenpen wir diese Kur^e
mit Klein („Ikos.", S. 167) die „Bringsehe Kurve-. Sie ist im B^
darstellbar als Schnitt einer Fläche zweiten und einer solchen dritten
Grades, die durch die Gleichungen:
I 9o T 91 + 9I + (pl + 9* = 0>
\ <po 4- <pi +- <pl + 9I 4- (p! = 0
gegeben sind. Diese Gleichungen aber sind uni^ittelbare Folgen der
Bring sehen Gestalt der Gleichung fünften Grades (9) S. 115. Den
120 mod 5 inkongruenten Substitutionen der @(-) entspreche^ 1^0 Kolll-
neationen der Bring sehen Kurve in sieh. Sie werden von den 60 geraden
Permutationen der (p gebildet, sowie den 60 ungeraden Permutationen,
letztere je vereint mit einem gleichzeitigen Zeichenwechsel, aller fünf
Koordinaten.
Aus (9) S. 115 ergeben sich die Darstellungen ton h^ and h^ in den
Formen (p^:
[ 20 h, (CO,, «2) == 9o* ~f <pI i- <pl - 9I H- 9>l
1 h^{co^, co^)-h^((o^, «2) = — 9o-91 • 92-93-^r
Mt Hilfe der Gleichung (10) S. 105 folgt weiter j^ls Bardellung von K
durch die Formen (pr:
(12) ^_.„^_2'^.5»i^^.
*) Vgl. .Modulfunkt.'- I, 569ff.
122
Bring sehe Gleichung fünften Grades.
Auf der Bringsciien Kurve wird hiernacli das einzelne System von 120
Punkten mit gegebenem K ausgeschnitten durch, die Fläche 20^*^" Grades:
(13)
23 . 0'
■'(nvy-^(s9't);=o.
Die Lösung der Galois sehen Resolvente der Bring sehen Gleichung läuft,
geometrisch gesprochen, darauf hinaus, hei gegebenem K die Koordinaten
eines der zugehörigen 120 PunUe auf der Bring sehen Kurve zu bestimmen..
Die übrigen 119 Punkte sind dann zugleich mit bekannt. Die
Gleichwertigkeit des Problems mit der Aufgabe der vollständigen Auflösung
der Bring scheu Gleichung ist einleuchtend.
§ 8. Bring sehe Kurve in Tetraederkoordinaten.
Unter Adjimktion von s stelle man aus den fünf Formen (py,{(o-^, co^)
jetzt vier linear-unabhängige Formen z^ (ca^, co^), • • •, ^^ («j, cOg) durch
die den Lagrangeschen Solventen nachgebildeten Ausdrücke:
(1) 5«;^ = 9o-r«*9i+«-''92 + ^^*93 + «'''94> /t = l, 2, 3, 4,
her, in denen sich dann die g), ihrerseits so darstellen:
(2) (p, = E-^z^ + 5-2^-^2 + £-3^^3 + f-*"^^, r = 0, 1, 2, 3, 4.
Als Potenzreihen dieser Formen z findet man aus (2) S. 117:
(3)
z^icoi^ CO,) =
z^((0^, «a) = ■
•)■
2^(1-22 + ...),
'•)
mit durchweo; reellen Koeffizienten. Die (Sj^^o "^^^ Permutationen bzw.
Substitutionen der (p transformiert sich auf eine Gruppe von 120 quater-
nären Substitutionen der Äjt, die erzeugbar ist aus den beiden den
Substitutionen S und T entsprechenden Substitutionen der Determinanten 1 bzw. — 1:
(4) Z[ — S^Z^, S'2==E^Z^, 4 = 5^^3, s[ = 8S..
(5)
yb , 1-
;J^ -_ 5^ ^ ^^ ^ _„
-V5.
l^-f5
-V5
1 — Vs
]öz[ =
l~-]h_
l-f V5_
Bringsche Kurre in Tetraederkpordinaten. 123
Man deute nun die z als „Tetraederkoordinaten" im Räume und
stelle die Bring sehe Kurve in ihnen dar. Die in (10) S. 121 links
stehenden Potenzsummen der cf gebßn auf die z^^ upigerechnet:
9o+9i +9l + --- = 10 (^,^,-^.-,„^3),
9o + 9i + 92 -^ • • • = 15 (^1 ^3 + ^l ~% T- ^l ~^2 - 4 ~^)-
Die Bring igelte Kurve wird dem^acli in Tetraederhovirdmaten durch:
(6) .-^.,^.^^3 = 0, ,u^ + 4h-4^,-4^^ = o
dargedeJlt. Die zweite Gleichung liefert die vqn C leb seh als „Diagonal-
fläche'- bezeichnete Fläche dritten Grades*). Bei den 120 quaternären
Substitutionen bleibt die linke Seite der ersten Gleichung (6) absolut
invariant, diejenige der zweiten blei|bt nur bei den 60 Substitutionen des
Xormalteilers ©g^^ invariant und erfährt im übrige^. Zeichenwechsel.
Soll das Problem der Lösung der Galois sehen Re^olvente der
Bring sehen Gleichung mittels der Sj^ angesetzt >verden, so sind die
Gleichungen (11) S. 121 auf die ^f. umzurechnen. Man gelangt, wepn
man die Ergebnisse mittels der ersten Gleichung (6) kürzt, zu zwei
Ausdrücken;
f X (^~i, ^2, ^3, ^J = Zf Z^ ~f Zl Z^ ~f Zl ^3 -r ^l -^ - 3 ^1 ^2 ~3 -"*>
(7) ^ 0(^1, ^,, ^3> ^J = ^1 + 4 + 4 -f 4
\ — 10 {zl ^3 z^ 4- 4 ^, ^^3 + zl z^_ z^ -r 4 ^i ^2),
in denen sich die Formen h so darstellen:
(8) - h,\ = ^{z,, z,, z^, ^J, Ä, = x(zp .2, ^3, z,).
Weit umständlicher ist die Upirechnung der Gleichung (6) S. 119 fur
das Differenzenprodukt P^^ auf die zj.. Man gelangt hier zu [dem Ausdruck
zehnten Grades:
,,, [ ^(~^> ^2, ~^3> ~^.) = 2 (5) (~^^' -11 ^^- ^^'^- i-'^ß ^^^*'-
l + 25 C| „-3i e,;^ — 50 4 4;i ^4;t — 75 -f ^Ifc^l;, — 150 4 ^Ifc 4/),
wo Ä die Zahlen 1, 2, 3, 4 durchläuft und (^] das Legeiidre sehe Zeichen
ist. An (8) reiht sieh dann die Gleichupg an:
(10) \h!^Wiz,,z„z„ z^y
Auf Grund von (10) S. 105 ergibt s^ch der Satz: Die Fanlilon K i^tcllt
sich als rationale FunMion auf der Bring sehen Kurre daf in der Qe&talt;:
(11) ^:(^—1): 1 = 0*:?F^:25ÜX=.
■*) Vgl. das Nähere m „Ikos.", S. :
124 I» ^- Bring sehe Gleichung fünften Grades.
Die Lösung der Galois sehen Besolvente der Bring sehen Gleiehung läuft
also darauf hinaus, bei gegebenem Werte -STdureh Lösung der Gleiehungen (6)
und (11) die zugehörigen 120 Wertsysteme für die Verhältnisse der ^^,
Zg.. g,, 0. ZU bestimmen.
§ 9. Parameterdarstellung der Bring sehen Kurve.
Die dureh die Gleiehung:
(1) ^j ^^ -4- ^2 -2^3 = 0
gegebene Fläehe zweiten Grades trägt zwei Seharen gerader Linien,
deren eine mittels eines Parameters X darstellbar ist dureh:
(2) z^-^Xz^ = 0, ^3 — ;l ^, = 0,
während die zweite mit dem Parameter ^ angebbar ist dureh :
(3) ^j — fi ^3 = 0, ^2 i" >" ^4 = ^•
Dureh jeden Punkt der Fläehe läuft eine Gerade der ersten und eine
solehe der zweiten Schar iiindureh*). Jedem Punkte der Fläehe (1) kommt
demnaeh ein bestimmtes Wertepaar X, ^ zu, so daß man die beiden
Parameter X, fi als „ Koordinaten "^ für die Punkte der Fläehe (1)
benutzen kann. Man wird demnaeh aueh die auf der Fläehe (1) liegende
Briagsehe Kurve mittels der Parameter X- ^ zur Darstellung bringen
können.
Zunächst möge das Verhalten der Parameter X, /i bei den 120 Raum-
koUineationen unserer Gruppe ©^20 festgestellt werden. Wir setzen:
(4) ;l^_1i_13, ^ = ?i=.-!i
und bemerken erstlieh, daß bei der KoUineation (4) S. 122 jede der beiden
Geradenseharen in sieh selbst übergeht. Die Parameter erfahren hierbei
die Substitution:
(5) X' = eX, ft' = E^ fi.
Bei der KoUiaeation (0) S. 122 aber werden beide Seharen ausgetauscht;
denn es geht z. B. die dureh ^^ === 0, ^3 = 0 gegebene Gerade der ersten
Schar in die durch:
~< _ ^; _ - 1 -f Vs"
===) Man beachte, daJß die geometrische Sprechweise hier im übertragenen
Sinne gebraucht ist, da sowohl die z als auch die Parameter A, /u. beliebige komplexe
Großen sind.
"^ VS ^ |5
e^ — £^ £—£*'
V5 " ys
..■ _ V5 "^ ys
15 Vö
Parameterdarstellung der B^ngsclien Kurve. 125
gegebene Gerade über, die def zweiten Scliar angehört. Xach kurzer
Zwischenrecbnung findet man aus (5) S. 122, daß dieser B^ollineation
die Substitutionen:
(6)
der Determinanten 1 entsprechen. Aub den Substitutionen (5) Ufhd (6)
erzeugt man eine Gruppe ©^20 '^^*" Ordnung 120 von Sutstitutionenpaareti,
die eine neue Darstellung unserer bisherigen (S^^q abgibt.
Der „ungeraden'• Permutation (ö^, 0.2, 6^, a^) der <5 entspricht als
Substitution der Formen (p:
(po = — cpo, (p'i = — <po, (po = — (p^, (p'i = — <P3' (p'i = — (pi,
und diese liefert auf Grund von (1) S. 122 als Substitution der Z)/.
Zi = Z„, ^3 = Z^, ~i = ■i^2' ~ 2 == ^1;
sowie damit als entsprechende (Substitution der Pa^-ameter :
(7) ;; =r —, a' = .1.
/^
Die Zusammensetzung der Substitutionen (7) und (ti) in dieser üeilien-
folge führt zu der Substitution
V5 V5_
ft == 7 ^2-"
"^ V5" '" Vs
(8)
J/i (5) «>^<^ (8) haben ivir fur h die erzeugenden Substitidionen S und T
der nicht-homogenen Ihosaeder-(^^^ wiedergewonnen [vgl. (1) S. 421,
während die Substitutionen von ^ aus denen von 1 durt^h Ersatz von s
durch 8^ hervorgehen'-^). Aus fieser DarfStellung des Korm^lteilers 0)^^^,
geht dann die ©^jo durch Zusatz der Substitutioa (7) der Periode i
hervor.
Zur Darstellung der Bring sehen Kurve benutzt man zweckmäßig
statt l, a homogene Variable a^, ^.-> ur^d ^u^, fi„ indem man X =z -ll
und ^ = ^^ setzt. Dabei genügt man den Gleichungen (4), indem man:
llc,
(9) z^ = 2.^^,, z^ = —Ki^i^ h = hH^ ^4 = hH
=) Dabei wechselt Vs entsprecjiend der &].eichupg (13) S. 4I das Vorzeichen.
126 I, ». Eringsche Gleichung fünften Grades.
vorschreibt. An Stelle von (5) und (6) aber treten die homogenen
unimodularen Substitutionen:
(10) l\^=zs^l^, A2 = £^A2, fti = £fti, ft2 = £*/^2-
f V5';l;=3 ^(£-£*)ftj-(«'-«')^2> V5^; = ^(£-£*);L,-(£2-£3);t,_^
Zur Darstellung der Bring sehen Kurve ist nun einfach die zweite
Gleichung (6) S. 123 mittels der Gleichungen (9) auf die l, fi umzurechnen.
Äh Parameterdardettung der Bring sehen Kurve findet man:
(12) Xf ^l ^2 + X! l^ {ii — Xi 11^ iil + Aj Xt ^f = 0.
Der Ausdruck sechsten Grades auf der linken Seite dieser Gleichung
ändert sich nicht bei Ausübung von (10), während er gegenüber der
Substitution (11) Zeichenwechsel erfährt. Er ist also invariant gegenüber
der Ikosaeder-@g(), die in der ®^^^ als Xormalteiler enthalten ist.
Trägt man in die rechten Seiten der Gleichungen (7) S. 123 für die z
die Ausdrücke (9) in den ^, ft ein, so gelangt man zu den beiden folgenden
Ausdrücken achten und zehnten Grades in den ^, ft, die wir gleich wieder
selbst durch X {X, (i) und $ (X, fi) bezeichnen wollen:
(13) X(X, ft) = Xt ftj l4 - U fti fta ~ ■^i '^a f*i + ^i ^i ft| — 3 Xi Xo fti fi|,
I ^ ß, fi) = ^f K + ^1 fi| — Ü ill + ll ill
Ebenso rechnet sich die Gleichung (9) S. 123 um in die Gestalt:
f wix, ii) = {XI' ~ iixtxl-xl')(ni' + n ii! ill - ill')
— 625 Xt XI ftf nl + 25 [(/.', ^2 ~f 3 ^^^ ;L| ) Qi^ llI — 2 ft^i uj)
(15) { - (A, ;i| - 3 X! XI) (ft? ftf -f 2 ft? ft|)
— (Xt XI — 2Xf Xl) (ft, fi| — 3ftf fi|)
— (X! XI T- AJ XI )(ii', ii, + 3 ft* ftl)].
In diesen Ausdrücken stellen sich die \, h^, h^ so dar:
(16) — \ \ = 0 (X, ft), \ hl = W {X, ii), \ = X {X, ft).
Die Darstellung der Funktion K als rationale Funktion auf der nunmehr
durch die Gleichung (12) gegebenen Bring sehen Kurve aber ist wieder:
(17) K:{E—1):1=0 {X, ft)* : W (X, ii)' : 256 X {X, iif.
Hieran kann man eine neue Formulierung des Problems der Lösung der
Galois sehen Resolvente der Bring sehen Gleichung reihen =*).
*) Über die Invariantentlieorie der aus (5) und (6) zu erzeugenden ©j^o
linearer Substitutionen vergleicbe man die Abhandlung von Gor dan „Über die
Auflosung der Gleichungen vom fünften Grade'*, Math. Ann, Bd. 13 (1878), sowie
die Angaben Kleins in .,Ges. Abh." II, 380.
Parameterdarstelliipag der Formen '?, W und X.
§ 10. Resolvente sechsten Grades der Bring ßchen Gleichung.
In der (S^^^o ^^^^ sechs konjugierte Teiler ©^ enthalten, derpn
einzelner als Xormalisator einen Teiler ©20 der Ordpung 20 besitzt.
Geht man auf die ursprüngliche Erklärung dey ^^^^ als mod 5 reduzierte
Ö*^^) zurück, so wird z. B. ei|ie der zyklischen Gruppen (S- aus der
Substitution (^' ^^
a U 1) erzeugt.
Der zugehörige Teiler ©^^ besteht
Flg. 16.
allen Substitutionen, die die Kongruenz y = 0 (mod 0) befriedigen. Durch
die gleiche Kongruenz y ~ 0 (mod 5) ist dann^ die der Gruppe ©^o ^^^'
sprechende Kongruenzgruppe fünfter Stufe erklärt, die ßinen Teiler ©,,,)
des Index 6 innerhalb der ©Ö liefert.
Um einen DB dieser Kongruenzgruppe ©(g) zu gewianeii, gelten wir
auf die S. 109 mit ©(24.) bezeichnete Kongruenzgriippe fünfter Stufe dps
Index 24 zurück, deren Substitutionen mod 5 i^itf ' '^"j und den Potenzen
dieser Substitution kongruent siad. Der Zusatz der Spiegelung ^' = — ^
an der imaginären ^-Achse führte zu der daselbst mit ©(24) bezeichneten
Gruppe, deren DB in Fig. 14 S. 111 dargestellt ist. Es handelt sich dabei
um ein Achteck, dessen acht Randk|-eise durchweg Symmetriekreise vqn
Spiegelungen der ©(24) waren. Dieses Achteck hat n]in in dem vqn
acht Kreisbogendreiecken umlagerten Pol
t == ^= der Substitution der Periode 4 • / 00
5y2
(1) r == -^-^—7-
5^-2y2
einen Mittelpunkt und wird durch diese der
©(6) angehörende Substitution und ihre
Potenzen in sich transformiert. Dpr Zusatz der
Substitution (1) zur ©(24) führt zu der durch
die Spiegelung t' = — t er^^eiterten
Gruppe ©(e), deren DB in Fig. 3-6 dargestellt
ist. Die beiden durch einen Pfeil
-verbundenen Seiten dieses Fünfecks sind v^ermöge
der Substitution (1) äquivalent, wählend die
drei anderen Seiten Symmetrjekreise von
Spiegelungen der ©(g) sind. Lagert man nun diesem DB &ein Spiegelbild
bezüglich der imaginären ^-Achse an, so gelangt man zu dem in Fig. 17
(S. 128) dargestellten DB unserer Kongruenzgruppe @(g).
Aus der Zusammengehörigkeit der ßandkurven dies^es DB erkennt
man, daß er vermöge der Funldion K auf eine sechsb^tterige Rjemann sehe
Fläche Fg über der Ä-Ebene mit folgender Verzweigung abgebildet wird:
128
I, 5. Bring sehe Gleiehung fünften Grades.
Bei K = 0 liegt ein vierblätteriger Verzweigungspunkt, den Bereichecken
— jl^, — ^ _* entsprechend, während die beiden übrigen Blätter bei
P 13V2
JS: = 0, den Ecken =—^~ entsprechend, isoliert verlaufen; bei ^ = 1
5V2
liegen drei zweiblätterige Verzweigungspunkte; bei Z" = oo findet sich
ein fünfblätteriger Verzweigungspunkt, der Spitze ^ = 0 entsprechend,
^^^ ^^ während das letzte Blatt bei
K = OD, der Spitze ^ = i <x>
entsprechend, isoliert verläuft.
Andere Verzweigungspunkte
treten nicht auf.
Daß diese Riemann sehe
Fläche Fg dem Geschlecht
j) = 0 angehört, ist bereits
aus der Zusammengehörigkeit
der Randkurven in Fig. 17
einleuchtend. Indem wir also
eine geeignete einwertige
Funktion r der Fläche
aussuchen und K als rationale
Funktion sechsten Grades von r
darstellen, wird diese Darstellung, als Gleichung sechsten Grades für r
bei gegebenem K aufgefaßt, eine jResolvente sechsten Grades der Bring sehen
Gleichung liefern. Die Auswahl von r geschieht in der Weise, daß wir
die Werte von r in irgend drei Punkten des DB vorschreiben. Es möge
zu diesem Zwecke festgesetzt werden:
(2) .(0)=oo. ,(.00) = 0, .(X|xij = ,^=li^)=-1,
d. h. r soll in dem fünfblätterigen Verzweigungspunkte bei K = cx> selbst
unendlich werden, im isoliert verlaufenden Blatte bei ^ = 00
verschwinden und im vierblätterigen Verzweigungspunkte bei E = 0 den
Wert — 1 haben.
Aus diesen Angaben sowie aus der eben beschriebenen Verzweigung
der Fläche Fg lesen wir für die Darstellung von K als rationale Funktion
sechsten Grades von r die beiden Ansätze ab:
_ (r^ -f ar + &)(r-f 1)* ^ ^ __ (z' -t-«r^-r^r + yf
(3)
K— 1 :
WO a, h, c, w, ß, y noch zu bestünmende Konstante sind. Indem man
die aus diesen beiden Gleichungen für die Ableitung von K nach r
folgenden Ausdrücke einander gleichsetzt, folgt nach kurzer Zwischen-
rechnung als eine in r identisch geltende Gleichung:
[ (T + iy{6z' + (4a + l)r' + Shz -h)
\ = (r^ + ar^ + ßz i- y) (or^ + 3ar' -^ ßr - y).
(4)
Resolvente sechsten Grades der Bringschen Gleichung. 129
Nun ist der erste Faktor rechter Hand zufolge der Ansätze (3) teilerfreipd
gegen (r + 1)^- Die identische Gleichung (4) spaltet sich demnach in
die zwei Gleichungen:
ot^ + Sar^ + ßr — y —■ o{x-^ If,
ör^ + (4a + l)T;2 + 3Z)r —b = 5(tS + «^2^ ^^4_y).
Also ist a = o,- ß = 15, y =- — o, und die Eintragung dieser Werte
in die zweite Gleichung liefert weiter « == 6, h = 25. Setzt man
endlich in die zweite Gleichung (3) die zusammengehörigen Werte
r = — 1, JST = 0 ein, so folgt:
e = (y — ß-^a—iy- == 25ß.
Damit ist folgendes Ergebnis gewopnen JDle aufzustellende Bepolvente
seehbten Gradet. der Bringschen Gleichung hat als Gleichtmg mit der t>-
heJcannten x und dem Parameter K die Gestalt ■
(5) ^:(^-l):l =.(r2-^6r~f25)(-p~f ])^
:(r^ + 5r'-}-loT—5)'
: 256 r.
In den beiden Ecken t = =—=— des PB wird ^ = 0. Die beiden
5]/2
zugehörigen Werte r sind die W^urzeln von (t^ -^ (ir -\- 25):
(6) ./±l,±i)=-3 + 4.
§ 11. Beziehung der Resolvente sechsten Grades zur Bringschen jKurve.
Der durch j; = 0 (mod 5) erklärte Teiler <>^2q stellt &ich bei Gebrauch
der quaternären ^^-Substitutioi^en durch die 20 Substitutionen dar, die
das Koordinatentetraeder in sich transformieren. In den Parametern, X
und fi geschrieben, wird die ©gp ^^^ den beiden Substitutionen (5) und (7)
S. 124ff. erzeugt, die sich bei homogener Schreibweise &o darstellen:
Aus (6) S. 123 geht hervor, daß die gemeinsamen Punkte der Bringschen
Kurve und der Koordinatenebeiien z^ = 0 allein die vier Tetraederecken
sind. Die zum ausgewählten Teiler ©^o gehörende Lösung t der Resolveni'e
sechsten Grades möge insbesondere x^ heißen^ die fünf übrigen aber x^,
r^, •••, T^. Es gehe r^ durch die Substiüition | ' j iq. Tq, diese Wurzel
aber durch ( ^' ''^ j in tj. über. Die 20 Nullpunkte der Funktion r» fallen
zu je fünf an vier Stellen der Bringschen Kuive zusammen, die einfach
Fnuke, Algebra. II. 9
130 Ii 5. Bringsche Gleichung fünften Grades,
die vier Ecken des ^-Tetraeders sind. Es handelt sich hierbei um die vier
Stellen, die von den Spitzen:
V2 3 .2V2
5 5y2 o
des DB der Fig. 14 S. 111 herrühren.
Die Darstellung von r« als rationale Funktion auf der Bring sehen
Kurve ist aus diesen Darlegungen leicht abzuleiten. Die Form ;
(2) i^oo = — h X^X.2 ^Uj Ug
reproduziert sich gegenüber den Substitutionen (1) bis auf das Vorzeichen.
Das Quadrat dieser Form:
(3) 1^^ = 2 51! H lil III = — 25 ^, ^2 ^3 ^4
liefert, gleich 0 gesetzt, im -e-j.-Raume die vier Ebenen des
Koordinatentetraeders, die die Bring sehe Kurve in den vier Tetraederecken schneiden.
Teilt man il)% durch die in (7) S. 123 gegebene biquadratische Form X,
deren 24 Nullpunkte auf der Bring sehen Kurve die Punkte mit K = oo
sind, so erhalt man eine zur Gruppe ®^^ und damit zum
Diskontinuitätsbereiche der Fig. 17 gehörende Funktion, die nur in den beiden Spitzen
^ = i 00 und ^ = 0 des DB verschwinden oder unendlich werden kann.
Die Anfangsglieder der Potenzreihen von i/;^ und X sind:
so daß der Quotient dieser beiden Formen das Anfangsglied 25 g und
also in der Spitze i^ =z i oa des DB einen einfachen Nullpunkt hat.
In der Spitze bei ^ = 0 liegt demnach ein Pol erster Ordnung.
Hiernach ist der Quotient bis auf einen konstanten Faktor mit der Funktion r
gleich. Dieser Faktor aber ist selbst gleich 1, da man aus der
Resolvente (5) fur lim r = 0 leicht abKest, daß die Reihenentwicklung von r
gleichfalls mit 25 g beginnt.
Die mit il;^ konjugierten Formen stellen wir dadurch her, daß wir
zunächst die zweite Substitution (1) und sodann die Substitution (11)
S. 126 ausüben. Dies führe zur Form t/;^, die dann durch wiederholte
Anwendung der ersten Substitution (1) zu den Formen t/;^, il)^. ij;^, ij;^
hinführt. Die bechb konjugierten Formen tl^ sind gegeben durcli:
\ T/;, = (an! -rl,l,~ 8'^ li) {8'^\a! + ^,^, - £2^>|), ^-^ 0,1, •-., 4,
und in ihnen stellen sich die Wurzeln der BesoJvente (5) S. 129 so dar:
_^^{i,iif _ ^,(1,117- ^ ^ ^
X (X, y) Xß, y) ' ' >
Hierdurch sind die "Wurzeln der Resolvente als rationale Funktionen auf
der durch (12) S. 126 dargestellten Bring sehen Kurve gegeben.
ßesolvente sechsten Grades und Bringsche K.xu-ve. JBI
Aus der Resolvente sechster). Grades folgt durch Multiplikation
mit hf:
hl (,;3 _^ 5 ^2 ^ 15-^ _ 5)2 ^ 256 {K— 1) hl % = hl hl r.
Setzt man hier für h^r = Xx entsprechend den letzten Glpichuagen il}^
ein, so folgt nach Ausziehen der Quadratwurzel;
t/;« + o ;», T/;* + ihhl T/;2 — 5 hl = £ h^ hl t/;.
Zur Bestimmung des Vorzeichens tj-age man: •
-©'<«
2 71
K = (-A (i-80g + ---). ^. = (—) (2-&ä^ + ---)
ein, worauf eine in q identisch bestehende Gleichung entstehen mi;ß. iJan
findet, daß das obere Zeichen gilt: Bie bcchs honjugierten Formen il^
befriedigen die Gleichung sechsten Grades:
(6) !/;<>+ o h^ T/;* + 15 hf T/;2 _ h^ hf i/; — 5 hf = 0.
Legt man zur Darstellung des Galqis sehen Körpers der Bringschen
Gleichung (9) S. llo unmittelbar die Wurzeln dieser Gleichung zugrunde,
so findet sich aus (1) S. 122:
— 5 ip^ = 25.0.^.0j^
— 2:^ g'v" 2— ^ ^' ^'+^ 2— ^'^' ^"^-'
wo V die Werte 0, 1, 2, 3, 4 ^u durchlaufen hat und die Indizes der q)
nötigenfalls mod 5 zu reduzieren sind. Da nxm in der letzten Glpichu^fig
rechts die erste Summe verschwindet und die dritte gleich dem negativ
genommenen Werte der zweiterji ist, so folgt a|s Darstellung von -^^ durch
die Wurzeln der Bringschen Gleichung (9) S. llo:
(7) — y 5 i/;^ == g)o g)i + g)i g), + g>2 (Pz ^ <Ps<Pi'T <Pi <Po-
Da das Verhalten der g) gegenüber den erzeugenden Sfibstiiutior^en der
®j,Q bekannt ist, so gewinnt man leicht entsprechende Ausdrücke fur die
übrigen Wuizeln der Resolvenie (6) in ^en tp.
Aui Grund der Gleichungen von S. Hoff, leitet man aus (7) leicht
auch noch die Darstellung der Wi^Tsel x^ der BeboJverde b<;chsten Gradet, (p)
S. 129 als FunUion des Galßisbchsn KorßfiTb der Qleichung fünften
Grades (o) S. llo al):
1280 Kx^ = fS<Jvö, + i(Jv+2f-
Da die sechs konjugierten Teiler ©g^ als Durchschnitt die (^^ haben, so
ist die Galois sehe Gruppe der Resolvente (o) S. 129 mit dpr Ö^gQ
isomorph; sie ist zugleich die Monodromiegvuppe dieser Gleichung.
9=^
132
I, 5. Bringsche Gleichung fünften Grades.
§ 12. Beziehung der Bring sehen Gleichung zur Resolvente
fünften Grades der Ikosaedergleichung.
Um die Beziehung der Bring sehen Gleichung zur Resolvente fünften
Grades der Ikosaedergleichung festzustellen, knüpfen wir an die
Gleichung (o) S. 11 o an und verstehen unter 6 die daselbst für den DB der
Fig. 15 erklärte einwertige Funktion. Die zugehörige Gruppe ©(g) werde
vermöge der Transformation co = ^^2 auf co umgeschrieben. Sie ist
alsdann kommensurabel mit der Modulgruppe, und zwar ist der
Durchschnitt ein Teiler @{?o) ^es Index 10 der ®^^\ der als Teiler des Index 2
in der ©(g) enthalten ist. Der DB dieser Gruppe @S ist in Fig. 18
dargestellt, die man von Fig. 15 S. 114 aus leicht verstehen wird. Die
Randkurven dieses DB hängen durch die in (2) S. 113 gegebenen Sub-
Fig. 18.
stitutionen Tj, T^, T^, T^ und die etwa T^ zu nennende Substitution
^' = ^ ~|- ^V- zusammen. Die drei in Fig. 18 angegebenen
Substitutionen, die die unteren Randkurven ineinander überführen, sind dann
einfach:
(1) r, = T,-T^, r^ = T^-T„ rs = T,-t-^
Auf CO umgerechnet Kefem sie die Substitutionen:
•^4-
F, =
(2)
zu denen dann noch für die beiden Geraden des DB die auf co
umgeschriebene Substitution T. =
/l,10^
lo, 1;
tritt. Alle vier Substitutionen
sind in der Modulgruppe enthalten, so daß wir hier in der Tat den
Durchschnitt der ©(g) mit der Modulgruppe @H vor uns haben.
Die Zuordnung der Randkurven zeigt unmittelbar, daß der DB der
Fig. 18 durch ö auf eine zweiblätterige Fläche des Geschlechts p = 1
über der ö-Ebene abgebildet wird. Man erkennt auch sofort, daß die
vier Verzweigungspunkte dieser Fläche von den drei Polen der
Substitutionen Tj, Tg, T3 und den beiden bezüglich der ©(g) äquivalenten Ecken
0) =:r -f- 5 -|- *■ herrühren. Zufolge (5) S. 115 liegen sie also in den drei
Nullpunkten der ganzen Funktion (ö^ _|_ 3 <j2 _|_ g ^ _|_ j g^ ^^^^ ^^^^ ^ __ 5^
Auf Grund bekannter Sätze notieren wir sogleich das Ergebnis: Zur
Kongruenzgruppen fünfter Sl;ufe @[^L und ©[^g^. 133
Darstellung der FunMionen def Gruppe ^(lo) ^cä, man zu 6 die folgende
Quadratwu/rzel zu adjungieren:
(3) y(ö_5)(<53-f 30^^80 + 16).
Die Gruppe ®(jo) liat als Teiler der Modulgruppe (
den Lidex 15
der Fig. 18 in das Dreiecksnetz der (3^'"\ sq gelangt man zu iem aus
Fig. 19.
15 Dreieckspaaren zusammen »e setz ten E)B der Fig. 19. E^ ist nun die-
@(^5) ein Teiler des Index 3 in einer von jepen fünf konjugiertem
Kongruenzgruppen fünfter Stufe i^erhalb der ]^odulgruppe, die die
Resolvente fünften Grades der Ikosaedergleichung:
(4) J: (J — 1) : 1 = (v^ — 11.' + 64) {V — 3)^
:v{v^ — 10v~\-4:6f
:— 17l>8
liefern *). Wir suchen nun eine bestimmte ui^ter den fünf Wurzeln dieser
Gleichung als Funktion v(co) von a aus, indem wir den ai;f der ikosa-
edrisch geteilten Kugel gelegenen Berßicli der Fig. 7 S. 59 4uf (\eii
Flg. 20.
in Fig. 20 dargestellten DB einer
der fünf konjugierten Kongruenx-
gruppen @(^) übertragen,
der Fig. 20 mit U^, U^, L\
zeichneten Substitutionen sind:
(3)
zu denen dann noch die in der Figu;- nicht näher angegebene Substitution
TJ^ = ( ' ^] tritt. Man zeigt sofort das Bestehen der Gleichungen:
(6) F, = U,- L\, Fa = U, ■ U^, V, = U,-U,- U„ T, = ^l
die die Gruppe @j3) üi der Tat als Teiler der ®'l^] charakteiisieren.
*) Es handelt sich um die (ileichung (6) S. 61. Die damalige Große Z is;t
als Funktion von m die Modulfunition erster Stufe J(«), die Unbekannte ? der
Gleichung werde als Modulfunktion durch v{ip) bezeichnet.
134 Ii 5. Bring sehe Gleichung fünften Grades.
Wir haben nun in v eine dreiwertige und in 6 eine zweiwertige
Funktion der Gruppe ©["s), so daß zwischen v und 6 eine algebraische
Relation bestehen muß, in der v auf den zweiten und ö auf den dritten
Grad ansteigt. Zur Aufstellung dieser Relation benutzen wir zunächst
die Tatsache, daß v und ö nur zugleich unendKch werden, namKch in
den Spitzen des DB. Schreiben wir die Relation als kubische Gleichung
für ö, so ist der Koeffizient des Gliedes mit ö^ konstant und kann gleich 1
genommen werden. Ebenso ist, wenn wir die Relation als quadratische
Gleichung für v schreiben, der Koeffizient des höchsten Gliedes konstant.
Weiter benutze man die Tatsache, daß die beiden Stellen mit ö = 0 von
den Punkten a =z -j^l ~^ i, C)=4;2-i-^ herrühren, denen die beiden
Nullpunkte der Funktion {v^— 10«? -f 45) entsprechen. Diese Angaben
liefern den Ansatz;
(7) 6^ -^{avA^ ß) ö^ ~f (a«) -f &) 0 ~f c {v^ — 10«) + 45) = 0.
Zur Bestimmung der fünf noch unbekannten Koeffizienten setze man
die Reihenentwicklungen:
f ö = -g~5-fl_2gö-f 4g5-7gf-12go-^ *-4g^-i ,
^^^ _1 2 4
\ V =z -ci 5 -|_ 4 -f 6 gs _ 20 gö -j
ein, deren erste aus (3) S. 118 bekannt ist. Die Reihe für v muß nach
Potenzen von q^ fortschreiten und mit der (— l)*^'* Potenz beginnen.
Man setze sie mit unbestimmten Koeffizienten an, trage sie in (4) ein
und fordere, daß die Reihe für J{a) gewonnen wird [vgl. (18) S. 89].
So gewinnt man die in (8) angegebenen Anfangsglieder. Trägt man die
Reihen (8) in (7) ein und ordnet nach ansteigenden Potenzen von g^, so
muß, da eine in o identische Gleichung vorliegt, der Koeffizient jeder
Potenz verschwinden. Hieraus ergeben sich lineare Gleichungen zur
Bestimmung der unbekannten Koeffizienten «, ß^ a, h, c. Man gelangt zu
folgendem Ergebnis: Zwischen den amgesueUen WurseJn 6 und v unserer
beiden Gleichungen fünften Grades besteht die jRelatiou:
(9) ö3 _ (.^ _ 1) ^2 ^ (3 ^. _ 21) ö _ (^.2 _ 10«, -f 45) = 0,
oder hei Anordnung nach Potenzen von o:
(10) v^ -!_ (ö2 _ 3ö _ 10)^. _ (ö3 ^ 02 _ 21 ö _ 45) 3= 0.
Eine Bestätigung des Ergebnisses entnehmen wir aus dem Umstand, daß
von den drei Stellen mit v = 0 eine bei o = + 5 -f- i liegt, wo ö = 5
gilt, während die beiden anderen bei co = i zusammenfallen. Der kubische
Ausdruck in der letzten Klammer der Gleichung (10) muß also das
Produkt von (ö — 5) mit einem Quadrat sein. In der Tat gilt:
6^ + d^ — 21 ö — 45 = (0 — 5) (ö -j- 3)2.
Bring sehe Gleichung und Resolveiite fünften Grades der Ikosaedergjeichung. 135
Eiae weitere Bestätigung Kefert die Lösung der Gleichung (10) naclfi v,
bei der sich die IrrationaKtät (3) einfinden muß Man erhält -vp^irkljch:
(11) 2 «) = — ö^ ~f a ö ~f 10 :^ V(ö -- o) (ö^Ts 0=^ ^ 8 (j + 16).
Die Transformation (11) führt die mit der Bring sehen Gleichung nahe
verwandte Gleichung (5) S. 115 in die ResoVvente fünften Grades (4) der
IkosaedergJeichung über, wobei die beiden ^Parameter- K und J der
Gleichungen durch die Relation (17) S. 107 verj:f^m^ft bind, die nach J ßuf-
gelösi so laufet:
(12) 3V = (2'K'- - 2 .3-^ • 23 £• -f 3^ ± (2' K-2- 3^) V^(X - 1).
Die direkte Bestätigung dieser Angabe kann man auch in der A.rt
vornehmen, daß man in (12) rechts der Gleichung (5) S. 115
entsprechend :
einträgt. Das Ergebnis läßt sich dann nach der nötigen
Zwischenrechnung in:
— 2° • 1728 / = ((2 vf— 22 (2 v) + 256) (2 c — 6)^
umformen, unter "Iv den Ausdruck (11) in ö verstanden. Dß;mit ist aber
die Gleichung (4) erreicht.
§ 13. Beziehung zwischen den beiden Resolveriten sechsten Grades.
Es möge auch noch kurz die entsprechende Entwicklung für die
Resolvente sechsten Grades (5) S. 129 der Bringschen Gleichifng und
die Resolvente gleichen Grades (3) S. 69 der Jkosaedergleich^g
angegeben werden. Schreibt man die in der letzten Gleichung auftretenden
Größen Z und | als Modulfunktionen / (p) und w (ca), so lautet die
fragliche Resolvente:
(1) /: (/— 1) : 1 = (w^ — lOw^ of
: (w' — 22 m: i- 125) (iv' —Apo— ly
: —1728 m:.
Der Aufstellung der Gleichung (5) S. 129 lag ein Teiler @(e) des
Index 6 der Gruppe ©<-) zugrunde, dessen DB pi Fig. 17 S. 128
dargestellt war. Die in jener Figur durch die Bezeichn^ingen L\, U^, • •
charakterisierten Substitutionen der ®(^ sind
Die @(p) enthält ^-Substitutionen beider Typen (vgl S. 100) Ihre
Substitutionen des zweiten Typus (1) S. 100 liefern einen Xormalteiler des
136
I, 5. Bringsche Gleiclimig fünften Grades.
Index 2, der also als Teiler der @^'^ durch ®§) zu bezeichnen ist. Seinen
DB gibt Fig. 21. Die durch die Pfeile näher bezeichneten Substitutionen
Fj, Fg, ••• sind:
: ü, = ('' f'\
Auf 0) umgerechnet haben wir hier die Substitutionen:
^U.
_( 9, 4'
, —37
-5, —3/
In dieser Gestalt liefert die ©(Jo) den Durchschnitt der @[g| mit der
Modulgruppe @ und ist als deren Teiler ©[^g) zu nennen. Die Eintragung
des Dreiecksnetzes der (^('") liefert den in Fig. 22 dargestellten DB der
@(^8)- Sie ist zugleich ein Teiler des Index 3 der durch y = 0 (mod 5)
charakterisierten Kongruenzgruppe fünfter Stufe, zu der die Resolvente (1)
der Ikosaedergleichung gehört.
Die zu den hier bevorzugten Gruppen gehörenden Wurzeln % und
w der beiden Resolventen sind als Funktionen der (
) zwei- bzw.
dreiwertig und sind deshalb wieder durch eine algebraische Relation
verbunden, in der r auf den dritten und w auf den zweiten Grad ansteigt.
Hier genügen bereits die Anfangsglieder der Reihenentwicklungen und
die Betrachtung der Werteverteilung unserer Funktionen im DB zur Ge-
Beziehung zwischen den beiden Resolventen sechsten Grades.
137
winnung der Relation. Wir notieren sogleich d^s Resultat: Die Ijeiden
ausgewählten Wurzeln r uvtd w der Gtleichungen sechden O-rades sind dtifch
die JRelation dritten G-rades:
(2) T^ +t^W -^OTW ^ W^ = 0
aneinander gebunden.
Die Verhältnisse gestalte;^ sich hier deshalb besonders einfach, weil
der DB der Fig. 22, wie man sieht das GrescMecM p == 0 hat. In der
Tat haben wir auch in (2) eine Relation des Geschlechtes 0. Deiften ^jpir
T und w als rechtwinklige Koordinaten, so liefert die Grleichung (2) eine
ebene Kurve dritten Grades wdt einem Doppelpunld inq. Xullpunl^t. jße-
kanntlich gewinnt man in diesem Falle eine einwertige Funktion X mittels
der Gleichung:
(3) m; +- A T =r 0,
d. h. geometrisch gesprochen, indem man die Kurve dritterji Grades rp.it
dem Geradenbüschel durch den Doppelpunkt schneidet. In X müssen
dann w und r rational darstellbar ^ein. In der Tat findet man aus (2)
und (3) sofort:
(4) w^ AHA-o) __Hl-o)
l~l
l — l
Für die Überführung der einen Gleichung sechsten Grades in die
andere vermöge der durch (2) gegebenen Transformation bedient man
sich zweckmäßig der Vermittlung der Größe X, während man andererseits
zwischen J und K die S. 103 eingeführte Funktion Q — ^
in der sich / und K nach S. 106ff. so darstellen:
einschaltet.
(5)
/ =
27 ö '
K =
138 ^, 6. Allgemeine Gleiclimig fünften Grades.
Man kann dann nämlich die leicht feststellbare Darstellung sechsten
Grades von Q in. k:
(6) ^:(^ + l):l = ß- ly ß~ 6): ß' ~2l -i- 6){k^ ~ 4.k- If :Q4:k
als Ausgangspunkt nehmen und aus ihr auf Grund von (4) und (5) die
beiden Gleichungen sechsten Grades herstellen. Erstlich folgt aus (6)
und (4):
16A(4^i- 1) == ß — lfß~6) + 16 A
= A* (A - 5)2 + 10 AHA - 5) (A - 1) + 5 (A - l)^
16A(4^+1) = (^iv'^10w-^o)ß — iy-,
(16kf-27Q = 64.27AHA —1)'(A —5) = — 1728wß — l)\
womit durch Vermittlung der ersten Gleichung (5) die Resolvente (1)
erreicht ist. Weiter folgt aus der zweiten Gleichung (4):
ir'-r^t + 25) ß — lf = ß^~2X^ o)\
(r+ 1)(A —1) = k^ — 4:X — l,
woraus man auf Grund von (6) weiter entnimmt:
(64 A)H« + 1)' = (t'-^ 61 + 25) (r + 1)*(A - 1/.
Teilt man diese Gleichung durch die wieder aus (6) und (4) folgende
Gleichung:
(64^)^4^ == 26Qtß — lf,
so gelangt man zufolge der zweiten Gleichung (5) zur Resolvente sechsten
Grades der Bring sehen Gleichung.
Sechstes Kapitel.
Allgemeine Gleichung fünften Grades.
§ 1. Allgemeine Gleichung und Hauptgleichung fünften Grades.
Xach I, 391 ist das Ergebnis der Galois sehen Theorie für die
allgemeine Gleichung fünften Grades in dem einfachen Satze enthalten, daß
bei Zugrundelegung des Funktionenkörpers, der aus dem rationalen
Körper durch Adjunktion der Gleichungskoeffizienten entsteht, die Galois-
sche Gruppe der Gleichung die symmetrische Permutationsgruppe (^^^o
ist, daß jedoch nach Adjunktion der Quadratwurzel der Diskriminante
die Galoissche Gruppe sich auf die alternierende ©g^ reduziert. Es ist
aber hiermit das Interesse an der allgemeinen Gleichung fünften Grades
keineswegs erschöpft. Wir haben in den vorangegangenen Kapiteln eine
ganze Reihe von Gleichungen fünften Grades betrachtet, sowie ihre
Beziehungen zueinander und zu ihren wichtigsten Resolventen untersucht.
Das gemeinsame Kennzeichen aller dieser Gleichungen war, daß sie je
Hauptgleichung funftei^ Grades und Ha^iptflaohe. ] 39
nur einen einsigen willkürlich wäMbare^ Parameter enthalten. Die ^1-
gemeine Gleichung fünften Grades hat, selbst weni^ wir den Koeffizienten
des höchsten Gliedes gleich 1 nehmet^ und vermittelst der Transformation (1)
in I, 165 den Koeffizienten des zweiten Gliedes verschwinden las&en,
immer noch vier willMrliche Parameter. Wird es vielleicht möglich
sein, die Anzahl dieser Parameter durch Tschirnhaustra^sformation weiter
zu reduzieren und schließlich sog^r die allgemeine Gleichung auf die
behandelten und durch transzendente Prozesse gelöstep Gleichungen der
vorigen Kapitel zurückzuführen?
Wir schreiben die allgepaeine Glejchung fünften Grades mit Bino-
mialkoeffizienten:
(1) x''i-lOax^-\-10hx^-i-6c.-j-d = 0,
wobei der Koeffizient des höchsten Gliedes gleich 1 genonunen ist und
das zweite Glied durch die eben schon genannte Transformation zum
Ausfall gebracht wurde. Die ^Koeffizienten a, h, c, d gelten ajs willkürlich
wählbare Parameter. Wir nehmen die S. ]21 bereits in Benutzung
genommene, von Klein eingeführte geometrische Deutmig der fünf an die
Bedingung:
(2) x^ ~f x^ -f x^^ x^-\-x^ = 0
gebundenen Wurzeln X]^ von (J.) als homogene Pentaederkoordinaten des
Raumes Rg von drei Dimensionen wieder auf. Die x-j^ sind algebraische
Funktionen der vier Parameter ß, h, e, d. Dem einzelnen System
von Werten dieser Parameter gehört alsdann ein bestimmter Punkt
X;^ =:r «^ des Rg ZU oder vielmehr, da die Reilienfolge der Wurzeln irgepd-
wie abgeändert werden mag, ein System von 120 Punkten des Rg, die
durch die 120 Vertauschungen der ocjc, also durch 120 ßine ©jg^ bildende
Kollineationen des Rg ineinander übergehen*).
Ist insbesondere auch noch der Koeffizient a gleich 0, so liegen
diese 120 Punkte auf der durch die Gleichung:
(3) x'o + x! -h xl + xl -^x!=0
gegebenen Fläche zweiten Grades, die Klein ^,ls „HaajfAflaehe"
bezeichnet, und die durch die 120 Kollineationen in sich transformiert
wird. Entsprechend heißt eine Gleichimg fünfte^ Grades (1) mit
verschwindendem a eine Haaptgleichung füniten Grades.
Es wird sich nun zunächst darum handeln, die allgßmeii^e
Gleichung (1) in eine Hauptgleichung zu transformieren. Damit in der
transformierten Gleichung sich nicht wieder ein Glied mit der vierl^en
Potenz der Unbekannten einfindet, hat man die Tschimhaustransformation
nach I, 167 in der Gestalt:
(4) x' = t, F, (x) -f t, F, (X) -t t, F, (x) -f t, F, {x)
=^) Vgl. hier überall „Ikos.", S. 162 ff.
140 I> 6. Allgemeine G-leichung fünften G-rades.
anzusetzen, wo die Bedeutung der Fq{x), F^(x), •-• aus (6) in I, 167
hervorgeht. Um zu einer Hauptgleichung zu gelangen, muß nach I, 180
die Bezoutiante verschwinden. Das ergibt eine quadratische Gleichung
für die t. Von diesen vier Größen können dabei noch drei willkürlich,
jedoch nicht durchweg verschwindend gewählt werden, woraus alsdann
die vierte Größe noch wunschgemäß aus einer quadratischen Gleichung
bestimmbar ist. Da nun die F^^ix), F^(x), ••• Funktionen steigender
Grade sind, so wird man die einfachsten Verhältnisse erzielen, wenn man
tf^ = 0, t^ = 0 setzt und t^ gleich einer von 0 verschiedenen Konstanten,
etwa gleich dem Koeffizienten 10a wählt. Schreiben wir also:
a, = t,F,{a,)-^10aF^{a,)
oder ausführlich:
(5) «^ = ^3 «i -f 10 a («1 -f 4 a), jt = 0, 1, • • ■, 4,
so beschreibt, geometrisch gesprochen, der Punkt «^ bei gegebenem
Punkte oCjc und noch willkürlichem ^3 eine durch den Punkt oci laufende
Gerade, die die Hauptfläche in zwei Punkten schneidet. Sie entsprechen
den beiden Werten ^3, die durch Lösung der vorhin genannten Gleichung
zweiten Grades für die t gewonnen werden.
Die zu lösende Gleichung zweiten Grades ist nun;
2 O3«i-+10«(«l + 4a))^ = 0
1 = 1
oder, wenn wir links die Quadrate entwickeln und die Potenzsummen
der «j. durch die Koeffizienten der Gleichung (1) nach L 102 ausdrücken,
sowie den überflüssigen Faktor — 20 a fortheben:
(6) ^2+ 30 6^4-100a (c~6aä) = 0.
Die beiden Lösungen, unter denen t frei wählbar ist, sind:
(7) ^ =—156 + 5 V24a3—4ac + 9&^
Der Radikand der hier auftretenden Quadratwurzel ist bei unabhängigen
Variablen a, h, c nicht das Quadrat eines rationalen Ausdrucks dieser
.Größen. Wir haben also das folgende Ergebnis gewonnen: Die allgemeine
Gleichung fünften Grades (1) ist nach AdjunJdion der Irrationalität:
(8) V24a3 —4ac +96ä
£um Körper (pi, a, h, c) mittels der Tschirnhaustransformation:
(9) x' = tx-^10a{x^ -}-4:a),
unter t eine der Größen (7) verstanden, in eine Hauptgleichung:
(10) a;'^+ 10 6'a;'ä-f 5 c'»'-f (?' = 0
üherführhar.
Es ist leicht zu zeigen, daß die Quadratwurzel (8) eine „akzessorische'-
Irrationalität der Gleichung (1) ist (vgl. I, 380). Anderenfalls wäre sie
Akzessorische Quadratwursiel zur Gewinnung einer Hafiptgleichung. ]41
eine rationale Funktion der Wurzeln « und müßte als solche, da sie
gegenüber den Permutationen der Wurzeln sich, abgesehen vom
Vorzeichen, reproduziert, zu einem Xorm^lteilßr der @ ,q gehören. Der
einzige solche Teiler aber ist die alternierende ©g^, und also w]irde die
Wurzel (8) durch die Koeffizienten und die Quadratwurzel der Diskripii-
nante rational darstellbar sein, und zwar insbesondere das Produkt der
Wurzel der Diskriminante mit einer rationalep Funktion der Koeffizienten
darstellen. Bei der Bauart der Warzel (8) ist dies ausgeschlossen, ^ie
ein Vergleich mit der in § 2 anzugebenden Diskriminante der
Hauptgleichung lehrt.
Übrigens folgt aus (o):
l[(.<^:-oc',) = l[{ci,-a,)- n (^+10a (c^,+ «,)),
i<k Kk i<k
WO das zweite Produkt rechter Hand eine symifnetrische Ifunktion (ier
Wurzeln ist. Hieraus ergibt sich der Satz: Die Quadfatwurzel der Dh-
kriminante der HauptgJeichmig (10) ibt, abgesehen von einem FaMor, der
eine FmiMion des Körpers (9?, a, b, p, V24 a^ — 4 <? c -j- 9 6^) id, gleich ^er
Quadratwurzel der Diskriminante der ursprünglichen Gleichung (1). Dies
ist mit der Gleichung (37) in I, 172 in rbe:peüistimmimg.
§ 2. Zwei Scharen von Hat^ptgleichuitigen als Resolventen.
Die erhaltene Hauptgleiohung fünften Grades schreiben w:|r unter
Fortlassung der oberen Indizes:
(1) »° 4-10Z>»2 ^-5cic-f f/= 0,
die zugehörigen Funktionen Fj^{x) sind:
(F,{x) =x,
I F, {x) = »^
^^^ ^ F^{x) =x^^&b,
. F^{x) := »*-f 10 6» +4r.
Wir fragen jetzt, ob es möglich ist, eine weitere Tschirnhaustransformation:
(3) X = t, F, (X) ^ t, F, (X) -t-1^ F, (x) -f t, F, {x)
in der Art auszuüben, daß die transformierte Gleichung eine
Hauptgleichung bleibt. Die Bezoutiante liefert nach I, 180 den mit — 2
multiplizierten Koeffizienten 10 a' der dritten Potenz der Unbekannten
in der transformierten Gleichung:
(4) — 20a' = '^B^i.t^tj,, i, k = 0, 1, 2, 3,
i,k
wobei Bii = Bj^^ gegeben ist durch:
(5) B,,= ^F,^^iui)F,^,{ai), z = 0, l, ...,4,
142 I' 6- Allgemeine Gleichung fünften G-rades.
unter a^, w^, •••, a^ die Lösungen der Gleichung (1) verstanden. Als
symmetrische Funktionen dieser Wurzeln drücken sich die Bi^ rational
in den Koeffizienten &, c, d der Gleichung (1) aus:
( B,, = 20 (cä -hd), B,, = SOhc, B,, = ^33 = 0,
(6^ I 5^3 = B^^ = —od, £„ = 120&^
[ ^13 = B,,= - 20c, B,, = - 80 6,
so daß wir aus (4) für 2 a gewinnen:
Xach (7) in I, 181 i&t die fünffache Diskriminante j JS^/, , 'der
Bezoutiante gleich der Diskriminante der Gleichung (1). Es ergibt sich
hieraus beiläufig der Satz: Die Dishriminante D der Hauptgleichung (1)
ist gegeben durch:
( D = o^id"- -{- 360 Vcd^ — 640 hc^d^ 256 c^ -r 3456 l^ d
^ ^ \ — 2160 Z^* 6-2).
Es ist nun leicht, zwei Scharen von Transformationen (3)
vorschriftsgemäß herzustellen. Wir bedienen uns zum Verständnis der hierhin
führenden Überlegung der S. 139 eingeführten geometrischen Deutung
von fünf Größen einer verschwindenden Summe als „Pentaederkoordinaten"
im Räume R3. Den einzelnen Punkt der Koordinaten x^, x^, x^, x^, x^
bezeichnen wir kurz durch das Symbol {xj^. Da x^ stets gleich der
negativ genommenen Summe der vier ersten Koordinaten ist, so könnten
wir uns auch auf diese beschränken, in denen wir dann gewöhnliche
homogene Raumkoordinaten haben.
Es ist nun zunächst einleuchtend, daß die vier Punkte {F^ {o''i)) =^ (^i-)'
{F^ {a.])), (F^ (a^.)), (F^ («^5.)) nicht in einer Ebene liegen. Es wären sonst
die vier Systeme zu je vier Zahlen:
F,{a,), F,{a,), F,{a,), F,(a,), i = 0, 1, 2, 3,
im Sinne von I, 69 linear abhängig, und also würde die Determinante
Fl («i) gleich 0 sein. Dann aber wären auch die vier Systeme:
■Fo (cci), F^ («i-), F^ («;.), F^ («i-), k = 0, 1, 2, 3,
linear-abhängig, d. h. es gäbe vier nicht durchweg verschwindende Zahlen
c'q, c\, c'.2, C3, für die die Gleichungen:
c; J'o («i-) + c;F^ («,) + c; F^ {a^) + c,F^ («,) = O, k = 0,l, 2, 3,
gelten. Dieselbe Gleichung für /,; = 4 wäre eine Folge der drei
vorstehenden Gleichungen*), und wir hätten in:
c; F^ {x) -f 6-; F^ {x) -r 4 F^ ix) -f 4 F^ (X) = 0
'^) Dies folgt mit Rücksicht auf die Gleichungen (9) m I, 102 aus der
allgemeinen Erklärung der, Funktionen F durch die Gleichungen (6) m I, 167.
Zwei Scharen von Ha^ptgieichungen. ]43
eine nicht identisch verschwindende Gleichung höchstens vierten Grades
mit fünf Lösungen a^, a^, •••, a^, was. solange D zjn 0 gilt,
ausgeschlossen erscheint. Wir nehmen demnach D d:: 0 au unci ziehen noch
die Folgerung, daß von den vier Punkten (^^(ajr;)), • • •, (F^(oci)) keine
drei in einer Geraden liegen.
Wir schreiben nun für die vier unbestimmten Größen t in (8):
^3 =:: t, t^ = bZ^, tj^ = bZ^, t^^ := ^Zq
und führen die Abkürzungen ein:
(9) F, {X) = 0 (^), z, F, {X) -T- z,F, (X) -rv,F,ix)=r W {x\
indem wir uns die Verfügung über r,, r,, r^ vorbehalten. Die Tschirn-
haustransformation ist dann:
(10) x = t ^ {X)-^ bW {x).
Sind die t bestimmt, während die t, b noch variable Parameter bind, so
beschreibt der Punkt:
(11) {x[) = {tQ{u,)--bW{u,))
eine durch den Punkt (0 (a^) = (cC]^ iiindurchlaufende Gerade. Diese
Gerade muß, falls die Transformation (10) stets wieder zu einer
Hauptgleichung hinführen soll, auf der Haupti'läche liegen. Durch den Punkt
(ay) aber laufen zwei Gerade der Hauptflache, die durch die
Tangentialebene des Berührungspunktes («jt) ausgeschnitten \v'erden. Es müßte aiso
der Punkt (^Jf (a^)) ein von («jt) verschiedener Pupkt auf der einen oder
der anderen dieser beiden Geraden sein. Xun beschreibt aber der Punkt:
(12) (?jr («,)) = (r^ F^ («,) + z, F, («,) -r ToF, («,))
bei variablen Parametern r die durch die drei Punkte (J^'j («/:)), (Z'2 («/)),
(J^3 («j;)) hindurchlaufende Ebene, die, wie \7ir wissen, den Punkt («;)
nicht enthält. Diese Ebene schneidet die Hauptflache in einem
Kegelschnitt, und auf diesem wird durch die Tangentialebene des Benihiungs-
punktes (uf) ein Paar von Punkten ausgeschnitten, von denen ]eder als
Punkt (W {ci];)) brauchbar ist. Wir bestimmen demng-ch die z derart,
daß den beiden Bedingungen:
(13) 2 ^ K) ^J^'K) = 0, S ?f {a,f = 0, A- :== 0, 1, .. -, 4,
k k
genügt wird, von denen die erste zum Ausdruck bringt, daß der Punkt
(W («/,)) auf der genannten Tangentialebene der Hauptflache liegt, wahrend
die zweite besagt, daß dieser Punkt der Hauptjlache angehört. Da
^ 0 {Ukf' = 0 gilt, so ist auch unmittelbar einleuchtend, daß die
k
zweite Potenzsumme der:
unabhängig von 0 und i verschwindet, falls die beiden Bedingungen (18)
erfüllt sind.
144 I> ö. Allgemeine Gleichung iunften Grades.
Diese Bedingungen schreiben sich nun explizite:
wo die Bii: die in (6) angegebene Bedeutung haben. Hieraus bestimmen
sich die Verhältnisse der z mittels einer Quadratwurzel. ]klan gibt der
Rechnung zweckmäßig die folgende Fassung: Zur Abkürzung setzt man:
-^00^0 -r -^10^1 + -^20^2 = -^0'
-Boi ^0 + ^11 ^1 ^ -^21 ^2 = -^1'
-^02 ^0 + -^12 ^1 + -^22 ^2 =^ -^2'
SO daß man die beiden Gleichungen (14) auch so schreiben kann:
( ^03-^0 + ^'13-^1 + ^23-^2 = ^.
^ ^^ \B,z, + B, z, -\-B,z,^ 0.
Mittels einer zunächst noch unbestimmten Gröi3e z^ stellen wir hieraus
die Gleichung her:
(16) {B, + z,B,,)z, 4- {B, + z,B,,)z, -f (^2 + r,B,,)r, = 0
und dürfen die zweite Bedingung (15) durch die Gleichung (16) ersetzen.
Diese Gleichung lösen wir durch die Annahme:
(17) ^,4-r3^o. = 0. B^-\-r,B^^ = 6z,, B,-r z,B,, = - 6z„
die wegen der noch verfügbaren Gröi3e z^ statthaft ist, und in der 0 eine
weitere noch zu bestimmende Gröi3e bedeutet. Die drei Gleichungen (17)
und die noch rückständige er&te Gleichung (15) ergeben zur Bestimmung
der z die Bedingungen:
( ^00 ^0 + ^lü T^i -t -B20 ^2 + -^30 ^3 = 0-
n Q^ ^01 ^0 "^ ^11 ^1 ^ *^^'2i — ö) ^2 ^ J^3i ^3 = 0,
.(lo) <j
-^02^0 — (-^'12 — 6)ri -f -BaaTa -!- B^.^z^ = 0,
l^^ostTo 4-^,3^, -i'23^2 = 0.
Damit diese Gleichungen ein System nicht durchweg verschwindender
Lösungen Zq, T■^, z.-,, z^ besitzen, ist das Verschwinden der vierreihigen
Determinante erforderlich:
(19)
Hier haben wir eine quadratische Gleichung für ö, und zwar eine reine
quadratische Gleichung, da nach Austausch der Zeilen und Spalten wegen
■Bit = -Btj ^ür — 6 dieselbe Gleichung gewonnen wird. Da für 0 = 0
^00-
^01.
-^02"
i' ,
Ao> -^20-
^n- -Bai —ö,
^12+ ö- ^22-
i.',,, 5,3 •
J^3
i^3
^3
0
Charakter der a djun gierten Irrationalitäten. 3 45
in (19) links die Diskrimiaspite der Bezoutiante vorliegt, so ist die
quadratische Gleichung für 6:
und wir
(20)
finden
zufolge
(6)
-Sl6'-^\P=^
0,
als die beiden Werte
'' = ^^5d-
von
ö:
Xach Eintragung des ausgewählten Wertes von 6 in (18) lösen wir dies
Gleichungssystem, indem wir r^, r^, z^ ^ß^ drpi richtig gewälilten Minoren
der Determinante (19) gleich setzen. Die berechneten r gehören dem
Körper (M, h, c, d, '^o D) an, während (; und s als verfügbare Parameter
bestehen bleiben.
Hiermit ist folgender wichtige Satz gewonnen: Nach Ädjmikt}on
der Quadratwurzel aus der f'unffacJim DibJcriminante der Gleichung (1)
oder der arsprünglichen Gleichung (1) S. 139=^) loann man mitteh der
Transformation (10) zwei Scharen pon Tschirnhauprebolventew der
Hauptgleichung (1) herstellen, die wieder Hauptgleichungen s^ind; hei ^eichen-
wechsel von \ö D gehen diese lieiden Scharen ineincmder uher.
Die erste oben adjungierte Quadratwui zel (8) S. 140 erwies s:tch
als akzessorisch. Über die zweite nunmehr adjungierte Quadratwurzel
\oD ist folgendes auszusagen* Wahrend der Faktor VD hehßnnfV^h eine
„naturliche- Irrationalität ist, stellt Vo eine „nfimensche" Irrationalität dßr,
die fur die ~allgemeine^ Gleichmig fünften Grades „ahzessoriSich" ^st.
Wäre nämlich V5 im Galois sc hen Körppr (d^t, cc^, a^, ••, «J der
Gleichung (1) enthalten, so würde diese Zahl zur alternierenden ^^^ gehören,
und man würde nach dem Lagrangeschen Satze (vgl. I, 391) eine
Darstellung :
Vs" := B (h, c, d) y^
von \6 haben, unter B eine rationale Funktion pait rationalen
Zahlenkoeffizienten verstanden. Der Vergleich mit Gleichung (8) zeigt, daß Vö
btets und nur dann eine natürliche Irrationalität der I-Jauptgleichang (Ij
ibt, wenn der Ausdruck:
(21) d"" -^ SQOh^cd^ — e^Ohc^d + 256 6-^ -^ MßQh^d—21ß0h^c^
das Quadrat eines rationalen Ausdrucks dcf i>, c, d mit ratimialen ^ahlen-
loeffizientm ist. Bei willkürlich variablen h. c, d ist dips niciht der Fall,
womit der ausgesprochene Satz bestätigt; ist. Im übrigen ist die ebpn
ausgesprochene Bedingung für die Natürlichkeit von ]/ 5 bei denjenigpn
Hauptgleichungen erfüllt, die wir S. 64ff als Resolventen fünften Grades
der Ikosaedergleichung kennenlernten. W^r erkannten ^uch bereits
"=) Vgl. den Schlußsatz von § 1, S. 141.
icke, .\lgebra. II.
146 I» 6- Aligemeine Gleichung fünften Grades.
S. 67 in Vs eine natürliche Irrationalität jener Gleichungen. Setzen wir
z. B. der Gleichung (11) S. 64 entsprechend:
h = — 4:2^, c = (px, d = — (f^,
so zieht sich der Ausdruck (21) in das folgende Quadrat zusammen:
y« -f 2 .123 ^5 ^5 ^ 12« ^2 x'' = <P' (<P' + 12' ff-
§ 3. Bring sehe Gleichung als Resolvente der allgemeinen Gleichung
fünften Grades.
Die beiden Scharen von Hauptgleichungen, die wir als Resolventeu
der allgemeinen Gleichung fünften Grades gefunden haben, entsprechen
im Räume R3 den Punkten zweier auf der Hauptfläche gelegenen Geraden,
die sich in demjenigen Punkte dieser Fläche überkreuzen, der durch die
Wurzeln der Gleichung (1) S. 141 geliefert wird. Wollen wir dabei nur
solche Hauptgleichungen zulassen, die keine neue Adjunktion nötig
machen, so werden freilich die beiden Parameter s und t der
Transformation (10) S. 143 dem bisher erreichten Körper entnehmen müssen.
Dagegen ist über die beiden bisher adjungierten Quadratwurzeln
hinaus eine weitere Adjunktion erforderlich, wenn wir eine
Hauptgleichung aus der einzelnen Schar aussuchen wollen, bei der auch noch
die dritte Potenzsumme der Wurzeln verschwindet. Diese Forderung
liefert für das Verhältnis der Parameter t, s die kubische Gleichung:
(1) 2(^^K-) + s^M' = o,
k
deren Koeffizienten nach der nötigen Ordnung Größen des Körpers
(9?, ü), c, d, \oD) sind*). Diese kubische Gleichung hat, wie wir später
sehen werden, eine Galois sehe Gruppe (^g. Zur Gewinnung einer Be-
solvente der Gestali:
(2) a;'^+ 5c'a;' + (^' = 0,
d. h. also einer „Bringschen Gleichung-', ist die weitere AdjunUion einer
Quadratwurzel und einer KuUkwurzel erforderlich.
Geometrisch ist der Sinn dieser Entwicklung einleuchtend. Der
durch die. Wurzeln einer Bringschen Gleichung gegebene Raumpunkt ist
neben der Hauptfläche auch noch auf der „Diagonalfläche- (vgl. S. 123):
(3) xl -h x't + xi ~f xl + a;| = 0
und also auf der „Bringschen Kurve^ (vgl. S. 121) gelegen. Diese Kurve
wird in der Tat von jeder Geraden der Hauptfläche in drei Punkten
geschnitten, wie sie in unserem Falle den drei Lösungen der kubischen
Gleichung (1) entsprechen.
=^) Man vergesse nicht, daß in den Koeffizienten b, c, d der Hauptgleicliung(l)
S. 141 bereits die erste akzessorische Quadratwurzel enthalten ist.
Hennitesche Losung der Gleichung fünften Grades. 147
Die Resolvente (2) läßt sich durch die lineare Transformation:
^ ' 5c' ' 256c*^
in die unter (12) S. 116 gewonnene Normalgestalt:
(5) ,;5_^(^^1^^, 0
der Bring sehen Gleichung mit einem einzigen „Parameter^ K überführpn.
Wir haben hiermit eine erste Art der „Auflösung^ der allgemeinen Glei-
chmig fünften Grades kennengelernt, wobei maq. beachteri wolle, daß
nach L 164 ff. mit der Auflösung einer Tschimhausresolvente stets auch
Wurzeln der ursprünglichen Gleichpug qls bekannt anzusehen sind. Die
Auflösung der allgemeinen Gleichung fünften Grades besteht in der
algebraischen BeduMion dieser ursprünglichen Gleichung fünften Grades mit
ihren fünf unbestimmten Koeffizienten auf die „einparametrpge^ GIeichmig(6);
wegen der Auflösung dieser Gleichung (^) hßben wir uns dann auf die
transzendenten Prozesse zu berufen, ße S-117 ff. beßprocfien sind.
Zu diesem Ergebnis war bereits 1858 Hermite in seiner oft
genannten Arbeit „Sur la resolution de l'equation du ciaquieme degre-'*)
gelangt. Seine Resolvente ist f reilicli niclit unmittelbar die Gleichung (5),
sondern baut sich als Bring sehe Gleichung etwas komplizierter aus dem
Jacobischen Integralmodul F und dem komplementären Modi(.l k'^ auf**).
Über W^ert und Bedeutung der bei Hermite zuerst a^ftretenden
„Auflösung der Gleichung fünften Grades du:pch elliptische Funktionen-' vgl.
man die Bemerkungen am Schluß des vierten Kapitels S. 99.
An der vorstehenden Entwicklung bleibt unbefriedigend, daß die
explizite Gestalt der kubischen Gleich^ng (1) bereit^ nicht mphr
angegeben wurde. Sie ist zwar durch Cayley wirklich berechnetj), hat
aber eine so umfängliche Gestalt, daß die ^veitere Verfolgung des
allgemein bezeichneten Entwicklungsganges in die Elinzelheitep der
Rechnung unersprießlich erscheint.
Endlich finde hier noch ejne Bemerkung über die Galois sehe Gruppe
der Gleichung (5) Platz. In den^ durch die bisherigen Adjunktionen
erreichten Körper ist die Quadratwurzel der Diskrin^inante der
Gleichung (5) nach (37) in I, 172 enthalten. Dagegen gehört diese
Quadratwurzel noch nicht dem Körper (dt, K) an und kann auch nicht durch
Adjunktion bloß numerischer Irrationalitäten erreicht werden, wie aus
der ersten Gleichung (7) S. 119 hervorgeht. Dem entspricht es, daß 4ie
Monodromiegruppe der Bring sehen Gleichung (5), wie schon S. 120
festgestellt wurde, die symmetrische ©jg^ ist.
=^) In den Compt. Rend., Bd. 46.
**) Vgl. „Ikos.", S. 148 oder „Ellipt, Funkt" II, 520. Vgl. auch oben
Gleichung (14) S. 116.
t) In der Abhandlung „On Tschirnh^usen's transforn^ation", Philosoph.
Transactions von 1861 oder „Gesammelte Werke", ]ßd. 4.
10*
148 I' 6. Allgemeine Gleichung fünften Grades.
§ 4. Diagonalgleichung fünften Grades mit einem Parameter.
Daß es möglich ist, ohne Lösung einer kubischen Hilfsgleichung,
d.h. ohne über den Körper {% h, c, d, VoD) hinauszugehen, zu einer
einparametrigen Resolvente zu gelangen, die gleichfalls enge mit den
elliptischen Funktionen zusammenhängt, ist bereits von Kronecker bei
seinen Untersuchungen über Gleichungen fünften Grades erkannt*).
Dieser Gegenstand hat vielfache Behandlungen gefunden und soll hier
zunächst nach einer Methode von Gordan**) dargestellt werden, die sich
am besten an die voraufgehenden Rechnungen von § 2 anschließt f).
Die fünf Systeme zu je fanf in § 2 betrachteten Größen: *
(1) 0(Di^f, 0(«,)^K), ^(ci,f, 0(«,), W{a^), i == 0, 1, ..., 4,
sind linear-abhängig (vgl. I, 7Iff.); denn die zugehörige fünfreihige
Determinante verschwindet, da die Summe der Elemente jeder Spalte
verschwindet [vgl. (13) S. 143]. Es gibt demnach fünf nicht durchgängig
verschwindende Größen L, M. N, m, n, für die die folgenden fanf
Gleichungen richtig sind:
(2) X0 ip^f + M^ (aO ^ (a,) + NWia,;f = m0 (a,) -^ nW(«^).
Zur Berechnung von X, M, N, m, n kann man aus dem entwickelten
Ausdruck von (2) die Potenzen af, aj, of, a^ mittels der Hauptgleichung
(1) S. 141 entfernen und gelangt so zu einer Gleichung vierten Grades
für jede der fünf Wurzeln a^, in der also jeder Koeffizient verschwinden
muß jj). Man findet auf diese Weise fünf Gleichungen, von denen zwei
die folgenden sind:
I Mr^ -f :V(3 crl + 12 b r^ r^ i- r|) — n r^ = 0,
^^'* I Mz^ -f X(— d xl — 2ez^r^^2h rf) — nr, = 0.
Aus diesen Gleichungen bestimmt man M, JSf, n als Größen des Körpers
Ä = (9^, h, c, d, VoZ>). Eine dritte der fünf Gleichungen erweist sich
vermöge der Relationen (14) S. 144 von den Gleichungen (3) abhängig.
Die beiden letzten Gleichungen drücken X und m in den schon
berechneten Größen M, X, n und mithin gleichfalls als Größen des
Körpers Ä aus.
Wir betrachten nun vorübergehend den Ausdruck
(4) L^'' -{-M^W -r NW
*) Brief an Hermite vom Juni 1858, veröffentlicht in (ien Compt. Rend.,
Bd. 46 und „Algebraische Mitteilungen" in den Berliner Monatsberichten von 1861.
=^*) „Über Gleichungen fünften Grades- (1886), Math. Ann., Bd. 28.
t) Man vgl. auch die Rechnungen, die Kiepert in § 8 seiner Abhandlung
„Auflosung der Gleichungen fünften Grades*', Joum. f. Math., Bd. 87 anstellt.
Weitere Nachweise folgen unten.
tt) Den Fall einer verschwindenden Diskriminante der Gleichung fünften
Grades dürfen wir als elementar beiseite lassen.
Herstellung einer Ihagonalgleiphung nach Gordan. 149
als quadratische Form mit unabhängig variabel gedachten 0, W. Diese
Form läßt sich auf vielfache Art als Aggregat zweier quadratischer
Glieder darstellen (vgl. I, 155 ff.). Eine bestimmte unter diesen Dar-
stellxmgen wird uns mit der auf die 3auptgleichung (1) S. I4I
auszuübenden Tschirnhaustransfonpaation versehen. Cm diese Darstellung
der Form (4) zu gewinnen, verstehen wir unter 0*, W zwei weitere
unabhängige Variable und bilden die identische Gleichung;
' ^ I 4(i0'2-f ilf0'?F'~f-.Y»p-'')(X^^-r.M"0^^A^«p-^)
unter 3 zi die Diskriminante ;
(6) ■ 3^ = Jf2_4^^
der quadratischen Form (4) verstß-nden '•^). Man trage hier 0' = n,
W' = — m ein und erkläre Jc^ 7 als zwei Größen des Körpers ^ durch:
(7) Ä; = 2 X « — Mm, J = Mn — 2NyH.
Die Determinante der vier Grqßen /.;, ?, m, n heiße ö:
(8) hp — lm ~ 8.
Aus (7) folgt dann für den ersten Klammerausdruck in (5) links:
Ln^—Mnm-^ Nwfi =^\8,
und man findet aus (5) als gewünschte Darstellung der Fon?i (4);
(9) 2 Ö(X02 -h M^W -f NW^) == {h0 + IWf -~3^(m0^ nWf.
Indem wir fortan unter 0 und W ^Jfieder unsere obiger^ Funktionen
verstehen, bauen wir aus den Basep der beiden iri (9) rechts stehenden
Quadrate die folgende Tschimhaustransformation auf:
und nehmen die Determinante $ zunächst von 0 verschieden an=^*). Die
Ausübung dieser Transformation auf die Jlauptgleichung (1) S. 141
liefere als transformierte Gleichung
(11) x'^ -f oa'x'^ + 106'a/3 _^ iQc'x'^ -4- od'x' + ß' == 0.
Ihre Wurzeln mögen durch a[ bezeichnet werden.
Xeben (11) führen wir noch zwei weitere Gleichungen fünften
Grades ein, deren Wurzeln durch:
(1'2) &^ = p=-, i =- 0, 1, .. •, 4,
*) Die Aufnahme des Faktors 3 hat den Zweck, die Schloßgleichung möglichst
einfach zu gestalten. Übrigens ist die erklari;e Gro^e J mit der sp bezeichneten
Modulform erster Stufe nahe verwandt.
*=") Die rechte Seite von (10) ist entgegen dem sonstigen Bra?xche als
„gebrochene" Funktion von x erklari,, wie dies übrigens in I, 164 bei Einfuhrung
der Tschirnhanstransformation wenigstens zuerst gleichfalls angenompien wurde.
150 I) 6- Allgemeine Gleichung fünften Grades.
erklärt seien, wobei für die erste Gleichung das obere und für die zweite
das untere Vorzeichen gelten soll. Als Darstellung von ßi in der
entsprechenden Wurzel Ki der Hauptgleichung hat man:
Gibt man aber in (9) den 0, W wieder die Bedeutung 0(cc^, ^(«t), so
läßt sich aus dieser Gleichung, falls man den links stehenden
Klammerausdruck durch {m0(ui) -\- nW(o(j)), entsprechend der Gleichung (2),
ersetzt und die rechts stehende Differenz der Quadrate in das Produkt
zweier Linearfaktoren zerlegt, die Folgerung ziehen:
Ä;0(a,) + lW{oO± V3^(w0K) + nW(u^)) ~
Für die Wurzeln ß^ der beiden fragKchen Gleichungen fünften Grades
gelten demnach auch die Darstellungen:
(14) 28 ßi = k0{a^) + Z?F(«,) + V3^(m0 {u^) + nW{ai))
in den entsprechenden Wurzeln a^ der gegebenen Hauptgleichung.
Hieraus ergibt sich aber das Verschwinden der ersten und zweiten
Potenzsummen der ß^ [vgl. (13) S. 143], so daß auch die beiden Gleichungen
mit den Wurzeln ßj, Hauptgleichungen fünften Grades sind.
Die Gleichung (11) muß also durch jede der beiden Transformationen:
x' = ^^V3^
in eine Gleichung fünften Grades für z imigeformt werden:
(^XV3^)5-^ oa'{zZfY3^Y^ Ho^X^ + VM + e' = 0,
in der nach Ordnung die GKeder ersten und zweiten Grades ausfallen.
Für die Koeffizienten a', h', • • • ergeben sich hieraus die vier Gleichungen.:
~3^V3^4- 9a'^ + 36'y3^4-c' = 0,
die paarweise addiert und subtrahiert ergeben:
I 9^2 + 186'^ 4-(?'= 0, 3a'^ + c' = 0,
l ^ + &' = 0, 9a zi + c' = 0.
Es sei nun erstKch ^ zfn 0. Dann Kefem die Gleichungen (15):
a = 0, h' = — zf, c = 0, d' = 9^1
Indem wir uns den Kachweis vorbehalten, daß die beiden Annahmen
8 =^ 0, ^ =lz 0, abgesehen von speziellen Gleichungen fünften Grades,
die als ausgeschlossen gelten dürfen, stets zutreffen, haben wir bei
Herstellung emer Diagonalgleichung nach Gordan. 151
Fortlassung der oberen Indizes folgendes Ergebnis gewonnen: Die
Hauptgleichung fünften Grades (1) S. 141 wird nach 4djun]ition der
Quadratwurzel VSD aus der fünffacher^ Disfiriminante du/roh die
Tschirnhaustransformation (10) in die „Diagonalgleichung" (vgl. S. 63):
(16) x^— lOzlx^-t4:6J^x-^e = 0
übergeführt, die ihrerseits durch die weitere Transformßtion:
in die „einparametrige Diagonalgleichung" ühergeTd:
(18) f — 10wy^-^4:6w^y-^Sw^ = 0.
Man beachte, daß die Irrat:(,onalität y'äzi nichit adjfingiert würde und
auch nicht in der Transformation (10) auftritt. Sie ist nur ein voriiber-
gehend benutztes Mittel zur Erleichterung der Rechnupg gewesen.
Es bleibt noch übrig, die Mögliehkeiien 6 = 0 und ^ = 0 zu
prüfen. Ist 8 = 0, so verschwindet die quadratische Form (4) für
0 := n, W = — m, hat also den Linearfaktor (m0 --j- nW). Der
andere Linearfaktor sei (fi0 -j- vW), wo auch fi, v Größen des Körpers ^
sind. Die Gleichung (2) liefert:
(19) (m0 («,) + nW(u^)) {{10 (a;) + vW{u)) = m0{a^) + nW{a^).
Da wir bereits die Gleichungen fünften Grades mit verschwindepder
Diskriminante ausgeschlossen haben, so kann der rechts stehepde in «^
höchstens auf den vierten Qrad ansteigende Ausdruck*) nicht für alle
fünf DCi verschwinden. Demnach gibt es mindestens ein «j, für das:
[i0ia,)^vW{c>O = 1
gilt. Also ist unsere Gleichung fünften Grades im Ejlörper ^ yeduzibel,
ein Fall, der gleichfalls ausgeschlossen werden d^rf. Damit erledigt sich
die Möglichkeit ^ = 0.
Ist zweitens 8^0, aber zi = 0, so übe man an Stelle von (10)
die Transformation:
x' = h0(x)-r1^'ix)
aus, so daß die transformierte Gleichung wieder eine Bauptgleichung ist.
Aus (2) und (9) folgt jetzt:
28{m0{a,) + nW(a^)) = (Ä0(«,) + Z?''(a,))l
Man hat also die beiden Gleichungen:
ak = Jc0(a,) -h lW(a,), a','- = 2S(w0(a,) -f nW(a,)),
aus denen das Verschwinden auch der dritten ui^d vierten Potenzsurame
der u'i folgt. Wir werden also zu einer reinen Gleichung fünften Grades
geführt, ein Fall, der gleichfq,lls a^s ausgesclilossen gelten darf.
*) m und n verschwinden nicht zugleich, da sonst m (2) alle fünf
Koeffizienten Lt M, -•-, n gleich 0 waren.
152 I? 6. Allgemeine Gleichung fünften Grades.
§ 5. Allgemeine Gleichung fünften Grades und Partialresolventen
der Ikosaedergleichung.
Durch die eben gewonnene Diagonalgleichung (16) ist die allgemeine
Gleichung fünften Grades an die Resolventen der Ikosaedergleichung
angeschlossen. In der Tat ist die genannte Gleichung (16) genau so
gebaut, wie die unter (5) S 63 gewonnene Resolvente der
Ikosaedergleichung, in die sie, was die Koeffizienten anlangt, einfach dadurch
übergeführt wird, daß man A und — e mit den Ikosaederformen y^ und t/;
gleichsetzt:
(1) ^ = Z> -e=i^.
Die Abhängigkeit der Wurzeln unserer Grleichung:
(2) x'' — lOzJx^ + 45^2^ + e = 0
von den beiden in der Gleichung noch enthaltenen Parametern ^ und — e
ist eben dieselbe, die wir zwischen den S. 62 eingeführten Formen fy and
den Ikosaederformen y, rf; im dritten Kapitel kennenlernten.
Hiermit ist eine zweite Art der Auflösung der allgemeinen Gleichung
fünften Grades gewonnen. Sie besteht aus dem algebraischen Teile der
Überführung der allgemeinen Gleichung fimften Grades durch wiederholte
Tschirnhaustranbformation in die Gleichung (2) und damit in die
jResolvente:
(3) /■5_iO;^/-B + 45;KV-i^ = 0
der Ikosaedergleichung und aus dem transzendenten Teile der Lösung der
Gleichung (3) durch Modulfunktionen (vgl. S. 98 ff.). Wir .haben hier im
wesentlichen diejenige Resolvente erhalten, die Brioschi*) in noch etwas
allgemeinerer Gestalt bei seinen ersten Untersuchungen über Gleichungen
fünften Grades gewonnen hatte**).
Die vorstehenden Bemerkungen sind an die zweiparametrigen
Gleichungen angeschlossen. Man kann an ihrer Stelle auch die ein-
parametrige Gleichung (18) S. 151 treten lassen, die durch die
Transformation :
(4) 4:y=-F, lQ2w=^-^
in die Resolvente (7) S. 63 der Ikosaedergleichung übergeht.
*) Es kommen die ersten Arbeiten von Brioschi im ersten Bande der
Annali di matematica (1858) in Betracht. Vgl. auch „Ikos.", S. 151, wo die mit
den Gleichungen (2) und (3) des Textes im wesentlichen übereinkommende spezielle
Brioschi sehe ßesolvente unter (26) angegeben ist.
**) Vgl. auch die Abhandlung von Brioschi „Sul metodo di Kjronecker per
la risoluzione delle equazioni di quinto grade'- von 1858 im ersten Bande der
„Atti del Istituto Lombardo"
Losung der Gleichung fiinften Qrades nach Kronecker und Brioschi. 153
Die gewonnene zweite Auflösung der allgemeinen Gleichung fünften
Grades*) ist jedenfalls der erstep Lqsungsmethode dadurch überlegen,
daß in ihrem algebraischen Teile außer den beider^ oft genannten
Quadratwurzeln keine weiteren Irrationalitäten ad|ungiert werden. Die erste
Methode erforderte demgegeniiber noch die liösung einer kubischen
Hilfsgleichung, die wir übrigens wegeii übergroßer Kompliziertheit nicht
einmal aufstellten. Dies Sachveihältnis kann ^uch dann nicht anders
werden, wenn wir über die Diagoiialgleichui^g zur Bring sehen Crleichung
vorzudringen versuchen. Indessen hat dißser letztere Weg doch den Vorzug,
daß die fragliche kuhibclie HiJfsghichting alßdamp eine behr zagangliche
Gestalt annimmt Es handelt sich dann nämliph einfach um die Relatioii (9)
S. 134 dritten bzw. zweiten Grades zwischen der Lösung v der Rßsolvente
fünften Grades (4)' S. 133 de|- Ikosaedergleichung und de|- zugehörigen
Wurzel 6 der Bringschen Gleichung (5) S 115 **). Die Diskripiinante dieser
kubischen Gleichung ist übrigens i^icht etwa das Quadrat eifier r^.tionalen
Funktion von v, woraus eine Bemerkung von S. 146 über die Galois sehe
Gruppe der kubischen Gleichung hervorgeht
§ 6. Ikosaedergleichung als Resolvente der allgemeinen Gleichung
fünften Grades.
Als einparametrige Resolvente hat Klein in der Theorie des Ikosa-
eders und der Gleichungen fünften Grades die IJcosaedergletchung in den
Mittelpunkt seiner Betrachtung gestellt. Dies setzt voraus, daß die fünfte
Wurzel der Einheit s, die \yie \5 eii^e akzessorische Irrationalität der
allgemeinen Gleichung fünften Grades ist, adjungiert wird. Insofern pnt-
spricht die Klein sehe Theorie der beka:finten Kronecker sehen Forderung,
überhaupt keine akzessorischen Irrationalitäten zum Gebrauch zuzulassen,
noch weniger, als die im vorletzten Paragraphen vollzogene
Transformation, die doch nur \'6 als numerische und für die allgemeine
Gleichung akzessorische Irrationalität benutzt. Aber gerade die Ikosa-
edertheorie, die in so hohem Grade zum Verständnis auch der gesandten
früheren Entwicklungen über Gleichurjigen fünften Qrades beigetragen
hat, zeigt uns, daß man beipi Festhalten an der Kronecl^ersehen
Forderung in Unkenntnis über wertvolle und interessante Entwi(iklungen
bleiben würde.
Den Übergang von der allgepaeinen Gleichung fynften Grades zur
Ikosaedergleichung hat Klein in ?wei Arten vollzogen. Die erste
Methode knüpft an die Hauptgleichung :
(1) X' + 106a;2 -^ ocsc + d = 0
*) Man konnte sie nach den Darlegungen von'Klem m „Ikos.", S. 151 als
die „Brioschi-Kroneckersche Methode"' bezeichnen und ihr gegenüber die in § 3,
S. 147 besprochene die „Hermitesche 4-'^flösungsmethode" nennen.
**) Koch einfacher ist die kabische Gleichung (2) S. 137 zwischen
entsprechenden Wurzeln der Resolvep.ten sechsten Grades.
154 I? 6. Allgemeine Gleichung fünften (trades.
an, setzt also bereits die Adjunktion der ersten akzessorischen
Quadratwurzel (8) S. 140 der ursprünglichen Gleichung (1) S. 139 voraus. Der
ITbergang von (1) zur Ikosaedergleichung vollzieht sich dann einfach
durch Wiederholung der Überlegung von S. 122 ff., wobei nur an einigen
Stellen ein Vorzeichenwechsel in den Formeln einzutreten hat.
Die in eine bestimmte Anordnung gebrachten Wurzeln x^, X-^, • • •, x^
der Hauptgleicbung (1) liefern einen gewissen Punkt auf der Hauptfläche,
die wir zunächst in „Pentaederkoordinaten'' darstellten. Der erste
Schritt ist, daß wir in Rg durch Benutzung der Lagrangesohen Solventen
Tetraederkoordinaten Zjc einführen:
(2) 5^fc = a^o -r s^x^ + f^^a^g + s^'^x^ + s^^x^ = (s^ x), h = i, 2,3,4-),
in denen sich die Pentaederkoordinaten umgekehrt so darstellen:
(3) a;^ = £-^^1 + £-2v^^^ £-3v^^ _j_ £-4v^^^ *. = 0, 1, •••, 4.
Die symmetrische Permutationsgruppe der x liefert für die z eine quater-
näre Substitutionsgruppe ®i20' ^^^ ^^^ ^^^ beiden Substitutionen:
yo ^1 = —-— ^1 + ^2 ^ - -J
(5)
1/- ' 1-V5
yo ^2 = •2']
Vo 4 = ■
2 ^ '
l+Vö
^3 + -^
1+V5
2 ^2~
1—Vö"
2 2
+ ^3 + ^
-■2^4)
-^4'>
^3 +
V5
)
erzeugbar sind **). Die Substitutionen der quatemären ©^g^ haben zur
Hälfte die Determinante 1, zur Hälfte — 1; die unimodalaren
Substitutionen liefern den Xormalteiler @g^. Die Gleichung der Hauptfläche
in Tetraederkoordinaten ist:
(6) ^^^^ + ^2^3 = 0.
Die Einführung der Koordinaten X, (i auf der Hauptfläche geschieht genau
wie S. 124 durch die Gleichungen:
(7) ;L__^ = !i, ^_fl___fi.
*) Bei Einhaltung der Bezeichnung (3) in I, 413 sollte die rechte Seite der
Gleichung (2) eigentlich (e~k^ x) heißen.
**) Hier liegt gegenüber den Formeln (5) S. 122 eine Vorzeichenabweichung
vor. Der Grund ist, daJß die jener Substitution zugrunde liegende Permutation
der Formen y noch mit einem gleichzeitigen Zeichenwechsel der y kombiniert
wax. Für die weiteren Formeln ist diese Vorzeichenabweichung ohne Folge, da
nur noch Quotienten der z zur Benutzung kommen.
Erste Klein sehe l^osung der Gleichung fünften Gr£(,(ies. 155
Die (Sjj2o setzt sich in eii^e Gipuppe von ^, ^i - Substitutionen um, die
aus den beiden Substitutionen (5) und (6) S. l'24ff. erzei^gbar ist. Die
Spaltung der ;L, fi in homogene Größen X^, X^ pnd ^^, fi^ gescMelifc wie
S. 125. Setzt man in Übereinstimmung mit (7):
(8) z^^X^ii^, z^=—X^ii^, ^^ = X^{i^, ^i==X^ii,^,
so hat man als homogene erzeugende Subst:|tutioüen die unter (10)
und (11) S. 126 angegebei^en. Der alternierenden Permutationsgrappe
der Xic entspricht jetzt homomorph die homogene Ikosaedergru^e, der X^, X^
und fij, fig gleichzeitig unterworfen sipd. Die erzeugenden Substitutionen
sind :
(9) X[ = £^1,
X^, X^ =
V5';l; =--
i6X', 3==
— Vs ii'i =--
8^X„
+ (£-
-is'
-Tis'
ill =
- £*)^1 —
-s')k-
-s')li,-
Si^l,
is'-
-(£-
-is'-
H =
-&^)K
- «*)^2
-s)ii^
(10)
— yS a.2 =: — (£* — £)fij — (£^ — £^)fi2-
Die ^-Substitution geht in die gleichzeitige fi-Substitutipn durch Ersatz;
von £ durch s^ über, wobei y5 Zeichenwechsel erfahrt.
Um jetzt von der Hauptgleichung (1) zur Ikosaedergleichung zu
gelangen, adjungieren wir auch noch die Quadratwyrzel '\[l) der in (8)
S. 142 berechneten Diskrimjnante D, womit, d^ e bpreits adjungiert ist,
auch y5i) rational bekannt ist. Die Gruppe der Gleichung (1) ist dann
die alternierende ©g^. Ihre Wurzeln nennen wir in der gewählten
Eeihenfolge jetzt wieder w^, «j, •••, a^ Dem Galois sehen Körper
(9t, £, a^, a^, ••-, a^) entnelimen wir die Funktion:
(11) '--tA
is\ «)
und bilden die ihr zugehörige Resolvente der Gleichupg (1) bei
Zugrundelegung des Körpers (9?, 6, c, d, s, \D). Den sechzig geraden
Permutationen der Uq, Kj, •••, w^ entsprechen die sechzig Ikosaeder-
substitutionen von X. Dip aus (4) oder (5) S. 56 zu entnehniende
rationale Funktion sechzigsten Graden von X:
ist bei diesen 60 Substitutionen invarj|.ant und demnach als Fupktioia der
Uq, a^, '--, ci^ eine zur alternierenden ©g^ gehörende, mithin im Körper
(% h, c, d, s, Y^) enthaltene Funktion. Als solche_ 4er variabel zu
denkenden Größen h, c, d, Yd heiße sie Ii(b, c, d, |/D). Dann id die
zur gewählten FunUion (11) gehörende Besolvente der Gleichung (1);
(13) 9(A, 1)^ + 1728 JS(6, c, d, iV)iiX, If = 0
156 I» 6- Allgemeine Gleichung fünften Grades.
die Ikosaedergleichung sechzigsten Grades mit dem einen Parameter JR. Sie
ist eine „Xormalgleichung'*, deren Galoissche Gruppe nach den
vollzogenen Adjunktionen mit der Ikosaeder-@6o isomorph ist.
Wir haben hiermit eine dritte Methode der Auflösung der allgemeinen
Gleichmig fünften Grades gewonnen *). Der algehraibche Teil dieser Äuf-
lösungsaH hedeht in der Transformation der allgemeinen Gleichung fünften
Grades in die einparametrige Ikosaedergleichung (13)**); über die
transzendente Lösung der Ikosaedergleichung durch Modulfunktionen ist bereits
S. 98ff. das Weitere ausgeführt.
Kleinf) stellt die „Ikosaedergleichung'* in Parallele zu den
„reinen Gleichungen'*, wobei der Lösung jener Gleichung durch
Modulfunktionen die transzendente Lösung der reinen Gleichungen durch den
Logarithmus entspricht. Der Anteil der Algebra an der Lösung ist dann
auf der einen Seite die Transformation der allgemeinen Gleichung fünften
Grades aaf die Ikosaedergleichung, auf der anderen Seite die Reduktion
allgemeiner zyklischer Gleichungen auf reine Gleichungen jf).
§ 7. Schar der Hauptresolventen.
Über die letzten Sätze des § 6 hinaus ist nun die Ikosaedertheorie,
wie schon angedeutet, für das Verständnis auch anderer, zum Teil schon
gegebener Entwicklungen sehr wertvoll. Insbesondere gehen wir nochmals
zurück auf die beiden Scharen von Hauptresolventen, die in § 2 S. 141 ff.
entwickelt wurden. Bei bestimmter Anordnung der Wurzeln wurden
uns diese beiden Scharen von Hauptresolventen durch die Punkte
derjenigen beiden Geraden der Hauptfläche geliefert, die zu den „Parameter-
werten'- :
gehören, unter a^, a^, ■ • •, a^ die Wurzeln der zunächst erreichten Haupt-
resolvente :
(2) x'° + lOhx^ j^^cx ^d =z 0
verstanden, und zwar in der gewählten Anordnung. Um die beiden
Scharen voneinander zu trennen, hatten wir \hl) zu adjungieren, wobei
die Bevorzugung eines bestimmten Vorzeichens dieser Quadratwurzel auf
die Auswahl einer bestimmten unter den beiden Scharen hinauslief. Wir
denken dasjenige Vorzeichen gewählt, das zur Geraden des Parameters l
hinführt. Es hat dann X den bestimmten Wert (1), während fi, um die
ganze Gerade zu beschreiben, alle möglichen Werte durchlaufen muß.
*) Will man auch hier eine Personalbenennung bevorzugen, so hat man die
Methode als Klein sehe zu bezeichnen.
**) Wegen der expliziten Darstellung von _g(&, c, d, ^D) vgl. man „Ikos.",
S. 182 ff., insbesondere die Gleichungen (35) und (36) S. 193 daselbst,
t) Vgl. „Ges. Äbh." II, 484.
tt) Vgl, die Entwicklungen m I, 413 ff.
ßesolventen der Ikosaedergleichung in der Schar der H^uptreiolventen. I07
Es ist nun zunächst möglich, die Wurzeln der 3auptresolventen def
ausgewählten Schar auf Grund der Formeln vqn § 6 in einfacher Weise
darzustellen. Wir erklären etw^ die Werte X-^, 2.^ durch:
(3) X, = (s, a), X^= — (£^ Di),
die also mit der Gleichung (2) und der Anordnung ihrer Wurzeln
bestimmt sind, und verstehen unter fi^, u^ zwei endliche und nicht zugleich
verschwindende Variable. Dcm^ sind entsprecfiend den Gleichungen (3)
und (8) § 6 die Wurzeln der Hauptresoheri,te gesehen diwch:
(4) Xy ^= E-''X^ii^-E~^''X^yi^^ B-^^X^lf,.j +B~^''X^ii^, *' = 0, 1, •••, 4.
Die Potenzsummen dieser Größen sind bereits, soweit wir sie hier
nötig haben, in den Rechnuagen von S. 123 ff. festgestellt. Benutzen wir
für die Potenzsummen die Bezeichnungen (1) in I, 101, so ergibt siph:
^i>4 = Xt^i^^l —XlX^ lit—S 11X1^1^4 +X^Xliio — Xt^i^i^,
i j)^ = xliiil -f /ii) — io;LU2i^ii^l i- io;L?;Lli^ii^2 + loxlxiiitn^
-f lOX^Xt^lid— Xl{{ii — }iT).
Der in der ersten Gleichung rechts stehendp Ausdruck möge durch
B{X, fi) bezeichnet werden, da er, glpich 0 gesetzt, die auf der Baupt-
fläche gelegene „Bringsehe Kurve'- dai-stellt. Füy die rechten Seiten
der zweiten und dritten Gleichimg (p) nehmen wir die schon in (13)
und (14) S. 126 eingeführten Be;zeichnungen X(X, fi) und 0{X, fi) wieder
auf. Man gelangt zu dem Satze: Die aubgewählte Schar der Haiipt-
resolventen ist dardeUhar in der Gedalt:
(6) a;° —oB{X, ii)x^ — oX(l, ii)x — ^{X, ji) = 0,
wo ^j, X2 durch (3) gegeben sind und ^j, ^g gwei endliche, nicht zugleich
verschwindende variable Farameter bedeuten.
Eine dieser Gleichungen :|st uns bereitb begegnet. Setzt man
nämlich:
(7) 11^ = XliXl — 7;Li), ft2 = XlOXl + XI),
so ergibt sich:
(8) X, = is^' Xl - s^^ XIX.) ßl - 7aD -h (f^U, Xl -r £' ^1) (7 Xl -j- X'^),
und damit haben wir in et\»/^as veränderter Anordnung die in (10) S. 64
erklärten fünf Formen h^{X.^, X^) wiedergewonrjien: Fur die JParameter-
werte (7) geht die Gleichung (6) ivi, die Uesolcente (11) S. 64 der Ilzosaeder-
gleichung über. Multipliziert man die Form achtep Grades K{X^, X^
mit der in (3) S. 62 gegebepen Form sechsten Grades f.y,{X^, X^), die die
Wurzel der Diagoualgleichuag (q) S. 63 war, so ergibt ^ich hei
zweckmäßiger Anordnung als Produkt:
(9) K{X„ X^) UX„ X^) = (£*' X, - a'^'X^)-Xi{2(iX\''— SdXUl - Xl')
-t (e^' l, - £'K)' ^1 (^1" — 39 X\X\ - 26 XW
158 I) 6- Allgemeine Gleichung fünften Grades.
A^tch diese fünf Formen sind die Wurzeln einer Besolvente fünften Grades
der Ikosaedergleichung, die sich der Schar (6) einordnet, nämlich für:
(10) \ ^ V i
^ ^ \ ^^^H ill'' - 39 mi - 26 ll\
wie man durch Vergleich von (4) und (9) sofort feststellt. Die drei
Koeffizienten dieser Resolvente sind Ikosaederformen der Grade 42, 56
und 70, also abgesehen von konstanten Faktoren gleich i^;^, y;^^ und
(p'"^. Man bestimmt diese Konstanten leicht und findet als Resolvente
fünften Grades der Formen (9):
(11) X^ —^0'^lX^—0'Ti(ffx—(^^'^ ~ ^.
Die Gleichung (8) können wir auch in die Gestalt setzen:
\{l^,l^ = (s^n^ —s^'l^)'ll{kl—7X1)-}-{£^'X,-}-sn^)'11(7X1-}-U).
Durch Zusatz der Gleichung (9) finden wir ein System linearer
Gleichungen für (£*^Aj — £^"^2) ^^^ (£^^^1 + £^^2)? dessen Determinante
man leicht zu (p(X-^, X^) berechnet. Xach Lösung dieser Gleichungen in
bezug auf (s*^ X^ — £^"^2)? (£'''^1 + £"^2) wolle man die gefundenen
Ausdrücke in
X, = (a^-X, — a^n^)ii^ ~f (a^n^ i- an,)ii^
eintragen und dabei statt der ^t^, fig neue Parameter m^, m^ einführen,
die man erklärt durch:
(XliXl''- SdXlXl-2QXl'')^,-Xl{2SXl''-S9 XUi-11")^^ = m^(pt,
\ — Xl(yXl ^X^fi^ + Xl{Xl — 7Xl)ii^ = m^fff.
Die lineare Schar der Wurzeln unserer Hauptresölvente (6) stellt sich dann
in der Gestalt:
(13) x,= m,{tK)^m,(x'fJt,)
dar, wo m^, m^ zwei endliche, nicht zugleich verschwindende Parameter
sind. Die Zusatzfaktoren tj; und 2^ bezwecken, die Ausdrücke rf;h^ und
l^fvhy ZU Formen gleichen Grades in X^, X^ zu machen. Zu den beiden
besonderen Resolventen wird man geführt, indem man erstens m^ = i^^S
Wg =: 0 und zweitens m^ ^= 0, m^^ = i~~'^ setzt.
Die Transformation der Hauptgleichung fünften Grades auf die ein-
parametrige Diagonalgleichung, die in § 4 S. 148 ff. ausgeführt wurde,
wird aus den letzten Darlegungen erst verständlich. Es ist nämlich die
Wurzelschar (13) eben dieselbe, die wir S. 143 durch:
x,^t^{a,)-^^W (av)
darstellten. Die besonderen S. 149 dieser Schar entnommenen Wurzeln:
(14) 'k^{a,)^lW{a,), m 0 (a,) ^-^ n W (a,)
Geometrische Deutupg dep Gordan sehen Transfprmatipn. 159
stellen sich in der Sohar (13) einfach ip den Gestalten /V^r, K dar, d. h.
sie liefern unsere beiden vorhin besonders betrachteten Regolveisten.
Für den Quotienten der Wurzeln (14) haben wir dann:
so daJ3 die x[, die Wurzeln der Diagonalgleichung (3) S. 152 sind.
§ 8. Zweiter Weg von der allgemeinen Gleichung zum» Ikosaeder.
Klein hat-noch eine zweite Methode entwicl^elt, von dßr allgemeinen
Gleichung fünften Grades zum Ikosaeder überzugehen. Wir gehen auch
auf diese Methode hier kurz ein, da sie einmal im folgenden Abschnitt
auf die Gleichungen sechsten Gradßs übertragen v^erdep soll und
andererseits mit den noch zu besprechenden Untersuchungen von Krqnecker
und Brioschi über Gleichungen fünften Grades enge zusammenhangt.
Die allgemeine Gleichung fünften Grades wird als gegeben
vorausgesetzt, ihre Wurzeln werden wie bisher durch a,,, ol^, • • •, a^ bezeichnet.
Adjungiert sei sogleich die Quadratwurzel der Diskriminante, plso eine
natürliche Irrationalität, so daj3 die Gruppe der Gleichung die
alternierende @gQ ist. Die neue Betrachtung beruht imn namentlich auf dem
Gebrauch der Besolvente sechsten Q-radnü der Glßichufig fünften Grades,
die zu den sechs konjugierten Teiler^ ©^^ vom Diedertypus gehört.
Unter S, T und TJ verstehen wir folgende drei Pern^utationen der ßg^,
die den gleichbenannten Ikosaedersubst:|.tutionen entsprechen:
S =:
-■2' "3? "4\
-3' «4' Hr
, '^2'
«0/
S und T erzeugen die ganze ©g^, und aus S und TJ entsteht eine erste
unter den Diedergruppen ©j^-
Die einfachsten Funktionen der ausgewählte^ ©j,, sind:
1 «0«! +aia2 + «2«3 + «3«4T-a4«f)'
[ «0^2 ~|- 01.^0!.^ -r a^«! -}- a^Kg -f- c'3C'0)
und es ist nach dem Lagrangeschen Safcze in einer unier ihnen und den
Koeffizienten der Gleichung sowie der Wurzel ^JD jede andere Funktion
der @jQ darstellbar. In den Arbeiten von J^ronecker und Brioschi sind
indessen andere Funktionen zugrunde gelegt. Kronecker gibt in seiner
ersten Mitteilung von 1858 nur kurz a^i, daß er mit dem Quadrat einer
ziemlich komplizierten Funktion fünften Grades der aj, gearbeitet habe *)
*) Die Funktion ist m „fkos.'-, S. 154, unter (29) angegeben.
160 I, 6. AUgememe Gleichung fünften Grades.
und notiert dann nur noch die mit dieser Funktion erhaltenen Ergebnisse.
Dabei macht Kronecker entgegen seinem später verfochtenen Prinzip
Gebrauch von akzessorischen Irrationalitäten. Bei Brioschi findet sich die
Funktion *):
(2) v^ =: («0 — «i) (a^ — Kg) («2 — «3) («3 — «4) («4 — «0)'
die nur erst bei S unverändert bleibt, aber bei Ausübung von V
Zeichenwechsel erfährt. Dasselbe gilt von der Funktion:
(3) w^ = («0 — a2)K — «4)K — «i)("i ~ «3)(c«3 — c<o)'
die mit v^ multipliziert als Produkt ]I) liefert:
(4) v^-w^^ iB.
Es gehe nun die Funktion v^o durch die Permutation T in ^^ über.
Vf^ aber durch S^ in v^; dann hat man ausführlich:
=: («0 — «2) («2 — «1) («1 — «4) («4 — «3) («3 — «0)'
— («1 — «3) («3 — Kg) («2 — Wo) («0 — aj (a^ — Kl),
(5) { v^ =: («2 — aj (a^ — «3) («3 — Kl) (a^ — a^) («o — «2)'
^3 — («3 — «0) ("0 — "4) («4 — «2) ("2 — «1) («1 — «3)'
v^ = (a^ — Kj) (Kj — a^) («0 — ^z) iP'-s — ^d iP'-z — ^i^-
Entsprechend bezeichnen wir die aus w^a hervorgehenden Funktionen
durch Wf^, u\. •••, w^. Aus (2) und (5) ergibt sich leicht: Die Wirkung
der Permutationen S und T auf die sechs Funktionen v ist:
g. I (S) v'^ = v^. v'(, = v^, v[ = v^, ^;; — v^, v'^ =: v^, r\ = v^,
1 (T) 'c'ao = Vf^, v'q = v^, v'i = v^, v'2 = —v^, v\ = —i\^ v\ = Vj^,
und genau dieselben Substitutionen erfahren die sechs Funktionen w, wie
aus (4) leicht hervorgeht. In:
(7) ßoo = (nio^ — nw^)^, ß,, = (mv^ -p mi\Y, ?' = 0, 1, •••, 4
haben wir demnach sechs konjugierte Scharen von Funktionen unserer
Diedergruppen ©^^ gewonnen, die sich bei Ausübung der Permutationen S
und T selbst so permutieren:
.3^ C ^ (ßoo, Ao> Al> /5-2> ^3. ßi] rp ^ /^oc, Ao> ßl^ ^2« Aa> ß^\
^ ' ^ß^. ßl^ ßi. ß,, ßi, ßoJ' W ß^, ßi^ A2. ßä, ßj '
Dabei sind m^ n zwei Parameter, über die wir noch verfügen können.
Die aufzustellende Resolvente sechsten Grades wird übrigens nicht
unmittelbar die Funktionen (7) zu Wurzeln haben, wenn sie auch mit
diesen Funktionen nahe verwandt ist. Wir kommen hierauf unten zurück
und verweilen zunächst bei den Quadratwurzeln der ß, die wir als
eindeutige Funktionen der Wurzeln a, so schreiben:
(9) ] ßoo = mv^ ~f niv^, ^|ßy = mv^ -\- nu\, v = 0, 1, ■ ■■, 4.
*) Die Indizes der Funktionen werden hier*wie S. 70 ff. gewählt.
Herstellung einer bihnearen Form ^ (s, t)- Kil
Gegenüber den Permutationen S und T zeigen sie das Verhalten der
Funktionen v und tv, d. b. ßie erfahrpn d^^e Permutationpn (8), wobei
jedoch \ß^, Y/Sg gegenüber T noch einen Zeichen Wechsel erleidei^. Hieran
schlieJ3en wir mit Klein"=) folgende Betracl^tung:
Wir adjungieren die fünfte Einheitswurzel a und fuhren die beiden
homogenen Variablen l^. X..^ ein, die den Ikosaedersubstitutionen
unterworfen werden sollen. Aus ihnen berechnen wir nach (12) S. 71 die
Verbindungen zweiten Grades:
(10) u^ r= l^l^, u^ =: l\, n^ = —ll
die nach S. 71 bei den Erzeugenden S und T die temg^ren Subst:(.tutionen:
(S) u'o = Uq, h[ := aa^, lü = £*w-^,
f V 5 «0 — '^o 4- W] -f '^ä'
(T) yjha, =: 2a, ^ (a^ ~ a')u, ^ (a-^ a')u„
I ]'ö <4 = 2«Q -|- (f + £*)**! ~ (f^ + £^)«o
erfahren. Die Quadratwurzeln (9) seien abgekürzt durch:
(11) ■^J^ = t^, ]Jr = t,, ^ = 0,1,..., 4
bezeichnet. Aus den drei GröJ3en « stellen wir folgende sechs
Ausdrücke :
(12) s^ = ]öU(^, ö, =z U(^^ a'u^-r a-'u^, v=0,l,---,4
her. Gegenüber den erzeugenden Substitutionen S i4nd T der ternareu
(^gQ der i(-Substitutionen zeigen die s das Verhalten:
(b) ö^ = ö^, ÖQ = öj, öl =: ö,, öo = Ö3, ö,, = S^. S4 = ÖQ,
d. h. die 0 zeigen genau dasselbe Verbalten wip die t bei den Peraiu-
tationen S, T der Wurzeln oc. Hieraus folgt der Satz: Die hilif^eare
Ve
(13) ß(s, t) =: ..o^oc-r S ^^^v
) -=0
verhalt sich invariant, falls mau auf die Uk eine gerade Permutation and
gleichzeitig auf X^, ^g ^wie der heideu ent^prechenden IJvßsaederöUhstitutioneu
ausübt, die eine und dieselbe fernare a-Suhötitatioip liefern.
Trägt man fur die 6 ihre Ausdrücke (12) in u^, w^, w^ ein und
ordnet in bezug auf die u, so nin^mt £1 die Gestalt:
(14) ß =: 2^o«o + ^i'h -r ^ä%
=*) Vgl. insbesondere die kurze Skizzß des Gedankenganges in „Ges. Abb."
II, 487 ff.
Fncke. Algebra. II. H
162 J» 6- Allgemeine Gleichung fünften Grades.
an, wo 2Af^, A.^, A^ gegeben sind durch:
(15) A, = t^^at^ + a% + e%i-a%,
Wir haben damit drei Funktionen fünften Grades der Wurzeln afc
konstruiert, die sich gegenüber den geraden Permutationen der ajt ihrerseits
linear und homogen substituieren. Gehen durch die einzelne Permutation
die u in ii und die A m A' über, so gilt, wie wir wissen:
Man sagt in diesem Falle, daJ3 sich '2A^, A^, A^ zu den m^, u^, a^
^hontragredienf^ substituieren. Insbesondere entsprechen den beiden
ternären w-Substitutionen S und T die beiden folgenden Substitutionen
der J.Q, A^, A^:
(S) A'o = Aq, A[ =r s^A^, A'2 = aA^,
i\6A'(, =: ^o-r A + A,
V5^; =: 2A, -}- (a' -^ a')A, ^ (^ + £*).!„
i^A', = 2A, ^ (6 + 6^)^, + (a' -r- e')Ä,.
Wir gelangen damit zu einer ©g^ ternärer A-Substitutionen, die sich aus
den entsprechenden Substitutionen der u einfach mittels des Ersatzes von e
durch s~^ gewinnen lassen.
Der tibergang zum Ikosaeder geschieht nun auf Grund bekannter
projektiv geometrischer Entwicklungen*). Die quadratische Form:
(16) zi = Al^A,A,
der Af^, A^, A^ ist gegenüber den Substitutionen der ©g^ invariant.
Deutet man A^, A^, A^ als homogene Koordinaten in der Ebene, so
wird durch ^ = 0 ein Kegelschnitt dargestellt, der durch die
00 3 KoUineationen:
( A', = (ad -r ß y) Ä^- ß8 A^ ^ ay A,.
(17) A[= -2y8A^i-8-'A^-yKi.^,
{ Ä2= i-2a ßA^ — ß^A^i-cc^A.^
in sich übergeführt wird. Es sei dabei ad — ßy = 1; dann ist auch
die temäre Substitution (17) unimodular.
Man kann die Punkte des Kegelschnitts bekanntlich durch einen
Parameter ^ darstellen, indem man:
(18) A,:A,:-A,^ f :^:1
*) Man findet diese ausführlich entwickelt m „Aut. Funkt." I, 12 ff.
Herstellung der ikosaedrisch substitmerten Große ^. 163
vorschreibt. Diese Parameterd^rstellung ist auf alle Punkte der
projektiven Ebene übertragbar: Einem beliebigen Punkte A^, -4^, Ä..,
der Ebene entsprechen als Parameter die beiden Werte:
(19) 5 = =^5^, £ = =^^iF^,
die im Sinne von (18) als Parameter den beiden Bert^hrungspunkten der
von jenem Punkte an den Kegelschnitt laufendeii Tangenten zi4kommen.
Bei Ausübung der Transformation (17) erfahren dann ^ und ^ kogredient
die Substitutionen:
(20) ^r^^lTß -, -^l±A.
-8' yl-id
Die in der ersten Grleichung (19) erklärte Grrcfße t, erfali^i gegeniiber der ©g^
der ternaren Ä-Siibditutionen eine ©g^ Unear-gehrochener Suhstittitianen,
und zivar zeigt die Rechnung, daß wir zur tirbprußglichen Normalform der
Ikosaeder-®gQ zurnckgefuhd werdeiß.
Um die algebraische Bedeutung dieses Ergebnisses zu erme&sen,
beachte man, daß zJ als Funktion der a;. gegenüber dep 60 geraden
Permutationen unverändert bleibt und also :patiorial in den Koeffizienten
der Gleichung fünften Grades und der Wurzel yjO darstellbar i&t*).
Wir haben damit folgendes Ergebnis gewonnen; Nuch AdjunJdion der
zweiten, and zwar akzessorischen'^'^) Quadratwurzel:
(21) 1z/=VA'+A^
hcöitzt man in:
(22) t = z:A±lA±AiÄ
eine Fuuldion der Wurzeln a^i, die stclt, gegenüber den geraden Yertauschungen
der cijc ikosaedrisch suhdituiert. Pie weitere Behandlung hat so zu
geschehen, daß man den Ausdruck ^ in die Jkosaedergleichnng (5) S. 56
für z einträgt und daraufhin Z rational in den Koeffizienten der gegebenen
Gleichung und den beiden adjungierte^i Quadratwurzeln ausdrückt. So
ist auf eine zweite Art die allgemeine Gleichung fünften Grades auf die
einparametrige Ikosaedergleiohung zurijckgeführt f)•
*) An numerischen Irrationalitäten wurdep wir hier nur ^5 notig haben;
übrigens sind naturlich die beiden ^n (7) eingeführten Parameter m, n noch
verfugbar.
**) Es geht dies aus dem unten zu behandelnden „Krpneckerschen Satze'- hervor.
t) Wir haben damit eine „zweite Klein sehe Losungsmethode" der Gleicjiung
fünften Grades gewonnen, bei der zum Unterschied gegen die erste die naturliche
Irrationaütat |(d zuerst adjungiert ist und dann erst die a^izessorische
Quadratwurzel. Über das gegenseitige Verhältnis beider Methoden spwie wegen der
weiteren Durchfuhrung der zweiten Methode ist auf ,Ikos,~, Abschn. II, Kap. 4
und 5 zu verweisen.
I, 6. Allgemeine G-leichung- fünften Grades.
§ 9. Formensystem der ternären Ikosaedergruppe.
Klein stellt in den Mittelpunkt seiner Entwicklung das „Formen-
prohlem" der temären Gruppe ©g^ der unimodularen ^4-Substitutionen als
„Problem der Ä". Die beiden in (19) S. 163 eingeführten variablen
Größen ^ und ^ werden je in zwei homogene Variable ^i, ^^ und ^j, ^,
gespalten, die kogredient die homogenen unimodularen Ikosaedersubsti-
tutionen erfahren sollen. Setzt man dann:
(1) Äo = l(^Jo + ^^^^)^ A^-U„ A = ^,f:.
so erfahren die A^^, A^, A,^ entsprechend die homogenen unimodularen
Substitutionen der temären Ikosaedergruppe ©g^, deren erzeugende
Substitutionen S, T bereits S. 162 angegeben wurden =^).
Eine erste invariante Form der ternären ©g^ ist die in (16) S. 162
eingeführte quadratische Form:
(2) J^Al+A,A^.
Deutet man die Aq, A-^, A^ als homogene Koordinaten in der Ebene, so
stellt zl = 0 einen Kegelschnitt dar, der eindeutig auf die Oberfläche
des Ikosaeders bezogen ist. Weitere invariante Formen bildet Klein,
indem er bzw. die 6^^, 10*^ und 15*^ Polare "•='==) der Ikosaederformen i,
cp und il; für ^^ ^^ ^^^ ursprüngliche und ^^, t,^ als neue Variable bildet
und in den zu gewinnenden Ausdrücken statt der t, auf Grund von (1)
die A einführt. Man gewinnt auf diese Weise drei invariante Formen
der Grade 6, 10 und 15 in den A.
Die erste dieser Formen mag noch durch Zusatz eines Gliedes a^^
vereinfacht werden, wo a eine Konstante ist; auch darf ein konstanter
Faktor zugesetzt oder fortgehoben werden. Als besonders einfach findet
man auf diese Weise die Form sechsten Grades:
(3) Ä (A, ^j, ^,) =. 8 At A^A,-2 AI AI AI - A^ (A! + AI) +- A^^ Al
Entsprechend darf die Form zehnten Grades vereinfacht werden, indem
noch, ein Bestandteil (ßAzt'^-'ry /J°) mit geeignet gewählten Konstanten ß
und y zugefügt vidrd. Hier ergibt sich als einfachste Form:
i M{A^, A^. A^ = 320 Al Al Al - 128 AI {Al -f AI)
(4) — 160 At AI AI -f 80 Al A, A., (A° + Al) + 20 A^ At AI
1 - 20 ^, A! AI (AI -f .4?) + {Al<^ ~\-Ar 4^6 A^ Al)
*) Man beachte, daß diese ternare Gruppe m der homogenen Gestalt eine @go
ist, während die homogene binare Ikosaedergruppe eine ©^go ist.
**) Vgl. (6) in I, 130.
Formen sechsten und zel^nten Grades der ternaren ©^q. 105
oder bei Benutzmig von 2 Ä^ an Stelle von A^ als ei^t,ie Verarjiderliche:
( M{A,, A,, A,) = 5 (2 A,Y A! Al - 4 (2 A,y (Ai -f- AJ)
(5) - 10i2A,yA!Ai + 10(2A,fA^A,(Al + A^,)^o(2A,fAtAl
\ - 10 (2 .4,) Af A! (AI i- Ai) + {AI' - A]'+ 6 Al AI).
Ein anderer rein algebraischer Wpg zur (Jewinnung fieser Fonnen,
der zugleich ihre geometrische Bedeutung klarlegt, ist der folgende:
Durch die Kurve sechsten Qrades A ^=^ 0 wird auf den^ Kegelschnitt
^ = 0 ein System von 12 nur untpr sich äquivalenten Pui.ikte
ausgeschnitten, die also die 12 Ikosaederecken sind. X^^^ werden aber je
zwei diametrale Ikosaederecken durch Xullse^izen der sechs linearen
Formen:
(6) g^ = y5A„ g, = A,^a-^A^ + a^A,. . =- 0. 1, '2, 3, 4,
auf dem Ikosaeder ^ :=z 0 ausgeschnitten, deren erste 41«" bpiden auf
dem Kegelschnitt zi = 0 gelegenen Pole (0, 0. 1) und (0, 1, 0) der
Substitution S liefert. Bei Ausübung der Substitutionen S und T zeigen
die linearen Formen (6) das Verhalten:
(S) g'^ = g^, go = g,, g'i = g^, g^ = fh, g\ = g^, d'^ =--ffo^
(T) g'^ = g^, g'^ = g^, g[ = g^, g',_ = — g,. g\ = -- g^, g\ == g^.
Hiernach liefert das Prodifkt der sechs Formen (6) eine invariante
Form sechsten Grades. Wiß man leicht feststellt, gilt zwischen dieser
Form sechsten Grades und der obigen Form A die Beziehung:
4
(7) .1,. II (A, ■+ £-> A, -f £> A,) = -A-T ^'.
r = 0
Um eine ahnliche Erklärung für die invariap.te Form zehnten Giades
zu gewinnen, bilden wir die fünf quadratischen formen:
I Ä-, = 4 AI - 2 A, A, ^ (r/ -f 1) (f^' A'i - a'^ AJ)
1 -2irj-2)A,(a^^A,-^a'A,)
für 0^ =r 0, 1, 2. 3, 4, wo r^ die folgende quadratische Irrationalität ist:
1 — / \ 15
(9) V = ^^
Gleich 0 gesetzt, liefern sie fünf Jfvegel schnitte, die den fünf konjugierten
Teilern ©^g ^'om Tetraedertypus zugeordnet sind. Per einzelne dieser
Kegelschnitte schneidet auf dem Ikosaeder ^ -= ö vier Flächenmitten
aus. Gegenüber den erzeugenden Substitutionen S und T der ©g^ zeigen
die Formen (8) das Verhalten:
(S) 7/o = \, K = \, Ti\ = \, ks = /.„ /.•; = 7^0,
(T) A-; = 7.„ 74 = 97.-,, 74=9^7.-,, k', = QH-^, JÜ = Qk„
I, 6. Allgemeine Gleichung fünften Grades,
-l-f iV3 ,
- ist. Die fünf Formen (8) sind die Formen niedersten
Grades, die gegenüber der^^^, abgesehen von multipWkativen dritten Einheits-
wiirseln, die 60 geraden Permutationen erfahren'-^). Wie man sieht, ist
das Produkt der fünf Formen (8) eine invariante Form zehnten Grades.
Gleich 0 gesetzt, schneidet sie, wie auch die Gleichung M = 0, auf
dem Ikosaeder ^ = 0 die 20 Flächenmitten aus. Die Darstellung des
Produktes der Formen (8) durch die Formen ^, A, M ist:
4
(10) Jj7.\ {A^. A^.A^) = --9i{öri~l) M + 4:80(rj~ 2) Az/^ -f- 1024^°.
Die 15 Substitutionen der Periode 2 stellen als Kollineationen
sogenannte „Jiarmonisclie PerspeUivitaten" dar. Sich selbst entsprechende
Punkte (Pole) einer solchen Kollineation sind erstens die gesamten
Punkte einer Geraden, der „ Perspektivitätsachse" sowie weiter ein
außerhalb der Achse gelegener Punkt, das „Perspektivifätszentrum". Die
übrigen Punkte der Ebene permutieren sich zu Paaren in der Weise, daß
zwei einander entsprechende Punkte mit dem Zentrum auf einer Geraden
liegen und durch dies Zentrum sowie den Schnittpunkt ihrer
Verbindungsgeraden mit der Achse harmonisch getrennt sind. In bezug auf den
Kegelschnitt ^ = 0 ist die Achse die Polare des Zentrums. Die
Perspektivitätsachsen der in der ©g^ enthaltenen Substitutionen der
Periode 2 sind durch die 15 Gleichungen gegeben:
(11) s''A,~e^A^ = 0, {l±]/5)A^-^e*^A^~^s'A, = 0, ^=o,l,---,4.
Es besteht der Satz: Dcit, Prodald der Unken Seiten der 15Gleichungen(il):
( K(A^, A„ A^) = — (AI — A'i) (1024 A]' — 3840 A^ A^ A^
I + 3840 AI AI AI - 352 Al {Al ^ A^) - 1200 A^ Af Al
I i- 160 AI A, A^ (AI ~f A'I) ^ 100 Al At AI
[ - 10 ^ Af AI (A! + AI) - (AI -f Alf')
oder hei Benutzung von 2 A^ als erster Veränderlichen:
( K(A,. A^, A,) = - (Ai - AI) ((2 A^' - 15 (2 AJ A, A,
- ^0C2A,rA!Al-11 C2A,)-^(Al +.4|) - 75(2^,)Mf.4|
^ 20 (2 A,)^ A, A (A! ^ AI) + 25 (2 A^f- At A.f
[ - 5 (2 A,) A! AI (AI + AI) - (Al -f Aiy-)
ist Us auf einen konstanten Faktor die einzige existierende invariante
Form 15^^'^ Grades. Eine (absolute oder relative) Invariante 15^^" Grades
*) Erst die von Klein in „Ikos.-, S. •2-22 erklarten fünf kubischen Formen dr
erfahren rein die 60 geraden Permutationen und geben zur Bildung der Bnoschisehen
ßesolvente fünften Grades Anlaß.
Volles Formensystem der terparen Ikosaederginippe. 167
gibt nämlich, gleich 0 gesetzt, eine Kurve 15*^" Grades, die das Ikosaeder
^ = 0 in einem System von 30 nur unter sicji äquivalenten Punkten
schneidet. Es gibt nur ein solches Punktsystem, nämlich die 30 Kanten-
halbieningspunkte, die von den 15 Achsen (11) ausgeschnitten werden.
Xun geht die Kurve lÖ*^'* Gerades durch die einzelne Perspektivität in
sich über und muß demnach, falls sie die zugehörige Achse glicht als
Bestandteil enthält, in jedem der beiden Schnittpunkte dieser Achse mit
dem Kegelschnitt ^ = 0 den letzteren entweder berühren oder daselbst
einen Doppelpunkt haben. In beiden Fällen zählt der Schratt der Kurve
15*^" Grades mit dem Kegelschnitt doppelt;, so daß wir 60 und nicht
30 Schnittpunkte erhalten würden. Die Kurve 15*^" Gfrades enthält
demnach eine und also alle Perspektivifcätsachsen, woraus die Behauptung
hervorgeht.
Weiter folgt leicht, daß X eine absolute Invßriante ist Wir haben
nämlich eine solche auch in der Funktionaldeterniinante von ^, A und M,
und diese ist nach dem gerade bewiesenen Satze bis auf einen konstapten
Faktor gleich N. Man zeigt in der Tat die Gültigkeit der Gleichi^ng:
(14) ^, ^, ^ =-10 X(A„,A„A,).
Es gilt nun der Satz: In /J, A, M and X hat man das volle System
invarianter Formen der ternaren l}MMeder-(^^^, in denen alle invarianten
Formen der ©g^ rational und ganz dafdelThar sind. Aus einer beliebig
vorgelegten Form sondere man zunächst die höchste in ihr enthaltene
Potenz von zJ ab. Der andere Faktor 0 ist dann gleichfalls eine
Invariante, und zwar eine absolute*). Die Kurve 0 = 0 schr^eidet auf
dem Ikosaeder ^ == 0 ein iiivariantes Punktsystem aus. Dieses bestehe
aus den ^-fach gezählten Ikpsaederecken, den u-fach gezählten
Flachenmitten, den v-fach gezählten Kantenmitten und wejter einer gewissen
Anzahl von Systemen zu je 60 äqifivalenten Punkten, das e^nzelr^e System
in einer gewissen MultipKzität %^ gezählt. Das einzelne dieser letzteren
Systeme, einfach gezählt, können -^ir n^n durch eine K urve 30sten Grades,
aA^Arß M^ = 0, bei zweckmäßiger Auswahl der Parameter a, ß
ausschneiden. Es läßt sich daraufhin eine Gleichung:
(15) A^- M" N' n {a^ Ä- + ß, MY' = 0
d^
^A'
dA
oA^
dM
C^o'
dzl
dj,'
dA
d4r
dM
dJ,'
dJ
^A,
dA
dA^
dM
dA.,
*) Gegenüber ,§ und T i^eigt namhch ^ das Verhalten <?' z=z a> 0 bzw.
4^' =1 i 0, und es muß ±_ s^ ei^e dritte Wurzel der Einheit sein, da Ä' • T von
der Periode 3 ist. Also ist x«' = 1. woraus die Behauptung folgt.
Ißg I, 6. Allgememe Gleichung fünften Grades.
aufbauen, mittels der wir auf dem Kegelschnitte ^ = 0 genau dasselbe
Punktsystem ausschneiden wie durch 0 = 0. Ist nun 0 nicht bereits
mit der linken Seite der Gleichung (15) bis auf einen konstanten Faktor
identisch, so wählen wir irgend einen weiteren Punkt auf dem Ikosaeder
.^ = 0, in dem alsdann die linke Seite der Gleichung (15) und die
Form 0 von 0 verschiedene Werte haben. Darauf hia läßt sich eine von
0 verschiedene endliche Konstante G derart bestimmen, daß die Gleichung:
(16) 0 — CA'- M" N' YL («. ^' - ßi ^T" = 0
für den gewählten Punkt zutrifft. Durch die nicht identisch
verschwindende Gleichung (16) wird alsdann eine Kurve dargestellt, die
einen ihrem Grade nach überzähligen Punkt, nämlich den eben gewählten^
auf dem Kegelschnitt ^ = 0 ausschneidet und also notwendig diesen
Kegelschnitt als Bestandteil enthält. Es möge ^ im ganzen ö^-fach als
Faktor in der liaken Seite der Gleichung (16) enthalten sein. Wir
haben dann zu setzen:
(17) 0=c Ä'- M" N' n ("' ^'+ß^ ^y ^ ^^-^x^
wo 0j eine invariante Form der ^^^ von geringerem Grade als 0 darstellt.
Indem man dieselbe Überlegung auf 0^ anwendet sowie den Prozeß
nötigenfalls wiederholt, gelangt man zum Beweise des aufgestellten Satzes.
Die Kurve SO^ten Grades aA^-^ß M^ = 0 mit nicht
verschwindenden a, ß schneidet den Kegelschnitt im allgemeinen in 60 verschiedenen
Punkten. Xur für ein gewisses Verhältnis a: ß fallen diese 60 Punkte
zu Paaren an den 30 Kantenmittelpunkten des Ikosaeders zusammen.
Einer dieser Punkte hat die Koordinaten J.^ = «, Ä^^ = A^ = 1.
Indem wir fordern, daß er auf der Kurve SO^ten Grrades liegt, ergibt sich^
daß die Koinzidenz der 60 Punkte zu Paaren für a = 12^, /3 = — 1
stattfindet. Die Kurve N^ = 0 liefert genau den gleichen Schnitt mit
dem Kegelschnitt zf = 0. Da man weiter zeigt, daß die Gleichung:
(18) iV^ + 1728^5 - M^ = 0
auch noch für den weiteren Punkt Ä^ = A^ =z 0, A^ = 1 des
Kegelschnitts erfüUt ist, so steht in (18) links eine durch zi teilbare Form:
(19) A^V l'^28^^ —M^= z/0^.
Die Form 0^ stelle man nun im Formensystem zl, A, • ■ ■ dar, wobei
sich zunächst ein Ansatz mit 11 Gliedern ergibt. Die Mehrzahl dieser
Glieder aber fäUt aus, da in (19) links die Potenzen ^o^^ ^o^^ A^'^, A^^
nicht auftreten. Der Ansatz reduziert sich so auf:
N^ + 1728^° — M^ = a AP zf''+ ß A^ Mzf' -f y A'zt^ + 6 A M"^''
-i- E A' MzJ.
Algebraische Beziehung zwischen (Jen ternarei^ Ikosaederformei^. 169
Die Koeffizienten a, ß, y, • • • bestimmt man sehr leicht durch Eintragung
der Ausdrücke der A, M, ■• • in c|en Ä und Vergleicl^ der Koeffizienten
rechts und links. Es ergibt sich der Sß,tz: Die zweite Potem der Forfn N
laßt sich in den iibrlgen, Formen äßü Sydemt! in folgender Ad ilarbtelleii:
(20) ^r-= — l728 A' + M^ -r 64 M^ ^^ — 640 A- Mzf'
4- UOOA^zi^—804 M^zl^^ 120d^Mzf.
Will man sich auf das Ikosaeder ^ = 0 beschränken, so hat mg-n ^ = ^
zu setzen, so daß an Stelle der Gleichungen (1) die iolgeudeu treten:
(21) ^io = t,t,> Ä^=-tl ^^2^tl
Die drei Formen A, M und iV liefein dann die Ikosaederformen ^, (p
und i/; wieder:
(22) M(.lo, A> 4,) =- <p(t„t,),
\ N{Ä„Ä„A,)= 1/^(^1-y.
§ 10. Jacob! sc]tie Gleichung sechsten Qradeß.
Die Funktion fünften Grades -.4^ der Wurzeln a der vorgelegten
allgemeinen Gleichung fünfien Grades bleibt bei cj^r Permutation S
unverändert, wahrend die Permutation U Zeichenwechsel von J.^ bewirkt.
In der Tat erfahren die in (11) S. 161 erklarten Ausdrücke t gegenüber V
die Substitution;
Also gehört Äq zur Dieder-Ö^^, die aus S und U erzeuget wird. Die
aufzustellende Resolvente sechstel^ Grades ä^er Gleichung fünften Grades
soll nun die sein, die:
(1) 7oo = o.Io'
zu einer ersten Wurzel hat, und deren übrige Wurzeln y^, j/p ■•■, y^
aus y^ durch die Permutationen T, ST, • • •, S^ T entstehen. Aus der
Wirkung von S und T auf die Ä entspiingt dann der Satz: Dte Qiiadi'ut-
warzeln der öecitö Losungen y de'' aufzuotellei'^den Beüolvente öecJ(öten
G-rades la^^en sich in den drei Größen A öo darstellen.
(2) ]'^ = \Ia„ ^'y; = 4^j^s^A^-^e-^A,, . == o, l, - ■., 4;
die Resolvente ist demnach eine „Jakohische Gleichung" sechsten Gradeö-^-).
Die Koeffizienten dieser Resolvente sechsten Grades sind Formen
der ternären Gruppe ©g^^ und als solche i^ den zi, A, ••■ darstellbar.
Wir setzen die Resolvente ii^ der Gestalt:
(3) z^ -i- aj^z'° -[- a^z*" -\- a^z^ -^ a^z^ -\- a^z -^ a^ = 0
*) Vgl. die S. 71 ff. gegebene Erklärung der Jacobi sehen Gleichungen.
170 Ii 6- Allgemeine Gleichung fünften Grades.
an und stellen die Potenzsummen ihrer Wurzeln;
4
als rationale ganze Funktionen der Formen Zl, A, M dar. Man findet
für die ersten fünf Potenzsummen nach kurzer Rechnung:
i), = 10 z/, i)2 = 30z/^ :P3 = 10(13z/^ —3^),
p^ = 70z/(9z/^ —4^), p^ = 10z/H313z/^—190^)+5M.
Die ersten fünf Koeffizienten der Gleichung (3) berechnet man jetzt nach
den Formeln (9) in I, 102, das Absolutglied stelle man als Produkt der
Wurzeln y und damit als fünffaches Quadrat der linken Seite der
Gleichung (7) S. 165 dar. Es findet sich:
a^=^-lQzl, a^ = S6zl^ a, == — ßO zi'-^ 10 A.
a^ = oozl^ — SOziA, a3 = — 26 z/5 4_ 30 ^2 ^ _ jVf,
a, = 6zf' — lOzl'A + oA-.
Hieraus geht hervor, daß man die Resolvente in eine einfachere Form
setzen kann, wenn man statt des bisherigen z in ihr (z — z/) als
Unbekannte einführt. Man findet nämlich den Satz: Die su den erklärten
Funktionen y gehörende Ite^olvente sechsten Grades der allgemeinen Gleichung
fünften Grade» ist:
( {z — Af — ^/i (z — ziY+ 10 A (z — ziy — M{z — z/)
^ \ -r (o A^ — zi M) = 0,
wo z/, A und M die invarianten Formen der ternäreu (^g^ i>ind, die sielt
rational in den Koeffizienten der gegebenen Gleichung und der Wurzel \ D
ausdrücken lassen.
Da die beiden in (7) S. 160 eingeführten Größen m und n noch
verfügbar sind, so haben wir hier mit einer Schar von Resolventen
sechsten Grades zu tun. Entsprechend heißt die erhaltene Gleichung (4)
bei unbestimmten m, n die allgemeine JakoUsche Gleichung sechsten Grades.
Kronecker hat nun den wichtigen Schritt getan, von hier zu einer
,.speziellen'" Jacobischen Gleichung überzugehen, mit der er Anschluß
gewann an die Jacobische Multiplikatorgleichung für die Transformation
fünften Grades der elliptischen Funktionen*). Es handelt sich in
unseren Bezeichnungen darum, m und n derart zu bestimmen, daß z/ ver-
öCltwindä. Xun ist z/ eine Form zweiten Grades in m, n, deren
=^) Der sich hier darbietende Weg stellt die eigentliche „Kronecker sehe
Methode der Losung der allgemeinen Gleichung fünften Grades- dar, wie er sie
bereits 1858 m seinem Briefe an Hermite andeutete. Brioschi hat nicht nur
die „Kroneckersehe Methode" ausfuhrlich behandelt, sondern ist dann auch,
Hermite folgend, zu der nachmals nach ihm benannten ßesolvente fünften Grades
zurückgekehrt (vgl. S. 152).
Kroneckersche Losung (Jer Gleichung fünften Grades. 171
Koeffi^enten rational in den Koeffizienten der Gleichimg fünften Grades
und VD darstellbar sind. Li ^ = 0 haben wir also eine Grleichung
zweiten Grades für das Verhältnis nt:n. }lan gelangt zu dem Satze;
Die allgemeine JacoUsche Gleichung (4) id nach AdjunUion einer zweiten
Quadratwurzel, die nach dem schon S. 163 erwähnten Satze von Kronecher
notwendig alsessoriöch ist, auf eine sj^ezielje Jacohische Gleichung mit
^ = 0, also auf die Gleichung:
(o) z' + 10 4 z^ — Mz -^oA^^O
reduzierhar, die ihrerseits sofort auf die jResolvente (7) S. 70 der Il-osaeder-
gleichung zuriicMommt und also nach S. 98 ff. durch ModiilfunlÜQnen
lööhar ist.
§ 11. Aufstellung einiger Hilfssätz^.
Die Transformation der allgemeinen Gleichung fünften Grades auf
eine Gleichung mit nur einem Parameter ^ar nach Adju|iktioQ zweier
Quadratwurzeln möglich, voq denen eine ..ak:?essorisch- ist.
Kronecker*) hat bereits 1861 die Behauptung aufgestellt, daß es nnmöglich
id, die allgemeine Gleichung fünften Graßcb hei alleinigem Gehrauch
„natürlicher- Irrationalitäten in eilte nur „einßarametrige- Gleichung zu tranb-
formieren.
Man gründet den Beweis dieses ,. Kronecker sehen Satzes- auf
verschiedene Hilfssätze, von denep ein erster der folgepde Satz vpn Luroth=^=^)
ist. Sind:
sioel ratimiale FunMionen von s, wo (p^ (ö) und t/;^ (ö) und ebenbO (p^ (b),
^2 (b) teilerfrertide ganze FunMionen darbtellen, die nicht ztigleich vom
Grade 0, d.h. }:onstant bind, bo l:ann mau eine lationßle FmtJdion X von
x^, x^ ho)%struieren:
(2) 2=: JS(»j. /,),
?M der x^ und x^ zugleich ratimial darstullhar bind:
(3) x^ = BAI), ^, = J^äC/v).
Zum Beweise dieses Satzes führen wir eine zweite von ö unabhängige
Variable t ein und bezeichnen die Werte der Funktionen (1) fur das
Argument t durch t/^, y^:
^1 (t) ^2 W
"') Vgl. die „Algebraischen Mitteilungen" m den Monataber. ^er Bßrl. Akad.
von 1861.
'■'*) Vgl. dessen Abhandlung „Beweis eines Satzes ubef rationale Kurven-,
Math. Ann. Bd. 9 (1875).
172 Ii 6. Allgemeine Gleichung fünften Grades,
Man hat dann in:
(5) (f, (s) ti (ß) - ^i (^) <Pi (i) = ^^ (^-^ tl ^ = 1' •^'
zwei nicht identisch verschwindende ganze Funktionen der beiden
Variablen s, t. Xach I, 44 denken wir diese Funktionen in ihre irreduziblen
Faktoren zerlegt und nennen das Produkt aller gemeinsamen, einzeln
sowohl ö als t enthaltenden Faktoren von X^ und X^ den ..größten
gemeinsamen Divisor- von X^ und X^. Er werde durch D (ö, t) bezeichnet,
und es werde:
(6) X, (., t)=^D (., t) X, (s, t), X, {s, t) = D (., t) X, (^, t)
gesetzt, wo Xii^j 0 ^^"^ X^i'^' 0 zwei ganze Funktionen sind, die keinen
ö und t zugleich enthaltenden Faktor mehr gemein haben. D (s, t) ist
nur erst bis auf einen von 0 verschiedenen konstanten Faktor erklärt;
wir denken diesen der Bestimmtheit halber irgendwie ausgewählt.
Bei Austausch von ö und f wechselt X^ (s, t) das Vorzeichen:
X, (., t)= -D {t, .) x^ {i, ^), X, (^ t)== -D {t, .) X, (t, .).
Demgemäß ist D (t, b) wieder ein gemeinsamer Divisor von X^, X^, und
zwar ein größter gemeinsamer Divisor, da sonst Xi und Xi noch einen »
und t enthaltenden Faktor gemein hätten. Hiemach ist JD (t, b) bis auf
einen konstanten Faktor gleich D (b, t). Dieser Faktor kann nur gleich
i:; 1 sein, da zweimaliger Austausch von ö und t zu D {s, t) zurückführt.
Wäre aber D (t, b) = D (s, t), so würde daraus:
folgen; also wäre Xi(ßj *) =^ *-*> ^- ^- Xti^j 0 würde als Funktion von t
für t := b verschwinden und mithin durch (t — s) teilbar sein, entgegen
dem Umstände, daß Xi (j>j 0 ^^d Xi (*) 0 keinen s und t enthaltenden
Faktor gemeinsam haben. Es gilt hiernach:
(7) D {t, s) = —D (s, 0-
Die ganze Funktion D (b, t) enthält somit den Faktor (s — f) und hat in
ö und t ein und denselben Grad jm > 1.
Die wirkliche Berechnung des gemeinsamen Divisors D {s, t) kann
nach dem bekannten ., Algorithmus des größten gemeinschaftlichen Faktors-
(vgl. I, 13 ff.) ausgeführt werden. Man hat dabei eine der beiden
Variablen, etwa t, zu bevorzugen und bei den Rechnungen auch
gebrochene rationale Funktionen von s zuzulassen. Man schreibe also unter
Bevorzugung von t:
.g. ( ^1 (0 = %t>^ + a^t'-' + ••• + a„
wo die a, h ganze Funktionen von s sind. Ist etwa h'^ 1, so beginnt
man mit der Division von X^ (t) durch X^ (t) und erhalte:
X,(t)= Q{t)X,{t)+P(t),
Beweis fies Lurothsehen Satzes. 173
WO Q (t) der Quotient und P (t) der Divisionsrest ist. Es ist klar, daß
JP{t), mit einer geeigneten ganzen Funktion von 0 allein muliipliz:(.ert,
eine wieder durch D (s. t) teiJ^bare ganze Funktion vop s, t liefert. Bei
Fortsetzung des Verfahrens e:phält man wie in I, 14 den größten
gemeinsamen Divisor vom vorletzten Divisionsrest her, der hier freilich erst
noch durch Multiplikation mit einer ganzen Funktion vor|. 0 allein von
seinen Xennern befreit werden muß.
Die letzte "Überlegung gestattet eine weitere wichtige Angabe über
die Bauart des gemeinsamen Pivisprs D (s, t). Wenn man schon rationale
gebrochene Funktionen von s bei der Rechnung zuläßt, mag man den
Divisionsprozeß statt an die Funktionen (8) auch an die beiden
Funktionen :
anknüpfen. Der vorletzte Divisipnsrest ist dann eine ganze Funktion
„^ten Q-rades von t, deren Koeffizienten rational in x^, x^ aufgebaut ^ind.
Wir nennen diesen Rest f(t, x^, x^) und haben aus ihm durch
Multiplikation mit einer gewissen ganzen Funktion g (0) von s allein den Divisor
D (s, t) herzustellen:
(9) D(.,t) = g{.)f(t,^„x,).
Man verstehe jetzt unter a u^d ß irgend zwei rationale Zahlen, fur
die die beiden Funktionen m^^^ Grades D (s, a) und D (0, ß) nicht
identisch ausfallen. Dann gewinnt man im Quotienten:
('°> ' - IM^ - f(ß, .7;^,) ~ ^("'■ ''^
eine rationale Funktion von /j, a;^, deren Koeffizienten dem Körper der
Koeffizienten der Funktionen (1) angehören. Wii' behaupten, daß hiermit
die unter (2) angesetzte Funktion gewonnen ist.
Um dies zu zeigen, setzen wir für 0 einen beliebigen Wert Sj ein
und betrachten die Gleichung D (s^, ^) ^^ 0 d^s Grades m für t, die dann
jedenfalls die Lösung t = b^ hat. Ihre gesamte^ Lösungen seipn:
(11) t = s„ s„ ..., s,.
Wir haben dann, da D {s, t) Teiler der beiden Fimktionen (5) ist:
(P^ i&^) i>^ (Sv) - ^>^ (^,) ^^ ip^) = 0, ^ ^ ^ ^ ., . . . ,,^
ffi (Si) i>^ (S«) - ^>^ (ö„) ^i (Si) ==0,
zwei Gleichungen, aus denen man leicht weiter:
(12) I ^^ ^'^'* ^^' ^""-^ "^^ ^"'^ ~ ^' ^''^ "^^ ^'"-"^ "" ^'
l ^z (Si) {(fz (S/.) ^^ (Sv) - (P^ (Sv) 1P^ (S^)) = 0
174 Ii 6- Allgemeine Gleichung fünften Grades.
folgert. Da aber (p^ (s) und ip^ (0) als teilerfremde Funktionen für s = s^
nicht zugleich verschwinden, so ist der unter (12) in Ellammern stehende
Ausdruck gleich 0:
(13) (p, (S„) i;, (S,) — y, (ö,) T/;, (S„) = X, (Sa, Sr) = 0, i = 1, 2,
so daß die beiden "Funktionen X^ (s, ^) und X^ (s, t) allemal verschwinden,
wenn man die Argumente mit irgend zwei Wurzeln (11) der Gleichung
D (s-^, t) = 0 gleichsetzt. Hieraus kann man den Schluß ziehen, daß
der für s = s^, t = s^ verschwindende Bestandteil der beiden
Funktionen Xj, notwendig der größte gemeinsame Divisor D{s, t) ist. Es
würden nämlich sonst die beiden in (6) eingeführten teilerfremden
Funktionen ;^^ (b, f) für Sil, Sv verschwinden müssen. Indessen gibt es
zufolge (4) in I, 47 zwei ganze Funktionen F(s, t), 0 (s, t), die in:
F(s, t)x,is, t) + 0(s, OZaCS' 0 = co(ß)
eine ganze Funktion co (ö) von ö allein liefern. Sollten also die
Funktionen 2i (s, i) für bu, öv zugleich verschwinden, so wäre s„ auf die endlich
vielen Lösungen von co (s) = 0 beschränkt. Also könnte D (s„, s^) zh 0
höchstens für endlich viele Lösungssysteme (11) zutreffen*). Dies ist
aber wegen der Stetigkeit von D (s, t) ausgeschlossen, so daß die
Gleichung gilt:
(14) D(.„, .,) = 0. u, .= 1,2,-.; m.
Hiemach haben für unser Größensystem (11) die tu Gleichungen:
D (.,, t) = 0, D (.2, 0 = 0, •. •, D (s«,, 0 = 0
j^ten grades mit der Unbekannten t alle ein und dasselbe Lösungssystem.
Schreiben wir demnach:
(15) D(., 0 = ^(0-J5,(s, 0,
unter }i (s) den Koeffizienten von t^ in der Gleichung D (ö, 0 = 0
verstanden, so werden für das einzelne System (11) die m ganzen Funktionen
Di(ö,, 0, I>i{h^ t), JD, (Ps, t), •••, I>i(s«i, 0 von t gleiche Koeffizienten
aufweisen, also identisch sein. Man hat insbesondere für die beiden oben
gewählten rationalen Zahlen a, ß:
1 D, («„ ß) = B, {s„ ß) = ... = D^ (s™, ß),
woraus man auf Grund von (15) die Gleichungen gewinnt:
B{s,,a) _I){s„a) D {b^, a)
(1'^)
D(s„ß) Dib„ß) D(s^,ß)
*) Man beachte, daß Sj willkürlich wahlbar ist, daß aber mit Sj das
Losungssystem (11) be^ttimmt ist.
Verallgemeinerter Lurothscher Satz. 175
Man schließt hieraus auf folgenden Satz: Auch die m Lösungen der
Gleichung m'^^^ Grades für 0:
(18) D{s, a) — lD{^, ß) = 0,
mit dem Parameter X bilden ^.Uemal ein System (11) zusan^mengehör^ger
Werte 0^, b^. •••, b„^.
Für jedes solche Wertsystem (11) ergejben sich nun ans:
X, (.„ b,) = 0, q>, (s,) ^, {s,) - tp, {s,) i,, (.,) =. 0
die Gleichungen:
^ ^ ^i (^i) ^ y» (^2) ^ ^ y» {^m)
■"* T/;,(s,) T/;,(52) ■" 1/;, (O'
aus denen man weiter folgert:
X, = — S ^^^ , ^ = 1, 2.
Hiernach sind die x^, x^ S}.mmetrische Funktionen der Wurzeln der
Gleichung m^^^ Grades (18), mithin i'ationale Funktionen der
Koeffizienten dieser Gleichung, d. h. rationale Funktionen von X. wobei die
Koeffizienten dieser rationalen Funktionen dem K örpe^- der Koeffizienten
der Funktionen (1) angehören. Die in dem zu beweisenden Satze
behaupteten Darstellungen (3) für x., x^ sind damit tatsächlich gewomien.
Hieran schließt sich der „verallgemeinerte Lürothsche Satz'': Sind
w > 2 rationale FauTdimien von b:
vorgelegt, wo im einzelnen Quotienten ZaJder und X'enner teilerfretnde, nicJd
zugleich dem Grade 0 angehörende ganze FunUiouen bind, bo Jcann ^oan
eine rationale FunMion:
(20) l = B{x^, x^, ■'-, xn)
konstruieren, in der die x^, »g, •••, ä;„ zugleicji ratj,onal darbtellbar bind.
Der Beweis gelingt durch den Schluß der vollständigen Induktion.
Man nehme den Satz für {n— 1) Funktionen (19) als gültig an. Man
kann also eine nicht-konstante rationale Funktion:
(21) fi = ^{x^, x,_, ■■■, »^_i)
angeben, in der die a;^, x^, •••, x^—i rational sind:
(22) X, == P,(ji), X, =-. P,J^), ■■■, x«_, = P«_,(^).
Man hat alsdann:
^23^ a — ^^'^ X — ^"^'^
176 !> 6. Allgemeine Gleichung funtten Grades.
WO die erste Gleichung aus (21) durch Eintragung der Ausdrücke (19)
für »j, »2, •••, Xn—i gewonnen wird. Xach dem für n = 2 bereits
bewiesenen Satze gibt es nun eine rationale Funktion:
/l = Qifi, Xn),
in der ft, und x^ ihrerseits rational darstellbar sind:
(1= Q^ (i), X,, = js« (;l).
Aus den vorstehenden Gleichungen folgt weiter:
X = Q{jP{x^^ Xg, •.., rx.^_i), »ji) = B{x^, Xg, •••, Xn),
t^ = P, {Q^ {X)) = B^ {X), ■■; »«_! = P«_i {Q, (X)) = Itr^-i W,
X,, = H^ iX),
womit der verallgemeinerte Lürothsche Satz bewiesen ist. Auch hier
gehören die Koeffizienten der Funktionen It dem durch die Koeffizienten
der Funktionen (19) gelieferten Körper an.
Leicht beweisbar ist der folgende zweite Hilfssatz: Id jede der
leiden Großen x, y eine rationale FunMion der anderen, so bind sie lineare
Funktionen voneinander. Es sei also:
wo beide Male Zähler und Nenner teilerfremde ganze Funktionen sind.
Die zweite Gleichung liefert (p (y) — xrf; (y) = 0 imd ergebe nach
abfallenden Potenzen von y geordnet:
% 2/™ -r «1 «z™"' + • • • + «m = 0,
wo die Koeffizienten a lineare Funktionen von x sind. Trägt man den
durch die er&te Gleichung (24) gelieferten Au&druck \on y in x ein,
so folgt:
als eine in x identisch bestehende Gleichung. Setzt man diese Gleichung
in die Gestalt:
— «o/"(^)™ = 5» (^)K/'(»)"'"'' + aj(x)^—^g (x) -i -f a^ g (xY'^-^).
so erweist sich y (x) als Teiler von a^ f (x)™. Da aber f (x) und g (x)
teilerfremd sind, so ist g (x) Teiler der linearen Funktion a^ und also
selbst Knear oder konstant. Entsprechend folgt aus:
-ar,g(xr = f(x){aJ(xr-^-^aJ(xr-^g(x)+.-.-^a^_,g{xr-^),
daß auch f(x) linear oder konstant ist, womit der Satz bewiesen ist.
§ 12. Resolventen mit einem Parameter.
Es sei die allgemeine Gleichung irgend eines Grades m > o
vorgelegt: ""
(1) ^™ + «, ^™-^ + a^z^-^ _|_ ... 4_ (j^ — 0,
Ansatz einer Eesolvente ii^it einem Parameter. 177
deren Wurzeln wir, um ihre unabhängige Veränderlichkeit besser zu
kennzeichnen, durch s.^, z^, •••, s^ bezeichnen. Audi die Koeffiziepten
ftj, Og, •••, a^ haben hier also als unabhängige Variable zi; gelten. Zum
Funktionenkörper (M, a^, a^, •••, a^) möge noch die Quadratwurzel ]'D
der Diskriminante der Gleichung adjangiert sein, wodurch sich die
Galois sehe Gruppe der Gleichung (1) auf die alternierende (3i ,
reduziert. Bei der Frage nach der Existenz eii^er Resolvente: "^
(2) f(x, p) = 0
mit einem einzigen Parameter p, deren Koeffizienten also rational in p
mit numerischen Koeffizienten aufgebaut &:(.nd, pehmen wir den
Standpunkt ein, daß ,.numerische- Irrationalitäten ohne Einschränkung ad-
jungierbar sind. Dagegen sollen, was die Abhp,ngigkeit von den
Variablen ^j, z^, •••,£^ angeht, allein „natürliche- Irrationalitäten, d.h.
rationale Funktionen der 5^, s^, •••, 2^,1 zugelassen werden. Es soll also
eine erste Wurzel x der Resolvente (2) eine rationale Funktion:
(3) x = g{z,, z,_, ••-, .-J
mit irgendwelchen numerischen Koeffizienten sein. Diese Fmiktion soll
noch nicht zur alternierenden (^j^ , gehören, da sonst in (2) eine „Partial-
2™-
resolvente" ersten Grades vorläge, die kein mit der Lösung der
Gleichung (1) gleichwertiges Problem darstellt. Durch die Permfitationen
der ®i , gehe die Funktion (3) x^. n'^ 1 \erschiedene Fuipiktiopen über,
2™-
die dann die Lösungen der Resolvente w*^» Grades (2) sind und durch
x^ = X, »2' ^3' " *) ^n bezeichnet werden mögen. Der Parameter p ist
nach Adjunktion von \D rational bekannt; als rationale Funktion der
Wurzeln z schreiben wir:
(4) i^ = Z(^n ^2' •••' ^m)-
Es lassen sich nun aus diesen Vorraussetzungen mit Bfilfe der Sp,tze
des vorigen Paragraphen verschiedene wichtige Folgeningen zieiien. Die
Gleichung (3) gehe durch die Permutatioi^en der @i , in die n ver-
schiedenen Gleichungen:
(5) a?fc = </fc(-*'i, ^2' •••' ~rJ' i=l, 2, ..-,«,
über, wo für fc = 1 die Gleichung (3) selbst vorliege. Es sei:
(6) ^F{x^, x^, • • •, x^^)
eine rationale Funktion der.^ und damit der z, die wjr dadurch zu einer
rationalen Funktion einer eipzigefl Variablen 0 machen, daß wir für die
^ die folgenden rationalen Funktionen von 0:
(7) z, = \ (s), ^a = K i^)' •■•■ -r^ = ^m (s)
Fncke, Algebra. II. 12
178 I' 6- Allgemeine Gleichung fünften Grades.
eintragen. Es soll die Tatsache bestehen, daß die Funktion (6) als
rationale Funktion von s identisch verschwindet. Dagegen soll:
(8) P = %{\i^yh(s), ■■; Kis))
eine nicht mit einer Konstanten identische rationale Funktion von s sein.
Unter diesen Umständen kann man beweisen, daß die FunUion (6) auch
bereits als solche der „unahMngigen- Variablen s^, z^, •••, x:^^ identisch
verbchwinden muß.
Um dies zu zeigen, ziehen wir die Monodromiegruppe der
Gleichung (2) heran, auf die sich die Galois sehe Gruppe dieser Gleichung
nötigenfalls nach Adjunktion geeigneter numerischer Irrationalitäten
reduziert. Die Permutationen der Monodromiegruppe:
/Xi, Xo ,
üben wir auf die Funktion (6) aus und bilden das Produkt aller
Funktionen F (»jj^ ,%,,•••, »^ ), das eine rationale Funktion von _p ist:
(10) n^K' ^'2' •••' x,^) = H{p).
Setzen wir nun fiir die s^, z^, •••, ^^ die rationalen Funktionen (7) ein,
so ist F{x^, »2, •••, Xrt) mit 0 identisch. Also verschwindet die linke
und mithin auch die rechte Seite von (10) identisch. Da aber _p nicht
konstant ist, so muß die im Zähler von H{p) stehende ganze Funktion
von p identisch verschwinden, d. h. lauter Koeffizienten 0 haben. Hieraus
folgt, daß das Produkt (10) auch schon vor der Eintragung der
Ausdrücke (7) für die s identisch verschwindet, also mindestens einen
verschwindenden Faktor hat. Ist aber einer gleich 0, so verschwinden sie
alle, da sie bei den Permutationen (9) der Monodromiegruppe ihren Wert
nicht ändern. Also verschwindet die Funktion (6) für die Wurzeln x^,
»2, •••, Xn, d. h. bei unabhängig variablen z^, z^, •••, z^.
Mittels des Lüroth sehen Satzes gelingt es nun, weiter folgende
Tatsache festzustellen: Die Wurzeln x^, jü^, • • •, x^ der Besolvente f {x, j)) = 0
mit einem Parameter p lassen sich ah rationale FunUion einer einzigen
Größe X darstellen, die selbbt eine rationale FunUion der x^, x^, • • •, x^
und also auch eine solche der m unabhängigen Variablen z^, z^, •••, z^, ist.
Man setze nämlich für die z wieder die rationalen Funktionen (7) von ö-
ein, die man, was keine Schwierigkeit hat, so gewählt denke, daß der
in (8) berechnete Ausdruck von p in b eine nicht mit einer Konstanten
identische rationale Funktion von ö wird. Dann werden auch die
Xj^, »2) •••> Xn rationale Funktionen von s, und es läßt sich nach dem
verallgemeinerten Lüroth sehen Satze eine rationale Funktion:
(11) k = B{x^, x^, •••,^«)
konstruieren, in der die rationalen Funktionen x^, x^, •••, x„ von s selbst
rational darstellbar sind:
(12) X, = B^ ß), X, = B, ß), ..., x,, = Bn ß).
Satz über Resol\enten mit einem Parameter. X79
Diese Gleichungen gelten in ö identisch Da p eip.e von einer
Konstanten verschiedene rationale Funktion von s geworden ist, so bleiben
sie nach dem eben bewiesenen ersten Satze a,uch dann noch gültig, wenn
wir den x wieder die Bedeutung fier Funktionen (o) der unabhängigen
Variablen z^, z^, • • •, s^^ verleihen. Die GröJ3e k wird dabei die ratioi^ale
Funktion:
(13) k = B{g,(z„ z,, .■■), g,{z^, z„ ...), ••■, g,,iz„ z„ ■.■))
der z;^, z^, •••, z^, wofür wir abkürzend schreiben:
(14) X = B(z„z„ .■.,zj.
llan übe jetzt auf die ~ die Permutationen der alternierenden (3i ,
aus. Ihr entspricht eine (^i , von Permutationeu (9) der Wurzeln der
Resolvente. Die einzelne Permutation (9) führt die Gleirhungen (11)
uud (12) über in:
(15) ;/ = E(x,^, »,2> •••, \),
(16) x,^ =r E^ß'), X,, = B.^{1'\ ■■•. ^,^^ = B,Al').
Tragen wir für die Xi^, -ii^- • ■ •, 'A in die ejrste dieser Gleichungen ihre
Ausdrücke (12) in X ein, so erweist sich X' als eine rationale Funktion
von l. Wenn wir andererseits in (11) für die x^. x^, •••, x,^ ihre
Ausdrücke (16) in X' eintragen, so ervy^eist sich umgekehrt auch X ^Is eine
rationale Funktion von /,'. Also hangen X und X' nach dem zweiten
Hilfssatze von § 11 (S. 176) linmr voneinander ab. Den ^ »«' verschiedenen
Permutationen (9) müssen \}n\ ver&chiedene lineare Substitutionen von a
entsprechen. Damit haben ^pr endlich folgenden grundlegenden Satz
gewonnen: Wenn die allgemeine Gleichung m^^'"- Grradeb (1) naclt Adjunl-
tion der Quadratwurzel aas de» Dibl^rlminante eine rationale Rebolverde [2.)
mit j.einem-' Parameter p hedtzt, bo laßt bich stetb eine rationale FmtMion
X =^ B{z^, z^, ■••, z^) der m Wurzeln kondruiefen, die gegenüber den
Sitbstitutionen der alternierenden Grrappe bellst eine (^i ^ linearer Suhsti-
tatlonen:
(17) r="'- + ^
erfahrt.
yX-YS
§ 13. Satz von Kronecker.
Wir sind jetzt imstande, den an^ Anfang von § 11, S. 171
aufgestellten Satz von Kronecker zu beweisen. Wir Löimen sogar
allgemeiner zeigen, daß die allge^ieine Gletcliang eineb G-rade» in > 5 kein"
rationale Bebolvente mit nur .,einer>f Parameter haben kann. Soll
nämlich eine solche Resolvente existieren, so läßt sich eiiiß rationale
Funktion X(Zj^, Zg, ••', z^) der rti unabhäi^gigen Variable a ^i- ~^, ■■■, z,„
X80 I» 6- Allgemeine Gleichung fünften Grades.
konstruieren, die bei Ausübung der geraden Vertauschungen der s eine
(^i linearer Substitutionen liefert. Es sind nun S. 3 5 ff. alle existieren-
den endlichen Gruppen linearer Substitutionen einer Variablen aufgezählt.
In Betracht kann überhaupt nur der niederste Grad m = 5 kommen, wo
die ®i^j die Ikosaeder-@gQ ist.
Man hat demnach nur noch folgende Frage zu beantworten: Ist es
möglich, eine rationale Funktion X von fünf „unabhängigen'* Variablen
z^, z^, •••, -^5 zu bilden, die bei den 60 geraden Vertauschungen der z
sechzig eine Ikosaeder-@gQ bildende lineare Substitution erfährt? Wir
stellen die rationale Funktion X als Quotienten zweier ganzer
Funktionen dar:
die wir abgekürzt X^ (^j), X^ (^jt) schreiben und als teüerfremd
voraussetzen dürfen. Irgend eine der 60 Permutationen führe z^ in s'j^ über,
so daß ^i, 4- •••) 4 die ^j, ^2' '"'' ■^s ^ "^^^ betreffenden Anordnung
sind. Dann gilt, falls unsere Frage zu bejahen ist:
,.^. A,(4) ^ a X^{z^)-^ ß X^{z^)
^^^ Ki^'i) 7 Ki^i^) -¥ 8 X^{z,)
Diese Gleichung besteht m den z identisch. Es ist demnach X^ {z'j^ bis
auf einen konstanten Faktor gleich dem rechts stehenden Zähler und
^2 C"^^) gleich dem Produkt des gleichen Faktors mit dem rechts
stehenden Xenner.
Wir nehmen diesen gemeinsamen konstanten Faktor in die
Koeffizienten a, /3, y, 8 auf. Dann entspricht jeder geraden Permutation der
z eine homogene lineare Substitution:
(3) X,(z'k) = ax,(z,) + ßh(^k), h(4) = rK(^k) -i-sx,(z,)
der beiden Funktionen X^, X^. Xach S. 42 ist die Ikosaeder-©g^ aus
zwei Substitutionen S und T erzeugbar, von denen S die Periode o und T
die Periode 2 hat, während S T eine Substitution der Periode 3 ist. Eine
Permutation der Periode v liefert eine Substitution (3), deren
Determinante {a8 — ßy) eine v*« Einheitswurzel ist. Den Permutationen S
und T entsprechen also Substitutionen, deren Determinanten eine fünfte
und eine zweite Einheitswurzel sind. Da aber ihr Produkt eine dritte
EinheitsWurzel ist, so sind alle diese Einheitswurzeln gleich -f 1. Alle
60 Substitutionen (3) sind demnach unimodular.
Man betrachte nun speziell die der Permutation T der Periode 2
entsprechende Substitution:
(4) 2.', = a X^ + ß X^, X'^ = fX,+8X^, Di8 — ßy=l.
Da die zweimalige Ausübung dieser Substitution zur identischen
Substitution führt, genügen die Koeffizienten den Bedingungen:
(5) «2^/37=1, (Dc + 8)ß = 0, (cc + 8)y = 0, 8^-\-ßy= 1.
Beweis des Kronecker sehen Satzes. 181
Ist mindestens eine der Zahlen ß, y von 0 verschieden, so folgt 8 = — a.
Dann liefert die letzte Gleichung (5) im AVidersprucJa zur letzten Gflei-
chung (4) die Folgerung ad — ßY-=—l. Also ist ß = 0, y == 0,
und man findet, da in (4) die identische Substitution nicht vorliegen
kann, als der Permutation T entsprechend die Substitution
Dann aber ist ST von der Periode 10 und Dficht, wie es doch zu fordern
ist, von der Periode 3. Damit ist ein Widerspruch aufgedeckt. Die
aufgeworfene Frage ist also zu vernei|ien, und der Kronecker bche Satz
ist bewiesen. Erst nach Adji^nktion der akzßssorisclien Quadratwurzel (8)
S. 140 ist die allgemeine Gleichung fünften Grades in eine Hajipt-
gleichung transfomiierbar, und diese ist dann allerdings nach Adjunktion
der ,.natürlichen- Irrationalität '\I) sowie der reinen Zahl \ 5 in eine
Gleichung mit nur einem Parameter überführbar.
Kronecker hat den fraglichen Satz, wie bereits S. 171 bemerkt
wurde, schon im Jahre 1861 ausgesprochen, aber einen Bewßis nicht
mitgeteilt. Den ersten Beweis des Satzes hat Klein veröffentlicht =^):
auch Gordan ist dann weiter auf den Gegenstand zurückgekommen•^•^).
Kroneckers eigene Erwäg-upgen konnten später aus hinterlassenen
Papieren festgestellt werden, worüber Klein in .,Ges. Abh.'' 11, 503
ausführlich berichtet hatf). Die vorliegende Darstellupg schließt sich in
der Hauptsache an Weber, Algebra II, an, für den seinerbcits im
wesentlichen Gordan vorbildlich w^r.
") Vgl. „Ikos.% S. 258ff. und diß 1877 verotfentlichte Abhai^dlung „Weitere
Untersuchungen über das Ikosaeder-, „Ges. Abh." II, 379.
'^") In der Abhandlung „Über biquadrati&che Gleichungen", Math. Ann.
Bd. 29 (1887). Über die gegenseitige Beziehung de:f Beweise von Klein und
Gordan vgl. man die Ausfuhrungen M. No et hers in seinem Bericht über Gordan,
Math. Ann. Bd. 75, S. 24ff.
t) Vgl. auch die Angaben Kleins in „Ges Abh.- II, 491.
Zweiter Abschnitt.
Endliche Gruppen ternärer Substitutionen
und zugehörige Gleichungen.
Erstes Kapitel.
Klein sehe Gruppe und zugehörige invariante Formen.
§ 1. Kongruenzgruppen siebenter Stufe in der Modulgruppe.
Xach I. 310 reiht sich an die Ikosaedergruppe <3^f^ als nächste
einfache nicht-metazykiische Gruppe eine @jgg der Ordnung 168 an. Es
war eine der schönsten und folgenreichsten Entdeckungen Kleins, daß
diese @jgg als eine G-rioßße ternärer linearer Soibstüufionen darstellbar
ist*). Auch verdankt man Kleins eigenen Arbeiten, denen dann weiterhin
Gor dan folgte, die reich entwickelte Theorie dieser temaren Gruppe
so daß es wohl gerechtfertigt erscheint, sie mit Kleins Xamen zu
belegen.
Einen besonders einfachen Eingang in die Theorie der Klein sehen
Gruppe gewinnt man über die Modulgruppe, indem man nach S. 91 ff
innerhalb der nicht-homogenen Modulgruppe die Haupthongruenzgrupße
biebenter Stufe ip^ bildet. Sie 1st nach (4) S. 92 ein Xormalteiler des
Index 168. &o daß das Komplement von ^2>i ^^^ ®i6s ^^^- -^^^^ kann
auch sagen, daß sich die nicht-homogene Modulgruppe ®, mod 7
reduziert, auf eine endliche Gruppe ©^gg zusammenzieht, und es ist daraufhin
leicht möglich, über die Struktur dieser 03jgg einige Angaben zu machen.
Wir bezeichnen die Substitutionen wieder wie in (5) S. 92, wobei
sich hier die Kongruenzen natürlich auf den Modul 7 beziehen. Da beim
Arbeiten mit der nicht-homogenen Modulgruppe ein gleichzeitiger
Zeichenwechsel der vier Koeffizienten ohne Änderung der Substitution V erlaubt
ist, so dürfen wir die Invariante j = a -)- d auf die vier Reste j = 0, 1,
*) 0. Jordan hat im Journ. f. Math. Bd. 84, S. 89ff. (1878) den Versuch
unternommen, alle endlichen Gruppen ternärer Substitutionen aufzustellen. Doch
hat er dabei gerade die beiden interessantesten Gruppen, nämlich die Klein sehe
Gruppe und die unten zu besprechende Valentmergruppe, übersehen.
Eeduktion der :y;odu|gruppe mod 7. 183
2, 3 beschränken. Wir ergänzen dann zunächst das Formelsystein (5)
S. 92 durch. Berechnung von F*:
(1)
7(?-l),
73 =
-I -- -.- - .._.2J)-(/-^l)j•
Hieraus ergibt sich als erster Satz: Im Komplement @j^g der Haupt-
hongruenzgruppe siebenter Stufe ip„ Jiat man SuhsßtiitiGnen der Perioden 2,
3, 7 und 4, je nachdem j = 0, 1, 2 oder 3 (mod 7) </i?^, abgesehen davon,
daß sich fur j = 2 auch die identische Subbtitution einstellt. Die Perioden 2
und 3 für j = 0 bzw. 1 stellt mai^. aus den Formeln (1) sofort fest. Für
j = 3 hat F^ die Invariante 0, so daJ3 F die Periode 4 hat. Für j = 2
erweisen sich V^ und F* als inve^-s, so daJ3 F die Periode 7 hat oder die
identische Substitution ist.
Um die Anzahl der Substitationßn der verschiedenen Periodep zu
bestimmen, haben wir nach S. 92 für den einzelnen Rest j =0, 1, 2, 3
die Anzahl inkongruenter Lösungen «, ß, y, d der Kongruenz:
(2) (xd — ßy=l (mod 7)
abzuzählen, wobei (wegen des erlaubten Zeichenwechsels der «, ß, y, d)
für j = 0 die Zahl a auf die Reste 0, 1, 2, 3 beschränkt werden darf,
sowie für j = 0, a = 0 die Zahl ß auf die Reste 1, 2, 3. Man gelangt
ohne Mühe zu dem Satze: I)i der Gruppe (^^^^ treten 21 Subbtitutloneu
der Periode 2 auf, 56 Subsiltwtio,t.eii, der Peuode 3, 48 bolche der Penode 7
nnd 42 der Periode 4, die s^bammen mit der Identität die c^^gg erbchopfen.
1st z. B. die Invariante j = a -j- ö = 1. so hat man an Stelle von (2):
— ßy^fx^—oc-^l (mod 7).
Für die beiden Reste a = 3 und 5 gilt also ßy = 0, eine jKongruenz, die
13 inkongruente Lösungen hat. Für die übrigen fünf Reste a hat flaan:
— ßy =a^ —a-^ Iz^O (mqd 7)
mit je sechs inkongruenten Iiösui|.gen. Al^o hat man in der Tat
2,13 + 5. tJ = 06
Substitutionen der Periode 3. Die übrigen Abzahlungen sind ebenso
leicht.
Infolge dieser Abzahlungen gibt es in der (3^^^ 21 zyklische Teiler
(S^ und in ihnen ebenso viele zy|vlische Teiler C^g, ferner 28 zyklische
Teiler (Sg und 8 zyklische Teiler C^^. E& ist die Frage, inwieweit die
zyklischen Teiler gleicher Ordm^ng konjugiert sind. Zu;- Entscheidung
hierüber knüpfen wir an die drei Substitutionen:
184 ■ 11, 1. Kleiasche Gruppe und zugehörige Formen.
die den S. 82 eingeführten und durch die Beziehung U-T-S = 1 ver-
Icnüpften erzeugenden Substitutionen der Modulgruppe entsprechen. Um
nun zunächst den Xormalisator der aus T zu erzeugenden zyklischen (^5^
zu bestimmen, haben wir alle Substitutionen F zu sammeln, die mit T
vertauschbar sind, also die Kongruenz V-T= T-V oder ausführlich:
befri(
w
tt=;)-rr;) .(-->
;digen. Man gelangt zu folgenden acht Substitutionen:
lu^i). (ro). fr?)' ii:%
iftj). nt)- n^' (?;j)-
die eine Diedergruppe (3^ bilden. Die in der ersten Zeile stehenden
Substitutionen bilden einen T enthaltenden zyklischen Teiler ®^, der die
Diedergruppe @g gleichfalls zum Xormalisator hat. Es ergibt sich der
Satz: In der ©^gg siiid 21 'konjugierte zyiähche Teller @^ tmd in ihnen
ebenso clele konjugierte Teller ©g enthalten, die als Normalisatoren 21 Jmu-
jtigierte Teller &^ vom Diedertypiis hsbltzen. Lidern man eine entsprechende
Entwicklung an die Substitution U anschließt, folgt weiter; In der 6>jgg
bind 28 konjugierte zyhlibche Teiler ©3 enthalten, die als Normalisatoren
28 konjugierte Diedergruppen ®g besitzen. Um endlich den Normalisator
der aus S zu erzeugenden zyklischen Gruppe ©^ zu gewinnen, haben wir
die der Kongruenz F> kS • V~^ = S^ oder ausführlich:
(") Ci;(\;lXJ;n (-^')
genügenden Substitutionen V zu sammeln. Man gelangt zu den 21
Substitutionen mit j; = 0:
<«) ilA)' (o;l)' (l:ih
sie bilden einen Teiler ©^^ der Ordnung 21, der außer der @^ noch aus
14 Substitutionen der Periode 3 besteht: In der ©^gg sind acht
konjugierte zyklische Teiler @^ und ihnen ah Normalisatoren zugehörig acht
kortjagierte Teiler 05^^ der Ordnung 21 enthalten, vmi denen einer durch
die Kongruenz j; = 0 (mod 7) charaUeribierf ist.
In der durch (4) gegebenen Dieder-@g sind zwei Vierergruppen
enthalten, denen die Substitution T gemein ist, und von denen eine aus:
(^) Criy g J). r
fO,—l\ /3, 2\ /—2, 3\ A^ 0\
' lo, ij
besteht. Dieselbe Vierergruppe ist auch noch in den Xormaüsatoren der
zweiten und dritten Substitution (7) enthalten. Wir haben also nicht
Zyklische und sonstige Teiler de:(- Gruppe (
185
zweimal 21, sondern nur zweimal 7 Vierergruppen ®^ Diese 14
Vierergruppen bilden nun entweder ein System konjugierter Teiler (3^ oder
zwei Systeme von je 7 konjugierten TeEern @^. Im ersten Falle hat
die einzelne ®^ als Xormalisaior eipe ©^g vom Tetraedertj^p^s. im zweiten
Falle eine Oktaeder-®^^. Der letztere Fall muß zutreffen, da die
Vierergruppe (7) Xormalteiler der Piedergruppe (4) ist und also im I^^ormali-
sator der Vierergruppe ein zyklischer Teilpr ®^ auftritt, was von der
Tetraedergruppe nicht gilt: Jn der @^^g sind zwßl Systeme von je sieben
l'ongugierten Teilern ©34 enthßUen, die den QMaedertypub lesitzen. Dies
sind die Teiler höchster Ordnung in der Gruppe @jgg.
Es ist jetzt leicht zu zeigen, daß die gewonnene (^^^^ einfach ibt. Ein
Xormalteiler muß vom einzelnen System konjugierter zyklischer Teiler
entweder alle oder keinen enthalten. Die Ordnung eines Xormalteilers
muß sich demnach in der Gestalt darstellen'
(8)
1 -r 21 £, ^ 42 £2 - 48 £3 + 56 £^,
wo die £ eine der Zahlen 0 oder 1 bedeuten, und übpgent» £3 nur dann
gleich 1 sein kann, wenn auch s-^ =
Summe (8) ein Teiler von 168 sejn,
so müssen, wie man leicht feststellt,
nur entweder alle £ gleich 0 oder
alle gleich 1 sein, &o daß die (^^
und die (^^^g die einzigen
Xormalteiler sind.
Für die Herstellung eines DB der
Hauptkongruenzgruppe ip^ siebenter
Stufe ist die Entwicklung von
S. 110 ff. vorbildlich. Dem aus
der Substitution S zu erzeugenden
zyklischen Teiler (3,^ der (^,gg
entspricht innerhalb der nicht-homogenen
Modulgruppe eine Kongruen:?gruppe
siebenter Stufe (^(24) des Index 24,
1 gilt. Soll aber der "^Vert der
deren Substitutionen
Kongruenzen:
(9)
V
durch die
(mod 7)
charakterisiert sind. Durch Zusatz
der Spiegelung U an der imaginären
cj-Achse wird (>)(.,^) zu einer Gruppe
(^(24) erweitert, deren DB das in
Fig. 23 dargestellte, von lauter Symmetrieh^bkreisen begrenzte Sechseck
ist. Bezeichnen wir diese Halbkreise je durch Xebeneinanderstellung
186 II, 1. Klein sehe Gruppe und zugehörige Formen.
der CO-Werte in ihren beiden Endpunkten, so gehören zu ihnen die
folgenden Spiegelungen:
— / 2 \ , ^
(ioo, 0), co' = —CO-, (0, -j, a = „-_ ^;
/2 1\ ,_13ö —4 /l 3x ,_ 8ä —3
VT'T> "^ -42«-13' U'T> ''-21«-8'
/3 1\ , 13ö —6 /l . \ , - ^ -,
(yy)' " ^28^-13' U'^°°j' «=-«-!'
die in der Tat alle der Gruppe ©(2*) angehören. Übrigens zählt man in
Fig. 23 ab, daß dieses Sechseck sich wirklich aus 24 Kreisbogendreiecken
der ö-Halbebene zusammensetzt.
Fügt man dem Sechseck der Fig. 23 sein Spiegelbild bezüglich der
imaginären co-Achse an, so entsteht ein DB der Gruppe (S\u). Von den
zehn den Bereich berandenden Halbkreisen sind je zwei bezüglich der
imaginären co-Achse symmetrische aufeinander bezogen. Die zugehörigen
Substitutionen gewinnt man einfach, indem man die erste der sechs eben
genannten Spiegelungen der Reihe nach mit den fünf übrigen kombiniert:
(«4>
--^, 0 -^
V 3 l)
1
¥"
3
y
2
~y
1
~T
(-|,^oo) ^(|,ioo)
2
1
3"'
3
1
^y
t)'
^-
i oo
7 CO -[- 1'
13ü3 + 4
42ü3^13'
8ü3 + 3
21ü3 + 8'
13ü3 + 6
28ü3 + 13'
a+l.
Die ersten vier Substitutionen, von denen eine parabolisch und drei
hyperbolisch sind, mögen Y^, V^, Fg, V^ genannt werden. An letzter
Stelle haben wir einfach die Substitution S.
Man übe nun auf den gewonnenen DB der (a)(24) die sechs
Substitutionen S-S S--, S-3 aus und füge ihm die sechs so entstehenden
Bereiche an. Von den sieben so aneinander gereihten Bereichen sind keine
zwei bezüglifh der Hauptkongruenzgruppe ^^ äquivalent.
Zusammengenommen Uefem sie demnach einen DB der Hauptkongr\xenzgruppe ^^.
Hier sind dann zunächst je die beiden in den Spitzen 0, +1, +2, j^S
zusammenhängenden Halbkreise durch die konjugierten parabolischen
Substitutionen:
Diskontmuitatsbereich der Hauptkongruenigruppe 9)^ 187
aufeinander bezogen. Ferner sind je die beiden in den sechs Punkten
i|)Z:|> il zusammenstoßenden Halbkreise durch parabolische
Substitutionen einander zugeordnet; es handelt sich dabei um die
Substitutionen :
'^ ^' ^ —\ -28, -28»'-^15 }' *-'^'-. •■' -
Daran reihen sich für die beiden äußersten Halbkreise und die beiden
geradlinigen Ränder die Substitutionen:
/ 7 24\ /24
lo, 1/
Fur die 14 noch übrigen Halbkreispaare hat man 2unach&t die Zusammeu-
ordnungen:
/ 1 2 s /I'd 8\ _ / 113, 35
3
-■^
V 7 3/ - 1—42, -13;-
(-T--^)-
3 1\ / ^ _ ^^'\ '-^ r / 55 2i\
Entsprechend sind die letzten 12 Halbkreispaare nach der Vorschrift:
zusammenzuordnen, wobei jedoch für o^ = 4, 5, b die in den linken
Klammern stehenden Halbkreisendpunkte, die in der angegebenen Gestalt
dem DB nicht mehr angehören würden, je um den Betrag 7 zu \-er-
mindern sind.
Jedem Teiler ©„ der ('»^jg^ entspricht eine KougrucnzgiTippe des
Index 168'^"S bestehend aus allen Substitutionen der ilodulgruppe, die
mod 7 mit den Substitutionen von 63u kongruent sind. So haben wir als
Gruppen von niederstem Index zwei Systeme von je sieben konjugierten
Kongruenzgruppen siebenter Stufe vom Index; 7, die den Oktaedergruppen ^b^^
entsprechen. Es ist wichtig, zu bemerken, daij die heldeh S-i/bteme con
je sieheit Kungruenzgnippeyi deb Index 7 innerhaJb der durch Spiegehingen
era-eüertoi, Blodnlgrappe konjugiert bind. Die unter (4) angegebene
Diedergruppe W^ enthält nämlich die beiden, wie oben festgestellt,
innerhalb der 0\^,j, nicht konjugierten Vierergruppen:
und:
(") (r;)-(i:s)-ej)-fi;t)'
188 n, 1. Klein seh« Gruppe und zugehörige Formen.
die durch die Spiegelung o' = — a ineinander transformieTt werden.
Die beiden diesen Vierergruppen zugebörigen Normalisatoren waren aber
zwei innerhalb der (^^gg noch nicht konjugierte Oktaeder-®^^.
§ 2. Erklärung der Klein sehen Gruppe.
An die gruppentheoretischen Darlegungen von § 1 schließt nun
Klein =^) die folgende grundlegende Überlegung an. Da die
Hauptkongruenzgruppe ^.j ein Xormalteiler der Modulgruppe ist, so wird der
DB der Gruppe ^^ durch alle 168 inkongruenten Substitutionen der
Modulgruppe in sich übergeführt. Bilden wir diesen DB mittels der
Funktion /(co) auf die /-Ebene ab, so entsteht eine 168-blättrige Fläche
über dieser Ebene, die entsprechend durch 168 eindeutige
Transformationen in sich übergeht. Ein einzelnes Blatt der Fläche geht dabei in
alle 168 Blätter über, so daß die Fläche von jedem Blatte aus gerade so
gebaut ist wie von jedem anderen**). Die Verzweigung der Fläche ist
die folgende; Bei / = 0 liegen 56 dreiblättrige Verzweigungspunkte,
bei J = 1 weiter 84 zweiblättrige und bei / = oo endlich 24
siebenblättrige. Weitere Verzweigungspunkte treten nicht auf. Auf Grund
der Regel (5) S. 112 wird nun festgestellt, daß das Geschlecht der 168-
hlattrigen Hache p = 3 ist.
Die letzte Tatsache begründet weiter die folgende
funktionentheoretische Überlegung: Auf unserer Fläche des Geschlechts 3
existieren drei linear-unabhängige Integrale erster Gattung, die eindeutige
Funktionen von co werden und als solche durch u^ (co), u^ (o), u^ (co)
bezeichnet seien. Gegenüber den 168 Transformationen der Fläche in
sich substituieren sich diese drei Integrale linear und nicht - homogen.
Bilden wir aus ihren Differentialen d^^■^, du^, du^ vermittelst des
gegenüber allen unimodularen Substitutionen invarianten Differentials:
(1) (co, d(o) = co^ -dco^ — co^-d(o^ = — cof -dco
die drei Modulformen siebenter Stufe (—2)*^^ Dimension:
diij^ du^ du^
^'^^ ""^ ~ (^^' ■"'' ~ J^'a)' ""' ~ (CO, dco)'
Sö werden diese gegemiber der homogenen Modulgruppe 168 homogene
lineare Substitutimien bildenj), die eine mit der ©^gg des § 1 isomorphe
G-ruppe bilden. Es ist dies diejenige temäre Gruppe, die wir ihrem
Entdecker zu Ehren weiterhin als die „Kleinsehe Gruppe- bezeichnen.
Aus bekannten funktionentheoretischen Sätzen folgerte Klein weiter
die Existenz einer invarianten Form vierten Grades F{x^, x^, x^ der
=") „Über die Transformation siebenter Ordnung der elliptischen Funktionen",
Math. Ann., Bd. 14 (1878) oder „Ges. Abb.- III, 90.
=^==) Klein bezeichnet sie dieserhalb als eine „regular verzweigte ßiemann-
sche Flache'-.
f) Alan beachte, daß die Xi-, x^, x^ als Modulformen gerader Dimension bei
der Substitution (a\ = — co,, co'o = — co« unverändert bleiben.
Einführung der Klein sehen Gruppe. ] 89
ternären (^^gg. Die 168-blättrige Eläche über der /-Ebene wird nänilich
leicht als nicht-hyperelliptisch erkannt =^). Die x liefern, als Verhältnis-
großen gesetzt, die sogenannten „Eormen y der Fläcjie und sirjid durch
eine homogene Relation vierten Grades:
(3) i^C»,, rr.^, »3) = 0,
verbunden**). Deuten wir die »j, »g, x^ als homogene Koordinaten in
der Ebene, so liefert die Gleichung (3) eine cloppelpunlptfreie Kurve
vierten Grades, die der Klein^chen Gruppe entsprechend durch 168 Kolli-
neationen ia sich übergeführt wird f).
Es ist leicht zu sehen, äa^ die hiqitadratibcJie Form F{x^, x^, x^)
eine absolute Invariante der Klein sehen (xruppe ibt. Den Erzeugenden (7)
S. 82 der Modulgruppe entsprechend i^t näpilich die Kleiasche Gruppe
aus zwei Substitutionen S und T erzeugbar, die die Beclingungen
befriedigen ;
(4) S'=l, T^==l. (S-Ty = l.
Bei Ausübung von S nimmt demnach F eine siebente Einheitswurzßl «
als Faktor an, und ebenso tritt bei T der Faktor + 1 auf. Da aber — a
eine dritte Einheitswurzel seip. muß, so ist £ = L, und es gilt das obere
Vorzeichen, woraus die Behai(.ptung hervorgeht.
§3. Darstellung der Klein sehen Gruppe in oktaedrischen Koordinaten.
In den Origüialarbeiten Kleins ist zur Darstellung der ternären
@jgg ein ia § 5 näher zu untersuchendes synunetrisches
Koordinatensystem zugrunde gelegt, das indessen die Adjunktion der siebenten
Einheitswurzel £ = e 7 nötig macht. Demgegenüber gelingt es bei
Autgabe der Symmetrie mit der quadratischen Irrationalität:
(1) , + ,. + ,. = :^L±iVI
auszukommen, was vom algebraischen Standpurjvt aas vorzuziehen ist.
Die Unsymmetrie der hier zi^nächst befolgten Da,rstellung beruht auf der
Bevorzugung einer der beiden Vie^ergr^pperfi (10), (11) S. 187 bzw. einer
der beiden zugehörigen Oktaedergruppe ®^^ Das eipzuführendp
Koordinatensystem soll entsprechend als ein „oktaedrisches- bezeichnet werden.
=^) Vgl. „Ges. Abh.'- III, 100. Vgl. auch die entsprechende Überlegung oben
S. 112 betreffend die damalige Riemannsche Flache Figo-
**) Ausführliches über die Flachen des Geschlechts j) = 3 findet man bei
Klein, ,.Ges. Abh.'- III, 435 ff.
t) Es handelt sich hier 11m diß sogenannjie „Xprmalkurve der Formen y~,
die bei j) = 3 dem vierten Grade angehört.
190
II, 1. Klein sehe Gruppe und zugehörige Formen.
Die Oktaedergruppe besteht in ihrer projektiven Gestalt aus den
Substitutionen, die die Figur des vollständigen Vierseits (vgl. Fig. 24) in
sich überführen ==•'). Die in der Figur stark ausgezogenen Geraden mögen,
wie angedeutet, die Seiten
^^o- ~^- des Koordinatendreiecks
sein, und dem Punkte A
mögen die Koordinaten
erteilt werden. Die (>}^^
besteht dann einfach aus
den 24 unimodularen
temären Substitutionen,
bei denen die Quadrate
Xi, xi, xi die sechs
möglichen Permutationen
erfahren. Der einzelnen
Permutation gehören wegen
der Forderung, daß die
Determinante der
Substitution gleich 1 sein soll,
stets 4 Substitutionen zu.
Die biquadratische
Form F(süj^. x^, x^) als
absolute Invariante der ®^^ ist eine symmetrische ganze Funktion zweiten
Grades der x'i, x|, x|, so daß wir den Ansatz gewinnen:
(2) F(x^, ^2, ^3) = a (xt i- 4 + »3) -r ^ (4 4 + x| ^
- xl xl).
Bevorzugen wir die andere der beiden Vierergruppen (10) und (11)
S. 187, so gilt der entwickelte Ansatz unverändert. Wir wollen für die
entsprechenden Koordinaten x'i, 0^2, x'^ schreiben und haben für die
biquadratische Form in ihnen den Ansatz:
(3) a' {x't^ -r x'i + al*) + V {x'i x'i" ~f xi x'i -^ x'i x:i).
Die den beiden Vierergruppen gemeiasame Substitution der Periode 2 sei
die harmonische Perspektivität ^■^) der Achse a;^ = 0 und des Poles
r^ = .^Cg == 0. Dann ist das Koordinatendreieck des zweiten Systems
i'x, x%, Xi im ersten durch die drei Geraden:
rfj = 0, a;^ ~|- ^3 = 0, x^ — a^g = 0
dargestellt. ISTun ist aber die Spiegelung co' = —«, die die beiden
Vierergruppen austauscht, eine symmetrische Umlegung der 168-blättrigen
Fläche in sich. Es werden also die zu den x^, x'^, % konjugiert
komplexen Werte S^, x'^, S3 linear mit den x^, x^, x^ zusammenhängen, und
*) Vgl. „Äutom. Funkt.- I, 71.
=*) Vgl. über harmonische Perspektivitaten S. 166.
B\quadratische Fonn F in oktaedrisclien Koordii^aten. 191
es wird der Übergang vom einen oktaedrisclien Koordinatensystem
J5j, x^, Xg zum anderen a,{, x'^, x\ durch eine Substitution de?- Gestalt:
(4) 7^ := ax^, ^2 = <3 (x^ -f x^), xä = y (/^ — x^)
vermittelt werden. Dies ist aber eine Substitution der Periode 2, so
daß ß = y gilt und also an Stelle von (4) auch, geschrieben vferde;p. kann:
(5) <}X[ = (9Xj, (jxä = Xg -j- vig, 0X'^ = r^2 —-^S'
unter ö und fi noch zu bestimmende Faktoren verstanden.
Wir haben nun die Forderung zu stellen, daß durch diese Si^b-
stitntion (5) die Formen (2) und (3) zusammenhängen. Die durch:
(6) a' {x{' + I',' ^ 7,') ^ V {x'i xi 4- x'i r;^ ^ xr^i) == 0
dargestellte Kurve vierten Grades*) sol] also durch (5) in die Kurve
F{x^, x.^, x^ = 0 übergehen. Man findet aber durch A^süb^ng cjer
Substitution (o) aus (6):
J «' {(i' 4 - 2 xl + 2 xl) + V (4 + 4) - 2 (B a' - l') x.| ^|
*- ( ~f 2 6' Ö^ (a;| a;f -f r^f 4) == 0.
Damit wir hier (bis auf einen konstanter^ Faktor) zur Form F(Xj, x^, x^)
geführt werden, müssen die Gleichuagen bestehen:
(8) ä'Ö* = 2ä' f h', 6ä' — 6' == 5'OK
Durch Elimination von «' und V folgt für $ die Gleichung:
(9) Ö« + Ö^ — 2 6' - 8 == 0.
Die reelle Lösung 6^ = 2 dieser für B^ kubischen Gleichung ist
imbrauchbar, da die Klein sehe G^-uppe nicht nur aus reellen Kollineationen
bestehen kann *'"••). Welche von den beiden Lösungen:
wir benutzen, ist gleichgültig, da ein Wechsel einfach au! ei^e Änderung
der Auswahl der Viexergruppe (10) bzw. (11) S. 187 hinauslauft. Wir
setzen:
und sehreiben ß in (5) gleich y 2 , damit die Substitution :
(11) V¥a = 6x^, \''2 7i = Xa + x„ V2"4 = ^\_ - ^.,
=^) Unter «', V werden wieder die zu a', V konjugiert komplexen Großen
verstanden.
**) Nach S. 6 ff. kann eine Substitution der Periocie 7 |iicht ausschließlich
reelle rationale Invarianten haben.
192 II, 1. Kleinsclie Gruppe und zugehörige formen.
die Periode 2 erhält. Indem wir ferner a' z= 1 setzen *), folgen aus (8)
für a und h' die Werte:
a' = 1, V = 3Ö.
Die Gleichung (7) geht dann über in:
(3 Ö -f 2) {xt -f a;| -f xl) - 6 (Ö - 2) (xl xl ~f xl xf ~f x! xl) = 0.
Wir erklären nun die Form F{x^, x^, x^) endgültig als die mit dem
Faktor ^ (3 ö ~f 2) multiplizierte linke Seite dieser Gleichung:
(12) F {X,, x^, x^) = x{ -f xt -f .^3^ -f 3 Ö {x\ xl -f xl xl ~f xl xl).
Zur Erzeugung der temären (S^gg genügt es jetzt, der ausgewählten
0324 irgend eine Substitution der zweiten ©g^ hinzuzufügen. Diese ®^
entsteht aus der ersten durch Transformation mittels der kurz durch U
zu bezeichnenden Substitution (11). Die Substitutionen bezeichnen wir
weiterhin kurz durch die in Klammem gesetzten Matrizen ihrer
Koeffizienten. Diejenigen der bevorzugten ©34 schreiben wir wie bisher uni-
modular, während sich die übrigen 144 Substitutionen am bequemsten
^oMomodular-, d.h. mit der Determinante 8 versehen, schreiben werden.
Wir entnehmen der ersten @^, die drei Substitutionen:
/O, 0, 1\ /— 1, 0, 0\ / 0, 0, —1\
(13) r=[0,-l,0\,V' = [ 0, - 1, 0 ), F" = ( 0,-1, 0 )
Vi, 0, 0/ \ 0, 0, 1/ V— 1, 0, 0/
und bilden die der ©^gg angehörende Substitution:
/-ö, -1, 1\
(14) s = r"-(u-^'r-u)-r = 1 0,-i, i •
V 0, 0.0/
Sie hat die Periode 7 und ihre Potenzen sind:
(15).
/—ö, — 1, 1\ /ö, 0, 0\ /-l, ö, — 1\
S = l ö,-1, 1, S^=- 1,-0,-1 , S'^= i,ö, 1,
\ 0, 0,0/ \l, 0,-1/ \ 0.0,—öl
/-i, 1, ö\ /ö, 1. i\ [-0. o,o\
S' = l 0,0, 0 , S^=3 o,-ö, ö , S«= -i,_i,ö .
\- 1, 1, - 0/ \ö, -1.-1/ \ 1, 1, 0/
Die Klein sehe Gruppe @^gg setgt sich aus der ®24 w**^ ^ß** Potenzen von S
nun einfach als Summe:
(16)
®168 =- ®24 + S-®,4 + S2-@! + ••• -f- S«.@,4
zusammen.
Die Substitutionen der einzelnen Nebengruppe S" • ®^^ lassen sich
leicht näher beschreiben. Man hat die Spalten der Matrix S" auf alle
sechs Arten zu permutieren. Dabei hat man, wenn es sich um eine
gerade Permutation handelt, entweder keine oder zwei Spalten im Vor-
*) Die biquadratische Form darf noch um einen konstanten Faktor
geändert werden.
Kleinsche Gruppe m pktaedrischen Koordinaten. 193
zeichen zu ändern; handelt es sich indessea tu^ eine ungerade
Permutation, so ist entweder eine oder es sind alle drei Spalten im Vorzeichen
zu ändern. Dies gibt in beiden Fallen vier Möglichkeiten. Die Periode
der einzelnen Substitution hängt von der Invariante j ab, die bei -pni-
modularer Schreibweise von der Summe un4 bei oktomoduLarer
Schreibweise von der halben Summe de|- Diagonalglieder geliefert wird. Es
treten folgende Invarianten auf:
(IV) i =: — 1, 0, 1, 0, 6.
denen die Perioden 2, 3, 4, 7, 7 entsprechep. Es gilt der leicht
feststellbare Satz: In der einzelnen Nßbengruppe S^ • ©24 ^^**^ ^^ts zwei Siib-
stitutionen der Periode 2, acht der Periode 3, sechs der Periode 4 und
endlich acht der Periode 7 efdhalten. Man hat beim Beweise nur zu
beachten, wie sich bei dea S])alter)ipermutationen und Vorzeiclien-
änderungen die Diagonalglieder der einzelnen Matrix ändern, und
wiederholt von der Relation 6 -f- ö == — 1 Gebrauch zu machen. Upter
Hinzunahme der Substitutionen der ®^^ finden sich 9 -r- 6 • "- = 21
Substitutionen der Periode ^wei, 8 -j-' ^ • 8 = 56 Substitutionen der
Periode drei, 6 -4- 6 • 6 = 42 solche der Periode vier und 6 • 8 von der
Periode sieben. Wir sind damit auf die schoa S. 183 festgestellte Anzahl
zurückgeführt.
Die Gruppeneigenschaft der 168 tßmären Substitutionen k^nn man
natürlich jetzt auch durch direkte Rechnung bestätige q. Man hat dabei
nur immer von den Relationen:
(18) Ö'^ = - ö - 2 , Ö^ = — ö — 2, ö -r Ö = - 1, 6-6 = 2
Gebrauch zu machen. Außerdem hat r|ian, falls zwei Substitutionen aus
Xebengruppen (16) kombiniert werden, die neurji Koeffizienten der
entstehenden Substitution um dea gemeinsamen Fakifcor 2 oder 4 zi; kürzen,
ie nachdem diese Substitution wieder einei Xebengr^ppe oder der ©g^
angehört. Auch ist es ein Leichtes, die absolute Invarianz der
biquadratischen Form (12) zu bestätigen. Es ißt hierbei hinreichend, wenn man
die Prüfung mittels einer einzigen Substiti^tion aus einer Xebengruppe
vollzieht, da die Invarianz gegenüJDer der ©34 zutage liegt.
Wir merken endlich noch den Satz an: Die Kleinbche Gruppe id
aas den beiden Substitutionen:
/— ö, — 1, 1\ /— 1, 0, 0'
(19) S=i ö, -1, 1 , T = ( 0,-i, 0
^ 0, ö, 0/ V 0' <^' 1
der Perioden 7 und 2 erseugbßr *). Da nämlich ,S • T die Periode 3 hat,
so erzeugen S und T einen Teiler der Ordnung 42 • v. Es gibt abei' in
*) Wir bezeichnen diese erzeugenden Substitutionen durch dieselben Symbole
wie die erzeugenden Substitutionen der Modulg^-uppe. Doph soll damit nicht
behauptet sein, daß die Substitutionen (19) die Wirkifng der Substitutionen (3)
S. 183 auf die Modulformen (2) S. 188 darstellen.
Fricke, Algebra. II. 13
194 II) 1- Klein sehe Gruppe und zugehörige Formen.
der ®jgg weder Teiler ©g^ noch Teiler ©^g. Ein Teiler (S)^ wäre
nämlich, da er kein Xormalteiler ist, sein eigener NormaJisator, so daß man
zwei konjugierte Teiler ®g^, ©g^ hätte. Da ihr Durchschnitt ein Normal-
teüer, also die ©^ ist,] so haben die beiden Teiler ©g^, ©§4 nur die
identische Substitution gemeinsam. Xach dem Sylow sehen Satze
enthalten die ©g^, ©84 zyklische Teiler ©2- ^^ müßten sich also die
21 konjugierten zyklischen ©^ in gleicher Anzahl auf die beiden Gruppen
®84' ®84 verteilen, was ein Widerspruch ist. Ebenso zeigt man, daß
keine Teiler © . auftreten.
§ 4. Geometrische Sätze über die Kollineationsgruppe ©^^g.
Der eiazelne Punkt (a;^, x^, x^) ist im allgemeinen einer unter 168
verschiedenen bezüglich der Kollineationsgruppe ©^gg äquivalenten Punkten.
Eine Herabminderung dieser Anzahl tritt indessen für die Pole der Kolli-
neationen ein, wie jetzt unter besonderer Berücksichtigung der durch
Xuüsetzen der biquadratischen Form F{x^, x^, x^) dargestellten Kurve
vierten Grades darzulegen ist. Abgekürzt möge diese Kurve weiterhin
durch das Symbol F bezeichnet werden.
Die 21 konjugierten Substitutionen der Periode 2 bedeuten
„harmonische PerspeMivitäten^. Ihre Pole bilden ein System von 21 nur
unter sich äquivalenten Punkten, die nicht auf der Kurve F liegen. Einer
unter diesen Punkten, nämlich der Pol der Substitution T, ist (0, 0, 1);
aus ihm stellt man die übrigen leicht durch die Substitutionen der ©jgg
her. Unter diesen Punkten sind neun reell; es handelt sich um die
Kreuzungspunkte zweier Geraden in Fig. 24 (S. 190) und um die drei
Ecken des Koordinatendreiecks. Die 21 Perspektivitätsachsen, zu denen
als reell die neun Geraden von Fig. 24 gehören, sind durch ^ullsetzen
der folgenden 21 linearen Formen j) (a;,, x^, x^ dargestellt:
p^ = '2x^, j5y=2»2, i5i4 = 2a;3,
p^ = - Bx^-x^ + x^, :Pg - dx^-x^-x^, Pi-o=+6x^ + 6x^,
P^=- dXj^-rdx^, p^ = X^-dx^-X^, p^^= -tX^-t dx^-X^,
P^ = -X^ + Bx^-X^, P^f^= X^-rdx^ + X^, Pj^^ = ■i-'ßXj^-dx^,
I>i- -x^ + x^ + dx^, Pii=dxi + 6x^, i^is = ■~^i + ^2~Öa;3,
P-^=- ßx^-rX^-i-X^, p^^= -ßx^+Bx^, ßiQ = +dXj^-X^-X^,
^6 =-Ox^i-dx^, pj^^= - x^-x^ + dx^, J520 = + a^i-ra;2 + öa;3,
wie man leicht aus (15) S. 192 folgert. Mit Rücksicht auf spätere
Anwendungen stellen wir fest, daß sich gegenüber der Substitution S je
die sieben untereinander angeordneten Formen p zyklisch permutieren:
{Po=I>v I>'i=P^, ■•■, i>;=i5o, i5;=i58, I>'s=I>c„ •••
(1)
i^o
i^s
i^lo
pu
Kg
=
=
=
=
=
A
JPo.
. P'e
Pie.^
Pi2' P
Ps>
Pi
=
I>u
16 =
1^20
--i>5.
-A>
= -
= -i>
= Pu
JP?-
i^'r
-i'u»
0. t
■
= -
P'l2
17 ==
-Prp
--P7>
= -Pl5>
= — i>2
Perspektivitatsachsen und sextattische Punkte. 195
Während die Wirkung der zweiten przeugenden Substiifcution T die
folgende ist:
' =ßä^ P'i == — Pi8>
(^) ^Ko= —i^ie.» -Pu = —i^u, i^lS =.Pi5> i^is =i>2Q> -PU = Vli,
Die Kurve vierten Grades F wird durch die 21 Achsen in 84 Punkten
geschnitten, die nur unter sicli äquivalent sind. Die vier Schnittpunkte
der einzelnen Achse werden durch die Substitutionen derjenigen Dieder-Og
untereinander ausgetauscht, die zur fraglichep Perspektivitäit als S^ormali-
sator gehört. Klein erkannte in jenen 84 Punkten sofort die
sogenannten „sextaMischen PunMe-' der E^'urve F, d. h. diejenigen Punkte,
in denen die Kurve von einepi Kegelschnitt sechspunktig berührt wird.
Cayley zeigte*), daß eine doppelpunktfieie Kurve w*®'^ Grades 3n (4w--9)
sextaktische Punkte hat, im Falle n = 4 also 84- Auf der 168-blätte-
rigen Riemann sehen Fläche über der /-Ipbene handelt ps sich einfach um
die 84 zweiblättrigen Verzweigungspunkte. Der fragliche Chara,kter der
84 Punkte wird unmittelbar anschaulich an dein reellen ^uge, den die
Kurve vierten Grades bei dem in § 5 zu erklärenden
Koordinatensysteme erhält. Hier werden drei Perspektivitatsachsen reell und stellen
Symmetrielinien der Kurve d^r (vgl. Fig. 25^ S. 198), deren einzelne die
Kurve in zwei reellen Punkiten schneidet. Ein Kegelschnitt, der die
Kurve F in einem dieser Punkte mindestens fünfpunktig schneidet, ist
eindeutig bestimmt. Er hat also die fragliche Achse gleichfalls zur
Symmetrielinie und schneidet somit die Kurve F in einer gefaden Anzahl
von Punkten, hier also in sechs Punkten.
Als Beispiel eines unter den 28 konjngierten Teilern (3^ nehmen
wir den ans der Substitution:
(2) x[ = x^, x'2 ^:= x^, x's = x^
zu erzeugenden. Der eine Pol (1, 1, 1) Kefert ein Systen^ von 28 nur
unter sich äquivalenten Punktpn, die nicht auf der Kurve F Kegen.
Dagegen Kegen die beiden anderen Pple:
(3) (1, (), ()^), (1, ()^ ()), Q = e~
auf der Kurve F und Kefern ein Systeni vqn 56 nur unter sich
äquivalenten Punkten. Es handelt sich hier un^ die 56 dreiblättrigen Ver-
zweigungspunkte der Riemamisehen Fläche über der /-Ebene oder in
kurventheoretischer Sprechweise um die 56 BerührungspunUe der
*) In den „Philosophical Transactions'*, Bd. 155, S. 545 (1854).
13*
X96 n, 1. Klein sehe Gruppe und zugehörige Formen.
28 Doppeltangenten der Kurve vierten Grades F. Der Beweis folgt
einfach durch Angabe der zur Substitution (2) gehörenden Doppeltangente:
(4) x^^x^ + Xs = 0.
Mittels der Substitutionen der @^gg stellt man aus (4) ohne Mühe
die 27 übrigen Doppeltangenten her. Die Lage der vier reellen unter
ihnen wird man in Fig. 24 (S. 190) leicht nachtragen.
Es bleiben jetzt auf der Kurve F als besondere Punkte nur noch
die 24, die den siebenblättrigen Verzweigungspunkten der Riemann sehen
Fläche entsprechen. Xun hat die Kurve vierten Grades F im System
ihrer 24 Wendepunkte, die durch ]^ullsetzen ihrer Hesseschen Form*):
i0{T^,x^, Xg) = 2 {xf -f- a;f -f «D — 5 6 {x^ «1 -f xf xt + «2 «!
l -j- X2X3 -r x\ %l -j- x\ xl) -{- 4 (ö — o)x\ x\ xl
ausgeschnitten werden, ein invariantes System von 24 Punkten. Da wir
auf der Kurve F nur ein solches System von 24 Punkten antrafen, so
entsprechen den 24 siebenblättrigen Verzweigungspunkten der Riemann-
schen Fläche die 24, WendepunUe der Kurve F. Wir kommen auf die
24 Wendetangenten sogleich ausführlicher zurück **).
Als nicht auf der Kurve F gelegen sind jetzt nur noch die 42 Pole
der 21 zyklischen Teiler ©^ zu nennen, die zu je zwei auf den 21 Per-
spektivitätsachsen liegen und zusammen mit den 21 Perspektivitäts-
zentren die gesamten Pole der ©^ liefern. Als Beispiele für dieses letzte
System zu 42 nur unter sich äquivalenten Punkten nennen wir die
beiden Pole:
(6) (e~, e~^, 0), (e"^, e^, 0)
der aus der Substitution:
(7) x'{ = — x^, x'.2 = x^, % = a-g
zu erzeugenden zyklischen Gruppe (S^. Wir folgern aus diesen Angaben
den später zu benutzenden Satz, daß die 42 fraglichen Pole der @^ auf
der Kurve sechsten Gerades liegen, die durch Xullsetzen der Hesseschen
Form (5) geliefert wird.
§ 5. Darstellung der Klein sehen Gruppe in Wendedreieckskoordinaten.
Ad die 24 Wendepunkte der Kurve F hat Klein eine Betrachtung
angeschlossen, die zu der von ihm benutzten Darstellung der @^gg'führt:
Die einzelne Wendetangente schneidet die Kurve F neben dem
Wendepunkt noch in. einem vierten Punkte. Alle 24 Wendetangenten liefern
in diesen 24 vierten Schnittpunkten ein System nur miteinander äqui-
*) Die Erklärung der Hesseschen Form ist in I, 152 durch Formel (21)
gegeben. Jedoch ist bei der Berechnung der rechten Seite der obigen Gleichung (5)
gegenüber jener Erklärung ein überflüssiger numerischer Faktor fortgelassen.
=^*) Man vgl. hier überall die Originalarbeit von Klein, „Ges. Äbh.'- HI, 90ff.
Einführung der Wended^^eieckskoorclinatep. 197
valenter Punkte, die, wie wir wissen, nur wieder die 24 Wendepunkte
selbst sein können: Der vierte SchnitipunJct einer Wendetangente mit der
Kurve F ist demnach stets uieder ein Wendepunkt. Man reihe nun an
eine erste Wendetangente in ihrem vierten Schr^ittpunkte mit p die
zugehörige Tangente als zweite Wendetangente, iiji derem vierten
Schnittpunkt die dritte Wendetangente usw. Die so entstehende Kette von
Wendetangenten muß sich nach piner Gliederanzahl, die ein Teiler von
24 ist, schließen. Man beachifce nun, daß der erstp Wendepunkt Pol eines
zyklischen Teilers ©^ ist, dessen Substitutionen die Wendetangente,
mithin den zweiten Wendepunkt, und damit überhaupt die ganze Kette in
sich überführen. Aber die ©^ hat drei Pole. jEs ergibt sich d^r Satz:
Die GliederanzaM der einzelnen Kette der Wendetangenten ist dr^i, so daß
bich die 24 Wendetangenten in add sogenannte „ Wendedreiecke^ anordnen.
Wir legen nun etwa das zu unserer Substitution S gehörende Dreieck
für ein neues Koordinatensystem 5,, s^, z^ zugrunde. Dann erscheint
die Substitution S in der Xormalgestalt (11) S. 11, wo die
Multiplikatoren fi siebente Wurzeln der Einheit sein müssen (vgl. S. 13). Die
„charakteristische Gleichung- (3) S. 5 der Substitution S ist:
(1) /i^ — Ö ,aM- Ö iii — 1 = 0.
Sie hat die drei Lösungen:
(-) \^x = «^ ."2 == «"' ."s = £^ f = e ^ ,
wo die Exponenten von £ dip drei quadratischen Xichtreste von 7 sind.
Die Substitution S hat also die Gestali-
(3) z\ = &^z^, z', = s'^'z^, z', = f^Jg.
Im Jformalisator (.^^^ der @^ sind Substitutionen der Periode 3
enthalten, die die drei Seiten [des ausgewählten Wendedreiecks zyklisch
permutieren. Man wähle die z so, daß eine dieser Permutationen durch.
(4) 5l = ^2, 4j = ^3, Z'z = ^y
gegeben ist*). Aus (3) und (4) erzeugt man sodann den fraglichen
Teiler ©a^- Das von Klein beifiutztß Koordin^tensysten^ ist also
dadurch charakterisiert, daß hei ihm einem der acht konjugierten Teiler ©^i
eine bevorzugte Stellung eingeräumt ist. Man hat nur ein System von
acht konjugierten Teilern ©g^, während maii zwei Systeme von je sieben
kanjugierten oktaedrischen Teilerp ©g hat, die bei der synupetrischen
Umformung U ineinander übergehen, ßei der Darstellung der Kleinsphen
Gruppe in „Wendedreieckskoordinaten^ id demmich zwar die Symmetrie
gewahrt, aber dies geht auf I^osten der AdjunUioß der debenten Einheitb-
ivurzel Jf, während bei der oben befolgten Darbtellung die (juadratische
Irrationalität 6 ausreichend war. Auch hat man bei Benutzung der
=*) Durch Auswahl des Koprdin£f.tendreiecks smd die Koordinaten z selbst
erst bis auf konstante Faktoren bestimmt.
198
II, 1. Klein sehe Gruppe und zugehörige Formen.
oktaedrischen Koordinaten den Vorteil, daß 24 Substitutionen der ©^gg
reell und besonders einfach ausfallen.
Die einzigen Ausdrücke vierten Grades der Koordinaten z, die
gegenüber der Substitution (3) absolut invariant sind, sind zfz^, ^i^^j
zlz^. Die invariante Form vierten G-rades der ©jgg hat demnach, da sie
auxih hei der Substitution (4) in sich übergehen muß, in dm WendedreiecJcs-
koordinaten die Gestalt:
(5) F(z^, z^, ^3) = zl z^ 4- zl ^3 + zl z^,
woraus man, für die zugehörige Hessesche Form sechsten Grades (nach
Fortlassung des Faktors 54) findet:
(6) <P {z^, ^2, ^3) = 5 zl zl zl — z^zl— z^ zl — ^3 zl-
Die Rationalität der Koeffizienten in (5) und (6) stellt natürlich einen
Vorteil der Wendedreieckskoordinaten dar.
Die Kurve F{z^, z^, z^) = 0 hat einen geschlossenen reellen Zug,
den Klein in seiner Originalarbeit nur«rst schematisch skizzierte. Später
ist diese reelle Kurve vonHaskell
in seiner Dissertation*) genau
untersucht und in der sich
ergebenden Gestalt von Klein in „Ges.
Abh." III, 134 aufgenommen.
Fig. 25 gibt den fraglichen
Kurvenzug wieder. Man bemerkt drei
reelle Perspektivitätsachsen, die
auf der Kurve die sechs reellen
sextaktischen Punkte ausschneiden.
Femer hat man drei reelle
Doppeltangenten mit reellen
Berührungspunkten (sechs Punkte b). Endlich
erblickt man sechs reelle
Wendepunkte c und zwei reelle
Wendedreiecke, von denen das stark ausgezogene das Koordinatendreieck ist**).
Die reelle Kurve geht durch sechs eine Diedergruppe @g bildende
Substitutionen in sich über. Die in der @g enthaltene zyklische ©3 wird
*) „Über die zur Kurve A^ fi-\-fi^ r-\-r^ A =z 0 im projektiven Sinne
gehörige mehrfache Überdeckung der Ebene'-, Gottingen 1889.
**) Klein hat diese Verhaltnisse in anschaulicher Weise dadurch
verständlich gemacht, daß er den S. 186 ff. beschriebenen DB der Hauptkongruenzgruppe
siebenter Stufe ^^ durch Zusammenbiegung aufeinander bezogener ßandkiirven
zu einer im ßaume gelegenen geschlossenen Flache umwandelt, die dann eine
„regulär-symmetrische" Einteüung in 2 • 168 Dreiecke tragt. Die Dreiecksseiten
setzen sich dabei zu 28 geschlossenen Symmetrielinien der Flache zusammen, von
denen eine bei den ausgewählten Koordinaten den reellen Kurvenzug der Fig. 25
Liefert. Die Abfolge der Eckpunkte der regulären Teüung auf der Symmetrielinie
ist dabei in der Tat dieselbe wie die der Punkte a, b, c in Fig. 25. Man findet
das Xahere in „Ges. Abh.'- IE. 129.
Erzeugende Substitutionen der ©^gg in Wende dreieckskoordinaten. 199
aus der Substitution (4) erzeugt, die kurz durcji TI bezeichnet werden
möge. Die drei noch hinzutretenden harmonischen Pej-spektivif^ten, von
denen wir eine mit T' bezeichnep wollen, sind dann sehr leicht
feststellbar. Wir bemerken zui|ächsi,, daß entsprechend der Struktur der
Dieder-@g die Gleichung T'-U = U^-T' gilt. Sie liefert für die
Substitution T' den Ansatz:
z'.2 = ß^i + y ^-2 +«•^■3;
Die Bedeutung der Koeffizienten jst einfach die, daß (a, /3, y) einer der
drei von den Ecken des Koordmatendreiecks verschiedepen reelle^. Werjide-
punkte ist. Wir können ihn beliebig unter 4i6sen Punkten wählen,
womit dann T' unter den drei reellen Perspektivit^ten eindeutig bestimmt
ist. Xun zeigt eine ganz kurze Rechnung, daß der reelle Punkt:
(£ — fS £2 — fS £^ — £3)
die beiden Formen (5) und (6) -verschwinden läßt und also einen der
fraglichen Wendepunkte liefert. Wir habep also für T' den weiteren
Ansatz:
Ö ^1 = (£ — £^) Z^ + (f^ — £°) ^2 -f (£* — E^) ^3,
ö 4 = (£' — e') ^1 + (£' - £') ^.2 + (£ - £') ^„
Eine ternäre Substitution der Periode 2 hat aber bei unimodularer
Schreibweise die Invariante j = — 1. Es gilt demnach:
- ö = (£ - £«) -j- (£^ - b') -i- (t^ - a') =-. i ff,
so daß die Substitution T' die Gestalt iiat:
i-iij^[ = {e - £6)^^ + (£2 _ £5)^^ ^ (gi _ ^3)^^^
<^') -^■V7 4 = (£2 — £5)^^4_(,4_£3).^^_(£ -£')^3>
[ - ^ V 7 4- = (£^ - £3) ^^ + (£ - f ß) ^.3 + (£^ - £^) ^3.
Aus T' und der unter (3) gegebenen Sdbstiiution S tpird die Klein sehe
Gruppe unter Zugrundelegung von WendedreiecJ^sJcoQrdinßten erzeugt *). -Per
direkte Nachweis der Invarianz von F(z^, ^2, z^ gegenüber T ist etwas
umständlicher zu führen als mit oktaedfischen Koordinaten.
*) Man zeigt nämlich sofort, daß T' • S die Invariante j = 0 un4 also die
Periode 3 hat. Die Jetzt erhaltenen Substitfitionen S, T' entsprechen genau den
Erzeugenden (1) S. 42 der Ikos£f,edergruppe.' At^ch in „Mqdulfuiikt." I, 704 ff.
Tverden die ternaren 2:-Substituti()nen 8 un4 T' benutzt. ]S,'ur sind die
Koordinaten dort Zi, Zi, z^ (statt hier Zi, z^, z^) genannt, und die hier mit S
bezeichnete Substitution entspricht der Substitution ca' = co — 1 der Modulgruppe
und ist also zu der dort mit S bezeichneten Substitution invers.
200 n, 1. Kleinsche Gruppe und zugehörige Formen.
Die Darstellung der gesamten ©^es ^ Wendedreieckskoordinaten
führt zu einem Bildungsgesetz, das der S. 42 geleisteten Darstellung
der Ikosaedergruppe genau entspricht. An die 7 Substitutionen:
/£3-, 0, 0 \
(7) 5-* = 0, £5^,0 , 'X. = 0, 1, -.-, 6,
\0, 0, £6^J
reihen sich zunächst die weiteren 49 Substitutionen S''-T' -S^, d. h.
ausführlich geschrieben;
l-i^Yz[= E^'^ + ^^-is -S^)z^ + 8^'' + ^'is^-s'')Z^^s'''^^^(E^-S^)z^,
(8) -iV7"4= s^" + ^'{e^ - s')z^-^ s^^- + ^\e' - s^)z^^ s^-'-r ^\e -b^)z^,
U i fiz\ =z e'"- ^ ^\s' - &')z^ - s^'- + '\s - s')z^-r s^^' + '^{s^-e')z„
wo 5£ und l die Zahlen 0, 1, 2, •••, 6 durchlaufen. Der Rest besteht
aus den 2 • 56 ähnlich gebauten Substitutionen:
(9) T" • S^, U''-S^--T'- S^ ;« =: 1, 2,
wo U die zyklische Permutation (4) der z ist.
Die Transformationsformeln des einen der beiden Koordinatensysteme
in das andere stellt man in der Art auf, daß man zunächst nach S. 4 ff.
die Pole (x^, x^, x^) der durch (19) S. 193 gegebenen Substitution S
berechnet. Man findet die drei Punkte:
(S^, -1-8-8^ S+S^), (£^ -!-£*-£, £*-r£^), (8^, - 1-8^ - 8^, 8'- 8%
Zwei dieser Tripel können auch durch diejenigen ersetzt werden, die aus
dem dritten durch zyklische Vertauschungen der x hervorgehen. Die
Gleichungen der Seiten des zugehörigen Poldreiecks sind daraufhin sofort
angebbar. Die z^, z^, z^ sind dann so anzusetzen, daß der zyklischen
Permutation der x die der z entspricht und die Substitution S in den z
die Gestalt (3) annimmt: Dem Zusammenhange zwischen den oktaedrischen
Koordinaten x^, x^, x^ und den Wendedreieckskoordinaten z^, z^, z^ kann
man die Gestalt geben:
{ 2-^= -r »1 — (£^ + £* + £°)»2 + (£* -f 8^)x^,
(10) ^2 = -r (£' + £')»! -I- -^2 - («' + «' + £')^3 >
l ^3 = — («^ + «* + «^)^i -r («* + £^)»2 -r
Lallan zeigt ohne Mühe, daß sich die unter (19) S. 193 gegebene
Substitution T auf die Koordinaten z in die aus (8) zu entnehmende
Substitution S^'T' -S^ umrechnet. Aus der Gestalt der Substitution S^-T'-S^
folgt nämlich leicht:
z[ + z,= (8' + 8^) {/. + z,), 4 + ^2 =-(£' + £' -r eWs + ^z),
sowie weiter unter Benutzung der Substitution (10):
^3 -p ^3 = 2 .^3 , Z[J^Z^=2 a-3 (8' + 8% Z', + Z, = — 2 T3 (f^ -^ 5^ -f f^).
Klein sehe Gruppe in Wendedreieckskoordinaten. 201
Aus (10) folgt somit für die der Substitution S^-T'-S^ entsprechende
Substitution der x:
(X[ 4- X^) — (£3 -^ E^ -j- £5) (4 + X^) -f (£* -r£^)(% — »s) == 0>
(£^ + 8')(x[ + x^) -r (4 + X,) - (£3 4- s^ -I- £5)(^; _ ^^) ^ 0,
— (£2 -p £^ -f- £°)(a?; -T- »i) + (£* + £')(»2 -f- »,) -r (% — %) = 0.
Die Determinante dieser für die (x[ -\- x.^), (x\ -\- x^, (% — x^) linearen
homogenen Gleichungen ist die der Substitution (10)^ also vor). 0 yer-
schieden. Somit gilt:
x[ ^ x^ = 0, 4 T- ^»2 = 0, x's — »3 == 0,
so daß wir die Substitution T von S. 193 erhalten.
§ 6. Zwei Systeme vpn quadra^tischen Oktaei^erformen.
Die bevorzugte Oktaedergruppe ©^^ hat; ^Is einfachste absolute Li-
variante diejenige zweiten Grades {xf -j- x| -\- xi). Diese ist also gegenüber
der gesamten Klein sehen Gruppe eine anter sieben konjugierten
quadratischen Oktaederformen, die de'(i sieben i^onjugierten Teilern ©g^ des einen
StfStems als Invarianten zugehören. Wir bezeichnen die mit 4
multiplizierte Form {Xi -\-xi -\-x^) durch ■4^^^{x■^, x^, x^) und stellen aus ihr
die weiteren sechs Formep d^rch Ausübung der Substitutionen
S, S^ •••, S' her:
^0 = 4:{x! ^ xi i- x!).
^,= - 2(Ö + 2)xl -f- (Ö + l){xl -h xh -f- 2{ß - B)x,x„
^^= — 2(Ö + 2)xl + (Ö + l){xl -r xl) -r- W — ^)x.,x^,
(1) ; ^3 = - 2(Ö + 2)0^1 -f (Ö -f l){xl - x!) - 2(6 - ^)x,x„
^,= - 2(Ö -f 2)x! -^ (Ö T l){x! r ^!) i- 2(Ö - ^)x,x„
t,= - 2{ß -f 2)0^1^ -^(e~\- l)(xl 4- xl) - '^{6 - S)x,x„
t^g = - 2(Ö -f 2)xi -f (Ö ^ l)(x! i- xt) -2(0-- S)x,x,.
Bei den erzeugenden Substitutionen S und T der @jgg erfahren diese
Formen die Permutationen:
(2) S = (i/;,, ip„ i,^., T/;3, T/.,, T/;,, t/;^), T = (i/;,, ^/;,)-(j^,, l/'s)-
Gegenüber der zyklischen Pennutation der x^, x^, x^ pennutieren sich
die drei Formen i/; zyklisch, deren Indizes die quadratischen Reste von
7 sind, und ebenso die drei Formen i/;^ mit den quadrat}.sch&n Nicht-
resten v.
202 n» 1- Klein sehe Gruppe und zugehörige Formen.
Die Ausübung der Substitution U (vgl. (11) S. 191) auf die Formen (1)
führt zu den sieben konjugierten quadratischen OUaederformen, die dem
zweiten System der sieben konjugierten Teiler ©g^ zugeMren:
^^ = (Ö -f l){x't -^r 4 -f xf) - (3Ö -f o){x^x^ -f 0^30;, -f x^x^),
^, = - (3Ö -f l){xl -f xl) + 2(6- l)xi,
'i,^= — (3Ö + l){xl -H xl) ~\-2{e — l)x!,
(3) ^ ^3 = (Ö -f l)ix! -f xi -f xl) -f (3Ö -f o)ix,x, + 0^30;, -a^.a;^),
^^ = — (3Ö -f l)(a;| -f %^) -f 2 (Ö - l)a;|,
^^ = (Ö ~f l){oo! -}- xl ~f a;|) ~f (3Ö -f o)(a;2a;3 — a^gä^i ~f x^x^),
^g = (Ö + l)(%2~f a;|~f a;|)-(3Ö~f o)(—a;2a;3+-a;3a;i~f a^io;,).
Diese Formen erfahren gegenüber den erzeugenden Substitutionen S und T
die Permutationen:
(4) S ;= (4},, -^„ ^2, ^3, %, ^5, p,), T = (^,, ^3) -(^5' ^e)-
Bei den zyklischen Permutationen der x zeigen sie dasselbe Verhalten
wie die Formen (1).
Unter den Formen ^ des einzelnen Systems kommen sechs, aber
natürlich auch nur sechs linear-unabhängige vor. Man hat nämlich
überhaupt nur die sechs linear-unabhängigen quadratischen Ausdrücke
^ij 4, •••; ^1^2' ^^^' ^^^^ leicht in den i/; des einzelnen Systems
darstellen lassen. Die Summe der Formen des einzelnen Systems verschwindet
identisch:
(5) 2 ^^ = 0' 2 ^^ = 0-
Indem man die Ausdrücke der Xi, x^, ••-, x^x^ durch die Formen des
einen Systems in die Darstellungen des anderen Systems einträgt, gewinnt
man die folgenden wichtigen Beziehungen:
(6) I f^^ = ^v + 3+^.+ 5+ ^. + «, ^^^^^^ ^^ ^ g^
vermöge deren sich die Formen jedes Systems in denen des anderen
darstellen, hi (6) hat man rechts die Indizes nötigenfalls mod 7 zu
reduzieren. Man überzeuge sich, daß zufolge (6) die Permutationen der
Formen des einen Systems einfache Folgen der Permutationen der Formen
des anderen Systems sind.
Da die zyklische Permutation der x diejenige der z nach sich zieht,
so sind die Formen t/;^ und 1/;^ auch in den z^, z^, z^ symmetrisch
gebaut. Man hat also für ij;^ den Ansatz:
^0 = « C-^' + ^1 + ^1) + 6(^2^3 + ^3^1 + ^1^2)-
Man findet aber aus (10) S. 200 nach kurzer Rechnung:
4-^4~\-4 = —ds'is'-8'>Y(x!+xi~\-xl~\-e{x,x,~\-x,x,-^x,x,)),
^i^3~\-^3^1~\-^1^2=—^^(^^—^^T(4~\'Xl-^xl — ^(X^X^-\-X^X^~\-X^X^))
Zwei Systeme von sieben Oktaßderformen. 203
Es wird weder die Permutatioaen (2) und (4) noch die Beziehungen (6)
stören, wenn man die sämtlichen in den z geschriebene^. Okfcaederforn^en
um einen gemeinsamen konstanten Faktor ändert. Wir erklären d[emn9,ch
die Oktaederform tp(^{z^, z^, z^ durch:
(7) ip^ = zl ~f zl + zl -f- Ö 1^2^3 + ^3^1 ~f s^z^
imd finden aus den beiden letzten Gleichungen die Beziehung:
(8) - Ö y, {z^, z,, z,) = £« (£^ - sy ^, {X,, X,, X,)
Man gelangt zu dem Ergebnis: Die OMaederformen der leiden Systeme
schreiben sich in den z^, z^, z^:
I yfy=z E^" Z^ -\- B^" zi ^ B^" zl -{-^ {e^'' Z^^Z^-^ E^" Z^Z^-^ E" Z^Z^,
wo V die Werte 0, 1, •••, 6 durchläuft; die Permutationen (2) und (4)
und ebenso die Beziehungen (5) und (6) bleiben in Kraft. Die Formen ly;,
ergeben sich unmittelbar aus (7) durch wiederholte Aiisübnng der
Substitution S. Aus ihnen berechnet man weiter die Formen ip^ am
einfachsten mittels der Beziehungen (6).
§7. System der Invaqantipn der Kleinschen Gruppe"^).
Kach S. 189 ist die biquadratische Form F eine absolute Invariante
der ©jgg- Die damalige Betrachtung zeigt, daß überhaupt jede invariante
Form der Kleinschen Gruppe eine absolute Invariante derselben ist. Kach
S. 18 lassen sich alle diese Formen in gewissen endlich vielep unter
ihnen rational und ganz darstellen. Dieße endlich vielen Fprmen bilden
das „volleFormensystem" der Gruppe @,^gg Klein hat gezeigt, daJ3 dieses
System aus vier Formen besteht; zu den uns bereits bekamiten Formen
F und ^ kommen nur noch zwei Formen liin2u, nämlich eine solche vom
J4ten ^jjj^ ejjQ^e solche vom 21^*^^* Grade. Den Beweis dieser
grundlegenden Tatsache führt Klein mittels geometrischer Überlegungen, die
sich auf die Kurve vierten Grades ^ = 0 stützen. Irgend eine
invariante Form der @jgg enthält entweder die Form F als Faktor, oder
sie Kefert, unter n ihren Grad verstanden, gleich 0 gesetzt eine Kurve
w*^" Grades, die die Kurve F = 0 in einepi invarianten System vpn
4w Punkten schneidet. Ein solches System stellt 4» nur untereinander
äquivalente Punkte dar. Diese invarianten Punktsysteme der Kurve
F =z 0 werden wir aber nach S. 194 ff. leicht charakterisieren können.
^) Bei der folgenden Unters(ichung ist der Gebrauch der
Wendedreieckskoordinaten Zl-, z^i Zz zweckmäßig, so d^ fur die invarianten formen vierten und
sechsten Grades die S. 198 eingefujirten, Bezeichnungen benutzt; werden.
204 III 1- Klein sehe Gruppe und zugehörige Formen.
An invarianten Punktsystemen auf der Kurve vierten Grades haben
wir nämlich erstlich die 24 Wendepunkte, die 56 Berührungspunkte der
Doppeltangenten und die 84 sextaktischen Punkte, sodann weiter
irgendwelche Systeme zu 168 äquivalenten Punkten, die von den eben
genannten besonderen Punkten verschieden sind. Irgend ein beliebiges
invariantes Punktsystem wird sich aus jenen besonderen Systemen in der
Art aufbauen, daß es die 24 Wendepunkte a-fach enthält, die 56
Berührungspunkte der Doppeltangenten |3-fach usw. Ist also n der Grad
irgend einer invarianten Form, die die Form F nicht als Faktor enthält,
so gilt für 4 n eine Gleichung:
(1) 4/^ =: 24« +56^~f 84j;—168d,
wo a, ß, y, 8 nicht-negative ganze Zahlen sind.
Zwei Formen, die nur um einen konstanten Faktor voneinander
verschieden sind, sehen wir als nicht wesentlich verschieden an. Dann
folgt aus (1) zunächst, daß es für w <^ 6 außer der Form:
(2) F{^^, ^2, ^3) = ^1^2 + 4^3 -f ^1^1
selbst keine Invarianten der Klein sehen Gruppe geben kann. Weiter
haben wir für n = ß nur die uns gleichfalls schon bekannte Form:
(3) * (^j, ^2, ^3) =: 5 z^ 4 ^1 — ^14 — ^2 ~3 — ^z 4 ■
Gäbe es nämlich eine zweite invariante Form ^' dieses Grades, so würde
sie, da für sie wieder «=1, |3 = 0, j; = 0, ^ = 0 zuträfe,
gleichfalls die Wendepunkte der Kurve vierten Grades zu Nullpunkten haben.
Dann aber ließe sich ein konstanter Faktor 1 so bestimmen, daß die
Kurve sechsten Grades ^' — l^ =z 0 noch einen beliebigen weiteren
Punkt mit der Kurve ^ = 0 gemein hätte. Also würde die Form
(^' — 1 ^), ohne identisch zu verschwinden, F als Faktor aufweisen, und
der andere Faktor wäre eine Invariante zweiten Grades, was nicht
möglich ist.
Für Formen der Grade » = 7, 8, • •-, 11 folgt aus (1) leicht, daß
sie F als Faktor haben müssen. Man hat also nur die beiden
Möglichkeiten F^ und ^. * für » =z 8 und » = 10. Für n = 12 reiht sich
eine Schar von Formen {v.F'^ -r- l^'^) an, die gleich 0 gesetzt:
(4) '^^« + 2*^ = 0
eine Schar invarianter Kurven zwölften Gradeb liefern, auf die wir unten
zurückkommen. Jede dieser Kurven hat in den Wendepunkten der
Kurve F rz=: 0 vierten Grades 24 Rückkehrpunkte; im übrigen bedeckt
die Schar die Koordinat^enebene in der Art einfach, daß durch jeden
Punkt der Ebene eine und nur eine Kurve der Schar hindurchläuft.
Für » =z 14 haben wir eine wesentlich neue Lösung der dio-
phantischen Gleichung (1), nämlich a = 0, /3 = 1, y := 8 =■ ^.
Klein erklärte eine invariante Form dieses Grades durch die mit den
Volles Pormensystem der E lein sehen Gruppe. 205
ersten Ableitungen von ^ geränderte B esse gehe Determinante von J'*).
Wir setzen:
dz,
d ^
d ^
(5) ^W{z^,z„z,) =
d^F
dzl'
0'F
'bz^öz.
d'^F
d z^ d z^
d^
£)e,'
d'^F
dz^dz^'
d'F
' dzl '
d'F
dz^ds^
g*
dz^'
c^F
dz^dz^
d^F
?jz^dz.
d^F
' d^r
8*
a^^s'
0
Xach der Berechnung von Gordan *=^) ist die entwickelte Gestalt dieser
Form:
*^ M ^ ^loz^zlzliztzl -^..,) -^ 18 {zlzl -..•)-l2^zlzUI{^l4 -•••),
wo in jeder Klaromer noch die aus dem ersten cfurch zyklische
Permutation der z entstehenden Glieder hinzuzusetzen ^ind Offenbar enthalt
^ die Form F nicht als Faktor, so daß die Kurve 14*^" G^-ades !F= 0
die 56 Berührungspunkte der Doppelt^ngenten auf ^ea Kurve vierten
Grades ausschneidet. Den gleichen Zweck erreicht paan übrigens mit
den beiden zerfallenden Formen 14*^" Grades:
6 6
(7) Yiw^i'i^ 'v ^3)> ri¥v(^i> ^v ^3)^
wo tpy und -y/^ die Oktaedeiformen (9) [S. 203 sind Man überzeugt
sich nun sehr leicht wie oben, daH alle invarianten Formen Ipen Q-raäeb
der Gruppe ©^gg eine Schar UJden, die ifi der Gewalt:
(8) ^W^lF'^
darstellbar ist. Speziell für die beiden Formen (7) stellt pan leicht die
Darstellungen fest:
(9) 13^"= ^+(70-62)^2^,1 n^>= 5»+(7 0-62)^2*.
Auf die durch Xullsetzen der Form (8) entstehejade Schar von Kurven
14ten Grades kommen wir unten noch zjirück.
Für die nächstfolgenden Grade » == 16, 18 und 20 erweisen sich
die invarianten Formen wieder durphweg als durch F, ^ und W rational
darstellbar. Die niederste in (1) zulässige unge|?ade Zahl n ist 21, mit
der Lösung a = ß = 8=^0, y = l dieser diophantischen Gleichung.
Es kann nur eine einzige inyariante Form 2lsten Grades X{Zj^, z^, z^)
^) Die Invarianteneigenschaft dieser Determiaante wird S. 332 ff. dargelegt.
**) In der Arbeit „Über die typische Darstellung ief ternaren biqiadratischen
Porm usw.^ Math. Ann. Bd. 17, S. 372 (1880).
en F,
dF
^'
d^
dz^'
*, !F durch:
'dF dF
8^2' S^3
d^ d^
dz^' dz^
dW d^
"8^' J7s
(11)
206 11? 1- Klein sehe Gruppe und zugehörige Formen.
geben. Jede solche Form liefert nämKch, gleich 0 gesetzt, eine Kurve
2lsten Grades, die zufolge (1) die 84 sextaktischen Punkte auf der Kurve
vierten Grades ausschneidet. Gäbe es nun zwei wesentlich verschiedene
Formen X und X', so könnte man zufolge einer schon vorhin dargelegten
Überlegung eine Form (X — l X') bilden, die nicht identisch verschwindet
und F als Faktor hat. Es bliebe als zweiter Faktor eine invariante
Form 17ten Grades, was nicht möglich ist. Klein erklärt die Form X
als Funktionaldeterminante der Formen F,
(10) — 14 X(^,,
Xach den Rechnungen von Gor dan hat man explizite:
[X{z,,z„z,)^zl'^zl'^zr-1 z,z,z,{zrz,^...)^2ll z,z,z,{,^zr^:.)
- 308^f 4^1 {zl^zl + •..)- 37 {zl^zl 4-...)- 289 {zlzl^ + .••)
-^ 4018 z^zi zi (z^ ^2' V ■ • •) -^ 6 3 7 ^f zi zl {z^ ^| + • • •)
^ im^z^z^z^izl'zl + ...)- Q279z!ziz!{ß^zl + .••)
^ 7007 zizizi (z^zi ^...)-10010^*^2'^1 (z;:zi ^...)
-3432^/^.J^J,
wo wieder in jeder Klammer die beiden Glieder zuzufügen sind, die aus
dem ersten durch zyklische Permutation der z entstehen. Diese Form
ist in das Produkt von 21 linearen Formen zerlegbar, die gleich 0 gesetzt
die 21 PerspeJdivitätsachsen darstellen. Das Produkt dieser 21 Linear-
formen ist nämlich eine invariante Form 21^*^" Grades, und wir haben
im wesentlichen nur eine solche Form.
Irgend ein System von 168 getrennt liegenden, bezüglich der ©^gg
äquivalenten Punkten der Kurve vierten Grades kann man durch eine
Kurve 42^"" Grades der Gleichung:
(12) xW^ + 2.0'' = 0
ausschneiden. Man kann nämlich den Wert x.l so wählen, dai3 die in
(12) links stehende Form an einer beliebig vorgeschriebenen Stelle der
Kurve vierten Grades verschwindet. Sie verschwiadet dann eben auch
an allen äquivalenten Stellen.
Es ist jetzt leicht, den folgenden Hauptsatz zu zeigen: Das volle
Formensystem der KJein sehen Gruppe besteht aus den Formen F^ #, ^
und X. Der Beweis gelingt durch den Schluß der vollständigen Induktion.
Eine ia einer beliebig vorgelegten Form als Faktor auftretende Potenz
von F denken wir fortgehoben. Die restierende Form f{z^, z^^ z^ habe
den Grad % und Kefere eine Kurve n'^^ Grades f =i 0, die auf der Kurve
Volles Formensystem der Klein sehen Gruppe. 207
vierten Grades ein invariantes Punktsystem ai^sschneidet, das entsprechend
der Gleichung (1) aus dem cc-fach gezpHten System der Wendepunkte,
dem /3-fach. gezählten System der Berührungspunkte der Doppeltangenten,
dem y-fach gezählten System der sextaktischen Punkte und aus d Systerfien
zu je 168 unter sich verschiedenen äquivalenten Punkten besteht*). Es
ist dann möglich, eine Form w*^" Grades:
d
(13) SB- Wß Xy. \\ (X, W^ ^ i, #0
Z —1
mit geeigneten Faktoren des Produktes aufzi|baue|i, die gleich 0 gesetzt
eine Kurve w*^" Grades mit genau demselben Schrfiittpunktsj'-stem auf der
Kurve ^ = 0 liefert. Man kann alsdann eine von 0 verschiedene
Konstante c so bestimmen, daß die Form n^^'^ Grades:
ä
noch einen (4» -f ^Y^^ Nullpunkt auf der Kurve .F == 0 an beliebiger
Stelle hat und also wegen dieses überzähligen JTullpunktes den Paktor F
besitzt. Daraus folgt die Möglichkeit der Darstellung
ä
f=c^ W^Xr. Yli^^W + A,*0 -r Ff,
der Form f, wo f, eine Form des Grades (w — 4) ist. Hiermit ist der
Schluß der vollständigen Induktion begründet, da bis zi^m G^ade w == 21
alle invarianten Formen' der @jgg durch F, ^, W und X rational i;nd
ganz darstellbar sind.
Zwischen den vier Formen F, ^, ^ und X der drei Variablen s^,
z^i ^3 muß nun eine algebraisphe Relation bestehen, (Jie wir noch
aufzustellen haben. Die Kurve 42^*^^^ Grawes (12) schneidet auf de^" Kurve
F =z Q ein System von 168 im allgemeinen getreimt liegenden Ipunkten
aus. K'ur für ;< == 0 fallen diese Punkte zu je 7 ip die 24 Wendepunkte,
für A = 0 zu je drei in die 56 Berührungspunkte der Doppeltangeni^en
und für einen noch festzustellenden Quotienten '/,:X zu je zweien in
die 84 sextaktischen Punkte. Diese letzteren Punkte werden, einfach
gezählt, durch X ■=. 0 ausgeschnitten. Durch Wiederholung der eben an
(13) angeschlossenen Uberlegupg gnlangen wir zu dem Ansatz:
(14) X^ ^^W^^l^' + F.f,
für die in Bede stehende Relation. Hier ist f^ eii^e Form 38»'^'! Grades,
die wegen dieses Grades eine rationale ganze Funktion von F, ^ imd W
allein sein muß. Der rationale Ausdruck von f^ in Fi ^ und W ist
leicht mit unbestimmten Koeffizienten anzusetzen. Zur Bestimmung der
Koeffizienten kann man den Umstand benutzen, daß die Eiijitragimg der
*) Diese S Systeme brauchen naturlich nicht durchweg yerscMeden zu i
208 II) 1- KJemsche Gruppe und zugehörige Formen.
Ausdrücke der Formen F^ ^, W, X durch die z^^, z^, z^ in (14) zu einer
in den z identisch bestehenden Gleichung -führen muß. Hieraus
entspringen lineare Gleichungen für die unbestimmten Koeffizienten^ aus
denen diese eindeutig berechenbar sind; denn die Relation (14) ist selbst
eindeutig bestimmt. Auf anderem Wege fand übrigens bereits Gor dan
in der eben genannten Arbeit den fertigen Ausdruck der Relation (14)
in der sogleich anzugebenden Gestalt: Zwischen den vier Formen des
vollen Systems der Klein sehen Gruppe ©jgg besteht die Relation-^
durch die das Quadrat der Form X als rationale ganze FunMion der drei
anderen Formen dargestellt ist.
§ 8. Invarianten der Klein sehen Gruppe in oictaedrischen Koordinaten.
Bedient man sich der ursprünglichen oktaedrischen Koordinaten, so
hatte die biquadratische Form nach S. 192 die Gestalt:
(1) F{x^, x^, x^) == xt ~f a;,* ~f %* ~f Sd(xix! + xix^ + x^xi).
Für die invariante Form sechsten Grades 0(x-^, x^, x^) gelte hier die
folgende Erklärung durch die Hessesche Determinante von F:
d^F d^F d^F
(2) 216(6 —1)0(x^, x„ x^):
Man berechnet dann leicht als entwickelte Gestalt von 0:
i0 = 2 (x^ ~f xi ~f x!) - 5 6{x^xi + xtxl^ x-lxl^ x^xi+ x^x^+xi xi)
^ ^ 1 —20{0-^2)x^x.!xi.
Die Formen" (1) und (3) sind symmetrische Funktionen von xf, a;|, xf
und stellen sich in den symmetrischen Grundfunktionen Sj, s^, Sg dieser
drei Größen (vgl. I, 100) in der folgenden einfachen Gestalt dar:
[ F=s'}-(Se-^6)s„
l 0= 2s-'-f (5Ö —l)s,S2 —7(oÖ ~f 7)S3.
Die Heranziehung dieser symmetrischen Grundfunktionen Sj, s^, s^
gestattet leicht auch die Bildung zweier Formen 14*^'! und 21^*^11 (^l-rades.
Eine Form 14tea Grades gewinnt man am einfachsten in dem durch 4
geteilten Produkte der sieben Oktaederformen (1) S. 201:
6
(o) 4:W(x^, x^, x^) = Yl ^vi^i, x,_, »3)
dx!'
d-F
dx^dx^
d^F
dx^dx^
di
'
'
Cj 8 ajg'
d^F
dx'i '
d'^F
dx^dx,
dx^dx^
d^F
dx^dx^
d^F
Pormensystem der Klein selben Gruppe in oVtaednschen Koordinaten. 209
oder ausführlicher ge&ehrieben:
(W== (x! + 4 -f xDllii (30 + 2) xt -r (B - 1) (xi -f- »/)
1 —Sßx^ (^1 + xl) -4- 30 (/9 - l) xl 'xl\
wo sich das Produkt auf die drei Faktoren bezieht, die aus de^i in der
Klammer angegebenen Ausdri(.ck durch die zyklischen Permutatipnen der
X hervorgehen. W ist eine symmetrische Funktion von xl, xl, xi, die
in den drei Grundfunktionen vonq. Grade 7 und voip. Gewichte 7 ist.
Da sie den Faktor s^ besitzt, so setzt man sie leicht siebengliedrig mit
unbestimmten Koeffizienten an. Yier von den Koeffizienten bestimmen
sich durch eine ganz kurze Rechnung, \^enn man x^= 0 setzt. Für die
drei übrigen Koeffizienten setze map. einige spezielle Wßrte der a;f, x|, «f.
wie z. B. xl = 1, ä;| = i, x? == — i oder x^ == 1, a;| =- q, x^ = q-
«in. Als entwickelten Ausdruck der Fprm W gewinnt man:
<7) +7^(53 0-3^.11)8,^1 +2.7^(421 ^y-3.883)ö^2Ö3
( — 2'-.73(UÖ -23)ö,s| +7^(7. iUy +23.67)ö,ö|.
Die Form 2lsten Grades köimte man als Funktionaldetermin^nte
von F, 0, 3*" in bezug auf die .<;,, x^, x^ dar&teilen, die sich in das
Produkt der Funktionaldetem^inante voifi F, 0, 3*" in bezug auf t^^, s^, Ö3.
und derjenigen von s^, s^, Ö3 in bezug auf die x^, x^, x^ spaltet. Die
letztere Determinante ist das Produkt von x^^x^x,^ und dem
Differenzenprodukte der xl, xi, xf, also die Quadratwurzel aus D-b^, unter D die
Diskriminante der kubischen Gleichung mit den Wurzeln x^, x'l^ /^ A-er-
standen, die sich nach I, 110 in den Grundfunktionen so darstellt.
<8) D = 4 4 — 4 ^i S3 + 18 ö, §2 S3 — 4 ö,^ — 27 5^
Man kann aber auch die Form 2P*^'i Grades X (a;,, x^, x^ miitels der
Linearformen (1) S. 194 durch die Gleichung erklären.
20
<9) 8(Ö - 1)X(^,, X,, X,) = ]][^^(^i' ^2' ^3)-
Man findet dann:
r X = ~{^f) -\-l)x^x^x^ (xl — x?) (x.f — xf) {xl ~ li)
^^^^ \ -11(^^0 -r 2)xt + x| + xi + 2(0 + 2)xlixi + xf) - 2xix!)
oder kürzer geschrieben:
{X--=^~{Sd-rl)ivi, llisl -r 2(Ö i- 1).^ + (3Ö ^ 1):.,*
1 -2(S~r3)x:jxl),
Fricke. Algebra. II. 14
210 II, 1. Klein sehe Gruppe und zugehörige Formen.
WO sich die Produkte wieder auf die zyklischen Permutationen der x
beziehen. Aus (11) ergibt sich durch Ausmultiplizieren der drei
Klammerausdrücke folgender entwickelte Ausdruck von X:
[ X == V^ (2*Si^ + 23 (3 Ö — 7)s* Sa + 2^. 3 (28 Ö + 3' • 5) s^s^
(12) __ (32.11 Ö+ 72) ,2 s|_ 2(5.19 Ö+3.151) s.s^Sg
[ +22(3 0 + 17)4 + (457 0 + 3.11.l9)ö|).
Den Ausdruck von X^ in den drei anderen Formen kann man mit
neun unbestimmten Koeffizienten ansetzen. Diese Relation besteht in
den Sj, Sg, Sg identisch. Indem man dies identische Bestehen fordert
und der Reihe nach Sg = 0, s^ == 0, Sg == 0 einträgt, gelingt die
Bestimmung der Koeffizienten. Die Rechnung ist indessen umständlich.
§ 9. System der acht Wendedreiecke.
Den acht konjugierten Teilern ©gi "^^^ IQein sehen Gruppe @jgg
gehören als Invarianten acht konjugierte kubische Formen zu, die gleich 0
gesetzt die acht Wendedreiecke darstellen. Da eines dieser Dreiecke das
Koordinatendreieck der z ist, so erscheint hiei der Gebrauch der
Wendedreieckskoordinaten am Platze. Die Bezeichnung der Indizes dieser acht
Formen, die wir ^^, cp^^ (p^^, •••, ^g nennen, rührt aus der Theorie der
Modulfunktionen siebenter Stufe her. Die erste Form <poc(^i, ^a, ^3)
liefere das Koordinatendreieck und sei genauer durch:
(1) cp^ = -7,,z,z,
gegeben. Sie gehe durch die Substitution T' von S. 199 in (p^ über,
und cpf^ werde durch die Substitution S^ von S. 197 in (p^ übergeführt.
Eine einfache Rechnung liefert dann folgende Gestalt der (p^:
i +2 8^-Z^zi + 2 8^-Z,4~\^2s^'Z,4, ^zz: 0, 1, 2, ..., 6.
Gegenüber den Substitutionen der Klein sehen Gruppe bilden die
acht kubischen Formen (p eine Gruppe ©^gg von 168 geraden Permutationen,
und zwar entsprechen den beiden erzeugenden Substitutionen S und T\
wie man leicht feststellt, die Permutationen:
.3s J ^ == (^Co» 9l' 92> 93> 94> 95' ^e)'
[ T' == (cp^, 9o)-(9i' 96)-(92' 93)'(9i' 9-o)-
Formenproblem der ®jgg und ßesolventen ßiebei^ten Grades 211
Zweites Kapitel.
Formenproblem der Klein sch^ifi Gruppe und
Gleichungen siebenten Grades.
§ 1. Ansatz des Formenpioblems UQd Resolvente siebenten Grawes.
Entsprechend den allge^ieinep Ansatzei^ von S. 19 ff. ist das „Formen-
problem" der temären Klein selben Gruppe @jgg in folgender Art zu
formulieren: Es sollen aus gegebenen Werten ßer vier inoarlaifden Formen F,
0, W X, die die zwischen diesen Formen besiehende Relation befriedigen
müssen, die Argumente, d. h. also entweder die x^, x^, x^ oder die z^ s^, z^
berechnet werden. Es handelt sich hier um ein „Galoissches Problem"
oder „Kormalproblem'- mit 168 Lösungen, insofern mit einer Lösung
alle 168 Lösungen rational bekannt siijid. In der Tat stellen sich ja alle
Lösungen in einer ersten durch die 168 Su|bstitiitionen unserer temären
Gruppe @^gg dar. Arbeiten wir mit den x^, x^, x^, so ist an numerischen
Irrationalitäten zum rationaleq Körper von vomheipein die ^aw^e algebraische
Zahl zweiten Grades B zu adjungieren. Werden die z^, z^, z^ bevorzugt,
so ist sogar die siebente Einheits,wurzel s, also eine ganze algebraische
Zahl sechsten Grades zu adjungieren.
Als „Totalresolventen- (vgl. I, 382) niedersten Grades hat man
zwei Gleichungen siebenten Grades, die dei^ beiden Sj^stemen von sipben
konjugierten oktaedrischen Teilern ®^^ zufgehören. Map stellt diese
Gleichungen sehr leicht in der Weise auf, daß man die Potenzsummen
der sieben Oktaederformen des einzelnen Systems in den Formen F, ^, W
darstellt und dann auf Grund der Regeln von I, I02|f. die Koeffizienten
der ßesolvente berechnet. ßei G-ebrauch der oktaedrischeß Koordinaten
hat die eine JResolvente [Formensybiem (L) S. 201] die Gedalt:
{ T/;^ —14(0+1) i^T/;^ + 14(0 — 1)01/;^ ~f 7 (1U> — 7) F^/.^
(1) -r 14(9 0 ~f 19)F07/^2 _,. 7(4(^_^ 11)^3 _ (17^^ 4_ll^,^2)^
( _ 4 jff = 0
und die zweite [Formensystem (3) S. 202] :
[ ^^~f 7(Ö + 2)F^^—7(3ö-f 1)01^^7(130^15)^2-^3
(2) — 14(130 —l)Fa>^2^7((31Öfo)F^ — 8(Ö-r 3)02)^
( — (4g«"-7(l3Ö~f 31)F2 0) .= 0,
bei Gebrauch der Wendedreieckskoordinaten ist die erste Beoolvente [efdes
Formensystem (9) S. 203]:
die bei Ersatz von 6 durch 8 unmittelbar in die zweite Ecbolpentc übergeht.
14=^
212 11, 2. Formenproblem der ©jgg und Gleichungen siebentea Grades.
Nach der vollständigen Lösung einer dieser Gleichungen siebenten
Grades sind nur erst die Quadrate und die zweigliedrigen Produkte der x
bzw. z rational bekannt. Die Berechnung dieser Größen selbst aus
den tIj erfordert noch die Ausziehung einer Quadratwurzel *). Man findet
nämlich, wenn man z. B. mit der Resolvente (1) arbeitet, aus (1) S. 201
leicht die folgenden Darstellungen der Quadrate und Produkte der x in
den il)^:
56 x! = (Ö 4- 4) 1/;^ -f (3 «9 — 2) {^p, + i^,), _
6ßxl ^ (ö + 4)T/;, + (3Ö-2)(^,-f i/;3),
Qox, == (6 -t 4:) ^, -^ (SB - 2) (^p^ + i^,),
(4)
6Qx,x,= -(Ö + 4)(t/;,-t/;.),
56 x,x,= -{8 ^ 4) (T/;^ - ^^),
öQx^X,= - (Ö ^ 4) (i/;, - T/;g),
woraus die gemachte Angabe hervorgeht. Die hinzutretende
Quadratwurzel ist unentbehrlich, da bei gleichzeitigem Zeichen Wechsel der x die
1^^ unverändert bleiben. Arbeitet man mit der Resolvente (3), so ist, wie
bemerkt, a zu adjungieren. Die Quadrate und Produkte der ^ werden
dann von den „Lagrangeschen Solventen-' (vgl. I, 413) der Wurzeln der
Gleichung (3) geliefert:
(5) <; '^4=^e''y^r, 14:^,,^ = -(e^l)^a^^^yj,,
wo V die Zahlen 0, 1, 2, - • •, 6 zu durchlaufen hat. Diese Gleichungen
gehen unmittelbar aus (9) S. 203 hervor.
§ 2. Spezielle Resolventen siebenten Grades.
Es gibt eine bemerkenswerte Art, die Resolventen siebenten Grades
auf einem direkten algebraischen Wege aufzustellen, der allerdings einer
transzendenten Begründung bedarf. Xach S. 187 (unten) entspricht dem
einzelnen Teiler <>\ innerhalb der (S)^gg (aller mod 7 inkongruenten
Substitutionen der Modulgruppe) eine Kongruenzgruppe siebenter Stufe
des Index 168 ^-^ innerhalb der Modulgrappe. So haben wir den zwei
Systemen von je sieben Oktaeder-®^^ entsprechend ^wei Systeme uon je
sieben honjtigierten Kongruenzgruppen des Index 7. Der DB einer
einzelnen dieser Gruppen muß aus den sieben zu den Substitutionen 1,
S^^. S-^, S-3 gehörenden Dreieckspaaren des Dreiecksnetzes der Modul-
*) Man beachte, daß durch die Angabe des Wertes der Form X ungeraden
Grades die Quadratwurzel eindeutig bestimmt ist.
Diskontinuitatsbereiclie fur die speziellen Eesolventen siebenten Grades. 213
gruppe zusammensetzbar seip, unter S die erzeugende Substitution
/I, 1\
der Modulgruppe verstanden; denn die zu dieser &ubstiti|tion gehö:pende
zyklische ®^ ist in der Oktaeder-@24 nicht enthalten. Der fragliche DB
ist in Fig. 26 wiedergegebea. Per Versuch zeigt aämlich, daß es im
wesentlichen nur eine einzige Art gibt, die Randkurven dieses Bereiches
zu Paaren einander zuzuordnen. In der Tat hat diese Zuoydnui^g so
zu geschehen, daß man bei der Abbildung des Bereiches vermittelst der
Modulfunktion erster Stufe J((o) zu e^ner sieber^blättrigen Riemann sehen
Flache über der /-Ebene mit zulässiger Verzweiguag gelangt. Dabei
sind aber Verzweigungspunkte nur bei / ^ 0, 1 und cx) zulässig, und
zwar an den beiden ersten Stellen nur drei- bzw. zweiblattrige
Verzweigungspunkte. Die Behauptuag, es gäbe ,im wesentlichen- nur die
in Fig. 26 angegebene Zuordnung der Randkurven des DB, ist sp zu
verstehen, daß die Zuordnung sowohl durch die Substitutionen S-^, S--,
S-^ als auch durch die Spiegelung U an der imaginären co-Achse und
endlich durch S-^ • ü, S-^ - U, S-^-U versetzt werden kann. Aut diese
Art aber erhalt man gera,de die DB aller 2-7 ^n Frage ötehendeii
Kongruenzgruppen.
Ehe die algebraische Ausbeute dieses Absatzes entwickelt wird,
gehen wir auf die mit der Modulgnippe kommensurable Gruppe (^(-) zurück,
auf die wir S. 100 ff. die Theorie der Bring sehen Gleichung tupften
Grades gründeten. Dieser Gruppe gehörte eine Einteilung der positiven
Arithmetisch waren die Substitutionen dieser (jiruppe mittels der
Irrationalität 12 zu erklären. Da 2 quadratischer Xichtrest von 5 i&t, so
lieferte die Hauptkongruenzgruppe fünfter Stufe einen Xormalteiler. des
Index 2-60 in der (^O. Hingegen ist 2 quadratischer Rest ^on 7, so
daß die Hauptkongruenzgruppe sieber^ter Stufe einen Xormalteiler des
Index 168 in der (5)^^ darstellt. Hter mubösn wir also auch wieder ~wet
Sydeme von je sieben konjugierten ^ongrmusgruppen dei, Liciex 7 antreffen,.
Mit K{^ werde die Funl^tion bezeichaet, die d^s Dreieckspaar des
neuen ]S^etzes auf die volle ^-Ebene abbildet !vgl. S. 104ff.j-") In den
*) Die damalige Funktion K{o}) mußte zufplge (11) S. 102 eigentlich durch
K(Z,^2) bezeichnet werden.
214 n, 2. Formenproblem der @igg und Gleichungen siebenten Grades.
drei Ecken der Winkel tj ?:, 0 nehme K die Werte 0, 1, oo an. Der
4' 2 '
DB der einzelnen der eben genannten Kt)ngruenzgruppen des Index 7
besteht dann wieder aus sieben nebeneinander gereihten Dreieckspaaren.
Verzweigungspunkte über der JST-Ebene können wieder nur bei ^ == 0,
1 und oo auftreten, und zwar an den ersten beiden Stellen nur vier- und
zweiblättrige bzw. zweiblättrige Verzweigungspxmkte. Der DB einer der
Gruppen ist in Fig. 27 dargestellt, aus dem die DB der übrigen Gruppen
Fig. 27.
wieder wie im eben besprochenen Falle ableitbar sind. Es gibt zwar,
wie der Versuch zeigt, noch drei weitere Zusammenordnungen der
Randkurven, die zu siebenblättrigen Riemann sehen Flachen mit zulässiger
Verzweigung über der jST-Ebene führen. Aber diese drei DB sind
syrometrisch xmd können deshalb für uns nicht in Betracht kommen.
Der DB der Fig. 26 wird durch die Funktion J{co) auf eine
siebenblättrige Fläche über der /-Ebene abgebildet, die bei / = 0 zwei
dreiblättrige Verzweigungspunkte trägt, bei / = 1 zwei zweiblätterige und
bei / = oo einen siebenblättrigen. Auf Grund der Regel (5) S. 112
stellt man als Geschlecht dieser Fläche j5 = 0 fest. Eine etawertige
Funktion der Fläche werde durch 6 bezeichnet und so gewählt, daß bei
/ = 0 in dem daselbst isoliert verlaufenden Blatte 6 verschwindet, und
daß ö = oo im Punkte / = oo zutrifft. Eine dritte Bestimmung, die
ö dann endgültig festlegt, bleibe vorbehalten. Die zwischen J und ö
bestehende algebraische Relation, die / als rationale Funktion siebenten
Grades von 6 darstellt, kann dann nach der von-Klein erdachten Methode*)
aus der Verzweigung der Riemann sehen Fläche allein bestimmt werden.
Aus der Lage der Punkte ö = 0 und oo und der fraglichen Verzweigung
folgt nämlich für die Darstellung von J" in (j ein Ansatz, den wir wie
früher (S. 60 und 128) in Gestalt der dreigliedrigen Proportion ansetzen:
(1) /:(J"-1):1 = 6 {6'- ^ aö ^llf : (6^ ^C6- ' dö + e){6^ + f6 ^ gf -.K
Im Absolutgliede der ersten Klammer rechts ist zur Kürzung der
weiteren Rechnung der Faktor 7 aufgenommen. Zufolge (1) muß nun
die identische Gleichung gelten:
(2) ö (ö^ -r a ö 4- 7 hf — Ä = (^s ^ cö^ ^ ^
e) (ö2 + fö + 9)\
=^) Vgl. insbesondere wegen der vorliegenden Relation „Ges. Abb.'- III, S. 83ff.
Erste spezielle Eesolvente siebenten Grades. 215
Hieraus ergibt sich durch Differentiation nach c die weitere identische
Gleichung :
(ö^ + aö + 7 6)2 (7 ö^ + 4aö f 71)) == (ö^ -^ fö A- g){7 ö* - (6c + 6f)6'
^(5^-f 4e/'+3^)ö2-f (4e + 3^/"4-2cp)ö-+ C^ef^dg)).
Da die beiden ersten Faktoren i^echts und linjis keinen Linearfaktor
gemein haben können, so spaltet sich die vorstehende Gleichung in die
beiden folgenden Identitäten:
7öV4aö + 7fe = 7 (ö^-^ fö ^ ^),
Für die unbekannten Koeffizienten bestehen derpjiacb. die Beziehungen:
4:a = 7f, 'b = g, ßc-rof—lAa, od+ 4:cf+Sg = 7 a^ ~^8b,
4:6 + Sdf + 2cg = 98a&, 2ef+äg == 343 b^.
Wäre nun a = 0, so würde /" == 0, c = 0, e = 0 folgen. Aus (1)
würde also folgen, dai3 0 = 0 bei / ^- 1 stattfindet, was indessen nicht
der Fall ist. Da hiernach a von 0 verschieden ist, können wir di^rck
Auswahl irgend eines von 0 verschiedenen Wertes für a die Funktion ö
endgültig festlegen. Es dient unseren Zwecken, wenn wir a :=^ 7 0 setzen.
Man hat dann:
a=7Ö, f = 4:d, c=13Ö, 19h — d'=27ü^o4.
Sdd + e = Woßb, dh + 80e = S4Sh^
wo aus der vierten und fünften Gleichnng Ausdrücke von d und e in Z^
folgen. Trägt man diese Ausdrücke in die letzte Gleichung ein, so ergibt
sich für h die quadratische Gleichung:
4 i!)2 + 11 (<9 -- 2) ö + 8 (3 Ö -h 2) = 0,
deren beide Lösungen uns zu zwei Gleichungen (1) hinführen. Sie
entsprechen den beiden unsymmetrischen DB, also den beiden Systemen
unserer konjugierten Kongruenzgruppen des Index 7. Wir wählen die
Lösung h = — ß — 3 und finden damit folgende Werte der ^Koeffizienten:
a =76, Z) = —(Ö + 3), c=13Ö, (^ = —(46 0-^111),
e = — 27 (5 6» — ^), /■ = 4 0,
während g mit l» gleich ist. Endlich ergibt sich h aus (2) für ö == 0:
h =, —eg^ = 27(6 6— 2) (Ö -^ 3)^ = — 121
Die Darstellung von J als rational^ FunUion sieherden Gerades von 6 if^t
geleistet durch die Grleichung:
(3) /:(/-!): L =
6(6'--1-7 6 6-7(6 + S)Y
: (ö^ -f 13 Ö ö'- (46 6 + 111)0-27 (5 Ö-2)) (ö'-r 4:0 6--(6 -r 3)f
: — 12^
216 il, 2. Pormenproblem der ©^gg und Gleichungen siebenten Grades.
Der DB der Fig. 27 wird durck KQ auf eine siebenblättrige Fläche
über der Z-Ebene abgebildet mit folgender Verzweigung: Bei K =■ 0
liegt ein zweiblätteriger und ein vierblätteriger Verzweigungspunkt, bei
K = 1 finden sicL zwei zweiblätterige Verzweigungspunkte und bei
iT = CO ein siebenblätteriger. Auch hier liegt das Geschlecht p = 0
vor. Die zugehörige einwertige Funktion werde mit r bezeichnet und
so gewählt, daß bei K = 0 im isolierten Blatte r = 0 und im
vierblätterigen Verzweigungspunkte T==«V7 = 20~fl ist, und daß t bei
K = CG selbst unendlich wird. Der Ansatz für die rationale Darstellung
von K als Funktion siebenten Grades von x ist dann:
E:(K-1):1 =t(r+ay{t-(26i-l)y:(T'+dx'-^cx+d)(x'+ex+ff:g.
Die Bestimmung der Koeffizienten a, h, •••, g nach der Methode von
Klein erfordert hier etwas mehr Aufwand von Rechnung. Die rationale
Darstellung von K als FMiktion siebenten Grades von z hat die Gestalt:
(4) K:{K--l):l =
y(^_(3ö-2)f(r-(2Ö-f 1))'
: (t3-2(4Ö - l)r^-(8ö-47)t + 16(30 - 1)) (r'- (3 ö ^ 1)t - (l9 - 2)f
■ 98.
Fassen wir nun die Gleichung (3) als eine solche vom siebenten Grade
für ö mit dem einen Parameter / auf, so hat diese eine Monodromie-
gruppe (Sjgg der Ordnung 168. Der zugehörigen Galois sehen Resolvente
des Grades 168 entspricht dann einfach jene regulär verzweigte Riemann-
sche Fläche von 168 Blättern, zu der wir bereits S. 188 vom DB der
Hauptkongruenzgruppe siebenter Stufe der Modulgruppe geführt wurden.
Danach ist einleuchtend, daß die Galois sehe Bebolvente der Gleichung (3)
einfach auf das Formenprohlem der Klein sehen Gruppe in dem besonderen
Falle der Gültigkeit der Gleichung F{z^, z^, z^ == 0 zu/rücJcJcommt, sofern
wir die Wendedreieckskoordinaten gebrauchen. In diesem Sinne nennen
wir die Gleichung (3) eine „spezielle Besolvmte siebenten Grades'' des
Formenproblems der Klein sehen Gruppe.
Die nähere Betrachtung bestätigt dies. Gut F == 0, so folgt aus
der Relation (15) S. 208:
(5) X^ = !P"3 -f 123 ^7
Durch die Gleichung :
(6) /: (J_ 1) : 1 = 5/3 .. X^ : -123 *^
erklären wir auf der Kurve vierten Grades F = 0 eine 168-wertige
Funktion, die iu je 168 bezüglich der Klein sehen Gruppe äquivalenten
Punkten der Kurve gleiche Werte annimmt, und die insbesondere in
den 24 Wendepunkten unendlich wird, in den 56 Berührungspunkten der
Doppeltangenten verschwindet und in den 84 sextaktischen Punkten
Herleitung der speziellen ßesolventen siebenten Grades fius der allgemeinen. 217
gleich 1 wird. Setzt man aber den Ausdruck (6) für J in (3) ein,
so folgt:
*^ ö (ö^ + 7 Ö ö — 7 (ö 4- 3))3 = !F3
oder nach Ausziehung der Kuhik^^nirze].:
Setzen wir aber hier zur Abkürzung:
(7) V^ö = y;,
gen wir in der Tat zu der aus (3) S. 21J für ^==0 sich*
ergebenden „speziellen Resolvente siebenten Grades" zurück:
(8) tp' + 16^ T/;* -- 7 (6 + 3) ^-3 ip — W= 0.
Eine entsprechende Beijachtung schließt sich an die Gleichung
siebenten Grades (4) für r mit dem einen Parameter K an. Auch sie hat
eine Monodromiegruppe der Ordnung 168, i^nd ihrer Galois sehen
Resolvente gehört eine regulär verzweigte 168-blätterige Rierpann sehe
Fläche über der jST-Ebene zu, die bei jST ^ 0, 1 und oo verzweigt ist.
Man hat an diesen Stellen 42 vierblätterige bzw. 84 zwei blätterige und
24 siebenblätterige Verzweigxmgspunkte. Das Geschlecht dieser Flache
berechnet sich demnach zu J5 = 10. Wie wir später noch ausführlicher
dartun werden, Jcommt die Galois bche Besolvente der Grleic}t,i4,ng (4) einfach
auf das Formenproblem der lilein bchen Grruppe fur den besonderen Fall
der Gültigkeit der Gleichimg bcchsten Grades ^{z^, z^, z^ = 0 zunicli.
In der Tat ist die hierdurch dargestellte EJ^urve sechsten Grades
singularitätenfrei und also vpm Geschlechte p == 10. An besonderen
Punkten haben wir aber auf dieser Kurve sechsten Grades einmal die
24 Schnittpunkte mit der Kurve vie^-ten Grades F = 0, sodann die
126 Schnittpunkte mit den 21 Pprspektivitätsachsen. Sie zerfallen in
ein System von 42 Punkten, die Pole von Substitutionen der Periode 4
sind, und ein weiteres System von 84 ipunkfen.
Auf der Kurve sechsten Grades wird unsere Funktion K durch die
Proportion erklärt:
(9) K:{K-1):1 ^W : X^ : 2«^^ F,
wobei man zu beachten hat, daß die Relation (1 5) S 208 im Falle der
Gültigkeit der Gleichung ^ i= 0 die Gestalt annimmt:
(10) X^ = W^-2^F'W.
Diese Angaben bestätigen wir einfach dadurph, daß die Eintragung des
Ausdrucks (9) von K in die Gleichung (4) zu derienige^ „besonderen
Resolvente siebenten Grades":
(11) ip'' — 10Fip''—l{20 + o)F^'ip^ + l{^fi — 'l)F^ip — W= 0
218 II, 2. Formenproblem 'der ©jgs ^^^ Gleichungen siebenten Grades.
führt, die aus der „allgemeinen E.esolvente'- (3) S. 211 für # = 0
hervorgeht. Wir finden nämlich aus der Gleichung (4) zunächst:
Fr{Fr -(36 — 2)Ff{Fr -(26 + 1)^' = W\
Setzen wir hier zur Abkürzung:
(12) V^ = ip
und ziehen rechts und links die Quadratwurzel, so erscheint die Relation (11)
wieder.
§ 3. Resolvetite achten Grades.
Xächst den 2 • 7 Oktaedergruppen sind die acht konjugierten ©g^
der Ordnung 21 die umfassendsten Teiler der @jgg. Ihnen sind die acht
konjugierten Wendedreiecke in der Art zugeordnet, da£ das einzelne
durch die Substitutionen seiner ®^^ in sich transformiert wird und also
eine invariante Form dritten Grades der ®^^ liefert. Es ist hier natürlich
der Gebrauch der Wendedreieckskoordinaten ^j, z^, z^ am Platze. Wir
bezeichnen die acht konjugierten kubischen Formen durch ^oo, 9>o' ^i»
•••) 96' ^^ "^^^ Schreibweise der Indizes oo, 0, 1, •••, 6, wie schon
S. 210 bemerkt wurde, einem in der Theorie der Modulfunktionen üblichen
Brauche entspricht. Die entwickelte Gestalt der Formen ist bereits
S. 210 berechnet: es fand sich:
(1) (f^ = —7 ^,^2^3,
(2) 9v = ^1 ^2 ^3 — «^' (^1 — ^2 ^3) — ^^ (4 — 4 ^1) ~ £*" (4 ~ 4 s^
+ 2 8^" Z^zl + 2 £^''^3^1 + 2 8*^" Z^4, r = 0, 1, 2, •• ., 6.
Die erste Form entspricht insbesondere dem Koordinatendreieck.
Die acht Formen (1) und (2) sind die Wurzeln einer Gleichung
achten Grades, deren Koeffizienten invariante Formen dritten, sechsten usw.
Grades der Klein sehen Gruppe sind. Da es für die ungeraden Grade
unterhalb 21 keiae invarianten Formen gibt, so fallen in der Gleichung
achten Grades alle Glieder mit ungeraden Potenzen der Unbekannten bis
auf das lineare Glied aus. Man hat für die Gleichung achten Grades
den Ansatz:
(3) <p^ -4- a^ (p^ -r (h ^^ + c F^) (p^ i- {d ^^ + e^ F^ + fWF) (p^
-i-gX(p + (h^^-^i^^F'-rlcF'i-IW^F) = 0,
wo a, &, c, .. •, l elf noch zu bestimmende numerische Konstanten sind.
Man berechnet sich nun sehr leicht die Darstellungen der
Potenzsummen jJg, JJ^, j5g der (p in den Formen F, <P, ••• und findet dann mit
Rücksicht auf das Verschwinden von jj^, p^, j5. aus (9) in I, 102 die
Koeffizienten von (p^, (p^, (p^ in (3). Zur Berechnung von g bediene
man sich des besonderen Wertsystems s^ = 1, z^ == z^ = 0, für das
F~ 0, * == 0, X = 1, (p^ = 0, (p, == — £2v
Aufstellung der allgepieinefx ßesplvente achten Grades. 219
gilt. Aus (3) aber folgt in diesem Falle einfach q)^ -{- g (p -= 0, so daß
g = 1 zutrifft. Das Absolutglied in (3) liefert, gleich 0 gesetzt, die
24 Wendetangenten. Die Forderung, daß dq,s Absolutglied mit ^3
verschwindet, führt auf Grund von (2), (3) und (6) S. 204 ff. auf:
h =zz Ä; == l i == ISh,
womit das AbsolutgKed bis auf einen konstanten Faktor bekaimt ist.
Diesen letzteren berechnet qian zweckmäßig d^^ch Beiiutzu|ag des
speziellen Wertsystems z-^ == ^^ = ^^ == 1. Man gelangt au dem
Ergebnis: Die acht Jcubischen Formen (l) und (2) der acht Jconjugierten
Teiler ©21 sind die Lösungen einer Jtesolvente achten Grades des Formen-
i der Klein sehen Gruppe, die die Gestalt ha(::
(4) 9« - 14 * 9« + 21 (3 *2 _. 2 ^3) ^4 _ 7 (10 * V 14 * F^ - WF) g)2
4- Xg> - 7 (*^ + 18 *2 ^3 J^F'+W^F) == 0.
Da die z ohne Änderung de|- cp noch upi eine geineinsa,me multipiikative
Kubikwurzel der Einheit abgeändert werden können, so ßind die ^,, 3^, ^3
allein aus den Wurzeln cp der Resolvente (4) nur erst mit Hilfe einer
Kubikwurzel berechenbar. Man findet zwar für die Quotienten der z
die rationalen Ausdrücke:
(5) f2 __ _ _v h ==, "1 £1 — 1
^3 2 Cpoo ' ^i 2 <Poo ' '^2 2 Cpao
wo V die Zahlen 0, 1, •••, 6 zu durchlaufen hat; dagegen erhält m^n
erst für die Kuben der z die rationalen Darstellungen:
.. 3__ S^ >'
Gleichwohl ist die Gleichung (4) eine Toialresolvenie des Formenproblems
der Klein sehen Gruppe, da mit Bekanntgabe des Werten der Foriq. F die
zur Berechnung der s zunächst erforderliche Kubikwurzel eindeutig
bestimmt ist.
Von den beiden speziellen Resolventen achten Grades, die für F = 0
und für $ == 0 eintreten, ist die ej'ste auch einer direkten funktionea-
theoretischen Betrachtung leicht z;ugänglich. Man hi^t hier mit der
Transformation siebenten Grades der elliptischen Modulfunktioiien ?u
tun*). Eine der acht konjugierten Kongruenzgrupp^n des Index 8
innerhalb der Modulgruppe, die den acht ©g^ entsprechen, hat den in
Fig. 28 abgebildeten DB. Er besteht au^ sieben nebeneinander gereihten
*) Vgl. „Ges. Äbhandl.'- III, 46 und 113 sowie „Modulfunkt." I, 741 ff.
220 II, 2. Fonnenproblem der ©^gs ^^^ Gleichungen siebenten Grades.
Dreieckspaaren und einem unten angefügten*)- Durch die Funktion /(co)
wird dieser DB auf eine achtblätterige Eiemannsche Fläche über der
/-Ebene mit folgender Verzweigung abgebildet: Bei J == 0 verlaufen
zwei Blätter isoliert, die anderen sechs hängen zu je dreien in zwei
Verzweigungspunkten zusammen; bei J == 1 finden sich vier zweiblätterige
Verzweigungspunkte und bei J == oo ein siebenblätteriger, während dort
ein Blatt isoliert verläuft.
Auch diese Fläche hat wieder das Geschlecht j5 == 0, so daß wir
mit einer einwertigen Funktion arbeiten können. Wir nennen sie z und
bestimmen, daß bei J" == oo im siebenblätterigen Verzweigungspunkte r == oo
und im isolierten Blatte r == 0 vorliegen soll, während eine dritte
Festsetzung vorbehalten bleibe. Für J als rationale Funktion achten Grades
von T hat man dann den Ansatz:
(7) J:(J—1):1 =: (t^ ^ar^ ß){r^^yr4-6f
mit neun noch zu bestimmenden Zahlen a, /3, • • •, wie aus der
beschriebenen Verzweigung hervorgeht. Es besteht nun die identische
Gleichung:
(8) (t- -f- a T -f |3) (t^ -f J' T -p ö)^ — e T = (r* + a T^ -f- 6 T^ -f c T -f äf-
Man differenziere diese Gleichung nach r, multipliziere das Ergebnis
mit X und bringe die vorstehende Gleichung in Abzug. Xach Ordnung
gelangt man zur weiteren identischen Gleichung:
(r^ -f- j^ T T ^)2 (7 r^ 4- (6 a + 4 j;) r^ -f (3 ^ + 3 a j; + ö) TV 2 ^ j^ T — ^^)
= {x^ -^ ax^ -r hx^ -^ cX -]- d) {1 x^ -{- oax^ -\-^hx"^ t cx — d).
Xun können die beiden in den ersten Klammern links und rechs stehenden
Ausdrücke Linearfaktoren nicht gemeinsam haben. Die vorstehende
Gleichung spaltet sich demnach in die beiden identischen Gleichungen:
lx^'{&a^4.y)x^+{pß+^ay-8)x'^'-2ßyx-ß8=^l{x^ + ax^^hT^~cx + d),
7 r* -f- 5 a r^ -f 3 6 t'- + c T — (^ == 7 (r2 ^ j; r + 8f.
'^) Es handelt sich hier einfach um die Kongruenzgruppe der Modulgruppe,
die durch ^ = 0 (mod 7) erklärt ist.
Berechnung der speziellen ßesqlvente achten Grades. 221
Hieraus ergeben sich zur Bestimmung der a, 8 • • • die (jleichungen:
ßa^4:y = 7 a, 5^ + 3aj;-L^==7 6,
2ßy =z7c, —ßd = 7d, ha =z lAy,
3 6 == 7/+ 14d, c = Uyd, d--=—7d^.
Durch die bisherigen Festsetzimgen über x ist diese Funktion nur erst
bis auf einen noch frei wählbaren konstanten Faktor bestimmt. A^ir
können über diesen so verfügen, daß y = — 5 wird. Daim folgt ^us
den acht vorstehenden Gleichungen:
a == — 14, a = — 13. 3 & == 175 -t- 14^,
c == — 70 6, d = —1 d',
3^ == 128 ^ L9^, ß == 49^.
Es folgt also 8 = l,b = 63, c = — 70, d = — 1, ß = 49. Endlich
findet sich e, indem man in der identischen Gleichung (8) rechts und
links die Koeffizienten von t gleichsetzt zu e == — 1728. Man gelangt
somit zu dem Satze: Die zu den acht Jconjugierten Jf^ongruenzgruppen
siebenter Stufe des Index 8 gehörenden mit x Jconjugierterp FtmUiorpen bind
die Wurzeln einer Gleichung ßchten Grades, die wir wie üblich in die
Gestalt Meiden:
(9) /:(/-l):l
(^2 _ 13 ^ ^ 49) (^2
(^4 __ 14 ^ ^ 63 r^ -
-1728r.
-ör+1)'
- 70 r — ly-
Es ist dies diejenige Gleichung, die B^lein bei de:p Transformation
siebenten Grades der elliptischen Funktionen als „Ersatz d^r i^odular-
gleichung erster Stufe- benutzt =^). Aus ihi leitet Klein durch einen
einfachen Übergang diejenige Gleichung ab, die er als „]klultiplikator-
gleichung erster Stufe- für Transformation siebenten Grades bezeichnet =^-^).
Es handelt sich hierbei einfach um den Vbergang von der Gleichung (9)
zu der aus (4) für ^ == 0 folgenden speziellen Eesolvente:
(10) ^8 _ 14 ^ ^6 ^ 63 ^2 ^4 __ 70 ^3 ^2 ^X(p — 1^' = 0.
Die beiden letzten Glieder der Propqrtion (9) geben namlfch bei Benutzung
der Gleichung (6) S. 216:
Multipliziert man mit ^ und zieht die Quadratwurzel, so folgt:
(*r)^—14 *(*r)3+63 *^(*r)'-70*3(^^)^X1 ^-7**== 0.
") VgU „Ges. Abh." III, 31 ff. und „Modulfunkt.-' II, 58ff.
'^*') Über den Zusammenhang der Funktion r mit der S. 87 eingeführten
Modulform erster Stufe ^(«i, Wg) sehe man „Ges. Abha^idl.'- III, 49 und
„Modulfunkt.'- II, 64.
222 II, 2. Forme np rob lern der ©^^g ^^^ Gleichungen siebenten Grades.
Der Vergleich mit (10) zeigt, daß wir:
(11) i¥^=cp
zu setzen haben, um von der Gleichung (9) aus zur speziellen Resolvente (10)
zu gelangen*).
"Über die besondere Resolvente (10) liegt noch eine weitere
ausgedehnte Literatur vor. Man hat hier mit einer Jacobischen Grieichung
zu tun, bei der die Quadratwurzeln der acht Lösungen sich in vier Größen
A(^, A-^, A^, J.3 in folgender Gestalt darstellen lassen**):
[ V^, ==A^ + e'^A,±s^'A,-rs"^'A,.
Besonders leicht lassen sich diese Entwicklungen darstellen, wenn man
die A(^, J-j, A^, A^ als Modulformen siebenter Stufe einführt und mit
ihren nach Potenzen von g = e'^*"' fortschreitenden Reihen arbeitet.
Jedoch gelang es Klein auch hier, eine von transzendenten Hilfsmitteln
unabhängige rein algebraische Theorie zu schaffen, die mit den
„Berührungskurven dritten Grades" der ebenen Kurve vierten Grades F = 0
arbeitet **=^).
§ 4. Allgemeine Gleichung siebenten Grades mit Galois scher Gruppe ©jg^.
Wie oben S. 153 ff. die Behandlung der allgemeinen Gleichung
fünften Grades auf die Ikosaedertheorie gegründet wurde, so hat Kleiny)
frühzeitig das Problem behandelt, die von ihm entdeckte ternäre Gruppe @jgg
für die Auflösung der allgemeinsten Gleichung siebenten Grades, deren
Galois sehe Gruppe mit jener ternären ©^gg isomorph ist, zu verwerten.
Es gelang ihm, die Lösung einer beliebigen Gleichung dieser Art
rational auf das Formenproblem der ternären @jgg zurückzuführen. Die
Reduktion auf ein spezielles Formenproblem mit F = 0 erforderte
indessen die Lösung einer Hilfsgleichung vierten Grades. Li
unmittelbarem Anschluß an Klein hat Gordan ff) diesem Gegenstande zwei
Abhandlungen gewidmet und über die Affektfunktionen der fraglichen
Gleichung ein weiterhin noch zu nennendes Theorem aufgestellt.
*) Man kann eine entsprechende Theorie fur die im Falle 0 =: 0 aus (4)
folgende spezielle Eesolvente achten Grades entwickeln. Nur ist diese Gleichung
der funktionentheoretischen Betrachtung nicht mehr so leicht zugänglich, da man
hier mit einer achtblattengen Eiemannsehen Flache „des Geschlechts _p = 1'-
zu arbeiten hat.
==*) Vgl. über den Begriff der „Jacobischen Gleichungen'- oben S. 71ff.
=•=*) Vgl. „Ges. Abhandl." III, 115ff. oder „Modulfunkt.'- I, 716ff.
t) „Ges. Abhandl.'- II, 407.
tt) nÜber Gleichungen siebenten Grades mit einer Gruppe von 168
Substitutionen'- I und II, Math. Ann., Bd. 20 und 25. Der Leser wird gut tun, zunächst
das Referat Klems über die Gordanschen Arbeiten in „Ges. Abhandl.'- II, 426 zur
Hand zu nehmen, da die Gordanschen Arbeiten infolge der Durchsetzung mit
ungeheuren Eechnungen immer etwas umständlich zu lesen sind.
Einführung der allgemeinen G|eichung siebenten Grades Bjit eii^er ©.gg- 223
Wir setzen die Gleichung siebenten Grades mit ausfallendem Gliede
sechsten Grades in der Gestalt an:
(1) f (x) = x^ ^ a^x"" -Y- a^3ü^ -\- a^x^ ^ ß^x- ~\- a^x -\- a,^ = 0;
ihre Wurzeln mögen mit a^^, a^^ a^, • ••, «g bezeichnet werden. Wir
haben die @jgg als Permutatipnsgruppe auf zwei Arten aus zwei Peimu-
tationen S und T erzeugen könnpn, nämlich aus dep beiden unter (2)
S. 201 bzw. (4) S. 202 angegebenen Permi^tationen. Die ersten beiden
Permutationen:
(2) S = (a^, «1, «2, «3, «4, «5, «e)' ^ = K' «5)-(p«2' «3)
mögen die Galois sehe Gruppe @jgg der Gleichung (1) erzeugen. Es tritt
dann zunächst die Frage auf, wie der ,.Affekt- (vgl. I, 386) der
Gleichung (1) zu charakterisieren ist.|
Um hierauf zu antworten, beinerke man, daß die ©^gg &wei Systeme
von je sieben konjugierten Teilern ©34 vom Oktaedertypus besitzt. Dem
zweiten System entsprechend hat die Gleichung (1) eine Rpsolvente
siebenten Grades, die wir in der Gestalt:
(3) f{x) = x'' -\- a^x^ -r ^3^* " ^4^^ + ^'5^^ + a^x -j- c^^ = 0
anschreiben, und deren Wurzeln ^vir ä^, ä^, •••, äg r|.ennep. Wie wir
diese Resolvente zu erklären haben, ist unmittelbar durch die
Gleichungen (6) S. 202 angegebep; wir stellen die Wurzeln ccy der Regol-
vente durch die a^ in der Gestalt:
(4) ÖKv = «v + 6-^ a,+5 H-«v-t 3? *'= 0, 1, •••, ß,
dar*). Dann fällt zunächst tatsächlich aych isi (3) das zweite Glied
aus. Im übrigen aber permutieren be:| Ausübung von (2) auch die a^
sich nur untereinander, indem sie entsprechend die TJnjLstelliingen.:
(5) S' == (Kq, a^, «2, «3, ä^, «5, «g), T' = (äo, ä^-iä^, a^
erfahren. Wir gelangen zur zweiten aus (4) S. 202 hervorgehenden
Darstellung der Permutations-©^ gg. M^ kann diese zweite Darstellung
auch auf folgendem Wege erhalten: Erzeugt i^an die erste Darstellung
aus S~"^ und:
S-'^-T-S = («0, «4)-(ai, «2).
so gelangt man durch Transformation Tc\xi der Substitution;
U = («,, Kg) • («2, a^) • («3, «4)
zu den Permutationen;
U-^-S-^'T-S-U = («0, c<3)-(c<5, «e)^
die formal mit (5) übereinstimmen.
^) Gordan schreibt links an Ste|le von ß 4en Faktor 2. Das geht auch,
ist aber unzweckmäßig, weil dann nämliph neben der „naturlic|ien'- Jrratiqnalitat d
der Kleinschen Gruppe im weiteren Verlaufe vermeidbare „akzessorische- Irra
tionalitäten sich einfinden wurden
224 n, 2. Formenproblem der ©igs i^d Gleichungen siebenten Grades.
Das Verhältnis der beiden Gleichungen (1) und (3) ist ein
gegenseitiges. Man findet nämlich aus (4) wegen Verschwindens der
Wurzelsummen umgekehrt:
(6) ÖKv = av4-a -f ä, +2 + av + 4j ?' = o, l, • • •, 6.
Es werden nun die symmetrischen Funktionen der Wurzeln der einen
Gleichung, auf Grund von (6) bzw. (4) auf die Wurzeln der anderen
Gleichung umgerechnet, Ausdrücke ergeben, die gegenüber der ©^gg
invariant sind. Man wolle insbesondere die Potenzsummen der a^ berechnen
und sie auf Grund der Formeln von I, 102 auf die Grundfunktionen
umrechnen. Man hat zunächst:
ö, = 0, 6, = 0, ds^ = ÖS2,
so daß man hieraus noch keine Affektfunktion gewinnt. Demgegenüber
gelangt man bei Berechnung der dritten Potenzsumme zu der Gleichung:
(7) i2-e)s, = 2A„
wo A^ der folgende siebengliedrige Ausdruck ist:
(8) y^g = a^ Kg Kg - «0 Kg a^ ^ a^ a^ a- - a^ a^ Wg -^ a^ a^ a^ - a^ a^ a^ - a^ a-^ a^.
In A^ Itahen wir die einfachste ÄffeUfunJdion der Gleichung (1) gewonnen,
in der nach dem Lag range sehen Satze in I, 378, alle iobrigen ÄffeU-
fiinUionen mit Hilfe der symmetrischen GrundfunUionen rational
darstellbar sind. In jedem Ausdruck zweiten Grades der a, der gegenüber der
@^gg invariant ist, erkennt man nämlich eine symmetrische Funktion der
Wurzeln. Andererseits ist die Funktion (8) der Wurzeln Uy gegenüber
der symmetrischen Gruppe, wie man leicht feststellt, in der Tat 30-förmig.
Aus (8) gewinnt man sogleich als eine Affektfunktion vierten Grades:
(9) A^ = aoa^aga^ -^ oCyCC^a^a.^ -f- a^a^a^a^ 4- a^a^a^a-^ + a^a^cc^aQ
+ «0 ^2 ^h '^b + (^(yf^x «3 «6 '
WO sich die Glieder in (8) und (9) rechts als supplementär entsprechen.
Durch Ausübung der Substitution:
(10) «0 = «0, «j = Kg, a.2 = Kg, «3 = a^i a^ = a^, «- = Wg, Wg = a^
gelangt man zu den Affektfunktionen:
A^ = «iWa^i + ^o^i^3 + c«gaoa2+asaßäj + a^agao + aga^ag^-agaaa
-t- «2 ä^ Wo äj -j- Kj äo Kg a^
der Gleichung (3).
Faßt man die Permutationsgruppe ©^gg der a^ als eine endliche
Gruppe „septenärer" linearer Substitutionen auf, so gibt es nach dem
Theorem von S. 18 eine endliche Anzahl zugehöriger invarianter Formen,
in denen alle diese Formen rational und ganz darstellbar sind. Den
näheren Aufschluß hierüber gibt ein Theorem von Gordan, dem im
Gordans Satz über die Äffektfunktionen der Gleichungen siebente^ Grades. 225
wesentliclien seine vorhin genannten Arbeiten gemdmet sind. Das
Gordan sehe Theorem lautet: Die invarianten Formevif der Perrfiutations-
@jgg der a^ sind rational und ganz darstellbar in d^n summarischen Grri^nd-
funMionen der a^ und denjenigev^ ÄffeUfunJdio^en, die aus den sym-
märischen G-rundfunMionen der a^, umgerechnet aii,f die a^, erhalten
werden. Dabei sind die G-rundfunMionen Sg, s^ und die aus s,, s^
entstehenden AffeUfanUionen rational durch die übrigen darstellbar; zwischen
den letzteren aber besteht noch eine Relation, in der s. und die „AffeU-
funJdion'- Sg auf den sechsten Grad ansteigen. Betreffs des Beweises
muß auf die Gordan sehe Darstellung selbst verwiesen werden.
Die von b^ gelieferte Affektfu^ktio^ ist, abgesehen von pymnqietrischen
Gliedern und dem Faktor 12:
2 (««V + 3 + «v + 5 ~f «V + e) a.
+ 3a,_5C«, + 6
Um daraufhin z. B. die Funktion A^ dem Gordan sehen Satze entspreehend
darzustellen, zerlege man das Produkt s^^A^ in die beiden Summen;
S j y^g = 2 (C'v + «v + 1 -4- Kr -r 2 + «V + 4) C'v + 3 C'v + 5 «v + 6
+ 2 («V T 3 -j- P«v -r 5 + a. -i- e) «v + 3 Wv + 5 «v + 6-
Die erste Summe erweist sieji als mit (»^ — AJ gleieh, sq daß wir, da
Sj = 0 ist, die Darstellung:
^i — s^+ 2 («V + 3 + «V + 5 + «1. + e) Cv + 3 a. -r 5 f<v 4- 6
finden.
Die Permutationen der Galoissehen @jgg lassen sieh mittels der Affekt-
funktion A^ sehr leieht ehara,kterisiereri. Man b^aehte zunäehst, daß die
Permutationen durehweg gerßde ^ind. Das einzelne Glied von A^ ynrd
dann dureh drei Permutatiorjien der Periode 2 in sich übergeführt, die
die anderen seehs Glieder unter sieh permutieren, So haben wir für das
erste Glied die Permutationen:
(11) («0' «1) • («2' «4)' («0' «?) • («i' «1)» («0' «4) • («1 > «2)-
Insgesamt liefern alle sieben Glieder von A^ auf diese Weise die 21 jper-
mutationen der Periode 2. ]Mfan bilde ferner aus den vier Faktoren des
ersten Gliedes von A^ die vier Tripel. Jedes geht djireh zwei einander
inverse zyklische Permutationen der Periode 3 in sieh über. Jeder dieser
Permutationen hat man no eh eine zyklische Permutation der am ersten
Gliede nicht beteiligten Wg, a^, Wg hinzuzufügen, und zwar nach folgender
Regel:
(12)
fK,
l(ao»
1 («0»
l(«2>
:e, Algebra
«2» a4)-K' %> «3)'
«4' «2)*K' «5> «^)'
Kj, aj . (Wg, U-, Kg),
«1. ao)-K' «5' «3)'
. II.
(a^, «2» '>^i)' (^'AJ '^bi ''^ß)-
(«2, «4, Ci(i)-{ciz, «5' «e)
(«4 , «1 , Kp) • (Wg , a- , Kg) ;
(«0, Mj, Ci^'(Di.j,, Kg, Kg)
15
226 n, 2. Formenproblem der ©igg ^^^ Gieichangen siebenten Grades.
Die 56 von allen sieben Gliedern von A^ entsprechend gelieferten
Permutationen sind die 56 Fermutationen der Periode 3 in der ©jgg. Das
erste Glied geht durch sechs Permutationen der Periode 4 in sich über,
die man (a^, a^, a^, cci) schreiben kann, wo a^, Uk, ai die sechs
Anordnungen der a^, a^, a^ durchlaufen soll. Diese Permutationen sind nur
erst ungerade. Man laat jeder noch eine Transposition zweier unter den
c^S) c'ö) c'e anzufügen:
Lx dieser Weise liefern die sieben Glieder von A^ die 42 Permutaüonen
der Periode 4t unserer ®jgg. In jedem der acht zyklischen Teiler ©^ ist
eine Permutation (a^^, a^, cti, afc, aj, a^, «„) enthalten, aus der der
Teiler ©^ herstellbar ist. Jedenfalls ist einer dieser Teiler aus:
(14) («0, «1, «2, «3, C4^, a^, Kg)
erzeugbar. Die übrigen sieben Permutationen (Kq, Kj, «i, •••) kann man
aus (14) vermöge der Transformation durch jene sieben Permutationen
der ®jgg herstellen, die «^ und a^ entweder unverändert lassen oder
austauschen. Es sind dies erstlich die drei Permutationen:
die die Permutation (14) bzw. in:
J(aO, «1, «3, «2, «6' "5' "4)' K' ^H «4' "6> "2' "ö' "3)'
[ (a^, Kj, Kg, a^, Kg, a, a^
transformieren, sodann aber die vier Permutationen:
(«o- ai)-(a2, aj, (a^, «i)'(«3, «g),
(«2, «3, K^, a6)*('''o? '''l)' ('''2' ^t^ ^^4' "3)"(«0) «l)>
die (14) bzw. in die inversen der folgenden vier Permutationen
transformieren :
a61 [^^^' "^' "®' "°' "^' '^^' '^*'^' ^"'" "^' "^' "°' "*' "*^' "^'''
[ (Kq, Kj, 0^2) «5) C'e' '''i' '''s)' ('''o' ^1' '''l' '''o' '''s' ^^2' ^<i)'
Aus den acht Permutationen (14), (15) und (16) entstehen durch
Wiederholung öLie 48 Permutationen der Periode 7 in der ©^gg.
§ 5. Zurückführung der Gleichung siebenten Grades auf das
Formenproblem der Klein sehen Gruppe.
Wie schon bemerkt, hat Klein die Lösung der allgemeinen Gleichung
siebenten Grades (1) S. 223 mit einer Galois sehen Gruppe @jgg rational
auf das Formenproblem der ternären ©j^g zurückführen können*). Wir
*) Vgl. „Ges. Äbhandl- II, 407.
Direkter Aufbau der Pei-muta^ions-^
j ipittels der Funktion A^-
227
beweisen diese Möglichkeit rjiach einem neigen ganz einfachen Verfahren
und vermeiden hierbei den Gebrauch der siebenten Einheitswur;?el e, ad-
jungieren vielmehr nur die quadratische Irrationalität 8.
Man führe zunächst rieben den okt^edrischen Punktkoordinaten
Xj, aJg, X3 die zugehörigen Linienkoordinaten u^, a.^, u^ ein. Sie
transformieren sich zu den x „kontragredient", d. 1^. so, daß (m^ a;^ -)- u^ x^ -j- Wg x^)
stets absolut invariant ist. Die den beiden Substitutionen (19) S. 193
entsprechenden erzeugenden Substitutionen der Klein sehen Gruppe in
Linienkoordinaten sind dann:
(S)
(T)
2ii[ = — 8 ^^ — ^2 + ^'3'
2 «4 = H u^ — u^ -j- u^,
: «^3,
SO daß die in Linienkoordinaten geschriebenen Substitutionen einfach
konjugiert komplex zu denen in Punktkoordinaten sind.
Die 21 Perspektivitätszentren werden durch JS'ullsetzer^ ebenso vjeler
linearer Formen ^^(ii^, n^, u^), P^{a-^^ u.^, u^), •••, F^^(u^, u^^ u^)
dargestellt, die aus den Formen (1) S. 194 für dje Perspektivitp,tsachsen
als ihnen konjugiert sofort abgeschrieben werden können:
(1)
A = '^'h^
Pj = - ÖMj- U^-U^,
P2= da^^Ou^,
P3 = - a^-liu^- u^.
-P4 = — «*i -^ ^2 ^ ^■^ ^3'
Pj. = ßu^^u^^ u^,
Pg = -eu^'ßu^,
A -2^,.
Pg -- dUj~U^^U^,
Pg = U^ - 8 tl^-U^,
P]0 = U^^ 0 U^-U^,
-^11 "= ß lii-rß li-2,
Pl2-= -0^2-0^3,
A3-= - tfi-'^<3-^^^3
P,,^2^3,
JP^^=- ßu^ + 0 «(3,
P^g = u^-ßu^~u^,
P„ = ßu^-ßa^^
P18 = -u^-rii^—ß a.^,
Pjg = ßU^~ U^-U^,
, P2o = Mi-«*ä^Ö^3.
Bei Ausübung von S und T verhaltep sich die Formen P(m,, u^, a^)
genau so wie die Formen p (a;^, x^, x^), worüber S. 194ff. zu vergleichen ist:
(S) (P„P,,P,,-..,Pe)-(Pp-
•••A3)-(A.. ^,.
,J^2o)>
{T)
K =
P'i =
P's =
P'n =
Pi,=-
Ko =
-A.
-As-
-A9>
A.-
-Ao.
As-
P'i
n
p'ä
p'i
p\
=
=
=
=
=
A'
-A>
P3,
-^ 20)
-A.
i^; =
^6 =
p;o =
A.==
i^;8 =
-A>'
-A.
-A..
A,,
-A.
^s
P7
Pj
p;
p
r=
=
1 =
5==
9 =
Pg,
-A,
-Ai
A2
-A.
228 II, 2. Formenproblem der ©^gs ^^^ Gleichungen siebenten Grades.
Das nächste Ziel soll nun sein, aus den sieben Wurzeln Uy der
Gleichung /"(a;) = 0 ein System von 21 konjugierten Funktionen
herzustellen, die sich gegenüber den erzeugenden Permutationen:
S = («0, Kj, «2, Kg, a^, Kg, «5, Kg), T = (Kj, Kg) • (Wg, Kg)
genau so verhalten wie die Formen P. Es ist leicht zu sehen, wie man
Funktionen dieser Art bilden kann. Man überlege, daß das Zentrum
P^ = 0 durch die Substitutionen einer diedrischen @g in sich
transformiert wird, die aus den beiden Substitutionen:
erzeugbar ist. Die erste liefert einen zyklischen Teiler (>\, bei dem P^
absolut invariant ist; bei den übrigen vier Substitutionen erleidet P^
Zeichenwechsel. Den Substitutionen (2) entsprechen die Permutationen:
(3) (Kj, ci^)-(a^, Kg, «3, aj, («i, «5)-(«2' "3)'
wie man durch Rückgang auf die Formen (1) S. 201, die ja die gleichen
Permutationen erfahren, feststellt. Man hat nun aus den a^ eine
gegenüber der @jgg von Zeichenwechseln abgesehen 2I-förmige Funktion
herzustellen, die bei der ersten Permutation (3) unverändert bleibt und bei
der zweiten Zeichenwechsel erfährt. Die einfachsten Funktionen, die
diesen Anforderungen genügen, sind die zweiten Grades:
(4) (a^ — a^) («2 ~ «3 — a^ — Wg)
und die kubische Funktion:
(5) (Kj — a-) («2 «3 — ci^ Kg).
Man würde indessen mit diesen Funktionen unmittelbar noch nicht zum
Ziele koromen, und zwar deshalb nicht, weil eine alsbald aufzustellende
bilineare Form identisch verschwinden würde. Doch genügt es für unsere
Zwecke, wenn wir in beiden Fällen den Faktor «o hinzufügen, der die
von den Funktionen erfüllten Bedingungen nicht stört*).
Indem wir etwa die Funktion (4) bevorzugen, fügen wir den
Faktor Uo hinzu und stellen durch wiederholte Ausübung von S und T
die 21 Funktionen her:
(6) |a + 7 =a,^(a, + .2-a,+3)(a, + 4 + a^ + g-a, + i-a, + 5), ^ = 0, 1,2,...,6.
l^v + u = a.^ («v -t- 4- «^ + e) («v + 1 -r «v + 5- «v + 2- «v + 3) 7
Schreibt man sich das System ganz aus, so erkennt man unmittelbar daß
diese 21 Funktionen sich bei Ausübung der Permutationen S und T
genau wie die Hnearen Formen P substituieren.
*) Die Wurzel a^ tritt in den Permutationen (3) nicht auf.
(9)
Bildung ternär substituierter Variablen x aus den Wurzeln a. 229
Man bilde nun die Supime der 21 Produkte Äji-P,,, die man als
Funktion von u^, u^, u^ und von pc^, a^, •••, Wg durch }i{u\ci) bezeichne:
20
(7) h{u\a) = ^Jk{cc)P,(u).
Dann besteht der Satz: Die FunUion h(u\oc) ist ahbolut inpariafit, so oft
die u einer Substitution der Klein sehen Gruppe u^nterworfen werden und
die oc die entsprechende Permutation erfahren. Mau ordne die Funktion (7)
nach den u an und findet:
(8) h (uIa) = u, x'i (a) + u-^x^ («) -r '«s-^z («)•
wo die X (a) die drei folgenden Funktionen der Wurzeln a, sind:
( ^1 (a) = (2 A — -43 — A -f- A - Ao — -^13 -^ Ae " ^is + Ao)
^0(A,-Ä,-r ^11 -f Ai) -r- Ö (- A -r A 4- A + As).
^2 («) = (—^1 + -4, -f A + 2^7 — ^8 — As -r As — Aä + ^^20)
-f 6 (^, -f ^4„ - A,, -f ^,,) + Ö (.43 -Ä,+ A,, ^ ^,g),
^3 («) = (^1 — -^3 + -^a + A — -^9 ^ ^,0 ^ 2 ^,, — ^,g — A^^)
-f 6 (A -r ^12 -f A-o — A^) -T B (A + Az — ^18 T Ao)-
Wir gelangen wegen der Inva^rianz von h(u\a) zy. dem wic^itigen Satze:
Die drei FunMionen vierten Grades der Wurzeln a^, die in (9) geiomi^en
bind, erfahren die Substitutionen der in Punliloordinaten gebchriebsnen
ternären Kleinschen Gruppe ©jgst /"ö^^^* die a den Pemmtatimien der
Galois sehen Gruppe der Gleichung f(x) = 0 unterwarfen werden. In
der Tat substituieren sich ja die x (a) mit den h kontragredient, also
kogredient mit den ursprünglichen Puaktkoordinaten Es bleibt nur
noch übrig zu beweisen, daß die Ausdrücke (9) nicht identisch
verschwinden. Würden sie aber identisch verschwinden, so würde dies auch
dann zutreffen, wenn man «3 -= «^ = «5 == «g == 0 setzt. In diesem
Falle findet man indessen:
x^ (a) = «0 «j «2 (2 «0 — «j — «2 — 0 («j — «2)),
^2 ('^) =^ ^0 ^1 '^^ ^\ + «2 — 2 «0 — 6 («1 -— «,)) >
^3 ^ = c'o <^i '^i ('*i — c'2) ^ '
wobei von der Relation 6 -f ^ + 1 =0 Gebrauch gemacht wurde *).
Die temäre Klein sehe Gruppe ®jgg ist bei diesen Rechnungen in
ihrer oben neu eingeführten auf das oktaedrische JCoordinatensys^em
bezogenen Gestalt benutzt. Dies ist in algebraischer Hinsicht wichtig,
weil, wie schon hervorgehoben wurde, auf diese Weise der Gebrafich der
*") Hatte man unmittelbar die Funktion (4) oder (5) genommen oder auch
nur a^ hinzugesetzt, so ware map auf entsprechendem Wege zu identisch
verschwindenden Ausdrucken x («) gelangt.
230 II) 2. Pormenproblem der ©jgg und Grleichungen siebenten Grades.
siebenten Einheitswurzel a vermieden wird und nur die quadratische
Irrationalität 6 zu adjungieren ist.
Durch die Gleichungen (9) ist nun in der Tat die Aufgabe der
Lösung unserer allgemeinen Gleichung siebenten Grades f(x) == 0 mit
einer Galoisschen Gruppe ©jgg rational auf das Formenproblem der
ternären Gruppe ©^gg zurückgeführt. Wir tragen für die x in die rechten
Seiten der Gleichungen (4), (7) und (12) S. 208 ff. die Ausdrücke (9) in
den Kv ein tmd erhalten dadurch vier rationale ganze Funktionen der a,,
die gegenüber der @^gg invariant sind und sich demnach auf Grund des
Gordan sehen Satzes (S. 225) rational und ganz in den Koeffizienten a^, ä^
der Gleichungen (1) und (3) S. 223 darstellen lassen =^). Die Aufgabe,
bei gegebenen Werten dieser vier Funktionen die x^, x^^, x.^ zu berechnen,
ist das „Formenproblem'^ der Klein sehen Gruppe: Nach ÄdjunMion der
numerischen Irrationalität zweiten Grades 6 ist die Lösung der Gleichung
siebenten Grades f(x) = 0 mit Galois scher ©^gg auf das Formenproblem
der Klein sehen Gruppe ratioruü reduziert, welches letztere die Galois sehe
JResolvente jener Gleichung vertritt und seinen „NormalcharaMer'' dadurch
kennzeichnet, daß alle 168 Lösungen in einer unter ihnen mit Hilfe von 0
linear darstellbar sind.
Klein hat noch das Problem behandelt, daß „allgemeine'-
Formenproblem der ternären Gruppe ©^gg auf ein „spezielles'- mit F = 0 zu
reduzieren, und findet, daß hierzu die Lösung einer akzessorischen
biquadratischen Gleichung hinreichend und notwendig ist**). Es gilt
dabei, einem beliebigen Punkte (x-^, x^, x^) der Koordinatenebene in
kovarianter Weise einen Punkt (^j, y^, y^ auf der Kurve vierten Grades
J' = 0 zuzuordnen. Dies kann z. B. in der Art geschehen, daß man die
lineare Polare de& Punktes {oü^, x^, x^ in bezug auf die Kurve vierten
Grades mit dieser Kurve zum Durchschnitt bringt, was die beiden
Gleichungen liefert:
X, (2 xl^Ü {xl ^ xl)) y, -f X, (2 xl + 3 ö {xl ~f xl)) y^
-^x,{2xl ^Ü{xl 4- xl))y, = 0,
^1 -r pI + ^3' + 3 Ö (yl yl + yl yl + yl yl) = 0.
Zur Bestimmung eines der vier Schnittpunkte ist hier in der Tat eine
Gleichung vierten Grades zu lösen. Diese Entwicklungen würden
wichtiger sein, wenn man bei der transzendenten Lösung des
Formenproblems der Klein sehen Gruppe allein auf elliptische Modulfunktionen
(Fall F = 0) angewiesen wäre und dann allerdings eine „akzessorische-
Gleichung in Kauf nehmen müßte. Dies ist indessen keineswegs der Fall.
==) Die Koeffizienten ä^ von (3) sind bei gegebener Gleichung (1) als deren
Affektfunktionen „rational bekannt".
**) Vgl. .,Ges. Abhandl." 11, 4-21.
Allgemeines über das Gren^kreistheorem der automorphßn Punktionen. 281
§ 6. Lösung der speziellen Formenprobleme der Klein sehen Gruppe.
Daß die Lösung des Formenproblems der Klein sehen Gruppe nicht
im Gebiete der Algebra zu suchep. ist, ist aus dem nicht-metazyklisphen
Charakter der ©^gg bekannt. Um die Abhängigkeit der x^, x^, x^ von
den Werten der Formen JP, 0, W, X oder auch die der z^, z^, z^ von
den Werten der F, fi?, W, X zu beschreiben, muß man demnach zu den
Hilfsmitteln der die Algebra übersphreitendep Funktionentheorie seine
Zuflucht nehmen. Der Grundgedanke ist dabei, daß man diß Abhängigkeit
der x^, ajg, x^ von den F, 0, W, X nicht direkt betrachtet, sondern zwischen
beide G-rößensysteme eine neue VerändefUche t, oder zwei fiomogene
Veränderliche ^j, ^2, die aus F, 0, W, X zu berechnen sind, einschaltet, in
denen alsdann sowohl die Formen F, 0, W, X wie auch insbesondere die
x^, x^, x^ eindeutig darstellbar sind. Es handelt sich hier urq. eine
sogenannte „uniformisierende Variable" ^, deren Existenz und Eigenart d]irch
das „Grrenzkreistheorem-' der ^utorp.orphen Funktionen gegeben ist*).
Dieses Theorem ist hier allerdings nur in den aUerniedersten Fällen
heranzuziehen. Es sei eine Iliemannsche Fläche des Geschlechts ^ = 0,
also etwa eine Ebene, gegeben, und auf ihr seien beliebige n Punkte
^1! 63; •••; ^n niarkiert, denen wir n gapze Zahlen Z^, /g, ••-, ?„, die > 2
sind, zuordnen. Man sagt, die Ebene (Rieman^ische Fläche) habe die
„Signatur" (0, n; ?j, l.^, •••, l^), wobei die erste Zahl d^s Geschlecht
darstellt. Dann existiert nach dem genannten Theorem auf der Ebene
eine und im wesentlichen auch nur eine „linea^r-potymorphe F]inktion" ^**),
die die geeignet zerschnittene Ebene auf den DB einer reellen
Substitutionsgruppe, in Gestalt eines der „positiven ^- H^lbebene•' angehörenden
Polygons mit n „festen Ecken" der Winkel ——, ——, ■••, —, abbildet.
'] '2 ^n
Man erteilt diesem DB gleichfalls die „Signatur" (0, n; I^, l^, •••, Z„).
Das (2n — 6)-fache Kontinuumf) der signierten Ebenen ist urfikehrbar
eindeutig auf das (2 n — 6)-fache Kontinuum der DB dieser Signatur
bezogen ff). Es kommen weiterhin nur die beiden niedersten Fälle
n = 3 und w 1= 4 zur Benutzung. Im ersten Falle hat m^ji stets einen
symmetrischen DB. Beschreibt man durch die drei Punkte c^, e^, e^
einen Kreis, so wird das Innere (und ebenso das Äußere) (iieses Kreises
auf ein Kreisbogendreieck der Winkel —, —, - der ^-Halbebene ab-
'1 '2 '3
gebildet, und wir gelangen, der ganzen ^ubstitiitionsgruppe entsprechend,
*) Vgl. „Ges. Abhandl.'- III, 627 und „Autom. Funkt.'- ß, 408ff.
**) Im allgemeinen unendlich-vieldeutige Funktion, die sich bei umlaufen
um die Punkte e linear gebrochen mit reellen Koefiiziepten substituiert.
f) Drei von den n Punkten e ka^in man durch lineare Substitution an fest
vorgeschriebene Stellen bringen. Es bleiben dann i^och (n — 3) „komplexe'-
Werte e frei wahlbar, so daß tatsächlich ein 2 (n — 3)-faches Kont^nuum vorliegt.
■ft) Man vgl. wegen alles Nähere^ „Autom. Funkt'- I, 383ff. und II, 440ff.
232 III 2. Pormenproblem der ©^gs ^"id Gleichungen siebenten Grades.
zu einer schlichten Bedeckung der ganzen ^-Halbebene mit einem Netze
solcher Dreiecke*). Im'^Falle» = 4 ist indessen der symmetrische
Fall ein besonderer.
Liegt beim Formenproblem der Kleinschen Gruppe der besondere
Fall F = 0 vor, so kann man entsprechend den Entwicklungen von
S. 182 ff. das Formenproblem auch durch ModulfunUionen lösen. Doch
ist das im Sinne der eben gegebenen Darlegungen als ein Umweg
anzusehen. Indessen gelangen wir hier zu der einzigen Entwicklung, die
bisher wirklich durchgeführt ist, und zwar unter Gebrauch der Wende-
dreieckskoordinaten z-^, z^, z^. Es sollen hier nur die Ergebnisse
zusammengestellt werden; wegen aller weiteren Ausführungen ist auf
„Modulfunktionen" zu verweisen. Im Falle F := 0 berechnen sich
zunächst die Modulformen erster Stufe g^, g^ und ^ (vgl. S. 86) aus
den Formen fi?, W, JC der Kleinschen Gruppe auf Grund der
Gleichungen **):
(1) 0 = —^, W=12g,zl\ X=2ieg^zl^.
Aus g^, g^ und zi berechnet man dann die Perioden Wj, Wg nach den
Regeln von S. 89 ff., womit man die uniformisierenden Variablen sowie
weiter die EntwicklungsgröJ3e q = e^^'" besitzt. Die Lösung des
Formenproblems der Kleinschen Gruppe wird dann einfach dadurch
geleistet, daJ3 man z^, z^, z^ als Modulfunktionen siebenter Stufe auffaßt
und als solche analytisch darstellt. Dies geschieht durch die
Reihenentwicklungen (vgl. „Modulf." II, 393):
(2)
\coJ
,, 2y(i_4ä2 + 3ä^ + 53«i--..),
wo durch den Stern in der dritten Reihe darauf aufmerksam gemacht
wird, daß das Glied mit q^ ausfällt f). Die Koeffizienten sind durchweg
ganze Zahlen, die nach einem einfachen zahlentheoretischen Gesetz aus
den Exponenten abgeleitet werden können (vgl. „Modulf." II, 588).
Endlich findet man Darstellungen der z durch die ^^-Funktion in
„Modulf." II, 394.
*) Die wenigen niederen Falle, in denen das Xetz die ganze g-Ebene
bedeckt, gelten im Texte als ausgeschlossen.
**) Vgl. „Modulf.'- I, 737.
t) Es liegt hier nur insofern eine kleine Unstimmigkeit vor, als der bisher
stets mit 8 bezeichneten Substitution nicht die so bezeichnete erzeugende
Substitution ci}[ = ßjj^ß>2, co'^ = C0.2 der ilodulgruppe entspricht, sondern deren
inverse Substitution co', = co. — ca^, mL z=z lo».
Losung des speziellen Formenproblems dei ©jgß durch Modulfunktionen. 233
Würde man, der älteren Auff^issung folgend, nicht mit dem Galois-
schen Problem arbeiten, sondern mit den niedersten Resolventen, nämlich
denen achten und siebenten Grades, so \\äirde|i im Falle ^ == 0 an Stelle
des Formenproblems die Modular- und ]M[ultiplikatorgleichungen für
Transformation siebenten Grades der elliptischeifi Funktiopen und ihre
Resolventen siebenten Grades treten. Man w]irde dann derei^ Wurzeln als
Modulfunktionen bzw. -former), siehentef Stufe in Reihen nach g
darzustellen haben.
In den vorhin allgemein entwickelten Ansatz ordnet sich nun der
Gebrauch der Modulfunktionen in folgender Art ein. Wir bilden zunächst
vermöge der Gleichung (6) S. 216 aus den Formen 0, W, Xdie GröJ3e /.
Über der J-Ebene war seinerzeit (S. 188) der Dß der
Hauptkongruenzgruppe siebenter Stufe als 168-blättrige Fläche gelagert, die uns zu
unserer Kurve vierten Grades ^ = 0 hinführte. Auf Grurjid des Grenz-
kreistheorems ist diese Entwicklung uirdsehrbar. Wir markieren in der
J-Ebene die drei Stellen e^ == 1, e^ —= 0, 63 = 00 und schreiben die
Signatur (0, 3; 2, 3, 00) vor. Dann ist die 'zugehörige linear-pqly-
morphe Funktion co (/), und unser Ansatz führt zuy Uniformisieriing
durch Modulfunktionen.
Hier versteht man nun den Upiweg, der beim Gebrauch der
Modulfunktionen gemacht wird. Man erzielt nämlich die Uniformisieriing
bereits mit der Signatur (0, 3; 2, 3, 7) und der zugehörigen polymorphen
Funktion ^ (/). Wesentlich ist nur, daJ3 siph dje 168-bläfctrige Flache
über der J-Ebene im K'etze der Kreisbogendreiecke der Winkel Vi -^j -^
2 3/
auf einen dieses Xetz nur einfach bedeckenden Bereich abbildet. Man
gelangt zu dem aus 168 Dreiecksp^aren zusammengeseiizten Bereich, den
man in „Ges. Abhandl." Ill, 126 oder in „Modulfunkt.'- I, 370
dargestellt findet, und der bei eingehenderen geometrischen Untersuchungen
der fraglichen Riemann sehen Fläche von jeher benutzt wurde *). Der
fragliche Bereich ist einfach wieder der DB der Hauptkongruenzgruppe
siebenter Stufe innerhalb der Gruppe der ^-Substitutionen, deren
arithmetischer Charakter in „Autom. Fpnkt." I, 606 ff. erklärt ist**). Die
Größe ^ ist eine eindeutige Funktion von a>, während umgekehrt co un-
endKch vieldeutig von ^ abhängt. Dies begründet den Vprrang von ^
vor CO für unseren Zweck der Uniformisierung. Indessen sind die
Darstellungen von s^, s^, s^m t, poch nicht näher untersucht.
Der Fall 5? == 0 unseres Formenproblems besitzt eijie g^nz
entsprechende transzendente Theorie, die indessep nur erst wenig entwickelt
ist. Man stelle zunächst fest, daß auf der Kurve sechsten Grades gB =: 0
*) Des besseren Überblicks halber ist die £ Halbebene bei jener Figur auf
die Flache eines Kreises linear transformiert.
**) Vgl. auch die Abhandlung des Verfassers ,,Über den arithmetischen
Charakter der zu den Verzweigungen (2, 3, 7) und (2, 4, 7) gehore|iden Dreiecks-
funktionen", Math. Ann., Bd. 41, S. 443.
234 II» 2. Formenproblem der ©igs ^^^ Gleichungen siebenten Grades.
die 24 konjugierten Pole der zyklischen Teiler ©^ liegen, desgleichen die
42 S. 196 näher bezeichneten Pole der zyklischen Teiler @^. Indessen
läuft die Kurve nicht durch die 21 restierenden Pole der @^ (21 Per-
spektivitätszentren), auch durch keinen Pol eines zyklischen Teilers ©g.
Dagegen wird die Kurve ^ = 0 außer in jenen 42 konjugierten Polen
noch in 84 weiteren konjugierten Punkten von den 21 Perspektivitäts-
achsen geschnitten. . Wir gehen nun auf die schon S. 217 erklärte
Funktion K auf der Kurve gB = 0 zurück, die durch:
(3) K: (K— 1) : 1 = W^ : X^ : 2^F' W
gegeben ist. Sie ist 168-wertig und nimmt ihren einzelnen komplexen
W'ert immer in 168 bezüglich der ©^gg äquivalenten Punkten an. Diese
Punkte liegen im allgemeinen getrennt; jedoch fallen sie für JST == 1 zu
je zweien in 84 getrennt liegenden Punkten zusammen, für JST = 0 zu
je vier in 42 und für JST =:; oo zu je sieben in 24 getrennt liegenden
Punkten. Wir folgern hieraus sofort: Mittels der Funktion E wird die
Kurve sechsten Grades abgebildet auf eine 168-blättrige Riemannsche
Fläche über der jST-Ebene, die 84 bei JST = 1 gelegene zweiblättrige
Verzweigungspunkte, 42 vierblättrige bei K = 0 und 24 siebenblättrige bei
K == oo hat, weitere Verzweigungspunkte aber nicht besitzt. Das
Geschlecht dieser Fläche bestimmt sich in der Tat zu j) = 10 in
Übereinstimmung mit dem Geschlecht der doppeltpunktfreien ebenen Kurve
sechsten Grades.
Wir markieren nun in der jST-Ebene wieder die Punkte e^ = 1,
gg = 0, 63 =3 oo und führen die zur Signatur (0, 3; 2, 4, 7) gehörende
polymorphe Funktion ^(K) ein und damit das Xetz der
Kreisbogendreiecke der Winkel ~, —, —• Als Hauptergebnis gilt der Satz; Im
Falle ^ = 0 wird die transzendente Lobung des Formenproblems der
Klein sehen Gruppe durch automorphe FunMionen der Gruppe der Signatur
(0, 3; 2, 4, 7) geliefert. Was in dieser Hinsicht bereits näher untersucht
ist, findet man in „Autom. Funkt."' I, 606 ff. und der eben genannten
Arbeit des Verfassers. Bekannt ist zunächst das arithmetische Gesetz
der zugehörigen Gruppe der ^-Substitutionen. Auch konnte leicht gezeigt
werden, daß ihre Hauptkongruenzgruppe siebenter Stufe wieder den Index
168 hat, und daß der zugehörige DB zur obigen 168-brättrigen Fläche
über der iT-Ebene hinführt. Die z^, s^, s^ sind also auch im Falle gB = 0
wieder „automorphe Funktionen siebenter Stufe".
Will man brauchbare analytische Darstellungen der z^, z^^ z^ haben,
so kann man entsprechend den Erfahrungen beim Falle ^ =: 0 den
Umweg gehen, daß man die polymorphe Funldion der Signatur (0, 3; 2, 4, 00)
einführt. Die zugehörige, mit der Modulgruppe kommensurable Gruppe
ist S. 100 ff. mit Hilfe der Irrationalität "fi dargesteUt. Die
Grundformen dieser Gruppe h^, \, h^ konnten als Modulformen zweiter Stufe
erklärt und in die Potenzreihen (9) S. 105 entwickelt werden. In ihnen
Transzendente Lösung des speziellen Pornienproblem^ mit ^ = 0. 235
stellen sich die Invarianten der Klein schea Gryppe im Falle 0 = 0
so dar:
(4) F=\, W= }ilh!, X --= \ \ Jit ■ ih„
was ein Vergleich der Gleichung (3) mit dpr von S. 105 \ier bekannten
Gleichung:
E:{K— 1):1 = ht : h! : 2oÖ/i,
bestätigt. Da 2 quadratischer Rest von 7 ist, so hat diß
Hauptkongruenzgruppe siebenter Stufe innerhalb der Gruppe der Signatur (0, 3; 2, 4, oo)
wieder den Index 168 wie :|nner]|ialb der Modulgruppe. In 2^, z^^ z^
haben wir das einfachste Fori^ensystem dieser Gruppe; als solche Forjnen
sind sie von der (— 2)**^^* Diinension und üire Quotienten liefern sechs-
wertige Funktionen. Die den Formeln (2) entsprechenden Reiken-
darstellungen sind indessen noch nicht näher untersucht.
§ 7. Lösung des allgemeiner* Formenproblems der Klein sehen Gruppe.
Wir sprechen vom „allgemeinen Formenproblem" der temären
Gruppe @J68) wenn keiner dpr beiden eben behandelten Fälle ^ == 0,
fi? = 0 vorliegt. Um jetzt die transzendente Lösmig dieses
Formenproblems vorzubereiten, führen wir die '^cloar der JLurven zwölften Grawes,:
(1) ;c*2_|_4_p3^'0
ein. deren jede durch die Substiti^tionen der ©^^g in sich transformiert
wird. Für v,-=^0 liegt die dreifach gezg,hlte B^urve vierten Grades ^ == 0
vor und für ^,-=-00 die doppelt gezählte Kurve sechsten G^-ades fi? = 0.
Mle übrigen Kurven (1) sind irreduzihel. Invariajite Faktoren der linken
Seite von (1) eines Grades m <C^ 12 könnten nur JF*, fi?, F^ und F- 0 ^ein,
die aber ausgeschlossen sind. Hätte also die linke Seite von (1) einen
Faktor f eines Grades m <^ 12, so wiiide dieser Faktor einem Teiler
der (^jgg eines Index /i ^ 1 angehören, und wir hatten als in der linken
Seite von (1) enthalten [i konjugierte Faktoren fi == f, f^, f^j • • -j fu-
Da /LI ^ 7 ist, so ware m = 1, und ipaan hätte die drei Möglichkeiten
fi = 7, 8 und 12. Indessen gibt es bei der ©^gg kein System von 7
oder von 8 oder von 12 konjugierten Linearformen.
Führt man statt der Wended^-eieckskoordinaten z^, z.^, z^ durch:
x:i/:l = j:^:z^:Z2
gewöhnliche kartesische Koordinaten x, y eii^, so wird die (Ueichung (1).
. 4:X^ -^Tiy^ -f ... z= 0,
wo alle nicht angegebenen Glieder den Grad 3 übersteigei^. Es ergibt
sich hieraus, daß die 24 Pole der ;^yklischen Teiler (^^, die die
gemeinsamen Grandpunkte aller Kurven des Büschels (1) sind, für die irre-
duziblen Kurven BiickTcehr^uuMe sind. Eine irrßduzible Ifurve (]), die
236 n, 2. Formenproblem der ©igs ^^^ Gleichungen siebenten Grades,
weiter keine singulären Punkte aufweist, hat nach einer bekannten Regel
das Geschlecht jp = 31.
Soll ein weiterer singulärer Punkt auftreten, so sind sogleich alle
bezüglich der ©^gg mit ihm äquivalenten Stellen singulare Punkte des
gleichen Charakters. Wir haben also zu untersuchen, was aus der
Kurve (1) wird, wenn wir den Parameter x so bestimmen, daß sie durch
eines der weiteren Polsysteme der Ö^gg hindurchlauft*). Es können
hierbei nur die 28 konjugierten Pole der zyklischen ©^ und die 21 Per-
spektivitätszentren in Betracht kommen, da die übrigen Pole immer nur
auf einer der beiden Kurven ^ == 0, $ = 0 liegen und also für die
iireduziblen Kurven (1) nicht in Betracht kommen.
Da 2j^ = 1, ^2=1, ^-g = 1 die Koordinaten eines der 28 Pole
der @3 sind, so lauft die irxeduzible Kurve der Gleichung:
(2) 4P_27*2„o
durch die 28 Pole der ©g hindurch, ilan stellt leicht fest, daß die
Kurve in den fraglichen 28 Polen DoppelpunUe aufweist, so daß ihr
Geschlecht auf /> = 3 zurückgeht. Wir haben hier die der Kurve
vierten Grades zwölfter Klasse ^ i= 0 nach dem Dualitätsprinzip
entsprechende Kurve zwölften Grades vierter Klasse vor uns, die den
28 Doppeltangenten und 24 Wendepunkten jener Kurve entsprechend
28 Doppelpunkte und 24 Rifckkehrpunkte hat.
Die durch die 21 Perspektivitätszentren hin durchlaufende irreduzible
Kurve zwölften Grades untersucht man bequemer mit den oktaedrischen
Koordinaten x^, x^, x^, wo man etwa das spezielle Zentrum x^ = 0,
ajg = 0 benutzen kann. Es zeigt sich leicht, daß die Kurve wieder
Boppelpunlie in den 21 Zentren hat, so daß das Geschlecht jetzt auf
p =z 10 herabgeht. Um den zugehörigen Wert des Parameters % zu
bestimmen, setze man:
x^ = 0, x^ = 0, x^ = £* (fä J- fS _ £* _ £^)
in die Transformationsformeln (10) S. 200 ein und findet:
2, = s'{8 -^8^-8^ — 8%
Z,=: e{8'-j-8'-e-E%
^3 =: £* (f^ — £° £* 8^).
Durch Ausübung der Substitution S^ gehe man von hier noch zum reellen
Perspektivitätszentrnm über:
^2 = £^ + £^ — £ — £^
„-3 = £2 + £& _ £4 _ £3_
^) Man beachte, daJJ 168 oder auch nur 84 weitere singulare Punkte nicht
«n können.
auftreten können.
Geometrische Grundlagen der Lösung des allgemeinen rormenproblems. 237
Eine kurze Rechnung zeigt dann, daß die durch diesen Punkt
hindurchlaufende Kurve der Schar (1) die Gleichung hat:
(3) ^'- 4- 4^^ = 0.
Wir notieren also den Satz: Die irreduziUen Kurven der Schar (1)
haben das Geschlecht p = 31 mit den heiden Äm^iahnißn (2) und (3), wo
die Geschlechtssahlen auf j) =-. 3 und j5 = 10 zurücTcgehen.
Man führe jetzt auch i^och die Schar der bezi^glich der ©^ g
invarianten Kurvten 14ten Q-rades vo^i der Gleichung:
(4) W—8lF^^=^0
ein, die sämtlich durch die 56 koi^jugierten Pole der zyklischen ©g and
die 42 konjugierten Pole der zyklischen @^ (Beriihrungspunkte der
Kurven 5? = 0 und W = 0) hiadurchlaufen. Abgesehen voa diesen
Punkten, durch die keine der irreduziblen Kurven (1) Jiindurchl^uft,
zieht durch den einzelnen Punkt der Ebene stets eine und pur eine
Kurve der Schar (4) hindurch.
Längs der einzelnen irreduziblen Kurve (1) wird nur|. X eine
eindeutige 168-wertige Funktion, die den einzelnen komplexen Wert in
168 bezüglich der ©^gg äquivalenten Punkten annimmt. Piese Punkte
sind im allgemeinen voneinander verschieden, jedoch mit folgenden
Ausnahmen: Erstlich fallen für A = c« die 168 Punkte zu je 7 in den
24 Polen der ©^ [Grundpunkten der Schar (1)1 zusammen. Sehen wir
weiterhin zunächst von den besonderen Kurvep (2) und (3) ab, so kommen
nur noch die 12-21 Schnittstellen der Kurve (1) mit den Perspektivitäts-
achsen in Betracht. Da die einzelne Achse durcii vier einen zyklischen
Teiler ©^ bildende Substitutionen ===) ir|. sich übergeht, so liefern ijire
Schnittstellen mit der Kurvte (1) drei Systeme vpn je vier äquivalenten
Punkten. Im ganzen hat man alsp auf der irreduziblpn Kurvte (1)
[abgesehen von den Fällen (2) und TB)] nur noch dreimal eip.
Zusammenfallen der 168 äquivalenten Punkte zu je 2;weien an 84 Punkten
festzustellen. Schließen wir die beiden speziellep Fälle (2) und (3) aus und
nehmen wir an, daß die dreimal 84 eben gewonnenen Stellen durchweg
getrennt liegen und zu den Werten A = ^;^, ^ = t^g und X = v^ führen,
so ergibt sich der Satz: Die einzelne Irreduzlhle Kurve (1) wird durch
die FunUion X auf eine 168-blättrige Flache ^her der X-Ehene abgebildet,
die nur an den vier Stellen X == v^, v^, v^ und oo oerzweigt td; Ußd zwar
liegen an jeder der ersten drei Stellen 84 zweihlattrige Verzweigdng'?,puAilie,
bei X ^= CO aber 24 siebenblättrige. Man überzeuge sich, daß diese Fläche
wie die Kurve (1) in der Tat das Geschlecht j) = 31 hat.
Die Lage der VerzweigTingsstellen v^, v^^ v^ ist nu^ naher zu
untersuchen. Für die in Frage kommenden Stellen der Koordinatenebene
*) Außerdem wird die Achse durch vier weitere a^s der zyklischen ©^ und
der eigenen Perspektivität zu erzeugende Substitutionen in sich übergeführt.
238 III 2. FormenprobleiD der ®i6g und Gleichungen siebenten Grades.
der ^j, -^g, ^3 verschwindet die Form X, so daß zufolge (15) S. 208 die
Gleichung gilt:
W^ + 2^.3^*7 —2^.1 IF^^IF^ —2^-P71^4- 2ö.l7P^*2|pr
+ 2*. 32. 7 P** y — 2" P^ * + 2^. 43 P« *3 __ 2^. 7 . G7 P^ ^^ = 0.
p]liminiert man F^ $ und W zwischen dieser Gleichung und den
Gleichungen (1) und (4), so ergibt sich:
(5) xU^— llx2A2 + x(x2+ 17 X —32. 7)A
+ (x^ + 43x2+ 7.67X +2.33) = 0
als kubische Gleichung für die drei Werte t\, Vc^^ v^. Wir spalten X in
den Quotienten Aj: Ag zweier homogenen Variablen, fügen, um aucli den
Verzweigungspunkt A = c» mit zu berücksichtigen, den Faktor Ag und,
um Binomialkoeffizienten zu gewinnen, den Faktor 12 hinzu und erhalten
so aus der linken Seite von (5):
(G) 4.3x^^1^2 —6.22x2-Aim +4(3x3+ 5U2_ ig9^);^^;^8
+ 12 (x^ + 43x2 + 469x + 54)^2^
als biquadratische „Verzweigungsform" unserer lG8-blättrigen Riemanii-
schen Fläche über der A-Ebene. Die durch (7) in I, 139 erklärten
Invarianten ^2, ^3 dieser Form stellen sich in x so dar:
I g^ = —22.3x^(3x2 —2.5.7x —33.7),
^^^ \ ^8 = —23.x*(32.7x^ + 7.13x2 + 33.7.17X + 36),
woraus man für die Diskriminante z/ findet:
(8) z/ = — 2^. 3« x^ (x + 27)3 (^ _ 1)4^
Für die absolute rationale Invariante J der Verzweigungsform [vgl.
Fon^iel (14) in I, 141] ergibt sich daraufhin:
(9) J: (J— 1): 1 = X (3 x2 — 2 . 5 . 7 X — 33. 7)^
: — (32. 7 x3 + 7 . 13 x2 + 33. 7 . 17 X + 3«)^
:27(x + 27)3(x—1)*.
Hieraus geht der wichtige Satz hervor: Bei den irreduziblcn
Kurven (1) tritt eine Ausartung der Eiemann sehen Fläche infolge Ver-
sehwindens der Dislcriminante z/ durch Zusammenrüclcen von VerzwcigungH-
stellen nur für x = — 27 und x =n 1, d. h. in den beiden besonderen
Fällen (2) und (3) ein.
Für X = — 27 nimmt die Gleichung (5) nach Fortlassung des
Faktors 27 die Gestalt an:
(3A + 1)2 (3 A —35) = 0.
Transzendente Lösung des allgemeinen Formenprobleins. 239
Aus (jrleichung (4) aber geht hervor, daß 3 A = — 1 im Punkte ^^ = 1,
^2 = 1, 'S^a =^ 1 zutrifft. Wir werden zu den 28 konjugierten Polen
der zyklischen Teiler ©g zurückgeführt, durch deren einzelnen die
Kurve (2) zweimal hindurchläuft*). Die 168-blätterige Riemannsche
Fläche über der A-Ebene hat nur noch die drei Verzweigungsstellen
A=::^, A= — l, k = oc; und zwar finden sich an der ersten Stelle
84 zweiblätterige Verzweigungspunkte, an der zweiten 56 dreiblätterige
und an der dritten 24 siebenblätterige. Wir sind damit zur Riemann-
schen Fläche des Falles F :z=: 0 zurückgeführt.
Für X = 1 nimmt die (ileichung (5) die Gestalt an:
(A —9)2(A -h 7) = 0.
Die Verhältnisse liegen hier ähnlich wie in dem gerade betrachteten
Pralle. Durch das einzelne Perspektivitätszentrum ziehen vier Achsen
hindurch (vgl. Fig. 24, S. 190). Jedes Zentrum ist Koinzidenzstelle von
vier Paaren bisher getrennt liegender Schnittpunkte der Achsen mit der
Kurve (1). Da die Kurve (3) aber zweimal durch jedes Zentrum
hindurchläuft, so entstehen bei der jetzt in Frage kommenden Koinzidenz zw^ei-
blätteriger Verzweigungspunkte 42 vierblätterige Verzweigungspunkte.
Die Kurve (3) wird demnach mittels der Funktion X auf eine 168-
blätterige Riemannsche Fläche mit den drei Verzweigungsstellen X = — 7,
X =i \) und A =^ oo abgebildet; und zwar finden sich an der ersten
Stelle 84 zweiblätterige Verzweigungspunkte, an der zweiten 42 vier-
blätterige und an der dritten 24 siebenblätterige. Wir haben damit die
Fläche des Falles $ = 0 wiedergewonnen.
Indem wir die beiden besonderen Fälle (2) und (3) zunächst wieder
ausschließen, führen wir für die mit den Punkten t\, v^, v^, oo signierte
A-Ebene auf Grund des (ilrenzkreistheorems die polymorphe Funktion J
.der Signatur (0. 4; 2, 2, 2, 7) ein. Sie bildet die geeignet zerschnittene
A-Ebene auf den DB einer Grenzkreisgruppe der Signatur (0, 4; 2, 2, 2, 7)
ab. Nach einem in „Autom. Funkt." I, 385 bewiesenen Satze bilden
die gesamten Gruppen dieser Signatur ein zweidimensionales Kontinuum.
das umkehrbar eindeutig auf das zweidimensionale **) Kontinuum der
signierten A-Ebenen bezogen ist. Die Grenzkreisgruppen der Signatur
(0, 4; 2, 2, 2, 7) sind alle isomorph und enthalten je einen Normalteiler
des Index 168.
Liegt keiner der Fälle (2) und (3) vor, so habe unser „allgemeines"
Formenproblem die Lösung ^^, z^, z^. Der Punkt dieser Koordinaten
lieo-t dann weder auf der Kurve F = 0 noch auf der Kurve # --. 0
*) Durch jeden Pol laufen drei Perspektivitätsachsen (vgl. Fig. 25, S. 198),
so daß der Pol Koinzidenzstelle von drei Paaren bisher zweiblätteriger
Verzweigungspunkte ist. Die bisher getrennt liegenden 84 Punktepaare ziehen sich in der
Tat auf die 28 getrennt liegenden Pole zusammen.
**) x ist ein „komplexer" Parameter.
240 n, 2. Formenproblem der ©j^g ^^^ Gleichungen siebenten Grades.
noch auch auf einer der Kurven (2) und (3). Durch ihn zieht also eine
und nur eine der irreduziblen Kurven (1) des Geschlechtes j) = 31
hindurch, auf der dann zugleich die gesamten 168 den Lösungen des
Formenproblems entsprechenden Punkte liegen. In der sti dem betreffenden
Parameterwerte y, gehörenden polymorphen FunUion t, von der Signatur
(0, 4; 2, 2, 2, 7) hahen wir die uniformiderende Variable gewonnen, die die
transzendente Lösung des Formenprohlems vermittelt; in t, sitid nicht nur
die an die Gleichung (15) S. 208 und die Belation (1) gelutidenen Formen
F, ^, W und X eindeutige FunUionen der Gesamtgruppe, sondern ebenso
sind die z^, z^, z^ als eindeutige automorphe FunUionen von t, eines
Normalteilers vom Itidex 168 dardelTbar.
Dieser Ansatz ist bisher noch in keinem Falle zur wirklichen
Durchführung gebracht. Auch ist diese Durchführung dadurch erschwert, daj3
man zur Darstellung der z^, z^, z^ als automorpher Funktionen von ^ nur
die praktisch recht unbrauchbaren Poincar^ sehen Reihen zur Verfügung
hat. Man wird sich auch hier damit helfen, daj3 man an Stelle der
polymorphen Funktion der Signatur (0, 4; 2, 2, 2 ,7) diejenige der
Signatur (0, 4; 2, 2, 2, oo) treten läj3t, was natürlich theoretisch einen
Umweg bedeutet. Der Vorteil aber ist, daJ3 man dann wieder Potenzreihen
nach der Exponentialfunktion g besitzt, die gut konvergieren und
überhaupt als „Potenzreihen'- brauchbarer sind als die Poiucaresehen Reihen.
Doch ist auch iu dieser Richtung noch nichts weiter zur Durchführung
gebracht.
Man wird noch fragen, was aus unserem Ansatz in den beiden
besonderen Fällen (2) und (3) wird. Die Antwort ist einfach: Es rücJcen
in beiden Fallen zwei elliptische Eclcen des DB zu einer parabolischen
zusammen, und man gelangt beide Male zur polymorphen FunUion der
Signatur (0, 3; 2, oo, 7). Vermutlich führen innerhalb dieser Gruppe die
Hauptkongruenzgruppen dritter und vierter Stufe zu unseren 168-
blätterigen Flächen. Doch ist darüber noch nichts weiter festgestellt.
Eine ausführliche Untersuchung über die symmetrischen Fälle der
Grenzkreisgruppen der Signatur (0, 4; 2, 2, 2, 7), und zwar sowohl algebraisch
wie transzendent, ist vom Verfasser ausgeführt*).
*) In der Arbeit „Entwicklungen zur Transformation fünfter und siebenter
Ordnung einiger speziellen automorphen Funktionen'-, Acta math., Bd. 17, S. 388ff.
(1)
Arithmetische Erklärung ei^ier neuen Substitutionsgruppe.
Drittes Kapitel.
Valentinergruppe und zugehörige invariante
Formen.
1. Einführung einer neijen unendliche^ Sulbstiti^tion^gruppe (
Wir verstehen weiterhin untey j und j die Lösungen:
. _ — 1 -r y5 T _ — 1 — VS
der ganzzahligen quadratischen Gleichung x- ~\- x — 1 = 0. Die
„ganzen Zahlen-' des quadratischen Zahjkörpers (ß, j) sind dann die in
der Gestalt (a -f- hj) mit irgendwelchen rationalen ganzen Zahlen ß, h
darstellbaren Zahlen. Wir bilden mit ganzen Zahlen Ä, B, 0, D des
Körpers {% j) und der Quadratwurzel \j lineare Substitutionen einer
komplexen Variablen ^ = ^ -- irj von der Bauart:
.,. ., _ (^ + i?Vi)^-(o-^vJ)
Es sollen also hier der erste und vierte Koeffizient zwei afe „konjugiert"
zu bezeichnende Zahlen {Az^B^j) seir^ und ebenso der zweite und der
negativ genommene dritte. Diebe Bauart hleiht hei Zubammenbet^ung zweier
Suhbtitutionen erhalten. Üben wir nan^lich auf ^' eine Substitution (2)
mit den Zahlen Ä', B', C, I)' aus, so entspringt eine Sut)stitution der
gleichen Bauart mit den ganzen Zahlen:
' A" = A'A-\-3 B'B — G'C ^jD'I),
B" = A'B -i-B'A -^ G'D—irC,
^^^ * G" = A'G -tJß'D f G'A—jD'B,
D" == A'D + B'G- C'B ^B'A
des quadratischen Körpers (5Ä, j).
Hieraus geht sofort hei-vor, dg.J3 alle unimodularen Substitutionen (2)
eine Gruppe bilden. Es besieht ^.ber weiter der wiphtige Sat^: Alle
quadrimodularen Substitutionen (2), d. h. alle Substitutionen (2) drr
Determinante 4;
(4) ^2 ^ C2 — j (B^ -f D^) = 4,
zu denen inbbesondere alle mit 2 ertceiterten animodularen Suhbtitutionen
geJiören, bilden gleichfalls eine Grrti,pße ©'. Es laßt sjch nämlich leicht
zeigen, daJ3 für jede quadrimodulare Substitution (2):
(5) A ~G, B = D (mod 2)
Fricke, Algebra. II. 16
242 Ilf S- Valentinergruppe Tuid zugeliorige Formen.
gilt. Sind also die beiden zusammenzusetzenden Substitutionen quadri-
modular, so folgt aus (3), da£ A", B", G'\ B" durch 2 teubar sind.
Kach Forthebung des Faktors 2 wird dann die zusammengesetzte
Substitution wieder quadrimodular. Die Gültigkeit der Kongruenzen (5)
zeigt man so: Es gibt mod 4 sechzehn Reste für die ganzen Zahlen des
Körpers (9?, j). Für die Summe {B^ ~f D^) der Quadrate zweier Zahlen
B, B gilt eine der vier Kongruenzen:
(6) ßä _|_ 2)2 = 0, 2, 2 + 2i, 2i (mod 4),
falls B = B (mod 2) ist, im Falle B ^B (mod 2) aber eine der sechs
Kongruenzen:
£2 _|_ 1)2 ^ 1, 3, 1 -|_ 3j, 3 ^i, 2 +i, 2 + Sj (mod 4).
Im letzten Falle B ^D (mod 2) würde sich aus (4) beziehungsweise:
Ä^~\-C^=j(B^+B')=j, 3i, 3 + 2i, l + 2j, 1+i, 3 + 3i (mod 4)
ergeben. Das sind aber gerade die sechs rückständigen Reste, die nicht
mit der Summe zweier Quadrate mod 4 kongruent sein können. Also
ist B = D (mod 2), und aus (4) folgt, den Kongruenzen (6) entsprechend:
^2-f C2=i(j?2 + D2) = 0, 2i, 2, 2~f2j (mod 4),
so daJ3 in der Tat auch die erste Kongruenz (5) gilt.
Weiter, besteht der Satz: Alle quadrimodälaren Suhstittdionen (2)
und aMe dimodularen, d. h. alle der Beterminante 2 :
(7) Ä" -^rG^—3 (5^ -^ D2) = 2
Mlden eine G-ruppe, in der die gewonnene Gruppe @' der quadrimodularen
Substitutionen einen Normalteiler des Index 2 liefert. Wir verstehen
unter U die besondere dimodulare Substitution:
(U) t' = -^-^
der Bauart (2). Bezeichnen wir zur Abkürzung die Substitution (2)
durch das Symbol [-4, B, C, B], so zeigt man leicht:
U-[A, B, G, B]'Ü-^ = [A, —B, C, B].
Hiemach ist U mit @' vertauschbar, und man hat in ® =: @' -f- ©' • f7
eine Gruppe, die @' als Xormalteiler des Index 2 enthält *). Es ist also
nur noch zu zeigen, daß die Xebengruppe @' • U gerade aus allen
dimodularen Substitutionen (2) besteht. Erstlich hat, wenn [A, B, C, B]
eine beliebige Substitution aus @' ist,
[A,B, 0, D].f7= [1(^ + 0,1(5-fD), _i(^_C), _|(i?-D)]
zufolge (5) vier ganzzahlige Beträge ^{A-\- G), ... und ist dimodular.
Ist andererseits V eine beliebige dimodulare Substitution, so ist
*) Die Substitution 7/2 gehört der Gruppe ®' an.
Arithmetische Erklärung einer neuen ßubstitutionsgruppe. 243
V- TJ~'^ = y quadrimodular und also F= F'- f7 in der Kebengruppe
@' • TJ enthalten.
Als letzten Satz notieren wir: Diß G-rtf^ppe ® aller quadrimodularen
.und dimodularen Substitutionen (2) J^at lavier reelle ^ubst^tutioßshoeffksienten
und ist durch die Spiegelung S an der ipiagirf.ären l-Achse:
{S) r == -1
wo t, zu t, Iconjugiert imaginär ist, zu einer 0-rup^e ® = ® -\- (3- S
erweiterungsfähig, in der @ ein Normalteiler des Index 2 ist. Der Be\>feis
geht unmittelbar aus der Gleichung hervor:
S.[A 5, 0, D]'S = [A, B, — G, — D].
§ 2. Dreiecksnietz und DB d^r Gruppe @.
Es soll festgestellt werden, welche Perioden bei etwaigen elliptischen
Substitutionen der Gruppe ® vorkommen können. Wechselt ^nan das
Vorzeichen von yS, so mögen die ganzen Zahlen A, B, G, T) eiper
Substitution [-4, B, G, D] in A^ B, G, D übergehen. Sie befriedigen die
Gleichung:
^' +^' + i±l(^ (ßs _|_ ;^2) ^ 4 bzw. = 2,
je nachdem die Substitution quadrimodular oder dimodular ist. Da die
A, B, C, D reell sind, so folgt:
(1) MI ^2 b?w. |1|<V2,
wo im ersten Falle das Gleichheitszeichen aur für die identische
Substitution zutrifft. Das Kennzeichen e|ner elliptischen Substiti(.tion ist
aber \A\ <^ 2 bzw. |-4j < '^2, je nachdem eine q^adrimoduIare oder di-
modulare Substitution vorliegt. Die gleichzeitigen Bedingungen j ^ [ <;; 2
und M I <^ 2 erfüllen nur die ganzen Zahlen:
(2) ^ = 0, i 1, ±j, ±j
und die gleichzeitigen Bedingungen \A\ << y2, \A\ <C ^2 ni^r die ganzen
Zahlen:
(3) ^ = 0 und ^ = + 1.
Bei den quadrimodularen Substitutionen ist der Wert -4 = ^r 1
unbrauchbar. Man hätte hier G=l (mod 2) und also:
A^-^G^ = 2, B2 _|_ 2)2 s 2 + 2 j (mod 4),
woraus B = D =j (mod 2) folgt. Wir setzen demnach:
(4) B = j -4- 2 &, D = j -f- 2 d,
244
II, 3. Valentinergruppe und zugehörige Formen.
WO h und d ganze ZaMen des Körpers (ß, j) sind. Xun folgt aus (4)
S. 241 für -4 = + 1 nach Multiplikation mit (j -f 1):
sowie wenn wir die Ausdrücke (4) von B und D eintragen:
2 - 2j T- 4i(& + d)~\^ 4.(1' + ^) = (i + 1){G' - 3).
Setzt man h -^ d = x und reduziert mod 8, so ergibt sich, je nachdem
C'^ = 1 oder = 5 (mod 8) gilt:
4tx^ ~\-4tjx = 4: bzw. = 4j (mod 8)
und also nach Fortnahme der Faktoren 4:
x^^jx-^l = 0 bzw. x^ ^jx -[-j = 0 (mod 2).
Beide Kongruenzen sind irreduzibel, woraus die Unbrauchbarkeit von
J. = + 1 hervorgeht. Für alle übrigen A aber werden wir
Substitutionen in (3 finden: Unter den qaadrimodularen Substitutionen treten an
Flg. 29.
cllijjtibchen Suhdit at Ionen bolche der Perlode 2, nämlich fur A = 0, and
weiter nar noch solche der Periode 5, nämlich fur A = tij und A = 4ii,
auf; anter den dimodalaren Sahstitutionen fanden sich nar elliptische der
Periode 2 fur A = 0 und bolche der Periode 4 für J. = — 1-
Wir stellen nun die drei in der erweiterten Gruppe (^ enthaltenen
Spiegelungen:
-^-rl ,-. .._ l-fJ + Vi
i.^) r
-i {T) r
iu) l'--
JtI ' ' " (i+i-Vi)e
zusammen, deren Symmetriehalbkreise der positiven ^-Halbebene durch:
(5) 1 = 0, 1^-4-^^21-1 =.0, r + 7?^ = (l+i)(l + VJ)
gegeben sind und das in der Fig. 29 sichtbare Kreisbogendreieck der
mit e,), ßj, ^2 bezeichneten und bei:
(«) ^ = (i+J
-VJ)-
y2
Spiegelungen in der nepen Gruppe @^. 245
gelegenen Ecken eingrenzen. Es handelt sich hier um ei^
Kreisbogendreieck der Winkel "ö" > t > ^ j ^"^ ^^-'^^ durch fortgesetzte Spiegelung
eine lückenlose und einfache Bedeckupg dßr ganzen ^-Halbebene mit
einem Xetze solcher Dreiecke entsteht (vgl. Fig. 29). Hiernach ist die
Grren^kreibgruppe der Signatuf (0, 3; 2, 4, 5) ein Teiler unserer aritli-
metiscJi erMärten G-ru^pe @.
Wir behaupten weiter, daß ^ußer den in dieser Grejizkreisgruppe
bereits vertretenen Spiegelungen weitere auch in der Gruppe @ nicht
enthalten sind. Dies ist leicht geometrisch, zur Evidenz zu bringen.
Ein Schnittpunkt zweier Symmetripkreise ist stets Pol einer elliptischen
Substitution. Liegt andererseits ay.i einem Symmetriek reise der Pol einer
elliptischen Substitution der Periode v, so laufen durch diesen Pol im
ganzen v Symmetriekreise hindurch, die sich unter den Wickeln —
schneiden. Enthält nun @ noch eine Spiegelung^ derpn Symmetriek|?eis
dem Xetze der Fig. 29 nicht angehört, so zieht auch noch ein solcher
Symmetriekreis durch das Innere des Dreiecks e^, e^, e^ hindurch. Dieser
Kreis kann durch keine der Ecken e^ und e^ laufen, da hier bereits die
kleinsten zulässigen W'inkel — und — vorliegen. Würde er d^rch e-^
er die Gegenseite e^, e^ im Imiern schneiden. Hiernach müßte der
fragliche Kreis wenigstens eine der beiden Seiten e^p^ und e^e^ inj Innern
schneiden. Soll nun ein Innenpunkt der Seite e^e^ Pol einer Substitution
der Periode 5 sein, so liefe durch ihn ein Synunetriekreis, der mit e^e^
den Winkel 4r bilden würde*). Dieser Kreis würde dje Seite e,e^ unter
einem Winkel 0" des Intervalls:
erreichen. Diesem Intervall gehört aber überhaupt keiner der zulässigen
W^inkel ^, ^ an, so daß der fragliche Pol nicht auftreten kanfi.
Genau so zeigt man, daß dem Innern der Seite e^e^ kein Pol eiaer
elliptischen Substitution der Periode 2 unserer Gruppe @ angehören kann.
Es würde ein die Seite e^e^ senkrecht kreu^jendefr Symmetriekreis a-^if-
treten, der e^ e^ unter einem Winkel d- des Intervalls (7) schneiden
müßte. Eben deshalb kann auch keia Pol einef Substitution der Periode 4
auftreten, denn deren Quadrat wäre ja yon der Periode 2. Die
Untersuchung etwaiger Pole zu den Perioden 5 und 4 im Innern von e^e^
*) Man denke diesen Symmetriekreis ai^s deifi Kreise ceae^d mittels einer
hyperbolisclien Substitution hergestellt, die den Halbkreis aeoeih zur Bahnkurve
liat und von a nacli b verschiebt.
246 Hl 3. Valentinergruppe und zugehörige Fonnen.
erledigt sich in derselben Art und mit dem gleichen Erfolg, nur tritt an
Stelle von (7) das Intervall:
Würde aber e^e^ m einem Innenpunkte e von einem neuen
Symmetriekreise senkrecht gekreuzt, so würde durch die zugehörige Spiegelung
entweder der Pol e^ oder e^ in einen äquivalenten Pol e'^ transformiert, der
der Dreiecksseite e^ßg angehört. Beides ist aber bereits als unmöglich
erwiesen.
Da in ® nur die Spiegelungen der Grenzkreisgruppe der Signatur
(0, 3; 2, 4 5) und keine weiteren enthalten sind, so wird das Xetz der
Fig. 29 durch alle Substitutionen von ® und also von @ in sich
transformiert. Die einzelne Substitution von @ wird demnach das Dreieck
6^6^63 entweder in sich oder in ein anderes Dreieck unseres Ketzes
transformieren. Das Dreieck wird indessen nur durch die identische
Substitution in sich transformiert, da die Eckpunkte e^, e^. e^ notwendig je
sich selbst entsprechen müssen. M&o ist das fragliche Kreisbogendreiech
ein DB der Gruppe ®, und damit haben wir in der in § 1 arithmetisch
erUärten Gruppe die GrenzJcreisgruppe der Signatur (0, 3; 2, 4, 5) er-
hmmt. Ein Dreieckspaar des ]!^etzes liefert uns einen DB der
ursprünglichen Gruppe ®. Diese Gruppe ist erzeugbar aus den Substitutionen:
(8) S = T-TJ, T=^fl-S, U=^-T,
die den Relationen genügen:
(9) S^ = 1, T^ = 1, U^ = 1, S-T-U=l
und entwickelt die Gestalten haben:
(1(3) ) Vi^i-K^, i+i + VJ/'
Wegen der vierten Belation (9) läßt sich @ au^h bereits aus den beiden
Substitutionen S und T erzeugen, die die Relationen befriedigen:
(11) S°=r 1, T^ = 1, {S-TY = 1.
Man kann ® statt dessen natürlich auch aus T und TJ sowie auch aus
TJ und S erzeugen.
§ 3. Hauptkongruenzgruppe dritter Stufe in der Gruppe ®.
Zur Gewinnung von Teilern der Gruppe ® kann man das Prinzip
der Kongruenzgruppen anwenden. Insbesondere bilden alle
Substitutionen von ®, die die Kongruenzen:
(1) i? = 0, C = 0, D = 0 (mod 3)
Diskontinuitatsbereicli und Dyeiecksnetz der neuen Grappe @oc. 247
befriedigen, einen als „HauptJcongruenzgru^pe dritter Stufe- zu
bezeichnenden Normalteiler eines endlichen Index ^i. Daß dje Kongruenzen (1)
einen Teiler erklären, geht aus der Zusammensetzungsregel (3) S. 241
hervor. Man hat hier nur nötigenfalls 2 A", 2 B", • • • an Stelle von
A", B", • • • zu schreiben, was abey nicht stört, da 2 zu 3 teileriremd ist.
Daß es sich um einen Xormalteiler handelt, geht aus den Gleichungen:
U'-'-lA, B, C, D]'U == [A, D, G, — B],
T-^-[A, B, G,D]-T= [A, -B,il+j)C-D, (l+j)(ö-D)]
mit Rücksicht darauf hervor, daß @ aus T and U erzeugbar ist
Die Bestimmung des Index ^ erfordert ejne etwas umständliche
Abzahlung. Gilt von zwei Substitutioaen V und V:
(2) A' ^öA, B' = 6B, C -=6C, B' = 6l) (mod 3),
wo 6 eine ganze Zahl des J^örpers (^,3) ist, so gehört V-Y-^ der
Hauptkongruenzgruppe dritte^ Stufe an Das zugehörige Komplement @a
erhalten wir demnach durch Reduktion der Gruppe @ mod 3, wobei zwei
Substitutionen, die die Kongruenzen (2) erfüllen, als nicht verschieden
gelten.
Bei der fragKchen Reduktion wird j eine „ GrßloisiiClie imaginäre
Zahl-', die als Wurzel der irreduziblen Kongruenz:
(3) f^j.^2=0 (mod 3)
zu erklären ist. Es ist zunächst wegen:
(4) A^ ^C^- j {B'' -f B^) = + 1 (mod 3)
mit den Determinanten + 1 und — 1 zu ipechnen. Im letzteren Falle
aber gelangen wir durch Erweiterung np.t dem die Kongruenz ö'-* ^ — 1
(mod 3) erfüllenden Faktor 6^1 —j zu einer Substitution der
Determinante 1. Es sind also alle inkongruenten Lösungen der Kongruenz:
(5) A^ + G^— j (B^ ^ Z>2) = 1 (mod 3)
abzuzählen, wobei zwei Lösungen, die d^rch gleichzeitigen i^eichenwechsel
von A, B, C, D ineinander übergehen, ßls njcht verschieden gelten*).
Wegen des letzteren IJmstandes dürfep wif A auf die fünf Reste:
(6) ^ = 0, 1, 1-i, i, 1-f-i (mod 3)
einschränken. Xun ist aber A diejenige Invariante der Substitution
[-4, B, C, D] der @^, die die Periode bestimmt. In der T^t gilt der folgende
Satz: Sieht man von der identischen Substitution ah, so hat [A, B, C, D]
die Periode 2, 3, 4 oder 6, je nachdem die erste, zweite, dritte oder eine
der heiden letzten Kongruenzen (6) gilt. Man hat nämJich:
(7) F^ = [A^ +1, AB, AG, AD],
(8) F^ = [A' — A^—1, AB(A^+ l), A C (A^ + 1), 4D{Ä^ i- 1)]-
*) Man beachte, daß die Kongruenz a^ = 1 (i^iod 3) nur die Lösungen
E 1 und a ^ — 1 hat.
248 II> 3. Valentinergruppe und zugehörige Formen.
Für ^ = 0 folgt also F^ = 1, okne daß F= 1 wäre. Für Ä^l-j
gut ^2 ^ 1 = 0 und also F* = 1, ohne daß F^ = 1 wäre. Für A~l
(oder besser = — 1) folgt:
F^ = [A, —B, —C, —D] = F-i (mod 3),
und also ist F entweder die identische Substitution, oder es liegt die
Periode 3 vor. Ist A = j, so findet man:
A^~A^—l=j^A, A^ + A^ — h
so daß F^ = F-i wird, ohne daß F= 1 wäre. Also hat F die Periode 5.
Dasselbe gilt, wenn A = 1 -{-j ist, da man hier für F^ die Invariante j
und also die Periode 5 feststellt
Um nun für die einzelne Periode die Anzahl der zugehörigen
Substitutionen festzustellen, bemerken wir zunächst, daß die Zahl 3 die fünf
quadratischen Reste hat:
0, 1, 1-i, -1+i, -1.
Durch Bildung der Summen zweier quadratischer Reste findet man den
Satz: Die Kongruenz:
(9) B^ + D^ ^ a + hj (mod 3)
ist durch 17 bzw. durch 8 inkongruente Zahlenpaare B, D zu befriedigen,
je nachdem a -j- 6 j = 0 oder ^ 0 (mod 3) gilt.
Ist nun erstlich -4^0 und also die Kongruenz;
B^-^D^ = (l-fi)(C2_i) (j^od 3)
zu lösen, so haben wir C auf die fünf Reste (6) zu beschränken. Für
C = 1 haben wir 17 Lösungen, für die übrigen vier Werte C je 8; doch
liefern die acht Lösungen für C = 0 nur vier verschiedene Substitutionen,
da man hier noch einen gleichzeitigen Zeichenwechsel von B und D
vornehmen kann. Die Anzahl der Substitutionen mit A = 0 ist also 45.
Für J. s 1 ist die Kongruenz:
B^+D^ ^(l+j)(P (mod 3)
zu lösen. Für C = 0 hat man 17 Lösungen, für die übrigen acht Reste
je 8. Man findet also neben der hierher gehörigen identischen Substitution
noch weitere 80 mit A = 1. Für A ^ 1-j hat man die Anzahl
inkongruenter Lösungen der Kongruenz:
B' + D' ^ (1 -f i) (C^ ^ 1) (jnod 3)
abzuzählen. In den beiden Fällen C = +(1 —j) hat man je 17 Lösungen
und für die sieben anderen Reste C je 8, im ganzen also 90 Lösungen.
In den beiden letzten Fällen A = j und A = 1 -f j sind die beiden
Kongruenzen:
B' + D'^{l+j)(G' + ^J), B' + D'^il+j){C^+l+j) (mod 3)
Komplement ©ggo der Hauptkopgruenzgnippe dritter Stufe in der @cc. 249
zu lösen. Da j und —l~j quadratische Mchtresfee sipd. so stehen
rechts für alle neun inkongruenten Zahlen C glicht durch 3 teilbare
Zahlen. Für jeden der neun inkongruenten Beste C hat m^n demnach in
beiden Fällen acht inkongruerite Lösungen, im ganzen gomit 2 • 72 solche
Lösungen. Die Gesamtzahl inkongruenter Substitutionen ißt:
45 + 1 + 80 + 90 -f- 2 • 72 = 360,
und man gelangt zu dem Satze: Das Komplement der HauptJcongruenz-
gruppe dritter Stufe in der Gruppe ® ist eine Gruppe ©gg^ der
Ordnung 360, in der außer der identischen Suh^itution 45 Substitutionen der
Periode 2, 80 Substitutionen dßr Periode 3, 90 Suhstitutionen der Periode 4
und 144 der Periode 5 enthalfen sind.
§ 4. Zyklische und verwi^ndte Teiler der Gruppe ©ggo«
Die in der ©gg^, enthaltenen zj^klischen Teiler ergeben sich aus dem
Schlußsatze von § 3. Die Frage, inwieweit sie konjugiert sind,
entscheidet man durch Aufstellung der zugehörigen Xormalisatoren. IJrst-
lich Kefert die Substitution [0, 0, 1, Q] ei^en Teiler <3^, dessen Xor-
malisator aus allen Substitutionen V := [A, B, C, D] besteht, die die
Bedingung:
V'[0, 0, 1, 0] = [0, 0, 1, 0]- F (mod 3)
oder entwickelt:
[G, D, ~A, —B\ = [0, — A — A B] (mod 3)
erfüllen. Es gilt also entweder B ^ D ~ 0 oder ^ s C = 0, so daß
man zu den acht Substitutionen geführt wird:
[ [1 -i, 0, 1 -i, 0], [0, 0, 1, 0], [1 -;, 0, - 1 +i, Ol, [1, 0, 0, 0],
|[0, 3, 0, 1], [0, 1, 0, -ij, [0, i, 0, - 1], [0, 1, 0, i].
Diese Substitutionen bilden eine Biedergruppe ®^, die ersten vier aber
den in der Diedergruppe @g enthaltenen zyMi&chen Teiler (3^. Jede mit
[1 —j, 0, 1 —j, 0] vertauschbare Substitution muß auch mit [0, 0. 1, Oj
vertauschbar sein, also der @g angehören. Man zeigt, daß [1 — j, 0, 1 —j, 0]
die zyklische @^ zum Xormalisator hat, diese (5)^ aber di^ Dieder-^^.
Es ergibt sich der erste Satz: Alle 45 Substitutionen der Perlode 2 i,lnd
konjugiert, desgleichen alle 90 Sut>stittit;ionen der Periode 4,- man hat
45 konjugierte zyklische @^ nnd als ihre Norwiallmtoren 45 konjugierte
diedrische Teiler @g. Der einzelne Teiler (Sj^ ist stets in fünf ®g
enthalten, aber nur in einer Diedergruppe Ög als Xormalieiler
Unter den 80 Substitutionen der Periode 3 sind speziell die beiden:
(2) V, = [1. 1, 0, 1 - j], 7a = [1, 1, 0, - 1 -hj]
250 n, 3. Valentmergruppe und zugehörige Formen.
enthalten, die nicht Jconjugiert sind. Es gäbe sonst eine Substitution V,
die die Bedingung V-V^ = V-, -V (mod 3) oder ausführlich die
Kongruenzen:
Ä ~\-jB+-(i +jD) ~ ±{A -rjB — a +i)J5)^
A4- B-{l-j)C =±{Ä4-B -(l-i)O),
OJ^j)B + G-jD =±({l+j)B + C+jD),
-(l-j)^-C-fD =±{(]-j)Ä-^C^D)
befriedigen würde. Die Annahme des unteren Zeichens führt zu der
unbrauchbaren Folge Ä~B=C = D = 0. Gilt aber das obere Zeichen,
so folgt:
(1—j)^-fC = 0, D = 0,
worauf sich aus (5) S. 247:
—jB^ = 1, B- = 2j + 2 (mod 3)
ergibt. Indessen ist (2 j -j- 2) quadratischer Xichtrest, so daß F^ und V^
nicht konjugiert sind.
Aus der Kongruenz:
[1,B, 0, (l-j)B]-[l,B', 0, {l-~j)B']
= [1,B-4B\ 0, (i-j) (£ + £')]
ergibt sich der Satz: Die neun Substitutionen [1, B, 0, (1 —j)B] bilden
einen kommutativen Teiler ©g, der außer der identischen Subditution acht
Substitutionen der Periode 3, urüer ihnen Fj enthält. Ebenso bilden die
neun Substitutionen [1, B, 0, (— 1 -\- j)B] einen lommutativen Teiler @g
mit acht Substitutionen der Periode 3, unter ihnen V^. Diese beiden ©g
sind die Xormalisatoren der Substitutionen V^ und V^; denn man findet
für eine Substitution [Ä, B, C. D], die z. B. mit F^ vertauschbar sein soll,
die Bedingungen (1 —j) B = D, C = 0, was zu den neun Substitutionen
[1, B, 0, (1 —j)B] zurückführt. Man hat hiernach zwei Systeme von ^e
40 konjugierten Substitutionen der Periode 3, wobei das eine System F,
und das andere V^ enthält.
Es soll festgestellt werden, welche unter den Substitutionen der
Gestalt [1, B', 0, (1 —j)B'] mit [1, 1, 0, 1 — j] konjugiert sind. Es
ist also die Frage, ob es eine Substitution F = [Ä, B, G, D] gibt, die die
F[l, 1, 0, 1 -j] ~ [1, B', 0, (1 -~j)B']-r
oder ausführlich geschrieben die Kongruenzen:
(Ä-^jB-{l+j)D =±{Ä + B'[jB-(l+j)D]),
.3. ) Ä + B + {l-~j)C =±{B + B'[A-(l-j)C]),
C -{{1 +j)B +jD) ^ ±{G + B'[(l +j)B +jD]),
[(l-j)A-G + D =±{D+B' [(1 -j)A ^ C])
Teiler ®^, ©g, @^, @g und ©g in der Gruppe ©sgo- 251
befriedigt. Gelten die unteren Zeichen, so liefert die zweit;e und die mit
(j — 1) multiplizierte vierte Kongruenz:
Ä-^(l—j)C = B~B'{A-(l- j) C),
Ä+ (1 ~-j) C = —(l -j)D -- B' (A - (} -j) C).
Man findet also:
~B'~(1 -j)D
und leitet daraus die vier Kongruenzeni ab:
£ + (l-i)2) = 0, j^-(l+^-)D = 0,
(1 +i)i?+i2) = 0, £2^-1)2 = 0.
Die erste und dritte Kongruenz (3) ergeben damit A = 0, C = 0, während
man im Widerspruch damit ^us der Kongrupnz (5) S. 247 die Folgerung
A^ -{- G^ = 1 zieht. Also siad in (3) die unteren Zeichen nicht
brauchbar. Gelten die oberen Zeichen, so liefern die mit (1 4- j) multiplizierte
erste und die mit j multiplizierte dritte Kopgruenz (3):
(B' - 1)(:B + (1 -j)D) = 0, (B' T- 1){B + (1 ^j)I)) = 0.
Durch Subtraktion dieser Kongruenzen voneinander fplgt bei Benutzung
von (5) S. 247:
£ + (1 —i) D = 0, A^ ^ C^ = 1.
Die mit ((1 —j) A — G) multiplizierte letzte Kongruenz (3) ergibt jetz-t:
((1 -3)A- Gf = B' ((1 -jf A' -G') = - B- {A^ + G^) - - B\
und da — l quadratischer Rest von 3 ist, so folgt, daß aifch B'
quadratischer Rest von 3 sein muJ3. Wir gelangen zu dem Ergebnis: Unter
den acU Substitutionen [1, B, 0, (t —j)-B] mit B ^ 0 sind die vier
konjugiert, in denen B quadratibcher jR,esl pon 3 id, und weiter die vier mit
quadratischen NicUresten B, so daß die kojfimutative ©g je vier Suhdltu-
tionen aus den beiden Systemen von 40 Tconjagierten Subßtitutionen der
Periode 3 enthalt. Jede Substitution der Periode 3 is'f mit ihrer inversen
Substitution konjugiert. Wegen der letzten Angabe hat man nur zu
berücksichtigen, daß — 1 qup^dratischei' Rest von 3 ist. übrigens wird
man diese Entwicklung auf 4ie zweite Substitution (3) leicht Sphritt für
Schritt mit dem gleichen Ergebnis übertragen.
Da die einzelne kommutative ©g je vier Si;bstiti)itionen aus beiden
Systemen von je 40 konjugierten Substitutionen der Periode 3 enthält
und jede Substitution dieser Periode nur in einer Gruppe @g (i^rem
Xormalisator) enthalten ist, so ergibt sich "v^eiter der Satz: Man hat in
der ®3g(, zehn kommutative konjugierte Teiler ®^, die also als NormaU-
satoren Teiler @3g der Ordnung 36 besitzen müssen*) Der zur @g der
Substitutionen [1, B. 0, (1 ~ j) B] gehörende Xormalisator ist durch
) Dies ist m Übereinstimmung mit den Sy^owsehen Setzen in I, 294.
252 II, 3. Valentmergruppe und zugehörige Formen.
7) = (1 —j)B charakterisiert. Er enthält die neun Substitutionen der
Periode 2:
(4) [0,B,l,(l-3)B]
und weiter die 18 Substitutionen der Periode 4:
(o) [l-.j,B,\-j,{l-3)Bl [l-j. 5, -1+i, (1-i)^]-
Die neun Substitutionen (4) bilden mit der ©g für sich einen Teiler @^g.
In der ©gg^ finden sich demnach zehn konjugierte Teiler ©3g und in ihnen
ebenso viele konjugierte Teiler ©,^g. Die einzelne zyklische ©^ tritt immer
in zweien unter den zehn konjugierten ©3g auf.
SoU die Substitution [j, 1 —j, 0, 0] der Periode 5 mit [Ä, B, C, D]
vertauschbar sein, so muß:
[jA-(l+j)B, (l-j)Ä + jB, jC-{l^j)D, (l-j)C+iD]
^[jA-(l+j)B, {l-j)Ä + jB, jC + {l+j)D, -{l-j)C+jD]
zutreffen. Hieraus folgt C = 0, D = 0, und die einzigen Substitutionen,
die diese Kongruenzen befriedigen, sind die fünf Potenzen von
[j, 1 -j, 0, 0],
wie man leicht durch die Aufsuchung aller Lösungen von A^ — jB^ = 1
feststellt. Die Substitution [j, 1 —j, 0, 0] ist also eine unter 72
konjugierten, so daß die gesamten 72 Substitutionen mit der Invariante j
[vierter Fall (6) S. 247] konjugiert sind und insbesondere je zwei inverse
unter ihnen konjugiert ausfallen. Genau die gleichen Aussagen gelten
von den 72 Substitutionen mit der Invariante (1 -j- j), die als die zweiten
Potenzen der Substitutionen mit A == j darstellbar sind. Übrigens wird
[j, 1 —j, 0, 0] durch [0, 0, 1, 0] in die inverse Substitution [j, — 1 +i,
0, 0] transformiert, so daß aus diesen beiden Substitutionen eine Dieder-
gruppe ©^0 erzeugt wird, die der Kormalisator des aus [j, 1 —j, 0, 0]
entstehenden zyklischen Teilers ©^ ist. Wir haben damit das Ergebnis
gewonnen: In der ©^g^^ sind 72 konjugierte Substitutionen der Periode 5
mit A = j und ebenso vi^le konjugierte Substitutionen der gleichen Periode
mit A = 1 -4-j enthalten; sie bilden 36 konjugierte zyklische Teiler ®.^,
denen als Xormalisatoren ebenso viele konjugierte Teiler ©j^^ vom Dieder-
typus zugehören.
Es läßt sich jetzt leicht zeigen, daß die G-ru^pe @3g^) „einfach" ist.
Ein ISTormalteiler enthält nämlich vom einzelnen System konjugierter
Substitutionen entweder keine oder alle Substitutionen. Dabei wird,
faUs die Substitutionen der Periode 4 auftreten, auch das System der
45 Substitutionen der Periode 2 im Normalteiler enthalten sein. Ebenso
werden entweder alle 144 Substitutionen der Periode 5 vorkommen oder
keine. Die Ordnung ^ eines Normalteilers ist demnach in der Gestalt:
,tt = 1 + 45 £, + 90 s^ £2 + 40 £3 + 40 £, + 144 s^
Teiler ©^g' ®36. ®Sf, ®io «nd ®24 iQ der Grappe ©360- 253
darstellbar, wo die e gleich 0 oder gleich 1 sind. Füi einen ecjiten
Teiler ist zunächst s^ = 0, sp daß ^ teilerfremd gegen 5 und also Teiler
von 72 sein muß. Somit ist auch s^ -— 0, und man hätte e^, a^, £^ so
zu bestimmen, daß:
ja = H- 45 f j ^ 40 £3 + 40 £,
in 72 aufgeht. Hieraus folgt s^ = 0, £3 = 0, s^ = 0, womit die
Behauptung bewiesen ist.
§ 5. Tetraeder-, Oktaeder- und Ikosaedergruppen in der (Sgg^,.
Die Forderung der Vertauschbaykeit der beiden Substitutiqnen
[0, 0, 1, 0], [0, B, G, B] der Periode 2 führt zu den Kongruenzen:
(1) C - 0, B- ^ 1)2 - — 1 — j (mod 3)
oder zu i? = 0, D = 0. Während die beiden letzten Kongruenzen zur
Substitution [0, 0, 1, 0] führen, werden die beiden Kongruenzen (1) von
den weiteren vier Substitutionen:
(2) [0, 1, 0, j], [0, 1, 0, - j], [0, J, 0, 1], [0, j, 0, - 11
und nur von diesen befriedigt. Es handelt sich um die vier
Substitutionen der Periode 2, die neben [0, 0, L, 0] in der Dieder-Ö)g (1) S. 249
enthalten sind. Der Struktur der Dieder-@g entsprechend gelangen wir
zu zwei jedenfalls in der @g nicht kon|^g•ierten Vierergruppen:
(3) [0,0,1,0], [0, 1, 0, j], ^0. j, 0, -1], [1,0,0,0],
(4) [0. 0, 1, 0], [0, 1, 0, -j], [0, j, 0, 1], [1, 0, 0, 0].
Da die einzelne Substitution der Periode 2 in zwei Yierergruppen
auftritt, so haben wir im ganzen 2 • 45 : 3 = 30 Vierergruppen in 4er ^^f^^,
die entweder alle konjugiert sind ode^ zwei Systeme zu je 15
konjugierten @^ liefern. Im ersten Falle hat die einzelne ©^ einen Xorm3,li-
sator @j2> der bekanntlich den Tetraedertypns besitzt, im zweiten Falle
einen Xormalisator ©3^ vom Oktaedertypus. Der zweite Fall liegt vor,
da der lN[ormalisator, wie wir schon wissen, eine Dieder-Öjy enthalt: I)ie
^3go enthalt zwei Sydeme von je 15 Iconjuglerten Teilern ©g^ vom QMaeder-
ty'ßus und in ihnen dann naturlieh auch zwei Systeme von je 15 honju-
gierten Tetraedergruppen (5)^2 '^^ Vierergrappen &^.
Die bisher befolgte Methode, von den zyklischen Teilern aus durch
Herstellung von Xormalisatoren zu nichtzyklischen Teüern zu gelangen,
versagt nun bei den wichtigsten Teilern unserer ©330, nämlich bei zwei
Systemen von je sechs konjugierten Teilern (^^^ vo^n Ikosaedertypus. Um
sie zu finden, knüpfen wir an die beiden Substitutionerf:
(5) S - [1 +j, 1 +j, 0, 0], T - [0, 1, 0, -j]
254 II) 3. Valentinergruppe und zugehörige Formen.
der Perioden 5 und 2 an *) und setzen diese Substitutionen in folgender
Art in eine neue Gestalt: Die ganze algebraische Zahl:
(6) £=-i + (l-i)Vi
genügt mod 3 der Kongruenz:
(7) £^ = 1,
und für ihre Potenzen gilt:
^ l e^-j + a-i)yi ^' = (1 +i)-(1 +3)U
^^ [s'^(l^j) + (l-^j)fj, £^H -i-(l-j)Vi.
Hieraus folgt weiter:
J 8 + s^ = j, £-^ + £3 = — 1 —i,
(9) £-£^-£^ + £' = 1 +2j =- Vö",
sowie durch Multiplikation der ersten und vierten Kongruenz (9):
£2 — £3 ^ — ys j Vi-
Die beiden letzten Kongruenzen setzen wir in die Gestalten:
(10) -^^-^'- -^^-'^'-
Mit Hilfe der eingeführten Zahl e schreiben sich die Substitutionen (5) so:
£ — £*
(11) o _ /«=> ^\ ^ - I ^ '
\ ^5 V5
Hier sind wir zu den erzeugenden Substitutionen (1) S. 42 der Ikosaeder-
gruppe zurückgeführt, wobei an Stelle der damaligen Gleichungen jetzt
Kongruenzen mod 3 treten und £ mod 3 die Rolle einer fünften
Einheitswurzel spielt.
Eine entsprechende Betrachtung kann man an die beiden
Substitutionen :
(12) s = [l-^i, i+i, 0,0], r = [o, 1, o,j]
anknüpfen, wobei £ im bisherigen Sinne gebraucht wird. Man gelangt
wieder zu den Gestalten (11), nur daß in der zweiten Substitution der
zweite und dritte Koeffizient entgegengesetzte Zeichen haben**).
*) Sie liefern m S • T = [1, 1 -\-j, —j, — 1] eine Substitution der Periode 3.
Hieraus wurde nach einem bekannten Satze der Gruppentheorie (vgl. „Modulfunkt.'-
I, 456) bereits folgen, daß S und T eine Ikosaeder-@60 erzeugen.
**) Bei der S. 42 betrachteten Ikosaeder-@go hatte man also auf die Sub-
stitutionsvanable die Spiegelung an der imaginären Achse vorzunehmen, um die
neue Gestalt der Gruppe zu erhalten.
Ikosaedrische Teiler ©go in der Gruppe ©^go- 255
Die beiden so erhaltenen Ikosae4ergnippen haben zwar die
Substitution S gemein. Sie sind aber nicht identisch, da sonst jn ihnen a,uch
die Substitution der Periode 4:
T'.T-[l~i, 0, 1-j, 0]
auftreten würde, was ausgeschlossep ist. Die einzelne @g^ ist ihr eigener
J^ormalisator *) und gehört demnach einem System von sechs kopju-
gierten Teilern ©g^ an. Da die ©g^ sechs zyklische ©^ enthält und im
ganzen 36 konjugierte ©^ in der ©gg^ auftreten, so findet sich die
einzelne ©- nur in einer unter den sechs konjugierten ©g^. Die beiden
oben aufgestellten ©g^ sind demnacli nicht konjugiert: In der Gruppe ©gg^
treten swei Systeme von je sechs konjugierten Teilern ©g^ vom Ikosaeder-
typus auf, die durch die beiden aus den Substitutionen (5) bzic. (12) su
erzeugenden ©g^ repräsentiert iverde^.
Indem man vom einzelnen echten Teiler nötigenfalls wiederholt zu
seinem ^^Tormalisator aufsteigt, muß man, da 4ie ©ggo eijifach ist, La jedem
Falle zu einem echten Teiler (^^ höchster Ordnung gelangen, der sein
eigener J^ormalisator ist. Dieser ist dann einer unter t konjugierten
echten Teilern, wo ^-t = 360 ist. Dje t Teiler ©^ haben, da die 0^^^^
einfach ist, als Durchschnitt nur d;e ©j. Zufolge des zweiten Satzes in
I, 335 gelangt man von diesep Teilern 3,us zu einer Darstellung der ©gg^
als transitive Permutationsgrüppe des Grades t- Also ist ^ ^ 6, und
man erkennt, daß die echten Teiler ©„ eine Ordnung a ^ 60 haben.
Die Ikosaedergruppen ©g^ der beiden Systeme sind (lie echten ^eiZer höchder
Ordnung der ©sgo? '>^d diese Gruppe ist als trandtive Perm^,tationsgruppe
sechsten Grades darstellbar, d. h. sie ist isomorph mit der alternierenden
Gruppe ©3go dieses Grades^*) Als solche werden ^h die ©gg^ bald
unmittelbar darstellen.
§ 6. Kongruenzgruppen vom Index 6 und zugehörige (Jleichungen
sechsten Grades.
Den zwei Systemen von Ikosaedergruppen ©g^ ipnerhalb der (^^gg^
entsprechen zwei Systeme von je sechs konjugierten Kongfuenzgruppen
dritter Stufe vom Index 6 innerhalb der in § 1, S. 241 ff., erklarten
Gruppe ©, die wir ihrem Indes: entsprechend mit ©(g) bezeichnen wollen.
*) Es wird sogleich bewiesen werden, daff die ©go die echten Teiler
höchster Ordnung der ©330 sind.
**) Die erste Erzeugende (10) S. 246 von der Periode 5 ist m einer und pur
einer ©go des einzelnen Systems enthalten. Ihr entspricjit alsp einß Pennutation,
bei der eine ©go sich selbst entspricht, wahrend die anderen fünf eine Permutation
der Periode 5, d. h. eine zyklische, mithin gerade Permutation erfahren. Die
Erzeugende T tritt in zwei Ikosaedergruppen ©go des einzelnen Systems auf.
Sie transformiert also diese beiden ©go ip sich und permutiert die übrigen vier ©go
zu Paaren, so daß wieder eine gerade Pennutation vorliegt. Die ©360 als
Permutationsgruppe sechsten Grades ist also diejenige der geraden Permutationen.
256
II, 3. Valentinergruppe und zugehörige Formen.
Wir stellen zunächst fest, daß die beiden Systeme dieser ©(g) innerhalb
der durch Spiegelungen erweiterten G-ruppe ® Jconjugiert werden.
Transformieren wir nämlich durch die Spiegelung an der imaginären ^-Achse,
so läuft dies darauf hinaus, da£ in der einzelnen ^-Substitution der zweite
und der dritte Koeffizient Zeichenwech&el erfahren. Hierbei tauschen
sich die Erzeugendenpaare (5) und (12) S. 253ff. zweier in ® noch nicht
konjugierten ©g^ in der Tat aus.
Wählen wir eine ©g^, die die unter (10) S. 246 gegebene erste
erzeugende Substitution S der Gruppe ® nicht enthält, so sind die fünf
den Punkt e^ in Fig. 29, S. 244, umgebenden Dreieckspaare bezüglich
der @(6) inäquivalent. Wir fügen noch, wie in Fig. 30, das Dreieckspaar
e'(, e^ e-i an und erhalten dann bei geeigneter Zusammenordnung der
Randkurven den DB einer unserer ©(g). Jedenfalls gehören die Seiten 60^2
und 60 4 zusammen. Im übrigen muß die Zusammenordnung
unsymmetrisch sein. Es zeigt sich, daß nur zwei Zusammenordnungen
brauchbar sind, nämlich die in Fig. 30 angegebene und die bezüglich des
Kreisbogens e^ e^ e'^ zu ihr
symmetrische. Führen wir nämlich die
Funktion L (^) ein, die das
Doppeldreieck der ^-Halbebene auf die
schlichte i-Ebene abbildet, und zwar
derart, daß in denEckpunl^ten e^, ^i) ^o
bzw. die Werte i r= 0, 1, 00
stattfinden, so wird der DB der Fig. 30
auf eine sechsblatterige Biemannbche
Flache über der L-Ebene abgebildet,
die folgende Verzweigung hat: Bei
X = 0 liegen ei/t zweiblätteriger tmd
ein vierblatterlger VerzweigungspunM,
bei L = 1 hat man zwei zweiblätterige
VerzweigungbpunUe und zicei isoliert verlaufende Blatter und bei L =: 00
einen ftinf blätterigen VerzweigungspunU und ein isoliert verlaufendes Blatt.
Damit haben wir eine bei unserem Dreiecksnetze zulässige Verzweigung
gewonnen. Man gewinnt die zur eben beschriebenen Fläche symmetrische
Fläche, wenn man die durch Spiegelung am Kreise e^ e^ e'^ aus Fig. 30
entstehende Zuordnung zugrunde legt. Man wird leicht feststellen, daß
alle anderen unsymmetrischen Zuordnungen der Randkurven des DB zu
unzulässig verzweigten Riemann sehen Flächen hinführen. Man hat
demnach in Fig. 30 den DB einer der zwölf Eongruenzgruppen ©(g) wirklich
gewonnen.
Grundlegend ist nun, daß die geioonnene sechsblatterige Biemannbche
Flache das Geschlecht j5 = 0 hat. Es existiert demnach eine eindeutige
automorphe Funktion x{^) der ausgesuchten Gruppe ©(g), die im DB
derselben jeden komplexen Wert nur einmal annimmt. Diese Funktion r
genügt als algebraische Funktion von L einer Gleichung sechsten Grades,
Berechnung der beiden ßesolventen sechsten Grades. 257
und umgekehrt ist L eiae rationale Funktion sechsten Grades von t.
Die Funktion r aber wollen wir dadurch eindeutig festlegen, daß wir
auf der Riemann sehen Fläche bei X = oo im isolierten Blatte r :^ 0
und ebenda im fünf blätterigen Verzweigungspunkte r = oo vorßchreiben,
während bei X = 0 im vie^-blätterigen Verzweigungspunkte r = 1
zutreffe. In bekannter Weise leiten wir da^n aus der Verzweigung der
Fläche für die rationale Darstellung von L durch, r den Ansatz ab:
(J) X:(X-1):1 = (r-^dfix-iy-.iT^^ar ^ß){r^^yx + 8^):hx.
Durch Differentiation nach r findet man aus (1)
hr^~ ^ {rAra){z— If (5 r} ~f (3 a - 1) r + fl),
6 r^ ^ = (r^ -^ j^ r + ö) (5 r* + (4 a + 3 j;) ^3 -f (2 a j; + 3 ^ + ö) r"
+ ßfz- ß8)
Die beiden rechts stehenden ganzen Funktionen sechsten Grades von r
sind identisch. Da indessen (r^ -\- yr -^ 8) keinen der linearen Faktoren
(r 4- a), (r — 1) enthalten kann, so galten die beiden identischen
Gleichungen :
5 r^ + (3 a — t) r + a = 5 (r^ -f j; r -f- ö),
oz^^{4.a^^y)r^^{2ay + ^ß^8)z^^ßyr-ß8 = 5(r~f «)(r- 1)^.
Die Vergleichung der Koeff:tzienten gleich hoher Potenzen rechts und
links liefert zur Bestimmung der unbekannten Konstanten a, a, ß, --i die
Gleichungen:
3a — 1 = 5 j^, a = ö8, 4a-]-3j'=5a — 15,
2aj; 4-3^ +d = 15—15a, ßy=-.löß — 5, ß8=oa.
Da a und 8 von 0 verschieden sind*), so folgt aus der zweiten und
sechsten Gleichung ß = 25. Aus der ersten, dritten und fünften
Gleichung folgt dann weiter;
(2) a = l(2a — 9), j; r^ |(3 a — 1), ö = | a.
Die Einführung dieser Ausdrücke und des Wertes ß in die vierte
Gleichung ergibt für a die quadratische Gleichung:
a^ -\-llß~\- H4 = 0.
Wir erhalten, wie es sein mi;ß, zwei W'erte a:
a = -i(ll±3iyT5),
sowie dann weiter aus (2) die entsprechenden Werte a, y, 8. Den
Koeffizienten h gewinnt man aus (]), indem paan -p = 1, X = 0 einträgt und
die inzwischen berechneten Werte a. a, ß, •■- beputzt
=^) Der Wert t = 0 findet bei L = oo statt,
icke, Algebra. II.
258 II> 3. Valentinergruppe und zugehörige Formen.
Auf diese Weise sind wir zu dem folgenden grundlegenden Ergebnis
gelangt: Die zu den leiden Systemen von je sechs konjugierten
Kongruenzgruppen dritter Stufe des Index 6 gehörenden automorphen FunUionen x (^)
genügen als algebraische FunUionen von L den leiden Gleichungen sechsten
Grades:
(3) X:(X— 1): 1 = 53(2r—(ll±3iVr5))ä(r— 1)*
:(5^2_(4o + 6iVT5)r~f 125) (10 r'
- (35 + 9 i Vl5) r-(11 ± 3 i Vl5)f
: + 2iO-3*-*Vl5r.
Verstehen wir unter yi die quadratische Irrationalität:
1 - n^is
(4) n = —^—,
so läßt sich die Gleichung (3) für das obere Zeichen in die Gestalt setzen:
(5) i:(i-l):l = 53(r-(3^-7)f (r-1)*
:(5Tä+2(67;-23)r-rl2o)(5r^-f (9 7?-22)r
:—12*(2 7;-l)r.
Die zweite Gleichung (3) geht aus (5) hervor, wenn man ?^ durch die
konjugierte Zahl ^ ersetzt.
§ 7. Galois scher Körper der Gleichungen sechsten Grades.
Unter den beiden erhaltenen Gleichungen sechsten Grades arbeiten
wir zunächst mit der Gleichung (5), der wir die Gestalt geben:
(1) 53(r~f (3,?-7))^(r-l)*~f 12*(2,^-l)ir=0.
Wegen der Bauart der Koeffizienten hat man hier zum rationalen
Körper 9^ zunächst die quadratische Irrationalität yi zu adjungieren und
nenne den entstehenden quadratischen Zahlkörper (9^, ti) kurz ^. Sodann
ist ^ durch Adjunktion von L zum Funktionenkörper (^, L)
auszugestalten. Der Durchschnitt der sechs Ikosaedergruppen des zur
Gleichung (1) gehörenden Systems ist die @j, und entsprechend ist der
Durchschnitt der sechs den ©g^ zugehörigen Kongruenzgruppen dritter
Stufe des Index 6 die Hauptkongruenzgruppe dieser Stufe des Index 360.
Bie Galois sehe Gruppe [Monodromiegruppe]*) der Gleichtmg (1) ist
demnach die alternierende Permutationsgruppe ©gg^ sechsten Grades.
*) Die Quadratwurzel der Diskriminante der Gleichung (1), d. h. ihr
Differenzenprodukt ist als Funktion der Gesamtgruppe @ jedenfalls eine rationale
Funktion von L. Nur ist die Frage, ob die Koeffizienten dieser rationalen
Funktion dem Körper ^ angehören, oder ob noch eine numerische Quadratwurzel
zu adjungieren ist.
ßiemannsehe Piaehe Fgso des Gresehleehts 10. 259
Wir nennen die sechs Wurzeln unserer Gleichung t-^, t^, •■ -, Tg. Der
Galois sehe Körper dieser Gleichung entsteht durch Adjunktioii von r^,
Tg, •••, Tg zu (^, L). Da indessen L rational in jedem t ist, so wird der
Galois sehe Körper bereits als Körper (^, t^, t^, •••, Tg) gewon^ien. Man
hat somit in t^ (g), t^ (g), • • •, Tg (£) ein Fuiiktionssystem für dje
Hauptkongruenzgruppe dritter Stufe, die wir ihrem Ir|.dex entsprechend durch
@(36o) bezeichnen. Auch ohne daß wir den DB dieses Xormalteilers
wirklich zeichnen, ist einleuchtend, daß er durch die Funktion L (^) auf
eine SQO-hlätterige Biemannsehe Fläehe über der L-Ehme abgebildet wird,
die nur bei i = 0, 1, oo verzweigt ist, und zwar trägt s:|e bei i == 0
90 vierblätterige Verzweigu|agspi;nkte, 180 zweiblatterige bei i == 1
und 72 fünf blätterige bei i := cx:>. Hieraus folgt nach bekannter Regel
(vgl. Gleichung (5) S. 112), daß cl,ie SBO-hldttertge Biemannsci^e Flache
das Geschlecht p = 10 hat.
Der DB des ^ormalteilers ©(seo) wird durch alle ^-3ubsiitutionen
in sich transformiert. Demgemäß gpstatiet dip 360-blätterige Rieraannsche
Fläche den mod 3 inkongruenten Substitutio^ien entsprechend 360
Transformationen in sich, für die wir zunächst die Darstellung durch die
360 geraden Permutationen der t^, Tg, •••, Tg besitzen. Das Ziel der
nächsten Entwicklung ist, die Gruppe der 360 Trg,nsfoimationen der
Riemann sehen Fläche in sich erhejblich einfacher darzustellen.
Wir beweisen zunächst, daß d^e Flache nicht hyperelliptl,sch Sßin Jcann.
Wäre sie nämlich hyperelliptisch, so würde auf ihr eine zweiwertige
Funktion ^(g) existieren, die entsprechend den Transformationen der
Fläche in sich entweder eine 'B^qq oder eine ©^g^ line£|,rer Substitutionen
von z liefern würde. Gruppen ©^g^ oder ©gg^ linearer Substitutionen einer
Veränderlichen ^ existieren indessen nicht (vgl. S. 35).
Auf unserer 360-blätteiigen Rienc^ann ^chen Fläche, die wir kurz
durch Fggo bezeichnen wollen, liefern ni(.n die „60-wertigen" t (^)
keineswegs das einfachste Funktiopssysfcem. Die zehn Verhältaisgrpßen (p^^,
^3' *■•> 9io' ^^^ °^^^ ^ bekannter Art den zehn linear-unabhängigen
Differentialen der ersten Gattung proportional setzt (vgl. „ Modidfunkt.'•
I, 543 ff. und II, 493 ff.) liefern hc^ ihren Quotienten bereits nur noch
18-wertige Funktionen. Setzt man die (p^, (p^, •••, 9)5^ ^^^ homogene
Koordinaten eines Raumes Rg von neui^ Dirpiensionen an, so wird (vgl.
„Modulfunkt." I, 569ff.) die Fläche Fsg,, auf eine Kurve 18*^" Grades
im Rg, die sogenannte „NormalJcurve der (p", abgebildet, die entsprechend
den Transformationen der Fläche in sich 360 eine G-rußße Uldertde
Kollineationen in sich erfährt. 4-ber selbst hiprmit haben wir noch
nicht das einfachste Funktionssystem der Fgg^ erh^ten.
Eine Verbesserung könnep wir zunächst auf folgende Art erzielen:
Die in den sechs Ikosaedergruppen des bevorzugten Systems enthaltenen
Tetraedergruppen sind alle konjugiert. Da in jeder Ikosaeder-^g^ fünf
Tetraeder-@j3 auftreten, an solchen ©^^ a,ber zwei Systeme von je
15 konjugierten Teilern in der @3go auftreten, so ist die einzelne
17*
260
II, 3. Valentinergruppe und zugehörige Formen.
Tetraeder-@j2 stets in zwei ©g^,, und zwar als deren Durclisclinitt enthalten.
Kombiniert man die sechs Jconjugierten Kongruenzgruppen dritter Stufe @(g)
in den 15 möglichen Arten zu Paaren, so ist der Durchschnitt der teiden ®(g)
des einzelnen Paares eine Kongruenzgruppe dritter Stufe @(3o) des Index 30,
und es entsprechen die in dieser Art entstehenden 15 konjugierten Gruppen (S)(3o)
den 15 Tetraeder-®^^ des einen in der ©gg^ enthaltenen Systems.
Einen DB für eine dieser Gruppen ©(30) kann man in der in Fig. 31
gegebenen sternförmigen Gestalt annehmen*). Die ©(30) ist der
Durclisclinitt zweier Gruppen ©(g) und ©(g), deren DB durch starkes Ausziehen
bzw. Punktieren der Ränder und ihrer Zuordnungen hervorgehoben sind.
Je fünf Dreieckspaare, die kranzförmig um den Mittelpunkt der Fig. 31
liegen, sind, bezüglich der ©(g) äquivalent, erweisen sich jedoch bezüglich
der ©(g) als inäquivalent, so daß tatsächlich keine zwei unter den
80 Dreieckspaaren bezüglich .des Durchschnitts ©(30) äquivalent sind.
Die Zuordnung der Randkreise ist zweimal durch Pfeile angedeutet,
übrigens durch Buchstaben in der Art, daß a auf a', h auf h' usw. bezogen
ist. Über der i-Ebene liefert dieser DB eine 30-blätterige Riemannsche
Fläche, die bei i = 0 einen zweiblätterigen und sieben vierblätterige
Verzweigungspunkte hat, bei i =z 1 vierzehn zweiblätterige und bei
L = OD sechs fünfblätterige. Hieraus ergibt sich der wichtige Satz,
*) Die Kreisbogendreiecke sind hier so gezeichnet, daß ihr gesamtes Netz
die Flache eines Kreises, nicht die positive ^-Halbebene, überspannt.
Sechsfach unendliche Funki(;ionenschar auf 4er Fl^-che F^go- 261
daß das Gebchlecht dieser Fläche p ^ 1 id; es handelt sich hier um
eine Grenzkreisgruppe der Signatar (0, 1; 2, 2, 2).
Zu den Gruppen ©(g)» ®(6) mögen dieFunlrtionen z^ (g), t^{^) gehören.
Die Funktionen haben ihre ISTullpunkte und Pole ausschlieJBlich in den
mit e bezeichneten Punkten des Dß dei &(so,) ■ I^ ^i liegt ein l^^uUpunkt
fünfter Ordnung von r^ (g) und ein Pol* erster Ordnung von r^{^), in e.^
umgekehrt ein XuUpunkt fünfter Ordnimg von r^ (^) und ein Pol erster
Ordnung von r^ (g). In e^, e^, e^ und e^ aber liegen übpreinstimmend
Pole erster Ordnung beider Punkt:|.onen, so daJ3 ihr Quotient dort endlich
und von 0 verschieden ist. Hiernach ist dej Quotient von z^ und r^,
für den man aus (1) die Darstellung:
/ON :^ ^ (^2 + '^y — ")- (t^ — 1)'
ableitet, eine sechswertige Funktion iip. PB der @(3o), die im Punkie e^
einen Pol sechster Ordnung und in e^ einen XuUpunkt dj|.eser Ordnung
aufweist, im übrigen aber endlich und von 0 verschieden ist. Auch die
Quadratwurzel des Quotienten (2) ist, wie 3,us der rechte^. Seite dieser
Gleichung hervorgeht, eine Funktion dpr Gruppe ©(so)- Doch gilt dies
nicht mehr von der sechsten Wurzel ur^seres Quotienten. Diese ist 2;war
auf der aus dem DB entstehenden Rien^ann sehen Fläche deß Geschlechtes
p =z 1 unverzweigt, aber nicht mehr eindeutig, da sie sonst pine einwertige
Funktion auf dieser Fläche sein würde. ,Es handfelt sich um eine
,, WarzelfunUion' auf der Fläche, die sich gegenüber den Substitutionen
der ©(30) erst bis auf multiplikative dritte Einheitswq.rzelü repi^oduziert.
Unverändert bleibt die sechste Wurzel bei den Substitutionen desjenigen
in der ©(30) enthaltenen Xoi-malteilers vom Index 3, der dem Xor^nal-
teiler ©^ vom Vierertypus innerhalb der Tetraeder-©j2 entspricht. Sieht
man zwei zueinander reziproke Quotienten als nicht wesentlich
verschieden an, so ergibt sich der Satz: Die lo webenüich verscMedeneu
Quotienten der sechs Verhaltnisgrbßen:
(3) ' V^ fe V^ VpT 1h fe
sind eindeutige automorphe FunMion^n derjenigen 15 };onjagierten Kongruenz-
gruppen ©(90) des Index 90, die den 15 hoßjuglßrten Vierergruppen de»
einen Systems entsprechen, und zwar dnd sie auf den zugeJwrigen DB
dreiwertige Funktionen.
DaJ3 die sechs Verhälti^isgröJBen (3) linear-uuäbihang^g sind, liann
man ohne besondere Mühe aus ihrem Verhalten gegenüber den Substitutionen
der ©3gQ entnehmen. Dagegen ist nur durchweine etwas weitergehende
funktionentheoretische Untersuchupg beweisbar, daß jede FunMlon der
Hauptlcongruenzgruppe ©(360)7 ^«"ß ^>^* DB dicber Gruppe zwölf wertig ist
262 III 3. Valentinergruppe und zugehörige Formen.
6
und ihre Pole in den zwölf NullpunUen von Vr^ Mt, in der sechsfach
unendlichen Schar der Funktionen:
6 C 6
W 6
mit den Parametern % darsleühar ist*).
Dies vorausgesezt kommen wir nun leicht durch Anwendung zweier
bekannter Sätze der Theorie der algebraischen Funktionen**), nämlich
des Riemann-Roch sehen Satzes und des Brill-Noether sehen
Reziprozitätssatzes, zum einfachsten Funktionssystem der Hauptkongruenzgruppe ©(seo)-
Xach dem ersten Satze gilt folgendes: Gibt man m Punkte auf einer
Riemann sehen Fläche des Geschlechtes j5, so enthält die allgemeinste
Funktion, die in jenen m Punkten Pole erster Ordnung hat, (m —J5 + ^ + 1)
willkürliche Konstante homogen und linear, wo t die Anzahl
linear-unabhängiger Verhältnisgröi3en (p ist, die in jenen m Punkten verschwinden.
In unserem Falle gilt m = 12, j5 = 10 und ^ = 3; wir haben eine
sechsfach unendliche Schar von zwölfwertigen Funktionen (4). Im
Sinne der geometrisch eingekleideten Theorie der algebraischen Funktionen
setzt man die sechs Gröi3en (3) zu homogenen Koordinaten eines Raumes
von fünf Dimensionen. In diesem Baume erscheint dann die Biemann sehe
Fläche Fgeo abgebildet auf eine irredudble Kurve zwölften Grades, die
der @3gQ entsprechend durch 360 KoUineationen in sich übergeführt wird.
Diese Kollineationsgruppe, die wir bald explizite darstellen werden,
besteht aus den 360 geraden Permutationen der Koordinaten, die dabei
in gewisser Art noch multiplikative dritte Einheitswurzeln annehmen.
Gebrauchen wir m, p, t vcn. eben angegebenen allgemeinen Sinne, so
hat der Brill-Xoethersche Satz folgenden Inhalt: Setzt man:
m' ■=z '2 p — 2 — m. t' = m — p -\-1 -\- 1,
so folgt aus dem Auftreten einer ^'-fach unendlichen Schar w-wertiger
Funktionen stets die Existenz einer ^-fach unendlichen Schar w'-wertiger
Funktionen, die zur ersteren Schar in einem Verhältnis der Reziprozität
steht. In unserem Falle ist w' = 6 und ^ = 3. Es ergibt sich der
grundlegende Satz: Auf der Biemann sehen Fläche Fggo existiert ein
System von drei Yerhdltnisgrößen x^, x^, x^, deren Quotienten sechswertige
*) Es handelt sich im Sinne der Theorie der algebraischen Funktionen um
eine sechsfach unendliche Vollschar von Spezialfunktionen (vgl. die gleich folgenden
Jv'^achweise). Die Richtigkeit des Satzes ergibt sich aus dem folgenden independenten
Aufbau der Valentinergruppe. Die unten zu gewinnenden beiden „allgemeinen"
Resolventen sechsten Grades des Formenproblems der Valentinergruppe werden
uns in der Tat für einen gewissen Spezialfall zu unseren beiden Gleichungen
sechsten Grades (3) S. 258 zurückfuhren.
**) Vgl. „Modulfunkt." I, 549 und 553.
Erste Erklärung der Valenünerginippe. 263
FunMonen der Fläche sind; es besteht somit zwischen den x eine homogene
irredudbele Belaiion sechsten Grades:
(5) Fix^, sp^, x^) = 0,
eine ebene Kurve sechsten Grades darstellend, die der ©gg^, entsprechend
durch 360 Kollineationen in ßich übergeführt wird. Diese Kollineatjons-
gruppe @3g(j ist 1889 auf anderem Wege von Valentiner gefunden*) und
soll nach ihm benannt werden. Die spätere Literatur über diese Grappe
wird noch genannt. Die sechs Yerhältnisgrößen (3) sind proportional
zu gewissen sechs linear-unabhängigen homogenen linparen Verbindungen
der Quadrate und Produkte xl, xl, a;|, x^x,_^, x^ap-^, x^x^ der x. Als, die
zehn VerhältnisgröJ3en (p kann man die Verbindungen dj-itten Grades:
xl, xi, xi, X1X2, Xi x^, xl x^i X2X1, xixi, a;|a;2, XiX^xi
der X benutzen. Daß sowokl diese, wie aifch die eben genannten sechs
quadratischen Verbindungen linear-unabhängig sind, geht aus der Tatsache
hervor, daß die niederste zwischen den v bestehende Beziehung die
irreduzibele Gleichung sechsten Grades (5) ist.
§ 8. Herstellung der Valentinergruppe.
Bei der Aufstellung der Vajentir^ergruppe kann man verschiedene
Koordinatensysteme benutzet^, je nachdem man beabsichtigt, 4en einen
oder den anderen Teiler der Gruppe besonders einfach darzustellen. Wir
benutzen zunächst iJcosaedrische Koordinaten s^, z^, 3^, bei deren Gebrauche
einer der Teiler ©g^ sich in der Gestalt der S. 161 ff. aufgestellten tem^ren
Ikosaeder-@g(j darstellt. Diese ©g^ enthielt insbesondere die drei nur
durch ihre Koeffizienten charakterisierten Substiiutionen:
/£, 0, 0
<1) S = ( 0, 1, 0
, 0, £^
0, 0,-
U =-- ( 0,-1.
■I, 0,
V5 ' Vö' VS
1 1 1
\~^' Vs' ^I
(unter £ die fünfte Wurzel der Einheit e « verstanden) und ist aus
den beiden ersten unter ihner). erzeugbar.
Die Herstellung der Va,lentinergnippe ist i^un ganz einfach. Wir
suchen uns • einen der Teiler ©^3 vom Tetraedeiptypus aus der ©g^, aus
und transformieren der Bequemlichkeit halber die z^, z^, z^ auf solche
oUaedrische Koordinaten x^, ap^, x^, daß die Tet^aedergruppe die S. 190
*) Vgl. dessen Abhandlung „De endehge Tfransformationsgruppers-Theorie"
in den Äbhandl. der Dänischen Akademie, sechste ßßihe, Bd. 5, S. 64. Jordan
hatte in seiner S. 182 genannten Untersuchung die Valentinergruppe übersehen.
264
II, 3. Valentinergruppe und zugehörige Formen.
zugrunde gelegte Gestalt annimmt, bei der die daselbst gezeichnete Fig. 24
des vollständigen Vierseits in sich übergebt. Diese ternäre ©^^ ist nur
in einer Weise zu einer ternären Oktaeder-@24 erweiterungsfähig. Die
Oktaedergruppe ist innerhalb der Valentinergruppe der Xormalisator der
Tetraeder-@j2. Der Ziibatz etwa einer Substitution der Periode 4 aus der
(^2^ zur anfangliehen Ikosaedef-(^^^ gestattet die ganze Valentinergruppe
her zustellen; denn die ©g^ ist ein umfassendster Teiler der ©gg^.
Zur Durchführung dieses Ansatzes wählen wir die ©^2; ^i^ ^i^
Vierergnippe (^^ der Substitutionen:
(2)
1, T, ü rnid T • ü :
V5
V5
2
1
2
8^ -r- s^
1
als Normalteiler enthält und in der sich weiter die folgende Substitution
der Periode 3 findet:
je je'- + £^) 2 £* £^(£ + £*) \
(3)
S*-T-S^ =
£^
(£-^
tl
1
w
2 s
£*
^4-
il
|5
1^
V5
Die oktaedrischen Koordinaten ;
Einheitswurzel e ^ verstanden,
Substitution:
\, aJg, x_^ führen wir, unter q die dritte
durch die nicht-singulare (vgl. I, 149)
-2(5^
-s')z,-z,)
\öj^ = ^i^^-&"■){-Z^-
(4) y^», = VS {z, - ^3),
' y 5 »3 = ()^ (£ — £*) {Z^ — 2 (£ ^ £*) ^2
ein, deren inverse die folgende Substitution ist:
f 2 \1j^ = if - 53) p2 ^^ _ y 5 ^^ __ (^
(^) -^ V^^2 = (£ - £*) p' »X - (£^- £^) p »3,
\ 2 Vo ^3 = (£2 - £3) ^2 ^^ _ y5 ^^ _ (^ _ ^,^ ^ ^^_
In den oktaedrischen Koordinaten stellen sich die Substitutionen T, U,
T • U in den Gestalten dar:
(b) T = (o,-1, 0), U = ( 0,1, 0), T.U = f 0,-1,0)
0.0, -1/ V 0, 0, 1/
Herstellung der VaJentinergruppe in oktaedrischen Koordinaten 2G5
während die Substitution (3) übergeht in:
/O, 0, ^os
(7) S* • T • S^ = ( eK 0, 0
\0, ^\ 0
Es ist für spater sehr folgenreich, daß hier der gemeinsaipae Faktor q^
in den Koeffizienten auftritt;. Kommt es uns eirjistweLlen nur auf
KoJUneationen an, so spielt dieser gemeinsame Faktor kejne Rolle, so
daß wir in (7) einfach eine zyklisc^ie Permutation der Koordinaten x vor
uns haben. Wir haben also tatsächtich die von S. 190 her bekannte
Gestalt der KoUiaeationsgruppe @^g vom Tetraedertypifs wieder erhalten.
Man kann nun bei Hereinnal^me der Oktaeder-®34 von S. 190 her
in zwei Weisen weitergehen. Entweder man entni^imt der &^^ etwa
eine Substitution der Periode i, die sicher noch nicht in der @^, enthalten
ist, rechnet sie auf die ikosaedrischen Koordinaten um und erzeugt aus
ihr und der (3^^ die ganze Yalentinergruppe. Oder man behalt die
oktaedrischen Koordinaten bei, lechnet auf Grund von (4) die erste
Substitution (1) auf die oktaedrischen Koordinalen x., x^, x^ um, v^as:
1~V5^ 1 -1-V^ ,\
-^-' 2^' 4 ^ \
1 , -i^V^ 1-V^
l-l-fV^ 1-rV^ 2 1
(8)
liefert und erzeugt aus dieser Substitution ^nd der iq. ihrer einfachsten
von S. 190 ff. her bekannten Gesialt erscheinenden Oktaeder-Öji die
ganze Yalentinergruppe. Der zweite Weg, der den Gebrauch der oJdandrischen
Koordinaten bedingt, ist in algehraischßr Hinsicht dec bessere, da man
hier, wie sich zeigen wird, mit der AdjmiMion einer einzigen numerischeu
Irrationalität vierien Grades auskommt, wählend man hei Gehrauch der
ikobaedribchen Koordinaten a und q oder eine mit ihnetf. aqptivalente
Irrationalität achten Grades adjungieren muß. Wir notieren demger^aß
das Ergebnis: Die VaJentinergruppe kann erzeugt werßeri, aus der
Substitution (8) und der ternaren OMaeder-®^^ in, ihrer einfachsten S. 190 ff.
angegebenen Gestalt. Wir behalten uns vor, dif erzeugende Substitution S
späterhin durch eine andere für die I^echnangen zweckmäßigere Substitution
zu ersetzen.
Da die Existenz der Yalentinergruppe pben durch eine nicht g^nz
einfache funktionentheoretische Überlegung bewiesen wurde, so ist ein
direkter Beweis erwünscht, daß die fraglichen Substitutionen wirklich
eine KoUineationsgruppe ©gg^ der Ordnung 360 erzeugen, die mit der
alternierenden Permutationsgruppe sechsten Grades isopaorpli ist. Damit
266 II, 3. Valentinergruppe und zugehörige Formen,
wird dann die Existenz der Valentinergruppe unabhängig von der
vorausgesandten transzendenten Theorie sichergestellt sein*).
Unter dem eben schon gemachten Vorbehalte betreffs Ersatz von S
benutzen wir als erzeugende Substitutionen der Valentinergrappe
einstweilen die Substitutionen der Perioden 3, 2 und 5:
/O, 1, 0\ /— 1, 0, 0\
(9) f7==( 0,0,1), V=i 0,0,1), S.
\1, 0, 0/ V 0, 1, 0/
Die ersten beiden Substitutionen erzeugen die bevorzugte Oktaeder-Og^.
Da diese ©^^ ein umfassendster echter Teiler der Valentinergruppe ist,
so erzeugt der Zusatz von S die Gesamtgruppe.
Die bevorzugte Ikosaeder-^g^j hatte als absolute Invariante die
quadratische Form (z^ z^ -j" ^i): ^^^ abgesehen von eiaem konstanten Faktor
sich in den oktaedrischen Koordiaaten a;^, x^, x^ auf die quadratische
Form:
(10) X!-^Q^XI-\~QXI
umrechnet (mittels der Substitution (5)). Man hat den sechs konjugierten
Ikosaeder-@gQ entsprechend sechs konjugierte Formen dieser Art. "Wir
setzen ihnen noch die Faktoren 2 hinzu, nennen sie die „Ikosaederformen'-
des einen der beiden Systeme und bezeichnen sie durch "(^(x-^, x^, x^)
oder auch kurz durch ^ ohne Angabe der Argumente **). Man berechnet
die Formen ^ einfach dadurch, daß man die erzeugenden Substitutionen (9)
wiederholt auf die mit 2 multiplizierte Form (10) ausübt. Man findet
das Ergebnis: Die sechs Jconjugierten JCkosaederformen des einen der
beiden Systeme sind:
'^1 = 2 (Xl -^ Q^ Xl + Q Xl),
^2 =: 2 (xl -T Qxi -j- Q^ X^),
^3 = — I ^ (^1 -r »I + «!) +- C^ — n) (+ »'2 a^3 + »S »1 ~ ^ 1^2)'
9i = —iv (4 + «I -r 4) + (2 — 1?) (~f x^ x^ — x^ x^ + x^ x.^),
^a = —^V (pl -\- ^l ± ^3) — (2 — ij) (-^ x^ »3 + i»3«1 -f x^ »2),
. ^6 = — i J? («1 -f -4 4- ^1) + (2 — n) (— »2 ^3 + ^3 ^1 + «1 ^2)'
wo iq die quadratische Irrationalität (4) S. 258 ist.
Man wolle nun die Wirkung der drei erzeugenden Substitutionen (9)
auf diese Formen explizite feststellen. Man findet:
(11)
{^)
(7)
(S)
^'l
^'l
^'l
= Q9i
= <P2>
= ^1.
9)2 = Q-(P2, 9^3 = (Pä^
fp2=<Pl^ (P3-(P3,
9)0= ()>3, Cps = QCp,
(fi
9>i
Cpi
= fps^ <P6 = (pö> cpe = fp4
= fPA' fph- (p^, cpe = cp^
= (p6> (p5- Q^cpe, (p'ä- Q
*) Umgekehrt werden wir hernach von der algebraischen Theorie unserer
Gruppe zur transzendenten leicht zurückgelangen.
**) Die Bezeichnung y behalten wir auch fur die Ikosaederformen des anderen
Systems bei, die weit übersichtlicher m den x gebaut sem werden.
Erstes System der sechß Ikosaederformep. 267
Wir betrachten jetzt zunächst nur „Kollineationpn'-, stellen durch XuU-
setzen der sechs Formen (11) die secM konjugierten IJcosaeßerJcegelscJiniüe
des einen Systems dar und sprechen kurz von einem Kegelschnitt ^.
Gegenüber den erzeugenden Kollineationen (9) eipfahren die seclis
Kegelschnitte ^ die folgenden drei geraden Permutatiqnen:
[ S = (^2, ^3, ^^, ^., ^g).
Die aus diesen Permutationen zu erzeugende Gruppe ist primitiv; denn
zufolge der Permutation S kann der Kegelschnitt ^^ weder mit einem
noch mit zwei weiteren Kegelschnitten zu einem System der Imprimi-
tivität zusammengehören. Die Griippe ist transitiv; denn ^^ häpgt schon
vermöge V und S mit allen übrigen ^ zusammen. Da in der Gruppe
die dreigliedrige zyklische Permutation U auftritt, so enthält sie nach
dem zweiten Satze in I, 347 die alternierende (ä^ggo sechsten Grades als
Teiler, und da alle drei Permutationen gerade sind, so id sie mit der
alternierenden Grruppe ©gg^ sechsten Grades identiüch.
Es mögen nun in der aus den drei Kollineationen (9) zu erzpugerjiden
Gruppe im ganzen v Kollineationen enthalten sein, die jeden einzelnen
der sechs Kegelschnitte ^ in sich überführen. Die v Kollineationen
permutieren dann insbesondere die vier Schnittpunkte:
(1, 1, 1), (1, - 1, - 1), (- l, 1, - 1), (- 1, - 1, 1)
der beiden ersten Kegelschnitte 9?^, ^2 untereinander. Man zeigt leicht
durch Rechnung oder geometrisch, daß alle Kollineationen, die diese vier
Punkte permutieren, unsere bevorzugt« Oktaeder-@24 bilden. U|ater
ihnen transformiert nur die identische B^ollipeation alle Kegelschnitte ^
in sich. Hieraus folgt der Satz Die Kollineationen (9) erzeugen eine
Kollineationsgruppe ©gg^ der Ordn%ng 360, die der alternierenden Per^u-
tationsgruppe sechsten Grades isomorph ist. Jliermit ist die Existenz der
Valentinergruppe unabhängig von der funktionentheoretischen Überlegung
von S. 259 ff. sichergestellt.
AUe drei Substitutionen (9) sind unirfiodular. Die aus ihnen zu
erzeugende Gruppe temärer unimodularer Substitutionen hat an
Ähnlichkeitssubstitutionen (vgl. S. 2) entvfeder nur die identische Substitution
oder die drei Substitutionen:
(13) x'^ — Q^x^, x'.2 = Q''x^, x^ = Q^x^, ^^ == 0, 1, 2.
Nun rechnet man sich leicht aus:
/«, 0, Cr
(14) s'^'(U'r'Tr)^-s^'U^ = Iq, e,Q
\0, 0, ^,
Hieraus ergibt sich der Satz: Die Valentinergruppe ist als. die aus den
Substitutionen (9) zu erzeugende Gruppe temärer unimodukarer Substitutionen
2(58 n, 3. Valentinergruppe und zugehörige Formen.
UMen in ihr einen Normcdteüer 6)3, dessen Komplement die KolUneations-
grupße ©gg^ '^^^
Es soU noch untersucht werden, ob in der ®iqqq ein mit der
KoUineationsgruppe (B^^q isomorpher Teiler existiert. Bezeichnet man
die drei Ähnlichkeitssubstitutionen (13) kurz durch die Sjonbole 1, q, q^,
so besteht die ©loso ^^^ ^^^ Tripeln einander ähnlicher Substitutionen W,
Q • W, Q^ ■ W. Insbesondere hat man an Substitutionen der Perioden 5
und 15 im ganzen 144 solche Tripel, die 144 Substitutionen der Periode 5
und 2-144 der Periode 15 liefern. Die ersteren 144 Substitutionen der
Periode 5 als einzige dieser Periode müßten alle im Teiler ©gg^ auftreten.
Eine entsprechende Überlegung zeigt, daß im Teiler die Substitution V
der Periode 2 und die Substitution U- V der Periode 4 auftritt. Also
findet sich auch U in der ©gg^. Die drei Substitutionen U, V und S
erzeugen aber zufolge (14) die Substitution q und damit bereits die
gesamte ®io8o- ^^ besteht demnach der Satz: In der ternären unimodu-
laren Valentinergruppe ©loso existiert kein mit der KoUineationsgrtippe <B^^^
isomorpher Teiler.
§ 9. Invariante sechsten Grades. Erweiterung der ©ggo«
Die S. 239 eingeführte Riemannsche Flache Fgg^j wird durch die
drei auf ihr existierenden Verhältnisgrößen x^, x^, x^ auf eine irreduzible
ebene Kurve sechsten Grades abgebildet, die durch die Gleichung:
(1) ^^(•^1) -^2' -^s) ^^^ *-*
dargestellt werde. Die links stehende Form sechsten Grades ist dann
gegenüber den Substitutionen der Valentinergruppe entweder relativ oder
absolut invariant. Es kann nur eine solche Invariante sechsten Grades
geben. Würde nämlich noch eine zweite existieren, so gäbe sie, gleich
0 gesetzt, eine Kurve sechsten Grades, die die irreduzible Kurve (1) in
36 Punkten schneiden würde, die gegenüber der ^^^^ nur unter sich
äquivalent sind. ]S[un sind aber auf der Fggo die Punkte im allgemeinen
zu je 360 äquivalent. Eine Verringerung dieser Anzahl findet nur bei
den Verzweigungspunkten statt, und ein System von 36
Verzweigungspunkten tritt nicht auf (vgl. S. 259),
Xun ist nach den Formeln (ll)ftS. 266 die dritte Potenzsumme
der Formen ^ eine absolute Invariante der Valentinergruppe, die nicht
identisch verschwindet, da in ihrem Ausdruck in den x das Glied mit xf
einen von 0 verschiedenen Koeffizienten hat. Also haben wir in jener
Potenzsumme die gesuchte invariante Form F{x^, x^, x^. Als absolute
Invariante der bevorzugten Oktaeder-Og^ist J'eine symmetrische Funktion
von x'l, x|, xl- Setzen wir noch eine multiplikative Konstante derart
Form sechsten Grades Fix-^, qs^, ccg) in ()ktae4rischen Koprdin^ten. 269
hinzu, daß der Koeffizient des nicht ausfallenden Gliedes mit xf gleich 1
wird, so gilt der Ansatz:
F = xf -i- xl ~\-xl ~\- a (x^ xi ~f x^ x'^ ~f a;| x{ -^ a;| x^ -j- x^ x^ ~f a;| xl)
-f- h xf xl a;|,
den wir auch noch einfacher in die Gestalt:
(2) F=(l-a) {xl -f xt -f xt) -f a (xt + xl ~\- xl) (x! ^ xl -f xl)
-f- & ^1 xl xl
setzen können. Zur Bestimmung von a und h kann man (statt die dritte
Potenzsumme der ^ wirklich auszurechnen) auch so verfahren, daß man
erstlich die beiden durch S äquivalenten Koordinateutripel:
(0, - 2 ()-, 0), i^- 1, ~~y-()^ -™y^ Qj
in (2) einträgt und die beiden entstehenden "^V'erte F gleichsetzt und
dann entsprechend mit den beiden Tripeln:
-V5 o -1 + V5^
,,, (^Vö^.,,MJ^^^,)
verfährt. Man gewinnt so für a und h die beiden Gleichimgen:
2B=19(l-a) + a^^:^"^^b,
3(l_a) + 6= I8(l_a)-f-—±^^^^,
durch deren Lösung man die Werte:
a = -|-(5-p^•VT5) = |(,^-3), ?> := 3 (5-^• VTö) = 6 (>;-^ 2)
findet. Die invariante Form secMten Qradee, F(a\, x^, x^) der Valeutiner-
gruppe hat hei Grehrauch der oMaedrisclien Koordinate^ die Gredalt:
(3) F = xl -^ xl -f- xl -^ l {ti — 3) {x\ xl + ^1 a;| + xo x'l -f xl xl
-^ xjxl -f xl xl) + 0 (?? -r 2) .^1^ xl xl;
sie id eine ahsoJiite Invariante der Grrupjje.
Das so gewonnene Ergebnis ist einer bemerkenswerten upd für die
Weiterentwicklung wichtigen Bestätigung f'^hig. Die S. 241 ff. eingeführte
Gruppe von ^-Substitutionen ist durch die Spiegelung an der imaginären
^-Achse zu einer Gruppe @ erweiterungsfähig, in der die H^uptl^ ongrüenz-
gruppe dritter Stufe ein Teiler des Index 2 • 360 ist. Die ©gg^ der
Transformationen der Kurvß sechsteu Grades F = 0 in sich ist
entsprechend einer Erweiterung auf eine ©a.seo ^ähig, wobei 360 lineare
Substitutionen von x^, x^, x^ in:
x'k = UkiXi -j- ct/,2% + c^ksXä, k = 1, 2, 3,
270 II) 3. Valentmergruppe und zugehörige Fonnen.
hinzukommen, unter Xi den zu Xi konjugiert komplexen Wert verstanden.
Es soll zunächst unter den neu hinzukommenden Substitutionen eine
geeignete „Spiegelang'' ausfindig gemacht werden. Diesem Ziele dient die
folgende Überlegung:
Der Xormalisator der unter (6) S. 264 gegebenen Substitution T
ist eine Dieder-Og, die zwei noch nicht innerhalb der ©ggo) wohl aber
innerhalb der ®2-36o konjugierte Vierer-®^ mit den gemeinsamen
Substitutionen 1 und T enthält. Die eine ©^ enthält außerdem noch U
und T-U mit den Perspektivitätsachsen x^ = 0, x^ = 0. Die andere
Yierergruppe besteht neben 1 und T aus den Substitutionen:
1, 0, 0\
0, 0, 1 j,
0, 1, oj
/-^'
0,
V 0, -
0,
0,
-1,
0^
— 1
0.
mit den Perspektivitätsachsen x^ -\- x^ := 0, x^ — x^ = 0. Durch die
aufzustellende Spiegelung werden also diese beiden Paare von Achsen
ausgetauscht, während die Achse a;^ = 0 von T in sich transformiert
wird. Nimmt man noch hinzu, daß durch die Spiegelung die beiden
Pole (0, 1, ihi) der in der obigen Dieder-Og enthaltenen zyklischen @^
aasgetauscht werden müssen, so gewinnt man für die Spiegelung den
Ansatz:
\2x'i = cix^, y2x'i = x^ -^ »3, \2x'. = ^2 — x^,
wo a, eine komplexe Zahl *) des absoluten Betrages 2 sein muß. Es muß
hiemach a derart bestimmbar sein, daß die für die x' gebildete Form
F(x'i, x'j, x's) nach Eintragung der vorstehenden Ausdrücke für die x'i,
X2, x'^, vielleicht von einer multiplikativen Konstanten abgesehen, in:
xt + xl + ^3 -f-1 (^ — 3) (xt xl -p xt xl + xl x! ^ •. •)
+ 6(^ + 2)S|i|^|
übergeht, unter ^ die zu rj konjugiert komplexe Zahl verstanden. Die
Rechnung zeigt, daß dies in der Tat zutrifft, wenn icir oc als die Jcon-
juglerte Zahl ß der folgenden ganzen algebraischen Zahl vierten G-raden:
(4) e = ^t;^^
wählen, deren Quadrat unsere Irrationalität rj ist. Damit haben wir das
folgende Ergebnis gewonnen: Die Erweiterung der Yalentinergruppe ©ggo
zur Gruppe ©a-seo ^^t vollziehlar mittels des Zusatzes der Substitution der
Periode 2;
(5) V"2o;; = e\, 1/24 = ^, + S3, V2% = ^2-%>
*■) Wäre a reell, so wäre die ganze Yalentinergruppe reell.
Endgültige erzeugende Substitutionen der Valent^nergruppe. 271
der man aueh die Grestalt verleihen Itann:
(6) \'2\ =z B x[, y 2 ^2 = a;2 -f %) V ^ ^3 == ^2 — ^^•
Eine erste Verwertung dieses Ergebnisses |^können wir daliiagejiend
vollziehen, daß wir die bisherige erzeugende Substitution S der Valentjner-
gruppe durch eine für die Rechnungen zweckmäJßigere Substitiftion
ersetzen. Die beiden Substitutionen TJ und F unter (9) S. 266 erzeugen
die bevorzugte ®^^. Der Zusatz irgead einer nicht in dieser @,^
enthaltenen dritten Substitution der ©3.330 genügt zur Erzeugufig dieser
Gruppe. Wir transformieren zunächst die Substitution:
X[ =0^2, % == äJj , X'-^ = iCg
durch die Spiegelung (5) und erhalten:
2x[ = B {x.^ -j- x^, 2 x'^ =- B Xi — «2 -p .C3, 2 % = ö Äj -j- x^ — x^.
Transformieren wir weiter durch U, so entsteht die dritte der folgei
Substitutionen:
/o, 1, ox ._-1,0,0. /-iiö, i,
(7) f7= 0, 0, 1|, r=l 0,0,1, W=[lo, 0,
\i, 0, 0/ V 0, 1, 0/ "^ i, iö,
die imimodular ist und die Periode 2 hat. Die Valentinergru^pe ©,^.360
ist aus den drei unimodularen SuhstituHonerp TJ, F, W der Perioden 3, 2
und 2 erseughar, so daß zur Darstellung dieser Grruppe die AßjunMion
der einen Mquadratischen Irrationalität 6 ziim rationale^ Körper ausreicht.
Mit B sind natürlich sowohl die dritten Wurzeln der Einheit q und q^
als auch \ o rational bekannt, wie aus den (jleichungen:
(8) 0-0 = 2, Ö-Ö = -^V3, B + ß=y5
hervorgeht ^).
§ 10. Zwei Systeme vofi je gech^ Ikosaederformen.
Dem einen System der sechs il^osaedrischen Teiler ©g^ der V^lentiper-
gruppe fanden wir die sechs konjugierten quadratischen
Ikosaederformen (11) S. 266 zugeordnet. Ihr Verhalten gegenüber der erzeugenden
Substitution W wird man leicht feststellen. Wir notieren gleich zu-
*) Der Vergleich mit den Entwicklungen von 3. 192 fuhrt zu dem
bemerkenswerten Satze: Aus den Substitutionen (7) \fird die EHemsehe Grippe ^jgg oder
die Valentinergruppe @io80 erzeugt, je nachdem man unter B d|e quadratische
Irrationalität 'X''' ■ oder die biquadra^ische i ~—'—- versteht. Man wolle
nur beachten, daß die Verbindung der ii^ der ©^gg enthaltenen Substitution
cci = ccg, x'^ = — Xi, x's = 3-3 mit der finter (15) S. 192 gegebenen
Substitution S^ bei unimodularer Schreibweise genaii zur jetzigen Substitution W fuhrt,
nur da£ ß die in (10) S. 191 angegebe^ie Bedeutung hat.
272 II) 3. Valentinergruppe und zugehörige Formen.
sammenfassend, daß sich die Formen ^ gegenüber den drei erzeugenden
Substitutionen U, V, W so verhalten:
(U)
(V)
Cpi = QCp,,
(P1 = (P2,
(p2-Q^cp2, cp's^cp^,
(p-2 = (Pi, fpi = (pzi
(Pi = (P3,
fpi = fpi^
95 = 95'
95 = 9g'
(p&=fpii
^>& = (ph^
<1)
91
92
93
=
=
=
71 Xt
v^'i
-^!
(W) (p[ = Q''(p^, cp2=Qcpe, 93=99i' 9^ = 94' fp5 = <Pö' 96 = 9'92-
Durch Ausübung der Substitution (5) § 9 auf die Form ^^ gewinnt
man eine erste Form (p-^ des zweiten Systems konjugierter Ikosaeder-
formen, aus der die übrigen fünf Formen am einfachsten durch geeignete
Substitutionen der bevorzugten Oktaeder-Og^ abgeleitet werden. Das
zweite System von sechs Jconjugierten Ikosaederformen ist:
4— xl + 2i}l'3x^x^,
^1 — ^3 — '2 ^■ y 3 x^ x^,
r}xl— a;| + 2^• V3 0^3a^i,
(p^ = — Xi -j- 7]xi — xi — 2i\Sx^x^,
(pT, = — Xi — xi -\- rjxi -^ 2i'^ Sx-^x^,
(pg = — iCi — xi -^ rj xi — 2i'^ Sx-^x^.
Die sechs Formen jedes der beiden Systeme sind voneinander
linear-unabhängig; denn es ist beide Male leicht möglich, die sechs
quadratischen Verbindungen der X-^, x^, x^ linear in den Formen des
Systems darzustellen. Es müssen demnach auch die Formen jedes
Systems linear in denen des anderen darstellbar sein, was sich sofort
bestätigt: Die Ikosaederformen (p stellen sich in den sechs Formen ^
deb anderen Systems so dar:
(2 — fj)(p^ = (^^ ^-^^)^ ^ (^^ ^ ^j _^ p2 (-^ _^ -^^^^
(2 — rj)(p^ = (^^ + ^^) + p2 (-^ ^ ^j ^ ^ (^, ^ -^)^
(2 — '?)93 = 9 (9i + 93 + 96) + P' (92 + 94 + 95)'
(2 — fj)(p^= Q (^^ + ^4 -I- 9.) + Q^ (92 + ^3 + ^e)'
(2 — >?)95 = Q^(9i + 93 + 95) + 9 (92 -f 94 + 96)'
(2 — '?)96 = 9' (9i -r 94 4- 96) + 9 (92 + 93 + 95)'
bcchs Gleichungen, die sich in die folgenden sechs Darstellungen der ^
durch die Formen (p invertieren:
' (2 - ^) 9i = (9, + (p^) + ^2 (^^ ^ ^j ^ ^ (^^ ^ ^^)^
(2 - ^)^^ = (^^ + 92) + () (93 + 9J -h ()' (95 + ^e).
(2 — ^) 93 = 9' (9i + 93 + 96) + 9 (92 + 94 + 95)'
(2 — ^) ^, = Q^ {cp^ Arcp^-Y(p;^ + Q (^2 + 93 + 96)'
(2 - 1?) 95 = 9 (9i + 93 + 9ö) -f- 9' (92 + 94 + 96)-
(2 — ^) 96 = 9 (9i 4- 94 + 96) 4- Q^ (92 -r 93 + 9ö)-
<2)
<3)
Geometrisches über die I}s;osae4erkegelschiiitte. 273
Der Vorzug des Systems der Formen (p ist in ihrer übersichtlicheren
Bauart in den x^, x^, x^ begründet. Ihr Verhalten gegenüber den
erzeugenden Substitutionen J7, V, W kann man entweder direkt aus (1)
bestimmen oder aus dem Verhalten der ^ auf Gnmd der Gleichungen (2)
ablesen. Beide Wege führen zu folgendem Ergpbnis:
(U) (p[ = (ps, (po = (Pi, fp'z= cp-^, cp[^ 93g, cp'^ = (p^, tjp;=cjp2,
(F) (p[=Cp^, (p'o = (p^, ^3= 96' ¥i= (Pb> 95=934. <3P6=CJP3,
(W) cp[ = cp^, <p2 = cp^, (p'z = Qfpi, <p'i=-Q-9z> 95 = 9i' 9b = f6-
Einige einfache geometrisciie Folgerungeii mögen sich hier
anschließen *). Durch NuUseti^en der Formen (p erhaltpn wir swßi Syßteme
von je sechs konjugierten Ikosaederkegelschnitten, deren einzelner im Sinne
von S. 164 als Abbild des Ikosaeders angesehen werden kann. Die
beiden Systeme zu je 20 konjugierten zyklischen ©^ verteilen sic^i auf
die Ikosaeder-@go in der Art, daß die einzelne Gruppe ©g imi^er in drei
Gruppen ©g^ enthalten ist. Indem wpan die sechs IJyObaeder-&^Q de^
einzelnen Systems auf die 20 möglichen Arten su dreien kombiniert^ sind die
Durchschnitte je dreier @go die 20 konjugierter^ ©3 dei> einet} Systems.
Über die zugehörigen Kegelschmtte aber gilt der Satz: Zwei unter den
drei Seiten des Poldreiecks der 6)3 sind Tßngenten des einzelnen l^^egel-
schnitts, die dritte Seite id die zugehörige BerUhrpongssehne. Durch Rech-
mmg bestätigt man dies sofort. M^n betrachte z. B. die drei durch
"^j z= 0, ^2 == 0, ^. =r 0 gegebenen Kegelschnitte, die zu der a,us U
zu erzeugenden Gruppe ©3 mit den drei Polen (L, 1, 1), (1, q, q^),
{1, Q^, q) gehören. Wir notieren noch den Sat^: Die 2'QO Pole- der ©3
Mlden zwei Systeme von je 60 nur unter sich äquivalenten Punkten, die
übrigens nicht auf der Kurve sechsten Grades F(x^, x^, x^) = 0
gelegen sind.
Kombiniert man eine Ikosaeder-®gQ des einen Systen:is mit einer des
anderen, was in 36 Arten paöglich ist, so ist der Purchschnitt zweier
zusammengeordneter ©g^ eitjie Dißder-©^,), deren es in der Tat 36
konjugierte gibt. Von den drei Polen der zugehörigen ©. liegei). zwei auf
dem einzelnen Kegelschnitt, der drittp ist der Pol der sie verbindenden
Sehne in bezug auf den Kegelschnitt. Es folgt: Jeßer Kegehchnitt des
einen Systems id mit jedem des anderen in doppelter Berührung; die beiden
Berührungspunkte liefern zwei Pole der ©5, der dritte ist der SchnittpunJd
der beiden gemeinsamen Tangenten. Man kann auch so sagen: Der
einzelne Ikosaederkegelschnitt wird von den sechs Kegelschnitten des
=^) "Wegen weiterer Ausfulirunge^ ist auf die Orjginalarbeiteu zu verweisen.
Am ausführlichsten ist die Valentinergruppe von F. Gerbaldi (Palermo) \Lntev-
sucht. Vgl. dessen in mehreren Fortsetzungen erschienene Arbeit „3m grappo
semplice di 360 collineazioni piane" in den B4n. 12 ff. der ßendiconti del circ.
mathem. di Palermo. Invariantentheo^etisch ist die Valentinergruppe schon früher
mit größtem Erfolge von A. Wim an (Lui^d) in der .Abhandlung „Über eine
einfache Gruppe von 360 ebenen KoUineationen", Math. Ann. Bd. 47, erforscht.
Fncke, Algebra. II. 18
274 II, 3. Valentinergruppe und zugehörige Formen.
anderen Systems in zwölf den Ikosaederecken entsprechenden Punkten
berührt. Da es auf dem Kegelschnitte nur ein System von 12 bezüglich
der @gQ nur unter sich äquivalenten Punkten gibt, so handelt es sich hier
um die zwölf von der invarianten Kurve sechsten Grades ausgeschnittenen
Punkte. Auf dieser Kurve gelangen wir zu den 72 unter sich
äquivalenten Punkten, die den fünfblättrigen Verzweigungspunkten der Fgg^
entsprechen. Damit folgt noch der Satz: Die 3 • 36 Pö?e der zyUiscJien
@5 zerfallen in zwei Systeme von 72 und 36 je nur unter sich äquivalenten
FunUen, von denen nur die ersteren auf der Kurve sechsten Grades liegen.
Die Rechnung bestätigt dies leicht. Die Pole der Substition S der
Periode 5 sind die Ecken des ikosaedrischen Koordinatendreiecks. Also
haben sie zufolge (4) S. 264 die oktaedrischen Koordinaten:
(4) {-Q{s'-s'), ±V¥, Q\e-e^)), {gia-a'), 0, q'(s'- b%
und die Verbindungsgerade der beiden ersten Punkte (4) hat nach (5)
S. 264 die Gleichung:
(5) QHe-s')x, + Q(e'-e')x, = 0.
Sie ist in der Tat die gemeinsame Polare des dritten Punktes (4) in
bezug auf die beiden durch:
iQx! + 4 + Q'^! = o, _
^^ \ — x!^'rjxl — x! + 2iySx^x, = 0
gegebenen Kegelschnitte, die den Formen ^^ und (p^ zugehören. Beide
Gleichungen (6) sind durch die beiden ersten Punkte (4) befriedigt und
ebenfallg die Gleichung F(Xi, x^, x^) == 0. Das Quadrat der in (5)
links stehenden Linearform stellt sich in den beiden quadratischen
Ikosaederformen ^^ und ^3 in der Gestalt dar:
(7) i V 3" {q^ (s - 8^) X^ + Q (£2 _ £3) x,Y == grj-^^-}/J ^3.
Die für die Theorie der allgemeinen Gleichung sechsten Grades
grundlegende Bedeutung der 36 mit dem Punkte (^ (e — s^), 0, q^ (e^- e^))
äquivalenten Punkte und der 36 mit der Geraden (o) äquivalenten
Geraden besteht darin, daß wir hier die kleinste Anzahl „linearer^ GeMlde
haben, die hezüglich der @3go nur unter sich äquivalent sind. Es ist
hinreichend, wenn wir dies" zunächst nur für die 36 Geraden weiter
verfolgen, da das Verhalten der 36 Punkte hernach aus dem der Geraden
nach dem Dualitätsprinzip zu entnehmen ist. Vor allem müssen wir an
Stelle der Geraden mit Linearformen arbeiten, die sich dann freilich
gegenüber den Substitutionen der Valentinergruppe nur erst bis auf
multiplikative sechste Einheitswurzeln permutieren. Durch
Multiplikation der linken Seite von (5) mit einem geeigneten konstanten Faktor
gelangen wir zur Linearform —Bx^ — {d — V)x^, die also dem
Formenpaar (p^, (p^ zugeordnet ist. Die 36 konjugierten Linearformen sind dann
unter Zusatz ihrer entsprechenden Formenpaare 'q>, (p durch folgende
Tabelle gegeben:
(92' 9l).
(92.93).
(92.95).
(9i. 92).
(9i. 94).
(9i. 96).
(96. 9,).
(94' 93)'
(93. 95).
(94. 92).
(93. 94).
(96.96).
System der 36 kopjugierten Lmearfprmep..
01 = ^x^^(6- 1)3-3,
cj,_ = (6-l)x^ + 6x^,
93 = 6x^^(6-l)x.^,
g,^(6-l)x,-6x„
9t = -6x^^{6-l)x^
275
(<P2. 92)' h =dx^_-(6-'i)x^,
(92. 9i)' i/s = - (Ö - 1) ^1 + Ö ^3'
(92. 9ß). ^9 =ÖXi-(Ö-l)a;2,
(9i.9i). 9io=-(6-'^)x2-6xs,
(9i. 93). 9,1 =-6 x^ -(6-l)x^,
(9i' 95). ^12 = - (6 - 1) «I - ^^ ^2'
^13 =
^16 =
Ö'l7 =
9l8 =
(6-l)x^-dx,,
(l-d)x^^x,-x^, ((^5,9,), 5',9 = (l-6)a;, - a:2-a;3,
x^~(l-d)x^-x^, ((^5,93), ^2o = -^'i + (l-Ö)a:',-X3,
•^l-^2 + (l ~^)^3. (95. 9o). ^'21 ="''^l~-^2~(l-^)-^3.
(l-Ö)»i + X2-a;3, (93,92), ^22=(l-f^)a;i-»2^/3,
-«l-(l-Ö)a?2-'^4- (96. 9i). 9-2B='^'l^('^-6)X2-^3r
Xi-x^_~(l-e)x., (9,,9ß), fifo^^--^]^^2^(^-0)■^■3,
(96
(94
(93
(94
(93
(96
(95
(95
(95
(93
(96
(94
92)
94)
96)
9i)
93)
95)
92)
94)
96)
9i)
93)
95)
^31 ■■
932 ■■
933 --
-V5
t-{^r-{^-6)x,+x,),
((l + /7)x,
-■3).
V5
V5
V5
V5
\5
ys
{x,-rx,^-{l-^^j))x,),
((1+0)»,+ ^2--^'3).
(-a;^ + (l+ö)a;2-r-^3).
(a;, - J52 + (1 +6)4-3),
((l+Ö)x,-»,-r3),
-(—«^ + (1 -rÖ)a?2 —X3),
-(-^i-A-f (l+Ö)»3),
-((1 -\-6)x^ — Xo_ + x^),
yy
2—(^i4- (1 +0)3^2 —-^3).
yy
18-
276 II, ä. Valenünergruppe imd zugehörige Formen.
Die Permutationen der Linearformen g gegenüber den erzeugenden
Substitutionen der Valentiner gruppe lassen sich ohne weiteres aus den
Permutationen der Formen ^, cp ablesen. Indessen muß man wegen der
hinzutretenden multipKkativen sechsten Einheitswurzeln doch die
Substitutionen U, V, W auf die Formen g ausüben. Man findet als
Permutationen der Indizes der Linearformen g] gleich unter Zusatz der in
Betracht kommenden sechsten Einheitswurzel:
/ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,
[ 2, 3, 1, 0, 6, 4, 8, 9, 7, 11, 12, 10, 14, 15, 13, 17, 18, 16,
19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, m\
20, 21, 19, 23, 24, 22, 26, 27, 25, 29, 30, 28, 32, 33, 31, 35, 36, 34/ '
/ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,
I-IO, -6, 5, -7, 3, -2, -4, -12, 11, -1, 9, -8, -19, 24, 17, -16, 15, 20,
19,20,21, 22,23,24, 25,26,27, 28,29,30, 31,32,33, 34, 35, 36\
-13,18,23,-22,21,14,-31,36,29,-28,27, 32,-25, 30, 35,-34, 33, 26/ '
u --
1, -^
«2 30, -(/^
13, 14,
3, ö26.
25, 26,
sö7, «214,
!, 3,
23, 13,
15,
-10,
27,
-ö6.
4,
22
16,
-16,
28,
36,
5,
29, -
17,
on,
29,
5,
6,
«2-27,
18,
-9.
30,
?1>
7,
o2 25,
19,
21,
31,
-31,
8,
-35, -
20,
-ö32.
32,
-ö2 20
9, 10, 11,
18, -15, o2i7, _
21, 22, 23,
19, 4, -o2.
33, 34, 35,
,-33, -^öl2, -8,
12,
«2 34,
24,
-24,
36^
28;
§ 11. Zwei Systeme von je 15 Oktaederformen.
Die zu den beiden Systemen von je 15 Oktaeder-©,^ gehörenden
quadratischen Oktaederformen sind weiterhin gleichfalls zu benutzen,
wenn sie auch nicht die Bedeutung der Ikosaederformen besitzen. Zwei
erste Formen aus den beiden Systemen zu je 15 konjugierten
quadratischen Oktaederformen haben wir in:
(1) t,^4t (x! + xl -f xl), i;i = ^irix! + 2 xl + 2 xf).
Die erste Form ist bekanntlich die absolute Invariante zweiten Grades
der bevorzugten Oktaeder-@24, und die zweite geht aus der ersten durch
die Transformation (5) S. 270 hervor. Mittels der Ikosaederformen stellen
sich diese beiden Oktaederformen in der Gestalt:
1 — ^ 1^1 == 2 (^3 -^ y^ + ^^ -f ^g)
dar. Die mit i^j bzw. -^^ konjugierten Formen gewinnt man am
einfachsten, indem man auf die vorstehenden Gleichungen wiederholt die
erzeugenden Substitutionen Z7, F, W ausübt. Man gelangt in den rechts-
Systeme der Oktaederformep. 277
seitigen Klammem beide Male zu den 15 ^nöglichen vieigliedrigen
Summen der sechs Ikosae(ierformen, wobei jedoch zwölfmal in zwei
Summengliedem noch die Koeffizienten q und q^ auftreten. Es ergibt
sich dabei als ein weiterhiiji zu benutzender Satz: Die 15 Jconjugperten
OMaederformen des einzelnen Sydems permutieren biclt, gegenüber den
erzeugenden Substitutionen TI, V, W, abgesehen von gelegentlich aufträenden
multipliliativen dritten Einheüswarzeln. Man braucht zum Beweise nur auf
die S. 272 ff. angegebenen Permutationen der Fopnen ^, (p
zurückzugreifen. Die Permutationen der Oktaederformen hier wirklich
herzustellen, ist nicht erforderlich.
Dagegen ist es für weitere Anwendungen erwünscht, explizite die
Darstellungen der Oktaederformen i;, tj; in den X-^, x.^, x^ zu besitzen:
Bei den Formen j/; treten folgende drei Typen auf:
i 4.{xl^xl^xt),
(3) 2rixl + {^-ri){xl^xl)~-l{l-^-ri)x,x^,
\{n — ^) (»1 + Q'A + ()^ x\) — '^ in -T1) {x^_ -^3 -T- Q ^3 ^1 + q'^ -^1 -^2) >
hei den Formen i^ aber nur die beiden Typen:
^^^ j 2irixl-r2xl~V'2xl),
11(3?; — 4) »? — !(?; — 4){ool + xl) -f ri i'\J^ x^ ix,_ + x^) -f Srjx^^x^.
Die erste Form (3) steht für sich, die [zweite Form (3) repräsentiert sech^
gleichgebaute Formen, die durch die Substitutionen der bevorzugten
Oktaeder-®,^ ineinander übergehen, die dritte Form (3) repräscfitieri.
entsprechend acht Oktaederfprmen. Ebenso repräsentieren die Formen (4)
drei bzw. 12 Oktaederformen. Bei der einfachen Bauart jener Oktaeder-Ög*
wird es nicht nötig sein, die beiden Systeme von je ] 5 konjugierten
Formen vollständig anzugeben.
Da die ®^^ drei zyklische ©^ enthält un(i in. der ©gg^ im ganzen
45 konjugierte zyklische ©^ auftreten, ßo findet sich die einzelne zyklische
Gruppe @4 jedesmal in. einer Oktaedergrjippe des einzelnen Systems.
Hieraus ergibt sich folgender Satz Der einzelne OUaederkegehahniit
befindet sich stets mit drei Kegelschnitten de$ anderen Systems in doppelter
Berührung; die 45 BerühruAigssehnen sind die PerspeUivitatsachsen der In
der Valentinergruppe enthßltencß 45 l^njugierten Kollineationen der
Periode 2. Zu diesen 45 Achsen gehören zunächst die neun Ge^raden
der Fig. 24, S. 190, die durch X^illsetzen der neun Linearformen:
(5) 4»^, 4»2, 4»3, 2Ö(»2±»3), 2 Ö (»3X^1)) 2Ö(äiXÄ2)
gegeben sind. Die zu den übrigen 36 Peispektivitatsachsen gehörenden
Linearformen setzen sich auß den beiden Typen:
(6) 2 (6 x,+x,_ + »3), 2 X, + (^ — 6) x, + (^ -f Ö) ^3
278 II, 3. Valentinergruppe und zugehörige Formen.
zusammen, wobei die erste Form (6) durch die Substitutionen der
bevorzugten 0ktaeder-(§24 "^ ganzen in 12 ähnlich gebaute Formen übergeht,
die zweite aber in 24*).
Wir kommen nochmals auf ein Paar von Oktaederkegelschnitten in
doppelter Berührung zurück, wobei die Berührungssehne eine der Per-
spektivitätsachsen ist. So gehört z. B. zu den beiden Kegelschnitten:
(7) Aix! -f xl + xl) = 0,2 (rjx! + 2x1 + 2x1) = 0
die durch x^ = 0 gegebene Achse, die auf den Kegelschnitten die beiden
Pole (0, 1, +'*) der zugehörigen zyklischen ©^ ausschneidet. Der dritte
Pol ist der Schnittpunkt der beiden Tangenten der Kegelschnitte (7)
in ihren beiden Berührungspunkten. Er ist zugleich das Perspektivitäts-
zentrum (1, 0, 0), das zur Achse x^ == 0 gehört. Auch die Kurve
sechsten Grades F =^= 0 läuft durch die beiden Punkte (0, 1, +^■) hindurch.
Da diese Kurve doppelpunktfrei ist und durch die fragliche Perspektivität
in sich übergeht, so hat auch sie mit den beiden Kegelschnitten (7)
in den Punkten (0, 1, +«) die Tangenten gemein. Man gelangt leicht
zu dem Satze: Der einzelne OMaederJcegeUchnitt wird von der Kurve
sechsten Grades F =^ 0 in zwölf zu Paaren zusammenfallenden PunUen
geschnitten, und die sechs so entstehenden Berührungs^unUe bind die sechs
OUaederecJcen. Umgekehrt folgt für die Kurve sechsten Grades der
Satz: Indem man das Produkt der 15 OMaederformen des einen oder des
anderen Systems gleich 0 setzt, gewinnt man eine 'bezüglich der ©gg^
invariante reduzihle Kurve 30^*^^^ Grades, die die Kurve sechsten Grades
i^'riirO an 90 nur unter sich äquivalenten PunMen berührt; sie
entsprechen den 90 vierblattrigen VerzweigungspunUen der Blemannsehen
Flache Fgeo-
Dem durch die beiden Kegelschnitte (7) festgelegten Büschel gehört
auch der durch:
(8) eiJx^-xi — xi = 0
gegebene Kegelschnitt an. Auch er berührt also die Kurve sechsten
Grades F = 0 in den beiden Punkten (0, 1, + i). Berechnet man aber
die gesamten zwölf Schnittpunkte des Kegelschnitts (8) mit der Kurve
F = 0, so folgt durch Elimination von (xi + »D aus den Gleichungen (8)
und F = 0 als Ergebnis Xi = 0. Alle zwölf Schnittpunkte koinzi-
dieren also an den beiden Stellen (0, l, :^i), an denen der Kegelschnitt (8)
von der geraden Linie X-^ = 0 geschnitten wird. Durch die Kollineation
x[= — »j, »2 = %, x's= — »3, die die Punkte (0, 1, + i) austauscht,
geht aber jede der beiden Kurven in sich über. Also fallen die zwölf
*) Die m den Formen (5) und (6) hinzugefugten Faktoren haben den Zweck,
daß sich die 45 Linearformen gegenüber den Substitutionen der Valentinergruppe
bis auf multiplikative sechste Einheitswurzeln permutieren. Es ist nicht notig,
dies weiter zu verfolgen.
Sextaktische Punkte der Kurve sechsten Grades F z= 0. 279
Schnittpunkte zu je sechs an den Stellen (0, 1, +i) zusammen. Hiernach
sind die 90 den vierhldttrigen Versweigungspunkten der Fläche Fggp
entsprechenden FunJcte der Kiirpe sechsten Grades SßcäaJdisch^').
Eine doppelpunktfreie Kurve seohsterji Grades hat 270 sextaktische
Punkte. Es ist leicht einzusehen, d^ß der J^esi der 180 übrigen sextaJc-
tischen Punkte der Kurve F =■ 0 von den 180 noch nicht genannten
SchnittpunMen mit den 45 PerspeUivitdtsachsen geliefert poerden, die den
180 sweihlättrigen VersweigungspunMen der JRiemannsehen Fläche
entsprechen. Der im einzelnen dieser Punkte mindestens fünfpunktig
berührende Kegelschnitt geht nämlich, da er eindeutig bestimmt ist, wie
die Kurve F = 0 selbst, durcji die beti^effende harmonische Perspek-
tivität in sich über. Dieserhalb muß er die Kurve F = Q in einer
geraden Anzahl von Punkten, alßo sechspi(.nktig, berührep.
Übrigens gelangt man auch von den [kosaederfprmen sehr leicht zu
den Perspektivitätsachsen. Diß Differenz der Kuben zweier
konjugierter Ikosaederformen zerfällt in das Produkt von sechß Linearformen,
die im System der 45 Formen (5), (6) enthalten sind. In der Tat
findet man:
[ q>i — ^1 = (»2 + ^) (»2—^3) (^3 + »1) C^a — «1) (»1 + »ä) (^1 — ^a)'
(9) (p! — yl = 12 ^ V 3 »2 »3 (Ö »j + »2 ^ x^) (B x^ — », — »3)
[ 0^1 IT ^2 — ^^3) (Ö ^1 — ^2 + %)
und beachte, daß die 15 Kubendifferenzen sowohl beim Formensystem 'q,
als auch beim System (p unterein^der äquivalent sind- Wir notieren den
für später wichtigen Satz: Jedes der beiden BifferenzenproduUe:
(10) Jl(^i-'<ff), Yli^i-^'i)
k<l k<J.
stellt Us auf einen konstanten FctMor das Qußdrat des ProduMes aller
45 Linearformen dar, die gleich 0 gesetzt, die Perspelftivitätsachsen hefern.
§ 12. Formensystem 4er Vftlentinergruppp.
A. Wiman hat in einer sehr wertvollen Untersuchung**), die ;^uersl(;
die allgemeine Aufmerksaip.keit auf die Valentinergruppe lenkte, das
volle Formensystem dieser Gruppe aufgestellt. Er bediente sich hierbei,
derjenigen invariantentheoretischen Hilfsmittel, die Klein bei der
Untersuchung der temären GrupjDe ©jgg angewandt hat, und gelangte zu ganz
analogen Ergebnissen wie iflein.
=^) Vgl. die Note S. 195.
**) „Über eine einfache Gruppe von 360 ebenen KoUmeationen'-, Math. Ann.
Bd. 47, S. 531 (1895).
280 II, 3. Valentinergruppe und zugehörige Formen.
Indem wir jetzt der Gleichförmigkeit wegen mit F unsere absolut
invariante Form sechsten Grades (3) S. 269 bezeichnen, bilden wir
zunächst deren Hessesche Form zwölften Grades und setzen:
g2_p g2_p g2_p I
(1) 3^.5^.., *(.„.„.,)=. g^-g-, g^. g^g^l.
g2_p g2_p g2_p I
Man hat dann in fi? eine absolut invariante Form zwölften Grades, deren
entwickelte Gestalt die folgende ist:
(2) *=. 2(i;,^-^~f ...)-6(^-3)(^/%^-i---.)-3(ll,? + 7)(»M~f ...)
— 12 (:q - 2^)%lxlxl (;r« 4- .. •) + 4(3,; -f 7) {xlxl ^ • • •)
-r 24 (3 ?; -— 4) »i^»|»| (»i*»| ^ ) — 60 (?; -f 16) »i*%*»|,
wo in den Klammern symmetrische Funktionen der »j, »,, »3 der
jedesmal angegebenen ,.Anfangsglieder'- oder „Leitglieder" stehen. Durch
gB =- 0 wird eine Kurve zwölften Grades dargestellt, die auf der Kurve
sechsten Grades .F = 0 ein invariantes System von 72 Punkten
ausschneidet. Es handelt sich um die 72 auf der Kurve .F = 0 gelegenen
Pole der zyklischen Teiler ©g, die die 72 Wenäe'^unUe unserer
doppelpunktfreien Kurve sechsten Grades sind.
Wir bilden ferner mit Wiman die mit den ersten Ableitungen von
fi? geränderte Hessesche Determinante von F (vgl. S. 332) und setzen:
g2_p g2_p g2_p g^
(3) — 2«.3^-5.^!F(»,,:r2,»3) :
Durch Ausrechnung, wenigstens der Anfangsglieder:
(4) !F= ;ri^O-f ;rf-f Ä;|«-f ...,
zeigt man, daß hier eine nicht identisch verschwindende absolut invariante
Form soften Grades vorliegt. Wir nehmen an, daß W die Form F nicht
als Faktor besitzt*), und bringen die Kurve sechsten Grades mit der
'd%l'
d'F
dx^dXj^'
d^F
dx^dx^'
d^
dx^'
dx^dx^
d'F
dx'i'
d'-F
dx^dx^
d^
dx^'
dXj^dx^
d'F
dx^dx^
d'-F
dxl'
ofiB
dx^'
dx^
d^
dx^
d^
dx^
0
=) Diese Annahme wurde man m der Weise darzulegen versuchen, da£ man
W fur einen geeignet auf der Kurve i^ = 0 gewählten Punkt als von 0
verschieden nachweist.
Herstellung neuer Formen dpjch anvariante Prozesse. 281
durch W = 0 gegebenen i^ivarianten Kurve 30***" Grades ziun
Durchschnitt. Man gelangt zu einem invarianten System von 180 Punkten
auf der Kurve sechsten Grades Es gibt miir z\^ei solche Systeme,
nämlich erstens das doppelt gezählte System der 90 Pole der zyklischen
Teiler ®^, die wir nach S. 279 als die sextaktischen Punkte „erster Arf
bezeichnen und zweitens das System der übrigen 180 Sclmittpunktp dei"
45 Perspektivitätsachsen mit der Kurve F = 0, die dip sesiaktischen
Punkte „zweiter Art" heißen mögen =^). "Clm die letzteren Punkte kani^
es sich nicht handeln. Durch die einzelne harmonische Perspektivitäi
wird nämlich die Kurve ÜP" = 0 in siclfi transfoi-mierl:. Da sie als
Kurve SO^*^'* Grades die 45 Perspektivitätsachsen nicht enthalten kann,
so müßte sie, falls ein sextaktischer Pui^kt zweiter Art auf ihr liegt,
daselbst entweder mit der Kurve F =^ 0 gleiche durch daß Perspek-
tivitätszentrum laufende Tangente haben oder einen mehrfaclien funkt
besitzen. Beide Male würde der Schnitt der B^urven ^ = 0, W := 0
im fraglichen Punkte doppelt zählen, so d^ß wir im ganzen 2-180 und
nicht 180 Schnittpunkte erhieltpn. Die Kurve 30«^^''' Grades W =^ 0
schneidet die Kurve F = Q in den je doppelt gemhlten 90 sextaUibchen
PunMen erster Art. Die unten wirklich zu benatzende (reduzible) Kurve
30sten Grades ^ = 0 wird die Kurve sechsten Grades an den fraglichen
90 Stellen berühren.
Wir bilden endlich die nicht identisch verschwindende Funktional-
determinante:
(5) X(x
der drei Formen F, 0, W^ die eine absolute Invariante 45**^", also
ungeraden Grades ist. Es Jcann, hon eifern konstanten FaMqr ahgeseheß, nu/r
„eine-^ invariante Form 45^^^ Grades geben; sie ist redusibel und liefert,
gleich 0 gesetzt, die 45 Pers'peMiMtätsacit,t>en. Durch X^=iO w|rd nämlich
auf der Kurve sechsten Grades ein invariantes Systpni vpn 270 Pimkten
ausgeschnitten, das entweder aus den gesamten sextaktischen Pimkten
oder aus den dreifach gezäi^lten sexta,ktisclien Punkten erster Art bpsteht.
da es andere Systeme von »270 nur -(inter sich äquivalenten I'unkten aijf
der Kurve sechsten Grades nicht gibt. Xun geht so^^ohl die Kurve
X = 0 wie die Kurve ^ = 0 durch die einzelne .Perspektivität ip sich
über. Enthält demnach die ersiere Kurve nicht die Perspektivitätsachse
selbst, so wird sie, wo sie durch eipen sextalctischen Punkt der Kurve
dF
cx^'
dx-^'
oF
dx^'
8*
bx^'
dx^'
dF
8 »3
8 »3
oW
=^) Auch die sextaktischea Punkte erster +irt liegen auf den Perspektivitats-
282 II> 3. Valentinergruppe und zugehörige Formen.
F = 0 hindurchläuft, diese letztere Kurve entweder geradzahlig
berühren oder einen mehrfachen Punkt geradzahliger Vielfachheit haben. In
den beiden letzteren Fällen zählt der Schnittpunkt beider Kurven in
geradzahliger Vielfachheit, was als nicht zutreffend erkannt wurde. Es
enthält also X = Ö eine und damit alle Perspektivitätsachsen. Man
kann auch algebraisch in folgender Art schließen. Es sei X zunächst
irgend eine absolut invariante Form ungeraden Grades. Da X bei der
in der Valentinergruppe enthaltenen Substitution:
unverändert bleibt und von ungeradem Grade ist, so erfährt sie bei der
Substitution ;ri = a?^, x'2 = x^, x'^ ■=^ x^, d. h. also bei Austausch
von »2 und »3, Zeichenwechsel. Somit hat X den Linearfaktor {x^ — x^
und also alle 45 konjugierten Linearfaktoren (5), (6) S. 277. Die
niederste invariante Form ungeraden Grades hat also den Grad 45 und
stellt bis auf einen konstanten Faktor das Produkt jener 45
Linearfaktoren dar.
Genau wie bei der Klein sehen Gruppe (vgl. S. 206 ff.) läßt sich nun
der Satz beweisen: Dm volle Formensystem der Valentinergruppe hesteht
aus den vier Formen F, 0, W, X der Grade 6, 12, 30 und 45. Zum
Beweise betrachten wir die Schar der Kurven 60^^^^* Grades:
(6) ^'^-^^W = 0
mit dem Parameter u. Durch geeignete Auswahl von ^ kann man
mittels der Kurve (6) jedes beliebig auf der Kurve F = 0 gewählte
System von 360 äquivalenten Punkten ausschneiden. Es treten dabei
die drei besonderen Fälle ein, daß, für |u, = 0 die 360 Punkte zu je fünf
in den 72 Wendepunkten zusammenfallen, für fi = 00 *) zu je vieren in
den 90 sextaktischen Punkten erster Art und für einen später zu
bestimmenden AVert (i zu je zweien in den 180 sextaktischen Punkten
zweiter Art. Es sei nun irgend eine absolut invariante Form ü
vorgelegt. Wir haben zu zeigen, daß Sl eine rationale ganze Funktion von
F, 5?, W, X ist. Die höchste in Sl aufgehende Potenz von F denken
wir fortgehoben, so daß die noch zu betrachtenden ü gegen F teilerfremd
sind. Ist der Grad m von Sl ungerade, so enthält Sl, wie man aus der
eben vollzogenen algebraischen Überlegung sofort folgert, die Form X
in höchster ungerader Potenz. Indem wir also auch die höchste in Sl
aufgehende Potenz von X fortheben, verbleibt nur noch eine gegen X
teilerfremde Form Sl von geradem Grade m zu betrachten. Die
zugehörige Kurve Sl = 0 schneidet auf der Kurve sechsten Grades die
180 .sextaktischen Punkte der zweiten Art entweder überhaupt nicht
oder in geradzahliger Vielfachheit aus. Diejenigen durch einen
sextaktischen Punkt hindurchlaufenden Zweige der Kurve Sl = 0, die die
Kurve sechsten Grades daselbst ungeradzahlig schneiden, treten nämlich
*) Wie wir in leicht verständlichem Sinne sagen dürfen.
Volles Formensystem der Valentinergi'uppe. 283
zu Paaren auf, indem die Zweige eiaes solchen Paares durch die
zugehörige Perspektivität ausgetauscht werden. Der Ges3,mtschnitt der
Kurven ü = 0 und ^==0 möge weiter die 72 Wendepunkte je a-fach.
die 90 sextaktischen P;inkte erster Art ß'-iack und endlich noch eine
Anzahl weiterer Systeme von je 360 Punkten enthalt;en. Da die Anzahl
der in die sextakitischen Punkte zweiter Art fallenden Schnittpunkte
gleichfalls ein Vielfaches von 360 ist, so gilt:
6 TO =: 72 u ~f 90 ß' -f 360 y.
Somit ist wegen des geraden m anck ß' gerade und werde gleich 2 ß
gesetzt. Wir können daraufhin ßine form :
(7) ^'^w^YK^^^^.w^)
k
aufbauen, die gleich 0 gesetzt genau dasselbe Punktsystem auf der Kurve
sechsten Grades ausschneidet wie ü == 0 imd also gleichfalls den Grad m
hat*). Es ist nun möglich, eine endliche von 0 verschiedene
Konstante c so zu bestimmen, daß die durch:
(8) Sl-c *- Wß Yl (*'^ ^ ft, W) = 0
Je
gegebene Kurve m^^ Grades die Kurve sechsten G^-ades noch in einem
neuen (6 m -\- l)sten Punkte schneidet. Dann enthält die in (8) links
stehende Form die irreduzible Funkt:).on JF mindestens iq. erst;er Potenz.
Tritt die höchste Potenz F'^ auf, so gilt identisch:
(9) £i = c ^-W^Hi^' + li,W-') -r-^'-ßi,
k
WO üj eine neue invariante Form des verminderten geraden Grades
W2j == m — ßv ist. Hierdurch ist die Bß,sis für ein induktives
Schlußverfahren gewonnen. Man hat, um 2;um Ziele zu kommen, nur noch zu
berücksichtigen, daß F, abgesehen voifi einpm konstanten Faktor, die
einzige invariante Form sechsten Grades ist, was übrigens auch in der obigen
Schlußweise schon enthalten ist.
Eine gewisse Kurve der Schar (6) schneidet auf der Kurve F == 0
die 180 sextaktischen Punkte der zweiten Art doppelt gezählt auÄ,.
Setzen wir den Faktor W hinzu, so schneidet die reduzible Kurve
9 Osten G-rades:
(10) W{^'^ i-^W^) =^ 0
alle 270 sextaktischen Punkte doppelt gezählt aus. Dies ist genau
dasselbe Schnittsystem, das auch durch die Gleichung X^ = 0 geliefert
"") Die Parameter fij, sind alle endlich und von 0 verschieden. Jeder Faktor
im Produkt (7) muß so oft hingeschrieben werden, als es die Yielfachheit des
betreffenden Schnittes erfordert. Die sextaktischen Punkte zweiter Art kommen
nötigenfalls mit unter den k Faktoren des Produktes im Ausdruck (7) m Betracht.
284 II, 3. Valentmergrappe und zugehörige Formen.
wird. Wie soeben schließen wir, daß es eine endliche von 0 verschiedene
Konstante a gibt, für welche die Form:
X^-aW{^-^ + aW')
den Faktor F gewinat. Der andere Faktor vom Grade 84 ist unserem
eben bewiesenen Satze zufolge eine rationale ganze Funktion von F, ^
und W. Es besteht somit der folgende Satz: Die vier Formen F, ^,
W, X des vollen Systems sind durch eine algebraische Belation:
(11) X' = a Wi^^ -4- ^ W) ^F-a (F, *, W)
aneinander gebunden, in der das Quadrat der Form X als rationale ganze
FunJdion der drei anderen Formen F, ^, W dargestellt wird. Wir
kommen auf diese Relation unten zurück [vgl. (6) S. 297].
§ 13. Neue Auswahl des Formensystems der Valentinergruppe.
An Stelle der Bezeichnung F für die invariante Form sechsten
Grades gebrauchen wir hinfort wieder die frühere F. Die Produkte :
(1) 0(x^, x^, x^) = Y[^J^^ '^{o!!i, x^^, x^) = JJ-^k
sind bei dem Verhalten der Formen q) gegenüber den erzeugenden
Substitutionen IT, V, W(vgl. S. 272 ff.) absolut invariante (reduzible) Formen
zwölften Grades der Valentinergruppe. Von ihnen steht von vornherein
fest, daß sie die Form F nicht als Faktor enthalten. Es ist demnach
möglich, jede dieser Formen an Stelle der Form ^ zu benutzen, ohne
daß die in § 12 gezogenen Schlüsse Einbuße erfahren. Wir wollen uns
weiterhin der sehr übersichtlich darstellbaren Form bedienen:
(2) 0 == UiiV^" - ^' - ^ly ^ 124^1)
(3)
= (r]-4:)(xl^-r-) + Q(Sr]-8)(xl'xi + :.)^3(18fj-3o)(x!xi + -)~--,
wo sich das Produkt auf die drei Faktoren bezieht, die aus dem wirklich
angegebenen durch zyklische Permutation der x^, x^, x^ herstellbar sind*).
Aus 0 und F können wir die Schar der invarianten Formen:
(3) 71^ ^IF^
zwölften Grades bilden. In dieser Schar (3) ist jede absolut invariante
Form zwölften Grades der Valentinergruppe enthalten. Eine beliebige
invariante Form Sl dieses Grades ist nämlich, wenn sie 0 oder F als
Teiler hat, in der Gestalt %0 bzw. XF^ darstellbar. Ist dies nicht der
Fall, so bringe man die Kurve Sl == 0 mit der Kurve sechsten Grades
zum Schnitt. Man gelangt zu einem invarianten System von 72 Punkten
*) Durch die in Klammern unter das Produktzeichen gesetzte Zahl ist hier
und weiterhin die Anzahl der Faktoren des Produktes angegeben.
Neues Formensystem de^ Valentinergruppe, 285
der Kurve jP = 0, also zu den Wendepunkten, die ^uch von der Kurve
0 = 0 ausgeschnitten werden. Man kann alsdann eine Konstante y, so
bestimmen, daß die Kurve £1—^Q =zi 0 in einem beliebigen von den
Wendepunkten verschiedenen Punkte die Kurve ^ = 0 schneidet. Dann
hat notwendig (ü — y,^) den Faktor F und also die Gestalt IF^,
woraus der Satz hervorgeht.
Hiemach ist sowohl ^ als auc}i die in (2) S. 280 dargestellte
Form ^ eine Form der Sch^r (3). So findet man z. B. leich-t für die
Form ^ die Darstellung:
(4) 18 * = - (^ 4- 7) ^ -f- 4(,; -^ l)f ^
aus der übrigens die Tatsache, daß ^ teilerfremd gegen F ist, u:fimittelbar
hervorgeht.
Reduzible invariante Formen SOs^^^^ Grades haben wir in den
Produkten :
15 _ 1^
(5) w{x^, x„ X,) = n^'^' ^(^' «2. %) = n^fc
der Oktaederformen beider Systeme. Kach einem S. 277 aufgestellten
Satze können diese Formen gegenüber den Substitutionen der
Valentinergruppe höchstens multiplikative dritte Eii|.heitswurzeln annehpien. Da
indessen die Valentinergruppe a]is z^ei Substitutionen S und T der
Perioden 5 und 2 erzengbar ist, bei denen die Formen (5) komplexe
dritte Einheitswurzeln nicht annehmen, so sm4 die Formen W, W
absolut invariant. Wir benutzen hinfort an Stelle der Fonn W die erste
der Formen (5), für die wir aus (4) S. 277 die Darstellung ablesen:
(6) ?F = 8n(ri^iM-2%^-l-2x|)
(3)
.n(^3^-4)xi2-|(,;-4)(»|-%2)-,;.-V3jr,(»,^^3)-.a^»^%),
(12)
wobei die Indizes an den Produktzeichen denselben Sinn haben, wie
in (2). Daß diese Form W weder 0 noch F als Faktor hat, ist
einleuchtend. Die Form W ist in der Gestalt:
W = aW ^h^^F~\-c(pF^ +-dF'
darstellbar; die Koeffizienten fertig zn berechnen, ist nicht erforderlich.
Im Anschluß an (5) und (6) S. 277 schreiben wfr endlich die vierte
Form des fortan zu benutzenden vollen Formensystems F, 0, W, X
der Valentinergruppe in der Gestalt an:
(7) X = x^x^ »3 {xi — »D (xl — x!) (x! — xi) • n (ö ^1 + ^. + ^3)
(1-2)
.Yl{2x,~\-(T]~e)x,-l-(^ + ß)x,).
286 IIj 3. Valentinergruppe und zugehörige Formen.
WO sich die Produkte auf die 12 bzw. 24 Faktoren beziehen, die aus
den angegebenen durch die Substitutionen der bevorzugten Oktaeder-
gnippe hervorgehen.
Xatürlich besteht auch zwischen den Formen des neuen Systems
eine Relation der Gestalt:
(8) X^ = aWi^'^ -f iiW^) +- F' a{F, 0, ?F),
wo Gr eine rationale ganze Funktion der F, 0, W vom 84sten Grade in
den »j, r»2, x^ ist. Die rechte Seite dieser Gleichung wird später in
nahe Beziehung zur Resolvente sechsten Grades des Formenproblems der
Valentinergruppe treten (vgl. S. 297).
§ 14. Gebrauch der ikosaedrischen Koordinaten.
Wenngleich die bisher dargestellte Theorie der Valentinergruppe
für die weiteren Entwicklungen eine ausreichende Grundlage liefern
würde, so mögen doch hier noch einige ergänzende, auch an und für sich
wertvolle Ausführungen über diese Gruppe folgen. Es soll zunächst
gezeigt werden, wie man die Behandlung der Gruppe bei Gebrauch der
schon S. 263 eingeführten ikosaedrischen Koordinaten 5^, s^, 2^
begründen kann. Die invarianten Formen der aus den Substitutionen S
und T (vgl. (1) S. 263) zu erzeugenden temären Ikosaedergruppe sind in
anderen Bezeichnungen S. 263 gegeben. Die beiden niedersten Formen
sind vom zweiten und sechsten Grade und haben in den z^, z^, ^3
geschrieben die Gestalten:
(1) ^,^3 -f-zl, z^sl — {s^ + 4)^2 — '^^i44 i- Q^^4h-
Die irreduzible Form sechsten Grades der in ikosaedrischen
Koordinaten 5j, ^2, ^3 geschriebenen Valentinergruppe muJ3, da diese Gruppe
die aus S und T erzeugte Ikosaedergruppe ©g^ enthält, darstellbar sein
als Summe der zweiten Form (1) und der mit einer noch zu
bestimmenden Konstanten a multiplizierten dritten Potenz der ersten Form (1),
also in der Gestalt:
(2) (1 + a)zl3! - {zl - 4)h + (3« - 'i)zUlzl + (3« + 8)^,^2*^3 + azi.
Es gibt in der Valentinergruppe GvaQ zweite mit der ersten ©g^ nicht
konjugierte Ikosaeder-Ögo, die mit der ersten den aus S zu erzeugenden
zyklischen Teiler ©5 gemein hat. Legen wir die zweite ©go i^ ü^^er
temären Gestalt mit den zugehörigen Koordinaten z'-^, z'2, z'^ zugrunde,
so konmien ihr die in den z'^, z'^, 4 geschriebenen Formen zu und die
Invariante sechsten Grades (2) der Valentinergruppe hat dann, vielleicht
abgesehen von einem konstanten Faktor, notwendig die Gestalt:
(3) (1 4- a') z\' z'i - (z',' -f z',') 4 -f (3 «' - 2) z[' z',' z','
+ {Sa' 4-8)^;4*4~f «'46.
Ansatz der Form sechsten Grades m ikosaedri^chen Koor4inaten. 287
Das Koordinatendreieck ist beiden Syßtemen gemeinscliaftlicli; denn es
ist das Poldreieck der Substitution S. Es gibt demnach einß
Substitution :
(4) Z[ == a^j, 4 := ßz^, s'i =z yz^,
die die Form (3) in die mit einer Konstanten h muHiplizierte Form (2)
überführt. Dies aber trifft stets und nur dann zu, wenn die folgenden
sechs Gleichungen gelten:
{l~\^a')^'y' = h(l-ra),
(5) \ (Sa- 2) «2 ^2 ,^2 ,^ 5 (3 ^ __ 2),
(3a'-| 8)aß'y = &(3«-f 8),
ß ß^ = ha.
Aus diesen Gleichungen sind die a, a', h, a, ß, y zu berechnen.
Keine der Konstanten a, a' \erscl^windet, d. h. die z\\^eite Form (1)
ist nicht bereits eine Form der Valentine^gruppe *). Dje Elimination
von 6 führt zu den Gleichungen:
a {a ~f 1) «^ y^ = ß^ ß' (a -p 1),
a{Sa'— 2)a^y- = ß^a'{Sa — 2),
^^^ ^ a(na'A-8)ay =r- ß^a'{^a-^8),
aa^ = a y'" = a! ß'".
Bezeichnet man die Zahl ay ■ ß~^ abkürzend durch d, so schreiben sich
die ersten drei Gleichungen (6) so:
(7) 3««' (d^ — 1) — 2ad^ 4- 2a = 0,
[ naa'(d—l)-^8ad — 8a' = 0,
woraus wegen Nichtverschwindens von a, a', aa' für ^ die Gleichung:
' ^3 — 1 , ^^ — 1 I
I 3 (^2 _ Y)^ _ 2 ^^ 2 ! := 0
I 3(^ -1), 8^, —81
folgt, die entwickelt die Gestalt annimmt:
(8) 10^(^- 1)2(4^2^7^ ^4) = 0.
Da «, ]3, y nicht verschwinden, so ist ^uch ^ von 0 verscjiiede^. Auch
die Lösung ^ =^ 1 ist unbraucl^bar. Da wir nän^lich das Aultreten
eines Faktors & bei Ausübung der Substitution (4) vorsahpn, dürfen wir
einen der Koeffizienten a, ß^ y frei wählen und setzen etwa j3 == 1. Da
>=) Man bestätigt dies aus (5) leicht. Wäre eine der Zahlei^ a, a' gleich 0,
so wurde auch die andere verschwinden, da weder ß noch h verschi^vinden. Aus (5)
bestimmt sich dann die Substitution (4) leicht als eine Potenz von S.
288 III 3. Valentinergruppe und zugehörige Foritien.
für Ä = 1 aus (7) die Gleichheit a =z a folgt, so ergibt sich aus (6)
und d = 1:
a^r==l, j;^=::l, o(j;=:l, «===: £', y = £~ ^
SO daß die Substitution (4) wieder eine Potenz von S sein würde. Es
bleiben demnach für 8 nur noch die beiden Wurzeln der quadratischen
Gleichung:
(9) 4 ö^ + 7 ö + 4 = 0.
Es mußten sich 2 Werte 8 ergeben, da oben unentschieden blieb, welche
unter den beiden S enthaltenden Ikosaedergruppen die vorangestellte
Gruppe ®gQ sein sollte. Wir entscheiden hierüber, indem wir die Lösung:
(10) ö = ^ =-rf
auswählen. Die Auflösung der drei linearen Gleichungen (7) für aa\
a^ a liefert weiter:
aa:a:a = 8d : 3(40 + ^^) • 3 ö (5 ö + 4),
woraus man folgert:
__ 8 _ brj—4: , _ 88 _ 5^ — 4
(11) a — Y^^s^r^) — —9 ^ ^ — 3^4^ + 5) — "T
Wie schon bemerkt, können wir ß willkürlich wählen. Wir
erklären ß durch die erste der folgenden Gleichungen, worauf sich die
weiteren leicht ergeben:
(12) ß^-lV' ay = ß'S = iri'.lij'=l.
Mit Benutzung des Wertes a folgt weiter:
„'«._ 5^-4 öv + 28 _bn-4_
<^P — ,) 3^— — - 9— — «'
SO daß aus den letzten Gleichungen (6) und (12) sich :
(13) a^ r= 1, y^ — 1, ay = 1, oc = f'', y = £-''
ergibt. Die Substitution (4) bleibt für unseren Zweck brauchbar, wenn
wir sie noch mit S~*' multiplizieren. Es läuft dies darauf hinaus, daß
wir a = 1, y = 1 setzen dürfen. Damit haben wir den Satz gewonnen:
Mittels der beiden ikosaedrischenKoordinatensystemen z^, z^, z^ und z\, z^, ^3
haben wir die invariante Form sechsten G-rades^ der Valentinergruppe in
den Gestalten:
(14)
+ 15(^ - 2)^,^^1^1 + 15 (^ + A)z^zU, + {öri - A)zl,
F' (0,, 4, 4) = 5 (^ + 1) e['i,',' - 9 (^1 + g',') 4
+ 15 (i) — 2) /i^ii','z'i'.+ 15<^ + 4) ^;^2*4 .+ (6 ^ - 4) 4"
Symmetrische Ikosaederkoordinaten. 289
anzusetzen; beide Koordinatensysteme hängen durch die Transformation:
(15) z[ — z^, 4 = —^rjz^, z'^ = z^
zusammen, die für die Formen (14) die Relation:
(16) F'{z[, 4, 4) = -\riF{z,, z^, z,)
nach sich zieht.
Da die Koeffizienten in den beiden Formen (14) konjugiert komplex
sind, so können wir die Kurve sechsten Grades F(z^, z^, e^) = 0 auch
durch die Gleichung F'(z^, z^, z^) = 0 geben, unter i den zu z
konjugiert komplexen Wert verstanden. Die linke Seite der letzten Gleichung
transformiert sich durch die Substitution:
(17) ^j = Z\, ^2 = — 1^-2, ^3 — ^nr
die wir auch :
(18) ^'; = ^j, 4 = _i^:^2, 4 = ^3
schreiben können, bis auf den Faktor —|iy wieder in die linke Seite der
(Tleichung F{z^, z^, z^ = 0. In (17) oder (18) haben wir somit eine
,,Spiegelung^'' wiedergewonnen, die die Kurve sechsten Grades in sich
überführt und die beiden Ikosaedergruppen ©g^ und @6o ineinander trans-
formioi.
Man kann übrigens ein symmetrisches ikosaedrisches
Koordinatensystem dadurch erklären, daß man neue Koordinaten x, y, z durch die
Transformation:
(19) ^=—?:y3^,, y = Oz^, z=-iiSz^
einführt. Die Spiegelung (17) stellt sich dann nämlich einfach in der
Gestalt:
(20) X = — X, y' = — y, / = — z
dar, woraus hervorgeht, daß die Form F in den x, y, z reelle
Koeffizienten haben muß. In der Tat geht die mit dem konstanten Faktor
d (rj — 2) multiplizierte Form. F, auf die symmetrischen
Ikosaederkoordinaten X, y, z umgerechnet, in die Form sechsten Grades:
(21) lOx^z^ _ 9 (^5 ^ ^6) ^ _ 45 ^2^2^2 _ 135 ^^4^ _^ 27 /
mit reellen rationalen ganzen Koeffizienten über. Wir haben hier also ein
Seitenstück zu den Wendedreieckskoordinaten bei der Klein sehen Gruppe,
in denen die Form vierten Grades der ©^^g gleichfalls reelle ganzzahlige
Koeffizienten hat. Dafür erfordert die Darstellung der Valentinergruppe
in den ikosaedrischen Koordinaten noch die Adjunktion der fünften
Einheitswurzel £.
§ 15. Gebrauch der kanonischen Koordinaten.
Hatten wir soeben die ikosaedrischen Koordinaten zu einem neuen
Wege benutzt, die Valentinergruppe und ihre Invariante sechsten Grades
zu gewinnen, so gibt es einen nicht minder interessanten, zum gleichen
Fricke, Algebra. II. 19
290
II, 3. Valentinergrappe und zugehörige Formen.
Ziele führenden Weg, der art die konjugierten Teiler ©gg der Kollineations-
gruppe ©3gQ anknüpft. Jeder dieser Teiler ©gg enthielt einen kommu-
tativen Normalteiler @g, der aus vier zyklischen ©g (je zweien aus den
beiden Systemen konjugierter ©g) zusammengesetzt war.
Mit der ©gg gewinnen wir Anschluß an die bekannte Theorie des
sysygetischen Büschels von Kurven dritten Grrades*) und der Hesseschen
Kollineationsgruppe ©g^g, die dieses Büschel und seine neun
Grundpunkte (die Wendepunkte der Kurven des Büschels) in sich transformiert.
Die einzelne Kurve ist dabei gegenüber einer ©jg invariant und eine von
12 konjugierten Kurven, die gegenüber der ©g^g die Permutationen einer
Tetraedergruppe bilden. Vier Kurven des Büschels zerfallen in die vier
Wendedreiseite, und vier Kurven sind äquianharmonisch; sie entsprechen
den vier Ecken und den vier Seitenmitten des Tetraeders. Sechs Kurven
des Büschels sind harmonisch; diese entsprechen den sechs Kantenmitten
des Tetraeders. Die einzelne harmonische Kurve des Büschels geht
gerade durch eine Kollineations - ©gg der in der Valentinergruppe
auftretenden Art in sich über und ist innerhalb der Hesse sehen Gruppe eine
von sechs konjugierten**).
Diese Angaben sind hier nur beiläufig gemacht. Will man sie etwa
bei Gebrauch der oktaedrischen Koordinaten bestätigen, so gehe man von
der @gg aus, die aus den beiden ersten der nachfolgenden Substitutionen:
(1)
/O, 1, 0.
f7= 0, 0, 1 ,
W, 0. 0/
/ !•
U' =
1-V5 ,
U^o,
/ - ^ß -^
W=I-^J, 0, -i
V-i P, 1
1 + V5 . i-Vs^
1 i + Vö
1—y"5 1 ,
: ^ O
A
erzeugbar ist. Die erste und dritte Substitution sind von der Periode 3
und vertauschbar. Die zweite Substitution ist von der Periode 4, xmd
es gut:
Also ist W im Xormalisator der aus den Substitutionen U'^-U'^
bestehenden konmiutativen ©^ enthalten, so daß durch Zusatz von TT zur ©g
*) Vgl. z. B. „Enzyklop. der math. "Wiss.~ Bd. 3, Teil 2, S. 493. Im ersten
Kapitel des nächsten Abschnitts kommen wir auf das fragliche Büschel
ausfuhrlicher zurück.
**) Innerhalb der Valentiner-@ggo, die mit der Hesseschen Gruppe den?
Durchschnitt @gg bildet, ist die harmonische Kurve naturlich eine von. zehn
konjugierten.
Syzygetisches Büschel von Kurven dritten Grades. 29]
der Teiler ©gg erzeugt wijrd. Die Poldreiecke vop U und P"' werden
durch Nullsetzen der beider^ zerlegbaren kabischen Formen:
(■^1 = ^f + xi + -i'l — Sx^i^x^,
J^ = -71 (xl ~f xi -r «D - B {xl x^_ + xl x^^xlx^-\ p xjx.^)
-|- 6 X^ »2 ^'3
dargestellt, aus denen die Gleichung des syzygetischen Büschels in def
Gestalt:
(3) '/z/, ^;l^^2 =-0
hervorgeht. Ohne besonderen Aufwand von Rechnung stellt man die
beiden letzten Wendedreiseite des Büschels und damit die Poldreiecke
der Substitutionen TJ-U' uiid If^-U' durch ^STullsetzen der Foniien
1^3 = - (2 t (1 - Vö) q) z/, - z/„
U, = - (2 + (1 + V5) 9'-) 4, - ^,
dar. Wir verfolgen dies nicht weiter, wollen vielmehr aus den
gegebenen Darlegungen einen neuen Absatz zur Gewiipiung der Valentiner-
gnippe und ihrer invarianten Fprm sechsten Grades herleiten.
Zur Darstellung der 18 Kollineationen, die jede ebene Kurve (Jrittep.
Grades in sich zuläßt, benutzt Klein*) ein „kanonisches
Koordinatensystem" ^j, ^2) ■^3) üi dem die Kurve die Gleichung gewinnt:
(5) 4 ^3 — 4 4 4- 9^ ^2 ^l i- 93 4 = 0,
wo g^ und g^ bis auf numerische Faktoren die beiden Arophold schep
Invarianten sind, die in den Koeffizienten der ursprünglich beliebig
angesetzten temären kubischen Fo^m vom v^.erten. und sechsten Grade sind.
Liegt insbesondere der har^on^che Fall vor, so ist ^, == 0, so daß die
Kurve dritten Grades durch:
(6) ^2^^_4^s^^^^^^| ^0
gegeben ist. Ohne Änderung des Koordinatendreiecks führen wir zur
Vereinfachung der Formeln noch die Transforip.ation aus ;
(7) ^] = 2/3 V2 i VS g^ y</2, ^2 = -h \9o, ^i = Vi 2 i ys
und behalten auch für die y den Namen der „kanonischen Koordinaten"
bei. Die Gleichung (6) geht bei Fortlassung eincfe, konstanten Faktors,
der allen Gliedern gemeinsam ist, über in :
(8) yU-^y,yl-¥^y,d=^ 0.
Wir werden unten einen sehr einfachen Übergang von der hier links
stehenden temären Form:
(9) f = yl + ^y^yl-^y,yl
*) Vgl. alles Nähere in „Ges. Abh." III, S. 217 oder „Modulfunkt.'- II, 246
19-
292 II, 3, Valentinergruppe und zugehörige Formen.
zur invarianten Form sechsten Grades der Valentinergruppe entwickeln.
Im übrigen ist der Grund dafür, dajß wir diese Methode zur Herstellung
der Valentinergruppe hier nur beiläufig behandeln, in dem Umstände zu
suchen, daß bereits die Aufstellung der ganzen ©gg der Kollineationen
der Kurve (8) in sich die Adjunktion neuer und umständlicher numerischer
Irrationalitäten nötig macht. Legt man als Koordinatendreieck eines der
vier Wendedreiseite zugrunde, so nimmt die Kurvengleichung die
bekannte Hesse sehe Gestalt an, und dann allerdings ist die Kollineations-@jg
außerordentlich einfach darstellbar*). Xun ist die durch 216 geteilte
Hessesche Form li von f gegeben durch:
j( 10) l = yl y^ — y^ yl — yl,
so daß das syzygetische Büschel durch:
(11) v,f^u,^ ^{yl-r^y,yt-\-^y^yl)-^ijfly,-yryl-yl) = o
dargestellt ist. Die vier in die Wendedreiseite zerfallenden Kurven (11)
bestimmt man leicht durch die Forderung, daß die linke Seite von (11)
einen Linearfaktor {y^ — ^ y^ haben soll. Man gewinnt für ^ eine
biquadratische Gleichung, die die vier durch den Wendepunkt (0, 0, 1)
hindurchlaufenden Wendelinien liefert. Wir wählen eine Wurzel it und
erhalten ein Wendedreieck, dessen Seiten durch:
( y_ 3 o-2 Vs" 2/1 + ^1/3 + 21^ ^2X1^^3 = 0
gegeben sind. In der Tat findet man durch Multiplikation dieser drei
Gleichungen die sich dem Ansätze (11) einordnende Gleichung:
t^{yl + ^y^yl ^^y,yl) + ^^^^^1^{yly,-y,yl-yi) = o.
Die mit geeigneten Konstanten multipKzierten linken Seiten der
Gleichungen (12) sind als neue Koordinaten einzuführen, um zur Hesseschen
Gleichungsform der Kurve dritten Grades zu gelangen. Wie man sieht,
sind für die wirkliche Aufstellung der ©^g neue Irrationalitäten zu
adjungieren.
Bei dieser Sachlage beschränken wir die weitere Entwicklung auf
die Herleitung der invarianten Form sechsten Grades der
Valentinergruppe. Die zunächst mit beKebigen Koeffizienten angesetzte ternäre
kubische Form f hat eine Schar von Kovarianten sechsten Grades in
den Variablen, und achten Grades in den Koeffizienten. Ist li die
Hesse sehe Form und bezeichnet man mit g die mit den partiellen ersten
'■^) Vgl. darüber das m „Modulfunkt.'- IL 251 ff., sowie unter S. 335ff.
Invanante Form sechsten Grades in kanonischen Koordinaten. 293
Ableitungen von h geränderte jHessesche Determinante der gegebenen
Grundform /':
(13)
8V
■dyl'
d^f
^2/a ^2/1
_d'l
d'f
dy^dy^'
d'f
dyi'
d'f
d-f oh
dy^^dy^' dy^
fS M j'
' S2/3 ^yi '^Vz'^y^ oyT dy^
dh dh oh
S.9j' g«/^' 8.2/3'
so haben wir in g eine e^ste Kovariante der genannten Grade. Die
Schar der Kovarianten ergibt sich bei Heranziehung der Aronhold scheu
Invariante S vierten Grades (in den ^Koeffizienten) in dei' Gestalt:
(14) yicj^XSfJi.
Im Falle unserer Form (9) mit numerischen Koeffizienten kommt
die gleichfalls numerische Invariante S i^icht weiter in Betracht. Die
Form g ist abgesehen von einem konstanten Faktor gegeben (Jurch:
{g = yl-'^ yt y, y, - yl (8 yt - 30 ^/f yl — 6 yt)
\ -y,y..{yt~^iylyl-^^iyl)
Für die in der Schar (14) enthaltene ., irreduzible •' Form sechsten
Grades F der Valentinergr^ippe darf ;c = 1 gesetzt werden. Schreibt
man Jl S = — ^, so ergibt sich der nur noch eine unbekannte Größe /«
enthaltende Ansatz:
\F= yl T- (3 a - 9) yt y, y^ + 30 yl yl yl - (2 ^ - 6) yl yl
I ~f2/l(C'^-8)^i' +(3ft+ 6)3/1)-.^!2/a(/*+1)2/1-(3/i-21).^t).
Zur Bestimmung von u bea,chte man, daß in der ©gg die Substitution
der Periode 4 enthalten ist:
(17) y'x = iy^, i/2 == — *«/2. y'i = yy
Die aus ihr zu erzeugende zyklische %^ hat innerhalb der @gg nuf sich
selbst zum Xormalisator. Dagegen hat sie innerhalb der Valentiner-
gruppe eine Dieder-®^ zum Xormalisa.tor, in dem noch vier Substitutionep
der Periode 2 vorkommen, die die Substitution (17) in ihre ipverse
transformieren. Sie werden also die Ecke (0, 0, 1) des
Koordinatendreiecks in sich transformieren i^nd die beiden anderen Ecken austauschen,
so daß sie bei unimodularer Schreib-v^eise die Gestajt:
(18) y\^=ay^_., y'^^a~^y^, y'i ~ ys
294 Hi 3. Valentinergrappe und zugehörige Formen.
haben. Gegenüber dieser Substitution müssen somit die beiden
biquadratischen Formen:
(19) (^-8)yt + ^(li-^^)yl, 0*+1)2/1-3(^-7)2/1
absolut invariant sein. Daraus ergeben sich die beiden Gleichungen:
(20) (^_8)a* = 3(^+2), (j,+1)^^ + 3(^-7)^0.
Durch Elimination von cc erhält man für ^ die quadratische Gleichung:
(ft +!)(/* + 2) -f (^ - 7) (^ - 8) = 0
mit den beiden Lösungen:
(21) ^ = 3 + 2iy5.
ilan kann hiernach das kanonische Koordinatensystem in zwei wesentKch
verschiedenen Arten auswählen. Wir bevorzugen das obere Zeichen in
(21) und bestimmen einen der vier zugehörigen "Werte a aus (20):
(22)
Es besteht hiernach der Satz: Bei G-eh'aiich der kanonischen Koordinaten
btellt sich die invariante Form bechsten Grades der VaJentinergruppe in
der Gestalt dar:
iF=yl-^^iyli>y^y, yt + 30 yl yl yl — 4« Vo yf pi
(23) +((-3 +2iV5)2/,* + 3(5 + 2iVö)2/|)2/|
l ~-2/,^^,((4-r2iV5)^,*+5(4-2*V5)2^|),
und die Valentinergrujo^e bclbd geht aiib der KolUneationsgruppe ©gg durch
Zusatz der Substitution der Periode 2 hervor:
2/1= 1 2/2, 2/2 =-—7==^—2/1, 2/3 = 2/3-
V3 V3|/^
Wegen weiterer Ausführungen über die Valentinergrappe sei auf
die S. 279 genannte Arbeit von Wiman, auf die Darstellung des
Verfassers in „Autom. Funkt.'" II, 617ff., sowie namentlich auf die 8,273
namhaft gemachten Untersuchungen von Gerbaldi verwiesen.
Eesolventen niederei^ Grades des Porpienproblems der ©ggo- 295
Viertes I^apitel.
Formenproblem der Valentinergruppe und allgem^äine
Gleichung sechsten Grades.
§ 1. Formenproblem der Valentinergruppe mid Resolvente
sechsten Grades.
Der Ansatz des Formenproblems der Valentinergruppe hat in üblicher
Weise zu geschehen: Es seien etwa fur die Formen F, 0, W, X vier die
Bdation (8) S. 286 befriedigende Werfe vorgeschriebe^, zu berechnen sind
entweder die zugehörigen Werte r^, x^, x^ ßelbst oder auch nur ihre
Verhältnisse X-^^:x^:Xy Das erste Problein hat 1080 Lösungen, die sich i^
einer unter ihnen durch die Substitutionen der Valentinergruppe ©i^gß
darstellen. Das zweite Proble^i läuft darauf Jiinaus, eilten zu den gegebener).
Werten F, 0, W, X gehörenden Punkt (a'^, x^, Xg) in der
Koordinatenebene der X zu bestimmen. Dieses Problem hat 360 L,ösungen, wobei
alle 360 Punkte aus einem unter ihnen durch die Kollineationen de;-
Valentinergruppe ©gg^ hervorgehen. Ist dieses Problem gelöst, so
erfordert die Lösung des umfassenderei^ Problems nur noch das Ausziehen
einer Kubikwurzel.
Die niedersten Resolventen des formulierten Problems sind erstlich
zwei Besolventen sechsten Crradeß, die zu den beiden Systen^en von je
sechs konjugierten Ikosaedergruppen gehören. Hipran reiht sich eine
Besölvente zehnten Grades, die za derf zehp konjugierten Teilern (Sgg
gehört. Endlich folgen zwei Besolventen 15^^ G-rades, die von den beideii
Systemen der Oktaedergruppen geliefert werden. Über alle diese
Resolventen hat Gerbaldi höchst ausgedehnte Rechmmgen angestellt. Es
gelingt ihm, die Resolventen sechsten u^d zehntep. Grades in fertiger
Gestalt anzugeben (in den §§ 44 und 55 seiner Abhandlungen). Der
Fall F ^= ö erwies sich fimktionentheoretisch zugänglich und ist
ausführlich und erschöpfend vom Verfasser untersucht und in „Auton^.
Funkt." II, 553ff. dargestellt. Es handelt sich um die Transformatiori
dritten G-rades derjenigen ßutoniorphen FunUlmien, die zur GrenzJcreis-
grtipße der Signatur (0, 3; 2, 4, 5) gehören. Diese Gruppe T^ar es, die
uns oben (S. 241 ff.) den Eingang in. die Theorie der Valentinergruppe
eröffnete. Insbesondere liefert die Resolyente zehnten (grades im Falle
F = 0 die „Transformationsgleichung" für den dritten Trangformations-
grad, die als Resolventen niedersten Grades zwei solche vom sechsten
Grade besitzt. Man findet ß. a. 0. nicht nur diese Gleichungen
zehnten und sechsten Grades, sondern auch die beiden Resolventen
]^5ten Grades fertig berechaet. Daß die Aufstellung dieser Gleichungen
ohne Benutzung transzendenter Hüfsnüttel allein du^ch algebraische
Methoden gelangt, gründet sich auf den Umstand, daß man in allen drei
Fällen mit Kongruenzgruppen des Geschlechtes _|> = 0 zu tun hatte.
296 III 4. Fonaenproblem der Valentinergruppe und Gleichung 6ten Grades.
Die einfachsten Formen der Teiler ©g^ sind die beiden Systeme zu
je sechs Ikosaederformen (p und ^. Nach S. 272 ff. permutieren sich
aber erst die Kuben der Formen des einzelnen Systems gegenüber den
Substitutionen der Valentinergruppe und bilden hierbei die alternierende
@3go des sechsten Grades. Die beiden einfachsten Resolventen sechsten
Grades werden demnach die Gleichungen für die dritten Potenzen der
Ikosaederformen (p, ^ der beiden Systeme sein. Es mag genügen, wenn
wir diejenige Gleichung aufstellen, die die Kuben der unter (1) S. 272
gegebenen Formen (p befriedigen. Man gehe so vor, daß man die
Potenzsummen der sechs Formen (p mit durch 3 teilbaren Graden etwa in den
Formen F, 0, W, die S. 284 ff. eingeführt wurden, zur Darstellung
bringt. Aus den Potenzsummen der Kuben ^f, <pi, • • • berechnen sich
dann nach I, 102 die Koeffizienten der Resolvente. Es ergibt sich der
folgende Satz: Die eine der beiden JResolventen sechsten Gradeb deb
FormenprohJems der Valentinergruppe, nämlich die Gleichung sechsten
G-rades, der die Kuben der Ikosaederformen cp genügen, hat, wenn wir mit Z
die Unbekannte bezeichnen, die Gestalt:
(1) Z«-f6(,^-i-2)J'Z^+(|(,^-3)0 + 6(ll72~fl)J^')Z^-(3(7?-M5)0F
- 4 (51 >j - 55)^^3) ^3 _ (^ (11 ^ _!_ 1) ^2 ^ I (29 ^ -!_ 39) 0 F^
- 3 (53 >j - 145) F') Z^ -f (i ?F -f il (123 ^i - 127) 0^ p
-l^ (1 71-^ o) QF^) Z ~\r ^^ = 0.
Bei dem nicht geringen Umfange der Rechnung, die zur Gewinnung
dieser Resolvente aufgewandt werden mußte, ist ein Vergleich mit der
schon früher von Gerbaldi berechneten Resolvente erwünscht. Wir
führen zu diesem Zwecke an Stelle von 0 die Form ^ auf Grund der
Gleichung (4) S. 285 ein und schreiben der Gleichförmigkeit wegen F
statt F; dagegen wird W beibehalten. Die Resolvente (1) nimmt dann
die Gestalt an:
(2) Z« + 6(,^ + 2)^.Z5-(|(,^-2)*-66^^2)Z^-(f(2,^-31)^*
-f(114r?-157)i?^S)Z^-(|l(2,;-f 3) *2_^(8^_|_ 17)^^2
-if (34,;-169)^*)Z2-f(i?Fn-1(31^-1) *2^
-f ^ (169,; -f 919) * ^3 -1 (835 yi - 207) F'^) Z
Um die Bezeichnungen Gerbaldis zu erhalten, führen wir die Formen Ä
und H sowie die Irrationalität c durch die Erklärungen:
(3) A:=—2F, H=-l^, c:=^n
ein. Die Gleichung (2) nimmt dann die Gestalt an:
(4) Z'-Q(c + l)ÄZ-'~\-{{c-l)H~\-33cÄ')Z'-{j;(4c-31)ÄH
+ li228c-ro7)A')Z'-{i-^(4c~\^3)H'~\^^,{lQc~\^ll)Ä'H
-|(68c-169)^^)Z2+-(i?F-^(62 6--l)^jy2
+ j^(338c-^9l9)^äjy+^(1670c-207)^5)Z
+ (lie + 1) A' -^Jc-4:) HY = iL
Allgemeine Resolventen sechsten Grades. 297
Dies ist in der Tat die Re^olve^te, die Gerbaldi in § 44 seiner
Abhandlung mitteilt. Es besteht ^ur der äi^ßerliche Unterschied gegenüber dey
Gleichung (4), daß Gerbalcji den Koeffizienten des linearen Gliedes als
selbständige invariante Form Gr des 30stei> Grades an Stelle von W
benutzt. Es ist einleuchtend, daß man sich aus dem Gesamtsystem def
invarianten Formen 30^*^^* Grades:
(o) aW -^h^^F+c^^'"^ + dF''
je nach Umständen eine geeignete auswählen darf.
Da die Gruppe der Gleichxmg (2) die alternierende ©gg^ ist, so ist
die Quadratwurzel ihrer Diskriaiinante rational bekannt. Dies geht auch
unmittelbar aus dem an (10) S. 279 angeschlossenen Satze hervor. Xach
ihm ist nämlich das Difl'erenzenprodukt der sechs Lösungen unserer
Gleichung sechsten Grades, abgesehen von einem konstanten Faktor, gleich
dem Quadrate der Form 45^*^^ Grades X Die Diskriaiinante der
allgemeinen Gleichung sechsten Grades ist bekannt ===). Es bestellt deinnach
keine grundsätzliche Schwierigkeit, diesep Ausdruck der Diskriminante
etwa in den Formen W, ^, F herzustellen. Es muß sich zeigen, daß er
das Quadrat eines rationalen A^sdrucks ^.n diesen Formen ist. Dieser
letztere Ausdruck ist dann bis auf einen konstanten Faktor gleich derA
Quadrat der Form X Wir gelangen so zu der iJöglichkeit, die
Relation (8) S. 286 oder auch (11) S. 284 wirklich herzustellen.
Es ist nun ein besonderer Erfolg der Gerbaldischen Untersuch^ngen,
daß sie bis zur fertigen Ausrechnung diese;- Relation wirklich \or-
gedrungen sind. Es handelt sich um die Fori^el (194) in § 60 der
Abhandlung von Gerbaldi. Wegen der Wichtigkeit dieser Formel soll
sie hier mitgeteilt werden Dabei bedei^ten F und ^ unsere bisher so
bezeichneten Formen, X jst alDgesehen von eineiA konstanten Eaktor
unsere Form 4o^i^^ Grades, die, gleich 0 gesetzt, die 45 Perspektivitat&-
achsen darstellt, und W ist eine für den vorliegenden Zweck besonders
geeignete, aus dem Systen^ (5) gewählte Form 30^*^" Grades**). Die
zwischen den Formen F, ^, W, X hsstehenfle Belatto^ id dann nach Ger
bald is jRechwimgen die folgende:
(6) X2 == !Fs + 3 (38 $° — 2^. 3' • o *^ F' ^ 2^ • 3-> • 5 • 31 ^^F'
— 2^. 3^. 5 ,11 *2 _p6 ^ 2^0. 35. 5 ^ _p8 _ 210.31 F'^) W
+ 2^ • 3« ^(36. 0 *^ — 2^. 3^ • 0 *6 ._p2_2*. 33.773 ^F^
— 2^.3^o.31**F*'+2i2-32.5.7*3_p8_9i3.32.52^2_pio
+ 21«. 3^ • 5 * Fy^ ■— 21^ o F'%
*") Ihr allerdings sehr umfänglicher Ausdruck ist z. B. mitgeteilt bei
SalmonFicdler, .,Algebra 4er ImearenTransformatioaen", 2. Aufl., S. 344 (1877).
*=^) W braucht also nicht gerade die oben so be/^eichnete Form (3) S. 280
298 n, 4. Formenproblem der Valentinergrappe und Gleichung 6ten Grades.
§ 2. Spezielle Resolventen sechsten Grades.
Wir erinnern zunächst an die beiden Gleichungen (3) S. 258, die
wir aus den damals betrachteten beiden Systemen konjugierter
Kongruenzgruppen dritter Stufe vom Index 6 ableiteten. Im Anschluß an (1) S. 258
können wir die eine dieser Gleichungen in die Gestalt kleiden:
144 .
(1) r2 + 3(r?-3)r2-3(2,^-5)r~f (37^-7)=z—=V(l-2,^)ir.
Aus ihr geht die andere Gleichung einfach dadurch hervor, daß man r}
durch rj ersetzt. Man findet, wenn man hernach rj wieder durch 1 — r}
ersetzt:
]^4^
(2) T'-3(ri±2)t' + B{2n + S)t-(^n~\-4:)=—^)/(2r)-l)LT.
■ ovo
Von einer dieser Gleichungen aus haben wir oben (S. 259 ff.) durch
eine nicht ganz einfache funktionentheoretische Überlegung die Valentiner-
gruppe eingeführt. Diese Überlegung soll jetzt dadurch sichergestellt
werden, daß wir von der Resolvente (1) S. 296 aus umgekehrt zu einer
der Gleichungen (1) oder (2) zurückgelangen können. Die S. 259 ff.
vielfach genannte 360-blätterige Riemannsche Fläche entspricht der Kurve
sechsten Grades jP = 0. Es handelt sich also hier um diejenige
in der allgemeinen Gleichung (1) S. 296 enthaltene „spezielle Resolvente",
die für JP = 0 eintritt und also die Gestalt hat:
^^^ l ~ (4 0)3 = 0.
Die in (1) und (2) auftretende Größe L ist eine 360-wertige
Funktion auf der Kurve sechsten Grades F = 0, deren Nullpunkte zu je
vier in den 90 sextaktischen Punkten erster Art (vgl. S. 281)
zusammenfallen, während die Pole zu je fünf in den 72 Wendepunkten liegen.
Demnach ist die rationale Darstellung von L auf der Kurve sechsten Grades
durch:
(4) L = c-^
geleistet, wo o eine noch zu bestimmende Konstante ist.
Um eine 60-wertige Funktion zu konstruieren, die zu einem ersten
ikosaedrischen Teiler ®g^ gehört, bezeichnen wir die zugehörige Iko-
saederform zweiten Grades mit (p^. Es handele sich etwa um die erste
Form (1) S. 272. Zum gleichen Teiler gehört auch das Produkt der
fünf übrigen Ikosaederformen tp^, cp^, ..., ^g. Wir erklären dann
zunächst unabhängig von (1) und (2) eine gewünschte Funktion x der ©g^
durch:
(ö) 4«"'
'/ • VlL <Ps <Pi fi, <Pe
Rückkehr zur speziellen ße^olven|;e sechsten Grades. 299
Die 60 Nullpunkte von x fallen zu |e 5 in den 12 Weiidepunktep der
Kurve sechsten Grades zusammen, die durch den Ikosaederkegelschnitt
gjj =z 0 ausgeschnitten werden. Die 60 Pole liegen in den übrigen
60 Wendepunkten, die bezüglich der ®^^ r^ur u|iter sich äquivalent sind.
Erweitern wir die rechte Seite der Gleichung (q) mit y^ und setzen, wie
S. 296, (pl = Z, so folgt:
(6) T;^t^, 2Z=— V^ 0^.
Zufolge (3) befriedigt also die in (5) eii^geführte Funktion 'f der Iko-
saeder-@g^ die Gleichung:
^3 ^3 ^3^ 6(7^ — 3)0 )j2 02^2 _ 3(11,; + l)02^0T-f (40)3
Man multipliziere diese Gleich^ng mit ff =^ — (^ ■»? -h 4) und teile
hierauf durch (4 0)^, wodurch man gewinnt:
x'-^in + 2)r2 -f 3(2,? -f 3)r-(3,? ^ ^^ = T^ ^(S^ + '^S)!^^-
Schreiben wir demnach unter Bestimmmig der bishpr noch unbekannten
Konstanten c an Stelle von (4) genauer:
so geht die letzte Gleichung genau in die Gleichung (2) über, so daß wir
tatsächlich zu der zweiten der S. 258 aufgestellten Gleichungen sechsten
Grades zurückgelangen. Damit ist der Schlußstein der hier beabsichtigten
Darstellung der Valentinergruppe gelegt.
§ 3. Notizen über die allgemeine Gleichung sechsten Grades.
Bald nach Herausgabe der „Volles, über das Ikos.'- unternahm es
Klein, die dort entwickelten Prinzipien auf die Auflösung der allgei^eineia
Gleichungen sechsten und siebei^ten Grades zu übertragep ===). Es gelang
in beiden Fällen, quatemärp Substitutionsgruppen dpr Ordnungen 6! und
I 7! zu erklären, die der sy:aimetrischßn Permutationsgruppe des Grades 6
und der alternierenden deß Grades 7 isomorph, sind. Diesen Gruppep
wurde dann die Rolle zugewiesen, die die Ikosaedergruppe bpi de^?
Auflösung der allgemeinen Gleichung fünften Grades spielte.
Diese Entwicklungen wurden, was die Glßichupigen sechsten Grades
angeht, mit dem Bekanntwerden der Valentinergi-uppe übejUüssig, da
es selbstverständlich vorzuziehen ist, an Stelle einer (][uatemären
Gruppe für die allgemeine Gleichung sechster). Grades nach Adjunktion
*) Vgl. die 1886 erschienene Abhandlung „Zur Theorie der allgemeinen
Gleichungen sechsten und siebenten Grades", üath. Apn. 3d. 28 oder „Ges.
Abhandl." II, 439.
300 Hl 4- Formenproblem der Valentinergruppe und Gleichung 6ten Grades.
der Quadratwurzel aus der Diskriminante die temäre Valentinergruppe
zu benutzen. Klein hat dann auch in seiner 1905 erschienenen Arbeit
„Über die Auflösung der allgemeinen Gleichungen fünften und sechsten
Grades" („Ges. Abhandl.-' II, 481) die Behandlung der Gleichung sechsten
Grades auf die Valentinergruppe gegründet. Er folgt hierbei seiner
zweiten in der Ikosaedertheorie entwickelten Lösungsmethode der
allgemeinen Gleichung fünften Grades, bei der die Ikosaedergnippe in
Gestalt einer temären ©g^ zugrunde gelegt wird (vgl. oben S. 159 ff.).
Die erste dabei zu lösende Aufgabe ist, aus fünf unabhängig veränderlichen
Größen Kj, Wg, •••, «5, nämlich den fünf Wurzeln der allgemeinen
Gleichung fünften Grades, durch eine Kette algebraischer Operationen
möglichst einfachen Charakters, drei Größen ^^, 3^, z^ zu konstruieren,
die die 60 Substitutionen der temären Ikosaedergmppe erfahren, falls
die oc den 60 geraden Permutationen unterworfen werden. Die
berechneten z^, ^2) ■2^3) in die invarianten Formen der temären ®^^
eingesetzt, liefern rational bekannte Größen. Die Aufgabe der Berechnung
der ^j, ^2) ■^s ^ii'5 bekanntgegebenen Werten jener invarianten Formen
ist das „Formenproblem der temären Ikosaeder-^g^". Das Ziel des
algebraischen Teiles der Theorie der allgemeinen Gleichung fünften
Grades war also die Reduktion dieser Gleichung auf das Formenproblem
der temären Ikosaeder-^g^. Der transzendente Teil der Theorie lehrt
dann weiter die Lösung des Formenproblems durch Modulfunktionen
(vgl. S.98ff.).
Für die "Übertragung dieser Theorie auf die allgemeine Gleichung
sechsten Grades hat Klein in der zuletzt genannten Arbeit einen ersten
Ansatz skizziert. Der eingeschlagene Weg führt indessen zu
Schwierigkeiten, und zwar infolge beständigen störenden Auftretens von dritten
Einheitswurzeln an unerwünschten Stellen. Dies liegi begründet in dem
Umstände, daß die Valentinergmppe zwar als Kollineationsgmppe eine ©gg^,
aber als temäre Substitutionsgruppe eine solche der Ordnung 8-360 ist,
während die Ikosaedergruppe auch als temäre Substitutionsgruppe eine ©g^
verbleibt. Die Idee, wie man die fragliche Schwierigkeit überwinden
kann, hat Klein ebenfalls gefaßt. Sie entsprang dem einfachen Gedanken,
neben Punktkoordinaten .c^, x^, x^ m der Ebene (etwa den oktaedrischen)
auch LinienJioordinaten u^, u^, u^ einzuführen und entsprechend mit
Zwischenformen zu arbeiten.
Diese Idee nahm Gordan auf und entwickelte sie in einer sehr
ausgedehnten Arbeit*). Seiner Eigenart entsprechend ist er an den
fraglichen Gegenstand mit den symbolischen Methoden der
Invariantentheorie herangegangen, ohne indessen zu abschließenden Ergebnissen zu
gelangen. Xach Gordan ist die Idee der „Kleinsehen Büinearformen-
(die gleich 0 gesetzt „Klein sehe Konnexe" liefem) von Coble**) bearbeitet,
=") „Über eine Kleinscbe Bilinearform", Math. Ann., Bd. 68 (1910).
*=*) „The reduction of the sextic equation to the Valentiner form problem",
Math. Ann., Bd. 70 (1910).
Geschichtliche Angaben über die Gleichung sechsten Grades. 301
und ihm gebührt das Verdienst, nach persönlichem Ideenaustausch mit
Klein die algebraische Seite unseres Problems auf einem ersten "V^ege
wirklich zur Durchführung gebracht zu haben. Auch Coble ist wesentlich
invariantentheoretisch eingestellt; grappentheo^etisch und geometrisch
dringt er noch nicht bis zur Erkenntnis der wahren Einfachheit des
Gegenstandes durch. Die nachfolgende Darstellung erwuchs aus einer
Untersuchung des Verfassers aus dem Winte^halbiahre 1924/"25, über
die in den „Gott. Xachr." vpn 1925 (Sitzung vom 15. Mai) berichtet ist.
Was endlich die transzendente Lösipig des Formenproblem& der
Valentinergruppe und damit der allgemeinen Gleichung sechsten Grades
angeht, so ist diese zunächst im besonderen Falle F = 0 durch unsere
oben (S. 241 ff.) zur Einfü|irung in die Theorie der Valent^lerg^ppe
gewählte Darstellung unmittelbar gegeben. Wir haben auf die
automorphen Funktionen der Grenzkreisgruppe der Signatur (0, 3; 2, 4, 5)
zurückzugehen und finden in ,.Autom. Funl^t'- II, 553ff. eine bereit^
ausführlich entwickelte Theorie. Wir besitzen in der auf den zehnten Grad
ansteigenden ,.Transformatipnsgleichung- für Transformation „dritten''
Grades diejenige Resolvente, die für die allgemeine Gleichung sechstel^
Grades dieselbe Rolle spielt, wie bei der allgei^einep Gleichung fünfter^
Grades die Modulargleichung für Transformation fünften Qrades der
elliptischen Funktionen. Liegt indessen der besondere Fall F = 0
nicht vor, so werden wir zur Gewipnung geeigneter uniforiAisierender
Variabler Erwägungen anzustellen haben, die sich den Entwickl^nger|.
von S. 235 ff. über die Kleip.sche Gruppe anschließen.
Ohne Bezugnahme auf die g-ntoi^orphen Funktionen ist ein di^'ekter
Ansatz zur transzendenten JLösuiig des Formenproblems der
Valentinergruppe von Lachtin*) q.nd Gordan'^^*) entwickelt. Mai^ berechne
etwa aus den oktaedrischen Koordinaten a^, x^, x^ äße d:pei Größen
nullter Dimension:
X-, X„ X.,
(1) Vi = 6-i:- ^2 == 6Z ' ^3=6^
\'f \'f Vf
und stelle aus den Formen F, 0, W die gleichfalls diese:p Dimension
angehörenden Quotienten:
(2) P=pi- ^ = j,,
her. Dann befriedigen die drei Größen (1) al& Funktionen der
unabhängigen Variablen u, v drei partielle Differentialgleichungen, welche die
,,, ., ^^'?/ ^^</ d^y -.. . , dy dy
zweiten Ableitimgen x—s, ?r^—•> k—ö) Ime^r in den ;—, ,;—. ^ au^-
ö^ ovüw ow^ öv Oiv
drücken. Lachtin zeigt, daß die Koeffizienten dieser Differentialgleicliungen
==) „Die Differential resolvente einer algebraischen Gleichung sechsten Grades
allgemein.er Arf-, Math. Ann., Bd. 56.
**) „Ü5>er die partiellen Differentialgleichungßn des Valentmerproblems",
Math. Ann., Bd. 61.
302 n, 4. Formenproblem der Valentinergruppe und Gleicliung 6ten Grades.
rationale ganze Funktionen von v und w sind, für deren Grade er obere
Schranken angeben konnte. Gordan drang bis zur wirklichen Aufstellung
der partiellen Differentialgleichungen durch. Damit war die Basis für
die Gewinnung von Potenzreihen der y als Funktionen von v, w erreicht.
Um nicht zu weitgehende transzendente Entwicklungen durchzuführen,
begnügen wir uns unten damit, den Anschluß an die für die Uniformisierung
in Betracht kommenden automorphen Funktionen zu entwickeln. Dieser
Standpunkt entspricht der allgemeinen Tendenz unserer Darstellung, die
auch bei den Gleichungen fünften und siebenten Grades befolgt wurde.
§ 4. Herstellung einer Klein sehen Bilinearf orm.
Zur Gewinnung einer „Kleinsehen Bilinearform", die die Reduktion
der allgemeinen Gleichung sechsten Grades auf das Formenproblem der
Valentinergruppe vermitteln wird, bedürfen wir zunächst eines Systems
konjugierter Linearformen der x^, x^, x^, die bezüglich der
Valentinergruppe nur unter sich äquivalent sind. Eine beliebige Linearform, die
durch keine von der identischen Substitution verschiedene Substitution
der Valentinergruppe in sich übergeführt wird, ist nun abgesehen von
multiplikativen dritten Einheits würz ein eine von 360 verschiedenen
konjugierten Formen. Es liegt aber in unserem Interesse, die Anzahl
verschiedener Formen möglichst herabzumindern. Würden wir z. B.
die Form:
zugrunde legen, die gleich 0 gesetzt eine Seite des Polardreiecks der
Substitution U der Periode 3 liefert, so würden wir abgesehen von
multiplikativen sechsten Einheits wurzeln zu nur 60 verschiedenen
konjugierten Formen gelangen. Diese Formen liegen der Coble sehen
Untersuchung zugrunde. Erheblich einfacher würde es schon sein, wenn wir
die 45 Perspektivitätsachsen heranziehen würden. Doch gelangt man
zimi einfachsten Ansätze bei Gebrauch der 36 Linearformen g, die S. 275
zusaromengestellt sind, und die gleich 0 gesetzt die Verbindungsgeraden
je der beiden auf der Kurve sechsten Grades gelegenen Pole der zyklischen
Teiler ©^ liefern.
Das Verhalten dieser 36 Linearformen g{x^, x^, x^ gegenüber den
erzeugenden Substitutionen f7, F, W ist S. 276 angegeben. Sie permutieren
sich untereinander; aber es treten dabei noch Zeichenwechsel und
multiplikative dritte Einheitswurzeln auf, und in diesem Umstände ist
die vorhin (S. 3Ü0) erwäimte Erschwerung unserer Entwicklung begründet.
Zur Überwindung dieser Schwierigkeit führen wir, der Idee Kleins
folgend, neben den x^, x^, x^ die zu ihnen „kontragredienten" Variablen
Mj, u^, W3 ein, die sich gleichzeitig mit den x so substituieren, daß der
bilineare Ausdruck:
(1^ (m, x) = u^x^-{- Mg x^ + M3 x^
Einführung der zu Xi, x^, % kontragradiepten Variablen Wj, u^, %• 803
absolut invariant bleibt. Geometrisch bedeuten die u^^ u^, u^ einfach
die den Punktkoordinaten «j, x^, x^ entsprechende;! Linienkoordipaten.
Aus der Gestalt der erzeugenden Subsiitutionen U, V^ W [vgl. (7) S. 271]
ergibt sich zunächst der Satz: Wird auf die x irgend eine Substitutiv
der VaJentinergruppe ausgeübt, so erfahren die u stets gleicfi^eitig die
Substitution mit den konjugiert komplexen Koeffizienten.
Die zu den S. 275 zusammengestellten 36 Linearformen ^ konjugiert
komplexen Linearformen der kontragredienten Variablen u bezeichnen
wir durch g:
(2)
g^ (u^, u^, M3) = ^9^2 + (ö — 1)%.
g^ (Mj, Uq, M3) == (ö — 1) %! + ö %,
5-36 K> ^ä' %) = --IT^^ (— ^1 + ^2 + (1 -^ Ö) ^h)-
Sie stellen gleich 0 gesetzt die 36 nicht auf der Kn,rve sechsten Qrades
gelegenen Pole der zyklisphen Teiler (S) dar und erfahren gegenüber
den erzeugenden Substitutionen U, jT, W der in den u geschriebenen
Valentinergruppe genau dieselben Substituf-tionen wiß die g (vgl. S. 2'
wobei nur jedesmal die Faitorei; q und q'^ auszutauschen sind. Hieraus
geht hervor, daß sich die 36 ProduMe gv{x)gv{u), falls die x und a
Jcontragrediente Variable die Substitutionen ^er Valentinergruppe erfahren,
glatt permviieren, ohne daß noch Zeichenwechsel oder mulßpliJcative dritte
Einheitswursdn auftreten. Wir geben die den erzeugende^ Substitutionen
TJ, V, W entsprechenden Permutationen hier nochpaals ausftihrlich an,
indem wir wie S. 276 der Kürze halber nur die Permuta,tioneQ der
Indizes notieren:
/l, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, \1, 18,
~ \2, 3, 1, 0, 6, 4, 8, 9, 7, 11, 12, 10, 14, 15, 13, 17, 18, 16,
19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36\
20, 21, 19, 23, 24, 22, 26, 27, 25, 29, 30, 28, 32, 33, 31, 35, 36, 34/'
V --
/ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. 14, 15, 16, 17, 18,
■ VlO, 6, 5, 7, 3, 2, 4, 12, 11, 1 9, 8, 19, 24, 17, 16, 15, 20,
19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36\
13, 18, 23, 22, 21, 14, 31, 36, 29, 28, 27, 32, 25, 30, 35, 34, 33, 26/'
/ 1, 2, 3, 4, 5, 6, 7. 8, 9, 10, 11, 12, 13, 14, 15, 16, 17. 18,
W=(
\30, 23, 13, 22, 29, 27, 25, 35, 18, 15, 17, 34, 3, 26, 10, 16, 11, 9,
19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36''
21, 32, 19, 4, 2, 24, 7, 14-, 6, 36, 5, 1, 3], 20, 33, 12, 8,
36\
28/
304 II, 4. Formenproblem der Valentinergnippe und Gleichung 6ten Grades,.
Wir führen nun die allgemeine Gleichung sechsten Grades in der
Gestalt;
(3) z^ + a^ ^^ + a^ s^ -^ a^r" -^ a^ ^^ ^ a^ ^ -f Og = 0
ein und nennen ihre Wurzeln a^, a^. a,^, a^, «-, «g. Die Quadratwurzel
der Diskriminante sei zum Körper (dt, a^, a^, •■■, a^ adjungiert, so daß
die Galois sehe Gruppe der Gleichung die alternierende Permutationsgruppe
sechsten Grades ist, die mit der Valentiner-(5)3^o isomorph ist. Diese
Permutationsgruppe @3go können wir aus drei Permutationen erzeugen, die
wir gleich wieder U, F. W nennen; sie mögen nämlich die Permutationen
der «j, «2, •••, «6 ^^^' die den S. 27 3 angegebenen Permutationen T, V, ^Y
der sechs Ikosaederformen q?^. 95.2. •••, cp^, abgesehen von den bei ihnen
gelegentlich auftretenden multiplikativen sechsten Einheitswurzeln, gleich-
gebaut sind. Die erzeugenden Permutationen der Galois sehen Gruppe ©gg^
der Gleichung (3) bind dann, wenn ivir sie in, ihren aus ZyMen
zusammengesetzten Gestalten angehen:
( ü = («j, «g. «-)•(«,. a^, «g),
(4) r= («3, «6)-K> «ö)-
I W= («j, «3) • («3, aj.
Das erste Ziel des algebraischen Teiles der Theorie der allgemeinen
Gleichung sechsten Grades ist nun, aus den als unabhängig variabel
gedachten Wurzeln a^, a^, ■■•, «e "^^^i Größen zu konstruieren, die die
Valentinersubstitutionen U, V, TT^erfahren, wenn die a den Permutationen (4)
unterworfen werden. Zu diesem Ende stellen wir uns zunächst die
Aufgabe, aus den a^, «.,. •••, «g in tunlichst einfacher Art 36 rationale
ganze Funktionen aufzubauen, die gegenüber den Permutationen (4) die
drei vorhin zusammengestellten Permutationen U, V, W der 36 Produkte
</> (a) g^ (u) erfahren. Es handelt sich um 36 konjugierte Funktionen
der 36 Teiler ©^^ vom Diedertypus. Es ist einleuchtend, wie man
diese Funktionen zu bilden hat. Die einfachste zur zyklischen
Substitution («2, «3, «4, «g, «g) gehörende Funktion, die gegenüber der
Galois sehen Gruppe 36-förmig ist, gehört dem zweiten Grade an und hat
die Gestalt:
«2 «3 -f <^3 «4 "T <^4 «o "T «5 «6 + <^6 ^2-
Aber wir würden aus einem noch näher zu besprechenden Grunde mit
dieser Funktion noch nicht zum Ziele kommen. Indessen genügt es,
den bei der genannten zyklischen Permutation nicht beteiligten Faktor «{
hinzuzusetzen, so daß wir also mit einer Funktion vierten Grades
arbeiten werden. Es ist leicht, die 36 gegenüber (S)^^^ eintretenden
Gestalten dieser Funktion herzustellen. Diese 36 Ausdrücke, die
wir durch A^(a), •••, -43g («) bezeichnen wollen, hat man dann in rieh-
Funktionen der 36 Diedergruppen ^^o- 305
tiger Weise den 36rProdu](iten g,(x)g^(u) zuzuordnen, was jn folgender
Art geschieht:
Aj = «1 («2 «5 + P«2 ^6 + «3 «4 + «3 «0 + ^«4 «g),
-lo = <^l («1 «4 ~r ^1 ''^ö + <^2 '''4 "^ ^2 ^ü ~r <^5 <^6)'
Jg = «5 (a, «2 + «1 «3 + «0 «4 + «3 «6 + "4 "e)'
-4^ = «2 («1 «3 + «1 «4 + «3 «6 -\- «4 «3 + «„ «e),
-^5 ^^= «4 («1 «2 + <^1 <^6 T~ ^2 ^6 "f '''3 ''^o + % ''^e)'
J.g r= a| («^ «^ -|- C4^ C4^ _4_ C4^ (^^ -j.. C4^ C4. _(_ „^ C4^)^
^7 = «2 («1 «5 + «1 «6 "i" "5 "4 + "3 "0 + ^^4 «5)'
^Ig r= a| («^ pig _|_ Ci^ Cig _|_ (^^ (^^ -|- (^^ (^^ _j_ g^. (^J^
-4g ::= a| («j «2 + «1 <^4 + "a ^3 "^ <^3 <^5 "T ''^4 <^o)-
^10 "^ "1 ("2 % + «2 "4 + "3 "5 + "4 ^6 + '^o "e)'
-4ii = «3 («] «2 + «1 «5 + «2 ^6 + "4 "5 + ^i "e)'
-4j2 r= a| («^ pig _!_ (^^ Cig _|_ (^^ (^^ _|. (^^ (^g _|_ (^^ (^^^^
-4i3 ^^= «1 («2 ♦'^3 ~\~ ^2^5 ~r <^5 <^6 + "4 <^5 + ''^4 ^^e)'
-4i4 = «I («1 «4 + «1 «6 ^ "a % "1"" "2 ^6 + "4 "0)'
J^j. r= a| («^ «^ _|_ (^^ cig _|_ C4^ (^^ 4- C4^ ci^ 4- CC3 «g),
^4jg = a| («j «4 -|- «j «5 -|- «^ «5 -f- «3 «g -f- «4 «g),
-4i7 ^= «4 («1 «3 + «j «5 -r «2 "5 "t" "a ^6 "T "3 "e)'
-4jg r= a| («j fZg -|- «j «4 — «2 «4 ~\~ <^2 '''5 + '''3 %)'
^19 ^^^ ''^i (''^ä "4 ~r '''2 '^^6 i~ '''& '''5 "i"' ^3 ^6 ~l~ ^^4 '''5)'
^■^20 ^^^ "3 (''^i ^5 ~\~ (^1(^6 '^ ^2 ^i H~ '''2 "5 ^ "4 ''^e)'
-4.21 ^^ "5 ("1 ^3 + «1 «4 i~ «2 «3 + «2 ^6 + ^i "ö)'
-422 ^^^ "2 (''^i ^^3 + <^i ''^e "i" "3 ^ö "i~ '''4 ^5 ~l~ ^i ^e)^
J.23 = «1 («1 P«5 — «1 «g — «2 "3 + "2 ^6 "1" ^^3 "0)'
-4,^ ^:= a| («j P63 -I- «j «5 + «2 «3 ~ «2 C<4 + «4 «5))
^25 "= "2 («1 «3 -^ «1 «0 ^ «3 «4 — «4 c<g 4- «5 «e)
J^g = «I («j «2 "^ <^1 <^3 + "') <^6 "1" '''3 ^0 "T ^'^o ''^e)'
J.,^ r= a| («^ «2 "h «1 «5 -*- «2 ^i "T «3 C<4 -^ «3 '^o)
-428 "^ "1 ("2 "4 + «2 "5 4~ "3 "4 " "3 ^6 "^ "0 "e)
^429 ^^= <^3 (<^l <^2 + <^1 '''4 "T «2 ^ö ^" '''4 "e ^~ ^0 ^6^1
A^(^ := a| («j «2 -i- «1 «4 -L «2 «6 ~" ^-3 "4 T" '^S ^b)
A^^ = «1 («j a^ -|- «j «g -^ «3 «4 -|- «3 «5 -^ «/j «g),
^32 r= a| («^ a, ^ ci^ (^_^ _j_ C4^ (^^ _|- (^2 «g -1- (/_^ «g)
YI33 ::= al («j «3 -|- «j «^ -f- «2 % + '''3 ^4 T «^'4 <^J'
-4^4 ^^= «1 («2 '''3 "^ <^2 ^^«5 "T «3 «4 "1" <^4 «0 ~ ^0 ^6^>
J3. r= a| (pc^ «2 + «1 «6 + '''2 '''4 ~1~ '''4 "0 ~r '^ö (^b)'
^36 = «5 («1 «2 + «1 «6 + "a "3 """ "3 "4 "^ "4 "e)'
Wie man leicht zeigt, erfaToren diese 36 FunM^onen der Wurzeln hei Aus-
ühung der drei Permutationm (4) in der Tat genau die ohpn fur die 36 Pro-
duUe gy {x) g^ (m) angegehe^en Perm^U/tatimien TT, Y, W.
Fncke, Algebra. II. 20
306 n, 4. Formenproblem der Valentinergruppe und Gleichung 6ten Grades.
Ein Schritt von grundsätzlicher Bedeutung ist nun die Herstellung
des folgenden 36-gliedrigen Aggregates:
(5) ^A,(a)gA^)V>(^),
das von Gordan als eine „Kleinsehe Bilinearform"^ bezeichnet wurde, da
die Idee der Heranziehung solcher Formen in der Tat von Klein
herrührt. Das Wesentliche an dieser Form ist, daß sie absolut invariant ist,
wenn die x und u als kontragrediente Variable zugleich die Substitutionen
der Valentinergruppe erfahren und gleichzeitig die sechs Größen a^, a^, ' • •, oc^
den diesen Substitutionen vermöge (4) zugeordneten Permutationen der
alternierenden ©ggo unterworfen werden.. In der Tat permutieren sich ja
bei den erzeugenden Operationen TJ, F, W einfach die 36 Glieder der
Summe (5). Gordan und Coble haben die Klein sehen Bilinearformen
dieser Art allgemein mit den symbolischen Methoden der
Invariantentheorie zu bearbeiten unternommen. Coble gelangt zu abschließenden
Sätzen über die Bildung aller Klein sehen Bilinearformen für die
Valentinergruppe. Er zeigt insbesondere, daß diese Formen in den a
mindestens den Grad 4 haben müssen. In der Tat ist für unsere weiteren
Zweclx nur eine solche Klein sehe Bilinearform brauM)ar, die in den x
und u weder identisch verschwindet noch auch auf dab ProduM einer FunMion
der a und der bilinearen Form (1) S. 302 zuritcMommt. Um dieser
Forderung zu genügen, haben wir oben in den Formeln für die Erklärung
der Ä (a) vor die fünfgliedrigen Klammerausdrücke je noch das Quadrat
einer Wurzel « gesetzt. Die fünfgliedrigen Klammerausdrücke hätten
zwar gruppentheoretisch dasselbe geleistet wie die von uns gewählten
-4(a); sie hätten indessen keine brauchbare Klein sehe Form (5) geliefert.
Diejenige Klein sehe Form, auf welche Coble bei seinen
invariantentheoretischen Entwicklungen geführt wird, ist von unseren Darlegungen
aus leicht zu verstehen. An Stelle des Produktes </j (x) g^ (u) tritt bei
ihm die Bilinearform:
(X^ Wg -f X^ U^ -f {X^U^ -X- X^ Wg) -f {X^ 2*2 -r ^2 %)
auf, die zu einer Dieder-@6 g^liört und also eine von 60 konjugierten
Formen ist. Man kann diese Form auch in die Gestalt setzen:
{x^ + a;2 + x^ (u^ -f 2*2 + %) — (^> ^)>
so daß der Coble sehen Theorie die 60 Seiten der Poldreiecke der
20 konjugierten zyklischen Teiler ©3 des einen Systems zugrunde liegen*).
An SteUe der Ä (a) gebraucht Coble eine auch schon früher aufgetretene
60-fÖrmige Funktion vierten Grades der Wurzeln, die sich durchweg aus
Wurzeldifferenzen aufbaut. Der letztere Umstand hat eine noch zu nennende
günstige Folge, die bei der hier vorliegenden Darstellung allerdings
entbehrt werden muß.
*) Das Symbol (u, x) ist in Gleichung (1) S. 302 erklärt.
Entwickelte Gestalt der benutzten Bihnearform. 307
Um die Brauchbarkeit der Form (5) da,rzuleg;en, ordnen wir sie nach
den Produkten w^Xj: und setzen sie also ia die Gestalt:
(6) i?ji (a) Wj x^ 4- £32 (a) u^x^^ \~ B^^ (a) n^ x.^-\ h -Bas («) "2 -^'s-
Die hierbei auftretenden Koeffizienten haben folgende Bedeutung:
(7) i?,, = 2 (^3 J^A^^A^i- ^„ f ^2, + ^28 -f ^zi -T Ai)
+ (^4j, +^,5 f ^,, + 4i8 -r -^20 f Al + ^3 + ^2*)
+ (3 - V5) {A,, + J, + A + A,, -f 4,3 f 4,, + A,, + 4,2)
3 —V'S
H 2 *^"^26 + Al + ^2ö + ^30 + ^82 + -^33 + ^^3- + ^33),
(8) B,^ = (^_ö)^-(^-6)A-(^-ö)43^(^-6)A2
^(1-0)^3- (l-Ö)A.rA5-(i-Ö)4xe-(l-Ö)A,-.l,,
- (1 - 6) A, - (1 - ö) ^20 + -^21 - (1 - 0)^22 - (1 - ^)^23 - -42,
-(1 + Ö)43,-(1-Ö)432^^33-(1 -6)^3,^(1 -Ö)43e-^6)'
(9) B,, = {^-B)A,-{n~e)A,~{^-6)A,^{n-H)A^,
+ (l-Ö)4,3-r4,, + (l-Ö)A5-(l-'5)A6-A7-(l--Ö)A,
-(l-ÖMx9-A20-a-Ö)^2X -(1-0)42,-^3- a -0)^2,
+ ^^-((l-rÖ)4,.^42ö-(l'ÖM27-(l-'^M2s-A9-(l-Ö)4,o
-(1 + 0)^31+432-(l-0)^33 ^-(1-^)^3,-^5-(i^ö)^3,)-
Die Ausdrücke für B^^, B^^, B^^ und £33, B^^, B^^ gehe^ hieraus durch
einmalige bzw. zweimalige Ausübung der Permatation U hervor, die je
drei 43^,+ !. A^^j^^^ A^v + i zyklisch permutiert. Es zeigt sich, daß B^^
und i?2i konjugiert komple:?: aufgebaut siqd, ebenso B^^ und B^^ sowie
1?23 und i?32. Man stellt mm leicht fest, daß B^^ die Gestalt Jiat:
1 — Vs"
-Bja = 2 ^'^ "^ ''"'* "^ "2 «3 («i — «^'2) H '
wo die nicht angegebenen Glieder mindestens einen der Faktoren a^, «^^
«g enthalten. Somit verschwindet B^.^ nicht identisch, so daß, wi^i
bewiesen werden sollte, die Form (6) weder idei^tisch verschwindet, noch
sich auf die Gestalt:
B (a) (u^ x^ + '>^i ^2 + ^3 ^3)
reduziert.
308 II, 4. Formenproblem der Valentmergruppe und Gleichung 6ten Grades.
§ 5. Zurückführung der allgemeinen Gleichung sechsten Grades
auf das Formenproblem der Valentinergruppe.
Das durch NuUsetzen einer Zwischenform dargestellte Gebilde
bezeichnet man allgemein als einen „Konnex", wobei der Grad in den x
die „Ordnung'' und der Grad der Zwischenform in den u die „Klasse" des
Konnexes heißt *). Insbesondere bezeichnet Coble einen Konnex erster
Ordnung und erster Klasse, der wie oben im Anschluß an die allgemeine
Gleichung sechsten Grades aufgebaut und durch die S. 306 genannte invariante
Eigenschaft ausgezeichnet ist, als einen „Kleinsehen Konnex". Ein Konnex
erster Ordnung und erster Klasse stellt eine 1-1-deutige
Punktkorrespondenz in der Ebene dar; dem einzelnen Punkte (x^, x^, x^) ist der Punkt
zugeordnet, der in Linienkoordinaten durch die Gleichung des Konnexes
gegeben ist.
Gehen wir sogleich zur Kleinschen Bilinearform (6) S. 307, so ist
natürlich die durch:
(1) 2-Bifc («)%% = (^j i, k = h 2, -d
dargestellte Punktkorrespondenz eben dieselbe, die man gewöhnlich durch
die KoUineation:
i^ 4 = -B21 ^1 + -B22 ^2 + -B23 ^3 ^
^ % = i?3i x^ + -B32 ^2 + -B33 ^3
darstellt. Das Verschwinden der Determinante der Substitution (2)
würde für die vorgelegte Gleichung sechsten Grades, wie wir noch sehen
werden, eine gewisse Relation sechsten Grades zwischen den Koeffizienten
a^, «2 ? • • • ? «6 ^^^^ ^^^^ ziehen. Entsprechendes gilt von der Forderung,
daß in (2) eine harmonische Perspektivität vorliege. Insofern wir hier
mit der „allgemeinen'- Gleichung sechsten Grades arbeiten, haben wir
anzunehmen, daß in (2) und also auch in (1) eine KoUineation mit drei
und nur drei sich seihst entsprechenden Punlien oder Polen vorliegt. Daß
im übrigen in (1) nicht der „identische Konnex- :
Wj x^ -f % % + % ^3 = 0
vorliegt, bei dem jeder Punkt sich selbst entspricht, ist bereits in § 4
gezeigt.
Wir wählen unter den drei Polen des Kleinschen Konnexes (1)
einen willkürlich aus und nennen seine Koordinaten |j, l^, I3. Es soll
der Zusammenhang dieser drei Größen mit der Gleichung sechsten Grades
festgestellt werden. Sie lassen sich, wie wir sogleich zeigen werden,
nach Lösung einer kubischen Hilfsgleichung rational aus den Wurzeha a
berechnen. Vor allem aber zeigen sie betreffs der @„,. ein Jcovariantcb
*) Vgl. z.B. Clebsch-Lindemann „Vorlesungen über Geometrie'- (1. Aufl.),
S. 9-24 ff.
Auswahl eines Poles des benutzten Klein sehen Konnexes. 309
Verhalten. Xehmen wir einen Wechsel des Koordinatensystems vor,
indem wir irgend eine Valentinersubstitution ausüben, und wenden wir
auf die Wurzeln a die zugehörige gerade Periputat^on 'an, so geht der
Konnex in sich über, so daß die |j, Ig, I3 gleichfalls die betreffende
Valentinersubstitution, für Punktkoordinaten geschrieben, erfahren In
den |j, I2, I3 haben wir also die gesmUen FunUionen der sechß Wurzeln
gewonnen, welche die Eigenschaft besitzen, die Yalentinersubstitutionen zu
erfahren, falls wir die Wurzeln a^, a^, •••, «^ den geraden Perfnutatlonen
unterwerfen. Xan beachte dabei wo|xl, daß siph die 1^, |,, I3 erst mit
Bilfe gewisser noch näher zu beschreibender Irrationalitäten aus den
Wurzeln berechnen. Es darf demnach nicht überrasphen, daß dei^
B60 geraden Permutationer^ der Wurzeln nicht eine ©3^0, sondern eine
®3-36o "^on Substitutionen der |j, 1^? I3 entspripht.
Zur Berechnung der |j, |,, Ig hat man nun zunächst die in ^
kubische Gleichung:
(3) B,„ {i~B,,, B,, 1 = 0
B,,, ß,„ (i-B,,
zu lösen, deren Wurzeln nach g. 7 die „irrationalen ly^varißnten^ der
Substitution (2) sind. In der entwickelten Gestalt der kubischen
Gleichung sind die Koeffizienten die ^rationalen Invarianten^ der
Substitution (2), die gegenübe:p einer Transformation der Substitution
unveränderlich sind. Als Funktionen der a sind demnach jepe Koeffizienten
unveränderlich gegenüber den Permutationen der alternierenden Gruppe;
sie sind demnach sogar, da sie als ganze Funktionen vierten, achten und
zwölften Grades der Wurzeln a.^, «g, • • •, «g den Grad 15 des
Differenzenproduktes nicht erreichen, symmetrisch in den Wurzeln a und also
rational und ganz in den Koeffizienten a^, «j? •••) <^6 ^^^ Gleichung-
sechsten Grades. Die entwickelte Gestalt dieser Hilfsgleichung dritten
Grades für [i ist:
(i^ — S(6 — \J) (a, 03 — 4 «4) ^^ — '^ (3 — Vö") (20 a^ a^ — 12 af a|
— 8 Ol «2 a^ -f 30 «1 a^ — 78 a^ a^ a^ -p 123 a^ ß^ a^ — 24 ai a^
— Ba^af —72a2ag-}-135a3a5 —288o|);[i —(16(7-3 VTiai^al
+ 72 (3 — fh^a^a^al + 216 (2 — Vi")«! 4- ..-) = 0,
wobei die nicht mehr angegebenen Terme des A.bso]|.utgliedes mindestens
einen der Faktoren a^, a., a^ enthalten*). Da zufolge (7)ff. S. 307 die
Diagonalglieder JS^^, i?,,, B^^ reelle Koeffizienten haben, während
*) Die Berechnung der n?.cht abgegebenen Glieder ist beschwerlich und sehr
zeitraubend. Coble kann an der entsprechenden Stelle semer T^ieorie eine
fertige, aber allerdings höchst umständliche und deshalb fur numerische Zwecke
wenig brauchbare Hilfsgleich^ng dritten Gracjes angeben, da ihm sein Ansatz
erlaubt, mit Semiinvarianten zu arbeiten.
(4)
310 II- 4. Formenproblem der Valentinergruppe und Gleichung 6ten Grades.
übrigens B^t^ und Bjt^ konjugiert komplex gebaut sind, so hat die Glei
chung (4) ausschKeßKch reelle numerische Koeffizienten, d. h. es tritt nur
2ioch y 5 , aber nicht mehr i yS in den Koeffizienten der kubischen
Gleichung (4) auf.
Die grundlegende Frage, ob die kubische Hilfsgleichung (4) eine
Oaloissche Gruppe @g der Ordnung 6 hat, kann auch ohne fertige
Berechnung des AbsolutgKedes bejaht werden. Wäre nämlich die
Quadratwurzel der Diskriminante der Gleichung (4) „rational bekannt",
so würde sie dies auch dann noch sein, wenn a^ = 0, a^ = 0, a^=z Q^
u^ = 0 gesetzt wird. In diesem Falle aber nimmt die kubische
Gleichung (4) die Gestalt an:
(5) ^3 ^ 18 (3 — yi") a^af yi — 216 (2 — y¥) at = 0
und ihre Diskriminante ist:
— 2« • 3« (2 — y¥)2 al (4 al + 27 al\
Ihre QuadratwTirzel gehört also dem zunächst zugrunde zu legenden
Körper (3^, ö, a^, «g, •••, a^ nicht an. Die Lösung der Gleichung (4)
erfordert demnach das Ausziehen zweier Wurzeln zweiten und dritten
Grades. Wir haben damit das wichtige Ergebnis gewonnen: 'Nach
AdjunMion der ganzen algebraischen Zahl vierten G-rades ß als numerischer
Irrationalität zum Körper (9?, a^, a^, • • •, a^), ferner einer nicht mehr
numerischen Quadratwurzel und einer ebensolchen Kubikwurzel*) [die sich
~bei der Auflösung der Hilfsgleichung (4) einstellen] sind durch rationale
Rechnungen, nämlich durch Auflösung linearer Gleichungen, aus den
Wurzeln a^, a^, • • •, a^ der allgemeinen Gleichung sechsten Grades (3)
S. 304 drei Größen |j (a), 1, (a), I3 (a) berechenbar, die bei den 360 geraden
Permutationen der Wurzeln die Valentinersubstitutionen erfahren.
Dieser Satz begründet die Zurückführung der allgemeinen Gleichung
sechsten Grades auf das Formenproblem der Valentinergruppe. Setzt
man die berechneten Ausdrücke |j (a), Ig (a), I3 (a) für die Argumente
aJj, x^, »3 in die invarianten Formen F, 0, W, X der Valentinergruppe
ein, so erhält man vier Ausdrücke in den Wurzeln a, die gegenüber den
geraden Permutationen derselben unverändert bleiben und also nach
Adjunktion der Quadratwurzel der Diskriminante der Gleichung sechsten
Grades rational bekannt sind. Die Berechnung der |j, ^^, I3 aus den
bekannten Werten F, 0, W, X löst das „Formenproblem der Valmtiner-
grußpe"; dieses ist also das „Normalproblem" oder „Galoissehe Problem^,
das an Stelle der „Galoissehen Besolvente" der allgemeinen Gleichung
sechsten Grades tritt. Dem Normalcharakter entsprechend sind mit einer
Lösung Ij, |,, I3 alle „rational bekannt", nämlich linear in der ersten
Lösung darstellbar. Gegenüber der Galois sehen Resolvente liegt inso-
*) Diese Wurzeln sind jedenfalls nicht beide „natürliche" Irrationalitäten
der Gleichung sechsten Grades, da sonst die Valentinergruppe nicht auf die
Ordnung 3 • 360 ansteigen könnte.
Gleichung 6ten (Grades und Formenproblem der Vfilentipergri^ppe. 311
fern ein Unterschied vor, als das Formenproblem nicht den Grad 360,
sondern 3 -360 hat. Es entspricht dies dem Umstände, daß die Zurück-
führung der Gleichung sechsten Grades auf da,s fragliche Formenproblem
nicht rational vollzogen werden gönnte, sondern dip Lqsimg einer
kubischen Hilfsgleichung nötig machte.
§ 6. Lösung des f ormenprobletns der Valentinergrvppe.
Bei der transzendenten Lösung des Formenprqblems der Valentiner-
gruppe könnte man zunächst, den Verhältnißsen bei den Grleicjiungen
fünften Grades folgend, den Versuch machep, ein beliebiges
Formenproblem durch Vollzug weiterer Adjunlitionen auf ein solches mit F = 0
zu reduzieren. Man hätte danii den transzendenten Teil des
Auflösungsprozesses der allgemeinen Glei(ihung seclisten Grades in der in „ Autom.
Funkt." II, 553 ff. entwickelten Theorie der Transformation dritten Graäeb
der auto'tnorphen Funktionen der Gren^hrei^gruppe von der Signatar
(0, 3; 2, 4, 5) unmittelbar zuy Hand. Die daselbst aufgestellte Trai^s-
formationsgleichung zehntpn Grades und ihre beiden Resolventen sechsten
Grades =^) (durchweg Gleichungen i^it nur einem Parapetei) wären (Jie
einfachsten Gleichungen, auf die die allgemeine Gleichung sechsten
Grades reduzierbar sein würde. Pieser Abschluß dey Theorie würde
genau den Entwicklungen entsprechen, die Ilermite, Kronecker u|id
Brioschi gegen Ende der fünfziger Jahre des vorigen Jahrhunderts über
die allgemeine Gleichung fünften Grades gaben.
Die Reduktion auf ein Problem mit F = 0 lauft geometrisch
darauf hinaus, einem beliebigen Punkte (^j, Ig, I3) der Ebene einen Punkt
der Kurve sechsten Grades F -= 0 kovariant zuzuordnen. Die einfachste
Art, dies auszuführen, scheint' die zu sein, daß man einen der sechs
Schnittpunkte der linearen Polare von (|j. Ig, I3) bezüglicl^ der Kurve
sechsten Grades mit dieser Kurve auswählt und dem Punktp (|j, 1^, Ig)
zuordnet. Aber hierbei würde selbst wieder eine Gleichung sechsten
Grades zu lösen sein. Bpi dieser Sachlage wird ipan von der Reduktion
auf ein Problem mit F -= 0 absehen müssen und einen Gedankengang
einschlagen, der an den Darlegungen von S. 235 ff- über die transzendente
Lösung des Formenproblems dpr Klein sehen Gruppe sein Vorbild hat.
Wir benutzen etwa die in der Relq,tion (6) S. 297 miteinander
verbundenen Formen F, ^, !P", X und legen die durch die Gleichung:
(1) 0{x^, x^, X3) — lF(x^, x^, x^f = 0
dargestellte Schar von E^urven zwölften Grades zugrunde. Die Kufve
zwölften Grades (1) ibt, abgebchen von gewissen drei Werten des Para-
mäers l, irreduzilel; nur fiir A = 00 reduziert bie sich auf die doppelt
gezählte Kurve bcchbten Grades F = 0, mid für gewibbC zwei endliche
*) Letztere sind die beiden oben (S. 257ff.) betrachteten Gleichungen
sechsten Grades.
312 II, 4. Formenproblem der Valentinergruppe und Gleichung 6ten Grades.
Werte dcb Parameters k erhalten wir je die sechs Ikosaederkegelschnitte der
beiden- Systeme. Invariante Formen eines Grades <; 12 gibt es nämlich,
abgesehen von F, bei der Valentinergruppe nicht, und die kleinste Anzahl
konjugierter Formen ist 6, die allein bei den beiden Systemen der
Ikosaederkegelschnitte wirklich vorliegt. Die sechs Ikosaederkegelschnitte
des einzelnen Systems überkreuzen sich in sechzig Punkten, die die
sechzig [äquivalenten Pole der zwanzig zyklischen Teiler ©g des
zugehörigen Systems sind.
Allen Kurven der Schar (1) sind als Grundpunkte gemein die 72
auf der Kurve ^ = 0 gelegenen Pole der zyklischen Teiler @g, die auf
der Kurve sechsten Grades die Wendepunkte sind. Im Übrigen lauft
durch jeden PunM der Ebene eine und nur eine Kurve der Schar (1)
hindurch. Jede Kurve der Schar (1) wird durch die 360 KoUineationen
der Valentinergruppe in sich transformiert. Sie ist im allgemeinen singu-
laritatenfrei und hat dann dab GrCbChlecM p = 55. Tritt ein mehrfacher
Punkt auf, so sind sogleich alle mit ihm äquivalenten Stellen mehrfache
Punkte des gleichen Charakters, Es kommen dabei, falls wir die redu-
ziblen Kurven ausschließen, nur das System der 36 nicht auf der Kurve
F =z ö gelegenen Pole der zyklischen Teiler ©^ und das System der
45 Perspektivitätszentren in Betracht. Die durch jene 36 Pole hiudurch-
laufende Kurve (1) hat daselbst Doppelpunkte, so daß das Geschlecht
auf j) = 19 herabgeht. Desgleichen hat die durch die 45
Perspektivitätszentren hindurchlaufende Kurve (1) daselbst Doppelpunkte und
also das Geschlecht j) = 10.
Wir führen nun neben der Schar (1) die durch die Gleichung:
(2) W{x^, x^, x^) — MF(x^, »2, x^f — 0
gegebene Schar von Kurven SO^ten Grades ein, deren einzelne gleichfalls
durch die 360 KoUineationen der Valentinergruppe in sich transformiert
wird. Sie hat also mit der einzelnen durch (1) gegebenen Kurve
12ten Grrades 360 bezüglich der ©gg^ äquivalente Punkte gemein.
Demgemäß wird:
(3) M = Z^»ii_^2^_^
F(x„x„x,y
auf der einzelnen Kurve (1) eine 360-wertige algebraische Funktion, die
den einzelnen komplexen Wert in 360 bezüglich der ©gg^ äquivalenten
Stellen annimmt. Diese 360 Stellen liegen im allgemeinen getrennt,
jedoch mit folgenden Ausnahmen: Erstens fallen die 360 Punkte mit
Jf = oo zu je fünf an den 72 Gnindpunkten des Büschels (1) zusammen.
Zweitens liefern die 540 Schnittpunkte der ausgewählten Kurve (1) mit
den 45 Perspektivitätsachsen drei Systeme zu je 180 äquivalenten
Punkten*); wir haben also noch dreimal ein Zusammenfallen der
'^) Man beachte, daß die einzelne Perspektivitätsachse durch acht eine
Diedergruppe bildende KoUineationen in sich übergeht, in der jedoch die
fragliche Perspektivität selbst enthalten ist.
Transzendente Lösung des Fprmenproblexns der Valentinergruppe. 313
360 Punkte zu Paaren an 180 Stellen zu konstatieren. Im üb:pigen
liegen je 360 Punkte der Kurve (1) mit gleichem 31 getrennt, fallß die
Kurve (1) irreduzibel ist und j) ^= 56 gilt, also keiner der beidep
besonderen Fälle mit j) = 19 bzw. p =z= 10 vorliegt. Indem man in die.
Relation (6) S. 297 den Perspektivitätsachgen entsprechend X := 0
einträgt und im übrigen 5? = XF^, W = MF'° setzt, ergibt sich nach
Fortheben von F^° die in 3f kubische Gleichung:
(4) ilfs -|_ 3 (38;L^ — 2^. 3'. 5 A* -r 2*. 3^. 5 . 31 ;L2 — 2^. 35. 5 .11 ;L^
~f 210. 3^. 5 ;L ~f 210. 3 L) 31 + 22. 36 (3« • 5 r — 2^ • 3' • 5 2«
~f 2*. 33. 773 ;L^ — 26. 35. 5 .11 r + 2^2. 32. 5 . 7 ;^3
— 2^3.32.52;L2^ 2^6.36.5;L-2^8.5) ^ Q^
deren drei Lösungen Jf = e^, ^,, e,^ die Werte der Funktion 31 sind,
bei denen Zusammenfall je der 360 Pu^te der Kurve (1) z.u Pa3,ren
stattfindet. Wir notieren als flrgebnis: Ibt die J^urve (1) irreduzibel and
liegt Jceiner der beiden Aa&nahmefaüe mit p =19 und p = 10 vor, sq
wird die Kurve zwölften G-rades (1) dwreli die FunUion (3) auf eine 360-
blätterige regular verzweigte BiemannscJie Fläche über der 3f-JEhene ab-
gebildet, die nur an den vier Stellen 31 --=^ e^, e^, e^, qo verzweigt ist,
und zwar liegen an. den ersten drei Stellen je 180 zwßiblatferige Ter-
zweigungspunUe und 72 funfblatf,erige bei 3£ = 00; diese Flache hßt
tatsächlich das Geschlecht j) == 55 und gestattet der Valentinergrußpe erd-
bprecliend 360 eindeutige Transformationen in sich.
Xach dem Grenzkreistheorem ist die einfachste „uAifo(misierendc
Variable" für die algebraischen Funktionea deip gewonnenen 360-blätte-
rigen Riemannschen Fläche diejenige polymorphe Funktion, die das
einzelne Blatt der Fläche auf den „DB"' einer Gren^krei&gruppe von. der
Signatur (0, 4; 2, 2, 2, 5) abbildet. Die Familie dieser
Grenzkreisgruppen ist zweidimensional =*) entsprechend dem Umstände, daß der
Faktor 2. in (1) ein Jcompleci(;er Parameter ist. In dey zugehörigen
Grenzkreisgruppe ist ein Xormalteiler des Index 360 enthalten, dessen
Quotientengruppe mit unserer (S^^q isomorph ist, und die voß sich aus
mittels ihres „DB"' zur qbigen 360-blätterigen I^iemannsehen Fläche
zurückführt.
Die transzendente Lösung des Formenproblems der Yalentinergruppe
hat nun aus folgenden Schritten zu geschehen: Die Werte (Jer Formen
F, 5?, W, X gelten als rational bekannt. Der :5Ugehörige Wert des
Parameters X ist aus (1) zu berechnen, womit die in Betracht kommende
Kurve zwölften Grades (1) gewonnen ist. Durch Auflösung der
Gleichung (4) gewinnt man die Verzweigungsstellen e^, e^^ e^ n^d 00 der
Jf-Ebene. Es sind alsdann zweckpiäßig an Stelle der polymorphen
Funktion ^ gleich zwei polymorphe Formen L, ^2 einzuführen, die man
=^) Man vergleiche „Äutom. F^nkt." I,
314 II) 4. Fonnenproblem der Valentinergruppe und Gleichung 6ten Grades.
als Lösungen einer gewissen linearen Differentialgleickung zweiter
Ordnung zu erklären kat. Für diesen Teil der Theorie findet man die
allgemeinen Grundlagen in „Autom. Funkt." II, 109ff. entwickelt. Die
Größen |j, l^t Is» ^^^ ^^^ Lösung des Formenprohlems abgehen, sind dann
eindeutige automorphe Formen der ^j, ^g» ^*"^ ^um Normalteiler des Index 360
in der zugehörigen Gruppe linearer ^-Substitutionen geMren, und man
hätte 0U ihrer wirklichen Darstellung die Poincare sehen Beihen
heranzuziehen.
Will man dieses Programm wirklich durchführen, so wird man, den
Erfahrungen bei den Gleichungen fünften Grades folgend, an Stelle der
Grenzkreisgruppen der Signatur (0, 4; 2, 2, 2, 5) besser mit denen der
Signatur (0, 4; 2, 2, 2, oo) arbeiten. Hier ändert sich grundsätzlich
nichts; aber man hat den Vorteil, daß man bei der Darstellung der |^,
lä' Is ^^ Stelle der Poincare sehen Reihen mit Potenzreihen der
Entwicklungsgröße :
arbeiten kann, die gut konvergent sind.
Was die beiden besonderen Fälle irreduzibeler Kurven (1) mit den
Geschlechtszahlen jö =19 und jö =10 anlangt, so artet die Signatur
(0, 4; 2, 2, 2, 5) m beiden Fällen durch Zusammenrücken zweier
elliptischer Ecken des ,.DB" in die Signatur (0, 3; 2, 5, oo) aus. Doch
gelangt man dabei nicht zu den einfachsten polymorphen Funktionen,
die man in jenen beiden Ausnahmefällen benutzen kann. Die letzteren
führen vielmehr zu den beiden Signaturen (0, 3; 2, o, 5) und (0, 3; 2,4, 5).
Jedoch sind diese Fälle, sowie auch die drei Fälle reduzibeler Kurven (1)
noch nicht näher untersucht.
§ 7. Theorem von Wiman.
Anhangsweise möge diesem Kapitel noch ein Bericht über sich hier
anschließende Untersuchungen hinzugefügt werden. Die bisherigen
algebraischen Entwicklungen ordnen sich, wie bereits wiederholt ausgeführt
wurde, einer gemeinsamen von Klein herrührenden Auffassung unter.
Die Aufgabe, eine reine Gleichung n"^^^ Grades »** = a zu lösen, kleidet
sich in ein „unäres Formenproblem''. Dem letzteren Kegt eine „unäre
Gruppe" zugrunde, nämlich die aus der Substitution»' = £ » zu erzeugende
zyklische Gruppe ©«, unter s eine primitive w^« Wurzel der Einheit
verstanden. Gegeben ist der Wert a der „invarianten Form" x'^ der @^. Bei
der „transzendenten Lösung" des Formenproblems ist ^ = In a = w • In »
die „uniformisierende Variable", in der x als „eindeutige automorphe
Funktion" ;r ::= e« darstellbar ist. Hieran reiht sich die „allgemeine
Gleichung fünften Grades", die auf das „binäre Formenproblem" des
Tkosaeders zurückgeführt wird, sodann die „ allgemeine Gleichung sechsten
Ausspruch des Wimanschen Theorems. 315
Grades-, die auf das „tej-näre Forpaenprobleipa" der Valentinergruppß
zurückkommt. In den beiden letzten Fällen jst die Quadratwurzel der
Diskrimüiante jeweils adjurigiert gedacht.
Es ist nun die Frage, wie diese Entwicklung fortzusetzen ist.
Zunächst ist es Klein gelungen (worauf wir noch zunickkommen), die
allgemeine Gleichung siebenten Grades nach Adjunktion de|- Quadrat^yrurzel
der Diskriminante auf ein „qu^tem^res Formenpro jolem" zu reduijieren.
Andererseits ist es stets möglich, die Aufgabe der Lqsung der allgeip.einea
Gleichung w'^en Grades als ein Foripenprobleip. mit (n — 1) homogenen
Variablen oder als ein solches in einem Baume von {n — 2) Dimensionen
aufzufassen. Man hat einfach die Gleichung mit ausfß,llendem Gliede
(n— 1)*^" Grades anzusetzen un.d die Wurzeln x^, x.^, ••-, »^, die wegen
Ausfalls des zweiten Gliedes der Gleichung die Relation:
x^ -\-x^-^ ••--{- Xn =^ 0
erfüllen, als überzählige Koordinatei). eines (n — 2)~dimensionalen ebenen
Raumes anzusetzen. Die Frage ist dann aber, ob sich nicht, wie in den
Anfangsfällen n = 5, 6, 7, auch weiterhin Reduktionen auf Fprmen-
probleme mit niedrigerer Dimensionenan^ahl vollziehen lassen. K^lein
hat in seinen 1893 in Evanston bei Chicago gehaltenen Vorlesungen ^)
die Vermutung ausgesprochen, daß eine solche Reduktion bei n = 8
nicht mehr möglich sei. Diese Vern^iutung hat Wim an bestätigt "==*). Im
Anschluß hieran ist es Wim an alsdann gelungen, das folgende
grundlegende Theorem zu beweisen: Es gibt für n'^1 Jxine KoTlineationü-
gruppe in einem Baume von weniger als ('^ — 2) Dimensionen, die mit der
symmetrischen oder auch nur mit der alternierenden Permutßtion^gruppe
des Grades n isomorph wdcef).
Es soll hier wenigstens im niedersten Falle n = 8 ein Beweis
dieses Wimanschen Theorems ausgeführt werden, der sich in der
Hauptsache an die Darstellung Webers in Bd. II seiner Algebra, S. 373ff.
anschließt. Es ist genug zu zeigen, daß es kßine pait der alternierenden
Gruppe des Grades 8 isomorphe I^ollineationsgruppe in einem Rauipe
von fünf Dimensionen (also bei sechs homogenen Variablen) geben kai^n.
Dann gibt es daselbst auch keine mit der S3immetrischen
Permutationsgruppe achten Grades isomorphe Kollineationsgruppe, und uni so ■\veniger
werden solche Kollineationsgruppen in einem Räume mit noch geringerer
Dimensionenanzahl vorkommen. Gibt es ^ber für die alternierende
Gruppe des Grades 8 eine isomorphe Kollineationsgruppp bej sechs
genen Variablen, so entspricht auch jedem Teiler der ersteren
=^) Vgl. Klein, „Evanston Colloquium" (New York 1894), S. 74.
**) „JsTote über die Vertauschungsgrappe von iicht Dingen'-, Gottmger
Kachrichten von 1897, S. 55.
t) Vgl. die Abhandlung von Wim an, „Über die Darstellung der symmetrischen
und alternierenden Vertauschungsgruppen als Kollmeatipnsgruppen von möglichst
geringer Dimensionenanzahl", lÜath. Ann. Bd. 52.
316 n, 4. Formenproblem der Valentinergruppe und Gleichung 6ten Grades.
Gruppe ein isomorpher Teiler in der Kollineationsgruppe. Der zu
erbringende Beweis des Wiman sehen Theorems beim Grade 8 beruht darauf,
daß für einen gleich zu nennenden kommutativen Teiler @g der
Permutationsgruppe die Annahme eines isomorphen Teilers der
Kollineationsgruppe im Räume von fünf Dimensionen auf einen Widerspruch führt.
Der fragliche kommutative Teiler @g enthält neben der identischen
Permutation die sieben geraden Permutationen der Periode 2 der acht
wieder durch oc^, «^, «3, • • •, «§ zu bezeichnenden Wurzeln *) :
S, = (1, 2). (3, 4). (5, 6). (7, 8),
S, = (l, 3). (2, 4). (5, 7). (6, 8),
^3 = (1, 4). (2, 3)-(5, 8). (6, 7),
(1) <; S, = (1, 5)-(2, 6). (3, 7)-(4, 8),
S, = (1, 6)-(2, 5)-(3, 8). (4, 7),
S, = (1, 7). (2, 8) .(3, 5)-(4, 6),
S, = (1, 8).(2, 7).(3, 6).(4, 5).
Man stellt sofort das Bestehen der folgenden vier Beziehungen fest:
I S,-S3 = S3.S, = S2, S^-S, = S,-S^ = S^,
^^■^ i S3 • s. = s, • S3 = s„ s, ■ S3- Sg = s„
aus denen hervorgeht, daß die Permutationen 8^=1, Sj, S^, •••, S„ in
der Tat eine Abelscihe Gruppe @g bilden, für die die drei Substitutionen
S^, S3, Sg eine „Basis'- bilden (vgl. I, 312).
Ist 9"? der Durchschnitt des Xormalisators von @g mit der
alternierenden Gruppe, so zeigt man leicht, daß alle sieben Substitutionen (1)
innerhalb ))l konjugiert sind. Denn die sechs Permutationen:
( (2, 3).(6, 7), (2, 4).(6, 8), (2, 5)-(4, 7)
1 (2, 6).(4, 8). (2, 7). (4, 5), (2, 8) • (4, 6)
gehören dem Teiler '^Jl an und transformieren S^ bzw. in S,, S3, •••, Sg,
so daß alle mit S^ und also auch je zwei unter ihnen innerhalb dl
konjugiert sind.
Es gilt nun der folgende Hilfssatz: Sind S^, Si, Si irgend drei
verschiedene Permutationen (1), so gibt es eine gerade Permiäation T, die S^
in sich und Sk in Si transformiert:
(4) T.S,-T-i = S„ T-Sk-T-^ = Si.
Dieser Satz gilt allgemein, wenn er für i = 1 gilt. Ist nämlich:
(o) T-S,.T-i = S,, T-Sk-T~^ = Si
*) Wir deuten hier und weiterhin die Permutationen der Wurzeln der
Gleichung achten Grades nur durch die Permutationen der unteren Indizes 1, 2,
Beweis des Theorpms von W;man fur » == 8. 317
für jede der 30 Kombinationen 7^, l zweier Indizes aus der Ileihe 2, 3, •• •, 7,
und ist ü die Permutation (3), die S^ in S^ transformiert, so setze mai}.:
Durch Transformation der Gleichungen (5) mit U folgt dann:
(6) T'-S,-T'~^ = S„ T'-Sjj-T'-^ = Sv.
Die 30 Paare S^-, Sy haben h' '^i, V ^ i, li' ^ T, da 7^ imd I von 1
und voneinander verschieden sind. Keine zwei dieser Paare sind
identisch, da dies die Identität der betreffenden Paare S'^-, Si zur folge hätte.
Die Gleichungen (6) beziehen sich ^Iso in der Tal auf alle 30
Kombinationen 7/, V zweier Indizes aus der Reihß 1, 2, •••, i— 1, i -|- 1, •••, 7.
Weiter läßt sich zeigen, d^ß, falls der S^tz für i = 1, ]: == 2 richtig
ist, er auch für i = 1 und beliebige Je, 7, also allgemein besteht. Ist
nämlich Z = 2, so fuhrt der Gebrauch von T~^ an Stelle von T sofort
zum Falle h = 2 zurück. Gilt aber 7.; > 2, l >> 2, so gelten der Afi-
nahme gemäß Gleichungen.
T"-S^-T"~^ = S^, T"-S^-T"-^ = Si.
Aus ihnen ergibt sich leicht:
(T".T'-iVS,-(T'-T"-i) ^ S,, {T' ■T'~^)-S}r{T'-T"-^) ^=Si,
so daß wir unseren Satz jetzt nur noch für i = 1, 7^ = 2 und beliebige^ /
zu zeigen haben. Wir finden aber leicht:
für 7 = 3, 4, 5, 6, 7, falls ^üx unter T bzw. die Permutation:
(1,2).(5, 6), (3, 5).(4, G), (3, 6) • (4, 5), (3, 7).(4, 8), (3, 8).(4, 7)
verstehen. Damit ist der Hilfssatz vollständig bewiesen. Übrigens
gehören alle Permutationen T depi Teiler 3^ an.
Wir nehmen nun an, daß eine piit der alternierenden Gruppe achten
Grades isomorphe Kollineationsgruppe in sechs homogenen Variablen j\,
^Tg, •••, »g existiere. In ihr haben wir daan den 9^ und @g entsprechende
Teiler, die gleich wieder 5)^ und ©§ heißen mögen; ebenso bezeichnen
wir die in ihnen enthaltenen Kollineationen, wie die entsprechenden
Permutationen, durch S^, T, ü. In der einzelnen der ^ugei^örigen
Substitutionen der »j, x^, • • •, x^, die wir gleichfalls wieder S^, T, U nennen,
sind dann nur erst die Quotienten der Koeffizienten eindeutig bestimmt;
doch denken wir diese Substitutionen irg-endwie bestimmt angeschrieben.
In den zwischen den Substitutionen bestehenden Eelationen, die den
Gleichungen (4) ff. entsprechen, treten dann zfinacl^st immer noch
Ähnlichkeitssubstitutionen auf, die wir durch A, A', • • • bezeichnen. Wir
erinnern daran, daß eine solche Ähnlichkeitssubstitutiop der x mit jeder
318 II, 4. Pormenproblem der Valentinergruppe und Gleichung 6ten Grades.
Substitution dieser Variablen vertauschbar ist (vgl. S. 3). Auch die
Quadrate der S^ sind Ähnlichkeitssubstitutionen, da die Kollineationen S^
die Periode 2 haben.
Es besteht nun die Tatsache, daß nicht nur je zwei Kollineationen S^,
S)c, sondern auch die Substitutionen S^, Sjc vertauschhar sind. Zunächst
haben wir für irgend drei verschiedene Indizes i, Ti, l aus der Reihe
1, 2, •••, 7 die Gleichungen:
(7) S,-Sk = Ä-S,rS„
(8) T• S,• T-i = ^'. Si, T-Sk-T~^ = A"■ Si
als für die Substitutionen gültig anzusetzen. Transformiert man die
Substitution (7) mit T und benutzt das Produkt der Gleichungen (8),
so folgt:
T'S^Sk-T-^ = A-A'Ä"-SiS, = A'A"-S^Si.
^STach Zusatz der Faktoren A'—'^, A"~'^ findet man:
(9) S,-Si = A-SrS,
mit der schon in (7) aufgetretenen Ähnlichkeitssubstitution A. Übt man
Sj, und dann die Substitution (7) aus, so folgt, da Sf als
Ähnlichkeitssubstitution mit S). vertauschhar ist;
(10) S,'Sk-S, = A-S!-Sj,.
Beginnt man mit (7) und läßt dann S^ folgen, so gelangt man zu:
Sf -Sk^ A-S^Sj,S, = A'- S! Sk.
Hiernach ist A^ = 1 und also A entweder die identische Substitution
oder die Substitution:
In beiden Fällen folgt aus (7) und (9):
(11) Sk-S, = A-S,-Sk, SrS,^A.S,-Si.
An Stelle von Si möge jetzt die Substitution Sjc • Si treten, deren
zugehörige Kollüieation gleichfalls in der @g enthalten ist. An die Stelle
von (8) treten dann die zwei Gleichungen:
(12) T'-S,-T'-^ = A"'-S„ T'-Sk-T'-^ = A"".S„Si.
An die Gleichungen (7) und (12) kann man dieselbe "Überlegung
anschließen wie oben an (7) und (8). An Stelle von (9) gelangt man zu
dem Ergebnis:
(13) S,.S,Si = A-S,SrS„ S^Si-S, = A-S,-S,Si
mit der bisherigen Substitution A. Übt man jetzt die Substitution (9)
und dann die erste Substitution (11) aus und beriicksichtigt, daß Sf eine
Ähnlichkeitssubstitution ist, so folgt:
SjrS!-Si = Sk-Si^S! = A'-S,Sk-SiS„ S,-SrS, = Si-S,-Sr,
Beweis des Theorems von Wiman fui n = 8. 319
und also liefert der Vergleich mjt der zweiten Gleiphung (13) endlich
Ä == 1 und, wie zu beweisea war, S^-S^ = S^-S^, d. h. die Vertai^sch-
barkeit auch der Substitutionen S.
I^ach S. 13 können wir durch geeignete Auswahl des
Koordinatensystems der X erreichen, daß etwa die Substitution S^ die „Xormal-
gestalt" :
(14) X[ =■ fl^X^, »2 = ^*2^2' »^ = f-s^t •••) »6 = ^6^6
annimmt. Hier sind die ft die irrationalen Invarianten oder ;,Multipli-
katoren'- der Substitution (vgl. S. 7). Da S^ eine Ähnlichkeitssubstitution
ist, so stimmen die ^, abgesehen vom Voi^zeichen, miteinander überein.
Wir können jetzt über die Scl^reibweise von S^ als Substitution so
verfügen, daß die Multiplikatoren gleich -j- 1 oder — 1 werden*). Es
seien « Multiplikatoren gleich — 1 und (B — «) gleich ~\- 1, Man kann
dann die x so angeordnet denken, daß die endgültige Gestalt von S^ als
Substitution diese ist:
(15) x'i = X^, •• ■, äo'a == —Xa, »«+ i = -f ^'ß + 1) * * ') ^6 == ^6'
Da S^ von der identischen Substitution verschieden ist, gehört die
Anzahl a dem Intervall 1 <; a <C 6 an.
Die Substitution S^ schreiben wir in der Gestalt an:
(16) xl = Cj,i x^ ~\- c^oX^ -\- • ■ ■ ~|- c^e ^^•
Fordern wir aber die Gleichheit der Substitutionen S^-S^ und S^-S^, so
ergibt, falls wir S^ in der vorläufigen Gestalt (14) benutzen, das Gesetz
der Zusammensetzung zweier Substitutionen (vgl. S. 3):
(17) iitCik = i^k-Ciic-
Ist somit fij zf: jx,^., so verschwindet 6^^. Aus der endgültigen Gestalt (15)
von S^ folgt somit, daß in der Matrix von S^ nur die «^ ünks oben und
die (6 — a)2 rechts unten stehenden Koeffizienten von 0 verschieden sein
können. Wenn wir demnach jetzt e|ne nur aifif die x^, x^, •••, x^
bezogene Transformation ausüben, die diesen Teil von S^ in die „Xormal-
gestalt-* (S. 13) überführt, so verhp-lt siph dieser Transformg-tion gegenüber
S^ wie eine Ähnüchkeitssubstjtution. behält also die Gestalt (15) bei. Ebenso
können wir durch eine nur auf Xa + i, •••, x^ bezogene Transformation
den Rest von S^ ohne Änderung von S^ auf die Xormalgestali bringen.
Also ' hat Sg nun endgültig die Gestalt (14). Da man übrigens ohne
Änderung von (15) die a ersten Koordinaten noch umordnen darf und
ebenfalls die (6 —«) letzten, so dürfen wir S^ in der Gestalt (14) so
annehmen, daß die ß ersten Multiplikatoren gleiph — 1, die dann
folgenden (a — ß) gleich ~\-1, die weiter folgenden y Multiplikatoren gleich
— 1 und die letzten (6 — « — y) gleich -}-- 1 sind.
*) Es kann freüicli immer noch der gemeinsame Factor — 1 allen
Koeffizienten zugefugt werden.
320 II) 4. Formenproblem der Valentinergruppe und Grleicliung 6ten Grades.
Xun werde S^ in der Gestalt (16) angesetzt. Wegen der Ver-
tauschbarkeit mit S^ können wieder nur die «^ links oben sowie die
(6 — aY rechts unten stehenden Koeffizienten von 0 verschieden sein.
Nun kommt aber auch noch die Vertauschbarkeit mit S^ hinzu. ^ In der
Matrix jener a^ Koeffizienten können erneut nur die ß^ links oben und
die (a — ß)^ rechts unten stehenden Koeffizienten von 0 verschieden
sein, und einen entsprechenden Schluß zieht man über die (6 — a)^ letzten
Koeffizienten c. Es ist klar, daß wir jetzt hintereinander vier
Transformationen, die sich einzeln auf ß, a — ß, y, 6 — a — y Variable
beziehen, derart ausüben können, daß ohne Änderung von S^ und S3
schließlich auch S^ die Normalgestalt (14) gewinnt. Natürlich dürfen
wir Sg wieder endgültig so schreiben, daß die Multiplikatoren durchweg
gleich ~|- 1 oder — 1 sind. Erinnern wir uns endlich der Gleichungen (2),
welche S^, S^, S^ und S^ aus S^, S3, S. aufbauen, so ergibt sich der
Satz: Man hann die Variablen x so wählen, daß alle sieben Substitutionen S
die G-estalt (14) haben, wo die Multiplikatoren ^ auf die Werte -{- 1 und
— 1 beschranM sind.
Man hat nun mehrere verschiedene Typen von Substitutionen S
unserer Art je nach der Anzahl n der positiven und v der negativen
Multiplikatoren. Bezeichnen wir den einzelnen Typus durch das Symbol
{7t, v), SO sind diese Typen (5, 1), (4, 2), (3, 3), (2, 4) (1, 0). Arbeiten
wir mit Kollineationen, so dürfen wir noch einen gemeinsamen Faktor
— 1 in die sechs Koeffizienten der einzelnen Substitution S aufnehmen.
Dann aber sind die Typen (5, 1) und (1, 0) nicht wesentlich verschieden
und ebensowenig die Typen (4, 2) und (2, 4), so daß wir bei den
Kollineationen nur drei wesentlich verschiedene Typen haben.
Innerhalb der Gruppe 9*? sind die sieben Substitutionen S konjugiert;
sie haben also nach S. 7 gleiche Systeme von Multiplikatoren (natürlich
von deren Anordnung abgesehen). Also gehören die Kollineationen S
alle einem und demselben Typus an. Es kann sich um keinen der
Typen (5, 1), (3, 3) handeln; denn zwei Substitutionen aus einem dieser
Typen geben zusammengesetzt eine Substitution des Typus (4, 2)*).
Hiernach gehören alle sieben Substitutionen S dem Typus (4, 2) an.
Man zählt leicht ab, daß es im ganzen 15 Substitutionen des Typus
(4, 2) gibt, die mit der identischen Substitution eine kommutative KoUi-
neationsgruppe @^g liefern. Irgend drei ihrer Substitutionen, die
voneinander und von der identischen Substitution verschieden sind, ergeben
die Basis für einen kommutativen Teiler ®g der ©^g. Wir greifen nun
diejenige @g auf, die als Teiler in der als existierend angenommenen
KoUineationsgruppe ^ enthalten ist Indem wir die einzelne
Substitution S kurz durch Zusammenstellmig der Vorzeichen ihrer Koeffizienten
bezeichnen, können wir die x so geordnet denken, daß die ©„ eine erste
*) Bei den Typen (5, 1), (3, 3) ist die Substitutionsdeterininante — 1, bei
(4, 2) aber gleich -f 1.
Beweis des Theorems von Wiman fur » = 8 321
Substitution S^ = (—, —, -f, -f, -j-, -f) enthält. Die (Sg hat dann
sicher noch eine zweite Substitution mit gleichen zwei ersten
Koeffizienten. Anderenfalls enthielten sie ja lauter Substitutionen, in denen
die beiden ersten Koeffizienten jeweils entgegepgesetzt wären; und dann
würde doch durch Zusammensetzung zweier solcher Substitutionen sofort
eine Substitution S entstehen, in der die beiden ersten Koeffizienten
gleich sind. Da wir ohne Änderung von Sj, die viey Variablen x^, ■•■, x^
noch umordnen können, so dürfen wir eine zweite Substitution Sh in der
Gestalt (-}-, -j-, —, —, -\-, -j-) gegeben annehmen.
Man gehe, unter Si irgend eine der übrigen fünf Substitutionen ve:p-
standen, auf die Gleichungen (8) zurück. Kombiniej-t man die erste
Gleichung (8) mit sich selbst, so folgt Ä'^ =- 1. Also ist A' entweder die
identische Substitution oder sie \^rechselt gleichzeitig die Vorzeichen aller ic.
Die letztere Möglichkeit ist ausgeschlossen, da das System der M]iltipli-
katoren von Sj, bei Transformation mit J' unverändert bleibt. Es gilt
also T ■ Si ==: Si- T, woraus wie oben folgt, daß in T nur die vier oben
links stehenden Koeffizienten uifid die 16 rechts unten stehenden von 0
verschieden sein können. Danij. aber folgt sofort aus der zweiten
Gleichung (8), daß auch in Si die beiden ersten Koeffizienten gleich sind-
Also stimmen in jeder der sieben Substitutionen S die beiden ersten
Koeffizienten überein. Man wolle nun dieselbe Betrachtung nur unter
Austausch der Rollen von S^ und Sj. ausführen. Man findet, daß in
jeder der sieben Substitutionen ß auch der dritte mit depa vierten
Koeffizienten übereinstimmt. Dann aber haben wif überhaupt nur mehr die
drei Substitutionen zur Verfügung:
(-, -, +, +, +, +), ( + , +, - - +, +),
(+. +. +, +. -. -).
so daß es gar keine für ur|.s branchbare @g gibt. Damit ist endlich das
Theorem von Wiman im Falle n = 8 bewiesen.
§ 8. Quaternäre Kollineationsgruppe für ()ie allgemeine Gleichung
siebenten Grades.
Soweit affektlose Gleichungen in Betracht kommen, ist dq,s Programm
unserer bisherigen algebraischen Entwicklungep zufolge des ^iman sehen
Satzes bereits mit dem Grade 7 erschöpfb. Darüber hinaus ist die
algebraische Reduktion der allgemeinen Gleichung n^^^ Grades ^uf ein
Formenproblem von weniger ^Is (^ — 2) Dimensionen unmöglich, man
hätte vielmehr den transzendenten Lösungsprozeß direkt an die Gleichung
n^^^ Grades selbst, die man als Formenproblem voi^ (»-- 2) Dimensionen
aufzufassen hat, anzuschließen. Xur beim Grade 7 erscheint es noch
möglich, die allgemeine Gleichung auf ein Iformenproblem von weniger als
fünf Variablen zurückzufüliren. In der Tat ist es Kleir). gelungen, durch
eine interessante liniengeometrische Betrachtung eine Kollineationsgruppe
Fricke. Algebra. II. 21
322 n, 4. Formenproblem der Valentinergruppe und Gleichung 6ten Grades.
im Räume von drei Dimensionen, also bei vier homogenen Variablen zu
konstruieren, die der alternierenden Permutationsgruppe des Grades 7
isomorph ist*).
Um wenigstens die Grundgedanken dieser Entwicklung hier kurz
zu skizzieren, nehmen wir die allgemeine Gleichung siebenten Grades
der „Hauptgleichung'- fünften Grades (vgl. S. 64) entsprechend sogleich
in der Gestalt an:
(1) z' ~f ttg^* -f a^z^ -^ a-^s^ -^ a^s -\- a,, = 0,
d. h. wir denken von vornherein durch Tschimhaustransformation eine
Gleichung hergestellt, in der das zweite und dritte Glied ausfällt. Die
Wurzeln der Gleichung, die a^, a^. •••. «g lieiße^ mögen, genügen dann
den beiden Gleichungen:
(2) S«fc = 0. 2 «1 = 0.
Mittels der siebenten Wurzel der Einheit s =^ e "^ bilden wir die
sechs Lagrangeschen Solventen (vgl. I, 413):
(3) ß,n= ao^s'^oi^^e^^a^^e^'^'a^^ r«^™«6' « = 1,2, •••,6,
und finden unter Benutzung der ersten Gleichung (2) die Wurzeln a in
den ß umgekehrt so ausgedrückt:
(4) 7a„ = £-«^j + £-2«^2^£-3«^^ £~^''ß6, » = 0,1,.. .,6.
Für die zweite Potenzsumme der Wurzeln a finden wir bei
Umrechnung auf die Größen ß:
(5) 7(al+a!^a!^---^al) = 'Hß^ße ^ ßoß, ~\-ß^ß,).
Unter S und T mögen die beiden folgenden Permutationen der
Wurzeln « verstanden werden:
(6) S = («0, «j, «2) ■• •) «b)' ^ = («3) «4)-
Nach dem ersten Satze von § 6 in I. 345 erzeugen diese Permutationen
S und T die symmetrische Permutationsgruppe des siebenten Grades.
Drückt man «^ nach (2) als negative Summe der übrigen Wurzeln aus,
so kann man die Permutationen (6) als lineare ganzzahlige Substitutionen
von «j, «2) •••■ «6 auffassen, und zwar hat dabei S die Determinante 1
und T die Determinante — 1. Sie erzeugen eine ©^^^g solcher
Substitutionen, die der symmetrischen Permutationsgruppe siebenten Grades
isomorph ist. Die unimodularen Substitutionen in dieser ©50^0 bilden
einen Xormalteiler ®>2h20' ^^^ ^^^ alternierenden Permutationsgruppe
siebenten Grades isomorph ist.
*) „Zur Theorie der allgemeinen Gleichungen sechsten und siebenten Grades",
Math. Ann., Bd. 28 (1886) oder „Ges. Abhandl.'- II, 439.
Quatemäje Gruppe fur die allgemeine Gleichi^ig siebenten Grades. 323
Man wolle nun diese Gruppe Ög^^o auf die ß^, ß^, "■, ß^
transformieren; die dieser Transformation dienende Substitution:
(7) ß^ = (£- - 1) «, + (£^- _ 1) «.^ 4- . . . ^ (£6» _„ 1) ^^^
wo w = 1, 2, . • •, 6 zu nehinen ist, ist nicht-singuläi\ Die Substitution S
rechnet sich einfach um auf die Gestalt:
(8) , ^; = £-»^^, ^^^ ^ 1^ .,, ...^ 6;
auch T ist nicht schwer anzugeben, wenn auch der Ausdruck etwas
komplizierter ist. Wir gelangen zu e^ner @504o ^^^^eßfe^ Substitutionen def
ßi> ß-2' ■"' ßö' ^^^ ^^^ ^^'^^'^ ^^^^^ ^^'' ^^^ ß verbindenden Gleichung:
(9) ß,ß, + ß.ßo-Tß^ß,==Q
zur absoluten Invariante haben und zur Hälfte unimodular sind, zur
Hoäfte die Determinante — 1 haben. XatüTlich besteht de|- Isomorphismus
zu den Permutationsgruppen siebenteii Grades fort.
Die letzten Angaben gestatten nun eine sehr einfache geometrische
Deutung im Räume von drei Dimensionen. Sind x^, x^, x^, x^ und
Uli y%i y%i Ui ^^^ homogenen K'oordinaten zweier Punkte, so siijd die
Plückersehen Linienkoordinaten jj^g, p^^, p^^, p„^, p^^, p^.^ der durch diese
beiden Punkte hindurchlaufenden Geraden durch:
(10) 9^): == J^iMk — -^icyi
gegeben und durch die in den x, y identische Relation
(11) Pi^lhi ^l'isPio^ -^PiiPo^ = 0
verbunden. Im übrigen sind die p^i,. alß hopioge^ie Linienjioordinaten
willkürlich variabel. Wir köuAen 4enua^ch die an die Relation (9)
gebundenen Größen ß-^, ß^, • • •, ßg als Linienkoordinaten ifti Räume deuten
und setzen zu diesem Zwecke etwa:
I ß, = A2> ^3 == PlZ' ß. = i^l4'
1 ßi = Psiy ßi = Pi2' ß-2 = P2%-
Die Darstellung der Wurzeln a in den Liaienkoordinaten ist zufolge (4)
die folgende:
(13) 1 an = £''Pn — ^^''-Pis — £^''Pii — £^''J^34 - ^^''Pi2 '- ^''"'P-iz-
Es besteht aber der Satz: Dem einzelnen Wertspstetn a^, «j, •••, (x.^
entspricht eindeutig eine Baumgerade, gegeben durch die berechneten
Koordinaten Pjjc; den 5040 durch die Perfnutationen der a entstehenden
Wertsystemen der Wurzeln aber entsprechen ebenso viele Bßumgerade, deren
Koordinaten p^jc durch die 5040 Svihstitutionen der oben fur die ß und
also p^]c gewonnenen ©jo^o au&, den Koordinaten einer ersten dieser Geraden
324 III 4. Formenproblem der Valentinergrappe und Gleichung 6ten Grades.
Die Rückkehr zu den Punktkoordinaten macht es nötig, neben ihnen
auch noch die ihnen entsprechenden Ebenenkoordinaten einzuführen.
Bezeichnen wir durch m^, u^, u^, u^ und v.^, v^, v^, v^ die Koordinaten
zweier Ebenen, so sind die Linienkoordinaten ihrer Sckoittgeraden
^12. äl3' äl4. 234' «42. «23 ^Urch:
<14) ä« — «*«^fc —%^'z
gegeben. Dabei gilt als Beziehung zu den Koordinaten p der gleichen
Oeraden*):
.^g I äl2 = -^34» äl3 = -^42- äl4 = -^23'
1 «34 = -Pia. «42 = -^13' «23 = -^U"
Nach einem von Klein aufgestellten Satze**) entspricht nun einer
linearen homogenen Transformation der Linienkoordinaten p, bei der die
in (11) links stehende quadratische Form absolut invariant ist, entweder
eine RaumkoUineation oder eine dualistische Transformation
(Auswechselung der Punkte und Ebenen), und zwar das erste oder zweite, je
nachdem die Determinante der Substitution der p, deren Quadrat gleich
-j- 1 ist, selbst den Wert -j- 1 oder — 1 hat. Xtm lieferten die 7! Per-
mutationen der Wurzeln a ebenso viele lineare Substitutionen der p^^,
tind zwar die i 7! geraden Permutationen solche der Determinante 1 und
der Rest solche der Determinante — 1. Damit erhalten wir das
Hauptergebnis: Der alternierenden Permutationsgruppe der sielen Wurzeln cc
entspricht eine isomorphe Gruppe ©3520 ^'^'^ JRaumJcoTlineationen, der
symmetrischen Gruppe aber ebenso eine ©5040» ^^e neben jenen 2520 Kdüinea-
tionen noch ebenso viele dualistische Umformungen des Baumes enthält.
Die erzeugenden Operationen, die den Permutationen (6) entsprechen,
mögen gleichfalls durch S und T bezeichnet werden. Die Permutation S
ergibt zufolge (8) und (12) für die p^j, die Substitution:
; P'i% = sPn, P'i3 = £^Piz, P'ii = £^Pii,
<1^> .0 . . -0
Pzi == e^Pzi, Pi2 = e'^Pio., P-2Z = s^Pis-
Die ihr entsprechende Kollineation S ist eindeutig bestimmt. Schreiben
wir sie als quatemäre »-Substitution, so ergibt sich:
(17) +x'i = x^, +X2 = Ex^, +x'z = e^x^, -T_x\-=z e'^x^,
wo entweder nur die oberen oder nur die unteren Zeichen gelten. Beide
Vorzeichen aber sind brauchbar. Durch die Operation T, die «3 und «^
austauscht, wird die Gleichung «^ — «3 == 0 oder in den p^-f, geschrieben:
(18) (£^-£^)(ff,, -1^3,) + (£ - fß) {p^^ -^^3) ^- if - £^) Op,3 -i),J = 0
*) Man vergleiche betreffs der Linienkoordinaten die Lehrbucher der ßaum-
geometrie oder auch die Referate von E. MuUer, „Die verschiedenen
Koordinatensysteme" in Bd. III, 1, 1 der Enzyklopädie, S. 722 ff. und von K. Zindler,
.Algebraische Lmiengeometrie", ebenda in Bd. Ill, 2, 2, S. 973 ff.
**) Vgl. „Ges. Abhandl." 11, 272.
Quaternäre Gruppe fur die allgemeine Q-leichung siebenten Gr^ides. 325
und damit der durch (18) dargestellte lineare Kopiplex in sich
übergeführt. Vermöge dieses Komplexes entspricht jedem Pui^kte des R^-umes-
eine Ebene (und umgekehrt) und diese dualistische Un^ormong liefert
die gesuchte Gestalt der Operation T. Tragen wir die Ausdrücke (10)
in (18) ein und ordnen nach den y, so ergibt sich:
Vi (—(«* — «^) -^2 — («^ — f°) "f's — (f — «^) »4)
^ y^ ((£* — s^) x^ -^{i- — f6) ^3 — {a- — £=) x^
■^ j/3 ((^^ — ^') ^'i — (^ — £') ^^2 ^ (f' — £^) ^4)
+ z/, ((£ - £«) «, ^ (^2 - £") r, - {a' - ^0 ^3) = 0
Unter Aufnahme eines Proportionalitatsfaktors 6 haben wir aLo die
dualistische Umformung T des Raumes in der Gestalt abzusetzen:
{ (3U^ =z * -r (f* — B^) X.2 -}- (£^ — £'') 3:3 -t- (£ — £^) if^,
] 6U^= — (a^ — £") »^ -h - - (£ — £') »3 - (£' - £°) »,,
I 0 M3 =z — (£^ — e"") a;^ -f- (£ — £^) ^2 — - — (£* — e^) x^,
l 0 M^ = — (£ — £&) X^ — (^2 — £^) a;,_ + (£* — f 3) ^^ ^ ^ ^
wo durch die Sterne auf das Ausfallen der vier Diagonalglieder
aufmerksam gemacht wird.
Zur Bestimmung des Faktors 6 bezieht Kleip die Substitution T
auf die durch 0^3 = 0, x^ = 0 gegebene Kante des Koordinatentetraederß-
Sie kann als Verbindungsgerade der beiden Tetraederecken:
( X, = 6, .r, = 0, x^ == 0, X, = 0,
(20) ' ' r.
l «/i = 0, «/2 =. ö, y^ == 0' ^i ~ ^
angesehen werden und hat demnach die Linieiikoordinaten:
(21) i>,2 = ö^ Pu = 0, P^, = 0, ß,,=--0, i>,2 = 0, J>23 = 0.
Den beiden Systemen von Punktkoordinaten (20) entsprechen aber
vermöge (19) die beiden Systeme von Ebenenkoordinaten:
(22) I
Für die Schnittgerade dieser beiden Ebenen findet man nach (15) die
Koordinaten:
[ -^12 = «34 = - 5 - £ - £^ Psi = äi2 = - 2 - s -- £^
(23) _pj3 = 2^2 = - £ f £2 ^ £^ - £6, _p^2 == q^^ = 8 - r - f' ^ £^
l Pii ^ «23 = - ^^ + ^^ 4- ^* - ^^ Piz = äu = £^ - f ^ - £* ~f a^.
Die beiden Systeme von Ei^oordinaten (21) und (2B) werden also durch
die Substitution T ausgetauscht. Gehen wir auf die Wurzeln a zurück,
0,
a' - £^
^2 =■ £^ — i*,
^2 = 0>
«(3 = £^—£^
6-3 = £ — £^
'f^
^■4
326 II, 4. Formenproblem der Valentinergrappe und Gleichung 6ten Grades.
die wir auf Grund von (13) berechnen, und lassen wir den unter (21)
gegebenen jo^ j^. die Werte «^, «^, • • •, «g entsprechen, den unter (23)
gegebenen aber die Werte «ö> <^i> ' •'• «et so müssen die Gleichungen:
«5 = «5, Ci'e = «(,
gelten. Xun. folgt aber aus (13) leicht:
7 «, = (J^ 7 «, = £ (j2^ 7 «2 = £2^2^ 7 «3 = £3 ^2^
7 «^ = £* 0-, 7 «, rrz £° a^, 7 Kg = £^ ()^,
7 «; = — 7, 7 «; = — 7 £, 7 «; = — 7 £2^ 7 «^ = — 7 £^
7«; = — 7 £3, 7«; = — 7 £^ 7«; = — 7 £«.
Wir finden, damit nicht nur den Faktor 6 == +^^7, sondern erhalten
wenigstens für die betrachteten speziellen Geraden eine Bestätigung der
auf den Ansatz (19) führenden Schluß weise. Als Ergebnis notieren wir:
Die Gruppe ©go^o 'von KolUneationen und dualistischen Umformungen det,
Baumes ist erzeugbar aus den leiden speziellen Operationen:
(T)
±i)llu^= * + (£* - £3) X^ ~f (£2 — £^) 0^3 -i- (£ - £«) X^,
4:iyyM2 — — (£* — £3)j;^-f * _(£_£6)a;g _|_(£2 _££)^^,
4-iy7M3 = — (£2_£5)rCj -f (£ — £«)X2 ^ * — (£* — £^)j5^.
-f i y7 M^ = — (£ — £^) x^ — (a^— £^) a?2 ~f (£* — £^) x^ -f V.- .
Wegen des doppelten Vorzeichens entspricht der Kollineationsgruppe (^2520
zunächst eine ©2-2520 quaternärer a; - Substitutionen. Die Frage, ob in
dieser ©2-2520 ^^ ^^ "^^^ Kollineationsgruppe isomorpher Teiler ©2520
von quatemären a?- Substitutionen enthalten ist, hat Klein gerade wie
die entsprechende Frage bei der Ikosaedergruppe im negativen Sinne
beantwortet.
Eine genaue Untersuchung der Kollineationsgruppe ©2590 ^^'^ ihrer
invarianten Formen ist noch nicht durchgeführt. Dagegen hat Klein
im letzten Teile seiner S. 322 genannten Abhandlung Ausführungen über
die Zurückführung der allgemeinen Gleichung siebenten Grades auf das
Formenproblem der ©2520 gegeben.
§ 9. Bericht über weitere Untersuchungen.
Wenn auch bei der allgemeinen Gleichung w*«" Grades für » >> 7,
wie in § 7 ausgeführt wurde, eine Reduktion auf ein Formenproblem
von weniger als (n — 2) Dimensionen unmöglich erscheint, so ist doch
nicht ausgeschlossen, daß bei Gleichungen mit einem Affekt noch
Anthmetische Erklänpig der einfachei^ Grappe ©50^. 327
die bisherige Methode der Auflösung, d. h. die Zurückführung aaf ein
Formenproblem möglichst geringer Dimension nebst transzendenter Lösung
des letzteren Erfolg verspricht. Insbesopdere wird es interessieren,
inwieweit hierbei die auf die Ordnung BQO nächstfolgenden beiden
einfachen nicht-metazyklischen Gruppen ©^^^ und ©gg^ (vgl. I, 310) eine
Rolle spielen mögen.
Die erste dieser beiden Gruppen ist von Cole gefunden*). Mit
ihr haben sich auch Wim an**) und der Verfasser f) beschäftigt. Jn
der zuletzt genannten Arbeit ist eine transzendente Begründung der
Gruppe @504 gegeben. Sie kpüpft an die Grenzkreisgruppe von der
Signatur (0, 3; 2, 3, 7), dje arithmetisch erklärbar ist mittek desjenigen
kubischen Körpers, der zuj' ganzen algebraischen Zahl:
(1) n=:e^ ^e ''
gehört. Diese Zahl rj genügt der kabisclien Ilesolvente:
(2) >?3 _|_ ^2 _ 2 ^ _ 1 ^0
der Kreisteilungsgleichung für den siebenten Teijungsgrad. Die
fragliche Grenzkreisgruppe baut sich dann aus den quadrimodularen
Substitutionen:
(3) ^ — , , ,
' -C + Z)V': —1, A — Byv—'i-.
auf. in denen Ä, B, G, D ganze Zahlen jenes kubischen Körpers sind,
die jedoch noch gewissen Kongruenzen mod 2 genügen müssen. In (\er
fraglichen Gruppe ist nun ein als Kongruenzgruppe zweiter 3tufe
erklärbarer Xormalteiler des Index 504 enthalten, deßsen Quotientengruppe
gerade unsere ©j^^ liefert. Es ergibt sich hierbei einmal eine sehr
bequeme Art, die Struktur der (5)^^^ zu untersuchen, andererseits wird die
@.Q^ auf dem fraglichen Wege funktionentheoretisch und algebraisch
zugänglich.
In letzterer Hinsiciit findet man leicht, daß das zur ©.^^
gehörende algebraische Problem als niederste Eesolvente eine solche vom
neunten Grade besitzt, die sogar in den^. durch dip genannte
Grenzkreisgruppe gegebenen Spezialfälle als (ileichung mit einein Parameter leicht
=^) Vgl. neben den schon in I, 310 genannten Arbeiten die Mitteilung „List
of the substitutiongroups of nine letters'-, Quarte^iy Joum., Bd. 26, wo die ©50*
als Permutationsgruppe von neun Dingen erklart ist.
**) Am Schlüsse der Xote „Über die Vertauschungßgnippe von acht Dingen'',
Gott. Xachr. von 1897, S. 62.
t) In der Abhandlung „Über eine einfache Gruppe von 504 Operationen",
Math. Ann., Bd. 52. S. 321.
328 n, 4. Formenproblem der Valentinergruppe und Gleichung 6ten Grades.
angebbar ist*). Wim an läßt a. a. 0. die Möglichkeit offen, daß jene
Gleichung neunten Grades auf ein Formenproblem in einem Räume von
sechs Dimensionen zurückführbar sei; eine weitere Herabminderung der
Dimensionenanzahl aber erklärt er als unmöglich.
Weit ausführlicher ist die Theorie der nächstfolgenden einfachen
nicht - metazyklischen Gruppe ©gg^ entwickelt. Die Hauptkongruenz-
gnippe elfter Stufe in der Modulgruppe hat den Index 660, und in der
zugehörigen Quotientengrappe hat man eine erste Darstellung der ®ggß. Die
Gleichungen niedersten Grades, die unsere ©gg^ zur Galois sehen Gruppe
haben, sind demnach die Modulargleichung zwölften Grades für die
Transformation elften Grades der elliptischen Funktionen und ihre beiden
von Galois entdeckten Resolventen elften Grades. Klein hat diesem
Gegenstande eine ausführliche Untersuchung gewidmet, die sich an seine
Theorie der temären (S^gg anschließt und mit dem gleichen Erfolge trotz
erheblich größerer Schwierigkeiten zu Ende geführt ist**).- Es gelingt
ihm, die Resolventen elften Grades, an denen sich bereits Hermite ohne
endgültigen Erfolg versucht hatte, in einfachster Gestalt fertig anzugeben,
und er entwickelt vor allem die Zurückführung der fraglichen
Gleichungen auf ein Formenproblem in fünf Variablen f). Für die dabei
eintretende Kollineationsgruppe im Räume von vier Dimensionen kommt
dann freilich nur ein „spezielles Formenproblem-' zur Geltung, dem bei
der temären ©^gg das besondere Problem mit verschwindender Invariante
vierten Grades F entspricht. Über das zugehörige allgemeine
Formenproblem sind Untersuchungen bisher noch nicht angestellt.
Seit langer Zeit sind diese Entwicklungen ausgedehnt auf die
Transformation eines beliebigen Primzahlgrades der elliptischen Funktionen.
Ist » >> 11, so ist die Modulargleichung des Grades {n ~|- 1) die niederste
Resolvente. Ihre Galois sehe Gruppe hat die Ordnung \n(n'^— 1) und
ist isomorph zur Quotientengruppe, die von der Hauptkongruenzgruppe
n^^^ Stufe des Index \n{n'^ — 1) in der Modulgruppe geliefert wird. Die
Darstellung der @jgg und ©gg^ durch Kollineationsgruppen verallgemeinert
Klein in der Art, daß er eine mit der Galois sehen Gruppe der
Modulargleichung isomorphe Kollineationsgruppe in \ {%—1) Variablen
konstruiert ff). Überhaupt sind die Transformations- und Teilungsgleiehungen
*) Es handelt sich um die Gleichung, mittels deren Goursat die Kommen-
surabilität der beiden Grenzkreisgruppen der Signaturen (0, 3; 2, 3, 7) und
(0, 3; 2, 7, 7) zum Ausdruck bringt; vgl. dessen „Eecherches sur l'equation de
Kummer", Akten der Finnischen Akad. m Helsingfors von 1888, Bd. 15, S. 90ff.
**) „Über die Transformation elfter Ordnung der elliptischen Funktionen",
Math. Ann., Bd. 15 oder „Ges. Abhandl." III, 140ff.
t) Vgl. auch die noch weit ausfuhrlichere Darstellung in „Modulfunkt.-'
II, 401 ff.
tt) Es ist hierüber zu verweisen auf die Abhandlungen Kleins, „Über
gewisse Teilwerte der i9'-Funktion'' und „Über die elliptischen ATormalkurven »ter
Ordnung" in den „Ges. Abhandl.'- III, 179 und 198. Vgl. auch „Modulfunkt.'-
II, 312 ff.
ilodulargleichupgen der elliptischen f'unktionen. 329
der elliptischen Funktionen, denen vop Anbeginii ab die Aufmerksamkeit
der Funktionentheoretiker zugewandt w^r, nicht nur sehr wertvolle
Beispiele zur Erläuterung der £t,llgemeinen Grundsätze der
Gleichungstheorie, sondern es haben jene Gleichungen in der geschichtl:(.chen
Entwicklung der Theorie der algebraischen Gleichungen insbesondere bei
Abel und Galois eine wesentliche und sehr fördernde Rolle gespielt. Die
nähere Behandlung dieser Gleichungen gehört indessen in die Theorie
der elliptischen Funktionen hinejn*).
*=) Es sei auf den zweiten Band vom Werke des Verfassers: „Die
elliptischen Punktionen und ihre Anwendungen" (Leipzig 1922) verwiesen, wo mai|
eine ausführliche Behandlung der fraglichen Gleichungen im Sinne der hier \er
tretenen allgemeinen Grundauffassungen dpr Algebra findet.
Dritter Abschnitt.
Geometrische Anwendungen der Gruppen?
theorie.
Erstes Kapitel.
Wendepunkte ebener Kurven dritten Grades.
§ 1. Kovarianten der ternären kubischen Form.
Es sei eine temäre kubische Form:
(1) F = a„j Xl + 0222 «2 ^
der drei Argumente x^, x^, x^ mit unbestimmten Koeffizienten a^^j, a^c^^^, •••
vorgelegt. Diese Form möge, wenn nur die Argumente hervorgehoben
werden sollen, durch F(x-^, x^, x^) oder kürzer durch F(x). und wenn
auch die Koeffizienten angedeutet werden sollen, durch F (x, a) bezeichnet
werden.
Eine beliebige nicht - singulare Substitution der drei homogenen
Variablen x^, x^, x^ sei gegeben durch:
(2) ^2 = «2.
i- a,2 % + «13 «3,
-f- OJ32 X'<i -j- «33 X'z;
ihre Determinante werde durch s bezeichnet. Die Form (1) hat alsdarm
gegenüber der Substitution (2) drei wichtige Kovarianten: Erstens die
Hessesche Determinante von F:
H{^, a) =
d^F
dxr
1 d^F
^^dx^ dx^'
^ d^F
c^F
dx^ dx^'
d^F
dxi '
d^F
d'^F
dx^ dx^
d^F
cx^ dx^
d^F
(3)
dXc^ dx^' CXg dx^' dx^
Kovarianteijt der ternaren ki|bischßn Fo^.'ni. 33 [
zweitens die mit den ersten Ableitungen von H gerändert Hessßsohe
Determinante von F:
:4)
iritte
:-5)
d^F d^F
dx'l' dp^ci^'
c^F d^F
J(x, a) = „
c^F d^F
dH dH
d x^' dx^^
:ns die Funktionaldeterminante von F, .
cF dF
d X^' d X.^'
TT, N dH dB
E(x, a) = ~—, -—,
^ cx^ a^ä'
0 ajj' dx^'
d'F
dx-^ dx^'
d^F
c'F
6x^ '
du
8^;
H und J:
dF
dx^
dx^''
dx^
dH
dx^
dH
8^
dH
dx^
0
Die Grade der Ausdrucke H, J, K in den Argumenten sind 3, 6, 9
und in den Koeffizienten 3, 8, 12; ihre Gewichte sind 2, 6, 9, so dg-ß
bei Ausübung der Substitution (2) die Ausdrücke H, J und K, gebildet
für die neuen Variablen a:' unc(. die neuen Koeffizienten, a, mit den
ursprünglichen Ausdrücken durch die Gleichungen verbunden sind:
I H(x', a) = s^H(x, ä), Jix, a!) = s^J{x, d),
I K(x', a) == b^K(x, a),
wahrend für die kubische Grundform (1) die Gleichung:
(7) F{x\ a) =F(j, a)
gilt. Übrigens behalten wir uns vor, die rechten Seiten der Gleichungen
(3), (4) und (5) noch um numerische Faktorep^ zu andern.
Die Kovarianz der Ausdrücke (3), (4) und (5) wurde bereits oben
bei den Formen F vierteil und sechsten Grades, die bei den ternaren
(iiuppen ®jgg und ^^bo auftraten, benutz^;. Das wi^-kliche Bestehen die&er
Eigenschaft zeigt man durch übertragijng der \ji I, 130 ausgeführten
Betrachtung auf temäre Formen. Man führt hierbei |j, 1^, ^3 als ipit
den X kogrediente Variable ein und knüpft an die aus (7) folgende
Gleichung:
(8) F{x ^t I', a) == F(x -i-11, a)
an. wo t ein Parameter ist. Entwickelt man beiderseits nach Potenzen
von t und setzt die Koeffizienten gleich hohe;- Potenzen von t rechts und
332 III: 1- Wendepunkte ebener Kurven dritten Grades.
links einander gleich, so ergeben sich insbesondere bei den Gliedern
mit t und f die Gleichungen:
(9)
cF(x', a)
dF{x, a)
i-l.
, dF{x', a)
OXs
dF(x, a)
(10)
',.^d^F(x', a)
d'F(x,a)
5i —^72
+2iu=?:.^;^+-
^ai^ls
8 a;^ d x'i
d-F(x, a)
Die Diskriminante der in (10) rechts stehenden quadratischen Form der
li) I2' Is' "^^^ unmittelbar unsere Hessesche Form (3) liefert, ist nach
I, 151 eine Invariante des Gewichts 2. Also sind die Kovarianz von
H und die Gleichung (6) für // bewiesen.
Entwickelt man die in der Gleichung:
H(x' ~\-t^', a) = s'H{x + tl, a)
rechts und links stehenden Ausdrücke nach Potenzen von t und setzt
die Koeffizienten der in t linearen Glieder einander gleich, so ergibt sich:
(11)
, dH(x\ a)
I ^21 f^H(x, a]
[ ^ \ dx^
■+|;
., dH(x', a) _
dx'z ~~
cH(x, a)\
' Wx^)
Aus (10) und (11) setzt man die Gleichung zusammen:
c^F(x', a)
(12)
, d'Fjx, a)
5l c^^'2 1
2 d^F{x, a)
cH{x, a')
CX.2 OX^
+ '
••)=
.21,1,4^:%^ + .
dH{x, ä)
dx
wo X' eine neue Variable sein soll und:
(13) ;l = .2a'
gilt. Wir fügen nun X als vierte Variable den |^, Ig, I3 bei und haben
dann in (12) rechts eine quaternäre quadratische Form der |j. Ig, I3, l-
Diese Form geht in die in (12) links stehende Form durch diejenige
«n>
«sp
«31>
0,
«12.
«22.
'^Vi.i
0,
«13'
«23'
«3V
0,
0
0
0
S^
Kovanantei^ der temaren kubischen Fofm. 333
quatemäre Substitution über, die aus (2) durch Zusatz der Gleichung (18)
entsteht, und deren Determinante:
(14)
ist. Die Diskriminante dey in (12) ^rechts stehenden Form i&t aber
unmittelbar unser Ausdruck (4), dessen Kovarianz und Gewicht 6 damit
eine Folge der Gleichung (16) in I, 151 ist.
Die Kovarianz der Funktionaldeterminante und ihr Gewicht 9 sind
nur durch eine einfache Rechnung beweisbar.
§ 2. Wendepunkte der ebepen K^ve dritten Grades.
Deutet man a;^, x^^ x^ als homogene Kooi^dinaten in der Ebene, sq
wird durch J" === 0 eine Kurve dritten Grades dargestellt, die wiy kurz
als die Kurve F bezeichnen. E]ine solche Kurve hat entweder das
Geschlecht j) rrz 1 oder 'j) =: 0. Der letztere besoi^dere Fall liegt vor,
wenn die Kurve einen Doppelp'iinkt hat. Daipi verschwindet die durch
Elimination der x aus den drei Gleichungen:
(1) 1^ = 0, |Z=0, V- = ^
0 X^ OX^ C %
zu gewinnende Diskriminante von F. Die folgenden Entwicklungen
sollen sich auf den „allgemeinen Fall" einer doppelpunktfreien Kurve
dritten Grades beziehen.
Durch XuUsetzen der zugehörioen Hesse sehen Forrp H von F wird
eine zweite Kurve dritten Grades dargestellt, die die „Hessesche Kurve"
der zugrunde gelegten Kijrve F gepannt wird und auch kurz als die
Kurve K bezeichnet werden möge. Es soll zupächst kurz die Bedeutung
dieser Kurve H für die Kjirve F in Erinnerui^g gebracht we?"den.
Da die Kurve F doppelpunktfrei ist, sq hat sie in jeden^ ihrer
Punkte eine bestimmte Tangente. Wir paachen durch Xeuwfihl der
Koordinaten X einen beliebig gewählten Punkt der Kurve F zur Ecke
a;^ rrz 0, a;2 = 0 des Koordinatendreiecks und wählen die Kurventangente
in diesem Punkte zur Seite x^ = 0 dieses Dreiecks. Die Porm F hat
dann die besondere Gestalt:
(2) i'' = ex^Xz -\- (aXi ^- 2hx-^x^ -j- cxf)x^
— (a a?!^ ~f 3 /3 x^ x.^~ Sy x^ xl -p ö jo]),
wo e =fz 0 ist. Die drei Schnittpunkte der Geraden x^ = 0 mit der
Kurve F bestimmen sich aus der Gleichung:
x| (8 »2 T" (^ ^s) = ö.
334 III« 1- Wendepunkte ebener Kurven dritten Grades.
Wir schließen hieraus, daß im Punkte x^ = 0, x^ = 0 stets und nur
dann ein Wendepunkt der Kurve F vorliegt, wenn c = 0 gut.
Für die Hesse sehe Form H der Form (2) berechnet man:
(3) —|ff= ce^x! + {(ace — h' e ~\- 3 e^y)x, ~\- S e^8x^)x! + ....
Soll die Hessesche Kurve auch durch den Punkt x^ = 0, x.^ = 0 der
Kurve F hindurchlaufen, so muß c e^ = 0 sein, also muß, da e =fz 0 ist. r
verschwinden. Auch läuft sie, falls c = 0 zutrifft, sicher durch diesen
Punkt x-^ = 0, x^ = 0 hindurch: Die Hessesche Kitrve H der gegebenen
Kwrve F lauft ditrch jeden WendepunJd dieser Kurve hindurch, und
umgekehrt ist jeder SchnittpunU der Kurve H mit der Kurve F ein Wende-
punU der letzteren. Eine Berührung beider Kurven kann an der
fraglichen Stelle nicht vorkommen. Es ist nämlich die Tangente der Kun-e //
daselbst durch:
{^ey — l'^)x^ + 3eda;2 = 0
gegeben. Soll sie also mit der Kurve F die Tangente gemein haben,
so würde d = 0 sein müssen. Für c = 0, 8 =^ 0 aber würde die
Form F reduzibel werden, was nicht zutreffen sollte. Beide Kurven
haben also neun getrennte Punkte gemein. Hieraus ergibt sich, daß eine
doppelpunJdfreie Kurve dritten Grades neun getrennt liegende Wende-
punJcte hat.
Man wähle jetzt ein neues Koordinatensystem in der Art aus, daß
die Gleichungen x^ :=: 0 und x^ = 0 die Wendetangenten in zwei
beliebigen Wendepunkten der Kurve F liefern, während die Gerade »3 = 0
die Verbindungslinie dieser Wendepunkte darstellt. Die Form F nimmt
dann eine Gestalt an, die sich auf das einzige Glied mit a;| reduziert,
sowohl wenn a;^ = 0 als auch wenn x^ = 0 gesetzt wird. Also gilt
nunmehr:
(4) F = x^x^(ax^~\-hx^~\-cx2) ^ exi,
wo wieder e zf= 0 gilt. Wäre hier etwa a = 0, so würde sich der Punkt
»2 = 0> ^3 = 0 als ein Doppelpunkt der Kurve herausstellen, dessen
Koordinaten dann in der Tat den drei Gleichungen (1) genügen würden.
Da ein solcher Punkt nicht auftreten sollte, so gilt a =j= 0; und ebenso
findet man, daß auch h dz 0 ist. Der Schnittpunkt der Geraden:
(0) ax^-^hx^ ~\-cx^ =z 0
mit der Seite x^ = 0 des Koordinatendreiecks ist also von den beiden
auf dieser Seite gelegenen Ecken dieses Dreiecks verschieden. Aus (4)
folgt, daß auch dieser Punkt ein Wendepunkt ist. Man gelang*t zu dem
Satze: Die VerUnäungsgerade irgend zweier Wendepunkte der Kurve dritten
Grades F schneidet auf dieser Kurve noch einen dritten Wendepunkt aus.
Man bezeichnet eine solche, drei Wendepunkte auf der Kurve F
ausschneidende Gerade als eine „Wendelinie-". Von jedem Wendepunkte
gehen vier solche Wendelinien aus, so daß man im ganzen zwölf
Wendelinien hat. Man kann die zwölf Wendelinien zu vier „ Wendedreiseiten~
Anzahl der Wendepunkte und der Wendel;nien. 335
in der Art subummen ordnen, daß die dt ei Seiten deb einzelnen dieser
Wendedreiseite aUe neun WendepunUe tragen. Man greife näiplich eine
erste Wendeünie L^ beliebig auf. Von einem nicht auf ihr gelegenen
Wendepunkte W^ ziehen d^rei W^endelinien nach den aijf L^ gelegenen
Wendepunkten. Die vierte von ihip. ausziehende Wendelinie sei L^.
Man hat dann neun Wendejinien, die die Punkte von L^ mit denen von
L^ verbinden. Außer L^ und L^ bleibt nur noch eine pinzige Wende-
liaie L^, an der kein auf L und L^ gelegener Wendepunkt beteiligt ist.
Auf X3 liegen also die drei letzten We^depijnkte, so daß m^n in X^, L^, X„
ein erstes Wendedreiseit hat. Pa jede Wendelinie an einem und nur
einem Wendedreiseit teilnimmt, so iiat man in der Tat vier solche
W end ed reiseite.
§ 3. Das singulare Koordinatensystem der Kurye dritten Gra()es.
Der eben angegebenen Gestalt (4) der kubischen Form F liegt ein
Koordinatendreieck zugrunde, dessen Seitp x^ j= 0 eine Wendelinie ist.
Man kann leicht zu einem neue^ Dreieck übergehe^, bei deip. auch die
beiden anderen Seiten Wendelinien sifid. Da a und 6 vop 0 A^^rschieden
sind, haben wir in:
(1) ' lx^ =z B^Xi -]^ sX.2 — iPXi, s = e ^ ==
[ x^ = x'2
eine nicht-singuläre Substitution, für die man:
— (ax^ -}- hx^ ~\- cx^) = a'i -r A — jf^^'z,
— ab.x^x^i^aXj^-j- hx^ + c^3) = j-'x -f- ^2^ — ^^^^3^ + c^i ^2^'.
findet. Die kubische Form (4) § 2 ßchreibt sich also iti den neuen Kq-
ordinaten so:
— ul-F = x'-^ -^ x',^ — {ahe -{- ^c^) xi" -y- ca'ix'^x'..
Der im dritten Gliede rechts auftretende Klammera^sdruck gilt als von 0
verschieden, da die Kurve anderenfalls die Ecke .^^ = 0, a^ = 0 des
Koordinatendreiecks zum Doppelpunkt haben würde. Die weitere
Substitution :
— ^abx'i = x[, — ]'ßhx2 =: x'i, S^ahx's == '^27 ahe-f-c^ x'.
führt unsere kubische Form F bei Fortlassung der oberen Indizes an
den neuen Variablen endlich in die sogenannte „Hei,bebche Notntalgestdlt~:
(2) F = xl ^ it| + it| ~f 6 Ö Xj ^2 '^3
über, in der nur noch ein einziger durch die Gleichung;
(3) _ _^-_ = 26
336 III, 1. Wendepunkte ebener Kurven dritten Grades.
gegebener Parameter 6 auftritt. Mit Klein*) bezeichnen wir das
hiermit erreichte Koordinatensystem x^, x^, x^ als das „singulare^. Das
Koordinatendreieck ist, wie bemerkt, ein Wendedreiseit. Die Seite a^g = 0
ist die bisher schon benutzte Wendelinie, und aus der Symmetrie der
Gleichung (2) in den a;^, x^, x^ geht hervor, daß auch die beiden anderen
Seiten solche Linien sein müssen.
Sieht man projektiv verwandte Kurven als nicht wesentlich
verschieden an, so gibt es zufolge (2) nur einfach unendlich viele wesentlich
verschiedene doppelpunJäfreie Ku/rven dritten Grades, die insgesamt als die
Kurven des Büschels (2) mit dem Parameter 6 darstellbar sind. Diesem
Büschel gehört mit der einzelnen Kurve stets auch deren Hessesche
Kurve an, da sich die Hessesche Form der Form (2) nach Fortnahme
des numerischen Faktors 216 zu:
(4) H = — e^ (x! ~f xl -^ xl) + (2 6^ -f 1) x^ x^ x^
berechnet. Man kann demnach auch von einer partikulären Kurve (2)
aus das ganze Büschel durch die Gleichung:
(5) zF-j-XH = 0
mit dem Parameter oi:X darstellen**). Die neun Grundpunkte des
Büschels sind die allen Kurven des Büschels gemeinsamen neun
Wendepunkte unserer Kurven, deren Koordinaten die folgenden sind:
no, 1, —1), ( 0. £, —8% ( 0, 8^, —8),
(6) (—1, 0, 1), (—8^ 0, 8), (—£, 0, 8^),
[ ( 1,-1, 0), ( 8, — £^ 0), ( 8^ —8, 0).
Die zwölf Wendelinien haben die Gleichungen:
ix-^ = 0, «2 = 0, x^ = 0,
^1+^2+^3 = 0, X^~\- 8X^~\'8^X^= 0, X^-j-8^X^~\- 8X^ = 0,
8X^~\'X^4- X^ = 0, X^ -{- 8X^~\- X^ = 0, X^~\- X^ -{- 8X^ = 0,
8^X-^-+- X^~\-X^ = 0, Xj^4-8^X^-^ X^ =0, a^i ~f X^ 4^8^X^:=:0.
Je drei Wendelinien, deren Gleichungen hier in einer Zeile stehen, liefern
ein Wendedreiseit. Die vier Wendedreiseite sind demnach durch
Nullsetzen der folgenden vier reduzibelen kubischen Formen darstellbar:
(8) A^=x^x^x^, z/v = a;i -j-a;.| ~f a;| — ^8''x^x^x^, »; — 0, l, 2.
Die vier „Kurven"" zt = 0 sind im Kurvenbüschel F = 0 enthalten j),
und zwar als die einzigen reduzibelen Kurven des Büschels, die man auch
dadurch erklären kann, daß sie die einzigen Kurven des Büschels sind,
*) Vgl. die Abhandlung „Über die elliptischen Xormalkurven der »ten
Ordnung'-, Ges. Abhandl. III, 198, § 6.
**) Man hat hier das sogenannte „syzygetische Büschel" von Kurven dritten
Grades vor sich.
t) Die Kurve zf^ — 0 fur den Wert ö := oo des Parameters.
Hessesche Qruppe @2i<i- 337
deren einzelne mit ihrer Hesseschen Kurve identibch id. Für die „Kurve"
z/oo = 0 ist dies einleuchtend. Im übrigen findet man durch Nullsetzen
der drei partiellen Ableitungen der form (2):
(9) x! = —2dx^x^, x\ = — 2 Ö .^3 r^i, xl r= — 2 ö a^i x^-
Sollen diese drei Grleichui^gen bei endlicliem f) und nicht zugleich
verschwindenden 'jHj gelten, sq darf kein x verschwinden. Durch
Multiplikation der drei Gleichungen (9) folgt alsp:
(10) 8 ry^ := - 1, (^ = - 1 £", ^ ^ 0, 1, 2,
womit wir die drei Formep /i^ gewinnen. Soli andererseits dje Hesse sehe
Form H bis auf einen von den x unabhängigen Faktor mit der Form F
identisch sein, so muß die Gleichung:
(:> ^3 _ 1) ^ e ^3 ^ 0
bestehen, was wieder zu cien Wertep (10) von ö hinführt.
§ 4. Kollineationsgruppen bei der ebenem KMrve dritten Grades.
Es ist einleuchtend, daß diejenigen KoUineationen, die die Figur cier
\ier Wendedreiseite in sich überführen. In ih^-er Gesamtheit eine Gruppe
bilden müssen. Man gelangt hierbei zu einer Kollineationsgrujj^e ©^jg
der Ordnung 216, die von C. Jordan als die ,.Hesbebch€ Gruppe'-
bezeichnet wurde'^). Die Hessepche (xriip^e enthalt neben anderen Teilern
vier konjugierte Teiler ®.^^ mtd afs ihren Durchschnitt einen Normal-
teiler @-,g. Die KoUineationen des Kormalteüers ®^g transformieren jedes
Wendedreiseit einzeln in sich T^nd fijhren zugleich jpde Kurve des Büschels
F = 0 in sich selbst über. Die einzelne Gruppe ©^ ist dadurch
erklärbar, daß sie die KoUineaiionerf. der Hesseschen Gruppe enthält, die
eines der vier Wendedreiseite invariant lassen.
Diese Angaben sind mittels dpr sipgulären Koordinaten sehr leicht
zu bestätigen. Soll eine Kollineation das Koordinatendreieck in sich
transformieren und die drei W endedreiseite zJy = 0 bis auf die
Reihenfolge reproduzieren, so kann man sie in die Gestalt setzen:
(1) X[ := a,, 4 '— S^'-^k, % == £^ -fh a, ß = 0, 1, 2,
wo.i, /.", 7 eine der sechs Ar^ordnungen der Indizes 1. 2, 3 isif;. Dies
ergibt in der Tat 54 KolHneationen. Den Xorm3,lteüßr @^g erhält man
für ß = — a (mod 3).
Unter den KoUineationen (1) greifen wir insbesondere die folgende
durch S zu bezeichnende:
(S) x'i = x^, x'2 =■ x^, X3 = i- »3
*) Diese ©oie >m<i i^^e Teilpr warben die einzigen wesentlich neuen temaren
Kollineationsgruppen, die Jordan bei semen Untersuchungen über endliche temäre
Gruppen (vgl S. 182) auffand.
Fncke, \igebra. 11. 22
338 III, 1. Wendepunkte ebener Kurven dritten Grades,
auf und reihen ihr die weitere Kollineation an,
( i^Sx'i = o;, + 0^3 + 5?3,
l i^S x's = 5?j 4- f^ 5?2 -j- £ 5?3,
die unimodular geschrieben ist. Man stellt leicht fest, daß S und T
folgende gerade Permutationen der Wendedreiseite bewirken:
(S) K. ^1. ^2).
(T) (^^, ^o)-(^i.^2)-
Aus S und T wird die gesamte alternierende Permutationsgruppe ©^^ der
vier Wendedreiseite erzeugt. Es folgt: Der Normdlteüer ©^g der Hesseschen
Gruppe liefert als Komplement eine ©^g, die mit der alternierenden Gruppe
vierten Grades und also mit der Tetraedergruppe isomorph ist.
Unmittelbar zur Tetraedergruppe wird man bei Rückgang auf die
Form F geführt. Die Kurven F = 0 unseres Büschels permutieren sieh
gegenüber der Hesseschen Gruppe ©^^g im allgemeinen zu je zwölf; dabei
gehen die zwölf Parameterwerte 6 aus einem unter ihnen durch die zwölf
linearen Substitutionen der Tetraedergruppe ©^^ hervor. Erzeugende
Substitutionen dieser Tetraeder-©j2 sind die beiden:
(S) e' = s6,
(T) 6'= ~^ + \
die, wie man leicht feststellt, den eben mit S und T bezeichneten KoUi-
neationen entsprechen*). Als besondere Fälle sind zu nennen erstlich
die den vier Tetraederecken entsprechenden Parameterwerte:
(2) 6 = ^, -i ~\e, -i£^
die die reduzibelen Kurven dritten Grades, d. h. die Wendedreiseite
liefern. Daran reihen sich die den vier Flächenmitten des Tetraeders
zugehörigen Werte:
(3) ö = 0, 1, £, £^
die den sogenannten „harmonischen Fall- liefern**). In diesen beiden
Fällen haben wir je nur vier bezüglich der Hesseschen Gruppe sich
austauschende Kurven, deren einzelne bei 54 eine ©^^ bildenden KoUinea-
tionen invariant bleibt. Endlich haben wir noch den besonderen Fall
der den Kantenmitten des Tetraeders entsprechenden sechs Werte:
(4) 6=-\±>^. --ipls, =lpls^
*) Man vergleiche auch die Angaben von S. 37 über die Tetraedergruppe.
**) Das zur Kurve dritten Grades gehörende elliptische Gebilde läJßt sich
dann auf eine zweiblattrige Eiemann sehe Fläche mit vier Verzweigungspunkten
von harmonischem Doppelverhaltnis beziehen.
Harmonischer und äquianhaifmonischer Fall. Tetraedergleichung. 339
mit sechs bezüglich der Gruppe ©gie ^^^^ austauschenden Kuryen dritten
Grades. Die einzelne dieser Kurven geht dann in sich über durch 3^
eine ©gg bildende Kolliaeationen; man spricht hier vqm .,äquian}ißrmo-
niscJien Fälle-.
Das Formensystem der Tetraedergruppe upd die Tetraedergleiphung
sind aus den vorstehenden Angaben sofort zu entnehmen. Wir spalten ö
in den Quotienten 6^ : ög zweier homogener Variablerji ß^, B^ und erklären
die erste Grundform g^ der Tetraedergruppe, deren Xullpunkie die vie^"
riächenmitten des Tetraeders sind, durch:
(5) ^3 = V2e,{ei-ei)
Daran reiht sich als zweite Grupdform h die durch:
i der cd.dd,
(6) 432 h = ' ^
dd^dO,' cdl \
zu erklärende Hessesche Form von ^^i sie hat entwickelt die Gestalt:
(7) /^ == - 3 Ö2 (8 6! + Öl)
und Kefert, gleich 0 gesetzt, die vier Tetraederecken. An dritter Stelle
ist die Funktionaldeterminapte g^, von g^ und Ji zu nennen, gegeben durch:
I dg.;, dj^
(8) — 144</3 =
W^' äö~
dh dh '
dJ,' Wo
10 df Ol — 61,
Kantenmitten des Tetraeders.
Die
ihre entwickelte Gestalt ist:
(9) gs = 8e
und ihre Nullpunkte sind die
Formen g^, g^ und h bilden das volleForme^syde^ den Täraederc/ruppe(S)-^^;
sie sind aneinander gebunden durch die jRelation:
(10) }i^=^ gl--27 gl
Ziehen wir die Gleichungen (5), (7) und (9) in die Proportion:
(11) gl: 27 g! : h^ -.= H 6! (6! — dir
:(8ß',-^20d!ßl-ßlf
■■ — Ol (8 6^ ~ Oir
zusammen, so haben wir die Tetraedergleichung gewonnen. . Die in
„Modulfunkt." I, 104 unter (1) in nichi -hoi^ogei^er Gestalt gegebene
Tetraedergleichung geht aus (11) du:rch die Substitution.
(12) Ö, : Ö, =- I: - 2
hervor.
340 III, 1. Wendepunkte ebener Kurven dritten Grades.
Wir notieren noch als besonderen Satz: Eine irreduzihele imd
dopßelpunUfreie Kurve dritten Grades gedaüet, abgesehen von den beiden
besonderen Fällen, die wir als harmonisch und aquianharmonisch bezeichneten,
um ganzen 18 eine ®jg bildende Kollineationen in sich, und zwar hat man
außer der identischen Kollineation acht solche der Periode 3 und neun von
der Periode 2; die letzteren sind harmonische PerspeUivitäten, die die neun
Wendepunkte zu Zentren und die zugehörigen neun harmonischen Polaren
zu Achsen haben*). Die neun Perspektivitäten sind innerhalb der @^y
konjugiert. Man beweise diese Angaben z. B. für den Wendepunkt der
Koordinaten a:;^ =r 0, j.^ =: 1, x^ = — 1, wo die Wendetangente und
die harmonische Polare durch die Gleichungen gegeben sind:
(13) 2 Ö «, — x.^ — »3 ~ 0, iCa — ^3 = 0.
§ 5. Das kanonische Koordinatensystem bei der Kurve dritten Grades.
Das bisher benutzte singulare Koordinatensystem x^, x^, x^ führt zu
einer Gleichung für die Kurve dritten Grades, deren Parameter d als
eine „irrationale Invariante- zu bezeichnen ist. Die zwölf konjugierten
Werte von 0 sind, wie wir fanden, die Lösungen der Tetraedergieichung.
Es soll ]etzt ein zweites Koordinatensystem eingeführt werden, das
Klein**) als „icanonisch^- bezeichnet, und das uns zu einer Kurven-
gleichnng mit rationalen Invarianten hinführen wird. Die neuen
Koordinaten mögen zunächst in vorlaufiger Gestalt y^, y^, y^ heißen. Die
Seite ;2/3 = 0 soll eine Wendetangente sein, die Seite y^ = 0 die
zugehörige harmonische Polare und die Seite y^ = 0 des neuen
Koordinatendreiecks eine noch näher zu bestimmende Gerade durch den
Berührungspunkt der gewählten Wendetangente y^ z= 0. Indem wir den Wendepunkt
der singulären Koordinaten :js^ = 0, x^ = 1, x^ = — 1 bevorzugen,
schreiben wir, den vorstehenden Angaben entsprechend:
(1) j ^2 = '^ 'J ^1 + ^2 -r -^.p
( .^3 = 2 6 ä;^ — x^ — a?3,
wo ri noch zu wählen ist. Ebenso behalten wir uns die Änderung der y
um geeignete konstante Faktoren zur endgültigen Fixierung der
kanonischen Koordinaten vor.
Die Ausdrücke der alten Koordinaten in den neuen sind:
l6x^ = y^ ^^3,
C^) \öx^^{e^7i)y, + dy^~yiy^, 0 =r 2 (6*-^ ??),
' \ö^z = —(ß + n)yi + By,_~riy^,
*) Vom einzelnen Wendepunkte gehen außer der Wendetangente noch drei
Tangenten an die Kurve. Die Berührungspunkte dieser Tangenten liegen auf
einer Geraden, die die „harmonische Polare'- des Wendepunktes heißt.
**) Vgl. die erste Note S. 336.
Einfahrung der kanonischen Koordinaten. 341
wo der Proportionalitätsfaktor 6 den rechts angegebenen Wert hat. Diß
bisherige auf die singulären Koordinaten bezogene Gleichung unserer
Kurve dritten Grades rechniet siph ai;f die y um in die Gestalt:
1 +(120^2- 12^2 rj Jr ^)y,yl + (6 Ö ^^^ - 2 ^^ ^ i)^|.
Es soll nun tj so bestimmt werden, daß rechter Hand der Koeffizient
des zweiten Gliedes verschwindet:
(4) 6Ö^-l8r^~T-3 ==0, ^=A-^^i.
Daraus ergeben sich für die Koeffizienten der Gleichung {S) in ß die
Ausdrücke:
6 0^ '
— _ (8 B^ T 1) (^^' — 1)
" 3Ö^ '
(8 Ö^ ^ 1) (8 ß' -T 20 /)3 — 1)
108 Ö6
und die Gleichung (3) geht nach Fortlassiing eines überflüssigen Faktors
in die Gestalt über:
I 3 (8 6^ -f 1)^ yl y, == 108 ß' y\ - 36 ß^ (Ö^ - 1) y^ y\
^""^ \ ^(8ß'-^20ß^-l)yl.
Wir Spalten jetzt wieder ß in ä,en Quotiepten der beiden homogenen
Größen öj, ß^ und multiplizieren die Gleichp.ng (o) mit ß^; sie kann
dann in die Gestalt gesetzt wej-den:
((8 ß! + Öl) i )/'^y,Y . (- y,) == 4 (3 ß^ y,f
- 12 ö, (ß! - ß!) (3 ß! y,) (- y,f - (8 ßl -^ 20 ßl ö| - Ö|) (- y,f
Wie man sieht, treten in den beiden letzten Gliedern die
Tetraederformen g^ und g^ auf. Indem wir das endgültige kanonische
Koordinatensystem z^, ^2, s^ durph die Festsetzung:
(6) (8 ßl -f 61) i V3 j/, =z,, 3 Öi^ y^ = z^, _ ^^ =. ^^ .
einfuhren, gewinnen wir als Gleichung der Kt^rve dritten Grades, bezogen
auf die kanonischen Koordinaten:
(7) zl ^3 = 4 zl — g,_ ^2 zl — </3 ^1,
wo rechter Hand diejenige Xormalgestalt der binären kubischen Form
gewonnen ist, die dem elliptischen Integral erster Gattung in der
Weierstrass sehen Gestalt entspricht'^).
*) Vgl. „Ellipt. Funkt.'' I, 123 und 153 sowie die unten folgenden Angaben
über die Beziehung zu den elliptischen Funkiionen.
342 III, 1- Wendepunkte ebener Kurven dritten Grades.
Aus (7) ergibt sich leicht die invariante Erklärung der zweiten
Seite des kanonischen Koordinatendreiecks. Die drei Schnittpunkte der
Kurve mit der harmonischen Polare z^ = 0, also die Berührungspunkte
der drei außer der Wendetangente vom bevorzugten Wendepunkte an die
Kurve laufenden Tangenten, sind durch die Nullpunkte der binären
kubischen Form:
(8) 9 (^2. ^3) = 4 4 — g^ z^ 4 — </3 zl
gegeben. Wir bilden nach Vorschrift von I, 130 die lineare Polare
dieser Form:
(9) 1^ ^. + ^ ^B = (12zl - g,zl) l, - (2g,z,,,^^ g,zl) t„.
dz^ 0^3
Tragen wir insbesondere dem Schnittpunkte der harmonischen Polare mit
der Wendetangente entsprechend z. ^ 0 ein, so ist der Nullpunkt der
linearen Polare durch ^2 = 0 gegeben, also auf der zweiten Seite
gelegen. Zusammenfassend können wir folgenden Satz zum Ausdruck
bringen: Bas 'kanonische Koordinatendreieck hat als Seite z^ = 0 eine
Wendetangente und als Seite z^ =■ 0 die zugehörige harmonische Polare,
während die Seite z^ = 0 als lineare Polare der Wendetangente in hezug
auf die drei anderen vom Wendepunkte an die Kurve laufenden Tangenten
bezeichnet werden darf.
Die ternäre kubische Form hat zwei rationale Invarianten, die von
A ronhold aufgestellt wurden und gewöhnlich mit S und T bezeichnet
werden. Die erste ist in den unbestimmt angesetzten Koeffizienten der
Form vom vierten Grade, die zweite vom sechsten Grade. Man findet
die entwickelten Ausdrücke der Invarianten S und T in Salmon-
Fiedlers „Analytischer Geometrie der höheren ebenen Kurven-''^),
S. 232 ff. der ersten Auflage. Trägt man in die daselbst gegebenen
Formeln insbesondere die Koeffizienten der Form (7) ein, so ergibt sich:
(10) -S = -^^„ T = if^3.
Hiermit bestätigt sich die oben gemachte Angabe, daß das kanonische
Koordinatensystem zu 'einer Gleichung der Kurve dritten G-rades mit
^rationalen^ Invarianten als Koeffizienten führt. Es steht dies keineswegs
im Widerspruch mit der Tatsache, daß das kanonische Koordinatendreieck
selbst in neun Arten wählbar ist; denn diese neun Dreiecke sind
konjugiert bezüglich der KoUineationsgruppe @jg der Kurve dritten Grades in
sich, so daß der Übergang von einem, zu einem anderen Dreieck die
Kurvengleichung unverändert läßt. Demgegenüber wurde das oben
benutzte singulare Koordinatendreieck durch jene 18 KoUineationen in sich
transformiert; dem Übergang zu einem anderen singulären
Koordinatendreieck entsprach demnach eine von der identischen Substitution
verschiedene Tetraedersubstitution des Parameters ß.
*) Leipzig 1873.
Beziehung des 'WendepunktprobleHis zur Tetraedergleichupg. 343
§ 6. Berechnung der Wenijeputifkte in kanonischen Koordinaten.
Unter den beiden benutztea noimalep. Gleichungen der Kurve dritten
Grades verdient die auf das kanonisclie Koordinatensystem bezogene
algebraisch insofern den Vorrang, als die Koeffizienten g^ und g^ als
rationale Invarianten der allgemeinen temären kubischen Form erkannt
wurden. Das Problem der Berechnung der Koordinaten der Wendepunkte
im kanonischen System kommt dann im wesentlichen a,uf den Übergang
zum singulären Koordinatensystem hinaus und ist (ienm£(,ch bereits in den
Formeln der letzten Paragraphen gelöst.
Im Sinne der Galoi^ sehen Theorie kann man folgenden Satz
aussprechen: Die Berechnung der kanonischen Koordinaten der neun
Wendepunkte einer ebenm Kurve dritten Qrades ist gleichwertig mit der Lösung
des Formenproblems der Tetraedergiruppe. Dieses Problem fordert die
Berechnung von ö^, 6^ ai^s gegebenen ui^d durch die Relation (10) S. 339
verbundenen Werten der Tetraederf'ormen:
(g, = 12 8,(8!-61),
(1) </3 .= 8 8! + 20 ßf 81 - 81,
{ h = -3d,(88f + ßl).
Führt man die absolute rationale Invariante / entsprechend der
Gleichung :
<2) /: (J_l): 1 =, gl,27 gl '.h^
ein, so kann man die Aufgabe auch so fassen, daß die „Tetraedergle^ehung'-;
(3) /:(/_l):l = 64Ö^(Ö^- 1)2
: (8 8" + 20 8^ — If
: - (8 8' + 1)'
^u lösen id, was bekanntlich das Ausziehen einer Kubikwurzel und zweier
Quadratwurzeln erfordeti*), und außerdem noph die Quadraticurse]:
ö.==±|/^
ausgezogen werden muß.
Hat man 8 und ög berechnet, so ^ind ()^ und die in (4) S. 341
erklärte Größe ti rational beka^int. Man beachte weiter, daJ3 die dritte
Einheitswurzel e eine natürliche Irrationalität der Tetraedergleichxmg
ist. Führen wir nicht-homogene Koordin.aten x, y durch die Fest^etzupg :
<5) z^:z^:z^ = y:x 1
ein, so wird die Kurvengleichung:
(6) f = 4:x^ — g^x — gs.
*) Vgl. „Ikos."', S. 97 oder die Ä.ngaben in. I, 343 ff. über die
Tetraedergruppe.
344 m» 1- Wendepunkte ebener Kurven dritten Grades.
und es liegt einer der Wendepunkte im Unendlichen. Die acht übrigen
Wendepunkte haben zu Paaren gleiche Abszisse x. Wir gewinnen
nämlich durch Rückgang auf die singulären Koordinaten (6) S. 336 der
Wendepunkte aus den Formeln (1) und (6) § 5 als die vier
Wendepunktsabszissen :
(7) a._3ö„ -30,2^—3, -3ö,2^Tj-^' ^^^2ö~f.^
Die beiden jeweils zugehörigen Ordinaten berechnen sich dann aus den
Abszissen einfach durch die Quadratwurzeln:
(8) 2/ = ±V4ä^ —</2» —ö's'
die natürlich nach Lösung der Tetraedergleichung und Berechnung der
Quadratwurzel (4) selbst „rational bekannt" sind.
Statt mit der Tetraedergleichung zu arbeiten, kann man auch an
die biquadratische Gleichung fur die vier endlichen WetideßunUsahszissen (7)
anknüpfen. Die Koeffizienten dieser Gleichung müssen rationale
Invarianten sein. In der Tat findet man durch Berechnung der
symmetrischen Grundfunktionen der vier Ausdrücke (7) auf Grund der
Formeln von § 4 als die fragliche biquadratische Gleichung:
(9) x^^^g,i'-g,x-i^g! = 0.
Nach Lösung dieser Gleichung, die die Tetraedergleichung zur Galois sehen
Resolvente hat, sind dann wieder die Quadratwurzeln (8) zu berechnen*).
§ 7, Beziehung zu den elliptischen Funktionen.
Die doppelpunktfreie ebene Kurve dritten Grades wird bekanntlich
durch elliptische Funktionen uniformisiert. Wir gehen auf diesen
Gegenstand hier nur beiläufig und ohne ausführliche Beweise ein, um die
einfache Darstellung der in den voraufgehenden Entwicklungen aufgetretenen
Gruppen mittels des elliptischen Integrals erster Gattung und seiner
Perioden anzugeben. Die uniformi&ierende Variable für die Koordinaten
der Punkte unserer Kurve dritten Grades ist das zu dieser Kurve
gehörende algebraische Integral erster Gattung. Bei der
funktionentheoretischen Sprechweise tritt an Stelle der Kurve als ihr eindeutiges
Abbild die zweiblätterige Riemannsche Fläche über der Ebene der
„ komplexen-^ Variablen x, die zur algebraischen Funktion :
(1) y — y4:x^ — g^x — g^
gehört. Die Fläche hat vier Verzweigungspunkte, die bei x = 00 und
in den drei endlichen Nullpunkten x = Cj^, e^, e^ des Radikanden in (1)
*) Die Gleichung (9) ist die spezielle Teilungsgleichung der Weierstrass sehen
jO-Funktion fur den dritten Teüungsgrad. Vgl. „Modulfunkt," II, 16 und „EUipt.
Funkt." II, 245.
Unifortnisierung der Kurve d^-itten Grades durch elliptische Funktionen. 345
liegen. Die fragliche unifqrmisierende Variable id dann einfach in G-e-
staJt des Weierstrasssehen JSformalintegraJs erster Gattung:
X
r dx
(2) ..,_
das sich hei Gebrauch der lißnmiibchen Koordinaten einfindet, gegeben, uii4
die Koordinaten x, y sind in u die eindeutigen elliptischen Funfctimien, di'i
Weierstraf>s einführte 'und durch.
(3) X =- fp(u), ij ^ p'iu)
bezeichnete'-^). Die Riemanq.sehe Fläche (Kurve dritten Grades) er&cheint
umkehrbar eindeutig abgebildel auf ein „Periodenparaßelogramm- der
M-Ebene, das wir geradlinig und mit den Ecken u =-- 0, lo^, ajj -t- ßjg, fii^
annehmen, unter Oj, co^ eiji „primitives Periodenpaar" des Integrals (2)
verstanden**). Punkte der w-Ebene a und u', die durch eine Gleichung
mit ganzen Zahlen m^, m^ zusammenhangen, liefern die gleichen Werte
sowohl für X als y und ergeben also den gleichen Punkt der Kurve.
Für die Verwendung der elliptischen Fiinktionen in der Theorie
der Kurven dritten Grades sind nun das Abel sehe Theorem und das
Additionstheorem der elliptisei).en Funktionen grundlegend. Xaeh dem
Abelsehen Theorem (vgl. „Elli|)t. Funkt." I. 214ff.) liegen drei Punkte
der Kurve dritten Grades mit den Integralwerten a^, ii^, u^ stets ur^d
nur dann auf einer Geraden, wenn die Summe (ti^ -f- «, -t- u^) eii^ gan^-
zahliges Multiplum (m^ «^ -j- m^ co^) der Periode ist, oder wenn (bei
Gebrauch einer zahlentheoretischen Sprechweise) die Summe (u^ -^ a^ — ii^)
kongruent 0 modulis Oj, co^ M'
(4) Mj — '«2 -f li^s = 0 (mod Oj, cüi^.
Sollen an einer dem Werte u entsprechenden Stelle der Kurve drei
konsekutive Punkte auf einer Geraden liegen, d. h. soll die Stelle einpn
Wendepunkt liefern, so maß 3 «* = Q (mod Oj, Og) sein Hierauf ergibt
sieh sofort: Die neun Stellen:
Ich. — liio^
(o) M = ^-^ -, /., f^ = 0,1, 2
des FeriodenparaJleJogran/yiis und nur diese liefern Wendejjurtl^e der Kurve.
Wir können demnach die neun Wendepunkte symbolisch du;"ch die neun
Restpaare (A, yi) mod 3 darstellen. Auch die Existenz der Wendelinien
ist unmittelbar einleuchtend. Es liegt nämlich rait zwei verschiedenen
*) Man vergleiche „Ellipt. Punkt." I, 152 und 19^.
=^-) Vgl. „EUipt. Funkt." I, 195.
346 III, 1. Wendepunkte ebener Kurven dritten Grades.
Wendepunkten {k-^, (i^), (X^, (i^) immer derjenige dritte ß^, ^3) auf einer
Geraden, für den:
A3 = — Aj — lä, ^3 = — fij — fia (mod 3) •
gilt.
Infolge des Additionstheorems (vgl. „Ellipt. Funkt." I, 204) gelten
für jeden komplexen Wert c die Gleichungen:
I ^Oiu^c) =Ii,{p{u), p'iu), pic), p'(c)),
( p'iu^c) ^B,{piu), p'{u), p{c), p'ic)),
wo rechts einfach gebaute rationale Funktionen der angegebenen
Argumente stehen. Durch:
I y' = Ii,{x,y, ^Oic), p'ic))
haben wir demnach eine umkehrbar eindeutige rationale Transformation
der Kurve dritten Grades in sich gewonnen, die wir kurz durch die auf
das Integral bezogene Gleichung u' = u -]- c darstellen können. Wir
gewinnen bereits alle diese Transformationen, wenn wir c auf das
Periodenparallelogramm einschränken; zu ihrer Darstellung werden wir also au <
Stelle der eben angegebenen Gleichung die Kongruenz:
(8) u = u ^ e (mod ca^, o,)
benutzen können. Diese Transformationen bilden eine „kontinuierliche
Gruppe- (unendlicher Ordnung). Sie ist auch noch erweiterungsfähig
durch Zusatz der dem Zeichenwechsel von u entsprechenden
Transformation x' = X, y' = — y. In transzendenter Gestalt haben wir
diese erweiterte Gruppe durch:
(9) w' = + w 4- f (mod «1, öo)
darznstellen. Fragt man nun, ob in dieser erweiterten Gruppe auch
„Kollineationen'- auftreten können, so liefert die transzendente Theorie
auch hierauf eine sehr einfache Antwort: Der Substitution (9) entspricht
stets und nur dann eine KolJineation der Kurve dritten Grades in sich,
wenn c der dritte Teil eines Periodenmultipliims ist; wir erhalten also eine
endliche Gruppe @jg von Kollineationen der Kurve dritten Grades in sich,
die sich transzendent durch:
(10) u =±u^ \y -^ (mod«1, öo)
darstellt. Es ist nicht schwer, aus den Formeln des Additionstheorems
die 18 Kollineationen unserer ©^g in kanonischen Koordinaten zu
entwickeln; man findet die Rechnung in ,,Modulfunkt." II, 249 durchgeführt.
Wendepunkte und Dreiteilung der elliptischen Funktionen. 347
Die vier verschiedenen Wendepunktsabszissen x, die wir duroh
Lösung der Gleichung (9) S. 344 finden, stellen sich jetzt mittels der
^-Funktion in den Gestalten:
dar. Es handelt sich um die vier verschiedenen endlichen „I'eüwerte dßr
p -Funktion-:
(12) ,= ^^(^'^+ü^)
vom dritten Teilungsgrade. Die Gleichung (9) S. 344 heißt entsprechend
die ^spezielle Teilungsgleichung'■ der ^-Funktion des dritten
Teilungsgrades. Die Teilwerte (11) sind „elliptische Modulformen- dritter Stufe,
insofern sie unverändert bleibei^ gegenüber den Substitutionen der
Hauptkongruenzgruppe dritter Stufe in der Modulgrappe *). Diese
Kongruenzgruppe ist ein Xormalteiler des Inde^ 12 in der gesamten ]\Iodul-
gruppe, dessen Komplement (3^^ ^^^ ^^^ Tetraedergrappe isomorph
ist**). Auf diese Weise werden wif zur Tetraedergruppe zurückgeführt,
mit der wir schon oben die G^Ioissche Gruppe der Gleichung (9) S. 344
isomorph fanden.
über die speziellen Teilungsgleichungen der elliptischen Funktionen
und ihre wichtigsten Resolver|.ten, die Modulargleichupgen, die in der
Entwicklung der Algebra seit Gauß' upd Abel^ Untersuchungen eine
höchst wichtige Rolle gespielt haben, sei allgemein auf „Ellipfc. Funkt.'- 11
verwiesen, betreffs der Teilungsgleichungen insbesondere auf S. 211 ff.,
betreffs der Modulargleichungen (dqrt „Transformationsgleichungen-
genannt) auf S. 342 ff.
§ 8. Begriff eifler Tripelgleichung neunten Grades.
Das Problem der Berechnung der neun Wendepunkte einer Kurve
dritten Grades ist in den bisherigen Entwicklungen nur erst in spezieller
Gestalt gelöst. Die Besonderheit liegt darin, daß wir die Kurve dritten
Grades sogleich in kanonischen Koordinaten gegeben annahn).en. Es soll
jetzt untersucht werden, wie sich die Lösnng unseres Problems bei
beliebig gegebener doppelpunktfrejer Kurve dritten Grades gestaltet,
wohei sich herausstellen muß^ welche algebraischen Prozesse über die
Lösung der Tetraedergleichung und die Auszjehung einer Quadratwurzel
hinaus noch durchzuführen sind, um ziir E-enntpis der
Wendepunktskoordinaten zu gelangen. Im Mittelpunkt dieser Betrachtung ^^ird der
Begriff der „Tripelgleichung neunter^ Grades- stehen, der zunächst naher
zu entwickeln ist.
*) Vgl. „ Modulfunkt." U, 7 ff.
'^) Vgl. „Modulfunkt.'- I, 354.
348 HI» 1- Wendepunkte ebener Kurven dritten Grades.
Wir denken die Gleichung der Kurve dritten Grades mittels
rechtwinkliger kartesischer Koordinaten x, y in der Gestalt F(a;, ^z) = 0
gegeben. Die Koeffizienten der Gleichung mögen zunächst nur der einen
Bedingung unterworfen sein, daß die Diskriminante der Gleichung nicht
verschwindet, damit kein Doppelpunkt auftritt. Durch Jlix, y) = 0 sei
die Hesse sehe Kurve der gegebenen Kurve dargestellt. Die Koeffizienten
von H sind in denen von F ganz und homogen vom dritten Grade.
Durch Anordnung nach Potenzen von y mögen wir finden:
F(x, y) = Ä,y' i- A/ - Ay ^^3 = 0.
^^^ ' H{x, y) = B,y' + B,y'^ B,y ^ B, =. 0,
wo Aj; und Bj; ganze Funktionen Jc^^^ Grades von x sind, die in den
Koeffizienten von F homogen vom ersten bzw. dritten Grade sind.
iS'umerische Irrationalitäten treten in den Bj; nicht auf.
Die Elimination von y aus den beiden Gleichungen (1) liefert uns
nach den Sätzfen über Resultanten in I, 113 eine Gleichung, deren linke
Seite als ganze ganzzahlige Funktion der A, B aufgebaut ist, und zwar
homogen vom Grade 3 sowohl in den A als in den B. Dabei ist sie in
den A und B zusammengenommen isobar vom Gewichte 9, so daß sie
in X auf den neunten Grad ansteigt. Schreiben wir demnach das Ergebnis
der Elimination von y in der Gestalt:
(2) f(-i) = G^x' -^G^x^ -rG,= 0
an, so sind die Koeffizienten G ganze ganzzahlige homogene Ausdrücke
zwölften Grades in den Koeffizienten von F. Die neun Lösungen der
Gleichung (2) aber sind die Abszissen der neun Wendepunkte unserer
Kurve dritten Grades. Wir nehmen an, daß diese neun Abszissen endlich
und voneinander verschieden sind, wodurch eine gewisse Beschränkung
in der freien Auswahl der Koeffizienten von F gegeben ist.
Das Fundament der folgenden Überlegung ist nun die Tatsache,
daß die Verbindungsgerade irgend zweier Wendepunkte der Kurve dritten
Grades auf dieser einen bestimmten dritten Wendepunkt ausschneidet,
woraus die Anordnung der neun Wendepunkte auf den zwölf Wendelinien
unmittelbar folgte. Durch beliebige zwei Wendepunkte der einzelnen
Wendelinie ist dabei jedesmal der dritte Wendepunkt dieser Linie
eindeutig bestimmt. Es soll festgestellt werden, welche algebraische
Eigenart der Gleichung (9) dieser Tatsache entspricht.
Ist x^ irgend eine W^endepunktsabszisse, so liefert, da die neun
W^endepunktsabszissen verschieden sind, die Eintragung von x^ in die
Gleichungen (1) zwei kubische Gleichungen für y, die die
Wendepunktsordinate y^ als einzige gemeinsame Lösung haben. Diese Lösung ist
durch einen rationalen Divisionsprozeß berechenbar. Man gelangt dabei
zu einer rationalen Darstellung:
(3) yi~(p (x^
Begriff einer Tripelgleichpno;. 3^9
von y^ durch a^, wobei diß Koeffizienten dieser Funktion g) ip deuen von*
F rational ohne numerische Irrationalitäten aufgebaut sind. Eß seien
nun Xi, und y^, = ^ (xj) die ]voordinate4i irgend eines zweiten
Wendepunktes. Dann ist die zu beiden gehörende Wendelinie durch die Gleichung:
y = y, + ^j^'-{x-x,)
dargestellt, die wir auch ^n die Gestalt setzei^ können.
(4) , = ^(,,)..SP(-!^^«:)(_,,)
Xi Xi
Sind Xi, yi die Koordinaten des dritten von dieser Wendeliiiie
ausgeschnittenen Wendepunktes, so wird die Eintragung des Ausdrucks (4)
für y in die erste Gleichang (1) eine kubische Gleichung in x mit den
drei Wurzeln x^, Xi, ii liefern. Entferrien wir also durch Division den
quadratischen Faktor {x — a^{x — Xi) au& dei linken Seite dieser
Gleichung, so verbleibt eine lineare Gleichung für j.i. Aup dteser
Gleichung berechnen wir fur Xi einen rationalen Auüdnu Jr.
(5) Xi = B{x^, xj.)
in x^, Xi mit Koefflstetden, die am denen von F ruttonqJ ohne numeiiüche
Irrationalitäten aufgebaut dnd; dahei bedeht diene Gleichung (5) hßi irgend
zwei verschiedenen WendepunTdsäbszii>i.en x^,, cij. jedesmal für die dritte von
der zageliorigen WendeUnie gelieferte Wendepunlisabi>dSh,e Xi.
Hieran schließt sich folgende Erklärung Eine algehraiöclie (gleichang
mit einer UnbeJcannten ohße gleiche Wurzeln, deren Koeffizienten eifern
vorgegebenen Körper ^ angehoreff,, soll ah eme ,.Trip3lgleichting~ bezeicJtnet
werden, wenn €ö eme rationale FunMion F^j zweier Vßnahlßn mä Koefft-sienten
aus §, vmi folgender Art gibt: Sind x-i und x^ zwei beliebige voheina/f.der
verschiedene Wurzeln der Gleichung, öo id Xi = F{x^, x^) deti. eine von
x^ und %-j^ verschiedene dritte Wurzel der Gleichung, und zwar boll die
Zusammenord'nung der Wurzeln zu Tripeln dabei eine solche sein, daß aut>
zwei behebigen Wurzeln des einzelnen Tnpeh stets die dritte Wurzel dieses
Tripels durch die Funlttßn B geliefert wird. Die Glejichung (2) ist eine
solche Tripelgleichung neunten Grades. Indem wir also für diesen Qrad
allgemeine Satze über die Auflösung der Tripelgleichungen entwickeln,
ist damit die Auflö&ung der Gleichung (2) zugleich mitbehandelt.
§ 9. Galois sehe Grippe einer Tripelgleichujig neunten Grades.
Es sei jetzt in der Gestalt:
(1) f{x) ^ G,cc' ^ Cj x' -f- C;x' -r -■■-^G, = 0
eine beliebige Tripelgleichung neunten Grades vorgelegt, fur die wir an
den Erklärungen und algebraischen Entwicklungen des § 8 festhalten.
Die Gewinnung der Galois sehen Gruppe dieser Gleichung beruht auf
einer sachgemäßen Bezeichnung ihrer neun Wurzeln. Es handelt sich
350 III» 1- Wendepunkte ebener Kurven dritten Grades.
'dabei für die Unterscheidung der Wurzeln einfach um die Heranziehung
der neun mod 3 inkongruenten Zaiilenpaare X, ^, die in § 7 bei den
Teilwerten der Weierstrasssehen Funktionen p, p' auftraten, und die
wir jetzt als Doppelindizes zur Bezeichnung der Wurzeln x =z axu. der
Gleichung (1) benutzen wollen. Der Erfolg wird zeigen, da£ wir bei
richtiger Verteilung der Doppelindizes auf die Wurzeln, die natürlich
durch die Beziehung zu den elliptischen Funktionen nahegelegt wurde,
zu einer ziemlich, einfachen Darstellung der Galois sehen Gruppe unserer
Tripelgleichung hingeführt werden.
Aus der Definition der Tripelgleichung folgt, daß jede der neun
Wurzeln in vier Tripeln vorkommt, und daß daher im ganzen 4.9:3 = 12
Tripel von Wurzeln auftreten. Wir greifen ein beliebiges unter diesen
zwölf Tripeln auf und bezeichnen seine drei Wurzeln durch a^o, a-^^, a^^^,
das Tripel selbst aber durch das Klammersymbol:
(2) («00, «12» «2l)-
Eine beliebige vierte Wurzel a^^ bestimmt mit den drei Wurzeln des
Tripels (2) drei weitere Tripel mit drei neu hinzukommenden,
voneinander verschiedenen Wurzeln, die wir a^^, a^g, a^^ nennen. Diese
Tripel sind also:
(3) (a^j, «00, «22)' Kl' «12' «10)' Kl' «21' «Ol)-
In der Tat können keine zwei dieser drei neuen W^urzeln gleich sein,
da sonst zufolge der Erklärung der Tripelgleichung die beiden zugehörigen.
Tripel (3) gleich sein müßten. Auch müssen sie von den drei Wurzeln (2)
verschieden sein, da sonst unter (3) das Tripel (2) wieder vorkäme,
während doch a^^ in (2) nicht auftritt.
Es bleiben jetzt nur noch zwei Wurzeln übrig, die wir durch a^^
und «20 in einer noch vorbehaltenen Anordnung zu bezeichnen haben.
Da die Wurzel a^^ bereits mit sechs Wurzeln zu den drei Tripeln (3)
verbunden ist und a^^ noch in einem vierten Tripel vorkommt, so ist
dieses vierte Tripel notwendig:
(4) Kl' «20' «02)-
Es gilt nun, die noch übrigen sieben Tripel festzustellen. Wir
suchen zunächst zum Wurzelpaar k^q, k^q, das bisher noch in keinem
Tripel auftritt, die dritte Wurzel zu bestimmen. Sie darf weder mit «oo
noch mit a^^ in einem' der bisherigen Tripel verbunden sein.
Ausgeschlossen sind also die Wurzeln Uj^^, a^^, a^^, a^^, a^^, so daß nur die
Wurzeln a^^ und qc-^q in Betracht kommen. Dieselben beiden Wurzeln «oi,
a^o bleiben auch nur übrig für das zum Paare «oo, «02 gehörende Tripel.
Xun hatten wir die Verteilung der Bezeichnungen «02, «20 ^^^ ^^^' beiden
zuletzt herangezogenen Wurzeln noch vorbehalten. Wir können demnach
diese beiden Bezeichnungen auch noch austauschen und damit erreichen,
daß zwei weitere Tripel gegeben sind durch:
(O) Ko' «90' «10)' Ko' «02' «Ol)-
Zwölf Wurzeltripel bei einer Tnpelgleichung neupten Grade^. 351
Von den Tripeln, die a^Q enthaltßii, s|.nd bereits zwei bekannt und
unter (3) und (5) gegeben. Die beiden noch zu bestiinmenden Tripel
mit «10 müssen die Wurzeln a^i, a^a, a^i, «22 enthalten. Die Paare a^^,
«21 und «oj, «02 führen aber zu ßcho^ gewonnenen Tripeln, so daß die
beiden noch fehlenden Tripel mit a^^ die folgenden sind:
(6) <.aio> «Ol' «22)' («10' «si' «02)-
Für a^i fehlt noch ein einziges Tripel. D9, diese Wurzel schon mit a^,
«21' So' «02' «10' «22 verbupden vorkommt, so ist das fehlende Tripel:
C^) («OJ' «12' «2o)-
EndKch stellt man durch Fortsetzung der Betrachtung die beiden folgenden
noch fehlenden Tripel fest:
(8) («02' «12' «22)' («20' «21' «22)-
Damit ist der wichtige Satz gewonnen: ßel der geivahlten Bezeichnung
der Wurzeln ci^u gehören zu einem Tripel älle^aJ drei Wurzeln ocx^^u^,
a^a, tt,, «;.3, «3 zusammen, für deren Indizes ßie Kongruenzen gelten:
(9) ^1+^2 + ^3 = 0, ^it,+ ^2 + ^3 = 0 (mod 3).
Das bei den Teilwerten der elliptischen Funktionen geltende Gesetz gilt
also allgemein für die Tripelgleichungen neunten Grades.
Für die Permutationen der neun Wuraeln unserer Tripelgleichufig (1)
führen wir jetzt eine Darstellung durch Kongruenzen mod 3 der Indizes X, ^
ein, die sich an die Entwicklungen in I, 44q anschließt ui^d aus den
damaligen Ansätzen auf induktiven^ Wege abgeleitet werden könnte.
Doch können wir auch bei den einfachen hier vorliegenden Verhältnissen
eine direkte Überlegung einschlagen. Wir schreiben:
(10) X' = g{l, ^), (i: = h{l, fi) (mod 3),
wo g und h zwei ganze ganzzahlige Fmiktionen yon A, (i sind, die in
keinem dieser beiden Argumente den zweiten Grad übersteigen*). Durch
diese Kongruenzen ist dei' einzelnen Wurzel azu die Wurzßl U/j u'
angeordnet. Es gilt der Satz: Man Jcann die ganzzahligen ICoeffizienteft,
in g und h so bestimmen, daß durch (10) eiße leliebig vor geschriebene
Permutation S = (axui o^-yj u<) ^er neun Wurzeln zur Darstellung kommf.
Man schreibe nämlich die beiden Kongruenzen (10) ausführlich:
! '^'^ ("00 + '^0lif* + «02;t*^)-(«10^«ll.'*^«12|i')^-(«20-«2l/+^«22i^^)'^''
1 fi' = (^00 -^ ^01 if* + ^02 f*^) ^ (^10 ' ^11 i^ + ^12 f*^) ^^ i\o "- ^21." ' ^22 ^"^) ^^
und betrachte sie einzeln. Die ganzen Zahlen a^j. der eisten Kongruenz
sind so zu bestimmen, daß den neun Restpaaren X, a vorgeschriebene
Zahlen X' entsprechen. Daraus ergeben si(;h für die neun zu bestimmenden
*) Zufolge des Fermat sehen Lehrsatzes wurden Funktionen, die m / und /t
den zweiten Grad übersteigen) nic^t mehr leisten als die Funktionen des Textes.
352 III, 1. Wendepunkte ebener Kurven dritten Grades.
Zahlen a^j^ neun lineare Kongru.enzen. Die Determinante dieser neun
Kongruenzen berechnet sich aber leicht als mod 3 mit — 1 kongruent.
Es gibt also (natürlich mod 3 genommen) ein unserer Forderung
genügendes Zahlensystem a^j^. Entsprechendes gilt von der zweiten
Kongruenz (11), womit unser Satz bewiesen ist.
Die Galois sehe Gruppe unserer Gleichung (1) besteht nun aus der
Gesamtheit derjenigen Permutationen ihrer neun Wurzeln, die jede
zwischen diesen Wurzeln bestehende Relation wieder in eine für sie
gültige Beziehung überführen. Die Begriffserklärung der Tr'pelgleichung
lehrt, daJ3 für jedes Wurzeltripel die Relation (5) S. 349 besteht, wo die
Koeffizienten der rationalen Funktion B dem zugrunde liegenden Körper Ä
angehören. Wesentlich neue Beziehungen aber bestehen zwischen den
Wurzeln nicht. Die hier in Frage kommenden Relationen sind also:
gebildet für alle Systeme von drei Wurzeln, die die Kongruenzen:
(13) Aj -^ A, + Äs = 0, 11^-^11^ + 11^=0 (mod 3)
befriedigen. Wir haben demnach alle Kongruenzen (11) heranzuziehen,
die die zwölf Wurzeltripel untereinander permutieren, also aus drei den
Kongruenzen (13) genügenden Restpaaren X^, ^i^; /I2. ;u,,; X^, ^i^ stets
\^Heder drei Eestpaare X\, ^[^ Ag, /u.^; A3, ^^ mit:
(14) ;i; 4- ;i; 4-;;, = 0, ;[*; + ^; -j- ^[i^ = 0 (mod 3)
herstellen.
Man setze nun erstlich in Übereinstimmung mit (13):
Aj = 0, Ap = 1, A3 = 2, yi^ = yi^ = ^«3 = yi (mod 3),
und findet aus (11) für die Bedingungen (14):
«20 + «21 if* + «22 i^^ = 0> ^0 + hii^ + &22 i^^ = 0 (mod 3).
Da diese Kongruenzen für alle drei Reste ^ gelten müssen, so sind die
sechs Zahlen a^^, a^^, a^^, 6,^, \^, &,, mit 0 mod 3 kongruent. Indem
man. zweitens wieder in Übereinstimmung mit (13) die besondere Auswahl:
/Ij = ^2 = A3 = A, ;u,^ = 0, ^2=1) 1^3 = '^ (mod 3)
trifft, zeigt sich entsprechend, daJ3 auch noch a^g, a^^, \^, h^^ = 0
(mod 3) sind. Es sind demnach höchstens die Kongruenzen:
A' = «00 + «Ol ^ -^ «10 ^ + «11 ^ i^ ] , . ^,
> (mod 3)
^ = ^0 - Vit^ + ^o^ + ^i^i^ I
brauchbar. Wir setzen drittens entsprechend (13):
k^ = H^ = 0, l^ = (i^ = 1, A3 = 1LI3 = 2 (mod 3)
und finden für die Kongruenzen (14):
2rt,, = 0, 2\^ = 0 (mod 3),
Gruppe der Tripelgleicjimig aeunten Grades. 353
SO da£ auch a^^ und h^^ piit 0 kongruent sind. Unter Wechsel der
Bezeichnungsweise der Koeffizienten haben wir fQr unßere Galoissche
Gruppe der Tripelgleichung (1) den allgemeinen Ansatz (11) apf die
•besondere Gestalt zu beschränken:
<lo) , M (mod 3).
Soll nun durch diese Substitution der Indizes 1, ^ eine Permi).tation
der Wurzeln axfi wieder in allen neun Wurzelig dargestellt werden, so ist,
wie man leicht feststellt, hierfür hinreichend und notwendig, d^j3 die
Determinante {ad — ßy) der Substitution (15) nicht du|-ch 3 teilbar ist,
daß also eine der Kongruenzen gilt:
(16) ad-^y= + l (mpdS).
Man beachte femer, daß dfei Zahlenpaare Aj, Uj; }.^, ii^; A3, ^3, die d:(.e
Kongruenzen (13) erfüllen, durch ciie Substitution (15) in drei Paai'e
J,j, ;u,j; X'.-^, 11^; A3, ;u,3 übergeführt werden, die dann auch stets die
Kongruenzen (14) befriedigen. Die Galoibsche G-riippe der Tripelgleicimng
neunten Grades (1) .besteht aus allen Permutationen ihreir nenn WurMß,
die von den linearen Substitutionen (15) geliefert werden; dabei sind die
f^i ß, 7) dj Aq, ^q ganze Zahlen, von denen die erden vier eine der beiden
Kongruenzen (16) erfüllen.
Die Gesamtheit der mod 3 inkongruenten Substitutionen (15) stellt
offenbar eine Gruppe dar, die wjr als die binare nicht-liomßgene Konyrueng-
gruppe dritter Stufe bezeicimen wollen*). Mit ihr ist unsere Galois sehe
Gruppe isomorph; denn es ist leicht zu sehen, daJ3 zwei nicht-kongruente
Substitutionen (15) stets auch zwei verschiedene Permutationen der neun
Wurzeln der Tripelgleichung ergeben. In dieser Gestalt als
Kongruenzgruppe wird sich unsere Gruppe der päheren Untersuchung sehr
zugänglich erweisen.
§10. Ordnung und Struktur der Galois sehen Gruppe
einer Tripelgleichung neunten Grades^
Die Ordnung der soeben erklärten Kongruenzgruppe dritter Sti^fe
ist gleich der Anzahl inkongruenter Substitutionen (15) §9 Um diese
Ordnung zu bestimmen, beachte man, daß zum einzelnen Zahlquadrupel u,
ß, y, 8, das eine der Kongruenzen (16) befriedigt, immer neun Substitutionen
gehören, da A,,, fio unabhängig yoneinander und von den a, ß, y, d
Kestsysteme modulo 3 zu durchlaufen haben. Von den 81 inkongruenten
Zahlquadrupeln a, ß, y, & befriedigen, ^ie man ieicht abzählt, 33 die
Kongruenz ad — ßy = 0. Die übrigen 48 Quadrupel befriedigen also
die Kongruenzen (16) §9, und z^ar gilt für 24 Quadrupel das obere
*) Der Begriff „Kongruenzgruppe'- ist also hier m anderem Sinne gebraucht,
wie bei den Teilern der Modulgruppe.
Fricke, Algebra. II. 23
354 ni? 1- Wendepunkte ebener Kurven dritten Grades.
und für die übrigen 24 das untere Vorzeichen: Unsere Kongruenzgruppe
imd damit die Galois sehe Gruppe der Tripelgleicliung (1) § 9 ist ein ©^g^
der Ordnung 432.
Die Dekomposition dieser ^^33 in eine Kette größter Normalteiler
ist sehr leicht zu leisten. Die zu (15) § 9 inverse Substitution ist:
j 2:^' ^ S^ — ßi^ — (SK — ß."0)'
[ + u' = — 7 A ~f a i[i ~f (y Ao — a^o)-
Man stellt daraus leicht fest, daß die neun Substitutionen:
(2) A' = A ~f Iq, ;[i' = fi ~f fig
einen J^ytimutativen Normalteiler @g bilden. Auf der anderen Seite bilden
die 48 Substitutionen:
(3) l' ^ aX-^r ßii, ii' ^yk-^öyi, dc8 — ßy ^±1
einen nicM-normalen Teiler ®^g, der als die homogene Kongruenzgruppe
dritter Stufe Ö)^g zu bezeichnen ist. Dieser Teiler @^g kann unmittelbar
als Komplement des Normalteilers ©g benutzt werden. Wenn man demnach
die @^8 dekomponiert und zu jedem zu gewinnenden größten Normalteiler
die @g der Substitutionen (2) hinzufügt, gewinnt man die Reihe der
Zusammensetzung (vgl. I, 280) für die Gesamtgruppe Ö^g^ wenigstens
bis zum Kormalteiler ^g.
In der homogenen Kongruenzgruppe ©^g ist nun zunächst ein
Kormalteüer ©^4 ^^^ Index 2, bestehend aus den Substitutionen :
(4) X'^aX-^ßii, ii: = yX + 8^, ad — ßy^l,
enthalten, der als die unimodulare homogene Kongrmnzgruppe dritter Stufe
zu bezeichnen ist. Auf diesen Teiler ©^4 ziebt sich die homogene
Modulgruppe (vgl. S. 78) bei Reduktion modulo 3 zusammen. In der ©g^
hat man den (nicht größten) Kormalteiler ®^, bestehend aus den beiden
Substitutionen:
(0) ^' = i ^, ^' = ± i"-
Das Komplement ist diejenige ©^g, auf die sich die nicht-homogene
Modulgruppe bei Reduktion mod 3 zusammenzieht. An dieser ©^^ ^^^^
stellt man ohne Mühe den Tetraedertypus fest, so daß man sich weiterhin
auf die Dekomposition der Tetraedergruppe ©^^ ^u stützen hat.
Hiemach ist die Reihe der Zusammensetzung unserer Gruppe ©^33
leicht angebbar. Man hat zunächst einen Kormalteüer ©„^g des Index 2,
der aus allen Substitutionen mit ad — ßy ^ 1 besteht. Entsprechend
dem Übergang von der Tetraedergruppe zum Kormalteiler ©^ vom
Vierertypus haben wir sodann einen Kormalteiler ©^g des Index 3 in der
Gruppe ©216; bestehend aus allen Substitutionen (15) §9, deren
Zahlquadrupel einer der acht Kongruenzen:
(«) (;,i)-±(ö;?). ±{Vo)' ±{tl)' ±{tl)
Zerlegung der Gruppe der Tripelgleichung neunten Grades. 355
genügen*). In der Vierergruppe hat man jetzt die Auswakl zwischen
drei Normalteüern ®^. Wir wählen in der ®^^ etwa den ]S[orm^lteiler ©gg.
dessen Substitutionen die beiden ersten Kongruenzen (6) befriedigen,
und weiter in dieser ©gg den Xormalteile;- ©^g aller Substitutionen, die
der ersten Kongruenz (6) genügßn. Hieran reiht sich weiter der schon
genannte kommutative Xorpialteiler @g aDer Siabstitutionen (2), bei dem
man dann endlich die Auswahl zwischen vjer zyklischen Normalteilern ©3
des Index 3 hat. Hiemach ist die Beße d^r Zusawimensetzung def
Galois sehen Gruppe ©^3^ ßiner Tripelgleichung neunten Grqdes durch:
(7) ®,^„ ®,,„ ©,„ ©3,, (k\„ ©„ ©3, @,
und also die Indexreihe durch 2, 3^ 2, 2, 2, 3, 3 gegeben, so daß jedß
Tripelgleichung neunten Grades eine mdazyJJische Gleichung (vgl 1,410) ibi.
Lassen wir die Wurzeln ocia der T4pelgleichujig dßn in (5) S. 345
gegebenen transzendenten Arguqienten:
der Wendepunkt der Kurve dritten Grades entsprechen, so liefert die
Kollineationsgruppe ©^g der Kurve ip sich den Normalteiler ©^g |n der
Reihe (7). Der Zusatz der unimodularen homogenen I^^ongruenzgruppe
dritter Stufe (Tetraedergruppe) prgibt in der Eeihe (7) die ®^^^, die sich
also mit der Hesseschen Gruppe ©g als isomprph erweist.
Beim Festhalten einer Wurzel der Tripelgleichung, z. B- der Wurzel a^Q,
gewinnt man einen nicht-normalen intransitiven Teiler ©^g der Galois sehen
Gruppe ©^32 der Tripelgleichung, der sich mit der homogenen Kongruenz-
gruppe aller Substitutionen (3) als isomorph erweist. Diese Gruppe ißt
insbesondere bei der Kurve dritten Grades sehr bekannt: Wir gelangen
swr Galois sehen Gruppe ©^^ der speziellen 'J'eölungsgleichung für den d^ittep
Teilungsgrad, die sich nach ÄdjunUion der Kubikwurzel c|!er Hinheii,, d. Jp.
der quadratiscJien Irrationalität \— 3, auf deren ,.Monodromiegruppe-' ©^^
reduziert. Diese ©3^ ist dann mit der homogenen mmiftodulßren Kongruena-
gruppe dritter Stufe isomorph ===*).
§11. Notizen über reelle Tripelgleichungen.
Wir schließen noch pia paar Bemerkungen über den besonderen
Fall an, da£ der zugrunde liegende Za,hlkörper und damit auch die
Koeffizienten der Tripelgleichung reell sind. Auch die Gleichung:
(1) ^h, ,"3 = ^ i^i-i, ^1 • "^2, ''2)
*) Gemeint sind natürlich die Kongruenzen'•
a S 1, ^ S 0, ^;/ s 0, ^ S 1,
a ^ _ 1, ^ =. 0, |;/ = 0, ^ = — 1,
**) Man vgl. das Nähere in „Bllipt. Funkt." II, 244 ff.
356 HI, 1. Wendepunkte ebener Kurven dritten Grades.
zwischen den drei Wurzeln eines Tripels hat dann reelle Koeffizienten.
Da die Wurzeln des Tripels hier in beliebiger Reihenfolge eingesetzt
werden können, so folgt als erster Satz: Sind in einem Tripel zwei
Wurzeln reell oder Jconjugiert komplex, so ist die dritte Wurzel reell.
Sind nun nicht alle neun W^urzeln der Tripelgleichung reell, so
treten mindestens zwei konjugiert komplexe Wurzeln auf. Sie liefern
ein Tripel, dessen dritte Wurzel reell ist. Die einzelne der beiden
komplexen Wurzeln kommt aber" noch in drei weiteren Tripeln vor,
und in diesen Tripeln finden sich nach dem eben aufgestellten Satze
mindestens noch drei weitere komplexe Lösungen. Da aber die Anzahl
dey komplexen Wurzeln gerade ist, so treteii jetzt deren mindestens
.sechs auf. Wir gelangen zu dem Satze: JEine reelle Tripelgleichung
neunten Grades hat entweder nur eine oder nur drei oder lauter reelle
Lösungen.
Liegen eine reelle Lösung und vier Paare konjugiert komplexer
Lösungen vor, so bilden diese vier Paare je vereint mit der reellen
Wurzel die vier Tripel, an denen die reelle Wurzel beteiligt ist. Von
besonderem Interesse ist der Fall von drei reellen und drei Paaren
konjugiert komplexer Wurzeln, weil dieser Fall bei der Gleichung für
die Wendepunkte einer reellen doppelptmktfreien Kurve dritten Grades
vorliegt. Wir wollen hier die drei reellen Wurzeln, die ja zusammen
eines der zwölf Tripel bilden, mit a^^Q, a^^, a^^ bezeichnen. Aus den
sechs komplexen Wurzeln bilde man dann zunächst die beiden Tripel:
(2) (a^j, «,2> «2o)' Ko' «21' ^^02)-
Li keinem dieser beiden Tripel können zwei konjugierte Wurzeln
vorkommen, da sonst die dritte Wurzel reell wäre. Es sind also die drei
Wurzeln des ersten Tripels (2) in irgend e.iner Reihenfolge den drei
Wurzeln des zweiten Tripels konjugiert. Hierbei zeigt sich noch der
Satz: Die drei Paare Jconjagiert Jcomplexer Wurzeln sind den drei reellen
Wurzeln zugeordnet in der Art, daß das einzelne Paar mit der zugeordneten
reellen Wurzel ein Tripel UJdet. Es kommt z. B. die reelle Wurzel «oo
außer im reeEen Tripel (a^o, «n, «22) ^^^^ ^^ ^^^ ^^^^ Tripeln:
(3) (a^o, «12- «ai)» Ko' «Ol' «02)' («00' «jc «20)
vor. Man nehme nun dem Satze entgegen an, da£ mindestens zwei unter
den drei Paaren:
(4)
«12' «21' «Ol' «02' «10' «20
Paare konjugiert komplexer W^urzeln darstellen würden, dann würden
für das dritte Paar auch nur zwei konjugiert komplexe Wurzeln
übrigbleiben. Man bilde nun das Tripel (a^j, «^2' «20) ^^^^ erwäge, daß mit den
drei Zahlen a^^, w^^, a^^ auch ihre konjugiert komplexen Zahlen a^^, a^^, «jo
die mit reellen Koeffizienten ausgestattete Gleichung (1) befriedigen.
Sätze über reelle TripelgleichungeQ neunten Grs^des. 357
mithin ein Tripel bilden. Dies ist aber nicht def Fall, da die Beding^ng (9)
S. 351 eines Tripels nicht erfüllt sein wiirde. Also fin4et siph ui^ter (4)
höchstens ein Paar konjugiert komplexer Wurzejn. Indem m^ eine
entsprechende Überlegung für die beiden anderen reellen Wurzeln a^^, a^^
durchführt, gelangt man Ißicht zum Beweise d^es Satzes.
Zweites Kapitel.
Doppeltangenten ebener Kurven vierten Grades.
§ 1. Anzahl der Doppelt^ngenten einer ebenen Kurve vierten Grades.
Die bei der Klein sehen Gruppe auftretende ebei^e Kurve vierten
Grades hatte 28 Doppeltangenten m^it 5Q getrennt liegenden
Berührungspunkten, die wir auf der Kurve in zwei Arten durch je sieben
Kegelschnitte ausschneiden konnten. Allgemein ist die Theorie der
Doppeltangenten ebener Kurven vierten Grades in algebraischer Hinsioht
beziehungsreich und interessant. Diese Theorie soll hier als letztes
Beispiel gruppentheoretische^ Anwendungen im Gebiete der analytischen
Geometrie behandelt werden.
Wir setzen eine irreduzible und doppelpunktfreie ebene Kurve
vierten Grades in homogeuen Koordinaten x^, x^, x^ di^rch:
(1) F(sp^, x^, x^) = 0
als gegeben voraus und schreiben die linl^e Seite der Gleichung ku^z F{x).
Ein einzelner Punkt der Kurve habe die Koordinaten x^, x^, x^. Die
Kurventangente in diesem Punkte ist in variablen Koordinaten |^, 1^, Ig
durch:
(2) ^^Ki^)+^2K(^)^t^Ki^) =0
dargestellt, wo Fl die partielle Ableitimg von. J" in bezug auf Xk ist.
Man wähle den Punkt (|^, ^^, I3) auf der T^agente beliebig, jedoch vom
Berührungspunkte verschieden; darpi durchläpft der Punkt:
(3) K + ^ii- ^2-^n„ ^3-^3)'
unter t einen variablen Parameter verstanden, die fragliche Tangente.
Um alle Schnittpunkte der Tangente (2) mit der Kurve vierten
Grades zu berechnen, haben wif die Koordinaten (3) in die Kurvengleichung
eiazutragen und die in t auf den vierten Grad ansteigende Gleichung:
(4) Fix, +t^,,x,-^t^„x,^t^,) = 0
nach t zu lösen. Entwickelt man die Ipike 3eite der Gleichung (4) auf
Grund von (8) in I, 41 nach P(^laren uAd damit zugleich nach Potenzen
von t, so fallen wegen (1) und (2) das Absolutglied und das GKed mit t
358 III, 2. Doppeltangenten ebener Kurven vierten Grades.
aus, entsprechend dem Umstände, daß zwei von den vier Wurzeln t
gleich 0 sind. Die dritte und vierte Wurzel genügen der quadratischen
Gleichung:
(5) P2(^II) + -Pb(^'1I)* + -P.(^II)^' == 0.
wo P,, (a;j|) oder ausführlich P^ix^, Oi,^, »slli, I2' I3) ^^^ '^*^ Polare
von F(x) in bezug auf den Punkt (|j, 1^, I3) ist. Benutzt man die
Beziehung (9) in I, 42, so schreiben sich diese Polaren ausführlich so am
einfachsten:
2-P2 = K(t)4±Ka)xi^----^2F';,{i)x,x,^),
Pg = F[ (I) x^^-^ F', (I) X, 4- K (I) »3.
Damit in der betrachteten Tangente eine Doppeltangente der Kurve
vierten Grades vorliegt, ist hinreichend und notwendig, daß die Gleichung
zweiten Grades (5) zusammenfallende Wurzeln hat, oder daß die Dis-
kri min ante J {x^, x^, %lli, Ig, I3) dieser Gleichung verschwindet:
(6) z/(^ II) = Pf ~ 4P2P, = 0.
Diese Gleichung ist in den x vom zweiten und in den | vom sechsten
Grade. Sie ist, falls der PunM (x-^^, x^, x^) auf der Kurve liegt [Gleichung(1)]
und falls der PunM (|j, Ig, I3) ein vom Berührungspunkte verbcMedener
PunM der Kurventangente im PmiMe (x-^, x^, x^) ist [CReichung (2)], die
notwendige und hinreichende Bedingung dafür, daß der PunM {x^, x^, x^
der BerilhrungspunM einer Doppeltangente der Kurve vierten Grades ist.
Die Gleichung (6) ist in eine Bedingung für den Berührungspunkt
(Xj^, x^, x^) eiaer Doppeltangente umzuwandeln, die frei ist von den |i, Ig, l^-
Wir befriedigen zunächst die Gleichung (2) für die |j, 1^, 1^ in
allgemeinster Art mittels dreier unbestimmter Größen 6^, h^, h^, indem wir:
[ li = \F;ix)-\F;^(x),
(7) l,::=\F[(x)-h,F;,(x),
[% = \F'^{x)-\F[{x)
setzen. Der geometrische Sinn dieser Lösung der Gleichung (2), die
nach Eintragung der Ausdrücke (7) für die | in den x identisch erfüllt
ist, ist offenbar der, daß wir auf der Tangente (2) den Punkt (|j. Ig, I3)
auswählen, in dem sie von der Geraden:
geschnitten wird. Die hier Hnks stehende Hneare Form, in den x
statt in den | geschrieben, möge kurz durch B {x) bezeichnet werden:
B {X) = fej «^ -p Ög ^ + &3 »3-
*) Mit F'^j^ ist die zweite partielle Ableitung von F nach x^ und ir^ gemeint.
Berechnung der Anzaiü deif Doppeltangenten. 359
Die Auswahl der linearen Form B (x) unterliegt nur der einen
Beschränkung, daß sie für die Koordinaten x^, x^, x^ des Berührungspunktes
unserer Tangente nicht verschwinden darf:
(8) BW^=0,
da anderenfalls entgegen unsei^er Annahme der Punkt (| t ^) der
Tangente der Berührungspunkt wäre.
Trägt man die Ausdrücke (7) der | in unsere Bedingung (6) für
den Berührungspunkt einer Doppeltangente ein, so nimmt diese Bedingung
die Gestalt an:
J (X^ , X^, X,,\\ F^ {X) — &3 F'^ (ä), ..)=:(}.
Der hier links stehende Ausdruck, de^ in den x vom 20^^^" und in
den unbestimmten Größen h voni sechsten Grade ist, möge kurz
D^-Tj, a?2, ^sl^i, 6,' ^3) o^^er D {x V) genannt werden. Die Bedingung
für den Berührungspunkt {x^, /^^ ^3) ^i^^r Doppeltangßnte lautet dan^T:
(9) Bipo li) = 0,
unter Hinzunahme der Ungleichung (8). Diese Ungleichung ist; wesentlich.
In der Tat läuft nach Auswahl der })^. \, h^ die Kurve 20^^^" Grades (9)
stets durch die vier Schnittpunkte der Gerade^ B (x) = 0 mit der Kurve
vierten Grades hindurch. Ist nämlich (x^, a^, x^) ein solcher
Schnittpunkt, so fallen die Punkte (|j. Ig, I3) und (^^, ^g, x^) zusammen, und
es werden für diese Koordinaten x^, x^, x^ nach (10) in I, 42 alle
Polaren P, gleich F{x), also gleich 0, so daß die Gleichung (6) und
damit die Gleichung (9) erfüllt ist.
Die eben gefundenen unserem Problem fremden Schnittpunkte der
Kurve F = 0 mit der Kurve 20sten Grades D (x h) = 0 sind nun
durch eine algebraische Weiterentwicklung dieser Gleichung (9) m
entfernen. Der Punkt (|j. Ig, |g) kann für unsere Zwecke durch jedßn
anderen vom Berührungspunkte (x^, x^, x^) verschiedenen Pifnkt:
(10) (^^i + /^li. ^•«2 + /^l2- ^-^3 ^ ftls), 14=^
der Tangente ersetzt werden. Wir stellen zunächst fpst, wie sich d[ie
Gleichung (7) bei diesem Ersatz veiphält. Entwickelt man die Gleichung:
F{x-tt(kx + iil)) = F{(l+lt)x-^litl) = (l^XtyF(x-^j^^^^
rechts und links nach Polaren [Gleichung (8) in I, 41], ^0 folgt mit
Rücksicht auf das Versch^;räiden dey nullten und ersten Polare:
fP^{x\lx + ii^)-YfI\(x ^x^- (i^) -^t'p^(x\kx + ^^)
= (1 -^ Xty iiH' P,(x'l) + (1 -^ 2.t)(iU^P^(a ^)^^H'P,(x |).
360 III) 2. Doppeltangenten ebener Kurven vierten Grades.
Ordnet man rechts nach Potenzen von t und setzt die Koeffizienten
gleich hoher Potenzen von t rechts und links einander gleich, so folgt:
P,(x\lx + ii^) = (i'P,(x\^) + 2Xii'P,(x\l), .
was man n^t Rücksicht auf das Verschwinden von P^ und P^ für die
vorliegenden Argumente auch aus den entwickelten Ausdrücken der
Polaren entnehmen kann. Der in (6) gegebene Ausdruck zi gehorcht
demnach für die hier in Betracht kommenden Argumente x, | dem Gesetze:
(11) zl(x\Xx + iil) = ^«z^(a;i|).
Wir bestimmen nun die Parameter k, ^ so, daß der Punkt (10) der
Schnittpunkt der Tangente (2) mit der beliebigen, jedoch nicht durch
den Berührungspunkt dieser Tangente laufenden Geraden:
A (x) = a^x^-{-a^x^-{- a^x^^ 0
wird. Entsprechend den Gleichungen (7) haben wir zu setzen:
;L a;^ + /Lt li = a^F^ (x) — a^F^ (x),
;L ajg + fi I2 = ag F[ (x) — a^ F^ (x),
^ ^3 + f^ I3 = «1 ^2 (^) — «2 ^1 (^)
und ziehen aus (11) die Folgerung:
(12) D(x\a) = ^'D(x\h).
Zur näheren Bestimmung von fi multipliziere man die soeben für die
(2.x -\- III) angegebenen drei Ausdrücke mit a,, a^, a^ und addiere,
woraus man:
(13) kA(x) + ^Ä(l) = 0
folgert. Multiplizieren wir dagegen die drei Gleichungen für die (Xx-\- ^^)
mit 6j, 62, feg und addieren sodann, so folgt wegen i? (|) = 0:
^' ^2. h I
kB (x) =^ a^, a^, ttg
Andererseits folgt aus (7):
F;(x), F'^{x), F^(x)
iF;(x), F^(x), F^(x)
und da die beiden hier rechts stehenden Determinanten entgegengesetzt
gleich sind, so folgert man mit Benutzung von (13):
^Ä(l) = — X fiB (x) == — X Ä (x),
Ä(x) = ^B(x).
Berechnung der Anzahl der Doppeltangenten. 361
Teilt man die Gleichung (12) durch die sechste Potenz der letzten
Gleichung, so folgt:
^ A(xy B{xf '
Der durch die sechste Potenz der linearen Form A (x) gdeiltß Ausdruck
D(x\a) ist für die hier in Frßge kommenden Argumente x von den a,,
Die Gleichung (14) ist unter der Voraussetzung bewiesen, daß der
Punkt (x^, x^, x^) ein beliebiger Pfinkt der gegebenen Kurve yierten
Grades ist. Die durch:
B (xf D(x\a) — A (xf D(x\h) = 0
gegebene Kurve 26sten Grades enthält deipnach die Kurve vierten Grades
als einen Bestandteil, so daß dip in der letzten Gleichung links stphendie
Form die irreduzible Form F{x>) nach I, 43 ff. als Teiler besitzt. Setzen
wir demnach :
(15) B{pcfJ){x a)--A{xfI){x h) = F(x)0(x a, h),
so haben wir in 0 (x\a, h) eine Form 22^*^^^ Grades der x, die sowohl
in den a als den h vom sephste^i Grade ist.
Um die Bauart dieser Form 0 leichter zu übersehen, nehmen wir
an, daß sich die Geraden A (x) == 0 und B (x) = 0 nicht apf der
Kurve F(a;) ==:; 0 schneiden, und wählen diese beiden Geraden <zur X-
und Y-Achse eines vorübergehend zu benutzenden kartesischen I^oordinatep.-
systems. Die Gleichung (15) besteht in den « identisch- Eechnen wir
sie auf die neuen Koordinaten X, Y um, so stehen linkß lauter Glieder,
die entweder durch Y^ oder durch X^ teilbß,r sind. Rechts stpht im
ersten Faktor ein Ausdruck ii^it nicht yerschwindendem Absolutgliede.
Würden, wenn wir im zweiten Faktor alle Glieder^ die nicht mindesteiis
einen der Faktoren X^, Y*^ entlialten, fortlassen, überhaupt noch Gliedpr
übrigbleiben, so würden von den Gliedern niedersten Grades beim
Ausmultiplizieren mit F (wegen des i^icht verschwindenden Absolutgliedes)
im Produkte nicht ausfallende Glieder herrühren, die keinen der
Faktoren X^, Y^ haben. Das aber widerspricht dem identischen Bestehen
der Gleichung. Hiemach ist es i^öglich, die Form 0 in die Gestalt
zu kleiden:
0(x\a,h) = A (xf 0, (x\a,h) — B (xf 0^ (^ \ a, {*),
wo 0j und 02 Formen Ißs^n Grades der x sind.
Aus (15) ergibt sich nun als identische Gleichung:
A(xf {D(x^h)-^F(x) 0, (x■ a, h)) = B {xf (D (x a) + F(x)0^(x'a, h)).
Auf Grund der Sätze in I, 43 ff. findet paan, daß A (xf ein Teiler der
rechts mit B (xf multiplizierten Fopn 20sten Grades ist. Man schreibe:
D(x\a) + F(x) 02 (X a, h) = A {xf W (x , ß, h)
362 III, 2. Doppeltangenten ebener Kurs'en vierten Grades.
und hat in W eiae Form 14*«'» Grades in den x. Wir kleiden diese
Gleichung in die Gestalt:
D (x lO) , , 0« (a; I a, h)
und tragen nunmehr ter die bisherigen unbestimmten Größen a, h spezielle,
etwa rationale Zahlen a^, a^, a^ und /3,, ß^, ß^ ein, für die wir die
beiden linearen Formen insbesondere A (x) und B (x) nennen *). Die
Form 14*^^* Grades Wix' a, ß), die außer von den x nur noch von den
Koeffizienten der Form F (x) abhängt, bezeichnen wir kurz durch X (x):
Aixf " ^^-"^ "^^^ Aixf
Durch Subtraktion der letzten Gleichung von der vorletzten folgt:
A(xy A(xf ^ ^ ^ '\ Ä(xy A(xy /
Schreibt man für die hier links stehende Differenz auf Grund von (15);
D(x a) D(x a) __ 0(x\a, a)
Ä(xy A(xy "" ^ \A{x)A{x)y'
so folgt.
W{x a,h)-Xix)-Fix)[^--^^^ AW~^P(^ÄW/
Durch Multiplikation dieser Gleichung mit der sechsten Potenz des
Produktes der beiden linearen Formen A {x) und A {x) gelangen wir zu
einer identischen Gleichung der Gestalt:
A {xf A {xf {W (a;, a, &) — X (x)) = F (x) ^ (ä),
wo Si(x) eine Form 22«^^^ Grades ist. Xun ist aber i^(ii:) teilerfremd
gegen A (x) und A (x), so daß Sl (x) durch die sechste Potenz des Produktes
dieser linearen Formen teilbar ist. Man findet;
W(x a,h) — X (x) ^ F(x)H (x),
wo H{x) eine Form zehnten Grades ist. Den hieraus sich ergebenden
Ausdruck von ^ (./j a, h) tragen wir in die Gleichung (16) ein und
erhalten bei Gebrauch der Abkürzung;
A (xfH(x) —0^(x\a,h)=a (x)
für die ganze Funktion 14*«^ Grades X{x) die Darstellung;
(!') Xix)- ^^^^ ,
wo Cr(x) eine Form 16*^" Grades ist.
*) Naturlich sind die rationalen Zahlen a. ß so zu wählen, daß sich die
Geraden A (x) = 0 und B (a?) = 0 nicht auf der Kurve vierten Grades schneiden.
Anzahl der Doppeltangenten. 363
Durch die Kurve 20^*^" Grades D (x a) == 0 werden auf der Kur\.e
vierten Grades F (x) = 0 alle Berhhrungspuiikte von Doppeltangenten
ausgeschnitten. Wie wir saher)., wei'den aber auch noch fremde Punkte
ausgeschnitten, nämlich die Schnittpunkte der Kurve vierten Grades mit
der Geraden A {x) = 0, die wir sp gewählt denken können, daß sie
durch keinen Berührungspunkt einer Doppeltangente hiadurchläuft.
Zufolge (17) werden alle Berühruiigspupkte der Doppe^tangenten auch durch
die Kurve 14*^" Grades X {x) =^ 0 atisgeschnitten. Jene fremden
Schnittpunkte aber können jetzt nicht mehr hiazukommpn; denn die Kurve
14ti,n Grades Z (a?) = 0 ist von der Auswahl der Geraden A (x) = 0
unabhängig. Damit ist der folgende Satz bewiesen: Auf der Kurve
vierten Grades F(x) = 0 liegen 56 BerührungsßunMe von DoppeUantjenterp;
die Zahl der BoppeUangenten ißt alßo 28. 3k]an könnte hiergegen m^r
noch einwenden, daß durch unsere Betrachtung die Zahl 28 pur erst a^s
obere Grenze für die Anzahl der Doppeltangenten erwiesen sei; es könpe
ja möglich sein, daß die Kurye F{x) == 0 allerp.al durch mehrfache
Punkte der Kurve 14*^" Grades X {x) = 0 hindurchlaufe. Daß dies nicht
zutrifft, lehrt das Beispiel der Kleinschep Kurve:
(18) xl »g -j- a'l x^ --j- xl x^ == 0,
die in der Tat 28 Doppelt^ngenten besitzt.
§2. Steiner sehe Komplexe von Dpppeltangenten.
Man wähle eine erste Doppeltangepte als Seite i^ = 0 des Ko-
ordiaatendreiecks. Sondert man dann aus allen Gliedern dey biquadratischen
Form jP, die x^ enthalten, diesen Ffiktor x^ ab, sq läßt sich F \n die
Gestalt:
(1) F =z X^(p (X^^, »2, ^3) 1^ (^2' ^3)^
setzen, wo tp eine kubische Form von x-^, x^, x^ jst und 1^ eine quadratische
Form von »,, x^. Für x^ = 0 muß pämlich die biqpadratische Gleichung
F = 0 für das Verhältnis x^: x^ zwei Doppelwurzeln haben. |jassen
wir im letzten GKede auch noch x^ zu, so können wir die Gestalt (1)
der biquadratischen Form in dreifach unendlich vielen Arten erzielen.
Ist nämlich l (x^, x^, x^) eine lineare Form mjt drei beliebig wählbaren
Koeffizienten, so können wir auch:
(2) F=x,((pi-2li; + x^ ;;^) - (i^ -r Ä .,)^
schreiben, wo in der ersten Klamme;- wieder eine kubische Form ^nd in
der zweiten eine quadratische i'orm steht,
Irgend eine zweite Doppeltangente sei durch Kullset:?en der in
den X linearen Form y.^ dargestellt. Wir fordern, daß der Kegelschnitt
tl; ^ Xx-^ = 0 durch die beiden Berührungspunkte dieser zweiten
Doppeltangente hindurchläuft, womit für die drei Koeffizienten von Ä zwei
lineare Bedingungen vorgeschrieben sind. Wir wählen y^ = 0 zur
zweiten Seite des Koordia^tendreieclcs und nennen der Gleichmäßigkeit
364 III, 2. Doppeltangenten ebener Kurven vierten Grades.
halber die dritte Koordinate z. Die erhaltene Gestalt der biquadratischen
Form aber schreiben wir gleich wieder so:
(3) F == x^(p{x^, y^, z) — ip(x^, y^, zf.
Für die Koordinaten der beiden Berührungspunkte der
Doppeltangente y^ = 0 verschwinden ip und F, also zufolge (3) auch (p. Da
in diesen beiden Punkten die Tangente durch y^ :=: 0 gegeben ist, so
verschwinden in beiden Punkten die partiellen Ableitungen von F nach
x^ und z:
dF , dtp ,^dt ^
dx^ ^ ^ ^dx^ ^dx^
—- = x^-~^— 2i;^~ = 0.
dz dz öz
Es folgt also, da an beiden Stellen cp und ip, nicht aber x^*),
verschwinden:
d x^ ' dz
Demnach ist die Gerade «/^ = 0 auch eine Doppeltangente der Kurve
dritten Grades g? = 0, so daß diese Kurve in die fragliche Gerade und
einen Kegelschnitt zerfällt. Entsprechend setzen wir (p = y^^ ^^^
haben für die biquadratische Form nach Auswahl zweier beliebiger
Doppeltangenten x^ = 0, y-^^ == 0 die Darstellung:
(4) F=x^y,x-t',
wo ;^ und tl; quadratische Formen sind.
Diese Gestalt unserer biquadratischen Form ist noch in einfach
unendlich vielen Arten erreichbar. Haben wir ein zweites Mal die Gestalt:
(5) F= x^y^X — W^
erhalten, so folgt als identische Gleichung:
(6) ^j^^y^(x-x)=. (W-t)(^ + '4')-
Man nehme nun an. x^ gehe in dem einen Faktor, y.^ aber im anderen
Faktor der rechten Seite dieser Gleichung auf. Dann verschwinden
im Schnittpunkte der beiden Geraden x^ = 0, y-^ == 0 beide Faktoren
{W +1^) und also auch ihre Differenz 21^, Infolge von (4) liegt
dieser Schnittpunkt auf der Kurve vierten Grades und ist ein Doppelpunkt
dieser Kurve. Da nun die Kurve als doppelpunktfrei vorausgesetzt
wurde, so ist die Annahme unhaltbar, und also ist x^ y^ Teiler nur eines
der beiden Faktoren in (6) rechts. Da wir über das Vorzeichen von W
*) Wurde die Gerade cci = 0 durch eine dieser beiden Stellen
hindurchlaufen, so wurden beide Gerade die Kurve daselbst zweipunktig schneiden. Die
Kurve hätte dann hier einen Doppelpunkt, und die Geraden Xi =^ 0, yi =: 0
wären zwei Tangenten vom Doppelpunkt an die Kurve. Indessen sollte die Kurve
doppelpunktfrei sein.
Doppeltangenten als Koordinatenachsen. 365
noch verfügen können, so dürfen w'ir annehmen, daß x^ y^ i|i (W — ip)
aufgeht. Dann gilt, da (!*' — ■^) voin zweiten Grade ist, die identische
Gleichung:
wo ^ eine Konstante ist. Aus (6) folgt:
und wir haben tatsächlich die einfach u^iendKch vielen Darstellungen:
(7) i,' = a;, ^, (;U -i- 2 ;[i </; + jti^ x^ y^) — (t-j- pL x^ y^f
unserer biquadratischen Fopn.
Es soll nun die Konstante fi derart bpstimmt \ferden, daß die
quadratische Form:
(8) Z + '^^i^^+f^'^ii/i
reduzibel wird und in zwei lineare Formen zerfällt, die alsdann durch
»2 und y^ bezeichnet sein mögen. Füy diesen Zerfall ist d^s Verschwinden
der Diskriminante der quadratischen Form (8) charakteristisch. Schreiben
wir explizite:
f9^ [ '^'^ ^" ^^ ^ "^^ ^' "^ ^^^ ^^ + 2 «1, x^ y^ 4- 2 a^^x^z-\^2 ß^^y^z,
I ^ = &n '4 + &22 yl + \z ^^ + 2 I),2 », 2/i + 2 &ig a;, ^ -^ 2 633 y^ z.
so liefert die Forderung verschw:|.ndender Diskriminp,nte für ^ die
Gleichung fünften Grades:
^ a„ -[- 2 ill bji, fij, -4- 2 u &J2 -f i iti^, «13 -^ 2 ^i 6^3
(10) «21 + 2 ^a bgi -r I ^lt^ «32 + 2 i[i 6,2, «23 +- - ^ ^23 I = 0-
«31 + 2 ^ 631' «32 + 2 ^ 6^2, «33 ~ 2 fi 633
Setzt man eine der fünf Wurzeln ^ dieser Gleichung in die Form (8) ein.
so zerfällt diese in zwei lineare Faktoren, Die den fünf Wurzeln ^
entsprechenden Zerlegungen der Fprm (8) nehmen wir x^y^, x^y^, •■•, x^^y^,
und die zugehörigen quadratischen Formen (i/; -|r ji x^ y^ mögen durch
^2' ^3' ■"' ^6 bezeichnet werden. Wir haben danüt dep folgenden Satz
gewonnen: Nach Auswahl eines 'beliebigen JPaares von I)oppeUarj,gen,ten
^j = 0, y^ =:z=: 0 der Kwrpe vierten Gerades laßt sich die GJeichaßg der
letzteren auf fünf Arten in die Gestalt:
(11) a)^yxXkiji, — i>l=(}, /t = -j, 3, ■••, 6,
Meiden, wo %., y^. fünf Paare II Mar er Formen und ipi. fimf Ihnen
entsprechende quadratische Formen sind.
Es ist aus (11) unmittelbar einle^chtelad, daß wir in x^^ = 0,
yj. =:: 0 Wieder ein Paar von Doppeltangenten der Kurve vierten Grades
dargestellt finden, deren vier Berührungspunkte gleiphfalls auf dem
Kegelschnitt tjj^ = 0 liegen. Man kann demnach ^em gewonnenen
Ergebnis auch folgende Gestalt verleihen: Nach Auswahl eines beliebigen
Paares von Doppeltangenten x^ == 0, 2/1 = 0 9^^^ ^^ f^'>^f zugehörige
3ßg III, 2. Doppeltangenten ebener Kurven vierten Grades.
weitere Paare u^^. = 0, ^jt = 0 pon der Art, daß die acht Berührungs-
punUe des einzelnen der fünf Quadrupel auf der Kurve vierten Grades
durch einen Kegelschnitt i/»^. = 0 ausgeschnitten werden*). Das System
der sechs Doppeltangentenpaare % = 0, ^/^ = 0 heißt nach Weber ein
„Steinerbcher Komplex" von Doppeltangenten**). Die frühere Sprechweise
„Steinersehe Gruppe- ist wegen der anderen Bedeutung des Begriffs
einer „Grappe- ia der Algebra unzweckmäßig.
Durch x^ = 0, y^ = 0 und x^ ■= 0, y^ = 0 seien jetzt irgend
zwei unter den fünf Paaren x^ = 0, yk = ^ ^on Doppeltangenten, die
wir dem Paare a;^ = 0, t/i == 0 zugeordnet fanden, dargestellt. Aus
den beiden Gestalten:
F :== x^y^x^y.2 — il^l, F = x^y^x^y^ ~ tl^l
der biquadratischen Form folgen die identischen Gleichungen:
■^1 l/i ^2 2/2 — tl = '^i y-i 'J^z Vz — ^f'
■^1 Z/i (^2 2/2 — *3 y%> = (^2 — "^s) (^2 + 1/^3)-
Wie oben schließen wir, daß x-^ y^ als Divisor in einem der beiden rechts
stehenden Faktoren enthalten ist, da die Kurve doppelpunktfrei sein
sollte. Wir dürfen demnach, da das Vorzeichen von ^3 noch gewechselt
werden darf, auf die weiteren identischen Gleichungen schließen:
(12) u-f^tl^ — i)^ — %, ^i y^~x^y^ = a (^3 4- i^^,
unter a eine von 0 verschiedene Konstante verstanden. Für die quadratische
Form z^2 ergibt sich hieraus die Gleichung:
2 a ^2 = «2 ^^ y^ J^^^y^_ ^^ y^^
und die biquadratische Form F gestattet die Darstellung:
(13) Aa^F =r 4:a^x^y^x^y^— (a^x^y^ + x^y^ ~ x^y^)\
=*) Die Forderung, daß von den zwölf hier in Frage kommenden
Doppeltangenten irgend zwei identisch ausfallen, hat eine Relation zwischen den
Koeffizienten a^^-, h^j. zur Folge. Man kann demnach zunächst die Koeffizienten
so bestimmt denken, daß in keinem Falle ein solches Identischwerden auftritt.
Aus funktionentheoretischen Erwägungen weiß man, daß die gesamten doppelpunkt-
freien Kurven vierten Grades ein einziges Kontinuum bilden. Der Zusammenfall
zweier Doppeltangenten bedingt aber (vgl. die voraufgehende Fußnote) das
Auftreten zweier Doppelpunkte, Bei den doppelpunktfreien Kurven vierten Grades
wird demnach das im Texte betrachtete System stets aus zwölf getrennten
Doppeltangenten bestehen.
**) Die ersten grandlegenden und weitreichenden Entdeckungen über das
Problem der Doppeltangenten der Kurve vierten Grades machte Steiner im
Jahre 1852; man vgl, dessen Abha,ndlung „Eigenschaften der Kurven vierten
Grades rucksichtlich ihrer Doppeltangenten'-, Joum. f. Math., Bd, 49, S. 265.
Unabhängig von Sterner hat zu der gleichen Zeit auch Hesse seine grundlegende
Arbeit „Über die Doppeltangenten der Kurven vierter Ordnung", Journ. f. Math.,
Bd. 49, S. 279 verfaßt.
Sternerscke Komplexe von Doppeltangentenpaaren. 367
K'un dürfen wir die Knearen Formen x^^, x^, x. noch um konstante
Faktoren ändern, ohne daß ihre Brauchbarkeit Einbuße erleidet. Statt
ihrer führen wir x'i, x'i^ % durcii folgende Gleichungen ein:
ax^^:= x-i, x^ ^= ax^, x^ = ax'^.
Lassen wir dann nach Transformation der Gleichung (13) auf die x die
oberen Indizes sogleich wieder fort, so ergibt sich nach Forthebung des
Faktors a^ aus der Gleichung (13) für das Vierfache unserer biquadratischen
Form F die Darstellung:
4i^= 4.x^y^x^^^ — {x^y^ -^ j^^y^- x^y.^f
oder in entwickelter Gestalt:
(14) l 4:F = 2 x^ y^ x^y^ + 2 x^y^ x^y^ + 2 x^ y^ x^ y^
I — «1 yl — A vi — A yl
Die Symmetrie der rechten Seite in den drei Indizes 1, 2, 3 ist von
grundlegender Bedeutung. Wir erkennen, dß-ß a,lle sechs Paare von
Doppeltangenten % = 0, yy^ == 0 im Steiner sehen Komplex
gleichberechtigt sind: Man wird immer wieder zu dem gleichen Steiner seh ,i,
Komplex geführt, wenn man die vorstehende Entwicklung an irgend eines
der fünf anderen Paare % = 0, «/j. = 0 statt an cp-^^ = 0, y^ = 0
anknüpft. Da sich aus den 28 Doppeltangepten im ganzen 378
Tangentenpaare bilden lassen, so folgt: Es gibt hei einer doppelpanktfreien Kurve
vierten Grades im ganzen 63 Steiner sehe Komplexe; jedes Ta^gentenpaar
gehört einem und nur einem dieser Komplexe an.
§ 3. Tripel und Quadrupel vqn Doppeltangenten,
Die einzelne Doppeltangente, die durch eipe Gleichung X]. = 0 oder
yf, = 0 dargestellt ist, wollen -yvir der Kürze halber durch bloße Angabe
der linken Gleichungsseite % oder y^ charakterisieren. Die sechs Doppel-
tangentenpaare des einzelnen Steiner schei|. Komplexes lassen sich wieder
zu 15 Paaren kombinieren
(1) %, yi] %, yj:, i, Ä z= 1, 2, .-•, 6
Das einzelne dieser 15 Tangenten quadrupel (1) ist dadurch charakterisiert,
daß die acht Berührungspunkte dieser vier Tangenten auf einem
Kegelschnitt gelegen sind und den vollen Schnitt der Kurve vierten Grades
mit diesem Kegelschnitt darstellen. Das gleiche Quadrupel wird auch
noch von zwei anderen Steiner^chen Kon^plexen geliefert, bei denen die
folgenden Paare von Doppeltangenteiapaaren vorliegen:
I «f, %; yi, yk,
l x^, yk, %, yt-
Im 'übrigen ist aus den Rechnungen des § 2 einleuchtend, daß man jedes
Quadrupel von Doppeltangenten, bei dem die acht Berührungspunkte auf
368 ni, 2. Doppeltangenten ebener Kurven vierten Grades.
einem Kegelschnitt liegen, in den Steiner scken Komplexen, und zwar
immer in drei solchen antrifft. Da wir 63 solclie Komplexe haben, so
folgt der Satz: Es gilt im ganzen 315 Quadrupel von Doppeltangenten
der Kurve vierten Grades von der Art, daß durch die acht Berührungs-
punJcte der Tangenten des einzelnen Quadrupels ein Kegelschnitt
hindurchläuft.
Die Tripel von Doppeltangenten betreffend hat Frobenius*) im
Anschluß an eine Untersuchung über Thetacharakteristiken folgende
Bezeichnung eingeführt: Ein Tripel von Doppeltangenten der ebenen Kurve
vierten Grades heißt ^syzygetisch^ oder „a^ygetisch-^, je nachdem die
sechs Berührungspunkte der drei Tangenten des Tripels auf einem
Kegelschnitt liegen oder nicht. Aus den bisherigen Darlegungen folgt ohne
weiteres der Satz: Drei Doppeltangenten, die einem und demselben
Steinersehen Komplex angehören, und zwar in der Art, daß zwei von ihnen ein
Paar dieses Komplexcb bilden, une z. B. die drei Tangenten x^, y^, x^,
bilden stets ein syzygetisches Tripel.
Weiter laßt sich ohne besondere Mühe der folgende Satz zeigen:
Drei Doppeltangenten, die einem und demselben Steiner sehen Komplex an-
gelwren, ohne daß irgend zwei von ihnen ein Paar dieses Komplexes bilden,
wie z. B. die Tangenten x^, x^, x^, liefern stets ein azygetisches Tripel. Zum
Beweise beachte man, daß die diei Geraden x^, x^, Xg nicht durch einen
Punkt laufen, da ein solcher Punkt zufolge (14) S. 367 der Kurve vierten
Grades angehören würde, und zwar als mehrfacher Punkt, was jedoch
ausgeschlossen ist. Wir dürfen demnach die fraglichen drei Tangenten
als Seiten des Koordinatendreiecks benutzen und mögen für die
Linearformen y^, y^, y^ in den x die Darstellungen finden:
[ ^1 = «11 »1 + «12 % 4- «13 ^3'
(3) I y^ = «21 Xj ~f «22 »2 + «23 »3'
[ 2/3 = «31 ^1 + «32 »2 ~1~ «33 ^3-
Aus der Kurvengleichung:
I 2 x^y^ %y^ + 2 x^y^ «,y^ ~f 2 x^y^ x^y^
\ — zt y^ — %i yi — xl yl = 0 ===)
läßt sich der Schluß ziehen, daß keiner der drei Koeffizienten a^^, a^^, «33
verschwinden kann. Wäre nämlich z. B. a^^ = 0, so würde die Tangente ^/^
durch den Schnittpunkt der Tangenten x^, x^ laufen, und dieser Punkt
vriirde zufolge (4) der Kurve angehören, und zwar wieder als mehrfacher
Punkt. Man berechne nun die Koordinaten der Berührungspunkte der
*) Vgl. dessen Abhandlung „Über die Beziehungen zwischen den 28 Doppel-
tajigenten einer ebenen Kurve vierter Ordnung'-, Journ. f. Math., Bd. 99, S. 275.
=«=*) Man kleidet diese Gleichung auch vielfach in die irrationale Gestalt:
V^^ + l'^^ + Vajgt/s ~ 0.
Syzygetische und azyget^sche Tnpe] von Doppeltangenten. 369
drei Tangenten x^, x^, %y Wir hahei^ zufolge (3) ui^d (4) die drei Paare
von Grleichungen zu lösen:
^ iC^ = 0, »3 («23 ^2 4- «23 ^3) — ■^o («32 ^2 + «33 '^s) = ^^
(5) \ X^ = 0, »3 («gj itj -j- «33 iTg) — iCj («jj iCj 4- «13 ^3) = 0^
(»3 = 0, »1 («jj ;rj — «j2 -^2) ■^a (<'^21 ■^l ~r «22 ^s) =^ *^J
von denen jedes Paar für eine der Tangenten die Berührimgspunkte
liefert. Sollten diese sechs Punltte nun auf einem Kegelschnitte liegen,
so sei dessen Gleichung:
A^ Xl ~f J.2 «1 -f Ä^ Xl -j- 2 A,-,^ X^ X3 -4- 2 A^^ Xg X^ -^ 2 A^^ X^ X., =:: 0.
Die drei unter (5) rechts stehenden Gleichungen zweiten Grades müßten
also ersetzbar sein durch die drei Gleichungen:
A^ xl -p -^3 X^ -f- 2 J.23 »2 Xg =: 0,
A^ xl -^ A^xi -t- 2 j1j3 Xj x^ == 0,
A^ xl 4- A, xl + 2 ^^2 «1 .^o = 0,
woraus wir, unter Cj, c^ und Cg drei Konstanten verstanden, die
Folgerungen ziehen:
A.^ =Z 6"j «22 • A^ = fj «33 ,
A^ = ^'a^oä' '-■^1 = <"2«in
^1 ^^^-^ ^"3«]!' ^"^2 ~~^ ^3 «22"
Da die «„, «22, «33 nicht verschwinden, so gilt:
^'l = ^'3) '^■3 = ~~ ^2' ''2 =^ '^1'
SO daj3 die Konstanten c verschwenden und danait auch A^ = 0. A^ = 0,
A^ = 0 gewonnen wird. Die Gleichung des fraglichen Kegelschnitts
müßte demnach:
^23 ^2 ^3 -r -^31 ^3 X^-^A^, Äj X, == 0
sein. Dann aber würde der Kegelschnitt durch die Ecken des Koordi-
natendreieoks laufen, während doch, wie wir wissen, diese Eckpunkte
nicht die Tangentenberührungspunkte sind. Damit ist iiie Behauptung
des letzten Satzes eingelöst.
Weiterhin bezeichnen wir auch ein Qaadrapel von Doppeltangenten
als .jbyzygdiseh^. wenn die acht Berührungspupkte der Doppeltangenten
des Quadrupels auf einem I^egelschniite liegen. Andererseits ßoll irgend
ein System von Doppeltangenten „aztjgetis^ch" heißen, wenn je drei aus
dem System zu entnehmende Doppeltangenten ein azygetisches Tripel
bilden.
Irgend einen ersten Steiner sehen Komplex bezeichnen wir wie
bisher durch:
<6) x^,y^, x^,y,, Xg,^^, x^,«/^, x^,y^, j^,y^.
Fricke, Algebra. II. -24
370 ni, 2. Doppeltangenten ebener Kurven vierten Grades.
Aus der Kurvengleichung:
^"i Vi »2 ^2 — ^1 == 0
ergibt sich dann, daJ3 der zum Tangentenpaare »j, x^ gehörende Komplex
auch das Paar y^, y^ enthalten muß, und daß im Komplex des Paares
x-^, y^ auch das Paar %^^ y^ auftritt. Wir reihen dementsprechend an
den Steiner sehen Komplex (6) die beiden folgenden Komplexe an:
(7) Äi,Ä2' y^y^^ •••'
(8) ■ ^1,2/2, ^2»^1' •••■
Aus den beiden letzten Sätzen ergibt sich, daß die Komplexe (6) und (7)
außer x-^, y-^, x^, y^ keine Doppeltangente gemein haben. Käme nämlich
z. B. die Doppeltangente oo^ auch im Komplex (7) vor, so wäre x-^, x^, x.
nach dem ersten Satze ein syzygetisches Tripel, während doch aus dem
zweiten Satze wegen der Stellung von x^, x^, %^ im Komplex (6) folgt,
daß diese Doppeltangenten ein azygetisches Tripel bilden. Die gleiche
Überlegung zeigt, daß überhaupt je zwei unter den drei Komplexen (6),
(7) und (8) außer x^^ x^, y^, y^ keine Doppeltangente gemein haben. Da
nun in jedem dieser Komplexe außer x^, y^, x^, y^ noch acht weitere
Doppeltangenten auftreten, so folgt: In den drei Komplexen (6), (7)
und (8) treten alle 28 Doppeltangenten auf, und zwar die Doppeltangenten
^i> 2^1 > ^2> 2/2 F dreimal, jede der übrigen aber einmal.
Alle in (7) und (8) auftretenden Doppeltangenten außer x^ und ^.^
bilden nun mit x^, y^ azygetische Tripel. Da wir das Paar x^, y^ zu
Anfang beliebig auswählten, so folgt: Mit einem helieMgen Paare von
Doppettangenten x-^, y^ Mlden genau zelin weitere Dopßeltangenten sysy-
gäibche Tripel, nämlich die sehn Doj)j)eItangenten, die dem ztim Paare x^, y^
gehörenden Steiner sehen Komplexe augeMren. Hiernach wird jedes syzy-
getische Tripel durch eine bestimmte vierte Doppeltangente zu einem
syzygetischen Quadrupel ergänzt. Der durch die sechs Berührungspunkte
des Tripels laufende Kegelschnitt schneidet auf der Kurve vierten Grades
auch noch die Berührungspunkte jener vierten Tangente aus. Jedes der
315 syzygetischen Quadrupel liefert uns somit vier syzygetische Tripel.
Da wir im ganzen 3276 Tripel von Doppeltangenten haben, so folgt:
Es gibt hei einer doppelpunUfreien Kurve vierten Grades 1260 t
lind 2016 azygetische Tripel von Doppeltangeuten.
§ 4. Paare und Tripel von Steiner sehen Komplexen.
Ein beliebiger unter den 63 Steiner sehen Komplexen, den wir
symbolisch mit Kj^ bezeichnen wollen, setze sich aus den folgenden sechs
Tangentenpaaren zusammen:
TO »1,2/1, »2'2/2, ^,2/3, »4,2/4, »5'2/5, »6'2/6-
Anzahlen der syzygetischen und der azygetischen Tripel. 371
Aus JSTj stellen wir wie in § 3 die beiden we^tereii Komplexe:
her, die im Verein mit K^, wie wir wissen, bereits alle 28
Doppeltangenten erschöpfen. Bei diesem Prozeß haben w d^s Pa^r:
der Tangentenpaare bevorzugt. Xun können wir aber im ganzen 15 Paare
von Tangentenpaaren aus dem Komplex K^ herausgreifen unci jedem Paar
entsprechend ein Paar von Komplesf.en bilden
TO *»>%. ViiVk^ •••>
TO '-^iiVk^ ^^k,Pi: ■'■,
die alle voneinander und von JST^ \erschieder|. sind. Sie erschöpfen
insgesamt 31 von den 63 Komplexen.
Um die übrigen Komplexe ^u gewinnen, durclilaufe z^ die 16
in Zg und K^ gegenüber K^ neu aufti'etenden Doppeltangenten. Die
32 Komplexe:
TO yi^^i' •••
sind dann voneinander und von den 31 schon hergestellter). Komplexen
verschieden, so daß wir in JST^, K.2, K^, K^ und K^ alle 63 Komplexe
gewonnen haben.
Es soll nun die Verteilung der Doppeltangenten auf die Komplexe K^
und K-^ näher untersucht werden. Eine beliebige unter den 16
Doppeltangenten ^^ werde herausgegriffen; sie gehöre, wie wir ojine Beschränkung
der Allgemeingültigkeit der Überlegung annehmen dürfen, dem
Komplex K^ an*) und bilde in ihm das Paar z^, s^. Die Komplexe K^
und Zg schreiben sich dann etwas ausführlicher so:
TO ^l'^l' •^2>^2> ••■'
TO 2/l'^l' 2/2>^2' ••^•
Wir stellen nun die folgenden drei Komplexe nebeneinander:
(ZJ »ii-s'i, "*'2)'^2' ■■''
TO »l'^2. ^^2'^1' ••^'
die wie die Komplexe Z^, Z^, Z^ alle 28 Doppeltangenten enthalten.
Demnach treten hier auch die beiden Tangenten x^, y^ ai(if, natürlich
==) Ist Zx m Z3 enthalten, so genügt der Austausch der Bezeichnungen x-^
und 2/1, um zur Annahme des Textes zu gelangen.
24*
372 III) 2. Doppeltangenten ebener Kurven vierten Grades.
nicht als Tangentenpaar, da sie als solches nur in K-^ enthalten sind. In
JSTg kann, wie wir schon wissen, weder x^ noch y^ vorkommen. Auch
können diese Doppeltangenten nicht beide in K^ oder beide in JSTg
enthalten sein; sonst wäre nämlich das Tripel x.^, %, y^ azygetisch, während
es doch wegen K^ syzygetisch ist. Da wir übrigens die Bezeichnungen x^
und 2/3 auch noch austauschen dürfen, so beschränken wir die
Allgemeingültigkeit der Betrachtung nicht, wenn wir annehmen, daß die
Doppeltangente »3 in K^ und y^ in K^ enthalten ist. Insbesondere gehöre x^
in K^ dem Paare »3,-^3 an. Die zweite Doppeltangente ^3 dieses Paares
kann nicht in iT^ enthalten sein; sonst wäre K^ wegen seines Paares x^, z^
unter den Komplexen Z^, K'^ enthalten. Also findet sich z^ in K^ oder
K^. Käme aber z^ in K^ vor, so wäre z^^ z^, z^ ein syzygetisches Tripel,
was wegen des Komplexes:
ausgeschlossen ist. Also steckt z^ im Komplex K^.
Man betrachte nun die beiden Komplexe:
(JI7) »2' ^3' '*2''^3' *■■■
Da »2, x^, y^, 2/3 ein syzygetisches Quadrupel bilden, so enthält K,j auch
das Paar y^, y^, so daß auch die Doppeltangenten y^, y^, z^, z^ ein
syzygetisches Quadrupel bilden. Somit gehören die Paare y^, z^ und
2/3, ^3 dem gleichen Komplexe an. Man hat demnach genauer:
{K^, x^,z^, x^,z.-,, Xs,z^, ■••,
TO i/l>^"j> .^2' ^2' ^3' ^"3' •••■
Die gleiche Betrachtung, die wir soeben für das Paar x^, y^
ausführten, kann man mit demselben Erfolge auch an jedes der drei letzten
Paare des Komplexes K.^ anschließen. Wir finden demnach als
endgültige Gestalt der Komplexe K^ und Er^:
(K^) X^,Z^. l^,Z^, %,^3) Ä^4)-4, -^öi^S) ^6f^6>
TO 2/1. ^l> 2/2'^2; 2/3' ^3' .</4'~^4' y-.^^öi ^6'^6-
Die sechs Doppeltangenten z^, z^. ••-, z^ bilden ein azygetisches System.
Da dem Komplex K^ das Paar z^, z^ angehört, so müssen die weiteren
vier Doppeltangenten z^, z^, z.^, z^ dem Komplex K^ angehören, und zwar
ohne daß irgend zwei von ihnen in K^ gepaart wären.
Man erinnere sich nun, daß der Komplex K^ irgend ein willkürlich
herausgegriffener war. und daß sich die 62 übrigen Komplexe aus den
30 Komplexen K'^, K^ und den 32 Komplexen K^, K^ zusanunensetzen.
Es ergibt sich somit der wichtige Satz: Irgend zwei Steiner sehe Komplexe
haben entweder ein syzygetisches Quadrupel von Doppeltangenten gemein
oder aber ein azygetisches System von sechs Doppeltangenten. Im ersten
Falle, also dem eines Paares K^. K^ oder K^, K^, sprechen wir von
einem „syzygetischen Komplexpaare ^. Zu jedem solchen Paare gibt es
Syzygetisciie und azygetische Kqmplextnpel. 373
noch einen bestimmten dritten Komplex, der dasselbe syzygetische
Quadrupel enthält. Drei solclie Komplexe, wie K^, Ei, K'^, bilden ein
„syzygetisches Komplextripel^. Zwei Steiner sehe Komplexe, die ein azy-
getisches System von sechs Doppeltangenten gemein haben, mögen ein
„a^ygetisches Komplexpaar'' bilden. Zu jedem solchen Komplexpaar
gehört dann noch ein dritter Komplex, der mit jedem Komplexe des Paares
selbst wieder ein azygetisches Paar bildet. lUfan spricht dann von einpm
„azygetischen Komplextripel", -^vie ein solches z. B. von den drei
Komplexen JSTj, K^, K^ gebildet wifd. In eii^em syzygßtiscl^en Komplpxtripel
treten alle 28 Doppeltangenten ^uf, in einpm azyget:(.schen indessen nur 18.
§ 5. Aronhold sehe Siebeii|systeme.
Aus der Existenz der Steiner sehen Komplexe ist einleuchtepd, daß
es azygetische Systeme zu sechs Doppeltangenten gibt. Durch Aronhold
ist die Aufmerksamkeit auf wicjitige azygäische Systeme pon sieben
Doppeltangenten gelenkt, die man n^ch ihm als „Aronholdsehe Siehensysteme-'
bezeichnet*). Die Existenz solcher Siebensysteme geht leicht aus den
Betrachtungen von § 4 hervor. Es sei in:
,j. I X^,yi, »2' 2/2' -^'S'^/S' ^4'2/4' •*5'2/5' »6' ^6'
irgend eia azygetisches Komplexpaa,r gegeben; dann haben wir z. B. in:
(2) x^, x^, »3, x^, x^, yg, Äg
ein Aronhold sches Siebensyslem. Die aus (2) herauszugreifenden Tan-
gententripel, die entweder keipe der beiden Doppeltangenten y^, z^ oder
nur eine von ihnen enth^ten, sind nämlich wegen (1) alle azygetisch.
Der zum Paare y^, z^ gehörende Komplexe, de|- das Komplexpaar (1) zum
azygetischen Komplextripel ergänzt (in § 4 durch K^ bezeichnet), enthalt
aber keine der Doppeltangenten x, so da,ß auch die fünf Tripel %, y^, z^
azygetisch sind.
Es besteht nun der folgende Sat?: Irgend sechs Doppeltang enten
eines Aronhold sehen Siebensystems Jcommen in einem und nur in einem
Steiner sehen Komplex vor. Haben wir ein beliebiges Siebensysteip:
SO soll zunächst bewiesen werden, daß die sechs Tangenten:
(4) X^, X^, »3, »4, "C-, »g
nicht in zwei verschiedenen Steiner sehen Komplexen vorkompaen können.
Würden zwei solche Koi^iplexe existieren, ^0 bezeichnen wir sie wie
*) Vgl. die Aronhold sehe Abhandlung „Über den gegenseitigen
Zusammenhang der 28 Doppeltangenten einer allgemeinen Kurve yierten Grades'-, Berliner
Monatsberichte von 1864, S. 499.
374 III, 2.'^ Doppeltangenten ebener Kurven vierten Grades.
unter (1). Dieses Komplexpaar ist dann azygetisch. Wir ziehen nun
auch noch den Komplex:
(3) y^,^^, ^2'^2' Vz^h^ 2/4>^4> 2/5>^5' 2/6'^6
heran, der das Paar (1) zum azygetischen Komplextripel ergänzt, und
bilden aus dem Komplex (5) das syzygetische Komplextripel:
[ 2/i,^i> 2/o,^2' i/3'^3' •••'
(6) y^,y^, ^,,^2, »i,»2> •••'
' 2/i-^2' 2/2' ^1'
In diesem Tripel müßten die fünf Doppeltangenten x^, x^, x.^, x^, x^
auftreten, und zwar offenbar allein im letzten Komplex (6); würde nämlich
im zweiten Komplex eines dieser % auftreten, so wäre das Tripel »j, x^, %
syzygetisch. Im letzten Komplex (6) sind aber nur noch vier
Tangentenpaare ungenannt. Sollen hier die fünf Tangenten x^, x^, •••, %
untergebracht werden, so müssen miadestens zwei x^, x^ gepaart seia. Dann
aber weist man sofort syzygetische Tripel x^, X)-, Xi nach, was dem
azygetischen System (3) widerspricht. Das System (4) kann also höchstens
in einem Komplex auftreten. Da die Bezeichnungen der sieben
Tangenten (3) noch beliebig getauscht werden können, so ist einleuchtend,
daß kein aus (3) entnehmbares System von sechs Doppeltangenten in
mehr als einem Komplex auftreten kann.
Um zu untersuchen, ob das aus (3) beliebig herausgegriffene System (4)
auch wirklich immer in einem Steiner sehen Komplex auftritt, entnehmen
wir dem System (4) zwei beliebige Doppeltangenten, etwa x-^ und x^, und
bilden den zu diesem Paare gehörenden Komplex:
»i,»2' 2/i'2/2' ••••
Eines der fünf weiteren Paare dieses Komplexes sei y-^, y^. Wir bilden
dann das syzygetische Komplextripel:
(Kj) x^,x^, y^,y^, •••.
(K^) x^,y^, x,,y^, •••.
was auf fünf Arten geschehen kann, da wir für y^, y^, wie gesagt, fünf
Tangentenpaare zur Verfügung haben. Im Tripel K-^, K^, K^ kommen
die fünf übrigen Tangenten x^, x^, »., x^, x^ sicher vor. In K^ kann
keine dieser Tangenten auftreten, da wir sonst ein syzygetisches Tripel
x^, »2, xj. hätten. Aus dem gleichen Grunde können sie in K^ und K^
nicht gepaart auftreten. Hiemach müssen sich die x^, x^, x^, x^, »7
entweder zu 3 und 2 oder zu 4 und 1 ungepaart auf die Komplexe K^, K^
verteilen. Wir prüfen die erste dieser beiden Möglichkeiten und schreiben,
da wir nötigenfalls noch die Bezeichnungen y^, y^ und damit auch K^, K^
austauschen können, den folgenden Ansatz:
TO «^l'2/l) -^2'2/2' ^3'2/3' »4'2/4- »5'2/5' •••)
(-£3) «^1.2/2' »2'2/l' ^6'2/6- »7'2/7>
Aronhold:sehe Siebei^systeme von Doppelta^genten. 375
bei dem also drei von den Tangente^ »3, x^, x^, x^, x., auf E^ und zwei
auf K^ entfallen*). Nun setze man noch den Komplex:
W ^6'-^7> .^yß>^7> •••
hinzu. E^ und K^ können kein azygetisches Komplexpaar bilden; denn
die Doppeltangenten x-^ und y^ können in K^ nicht auftreten, da die
Tripel x-^, Xq, »^ und y-^, y^^. y^ zufolge (3) und JSr3 ^zyge^isch sind. Also
bilden K^ und K^ ein syzygetisches Komplexp^ar upd halben demzufolge
ein syzygetisches Tangentenquadrupel gemein. Wie ma,n aber auch aus
K^ ein Paar von Tangentenpaaren herausgreift, inpner wird in diesem
Paare mindestens eine Tangente % aus der Reihe x^, x^, x^, x^, x^
enthalten sein. Diese Tangente % tritt dann auch in K^ auf, und alsQ wäre
Xf:- Xq, Xri entgegen dem Siebensystem (3) ein syzygetisches Tripel. Die
fünf Tangenten »3, •••, x^ verte:|len ^ich hiernach auf Zg und K^ sp, daj3
in einem Komplex vier u|id im anderen eine Tangente auftritt. Wir
dürfen (wegen der Vertauschbarkeit -von ;?/,, y^ in K^ vier und in K^ eine
annehmen. Es finde sich x;,^ in K^, während d,ie übrigen vier Tangenten
x\. Xj^, Xi, x^ in JSTg enthalten sind:
(^2) »1,^1, ^2-2/2- ^i>2/»> Hl Vi, xi,y^, Xm,y„^.
TO »i>^2' -^a'^/r ^n^yn, •■-,
Man erinnere sich nun, daß wir im ganzen fünf Komplexpaare dieser
Art bilden können. Dabei können keine zwei Paare von Komplexen sich
einstellen, bei denen in K^ die gleiche T^ngerjite x,^ auftritt. Es müßte
ja sonst zwei Komplexe mitj dem System x^, x^, %, Xjc, Xi, x^ geber)., was,
-wie wir schon wissen, nicht der Fall ist. Soipit tritt auch x,^ einpial in
K^ auf; dann aber haben wir in:
(■^2) »l'2/l' *^2'2/2' %'2/3' '-^i^Vv •^5'2/^' ^6'2/6
denjenigen Steiner sehen Komplex vor uns, dessen Existenz noch zu
beweisen war.
§ 6. Neue Bezeichnungen der Doppelt^ngenten jiebst Folgerungen.
Im Anschluß an Hesse (vgl. die Xote S. 366) hat Cayley**) eine
neue Bezeichnung der Doppeltangenten eingeführt., die zu eine;- sehr
brauchbaren Darstellung der Systeme vor; Doppeltangen^en durch
figürliche Symbole f) geführt l^at. Dieser Entwicklung liegt die Aiisw'atl
irgend eines Aronhold sehen Siebensyßtems:
(1 ^ X, , Xn, X^, Xa^ , X^, Xq , d q
*) Es ist fur die nachstfplgen4e Schlußweise glßichg^ltig, ob «g und .r^ oder
zwei andere unter den fünf Tangenten cc^: a?3, • •-, ^C; in ^3 auftretßn.
*=*) Vgl. dessen Abhandlung .,Xote sur l'algprithme des tangentes double d'une
courbe du quatrifeme ordre*-, Journ. f. Math., Bd. 68, S. 176.
t) Vgl. Salmon, „Treatise on the higher plane cuives" oder die deutsche
Bearbeitung von Fiedler, .,4nalytische Geometrie der höheren ebenen Kurven",
S. 285. Leipzig 1873.
376 III, 2. Doppeltangenten ebener Kurven vierten Grades.
zugrunde, dessen Tangenten wir noch kürzer auch kurz durch die sieben
Ziffern 1, 2, 3, 4, 5, 6, 7 bezeichnen. Es werde nun die Doppeltangente 1
zunächst abseits gestellt und der nach § 5 eindeutig bestimmte Komplex
der übrigen sechs Tangenten (1) eingeführt:
(2) x^,y^, »3,2/3, x^,y^, x.^,y.^, x^,y^, x^,y^.
Die Tangente y^ ist durch die ausgesonderte Tangente x^ als die mit x^
gepaarte Tangente dieses Komplexes eindeutig bestimmt und kann
demnach durch das Symbol [1, 2] eindeutig charakterisiert werden. Es ist
klar, da£ wir in derselben Weise überhaupt die in (2) auftretenden
Doppeltangenten y^ durch [1, a^] bezeichnen können. Sondern wir aus
dem Siebensystem (1) die Tangente Xa aus, so können wir entsprecliend
sechs Doppeltangenten [«,, v] mit den sechs von fi verschiedenen Ziffern v
erklären.
Da wir die sieben Tangenten im Systeme (1) noch beliebig
austauschen können, so erscheinen alle Tangenten [fi, v] als gleichberechtigt.
Diese Gleichberechtigung überträgt sich auch auf Tangentensysteme
[fi, v], [fx, v'], ■••■ Ein Satz, bei dem keine Auszeichnung einer
Tangente oder eines Tangentensystems vorliegt, überträgt sich vom System
[fi, 0^], [fi'j v'], • ■ • sofort auf alle Systeme, die aus ihm durch irgend
eine auf die Ziffern 1, 2, •••, 7 auszuübende Permutation entsteht. Wenn
wir demnach z. B. zeigen können, daß die beiden Tangenten [1, 21 und
[2, 1] identisch sind, so wird sich daraus sofort ergeben, daß überhaupt
für jede Kombination ji, v die beiden Tangenten [^i, v\ und [v, ,u]
miteinander identisch sind. Um aber die Identität von [1, 2] und [2, 1]
darzutun, bilde man den zum System x^, x^, x^, x-, x^, x^ gehörenden
Komplex, der mit dem Komplex (2) mehr als vier Tangenten gemeinsam
enthält und also mit diesem Komplex ein azygetisches Paar bildet. Dieser
Komplex hat notwendig die Gestalt:
(3) a?j, 2/2, •^s, ~3, -1^4, -^4, -^i > ■^ö) -^6' ■^e' ■^T) ■2^7 ;
denn er enthält neben den Paaren mit x^, x^, •••, x^ ein Paar mit x^
und einer der Tangenten des ersten Paares x^, y^ von (2), also mit y^,
da »2 im Komplex (3) nicht auftreten kann. Es läßt sich demnach y^
auch als Tangente [2, 1] darstellen, womit unsere Behauptung
bewiesen ist.
Die sechs Tangenten [1,2], [1,3], [1,4], •••, [1,7] sind als
Glieder des Komplexes (2) voneinander verschieden. Es sind demnach
überhaupt je sechs Tangenten [fi, v] mit der gleichen Ziffer fx
verschieden, und dasselbe gilt (wegen des Gesetzes [^, v] = [v, fij)
von je sechs Tangenten mit derselben Ziffer v. Die beiden
Komplexe (2), (3) enthalten, wie wir wissen, 18 verschiedene Doppeltangenten.
Insbesondere ist also z. B. die Doppeltangente ^3 = [2, 3] von der
Doppeltangente ^^ =: [1, 4] verschieden. Wir schließen hieraus sofort
weiter auf den Satz: Irgend zwei DoppeJtangenten [^i, v] und [fi', v'] ohne
Xeue Bezeichnungen fur die Doppeltangentea. 377
gemeinsame Ziffer sind stets verschieden. Hiemach entsprechen 4en
21 Kombinationen der sipben Ziffern 1, 2, ••-, 7 zu Paaren 21
verschiedene Doppeltangenten, die mit den offenbar von ihpen verschiedenen
Doppeltangenten 1, 2, •••, 7 alle 28 Doppeltangenten erschöpfen.
Als eine erste Folgerung können wir jetzt dßn Satz beweisen, daß
fo }vein azygetisches System von acht Dop^eltangenten gilt, also aucji Jximb
•von mehr ah acht Doppeltangenten. Zum Beweise fügen wir dem beliebig
gewählten azygetischen Systeme def Doppeltangenten (1) eine der 21 von
ihnen verschiedenen Tangenten [f*, v] an und dürfen \yegen der
Gleichberechtigung dieser Tangenten etw^ y^ = [1^ 2] wählen. Dann liegt in
x^. y^, »3 zufolge (3) ein syzygetisches Tri])el vor, womit unser Satz
bewiesen ist.
Übrigens gestalten wir die Bezeichnungsweise noch gleichipäßiger,
wenn wir auch noch die Ziffe;- 8 ip Gebrauch ne^imen und die
Doppeltangenten 1, 2, •••.7 fortan durch [1, 8], [2, 8], •••, [7, 8] oder auch,
unter Ausdehnung des Gesetzes [^, v] = [v, iij, durch [8, Ij, [8, 2], ••■.
8, 7j bezeichnen. Die 28 Doppeltangenten entsprechen dann den 28
Kombinationen der acht Ziffern 1, 2, ••-, 8 zu Paaren. Xur dürfen \vir
dabei nicht übersehen, daß bei der Erklärung unserer Bezeichnungsweise
die Ziffer 8 eine Sonderstellnng einnimmt. Das wiederholt benutzte
Gesetz von der Gleichberechtigung der Tangenten [u, v\ darf den^nach
bei solchen Systemen von Tangenten, bei denen die Ziffer 8 im Spiele
ist, nicht unbeschränkt benutzt werden.
Die neue Bezeichnung der Doppeltangenten wird nun besonders
wertvoll, wenn wir sie :?u einer weiteren figürlichen Daistellimg der
Doppeltangenten und der Systeme solcher fortentytrickeln. Die einzelne
Doppeltangente [^i, v] deuten wir durch einen Strich I an, an dessen
beiden Enden wir die Ziffern ^ und v angeschrieben denken- Ein
Doppeltangentenpaar [fi, v]. [{i', v'] wird symbolisch duj-ch dßS Zeichen i i
angedeutet, falls die vier Ziffe^-n fi, v, fi', v' verschieden sind, und durch
das Symbol V, falls [ji, v] mit [^', v'\ eine Ziffer gemeinsam hat. IIan
wird hiernach für die Tripel von Doppeltangenten sofort die folgenden
fünf durch die Symbole:
(4) ,!, V, ^, n, V
darzustellenden Möglichkeiten unterscheiden.
Ehe wir weitergehen, soll sogleich untersucht werden, wie sich rp.it
Hilfe der Zeichen (4) die syzygetischen und die azygetischen Tripel
darstellen mögen. Zu diesem Zwecke ergänzen ^vir die beiden Steinpr sehen
Komplexe (2) und (3) zum azygetischen Komplextripel
(5)
»2'2^2'
Xi,y^,
X^.X^,
»3-2/3>
»3, ^3,
2/3>^3>
^iiVi^
»4,^4)
y^r^i,
Xg
Xj
2/5
-2/0'
^^y
> ■'5'
•^6.2/6'
•^6' ■^6'
y,.^,,
x,,y,
x^,^^.
y,,z,.
378 III^ 2. Doppeltangenten ebener Kurven vierten Grades.
Wir untersuchen nun die Zeichen (4) einzeln und beginnen mit \J/, wo
wir wegen der Sonderstellung der Ziffer 8 drei Arten von Tripeln zu
unterscheiden haben, je nachdem die Ziffer 8 in keiner, in einer oder in
allen drei Doppeltangenten auftritt. Als Repräsentanten dieser drei
Arten können wir die folgenden drei Tripel benutzen:
I [1, 5], [1, 6], [1, 7] = 2/5> y,- y-r
(6) [1, 6], [1, 7], [1, 8] = 2/6, y,. h-
[ [1, 8], [2, 8], [3, 8] = X,. x^, T,.
Xach dem dritten Satze in § 3 sind die beiden ersten Tripel wegen des
dritten Komplexes (o) azygetisch. Das dritte Tripel (6) ist als
Bestandteil des Siebensystems (1) azygetisch. Beim Zeichen V hat man vier
Arten von Tripeln zu unterscheiden, die repräsentierbar sind durch:
y.-
I \A. Hl n. 41 [9 .qi r=z V. t, .
(7)
[3, 8],
[4, 8],
[1' 2],
[1. 4].
[4, 8],
[1, 4],
[1, 3],
[1, 5],
[1, 2] = x^.,
[2, 3] = x,.^
[4, 8] = y,.
[2, ^ = y,:
Man erkennt das erste, dritte und vierte Tripel sofort wegen der
Komplexe (5) als azygetisch. Ebenso ist das zweite Tripel azygetisch. da
zwar das Paar c^, y^, aber nicht die Doppeltangente 0^ im ersten
Komplex (5) auftritt. Für das Symbol \/ haben wir zwei Arten von Tripeln,
repräsentiert durch:
[ [1, 8], [2. 8], [1, 2] = x„ X,. y,.
I [1. 2], [1, 3], [2, 3j =. 2/,, ^3, z,.
Beide sind azygetisch, da zwar die Paare x^. x^ und ^3, s^ dem dritten
Komplex (5) angehören, nicht aber die Doppeltangente y^. Auch für
das Symbol | haben wir zwei Arten von Tripeln, die repräsentierbar
sind durch:
y. I [1- 31, [2, 4], [5, 8] = 2/3, z,, X,,
1 [1, 3], [2, 4], [5, 6] = ^3. z,, [5, 6].
Zur Entscheidung über die Katur dieser Tripel bilden wir das syzy-
getische Komplextripel:
0-^) \ yz,yi, ^3,^4, %,»4, ■■•■
1 ^3>^3, 2/4» ^4'
in dem alle Doppeltangenten, also auch [5, 8] und [5, 6] auftreten. Doch
können sie sich weder im zweiten noch im dritten Komplex (10) finden,
da die beiden Tripel:
//3, y^, [5, 8] = [1, 3]. [1, 4], [5, 8j,
y,. ^3. 15, 8] = [1, 3], [2, 3], [5, 8],
Figürliche Bezeichnungen der Tripel und Quadrupel. 379
und ebenso die beiden Tripel:
2/3, y,, [5, 6] = [1, 3]. [1, 4], [5. 6].
y„ ^3, [5, 6] = [1, 3], [2. 3], [5, 6j
übereinstimmend das Zeichen V besetzen und also a,zygetisch sind. Also
sind die beiden Tangenten [5, 6] und [5. 8] im ersten Komplex (10)
enthalten, so daß beide Tripel (9) syzygetisch sind. Bei dem noch
übrigbleibenden Zeichen Fl hat man wieder (Jrei Arten von Trippln, die
repräsentiert werden können durch:
i [1, 2], [2, 3], [3, 4] == y„ z„ [3, 4].
(11) [1,2], [2, 3], [3. 8] =2/,, z,, ^3,
[ [1, 8], [2, 8], [2. 3] == »,, %^, ^3.
Die beiden letzten Tripel erkennt inan aus (5) spfort als syzygetisch.
Wegen des ersten Tangententripels (11) bilde man das syzygetisch«
Komplextripel:
{y^,3^, ^1,^3, •••,
2/2, »p ^3,a;3.^ ....
2/2-»3, s^,x^, ....
Die beiden letzten Komplexe könnpn dje Doppeltangente [3, 4] nicht
enthalten; denn die beiden Tripel:
y,, X,, [3, 4] = [1. 2], [1, 8], [3, 4],
y„ ^3, [3, 4] := [1, 2], [3, 8], ^3, 4]
haben das Zeichen VI und sind also azygetis(ih. Ä.lso ist die Tangente
[3, 4] im ersten Komplex (12) enthalten, so daß auch das erste Tripel (Ij)
syzygetisch ist. Unter Zusammenfassung der Ergebnisse finden wir den
Satz: Alle Tripel von Doppeltangenteif mit den symbolischen Zeichen:
IM, n
öiml syzygetisch und alle Tfipel m,it (^m Zeichen:
VI, \k' V
sind azygetisch. Bemerkenswert ist, daß in diesem Ergebnis die
Sonderstellung, die die Ziffer 8 im L,aufe der bisherigen Entwicklung spielte,
nicht mehr hervortritt.
Eine unmittelbare Folge hieraus ist der weitere Satz: Alle QiKidrapel
von Doppeltangenten mit den heißen Zeichen:
MM, G
sind syzygetisch, wahrend ajle Quadrupel i^it den Zeichen-
^., VI, ^1. VV
azygetisch bind. Wie man nämlich auch einen St^-ich fortnehmen mag,
es bleibt stets das Zeichen eines syzygetißchen bzw azygetischen Tripels.
380 ni, 2. Doppeltangenten ebener Kurven vierten Grades.
Alle übrigen Quadrupel sind weder syzygetisch noch azygetisch. In
einem hierher gehörigen Quadrupel ist mindestens ein syzygetisches
Tripel und mindestens ein azygetisches enthalten. Ein Beispiel ist das
Quadrupel:
[1, 2], [2, 3], [3, 1], [1, 4],
dem das Zeichen \7_ zukommt*).
Wir betrachten endlich die symbolischen Zeichen der Aronhold sehen
Siebensysteme. Eine solche Figur besteht aus sieben Strichen, die so
zusammenhängen müssen, daß nicht mehr als acht verschiedene
Endpunkte von Strichen vorKegen; denn wir haben nur acht Ziffern zur
Verfügung. Aus der Figur darf sich auf keine Weise durch Herausnahme
von vier Strichen eine der beiden Figuren |||, Fl herstellen lassen; denn
im Siebensystem tritt kein syzygetisches Tripel von Doppeltangenten
auf. Die Figur kann demnach nur aus einem zusammenhängenden
Strichsystem oder aus zwei solchen bestehen; denn kämen drei Strichsysteme
vor, so könnten wir durch Fortnahme von vier Strichen stets die
Figur III herauslösen. Wir wollen entsprechend die Figur des
Siebensystems als .,einteilig" bzw. als „zweiteilig" bezeichnen. Als einer der
Teile kann V auftreten. Im übrigen aber kann kein Teil mehr als einen
Punkt aufweisen, von dem mindestens zwei Striche ausziehen, da man
sonst die Figur Fl herausheben könnte.
Ist die Figur des Siebensystems einteilig, so besteht sie aus einem
siebenstrahligen Sterne -i^, wie aus den eben gegebenen Darlegungen
hervorgeht. Da man jede der acht Ziffern in das Zentrum stellen
kann, so haben wir acht Möglichkeiten, und unser anfängliches
Siebensystem (1) :
[1, 8], [2, 8], [B, 8], [4, 8], [5, 8J, [6, 8], [7, 8j,
stellt eines der acht hierher gehörigen Systeme dar.
Ist die Figur zweiteilig, so kann der eine Teil weder aus einem
Striche, noch aus zwei Strichen, noch aus einem dreistrahligen Sterne
bestehen. In diesen Fällen müßte nämlich der andere Teil ein Stern
mit bzw. sechs, fünf oder vier Strahlen sein. Stets würde dabei die
Zahl der verschiedenen Strichendpunkte größer als 8 sein. Es bleibt nur
die eine MögKchkeit übrig, daß der eine Teil V und der andere Teil
ein vierstrahliger Stern ~V- ist. In der Tat kann man auch aus der
Figur:
V ^A^
*) Wie bereits S. 368 festgestellt wurde, gibt es 315 syzygetische Quadrupel.
Beiläufig bemerken wir, daß es 5040 aaygetische Quadrapel gibt, wahrend der
Rest aus 15120 Quadrupeln besteht. Vgl. das S. 375 genannte Werk von Salmon-
Fiedler, S. 285.
Pigurhche Bezeichnungen der Siebensysteme. 381
auf keine Weise durch Fortnahme yon yier strichen eines der beiden
Bilder der syzygetischen Tripel herstellen. Ein Beispiel eines liierher
gehörenden Aronholdsehen Sieli^ensystems ist:
[1, 2], [1, 3], [2, 3], [4, 5j, [4, ö], [4, 7], [4, 8].
Nun haben wir (|) === 56 Tripel, die als sypibolisches Bild A haben.
Il^ach Auswahl eines dieser Tripel bleiben fünf Ziffei-n zur Verfügui^g, von
denen wir eine beliebige in das Zentram des vierstrc^hligen Sternes stellen
können. Wir haben also 56-5 = 280 Siebensysteme der beschriebenen
zweiteiligen Figur. Also bestejit der Satz: Es gibt insgesamt 288 Aron-
Jioldsche SiehmsySterne, die sieh zu 8 hßw. 280 auf die beiden Figuren
verteilen:
Aus der Verschiedenheit dieser beiden Symbole darf keineswegs der
Schluß auf die Existenz von zwei Typen Arpnholdschßr Siebensystei^e
gezogen werden. Unsere ganze symbolische Bezeichniing hangt ja von
der freien Auswahl des ersten Siebensystpms (1) ab- Ersetze^ wir dieses
Siebensystem durch eine^ der 280 Siebensysteme, die wir eben beim
Zeichen V -V- fanden, so erhält dies neu zugrunde gelegte System ^Is
eines unter gewissen acht Systemen jetzt das Zeichen -^^.
Die syzygetischen Quadrupel von Doppeltangentei^ sind, wie obpn
bemerkt, durch zwei symbolische Figuren dargestellt, pämiich entweder
durch vier getrennte Striphe oder durch ein Quadrat. Die sechs
Tangentenpaare eines Steiner sehen Komplexes geben zu zweien kombiniert
stets ein syzygetisches Quadrupel, ilan stellt daraufhin ziemlich leicht
fest, daß es der Bezeichnung nach zwei Typen von Steiner sehen
Komplexen gibt. Ein Komplex des ersten Typus ist:
I [1, 2] [3, 4], [I, 3J [2, 4], [l, 4J [2, 3], ,5, 6] [7, 8].
1 [5, 7] [6, 8], [5, 8] [6, 71.
Das Charakteristische ist hier, daß in drei Pg-aren von Doppeltangenten-
paaren vier unter den acht Ziffern l, 2, ••-, 8 auftreten, in den anderen
drei Paaren aber der Eest der acht Ziffern. Ein Komplex des zweiten
Typus aber liegt vor in:
( [1, 7] [1, 8], [2, 7] [2, 8], [3, 7] [S, 8], [4, 7] [4, 8^
1 L5, 7| [5, 8], i6, 7] [6, 8]'.
Hier kommen zwei unter den acht JZiffei^ in den beiden Tangenten jedes
Paares vor; die übrigen sech^ Ziffern c^ber verteilen sich auf die sechs
Paare des Komplexes.
382 III) 2- Doppeltangenten ebener Kurven vierten Grades.
§ 7. Sätze von Aronhold.
Grundlegend für die algebraische Behandlung des
Doppeltangentenproblems ist folgender von Aronhold*) aufgestellte Satz: Ist bei einer
Kurve vierten Grades irgend eines der 288 Siebensysteme von
Doppeltangenten gegeben, so Jcönnen daraas alle übrigen Doppeltangenten rational
berechnet werden.
Zum Beweise dieses Satzes denken wir ein beliebiges Aronhold sches
Siebensystem:
(1) x^, »3, Xg, X,, x^, x^, x^
gegeben, was explizite in folgender Art geschehen kann. Die drei
Doppeltangenten x-^^, x^, x^, die ein azygetisches Tripel bilden, laufen
nach S. 368 nicht durch einen Punkt und können deshalb als Seiten eines
Koordinatendreiecks benutzt werden. Wir wollen alsdann das
Siebensystem (1) dadurch explizite gegeben denken, daß wir x^, a;., x^, x^ als
lineare Formen der x^, x^, x^ bekanntgeben:
ix^ = ttj»j ~|- a^x^ ~|- a^x^,
X. rziz 6 X -4- 6 a;, -4- 6, a;,,
1 1 T 2 2 T 3 3>
x^ = ä!j a;^ ~f d^ x^ ~f d^ x^ **).
Wir heben nun aus dem Siebensystem (1) der Reihe nach die drei
ersten Doppeltangenten heraus und bilden jeweils für die sechs
zurückbleibenden Doppeltangenten den Steiner sehen Komplex. Kach (2) und (3)
S. 376 sind diese Komplexe:
f^ä'ls' «S'lä' ^4-l41- «S'löl' «e'lei' »7>l71'
(3) «3-ll> ^1>I3' •^4>l42> ^5'l52> ^H^löä' «7>l72>
[a;,,|,, a;^,^,, »,,|,3, a;.,|,3, x^,^^^, x^,tn^
wo wir die neu hinzutretenden Doppeltangenten allgemein durch |
bezeichneten und durch untere Indizes unterscheiden. Xach den
Bezeichnungen von § 6 gilt:
I, = [2, 3], I, = [3, 1], |3 = [1, 2], I,, = [1, 4], ....
Aus (3) ergibt sich noch als ein weiterer Steiner scher Komplex:
(4) - x^,ti, «ä-lä' «3.l3> •••.
der mit jedem der Komplexe (3) ein syzygetisches Paar bildet und also
keine der vier Doppeltangenten x^, x^, x^, x^ enthält.
^) Vgl. die m der Note S. 373 genannte Abhandlung.
=^*) Da keine drei unter den sieben Tangenten (1) durch einen Punkt laufen,
so sind die zwölf Koeffizienten in (2) durchweg von 0 verschieden und es
verschwindet auch keine der Matrix dieser Koeffizienten zu entnehmende zwei- oder
dreireihige Determinante.
Berechnung aller Doppelt^ngenten aus einem gegebenen Siebensystem. 333
Unser Ziel soll nu^ sein, daß wjr die Doppelt^ngenten |j, I2, I3
berechnen, und zwar dadurch, daß wir l^j'^g, I3 als lineare Formen der
x-^, x^, »3 angeben. Die drei Formen |j, l^, I3 werden dabei zunächst
noch je um einen willkürlichen Faktor unbestimmt bleiben. Wir können
die Willkür dieser Faktoren dadurch beschränken, daß wir die Rechnungen
von S. 366ff., wie sie für die damaligen Tangenten a;^, ijy x^. y^. a;,, y^
durchgeführt wurden, auf unsere jetzigep Taiigentpn a;^, |j, x^, ^^. x^, ^.
beziehen und insbesondere alsp die folgende Gleichung der Kurve vierten
Grades fordern:
f 2 »212 5^313 4- 2 ^313 a-j Ij + 2 x^ I, x^ I2
Doch werden auch dann die |j, l^, I3 ipn einen gemeinsamen konstanten
Faktor unbestimmt bleiben, woran man sich unteii erinnern wolle.
Die biquadratische Form kqnnen wir in folgende drei einander
identisch gleiche Gestalten setzen:
(6) F = 4 »212 x^ I3 — i,^ = 4 x^ I3 x^ I, — i^l = 4*, I, x^ |, — t//^
wobei die quadratischen Formen i/; durch:
I T/;, = — a^ili ~f a^als-f a;3|3,
(7) T/;^ = ---^i^i — X^t^ + ^sts,
[ ^s= -T ^1 li ^ «2 I2 — «3 I3
gegeben sind*). Zufolge (3) haben wir auch in x^, I3, x^, |^j ein syzy-
getisches Quadrupel. Wir können daher bej geeigneter Verfügung über
einen in die Linearform |^j aufzunehmenden konstanten Faktor die
biquadratische Form F auch in die Gestalt kleiden
(8) F= 4x,tsXj^^-%',
wo 2 *üiß bis auf das Vorzeichen bestimmte quadratische Form ist.
Aus (8) und der ersten Darstellung (6) von F folgt die in den
Xj^, x^, x^ identische Gle:|chung:
4 X, I3 (^312 - »4 L^) = (^1 - %) (^1 + X)-
Genau wie S. 364 schließen wir, daß x^^^ nur in einem der beiden rechts
stehenden Faktoren als JDivispr enthalten spin l^ann. Wir wählen das
noch verfügbare Vorzeichen von 2 so, daß d:|es der ergte Faktor ist. Es
gibt dann einen von 0 verscjiiedepen konstanten Faktor l^, derart, daß
(^1 — %) ^^^ '^^i-^its identisch wird, worauf sirh dip letzte Gleichung
in die beiden Gleichungen spaltet:
^1 - Z = 2 ;L, X, I3, X, (i;, -f x) = 2 (0^312 - -^4 Li)-
Ersetzt man in der hieraus folgenden Gleich(ing:
^1 ^1 = ^4 -^2 I3 + «3 I2 — »4 Li
*) Vgl. S. 366. Statt 4 F ist hier kurz JF geschrieben.
384 ni, 2. Doppeitangenten ebener Kurven vierten Grades,
die quadratische Form tj;^ durch ihren Ausdruck (7), so folgt:
^i Li = «3 lä — ^1 (— «1 ll + ^2 lä + ^3 Is) + ^f «2 Is-
Genau entsprechende Betrachtungen kann man an die beiden syzygetischen
Quadrupel x^, |j, x^, l^^ und x^, ^^, x^, l^g unter Benutzung der zweiten
und dritten quadratischen Form (7) anknüpfen. Wir erhalten auf diese
Weise insgesamt drei Gleichungen, die bei zyklischer Vertauschung der
drei Indizes 1, 2, 3 ineinander übergehen:
I x^ I,, = 0^3 I2 — ^1 (»3 Is — ^1 li + «2 I2) + ^! «2 Is'
(9) «4 I42 = «1 Is — ^2 («1 li — «2 I2 + «s Is) + ^1 «s li >
l «4 I4S = »2 li — '^s («2 li — «s Is + «1 li) + ^1 «112-
Es sollen nun die Konstanten l bestimmt werden. Wir teilen die
zweite Gleichung (9) durch 2.^, die dritte durch 2.^ und addieren sie
sodann. Es folgt als eine in den a;^, x^, x^ identisch bestehende Gleichung:
Das Tripel der Doppeitangenten a;^, |j, x^ ist zufolge (3) azygetisch, so
daß sich diese drei Tangenten nicht in einem Punkte schneiden (vgl.
S. 368). Zufolge der letzten Gleichung läuft also die durch:
^2«s-i--r = 0
dargestellte Gerade durch den Schnittpunkt der Tangenten x^, x^.
Umgekehrt wird sich denmach x^ als lineare Form der x^, x^, x^ so
darstellen lassen:
: a a?j ~f «' [l^ ajg -f ^ V
Aber diese Darstellung ist uns unter (2) bekanntgegeben. Wir folgern,
daß das Produkt l^ l^ mit dem Quotienten a^: a^ gleich ist. Unter
Einführung einer neuen Konstante yi^ schreiben wir dementsprechend:
(11) 1^=: yi^a^, — = ^^a^.
Weiter folgt:
^2 *''s 4" -j^ = {^1 »4 — l^i ß] «1,
und aus (10) berechnet man leicht die weitere in den x^, x^, x^ identisch
bestehende Gleichung:
a, X, ^^'
,t' + t-'''-^-) = <-''-<•' + '■■''■> «' + 1 + 1)-
Berechnung aller Doppeltangenten ai;s einem gegebenen Sißbensystem. 3So
Da x^ und x^ verschiedene Doppeltangepten sind, so spaltet sich diese
Gleichung in die beiden folgenden:
y^x^=^ — (i^ (2 -f a, fi^) |j + ii -i- ii,
(12)
^4ä j b43 .
Wir hatten in (10) die zweite und dritte Gleichung (9) kon^biniert.
Vereinigen wir entsprechend die dritte und erste und sodann die erste
und zweite, so finden wir bei dem gleichen Vorgehen zwei weitere
Gleichungspaare, die einfach aus (12) duych zyklische Vertauschung der
drei Indizes 1, 2, 3 hervorgehen. So erscheint zunächst die ersfe
Gleichung (12) als eine der folgenden drei Gleichungep:
(13)
- ^1 (2 ~f «1 fii) li •
. ^
«0 a^
An Stelle der »j, x^, x^ kann man auch die |j, Ig, 1^ als Koordinalen
gebrauchen. Die drei hier vorliegenden Darstellungen von x^ in cfen
li) Is' Is i^üssen dann miteinander identisch sein, woraus wir die
Folgerungen ziehen:
-^(2-f a^^u,)
1
1
1
= -^(2^a,^.
Es folgt o^j = 0^2 = '^3) ^0 daß ^vir bei dpn a^ die Indizps fortlassen
können. Weiter folgt:
— ttj ;u,j (2 ~|- <?j ;u,j) = 1, i«'i = ,
— «2 ;[i2 (2 ~f ^2 /ig) = ], ^«2 = — --,
— ^3if*3(2 4-%^3) = ^> f*3=— --•
"3
Die Gleichungen (13) nehmen übereinstipimend die Gestalt an:
vx^
Fricke. Algebra. II. 25
Si , S2 I S3
386 ni, 2. Doppeltangenten ebener Kurven vierten Grades.
woraus wir mit Benutzung von (2) folgern:
(14) V (a,x^ + a^oc^ + a,x^) = -^ -r ^ -r -^ ■
U}y t*q Ctg
Durch Eintragung der berechneten Werte ^ in (il) und in eine
entsprechend abzuleitende Gleichung für X^ erhält man als die gesuchten
Werte der drei Konstanten X:
Xun ist auch die zweite Gleichung (12) eine unter dreien, die durch
zyklische Permutation der Indizes 1. 2, 3 ineinander übergehen. Ersetzen
wir in diesen Gleichungen die u durch ihre inzwischen berechneten
W^erte und lassen bei den v die Indizes fort, so finden wir bei
Zeichenwechsel:
Durch
Addition dieser
1.1
1.1
^1
«2
«3
Gleichungen folgt
543
= -
V {a-^ X
+ ^ «3 -^2
bei Benutzung
1 + a, ^2
+ «3
von
h\
(14):
und also gelten für |^^, l^^; l.s folgende Darstellungen:
(16)
«1 /
§43 = — (^(«1 'l 4-02-^2)
Hier ist nun noch die Konstante v unbekannt. Um weitere
Angaben über sie machen zu können, bemerken wir, daß wir bei der auf das
Formelsystem (7) folgenden Betrachtung das System der drei
Tangentenpaare x^, 1^^; »^, 1^2; ^4) I43 bevorzugt haben. Wir können genau
entsprechende Entwicklungen an die drei Systeme:
(1'^) -i., |»i> ^-j, 1*2- •*». 1^8- i = 5, 6, 7,
die wir den drei Komplexen (3) entnehmen, anschließen, wobei die drei
letzten Gleichungen (2) zur Benutzung gelangen. Es kommen dann vier
Berechnung aller Doppeltangenten fius einem gegebenen Siebei^system. 387
Konstanten v in Betracht, die wir durch die Bezeichnungen v^, Vr,, v^, v,,
unterscheiden. An Stelle von (14) tritt ein Systpm vpn vipr Relationen:
(18)
V^ («1 ^'i -f 0,2 -^2 + Öts ■^s) =
V^ (&j X-j -]- &2 4^2 + ^3 "^s) = "
Veic^^i +6-2^2 -i-Cs^s) =
, I2 , I3
^i^ + i^,
^2 ^'3
[ §2 i S3
Hier haben wir mer lineare Gleichungen zur Beistimi^ung der drei
linearen Formen |j, ^^, I3. Eine dieser Gleichungen muß also eip.e Folge
der drei anderen sein. Um die Bedingung für diese Abhängigkeit in
symmetrischer Weise anzusetzen, führen wir vier Grpßen n^, jf,, '/g, 01,^
ein, die den drei Gleichungen:
(19)
a^ ' fe, ' c, ' d^
«2 \ c^ '^ d^
^ 0,
: 0
genügen sollen. Die Größen % sipid Merdurch bis a]if eipen allen
gemeinsamen willkürlich bleibenden Faktor bestimpit. Die fragliche
Abhängigkeit der Relationen (18) kommt dann durch das Bestehen der drei
weiteren Gleichungen:
[ Oj a^ v^ -r ^15^5 v^ -j- c^ sfg v^ -4- d^ '/^ v,^ = 0.
(20) «2 n^ v^ -r &2 5*5 "^5 ~r ^^'2 5*6 "^e ~r ^2 5*71^7 == 0'
[ 03 ^f^ 0^^ -j" &3 ^C^ 0^5 -t- C3 ;fg a^g -j- (^3 Tlrj Vr; == 0
zum Ausdruck. Aus diesen Gleichi(.ngen berechnen sich die v^. v^, Vq, Vj
bis auf einen ihnen allen gemeinsamen willkijrlich bleibenden Faktor.
Daß sich hier ein solcher unbestimmter Faktor einfinden ipauß, ist
oben [gleich hinter der Gleichung (5)] bereits ai^sdrücklich betont. In
der Tat tritt dieser Faktor als ein gemeinsamer in den Lösungen |j, ^^j I3
der Gleichungen (18) auf und stellt sich ebenso in den Darstellungen
ein. die wir daraufhin füy |^j, ^^^, f^g aus (16) herleiten, ebenso endlich
in den Darstellungen der neun Doppeltapigen ten l^i, |^,, l^a, die wir aus
den drei weiteren sich an (16) anschließenden Gleichnngssystemen
entnehmen. Die Berechnung der 15 Doppeltangenten:
li) Sik
f --
: 4, 5, 6, 7, k = 1, 2, 3
388 III> 2. Doppeltangenten ebener Kurven vierten Grades.
selbst aus dem vorgelegten Aronhold sehen Siebensystem (1) aber ist
wirklich geleistet. Es fehlen nur noch die sechs Doppeltangenten:
[4, 5], [4, 6], [4, 7], [5, 6], [5, 7], [6, 7].
Wir gewinnen sie sämtlich, wenn wir bei Bildung dreier Steiner sehen
Komplexe von der Art (3) nicht wie damals die drei Doppeltangenten
x^, x^, »3, sondern x^, »g, »5 auszeichnen. Der aufgestellte Satz von
Aronhold ist damit vollständig bewiesen.
Ein zweiter Satz von Aronhold besagt: Für helieUge sieben Gerade
in der Ebene Jcann man im allgemeinen, d. h. wenn gewisse rationale
Funktionen der Koeffizienten in den Gleichungen der Geraden nicht verschwinden,
durch rationale Bechnungeu die Gleichung einer doppeltpunUfreien Kurve
vierten Grades herstellen, die jene sieben Geraden zu einem Siebensystem
von Doppeltangenten besitzt Der Beweis folgt einfach durch IJmkehrung
der durchlaufenen Entwicklung. Von den sieben Geraden dürfen keine
drei durch einen Punkt laufen. Wir wählen drei von den Geraden zu
Achsen x^ = 0, ^Tg = 0, »3 = 0 des Koordinatendreiecks und stellen
die vier anderen durch Kullsetzen der vier unter (2) gegebenen linearen
Formen x^, »5, x^, x^ dar. Dann darf keine der Matrix der zwölf
Koeffizienten a, b, c, d zu entnehmende Determinante*) verschwinden. Im
übrigen seien die a, h, c, d zunächst willkürliche Variable. Die |j, |,, I3
bestimmen sich jetzt aus (18), (19) und (20) rational als lineare Formen
der x^, »2, x^, worauf man weiter gleichfalls rational die l^^, l^a, l^g
aus (16) und den drei entsprechenden Gleichungssystemen für ^ = 5, 6, 7
berechnet. Die Eintragung der für |j, ^^, I3 gewonnenen Ausdrücke in
die Gleichung (5) ergibt die auf rationalem Wege gewonnene Gleichung
einer Kurve vierten Grades. Die Diskriminante dieser Gleichung kann nicht
identisch verschwinden, da wir ja oben umgekehrt von unserer doppelt-
punktfreien Kurve, die eine von 0 verschiedene Diskriminante hat, zu
Gleichungssystemen (18), (19), (20) hingelangen konnten, die sich unserem
jetzigen Ansatz (wegen der vorausgesetzten Willkür der a, b, c, d)
notwendig einordnen müssen. Endlich kann man von den Gleichungen (18)
und (16) zur Darstellung (8) von F und zu den entsprechenden
Darstellungen gelangen, bei denen der Index 4 durch 5, 6 und 7 ersetzt
erscheint. Diese Darstellungen gestatten den Schluß, daß x^, x^, so^, »^
mit »j, x^, »3 ein Aronhold sches Siebensystem für die gewonnene Kurve
vierten Grades bilden.
§ 8. Galois sehe Gruppe der Doppeltangentengleichung.
Es soU nun das Doppeltangentenproblem der ebenen Kurve vierten
Grades im Sinne der Galois sehen Gleickungstheorie entwickelt werden.
Es wird eine temäre biquadratische Form F vorgelegt, deren 15 Glieder
*) Die Koeffizienten selbst gehören der Matrix als „einreihige"
Determinanten an.
Herstellung der Doppeltangent engleichung. 389
unbestimmte Koeffizienten haben. Zugrunde zu legen ist der Körper ^,
der aus dem rationalen Körper durch Adjunktion der 14 unabhängigen
Quotienten jener 15 Koeffizienten entsteht Die 28 Doppeltangenten
sind darstellbar durch Nullsetzen einer reduziblen. nänilich eben in
28 lineare Formen zerf9,Ubaren Kovarjante 28stpn Grades der Form F.
Wir bringen diese Kovarianfce etwa zum Schnitt mit einer Seite des
Koordinatendreiecks, die wir so gewählt denken, daß sich auf ihr keine
zwei Doppeltangenten schneiden. Die 28 Schnittpuakte werden ciana
durch eine Gleichung 28^*^^^ (jrades ohne mehrfache Wurzeln bestimmt,
die wir kurz die „Doppeltangentengleichung" nennen wollen.
Um diesen Ansatz aoch etwas genauer zu bezeichnen, gestalten wir
das Koordinatensystem |n ein ge^^öhnliches kartesisches System x, y um
und nehmen an, daß sich ai;f der »-Achse keine zwpi Doppeltangenten
schneiden. Die Kurve viertea Grades sei djirch die Gleichung:
(1) F{x, y) --= 0
gegeben. Eine einzelne der 28 Doppeltangenten, d\e diß x-Achse im
Punkte der Abszisse | schneidet, stellen wir durch:
(2) y = ß(x~^)
dar. Wir haben alsdann in 6, | ein Wertepaar, für das die in x
biquadratische Gleichung:
(3) F{v, ß(x-^)) =-.0
zwei Doppelwurzeln hat. Aach wird umgekehrt jedes Wertepaar (I, |,
für das die Gleichung (3) diese ^Eigenschaft hat, in (2) eine
Doppeltangente liefern. Man ordne die biquadratische Gleichung (3) nach
Potenzen von X und findet leicht, daß sie stets und nur dann zwei
Doppelwurzeln hat, wenn gewisse zwei a^s den Koeffizieaten der biquadratischen
Gleichung leicht herstellbare Relationen:
(4) 9^(ft,|) = 0, 9,(6, l) = 0
zutreffen. Die Elimination von ß aus diesen beiden Gleic^iungen liefert
uns die Doppeltangentengleicliung. Für die einzelne Lösung | berechnen
wir den zugehörigen Wert ß ßls gemeinsame Lösung der Gleichimgen (4)
in Gestalt einer rationalen Funktion von |:
(5) Ö=-JS(|).
Die Wurzeln | der Doppeltangentengleichung ordnen wir, wie die
Doppeltangenten selbst, in syzygetische und ^.zygetischß Tripel und
Quadrupel, in Steiner sehe Komplexe und in Aronholdsche Siebensysteme.
Wir bezeichnen die Wurzeln auch, entsprechend den Doppeltangenten,
d.^rch die Symbole [^i, v\, wo [i, v zwßi verschiedene Ziffern der Reihe
1, 2, 3, •••, 8 sind und stets [v, ff] = {{i, v] gilt.
Sind nun t-^ (x, y) = 0 und t^ (x, y) == 0 die Gleichungen zweier
Doppeltangenten, so können wir nach den Rechnungen von S. 364ff. auf
390 III. 2. Doppeltangenten ebener Kur%-en vierten Grades.
rationalem Wege die Funktion vierten Grades F {x. y) in die Gestalt
setzen:
(6) F{x, y) = tJ,_cp-^\
wobei durch i/; = 0 ein Kegelschnitt durch die vier Berührungspunkte
der beiden Doppeltangenten t^ = 0, t^ = 0 dargestellt ist. Unter der
Kegelschnittschar:
9 + 2 ;. T/; + X- tJ^ = (J
mit dem Parameter l gibt es alsdann fünf, den Werten Z^, Ag. • • •. /.g des
Parameters entsprechend, die in Geradenpaare zerfallen. Bilden wir das
Produkt:
(7) 0 ='[[((pi-2k^1l^^A^tJ,).
bezogen auf jene fünf Werte A, die die Wurzeln der Gleichung (10) S. 365
sind, so ist dies Produkt rational durch die Koeffizienten von F und die
von t^ und t^ darstellbar. Dabei ist 0 eine Funktion zehnten Grades
von X, y, die reduzibel ist. Die zehn linearen Faktoren, in die 0 spaltbar
ist, stellen gleich 0 gesetzt die fünf Doppeltangentenpaare dar, die mit
dem Paare t^ = ö, t^ = ö einen Steiner sehen Komplex bilden.
Da die Werte 6 durch ihre zugehörigen Werte | in der Gestalt (5j
rational darstellbar sind, so können die Koeffizienten \ on 0 auch rational
durch die beiden zu t^ und t^ gehörenden Wurzeln |-^. f, der
Doppeltangentengleichung im Körper ^ dargestellt werden. Setzt man sodann
in der Gleichung 0 = 0 die Ordinate y = 0. so gewinnt man eine in |
auf den zehnten Grad ansteigende Gleichung:
(8) ^(1,, l2-l) = 0-
deren Koeffizienten rationale Funktionen von |,. |, (im Körper Ä) sind,
und deren zehn Lösungen | diejenigen zehn Wurzeln der
Doppeltangentengleichung sind, die mit den beiden Wurzeln |j, |, die syzygetischen
Tripel zusammensetzen. Hieraus geht folgender Satz hervor: Es gibt eine
im Körper ü rationale Funktion ^d^. Ig, Ig) mit drei Argumenten, die
stets und nur dann verschwindet, wenn |j, I2, I3 ein syzygetisches Tripel
von Wurzeln der Doppeltangentengleichung bilden.
Entsprechend den Sätzen von S. 382 ff. ist durch ein Aronhold sches
Siebensystem von Wurzeln:
(9) l.> I2, la. L, k- l6> I7
jede Wurzel der Doppeltangentengleichung rational ausdrückbar. Es
folgt aus den damaligen Entwicklungen, daß wir z. B. für die Wurzelfi, 2r
oder |j2 eine Darstellung:
(10) I.. = ^(l.,l.lla>l.>l5. le. I7)
haben, wo W eine rationale Funktion bedeutet, die sich nicht ändert,
wenn man |j und 1, vertauscht, oder wenn man auf I3, |^, •••, |^ eine
beliebige Permutation ausübt. Setzt man aber in (10) an Stelle von
Aufstellung der G-alois sehen Gruppe dep DoppeltaUfgeatengleichung. 391
|j, I2 ^^ ^Sisa: |u, |v, ^o geht 1^^ in die "Wurzel |„, odej- [a, v] über.
Im übrigen erinnern wir noch da),ran, daß den Wurzeln (9) selbst die
symbolischen Bezeichnungen [1, 8], [2. 81, •••, [7, 8] zukommen.
Hiernach entspricht jeder Permutation der sieben Wurzeln de^
Siebensystems (9) eine bestimmte Permutation der gesamten 28 Wurzeln unserer
Doppeltangentengleichung. Ersetzt man aber weiter das Aronliold sphe
Siebensystem (9) durch irgend ein anderes unter den 2ö8 Siebensystemen,
so zieht dies wiederum zufolge der Darstellungen (10) eine Permutation
der 28 Wurzela unserer Doppeltangentengleichung ng^ch sich. Es gilt
alsdann folgender Hauptsp.tz: Die Gäloi^sche Grruppe der Doppeltangente'n-
gleichung wird erhalten, wenn )nan von, der Darstellung aller 28 Wurzeln
Im durch das Siebensystem (9) zu den entsprechenden Darstellungen durch
alle 288 Siebensysteme ühßrgeht und außerdem in jedem der 288 Falle die
sämtlichen 71 Permutationen der 28 Wurzeln herstellt, die durch die
gesamten Permutationen der sieben Ww^eln des Sdebefisystems eitstehen. Um
dies zu zeigen, müssen wir an der fraglichen Gruppe der 288 ■ 7!
Permutationen die notwendigen und hinreichenden Kennzeichen nachweisen,
die in I, 372 ff. für die Galois sehe Gruppe einer Gleichung ent-
mckelt sind.
Erstlich ist zu beweisen, daß jede Permutation S der Wurzeln $, die
alle zwischen den | bestehenden rationalen Relationei). wieder in solphe
überführt, der Gruppe jei^er 288-71 Permutationen angehört. Aach jede
Potenz von S, also auch S~K wird dann jede zwischen den Wurzeln
gültige Relation wieder in eine solche umformen. Da nun die Gleichu|ig:
(11) ^(ll. l.-l3) = 0
für jedes syzygetische Tripel, aber für kein azygetisches gilt, so wird
durch S jedes syzygetische Tripel wieder in e|n solches übergeführt. Ajser
auch jedes azygetische Tripel geht bei Ausübung von S nieder in ein
azygetisches über: sonst würde ja durch S~^ ein syzygetisches Tripel in
ein azygetisches übergeführt. Hiernach trß,nsformiert S das Siebeu-
system (9) wieder in ein Siebensystem:
(12) 1;. 1;, 1;, 1;. 1;, 1;. 1;,
so daß es unter den 288 • 71 oben erklärten Perm^itationen eine, S', gibt,
die auf die Wurzeln (9) die gleiche Änderung ausübt wie S. !Xun gßht
aber auch die-Relation:
"(13) |.>i = ^^(|., I.U«, I.. •••)
durch S wieder in eine giiltige Gleichung über:
1;. = '4^(1:., i;.li:.. i;,---)-
Rechts steht der Ausdruck derjenigen Wurzel, in die |^^ durch S"
übergeführt wird. Also ist S, wie zu beweisen war, mit S' identisch und
damit unter den 288 «7! Permutationen enthalten.
392 III? -■ Doppeltangenten ebener Kurven vierten Grades,
Es ist zweitens zu zeigen, daß irgend eine zwischen den 28 Wurzeln
der Doppeltangentengleichung wirklich bestehende rationale Relation mit
Koeffizienten des Körpers ^ durch jede der 288-7! Permutationen
wieder in eine wirklich gültige Relation übergeführt wird. Eine solche
Relation sei in:
(14) ß(lx.l2.'--.l7.ll2. ••'.«.•• 0 = 0
vorgelegt, wo a, ••• die Verhältnisse der Koeffizienten der
Kurvengleichung sein sollen. Man kann nun zunächst die l^g, ••• nach (13)
rational durch die |^, Ig, •••, 1^ im Körper ^ darstellen. Sodann lassen
sich nach dem ersten Satze von § 7 S. 382 ff., nach welchem die Kurve
aus einem vollständigen Siebensystem ihrer Doppeltangenten rational
berechenbar ist, die Größen a, • • • rational mit numerischen Koeffizienten
in den sieben (rrößenpaaren:
(15) |„Ö„ I2.Ö2. I3.Ö3. •••. I7.Ö7
darstellen. Die dadurch entstehende Gleichung muß, da nach dem zweiten
Satze von § 7 S. 388 zu irgend sieben Geraden als Doppeltangenten
eine Kurve vierten Grades gehört, in den Größen (15) identisch bestehen.
Sie wird also richtig bleiben, wenn man die sieben Größenpaare (15)
beliebig permutiert oder auch dieselben durch die sieben Größenpaare irgend
eines anderen der 288 Siebensysteme in beliebiger Anordnung ersetzt.
Das aber läuft einfach darauf hinaus, daß die Gleichung (14) gültig bleibt,
wenn man die Wurzeln | einer der 288 • 7! Permutationen unterwirft.
Damit ist die ©288-7! ^Is die Galois sehe Gruppe der
Doppeltangentengleichung erkannt.
§ 9. Erzeugung der Galois sehen Gruppe der Doppeltangentengleichung,
Für die 28 Wurzeln der Doppeltangentengleichung benutzten wir
die Bezeichnung 1^, l^t • *'> I7) I12) lis» "•) ^&t Daneben hatten wir
die etwas mehr symmetrische Bezeichnung [u, v], wo ^u, v zwei
verschiedene unter den Ziffern 1, 2, ••-, 8 sind und [v, yi] = [ft, v] gilt.
Die Ordnung unserer Galois sehen Gruppe stellten wir bereits fest zu:
288-7! = 36-8! = 1451520.
In dieser Gruppe ©288-7! haben wir einen Teiler ©7., der von den
7! Permutationen der Wurzeln |j, Ig> • ••-, I7 geliefert wird und also mit
der symmetrischen Permutationsgruppe des Grades 7 isomorph ist. Die
Wurzeln |^^ mit Doppelindex permutieren sich dabei entsprechend ihren
Darstellungen:
(1) |uv = ^(|u, l.jl.. Ia, -••)-
Aus den Entwicklungen von S. 377 ff. ergab sich, daß bei der Anordnung
der W^urzeln der Doppeltangentengleichung in syzygetische und azygetische
Tripel und Quadrupel, in Steiner sehe Komplexe und in Aronholdsche
Siebensysteme die Ziffer 8 als Index völlig gleichberechtigt mit den
Teiler ®g, m der Griippe der Doppeltangentengleichui^g. 393
Ziffern 1, 2, ■••, 7 auftritt. Allein auf diesen Anordnungen ^.ber
beruhen die gesamten Folgerungen, die wir über die Relationen ^wischen
den Wurzeln und über die Galois sehe Gruppe der
Doppeltangentengleichung gezogen haben. Benutzen wir demnach die symmetrische
Bezeichnung [^u, v] der Wurzeln, so ^^rerden jene Relationen ai^ch gegenüber
jeder der 8! Permutatioaen der Ziffern 1, 2, •••,8 wieder in gültige
Relationen jiibergehen. Die GaUis,sche Gruppe ©sg.g' ^oA demnaclt auch
einen Teiler ©gi der Ordnung 8! und des Index 36, der ftiit rfer bym-
metrischen Permutationsgfuppe des Grawes 8 isomorph ist v(,nd d/tirdi die
fraglichen 81 Permutationen hergestellt wird.
Beim Teiler ©^j geht das Siebensystem:
(2) [1,81, [2,8], [3,8], •.., |7, 8]
in sich selbst über. Gegenüber dem genau aten Teiler ©gi abei perpiu-
tieren sich diejenigen acht Siebensysteme untereinander, denen da^ Syi^bol
-i^ zukommt. Wollen wir also jetzfc durch Ilinzunahme der sieben
Xebengruppen, die zum Teiler ©gi gehören, die Gesamtgruppe herstellen,
so sind solche Permutationen herapzuziehen, bei denen ein Siebensystem
des eben genannten Symbols in ein solches vom Syr^ibo'l V -^
übergeht. Xun kann ein Sieben^ysteip vom Symbol -i^, z. B. das»
Siebensystem (2), gerade in 35 wesentlich verschiedenea Arten ia eii^
Siebensystem des zweiten Symbols übergeführt werden; denn wir köimen aus
dem siebenstrahligen Stepie ajif (l) = 35 Arten ein Tripel von Strahlen
herausgreifen und aus den drei Zahlen an den Spitzen dieser Strahlen
das Dreieck V bilden. Diese 35 Arten des Übergangs vom
Siebensystem (2) zu einem Siebensystem des zweiten Symbols sind wieder lait-
einander gleichberechtigt, so daß uns eifi spezielles Beispiel eines solchen
Übergangs allgemein über die Eigenart der zugehörigen Permutation der
Wurzeln | unterrichten ^vird.
Kehmen wir etwa als Beispiel die Perm^tatioa S, die für die
Wurzeln des ersten Siebensystems (2) so lautet:
.ON c _ (iU 8], [2, 8], ^3, 8], .[4, 8], [5, 8], [6, 8], [7, 8]\
^^^ '^ — l[2, 3], [3,1], [1,2], [4,8], [5,8], [6,8], [7, 8]^
Bei dieser Permutation sind die Ziffern 1, 2, 3 gleichberechtigt ]ind
ebenso die vier Ziffern 4, 5, 6, 7. Bier ist nun festzustellen, in welche
Wurzel die einzelne Wurzel [{i, v], an der die Ziffer 8 nicht beteiligt ist,
übergeht. Wegen der gerade genannten Gleichberechtigungen isfc es
hinreichend, die drei Wurzeln [1, 2], [1, 4], [4, 5] zu betrachte^. Wir bilden
zu diesem Zwecke erstlich den Steinersphen Komplex:
(4) [2, 8] [1, 2], [3, 8] [1, 3], [4, 8] [1, 4], [p, 8] [1, 5], [6, 8] [1, 6], [7. 8] [1, 7],
der den Typus (14) S. 381 hat. Aus (3) liest man ]inmittelbar ab, in
welche Wurzeln die seclis Wurzeln [2, 8], [3, 8], •••, [7, 8] durch S
übergeführt werden. Der aus (4) entstehende Koipaple^^ enthält jedenfalls
die Wurzeln [4, 8], [5, 8], [6, 8], [7, 8] in den vier letzten Paaren von
394 HI, 2. Doppeltangenten ebener Kurven vierten Grades.
Wurzeln. Mithin hat er wieder den Typus (14) S. 381, und man stellt
daraufhia leicht fest, daß man zu:
[3, 1] [3, 8], [2, 1] [2, 8], [4, 8] [1, 4], [5, 8] [5, 1], [6, 8] [6, 1], [7, 8] [7, 1]
gelangt, also wieder zum Komplex (4) zurück. Somit transformiert die
Permutation S die Wurzel [1, 2] in [3, 8] und die Wurzel i;i, 4] in sich
selbst. Wir betrachten zweitens den Komplex:
(o) [1, 8] [1, 4], [2, 8j [2, 4], [3, 8] [3, 4], [5, 8] [5, 4], [6, 8] [(5, 4], [7, 8] [7, 4],
die den Typus (14) S. 381 besitzt. Wie soeben finden wir leicht, daß
wir bei Ausübung der Permutation S aus (5) den folgenden Komplex:
[2, 3] [1, 4], [3, 1] [2, 4], [1, 2] [3, 4], [5, 8] [6, 7], [6, 8] [5, 7], [7, 8] [5, 6]
erhalten, der den Typus (13) S. 381 besitzt. Durch S wird hiemach die
Wurzel [4, 5] in [6, 7] übergeführt. Unter Zusammenfassung haben wir
für S die Darstellung:
(OS e_ /[l'^L [1,4], [4,5], ...^
^^ ~ U3, 8], [1, 4], [6, 7], ...;■
Das Ergebnis läßt sich unter Berücksichtigung der Gleichberechtigung
der drei Ziffern 1, 2, 3 und derjenigen der vier Ziffern 4, 5, 6, 7 leicht
allgemein aussprechen, wenn wir der Bezeichnung S zur besseren
Charakteristik der Operation (3) in sofort verständlicher Weise die
Zusammenstellung der vier Ziffern 4, 5, 6, 7 als Index anhängen. Durch die
Bezeichnung Si^ 5^ 6,7 ist die fragliche Permutation dann eindeutig bestimmt.
Die Reihenfolge der vier Indizes ist natürlich gleichgültig, und wir
erhalten alle 35 Permutationen S, wenn wir aus der Ziffernreihe
1, 2, 3, ••-, 7 die 35 Kombinationen zu vieren herausgreifen. Wir lesen
aus (3) und (6) gleich folgendes allgemeine Ergebnis ab: Durch eine
Permutation Sa^, a^, a^, «^ w«^ö! die einzelne Wursel [^it, v] in sich selbst
übergeführt, falls nur eine der Ziffern ^, v im Quadrupel a^, a^, Wg, «^
auftritt; finden sich beide Ziffern ^, v im Quadrupel a^, a,, «3, «^ oder
Lvmmt in diesem keine der Ziffern a, v vor, so geht [(i, v] in [[i', v'] über,
tco fi, V, fi', v' jenes Quadrupel ist oder die vier übrigen unter den acht
Ziffern darstellen. Hieraus ergibt sich sogleich weiter: Alle 35
Permutationen S haben die Periode 2. Die Gesamtgruppe ®36-8! ^^^^ erzeugen
wir nun einfach durch Hinzunahme der 35 Nebengmppen zum Teiler ©g»:
(7) @,6.8! =r @g; + SW-@8,-f S(2)-@8!-i-... + S(35).@8!,
WO wir die 35 Permutationen S der Kürze halber durch obere Indizes
imterschieden haben.
Um ein paar weitere noch zu benutzende Formeln aufzustellen, ist
es zweckmäßig, die Permutation S4 5 g 7 auch durch S^ .3 3 g darzustellen,
indem wir die anderen vier Ziffern als Indizes benutzen. Wir verfahren
auch bei einer beKebigen Permutation Sß.^^ a^^ «3, «^ so, wobei dann also
in der zweiten Darstellung der Permutation immer die Ziffer 8 als Index
Erzeugung der Gruppe deip DoppeltangenteAgleichung. 395
auftritt. Auch bei dieser neuen Darstellung ist die Reitienfolge der
Ziffern im Index gleichgültig. Der eben aufgestellte Hauptsatz tiber die
Wirkung der Permutationen S erleidet auch in der Form keipe Änderung
bei Gebrauch der zweite^ Schreibweise unserer Permutationen. Nach
dieser Verabredung köi^nen wir zwßi verschiedene Permutationen
Sa^^ a^^ «3, a^i Sa\, c^, a'^. a' üni^er SO schrcibcfl, daß ihre beiden Indizes
entweder zwei oder drei Ziffej-n gemein habpn. Es wäre ja auch
möglich, daß die beiden Indizes nur einp Ziffer gemein haben. Pann genügt
es aber, die eine Permutation durch die andere zur Verfügung stehende
Bezeichnung zu belegen, um einen der beiden bezeichneten Fälle zu
erhalten, nämlich den, daß die beiden Indizes drei Ziffern gemein haben.
Bei der Verwendung unspres eben gewonnenen iiauptsatze& treten nun
die Indizes 1, 2, 3, ••-. 8 wieder gleichberechtigt auf.
Unter T verstehen wir die Permutation de» Teilers @^t. die der
Permutation:
(8) f^' •^' •^' ^' ^' ^' '• ^)
\ a^. «o, ^'3. «i- «5, «6' "-' "8^
der acht Ziffern entsprich^t. Die Permutation, djie einer Transposition
der beiden Ziffern ^. v zugehört, sei durclfi (it, v) bezeichnet. Wir
notieren dann zunächst in Übereinstimmung mit dem z^j^^eitep der beiden
obigen Sätze:
(y) s.„.. ., ..-V.„«3-, == 1
Weiter merken wir die (rleichung an"-):
(10) T-S,.,. , = K.^.c.,^arT,
aus der hervorgeht, daß die 35 Permutationen S miteinander
gleichberechtigt sind. Es ist nicht nötig, die Richtigkeit der Gleichupg (10)
für alle 28 Wurzeln | durch2uprüfen. Es genügt wegen der
Gleichberechtigung der acht Ziffern, allein die drei Wurzeln j"!, 2(, [1, oj und
1^5. 6] zu prüfen: das Symbol i^it. v\ der erstep Wurzel hat zwei Ziffern
mit dem Quadrupel 1, 2, 3. 4 gemein, das der z^^eitei^ eine Ziffer und
das der dritten keine. Wiederholt zu verwenden hg,t man hier und
sogleich den vorhin aufgestellten Satz über die Transformation der
Wurzeln [;u,, v] durch die Permutation S. Es wird nun in der Tat [1, 2'
sowohl durch die in (10) links wie die rechts stehende Pern^utation
in [wg. a^J transformiert. Desgleichen wiyd [1, 5 übereinstimmend
in [Kj, a.] übergeführt ^nd ^p, 6j in [a., cCg]. Damit steht die
Relation (10) fest.
Bei der Kombination zweier Pern^utationen S brauchen wir, wie
schon bemerkt, nur zu upterscheiden, ob die Indjzes der beiden S drei
Ziffern oder zwei Ziffern gemeinsan^ habpn. In beiden Fällen genügt es.
*) Man erinnere sich, ^aä in syiiit»olischen Prpduktßn vop Gruppenelementen
die Faktorenfolge von rechts nach hnks zu lesen ist.
396 ni, 2. Doppeltangenten ebener Kurven vierten Grades.
ein Beispiel zu betrachten, da die übrigen Fälle als mit ihnen
gleichberechtigt sich entsprechend erledigen. Wir merken die beiden Regeln an:
(11) Si, 2, 3, 5 • Si, 2, 3, 4 = Si, 2, 3, 4 • (4, 5),
(12) S,, 2,5,6 • S,, 2,3,4 = S,, 2,7,8 • 0, 8) • (5, 6) • (3, 4) • (1, 2).
Bei der Regel (11) genügt es, die acht Wurzeln [1, 2], [1, 4], [1, 5],
[1, 6], [4, 51. [4, 6], [5, 61. [6, 7] zu prüfen. Die einzelne unter ihnen
wird in der Tat durch die in (11) einander gleich gesetzten Permutationen
in ein und dieselbe Wurzel transformiert. Auch die letzte Regel (12)
wird man leicht beweisen.
§ 10. Einfachheit der Gruppe der Doppeltangentengleichung.
Um eine Kompositionsreihe der Galois sehen Gruppe ©sg.s! der
Doppeltangentengleichung aufzustellen, gehen wir auf die Zerlegung:
(1) @36.8! = ®Sl+SM.@sl 4-S(2).@3, -f ... ^S(35).@3j
zurück, wo der Teiler ®g< mit der symmetrischen Permutationsgruppe
des Grades 8 isomorph ist. Der Teiler ©gi ^^^ seinerseits einen und
nur einen*) Xormalteuer ©4.71, der mit der alternierenden
Permutationsgruppe des Grades 8 isomorph ist, und gestattet demnach die Zerlegung:
(2) @g, = @,.,j^ f7-@4.7!,
wo U eine Permutation ist, die von einer ungeraden Permutation der
acht Ziffern, z. B. einer Transposition, geliefert wird.
Es sei nun G9„ irgend ein Kormalteiler der Gesamtgruppe, dessen
Ordnung ^a jedoch größer als 1 sein soll, der also nicht aus der
identischen Permutation allein bestehen soll. Der Durchschnitt 1j(®u, ©gl)
ist dann ein Xormalteiler der Gruppe ©gi, der entweder nur aus der
identischen Permutation besteht oder den Teiler ©4.71 enthält. Wir
notieren als ersten Satz: Hat der Normalteüer ©„ außer der identischen
Permutation noch eine weitere Permutation mit ©gi gemein, so enthält er
die Gruppe ©4.7;-
Es liege nun der Fall vor, daß ©„ die Gruppe ©4 .7; enthält. Dann
kommt in ©„ z. B. diejenige Permutation der Wurzeln | vor, die der
dreigliedrigen zyklischen Permutation (6. 5, 4) entspricht. Diese
Permutation der I möge selbst durch das Sjonbol (6, 5, 4) bezeichnet
werden. ©„ enthält als Xormalteiler auch alle mit (6, 5, 4) konjugierten
Permutationen, also z. B. auch:
(3) Si,2,3,5-(6, 5, 4).S,,2,,,5,
da die Permutation S^^ 2,3, 5 die Periode 2 hat. Xach der Regel (10)
S. 395 aber gilt;
Si, 2,3,5 • (6, o, 4). Si, 2,3,5 = Si, 2,3,5 • Si, 2,3,4 • (6, o, 4).
*) NaturKch abgesehen von den Teilern ©^ und ©g! der Gruppe ©gN
Untersuchui^g etwaiger Norn^alteiler der @^g g, 397
Wenden wir auf das Produkt der beiden erste^ Faktoren rechts die
Regel (11) S. 396 an, so weisen wir in @„ auch die Permutation
^1,2,3,4 • (4, 5) • (6, 5, 4) und also, da (6, 0, 4) in ®„ auftritt, a^ch
^1,2,3, 4 • (4, o) nach. Damit kommt in &,, jede Permutation des Systeips:
Sl,2,3,4-(4, 5).®,.,!== S, .2,3,4-((4, 0).@,.,,) = Si,2,3,4-?'?4.7!
vor, wenn wir der Kürze halber die im letzten Gliede def Formel (2)
auftretende Xebengruppe durch das Symbol '^i.'ji bezeichnen.
Dies Ergebnis gestattet eine wesentliche Verallgemeinerung. Wir
verstehen unter T die der Penpautaiion:
(4^ /l, 2, 3, 4, 5, 6, 7, 8\
der acht Ziffern entsprechende Permutation des Teilers ©§,. Dabei
denken wir a^, Wg, «3, a^ willkürlich gewählt und können dann über die
Anordnung a-, «g, a^, Wg des ^iffemrestes immer noch so verfugen, daß
die Permutation (4) nach Wunsch gerade oder ungerade ausfällt, also T
in ©4.7! bzw. 9^4.7! enthalten ist. Wahlen wir eine gerade Pen>iu-
tation T, so gilt:
r-i.9^4.7! = 9^4.7',
und da Si^ 2,3, 4 • 9?4.7' ^^^ T in ©„ auftreten, so findet sich in @„ auch
das ganze Permutationensystem:
(5) T-S,,2,3,4-T-i.9^4.7. = S.,.,, .3, .,.9^4.7!.
Die rechte Seite dieser Grleicbung entsteht aus der jinken auf Gri^nd
der Regel (10) S. 395.
Auch die Permutation:
Sl,2,3,4-(4, 6)-(3, 5).S,,2,3,4
gehört als mit (4, 6) • (3, 5) konji^giert den). Xormaltßiler ©„ an. Auf
Grund der Regel (10) S. 395 köi^nen wir diese Perpiutaiion ^uch so
schreiben:
Sl,2,3,4-Sl,2,^,6-(4. 6). (3, 5).
Formen wir weiter mit der Regel (12) S. 396 um, so gelangen wir zu
der Gestalt:
Si, 2,7,8 • (7, 8). (3, 4). (5, 6). (1, 2) • (4, 6) - (3, 5)
= Si,2,,,8-(1, 2)'(3, 6)-(4, 5)-(7. 8).
Da die hier rechts mit Si^ 2,7, s multiplizierte Perm^tatiofi dei' | von
einer geraden Permutation der acht puffern herrührt ur^d also dem
Teiler @„ angehört, so finden sich auch Si, 2,7, s "^d damit alle
Permutationen des Systems:
(6) Si,,,7 8-®4.7!
im Xormalteiler ®„. Wie wir nun yorhi^i aus de^i Auftreten von
-Si, 2 3 4 •9'?4.7! in ®u sphlossen, daß sich überhaupt jedes System
Sß^, ß2, ß3, a4"^^4-7! ^^ ®f' findet, so ergibt sich jetzt, daß mit dem
398 III, 2. Doppeltangenten ebener Kurven \ierten Grades.
System (6) die gesamten Permutationen des Systems -S^^, ß,, «3, ß^ • ®4.7;
in @ti vorkommen, wo a^, ag, %? «4 irgend ein Quadrupel von Ziffern
der Reihe 1, 2, •••, 8 ist. Fügen wir das System (5) hinzu, so haben
wir in @„ das System;
also jede der Xebengruppen in (1) rechts nachgewiesen. Mit Si^ 2, s, 4 • ^s:
kommt auch Si^ 2,3, 4 selbst und damit auch:
K 2, 3, 4 ■ (Si, 2. 3, 4 • ®8!) = (Sl, 2, 3, 4 • ^i, 2, „, 4) ' ©8! = @8!
vor; ®,t ist also die Gesamtgruppe. Unter Hinzunahme des ersten Satzes
folgt als zweiter Satz: £m Normalteihr- @„, der mit dem Teiler ©gi aii^ßer
der identischen Permutation noch mindestem eine weitere Permutation
gemeinschaftlich hat, ist mit der Gesamtgruppe identisch.
Soll ein von @^ und (^36.8' verschiedener Xormalteiler ©„ existieren,
so müssen dessen Permutationen, abgesehen von der identischen, durchweg
den 35 in (1) rechts stehenden Xebengruppen angehören. Irgend eine
Permutation S^^, c.,, «3, «^ kann aber nicht in ©„ auftreten. Da nämlich
diese 35 Permutationen zufolge (10) S. 395 alle untereinander konjugiert
sind, so treten im Xormalteiler ©« mit einer alle 35 auf. Dann muß
sich auch die Permutation:
Si, 2,3,4 • ^1,2.3.5 • -^'1 2,3,4 = (4, 0)
finden ivgl. (11) S. 396j. Diese aber gehört der Gruppe (^gj an, was im
Widerspruch zu der jetzt gültigen Voraussetzung ist.
Es müJßte demnach in @« eine Permutation:
auftreten, wo V eine nicht identische Peimutation de& Teilers ©g! ist.
Dann aber findet sich im Xormalteiler O^« auch jede mit (7) konjugierte
Permutation:
(8) {T-^-^a,.a,,a,,a,-T)-^T-^.V.T).
Wir können nach (10) S. 395 die Permutation T aus dem Teiler @gi
derart wählen, daß die in der ersten Klammer unter (8) stehende
Permutation gleich Si^ 2^ .3^ 4 wird. Die zweite Klammer umschließt eine
nicht identische Permutation des Teilers @gi. die U genannt werde und
der nicht identischen Ziffernpermutation:
^9) /l, -2, 3, 4, 5, 6, 7, 8^
V«i, «2' "35 «4' «5' «6' «7' "■&'
entspreche. In der oberen Reihe (9) findet sich mindestens eine Ziffer i,
fur die a, nicht gleich i ist. Diese Ziffer / kommt in einem der beiden
Quadrupel vor:
(10) 1, 2, 3, -i, 5, 6, 7, 8.
Im gleichen Quadrupel stehen noch drei Ziffern, von denen mindestens zwei
von «j verschieden &ind. Eine von diesen beiden, die h genannt werde,
Eintachheit der Gruppe der Doppeltangentengleichuag. 399
wählen wir aus und halfen dann sicher in (/. Ti) und (a^, a^.) zwei
verschiedene Permutationen, da a^ weder gleich i nocli gleich fc ist. Aus (9)
folgern wir:
(11) r,(i, ;o-r-i = (o,, a,.).
Xeben S^^., 34- U gehören auch die Permutationen :
dem Kormalteiler an, deren erste z|i S-^^ 2 3,i-'C invers ist. während die
zweite mit dieser Substitution konjugiert ist. Iin Xormalteilei findet
sich also auch:
U-'-S^,,.s.,-(i, k)-S^,,,s,,-U.(i, k)
und damit auch:
(1-^) S,, 2.3, 4 • (^ k) • Si, a, 3, 4 • ^^- (^ ^^-) • U-\
Xach (10) S. 395 gilt:
da die Ziffern t, 7. einem |ind demselben Quadrupel (10) angehören. Die
Permutation (12). die in ©„ auftritt, läßt sicl^ also auch so schreiben:
(*•. k) (Si, 2,3,,)' • V- {% f^ ■ ^J~' = (h k) • (U- (i, k). C-1) = (^ /.). («„ «,)
und ist. da (i, k) z^ (a^, 0^^ gilt, e|ne n^icht identische Permutation des
Teilers ©gi- Damit sind wir aufs neue zu einem "Wi4erspiuch geführt.
Es gilt also der Satz: Es gibt in der Gialotsbchen Gruppe der TJoppßl-
tangentengleicJiung keinen von der ®^ vert^cJüedßnen echten Normalteder, 00
daß diese Gruppe @36. gi einfacji ist.
Die Grundsätze der Galois sehen Theorie (vgl. I, 383 ff.) liefern also
hier keine Erleichterung von der Art. daß ^vir die Lößung der Poppel-
tangentengleichung auf eine Kette von Lösungen mehrerer Resolventen
mit Galois sehen Gruppen geringerer Ordnungen zurückführen könnten.
Insbesondere ist also eine Lösung mit Hilfe zyklischer Gleichungen ai^s-
Übrigens müssen die geraden Perrnjitationen der Wurzeln |, die in
der Gruppe ©sb.g' enthalten sind, notwendig einen Xorm^lteiler
derselben bilden. Da das Quadrat jeder Permutation eine gerade
Permutation ist, und in der ©36.3' Permutationen mit Perioden, die ^ 2 sind,
auftreten, so ist jener Xormalteiler mit der Gesamtgruppe gleich. Wir
notieren also noch den Satz: Die Galoisbche Gruppe der DoppeJtangerden-
gleidmng 28^^'"' Grades ist in der ßltern^erenden Fermutationsgruppe deb
Grades 28 als Teiler mthalten, bo dßß die Diäkrimi,naMe jener Gleichung
in dem zugrunde liegenden Korper ein reifies Quadrat darstellt.
400 III. 2. Doppeltangenten ebener Kurven vierten Grades.
§ 11. Transitivität der Gruppe der Doppeltangentengleichung.
Die Galois sehe Gruppe der Doppeltangentengieichung ist sicher
transitiv; denn es gibt bereits im Teiler ©gi ^^^^ Permutation, die die
Wurzel [1, 2] in eine beliebig vorgeschriebene Wurzel [fi, v] überführt.
Soll die Gruppe mindestens zweifach transitiv sein, so ist hierfür
hinreichend und notwendig, daß es unter den Permutationen, die [1, 2] in
sich überführen, eine gibt, die die Wurzel [1, 3] in eine beliebig
vorgeschriebene von [1, 2] verschiedene Wurzel [fi, v] überführt. Nun geht
[1, 3] durch die Permutation (1, 2), die [1, 2] in sich überführt, in die
Wurzel [2, 3] über. In ©g' aber sind weiter Permutationen enthalten,
die [1, 2] unverändert lassen und [1, 3] in [1, 4], [1, 5], [1, 6], [1, 7], [1, 8],
die Wurzel [2, 3] aber in [2, 4], [2, o], [2, 6], [2, 7], [2, 8] überführen.
Im Teiler, der [1, 2] unverändert läßt, ist also [1, 3] sicher mit allen
Wurzeln [1, v] und [2, v], abgesehen von [1, 2], verbunden (vgl. I, 332).
In diesem Teiler tritt auch eine Permutation auf, die das erste der beiden
Siebensysteme:
[1, 2j, [1. 3], [1, 4], [1. 5J, [1, 6], [1, 71, [1, 8],
[1, 2], [4, 5J, [3, 4], [3, 5], [1, 6], [1, 7]. [1, 8]
in das zweite überführt, so daß [1, 3] mit [4, o] verbunden ist. Endlich
ist [4, oj bereits im Durchschnitt des fraglichen Teilers mit der Gruppe
(^)8! mit allen [fi, v] verbunden, an denen die Ziffern 1 und 2 nicht
beteiligt sind. Dreifach transitiv kann die ©se . g) nicht sein; denn es kann
kein syzygetisches Wurzeltripel durch eine ihrer Permutationen in ein
azygetisches übergeführt werden. Die G-aloissche Gruppe @36-8! ^ß»'
Doppeltangentengieichung ist genau zweifach transitiv.
Adjungiert man eine einzelne Wurzel der Doppeltangentengieichung,
so genügen die 27 übrigen Wurzeln einer Gleichung, deren Koeffizienten
dem erweiterten Körper angehören. Ihre Galois sehe Gruppe ® aber ist
der Teiler der ©se.gi, der im Sinne von I, 378 ff. zur adjungierten
Wurzel gehört, also aus allen Permutationen der ©^g - s! besteht, die die
adjungierte Wurzel unverändert lassen. Diese Gruppe @ ist für die
übrigen 27 Wurzeln, wie wir sahen, noch transitiv, so daß die Grleich/ang
2'ji-un G-yades im erweiterten Körper irredmihel ist [vgl. I, 373]*).
*) C. F. Geiser hat in der Abhandlung „Über die Doppeltangenten einer
ebenen Kurve vierten Grades", Math. Ann. Bd. 1, S. 129, den Satz aufgestellt,
daß eine ebene Kurve vierten Grades stets als Schnitt eines Tangentenkegels
aufgefaßt werden kann, der von einem Punkte einer Fläche dritten Grades an
diese Flache laufe. Hieraus ergibt sich ein interessanter Zusammenhang zwischen
den 28 Doppeltangenten der Kurve mit den 27 Geraden der Flache dritten Grades.
Aus diesen Entwicklungen kann man den Schluß ziehen, daß die Gabis sehe
Gruppe der Gleichung 27sten Grades, von der die Losung des Problems der 27
Geraden auf der Flache dritten Grades abhängt, isomorph ist mit der Gruppe der im
Texte betrachteten Gleichung 27sten Grades.
Zweifache Transitivitat der Gruppe @36 b<- 401
Adjungiert man zwei Wurzpln, so gestalten sieb d^e Verhältnisse
anders. Die Galois sehe Gruppe der übrigbleibenden Gleichung 26sten Grades
ist in der Tat intransitiv, so dßß diese Gleichung redumhel wird. Es
spaltet sich ein Faktor zehnten Grades ab, der gleich 0 gesetzt die schon
unter (8) S. 390 gewonjiene Gleichung:
(1) ^(|) = 0
zehnten Grades mit Koeffizienten des durch dip Adjunktion cfer beiden
Wurzeln erweiterten Körpers liefert. Die zehn Lösungen geben
diejenigen Wurzeln, die mit den beiden adjungierten Wurzein syzygetische
Wurzeltripel bilden.
Wir weisen endKcli noch auf die oft genannte Gruppe ©gi liin, die
als Teiler der Galois sehen Gruppe ^ze ■ i,\ den Index 36 hat. Diese
Gruppe ist einfach transitiv. Es ist nämlich die Wurzel [1, 2^ durch
die ®8! noch mit allen Wurzeln [^. v] verbunden. Durch den zu ^1, 2^
gehörenden Teiler von ©g, ist aber z. B. die Wurzel [1, 3] nicht mit
[4, 5] verbunden, so daß nur noch einfache Transifcivität vorliegt. Man
verstehe nun unter a?^, x^, •••, x^ die acht Wurzelprodukte;
( x^ = [1, 21 -[1,3]. ^1, 4j. [I. 5] • :i. {\ ■ X 7] • [1, 8;
(2) X., r= [2, 11. [2, 3]. [2, 4, - [2, 51. ^^2, 6] • 2. 7 • [2, 8j.
Die symmetrischen Funktionen dieser ^cht Produkte sind Funktionen des
Teilers ©gi- Als solche sincl sie nach dem Lagrangeschen Satze (I, 379)
in einer zweckmäßig gewählten, zur ©g; gehörenden Funktion rational
darstellbar, die ihrerseits die Lösung einer Gleichung 36^'«" Grades mit
Koeffizienten des ursprünglich zugrunde gelegten l^örpers ist. Xach
Adjunktion der fraglichen Wurzel dieser Gleichung werden die acht
Größen (2) die Lösungen einer affektfreien Gleichung achten Grades mit
Koeffizienten des eben erweiterten Körpers.
§ 12. Realität der Doppeltangenten bei reellen Kurven vierten Grades.
Die Gleichung unserer doppelpunktfreien Kurve vierten Gr&des habe
jetzt reelle Koeffizienten, so daß der zugrunde liegende Z^hlköj-per reell
ist. Mit jeder komplexen IjösuE|:g | der Doppeltangentengleichung ist
dann auch die zu | kopjugiert komplexe Zahl | eine Lösung der
fraglichen Gleichung, so daß die nicht reellen Doppeltangenten eüiander zu
Paaren konjugiert sind. Für drei syzygetische Doppeltangenten ist die
Gleiehung (8) S. 390 charakteristisch, deren Koeffizienten jptzt reell sind.
Es wird demnach irgend ein syzygetisches System von Doppeltangenten
oder Wurzeln | der Doppeltangentengleichu^g wieder ein solches System
liefern, wenn wir alle Wur:?eln ^ zugleich durch ihre konjugierten
ersetzen. In derselben W>.ise folgt aus einem azygetischen System natür-
lieh wieder ein azygetisphes.
Fricke. Algebra. II. ' 26
402 III, 2. Doppeltangenten ebener Kurven vierten Grades.
Um nicht bei Betrachtung von Steiner sehen Komplexen das Wort
„komplex" in doppeltem Sinne zu gebrauchen, sprechen wir besser von
„konjugiert imaginären" Doppeltangenten oder Wurzeln der
Doppeltangentengleichung. Ein Steiner scher Komplex K liefert nun bei Ersatz
aller seiner Wurzeln oder Doppeltangenten | durch ihre konjugiert
imaginären I wieder einen Komplex, Ist dieser zweite Komplex mit dem
ersten identisch, so bezeichnen wir K als einen „reellen Komplex^; im
anderen Falle sprechen wir von einem Paar „Jconjugiert imaginärer
Komplexe" und nennen den einzelnen einen „imaginären Komplex". In
einem reellen Komplex kann niemals eiae reelle Tangente | mit einer
nicht reellen rj gepaart vorkommen. Der Komplex würde sonst neben
dem Paare |, rj das Paar |, rj enthalten, während doch zwei Paare eines
Komplexes nie eine Doppeltangente gemein haben. In einem reellen
Komplex sind also entweder zwei reelle Tangenten gepaart oder eine
imaginäre I mit ihrer konjugierten |, oder drittens zwei nicht konjugierte
imaginäre Tangenten |, rj. Im dritten Falle tritt in dem gleichen
Komplex dann auch das zu |, r] konjugierte Paar der Doppeltangenten
I, ^ auf.
Auch eia Aronhold sches Siebensystem, das wir symbolisch durch A
bezeichnen wollen, geht bei Ersatz aller sieben Doppeltangenten durch
ihre konjugiert imaginären wieder in ein Siebensystem Ä über, das wir
als zu A konjugiert bezeichnen. Gilt A = A, so heißt A „reell"
anderenfalls „imaginär". In einem reellen Siebensystem ist immer eine
ungerade Anzahl von reellen Doppeltangenten enthalten, mindestens
also eine.
Wir behandeln zunächst die Frage, ob alle 28 Doppeltangenten
imaginär sein können. Trifft dies zu, so wählen wir irgend ein Paar
konjugiert imaginärer Tangenten |, | und setzen eine dritte
Doppeltangente rj hinzu, die mit dem Paare |, | ein azygetisches Tripel bildet,
und die der Annahme gemäß gleichfalls imaginär ist. Der zum Paare |, jy
gehörende Steiner sehe Komplex K kann | nicht enthalten (da sonst |, r], f
ein syzygetisches Tripel darstellen würden) und ist demna,ch von seinem
konjugierten Komplex K verschieden, also nicht reell. Wir schreiben :
(^) 1.»?. tvVl^ l2''?2. l3.'?3. ti,Vi> lö.'^ö.
(K) 1,^, li,^,, la,^, 13,^3, 1^,^^, \,%>
wo, wie immer, f^ zu 1^ und 7}v zu rj^ konjugiert imaginär ist.
Ein solches Paar ist nun entweder syzygetisch oder azygetisch (vgl.
S. 372). Im ersten Falle haben K und K vier Doppeltangenten gemein,
während die übrigen 16 Doppeltangesten durchweg verschieden sind. Die
vier je zweimal auftretenden Tangenten bilden in K und ebenso in K zwei
Paare; die beiden Paare von K gehen durch Austausch zweier Tangenten
in die Paare von K über. Nun kommt aber, wie wir schon wissen,
Unmöglichkeit von lanter imaginären Doppeltangenten. 403
I nicht ia K und eben deshalb | nicht in K vpr. Also sind die Paare
I, 71 und f, ^ nicht an den zweimal auftretenden Tangenten beteiligt Da
die fünf letzten Paare in K noch belie]3ig umgeordnet werden können, so
nehmen wir an, daß Id »^j, I3, Jjg ^ip zweimal auftretenden Tangenten
sind. Wir fragen, ob eine dieser Tangenten, die wir etwa an die erste
Stelle gesetzt denken ui^d also |^ nennen, i^nerhalb K in eiaem der drei
letzten Paare stecken Ijönnte. Wir denken dann die Tangente sq
geordnet, daJ3 I3 = |j zutrifft. Dann wäre aber auch I3 -= li, so daß
auch das vierte Paar l^^ t}^ der Annahme entgegen ^n den doppelt
auftretenden Tangenten beteiligt wäre. Hieniach müssen die Tangenten
li' *?!) lä' '^a» ^^^ ^^^ Reihenfolge abgesehen, mit de|i Tangenten |j, ^j,
I2, ^3 identisch sein. Es kann aber nicht |^ = \ seia, weil keine reelle
Tangente vorkommen sollte. Es kann auch nicht |j = ^^ ^eia, weil
sonst 7^1 = Ij, wäre, wqraus K = E folgen würde. Es kani^ drittens
nicht 1^ = I2 sein, weil sonst da,s zweite ynd dritte Paar von K durch
Austausch von |^ und 1^ in f^as zweite und dritte Paa,r voi^ E iiberginge,
also 'jji = ^1 lind damit reell wäre. Zu dem gleichen Ergebnis würde
die vierte Annahme |j = rj^ führen. Diese Überlegung zeigt, daß
überhaupt das Auftreten zweier syzygetischer, einapder konjugierter
Komplexe mit der Voraussetzung ausschließlich imaginärer Doppeltangeiiten
unvereinbar ist.
Es bleibt nur die Möglichkeit, das Paar iJT, K als azygetisch
anzunehmen. Das einzelne Paar enthält dani]L eine Tangente, die auch im
anderen Komplex auftritt, während die zweite Tangente dort sich nicht
findet. Nun tritt aber | üqa zweiten Komplex K nicht auf. E^ ist
nämKch | als imaginär von | versphieden; es ist femer | ::^ ^, da sonst
K = K wäre; es ist endlich | in keinem der letzten fünf Paare vop K
enthalten, da |, rj, | ein azygetisches Tripel ist. Also kommt rj iji K
vor (natürlich nicht im ersten Paare), i^nd wir können die Anordnung so
treffen, daß vj 7= rj^^ und dann anch rj^ = r} i^t. Yom dritten Paare
I2, 7]^ nennen wir die auch in E auftretende Tangente rj^- Pa die beiden
ersten Paare schon vergriffe^ sind ui|d r}^ offenbar wieder nicht im
Paare Ig, ^3 vorkommen kann, so dürfefi wir 1^2 = Vs "^^ dann rj^ = j^g
setzen. Unsere beiden J^ompiexe lauten also:
W IV' li.i l2'%' lä)^. •••.
(^) lv> lvV> la.^s. l3.'22. ••••
Man bilde nun die beiden Koipplexe:
m iv., ••••
Diese Komplexe sind voneinander verschieden. Es ist nämKch rj weder
gleich ri noch gleich rj2', auch kann 7} in keinem anderen Paare von K'
404 HI, 2. Doppeltangenten ebener Kurven vierten Grades.
vorkommen, da sonst das Tripel ij, rj, rj^ syzygetisch wäre, während doch
diese Tangenten in drei verschiedenen Paaren von K auftreten und also
nach S. 368 ein azvgetisches Tripel liefern. Auch rj^ kommt in K' nicht
vor, da auch das Tripel rj, rj^, ^2 azygetisch ist. Hiemach bilden K' und
K' ein Paar konjugierter „syzygetischer" Komplexe, und mit dem
Auftreten eines solchen Paares ist, wie wir bereits wissen, die Annahme
ausschließlich imaginärer Doppeltangeuten unvereinbar. Diese Annahme
ist also unhaltbar. Da wir nicht eine ungerade Anzahl imaginärer
Doppeltangenten haben können, so folgt als erster Satz: Unter den
28 Do^peltangenten sind immer mindestens zwei reell.
Es soll nun bewiesen werden, daß immer mindestens vier reelle
Doppeltangenten auftreten. Wir bezeichnen die beiden sicher
existierenden reellen Doppeltangenten durch x und y^) und bilden den zum Paare
X, y gehörenden reellen Komplex K. Die fünf übrigen Paare von K sind
entweder reell, oder das einzelne dieser Paare ist sich selbst konjugiert
wie I, I, oder sie sind einander zu zweien konjugiert wie |, rj und |, rj.
Da die Anzahl 5 ungerade ist, so findet sich mindestens ein Paar, das
entweder reell oder sich selbst konjugiert ist. Ist das Paar reell, so
haben WT.r unter Hinzunahme von x, y ein syzygetisches System von
vier reellen Doppeltangenten, und dann ist unsere Behauptung bereits
bestätigt. Wir haben also anzunehmen, daß ein Paar |, | auftritt, und
bilden dann das syzygetische Komplextripel:
(A',) r,y. 1,1, ....
Ä) ^,t, y-l li-^i, ••-
Da K^ und K^ konjugiert sind und außer x, |, y, | gemeinsame
Doppeltangenten nicht aufweisen, so sind alle weiteren in K^ und K^
auftretenden Doppeltangenten |^, ?^^, •.• imaginär. Man bilde weiter die beiden
einander konjugierten Komplexe:
(A's) ^.§\, Im- •••'
(Jq ^,i„ 1,^1' ••••
Die Doppeltangente y tritt nicht in Ä'g auf und damit auch nicht in K^,
da sonst x, |, y nach S. 368 ein azygetisches Tripel bilden würden, was
dem Komplex A', widerspricht. Aus demselben Grunde kann wegen K^
die Doppeltangente | nicht in iCg und | nicht in K^ auftreten.
^Sind nun erstlich die beiden Komplexe K^. K^ syzygetisch, so muß |j
in iCg vorkommen und |^ in Z3; und zwar sind dabei nach der Bauart
syzygetischer Komplexe |^ und |^ mit einer und derselben Doppeltangente
*) Reelle Doppeltangenten mögen bei den nächstfolgenden Entwicklungen
durch lateinische Buchstaben, imaginäre aber durch griechische gekennzeichnet
werden.
Unmogliclikeit von nur zwei reellen Doppeltapgenten. 405
gepaart, die sich selbst konjugiert, also i-eell ist i^nd s heiße, piese
Tangente s ist von x und 2/ verßchieden und piuß in K^ auf^reter)., da
nach S. 373 die Komplexe K^, K^, K^ alle 28 Doppeltangenten enthalten
und Zg, Zg außer x, y, wie wir wissea, ni^r imaginäre Doppeltangenten
aufweisen. In K^ ist 2 mit einer reellen Doppeltangente t gepaart, so
daß wir im fraglichen Falle zweier s^zygetischer Komplexe li^, K„ ein
syzygetisches Quadrupel reejler Doppeltang enteil j,. //, z, ^ nachgewiesen
haben.
Nun können aber auch die l^omplexe K^, K. ein azj-getisches Paar
bildeil. Dann tritt |^ nicht in ^3 a^f. Da a]ich, wie ^r schon
feststellten, I in JSTg nicht vorkommt, so findet sictf tj^ in JST^. Die mit ?^^
in K^ gepaarte Doppeltangente tritt dann nicht in K^ auf und ist also
imaginär; wir nennen sie ^^. Tritt nup in den drei letzten Paaren
überhaupt noch eine reelle Tangente auf, so ist sje weder gleich x noch
gleich y. Sie heiße z und führt genau wie oben z^ einem in K^
enthaltenen reellen syzygetischen Quadrupel. Kommen in d^n drei letzten
Paaren von K^ aber nur imaginäre Tangenten vpr, so sei das vierte Paar
von K^ durch I3, 7^3 bezeichnet. Da K^ nicht reell ist, so können |„
und 7^3 nicht konjugiert sein. Ist I3 die auch in K^ auftretende
Doppeltangente, so haben wir:
TO '^''li-' ^'»?i' ^2'^/i' Is.^js- l^n^- •••'
Ä) ^li- Inv Lv,. h,vz- hrn.- ••••
Die beiden letzten Paare 1^, '^. und I5, ^^ müsseii dar^n eine gemeinsame
Doppeltangente haben. Es kann abe;- nicht |^ ==:: ^^ sein, \^reil sonst
1^ == ?^. folgen würde und K^ -— K.^ seir^ müßte. Also ist entweder
I5 == I5 oder rj.^ == rj^. In beiden Fällen tritt also eine reelle
Doppeltangente auf, die wir besser durch z bezeichnen und von der auß wir den
Beweis wie oben zu Ende führen: Unter den 28 Doppeltange'nten Jconpmen
immer mindestens vier reelle vor, die ein syz'ygdisches (Quadrupel bilden.
Ist außer den vier jetzt als existierend erkannten reellen
Doppeltangenten eines syzygetischen Quadrupels mindestens noch eine reelle
Doppeltangente vorhanden, bo läßt sich zeigen, daß acht reelle
Doppeltangenten existieren, die in einem Steine;-sehen Komplexe vier Paare
bilden. Die vier zunächst festgestellten reellen Doppeltangenten des
syzygetischen Quadrupels nepnen wir t, y, v, w und bilden (Jas syzy-
getische Komplextripel:
(K^) x,'t/, 'If- ii\ • ••,
(Zg) x,v, y. w, ••-,
(Z3) ip. w, y,v^ - • •.
Der Beweis der aufgestellte^ Behauptung soll indirekt geführt werden.
Wir nehmen an, daß keiner der drei Komplexe K^, K^, K^ vier reelle
406 III, 2. Doppeltangenten ebener Kurven vierten Grades.
Taijgentenpaare enthalte. Sie sollen also höchstens drei oder nur die
beiden angegebenen reellen Paare enthalten, woraus sich ein Widerspruch
herleiten läßt. Jedenfalls hat einer der drei Komplexe noch ein weiteres
reelles Paar; denn sie enthalten zusammen alle 28 Doppeltangenten, und
eine fünfte reelle Tangente sollte auftreten. Wir dürfen annehmen, daß
K, das dritte reelle Paar p, q aufweist. Dann bleiben in JST^ noch drei
imaginäre Paare. Zwei unter ihnen können konjugiert imaginär sein;
sicher aber tritt ein sich selbst konjugiertes Paar q, q auf, so daß wir K.^
ausführlich:
(K^) X, y, V, w, p, q, q,q, ■•■
schreiben können. Ein beliebiges imaginäres Paar von K^ heiße |, rj:
(K^ x,v. y,w, ^,r], •••.
Dann läßt sich zeigen, daß | und r} nicht konjugiert sein können. Reihen
wir nämlich den zu K^ syzygetischen und zu K^ azygetischen reellen
Komplex:
TO ^'l->' 2/. 2, •••
an, so kommt eine der Tangenten |, rj, etwa |, in K^ vor, die andere, rj
aber nicht. Würde aber rj zn ^ konjugiert sein, so würde mit | auch rj
im reellen Komplex K^ auftreten. Hiemach kann in K^ und, wie wir in
derselben Art schließen, auch in K^ kein sich selbst konjugiertes
imaginäres Paar auftreten. Die imaginären Paare in K^ und K^ sind also zu
je zweien konjugiert, so daß sich in jedem dieser Komplexe nicht drei,
sondern vier imaginäre Paare finden. Man hat demnach sechs reelle und
22 imaginäre Tangenten.
Das azygetische Komplexpaar K^, K^ schreiben wir ausführlicher:
(K^) x,v, y,w, ^.Tj, 1,7}, ••.,
(A',) x,p, y,q, H 1,1, ■•'.
wo ^ nicht in Kc^ vorkommt, also auch nicht gleich | sein kann und, als
mit der imaginären Tangente | im reellen Komplex K^ gepaart, eine
neue imaginäre Tangente darstellt. Der Komplex:
TO l.l. v^v^ ti ■■■
ist mit JTg und K^ syzygetisch und weist demnach keine der sechs
reellen Doppeltangenten x, y, v, w, p, q auf. K^ und die konjugierten
Komplexe:
TO «,l, ^•.^, ]9,t, ■",
TO ' x.l v,^, p,l, ...
bilden ein azygetisches Tripel. Die drei reellen Doppeltangenten y, w, q
treten in JSTg und K^ nicht auf; wir hätten sonst in x, y, p, desgleichen
in V, w, X, endlich m p, q, x azygetische Tripel, was gegen K^ verstößt.
Hiemach ist jeder der Komplexe K^, K^ azygetisch zu K-^. so daß von
Fall von acht reellen Dpppeltangenten. 407
dem in JSTj auftretenden Paare q, q eine Tangente, etwa q, in K^ auftritt,-
die andere, q, findet sich dann in -Kg- Da reelle Tangenten nicht mehr
zur Verfügung stehen, so ist ^ in JSTg i^it einer imaginärep von q
verschiedenen Tangente gepaart, die durch ö bezeichnet werde. Man hat
dann:
TO a;,|. v,ri, p,^, q,6, 6,z, •••,
TO ^'i' *'''^' P>i 9'^' <5'^' •••'
wo r und r konjugiert imaginäre Tangenten sind. Jet:?t bleibt nur npch
ein Paar imaginärer Tangenten %, l in iJTg und das konjugierte Paar jc, \
in JSTg. Damit aber tritt der Widerspruch zutage. Eine der beiden
Tangenten %, l, etwa die an die erste Stelle gesetzte Tangente y,, muß
auch im Paare ji, X auftreten. Da aber y, nicht gleich yc ist, sp würde
y =1 A und also l =2 % folgen, d. h. es wäre JSTg entgegen dßn Tatsachen
reell. Damit haben wir folgenden zweiten Satz gewonnen: Kommt außer
dem sysygetischen Quadrupel reßller Doppeltangenter(> noch mindestenb eine
fünfte reelle Do;ppeltangente vor, so treten mindestens acht reelle
Doppeltangenten auf, die in einem Steiner sehen Komplexe vier reelle Paare bilden.
Wir gehen wieder einen Schritt weiter und prüfen, welche
Folgerungen gezogen werden können, wenn in einem Kpmplex:
TO «i>2/i> «2'%' ^3>2/^> '^i^yii «^>2/5> •••
mindestens fünf reelle Paai'C Xy, y^ enthalten sind. Es läßt sich beweisen,
daß dann alle 28 Doppeltangenten reell siad. Tritt zupächst, abgesehen
vielleicht vom letzten Paare des Komplexes K^, nocl^ mindestens ein
imaginäres Paar |, | auf, so ist der dijrch dieses Paar erldärte reelle
Komplex K^ syzygetisch zu Z^; dßnn keine Tangente des Paayes |, |
kommt in K^ vor. K^ und K^ haben demnach vier Tangenten, die sowohl
in Zj wie in K^ zwei Paare bilden, gemeinsam. Hieran kann das letzte
Paar von JST^ nicht beteiligt sein, weil son^t im reellen Komplex K^^
imaginäre Doppeltangenter). mit reellen gepaart wä,ren. Wir denken die
Bezeichnungen der Doppeltangenter). x, y so verteilt, daß K^ gegeben
ist durch:
TO ^i>»2> Vi^y^i l>l----
Man ergänze K^ durch die beiden einander konjugierten Komplexe:
(^3) ^rl> ^"2>l, •••>
TO «i>l> »2>l. •••
zu einem syzygetischen Tripel. Außer den vier eben namhafip gemachten
Tangenten x^, x^, |. | haben K^, K^ keiae Tangenten gemeinsam. Die
16 übrigen Doppeltangenten von K^ und K^ sind also imagiaär. Das
ist aber nicht möglich, da Zg zu K^ azygetisch ist und also noch drei
von den sechs reellen Tangenten x^, y^^, x^, y^, x^^ 2/5 enthalten muß.
408 ^^■> -• Doppeltangenten ebener Kurven vierten Grades.
Die Annahme der Existenz aucli nur einer einzigen imaginären Tangente ^
außerhalb K-^ ist demnach unhaltW.
Es könnte nun aber noch K^ die Gestalt haben:
(K^) x^,y^, »2,2/2, ^^,^3, x^-y^, x.,y'o, n^n-
Aber auch dies ist abzuweisen; denn der mit K^ syzygetische Komplex:
könnte nicht reell sein und hätte doch vier reelle Paare, da nur noch
reelle Doppeltangenten verfügbar sind. Es gilt also der dritte Satz:
Kommen in einem Steiner sehen Komplexe fünf Paare reeller Doppeltangenten,
cor, bo sind alle 28 Doppeltangenten reell.
Wir nehmen endlich an, daß mehr als acht, aber nicht alle
Doppeltangenten reell seien. Dann können wir von folgendem syzygetischea
Komplextripel ausgehen;
(-STi) ^1,2/1, »2,2/2, »3,2/3, »4,2/4, •••,
(Z,) »^.»2, y^.y,, z^,^^_,
Xach dem vorletzten Satze existiert nämKch ein Komplex K-^, der dann
noch zwei imaginäre Paare enthält, da nicht alle 28 Doppeltangenten
reell sein sollen. Da das Tripel JST^, K^, K^ alle 28 Tangenten enthält,
so kommt die neunte reelle Tangente s^ in K^ oder K^, etwa in K^, vor
und ist dort mit einer zehnten reellen Tangente 2^ gepaart. Man bilde
den mit K^ syzygetischen Komplex:
{K^) »,,^'j, »2,^2, ...,
der mit K.^ azygetisch ist. da zwar »^, aber nicht z^ in K^ vorkommt.
iQ muß also aus den Paaren »3, y^ und x^, y^ von K^ je eine
Doppeltangente enthalten, etwa ». und »^, so daß wir zu schreiben haben:
(K^ »1,5^1, »2,-'',, -i^z^^z, x^,^i, ••'•
Die beiden Doppeltangenten 0^, z^ treten nicht in dem zu K^ azygetischen
Komplex K^ auf. Sie kommen aber auch nicht in K^ vor, da K^ und K^
syzygetisch sind und schon die vier Tangenten »,, »g, ^j, z^ gemein
haben. Also kommen ^3, ^^ in K^ vor. wo sie indessen kein Paar bilden.
Es wäre ja sonst »j, ^3, z^, zuwider dem Komplex JST^, ein syzygetisches
Tripel. Somit hat K^ die Gestalt:
(A3) ^1-2/2, %,i/i, ^3-^3, -^4,^4, "■
mit zwei weiteren reellen Tangenten ig, t^. Die vier noch fehlenden
aber sind gemäß der Voraussetzxmg imaginär.
Wiederholen wir jetzt diese Überlegung für das Tripel:
(^"1) -^i'i/i. *2>2/-2> ^3.^3> «4.^*> •••,
(Z; = Z3) »j,2/2, »2,«/i, ^3,^3,
Vier mögliche Falle reeller Doppelt^ngenten. 409
so finden wir, daß auch K^ vier Paare reeller Dpppeltangenten aufweist.
Also haben wir als vierten Saifcz: Sind r^ehr (üs aeht reelle Doppeltangentm
vorhanden, ohne daß oTle 28 reell sind, so hat man 16 reelle
Doppeltangenten, die in den drei Komplexen ßines byzygdiscfien 'J'ripels je vier
reelle Paare ausmachen.
Hiermit sind alle Möglichkeiten erschöpft. Wif fassen d:^e
Ergebnisse nochmals zusammeifi: Betreffs der Bealität der Doppeltangenten einer
b'mgularitätenfreien ebenen K'urve pierten G-rßdes sind allein folgende vi^r
Falle möglich:
I. Vier reelle Doppdtange/den eineb syzygetiscTten Quadrupel^.
n. Acht reelle Doppeltangenten, die vier Paare eine^. Steiner sehen Xodi-
plexes Mlden.
III. Sechzehn reelle Doppeltangenten, die in den drei Komplexen einet,
sysygelischen Tripels je vier reelle Paare Wden.
IV. Alle 28 Doppeltangenten reell.
§ 13. Existenzbeweis der vi^r F^lle reeller Doppelt^ngenten.
Wir prüfen nunmehr, ob die vier eben als allein zulässig erkannten
Fälle reeller Doppeltangßnten auch wirklich auftreten. Dip Betrachtung
gründen wir auf den Satz (vgl. § 7, S. 382 ff.), daß man fiir ein System
von sieben gewählten Geraden der Ebene durch rationale Rechnungen eine
Kurve vierten Grades zu berechriien imstande ist, für die jene sieben
Geraden ein Aronhold sohes Siebensystem von Doppeltangenten bilden.
Unter den sieben Geraden können auch imaginäre vorkommen. D^mit
aber die Kurvengleichung reell ausfällt, habpn wir zi^ fordern, daß mit
jeder imaginären Geraden, auch ihre konjugierte im System auftritt. Man
hat demnach folgende vier Fälle zu unterscheiden.
I. Eine reelle Gerade und drei Paare konjugiert imaginärer
Geraden.
II. Drei reelle Gerade und z\^ei Paare konjugiert imaginärer
Geraden.
III. Fünf reelle Gerade und ein Paar konjugiert icfiaginärer Geraden.
IV. Sieben reelle Gerade.
Diese vier Falle werden nun gerade gpnau zu den v|,er Fällen am
Schlüsse von § 12 hinführen, womit der Existenz beweis dieser Fälle
geführt sein wird. Man erkennit dies sehr leicht, wenn man sich der
Bezeichnung der Doppeltangenteifi durch sieben Ziffe^Ti bedient, wie wir sie
S. 376 einführten. Wir halten an der ersten Dar stell vmgs^^eise fest, bei
der die sieben Tangenten eines ersten Aronhold sehen Siebensystems durch
je eine Ziffer bezeichnet werden, die 21 übrigen Tangenten aber durch
Ziffempaare. Xur wird es zweckmäßig sein, daß wir durch die Wahl
der Ziffern sogleich kennzeichnen, welcher yon den vier soeben
unterschiedenen Fällen vorliegt. Im Falle I bezeichnen wir also die sieben
410 IIIj 2. Doppeltangenten ebener Kurven vierten Grades.
Tangenten des gegebenen Siebensystems durch 1, 2, 2, 3, 3, 4, 4, im
FaK II durch 1, 2, 3, 4, 4, 5, 5 usw.
I. Es liege nun der erste Fall vor mit dem gegebenen reellen Aron-
holdsehen Siebensystem:
(Ä) 1, 2, 2, 3, 3, 4, 4.
Wir bilden den Komplex K vom Typus (14) S. 381:
(K) 1, [1, 2], 2, [2, 2], 3, [2, 3], 3, [2, 3], 4, [2, 4], 4, [2, 4]
und behaupten, daß der ihm zugehörige konjugierte Komplex durch:
(K) 1, [1, 2], 2, [2, 2], 3, [2, 3], 3, [2, 3], 4, [2, 4], 4, [2, 4]
gegeben ist. Erstlich nämlich haben wir hier einen Steiner sehen
Komplex, da wieder der Typus (14) S. 381 vorliegt. Der zu K konjugierte
Komplex enthält in seinen sechs Paaren die Doppeltangenten 1, 2, 3, 3, 4, 4
und ist nach einem Satze von S. 373 durch diese sechs von den sieben
Tangenten des Aronhold sehen Siebensystems A eindeutig hestimmt. Also
ist K der zu K konjugierte Komplex. Wäre K = K, also K reell, so
wäre das Paar 2, [2, 2], das mit dem Paare 2, [2, 2] die Tangente [2, 2]
gemein hat, mit diesem Paare 2, [2, 2] identisch. Aber es gilt 2 zfz 2.
Wir haben also zwei konjugiert imaginäre Komplexe K, K vor uns, die
offenbar azygetisch sind. Gemeinsam sind den beiden Komplexen allein
die sechs Doppeltangenten 1, [2, 2], 3, 3, 4, 4. Die Tangenten [1, 2]
und [1, 2] sind verschieden, und da sie einander in K und K entsprechen,'
so sind sie konjugiert imaginär. Auch [2, 2] und [2, 2] entsprechen
einander in K und K, sind also konjugiert imaginär; da sie aber einander
gleich sind, so ist [2, 2] reell. K liefert als zu [2, 3] konjugiert [2, 3].
Da aber [2, 3] nicht in K auftreten kann, so sind [2, 3] und [2, 3]
verschieden, so daß [2, 3] imaginär ist. Ebenso findet man, daß die
Doppeltangenten [2, 3], [2, 4], •. • imaginär sind. Da offenbar die drei letzten
Ziffempaare in A gleichberechtigt sind, auch die beiden Ziffern v, v des
einzelnen Paares ausgetauscht werden können, so ergibt sich der Satz:
Im ersten Fälle hat man die vier reellen Doppeltangenten:
(1) 1, [2, 2], [3, 3], [4, 4],
die 24 übrigen sind imaginär, womit der Fall I, § 12 erreicht ist. Daß
wir in (1) ein syzygetisches Quadrupel gewonnen haben, zeigt der nach
Vorschrift von (13) S. 381 gebildete Steiner sehe Komplex:
1, [2, 2], 2, [1, 2], 2, [1, 2], [3, 3], [4, 4],
[3, 4], [3, 4], [3, 4], [3, 4],
in dem die reellen Doppeltangenten das erste und vierte Paar aufbauen.
n. Wir geben zweitens das Siebensystem:
(-4) 1, 2, 3, 4, 4, 5, 5
Verwirklichung der Fälle I und H reeller Doppeltangenten. 411
mit drei reellen und zwei Paaren konjugiert imagiaq.ren Tangenten. Hier
arbeitet man zweckmäßig mit den drei folgenden Komplexen:
(JT,) 2, [1, 2], 3, [1, 3], 4, [1, 4], 4, [1, 4], 5, [1, 5], 5, [1, 5],
TO 1, [1, 4], 2, [2, 4], 3, [3, 4J, 4, [4, 4], Ö, [4, 51, 5, [4, 5],
TO 1, [1, 4], 2, [2, 4], 3, [3, 4], 4, [4, 4], 5, [4, 5], 5, [4, 5],
die dem Typus (14) S. 381 angehören. Der mit jT^ kpnjugierte
Komplex enthält die sechs Doppeltangenten 2, 3, 4, 4, 5, 5 des
Siebensystems Ä. Er ist nach dem Satze von S. 373 hierdurch eindeui^ig
bestimmt und demnach mit K^ identifäch, so d^ß K^ reell ist. Es folgt
hieraus, daß [1, 2] und [1, 3] reell sind, [l, 4] und [1, 4] aber konjugiert
imaginär sein müssen, wie auch [1, 5] und [1, 5]. Aus dem wiederholt
genannten Satze von S. 373 folgt weiter, daß E^ und K^ konjugiert
imaginär sein müssen. Wie oben ergibt sich, dal^ [4, 4] reell ist, und
daß [4, 5] und [4, 5] konjugiert: imaginär sind nnd ebenso [4, ö] nnd
[4, 5]. Die Ziffern 1, 2, 3 sind gleichberechtigt, ebenso die ^iffempaare
4, 4 und 5, 5. Wir notieren also das Ergebnis: Im zweiten Falle hat
man acht reelle Doppeltangenten:
(2) 1, 2, 3, [2, 3], [3, Ij, [1, 2], [4, 4], [5, 51
und zwanzig imaginäre:
I 4, 5, [1, 4], [1, 5], [2, 4], [2, 5], [3, 4], [3, 5]. [4, 5], [4, 5],
1 4, 5, [1, 4], [1, 5], [2, 4], [2, 5], [3, I], [3, 5], [4, 5], [4, 5],
wobei je zwei Jconjugierte U7f,tereinander geordnet sind. Hiermit hohen wir
den Fall II von § 12 erreicht. Es muß filso einen reellen Steiner sehen
Komplex geben, in dem die acht Tangepten (2) za vier Paaren ^^ereint
auftreten. Dieser Komplex ist:
1, [2, 31, 2, [3,1], 3, [1,2], [4, 4] [5, 51. [4, 5], [4, 5]. [4, 5]. [4, 5];
er gehört dem Typus (13) S. 381 an.
III. Im dritten Falle haben wir von dem Siebensystem:
{A) 1, 2, 3, 4 o, ß, 6
mit fünf reellen Doppeltangentea und einem P^are konjugiert imaginärer
auszugehen. Wir bilden die drei E-omp]exe des Typus (14) S. 381:
{K^) 2, [2, 1], 3, [3, 1], 4, [4, 1], 5, [5, 1], 6, [6. 1], 6, [6, Ij,
{K^) 1, [1, 6], 2, [2, 61, 3, [3, 6j, 4, [4, 6], 5, [5, 6], 6, [6, 6],
{K^ 1, [1, 6], 2, [2, 6], 3, [3, 6], 4, [4, ß], 5, [5, 6], 6, [6, 6].
Der zu K^ konjugierte Koinple:^ enthält die sechs Poppßltangenten 2, 3,
4, 5, 6, 6 des Aronhold sehen Siebepsystßms A und ist demnach mit K^
identisch, d. h. K^ ist reell. Ebenso erkennt man, daß K^ zu K^ kon-
412 in, 2. Doppeltangenten ebener Kurven viei-ten Grades.
jugiert ist. Auch die Fortsetzung der Überlegung gestaltet sich wie in
den beiden voraufgehenden Fällen. Man gelangt zu dem Ergebnis: Im
dritten Falle treten sechzehn reelle Doppeltangenten auf:
1, 2, 3, 4, 5
il, 2], ^1, 3^, [1. 4], i^ 51, [2, 8], [2, 4], [2, 5; [3, i]. [3, 5], ^4, 5],
\6, 6],
während die uhrigen ztcolf Doppeltangenten zu Paaren Jconjugiert imaginär
6, [1, 6], [2, 6], [3, 6(, [4, 6], [5. 6],
B, [1, 6], [2, 6], [3. 6j, [4, 6], [5, 6^.
Damit ist der Fall III von, § 12 reaVibiert. Hier muß ein syzygetisches
Komplextripel nachweisbar sein, das in jedem Komplex vier reelle Paare
und zwei imaginäre, einander konjugierte Tangentenp^are aufweist. Ein
solches Tripel haben wir z. B. in:
1, 2, [1, 3., ^2, 31. :i, 4]. [2,4], ,1, 5], [2, 5], [1, ^l i^, 6], [1, 6], [2, 6],
3,4, [1, 3j, ri,4j. f2, 3]. [2,41, [5. 3], [5, 4j, 13, 6], [4, 6], [3, 6], [4, 6],
1,21, [3,4j, [1. 3], [2,4j. il,4], [2,3], 5, [6, 6], 6, [5, 6], 6, [5, 6,.
Die beiden ersten Komplexe besitzen den Typus (14) S. 381, während
der dritte Komplex zum Typus (13) S. 381 gehört, übrigens gewinnt
man bei Permutation der Ziffern 1, 2, 3, 4, 5 immer wieder brauchbare
syzygetische Tripel.
IV. Der letzte Fall erledigt sich unmittelbar. Wenn nämlich
sieben reelle Gerade als die sieben Doppeltangenten eines A ronhold sehen
Siebensystems gegeben sind, so sind alle 28 Doppeltangenten reell; denn
sie berechnen sich aus jenen sieben nach S. 382 ff. durch rationale Eech-
nungen. Somit treten alle vier in § 12 aU möglich erkannten Fälle reeller
Doppeltafhgenten der reellen ebenen Krarven vierten, Grades auch wirlüich
auf. In den vorstehenden Zeilen ist übrigens noch keineswegs bewiesen,
daß bei jeder reellen Kurve vierten Grades ein reelles A ronhold sches
Siebensystem existiert. Ob also bei ^eder reellen Kurve vierten Grades
die reellen Doppeltangenten und die imaginären Paare in obiger Art
aufgestellt werden können, soll nicht behauptet werden.
Endlich sei noch bemerkt, daß aus der Realität einer Doppeltangente
noch nicht die Realität der beiden Berührungspunkte folgt. Diese hängen
erneut von einer reellen quadratischen Gleichung ab, die dann eben reelle
oder konjugiert komplexe Lösungen haben mag. In dieser Hinsicht ist
die durch Nullsetzen der biquadratischen Form (5) S. 198 gegebene
„Kleinsehe Kurve vierten Grades-':
(4) ^f^2 + 4^3-f ^f^i = 0
Verwirklichung der Fälle III ufid lY reeller Doppeltangenten. 418
lehrreich. Eine der vier zupi mipdestßn reell ausfallenden Doppeltangenten
sei durch:
(5) a.^'j i-a,^^ ^a^s^= 0
gegeben. Sie geht durch die sechs Substitutionen:
s[ = S^'^^, z'-2 = £^'^.,> ?i =: i-^'3^, V — 1. 2, 3, •••. 6.
unter £ die primitive siebente Einheitswurzel e "' verstanden, in sechs
paarweise konjugiert imaginäre Doppeltangenten:
(6) a^^""^ z^-\-a^E^^ z^A^ a^i:^^ z^^=z <<)
über. Die Klein sehe Kurs^e hat also vier reejle und zwölf I*aare konjp-
giert imaginärer Doppeltangenten. Die Crleichungen de:p reellen '\Vende-
tangenten sind leicht anget)bar. Ma,n zeigt nämlich durch Ausrechnung
das identische Bestehen der folgenden Gleichung:
(7) _7(>f^,+^?^3^ ^|^i) =
(^1 +^2 -^3)-n((^ -h £«-2)5, +(.^ ^£^-2)r, + (£^ -£^-2)23)
- 7 {z\ -l- 4 ^zl^% {z,z, ^ z,z, + z, z^)\
wo sich das Produkt auf diejenigen drei Linearfakt;oren bezieht, die aps
dem angegebenen durch zykliscl).e Permutation der ä^, z^, z^ hervo:pgehen.
Die vier Linearfaktoren in^ ersten GJiede der rechten Seite von (7) geben,
gleich 0 gesetzt, die vier reellen Doppeltangenten. Pie quadratische
Form im letzten Gliede vpn (7) liefert den Kegelschnitt duych die acht
Berührungspunkte der Doppelt^ngenten des reellen sy:?ygetische|i
Quadrupels. Wie schon ein Blick auf Fig. 25 S. 198 lehrt, hat die reelle
Klein sehe Kurve nur drei Doppeltangenten mit reellen
Berührungspunkten. Die vierte reelle Doppelt^ngente:
die unendlich ferne Gerade der Eberfe de:p Fig. 25, hat die beiden
konjugiert komplexen Berührungspunkte:
Die verschiedenen Gestalten de:p reellen Kurven vierten Grades sind
ausführlich von Zeuthen*) untersucht worden. Klein**) hat einen
unmittelbar anschaulichen Eingang in diesen Gegenstand gewonnen, indem
er an eine Kurve vierten Grades anknüpft, dip in zwei sich schneidende
Ellipsen zerfällt, und auf diese den „Prozeß der Auflösung der
Doppelpunkte- anwendet. Nimmt man z. B. bei gewöhnlichen rechtwinkligen
=^) „Sur les differentes formes des courbes du quatr;eme ordre'-, Math. Ann.
Bd. 7 (1874).
*=^) „Über den Verlauf der Abel sehen Integrale ttei den Kurven vierten
Grades'- § 5, Math. Ann. Bd. 10 (1876) qder „Ges. Abb.-' II. 111.
414 ni, 2. Doppeltangenten ebener Kurven vierten Grades.
Koordinaten x, y den Ausgang von den beiden kongruenten, sich
überkreuzenden Ellipsen:
^ = 62 ^2 _^ «2 ^2 _ 1 „ 0^
T/; = a^ a;2 -f &2 «/2 — 1 =3 0
und verstellt unter b eine sehr kleine reelle Zahl, so liefert die Gleichung:
y . i/; — ö = 0,
je nachdem b positiv oder negativ ist, eine zweiteilige „Gürtelkurve"
oder eine „vierteilige Kurve", wie sie in der Fig. 32 und der Fig. 33
Fig. 32. Fig. 33.
dargestellt sind. Im ersten Falle hat man vier reelle Tangenten mit
reellen Berührungspunkten. In der vierteiligen Kurve liegt der extreme
Fall von 28 reellen Doppeltangenten vor. Betreffs der übrigen nach
Klein sehen Verfahren gewinnbaren Kurvengestalten vgl. man die
genannte Abhandlung.
Register.
1 Strieh bedeutet die "WiederJiolung des Stichwort
einzelnen Stiebwonfe lolgen die Angaber
s. pie Zahlen g^ben die Seit
nach steigender Seitenzahl.]
Absolute Invariante einer Gruppe 14.
Ähnliche Substitutionen 3.
Ähnlichkeitssubstitutio:^ 2.
ÄquianharmonischerFall bei ebenen
Kurven dritten Grades 339.
Äquivalenz von Punkten bezüglich
einer Gruppe 33, 47.
Aronholdsche Invarianten der ter-
nären kubischen Form 342.
Aronholdsche Sätze ube^" Erzeugung
einer Kurve vierten Grades 382, 388.
Aronholdsche Siebensysteme von
Doppeltangenten 373.
Assoziatives Gesetz bei
Substitutionen 3.
Äzygetische Quadrupel von
Doppeltangenten 369.
Äzygetische Systeme von
Doppeltangenten 369.
Äzygetische Tripel von
Doppeltangenten 368. — — yon Stemei-
schen Komplexen 373.
Bahnlinie einer Substitution 28.
Bilinearformen, Kleinsciie — 300,
302.
Brill-Kother scher ßeziprozitats-
satz 262. {
Bringsche Gleichung fui^ften Grades
116, 146. Transzendente Lösung der
—n — 117. Galoisscher Körper der
—n — 120.
Bringsche Kurve 121. Parametei-
darstellung der —n — 126.
Brioschische ßesolvente der
allgemeinen Gleichung fünften Grades 152.
Charakteristische Gleichung einer
Substitution 5.
Deterfliinante einer Substitution 2.
Diagoifialflache von Clebsch 123.
Diagofialgleichung fünften Grades
63, 151.
Diametralsymmetrie 44.
Diede^gruppe 37.
Differentialgleichu:pgen zur Losung
des Formenproblems der Valeptmer-
gruppe 301.
Diophantische Gleichung fur Poly-
edefgruppen 34.
Diskontinuitatsbereich einer Gruppe
47. — der Mpdulgruppe 81, 83.
Doppeltangenten der ebenen E^urven
vierten Grades 357 ff., ihre Anzahl
363. Realität der — 401 ff.
Doppeltangentengleichung 389.
Drehungen dey Ki).gel, analytisch
dargestellt 30.
DreiepksnetiS der Modulgrifppe 80.
Dual'istisc^ie Umformupgen im
ßai^me 325.
Eflliptischp Substitution 26.
Erlaubte ^.banderui^g eii^es Diskonti-
nuitatsbe^eiches 48.
IJrweitorung der Polyedergruppen 45.
— der ilodulgruppe 78. — der Va-
lentinergi-uppe 270.
Faktorensystem einpr Grpppenmvari-
ante 15.
Fixpunkt einer Substitution 5.
Fläche dritten Gra4es, Problem der
27 Geraden 400.
Formenproblem einer endlichen Gruppe
20. Algebraische Bedeutung der —e
22. — der Ikosaedergrappe 55. —
der Modulgruppe 89. — der Klein-
416
Register.
sehen Gruppe 211. — der Valentiner-
gnippe 295.
Formensystem der Ikosaedergruppe 55.
— der Klein .sehen Gruppe 2Ü6, in
oktaednschen Koordinaten 208.' —
der Valentine rgruppe auf Grund
invarianter Prozesse 280, durch Produkt-
bildungen 284.
Fundamentalpolygon 47.
Gleichung, charakteristische fur eine
Substitution 5, —, diophantische fur
die Polyedergruppen 34. Jacobische
— 71. Bring sehe — fünften Grades
116. Hermitesche — fünften Grades
116. Allgemeine — siebenten Grades
mit einer Gruppe ©^gg 222.
Allgemeine — sechsten Grades 300.
Gordanscher Satz über den Affekt
bei Gleichungen siebenten Grades 225.
Größter zyklischer Teiler einer
Gruppe 33,
Grundformen der Ikosaedergruppe 53.
Gruppe linearer Substitutionen 12.
Zyklische — 36. Hamilton sehe —
51. Reine — 51. Klein sehe — 188.
— der Tripelgleiehung neunten Grades
355. —derDoppeltangentengleiehung
391.
Gurtelkurve vierten Grades 414. i
Hamiltonsehe Gruppe 51.
Harmonische Perspektivitat 166.
Harmonische Polare bei einer ebenen
Kurve dritten Grades 340,
Harmoniseher Fall bei einer ebenen
Kurve dritten Grades 291, 338.*
Hauptflaehe bei der allgemeinen
Gleichung fünften Grades 139.
Hauptfunktion (Modulfunktion) fünfter
Stufe 97.
Hauptgleiehung fünften Grades 64, ''
139. Scharen von —en fünften Grades '
reich 145,
Hauptkongruenzgruppe »^ter Stufe '
in der Modulgruppe 91. — fünfter ,
Stufe m der Modulgruppe 93. — i
siebenter Stufe in der Modulgruppe ,
182, zugehöriger
Diskontinuitätsbereich 185,
Hermit es ehe Gleichung fünften Grades
116.
Hermitesehe Losung der Gleichung '
fünften Grades 147.
Hessesehe Gruppe ©.jie 290, 337.
Hessesche Normalgestalt der ter-
nären kubischen Form 335.
Hessesehe Kurve der ebenen Kurve
dritten Grades 333.
Hyperbolische Substitution 26.
Hypergeometrisehe
Differentialgleichung bei der Modulgruppe 90.
Identischer Konnex 308.
Identische Substitution 3.
Ikosaederf ormen bei der Valentmer-
grappe 266, 272.
Ikosaedergleichung 56.
Ikosaedergruppe 41. Erzeugung und
Normaldarsteilung der — 42.
Zerlegung der — 43. Ternare Gestalt
der — 162.
Ikosaederkegelschnitte bei der Va-
lentinergruppe 267.
Ikosaedrisehe Koordinaten bei der
Valentinergruppe 263, 286.
Symmetrische 289.
Ikosaedrisehe Kugelteilung 47.
Integralmodul k- (^) als Hauptfunktion
105,
Invarianten einer Substitution 7. —
einer Gruppe linearer Substitutionen
14. Existenz der — einer Gruppe
16, BildungsgesetiS der — einer Gruppe
17. Existenz relativer — 19. — der
Ikosaedergruppe 53. — der Klem-
sehen Gruppe 204,206, m oktaednschen
Koordinaten 208. — sechsten Grades
der Valentinergruppe 169.
Inverse Substitution 4.
Inversion an einem Kreise 45.
Inversionskreis 45.
Jaeobische Gleichung 71. — —
sechsten Grades 169. — — achten
Grades 222.
Kanonische Koordipaten bei der
Valentinergruppe 291. bei der
ebenen Kurve dritten Grades 291, 340.
Kettenbruchentwieklung der
Substitutionen der Modulgruppe 83.
Kleinsehe Bilinearformen 300, 302,
Kleinsehe Gruppe 182, 188. Zyklische
und andere Teiler der —n — 184.
— — in oktaedrisehen Koordinaten
189. Erzeugung der —n — 193,
— — in Wendedreieckskoordinaten
199.
Kleinsehe Konnexe 300.
ßegjstei
417
Kleinsche- LosuDrgen der Gleichung
fünften Grades 156, 159.
Kommensurabele Gruppen 102,
Kommutative Substitutionen 3,
Kongruenzgruppen fünfter Stufe m
der Modulgruppe 94. — siebenter
Stufe in der Modulgruppe 182. —
dritter Stufe bei der Valent;nergruppe
247. — dritter Stufe bei Tnpel-
gleichungen 353,
Konnex, Kleinsche —e 3CK), Klasse
und Ordnung eines —es 308.
Identischer — 308.
Kovarianten bei Gruppen linearer
Substitutionen 15, — de^ ternären
kubischen Form 330.
Kreisverwandtschaft 27,
Kroneckersche Losung der Gleichung
fünften Grades 170.
KroneckerscherSatz über^^esolventen
mit einem Parameter 179.
Kugeldrehungen, analyt:^sch
dargestellt 30.
Kugelteilung, ikosaednsche 47,
Linearformen, konjugierte bei der Va-
lentinergruppe 274.
Linear-polymorphe Funktionen
gegebener Signatur 231.
Linienkoordinaten, ihre Einführung
bei der Valentinergruppe 300. — im
Räume 323,
Loxodromische Substitution 2ß.
Lurothscher Satz 171.
Matrix einer Substitution 2.
Modulargleichungen der ßlbptischen
Funktionen 328.
Modulform 84, —en g^, g^, J 87.
Modulfunktion 84. — J(ö,-) 85. — en
fünfter Stufe 97.
Modulgleichung 88.
Modujgruppe 76. Homogene — 78,
Erweiterte — 78. Dreiecksnetz der
■j- 80. Diskontmuitatsbereich der —
81. Erzeugung der — 82. Pormen-
problem der — 89.
Multiplikative Substitution 2, 11.
Multiplikatoren einer Substitution
2, 7.
Niveaulinie einer Substitution 28.
Normalgestalt einer Substitution 11.
Xormalkurve der Formen f bei der
Valentinergruppe 259.
Fr icke. Algebra, II.
Oktaederformen bei der Kleinschen
Gruppe 201, — bei der
"Valentinergruppe 276.
Oktaedergruppe 39.
Oktaederkegelsc|initte bei der
Valentinergruppe 277.
Oktaed^-ische Koordinaten bei der
Valentinergruppe 263.
Parabolische Substitution 26.
Pentaederkoordinaten im Räume 121.
Perspektivitat, harmonische 166,
Pol einer Substitution 5.
Polyedergruppen 36, 41. Erweiterte
— 45, Homogene — 50,
Polymorphe Punktionen gegebener
Signatur 231,
Prpdukt zweier Si+bstit^tionen 3.
Prpjektion, stereograpbische 29.
Quadritnodulare Substitution 241.
Quaternare K ollineationsgrnppe
beider allgemeinen Gleichung siebenten
Grades 326.
Quaternionengruppe 51.
Relative Invariante einer (Jruppe 14,
ßesolvente funftenGrades der Ikosaeder-
gleichung 61, 63. — sechsten Grades
der Ikosaedergleichung 69, 70. —
sechsten Grades der Bringschen
Gleichung 129, Hermii^esche — der
Gleichung funftpn Gifades 147. Bri-
oschische — der GJeichung fünften
Grades 152, Kroneckersche — der
Gleichung fünften Grades 170 —n
mit einem Parairfeter 177. Allgemeine
und spezielle — n siebenten Grades
bei der Kleinschen Gruppe 211, 215,
217. —n achten Grades bei der
Kleinsehen Gruppe 221 Spezielle —
sechsten Grades bei der
Valentinergruppe 2p8, 298. Allgemeine —
sechsten Grades, bei der
Valentinergruppe 296.
ßeziprpzitatssalz von BriU und Kother
262.
ßiemann-Rochscher Satz 262.
Sextaktisc^e Punkte auf der Kurve
vierten Gr3,des der Kleinschen Gruppe
195, — — erster und zweiter Art
bei der Kurve sechsten Grades der
Valentmergi-uppe 281.
27
418
Register,
Signatur einer Ebene oder einer Rie-
mann sehen Fläche 231.
Singulare Koordinaten bei der ebenen
Kurve dritten Grades 336.
Singulare Substitution 2.
Spezialfunktionen auf einer Riemann-
scben Fläche 262.
Spezielle Teilungsgleichung der
p-Funktion fur den dritten
Teilungsgrad 347.
Spiegelung an einem Kreise 45.
Stereographische Projektion 29.
Steinersche Komplexe von
Doppeltangenten 366.
Substitution, lineare homogene mit
n Variablen 2. —en, singulare und
nicht-singuläre 2. Multiplikative — 2.
Identische — 3. Vertauschbare oder
kommutative —en 3. Ähnliche —en 3.
Inverse — 4. Normalgestalt einer —
11. Multiplikative — 11. Homogene
und nicht-homogene — 25.
Elliptische, parabolische, loxodromische
—en 26. —en erster und zweiter
Art 44.
Symmetriegesetz 85.
Symmetriekreis einer Spiegelung 45.
Syzygetische Quadrupel von
Doppeltangenten 369,
Syzygetisches Büschel von Kurven
dritten Grades 290, 336.
Syzygetische Tripel von
Doppeltangenten 368. — — von Steiner-
schen Komplexen 373.
Teilungsgleichungen der elliptischen
Funktionen 328.
Ternare kubische Formen und ihre
Kovarianten 330,
Tetraedergleichung 339,
Tetraedergruppe 38, 338.
Formensystem der — 339,
Transformation einer Substitution 6.
— durch reziproke Radien 45,
Transformationsgieichungen der
elliptischen Funktionen 328.
Transzendente Lösung der Ikosaeder-
gleichung und ihrer Resolventen 99.
Transzendente Lösungder Bringschen
Gleichung 117, — — des
Formenproblems der Klein sehen Gruppe 232,
234, 240. des Formenproblems
der Valentinergruppe 311,
Tripelgleichung 349. Gruppe der —
neunten Grades 355, Reelle —en
neunten Grades 356.
Uniformisierende Variable der Iko-
saedergleichung 98. — — bei der
Klein sehen Gruppe 231. bei
der Valentinergruppe 313. der
ebenen Kurve dritten Grades 344.
Unimodulare Substitution 25.
Valentinergruppe, erste Erklärung
263. — in oktaedrischen Koordinaten
265. Erzeugung der — 267, 271.
— in ikosaedrischen Koordinaten 286.
Vertauschbare Substitutionen 3,
Vierergruppe 37.
Vierteilige Kurve vierten Grades 414.
Voll schar von Spezialfunktionen auf
einer Riemann sehen Flache 262,
Weierstrass sches Normalintegral
erster Gattung 345,
Wendedreiecke bei der Kurve vierten
Grades der Klein sehen Gruppe 210,
Wendedreieckskoordinaten bei der
Klein sehen Gruppe 197,
Wendedreiseite der ebenen Kurve
dritten Grades 334,
Wendelinien der ebenen Kurve dritten
Grades 334.
Wendepunkte der ebenen Kurve dritten
Grades 334,
Wimanscher Satz 3I9,
Wurzelfunktionen auf einer Riemann-
schen Flache mit _p = 1 261.
Zusammensetzung von Substitutionen
3. — der Kugeldrehungen 32.
Zwischenformen bei der Valentiner
gruppe 300.
Zyklische Gruppen 36.