Lehrbuch der Algebra. Band 1, 2 - Weber H.

Автор: Weber H.
Теги: algebra mathematik algebra-lehrbuch
Год: 1898
Похожие
Geodaesie, Fortsetzung von Band 4
Rechenmethoden der Physik
Kryptographie in C und C++ Zahlentheoretische Grundlagen, Computer-Arithmetik mit großen Zahlen, kryptographische Tools
Lehrbuch der Algebra
Текст
                    Cornell University Library
reformatted this volume
to digital files to preserve
the informational content
of the deteriorated original.
The original volume was scanned
bitonally at 600 dots per inch
and compressed prior to storage
using ITU Group 4 compression.
1997

WLmvttmty fpitomg
BOÜGHT WITH THE INCOME
FROM THE
SAGE ENDOWNENT FUND
THE GIFT OF
Süenry m.
189X

s
LEHRBUCH
DBS.
ALGEBRA
ERSTER BAND

LEHEBÜCH
DEE
ALGEBRA
VON
HEINRICH FEBER
PROFESSOR DER MATHEMATIK'AS DER, UNIVERSITÄT STRÄSSBÜRG
ZWEITE AUFLAGE
EESTEE BAND
BRAÜNSCHWEIG
DRÜCK UND VERLAG VON FRIEDRICH VIEWEG UND SOHN
18 9 8

Alle Hechte, namentlich dasjenige der Uebersetzung in fremde Sprachen,
vorbehalten.

VORWORT ZUR ERSTEN AUFLAGE.
J3ei der Entwickelung, welche die Algebra in den letzten
Jahrzehnten genommen hat, dürfte eine zusammenfassende Dar-
Darstellung und Verknüpfung der verschiedenen theoretischen Be-
Betrachtungen und mannigfachen Anwendungen auch nach dem für
seine Zeit trefflichen Lehrbuch von Serret nützlich sein.
Seit Jahren hege ich den Plan eines solchen Unternehmens,
das ja gross und weitaussehend erschien, und mancherlei Vor-
Vorarbeiten erforderte. Erst nachdem ich in Universitätsvorlesungen
mehrmals das Gebiet im Ganzen durchwandert und einzelne
Theile spezieller behandelt hatte, entschloss ich mich, an die
Ausführung des Werkes zu gehen, von dem jetzt der erste Band
vollendet vorliegt.
Es war meine Absicht, ein Lehrbuch zu geben, das, ohne
viel Vorkenntnisse vorauszusetzen, den Leser in die moderne
Algebra einführen und auch zu den höheren und schwierigeren
Partien hinführen sollte, in denen das Interesse an dem Gegen-
Gegenstande erst recht lebendig wird. Dabei sollten die erforderlichen
Hülfsmittel, die elementaren sowohl als die höheren, aus dem
Gange der Entwickelung selbst abgeleitet werden, um die Dar-
Darstellung von anderen Lehrbüchern möglichst unabhängig zu machen.
Zwei Dinge sind es, die für die neueste Entwickelung der
Algebra ganz besonders von Bedeutung geworden sind; das ist
auf der einen Seite die immer mehr zur Herrschaft gelangende
Gruppentheorie, deren ordnender und klärender Einfluss überall
zu spüren ist, und sodann das Eingreifen der Zahlentheorie.

VI Vorwort zur ersten Auflage.
Wenn auch die Algebra zum Theil über die Zahlentheorie hin-
hinausgeht, und in andere Gebiete, z. B. die Functionentheorie, oder
in ihren Anwendungen auch in die Geometrie hinüber greift, so
ist doch die Zahlenlehre immer das vorzüglichste Beispiel für
alle algebraischen Betrachtungen, und die Fragen der Zahlen-
Zahlentheorie, die heute im Vordergrund des Interesses stehen, sind
vorwiegend algebraischer Natur. Hierdurch war der Weg be-
bezeichnet, den ich in meiner Arbeit zu gehen hatte.
Der grosse Stoff ist in zwei Bände vertheilt. Der erste Band
enthält den elementaren Theil der Algebra, den man mit einem
hergebrachten Ausdruck als Buchstabenrechnung bezeichnen
kann, sodann die Vorschriften über die numerische Berechnung
der Gleichungswurzeln und die Anfänge der Galois'schen Theorie.
Der zweite Band, der dem ersten hoffentlich in kurzer Zeit
folgen wird, soll die allgemeine Theorie der endlichen Gruppen,
die Theorie der linearen Substitutionsgruppen und Anwendungen
auf verschiedene einzelne Probleme bringen und soll abschliessen
mit der Theorie der algebraischen Zahlen, wo der Versuch
gemacht ist, die verschiedenen Gesichtspunkte, unter denen diese
Theorie bisher betrachtet worden ist, zu vereinigen.
Endlich soll der zweite Band ein alphabetisches Register
über beide Bände bringen.
Wie es bei einer Disciplin, die in rascher Entwickelung
begriffen ist, und an der von den verschiedensten Seiten gearbeitet
wird, nicht anders sein kann, ist auch in der Algebra der Sprach-
Sprachgebrauch und die Bezeichnungsweise sehr mannigfaltig und häufig
nicht übereinstimmend. Dadurch wird eine einheitliche Dar-
Darstellung und das Eindringen in die verschiedenen Arbeiten sehr
erschwert.
Ich habe mich daher bemüht, eine möglichst zweckmässige
Ausdrucksweise einheitlich beizubehalten, und habe mich dabei
vielfach mit Fachgenossen berathen. Ich darf die Hoffnung aus-
aussprechen, dadurch zur Befestigung einer einheitlichen Termino-
Terminologie beigetragen zu haben.
Die Literaturnachweisungen und historischen Notizen, die
in dem Buche gegeben sind,.machen in keiner Weise den An-
Anspruch auf Vollständigkeit, wenn ich auch bemüht gewesen bin,

Vorwort zur ersten Auflage. VII
nach Möglichkeit die wichtigsten Quellen und literarischen Hülfs-
mittel an geeigneter Stelle zu erwähnen.
Es ist mir eine angenehme Pflicht, so manchem Freunde und
Collegen, der an dem Fortschreiten meiner Arbeit regen und
thatkräftigen Antheil genommen hat, hier meinen Dank auszu-
auszusprechen. Zuerst gilt dieser Dank meinem Freunde Dedekind
für seine treue Hülfe bei der Correctur, und wenn er auch auf
den Plan und die Ausführung meines Werkes keinen Einfluss
ausgeübt hat, so möchte ich doch nicht unerwähnt lassen, dass
ich schon vor vielen Jahren durch ein Heft einer Vorlesung, die
er im Winter 1857/58 in Göttingen über höhere Algebra, ins-
insbesondere über die Theorie von Galois gehalten hat, ein noch
lebhafteres Interesse für diese Theorie gewonnen habe, die vordem
auf unseren Hochschulen in solcher Vollständigkeit wohl noch
nicht vorgetragen war.
Auch der mannigfachen Anregung und Belehrung habe ich
hier zu gedenken, die ich meinem Freunde und Collegen F. Klein
verdanke, der das Fortschreiten der Arbeit mit regstem Interesse
begleitet hat und dessen sachkundiger, stets bereitwilligst ge-
gegebener Rath in manchen Theilen des Buches von grossem Einfluss
gewesen ist.
Ich kann hier nicht alle Fachgenossen und Freunde namhaft
machen, die mich durch ihren Rath unterstützt haben, wie der
Leser an den betreffenden Stellen finden wird. Aber der Herren
E. Hess in Marburg, Fr. Meyer in Clausthal, R. Fricke in
Braunschweig, die durch kundige und sorgfältige Ausführung
der mühevollen Correctur der Druckbogen Genauigkeit und
Richtigkeit des Textes gefördert haben, muss ich hier noch
gedenken.
Endlich gilt mein Dank der Verlagsbuchhandlung, die durch
bereitwilliges Eingehen auf meine Wünsche, durch Sorgfalt in
Druck und Ausstattung wesentlich zum Gelingen des Ganzen
beigetragen hat.
Göttingen, im November 1894.
Der Verfasser.

VORWORT ZUR ZWEITEN AUFLAGE.
JL/as Lehrbuch der Algebra geht hiermit zum zweiten Male
in die Oeffentlichkeit. Plan und Gang der ersten Auflage sind
durchweg beibehalten. Trotzdem ist das ganze Gebiet wiederholt
durchgearbeitet, und manches Neue ist hinzugenommen, theils zur
Berichtigung einzelner Irrthümer oder zur Erhöhung der Klarheit
und Verständlichkeit, theils um durch Berücksichtigung neuer
Arbeiten der Vollständigkeit näher zu kommen. Eine wesentliche
Erweiterung hat die Theorie der Elimination im vierten Abschnitt
gefunden.
Es ist mir abermals eine erfreuliche Pflicht, den zahlreichen
Freunden des Buches, die mich durch Mittheilungen in der Neu-
Neubearbeitung unterstützt haben, meinen Dank zu sagen. Ausser
den in der Vorrede der ersten Auflage Genannten gilt dieser
Dank vorzugsweise den Herren Hensel, Frobenius, Netto,
sowie einem unbekannten Freunde und sorgfältigen Leser des
Buches.
Strassburg, im Januar 1898.
Der Verfassern

INHALT DES ERSTEN BANDES.
Seite
Einleitung 1
Erstes Buch.
Die Grün dlagen.
Erster Abschnitt.
Rationale Functionen.
§. 1. Ganze Functionen . • 25
§. 2. Ein Satz von G a u s s .27
§. 3. Division 30
§. 4. Theilung durch eine lineare Function 32
§. 5. Gebrochene Functionen; Theilbarkeit 34
§. 6. Grösster gemeinschaftlicher Theiler 37
§. 7. Producte linearer Factoren 41
§. 8. Der binomische Lehrsatz 45
§. 9. Interpolation 47
§. 10. Lösung des Interpolationsproblems durch die Differenzen ... 49
§. 11. Arithmetische Reihen höherer Ordnung 50
§. 12. Der polynomische Lehrsatz 53
§. 13. Derivirte Functionen 54
§. 14. Derivirte eines Productes 57
§. 15. Partialbrüche 59
§. 16. Entwickelung eiuer gebrochenen Fuuction nach fallenden Potenzen
der Variablen 62
§. 17. Ganze Functionen mehrerer Veränderlichen: Formen 64
§. 18. Die Derivirten von Functionen mehrerer Variablen 67
§. 19. Das Euler'sche Theorem über homogene Functionen 70
§. 20. Zerlegbare und unzerlegbare Functionen 71
Zweiter Abschnitt.
Determinanten.
§. 21. Permutationen von n Elementen 78
§. 22. Permutationen erster und zweiter Art 79
§. 23. Determinanten 82

X Inhalt des ersten Bandes.
Seite
§. 24. Hauptsätze über Determinanten 84
§. 25. Unterdeterndinanten 86
§. 26. Die Unterdeterminanten im weiteren Sinne 91
§. 27. Lineare homogene Gleichungen .r 96
§. 28. Elimination aus linearen Gleichungen 102
§. 29. Unhomogene lineare Gleichungen 104
§. 30. Multiplikation von Determinanten 108
§. 31. Determinanten der Unterdeterminanten 113
§. 32. Determinantensatz von Sylvester 115
Dritter Abschnitt.
Die Wurzeln algebraischer Gleichungen.
§. 33. Begriff der Wurzeln. Mehrfache Wurzeln 117
§. 34. Stetigkeit ganzer Functionen 119
§. 35. Vorzeichenwechsel von f(x). Wurzeln von Gleichungen nn- ^
geraden Grades und von reinen Gleichungen '. 123
§. 36. Lösung reiner Gleichungen durch trigonometrische Functionen >127
§. 37. Befreiung einer Gleichung vom zweiten Gliede ' . 130
§. 38. Cubische Gleichungen. Cardanische Formel , . 132
§. 39. Der Cayley'sche Ausdruck der Cardanischen Formel . . . 134
§. 40. Die biquadratische Gleichung 135
§. 41. Beweis des Fundamentalsatzes der Algebra 137
§. 42. Algorithmus zur Berechnung der Wurzeln 143
§. 43. Zahlenwerthe ganzer Functionen 147
§. 44. Stetigkeit der Wurzeln 148
Vierter Abschnitt.
Symmetrische Funetionen.
§. 45. Begriff der symmetrischen Functionen. Symmetrische Grund-
functionen 154
§. 46. Die Potenzsummen 156
§. 47. Beweis des Hauptsatzes für zwei Variable 160
§, 48. Allgemeiner Beweis des Hauptsatzes 161
§. 49. Zweiter Beweis des Satzes von den symmetrischen Functionen 163
§. 50. Discriminanten 167
§. 51. Kennzeichen für die Anzahl der verschiedenen Wurzeln . . . 170
§. 52. Discriminanten der Formen dritter und vierter Ordnung . . . 172
§. 53. Resultanten 175
§. 54. Bestimmung der gemeinschaftlichen Factoren 179
§. 55. Elimination. Theorem von Bezout 185
§. 56. Elimination aus drei Gleichungen . . . ' . . . . 190
§. 57. Grad und Gewicht der Resultanten. Das Theorem von Bezout 193
§. 58. Tschirnhausen-Transformation ¦. . 199
§. 59. Anwendung auf die cubischen und biquadratischen Gleichungen 202
§. 60. Die Tschirnhausen-Transformation der Gleichung 5ten Grades 204

Inhalt des ersten Bandes. XI
Seite
Fünfter Abschnitt.
Lineare Transformation. Invarianten.
§. 61. Einführung der linearen Transformation 207
§. 62. Quadratische Formen 208
§. 63. Transformation der quadratischen Formen iu eine Summe von
Quadraten 210
§. 64.. Trägheitsgesetz der quadratischen Formen 212
§. 65. Transformation von Formen wten Grades 214
§. 66. Invarianten und Covarianten 216
§. 67. Lineare Transformation der binären Formen 219
§. 68. Binäre cubische Formen 223
§. 69. Das volle Formensystem der binären cubischen Form 226
§. 70. Biquadratische Formen 229
§. 71. Auflösung der biquadratischen Gleichung 231
§. 72. Die Covarianten 233
§. 73. Das volle Invariantensystem der binären biquadratischen Form 236
Sechster Abschnitt.
T s eMrnli au sen- Transformation.
§. 74. Die Hermite'sche Form der Tschirnhausen-Transformation . 240
§. 75. Invarianteneigenschaft der Tschirnhausen-Transformation . . . 242
§. 76. Ausführungen über den Hermite'schen Satz 245
§. 77. Transformation der cubischen Gleichung 248
§. 78. Allgemeine Ausführung der Transformation 253
§. 79. Die Bezoutiante 255
§. 80. Transformation der Gleichung fünften Grades 260
§. 81. Normalform der Gleichung fünften Grades 263
Zweites Buch.
Die Wurzeln.
Siebenter Abschnitt.
Realität der Wurzeln.
§. 82. Allgemeines über Realität von Gleishungswurzeln und über
Discriminanten 271
§. 83. Discussion der quadratischen und cubischen Gleichung .... 273
§. 84. Discussion der biquadratischen Gleichung 276
§. 85. Die Bezoutiante und ihre Bedeutung für die-Wurzelrealität . . 281
§. 86. Die Trägheit der Formen zweiten Grades 284
§. 87. Quadratische Formen mit verschwindender Determinante . . . 287
§. 88. Quadratische Formen mit nicht verschwindender Determinante 290
§. 89. Anzahl der positiven und negativen Quadrate 291
§. 90. Anwendung auf die Bezoutiante 296

XII Inhalt des ersten Bandes.
Seite
Achter Abschnitt.
Der Sturm'sehe Lehrsatz.
§. 91. Das Sturm'sche Problem 301
§. 92. Die Sturm'schen Ketten 302
§. 93. Erstes Beispiel: Kugelfunctionen 304
§. 94. Zweites Beispiel 307
§. 95. Die Sturm'schen Functionen 311
§. 96. Hermite's Lösung des Sturm'schen Problems 313
§. 97. Bestimmung der Hermite'schen Form S 314
§. 98. Die Determinante der Hermite'schen Form 316
§. 99. Formulirung der Aufgabe durch Hurwitz 318
§. 100. Grundzüge der Charakteristikentheorie 323
§. 101. Charakteristik eines Systems von drei Functiönen 325
§. 102. Beziehung der Charakteristik zu den Schnittpunkten 327
§. 103. Anwendung der Charakteristiken auf die Eingrenzung der
complexen Wurzeln einer Gleichung 329
§. 104. Bestimmung der Charakteristik 331
§. 105. Gauss' erster beweis des Fundamentalsatzes der Algebra . . 333
§. 106. Der Satz von Hurwitz 335
Neunter Abschnitt.
Abschätzung der Wurzeln.
§. 107. Das Budan-Fourier'sche Theorem 341
§. 108. Die Newton'sche Hegel 345
§. 109. Der Cartesische Lehrsatz 350
§. 110. Das Jacobi'sche Kriterium 353
§. 111. Kleins geometrische Yergleichung der verschiedenen Kriterien 354
§. 112. Bestimmung einer oberen Grenze für die Wurzeln 358
§. 113. Abschätzung der imaginären Wurzeln 360
§. 114. Das Theorem von Holle 361
§. 115. Die Sätze von Laguerre für Gleichungen mit nur reellen
Wurzeln 364
Zehnter Abschnitt.
Genäherte Berechnung der Wurzeln.
§. 116. Interpolation. Regula falsi ' 372
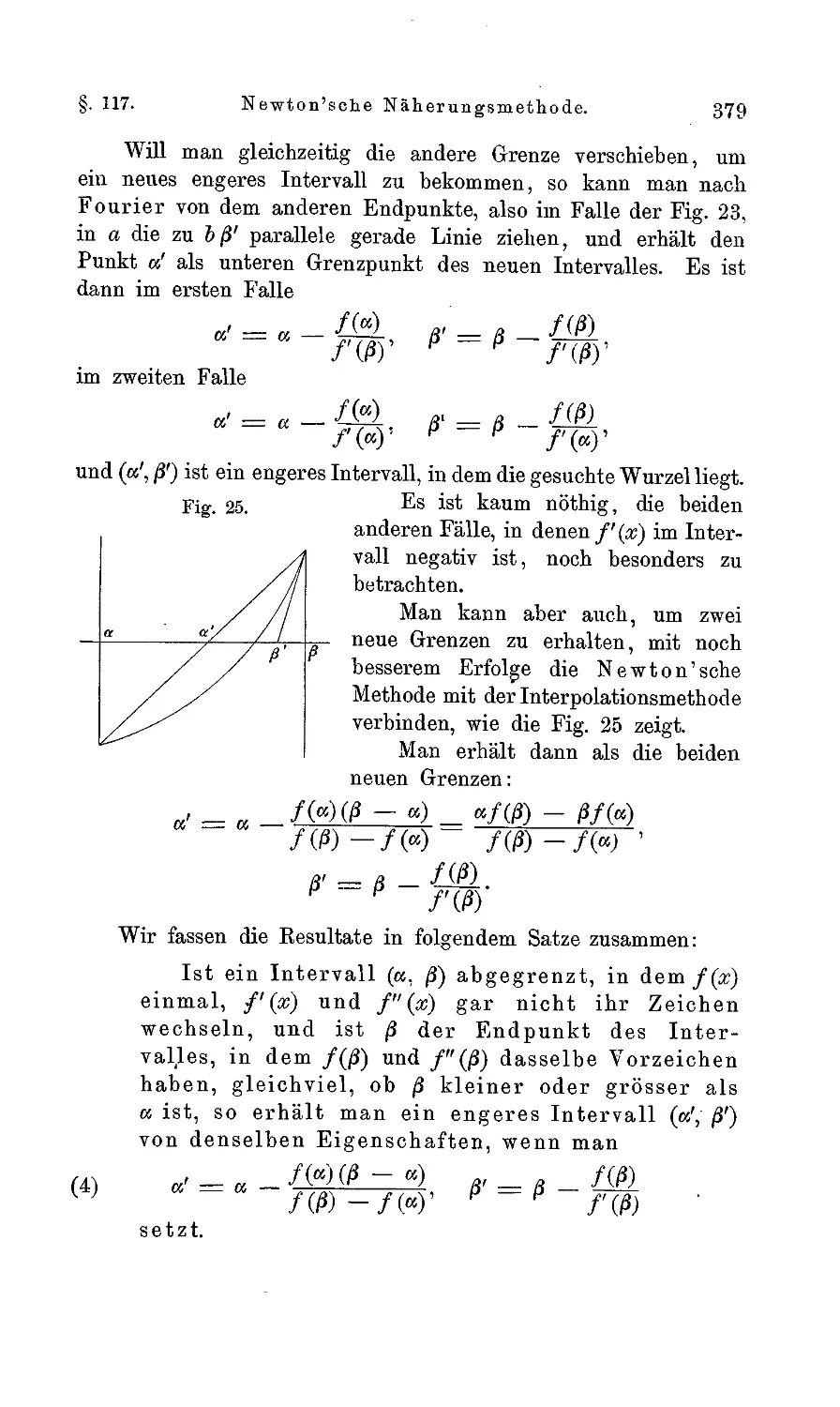
§. 117. Die Newton'sche Näherungsmethode 376
§. 118. Die Näherungsmethode von Daniel Bernoulli und ver-
verwandte Methoden 383
§. 119. Die Näherungsmethode von Gräffe 386
§. 120. Trigonometrische Auflösung cubischer Gleichungen . . . * . 391
§. 121. Die Gauss'sche Methode der Auflösung trinomischer Glei-
Gleichungen 393
§. 122. Berechnung der imaginären Wurzeln einer trinomischen
Gleichung 397

§•
§•
§•
§•
§•
§¦
§.
§¦
§•
§•
§.
§•
§•
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
Inhalt des ersten Bandes. XIII
Seite
Elfter Abschnitt.
Kettenbrücke.
Verwandlung rationaler Brüche in Kettenbrüche 400
Kettenbruchentwickelung irrationaler Zahlen 403
Die. Näherungsbrüche 404
Lösung unbestimmter Gleichungen mit zwei Unbekannten . . 407
Convergenz der Näherungsbrüche 411
Aequivalente Zahlen 413
Entwickelung äquivalenter Zahlen in Kettenbrüche ...... 417
Quadratische Irrationalzahlen 419
Reducirte Zahlen mit negativer Discriminante 428
Reducirte Zahlen mit positiver Discriminante 427
Entwickelung reeller quadratischer Irrationalzahlen in Ketten-
Kettenbrüche . 429
Beispiele 435
Die Pell'sche Gleichung ^ 438
Ableitung aller Lösungen der Pell'sehen Gleichung aus der
kleinsten positiven 442
Genäherte Berechnung der reellen Wurzeln einer numerischen
Gleichung durch Kettenbrüche 445
Rationale Wurzeln ganzzahliger Gleichungen. Reducible
Gleichungen 447
Zwölfter Abschnitt.
Theorie- der Einheitswurzeln.
§. 139. Die Einheitswurzeln 452
§. 140. Primitive Einheitswurzeln 455
§. 141. Gleichungen für die primitiven Einheitswurzeln wten Grades . 458
§. 142. Die Discriminante der Kreistheilungsgleichung ....... 462
§. 143. Primitive Congruenzwurzeln 466
§. 144. Multiplikation und Theilung der trigonometrischen Functionen 474
§. 145. Vorzeichenbestimmung. Quadratische Reste . . . 480
Drittes Buch.
Algebraische Grossen.
Dreizehnter Abschnitt.
Die Galois'selie Theorie.
§. 146. Der Körperbegriff 491
§. 147. Adjunction 493
§. 148. Functionen in einem Körper 494
§. 149. Algebraische Körper 497
§. 150. Gleichzeitige Adjunction mehrerer algebraischer Grossen . . . 499

XIV Inhalt des ersten Bandes.
Seite
§. 151. Primitive und imprimitive Körper ¦ . 501
§. 152. Normalkörper. Galois'sche Resolvente 505
§. 153. Die Substitutionen eines Normalkörpers 508
§. 154. Zusammensetzung der Substitutionen 511
§. 155. Permutationsgruppen 513
§. 156. Galois'sche Gruppe 517
§. 157. Transitive und intransitive Gruppen 523
§. 158. Primitive und imprimitive Gruppen 524
Vierzehnter Abschnitt.
Anwendung der Permutationsgruppen, auf
Gleichungen.
§. 159. Wirkung der Permutationsgruppen auf Functionen von un-
unabhängigen Veränderlichen 529
§. 160. Zerlegung von Permutationen in Transposition und in Cyklen 533
§. 161. Divisoren der Gruppen, Nebengruppen und- conjugirte Gruppen 542
§. 162. Reduction der Galois'sehen Resolvente durch Adjunction.
Normaltheiler einer Gruppe 548
§. 163. Die Gruppe der Resolventen 553
§. 164. Reduction der Galois'schen Gruppe durch Adjunction belie-
beliebiger Irrationalitäten 555
§. 165. Imprimitive Gruppen 558
Fünfzehnter Abschnitt.
Cyklisehe Gleichungen.
§. 166. Cubische Gleichungen 564
§. 167. Permutationsgruppen von vier Elementen 566
§. 168. Auflösung der biquadratischen Gleichungen 570
§. 169. Abel'sche Gleichungen 575
§. 170. Reduction der Abel'sehen Gleichungen auf eyklische .... 579
§. 171. Resolventen von Lagrange 584
§. 172. Auflösnng der cyklischen Gleichungen 588
§. 173. Theilüng des Winkels 593
Sechzehnter Abschnitt.
Kreistheilung.
Irredueibilität der Kreistheilungsgleichung 596
Die Kreistheilungsperioden und die Periodengleichungen . . . 601
Gauss'sche Methode zur Berechnung der Resolventen .... 606
Zurückführung der Kreistheilungsgleichung auf reine Glei-
Gleichungen 610
Eigenschaften der Zahlen ty 617
Die Gauss'schen Summen 621
Die Perioden vou Vs(w— 1) und % (w— 1) Gliedern 628
Die complexen Zahlen von Gauss 635
Der Körper der dritten Einheitswurzeln 641
§.
§•
§¦
§•
§•
§•
§•
174.
175.
176.
177.
178.
179.
180.
181.
182.

Inhalt des ersten Bandes. XV
Seite
Siebzehnter Abschnitt.
Algebraische Auflösung von Gleiehungen.
Reduction der Gruppe durch reine Gleichungen 644
Metacyklische Gleichungen 646
Einfachheit der alternirenden Gruppe 649
NichtmetacyMische Gleichungen im Körper der rationalen
Zahlen 652
Auflösung durch reelle Radicale 655
Metacyklische Gleichungen von Primzahlgrad 658
Anwendung auf die metacyklischen Gleichungen 5*en Grades . 670
Die Gruppe der Resolvente 676
Achtzehnter Abschnitt.
Wurzeln metaeykliselier G-leieliungen.
§. 191. Stellung der Aufgabe. Hülfssatz 680
§. 192. Sätze über die Resolventen 683
§. 193. Wurzeln metacyklischer Gleichungen 688
§. 194. Befreiung von den beschränkenden Voraussetzungen 691
§. 195. Realitätsverhältnisse 697
§. 196. Metacyklische Gleichungen 5*en Grades 698
§.
§•
§•
§.
§•
§•
§•
§•
183.
184.
185.
186.
187.
188.
189.
190.

EINLEITUNG.
Wir setzen bei unseren Betrachtungen die natürlichen
Zahlen 1, 2, 3 . . . und die Regeln, nach denen mit diesen
Zahlen gerechnet wird, als bekannt und gegeben voraus. Die
fundamentalen Rechenarten, die sogenannten vier Species, sind
die Addition, die Multiplication, zu der als Wiederholung
das Potenziren gehört, die Subtraction und die Division.
Die beiden ersten heissen die directen Rechenoperationen; sie
sind dadurch ausgezeichnet, dass sie im Reiche der natürlichen
Zahlen unbegrenzt ausgeführt werden können. Die erste der
indirecten oder inversen Operationen, die Subtraction, lässt sich
nur dann ausführen, wenn der Minuend grösser ist als der Sub-
Subtrahend.
. Die Aufgabe der Division kann man auf zwei Arten auf-
auffassen. Bei der ersten elementaren Auffassung wird gefragt, wie
oft der Divisor im Dividenden enthalten ist. Eine Zahl ist
nicht in einer kleineren enthalten. Ist aber der Dividend gleich
oder grösser als der Divisor, so giebt die Beantwortung der
Frage einen Quotienten und in den meisten Fällen einen Rest,
der kleiner als der Divisor ist. Wenn kein Rest bleibt, so sagt
man, die Division geht auf, oder der Dividend ist durch
den Divisor theilbar, oder der Divisor ist ein Factor oder
Theiler der Zahl, die den Dividenden bildet.
Diese Aufgabe, die sich schon auf den ersten Stufen der
Rechenkunst einstellt, führt zu einer tiefer liegenden Unter-
Unterscheidung der Zahlen, die das Fundament aller Zahlentheorie ist.
Da ein Factor nie grösser sein kann als die Zahl, deren
Factor sie ist, so hat jede Zahl nur eine endliche Anzahl von
Factoren. Jede Zahl ist durch 1 und durch sich selbst theilbar,
und eine Zahl, die sonst keinen Theiler hat, heisst eine Prim-
Primzahl. Die Zähl 1 selbst pflegt man aus Zweckmässigkeitsgründen
"Weber, Algebra. I. 1

2 ¦ Einleitung.
nicht als Primzahl zu bezeichnen. Sind zwei Zahlen durch eine
dritte theilbar, so ist auch die Summe und die Differenz der
beiden ersten durch die dritte theilbar; und ist eine Zahl durch
eine zweite, diese durch eine dritte theilbar, so ist auch die erste
durch die dritte theilbar.
Zwei Zahlen haben immer den gemeinsamen Theiler 1. Wenn
sie keinen anderen gemeinsamen Theiler haben,' wie z.B. die
Zahlenpaare 5 und 7 oder 21 und 38, so heissen die beiden Zahlen
relative Primzahlen oder auch theilerfremde Zahlen.
Unter den gemeinsamen Theilern von irgend zwei gegebenen
Zahlen wird einer der grösste sein, und es ist eine sehr wichtige
Aufgabe, diesen grössten gemeinschaftlichen Theiler zu finden.'
Dazu führt ein Verfahren, das unter dem Namen Algorithmus
des grössten gemeinschaftlichen Theilers bekannt ist,
und sich schon bei Euklid1) findet. ¦
Sind a, % die beiden Zahlen, so nehme man die grössere
von ihnen, die a sei, als Dividenden, die kleinere at als Divisor,
und bestimm^* den Quotienten #i; und wenn die Division nicht
aufgeht, den Rest. a?, also a = qt % -f- a2, so dass a2 <C ax ist.
Jeder gemeinschaftliche Theiler von a und ax ist dann auch ge-
gemeinschaftlicher Theiler von ax und a2 und umgekehrt. Verfährt
man mit %, a3 ebenso wie mit a und at und setzt, wenn die Division
nicht aufgeht, % = g2 a2 + «3, so ist wieder 03 <C «2, und jeder
gemeinschaftliche Theiler von % und a.2 ist auch gemeinschaft-
gemeinschaftlicher Theiler von a2 und az und umgekehrt. Fährt man auf
diese Weise fort zu dividiren, so muss, da die Zahlen a,Oi,a2,«3...
immer abnehmen, nothwendiger Weise die Division nach einer
endlichen Anzahl von Schritten aufgehen, und es muss also zuletzt
ein Paar von Gleichungen av_2 = <fr-i «v—i -j- ar, ar—i = <Z»ßv
auftreten. Dann ist av ein gemeinschaftlicher Theiler aller vor-
vorausgehenden a, also auch von a und aa, und jeder gemein-
gemeinschaftliche Theiler von a und at ist Theiler von av. Also ist
ar der grösste gemeinschaftliche Theiler von a und %,
und wir sind zugleich zu dem Satze gelangt, dass jeder gemein-
gemeinschaftliche Theiler zweier Zahlen in ihrem grössten gemein-
gemeinschaftlichen Theiler aufgehen muss.
. Sind a und % relative Primzahlen, so ist der letzte Divisor
av = 1. Multiplicirt man unter dieser Voraussetzung die vor-
J) Elemente, Buch YII, II, Bd. II der Heiberg'scten Ausgabe (Leipzig,
Teubner, 1883). :

Zerlegung in Primzahlen. 3
stehenden Gleichungen mit irgend einer Zahl b, so folgt, dass
b der grösste gemeinschaftliehe Theiler von a b und ax b ist, und
dass also jeder gemeinschaftliche Theiler von ab und aj oder
von a und aj b Theiler von b sein muss. Ist also % relativ
prim zu a und zu b, so ist es auch relativ prim zu ab, und aus
der speciellen Annahme, dass a^ eine Primzahl sei, ergiebt sich,
dass ein Product nur dann durch eine Primzahl theilbar sein
kann, wenn wenigstens einer der Factoren durch sie theilbar ist.
Ist also das Product ab durch ax theilbar und ist % relativ
prim zu a, so muss b durch a1 theilbar sein.
Sind a, b irgend zwei Zahlen mit dem grössten gemeinschaft-
gemeinschaftlichen Theiler d und ist a = da', b = dV, so sind a! und V
relativ prim zu einander. Jede Zahl m, die zugleich ein Viel-
Vielfaches von a und von b ist, hat die Form m = 'am' = da!m'
und darin muss a'm' ein Vielfaches von V sein, also muss auch
m! ein Vielfaches von V sein, d. h. jede Zahl, die zugleich ein
Vielfaches von a und von b ist, ist durch a'b'd theilbar. Diese
Zahl a'b'd, die selbst ein gemeinschaftliches Vielfaches von ä
und b ist, heisst daher das kleinste gemeinschaftliche Viel-
Vielfache von a und b.
Wenn eine Zahl durch zwei relative Primzahlen theilbar ist,
so ist sie auch durch ihr Product theilbar, und wenn also eine
Zahl m durch mehrere Zahlen theilbar ist, von denen je zwei zu
einander relativ prim sind, so ist sie auch durch das Product
aller dieser Zahlen theilbar.
Jede Zahl m, mit Ausnahme von 1, ist durch eine Primzahl
theilbar. Denn ist m nicht selbst eine Primzahl, so hat m einen
von 1 verschiedenen Theiler m', der kleiner als m ist. Ist m'
auch keine Primzahl, so hat es einen kleineren Theiler m", der
grösser als 1 ist, und der auch Theiler von m ist, u. s. f., und
so gelangt man auf einen Primzahltheiler von m.
Eine Potenz aa einer Primzahl a kann durch keine von a
verschiedene Primzahl b theilbar sein, weil eben sonst a durch
b theilbar sein müsste. Folglich kann a" keine anderen Theiler
haben, als Potenzen von a, deren Exponent nicht grösser als «
ist. Potenzen verschiedener Primzahlen, wie aa, b?, sind daher
stets relativ prim.
Hierauf gründet sich der Beweis des wichtigen Satzes, dass
eine Zahl m immer und nur auf eine einzige Weise als ein
1*

4 Einleitung.
Pro'duct von Primzahlen dargestellt werden kann. Denn da der
Theiler nicht grösser sein kann als der Dividend, so kann m
sicher nur durch eine- endliche Anzahl von Primzahlen theilbar
sein. Ist a eine von diesen Primzahlen und a" die höchste Potenz
von a, die in m aufgeht, so ist auch « eine bestimmte Zahl. Es
seien nun ebenso bß, C . . . die höchsten Potenzen der .übrigen in
m aufgehenden Primzahlen b, c . . ., durch die sich m theilen lässt,
dann muss, da je zwei der Zahlen aa, fr*, C . . . relativ prim
sind, m auch durch das Product aa fr*' c* . . . theilbar sein, und
es muss m diesem Producte gleich sein, da sonst noch eine andere
Primzahl oder eine höhere Potenz einer der Primzahlen a, b, c . . .
in m aufgehen müsste.
Wir geben nun eiuen Ueberblick über diel in der Mathe-
Mathematik nothwendigen und allmählich eingeführten] Erweiterungen
des Zahlenbegriffes.
Wir verstehen unter einer Mannigfaltigkeit oder Menge,
oder dem abkürzenden Zeichen -K ein System von Objecten oder
Elementen irgend welcher Art, das so in sich abgegrenzt und
vollendet ist, dass von jedem beliebigen Object vollkommen be-
bestimmt ist, ob es zu. dem System gehört oder nicht, gleichviel,
ob wir im Stande sind, in jedem besonderen Falle die Ent-
Entscheidung wirklich zu treffen oder nicht.
Eine Menge heisst geordnet, wenn von irgend zwei/unter-
zwei/unterschiedenen/ihrer Elemente immer ein in sich vollkommen^ be-
bestimmtes als das grössere gilt, und zwar so, dass aus a >> b,
b >> c stets a > c folgt. Ist a >> b und 6 > c oder a >> b > c,
so sagen wir, dass b zwischen a und c liegt.
Die natürlichen Zahlen bilden eine geordnete Menge; zwischen
zwei auf einander folgenden ihrer Elemente liegt kein weiteres
Element. Eine solche Mannigfaltigkeit heisst eine discrete.
Eine geordnete Menge von der Eigenschaft, dass zwischen je
zwei Elementen immer noch andere Elemente gefunden werden,
heisst dicht. Eine dichte Menge kann man bilden, wenn man
die natürlichen Zahlen in Paaren zusammenfasst, und diese Paare
als Elemente einer Menge auffasst. Diese Paare sollen Brüche
genannt und mit m: n oder — bezeichnet werden, und zwei solche
Brüche m:n und m':n' werden, einander gleich gesetzt, wenn
mn' = nm' ist. Fasst man alle iunter einander gleichen^ Brüche

. Schnitte. 5
zu einem Element zusammen, so erhält man eine Mannigfaltig-
Mannigfaltigkeit, die geordnet ist, wenn man noch festsetzt, dass m: n grösser
als ml: n' ist, wenn mn'\> nm' ist. Dass diese Mannigfaltigkeit
dicht ist, sieht man so ein: sind (i = m : w, ft' = m! : n' zwei
Brüche und ii^>(i', so kann man, wenn h eine willkürliche
Zahl ist,
hmn' , hm' n
hnnn hnn'
setzen, und darin ist hmn' ^> Jim'n. Man kann h immer so
annehmen, dass zwischen hmn' und hm'n noch Zahlen liegen,
und wenn jo eine solche Zahl ist, so liegt p : hnn' zwischen p
und 11'.
Die Punkte einer geraden Linie kann man auch als eine
geordnete Menge auffassen, wenn man unter grösser und kleiner
irgend eine Ortsbeziehung, z. B. weiter rechts und weiter links
oder höher und tiefer versteht. , /
/
Eine Eintheilung einer geordneten Menge 2JI in zwei Theile
A, B der Art, dass jedes Element a von A kleiner ist als jedes
Element b von B, wird ein Schnitt in Tt genannt und wird
passend durch (A, S) bezeichnet. Ein solcher Schnitt entsteht,
wenn man irgend ein Element (t, von -K herausgreift, alle
kleineren Elemente zu A, alle grösseren zu B und [i selbst nach
Belieben zu A oder zu B rechnet. (Es entstehen, genau gesagt,
je nachdem man das eine oder das andere thut, zwei Schnitte,
die wir aber immer als gleich betrachten wollen?) Wenn in einem
Schnitt (A, B) entweder A ein grösstes oder B ein kleinstes
Element p enthält, so sagen wir, dass (i den Schnitt (A, B) er-
erzeugt. Es kann aber auch der Fall vorkommen, dass weder A
ein grösstes noch B ein kleinstes Element besitzt.
Wenn jeder Schnitt in einer dichten Menge durch
ein bestimmtes Element p erzeugt wird, so heisst die
Menge stetig.
Stetigkeit sowohl als Dichtigkeit sind Eigenschaften, die der
Natur der Sache nach unserer Sinneswahrnehmung unzugänglich
sind; sie lassen sich daher auch an Dingen der Aussenwelt, an
Raumgrössen, Zeiträumen, Massen, niemals mit Strenge nach-
nachweisen, wie sehr sie uns auch im Wesen unserer Anschauung
zu liegen scheinen. Es lassen sich aber sehr wohl reine Begriffs-

6 Einleitung.
Systeme construiren, denen die Dichtigkeit ohue die Stetigkeit
oder auch Dichtigkeit und Stetigkeit zukommenl).
Ein Beispiel einer dichten Menge bieten die rationalen
Brüche. Diese Mannigfaltigkeit, die wir mit 91 bezeichnen wollen,
ist keine stetige. Denn nehmen wir irgend einen rationalen
Bruch p = m : n, worin m und n keinen gemeinschaftlichen
Theiler haben und nicht beide Quadratzahlßn sind, so ist (t, nicht
das Quadrat eines rationalen Bruches. Denn wäre (t, = p^ : g2,
so würde mg2 = np2 folgen, und daraus, wenn auch p und q
ohne gemeinschaftlichen Theiler angenommen werden, m = p2,
n — g2, was durch die Voraussetzung ausgeschlossen ist. Wenn
wir also einen Schnitt (A, B) in der Mannigfaltigkeit 91 bilden,
indem wir jedes Element a von 91 zu A rechnen, dessen Quadrat
kleiner als (i ist, und jedes Element b zu B, dessen Quadrat
grösser als (i ist, so ist weder in A ein grösstes noch in B ein
kleinstes Element enthalten, und, der Schnitt (A, B) wird nicht
durch ein Element in 91 erzeugt.
Denn angenommen, es sei a = p : q irgend ein Element in
A, also p2 : q2 •< m : n oder np2 <«f; dann nehmen wir
eine natürliche Zahl y beliebig und wählen eine andere natür-
natürliche Zahl x so, dass x >> y und x (mq* — np2) >> ny B p -f- 1),
woraus folgt:
s2(»f — w^2) > nx«/Bp -f- 1) > n Bpxy + J/2), .
also auch
mq2x2 >• n(px -\- y)K
Setzen wir also a' = (px -f- y) : qx, so ist al > a und a'2 -< (i,
also.a' auch in A enthalten; und ebenso kann man zeigen, dass
es in B kein kleinstes Element giebt.
Die Mannigfaltigkeit 91 kann uns aber als Ausgangspunkt
dienen, um eine stetige Menge zu construiren. Die Gesammtheit
aller Schnitte in 91 ist gewiss eine Mannigfaltigkeit, die mit ©
bezeichnet sein mag. Betrachten wir zwei verschiedene ihrer
Elemente « = (A, B), «' = (A\ B'), so wird entweder A ein
Theil von A' oder A' ein Theil von A sein. Denn wenn irgend
2) Dies ist von Dedekind nachgewiesen, dem wir überhaupt die
oben gegebene Definition der Stetigkeit verdanken. Vgl. die Schriften von
Dedekind, „Stetigkeit und irrationale Zahleu", BrauDschweig 1872, 1892.
„Was sind und was sollen die Zahlen?", Braünschweig 1888, 1893. Andere
Mannigfaltigkeiten, denen die Stetigkeit zukommt, sind von Weierstrass
und G. Cantor gebildet.

Stetigkeit. 7
ein Element a m A gehört, so gehört auch jedes kleinere Ele-
Element von 91 zu A. Ist A ein Theil von A', so wollen wir a
kleiner als «' nennen, und dadurch ist die Menge © zu einer
geordneten geworden.
~~~ Sehen wir die durch die rationalen Brüche erzeugten Schnitte
als gleichwertig mit diesen rationalen Brüchen selbst an und
nennen sie kurz rationale Schnitte, so enthält die Menge © die
Menge 9t, und © ist also jedenfalls eine dichte Menge. Die
Menge © ist aber auch stetig; denn bezeichnen wir die Theile
von © durch die grossen deutschen Buchstaben 51, SB ... und be-
betrachten irgend einen Schnitt C1, SB) in der Mannigfaltigkeit der
Schnitte, so können wir ein Element in © bestimmen, a = (A, B),
indem wir in A jeden rationalen Bruch aufnehmen, der einen der
Schnitte von 2t erzeugt, und alle anderen rationalen Brüche, die
also die rationalen Schnitte in SB erzeugen, nach B werfen.
Dieser Schnitt a in 91 erzeugt den Schnitt Bt, SB) in ©. Dies
wird nachgewiesen sein, wenn gezeigt ist, däss jedes Element «'
in ©, was kleiner ist als a, zu 2t gehört, und jedes Element ß
in ©, was grösser ist als a, zu 33.
Sei also «' = (A\ B') und a' <[ a, dann giebt es rationale
Brüche in A, die nicht in A' enthalten sind; es giebt also ein
rationales (i, so dass. a' <; fi <; a, und dieses p erzeugt einen
Schnitt, der in 21 enthalten ist, gehört also selbst zu 2t; da «'
<^ li ist, so gehört auch a' zu 2t. Ganz ebenso zeigt man, dass
jedes ß\ das grösser als a ist, zu SB gehört, und damit ist die,
Stetigkeit von © nachgewiesen.
Diese sehr abstracte Betrachtungsweise giebt uns die Sicher-
Sicherheit, dass die Annahme einer stetigen Menge keinen Widerspruch
enthält, dass solche Mengen wenigstens im Reiche der Gedanken'
existiren. Die Geometrie wie die Analysis, die immer gern an'
die geometrische Anschauung anknüpft, hat lange stillschweigend'
die Existenz stetiger Mengen, z. B. bei den Punkten einer ge-
geraden Linie oder irgend eines anderen zusammenhängenden'
Linienzuges, als eine Art von Axiom angenommen. Auch der
Unterschied zwischen dichter und stetiger Menge, der der Unter-
Unterscheidung commensurabler und incommensuräbler Strecken zu
Grunde liegt, ist den Alten nicht entgangen i).
1) Euklid, Elemente, Bach X.

8 Einleitung.
Auch wir wollen in der Folge nicht auf das Hülfsmittel der
geometrischen Anschauung verzichten, und z.B. die Punkte einer
geraden: Linie unbedenklich als eine stetige Menge betrachten.
Eine geordnete Menge 2JI heisst messbar unter folgenden
Voraussetzungen: Addition und Vervielfältigung sind in Ü){ all-
allgemein ausführbar, ebenso Subtraction eines kleineren von, einem
grösseren Element, d. h. aus irgend zwei Elementen a, & (die
auch identisch sein können) kann nach einer bestimmten Vor-
Vorschrift ein neues Element, a -f- b, von 3Jt abgeleitet werden, so
dass a -\- b grösser als a und als b ist, und dass die bekannten,
in den Formeln a -f- b = b -j- a, (a -\-b) -\- c — a -\- (b -\- c)
ausgedrückten Regeln der Addition gelten; nnd zu zwei Ele-
Elementen a, c, von denen das zweite grösser ist, kann ein drittes
Element b gefunden werden, so dass a -f- b = c ist, was auch
durch das Zeichen der Subtraction b == c — a ausgedrückt wird.
Zwei ungleiche Elemente von -K haben also immer eine bestimmte
Differenz. Aus diesen Voraussetzungen folgt, dass eine Summe
grösser wird, wenn einer der Summanden sich vergrössert. Die
wiederholte, etwa »w-malige Addition desselben Elementes a heisst
Vervielfältigung und ihr Ergebniss wird mit ma bezeichnet.
Es kommt endlich noch eine Voraussetzung hinzu, nämlich die,
dass bei jedem gegebenen a ein hinlänglich hohes Vielfaches ma
grösser ist, als ein beliebig gegebenes anderes Element b. Unter
den Elementen einer messbaren Menge giebt es also kein grösstes.
In einer dichten messbaren Menge giebt es auch kein
kleinstes Element; denn wäre, a das kleinste und b ein beliebiges
Element, so könnten zwischen b und b -\- a keine Elemente
liegen, weil, wenn b <^ c <C b -f- a wäre, aus der Definition
der Messbarkeit folgen würde, dass af = c — b kleiner als a
wäre. Es folgt auch umgekehrt, dass eine messbare Menge, in
der kein kleinstes Element vorkommt, dicht ist. Denn sind a
und a -\-b irgend zwei Elemente, so braucht man ja zu a nur
ein Element zu addiren, was kleiner als b ist, um ein Element
zwischen a und a -\- b zu erhalten.
Ist eine Menge stetig, so lassen sich die Voraussetzungen
für die Messbarkeit noch vereinfachen, weil dann die Subtraction
eine Folge der Addition ist. Sind nämlich a und c zwei Ele-
Elemente einer stetigen geordneten Menge 9JJ, in der die Addition

Messbare Mengen. 9
besteht, und ist c 5> a, so erhält man einen Schnitt (A, J5) in
9JI, wenn man alle Elemente: x, für die a -j- x ^ c ist, nach ^4,
und für die a -f- x >> c ist, nach 2? verweist. Dieser Schnitt wird
durch ein Element b erzeugt, für das a -f- b = c sein muss.
Die natürlichen Zahlen bilden nach unserer Definition eine
messbare Menge, in der ein kleinstes Element, nämlich 1, vor-
vorkommt. Die Mannigfaltigkeit der rationalen Brüche wird eben-
ebenfalls messbar, wenn man Addition und Subtraction nach den
bekannten Regeln der Bruchrechnung erklärt. Besonders wichtig
und gleichsam typisch für die messbaren Mengen ist die Mannig-
Mannigfaltigkeit der geradlinigen Strecken oder Längen einer Linie,
die einfach durch Aneinanderlegen addirt werden. Auch Stoff-
Stoffmengen, durch die Wage verglichen, und Zeiträume, mit der Uhr
gemessen, liefern: Beispiele messbarer Mengen. Die Art des
Messens liegt nicht in der Natur der Mannigfaltigkeit selbst,
sondern wird durch den denkenden Beobachter hineingelegt; so
würde es z. B. ebenso gut zulässig sein, unter der Summe a -\-b
zweier Strecken a und b die Hypotenuse eines rechtwinkligen
Dreiecks mit den Katheten a, b zu verstehen, statt, wie es ge-
gewöhnlich angenommen wird, die aus a und b durch Aneinander-
Aneinanderlegen zusammengesetzte Strecke.
Um die stetige Menge © der Schnitte in der Mannigfaltig-
Mannigfaltigkeit der rationalen Brüche 91 zu einer messbaren zu machen,
beachte man zunächst Folgendes.
Ist a, = (A, B). ein Element in @ und (i ein beliebig ge-
gegebener rationaler Bruch, so kann man immer ein Element a! in
A so bestimmen, dass a! -f- (i = V in B enthalten ist.. Denn
wählt man iu A, B zwei beliebige Elemente a, b, so kann man
die natürliche Zahl m so bestimmen, dass m\x, ^> b — a ist,,so
dass a -f- m p in B enthalten ist. Ist dann h die kleinste ganze
Zahl, für die a -f- h ^ in 33 enthalten ist, so ist a-\-Qi— l)ji ¦= al
in A und also a! -\- (i = V in B enthalten.
Wir verstehen nun unter der Summe (A, B) + (A\ B')
= (J.", B") oder «-(-«' = a" den Schnitt in 9i, den man erhält,
wenn man einen rationalen Bruch a" nur dann nach A" verweist,
wenn.ein a in A und ein a' in A' existirt von der Beschaffen-
Beschaffenheit, dass a" ^ a -f- a' ist. In der That ist (A", B") ein Schnitt;
denn ist a" in A" enthalten, so gilt dasselbe von jedem-, kleineren
Bruch, und es giebt Brüche, die in A", und Brüche, die nicht in
A" enthalten sind, nämlich die Brüche von der Form a--\- a'

10 : Einleitung.
und b ^- b'. Es ist ferner «" grösser als a und a'. Denn A"
enthält zunächst alle A, und wenn a' ein beliebiger Bruch in A'
ist, so kann man a in A so wählen, dass das Element a -\- a'
von A" in B enthalten ist; also ist A" umfassender als A. Die
durch rationale Brüche (i, p' erzeugten Schnitte ergeben durch
Addition den durch (i -\- p' erzeugten Schnitt.
Die Bedeutung dieser Definition erweist sich in folgendem Satze:
Ist 9Jt eine stetige messbare Mannigfaltigkeit,
und 50?! ein Theil von -DJ, der gleichfalls stetig und
nach der in 2Jt geltenden Regel messbar ist, so ist ^\
mit 2JI identisch.
Der Beweis ergiebt sich folgendermaassen:
1. Ist 2Jtx von -K verschieden, so giebt es in W Elemente «,
die kleiner sind als alle Elemente von SDlj.
'Denn sei a ein nicht in Wx enthaltenes Element von "JR.
Wenn es in SJij Elemente giebt, die kleiner als a sind, so bringt
a einen Schnitt (A1: _BX) in l!fft1 hervor, den man erhält, wenn man
alle Elemente von 9Jlx, die kleiner als a sind, in Ax aufnimmt, die
anderen in Bx. Dieser Schnitt muss aber wegen der voraus-
vorausgesetzten Stetigkeit von 2Jtx auch durch ein Element ax m W\
erzeugt werden, und weil 5KX ein Theil von -K ist, so muss %
auch in 9)i vorkommen. Wenn aber a nicht in 9)ix vorkommt,
so sind a und ax von einander verschieden, und kein "zwischen
a und % gelegenes Element von W kann zu 9)ix gehören. Denn
ist z. B. «<«], und bt ein Element von ^, was der Bedingung
a <C bi <C % genügt, so müsste &x, weil es kleiner als ax ist, zu
Alt und weil es grösser als a ist, zu Bx gehören.
¦ Folglich giebt es kein Element in 3Jlx, was kleiner ist als
<h — o (oder a — %), w. z. b. w.
2. Wir bestimmen nun einen Schnitt (.4, S) in 9I so, dass
' in B alle Elemente von -K aufgenommen werden, von denen ein
Element in üüij erreicht oder übertrofien wird, nach A also nur
die Elemente «, die kleiner sind als alle Elemente von üftj.
Dieser Schnitt werde durch das Element a in -K erzeugt. Ist
dann a' irgend ein Element in Tt, und a' >> a, so giebt es
zwischen a und a! immer ein und folglich auch beliebig viele
Elemente von 2J?X, während es in ^ kein Element giebt, was
kleiner als a ist. Nimmt-man nun

Nicht messbare Mengen. 11
al — a <C a, » < «i < öj < «',
worin a^, at zwei von einander verschiedene Elemente von Wi-i
sind, so ist a2 — «i <C ai un(i doch ist, wegen der Messbarkeit,
die Differenz a2 — ax in 9Jlj enthalten, worin ein Widerspruch liegt.
Es giebt also in 2JI kein Element, was nicht auch in Üftj
enthalten wäre.
: r
Der: zuletzt bewiesene Satz gilt/nicht mehr für stetige Mengen,
denen die Messbarkeit nicht, zukommt. Um dies^ an einem, Bei-
Beispiel zu zeigen, nehmen wiri die/oben definirte jMannigfaltigkeit
© der Schnitte a, und fügen noch ein mit 0 zu bezeichnendes
Element hinzu, welches kleiner, sein soll als alle a. Diese Menge
bezeichnen wir mit %.x. Hierauf wird eine neue Menge 5l2 con-
struirt, die aus den Paaren («, ß) besteht, worin «/und ß je ein
beliebiges Element aus 9XX darstellen. Diese Elemente werden so
geordnet, dass die kleineren « den grösseren a vorangehen, während
b;ei gleichen a die Elemente mit kleineren ß vorangehen. Die
Menge 5l2 enthält hier, wenn wir a = («, 0) annehmen, die Menge
3tx, ohne mit ihr identisch zu sein. Die Stetigkeit kommt hier
beiden Mengen zu, nicht aber die Messbarkeit.
Ebenso kann man noch reichere Mengen 313 bilden, die aus
den Elementen (a, ß, y) besteh/en, worin jedes der Zeichett a, ß, y
die Elemente von 9Ij durchläuft, u. s. f.
"Ein anderes lehrreiches Beispiel einer stetigen, nicht mess-
messbaren Menge erhält man, wenn man auf einer geraden Linie,
etwa von links nach rechts auf einander folgend, drei feste Punkte
a, b, c annimmt, und dann die Menge, 9Jt der Punkte dieser
Geraden betrachtet, die links von a und rechts von c liegen, und
den einen zwischenliegenden Punkt b hinzufügt. Hier ist sogar
in unserer räumlichen Anschauung eine Lücke \von endlicher
Ausdehnung vorhandenJ). Dass diesie Menge trotzdem noch als
eine stetige bezeichnet wird, rechtfertigt sich, wenn inan die ent-
entsprechende Mannigfaltigkeit in der Zahlenreihe aufsucht..
Wir greifen aus der Menge © eine Theilmenge ©x heraus,
indem wir alle Schnitte/'«< 1 und ß ^> 3 und ausserdem die
Zahl 2 in ©x aufnehmen.
l) Auf diese Art stetiger Mengen hat mich G. Cantor aufmerksam
gemacht.

12 Einleitung.
Die Elemente von @x haben eine durch © bestimmte Ord-
Ordnung, und man kann die Elemente von ©x in völlig eindeutiger
Weise .auf die Elemente.von © beziehen, so dass die Ordnung
gewahrt bleibt. Man ordne nämlich die Elemente a <; 1 in ©x
denselben Elementen in © zu, das Element 2 in ©x dem Element
1 in @, jedes Element ß >> 3 in ©j dem Element ß — 2 in ©.
Es haben idann, wenn man von © zu ©x übergeht, die Elemente
gewissermaassen nur andere Namen erhalten.
Wir gehen nun über zu der Definition der Verhältnisse,
die von Alters her als Grundlage der Zahlenlehre betrachtet
werden, und folgen dabei zunächst Euklid1).
Wenn man die Elemente einer stetigen messbaren Menge 9Jt
zu Paaren verbindet, und diese Paare an sich als Elemente be-
betrachtet, so entsteht eine neue Mannigfaltigkeit; wir bezeichnen
ein solches Paar mit a : b, oder auch mit -j-, unterscheiden aber,
wenn a und b verschiedene Elemente sind, a : b von b : a, und
nennen a den Zähler und b den Nenner von a : b. Diese Paare
wollen wir Verhältnisse nennen und wollen diese neue Menge
nun ordnen und messbar machen.
Nehmen wir zunächst an, dass zwei ganze Zahlen m, n exi-
stiren, so dass na = mb wird, wie es z. B. immer der Fall ist>
wenn a, b zwei natürliche Zahlen oder zwei commensurable
Strecken sind; dann ist, wenn p, q zwei andere ganze Zahlen sind,
dann und nur dann qa = pb, wenn mq = np ist. Denn aus
na = mb folgt qna = qmb, und wenn also qa = pb ist,
pnb = qmb, und folglich pn,= qm. 'Das Zahlenpaar p, q ist
durch diese Forderung vollständig bestimmt, wenn noch die Be-
Bedingung hinzukommt, dass p, q relative Primzahlen sein sollen.
Dann kann, wenn h eine beliebige ganze Zahl ist, m = hp,
n z=Jiq sein. In diesem Falle nennen wir das Verhältniss a : b
ein rationales und setzen es gleich dem rationalen Bruch m : n
oder p : q. Diese rationalen* Brüche können hiernach als Ver-
Verhältnisse ganzer Zahlen aufgfefasst werden.
Alle unter einander gleichen rationalen Verhältnisse bilden eine
rationale Zahl, und die rationalen Zahlen bilden, wie die ratio-
rationalen Brüche, eine geordnete, dichte und messbare Mannigfaltigkeit.
i) Elemente, Buch V.

Verhältnisse. 13
In die Mannigfaltigkeit der rationalen Zahlen ordnen sich
die natürlichen Zahlen selbst mit ein, wenn man unter einer
natürlichen Zahl m das Verhältniss m : 1 versteht.
Wir kehren jetzt zu irgend einer messbaren Mannigfaltigkeit
9JJ zurück und nehmen aus ihr irgend zwei Elemente a und b.
Wählt man, was immer möglich ist, zwei natürliche Zahlen >», w,
so dass «« > mb, so heisst das Verhältniss a : b grösser als
das rationale Verhältniss m : n oder
am
und wenn m : n > p : q, so ist auch a : b > p : g.
Ebenso folgt, wenn n' a <^ m'b ist,
a rrt_
Ist a : i ^> m : n, so kann man eine und folglich auch be-
beliebig viele rationale Zahlen nii -. nx finden, so dass
a nii in
ist, d. h. man kann zwischen a :b und m : n beliebig viele
rationale Verhältnisse einschalten. Um dies zu zeigen, wähle
man eine beliebige ganze Zahl h und bestimme die ganze Zahl h
so, dass h(na — mV) > hb wird, was immer möglich ist;
dann ist
a hm -\- fc m
T> hn >"w"'
Und ebenso folgt, wenn n'a <^m' 6, ~ti (m! b — n! a) >> 7c' a ist,
a h'm' m!
Wenn nun a : b und « : ß irgend zwei Verhältnisse sind,
die wir der Kürze wegen auch mit e, s bezeichnen wollen, deren
Elemente derselben oder auch verschiedenen Mannigfaltigkeiten
angehören, so sind zwei Fälle möglich: 1) Es liegt kein ratio-
rationales Verhältniss [i zwischen e und s, oder 2) es liegt ein ratio-
rationales Verhältniss zwischen e und s.
Im Falle 1) heissen die peiden Verhältnisse e nnd s ein-
einander gleich, und man sieht, dass zwei Verhältnisse, die einem
dritten gleich sind, auch unter einander gleich sind; denn ist
e <Z (i << £, so ist jedes andere Verhältniss e' entweder kleiner
oder gleich oder grösser als p. Ist e' gleich /*, so liegen so-

14 Einleitung.
wohl zwischen e und e' als zwischen e' und s rationale Verhält-
Verhältnisse. Ist aber e' kleiner als: (i, so liegt p, zwischen e' und s,
und ist e' grösser als p, so liegt (i zwischen e und e'; also kann
e' nicht zugleich gleich e und gleich s sein. ;
— Im Falle 2) heissen die Verhältnisse e, s ungleich. Es
kann also entweder «) e <; [i -< s oder ß) e > \t! > ,s sein, und
diese beiden1 Fälle schliessen sich aus, weil aus e < (i < j,
s <C ft' folgt, dass f«. << ft', und folglich e -< ft' ist.
Die Grössenbeziehung 2 «) oder 2 ß) bleibt auch bestehen,
wenn e oder £ durch ein ihm gleiches Element ersetzt wird.
Denn ist f«. < s und f«. ^ s\ so liegt zwischen ^ und s' ein
rationales Verhältniss und s, s' sind nicht gleich.
Im Falle 2 «) heisst e kleiner als s, im Falle 2 ß) heisst
e grösser als £.
Zwischen zwei ungleichen Verhältnissen kann .man eine be-
beliebige Anzahl rationaler Verhältnisse einschieben.
Wenn wir nun alle unter einander gleichen Verhältnisse zu-
zusammenfassen, so erhalten wir einen Gattungsbegriff, den wir als
Zahl im allgemeinen Sinne des Wortes bezeichnen. Die Zahl ist
also ein Name oder Zeichen für eine gewisse Mannigfaltigkeit,
deren Elemente eben die/mit einem unter ihnen gleichen Ver-
Verhältnisse sind1). Unter diesem Zahlbegriff sind die rationalen
Verhältnisse und folglich auch die natürlichen Zahlen als die
Verhältnisse m : 1 mit enthalten und bilden die rationalen
Zahlen.
Zahlen, die nicht aus rationalen Verhältnissen entspringen,
heissen irrationale Zahlen.
Nach dem, was bis jetzt ausgeführt ist, bilden die Zahlen
eine geordnete Menge, und man kann ihre Ordnung fest-
feststellen, wenn für jede Zahl irgend eines der\ darunter enthal-
enthaltenen Verhältnisse als Eepräsentant gewählt wird.
Von zwei Verhältnissen mit demselben Nenner und un-
ungleichen Zählern ist das das grössere, dessen Zähler grösser ist,
und von zwei Verhältnissen mit demselben Zähler und ungleichen
Nennern ist das das kleinere, dessen Nenner grösser ist.
l) Auf den Gattungsbegriff lassen sich auch die natürlichen Zahlen in
einfacher und folgerichtiger Weise zurückführen.

Zahlen. 15
Sind nämlich a, a1, b beliebige Elemente einer messbaren
Menge und d > a, so wähle man zunächst eine ganze Zahl n
so., dass na > b und n {a! — a) > b. Hierauf nehme man
die kleinste ganze Zahl m, die der .Bedingung mb > na ge-
genügt; dann ist na <z mb, aber mb < na'. Denn wäre mb
^> w a' J> w a -|- w (a' — a), so wäre mb > na -\- b; also
wäre gegen die Voraussetzung schon {m — l)b > na. Dann ist
a m a!
y<¥<:T'
also a:b < a':&; und ganz ebenso kann man beweisen, dass,
wenn b' > b ist, a ¦. b ;> a : V wird.
Man drückt diesen Satz auch so aus, dass ein Verhältniss
zugleich mit dem Zähler wächst und mit wachsendem Nenner
abnimmt.
Hieraus ergiebt sich auch leicht der folgende Satz: Sind
a, b, c, d Elemente derselben messbaren Menge und ist a : b
= c : d, so ist auch a : c = b : d.
Denn angenommen, es wäre a : c < b : d, so müsste es zwei
ganze Zahlen m, n geben, so dass
n a < m c
nb > md.
Dann aber wäre nach dem eben bewiesenen Satze na : nb <
mc : md, also auch a : b < c : d, entgegen der Voraussetzung.
Hieran schliesst sich nun folgender Hauptsatz. Wenn
von den vier Grossen a, b, c, d irgend drei aus einer
stetigen messbaren Menge beliebig gegeben sind, so
lässt sich die vierte in derselben Menge so bestim-
bestimmen, dass a : b = c : d ist.
Der Satz ist eine unmittelbare Folge der vorausgesetzten
Stetigkeit. Denn wenn man z. B. ein Element x von 9Jt in A
oder in S aufnimmt, je nachdem x : b kleiner oder grösser als
c : d ist, so erhält man einen Schnitt, der durch ein Element a
erzeugt wird, das der Bedingung a : b = c : d genügt. Es gilt
aber dieser Satz auch in gewissen nicht stetigen Mengen, z. B,
für die rationalen Brüche.
Hieraus folgt, dass man als Repräsentanten zweier Zahlen
immer zwei Verhältnisse wählen kann, deren Elemente derselben
Mannigfaltigkeit angehören, und die denselben beliebig zu wählen-
wählenden Nenner haben. Die Addition wird dann so erklärt, dass

}Q Einleitung.
a . b a -\-b
e ' e c
ist. Diese Regel umfasst als speciellen Fall die Addition der
rationalen Brüche, und um sie allgemein zu rechtfertigen, braucht
dann nur noch gezeigt zu werden, dass, wenn a : c = a' : d und
b : c = V : c',. auch (a -\- b) : c = {a! ~-\- V) -. d sein muss. Wir
beweisen dies, indem wir zeigen, dass, wenn a : c = a': d und
(a -f- b) : c > (a' -)- b'): c' ist, auch b : c > 6' : d sein muss. Es
sei also, wenn m und n zwei ganze Zahlen sind,
a -{-b m a' -\- V
~~c~ >^> d ;
dann ist n (a + 6) > mc und ind ^> na' -\- b. Dann ist um
so mehr md >¦ w a' und wegen a: c — a': d auch «ic>»«.
Es ist also auch
& m c — n a md — na' V
c «c ' nd d '
Andererseits folgt aber leicht aus der Voraussetzung a : c
= al : c', dass auch
mc — na md — na'
nc nd
ist, also b:c^> b' :d, w. z. b. w.
Hiermit ist also nachgewiesen, dass auch die Zahlen, wie wir
sie definirt haben, eine meSsbare Menge bilden. Sind a und c
einer stetigen Mannigfaltigkeit entnommen, so bilden auch bei
feststehendem c die Verhältnisse a: c eine stetige Menge und es
folgt also, da es überhaupt stetige Mengen giebt, dass auch die
Zahlen eine stetige Menge bilden.
Sind «, ß, y, d jetzt Zahlen, so kann man aus der Proportion
a: ß = y: § eine beliebige der vier Zahlen durch die drei anderen
gegebenen: bestimmen. Setzt man 8 = 1 und sucht «, so erhält
man die Multiplication a = ßy, und die Vertauschbarkeit
der Factoren ist eine Folge des Satzes, dass a:y = ß:d aus a:ß
= y.d folgt. Sucht man y, so erhält man die Division; und aus
der oben gegebenen Definition der Addition folgt die Grund-
Grundformel a(ß-\-y) = ct,ß-\-ay. Die vier Grundrechnungsarten sind
also in dem Gebiete der Zahlen ausführbar mit der einzigen
Beschränkung, dass bei der Subtraction der Subtrahend kleiner
sein muss als der Minuend.

Zahlenreihen. 17
Die Construction eines Schnittes in der Reihe der Zahlen
liefert stets den Beweis für die Existenz einer Zahl, die bestimmten
Anforderungen genügt. So erhält man einen Schnitt (A, JB),
wenn man alle und nur die Zahlen, deren Quadrat kleiner als
eine bestimmte Zahl « ist, in A aufnimmt; diesem Schnitt ent-
entspricht eine bestimmte Zahl, deren Quadrat gleich « ist und die
mit V« bezeichnet wird, und dadurch wird die Existenz der
Quadratwurzeln nachgewiesen.
Auf die Schnitte lassen sich auch die von G. Cantor zur
Definition der Irrationalzahlen eingeführten Zahlenreihen
zurückführen l).
Nach Cantor ist unter einer Zahlenreihe irgend ein un-
unbegrenztes, in hestimmter Weise geordnetes System von Zahlen
zu verstehen:
8 = #!, x2, xs, Xi . . .
von der Beschaffenheit, dass es eine bestimmte Zahl g giebt,
unter die keine der Zahlen S heruntersinkt, und dass, wenn d
eine beliebig gewählte Zahl ist, und xn, xm verschiedene Ele-
Elemente aus S sind, xn — xm oder xm — xn immer kleiner bleibt
als d, wenn m und n eine hinlänglich grosse Zahl überschritten
haben.
Es giebt immer Zahlen, die von den Zahlen einer solchen
Reihe nicht überschritten werden; denn hat man 8 gewählt und
n passend bestimmt, so überschreitet xm, welchen Werth auch
m haben mag, niemals die grösste der Zahlen x±, x% . . . xm
xn -\- 8. Andererseits giebt es auch Zahlen, die von unendlich
vielen xn überschritten werden, z. B. jede Zahl, die kleiner ist
als g. Man erhält nun einen Schnitt (A, JB), wenn man die
Zahlen nach JB wirft, die, wenn n einen hinlänglich hohen
Werth hat, von keinem xn mehr überschritte^ werden (die also
von keinem oder nur von einer endlichen Anzahl von ocn über-
überschritten werden), und alle anderen Zahlen (die also von unend-
unendlich vielen xn überschritten werden) nach A. Wird dieser Schnitt
durch die Zahl « erzeugt, so giebt es, wie klein auch 8 sei,
immer unendlich viele Zahlen xn zwischen a — s und a, und
man kann sagen, dass diese durch S vollkommen bestimmte Zahl
x) Cantor, Ueber die Ausdehnung eines Satzes aus der Theorie der
trigonometrischen Reihen. Mathematische Annalen, Bd. 5 A872)- vergl.
auch Heine, Elemente der Functionenlehre. Journal für Mathematik,
Bd. 74 A872).
Weber, Algebra. L 2

18 Einleitung.
« durch die Zahlenreihe S erzeugt wird. Nach Cantor ist die
Zahlenreihe S geradezu die Definition der Zahl «. Selbstver-
Selbstverständlich kann eine und dieselbe Zahl « durch sehr verschiedene
Zahlenreihen erzeugt werden. Diese Zahlenreihen sind aber alle
als unter einander gleich zu betrachten. Man kann unter Anderem
die Zahlen von S alle als rationale Brüche annehmen. Es lässt
sich auch umgekehrt leicht nachweisen, dass man zu jeder
gegebenen Zahl « immer Zahlenreihen S angeben kann, durch
die a erzeugt wird, so dass also die Gesammtheit der Zahlen-
Zahlenreihen S gleichfalls eine stetige Menge bildet.
Bei der Erklärung der Grundrechnungsarten hat sich bei
der Subtraction eine unbequeme Beschränkung ergeben, von der
wir uns frei machen durch Einführung der Null und der nega-
negativen Zahlen.
Es möge x jedes Element des bisher definirten Zahlensystems
bedeuten, das wir jetzt als das System der positiven Zahlen
bezeichnen wollen. Wir nehmen dies Zahlensystem ein zweites
Mal und bezeichnen zum Unterschied in diesem zweiten System,
das als das System der negativen Zahlen bezeichnet werden
soll, jedes Element mit — x. Das zweite System ordnen wir nun
dem ersten gerade entgegengesetzt, so dass überall, wo in dem
System x „grösser" steht, in dem System —¦ x „kleiner" gesetzt
wird, und umgekehrt. Addition und Subtraction werden in — x
ebenso erklärt wie in xr so dass (— x) -f- (— y) = — (x -\- y);
(— x) — (— y) = — (x — y) sein soll.
Wir wollen aber diese beiden Zahlensysteme in der Weise
zusammenordnen, dass jedes — x kleiner sein soll als jedes x.
Wir erhalten so eine geordnete Menge, in der kein grösstes und
kein kleinstes Element vorhanden ist. Dieses System ist auch
im Allgemeinen stetig, nur der einzige Schnitt (— x, x) wird
durch kein Element erzeugt, und hier, wo beide Systeme zu-
sammenstossen, ist also noch eine Verletzung der Stetigkeit vor-
vorhanden. Um die Stetigkeit herzustellen, müssen wir also dem
Schnitt (— x, x) entsprechend noch eine Zahl Null oder 0
hinzufügen, die eben durch diesen Schnitt definirt ist. Dann
haben wir eine geordnete stetige, beiderseits unbegrenzte Menge,
die vollständige Reihe der reellen Zahlen.
In dem so erweiterten Zahlenbereiche erklären wir nun die
Addition allgemein, indem wir definitionsweise setzen:

Negative Zahlen. 19
x -f- (-- x) = 0, a; + 0 = x,
x -+- (— y) = x — y, wenn' a; >¦ y, = — (y — x), wenn y > x.
Bei dieser Erklärung der Addition gelten, wenn zx, 0.,, 03
irgend drei Zahlen des ganzen Zahlenbereiches sind, die Gesetze:
*1 + *ä' = ^2 + *1, (*1 + ^a) + ^3 = ^1 + (>2 + %),
die man das commutative und das associativ.e Gesetz nennt. Man
bildet die Summe aus einer beliebigen Anzahl von Summanden,
indem man nach Belieben der Reihe nach je zwei Summanden
zu einer Summe vereinigt. Die Subtraction braucht nicht mehr
besonders berücksichtigt zu werden, wenn man sx — s2 durch
sx -\- (— z2) erklärt und — (— z) = z setzt.
Man stellt die Zahlenreihe anschaulich durch Punkte dar,
indem man von einem festen mit 0 bezeichneten Punkte einer
geraden Linie die positiven Zahlen als Strecken nach der einen,
etwa der rechten, die negativen Zahlen nach der anderen (linken)
Seite aufträgt. Das Bild der Summe zweier Strecken z-^ -\- 3%
erhält man, wenn man von dem Punkte zx aus die Strecke von
der Länge + z2 nach der rechten oder nach der linken Seite
abträgt, je nachdem ^2 positiv oder negativ ist.
Die Multiplication und Division wird in dem erweiterten
Zahlenbereich durch die Gleichungen
x {—y) = (— x) y = — xy
(—x) (—y) = xy, 01 = 0
erklärt. Die Division als die Umkehrung der Multiplication ist
immer möglich, ausser wenn der Divisor Null ist.
Für ein Product aus mehreren Factoren und für den Quo-
Quotienten zweier solcher Producte gilt der Satz, dass sein Werth
positiv oder negativ ist, je nachdem die Anzahl der überhaupt
darin (im Zähler und Nenner) vorkommenden Factoren gerade
oder ungerade ist.
Eine fernere Erweiterung des Zahlbegriffes bestellt in der
Einführung der complexen Grossen. Wir combiniren je zwei
Zahlen der gesammten Zahlenreihe zu Paaren (x, y), und be-
betrachten zwei solche Paare (x, y) und (a, b) nur dann als gleich,
wenn x = a, y = i ist. Diese Zahlenpaare bilden eine Mannig-
Mannigfaltigkeit , deren Elemente zwar nicht geordnet werden, mit
denen aber die Rechenoperationen der Addition, Subtraction,
2*

20 Einleitung.
Multiplication und Division vorgenommen werden sollen, nach
folgenden Regeln. Es sei
O, y) + («> &) = O + «, 2/ + &)>
(a>, y) (a, 6) = (*« — yb, xb + ya),
und wir setzen ausserdem fest, dass (x, 0) = x sei, was diesen
Gleichungen nicht widerspricht. Es ist (x, y) nur dann = 0,
wenn x und y beide gleich Null sind. Ferner bezeichnen wir
zur Abkürzung @, 1) mit i. Dann ergeben obige Gleichungen
die Folgerungen:
(x, 0) @, 1) = @, x) oder = ix,
(x, 0) + @, y) = (x, y) = x + yi,
% + yi + a 4- bi == O + «) + B/ + 6)*
und die Umkehrung der Addition:
# + yi — (a + ii) = (x — a) + i (y — b),
ferner die Multiplication:
(x -(- yi) (a -\~ bi) = xa — yi -j- i(a;6 -(- 2/a)> *2 = — 1>
(ä 4- yi) (x — yi) = x** + j/2, .
. . , . T . (a — bi) (x + V*)
g + y» = (a + 6«V (a» + 5^
oder
x -\- yi ax -\- by -\- i {ay — bx)
a -\-bi ~ «2 + ß '
wodurch die Division erklärt ist, ausser wenn a -\- bi = 0 ist.
Zahlen von der Form ix heissen rein imaginäre Zahlen
und i die imaginäre Einheit. Eine Zahl ix soll positiv oder
negativ imaginär heissen, je nachdem x positiv oder negativ
ist. Die Zahlen a -\- bi heissen imaginär oder complex. Das
System der reellen und der rein imaginären Zahlen sind
darunter als Specialfälle enthalten.
Es sind also in dem Gebiete der complexen Zahlen
x -\- yi die Grundrechnungsarten unbegrenzt auszuführen (mit
Ausnahme der Division durch Null), und die Rechnung mit den
reellen Zahlen ist ein Specialfall davon.
, Man stellt die complexen Zahlen e = x -\- yi nach Gauss
geometrisch durch die Punkte einer Ebene dar, indem man ein
rechtwinkliges Coordinatensystem zu Grunde legt und den- Punkt
mit den Coordinaten x, y als Bild des Zahlwerthes s betrachtet.
Die Punkte der #-Axe stellen in der oben besprochenen Weise

Imaginäre Zahlen. 21
die reellen Zahlen x dar. Die Punkte der y-Kxe sind die Bilder
der rein imaginären Zahlen yi. Der Coordinatenanfangspunkt
ist das Bild der Zahl 0. Der Radius vector vom Nullpunkte nach
dem Punkte s hat den Zahlwerth q = Vx2 -+- y*, und wird der
absolute Werth oder der Betrag oder, nach älterer Ausdrucks-
Ausdrucksweise, der Modulus der complexen Zahl z genannt.
Die einzige Zahl 0 hat den absoluten Werth 0. Jede positive
Zahl kommt bei unendlich vielen complexen Zahlen als absoluter
Werth vor und die Bildpunkte aller Zahlen mit demselben abso-
absoluten Werthe liegen auf einem Kreise, dessen Mittelpunkt im
Coordinatenanfangspunkte liegt.
Zwei imaginäre Zahlen, die sich nur durch das Vorzeichen
von i unterscheiden, also x -(- yi und x — yi, heissen conjugirt
imaginär. Ihr Product ist das Quadrat des absoluten Werthes
von jeder von ihnen
Wenn von zwei conjugirt imaginären Zahlen die eine gleich
Null ist, so ist auch die andere gleich Null, und man kann also
in jeder richtigen Zahlengleichung i durch — i ersetzen, ohne
dass die Richtigkeit gestört wird.
Wir wollen noch den oft angewandten Satz anführen, dass
der absolute Werth einer Summe zweier von Null verschiedener
complexer Zahlen niemals grösser ist, als die Summe der abso-
absoluten Werthe der Summanden, und nur dann gleich, wenn das
Verhältniss (der Quotient) beider Summanden reell und positiv
ist. Sei nämlich
8 = x + yi, c = a + bi, Z = (x -f a) -f- (y + b)i,
q* = x^ + y\ r2 = tt* + b2, B2 = (x + aJ + (y + i)%
dann ist
das ist sicher positiv, wenn ax -\- by <j; 0 ist. Wenn aber
ax -\- by >¦ 0 ist, so folgt aus
r2^2 — (ax + byJ = (ay — bx)\
dass rg ^ ax -\- by ist, und nur dann gleich, wenn ay — bx
= 0. Daraus also ergiebt sich, dass r -f- g ^> H ist und nur
in dem besonderen Falle r -\- q = H, wenn ay — bx = 0,
ax -(- by ^> 0, woraus das Gesagte folgt.
Bei der geometrischen Darstellung ist dieser Satz ein Aus-
Ausdruck dafür, dass in einem Dreieck eine Seite kleiner ist, als
die Summe der beiden anderen. Der Satz hat noch die andere

22: . Einleitung.
Folge, dass der absolute Werth einer Summe nicht kleiner sein
kann, als die Differenz der absoluten Werthe der Summanden.
Denn wenden wir den vorigen Satz auf die Summe c == Z — s
an, so folgt r ^ B -\- q oder
B %-r — Q.
Die Gleichheit findet hier nur dann statt, wenn der Quotient
e : c reell und negativ ist.
Es ist noch ein Wort über das wichtigste Hülfsmittel der
Algebra, die Buchstabenrechnung, zu sagen. Die Anwendung
dieses Hülfsmittels ist so allgemein, dass man bisweilen das Wort
Buchstabenrechnung geradezu synonym mit Algebra gebraucht.
Die Regeln, wie mit solchen Buchstabenausdrücken gerechnet
wird, setzen wir als bekannt voraus. Gleichungen zwischen
Buchstabenausdrücken können von zweierlei Art sein; entweder
es sind sogenannte Identitäten, d. h. die zwei einander gleich
gesetzten Ausdrücke können durch Anwendung der Eechenregeln
so umgeformt werden, dass beide Ausdrücke genau überein-
übereinstimmen. Man erhält dann aus solchen Bachstabengleichungen
richtige Zahlengleichungen, wenn die Buchstaben durch irgend
welche, sei es reelle, sei es complexe Zahlen ersetzt werden,
vorausgesetzt, dass dabei nicht die Forderung der Division durch
Null auftritt. Die Buchstaben in solchen Gleichungen werden
oft auch als Variable bezeichnet, weil man sich vorstellen kann,
ohne je zu einem Widerspruch zu gelangen, dass für die Buch-
Buchstaben nach und nach andere und andere Zahlwerthe gesetzt
werden.
Eine andere Art von Gleichungen zwischen Buchstabenaus-
Buchstabenausdrücken haben nicht diesen Charakter der Identität. Sie enthalten
vielmehr eine Forderung, die an solche Zahlen gestellt wird, die
man, ohne die Gleichungen unwahr zu machen, für die Buch-
Buchstaben einsetzen darf. Die Algebra hat die Aufgabe, Zahlwerthe
zu ermitteln, die einer solchen Forderung genügen, die Gleichung
zu lösen. In diesen Gleichungen werden die Buchstaben auch
als „Unbekannte" bezeichnet. Es kommen sehr häufig in ein
und derselben Gleichung Buchstaben von zwei Arten vor, solche,
für die beliebige Zahlwerthe gesetzt werden sollen, und andere,
deren Zahlwerth erst ermittelt werden soll.

EESTES BUCH.
DIE GRUNDLAGEN.

Erster Abschnitt.
Rationale Funetionen.
§. 1.
Ganze Functionen.
Nächster Gegenstand der Betrachtung sind ganze rationale
oder auch kurz ganze Functionen einer Veränderlichen.
Wir verstehen darunter Ausdrücke von folgender Form:
A) f(x) = aoxn + a^»-1 + a2tf»-2 -| 1- dn-iX -f- an,
worin n ein ganzzahliger Exponent, der Grad der Function f(x)
ist. Der Grad ist eine natürliche Zahl. Bisweilen ist aber
auch nützlich, von ganzen rationalen Functionen Oten Grades zu
sprechen, worunter ein von x unabhängiger Ausdruck verstanden
wird, x heisst die Veränderliche, a0, %, a2 ... «„_!, an die
Coefficienten. Sowohl x als a0, Oj . . . an sind Symbole für
unbestimmte Grossen, mit denen nach den Regeln der Buch-
Buchstabenrechnung verfahren wird, für die auch unter Umständen
bestimmte Zahlwerthe gesetzt werden können (vgl. die Einleitung).
Wenn die Function fix) in der Weise wie in A) geschrieben
ist, so nennen wir sie nach absteigenden Potenzen von x
geordnet. Die Summanden können in jeder beliebigen anderen
Reihenfolge angeordnet, also z. B. auch nach aufsteigenden Po-
Potenzen von x geordnet sein:
f(x) = a„ -)- a„-!X + • • • + «ja:«-1 -)- aoa^.
Durch Addition (Subtraction) und Multiplication ganzer
rationaler Functionen entstehen wieder ganze rationale Func-
Functionen. Die Vorschriften der Buchstabenrechnung geben un-
unmittelbar die Bildungsgesetze dieser neuen Functionen.
Bei der Addition ist der Coefficient irgend einer Potenz xv
in der Summe gleich der Summe der Coefficienten von xv in den
einzelnen Summanden. Der Grad der entstandenen Function ist

26 Erster Abschnitt. §. 1.
gleich dem höchsten der Grade der Summanden und kann sich
nur in dem besonderen Falle erniedrigen, wenn der höchste
Grad in mehreren Summanden vorkommt und die Summe der
Coefficienten der höchsten Potenzen gleich Null ist.
Bei der Multiplication zweier öder mehrerer ganzer rationaler
Functionen entsteht eine Function, deren Grad gleich der Summe
der Grade der Factoren ist.
Um für das Product das Bildungsgesetz der Coefficienten zu
übersehen, setzen wir
A(x) = a^x™ -)- «jx™-1 4-
W B(x) = 6az« + \oc"-t +
C) A(x)B{x) = C(x) — coxm+n -
und erhalten
d = a0 b\ -)- ax b0,
c2 = a0 b2 -\- av \
oder in allgemeinen Zeichen, wenn v eine der Zahlen 0, 1, 2 ...
m -(- n bedeutet:
D) cv = a^bv -f- »ihv-i -f- a2bv—^ -[-••• a.-i\ + av60,
worin alle a, deren Index grösser als m, und alle b, deren Index
grösser als n ist, gleich Null zu setzen sind. Denn cv ist der
Coefficient von xm+M~", und es entsteht also cvxm+n~v durch
Multiplication aller Glieder von der Form a^x—^ mit allen
Gliedern der Form bv-.floen~v+ii und darauf folgende Addition.
Sind «o und b0 = 1, so ist auch c0 = 1.
Hat in allen Factoren eines solchen Productes die
höchste Potenz von x den Coefficienten 1, so ist auch
im Product der Coefficient der höchsten Potenz = 1.
Aus diesen Vorschriften für die Rechnung mit ganzen Func-
Functionen folgt, dass die Regeln des Rechnens, die sich in Formeln'
wie ab = ba, (abjc = a(bc), (a -(- b)c == ac >-\- bc und ähn-
ähnlichen aussprechen, auch wenn a, b, c ganze Functionen von x
sind, gelten, und zwar in dem Sinne, dass ganze Functionen nur
dann als gleich gelten, wenn gleich hohe Potenzen gleiche Coeffi-
Coefficienten haben. ¦ ' ~
Unter ganzen Functionen mehrerer Veränderlichen verstehen
wir Summen von Producten Ton ganzen, positiven Potenzen der
Veränderlichen x, y, s . . . mit irgend welchen Coefficienten,-die

§. 2. Rationale Functionen. 27
als constant gelten. Man kann sich diese Functionen entstanden
denken aus den Functionen einer Veränderlichen x, wenn man
darin die Coefficienten. a0, % . . . a» selbst wieder als ganze
rationale Functionen von anderen Verhältnissen y, 0 ... auf-
fasst. So entstehen Functionen von m Veränderlichen aus Func-
Functionen von m — 1 Veränderlichen. Alle Glieder einer solchen
Function sind von der Form xr ys z* . . ., multiplicirt mit einem
Coefficienten, und wenn die Function gehörig zusammengefasst
ist, so kommt jede Combination der Exponenten r, s, t . . .nur
einmal vor. Zwei so geordnete ganze Functionen gelten nur
dann als einander gleich, wenn sie dieselben Producte xrys0t . . .
mit denselben Coefficienten enthalten; und eine geordnete ganze
Function ist nur dann gleich Null, wenn alle ihre Coefficienten
verschwinden.
§• 2.
Ein Satz von Gauss.
Wir wollen sogleich eine Anwendung der Multiplicationsregel
zweier ganzer rationaler Functionen machen zum Beweise eines
Satzes von Gauss, der uns später noch nützlich sein wird,
hier aber zur Einführung in die ßechnungsweise und als Beispiel
dienen soll1).
Wir betrachten hier den Fall, dass die Coefficienten in den
Functionen A(x), B(x) ganze Zahlen sind, so dass nach D)
auch die Coefficienten von C(x) == A(x)B(x) ganze Zahlen sind.
Wenn die sämmtlichen ganzzahligen Coefficienten a0, «j,... am
einer Function A(x) keinen gemeinschaftlichen Theiler haben, so
heisst die Function A(x) eine ursprüngliche oder primitive
Function, und der Satz, den wir beweisen wollen, lautet:
Wenn A (x) nnd B (x) ursprüngliche Functionen
sind, so ist auch ihrProduct C(x) eine ursprüngliche
Function.
Der Beweis ergiebt sich fast unmittelbar aus dem Anblick
der Formel D), §.1.
Wenn nämlich die sämmtlichen Coefficienten c0, cv c2... cm+n,
wie sie dort angegeben sind, einen gemeinschaftlichen Theiler
haben, der grösser als 1 ist, so muss es auch wenigstens eine
Gauss, Disquisitiones antkmeticae, Art. 42.

28 Erster Abschnitt. §• 2.
Primzahl geben, die in allen diesen Coefficienten aufgeht. -Es
sei p eine solche Primzahl; diese kann nach der Voraussetzung,
dass A(x), B(x) ursprünglich seien, weder in allen a0, <h • • • am,
noch in allen 60, bx . . . b„ aufgehen.
Es möge nun p aufgehen in:
a0, % ... «r-i) aber nicht in ar,
in
60, &i . . . &s_i, aber nicht in bs,
dann ist nach Voraussetzung r ^ m und kann auch gleich Null
sein, wenn p schon in a0 nicht aufgeht. Ebenso ist s <n.
Bilden wir nun nach D) cr+s und ordnen es in folgender
Weise:
qn cr+s = arbs -)- ar-ibs+1 -f- a,.-2&s+2 + • • •
so sieht man unmittelbar, dass cr+s nicht durch p theilbar sein
kann, wie doch angenommen war; denn das erste Glied arbs ist
durch ja nicht theilbar, während alle anderen Glieder, da sie mit
einem der Coefficienten a0, % ... ar-i, b0, bi ¦ • ¦ bs-i multiplicirt)
sind, durch p theilbar sind. Die Annahme also, dass C(x) nicht
ursprünglich sei, während es A (x) und B (x) sind, führt zu einem
Widerspruch.
Dieser Satz lässt sich übertragen auf Functionen von meh-
mehreren Veränderlichen. Wir nennen eine ganze rationale Function
von m Veränderlichen mit ganzzahligen Coefficienten ursprüng-
ursprünglich oder primitiv, wenn die Coefficienten keinen gemeinsamen
Theiler haben, und wir sprechen den Satz aus, dass das Pro-
duct von zwei ursprünglichen Functionen wieder
eine ursprüngliche Function ist.
Um seine Wahrheit einzusehen, brauchen wir nur in der
oben durchgeführten Betrachtung die Coefficienten a0, a^, a2 . . .
bo, bu b2 . . . nicht als ganze Zahlen, sondern als ganze rationale
Functionen von [i — 1 Veränderlichen y, z . . . anzunehmen und
eine solche Function durch eine Primzahl p theilbar zu nennen,
wenn alle ihre Coefficienten durch p theilbar sind. Setzen wir
dann voraus, der zu beweisende Satz sei bereits für Functionen
von ji. — 1 Variablen bewiesen, dann ergiebt die Formel A)
seine Richtigkeit für Functionen von ji. Variablen, also seine
allgemeine Gültigkeit durch den Schluss der vollständigen In-
duction oder den Schluss von fi v— 1 auf ji..

§; 2. Kationale Functionen. 29
Durch dieselbe Betrachtungsweise schliesst man auch, dass
ein Product von zwei oder mehreren ganzen Functionen nicht
verschwinden kann, wenn nicht einer seiner Factoren ver-
verschwindet. Denn eine verschwindende Function ist durch j e d-e
Primzahl j) theilbar.
Eine imprimitive Function ist eine solche, deren ganzzahlige
Coefficienten alle einen gemeinsamen Theiler haben. Den grössten
dieser Theiler nennen wir den Theiler der Function. Dann,
können wir den bewiesenen Satz auch so ausaprßßhen:
Der Theiler eines Productes zweier ganzer Func-
Functionen ist gleich dem Product der Theiler beider
Functionen.
Denn sind PA und QB zwei ganze Functionen mit den
Theilern P und Q, so sind A und B ursprüngliche Functionen.
Also ist auch AB = C eine ursprüngliche Function und PQ
ist der Theiler der Function PA . QB = P QC.
Wir können dem Satze, insofern er sich auf Functionen
. einer Veränderlichen bezieht, ohne seinen Inhalt wesentlich zu
ändern, folgende Fassung geben, in der er besonders nützlich ist.
Sind
<p (x) = #» -f~ "i x™—1 + w2 x™—* -[- • • • -f- am
1>(x) = x» -f- ftaf-» + ß2x»-* -\ h ß»
zwei ganze rationale Functionen, in denen die höchsten
Potenzen von x den Coefficienten 1 haben, während die
übrigen Coefficienten rationale Zahlen sind, so können
in dem Product
<p(x)ip(x) — xm + n 4- y1xm+n~1 -f- y2xm + n-2 + • • • + 7m + n
die Coefficienten y nicht alle ganze Zahlen sein, wenn
die Coefficienten w, ß in q>(x) und tl>{x) nicht alle ganze
Zahlen sind.
Denn bezeichnen wir den kleinsten Hauptnenner der Coeffi-
Coefficienten w von <p mit a0, der Coefficienten ß von ip mit b0, so
sind a0 <p(x) — A(x), boip(x) = B(x) primitive Functionen von x.
Ihr Product a0 b0 <p (x) ty (x) hätte, wenn die Coefficienten y ganze
Zahlen wären, den Theiler a0 bo und wäre also, wenn a0 und b0
nicht beide gleich 1 wären, nicht primitiv; dies aber wäre ein
Widerspruch mit dem oben bewiesenen Satze.

30 Erster Abschnitt. §. 3.
&. 3.
Division.
Es seien, wie bisher
A = A(x) = aoxm -|- «x«™-1 + • • •
( ' B = B(x) = &„«»+&! o"-1 -|
zwei ganze rationale Functionen von a;; es soll jetzt vorausgesetzt
werden, dass m 5; n sei und dass a0 und &0 von Null verschieden
sind. Dann ist die Differenz
B) A — £ #»—.B
auch eine ganze rationale Function von x, deren Grad aber
kleiner ist als m, da die höchste Potenz in beiden Gliedern
der Differenz denselben Coefficienten hat und also herausfällt.
Wir setzen diese Differenz:
C) Ä = A'(x) = a'ox™' -\- a'ix'-1 -\- ¦ • •, m' < m.
Ist nun m' noch ^ n, so können wir in B) A' an Stelle von
A setzen und dieselbe Schlussweise wiederholen.
So ergiebt sich eine Kette von Gleichungen:
A — %- x™-n B = A',
D) K B — A,
A" — ^ x^"-"B = A"\
und diese Kette lässt sich so lange fortsetzen, bis der Grad der
entstandenen Function kleiner als n geworden ist. Da nun in
der Reihe der Functionen A, A', A" . . . der Grad jeder folgenden
jnindestens um eine Einheit erniedrigt ist, so besteht die
Kette der Gleichungen D) höchstens aus m — n -\- 1 Gliedern;
sie kann aber auch weniger Glieder enthalten, wenn sich gleich-
gleichzeitig mehrere Potenzen herausheben. Addiren wir die sämmt-
lichen Gleichungen D), bezeichnen die letzte der Functionen
A, A' . . . mit C und setzen zur Abkürzung
E) Q=°f ^-»+!^'-»+...,

§. 3. Division. 31
so dass auch Q eine ganze rationale Function von x ist, so
folgt
F) A = QB + G.
Die hier geschilderte Operation, durch die aus A, B die
Functionen Q, G gefunden werden, heisst Division. A ist der
Dividendus, B der Divisor, C der Rest und Q der Quo-
Quotient. Der Grad des Restes ist immer niedriger als
der Grad des Divisors.
Die Coefficienten der Functionen Q und C sind aus den
Coefficienten a und b durch Addition, Subtraction, Multiplication
und Theilung zusammengesetzt. Im Nenner kommen aber nur
Potenzen von b„ vor, und wenn also b0 = 1 ist, so sind die
Coefficienten von Q und C ganze Functionen der a und b. Die
höchste Potenz von bt), die im Nenner auftreten kann, ist die
(m — n -\- l)te, da in der Kette D) in jeder folgenden Gleichung
im Nenner einmal der Factor b0 hinzukommt. Es kann aber in
besonderen Fällen die höchste Potenz von b0 in allen Nennern
niedriger sein.
Nehmen wir z. B. für A eine Function dritten Grades
G) f(x) = «o«3 + «l«2 + «2^ + «3
und für B die sogenannte erste Derivirte von f(x), die vom
zweiten Grade ist
(8) /'(«) = 3 0,«» + 2 0!« + a2,
so erhält man:
c _ ßa0a2 — lal ^ 9a,«,- a^a%
J . 9a0 •" 9a0
Wie man. die in den Gleichungen D) vorgeschriebene Rech-
Rechnung zweckmässig anordnet, darf hier aus den Elementen als
bekannt vorausgesetzt werden. Wir machen auf die Analogie
aufmerksam, die zwischen dieser Rechnung und der Division
im dekadischen Zahlsystem besteht. Eine Function fix) stellt
eine dekadisch geschriebene Zahl dar, wenn die Coefficienten
a0, Oj ... ganze Zahlen zwischen Null (einschliesslich) und 10
(ausschliesslich) sind, und x = 10 gesetzt wird. Lässt man in
den Coefficienten auch Zahlen zu, die grösser als 10 sind, so
kann man eine Zahl auf verschiedene Arten durch f(x) dar-
darstellen. Man wendet dies bei dem Divisionsverfahren an, um auf

32 Erster Abschnitt. §. 4.
die einfachste Weise in den Resultaten gebrochene und negative
Coefficienten zu vermeiden.
Ebenso wie man bei der Rechnung mit dekadischen Zahlen
eine nicht aufgehende Division durch die Decimalbrüche fort-
fortsetzen kann, so kann man auch bei der Division von Functionen
die Rechnung noch weiter führen.
Ist nämlich jetzt 9(x) eine Function mten Grades und/(#)
eine Function #en Grades, wobei über die Grössenbeziehung von
m und n nichts festgesetzt werden soll, so nehme man einen
beliebig hohen Exponenten v, und wende die Regel der Division
durch f{x) auf die Function xv<I>(x) an. ' Bezeichnet man einen
Rest von höchstens (n — l)tem Grade mit <&„(¥), so ergiebt sich:
A1) a?Q(x) —f(x) {cn-m-1x™-»+* + cn-mxm-n+*-1 -\
+ c,^} + *,(*).
Die Coefficienten c„_m_i, c„_m, cw_m+i . . . sind rational
aus den Coefficienten von f(x) und <P (x) gebildet. Der Coeffi-
cient cx ist von der Wahl von v unabhängig, sofern nur v > x ist.
Denn wenn man in A1)
f(x) = aox» + «i«»-1 -\ \- an
®(x) = b^x™ + b1xm~1 -) \- bm
setzt, so erhält man zur successiven Berechnung der c„_m_x
cn-m, cn-m+1 ... die Gleichungen
floCn-m-l = ^0
,, m «0 C„_m -(- «j Cn—m-\ = ^1
flo^ m + 1 ~y~ ®lCn—m ~\~ (^2^n — m—2 == 
und diese Kette von Gleichungen kann beliebig weit fortgesetzt
werden, wobei die a, deren Index grösser als n, und die b, deren
Index grösser als m ist, gleich Null zu setzen sind.
§.4.
Theilung durch eine lineare Function.
Wir wollen die allgemeine Vorschrift für die Division noch
auf einen besonderen Fall anwenden. Es sei der Dividend
A) f(x) = aoxn + a^"-1 + a2«»-2 -\ \-a„
beliebig, dagegen der Divisor vom ersten Grade oder, wie man
auch sagt, linear. Wir wollen auch den Coefficienten der ersten

§. 4. Division durch lineare Funotionen. 33
Potenz von x im Divisor = 1 voraussetzen und also den Divisor
in der einfachen Form (x — a) annehmen, worin a beliebig
bleibt. Der Quotient Q ist in diesem Falle vom (n — l)ten Grade
und der Rest G vom Oten Grade, d. h. von x unabhängig. Setzen
wir also
B) /(*) = (x-a)Q + C,
so enthält C die Variable x nicht mehr, und wenn wir
C) Q = qox«-i + qLx"^ + ••• + qn-*x + gn_a
setzen, so folgt aus B):
D) f(x) = qox»^- ft«»-H h <ln
und aus der Vergleichung mit A):
E)
F)
Daraus
erhält
= «0
¦— Oq m
= aoa-
0.1
¦ 0a
q.n-1
C
man
4-
i
2 +
— «3o
— Mi
— uqn-2
«On-l
dt
«1« +
= «!
— a2
= »n-l
= an.
«2
2 -) aM_a
C entsteht aus /(ic), wenn man a; = « setzt, und kann also
auch mit /(«) bezeichnet werden.
Demnach haben wir auch die Formel
G) /(^-/W^
v y a; •—• a *v y
worin ^ (a;) eine ganze Furiction vom Grade w — 1 ist.
Wenn wir in den Ausdrücken F) an Stelle der unbestimmten
Grosse a das Zeichen x setzen, so entsteht daraus eine Reihe
von ganzen rationalen Functionen von x, die wir, wenn wir der
Einfachheit halber a0 = 1 setzen, so schreiben:
Weber, Algebra. I.

34 ... Erster Abschnitt. '" §; 5;
/o =1, ' ' ¦;¦¦; ;¦¦"
/i = # + «i,
(8) /a — tf2 + «^ + a2,
Diese Functionen fo, fi • • • fn-i werden uns später noch
gute Dienste leisten. Für jetzt fügen wir noch folgende Bemer-
Bemerkungen bei.
Man kann nach (8) die Potenzen 1, x, x2 . . . xn~1 von' x,
linear ausdrücken durch die Functionen /0, fx . . . fn—i, und zwar
so, dass in den Coefficienten nur ganze rationale Verbindungen
der a vorkommen, z. B.
1 =/o,
x = /i — «i/o,
*2 =/2 — «1/1 + («i2 — «2)/o,
und daraus folgt, dass man jede ganze rationale Function von;a;,
deren Grad nicht grösser als n — 1 ist, gleichfalls linear durch
/oi /ii • • -i fn—i ausdrücken kann in der Form
(9) Wo +yifl-\ H Vn-lfn-l,
worin die Coeficienten y0, yt . . . y„—i von x unabhängig sind.
Ist also F(x) eine beliebige ganze rationale Function von x,
so kann man nach §. 3, indem man f(x) als Divisor betrachtet
A0) F(x) = Qf(x) + ,2/c/o + yj, -\ 1- yn-xfn-V
setzen, worin auch Q eine ganze rationale Function von x ist.
Zur recurrenten Berechnung der Functionen fv(x) ergiebt
sich aus (8) die Eelation: ..,;'¦ ¦
A1) . fvip) — xfv-i(x) = ar.
§. 5:
Crebrochene Functionen; Theil-barkeit.
Wenn F(x) und/(#) zwei ganze rationale :Functionen, von x
sind, so heisst der Bruch ,. .. •
{) • fix) ¦'¦- '"
eine gebrochene rationale oder auch kurz gebrochene
oder rationale Function von x.

§. 5. Theilbarkeit ganzer Functionen. 35
Ist der Grad des Zählers niedriger als der Grad des
Nenners, so heisst die Function echt gebrochen, im entgegen-
entgegengesetzten Falle unecht gebrochen.
Nach §. 3 lassen sich die ganzen rationalen Functionen Q
und <p(x) so bestimmen, dass
B) F(x) = Qf(x) + cp(x),
und der Grad von tp(x) kleiner als der Grad von f(x) ist; dem-
demnach ist
7M 7W
und daraus der Satz:
Jede gebrochene Function kann in die Summe aus
einer ganzen und einer echt gebrochenen Function zer-
zerlegt werden.
Ist n der Grad von f(x), so ist der Grad von q> (%) höchstens
n — 1, er kann aber auch niedriger sein; insbesondere kann
auch der Fall eintreten, dass q>(x) identisch verschwindet.
Dann heisst die Function F(x) durch f(x) theilbar.
Die Function
F(x)
ist in diesem Falle nur scheinbar gebrochen, in Wirklichkeit der
ganzen Function Q gleich.
Die Formel
D) ± A — xm~x -\- xm~2 -f xm-3 -| 1-1
giebt hierfür ein einfaches Beispiel. Es ist dies die bekannte
Formel für die Summe der geometrischen Progression
1 -)- x -\- #2 + • • • -f x™-1.
Für die Heilbarkeit von Functionen gelten dieselben Ge-
Gesetze, wie für die Theilbarkeit der Zahlen, insbesondere die
folgenden: '
1. Wenn die Function F(%) durch die Function
f(x), f(x) durch eine dritte Function q>(x) theilbar ist,
so ist auch F(x) durch <p(x) theilbar.
Denn ist
' ¦ ¦. ¦ : F= Qf, ^ f=q9i _, , _ ..1 . \
worin Q und q ganze rationiale Functionen. sind, so¦ ist ,'.'.". :
;.' .:. ; F—Qq<p, - ;'.-.-; ..' - :: .:.!
und da Q q eine ganze rationale Function ist, F durch q>> theilbar.
3*

36 Erster Abschnitt. §. 5.
2. Ist F(x) durch f(x) theilbar und Q eine beliebige
ganze rationale Function, so ist auch QF(x) durch f(x)
theilbar.
3. Ist F(x) und/(#) durch q> (x) theilbar, so ist auch
F(x) +f(x) durch cp(x) theilbar, oder allgemeiner:
4. Sind jp7!, F2 . . . durch f(x) theilbar und Q„ Q2 . . .
beliebige ganze rationale Functionen, so ist auch
QiFi + Q3F2 + • • • durch f(x) theilbar.
Der letzte Satz umfasst die beiden vorhergehenden und wird
einfach so bewiesen.
Sind Fu 1^ ... durch / theilbar, so kanu man die ganzen
rationalen Functionen ©j, <P.2 . . . so bestimmen, dass
F^VJ, . Fa = *,/...
und folglich
Q1F1 + ft-fi H = (öi®i + ft®2 H )/•
Da nun Q1^>1 -\- Q^z -\- • • • eine ganze rationale Function
ist, so ist der Satz bewiesen.
5. Jede Function ist durch sich selbst theilbar.
In Bezug auf die Theilbarkeit oder Untheilbarkeit von Func-,
tionen wird nichts geändert, wenn die Functionen mit beliebigen
von x unabhängigen Factoren multiplicirt werden.
Eine von x unabhängige, von Null verschiedene Grosse kann
als Function nullten Grades aufgefasst werden. Nennen wir eine
solche Grosse eine Constante, so können wir sagen:
6. Jede Function ist durch jede Constante theilbar.
Wenn eine Function durch eine andere theilbar ist, so ist
der Grad des Quotienten gleich der Differenz des Grades des
Dividenden und des Grades des Divisors. Ersterer kann also
nicht kleiner sein als letzterer. Sind die Grade gleich, so ist
der Quotient eine Constante, und daraus folgt: .
7. Wenn von zwei ganzen rationalen Functionen
gleichen Grades die eine durch die andere theilbar
ist, so unterscheiden sie sich nur durch einen con-
stanten Factor von einander, und es ist auch die
zweite durch die erste theilbar.
8. Nach §. 4 ist die nothwendige und hinreichende
Bedingung dafür, dass die Function f(x) durch die
lineare Function x — a theilbar ist, die, dass /(«)
= 0 sei

§. 6. Grösster gemeinschaftlicher Theiler. 37
§.6.
Grösster gemeinschaftlicher Theiler.
Es ist eine Aufgabe von fundamentaler Bedeutung, zu ent-
entscheiden, ob zwei ganze rationale Functionen ausser den Con-
stanten noch einen anderen gemeinschaftlichen Theiler haben.
Man findet die Lösung durch den Algorithmus des grössten
gemeinschaftlichen Theilers ganz in derselben Weise, wie
die entsprechende Frage in Bezug auf die Theilbarkeit ganzer
Zahlen beantwortet wird. (S. die Einleitung.)
Es seien
A) f(x) = 4 <p(x)=A'
zwei gegebene Functionen; der Grad von <p (x) möge niedriger
oder wenigstens nicht höher als der von f(x) sein.
Wir dividiren A durch A' und bezeichnen den Rest, dessen
Grad niedriger ist als der Grad von A', mit A", also:
A = Q'A> + A";
nun dividiren wir A durch A' und bezeichnen den Eest mit A'",
und fahren so fort in der Bildung der Functionenreihe:
B) A, A\ A", A" . . .,
deren Grade n, n', n", n'" . . . immer abnehmen und folglich nach
einer endlichen Anzahl von Divisionen auf Null heruntergehen.
Der letzte Rest vom Grade Null, der also eine Constante ist, sei
AW. Dann haben wir die Kette der Gleichungen:
A = Q'A' + A"
A' = Q"A" + A"
C)
worin Aw eine Constante ist.
Wenn nun A, A' irgend einen gemeinsamen Theiler haben,
so ist dieser nach den Sätzen des vorigen Paragraphen, wie der
Anblick der Gleichungen C) lehrt, auch Theiler von A", A'",
A"" u. s. f. bis Am. Ist J.w eine von Null verschiedene Con-
Constante, so kann also kein von x abhängiger Theiler von f(x)
und cp(x) existiren. Solche Functionen heissen theiler fremd
oder relativ prim. Man sagt auch, indem man nur die von %

38 Erster Abschnitt. §. 6.
abhängigen Theiler berücksichtigt, die Functionen haben
keinen gemeinsamen Theiler.
Die Bedingung, dass die beiden Functionen einen gemein-
gemeinsamen Theiler haben, ist also:
D) ¦ Am = 0.
In diesem Falle ist Ä(v~1) Theiler von A(v~2\ wie die letzte
Gleichung C) zeigt, und nach der vorletzten dieser Gleichungen
Theiler von A!y~S) u. s. f., also auch Theiler von A und A\ d. h.
von f und cp. Und da umgekehrt jeder gemeinsame Theiler von
A, A' auch Theiler von A("~1) ist, so heisst A(v~v der grösste
gemeinsame Theiler von / und <p. Der Algorithmus C)
zeigt, dass man Aw oder A(v~x) aus den Coefficienten von / und cp
durch die rationalen Rechenoperationen ableiten kann,
und zwar so, dass immer nur durch die Coefficienten der höchsten
Potenzen von x in den Functionen A, A', A" . . ., die von Null
verschieden sind, dividirt wird.
Wir wollen diese Betrachtungen auf zwei Beispiele an-
anwenden.
Es seien zunächst:
,-v A = aox2 -j- a\x + «2
W B = bhX> + blX + b2
zwei Functionen zweiten Grades, also a0, i0 von Null ver-
verschieden. .
Der erste Schritt ist die Bildung der Gleichung
"F) A = £b + C,
worin •
G) C =cox -f c„ ¦
und
\°) Co v , Ci r
Ist c0 = 0; also G constant, so haben A, B nur dann einen
gemeinsamen Factor, wenn auch cx = 0 ist, und dann ist A
durch B theilbar, d. h. A und B unterscheiden sich nur durch
einen constanten Factor. Ist aber c0 von Null verschieden, so
setzen wir die Rechnung fort, indem wir
B = QC+D
setzen, worin (nach §. 4, wenn dort « = — cx : c0 gesetzt wird)

§. 6. Quadratische, und cubische Functiou. 39
/q\ '. j\ Qq Q{ — fei co fr ~t
o
Ist D von Null verschieden, so sind A, B ohne gemein-
gemeinschaftlichen Theiler. Ist aber D = 0, so ist 0 der grösste ge-
gemeinschaftliche Theiler von A und B.
Setzt man die Werthe c0, fr aus (8) in (9) ein, so erhält
man mit Weglassung des Nenners boc^ die Bedingung für die
Existenz eines gemeinsamen Theilers C von A und B in der Form
A0) ao26| -\- «22&02 — 2«o«2&<A — ai«2&<A — a^^b^
-j- a0a2b? -(- c^&o&j = 0
oder
A1) (ao62.— &o«2J + (»o&i — «i&o) («2&i — «1^2) = 0. •
Diese Bedingung ist auch erfüllt, wenn c0 und cx gleich
Null sind, und ist also die nothwendige und hinreichende Be-
Bedingung dafür, dass A, B einen gemeinsamen Theiler haben.
Die linke Seite von A0) oder A1) heisst die Kesultante
der Functionen A und B.
Als zweites Beispiel nehmen wir das schon im §. 3. gewählte.
Setzen wir
fi.X)= «0^3 + alX2 + «2^ + «3 = Ä
/'(*) = 3ao^2 + 2% a; +a2 = J5,
und setzen a0 von Null verschieden voraus, so haben wir nach §. 3:
A3) ¦ A = QB + C, ' ;
A4) 0 = c0* + Cii
worin ' y
90» . ' Cl~ 9^
Wenn c0 gleich Null ist, so ist hiermit der Algorithmus schon
geschlossen; wenn cx von Null verschieden ist, dann haben A und
B keinen gemeinsamen; Theiler; ist aber cx auch gleich Null, so
ist B selbst der grösste gemeinsame Theiler von A und B, d. h.
A ist durch B theilbar. Die Bedingungen hierfür sind also:
A6) _..-..- 3 ao.a? — «i2 =. 0, 9 a0a3 — a-^a^ = 0.
Ist Co nicht gleich Null, so gehen wir einen Schritt weiter
und setzen
A7) . B =PC + D,
worin, D constant wird und den.Ausdruck erhält:
3ct0C2

40 Erster Abschnitt. §: 6.
Ist dieser Ausdruck von Null verschieden, so sind A und B
theilerfremd, ist er gleich Null, so haben A und S den grössten
gemeinschaftlichen Theiler G. Setzen wir für c0, q dieWerthe(lö)
ein, lassen den Nenner weg, heben noch den von Null verschie-
verschiedenen Factor 9a0 heraus und kehren das Vorzeichen um, so
erhält diese Bedingung nach einfacher Kechnung die Gestalt:
A9) a-fa/ -\- 18ao«i«2«3 — 4ao«23 — ^afcts — 27a02a32 = 0.
Sie ist, wie man leicht durch Kechuung oder auch aus A8)
sieht, auch dann erfüllt, wenn die Bedingungen A6) bestehen,
und ist also die nothwendige und hinreichende Bedingung dafür,
dass f(x) und f'(x) einen gemeinsamen Theiler haben. Die
linke Seite von A9), die eine ganze rationale und homogene
Function der Coefficienten von f{x) ist, heisst die Discrimi-
nante der Function f(x).
Wir leiten noch einen Satz aus dem Algorithmus C) her,
der oft angewandt wird.
Aus der ersten dieser Gleichungen folgt:
B0) A" = A — Q'A\
und wenn man diesen Werth von A" in die folgende Gleichung
einsetzt:
A'" = A + Q'Q")Ä — Q"A
also, wenn mit p, p' ganze rationale Functionen bezeichnet
werden,
B1) A'" = pA+ p'A'.
Setzt man die Ausdrücke B0), B1) in die dritte Gleichung C)
ein, so ergiebt sich für AI'" wieder ein Ausdruck von der Form
B1) und so kann man fortfahren, und erhält schliesslich:
B2) A(r) = P A -f- P'A',
worin P, P' ganze rationale Functionen sind, deren Coefficienten
durch rationale Kechenoperationen aus den Coefficienten von A
und A' zusammengesetzt sind.
Die Gleichung B2) bleibt richtig, wenn man P durch P — Q A'
und P' durch P' -\- QA ersetzt, worin Q eine beliebige ganze
Function von x ist. Sind nun n und n' die Grade von A und A',
so kann man Q nach §. 3 so bestimmen, dass der Grad von
P— QA' nicht grösser als ri — 1 wird, und dann folgt, da in
B2) die höchsten Potenzen von x sich wegheben müssen, dass
der Grad von P' -)- QA nicht höher als n — 2 sein kann.

§. 6. Producte linearer Functionen. 41
In der Formel B2) ist J.w eine Constante. Besonders
wichtig ist dieser Satz in dem Falle, wo A^ von Null verschie-
verschieden, also A, A' relativ prim sind. Setzen wir in diesem Falle
P = A<r)F(x), F' = Am®(x),
so können wir nach Weglassung des Factors A(v) dem Satze fol-
folgenden Ausdruck geben:
I. Sind f(x) und cp(x) zwei ganze Functionen ohne
gemeinsamen Theiler von den Graden n und m,
so kann man zwei andere ganze Functionen
F(x) und # (x) bestimmen, deren Grade nicht
höher als m—1 und n—1 sind, die der Gleichung
B3) F(x)f(x) + 0(x)tp(x) = 1
identisch genügen.
Der Satz lässt sich noch verallgemeinern. Multipliciren wir
die Gleichung B3) mit einer beliebigen ganzen Function %(x),
so folgt:
B4) F(x) X (x)f(x) + $>(x)X (x) <p(x)^% (x),
und nach §. 3 können wir
B5) *(x)%(x) = QW(x) + 4>(x)
setzen, so dass Q(x), 1>(%) ganze Functionen von x sind, und der
Grad von if>(x) kleiner ist als der von f(x). Setzen wir dies
in B4) ein und setzen an Stelle von F(x)%(x) -\- Q(x)q>(x)
wieder F(x), so erhalten wir:
F(x)f(x) + 9 («)*(«) = %{x).
Wir können daher den vorigen Satz so verallgemeinern:
II. Sind/(a;), q>(x), %(x) gegebene ganze rationale
Functionen, und f(x) und <p (x) ohne gemein-
gemeinsamen Theiler, so lassen sich die ganzen
rationalen Functionen F(x), ip(x) und zwar il>(x)
von niedrigerem Grade als fix) so bestimmen,
dass die Gleichung
B6) F(x)f (x) +1>(x)<p (x) = x (oo)
identisch befriedigt ist.
Producte linearer Factoren.
Nach §. 1 erhalten wir durch Multiplication ganzer Func-
Functionen ebensolche Functionen von höherem Grade, und zwar be-

42 Erster Abschnitt. §.7.
stimmt sich der Grad des Productes durch die Summe: der Grade
der einzelnen Factoren.
Wenn wir also n lineare Factoren mit einander, multi-
pliciren, so entsteht eine Function wten Grades, deren Bildungs-
Bildungsweise wir etwas genauer untersuchen müssen.
Wir wollen die linearen Factoren in der einfachen Form
x — a15 x — «2, . . ., x — Kn annehmen, und setzen, da der
Coefficient der höchsten Potenz = 1 ist,
A) fix) = (x — aj (x — O . . . (x — O
= #"-!-«! X" — 1 -f-
Eine leichte Ueberlegung lässt folgendes Bildungsgesetz der
Coefficienten aa, a2 . . . an erkennen:
Es ist — üi gleich der Summe «, a2 gleich der Summe
derProducte von je zweien der et,, — a3 die Summe der Pro-
dücte von je dreien der «, allgemein (— 1)" av die Summe der
Producte von je v der Grossen a, oder in Formeln ausgedrückt:
¦ ¦ " — a, = Eax
«2
^ '.¦-¦' ' ¦ : : (— Vf av =
(— lfan:=
Um aber noch deutlicher die Richtigkeit dieses Bildungs-
Bildungsgesetzes einzusehen, bedient man sich der vollständigen In-
duetioh.
Man bestätigt die Richtigkeit zunächst in den ersten Fällen
durch wirkliche Ausführung -der Multiplication
(X- «x) (X «2) = X?
Nehmen wir die Richtigkeit unseres Bildungsgesetzes bei
n — 1 Factoren als bewiesen an und setzen:
ix ~ ax) (x — «2) ... (x — «„_!) = z»-1 -\- a!Xn-2 + ••• a'n-x,
so findet man durch Multiplication mit x — ccn:

§. 7. Producte linearer Faetoren. 43
a1 = a[ — «„
"«2 = «2 «n«l
«3 = «3 «»«2
C) ........
«v = flv — nnav—i
und daraus ist die Richtigkeit der Formeln B) unmittelbar er-
ersichtlich.
Es ist von Wichtigkeit, die Anzahl der Glieder zu bestim-
bestimmen, die in jeder der Summen B) vorkommen. Wir bezeichnen
die Anzahl derTerme, die in der Summe (—Vfav vorkommen, mit
B^; es ist die Anzahl der Combinationen ohne Wiederholung
von n Elementen zur vUn Classe (d. h. von je v verschiedenen
der n Elemente). Um sie zu bestimmen, denke man sich zu-
zunächst die Btüi Combinationen zur (y — l)ten Classe gebildet.
Aus jeder dieser Combinationen kann man durch Hinzufügung
je eines der fehlenden n — v -\- 1 Elemente n — v -j- 1 Combi-
Combinationen zur vien Classe ableiten. Auf diese Art aber wird jede
Combination frnal, nämlich durch Hinzufügung jedes ihrer Ele-
Elemente gebildet, so dass man die Relation
erhält, während B^ offenbar denWerth n. hat. Wenn man also
die aus D) folgenden Gleichungen
= n
\ 2~~
multiplicirt, so folgt
,„, w.) _ n (n - 1) (n - 2) . .. (n - v +ü)
(b) ±tv — 1.2.3...V
Wir werden in der Folge oft, wenn m eine beliebige positive
ganze Zahl ist, das Zeichen ' ¦
G) II (m\ =1.2.3.. . w, iT@) = 1
benutzen, so dass
(8) II(m) = nll(m — 1).

44 Erster Abschnitt. §. 7.
Mit Hülfe dieses Zeichens lässt sich der Ausdruck für _B(„n)
übersichtlicher so darstellen:
(9) Bv —H»-y-i2(
der, wenn Bi"* = 1 gesetzt wird, auch noch für v = 0 und v = n
gilt, und die Unveränderlichkeit von B^ bei der Vertauschung
von v mit n — v erkennen lässt.
Das Product II (m) wird auch die Facultät von m genannt
und mit
1 . 2 . 3 . . . m = m\
bezeichnet.
Die Ableitung der Formel D), die wir soeben nach den
Vorschriften der Combinationslehre gegeben haben, ist zwar
vollkommen richtig und einleuchtend, erfordert aber zur ge-
genauen Begründung einige Ueberlegung, die sich nicht gut in kurze
Worte fassen lässt. Wir wollen daher nachträglich noch durch
das Mittel der vollständigen Induction die Richtigkeit beweisen.
Die Formeln C) geben nämlich die folgenden Recursions-
formeln:
A0)
Nun lässt sich die Formel F) für die ersten Werthe von n
sehr leicht durch Abzählen bestätigen. Nimmt man sie für
n — 1 als richtig an, so ergiebt A0):
(B) 12 (w—1) 77 (w — 1)
woraus nach (8)
n(n)
-n(v)n(n-vy
und hierdurch ist die Allgemeingültigkeit der Formel (9) bewiesen.
Aus der Bedeutung von B^ ergiebt sich, und wird auch
aus den Formeln A0) durch vollständige Induction bewiesen,
dass die B^ positive ganze Zahlen sind.

§. 8. Binomial-Coefficienten. 45
§.8.
Der binomische Lehrsatz.
Wenn wir in der Formel A) des vorigen Paragraphen die
bisher willkürlichen Grossen «j, «2 . . . an einander gleich setzen,
so erhalten wir den binomischen Lehrsatz, der in nichts
Anderem besteht, als in der Ordnung der wten Potenz eines
Binomiums x -f- y nach Potenzen von x. Wenn wir nämlich
setzen, so ergiebt die Formel B)
worin nach der Definition des vorigen Paragraphen B("} die An-
Anzahl der Terme der Summe bedeutet, die alle einander gleich
und gleich (— l)** yv werden.
Demnach ergiebt sich
oder entwickelt geschrieben:
(x -\- y)n = x™ -|- nxn~1y -| ^—-^—^ xn~iy2 -{- • • • -\- y"
die letzte Summe über alle nicht negativen ganzzahligen Werthe
«, ß erstreckt, die der Bedingung a -f- ß = n genügen.
Hiernach heissen die Coefticienten B^ die Binomial-
coefficienten.
Wir setzen der Uebersicht wegen eine kleine Tabelle der
ersten Werthe der Binomialcoefficienten hierher:
» = 1 1,1,
n = 2 1, 2, 1,
n = 3 1, 3, 3, 1,
n = 4 1, 4, 6, .4, 1,
«=5 1, 5, 10, 10, 5, 1,
»= 6 1, 6, 15, 20, 15, 6, 1,
»= 7 1, 7, 21, 35, 35, 21, 7, 1.

46 Erster Abschnitt. §. 8.
Wir wollen unter den verschiedenen Eigenschaften der Bino-
mialcoefficienten zwei ableiten, von denen wir nachher eine
interessante Anwendung machen werden.
Aus A) ergeben sich, wenn man x, y durch 1, x ersetzt, und
n = 0, 1, 2, 3 . . . nimmt, die Formeln
1 -f x = B@1) -f B?x
B) A + x)' = Bf -f Bfx + Bfx*
A -f xy = B$> + B^x + B?>x>-\
Wir machen nun von der Summenformel der geometrischen
Reihe Gebrauch:
1 + A + *) + A + x)» + ..: + A + xY = (-i + X)
Uz
die man aus §. o D) erhält, wenn man dort x durch 1 "—(— o? er-
ersetzt. Entwickelt man hier wieder A -f- a;)M+1 nach der Bino-
mialformel, indem man in der letzten Formel B) n in n + 1
verwandelt und. Bo>+1) = 1 setzt, so erhält man für die rechte
Seite:
C) A + *)n+1 - 1 = JJJ.+1) + Bin+i)x + . . . + 50.+«^.
00 ' ' '
Vergleicht man dies mit der Summe der rechten Seiten von
B) und setzt den Vorschriften des §. 1 gemäss die Coefficienten.
entsprechender Potenzen von x einander gleich, so folgt:
-p(n) T>(n + 1)
• . . -D» ' -— -En + 1 i
oder allgemein -
E) .BW _jl'.#'+» _| )-&?> = &&» '
W'enn man aber die Gleichungen B) der Reihe nach mit
-t>0 5 -Dl ) -f- -L>2 , • • \± -D„ ,
inultiplicirt (wo das, obere Zeichen bei geradem, das untere bei
ungeradem n gilt), so/ergiebt die;Summe,der linken Seiten nachA),
Bf - B^ A -f x)~+ BV\l ¦•+ *J - • • -'± B(:\l +'¦«)«
= [!-(!+ *)]- = (- *)»,

§. 9. Interpolation. 47
und die Gleichsetzung der Coefficienten gleich hoher Potenzen
auf der rechten und linken Seite liefert das Formelsystem
0 = .BM0 — .BW + BfB{n) ±
0 =
± 1 = ± &?&?•
Dies Formelsystem lässt sich in umgekehrter Reihenfolge
mit Benutzung der Relation B^ = B("-v auch so darstellen:
1 = B^B^
0 = B^B^ — Bfr-^B?*
G) 0 = EPBP - Bf-^BP + B^-^B^
0 = B^B^ - B^lfB?* + B(:z?B(? + B$>B(:i)
oder auch in zusammenfassender Bezeichnung:
(8) h (— XfB^-pB^ =1 ^ = 0
0,|«
= 0 [i = 1, 2 . . . w.
§.9.
Interpolation.
Wir wollen von den zuletzt gewonnenen Formeln eine An-
Anwendung machen auf eine Aufgabe aus der Theorie der Inter-
Interpolation.
Es soll eine ganze rationale Function wten Gra-
Grades bestimmt werden, die für n -j- 1 gegebene Werthe
der Veränderlichen x vorgeschriebene Werthe hat.
Es handelt sich also um die Bestimmung der n + 1 Coeffi-
Coefficienten a0, «!,... an in
A) . , f{x) = aox» -f- diX»—1 -f • • -On-xX + an
aus den w -f- 1 Gleichungen
B) - /(«) == ^o, /K) = ^ ... /K) == A,
wenn a0, «j ... «n die gegebenen Werthe von *, und Ao, Ax ... An
die entsprechenden Werthe von f{x) sind. Die Gleichungen B)
sind ein System von Gleichungen ersten Grades für die Unbe-
Unbekannten «o, «i,, • '._•¦> an, die sich im Allgemeinen durch Deter-
Determinanten auflösen lassen, wie wir im nächsten Abschnitt sehen

48 Erster Abschnitt. §. 9
werden. Wir kommen später auf diese Aufgabe zurück, be-
behandeln sie aber jetzt unter der besonderen Voraussetzung, dass
die gegebenen Werthe von x die n -\- 1 ersten ganzen Zahlen
0, 1, 2, ... n seien.
Die Binomialcoefficienten B^\ wie sie durch §. 7 F) definirt
sind, behalten ihren guten Sinn, auch wenn n keine ganze Zahl
ist, wie bisher vorausgesetzt war, sondern eine beliebige veränder-
veränderliche Grosse. Es ist dann
C) Bv - 1 . 2 . 3 . . . v
eine ganze rationale Function vten Grades von x1). Der Coeffi-
cient von xv ist von Null verschieden und daher kann auch xv
ausgedrückt werden durch B^f1 und durch niedrigere Potenzen
von x. Es lässt sich also auch jede ganze Function wten Grades
fix) von x linear ausdrücken durch Bf\ B^ . . . B^ in der
Form:
D) f(x) = M0BP + MtB^ + • • • + MnBt\
worin ilf0, M1 ... Mn Constanten sind, und die Function fix)
ist bestimmt, wenn diese Constanten bestimmt sind.
Es sei nun nach unserer Voraussetzung/@),/(l),/B) .. •/(«)
gegeben; da nach C) B^ immer verschwindet, wenn x einen der
Werthe 0, 1, 2, ... v — 1 hat, so ergeben sich aus D) die fol-
folgenden linearen Gleichungen für die Unbekannten M:
/(O) =
/(l) =
E)
Diese Gleichungen .sind nun in Bezug auf Jf0, Mx . . . M„
aufzulösen, was sehr leicht mit Hülfe der Schlussgleichungen (8)
des vorigen Paragraphen geschieht. Die erste Gleichung E) er-
giebt nämlich direct
F)Mo
x) Die Bedeutung dieser verallgemeinerten Binomialcoeffieienten für
die EntwickelQng 4er Potenzen des Binoms gekört nicht Werner, sondern
in die Analysis.

§. 10. Interpolationsproblem. 49
Multiplicirt man die erste Gleichung E) mit Bf\ die zweite
mit — -Bix) und addirt, so erhält man nach dem erwähnten
Formelsystem (auf n = 1 angewandt):
und so allgemein, indem man die v ersten Gleichungen E) der
Reihe nach mit B(J\ — BP, + B%> ¦ ¦ ¦ ± B? multiplicirt und
addirt:
wodurch nach D) die Function F(x) bestimmt und die Aufgabe
gelöst ist. Es ist klar, dass, so lange wir über die Werthe /@),
/(l), . . ./(«) keine besondere Voraussetzung machen, in dieser
Form jede beliebige ganze rationale Function von x dargestellt
werden kann.
§. 10.
Lösung des Interpolationsproblems durch die
Differenzen.
Die Definition der ganzen rationalen Function B^
m Rw — * Qc ~ 1) • • • fr — * + 1)
K } " ~~ 1 . 2 . 3 ... v
giebt die früher schon für den speciellen Fall eines ganzen
positiven x bewiesene Relation:
Daraus erhalten wir für die Coefncienten Mo, Mt . . . Mn eine
Bestimmungsweise, die für die praktische Rechnung viel be-
bequemer ist, als die Anwendung der Formeln des vorigen Para-
Paragraphen.
Es ist nämlich nach den Formeln D) und F), §. 9,
und wenn wir darin x durch x -)- 1 ersetzen und die Differenz
bilden, mit Rücksicht auf B)
E) /ix = Mx -j- M^Bf* -\- M%B'ii -j- • • • -f- MnB(nLi,
woraus sich ergiebt [da E) eine Gleidhung von derselben Art
wie C) ist, nur dass n — 1 an Stelle von n getreten ist]:
Weber, Algebra. I. a

50
Erster Abschnitt.
M, = z/0 = /(l) - /@).
5. 11.
Setzen wir
F)
¦^x + 1 ^x — -^x i
so wird also hiernach
Mo = /@), 3/i = 4>,
und die Formel C) ergiebt
G) f(x) = /(o) + z/0 j^"' + ^0 5?) H h 4*)Ä"),
und ebenso kann man die Functionen z/,,., z/^, z/^' . . . ausdrücken:
= 4'o ...Mn =
(8)
Die z/,., J'm z/ä, • • • 4(" r) sind ganze rationale Functionen
der Grade n — 1, n — 2, ... 0, die letzte von ihnen also con-
stant. Um sie alle darzustellen, braucht man nur die Werthe
/@), z/0, z/q, z/ö, . . . 40n~1\ die man am leichtesten berechnet,
wenn man eine Tabelle anlegt, die für den Fall n = 3 z. B.
folgende Form haben würde:
/@)
/(l)
und, wenn die/@),/(l), . . . gegeben sind, durch einfache Sub-
tractionen berechnet wird.
§• 11.
Arithmetische Reihen höherer Ordnung.
Das Vorhergehende ist die Grundlage für die Theorie der
arithmetischen Reihen höherer Ordnung.
Wir bezeichnen mit
A) t»0, «1, «2, «3, • • • ¦
irgend eine unendliche Reihe von Grossen und mit

§. 11. Arithmetische Reihen. 51
B) Jo = «! — Mo, J\ = M2 — «i, z/2 = % — M2 . . .
die Reihe ihrer Differenzen, mit
C) /r*=.Ax — Ao, z/i = 4, — A± . . .
die Reihe ihrer zweiten Differenzen u. s. f.
Es ist klar, dass die Reihe A) vollständig bestimmt
ist, wenn ihr erstes Glied und die Reihe ihrer ersten Differenzen
gegeben ist; denn es ist
«1 = «0 + 4), «2 = «0 + ^0 + ^1 • • •>
Mm = Mo + ^0 + ^1 + • • • + ^m-1-
Ebenso ist die Reihe A) völlig bestimmt, wenn die beiden
ersten Glieder und die Reihe ihrer zweiten Differenzen gegeben
ist u. s. f. Die Reihe A) wird eine arithmetische Reihe
wter Ordnung genannt, wenn die Reihe ihrer wten Diffe-
Differenzen constant ist, also die Reihe der (w -j- l)ten Differenzen
aus lauter Nullen besteht.
Man erhält eine arithmetische Reihe wter Ordnung, wenn
man in einer ganzen Function wten Grades f(x) für x die
Zahlen 0, 1, 2, 3 ... einsetzt.
Denn setzt man
An-l) An —2) Än — H)
so ist Jx vom (n — l)ten, A'x vom (n — 2)ten Grade in Bezug
auf x, und also J^1^ constant.
Ist nun
Mo, Mj, M2 • • •
eine arithmetische Reihe wter Ordnung, so ist die ganze Reihe
vollständig bestimmt, wenn die n Werthe m0, Mi, m2 . . . m„_j und
ausserdem die constante wte Differenz gegeben sind. Diese
letztere ist aber bestimmt, wenn auch noch das (n -)- l)te Glied
m„ gegeben ist. "Wir können also den Satz aussprechen:
Eine arithmetische Reihe wter Ordnung ist voll-
vollständig bestimmt, wenn ihre w -\- 1 ersten Glieder
gegeben sind.
Da nun eine Function f{x) vom wten Grade gleichfalls durch
die willkürlich gegebenen Werthe
4*

52 Erster Abschnitt. §.11.
völlig bestimmt ist, so folgt, dass aus den ganzen ratio-
rationalen Functionen wten Grades f(x) alle arithmeti-
arithmetischen Reihen nter Ordnung erzeugt werden, wenn
man darin für x die Reihe der natürlichen Zahlen
setzt.
Der Ausdruck des allgemeinen Gliedes ist dann durch die
Formel G) des vorigen Paragraphen gegeben.
Die Summen der m -\- 1 ersten Glieder einer arithmetischen
Reihe wter Ordnung
bilden eine arithmetische Reihe (n -j- l)ter Ordnung, da ihre
ersten Differenzen
Sm-t-l Sm = Um + i
eine arithmetische Reihe wter Ordnung bilden.
Es lässt sich also mit Hülfe der Formel G) des §. 10 die
Summe sm allgemein bestimmen, wenn man s0, sx . . . sn+1 als
bekannt annimmt.
Um die erzeugende Function F(x) von sm zu finden, wenn
f(x) die erzeugende Function von um ist, setzt man
und hat dann in der Formel G), §. 10:
F(x) = F@) -f B0Bix) + D'0Bf -\
zu setzen:
. D0 = -F(l)--F@)=/(l), D'o=/B)
A = FB) - F(l) =/B), Di =/C) -/B) =
So erhält man:
F(x) =/@) +/A)-B?) + ^^ + 4-B?} H
Nehmen wir z. B. /(«) = x2, so giebt uns j'(w) die Summe
der m ersten Quadratzahlen. Es ist

§. 12. Der polynomische Lehrsatz. 53
also F(x) = x -f- 3 - ^ \~ 2 = ^—5
_ a;(a;4- 1) B a; + 1)
~~ 6
Für f(x) = xz ergiebt dieselbe Rechnung:
Die Summe der m ersten Cuben ist also gleich dem Quadrat
der wten Trigonalzahl.
§• 12.
Der polynomische Lehrsatz.
Im §. 8 ist für den binomischen Lehrsatz die Form ab-
abgeleitet :
A) (X i yy _ jj(w) "V ^ ,
<2j JI(«) n (ß) ^ ,...„
in der sich die Summe auf alle Combinationen zweier Zahlen
«, ß erstreckt, deren keine negativ ist und die der Bedingung
B) « + ß = n
genügen.
Diese Form gestattet, zunächst durch Induction, eine Ver-
Verallgemeinerung auf die »te Potenz eines Polynoms:
mit der Bestimmung, dass «, ß, y . . . alle positiven oder ver-
verschwindenden ganzzahligen Werthe durchlaufen, die der Be-
Bedingung
D) « + 0 + y + . • . = n
genügen. Um aber die Eichtigkeit dieser Formel allgemein zu
beweisen, nehmen wir an, sie sei bewiesen, wenn das Polynom
ein Glied weniger enthält, wie sie es in der That ist, wenn das
Polynom nur zwei Glieder enthält.
Wir setzen dann
E) . u = y-\-e-\
und wenden auf {x -\- u) die Formel A) an, aus der sich er-
ergiebt :

54 Erster Abschnitt. §. 13.
a>v XaUv
F) (x + y + m +..•)•= ü(») ^ 77(WO7(,)
mit der Beschränkung
G) k -\- v = n.
Nun ist aber nach der Annahme schon bewiesen:
(8) * = n(v) V
(9) /S + y H = v,
und wenn dies in F) eingesetzt wird, so ergiebt sich unmittel-
unmittelbar die Formel C), und G) geht in D) über.
Die Coefficienten
die ihrer Bedeutung nach ganze Zahlen sind, heissen die Poly-
nomialcoefficienten.
Beispielsweise erhält man für die dritte Potenz des Trinoms:
A1) (X -\- y + ZY = «3 _|_ yZ _|_ g% _^_ %Xiy _|_ 3^^
-\-Sx20-\-Sx^-\-ßy2z-{-3yz2-\-6 xyz.
Wenn » eine Primzahl ist, so hat in A0) der Zähler den
Factor n, während der Nenner JT(a)J7(/3) JT(y) . . . den Factor n
nur dann enthält, wenn eine der Zahlen «, ß, y . . . gleich n,
die übrigen gleich Null sind. Es folgt hieraus, dass die Poly-
nomialcoefncienten P«"^ . . . alle durch n theilbar sind, mit
Ausnahme der Coefficienten von x", yn, z*, . . . die gleich 1 sind.
Von diesem wichtigen Satze werden wir später häufig Ge-
Gebrauch machen.
§¦ 13.
Derivirte Functionen.
Es sei
A) f(x) = aoxn + a^-1 + a2a;n-2 -| \- an
eine ganze rationale Function »ter Ordnung.
Wenn wir darin x durch ein Binom x -\- y ersetzen, so
können wir auf jedes einzelne Glied den binomischen Lehrsatz
anwenden, und können das Ergebniss nach fallenden oder nach
steigenden Potenzen von x oder von y ordnen. Wir wollen die
Ordnung nach steigenden Potenzen von y ausführen. Die höchste

§. 13. Derivirte Functionen. • 55
Potenz von y, die vorkommt, ist die wte, und der Coefficient der
nullten Potenz von y ist dieFunction/(a?) selbst, wie man erkennt,
wenn man y = 0 setzt. Wir setzen also, indem wir die anderen
Coefficienten mit
1 W' JTB)' JZC)
bezeichnen,
B) /(* + y) = /(*) ^
±4ö
0, n v '
Die Functionen /'(x), f"(x),/'"(x) . . . heissen die erste,
zweite, dritte, . . . Derivirte oder Abgeleitete von f(x).
Es sind ganze Functionen von x und ßv)(x) kann den Grad
n — v nicht übersteigen, da die Summe der Exponenten von x
und y in keinem Gliede den Grad n übersteigt.
Die erste Derivirte, die also der Coefficient der ersten
Potenz von y in der Entwickelung von/(a; -f- y) nach
steigenden Potenzen von y ist, erhält man durch Anwen-
Anwendung des binomischen Lehrsatzes auf A):
C) f'(x) = na^x*-1 + (n — l)^"-2 + (n — 2)a2xn~3 -|
Der Hauptsatz über die derivirten Functionen ergiebt sich
aus B), wenn wir x in x -\- s oder y in y -\~ s verwandeln:
J 2 tt
0,n ^ ' 0,n ^ '
Bezeichnen wir mit /**>¦"> (x) die (tte Derivirte von /W («),
so ist nach B)
E) /« (x + e) = 2 ^10^
0,n —»
und nach dem binomischen Satze:
Setzen wir dies in D) ein, so folgt:
G)
Die letzte Summe ist über alle nicht negativen Zahlen ß, y
zu erstrecken, deren Summe den Grad n von fix) nicht über

56 Erster Abschnitt. §. 13.
steigt. Dieselben Zahlencombinationen durchlaufen aber auch die
Exponenten v, {i auf der linken Seite, und die Vergleichung der
Coefficienten gleicher Potenzen und Producte ergiebt (nach §. 1):
also den Satz:
Die (tte Derivirte von der vten Derivirten ist die
(v -f- (t)te Derivirte der ursprünglichen Function.
Man erhält also die sämmtlichen höheren Derivirten, indem
man nach der Regel C) aus jeder vorangehenden die erste Deri-
Derivirte bildet:
/(*) =
(9) /(*) =
/' (x) = n (n —-1)UqX»-2 -|- (» — 1) (» — 2) i
Eine etwas einfachere Form nehmen diese Derivirten an,
wenn man sich einer anderen Bezeichnungsweise bedient, die
häufig im Gebrauch und für gewisse Zwecke fast unentbehrlich
ist, die wir im Anschluss hieran besprechen wollen.
Es liegt wegen der Unbestimmtheit der Coefficienten
«oi «i • . • «n offenbar keine Beschränkung darin, wenn wir eine
ganze rationale Function »ten Grades so darstellen:
A0) f(x) = aox» + JBfV«»-1 + B^a2xn-2 -\ \-an,
oder ausführUch:
A1) /(*) = aox» + »Oi«—i + ^-=^ a,x«-> -\
Wenn eine Function /(a;) so dargestellt ist, werden wir sagen,
sie sei „mit den Binomialcoefficienten geschrieben".
Grössere Uebereinstimmung zeigen hierdurch bereits die
Formeln (9), die dann so lauten:
f(x) = n(n1)
+
n
»(» _
2)aix»-*

§. 14. Derivirte eines Productes. 57
worin die rechten Seiten alle auch mit den Binomialcoefficienten
geschrieben erscheinen. Wir werden später den Nutzen dieser
Bezeichnungsweise noch weiter kennen lernen, müssen aber schon
hier hervorheben, dass die Wahl der einen oder anderen Dar-
Darstellungsweise doch nicht ganz gleichgültig ist, die erste oft
auch den Vorzug verdient. Besonders in den Fällen, wo die
Coefficienten Zahlen sind und es auf das zahlentheoretische Ver-
Verhalten dieser Coefficienten ankommt, darf man nicht ausser Acht
lassen, dass durch die Binomialcoefficienten ein der Sache
fremdes numerisches Element eingeführt wird. Dass Gauss in
der Theorie der quadratischen Formen (in den Disq. ar.) die
Schreibweise mit den Binomialcoefficienten anwendet, wenn er
die quadratischen Formen durch ax* -\- 2b xy -\- cy% darstellt,
und dass diese Bezeichnung allgemein Eingang gefunden hat,
hat in der Zahlentheorie zu einer unnöthigen und sehr bedauer-
bedauerlichen Complication geführt.
§. 14-
Derivirte eines Productes.
Die derivirten Functionen, die wir hier betrachtet haben,
sind keine anderen als die aus der Differentialrechnung bekannten
Differentialquotienten; wir haben den Begriff aber hier, wo es
sich um ganze rationale Functionen handelt, ohne Anwendung
der Infinitesimalrechnung gewonnen aus den Entwickelungscoeffi-
cienten der Potenzen von y in derFunction/(a; -\- y). Bezeichnen
wir die vte Ableitung von f{x) mit Dvf, so ist nach B), §. 13:
und darans ergeben sich sofort die beiden Grundsätze, die sich
in den Formeln
B) Dv(Cf) = CDrf,
C) D,(/ + y) = Dvf + D,v
ausdrücken, worin C eine Constante, <p eine zweite ganze ratio-
rationale Function von x ist.
Eine Verallgemeinerung der Formel B) giebt die Darstellung
der Derivirten des Productes ftp. Setzt man nämlich nach A)
abkürzend

58 Erster Abschnitt. §. 14,
f(x -\- y) = m0 -\- y ut -f- y2u2 -\- • • • yn un
also
D)
q> (x -f- y) = v0 -f- yvx + t/2v2 -\ • ymvm,
M
so ergiebt die Ausführung der Multiplication der beiden Formeln
D), wenn man in dem Product den Coefficienten von y" auf-
aufsucht :
F) n
oder
G) Dv [ftp) = tp Dvf + .#> X»v_x
worin jBir), jB^v) ... die ßinomialcoefficienten sind. In ähnlicher
Weise kann man unter Anwendung der Polynomialcoefficienten
die Deriräten eines Productes von mehr als zwei Factoren
bilden.
Wir wollen die erste Derivirte, die wir jetzt mit D statt
mit Dx bezeichnen, für ein Product von »Factoren danach bilden.
Für zwei Factoren erhalten wir nach G):
und allgemein, wenn wir die Factoren mit ttj, w2. • ¦ • M» i die
Derivirten mit u[, «4 . ... u'n bezeichnen:
(8) Z»(miM.2 ...u„)
= U\U.2 . . . U„ -\- Mx«2 ...«» + '•• +
oder kürzer:
. . . u„) -^-i Duv
. . . Un ^-* Uv
Wenn wir also ein Product aus linearen Factoren
(9) f(x) = (x — O (x — a2) . . . (x — «„)
betrachten, so erhalten wir, da die ersten Derivirten von x — «L,
x — c«2, . . . x — an sämmtlich gleich 1 sind,
f'(x) == (x — «j) (x — a3) ....(* — «„)
+ (« — «i) (« — «3) . . . (X — «„)
+ (x — %) (« — k2) . . . (x — a„_i),
wofür man auch setzen kann:

§. 15. Partialbrüche. 59
(ii) f{x) =
X
Ein sehr wichtiges Resultat ergiebt sich hieraus, wenn x
gleich einem der Wertbe «l5 «2 . . . a„ gesetzt wird, nämlich
/' («0 = («i — «2) («1 — «3) • • • («1 — ««)
A2) /'W = (Ki ~ a^ (a* — cc-i) . . . («a — an)
/'(«„) = (ccn — «,) («n — Oj) . . . (a„ — «„_!).
§. 15.
Partialbrüche.
Die zuletzt abgeleiteten Formeln können dazu dienen, die in
den Paragraphen 9 und 10 behandelte Interpolationsaufgabe in
einer neuen Form zu lösen. Es habe/(a?) dieselbe Bedeutung wie
oben, nämlich
(!) f(x) = 0 — O (x — «2) • • • 0 — O,
und «!, «2 . . . «n seien beliebige, jedoch von einander verschie-
verschiedene Grossen. Wir setzen zur Abkürzung
= (* - «2) (* - «.0 • • • (* - O
B) /«(Ä) = /ZT^ = (» — «1) (* — «»)...(« — «»)
/»(*) ¦= ~^ = (* — «1) (*-«,)...(*- «•-1),
so dass nach den Formeln A2) des vorigen Paragraphen/x («^
—/'(ai)> /i(a2) = 0, ebenso allgemein, wenn (i und v ver-
verschiedene der Indices 1, 2 ...» sind:
C) /,(«,)=/'(«,), /,(«^) = 0.
Wenn nun Au A2, . . . An ein System gegebener Grossen ist,
so hat die ganze Function (n — l)ten Grades
wegen C) die Eigenschaft, für x = av in Av überzugehen, und
es ist also eine ganze Function (n — l)ten Grades q>(x) dar-
dargestellt, die für n Werthe von x gegebene Werthe annimmt, wie

60 Erster Abschnitt. §. 15.
in §. 9. Für besondere Werthe der Av und «v kann der Grad
von <p (x) auch noch niedriger werden. Die Formel D) ist die
Interpolationsformel von Lagrange. Sie lässt sich nach B)
auch so darstellen:
¦ | 9 K)
und hierin kann <p(%) jede beliebige ganze Function (n — l)ten
oder auch niedrigeren Grades bedeuten. Ist <D(x) eine Function
von höherem als (n — l)ten Grade, so kann man nach §. 3:
F) ®G*) = G/(*) + v(*)
setzen, worin Q eine ganze Function und q>(x) höchstens vom
(n — l)ten Grade ist Zugleich ist aber wegen A)
G)
und folglich
/O) ~ v ^ /' («i) (*—«i) ^ /' K) 0 - «2)
^ ^/'(*„) (X-Vn)
Durch diese Formel ist der Bruch &(x):f(x) in eine Summe
aus einer ganzen Function Q und aus Brüchen mit constantem
Zähler und linearem Nenner zerlegt. Diese Brüche heissen
die Partialbrüche der gebrochenen Function <D(x) -f(x). Sie
spielen bekanntlich eine wichtige Rolle in der Integralrechnung.
Wir leiten aus diesen Resultaten noch einige Folgerungen
ab: Setzen wir q>(x) = xm+1, so bleibt die Formel E) anwend-
anwendbar, wenn m<^n — 1 ist. Setzen wir voraus, dass von den Grossen
«l5 «2, ...,«„ keine verschwindet, so wird die linke Seite von E)
gleich Null für x = 0, und wir erhalten den Satz:
m = 0,l, % ... n — 2.
Für 3> (x) = xn kann die Formel (8) angewandt werden, in
der sich Q = 1 ergiebt, und es folgt:
»—1 «—2 n—1
^1"*i_ . . . 1 ^2 — 1
Die Formeln (9) und A0) gelten auch dann noch, wenn

§. 15. • Partialbrüche. 61
eine der Grossen « verschwindet. Dies ist ohne Weiteres klar,
wenn m ;> 0 ist. Aber auch für m — 0 ergiebt sich (9) in
diesem Falle aus der Formel E), die für q>(x) = x, «x = 0
so lautet:
x «2 . | an
f'(x) - (* —O/>2) "i r (x _««,,)/'(«,,)'
was für x = 0 wieder die Formel (9) ergiebt.
Wir haben bei diesen Betrachtungen ausdrücklich ange-
angenommen, dass die Grossen «l5 «2, . . ., «„ von einander ver-
verschieden sind; anderenfalls würden einige der Grossen /' (<%),
/'(a2), . . ., /'(«„) verschwinden. Verstehen wir aber allge-
allgemeiner unter f(x) ein Product aus Potenzen von einander ver-
verschiedener Linearfactoren der Form x — «, und unter &(x) eine
beliebige ganze Function, so lässt sich auch jetzt noch die ge-
gebrochene Function &(x) : f(x) in .eine ganze Function und
eine Summe von Partialbrüchen zerlegen, wenn wir allge-
allgemeiner unter Partialbrüchen Brüche verstehen, die einen
constanten Zähler und eine Potenz des Binoms (x — «)
im Nenner enthalten.
Um dies durch vollständige Induction nachzuweisen, setzen wir
A1) /(*) = (* —«)a/i(«)
und verstehen unter fx (x) ein Product aus Potenzen von Linear-
Linearfactoren, unter denen x — « nicht mehr vorkommt.
Nun lässt sich nach §. 5 die Constante A so bestimmen, dass
A2) 0 (x) — Afx (x) = (x — «) 0, (x)
durch (x — «) theilbar wird. Es ist nur
a — #(a)
zu setzen, und dann ergiebt sich aus A1) und A2):
f
f(x) {x-ayf^a)^ {x-ay-\fx{xy
Auf den zweiten Bruch auf der rechten Seite dieser Formel,
der den Factor (x — «) einmal weniger im Nenner enthält, als
der ursprünglich gegebene Bruch (&(#) :f(x), lässt sich dasselbe
Verfahren wieder anwenden, und damit kann man so lange
fortfahren, bis die gewünschte Darstellung durch Partialbrüche
erreicht ist.

62 . Erster Abschnitt. §. 16.
§• 16.
Entwickelung einer gebrochenen Function nach
fallenden Potenzen der Variablen.
Wir haben im §. 3 für einen beliebigen positiven Expo-
Exponenten v die Formel abgeleitet:
A) a?Q(x)
worin /, (Z>, <bv ganze Functionen von x der Grade n, m, n — 1
waren, und worin die c und ebenso die Coefficienten von (Z>1
rational aus denen von / und von <Z> abgeleitet sind. Dividirt
man diese Formel durch xvf(x), so folgt:
B) j±-± = C„^m-1Xm~n -f Cn-mZ™-"-1
+ ... + Cv_x , + _.
De,r. ins Unbestimmte fortgesetzte Theil dieses Ausdrucks
C) C-m-l r»-» + Cn_m X'»-»-1 -)
heisst die Entwickelung des Bruches #(«):/(«) nach fal-
fallenden Potenzen von x und die c,- die Entwickelungscoeffi-
cienten. Das weggelassene Glied x~*<&v(x) : f(x) heisst der
Rest. Mit welchem Rechte man unter Umständen die Entwicke-
Entwickelung für die Function selbst setzen kann, ist eine Frage, die in
die Analysis gehört, auf die wir hier nicht einzugehen brauchen.
Wenn 0(x) : f(x) eine echt gebrochene Function ist, so
enthält die Entwickelung nach fallenden Potenzen nur negative
Exponenten von x. Ist aber (& : / unecht gebrochen, so scheidet
sich noch eine ganze Function oder eine Constante ab. Der
Theil mit negativen Potenzen
X """ X'i "T" X\ "^ ' ' '
ist der wichtigste. Er ist für alle Functionen (& derselbe, die
bei der Theilung durch f denselben Rest geben.
Die Entwickelung B) ist in dem Sinne eindeutig bestimmt,
dass, wenn wir einen Ausdruck von der Form annehmen:

§. 16. Entwickelung einer gebrochenen Function etc. 63
y±) ,, T" Wi — m — l <*¦ T^ yn—m <*¦
und nur voraussetzen, dass in der gebrochenen Function £1
der Grad des Nenners höher sei als der Grad des Zählers, dann
nothwendig
,,, , n &(x)
E) « = «, a = ±f
sein muss. Es folgt nämlich zunächst aus der Annahme D)
durch Multiplication mit xvf(x), dass £lf(x) eine ganze Function
von x ist, deren Grad also nach unserer Annahme höchstens
= n — 1 ist, und dann werden die c'i durch Vergleichung mit
der Formel A) den a gleich gefunden, was dann für Sl den Aus-
Ausdruck E) nach sich zieht.
Daraus folgt weiter, dass man die Entwickelungscoefficienten
für die Summe von zwei oder mehr gebrochenen Functionen er-
erhält, wenn man die entsprechenden Coefficienten der einzelnen
Summanden addirt, und dass man die Entwickelung eines Pro-
ductes zweier Functionen dadurch bilden kann, dass man hin-
hinlänglich weit fortgesetzte Stücke der Entwickelungen der ein-
einzelnen Factoren mit einander multiplicirt, und das Ergebniss
wieder nach absteigenden Potenzen der Variablen ordnet. Hier-
Hierbei kann man einfach die Regel der Multiplication (§. 1) auf
ganze Functionen von 1 : x anwenden.
Für den einfachen Bruch
1
X — K
ergiebt sich die Entwickelung
1 + ^. + ^ + ^! + ..
X ~ X'2~ X* ~^X* ¦ '
wie man leicht aus §. 3, A2) findet, und daraus, wenn man einen
nach §. 15, (8) in Partialbrüche zerlegten Bruch hat:
|
r/'(
für die Coefficienten c0, cu c2 • • • die folgenden Ausdrücke:
worin sich das Summenzeichen auf «j, cc3, ...,«„ erstreckt.

64 Erster Abschnitt. §. 17.
Nehmen wir insbesondere 0 (x) = f (x) an, so werden
die Grossen c0) cl5 c2 • • • identisch mit den Summen der Potenz
der k:
F) c0 = n, d = 2 Ki, C2 = 2 af, . . .
§. 17.
Ganze Functionen mehrerer Veränderlichen: Formen.
Wir haben bisher vorzugsweise die ganzen rationalen Func-
Functionen von einer Veränderlichen betrachtet; wir können uns
aber nicht immer darauf beschränken und haben ja auch schon
oben Functionen mehrerer Veränderlichen benutzt. Unter einer
ganzen rationalen Function nten Grades mehrerer Veränderlichen
F(x, y, 0, . . .) verstehen wir eine Summe von Gliedern:
ß
worin k, ß, y . . . ganzzahlige, nicht negative Exponenten sind,
deren Summe u -f- ß -f- y -(-.... den Werth n nicht übersteigt,
und wenigstens in einem Gliede auch wirklich erreicht. Der
Grad wird also bestimmt durch den grössten Werth, den die
Summe a -f- ß -\- y -}-••• annimmt. Die J.«,ß,Y... -können be-
beliebige Grossen darstellen und heissen die Coefficienten.
Wenn die Summe der Exponenten a -f- ß -f- y -f- • • • in
allen Gliedern denselben Werth hat, so heisst die Function
homogen.
Eine fundamentale Eigenschaft der homogenen Func-
Functionen wten Grades ist die, dass, wenn alle Va-
Variablen mit demselben Factor vervielfältigt wer-
werden, der Erfolg derselbe ist, wie wenn die Function
mit der wten Potenz vervielfältigt wird; in Zeichen,
wenn t eine beliebige Veränderliche bedeutet:
A) F(tx, ty, ts ...) = t«F{x, y,e...)\
denn ersetzt man in dem Product x" y? zy . . ¦ die Variablen
durch tx, ty, tz, . . ., so erhält es den Factor
ta + fl + y + •••.
hat nun a -\- ß -\- y -\- ¦ • • in allen Gliedern denselben Werth
n, so kann der Factor tn vor die Summe F herausgenommen
werden. Hat aber die Summe cc -f- ß -\- y -f- • - • in den ein-
einzelnen Gliedern verschiedene Werthe, so kann ein solcher ge-
gemeinschaftlicher Factor nicht herausgenommen werden, wenig-

§. 17. Formen. 65
stens nicht, ohne dass noch verschiedene Potenzen von t in
den einzelnen Gliedern bleiben.
Durch Vermehrung der Veränderlichen kann man jede
nicht homogene Function in eine homogene von gleichem Grade
verwandeln. Ist nämlich m — 1 die Anzahl der Variablen in
einer nicht homogenen Function wten Grades, so setzen wir
und erhalten in
n -p fx± 3-2 #3
eine ganze homogene Function wten Grades der Variablen
xx, x2 ¦ . . Xm, die wir mit
y^it ^2 • • • ^tn)
bezeichnen.
Es empfiehlt sich bisweilen, die homogenen Functionen meh-
mehrerer Variablen mit den Polynomialcoefficienten zu
schreiben.
Wir setzen daher
B) O(x x x )
^ n(n) . a a
(a2) . ..n{ccm) JLa»"'---am x^ ^¦¦¦xm
wo sich die Summe auf alle nicht negativen, der Bedingung
C) % -4- cc2 -\- ¦ • • -(- am = m
genügenden Zahlen erstreckt. Diese Bezeichnungsweise, ohne die
Beschränkung C), ist auch auf nicht homogene Functionen an-
anwendbar.
Man kann aber die homogene Function auch so darstellen:
D) 0 fa, X2 . . . Xm) = Z ÄVu »s . . . *„ Xn XH . . . Xv
worin jeder der Indices vt, v2 . . . vn von den übrigen unabhängig
die Werthreihe 1, 2 . . . m zu durchlaufen hat. Die Summe D)
besteht also aus mn Gliedern, die aber nicht alle von einander
verschieden sind. Das Product xVl %vt... %vn bleibt nämlich un-
geäudert, wenn die Indices vu v2 . . . vn beliebig unter einander
permutirt werden. Die Anzahl der Permutationen von n Ele-
Elementen beträgt aber II (n). Sind unter diesen Elementen je
Weber, Algebra. L 5

66 Erster Abschnitt. §. 17.
«!, «2 . . . einander gleich, so reducirt sich die Zahl der Permu-
Permutationen auf
woraus sich ergiebt, dass in D) irgend ein Product x^xl*... genau
mal vorkommt. Setzt man also noch fest, dass AVlt ,.„...» sich
nicht ändern soll, wenn die Indices beliebig permutirt werden,
so erweisen sich die Bezeichnungsweisen B) und D) als iden-
identisch, wenn durch Zusammenfassen gleicher Factoren
XVl Xr, . . . Xyn = X? X\* . . . 0T«m
und
gesetzt wird.
Bezeichnen wir die Anzahl der Glieder, die in der Function
0 [nach B)] auftreten, mit (m, »), so findet man, indem man zu-
zunächst die Glieder zählt, die den Factor xx haben und dann
die übrigen, die eine homogene Function wter Ordnung von den
übrigen m — 1 Variablen bilden, die ßecursionsformel:
E) (*», n) = (m, n ~ 1) + (m — 1, »),
mit deren Hülfe man durch vollständige Induction den Ausdruck:
(e>\ (m m\ — m (w + 1) • • • 0" + " — 1) _ J7 (m + n — 1)
der sowohl für n = 1 als für m = 1 richtig ist, als allgemein
gültig erkennt.
Die ganzen homogenen Functionen werden auch Formen
genannt. Man unterscheidet nach der Anzahl der Variablen
unäre (einfache Potenzen), binäre, ternäre, quaternäre
Formen. Die binären Formen sind es, die uns hier besonders
interessiren, deren Theorie im Wesentlichen identisch ist mit
der Theorie der ganzen rationalen Functionen einer Veränder-
Veränderlichen. Man gelangt von den binären Formen zu diesen Func-
Functionen zurück, wenn man eine der homogenen Variablen als con-
stant ansieht, z. B. ihr den Werth 1 giebt.

§• 18. .Rationale Functionen. 67
§• 18.
Die Derivirten von Functionen mehrerer Variablen.
Wir haben im §. 13 die derivirten Functionen einer ganzen
rationalen Function einer Veränderlichen definirt. Der Begriff
lässt sich unmittelbar übertragen auf Functiouen mehrerer
Variablen, indem man die Ableitungen in Bezug auf jede Variable
für sich, als ob sie die einzige wäre, bildet. So erhält man,
wenn man etwa wie in §. 17
A) F(x, y,z...) = SA
setzt, die' erste Derivirte nach x:
B) F' (x) =
oder nach y:
C) F'(sf)
u. s. f. Aus diesen Functionen kann man nach denselben Regeln
wieder die Ableitungen nach den verschiedenen Variablen bilden
und erhält so die höheren Ableitungen.
Um die Resultate übersichtlicher darzustellen, sei 3> (xa, x2... xm)
eine ganze rationale Function wter Ordnung der m Veränderlichen
Xi, x2 . . . xm. Wir ersetzen diese Veränderlichen durch Binome:
X\ -\~ |i, X2 -\~ g2v • • •» xm ~T Sm
und entwickeln in jedem Gliede der Function
*(«1 + In «2 + l2, • • ••> ^m + im) = $(X -f i)
durch Ausführung der Multiplication
(X, + Ix)«' (X2 + &)«. . . . (Xm + Infm
nach Potenzen von li, & • • • im- Fassen wir gleiche Potenzen
und Producte der Variablen £ je in ein Glied zusammen, so
ergiebt sich in der Bezeichnung B) §. 17 für &(x -\- |) eine
Darstellung, die in der Differentialrechnung die Taylor'sehe
Entwickelung heisst:
D;
Die Coe'fficienten, die wir mit
bezeichnen, sind Functionen der Variablen x und heissen, wenn
5*

68 Erster Abschnitt. §. 18.
Ki —1~ oea —|— - - • —J— Km = v ist, die Derivirten vter Ordnung
der Function (P.
Man stellt sie auch nach der in der Differentialrechnung
gebräuchlichen Bezeichnungsweise so dar:
E) #»i,«....«„® = 0a;
Das Bildungsgesetz der Derivirten lässt sich in folgende
Sätze zusammenfassen, wobei wir der Kürze wegen die Indices
bei dem Zeichen D weglassen.
I. Ist G eine Constante, so ist
= CD®.
II. Sind 0 und *P" irgend zwei Functionen, so ist
I)(® -\--W).*= D0 -f DW.
Beides folgt unmittelbar aus D).
Wir können also leicht die derivirten Functionen allgemein
bilden, wenn wir sie für den specieilen Fall kennen, in dem <P
ein Product von Potenzen ist, also wenn wir
kennen, worin die (x beliebige, nicht negative Exponenten sind.
Nun ist aber
und folglich:
F) fc + I0 • • • (a» +
und es ergiebt also die Vergleichung mit D) und F):
G) T) (VUl r1*™)
\' J J-'al ...am \ß>i . • • %m )
!
so lange «j ^ f<j . . . am ^ [im. Dagegen ist
sobald einer der Indices cc grösser ist als der entsprechende
Exponent (i.

§. 18. Rationale Functionen. 69
Bezeichnen wir nun mit ßi, ßa . . . ßm ein zweites System
von Indices, und bilden von der Function G) die Ableitung
Jjflu |js... ßm, so ergiebt sich durch nochmalige Anwendung der-
derselben Formeln G) und (8):
(9) 2>A...^^...^(^..a^) = 2>A + a1.../jw + ^D1...aÄ"),
und daraus folgt nach II. die allgemeine Gültigkeit des Satzes:
HL ^1,...ßmDa1,...am^ = I)ßl + ai,...ßm + amO>,
was eine Verallgemeinerung des Satzes (8), §.13 ist, und man
kann also die höheren Derivirten durch fortgesetzte Ableitung
der niederen bilden.
Für die ersten Derivirten einer Function <Z>
A, 0 . . . 0 #, Do, 1 ... 0 #, ... -Do, 0 ... 1 0
brauchen wir auch die kürzeren Zeichen
&'(xj, & (x3), . . . & (xm),
ebenso für die zweiten
Dit 0 ... 0, Dl, 1 ... 0, . .
die Zeichen
0" (x„ Xl\ 0" fo, x,) = 9" («,, x,), . . .
Auch diese Bezeichnung lässt sich verallgemeinern nnd
würde zu einem der Formel D), §. 17 entsprechenden Ausdruck
führen. Alles dies behält seine Gültigkeit, mag die Function 0
homogen sein oder nicht.
Wir erwähnen des häufigen Gebrauches wegen die Formeln
für die quadratischen Formen besonders. Setzen wir
A0) ®(x) = 2aitlcscixk,
worin i, To von einander unabhängig die Reihe der Zahlen
1, 2 . . . m durchlaufen und a^ Ä = a^ i ist, so ist
Va#'(*i) = <h, i X\ + «i, 2 «2 H V «i, mXm
A1) Va &' («2) = «2, 1 «1 + «2, 2 «2 + • • • + «2, m«m
1/2 ©'(iCm) = «m, 1^1 + «m, 2^2 + • • • + «in,».*«.,
und wir setzen noch
A2) 9(x, i) = 0A 7) = Sii0'(xt) =
Dann ist
A3) 0(x-j-g) = 0 [x) -

70 Erster Abschnitt. §. 19.
Die Function <&(#,•£) wird die Polare von 9 genannt. Sie
ist linear und homogen sowohl in Beziehung auf die x, wie in
Beziehung auf die £. ¦
Sie kann ausgedrückt werden durch
A4) Q>(x,£) = 2Zaile!iixle
und genügt der Bedingung
A5) ®(x,x) = 2®(x).
§. 19.
Das Euler'sche Theorem über homogene Functionen.
Aus den vorstehenden Entwickelungen lässt sich mit Leich-
Leichtigkeit ein Fundamentalsatz über- homogene Functionen her-
herleiten, der von Euler entdeckt und nach ihm benannt ist.
Wir erhalten ihn am einfachsten aus der Formel D) des
vorigen Paragraphen, wenn wir darin 3>.als homogene Function
annehmen. Ist dann t eine beliebige Veränderliche und
A) & = txu ga = tx2 . . ., gm = txm,
so ergiebt die Fundamentalformel §. 17 A) für die homogenen
Functionen
Wendet man auf der linken Seite von B) den binomischen
Satz an, und setzt dann die Coefficienten gleich hoher Potenzen
von t beiderseits einander gleich, so ergiebt sich für jedes
v = 1, 2 ... n:
a
= 2
worin sich die Summe auf alle der Bedingung
D) «l+«2"j (- K* = V
genügenden Werthsysteme der a erstreckt.
In dieser Form ist das zu erweisende Theorem in seiner
Allgemeinheit enthalten. Für den besonderen Fall v = 1
erhalten wir die Formel
E) n^{xx, x2 . . . xm) =.x1

§. 20. Zerlegbare und unzerlegbare Functionen. 71
wovon die Formel A5) des vorigen Paragraphen ein specieller
Fall ist, und für v = 2:
F) n(n — 1) <&(*!, %2 ¦ . . xm) = E xt xh 0" (#f, «*,),
worin die Summe von i = 1 bis * = m und von 1c = 1 bis
i = m zu erstrecken ist, so dass jedes Glied mit ungleichen i, 1c
zweimal in der Summe auftritt.
Setzen wir, wenn die cc der Bedingung D) unterworfen sind
G) &v(£, x) = 2j
so ist nach D) des §. 18:
(8) 9(x + i) = ®{x) + 0t (x,® + *,(«,ö H (- 04^,1),
und da die linke Seite ungeändert bleibt, wenn a; mit § ver-
vertauscht wird, so ergiebt sich die Relation:
(9) $«-* (x, 8 = 0, (& «),
also insbesondere
A0) ®.(«,«) = ®(ö.
Die Function #„ (x, |) wird, als Function von x betrachtet,
die vte Polare der Function 0 für das Werthsystem §
genannt.
Wir wollen die Formel C) noch für den Fall einer binären
Form (m = 2) specialisiren.
Wir bezeichnen die Variablen mit x, y und setzen zur
Abkürzung
0 {x, y) = u, I)hi r_a 0 =f uh
und erhalten aus D)
vX) n{n-v) ff n(h)ii(v - h) UhX y '
worin v jeden beliebigen Werth, der nicht grösser als n ist,
annehmen kann.
¦ ¦ " §.20.
Zerlegbare und unzerlegbare Functionen.
I ' Das Product von ganzen Functioneu ist wieder eine ganze
Function, die, wenn die Factören von Null verschieden sind,
selbst von Null verschieden ist (§. 2), und deren Grad gleich

72 Erster Abschnitt. §..20.
der Summe der Grade der Factoren ist. Dies ist zunächst evi-
evident, wenn die Factoren, und folglich auch das Product, homo-
homogene Functionen sind, und es folgt dann allgemein aus der
Bemerkung, dass sich jede nicht homogene ganze Function in
eine Summe von homogenen Functionen verschiedener Grade zer-
zerlegen lässt, deren höchster den Grad der Function bestimmt.
Wir haben nun unter den ganzen Functionen. solche zu
unterscheiden, die als Producte von zwei oder mehr ganzen
Functionen, deren keine vom nullten Grade (also constant) ist,
dargestellt werden können, und solche, bei denen dies nicht mög-
möglich ist. Die ersten heissen zerlegbar, die anderen unzer-
unzerlegbar.
Wenn eine ganze Function zerlegbar ist, so ist der Grad .
jedes der Factoren niedriger als der Grad der Function selbst.
Eine lineare Function ist also immer unzerlegbar, und jede
ganze Function lässt sich in eine endliche Zahl unzer-
unzerlegbarer Factoren zerlegen.
Wir nennen eine ganze Function W durch eine andere w
theilbar, wenn eine dritte ganze Function (oder auch eine Con-
stante) w' existirt, so dass
W =. ww'
ist. Daraus folgt dann, dass, wenn U eine durch w theilbare und
V eine beliebige ganze Function ist, auch das Product UV
durch w theilbar ist, und dass, wenn U, U', U" . . . durch w
theilbare, F, F', V" . . . beliebige ganze rationale Functionen sind,
auch UV-\- U'V -f TJ"V" -| durch w theilbar ist.
Ist W durch w theilbar, so sagt man auch, w geht in
W auf.
Zwei ganze rationale Functionen U V, die nicht durch eine
und dieselbe ganze rationale Function theilbar sind, heissen
relativ prim oder theilerfremd.
Wir beweisen den Satz:
I. Sind ü, F, v ganze Functionen irgend welcher
Veränderlichen, sind U und v relativ prim und
UV durch v theilbar, so ist F durch v theilbar.
Dieser Satz entspricht genau einem bekannten Fundamental-
satz aus der Lehre vou den ganzen Zahlen, dass nämlich, wenn
ein Product von zwei ganzen Zahlen durch eine dritte ganze

§. 20. Zerlegbare und unzerlegbare Fuuctionen. 73
Zahl theilbar ist, die zu dem einen Factor theilerfremd ist, der
andere Factor durch diese Zahl theilbar sein muss.
Wir beweisen ihn durch vollständige Iiiduction. Sind U,Vv
nur von einer Veränderlichen x abhängig, so ist der Satz
richtig; denn nach §. 6 (Satz I) kann man in diesem Falle, wenn
U und v relativ prim sind, zwei andere ganze Functionen P und
j) von x so bestimmen, dass
woraus durch Multiplication mit V
p u.r + pVv = v
folgt, und daraus ersieht man, dass, wenn UV durch v theilbar
ist, auch V durch v theilbar sein muss.
Wir nehmen also an, der Satz, den wir beweisen wollen, sei
für Functionen von n und weniger Veränderlichen bewiesen, und
wir leiten daraus seine Richtigkeit für Functionen von n -J- 1
Veränderlichen ab.
Dazu ist erforderlich, dass wir aus dein als richtig voraus-
vorausgesetzten Theorem I. einige Folgerungen ziehen, als deren Schluss
sich dann die Gültigkeit des Theorems für die nächst höhere
Variablenzahl ergiebt.
Ist v eine unzerlegbare Function, so ist eine andere Fuuc-
tion U derselben Veränderlichen entweder relativ prim zu v oder
durch v theilbar. Daraus folgt nach I., dass ein Product von
zwei Functionen JJV nur dann durch v theilbar sein kann, wenn
einer der beiden Factoren durch v theilbar ist. Dasselbe gilt
für ein Product von mehreren Functionen, und so folgt aus I.
das Theorem:
IL Ein Product aus mehreren ganzen Functionen ist
nur dann durch eine unzerlegbare Function v
theilbar, wenn wenigstens einer der Factoren
des Productes durch v theilbar ist.
Wenn eine ganze rationale Function U auf zwei Arten in
unzerlegbare Factoren zerlegt ist,
[/¦= vv'v" ¦ • • = ww'w" . . .,
so muss nach II. wenigstens einer der Factoren v, v', v" . . .
durch w theilbar sein, also etwa v. Dann aber kann, da auch
v unzerlegbar ist, v von w nur durch einen constanten Factor
verschieden sein.

74 Erster Abschnitt. §.20.
Demnach ist, wenn c dieser constante Factor ist,
c v' v" • • • = w' w" . . .,
woraus folgt, dass eine der Functionen v\ v" . . ., etwa v', durch
w' theilbar ist, und sich also von w' nur durch einen constanten
Factor unterscheidet u. s. f.
Wir erhalten also als zweite Folgerung aus dem Theorem I:
III. Eine ganze Function kann, von constanten Fac-
toren abgesehen, nur auf eine Art in unzerleg-
unzerlegbare Factoren zerlegt werden.
Hieraus ergiebt sich der Begriff des grössten gemein-
gemeinschaftlichen Theilers von zwei oder mehr ganzen rationalen
Functionen U, V. . . Man versteht darunter das Product aller
unzerlegbaren Factoren, die in den Zerlegungen jeder der Func-
Functionen U, V. . . vorkommen, oder die Function möglichst hohen
Grades, die in allen Functionen U, V. . . aufgeht. Nach III. ist
diese Function, von einem constanten Factor abgesehen, für jedes
Functionensystem U, V. . . vollständig bestimmt.
Mehrere Functionen U, V, W. . . heissen relativ prim, wenn
keine zwei von ihnen einen gemeinsamen Theiler haben.
Alle diese Definitionen und Sätze sind genau analog mit
sehr bekannten Sätzen der elementaren Zahlenlehre, die dort
als Folgerungen des Algorithmus des grössten gemeinschaftlichen
Theilers auftreten, nur dass hier die unzerlegbaren Functionen
die Rolle der Primzahlen übernehmen.
Wir führen noch einen solchen Satz an:
IV. Sind m, v relativ prim und Uu, Uv durch w theil-
theilbar, so ist U durch w theilbar.
Denn zerlegt man die ganzen rationalen Functionen U, u, v, w
in ihre unzerlegbaren Factoren, so muss irgend ein Factor von
w, da er nicht in u und v zugleich vorkommen kann, in U auf-
aufgehen. Hebt man ihn aus U und w weg, so kann man ebenso
für einen nächsten Factor von w schliessen u. s. f.
Wir betrachten nun ganze rationale Functionen einer Ver-
Veränderlichen t .... .-¦¦¦¦
., "• '/(*) — t«o*" -f m^-1 h + «*_!* -f um, ¦ ¦ ¦¦
dereu Coefficienten ganze rationale Functionen von n Veränder-
Veränderlichen «sind,, von denen t unabhängig ist. '.. ¦ ¦
Sind die Coefficienten u0, u{ . . . um ohne gemeinsamen

§. 20. Zerlegbare und unzerlegbare Functionen. 75
Theiler, so heisst f(t) primitiv, im anderen Falle wird der
grösste gemeinschaftliche Theiler der Coefficienten u0, ut ¦ ¦ . um
der Theiler der Function f(t) genannt (vergl. §. 2).
Wir schliessen, immer unter Voraussetzung der Gültigkeit
von I:
V. Das Product von zwei primitiven Functionen f(t)
und (p{t) ist wieder eine primitive Function und
der Theiler eines Productes zweier imprimitiver
Functionen ist gleich dem Product der Theiler
beider Factoren.
Der Beweis ist ganz so wie für den entsprechenden Satz
in §. 2.
Es seien
W <p (t) = M" -f t>! P-1 -\ 1- t>„
zwei primitive Functionen und
B) F(t) = Uo P»+t* + Di *» + "-» -\ 1- D"m+„
ihr Product. Es ist dann, wenn r und s irgend zwei Ziffern aus
den Reihen 0, 1 ... m, und 0, 1, 2 ... ft bedeuten (§. 2)
C) . Ur + s = UrVs -\- Ur-!VS + 1 -{-'••
-j- Ur+iVs-t -j
Wenn nun w irgend eine unzerlegbare Function ist, die
weder in allen ur noch in allen vs aufgeht, so wählen wir in C)
r und s so, dass ur das erste nicht durch w theilbare u ist, also
ur-i, Mr_2 . . . durch w theübar sind, und dass ebenso vs das
erste, nicht durch w theilbare v wird. Dann kann auch Ur + S
nicht durch w theilbar sein, weil alle Glieder, mit Ausnahme
des ersten, durch w theilbar sind, d. h. F(t) ist primitiv.
Daraus folgt unmittelbar, wenn p und q irgend welche ganze
rationale Functionen der x sind, dass pq der Theiler des Pro-
Productes der beiden imprimitiven Functionen pf(t), qfp(t) ist, also
der zweite Theil des Satzes V. Daraus folgt weiter:
VI. Wenn eine ganze rationale Function F(t) der
n -\- 1 Variablen x und t in zwei Factoren zer-
zerlegbar ist, die in Bezug auf t ganz, in Bezug auf
die x wenigstens rational sind, so ist sie auch in
zwei Functionen zerlegbar, die in x und t ganz
und rational sind.

76 . Erster Abschnitt. §. 20.
Denn nach der Voraussetzung giebt es eine ganze rationale
Function w der x allein und zwei ganze rationale Functionen
der x und t, ft (t), cp. (t), so dass
i
und nach V. muss w in dem Product der Theiler von f. (t) und
9j (t) aufgehen, so dass wir auch
erhalten, worin f(t), <p (t) gleichfalls ganze rationale Functionen
von x und t, und zwar in Bezug auf t von demselben Grade wie
/i (t) und 9j (t) sind, w. z. b. w. — Hieraus schliessen wir weiter,
dass zwei Functionen .F(<),/(<), die als ganze rationale Functionen
der n -\- 1 Veränderlichen x und t betrachtet, in dem oben defi-
nirten Sinne relativ prim sind, sich auch, als Functionen von t
allein betrachtet, und nach dem Algorithmus des grössten gemein-
gemeinschaftlichen Theilers behandelt (§. 6), als relativ prim erweisen
müssen. Denn wenn sie einen gemeinsamen Theiler hätten, der
in Bezug auf t ganz, in Bezug auf die x gebrochen wäre, so
Hesse sich eine ganze Function T von x und t und eine ganze
Function P der x allein so bestimmen, dass
PF(t) = TF.it), P/{t) = Tf.it)
wäre, worin Fu /i ganze Functionen ohne gemeinsamen Theiler
sind. Wenn also Pl5 fr, M die Theiler der Functionen Ft(t),
/j (£), T sind, so sind P. und fr relativ prim, und P. M und pk M
sind durch P theilbar, also ist nach IV. auch M durch P theilbar;
mithin sind Fit) und fit) durch die ganze Function T:P theilbar,
also nicht relativ prim, wie doch vorausgesetzt war.
Es ergiebt sich also nach §. G, dass sich zwei ganze Func-
Functionen Q, q von x und t und eine ganze Function X von den
x allein so bestimmen lässt, dass die Identität
D) QFit) + qfit) = X
besteht.
Ist nun &H) eine weitere ganze Function von x und t, so
folgt aus D) durch Multiplication mit <&(£)
Q ^ (t) Fit) + 2 <D @ /(*) = X * it),
und wenn also 3>(f) Fit) durch f(t) theilbar ist, so ist auch
X 0 it) durch fit) theilbar.
Demnach können wir, wenn <jp(£) und i>it) wieder zwei
ganze Functionen von x und t bedeuten, setzen:

§. 20. Zerlegbare und unzerlegbare Functionen. 77
{) F(tH(t) =
Multiplicirt man die zweite dieser Gleichungen mit X und
setzt aus der ersten für X&(t) den Ausdruck <p(t)f(t) ein, so
lässt sich f(t) wegheben und es folgt
<p(t)F(t) = Xt(t).
Es muss also X sowohl im Theiler von cp(t)f(t) als in dem
von <p(t)F(t) aufgehen, und da f(t) und F(t) und mithin auch
ihre Theiler relativ prim sind, so muss X im Theiler von <p(t)
aufgehen (nach IV). Setzen wir demnach
so folgt aus E)
*(<) = 9l (<)/(*),
d. h. 0(t) ist durch f(t) theilbar; also:
VII. Sind F(t) und/(f) relativ prim und ®(f)F(t) durch
f(t) theilbar, so ist &(t) durch f(t) theilbar.
Dies aber ist nichts Anderes als das Theorem I. für Func-
tionen von n -\- 1 Variablen, und I. somit allgemein bewiesen.
Zugleich sind damit auch die aus I. gezogenen Folgerungen
bewiesen, insbesondere die, dass eine Function von einer belie-
beliebigen Anzahl von Variablen, abgesehen von constanten Factoren,
nur auf eine Art in unzerlegbare Factoren zerlegt werden kann.

Zweiter Abschnitt.
Determinanten.
§• 21.
Perniutationen von n Elementen.
Wir betrachten ein System von n unterschiedenen Elementen
irgend welcher Art, z. B. die n Ziffern
1, 2, 3 ... n,
deren Complex in dieser bestimmten Anordnung wir mit 91 be-
bezeichnen wollen. Die Elemente von 9t lassen sich auf verschie-
verschiedene Art anordnen, z. B.:
2, 1, 3 ... n.
Der Uebergang von einer Anordnung zu einer anderen heisst
eine Permutation.
Bezeichnen wir die Anzahl der verschiedenen Anordnungen,
die nur von der Anzahl n der Elemente abhängen kann, mit
II(n), so ergiebt sich zunächst IIA) = 1, 11B) = 2, uud um
die Zahl allgemein zu bestimmen, denken wir uns zu n — 1
Elementen ein wtes hinzugefügt. In jeder Anordnung der n — 1
Elemente kann nun das wte Element an n verschiedene Stellen
gesetzt werden, nämlich vor das erste, zwischen das erste und
zweite, zwischen das zweite und dritte u. s. f., endlich nach dem
(n — l)ten, und alle die so entstandenen Anordnungen sind von
einander verschieden. Daraus folgt:
A) JI(n) = nJI(n— 1),
woraus sich durch vollständige Induction
B) n(n) = 1.2.3 ...»
ergiebt. so dass das Zeichen II(n) hier dieselbe Bedeutung hat,
wie im ersten Abschnitt (§. 7).

§. 22. Permutationen erster und zweiter Art. 79
Irgend eine Anordnung des Systems 31 bezeichnen wir mit
91', oder ausführlicher, wenn «j, «j . . . «„ die Ziffern 1, 2 ... n
in irgend einer Reihenfolge bedeuten, mit
C) 21' = «!, «, , . . a».
Man kann auf sehr verschiedene Arten aus einer Anordnung
eine beliebige andere ableiten, d. h. eine Permutation ausführen.
Unter den verschiedenen Möglichkeiten sind für uns die durch
sogenannte Transpositionen, d. h. durch successive Ver-
Vertauschung von nur zwei Elementen ausgeführten, von besonderem
Interesse. Durch mehrere, nach einander ausgeführte Transposi*
tionen lässt sich aus jeder Anordnung, z. B. aus % jede andere
91' herleiten. Man kann zu diesem Zwecke etwa so verfahren, dass
man in 3t zunächst das Element 1 mit dem, was in 31' an erster
Stelle steht, also mit «,, vertauscht (falls nicht at = 1 ist), dann,
wenn «2 nicht schon = 2 ist, 2 mit «2 u. s. f.
Um z. B. von A, 2, 3, 4) zu D, 3, 2, 1) zu gelangen, bildet
man die Anordnungen
A, 2, 3, 4), D, 2, 3, 1), D, 3, 2, 1).
Bezeichnen wir eine Transposition kurz durch die beiden
vertauschten Ziffern, also die Vertauschung von 1 mit 2 durch
A, 2), so haben wir hier nach einander die Transpositionen
A, 4), B, 3) ausgeführt.
Es ist zu bemerken, dass der Uebergang von einer Anord-
Anordnung zu einer bestimmten anderen auf unendlich viele verschie-
verschiedene Arten durch auf einander folgende Transpositionen erreicht
werden kann. So geht die Anordnung A, 2, 3, 4) auch durch die
Transpositionen A, 2), A, 3), B, 4), A, 2) in D, 3, 2, 1) über.
Man kann auch etwa zunächst beliebig oft blindlings trans-
poniren, und dann erst anfangen, die Transpositionen in der
angegebenen Weise planmässig einzurichten.
§• 22.
Permutationen erster und zweiter Art.
Die II (n) Anordnungen von n Elementen lassen sich nach
folgendem Gesichtspunkte in zwei Arten zerlegen.
Aus den n Elementen unseres Systems lassen sich —L—'-
und nicht mehr Paare bilden. Wir wollen nun den n Elementen

80 Zweiter Abschnitt. §. 22.
1, 2, .'¦.'. n in bestimmter Weise n reelle Zahlwerthe %, a2, . • • an
zuordnen, und aus diesen Zahlwerthen die —^r—'- Differenzen
«i — «a, cti — as . . . bilden, wobei der niedrigere Index dem
Minuenden angehören soll. Das Differenzenproduct
A) P — (% — a2) («i — a%) ...(«! — a„)
(«2 — as) . . . (a2 — an)
(an_! — an)
wird, wenn die ax, a2 . . . an von einander verschiedene Zahl-
Zahlwerthe sind, einen von Null verschiedenen Werth haben, z. B.
einen positiven, wenn ai ^> a2 ^> as . . . ^> an angenommen war.
Wenn wir nun die Indices 1, 2, 3 ... n irgendwie unter ein-
einander vertauschen, also etwa von 21 zu 21' übergehen, so geht
P in
B) P' = (aai — a«2) (aai — aa,) . . . (aai — a«M)
(a«2 — aUa) . . . (aUi — a«n)
über, und dies Product besteht, abgesehen vom Vorzeichen, aus
denselben Factoren wie P, d. h. es ist P' entweder gleich P
oder entgegengesetzt zu P.
I. Wir rechnen nun die Anordnung 21' und also
auch die Permutation, die 21 in 21' verwandelt,
zur ersten oder zur zweiten Art, je nachdem
P mit P' gleich oder entgegengesetzt ist, so
dass 21 selbst zur ersten Art gehört.
II. Durch eine einfache Transposition (h, &), worin
Ä, 1c irgend zwei der Ziffern 1, 2 ... n bezeich-
bezeichnen, ändert sowohl P als P' sein Vorzeichen.
Denn die Factoren, die h und 1c gar nicht enthalten, werden
durch diese Transposition nicht berührt; dann haben wir in
P und P' den Factor + (ah — aft) und die Factorenpaare
+ (% — «r) («s — av), wo v die Reihe der Zahlen 1, 2 . . . n,
mit Ausnahme von h, 1c durchläuft. Der erstere Factor ändert
aber sein Zeichen, während das Factorenpaar ungeändert bleibt
bei der Transposition (h, h). Daraus folgt:

§. 22. Permutation erster und zweiter Art. 81
III. Die Permutationen der ersten Art sind aus
einer geraden Anzahl von Transpositionen
zusammengesetzt, und die der zweiten Art
aus einer ungeraden Anzahl.
Zu der ersten Art ist dann auch die sogenannte identische
Permutation zu rechnen, die 2t • ungeändeft lässt.
! Daraus ergiebt sich noch die Folgerung: Auf wie verschie-
verschiedenen Wegen man auch 21' aus 21 durch Transpositionen ab-
ableiten mag, die Anzahl dieser Transpositionen ist bei allen diesen
Arten übereinstimmend gerade oder ungerade (je nachdem 2t'
zur ersten oder zur zweiten Art gehört).
Wenn wir in den sämmtlichen Anordnungen
21, 21', 21" ...
der n Elemente eine Transposition, etwa A, 2), vornehmen, so
geht jede dieser Anordnungen in eine bestimmte andere über,
etwa 21 in SS, 21' in 33', 2t" in 33" . . ., und wenn wir dieselbe
Transposition noch einmal wiederholen, so geht 33 wieder in 21,
33' wieder in 21' ... über. Daraus folgt, dass die Anordnungen
33, 33', 23" . . . alle von einander verschieden sind und folglich
in ihrer Gesamnitheit mit der Gesammtheit der 2t überein-
übereinstimmen. Da nun, wie wir oben gesehen haben, die sämmtlichen
Differenzenproducte
die aus P mit den verschiedenen Anordnungen 2t, 21', 2t"...
gebildet sind, durch eine Transposition das Zeichen ändern, so
folgt, dass jedem 2t der ersten Art ein 33 der zweiten Art ent-
entspricht und jedem 2t der zweiten Art ein 23 der ersten Art.
IV. Hiernach ist die Anzahl der Anordnungen der
ersten Art ebenso gross, wie die Anzahl der
Anordnungen der zweiten AiJ;, nämlich — 77 (wI).
Für n = 3 haben wir die folgenden sechs Anordnungen,
von denen die erste Horizontalreihe die erste Art bildet:
a) A, 2, 3), B, 3, 1), C, 1, 2)
K C, 2, 1), B, 1, 3), A, 3, 2)
J) Diese Sätze sind hier aus der Betrachtung des Productes P, also
einer • Zahlgrösse, gewonnen. Wie man ohne Benutzung einer solchen
Function zu denselben Ergebnissen gelangen kann, werden wir im XIV. Ab-
Abschnitt sehen.
Weber, Algebra. I. g

82
Zweiter Abschnitt.
§.. 23.
§. 23.
Determinanten.
Wir betrachten jetzt ein System von w2 beliebigen Grossen,
mit denen die rationalen Rechenoperationen ausgeführt werden
können. Zu einer einfachen Bezeichnung dieser Grossen wählen
wir einen Buchstaben mit einem doppelten Index af>, worin
i sowohl als Je die Reihe der Ziffern 1, 2, 3 ... n durchlaufen soll.
Zur besseren Uebersicht ordnen wir diese Grossen in ein Quadrat,
so dass alle a mit demselben oberen Index in einer Horizontal-
Horizontalreihe, alle a mit demselben unteren Index in einer Verticalreihe
stehen, und bezeichnen dies Quadrat mit z/, also:
a«, a«, a?) . . . a«
af), of), af> . . . affl
a?\ af\ af> . . . af
A)
z/ =
a[n\
Der Kürze halber nennt man die Horizontalreihen Zeilen,
die Verticalreihen Colonnen oder Spalten. Die Grossen e4ft)
heissen die Elemente des Systems z/.
Wir wollen aber unter dem zwischen verticalen Strichen
eingeschlossenen Quadrat nicht nur den Complex der Grossen a
verstehen, sondern eine bestimmte arithmetische Verbindung
dieser Grösseu, die sich ausrechnen lässt, sobald die a numerisch
gegeben sind, und die wir jetzt beschreiben wollen.
Man bilde das Product aller Elemente a, die in der von
links oben nach rechts unten gehenden Diagonale stehen:
B) M = aW cd® aW . . . a(M).
leite daraus II(n) Producte M, M', M" . . . her, indem man
die unteren Indices permutirt, und gebe jedem so entstandenen
Product das positive oder negative Zeichen, je nach-
nachdem die angewandte Permutation zur ersten oder
zur zweiten Art gehört, also nach der Bezeichnung des
vorigen Paragraphen:
C) Jf' = £o«o«...aW.
Die Summe aus diesen Producten
M + M + M " + ••• = EM

§. 23. Determinanten. 83
soll z/ sein, z/ wird die Determinante der w2 Elemente af>
genannt, und zwar, wenn die Unterscheidung nothwendig ist,
eine w-reihige Determinante (auch Determinante wten
Grades oder wter Ordnung). Das Glied M dieser Summe,
d. h. also das Product "aller in der Diagonale des Quadrates
stehenden Elemente, wird das Hauptglied genannt.
Nehmen wir z. B. n = 2, so erhalten wir
D) // = flpaf-fl«a(a\
und für n = 3 [nach C) des vorigen Paragraphen]:
4 = a<paf>af> + a^af^af -f
*• ' —
F)
= ad — bc.
ab'c" -\-bc'a" -\- ca'b"
oder in anderer Bezeichnung:
a, b
c, d
a, b, c
a', b', &
a", b", c"
Es ist dem Leser zu empfehlen, die Berechnung solcher
Determinanten an Zahlenbeispielen einzuüben.
Die Bezeichnung A) ist in vielen Fällen zu umständlich; es
sind daher noch andere, kürzere Zeichen im Gebrauch. So setzt
Jacobi, indem er nur das Hauptglied der entwickelten Deter-
Determinante ausführlich schreibt:
(8) z/ = 2 •+- «W a<2> . «(»)
und Kronecker noch kürzer:
(9) z/ = | af |.
Beide Bezeichnungen sind aber nur dann ganz deutlich,
wenn die Elemente in der hier vorausgesetzten Weise durch
zwei Indices bezeichnet sind, und durchaus unanwendbar, wenn
die Elemente z. B. numerisch gegeben sind.
Es kommen bisweilen Determinanten vor, bei denen
af> = -ap
ist, bei denen also in A) die symmetrisch zur Diagonale des
Quadrates stehenden Elemente einander gleich sind. Wir werden
in diesen Fällen gewöhnlich beide Indices (um ihre Gleichwerthig-
keit anzudeuten) unten hinsetzen, also
ai,lc =• <h,i
setzen. Solche Determinanten heissen symmetrisch.
0*

84 Zweiter Abschnitt. §. 24.
§• 24.
Hauptsätze über Determinanten.
Aus dem Begriff der Determinante ergeben sich leicht die
ersten Sätze, die für die Anwendung geeignet sind.
Wenn wir in dem Product [§. 23, C)]
A) M> = ±a%a%...a%
die Factoren umstellen, so ändert sich sein Werth nicht. "Wir
können also die Factoren auch so anordnen, dass die unteren
Indices in ihrer natürlichen Eeihenfolge 1, 2 . . . n erscheinen.
Dabei werden dann die oberen Indices in einer gewissen Weise
permutirt erscheinen, also M' die Form erhalten:
B) ±af*afi> ...a{ln\
worin
(ft, &.../}») = 33,
ebenso wie
(«!, «2 ... «„) = 31
eine Anordnung der Ziffern 1, 2 . . . w bedeutet. Man kann
die Anordnung 93 dadurch erhalten, dass man in den Factoren
von M' die Transpositionen, die zu 51 geführt. haben, von der
letzten anfangend, rückgängig macht, um in der Reihe der
unteren Indices wieder die ursprüngliche Anordnung zu erhalten.
Die dabei sich ergebende Reihenfolge der oberen Indices ist dann
die Anordnung 93. Es folgt daraus, dass 33 zur ersten oder zur
zweiten Art gehört, je nachdem 31 zur ersten oder zur zweiten
Art gehört, da beide durch die gleiche Anzahl von Transposi-
Transpositionen entstehen. Die Gesammtheit der 18 stellt ebenso wie die
Gesammtheit der 51 alle Permutationen der n Elemente dar, da
zwei verschiedene 51 niemals zu demselben 18 führen können.
Damit ist bewiesen: •
I. Die Determinante <d kann auch dadurch gebildet
werden, dass man in dem Hauptgliede a<l>a<2>... «W
die oberen Indices auf alle möglichen Arten per-
permutirt, jedem der so gebildeten Producte das
positive oder negative Zeichen giebt, je nachdem
die angewandte Permutation zur ersten oder
zweiten Art gehört, und dann die Summe aller
dieser Producte nimmt.

§. 24. Determinanten. - 85
In der Darstellung §. 23, A) von z/ werden durch die oberen
Indices die Zeilen, durch die unteren Indices die Colonnen
gekennzeichnet,. und demnach können wir diesem Satze auch den
folgenden Ausdruck geben:
II. Eine Determinante ändert sich nicht, wenn die
Zeilen zu Colonnen und die Colonnen zu Zeilen
gemacht werden.
Wenn wir in den sämmtlichen Anordnungen 91, 91', 91" ...
der n Elemente irgend zwei Elemente mit einander vertauschen,
so bleibt die Gesammtheit dieser Anordnungen ungeändert, aber
es geht jede Anordnung erster Art in eine Anordnung zweiter
Art über und umgekehrt. Wenn wir also in den Gliedern
M, M', M" . . ., aus denen z/ zusammengesetzt ist, irgend zwei
untere Indices vertauschen, so geht jedes Glied mit positivem
Zeichen in ein anderes über, das in 4 mit dem negativen Zeichen
behaftet war und umgekehrt, also es ändert d sein Vorzeichen.
Daraus folgt mit Hülfe von II. der Satz:
III. Wenn man in z/ zwei untere oder zwei obere In-
Indices mit einander vertauscht, so ändert die
Determinante nur ihr Vorzeichen.
Etwas anders ausgedrückt:
Wenn man zwei Zeilen oder zwei Colonnen mit
einander vertauscht, so ändert die Determinante
nur ihr Vorzeichen,
und daraus allgemeiner:
IV. Wenn in einer Determinante die Zeilen oder die
Colonnen permutirt werden, so ändert sich der
absolute Werth nicht, und das Vorzeichen ändert
sich nicht oder geht in das entgegengesetzte
über, je nachdem die angewandte Permutation
zur ersten oder zweiten Art gehört.
Aus III. erhält man den folgenden Fundamentalsatz:
V. Wenn in zwei Zeilen oder in zwei Colonnen die
an gleicher Stelle stehenden Glieder einander
gleich sind (kürzer ausgedrückt: wenn zwei Rei-
Reihen einander gleich sind), so hat die Deter-
Determinante den Werth Null.
Denn die Vertauschung der zwei Reihen ändert nach III.
das Zeichen, kann aber andererseits, da beide Reihen, identisch

86 Zweiter Abschnitt. §. 25.
sind, nichts ändern, so dass für z/ nur der Werth Null übrig
bleibt.
Man drückt den Satz V nur anders aus, wenn man sagt:
VI. Man erhält eine verschwindende Determinante,
wenn man die Elemente einer Reihe durch die
entsprechenden Elemente einer anderen Reihe,
oder, kurz gesagt, wenn man einen unteren oder
oberen Index durch einen anderen ersetzt.
§. 25. .
Unterdeterminanten.
In jedem Gliede der entwickelten Determinante
2 ±a<»af> .. . a«,
deren Werth wir jetzt mit A bezeichnen wollen, kommt jede
der Zahlen 1,2...« ein und nur einmal als unterer Index
vor. Es wird also ein gewisser Complex von Gliedern den Factor
ap> enthalten, ein anderer Complex den Factor a<2> u. s. f., end-
endlich ein Complex den Factor af>; jedes Glied der Determinante
kommt in einem und nur in einem dieser Complexe vor.
Bezeichnen wir also den ersten dieser Complexe mit a<J> Af>,
den zweiten mit af> A{2\ den letzten mit a<n> A[n\ so können wir
die Determinante folgendermaassen darstellen:
A) ' Ä = aWAV -f a<2> A{» -| 1- a<»> A<?\
An Stelle des unteren Index 1 hätten wir ebenso gut jeden
anderen, v, herausgreifen und daher
B) A = a« Af + af A? + h <& ^
setzen können. Darin bedeutet das Product a^Ar den
Complex aller Glieder der Determinante, die den Factor
aV enthalten.
Da dieselben Regeln wie für die unteren so auch für die
oberen Indices gelten, so kann man die Determinante auch noch
in der folgenden Weise schreiben:
C) A = aVAV + «M0 H h ^^\
worin (i gleichfalls jeden der Indices 1,2...« bedeuten kann.

§.25.
Unterdeterminanten.
87
Die hierdurch vollständig definirten Grossen J.£u) heissen die
Unterdeterminanten der Determinante A. Um ihre Bildungs-
Bildungsweise genau kennen zu lernen, betrachten wir zunächst den
Complex ail)A?\ Man erhält ihn, wenn man in dem Product
„B)
An)
den unteren Index 1 ungeändert lässt und nur die übrigen In-
dices 2, 3 ... n auf alle Arten permutirt und die Summe der
entstandenen Glieder mit Rücksicht auf die Zeichenregel bildet,
d. h. es ist A^ die (n — 1)reihige Determinante:
D)
,,B)
«2 ,
(8)
«3
«2 , «3
oder die Determinante, die man aus A erhält, wenn man in dem
A darstellenden Quadrat [§. 23, A)] die erste Zeile und die erste
Colonne weglässt.
Daraus ergiebt sich leicht die Bedeutung von Jiu); man
kann, indem man v — 1 Zeilenvertauschungen vornimmt, die
vte Zeile zur ersten machen, und wenn man noch ft — 1 Ver-
Vertauschungen der Colonnen hinzunimmt, die ftte Colonne zur
ersten; im Uebrigen bleiben die Reihen in ihrer Aufeinanderfolge
ungeändert. Die Determinante selbst hat den Factor (— 1}"+"
angenommen und ist dem absoluten Werthe nach ungeändert
geblieben (§. 24, IV). In der so umgeänderten Reihenfolge ist aber
das Element aV an die Stelle des Elementes a^ getreten, und
daraus schliesst man auf folgendes Bildungsgesetz:
Man erhält die Unterdeterminante A^ dadurch,
dass man in dem die Determinante darstellenden Qua-
Quadrat die beiden Reihen weglässt, die sich in aj;u) kreuzen,
und den Factor (— 1)"+'' hinzufügt.
So erhält man z. B. für die dreireihige Determinante die
folgende Darstellung:
E)
a, 5, c
d, V, d
a", V, c"
= a
V,
b",
&
c"
— b
a',
a",
c'
c"
4-c
d,
a",
V
b"
_ c>v>) .j. b(c'a" — d c") + e(db" — b'a").

88 Ä Zweiter Abschnitt. §. 25.
Da der untere Index v in if' gar nicht vorkommt, so
ändert sich Af^ nicht, wenn der untere Index v durch einen
anderen ersetzt wird. Dann aber verschwindet nach §. 24, "VI.
die Determinante. Wir erhalten demnach aus B) die folgende
wichtige Relation, in der (t, v irgend zwei von einander ver-
verschiedene Ziffern 1, 2 ... n sein können:
F) 0 = <Af -f af Af-\ h o?} Ä?\
und ebenso bekommt man aus C):
G) 0 = «?'> AP + a^ A?^ h «2° A*>.
Beispielsweise ergiebt sich aus E), wenn a, 5, c durch
a', &', c' ersetzt werden':
(8) et (V c" — c' b") -f V (c'a" — «' c") + c' (et l" — 5' a") = 0,
eine Formel, von deren Richtigkeit man sich durch die einfachste
Rechnung überzeugt.
Wenn wir die Relation F) mit einem beliebigen Factor X
multipliciren und zu B) addiren, so erhalten wir die Formel:
(9) A = (a?> + l af) A*> + (o» + l af) A? +
\-(aP + X<P)AP,
die uns den folgenden Satz ausdrückt:
VII. Die Determinante ändert ihren Werth nicht,
wenn man zu den Elementen einer Zeile die
mit einem beliebigen gemeinschaftlichen Factor
multiplicirten entsprechenden Elemente einer
anderen Zeile addirt.
Derselbe Satz gilt auch von den Colonnen. Er wird zur
Vereinfachung und numerischen Berechnung von Determinanten
oft mit Nutzen verwendet. Wir fügen noch folgende Sätze bei,
die sich aus den Darstellungen B), C) sofort ablesen lassen.
VIII. Wenn alle Elemente einer Zeile oder einer Co-
lonne einen gemeinschaftlichen Factor haben, so
kann dieser weggelassen und als Factor vor die
Determinante gesetzt werden.
Denn es ist nach B):
jp a?} AP + p af Af -\ 1- p ain) A^ =pA.
IX. Wenn in einer Zeile oder in einer Colonne alle
Elemente bis auf eines verschwinden, so.reducirt

§• 25.
Unterdeterminanten.
sich die Determinante auf das Product dieses
einen Elementes mit der entsprechenden Unter-
Unterdeterminante.
Denn wenn a^\ af1 . . . a^ mit Ausnahme von ai* ver-
verschwinden, so ist nach B):
der Werth von A ist dann von den a&\ aW . . . «2° (mit Aus-
Ausnahme von a?^) ganz unabhängig.
Um von diesen Sätzen eine Anwendung zu machen, wollen
wir den Werth ,der Determinante
1, a, a*
1, 5, 5*
bestimmen, worin a, b, c beliebige Grossen seien.
Multipliciren wir die zweite Colonne mit a und subtrahiren
sie von der dritten, darauf die erste mit a und subtrahiren sie
von der zweiten, so folgt nach VII:
1, 0, 0
1, 5-—a, 5{5 — a)
1, e — a, c(c — a)
und nach IX:
und endlich nach VIII:
A0) z/ = (b — a) (c — a)
5 — a, 5E — ä)
c — a, c(e — a)
1, e
— a)(c — a) (c—b).
Auf die gleiche Weise kann man auch die w-reihige Deter-
Determinante
1, öj, al . . . a?-1
1, Cto% Q/a . . . Cl,
n—1
P2
an, al . . . al 1
behandeln und findet ihren Werth gleich
(a2 — «0 (a3 — <%) . . . (an
(a3 — a2) . . . (an
A1)
— a2)
(a„ — aM_i

90 Zweiter Abschnitt. §.25.
Ordnet man die Colonnen in umgekehrter Reihenfolge, so
sind dazu, je nachdem n gerade oder ungerade ist,
n ' «— 1
_ oder —r-
Vertauschungen erforderlich, so dass sich die so geordnete
Determinante von J durch den Factor
n(n—1)
(-1) 2
unterscheidet. Es kommt auf dasselbe hinaus, wenn man den
—^—n Factoren des Productes A1) das entgegengesetzte
Vorzeichen giebt.
Es besteht also zugleich mit A1) die Gleichung:
(% —a2) (%—%) ... (%—«»)
A2)
_ (a2—a3) . . . (a2 — o»)
(a„_! — an).
Wir wollen hier noch eine Bezeichnungsweise der Unter-
Unterdeterminanten erwähnen, die der Differentialrechnung entnommen
ist und oft mit Nutzen verwendet wird, besonders wenn es sich
um die Bildung von Derivirten handelt.
Wenn die Grossen ajp als unabhängige Variable betrachtet
werden, so ist die Determinante A in Bezug auf jede von ihnen
nur vom ersten Grade. Die nach aP genommene Ableitung oder
der Differentialquotient ist also gleich dem Coefficienten von
af\ also:
Wenn demnach z. B. die af* Functionen einer Variablen t
sind, so ist auch A eine Fnnction von t, und man erhält nach
den ersten Regeln der Differentialrechnung die Ableitung von A
in Bezug auf t in der Form
wenn * die Ableitung von af* nach t bedeutet.
o t
Wenn wir die a^ als von einander unabhängige Variable
betrachten, so ist die Determinante
A = £ ™

§. 26. Höhere Unterdeterminanten. 91
eine homogene Function wten Grades von n Variablen, jedoch
von der besonderen Eigenschaft, dass jede einzelne Variable nur
linear darin vorkommt. Aus der Darstellung durch die Unter-
Unterdeterminanten B), C) lässt sich leicht schliessen, dass diese
Function unzerlegbar ist. Denn ist F der unzerlegbare
Factor von A, der die Variable af^ enthält, so muss dieser
Factor F wegen B) eine lineare homogene Function der Variablen
a(r\ <42) . . . ain) sein, und wegen C) eine lineare Function der
Variablen ctf\ 4° . . . a(>? (§. 20). Es enthält daher F alle
Variablen af und ist folglich mit A identisch. Wir sprechen
also noch den Satz aus:
X. Die Determinante ist eine unzerlegbare Function
ihrer »^-Elemente.
§. 26.
Die Unterdeterminanten im weiteren Sinne.
"Wir können nun die Betrachtungen des vorigen Paragraphen
in folgender Weise verallgemeinern.
Wie wir vorhin von der Aufgabe ausgegangen sind, alle
Glieder in der entwickelten Determinante A aufzusuchen, die
den Factor aW enthalten, so wollen wir jetzt alle die Glieder
aufsuchen, die den Factor
^ af . . . a«
enthalten, worin v eine beliebige Zahl unter « sein kann.
Diese Glieder erhalten wir aus dem Hauptgliede
.«?> <> . . . a« <*;& . . . <,("),
¦wenn wir bei der Permutation der unteren Indices 1, 2 ... v
ungeändert lassen und nur v -\- 1, . . . n auf alle Arten permu-
tiren unter Berücksichtigung der Vorzeichenregel.
Demnach ist der Inbegriff der gesuchten Glieder *
A) apafK. . a<;)
I. Die hier als Factor auftretende Determi-
Determinante von n — v Reihen, die wir mit A\\\\;;rv

92 Zweiter Abschnitt. §. 26.
bezeichnen, entsteht aus A durch Weglassen
der v ersten Zeilen und Colonnen.
Dieses Resultat wollen wir nun auf folgende Art verall-
verallgemeinern :
"Wir wählen irgend v Elemente
aus, jedoch so, dass nicht zwei Elemente in derselben Zeile oder
in derselben Colonne vorkommen, d. h. so, dass nicht zweimal
derselbe untere oder derselbe obere Index vorkommt, und be-
bezeichnen den Inbegriff der Glieder der Determinante, die das
Product dieser Elemente als Factor enthalten, mit
B) aW oW ... aC"> 4/»" fr •••/»».
Man kann durch Umstellen von Zeilen und Colonnen, wo-
wodurch höchstens das Zeichen der Determinante geändert wird,
immer erreichen, dass die Elemente
C) fljf, o(W . . . «(f) .
an die Stelle der Elemente
oW, af) . . . a«
gelangen; dann aber lässt sich die Regel I. auf die Bestimmung
von Aa*t„l'.'.'.ar anwenden und es ergiebt sich:
II. Man erhält (vom Vorzeichen abgesehen) -A«)', 4'.!!<*»
als (w — i/)-reihige Determinante, wenn man in
A alle Zeilen und Colonnen weglässt, die
sich in einem der Elemente C) schneiden, und
die übrig bleibenden Zeilen und Colonnen in
ihrer Reihenfolge stehen lässt.
Für die Zeichenbestimmung aber ergiebt sich folgende Vor-
Vorschrift.
Man ordne die unteren und die oberen Indices 1, 2 ...»
in der Weise:
D) «j, «2 . . . «„, ccv+1 . . . «„
E) ßt, ß2 ¦ ¦ ¦ ßv, ßv+\ • ¦ • ßm
indem man ccv+1 . . . ccn und ebenso ßv+t . . . ßn der Grosse
nach auf einander folgend annimmt.
III. Die in II. beschriebene (n — i/)-reihige Deter-
Determinante erhält das positive oder negative
Zeichen, je nachdem die beiden Anordnungen

§. 26. Unterdeterminanten ^ter Ordnung. 93
D) und E) der Ziffern 1, 2 ... n beide zu der-
derselben oder zu verschiedenen Arten gehören.
Denn die Determinante ändert ihr Zeichen durch jede Ver-
Vertauschung zweier unterer oder zweier oberer Irrdices. Um den
allgemeinen Fall B) auf den besonderen Fall A) zurückzuführen,
hat man so viele Transpositionen oberer und unterer Indices
vorzunehmen, dass die Permutationen D) und E) beide in die
ursprüngliche Anordnung 1, 2, 3 . . . n übergehen, und ebenso
viele Zeichenwechsel haben stattgefunden.
Die so definirten Grossen
(?!, |}s. . ./}„
-ä.alt a2...av
heissen die vten Unterdeterminanten oder Unter-
Unterdeterminanten t>ter Ordnung. Sie sind dargestellt durch
(n — v)- reibige Determinanten.
Aus III. folgt in Bezug auf diese Unterdeterminanten
der Satz:
IV. Die Unterdeterminante ÄJ^ul'.'.'. a, ändert nur
ihr Vorzeichen, wenn zwei ihrer unteren oder
zwei ihrer oberen Indices vertauscht werden,
oder allgemeiner: sie bleibt dem absoluten
Werthe nach ungeändert, wenn die Anord-
Anordnung der Indices %, «2 • • • ocv durch irgend eine
andere Anordnung ersetzt wird und ändert
das Zeichen oder nicht, je nachdem diese
Permutation zur zweiten oder zur ersten Art
gehört.
Bezeichnen wir aber mit u[, «2 . . • «', irgend eine Anord-
Anordnung der «!, «2 . . . ccv, so enthält die Determinante A auch den
Complex der Glieder
l ™a' a * " * av J^ali Ö2 • • • av'
und wenn wir also alle diese Glieder sammeln, so erhalten wir
den Complex:
Die.hier auftretende v-reihige Determinante

94
Zweiter Abschnitt.
§• 26.
„(fix) „(fiO M
„(fit) „(?*> Jh
wollen wir die zu -44,4'"«» complementäre Unterdeter-
Unterdeterminante nennen und mit B„l 4¦'¦'¦ '¦Z bezeichnen. Sie enthält
genau die Zeilen und Colonnen, die in .4«,*'«*"'.«* fehlen und
stimmt, abgesehen vom Vorzeichen, mit der Unterdeterminante
(n — v)ter Ordnung
aPv + i •¦ ¦ fin
überein.1 Der Complex der Glieder F) wird also bezeichnet mit
Wählen wir nun für ocj, a2 ...«»¦ jede Combination von v
der Ziffern 1, 2 . . . w, deren Anzahl (nach §. 7) B^ ist, so
erhalten wir, indem wir /515 /32 . . . ß„ festhalten, ebenso viele
Complexe der Form G), und jedes Glied der Determinante A
kömmt in einem und nur in einem dieser Complexe vor.
V. Demnach erhalten wir, wenn wir alle Ausdrücke
G) summiren, die Determinante A:
iq\ A £ Ah'fc---?v -oft. fit ••¦/»»
\y) ¦&¦ •^ ¦Ä«i, at...av -Dax, as... av
Selbstverständlich kann man auch die Combination der «
festhalten und in Bezug auf die ß summiren.
Dies ist der Satz von Laplace.
Als häufig vorkommender specieller Fall mag der erwähnt
werden, wo ß1, /32 . . . ßv = 1, 2 . . . v und wo aW = 0 ist,
wenn r einen der Werthe 1, 2 . . . v und gleichzeitig s einen
der Werthe v -\- 1, ... n hat. Dann werden alle A\'^ «2;;; lv =0»
mit Ausnahme von A\\ t'.'.'.l, und man erhält
A Jl, 2 .••» TDl, 2 ... v
¦**¦ -, 2 .. . v -Dl, % ... v
Der Satz wird durch folgendes Diagramm veranschaulicht,
in dem das ganze Quadrat die Determinante A vorstellt, und
wo in dem schraffirten Rechteck lauter Nullen stehen. Sind

§• 28.
Unterdeterminanten j'ter Ordnung.
95
dann B und C die in den beiden kleinen Quadraten stehenden
Determinanten von v und n — v Reihen, so ist
(9) A = B C.
Noch eine andere Darstellung der Determinante A durch
die ersten und zweiten Unterdeter-
Unterdeterminanten erhält man auf folgende
Weise.
Man wähle in A irgend zwei
Reihen aus, die sich in einem Ele-
Elemente, etwa in aW, schneiden. In jedem
Gliede von A kommt ein Element mit
dem unteren Index v und ein Element
mit dem oberen Index (i vor. Wir
haben also zunächst in A den Com-
plex ai^ AvU) und ferner die verschie-
verschiedenen Complexe afp a^ Ai^ worin i jeden von fi verschiedenen
und Tc jeden von v verschiedenen Index bedeuten kann.
VI. Wir können daher setzen:
B
C
oder nach IV.
Wir bemerken zu diesem Satze noch, dass A^,% die dem Ele-
Elemente «W entsprechende erste Unterdeterminante der
(w— 1)reihigen Determinante A^ ist; denn J.^ ist der Coefficient
von ai^ a-i? in der Entwickelung von A und A^ der Coefficient von
äf\ folglich A^]l der Coefficient von a® in der Determinante Af\
Man kann nach diesem Satze die sogenannte geränderte
Determinante
s«, a« . . . a«, «!
««, af
u.2
x, v2 . . . vn, q
nach den Elementen der letzten Zeile und Colonne entwickeln
und erhält
A2)
CT= 2J. —
v* Af

Zweiter Abschnitt.
'§. 27.
Man erhält diese Gleichung aus A0), wenn man n in n -\- 1
verwandelt, und die Elemente der letzten Zeile und Colonne
durch eine andere Bezeichnung auszeichnet.
Ersetzt man q durch q — u, worin u wieder eine beliebige
Grosse ist, so ergiebt sich die oft angewandte Formel:
A3)
[), af
"i '
. ,vn, q — u
= U— Au,
¦worin U die Bedeutung A2) hat.
Auch bei den höheren Unterdeterminanten ist bisweilen
die Bezeichnung durch Differentialquotienten zweckmässig, so
dass z. B.
A4)
gesetzt wird.
8 af d aW
§. 27-
Lineare homogene Gleichungen.
Die häuptsächlichste Anwendung der Determinanten, der
die ganze Theorie ihren Ursprung verdankt, ist die Auflösung
linearer Gleichungen.
Wir wollen hier die Aufgabe gleich in allgemeinster Weise
in Angriff nehmen, da die specielle Form kaum eine Verein-
Vereinfachung ist und sich nachher leicht aus dem allgemeinen Resul-
Resultate ableiten lässt.
Wir betrachten ein System von m Gleichungen ersten Grades,
in denen n Unbekannte x^ x2 . . . x„ homogen vorkommen:
af)
af x
\-
xn = 0
-\ \-
= 0,
¦worin die Coefficienten af> als gegebene Grossen betrachtet
¦werden. Ueber die Zahlen m, n wollen wir vorläufig noch gar
keine Voraussetzung machen, sondern uns allgemein die Aufgabe

§..27. Lineare homogene Gleichungen. 97
stellen, alle Werthsysteme der Xj_, x2 . . . xn zu ermitteln, die
den Gleichungen A) genügen.
Eine Lösung der Gleichungen A) können wir sofort angeben:
sie sind nämlich, was auch die Coefficienten af?) sein mögen,
erfüllt, wenn
B) ajj = 0, #2 = 0, ... xn = 0.
Einen anderen extremen Fall können wir noch erwähnen;
wenn nämlich die Coefficienten af> sämmtlich den Werth Null
haben, dann sind die Gleichungen A) für beliebige Werthe
von xv x2 . . . xn befriedigt.
Der allgemeinen Beantwortung der Frage schicken wir fol-
folgende Bemerkungen voraus.
Wir schreiben das System der Coefficienten von A) in Form
eines Rechtecks
Ein solches Schema, das für sich noch keine numerische
Bedeutung hat, heisst eine Matrix, insofern es als Quelle einer
grösseren Anzahl von Determinanten betrachtet wird.
Die der Matrix entstammenden Determinanten er-
erhält man, wenn man beliebige Zeilen und Colonnen weg-
lässt, in beliebiger, nur insoweit bestimmter Anzahl,
dass die übrig bleibenden Elemente ein Quadrat bilden,'
lind dieses Quadrat als Determinante auffasst. , ¦ :¦,
So erhält man aus der Matrix einreihige, zweireihige ü. s. f.
Determinanten. Die höchsten Determinanten sind n- oder
m-reihig, je nachdem n oder m die kleinere Zahl ist (oder w-reihig,
wenn n = m ist). , ;
Wir machen nun die Annahme, dass unter den v-reihigen
Determinanten der Matrix wenigstens eine von Null "ver-
"verschieden sei, während die (v -f- 1) reihigen und folglich auch
die höheren Determinanten, falls solche vorhanden sind, alle
verschwinden sollen, v kann jede Zahl sein, die nicht grösser
als die kleinere der beiden Zahlen ri oder^ n( ist (oder. falls
n = m ist, diesen gemeinschaftlichen Wertlv nicht iiberfeifft).
Eine solche Zahl -v wird sich immer- finden lassen, wenn wir
Weber, Algebra. I. 7

98
Zweiter Abschnitt.
§•27.
den schon erledigten, ganz interesselosen Fall ausschliessen, dass
alle Coefficienten af> verschwinden.
Wir können, ohne die Allgemeinheit zu beschränken, zur
Vereinfachung der Bezeichnung annehmen, die nicht verschwin-
verschwindende v-reihige Determinante sei
D)
A ==
a[%
Denn offenbar steht es uns frei, das Gleichungssystem A) in
beliebiger Weise anzuordnen, und ferner können wir die Bezeich-
Bezeichnung der Unbekannten x so wählen, dass irgend v von ihnen
die v ersten sind.
Die Unterdeterminanten von A bezeichnen wir wie früher
mit Af>, worin i, h von 1 bis v gehen.
Wenn nun zunächst v = n ist, was voraussetzt, dass m
nicht kleiner als n ist, so haben die Gleichungen A) keine
andere Lösung, als die in den Gleichungen B) enthaltene.
Denn greifen wir die n ersten der Gleichungen A) heraus:
9. 2 I « tt
Of) X1
x2
o«> xn == 0
«! +
^ «« = 0,
multipliciren diese der Reihe nach mit J.^, J.'? . . . Aft\ worin
ft jeder der Indices 1, 2 . . . n sein kann, und addiren sie, so
folgt, weil nach §. 25 B) und F)
f af = 0 oder = A
ist, je nachdem X von (i verschieden ist oder nicht,
AXa = 0,
und da nach unserer Voraussetzung A von Null verschieden ist,
Xf, = 0.
Damit ist bewiesen:
I. Wenn ein System von m linearen homogenen
Gleichungen mit n Unbekannten eine Lösung hat,
bei der nicht alle Unbekannte verschwinden, so

§. 27. Lineare homogene Gleichungen. 99
müssen, wenn m f> n ist, sämmtliche w-reihige
Unterdeterminanten der Matrix der Coefficienten,
C), verschwinden.
Wir heben den am meisten angewendeten besonderen Fall
m = n hervor und geben dem Satze für diesen Fall den folgen-
folgenden Ausdruck:
II. Wenn ein System von n linearen homogenen
Gleichungen mit n Unbekannten eine von Null
verschiedene Determinante hat, so haben sämmt-
sämmtliche Unbekannte den Werth Null, oder:
Wenn ein System von n linearen Gleichungen
mit ebenso vielen homogen vorkommenden Un-
Unbekannten eine Lösung hat, bei der nicht alle
Unbekannten verschwinden, so verschwindet die
Determinante des Systems.
Unter der Determinante eines Systems von n linearen
homogenen Gleichungen mit n Unbekannten ist hier die
Determinante aus den »2 Coefficienten dieser Gleichungen ver-
verstanden.
Wir betrachten ferner den Fall, dass v kleiner als n ist.
Da m gleich oder grösser als v sein muss, so wählen wir die v
ersten Gleichungen des Systems A), und schreiben sie so:
F) 1 l ' 2 2 ~ ~ * " + 1 +
Wir bezeichnen wieder mit (i einen der Indices 1, 2 . . . v,
multipliciren die Gleichungen F) der Reihe nach mit A$\
Af . . . A^ und addiren sie. Daraus folgt, wie vorhin, mit
Benutzung von §. 25, B), F):
G) Axfl — — Cv+^pXr + i — ... — Cn^x„,
wenn zur Abkürzung gesetzt ist:
(8) &,r — h af Af, l = v + 1, v + 2, . . . n.
Nach §. 25, B) ist Gitfi die Determinante, die aus der durch
D) definirten Determinante dadurch hervorgeht, dass man die
7*

100
Zweiter Abschnitt.
§• 27.
Elemente der fiten Colonne a«, af> ... a« durch af, af ... a^
ersetzt.
Durch G) sind nun, da A von Null verschieden ist, die
Xi, x2 . . . xv linear ausgedrückt durch xv + 1, . . . xn und durch
die bekannten Grossen.
Es ist nun noch zu zeigen, dass durch die Ausdrücke G)
die Gleichungen A) befriedigt sind, welche Werthe auch
Xv + i, ... xn haben mögen, dass also n — v von den Unbe-
. kannten willkürlich bleiben, von denen die übrigen v nach G)
abhängig sind.
Um die Wahrheit dieses Satzes einzusehen, haben wir nur
die Ausdrücke G) in die Gleichungen A) einzusetzen. Man ver-
vereinfacht die Rechnung sehr durch Anwendung eines Summen-
Summenzeichens 2, bei dem wir, wie schon oben, die Summationsbuch-
staben oben, die Grenzen unten anhängen. Zunächst können wir
dann..die Gleichungen G) so schreiben:
(9) Ax„ = — 2 2 af Af xh, (i = 1, 2 . . . v.
Wir multipliciren, wenn 1c irgend eine der Ziffern 1, 2
bedeutet, mit a® und summiren in Bezug auf (t:
10) A2a^x„ = —Zxh i? i a^ a\f Af, ft = 1, 2 .
1, v v + i,n 1, y l, v
Dazu addiren wir beiderseits die Summe *
m
m.
AZ
xh
und erhalten
A1)
AZaf x^
1,» v
af
1,» -1,»
/
Der Factor von xh in der Summe auf der rechten Seite ist
, nach §. 26, A2). die Determinante
A2)
aP-\ aW
af,
a<?\
af>,
und, verschwindet daher, wenn Je <,v ist, nach .§. 24, V., weil
zwei Zeilen übereinstimmen, wenn aber 1c >. v ist, nach der

§. 27. Lineare homogene Gleichungen. 101
Voraussetzung, weil dann A2) eine v -j- 1 reihige Determinante
der Matrix C) ist. Wir bekommen also aus A1), da A von
Null verschieden ist,
A3) iafxf, = 0, Tc=l,2...m,
i,»
d. h. das System der Gleichungen A) ist durch G) befriedigt.
Damit ist bewiesen:
III. Wenn in einem System von m linearen homogenen
Gleichungen mit n Unbekannten alle v -\- 1 reihi-
reihigen Unterdeterminanten der Matrix der Coeffi-
cienten verschwinden, so hat das System eine
Lösung, in der mindestens n — v von der Unbe-
Unbekannten willkürlich bleiben. Ist »i < «, so giebt
es immer eine Lösung, in der mindestens n — m
der Unbekannten willkürlich bleiben;
und hiervon ist ein häufig vorkommender specieller Fall:
IV. Wenn die Determinante eines Systems von n line-
linearen homogenen Gleichungen mit ebenso viel
Unbekannten verschwindet, so können die
Gleichungen so befriedigt werden, dass nicht
alle Unbekannte verschwinden.
Wir wollen von dem so bewiesenen Satze noch den anderen
Fall hervorheben, dass m = n — 1 und v = n — 1 ist. In
diesem Falle bleibt nur eine der Unbekannten beliebig und die
Verhältnisse der Unbekannten sind völlig bestimmt. Wir
können diesem Resultate folgenden Ausdruck geben:
Bezeichnen wir die (n—1) reihigen Determinanten der Matrix
mit abwechselndem Vorzeichen genommen durch
A.I, Ajj . , . A„
und nehmen an, dass wenigstens eine von diesen Grossen von
Null verschieden sei, so ist die Lösung des Systems:

102 Zweiter Abschnitt §. 28.
\- aVxn = 0
A5)
a[»-1>xl -f af-Vx* -\ 1- a%-»xn — 0
gegeben durch die Verhältnisse
A6) xx : x% : ¦ • • : xn = AY : Ä-2 : • ¦ ¦ : An.
So erhalten wir für n ^ 3 die Lösung des in der Geometrie oft
vorkommenden Gleichungssystems
(. , ax' -\- by -(- C0 = 0
*• ; a'x+b'y-\-e!e = 0
in der Form
A8) x : y : s = bc' — cb' : cd — ad : ab' — ba'.
§• 28.
Elimination aus linearen Gleichungen.
Es kommt bisweilen vor, dass es sich bei einem gegebenen
System linearer Gleichungen nicht sowohl um die wirkliche Er-
Ermittelung der Unbekannten handelt, als um die Beurtheilung der
Möglichkeit ihrer Lösung, also um die Aufstellung der Bedingungs-
Bedingungsgleichungen, die zwischen den Coefficienten bestehen müssen,
wenn Lösungen oder Lösungen von bestimmter Art überhaupt
vorhanden sein sollen. Die Aufstellung dieser Bedingungs-
Bedingungsgleichungen heisst Elimination. Implicite ist die Lösung
dieser Aufgabe schon im Vorhergehenden enthalten; wir wollen
aber noch ausdrücklich auf einigel hierher gehörige Fragen
zurückkommen.
Wir betrachten, wie im vorigen Paragraphen, ein System
von m linearen Gleichungen mit n homogen vorkommenden
Unbekannten, und fragen: wann hat dies System eine Lösung,
bei der nicht alle Unbekannten verschwinden? Wir haben schon
gesehen, dass dies immer der Fall ist, wenn n >> m ist.
Ist aber n 5 w*, so ist die nothwendige und hin-
hinreichende Bedingung für eine solche Lösung die, dass alle
w-reihigen Determinanten der Matrix verschwinden. Denn wenn
eine von diesen nicht verschwindet, so sind nach §. 27, II. die
Werthe der Unbekannten nothwendig Null, während, wenn sie

§. 28. Elimination. 103
alle verschwinden, eine Zahl v <^ n gefunden werden kann, so
dass alle (y -j-1) reihigen Determinanten der Matrix Null sind,
während von den v-reihigen wenigstens eine nicht verschwindet,
so dass also nach §. 27, III eine Lösung von der verlangten Art
vorhanden ist.
Die Anzahl der aus einer Matrix von m Zeilen und n Colon-
nen zu bildenden n-reihigen Determinanten ist, wenn n üg m ist)
gleich der Anzahl der Combinationen von in Elementen zur
wten Classe ohne Wiederholung, also (nach §. 7) gleich:
m (m—1) . . . (in — w-f- 1)
r72...n '
und so gross wäre also die Anzahl der Bedingungen. Ist n = m,
so ist diese Zahl = 1 und wir erhalten den Fall §. 27, II. und
wie zu erwarten war, eine Bedingung. Im Allgemeinen ist aber
diese Anzahl der Bedingungen, obwohl sie alle erfüllt sein
müssen, grösser als nöthig ist, weil einige von ihnen nothwendige
Folgen der übrigen sind.
Um ein System von notwendigen, hinreichenden und von
einander unabhängigen Bedingungen zu erhalten, fassen wir die
Fragestellung etwas präciser und fragen nach den Bedingungen:
dass aus einem System von m linearen, homogenen
Gleichungen mit n Unbekannten v von den Un-
Unbekannten durch n — v willkürlich bleibende
vollkommen bestimmt werden können.
Auch diese Frage ist in §. 27 eigentlich schon beantwortet.
Es muss unter den v-reihigen Determinanten eine von Null ver-
verschieden sein, während die (y -\- l)reihigen alle verschwinden.
Es genügt aber schon, wenn es von einer kleineren Anzahl der
(v -j- 1)reihigen Determinanten feststeht, dass sie verschwinden.
Nehmen wir an, die Unbekannten #» + 1, xv+z • • ¦ %n sollen
willkürlich bleiben, xx, x2 . . . xr durch sie bestimmt sein, und
nehmen die Determinante:
Ä=
a«
als von Null verschieden an.

104
Zweiter Abschnitt.
§•28.
'¦ Wir berechnen'die" Unbekannten xly x2 . . .- xv nach §. 27, (9)
und bilden die Summen §.27 A1), deren Verschwinden besagt,
dass das gegebene Gleichlingssystem wirklich befriedigt ist. Die
Bedingungen werden also: " .
B)
a<2>, af . . . af>, af
af, a«
oder anders geschrieben:
C)
o«), af
= 0,
und diese Bedingungen genügen auch. Die Gleichung B) oder
C) ist aber identisch befriedigt, wenn h = 1, 2 . . . v oder
Ja = 1, 2 ... v ist, und giebt also für diese Werthe keine
Bedingung für die Coefficienten. Solche Bedingungen ergeben
sich nur für
. h = v -\- 1, v -f 2 . . . n -
w ¦ k = v + 1, v -f 2 . . . m,
also
E) (» - v) (m - v\
der Zahl nach.
Diese Bedingungen sind aber wirklich von einander unab-
unabhängig , d. h. es folgt keine aus den übrigen; denn die linken
Seiten von C) können durch geeignete Annahmen über die Coef-
Coefficienten a für jede Indexcombination aus der Reihe D) einen
ganz beliebigen Werth erhalten, wie man erkennt, wenn man
sämmtliche a®, a® mit Ausnahme von affi gleich Null setzt.
'§. 29. * ¦
Unhomogene lineare Gleichungen.
Wir haben die Aufgabe, der. Auflösung linearer Gleichungen
in den bisherigen Betrachtungen dadurch nicht unwesentlich
vereinfacht und auf allgemeinere Gesetze zurückgeführt, dass
wir die Gleichungen in Bezug auf die Unbekannten homogen

§. 29. Unhomogene Gleichungen. 105
vorausgesetzt haben. In den Anwendungen kommen aber häufig
die Unbekannten nicht homogen vor, und wenn auch principiell
der eine Fall von dem anderen nicht wesentlich verschieden ist,
so wollen wir doch den Fall der nicht homogenen Gleichungen
noch besonders betrachten. Wir können ihn aus dem Fall der
homogenen Gleichungen dadurch ableiten, dass wir die Forderung
hinzufügen, eine bestimmte der Unbekannten soll den Werth 1
haben. Wenn diese Unbekannte unter denen vorkommt, die das
Problem willkürlich lässt, so entspringt daraus gar keine
Schwierigkeit, weil wir sie ja nur = 1 zu setzen brauchen.
Gehört sie aber zu denen, die durch die übrigen bestimmt sind,
so müssen noch gewisse Bedingungen erfüllt sein, die besagen,
dass der Werth 1 für diese Unbekannte zulässig ist.
Wir wollen hier die Frage selbständig und in etwas geän-
geänderter Bezeichnung behandeln, beschränken uns aber der Ein-
Einfachheit halber auf den wichtigsten Fall, wo die Anzahl der
Unbekannten mit der Anzahl der Gleichungen übereinstimmt.
Es sei folgendes System von Gleichungen in Bezug auf die
Unbekannten %, x2 . . . x„ aufzulösen:
aVx1 + afx, -| \- aUxn = y,
(]} o« xx + afx% H h «i2) *• = 2/2
a^x1 + af>x.2 -\ 1- a™xn = yn,
worin dieCoefficientenaf-V und die unabhängigen Glieder yv y^...yn
als gegeben betrachtet werden. Wir bezeichnen mit
B) Ä = 2± af> af . . . «w
die Determinante des Systems und wie früher mit Af^ die
ersten Unterdeterminanten von A. Ist h einer der Indices
1, 2 ...» und multipliciren wir die Gleichungen A) der Reihe
nach mit A*\ A® ... A^ und addiren sie dann, so erhalten wir
C) xx i? af Af + x2 h 4> A$-\ h xn h a® Af = Syt Af.
Nach §. 25, B) und F) verschwinden hier die Coefficienten
der a?j, x2 . . . xn mit Ausnahme des einen Coefficienten von ajÄ,
der den Werth A erhält, und sonach ergiebt sich:
D) Axlc = ZtjiAg,
und für den Fall, dass A von Null verschieden ist,
können hieraus die Werthe der Unbekannten eindeutig

106
Zweiter Abschnitt.
§.29.
so berechnet werden, dass dadurch die Gleichungen A)
wirklich befriedigt sind [§. 25, C), G)].
Setzen wir A® = A cc®, so können wir die Lösung in der
Form schreiben:
Xl = af>yx + «W yt ^ [~ «^V»
deren Analogie^mit dem System A) in die Augen fällt.
Wenn aber A = 0 ist, so lehren die Gleichungen D) nichts
über die Werthe der x, sondern sie geben nur ein System von
Bedingungen an, denen die y sicher genügen müssen, wenn die
Gleichungen A) überhaupt lösbar sein sollen. Um zu einem
allgemein gültigen Resultat zu kommen, verfahren wir ganz
ähnlich wie bei den homogenen Gleichungen. Wir nehmen an,
dass ausser der Determinante A auch noch alle Unterdeter-
Unterdeterminanten bis zu einer gewissen Ordnung Null sind. Wir be-
bezeichnen eine nicht verschwindende v-reihige Unterdeterminante mit
F)
B =
o«, o
o«
o«, a« . . . o«
ihre Unterdeterminanten mit B£\ worin h, h nur die Werthe
von 1 bis v durchlaufen, und setzen nun voraus, alle (y -)- 1)-
reihigen Unterdeterminanten von A verschwinden.
Wenn wir die ersten v Gleichungen des Systems A) mit
B%\ B$ ...Bf? multipliciren und addiren, so folgt [§.25, B), F)]:
G)
Bxk =
'/t y% — z, xs z, Hit a-k ,
»¦ + 1,1- l,r
Hierdurch sind v der Unbekannten x durch die übrigen
bestimmt, und wir setzen, um zu sehen, inwieweit hierdurch die
Gleichungen A) befriedigt sind, die Ausdrücke in A) ein. Wir
multipliciren hierzu G) mit a<*), wo A die Werthe 1, 2 ...»
durchläuft, und summiren in Bezug auf fc. So folgt:
(8) B X afxu = 2 Bfa^
— z, xs
* + !,» 1,»
a
(?) „$¦)

§. 29. Unhomogene Gleichungen. 107
und wenn wir beiderseits
B h afook
v + l,n
addiren:
(9) B 2 aPxt = 2 Bf a$ yt + 2 xs (b af - 2 Bf af
l,n 1,* » + 1,» \ 1>*
Nun ist nach §. 26, A2) der Coefficient von xs auf der
rechten Seite eine (v -f- 1) reihige Unterdeterminante von A und
also nach der Voraussetzung gleich Null. Nach A) soll
2 agix* = yi
sein, und folglich genügen die Ausdrücke G) dann und nur
dann den Gleichungen A), wenn
A0) Byx = %$Bfog>yt
l,v
ist. Diese Gleichung ist, wenn X 5 v ist, wegen §. 25, B), F)
immer befriedigt. Ist aber l = v -\- 1, v -f- 2 . . . n, so sind
n — v Bedingungen für die y in A0) enthalten, die, da jede
Bedingung eine neue der Grossen y enthält, von einander unab-
unabhängig sind. Ist eine dieser Bedingungen nicht erfüllt,
so hat das gegebene Gleichungssystem keine Lösung.
Wenn wir in dem Gleichungssystem A) die x nicht als
Unbekannte, sondern als Veränderliche betrachten, so werden
auch die y veränderliche Grossen sein. Bei dieser Auffassung
nennen wir das System A) eine lineare Substitution, inso-
insofern dadurch der Uebergang von einem System von Variablen,
zum anderen vermittelt wird. Nur wenn die Determinante A,
die wir jetzt die Substitutions-Determinante nennen, von
Null verschieden ist, werden die y als unabhängige Variable an-
angesehen werden können. Ist dies der Fall, so ergiebt das System
E) die Darstellung der Variablen x durch die y oder die zu A)
inverse Substitution.
Das bisher Bewiesene wollen wir schliesslich noch in einen
allgemeinen Satz zusammenfassen.
Ein System von m linearen Functionen j^, y2 . . . ym der
n-Veränderlichen x1: x2 . . . xn, das durch die Ausdrücke:
A1) yi = af>x1Jra^x2^-a^xn, i = 1, 2 . . . m
bestimmt ist, heisst linear unabhängig, wenn eine Gleichung

108 Zweiter Abschnitt. §. 30.
A2) hyi + hy-2-] \-i»y* = o
mit constanten Coefficienten Xu A2 . . . lm identisch (d. h. für alle
xx . . . x„) nur dann bestehen kann, wenn die l alle verschwinden.
Im entgegengesetzten Fall heisst das System yt linear ab-
abhängig. Dann gilt der Satz:
V. Wenn die Functionen ylt y2 . . . ym linear unab-
unabhängig sind, so lassen sich die %, x% . . . xn
immer so bestimmen, dass die t^, y% . . . ym beliebig
gegebene Werthe erhalten.
Die Richtigkeit dieses Satzes ergiebt sich aus der Erwägung,
dass nach §. 27, I und III die y< nur dann, und immer dann
linear unabhängig sind, wenn m < n ist, und wenn aus der
Matrix der Coefficienten a® wenigstens eine nicht verschwindende
»w-reihige Determinante gebildet werden kann.
§. 30.
Multiplication von Determinanten.
Der Satz, den wir jetzt noch beweisen wollen, lehrt, wie
man das Product zweier Determinanten von gleich viel Reihen
durch eine einzige Determinante von ebenso viel Reihen dar.
stellen kann. Man wird am einfachsten darauf geführt, wenn
man die Auflösung von zwei Systemen linearer Gleichungen
betrachtet.
Es seien jetzt die Coefficienten af\ bf\ wenn i, h die Reihe
der Zahlen 1, 2 ... n durchlaufen, beliebige veränderliche
Grossen, ebenso die Grossen a?,-, yi, £», die nur an die Relationen
gebunden sind:
A) S afxi = yk,
B) . Zlfyie = zh:
Wenn nun die Aufgabe gestellt wird, die "Variablen x durch
die Variablen z zu bestimmen, so kann diese Aufgabe auf dop-
doppelte, Art gelöst werden. Man kann nach §. 29, D) die
Gleichungen A) in Bezug auf x, die Gleichungen B) in Bezug
auf y auflösen, und die letzteren Ausdrücke in die ersteren ein-
einsetzen. Bezeichnen wir mit A, _B die Determinanten der beiden
Gleichungssysteme, also:

§.30.
Multiplioation von Determinanten.
109
A =
af\ af . . . oW
»(> a<
6«, &« .
b<*>, bf .
bf
und mit Af\ Bf* die ersten Unterdeterminanten, so erhält man
C) Axt =
D) Byt =
und durch Substitution von D) in C):
Man kann aber auch so verfahren, dass man aus A) die
Ausdrücke für y in B) einsetzt, wodurch man, wenn
F)
gesetzt wird, erhält:
0)
Wenn man nun
(8)
C =
cf\
setzt, und mit C^ die Unterdeterminanten von C bezeichnet, so
ergiebt die Auflösung von G):
(9) C& =Seh Cih\
und die Vergleichung von E) mit (9) ergiebt
A0) AB == G,
und für die Unterdeterminanten
A1) CP = ZAfBi\
In dieser Schlussweise ist aber noch eine Lücke, bedingt
durch den Zweifel ob sich E) von (9) nicht durch einen beiden
Seiten gemeinschaftlichen Factor unterscheiden könnte. Diesen
Zweifel kann man durch eine sehr einfache Ueberlegung begegnen,
die sich auf die Unzerlegbarkeit der Determinante (§. 25, X) und
auf die Betrachtungen des §. 20 stützt. Es ergiebt sich nämlich

110 Zweiter Abschnitt. §. 30.
zunächst durch die Vergleichung von E) und (9), wenn alle
aÄ*' ^ ^ a^s unabhängige Variable betrachtet werden:
CZzh hÄf Bf = ABZzh Cf\
und daraus
Nach §. 20 muss der unzerlegbare Factor A in einem der
Factoren der linken Seite aufgehen, und da die A^ von nie-
niedrigerem Grade sind als A, so kann dies nur C sein. Aus dem
gleichen Grunde muss B in G aufgehen und die Vergleichung
der Grade und des ersten Gliedes giebt G = AB.
Man kann aber auch auf einem mehr rechnenden Wege zum
Ziele gelangen.
Wir wollen das Hauptglied der Determinante G nach F)
bilden, indem wir mit sl5 s2 . . . s„ von einander unabhängige
Summationsbuchstaben bezeichnen, die von 1 bis n laufen:
• . • Cn
«1,
Die Pennutation der unteren Indices der c entspricht der
Permutation der unteren Indices der a, und wenn man also mit
Rücksicht auf die Vorzeichenregel die Determinante G bildet, so
erhält man
A3) S-_
. . Vn £i 2C $1 •M'2 • • • "w
Nun ist
y? -\- n(s0 n,C3) n} n)
— 12 n
nach §. 24, VI. immer dann gleich Null, wenn unter den sx, s.2...s„
zweimal dieselbe Ziffer vorkommt; es behalten also nur die
Glieder in A3) einen von Null verschiedenen Werth, in denen
Sj, s2 . ... sn eine Anordnung der Indices 1, 2 . . . n ist, und
zwar ist dieser Werth -\-A oder —A, je nachdem diese Anord-
Anordnung zur ersten oder zur zweiten Art gehört (§. 24, IV).
Demnach wird die rechte,Seite von A3):
A s i x öi' »2 . . . on ,

§. 30. Multiplioation von Determinanten. 111
die Summe erstreckt über alle Permutationen sl7 s2 . . . sn. Diese
Summe ist aber gerade die Determinante B und daher die
Formel
C = AB
bewiesen.
Das in der Formel F) enthaltene Bildungsgesetz der Ele-
Elemente cf> können wir in Worten so ausdrücken:
Um die Elemente der Determinante G, die das
Product der beiden Determinanten A, B ist, zu
erhalten, multiplicirt man die Elemente je einer
Colonne von^. mit den entsprechenden Elementen
einer Colonne von B und addirt die Producte.
Nach den Sätzen über die Determinanten kann man die
Form von G in mannigfacher Weise abändern. Wir wollen
darüber Folgendes bemerken.
Wenn man zwei Colounen in A oder in B vertauscht, so
andern sich die Elemente cf> nicht, sondern vertauschen sich
nur unter einander.
Wenn man aber zwei Zeilen in A oder in B vertauscht, so
ändern sich die c^, indem die Factoren in den einzelnen Pro-
ducten der Summe anders zusammengefasst werden; wenn man
aber entsprechende Vertauschungen in den Zeilen von A und
von B gleichzeitig vornimmt, so bleiben die cf> ungeändert,
weil dadurch nur die einzelnen Glieder der Summe vertauscht
werden.
Indem man in A oder in B oder in beiden zugleich die
Zeilen zu Colonnen macht, erhält man noch drei verschiedene
Arten für die Bildung des Products zweier Determinanten in
Determinantenform. Letzteres kann man auch so ausdrücken:
Um das Product zweier Determinanten zu bilden,
kann man die Elemente der einzelnen Zeilen
oder Colonnen des einen Factors mit den ent-
entsprechenden Elementen der Zeilen oder der Co-
Colonnen des anderen Factors multipliciren und die
Producte addiren, und diese Productsummen als
Elemente einer neuen Determinante auffassen.
Auf ein Product zweier Determinanten mit verschiedener
Elementenzahl lässt sich die Multiplicationsregel dadurch an-

112 . Zweiter Abschnitt. §. 30,
wenden, dass man die Determinante mit geringerer Reihenzahl
durch den Satz §. 25, IX. in eine andere mit mehr Reihen ver-
verwandelt.
Das Multiplicationstheorem gestattet noch eine Verall-
Verallgemeinerung, die sich mit denselben Mitteln ableiten lässt.
Wir erweitern die Formel F) dahin, dass wir setzen
A4) cf> = 2 aP 6?\
l,m
worin wir aber jetzt die Anzahl m der Summanden auf der
rechten Seite grösser als n annehmen wollen, während i und h
nach wie vor von 1 bis n laufen sollen.
Wir bilden nun das Product wie in A2), und bilden die
Determinante A3) ganz wie oben, nur mit dem Unterschiede,
dass die Summationsbuchstaben s17 s2 . . . s„ jetzt von 1 bis m
laufen.
Wählen wir unter den Ziffern 1, 2 ...» irgend eine Com-
bination von n verschiedenen Ziffern «j, k2 . . . «„aus, so enthält
die jetzt erweiterte Summe A3) alle Producte von der Form
s ± <&° <&>... ay, s ± bp> if*... *4H
aber keine anderen Glieder, und die Determinante der 4A) ist
also gleich der Summe aller dieser Producte. Wir haben also
den folgenden Satz:
Wenn die Elemente der Determinante
fi -y I .0) .,B) J")
die Form A4) haben, worin m >> n ist, so wähle man
unter den Ziffern 1,2 . . . m auf alle möglichen Arten
n verschiedene aus, die in einer beliebigen, aber festen
Reihenfolge mit %, cc2 . . . <x„ bezeichnet werden. Ist
dann
jLa — ¦" it «i «2 . . ¦ a„
A5)
Ba = s± if° if*... i{:«),
so ist
A6) C=2AaBa,
wenn sich die Summe auf alle möglichen Combinationen
der k erstreckt.
Die Anzahl der Glieder dieser Summe ist gleich der Anzahl

§.31.
Determinanten der Unterdeterminanten.
113
der Combinationen ohne Wiederholung von m Elementen zur
»ten Classe, also (§. 7):
m (m — 1) (m — 2) . . . (m — n -j- 1)
1 . 2 . 3 . . . n
§• 31.
Determinanten der Unterdeterminanten.
Wir machen hier gleich eine Anwendung von dem Multi-
plicationsgesetz der Determinanten.
Es sei wie bisher:
A)
und
B)
A =
%f\ af . . . al
ß)
Af\ Af . . .
. A
(n)
A(n) A'.n)
das System der Unterdeterminanten. Bilden wir aus B) die
Determinante, die wir mit A bezeichnen wollen, so können wir
auf das Product AA die Multiplicationsregel anwenden. Dies
giebt aber nach §. 25, C) und G):
J, 0 ... 0
0, A ... 0
A/l =
= An,
0, 0 ... A
und daraus durch Division mit A:
C) A == An~\
Es ist also A die (n — l)te Potenz von A. Bei dieser
Ableitung ist allerdings zunächst vorausgesetzt, dass A von Null
verschieden sei. Da aber C) in Bezug auf die Elemente af*
eine Identität ist, d. h. auch dann gilt, wenn diese Grossen
unabhängige Variable sind, so folgt, dass auch noch in diesem
Ausnahmefall die Formel C) gilt, d. h. dass,- wenn A ver-
verschwindet, auch A verschwindet.
Weber Algebra. I.
8

114
Zweiter Abschnitt.
§.31.
Dies Ergebniss ist ein specieller Fall eines 'allgemeineren-
Satzes, nach dem jede beliebige Determinante der Matrix B)
gebildet werden kann. Betrachten wir die D-reihige Unterdeter-
Unterdeterminante
D)
w
A™,
aus der man durch Permutation der oberen und unteren Indices
alle anderen v-reihigen Unterdeterminanten ableiten kann, so
kann man die Multiplicationsregel anwenden, indem man dy
nach der Bemerkung des letzten Paragraphen in eine w-reihige
Determinante verwandelt:
E)
-eil i -"-2 • • • -a-y , Ji-v + i • . . -n-n
0, 0
0, 1
0
0, 0 ... 0, 0 ... 1
wobei n — v Zeilen und Colonnen beigefügt sind, von denen die
ersteren ausser in den Diagonalgliedern lauter Nullen haben.
Bildet man jetzt das Product Adv, so folgt
F) AA =
A,
o,
o,
o,
0
0
0
0
und dies ist nach dem
... 0,a
. . . A, a,
... 0, a!
... 0, a[
Satz IX.,
a(«)
%u...
r+l1). • •
§. 25
. . c&+1
a
i)
n
«S?
at
)
3
Dividirt man hier durch A und wendet die Bezeichnung des
§. 26 an, so folgt
G) j* = A'^Aft::::.

§¦ 32.
Determinantensatz von Sylvester.
115
Für v = 2 ergiebt sich das specielle Resultat
(8)
Die Formel (8) werden wir später öfter benutzen. In der
Bezeichnung durch die Differentialquotienten lässt sie sich so
darstellen
_ dA dA dA dA
p 8 af ~ 8 a<-p 8 af 8 af 8 a<£)'
Besonders wichtig ist sie in dem Falle, wo A eine sym-
symmetrische Determinante ist, wo also af> = aj>) ist; dann
ist auch
ZA _ dA
worin bei der Differentiation nicht Rücksicht genommen ist auf
die Abhängigkeit af> = ag>; dann wird die Formel (9)
dA /8iV
)
A0)
A
?) 8 af> ~~ 8 a« 8 af \d af>)
§. 32.
Determinantensatz von Sylvester.
Die zuletzt erhaltenen Resultate lassen sich noch in einer
anderen Weise verallgemeinern nach einem Satze von Sylvester,
den wir hier noch nach dem Vorgange von Frobenius beweisen
wollen.
Es sei
A) A = 2±cPctf>...c&y
eine Determinante, r irgend eine Zahl < n und
B) Ar=Z±aWafK..arr)
von Null verschieden. Mit A^ bezeichnen wir jetzt die Unter-
Unterdeterminanten von Ar (nicht von A), und bilden das Product
der beiden Determinanten

116
Zweiter Abschnitt.
§.32.
dessen Werth, was auch die T sein mögen, nach §.31 C) und
§. 25, IX. den Werth
D) AAnr~x
hat. Bestimmen wir die Y und eine weitere Reihe von Grossen
B^ aus den Gleichungen
-.. + a? Ff + af^Ar = 0
aV Yf + «?> 4- = 0
et, = r -\- 1^. . .. n
so folgt durch Elimination von Yf . . . Y(p nach §. 29, II. und
§• 36, A3)
F)
a(*> . . . o« af
a« . . . a«, af
a^ . . . a(r\ affl
et ct. ' it.
und die Multiplication der beiden Determinanten C) ergiebt
Ar, , 0, 0, , 0
, . . ., il-fj-i, JJr+i , . . ., -D^4
worin die X gewisse r-reihige Determinanten sind, auf deren
Kenntniss es nicht ankommt Der Werth dieser Determinante
ist aber nach §. 25, IX.
und hieraus und aus D) ergiebt sich die Relation von Syl-
Sylvester:
G) 2 ± B?+P . . . B£° = Anr-r~x A,
wo die Bf die Bedeutung F) haben, und die für r = n — 2
in die Relation §. 31, (9) übergeht1).
x) Sylvester, Philosophical Magazine 1851. Frobenius, Crelle's
Journal, Bd. 86, S. 53. Sitzungsberichte d. Berliner Akademie 1894, XII, XXIII.

Dritter Abschnitt.
Die Wurzeln algebraischer Gleichungen.
§. 33.
Begriff der Wurzeln. Mehrfache Wurzeln.
Nachdem in den beiden ersten Abschnitten die algebraischen
Grossen mehr von der formalen Seite betrachtet waren, wobei
es sich um identische Umformungen von Buchstabenausdrücken
handelte, in denen die Buchstaben durchweg als Symbole für
variable Grossen aufgefasst werden konnten, treten nun die
Zahlengrössen mehr in den Vordergrund.
Wir verstehen hier unter Zahlen, gemäss dem in der Ein-
Einleitung Festgesetzten, reelle oder imaginäre Grossen von der
Form a-\- bi, und stellen die reellen Grossen zur Veranschau-
Veranschaulichung durch die Punkte einer geraden Linie, die imaginären
durch die Punkte einer Ebene dar. Unter dem absoluten
Werth einer imaginären Grosse a -\-bi verstehen wir ]/a2-j-&2
und bezeichnen ihn nach Weierstrass mit
| 0 + 6» |.
Es sei nun
A) f(z) = aox» -^a^»-1 + o,«»-» -| \-an
eine ganze Function von x, worin die Coefficienten irgend welche
reelle oder imaginäre Zahlen sind, und der erste, a0, von Null
verschieden vorausgesetzt wird. Wenn a eine Zahl ist, die für x
gesetzt die Function f{x) zu Null macht, die also der Bedingung
/(«) = 0 genügt, so heisst « eine Wurzel der Gleichung
f(x) = 0.

118 Dritter Abschnitt. §. 33.
Wir sagen auch kurz, a ist eine Wurzel von f(x). Nach
§. 4 lässt sich dann f(x) durch x — « ohne Rest theilen, so
dass man
B) f(x) = (x-a)f1(x)
setzen kann, worin fx (x) nur vom (n — l)ten Grade ist, und den-
denselben ersten Coefficienten a0 hat, wie f(x), also
fx (x) = a0 x»-1 -f- a\ xn~2 -|
Die Coefficienten von _/i (x) sind in §. 4 F) angegeben.
¦Jede Wurzel von fi(x) ist also zugleich Wurzel von f(x)
und umgekehrt ist jede Wurzel von f(x) entweder = « oder
eine Wurzel von fx (x). Wenn eine Wurzel a von f(x) bekannt
ist, so ist die Aufgabe, die übrigen zu finden, auf die Lösung
einer Gleichung (n — l)ten Grades zurückgeführt.
Das Ziel der Betrachtungen dieses Abschnittes besteht in dem
Nachweis, dass jede Function f(x) vom nten Grade wenigstens
eine Wurzel hat. Dieser Satz heisst der Fundamentalsatz der
Algebra. Zunächst ziehen wir aus B) die wichtige Folgerung:
L Eine Gleichung nten Grades kann nicht mehr als
n Wurzeln haben.
Denn hätte / (%) mehr als n Wurzeln, so hätte fx (x), was
nur vom (n — l)ten Grade ist, mehr als n — 1 Wurzeln. Eine
Gleichung ersten Grades hat aber nicht mehr als eine Wurzel,
woraus die Richtigkeit unseres Satzes durch vollständige Induction
folgt. Man giebt ihm bisweilen auch den Ausdruck
II, Wenn eine Function nten Grades f(x) mehr als
n Wurzeln hat, so müssen alle ihre Coefficienten
Null sein.
Ist ß eine Wurzel von _/i (x), so lässt sich ebenso setzen
/i (*) = (* — /») f» (*), f(x) = (x — «)(x- ß)f2 (x),
worin f3(x) = a0xn—2 -)-••• nur vom (n — 2)ten Grade ist.
Nimmt man also an, dass jede der Functionen, die man durch
diese Division erhält, fi(x), f$(x) . . . wenigstens eine Wurzel
habe, so erhält man schliesslich
C) f(x) = ao(x — a) (x — ß) . . . (x — v),
und wir können also den Satz, den wir vorhin als das Ziel
unserer Betrachtungen bezeichnet haben, auch so aussprechen:
Es soll bewiesen werden:

§. 34. Stetigkeit. 119
Eine Function nten Grades lässt sich in n lineare
Factoren zerlegen.
Die Grossen a, ß . . . v sind dann alle Wurzeln von f(x)
und ihre Zahl ist also n. Es ist aber nicht ausgeschlossen, dass
unter den k, ß . . . v dieselbe Zahl mehrmals vorkommt. Dann
würde / (x) weniger als n Wurzeln haben, während doch der
Satz bestehen bleibt, dass f(x) in n lineare Factoren zerlegbar
ist. Um die Uebereinstimmung herzustellen, ist man überein-
übereingekommen, wenn x — a mehrmals in f (x) aufgeht, a unter den
Wurzeln mehrfach zu zählen und also von einfachen, zweifachen,
dreifachen etc. Wurzeln zu sprechen.
Führen wir die derivirten Functionen ein, indem wir in §. 13,
B) k und x — a an Stelle von x und y setzen, so folgt:
D) f(x) = /(«) + (*-«) /' («) + ^=^ /" («)
Wird also nun wieder angenommen, dass /(«) verschwindet,
so ergiebt sich
also
Es ist also a eine Doppelwurzel von f(x), wenn mit /(«)
gleichzeitig /'(os) verschwindet. Auch die Formel D) zeigt, dass
nur unter dieser Voraussetzung f(x) durch (x — «J theilbar
ist. Diese Schlussweise lässt sich weiter ausdehnen und führt
zu dem Satze:
III. Die nothwendige und hinreichende Bedingung
dafür,' dass « eine »«-fache Wurzel von f(x) ist,
ist die, dass /(«), /'(es), /"(«), • . . /^-^(a) ver-
verschwinden, ßm)(cc) nicht verschwindet.
§• 34.
Stetigkeit ganzer Functionen.
Wenn, wie bisher
A) f(x) = a0 x» -f 0! x»-1 -) \-an
eine ganze Function von x ist, so beweisen wir zunächst fol-
folgenden Satz:

120
Dritter Abschnitt.
§.34.
IV. f{x) wird zugleich mit x unendlich gross.
Das will sagen, wenn C eine beliebig gegebene positive
Zahl ist, so kann man die positive Zahl It so wählen, dass
\f(x)\>C
wird, sobald der absolute Werth von x grösser als It wird; oder
geometrisch ausgedrückt: man kann in der »-Ebene einen Kreis
um den Nullpunkt so beschreiben, dass ausserhalb dieses Kreises
der absolute Werth von fix) nicht mehr unter C herabsinkt,
wie gross auch C angenommen ist. Der Satz ist einleuchtend
für den Fall einer einfachen Potenz x"; denn ist r der absolute
Werth von x, so ist r* der absolute Werth von xn, und r* ist,
sobald r grösser als 1 geworden ist, grösser als r und wächst
also mit r ins Unendliche.
Um den Satz allgemein zu beweisen, bezeichnen wir die
absoluten Werthe von x, a0, a1? a2 . . . an mit r, c0, cu c2 . . . c„.
Dann ist
BV fix) — r* aa A - -I—2. _i_ . . . __2.
und, weil nach den in der Einleitung bewiesenen Sätzen der
absolute Werth einer Summe nicht kleiner als die Differenz und
nicht grösser als die Summe der absoluten Werthe der Sum-
Summanden sein kann,
xn
1 _|_ _-L 4_ _
x x2 ~*~ aJ*
e2
Da die c0, cx . . . c„ fest gegebene Constanten sind, so kann
man E so gross wählen, dass, sobald r > It ist,
y l ^2 I yn
beliebig klein, z. B. kleiner als x/a Co wird; dann ist
, a« , , an
a0 -\-
und also nach B)
also, wenn man
x
> Va Co,
annimmt,

§. 34 Stetigkeit. 121
C)
Hieran schliesst sich der Satz
V. f(x) ist eine stetige Function von x.
Damit soll Folgendes gesagt sein: Ist der absolute Werth
von x kleiner als eine beliebige endliche Grosse R, so kann
man, wie klein auch die positive Grosse ca angenommen wird,
eine positive Grosse e derart finden, dass
D) l/(* + A)-/(*)!<«
wird, so lange der absolute Werth p von h kleiner als s bleibt,
und zwar so, dass s nur von der Wahl von ca, nicht aber von x
abhängig ist (gleichmässige Stetigkeit).
Nach §. 13, B) ist
E) /(* + h)-f(x) = hf{x) ^ ^
Nehmen wir nun den absoluten Werth von h kleiner als 1
an, so ist der absolute Werth der in der Klammer stehenden
Grosse
F) /'(x) -(- — /" (x) -)-•••-)- »o hn~i
kleiner als eine bestimmte von Null verschiedene Zahl k, die
man erhält, wenn man in F) h durch 1, die Coefficienten
«o > % ... an—i durch ihre absoluten Werthe und x durch B
ersetzt, weil dadurch jedes einzelne Glied der Summe F) durch
seinen absoluten Werth oder durch eine grössere Zahl ersetzt
wird. Wählt man £ so klein, dass
£k < ca
ist, so ist wegen E) die Forderung D) erfüllt, so lange
Q < £
bleibt.
Wir können dem Satze von der Stetigkeit der Function
f(x) noch einen etwas anderen Ausdruck geben, der uns für die
Folge wichtig ist. Nach dem Satze, dass der absolute Werth
einer Summe von zwei Gliedern der Grosse nach zwischen der
'Summe und der Differenz der absoluten Werthe der Glieder
liegt (vergl. Einleitung, S. 21, 22), erhalten wir aus E), wenn wir

122 Dritter Abschnitt. §. 34.
9>(A) = hf(x) + T^f"(x) + • • • +• »"«o
setzen,
\f(x) | - | 9(Ä) ! < |/(* + A) | < \f<x) | + I 9>(A) I.
oder
- I -9>(A) l< l/(* + A) I - I/O») I < I 9(A) |.
Nun ist, wenn q < £ ist, | cpQi) | < co, und wir können also
auch sagen
VI. Der absolute Werth der Differenz
I/O«+ A)|-|/(*) I
ist kleiner als eine beliebig gegebene Grosse co,
sobald der absolute Werth von h kleiner als ein
genügend kleines s ist.
Daraus können wir noch schliessen, wenn wir x. = y -\- ig
setzen, und h entweder reell oder rein imaginär annehmen, dass
\f{y-\-zi)\ bei feststehendem z eine stetige Function von y
und bei feststehendem y eine stetige Function von z ist.
VII. Sind die Coefficienten a0, %...«„ und die Va-
Variable x reell, so kann man x dem absoluten
Werthe nach so gross wählen, dass das Vor-
Vorzeichen von fix) mit dem Vorzeichen des ersten
Gliedes aox" übereinstimmt, also bei positivem a0
und geradem n positiv, bei ungeradem n für
negative x negativ und für positive x positiv
wird.
Denn man kann in
x dem absoluten Werthe nach so gross wählen, dass der absolute
Werth von
«1 I «2 , _|_ fl«
X ' X "¦" ' ' Xn
unter den von cto heruntersinkt und also der Klammerausdruck
das Vorzeichen von a0 hat, was es dann für jedes absolut
grössere x beibehält.. .

§. 35. Vorzeichenwechsel. ]23
§. 35.
Vorzeichenwechsel von f(x). Wurzeln von Gleichungen
ungeraden Grades und von reinen Gleichungen.
Auf Grund der Sätze des vorigen Paragraphen können wir
das folgende wichtige Theorem beweisen:
VIII. Sind die Coefficienten von f(x) reell und exi-
stiren zwei reelle Werthe a, b von x, so dass f(a)
und f(b) entgegengesetzte Vorzeichen haben, so
giebt es zwischen a und b wenigstens eine Wurzel
% der Gleichung f(x) = 0.
Wir wollen annehmen, es sei a < b und f(a) negativ, f(b)
positiv. Wir theilen die Zahlen zwischen a und b so in zwei
Theile 91 und SB, dass eine Zahl « zu 91 gehört, wenn zwischen
« und a, die Grenzen eingerechnet, kein x liegt, wofür f(x)
positiv wird, und eine Zahl ß zu SB, wenn zwischen ß und a
wenigstens ein Werth von x liegt, für den f (x) positiv
wird. Ein Drittes ist offenbar nicht möglich und jede Zahl
zwischen a und b ist also in 91 oder in SB untergebracht. Wir
rechnen noch die Zahlen, die kleiner als a sind, zu 9t, und die
grösser als b sind, zu SB.
Gehört « zu 91, so gehört auch jedes x, was kleiner ist als
«, zu 91, und gehört ß zu SB, so gehört jedes grössere x zu SB.
Es ist also jedes ß grösser als jedes « und die beiden
Zahlengebiete 91, SB bilden einen Schnitt (Einleitung, S. 5) der
durch eine Zahl § erzeugt wird, so dass jede Zahl «, die
kleiner als § ist, zu 91 gehört, jede Zahl ß, die grösser als g
ist, zu SB.
Ist nun für irgend eine Zahl x0 der Werth von f(x0) negativ
oder positiv, so lässt sich nach V. des vorigen Paragraphen eine
positive Grosse s so bestimmen, dass für jedes x zwischen x0 — e
und x0 -|- « die Werthe von f(x) immer negativ oder immer
positiv sind. Daraus ergiebt sich, dass /(£) weder negativ noch
positiv sein kann und also Null sein muss. Denn wäre /(§) negativ,
so wäre auch f(x) zwischen § und § -|- e negativ; diese Werthe
würden also zu 21 gehören, während sie doch grösser als £ sind;
und wäre /(£) positiv, so wäre f(x) positiv, so lange x zwischen
| — £ und | liegt; diese Werthe würden also, obwohl sie kleiner
als | sind, zu SB gehören, und beides ist nach der Definition von

124 Dritter Abschnitt. §. 35.
§ unmöglich. ¦ Ganz ähnlich kann geschlossen werden, wenn f(a)
positiv und f(b) negativ ist und nnser Satz ist also erwiesen.
Hieraus ziehen wir zwei wichtige Folgerungen: Wenn /(§)
verschwindet, so lässt sich ein Intervall
| — £ <X <%-\- S
so bestimmen, dass f(x) ausser für x = § in diesem Intervall
nicht verschwindet. Es sind dann vier Fälle in Bezug auf die
Vorzeichen von / (x) in den beiden Intervallen § — s < x < §
und | < x < % -\- s möglich, die im folgenden Schema zusammen-
zusammengestellt sind:
§-£<£<! + *
!•/(*) + -
2.f(x) - +
,3. /(*) + +
4. f{x) - -.
Ist /w(a?) die erste unter den Derivirten von f(x), die für
x = | von Null verschieden ist, so zeigt die Formel [§. 13, B)]
dass diese vier Fälle durch folgende Kennzeichen unterschieden
sind:
1. v ungerade /« (£) < 0
2. v ungerade /« (£) > 0
3. v gerade /« (£) > 0
4. v gerade /« (|) < 0.
Wir sagen, dass im ersten Falle /(#) abnehmend, im
zweiten wachsend durch Null geht. Im Falle 3. ist /(§) = 0
ein Minimum, im Falle 4. ein Maximum.
Wenn insbesondere /'(§) von Null verschieden, § also eine
einfache Wurzel ist, so ist das positive oder negative Vorzeichen
von /' (|) das Kennzeichen für das Wachsen oder Abnehmen der
Function f(x) beim Durchgang von x durch |.
Wir beweisen mit diesen Hülfsmitteln noch zwei weitere
wichtige Sätze.
IX. Die Gleichung
xn — a = 0
hat, wenn a eine positive Zahl ist, eine und nur
eine positive Wurzel.

§. 35. Wurzeln reiner Gleichungen. 125
Denn setzen wir
A) f(x) = x"-a,
so ist f(x) nach §.34, VII. für ein hinlänglich grosses positives x
positiv, und für x = 0 negativ; also giebt es einen positiven
Werth von x, den man mit ]/ä bezeichnet, für den f(x) ver-
verschwindet.
Dass es aber nur einen solchen Werth geben kann, folgt
daraus, dass xn, so lange x positiv bleibt, mit x fortwährend
wächst
Ist n ungerade, so existirt auch für negative a eine und
nur eine negative Wurzel von A), was ebenso bewiesen wird.
X. Eine Gleichung ungeraden Grades mit reellen
Coefficienten hat immer wenigstens eine reelle
Wurzel.
Denn nach §. 34, Satz VII. kann f(x), wenn der Grad un-
ungerade ist, sowohl positiv als negativ werden und f(x) = 0 hat
also nach VIII. eine Wurzel. Wir beweisen endlich noch
XI. Eine reine Gleichung hat immer eine Wurzel.
Unter einer reinen Gleichung verstehen wir eine Gleichung
von der Form
B) xn — a — 0,
wo a eine beliebige reelle oder complexe Grosse ist,
Dass diese Gleichung für ein reelles positives a immer eine
Wurzel hat, ist oben schon bewiesen, und für a = 0 wird sie
offenbar durch x = 0 befriedigt.
Der allgemeine Beweis kann in zwei Theile zerlegt werden;
es genügt nämlich, wenn wir zunächst n = 2, dann n ungerade
voraussetzen. Denn existirt die Grosse ~^ä und ^f a oder V'a für
jedes a, so ist auch die Existenz von
also von 1/a für jedes beliebige n sichergestellt. Es würde
sogar genügen, die Existenz von p*'a für den Fall zu beweisen,
dass n eine Primzahl ist. Daraus ist aber zunächst kein beson-
besonderer Vortheil zu ziehen.
Wir bezeichnen die complexe Grosse a mit b -\- c i und
setzen, da x im Allgemeinen auch complex sein wird,
x = y -\- i s.

126 Dritter Abschnitt. §. 35.
Dann haben wir zunächst zu zeigen, dass
C) (y + t*)» = & + »c
welche reellen Werthe auch b, c haben mögen, durch reelle y, s
befriedigt werden kann. Die Gleichung C) ist aber erfüllt, wenn
D) 2/2_22 = &) 2yz = c,
also
. (yt _|_ ^2J _ £2 _|_ C2
und folglicli
E) «/2 -f 22 = Vb2 + c2.
Nach IX. existirt immer eine positive Quadratwurzel V&2 -\- cK
Aus D,) und E) folgt nun
b + VP-+T2 — & 4-
* = 2 ' * =2 '
und die beiden Grossen + b -\- 'Vb^_-\-_ci sind offenbar positiv,
da &2 + c2 > &2, also auch V&2 -j- c2 > V^ Wir erhalten
daraus
2
2
worin aber das eine Vorzeichen durch das andere bestimmt ist
durch die Bedingung
2yz = c;
eines der beiden Vorzeichen aber bleibt willkürlich, so dass wir
nicht nur eine, sondern zwei (entgegengesetzte) Lösungen von
C) erhalten.
Es sei ferner n ungerade; wir nehmen die zu lösende
Gleichung in der Form an
F) {y -\- i z)n = b 4- c i.
Ist c = 0, also a reell, so können wir z = 0 setzen und
erhalten nach IX. einen reellen Werth von x.. Nehmen wir aber
c von Null verschieden an, so folgt aus F) (Einleitung, S. 21)
G) (y — izf = b — c i.
Multipliciren wir die beiden Gleichungen F), G) mit ein-
einander, so folgt
tyt _|_ giy> _ -ja 4. c\
und daraus (nach IX.)

§. 36. Keine Gleichungen. 127
(8) «/a _|_ Si = yb* + c2,
wodurch der absolute Werth von x bestimmt ist. Es ergiebt
sich ferner aus F) und G)
-*<o = 0-
) =
2 2
Nun ist cp(y,z) eine ganze homogene Function wtenGrades
der beiden Veränderlichen y, 0, und zwar mit reellen Coeffi-
cienten (da die Vertauschung von i mit —¦ i in <p(y, z) nichts
ändert), und wenn wir nach absteigenden Potenzen von y ordnen,
so ist das erste Glied cyn, also nach Voraussetzung von Null
verschieden. Setzen wir nun
V = *>e,
so erhalten wir aus (9)
A0) cp (A, 1) = 0,
also eine Gleichung wten Grades für X, die nach X. gewiss eine
Wurzel hat. Ist l bestimmt, so folgt aus (8)
Hierdurch sind die Gleichungen (8), (9) thatsächlich befrie-
befriedigt; aus (9) aber folgt
(y + * z)n («/ — * z)n
b -\- ic b — *c '
und aus (8), dass der gemeinsame Werth dieser beiden Brüche
+ 1 ist. Wir haben daher
(y -j- ig)» = ± (b -j- ci), (y — iz)n = ± (b — ci),
und es kann also das Vorzeichen der Quadratwurzel in A1) so
bestimmt werden, dass die Gleichungen F) und G) erfüllt sind
§. 36.
Lösung reiner Gleichungen durch trigonometrische
Functionen.
Weit vollständiger und einfacher kann die Auflösbarkeit
einer reinen Gleichung dargethan werden, wenn man die trigono-
trigonometrischen Functionen und ihre einfachsten Eigenschaften als
bekannt voraussetzt. Freilich sind diese Functionen der eigent-

128 '; Dritter Abschnitt. §. 36.
liehen Algebra fremd und darum ist es befriedigender die
principiellen Fragen, so wie es im Vorhergehenden geschehen
ist, und auch noch später geschehen soll, ohne ihre Hülfe zu
beantworten. Für die Anwendung und eine bequemere An-
Anschauung wollen wir aber dieses Hülfsmittel doch nicht ent-
entbehren.
Setzen wir, wenn b, c reelle Zahlen sind,
A) b = r cos cp, c = r sin cp,
so ist, wenn wir r positiv annehmen, der Winkel q> hierdurch
bis auf ein Vielfaches von 2 n bestimmt. Er wird völlig be-
bestimmt sein, wenn wir ein Intervall von der Grosse 2 % fest-
festsetzen, in dem er liegen soll, z. B.:
— a < y ^ a.
In geometrischer Auffassung sind r, cp die Polarcoordinaten
des Punktes, dessen rechtwinklige Coordinaten b, c sind.
r ist der absolute Werth der complexen Grosse a = b -\- c i
und cp wollen wir die Phase dieser complexen Grosse nennen.
Das Product zweier complexen Grossen
, . a = r (cos (p -\- i sin cp)
\ ' a' — r' (cos <p' -\- i sin cp'),
ergiebt sich in der Form
C) aa' = rr'[cos (cp -|- cp') -j- isin (q> + <p')],
und daraus erhält man, wenn n eine beliebige ganze positive
(oder selbst negative) Zahl ist, den nach Moivre benannten
Lehrsatz:
D) (cos (p -f- * sin (jp)" = cos n cp -\- isrnn cp,
der dazu geführt hat, die Grosse cos cp -j- * sin cp als Exponential-
funetion mit imaginärem Exponenten zu betrachten, und demnaeh
cos cp -\- isin cp = eif
zu setzen. Dadurch erhalten die Formeln C) und D) die
Gestalt
E) e»>e*r/1' = e*w+'/>'M (fvy — &»<?.
Wenn wir demnach
F) a = r (cos q> -\- i sin cp),
setzen und unter pV dem nach §. 35,. IX. existirenden und völlig
bestinämten positiven Werth verstehen, dessen fite Potenz == r
ist, so ist .

§• 36.
G)
Reine Gleichungen.
= l/V (cos—4-^sin—)
eine Grosse, deren nte Potenz = a ist, also eine Wurzel der
Gleichung
(8) x" = a,
wenn unter n eine beliebige positive ganze Zahl verstanden wird.
Derselben Forderung genügt aber auch jeder der Werthe
,„, i«/~r /<P -4~ 2hx\ . . . /w 4- 2kit\
(9) xjc ?= \/r \ cos ( -—! ) -+- % sm -—!
wenn k eine beliebige ganze Zahl ist. In (9) sind aber n und
nicht mehr verschiedene Werthe enthalten, die man erhält,
wenn man
A0) h — 0, 1, 2, . . . n — 1
setzt; denn vermehrt man h um ein Vielfaches von n, so ändert
(9) seinen Werth nicht, während die n Werthe A0) lauter ver-
verschiedene Werthe von x ergeben, weil sie verschiedene Phasen
haben.
Die Gleichung (8) hat demnach nicht nur eine,
sondern n verschiedene Wurzeln.
Fig. 1.
Die geometrischen Bilder der
Werthe x^ liegen alle auf
einem Kreise mit dem Radius
pV, und zwar um den Winkel
2 n : n von einander entfernt.
Man erhält den ersten dieser
Punkte dadurch, dass man den
gegebenen Winkel <p in n gleiche
Theile theilt. Der Radius pV ist
grösser oder kleiner als r, je
nachdem r kleiner oder grösser
als 1 ist. Die beistehende Fig. 1
zeigt diese Verhältnisse für n = 3 unter der Voraussetzung, dass
r > 1 ist.
Man kann die verschiedenen Werthe von % dadurch erhalten,
dass man den ersten von ihnen
n
¦ • 9
sm —
n.
mit den verschiedenen Werthen von
Weber, Algebra. I.

130 Dritter Abschnitt. §. 37.
A1) £fc = cos 1- «sin
K J n ' n
multiplicirt. Die Grossen £k sind Wurzeln der Gleichung
A2) xn = 1,
und heissen die nten Einheitswurzeln. Es sind n und nur n
verschiedene Werthe, von denen bei ungeradem n nur einer (für
(n\
für h = 0 und ft = —) reell sind.
Die geometrischen Bilder der nten Einheitswurzeln sind die
Eckpunkte eines dem Kreise mit dem Radius 1 einbeschriebenen
regelmässigen w-Ecks. Ihre algebraische Bestimmung ist Gegen-
Gegenstand der Kreistheilungslehre. Bezeichnen wir den Werth
von £fc für Tc = 1 mit e, setzen also
jL 7t , . . itTC
s = cos — 4- * sm —,
n n
so ist nach dem Moivre'sehen Satze
£fc = £k,
so dass alle »ten Einheitswurzeln als Potenzen von einer unter
ihnen dargestellt sind..
§. 37.
Befreiung einer Gleichung vom zweiten Gliede.
Die Gewissheit der Existenz der Wurzeln reiner Gleichungen
setzt uns in den Stand, die Wurzelexistenz bei den Gleichungen
zweiten, dritten und vierten Grades oder, wie man auch sagt, bei
den quadratischen, cubischen und biquadratischen Gleichungen
nachzuweisen, indem wir die Bestimmung ihrer Wurzeln auf die
Lösung reiner Gleichungen zurückfuhren. Wir werden auf
diese Frage später von verschiedenen allgemeineren Standpunkten
zurückkommen, besprechen aber hier in der Kürze die älteren
Methoden der Auflösung, die, wenn sie auch wenig Einblick in
den allgemeinen Zusammenhang dieser Fragen gewähren, doch
in der Anwendung sehr einfach sind. Sie erwecken den Schein,
als ob es sich um eine der Verallgemeinerung auf höhere
Gleichungen fähige Methode handle, was aber nicht der Fall ist.
Zunächst folgende allgemeine Bemerkung. Nehmen wir der Ein-
Einfachheit halber in der Function

§. 37. Die Wurzeln algebraischer Gleichungen. 131
A) f(x) = ocn + <h a;—1 + a2 a;1—2 H )- an
den Coefncienten von a;n gleich 1 an, was man im Allgemeinen
durch Division mit dem Coefncienten von ccn erreicht, so können
wir durch eine einfache Substitution
B) ' * = *-¦£,
fipo) in eine andere Function wten Grades <p(jf) transformiren,
in" der das zweite Glied yn~1 nicht vorkommt; denn es ist nach
dem binomischen Lehrsatz
fi i
xn _ yn _ ai yn-1 + _____ a*yn-i _J
^n-2 _ yn-% . . #)
also
Wenn wir die Transformation für die Fälle n = 2, 3, 4
wirklich ausführen, so erhalten wir
n — 2 <p(y) = 2/2 _)_ a
C) » = 3 9 («/) = 2/8 -)- a y -\- b
n = 4 9(«/) = «/* -f ay% -f &«/ + c,
wenn wir setzen
für w = 2: a = j- + a2i
für n = 3: a := ^- -|- a2
o
D) 27 3
für » = 4: a = — —^- -\- a%
o
256 ~f 6~ 4 "" a*'
und die Lösung der Gleichung f(x) = 0 ist durch B) auf die
Lösung von cp(y) = 0 zurückgeführt. Diese ergiebt zunächst
für » = 2
9*

132 Dritter Abschnitt. §. 38.
und folglich
Wir haben also zwei Wurzeln
E)
j ) V% — 4 a2
P — ~
§. 38.
Cubische Gleichungen. Cardanische Formel.
Die Gleichung dritten Grades nehmen wir in der
reducirten Form an
A) y3 + ay -\- b = 0
und führen zwei neue Unbekannte u, v ein, indem wir
B) y = u -\- v ¦ ¦
setzen. Dies in A) eingesetzt, ergiebt
C) u3 -\- v3 -)- C uv -)- a) (u -)- v) -)- b = 0.
Wir bestimmen eine der beiden Grossen u, v durch die
andere nach der Gleichung
D) 3 u v = — a,
und erhalten aus C)
E) m3 -J- w3 = — b.
Aus D) und E) aber lassen sich u3 und «3 durch eine
Quadratwurzel bestimmen. Man erhält nämlich
_ , 4 a3
~ "i" 27
Setzen wir zur Abkürzung
G) E==X + 27'
so findet sich
M3 — «3 — 2 ]/R

§. 38. Die Wurzeln algebraischer Gleichungen. 133
Wir geben der YB, eines der beiden Zeichen und erhalten
nach E)
! V = - \ - VE,
und also
(9) y =
Die Multiplication der beiden Ausdrücke (8) ergiebt
und zeigt, dass, wenn für t* ein bestimmter unter den drei
Werthen der Cubikwurzel genommen wird.
00)
jedenfalls einer der drei Werthe von y — 1_ V-R ist. Aus D)
folgt aber, dass, nur wenn wir diesen Werth für v nehmen,
die Gleichung A) durch y = u -\- v befriedigt ist. Wir erhalten
so, den drei Werthen von u entsprechend, drei Wurzeln der
Gleichung A). Aus der Existenz einer Wurzel der cubischen
Gleichung ergiebt sich aber auch dadurch schon die Existenz
von dreien, dass bereits nachgewiesen ist, dass die quadratische
Gleichung zwei Wurzeln hat.
Um aus der einen Wurzel (9) die beiden anderen abzuleiten,
setzen wir
« = u -j- v,
und dividiren yz -\- ay -\- b durch y — a. Der Quotient, dessen
Wurzeln die beiden anderen Wurzeln ß, y der cubischen
Gleichung A) sind, ist
2/2 -f ay _|_ «2 -f a = 0,
woraus man nach D) des vorigen Paragraphen
— «d=V— 3«2 — 4a
y- _
findet. Setzt man hierin « = u -|^ v, und nach D) a = — 3 u vt
so folgt:

134 Dritter Abschnitt. §. 39.
= — (u + v) ± V — 3 (u
uv
__ — (u -)- v) ± V — 3 (u — v)
_
Setzen wir also
woraus
A2); £2 +£
£2 = ~
2
folgt, so erhält man die drei Wurzeln der cubischen Gleichung F)
a = t* -)- t?
A3/ /S = su + £2t?
y = s2u-\- sv.
Darin ist s eine von 1 verschiedene dritte Einheitswurzel,
die hier ohne die trigonometrischen Functionen algebraisch aus-
ausgedrückt ist. Setzt man eu oder e2u für u, also s2v, sv für v,
so vertauschen sich die drei Grossen «, /3, y unter einander.
Der Ausdruck (9) für die Wurzel einer cubischen Gleichung
wird die Cardanische Formel genannt.
§. 39.
Der Cayley'sche Ausdruck der Cardanischen
Formel.
Jede Cubikwurzel hat, wie wir gesehen haben, drei ver-
verschiedene Werthe, die man aus einem von ihnen erhält durch
Multiplication mit 1, s, a2. So hat also auch jede der beiden
Grossen u, v, wie sie durch (8), §. 38 definirt sind, drei Werthe
und die Summe u-\-v hat also, wenn man nur die Bedingungen
(8) berücksichtigt, neun verschiedene Werthe; von diesen
geben aber nur drei Lösungen der cubischen Gleichung, und
erst durch Zuziehung der Relation D), §. 38
A) 3 uv = — a
werden unter den neun Werthen die brauchbaren ausgesondert.

§. 40. Biquadratische Gleichungen. 135
Dies ist ein Mangel der Cardanischen Formel, die hiernach
für sich noch nicht genügt, um die Wurzeln der cubischen
Gleichung eindeutig zu geben. Diesem Mangel hat Cayley
durch die folgende Darstellung abgeholfen. Man definire zwei
neue Grossen |, rj durch die Gleichungen
B) U=^7], « = |1J»,
woraus sich durch Multiplication mit Benutzung von A)
C) ^
ergiebt; folglich ist, wenn dieser Werth in B) eingesetzt und für
u, v ihre Ausdrücke §. 38, (8) substituirt werden,
und wenn man also jetzt die Wurzel y der cubischen Gleichung
in die Form
E) y = Sn (£ + n)
setzt, so erhält man einen Ausdruck, der, wenn man, von ein-
einander unabhängig, g durch g, s f, e2!-, und 7] durch rj, srj, £2tj
ersetzt, nicht neun, sondern nur die drei Werthe
F) epTj + e^r]*
£2£2^ + £^2
annimmt. Giebt man ausserdem der in D) vorkommenden
Quadratwurzel das entgegengesetze Zeichen, so werden |, q mit
einander vertauscht, und die drei Wurzeln F) nur unter einander
permutirtJ).
§• 40.
Die biquadratische Gleichung.
Ein ähnlicher Weg, wie bei der Lösung der cubischen Glei-
Gleichung durch die Car danische Formel, lässt sich zur Lösung
der Gleichung vierten Grades
A) yi + «2/2 + 62/ + c = 0
einschlagen.
x) Cayley, Phil. Mag., vol. XXI, 1861. Colleoted mathematical papers,
vol. V, Nr. 310.

136 Dritter Abschnitt. §. 40.
Wir setzen
2 y = u -j- v -\- w,
und erhalten, wenn wir zur Abkürzung
B) s = u2 -f- v2 -\- w2, t =
setzen,
\(
162/4 = s2 -)- 4s (vw -f- wu -\- uv) -\- At
-\- 8 u v w (u + v -f- w).
Wenn man dies in A) einsetzt, so findet sich
s2 -\~ it -)- 4as + 16c -)- 8(w»w + 6) («t + » + w)
—|— 4 (s —|— 2 a) (v w -\- w u -f- «t ü) = 0.
Diese Gleichung wird aber durch die Annahme befriedigt
s-f-2a = 0, «tt;M; + 5 = 0, s2 + 4* + 4 as -(- 16c = 0.
Mit Hülfe der ersten dieser drei Gleichungen wird die dritte
t = a2 — 4 c,
und, wenn man für s, t die Werthe B) zurücksetzt,
U2 _|_ V2 _|_ W2 — 2 ÖS
C) v2w2 -f w2w2 + w2t?2 = a2 — 4c
%»M) = — b.
Nach §. 7 sind diese Gleichungen dann und nur dann
befriedigt, wenn w2, t?2, w2 die Wurzeln der cubischen Gleichung
D) s* -j- 2 az2 -\- (a2 — 4 c) 0 — 62 = 0
sind, und wenn die Vorzeichen von u, v, w so bestimmt werden,
dass die letzte der Gleichungen C) befriedigt ist. Diese letztere
Bedingung lässt noch vier verschiedene Vorzeichenbestimmungen
zu, so dass man die vier Wurzeln der biquadratischen Gleichung
in folgender Weise erhält:
2«= u -\- v -\- w
,., 2/3= u — v — w
2y = — u -\- v — w
2 8 .= — u — v -\- w.
Die Lösung der biquadratischen Gleichung ist. damit auf
die der cubischen Gleichung D) zurückgeführt.
Diese Gleichung heisst eine cubische Resolvente der
biquadratischen Gleichung.

§. 41. Fundamentalsatz. 137
§• 41-
Beweis des Fundamentalsatzes.
Wir gehen nun an den Beweis des Fundamentalsatzes
der Algebra, dass jede Gleichung f(x) = 0 wenigstens eine
Wurzel hat. Wir schicken einige allgemeine Sätze voraus:
1. Wenn 8 ein beliebiges System reeller Zahlen be-
bedeutet, die alle grösser sind als eine bestimmte
positive oder negative Zahl G (d. h. ein System,
das keine unendlichen negativen Zahlen enthält),
so existirt eine untere Grenze für die Zahlen 8.
Unter einer unteren Grenze g ist eine solche Zahl zu
verstehen, die von keiner Zahl des Systems 8 unterschritten
wird, aber so beschaffen, dass, wenn d eine beliebig gegebene
positive Grosse ist, zwischen g und g •-(- 8 (mit Einschluss der
Grenzen) immer noch wenigstens eine Zahl des Systems 8 liegt,
wie klein auch S sein mag.
Der Beweis ergiebt sich unmittelbar aus der Möglichkeit
eines Schnittes B1, 23), den man so construirt, dass man eine
Zahl a nach 3t wirft, wenn sie von keiner Zahl des Systems 8
unterschritten wird, und eine Zahl ß nach 23, wenn sie
wenigstens von einer Zahl in S unterschritten wird. Die durch
diesen Schnitt bestimmte Zahl g wird von keiner Zahl in S
unterschritten, denn sonst gäbe es auch Zahlen, die kleiner als
g sind, und also zu 21 gehören, und die doch von Zahlen in S
unterschritten werden, während andererseits jede noch so wenig
über g liegende Zahl ß zu 23 gehört und also von einer Zahl
in 8 unterschritten wird. Das sind aber die charakteristischen
Merkmale der unteren Grenze.
2. Ist S' ein Theil von 8, so haben auch die Zahlen
8' eine untere Grenze g', und diese ist entweder
gleich g oder grösser als g.
Denn kleiner als g kann sie nicht sein, da sonst Zahlen in
S' und folglich auch in 8 vorkämen, die unter g liegen.
Es sei nun f(x) eine reelle Function von x, die in dem
Intervall
A) a <! x <f 6

138 Dritter Abschnitt. §. 41.
nur endliche Werthe hat, und die ausserdem in diesem Intervall
stetig ist; das will, in Uebereinstimmung mit §. 34, V und VI,
besagen, dass
B) . /(* + *)-/(*)•
dem absoluten Werthe nach in dem ganzen Intervall unter einer
beliebig gegebenen Zahl rj liegt, wenn das positive h kleiner als
eine gewisse Zahl s ist. (Für x = a nehmen wir in B) nur
das obere, für x = b nur das untere Zeichen, um mit x + h
nicht aus dem Intervall herauszukommen.)
Für die Werthe einer solchen Function in dem Intervall
giebt es nach 1. eine untere Grenze g, und wir beweisen nun
den Satz:
3. dass die Function f(x) den Werth g für irgend
einen Werth | des Intervalles annimmt, wonach
die untere Grenze zu einem Minimum der Func-
Function f(x) in dem Intervall wird.
Der Beweis ist folgender. Die untere Grenze der Functions-
werthe in einem Theil des Intervalles A) ist nach 2. entweder
gleich oder grösser als g.
Wenn nun f(a) = g ist, so ist das zu Beweisende richtig;
ist aber /(«)>#, so kann man wegen der Stetigkeit von f(x)
ein Intervall a ^ x ^ a -)- h angeben, in dem f(x) > g bleibt
und also die untere Grenze von f(x) grösser als g ist.
Wir construiren nun in dem Intervall A) einen Schnitt
C1, 33) der Art, dass wir einen Werth « des Intervalles A) zu
91 rechnen, wenn die untere Grenze von f(x) in dem Intervall
a <! x <! « grösser als g ist, und einen Werth ß zu 33, wenn
die untere Grenze im Intervall a ^ x ^ ß gleich g ist.
33 kann möglicherweise aus dem einzigen Werthe b bestehen;
dann aber muss f(b) = g sein, und unsere Behauptung ist für
x = b erfüllt; denn wäre f(b)>g, so könnte man eine Grosse
g' zwischen f(b) und g und wegen der Stetigkeit ein Intervall
b — h ^ x <*b so annehmen, dass in diesem Intervall alle
Functionswerthe f(x) grösser als g', ihre untere Grenze also
gleich oder grösser als g' und daher sicher grösser als g wäre.
Da aber b — h zu 91 gehört, so ist auch in dem Intervall
a <J x ^ b — h und folglich in dem ganzen Intervall A) die
untere Grenze grösser als g, gegen die Annahme.

§. 41. Fundamentalsatz. 139
Ist also f(b) > g, so definirt der Schnitt B1, 23) eine Zahl |
im Inneren des Intervalles A), von der wir nun zeigen können, dass
sein muss.
Ist /(!)># und f(£)>g'>g, so können wir wegen der
Stetigkeit von f(x) ein Intervall
£ — h^x^Z + h
bestimmen, in dem alle Functionswerthe f(x) grösser als g' und
also ihre untere Grenze grösser als g ist. Da aber | — h zu 21
gehört, so ist auch in dem ganzen Intervall
a < x < i- -\- h
die untere Grenze von f(x) grösser als g, während doch £ -j- h
zu 23 gehört, worin der Widerspruch liegt.
Es sei jetzt f(x) eine ganze rationale Function mit beliebigen
complexen oder reellen Coefficienten, und die Variable oo soll
gleichfalls complexe Werthe haben können.
Nach §. 34, IV kann, wenn C ein beliebiger positiver Werth
ist, die positive Grosse B so angenommen werden, dass
D) \f{x)\>C
ist, sobald
E) | x | ^ B
wird. Zur Veranschaulichung stellen wir das durch die Un-
Ungleichung
| x | < B
begrenzte Gebiet (B) für die Variable x durch eine Kreisfläche
vom Radius B in der Ebene der Variablen x = y -\- i s dar.
Wenn wir' C grösser annehmen, als irgend einen Werth
von | f(x~) | im Inneren des Gebietes (B), zum Beispiel grösser
als | /@) |, so wird \ f(x) \ gewiss im Inneren des Gebietes
(B) kleiner werden als an der Begrenzung. Da nun im ganzen
Inneren von (B) die Function | f(x) \, die wir zur Abkürzung
jetzt mit X bezeichnen wollen, nicht negativ wird, so giebt es
für die Werthe von X eine untere Grenze g und wir haben den
Satz zu beweisen;
4. Es existirt ein Werth £ von x im Inneren des
Gebietes (B), so dass
F) 1/AI=0

140
Dritter Abschnitt.
Fig. 2.
wird, dass also die untere Grenze auch hier
ein Minimum ist.
Die untere Grenze von X in irgend einem Theile des Be-
Bereiches ist entweder gleich g oder grösser als g.
Ein Grössengebiet, das durch die Ungleichheitsbedingungen.
G) | x | ^ B, — B<^y<^a
bestimmt ist, wird in unserer Fig. 2 durch das Segment (PQa Q'),
das wir das Segment (P, «) nennen wollen, dargestellt. Wir
bestimmen nun zunächst
einen Werth rj von y
durch einen Schnitt B1,23)
folgendermaassen:
Eine Zahl « zwischen
— B und -f- B wird in
21 aufgenommen, wenn,
die untere Grenze von
X in dem Segment (P, u)
grösser als g ist, und
ein Werth ß wird in 33
aufgenommen, wenn die
untere Grenze von X in
dem Segment (P, ß)
gleich <jr ist. Dieser Schnitt.
B1, SB) definirt eine Zahl
7] von der Eigenschaft, dass die untere Grenze von X in dem
Bereich (P, y), wenn y < tj ist, grösser als g, und wenn y > -q
ist, gleich g ist.
Nun ist nach §. 34, VI
eine stetige Function von s in dem Intervall
(8) — MB? — yf ^ e ^ ViZ2 — n\
was in der Fig. 2 durch Jf, JM7 bezeichnet ist.
Diese Function erhält also nach 3. für irgend einen Werth t,
von s in diesem Intervall einen Minimumwerth y, so dass, wenn
gesetzt wird,
(9)
wird.
1/A) 1 =

§. 41. Fundamentalsatz. 141
Es ist nun ferner leicht einzusehen, dass y = g sein muss,
denn da g die untere Grenze aller Werthe von X innerhalb (B)
ist, so kann y zunächst nicht kleiner als g sein.
Es kann aber y auch nicht grösser als g sein; denn alle
Werthe, die X auf der Strecke MM' annimmt, sind J? y; ist
aber y > g, so kann man eine Grosse g1 so annehmen, dass
y > g' > g ist, und wegen der in §. 34, VI bewiesenen Stetigkeit
von X lassen sich die Zahlen «, ß so bestimmen, dass
«< n <ß
und dass in dem ganzen Bereich (P, ß) — (P, «) = («, ß)
(QNN'Q1 in der Fig. 2) X grösser als g1 bleibt. Folglich ist
die untere Grenze von X in («, ß) grösser als g. Da nun die
untere Grenze von X in (P, «) grösser als g ist, so ist sie auch
in (P, /3), was aus (P, «) und («, /3) zusammengesetzt ist, grösser
als g; ß gehört aber zu 23, woraus ein Widerspruch mit der
Definition von 23 folgen würde.
" Es bleibt also nur übrig, dass y = g ist, und der Satz 4.
ist damit nachgewiesen, nämlich, dass es einen Werth | im In-
Inneren von (E) giebt, für den
\f(M)\=9
ist, dass also | f(x) | einen Minimuinwerth erreicht. Wir be-
beweisen nun:
5. Wenn a irgend ein Werth von x ist, für den
f(a) von Null verschieden ist, so lässt sich h
so annehmen, dass
ausfällt.
Daraus folgt dann, dass, wenn /(£) von Null verschieden
wäre, g nicht das Minimum der Function \f(%) | sein könnte;
da dies aber bewiesen ist, so muss
A1) /(ö = 0
sein, und | ist eine Wurzel der Gleichung f(x) = 0. Der
Fundamentalsatz wird also dann bewiesen sein.
Beim Beweise von 5. machen wir Gebrauch von dem schon
bewiesenen Satz (§. 35), dass eine reine Gleichung immer eine
Wurzel hat.
Von den derivirten Functionen /'(«),/"(«) • ¦ • können einige
verschwinden; die letzte/<">(«), die gleich II(n)a0 ist, ist aber

142
Dritter Abschnitt.
§. 41.
von Null verschieden; es mögen also /' («), /" («)... /('"
verschwinden, /W(«) nicht verschwinden. Wir haben
nach §.13
Jim
A2) /(« -f K) =/(«) + j^y—. /(») («) +
»+«
/(
Wir wählen, was nach §. 34, V stets möglich ist, eine
tive Zahl £ so, dass
|
+\ /(m)(«) t(»-|l)(»+ 2) /(
ist, sobald
A4) | h | < £,
und einen postitiven echten Bruch d so, dass
dann
posi-
posi< 1
was, wenn /(«) nicht verschwindet, gleichfalls möglich ist. Dann
bestimmen wir (auf Grund von §. 35) h aus der Gleichung
woraus nach A5)
h | < £
folgt. Aus A2) ergiebt sich jetzt, wenn man für hm den Werth
aus A6) setzt,
/(« + *) = (!-*)/(«)
also
A7)
2) /(»•) («)
1)/(»»(«)
2) /<m>(«)
und wegen A3)
A8)
w. z. b. w.
Damit ist also der Beweis des Fundamentalsatzes beendigt.

§. 42. Die Wurzeln algebraischer Gleichungen. 143
§• 42.
Algorithmus zur Berechnung der Wurzeln.
Der im vorigen Paragraphen gegebene Beweis für die Exi-
Existenz einer Wurzel einer algebraischen Gleichung lässt zwar an
Bündigkeit nichts zu wünschen übrig, er hat aber noch den
Mangel, dass er nicht die Schritte erkennen lässt, wie man eine
Wurzel durch ein convergentes Rechnungsverfahren berechnen
kann. Wir fügen also noch die folgenden Betrachtungen hinzu,
die diesem Mangel, wenn auch nur theoretisch, abzuhelfen be-
bestimmt sind. Sie geben noch einen zweiten Beweis des Funda-
mentalsatzes, der in der Hauptsache von Lipschitz stammt
(Lehrbuch der Analysis, Bd. I, §. 61 ff.; Vereinfachungen sind
dem Verfasser von Dedekind und Frobenius mitgetheilt).
Wenn die beiden ganzen rationalen Functionen f(x) und
f'(x) einen gemeinsamen Theiler haben, so kann dieser nach
§. 6 durch rationale Operationen gefunden und beseitigt werden.
Wir dürfen also voraussetzen, dass/(a;) und/'(#;) keinen gemein-
gemeinsamen Theiler haben, dass sie also für keinen Werth von x beide
zugleich verschwinden.
Wir setzen nun voraus, dass die Wurzelberechnung für eine
Function (w — l)ten Grades schon gelungen sei, und nehmen
demnach /' (x) in lineare Factoren zerlegt an. Demnach sei, wenn
A) f(x) = xn + «j x«-1 + a2 a;"-2 -| •,
ist,
B) f'(x) = K" + (n — l)«^"-2 • • •
= n(x — ft) (x — ßt)...(x — ßn-i),
worin die ßu ß2 . . . /?«_! als bekannte Zahlen angesehen werden,
die auch theilweise identisch sein können. Nach unserer Voraus-
Voraussetzung werden die absoluten Werthe
C) |/(A)|, |/G32)|,--.|/(/3«-i)|,
die wir mit
D) &n b2 . . . &n_i
bezeichnen, alle von Null verschieden sein; wir wollen die Be-
Bezeichnung so gewählt annehmen, dass öj der kleinste unter ihnen

144
Dritter Abschnitt.
§. 42.
sei, oder wenigstens keinen der anderen an Grosse übertrifft.
Nach dem Satz 5, §. 41 lässt sich dann ein Werth « von x so
bestimmen, dass der absolute Werth a von/(«) kleiner als 6j
wird, also:
E) a < bx ^ 62 <; 63 . . . 5S 6n-i-
Wir begrenzen nun ein Gebiet G für die Variable x derart,
dass ausserhalb dieses Gebietes der absolute Werth von f(x)
immer grösser als a ist, so dass G alle Punkte x enthält, in
denen | f(x) | < a ist (aber auch noch andere Punkte). Dies ist
nach §. 34, IV dadurch möglich, dass wir vom Nullpunkte als
Mittelpunkt einen die Punkte «, ßv ß2 . . . /3n_i einschliessenden
Kreis (B) von hinlänglich grossem Radius B legen und die Punkte
ßi, j32 . . . ßn-i, in denen \f(x) | ja grösser als a ist, durch
kreisförmige Hüllen von so kleinen, aber nicht verschwindenden
Radien q1, q2 . . . pn_1 von diesem Kreise ausscheiden, dass im
Inneren aller dieser Kreise (p^, (p2) ... (p„_i) der absolute Werth
|/(«) | grösser als a bleibt (§. 34, V). Dann umschliesst keiner
pj„ 3 dieser Kreise den Punkt
k, in dem | f(x) \ = a
ist. Das von den Kreisen
(B), (Pl) • • • (P»-i) be-
grenzte zusammenhän-
zusammenhängende Flächenstück ist
das Gebiet O.
Wir bestimmen nun
eine Zahlenreibe
05, 06', «", 06'" . . .
derart, dass die absoluten
Werthe von /(«), /(«'),
/(oc") . . ., die wir mit
a, a', a", a'" . . .
bezeichnen, immer ab-
abnehmen. Die so bestimmten Punkte a, oc', a," bleiben alle im
Inneren des Gebietes G, weil ja in ihnen \f(x) | < a ist.
Wir bedienen uns dazu eines Verfahrens, ganz ähnlich dem
zum Beweis des Satzes 5, §. 41 angewandten, nur dadurch verein-
vereinfacht, dass /'(«) schon von Null verschieden ist. Wir setzen,
indem wir unter 8 einen noch näher zu bestimmenden, positiven,
echten Bruch verstehen, in der Entwickelung

§. 42. Die Wurzeln algebraischer Gleichungen. 145
F) /(« + A) =/(«) + A/'(«) + |7"(«) + • • •
und erhalten
/'(«)» 3 /'(«K
Nun ist nach B)
/'(«) = n(a - ßL) (a — ßa) ...(« — /?„_,),
also, wenn wir die absoluten Werthe von (« — ft), (« — ßz) ¦ • •
{« — /3«_i) durch y1} r2 . . . rn-x bezeichnen,
|/'(«) | = w »i r2 . . . r«—i-
Da nun « ausserhalb des um jSi beschriebenen Kreises qx
liegt, so ist rx > pj, und ebenso r2 > q2 • • •) und folglich
also | /' («) | grösser als eine von der Lage von « innerhalb O
unabhängige positive Zahl Tc. Daraus ergiebt sich, dass man eine
hinlänglich grosse positive Zahl Q, die gleichfalls von der Lage
von a und von dem echten Bruch 8 unabhängig ist, so wählen
kann, dass
j \y*) J \ /
und dass zugleich
Q>i
ist. Man kann Q erhalten, wenn man auf der linken Seite
von (9) in den Nennern /'(«) durch Ä, 8 durch 1, sonst alle
Glieder durch ihre absoluten Werthe, endlich den absoluten
Werth von a, durch den grössten Werth R ersetzt, und die so
gewonnene Zahl, wenn nöthig, noch bis über 1 und sonst noch
beliebig vergrössert. Dann ergiebt sich aber aus (8), wenn
A0) a+A = «1, \f(u)\ = a, 1/@1I = 0!
gesetzt wird,
Setzt man hierin und in G), was gestattet ist, 8 = 1 : Q,
so folgt
Weber, Algebra. I. in

146 Dritter Abschnitt. .§. 42.
A2) al<
Wir leiten nun durch dasselbe Verfahren aus k1: Oj ein
zweites Grössensystem oc2, a2 ab, dann aus «2, % ein drittes,
e%, as, u. s. f. und erhalten so für die Reihe abnehmender posi-
positiver Zahlen a, a15 a2, «s • • • die Umgleichungen
A3) % < a ®, a2 < «i © • • . a» < «»-i ©>
worin
ein positiver echter Bruch ist. Aus A3) folgt aber durch Multi-
plication
av < a&v
und daraus
A4) Lim a, = 0.
Nun ergiebt sich aus A1) und A2)
woraus für jeden Index v
/¦ie\ I , 2(«v Uv+i)
A5) |«v — es,+1 | < -i jg ^-;<
Nun ist, da der absolute Werth einer Summe kleiner ist, als
die Summe der absoluten Werthe, für irgend zwei Indices (t, v,
deren erster der kleinere ist, nach A5)
| dp — a, | < | o«^ — «vi-! | -f" I «H-i — af«+2 I -\ \~ I «»-i —«v |
2 2 2
< j («/* — «f+0 + j K+i — «f+a) H h j (a"-1 ~ a-)
und daraus
A6) K-M<^^
und mit Hülfe von A4)
Lim | «j, — o» | = 0,
wenn jt und v unbegrenzt wachsen.
Damit ist ausgedrückt (nach dem in der Einleitung erklärten
Begriff der Zahlenreihe, S. 17), dass sich die Zahlen «, c^, «2 ...
einer bestimmten Grenze nähern, die wir mit f bezeichnen wollen.

§. 43. Zahlenwerthe ganzer Functionen. 147
Aus der Stetigkeit der Function / (x) folgt aber dann leicht,
dass /(£) =0 sein muss; denn wäre | /(§) | > 0, so könnten,
da die «w dem Werthe § beliebig nahe kommen, die absoluten
Werthe aW von /(«<*>) nicht unter jeden positiven Werth herunter-
heruntersinken, was wir doch von ihnen nachgewiesen haben.
§. 43.
Zahlenwerthe ganzer .Functionen.
Aus dem Fundamentalsatz von der Wurzelexistenz ergeben
sich einige Sätze über die numerischen Werthe ganzer Functionen,
die, so einfach sie sind, doch besonders hervorgehoben werden
müssen:
1. Sind ®j (x, y,e.. .), #2 («, y, e ...), ®8 0, y,z ...),..
ganze Functionen der Veränderlichen x, y, z . . .
mit numerischen Coefficienten, die in keiner der
Functionen alle zugleich verschwinden, so kann
man für die Veränderlichen auf unendlich viele
Arten solche Zahlenwerthe setzen, dass keine
der Functionen ®j, #2, <DS . . . verschwindet.
Der Satz ist zunächst evident, wenn die Functionen 3>j, 3>2,
<P3 . . . nur von einer Variablen abhängen; denn dann giebt es
überhaupt nur eine endliche Anzahl von Zahlwerthen für diese
Veränderliche, die eine dieser Functionen zum Verschwinden
bringen.
Dann aber können wir die Kichtigkeit des Satzes für
Functionen von n -j- 1 Veränderlichen leicht einsehen, falls wir
ihn für Functionen von n Veränderlichen als erwiesen betrachten.
Denn ordnen wir die Functionen nach der (n -)- l)ten Veränder-
Veränderlichen t, so können wir für die übrigen n Veränderlichen nach
Voraussetzung solche Werthe setzen, dass in keiner der Func-
Functionen die Coefficienten aller Potenzen von t verschwinden; dann
haben wir Functionen der einen Veränderlichen t und können
für diese einen solchen Werth setzen, dass keine der Functionen
verschwindet. Damit ist der Satz bewiesen, und man sieht, dass
er auch noch richtig bleibt, wenn für die absoluten Werthe der
Zahlen, die für die Variablen zu setzen sind, beliebige obere
Grenzen festgesetzt sind, oder wenn gefordert wird, dass nur
rationale Zahlen für die Variablen zu setzen seien.
10*

148 Dritter Abschnitt. §• 44
2. Haben keine zwei der Functionen &1: <&2, 03 ¦ ¦ ¦
einen gemeinschaftlichen Factor (§. 20), so kann
man für die Variablen solche Werthe setzen, dass
eine dieser Functionen, die nicht eine Constante
ist, verschwindet, während die übrigen von Null
verschiedene Werthe erhalten.
Um diesen Satz zu beweisen, nehme man an, es sei t eine
der Variablen, die in (Pj wirklich vorkommt. Dann kann man
für jede Funktion ®* aus der Reihe ®2, <P8 . . . nach dem Algo-
Algorithmus des grössten gemeinschaftlichen Theilers die ganzen
Functionen ©,-, <&, X{, deren keine identisch Null ist, so be-
bestimmen, dass
A) BiVi + %*! = Xt
wird [§. 20, D)], dass X» von t unabhängig und nur von den
übrigen Variablen x, y '. . . abhängig ist Nun setze man für die
letzteren Variablen x, y . . . solche Werthe (nach dem Satze 1.),
dass alle Functionen X{ von Null verschieden sind, und dass. Ot
nicht von t frei wird, sondern in eine Function f(t) übergeht.
Endlich setze man für t eine Wurzel der Gleichung f(t) = 0.
Dann verschwindet ®l5 während nach A) keine der Functionen
G>i verschwinden kann. Dies aber fordert der Satz 2.
§. 44.
Stetigkeit der Wurzeln.
Wir beschliessen diesen Abschnitt mit dem Beweis des Satzes:
Die Wurzeln einer algebraischen Gleichung
sind stetige Functionen der Coefficienten.
Wir haben zunächst die Bedeutung dieses Satzes zu erklären.
Es sei
A) f(x) ~xn~\-al x»-1 -{- a2 xn~2 ~\
eine ganze rationale Function von x vom nten Grade. Nach dem,
was in den vorangegangenen Paragraphen bewiesen ist, lässt sich
f(x) in n lineare Factoren zerlegen, die zum Theil einander
gleich sein können. Wir setzen, indem wir gleiche Factoren zu-
zusammenfassen und die Wurzeln mit k, ß, y . . . bezeichnen,
B) f{x) = {x- af (x - ßf (x - yf . . ,
worin a, b, c . . , ganze positive Zahlen sind, deren Summe
gleich n ist.

§• 44.
Stetigkeit der Wurzeln.
149
Die Wurzeln a, ß, y . . . werden sich mit den Coefficienten
«i, «2, «s •'• • ändern, auch der Grad ihrer Vielfachheit kann ein
anderer werden.
Wir bezeichnen die Aenderungen von au a2 • • . mit eu £2 ...
und setzen
C) 9>(s) = eia;-i +6, ««-* + ...
Wir umgeben die Punkte a, ß, y . . . mit Gebieten von
beliebiger Kleinheit, jedoch so, dass diese Gebiete sich gegen-
gegenseitig ausschliessen, etwa dadurch, dass wir die Punkte k, ß, y ...
durch Kreisperipherien mit den Radien p, g', q" . . . einschliessen,
und bezeichnen diese Gebiete durch (g), (gr), (g") . . .
Wenn die absoluten Werthe von s1, e2 • • • unter hinläng-
hinlänglich kleinen Werthen liegen, so können wir von der Function
/i (x) zunächst beweisen,
dass sie keine Wurzeln ausserhalb der Gebiete
(P), (?'), (9") ¦ ¦ • hat,
und zweitens,
dass die Anzahl der Wurzeln von fi(x) inner-
innerhalb (g) genau a, innerhalb (q') genau b, inner-
innerhalb (q") genau c u. s. f. beträgt.
Bei dem letzten Theil des Satzes ist aber zu beachten,
dass, wenn fi(%) mehrfache Wurzeln hat, diese nach ihrer
Vielfachheit gezählt werden müssen.
Fig. 4. Wir construiren nach §. 34, IV
in der Ebene x einen Kreis mit
dem Radius H und dem Null-
Nullpunkt als Mittelpunkt, der die
Gebiete (q) , (gJ), (g"). . . ein-
schliesst, so dass ausserhalb dieses
Kreises keine Wurzeln von /t (x)
mehr liegen, und bezeichnen das
innerhalb dieses Kreises, aber
ausserhalb (g), (g1), (g") . . .
liegende Gebiet mit Gr. Es ist
dazu noch zu bemerken, dass B
von den «l5 s2 . . . unabhängig
angenommen werden kann, so lange für die absoluten Werthe
dieser Grossen eine bestimmte obere Grenze festgesetzt wird.

150 Dritter Abschnitt. §. 44.
Ist nun x ein Punkt des Gebietes Cf, so ist der absolute
Werth von x — « grösser als q, der von x — ß grösser als
q', u. s. f., und mithin nach B)
E) \f(x)\>(f'^Q"':..
Ist nun «i eine Wurzel von /j (x), so folgt aus D)
F) /(k1) = — <p («j),
und «j kann daher nicht in dem Gebiete G liegen, wenn man
dafür sorgt, dass innerhalb Q überall
G) \<p(x)\<9°<>'* <,'"...,
was durch genügende Verkleinerung der oberen Grenze von «x, £2 • •.
immer möglich ist. Hiermit ist der erste Theil unserer Behauptung
erwiesen, dass, wenn die Ungleichung G) befriedigt ist, keine
Wurzeln von fr (x) ausserhalb der Gebiete (q), (q1), (q") ... liegen.
Um den zweiten Theil zu beweisen, setzen wir
(8) /(*)¦=?(«)(*-«)•,
(9) t(x) = (x- ßf(x — yy...
Wir wählen nun eine positive Zahl A, die aber von q un-
unabhängig sein soll, so dass, so lange x im Inneren oder an der
Peripherie des Gebietes (p) liegt,
A0) | 1>(x) \>A, (für | x — « | ^ 9)
bleibt. Eine solche Zahl erhalten wir z. B., wenn wir l gleich
der Hälfte des kleinsten unter den Abständen (es, ß), (a, y) .. .
annehmen und
setzen; dann ist die in A0) ausgedrückte Forderung wenigstens
so länge erfüllt, als q kleiner als l ist. Ist nur ein einziger
Punkt a vorhanden, so ist ip (x) = 1 zu setzen, und für A kann
jeder beliebige echte Bruch gesetzt werden.
Es seien nun c^, «2 • • • die Wurzeln von fr (x)' innerhalb
(q), und %, % ... die Grade ihrer Vielfachheit, und ßr, ß2 . ¦ .,
bx, 63 • • •> 7\i 7i • • •¦> Ci) c2 . . • sollen dieselbe Bedeutung für die
Gebiete (q'), (q") . . . haben; es ist dann
A1) n = «!-)- a2 -\ 1- &! + b2 + • • • + Ci + c2 -\ ,
da die Gesammtzahl aller Wurzeln gleich n sein muss. Die
Function fx (x) lässt sieh dann so darstellen:
A2) fx (x) = ^ {x) (x — uCfi (x - «,)«« . . .,

§. 44 Stetigkeit der Wurzeln. 151
worin
A3) ft (x) = (x — ß^ (x - ß,)h . . .
Nun können wir eine von q, q', q" unabhängige positive
Zahl B bestimmen, so dass, so lange x innerhalb oder an der
Grenze von (q) bleibt
A4) \1>1(x)\<B (für | x — u [ ^ q).
Wir können z. B. eine Grosse L wählen, die grösser ist als
die doppelte Entfernung des Punktes k von einem der Punkte
ß, y . . . und jedenfalls grösser als 1 und dann
.B> Ln
annehmen.
Nun folgt aus D)
A5) l/(*)l<l/i(*)l + l9>(*)|,
also nach (8) und A2)
A6) \t(x)\.\x — K\a<\ip1(x)\.\x~(xl\ai.\x — (x2\^...-\-\^(x)\,
und wenn wir nun «auf der Peripherie von (q) annehmen, also
| x — a | = q
setzen, so ist
\ x — «j | < 2 p, \ x — ctg | < 2 p . . .
folglich nach A0) und A6)
A7) (fA<B(fy*+*+—B + | <p(x) |.
Wir wollen nun die oberen Grenzen für die Coefficienten
£1( a2 • • • von (p so klein annehmen, dass
| <p(x) | <(pA'
wird, worin A' eine Zahl bedeutet, die kleiner als A ist; dann
folgt aus A7)
A8) A — A' < 2ai + n2 + --- p-«+«i+««+--- B.
Dies aber würde für ein hinreichend kleines p nicht mehr
möglich sein, wenn a grösser als die Summe «j -J- a2 -(-•••
wäre. Es folgt also
A9) a 5! % + a2 H •
Ebenso lässt sich beweisen, dass
i> ^ 61 + h H
B0) c ^ Cl + c2 H
sein muss. Da aber die Summen der linken Seiten sowohl als

152 Dritter Abschnitt. §: 44.
der rechten in den Ungleichungen B0), B1) gleich n sein
müssen, so können nur die Gleichheitszeichen bestehen, also:
a = ax -f- a2 -(-•••
¦ ' 6^6!+ 6, + ...
C = Ci -f- C2 -f- •.- •
wodurch auch der zweite Theil unseres Satzes bewiesen ist.
Wir wollen dem bewiesenen Satze noch folgende, auf den
Fall mehrfacher Wurzeln bezügliche Bemerkung beifügen.
Die nothwendige und hinreichende Bedingung dafür, dass
f(x) = 0 überhaupt mehrfache Wurzeln habe, ist die, dass f(x)
und f'(x) einen gemeinsamen Factor haben. Wenn man also
nach den im ersten Abschnitt entwickelten Principien den Algo-
Algorithmus des grössten gemeinsamen Theilers auf diese beiden
Functionen anwendet, so erhält man die Bedingung gemeinsamer
Factoren daraus, dass man den letzten constanten Rest gleich
Null setzt, in Gestalt einer Gleichung zwischen den Coefficienten:
F(a1, aa...a„) — 0,
worin F eine ganze rationale Function der Argumente al5 a2.... a„
ist, die die Discriminante von/heisst, deren Eigenschaften
und Bildungsweise im nächsten Abschnitt noch eingehender
behandelt werden soll; jedenfalls kann, da es überhaupt Glei-
Gleichungen »ten Grades ohne mehrfache Wurzeln giebt, F nicht
identisch verschwinden.
Betrachten wir also jetzt
F(at -)-<¦!, a2 -\- b2 ... a„ -f- £„),
so wird auch diese Function, wenn die «], «2 • • • an bestimmte,
die £lt s2 • • • £» aber unbestimmte Zahlen sind, nicht identisch
verschwinden,. und man kann über die s so verfügen, dass ihr
Werth von Null verschieden ausfällt, auch dann noch, wenn
für die absoluten Werthe der 6 eine beliebige obere Grenze
festgesetzt ist (§. 43).
Man sieht also aus. diesen Betrachtungen, wie eine a-fache
Wurzel k von f(x) bei stetiger Veränderung der Coefficienten in
a einfache Wurzeln aus einander strahlt, so dass man auch von
diesem Gesichtspunkte berechtigt ist, die «-fache Wurzel als
durch das Zusammenfallen von a einfachen Wurzeln entstanden
zu betrachten.

§. 44. Stetigkeit der Wurzeln. 153
Nehmen wir den Coefficienten der höchsten Potenz von x
nicht gleich 1 an, untersuchen also die Gleichung in der Form
B1) . aoxn -\- «!x"-1 -\- a2x»-2 -\- ¦ • • + an-xx -\- an = 0,
so sind, wenn an = 0 ist, eine oder mehrere der Wurzeln gleich
Null, und die Gleichung B1) lässt sich durch x oder eine höhere
Potenz von x dividiren, wodurch eine Gleichung von entsprechend
niedrigerem Grade entsteht, in der das letzte Glied von Null ver-
verschieden ist. Wir wollen also von vornherein a„ von Null ver-
verschieden annehmen und nun in B1)
B2) x = -
y
setzen. Durch Multiplication mit yn und Division mit a„ geht
dann B1) über in
B3) VnJr~- T-1 + --- + t-» + 7L = °»
an a„ an
und wir können auf die Wurzeln dieser Gleichung den vorhin
ausgesprochenen Satz anwenden, indem wir a0 = 0 annehmen,
so dass eine der Wurzeln von B3) verschwindet. Wir erlangen
so den Satz:
Man kann in der Gleichung B1) a0 so klein annehmen, dass
eine ihrer Wurzeln über alle Grenzen gross wird, während die
anderen sich beliebig wenig von den Wurzeln der Gleichung
(n — l)ten Grades
% x"-1 -\- a2 %"~2 -\~ • • • -j- o-n-\ x -\- an = 0
unterscheiden.
Man drückt das auch so aus, dass mit verschwinden-
verschwindendem öf0 eine der Wurzeln von B1) unendlich wird.
Wenn auch noch aY oder aY und a2 verschwinden, so werden
zwei oder, drei Wurzeln unendlich u. s. f.
Es rechtfertigt sich hierdurch der bisweilen gebrauchte
Ausdruck, dass eine Gleichung wten Grades durch Unendlichwerden
einer Wurzel in eine Gleichung (n — l)ten Grades übergehe.

Vierter Abschnitt.
Symmetrische Functionen.
§. 45.
Begriff der symmetrischen Functionen.
Symmetrische Grundfunctionen.
Wir betrachten in diesem Abschnitt ganze Functionen
beliebigen Grades von einer beliebigen Anzahl, n, von Veränder-
Veränderlichen
«i, a2 ... an.
Eine solche Function heisst symmetrisch, wenn sie
ungeändert bleibt, wenn die Variablen aL, k2 . . . an
einer beliebigen Permutation unterworfen werden,
und solche symmetrische Functionen sind es, deren Eigenschaften
und Bildungsgesetze wir jetzt genauer kennen lernen müssen.
Damit eine Function *&(<*!, a2 .. . ey) symmetrisch sei, ist es
genügend, dass sie sich bei der Vertauschung von je zweien der
Argumente a15 o^ . . . an nicht ändere, weil nach §. 21 alle
Permutationen durch eine Keihe von Transpositionen gebildet
werden können.
Die Function <& wird im Allgemeinen nicht homogen sein,
sondern Glieder verschiedener Dimension enthalten; wenn man
aber alle Glieder gleicher Dimension zusammenfasst, so lässt
sich jedes 0 durch eine Summe homogener Functionen ver-
verschiedener Grade darstellen, und wenn <& symmetrisch sein soll,
so muss jeder homogene Bestandtheil eines bestimmten Grades
für sich symmetrisch sein, da durch die Permutationen der
Variablen die Dimensionen der Glieder nicht geändert werden.

§. 45. Symmetrische Grundfunction. 155
Wir können uns hiernach auf die Betrachtung homogener,
symmetrischer Functionen beschränken, aus denen alle
anderen sich zusammensetzen lassen.
Hiernach ist es leicht, die allgemeine Form einer symme-
symmetrischen Function anzugeben. Wir erhalten sie, wenn wir in
einem Gliede einer solchen Function
(ähnlich wie bei der Bildung der Determinanten) die unteren
Indices auf alle mögliche Art permutiren und die Summe aller so
gebildeten Glieder nehmen. Eine solche Function können wir einen
Elementarbestandtheil einer symmetrischen Function nennen.
Nehmen wir mehrere solche Elementarbestandtheile, multipliciren
sie mit beliebigen, von den a unabhängigen Factoren und
addiren sie, so erhalten wir die allgemeinste symmetrische Func-
Function. Die Anzahl der Glieder eines dieser Elementarbestand-
Elementarbestandtheile ist, wenn die Exponenten vx, v2 . . . vn alle von einander
verschieden sind, II(n); wenn aber ein und derselbe Exponent v
mehrmals vorkommt, so hat man die Permutationen, die keine
verschiedenen Glieder geben, wegzulassen. Es ist z. B. bei drei
Veränderlichen, wenn vL, v2, v3 verschieden sind, ein Elementar-
Elementarbestandtheil :
wenn aber v3 = v% ist
«n a»s «j» -f- «ji«»«etj« -f- «n «j-s«»«.
Das einfachste Beispiel einer symmetrischen Function ist die
Summe der Variablen
«l + «! + «H h «n-
Ebenso gehört das Product «j, a.2 . . . an dazu.
Diese beiden sind die extremen Fälle einer Keine von sym-
symmetrischen Functionen, die wir die symmetrischen Grund-
functionen nennen und folgendermaassen erhalten.
Das Product
A) f(x) = {x — «,) (x — k.2) . . . (x — «„)
ist, was auch x sein mag, wenn nur x von den et, unabhängig
ist, eine symmetrische Function von et,, <% , . . an. Wenn wir
also die Multiplication der einzelnen Factoren ausfuhren und

156 Vierter Abschnitt. §. 46.
nach Potenzen von x ordnen, so sind die Coefficienten der ein-
einzelnen Potenzen von x gleichfalls symmetrische Functionen. Denn
sie ändern sich bei der Vertauschung der u ebenso wenig wie
die Function f(x), Wir setzen
B) f{x) = x" -\- a^-1 -\- a^x«-2 -| f- an^x -\- an.
Die Functionen au a2 . . . an sind die Coefficienten der alge-
algebraischen Gleichung, deren Wurzeln «l5 a2 . . . an sind. Sie
werden die symmetrischen Grundfunctionen genannt.
Diese symmetrischen Grundfunctionen haben wir schon im §. 7
gebildet; es ist, wie wir uns erinnern, ax die mit negativem
Zeichen genommene Summe der a, a2 die Summe der Producte
zu zweien, a% die mit negativem Zeichen genommene Summe der
Producte zu dreien u. s. f., endlich an das Product sämmtlicher
«, mit positivem oder negativem Zeichen, je nachdem n gerade
oder ungerade ist. Wir setzen abkürzend
aL = — 2 «i
«2 = + 2 ««1 ««2
C) a% = — 2 ««i «2 «3
Das Ziel unserer Betrachtungen ist der Beweis des Haupt-
Hauptsatzes, dass sich alle symmetrischen Functionen der et
rational durch die Grundfunctionen ausdrücken lassen.
§. 46.
Die Potenzsummen.
Wir beschäftigen uns zunächst mit einer anderen speciellen
Art symmetrischer Functionen, den Potenzsummen. Bedeutet
nämlich v irgend einen ganzzahligen positiven Exponenten, so gehört
(i) Sr = < + «; + • • • + *:
offenbar zu den symmetrischen Functionen, und sr wird die
vu Potenzsumme genannt. Wir wollen Formeln ableiten, nach
denen die Potenzstimmen durch die Grundfunctionen ausdrück-
ausdrückbar sind.
Wir bezeichnen in der Folge immer, wenn <p (x) irgend eine
Function von x ist, mit

§. 46. Potenzsummen. 157
die Summe, die wir erhalten, wenn x in q>(x) durch jede der
Variablen au a2 . . . an ersetzt und die so gebildeten Functionen
addirt werden, also
S[q>(et)] = (p («x) + (p(et,,) -\ \- (p («„).
Hiernach ist z. B.
5 (es») = s, ¦
die vte Potenzsumme.
Wir dividiren nun/(a;) nach §. 4 durch eine beliebige lineare
Function x — a und erhalten
worin [§. 4, (8)]:
/i («) = « + «i
g («) =:«¦! + «!« + a2
C) /3 («) = «3 -(- ax et2 -)- a2« -|- a3
3 -^ \- an^.
Wir setzen in B) für a jede der Grossen «„ «a . . . es», wo-
wodurch /(«) = 0 wird und bilden die Summe S.
Die linke Seite ergiebt dann nach §. 14, A1)
+ (» — l)«!^-2 -f- (w — 2)a2a^-3 + • • • + «n-i,
während die rechte Seite
E) »*-* + «-«SQ/i(«)] + «-^-SfQ/iC«)] ^ h S[/-i(«)]
wird, und die Vergleichung der Coefficienten gleicher Potenzen
Ton x in D) und E) ergiebt
«)] =(»-2)o,
Es ist aber nach A) und C)
S„_2 -4-

158 Vierter Abschnitt. §. 46.
und demnach erhält man aus F) das folgende von Newton
herrührende Formelsystem*):
0 = Si + «i
0 = s2 + % Si + 2 a2
G) 0 = s3 -+- % s2 + a2 sx -+- 3 Oj
0 = S„_2 -j- «x S„_2 + % S»-8 H h (» — 1) «»-!•
Dies Formelsystem lässt sich aber noch weiter fortsetzen;
denn da
«[/(«)] = 0, S [«/(«)] = 0, S [««/(«)] = 0...
ist, so folgt
0 = «n + «1 S«-l +
0 = s„+1 -\- axsn -f
0 = s„+2 + «i sn+i + «2s„ + • • • + «»
Durch die Formeln G), (8) ist nun die Aufgabe gelöst, der
Reihe nach die Functionen sL, s2, s3 . . . bis zu beliebiger Höhe
als ganze rationale Functionen der symmetrischen Grund-
functionen darzustellen, z. B.:
Sl == — eh.
s2 = -j- a\ — 2 a2
(9) s3 = — al -f- 3 «i a2 — 3 %
s4 = + ai — 4 af a2 + 4 <h <h + 2 a| — 4 a4
••.....••5
und die Bildungsweise dieser Ausdrücke zeigt, dase die Coeffi-
cienten in diesen Darstellungen ganze Zahlen sind.
Man kann auch umgekehrt mittelst der Formeln G) und (8)
die symmetrischen Grundfunctionen au a2, % . . . rational durch
die Potenzsummen s^, s2, s3 . . . ausdrücken. Diese Darstellung
ist aber insofern weit weniger einfach, als die Coefficienten nicht
ganze, sondern gebrochene Zahlen sind, z. B.
(*! = — $!
A0) 2 a2 = + sl — s2
6a8 = — sf -+- 3sxS2 — 2s3
') Newton, Arithmetica universalis, edit. s'Gravesande, p. 592.

§. 46. Potenzsummen. • 159
Man kann das Formelsystem (8) auch nach der entgegen-
entgegengesetzten Kichtung fortsetzen, wenn man die Gleichungen
8 [«-1 /(«)] = 0, 8 K2 /(«)] = 0 . . .
bildet. Man erhält dadurch ein Mittel, um die Potenzsummen
Sv auch für negative Exponenten v durch die Grundfunctionen
auszudrücken. Diese Summen der negativen Potenzen gehören
gleichfalls zu den symmetrischen Functionen, wenn auch nicht
mehr zu den ganzen, sondern zu den gebrochenen. Sie
gehen erst durch Multiplication mit Potenzen des Productes
aL a2 . . . an in ganze Functionen über. Der Vollständigkeit wegen
setzen wir die zwei ersten dieser Formeln hierher:
0 = s„_i + <hsn_2 -f- a2s„_3 -f- • • • -f- »«„-i -j- ans_i
0 = s„_2 + «! s„_3 -f- «2 s*-i + * h «n-i«-i + a»s_3,
die sich nach G) auch so darstellen lassen:
«„_! + a„s_! = 0, 2 a„_2 + a„_iS_i + a„s-2 = 0.
Die in §. 15 abgeleiteten Formeln (9) und A0) ergeben für
die Functionen /„ die später anzuwendenden Relationen
8 4rr = 0 v = 0, 1, 2 ...» - 1
A2) '»
O /n-l(«) _ !
/'(«) "~
Im §. 4 haben wir für die Functionen fv{x) bereits die
Relation kennen gelernt:
fv (x) — xfv-i (x) = ar.
Daraus ergiebt sich
und daraus nach §.15 (9), so lange fi < n ist,
Dies führt aber mit Hülfe von A2) zu dem Satze
= 1 [i -\- v = n — 1,
der für jedes v gültig ist, so lange ft < n ist.
Diese Formeln bleiben auch dann noch richtig, wenn der
Coefficient der höchsten Potenz von x in f(x) nicht gleich 1 ist,
wenn also

160 Vierter Abschnitt. §. 47.
f(x) = a0 x" -)- «! a;"-1 4 ••• + «»»
und
A4) fr(x) = aox^-\-a1x^-] \-av
gesetzt ist.
§. 47.
Beweis des Hauptsatzes für zwei Variable.
Wir gehen nunmehr zum Beweis des Fundamentalsatzes der
Theorie der symmetrischen Functionen über, dass sie alle rational
durch die symmetrischen Grundfunctionen ausdrückbar sind. Da
wir die Yollständige Induction als Beweismittel anwenden, so
leiten wir den Satz zunächst unter der Voraussetzung ab, dass
nur zwei unabhängige Veränderliche a, ß gegeben seien, aber auf
einem Wege, der zugleich für den allgemeinen Beweis den leiten-
leitenden Gedanken hervortreten lassen wird.
Wir bezeichnen die symmetrischen Grundfunctionen mit
A) a = _(a + /3), b = aß
und setzen demgemäss
B) f(x) = (x — a) (x — ß) = x* -f ax -\- b.
Es sei nun S(a, ß) irgend eine ganze rationale und sym-
symmetrische Function von a und ß. Wir können für ß aus A) den
Werth — (a -\- a) einsetzen und erhalten, wenn wir nach Po-
Potenzen von k ordnen,
C) S(a, ß) = S(a, — a — a) = A0ot,m -\- Äxa™-1
-\ -f- A>-i<« + Am
worin die Coefficienten Ao, Ax . . . Am nur von a und von den
in 8 etwa noch vorkommenden Coefficienten abhängen. Wir
bemerken aber ausdrücklich, dass, wenn in S(a, ß) keine ge-
gebrochenen , Zahlencoefficienten vorkommen, auch in den Coeffi-
Coefficienten Ai A • • • A» keine Brüche auftreten.
Wir setzen nun
D) ®(x) = A^m + Ao1"-1 H h Am-ix -\- An,
dividiren 9(x) durch f(x) (nach §. 3) und erhalten einen Quo-
Quotienten Q und einen Rest, der in Bezug auf x höchstens vom
ersten Grade ist, also:
E) O(x)=

§. 48. Allgemeiner Beweis des Hauptsatzes. 161
hierin sind .nun A und B ganze Functionen von a und b, und
auch sie enthalten keinerlei gebrochene Zahlencoefficienten,
wenn in S keine solche vorkommen. Wenn wir nun x = a
setzen, so ergiebt sich aus E) und C), da f(a) verschwindet,
F) 8(u,ß) = A-\-B«.
Da aber S(cc, ß) und ebenso A, B symmetrisch sind, so folgt
durch Vertauschung von a und ß
G) 8(a,ß) = A + Bß.
Hieraus schliesst man, da « und ß von einander unab-
unabhängige Variable sind, dass B = 0 und folglich
(8) <8(«, ß) = A
sein muss, womit der Fundamentalsatz für diesen Fall bewiesen ist.
§• 48.
Allgemeiner Beweis des Hauptsatzes.
Wir setzen nun voraus, der Fundamentalsatz sei bewiesen
für symmetrische Functionen von n — 1 Veränderlichen und
leiten ihn durch ein Verfahren, was dem in §. 47 angewandten
ganz analog ist, für n Variable her.
Es sei wieder
A) S = £(«!, «2 ...«„) ,
eine ganze symmetrische Function der n Veränderlichen «l5 a2... &,„.
Wenn wir sie nach Potenzen von c^ ordnen und demgemäss
setzen
B) 8 = So < + S1 ««-1 -| h <Vi«! + 8»
so sind die Coefficienten <S0, St . . . /Su ganze symmetrische
Functionen der n — 1 Veränderlichen «2, . . . «„.
Bezeichnen wir die symmetrischen Grundfunctionen dieser
letzteren Variablen mit %, d% . . . ö4_i, so können wir die Coeffi-
Coefficienten $o, $i ... S^ nach unserer Voraussetzung rational durch
diese ausdrücken. Es ist aber nach §. 46, B) und C)
a'i = /i (ph) — <*i + «i
«2 =/2 («0 = «i2 + «i «l + «2
«3 — /3 Ol) = «1 + «1 «l2 + «2 «1 + %
Weber, Algebra. I.

162 Vierter Abschnitt. §. 48.
d. h. die Coefficienten Sai ^ ... S,, können ganz und rational
durch c«!, «!, a% . . . an ausgedrückt werden. Wenn wir also,
nachdem diese Ausdrücke eingeführt sind, in B) aufs Neue nach
Potenzen von ax ordnen, so erhalten wir
C) S = Äo «j» + Al «»-1 -\ (- A.-1 «i + Äm,
worin im Allgemeinen m ein von ft verschiedener Exponent sein
wird, und die Coefficienten Ao, ,A1 . . . Am ganz und rational von
al5 %...«„ abhängen. Wir setzen wieder
D) ®(x) = Aoaf-\- ALcc»>-i -j 1- Am-iX + A„
und dividiren <&(x) durch
f(x) = xn -\- a,! x"-1 -f- cr2 ^»-2 -)- • • • + an
= (x — «j) (a; — «2) . . . (x — «„).
Es ergiebt sich ein Quotient und ein Best, der in Bezug
auf x höchstens vom Grade n — 1 ist. Wir setzen also
E) ®(x)=Qf(x)-\-ip(x)
F) 10) = Co x»-i + d*«-• H [. Cn^x + CUx,
und hierin sind Co, Cj . . . (?„_! ganze rationale Functionen von
«d a2 • • • am in denen, wenn Ä in seiner ursprünglichen Form
keine gebrochenen Coefficienten enthält, auch keine Brüche vor-
vorkommen.
Nun ist aber, da /(aj) verschwindet, und S — i&fa) ist,
nach E)
G) S=*(«i)
und hierin kann, da S symmetrisch ist, at durch a2, «ä . . . ccn
ersetzt werden. Hieraus ergeben sich die folgenden n Glei-
Gleichungen :
c0«j-i + c,«r2 H h <^«-2«i + (c*-! - iS) = 0
ci «r2 H h <^»-2«2 + (c»_i - s) = 0
«r1
Co «T1 + Ci <~2 H h ^»-2«n + (C_x - S) = 0.
Betrachten wir dies System als ein System homogener
linearer Gleichungen mit den n Unbekannten
Gf,, Ci ... Gn—2i Cn—X — S,
so ist seine Determinante

49. Zweiter Beweis des Hauptsatzes. 163
die nach §. 25, Formel A2) gleich dem Product aller Differenzen
«1 — «25 «i — «3 • • • ist, von Null verschieden, und folglich ist
nach dem Satz II. in §. 27:
Go = 0, d = 0 . . . GM-2 = 0
und
(9) S=O-i,
worin der zu beweisende Fundamentalsatz enthalten ist.
Zu demselben Resultat gelangt man auch durch den Satz II,
§. 33; denn da die Function (n — l)ten Grades von a;
Q /y.n—1 _|_ Q <ri—2 _|_ . . . _1_ Q x —I— C S
für x = «i, «2 . . . an, also für mehr als w — 1 Werthe ver-
verschwindet, so müssen ihre Coefficienten alle Null sein.
Der Beweis, den wir hier für das Fundamentaltheorem im
Anschluss an Cauchy1) gegeben haben, bietet zugleich ein
Mittel, in besonderen Fällen den Ausdruck einer symmetrischen
Function durch die Grundfunctionen wirklich zu berechnen.
Dieselbe Möglichkeit bieten auch die anderen Beweise, die für
das Theorem bekannt sind. Wir wollen noch einen zweiten
Beweis hier mittheilen, der zu einer oft einfacheren Berechnungs-
Berechnungsart führt2).
§. 49.
Zweiter Beweis des Satzes von den symmetrischen
Functionen.
Es sei S eine ganze symmetrische Function der Variablen
«i, «2 • • • «m- Die einzelnen Glieder dieser Function sind alle
von der Form
') Cauchy, Exercices de mathematiques, 4^m« annee.
2) Waring, Meditationes algebraicae. Gauss, Demonstratio nova
altera theorematis omnem functionem algebraicam rationalem integram
unius variabilis in factores reales primi vel secundi gradus resolvi posse.
Werke, Bd. III, S. 36.
11*

164 • Vierter Abschnitt. §. 49.
Map a\* . . . «*",
worin M ein von- den « unabhängiger Coefficient ist. Diese
Glieder sollen nun in bestimmter Weise angeordnet werden. Es
soll, nachdem die Reihenfolge der Variablen u1, «2 . . . «„ fest-
festgesetzt ist, von zwei Gliedern
A = Map al* . . . an, AI = M' <'i <« ...«*"
A das höhere genannt werden, wenn die erste der Differenzen
l>! — VU V2 — V2 . . . Vn — Vm
die von Null verschieden ist, einen positiven Werth hat, wenn
also entweder v1 > v\ oder v1 = v{, v2 > v'% oder v1 = v[, v2 = v'i,
v% > v'b etc.
Da wir alle Glieder, in denen sämmtliche Exponenten
vu v2 . . . vn übereinstimmen, in ein Glied vereinigt voraussetzen,
so ist hiernach von je zwei Gliedern entschieden, welches das
höhere ist, und wenn A höher als A!, A' höher als A" ist, so
ist auch A höher als A".
Ist nun nach dieser Anordnung
A = Map «**... «*w
das höchste Glied unserer Function <S, so folgt, dass
sein muss; denn wäre vi < v2, so würde das Glied
Jlf «** c^i . . . «*M,
das wegen der Symmetrie gleichfalls in 8 vorkommen muss, in der
Ordnung höher stehen als A, gegen die Voraussetzung. Ebenso
folgt, dass v2 5 vz sein niiss, denn wäre v2 < v8, so würde
M<i <3 «r*. •. «""
Lad n
höher stehen als J. u. s. f. Wir schliessen also, dass die Expo-
Exponenten in A
vu v2, vs . . . vn
eine abnehmende oder wenigstens niemals wachsende
Zahlenreihe bilden, oder dass die Differenzen
n — v2, v2 — i/3, ... vn_x — vn
alle positiv oder wenigstens nicht negativ sind.
Wir schliessen zweitens, dass in keinem Gliede der Function
8 ein höherer Exponent als vv vorkommen kann; denn sonst

§. 49. Zweiter Beweis des Hauptsatzes. 165
würde auch ein Glied vorkommen, in dem a^ diesen höheren
Exponenten hätte, und dies wäre gegen die Voraussetzung von
höherer Ordnung als A. Es sind also die Glieder, die in einer
symmetrischen Funetion überhaupt vorkommen können, von den
Coefficienten abgesehen, durch das höchste Glied vollkommen
bestimmt, und die Anzahl der möglichen Glieder ist bei gegebenem
höchsten Gliede nur eine endliche.
Wir ordnen die symmetrischen Functionen nach der Expo-
Exponentenreihe ihres höchsten Gliedes
Oi, v2 . . . vn)
in der Weise an, dass von zwei solchen Functionen 8, 8' mit
den Exponentenreihen (^, v2 . . . vn) und (v[, v'% . . . v'n) S als
die höhere gilt, wenn die erste nicht verschwindende unter den
Differenzen vx — v\, v2 — v'% . . . vn — v'n positiv ist.
Die niedrigste Ordnung ist hiernach die, in der alle diese
Exponenten = 0 sind, und die symmetrische Funetion also eine
Constante wird. Die nächst niedrige Ordnung ist
A, 0, 0 ... 0),
der die einzige symmetrische Funetion
entspricht. Die nächstfolgende Ordnung ist
A, 1, 0 ... 0),
der die symmetrische Funetion
M % -)- M' a2
entspricht, und so erhalten wir in den n ersten Ordnungen die
Grundfunctionen selbst und ihre linearen Verbindungen, und
keine anderen.
Die nächstfolgende Ordnung ist charakterisirt durch
B, 0, 0 ... 0)
und enthält die linearen Verbindungen der Grundfunctionen mit
der Summe der Quadrate.
In allen diesen Fällen ist die Darstellbarkeit der symmetri-
symmetrischen Functionen bereits bewiesen, und wir werden also jetzt
den allgemeinen Beweis dadurch führen, dass wir die Darstellung
der Funetion 8 von der Ordnung (vt, i/2 . . . vn) durch die
Grundfunctionen unter der Voraussetzung ableiten, dass sie für
die Functionen niedrigerer Ordnung schon bekannt sei, also durch
das Schlussverfahren der vollständigen Induction. '

166 Vierter Abschnitt. §. 49.
Wir bemerken hierzu, dass durch die Multiplication zweier
symmetrischer Functionen 8 und #', deren höchste Glieder
A = Mof* «£ . . . «*», AI = M' <i «£'« ...«*"
sind, eine symmetrische Function entsteht, deren höchstes Glied
das Product
A AI = JOf'a*i+'"ia£s+1 . . . «**"+1/"
ist. Denn nehmen wir an, es gebe in SS' ein höheres Glied
als AA', das aus der Multiplication der beiden Glieder
B = JV»ui a£s . . . «'"M, B' = N' a{"i «"'2 . . . «""
entsteht, also
BB' = Mt(fi+.";«;»+c; ... <%»+ll\
und es sei nicht gleichzeitig B = A und 5' = .4/, so wäre die
erste der Differenzen
fh — vl + Fl ^i) f*2 vl -\- F2 V2, • • • F» vn + F» — v»i
die von Null verschieden ist, positiv, was unmöglich ist, da die
erste nicht verschwindende unter den Differenzen
(h — vn f% — va . . . [in — vn
und unter den Differenzen
f*i — v'lt (i'a — v'2 . . . [i'n — ^
nach der Voraussetzung negativ ist. Durch Wiederholung dieses
Schlusses ergiebt sich der allgemeinere Satz, dass man das
höchste Glied eines Productes aus mehreren Factoren erhält,
wenn man die höchsten Glieder der einzelnen Factoren multi-
plicirt.
Die höchsten Glieder der symmetrischen Grundfunctionen
al5 «2i «g . • • a»
sind nun, abgesehen vom Vorzeichen,
«!, «! «2, «1 W2 W3l • • -, «1 «2 «3 • • • W>M
und wenn wir also das Product bilden
P — -j- JK"a^*a;is-*» . . . a*ü71~~1'M a^M,
so erhalten wir eine symmetrische Function, deren höchstes
Glied gleichfalls A ist, wie in 8.
Die Differenz
8 — P = S'
ist also wieder eine symmetrische Function, deren höchstes Glied
niedriger ist als das von S, und die wir nach der Voraus-

§. 50. Discriminanten. 167
Setzung rational durch die Grundfunctionen darstellen können.
Da P ebenso dargestellt ist, so ist das Ziel erreicht. Es erhellt
auch hier wieder, dass durch die Darstellung mittelst der Grund-
Grundfunctionen keine Brüche eingeführt werden, wenn ursprünglich
in S keine enthalten sind.
Diese Methode der Berechnung symmetrischer Functionen
giebt uns zugleich Aufschluss über den Grad der ganzen ratio-
rationalen Function von Oj, a2 . . . a„, durch die eine bestimmte
symmetrische Function der «j, «%...«„ ausgedrückt wird.
Wenn nämlich (vx, v2 . . . vn) die Ordnung der symmetrischen
Function ist, so ist vx der Grad von P in Bezug auf sämmtliche
av. a2 ... an, und in dem entwickelten Ausdruck für 8 kann kein
Glied höheren Grades vorkommen; auch kann das Glied P durch
keines der folgenden Glieder zerstört werden, da P durch die
Ordnung von 8 völlig bestimmt ist, und die Ordnung von S'
und aller folgenden symmetrischen Functionen niedriger ist, als
die Ordnung von S.
Setzen wir an Stelle von %, a2 . . . an:
*i «2 an
aa' a0 «o '
so ist aj» 8 eine ganze homogene Function vtten Grades
von a0, ß] . . . an, und man kann 8 nicht durch Multiplication
mit einer niedrigeren Potenz von a0 in eine ganze Function der
a verwandeln. Der Exponent v1 ist also bestimmt durch
die höchste Potenz, in der irgend eine der Wurzeln k
in 8 vorkommt.
§. 50.
Discriminanten.
Die im Vorhergehenden gewonnenen Sätze lehren, sym-
symmetrische Functionen der Wurzeln einer Gleichung rational durch
die Coefficienten der Gleichung auszudrücken; die Resultate sind
zunächst abgeleitet unter der Voraussetzung, dass die Wurzeln,
oder, was nach dem dritten Abschnitt damit gleichbedeutend ist,
die Coefficienten unabhängige Variable waren; sie können aber
nicht falsch werden, wenn dafür bestimmte numerische Werthe
gesetzt werden, da wenigstens bei den ganzen symmetrischen
Functionen keine Nenner vorkommen, die verschwinden können.

168 Vierter Abschnitt. * §. 50.
Wir machen zunächst einige Anwendungen auf besondere
symmetrische Functionen, die für die Folge wichtig sind. Schon
im §. 22 ist bemerkt worden, dass das Differenzenproduct
A) P = («! — Ojs) («! — «3) . . . («! — Kn)
(«3 «3) ... («2 — «»)
durch Umstellung zweier Elemente nur das Vorzeichen ändert.
Das Quadrat dieses Productes wird also bei allen Vertauschungen,
zweier der Variablen a und demnach auch bei allen Permu-
Permutationen umgeändert bleiben, d. h. eine symmetrische Function
der Variablen sein. Die Ordnung dieser symmetrischen Function
ist, wie man aus A) sieht, gleich
B n — 2, 2 n — 4, ... 2, 0).
Wenn wir also die Function f(x), deren Wurzeln die au a%... an
sind, in der Form annehmen
f(%) — aoxn -\- axxn~Y -j- «2%"~2 + • • • + «n-i* + «n,
so dass die höchste Potenz von x nicht gerade den Coefficienten
1 hat, so ist P2 eine ganze rationale Function von
die durch Multiplication mit afn~i in eine homogene Function
von a0, %, . . . an übergeht. Wir nennen diese homogene Func-
Function, die also durch
C) ao2«-2P2 = D
definirt ist, die Discriminante der Function f(x). Setzen
wir aa = 1, so erhalten wir die unhomogene Form der
Discriminante1).
Das Verschwinden der Discriminante ist die noth-
wendige und hinreichende Bedingung dafür, dass
zwei der Werthe at, «2 . . . k„ einander gleich werden.
Wir können für die Discriminante noch einen zweiten Aus-
Ausdruck aufstellen.
Es ist nach §. 14, A2)
n(n—1)
*) Die Discriminante ist, vom Factor (— 1) 2 «o"~% abgesehen,
dasselbe, was Gauss die Determinante der Function nennt A. c, art. 6).

§¦ 50.
Discriminanten.
169
D)
— «3) . . . («j — «„)
— a3) . . . («2 — «„)
/' («n) = «0 («» — «*i) («« «2) • • • («n — «m-i),
folglich, da hier jeder Factor (uh — e%) zweimal mit entgegen-
entgegengesetzten Zeichen vorkommt,
E) D = (- 1) 2 «r2 /' («a) /' («2) • • • /' K>
Um die Discriminante wirklich darzustellen, haben wir zu-
zunächst ein allgemeines Mittel. Es war nach §. 25
F) (-1)
'P =
1, «!, «f
und wenn wir nach §. 30 das Quadrat dieser Determinante durch
Multiplication nach Verticalreihen als eine neue Determinante
darstellen und
»»= «r + «m— «r
setzen
G)
5.7,
• . • Sn—1
. . . Sn
s23).
Die Grossen sm sind aber die Potenzsummen, die wir schon
im §. 46 durch die Coefficienten ausgedrückt haben; nur sind an
Stelle der ax, a^ . . . an die Quotienten B) zu setzen.
So finden wir z. B. für n = 2
(8) D — a02 (s0 s3 — sf) = ö^2 — 4 a0 a2
und für w = 3
(9) D = a04 (s0 s2 s4 — s0 s32 -f 2 sx s2 s3 — sfs
Hierin ist nach §. 46 zu setzen
s0 = 3, «o sl = — %
— 27 a02a32.
ao S3 = — «i + 3 a0 «1 «2 — 3 a02 %
a*s4 = af ¦— 4a0 afa.2 -f- 4 a02 c^ a3
wodurch man erhält
A0) D = O]2^2 + 18 «o «1 «2 «3 — 4 a0 «| —

170 Vierter Abschnitt. §. 51.
Die Discriminante I) ist eine unzerlegbare Funciion
der Variablen a0, % . . . an (§. 20).
Denn angenommen, JD habe einen rationalen Theiler Du
so muss Dx homogen sein, und lässt sich daher, von einer Potenz
von a0 als Factor abgesehen, rational durch die Variablen
«!, «2 • • • an ausdrücken. Da nun D durch keine Potenz von a0
theilbar ist, so muss Dt, wenn es nicht constant ist, die Variablen
ß15 «2 . . . e*n enthalten und muss daher wegen C) durch eine der
Differenzen a,- — «fc theilbar sein. Da aber andererseits Dx in
Bezug auf die «j, «2 . . . k„ symmetrisch ist, so ist es auch
durch das Quadrat von «,• — «fc und durch das ganze Product
P2 theilbar, also, von einem constanten Factor abgesehen, mit
D identisch.
§• 51.
Kennzeichen für die Anzahl der verschiedenen
Wurzeln.
Das Verschwinden der Discriminante D ist, wie wir gesehen
haben, die Bedingung dafür, dass zwei unter den Wurzeln
«!, «2, • . . ot,n der Gleichung f(x) = 0 einander gleich werden.
Man kann aber diesen Satz noch verschärfen und so ein genaues
Kennzeichen für die Anzahl der verschiedenen Wurzeln
von f(x) = 0 herleiten.
Wenn, wie bisher, s0, sx, s2, . . . die Potenzsummen der k
bezeichnen, so setzen wir nun für ein beliebiges v ^ n
A) D, =
j, . . . Sv
so dass, wenn a0 = 1 angenommen wird, Dn mit der Discrimi-
Discriminante D von f(x) übereinstimmt. Um diese Functionen Dv durch
die Wurzeln «,¦ auszudrücken, beweisen wir. folgenden Satz:
1. Man wähle beliebig v unter den Grossen «j
aus, etwa k1: «2 . . . av, und bezeichne das
Differenzenproduct [§. 50, A)] dieser v Grossen
mit

§. 51. Kennzeichen f. d. Anzahl d. verschiedenen Wurzeln. 171
B) P, =
1, «!,... «J-1
i,«,,... «r1
D, =
2 Wj Wj
2 K{ Kt
2^ &h
Dann ist;
worin sich die Summe 2 auf alle möglichen
Arten, die v Grossen Oj, a.2, . . ., kv auszuwählen
bezieht.
Man kann diesen Satz auch so ausdrücken, dass Dv die
Summe der Discriminanten aller der Gleichungen ist, die irgend
v von den Grossen k{ zu Wurzeln haben.
Um ihn zu beweisen, sei v irgend eine unter n gelegene
Zahl. Schreiben wir dann die Determinante Dv in der folgenden
Form:
v-i 0 1 ¦«-! 0 v—1
2 <*. k{ , ... 2 «*,• «f
V r/1 r/1 V /v1 r/~1
2«. »,,.-.1«, «,
so können wir den Schlusssatz des §. 30 anwenden, wenn wir dort
„(.*) j.(«) „*—i
n h s
setzen, und dann geht die Formel A6), §. 30 unmittelbar in die
Formel C) über.
Daraus erkennen wir zunächst nach §. 49, dass a%v~iDv eine
ganze Function der a0, %, . . . a„ ist, die den Factor a0 nicht
mehr hat. Es ergiebt sich aber auch daraus die folgende Be-
Bedeutung der Dv für die Erkennung der Wurzelgleichheit:
2. Die nothwendige und hinreichende Bedingung
dafür, dass unter den k1, m2, ...,«„ nicht mehr
und nicht weniger als q verschiedene vor-
vorkommen, ist
-fy+i = 0, D?+3 = 0, . . . Dn = 0,
D? von Null verschieden1).
Denn ist v grösser als q, so kommen in jedem der Diffe-
renzenproducte P„ der Formel C) zwei gleiche k vor, und sie
verschwinden also alle. Ist aber v = q, so enthält die Summe
x) Dieser schöne Satz ist von L. B a u r gefunden und dem Verfasser
mitgetheilt (Mathematische Annalen, Bd. 50).

172 Vierter Abschnitt. §. 52.
C) ein nicht verschwindendes Glied, nämlich das Differenzen-
product der q verschiedenen Grossen ku «2, . . ., «?, während
alle anderen Glieder der Summe verschwinden.
§• 52.
Discriminanten der Formen dritter u"nd vierter
Ordnung.
Bei den Functionen dritter und vierter Ordnung haben wir
zur Berechnung der Discriminanten in den Auflösungen der
Gleichungen dieser beiden Grade (§. 38, §. 40) ein einfaches Mittel.
Was zunächst die Gleichung dritter Ordnung betrifft, so
waren die drei Wurzeln von
A) x°- + ax + b = 0
in der Form dargestellt:
m = u -\- v
B) ß = su -f- s^v
y = 62M-(- ev,
worin
(S)
die complexen dritten Einheitswurzeln sind und m, v durch
§. 38, (8) bestimmt sind.
Aus <3) folgt
D) a— e* = V-r
und aus B)
a — ß = V— 3 («2« — ev)
k — y = — V— 3 (eu — e2v)
ß — y = V— 3 (tt — i;).n
Hieraus durch Multiplication
E) (« — /S) (« — y) (ß - y) = 3 Y=3 (tt» — »»>
Erhebt man ins Quadrat, so erhält man für die Discri-
minante der cubischen Gleichung A) nach §. 38, F)
F) D = — B7 &2

§. 52. Discriminan^en. 173
Hieraus erhält man die Discriminante der allgemeinen Function
G) a0 x% -j- ax x* -\- a2 x -\- a3,
wenn man für a und b die Ausdrücke §. 37, D) einsetzt, in
denen man %, a2, az durch
% a% <h
ersetzt, und mit a04 multiplicirt [§. 50, C)]. Man erhält so
3 a0 «2 — «i3
, 2al — 9 «o «i % -f- 27 a02 %
°~ 27< '
und folglich
(8) D = - 2^ {B af - 9 a0 % a2 + 27 a02a3
Wenn man das Quadrat und den Cubus ausrechnet, so
kommt man zu der Formel A0) §. 50 zurück; es ist aber be-
merkenswerth, dass die Formel (8) scheinbar den Nenner 27 a02
enthält, der sich beim Ausrechnen forthebt.
Ebenso können wir bei den biquadratischen Gleichungen
verfahren. Wir erhalten, wenn «, ß, y, ö die Wurzeln der bi-
biquadratischen Gleichung
(9) a^-f- ax2 -\- hx -\- c = 0
sind, nach §. 40, E)
« — ß = v -j- w, y — ö = v — w,
A0) cc — y = tc -j- tt, d — ß = w —¦ u,
cc — d = u -\- v, ß — y = u — v.
Danach wird die Discriminante der Gleichung (9)
D = (|>2 — W2J (W2 — M2J (U2 — V2J,
d. h. es ist D gleich der Discriminante der cubischen Resolvente
§. 40, D)
A1) s% + 2a.?2 -f («2 — 4c) s — Z>2 = 0,
deren Wurzeln u'\ v2, w2 sind.
Wenn man diese Discriminante aber nach der Formel A0),
§. 50 bildet, indem man
a0 = 1, öSj = 2 a, a2 = a2 — 4 c, % = — 52

174 Vierter Abschnitt. §. 52.
setzt, so folgt
A2) D= — 4a3&2_|_ U4ac62+ 16a*c
— 128 a2e2 + 256 c3 — 27 R
Wenn man dagegen zur Bildung der Discriminante der
cubischen Gleichung A1) die Formel (8) anwendet, so erhält man
A3) 27 D= 4(a2 -f 12 c)» — B «3 _ 72 ac + 27 Z>2J.
Man leitet hieraus die Discriminante der allgemeinen Func-
tion vierten Grades
A4) f(x) = «o #* -|- ^i %3 -\- a2x2 -\- asx -j- a4
ab, indem man nach §. 37, D) a, 5, c durch
— 3 a* .
«1 «1 «2 , -
1 2"" + ^
— 3 aj4 , «j3 a2 % «3 ,
~256 "" T6 4~ ' üi
ausdrückt, dann %, a2, a3, a4 durch
ersetzt und mit a06 multiplicirt.
Setzt man nach Ausführung dieser einfachen Rechnung zur
Abkürzung
A5) A = a| — 3 % a3 -j- 12 a0 «4,
A6) 5 = 27 fflj2^ + 27 a0 <as| + 2 a23 — 72 a0 a2 a4 — 9 % a2 a3,
so erhält man aus A3)
A7) 27D = 4:A3 — B2.
Die Grossen A und B, die uns im nächsten Abschnitt noch
beschäftigen werden, heissen die erste und zweite Invariante
der biquadratischen Function /. Man kann also nach A7) die
Discriminante rational durch diese Grossen ausdrücken, jedoch
nicht so, dass die Coefficienten ganzzahlig werden; führt man die in
A7) vorgeschriebene Rechnung aus, um D durch die Coefficienten
aa, «!, «2) az selbst darzustellen, so muss sich der Factor 27
noch fortheben lassen. Wir wollen den langen Ausdruck, dessen
Berechnung keinerlei Schwierigkeit bietet, nicht hierher setzen.

§. 53. Resultanten. ^ 175
§. 53.
Resultanten.
Eine andere Anwendung der Theorie der symmetrischen
Functionen, die übrigens die Discriminantenbildung als speciellen
Fall enthält, ist die Bildung der Resultanten.
Es seien
A) /(a?) = o0Ä» + «1»»-1 + oa»»-!'H h«»,
B) <p(x) = boxm-jt-blxm-1 + b2xm-z H \-bm
zwei ganze rationale Functionen vom wten und mtm Grade und
«i, «2, ... an seien die Wurzeln der ersten, so dass auch
C) f{x) = a0 (x — «j) (x — ai)...(x — ccn)
gesetzt werden kann.
Nun ist das Product
<P («i) 9 («2) • • • 9> («»)
eine symmetrische Function der Wurzeln von f(x) und kann
also ganz und rational durch
«i «2 _ _ «n
fflo' ao «0 .
ausgedrückt werden. Die Ordnung dieser symmetrischen Func-
Function ist (m, m . . . m) (§. 49) und daher ist
D) R = a™q> (%) q> («,)... q> (an)
eine ganze rationale und homogene Function mter Ordnung von
a0, aj ... aTC. Sie ist auch, wie ihr Ausdruck zeigt, eine ganze
homogene Function wter Ordnung von b0, 5X . . . bm. Sie wird die
Resultante der beiden Functionen f(x) und q>(%) genannt.
Diese Bezeichnung rechtfertigt sich durch eine zweite Darstellung.
Bezeichnen wir die Wurzeln von q>(x) mit &, ß2 . . . ßm,
setzen also
E) g>(x) = bo(x- ßt) (X-ß3)...(x — ßm),
so wird nach D)
F) B = a?b?II (cn - ft),
worin das Productzeichen II sich auf alle Indices i = 1, 2 . . . n,
Tc = 1, 2 . . . m bezieht.

176 Vierter Abschnitt. §. 53.
Dieser Ausdruck zeigt nun, dass R, abgesehen von dem
Factor (— l)mn, in der gleichen Weise von <p (x) abhängt, wie
von f(x), und dass wir also auch setzen können
G) (_ iyn R = bn /(&)/(&) . . . f(ßm).
Die Discriminanten sind hiernach ein specieller Fall der
Resultanten, den man erhält, wenn man für <p (x) die Derivirte
f'(x) nimmt. Wie bei den Discriminanten, kann man auch von
der Resultante nachweisen, dass es eine unzerlegbare Function
der Variablen a, b ist.
1. Das "Verschwinden der Resultante von f(x) und
q>(x) ist die nothwendige und hinreichende
Bedingung dafür, dass die beiden Gleichungen
f(x) = 0 und <p (x) = 0
eine gemeinsame Wurzel und folglich die
Functionen fix) und q>(x) einen gemeinschaft-
gemeinschaftlichen Theiler haben.
Die Gleichung, die durch Nullsetzen der Resultante entsteht,
wird auch die Endgleichung aus f(x) — 0 und q>(x) = 0
genannt und die Aufstellung der Endgleichung die Elimination
von x.
Zur Berechnung der Resultanten kann man den Algorithmus
des grössten gemeinsamen Theilers anwenden (§. 6). Ist nämlich
m ^ n, so kann man eine ganze Function Q und eine eben-
ebensolche Function ip(x), deren Grad kleiner ist als m, so be-
bestimmen, dass
f(x)= Q9(x) + ^(x),
also, wenn man für x eine der Wurzeln ß( setzt,
(8)
ist ml der Grad von 4>(x), so ist
(9) h
die Resultante von q>(x) und ip(x) und daher
A0) ±R = bl-m'R'.
Die Bildung der Resultante R ist hierdurch auf die Bildung
von R' zurückgeführt. Man kann nun q>.(x) wieder durch i>(x)

§. 53. Resultanten. 177
theilen, und führt so die Bildung von B' auf die Bildung einer
Resultante von Functionen immer niedrigeren Grades zurück, bis
man schliesslich auf eine Constante, d. h. eine Function der
Coefficienten a, b kommt, die mit der gesuchten Resultante iden-
identisch sein muss.
Die Berechnung der Resultanten ist meist sehr weitläufig.
Wir wollen nur das einfachste Beispiel der Resultante zweier
quadratischer Functionen anführen:
f{x) = a0 x2 + ax x -\- a2
cp(x) = b0x2 + bxx-\- ~b%.
Man kann hier direct das Product
B = a02F0 «¦> +£>!«!+ b2) (b0a* + bt «2 + b2)
berechnen, und erhält, wenn man
«0 («1 + «ä) = «11 «o «1 «2 = «2
setzt,
A1) B = agh* + a22502 — b0bt ax a2 — a0 «1 h h
-\- b0 b% a? -\- a0 a2 6/ — 2fföJ0 <h b2,
oder, was damit identisch ist,
A2) B = («o &2 — «2 &0J — («o h — <h \) (% &2 — <h bi)-
Die einzelnen Glieder der Resultante der zwei Functionen
f(x) und 93 (x) vom wten und mien Grade haben, von einem numeri-
numerischen (ganzzahligen) Factor abgesehen, die Gestalt
A3) a;.«?...<.S'ff...e,
worin, wie aus den oben bestimmten Graden hervorgeht,
. ' ' vo + vi +. \- vn=m
Wir können aber noch eine andere Relation zwischen diesen
Exponenten angeben.
Da nämlich [nach F)] B eine homogene Function wwton
Grades von den n -\- m Variablen «, ß ist, da ferner a0 vom
nullten, % vom ersten, a2 vom zweiten etc. Grade in den a,
allgemein a& und bk vom &ten Grade in diesen Variablen sind,
so folgt
vi-f 2va-f 3vs-| \-nvn
Weber, Algebra. I. 19

178 Vierter Abschnitt. §. 53.
Wenn wir den Index Tt von a^ oder bb das Gewicht der
betreffenden Grosse nennen und unter dem Gewicht eines
Productes die Summe der Gewichte der einzelnen
Factoren verstehen, so können wir der Formel A5) auch
den wörtlichen Ausdruck geben:
2. Alle Glieder der entwickelten Resultante
haben ein und dasselbe Gewicht mn.
Summen, deren Glieder alle dasselbe Gewicht haben, heissen
isobarische Functionen, und das Gewicht eines jeden
Gliedes heisst das Gewicht der Function. Durch Multiplication
mehrerer isobarischer Functionen entstehen wieder isobarische
Functionen, und das Gewicht des Productes ist die Summe der
Gewichte der Factoren.
Die Resultanten sind isobarische Functionen der Variablen
«fc, hc vom Gewichte mn.
Die Functionen / und <p selbst kann man dadurch zu iso-
isobarischen machen, dass man der Variablen * das Gewicht 1
beilegt.
3. Ersetzt man die Variablen in einer isobari-
isobarischen Function durch homogene Functionen
irgend welcher anderer Variablen vom Grade
des Gewichtes der betreffenden Variablen, so
entsteht aus der isobarischen Function eine
homogene Function der neuen Variablen,
deren Grad dem Gewichte der Function
gleich ist.
Wenn die Functionen f(%), q>(x) durch Ordnen zweier
homogener Functionen der Variablen x, y, s . . . vom Grade n
und m nach einer der Variablen x entstanden sind, so sind die
Coefficienten as, b^ homogene Functionen vom Grade 1c der
Variablen y, z . . . und aus 2. und 3. ergiebt sich der Satz:
4. Durch Elimination einer Variablen x aus zwei
homogenen Functionen wten und wten Grades
ergiebt sich eine Endgleichung vom Grade mn
in den übrigen Variablen.
Giebt man den Variablen a*, 5& nicht die Gewichte Tc, son-
sondern (N -j- Tc) und (M -\- le), worin N, M irgend zwei Zahlen
sind, so wird das Gewicht der Resultanten von / und <p, wie aus
A4) und A5) hervorgeht,

§. 54. Bestimmung der gemeinschaftlichen Factoren. 179
A6) mN-{- nM -\- mn.
Dies ist auch der Grad der Besultanten, wenn die a& und 5A
durch Functionen von neuen Variablen der Grade N -j- h und
M -\-lc ersetzt werden.
§• 54.
Bestimmung der gemeinschaftlichen Factoren.
Eine elegante Lösung des Eliminationsproblems, wodurch
wir zugleich die gemeinschaftlichen Factoren der beiden Func-
Functionen f(x) und <p(%) erhalten, ergiebt sich, wenn man die in
§. 4 eingeführten Functionen f3 (x) benutzt. Wir definiren aber
jetzt diese Functionen so:
/o 0») = «o
¦ft (x) = a0 x -f- %
A) ft (a?) =
fn(x) = aoxn -\- ^x»-1 -\- azx»-2 -j • -)- am
so dass /„(#) mit der ursprünglich gegebenen Function f(x)
identisch ist. Es ist aber fs (x) eine ganze Function sten Grades
von x, und wenn wir
B) /(*)==*—/.(a)+ #(aO
setzen, so ist
C) F. (x) = as+1 X»-*-* + as+2 x»-*-* -| \-an
eine ganze Function vom Grade n — s — 1.
Dieselbe Bedeutung mögen q>s{x) und 9s{x) für die Function
<p (x) vom Grade m haben, so dass
<p (x) = xi»-* <ps (x) -|- 0S (x)
D) <ps(x) = Z>0 «• + 6i a^-1 H h^
#s (a?) = Z»s+1 a;"'-5-1 + 5s+2 a?»-«-2 -| 1- &m.
Daraus ergiebt sich, wenn man s in B) und D) durch n — s
und m — s ersetzt: ;
E) q>fn-s —f<pm-s = (xs 9>OT_S + ^w_s)/n_s
— (xsfn-s -f Fn_s) q>m_s = #OT_S/„_S — Fn_s 93m_s.
Nehmen wir nun an, es sei :.
F) »^ m,
12*

180 Vierter Abschnitt. §. 54.
so ist die Function auf der rechten Seite der Gleichung E) vom
Grade n — 1 in Bezug auf x. Wir setzen, indem wir s durch
n — s -\- 1 ersetzen,
G) $>/_! = A%sxn~^ + A%sxn~* -| hA« +/9>m-»+.-i,
worin gjm_n+s_x = 0 zu setzen ist, wenn m — n -\- s — 1
negativ wird.
Die Coefficienten J.r> s sind darin homogene lineare Functionen
sowohl von den Coefficienten a< als von den Coefficienten b{. Sie
sind zugleich isobarisch vom Gewichte
(8) m — n -\- s -\- r — 1,
wie man am einfachsten erkennt, wenn man nach der Vorschrift
des vorigen Paragraphen der Variablen x das Gewicht 1 beilegt,
wodurch die Functionen /s, <ps in isobarische Functionen mit dem
Gewichte s übergehen.
Wenn das Gewicht einen negativen Werth erhält, so ist die
Function gleich Null.
Beispielsweise ist, wenn n > m ist,
und wenn n = m ist,
-A.1>s = aobs — h0 as.
Wir wollen aber die Formel G) nur so lange anwenden,
als s > n — m ist, so dass darin nur positive Werthe von
m — n -\- s vorkommen, also für
s = n — m -)- 1, n — m -\- 2, . . ., n.
Ist s <J n -r- m, so wollen wir setzen
(9) <p a?-1 = Ä^x»-1 +. A^x"-* -| \- An,s
s = 1, . . ., n — m.
Diese Ar, s sind dann lineare Functionen der b allein. Sie
sind nämlich, soweit sie nicht Null sind, geradezu den b gleich,
so dass
A0) Ar,s — bn-n+t+r-l, » — W + r^r + S^» + l
und = 0, wenn m — n -\- s -\- r — 1 negativ oder grösser
als m ist. Dann ist auch hier das Gewicht von Ar>s gleich
m — n -\- s -\- r — 1, falls Ar, s nicht gleich Null ist.
Um die Formeln (8), (9) zu vereinigen, wollen wir noch ein
Zeichen ps einfuhren, so dass
A1) ps = x8-1 für s = 1, . . ., n — m
= /3-i „ s = n — m -\- 1, n — m -\- 2, . . ., n,

§. 54 Bestimmnng der gemeinschaftlichen Factoren. 181
und ps eine Function (s — l)ten Grades von x ist. Dann lassen
sich die Gleichungen (8), (9) in die eine zusammenfassen:
A2) q>ps = A^X»-1 + A,s«n-2 -\ h^v + «'/>
worin qs = cpm^^^! oder (für negative m — n -j- s — 1)
= 0 ist.
Wenn nun für irgend einen Werth von x die Functionen
f(x) und q> (x) zugleich verschwinden, so muss die Determinante
des Systems verschwinden, das aus A2) hervorgeht, wenn wir
/ und <p = 0 setzen (§. 27, II). Die Bedingung hierfür ist also,
wenn wir
-™1, 1> -4-2, 1 • • • -o-m, 1
,¦• n\ -p -, 2> -^-2, 2 • • • -o-M, 2
-n-1, Mi -42, n • • • -^m, n
setzen, iJ = 0, und R ist daher die Resultante für / und <p.
Man sieht auch hieraus sofort, nach den oben gegebenen Grad-
und Gewichtsbestimmungen der J.r>s, dass R in Bezug auf die a
vom Grade m, in Bezug auf die b vom Grade n und vom
Gewichte mn ist, wie es sein muss.
Wir wollen über die Determinante R und ihre Unter-
Unterdeterminanten eine Reihe wichtiger Sätze ableiten.
I. Wenn die beiden Functionen f und q> einen
gemeinschaftlichen Theiler vom Grade n — r
haben, so verschwinden alle Unterdetermi-
Unterdeterminanten von R mit r -\- 1 Reihen.
Um ihn zu beweisen, greifen wir aus der Reihe der Indices
1, 2, . . ., n irgend r -\- 1 heraus, «j, c^, . . ., «r+1, und bilden nach
A2) die Gleichungen
A4)
Wenn nun cl5 c2, . . ., cr+1 irgend welche Constanten sind und
P=C1pai -j-CzPas -) \~ Cr+lPar+1
A5) 0 = cx qai +c2qa2 -| 1- cr
Cs :== Ci -o-s,«! ~r C2 -^-», «ä ~r " ' * ~r cr
gesetzt wird, so folgt aus A4)

182 Vierter Abschnitt. §-54.
A6)
Nun kann man (§. 27, III) unter allen Umständen die Con-
stanten cl5 c2, . . ., cr+J so bestimmen, dass
A7) C, = 0, C2 = 0, . . ., Cr = 0
ist, und dann ist die Function C(x) auf der linken Seite von
A6) höchstens vom Grade n — r — 1 in Bezug auf x. Wenn
aber / und <p einen gemeinsamen Theiler (n — r)*131 Grades
haben, so muss dieser nach A6) auch in C(x) enthalten sein,
und dies ist nur möglich, wenn zugleich mit A7) auch die
Gleichungen
A8) Cr+i = 0, a+2 = 0, . . ., C„ = 0
befriedigt sind. Dann aber müssen nach §. 27, I. alle (r -\-1)-
reibigen Unterdeterminanten der Matrix
verschwinden, w. z. b. w.
Es gilt auch der umgekehrte Satz:
II. Wenn sämmtliche Unterdeterminanten von B
mit r -\- 1 Reihen verschwinden, so haben die
Functionen / und q> einen gemeinschaftlichen
Theiler vom Grade n — r.
Nehmen wir nämlich an, dass alle Unterdeterminanten von
(r -\- 1) Reihen der Matrix A9) verschwinden, so kann man die
Constanten cu . . ., cr+i so bestimmen, dass die Gleichungen A7),
A8) befriedigt sind und folglich C(x) verschwindet, ohne dass
alle d verschwinden. Nehmen wir
B0) «n a2, . . .,•«,.+! == 1, 2, . . ., r + 1
an, so ist nach A5) P höchstens vom Grade r, und aus A6)
folgt, dass <pP durch / theilbar ist. Demnach muss q> einen
Theiler mit / gemein haben, dessen Grad mindestens = n — r ist.
Wenn wir die Determinanten
B1) Br = 2 ±A1AA2>2. .. Artr
die Hauptunterdeterminanten von B nennen, so dass
speciell Bn = B ist, so können wir dem zuletzt bewiesenen Satze
die folgende weitergehende Fassung geben:

§. 54. Bestimmung der gemeinschaftlichen Factoren. 183
III. Die nothwendige und hinreichende Bedingung
dafür, dass / und <p einen grössten gemein-
gemeinschaftlichen Theiler vom Grade n — r, aber
nicht von höherem Grade, haben, ist die, dass
Rn, -ß„—i, . . ., -Rr+l
verschwinden, während Mr von Null ver-
verschieden ist.
.Nehmen wir nämlich an, / und q> haben einen gemein-
gemeinschaftlichen Theiler vom Grade n — r — 1, und es verschwinde
äusserdem Br+1, dann machen wir über die « die Annahme B0)
und können wegen Er+1 = 0 die Constanten c,-, nicht alle ver-
verschwindend, so bestimmen, dass
Cx = 0, 0, = 0, . . ., Cr+1 = 0
wird. Dann ist C(x) höchstens vom Grade n — r — 2, und
muss daher, da es durch jeden Theiler von / und <p, also durch
eine Function (n — r — l)ten Grades theilbar ist, identisch Null
sein. Daraus können wir aber wie oben schliessen, dass / und <p
einen gemeinschaftlichen Theiler vom Grade n — r haben.
Da Ar,s nach A0) gleich Null ist, wenn r-\-s<n — m -f- 1,
und gleich i0, wenn r -\- s = n — m -j- 1, so ist
B2) Bn^ - (- if(n~mnn-m-i) irm-
Dies ist also von Null verschieden, so lange <p wirklich den
Grad m erreicht, in Uebereinstimmung damit, dass in diesem
Falle der grösste gemeinschaftliche Theiler von / nnd <p den
Grad m nicht übersteigen kann.
IV. Wenn die Voraussetzungen des Satzes III er-
erfüllt sind, so lässt sich der grösste gemein-
gemeinschaftliche Theiler Tr von / und <jp durch die
folgende Determinante darstellen:
B3) Tr =
ltl, Ä^.-.Ar-i,!, Ar>1 xn~r + Ar + ^z»-1—1 -\ 1- AnA
i,2, A%2,...Ar-lti, Ar,2 xn~r -f- Ar+1,2*"-»—1 -j- 1- A,
n J2,r,---^r-l,r, Ar,r 0Cn~r + Ar+ hrXn~'—1 -\ \~ An>
Diese Function ist nämlich vom Grade (n — r) und der
Coefficient von xn~r ist gleich Rr, also, nach Voraussetzung, von
Null verschieden.
Es ergiebt sich aber aus A2)

184
Vierter Abschnitt.
§¦ 54.
fPsfqs Ä1,sx A2,sx^r-i,. a;\
und folglich erhält man nach dem Determinantensatz von der
Addition der Colonnen (§. 25, VII)
B4)
r-1,2,
,r, -Ar, • • • Är-hr, (p pr — fq
oder, wenn wir nach den Elementen der letzten Colonne ordnen
und
B5)
P —
j. r —
-a.1,2) -a.2,2, • •
r—1,15
r—1,2)
-o.l,n
setzen
B6) Tr = Pr<P — Qrf,
worin Qr aus Pr hervorgeht, wenn man die pi durch die #»• ersetzt.
Haben also, wie vorausgesetzt, / und <p einen gemeinschaft-
gemeinschaftlichen Theiler (n — r)ten Grades, so muss dieser auch in Tr
aufgehen, und also, da die Grade übereinstimmen, mit Tr iden-
identisch sein.
Die Function Tr ist in Bezug auf die Coefficienten b von q>
homogen und vom Grade r, in Bezug auf die Coefficienten a von
/ ist der Grad aber nur r — n -\- m, da die ersten n — m
Zeilen der Determinante B3) die a nicht enthalten. Bezeichnen
wir den Grad von Tr in Bezug auf x mit s, setzen also n — r
= s, so ist der Grad von Tr in den a gleich m — s in den b
gleich n — s.
Um das Gewicht von Tr zu erhalten, geben wir der Variablen
x wieder das Gewicht 1. Dann ist die Determinante B3) eine
Summe von Producten, deren Gewicht man nach (8) erhält, wenn
man in
m — n + h -\- h — 1
die Zahlen h und k beide in irgend einer Reihenfolge von 1 bis
r gehen lässt und die Summe aller dieser Ausdrücke nimmt.
Da hiernach die Summe aller h -\- h gleich r (r -j- 1) ist, so
ergiebt sich das Gewicht gleich r (m — n -f- r), oder, wenn
wieder n — r = s gesetzt wird, gleich (n — s) (m — s). Es
folgt also:

§. 55. Elimination. 185
V. Die Function TM_S ist vom Grade s in x, m — s
in den Coefficienten von /, n — s in den Coeffi-
cienten von <p, und isobarisch und vom Gewicht
(m — s) (n —- s).
Wenn B, aber nicht die Unterdeterminante i?m_i, gleich Null
ist, also nur eine gemeinschaftliche Wurzel von/ und <p vorhanden
ist, so kann man die verschiedenen Potenzen der Unbekannten
aus den Gleichungen A2) bestimmen, die dafür ergeben:
-4i,»a!"-1 + A^af-* -\ 1- An,. = 0, s = 0, 2, . . ., n — 1,
nnd man erhält also, wenn man die Unterdeterminanten von 2?
mit R^k bezeichnet:
„
O/
---7t, 71 -"-"?!, 1t -"-"Tt,"
Darin ist -R„)M = -ßn—n und wenn wir -R„_1)B = 5«-i setzen, so
ergiebt sich
B8) x = ^=-1-
§• 55.
Elimination. Theorem von Bezout.
Wenn in den beiden Functionen
V J ff* f/y\ - 7) //iWJ- __!_ 7) /yWl—1 I ... I 7)
die Coefficienten a, b selbst wieder ganze Functionen einer
Grosse y sind, so wird auch die Resultante eine ganze Function
von y werden, die wir mit F(y) bezeichnen wollen. Die Bildung
dieser Gleichung ist die Elimination von x aus den beiden
Gleichungen A).
Die Gleichung
B) F(y) = 0
hat alle die Werthe von y zu Wurzeln, wofür die beiden
Gleichungen
eine gemeinsame Wurzel haben. Ist die Bedingung B) befriedigt,
so findet man die Werthe von x, die den zwei Gleichungen
C) genügen, indem man den grössten gemeinschaftlichen Theiler
von f{x) und cp(x) aufsucht. Dieser gemeinschaftliche Theiler

186 Vierter Abschnitt. §.55.
ist vom ersten Grade und bestimmt also x rational, wenn
nur eine solche gemeinschaftliche Wurzel vorhanden ist. Sind
mehrere gemeinschaftliche Wurzeln vorhanden, so erfordert die
Bestimmung von x noch die Lösung einer Gleichung höheren
Grades.
Gehört zu jeder Wurzel der Resultante nur eine gemein-
gemeinschaftliche Wurzel x, so ist die Zahl der Werthepaare x, y, die
den Gleichungen C) genügen, gleich dem Grade der Resultante
in Bezug auf y. Sind also die Coefficienten a vom Grade v, b
vom Grade ft in Bezug auf y, so ist nach der Gradbestimmung
des §.53 der Grad der Resultante
D) nv -\- m[i;
so gross ist also die Anzahl der gemeinsamen Wurzelpaare.
Diese Zahl kann aber noch dadurch modificirt werden, dass
möglicherweise die Coefficienten so beschaffen sein können, dass
die höchste Potenz von y aus der Endgleichung wegfällt. Man
würde dann die Uebereinstimmung der Zahl mit D) nur durch
die Hinzufügung unendlicher Wurzeln retten können. Auch
mehrfache Wurzeln geben zu Bedenken Anlass. Man begegnet
diesen Uebelständen theilweise dadurch, dass man die homogene
Form der Gleichungen zu Grunde legt, eine Form, in der sich
das Eliminationsproblem besonders in der Geometrie einstellt.
Wenn nämlich die Function f (x) aus einer homogenen
Function wter Ordnung der drei Variablen x, y, s (einer ternären
Form) durch Ordnen nach Potenzen von x hervorgegangen ist,
so sind die Coefficienten a„, %, a2 . . . a„ homogene Formen der
beiden Variablen y, 0 von dem Grade, den der Index angiebt,
also a0 eine Constante, a^ eine lineare, a2 eine quadratische
Form u. s. f., und Entsprechendes gilt von den Coefficienten
i0, ii . . . bm der Function q> (x).
Bedeuten x, y, z Dreieckscoordinaten in der Ebene, so sind
f(x) = 0, q>(x) = 0 die Gleichungen einer Curve wter und einer
Curve mter Ordnung, und die gemeinsamen Wurzeln dieser beiden
Gleichungen (die Verhältnisse x:y.d) bedeuten die Schnittpunkte
der beiden Curven. Die Endgleichung, die man durch Elimi-
Elimination von x erhält, ist eine homogene Gleichung, deren Grad
sich aus A5), §. 53 gleich nm ergiebt.
Eine Verminderung des Grades kann hier nicht stattfinden;
immer ist die Endgleichung eine homogene Gleichung des ninten

§. 55. Elimination. 187
Grades für die beiden Unbekannten y, 0. Die einzige Ausnahme,
auf die hier zu achten ist, ist die, dass die Resultante identisch
(für alle y, s) verschwindet, dass also unendlich viele gemein-
gemeinsame Wurzeln vorhanden sind. Dieser Fall tritt dann, aber auch
nur dann ein, wenn / und q> als Functionen der Variablen x, y, 0
betrachtet, einen gemeinsamen Theiler haben (§. 20). Hierher
ist auch der Fall zu rechnen, dass / und q> einen nur von y, 0
abhängigen gemeinsamen Theiler haben, der dann auch als
Factor der Resultanten auftritt. Hier giebt es zwar nur eine
endliche Zahl von Werthepaaren y.0, zu diesen aber unendlich
viele Werthe von x.
In der Geometrie haben diese Fälle die Bedeutung, dass die
beiden Curveri einen Curventheil und nicht bloss einzelne Punkte
gemein haben.
Was sich von einem strengen algebraischen Standpunkte über
diese Frage sagen lässt, ergiebt sich aus §. 54 Wir wollen die
Coefficienten a^, bi in A) als ganze Functionen iten Grades
einer Variablen y ansehen, so dass das Gewicht mit dem Grade
in Bezug auf y übereinstimmt.
Wenn / und q> als Functionen von x und y einen gemein-
gemeinschaftlichen Theiler haben, so giebt es unendlich viele gemein-
gemeinsame Lösungen von / = 0 und <jp = 0. Im anderen Falle
bilden wir durch Elimination von x die Resultante B, die eine
ganze Function muten Grades von y ist. Der Grad kann sich
dadurch erniedrigen, dass die Coefficienten einiger der höchsten
Potenzen verschwinden. Es giebt also jedenfalls nicht mehr als
nin Werthe von y, für die B verschwindet. Ist ß einer dieser
Werthe, so ist B durch y — ß theilbar. Wenn nun aber für
y = ß die beiden Functionen / und q> einen grössten gemein-
gemeinschaftlichen Theiler vom Grade s oder n — r haben, so sind
nach §. 54, I, III die sämmtlichen Unterdeterminanten von B
von r-f 1 Reihen durch (y — ß) theilbar, während Br nicht
durch y — ß theilbar ist. Daraus ergiebt sich aber, am ein-
einfachsten aus dem Sylvester'schen Theorem [§. 32, G)], dass
B selbst durch (y — ß)" theilbar ist. Es kann aber B auch
noch durch eine höhere Potenz von y — ß theilbar sein. Jeder
Theiler sten Grades von / und <p absorbirt also mindestens s
Wurzeln von B = 0, und wir erhalten hieraus das nach Bezoiit
benannte Theorem in folgender, in geometrisches Gewand ge-
gekleideter Gestalt.

188 Vierter Abschnitt. §. 55.
I. Zwei Curven nter und wter Ordnung, die keinen
Curventheil gemein haben, schneiden sich, höch-
höchstens in nm Punkten.
Dass die Maximalzahl mn für jeden Werth der Zahlen n und
m unter Umständen erreicht werden kann, ersieht man aus dem
Falle, dass / und <p in lauter in Bezug auf x und y lineare
Factoren zerfallen.
Will man, wie es in der Geometrie gebräuchlich ist, in dem
Satze den Zusatz „höchstens" weglassen, so muss man unend-
unendliche Wurzeln mitrechnen, was man durch Einführung homogener
Variablen umgehen kann. Man muss aber auch noch Fest-
Festsetzungen treffen, wonach in gewissen Fällen einige der Schnitt-
Schnittpunkte mehrfach zu zählen sind.
Nur wenn wir uns der oben erwähnten homogenen Form be-
bedienen, oder, was auf dasselbe hinauskommt, wenn wir unendliche
Werthe der Unbekannten zulassen, können wir den Satz aus-
aussprechen, dass zwei Gleichungen mit zwei Unbekannten
immer wenigstens eine Lösung haben.
Die Theorie der Elimination setzt uns nun in den Stand,
folgende Aufgabe zu lösen.
II. Es sei ein System 8 von Gleichungen fx = 0,
f2 = 0, /3 = 0, . . . zwischen den Unbekannten
x, y, g, . . . gegeben. Die Anzahlen der Gleichun-
Gleichungen und der Unbekannten sollen beliebig sein
und brauchen nicht mit einander überein-
übereinzustimmen. Es sollen alle Werthe der Unbe-
Unbekannten ermittelt werden, die diesen Glei-
Gleichungen zugleich genügen, wenn solche vor-
vorhanden sind, und im entgegengesetzten Falle
nachgewiesen werden, dass keine vorhanden
sind.
In dem Falle, wo nur eine Unbekannte vorhanden ist, hat
man zur Lösung dieser Aufgabe zu untersuchen, ob die Func-
tionen /1,/2,/s, • •. einen gemeinschaftlichen Theiler haben, und
wenn ein solcher gefunden ist, giebt uns sein Verschwinden die
Werthe der Unbekannten durch Auflösung einer algebraischen
Gleichung mit einer Unbekannten. Wir nehmen also die Auf-
Aufgabe für eine geringere Anzahl von Unbekannten, als die gegebene,
als gelöst an, und wenden die vollständige Induction an.

§. 55. Elimination. 189
Wenn von den gegebenen Gleichungen nur eine, etwa
fx = 0, die Unbekannte x enthält, so setze man in diese eines
der Werthsysteme der y, 0, . . . ein, die den übrigen Gleichungen
genügen, die, nach der Voraussetzung, als schon gefunden be-
betrachtet werden. Dann sind drei Fälle möglich: Entweder fx
verschwindet identisch, dann gehören zu diesem Werthsystem
der y, 0, . . . unendlich viele Werthe von x, oder es geht x aus
/1 heraus, ohne dass /i verschwindet, dann giebt es keinen Werth
von x, oder endlich es ergiebt sich eine algebraische Gleichung
für x, die eine endliche Anzahl von Wurzeln hat.
Hierauf können wir nun das allgemeine Problem in folgen-
folgender Weise zurückführen. Wir nehmen aus dem System zwei
Gleichungen heraus, die die Variable x enthalten:
f=aoxn-\~a1 xn~1 -f- • • • -j- an
q> = b0 xm -j- h %m~Y -j H im,
deren Coefficienten ganze Functionen der y, 0, . . . sind. Diese
müssen in Bezug auf x einen gemeinschaftlichen Theiler vom
ersten, zweiten, dritten,... Grade haben. Die Bedingungen dafür
lassen sich nach §. 54 als rationale Gleichungen zwischen den
y, 0, . . . darstellen, und ebenso ergiebt sich dann der grösste
gemeinschaftliche Theiler von / und <p als rationale Function
von x, y, 0, . . . Dadurch ist dann das System 8 auf ein anderes
System 81 zurückgeführt, das zwar mehr Gleichungen enthalten
kann als 8, in dem die Unbekannte x aber in einer Gleichung
¦weniger vorkommt als in 8. Durch Wiederholung dieses Ver-
Verfahrens ist dann die Aufgabe gelöst. Es ist hierbei aber noch
zu bemerken, dass man die verschiedenen Systeme SL be-
betrachten muss, die sich aus der Annahme verschiedener Grade
¦des gemeinschaftlichen Theilers von/und q> ergeben; auch muss
man darauf Rücksicht nehmen, dass möglicherweise a„, ba ver-
verschwinden können, wenn man es nicht vorzieht, diese Möglichkeit
dadurch auszuschliessen, dass man durch eine lineare Substitution
in allen Gleichungen von 8 den Coefficienten der höchsten
Potenz von x constant macht. Man erreicht dies etwa dadurch,
dass man
y = x -f- ayu 0 = x -\- ßeY, . . .
setzt, worin «, ß, . . . beliebige, nicht verschwindende Constanten
sind.
Wenn sich im Verlaufe der Rechnung Gleichungen einstellen,

190 Vierter Abschnitt. §. 56.
die einen rationalen gemeinschaftlichen Theiler haben, so kann
man diesen abspalten, und die Aufgabe in mehrere einfachere
der gleichen Art zerlegen. Es kann auch vorkommen, dass in
den auf einander folgenden Systemen von Gleichungen eines auf-
auftritt, dessen Gleichungen alle einen gemeinsamen Theiler haben.
Enthält dieser mehrere der Unbekannten, so entspringt aus ihm
ein System von unendlich vielen Lösungen, bei denen allen in
diesem Factor vorkommenden Unbekannten, ausser einer, be-1
liebige Werthe ertheilt werden können.
III. Das Problem II wird also nach dem geschil-
geschilderten Verfahren immer gelöst durch Auf-
Auflösung einer Kette von algebraischen Glei-
Gleichungen mit nur einer Unbekannten unddurch
Einsetzen willkürlicher Werthe für gewisse
der Unbekannten.
§. 56.
Elimination aus drei Gleichungen.
Die Principien der Elimination, die wir im Vorhergehenden
auf zwei Gleichungen angewandt haben, lassen sich auf mehrere
Gleichungen mit mehreren Unbekannten ausdehnen. Wir wollen
auf den Fall von drei Gleichungen mit zwei Unbekannten etwas
näher eingehen.
Es seien
A) f(x,y) = 0, <p(x,y) = 0, 4> (x, y) = 0
die drei gegebenen Gleichungen von den Graden n, m, l und wir
setzen
B) f(x, y) = aox»-{- a.x—1 -\ \-am
darin aber sei
C) aÄ = a^y* -+- a^f1 H h «*,*•
In ganz entsprechender Weise bezeichnen wir die Functionen q>
und ip, deren Coefficienten i und c sein mögen, so dass
. i> — C0Xi + C^-l -\- \-Ci
{J c* = cKay" -f Cs,!^-1 H fcft)ft
wird.
Wir bilden nun zunächst aus den beiden Functionen / und
q> nach §. 54 die Resultante B„. Wir setzen dann unter der

§. 56. Die Resultante. 191
Voraussetzung, dass Bn—i von Null verschieden ist [nach §. 54,
B8)]:
E) x = |l=L
in «/> (a;, y) ein, und erhalten
Die rechte Seite dieses Ausdrucks ist eine ganze Function
von y, deren Grad ft wir hier nicht näher zu bestimmen brauchen.
Er lässt sich übrigens mit Hülfe der Gleichungen B7), §. 54
noch erniedrigen, worauf es hier nicht ankommt.
Wir ordnen F) nach Potenzen von y und setzen
G) Bln-iip(x,y) = W(y) = C^y11 -\- Ci^-1 -\- ¦ ¦ ¦ -f- C|u.
Worauf es hier allein ankommt, ist, dass die Co, Ct,. . ., Cft ganze
Functionen der a, b und lineare Functionen der c sind.
Wir denken uns ferner die Resultante Bn nach Potenzen
von y geordnet und erhalten
(8) Bn = Aoymn -\- A1ymn-1 -j- • • • -\~ Am„,
worin die Coefficienten Ai ganze Functionen der a, b allein sind.
Nun bilden wir die Resultante [W, Bn] der beiden Func-
Functionen G), (8). Diese ist eine ganze Function der a, b, c, homogen
in Bezug auf jede der drei Variablen-Reihen a, b, c, deren Grad
in Bezug auf a, b einstweilen nicht näher bekannt ist, deren Grad
in Bezug auf die C und folglich auch in Bezug auf die c (nach
§. 53) gleich mn ist.
Wir sondern nun von der Function [W, Bn~\ einen von den
a, b allein abhängigen Factor B möglichst hohen Grades ab,
und setzen
(9) [W, Bn] = B£l,
so dass £1 keinen von den c unabhängigen Factor mehr enthält.
I. Die auf diese Weise, bis auf einen numerischen
Factor vollständig bestimmte rationale Fuuction
der a, b, c, die in Bezug auf c vom Grade mn ist,
nennen wir die Resultante der drei Functionen
Hier ist nun zunächst zu bemerken, dass der Factor D
nicht verschwinden kann, wenn die Resultante der beiden Func-
Functionen Bn und i?„_! die wir mit z/ bezeichnen wollen, nicht
verschwindet; denn wenn [W, B„] verschwindet, so haben W = 0
und Bn = 0 eine gemeinsame Lösung y. Wenn z/ nicht ver-

192 Vierter Abschnitt. §. 56.
schwindet, so kann Mn nicht identisch verschwinden, und Mn—i
kann für dieses y nicht Null sein; also giebt es eine gemeinsame
Lösung x von der Form E) von / = 0 und <jp = 0, die dann
auch 4> zu Null macht. Wenn aber das von den c unabhängige
B gleich Null ist, so bleibt [W, En] Null, welche Werthe auch
die c haben mögen, und man kann die c so annehmen, dass
t\i = 0 keine Lösung mit / = 0 und q> = 0 gemein hat. Wenn
also B = 0 ist, so muss z/ verschwinden. Damit ist Folgendes
bewiesen:
II. Wenn für die a, i, c solche Werthe gesetzt sind,
dass ß = 0 und z/ nicht = 0 wird, so haben die
drei Gleichungen / = 0, <p = 0, «/> = 0 eine ge-
gemeinsame Lösung
und umgekehrt:
III. Haben /=0, q> = 0, ip = 0 eine gemeinsame
Lösung, und ist z/ von Null verschieden, so ver-
verschwindet £1.
Es ist nicht leicht, sich auf rein algebraischem Wege von
der unnöthigen Voraussetzung frei zu machen, dass z/ von Null
verschieden sei. Einfacher aber gelangt man dazu durch Be-
Benutzung der Stetigkeit.
Angenommen, die drei Gleichungen A) haben eine gemeinsame
Lösung x, y, während z/ = 0, aber £1 von Null verschieden ist
Dann kann man die a, b beliebig wenig, aber so ändern, dass
z/ einen von Null verschiedenen Werth erhält. Betrachtet man
x, y als Lösung von / = 0 und <p = 0, so werden diese Grossen
durch algebraische Gleichungen bestimmt, deren Coefficienten
rational von a, b abhängen, und die sich also bei hinlänglich
kleinen Veränderungen von a, b um beliebig wenig ändern
(§. 44). Sie mögen in x\ y' übergehen. Dann kann man die
Coefficienten c noch so ändern, dass ip (%', y') wieder verschwindet,
und diese Aenderungen der c sind ebenfalls beliebig klein. Man
kann also schliesslich diese Aenderungen alle so klein annehmen,
dass ii nicht Null wird, und dann erhält man einen Wider-
Widerspruch gegen III.
In ähnlicher Weise lässt sich zeigen, dass auch wenn &l
und z/ zugleich verschwinden, die drei Gleichungen A) eine
gemeinsame Lösung haben. Wenn zunächst / und q> einen ge-
gemeinsamen Theiler haben, so wird dieser und folglich auch/
und (jp mit 4>. eine gemeinsame Wurzel haben.

§. 57. Theorem von Bezout.' 193
Wenn dies nicht der Fall ist, so giebt es nur eine endliche
Anzahl von Wurzeln x, y von / und <p. Wir wollen annehmen,
dass für keine von diesen ip (x, y) verschwindet. Wir variiren
nun a, b, c so wenig, dass alle diese tj> (x, y) von Null ver-
verschieden bleiben, jedoch so, dass /l von Null verschieden wird,
während ß Null bleibt. Dann haben wir einen Widerspruch
gegen (II). Damit ist also bewiesen:
IV. Die nothwendige und hinreichende Bedingung
dafür, dass die Gleichungen /= 0, cp = 0, ^ = 0
eine gemeinsame Lösung haben, ist ß = 0.
Es ist hierbei jedoch noch zu bemerken, was wir bei der
Beweisführung der Kürze wegen nicht ausdrücklich hervorgehoben
haben, dass der Satz II, und demgemäss auch III und IV nur
dann allgemein gültig sind, wenn man auch unendliche Werthe
von x, y zulässt, oder besser, wenn man die gegebenen Gleichungen
in der homogenen Form
f(x, y, z) = 0, cp (x, y, z) = 0, 4> (x, y, z) = 0
annimmt, wobei dann auch z = 0 unter den Lösungen auftreten
kann.
§• 57.
Grad und Gewicht der Resultante. Das Theorem
von Bezout.
Näheren Aufschluss über die Natur der Resultante £1 von
drei Gleichungen erhalten wir, wenn wir einen speciellen Fall
betrachten, den nämlich, dass die drei Functionen /, cp, tp in
lineare Factoren zerfallen.
Es sei
/ = n («w x + o« y + <>)
1, n
A) 9=jlßf>x
= n (y W x +
) y
worin die a, ß, y nun als unabhängige Variable gelten. Dieser
Fall geht aus den allgemeinen dadurch hervor, dass man für
die a, 6, c gewisse homogene Functionen a', b\ c' der Variablen
Weber, Algebra. I. 13

194 Vierter Abschnitt. §. 57.
a, ß, y setzt, und zwar sind die a vom wten Grade in den «, die
b vom witen Grade in den ß, die c vom Zten Grade in den y. Das
Ersetzen der a,b, c durch diese Functionen «', 6', c' wollen wir
der Kürze wegen die Substitution © nennen.
Die Functionen /, <p, ^, ß mögen durch die Substitution ©
in /, <p', ^', ß' übergehen. Es werden f, <p', ip' immer dann,
aber auch nur dann, eine gemeinsame Wurzel haben, wenn eine
der Determinanten
B)
«w,
verschwindet. Die Anzahl dieser Determinanten beträgt Imn.
Daraus folgt, dass auch £1' durch jede der Determinanten
B), und folglich auch durch ihr Product theilbar sein muss.
Daraus ergiebt sich nun der Beweis des folgenden wichtigen
Satzes:
I. Die Resultante ß ist als Function von a, b, e un-
unzerlegbar.
Es sei nämlich ßn ein in Bezug auf a, 6, c rationaler Theiler
von ß, und durch die Substitution © gehe ßx in ßi über. Es
muss dann ßi wenigstens durch eine der Determinanten zlh,i,ic
theilbar sein. Da aber, wenn die Indices h, i, Je durch irgend
drei andere h', i', Je' ersetzt werden, die a', b', c' und mithin auch
ßi ungeändert bleiben, so muss ßi durch die sämmtlichen
Determinanten B) und also auch durch deren Product theilbar
sein. Da das Product aber in Bezug auf die c' vom Grade mn
ist, so ist auch ii1 nicht von niedrigerem Grade in. Bezug auf
die e. Da es aber auch nicht von höherem Grade sein kann,
und da überdies nach Voraussetzung ß keinen von den c unab-
unabhängigen Theiler hat, so ist ßx (von einem numerischen Factor
abgesehen) mit ß identisch.
Diese Betrachtung zeigt nun zugleich, dass ßi in Bezug auf
die «', V und folglich ß in Bezug auf die a, b mindestens
vom Grade ml und nl sein muss.
Wenn wir aber nun die ganze Betrachtung des vorigen und
dieses Paragraphen wiederholen, nur mit dem Unterschiede, dass
wir / an die Stelle von tp, also die a an die Stelle der c treten
lassen, so erhalten wir statt ß eine Function Slf, die in Bezug

§. 57. Theorem von Bezout. 195
auf die a vom Grade ml ist. Nach §. 56^ IV. verschwindet aber
£1/ immer, wenn £1 verschwindet; und folglich muss £lf durch das
unzerlegbare £1 theilbar sein (§. 43, 2.). Daraus ergiebt sich,
dass £1 in Bezug auf die a höchstens vom Grade Im ist, und
da dieselbe Betrachtung ein drittes Mal wiederholt werden kann,
so ist bewiesen:
II. Die Resultante £1 dreier Functionen von drei
Variablen von den Graden n, m, l ist vom Grade
ml in den Coefficienten der ersten, In in denen
der zweiten und nm in denen der dritten Function.
Daraus ergiebt sich, dass die Function £1' dem Producte
der Determinanten B) gleich ist, oder die Formel
C) fi' = J7^M>fc.
Diese Formel gestattet die Bestimmung des Gewichtes von
£1, das wir erhalten, wenn wir den Coefficienten a^*, b^-k, e&,&
das Gewicht h beilegen, so dass [nach §. 53, C)] /, <p, ty in
homogene Functionen wten, mten, Zten Grades übergehen, wenn für
die Coefficienten homogene Functionen neuer Variablen vom
Grade des Gewichtes gesetzt werden.
Das Gewicht fc ergiebt sich nämlich für die aj^jt, %,&;, <4,fo>
wenn wir in A) den «l5 «ä, ßx, ß2, yu y2 das Gewicht 0, und den
ai i ßi i 7z das Gewicht 1 beilegen. Dadurch erhält aber z/Äi ^ fc
das Gewicht 1 und £1' das Gewicht Imn. Dies ist dann aber
auch das Gewicht von £1, das sich durch die Substitution @ nicht
ändern kann. Diesem Satze über das Gewicht können wir den
folgenden Ausdruck geben, in dem es das Bezout'sche Theorem
enthält.
III. Durch Elimination von zwei Unbekannten aus
drei Gleichungen Zten, mten, wten Grades ergiebt
sich für die dritte eine Endgleichung vom Grade
Imn.
Um daraus (wie in §. 55, I.) den geometrischen Satz ab-
ableiten zu können, dass sich drei Flächen von den Graden l, m, n,
die nicht unendlich viele Punkte gemein haben, höchstens in
Imn Punkten schneiden, wäre noch zu zeigen, dass die End-
Endgleichung in s, wenn zu demselben Werthe 0O vom s mehrere,
etwa v Werthe von x, y gehören, wenigstens durch (z — 0O)V
theilbar ist.
13*

196 Vierter Abschnitt. §. 57.
Dieser Beweis würde auf algebraischem Wege nicht ohne
Weitläufigkeit zu führen sein. Man kann diesem Mangel aber
auch durch eine Stetigkeitsbetrachtung abhelfen, die hier, in
geometrischem Gewände, kurz angedeutet sein mag. Nehmen
wir an, die drei Flächen /, <p, ^ haben für einen Werth s = 0O
v Schnittpunkte. Wir geben dem System der Flächen /, <p, ip,
ohne ihre Gestalt und gegenseitige Lage zu ändern, eine unend-
unendlich kleine Drehung um eine Axe, die in der Ebene 0 =¦ 0O
liegt, aber mit keiner der Verbindungslinien der in dieser Ebene
angenommenen v Schnittpunkte parallel ist. Dann sind nach der
Drehung die ^-Ordinaten dieser Punkte alle von einander ver-
verschieden; sie mögen gu g% . . . gv geworden sein. Diese Drehung
findet aber ihren analytischen Ausdruck in gewissen Ver-
Veränderungen der Coefficienten a, b, c von /, <p, i\>, die zugleich
mit der Drehung unendlich klein werden. Wenn nun die Re-
Resultante £l(g) durch diese Drehung in ß' übergegangen ist, so
ist ß' durch (g — g{) @ — g2) . . . @ — gr) theilbar; und da
die Drehung beliebig klein genommen werden kann, so ergiebt
sich daraus nach §. 44, dass ß @) durch @ — 0o)r theilbar sein
muss.
Wir wollen hier noch einmal auf die Bildung der End-
gleichung von zwei homogenen Gleichungen mit zwei Unbe-
Unbekannten, also auf die Bestimmung der Schnittpunkte zweier
Curven zurückkommen. Es seien diese beiden Gleichungen vom
Grade n und m
D) f(x, y, 0) = 0, tp 0, y, 0) = 0,
mit den Coefficienten a und b.
Die Endgleichung ergiebt sich in einer symmetrischen Form,
wenn man eine lineare Gleichung
E) ux -\- vy + wg = 0
mit unbestimmten Coefficienten w, v, w hinzufügt, und dann aus
den drei Gleichungen E) und F) die x, y, 0 eliminirt. Man
erhält dann nach B) eine Endgleichung
F) ß («, v, w) = 0,
die in Bezug auf u, v, w homogen und vom Grade mn ist. In
den a ist sie vom Grade m, in den b vom Grade n. Setzt man
in ß («, v, w) z. B. u = 0, v = 1, w = — y, 0 = 1, so ergiebt
sich die Endgleichung für y in der früheren Gestalt.

§.57. Die Resultante. 197
Die Function ß verschwindet, wenn die Gleichungen D) und
E) eine gemeinsame Lösung haben, d. h. so oft die durch E)
dargestellte gerade Linie durch einen Schnittpunkt der beiden
Curven / und cp hindurchgeht, und wenn daher u, v, w homogene
Liniencoordinaten bedeuten, so ist ß = 0 im Sinne der analy-
analytischen Geometrie die Gleichung des Schnittpunktsystemes der
beiden Curven / und <p x).
Die Function ß («, v, w) ist zwar als Function der Variablen
a, b, u, v, w unzerlegbar; sie enthält aber für jedes besondere
Zahlensystem a, b, wofür sie nicht identisch verschwindet, lineare
Factoren in Bezug auf u, v, w, nämlich, wenn x, y, 0 die Coordi-
naten eines der Schnittpunkte sind, den Factor ux -\- vy -f- v0.
Haben wir also m n verschiedene Schnittpunkte, so zerfällt
£l(u,v,w) in mn lineare Factoren.
Hieraus kann man nun wieder durch Stetigkeitsbetrach-
Stetigkeitsbetrachtungen nachweisen, dass ß auch im allgemeinen Falle, wenn es
nicht identisch verschwindet, in m n lineare Factoren zerleg-
zerlegbar ist.
Um dies zu zeigen, seien P1? P3, . . . mit den Coordinaten
xii 2/i > #1 > x%t yii 0i • • ' die Schnittpunkte von / und <p.
Wir können den Coefficienten a, b unendlich kleine Aende-
rungen ertheilen, so dass die Resultante mn verschiedene
Wurzeln erhält, und folglich die variirten Curven /', cp' mn
getrennte Schnittpunkte. Von diesen Schnittpunkten wird eine
gewisse Zahl v1 unendlich nahe bei Px liegen, deren Complex
wir mit PJ bezeichnen wollen, ebenso werden v.2 Punkte P%
unendlich nahe bei P2 liegen u. s. f., so dass
vx -f- v2 -f- • • • = m n
ist. Es sei dann
U-l =ux1 + vyx + W0l
der dem Punkte Pt entsprechende Factor von
ß = ß (u, v, w)
und sei demnach
ß = TJ-i. ßi.
Durch die angegebene Variation der a, b gehe ß in ß'
x) Diese Darstellungsweise der Resultanten findet sich, für den Fall
von drei Flächen zweiten Grades, bei Hesse, Analytische Geometrie des
Raumes (Leipzig, Teubner, 1. Auflage 1861, 3. Auflage 1876).

198 Vierter Abschnitt. §. 57.
über; dann hat ß' die den vx Punkten PJ entsprechenden vx
linearen Factoren d, DT, . . . und es sei
ß' = UJ ßj
so dass ßi noch durch TJ'-l ¦ . . theilbar ist.
Wenn nun ßx nicht durch Uj, theilbar wäre, so könnte man
über die «, v, w so verfügen, dass Z7X = 0, und ßx von Null
verschieden wäre.
Dann würde man aber, da die Variationen beliebig klein
genommen werden können, und ßi dem Si^ also beliebig nahe
gebracht werden kann, ein System vom Werthe u, v, w finden
können, für die TJ'i verschwindet, während ßi von Null ver-
verschieden ist. Dies ist aber unmöglich, weil ßi durch Z7i' theil-
theilbar ist. Folglich muss ß durch J7i theilbar sein, und durch
Wiederholung dieses Schlusses findet man, dass ß durch U[l
theilbar ist. Wir haben also das Bezout'sche Theorem in
folgender schärferen Form.
IV. Die Resultante Sl(u,v,w) der beiden Curven / und
<p verschwindet entweder identisch, und dann
haben/ und <p unendlich viele gemeinschaftliche
Punkte; oder es zerfällt £l(u,v,w) in mn lineare
Factoren, die auch zum Theil einander gleich
sein können, deren jeder, für sich gleich Null
gesetzt, die Gleichung eines der Schnittpunkte
der beiden Curven darstellt.
Diese Formulirung des Satzes von Bezout giebt dann auch
eine zweckmässige Bestimmung darüber, mit welchem Grade
der Vielfachheit man jeden Schnittpunkt der beiden Curven zu
zählen hat.
Diese Betrachtungen sind, wie man leicht erkennt, einer
Verallgemeinerung für den Fall einer grösseren Anzahl von
Gleichungen mit einer gleich grossen Anzahl von Unbekannten
fähig. Man hat z. B., um zu dem nächsten Falle überzugehen,
aus den Voraussetzungen des §. 56 aus drei Gleichungen
f(pc, y) = 0, <p (x, y) = 0, ij> (x, y) = 0, die eine gemeinsame Lösung
haben, für diese Werthe von x, y rationale Ausdrücke durch die
Coefficienten von /, <p, i\> abzuleiten. Wir wollen hier aber nicht
näher darauf eingehen.

§. 58. Tschirnhausen-Transformation. 199
§. 58.
Tschirnhausen-Transformation.
Wir machen von der Theorie der symmetrischen Functionen
und der Resultantenbildung noch eine wichtige Anwendung auf
die von Tschirnhausen1) herrührende Transformation alge-
algebraischer Gleichungen.
Es sei
A) f{x) = xn -f ö!^-1 + a^x"-* -j [. an^x -f an
irgend eine Function wten Grades, und
irgend eine (ganze oder gebrochene) rationale Function von x,
bei der wir nur die eine Voraussetzung machen, dass f(x) und
fy (x) keinen gemeinsamen Theiler haben sollen. Nach
dem Schlusssatz von §. 6 können wir dann die Functionen F(x)
und <p (x), letztere höchstens vom Grade w— 1, so bestimmen, dass
C) % (x) = F(x)f(x) + <p (x) i> (x)
wird, so dass, sobald für x eine Wurzel der Gleichung
D) f(x) = 0
gesetzt wird,
4$ = 9 ix)
wird. Da wir nun die Werthe von y nur für solche Werthe
von x, die Wurzeln von D) sind, betrachten werden, so
verlieren wir nichts an Allgemeinheit, wenn wir von vornherein
y = cp(x),
also gleich einer ganzen Function (« — l)ti!n Grades setzen. Es
sei also
E) y = (pix) = «o + «! x + «j,x* -) (- an^xn-\
worin die Coefficienten a vorläufig noch ganz unbestimmt bleiben.
Bezeichnen wir mit
F) Xlt X2, . . ., Xn
*) Acta eruditorum, Leipzig 1683.

200 Vierter Abschnitt. §. 58.
die Wurzeln der Gleichung D), so ergeben sich aus E) die ent-
entsprechenden Werthe von y:
G) yr = <p (x{), 2/2 = y (xa) . . . yn = <p (x„),
und das Product
(8) Q(y) = (y — yj (y — y2) . . . (y — yn)
ist eine symmetrische Function der Grossen F), die sich
also rational durch die Coefficienten von /(a;) aus-
ausdrücken lässt.
In dieser Weise dargestellt, möge <Z>(j/) den Ausdruck haben
(9) <P(y) = y» + hy^ + hy»-* -] [- bn^y + bn.
Die Coefficienten bv werden nach §. 7 durch die yi bestimmt
mittelst der Formeln
h = — Züi, h = Zyiüv h = — Et/iUaüs, ¦ •
woraus sich ergiebt, dass bv eine ganze rationale und
homogene Function vten Grades von den Variablen
a0, «!,..., «M_j ist.
0 (i/) ist nichts Anderes als die Resultante der beiden
Gleichungen
A0) /(*) = <>, <p(x) - y = 0,
und nach §. 54 kann man auch umgekehrt die gemeinsame
Wurzel x dieser beiden Gleichungen A0), wenn y einem der Werthe
Vn Vii • • -1 Vn gleich wird, rational durch die Coefficienten von
A0), d. h. rational durch a4, a{, y ausdrücken, vorausgesetzt, dass
nur eine solche gemeinsame Wurzel vorhanden ist.
Dies wird dann eintreten, wenn die n Werthe yu y2, . • ., yn
von einander verschieden sind. Dann erhält man einen Ausdruck
* = ßo + ßiy + ß*y* -\ h ßn-iy"'1,
der gültig ist, wenn für x einer der Werthe F) und für y der
zugehörige Werth G) gesetzt wird. Die Grossen ßi sind aus
den <Xi und «^ rational zusammengesetzt.
Kommen aber unter den Werthen yx, y2, . . ., yn mehrere
gleiche vor, so erfordert die Bestimmung der zugehörigen Werthe
der x noch die Auflösung einer Gleichung des entsprechenden
Grades. Dieser Grad ist aber immer kleiner als w, da
die Function q> (x) höchstens für n — 1 Werthe von x denselben
Werth y erhalten kann. Wenn also die Gleichung
A1) <P(y) = 0

§. 58. Tschirnhausen-Transformation. 201
vollständig gelöst ist, so ist damit auch die Gleichung A) voll-
vollständig gelöst [wenn A1) nur verschiedene Wurzeln hat] oder
wenigstens auf die Lösung einer Gleichung niederen Grades
zurückgeführt [wenn A1) gleiche Wurzeln hat].
Demnach betrachten wir A1) als eine Umformung der
Gleichung A), und die Bildung von A1) aus A) heisst die
Tschirnhausen-Transformation der Gleichung A).
Der Zweck einer solchen Transformation ist, die Coeffi-
cienten a{ so" zu bestimmen, dass <& (y) eine einfachere Gestalt
erhält als f(x).
Man kann die Coefficienten bv bilden, wenn man die Potenz-
Potenzsummen der yi kennt (§. 46).
Bezeichnen wir die Summen der mten Potenzen der Xi mit
sm, der yi mit öm, also
sm = Sx™, <sm = Syy,
so können wir öm durch die sm auf folgende Art bilden.
Wir entwickeln zunächst y™ nach dem polynomischen Lehr-
Lehrsatz (§. 12), setzen also
A2) ym =
worin die Summe sich auf alle nicht negativen ganzzahligen
Werthe von v0, v\, . . ., v„_i erstreckt, die der Bedingung
A3) v0 + vx -) 1- v„_j = m
genügen. Setzen wir dann in A2) x^ xit . . ., xn für x und bilden
die Summe der so erhaltenen Werthe von y^, y*g, . . ., ym, so folgt
A4) öm =
) • • • ^M "-1
Hierdurch ist öm als ganze homogene Function mter Ordnung
der «0, «!,..., «„_! dargestellt. Eine etwas vereinfachte Schreib-
Schreibweise erhält man nach der zweiten Darstellung von Formen
(§. 17). Lassen wir ^t, /t2, . . ., pm unabhängig von einander die
Reihe der Zahlen 0, 1, . . ., n — 1 durchlaufen, so wird, wenn in
einer Combination v0 mal der Index 0, vx mal der Index 1, v2 mal
der Index 2, ... v„_!mal der Index n — 1 vorkommt,
Vo + vi + vi H h "*-i = m
und

202 Vierter Abschnitt. §. 59.
Cl+ftH • + f*m = Vx + 2f2 + • • • -f (W — 1)V„-1,
und danach kann der Ausdruck für öm so dargestellt werden: ;
/*
A5) 6m = Ss^+^ + .-.+^a^tt^ . . . aßm.
Beispielsweise wird
A6) ö2 =
h, i, fc
worin h, i, h die Reihe der Zahlen 0, 1, 2, . . ., n — 1 durchlaufen.
§. 59.
Anwendung auf die cubischen und biquadratischen
Gleichungen.
Das Ziel, das schon Tschirnhausen bei dieser Trans-
Transformation im Auge gehabt hat, bestand darin, durch Bestimmung
der Substitutionscoefficienten aa, «i, • . ., «K—i in der umgeformten
Gleichung <I> (y) = 0 so viele Glieder zum Verschwinden zu
bringen, dass die Gleichung lösbar wird. Es gelingt dies leicht
bei den Gleichungen dritten und vierten Grades, wenn es auch
nicht einfach ist, und nicht ohne weitläufige Rechnungen mög-
möglich scheint, die sonst bekannten Formeln auf diesem Wege
abzuleiten.
Nehmen wir zunächst die cubische Gleichung
A) xz -\- a x2 -)- b x -\- c = 0,
die wir durch die Substitution
B) y = et -j- ßx -\- yx2
umformen. Um die Gleichung für y
C) y3 -j- Ay2 -\- By -\~ C=0
auf eine reine cubische Gleichung zurückzuführen, haben wir die
Verhältnisse a:ß:y aus den beiden Gleichungen
D) A = 0, B = 0
zu bestimmen, von denen die erste linear, die zweite quadratisch ist.
Die Gleichungen D) sind gleichbedeutend mit

§. 59. Gleichungen dritten und vierten Grades. 203
und ergeben also nach A6) des vorigen Paragraphen
«s0 + ßsL -\-ys2 = 0,
«2S0 -f 2aßs1 + 2uys2 -f /32S2 + 2ßyss -f y2s4 = 0,
worin s0 = 3 ist. Multiplicirt man die letztere Gleichung mit
s0 und zieht das Quadrat der ersten davon ab, so folgt
F) ß* (So s2 - sf) + 2 ß y (s0 s3 — Sl s2) + r^(So §4 _ S|) = o.
Die Discriminante dieser quadratischen Gleichung
(S0 S3 — SX S2J — (So S2 — S/) (So Si — Sl)
giebt entwickelt
So (So S2 Si So S3 — Si S4 — S| -(- 2 Si S2 S3),
ist also, wenn x; die Discriminante der cubischen Gleichung A)
bedeutet [§. 50, (9)] gleich — 3D, und "die Auflösung von F)
giebt also
ß _ — (s0s3 — s2 s2) + V —3D
G)
y s0 s2 — $(
Damit ist die Gleichung C) auf eine reine Gleichung zurück-
zurückgeführt, die zu ihrer Lösung nur noch das Ziehen einer Cubik-
wurzel erfordert. Welches Vorzeichen wir der in G) vorkommen-
vorkommenden Quadratwurzel geben wollen,' steht in unserem Belieben.
Um die Tschirnhausen-Transformation für die biquadratische
Gleichung zu benutzen, kann man etwa so verfahren, dass man
in der umgeformten Gleichung
(8) yi + hxy* + b2y* -f bsy 4 &4 = 0
die «o, «i, «2, «j so bestimmt, dass
(9) &i = 0, b3 = 0
wird, wodurch (8) in eine quadratische Gleichung für y2 über-
übergeht, aus deren Wurzeln noch die Quadratwurzeln gezogen
werden müssen, so dass, nachdem die Gleichungen (9) gelöst
sind, noch zweimal eine Quadratwurzel gezogen werden muss.
Wenn man mittelst der ersten Gleichung (9) aus der zweiten
a0 eliminirt, so entsteht eine homogene cubische Gleichung
zwischen c^, a2, as. Man kann daher eines von den beiden Ver-
Verhältnissen k1:u2:cxs beliebig annehmen, z. B. a3 = 0 setzen, und
erhält zur Bestimmung des anderen eine cubische Gleichung.
Dadurch ist dann die Lösung der biquadratischen Gleichung auf
die einer cubischen und auf Quadratwurzeln zurückgeführt.

204 Vierter Abschnitt. §. 60.
§. 60.
Die Tschirnhausen-Transformation der Gleichung
fünften Grades.
Will man auf die Gleichung fünften Grades
A) X' -f- Oj X* -f" a2 X°" + «3 #* + ai X + ai = 0
die Tschirnhausen-Transformation anwenden, so hat man
B) # = ao-pa1aj + a2aj2-|- a3 «3 + a4 a?*'
zu setzen, und erhält die Transformirte
C) t + Kt + 6ay« + 632/2 + &42/ + &5 = 0.
Der nächstliegende Gedanke, wäre nun, die Verhältnisse der
fünf Unbekannten a so zu bestimmen, dass
D) hx = 0, h = 0, &3 = 0, &4 = 0
würde, wodurch C) auf eine reine Gleichung zurückkäme, und
dies war auch das Ziel, das Tschirnhausen im Auge hatte.
Aber von den vier Gleichungen D) ist die erste linear, die
zweite quadratisch, die dritte vom dritten und die vierte vom
vierten Grade. Die Endgleichung, die man daraus ableiten kann,
wird daher (nach §. 57, III.) vom Grade 2.3.4 = 24, und daher
kann daraus für die Lösung der Gleichung fünften Grades kein
Nutzen gezogen werden. Man sucht daher zunächst nur den
beiden Gleichungen zu genügen:
E) \ = 0, b2 = 0,
wodurch die Gleichung C) in eine Form übergeht, die nach
F. Klein (Vorlesungen über das Ikosaeder) eine Haupt-
gleichung fünften Grades genannt wird.
Zur Befriedigung der beiden Gleichungen E) haben wir die
Verfügung über die vier Verhältnisse a0 : % : a2 : Ms '¦ aii un^ wir
können diese Grossen noch auf mannigfaltige Art zur Verein-
Vereinfachung der Gleichung fünften Grades benutzen.
Wir kommen in einem späteren Abschnitt ausführlicher auf
diesen Gegenstand zurück und beschränken uns hier darauf, die
Ziele im Allgemeinen zu bezeichnen. Der Anschaulichkeit wegen
bedienen wir uns einer geometrischen Einkleidung, die übrigens
zum Verständniss der algebraischen Theorie, wie sie später
gegeben werden soll, durchaus nicht wesentlich ist.

§. 60. Hauptgleichung fünften Grades. 205
Wenn wir mit Hülfe der linearen Gleichung b\ = 0 von
den fünf Grossen k die eine, etwa a0, durch die übrigen aus-
ausdrücken, so können wir die vier übrigen ax, «<,, «3, ai als homo-
homogene Coordinaten eines Raumpunktes betrachten. Die Gleichung
b2 = 0 stellt dann eine Fläche zweiter Ordnung dar, bs = 0
eine Fläche dritter Ordnung, bi = 0 eine Fläche vierter Ord-
Ordnung, b-0 = 0 eine Fläche fünfter Ordnung.
Wollte man also 62, bs, bt zugleich zu Null machen und
dadurch die gegebene Gleichung auf eine reine reduciren, so
müsste man einen der 24 Schnittpunkte von drei Flächen zweiter,
dritter, vierter Ordnung bestimmen, der von einer Gleichung
24ten Grades abhängt.
Statt nun so zu verfahren, sucht man auf der Fläche
b% = 0 eine gerade Linie zu bestimmen. Solcher gerader Linien
giebt es auf jeder Fläche zweiter Ordnung eine oder zwei
Schaaren (reell oder imaginär), und man kann eine dieser Geraden
durch Quadratwurzeln bestimmen, wie weiter unten aus-
ausgeführt werden soll. Die Ermittelung eines Schnittpunktes einer
dieser geraden Linien mit der Fläche bz = 0 führt dann auf
eine Gleichung dritten Grades, und wenn man noch durch Be-
Bestimmung eines gemeinsamen Factors der et, den Coefficienten
b± = 1 macht, so erhält die Gleichung für y die Gestalt
F) 2/5 + 2/ + & = 0,
wodurch y als algebraische Function einer Variabein b bestimmt ist.
Diese Gleichungsform wird gewöhnlich nach dem englischen
Mathematiker Jerrard genannt, der sie im Jahre 1834 bekannt
machte. Sie ist aber schon viel früher A786) von E. J. Bring
in Lund publicirt worden1). Wir nennen sie daher die Bring-
Jerrard'sche Form.
Ebenso gut könnte man durch eine Gleichung vierten Grades
&4 = 0 machen, und würde eine zweite Normalform der Gleichung
fünften Grades erhalten:
G) r + t + & = 0,
die die gleiche Berechtigung hat, wie die Bring-Jerrard'sche
Form.
Für die Lösung der Gleichung fünften Grades freilich wird
durch diese Betrachtungen nichts gewonnen. Ihr Nutzen besteht
Vgl. F. Klein, Vorlesnagen über das Ikosaeder, S. 143.

206 Vierter Abschnitt. §. 60.
darin, dass die Gleichung fünften Grades auf eine Normal-
form zurückgeführt wird, die nur von einem veränderlichen
Coefficienten abhängt. Dies kann auf unendlich viele verschiedene
Arten, erreicht werden, und gelingt am einfachsten, nämlich ohne
Lösung einer Gleichung dritten oder vierten Grades, wenn man
die Gleichung fünften Grades bs = 0 selbst als eine Umformung
der gegebenen Gleichung fünften Grades betrachtet. Hat man
nämlich die Gleichung b6 = 0 gelöst, so wird einer der fünf
Werthe von y gleich 0, und die gegebene Gleichung fünften
Grades ist damit zugleich gelöst.

Fünfter Abschnitt.
Lineare Transformation.
§. 61.
Einführung der linearen Transformation.
Wenn wir in irgend welchen Functionen, die von den m
Veränderlichen a%, x2, ¦ . ., xm abhängen, für diese Veränderlichen
lineare Ausdrücke einsetzen, die von m neuen Veränderlichen
x'h x'2, . . ., x'm abhängen
(i) ?r:v: ::7+:':+<"-:
so nennen wir dies eine lineare Substitution, und das Er-
gebniss eine lineare Transformation.
Die Grosse
B)
«w, «f),.. .,
heisst die Substitutionsdeterminante. Sie muss immer
von Null verschieden sein, da sonst durch A) eine Abhängigkeit
zwischen den Variablen xx, x2, . . ., xm ausgedrückt wäre.
Durch eine lineare Substitution geht jede homogene Func-
tion der Variablen x in eine homogene Function desselben
Grades der Variablen x' über.

208 Fünfter Arbschnitt. §. 62.
So geht beispielsweise jede lineare Function
i
y = SciiXi
in eine ebensolche Function
y< = Ea-x'i
über, worin
C) a!h
Betrachten wir m solcher linearer Functionen
i
*«m>—•Mflfe^' = 2 a>i,v%i v = 1, 2,..., m,
so erhalten wir m transformirte Functionen
y'v = U^vx'i v = 1, 2,..., m.
Die Determinanten der Systeme yn y'v
4 = 2 + (h,lCl2,2 • • • Om,m, 4' = 2 + 0^,10^,2 • . • 0!m,m
stehen nach dem Multiplicationsgesetz der Determinanten in der
Abhängigkeit
D) J' = r4,
so dass die eine nicht ohne die andere verschwindet.
§• 62.
Quadratische Formen.
Von besonderer Wichtigkeit ist die Transformation der
homogenen Functionen zweiten Grades oder der quadratischen
Formen. "Wir bezeichnen sie, wie schon im ersten Abschnitt, so:
A) g>(%7 ^25 • • -i ay)
Durch die Substitution §. 61, A) geht <p über in
B) * (x'v x'2, . . ., x'm) = 2a'i!htiü.
Setzen wir x -(- £ für % und ebenso x' -f- |' für x1, so dass
die |' mit den -| in derselben Abhängigkeit stehen, wie die af
mit den x, so erhalten wir, wenn wir zur Abkürzung
| <p' (xt) = ut, \ 0' (xi) = u'i
setzen, durch Vergleichung der Glieder der ersten Dimension
[§. 18, A2), A3)]:

§. 62.
C)
also,
D)
wie
Nun
in
ist
§•
Quadratische Formen.
2?g,«, = 27g;«^
61, C)
209
und demnach giebt uns D) die Transformation von m linearen
Functionen. Die Coefficienten des transformirten Systems sind
a^j, und des ursprünglichen, die man durch Einsetzen des ersten
Systems E) in D) erhält,
F) bk,h
Die Determinante des ersteren Systems
H' = S + ffli,i «3,2 • • • S
ist nach §. 61, D)
und nach F) ist die Determinante der by,^
Wenn wir also
G) H = S ± ahl 02,3 ... anhm
setzen, so haben wir den wichtigen Satz
(8) H' = r"K
Die Determinante H wird die Determinante der Form
(p (x) genannt.
Sie ändert sich also bei der linearen Transformation der
Function q> nur um den Factor r2, und sie kann bei der trans-
transformirten Form nicht verschwinden, wenn sie es bei der ursprüng-
ursprünglichen nicht thut.
Das Verschwinden der Determinante H hat die Be-
Bedeutung, dass die Function <p(x) sich auffassen lässt
als eine Function von weniger als m Veränderlichen,
die lineare Functionen der x sind.
Denn wenn erstens durch eine lineare Transformation y (x)
in die Function <£ (x1) übergeht, die von einer der Veränderlichen)
etwa von x'v unabhängig ist, so verschwindet H', da die Elemente
in einer der Zeilen (und Colonnen) alle verschwinden, und also
ist wegen (8) auch H = 0.
Zweitens aber ist H die Determinante des Systems linearer
Gleichungen
Weber, Algebra. I. 14

210 ¦ Fünfter Abschnitt. §. 63.
(9) .q>'(Xi) = 0, » = l, 2...m,
und wenn diese Determinante verschwindet, so giebt es (§. 27, IV.)
ein Grössensystem
A0) 4°>, af > . . . a*»>,
dessen Elemente nicht alle verschwinden, und die, für die % ein-
eingesetzt, den Gleichungen (9) genügen.
Nun hat man aber, wenn a?,-, x\ irgend zwei Grössensysteme
sind, und X ebenfalls eine willkürliche Grosse bedeutet, die iden-
identischen Gleichungen
A1) <p(x + lad) = <p(x) k
[§. 18, A2) bis A5)], so dass, wenn für x\ die Werthe xT gesetzt
werden
ganz unabhängig von X wird. Wenn wir nun annehmen, es sei
scfV> von Null verschieden und wir setzen
ferner:
A3)
y.2 = x2CC^> -
ya = x3 af> — xx xf>
, = xmxf —
so folgt:
A4) 4°>2 (p(x) = 9 @, 2/2, 2/3 ••• 2/m)>
wodurch 9 (a;) durch die m — 1 Veränderlichen y2, y3 . . . ym aus-
ausgedrückt ist.
§. 63.
Transformation der quadratischen Formen in eine
Summe von Quadraten. ¦
Wir machen von dem zuletzt bewiesenen Satze sogleich eine
wichtige Anwendung auf die Discriminante der Function A1)
(als Function zweiten Grades von X betrachtet), wobei nicht
mehr vorausgesetzt wird, dass die Determinante der Function <p
verschwiudet. Diese Discriminante ist
A) * {x) = [2 xt <p' {x'i)Y - 4 <p (a) <p (*0-

§. 63. Quadratische Formen. 211
Setzen wir in ihr x{. -\- X x\ an Stelle von x„ so ergiebt sich,
wenn man für q>(x -\- Xx') den Ausdruck §. 62, A1) substituirt
und ZJx'i (p' (x'i) = 2 q> (x'~) setzt,
ip(x-\- Ix1) = 4>(x),
woraus hervorgeht, dass il>(x) nur von m — 1 linearen Verbin-
Verbindungen der m Veränderlichen abhängt. Setzt man für x'v x\...x'm
beliebige specielle Werthe, für die <jp (x1) nicht verschwindet, und
nimmt x\ von Null verschieden an, so wird
x'lt\>(xu x2, . .. xn) == tp@, Xtx\ — xxx'2, . .. xmx\ — xxx'm),
also eine Function der m — 1 Veränderlichen
y3 = x.2 x\ — xx #2,. . . ym = xm x\ — xx x'm
Man kann dies auch dadurch bestätigen, dass
für xx, #2 . . . xm = x'x, x'2 . . . x'm alle zugleich verschwinden,
dass also die Determinante der Function tp verschwinden muss.
Die Formel A) enthält nun ein sehr wichtiges Resultat, das
sich am besten übersehen lässt, wenn wir dieser Formel folgende
Gestalt geben.
Wir setzen
) )
und erhalten
C) 9(x) = rx2 + xB/2,y% ¦¦¦ ym\
wodurch <p (x) dargestellt ist als Summe aus einem Quadrat einer
linearen Function yx und einer Function % von m — 1 Variablen.
Dabei ist Yx nicht linear ausdrückbar durch y2, ys . . . ym; denn
für Xx, x.2, . . . xm = x'v x\, . . . x'm werden y^ ys . . . ym gleich
Null, während Yj =~\/(p(x'), also von Null verschieden wird.
Daraus folgt der wichtige Satz
Eine quadratische Form von m Veränderlichen
lässt sich immer darstellen als eine Summe von
Quadraten von in oder weniger von einander unab-
unabhängigen linearen Functionen.
Dieser Satz ist offenbar richtig für eine Function von einer
Variablen, die ja selbst ein Quadrat ist. Aus C) folgt aber die
Richtigkeit des Satzes für eine Function von m Veränderlichen,
wenn seine Richtigkeit für eine Function von m — 1 Veränder-
Veränderlichen vorausgesetzt wird.
14*

212 Fünfter Abschnitt. §.64.
Die Darstellung ist, wie B) zeigt, auf unendlich viele ver-
verschiedene Arten möglich, da die willkürlichen Grossen x1 noch
in dieser Formel vorkommen.
Eine Darstellung durch weniger als m Quadrate ist nur dann
möglich, wenn die Determinante der Function <p verschwindet.
Da. in dem Ausdruck B) für Yt eine Quadratwurzel vor-
vorkommt, so kann Yx reell oder imaginär sein, selbst wenn die
Coefficienten von q> und die x und x' reell vorausgesetzt werden.
Setzen wir aber in dem Falle, wo Y1 imaginär ist, i Yt an
Stelle von Y1: so können wir unseren Satz auch so aussprechen:
Eine reelle quadratische Form von m Veränder-
Veränderlichen lässt sich als Summe von höchstens m positiven
oder negativen Quadraten reeller linearer Functionen
der x darstellen l).
Zur Veranschaulichung dieser Betrachtungen mag noch be-
bemerkt werden, dass im Sinne der analytischen Geometrie das
Verschwinden der Determinante der Function <p bei drei Variablen
die Bedingung ist, dass der Kegelschnitt q> = 0 in ein Linien-
Linienpaar zerfällt, und bei vier Variablen, dass die Fläche <p = 0 in
einen Kegel übergeht. Die in A) eingeführte Function $ stellt,
gleich Null gesetzt, für vier Variable, den Tangentenkegel der
Fläche 93 = 0 dar, der seine Spitze im Punkte x', hat.
§• 64.
Trägheitsgesetz der quadratischen Formen.
Für die Zerlegung einer quadratischen Form in Quadrate
gilt nun der folgende Satz, der von Sylvester den Namen des
Gesetzes der Trägheit der quadratischen Formen erhalten hat
(Philos. Mag. 1852).
!) Für die allgemeine Theorie der linearen Transformation der Formen
zweiten Grades sind ausser den Untersuchungen von Jacobi und Hesse
(Hesse, „Vorlesungen über analytische Geometrie des Raumes", dritte
Auflage, besorgt und mit Zusätzen versehen von Gundelfinger, Leipzig
1876) besonders die Arbeiten von Weierstrass und Kronecker (Monats-
(Monatsberichte der Berliner Akademie 1868, 1874) von Bedeutung. Eingehende
historische Darlegung der Entwickelung der Frage in dem „Bericht über
den gegenwärtigen Stand der Invariantentheorie" von Franz Meyer
(erster Jahresbericht der deutschen Mathematiker-Vereinigung, Berlin 1892).

§. 64. • Trägheitsgesetz. 213
Wie man auch eine reelle quadratische Form cp (x)
in die Summe von positiven und negativen Quadraten
linearer Functionen zerlegen mag, die Anzahl der posi-
positiven und negativen dieser Quadrate, und also auch ihre
Gesammtzahl, ist immer dieselbe, vorausgesetzt, dass
zwischen diesen linearen Functionen keine lineare Ab-
Abhängigkeit besteht.
Der Beweis dieses wichtigen Satzes ist sehr einfach.
Es seien
A) <p(x)= Yj+Y* + .••Yi — Y? — Y* iy
= Z\ + ZI -j ZI - Z* - Z'l - Z$
zwei Zerlegungen von cp (x) in Quadrate. Es seien also
Ti, Y2 . . . Yn T\, Y'2 . . . Yv' homogene lineare Functionen von
x, zwischen denen keine lineare Relation mit constanten Coeffi-
cienten besteht und also v -\- v' ^ m; dieselben Voraussetzungen
werden über die Functionen Z„ Z2...Zfl, Z[, Z'ii...Zfl, gemacht,
so dass auch ft -f- fi' 3^ m ist.
Angenommen, es sei
v O,
dann können wir die Variablen x den linearen Gleichungen
, Yx = 0, T2 = 0 . . . Yv = 0
{"> Z\ = 0, Z'a = 0 . . . Zp = 0
unterwerfen, deren Anzahl v -\- ft' kleiner als m ist.
Wenn nun die sämmtlichen Functionen Z^ Z2 . . . Z^ linear
abhängig wären von den Functionen Ti, Y2... Yn Z'v Z'2...Z'p,,
so könnte man aus diesen [i Gleichungen durch Elimination der
v Variablen Yt, Y2 . ¦ ¦ Yv eine lineare Gleichung zwischen den
ZL, Z2 . . . ZiU, Z'x . . . Z'^t herleiten, die nach Voraussetzung nicht
bestehen soll. Es ist also das Verschwinden sämmtlicher
Zu Zi . . . Zu nicht eine nothwendige Folge der Gleichungen B),
und wir können zu den Gleichungen B) noch eine nicht homo-
homogene hinzufügen, etwa
Z1 = l;
dann haben wir für die m Unbekannten x ein System von m
oder weniger Gleichungen, die von einander unabhängig sind,
sich also nicht widersprechen. (§. 29, V).
Dann ergiebt aber die zweite Darstellung A) für cp (x) einen
positiven Werth, während die erste einen negativen oder ver-

214 Fünfter Abschnitt. §. 65.
schwindenden Werth giebt, worin ein Widerspruch liegt. Es
folgt also
v :> &
und da man ebenso schliesst
so bleibt nur v = [i übrig. In gleicher Weise kann man be-
beweisen, dass v' = fi' ist, wodurch unser Satz vollständig be-
bewiesen ist.
§. 65.
Transformation von Formen wten Grades/.
Wenn eine Form wten Grades von m Veränderlichen, F(x),
durch eine lineare Substitution [§. 61, A)] transformirt wird in
0{x'), so wird gleichzeitig die lineare Function der Veränder-
Veränderlichen |l5 |2 .. . |m
A) S^F(xt)
durch dieselbe auf |< angewandte Substitution in
B) i?S*(a4)
transformirt, weil beide Ausdrücke den Coefficienten der ersten
Potenz von t in der Entwickelung von
nach Potenzen von t darstellen (§. 18). Desgleichen wird die
quadratische Function
C) 2kkF"(xixk) .
in
transformirt.
Wenden wir das erste Resultat auf ein System von m Func-
tionen F1 (x), Fz (x) . . . Fm (x) von beliebigen Graden an und
bezeichnen mit J die Determinante
. . . Fx{xn)
. . . Ft(xm)
J&), Fm(x2) . . . Fm(xm)
während wir mit A' die entsprechende, aus den Functionen
Oi, 0} . . . 0m gebildete Determinante bezeichnen, so erhalten

§. 65.
Functional-Determinante.
215
wir nach §. 61, D), wenn wir wieder mit r die Substitutions-
Substitutionsdeterminante bezeichnen,
E) J' = r/1.
Die Function J heisst die Functional-Determinante
der m Functionen Fx, F2 . . . Fm.
Desgleichen erhalten wir aus der Transformation C), D),
wenn wir mit H die Determinante
"(xv xj, F'fa, x2) ... F'(x1, xm)
F'{x^ x{), F'(x2, x2) . . . F'ix» xm)
F'(xm, xj, F'(xm Xi) ... F'(xm, xm)
und mit E' die entsprechende Determinante für die transformirte
Function <E> bezeichnen, nach §. 62, (8)
jET heisst die Hesse'sche Determinante1) der Function
F. In beiden Formeln E) und F) bedeutet r die Substitutions-
Substitutionsdeterminante.
Aus den Formeln B), C) F) ergiebt sich ferner, dass die
Function
G) Z
durch die auf die | und die x gleichzeitig angewandte Substi-
Substitution in
S & & O>" (x-, 4) +
(8) ^g
übergeht, wenn X ein unbestimmter Coefficient ist. Betrachten
wir also das System von n -j- 1 Variablen |l5 |27 • • • Im» A, so
geht dies durch eine lineare Substitution, die aus §. 61, A)
durch Hinzufügung der Gleichung V = r2l hervorgeht, und
deren Determinante
«CD, „(i), ... «0) 0
0, 0,
0,
J) GeBannt nach Hesse, der in geometrischeB Untersuchungen,
namentlich in der Theorie der Curven dritter Ordauag trad ia Eliminations-
problemen diese Determinante vielfach anwandte und ihre Bedeutung
erkannte.

216 Fünfter Abschnitt. §.66.
ist in das System |'1}' |'2, . . . gm, V über und die quadratische
Form G) wird dadurch in die quadratische Form (8) transformirt.
Wenden wir also auf diese Form den Satz §. 62 (8) an, und
bezeichnen die Hesse'sehe Determinante der Form G), also
wenn JET fa), H'(xz), . . . H (xm) die Ableitungen von R sind, die
Determinante
F"(xx, x,), F'(xu x%), . . . F'(xlt xm), R'(xx)
F"(x2,xL), F'(x^x%\. . . F'(x2,xm), H'(x2)
(9)
F"(xm,x{),F'(xm,x,):. . . F*(xm,xm), H'(xm)
0
mit C, so besteht die Eelation
A0) C = r* C
wenn C dieselbe Bedeutung für die transformirte Function 0
hat, wie C für F. Eine ähnliche Beziehung ergiebt sich auch,
wenn man in (9) die H' (xi) durch die Ableitungen F (xi) ersetzt.
Dann aber geht die Determinante (9) in das Product HF über,
und wir erhalten also kein neues Eesultat.
' §. 66.
Invarianten und Covarianten.
Bei. der linearen Transformation der homogenen Functionen
treten immer gewisse Functionen der Coefficienten auf, die, wenn
man die Coefficienten der gegebenen Form durch die Coefficienten
der transformirten Form ersetzt, sich nicht anders ändern, als
dass sie einen Factor annehmen, der eine Potenz der Substitutions-
Substitutionsdeterminante ist. Auch bei gleichzeitiger (simultaner) Trans-
Transformation eines Systems von mehreren Formen kommen solche
Functionen vor, die von den Coefficienten aller Formen des
Systems abhängen. Solche Functionen sind z. B. bei einem
System von n linearen Formen die Determinante des
Systems, und bei einer quadratischen Form die Deter-
Determinante dieser Form.
Man nennt diese Functionen Invarianten der Form, oder
wenn sie von mehreren Formen abhängen, simultane Inva-
Invarianten des Systems.

§. fi6. ' Invarianten und Covarianten. 217
Wenn also I(a) eine Function der Coefficienten a einer
Form F(x) ist, und wenn a' die Coefficienten der transformirten
Form &(%') sind, so heisst I(a) eine Invariante, wenn die iden-
identische Relation
A) J(a') = rU(a)
besteht. Der Exponent % heisst das Gewicht der Invariante.
Ist dieser Exponent Null, so heisst /eine absolute Invariante.
Man betrachtet meist nur ganze rationale Invarianten,
d. h. solche Functionen I, die von den Coefficienten a rational
abhängen und überdies ganze homogene Functionen von
ihnen sind. Die simultanen Invarianten sollen in Bezug auf die
Coefficienten einer jeden der Formen, von denen sie abhängen,
homogen sein.
Ausser den Invarianten giebt es auch Functionen, die neben
den Coefficienten die Variablen selbst noch enthalten, im Uebrigen
aber dieselben Eigenschaften wie die Invarianten A), „die In-
varianteneigenscbaft" haben; also, wenn C(x, a) eine solche
Function ist:
B) C{af, a') = rl C(x, a).
Solche Functionen heissen Covarianten der Form F{x).
Die Functionaldeterminante ist eine simultane Covariante eines
Systems von m Functionen und die Hesse'sehe Determinante
einer Function von höherem als dem zweiten Grade, ist eine
Covariante einer einzelnen Form. Ebenso ist die im vorigen
Paragraphen betrachtete Function C eine Covariante von F.
Auch unter den Covarianten betrachtet man vorzugsweise ganze
rationale und homogene Functionen von x und von a.
Ist m die Anzahl-der Variablen x, n der Grad der Function
F(x), v und fi die Grade von C(x, a) in Bezug auf die x und
a, so besteht zwischen den Zahlen A, [i, v, m, n die Relation
C) n ft = m i. -f- v,
die man dadurch beweist, dass man den Grad der rechten und
linken Seite von B) in Bezug auf die Substitutionscoefficienten
vergleicht. Die a! sind nämlich in den Substitutionscoefficienten
vom wten Grade, r vom »»ten Grade, x vom ersten Grade, woraus
sich C) ergiebt. Die entsprechende Formel für die Invarianten
erhält man, wenn man v = 0 setzt, wie denn überhaupt die
Invarianten als specieller Fall der Covarianten betrachtet werden
können.

218 Fünfter Abschnitt. §.67.
Ein allgemeines Gesetz zur Bildung von Invarianten und
Covarianten, das wir in den besonderen Fällen des §. 65 schon
gebraucht haben, wollen wir kurz besprechen.
Wenn wir nach §. 18, D) die Function
F(xL + «|„ x% + i|2 . . . xm -\- t£m)
nach Potenzen von t ordnen, so erhalten- wir für den Coefficienten
von V
«1 + «2 +••• + «»» = V-
Wenn wir auf die Variablen | und x gleichzeitig die lineare
Transformation A), §. 61 anwenden, so geht _Fr(#,|) in <E>„ (x\ |')
über, was man aus Fv erhält, wenn man gleichzeitig alle Buch-
Buchstaben x, |, a durch x', |', a' und F durch <E> ersetzt.
Daraus folgt:
I. Betrachtet man Fv(x, |) als Form vten Grades
von | und bildet eine Invariante dieser Form,
deren Coefficienten also noch von den x ab-
abhängen, so erhält man eine Covariante der
Form F.
Und da die Variablen x ¦ und | derselben Transformation
unterliegen, so ergiebt sich ebenso:
II. Bildet man eine Covariante der Function
Fv(x, |) als Function von | betrachtet, und er-
ersetzt darin die | durch die x, so erhält man
eine Covariante der ursprünglichen Function
F(x).
Die gleichen Sätze gelten auch für simultane Invarianten
und Covarianten.
Von den Functionen Fv(x, |) gilt der Satz
E) Fv(x, |) = *'„_>.(!, x),
der sich durch die Vergleichung entsprechender Potenzen von t
auf beiden Seiten der Identität
F(x, + *&... aw + *£») = t-F^x, -f |i . . . ir-1xm + |m)
ergiebt.
Die Functionen

§. 67. Binäre Formen. 219
"werden die Polaren der Function F(x) genannt, und zwar
lieisst Pv(x, |) die vte Polare. Auch von ihnen gilt der Satz
Pv(x, g) = p„_, (g,«).
Der constante Factor iT(v) TJ{n — v): II(n) ist zugesetzt,
damit, wenn die Form F(x) mit den Polynomialcoefficienten
geschrieben ist, die Functionen Pr möglichst einfache Coefficienten
erhalten.
Für die binäre Form f(x, y), auf die wir im Folgenden
diese Definitionen hauptsächlich anwenden werden, ergeben sich
für die Polaren folgende Ausdrücke:
und allgemein
n(» — 1) . . • (n — v -f 1)
Wenn man zu einem System von Covarianten einer
Form F wieder Covarianten bildet, so erhält man, wie
unmittelbar einzusehen ist, Covarianten der ursprüng-
ursprünglichen Form.
So erhält man z. B. im Falle dreier Variablen, wenn man
aus den drei in §. 65 betrachteten Formen F, H, C die Func-
tionaldeterminante bildet, die neue Covariante von F:
F) K= F'(x,), H'(x,), C'(x2)
j. i«x/g ij J.-L [*&% u \j yy^z)
die nach C) das Gewicht 9 hat, also der Bedingung
G) K' = r9K
genügt.
§. 67.
Lineare Transformation binärer Formen.
Eine ganze rationale Function wten Grades von x
A) fix) = «o #" -(- <h xn~1 -(- a2xn~i -\- • • ' -\- a„—iX -(- an

220 Fünfter Abschnitt. §. 67.
wird in eine binäre Form verwandelt, wenn man x durch x : y
ersetzt und mit «/" multiplicirt:
B) /O, y) = «os" + «i«"~1 V-+a%a?"-V -| \-anr-
Wenn man die Wurzeln von /(#)¦ kennt, so kann man /(#)
in n lineare Factoren zerlegen:
C) f(x) = a0 (x — c^) (x — a2) . . . (x — «„),
und daraus ergiebt sich
D) /(«» V) = ao(x — «!«/) (# — «2«/)... (a; — «„«/).
Ersetzt man aber auch «l5 «2 . . . «„ durch Verhältnisse
C6j: j81} «2: /S2, . . . «n: ß», so erhält man
E) /(«, ^) = -^(«^1 — y«i) {xß2 —ya%). .. (xßn — yccn),
wenn
«o = A ßi ßa • • ¦ ßn
gesetzt wird.
Für die Factoren von f(x, y), die uns jetzt öfter begegnen,
führen wir als Abkürzung das Zeichen, ein
F) . . xßl — ya1 = (xß1).
Ebenso werden wir setzen
G) xt y2 — Xi y1 = (xL y%),
worin xu yx und x2, y2 zwei beliebige Variablenpaare sind. Wenn
wir die inhomogene Darstellung anwenden, so setzen wir noch
kürzer
,g. x — «j. = @, 1), x — «2 = @, 2), . . . x — «„ = @, n)
^ J «i — a2 = A, 2), ... «j — «fc = (i, h).
Machen wir in der Form B) eine lineare Substitution
x = ax'-\~ßy'
mit der von Null verschiedenen Determinante
A0) r = a§ — ßY;
so geht die Form f(x, y) in eine Form wten Grades F(x', y1)
über, und es ist
A1) F(af, y') = a'ox'» + «i^-1«/' + aia/—V* H <y"n-
Die Coefficienten ab, a\ . . . a'n der transformirten Form er-
erhält man als lineare und homogene Ausdrücke in den Coeffi-
Coefficienten Oo, ax . . . o» und als homogene Ausdrücke wten Grades
in den Substitutionscoefficienten a, ß, y, d. Man erhält so, wenn
man x' = 1, y' = 0 oder x' = 0, y1 = 1 setzt,
A2) oi =*/(«, y),- ait=f(ß,8).

§.67. Binäre Formen. 221
Die übrigen Coefficienten a' kann man durch die Derivirten
der Function f(x, y) ausdrücken, z. B.
was wir nicht weiter ausführen.
Wenn wir auf die beiden Variablenpaare #, y und «&, /3fc
gleichzeitig die Transformation (9) anwenden, so erhalten wir
die linearen Factoren von f(x, y) transformirt, nämlich
A3) &ß*) = r(xßk),
wie man aus der Multiplicationsregel der Determinanten oder
auch durch directes Ausrechnen findet. Diese Factoren {xß-^)
sind also auch Covarianten von f(x,y), freilich aber irratio-
irrationale, da.sie nicht rational von den Coefficienten von f(x) ab-
abhängen. Ebenso ergiebt sich
A4) KÄ) = r(akft),
wonach die Determinanten (außk) als irrationale Invarianten
zu betrachten sind. Wir wollen nun darlegen, wie man daraus
rationale Invarianten und Covarianten bilden kann.
Wir betrachten zu diesem Zweck am besten die lineare
Transformation in der nicht homogenen Gestalt
05) *
und wenden diese auf die Function f(x) in A) an. Es folgt
dann, wenn
F(af) = äox1" + a'ix'"'1 -f a^a;'»-2 -| \- a>n
gesetzt wird
A6) F(af) = (Vaf + 8)*f(x).
Diese Gleichung schreiben wir auch so:
Fix1) = (ax' + ß)"(a0 + a, I + a2 I • • •),
woraus, wenn man x' = — d:y, also x = <x> setzt,
oder, wenn ai, «2, ... «» ebenso von 0^, «2, ...-«„ abhängen, wie
x' von x, also
F{x') = aj(a/ - «;) (»' - «'2) ...(«' — <)
gesetzt wird,
A7) r»a0 = ai(y«; + ») (y«'2 + »)... (y«„ + 8)
folgt.

222 Fünfter Abschnitt. §. 67.
Nun ist nach der Transformation A5)
x — <h = r{x' — aj)
*)
Wir bilden nun ein Product P aus irgend welchen der
Factoren
@, 1), @, 2) ... @, »)
A, 2), A, 3) ... (» - 1,»),
jedoch so, dass darin jede der Ziffern 1, 2 ... n im Ganzen
gleich oft, etwa fxmal vorkommt. Der Index 0, d. h. die
Variable x, möge i/mal vorkommen, und die Gesammtanzahl der
Factoren soll q betragen. Es ist dann, da jeder Factor zwei
Indices enthält,
A9) v-\-np = 2q.
Dann ergiebt sich aus A7) und A8), wenn P' aus P durch
Vertauschung von x, «j mit x', a\ hervorgeht
B0) a'f P = ajy»i"-a (y x' -\- 8)VP.
Wir bilden nun
B1) C(x,y,a) =
die Summe genommen über alle Werthe, die man aus P erhält,
wenn man die Indices 1, 2,3...» auf alle mögliche Arten
mit einander vertauscht. Diese Summe ist dann eine sym-
symmetrische Function der Wurzeln von A) und lässt sich also als
ganze rationale Function der Verhältnisse a^-.a^ a2:ao-"fll»:ao
ausdrücken, so dass kein Glied die (tte Ordnung übersteigt (§.49)..
Die Function C(z, y, a) ist also eine ganze homogene Function
von o0, % ... a„ von der ftten Ordnung und eine ganze homogene
Function von x, y von der vten Ordnung. Da sie nach A9), B0)
der Bedingung
B2) _C(x\ y', a') = r*C(x,y,a),
B3) A = wft — q, 2/L = wfi. — v
genügt, so ist sie eine Govariante und in dem besonderen
Falle, wo v = 0 ist, eine Invariante.
Das Gewicht X ist, wie der zweite Ausdruck zeigt, immer
positiv oder Null, da n[i mindestens gleich v ist. Der äusserste

§. 68. Binäre cubische Formen. 223
Werth n(i = v oder 1=0 kommt nur dann vor, wenn in P
jeder der Indices 1, 2, 3 ... n nur mit 0 verbunden vorkommt,
also P eine Potenz von f(x) selbst ist.
§. 68.
Binäre cubische Formen.
Eine binäre quadratische Form giebt keine anderen in-
invarianten Bildungen als die Discriminante. Mit diesen befassen
wir uns daher nicht, und gehen gleich zur Betrachtung der
cubischen Formen
A) f{x,y) = a{jx*-\-axxt*y-\ra.1xy'>-\-a%y%
über. Hier bilden wir als erste quadratische Covariante die
Hesse'sehe Determinante. Wir wollen hier immer die Regel
befolgen, dass wir die Formen mit ganzzahligen Zahlencoeffi-
cienten ohne- gemeinsamen Factor schreiben. Dann müssen wir
in der aus den zweiten Ableitungen von A) gebildeten Deter-
Determinante den Factor 4 abwerfen und erhalten als erste Covariante
oder
B) H = A,
wenn zur Abkürzung
Ao \
C) Ai = 9ffioö!j — dx a2
A% = 3 % a% — a|
gesetzt ist.
Die Discriminante dieser quadratischen Form ist eine Inva-
Invariante der gegebenen cubischen Form. Sie enthält aber den
Factor 3 in allen numerischen Coefficienten, und demnach
setzen wir
D) 3D=4AA-i/,
und dann stimmt D mit der Discriminante der cubischen
Form [§. 50, A0)] überein:
E) D = alal -\- 18ao%<V'3 — 4ao%3 — ±a\a% — 27afiag.
Eine weitere cubische Covariante erhalten wir, wenn wir die
Functionaldeterminante von f(x, y) und H(x, y) bilden:

224 Fünfter Abschnitt. §. 68.
F) Q (x, y) = f (x) H> (y) - /' (y) H> (x)
oder
G) Q—
Axx-\- 2Aly
in der sich kein numerischer Factor wegheben lässt. Wir setzen
die ausgerechneten Coefficienten von x3, x2y, xy2, ys, deren Bil-
Bildung keine Schwierigkeit macht, der Reihe nach hierher:
27 a02o3 — 9 a0 Oj o2 -j- 2 of,
— 27 a0 a2 a$ -\- 18 a?a3 — 3
— 27ao»32 + 9 »10203 — 2o23.
Das Verhalten von S, D, Q bei linearer Transformation
ergiebt sich aus §. 66, B), C); sind IZ7, B', Q' die entsprechenden
Bildungen für eine transformirte Form, so hat man
(8) H' = r2H, B = r*D,- Q' = r* Q.
Die Covarianten können wir benutzen, um die cubische Form
auf eine Normalform zu transformiren, die zugleich die Lösung
der cubischen Gleichung giebt.
Wir wählen die Normalform
(9) fix, y) = F{1 n) = £3 + ^
worin §, v\ lineare Functionen von x, y sind; eine Form, die, wie
sich gleich ergeben wird, immer hergestellt werden kann, wenn
D nicht verschwindet, also die Gleichung / = 0 nicht zwei
gleiche Wurzeln hat. Die Lösungen von / = 0 ergeben sich
dann aus den linearen Gleichungen
l + n = 0, I + Bf! = 0, 1 ¦ + e'n = 0,
worin a eine imaginäre dritte Einheitswurzel ist.
Um für die Normalform (9) die Formen S\ D', Q' zu bilden,
haben wir a'o = a's = 1, a[ = a'% = 0 zu setzen und erhalten
1P = 9 |ij, Df=- 27, Q> = 27 (I» — ij»).
Wenn die Normalform (9) durch lineare Transformation aus
der allgemeinen Form fix, y) abgeleitet ist, so ergiebt sich
nach (8) ,
9£
- 27 = reD

§. 68. Binäre cubische Formen. 225
Daraus folgt
#
also, wenn für r3 aus der ersten Gleichung der Werth 9: V— 3 D
gesetzt wird,
6|« y=WD = + Q
6r}3]/— 3D = -
woraus £ und v\ durch zwei Cubikwurzeln bestimmt sind, von
denen nach der ersten Gleichung A0) die eine durch die andere
ausgedrückt werden kann.
Darin liegt auch der Beweis, dass, wenn D von Null ver-
verschieden ist, die Normalform durch lineare Transformation her-
hergestellt werden kann. Denn unter dieser Voraussetzung zerfällt
H in zwei von einander verschiedene lineare Factoren, und wenn
man diese, von constanten Factoren abgesehen, für die neuen
Variablen |, v\ einer linearen Transformation wählt, so wird
Äü = 0, A'2 = 0; es folgt aber aus den identischen Relationen
O (X§ -£Lq ~~\— Oi\ -^-2 ^2 -^-1 5 ^2 "^^0 —I— " ^0 -^-2 -~~ ^1 -^-li
wenn nicht zugleich A\ = 0, was durch das nicht verschwindende
D ausgeschlossen ist; a[ = 0, d% = 0, d. h. die transformirte
Form von f enthält nur die Cuben von £ und jj.
Eliminirt man |, jj, r aus den Gleichungen A0), so erhält man
zwischen den Covarianten folgende identische Relation
A2) 4fis -j- #2 _|_ 27 Dp = 0.
Um die Transformation in die Normalform auszuführen, d. h.
die Functionen |, rj wirklich zu finden, zerlegt man die Function
H in ihre linearen Factoren
4AoH=BAox-\-Aiy-\-y— 3Dy) BA0x -\- Ax y—]/— 3 Dy).
Dann unterscheiden sich |, i\ von diesen beiden Factoren von H
nur um je einen constanten Factor. Wir setzen also, wenn wir
zwei constante Factoren mit h, k bezeichnen,
2g
2n = hBAoX + A, y -f ]/— 3Dy),
woraus sich durch Multiplication mit Rücksicht auf die beiden
ersten Gleichungen A0) ergiebt:
A4) 3hJcA0f— D = 1,
Weber, Algebra. I. ' jg

226 Fünfter Abschnitt. §. 69.
und die Gleichungen A1) geben durch Vergleichüng der Coeffi-
cienten von xz
6h3A*]/—3D = + q0 + 3 ]/— 3Da0
A5)
6 fcs A* ]/_ 3_ J) — — q0 _|_ 3 V—- 3 D a0,
wo g'o der Coefficient von #3 in <jM also
A6) #0 = 27 a02 a3 — 9 »o «i «2 + 2 «i
ist.
Dass die Vorzeichen von V— 3D mit Rücksicht auf die
Vorzeichen in A1) so zu nehmen sind, wie es in den Formeln
A3) geschehen ist, ergiebt sich am einfachsten, wenn man die
Rechnung für den besonderen Fall a0 = 0, % = 0 durchführt,
in dem die Vergleichung von A1) mit A3) die Identität
(axx — ea2yy = afxz — 3sala2x2y -j- 3 a2 a^a^xy* — a£y8
ergiebt, wenn e eine imaginäre dritte Einheitswurzel ist.
§. 69.
Das volle Formensystem der binären cubischen Form.
Wir wollen noch nachweisen, dass die Invarianten und
Covarianten der cubischen Form durch die Functionen D,f, H, Q
erschöpft sind, d. h. dass sich alle Invarianten und Covarianten
einer cubischen Form rational durch diese vier Formen aus-
ausdrücken lassen.
Sei also
C = C(x, y, a)
eine Covariante vom Grade v in den Variablen und vom Grade
(i in den Coefficienten, von der wir voraussetzen wollen, dass sie
nur ganzzahlige numerische Coefficienten hat.
Es ist dann für irgend eine transformirte Form [§.66.B), C)]
A) C=C($,ri,a')
B) *=^
Wir verstehen jetzt unter |, t\ die Variablen unserer oben
betrachteten Normalform. Bezeichnet dann e eine dritte Einheits-
Einheitswurzel, so ist
eine lineare Substitution mit der Determinante 1, durch die die
Normalform §. 68, (9) in sich selbst übergeht. Es folgt also,

¦§. 69. Das volle Formensystem der cubischen Form. 227
dass sich, C nicht ändern kann, wenn |, r) durch e f, a2 jj ersetzt
werden; es kann also C" nur von £?j, |8, jj3 rational abhängen.
Die Vertauschung von f mit t\ entspricht einer Substitution
mit der Determinante — 1; dadurch bleibt also C" ungeändert
oder ändert sein Zeichen, je nachdem X gerade oder ungerade
ist. Es besteht daher C aus einer Summe von Gliedern der Form
worin M ein ganzzahliger Factor ist (da wir die numerischen
Coefficienten in G und also auch in C als ganze Zahlen voraus-
vorausgesetzt haben), und das obere oder untere Zeichen gilt, je nach-
nachdem X gerade oder ungerade ist. Im letzteren Falle ist dieser
Ausdruck durch £3 — jj3 theilbar und der Quotient ist durch
|3 -f- jj3 und 1^ rational und ganzzahlig ausdriickbar (weil eine
symmetrische Function von zwei Grossen so durch die Summe
und das Product dargestellt werden kann). Setzen wir also % = 0
oder = 1, je nachdem X gerade oder ungerade ist, so ergiebt
sich für C ein Ausdruck von der Form
worin die M ganzzahlige Coefficienten sind und «, ß eine Reihe
positiver ganzer Zahlen durchlaufen, die der Bedingung
C) 3tr -|- 3ß -f- 2 a —v
genügen. Aus A) ergiebt sich also, wenn wir mit einer hinläng-
hinlänglich hohen Potenz von 3 multipliciren und |?j, £3 -\- jj3, £3 — 9j3
nach §. 68, A0) durch H, /, Q, und r durch D~* ausdrücken,
D) 3aC= <F2MD*E*f,
worin
E) 6 y = X — 3 z — 2 a,
und worin die M gleichfalls ganzzahlige Factoren sind.
Zu jedem Werth von y gehört nach E) ein bestimmter
Werth von « und nach C) ein bestimmter Werth von ß; ebenso
sind durch einen Werth von a oder von ß jedesmal die beiden
übrigen Zahlen bestimmt, so dass in D) jeder Exponent von
D, H oder / nur einmal vorkommt.
Dass y eine ganze Zahl ist, folgt leicht aus B), C), E);
denn da nach der Definition X — 3r eine gerade Zahl ist, so
ist zunächst 3 y eine ganze Zahl, und da ferner nach B) und C)
15*

228 Fünfter Abschnitt. §. 09.
so ist 6y und mithin 3y durch 3 theilbar. Hieraus folgt, dass
auch ö eine ganze Zahl ist.
Dass aber y auch positiv sein muss, sehen wir so ein:
Angenommen, auf der rechten Seite von D) kommen auch
negative Potenzen vonD vor, so multipliciren wir diese Gleichung
beiderseits mit einer so hohen Potenz von D, dass rechts keine
negativen Potenzen von D mehr auftreten, dass aber auch die
rechte Seite nicht den Factor JD erhält. Setzen wir in der so
gewonnenen Gleichung
F) a0 = 0, % = 1, a2 = 0, az = 0,
so wird
G) D = 0, H=—x\ f=x*y, Q = 2x\
Es würde also die linke Seite verschwinden, während die rechte
Seite nicht verschwindet, worin ein Widerspruch liegt.
Wir können aber endlich auch noch beweisen, dass auf der
linken Seite von D) keine Potenz von 3 auftreten kann, die
nicht in allen Factoren M enthalten ist, und sich also fort-
fortheben lässt.
Wir haben im §. 2 den Satz bewiesen, dass das Product
zweier primitiver ganzer rationaler Functionen von beliebigen
Variablen wieder eine primitive Function ist. Dabei ist unter
einer primitiven Function eine solche verstanden, deren Coeffi-
cienten ganze Zahlen ohne gemeinsamen Theiler sind. Es handelt
sich nun hier darum, nachzuweisen, dass eine Summe der Form
worin die M ganze Zahlen ohne gemeinsamen Theiler sind, nicht
imprimitiv werden, und speciell den Factor 3 erhalten kann,
wenn für Q, D, H, f ihre Ausdrücke in den a, x, y gesetzt
werden. Nach dem erwähnten Satze genügt es, da Q eine primi-
primitive Function ist, dies nachzuweisen für die Form
(8) EMDyHaf.
Hierin können wir überdies alle Glieder weglassen, deren M
den Factor 3 schon hat, und endlich können wir wieder nach
dem erwähnten Satze annehmen, dass der Ausdruck nicht durch
D theilbar sei, dass er also ein Glied mit y = 0 enthält.
Nehmen wir also an, es habe unter diesen Voraussetzungen der
entwickelte Ausdruck (8) den Theiler 3, und substituiren nun die
besonderen Werthe F), G), d. h. setzen wir D = 0, H = —x2,

§. 70. Biquadratische Formen. 229
f = x*y, so reducirt sich der Ausdruck auf das einzige Glied,
in dem y = 0, 2 « = l ist,
und es würde also folgen, dass dies M den Theiler 3 haben
miisste, was gegen die Voraussetzung ist. Damit ist also be-
bewiesen :
Jede ganzzahlige Covariante der cubischen Form
kann ganz und rational und mit ganzzahligen Coeffi-
cienten M dargestellt werden durch einen der beiden
Ausdrücke
Die Invarianten sind als Specialfall unter den Covarianten
enthalten und sind sämmtlich Potenzen von D.
§. 70.
Biquadratische Formen.
Wir gehen nun zur Betrachtung der biquadratischen Form
A) f(x, y) = aü x* -j- ax x* y -\- a2 x* y2 -j- azxyt -\- cs4 yi
über.
Wir haben zunächst die Hesse'sehe Determinante als Cova-
Covariante vierter Ordnung, die wir, um sie von einem Zahlenfactor
zu befreien, durch 3 theilen:
12 a0 x2 -\- 6 ax x y-j- 2 a2 y\ 3 <h x% -(- 4 a% xy ~\-
3»!
oder
worin
Aü = 8 »o % — 3 a2, A± = 8 a2 »4 —
^Lj = 24 a0 a3 — 4 % »25 -^-3 = 24 ci^ a4
^2 = 48 «o ^4 -f- 6 % a3 — 4 a22,
und eine Covariante sechsten Grades
W 12 Ä'(*), S»(y)
Die Invarianten der biquadratischen Form bilden wir am
einfachsten nach §.67 aus den Wurzeldifferenzen.

230 Fünfter Abschnitt. . §. 70.
Wir erhalten so eine Invariante von der zweiten und eine
von der dritten Ordnung in den Coefficienten:
D) A = $ a> [A2)^ C4J + A3J B4J + A4J B3J]i
E) J8 = a*27A2)»C4)*A3)D2),
Ausdrücke, die sich übersichtlicher schreiben lassen, wenn man
F) V = A2) C4), F = A3) D2), W = A4) B3)
setzt, nämlich
G) B=: a$\U\V— PF) + V\W-V)-^W^{TJ— F)]
Zur Berechnung dieser Grossen sind die nöthigen Formeln
schon in §. 52 entwickelt. Nach den dortigen Formeln A0)
ergiebt sich
(8) U = »2 — w2, V = w2 — u2, W = m2 — w2,
und m2, w2, w2 sind die Wurzeln der cubischen Resolvente
(9) zs -\-2as* -{-(a* — ±c)s — b* = 0.
Die Ausdrücke für A, B ergeben sich nun aus der Be-
Bemerkung, dass die drei Grossen
yl = a0 (F— W) = »o (w2 + »2 + w2 — 3 «2)
A0) 2/2 = »o ( W— U) = a0 (u2 -f- t;2 + w2 — 3 ü2)
yg = «0 (U — F) = »o («2 + «2 + w2 — 3 w2)
wegen G) und (8) die Wurzeln der cubischen Gleichung
A1) y»-8Ay + B = 0
sind. Die Gleichung A1) muss also aus (9) durch die Substi-
Substitution
y = — a0 B a ~\- 3 z)
hervorgehen, und es ergiebt sich daraus
A = a%(a*-{- 12 c)
B — «08Ba3 _ 72ac + 27&2),
und durch die Coefficienten a0, a-^, a2, äz, a± ausgedrückt:
A2) A = a$ — 3 ax a3 -}- 12 a0 a4
A3) JB = 27 »j2 a4 -(- 27 a0 a32 -j- 2 a23 — 72 a0 «2 a4 — 9 a, «2 a3,
so dass A, B dieselbe Bedeutung haben, wie in §. 52.
Auch die Discriminante der biquadratischen Gleichung als
eine dritte, aber von A und B abhängige Invariante

§.71. Biquadratische Gleichungen. 231
A4) D = < V2 F2 W2
haben wir an der erwähnten Stelle schon gebildet und gefunden
A5) 21D = ±A* — B\
Nach der Formel des §. 67, 2/1 = n(i — v, erhalten wir
für die bis jetzt gefundenen invarianten Bildungen, die wir für
eine transformirte Form mit Accenten bezeichnen, folgende Re-
Relationen
§. 71.
Auflösung der biquadratischen Gleichung.
Wir wollen eine Normalform durch eine lineare Substitution
mit der Determinante 1 herstellen, zu deren Ableitung wird die
gegebene biquadratische Form in lineare Factoren zerlegt an-
annehmen :
A) /(*> V) = «o (« — <*y) {% — ßy) (% — y y) (x — 8y).
Wir setzen
B) r
y]/a — ß= | — fl,
also
x — ay = — ]/« — ß
{% — 7 y) V« — ß = {ß — y) | — (« — y) n
(X - §y)\/K-ß ^=(ß — S)i — (K-d)V,
und dadurch geht f(x, y) über in
D) F(&, n) = < £3n + < i2n2 + < ^3,
und die Invarianten für diese Form sind
A' — A — a'l — 3 a\ a'z,
E) B' = B = 2 a'l — 9 a[ a\ o'„
D' = D = a'l dl a'l — 4 »'•> a,8.
Die Coefficienten a\, a'2, a'3 sind nach C) leicht durch die «, /3, y, d
auszudrücken:

232 Fünfter Abschnitt. §. 71.
a\ = a0 (ß- y) (ß - 8)
F) a'3 = a0 (a — y) (a — 6)
a\ = - oo[(« - y) (|5 - 8) + (« - *) (ß - y)]
Durch Vertauschung der Wurzeln können wir die Normal-
Normalform D) auf sechs verschiedene Arten herstellen, die aber nur
drei verschiedene Werthe von a'2 liefern. Diese drei Werthe
sind, wenn wie oben
U= (« -ß)(y — S),
G) y = (« - r) (* - Ä,
tf= (« - 8) (ß - y),
U+ F+ TF=O
gesetzt wird,
a'2 = a0(F - W),
(8) < = ao(PF-C/),
<=«o(CT -F).
Kennt man die a'2, a'%, a'£, so kann man auch die U, V, W
bestimmen durch
3 a0 U = a" — o!'%
(9) 3a0V=ä2-al
3 es0 W= a1; — a'2,
woraus hervorgeht, dass, wenn von den drei Grossen a'2, a2, a'2"
zwei einander gleich sind, eine der Grossen U, V, W ver-
verschwindet, also zwei der Wurzeln der biquadratischen Gleichung
einander gleich sind, und folglich ihre Discriminante verschwindet.
Setzen wir noch
A0) ay + */J = t>,.
ud -j- ßy = w,
so ist
a0 (« -j- « + w) = »2,
[die Summe der Producte der Wurzeln vonf(x,y) zu je zweien],
TJ = v — w,
. F = w — u,
¦ W= u — v,
also
3 a0 u = a% — a'2,
A1) 3aav = a2 —¦ a2,
3 aow = ft2 — ffj1'

§. 72. Covarianten. 233
Es sind also mit den Grossen a'2, a2, a'£ zugleich die u,v,w
bekannt. Wenn man aber die Grossen «, v, w kennt, so ist
die Lösung der biquadratischen Gleichung auf Quadratwurzeln
zurückgeführt. Denn es ist
aß -\- yd = u, aoaß.yS = ai
und daraus
Da man nun ebenso die Producte
ccy, ccd, ßy, ßd
bestimmen kann, so kann daraus a2 etwa aus
aß . ay
berechnet werden.
Die Grossen a'2, a2, a2' sind aber, wie wir schon im vorigen
Paragraphen gesehen haben, die Wurzeln der cubischen Gleichung
A2) 0S — 3Ä0 JrB = 0.
Dies ist wohl die einfachste Form, die man der cubischen
Resolvente der biquadratischen Gleichung geben kann.
§. 72.
Die Covarianten.
Wenn wir die Covariante E, nach §. 70, B) für die trans-
formirte Form
A) f(x, y) =
bilden, so erhalten wir
B) — E = 3 a? |* + 4 a\ a'2 g» n - F a\ a's — 4 ä*) g* ij»
+ 4a'8a'ggij* + 3o?ij*,
und daraus folgt
C) E + 4 «;/ = —• 3 « |2 - a'8 n*y.
Es ist also diese Verbindung, von dem Factor — 3 ab-
abgesehen, das Quadrat einer quadratischen Form, und dasselbe
gilt, wenn wir a'2 durch a\, a'£ ersetzen. Wir setzen also zur
Abkürzung

234 Fünfter Abschnitt. §. 72.
lT+4a'/=—3>|.
Von den drei Functionen ipt, i/>2, ip3 können keine zwei
einen gemeinschaftlichen Theiler haben, wenn die
Discriminante D von Null verschieden vorausgesetzt wird. Denn
dann sind auch die drei Grossen a'2, a2, a2' von einander ver-
verschieden. Wenn also i\>x und ty3 verschwinden, so müssen H und
/ verschwinden, d. h. ein gemeinsamer Theiler von ipt und ^2
müsste gemeinsamer Theiler von H und / sein. Nun war aber f
ein beliebiger Lineartheiler von /. Dieser kann nach B) nur
dann • Theiler von H sein, wenn a'3 = 0 ist, also wieder, wenn
die Discriminante D verschwindet [§. 71, E)].
Nun ist die Functionaldeterminante T von / und H identisch
mit der Functionaldeterminante von / und H -\- Xf, was auch
X sein mag, und daraus ergiebt sich, wenn X = 4a'2 gesetzt
wird:
T=-\^\F (g) t\ fo) - F' (V) t\ (g)]..
Es ist also T theilbar durch ijt-y, und aus gleichen Gründen
durch ij>2 und ipz, und folglich ist T bis auf einen von |, v\ un-
unabhängigen Factor identisch mit dem Product tyx $% i^3.
Bilden wir demnach das Product der drei Gleichnngen D),
so folgt mit Bücksicht auf die cubische Gleichung §. 71, A2),
der die Grossen a'2, a2, a2' genügen:
H3 — iSAHf — UBf = cTa,
wo c eine noch zu bestimmende Constante ist. Nach §. 70, A6)
bleibt c bei einer linearen Transformation ungeändert, und man
findet also seinen Werth, wenn man aus der Normalform A), B)
die Glieder mit der höchsten Potenz von | beiderseits einander
gleich setzt, c = — 27.
Wir haben also zwischen den Invarianten und Covarianten
die folgende identische Relation
E) Hz — 48 A Ef — 64 Bf = — 27 T2.
Die Functionen ^, ij>2, i/>3 sind gleichfalls Covarianten, frei-
freilich mit Coefficienten, die in den Coefficienten von / nicht ratio-
rational sind. Wir können sie leicht durch die Wurzeln a, ß, <y, d
von / = 0 ausdrücken. Setzt man zur Vereinfachung y = 1,
so folgt nach §. 71, C) und F)

§. 72. Covarianten. - 235
tfi = «i I2 — a'z V2
_ „ (ß — y)(ß- S) (x — «)» - (« — y) (« - fl) (g - ft»
-a° ^^Tß :
Darin aber lässt sich <x — ß im Zähler und Nenner weg-
wegheben, und man kann ^ in zwei Formen darstellen; um ip2 und
¦4>s zu erhalten, braucht man dann nur ß, y, 8 cyklisch zu ver-
vertauschen.
Man findet so:
^1 = (y - ß) (x - u) (x — d) — (a - 8) {x - ß) (x - y)
= (8 — ß)(x — «) (x — y) — (a — y) (x - ß) (x - 8)
F) h = (8-y)(x-a)(x—ß) — (a- ß) (x - y) (x - 8)
= (ß — <y)(x— «) (x — 8) — (u — 8) (x — r)(x — ß)
fl = (ß -8)(x-a) (x — y) — (a- y) (x - 8) (x - ß)
= (y - 8) (x - u) (x — ß) — (a- ß) (x - 8) (x - y).
Die Grossen tyf, ^22, ^32 kann man auffassen als die Wurzeln
einer cubischen Gleichung, deren Coefficienten Covarianten sind.
Man erhält diese Gleichung leicht aus D) in der Form
Diese Gleichung ergiebt nach §.71, A2) und mit Benutzung
des Ausdruckes E) für T2
G) s*-
Es ist noch von Interesse, die Discriminante dieser Gleichung
zu bilden. Man erhält sie am einfachsten aus dem Ausdruck
wenn man die Ausdrücke D) einsetzt und dann für (a'2 — a'^J
(a'z — a'g'J (a'ä — a'ä'J die Discriminante der Gleichung §. 71, A2)
27D^LS — .B2) = 36D
setzt, wo dann D die Discriminante von / ist. Man erhält so
(8) z/ = 212D/6.

236 ' Fünfter Abschnitt ' §. 73.
§• 73.
Das volle Invariantensystem der binären
biquadratischen Form.
Wir wollen noch beweisen, dass mit den Bildungen A, B
das System der unabhängigen Invarianten der binären, biquadra-
biquadratischen Form erschöpft ist. Während man sich aber gewöhnlich
mit dem Nachweis begnügt, dass jede Invariante eine ganze ratio-
rationale Function von A, B ist, wollen wir, wie wir es schon in
§. 69 für die Covarianten der cubischen Form getban haben,
auch die Frage nach den numerischen Coefficienten berühren,
und hier zeigt sich eine neue Erscheinung.
Die Invariante D z. B. ist zwar nach §. 70, A5) rational
durch A, B ausgedrückt. Aber die Zahlencoefficienten sind nicht
ganze Zahlen, sondern haben den Nenner 27, obwohl die Coeffi-
Coefficienten in der entwickelten Function D alle ganze Zahlen sind.
Wir betrachten also jetzt als ganze Invarianten ganze
rationale homogene Functionen (tten Grades der fünf Veränder-
Veränderlichen a0, au a2, a3, a4
A) I(a0, Ox, a2, a3, a4) = I(ä),
deren Coefficienten ganze Zahlen sind, und denen die Inva-
Invarianteneigenschaft
B) I> = r^I
zukommt, wenn V oder I(a') dieselbe Function der Coefficienten
einer transformirten Function ist.
Solche Invarianten sind A, B, D, zwischen denen die Rela-
Relation besteht:
C) 27 D= IA3 -B%
und unser Ziel ist, zu beweisen, dass alle ganzen Invarianten
ganze und ganzzahlige rationale Functionen von diesen dreien
sind.
Wenn wir die Function I' in der Normalform D) des §.71
bilden, so erhalten wir zunächst aus B), da r = 1 ist,
I(a) = I @, äv «;, a's, 0),
und diese Function I kann nur von a'2 und dem Product a\ a's
abhängen; denn die Substitution

§. 73. Das volle Invariantensystem. 237
deren Determinante = 1 ist, lässt die Normalform §. 71, D) und
in ihr a'2 ungeändert, während a\, a's in X2 a'v a's: A2 übergehen,
und darin ist X eine -willkürliche Grosse.
Wenn wir also
«2 = S
setzen, so ist
D) 1=9 ((*>;,,«),
wenn 95 eine ganze, rationale, ganzzahlige Function der beiden
Argumente a\ a's und 0 ist.
Nun ist aber nach §.71, E)
3 a\ a'a = 02 — A,
und wenn wir also D) mit einer geeigneten Potenz von 3, etwa
3", multipliciren, so erhalten wir
E) grI=1>(A,s),
worin tp wieder eine ganzzahlige Function von A und 0 ist.
Nach §. 71, A2) ist aber
0* = SA0 — B,
und hiernach können wir alle höheren Potenzen von 0 durch
die erste und zweite ausdrücken, erhalten also
F) VI=%(A,B,0),
worin % in Bezug auf 0 höchstens vom zweiten Grade ist.
Die linke Seite von F) bleibt aber ungeändert, wenn 0
durch a'2, a'2, a'g', also durch drei verschiedene Wertbe, ersetzt
wird, und folglich kann die Function % die Variable 0 überhaupt
nicht mehr enthalten (§. 33, II).
Es ist daher
G) BVI=%(A,B),
worin % eine ganzzahlige, ganze, rationale Function ist.
Wenn wir in G) nach C)
S2 = 1A3 — 27 B
setzen, so folgt, dass G) eine der beiden folgenden Formen hat
(8) BvI=<Z(A,B)y B$(A,I)),
je nachdem der Grad von I gerade oder ungerade ist.

238 Fünfter Abschnitt. §. 73.
Ist I eine ursprüngliche Function der a, d. h. eine
solche, deren Zahlencoefficienten keinen gemeinsamen Theiler
haben, so können die Coefficienten der Functionen <P jedenfalls
keinen anderen gemeinschaftlichen Theiler haben, als eine Potenz
von 3.
Was uns zu beweisen obliegt, ist, dass sie alle durch
3r theilbar sind, oder was dasselbe ist, dass, wenn wir
<5(^L, D) als ursprüngliche Function voraussetzen, v = 0
sein muss.
Es ist also die Frage: Können aus der ursprünglichen
Function <&(A, D) oder B<I>(A, D) Functionen mit dem Theiler
3 entstehen, wenn man die A, B, D durch ihre Ausdrücke in
den a ersetzt? Da B ursprünglich ist, so kann nach §. 2 die
in den a ausgedrückte Function 5$(i, D) nur dann den
Theiler 3 haben, wenn ihn <£(A, D) hat.
Also ist die Frage darauf zurückgeführt: Kann die ur-
ursprüngliche Function <&(A, D), den Theiler 3 erhalten, wenn
A, D durch ihre Ausdrücke ersetzt werden?
Dass diese Frage verneint werden muss, können wir leicht
so einsehen. Wir denken uns zunächst in 0 (A, D) alle die
Glieder beseitigt, deren Coefficienten durch 3 theilbar sind;
denn offenbar müssen auch die übrigen Glieder noch dieselbe
Eigenschaft behalten, durch Substitution der Ausdrücke für
A, D den Theiler 3 zu erhalten.
Wir können zweitens annehmen, dass <&(A, D) nicht den
Factor D hat, denn durch Weglassen dieses Factors würde nach
dem schon erwähnten Satze (§. 2) die fragliche Eigenschaft nicht
aufgehoben.
Dann aber müsste aus 0 (A, D) eine durch 3 theilbare
Zahl entstehen, wenn alle a, mit Ausnahme von a2, gleich Null,
02 = 1 gesetzt werden. Dadurch wird D = 0, A = 1, und es
müsste also 0 A, 0) eine durch 3 theilbare Zahl sein; dies ist
aber der Coefficient der höchsten Potenz von A in <3>(A, D), der
nach Voraussetzung nicht durch 3 theilbar ist. Damit haben wir
also bewiesen:
Jede ganzzahlige Invariante der biquadratischen
Form lässt sich rational und ganzzahlig durch
A, B, D darstellen, und zwar in einer der beiden
Formen

§. 73. Das volle Invariantensystem. 239
Dass auch umgekehrt jeder solche Ausdruck, wenn er in
den Coefficienten a homogen ist, eine ganzzahlige Invariante
darstellt, ist von selbst klar1).
l) Die Theorie der Invarianten findet man ausführlich dargestellt in
den Werken: Clebsch, „Theorie der binären algebraischen Formen".
Leipzig 1872. Faä di Bruno, „Einleitung in die Theorie der binären
Formen". Deutsch von Walter. Leipzig 1881. P. Gordan, „Vorlesungen
über Invariantentheorie", herausgegeben von Kerschensteiner, Leipzig
1885. Vergl. auch Franz Meyer, „Bericht über den gegenwärtigen Stand
der Invariautentheorie" im Jahresbericht der deutschen Mathematiker-
Vereinigung 1890/91 (Berlin 1892). In Bezug auf die zuletzt behandelte
Frage s. H.'Weber, „Zur Invariantentheorie". Göttinger Nachrichten 1893.

Sechster Abschnitt.
Tschirnhausen-Transformation.
§. 74.
Die Hermite'sche Form der Tschirnhausen-
Transformation.
Wir haben im vierten Abschnitt den Grundgedanken der
Tschirnhausen-Transformation schon kennen gelernt.
Die Aufgabe war die, eine algebraische Gleichung wten
Grades
A) f{x) = aox» + dx"-1 -\ H an-ix + an = 0
durch eine Substitution (n — l)ten Grades
B) y = «o -\- % x -f- «2 #2 -\- ¦ ¦ ¦ + an_i a;"-1
umzuformen, um in den willkürlichen Goefncienten a Mittel zu
gewinnen, die Gleichung zu vereinfachen.
Hermite hat dadurch, dass er der Substitution B) eine
besondere Form gab, diese Aufgabe sehr vereinfacht und mit
der Invariantentheorie in Verbindung gebracht1).
Hermite benutzt dabei die Functionen /0, /i,/2 . . •/»—i,
die uns schon früher beim Eliminationsproblem gute Dienste
geleistet haben, durch die sich die Potenzen von x bis zur
(n — l)ten rational ausdrücken lassen.
Wir bezeichnen hier mit x eine Wurzel der Gleichung A),
während unter t eine unbestimmte Veränderliche verstanden sein
soll. Dann ist (wie im §. 4 und §. 46)
J) Hei-mite, Sur quelques theoremes d'algebre et la resolution de
l'equation du quatrieme degre, aus den Comptes rendus der Pariser Aka-
Akademie besonders erschienen. Paris 1859.

§. 74. Hermite'sche Form d. Tschirnhausen-Transformation. 241
C)
und
/0 (#) = a0
/l (#) = «0 * + «1
D) /2(#) = ao#2 + Oi« -f a%
fn_x{x) = ao^-1 + o^-2 + a2^-3 -| \- aM_!
Wir nehmen nun die Substitution B) in der Form an
E) y = 4- i/o (*) + <»_«/! (*)+ — +*i /»-2 (*) + <b/—i (*),
worin die tn—ii tn—2 ¦ • • hi to <&e an Stelle der ex, getretenen
unbestimmten Grossen, und nicht mit den Potenzen von t zu
verwechseln sind. Es geht aber y aus dem Ausdruck C)
hervor, wenn th durch 4 ersetzt wird.
Bezeichnen wir durch das vor eine Function gesetzte Zeichen
8, dass die Summe über sämmtliche Wurzeln x der Gleichung A)
zu nehmen ist, so^haben wir, wie im §. 46:
8 [/o OO] = na0
S[/,W] =(»1-1H!
F) Slf2(x)] =(n-2)a2
8[fn-1(x)] = aM_!,
also:
G) S(y) = naot„-! -(-(»—l)a1i„_2H f- 2an_2*1
ein Ausdruck, der sich aus /' (f) ergiebt, wenn th durch t^ ersetzt
wird [§. 46, D)].
Eliminiren wir mit Hülfe von G) die Variable tn—i aus E)i
so folgt
(8) y
wenn
E
n ^
; =/i -
) = t„-2
n — l
n
¦Fo(*) +
_l_ 2l
w
— 2
1
„_a =/„-i — — aB_1 = a0iC|-1 + a1a;''-2-| 1
/fr
B1 0 + 1|1
/fr 7»
so dass
Weber, Algebra. I. -^q

242 Sechster Abschnitt. §. 75.
A0) 8[Fo(x)] = 0, 8\Ft(x)] = 0,...S[F.-,(x)] = 0.
Setzen wir nach C)
A1) F(t, x) = /^- - -
so geht die rechte Seite von (8) aus F(t, x) hervor durch die
Ersetzung von V durch %.
Nehmen wir von vornherein y in der Form
A2) y — tn-2F0 (x) + *„_3 Fx (x) -| (- t0 Fn-2 (x)
an, so ist die Gleichung
A3) . 8(y) = 0
identisch befriedigt. Welchen Nutzen diese Form der Substitution
gewährt, werden die nächsten Betrachtungen zeigen.
§• 75.
Invarianten-Eigenschaft der Tschirnhausen-
Transformation.
Es ist jetzt der Einfluss zu untersuchen, den eine lineare
Transformation, der wir die Function f(x) unterwerfen, auf die
Tschirnhausen-Transformation hat.
Wir machen in f(x) die lineare Substitution
wodurch wir erhalten
so dass 95 (|) eine ganze rationale Function n ten Grades und
9(|) = 0 die durch A) transformirte Gleichung f(x) = 0 ist.
Wir leiten nun eine Function 0 (r, |) ganz in derselben
Weise aus 95 (!) ab, wie wir im vorigen Paragraphen F(t, x) aus
f(x) abgeleitet haben, nämlich
worin t ebenso wie t eine Variable ist und die Functionen
<&0 (!), <&j (!) . . . <&„_2(!), ebenso aus ! und den Coefficienten

§. 75. Invarianten-Eigenschaft. 243
von (jp (|) gebildet sind, wie die entsprechenden Functionen
Fo (x), F-l (x) . . . Fn-2 (x) aus x und den Coefficienten von f(x).
Wenn wir nun andererseits in F(t, x) gleichzeitig mit der
Substitution A) die Substitution
ausführen, so erhalten wir
E) Cy*+ *)"/(*) = vto.
F) (yl + *)(y* + *)(*-*) = r(r-|),
und, indem wir von E) die Ableitung, am einfachsten durch
Differentiation mittelst der Formel
ät__ . r
dx ~~ (yx -\- §y
bilden,
G) r (y x + df-1 \f (*) = (y v + d) I 9> (t) - y q> (r).
Aus E), F) und G) folgt
= ^
(„ + v
und durch Subtraction beider Formeln
r
\ ) t — | n
also
(8)
oder, ausführlicher geschrieben
(9) «—" ©o + *"-8 ®
"Wir setzen nun, indem wir in F(t, x) die Potenzen ik durch
beliebige Variable % ersetzen und ebenso in <&(t, |) th durch th,
so dass die Substitutionen der Tschirnhausen-Transformation
A1) y = Y(t, x), y=H(T, |)
lauten [§. 74, A2)],
16*

244 Sechster Abschnitt. §. 75.
Die Gleichung (9), die in Bezug auf % identisch ist, bleibt
aber auch richtig, wenn nach Ausführung der angedeuteten
Potenzirung rechts zh durch rft ersetzt wird, und sie lehrt also,
dass zwischen den Functionen Y(t, x), H(r, §) die Relation besteht
A2) H(r, |) = r Y(t, x),
wenn wir die t von den % in folgender Weise abhängen lassen:
Man setze
^«-2 = («r -j- jS)«-^
und ersetze nach Ausführung der Potenzen th durch vh.
Es sei nun s eine beliebige Veränderliche, und wir multi-
pliciren, ehe wir die Potenzirungen in A3) ausführen, diese
Gleichungen der Reihe nach mit
dann bekommen wir links eine ganze rationale Function von s
vom (n — 2)ten Grade
A4) T(e) = tn_2 — (n- 2) *„_8 e
und die rechte Seite ergiebt nach dem binomischen Satze
[(« + ß) — Hr* + <J)]M-2 = [*(« - v*) + (ß-
was, wenn wir
setzen, in
übergeht.
"Wenn wir hierin die Potenz (r — £)re~2 nach dem bino-
binomischen Satze ausführen, und dann rh durch tk ersetzen, so
erhalten wir eine Umformung der Function T (s). "Wir setzen also
und erhalten die identische Umformung

§. 76. Der Hermite'sche Satz. 245
A6) (y t + *)-« T
worin der Zusammenhang zwischen den Coefficienten £ und r
durch die symbolischen Gleichungen A3) ausgedrückt, also der-
derselbe ist, wie in den Functionen Y und H.
Es ist also hiernach r"-2®(£) die Umformung der
Function {yt, -f- dI»-2 T(,s) durch dieselbe lineare Sub-
Substitution, durch die (y% -\- $)nf(ß) in <p(£) übergeht.
Bezeichnen wir die Coefficienten dieser umgeformten Func-
Function, also die Grossen rn~ 2vk mit tf, so ergiebt die Gleichung A2),
die in Bezug auf % linear ist,
A7) S(t', g) = t—i T(t, x).
Aus Y(t, x) gehen nun n Functionen hervor, wenn man
für x die n "Wurzeln von f(x) setzt. Jede homogene rationale
symmetrische Function dieser n Functionen ist rational durch
die Coefficienten von f{x) ausdrückbar, und wenn wir also eine
solche Function mit K(t, a) bezeichnen, so ergiebt die Gleichung
A7), wenn wir die Coefficienten von q> (§) mit a' bezeichnen,
A8) K(f,a') = r*<n-»K(t,a%
wenn v den Grad der symmetrischen Function bedeutet. Damit
ist der schöne Satz von Hermite bewiesen:
Die Coefficienten in der durch die Tschirnhausen-
Transformation
y = Y(t, x)
umgeformten Gleichung f(x) = 0 und alle symme-
symmetrischen Functionen der n Werthe y sind simultane
Invarianten der beiden Functionen
§• 76.
Ausführungen über den Hermite'schen Satz.
Durch die Betrachtungen des letzten Paragraphen hat sich
ergeben, dass, wenn wir
A) y = tn-iFo(x) -f- tn_sF,(x) \-t0Fn_2(x)
setzen, die symmetrischen Functionen der n Werthe yu y2 . . . yn,
die man aus y erhält, wenn man für x die n Wurzeln von

246 Sechster Abschnitt. §. 76.
f(x) = 0 setzt, simultane Invarianten von zwei Formen wten und
(n — 2)ten Grades, f(g), T{z) sind.
Eine solche ganze rationale und homogene symmetrische
Function vtea Grades
P (Mi, y* • ¦ ¦ y»)
ist wegen A) offenbar eine homogene Function vten Grades der
Variablen t. Sie ist ebenso eine homogene Function vten Grades
in den a, da der Ausdruck A), wie er die a explicite enthält,
linear ist, und da die symmetrischen Functionen der x nur von
den Verhältnissen at: a0, a2: «0, . . . an: a0 abhängen. Bei dem
Ausdruck von P durch die a könnte aber möglicherweise eine
Potenz von a0 im Nenner bleiben, und wir haben noch nachzu-
nachzuweisen, dass dies nicht eintritt.
Setzen wir
und bestimmen die Potenz a* so, dass K(t, a) eine ganze Func-
Function der a ist, aber für a0 = 0 nicht mehr verschwindet, so
wird folgen, dass % = 0 sein muss, wenn wir nachweisen, dass
für a0 = 0 die sämmtlichen y endliche Werthe behalten.
Wenn wir a0 = 0 werden lassen, während die übrigen a
ungeändert bleiben, so wird eine der Wurzeln x, wie wir im
§. 44 gesehen haben, unendlich wachsen. Dass aber das zugehörige
y gleichwohl endlich bleibt, ergiebt sich aus der in Bezug auf t
identischen Gleichung §. 74, A1)
B) rZ~ - \f® = ^Foix) + t»sF1(x)+~-+Fn-2(x),
aus der zu ersehen ist, dass, wenn a0 = 0 und x unendlich wird,
die Functionen
F0(x), F^x) .. . Fn-a(x)
gleich den Coefficienten von /'(*), also gleich
n — 1 1
0, — Ox..., --«.-!
werden. Es bleiben also auch die y endlich, und P (yt, y2 . . . yn)
ist gleich einer ganzen rationalen Invariante vom Grade v
sowohl in den t als in den a.
Wenn wir also die Gleichung für y in der Form annehmen:
C) r + Piir-* + p*r~'-\ h-?» = o>
so ist P» eine solche Invariante vten Grades.

§. 76. Transformation der oubisohen Gleichung. 247
Eine Invariante vom Grade n (n — 1) ist auch die Discri-
minante d der Gleichung C), oder das Quadrat des Differenzen-
productes
D) n = (y, — y2) {y, — yt) ¦ ¦ •
(lf> — y») • • •
Um über die Bildung dieser Grosse näheren Aufschluss zu
bekommen, erinnern wir uns, dass wir y erhalten, wenn wir in
t — x n
P durch tic ersetzen. Wir erhalten also y^ — y2 aus der Formel
E) * - y, = & - *)
wenn wir dieselbe Vertauschung machen.
Der Quotient
/@
(* — Xi) (t — Xh)
ist eine ganze rationale Function von t vom Grade n — 2. Er-
Ersetzen wir darin V durch th, so möge er in tith übergehen; wir
haben dann
F) yi — yh — (%i — xh)tijk.
Wenn wir also
G) a«-^& = t1,2t1,B.-.t1,n
t%,Z • • • t%n
tn—l,n
setzen, so ist & eine homogene ganze Function vom Grade
x/2 n (ti — 1) in Bezug auf die t, und sie ist ausserdem als sym-
symmetrische Function der x rational durch die Coefficienten a dar-
darstellbar.
Aus F) folgt aber, wenn D, wie im §. 50, C) die Discri-
minante von fix) bedeutet,
(8) J z= D ®\
woraus zu schliessen ist, dass & eine Invariante ist, die den
Nenner a0 nicht mehr enthält, z/ ist in den Coefficienten a
vom Grade n (n — 1), während D nach §. 50 vom Grade 2 n — 2
ist; daraus folgt, dass & vom Grade ]/s (n — 1) (n — 2) in den
Coefficienten a ist.
& ist eine sogenannte zerlegbare Form 1/2 n (n — l)ten
Grades in den Variablen t; denn sie lässt sich nach G) in lauter

248 Sechster Abschnitt. §. 77.
lineare Factoren zerlegen, die freilich nicht rational in den
a sind.
Wir haben schon im §. 58 darauf hingewiesen, dass bei der
Tschirnhausen-Transformation auch x rational durch y ausdrückbar
ist; und dasselbe gilt also auch für jede rationale Function von x.
Betrachten wir irgend eine solche Function cp (x), die auch
noch die Coefficienten a und t enthalten kann, aber immer für
beide Arten von Variablen ganz und homogen vorausgesetzt sei,
so können wir setzen
(9) <p (x) = Co + C\ y -f- C, yi -\ + O.-i yn~\
worin die Co, Q,... Cn—i rational in a und in t ausdrückbar sind.
Stellen wir die Gleichung (9) für x = «x, x% . . . xn,
y = yu y2, . . . yn auf, so erhalten wir für die Bestimmung der
C ein System linearer Gleichungen, dessen Determinante
A0)
also gleich &]/D ist. Der Zähler des Ausdruckes für Cr geht
aus der Determinante A0) hervor, indem man die Elemente der
(v -f- l)ten Colonne durch q>(x^), cp(x2) . . . 'cp(x„) ersetzt, und
folglich hat der Zähler, wenn man Alles durch die xt ausdrückt,
den Factor VD (weil er verschwindet, wenn zwei Xi einander
gleich werden).
Wir können also setzen
1,
1,
1,
2/i,
2/2,
2/«,
yl-
yl-
yl.
¦ • y\
¦ ¦yl
¦ -r
~i
—i
—i
worin Qv eine ganze rationale Function der t und der a ist, die
höchstens noch eine Potenz von a0 im Nenner enthalten kann.
Wir bekommen dann
A1) 0<p(x)=Qo+ Qiy+ Q2y* ^ f- Qn-ir-1-
Die Coefficienten Qv sind aber keine Invarianten und ihre
Berechnung ist in den meisten Fällen schwierig.
§• 77.
Transformation der cubischen Gleichung.
Der Hermite'sche Satz (§. 75) reicht für die cubische Glei-
Gleichung aus, die Transformation ohne weitere Rechnung auszuführen

§. 77. Cubisehe Gleichung. 249
Wir haben dazu, wenn wir homogene Variable gL, zs2 an-
anwenden, simultane Invarianten der cubischen Form
A) /fa, ga) = a0g? -f ax g*ga -\- a2 g: e* -f a3 4
und der Linearform
B) T= — toe1 + t1ea
zu bilden. Wenn wir aber die lineare Substitution
auf T anwenden, so ergiebt sich
— «0^-1-^*2 = — f0 z\ + fj /2,
wenn
1 = 14«- *ir,
*i = — *o 0 + *i Ö,
oder
^o = r*; + <H'o.
Diese Substitution geht aus C) hervor, wenn man glt ga,
g'1, g"a durch rt„ rt0, Hv t'o ersetzt. Wenn nun I(a, tu t0) eine
simultane Invariante von / und T ist, homogen und vom vten
Grade in t0, ^ und vom Gewicht l, also
l(a\fv fo) = ril(a, <x, U
so folgt durch diese Vertauschung
J(a', z\, 0'2) = r*-*I(a, ^, *),
d. h. es ist J(a, ^x, ^2) eine Covariante von /.
Man erhält also alle simultanen Invarianten von f
und Taus den Covarianten von/, wenn man darin glt s^
durch tx, t0 ersetzt.
Die Covarianten von / haben wir aber in §. 68, 69 voll-
vollständig kennen gelernt.
Danach ist es leicht, die cubische Gleichung zu bilden, die
sich aus der Substitution §. 74, A2)
E) y = t
für y ergiebt. Schreiben wir die Gleichung in der Form
2/3 + P22/ + P8= 0,
so sind P2, P8 Covarianten von /, und zwar P2 von der zweiten,
P3 von der dritten Ordnung, sowohl in t als in a.

250 Sechster Abschnitt. §. 77.
Da nun P2 und P3 Covarianten der cubischen Form sind,
so können sie sich nach §. 68 und 69 von den beiden dort defi-
nirten Functionen
H(tut0), Qfat,,)
nur um constante, d. h. numerische Factoren unterscheiden. Diese
constanten Factoren lassen sich durch irgend eine specielle
Annahme bestimmen.
Wir können z. B. annehmen
*! = 1, t0 = 0, a0 = 1, % = 0,
dann wird y ¦= x, also
P2 = a2, X3 = 0S3.
Andererseits ergiebt sich aber nach den im §. 68 gegebenen
Formeln B), C), G) für diese besondere Annahme
#(l,.0) = 3a2, 0A,0) = 27 a,,
woraus man allgemein schliesst
P2 = I H (tu «,), P3 = ^ Q ft, U
so dass wir für y die cubische Gleichung erhalten
F) y* + \ s&> *o)y + ^ oft, A>) = 0.
Die Discriminante d dieser cubischen Gleichung ist
also mit Anwendung der Relation §. 68, A2)
G) 8 Q2 "
(8)
wenn D die Discriminante der gegebenen cubischen Gleichung
ist, in Uebereinstimmung mit den allgemeinen Resultaten des
vorigen Paragraphen.
Wollen wir hierauf die Auflösung der cubischen Gleichung
gründen, so müssen wir zunächst nach den Vorschriften des
vorigen Paragraphen x rational durch y darstellen. Wir setzen
(9) ao/ft, t0) x = Qo -\- Ql y + Q2 y\
Die Berechnung der Coefficienten Q ist leicht auszuführen,
wenn man diese Gleichung für x1} xs, a;3, und entsprechend
yu Vi, V% aufstellt.

§. 77. Cubische Gleichung. 251
Wir wollen über den Gang der Rechnung, die nur die Dar-
Darstellung symmetrischer Functionen der Wurzeln einer cubischen
Gleichung durch die Coefficienten nach den Vorschriften des
vierten Abschnittes (§. 48, 49) erfordert, einige Andeutungen
machen. Nimmt man zunächst die Summe der drei Gleichungen
(9), so erhält man nach F)
3 Qo = | H&, t0) Q, — ax/&, *0),
so dass also nur noch Q1 und Q^ berechnet zu werden brauchen;
diese findet man, wenn man die für x = x1 gebildete Gleichung
(9) mit
2/2 — 2/s = «o (%% — Xt) (*i — *o «i)
und mit
multiplicirt, und die drei durch cyklische Vertauschung der In-
dices 1, 2, 3 gebildeten analogen Gleichungen addirt.
Man hat dann nur Gebrauch zu machen von den Formeln
- x.) =
und findet so
Setzen wir zur Vereinfachung tx = t, t0 = 1, gehen also zu
den inhomogenen Ausdrücken über, so ergiebt sich
A0) Ca0x + ad/(«) = -|fi(*) + yf (*) - 3y»,
während die Gleichung für y lautet
A1) tJr\^
wenn wir S(t), Q(t) für H(t, 1), Q(t, 1) setzen.
Um nun die cubische Gleichung zu lösen, bestimmen wir t
aus der quadratischen Gleichung
Hit) = 0.

252 Sechster Abschnitt. §. 77.
Wir wollen für den Augenblick zur Abkürzung
A2) q = ]/— 3D
setzen; dann folgt aus G)
A3) Q = 3 Qf(t),
und aus A1)
und der Ausdruck A0) ergiebt
A5) C a0 x + at) /(«) = y/':(«) — 3 ^.
Um die Uebereinstimmung dieses Resultats mit der Car-
danisehen Formel herzuleiten, gehen wir auf den §.68 zurück,
und setzen in den dortigen Formeln x = t, y = 1.
Wegen A3) wird, nach §. 68, A1), A3)
n — o,
und folglich
2Äot-\- Ä! = — q, £ = — hQ,
ferner nach §. 68, A0)
/(*) = f8, /'(*) = 3 £2f,
worin |' = hA0 nach §. 68, A3) die Ableitung von | nach t ist,
Danach folgt aus A4)
y
und aus A5)
Baox + a, = —
oder nach §. 68, A4)
A6) 3 a0 x -+- ax =
worin nach §. 68, A5)
Nehmen wir a0 = 1, ax = 0 an, so erhalten wir aus A6)
die Cardanische Formel (§. 38)

§. 78. Allgemeine Ausführung der Transformation. 253
§. 78.
Allgemeine Ausführung der Transformation.
In der allgemeinen Durchführung der Tschirnhausen-Trans-
Tschirnhausen-Transformation in der Hermite'schen Form können wir noch einen
bedeutenden Schritt weiter gehen.
Wir betrachten zunächst die allgemeine Substitution §. 74, E)
A) y = U-l /o + tn-2 /i + t»-t /„ H V «b/.-l,
aus der wir die speciellere Form §. 74 A2) erhalten, wenn wir
die Variablen t an die eine lineare Bedingung
B) S(y) = naotn-i -f- (» — 1)M„_2 -\ (- an-itü — 0
binden, was aber fürs Erste noch nicht geschehen soll.
Durch die Functionen /0, /i, f2 . . . /„_i lassen sich nach
§. 74, D) alle Potenzen von x und also auch alle rationalen
Functionen von x linear und homogen darstellen.
Wenn wir diese Darstellung für die verschiedenen Potenzen
Ton y finden können, so lässt sich durch Elimination der f{ die
Gleichung wten Grades für y bilden.
Denselben Zweck erreichen wir aber noch einfacher, wenn
wir die » Producte yfs linear durch die / darstellen. Denn
wenn wir die Gleichungen haben
C) yf. = E0,sf0 + £i,s/i + E2,sf2 -] 1- En-liSfn-i
s = 0, 1, 2 ...» — 1,
so erhalten wir durch Elimination von /0, /x . . . fn_1 aus dem
System C)
Eo, 0 y-i E\, o, i?2, 0 • • . En—1, 0
Eo>l5 -Ei,! — y, E2,i ... En-itl
D) E =
= 0,
E0,n—li Eitn — i, E2,n—1 • • • En — i,n — l — V
also eine Gleichung wten Grades für y, die die gesuchte trans-
formirte Gleichung ist. Alles ist daher zurückgeführt auf die
Bestimmung der Coefficienten Er>s, die, wie aus A) hervorgeht,
jedenfalls lineare Functionen der Variablen t sind. Insbesondere-ist
E) J&o, 0 == a0 ^n—1) E\t o = <Z<>tn — 2> • • • En — 1,0 = dota.
Um die übrigen E zu berechnen, bemerken wir, dass nach
der Definition §. 74, D) zwischen den Functionen / die folgenden
Relationen bestehen:

254 Sechster Abschnitt. §. 78.
xfo = /i — «i
S/i = /« — «2
F) . . . . ¦
#/» — 2 /» —1 «» — 1
%Jn — 1 == *»i
Ton denen die letzte eine Folge der Gleichung f(x) = 0 ist.
Wenn wir nun die Reihe der Variablen t0, tx . .. tn-\ fort-
fortsetzen, indem wir die neuen Variablen t„, tn + 1, tn + 2 . . . durch
folgende Gleichungen definiren
a0tn -f- a-L tn—i -f- a2tn-2 -{-••• -\- ant0 = 0,
G) *o^» + l ~~\~ al tn -\~ a2^n — i -f- ••'-)- *n^l = 0,
a0 4+2 + «i*»+i + »2*» + • • • + anh = 0,
so erhalten wir, wenn wir die Gleichungen F) der Reihe nach
mit t„—i, £„_ 2 . . . t0 multipliciren und addiren,
(8) xy = tn/, + tn-!/H h <i /.-i,
und wenn wir nun F) ebenso mit tm tn—-y . . . tx multipliciren,
nach (8)
afly = tn+1f0 + tnfx-\ 1- «,/._!.
So ergiebt sich das folgende System
y = tn-i /o + tn-2 /i + • • • + t0 fn-!
xy = tn /o + *»-i fi~\ h h fn-i
(9)
und wenn wir diese Gleichungen wieder mit as, a«_i • ¦ •
multipliciren und addiren, so folgt der gesuchte Ausdruck
yfs = Eo,efo + El,*fl + • * • + -E"»-l,s/»-D
worin nach G)
= *s + l^n — 2 * " * — Clnts—1
s —2 "P %4 ttt
A0) jE"s-1)S = «o*» +
-Ss, s ==: *0^n —1 -j~
Es + itS= a0t„—2 -f-
— i,g=

§. 79. Die Bizoutiante. 255
Hierzu ist noch zu bemerken, dass die überzählig eingeführten
Variabein tm tn+1 ... in der zweiten Form von Eo,„ E1<s... Es^1>s
bereits wieder eliminirt sind, und dass die Variable tn-\ nur
in jE1,,, 5 vorkommt.
§• 79. ¦
Die Bezoutiante.
Die Gleichung D) des vorigen Paragraphen wird, entwickelt,
die Gestalt haben
yn _|_ pir-! _J_ P2yn-2 _| f- P, = 0,
oder wenn wir £„_! so bestimmen, dass S(y) = 0 wird,
(i) sr + Psy-M \-p» = o;
darin ist dann
— 2Pa = 8(y»)
eine Function zweiten Grades in Bezug auf die t und in Bezug
auf die a. Diese Function ist für viele Anwendungen besonders
wichtig und hat von Sylvester den Namen Bezoutiante
der Function f(x) erhalten, zu Ehren des französischen Mathe-
Mathematikers Bezout, der schon im vorigen Jahrhundert die ersten
richtigen Ausführungen über Elimination gegeben hat1).
Nach den Formeln des letzten Paragraphen lässt sich diese
Function verhältnissmässig einfach berechnen. Wir führeu zu-
zunächst neben den Variablen i„_j, £„_2 . . . t0 noch ein zweites
System davon unabhängiger Variabein rn_1; r„_2 . . . t0 ein und
setzen
/2\ y — *»-i/o + t»-afi +¦•••+ tofn-i
> z =. r„-i/0 + ^»-2/1 ~\ h *o/»-i-
Statt nun 8(y2) zu bilden, berechnen wir zunächst S(y#),
woraus dann S(t/2) hervorgeht, wenn man die x gleich den t setzt.
Wenn man die Formel C) des vorigen Paragraphen
C) yfs = Eo,sfo + E^f, j h En-^fn-,
mit rn_s_j multiplicirt und dann in Bezug auf s von 0 bis n — 1
summirt, so findet man
D) y*=fo 2 JKo,.r«-.-i
0,n — 1
s s
l £ El,sTn — s-l -\~ ' ' ' ~H /»—1 "^ -E"n-l,s^»-s-l-
0,» —1 0,» — 1
J) Sylvester, On a theory of the syzygetic relations of two rational
integral fonctions etc. Phil, transactions vol. 143 A853).

256 Sechster Abschnitt. §. 79.
Nun ist nach §. 74, F)
Sfo = na0, ä/j = (n — 1) al5 . . . Sfn-i = a„_j,
so dass man erhält
o ,
0,» —1
s
-\- (n—l) dx 2 jE'liSrn_s_1
o,» —i .
0,»—1
Hierin ist nun der Coefficient von r„_i
na0E0,0 + (» — 1) «i-Ei.o + •••'+
¦also nach C)
Da nun S(^) mit dem Gliede waor„_i anfängt, so wird in
der Differenz
E) 8(jfg) - \ 8(y) S(g)
kein Glied vorkommen, das mit r„_j multiplicirt ist. Da dieser
Ausdruck aber ausserdem in Bezug auf t und r symmetrisch ist,
so enthält er auch nicht £»_i, uud wir körinen bei seiner Bildung
einfach tn—-y und t„—1 = 0 annehmen.
Wir setzen nun
S(y) = naotn-! + <p(t),
worin
F) <p(f) = (»— 1H^^-2 + (w — 2)a2tf„_3 -| (- an_i*o.
Dann wird
G) I
1,»—1
1,»—1
+ a„_! Z1 jE„_i,s r„_s_j — — (p (t) <p (r),
l,n—1 **
wobei jedoch zu bemerken ist, dass £„_i = 0 anzunehmen, also
zu setzen ist, während die übrigen E durch die Formeln A0) des
vorigen Paragraphen bestimmt sind.

§. 79. Die Bezoutiante. 257
Der Ausdruck auf der rechten Seite von G) ist eine bi-
lineare Function der t und r; er möge entwickelt die Form
haben
0,n— 2 0,M —2
mit der Bedingung Bn,k = Bk,h- Die Bezoutiante ergiebt
sich dann, wenn man t = t setzt, also
(8) B = 2 B^ktjtfa,
0,n— 2
worin die Coefficienten J9Ä>S quadratische Functionen der a sind;
und aus G) folgt
(9) Sine) - \ S(y) 8(e) = 2? J?»,» ferh
A0) 5(y») = \ [8(y)f + 5.
Nach der Formel (8), §. 74 ist
V—\ 8C/) = tn-sFo + k_8J?\ -| f-
IV
und wenn wir beides multipliciren,
yz - ~ [yS@) + ,8C,)] + ^ 5(y) 8(*)
h,k
0,» —2
Summiren wir diese Formel über alle Wurzeln #, d. h. nehmen
wir die mit S bezeichnete Summe, so folgt
8(ffg) — i SCj) 8@) = 2;
und die Vergleichung mit (9) lehrt:
Wir bezeichnen mit d die Determinante der Function B,
setzen also
^=^± -Bo, 0^1,1 ¦ • • -B»— 2,» —2-
Nach dem Multiplicationssatze der Determinanten und mit
Rücksicht auf die Formeln [§. 74, A0)]:
SF0 = 0, SJ\ = 0, . . . S'FM_ä = 0
Weber, Algebra. I. jy

258
Sechster Abschnitt.
§.79.
ist aber, wenn wir
1, -F„Oi)> J\(*i) • • • Fn_2(x1)
0 =
1, F0(xn), F, (
setzen, nach A1)
A2) 0>2 =
Beachtet man nun die Ausdrücke (9) in §. 74 für die Func-
tionen Fo, Fx . . . Fn_2, so ergiebt sich leicht nach dem Satze,
dass man in einer Determinante eine mit einem beliebigen Factor
multiplicirte Colonne zu einer anderen Colonne addiren kann
(§. 25, VII), für 0 der Ausdruck
1, x.2, xl
1,
Hier-
Hierdessen Quadrat nach §. 50 die Discriminante von f(x) ist.
nach haben wir also nach A2) den wichtigen Satz:
Die Determinante der Bezoutiante von fix) ist der
»te Theil der Discriminante von f(x).
Die Berechnung der Bezoutiante hat nach unseren Formeln
gar keine Schwierigkeit mehr und gestaltet sich ziemlich einfach.
Für n = 3 erhält man das schon aus der Formel F) des §. 77
zu schliessende Resultat
. B = — jH (tu t0).
Für die Berechnung der Bezoutiante der biquadratischen
Form wollen wir zur Veranschaulichung des Vorhergehenden
das Formelsystem vollständig aufführen, indem wir die Durch-
Durchführung der wenig längeren Rechnung für die Form fünften
Grades dem Leser überlassen.
Es ist für die Form vierten Grades nach G) und §. 78, A0)
f(x) — a0 xi -j- ax x* -f- a2 «2
-&2,1 == ö0 ^2 ~P "] ^1
-^3,1 —~ Ö^O ^1 H^ ^1 ^0
a% x -f- a4
2a2

§• 79.
Die Bezoutiante.
259
-^0,2
-E"l,2
-^2,2
-E"?„2
-E"o,3
#1,3
-^2,3
-^3,3
= — % t.2 — % £j
= % £j % #o
= % £2 ~f~ a2 h
= !¦ %^2 + % ^1
"= % &2
= — %«!
= %A)
= % 4 ~f" CB ^]
+ % t,)
+ %^0
4«0 tx
3 % ti
2%rx
%rx
4%r0
3% r0
2%r0
%r0.
Man hat diese Ausdrücke mit den rechts daneben gesetzten
Factoren zu multipliciren und zu addiren, dann noch
— i 9 (*) <P @
2 % <! -j- % <0) C % t2 ~\- 2 % rx -}- % r0)
hinzuzufügen und die Coefficienten von rÄ^ aufzusuchen. So
eEgiebt sich:
J92,2 = — j(8o0a2 — 3%2), 5o,i = —-^
l _ .9 Ti J-
— ^c
A4) i?i;i = — 4 a0 «4 — 2 % «3+%,2> 2?i,2 =
^0,0=^ — -j (8 % «4 — 3 %2), J30,2 = — -j A6 % «4 — % %j).
Auf dieselbe Weise kann man bei einer Form fünften Grades
verfahren, und findet für die Coefficienten der Bezoutiante fol-
folgende Ausdrücke:
— 10% c%
= 6a| —
5 B3j3 =
5J?o,i =
5 2?o,2 =
5 j?o,3 =
X B
O -£>1,2
5 #1,3 =
5BM =
3% a
2 a.2 a
2%a
3%a
4 15%%
4 — 20 % a3
4 — 25 % %
3 — 10 Qj\ &$ — Zv Ct>Q Ü
3 — 20 % %
2 — 15%%.
17*

260 Sechster Abschnitt. §. 80.
§• 80.
Transformation der Gleichung fünften Grades.
Diese Entwickelungen sollen nun angewandt werden, um
die Transformation der Gleichung fünften Grades, wie wir sie
im §. 60 skizzirt haben, durchzuführen.
Es lässt sich auf unendlich viele Arten ein Werthsystem
*o> *i> ^2) h so bestimmen, dass die Bezoutiante B verschwindet;
im Allgemeinen ist dazu die Auflösung einer quadratischen
Gleichung erforderlich. Wir können z. B.
t2 — 0, tz = 0
setzen und das Verhältniss t0: tt aus der quadratischen Gleichung
Bo,ot;- + 2 £0,1*0*1 + £1,1^ = 0
bestimmen. Diese Werthe von t enthalten dann die Quadrat-
Quadratwurzel .
Statt dessen kann man aber auch andere Bestimmungen treffen
und bekommt andere und andere Quadratwurzeln. In der Aus-
Auswahl dieser Quadratwurzel liegt etwas Willkürliches und Un-
Unbestimmtes.
Wir greifen unter diesen verschiedenen Bestimmungsweisen
eine heraus und transformiren damit die gegebene Gleichung
fünften Grades in eine Hauptgleichung, d. h. in eine solche,
in der die dritte und vierte Potenz der Unbekannten nicht vor-
vorkommt, oder wir nehmen an, nach F. Klein's Vorgang, die zu
transformirende Gleichung sei von Haus aus eine Haupt-
gleichung
A) f(x) = aox» + «3x* ~\- aAx -\- «5 = 0.
Wir wollen aber noch ausdrücklich hervorheben, dass nach
§. 76, (8) durch diese vorläufige Tschirnhausen - Transformation
die Discriminante der gegebenen Gleichung nur um einen Factor
®2 geändert wird, worin ® rational von den angewandten t,
also auch von der zu ihrer Bestimmung benutzten Quadratwurzel
abhängt.
Unter der Voraussetzung A) werden nun die Coefficienten
der Bezoutiante nach den Formeln des vorigen Paragraphen
folgende:

§. SO. Hauptgleichung fünften Grades. 261
5 i?o,o = 4a| — 10 «3 «5, 5J90,i = Sa3a4
5 J91;i = 6 a|, 5 J3o,2 = 0
B) 5J92,2 = — 20a0a4, öB0,s = — 25ao«r,
5J93,3 = 0, 5J51B = — 25a0a3
5J9i>s = — 20a0a4, 5J92,3 = — 15 aoa3.
Wenn man hieraus die Determinante berechnet, so erhält
man ohne Schwierigkeit nach §. 79, A2) für die Discriminante
der Hauptgleichung fünften Grades
C) D = a08 E*a<}a£ -f- 28a0o? + 225Oaoa33a4a^
— 1600 a0 «s a|a8 -f- 108a35a6 — 27a34a|).
Da nun hier J9S,3 = 0 ist, so haben wir ein Werthsystem
der t, wofür die Bezoutiante verschwindet, nämlich
t0 = 0, tx = 0, i2 = 0.
Wir nehmen nun unsere Tschirnhausen - Substitution in fol-
folgender Form [§. 74, A2)]
D) y = tzF0 + t2 («ä J\ +ßlF2 + «0 i^3),
und wollen über die «0, «l5 k.2 so verfügen, dass die Gleichung
fünften Grades für y unabhängig von tz, t2 zu einer Haupt-
Hauptgleichung wird, dass also S (j/2) identisch für alle t2, ts ver-
verschwindet.
Da S (Ff) = J53K hier verschwindet, so geschieht dieser
Forderung nach §. 79, A1) Genüge, wenn wir «0, ax, «2 so
bestimmen, dass
E) «(fJ?M + alJB1|i + «lAa
-[- 2 cs0 «i -Bo,i + 2 «0 «2 J90!2 + 2 «! «2 J?i,2 = 0,
F) a0 JB0,b -\- «i J5i,3 + «2 -22,3 = 0.
Diese Gleichungen führen durch Elimination von einer der
drei Grossen « auf eine quadratische Gleichung für das Ver-
hältniss der beiden anderen. An sich ist es nicht nothwendig,
irgend einen besonderen Fall auszuschliessen, auch nicht den,
dass JB0,s, 2?i,8, J?2,3 alle drei verschwinden; man hätte dann nur
für die « irgend eine Lösung der Gleichung E) zu nehmen.
Um aber nicht weitläufig zu sein, wollen wir annehmen,
dass 2?o,3 von Null verschieden sei, weil die hierdurch aus-
ausgeschlossenen Fälle, in denen eine Wurzel der gegebenen Glei-
Gleichung Null oder unendlich wird, hier eigentlich kein Interesse
bieten, weil sie auf eine Gleichung niedrigeren Grades zurück-
zurückkommen. Die Behandlung bleibt übrigens ganz dieselbe, wenn

262
Sechster Abschnitt.
§• 80.
(8)
wir annehmen, dass eine andere von den drei Grossen B0,s,Bi.$-, 2?2,s
Ton Null verschieden ist.
Um nun die Gleichungen E), F) in symmetrischer Weise zu
behandeln und namentlich zu erkennen, welche Quadratwurzel
zu ihrer Lösung erfordert wird, verfahren wir so. Wir setzen
zur Abkürzung
#0 = «0-^0,0 ~\~ al#0,l ~\~ «2 #0,2
G) J5j = «0J9lj0 + «i#i,i + «2 #1,2
B2 = «0J92i0 -\- KyB^l -\~ #2#2,2-
Dann können wir die Gleichungen E) und F) so darstellen:
cco#o + «i#i +«j#2 =0
«0 #0,3 + «1#1,3 + «2#2,3 = 0.
Wir multipliciren die zweite mit einem unbestimmten Factor
«., und addiren sie zur ersten, wodurch wir erhalten
eine Gleichung, die erfüllt ist, wenn wir setzen
Bo + «3 J90,3 = 0
#2 ~j~ a3#2,3 = ÖOCj.
Aus diesen drei Gleichungen, in Verbindung mit der Gleichung F),
haben wir die Unbekannten «0, csx, cs2, «3, ö zu bestimmen. Wir
setzen die Gleichungen zunächst ausführlich hierher:
«0#0,0 + «l#0,l + «2 #0,2 . +«3 #0,3 = 0
' «0J92,0 + «j(_B2,l + ö) + «2 #2,2 • + C-3#2,8 = 0
a0 #8,0 ~|- Kl#8,l -f- ai#3,2 ¦ = 0)
und wenn wir hieraus «0, ux, a2, «3 elimiuiren, so ergiebt sich
eine quadratische Gleichung für 6, nach deren Lösung man die
Verhältnisse «0: ax : «2: «8 aus linearen Gleichungen bestimmen
kann.
Die quadratische Gleichung für tf aber lautet in Deter-
Determinantenform
#0,0) #0,li #0,2)
#1,0) #1,1) #1,2
#2,0) #2,1 + 6) #2,2)
#3,0) #8,1) -#3,2)
#0,3
#2,3
= o.

.§. 81. Normalform der Gleichung fünften Grades. 263
Da sich die linke Seite durch Vertauschung von 6 mit — 6
nicht ändert, so ist es eine reine quadratische Gleichung und
sie giebt mit Rücksicht auf §. 79, A2)
Biz <P - \D = 0,
wenn D die Discriminante der gegebenen Gleichung ist. Wir
bekommen also nach B)
A2) 5aoa5ö =
worin das Vorzeichen beliebig ist.
§. 81.
Normalform der Gleichung fünften Grades.
Wie schon früher bemerkt, ist das hauptsächlichste Ziel
dieser Betrachtungen, eine Normalform der Gleichung fünften
Grades herzustellen, die nur von einem unbestimmten Coeffi-
cienten, einem Parameter, abhängt. Eine solche Normalform
ist die Bring-Jerrard'sche Form. Um diese zu erhalten, haben
wir nach D) des vorigen Paragraphen
A) y = tiF0 + ta («,JFi -\-UlFt + a0Fs)
zu setzen, so dass identisch
S(y) = O, S(y») = 0
wird, und dann ist das Verhältniss ts : t2 aus der cubischen
Gleichung
zu bilden. Diese cubische Gleichung lässt sich wirklich bilden,
wenn auch ihr Ausdruck lang wird. Die hierzu nöthigen Formeln
sind von Cayley berechnet1).
Es ist das Ergebniss einer merkwürdigen Untersuchung von
Gordan, dass man eine andere, die Brioschi'sche Normalform
ohne neue Irrationalität erhalten kann, und wir wollen zum
Beschluss dieser Betrachtungen über die Tschirnhausen - Trans-
Transformation dies Resultat noch ableiten2).
Wir halten an den Voraussetzungen des vorigen Paragraphen
fest und setzen für den Augenblick zur Abkürzung
*) Cayley, on Tschirnhausen's Transformation, Phil. Trans. 1861,
Mathematical Papers, Tom. IV, Nr. 275.
2) Gordan, Mathematische Annalen, Bd. 28, 1886.

264 Sechster Abschnitt. §. 81.
B) u = F0, v
worin c^, «j, «2 die im vorigen Paragraphen bestimmten Werthe
haben sollen. ¦
Nach derjFormel §. 79, D) lassen sich die drei Functionen
M2, U V, V2
linear und homogen durch fo, flt f2, fz, fi darstellen, und weil
C) S(u2) = 0, S(uv) = 0, S(v2) = 0
ist, so werden diese Ausdrücke auch in Fo, F1} Ft, 1% linear
und homogen (§. 74).
Die Rechnung ist nach den Formeln der §§. 78, 79 leicht
auszuführen, soll aber hier nicht weiter verfolgt werden, da es
uns nur auf die Darlegung des Grundgedankens ankommt. Wir
wollen nur bemerken, dass die Coefficienten in den Ausdrücken
für m2, uv, v2 linear in den Coefficienten der ursprünglichen
Gleichung fünften Grades und quadratisch in den «0, «x, «2
sind. Wenn wir nun aus diesen Ausdrücken mit Hülfe von B)
die Functionen Fo, Fx, Ft, Fz eliminiren, so erhalten wir eine
Relation von der Form
D) pu2 -\- 2quv -\- rv2 = au + bv,
worin die p, q, r, a, b von den Coefficienten a< und cti rational
abhängen und jedenfalls nicht alle zugleich verschwinden.
Setzen wir für den Augenblick
pu2 -j- 2quv -\- rv2 = <p(u,v),
so ist nach §. 63
4 <p («', v') <p («, v) — [w' <p' (u) + v' <p' (v)f
das Quadrat einer linearen Function von «, v, so dass dadurch
<p (u, v) in die Summe von zwei Quadraten zerlegt wird. Wählen
wir u' = b, v' = — a, so folgt
<p F, — a) <p (u, v) = [b (pu -j- qv) — a (qu -j- rv)]2
+ (pr — g»)(au-\-
oder wenn man zur Abkürzung
pb2 — 2qab -\- ra2 = m,
bp — aq = a',
E) bq — ar = V,
q2 — pr = c
setzt,
F) m(j>u2-\- 2quv -\-rv2) = (a'u -j- b'vJ — c(au-\-

§. 81. Normalform der Gleichung fünften Grades. 265
und nach D) kann diese Gleichung auch so dargestellt werden:
G) m (au -+- bv) = (a'u -f b'vJ — c (au -f bvJ.
Man setze nun
(8) y = —u ~T_, v,
und bilde die Gleichung fünften Grades, deren Wurzeln die fünf
Werthe von y sind:
darin lassen sich die Coefficienten c auf folgende Weise näher
bestimmen.
Aus (8) leiten wir ab
y i 1/7 = a'u + b'v -\- Vc (au-\- bv)
' au -j- bv
und daraus nach G)
y 4- Vc =
a'u -\- b'v — Vc (au -\- bv)
r= = a'u -j- b'v — Vc (au -\- bv).
y + Vc
Daraus folgt aber nach C)
Wenn wir also aus (9) die Gleichung ableiten, deren Wurzeln
die Werthe
1 = y + Vc
sind, also _
setzen, so muss eine Gleichung für § entstehen, in der die Coeffi-
Coefficienten von t-* und §3 verschwinden, und zwar welches Zeichen
wir auch der Quadratwurzel Vc geben. Dadurch erhält man vier
Gleichungen zwischen den Coefficienten cv der Gleichung (9).
Die Gleichung für § wird nämlich:
(l - g WN + *! (l - $ Vöy + ^ (l - § V^K
+ c,|» A _ | WJ + c& (l - | Vt) + c51» = 0.
Setzt man hierin die Coefficienten von §* und |3 gleich 0,
so folgt:

266 Sechster Abschnitt. §. 81.
5 Vc4 - 4d Vcs + 3c2 Vc2 — 2c3 Vc" + c4 = 0,.
— 10 Vc3 + 6Ci Vc— 3c2 Vc" + c3 =0,
und diese Gleichungen zerfallen wegen des doppelten Zeichens
von Vc in die vier
5 c3 + 3 c2 e -f- Ci = 0,
4Clc + 2c3 =0,
10 c + 3 e2 =0,
6 ex c -j- c-i =0.
Aus der zweiten und vierten dieser Gleichungen folgt
Ci = 0, es = 0,
und dann aus der dritten und ersten
c3 = — y c, c4 = 5 c2,
so dass also die Gleichung für y die Gestalt erhält
A0) i/a _^C2/3 +
Diese Gleichung hängt noch von den beiden Parametern c5
und c ab; man kann sie auf eine Gleichung mit einem Para-
Parameter reduciren durch die Substitution
wodurch sie die einfache und elegante Form erhält
A2) 0° — 10^3 + 45^ + y = 0.
Dies ist die Brioschi'sche Normalform. Die Substitu-
Substitution A1) leidet aber an dem Uebelstande, dass sie noch eine
Quadratwurzel enthält, während in den Formeln (8) und A0)
nur die zwei im vorigen Paragraphen besprochenen Quadrat-
Quadratwurzeln vorkommen. Man kann aber auch nach einer Bemerkung
von Klein auf rationalem Wege aus A0) zu einer Normalform
kommen, die nur einen Parameter enthält.
Setzt man z. B.
so erhält man aus A0) die Gleichung
A4) 0^ -\- 150* — lOy02 -f 3y2 = 0.

§. 81. Normalform der Gleichung fünften Grades. 267
Es ist bei dieser Transformation stillschweigend die Voraus-
Voraussetzung gemacht, dass die in E) mit m und c bezeichneten
Grossen nicht Null seien.
Ist m = 0, so ist in der Formel D) pu2 -\- 2quv -\- rv1*
durch au -\- bv theilbar, es muss dann also wenigstens für
einige der Wurzeln die Gleichung
au -(- bv = 0,
d. h. eine Gleichung von nicht höherem als dem vierten Grade
bestehen.
Ist c = 0, also pu2 -\- 2 quv -\- rv% ein Quadrat einer
linearen Function, so ergiebt sich aus G) und C), dass, wenn
y = a'u -\- b'v
gesetzt wird,
S(y) = O, S(y*) = O, 8(y*) = 0
ist, dass also die Bring-Jerrard'sche Form in rationaler
Weise herstellbar ist.
Wir können schliesslich die Resultate dieser Betrachtungen
dahin zusammenfassen:
Die Hauptgleichung fünften Grades lässt sich
durch eine Transformation, die als einzige Irratio-
Irrationalität die Quadratwurzel aus der Discriminante
enthält, auf eine Normalform mit einem Parameter
transformiren.

ZWEITES BUCH.
DIE WURZELN.

Siebenter Abschnitt.
Realität der Wurzeln.
§. 82.
Allgemeines über Realität von Gleichungswurzeln
und über die Discriminante.
In diesem Abschnitt werden wir uns mit der Frage beschäf-
beschäftigen, wie viele Wurzeln einer algebraischen Gleichung reell
sind. Die Coefficienten der Gleichung werden dabei als reelle
Zahlen vorausgesetzt. Wir wollen solche Gleichungen kurz
reelle Gleichungen nennen und beginnen mit einigen allgemeinen
Betrachtungen.
Die reelle Gleichung nten Grades
/(*) = <>
hat, wie wir im dritten Abschnitt gesehen haben, n Wurzeln, die
entweder reell oder imaginär, d. h. von der Form § -(- ir\ sind, mit
reellen §, r\. Die Zahl von n Wurzeln ergiebt sich aber nur dann
allgemein, wenn wir unter Umständen eine Wurzel mehrfach
zählen, nämlich (m-j-l)fach, wenn mitf(x) zugleich die m ersten
Derivirten von f(x) verschwinden. Da nun ein complexer Aus-
Ausdruck von der Form X -j- iY nur dann gleich Null ist, wenn
die beiden reellen Bestandtheile X und T einzeln verschwinden,
wenn also, mit X -j- i T zugleich X — iY verschwindet, und da
ferner bei reellen Coefficienten, wenn /(§ -j- irf) = X-\-iY
ist, sich/(§ — irj) = X — iY ergiebt, so folgt aus/(§-f irj) = 0,
dass zugleich /(§ — itj) = 0 sein muss, dass also zu jeder
imaginären Wurzel § -j- irj eine zweite davon verschiedene
imaginäre | — iy, d. li. die conjugirt imaginäre Wurzel
gehört. Da mit den Derivirten /'(§ -j- irj), /"(§ -\~ irf) . . . zu-
zugleich die conjugirten Grossen /' (§ — irf), /" (§ — i rj) . . . ver-

272 Siebenter Abschnitt. §. 82.
schwinden, so folgt, dass conjugirt imaginäre Wurzeln
denselben Grad der Vielfachheit haben.
Daraus folgt, dass die imaginären Wurzelu immer in gerader
Zahl vorkommen, und dass eine Gleichung ungeraden Grades
immer mindestens eine reelle Wurzel haben muss.
Unser nächstes Ziel wird das sein, die Zahl der reellen
Wurzeln, ohne die Gleichung aufzulösen, direct aus den Werthen
gewisser rationaler Functionen der Coefficienten der
Gleichung zu bestimmen.
Eine sebr wichtige Rolle spielt hierbei die Discriminante,
auf deren Bedeutung für unsere Frage wir zunächst eingehen
müssen.
Wir haben in §. 50 die Discriminante erklärt als das Product
aus den Quadraten der sämmtlichen Wurzeldifferenzen
(*! — x2y,
noch multiplicirt mit a|n~2, wenn a0 der Coefficient der höchsten
Potenz der Unbekannten in der gegebenen Gleichung ist, und
wir haben dort gezeigt, wie die Discriminante als rationale
Function der Coefficienten berechnet werden kann. Der Factor
a20"- ist immer positiv und könnte hier ohne wesentliche Be-
Beschränkung der Allgemeinheit auch gleich 1 vorausgesetzt werden.
Wir wollen, wie schon früher, für die Discriminante das Zeichen
D gebrauchen.
Die Discriminante verschwindet dann und nur dann,
wenn unter den Wurzeln zwei gleiche vorkommen.
Nehmen wir an, dass f(x) durch Absonderung des grössten
gemeinschaftlichen Theilers von f(x) und /' (#), was durch ratio-
rationale Rechnung geschieht, von mehrfachen Factoren befreit sei,
so wird also D nicht verschwinden.
Sind xx und x2 reell, so ist (x-, — x2J positiv. Ist xx reell
und x2 imaginär, so giebt es eine zu ar2 conjugirte Wurzel x'%,
und das Product
(»! — x2) ix,, — x'a)
ist als Product zweier conjugirt imaginärer Grossen positiv, also
auch sein Quadrat.
Sind xx und x2 beide imagiuär, aber nicht conjugirt, so ist
das Product
(Xi fl;2) (Xi — X'st)
und sein Quadrat positiv.

§. 83. Wurzeln der cubischen Gleichung. 273
Sind aber endlich x1 und x% conjugirt imaginär, so ist ihre
Diiferenz rein imaginär und deren Quadrat negativ.
Es kommen also in dem Product, durch das wir die Discri-
minante erklärt haben, genau so viel negative Factoren vor, als
es Paare conjugirt imaginärer Wurzeln giebt, und wir schliessen
daraus auf den wichtigen Fundamentalsatz:
Ist f(x) — 0 eine reelle Gleichung ohne mehrfache
Wurzeln, so ist die Discriminante positiv oder negativ,
je nachdem die Anzahl der Paare conjugirt imaginärer
Wurzeln gerade oder ungerade ist.
Der Fall, wo nur reelle Wurzeln vorhanden sind, gehört zu
denen, wo die Discriminante positiv ist.
Für die Fälle der quadratischen und cubischen Gleichungen,
in denen nur ein Paar imaginärer Wurzeln auftreten kann, ist
durch diesen Hauptsatz bereits die Unterscheidung der ver-
verschiedenen Fälle, die in Bezug auf die Wurzelrealität möglich
sind, die Determination, vollendet.
§. 83.
Discussion der quadratischen und cubischen
Gleichung.
Für die quadratische Gleichung
a0 x% -(- aj x -\- a2 = 0
haben wir (§. 50)
D = a? — 4 a0 a2 > 0 reelle Wurzeln,
< 0 imaginäre Wurzeln.
Für die cubische Gleichung
a0 x3 -|~ % x% -j- a2 x -f- a3 = 0
ist
T> = al a22 -j- 18 a0 a} a^a% — 4 a0 a23 — 4 af a% — 27 a02 a32,
D > 0 drei reelle Wurzeln,
D < 0 eine reelle, zwei imaginäre Wurzeln.
Auch der Fall D = 0 giebt hier zu keinen weiteren Unter-
Unterscheidungen Anlass; denn in diesem Falle sind die beiden
Wurzeln der quadratischen Gleichung einander gleich und reell,
von den drei Wurzeln der cubischen Gleichung zwei einander
gleich und alle drei reell; denn eine imaginäre Wurzel kann hier
Weber, Algebra. I. 13

274 Siebenter Abschnitt. §. 83.
nicht doppelt vorkommen, weil sonst auch die conjugirte doppelt
vorkommen würde, und ebenso wenig kann die einzelne Wurzel
imaginär sein, weil sonst eine zweite vorhanden sein müsste.
Es kann sich bei der cubischen Gleichung nur noch darum
handeln, die Bedingung dafür aufzusuchen, dass alle drei Wurzeln
einander gleich sind.
In diesem Falle muss die linke Seite der cubischen Gleichung
ein vollständiger Cubus sein, also
a0 x* -(- Oj x* -j- a2x -j- a3 = a0 (# — wK-
Die Vergleichung beider Seiten dieser in Bezug auf x identischen
Gleichung ergiebt
«! = — 3 a0 a, a2 = 3 a0 «2, a3 = — a0 «3,
woraus man durch Elimination von a erhält
A, a* — 3a0a2 = 0,
^ ax a2 — 9 aQ a3 = 0.
Daraus ergiebt sich als Folge (indem man die erste dieser Glei-
Gleichungen mit a2l die zweite mit ax multiplicirt und subtrahirt)
al — 3 % a3 = 0;
und wenn diese Bedingungen erfüllt sind, so folgt daraus um-
umgekehrt
d. h. die Gleichheit aller drei Wurzeln.
Bei der cubischen Gleichung
können wir ausser über die Realität auch noch über die Vor-
Vorzeichen der Wurzeln vollständig entscheiden.
Bezeichnen wir nämlich mit oc, ß, y die drei Wurzeln, so ist
B) a1= — («+/3+y), «2 = «ß+«r+ßr> % = — Kßy*
Ist nun D < 0, also nur eine Wurzel, etwa «, reell, so ist
ßy positiv und a wird negativ oder positiv sein, je nachdem c%
positiv oder negativ ist. Ist aber J) positiv, also alle drei Wurzeln
reell, so ist, wenn «, ß, y positiv sind, nach B)
C) % < 0, a2 > 0, a3 < 0;
diese Bedingungen sind nothwendig dafür, dass alle drei Wurzeln
positiv sind. Sie sind aber auch hinreichend; denn wenn eine

§. 83.
Wurzeln der cubischen Gleichung.
275
oder drei Wurzeln negativ sind, so ist a3 > 0. Sind aber zwei
Wurzeln, etwa ß, y, negativ, so ist entweder
«! ;> 0 oder a > — (ß -j- y).
In letzterem Falle aber folgt
a2 < ßy - (ß + rJ = - ß2 - ßy - y\
also a3 negativ.
Ist endlich eine Wurzel gleich 0, so muss nothwendig a%
verschwinden.
Indem man x durch — x ersetzt, schliesst man, dass für drei
negative Wurzeln die nothwendige und hinreichende Bedingung
die ist
D) «! > 0, a2 > 0, a3 > 0.
Wir erhalten daher unter Voraussetzung einer positiven
Discriminante folgende Tabelle:
ßj ÖS2
- +
+ +
- +
«3
—
+
x
3
!¦
0
wo in der letzten Columne die Zahl der positiven Wurzeln
angegeben ist. Wir können das Eesultat dieser Betrachtung so
aussprechen:
Bei positiver Discriminante ist die Anzahl der posi-
positiven Wurzeln der cubischen Gleichung gleich der An-
Anzahl der Zeichenwechsel in der Reihe
1, «i, a2, «3,
wenn wir unter einem Zeichenwechsel die Aufeinanderfolge einer
positiven und einer negativen oder einer negativen und einer
positiven Grosse verstehen.
Wenn eine der beiden Grossen au a2 verschwindet, so haben
wir, da dann nicht alle Wurzeln von gleichem Zeichen sein
können, eine oder zwei positive Wurzeln.
18*

276 Siebenter Abschnitt. §. 84.
Wenn a3 = 0 ist, so reducirt sich die Discriminante auf
ai(af — 4a2),
und wenn diese positiv ist, so hat die cubische Gleichung eine
verschwindende und noch zwei andere reelle Wurzeln. Diese
sind positiv, wenn
% < 0, a2 > 0,
negativ, wenn
«i > 0, a% > 0,
und es ist eine von ihnen positiv und eine negativ, wenn
= 0, a2 < 0
ist.
§• 84.
Discussion der biquadratischen Gleichung.
Bei den Gleichungen vierten und fünften Grades existiren
entweder keine oder zwei oder vier imaginäre Wurzeln. Ist die
Discriminante negativ, so hat man zwei imaginäre Wurzeln. Bei
positiver Discriminante können entweder vier oder keine ima-
imaginären Wurzeln vorhanden sein. Diese beiden Fälle zu unter-
unterscheiden, wird weiterhin unsere Aufgabe sein. Wir wenden uns
aber zunächst zu einer elementaren Betrachtung der biquadra-
biquadratischen Gleichung, die wir der Einfachheit halber in der ver-
verkürzten Form
A) x*-\- a'^-f bx-\- c = 0
annehmen wollen, von der wir leicht zur allgemeinen Form
zurückkehren können.
Bezeichnen wir die Wurzeln mit a, ß, y, d und setzen, wie
in §. 52
a — ß = v -\- w, y — d = v — «?,
B) « — y = w -[- m, d — ß = iv — u,
a — ö = u -\- v, ß — y — u — v,
so sind m2, v2, w2 die Wurzeln der cubischen Resolvente
C) 2/3 +2«2/2-f («2 — 4cJ/— &2 = 0,
und die Discriminante D dieser cubischen Gleichung, die durch
D) 27D = 4(a2+ i2c)s — B«s — 72ae+ 27 &2J
bestimmt ist, ist zugleich die Discriminante der biquadratischen

§. 84. Wurzeln der biquadratischen Gleichung. 277
Gleichung A), und die Vorzeichen der Grossen u, v, w sind
durch die Bedingung
E) u v iv = — b
beschränkt [§. 40, C)].
Wenn die Discriminante negativ ist, so hat die Gleichung
C) ebenso wie A) zwei conjugirt imaginäre Wurzeln.
Ist D positiv und alle vier Wurzeln «, ß, y, 8 reell, so
werden auch u, v, w reell und also ihre Quadrate, d. h. die
Wurzeln von C), positiv.
Sind alle vier Wurzeln imaginär, etwa a mit ß und y mit 8
conjugirt, so folgt aus B), dass v und w rein imaginär, u reell
ist; also hat in diesem Falle die Gleichung C) eine.positive und
zwei negative Wurzeln.
In beiden Fällen kann aber auch, wenn b verschwindet, eine
der Grossen u, v, w gleich Null sein.
Mit Rücksicht auf die Ergebnisse des letzten Paragraphen
über die cubische Gleichung kommen wir also zu folgendem
Resultat:
Die nothwendige und hinreichende Bedingung
für die Existenz von vier verschiedenen reellen
Wurzeln ist
F) JD > 0, a < 0, a2 — 4e> 0.
In allen anderen Fällen, wo D positiv ist, hat die Gleichung
vier imaginäre Wurzeln.
Wir können auch für D = 0, also im Falle der Gleichheit
zweier Wurzeln, die Discussion vollständig durchführen.
Nehmen wir y = ö an, so folgt aus B), da wir die An-
Annahme u-^-ß-\-y-\-8 = 0 gemacht haben,
2v — 2w = k — ß
2u = u-\- ß — 2y = 2(u-{- ß)
und daraus nach C)
- 4a = 2(a + /3)s-]-(«_ ßf
16(«** - 4C) = (« - ßy [8(« + ßy + (« - ßn
Um zunächst den Fall zu erledigen, dass auch a = ß ist,
so erhalten wir aus G) dafür die Bedingung a2 — 4 c = 0, und
die erste Gleichung G) zeigt, dass a negativ ist, wenn a und y
reell, dagegen positiv, wenn a und y conjugirt (und dann wegen
a -\- y = 0 rein imaginär) sind. Daraus folgt:

278 Siebenter Abschnitt. §. 84.
Die biquadratische Gleichung hat zwei Paare gleicher, reeller
Wurzeln, wenn
(8) D = 0, a < 0, a2 — 4c = 0
und zwei Paare gleicher imaginärer Wurzeln, wenn
(9) D — 0, a > 0, a2 _ 4 c _ 0.
Ist aber a von ß verschieden, so muss y reell sein und G)
zeigt, dass, wenn a und ß reell sind, a negativ und at2 — 4e
positiv ist, dass dagegen, wenn a und ß conjugirt imaginär sind,
entweder a positiv oder a1 — 4c negativ sein muss, da in die-
diesem Falle (« — ßy negativ ist, und wenn 2(« + ßJ+(«—ß)-
positiv ist, jedenfalls auch 8(w-)- /3J-{-(a— /3J positiv sein muss.
Wir können also F) dahin ergänzen, dass wir sagen:
Die nothwendige und hinreichende Bedingung für
die Existenz von vier reellen Wurzeln, von denen auch
zwei (aber nicht mehr) einander gleich sein können, ist
A0) D ^ 0, a < 0, «2 — 4 c> 0.
Die nothwendige und hinreichende Bedingung für
drei gleiche Wurzeln, die nothwendig alle reell sind, ist
nach B)
es muss also die cubische Resolvente C) drei gleiche Wurzeln
haben, und dafür sind nach §. 83 A) die nothwendigen und hin-
hinreichenden Bedingungen
o.+ 12C = 0
K ' 2«3 — 8ac-\- 9&2 = 0.
Nach §. 52 A5), A6) sind die beiden Invarianten A und B
der biquadratischen Gleichung
A = a* -\- 12c, JB = 2«3 — 72ae -)- 27R
Also können wir die Gleichungen A1) auch so schreiben:
A = 0, J3-f-4aJ. = 0,
so dass A1) gleichbedeutend ist mit
A = 0, B = 0.
Durch Elimination von c kann man aus A1) auch noch die
Gleichung ableiten:
A2) 8 «s _j_ 27 &2 = o.
Endlich ist noch die Bedingung für die Gleichheit
aller vier Wurzeln
a = 0, 6 = 0, c — 0.

§. 84.
Dis er iminantenf lache.
279
Man kann diese Verhältnisse sehr anschaulich machen durch
eine geometrische Deutung, und wenn auch geometrische Be-
Betrachtungen nicht eigentlich in unserem Plane liegen, so wollen
wir doch nicht unterlassen, den Leser darauf gelegentlich hin-
hinzuweisen.
Deutet man a, b, c als rechtwinklige Coordinaten im Räume,
so ist jeder Raumpunkt als Träger einer gewissen biquadratischen
Gleichung von der Form A), f(x) = 0, zu betrachten; alle
Gleichungen, die eine bestimmte Zahl x zur Wurzel haben,
werden durch Punkte einer Ebene [f(x) = 0] repräsentirt. Die
Gleichung D = 0 ist die Gleichung einer krummen Oberfläche
(fünften Grades), der Discriminantenfläche, die von den
Schnittlinien der Ebenen f(x) = 0, /' (x) = 0 erzeugt wird, und
also eine abwickelbare Fläche ist. Sie ist die Einhüllende aller
Ebenen f(x) = 0.
Die Fläche hat eine aus zwei Zweigen bestehende Rückkehr-
Rückkehrkante, die durch die Gleichungen A1), A2) dargestellt ist, und
eine Doppellinie, die durch die Gleichungen 6 = 0, a2 — 4 e = 0
bestimmt ist und also die Gestalt einer Parabel hat. Auf der
Seite der negativen a durchsetzt sich in dieser Parabel die
Fig. 5.
in
Fläche selbst. Auf der
Seite der positiven a
setzt sich die Parabel
als isolirte Linie fort.
Die Discriminanten-
Discriminantenfläche theilt den gan-
ganzen Raum in drei
Fächer, von denen zwei
nur längs der Doppel-
Doppelparabel zusammen-
zusammenhängen, und diese
Fächer enthalten die
Punkte, denen keine,
zwei und vier reelle
Wurzeln entsprechen.
Nennen wir für den
Augenblick diese drei Fächer [0], [2], [4], so grenzt [0] an [4]
nur längs der Doppelparabel, während [0] sowohl als [4] längs
der Flächentheile an [2] grenzen. Wir wollen mit [0, 2] und
[2, 4] die Grenzflächen von [0], [2] und von [2], [4] bezeichnen.

280 Siebenter Abschnitt. §. 84.
Der isolirte Theil der Parabel setzt sich in das Innere von [0]
fort. Die Rückkehrkanten liegen auf dem Theil der Fläche, der
[4] von [2] scheidet
Im Coordinatenanfang stossen die drei Raumtheile und ihre
Grenzflächen und Grenzlinien zusammen. Die Punkte der
Flächentheile [0, 2] stellen Gleichungen mit zwei gleichen und
zwei imaginären Wurzeln dar, die Punkte von [2, 4] Gleichungen
mit zwei gleichen und zwei davon verschiedenen reellen Wurzeln.
Auf der Doppelparabel finden zweimal zwei gleiche Wurzeln
statt, und zwar auf dem Theil, in dem [0] an [4] grenzt, reelle,
in dem isolirten Theil imaginäre.
Die Punkte der Rückkehrkanten repräsentiren Gleichungen
mit drei gleichen Wurzeln und der Coordinanten - Anfangspunkt
die Gleichung mit vier gleichen Wurzeln.
Auf die Discriminantenfläche und ihre Bedeutung für die
Discussion der biquadratischen Gleichung hat zuerst Kronecker
hingewiesen. Ein Modell der Fläche ist von Kerschensteiner
construirt*).
Der analytische Ausdruck für die Bedingungen der Realität
der Wurzeln lässt sich in eine Gestalt bringen, in der nur die
Covarianten der biquadratischen Form vorkommen2).
Den Ausgangspunkt dazu bilden die Ausdrücke für die
Functionen ipt, ip2, il>a, die §. 72, F) gegeben sind. Wenn wir
in jenen Ausdrücken a mit ß vertauschen, so gehen ipx, il>2, i>% in
^li —^31 —^2 über, und wenn wir gleichzeitig a mit ß und y
mit d vertauschen, i^, if>2, ip3 in ^15 — ip2, — ij>3. Daraus ergiebt
sich Folgendes:
Setzt man für die Variable x einen beliebigen reellen Werth
und sind die Wurzeln «, ß, y, d der biquadratischen Form alle
reell, so sind auch if^, fa, ij>3 reell.
Sind «, ß conjugirt imaginär, y, d reell, so ist die Ver-
!) Kronecker, Monatsbericht der Berliner Akademie vom 14. Februar
1878. Eine Beschreibung des Modells findet sich in dem von Dyck heraus-
herausgegebenen Katalog mathematischer Modelle, München 1892, dem die Fig. 5
auf voriger Seite entnommen ist.
2) Clebsch, „Theorie der binären Formeu", §. 47. Faä di Bruno,
„Theorie der binären Formen", deutsch von Walter (Leipzig 1881), §. 20,
woselbst sich ein wesentlicher Zusatz von Nöther findet.

§. 85. Bezoutiante und Wurzelrealität. 281
tauschung von a und ß gleichbedeutend mit der Vertauschung
von i mit —i. Es sind also in diesem Falle ^ reell, ^2, —^3
conjugirt imaginär.
Sind endlich «, ß und y, d zwei Paare conjugirt imaginärer
Wurzeln, so werden « mit ß und y mit d vertauscht, wenn i in
— i übergeht; also sind in diesem Falle ti reell, ^2> ^3 rein
imaginär.
Sind vier Wurzeln reell, so werden ipf, ip-g, i/>| reell und
positiv.
Sind zwei Wurzeln reell, so ist ipf- reell und positiv, ^|, ipg
sind conjugirt imaginär.
Sind vier Wurzeln imaginär, so ist ij>f positiv, ^»|, ip£ sind
reell und negativ.
Nun haben wir im §. 72, G) die cubische Gleichung auf-
aufgestellt, deren Wurzeln ipf, il>£, ipg sind, und haben auch ihre
Discriminante gebildet. Im vorigen Paragraphen haben wir ein
Kennzeichen für die Anzahl der positiven Wurzeln einer cubischen
Gleichung kennen gelernt, woraus sich folgendes Eesultat ergiebt:
Ist D < 0, so hat die biquadratische Gleichung zwei reelle
und zwei imaginäre Wurzeln.
Ist D > 0, so müssen, wenn vier reelle Wurzeln vorhanden
sein sollen, in der Reihe
1, H, H* - WAf, — T2
drei Zeichenwechsel vorkommen, d. h. es muss
H<0, I?-WAf>0
sein. Bei den drei anderen noch möglichen Zeichencombinationen
sind alle vier Wurzeln imaginär. Hierbei aber kann für x ein
beliebiger reeller Werth gesetzt werden.
§. 85.
Die Bezoutiante und ihre Bedeutung für die
Wurzelrealität.
Für die Untersuchung der Realität der Wurzeln einer be-
beliebigen reellen Gleichung in allgemeineren Fällen kann die
Function mit Nutzen angewandt werden, die wir im §. 79 als
Bezoutiante der Gleichung bezeichnet haben.

282 Siebenter Abschnitt. §. 85.
Ist
A) f{x) = ot» -\- a^-1 + a2a^-2 -| 1- a„ = 0
irgend eine reelle Gleichung «ten Grades, so war die Bezoutiante
folgendermaassen definirt:
Man setze
B) y = tn^f, (x) -\~ tn-2ft (x)-{ h «o/.-i («),
worin die t0, tt, . . ., i^—x unbestimmte Variable bedeuten und
fo(x) = 1, fx(x) = x -f ay, f2(x) — x* -\- axx + o2r. . .
Es ist dann [§. 79, A0)]
C) ^
wo B eine quadratische Form der n — 1 Variablen t0, tu..., f„_2
ist mit Coefficienten, die rational aus den Coefficienten «j zu-
zusammengesetzt sind. Diese Function B haben wir als Bezoutiante
definirt und für die Fälle n — 4 und n = 5 wirklich gebildet.
Nun sind in der Summe auf der linken Seite von C)
D) . y! + yt + yl-\ h yl,
die 2/1, y2, ..., y„ lineare Functionen der Variablen t0, tu ..., #»_!,
und wir haben also in der Formel C) eine Transformation der
quadratischen Form
E) \ [S(y)f + B = 0 (t0, tx,..., tn-i)
auf eine Summe Ton n Quadraten.
Wir machen fürs erste keinerlei beschränkende Voraus-
Voraussetzungen über Gleichheit oder Verschiedenheit der Wurzeln Ton
/(a;)und müssen nun zunächst untersuchen, inwieweit die linearen
Functionen yv y%, . . ., y„ von einander unabhängig sind. In dieser
Beziehung gilt der Satz:
Sind Xy, x$, . . ., xy von einander verschiedene Wur-
Wurzeln der Gleichung A), so sind yt, y2, . . ., yv linear unab-
unabhängig.
.Denn angenommen, es existire zwischen yu y2, . . ., yv eine in
Bezug auf die t identische lineare Relation
«i 2/i + «2 2/2 + • • • + «v yv = 0,
deren Coefficienten a von den t unabhängig und nicht alle gleich
Null sind, so würde diese in die folgenden Gleichungen zer-
zerfallen:

§. 85.
Bezoutiante nnd Wurzelrealität.
283
«1 /o
«1 fl
«2 /o
«2 /l
«v/0 (»,) = 0,
«v/i (O = o,
«2 f„-l(x3) + • 1- «v/„-l(»,) = 0.
Da nun v ^ n ist, so muss die Determinante der v ersten
von diesen Gleichungen verschwinden, also
oder
= 0,
1, X2 -f %, «I + «1 «2 + «2 • • •
= 0.
/y __L ff fy* | /y /y | i-t
*A/y ^*li *^V '—— \Aj\ <JUy —j— l*o • • i
Diese Determinante lässt sich aber durch wiederholte An-
Anwendung des Satzes von der Addition der Colonnen §. 25, (VII)
auf die Form bringen:
I/v» /v* ^ /y*V — X •— / /y /y i / /y> /y \ / /v> /y \
5 15 11 * * *) ^ j V 1 ^"'^ ^2/ VI ^"'^ ""'$/ • * * \ 1 wy I
f /y /y \ f /y /y> i
1
1,
1
(^-r—1 Xv)i
und kann also nicht verschwinden, wenn, wie vorausgesetzt war,
die xx, x<}, . . ., xr verschieden sind.
Wenn wir daher in der Summe D) alle unter einander
gleichen Glieder zusammenfassen, so bleiben so viele Qua-
Quadrate linear unabhängiger Functionen übrig, als die
Gleichung A) verschiedene Wurzeln hat.
Wenn nun xx eine reelle Wurzel von A) ist, so ist yl ein
positives Quadrat in der Summe D). Sind aber xx und x2 con-
jugirt imaginär, so zerfallen auch yx und y2 in zwei conjugirt
imaginäre Bestandtheile
2/i = «* + vii Vi—u — vi,
wo u und v lineare reelle Functionen von den t sind. Demnach
wird
Es ist also durch D) die durch E) definirte Function &(t)
in eine Summe von Quadraten zerlegt, deren Anzahl gleich der

284 Siebenter Abschnitt. §. 86.
Zahl der verschiedenen Wurzeln \onf(x) = 0 ist, und unter
denen so viele negative sind, als unter diesen von einander ver-
verschiedenen Wurzeln Paare imaginärer Wurzeln vorkommen.
Diese Anzahlen bleiben aber nach dem Trägheitsgesetz der
quadratischen Formen (§. 64) bei jeder anderen linearen reellen
Transformation der quadratischen Form in eine Summe von
Quadraten dieselben. Nun ist S(y) eine reelle lineare Function
der t, und B enthält die Variable tn—i nicht mehr; hiernach
ergiebt sich aus der Formel E) der Satz:
I. Wenn die Bezoutiante B durch reelle lineare
Transformation in eine Summe von % positiven
und v negativen Quadraten, die nicht auf eine
kleinere Zahl reducirt werden können, zerlegt
ist, so ist % -\- v -\- 1 die Zahl der verschiedenen
Wurzeln von f{x) = 0; und v ist die Anzahl der
darunter enthaltenen Paare conjugirt imaginärer
Wurzeln, % — v -j- 1 die der reellen.
Ist die Determinante von B, also auch die Discriminante
von f{x) (§. 79) von Null verschieden, so ist % -j- v = n — 1
und v ist kleiner oder höchstens gleich | n.
Die Bezoutiante ist also eine quadratische Form von einer
besonderen Natur, die sich eben darin ausspricht, dass unter
den Quadraten, in die sie sich zerlegen lässt, höchstens | n nega-
negative vorkommen können.
§. 86.
Die Trägheit der Formen zweiten Grades.
Durch den Satz des vorigen Paragraphen sind wir auf die
Untersuchung der homogenen Functionen zweiten Grades mit
reellen Coefficienten hingewiesen. Ueber diese Functionen haben
wir in §. 64 unter dem Namen des Trägheitsgesetzes einen
Satz kennen gelernt, der für das Folgende die Grundlage bildet.
Der Satz besteht darin, dass, wie man auch eine quadratische
Form von m Veränderlichen in eine Summe von positiven und
negativen Quadraten von linear unabhängigen linearen Functionen
transformiren mag, was auf unendlich viele verschiedene Arten
möglich ist, die Anzahl der positiven und ebenso die der negativen
Quadrate immer dieselbe ist.

§. 86. Trägheit der Formen zweiten Grades. 285
Bezeichnen wir mit % die Anzahl der positiven und mit v
die Anzahl der negativen Quadrate, so ist % -\- v höchstens
gleich m.
Wenn wir den Unterschied m — % — v mit q bezeichnen,
so kann, wenn wir die allgemeine quadratische Form von m
Variablen als Summe von m Quadraten darstellen, q als die An-
Anzahl der Quadrate mit verschwindenden Coefficienten bezeichnet
werden.
Die drei Zahlen je, v, q, von denen keine negativ sein kann
und deren Summe gleich der Anzahl der Variablen ist,
A) % -f v -f q — m,
sind also für eine bestimmte quadratische Form unveränderlich.
Wir werden sie die charakteristischen Zahlen der quadra-
quadratischen Form nennen1).
Wir haben nach Mitteln zu suchen, um aus den Coefficienten
der quadratischen Forin die Zahlen je, v, q zu ermitteln. Wenden
wir diese Mittel auf die Bezoutiante an, so erhalten wir Kenn-
Kennzeichen, um aus den Coefficienten einer Gleichung auf die Anzahl
ihrer reellen Wurzeln zu schliessen.
Es sei also jetzt, wie in §. 62
B) 9(i, )
1, m .
eine quadratische Form von m Veränderungen mit reellen
Coefficienten o,-)ft.
Die Determinante
C) R = Z ± «1,1, «2,2, • • -, ÖW,m
zeigt durch ihr Verschwinden an, dass y durch lineare Trans-
Transformation in eine Function von weniger als m Variablen trans-
formirt werden kann, dass also q grösser als Null ist.
Die Determinante R ist eine symmetrische Determinante.
Unter ihren Unterdeterminanten verschiedener Ordnung kommen
gewisse vor, die wieder symmetrische Determinanten sind, nämlich
die, die man aus R erhält, wenn man Zeilen und Colonnen, die
sich in Diagonalgliedern schneiden, ausstreicht, die also, wenn
*) Nach Frobenius heisst n -f- v der Kang, n — v die Signatur
der quadratischen Form („Ueber das Trägheitsgesetz der quadratischen
Formen"; Sitzungsberichte der Berliner Akademie 1894).

286
Siebenter Abschnitt.
§.86.
«, ß, y . . . irgend welche unter den Indices 1, 2,. . ., m bedeuten,
durch
zu bezeichnen sind. Diese wollen wir die Haupt-Unterdeter-
Haupt-Unterdeterminanten von R nennen.
Wir wollen die Anzahl der Haupt-Unterdeterminanten be-
bestimmen.
Die Anzahl der j* -reihigen Haupt-Unterdeterminanten ist
gleich der Anzahl der Arten, wie man aus der Reihe der Indices
1, 2, 3, . . ., m Gruppen von j* verschiedenen auswählen kann, also
gleich der Anzahl der Combinationen von m Elementen zu je ;*,
und diese Zahl ist gleich dem Binomialcoefficienten B^K Die
Anzahl aller Haupt-Unter determinanten ist also, wenn wir die
Determinante R selbst und ausserdem noch die Einheit als eine
nullreihige Determinante mitzählen,
i i ™ i m(m — 1)
1.2
= 2»'.
Es ist aber meist nur ein kleiner Theil von diesen wirklich
zu berücksichtigen.
Die Indices 1, 2, 3,...,m lassen sich auf II (m) = 1 .2 .8...m
verschiedene Arten anordnen; wenn wir mit irgend einer dieser
Anordnungen die Determinante bilden
<h,
«2,1,
so lässt sich eine Reihe von Haupt-Unter determinanten daraus
ableiten, wie es durch die Striche angedeutet ist, d. h. so, dass
man jede vorhergehende aus der nachfolgenden erhält, indem
man die letzte Zeile und Colonne weglässt; es ist also
:== -"•
Ein solches System soll, wenn es in absteigender Reihe

§. 87. Verschwindende Determinante. 287
geordnet ist, eine Kette von Haupt-Unterdeterminanten
heissen. Solcher Ketten lassen sich II(m) verschiedene bilden, in
denen allen das erste Glied B, das letzte Glied 1 ist.
§. 87.
Quadratische Formen mit verschwindender
Determinante.
Wenn die in C), §. 86 definirte Determinante B der quadra-
quadratischen Form cp (xu x2, . ¦ ., xm) verschwindet, so lässt sich, wie wir
schon im §. 62 gesehen haben, q> durch weniger als m von ein-
einander unabhängige lineare Functionen von x ausdrücken. Wenn
wir mit m—Q die kleinste Zahl von Variablen bezeichnen, durch
die sich cp ausdrücken lässt, so hat q dieselbe Bedeutung, wie
im vorigen Paragraphen.
Wenn sich nun unter den Haupt-Unterdeterminanten von R
eine Ä-reihige findet, die von Null verschieden ist, etwa
Bfr — -S1 i «i,l «2,2) • • •; «7t,7tj
so ist, wenn wir
xk+1 = 0, Xk+z = 0, . . ., xm = 0
setzen,
cp fa, x2, . . ., xb 0, 0, . . ., 0)
eine quadratische Form von k Variablen xt, x2, ¦ ¦ ., xk, deren
Determinante B^ von Null verschieden ist, die sich sonach nicht
durch weniger als Je Variable ausdrücken lässt. Um so weniger
kann also bei unbeschränkt veränderlichen %v z2, . . ., xm die
Function cp von weniger als h Variablen abhängen und es folgt
A) Q^m — h.
Wir nehmen nun an, die Form cp (xu x2, . . ., xm) lasse sich
durch Je von einander unabhängige lineare Formen von x aus-
ausdrücken, die wir mit
gl = ßf] xx + $> x, H h ® ^ + &+i ^+H h ß™ x™
= ßf X, + ßf X, -\ h ßf ^ + ßSll «fc+H h ß% 00m
B) 02
glc = ßf> Xl+ßfx^ h ß™ **+^Äi «*+H V ß™
bezeichnen wollen.

288 Siebenter Abschnitt. §. 87.
Da i?!,^,...,^ von einander linear unabhängig sein sollen, so
muss unter den aus der Matrix
ff-) ff) ff)
oB) «B) aB)
Pl i P2 j • • ., Pm
M M oQc)
Pl j /-»2 1 • • •) Pm
zu bildenden Jc-reinigen Determinanten wenigstens eine von Null
verschieden sein. Denn wären sie alle gleich Null, so liessen
sich die Unbekannten Aj, &2, . . ., h^, die nicht alle verschwinden
sollen, aus den Gleichungen
Kßf + hßf ^ 1- Mf = 0, s = 1, 2, 3, . . ., m
bestimmen, und die su £2, ...,£* würden einer Gleichung
genügen, also nicht unabhängig sein (§. 27).
Wir können aber, ohne die Allgemeinheit zu beschränken,
annehmen, dass die Determinante
*i Pi P2 • • •¦ Pjt
von Null verschieden sei, und dann können wir die Gleichungen
B) in Bezug auf die Variablen xu xa, ...,%% auflösen.
Diesen Auflösungen geben wir die Form
x = y -\- «A) x -4~ ¦ • ¦ -4- am x
/-gx ^2 = 2/2+ «ft + 1% + 1 -\- ¦ • • -\- Cim Xm
x-k = 2/ä + «fc + i xt + i -| h d$%m,
worin die ys lineare homogene Verbindungen der ss sind, die
aus den Gleichungen
o(l) I o(l) _j_ _ I o(l)
bestimmt werden, während die « neue Coefficienten sind, die in
einer leicht zu übersehenden Weise aus den ß abgeleitet werden,
auf deren Bildung es uns hier nicht weiter ankommt.
Nun lässt sich nach der Voraussetzung die Function
cp(a^,x2, ..., xm) durch gx,#ä, ..., gk, also auch durch yx,y2, ..., y*

§. 87. Verschwindende Determinante. 289
allein ausdrücken. Bezeichnen wir diesen Ausdruck mit
®(Vu Vi, • ¦ •) 2/jt), so haben wir [durch Vermittelung von C)] die
Identität
D) cp(Xi, xt, . . ., Xtc, xk + 1 . . . xm) = ®(yu y2, . . ., yk),
und wenn wir darin Xjc + 1, x-k+z, . . ., xm = 0 setzen,
E) 0(xi_, x^ . . .,xlt) = (p («!, x2, . . ., xh, 0, 0, . . ., 0),
wodurch, da es auf die Bezeichnung der .Variablen nicht an-
ankommt, <5 vollständig bestimmt ist; wir können daher setzen
2/2, • • -, 2/ä) = 9 B/15 yii ¦ • •) y-xr, o, o,..., o)
0 entsteht also aus cp dadurch, dass man die m — h letzten
Variablen (bei der hier gewählten Anordnung) gleich Null setzt:
r,s
G) #(«!, . . .,Xk) = 2 ar>sXrXs.
Die Determinante von ^ ist eine der Haupt-Unterdeter-
Haupt-Unterdeterminanten von R, und zwar erhält man sie, indem man in B die
m — Je letzten Zeilen und Colonnen wegstreicht.
Nehmen wir an, dass cp sich nicht durch noch weniger als
lc Variable ausdrücken lässt, dass also Je = m — q sei, so kann
die Determinante dieser Function 0 nicht verschwinden.
Hieraus und aus dem zuvor Bewiesenen ergiebt sich nun
der Satz:
II. Wenn alle Haupt-Unterdeterminanten von B von
mehr als Je Reihen verschwinden, während unter
den Haupt-Unterdeterminanten von Je Reihen
wenigstens eine von Null verschieden ist, so ist
q = m — Je.
Denn aus G) folgt, dass, wenn q = m — Je ist, wenigstens
eine fe-reihige Haupt-Unterdeterminante von Null verschieden
sein muss, und aus A), dass, wenn auch noch eine Haupt-Unter-
Haupt-Unterdeterminante von mehr als Je Reihen von Null verschieden ist,
q < m — Je
ist. Wenn also q = m — Je ist, so kann keine Unterdeterminante
von mehr als Je Reihen von Null verschieden sein.
Sind 3t, v, q die charakteristischen Zahlen der Form <p, so
sind 7t, v die Anzahlen der positiven und negativen Quadrate,
in die sich die durch G) bestimmte Form 9 zerlegen lässt, und
Weber, Algebra. I. jg

290 Siebenter Abschnitt. §.88.
die Bestimmung der Zahlen 3t, v braucht also nur noch für
letztere Fuhction, deren Determinante von Null verschieden ist,
durchgeführt zu werden. '
§.88.-
Quadratische Formen mit nicht verschwindender
Determinante.
Bei der Untersuchung der Formen <p (%, x2, . . ., xm) mit nicht
verschwindender Determinante machen wir von einem Deter-
Determinantensatz Gebrauch, den wir im §. 31 bewiesen haben, und
an den wir hier erinnern wollen.
Ist A eine Determinante von m Reihen, und sind Af) ihre
ersten, Affi ihre zweiten Unterdeterminanten, so ist
A) - A^Af-AfA^^AA^. .
Ist A eine von Null verschiedene symmetrische Deter-
Determinante, so ist A(x = A(P und wir können die Formel A) so
schreiben:
B) A? Af — Af = AA\X
Darin kann i jeden der Indices 2, 3, . . ., m bedeuten. Wenn
A*P = 0 und A\\li = 0 ist, so folgt hieraus, dass auch A® = 0
sein muss, und daraus schliessen wir, dass nicht zugleich
verschwinden können, da sonst auch
JB) jC) A(m)
-fl-1 ) -o-l ! • • •¦> -o-l 1
also auch, gegen die Voraussetzung, A verschwinden würde (§.25).
Wenden wir dies auf die jetzt von Null verschieden an-
angenommene Determinante i? = Rm unserer Function q> an, so
folgt, dass zwar die erste Haupt-Unterdeterminante -Bm_1? dann
aber nicht alle zweiten Haupt-Unter determinanten -ßm_2 ver-
verschwinden können. Dieselbe Schlussweise lässt sich anwenden,
wenn wir R durch ein nicht verschwindendes i?m_l5 i?TO_2 • • .
ersetzen, und wir gelangen also zu folgendem wichtigen Satz:
III. Man kann, wenn B von Null verschieden ist, die
Indices 1, 2, . . ., m so anordnen, dass in der Kette
der Haupt-Unterdeterminanten
C) Rm, Rm—i) • • •; Hit Hn

§. 89. Anzahl der positiven und negativen Quadrate. 291
nicht zwei auf einander folgende Glieder ver-
verschwinden.
Die Determinantenrelation B) ergiebt, wenn man
Ä = Sk+i, (h= 1, 2, .. ., m — 1)
setzt, eine Gleichung zwischen drei auf einander folgenden Gliedern
der Kette C), die wir so schreiben können:
D) RkSk — T-k = Ric-iRit+n
worin 8% und T^ gewisse Unterdeterminanten von M, also ganze
rationale Functionen der Coefficienten a^ sind.
Näher bezeichnet, sind i4, St, T% erste Unterdeterminanten
von -Rfc+i, und zwar ist
Eine dem Satz C) entsprechende Anordnung der Indices
wollen wir für die Folge als gewählt voraussetzen. Dann ist,
wenn i4 verschwindet, i4—i und i4+i von Null verschieden und
D) zeigt, dass sie entgegengesetzte Vorzeichen haben, also:
IV. Wenn ein inneres Glied einer Kette von Haupt-
Unterdeterminanten verschwindet, so haben die
beiden angrenzenden Glieder entgegengesetzte
Vorzeichen.
§. 89.
Anzahl der positiven und negativen Quadrate.
Um die Anzahl der positiven und negativen Quadrate einer
Form mit nicht verschwindender Determinante zu bestimmen,
nehmen wir zunächst an, dass in der Kette der Haupt-Unter-
Haupt-Unterdeterminanten
-"mi -"m—1? R>m—2) • • •¦, -R\i -^o :== 1
kein Glied verschwinde. Wir können dann den Coefficienten X
so bestimmen, dass die Determinante der Form
A) t = y (»i, «2, xs, . . ., xm) — Xx2m
verschwindet. Die Determinante ist nämlich
19*

292 . Siebenter Abschnitt. §. 89.
und sie verschwindet, wenn
gesetzt wird.
Die Function ip lässt sich dann durch m — 1 Variable y
ausdrücken, und man erhält nach der Formel F), §. 87
1? Oi, a;2, . . ., xm) — i\> (yv y2, . . ., fm_x, 0),
oder nach A)
B) (p (xu »ä, . . ., xm) = -j~- x2m -f (p (y1: y2, . . ., 2/OT_i, 0),
und die Untersuchung der Function (p von m Variablen ist dadurch
auf die Untersuchung von qpx (y) = cp (y^ y3, . . ., «/m_i, 0) von
m — 1 Variablen zurückgeführt, deren Determinante gleich i?m_1?
also von Null verschieden ist. Je nachdem Rm : .Bm_i positiv
oder negativ ist, wird die Function (p(x) ein positives oder ein
negatives Quadrat mehr haben als cpL (y).
Durch Anwendung des gleichen Verfahrens auf cpx (y) und
die folgenden Functionen ergiebt sich der Satz:
Die Anzahl der positiven und negativen Glieder der Reihe
i?m_x' Hm—i1 ' Ro
stimmt überein mit der Anzahl der positiven und negativen
Quadrate, in die sich die Function (p (x) zerlegen lässt.
Wir wollen diesem Satze noch einen etwas anderen Ausdruck
geben, schicken aber folgende Erklärung voraus.
Wenn eine Reihe von Null verschiedener reeller Zahlen in
bestimmter Anordnung vorliegt, so können die Vorzeichen dieser
Grossen in mannigfaltiger Weise wechseln; folgen zwei Grossen
von gleichem Zeichen auf einander, so findet eine Zeichenfolge
(Permanenz) statt, folgt aber auf eine Grosse eine andere von
entgegengesetztem Zeichen, so haben wir einen Zeichenwechsel
(Variation).
Betrachten wir nun von diesem Gesichtspunkte die Reihe
der Grossen
-£lm, ±im — 1, _tim — 2l • • •, -"lj -f^O)
so findet beim Uebergange von i4 zu i4—i eine Zeichenfolge oder
ein Zeichenwechsel statt, je nachdem der Quotient R^ : i?j:_i
positiv oder negativ ist.

§. 89. Zeichenfolgen und Zeichenwechsel. 293
Wir können also auch den folgenden Satz aussprechen:
V. Ist jt die Anzahl der positiven, v die der nega-
negativen Quadrate von cp, so ist n gleich der'Anzahl
der Zeichenfolgen, v gleich der Anzahl der
Zeichenwechsel in der Kette
D) Rm Rm—i, üm—2, • • •) -ßii -ßo-
Diese Fassung des Satzes hat den Vorzug, dass sie sich auf
den Fall übertragen lässt, dass in der Reihe D) einzelne innere
Glieder verschwinden, wenn nur nicht zwei auf einander folgende
Glieder Null sind (was nach §. 88, III. immer angenommen werden
kann). Wenn nämlich Rk = 0, 14-1, 14+i von Null verschieden
sind, so haben nach §. 88, Satz IV. 14-i und 14+ i verschiedene
Vorzeichen. In der Reihe
-"fc+i} 14) 14—i
findet also ein Zeichenwechsel und eine Zeichenfolge statt,
gleichviel ob wir das verschwindende Bk durch eine positive oder
eine negative Grosse ersetzen.
Wenn wir nun die Kette D)
J^mi J^m — 1) • • ") -"ii -)
in der einzelne Glieder verschwinden, durch eine andere ersetzen,
E) JR'm, R'm—i, ¦ . ., R'i, -ßo,
in der kein Glied verschwindet, und in der den nicht verschwin-
verschwindenden Gliedern der Reihe D) Glieder von demselben Vorzeichen
entsprechen, so haben die Reihen D) und E) gleich viele Zeichen-
wechsel, welches Zeichen auch die den verschwindenden H ent-
entsprechenden B' haben mögen.
Es sei nun i>{x) eine zweite beliebige quadratische Form
der Variablen x, mit der wir die Form
F) q>' = cp + s 4>
bilden, worin s ein noch unbestimmter Coefficient ist. Wir
werden nun sogleich zeigen, dass wir s so wählen können, dass
cp' und cp dieselbe Zahl von positiven und negativen Quadraten
haben, dass aber in der' Kette der Haupt-Unterdeterininanten
14 der Form cp' keine verschwindenden Glieder vorkommen, und
dass endlich einem nicht verschwindenden 14 ein 14 von dem-
demselben Vorzeichen entspricht. Dann können die Zahlen it, v
für cp und für cp' sowohl aus der Reihe D), als auch aus der
Reihe E) ermittelt werden, und die Anzahl der Zeichen-

294
Siebenter Abschnitt.
§• 89.
Wechsel, die in beiden gleich ist, giebt die Anzahl v der nega-
negativen Quadrate.
Um nun den Nachweis zu führen, dass der Coefficient s in
der angegebenen Weise bestimmt werden kann, nehmen wir an,
es sei q> irgendwie in eine Summe von Quadraten verwandelt
G) cp = Ajy\ -f- A2y% -)-••• -\- KiVm,
und ^, in den Variablen yx, y2, . . ., ym dargestellt, habe den
Ausdruck
Die Zahlen «, v für die Function cp' werden dann aus der
Kette der Haupt-Unterdeterininanten von
(9)
-\- £02,2
£02,»)
Sßm,
£ 0«i,l5 £0m,2 . . • Aj
nach dem Satze V. bestimmt.
Nun kann man aber s so klein annehmen, dass diese Haupt-
Unterdeterminanten dem Zeichen nach übereinstimmen mit
Aj^ A3 . . . ATO, Aj A2 A3 . . . ATO_1, . . ., Aj, A2, A15 1,
und dann ist die Anzahl der positiven und negativen Quadrate
von cp' gleich der Anzahl der positiven und negativen unter den
Coefficienten A, von denen keiner verschwindet, d. h. die Zahlen
it und v sind für cp und cp' dieselben.
Sind nun die Coefficienten von ty, in den ursprünglichen
Variablen ausgedrückt, J,-jto also
so ist eine der Haupt-Unterdeterminanten von cp'
und ist also eine ganze rationale Function fcten Grades von e,
worin die Jf15 Jlf2, . . ., Jf^ rational von den aiilc, hilc abhängen.
Insbesondere ist
und man kann die iitlc immer so annehmen, dass Mje von Null
verschieden ist. Nach §. 34 kann man also s so annehmen, dass,

§. 89. Zeichenfolgen und Zeichenwechsel. 295
wenn Ry von Null verschieden ist, R'k dasselbe Zeichen hat, wie
ü?fa und wenn Ry, verschwindet, R'y nicht verschwindet.
Wir können das hierdurch Bewiesene mit den Ergebnissen
des §. 87 in eine allgemeine Regel zur Bestimmung der Anzahl
der negativen Quadrate, auch für den Fall verschwindender
Determinante, zusammenfassen.
VI. Um die charakteristischen Zahlen «, v, q der
Function cp(x) zu bestimmen, ordne man die
Variablen a^, a%, . . ., xm so an, dass in der Kette
der Haupt-Unterdeterminanten
A0) Rm, Rm—1, • • ; Hi, R6
eine möglichst kleine Anzahl von Anfangs-
Anfangsgliedern verschwindet, und dass von den folgen-
folgenden Gliedern nicht zwei neben einander stehende
verschwinden; q ist dann die Anzahl der ver-
verschwindenden Anfangsglieder, v die Anzahl der
Zeichenwechsel und % = m — v — q x).
Zu bemerken ist noch, dass man die Anzahl der Zeichen-
Zeichenwechsel in der Reihe A0) auch von rechts nach links abzählen
kann, d. h. dass man dieselbe Anzahl von Zeichenwechseln findet,
wenn man die Reihe in umgekehrter Ordnung schreibt.
Bezeichnen wir mit «, v, q die charakteristischen Zahlen der
Form cp und bilden die Form
<p' = <p -\- sty,
so können wir i\> so bestimmen, dass die Determinante von <p'
nicht identisch für jedes £ verschwindet. Dann sind n', v', 0 die
charakteristischen Zahlen von q>' und
A1) X> -\-v' = 7t + V -{- Q.
Es ist dann in G)
ATO = 0, nm—i = 0, . . ., A,m — q+i = 0,
Am_?, AOT_?_!, . . ., Ax von Null verschieden, i
1) Hierüber ist zu vergleichen Gundelfinger's Zusatz zur dritten
Auflage von Hesse's analytischer Geometrie des Raumes. Frobenius,
„Ueber das Trägheitsgesetz der quadratischen Formen". Sitzungsberichte
der Berliner Akademie 1894. Frobenius giebt ein Verfahren an, um die
Signatur, also die Differenz n — v, in gewissen Fällen auch dann aus der
Kette G) zu bestimmen, wenn darin beliebige Glieder verschwinden, so
dass ein vorheriges Ordnen der Indices entweder ganz vermieden oder
wenigstens eingeschränkt wird.

296 Siebenter Abschnitt. §. 90.
In der Kette der Haupt-Unterdeterminanten von (9) stimmen
dann bei hinlänglich kleinem e die m — q Endglieder im Vor-
Vorzeichen überein mit
1, A1? Ai A2, . . ., Ax A2 . . . ATO_£,,
und die Anzahl der in dieser Kette vorkommenden Zeichenfolgen
ist daher mindestens gleich der Anzahl der positiven X und
die Anzahl der Zeichenwechsel mindestens gleich der Anzahl
der negativen L Es ergiebt sich hieraus
A2) «' ^> », t/ JS v.
Nennen, wir eine Form q>, deren charakteristische Zahlen
it = m, v = 0, p = 0 sind, die also als Summe von n positiven
Quadraten von einander unabhängiger linearer Functionen dar-
darstellbar ist, eine positive Form, so gilt der Satz, dass für eine
positive Form keine der Haupt-Unterdeterminanten verschwinden
kann. Denn eine positive Form kann für kein reelles Werth-
system der Variablen xu x2, . . ., xm verschwinden, ausser wenn
diese Variablen alle gleich Null sind. Wenn aber nun die
Haupt-Unterdeterminante i?s = 0 ist, so ist die Function von
Ti Variablen
cp (xu x2, . . ., xk, 0, . . ., 0),
deren Determinante eben Bk ist, durch weniger als n lineare
Functionen der xv x2, . . ., #*, etwa yv yt, .. ., y^—i, darstellbar,
und die Function <p verschwindet daher, wenn
«/i = 0,..., «/fc-! = 0, xt+1 = 0, . . ., xm — 0,
ist. Dies ist ein System linearer Gleichungen, das durch nicht
verschwindende x befriedigt werden kann. Daraus ergiebt sich
VII. Die nothwendige und hinreichende Bedingung
für eine positive Form ist die, dass die Glieder
der Kette G) alle positiv sind.
Den entsprechenden Satz für eine negative Form erhält man,
wenn man VII. auf die Form — cp anwendet. Positive und nega-
negative Formen werden auch unter dem Namen der definiten
Formen zusammengefasst.
§. 90.
Anwendung auf die Bezoutiante.
Die genaue Discussion der Trägheit der quadratischen
Formen hatte für uns den Zweck, die Anzahl der reellen und

§. 90. Anwendung auf die Bezoutiante. 297
imaginären Wurzeln einer algebraischen Gleichung durch Ab-
Abzählung der positiven und negativen Quadrate der Bezoutiante
zu bestimmen. Ist n der Grad der Gleichung, so ist ihre
Bezoutiante eine quadratische Form von n — 1 Veränderlichen,
und im §. 79 haben wir sie für n = 3, 4, 5 vollständig gebildet,
und die Wege kennen gelernt, wie man auch in anderen Fällen
zu ihrer Berechnung gelangen kann.
Wir haben schon früher bemerkt, dass die Bezoutiante nicht
eine allgemeine quadratische Form ist, sondern dass sie die be-
besondere Eigenthümlichkeit hat, dass die Anzahl v ihrer negativen
Quadrate niemals grösser als \n werden kann. Diese Eigen-
Eigenthümlichkeit muss in gewissen Ungleichheitsbedingungen zwischen
den Coefficienten ihren Ausdruck finden, die aber zur Zeit noch
nicht bekannt sind. Nur in dem Falle n = 3 können wir den
algebraischen Charakter dieser Beschränkung vollständig angeben.
Für die cubische Gleichung
f(x) = a0 x* -\- % x2 -(- % x -\- a3 = 0
ist die Bezoutiante nach §. 79, A3) nichts Anderes, als die
Hesse'sche Covariante (§. 68)
-1 H&, *,) = — ! D, n + A *i *o + A *<?)•
Es besteht aber, wenn D die Discriminante, also
SD = <LA0A2 — AI
ist, die Relation
4#3_j_ Q2 _^_ 27Dß = 0,
mithin, wenn wir darin £0 = .0 setzen,
A) 4^03 + <z0ä + 27Z>a0ä = 0,
wenn
q0 = 27a02a3 — 9a0<% <h + 2a>i
ist. Diese Relation zeigt, dass Aa und D nicht zugleich positiv
sein können, und dass also die Form — H nicht in zwei
negative Quadrate zerlegbar ist. ,
Wir wollen den allgemeinen Satz des vorigen Paragraphen
noch auf die biquadratische Gleichung anwenden, die wir der
Einfachheit halber in der Form
B) x± + ax2 + ^x + c = 0
annehmen. Um die Coefficienten der Bezoutiante zu bilden,
haben wir in den Formeln §. 79, A4)
«0> (hl «25 «3) «4
durch

298 Siebenter Abschnitt. §. 90.
1, 0, o, b, c
zu ersetzen. Wir erhalten so
£22 —_ 2a, £M = a2 — 4c, JB0,o = — |(8ac ~ 3&2)'
Bo>1 = \ab, JB2,o = — 4 c, _BM = — 3 b.
. Wir ordnen die Determinante so an:
— 2 a, — 3 b, —4c
— 3 5, a2 — 4 c, \ab
— 4c, fa&, —i(8ac —3&2
und erhalten die Kette der Haupt-Unterdeterminanten
C) -D, — 2as + 8ac — 9&V — 2a," 1)
wenn J> die Discriminante bedeutet, die nach §. 53, A3) bestimmt
ist durch
D) 27 D = 4 (a2 + 12 c)s — B «3 _ 72 a c -f 27 &2J.
Das Kennzeichen dafür, dass alle vier Wurzeln reell sind,
ist hiernach
E) B > 0, — 2 a» + 8 a c — 9 b2 > 0, — 2 a > 0.
Dies Kennzeichen ist scheinbar verschieden und jedenfalls
weniger einfach, als das in §. 84 aufgestellte
F) D > 0, a < 0, a2 — 4e> 0.
Wir wollen aber nun noch nachweisen, dass beides genau
dasselbe besagt.
Zunächst ist sofort zu übersehen, dass F) erfüllt sein muss,
wenn E) erfüllt ist, denn
— 2 a (a2 — 4 c) — 9 62
kann nicht positiv sein, wenn a und a2 — 4c negativ sind; um
aber umgekehrt einzusehen, dass aus F) die Bedingungen E)
folgen, müssen wir den Werth von D in Betracht ziehen.
Wir setzen zur Abkürzung
G) « = — 2a, |3 = — 6as-|-24ac — 27J2, j> = 3a2 — 12c,
so dass die Bedingungen E)
a > 0, |3 > 0, D > 0,
die Bedingungen F)
a>0, r>0, .D>0
lauten; dann ist nachzuweisen, dass, wenn «, <y und J> positiv
sind, auch ß positiv sein muss. Hierzu drücken wir D in D)
nach G) durch «, ß, <y aus und erhalten
27 D — 4(«2 — y)8 — [2«(«2 — y) — ß]K

§. 90. Biquadratische Gleichung. 299
Wenn D positiv ist, so muss hiernach gewiss «2 — y positiv
sein. Setzen wir also
u? — y = <S2,
so ist «2 > d2, also, wenn d positiv genommen wird,
«> d
und
27 D = 4<S« — Bad* — |3J.
Hiernach kann D bei negativem |3 nicht positiv sein; denn
ist ß negativ, so ist
2«<S2 — |3> 2«<S2> 2^3,
also 4 de — B a <S* — |3J negativ.
Es ist hiermit direct nachgewiesen, dass die Kriterien E)
und F) genau dasselbe besagen.
Nach der im §. 84 gegebenen geometrischen Interpretation
bedeutet ß = 0 eine Fläche dritter Ordnung, die durch die
Parabel b = 0, y = 0 hindurchgeht, und die, soweit negative
Werthe von a in Betracht kommen, ganz in dem Raumtheil ver-
verläuft, in dem D negativ ist.
Um für die Gleichung fünften Grades ein Beispiel vor Augen
zu haben, betrachten wir die Gleichung
x'" -\- x* + a = 0.
Wir haben also in unseren allgemeinen Ausdrücken §. 79
oder auch §. 80, B), C) zu setzen
a0, au a2, a3, a4, a-0 =
1, 0, 0, 1, 0, o,
und wir erhalten für die Determinante der Bezoutiante
— 2 a, 0, 0, —5a
0, f, — 5 a, 0
0, — 5 a, 0,-3
— 5 a, 0,-3, 0
und für die Discriminante
D = 108 a + 3125 aK
Eine Kette von Haupt-Unterdeterminanten ist
13' 108
(8) 12), 50 a\ -^—, -2 a, 1.
Die Discriminante ist negativ, wenn
(9) ¦ 0 <-a<]/}
3125'

300
Siebenter Abschnitt.
90.
sonst positiv, besonders also für alle positiven a positiv. Man
sieht, dass bei positiver Discriminante in (8) immer zwei
Zeichenwechsel, bei negativer Discriminante, wo auch a negativ
ist, ein Zeichenwechsel stattfindet.
Unsere Gleichung hat also, so lange a in dem Intervall (9)
liegt, zwei imaginäre Wurzeln, wenn es ausserhalb dieses Inter-
valles liegt, vier imaginäre Wurzeln, niemals vier reelle Wurzeln.
Ein rein numerisches Beispiel bietet die der complexen
Multiplication der elliptischen Functionen entnommene Gleichung
x$ _ xz _ 2 a;2 — 2 x — 1 = 0.
Für die Determinante der Bezoutiante erhalten wir aus §. 79:
— 4
5 '
— 3
5 '
4
~5'
5,
— 3
5 '
4
5'
33
T'
8,
4
51
33
5'
46
1P
6,
i 6
und die Kette der Haupt-Unterdeterminanten
472 94 , — 4
T' "'
1,
1,
so dass die Discriminante unserer Gleichung 472 ist. Die
Gleichung hat also zwei Paar imaginäre und eine reelle Wurzel.
Das zweite Glied dieser Kette 94 : 5 braucht man, wenn man
die Discriminante kennt, nicht zu berechnen, ja es genügt schon
die Kenntniss des negativen Vorzeichens im vorletzten Gliede,
um die vorstehende Entscheidung über die Realität der Wurzeln
zu treffen.

Achter Abschnitt.
Der Sturm'sche Lehrsatz.
§• 91,
Das Sturm'sche Problem.
Die im vorigen Abschnitt behandelte Frage nach der Anzahl
der reellen Wurzeln einer Gleichung ist ein specieller Fall eines
allgemeineren Problems, das den Gegenstand dieses Abschnittes
ausmachen soll, und das die Grundlage ist für alle Methoden
der genäherten numerischen Berechnung von Gleichungswurzeln.
Es handelt sich um die Frage: wie viele reelle Wurzeln
einer reellen numerischen Gleichung liegen zwischen
zwei gegebenen reellen Zahlwerthen a und b?
Ist dies entschieden, so handelt es sich weiter darum, die
Grenzen a, b so weit einzuengen, dass nur noch eine Wurzel
der gegebenen Gleichung zwischen ihnen liegt, und sie endlich
einander so weit zu nähern, dass jede von ihnen als ein ge-
genäherter Werth dieser Wurzel betrachtet werden kann.
Nehmen wir a = — oo, b = -\- oo, oder doch a negativ, b
positiv so gross an, dass jenseits dieser Grenzen keine Wurzeln
mehr liegen können, so fällt diese Aufgabe mit der im vorigen
Abschnitt behandelten, die Anzahl aller reellen Wurzeln zu be-
bestimmen, zusammen.
Wir wollen zunächst zeigen, wie sich das allgemeine Problem
auf das specielle zurückführen lässt, wie also unsere jetzt auf-
aufgeworfene Frage, im Princip wenigstens, durch die Betrachtungen
des vorigen Abschnittes beantwortet ist. Es möge sich zunächst

302 Achter Abschnitt. §. 92.
darum handeln, die Anzahl der positiven Wurzeln einer
Gleichung f(x) = 0 zu ermitteln. Setzen wir x = y2, so wird
jedem reellen Werth von y ein positiver Werth von x ent-
entsprechen, und umgekehrt entsprechen jedem positiven Werth von
x zwei reelle, entgegengesetzte Werthe von y. Die Anzahl
der positiven Wurzeln von f(x) ¦= 0 ist also halb so
gross, als die Anzahl der reellen Wurzeln von f(y2)
= 0. Setzen wir ferner
x — a
y = T^x-^
so wird, während x von a bis b geht, y durch positive Werthe
von Null bis Unendlich gehen, und wenn wir durch diese Sub-
Substitution f(x) in F(y) transformiren, so wird f(x) = 0 ebenso
viele Wurzeln zwischen a und b haben, als F(y) = 0 positive
Wurzeln hat, mithin halb so viel als F(s2) = 0 reelle Wurzeln
hat. Unsere Aufgabe ist also dadurch in der That auf die
Ermittelung der Anzahl der reellen Wurzeln einer gewissen
anderen Gleichung zurückgeführt, deren Grad doppelt so gross
ist, als der Grad der gegebenen Gleichung. Diese Zurück-
Zurückfuhrung des Problems giebt aber seine Lösung nicht in der
einfachsten Form, und wir müssen nach einer einfacheren Be-
Beantwortung der Frage suchen.
§. 92.
Die Sturm'schen Ketten.
Zu einer Lösung des Problems, das wir uns im vorigen
Paragraphen gestellt haben, führt uns folgende Betrachtung.
Es seien « und ß irgend zwei reelle Zahlen und « < ß.
Es sei ferner fix) eine gegebene ganze rationale Function von
x, von der ermittelt werden soll, wie viele ihrer Wurzeln in
dem Intervall z/
« < x < ß
liegen. Wir nehmen an, dass «, ß nicht selbst zu den Wurzeln
von f(x) = 0 gehören, dass also /(«) und f(ß) von Null ver-
verschieden sind. Ausserdem wollen wir noch fürs erste annehmen,
dass f(x), wenigstens in dem Intervall z/, keine mehrfache Wurzel
habe, dass also für keinen Werth des Intervalls f(x) und f (x)
zugleich verschwinden sollen.

§. 92. Die Sturm'schen Ketten. " 303
Wir nehmen an, dass wir auf irgend eine Weise eine Reihe
von m -\- 1 stetigen Functionen herstellen können
(i) . ./(*),-/i(*), h D ...,/«(*), ' («)
denen folgende Eigenschaften zukommen:
1. Von den Functionen/,, sollen im Intervall /l nicht
zwei auf einander folgende zugleich verschwinden.
2. Die letzte von ihnen, fm(x), soll im Intervall J
überhaupt nicht verschwinden, also ein unver-
unveränderliches Zeichen behalten.
3. Wenn ein mittleres Glied, etwa/„(a;), für irgend ein
x im Intervall <d verschwindet, so sollen für dieses
x die beiden angrenzenden Functionen fv-i(x) und
fv+1(x) entgegengesetztes Vorzeichen haben.
4. Wenn/(V) im Intervall z/ verschwindet, so soll
/i (x) für diesen Werth von x dasselbe Vorzeichen
haben wie f'(x).
Eine solche Functionenreihe($) wollen wir eine Sturm'sche
Kette nennen. Wie man sie bilden kann, werden wir später
sehen; zunächst sollen aus der Definition Folgerungen gezogen
werden.
Für jeden Werth von x, für den keine der Functionen von
(ß) verschwindet, hat jede dieser Functionen ein bestimmtes
Vorzeichen. Wir zählen einen Zeichenwechsel, so oft beim
Durchlaufen der Kette von links nach rechts auf ein positives
Glied ein negatives oder auf ein negatives Glied ein positives
folgt. Die Anzahl der so gezählten Zeichenwechsel (Variationen)
für einen bestimmten Werth von x wollen wir mit V(x) be-
bezeichnen. Wenn ein mittleres Glied /„ (x) verschwindet, so haben
wir nach 3. beim Uebergang von /,,_] (x) zu fv+1 (x) einen Zeichen-
Zeichenwechsel zu zählen.
Sind «, ß zwei Werthe, für die keine der Functionen /„ ver-
verschwindet, und lassen wir nun x stetig wachsen von « bis ß, so
wird eine Aenderung in der Zahl der Zeichenwechsel nur dann
eintreten können, wenn eine der Functionen von (R) ihr Zeichen
wechselt, also durch den Werth Null hindurchgeht (wegen der
vorausgesetzten Stetigkeit).
Ist dies aber eine mittlere Function, so ändert sich die
Zahl der Zeichenwechsel nicht (nach 3). Denn in
/»—n /v) fv + i

304 Achter Abschnitt. §. 93.
findet vor und nach dem Durchgange von /„ durch Null immer
ein Zeichenwechsel statt, weil fv + i und /v_i entgegengesetzte
Zeichen haben.
Wenn aber f(x) durch Null geht, so geht beim Durchgange
wegen 4. ein Zeichenwechsel verloren. Denn geht/(a;) von nega-
negativen zu positiven Werthen, so ist (vergl. §. 35) f(x) und mithin
fi(x) positiv und die Vorzeichen ändern sich so:
+ +
und wenn f{x) von positiven zu negativen Werthen übergeht, so
ist/'(#) und fx (x) negativ, also die Zeichen so:
/D/iW
¦ + -
i
mithin ist in beiden Fällen ein Zeichenwechsel verloren
gegangen.
Da nun fm (x) nach 2. sein Zeichen nicht wechselt, so folgt,
dass V (k) — V(ß) gleich der Anzahl der zwischen « und ß
gelegenen Wurzeln von f(x) = 0 ist, oder:
Die Anzahl der Wurzeln von f(x) = 0 zwischen «
und ß ist gleich dem Ueberschuss der Anzahl der
Zeichenwechsel der Kette für x = a über die Anzahl
der Zeichenwechsel für x = ß.
Wenn für x = « oder x = ß eine oder einige der mittleren
Functionen von ($) verschwinden sollten, so ist es wegen 3. gleich-
gleichgültig , ob wir diesen verschwindenden Werth durch einen posi-
positiven oder einen negativen ersetzen.
§. 93.
Erstes Beispiel: Kugelfunctionen.
Ehe wir nun zu den allgemeinen Methoden übergehen, nach
denen Sturm'sche Ketten zu bilden sind, wollen wir einige
Beispiele betrachten, in denen sich durch besondere Umstände
solche Ketten darbieten.
Wir betrachten zunächst die sogenannten Kugel func-
functionen, die in der mathematischen Physik und Mechanik viel-
vielfach gebraucht werden.

§. 93. Kugelfunctionen. 305
Unter Kugelfunctionen versteht man ein System ganzer
rationaler Functionen von steigendem Grade, das folgendermaassen
definirt ist:
Po(*)=l
P1 (x) = x
P8(s) =§(**-!)
P,(«) = |(«8-f x)
D . . 1 . 3 . . . Bn — 1) / w(w — 1) „
jrn{X) — 1.2...W V 2Bn —1)
WQ - 1) (n - 2) (n - 3) _ \
~r 2 . 4 B n — 1) B n — 3) ' " '/
so dass P„(a;) eine ganze rationale Function wten Grades ist,
und, je nachdem n gerade oder ungerade ist, nur die geraden
oder- nur die ungeraden Potenzen enthält. Durch Anwendung
des Zeichens IJ(n) kann man den allgemeinen Ausdruck für die
Kugelfunctionen auch so darstellen:
worin die Summe in Bezug auf [i von p = 0 an so weit zu er-
erstrecken ist, als n — 2 p nicht negativ wird.
Zwischen diesen Functionen bestehen die folgenden Rela-
Relationen, die sich nach Einsetzen des Ausdruckes A) durch ein-
einfache Vergleichung der Coefficienten gleicher Potenzen von x
verificiren lassen,
B) nPn{x) — Bn - l)x Pn-x(%) + (n — 1) P»_a(«) = 0
P^x) -xP0(x) = 0
C) A — x*) P'n(z) + nxPn(x) - nP„_!(*) = 0.
Aus der letzten Gleichung folgt für sj = il
±P»(±1) = P—i(±l),
also
D) P»(l)=l, P„(-l) = (-l)».
Aus B) und C) folgt nun, dass die Functionen Pn, von
einem beliebigen m an abwärts geordnet,
E) Pmi Pm — lt Pm—% • • • Po
in dem Intervall von — 1 bis -|— 1 die Eigenschaften einer
Sturm'schen Kette haben. Denn wenn P„ und Pn—\ für irgend
Weber, Algebra. I. 20

306 Achter Abschnitt. §. 93.
ein x zugleich verschwänden, so müsste nach B) auch P„_2,
folglich P„_8 etc. bis Po verschwinden, was unmöglich ist, da
Po = 1 ist. Hiernach ist §. 92, 1. erfüllt, und weil Po = 1 ist,
so ist auch die Bedingung §. 92, 2. für jedes beliebige Intervall
befriedigt.
Ist P»_i = 0, so ist nach B) P„ und P„-2 von entgegen-
entgegengesetztem Vorzeichen, wie die Bedingung §. 92, 3. fordert.
Aus C) folgt, dass niemals P„(x) und P'n(%) zugleich ver-
verschwinden, da sonst auch Pn—1(x) verschwinden müsste, und
endlich ergiebt sich aus C), dass, wenn Pn(x) verschwindet
und — 1 < x < 1 ist, Fn(x) und P„_i(.¦*:) dasselbe Vorzeichen
haben.
Setzen wir nun in E) für x die Werthe — 1, -\~ 1 ein, so
folgt aus D), dass für x = — 1 in E) lauter Zeichenwechsel
stattfinden, für x = -\- 1 gar kein Zeichen Wechsel; und daraus
folgt:
D^e Gleichung Pm(x) = 0 hat m reelle Wurzeln
zwischen x = — 1* und x = -f- 1, und da Pm vom «wten
Grade ist, so sind dies alle Wurzeln.
. Wir können aber einen noch etwas weiter gehenden Schluss
ziehen. Nehmen wir ein Intervall /l = («, ß), in dem zwei und
nicht mehr Wurzeln f, tj von Pm = 0 enthalten sind, so gehen
beim Uebergang von « zu ß in der Kette E) zwei Zeichenwechsel
verloren. Wir nehmen « so nahe an f, ß so nahe an ij, dass
Pm_i(«) mit Pm_i(f) und Pm_j (ß) mit ?m-1(ri) von gleichem
Vorzeichen ist. Wenn Pm beim Durchgang durch f vom Nega-
Negativen zum Positiven geht, so geht es beim Durchgang durch rj
vom Positiven zum Negativen; es ist also Pm(l) und folglich
Pm_i(|) und Pm_i(«) positiv, P'm{r[) und folglich Pm_1(i)) und
Pm-i(ß) negativ, und das Umgekehrte findet statt, wennPTO beim
Durchgang durch f vom Positiven zum Negativen geht. Man sieht
also daraus, dass beim Uebergang von a zu ß in
-t*m} -^ m — 1
ein Zeichenwechsel verloren geht, also muss bei dem gleichen
Uebergang, und folglich auch bei dem Uebergang von f zu r\ in
der Kette
¦*m — h -£»» — 2 • • • -M>
gleichfalls ein Zeichenwechsel verloren gehen; daraus
schliessen wir auf den Satz:

§. 94. Die Säculargleichung. 307
Zwischen zwei auf einander folgenden Wurzeln
von Pm = 0 liegt eine und nur eine Wurzel von
Pm-l = 0.
§• 94.
Zweites Beispiel.
Als zweites Beispiel betrachten wir eine Gleichung, die wir
der Kürze wegen die Säcular-Gleichung nennen wollen, weil
die Untersuchung der säcularen Störungen der Planeten zuerst
auf sie geführt hat1). Sie ist auch sonst wohl unter diesem
Namen bekannt, kommt aber auch in vielen anderen Unter-
Untersuchungen vor, z. B. bei der Bestimmung der Hauptaxen einer
Fläche zweiten Grades, in der Theorie der kleinen Schwingungen;
ihre allgemeine analytische Bedeutung liegt darin, dass sie eine
besondere, die sogenannte orthogonale Transformation einer qua-
quadratischen Form in eine Summe von Quadraten liefert. Wir
wollen hier die Gleichung nehmen, wie sie vorliegt, ohne Be-
Beziehung auf irgend eine Anwendung, und wollen sie nach unseren
allgemeinen Sätzen discutiren.
Es sei a^fc, wenn i und k die Reihe der Indices 1, 2, 3 ... n
durchlaufen, irgend ein System reeller Grossen und
A) «<,» = «M
vorausgesetzt. Wir betrachten die symmetrische Determinante
X
B) Ln(x) =
die eine ganze rationale Function wten Grades von x ist, in der
xn den Coefficienten (— 1)" hat. Die Gleichung L„(x) = 0 soll
der Gegenstand unserer Betrachtung sein.
Wir bilden die mit abwechselnden Zeichen genommene Kette
der Haupt-Unterdeterminanten
C) Ln(x), -£„_!<», Ln-a(x) ...,(- lf-'L^x), (- 1)",
!) Laplace, Histoire de l'Aoademie des Sciences 1772. Von neueren
Werken kann man darüber vergleichen Dziobek, Theorie der Planeten-
bewegung, Leipzig 1888.
20*

308 Achter Abschnitt. §. 94.
und wollen nun nachweisen, dass, wenn wir die Voraussetzung
hinzufügen, dass von den Grossen C) keine zwei auf
einander folgende zugleich verschwinden, wir eine
Sturm'sehe Kette vor uns haben.
Es ist dies eine einfache Folgerung aus der Formel, die wir
schon im §. 88 zu einem ähnlichen Zwecke benutzt haben, und
die wir so darstellen können:
D)
worin Sk und Tk ganze rationale Functionen von x sind.
Wir haben nur zu zeigen, dass die Forderungen §. 92, 1. bis
4. befriedigt sind. Davon ist aber 1. in die Voraussetzung auf-
aufgenommen, 2. ist erfüllt, da das letzte Element gleich + 1 ist.
Aus der Formel D) folgt, dass, wenn Lh = 0 ist, Lk—i und Z^+i
entgegengesetzte Zeichen haben, dass also die Bedingung 3.
erfüllt ist.
Es bleibt nur noch die Bedingung 4. übrig. Wenden wir
aber die Formel D) auf k = n — 1 an, so lautet sie
dLn dL» ( dLn
55^
Oan,n 0 an — l, n — 1
und daraus folgt, dass, wenn Ln := 0 ist,
gleiche Zeichen haben; und ebenso kann man schliessen, dass
alle Haupt-Unterdeterminanten von Ln
dasselbe Zeichen haben.
Nun ist aber die Derivirte von Ln (vergl. §. 25)
und hat also für einen Werth x, für den Ln{x) verschwindet,
das entgegengesetzte Zeichen, wie Ln—i, was eben die Forde-
Forderung 4. verlangt. Daraus folgt der Satz:
I. Sind «, ß zwei reelle Werthe, k < ß, so ist die
Anzahl der zwischen « und ß gelegenen Wurzeln
von Ln(x) gleich dem Ueberschuss der Anzahl
der Zeichenwechsel der Kette C) für x = «
über die Anzahl der Zeichenwechsel für x = ß.

§. 94. Die Säculargleichung. 309
Die höchste Potenz von x, die in Lk(x) vorkommt, ist, wie
schon oben bemerkt,
(- 1)*^,
und wenn der absolute Werth von x hinlänglich gross ist, so
wird das Vorzeichen dieses Gliedes über das Vorzeichen von
Lk (x) entscheiden. Nehmen wir also für « einen genügend
grossen negativen, für ß einen genügend grossen positiven Werth,
so finden in C) für x = « lauter Zeichen Wechsel, für x = ß
lauter Zeichenfolgen statt. Es werden also n Wurzeln zwischen
« und ß liegen, und daraus folgt der Satz:
II. Die Gleichung Ln(x) = 0 hat lauter reelle'
Wurzeln.
Diese beiden Sätze sind aber nur von beschränkter Anwend-
Anwendbarkeit, so lange wir uns nicht von der Voraussetzung frei
machen können, dass in der Kette der Z% nicht zwei auf ein-
einander folgende Glieder zugleich verschwinden sollen. Von dieser
Beschränkung können wir den Satz aber durch folgende einfache
Ueberlegung befreien.
Nehmen wir an, für irgend einen Werth von x verschwinde
Lj„ aber nicht L%—i] wir können dann die Grossen aÄ + 1)f, die in
Lk nicht vorkommen, so bestimmen, dass Lfc+i für diesen Werth
von x nicht verschwindet; denn es kann L^ + i nicht identisch
für alle a»+i,< verschwinden, weil es das Glied
enthält [§. 26, A2)].
Hiernach können wir, wenn in der Kette
E) Lm —£»_i, £»_a • • • ± A) +1
einige auf einander folgende Glieder für irgend einen Werth von
x verschwinden, durch Abänderung der a^ eine andere Reihe
F) L'n, —-£4-i, £»—2 • • • i L'u +1
ableiten, in der keine zwei auf einander folgenden Glieder für
irgend einen Werth x (des Intervalles « . . . ß) verschwinden.
Zugleich können die aj,», von denen die L' abhängen, so
angenommen werden, dass sie sich von den a^ um weniger
als eine beliebig gegebene Grosse co unterscheiden.
Wenn nun die Zahlen «, ß so angenommen sind, dass in
der Reihe E) kein Glied für x = « oder x = ß verschwindet,
so können wir ra so klein annehmen, dass für x = « und x = ß

310 Achter Abschnitt. §. 94.
entsprechende Glieder von E) und F) dasselbe Vorzeichen haben.
Durch unseren Satz ist aber die Anzahl der Wurzeln von L'n = 0
zwischen a und ß durch die Zeichen der Reihe F) bestimmt.
Nun lässt sich andererseits wieder o so klein annehmen,
dass die Wurzeln von L'n = 0 von denen von Ln = 0 beliebig
wenig unterschieden sind (§. 44).
Es kann zwar eine Doppelwurzel von Ln = 0 in zwei ein-
einfache Wurzeln von L'm = 0 übergehen; aber da L'„ = 0 keine
imaginären Wurzeln hat, so sind diese reell; und dasselbe findet
statt, wenn L„ = 0 mehrfache Wurzeln hat.
Hiernach behalten die Sätze I. II. ihre Gültigkeit,
wenn die Voraussetzung aufgegeben wird, dass in der
Kette der Lk keine auf einander folgenden Glieder ver-
verschwinden; nur müssen die mehrfachen Wurzeln dabei
nach ihrer Vielfachheit gezählt werden.
Hieraus können wir eine merkwürdige Beziehung der Säcular-
gleichung zu dem Trägheitsgesetz der quadratischen Formen
herleiten, die in der Geometrie, bei der Bestimmung der Haupt-
axen einer Fläche zweiten Grades wohl bekannt ist.
Wir betrachten neben der Function Ln(x) die quadratische
Form
G) <p (xx, X2, . . ., Xn) = 2Oi,n0Ci%n\
dann ist Ln(s) für ein beliebiges £ die Determinante der Form
(8) 9'=9—6(«? + «! \-xl).
Die Gleichung Ln{x) = 0 möge P positive, N negative und
B verschwindende Wurzeln haben. Wir nehmen £ positiv an, aber
so klein, dass alle positiven Wurzeln von L grösser als £ sind,
und ausserdem so, dass kein Glied der Reihe C) für x = £
verschwindet. Dann ist
(9) Ln(s), Ln^(B),..., L^s^l
eine Kette von Hauptunterdeterminanten für die Function <jp',
und wenn wir also mit %\ v', 0 die charakteristischen Zahlen von
q>\ bezeichnen, so ist %' (nach §. 89, V.) gleich der Anzahl der
Zeichenfolgen, v' gleich der Anzahl der Zeichenwechsel in der
Kette (9).
Wenn wir aber das Theorem I. anwenden, indem wir « = £
setzen, und ß grösser als alle Wurzeln von Ln (x) annehmen, so
dass in der Kette C) für x = ß nur noch Zeichenfolgen vor-

§. 95. Die Sturm'chen Functionen. 311
kommen, so giebt uns die Anzahl der Zeichenwechsel in C) für
x = £, die mit der Anzahl der Zeichenfolgen in (9) überein-
übereinstimmt, die Zahl P der positiven Wurzeln von Ln (x) = 0. Dem-
Demnach ist, weil ausserdem noch 3t'-\-v' = P-^-N-\-B = n ist,
A0) jr' = P, v' = N-{-B.
Wir nehmen nun die Functionen q> und <jp' in folgender
Weise in ihre positiven und negativen Quadrate zerlegt an:
A1) <p = y» + j/H \-y*-g* — e2 0*.
A2) 9'=9-«(«? + asH \-xl)
= r» + rn 1- y% -zi-zi zi
Wenn nun % -\- v' < n ist, so können wir die x1, x2,..., xm
zum Theil wenigstens von Null verschieden, so bestimmen, dass
Vi = 0, y, = 0, . . ., yn = 0, Z, = 0, Z2 = 0, . . ., Zt> = 0.
Dann aber ergiebt die erste Darstellung A2) mit Hülfe von
A1) einen negativen, die zweite einen positiven (oder verschwin-
verschwindenden) Werth von <p', so dass die Annahme % -\- v' < n un-
unstatthaft ist. Es ist also % -\- v' ^ n = %' -\- v', also nach A0)
Andererseits folgt aber aus §. 86 A2)
P^rc,
was nur mit einander verträglich ist, wenn
A3) % = P
ist. Ebenso können wir nun auch beweisen, indem wir statt
eines positiven ein negatives s zu Hülfe nehmen, dass v = N
und folglich q = B sein muss.
Wir sprechen dies noch als einen Satz aus:
III. Die charakteristischen Zahlen sr, v, q der quadra-
quadratischen Form y sind gleich den Anzahlen der
positiven, negativen und verschwindenden Wur-
Wurzeln der zugehörigen Säculargleichung.
§. 95.
Die Sturm'schen Functionen.
Nach diesen besonderen Beispielen wenden wir uns zur Be-
Betrachtung des Verfahrens, durch das man in allen Fällen eine

312 Achter Abschnitt. §. 95.
Sturm'sche Kette erhält1). Die Bildungsweise dieser Functionen
ist principiell ausserordentlich einfach, wenn auch in der prak-
praktischen Ausführung meist nicht durchführbar.
Wir beschränken uns hier auf die Betrachtung von Glei-
Gleichungen ohne mehrfache Wurzeln, oder wir nehmen an, dass
vor der Anwendung des darzulegenden Verfahrens f(x) von jedem
gemeinschaftlichen Factor mit seiner Derivirten /' (x) befreit sei.
Wenn wir dann
A) /i (*)=/'(*)
annehmen, so ist sicher die Bedingung §. 92, 4. befriedigt. Nun
verfahren wir so, als ob es sich um die Aufsuchung des grössten
gemeinschaftlichen Theilers von f(x) und fx (x) handle, indem
wir dabei jedesmal das Vorzeichen des Restes umkehren; wir
bilden also durch Division die Gleichungen
B) /i = #2/2 —/s
fm—2 == im—lfm—2 fmi
worin die g15 q2, . . ., #m_i und ebenso die /15 /2, ...,/», ganze
rationale Functionen von x sind; die Grade der Functionen
/,/i,/a, • • ;fm nehmen ab und man kann daher die Operation
so weit fortsetzen, dass fm constant ist, oder wenigstens in dem
betrachteten Intervall nicht mehr verschwindet. Dass fm nicht
Null werden kann, ist eine Folge der Voraussetzung, dass / und
fx ohne gemeinsamen Theiler sind..
Dass man dann in der Reihe
C) /,/1,/a,...,/«-
wirklich eine Sturm'sche Kette hat, ergiebt sich unmittelbar,
wenn man die Kriterien §.92, 1. bis 4. durchgeht. Denn wenn
zwei auf einander folgende der Functionen C) zugleich ver-
verschwinden, so verschwinden nach B) auch alle nachfolgenden;
dies ist aber unmöglich, weil fm von Null verschieden ist.
Ist aber /„ (x) = 0, so folgt aus B)
womit alle die Forderungen des §. 92 befriedigt sind.
x) Stürm, Mem. sur la resolution des equations numeriques. Mem.
de l'academie de Paris. Sav. etrang. VI, 1835. Auszug in Bull, de Ferussac
XI, 1829.

§. 96. Hermite's Lösung des Sturm'sehen Problems. 313
Es ist, wie sich von selbst versteht, gestattet, die Functionen
der Reihe C) mit positiven, z. B. constanten Factoren zu multi-
pliciren, ohne dass sie aufhören, eine Sturm'sehe Kette zu bilden.
Für n = 2 können wir demnach als die Sturm'sehen
Functionen folgende nehmen:
f(x) = x* -j- ax -j- i
f1(x)=2x-\- a
§. 96.
Hermite's Lösung des Sturm'schen Problems.
Ein anderer "Weg zur Lösung des Sturm'schen Problems,
der zu einfacheren Resultaten führt, wenigstens was die Durch-
Durchführung der Rechnung im Einzelnen betrifft, ist von Hermite
eingeschlagen, der an das Trägheitsgesetz der quadratischen
Formen und die Tschirnhausen-Transformation anknüpft1).
Es sei
A) fix) = aoxn -|- axxn~x -| • -j- an_xx + an = 0
die vorgelegte Gleichung und
(«) %u x2, . . ., xn
ihre Wurzeln, die wir von einander verschieden annehmen.
Wir benutzen wie in §. 74 die Functionen
C) /0 (x), /x (x), f2 (x), . . ., /„_! (x),
und setzen wie dort, indem wir unter t0, tt, . . ., tn—t unabhängige
Variable verstehen,
D) y = t„-!/0 (x) + tf„_2 fi(x)~\ h *i /»-a<#> + *o/n-i(«)•
Es mögen yu y2, . . ., y„ die Werthe sein, die y für x = xu
x2, . . ., xn annimmt.
Ist nun « ein beliebiger reeller Werth, so setzen wir
E) Ha = (xx — a)yl -\- (x2 — «)y$ -) \-(x„ — a)yl
Dies ist eine quadratische Form der n Variablen t, und wir
wollen zunächst die Zahl ihrer negativen und positiven Glieder
bestimmen. Ist X\ eine reelle Wurzel, also auch y1 reell, so ist
x) Hermite, Remarques sur le theoreme de M. Sturm. Comptes
rendus der Pariser Akademie, T. 36 A853).

314 Achter Abschnitt. §. 97.
das Glied (xi — <x)yl positiv oder negativ, je nachdem x1
grösser oder kleiner als « ist. Bilden aber xx, x2 ein imaginäres
Paar, so sind auch yt, y2 conjugirt imaginär, und
(x1 — a)yl + (x2 — a)y$
zerlegt sich in ein positives und negatives Quadrat. Dies
ergiebt sich wie im §. 85, wenn man yx\' xx — « = u -\- iv,
y2]/^2 — a = u — iv setzt.
Daraus folgt, dass die Anzahl Na der negativen Quadrate
in Ha gleich ist der Anzahl der imaginären Paare, vermehrt um
die Anzahl der reellen Wurzeln, die kleiner als « sind.
Nehmen wir also eine zweite reelle Zahl ß > «, bilden die
Function Hp und bezeichnen mit Np die Anzahl ihrer negativen
Quadrate, so ist die Differenz
IVß — ±ya
gleich der Anzahl der reellen Wurzeln zwischen « und ß.
Man erhält also ein Mittel zur Bestimmung dieser Zahl,
d. h. zur Lösung des Sturm'schen Problems, wenn man die
Coefficienten der Function Ha als Functionen der Coefficienten
von/(#) und von « darstellt, und dann die Zahl Na untersucht.
§• 97.
Bestimmung der Hermite'schen Form H.
Zur Bestimmung der Hermite'schen Form H können wir
die Mittel anwenden, die wir im sechsten Abschnitt kennen gelernt
haben. Wir haben im §. 79 die Formel abgeleitet:
A) yfs = EOtSfo + Ehsfx ~\ 1- £„_!,,/„_!.
Mit Benutzung der Relationen [§. 78, F)]
xj0 =/i — %, xjj = f2 — a2, ¦ • ., xfn^i = — am
folgt hieraus
^2) xyf» = -Eo,»/i + -Ei,s/2 + • • • + ¦#«-2,s/«-i
Wir bestimmen also noch eine Functionenreihe _E_i,s durch
die Gleichung
C) a^E—^s -]- aiEOtS -\- a2 E1>s -(-¦** ~\~ an^n—i,s = 0,
und erhalten dann aus A) und B)

§. 97. Bestimmung der Hermite'schen Form U. 315
(x — a)yfs = (E_hs — aEo,.)fo
Die Function .ELi,» lässt sich aber durch die Relation
[§• 78, G)]
«0 Ws + «i^m + s —1 -(-••• + ßnk = 0
ganz in der gleichen Weise ausdrücken, wie die übrigen E, so
dass wir folgendes System von Formeln erhalten [§. 78, A0)]:
JE—itS = aotn + s -j- ax tn + s—i -\- • • • -j- astn
= ßs + i^j—1 • • " 0>nts
Eo,s == (h^n + s — 1 -j- öi^n + s —2 ~T " ' ' "T" 0>stn — l
, s — 2 ~p öi^n + s —3 ~)~ * * * "T" ttstn — 2
=
E)
Es—itS = ai)tn -)- a-itn—i -j- • • • -j- astn—s
= ös ^. i IM — s — j • • • ß„
-Es,« = «o4-l ~|- öj^„_2 ~H " • " "f" O'stn — s — 1
Es + i,s =z do^n — 2 ~~T~ O'itn — S ~\~ ' ' ' ~\~ ®stn — s — 2
Führen wir ein zweites System von Variablen x ein und setzen
0 = T„_i/0 -|- Tn_2/i -(-*•• + *o /n-l)
so ergiebt sich aus D) mit Benutzung der Formeln [§. 74, F)]
F) S[(sc — <z)y0] = nao 2 C
0, n—1
(w—
o,»—i
\ „! („2,s nl,s)nsl
0,«—1
und dies geht geradezu in die Function H über, wenn wir t = t
setzen.
Nehmen wir als Beispiel den Fall n = 3, so ergiebt sich
E—it 0 = (h ^2 Ö2 ^1 <*3 ^01 -, 0 == ö0 4i
-E—1, 1 = *ä ^2 Ö3 hl EOt i = — rt2 ^1 «'3 ^0>
-E-l, 2 — % ^2) -E», 2 = <*s <x,

316
Achter Abschnitt.
§.98.
-£i2, 0 == *0 *0>
'1 "ll 2, 1 **0 *1 ~T~ ^*1 t'Oi
und hieraus kann man die Coefficienten der Form H nach F)
leicht berechnen:
.02,2 = — «o (#i ~~h 3 a0 «)
xii, i = — 3 öq Ö3 — ü>i ü>2 — 2 (ßj — öq ö2) w
XIo, 0 ^—^ ^2 ^3 ~|~ (¦" ^1 ^3 ^2) ^
-Hi, 0 = — 2 «[ a3 -f- C «o % — % «2)«
£T2,1 = — 2 a0 (a2 + «i«)
¦Ho, 2 = — «0 C «3 + «2 «)•
§.98.
Die Determinante der Hermite'schen Form.
Für die Frage nach der Anzahl der negativen Quadrate der
Form H ist die Kenntniss ihrer Determinante von Wichtigkeit.
Diese Determinante lässt sich allgemein auf folgende^ Art be-
berechnen.
Setzen wir
i 7c
H = 2J 2 Hit je tit-k,
0, n—1
so sind die Coefficienten i?iOc, deren Determinante gebildet werden
soll, durch die Formel §. 97, F) gegeben. Es ist H^j, der Coeffi-
cient von titje in jener Formel, also
H^je = S(X — <*) fn-i-t fn-je-t.
Die Determinante aus diesen n2 Grossen lässt sich aber
nach dem Multiplicationssatz in die Form setzen:
X
(xn — «) /0 (xn), (x„ — «) /x (xn), . . ., (a;w — «) /„_!
/o («0, /1 («1), • • ., /n-i («1
/o 00, /l (*n), • • •, fn-1 («n)
oder auch, da
«o («1 — «) (a?2 — «)••• O» — «) = (— !)M /(«)
ist, in die Form

§.98.
Die Determinante der Hermite'schen Form,
/o (Ph), /i (Ph), ¦ ¦ -, /n-i («i
317
/o {%n)i J\ (%n)i • • •> /» —1 (#n)
Die hier noch vorkommende Determinante der fh
Product der beiden folgenden:
t) ist das
a0, 0,
a15 «ei
., 0
•, 0
O"n — li an—i
1, $21
Das Quadrat dieses Productes ist aber, wenn D die Discri-
minante der Function f(x) bedeutet (§. 50), gleich a$ D, so dass
sich für A ergiebt
A) ^ = (-l)»Oo/(«)Ä
Da nach der Voraussetzung D nicht verschwinden soll, so
wird <d also nur dann verschwinden, wenn für « eine der Wur-
Wurzeln von f{x) = 0 gesetzt wird, und dies soll auch aus-
ausgeschlossen sein.
Bezeichnen wir eine. Kette von Haupt - Unterdeterminanten
von z/, mit der niedrigsten angefangen, mit
-^1 («), -^2 («), • • •, 4„ («) = ^,
so ist nach §. 89, V. die Anzahl der Zeichenwechsel in
B) 1, ^(«), 4<*), ¦¦-, ^»(«)
gleich der Anzahl JV« der negativen Quadrate in H, und wenn
wir also die entsprechende Zahl Np in
abzählen, so ist Np — Na die Anzahl der zwischen « und ß
gelegenen Wurzeln von f(x).
, Für die cubische Gleichung ergeben sich die Ausdrücke aus
dem Schluss des vorigen Paragraphen. Wir bilden die Kette
1 1 / \ 1
W I TT TT 7T2 \ A
**0) ~Z~ -, 2j ~ I -,2 -,1 -,2 h —-^)
&Q (Aiq \ . J Ct/Q
die offenbar dieselbe J.nzahl von Zeichenwechseln hat wie B),
und erhalten so die Functionen
a0, — 3a0« — «!>
«j2 — 3 a0 a2) -|- « B al -\- 9 a02 a3 — 7«

318 Achter Abschnitt. §. 99.
Nehmen wir zur Probe «= — oo, ß = -\- <n, so. erhalten
wir, wenn noch a0 = 1 gesetzt wird, die Zeichenbestimmung
1, +1, K-3a2), 0,
1, — 1, (af - 3 a,), - D.
Man muss bei der Abzahlung beachten, dass, wennD positiv
ist, a\ — 3 a2 nicht negativ sein kann [§. 52, (8)].
§• 99.
Formulirung der Aufgabe durch Hurwitz.
Anlässlich einer besonderen Frage, auf die wir weiter noch
zurückkommen, hat Hurwitz eine Darstellung des Sturm'schen
Problems gegeben, die zu besonders einfachen Resultaten führt1)-
Es sei
A) f(g) = *»„*• + «h *»~H h o»
eine ganze Function wten Grades der Variablen g. Es sei ferner
3>(>) eine zweite ganze Function von beliebigem Grade. Wir
suchen nach §.16 die Entwickelung des Bruches <b(z):f{z) nach
fallenden Potenzen, und bezeichnen den Theil dieser Entwicke-
Entwickelung, der negative Potenzen von g enthält, mit
B) Co^-i + c^-2-^ = 27 <**-*-i.
o,...
Es sei nun weiter
C) 0(g) = to + t10-\ h tm-l^'1
eine ganze Function von einstweilen noch beliebigem Grade
(m — 1), deren Coefficienten t0, tx, . . ., tm-x unabhängige Va-
Variablen sind. Wir bilden die Entwickelung nach fallenden Po-
Potenzen von z für den Bruch
0, m—l
wofür wir nach B) mit Benutzung der Regeln des §.16 erhalten
oder, nach absteigenden Potenzen von z geordnet,
D) S e-1-1 2' d+i
Mathematische Annalen, Bd. 46.

§. 99. Formulirung der Aufgabe durch Hurwitz. 319
Bezeichnen wir den Rest der Division von & @) durch f(z)
mit ®! (z) und setzen
®i (*) = <i + *i H h 4-i«—*,
so sind die ^, t\, . . ., 4-i lineare homogene Functionen der
Variablen t0, t^ . . ., tm-i- Es geben aber nach §. 16 die beiden
Brüche
9(g)@(g)' <P(*)Si(g)'
{) /(*) /(*)
bei der Entwickelung nach fallenden Potenzen von 0 dieselben
Glieder mit negativen Exponenten, und daraus folgt, dass die
in der Entwickelung D) auftretenden quadratischen Formen der
m Variablen ti «•,&
Tx = 2 cx + i + ictitjc
auch als quadratische Formen der n Variablen i\ ausgedrückt
werden können. Sind also itx, v?., Qx die charakteristischen Zah-
Zahlen vonT;t, so ist qx mindestens = m —n. Von nun an wollen
wir m = n setzen, also unter ©{0) eine Function (n — l)ten
Grades verstehen. Wir betrachten hauptsächlich die Function To,
die wir auch kurz mit T bezeichnen, also die quadratische Form
i ic
F) T = Z d+ttitk,
1,M —1
und bezeichnen ihre charakteristischen Zahlen mit it. v, q. Dann
ergiebt sich aus dem soeben Bewiesenen zunächst:
1. Wenn /(#) und O@) nicht relativ prim sind, so ist
q > 0, also T keine definite Form.
Denn wenn wir den grössten gemeinschaftlichen Theiler von
/ und O herausheben, so entstehen aus E) Brüche von derselben
Gestalt, in denen 0 dasselbe geblieben ist, während sich der
Grad des Nenners erniedrigt hat. Ist n' dieser erniedrigte Grad,
so ist m — n' und folglich auch q positiv. Wir können ferner
noch beweisen:
2. Wenn f{0) und f@) einen gemeinschaftlichen
Theiler haben, so ist T keine definite Form.
Denn wenn f(ß) und f @) einen gemeinsamen Theiler haben,
so lässt sich eine reelle Function Q @) (vom ersten oder zweiten
Grad) so bestimmen, dass
ist. Dann ist Qft @) von niedrigerem als ntem Grade, und wir
können die Coefficienten t0, t^ . . . 4—1 so bestimmen, dass
& = Qfi (e)

320 Achter Abschnitt. §. 99.
wird. Dann ist aber ® (eJ durch f{z) theilbar, und O(g) ®(sJ :
ist eine ganze Function. Es kommen dann also in der Ent-
wickelung nach fallenden Potenzen keine negativen Potenzen
mehr vor, und es wird Dicht nur T, sondern alle Functionen Ti
gleich Null.
Es giebt also von Null verschiedene Werthe der Variablen
tt, für die T verschwindet, was bei definiten Formen nicht mög-
möglich ist.
Wenn wir annehmen, dass die Function f(s) keine mehr-
mehrfachen Factoren hat, so können wir, wenn die Wurzeln von f{z)
bekannt sind, die Functionen T% leicht in eine Summe von Qua-
Quadraten zerlegen. Es ist nämlich dann, wenn das Summenzeichen S
sich auf die Wurzeln
X X^ X%i . . ., Xn
von f(z) erstreckt, und Gr{z) eine ganze Function bedeutet,
nach §.15
und wenn wir hierin 1 : (s — x) nach §.16 nach fallenden Po-
Potenzen von s entwickeln, so ergiebt sich
(8) Tx _ 6
T ^
Tx _ 6 f(x)
Die Functioiien
& (Xj) = to-\-t1X1 -\- ¦ ¦ ¦ ~\- tn-i
® (%i) = t0 + ttx2 -\~ ¦ ¦ • 4- tn-x
deren Determinante gleich dem Differenzenproduct der X{ und
folglich von Null verschieden ist, sind von einander linear unab-
unabhängige, lineare Functionen der ti und durch (8) ist also T% in
eine Summe von n Quadraten zerlegt. Setzen wir
A0)
so ergiebt sich (für l = 0)
A1) T = y- -t- wf -4- • • • -4- y„.
Unter der Voraussetzung reeller Coefficienten von / und <P
lassen sich nun die für die Trägheit der Function T charakteri-
charakteristischen Zahlen sr, v, q bestimmen.

§. 99. Formulirung der Aufgabe durch Hurwitz. 321
«
Zunächst ist ersichtlich, dass y? aus der Summe A1) dann,
und nur dann, wegfällt, wenn <& (xi) = 0 ist, also wenn Xi eine
gemeinschaftliche Wurzel von / und O ist. Es ist also q gleich
dem Grade des grössten gemeinschaftlichen Theilers von / und
O, und gleich Null, wenn / und <& relativ prim sind.
Ist Xi, x2 ein imaginäres Paar, und <t>(%i) von Null ver-
verschieden, so ist
Vi = P + Q* 2/2 = P — Qi
und folglich
Dieses Paar giebt also einen Beitrag von einer Einheit zu jr
sowohl als zu v.
Für ein reelles x ist aber y2 positiv oder negativ, je nach-
nachdem <& (x) und /' (x) gleiche oder verschiedene Zeichen haben.
Hieraus ergiebt sich folgende Bestimmung für die charak-
charakteristischen Zahlen jr, v, g der Form T.
q ist gleich der Anzahl der verschwindenden <&(x).
¦it ist gleich der Anzahl der imaginären Paare mit nicht
verschwindenden <&(x), vermehrt um die Anzahl der
A2) reellen Wurzeln mit positivem O(x)f'(x).
v ist gleich der Anzahl der imaginären Paare mit nicht
verschwindenden <&(#), vermehrt um die Anzahl der
reellen Wurzeln mit negativem <b(x)f'(x).
Wir machen hiervon einige besondere Anwendungen.
Der Fall, dass T eine definite Form ist, dass also q und
v = 0 oder q und % = 0 sind, kann nur dann eintreten, wenn
0 und / relativ prim sind, wenn f(x) nur von einander ver-
verschiedene reelle Wurzeln hat, und wenn ausserdem G>(x)f(x)
für alle Wurzeln von fix) dasselbe Zeichen hat. Sind « und ß
zwei der Grosse nach auf einander folgende von diesen Wurzeln,
so haben /' («) und /' (ß) entgegengesetzte Vorzeichen. Es müssen
daher auch <J>(a) und &(ß) entgegengesetzte Vorzeichen haben.
Es muss also zwischen « und ß eine ungerade Zahl von Wurzeln
von O(x) — 0 liegen. Unter diesen Voraussetzungen ist auch
umgekehrt T eine definite Form, die im Zeichen mit O(x)f'(x)
übereinstimmt. O kann also, wenn T eine definite Form sein
soll, nicht von niedrigerem Grade sein als n — 1. Ist O auch
nicht von höherem Grade, so muss zwischen je zwei Wurzeln von
f(x) eine und nur eine Wurzel von O(x) liegen, oder wie wir
Weber, Algebra. I. 21

322
Achter Abschnitt.
§. 99.
uns auch ausdrücken können, die Wurzeln von f{x) sind durch
die Wurzeln von O(x) von einander getrennt.
Die Form T wird speciell eine positive sein, wenn wir ausser-
dem noch annehmen, dass c0 positiv ist, und dies wird dann ein-
eintreten, wenn die Coefficienten der höchsten Potenzen von 0 in
f(z) und O(s) dasselbe Zeichen haben. Da wir nun in §.89 VII.
die nothwendige und hinreichende Bedingung für eine positive
Form aufgestellt haben, so können wir jetzt folgenden Satz aus-
aussprechen, wenn wir
oi Ci, ...... cv
C2,
»i Cv
= Cv
setzen.
3. Die nothwendige und hinreichende Bedingung
dafür, dass die Gleichung wten Grades f(x) = 0
nur von einander verschiedene reelle Wurzeln
hat, die durch die Wurzeln der Gleichung (n — l)ten
Grades O(x) = 0 von einander getrennt sind, ist,
wenn die Coefficienten der höchsten Potenzen
von / und O von einerlei Zeichen sind, die, dass
die Determinanten
Cr r* r1 (~*
alle positiv sind.
Wenn wir <&(#) =/'(#) setzen, so ist <&(#) : f @) = 1, also
immer positiv. Zugleich gehen in diesem Falle die c0, cl5 c2, . . .,
(nach §. 16) in die Potenzsummen s0, sx s2, . . ., über. Setzen
wir dann
V) Sv + i, . . ., S3v
so ist (wenn a0 = 1 angenommen wird) Dn—X die Discriminante
von / und es folgt der Satz
4. Die nothwendige und hinreichende Bedingung
dafür, dass die Gleichung wten Grades / (x) = 0
nur reelle von einander verschiedene Wurzeln
hat, besteht darin, dass
-Do, -Dl5 .D2, . . ., Dn—i
positiv sind.

§. 100. Charakteristikentheorie. 323
Nimmt man 3> (x) = (x — a) /' (x) an, worin a eine belie-
beliebige reelle Zahl ist, die nicht zu den Wurzeln von f{x) gehört,
so ist, wenn f(x) nur einfache Wurzeln hat, q = 0, und, mag
nun f(x) imaginäre Wurzeln haben oder nicht, es ist % — v die
Anzahl der reellen Wurzeln, die grösser als a sind, vermindert
um die Anzahl der unter a liegenden Wurzeln. Die Differenz
% — v nimmt also jedesmal um zwei Einheiten ab, wenn a
wachsend durch eine Wurzel von f(x) hindurchgeht. Dies ist in
Uebereinstimmung mit §. 96.
§. 100.
Grundzüge der Charakteristikentheorie1).
Die Sturm'schen Sätze werden in ausserordentlicher Weise
durch die Charakteristikentheorie von Kronecker verallgemei-
verallgemeinert, die dasselbe Ziel wie der Sturm'sehe Satz für Gleichungs-
Gleichungssysteme mit beliebig vielen Veränderlichen verfolgt. Wir be-
beschränken uns hier auf die Betrachtung des einfachsten Falles,
den wir zur Einschliessung der complexen Wurzeln einer Glei-
Gleichung anwenden wollen; auch bedienen wir uns hier unein-
uneingeschränkt der geometrischen Anschauung und der Bezeichnungs-
Bezeichnungsweise der Differentialrechnung.
Wir betrachten zunächst zwei reelle Functionen cp (x, y),
ip (x, y), und deuten die reellen Variablen x, y als rechtwinklige
Coordinaten in einer Ebene. Die Gleichungen
A) cp (x, y) = 0, ip (x, y) = 0
stellen dann zwei Curven dar, die wir kurz die Curve cp und die
Curve ip nennen. Wir nehmen zunächst an, diese Curven seien
geschlossen und erstrecken sich nicht ins Unendliche. Wir nehmen
ausserdem an, cp sei im Inneren der Curve cp negativ, im
Aeusseren positiv; ebenso ip im Inneren von ty negativ, im
Aeusseren positiv.
Bezeichnen wir, wie die Fig. 6 (a. f. S.) zeigt, den Winkel, den
die Normale n in irgend einem Punkte von cp, in der Richtung,
in der cp wächst, also nach aussen gezogen, mit der Richtung der
positiven x-Axe bildet, mit &, so ist, wenn cp'(x) und g>'(y) die
partiellen Ableitungen von q> sind, und die Quadratwurzel positiv
genommen ist,
J) Kronecker, Monatsberichte der Berliner Akademie, März u. August
1869, Februar 1873, Februar 1878.
21*

324
cos 9- =
Achter Abschnitt.
y'O)
§. 100.
sin
Ziehen wir die Tangente t so, dass sie zu der eben bezeich-
bezeichneten Normale n so liegt, wie die positive y-Axe zur positiven
#-Axe und bezeichnen den Winkel, den sie mit der positiven
x-Axe bildet, mit |, so ist
COS | =
sin | =
Bezeichnen wir den Fortschritt auf q> in der Richtung t als
den positiven und sind dx, dy die Projectionen dieses Fort-
Fortschrittes, so sind dx und dy proportional und im Zeichen über-
übereinstimmend mit — <p'(y), <p'(#)) und wenn 3> eine beliebige
andere Function ist, so ist
d& = &{x)dx -+- ®'(y)dy
im Vorzeichen übereinstimmend mit der Functionaldeter-
minante
B) [<p, «P] = cp' (x) 9' {y) - cp' (y) & (x).
Bei der üblichen Annahme über die Coordinatenrichtung ist
die positive Fortschrittsrichtung die, bei der das Innere der
Fig. 6.
Fläche zur Linken
liegt.
Wenn nun die
positive Fortschritts-
Fortschrittsrichtung auf cp an
einem der Durch-
Durchschnittspunkte der
Curven <p, ty in das
Innere von ij> hinein-
hineinführt, so ist d tji, also auch die
Functionaldeterminante [cp, ip] nega-
negativ, und im entgegengesetzten Falle
positiv (Fig. 7). Wir nennen einen
Schnittpunkt von cp und ip einen
Austrittspunkt A(cp, ip) oder einen Eintrittspunkt E(cp, ij>), je
nachdem die positive Fortschrittsrichtung von <p aus dem Inneren
von ip ins Aeussere oder vom Aeusseren ins Innere führt, und
haben also den Satz:
an einem A(cp,ip) ist [cp, ^] > 0

§. 101. Charakteristik eines Systems von drei Functionen. 325
Die Anzahl der A(cp,ip) ist ebenso gross, wie die der E(cp, ij>);
und wenn wir cp mit i\> vertauschen, so gehen die A(cp,ip), E(cp,ij>)
in E(tp, cp) und A(ip, cp) über.
Die zwei Functionen cp, ip bestimmen in eindeutiger Weise
einen Flächenraum, der dadurch charakterisirt ist, dass in ihm
das Product cp-tp negativ ist. Wir wollen ihn den Binnenraum
(cp, tj)) oder (tj), cp) nennen. In unserer Fig. 7 ist es die schraf-
firte Fläche.
§. 101.
Charakteristik eines Systems von drei Functionen.
Wir nehmen nun zu den beiden Functionen q>, i\> eine dritte
f(x, y) hinzu. Die durch die Gleichung / = 0 dargestellte
Curve, oder die Curve / soll gleichfalls im Endlichen geschlossen
sein, und wir wollen ausserdem noch annehmen, dass sie durch
keinen der Schnittpunkte von cp und tj) hindurchgeht.
Wir geben diesen drei Functionen eine bestimmte cyklische
Reihenfolge
/, <P, *,
so dass auf tp wieder / folgen soll, und verbinden mit dieser
Reihenfolge eine bestimmte, etwa die positive Fortschrittsrichtung
auf jeder der drei Curven. Wir wollen festsetzen, dass mit der
umgekehrten Reihenfolge
auf jeder der drei Curven die entgegengesetzte, also die negative,
Fortschrittsrichtung verbunden sei.
Fig. 8. Wir durchlaufen nun, bei der-
ersten Reihenfolge, die Curve / in
positivem Sinne, und achten auf die
Schnittpunkte von / und cp. Ein
solcher soll ein Austrittspunkt A (f; y>,ip)
genannt werden, wenn die positive
Richtung von / aus dem Inneren des
Binnenraumes (cp, ij>) in das Aeussere,
und ein Eintrittspunkt E(f; cp, tj)), wenn
er aus dem Aeusseren in das Innere führt.
In der Fig. 8 sind die Punkte a die Austrittspunkte, der
Punkt e ein Eintrittspunkt.

326 Achter Abschnitt. §. 101.
Die Gesammtanzahl der Ein - und Austrittspunkte stimmt
überein mit der Anzahl der Schnittpunkte von / und cp, und ist
also, da beide Curven geschlossen sind, eine gerade Zahl. Ist
a die Anzahl der Punkte A(f; cp, tp), e die Anzahl der Punkte
E(f; cp, il>), so ist also auch e — a eine gerade Zahl und
i(e — a) — Jc
eine ganze Zahl, die nach Kronecker die Charakteristik des
Functionensystems /, g>, ip heisst. (Im Falle der Fig. 8 ist
sie gleich — 1.)
Wenn wir die Functionen /, cp, ip cyklisch vertauschen, so
erhalten wir drei Bestimmungen für die Charakteristik, und wenn
wir die Reihenfolge umkehren und dabei nach der getroffenen
"Vereinbarung auch die positiven Eichtungen durch die negativen
ersetzen, drei weitere. Diese Bestimmungen sind, wenn wir jetzt
die Symbole A (f; <p, ip), E(f; cp, ip) zugleich als Bezeichnung
für die Anzahlen der betreffenden Punkte brauchen,.
1. ±[E(f;cp,ip)-A(f;cp,ip)l
2. K^(9>;*,/)-^(g>; *,/)],
•3. f [#(*;/, <p) - AA>; f, g>)],
4. l[E(f;ip,y)-A(f;ip,cp)l
5. ![E(iP;cp,f)-A(iP;cp,f)l
6. H^(9>;/.*)-^(9>;/»*)]>
und es gilt nun der fundamentale Satz, dass diese sechs
Bestimmungen dieselbe Zahl ergeben.
Um ihn zu beweisen, durchlaufen wir die Curve / in posi-
positivem Sinne, und achten auf die sämmtlichen Schnittpunkte mit
cp und ip. Der Weg längs der Curve / wird dabei ebenso oft in
den Binnenraum (cp,ip) eintreten müssen, wie er aus ihm heraus-
heraustritt, weil er wieder in seinen Ausgangspunkt zurückkehren
muss. Die Curve / tritt aber ein in den Punkten E (f; % ip)
und A(f; ip, q>) und tritt aus in den Punkten A(f; <p, i\>) und
E(f; ip, q>). Also ist
E(f; <p, *) + A(f; n,, cp) = A(f; cp, *) -f E(f; *, g>),
wodurch die Uebereinstimmung von 1. und 4. nachgewiesen ist.
Wenn wir nun zweitens die Curve cp in negativem Sinne
durchlaufen, und auf ihre Schnittpunkte mit / achten, so ergiebt
sich, dass jeder Punkt E(f; cp, ip) zugleich ein Punkt E(cp;f,tp),
und jeder Punkt A(f; g>, ip) ein Punkt A(q>; /, ip) ist. Denn
in der Fig. 9, worin der Punkt a irgend einen der Schnitt-

§. 102. Charakteristik-Beziehung zu den Schnittpunkten. 327
punkte von / und cp darstellt, ist dieser Punkt ein E(f; cp, ip)
und zugleich ein E(cp; f, ip), wenn ip in a positiv ist, und ein
A(f; cp, ip) und zugleich ein A(cp;f, ip), wenn ip in a, negativ ist.
Fig. 9.
Daraus folgt die Üebereinstimmung
von 1. mit 6. Es folgt ferner durch
nochmalige Anwendung des ersten
Schlusses die Üebereinstimmung von
6. mit 2. und dann durch Anwendung
des zweiten Schlusses die von 2. mit 5.
und endlich des ersten die von 5.
mit 3., also die Uebereinstim-
^ mung aller sechs Ausdrücke.
Man ist daher berechtigt, die so bestimmte Zahl schlechtweg
als die Charakteristik des Functionensystems (/, cp, ip)
zu bezeichnen.
§. 102.
Beziehung der Charakteristik zu den Schnittpunkten.
Man hat nun zu beachten, dass die Bezeichnung der Schnitt-
Schnittpunkte zweier Curven als Ein- und Austrittsstellen in §. 100
wesentlich verschieden ist von der in §. 101. Dort kam nur die
Beziehung der Punkte zu den beiden sich schneidenden Curven
in Betracht, während in §. 101 noch die Beziehung zu einer
Fig. 10.
dritten Curve in Frage kam; dies ist in
den gewählten Bezeichnungen E (cp, rp),
A(cp,i\>) und E(J; cp,ip), A(f; cp, ip) voll-
ständig ausgedrückt. Nun müssen wir
aber genauer untersuchen, wie sich die
beiden Bezeichnungsweisen zu einander
verhalten.
Wir wählen der Deutlichkeit halber
eine etwas einfachere Figur als oben,
die zugleich alle möglichen Verhältnisse
veranschaulicht (Fig. 10).
In einem Punkte E(cp, ip) tritt die cp- Curve in die Fläche
der Curve ip ein, d. h. es geht ip von positiven zu negativen
Werthen. Ist dann zugleich / positiv, so ist dieser Punkt ein
E(cp; ip,f), wie der Punkt 1 in unserer Figur, ist aber/ negativ,
so ist es ein A(cp; ip,f), wie der Punkt 3. So haben wir:
t

328 Achter Abschnitt. §. 102.
Ein Punkt E (cp, ip) ist ein
E(cp; il>,f), wenn/> 0, (Punkt 1 der Fig. 10)
A(cp; ip,f), wenn / < 0, (Punkt 3 der Fig. 10).
Ein Punkt A(cp, ty) ist ein
E(cp; ip,f), wenn / < 0, (Punkt 2 der Fig. 10)
A{cp; i\>,f), wenn/> 0, (Punkt 4 der Fig. 10).
Nun ist in den Punkten E(<p, ip) die Functionaldeterminante
[cp, if\ negativ, in A(cp, ty) positiv (§. 100), und wir können also
das Bewiesene so zusammenfassen:
Es ist E(cp; i>,f) die Anzahl der Schnittpunkte von cp, ip, in
denen [cp, ^] / < 0,
A(cp; tj), /) die Anzahl der Schnittpunkte von cp, i\>, in
denen [cp, tj)] f > 0;
also ist die Charakteristik gleich dem halben Ueberschuss der
ersten Zahl über die zweite.
Diesem Satz können wir folgenden Ausdruck geben, wobei
er von Grössenverhältnissen gänzlich unabhängig erscheint und
nur von den Lagenverhältnissen der Curven und ihrer Schnitt-
Schnittpunkte abhängt.
Unterscheiden wir die Schnittpunkte von cp, tj), je nachdem
sie Austrittspunkte A(cp, tj)) oder Eintrittspunkte E(cp, tp) sind,
durch das Zeichen a und s, ebenso, je nachdem sie äussere oder
innere Punkte zu der Curve / sind, durch a und s, geben dann
den Punkten a, s und s, a den Charakter -\- 1, den Punkten
«, « und s, s den Charakter — l1), so ist die Charakte-
Charakteristik des Functionensystems (f, cp, -ty) gleich der halben
Summe der Charaktere der sämmtlichen Schnittpunkte
von cp, ip.
Die Sätze und Begriffsbestimmungen, die wir hier gegeben
haben, bleiben unverändert bestehen, auch wenn die betrachteten
Curven aus mehreren in sich geschlossenen Zügen bestehen;
auch können Doppelpunkte bei den Curven vorhanden sein; es
muss nur von jeder Fortschrittsrichtung auf einer der Curven
x) Kronecker versteht unter Charakter eines Punktes etwas Anderes.
Nach seiner Definition (Monatsbericht der Berliner Akademie, 4. März 1869)
ist nämlich der Charakter eines Schnittpunktes von q> und \p die Charak-
Charakteristik eines Curvensystems, das mau aus /, g>, xp erhält, wenn man /
durch eine Curve ersetzt, die nur diesen einen Schnittpunkt von tp, ip um-
schliesst.

§. 103. Eingrenzung der complexen Wurzeln. 329
völlig bestimmt sein, ob sie als positiv oder als negativ zu be-
betrachten ist, d. h. es muss jedes Stück einer Curve / oder q>
oder ip Flächehtheile von einander trennen, in denen die Func-
tionen / oder q> oder ip entgegengesetzte Vorzeichen haben.
Auszuschliessen sind nur die Fälle, in denen eine der Curven
durch einen Doppelpunkt der anderen hindurchgeht, oder in
denen die Curven einander berühren, oder in denen die drei
Curven/, g>, ip durch einen Punkt gehen; denn in diesen Fällen
würde die Bestimmung eines Punktes als Eintrittspunkt oder
Austrittspunkt zweifelhaft werden.
Erstrecken sich die Curven ins Unendliche, so muss man
sie, um unsere Sätze anwendbar zu machen, durch willkürlich
hinzugefügte Curvenstücke abschliessen, wie wir im nächsten
Paragraphen sehen werden.
§. 103.
Anwendung der Charakteristiken auf die Eingrenzung
der complexen Wurzeln einer Gleichung.
Es sei jetzt
g = x -\- yi
eine complexe Veränderliche und
A) F{e) = g> («, y) + » * (x, y)
eine ganze rationale Function von g mit reellen oder complexen
Coefficienten, und darin y (x, y), ip (x, y) reelle Functionen der
reellen Veränderlichen x, y. Wir setzen voraus, dass F(g) und
F' (s) nicht zugleich verschwinden. F(ß) verschwindet nur in
den Schnittpunkten der beiden Curven tp und ip. Die Ableitung
von A) ergiebt
F(*) = <p'(x) + iip'(x) = - i<p'(y) + ip'(y),
also
B) g>'(*) = *'(y). g>'(y) = — *'(*),
und folglich
C) [<p, V] = tp' (x) H,' (y) — <p> 0/) V (x)
= <p'(xy + <p'(yy = i,'(x)* + 1>'(y)>.
Hieraus folgt, dass die Functionaldeterminante [q>, ip] nie-
niemals negativ wird und nur da verschwindet, wo q>' (x) und q>' (y),
also auch ip'(x) und ip' (y) zugleich verschwinden.

330
Achter Abschnitt.
§. 103.
Dies tritt aber nie in einem Schnittpunkte von cp und ip ein,
da sonst hier F (z) und F' (g) zugleich verschwinden würden.
Die positive Fortschrittsrichtung ist in jedem Theil der Curve cp
oder ip völlig bestimmt durch das Vorzeichen der Function in
den angrenzenden Flächentheilen; auch etwaige Doppelpunkte, in
denen (p, cp'(x) und cp'' (y) zugleich verschwinden, machen dabei
keine Ausnahme.
Da die Functionaldeterminaiite \cp, ip] in allen Schnittpunkten
der Curven cp, ip positiv ist, so sind alle diese Punkte Austritts-
punkte A(q>, ip), und daraus folgt, dass die Curven cp und ip nicht
geschlossen sein können, sondern sich ins Unendliche erstrecken
müssen, da sonst auf eine Austrittsstelle nothwendig eine Ein-
Eintrittsstelle folgen müsste. Im Uebrigen bestimmen auch hier die
Curven g>, ip einen Binnenraum, in dem das Product cp ip negativ ist.
Wir fügen nun zu den beiden Functionen cp, ip eine dritte
Function/ hinzu, die, gleich Null gesetzt, eine geschlossene
Curve darstellt, und bestimmen die Charakteristik des Func-
tionensystems ganz in der früheren Weise, indem wir längs der
Curve / fortschreiten
(l)Jc = l[E(f;cp,ip)]-A(f; cp,ip)]=±[E(f;ip,cp)-A(f;ip,<p)].
So ist z. B. in der Fig. 11 die Charakteristik Je = 2.
Fig. 11. Fig. 12.
Um unsere Sätze anwenden zu können, müssen wir die Curven.
cp, ip irgendwie durch willkürlich hergestellte "Verbindungen, die
aber alle ausserhalb / verlaufen sollen, zu geschlossenen machen.
Die Charakteristik dieses Systems ist dann gleichfalls durch A)

§. 104. Bestimmung der Charakteristik. 331
bestimmt. Als Beispiel ergänzen wir die Fig. 11 durch Fig. 12,
in der diese abschliessenden Verbindungen gezeichnet sind. Die
so hinzugefügten Schnittpunkte können theils Austrittspunkte
A(cp, ip), theils Eintrittspunkte E(cp, tj)) sein. Wir wollen ihre
Anzahlen mit
A'(<p, t\>), E'(<p, t\>)
bezeichnen, während A (q>, i\>) die Zahl der ursprünglich vor-
vorhandenen Schnittpunkte bedeutet. Immer muss jetzt
B) A (<p, *) + A' (cp, n,) = E' (tp, *)
sein. Wir theilen die Punkte A (cp, tp) in zwei Gruppen Aa (q>, tj))
Ae (g>, ij)), von denen die ersten ausserhalb, die anderen innerhalb
von / liegen sollen. Dann haben wir folgende Charaktere der
Schnittpunkte
Aa (% 1p) — 1,
-4« (<P, *) + 1,.
A' (<p, i,) — l,
W (cp, *) + 1.
Der doppelte Werth der Charakteristik ist dann, wenn wir
der Einfachheit halber die Bezeichnung (<p, ip) weglassen (§. 101)
C) - Aa±A£ — A' + E' = 2k;
dazu die Gleichung B) addirt, ergiebt
D) k = As,
d. h. die Charakteristik ist gleich der Anzahl der im
Inneren von / gelegenen Schnittpunkte von g>, i>.
Damit haben wir also ein Mittel gefunden, um die Anzahl
der Wurzeln der Gleichung
F(g) = 0,
deren geometrische Bilder im Inneren einer beliebig gegebenen
Curve liegen, aus der Charakteristik zu bestimmen. Die will-
willkürlich hinzugefügten äusseren Verbindungen spielen hierbei gar
keine Rolle mehr und können vollständig unterdrückt werden.
§. 104.
Bestimmung der Charakteristik.
Um den im Vorigen bewiesenen Satz anwendbar zu machen,
müssen wir noch zeigen, wie wir die Charakteristiken wirklich

332
Achter Abschnitt.
104.
bestimmen können. Denken wir uns zu diesem Zweck die Curve/
so in Theilstrecken getheilt, dass in einer von ihnen nur ein -
Schnittpunkt mit der Curve <p oder ein Schnittpunkt mit der
Curve ip liegt, und bezeichnen wir mit a (Fig. 13) den Anfang,
mit b das Ende einer solchen Strecke, mit | den in ihr liegenden
Schnittpunkt von / mit <p, so wird der Punkt | ein Punkt
E(f; <p, ip) sein, wenn das Product q> ip in a positiv ist, und ein
Punkt A(f; q>, ip), wenn <p ip in a negativ ist; und damit ist die
Fig. i4. Möglichkeit gegeben,
+i aus den Vorzeichen
der Functionen cp, ip
in den Theilpunkten
der Strecken die Cha-
Charakteristik vollständig
zu bestimmen. Wie
wir aber die Curve /
in solche Theilstrecken
eintheilen, das lehrt uns der Sturm'sehe Lehrsatz. Wir
denken uns zu diesem Zweck x und y als Functionen einer
Variablen t dargestellt, die längs der Curve / alle reellen Werthe
von — oo bis -\- oo (oder auch nur die Werthe eines end-
endlichen Intervalles) durchläuft. Dadurch gehen tp und ip auch
in Functionen der Variablen t über und man hat die Lage
ihrer Wurzeln nach dem Sturm'sehen Lehrsatz zu unter-
untersuchen.
Ist z. B. wie in Fig. 14 die Curve / ein Kreis mit der
Gleichung
(x — aJ -|- (y — ßJ = q%
so können wir setzen:
1 — t2
2t
x — k =
y-ß =
und t durchläuft einfach alle Werthe von — oo bis -+- oo, während
der Punkt x, y sich über den ganzen Kreis in positivem Sinne
bewegt. q> und ip gehen, mit einer geeigneten Potenz von \-\-P
multiplicirt, in ganze rationale Functionen von t über, die die
Anwendung des Sturm'sehen Satzes gestatten.

§. 105. Fundamentalsatz der Algebra. 333
§. 105.
Gauss' erster Beweis des Fundamentalsatzes der
Algebra.
Gauss hat für den Hauptsatz der Algebra, dass eine Glei-
Gleichung nteu Grades n Wurzeln hat, drei verschiedene Beweise
gegeben. Der erste von diesen, der sich in seiner Doctordisser-
tation findet, und den er später noch weiter ausgeführt und
anders dargestellt hat, beruht, wenn auch in anderer Einkleidung,
auf dem Gedanken, der dem Charakteristikenbegriff zu Grunde
liegt1). Danach gestaltet sich dieser Beweis in seinen Grund-
Grundzügen folgendermaassen.
Es sei g = x -\- yi und
A) F{z) = <p(x,y) + iil>{x,y)
eine ganze rationale Function von 0 vom wten Grade mit reellen
oder complexen Coefficienten, in der gn den Coefficienten 1 hat,
also
B) F(ß) = sn + t*!*»-1 + a2 s»-2 -| \- an.
Wir setzen wieder voraus, dass F(s) und F'@) keinen ge-
gemeinsamen Theiler haben, und der Beweis, dass F(s) für n
Werthe von.0 verschwindet, beruht nun darauf, dass, wenn wir
für / einen Kreis von hinlänglich grossem Radius wählen, die
Charakteristik des Functionensystems f, cp, ty direct bestimmt
werden kann und sich gleich n findet. Dann folgt nach §. 103,
dass in dem so gewählten Kreise n Punkte g liegen, in denen
F(g) verschwindet.
Wir bedienen uns der Polarcoordinaten, und setzen, da
%, «2, a3, . . ., an auch complex sein können,
worin j)l7 p2, ... j>„, JR positiv sind und die Winkel qu g2, ... q^ %¦
in irgend einem Intervall vom Umfang 2 % gewählt werden können.
!) Gauss, Demonstratio nova theorematis omnem functionena alge-
braicana rationalem integram unius variabilis in factores reales primi vel
secundi gradus resolvi posse A799). Beiträge zur Theorie der algebraischen
Gleichungen A849). Kronecker, Monatsberichte der Berliner Akademie,
21. Februar 1878.

334
Achter Abschnitt.
§. 105.
Hierdurch wird
cp (x, y) = Bn <
(8) +...+i>„cosgn
ij/ (x, y) = B" sin n & -j- p1 Bn sin [(n —
+ • • • + J>» sin qn,
und wir bilden auch noch die nach # genommenen Ableitungen
-f qn_
= nBn cos n %¦ -\- (n —
cos [(» —
9w
3(ü
Wir theilen jetzt die Kreisperipherie mit dem Radius B in
4 n Theile ein von der Winkelgrösse
4»'
indem wir bei # = — » anfangen. Die Theilpunkte sind also
— <o, <o, 3 <o, 5 », . . . (8 n — 3)»,
und die Intervalle mögen der Reihe nach mit 1, 2, 3, ... in
bezeichnet sein, so dass das mit v bezeichnete Segment die
Grenzen B v r— 3) co und
Bv — l)co hat. Die Fig. 15
zeigt diese Eintheilung für
n = 3.
In den Intervallen
1, 3, 5 ... (in — 1)
ist cos n #, absolut genom-
genommen, grösser als 1:1/2, und
abwechselnd von positivem
und negativem Vorzeichen.
In den Intervallen
2, 4, 6 in
_ ist sin n & absolut grösser
als 1 : ]/2 und gleichfalls abwechselnd von positivem und nega-
negativem Vorzeichen.
Man kann ahevB so gross annehmen, dass in den Intervallen
1, 3, 5 ... D n — 1) das Vorzeichen von <p und -y-w mit dem
Jlw
13u>
15 @
2lu>

§. 106. Der Satz von Hurwitz. 335
von cos n #, und in den Intervallen 2, 4, 6 ... 4 n das Vorzeichen
von i> und —=-£ mjt dem von sin n & übereinstimmt.
Da also cp in den Intervallen 2, 4, 6 ... 4w sein Zeichen
ändert, so muss es in jedem dieser Intervalle durch Null gehen,
und da die Abgeleitete -~ ihr Zeichen nicht ändert, so kann
a v
es nur einmal in jedem durch Null gehen.
Ebenso ist zu schliessen, dass 4> in jedem der Intervalle
1, 3, 5 ... 4 n — 1 einmal und nur einmal durch Null geht.
Wir haben also eine Eintheilung der Kreisperipherie, wie sie im
vorigen Paragraphen zur Bestimmung der Charakteristik verlangt
wurde, und da in den Theilpunkten », 5», 9ra...D» — 3)» das
Product cp ip positiv ist, so kommen auf der Kreisperipherie keine
Punkte A(f; cp, ip) vor und die Anzahl der Punkte E(f; cp, i>) ist
2»; die Anzahl der Wurzeln von F(s) ist also gleich n, was zu
beweisen war. Ebenso führt das entgegengesetzte Umkreisen
von / niemals auf einen Punkt A (/; cp, ij>) und die Anzahl der
Punkte E(f; 4>, cp) ist ebenfalls 2n.
IT H IT
Die Punkte % =¦ — und # = — der Kreisperipherie liegen
in den Intervallen n -j- 1 und Bn -\- 1, haben also bei geradem
n einen ungeraden und bei ungeradem n einen geraden Index.
Es liegt also in diesen Intervallen bei geradem n je ein Schnitt-
Schnittpunkt von -ty und kein Schnittpunkt von cp und bei ungeradem n
je ein Schnittpunkt von cp und kein Schnittpunkt von ip. Es
folgt hieraus:
Theilt man den Kreis / durch die y-Axe in zwei
Halbkreise, so liegen auf jedem dieser Halbkreise
n Punkte E(J; cp, ip) bei geradem n,
n Punkte JE(f; ij), cp) bei ungeradem n.
Diese Bemerkung giebt uns ein Mittel, um über die Ver-
theilung der Wurzeln auf die beiden Halbkreisflächen aus dem
Verhalten der Functionen cp, ij/ auf der y-Axe Schlüsse zu ziehen.
§. 106.
Der Satz von Hurwitz.
In der schon früher (§. 99) erwähnten Abhandlung hat
Hurwitz die Bedingungen dafür aufgestellt, dass eine reelle
Gleichung nur Wurzeln mit negativem reellem Theil habe.

336 Achter Abschnitt. §. 106.
Behalten wir der Symmetrie wegen den Coefficienten a„ bei,
den wir gleich 1 annehmen können, und den wir als positiv
voraussetzen wollen, so sei die gegebene Gleichung
A) F(e) = <*>#> + a,«—H h«»^0-
Die a0, %, . . ., an sollen jetzt reelle Zahlen sein. Setzen
wir für s einen rein imaginären Werth y i, so wird s in folgender
Weise zerlegt. Wir setzen:
B) F1 {y) = aoy« — a^y»-* -f aiy"~i
F^^^a^r-1 — azyn~B + a-oV"-6 >
und dann ist
C) F(yi) = i*(F1—iF<l).
Wir haben also nach der Bezeichnung des vorigen Para-
Paragraphen
cp @, y) = ± F„ i> @, y) = + Fi bei geradem n
( ) cp(O, y) = + F%, i> @, y) = rp Ft bei ungeradem n.
Wenn nun alle Wurzeln von F negative reelle Theile haben
sollen, so darf zunächst F± und F2 für kein reelles y zugleich ver-
verschwinden, weil sonst F eine reine imaginäre Wurzel hätte. Es
müssen ferner alle Wurzelpunkte in dem Halbkreis liegen, der in
unserer Fig. 15 durch die Punkte 4, 7,10 bezeichnet ist. Wenn wir
also die Begrenzung dieser Halbkreisfläche als /-Curve betrachten,
so müssen auf ihr 2 n Punkte F(f; cp,ij)) und 2 n Punkte E(f;ij/,tp)
liegen. Folglich müssen nach dem Schlusssatze des letzten Para-
Paragraphen auf dem geradlinigen Durchmesser
n Punkte E(f; cp, ip) bei geradem n
n Punkte E(f; $, ij)) bei ungeradem n
liegen. Daraus aber ergiebt sich nach D) für beide Fälle, dass
auf dem Durchmesser n Wurzeln von Fx = 0 liegen müssen,
und dass in diesen Punkten F\ (y) F% (y) positiv sein muss,
damit es Punkte E(f; cp, ip) oder E(f; ip, cp) sind.
Da n solche Punkte vorhanden sein müssen und Fx nur
vom «ten Grade ist, so kann F[(y) hier nicht zugleich mit F-y{y)
verschwinden.
Es treten also hier die Voraussetzungen des Satzes §. 99, 3.
in Kraft, wenn wir an Stelle der dort vorkommenden Functionen
/ und E hier Ft und F% setzen. Um ihn anwenden zu können,
müssen noch die Determinanten Cv und also zunächst die Coef-
Coefficienten c„ der Entwickelung des Bruches Ft: Fx nach fallenden
Potenzen von y berechnet werden.

§. 106.
Der Satz von Hurwitz.
337
Hier hängt aber die Function yF2:F1 nur von y* ab, und
folglich kann die Entwickelung nach fallenden Potenzen von y
auch nur die geraden Potenzen enthalten, d. h. es sind c2, c3,
c5, . . . = 0. Dann aber zerfällt die biquadratische Form T
[§. 99, F)] in die beiden Formen
von denen die erste nur die Variablen t0, t$, t^ . . ., die andere
nur die Variablen tu t3, t$, . . . enthält. Für unseren Fall muss
also jede dieser Formen definit, und zwar positiv sein.
Wir setzen jetzt für ein gerades n
Ea)
und
E")
0
für
C"
<-o, c2, .
Ci, Ct, .
Cn — 2i Cn, '
ein ungerades
Co, Cj, .
C2, C4, .
(
'» — 1, Cn +1,
¦ ; Cn-l
' •, Cn
. ., C2„_4
n
• ¦ ; Cn — i
• • ; Cn+1
• • -1 C2n_2
C" =
pn
c2,
Ci,
Cn,
Ci,
Ci,
Cn-
Cl, -.
%, ¦ .
Cn + 2, ¦
Ci, ¦ .
cs, . .
li Cjj + i,
• ;Cn
¦ ; Cn+2
• ; Cin —
¦ ; Cn-i
• ; Cn + 1
..., C2«_
und erhalten nach §. 89, VII. den Satz:
1. Damit die Gleichung F(s) = 0 nur Wurzeln mit
negativem, reellem Theil besitze, ist nothwendig
und hinreichend, dass die Determinanten C, 0"
nebst allen ihren Hauptunterdeterminanten po-
positiv seien.
Selbstverständlich genügt es (nach §. 89) festzustellen, dass
eine Kette von Hauptunterdeterminanten von C\ C" positiv ist.
Zur Berechnung der Coefficienten c0, c2, c4, . . . ergiebt sich
aber folgendes einfache Verfahren.
Man bilde das Product
In diesem Product können keine negativen Potenzen von y
vorkommen, und die Coefficienten der positiven Potenzen müssen
mit den Coefficienten der entsprechenden Potenzen in yF2 (y)
übereinstimmen. Daraus ergeben sich nach B) die folgenden
Gleichungen zur successiven Berechnung von c0, c2, c4, . . .
Weber, Algebra. I. 22

338
Achter Abschnitt.
§. 106.
F)
Oi = O,q Cq
— ÖS3 = OSq C% —
Qjf -— C(/q Cß
\C2 —
Hurwitz hat diesen Bedingungen noch eine andere Gestalt
gegeben, die formell einfacher ist, obwohl sie die Berechnung
höherer Determinanten erfordert.
Wir wollen hier, um die Uebersicht nicht durch allzu grosse
Formeln zu erschweren, die Rechnung nur in einem Beispiel durch-
durchführen, aus dem aber der Gang im Allgemeinen vollkommen zu
ersehen ist.
Wir setzen die zweite Hauptunterdeterminante c0 c± — e|
C in die Form
1, 0, 0, 0
0, Co, c2, Ci
0, 1, 0, 0
0, 0, Co, c2
und niultipliciren sie in der letzten Gestalt mit
«o, 0, 0, 0
: «21 ft0l 0, 0
aM — a.2, a0, 0
— ÖSg, ÖS4, fl.2, ÖSq
Dadurch ergiebt sich nach F)
a0, 0, 0, 0
¦ $2, o±) öEq, 0
1,
o,
o,
o,
o,
1,
o,
o,
o,
C2)
0
0
Ci
Ci
— Oi,, — fto, O,
= «0
, 0
a-0,
a3
und die zuletzt angegebene Determinante muss daher positiv
sein. Ebenso behandle man die Hauptunterdeterminanten von
C", indem man z. B.
1, 0, 0, 0
0,' 1, 0,' 0
0, Co, C-2, Ci
setzt, wofür man den Ausdruck erhält:

§. 106.
Der Satz von Hurwitz.
339
»!, ao> 0, 0
as, a2, au a0
«5, ai, »3> O"t
a7, a6, a-0, a4
was also ebenfalls positiv sein muss.
Hieraus ergiebt sich der Hurwitz'sche Satz:
2. Die nothwendige und hinreichende Bedingung
dafür, dass die Gleichung F = 0 nur Wurzeln
mit negativem, reellem Theil habe, besteht darin,
dass ausser a0 die n ersten Glieder der Kette
der Hauptunterdeterminanten Au A2, . . ., A„ der
Determinante
«!, a0, 0, 0, 0, 0 ...
a3, a2, au a0, 0, 0 ...
a5, a4, %, a2, »!, a0 . . .
a7, a6, a5, a4, %, a2. . .
positiv sein müssen.
Dieser Satz ist zunächst nur unter der Voraussetzung abge-
abgeleitet, dass F(s) keine mehrfachen Wurzeln hat, oder dass die
Discriminante dieser Function nicht verschwindet. Wir können
uns aber von dieser Beschränkung leicht nachträglich frei machen.
Wenn zunächst die in 2. vorkommenden Determinanten
sämmtlich positiv sind, so ist die quadratische Form T eine
positive, und dann können nach (§. 99, 1.) Fi und F2 keine
gemeinschaftliche Wurzel haben. Es kann also F keine rein
imaginäre Wurzel haben.
Es kann aber F dann auch keine Wurzel mit positivem,
reellem Theil haben, denn sonst könnte man die Coefficienten
von / so wenig ändern, dass die Determinanten 2. positiv bleiben,
dass Wurzeln mit positivem, reellem Bestandtheil bleiben, und
dass die veränderte Function F keine mehrfachen Wurzeln mehr
hat. Dann erhält man aber einen Widerspruch mit dem
Satze 2.
Ebenso kann man umgekehrt schliessen, dass, wenn F(s)
nur Wurzeln mit negativ imaginärem Theil hat, keine der Deter-
Determinanten 2. negativ sein kann.
Es bleibt also nur noch nachzuweisen, dass unter dieser
Voraussetzung über die Wurzeln von F keine der Determinanten 2.
22*

340
Achter Abschnitt.
§. 106.
verschwinden kann. Nehmen wir, um dies zu beweisen, an, es
sei etwa
«!, a0, 0, 0
«3, «2l «15 «0
«51 «41 «31 «2
«71 «6, «5, «4
die erste verschwindende unter diesen Unterdeterminanten. Es
hat hierin w, den Coefticienten
der nach Voraussetzung negativ ist. Wenn wir also F in F'
= F -j- s0 verwandeln, so können wir die Coefficienten von O
so bestimmen, dass bei hinlänglich kleinem positivem oder nega-
negativem £ die Function F' keine gleichen Wurzeln mehr hat, und
dass die reellen Theile dieser Wurzeln negativ bleiben. Durch
die Substitution F' für F möge At in A\ übergehen.
Ordnen wir Ai nach Potenzen von g, so verschwindet der
Coefficient der ersten Potenz von £ nicht identisch, und folglich
können wir das Zeichen von £ noch so bestimmen, dass Ai nega-
negativ wird. So ergiebt sich auch hier ein Widerspruch gegen den
Satz 2.

Neunter Abschnitt.
Abschätzung der Wurzeln.
§. 107.
Das Budan-Fourier'sche Theorem.
Die Functionen der Sturm'sehen Ketten lösen zwar voll-
vollständig und ausnahmslos das Problem der Bestimmung der Anzahl
der Wurzeln einer Gleichung zwischen gegebenen Grenzen; aber
ihre wirkliche Berechnung ist meist schwierig und oft unaus-
unausführbar. Man kennt eine Reihe von Sätzen zur Abschätzung
der Zahl der Wurzeln zwischen gegebenen Grenzen, die viel ein-
einfachere Regeln liefern, aber freilich auch die Frage nicht voll-
vollständig beantworten, sondern nur eine Maximalzahl geben, worüber
die Anzahl der Wurzeln nicht hinausgehen kann. Diese Regeln
sind oft für die Anwendung sehr nützlich und ausreichend, und
sie dürfen daher hier nicht fehlen.
Wir betrachten zunächst ein Verfahren, das von Budan
herrührt, dann aber von Fourier benutzt und erweitert wurde1).
Betrachten wir an Stelle einer Sturm'sehen Kette die Reihe
der Ableitungen einer reellen Function f(x) vom wten Grade
A) f(x),f'(x),f"(x), ..,/«(x),
worin also /(n) (x) eine Constante ist, die wir von Null verschieden
und positiv voraussetzen. Sie ist, von einem positiven Zahlen-
factor abgesehen, der Coefficient von xn in f(x).
!) Budan, Nouvelle methode pour la resolution des equations nume-
riques A803 der Pariser Akademie vorgelegt). Fourier, Analyse des
equations determinees. Paris 1831. Ueber das Geschichtliche dieser Frage
vergleiche man Lagrange, Traite de la resolution des equations, Note VIII
(Werke, Bd. 8).

342 Neunter Abschnitt. §. 107.
Es seien wieder a und ß > cc zwei reelle Zahlen, die das
Intervall (u,ß) bestimmen, in dem die Anzahl der reellen Wurzeln
von f(x) gezählt werden sollen.
Wir wollen zunächst annehmen, dass in dem Intervall (a, ß)
nicht zwei Glieder der Reihe A) zugleich verschwinden, und
dass für x = et, x = ß kein Glied der Reihe verschwindet.
Lassen wir nun x von a bis ß stetig wachsen, so kann in
der Vorzeichenfolge der Reihe A) nur dann eine Aenderung
eintreten, wenn eine der Functionen durch Null geht. Wenn
f^ipe) für x = § durch Null geht, so geht/A>) (#), je nachdem
f<y+i)(x) positiv oder negativ ist, von negativen zu positiven oder
von positiven zu negativen Werthen über, und es geht also
zwischen /W und f<v+1') beim Durchgang durch § ein Zeichen-
Zeichenwechsel verloren. Dies gilt auch, wenn /<"> die Function f{x)
selbst ist. Wenn aber fw eine der Derivirten ist, so geht ihr
eine Function f(-v~1'> voran, und da f(y~1) nach Voraussetzung für
x = % nicht Null ist, und /W beim Durchgang durch % sein
Zeichen wechselt, so findet zwischen /(r—^ und /M beim Durch-
Durchgang durch | entweder ein Verlust oder ein Gewinn von einem
Zeichenwechsel statt. Wenn also ein inneres Glied der Reihe A)
durch Null geht, so bleibt die Anzahl der Zeichenwechsel unge-
ändert, oder es gehen zwei Zeichenwechsel verloren.
Geht aber f(x) selbst durch Null, so geht ein Zeichenwechsel
verloren.
Daraus folgt das Theorem:
I. Die Anzahl der zwischen a und ß gelegenen
Wurzeln von /(«) ist höchstens so gross, wie die
Zahl der zwischen a und ß verlorenen Zeichen-
Zeichenwechsel, und wenn sie kleiner ist, so ist der
Unterschied eine gerade Zahl.
Mit Benutzung einer Formel können wir auch sagen:
Ist V(x) die Anzahl der Zeichenwechsel (Variationen), die
die Reihe A) für irgend einen Werth x darbietet, so ist die
Anzahl der zwischen « und ß gelegenen Wurzeln von f(x)
B) F(a)_F@)_2Ä,
worin h eine nicht negative ganze Zahl ist.
Der Beweis des Satzes I. bedarf noch einer Ergänzung für
den Fall, dass in der Reihe A) mehrere auf einander folgende
«Glieder zugleich verschwinden.

§. 107. Das Budan-Fourier'sehe Theorem. 343
Es mögen also für einen Werth f von x zwischen « und ß
in der Reihe
C) /«(*), /<'+»(aO, • • , /"+"-»(*),
alle Glieder, mit Ausnahme des letzten, verschwinden, und das
letzte /(»+/*) (x) möge etwa einen positiven Werth haben.
Wir grenzen um f zwei Intervalle 8X, d2 ab, so dass alle
Werthe von x im Intervall 8t kleiner, im Intervall d2 grösser
als | sind, und nehmen diese Intervalle so klein, dass die Func-
tionen C) ausser in f darin nicht verschwinden, also auch/c+M)(a;)
positiv bleibt.
Da nun, wenn/c+^a;) positiv ist, /(»+/*—*>(x) mit x zugleich
wächst, so ist
/(» + /*-» (#) in dj negativ,
in d2 positiv.
Daraus folgt, dass /(»+/* ~^(x) in d1 abnimmt, in d2 wächst,
also in beiden Intervallen positiv ist, und so schliessen wir
weiter auf die Vorzeichenfolge in der Reihe C):
D) /W (x), /C+1) (x), /(» + « (X), . . ., /(-+,«-« (x), /»+/«(*)
^,(-1)« -(-l)" (-iy ... - +
*., + + + + +
d. h. in der Reihe C) werden beim Durchgang durch f aus
lauter Zeichenwechseln Zeichenfolgen, und es gehen in der Reihe
C) (i Zeichenwechsel verloren.
Ist/("+¦")(!) negativ, so sind alle Zeichen in D) die ent-
entgegengesetzten, und der Schluss bleibt sonst derselbe.
Wenn nun v = 0, d. h. f^(x) die ursprüngliche Function
f(x) selbst ist, die dann in f eine (ft*^p"l) fache Wurzel hat, so
findet also beim Durchgang durch f auch in der Reihe A) ein
Verlust von ft Zeichenwechseln statt.
Ist aber v > 0 und die dem /w (x) vorangehende Function
ßv~1)(x) von Null verschieden, so haben wir folgende Zeichen:
1. (i gerade:
a) Z«"-« (*),/«(*), b) /«—»(*),/<">(*)
8» + + +
a» + + - +

344 Neunter Abschnitt. '§. 107.
2. (i ungerade: '
Es geht also bei geradem (t zwischen /(r~1) und /<r> kein
Zeichenwechsel verloren, bei ungeradem (i geht ein Zeichenwechsel
verloren oder es wird einer gewonnen. Es ist also der Yerlust
an Zeichenwechseln beim Durchgang durch f in der Reihe
E) /(^-1),/(r>,/(r + 1>, ..,/<*-">
bei geradem (i gleich (t, bei ungeradem (i gleich (t + 1, also
immer eine gerade Zahl und nie negativ.
Wir können diesen Ergebnissen einen übersichtlichen ana-
analytischen Ausdruck geben, der ihre Bedeutung besser erkennen
lässt.
Wir bezeichnen mit V(x) wie früher die Anzahl der Zeichen-
Zeichenwechsel in der Reihe A) für einen bestimmten Werth von x,
jedoch mit der näheren Bestimmung, dass, -wenn für einen Werth
von x einige der Glieder der Reihen verschwinden, diese bei
Abzählung der Zeichenwechsel einfach übergangen werden. Wir
können dann V(x) als eine Fünction von x auffassen, die sich
aber nur um ganze Zahlen ändern kann, also unstetig ist für
die Werthe von x, für welche einige Glieder der Reihe A) ver-
verschwinden. Wir wollen dann mit V(x — 0) und V(x -j- 0) die
Werthe der Fünction V(x) unmittelbar vor und unmittelbar
nach einer solchen Stelle bezeichnen. Dann zeigt die Betrachtung
von E), dass in allen Fällen
F) F(f + 0) = F(f)
ist, und dass, wenn f eine (t-fache Wurzel von fix) ist,
G) r(f-0) = F(f) + p + 2Ä,
worin h eine nicht negative ganze Zahl ist.
Daraus ergiebt sich also, wenn wir zunächst daran festhalten,
dass für x = « und x = ß keine der Functionen A) ver-
verschwindet, dass F(«) — V(ß) sich von der Summe aller Zahlen
(t, d. h. von der Anzahl der im Intervall («, ß) gelegenen Wurzeln,
jede nach dem Grade ihrer Vielfachheit gerechnet, um eine
gerade, nicht negative Zahl unterscheidet, und damit ist also
das Theorem I. von seiner Beschränkung befreit.

§. 108. Die Newton'sche Regel. 345
Wir können aber auch noch die Voraussetzung aufgeben,
dass für et, und ß keine der Functionen A) verschwindet, wenn
« und ß nicht unter den Wurzeln von f(x) vorkommen.
Denn dann ist unser Theorem anwendbar auf zwei Werthe,
von denen der erste etwas grösser als «, der andere etwas kleiner
als ß ist, und die dieselben Wurzeln einschliessen, wie « und ß;
d. h. es ist, wenn wir mit j die Anzahl dieser Wurzeln bezeichnen
und da
F(« + 0) = F(«), V(ß — 0) = V(ß) + 2 Ä',
so folgt
was wieder der Ausdruck unseres Theorems ist.
Wenn aber « oder ß selbst zu den Wurzeln von f(x) gehört,
dann ist unser Theorem nur dann richtig, wenn diese Grenz-
werthe nicht mit zum Intervall gezählt werden.
Das Budan-Fourier'sche Theorem giebt zwar nicht, wie
der Sturm'sche Satz, eine vollständig sichere Entscheidung über
die Zahl der Wurzeln in einem Intervall, es kann aber doch in
manchen Fällen den Sturm'schen Satz ersetzen; denn hat man
das Intervall («, ß) so weit eingeschränkt, dass kein oder nur
ein Zeichenwechsel von a bis ß verloren geht, so folgt mit
Sicherheit, dass im ersten Falle keine, im zweiten eine und nur
eine Wurzel im Intervall liegt.
Die Abgrenzung der Wurzeln kann also durch die Budan'sche
Reihe nur dann vollständig gegeben werden, wenn nicht beim
Durchgang durch einen Werth f gleichzeitig mehrere Zeichen-
Zeichenwechsel verloren gehen. Dies Verhalten kann, wie klein auch das
Intervall («, ß) gewählt sein mag, nicht mit Sicherheit erkannt
werden, und man wird also, wenn nach einer angemessenen Ein-
Einengung des Intervalles die Abgrenzung nicht gelungen ist, doch
zu einem anderen Verfahren, in letzter Instanz zum Sturm'-
Sturm'schen Satze greifen müssen.
§. 108.
Die Newton'sche Regel.
Eine Ergänzung der vorstehenden Regel, die eine weitere
Annäherung an die genaue Festsetzung der Grenzen der Wurzeln

346 Neunter Abschnitt. §. 108.
gestattet, giebt die jetzt zu besprechende, von Newton her-
herrührende, aber erst von Sylvester bewiesene Vorschrift1).
Es sei wieder
A) f(x) = a^xn -\- axxn~x -\ • -(- an^x + an = 0
die zu untersuchende Gleichung. Wir setzen, indem wir mit
n(m) wie immer das Product 1. 2. 3 . . . m und mit/(r> (#) die
vte Derivirte bezeichnen,
C) Fv{x)=ß{x)—fv+1(x) fv-i(x),
mit dem Zusatz, dass
D) F„=F=l, Fn=fn,
also, worauf es wesentlich ankommt, positiv sein sollen.
Für die Abgeleiteten der Functionen /„, F* erhalten wir aus
B) und C)
E) /,(*) = (» —«0/, + 1,
F) f,F,(x) = (n — v — l) (F*fv+1 + F,+ify-i).
Da es auf die positiven Zahlenfactoren nicht ankommt, so
können wir die Budan'sche Reihe durch die Reihe der Func-
Functionen
/1 /li JZi • • •> Jn
ersetzen.
Die New ton'sehe Regel macht nun von der Doppelreihe
Gebrauch:
*• ' F ~F ~F F
-T, M%i J?2, . . ., -TM.
Wenn wir zwei auf einander folgende Glieder dieser Doppel-
Doppelreihe, wie
für einen Werth von x betrachten, für den keine der vier Func-
Functionen verschwindet, so sind in Bezug auf die Zeichenfolge die
nachstehenden Fälle möglich:
*) Newton, Arithmetiea universalis. Sylvester, Transactions of
the R. Irish Academy, t. 24 A871). Phil. Mag., 4. ser., t. 81. Vergl. auch
Petersen, Theorie der algebr. Gleichungen. Kopenhagen 1878.

§. 108. Die Newton'sche Regel. 347
a) ~*~ Jr, Jr~Jr, ~" ~, , P P,
b) +-' i+' +-' -+'FF'
c) +i — i +~' -+'pF'
d) ++' i-' ++' --'FP-
Dies Verhalten bezeichnen wir mit folgenden Ausdrücken
und Symbolen:
a) Folge-Folge (Permanenz-Permanenz) P p,
b) Wechsel-Wechsel (Variation-Variation) VV.
c) Folge-Wechsel (Permanenz-Variation) P F,
d) Wechsel-Folge (Variation-Permanenz) V P.
Die zwei Sätze, die wir beweisen wollen, lauten:
II. Die Anzahl der zwischen « und ß gelegenen
Wurzeln von fix) ist entweder genau so gross
oder um eine gerade Zahl kleiner, als die
Zahl der beim Uebergang von « zu ß in der
Doppelreihe G) verlorenen Wechsel-Folgen.
III. Die Anzahl der zwischen « und ß gelegenen
Wurzeln von fix) ist entweder genau so gross
oder um eine gerade Zahl kleiner, als die
Zahl der beim Uebergang von « zu ß in der
Doppelreihe G) gewonnenen Folge-Folgen.
Von diesen beiden Sätzen, die nicht immer dieselbe obere
Grenze für die Zahl der Wurzeln geben, wird man den anwenden,
der die niedrigste Grenze giebt.
Wir machen beim Beweis dieses Satzes die folgenden Vor-
Voraussetzungen, von denen wir uns zum Theil später wieder
befreien werden:
1. fix) hat keine doppelten oder mehrfachen Wurzeln.
2. Von den Functionen fv(x) verschwinden nicht zwei be-
benachbarte für denselben Werth von x.

348
Neunter Abschnitt.
108.
3. Auch von den Functionen Fv{x) verschwinden nicht zwei
benachbarte für denselben "Werth von x.
4. Eine Folge von 2. ist [nach Formel C)], dass nicht
fv (%) und Fr (x) für denselben Werth von x verschwinden.
5. Für x = a und x = ß selbst soll keine der Functionen
fv, Fr verschwinden.
Der Beweis der Sätze II. und III. ist nun folgender:
Lassen wir x, stetig wachsend, von « bis ß gehen, so kann
eine Aenderung in der Zeichenfolge nur dann eintreten, wenn
eine der Functionen fv .oder JF„ durch Null hindurchgeht, und es
kommt nur darauf an, den Effect zu untersuchen, den ein solcher
Durchgang durch Null in den verschiedenen Fällen hervorruft.
Nehmen wir zunächst an, es gehe eine der mittleren Functionen
/, etwa fv, durch Null, wobei also 0 < v < n. Je nachdem fv+1
positiv oder negativ ist, wird /„ wachsen oder abnehmen. Es
wird also im ersten Falle /„ (x — 0) negativ, fv (x -\- 0) positiv
sein, und im zweiten Falle umgekehrt; ausserdem folgt aus C),
dass, wenn fv = 0 ist, Fv-% und JPr+1 positiv sind, und JF„ das
entgegengesetzte Vorzeichen von fv—ifv+i hat. "Wir stellen die
hiernach bleibenden Möglichkeiten tabellarisch zusammen, lassen
aber in der Aufzählung solche Fälle weg, die durch gleichzeitige
Vorzeichenänderung der drei Functionen /»—i,/r,/»+i aus den
aufgeführten entstehen, da diese offenbar keine verschiedenen
Resultate ergeben. Es bleiben uns hiernach nur zwei Fälle:
f(x-
/(* +
F
0)
0)
v —
+
+
+
1,
~ +
+ +
— +
1
In diesen Fällen ist also
PP, VP
VP, PP
noch ein PP verloren
x - 0 VV, VV
x + o pv, pv
Es wird also weder ein VP
oder gewonnen.
Wenn aber f(x) selbst durch Null geht, so haben wir, wenn
wir fx ix) positiv voraussetzen, was mit .Rücksicht auf die vorher
gemachte Bemerkung genügt,

§. 108.
Die Newton'sche Regel.
349
F
0)
0)
0
+
+
1
t
+
Es geht also hier ein VP in ein PP über, d. h. es wird
ein VP verloren, ein PP gewonnen.
Wenn endlich Fr durch Null geht, wo natürlich 0 < v < n
sein muss, so ist das Verhalten folgendes:
Wenn F„ = 0 ist, so müssen nothwendig /»_! und fv+1
gleiche Vorzeichen haben, da sonst JP„ aus zwei positiven Gliedern
bestehen würde, und nicht verschwinden könnte. Es ist ferner
F'v(x) nach F) vom selben Vorzeichen wie das Product/„_!/,, JF„+1,
und also hat Fv(x — 0) das entgegengesetzte, Fv(x -\- 0) das
gleiche Vorzeichen, wie das Product.
Auch hier können wir in der Aufzählung die Fälle weglassen,
die aus den aufgeführten durch gleichzeitige Zeichenänderung
in allen drei Functionen fr_1, fv, fv+1 oder Fv-t, F„ Fv+1 ent-
entstehen, und es bleiben also folgende Fälle:
f
F(x — 0)
f
F(x — Ö)
V 1, V, V -\- 1
+ - +
+ + +
V 1, V, V -)- 1
+ + +
Die Zeichenwechsel sind in diesen vier Fällen:
X
X
— 0
+ o
pv,
pp,
PV
pp
pp,
PV,
PV
pp
VP,
vv,
VP
vv
vv,
VP,
VP
vv
Im ersten F&lle werden zwei PP gewonnen, im zweiten
und vierten Falle tritt- keine Aenderung ein, im dritten Falle
gehen zwei VP verloren.

350 Neunter Abschnitt. §. 109.
Damit aber sind die Sätze II. III. bewiesen.
Die Voraussetzungen 2., 3., dass von den Functionen fv und
Fv nicht zwei benachbarte für dasselbe x verschwinden sollen,
können wir aufgeben. Denn wenn wir an der ersten Voraus-
Voraussetzung festhalten, dass keine mehrfachen Wurzeln vorhanden
sind, so können wir den Coefficienten av so kleine Aenderungen.
ertheilen, dass erstens die Voraussetzungen 2., 3. befriedigt sind,
und zweitens die zwischen « und ß gelegenen Wurzeln sich so
wenig ändern, dass keine von ihnen aus dem Intervall heraus-
heraustritt. Da die Wurzeln nur einzeln vorkommen, so können dabei
reelle Wurzeln nicht in imaginäre übergehen.
Ob der Satz bei richtiger Zählung der mehrfachen Wurzeln
auch noch im Falle mehrfacher Wurzeln gültig bleibt, mag dahin
gestellt bleiben.
§. 109.
Der Cartesische Lehrsatz.
Der Cartesische Lehrsatz, der auch nach Harriot1)
benannt wird, giebt eine Regel zur Abschätzung der Zahl der
positiven Wurzeln. Wir können ihn einfach als speciellen Fall
des Budan'schen Theorems betrachten, indem wir « = 0 und
ß = oo oder wenigstens so gross annehmen, dass die Functionen
A) f(x),f(x),f"(x),..,ß»>(x)
für x > ß alle dasselbe Zeichen haben. Dies Zeichen stimmt
überein mit dem Zeichen des Coefficienten der höchsten Potenz
von x in f(x) und kann positiv angenommen werden.
Ist
f(x) = aoxn -\- fflja^-1 -(- a2a;"-2 -)-...-)- an-Xx -\- o»,
so erhalten die Functionen A), von positiven Zahlenfactoren
abgesehen, für x = 0 die Werthe
B) G5M, an—i, an—2, • . ., o&o)
und daraus ergiebt sieh also das Theorem:
IV. Die Anzahl der positiven Wurzeln der Gleichung
f(x) = 0 ist gleich oder um eine gerade Zahl
1) Harriot, Artis analyticae praxis ad aequationes algebraicas resol-
vendas 1631. Gauss' Werke, Bd. III, S. 67. Lagrange, 1. c.

§. 109. Der Cartesisehe Lehrsatz. 351
kleiner, als die Anzahl der Zeichenwechsel in der
Reihe der Coefficienten von/(«), wobei etwa ver-
verschwindende Coefficienten einfach zu übergehen
sind und die Wurzel x = 0, wenn sie vorhanden
ist, nicht mitzählt.
Um auch die Anzahl der negativen Wurzeln abzuschätzen,
kann man entweder das Budan-Fourier'sche Theorem auf das
Intervall (— oo, 0) anwenden, oder man ersetzt x durch —x,
d. h. man ändert die Vorzeichen von d, a3, a-3, . . . und wendet
dann das Theorem IV. an.
In ähnlicher Weise wollen wir das Newton'sche Kriterium
des §. 108 specialisiren.
Wir bemerken dazu, dass
und folglich
X
n(n)
[v(n — v) ai—, — (y -f- 1) (n — v + 1) an-v-ian-v+1]
wird, dass ferner die Reihe der/»(#) für x=-\-co nur Zeichen-
Zeichenfolgen, für x = — oo nur Zeichen Wechsel darbietet.
Wenn wir also
C) Ay — v(n — v)a? — (v -(- 1) (n — v -(- l)ar_ia»+i,
Ao = l, A* = \
setzen, so dass Ay, von einem positiven Factor abgesehen, mit
JF„_„(O) übereinstimmt, so folgt, dass für x — 0 die Doppel-
Doppelreihe G), §. 108, in umgekehrter Ordnung geschrieben, den Vor-
Vorzeichen nach übereinstimmt mit
G50) %) a2i • • •¦> ®n
Ao, Ai, A2i . . ., An.
Beim Uebergang zu x = -\- oo sind in der Reihe /(«),
ft (x), ...,/„ (x) alle Zeichen Wechsel und beim Uebergang zu
x = — oo alle Zeichenfolgen verloren gegangen, also in der
Doppelreihe der /,, Fv für x = -(- oo alle VP, für x = — oo
alle PP.
Danach können wir nach §. 108, II. III. folgende beiden
Theoreme aussprechen:

352 Neunter Abschnitt. .§. 109.
V. Die Zahl der positiven Wurzeln von/(#) ist so
gross oder um eine gerade Zahl kleiner, als die
Zahl der Wechsel-Folgen in der Doppelreihe D)_
VI. Die Zahl der negativen Wurzeln von f(x) ist so
gross oder um eine gerade Zahl kleiner, als die
Zahl der Folge-Folgen in der Doppelreihe D).
Die Summe der Anzahlen der VP und der PP ist aber
gleich der Anzahl der Zeichenfolgen in der einfachen Reihe
E) Ao, At, A2, . . ., An,
und wir erhalten also noch aus V. und VL:
VII. Die Anzahl aller reeller Wurzeln von f(x) ist so
gross oder um eine gerade Zahl kleiner, als die
Zahl der Zeichenfolgen in der Reihe E).
Die Gesammtanzahl der Zeichenwechsel und Zeichenfolgen
in der Reihe E) ist so gross, wie die Zahl aller reellen und
imaginären Wurzeln zusammengenommen, nämlich n. Denn der
Fall, dass in der Reihe E) einige Glieder verschwinden, ist hier
auszunehmen. Da überdies das erste und letzte Glied der
Reihe E) dasselbe Vorzeichen haben, so ist die Anzahl der
Zeichenwechsel in dieser Reihe eine gerade Zahl. Wir können
also zu VII., ohne damit etwas Neues zu sagen, noch das
Theorem hinzufügen:
VIII. Die Anzahl der imaginären Wurzeln von f(x) ist
mindestens gleich der Anzahl der Zeichen-
Zeichenwechsel in der Reihe E).
In der Fassung der beiden letzten Sätze ist es gleichgültig,
ob einige der Coefficienten al5 a2, ..., an verschwinden, wenn nur
keines der Av Null ist.
Bei der cubischen Gleichung
a0 x3 -\- G&x x2 -\- a2 x -(- a8 = 0
ist
.4 = 2 (a2 — 3 a0 a2)
A2 = 2 0! — 3 ax Og),
und in der Reihe
1, Ax, A2, 1
kommen also zwei Zeichenwechsel vor, wenn von den beiden
Grossen Ax, A2 eine oder auch beide negativ sind, und in diesen
Fällen hat also die Gleichung zwei imaginäre Wurzeln.

§. 110. Das Jacobi'sehe Kriterium. 353
Sind aber At und A2 positiv, so ist die Entscheidung aus diesem
Satze allein nicht zu treffen; es ist dann nöthig, noch die Grosse
B = 9 a0 a3 — ax a2
in Betracht zu ziehen, und das Zeichen von
ZD = AxAs — B*
zu untersuchen (§. 68).
Im Falle der biquadratischen Gleichungen hat man die drei
Ausdrücke zu betrachten:
= 3af — 8a0a2,
Sind die Zeichen der Reihe nach 1 , so hat man vier
imaginäre Wurzeln. Sind die Zeichen alle drei positiv, so können
vier oder zwei oder keine imaginäre Wurzeln vorhanden sein;
in allen anderen Fällen hat man zwei oder vier imaginäre
Wurzeln.
§. 110.
Das Jacobi'sehe Kriterium.
Um die Anzahl der Wurzeln abzuschätzen, die zwischen
zwei Grenzen cc, ß liegen, hat Jacobi eiu Kriterium aus dem
Cartesischen Lehrsatz abgeleitet. Wenn nämlich
A) f(x) = 0
die vorgelegte Gleichung nten Grades ist, von der entschieden
werden soll, wie viele Wurzeln sie zwischen den beiden Grenzen
«, ß hat, so setzt Jacobi1)
x — et et -4- ßy
und bildet nun die Gleichung
C) (i + y*f(j^rf) = 9C/) = hr + hr-1 H \-K
worin die b0, b^ . . ., bn ganze homogene Functionen nUn Grades
von cc und ß und lineare Functionen der Coefficienten von f(x)
]) Observatiunoulae ad theoriam aequatiouum algebraiearum perti-
nentes. Crelle's Journal, Bd. 13. Gesammelte Werke, Bd. III.
Weber, Algebra. I. 23

354 Neunter Abschnitt. §. 111.
sind. Wenn nun x von a bis ß wächst, so geht y, gleichfalls
wachsend, von 0 bis co. So viele Wurzeln also fix) zwischen
a und ß hat, genau so viele positive Wurzeln hat cp (y).
Es folgt also aus dem Cartesischen Satz:
IX. Die Anzahl der Wurzeln von/(a;) zwischen k und ß
ist so gross oder um eine gerade Zahl kleiner,
wie die Anzahl der Zeichenwechsel in der Reihe
bw &n h, ¦ • -i bu.
Während also bei dem Budan'sehen Theorem die Vorzeichen-
Vorzeichenwechsel in zwei Werthreihen abzuzählen und zu vergleichen
sind, verlangt das Jacobi'sche Kriterium nur die Abzählung
der Vorzeichenwechsel in einer Werthreihe.
Auf dieselbe Weise lässt sich auch die Newton'sehe Regel
umgestalten, wenn man die Grossen
Br = v(n — v) b} — (y -\- 1) (n — v -\- 1) bv—ibr + i
in Betracht zieht, und man erhält so den Satz:
X. Die Anzahl der Wurzeln von/(a;) zwischen k und ß
ist so gross oder um, eine gerade Zahl kleiner,
wie die Zahl der Wechsel-Folgen in der Doppel-
Doppelreihe
§. 111.
Kleins geometrische Vergleichung der verschiedenen
Kriterien.
Um die Tragweite der verschiedenen Kriterien unter ein-
einander zu vergleichen, hat Klein eine geometrische Interpretation
angewandt, die wir jetzt besprechen wollen. Wenn man nicht
mit Räumen von mehr Dimensionen operiren und damit die
geometrische Anschauung verlieren will, muss man sich hierbei
auf die ersten Fälle beschränken, und wir beginnen also mit den
quadratischen Gleichungen
A) a;*'_|_ ax + b = 0.
Sehen wir a und b als rechtwinklige Coordinaten in einer
Ebene an, so ist jeder Punkt dieser Ebene das Bild einer und

§. 111. Geometrische Interpretation. 355
nur einer quadratischen Gleichung, und umgekehrt hat jede
quadratische Gleichung mit reellen Coefficienten einen Punkt der
Ebene zum Bilde.
Die Gleichung
B) a2 — 46 = 0
stellt eine Parabel dar, auf der die Bilder der Gleichungen mit
gleichen Wurzeln -liegen. Die inneren Punkte, d. h. die in der
Höhlung der Parabel liegenden, stellen die Gleichungen mit ima-
imaginären Wurzeln, die äusseren Punkte die Gleichungen mit reellen
Wurzeln dar.
Wir bilden nun nach §. 95 die Sturm'sehe Kette
C) x* -j- a x + 6, 2x + a, a* — 4 6,
und untersuchen die Zeichenwechsel. Ist x constant und a, 6
variabel, so ist
x2-\-ax-{-b = 0
die Gleichung der Parabeltangente in dem Punkte
a = — 2x, b = x2,
und zwar ist x2 -f- a x -\- b positiv in dem Theil der Ebene, der
zugleich die Parabel enthält.
Durch diese Tangente und durch die Parabel wird die
Ebene in vier Felder getheilt, in denen in der Reihe C), wie in
der Fig. 16 (a. f. S.) angedeutet ist, 0, 1, 2 Zeichen Wechsel vor-
vorkommen.
Wenn man also x = et und x = ß setzt, so erhält man
zwei solche Tangenten und eine Eintheilung der Ebene in vier
Felder, worin die repräsentirenden Punkte für solche Gleichungen
liegen, die zwischen es und ß keine, eine oder zwei Wurzeln
haben. In der Fig. 17 sind diese vier Felder durch die betreffenden
Ziffern gekennzeichnet.
Es ist der Unterschied zwischen solchen Punkten, von denen
aus keine, eine oder zwei Tangenten an die Parabel gezogen
werden können, die ihren Berührungspunkt zwischen a und ß
haben. Die Fig. 17 also giebt die genaue und vollständige
Unterscheidung der verschiedenen Fälle.
Vergleichen wir nun hiermit den Budan'sehen Satz, so
haben wir die drei Functionen /(#),/' (x),f"(x), also
D) x*-{-ax-{-b, 2x -f a, 1
in Bezug auf die Zeichenwechsel zu untersuchen.
23*

356
Neunter Abschnitt.
§• Hl.
Die beiden geraden Linien
x* -f- ax + 6 = 0, 2x -\- a = 0
theilen die Ebene in drei Felder, in denen die Reihe D) die in
der Fig. 18 angedeuteten Zeichenwechsel bietet.
Fig. 16. Fig. 17.
Nehmen wir wieder zwei Werthe x = « und x = ß, so
ergeben sich sechs Felder, in denen der Verlust an Zeichen-
Fig. 18. Fig. 19.
wechseln in der Fig. 19 angegeben ist. In den mit 0 und 1
bezeichneten Feldern giebt also der Verlust an Zeichenwechseln
•die richtige Anzahl von Wurzeln. In dem Felde 2 dagegen
ist die Entscheidung zwischen zwei und keiner Wurzel nicht
getroffen.

§. 111. Geometrische Interpretation. 357
Nehmen wir nun das Jacobi'sche Kriterium (§. 110).
Danach müssen wir, um die Anzahl der zwischen a und ß
gelegenen Wurzeln abzuschätzen, die Gleichung A) erst trans-
formiren auf
(« + ßyy + a(« + ßy) A + y) + 6A + y)» = 0,
oder
(ß' + «0 + 6) y* + [2 «/J + a (a + £) + 2 6] y
+ («2 + «« + &) = 0,
und es ist nun die Anzahl der Zeichenwechsel in den drei
Functionen
60 = j8» + O|8 + 6
&! = 2cc/3 + a(cc -f /3) -f 2&
&2 = cc2 -)- acc -(- b
abzuzählen. Der erste und der dritte dieser Ausdrücke stellen,
gleich Null gesetzt, die beiden vorhin betrachteten Parabel-
Parabeltangenten dar. Der mittlere, 2 a ß -\- a (a -\- ß) -\- 2 b, ver-
verschwindet für a = — 2 cc, b = ofi und für a = — 2/3, b = /32
stellt also die Verbindungslinie der beiden Punkte a, ß dar, und
zwar so, dass er auf die Seite, die den Schnittpunkt der beiden
Fig 20. Tangenten enthält, negativ wird [in diesem
Schnittpunkte seihst ist er gleich — (ß — ccJ].
Wir erhalten hier fünf Felder mit keinem,
einem oder zwei Zeichen wechseln, wie die
Fig. 20 angiebt.
Man sieht aus dieser und der vorigen
Figur, dass der Raum der Unentschiedenheit
bei Anwendung des Jacohi'schen Kriteriums ein Theil von dem
ist, der sich für das Budan-Fourier'sche Theorem ergiebt, und
dass also ersteres in diesem Falle vor letzterem den Vorzug ver-
verdient, entgegen einer Bemerkung von Jacohi, der dem Budan-
Fourier'schen Kriterium vor dem seinigen den Vorzug giebt.
Ob dies auch bei Gleichungen höheren Grades noch richtig ist,
bleibt freilich noch zu untersuchen1).
Um das Newton'sche Kriterium in der Form §. 110, X. auf
quadratische Gleichungen anzuwenden, hat man noch Bo, JBi, B2
J) Vgl. F. Klein, Geometrisches zur Abzahlung der reellen Wurzeln
einer algebraischen Gleichung in Dyck's Katalog mathematischer Modelle
(München 1892).

358 Neunter Abschnitt. §. 112.
zu bilden, von denen aber Bo, _B2 immer positiv sind, und daher
durch 1 ersetzt werden können. Für Bt ergiebt sich aber
(a2 — ib) (cc — ßy und man hat also die Anzahl der Wechsel-
Folgen in der Doppelreihe
b0, bu &2
1, B» 1
abzuzählen, was in diesem Falle die genaue Anzahl der Wurzeln
ergiebt.
§. 112.
Bestimmung einer oberen Grenze für die Wurzeln.
Wir haben schon im dritten Abschnitt von dem Satze Ge-
Gebrauch gemacht, dass man immer eine positive Zahl finden kann,
die grösser ist als die absoluten Werthe sämmtlicher Wurzeln
einer gegebenen Gleichung. Es kommt aber jetzt darauf an,
eine möglichst einfache und zugleich möglichst genaue Bestim-
Bestimmung einer solchen oberen Grenze zu geben.
Wir betrachten zunächst nur die reellen Wurzeln, und suchen
also eine positive Zahl, die grösser ist als die grösste positive
Wurzel einer gegebenen Gleichung f(x) = 0.
Eine solche Bestimmung giebt uns das Budan'sche Theorem.
Nehmen wir den Coefficienten der höchsten Potenz von x
in f{x) gleich 1 (oder wenigstens positiv) an, so kann man die
positive Zahl et immer so gross annehmen, dass
A) /(«),/»,/», •••,/«<»
alle positiv werden. Dann geht in der Eeihe der Functionen
f(x),f'(x),f"(x), ...,/<»>(*)
zwischen x = ot, und x = co kein Zeichenwechsel mehr verloren,
und es kann also auch nach dem Theorem I. (§. 107) keine Wurzel
von f{x) zwischen ot, und co liegen.
Will man aus dem gleichen Satze für die negativen Wurzeln
eine untere Grenze haben, so nehme man die positive Zahl ß so
an, dass
B) (_ 1)" /(_ ß), (- 1)—i /' (- ß), . . , /W (- ß)
alle positiv werden, dann hat die Gleichung f(x) = 0 sicher
keine negative Wurzel unter — ß.
Diese Bestimmung der Grenzen rührt schon von Newton her.

§. 112. Obere Grenze der Wurzeln. 359
Eine andere Bestimmung einer oberen Grenze, die für die
Eechnung einfacher ist, hat Laguerre angegeben1). •
Er benutzt statt der Ableitungen f(x), f'(x), f "(%)¦, • • • die
Functionen f0 (x), fx (x), /2 (%), . . ., fn-i (%), die wir schon mehr-
mehrfach, besonders in der Tschirnhausen-Transformation, gebraucht
haben.
Wir haben diese Functionen im §. 4 definirt durch
fo(x) =1
/i 0») = x + ax
A (x) = x2 -+- «! x + a2
a.2 x«~s -)
/(«) = /n («) = ^ + «1 a;n + «2 ^n~2 -|
und für sie die Eecursionsformel aufgestellt:
/r (ä) — Zfv-i C0) = «».
Man hat nun, wie schon an der angeführten Stelle ge-
gezeigt ist,
C) f{x) = (« — «) [«-*/, («) + a-»^ («) H h/U («)] +/(«).
Der Anblick dieser Formel zeigt, dass, wenn et eine Zahl
ist, die die Functionen
D) /o («), /i («), /, («), • • , fn-l («), /(«)
positiv macht, kein positives x grösser als a existiren kann, was
f(x) zu Null macht, da dann auf der rechten Seite von C) lauter
positive Glieder stehen.
Wenn also ein positives a so bestimmt ist, dass die Func-
Functionen D) alle positiv sind, so ist dies eine obere Grenze für
die positiven Wurzeln von f(x).
Ebenso erhält man eine untere Grenze —ß für die negativen
Wurzeln, wenn man die positive Grosse ß so bestimmt, dass
E) /, (- ß), -/i (- ß), A (- /*),••• (- !)n /(- ß)
alle positiv werden.
Diese Bestimmung der Grenzen ist zwar in der Eechnung
einfacher zu handhaben, giebt aber doch unter Umständen minder
genaue Grenzen als die Newton'sehe Bestimmung.
J) Laguerre, Nouvelles Annalesd.math., 2.ser., t.XIX, 1880. Journal
de math., 3. ser., t. IX, 1883.

360 Neunter Abschnitt. §. 113.
Wenn man nämlich C) fortgesetzt nach x differentiirt und
dann x = a setzt, so erhält man unter der Voraussetzung, dass
die Grossen D) alle positiv sind, für die Derivirten /' (x), f" (x), .. .
Ausdrücke, die für x = a aus lauter positiven Gliedern bestehen.
Wenn also die Ausdrücke D) positiv sind, so sind nothwendiger
Weise auch die Derivirten A) alle positiv, während das Um-
Umgekehrte nicht nothwendig der Fall ist.
Um eine obere Grenze für den absoluten Werth der ima-
imaginären Wurzeln, der auch für den Fall complexer Coefficienten
noch gültig ist, zu finden, betrachten wir die Function
worin die Coefficienten a15 a2, . . ., a„ reell oder imaginär sind.
Wir bezeichnen den absoluten Werth einer complexen Grosse a
wie früher durch |a| und haben dann, wenn wir annehmen, der
absolute Werth von x sei grösser als 1,
< I <h | + I «2 | H \- | «n | = «•
X ' ' Xn~^
Nehmen wir also x so an, dass sein absoluter Werth
grösser ist als jede der beiden Zahlen 1 und cc, so kann der
Ausdruck
nicht verschwinden, da der absolute Werth von x grösser ist, als
der absolute Werth der Summe aller übrigen Glieder der rechten
Seite.
Wenn wir also, je nachdem a grösser oder kleiner als 1
ist, einen Kreis mit dem Eadius et oder 1 um den Nullpunkt als
Mittelpunkt legen, so liegen ausserhalb dieses Kreises gewiss
keine Wurzeln von f(x) mehr.
§. 113.
Abschätzung der imaginären Wurzeln.
Wir haben im §. 103 gesehen, wie wir aus der Charakteristik
eines gewissen Curvensystems die genaue Anzahl der complexen
Wurzeln einer Gleichung bestimmen können, die im Inneren
einer geschlossenen Curve liegen. Auch dies Kennzeichen lässt

§. 114. Theorem von Kolle. 361
sich vereinfachen, wenn man nicht mehr die genaue Anzahl der
Wurzeln, sondern nur eine obere Grenze für diese Zahl finden
will, was in vielen Fällen auch zur genauen Bestimmung aus-
ausreicht.
Es sei also, wie in §. 103
A) F(z) = cp (x, y) + *> (x, y)
eine reelle oder complexe Function des complexen Arguments
z .= x -\- yi; darin seien cp und i> reelle Functionen von x und?/,
und es werde nun eine geschlossene Curve / gezeichnet. Wir
haben dann den Satz:
XL Wenn die Curve / durch die Curve cp in 2m
Segmente getheilt wird, in denen cp abwechselnd
positiv und negativ ist, so ist die Zahl der inner-
innerhalb / liegenden Wurzeln von F(z) höchstens
gleich m; und dasselbe gilt auch, wenn/ durch i>
in 2m solcher Segmente getheilt wird.
Der Satz ist eine unmittelbare Folge des Charakteristiken -
satzes §. 103; denn danach ist
und wenn nun die Curve / von der cp -Curve in 2» Punkten
geschnitten wird, so ist
also
h = m — A (f: qp, -ijj).
Darin ist aber nach dem erwähnten Satze h gleich der
Anzahl der im Inneren von / liegenden Wurzeln von F, und
A (f; cp, ifr) ist eine jedenfalls nicht negative Zahl. Ganz ebenso
kann man mit der Formel
verfahren.
§. 114.
Das Theorem von Rolle.
Wenn die Gleichung f(x) = 0 zwei reelle Wurzeln a und ß
hat, von denen die erste eine a-fache, die zweite eine 6-fache
ist, so können wir

362 Neunter Abschnitt. §. 114.
setzen.
Ist nun a < ß, und liegt zwischen a und ß keine Wurzel
von f(x) = 0, so wird/(x) und fx (x) in diesem ganzen Inter-
Intervall ein unverändertes Vorzeichen haben. Bilden wir von A)
die Ableitung, so ergiebt sich
(x-K) (X-ß)f(x)
B) W)
= a{x - ß) + b(x - «) + (x - «) {x - |8L^-
Die rechte Seite dieses Ausdruckes wird für x = cc negativ,
nämlich a(cc — /3), und für a; = ß positiv, nämlich b(ß — cc),
und muss also, während x von ot, bis /3 geht, einmal, oder allge-
allgemeiner eine ungerade Anzahl von Malen durch Null gehen. Auf
der linken Seite von B) haben (x — cc) {x — ß) und fix) ein
unverändertes Vorzeichen, und also muss f'(x) eine ungerade
Anzahl von Malen durch Null gehen. Daraus folgt das Rolle'sche
Theorem:
XII. Sind et und ß zwei auf einander folgende
Wurzeln von f (x) = 0, so liegen zwischen
k uttd ß (ohne die Grenzen mitzurechnen)
Wurzeln von f'(x) = 0 in ungerader Anzahl,
also mindestens eine.
Wichtige Folgerungen ergeben sich hieraus für den Fall, dass
die Gleichung f(x) = 0 nur reelle Wurzeln hat. Sind diese,
der Grosse nach geordnet, cc, ß, y,..., und ist cc eine a-fache, ß eine
&-fache, y eine c-fache etc. Wurzel, so hat f (x) = 0 in cc eine
(a — l)-fache, in ß eine (b — l)-fache, in y eine (c — l)-fache Wurzel
und zwischen cc und /3, zwischen ß und y u. s. f. je mindestens
eine reelle Wurzel. Die Gesammtzahl dieser Wurzeln ist aber
a —(— & —(— c —(-- • - - — 1 = n — 1,
und da f'(x) vom (n — l)ten Grade ist, so wird diese Minimalzahl
auch nicht überschritten. Daraus folgt der Satz:
XIII. Hat/(a;) = 0 nur reelle Wurzeln, so hat auch
f'(x)z=0 nur reelle Wurzeln, und von diesen
sind die, die nicht mit mehrfachen Wurzeln
von f (x) zusammenfallen, einfache Wurzeln,
die von den Wurzeln von fix) getrennt werden.

§. 114. Theorem von Kolle. 363
Wenn wir dies Theorem wiederholt anwenden, so können
wir es folgen denn aas sen verallgemeinern:
XIV. Hat f (x) nur reelle Wurzeln, so haben auch
f'(x), f"(x), f'"(x) . . . nur reelle Wurzeln. Hat
eine dieser Functionen/M(a?) eine a-fache Wurzel
«, und ist a > 1, so ist « eine (a-j-r)-fache Wurzel
¦vonf(x).
Diese Sätze werden wesentlich verallgemeinert, wenn man
eine lineare Transformation darauf anwendet*).
Dies wird leichter ausgeführt, wenn man die homogene
Schreibweise anwendet, also unter fix, y) eine ganze homogene
Function «ten Grades versteht. Bildet man für einen beliebigen
Werth £ : q die Polaren dieser Function (§. 66):
C)
nzf" (y,y,y)}
so bleiben diese Functionen ungeändert, wenn man f, vj und x, y
gleichzeitig durch eine lineare Transformation umformt, und für
/ und seine Ableitungen die entsprechenden transformirten Func-
Functionen setzt. In Bezug auf die Realität der Wurzeln wird durch
eine reelle lineare Transformation nichts geändert. Nun lässt sich
aber, wenn f, vj reell sind, die reelle lineare Substitution so be-
bestimmen, dass die transformirten Werthe f = 1, ij' = 0 werden,
und dadurch gehen, wenn man noch y = 1 setzt, die Polaren
in die Derivirten der Function f(x) nach x über (abgesehen von
Zahlenfactoren).
Daraus folgt, dass in den Sätzen XIIL, XIV. die Deri-
Derivirten/'^),/"^) ... durch die Polaren Pi(x,f), P2(a;,|) ...
für ein beliebiges, reelles |, v\ ersetzt werden können.
Wir machen hiervon die Anwendung auf die Gleichung, die
man erhält, wenn man die (n — 2)te Polare gleich Null setzt:
x) Laguerre, Nouvelles Annales de mathematiques, 2. Ser., Vol. 19,
1880.

364 Neunter Abschuitt. §. 115.
i, i) + 2 x yf (i, v) + rr {% n) = o.
Hat /(#,y) = 0, wie wir voraussetzen, nur reelle Wurzeln^
so muss auch die quadratische Gleichung D) reelle Wurzeln
haben, d. h. es muss die Hesse'sche Determinante
E) /"(!,£)/" A?, i?)-/"(^J
für alle reellen f, v\ negativ sein. Sie kann nur dann ver-
verschwinden, wenn D) zwei gleiche Wurzeln hat, und dies ist nach
XIV. nur dann möglich, wenn f(x,y) die nte Potenz einer linearen
Function ist. In diesem Falle verschwindet die Determinante
E) identisch. Wenn wir also von diesem Falle absehen, so folgt,
dass für eine Gleichung mit nur reellen Wurzeln die
Gleichung, die man durch Nullsetzen der Hesse'schen
Determinante erhält, nur imaginäre Wurzeln hat.
Wollen wir zur inhomogenen Darstellung zurückkehren, so
können wir mit Benutzung des Etrler'sehen Satzes
*/(*) + yf'(y) =»/(*)
F) xf" (x, x) + yf" (x, y) = (n- 1)/ (x)
*f (y, *) + yf" (y, ?) = (»- i)/' (y)
setzen, und damit /' (y), f" (x, y), f" (y, y) eliminiren. Man erhält
so, wenn man y = 1 setzt,
f(!t) =nf{x)-xf{x)
G) f'(x,y)= (n-l)f(x)-xf"(x)
f'(y,y) = n(n- \)f{x) - 2(» - \)xf(x) + ^/"D'
also wenn
(8) (n - 1) H(x, y) = /" (x, x) f" (y, y) - /" (x, y)*
gesetzt wird:
(9) H(x, y) = H(x) = nf(x)f" (x) - (n — 1)/' (x)\
H(x) ist in Bezug auf x höchstens vom Grade 2 n — 4.
§. 115.
Die Sätze von Laguerre für Gleichungen mit nur
reellen Wurzeln.
Von den zuletzt abgeleiteten Sätzen hat Laguerre eine
Anwendung auf Gleichungen mit nur reellen Wurzeln gemacht,
die wir noch keimen lernen wollen.

§. 115. Sätze von Laguerre. 365
Es sei f(x) = 0 eine Gleichung wten Grades mit n reellen
Wurzeln «, «l5 «2 . . ., die wir von einander verschieden vor-
voraussetzen.
Ist x eine veränderliche Grosse, so haben wir die schon
mehrfach angewandte Formel [§. 14, A1)]:
( ' \x — cc)~ f{x) '
worin sich das Summenzeichen S auf die verschiedenen Wurzeln
«, «i, «2) • • • bezieht. Wenn wir hiervon nochmals die Ableitung
nach x bilden, so folgt
K) (x — «J /(a;)«
und wenn wir auf der rechten Seite die Function H [§. 114, (9)]
einführen,
C) S X _f(xY-H(x)
Wendet man auf diese Formel eine lineare Transformation
an, bei der dem Werth x = co ein beliebiger anderer reeller
Werth der neuen Veränderlichen entspricht, so erhält man eine
allgemeinere Formel, die wir zunächst ableiten wollen. Wir
führen homogene Variable ein, indem wir x durch x : y und «
durch « : /3 ersetzen. Dadurch wird C)
nun wenden wir eine beliebige lineare Transformation an:
x = aa/ + &«/', « = aa' -\- bß',
() y=cx' + dy\ ß = ca!+dß',
oder aufgelöst:
rx1 = dx — by,
F) ry' = — cx -\- ay, r = ad — bc.
xß — ycc = r(x'ß' — y' k').
Wenn durch diese Transformation
f(x,y) = <p(x',y')
wird, so wird
rf'(x) = dcp'(x')-ccp'(y'),
und wegen der Covarianteneigenschaft der Function H (§. 65)

366 Neunter Abschnitt. §. 115.
wenn H' ebenso aus cp abgeleitet ist, wie H aus /. Hiernach
folgt aus D):
G) S
In dieser Formel können, da dies nur Sache der Bezeich-
Bezeichnung ist, bei x', y', «', ß', H' die Accente weggelassen und / an
Stelle von (p gesetzt werden. Es bleiben die beiden willkürlichen
Grossen c und d darin.
Setzen wir der eleganteren Bezeichnung wegen noch c = —17,
d = |, so erhalten wir also:
3 —i?«V__[g/(aQ
\xß-ya)- nf{x,yy
und in dieser Form bleibt sowohl die rechte als die linke Seite
vollkommen ungeändert, wenn wir auf die Variablenpaare x, y;
1,1?; «, ß gleichzeitig eine beliebige lineare Transformation
anwenden.
Die Formel (8) ist eine identische; sie gilt für jede Func-
tion f(x,y) und für alle Werthe der Variabelen x, y-, f, vj. Jetzt
aber machen wir die Voraussetzung, dass fix, y) nur reelle
Wurzeln habe, dass also die «, ß reell seien, und wir setzen
auch |, vi und x, y als reell voraus. Beide Seiten der Gleichung (8)
sind dann wesentlich positiv. Wir bezeichnen ihren gemeinsamen
Werth durch P, und bestimmen nun eine Grosse X : Y durch
die quadratische Gleichung
Xy - Yx
oder
(9) 9 =.(Xy — Yxy P — (Xn — Ff)» = 0.
Diese Gleichung hat zwei reelle Wurzeln, die man aus
Xri — 71 = ±]/P (Xy — Yx)
erhält. Ueber die Lage der Wurzeln dieser Gleichung können
wir aber Folgendes aussagen:
Setzen wir X = x, Y = y, so wird 9 negativ.
Setzen wir aber X = «, Y= ß, wenn a : ß irgend eine
der Wurzeln von / = 0 ist, so ist
,_ . _/f/»-fl«Y
\Xy - Yx)

§. 115. Sätze von Laguerre. 367
also gleich einem Gliede der Summe
und daher kleiner als P. Daraus folgt, dass <& für X : Y = « : ß
positiv ist.
Wenn wir nun die Werthe der sämmtlichen «: ß und x : y,
der Grosse nach cyklisch geordnet, etwa auf einem Kreise an-
anordnen, und den Werth X: Y durch einen variablen Punkt dieses
Kreises darstellen, und die betreffenden Punkte mit «, x, X
bezeichnen, so geht <& durch Null, wenn X von x aus nach vor-
vorwärts oder nach rückwärts bis zu den nächst gelegenen Punkten,
die wir mit «j und «2 bezeichnen wollen, geht. Sind also Xu X2
die Wurzeln der Gleichung (9), so haben wir folgende Anordnung
auf dem Kreise
A0) . «!, Xx, x, X2, «2,
und (Xj, X3) stellt ein Intervall dar, in dem zwar der
beliebig gewählte Punkt x, aber kein Wurzelpunkt der
Gleichung/== 0 liegt. Xt und X2 sind also den beiden
nächst gelegenen Wurzeln «l5 «2 näher als der Ausgangs-
werth x.
Dies gilt, welche Lage auch der zweite willkürliche Punkt |
haben mag. Es werden davon zwar die Punkte Xx, X2 abhängig
sein; immer aber werden sie in dem Intervall («,, x) und (x, a2)
liegen.
Es entsteht nun die Frage: wie ist der Punkt £ zu wählen,
damit Xj möglichst nahe an «x oder X2 möglichst nahe an «2
liege, oder vielmehr, da es auf die Kenntniss von £ selbst nicht
ankommt, welches ist der möglichst nahe bei «: gelegene Punkt
Xi und der möglichst nahe bei «2 gelegene Punkt X2?
Denken wir uns den Punkt X gegeben, so ist (9) eine
quadratische Gleichung für den Punkt f; zu jeder Lage von X
gehören also zwei Lagen von f. Aber nur solche Werthe von
Xj oder X2 sind in A0) zulässig, für die diese quadratische
Gleichung reelle Wurzeln ergiebt. Also nur solche Werthe von
Xj und X2 können vorkommen, bei denen die Discriminante
von (9) in Bezug auf £ positiv ist, und wir erhalten die Grenz-
Grenzlagen von Xj und X2, wenn wir die Discriminante von (9)
gleich Null setzen. Die Coefficienten von |2, 2fij, i?2 in (9)
sind aber

368 Neunter Abschnitt. §. 115.
?ä {Xy - Yxf -
und die Discriminante erhält man, wenn man von dem Quadrat
des mittleren das Product der beiden äusseren abzieht, nämlich,
mit Benutzung der Relation xf (x) -\- yfr(y) = »/:
K» - VE(Xy ~ Yx)* + [Xf(x)
und man erhält also die Grenzwerthe von X : Y aus der Gleichung
A1) [Xf (x) + Yf (j,)]» + (» - 1) (Xy - Yx? H = 0,
die in Bezug auf X : Y quadratisch ist. Hier steht H der
Kürze wegen für H(x, y).
Da H negativ ist, hat diese Gleichung zwei reelle Wurzeln,
die man aus
A2) Xf (x) + Yf (y) = ± (Xy - Yx) V(l - n) H
findet.
Diese Formel umfasst mehrere besondere Resultate, die man
erhält, wenn man die homogene Form verlässt.
Nehmen wir zunächst y = 0, also x : y unendlich und
setzen Y = 1, so ergeben sich zwei Werthe Xl5 X3, zwischen
denen die Gesammtheit aller Wurzeln von f(x) enthalten ist.
Setzen wir
f(x,y) = a^x» -\- aicr-iy -\- a2xn~2y^ -] ,
so wird
A3) H = [2na0 a.2 — (n — l)
und man erhält diese beiden Werthe aus
A4) «o, X — — ax + ]/(n — lJ«^ — 2n(n —
Lässt man x : y unbestimmt, kehrt aber zur inhomogenen
Form zurück, indem man y = 1, Y = 1 setzt und die Formeln
G) und (9) des §. 114 anwendet, so erhält man aus A2)
A5) x — X = nf{x)
K f(x)±]/{n~\ff(xy-n(n-l)f(x)f"{xy
und diese Werthe haben folgende Bedeutung:

§. 115. Sätze von Laguerre. 369
Liegt x zwischen zwei Wurzeln «j, «2 von f(x), so liegt von
den beiden durch A5) dargestellten Werthen von X der eine
näher an au der andere näher an «3, aber beide noch innerhalb
des Intervalles («x, «2).
Ist aber x grösser als die grösste, oder kleiner als die
kleinste Wurzel von f(x), so liegen die sämmtlichen Wurzeln
zwischen den beiden Werthen von X, während x ausserhalb liegt,
oder es liegt x zwischen den beiden Werthen von X, und alle
Wurzeln von f(x) ausserhalb. Liegt x nahe an einer Wurzel,
so giebt einer der beiden Werthe von X einen noch genaueren
Werth dieser Wurzel.
Wir nehmen als Beispiel (mit Laguerre) die Kugelfunc-
tionen, von denen wir schon früher (§. 93) nachgewiesen haben,
dass sie nur reelle Wurzeln haben, die alle zwischen — 1 und
-\- 1 liegen. Die Function
v . . 1.3...Bw —1) / n(n— 1) „ . \
p-(*> = i,2...» r-2B»-i)x + -)
hat die Eigenschaft, dass
2)
n { } ~ 8
ist. Man beweist dies leicht durch vollständige Induction, indem
man in den ersten Fällen n = 2, 3 ... die Formeln direct
nachweist, und dann aus der ßecursionsformel
A - x*)Fn(x) + nxPn(x) — nP^x) = 0
durch zweimalige Ableitung die Richtigkeit für den Index n nach-
nachweist, falls.sie für den Index n — 1 vorausgesetzt wird.
Wenn wir dann in A5) x — 1 setzen, so erhalten wir einen
Werth von X, der kleiner als 1, aber noch grösser als die
grösste Wurzel von P„ ist, nämlich
2
X= 1 -
n
Für n = 7 z. B. ergiebt sich
X = 0,94967 . . .
Weber, Algebra. I. 24

370 Neunter Abschnitt. §. 115.
Der genauere Werth der grössten Wurzel ist nach der
Berechnung von Gauss (Gauss' Werke, Bd. IIIj S. 195):
0,94911 . . .;
X zeigt also erst in der vierten Decimale den Ueberschuss über
den Werth dieser Wurzel.
Ebenso wie durch Xu X.2 ein Intervall bestimmt ist, in dem
gar keine Wurzel der Gleichung liegt, so kann man auch ein
Intervall bestimmen, in dem gewiss Wurzeln liegen. Auch hierbei
geht man am besten von der homogenen Form aus und benutzt
die lineare Transformation.
Sei also wie vorher f(x,y) eine Form n^11 Grades mit lauter
reellen Wurzeln; und seien ferner x : y, | mj, £' : vf drei reelle
Werthe, von denen zwei willkürlich sind, und von denen der
dritte durch die Eelation
[1/ (*) + nf (s/)] [IT (*) + n'f
von den beiden anderen abhängt. Die Gleichung A6) bleibt
ungeändert, wenn wir die drei Grössenpaare x, y; |, ij; f, vf
gleichzeitig derselben linearen Transformation unterwerfen. Daher
können alle Schlüsse, die wir aus einer speciellen Form dieser
Gleichung ziehen, verallgemeinert werden. Die lineare Substitution
lässt sich so bestimmen, dass für die neuen Variablen y = 0,
| = 0 wird; dann ergiebt A6) für £', vj' die Gleichung
oder also, wenn man a0 = 1, rf = 1 annimmt,
Es ist aber, wenn wir, wie oben, mit « die Würzein von /
bezeichnen,
a* — 2 a2 = 8(cc% ax = — S («);
also wird
Dafür lässt sich auch setzen:
iSf[«(«-|')] = O,
und daraus ergiebt sich, da alle « reell sein sollen, dass die

§. 115. Sätze von Laguerre. 371
Producte «(« — f) weder alle positiv noch alle negativ sein
können, oder mit anderen Worten, es muss ein Theil der Wurzeln
zwischen 0 und f', ein anderer Theil ausserhalb dieses Intervalles
liegen.
Daraus folgt nun durch Anwendung der linearen Trans-
Transformation allgemein, dass auf dem Kreise, der die Punkte
«, x, |, |' trägt, wenn f, f durch A6) verknüpft sind, in
jedem der beiden Theile, in die der Kreis durch f und
f getheilt wird, wenigstens eine der Wurzeln « liegt.
Der Punkt x und einer der Punkte f, f sind willkürlich; der
dritte Punkt ist durch A6) bestimmt.
24*

Zehnter Abschnitt.
Genäherte Berechnung der Wurzeln.
§. 116.
Interpolation. Regula falsi.
Mit der Abgrenzung der Intervalle, in denen nur je eine
Wurzel einer algebraischen Gleichung liegt, ist die Möglichkeit
gegeben, die reellen Wurzeln mit beliebiger Genauigkeit nume-
numerisch zu berechnen, indem man das Intervall mehr und mehr
einengt, z. B. fortgesetzt halbirt. Theilt man ein Intervall von
der Grosse 1 fortgesetzt in zehn Theile, so liefert jeder neue
Schritt eine weitere Decimalstelle.
Wenn einmal erst eine Wurzel von allen übrigen abgesondert
ist, so hat man bei der weiteren Einengung des Intervalles immer
nur das Vorzeichen der Function f(x) selbst zu berücksichtigen.
Die dazu nöthigen Rechnungen können sehr erleichtert werden
durch die Anwendung der Interpolationsformel, die wir im ersten
Abschnitt kennen gelernt haben.
Wir haben nämlich in §. 10, G) eine Formel hergeleitet, nach
der man eine Function wten Grades, die wir jetzt mit cp(!f) be-
bezeichnen wollen, bestimmen kann, wenn n -\- 1 auf einander
folgende Werthe cp @), cp A), . . ., cp (n) gegeben sind. Diese
Formel ist, wenn
A) ¦*' ~ 1 .2. 4 . .. v
4 = 9A + 1)-9A),
B)
4"-» =
gesetzt wird
4 =4+i — 4

§. 116. Eegula falsi. ' 373
C) <p (£) = <p @) + JoB? + ^Bf -f h 4—"^
Der Werth der Formel liegt darin, dass die Reihe der
Differenzen z/0, zT0, Zl'ö . . . in vielen Fällen so rasch abnehmende
Zahlenwerthe bietet, dass man sich mit einigen der ersten Glieder
der Reihe C) begnügen kann.
Ist nun f(x) die zu untersuchende Functioa und («, ß) das
Intervall, in dem eine der gesuchten Wurzeln liegt, so setzen
wir, indem wir unter m irgend eine geeignete ganze Zahl ver-
verstehen,
* ß — a i * t-
S = ^~> * = « + **
und wenn wir also
setzen, und die Formel C) auf qp(|) =f(x) anwenden,
D) f{x) =/(,) +^ (x - «) + § (X ~ K) ^-"-
Man könnte ebensogut auch von dem anderen Endpunkt ß
des Intervalles ausgehen, und müsste dann in C)
x = ß-d£
setzen. Man würde dann erhalten
4. =/(*-*)-/(*)
Wenn man die Gleichung
y =/(*)
als Gleichung einer Curve in einem rechtwinkligen Coordinaten-
system x, y deutet, so lassen sich die Verhältnisse geometrisch
veranschaulichen.
Wenn man z. B. die Gleichung D) auf das Intervall von « bis
(« -\- 8) anwendet und sich mit der Berücksichtigung der ersten
Differenz begnügt, so heisst das in der Sprache der Geometrie,
dass man den zwischen den beiden Curvenpunkten «, /(«) und
a -\- 8, /(« -j~ 8) verlaufenden Gurvenbogen durch die Sehne
ersetzt. Berücksichtigt man auch die zweite Differenz, so wird

374 Zehnter Abschnitt. §. 116.
der durch die drei auf einander folgenden Punkte mit den
Abscissen «, a -\- 8, a -j- 2 8 gehende Curvenbogen durch den
Bogen einer Parabel ersetzt, die durch dieselben Punkte geht
und deren Axe der Ordinatenaxe parallel ist; und diese Parabel
wird sich der Curve noch enger anschliessen als die Sehne. Je
kleiner das Intervall 8 ist, um so weniger werden die höheren
Differenzen von Einüuss sein.
Wie weit man also bei der Annäherung zu gehen hat, das
hängt nicht nur von der Genauigkeit ab , mit der man f(x) zu
kennen wünscht, sondern wesentlich auch von der Dichtigkeit
der Werthe «, « -)- 8, « -)- 2 8 . . ., für die die Function bekannt
ist. Auf diesen Sätzen beruht die Einrichtung unserer Tabellen-
Tabellenwerke, besonders der Logarithmentafeln. Es handelt sich dabei
freilich nicht um ganze rationale Functionen; allein bei den
stetigen Functionen überhaupt gelten hier dieselben Gesetze.
Man findet in den Tafeln daher auch neben den Werthen
/(«), /(« -f 8), /(« -\- 28) . . . die Werthe der ersten oder der
beiden ersten Differenzen angegeben. Bei den gebräuchlichen
siebenstelligen Tafeln genügt die erste Differenz. In der zehn-
stelligen Tafel „Thesaurus logarithmorum" von Vega sind auch
die zweiten Differenzen angegeben und müssen bei ganz scharfen
Rechnungen berücksichtigt werden.
Unsere Interpolationsformeln lassen sich mit Nutzen an-
anwenden, um die Wurzeln der Gleichungen-zu berechnen, oder,
genauer ausgedrückt, die auf anderem Wege gefundenen Nähe-
rungswerthe zu verbessern.
Wir können die Aufgabe so formuliren, dass zu einem
gegebenen, zwischen /(«) und /(« -\- 8) gelegenen Werth von
f(x) der zugehörige Werth von x gefunden werden soll.
Wir betrachten x = « als einen ersten Näherungswertli.
Setzen wir nun
/(*)-/(«) = 4
so ist, wenn die Function f(x) zwischen x = « und x = a -\-8
nur wächst oder nur abnimmt, z/ ein gegebener Werth von dem-
demselben Zeichen wie z/„ =f(a -\- 8) — /(«) und absolut kleiner
als z/„. Setzen wir noch x — « = w, so giebt die Formel D)
Bleiben wir zunächst bei der ersten Differenz stehen, so
ergiebt sich als erste Correction

§. 116. Eegula falsi. 375
G)
und wenn wir nun
= d 4- + «*'
setzen, so fQlgt aus F), wenn man im zweiten Gliede u' weglässt,
also als zweite Correction:
Die erste Correction G) erhält man dadurch, dass man den
zwischen « und « -j- 8 verlaufenden Curvenbogen durch die
Sehne ersetzt, wie oben, die zweite Correction (8) dadurch, dass
man den Bogen zwischen «, « -j- S, « -f- 2 8 durch eine Parabel
ersetzt, die durch dieselben Punkte geht, die aber jetzt ihre Axe
mit der x-Kxe parallel hat.
Nehmen wir als Beispiel die Gleichung
f(x) — xs — 2x — 2 = 0,
die zwischen 1,7 und 1,8 eine reelle Wurzel hat.
Man berechnet
x = 1,7, f(x) = — 0,487, zla — 0,719, Ja = 0,108
1.8, = -f 0,232, = 0,827,
1.9, = 1,059.
Da f(x) = 0 sein soll, so ist
J = 0,487
zu setzen und die erste Correction zu os = 1,7 ist nach G)
u = 0,06773,
die zweite Correction ergiebt nach (8)
u' = 0,00164,
also
« + u + u' = 1,76937.
Der auf andere Weise berechnete genauere Werth ist 1,76929...
Wir haben also ein in den ersten drei Decimalen genaues Re-
Resultat. Wir haben aber hier kein anderes Mittel, um die Genauig-
Genauigkeit von vornherein zu schätzen, als die Abnahme der Differenzen
J, /J\ J". . Ist J' so klein, dass es ausserhalb der Grenzen

376 Zehnter Abschnitt. §. 117
der beabsichtigten Genauigkeit fällt, so giebt die Berücksichtigung
der ersten Differenz ein genaues Resultat. Die hier aus einander
gesetzte Vorschrift zur Wurzelberechnung wird die Regula falsi
genannt.
Die einfachste, für die erste Annäherung geeignete Form
dieser Vorschrift ist die:
Liegt zwischen « und ß eine Wurzel« der Gleichung f(x) = 0
und ist f(a) = — a, f(ß) = b, so ist
(9) x = ^L±±t
ein genäherter Werth von x. Dies ist nur eine andere Schreib-
Schreibweise für die Formel G).
Die Newton'sche Näherungsmethode.
Eine Methode, die zur genäherten Berechnung der WTurzeln
einer Gleichung meist besser ist als die Interpolation, rührt von
Newton her und wurde von Fourier ausgebildet und genauer
untersucht.
Die Methode besteht einfach in Folgendem. Es sei
A /(*) = 0
die aufzulösende Gleichung und es sei ein Werth x = « ge-
gefunden, den man als eine gewisse Annäherung an eine Wurzel
betrachten kann. Wir setzen in A)
x = a -\- h,
und erhalten
/(« + h) =/(«) + hf («) + ^i /"(«) + ...
Wenn man nun h aus der Gleichung bestimmt
/(«) + */'(«) = 0,
was voraussetzt, dass /' («) von Null verschieden ist, so wird
und wird also, wenn h eine kleine Zahl ist, da nur das Quadrat
und höhere Potenzen von h vorkommen, einen kleinen Werth
haben. Es wird also unter den geeigneten Voraussetzungen

§. 117. Newton'sehe Näherungsmethode. 377
als eine bessere Annäherung an den wahren Werth der Wurzel
zu betrachten sein.
Ersetzt man dann « durch «', so wird man in
eine noch bessere Näherung erhalten u. s. f.
Es bleiben hier aber noch folgende beiden Fragen zu beant-
beantworten :
1. Unter welchen Voraussetzungen ist «' wirklich ein besserer
Werth als «?
2. Wie kann man den Grad von Genauigkeit schätzen, den
man so erreicht?
Diese Fragen hat Fourier beantwortet; er macht aber dabei
folgende Voraussetzung:
Es ist eine Wurzel von /(») in einem Intervall («, ß)
eingeschlossen, das keine zweite Wurzel enthält.
In dem Intervall («, ß) istf'(x) von Null verschieden
und/"(#) auch von Null verschieden.
Was die letztere Voraussetzung betrifft, dass /" (x) im Inter-
Intervall von Null verschieden ist, so ist sie nur gemacht, um ein-
einfacher auszudrückende Bedingungen für die Anwendung der
Methode zu erhalten. An sich ist ihre Brauchbarkeit bei genügen-
genügender Einengung des Intervalles davon nicht abhängig. Wenn aber
f(x) und /"(.«) keinen gemeinsamen Theiler haben, also nicht
zugleich verschwinden, so kann man die Fourier'sehe Voraus-
Voraussetzung durch Einengung des Intervalles immer erfüllen, und
wenn f(x) xmdf'(x) einen gemeinsamen Theiler haben, so kann
man diesen zuvor absondern und dann auf die einzelnen Factoren
von f(x) die Näherungsmethoden anwenden.
Am einfachsten übersieht man die Verhältnisse in der Geo-
Geometrie, wenn man y =f(x) als Gleichung einer ebenen Curve
in einem rechtwinkligen Coordinatensystem deutet.
Die Gleichung
C) y = /(«) + (* -«)/(«)
ist die Gleichung der Curventangente in dem Punkte «, /(«)
und die Newton'sehe Näherungsmethode kommt also darauf
hinaus, dass man die Curve in dem Interwall («, ß) in erster
Annäherung durch die Tangente in einem der Endpunkte ersetzt,
anstatt wie bei der Interpolationsmethode durch ihre Sehne.

378
Zehnter Abschnitt.
§¦ 117.
Wenn der zweite Differentialquotient in dem Intervall («, ß)
verschwindet, also die Curve einen Wendepunkt hat, so kann der
Fall eintreten, dass beide Endtangenten aus dem Intervall hin-
hinausführen; dann ist die Newton'sche Methode also nicht an-
anwendbar (Fig. 21). Es kann aber auch, wenn das Intervall («, ß)
schon genügend eingeengt ist, der andere Fall eintreten, dass
Fig. 22.
Fig. 21.
beide Tangenten nach inneren Punkten des Intervalles führen
(Fig. 22). Indessen wird in diesen Fällen immer die Regula
falsi eine bessere Annäherung geben.
Wir wollen aber jetzt annehmen, dass /' (x) und /" (x) in
dem Intervall («, ß) nicht verschwinden. Dann ändert die Curve
den Sinn ihrer Krümmung nicht, und dann hat gewiss immer
Fig. 23. Fig. 24.
eine der beiden Endtangenten ihren Schnittpunkt mit
der «-Axe im Inneren des Intervalles.. Dies trifft sicher zu, wenn
die Tangente in dem Endpunkte des Intervalles genommen wird,
in dem f(x) und f"{x) dasselbe Vorzeichen haben. Die
beiden Fig. 23 und 24 veranschaulichen das Verhältniss bei
positivem /' (x) und positivem und negativem /" (x).
Es ist also im ersten Falle ß', im zweiten «' ein besserer
Annäherungswerth, als ß und «.

§• 117.
Newton'sehe Näherungsmethode.
379
Will man gleichzeitig die andere Grenze verschieben, um
ein neues engeres Intervall zu bekommen, so kann man nach
Fourier von dem anderen Endpunkte, also iin Falle der Fig. 23,
in a die zu i ß' parallele gerade Linie ziehen, und erhält den
Punkt «' als unteren Grenzpunkt des neuen Intervalles. Es ist
dann im ersten Falle
* = --$5- ' = >-%!
im zweiten Falle
und («', ß') ist ein engeres Intervall, in dem die gesuchte Wurzel liegt.
Fig. 25.
Es ist kaum nöthig, die beiden
anderen Fälle, in denen fix) im Inter-
Intervall negativ ist, noch besonders zu
betrachten.
Man kann aber auch, um zwei
neue Grenzen zu erhalten, mit noch
besserem Erfolge die Newton'sehe
Methode mit der Interpolationsmethode
verbinden, wie die Fig. 25 zeigt.
Man erhält dann als die beiden
neuen Grenzen:
„, _ u /(")(/» ~ «) _ «f(ß) ~ ßf(«)
cc -— co —
lißl
f'iß)
ß' = ß-
Wir fassen die Resultate in folgendem Satze zusammen:
Ist ein Intervall («, ß) abgegrenzt, in dem/(a?)
einmal, /'(%) und /"(%) gar nicht ihr Zeichen
wechseln, und ist ß der Endpunkt des Inter-
Intervalles, in dem f(ß) und f"(ß) dasselbe Vorzeichen
haben, gleichviel, ob ß kleiner oder grösser als
« ist, so erhält man ein engeres Intervall («', ß')
von denselben Eigenschaften, wenn man
setzt.
/iß) -
riß)

380 Zehnter Abschnitt. §. 117.
Um diese Resultate der geometrischen Anschauung ana-
analytisch zu beweisen, nehmen wir an, es sei im Intervall f'(x)
und /" (x) positiv, also « < ß, und
/(«)<0, f(ß)>0.
Wir beschränken uns auf die Betrachtung dieses einen
Falles, da die drei anderen genau in derselben Weise zu be-
behandeln sind.
Wir bilden die Function
und deren erste Derivirte
Der Zähler dieses Ausdruckes
*(x) = -(ß- x)f{x) +/(/J) -f{x)
verschwindet für x = ß, und seine Derivirte ist
V(x) = -(ß-x)f'{x),
also im Intervall negativ. Daraus folgt, dass tyix) im Intervall
mit wachsendem x abnimmt und daher, weil es für den grössten
Werth x = ß verschwindet, positiv bleibt. Folglich ist auch
qp' ix) positiv und cp ix) wächst im Intervall mit wachsendem x
beständig. Wir haben demnach
« < x < ß.
Setzen wir nun
so wird
und nach E) folgt, dass diese Differenz positiv ist, also
u < «' < ß' < ß.
Setzt man dann in E)
x = a' und * = ß'
und beachtet, dass
ß ,j -(ß- *)f(ß) ß ß,

§. 117. Newton'sehe Näherungsmethode. 381
so ergiebt sich
/(«')<0, /(/?') >0.
Es ist also die gesuchte Wurzel zwischen et! und ß' enthalten,
und das Intervall (et1, ß') ist kleiner als (et, ß).
Setzen wir in diesen Ausdrücken «', ß' an Stelle von et,, ß,
so erhalten wir ein neues, noch engeres Intervall u. s. f.
Was die Convergenz dieses Verfahrens betrifft, so können
wir uns darüber folgendermaassen vergewissern. Wir setzen
nach F):
A\ ß' — K' — * fr- a\ —/08) </("> ~ fW + (ff - »)/'(fl){
V) ß-a~ *^W - (ß_ K)f(ß) {f(ß) _f{a}]
Zähler und Nenner sind hier durch (ß — «K theilbar, und
wenn wir den gemeinsamen Factor (ß —- et)'2 wegheben und f, rj
für et, ß setzen, so erhalten wir einen Ausdruck von der Form
worin i\I und i>2 ganze rationale Functionen der beiden Variablen
|, rj sind.
Ist x die im Intervall («, /3) gelegene Wurzel, so werden die
beiden Functionen r\)x und 4>2 nach unseren Voraussetzungen
über f(x) nicht gleich Null, wenn
(8) « < | < #, a; < m 5 /S.
Die Function <5 (|, ^) ist für | = «, ^ = ß, aber auch für
jedes andere Werthpaar in dem Intervall («, /S), wofür /(|)
negativ,/(ij) positiv ist, kleiner als 1, da jedes solche Intervall
(|, rf) an Stelle von («, ß) genommen werden könnte.
Da nun <&(f, ¦»?) eine stetige Function der beiden Veränder-
Veränderlichen |, rj ist, so lange diese in dem Bereich (8) bleiben, so
muss in diesem Bereich die Function 3>(f, r[) einen Maximum-
werth haben, und dieser muss kleiner als 1 sein, weil <&(£, rj)
auch noch in den Grenzfällen j- = %, rj = % kleiner als 1 bleibt.
Es lässt sich also ein positiver echter Bruch & angeben,
so dass
* (I, n) < ®
ist, so lange |, rj dem Bereich (8) angehören. Dann folgt aus G)
ß' — «' < (ß — os) &.
Ebenso folgt, wenn wir auf dieselbe Weise von dem Intervall
(«', ß') zu einem engeren Intervall («", ß") fortschreiten,

382 Zehnter Abschnitt. §. 117.
ß" — «" < (ß' — «') 8',
worin ®' dieselbe Bedeutung für «', /3' hat, wie & für «, ß. Da
aber «', ß' dem Bereich (8) angehören, so ist ©' nicht grösser
als & und statt &' kann anch & gesetzt werden. Es folgt also:
ß« _ «" <(£_«) @2;
und so schliessen wir weiter
ß(y) _ «W <(ß — a)®\
Die Intervalle nehmen also mindestens so stark ab, wie die
Glieder einer fallenden geometrischen Progression.
Als Beispiel mag die Gleichung dienen:
x* — 2 #2 — 2 = 0,
die eine Wurzel zwischen
« = 2,25 und ß — 2,36
hat.
Man erhält ausv den Formeln D) für
ß' = 2,35931 . . ., «' = 2,359298 . . .,
so dass ein in der vierten Decimale genauer Werth der Wurzel
2,3593
ist. Für diesen Werth selbst ist, wie eine genauere Rechnung
ergiebt, f(x) noch negativ, so dass er für a' genommen werden
kann. Der nächste Schritt der Annäherung ergiebt
2,359304.
Auf demselben Princip, das der Newton'schen Auüösungs-
methode zu Grunde liegt, beruhen auch die Methoden von
W. G. Horner und Joseph Horner, die wir hier nur erwähnen
können. Bei beiden ist das Ziel eine zweckmässige Anordnung
der Rechnung, und, besonders in der ersten, ein dem dekadischen
Zahlensystem angepasster Algorithmus, nach Analogie der
Divisionsregeln der niederen Arithmetik. Ein schnelles und
sicheres Rechnen nach diesen Methoden erfordert viel Uebung1).
l) W. Gr. Horner, A new method of solving numerical equations of
all Orders, by continuous approximation. Communicated by Davies Gilbert.
Philosophical Transactions 1819. Joseph Horner, Approximation to
the roots of algebraic equations in a series of aliquot parts. Quarterly
Journal of Mathematies, Vol. III, 1860.

§. 118. Bernoulli'sehe Näherungsmethode. 383
Die Näherungsmethode von Daniel Bernoulli und
verwandte Methoden.
Die Methode zur genäherten Auflösung einer Gleichung, die
von Daniel Bernoulli herrührt1), beruht darauf, dass, wenn
man eine Reihe reeller Grossen hat, die Potenzen der grössten
unter ihnen um so mehr die gleich hohen Potenzen der übrigen
überwiegen werden, je höher die Potenzen sind.
Sind a, ß, y . . . beliebige reelle oder complexe Grossen,
so jedoch, dass der absolute Werth von a grösser ist, als der
absolute Werth aller übrigen, dass also die absoluten Werthe
der Brüche ß:u,y:a... echte Brüche sind, so ist
V ) „m —1 _U Rm—l I „,m— 1 I
und je grösser m wird, um so mehr wird sich dieser Ausdruck
wie die zweite Darstellung zeigt, der Grenze oc nähern.
Sind a, ß, y . . . die Wurzeln einer algebraischen Gleichung,
so ist die linke Seite von A) der Quotient der wten und (m — l)ten
Potenzsumme, und wir erhalten also den Satz:
Der Quotient der mtea und (m — l)ten Potenz-
Potenzsumme nähert sich mit wachsendem m der absolut
grössten unter den Wurzeln.
Nimmt man m negativ an, und setzt a absolut kleiner als
ß, y . . . voraus, so folgt auf die gleiche Weise:
Der Quotient der — wten und — (m -j- l)*?n
Potenzsumme nähert sich mit wachsendem m der
absolut kleinsten unter den Wurzeln.
Da man die Potenzsummen als symmetrische Functionen
durch die Coefficienten berechnen kann, so braucht man nur ein
hinlänglich grosses m zu nehmen, um einen angenäherten Werth
der absolut grössten und absolut kleinsten Wurzel zu erhalten.
D. Bernoulli, Commentationes Petropolitanae. Bd. III.

384
Zehnter Abschnitt.
§. 118.
Wenn aber unter den Wurzeln der Gleichung solche vor-
vorkommen, die denselben absoluten Werth haben, und dieser der
grösste oder der kleinste ist, so ist diese Methode nicht anwend-
anwendbar, also z. B. nicht auf reelle Gleichungen, bei denen ein Paar
imaginärer Wurzeln vorkommt, das die reellen an absolutem
Werth übertrifft.
Wenn aber die grösste Wurzel zwar einzeln vorkommt, aber
die nächstfolgende nicht viel übertrifft, so wird das Verfahren
nur langsam einige Genauigkeit geben.
Jacobi hat die Bernoulli'sche Methode nach einer Rich-
Richtung ergänzt1).
Nehmen wir an, es seien
unter den Wurzeln xlt x2, . ¦ ., xn solche, deren absolute Werthe
grösser sind, als die absoluten Werthe der folgenden xk+1, xk+2,
. . ., x„ und setzen
B) Pm + 1 =
so werden, wenn wir
C) (x — Xi) (x — x2)... (x — xk) = x* -f- AiX^~x -\- • • • -|- Ak
setzen, die Coefficienten Au A2, . . ., Ak den Gleichungen genügen
t-fc—a A2-f~-
t-fc-i A2-\--
Wenn man den Gleichungen D) noch die Gleichung
x* + A^-1 + A«*-2 H \- Ah = 0
zugesellt und die Ax, A2, . . ., Ak eliminirt, so ergiebt sich die
Gleichung fcten Grades ¦
x*, x*-*, ... 1
Pm + hi Pm + k—1) ' ' - Pm.
Pm+k + li Pm + lci ' * • Pm + 1
+ 2k—li
Pm + k — 1
Observatiunculae etc. Werke, Bd. 3, S. 280.

§. 118. Bernoulli'sche Näherungsmethode. 385
deren Wurzeln xu x2, -...,#& sind. Die Grossen pm, pm+i, . . .,
können aber mit um so grösserer Genauigkeit durch, die ent-
entsprechenden Potenzsutnmen aller Wurzeln ersetzt werden, je
grösser m ist.
So bekommt man z. B. für Je = 2:
a _j_ PmPm + S — Pm+lPm + 2 , pli + 2 —Pm+lPm+3 __ q
Pm + 1 — PmPm+2 Pm + 1 — PmPm + 2 ' ~ '
eine Gleichung, die man anwenden kann, wenn bei einer reellen
Gleichung ein Paar conjugirter Wurzeln den absolut grössten
Werth haben.
Wenn man die Bernoulli'sche Methode auf die Summe
der negativen Potenzen anwendet, so erhält man, wie schon
bemerkt, eine Annäherung an die absolut kleinste Wurzel. Man
kann aber, durch Verlegung des Anfangspunktes, jede Wurzel'
zur absolut kleinsten machen, wozu freilich die Kenntniss eines
bis zu einem gewissen Grade genäherten Werthes nöthig ist.
Eine Formel, die für alle Fälle ausreicht, hat Fr. Meyer
gegeben !). Es seien c^, a2, us, . . ., a„ die Wurzeln der Gleichung
f(x) = 0, die reell oder imaginär sein können. Man suche einen
Punkt p in der «-Ebene, so dass sich um p als Mittelpunkt ein
Kreis beschreiben lässt, der nur einen der Punkte aua2, . . ., ccn
enthält, etwa den Punkt al5 dass also die absoluten Werthe von
E) i> — «i p — «i p — «t
p — a2 ' p — a3 ' ' ' '' p — un
echte Brüche sind. Solche Punkte existiren immer; sie müssen
nöthigenfalls nach der Sturm'sclien Methode gefunden werden.
Wählt man ausserdem noch eine beliebige Function cp (x), die
mit f(x) keinen gemeinsamen Theiler hat, z. B. q>{x) = 1, und
bildet die symmetrischen Functionen
«i f («i) _j_ «2 9 0*2) 1 1 «tt 9 («»)
_ (p — <*i)m "*" (p — «,)»  *" (p — «.)"
* (p — «)m "•" '
(p — axy * (p —
so nähern sich diese mit wachsendem w der Grenze «i, und zwar
um so schneller, je kleiner die absoluten Werthe der Brüche E)
bereits sind.
!) Mathematische Annalen, Bd. 33.
Weber, Algebra. I. 25

386 Zehnter Abschnitt. §. 119.
Die Richtigkeit hiervon zeigt sich sofort, wenn man die
Formel F) in der Weise schreibt:.
^ |-
Wir wollen schliesslich noch auf die neueren Untersuchungen
von Fr. Cohn hinweisen, in denen diese Methoden der näherungs-
näherungsweisen Lösung algebraischer Gleichungen weiter ausgebildet und
auch nach der functionentheoretischen Seite hin untersucht
sind !).
§. 119.
Die Näherungsmethode von Gräffe.
Auf einem ähnlichen Gedanken, wie die Bernoulli'sche
Näherung, beruht auch ein Verfahren, das von Gräffe an-
angegeben und von Encke weiter ausgebildet ist2), und das sich
besonders zu einer praktischen Durchführung der numerischen
Rechnungen eignet.
Sind, wie oben, a, ß,y ... die Wurzeln einer Gleichung und
ist a die absolut grösste unter ihnen, so dass keine der anderen
der Wurzel a an absolutem Werth gleichkommt, so hat
A) y«m + ßm -f- y
mit unbegrenzt wachsendem m den Werth a zur Grenze; es ist
sogar die Convergenz gegen a noch besser, als bei dem im
vorigen Paragraphen betrachteten Quotienten
Mm _|_ ßm, _J_ ym _|_ . . .
um-l _J_ ^m-i _|_ ym-1 _J_ . . .'
wie man erkennt, wenn man nach dem verallgemeinerten binomi-
binomischen Lehrsatz:
J) Fr. Cohn, Ueber die in recurrirender Weise gebildeten Grossen
und ihren Zusammenhang mit den algebraischen Gleichungen. Mathe-
Mathematische Annalen, Bd. 44 A894).
2) Gräffe, Die Auflösung der höheren numerischeu" Gleichungen,
als Beantwortung einer von der Berliner Akadamie gestellten Preisfrage,
Zürich 1837. Encke: Crelle's Journal, Bd. 22 A841).

§. 119. Gräffe'sche Näherungsmethode. 387
j
setzt.
Die absolut kleinste unter den Wurzeln erhält man nach
demselben Princip als Grenzwerth von
B)
+ + +
m ' ßm- ytn >
und wenn p ein beliebiger Werth ist, so erhält man die dem
Werth p am nächsten liegende Wurzel als Grenzwerth von
C) p
L
(u — p)m (ß — p)m
Wenn man die Gleichung f(x) durch die Substitution
_ 1 __ 1
transformirt, so gehen die Ausdrücke B), C) aus dem Ausdruck
A) hervor, auf den wir uns daher jetzt beschränken wollen.
Wendet man die Formel A) auf eine reelle Gleichung an,
so ist am -\- ßm -\- ym -(-... eine reelle Zahl; und wenn die
absolut grösste Wurzel oc reell ist, so ist auch die mie Wurzel
reell zu nehmen. Ist aber m eine gerade Zahl, so muss man,
um über das Vorzeichen zu entscheiden, noch wissen, ob « positiv
oder negativ ist. Nöthigenfalls wird darüber durch Einsetzen
des gefundenen Näherungswerthes in die gegebene Gleichung
entschieden.
Ebenso wird man, wenn man die Formel A) auf eine ima-
imaginäre Gleichung anwendet, entscheiden müssen, welche der ver-
verschiedenen wten Wurzeln die richtige Annäherung giebt.
Die Ausdrücke
sm = «» -\- ßm -f- y» -f . . .
lassen sich besonders einfach dann berechnen, wenn man für m
die auf einander folgenden Potenzen von 2, also m = 2, 4,8,16...
setzt, und liefern dann sehr gute Resultate.
Es ist s2 der negative Coefficient der (w — l)ten Potenz der
Unbekannten in der Gleichung, deren Wurzeln die Quadrate der
25*

388 Zehnter Abschnitt §. 119.
Wurzeln von f(x) sind. Diese Gleichung wird aber leicht auf
folgende Weise gebildet.
Man fasse in fix) die Glieder mit geraden und mit ungeraden
Potenzen von «zusammen und setze demnach
f{x)= <p(x*)-\-xil>(x*).
Es ist dann
fx («) = y (xy — xip (xy = o
die Gleichung, deren Wurzeln die Quadrate der Wurzeln von
fix) sind. Behandelt man ft(x) ebenso, so erhält man eine
Gleichung, deren Wurzeln die vierten Potenzen der Wurzeln von
f{x) sind u. s. f.
Die Ausführung dieser Rechnung ist sehr einfach und führt
oft nach wenigen Schritten zu einer guten Näherung.
Wir betrachten einige Beispiele.
Zunächst nehmen wir die Gleichung
D) . «3 — 2x — 2 = 0,
die eine reelle positive und zwei imaginäre Wurzeln hat. Die
reelle Wurzel ist grösser als 1,7, und da das Product aller drei
Wurzeln gleich 2 und A,7K > 2 ist, so ist der absolute Werth
der beiden imaginären Wurzeln kleiner als die reelle Wurzel.
Also ist die reelle Wurzel die absolut grösste und die Gräffe'-
sche Näherungsmethode muss auf sie führen. Man bekommt nun
die Gleichungen, deren Wurzeln die zweite, vierte, achte... Potenz
der Gleichung D) sind:
xs — 4x2 -\- £x — 4 = 0
x?' — 8x* — lßx — 16 = 0
xz — 96 «2 — 162 = 0
und
x = ^96 = 1,7692 . . .
ist bereits ein in den vier ersten Decimalen genauer Werth.
Der nächste Schritt würde kein anderes Resultat ergeben (weil
die erste Potenz der Unbekannten in der letzten Gleichung fehlt);
aber der darauf folgende ergiebt den in der sechsten Decimale
genauen Werth
32
x = V85032960 = 1,769293 . . .
Wir wollen noch ein zweites Beispiel- einer Gleichung fünften
Grades betrachten, das Gelegenheit bietet, mehrere der Sätze
des vorigen Paragraphen anzuwenden. Das Beispiel ist, wie die

§. 119. Grräffe'sehe Näherungsmethode. 389
früheren, der Theorie der complexen Multiplication der ellipti-
elliptischen Functionen entnommen. Es ist die Gleichung fünften
Grades
E) «5 _ #3 _ 2 ä>a. — 2x — 1 = 0.
Wir leiten daraus die Gleichung ab, deren Wurzeln die
Quadrate der Wurzeln von E) sind, indem wir in
{x= — x* — 2x)<* — Bx* -\- l)^ = 0
x2 durch x ersetzen. Dies giebt
F) x* — 2x* — 3«s _ i = o,
und wenn wir dasselbe Verfahren zunächst noch zweimal anwenden,
so erhalten wir die Gleichungen, deren Wurzeln die vierten und
achten Potenzen der Wurzeln von E) sind:
G) x= — 10a* + 9«s _ 4^2 _ x = o,
(8) x= — 82** + x* — 36«2 — 8x— 1 = 0.
Die letzte dieser Gleichungen eignet sich zur Discussion.
Sie hat nach dem Cartesischen Lehrsatz (§. 109) wenigstens eine
positive Wurzel; und da die linke Seite von (8) für x = 1
negativ ist (= — 125), während sie für ein unendlich wachsen-
wachsendes x positiv wird, so hat (8) eine reelle Wurzel, die grösser
als 1 ist.
Wenn wir für die Gleichung (8) die in dem Newton'sehen
Kriterium (§. 109) vorkommenden Functionen
1, 4 al — 10 a0 a2, 6 af — 12 ax as
6a|— 12a2at, 4a| — 10% a5, 1
bilden, so erhalten wir die Vorzeichen
+ + - + - +
und (8) hat also nach §. 109, Lehrsatz VIII. vier imaginäre
Wurzeln. Die positive Wurzel ist jedenfalls grösser als 1, da die
linke Seite von (8) für x = 0 und x = 1 negativ ist.
Um nun zu entscheiden, welche der Wurzeln den grössten
absoluten Werth hat, wollen wir in (8) x = 1 : z setzen, und
dann nach §. 103, 104 untersuchen, wie viele Wurzeln im Inneren
des Einheitskreises in der 5-Ebehe liegen. Setzen wir also in
£5 -)_ 8 0i + 36 £3 _ zi -|_ 82 s — 1
g = cos fr -f- «sin ¦fr, so erhalten wir den reellen und imaginären
Theil:

390 • Zehnter Abschnitt. §. 119.
cp = cos 5 fr -\- 8 cos 4 fr -j- 36 cos 3 fr — cos 2 -9- -|- 82 cos fr — 1
ip = sinö-ö1 + 8 sin4'9i -f 36 ainZfr — sin2# -|- 82 sin«-.
Es lässt sich nun zeigen, dass i\> positiv ist, wenn 0 < fr < n
und folglich negativ, wenn 0 > fr > — jt, dass also der Einheits-
Einheitskreis in zwei Segmente getheilt ist, in denen i/> entgegengesetzte
Vorzeichen hat. Daraus folgt nach §. 113, XL, dass im Inneren
des Kreises nur eine Wurzel liegen kann, und dies ist die reelle
Wurzel, während die imaginären Wurzeln ausserhalb liegen. Es
folgt dann daraus für die Gleichung (8), dass die reelle Wurzel
den grössten absoluten Werth hat, und dass also dieser durch
die Gräffe'sche Methode gefunden wird.
Um nun diese Eigenschaft der Function i/> nachzuweisen,
setzen wir 2coS'9i = §, und wenden die goniometrischen For-
Formeln an:
sin5# = sin#(£4 — 3 & + 1)
sin 4-fr = sin fr (§3 — 2 §)
sin 3 & = sin fr (§a — 1)
sin 2 fr = sin fr §.
Dadurch erhalten wir
1> = sin#[£* + |»(8| + 33) + D7 - 17$],
woraus man. sofort sieht, dass der Factor von sin fr positiv bleibt
so lange § zwischen — 2 und -|-2 liegt.
Die Gleichung (8) giebt nun selbst schon einen ziemlich
guten Näherungswerth für die reelle Wurzel
x = f 82 = 1,73471.
Ein genauerer Werth, den man erhält, wenn man noch zwei
Schritte weiter geht, ist 1,73469, der in der fünften Decimale
noch richtig ist.
Eine Einschliessung der gesuchten Wurzel in zwei Grenzen
giebt diese Methode nicht. Das Kennzeichen, ob ein genügender
Grad von Genauigkeit erreicht ist, besteht darin, dass, wenn su,
Sp zwei auf einander folgende, zur Berechnung benutzte Potenz-
Potenzsummen der Wurzeln sind, diese sich mit genügender Genauigkeit
verhalten, wie die ftte zur (i'tea Potenz einer Grosse, oder dass
annähernd
ftlogv — (i'logsu = 0
ist. Man muss aber diese Prüfung bei mehreren auf einander

§.120. Cubische Gleichungen. 391
folgenden Gliedern vornehmen, da in besonderen Fällen diese
Relation scheinbar erfüllt sein kann und bei der späteren Rech-
Rechnung wieder aufhört.
§; 120.
Trigonometrische Auflösung cubischer
Gleichungen.
Wir besprechen nun noch einige auf Gleichungen von
speciellen Formen anwendbare Methoden der numerischen Auf-
Auflösung. Das Ziel dieser Methoden ist, die allgemein verbreiteten
Tafeln der trigonometrischen Functionen und der Logarithmen
für die Auflösung von Gleichungen nutzbar zu machen. Wir
wenden uns zunächst zur Betrachtung der cubischen Gleichungen,
die wir immer in der reducirten Form
A) «s + ax -\-b = 0
annehmen, worin a und b reelle Zahlen sind. Da die Ver-
Vertauschung von x mit — x gleichbedeutend ist mit der Ver-
Vertauschung von b mit —b, so können wir uns auf die Annahme
beschränken, dass b negativ sei, und es bleiben dann noch drei
verschiedene Fälle zu betrachten. Wir setzen b = — g und, je
nachdem a positiv oder negativ ist, a = ^z e. Dann haben wir
a) xs -f- ex — g = 0
b) x* — ex — g = 0, J < 17
c) x* — ex — g = 0, 27 > T '
Die Grenzfälle, dass eine der Grossen e, g, 4e3 — 27g'} ver-
verschwindet, schliessen wir aus.
Um die Cardanische Formel anzuwenden (§. 38), setzen wir
wo das obere Zeichen im Falle a), das untere in den Fällen b)
und c) gilt. In den Fällen a) und b) ist nur eine Wurzel reell,
in dem Falle c) (dem Casus irreducibilis) sind alle drei Wurzeln
reell. Die Cardanische Formel giebt
* = yi + v* +
'V f -

392 Zehnter Abschnitt. §. 120.
Wir verfahren" nun so in, den drei Fällen:
a) Wir führen einen Winkel -91 ein, den wir zwischen 0° und
90° wählen können, durch die Gleichung:
also
*= V-rlV*»tg* + ;^5+ Ucotgtf-
* VA »\
-^ — y tg -;,
und wenn wir noch einen Winkel cp aus
E) tg — = tg qp3
bestimmen, so ergiebt sich
F)
Die Winkel ¦81, 9 und zuletzt « findet man aus den logarith-
logarithmisch trigonometrischen Tafeln nach den Formeln D), E), F).
Um die imaginären Wurzeln zu erhalten, ersetzt man tgcjp
durch q tg (p, wenn p eine imaginäre dritte Einheitswurzel
bedeutet.
b) Im zweiten Falle bestimmen wir den Winkel &, gleich-
gleichfalls im ersten Quadranten, aus
2 V 27 sin«-
cotg®
x = \/ —
(8)
(9) "-"fl sin~T,
c) Im letzten Falle endlich, wo drei reelle Wurzeln vor-
vorhanden sind, setzen wir

§. 121. Trinomische Gleichungen. 393
x = l/-|- (j^cos fr -j- i sin fr -{- ]fcos# — i sin fr),
oder nach dem Moivre'schen Satze:
A1) x = 2 Vir cos i- *•
Nimmt man ¦£>• wieder im ersten Quadranten, so erhält man
für die beiden anderen gleichfalls reellen Wurzeln
x-{-& Afe x — fr
OS- -2)/ycos^—•
Alle diese Formeln sind für die logarithmische Rechnung
eingerichtet.
§. 121.
Die Gauss'sche Methode der Auflösung trinomischer
Gleichungen.
Gauss hat eine Methode angegeben, um die Wurzeln einer
Gleichung, die nur drei Glieder enthält, in einfacher Weise
numerisch aufzulösen. Solche Gleichungen kommen häufig vor
und umfassen als Specialfälle alle quadratischen und die redu-
cirten cubischen Gleichungen.
Es wird zunächst von einer solchen Gleichung, deren all-
allgemeine Form
A) xm+n -j- ax™ -\- b = 0
ist, nur die positive Wurzel, wenn sie existirt, gesucht. Die etwaige
negative ergiebt sich, wenn man x durch —x ersetzt.
Nach den Vorzeichen von a, b hat man drei Fälle zu unter-
unterscheiden, da, wenn beide Vorzeichen positiv sind, keine positive
Wurzel vorhanden ist. Wir betrachten also, indem wir mit e
und g positive Zahlen bezeichnen, die drei Fälle:
a) xm+n + exm — g = 0,
b) xm + n — exm — g = 0,
c) a^ + n — exm -\- g = 0.

394 Zehnter Abschnitt. §. 121.
n den beiden ersten Fällen haben wir nach dem Cartesi-
schen Lehrsatz je eine positive Wurzel, im dritten können zwei
oder keine positive Wurzel vorhanden sein.
Wir setzen nun mit Gauss
und suchen die drei Gleichungen a), b), c) durch passende Sub-
Substitutionen auf die Form:
sin2 © -f- cos2 © = 1
zurückzuführen. Wir setzen:
„ xm + n . ^ e%m ^ i- sin@2m
= sin ©2, = cos ©2, l =
9 9
sin ©2m
B) b) gx-™-» = sm@*, ex~» = cos©2, * =
c) — = sin ®\ y—— = cos ©2, l — sin©2mcos©2«.
} e e
Die letzte Gleichung ergiebt die Unterscheidung der beiden
Fälle, in denen die Gleichung c) zwei oder keine positive
Wurzel hat.
Man erhält nämlich für das Maximum von sin@2mcos@2K
nach den Regeln der Differentialrechnung
mmnn
(m 4- w)m+K'
das für tg©2 = m : n erreicht wird. Wenn also l unter dieser
Grenze liegt, so haben wir in c) zwei reelle Wurzeln, sonst
keine. In den Formeln B) ist l eine gegebene Grosse, und man
hat nun aus den Tafeln den Winkel © zu suchen, der diesen
Gleichungen genügt. Wenn man. noch gar keine Kenntniss über
die ungefähre Lage dieses Winkels hat, so ist es zweckmässig,
für die erste Annäherung eine etwa von Grad zu Grad fort-
fortschreitende, auf zwei Decimalen abgekürzte Tafel zu benutzen,
um den so gefundenen Werth mit Hülfe genauerer Tafeln zu
verbessern.
Gauss benutzt nicht die trigonometrischen Tafeln, sondern
die von ihm zuerst eingeführten Additions- und Subtractions-
Logarithmen. Wir wollen dies an einem der Fälle in der Kürze

§. 121. Trinomisohe Gleichungen. 395
zeigen. Die Einzelheiten für die praktische Anwendung der
Methode sind in der Gauss'schen Abhandlung zu suchen1).
Die Tafeln der Additions- und Subtractions-Logarithmen,
wie sie zuerst von Gauss eingeführt und berechnet sind, und
wie sie sich jetzt auch in den gebräuchlichen Tabellenwerken
finden, geben zu drei Zahlen, die grösser als 1 sind:
a, b = 1 -| , c = 1 -f- a,
et
die Brigg'schen Logarithmen:
A, B, C.
Ist © ein Winkel im ersten Octanten, so kann man setzen:
C)- a — cotg ©2, b = —l—, c = -^-~, 0 < © < 45°,
v J s ' cos @2' sin @2' '
und wenn © im zweiten Octanten liegt:
D) a = tg ©2, b — —^ c = —17^, 45« < © < 9Oo.
v J ö ' sin @2' cos ©2
Wir wollen dies auf den Fall b) anwenden; dabei ist zu
unterscheiden, ob l kleiner oder grösser als 2m ist, weil davon
abhängt, ob © im ersten oder zweiten Octanten liegt. Es sind
also wieder zwei Fälle zu unterscheiden:
«) l < 2m,
fom j^m foni -}- n
an am+n cn '
E) xm+n — gc, xn = eb, od = — •
ß) A>2»
a + b = ac = —;—,
bn
» = gb, xn = ec, xm = —•
ß O)
Im Falle «) würde man also
F) log l = m B — n Ä
setzen und danach aus der Tafel die zusammengehörigen Werthe
von A und B aufsuchen. Hat man diese gefunden, so ergiebt sich
G) mlogx = A -\- logg — löge.
1) Beiträge zur Theorie der algebraischen Gleichungen, zweite Ab-
Abtheilung A849). Gauss Werke, Bd. III, S. 85.

396
Zehnter Abschnitt.
§. 121.
Um den Gebrauch dieser Formeln an einem Beispiel zu
erläutern, wollen wir die Gleichung betrachten:
*s — 2 x — 2 = 0,
also e = g = 2, m = 1, n = 2, A = | setzen. Die Formel F)
giebt also
(8) : 2Ä — B = 0,3010300
und G)
(9) log x = A.
Um den ersten Näherungswerth von A zu finden, benutzt
man einen kleinen Auszug aus der Tafel:
A = 0, B = 0,301
A = 0,1, B — 0,254
A — 0,% JB = 0,212
A = 0,3, I? = 0,176
Es ergiebt sich daraus:
0,2
0,3
2A — B
0,188
0,424
Fehler
— 0,113
,123
Man kann hierauf die Interpolationsmethode anwenden, um
einen genaueren Werth von A zu erhalten, indem man den
Gesammtfehler von 0,236 nach Verhältniss der Theilfehler auf
beide Werthe von A vertheilt, also
0,1
A = 0,2
setzt.
0,236
0,113 = 0,247 . . .
Mit Hülfe einer siebenstelligen Tafel von Zach erhält man nun:
A
0,247
0,248
B
0,1948581
0,1944969
2A — B
0,2991419
0,3015031
Fehler
— 0,0018881
+ 0,0004731
und durch abermalige Anwendung der Interpolation
A = 0,2477996
oder
x = 1,769292.
Eine etwas andere Anordnung der Rechnung ist den neuer-
neuerdings erschienenen „Tafeln zur Berechnung der reellen Wurzeln
sämmtlicher trinomischer Gleichungen'? von Gundelfingen
(Leipzig 1896) zu Grunde gelegt.

§. 122. Imaginäre Wurzeln. 397
Dort wird z. B. die Gleichung b) in die Form gesetzt
9 9
Ist dann
n
9 9
so folgt
A0) 1 -f 10A = 10-8
und
A1) logx= =
also
A2) A i B = lose : loggr.
J m -\- n m -\- n
Die Tafeln von Gundelfingen enthalten nun ausser den
zusammengehörigen Werthen von A, B noch die Werthe von
A — (iB für ein echtgebrochenes ft von (i = 0,05, (i = 0,1,
(i = 0,15, . . ., so dass man, wenn man die rechte Seite von A2)
berechnet hat, aus der Tafel direct genäherte Werthe von
A, B findet, die dann nach A1) genäherte Werthe von logz
ergeben.
Die Methode von Gauss ist auch auf Gleichungen mit mehr
als zwei Gliedern ausgedehnt wordenJ).
§. 122.
Berechnung der imaginären Wurzeln einer
trinomischen Gleichung.
Gauss hat auch für die Berechnung der imaginären Wurzeln
einer trinomischen Gleichung ein Verfahren angegeben, das wir
hier noch kurz besprechen wollen. Wir machen die Annahme
reeller Coefficienten, obwohl die Methode auch auf den allge-
allgemeinen Fall anwendbar ist. Wir wollen die Gleichung in die
Form setzen:
A) xm + u — ex™ — g= 0,
brauchen uns aber hier nicht auf positive Werthe von e und g
zu beschränken.
!) A. Wiener, Sohlömiloh's Zeitschrift, Bd. 31. R. Mehmke, ebenda,
Bd. 36.

398 Zehnter Abschnitt. §. 122.
Wir setzen
x ,
und erhalten, indem wir den imaginären Theil in A) für sich
Null setzen,
solcher Gleichungen erhalten wir aber noch zwei, wenn wir A)
mit x~m und mit x~m~n mültipliciren. Dies giebt
C) ^ + m_— <7sinmO-
v J e sinn fr '
und von diesen drei Gleichungen folgt jede aus den beiden
anderen. Wenn man r aus zwei von ihnen eliminirt, so ergiebt
sich, wenn, wie oben
gesetzt wird,
,., . sin n &* sin m O1™
^ - *¦ ' sin(n->rm)&n+m'
Man kann, da man von den beiden conjugirten Wurzeln
nur die eine zu berechnen braucht, & auf den ersten Quadranten
beschränken, muss aber dann unter Umständen auch r negativ
annehmen.
Wie man nun aus der Formel E) mittelst der trigono-
trigonometrischen Tafeln den Winkel & und dann aus einer der drei
Formeln B), C), D) den zugehörigen Werth von r berechnet,
das wollen, wir nun an dem vorhin betrachteten Beispiel
a;» — Ix — 2 = 0
noch nachweisen.
Hier wird die Gleichung E)
, . 1sin 2 O12 sin %¦
W  ~~ sin
oder
G) 3 log sin 3 & — 2 log sin 2 & — log sin & = 0,3010300,
woraus zunächst ersichtlich ist, dass der Winkel & in dem Inter-
Intervall von 0 bis 60° liegt. Man findet zunächst nach wenigen
Versuchen, dass & zwischen 33° und 34° liegt, und wenn man
dann für diese beiden Werthe die Differenz
(8) 3 log sin 3 & — 2 log sin 2 & — log sin & — 0,3010300

§. 122. Imaginäre Wurzeln. 399
berechnet, so erhält man zunächst auf drei Decimalen ,
0,026, — 0,013,
und hieraus ergiebt sich durch Interpolation der genauere Werth
& = 33» 40'.
Hierauf berechnet man die Differenz (8) mit etwas grösserer
Genauigkeit, etwa auf fünf Stellen für einige Winkel in der
Nähe der Werthe 30° 40', von Minute zu Minute fortschreitend,
und findet aus der Vorzeichenänderung, dass & zwischen
33° 41' und 33» 42'
liegt. Wenn man nun für diese beiden Werthe die Rechnung auf
sieben Stellen durchführt, so ergiebt sich wieder durch Inter-
Interpolation der genauere Werth
& = 33» 4i' 20,6".
Aus den Formeln C) oder D) sieht man, dass hier r negativ
ist, und man erhält r sehr einfach aus einer dieser Gleichungen.
Man findet die Brigg'sehen Logarithmen:
log(— r) = 0,0266148
log cos & = 9,9201547 — 10
log sin«- = 9,7440468 — 10.
Also sind die beiden imaginären Wurzeln:
— 0,88464G ± 0,589740 *.

Elfter Abschnitt.
Kettenbrücke.
§• 123.
Verwandlung rationaler Brüche in Kettenbrüche.
Wenn man eine natürliche Zahl m durch eine andere n
nach den gewöhnlichen Regeln dividirt, so erhält man einen
Quotienten und einen Rest, der positiv und kleiner als der
Divisor n ist. Bedeutet a den Quotienten und r den Rest, so ist
A) m — an -j- r.
Alle Zahlen m, m', m", ..., die denselben Rest geben, heissen
restgleich oder congruent nach dem Modul n, und man
drückt dies nach Gauss durch das Zeichen aus:
B) m = m' (mod. n).
Eine solche Formel wird eine Congruenz genannt.
Wenn wir also das System der Zahlen
r = 0, 1, 2, . . ., n — 1
betrachten, so ist jede beliebige (positive oder negative) ganze
Zahl m einer und nur einer von diesen Zahlen nach dem
Modul n congruent. Dieselbe Eigenschaft hat aber auch jedes
System von Zahlen
S = fM0, IMi, OT2, . . ., OT„_i,
die so ausgewählt sind, dass unter ihren Resten alle Zahlen r
(und jede nur einmal) vorkommt. Es ist dann jede beliebige
Zahl m einer und nur einer der Zahlen s nach dem Modul n

§. 123. Volles Restsystem. 401
congruent. Ein solches Zahlensystem wollen wir ein volles
Restsystem für den Modul n nennen. Ein solches volles
ßestsystem bilden z. B. bei ungeradem n die Zahlen
_
' ' ' '
Die Zahlen r heissen die kleinsten (oder kleinsten posi-
positiven) Reste, die Zahlen g die absolut kleinsten Reste.
Durchläuft s ein volles Restsystem für den Modul n, und
hat a mit n keinen Theiler gemein, so durchläuft auch as ein
volles Restsystem für denselben Modul. Denn wären unter den
Zahlen as zwei verschiedene, as1 und a%, die denselben Rest
geben, so müsste ihre Differenz a (sx — s2) durch n theilbar sein,
und da a mit n keinen Theiler gemein hat, so müsste Si —• s3
durch n theilbar sein, was nicht möglich ist, wenn sx, s2 zwei
verschiedene Zahlen eines vollen Restsystems sind.
Um nun die in A) angedeutete Division fortzusetzen, wollen
wir m, n, r durch m, w^, m2 bezeichnen, und dann wieder den
Quotienten und den Rest der Division von inx durch m.2 mit
al5 w% u. s. f. Setzen wir ausserdem noch a0 für a, so ergiebt
sich eine Reihe von Gleichungen:
m = a0 m1 -\- m%
»»i = Oj m.2 -\- m%
C) »«2 = «2 m% -f- m4
mv—\ = av-imv -f- »*r + 1,
die sich so lange fortsetzen lässt, als keiner der Reste ver-
verschwindet, d. h. so lange, als keine der Divisionen aufgeht.
Weil aber
m1 > m% > ms > • • •
ist, so muss, da es nur eine endliche Anzahl von positiven Zahlen
giebt, die kleiner als m1 sind, nach einer endlichen Anzahl von
Theilungen die Division aufgehen. Wenn mv durch mv + i theilbar
ist, so ist w»+i der grösste gemeinschaftliche Theiler
von m und mv
Denn mr + i ist dann nach den Gleichungen C) Theiler aller
vorausgehenden m^, und umgekehrt ist jeder gemeinsame Theiler
zweier benachbarter ma auch Theiler aller folgenden, also auch
von mv + i- x
Weber, Algebra. I. 26

402 Elfter Abschnitt. §. 123.
Wenn daher m und m^ ausser 1 keinen gemeinsamen Theiler
haben (wenn sie also theilerfremd oder relativ prim sind),
so muss ffl»^i = 1 sein, und wir können die Gleichungen C) so
darstellen:
J m1 ' OTj
m, . m-i mv-i , 1
—l- = ax -\ -, • • •, = a„_i -\
Dies giebt die Entwickelung des Bruches m: m^ oder m : n
in einen Kettenbruch. Wir erhalten successive
,.. m .Im .1
E) — = a0 -\ , — = a0 -\
v J n ' m n
n ' m, n ,1
— Oj -\ '
m w%
und endlich
F) f
(h
¦ l
1 m,
wofür wir, des bequemeren Druckes wegen, auch
m / mx\ m / m.2\
n ~~ \ °' mj' n ~~~ V °' ^ mj
m , .
— = (Ct>a, di, d-2, . . ., ffli>_i, mv)
setzen.
Hierzu ist noch Folgendes zu bemerken: Jeder positive
rationale Bruch lässt sich in die Form m : n setzen, so dass m
und n relativ prim sind, und daher können wir jeden solchen
Bruch in einen Kettenbruch von der Form F) oder G) ent-
entwickeln. Auch für negative rationale Brüche gilt dies, wenn wir
für die Zahl a0 auch negative Werthe zulassen. Die au a2,..., av_i, mr
sind aber auch dann positive ganze Zahlen. Diese Zahlen sind
vollkommen und unzweideutig bestimmt. Nur in einer Beziehung
steht uns noch eine Willkür offen.
Es ist nämlich nach der bis jetzt getroffenen Bestimmung
der letzte der Theilnenner mv grösser als 1, da wir angenommen

§. 124. Irrationale Zahlen. 403
haben, dass mv + i der erste unter den Resten sein sollte, der
gleich 1 ist. Demnach könneu wir, wenn av eine positive ganze
Zahl ist, entweder
mv = av,
oder
mv = a, -\- y
setzen und erhalten daher die zwei Darstellungen durch Ketten-
Kettenbrüche :
m .
— = («0, «1, «2, • • •) Ov)
= («o, «li «2> • • •) «») !)•
I. Es lässt sich also jeder rationale Bruch in einen
Ketteribruch entwickeln, der nach Belieben eine
gerade oder eine ungerade Anzahl von Theil-
nennern hat.
Die in den Formeln E) vorkommenden Zahlen
• »j m2 ms
j»2' w%' m^ ' ' ''
nennen wir die Schlusszahlen des Kettenbruöhes, die Zahlen
a0, «!, «2i • • • sollen die Theilnenner heissen (obwohl «0 nicht
eigentlich als Nenner auftritt).
Ersetzen wir m durch eine nach dem Modul n congruente
Zahl m\ so unterscheiden sich die beiden Brüche m : n und
m' : n nur um eine ganze Zahl; die Kettenbruchentwickelungen
unterscheiden sich also nur in ihren ersten Gliedern a0.
§. 124.
Kettenbruchentwickelung irrationaler Zahlen.
Wenn x eine reelle irrationale Zahl ist, so wird es immer
eine und nur eine ganze Zahl a0 geben, so dass x zwischen a0
und a0 -f- 1 liegt. a0 ist positiv, wenn x grösser als 1 ist, Null,
wenn x ein positiver echter Bruch ist, und negativ, wenn x
negativ ist. Setzen wir also
X\
so ist x1 ein positiver unechter Bruch, also wenn «x die zunächst
unter xx gelegene ganze Zahl ist, % positiv. Wir setzen
26*

404 Elfter Abschnitt. §. 125.
Xy = Oi + —,
2
+
so dass %, #2, ...,#« positive unechte Brüche, %, «2, . . ., an—i
ganze positive Zahlen sind.
Nach der Bezeichnung des vorigen Paragraphen ist also x
gleich dem Kettenbruch
(«0) <*1) Ö2? • • •¦> a«—li *»»)•
Diese Kettenbruchentwickelung lässt sich aber, wenn x
irrational ist, unbegrenzt fortsetzen, d. h. wir können n
beliebig gross annehmen. Es entsteht der folgende aus dem
vorangehenden dadurch, dass man
xn = an -f- —
• if-M + l
setzt. Auch hier nennen wir die ganzen Zahlen «0, %, a^ ..., an—i
die Theilnenner, xn die Schlusszahl.
Die Kettenbruchentwickelung der rationalen Zahlen ist als
Specialfall darin enthalten.
§. 125.
Die Näherungsbrüche.
Wenn wir einen Kettenbruch
A) X = (Oo, %, «2, • . ., «„-i, Xn),
worin wir xn als eine variable Grosse ansehen können, in einen
gewöhnlichen Bruch verwandeln, so erhalten wir im Zähler und
im Nenner einen linearen Ausdruck in xn. Es wird also
x —
) v -X- n '
«*« -f- V»—i
worin Pre, Qn, P„_!, Qn—\ ganze rationale Functionen der
«0) «i) <hi • ¦ •, an—i sind. Dass dies richtig ist, ergiebt sich für
die ersten Werthe n = 1, 2, . . . durch unmittelbare Rechnung:

§. 125. Näherungsbrüche. 405
§
x1
_ («0 «1 +
Wenn wir die Formel B) für n schon als bewiesen voraus-
voraussetzen, so erhalten wir, wenn wir
xn = an
setzen:
(£»«»+ Qn-OUBn + l + Qn
Das ist aber die Formel, die sich aus B) durch
Vertauschung von n mit n -\- 1 ergiebt, wenn wir das
folgende Bildungsgesetz für die P„, Qn annehmen:
P „ T> _J_ T>
K ' Qn + 1 = ««£« + Qn-l-
Diese Formeln bestimmen vollständig die P„, Qn für n = 2,
3, 4, . . ., wenn wir noch die Bestimmung hinzufügen:
P. = l, Px = «o,
W <2o = 0, & = 1.
Die Brüche
n Pi ^
öo' öi' Q% '' '
von denen der erste mit dem Nenner Null nur formell, der Ueber-
einstimmung wegen, eingeführt ist, heissen die Näherungs-
Näherungsbrüche des Kettenbruches A), P„ der Zähler und Qn der Nenner
des wten Näherungsbruches.
Das Bildungsgesetz C) zeigt, dass, wenn die a ganze Zahlen
sind, auch P„ und Qn ganze Zahlen sind. Sind die Theilnenner
von % an positiv, so sind die Nenner Qu Q2, Qs, . . . alle positiv
und wachsen mit n, und zwar, da es ganze Zahlen sind, ins
Unendliche. Nur in dem besonderen Falle, wo % = 1 ist, ist
$j = Q2 = 1 und das Wachsen beginnt erst von QB an, und
wir können also den Satz formuliren:
II. Sind Qn-i, Qn die Nenner von zwei auf einander
folgenden Näherungsbrüchen, so ist
0 <; Qn-i <S Qn, Qn= » für » = 00,
wo die Gleichheit mit der unteren Grenze 0 nur

406 Elfter Abschnitt. §. 125.
bei n = 1, mit der oberen Grenze Q„ nur bei n = 2
vorkommen kann. Es ist also, wenn n > 2 immer
0 < Qn-x < Qn-
Die Pl5 P2, P8, . . . sind, wenn a0 positiv ist, gleichfalls alle
positiv, wenn «o negativ ist, so sind sie alle negativ, mit etwaiger
Ausnahme von P2 = «0 «x -)- 1, was gleich Null sein kann.
Die Qn sind von «0 ganz unabhängig. In welcher Weise die P«
von «0 abhängen, können wir auf folgende Art erkennen.
Nehmen wir die Zahlenreihe
%, «2, «8, «4, ...
als gegeben an und betrachten die Recursionsformel
E) Tn+i = anTn + Tn-u
so ist dadurch Tn vollständig für alle n bestimmt, wenn To und
Tj gegeben sind.
Nehmen wir zwei specielle Fälle Q„ und B„, die durch die
Bedingungen
Bo — 1, Et — 0
F) Go = 0, & = 1
bestimmt sind, so erhält man die allgemeine Lösung der Glei-
Gleichung E) in der Form
G) Tn= T0Bn-{- TiQn
und hierin ist also auch
(8) P« = Bn + «0 &
enthalten. Wenn wir zwei Lösungen von E) betrachten, Tn und
S„, also:
^ 5 ( ^
so folgt durch Elimination von an
Tn + lSn — ^«^„+1 = — (TnSn—l Tn — i Sn),
oder wenn wir
^nSn + l — SnTn + i = <4n
setzen,
(9) 4n= — -dn-X = 4n-t = ¦¦¦ = (— 1)»Z/O.
Für Tn = Bn und Sn = Qn ist aber Jo = 1, [nach F)],
also nach (9)
Bn Qn + l — QnBn + i = (—1)»,
oder, indem man n in n — 1 verwandelt und das Zeichen beider-
beiderseits umkehrt:
A0) Bn Qn-i - Qn Bn-i = C- 1)".

§. 126. Unbestimmte Gleichungen. 407
Wendet man dies auf zwei Functionen Tn, Sn an, die durch
Tn =T0Rn+ Tj. Qn, S„ = So i?„ + S, Qn
definirt sind, so folgt
Tn 8n-t - Sn Tn_x = (-1)« (To S, - Tx So),
also im Besonderen
A1) P» Qn-X - QnPn-l = (~ 1)».
Diese Formel, von der wir noch mannigfache Anwendung
machen werden, zeigt, dass die Zahlen PM, Qn ohne gemeinsamen
Theiler sind, dass also die Näherungsbrüche Pre: Qn nicht durch
Heben reducirt werden können.
Ist der Kettenbruch ein endlicher, ist also die Schlusszahl
xn—i = an—x eine ganze Zahl, so setzen wir die Bildung der
Näherungsbrüche nicht weiter fort als bis zu
Pn Pn—lCtn—1 ~f" P«—2
Qn Qn-1 Un-1 + Qn-2 '
und die Formel B) zeigt, dass dann der letzte Näherungsbruch
mit dem Werthe des Kettenbruches übereinstimmt.
§• 126.
Lösung unbestimmter Gleichungen mit zwei
Unbekannten.
Die zuletzt gefundenen Formeln führen zur Lösung einer
Aufgabe, die in vielen Anwendungen vorkommt:
Es seien a, ß zwei gegebene ganze Zahlen
ohne gemeinsamen Theiler, es sollen zwei andere
ganze Zahlen gefunden werden, die der Bedingung
genügen:
A) ay - ßx = 1.
Diese Aufgabe hat, wenn sie überhaupt lösbar ist, unendlich
viele Lösungen, die alle aus einer von ihnen abgeleitet werden
können.
Ist nämlich x0, y0 eine Lösung, also
B) ay0 — ßx0 — 1,
so folgt durch Subtraction von A) und B)
K {y — j/o) = ß (% — «o),
woraus zu schliessen ist, da et, mit ß keinen gemeinsamen Theiler

408 Elfter Abschnitt. §. 126.
hat, dass x — Xo durch a theilbar ist; setzen wir demnach, indem
wir mit h eine willkürliche ganze Zahl bezeichnen,
x = x0 -\- h a,
so folgt
und in dieser Form sind alle Lösungen von A) enthalten.
Wir brauchen also nur noch eine Lösung von A) zu suchen,
die wir immer auf folgende Weise erhalten. Wir setzen ß als
positiv voraus, was die Allgemeinheit nicht wesentlich beschränkt,
da wir eventuell x m —x verwandeln können, und entwickeln
nach §. 123 die rationale Zahl et, : ß in einen Kettenbruch:
a ¦ , N
-j = (Oo, «i, «2) • • -l «»-1>
Hiervon bilden wir die Näherungsbrüche
£_0 £_l M Pn—l Pn
Vo* &' &' ¦"' G—i' Qn
so dass
ü — Eil
ß Qn'
Da aber a, ß sowohl als Pre, Qn ohne gemeinsamen Theiler
sind, und da ß und Q„ positiv sind, so folgt
U = Pn, ß = Qn.
Da nun ferner nach §. 125
Pn Qn-\ — Q»Pn-l = (- 1)"
ist, so folgt, dass
C) x = (-iyPn-u y = (-l)"G—i
ganze Zahlen sind, die der Gleichung A) genügen, womit also
die Aufgabe vollständig gelöst ist.
Die Rechnung ist bei massig grossen Zahlen ziemlich einfach.
Setzen wir z. B. a = 24335, ß = 3588, so erhalten wir
zunächst nach §. 123 den Kettenbruch:
= F, 1, 3, 1, 1, 2, 6, 2, 1, 1, 4),
und die Näherungsbrüche
J_6^7_273461156^997^ 2150 3147
0' T' T' 4' 5' 9' 23' 147' 317' 464'
5297 24335
781 ' 3588 '

§. 126. Unbestimmte Gleichungen. 409
und da hier n = 11, also ungerade ist, so hat man zu setzen:
x — — 5297, y = — 781.
Dies sind die absolut kleinsten Werthe von x, y, die der
Gleichung A) genügen.
Die kleinste positive Lösung erhält man daraus, wenn man
w und ß dazu addirt, also
x = 19038, y = 2807.
Hierauf wird auch die Lösung der allgemeineren Gleichung
D) ay — ßx = y
in ganzen Zahlen x, y zurückgeführt.
Zunächst ist klar, dass, wenn D) überhaupt lösbar sein soll,
jeder gemeinsame Theiler von et, und ß auch Theiler von y sein
muss. Ein solcher gemeinsamer Theiler wird dann durch Division
weggeschafft. Wir nehmen also auch hier an, dass et, und ß
keinen gemeinsamen Theiler haben. Dann folgt ebenso wie
oben, dass alle Lösungen von D) aus einer von ihnen, a;0, y0,
erhalten werden in der Form
x = x(i -{-ha, y = yo-{-hß,
worin h eine unbestimmte ganze Zahl ist. Setzt man dann in D)
% = r I, y = v%
und theilt durch y, so geht D) über in
«ij — j8g = 1,
also in eine Gleichung von der Form A).
Die Lösung wird zu einer völlig bestimmten, wenn noch
eine Bedingung gegeben ist, aus der h bestimmt werden kann,
z. B. die, dass y zwischen 0 und ß liegen soll, mit Einschluss
der einen der beiden Grenzen. Wir wollen dies in folgendem
Lehrsatze zusammenfassen:
III. Die unbestimmte Gleichung
et,y — ßx = y
hat, wenn a, ß, y ganze Zahlen und et, und ß ohne
gemeinsamen Theiler sind, immer eine ganz-
ganzzahlige Lösung x, y und nur eine, wenn noch die
Bedingung
o ^ y < ß,
oder
0 < V ^ ß
hinzukommt.

410 Elfter Abschnitt. §. 126.
Nach dem oben Bemerkten giebt es aber auch immer
Lösungen der Gleichung D), wenn y durch den grössten gemein-
gemeinschaftlichen Theiler von « und ß theilbar ist. Insbesondere
können wir den Satz aussprechen: Der. grösste gemein-
gemeinschaftliche Theiler 8 zweier Zahlen «, ß lässt sich in
der Form
ccx — ßy — 8
darstellen, worin x, y ganze Zahlen sind.
Das Theorem III. lässt sich in folgender Weise verallge-
verallgemeinern :
IV. Sind «!, a2, w8, . . . gegebene ganze Zahlen in
beliebiger Anzahl, ohne einen allen gemeinsamen
Theiler, m eine beliebig gegebene Zahl, so lassen
sich immer die ganzen Zahlen x1, x2, xB, ... so
bestimmen, dass
E) m = «! xx -f- «2 x2 -j- «3 xs -j- • • •
wird.
Besteht die rechte Seite von E) nur aus zwei Gliedern, so
fällt dieser Satz mit dem Theorem III. zusammen. Nehmen wir
also die Möglichkeit, eine Formel E) zu befriedigen, als bewiesen
an, wenn die rechte Seite aus weniger Gliedern besteht, so können
wir, wenn 8 der grösste gemeinschaftliche Theiler von «2, «3, ...
ist, da 8 relativ prim zu c^ sein muss, die beiden Gleichungen:
8 = aiyi-\- asys-\ •
m = c^ Xi -{- 8 x
durch ganzzahlige x, a^, y2, ys, ... befriedigen. Dann ist aber
die Gleichung E) durch
xt, x2 = xy^ xs=xys...
befriedigt.
Das durch den Satz III. gelöste Problem wird in der Zahlen-
Zahlentheorie auch so ausgedrückt:
V. Sind a, ß, y gegebene Zahlen, so soll eine Zahl y
gefunden werden, die der Congruenz
ocy = y (mod ß)
genügt. Diese Aufgabe hat immer eine Lösung,
wenn y durch den grössten gemeinschaftlichen
Theiler von a und ß theilbar ist.

§. 127. Convergenz der Näherungsbrüche. 411
Das letzte Theorem führte zur Lösung der folgenden
Aufgabe:
VI. Es ist eine Keihe positiver ganzer Zahlen
jWj, w%, ms, . . . gegeben, deren keine zwei einen
gemeinsamen Theiler haben. Es ist eine ganze
Zahl z zu bestimmen, die bei der Theilung
durch w%, «w2, ms, . . . gegebene Reste rx, r2, r3, . . .
g i e b t.
Diese Aufgabe ist immer lösbar, und eine Lösung wird auf
folgende Weise gefunden:
Wir wollen mit
m = mi W/i ms . . .
das Product der Zahlen mxm%m% . . . bezeichnen und
m = «i«! = m-2 «2 = ms o% . . .
setzen, so dass nach unserer Voraussetzung «j = »%»% . . .
relativ prim zu ml5 ebenso a2 zu w2 u. s. f. ist. Dann bestimmen
wir nach V. die Zahlen xu x2, xs, . . . aus den Congruenzen
«! Xx = rx (mod »%), a% x2 = r3 (mod m2), as xB = rB (mod jw8), ...
und erhalten, da a2, «3, ... durch mx u. s. f. theilbar sind, die
gesuchte Zahl in der Form
X = Kx Xx -\- 0i2 X2 -\- ds Xs -\- • • •
Hierzu kaun noch ein beliebiges Vielfaches von m gefügt
werden.
Die in diesem Paragraphen betrachteten Gleichungen ge-
gehören zu den sogenannten Diophantischen Gleichungen,
worunter man im Allgemeinen Gleichungen versteht, die eine
grössere Zahl von Unbekannten enthalten, als nach den Regeln
der Algebra daraus bestimmt werden können, worin aber die
Unbekannten noch durch die weitere Forderung beschränkt sind,
dass es ganze Zahlen sein sollen.
Convergenz der Näherungsbrüche.
Wir nehmen jetzt an, dass die Reihe der Zahlen ax, a2, a3, ...
eine unbegrenzte sei, und bilden die Differenz zweier auf einander
folgender Näherungsbrüche:

412 Elfter Abschnitt. §. 127.
A) P» P»-i_ (—1)"
Qn Qn—i QnQn — 1
Diese Differenz hat also bei geradem n das positive, bei
ungeradem n das negative Zeichen und nimmt, dem absoluten
Werthe nach, mit unendlich wachsendem n unbegrenzt ab. Bilden
wir noch aus A):
P' p ( 1 \n ( 1 \n +1
,,.,) _n -T«-2 _ l lJ _j_ V l)
W 'Qn Qn-Z QnQn-1 ^~ Qn-lQn-%
(-1)" / J_ _ _J\
Qn-1 \Qn Qn-J'
so folgt, da Qn—2 < Qn ist, dass diese Differenz bei geradem n
negativ, bei ungeradem n positiv ist.
Hieraus folgt, dass die Reihe der Näherungsbrüche mit
geradem Index
V T> V
V2 Yi Vß
eine abnehmende, die Reihe der Näherungsbrüche mit unge-
ungeradem Index
V V V
Vl V^ ^j5
eine zunehmende ist.
Nun ist nach §. 125
• x=PnXn-\-Pn-X "
Qn%n-\- Qn-\
also
und da Qn, Qn-n %n positiv sind, so sind alle Zahlen der Reihe C)
grösser als x, alle Zahlen der Reihe D) kleiner als x.
Der Unterschied E) sinkt mit unendlich wachsendem n
unter jede Grenze und ist, da zn>a„, also Qnx„-{- Qn-i> Qn+i
ist, dem absoluten Werth nach kleiner als
1
F) TTTt '
V» Vn + i
und um so mehr kleiner als 1 : Qn.
Die Zahlen der Reihe C) nähern sich also abnehmend, die
der Reihe D) zunehmend der Grenze x. Der Ausdruck F) giebt
ein Maass für den Fehler, den man begeht, wenn man x durch
den Näherungsbruch P„ : Qn ersetzt.

§. 128. Aequivalente Zahlen. 413
Die Näherungsbrüche sind also angenäherte
Ausdrücke von Irrationalzahlen durch rationale
Brüche.
Dass diese Näherungsbrüche bei gleichem Grade der An-
Annäherung an die Irrationalzahl x die möglichst einfachen sind,
das wird durch folgenden Satz ausgedrückt:
VII. Es lässt sich zwischen den zwei rationalen
Brüchen
Pn Pn — 1
kein anderer rationaler Bruch einschieben,
dessen Nenner kleiner als Qn oder auch nur
gleich Q„ ist.
Angenommen, es liege der rationale Bruch M: N zwischen
den Näherungsbrüchen Pn : Qn und Pn~i ¦ Qn-i- Dann ist die
Differenz
Pn -P« —1
~Qn ~ Qn-1
absolut grösser und vom selben Vorzeichen wie
M Pn^
N Qn-X '
also
Multiplicirt man beiderseits mit NQn-i, so folgt nach A)
uud da rechts eine positive ganze Zahl steht, die also mindestens
gleich ] ist, so folgt
N> Qn-
§. 128.
Aequivalente Zahlen.
Die Kettenbrüche führen uns auf die Betrachtung einer
besonderen Art von linearen Substitutionen, die in der Algebra
und Zahlentheorie überhaupt eine grosse Bedeutung haben, und
die wir etwas näher betrachten wollen.

414 Elfter Abschnitt. §. 128.
Sind x und y zwei Zahlen oder auch veränderliche Grossen,
die in der Abhängigkeit von einander stehen
/IN KX ~f~ ß
A> • y = t^R'
worin «, ß, y, tf ganze Zahlen sind, die der Bedingung
B) ad — ßy = s = ±l
genügen, so nennen wir x und y mit einander äquivalent'1).
Wir nennen sie eigentlich oder uneigentlich äquivalent,
je nachdem £ = -\- 1 oder £ = — 1 ist. Diese Beziehung ist
eine gegenseitige, denn aus A) folgt
C) x = 8y~l ¦
— yy + «
Wenn zwei Grossen mit einer dritten äquivalent
sind, so sind sie auch mit einander äquivalent.
Denn ist
D) x = —.—-j—~,
v ' y' e -f- d"
so folgt aus A)
" + ß"
wenn
a" = a«' + /Jy',- ß" = Kß'
{ ' y" = y«' + 8y\ d" = y ß' + d d',
G) a» fl" _ j3» r" _ („ § _ ^ y) (y ö' _ /}' r'),
oder
(8) s" = s e'.
Die Substitution E) heisst aus A) und D) zusammen-
zusammengesetzt.
Es macht sich das Bedürfniss nach einer abgekürzten Be-
Bezeichnung dieser Substitutionen geltend. Da es häufig nicht auf
die Variablen, sondern nur auf die Substitutionszahlen a, ß, y, 8
ankommt, so bezeichnet man die ganze Substitution A).durch
die Substitutionszahlen oder auch nur durch einen einfachen
Buchstaben
-1) Vgl. Dedekind, Schreiben an Herrn Borchardt über die Theorie
der elliptischen Modulfunctionen. Oelle's Journal, Bd. 83 A877).

§. 128. Äequivalente Zahlen. 415
und schreibt dann, wenn es nöthig ist, die Gleichung A) so:
Die Zusammensetzung zweier Substitutionen bezeichnet man
durch Nebeneinandersetzen der Zeichen, wobei aber auf die
Reihenfolge zu achten ist, also
«,ß\(<ß'\_("",ß"\
)W)\)
oder
A1) SS' = S".
Die Formeln F) enthalten die Vorschrift, nach der eine
zusammengesetzte Substitution zu bilden ist. Man kann sie aus
der Multiplicationsregel der Determinanten ableiten, muss aber
beachten, dass im ersten Factor nach Zeilen, im zweiten nach
Colonnen summirt werden muss, wie eben die Formeln F)
zeigen.
Ebenso wie man zwei Substitutionen zusammensetzt, kann
man auch die Zusammensetzung von mehreren bilden:
S Si S% Ss . . .
Bei der Bildung der zusammengesetzten .Substitution dürfen,
im Allgemeinen wenigstens, die Componenten nicht vertauscht
werden; wohl aber kann man nach Belieben zwei benachbarte
zu einer zusammenfassen, dann wieder zwei u. s. f., d. h. es gilt
zwar nicht das commutative, wohl aber das associative
Gesetz.
Dies folgt unmittelbar daraus, dass, wenn x durch xx, xx
durch x2, x2 durch xs ausgedrückt ist, der Ausdruck von x durch
x6 entweder dadurch gefunden werden kann, dass man zuerst
Xi in x durch x2 und dann x2 durch xz ausdrückt, oder dass
man zuerst xx durch xs ausdrückt und dies in dem Ausdruck
von x durch xx einsetzt.
Nach (8) ist eine zusammengesetzte Aequivalenz eine eigent-
eigentliche oder uneigentliche, je nachdem sich unter den Compo-
Componenten eine gerade oder eine ungerade Zahl von uneigentlichen
findet.
¦ Wenn man die beiden Substitutionen
*)

416 Elfter Abschnitt. §. 128.
zusammensetzt, so erhält man, gleichviel welche von beiden man
an die erste Stelle setzt,
<»> C:
Diese Substitution ist nach A) gleichbedeutend mit y = x;
sie ändert nichts und wird die identische Substitution
genannt und wohl auch kurz durch 1 bezeichnet. Demnach
nennt man die beiden Substitutionen A2) zu einander reciprok
und bezeichnet sie mit
S, S~\
oder man setzt
\—sy, saj
Durch die Zusammensetzung mit der identischen Substitution
A3) bleibt jede andere Substitution ungeändert.
Wir leiten hieraus sehr einfach den Beweis des Satzes ab:
VIII. Alle rationalen Zahlen sind unter einander
äquivalent, und zwar sowohl eigentlich als
uneigentlich.
Sind nämlich m : n und ml : n' zwei rationale Brüche und
m und n sowohl als ml und n' ohne gemeinsamen Theiler, so
können wir, wenn s, s' nach Belieben ±1 sind, die Zahlen (t, v
und jt', v' nach §. 126 so bestimmen, dass
mv — wjt = a, m!V — w'ft' = s'
wird, dass also
M - ( ^
\y,
eine lineare Substitution, und
__/a,ß
\ w, v'J
zwei lineare Substitutionen äind. Es ist dann auch
MM'~l =
woraus folgt:
m = am' -\- ßn', n = ym' -f- 8n',
also
m n
n ml

§. 129. Aequivalente Zahlen. 417
was zu beweisen war. Die Aequivalenz ist eine eigentliche oder
eine uneigentliche, je nachdem e = e' oder b = — e' ist.
Jede Zahl ist mit ihrer entgegengesetzten und mit ihrer
reciproken uneigentlich äquivalent, denn es ist
§. 129.
Entwickelung äquivalenter Zahlen in Kettenbrüche.
Wenn von zwei äquivalenten Zahlen die eine irrational ist,
so ist es die andere auch, und wenn die eine' reell ist, so ist es
auch die andere. Wir machen diese beiden Annahmen, setzen
also in
A) y==c^L±l ad_^r==£
v J y y x -f- d ^"
x als irrational und reell voraus, und wollen nun untersuchen,
wie sich aus der Kettenbruchentwickelung von x die Ketten-
bruchentwickelung von y herleiten lässt.
Es sei also x in einen Kettenbruch mit der Schlusszahl xn
entwickelt:
B) x = (a0, «!, a.2, . . ., a„_i, xn\
worin wir n vorläufig unbestimmt lassen.
Durch die Näherungsbrüche ausgedrückt, wird
Wenn wir dies in A) substituiren, so folgt
worin nach §. 128, A0) und F), G)
Rn = a Pn + ß Qm Rn^ = « PM_! + ß Qn-X
{b) stt = rPn + d Qn, 8n-i = r P«-i + * Qn-i
F) Rn 8n-l — Sn Rn-t = (— 1)" B.
Setzt man Sn in die Form
Weber, Algebra. I. 27

418 Elfter Abschnitt. §.129.
so ergiebt sich, da sich P„ : Qn dem Werthe x bis auf jeden
beliebigen Grad annähert und Q„ positiv ist, dass, wenn n gross
genug gewählt ist, S„ im Vorzeichen mit
(yx + *)
übereinstimmt. Da x irrational ist, so ist diese Grosse von Null
verschieden, und wir wollen sie als positiv voraussetzen. Wäre
sie negativ, so hätten wir, um sie positiv zu machen, nur die
Vorzeichen der vier Zahlen «, ß, y, 8 gleichzeitig zu ändern, wo-
wodurch A) ungeändert bleibt.
Es wird also 8n für hinlänglich grosse n positiv sein. Nun
folgt aber aus E) mit Rücksicht auf §. 125, C):
S« + l = 0>n Sn -f- So—i,
¦woraus man schliefst, dass, wenn n so gross ist, dass Sn—z und
die folgenden 8 positiv sind, S„ mit n zugleich wächst, also:
G) S„ > 8H-i> 0.
Wir entwickeln nun den rationalen Bruch Bn : Sn in einen
endlichen Kettenbruch
(8) ^ = F„ h, 6„ . . , &«_!),
und bezeichnen den vorletzten Näherungsbruch mit R' : S', so
dass wir die Relation haben:
(9) BnS'- SnR' = (-l)»\
Nach dem Satze I. in §. 123 können wir aber m nach
Belieben gerade oder ungerade voraussetzen, und wir wollen so
darüber verfügen, dass
(— 1)>» = (— 1)» «
wird. Ausserdem ist, wie wir aus §. 125, II. wissen,
A0) Sn ^ S' ^ 0,
worin aber das Gleichheitszeichen in der unteren Grenze nur für
m = 1 und in der oberen Grenze nur für m = 2 und \ = 1,
also überhaupt nur, wenn S„ = 1 ist, vorkommen kann, und
dies kann man nach G) vermeiden, wenn man n gross genug
annimmt.
Da aber nach §. 126, III. durch die Bedingungen (9), A0)
die Zahlen 8', B' völlig bestimmt sind, und Sn-i, jß„—i nach
F), G) denselben Bedingungen genügen, so folgt
S' = ön —1', JR' =r JBM_!.

§. 130. Quadratische Irrationalzahlen. 419
Hieraus ergiebt sich nun weiter, dass der Kettenbruch mit
der Schlusszahl xn
A1) F0, lu b2, . . ., bm-u xn)
den ¦ Werth hat
also mit ?/ übereinstimmt.
Wenn man nun x„ weiter in einen Kettenbruch entwickelt
xn = (am ccn^.i, cin + ib) • • •)'
so erhält man aus B) und A1):
x = (a0, al5 a2, . . ., an—i» *«) a« + i> ö« + 2> • • •)
oder in Worten ausgesprochen den Satz:
IX. Die Kettenbruchentwickelungen zweier äqui-
äquivalenter Zahlen stimmen von einem gewissen
Theilnenner an mit einander überein.
Wir können noch hinzufügen, dass, wenn die Aequivalenz
eine eigentliche ist (s = -j- 1), die Zahl der den überein-
übereinstimmenden vorangehenden Theilnenner in beiden gerade, oder
in beiden ungerade ist, und dass, wenn die Aequivalenz un-
uneigentlich ist, diese Zahl in der einen gerade, in der anderen
ungerade ist.
Dass der Satz auch umgekehrt gilt, ist leicht einzusehen.
Denn wenn zwei Kettenbrüche von einem gewissen Theilnenner
an übereinstimmen, so können sie so geschrieben werden, dass
sie dieselbe Schlusszahl haben. Nun ist der Werth eines Ketten-
Kettenbruches aber immer äquivalent mit jeder seiner Schlusszahlen
[§. 125, B)]; also sind auch zwei Kettenbrüche mit
gleicher Schlusszahl unter einander äquivalent.
§. 130.
Quadratische Irrationalzahlen.
Einfache und schöne Gesetze ergeben sich, wenn man die
Kettenbruchentwickelung auf die Bestimmung der Wurzeln einer
quadratischen Gleichung anwendet. Die Wurzel einer ganz-
ganzzahligen quadratischen Gleichung hat die Form
A) a = x + yVd,
27*

420 Elfter Abschuitt. §. 130.
worin x, y, d ganze oder gebrochene rationale Zahlen sind. Wir
können aber, ohne die Allgemeinheit zu beschränken, d als
ganze Zahl und ohne quadratischen Theiler voraussetzen;
denn wenn d einen Nenner hat, so können wir mit diesem
Nenner erweitern und können die Wurzel aus dem quadratischen
Nenner und aus einem etwaigen quadratischen Theiler des
Zählers zu y rechnen; wir nehmen dann weiter an, dass d nicht
gleich 1 ist, da sonst to rational wäre; d kann positiv oder
negativ sein, und davon hängt es ab, ob to reell oder
imaginär ist.
Wir wollen das Vorzeichen der Quadratwurzel Vd eindeutig
bestimmen, was etwa dadurch geschehen kann, dass man bei
positiven d auch Vd, und wenn d negativ ist, — * Vd positiv an-
annimmt oder, anders ausgedrückt, dass man Vd positiv reell
oder positiv imaginär annimmt.
Aendern wir das Vorzeichen der Wurzel, so erhalten wir
B) to' = x — y Vd,
was die zu to conjugirte Zahl genannt wird. Sie entsteht
auch aus to durch Aenderung des Vorzeichens von y. Das Pro-
duct der beiden Zahlen to, to'
to to' = ,-r2 — y%d
heisst die Norm von to (oder auch von to'). Die Norm eines
Productes zweier quadratischer Irrationalzahlen ist
gleitfh dem Product der Normen.
Die Norm einer imaginären Zahl to ist immer positiv. Bei
reellen quadratischen Irrationalzahlen kann die Norm positiv
oder negativ sein.
Die Zahlen to und to' sind die Wurzeln einer Gleichung mit
rationalen Coefficienten:
C) to2 — 2xa -\- («2 — yzd) = 0.
Um sie in eine ganzzahlige Gleichung zu verwandeln,
setzen wir
D) X2 — yzd = — —, 2x = —,
c c
worin- a, b, c ganze Zahlen ohne gemeinsamen Theiler sind, und
erhalten aus C)
E) c to2 = a -f- b to,
also eine ganzzahlige primitive Gleichung.

§. 130. Quadratische Irrationalzahlen. 421
Die Zahlen a, b, c sind durch D) nur bis auf ein gemein-
gemeinsames Vorzeichen bestimmt.
Die Discriminante von C) ist
F) D = &a + 4ac = 4ca«M
und soll auch die Discriminante der Irrationalzahl co
heissen. D ist also eine ganze Zahl, die im Vorzeichen mit d
übereinstimmt und die durch d theilbar ist; denn ist p ein Prim-
theiler von d, der also in d nach Voraussetzung nur einmal auf-
aufgeht, so kann p nicht im Nenner von 2cy aufgehen und muss
also nach F) in D aufgehen. Also ist auch 2cy eine ganze
Zahl und der Quotient D : d ist eine Quadratzahl.
Um die Vorzeichen von a, b, c zu bestimmen, wollen wir
festsetzen, dass die ganze von Null verschiedene Zahl 2cy
positiv sein soll, dass also c und y im Vorzeichen überein-
übereinstimmen. Wenn wir nun
setzen, also VD ebenso wie Vd positiv reell oder positiv imaginär
annehmen, so ergiebt sich nach D) und F)
oder, was dasselbe ist
. 2a , —2a
<8>
Es ist daher nicht nur das Zahlensystem a,b,c durch
<a eindeutig bestimmt, sondern auch umgekehrt co durch
o, b, c. Setzen wir, um diese Zugehörigkeit auszudrücken
(9) to = {a, b,c},
so ist die conjugirte Zahl to' zu bezeichnen durch
A0) co' = { — a, — b, — c}-
Da eine gerade Quadratzahl durch 4 theilbar ist, eine
ungerade, durch 4 getheilt, den Eest 1 lässt, so ergiebt sich
aus F), dass
A1) Z> = 0 oder = 1 (mod 4)
sein muss.
Wir wollen noch untersuchen, wie sich die Zahlen a, b, c, D
ändern, wenn wir von a zu einer äquivalenten Zahl oo1 über-
übergehen. Es sei also

422 . Elfter Abschnitt. §. 130.
* yto -j- d
Setzen wir _ _
co = x -\-yVd, co1 = xx + yx]/'d,
so folgt, wenn man in A2) den Nenner rational macht,
2 yd'x + 82'
und wenn m1 der quadratischen Gleichung
A5) Cj ojj2 = % -(- 6j ojj
genügt, nach A2) und E):
6L_ — 2aay + 6foig + ßy) -\- 2cß8
i
4- cß2
ferner nach D) und A3):
syc = (—ay2 -\- byd -\
Wir setzen hiernach
— £«! = — a«2 -(- baß -\- cß2,
A6) a6i = — 2aay + &(«* + /3r) -f- 2c/3d,
a Ci = — ay2 _)_ byd -f cd2,
und folglich
A7) 2/c — ^d,
so dass ylei positiv ist.
Aus A6) ergiebt sich durch Auflösung
sa = ax d* -f 6, ß d — e1 ß2,
A8) Bl = 2a1y8 -\-bx(a8 -[- ßy) — 2c1aß,
— sc = a1y2-\-b1Ky — cx a2,
woraus zu schliessen ist, dass die durch A8) bestimmten Zahlen
«!, bt, d keinen gemeinsamen Theiler haben. Ferner ergiebt sich
noch durch einfache Rechnung, oder auch nach dem Multipli-
cationssatze der Determinanten
A9) b2 -f iac = bl + ia1c1 = D.
Aus A7) und A8) schliessen wir, dass die Zahlen a^, bu cx
dieselbe Bedeutung für a1 haben, wie a, b, c für to, und dass daher

§. 181.
Reducirte Zahlen.
423
B0) <Ol ^
zu setzen ist.
Durch A9) ist dann der Satz bewiesen:
Aequivalente Irrationalzahlen haben nicht nur
dieselbe Irrationalität, sondern auch dieselbe Dis-
criminante.
§• 131.
Reducirte Zahlen mit negativer Discriminante.
Die bisherigen Betrachtungen sind gleichmässig auf die beiden
Fälle der reellen und imaginären quadratischen Irrationalzahlen,
also auf positive und negative Discriminanten anwendbar. Jetzt
Fig. 26. aber müssen beide Fälle von ein-
einander getrennt werden, und wir
beginnen mit den negativen Dis-
Discriminanten. Es handelt sich
also um imaginäre Zahlen:
A) ca =x-\-y V d = !¦-\-irj,
worin § und rj reell sind; es ge-
genügt, von den beiden conjugirten
Zahlen g-f-*)j, § — ir\ die eine zu betrachten. Wir nehmen
also rj positiv aii und setzen folgende Definition fest:
Eine complexe Zahl ca = § -f- irj heisst bei positivem
rj reducirt, wenn
Betrachtet man f, rj als rechtwinklige Coordinaten in einer
Ebene, so wird jede Zahl ca durch einen Punkt dieser Ebene
veranschaulicht, und die Lage der Punkte, die den reducirten
Zahlen entsprechen, wird durch das in d§r Fig. 26 schraffirte
Feld (mit Einschluss der Grenzen), das wir das Grundfeld nennen,
veranschaulicht.
Aus den Bedingungen B) folgt dann noch, was auch in der
Figur leicht zu bestätigen ist,
C) n*^h c
Geht man nun von einer Zahl co zu einer äquivalenten Zahl
cat über, so ergiebt die Formel A2) des vorigen Paragraphen

424 Elfter Abschnitt. §. 131.
und diese Formel zeigt, dass % dasselbe oder das entgegen-
entgegengesetzte Zeichen wie rj hat, je nachdem £ = -\- 1 oder = — 1
ist, also je nachdem die Aequivalenz eine eigentliche oder eine
uneigentliche ist.
Beschränken wir uns also auf Zahlen mit positiv imaginärem
Bestandtheile, so kommt nur die eigentliche Aequivalenz in
Betracht, und wir beweisen jetzt den Fundamentalsatz:
1. Jede imaginäre quadratische Irrationalzahl
x -f- y]/d mit positiv imaginärem Bestandtheil
ist mit einer reducirten Zahl äquivalent.
Verstehen wir unter a die dem § nächstgelegene ganze Zahl,
so wird a> — a der ersten der Bedingungen B) genügen, dass
nämlich — f ^ § — a^l isk
Wenn nun
E) r2 = (§ — aJ -f- i?a = (ra — «) (co' — a)
grösser oder gleich 1 ist, so ist a> — a, was mit a> äquivalent ist,
bereits reducirt; anderenfalls setzen wir, indem wir eine Ketten-
bruchentwickelung anwenden,
F) m = * - i-,
so dass auch o>i = §i + ifji mit o äquivalent ist. Die Zahl <ax
behandeln wir nun wieder ebenso wie co, indem wir, wenn a>1 — «j
noch nicht reducirt ist,
G) ah = «! — —
setzen u. s. f. Betrachten wir die Reihe der nach Analogie von
E) gebildeten Grossen
rl = (|t - «,)« + nl r* = fa — a& + v>, . . .,
so konimt es also jetzt nur darauf an, nachzuweisen, dass wir
nach einer endlichen^ Zahl von Schritten dieser Art zu einem r%
kommen, das gleich oder grösser als 1 ist.
Nach F) ist aber
r» = (m — «) K — «) = , „
und danach ergiebt die Vergleichung der imaginären Theile auf
beiden Seiten von F):

§. 131. Reducirte Zahlen. 425
Ebenso folgt die Reihe der Gleichungen
(8) r\ = r2^, r^ = r?r}2, rjs = r|ij8, . . .
Nun ist aber irj — yVd, und also nach der Formel F), §. 130
und weil hier y positiv ist, so ist c eine positive ganze Zahl.
Weil aber äquivalente Zahlen dieselbe Discriminante haben, so
folgt ebenso: _
V . V3
worin c, cl5 e2, . . . eine Reihe positiver ganzer Zahlen ist.
Danach erhält man aus (8):
(9) d = rH, c2 = r/Cj, c3 = r?c2, . . .
So lange aber die Zahlen r2, rf, . . ., r% kleiner als 1 sind, folgt
hieraus
A0) c > d > c2 . . . > c, + i,
und weil es nur eine endliche Anzahl positiver Zahlen geben
kann, die kleiner als c sind, so muss diese Reihe abbrechen,
womit unser Satz 1. bewiesen ist.
Die reducirten Zahlen, deren Bilder an der Begrenzung des
Grundfeldes liegen, sind paarweise äquivalent, nämlich
a) ea = — \ -f- irj und <o1 = (o-{-l—±-\-irj
(a und a' in der Figur),
b) o) = — | + in und coY = — — — | -)- irj,
wenn ]¦* -\- rj* = 1 ist (b und V in der Figur). Es gilt aber
ferner der Satz:
2. Von den Fällen a), b) abgesehen, sind keine zwei
reducirte Zahlen äquivalent.
Nehmen wir nämlich zwei nicht identische reducirte Zahlen an,
A1) ß> = I + n i, ß>i = §i + Vi h
und setzen voraus, was die Allgemeinheit nicht beeinträchtigt,
A2) Vi ^ V,
so folgt aus der Formel D):
r\
also wegen A2):
A4)

426 Elfter Abschnitt, §. 131.
also auch, nach C):
A5) i^r2^2^fr2;
also sind zwei Möglichkeiten:
«) y = 0, ß) r = ±l.
Im Falle a) ist «d = 1, also a = d = ± 1, aus A3) er-
giebt sich ^ = ¦>?, ferner aus D):
Dies ist aber nur dann mit den Bedingungen B) verträglich,
wenn entweder gt = g, ß = 0, und also <»i mit oj identisch ist,
oder wenn ß = + 1 und §, = — % = + | ist, also in dem
Falle a).
Im Falle ß) ist nach A4) (g ± dJ <| 1, und also entweder:
d = 0, /3y = — 1 und £2 -f- ??2 = 1, ^ == ^, ferner nach D)
§! :=: ± « — £, also, da fi = | ausgeschlossen ist, ^ = -r- §,
« = 0, das ist der Ausnahmefall b),
oder: d = + 1, also (g + lJ -f- j?2 ^ 1, und folglich nach
C) (| ± lJ ^ \. Weil aber (| ± 1) nach B) dem absoluten
Werth nach mindestens gleich \ sein muss, so folgt hieraus
g = q= |, j?2 = f; mithin nach A3) ^2 = i?2 = f, und nach
B) gxa = -j, g, = + |, was sowohl unter dem Fall a) als unter
dem Fall b) enthalten ist.
Hiermit ist also der Satz 2. bewiesen. Dem fügen wir nun
noch als dritten Satz hinzu:
. Zu einer gegebenen negativen Discriminante D
giebt es nur eine endliche Anzahl reducirter
Irrationalzahlen.
Aus der Darstellung der Irrationalzahlen §. 130, G):
b t b f--D
und aus der Ungleichung C) ^2 ^> f folgt
oder
-D
3 ' , ...
also giebt es, wenn D gegeben ist, nur eine endliche Zahl
von Werthen der positiven ganzen Zahl c. Ferner folgt aus
2 =3 » ^S 2 '
— c <L b <, c.

§. 132.
Reducirte Zahlen.
427
Also giebt es zu jedem Werth von c nur eine endliche Zahl
von Werthen für b, w. z. b. w.
Vereinigt man alle unter einander äquivalenten Zahlen zu
einer Zahlclasse, so haben wir dann also nach 1. bewiesen:
4 Die Anzahl der Classen von imaginären qua-
quadratischen Irrationalzahlen einer gegebenen
Discriminante ist endlich.
§. 132.
Reducirte Zahlen mit positiver Discriminante.
Wir haben nun eine ähnliche Untersuchung durchzuführen
für ein positives d, also für reelle quadratische Irrational-
Irrationalzahlen. Eine solche Zahl co = x -f- y Vd soll reducirt heissen,
wenn sie folgenden Bedingungen genügt:
co ist positiv und grösser als 1, und die mit co
conjugirte Zahl co' ist negativ und dem absoluten
Werthe nach kleiner als 1,
oder in Zeichen:
A) 0 < y Vd — x < 1 < y Vd + x.
Deutet man in einer Ebene x, y als rechtwinklige Coor-
dinaten, so dass die Punkte der Ebene die Bilder der Zahlen co
werden, so liegen also die Bilder
der reducirten Zahlen in dem
Theile der Ebene, der in der
Fig. 27, die der Annahme d = 2
entspricht, schraffirt ist.
Wir nehmen hier eigentliche
und uneigentliche Aequivalenz zu-
zusammen und beweisen zunächst die
Sätze:
1. Jede Zahl ca ist mit einer reducirten Zahl
äquivalent.
Man sieht dies leicht ein, wenn man co in einen Kettenbruch
entwickelt und bis zur Schlusszahl co„ geht:
B) oo = (a0, «!, «2, . . ., «„_,, con).

428 Elfter Abschnitt. §. 132.
Dann ist co mit con äquivalent, und con ist, sobald n grösser
als 0 ist, positiv und grösser als 1. Da con mit co äquivalent ist,
so handelt es sich nur noch um den Nachweis, dass, wenn n
hinlänglich gross ist, die zu con conjugirte Zahl co'n negativ und
absolut kleiner als 1 ist. Dies aber ersieht man aus nach-
nachstehenden Formeln: Aus B) folgt, wenn P„ : Qn die Näherungs-
Näherungsbrüche sind,
_ Pncon -f Pn_x
oder durch Auflösung
(*\ n — ^n-i m - Pn-i _ Qn-1 (— 1)"
{) n~~ Qnco-Pn - Qn Q«{Q«co-Pn)
Verwandeln wir in dieser Gleichung Vd in — Vd, so geht
gleichzeitig co in co', con in co'n über und wir erhalten aus C)
n /¦¦.' t> n /¦» '
/ V» — l"» — -fn—l Vit—1 V»—1
<?»<»' — Pn ~~ QV , P„ '
m--Qn
E)
1
V» V«-i
(—D*
Wenn nun n hinlänglich gross angenommen wird, so unter-
unterscheiden sich
/ °» / "n — l
CO -y-, OJ ^
Vn V»—i
beliebig wenig von der nicht verschwindenden Differenz co' — co
= —2yVd, wonach D) zeigt, dass co'n negativ ist. Aus E) aber
folgt, dass co'n -\- 1 positiv ist, da Q„ — Qn—i als positive ganze
Zahl mindestens gleich 1 ist, und
1
für ein hinlänglich grosses n beliebig klein wird; und dadurch
ist der Beweis des Satzes 1. geführt.
Da die conjugirte Zahl von der conjugirten co' die ursprüng-
ursprüngliche Zahl co ist, so folgt aus der Definition der reducirten
Zahlen,
dass co und — 1 : co' gleichzeitig reducirt sind.

§. 133. Reelle quadratische Irrationalzahlen. 429
2. Ist ca reducirt und für ein ganzzahliges a
F) ca = a + —,
so ist ca1 dann und nur dann reducirt, wenn « die
grösste in ca enthaltene ganze Zahl ist, wenn also
G) k < co < a -f- 1-
Ist die Bedingung G) erfüllt, so ist cax positiv und grösser als
1, und
<8) < = 1^
ist, da ca' negativ ist, ein negativer echter Bruch; also ist cal
reducirt. Dagegen kann cal nicht reducirt sein, wenn a > ca ist,
da dann oj] negativ ist, oder wenn « -j- 1 < ca ist, da dann car
kleiner als 1 ist.
Setzt man (8) in die Form
(9) - h = <* + -V»
so ist, da — 1 : ca' und ¦— 1 : ca't zugleich mit ca und caL redu-
reducirt sind, a die grösste in — l: «»i enthaltene ganze Zahl, und ca'
ist nach (9) durch ca't, also auch ca durch caY völlig bestimmt.
Hieraus folgt:
3. Entwickelt man eine reducirte Zahl ca in einen
Kettenbruch, so sind alle Schlusszahlen can wieder
reducirte Zahlen, und durch eine dieser Schluss-
Schlusszahlen can ist sowohl die folgende can+1 als die
vorangehende <»„_! vollkommen bestimmt.
§. 133.
Entwickelung reeller quadratischer Irrationalzahlen in
Kettenbrüche.
4. Für eine gegebene Discriminante giebt es nur
eine endliche Anzahl reducirter Zahlen.
Die Richtigkeit dieses Satzes sieht man leicht ein, wenn man
nach §. 130 die Irrationalzahl ca in die Form setzt:

43a Elfter Abschnitt. §. 133.
... b 4-VD —2a
Die conjugirte Zahl ist
B) co' = ~
1 ' 2 c
Soll a> reducirt sein, so ist
C) Q< D2~b
Es muss also, da VD positiv ist, c positiv sein und
D) 0 < VD — b < 2 c < VD -|- b.
Eine zweite Form dieser Bedingungen erhalten wir aus der
zweiten Darstellung
E) 0 < VD — b < 2 a < VD + b.
Es sind also a, b, c positiv und b kleiner als als VD.
Bedeutet X die grösste in YD enthaltene ganze Zahl, also
k < YD < k + 1,
so hat b einen der Werthe 1, 2, 3, . . ., k, jedoch mit der Be-
Beschränkung, dass bei geradem D nur die geraden,, bei ungeradem
D nur die ungeraden unter diesen Zahlen für b zu nehmen sind.
Es ist dann a und c so zu bestimmen, dass
F) —^— = ac,
und dass
k — b + 1 ^ A-j-6
und a muss zwischen denselben Grenzen liegen. Nur einer von
diesen beiden Grenzwerthen ist eine ganze Zahl, der andere kann
für die untere Grenze durch die nächst grössere, für die obere
Grenze durch die nächst kleinere ganze Zahl ersetzt werden.
Es ist also für b nur eine endliche Zahl von Werthen zulässig;
dann ist (D — ö2) : 4 nur auf eine endliche Anzahl von Arten
in zwei Factoren zerlegbar, und von diesen Zerlegungen sind nur
die beizubehalten, in denen beide Factoren der Bedingung G)
genügen. Ausserdem sind noch solche Combinationen wegzu-
wegzulassen, in denen a, b, c einen gemeinsamen Theiler bekommen.
Darin liegt das Mittel, um für ein gegebenes D alle reducirten
Zahlen wirklich zu bestimmen, und dann ist nach §. 130, (9)

§. 133. Reelle quadratische Irrationalzahlen. 431
weil y und c hiei* positiv sind. Aus §. 132, 3. und §. 133, 4. er-
gieht sich nun der folgende wichtige Satz:
5. Die Kettenbruchentwickelung einer reducirten
Zahl co ist periodisch,
d. h. wenn co in einen Kettenbruch
(9) co = («0, %, a2, . . .)
entwickelt wird, so kehren immer nach einer bestimmten Anzahl
von Theilnennern dieselben Theilnenner in derselben Reihenfolge
wieder, also, wenn die Periode aus v Gliedern besteht, so ist
«ir—l = «2V—1 = «3V — 1 • • •,
und es genügt also, den ganzen Kettenbruch durch die Periode
zu bezeichnen, etwa so:
A0) m = [«0, «j, . . ., «r_j].
Dieser Satz ist offenbar gleichbedeutend damit, dass die
Schlusszahl cov des Kettenbruches (9) mit co selbst identisch ist,
und darin liegt auch der Beweis der Behauptung. Denn die
Schlusszahlen cov gehören als äquivalente Zahlen alle zur selben
Discriminante, und daher ist nach 4. die Zahl aller möglichen
Schlusszahlen nur eine endliche. In der Reihe der Schlusszahlen
co, o}1? oj2 . . . muss daher einmal eine schon dagewesene zum
zweitenmal auftreten. Ist cor die erste, die zum zweitenmal auf-
auftritt, so muss co„ = co sein, da sonst nach §. 132, 3. auch gj„_i
zum zweitenmal auftreten würde.
Es lassen sich also die sämmtlichen, zu einer Discriminante
gehörigen reducirten Zahlen in Perioden anordnen:
A1) co, cou o2, . . ., «„_!,
so dass, wenn
«0, «!, «2> . . ., «„_!
die grössten darin enthaltenen ganzen Zahlen sind,
m = [a0, «!, . . ., a„_i]
<°1 — [«1) «25 • • •» «f-15 «o]

432 Elfter Abschnitt, §. 133.
ist, womit die Kettenhruchentwickelung für jede von diesen
Zahlen gegeben ist.
Ist durch eine Periode das ganze System der zur Discri-
minante D gehörigen reducirten Zahlen noch nicht erschöpft, so
bildet man eine zweite Periode u. s. f. Da durch eine Zahl co
sowohl die in der Periode vorhergehende, wie die nachfolgende
völlig bestimmt ist, so enthalten zwei verschiedene Perioden nie-
niemals eine gemeinschaftliche Zahl.
Von diesen Perioden gilt nun der Satz:
6. Reducirte Zahlen aus derselben Periode sind
äquivalent, aus verschiedenen Perioden sind nicht
äquivalent.
Der erste Theil der Behauptung ist von vornherein klar, da
reducirte Zahlen derselben Periode Schlusszahlen von einander
sind; der zweite Theil ist durch den Satz §. 129, IX. bewiesen,
dass äquivalente Zahlen, bei hinlänglich weit fortgesetzter Ketten-
bruchentwickelung, schliesslich dieselben Schlusszahlen bekommen.
Sind also beide Kettenbrüche periodisch, so müssen sie derselben
Periode angehören.
Hat man für eine gegebene Discriminante D nach den am
Anfang des Paragraphen gegebenen Vorschriften das vollständige
System der reducirten Zahlen entwickelt, so ist es leicht, diese
Zahlen in Perioden zu ordnen und die Theilnenner a des Ketten-
Kettenbruches zu finden. Es sei nämlich
eine von diesen Zahlen,
die ihr in der Periode unmittelbar folgende Zahl, so dass
A4) co = a -| , co1 =
co — a
ist, wenn a die grösste in co enthaltene ganze Zahl bedeutet.
Nach A2) und A4) ist dann
2c
co.
\-b — 2ca
und die Vergleichung mit A3) giebt
A5) ax = e, bi = 2 ca — b.-

§. 133. Periodische Kettenbrüche. 433
Wenn umgekehrt zwei der zu D gehörigen reducirten Zahlen
{a, b, c), {«!, &j, Ci], in der durch A5) dargestellten Beziehung
stehen, worin « irgend eine ganze Zahl ist, so folgt die zweite
der ersten in der Periode unmittelbar nach. Denn aus A5)
folgt A4), und daher muss « nach 2. die grösste. in co enthaltene
Zahl sein.
Die Zahl c^ ist also aus co durch die Bedingungen A5)
vollständig und eindeutig bestimmt.
7. Man ordnet also die Zahlen {a, b, c), von einer
beliebigen unter ihnen ausgehend, von links
nach rechts in der Weise, dass die letzte Zahl c
der vorangehenden zugleich die erste Zahl ax der
folgenden wird, und dass die Summe der beiden
mittleren Zahlen b -)- bx durch 2 c theilbar ist.
Diese Anordnung ist nur auf eine Art möglich,
und der Quotient b -f- b^ :2c ist die Zahl «, die
als Theilnenner im Kettenbruch auftritt.
Betrachten wir nun irgend eine primitive ganzzahlige qua-
quadratische Gleichung
A6) i + Bß+Cßs = 0,
in der A, B, C ganze Zahlen ohne gemeinsamen Theiler sind,
die der Bedingung
B* — AAC = D
genügen, so sind die beiden Wurzeln £1, £1' dieser Gleichung
quadratische, zur Discriminante D gehörige Irrationalzahlen, und
wenn wir sie in Kettenbrüche entwickeln, so werden wir nach
§. 132 endlich auf Schlusszahlen co1, ra2 kommen, die zu den
reducirten gehören, und die also in den oben besprochenen
Perioden enthalten sein müssen.
Es ist noch festzustellen, ob diese Schlusszahlen Oj, ra2 in
derselben oder in verschiedenen Perioden enthalten sind.
Nach 6. sind sie dann und nur dann in derselben Periode
enthalten, wenn £1 und £1' mit einander äquivalent sind. Nennen
wir solche quadratische Irrationalzahlen, die mit ihren conju-
girten äquivalent sind, zweiseitige Zahlen1), so können wir
also sagen, dass die Kettenbruchentwickelung der Wurzeln der
2) „Zweiseitig" brauchen wir Dach Dedekind's Vorschlag statt des
Gauss'schen anceps oder des sonst üblichen ambig: Dirichlet-Dede-
kind, Vorlesungen über Zahlentheorie. 4. Auflage, 1894, S. 139.
"Weber, Algebra. I. 28

434 Elfter Abschnitt. §. 133.
Gleichung A6) zu einer oder zu zwei verschiedenen Perioden
führt, je nachdem die Wurzeln zweiseitig sind oder nicht.
Welcher von beiden Fällen eintritt, kann man an der Periode
selbst erkennen.
Wenn nämlich ra eine reducirte Zahl ist, und ra' conjugirt
zu ra, so ist auch — 1 : ra' reducirt (§. 132); und wenn &i äqui-
äquivalent ist mit ra, so ist £1' äquivalent mit ra', also auch mit — 1: ra'.
Ist
ra = {a, i, c},
so ist nach A2):
Nach §. 132, (9) schliesst sich also — 1 :ra' ebenso an — l:ra,
an, wie col an ra. Ist daher die Periode von ra
ra, Oj, ra2, . . ., ra„_i,
so ist die Periode von — 1 : ra':
— 1 — 1 — 1 — 1
ra'v—i' c»_a rai ' ra'
Ist die Periode der Kettenbruchentwickelung von ra
A7) [«0, «!, . . ., «„_!],
so ist sie für — 1 : ra':
A8) [«v-l, «v_2, . . ., «„],
also die umgekehrte.
Ist nun ra mit ra', also auch mit — 1: ra' äquivalent, so müssen
nach 6. diese beiden Perioden mit einander übereinstimmen, wenn
man bei einem geeigneten Gliede beginnt, oder die Periode von
ra muss umkehrbar sein.
Das besagt: Es müssen sich in der Kettenbruchentwickelung
für ra zwei Elemente so auswählen lassen, dass die Entwickelung
gleich lautet, wenn man sie von der einen dieser Zahlen nach
links oder von der anderen nach rechts fortschreitend liest. In
Zeichen: es muss für irgend ein passend bestimmtes Je und für
» = 0, 1, 2, . . ., v — 1
a{ = ak_i
sein. Wenn die Periode umkehrbar ist, so ist auch umgekehrt
(nach 6.) ra mit — 1 : ra', also auch mit ra' äquivalent. Daraus
also das Resultat:
8. Zweiseitige Zahlen haben in ihrer Kettenbruch-
Kettenbruchentwickelung eine umkehrbare Periode und um-

§. 134. Beispiele. 435
gekehrt sind Zahlen, die in der Kettenbruch-
entwickelung eine umkehrbare Periode haben,
zweiseitig.
Schliesslicli wollen wir noch bemerken, dass durch die Eigen-
Eigenschaft, in einen periodischen Kettenbruch entwickelbar zu sein,
die reellen quadratischen Irrationalzahlen von allen anderen
Zahlen unterschieden sind. Denn ist a eine in einen Ketten-
Kettenbruch entwickelte Zahl, und sind con, com zwei Schlusszahlen
dieses Kettenbruches, so ist
Pn Mn H~ -fit — 1 Pm&m ~\~ Pm—1
~~ Qn&n + Qn-1 ~ Qm^m + Qm-1 '
Wenn nun der Kettenbruch periodisch ist, gleichviel, ob die
Periodicität gleich von Anfang beginnt oder erst im Verlaufe
der Entwicklung, so ist, für zwei verschiedene Werthe von n
und m, con = ram, und man erhält also durch Elimination von
an eine quadratische Gleichung für ra, die man in die Form
setzen kann:
Pu — ra Qn, PM_i — coQn-i
Pm — C Qm, -Pm-1 — « Qm-1 ~
§• 134.
Beispiele.
Wir wollen einige Beispiele für die Bestimmung der redu-
cirten Zahlen und Perioden hier durchführen, um die Anwendung
der Methode zu zeigen; die Beispiele lassen sich natürlich ganz
nach Belieben vermehren.
1. D — 29.
Wir bestimmen zunächst nach §. 133 die sämmtlichen zu
D gehörigen reducirten Zahlen. Die grösste in VD enthaltene
ganze Zahl X ist hier = 5; also kann b nur die Werthe haben:
l = 1, 3, 5,
woraus
p6'
ac = =7,6,1.
Die Grenzen, in denen a und c liegen müssen, sind nach
§. 133, G) für die drei Werthe von b:
3, 3; 2, 4; 1, 5.
Man erhält also nur die einzige reducirte Zahl:
{1, 5, 1}.
28*

436 Elfter Abschnitt. §. 134.
Die Periode besteht aus einem einzigen Gliede, und der
Kettenbruch für co ist:
5+V29 .... ,
m = —- = E, 5, 5 . . .)•
2. D = 116 = 4. 29.
Hier ist X = 10 und h hat einen der Werthe
l = 2, 4, 6, 8, 10,
also
ac = 28, 25, 20, 13, 4;
die Grenzen für a und c sind
5, 6; 4, 7; 3, 8; 2, 9; 1, 10,
also, da die Fälle, in denen a, i, c den gemeinschaftlichen Factor
2 haben, noch wegzulassen sind, ergeben sich die reducirten
Zahlen:
{5, 4, 5}, {4, 6, 5j, {5, 6, 4}, {1, 10, 4}, {4, 10, 1},
die sich so in eine Periode ordnen, wobei das erste Glied am
Ende noch einmal zugesetzt ist:
{4,10,1}, {1,10,4}, {4,6,5}, {5,4,5}, {5,6,4}, {4,10,1},
und für co ergiebt sich die Kettenbruchperiode:
5 -f- V29 = [10, 2, 1, 1, 2].
3. D = 76 = 4. 19, k = 8,
6=2, 4, 6, 8,
ac — 18, 15, 10, 3.
Grenzen für a und c:
4, 5; 3, 6; 2, 7; 1, 8;
also sind die reducirten Zahlen:
{3, 4, 5}, {5, 4, 3}, {2, 6, 5}, {5, 6, 2}, {1, 8, 3), {3, 8, 1}.
gijj Wir erhalten eine Periode:
{3, 8, 1}, {1, 8, 3}, {3, 4, 5}, {5, 6, 2}, {2, 6, 5}, {5, 4, 3}, {3, 8, 1},
und die Periode des Kettenbruches für 4 -f- Vl9 wird
[8, 2, 1, 3, 1, 2].
4. D = 37, X = 6,
b = 1, 3, 5,
ac = 9, 7, 3;
Grenzen für a, c:
3, 3; 2, 4; 1, 5;

§. 134. Beispiele. 437
reducirte Zahlen:
{3, 1, 3}, {1, 5, 3}, {3, 5, 1};
Periode:
{3, 5, 1}, {1, 5, 3}, {3, 1, 3}, {3, 5, 1};
Kettenbruch:
5 +V37
2 = t ' ' J*
In allen diesen Fällen sind die Perioden umkehrbar.
5. D = 148 = 4. 37, l = 12,
6 = ' 2, 4, 6, 8, 10, 12,
ac = 36, 33, 28, 21, 12, 1;
Grenzen für a, c:
6, 7; 5, 8; 4, 9; 3, 10; 2, 11; 1, 12;
reducirte Zahlen:
{4, 6, 7}, {7, 6, 4}, {3, 8, 7}, {7, 8, 3}
{3, 10, 4}, {4, 10, 3}, {1, 12, 1}.
Hier erhalten wir drei Perioden von 1, 3 und 3 Gliedern:
{1, 12, 1}, {1, 12, 1},
{3, 10, 4}, {4, 6, 7}, {7, 8, 3}, {3, 10, 4},
{4, 10, 3}, {3, 8, 7}, {7, 6, 4}, {4, 10, 3}
und die Kettenbruchperioden
[12], [2, 1, 3], [3, 1, 2];
von diesen ist die erste umkehrbar, die anderen beiden gehen
durch ümkehrung in einander über.
6. D = 136 = 4. 34, X — 11,
b = 2, 4, 6, 8, 10,
ac — 33, 30, 25, 18, 9;
Grenzen für a, c:
5, 6; 4, 7; 3, 8; 2, 9; 1, 10;
reducirte Zahlen:
{5, 4, 6}, {6, 4, 5}, {5, 6, 5}, {2, 8, 9}, {9, 8, 2}
{3,8,6}, {6,8,3}, {1,10,9}, {9,10,1}, {3,10,3};
Perioden:
{5, 4, 6}, {6, 8, 3}, {3, 10, 3J, {3, 8, 6}, {6, 4, 5}, {5, 6, 5}, {5, 4, 6};
{9, 10, 1}, {1, 10, 9}, {9, 8, 2}, {2, 8, 9}, {9, 10, 1};
Kettenbruchperioden:
[1, 3, 3, 1, 1, 1], [10, 1, 4, 1].
Wir haben also hier zwei verschiedene Perioden, die beide
umkehrbar sind.

438 Elfter Abschnitt. §. 135.
§. 135.
Die Pell'sche Gleichung.
Ist co eine zu der positiven Discriminante D gehörige redu-
cirte Zahl, so erhält man durch die Kettenbruchentwickelung:
co
und es ist con = co immer dann, wenn n ein Vielfaches von der
Gliederzahl v der Periode ist. Dann aber folgt aus A):
B) Qn ra* = (Pn - Qn_,) co + Pn_,.
Es genüge nun co der quadratischen Gleichung §. 130, E):
C) cco* = a + bco, D = b* + 4ac,
und aus dieser muss, da a, b, c ohne gemeinsamen Theiler sind,
die Gleichung B) durch Multiplication mit einer ganzen Zahl
folgen. Bezeichnen wir diese ganze Zahl mit w, so ist also
D) Q„ = UC, P„-i = ttff, P„ Qn-l = Ul.
Setzen wir noch
E) ' Pn-^Qn-1 = t, ;.
so folgt:
^ t -f- üb
F) t-^
Nach §. 125, A1) ist
PnQn-l—
und daraus:
G) P —
Die Gleichung G) heisst die Pell'sche Gleichung. Die
Aufgabe ist die, für ein gegebenes D alle ihre ganzzahligen
Lösungen t, u zu finden. Da, wenn t, u der Gleichung genügen,
auch ±t, +u ihr genügen, so können wir uns auf die Ermitte-
Ermittelung ihrer positiven Lösungen beschränken.
Die Formeln D), E) geben uns eine unendliche Zahl solcher
Lösungen; wir haben nur für n ein beliebiges Vielfaches der
Periodenzahl v zu wählen, für u den grössten gemeinschaftlichen
Theiler von Qn, PM_i, Pn — Qn—i, oder auch einfach die Zahl
Qn : c zu setzen, und t aus E) oder auch, nachdem u bestimmt
ist, direct aus G) zu ermitteln.

§. 135. Die Pell'sche Gleichung. 439
Ist v ungerade, und n ein ungerades Vielfaches von v, so ist
(8) P — B w2 = — 4,
ist aber v gerade, oder n ein gerades Vielfaches von v, so ist
(9) #> —D»* = 4.
Die Gleichung (9) hat die selbstverständliche Lösung t = ± 2,'
m = 0; in allen anderen Lösungen von (8) oder (9) sind t und
u von Null verschieden und wir betrachten hier nur die positiven
Lösungen.
Wir wollen nun nachweisen, dass man aus einer beliebigen
Gleichung von der.Form C) durch die Formeln D), E) alle
Lösungen von (8) und (9) erhält.
Nehmen wir also an, es sei t, u irgend eine positive Lösung
der Gleichung (8) oder (9), und a = \a, b, c) eine zur Discri-
minante D gehörige reducirte irrationale Zahl. "Wir bestimmen
durch die Gleichungen F) P„, Qm Pn—i, Qn—i, die offenbar ganze
Zahlen werden, da t und üb entweder beide gerade oder beide
ungerade sind. Aus der Gleichung C), der co genügt, ergiebt sich
dann B), woraus wieder auf
Qn C + Qn-1
zu schliessen ist; und aus (8) oder (9) ergiebt sich
A1) PnQn-l — QnPn-X = + 1,
worin, wie auch in den folgenden Formeln, das obere oder das
untere Zeichen gilt, je nachdem t, u die Gleichung (8) oder (9)
befriedigt. Nun folgt aber aus F)
0-0 _
91
und weil {a, b, c\ eine reducirte Zahl ist, so ist 2c -f- b > VT)
[§. 133, D)], also _
n n ^ uVD — t _ u*D — P _ ±2
O-«-^ 2 -2(
da aber u und t positive ganze Zahlen sind und B > 1, so ist
uVD -\- t > 2, also Qn — Qn-i > 0 für das obere und > — 1
für das untere Zeichen.
Weil nun Qn — Qn-i eine ganze Zahl sein muss, so ist
sie hiernach gleich oder grösser als Null, und wir haben
Qn-l ä Q„
wo das Gleichheitszeichen nur im Falle des unteren Zeichens,
also im Falle der Gleichung (9) möglich ist.

440 Elfter Abschnitt. §. 135.
Ferner ist (da nach §. 133, D) l < V~D ist)
also ^M_! Null oder positiv, und Null kann nur im Falle des
oberen Zeichens, also im Falle der Gleichung (8) auftreten.
Daraus schliessen wir
A2) 0 ^ £„_! ^ Qn,
wo das Gleichheitszeichen in der unteren Grenze nur im Falle
der Gleichung (8), also der oberen Zeichen, in der oberen Grenze
nur im Falle der Gleichung (9), also der unteren Zeichen vor-
vorkommen kann.
Wir entwickeln nun den rationalen Bruch PM : Qn in einen
endlichen Kettenbruch
7f = («0) «1, «2) • • •) «K-l)>
indem wir n nach §. 123, I. so annehmen, dass
(- l)M = =F l
wird. Bedeutet dann P' : Q' den vorletzten Näherungsbruch,
so ist
PnQ'-QnP'=+h
und es ist nach §. 125, II.:
0 ^ Q' ^ Qn,
wo das Gleichheitszeichen in der unteren Grenze nur für n = 1,
also im Falle der oberen Zeichen, in der oberen Grenze nur für
n = 2, also der unteren Zeichen vorkommen kann, ebenso wie
in A2). Daraus folgt nach §. 126, III.:
Q' = &_,, P' = ?„_,,
und es ist also nach A0)
(«0, «!, «2, . . ., «„_!, ra) = ra,
d. h. [«0, «!, «2, . . ., «„_]] ist eine Periode des Kettenbruches für
ra, aus der nach den Formeln D), E) die Lösung t,-u von G)
hergeleitet wird. Damit ist bewiesen, dass wir auf -diese Weise
alle Lösungen der Gleichung G) finden.
Hieraus lassen sich noch einige wichtige Folgerungen ziehen.
Sind t, u und tu «j zwei Lösungen der Gleichung (8) oder
(9), wobei nicht ausgeschlossen ist, dass fdr die eine die Gleichung

§. 135. Die Pell'sche Gleichung. 441
(8), für die andere die Gleichung (9) gilt, so folgt in allen Fällen
A3) P — t?^D («2 — O — 8.
Nehmen wir nun u>u1 an, so ist m2 — u? — (u — Wj) (u-f-«i) 55 2,
und da D = 0 oder = 1 (mod 4) und kein Quadrat ist (§. 130),
so ist D mindestens =¦ 5. Nach A3) ist daher auch t > tu
und wir schliessen, dass, wenn u wächst, auch t wachsen muss,
dass also, wenn u einen möglichst kleinen positiven Werth hat,
auch t möglichst klein ist. Man kann also von einer kleinsten
positiven Lösung reden, die wir mit T, U bezeichnen wollen. Man
erhält sie, wenn man in den Formeln D), E) n möglichst klein,
also gleich der Gliederzahl v der Periode setzt. Ist daher v
gerade, so ist nur die Gleichung (9), nicht die Gleichung (8)
lösbar; ist aber v ungerade, so ist sowohl (8) als (9) lösbar. Da
dies nur von der Discriminante D, nicht von der besonderen
Zahl co abhängen kann, so folgt:
9. dass bei einer Discrimininante die verschiedenen
Perioden entweder alle eine gerade oder alle
eine ungerade Gliederzahl enthalten.
Ist D gerade, also durch 4 theilbar, so muss auch t gerade
sein, und die Gleichung G) lässt sich Glied für Glied durch 4
theilen. Ist D ungerade, so sind auch t, u entweder beide gerade
oder beide ungerade; sind sie beide ungerade, so sind ihre Qua-
Quadrate, wie alle ungeraden Quadratzahlen, nach dem Modul 8 mit
1 congruent, also muss D = 5 (mod 8) sein. Aber es ist nicht
immer möglich, wenn D = 5 (mod 8) ist, die Gleichung G)
durch ungerade Zahlen zu lösen i). Ist D = 1 (mod 8), so
müssen t, u gerade sein.
Die Beispiele des §. 134 geben, auf diese Weise behandelt,
die folgenden kleinsten positiven Lösungen der Pell'sehen
Gleichung, wobei der Factor 4, wo es möglich ist, weggehoben ist.
. 52 — 29.12 = _ 4
702 _ 29.132 = — 1
1702 — 19.392= i
62 — 37.12 = — 1
35* — 34.62 _ i.
*) Vergl. Ca'yley, Note zur l'equation x2— Dy2= + i, X» = 5 (mod 8),
Crelle's Journal, Bd. 53. Mathematical papers, Vol. IV. Tafeln für die
Lösungen der Pell'sehen Gleichung in der Form y2 =: ox2 -j- 1 hat
Degen berechnet (Canon Pellianus, Havniae 1817). Auch in Legendre's
Zahlentheorie (deutsch von Maser) findet sich eine solche Tafel.

442 Elfter Abschnitt. §. 136.
§. 136.
Ableitung aller Lösungen der PelPschen Gleichung
aus der kleinsten positiven.
Ist t, u irgend eine Lösung der Pell'sehen Gleichung, so
ist der Ausdruck
P — Du*
4
der den Werth + 1 hat. die Norm der beiden conjugirten Zahlen
i± »t/B t-rfB (§ 130>
"Wir wollen sie die zu VI) gehörigen Einheiten nennen.
Darunter sind auch die Zahlen + 1 enthalten (für u — 0).
Sind also (tt, %), (t2, w2) irgend zwei (positive oder negative)
Lösungen der Pell'sehen Gleichung
p — Dui = ± 4,
so haben die beiden Zahlen
&i — 2' ®* ~2
die Norm + 1, und das Gleiche gilt also auch von ihrem Product
Darin ist
h =
und t$ und ms sind, wie man sofort sieht, ganze Zahlen.
Denn wenn D gerade ist, so sind tu t2 gerade, und wenn D
ungerade ist, so sind tu Ui entweder beide gerade oder beide
ungerade, und ebenso t2, m2. Es ist also ®3 gleichfalls eine zu
V.D gehörige Einheit, und es folgt, dass das Product zweier
(und folglich auch mehrerer) Einheiten wieder eine Ein-
Einheit ist.
Ist & eine beliebige irrationale Einheit, so ist +®—1 die
zu ® conjugirte Einheit. Es gehören unter den von ^ 1 ver-
verschiedenen Einheiten immer vier zusammen, .
+ ®, ± ®~\
unter denen eine positiv und grösser als 1 ist. Diese, entspricht

§. 136. Die Pell'sche Gleichung. 443
den positiven Werthen von t, u; eine zweite ist positiv und
kleiner als 1 und die beiden anderen sind negativ. Ist T, U die
kleinste positive Lösung der.Pell'schen Gleichung, so ist
0 __ t + üVT>
die kleinste unecht gebrochene zu ~\/~D gehörige positive Einheit,
und wir können nachweisen, dass in der Form + ®n, worin n
eine ganze Zahl bedeutet, alle zu ~\/~D gehörigen Einheiten ent-
enthalten sind. Es genügt dazu, zu zeigen, dass der Ausdruck @*
für ein positives n alle Einheiten, die grösser als 1 sind, liefert.
Dies ist aber sehr einfach; denn ist ®j irgend eine von diesen
Einheiten, so wird sie zwischen zwei auf einander folgenden
Potenzen von & liegen, da diese Potenzen mit dem Exponenten
ins Unendliche wachsen; also
&n <i ®! < &n + \
mithin
1 <; @i &-n < &.
Da aber &1 &~n gleichfalls eine Einheit ist, so ist, wenn nicht
das Gleichheitszeichen gilt, &x ®~n grösser als 1 und kleiner als
0, was gegen die Voraussetzung ist, dass & die kleinste unecht
gebrochene Einheit sei; es muss also
®, = 0n
sein, was zu beweisen war.
Anmerkung, die Gauss'sche Theorie der quadratischen
Formen betreffend1).
Wir fügen, um die Verbindung unserer Betrachtungen mit
der sonst bekannten Gauss'sehen Theorie der quadratischen
Formen herzustellen, einige Bemerkungen bei, die in unserem
Zusammenhange nicht gerade erforderlich sind, und die daher
auch übergangen werden können.
Aus jeder quadratischen Irrationalzahl
co = {a, b, c)
können wir eine bestimmte primitive quadratische Form (nach
der Gau ss'sehen Bezeichnung)
!) Vergl. Disq. ar. art. 183 ff., Dirichlet-Dedekind, Vorlesungen
über Zahlentheorie. Vierte Auflage. §. 62, §. 72 ff.

444 Elfter Abschnitt. §. 136.
9 = (Ä, B, C) = (— a, f 6, c) oder = (— 2 a, b, 2c)
(je nachdem b gerade oder ungerade ist) ableiten, deren Deter-
Determinante = D : 4 oder = D ist. Aus der conjugirten Zahl
co' = {— a, —5, — c}
erhalten wir dann die Form — 9, deren Coefficienten denen von
9 entgegengesetzt sind. Die Zahlen co und co' sind die Wurzeln
der Form 9 = 0 oder — 9 = 0. Ebenso sind — co und — co' die
Wurzeln der zu 9 entgegengesetzten Form 9' = (A. — JB, C).
Bei Gauss werden nun nur solche Formen derselben Deter-
Determinante in eine Classe vereinigt, die eigentlich äquivalent sind,
und es ist noch die Beziehung der Gauss'schen Classenzahl zu
der Zahl der Classen der co oder zu der Anzahl der zu einer
bestimmten Discriminante gehörigen Kettenbruchperioden fest-
festzustellen. Dazu führen folgende Sätze:
1. Die beiden Formen 9 und —9 sind dann und nur
dann uneigentlich äquivalent, wenn die Glei-
Gleichung P — Du2 = — 4 in ganzen Zahlen lös-
lösbar ist.
Diesen Satz wollen wir aus der Theorie der quadratischen
Formen hier voraussetzen. Er kann entweder aus der Betrach-
Betrachtung der Perioden der reducirten Formen oder auch ohne diese
Theorie auf demselben Wege bewiesen werden, wie man die
Transformation einer quadratischen Form in sich selbst auf die
Lösung der Pell'schen Gleichung zurückführt.
2. Wenn co mit co' eigentlich äquivalent ist, so ist
9 mit —9 eigentlich äquivalent.
Dies zeigen die Formeln §. 130 A5), wenn man darin al = — a,
bx = — b', Cj = — c, s = 1 setzt. Ebenso ergiebt sich aus diesen
Formeln:
3. Wenn ra mit co' uneigentlich äquivalent ist, so ist 9
mit sich selbst uneigentlich, also 9 mit 9' eigent-
eigentlich äquivalent.
Die beiden letzten Sätze gelten, wie man aus denselben
Formeln erkennt, auch umgekehrt.
Wir fassen jetzt die vier Formen
# = 9, — 9, 9', — 9'
und die vier Zahlen
ii, = 03, — co, co', — a>'

§. 137. Berechnung Von Gleichungswurzeln. 445
zu je einem Complex <& und £1 zusammen, die einander eindeutig
zugeordnet sind. Ersetzen wir co durch eine äquivalente Zahl cou
so erhalten wir einen Complex Slx und diesem entsprechend einen
Complex <&!, dessen Formen sich den Formen 3> so zuordnen
lassen, dass je zwei entsprechende eigentlich äquivalent sind.
Wir unterscheiden nun die beiden Fälle
a. Wenn P — Z)u2 = — 4 lösbar ist, also die Anzahl der
Periodenglieder des Kettenbruches für a ungerade, so ist 9 mit
— <p uneigentlich, also mit — 9' eigentlich äquivalent und 3>
repräsentirt zwei Gauss'sche Classen, oder, wenn 9 mit sich
selbst uneigentlich äquivalent ist, eine Anceps-Classe. Ebenso
repräsentirt £1 zwei Classen von Zahlen co, oder, wenn co und co'
äquivalent sind, nur eine. Hier ist aber co mit sich selbst
uneigentlich äquivalent, folglich ist, wenn co mit co' überhaupt
äquivalent ist, auch uneigentliche Aequivalenz vorhanden, und
dann gehört also (nach 3.) 9 in eine Anceps - Classe. In dem
Falle a. ist also die Gauss'sche Classenzahl gleich
der Anzahl der Classen der Zahlen co.
b. Wenn P — Du* = — 4 lösbar, also die Anzahl der
Periodenglieder gerade ist, repräsentirt 3> vier oder zwei
Gauss'sche Classen, letzteres, wenn entweder 9 mit —9 oder
9 mit cp' eigentlich äquivalent, wenn also co mit co' überhaupt
äquivalent ist. In dem Falle b. ist also die Anzahl der
Gauss'schen Classen doppelt so gross als die Anzahl
der Classen der co.
§. 137.
Genäherte Berechnung der reellen Wurzeln einer
numerischen Gleichung durch Kettenbrüche.
Auf die Theorie der Kettenbrüche gründet, sich ein von
Lagrange herrührendes Verfahren, um die reellen Wurzeln
einer numerischen Gleichung mit beliebiger Annäherung zu be-
berechnen, das sich jetzt mit wenig Worten aus einander setzen
lässt.
Es sei f(x). = 0 eine reelle Gleichung, die wenigstens eine
reelle Wurzel hat. Nach einer der verschiedenen Methoden des
VIII. und IX. Abschnittes können wir dann immer eine ganze
Zahl a0 finden, so dass zwischen a0 und a0 -\-1 eine oder mehrere

446 Elfter Abschnitt. §. 137.
der Wurzeln von f(x) liegen. Transformiren wir also f(x) durch
die Substitution
. 1
x = «o + —•
xx
in fL (ajj), so wird f± (xx) eine oder mehrere Wurzeln haben, die
grösser als 1 sind. Wir bestimmen also eine positive ganze
Zahl au so dass zwischen ax und ax -\- 1 eine oder mehrere der
Wurzeln von/1(a;1) liegen, und transformiren fx {xx) durch die
Substitution
% = «!+ —
x2
in f% (x2). Die Gleichung /2 = 0 hat dann wieder mindestens
eine Wurzel, die grösser als 1 ist, und die also zwischen den
beiden positiven ganzen Zahlen a2 und a2 -|- 1 liegt, u. s. f.
Schliesslich wird man auf diese Weise dazu kommen, eine einzige
Wurzel zu isoliren, und man erhält in der Keine der Näherungs-
Näherungsbrüche
(a0), (»o, «0, (a0, «1, a.2), (a0, <h, «2> «s) • • •
eine Eeihe rationaler Zahlen, die abwechselnd über und unter
einer der Wurzeln x liegen und sich dieser Wurzel unbegrenzt
annähern. Ist man so bis zu dem Näherungsbruch
^ F*
(a0, »!, a2, . . ., av-i) — -jr-
V" •
vorgedrungen, so unterscheidet sich dieser von dem wahren Werth
von x um weniger als 1 : Q$. Die Grosse des Nenners giebt
also unmittelbar ein Maass für die bereits erreichte Genauigkeit.
In den gewöhnlichen Fällen wird man die Zahlen a0, o,, a2...
einfach dadurch erhalten, dass man auf die Zeichenwechsel der
Functionen /, /l5 /2 . . . achtet.
Um dies Verfahren an einem Beispiel zu erproben, nehmen
wir die cubische Gleichung, die wir schon früher betrachtet
haben:
xz — 2 x — 2 = 0.
Sie hat eine Wurzel zwischen 1 und 2, also haben wir a0 = 1
zu setzen.
Man erhält, wenn man die oben angegebene Transformation
wirklich ausführt, die folgende Kette von Gleichungen:
x3 — 2 x — 2 = 0, ao = l
3 a?3 — a?2 — 3 x — 1 = 0, ax = 1

§. 138. Kationale Wurzeln. 447
- 8 x — 3 = 0, a2 = 3
— 22«2 — 14« — 2 = 0, «3 = 2
46«s _ 6«2 — 32« — 9 = 0, at= 1
«3 — 94«2 — 132« — 46 = 0, a5 = 95
3561 «s — 9083 *2 — 191« — 1 = 0, ae = 2,
also
v — A 1 3 9 1 QI 9 ^
<ßj —— l ¦*¦} •*• j *Jj -^j -1-5 £7v} j£i • . * 1
und die Näherungsbrüche:
J_ 2_ _7_ 16 23 2201 4425
1 ' 1 ' 4 ' 9 ' 13' 1244' 2501
Wenn wir die beiden letzten Brüche in Decimalbrüche ver-
verwandeln, so erhalten wir für « die beiden Grenzen:
* 1,7692926; 1,76929228,
und der Fehler in der letzteren etwas zu kleinen Zahl ist
kleiner als
0,00000016.
Dass man hier nach wenig Schritten ein gutes Resultat
erhält, beruht auf dem Umstände, dass hier ziemlich früh ein
grösserer Theilnenner 95 auftritt. In den meisten Fällen be-
bekommt man für die Theilnenner kleine Zahlen; dann wachsen
die Nenner der Näherungsbrüche langsam, und man erhält nur
mühselig ein Resultat von grösserer Genauigkeit.
Die Auffindung grösserer Theilnenner, z. B. 95, wird durch
die Bemerkung erleichtert, dass, wenn eine Wurzel einer Gleichung
einen grossen Werth hat, der negative Coefficient der zweithöchsten
Potenz der Unbekannten eine, wenn auch nur rohe Annäherung
an diese Wurzel giebt, wie z. B. in der vorletzten der obigen
Gleichungen 94 an 95.
§. 138. *
Rationale Wurzeln ganzzahliger Gleichungen.
Reducible Gleichungen.
Wir schliessen diesen Abschnitt mit einer Betrachtung über
ganzzahlige Gleichungen, die, wenn sie auch nicht unmittelbar
mit der Theorie der Kettenbrüche in Beziehung steht, doch hier
am passendsten eine Stelle findet.

448 Elfter Abschnitt. • §. 138.
Wenn man es mit Gleichungen zu thun hat, deren Coeffi-
cienten rationale Zahlen sind, so wird man zunächst nach
etwaigen rationalen Wurzeln suchen. Wenn die Gleichung
f(x) = aoxn -j- ctix»-1 -j- a2xn~2 + • • • + an-\X -\- an = 0
rationale Coefficienten hat, so können wir immer annehmen, dass
diese Coefficienten ganze Zahlen sind; man hat nur nöthig, um
den Fall gebrochener Coefficienten darauf zurückzuführen, die
ganze Gleichung mit einem gemeinschaftlichen Vielfachen aller
Nenner zu multipliciren.
Wir können aber auch noch weiter annehmen, dass a0 = 1
sei; denn setzen wir in dem Product a^~1f(x)
a0 x = %i,
so wird die Gleichung
x\ + os, x\~x + »o «2«i~2 -\ 1- a™-1 an = 0.
Wir wollen also jetzt annehmen, dass in der Gleichung
A) xn + ^x»-1 -\- aixn-i + • • • + an-xx -\- a.n = 0
die Coefficienten %, a2, . . ., an ganze Zahlen sind. Eine ratio-
rationale Wurzel von (l)'kann nicht eine gebrochene Zahl sein;
denn nehmen wir an, es werde A) befriedigt durch den Bruch
wo p und g ganze Zahlen ohne gemeinsamen Theiler sind, und
g positiv und grösser als 1 ist, so folgt durch Multiplication
mit q"-1
+ «F" +
2 -\ 1- anqn-1 = 0.
Es müsste also pn : q eine ganze Zahl sein, was unmöglich ist.
Wenn nun die Gleichung A) dadurch befriedigt werden kann,
dass man für x eine ganze Zahl setzt, so muss diese ganze Zahl,
wie die Gleichung A) zeigt, nothwendig ein Theiler von an sein,
und man hat also nur die verschiedenen Divisoren von a„, mit
positivem und negativem Zeichen behaftet, versuchsweise in die
Gleichung einzusetzen.
Auf die Frage nach rationalen Wurzeln einer ganzzahligen
Gleichung kommt auch die allgemeine Frage zurück, ob eine
ganze rationale Function
f(x) = xn + os, x»-1 + os2 x»-2 -\ 1- an-i x + osn,
deren Coefficienten osl7 os2, . . ., an ganze Zahlen sind, durch eine
rationale Function von niedrigerem Grade v:

§. 138. Reducible Gleichungen. 449
(p(x) =r xr + alxv~1 -f-
mit rationalen Coefficienten «j, «2, . . ., «r theilbar sein kann.
Wenn f(x) durch <jp(a?) theilbar ist, so ist der Quotient i>(x)
wieder eine ganze rationale Function mit rationalen Coefficienten
vom Grade n — v:
i>(x) = Xn~* + ß-LX*"*-1 -| \- ßn-v-iX + ßn-v,
und da f(x) auch durch i>(x) theilbar ist, so können wir bei
der Entscheidung unserer Frage v < \n annehmen. Ausserdem
folgt aus §. 2, dass die Coefficienten « und ß von <p und tj>
ganze Zahlen sein müssen.
Um nun über die Möglichkeit einer solchen Theilung zu
entscheiden, nehme man die Function <jp (x) mit unbestimmten
Coefficienten «, und dividire f{%) durch <jp (x) (nach §. 3). Es
ergiebt sich dann ein Rest vom Grade v — 1, und wenn man
dessen Coefficienten, die sämmtlich rationale Functionen der m
sind, gleich Null setzt, so erhält man v Gleichungen, denen diese
Coefficienten genügen müssen. Man kann durch Elimination (§.55)
eine Gleichung herstellen, die nur noch eine dieser Unbekannten
enthält, und die dann eine ganzzahlige Wurzel haben muss. Es
wird aber oft zweckmässiger sein, diese Elimination nicht wirk-
wirklich auszuführen, sondern direct zu versuchen, dem System der
v Gleichungen durch ganzzahlige Werthe der « zu genügen. Die
Auswahl der zu erprobenden Zahlen kann durch manchen Kunst-
Kunstgriff, der auf zahlentheoretischen Sätzen beruht, sehr eingeschränkt
werden.
Wir wollen beispielsweise eine Gleichung zehnten Grades
aus der Theorie der elliptischen Functionen entnehmen, wo
solche Aufgaben sehr häufig in der Weise vorkommen, dass die
Zerlegbarkeit in Factoren bestimmten Grades theoretisch fest-
feststeht, und wo es sich dann darum handelt, diese Factoren zu
finden1). Eine solche Gleichung ist
#10 _ 36 #8 + 528«« — 3897«* -(- 14354 «2 — 21025 = 0.
Wir fragen, ob die linke Seite in zwei Factoren fünften
Grades zerlegbar ist. Wenn der eine der beiden Factoren
l) Vergl. des Verfassers Werk: „Elliptische Functionen und algebraische
Zahlen", Braunschweig 1891. Das hier behandelte Beispiel aus der Theorie
der Transformation 47sterlGrades ist aus der Abhandlung genommen: „Ein
Beitrag zur Transformationstheorie der elliptischen Functionen etc." von
H. Weber A893). Mathematische Annalen, Bd. 43.
Weber, Algebra. I. 29

450: ' Elfter Abschnitt. §. 138.:
ß%3 -\-yxi -f- d# +'£
ist, so ist der andere, da.in der gegebenen Gleichung keine
ungeraden Potenzen vorkommen,
a;5 — a& -\- ßx% — y^2 _^_ ## — s,
und es muss also sein:
X™ — 36 a:* + 528 jr6 — 3897 a* + 14354a;2 — 21025
Setzt man entsprechende Coefficienten einander gleich, so
folgt:
1. •«« — 2/3 = 36,
; 2. /S*-f- 2d — 2ocy = 528,
3. y2_)_2«£ — 2ßS — 3897,
4. ö«-— 2y« = 14354,
5. £2 = 21025,
und es sind nun ganzzahlige Werthe von «, ß, y, d, s zu suchen,
die diesen fünf Gleichungen genügen. Zunächst erhält man aus 5.:
£ = 1/21025 = 145 = 5 .29,
und' man kann £ positiv annehmen, weil das von x unabhängige
Glied jedenfalls in einem der beiden Factoren .positiv ist. Die
Gleichung 4. ergiebt, wenn man rechts den Rest nach dem Modul
145 nimmt,
D) d2 = — 1 (mod 145),
und diese Congruenz hat die vier Lösungen
8 = ± 12, ±17 (mod 145).
Da 8 nach 4. ausserdem gerade sein muss, so könnte d folgende
Werthe haben:
8 = ± 12, ± 128, ± 162.
Weiter wird man vorläufig nicht gehen, da grosse Zahlwerthe für
8 von vornherein unwahrscheinlich sind. Diesen Werthen von d
entsprechend erhält man aus 4. für y:
y = — 49, 7, 41.
Wenden wir noch den Modul 5 an, so folgt:
yi = l, — 1, .1 (mod 5)
und aus 3.:
ß=±l, ±2, ±1 (mod 5)
und aus 1.:
«* = 1 ± 2, ¦ 1 + 1, 1 ± 2 (mod 5).

§. 138. Reducible Gleichungen. 451
Daraus ergiebt sich, da nur 0, 1 und 4, nicht 2 und 3 nach
dem Modul 5 mit einem Quadrat congruent sein können, dass
in 8 die Zeichen so genommen werden müssen:
8 = — 12, -)- 128, — 162
«= ± 2, 0, ±2 (mod 5).
Die Gleichung 2. zeigt noch, dass der mittlere Fall auszu-
schliessen ist, da die rechte Seite nicht durch 5. theilbar ist.
Dass auch 8 = — 12 ausgeschlossen werden muss, ergiebt sich
aus der Gleichung 2., die für 8 = —12, y = — 49 die Congruenz
ß2 = 6 (mod 7)
zur Folge hat, die aber nicht lösbar ist.
Es bleibt also nur noch übrig:
d = — 162, y = 41.
Aus 3. folgt für ß die Congruenz:
17 ß == 93 (mod 145)
oder
ß = — 1 (mod 5), 2 ß = — 1 (mod 29),
also •
ß = 14 (mod 145).
Nimmt man /3 = 14 an, so folgt « = — 8, und alle Glei-
Gleichungen 1. bis 5. sind befriedigt. Es hat sich also damit die
Zerlegung ergeben, die nachträglich leicht zu verificiren ist:
#10 _ 36 #8 _J_ 528 x6 — 3897«* + 14354 x2 — 21025 =
(«5 _ 8x* + 14a;s _|_ 41^2 _ \Q2x -\- 145)
(a>5 +8ä*+14a>3 — 41a:2 —162 a: — 145).
29*

Zwölfter Abschnitt.
Theorie der Einheitswurzeln.
§• 139.
Die Einheitswurzeln.
Unter einer Einheitswurzel versteht man allgemein eine
reelle oder imaginäre Zahl von der Beschaffenheit, dass irgend
eine ihrer Potenzen mit einem ganzzahligen Exponenten gleich 1
ist. . Diese Einheitswurzeln haben wir schon im §. 36 kennen
gelernt und durch trigonometrische und Exponentialfunctionen
dargestellt. Wir haben ferner specielle Fälle, z. B. im §. 38 die
dritten Einheitswurzeln, benutzt, die dort ohne trigonometrische
Functionen ausgedrückt wurden.
In allen tiefer gehenden Untersuchungen über algebraische
Gleichungen ist nun eine genauere Kenntniss der Einheitswurzeln
und ihrer Eigenschaften unerlässlich. Wir werden uns daher in
diesem Abschnitt mit dem elementaren Theil der algebraischen
Theorie der Einheitswurzeln eingehender beschäftigen, ohne von
ihrer Darstellung durch trigonometrische Functionen Gebrauch
zu machen. Wegen der geometrischen Anwendung auf die Con-
struction der regulären Vielecke, auf die wir schon im §. 36
hingewiesen haben, wird die Theorie der Einheitswurzeln auch
die Kreistheilungstheorie genannt. Sie ist im Wesentlichen
eine Schöpfung von Gauss1).
Wenn die wte Potenz einer Zahl *• gleich 1 ist, wenn also
die Gleichung
l) Gauss, Disq. ar. Sectio VII.

§.139. Einheitswurzeln. 453
für ein ganzes positives n befriedigt ist, so heisst r eine wte
Einheitswurzel oder eine Einheitswurzel vom Grade n.
Es sind also alle wten Einheitswurzeln, und nur diese, Wurzeln
der Gleichung nten Grades
B) fix) — xn — 1 = 0.
Es ist
C) f(x) = nxn-1,
und folglich hat/(«) mit/'(a:) keinen Theiler gemein; also hat
f(x) keine mehrfachen Wurzeln, und es giebt n und nicht mehr
von einander verschiedene nte Einheitswurzeln.
Ist r eine nte Einheitswurzel, so ist es auch jede ganze
Potenz von r, denn aus rn = 1 folgt rÄn = 1, wenn Je eine be-
beliebige positive oder negative ganze Zahl ist (auch Je = 0 nicht
ausgeschlossen); also ist auch rÄ eine nte Einheitswurzel. Da es
aber nur n Einheitswurzeln vom Grade n giebt, so sind die
Potenzen rÄ nicht alle von einander verschieden. Hierüber gilt
nun Folgendes:
Wenn sich zwei Zahlen k, h' um ein Vielfaches von n unter-
unterscheiden, wenn also
D) V = Je (mod n)
ist, so ist auch
E) r* == rv.
Denn ist h' = h -J- h n, so ist
woraus, da r» = 1 ist, die Gleichung E) folgt.
Es sind also in der Reihe der Zahlen
F) 1, r, r\ r\ . . ., r»-1
gewiss alle von einander verschiedenen rÄ enthalten; aber es
müssen nicht umgekehrt die Grossen F) alle von einander ver-
verschieden sein.
Nehmen wir an, es seien Je und Je' = Je -J- jt zwei Zahlen
der Reihe
0, 1, 2 ... n — 1,
und
r* =
so folgt, dass r'* = 1 sein muss. Es kann also in der Reihe F)
kein früher dagewesenes Glied wiederkehren, ehe das erste Glied

454 Zwölfter Abschnitt. §. 139.
1 zum zweiten Male vorkommt, und wenn (i die kleinste posi-
positive Zahl ist, für die ru = 1 ist, so sind die Zahlen:
G) 1, r, r», . . ., r"-1
alle von einander verschieden.
Es muss dann jt ein Theiler von n sein. Denn durch
Division lassen sich die ganzen Zahlen h, (i' so bestimmen, dass
n = h[i -f- ft'; 0 <I (i' < (i-
Dann ist aber auch, wie aus
hervorgeht, r'4' = 1, d. h. da jt die kleinste positive Zahl sein
soll, für die ru = 1 ist, (i' — 0, und folglich n durch (i theilbar.
Es ist also r zugleich (ite Einheitswurzel, aber
nicht Einheitswurzel von noch niedrigerem Grade.
Man nennt die Zahl r eine primitive wte Einheits-
wurzel, wenn sie nicht zugleich Einheitswurzel eines
niedrigeren Grades ist.
Aus dieser Definition folgt, dass die Zahlen der Reihe F),
wenn r eine primitive nte Einheitswurzel ist, alle von einander
verschieden sind, und dass sämmtliche «ten Einheitswurzeln
darunter enthalten sind, dass sie aber nur einen Theil der wten
Einheitswurzeln ausmachen, wenn r eine imprimitive nte Einheits-
Einheitswurzel ist.
Jede Einheitswurzel, deren Grad ein von n verschiedener
Theiler von n ist, ist zugleich imprimitive wte Einheitswurzel.
Ist r zugleich wte und wte Einheitswurzel, so ist es
auch [ite Einheitswurzel, wenn (i der grösste gemein-
gemeinschaftliche Theiler von n und m ist.
Denn nach §. 126 kann man die ganzen Zahlen x, y so be-
bestimmen, dass
mx ~\- ny = (i
wird, und folglich ist
Dem entspricht der andere Satz:
Sind ru r2 . . . Einheitswurzeln der Grade %, n2 . . .,
so sind sie alle zugleich Einheitswurzeln des Grades w,
wenn m irgend ein gemeinschaftliches Vielfaches von
»%, w2 • • • bedeutet.

§. 140. Primitive w*« Einheitswurzeln.
'..;"¦¦ §• 140. "'' . >
Primitive Einheitswurzeln.
Dass primitive Einheitswurzeln für jeden Grad n existiren,
haben wir im vorigen Paragraphen noch nicht bewiesen. Wir
müssen dies zunächst nachholen und werden dabei auch die
genaue Zahl der primitiven Einheitswurzeln feststellen.
Sei der Grad n in zwei Factoren a, b zerlegt, die zu ein-
einander relativ prim sind, also
n = ab,
und sei a eine ate, ß eine bte Einheitswurzel. Dann ist das
Product
A) r = aß
eine wte Einheitswurzel. Sind «', ß' zwei andere ate und 6te Ein-
Einheitswurzeln, so ist r' = <x'ß' auch eine »te Einheitswurzel, und
es ist zu zeigen, dass ¦ r' von r verschieden ist, wenn nicht gleich-
gleichzeitig « = <x' und ß = ß' ist.
Da nämlich a, b relativ prim sind, so kann man nach §. 126
die ganzen Zahlen x, y so bestimmen, dass
B) ace-\-"by = 1
ist; und dann folgt aus A)
• a =>*!', ß = raic.
Demnach ist et, und ß durch r vollständig bestimmt, und
wenn a' ß' auch gleich r sein soll, so muss a = <x', ß = ß' sein.
Lässt man also in A) cc alle aten, ß alle bten Einheitswurzeln
durchlaufen, so erhält r genau ab = n verschiedene Werthe,
und es folgt:
I. dass in der Form aß alle wten Einheitswurz'eln
darstellbar sind,
und weiter:
II. dass r dann und nur dann eine primitive nte
Einheitswurzel ist, wenn a eine primitive ate
und ß eine primitive bte Einheitswurzel ist.
Denn erstens sei ft der kleinste positive Exponent, für den
r" = 1 ist; dann ist auch cc"' /?¦" = 1 und daraus folgt nach B),
wenn man beiderseits zur Potenz by und ax erhebt,
v? = 1, ßf = 1.

456 Zwölfter Abschnitt. §. 140.
Wenn nun [i < n ist, so kann es nicht zugleich durch a
und durch b theilbar sein, und also können auch a und b nicht
beide die kleinsten positiven Exponenten der Potenzen von a und
ß sein, die gleich 1 werden, d. h. also, wenn r nicht primitive
#e Einheitswurzel ist, so sind auch a und ß nicht zugleich
primitive ate und bte Einheitswurzeln, oder wenn cc und ß primi-
primitive ate und 6te Einheitswurzeln sind, so ist ihr Product r primi-
primitive nte Einheitswurzel. Auf der anderen Seite ist klar, dass,
wenn a oder ß Einheitswurzel von niedrigerem Grade als a oder
b ist, auch r Einheitswurzel von niedrigerem als dem nien Grade
sein wird.
Zerfällt n in mehrere Factoren a, b, c . . ., von denen je
zwei zu einander relativ prim sind, und sind <x, ß, y . . . Einheits-
Einheitswurzeln der Grade a, b, c . . ., und setzt man
C) r = aßy ,. .,
so schliesst man durch mehrmalige Anwendung der vorigen Sätze,
dass in C) alle wten Einheits würz ein, und jede nur einmal, ent-
enthalten sind, und ferner, dass r dann und nur dann primitive
wte Einheitswurzel ist, wenn «, ß, y . . . primitive Einheitswurzeln
der Grade a, b, c . . . sind.
Bezeichnen wir jetzt die Anzahl der primitiven ntetL Einheits-
Einheitswurzeln durch g?(w), so folgt aus dem hier Bewiesenen
D) <p(n) = <p(a)<p{b)<p{c) .. .,
wenn
n = abc . . .,
und a, b, c . . . Zahlen sind, die, je zwei und zwei, zu einander
relativ prim sind.
Nun kann man jede Zahl n auf eine und nur auf eine Weise
in ein Product von Primzahlpotenzen zerlegen
n = p"p?ip*2 . . .,
worin jp, pu jp2 . . . verschiedene Primzahlen und ic, »1? n2 ...
positive Exponenten sind, so dass aus der Formel D) folgt:
E) <p O) = <p O*) <p Ofi) y (p**)
und dass es also nur noch darauf ankommt, zu entscheiden, ob
und wie viele primitive Einheitswurzeln des Grades pn existiren.
Diese Frage ist aber sehr einfach zu entscheiden. Wenn
nämlich q eine Einheitswurzel vom Grade jp* ist, so ist der
niedrigste Grad, zu dem q als Einheitswurzel gehört, ein Theiler
von p", also eine Potenz von p, und wenn er also nicht gleich

§. 140. Primitive rate Einheitswurzeln. 457
pn ist, ein Theiler von p*—1, d. h. jede nicht primitive Einheits-
Einheitswurzel vom Grade p" ist zugleich Einheitswurzel vom Grade
pa~1. Da es aber p" Einheitswurzeln vom Grade p" und nur
pn—i Einheitswurzeln vom Grade p7t~1 giebt, so müssen
primitive Einheitswurzeln des Grades pn vorhanden sein. Daraus
erhält man nach E) die Anzahl aller primitiven wten Einheits-
Einheitswurzeln
F) 9(n) =
worin das Productzeichen H sich auf alle von einander ver-
verschiedenen in n aufgehenden Primzahlen bezieht. Nur für den
Fall n = 1 passt die Formel F) nicht mehr; in diesem Falle
ist cp A) = 1 zu setzen. Die Zahl cp (n) ist also niemals gleich
Null. Da es hiernach für jeden Grad n wenigstens eine primi-
primitive Einheitswurzel r giebt, so lassen sich alle wten Einheitswurzeln
durch die Potenzen von r darstellen:
\') xi 'i ' i ' i • • •> '
Ist rÄ irgend eine Potenz von r, so wird dann und nur dann
rtm __ i semj wenn ]zm durch n theilbar ist. Ist also n = n'n"
und n' der grösste gemeinsame Theiler von Tt und n, so muss m
durch n" theilbar sein, und n" ist der Exponent der niedrigsten
Potenz von rÄ, die gleich 1 wird, d. h. rk ist eine primitive n"te
Einheitswurzel. Es folgt hieraus der Satz:
III. Ist r primitive nte Einheitswurzel, so ist rÄ dann
und nur dann primitive nte Einheitswurzel, wenn
h relativ prim zu n ist.
Nehmen wir k aus der Reihe der Zahlen 1, 2, 3 ... n, so
ergiebt sich der Satz der Zahlentheorie, dass cp(n) gleich der
Anzahl der Zahlen ist, die nicht grösser als n und rela-
relativ prim zu n sind. Dies ist die ursprüngliche Definition des
in der Zahlentheorie allgemein gebrauchten Zeichens cp(n).
Ist h relativ prim zu n, so kann man eine ganze Zahl x so
bestimmen, dass Jcx = 1 (mod ri) wird. Sind dann r, rx zwei
nte Einheitswurzeln, so kann nur dann rÄ = r\ sein, wenn r = r1
ist, wie sich durch Erheben zur Potenz x ergiebt. Daraus folgt
nach III.:

458 Zwölfter Abschjiitt. , . §. 141.
IV. Ist h relativ prim zu »und durchläuft r die
Reihe der primitiven nten Einheitswurzeln, so
durchläuft rÄ dieselbe Zahlenreihe, wenixauch
in anderer Ordnung.
Endlich führen wir noch den Satz an:
V. Ist n eine Primzahl, so ist jede wte Einheits-
wurzel mit Ausnahme von 1 primitive w*6 Einheits-
Einheitswurzel.
§. 141.
Gleichungen für die primitiven Einheitswurzeln
nien Grades.
Alle ntetL Einheitswurzeln sind, wie wir gesehen haben,
Wurzeln einer Gleichung /„ (x) = 0, wenn
A) fn{x) = S" — 1
ist; wenn wir die Function fn(x) von allen Factoren befreien,
die sie mit anderen Functionen derselben Form/ni(a;) gemein hat,
was durch rationale Operationen geschieht (§. 6), so erhalten,wir
eine Gleichung Xn.= 0, der die primitiven ntetL Einheitswurzeln
und nur diese genügen, und Xn hat die Form
B) Xn — xv -f.«! x"-1 -\-• •¦ ¦-\- ar.
Der Grad v ist gleich <p (n) und die Coefficienten at, a2> ¦• ¦¦, <h
sind rationale Zahlen.
Beim Aufsuchen der gemeinschaftlichen Factoren von fn und
fni können wir uns für % auf die Theiler von n beschränken.
Wie man die Function Xn einfach bilden kann, werden wir gleich
, noch näher sehen. Wir beweisen aber zunächst einen allgemeinen
. Satz über diese Functionen.
Die wten Einheitswurzeln umfassen alle primitiven jttei1 Ein-
Einheitswurzeln, worin (i irgend ein Theiler von n ist, n selbst und
1 eingeschlossen, da als primitive erste Einheitswurzel eben die
. Einheit 1 selbst zu betrachten ist. Lassen wir also (i alle Divi-
Divisoren von n durchlaufen und beachten, dass zwei verschiedene Xu
niemals einen gemeinschaftlichen Theiler haben, und dass sowohl
/„(#) als Xju keine mehrfachen Factoren enthalten, so folgt:
C) fn{x) =

§. 141. Einheitswurzeln. 459
worin sich das Productzeichen II auf alle Theiler jt von n
bezieht.
Daraus erhalten wir nebenbei einen Beweis des zahlen-
zahlentheoretischen Satzes:
D) n
wenn wir den Grad der Functionen auf der rechten und der
linken Seite von C) einander gleich setzen.
Andererseits schliessen wir nach dem Gauss'sehen Theorem
(§. 2), dass die Coefficienten der sämmtlichen X^ ganze Zahlen
sind. Denn kämen darunter auch gebrochene Zahlen vor, so
könnte das Product nicht lauter ganzzahlige Coefficienten ent-
enthalten, wie es doch nach C) und A) sein muss.
Alle Functionen /„ (x) haben den Theiler x — 1, und wenn
wir die Theilung ausführen, so ergiebt sich
E) ^Lill. = z»-l _J_ xn-2 I UO-1.!
w x — j i i ii.
Hieraus schliessen wir, dass, wenn r irgend eine primitive
oder nicht primitive nte Einheitswurzel ist, mit alleiniger Aus-
Ausnahme von r = 1, immer
F) 1 -j- r + r2 -| (- r»-1 = 0,
während für r = 1 die Summe auf der linken Seite von F)
offenbar den Werth n hat.
Wenn n eine Primzahl ist, so giebt es ausser 1 keine im-
imprimitiven wtei1 Einheitswurzeln, und daher ist, wenn n eine Prim-
Primzahl ist, was wir dadurch andeuten wollen, dass wir p dafür
setzen,
G) Xp = x*>-1 + XP-* -] 1- # + 1.
Ebenso einfach lässt sich Xn bilden, wenn n eine Prim-
Primzahlpotenz ist, also
n = pn,
oder, wenn wir zur Abkürzung p"—1 =.p' setzen:
n = p' p.
Die wten Einheitswurzeln bestehen in diesem Falle aus den
primitiven wten Einheitswurzeln und aus den ^'ten Einheitswurzeln,
und es ist also
(8) Xn = ^7—f =

460 Zwölfter Abschnitt. §. 141.
Ist p' > 1, also % > 1, so fehlt in dieser Gleichung das
Glied mit der (v — l)ten Potenz der Unbekannten, dessen Coeffi-
cient der negativen Summe der Wurzeln gleich ist. Wir haben
also den Satz:
VI. Die Summe aller primitiven nten Einheitswurzeln
ist, wenn n eine höhere Potenz einer Primzahl
ist, immer gleich Null.
Zur allgemeinen Bildung von X„ wollen wir ein recurrentes
Verfahren anwenden; wir nehmen Xn als schon gebildet an,
bezeichnen mit p eine in n nicht aufgehende Primzahl, mit p'
wie oben die {% — l)te Potenz von p, und bilden nun Xnp>m
worin natürlich p' auch gleich 1 sein kann.
Bezeichnen wir mit r die primitiven ntetL Einheitswurzeln,
mit a jede Einheitswurzel des Grades pp', und mit a! jede Ein-
Einheitswurzel des Grades jp', so erhält man die sämmtlichen primi-
primitiven Einheitswurzeln des Grades npp', wenn man von den
sämmtlichen ra die ra' wegnimmt (§. 140, II.). Die ra sind aber
die Wurzeln der Gleichung:
weil die Grossen
(r a)vp' .== r**1,
von der Reihenfolge abgesehen, mit den r selbst übereinstimmen
(§. 140, IV.). Ebenso sind die ra' die Wurzeln der Gleichung
X„«) = 0,
und daraus ergiebt sich
m x (x)-Xn(xPpr)
Hiervon macht auch der Werth n = 1 keine Ausnahme,
wenn wir unter Xx die Function x — 1 verstehen. Danach
können wir Xn in allen Fällen verhältnissmässig einfach bilden.
Wir betrachten einige besondere Fälle.
Nehmen wir an, es enthalte n nur zwei von einander ver-
verschiedene Primzahlen p, q und sei also
n=pp'qq',
dann ergiebt die Formel (8) und (9):
(X» —
XP! — \)
B — l) («2 — l)

§. 141. Einheitswurzeln. 461
eine Formel, die sich leicht durch vollständige Induction folgender-
maassen verallgemeinern lässt.
Bezeichnet man mit ^ alle Zahlen, die aus n entstehen,
wenn man n durch eine gerade Zahl verschiedener Primtheiler
von n dividirt (n selbst eingeschlossen), mit jt2 die Zahlen, die
aus n entstehen, wenn man n durch eine ungerade Zahl solcher
Primtheiler dividirt, so ist
Der Beweis ergiebt sich aus (9) für npp', wenn man an-
annimmt, die Richtigkeit sei für n schon bewiesen.
Bedeutet r jede der primitiven ntetL Einheitswurzeln, so sind
bei ungeradem n die —r die primitiven 2wten Einheitswurzeln
(§. 140, L, II.). Demnach ist bei ungeradem n
A1) X,n(x)=Xn(-x).
Ist n eine Potenz von 2, so ist nach (8): •
A2) Xn = -n J-=3l+].
Setzen wir in der Formel (8) x = 1, so erhält X„ den
Werth p, wenn n eine Potenz von p ist. Dagegen ergiebt die
Formel (9), wenn n > 1 ist, für X„M- den Werth 1 (für n = 1
würde auf der rechten Seite Zähler und Nenner = 0).
Wir erhalten also den Satz:
VII. Die Function Xn erhält für x = 1 den Werth p,
wenn n eine Potenz der Primzahl p ist, und
den Werth 1, wenn n mehr als eine Primzahl
als Theiler hat.
Ist p eine in n aufgehende Primzahl und
n = pn\
so ist
A3) =-; ~ = a^'ü*-1) + a^(p-» _| 1- «-' + 1,
und diese Function verschwindet, wenn x- gleich irgend einer
primitiven wtel1 Einheitswurzel « gesetzt wird. Sie ist daher
durch Xn theilbar, und es muss also eine ganze Function Yn
von x geben, die nach §. 2 ganzzahlige Coefncienten hat, so dass
A4) xn'<J>-» + a^'ö>-2> -| + x«' + 1 = Xn Yn

462: Zwölfter Abschnitt. §. 142.
wird. Ist nun <x' irgend eine n'te Einheitswurzel, also cc'n' = 1,
so folgt aus A4)
A5) Xn(a')Tn(a')=p,
also eine Zerlegung der Primzahl p in zwei Factoren, die ganze
Functionen einer Einheitswurzel von beliebigem Grade n' sind.
§• 142.
Die Discriminante der Kreistheilungsgleichung.
Die Einheitswurzeln vom Grade n lassen sich in transcen-
denter Form darstellen durch
,,. — 2 3rfc . . . 2 3T&
A) r = e n = cos \- % sm
Diese Einheitswurzel ist primitiv oder nicht, primitiv, je
nachdem h theilerfremd zu n ist oder nicht. Die einfachste
unter den primitiven erhält man für Je = 1, nämlich
2«t Ojj 2j[
B) ra = e n = cos 1- * sin — = a + b i.
Der Winkel 2 sr : n ist der wte Theil der ganzen Kreisperi-
Kreisperipherie. Die verschiedenen Theilpunkte, die man erhält, wenn man
Fig. 28. diesen W7inkel von einem beliebigen Anfangs-
Anfangspunkte an auf der Peripherie aufträgt, be-
bestimmen das dem Kreise eingeschriebene
reguläre w-Eck.
Die Theilpunkte lassen sich construiren,
wenn man r und damit a und b (oder auch
nur eine dieser beiden Grossen) kennt. Insbesondere ergiebt sich
für die Seite s des regulären w-Eckes, wenn der Radius c des
umgeschriebenen Kreises gleich 1 angenommen wird,
n
Die übrigen Grossen r stehen in derselben Beziehung zu den
anderen Theilpunkten. Wegen dieser geometrischen Bedeutung
nennen wir die Gleichung X„ = 0, deren Wurzeln die Grossen A)
sind, die Kreistheilungsgleichung.
Wir bestimmen jetzt die Discriminante der Kreistheilungs-
Kreistheilungsgleichung Xn = 0, beschränken uns aber auf den Fall, dass »
eine ungerade Primzahl ist.

§. 142. Discriminante der Kreistheilungsgleichung. 463
Es ist dann
C) Xn = a;—1 + »»-» + • • • + x -f 1,
und da nur die eine imprimitive iite Einheitswurzel 1 existirt,
so ist
D) fn(x) = s- — 1 = (s - 1) Xn,
also
E) fn(x) = fix»-* = X. + (*—!) ^n-
Ist nun D die Discriminante von X». so ist nach §. 50, E)
F) D-= (— 1) 2
worin sich das Productzeicheu II auf alle Wurzeln r der Gleichung
X« = 0 erstreckt, und worin, da n ungerade ist,
n(n — 1) n — l
gesetzt werden konnte.
Es ist aber nach E)
/7 I <W vH—'1 — ~— (np __ 1 *\ X f<J*l
III /(< / ¦ 1 / ^^ X I -ti-rt \* _/ 7
und da das Product aller r gleich 1 ist (weil es gleich dem von
x unabhängigen Grliede in X„ ist), und da
also
II(r — 1) = Xn(l) = n, (§. 141)
so folgt aus F) und G)
(8) D = (—1)~*~ n»-\
Die Wurzeln von Xn sind, wenn r eine von ihnen ist, alle
in der Form enthalten
v y2 <r%
und wenn wir also das Differenzenproduct
(9) P = (r — r2) (r — rs) . . . (r —
einführen, so ist (§. 50)
D = P\
Es ist also auch nach (8)
n—3
A0) P = n~

464 Zwölfter Abschnitt. §. 142.
wodurch P, abgesehen vom Vorzeichen, bestimmt ist. Es ist P
reell, wenn n = 1, und imaginär, wenn n = — 1 (mod 4) ist,
also reell für n = 5, 13, 17, 29, 37, . . ., imaginär für n = 3, 7,
11, 19, 23, 31, ... Das Vorzeichen, das wir in A0) der Wurzel
zu geben haben, hängt davon ab, welches r wir in dem Ausdruck
(9) gewählt haben.
Wählen wir ein bestimmtes r, z. B. r — r0, so können wir
das Vorzeichen in A0) noch bestimmen. Um dies auszuführen,
theilen wir die binomischen Factoren von P,
r* — ***, v < ft,
deren Anzahl \{n — 1) (n — 2) beträgt, in zwei Classen. Die
Differenzen der einen Classe bilden das Product
/ n—l n + l\
A1) Q — (r — r«-1) (r2 — r"~2) . . . \r 2 — r 2 ),
das also alle die Factoren enthält, in denen ft -\- v = n ist.
Die übrigen Factoren lassen sich in Paaren von folgender
Form zusammenfassen
A2) B = (rv — ru) (r»-M — r»—").
Die Anzahl der Factoren in Q ist \{n — 1), und also ist
die Anzahl der Paare B
1 /(n — 1) (n — 2) _ n— 1\ _ (n — 1) (w— 3)
7 \ 2 ~2 ) ~ 4
und diese Zahl ist immer gerade, da einer der beiden Factoren
n — 1, n — 3 durch 4 theilbar ist.
Nun ist, wenn
27tilc
r = e "
ist,
B = — 2 + f-* + f-M = — 2 (l — cos
d. h. B ist immer negativ. Folglich ist das Product aller B eine
positive Grosse.
Es ist ferner
A3) <) = B*J sin __ sin— sin i1
nn ,
und das Vorzeichen hiervon ist von h abhängig. Nehmen wir
aber 7; = 1, also r = r0, so sind alle die Winkel
2 % 4 % (n — 1) %
n ' n ' ' n

§. 142. Discriminante der Kreistheilungsgleichung. 465
zwischen Null und % gelegen und die Sinus alle positiv. Wir
schliessen hieraus nach A0), dass in diesem Falle
«—1 »— 3 _
A4) P = i~n~Vn
ist, und Vn positiv zu nehmen ist.
Das Vorzeichen des Productes der B hängt von der Wahl
von r nicht ab, sondern nur von der Beschaffenheit von n. Es
ist daher von Interesse, das Product Q, dessen Vorzeichen von
der Wahl von r abhängt, für sich zu bestimmen. Wir erhalten
es auf folgende Weise:
Multipliciren wir den Ausdruck A1) mit
und sodann mit
n — l nß — l
T—"^ . T—2 ¦ ¥—'^ Y 2 ^^ T ^
so erhalten wir
tfi—i
r e q _ (r2 _ i) (ri — i) . . . (r»-i _
r 8 Q = A — r»-a) A — r»-*) . . . A — r).
Da nun die Exponenten 2, 4,..., n— 1, vi—2, n — 4,..., 1
zusammen alle Zahlen 1, 2, . . ., n — 1 umfassen, so ergiebt sich
durch Multiplication dieser beiden Ausdrücke:
Q ()( ) {f,
also
n — l _
A5) Q = ± i~ Vn.
Die Vergleichung mit A3) ergiebt
A6) 2 2 sin sm • • • sm =
Das Vorzeichen in dieser Formel hängt, wie in A5), noch
von h ab; es ist aber das positive, wenn h = 1 ist. Im Uebrigen
wollen wir über dies Vorzeichen, das weiterhin noch genauer
untersucht werden wird, noch einen wichtigen Satz ableiten.
Nach der Definition A1) ist Q eine ganze rationale Function
von r, die, wenn man sie nach Potenzen von r ordnet, ganze
rationale Zahlencoefficienten erhält. Setzen wir also
r = **,
Weber, Algebra. I. g()

466 Zwölfter Abschnitt. §. 143.
sö wird ' - ' '
worin F das Zeichen für eine rationale Function ist, deren
Coefficienten von h nicht abhängig sind. Setzen wir nun für Je
der Reihe nach die Werthe
h = 1, 2, . . . n — 1,
so stellt r\ alle Wurzeln der Kreistheilungsgleichung Xn = 0
dar, und die Summe
iQ = F(r0) + F(r> )+;•• + 2^-*)
ist eine symmetrische Function der Wurzeln dieser Gleichung;
sie lässt sich also rational durch die Coefficienten der Gleichung,
d.h. durch rationale Zahlen ausdrücken und ist mithin selbst eine
rationale Zahl. Andererseits ist aber nach der Formel A5)
lö = A»~ä~ Vn,
wenn h eine ganze Zahl bedeutet, nämlich die Anzahl der Fälle, in
denen in A5) das positive Zeichen zu nehmen ist, vermindert um
die Anzahl der Fälle, in denen das negative Zeichen gilt. Beides
ist aber nur dann mit einander verträglich, wenn h = 0 ist;
und damit ist der folgende Satz bewiesen:
1. Durchläuft h die Reihe der Zahlen 1,2,3,...,»—1,
so gilt in" der Formel A6) ebenso oft das positive
wie das negative Zeichen.
Es braucht kaum besonders erwähnt zu werden, dass man
für lc auch ein anderes volles Restsystem von n, mit Ausschluss
der durch n theilbaren Zahl, nehmen kann.
§. 143.
Primitive Congruenzwurzeln.
Parallel mit der Theorie der Einheitswurzeln geht eine
Theorie der sogenannten binomischen Congruenzen, ohne die in
der Theorie der Kreistheilungsgleichungen weitere Schritte nicht
gemacht werden können, deren Grundzüge passend hier ein-'
geschoben werden, wo sich die Analogie mit der Theorie der"
Einheitswurzeln deutlich zeigt.

§. 143. Primitive CongruenzwurzeJn. 467
Es sei also jetzt n eine Primzahl und
A) f(x) =-«o %m + % x™-1 H 1- a»-i« + »»
eine ganze Function von x, deren Coefficienten a ganze Zahlen
sind, und a0 nicht durch n theilbar. Setzen wir für x eine solche
ganze Zahl «, dass /(«) durch » theilbar wird, so sagen wir
(nach Analogie der Gleichungen), « sei eine Wurzel der Con-
Congruenz mten Grades:
B) f(x) = 0 (mod n).
Wird « um ein Vielfaches von n vermehrt, so bleibt es
Wurzel der Congruenz B). Solche nach dem Modul n con-
gruente Wurzeln gelten nicht als verschieden. Unter dieser
Voraussetzung können wir den Satz aussprechen:
1. Eine Congruenz wten Grades für einen Primzahl-
Primzahlmodul kann nicht mehr als m verschiedene
Wurzeln haben.
Der Satz ist richtig für »»=1, denn dieCongruenz a0x-{-a=0
(mod n) hat nur eine Wurzel, nämlich, wenn a'o so bestimmt wird,
dass a0 a'o = 1 (mod m) ist, w = — a a'o (mod n). Wir nehmen
unseren Satz also jetzt als bewiesen an für den Grad m — 1
und leiten seine Richtigkeit für den Grad m daraus her. Nach
§. 4 können wir, wenn zunächst « beliebig ist, setzen
/q\ J W J \ 1 / r„\
worin fi (x) eine ganze Function vom (m — l)ten Grade ist, die,
wenn a eine ganze Zahl ist, ganzzahlige Coefficienten bat. Wenn
also /(«) = 0 ist, so folgt aus C)
D) • f(x) = (x — «)/! (x) (mod n).
Jede Wurzel ß der Congruenz B) muss also der Bedingung
(ß — «) /j (ß) = 0 (mod n) genügen. Also ist entweder ß — w
oder /i (ß) durch n theilbar.
Nun giebt es nach Voraussetzung höchstens m — 1 Werthe
ß, für die fx (ß) durch n theilbar wird; giebt es also noch eine
mte Wurzel von D), so muss diese gleich « sein.
Wenn also eine Congruenz von der Form f(x) = 0 (moin)
mehr Wurzeln hat, als ihr Grad beträgt, so schliessen wir, dass
die Congruenz identisch ist, d. h. dass alle Coefficienten von f(x)
durch n theilbar sein müssen.
30*

468 Zwölfter Abschnitt. §. 143.
Dieser Satz ist, wie man sieht, ganz analog dem alge-
algebraischen Satze, dass eine Gleichung nicht mehr Wurzeln haben
kann, als ihr Grad angiebt. Es lässt sich aber nicht der andere
Satz übertragen, dass jede Gleichung auch wirklich so viele
Wurzeln hat. Eine Congruenz mten Grades kann weniger, selbst
gar keine Wurzeln haben. Um so bemerkenswerther ist eine
besondere Congruenz, bei der die Zahl der Wurzeln immer dem
Grade gleichkommt, auf Grund eines Lehrsatzes, der der
Fermat'sche Lehrsatz genannt wird, und den wir hier so
formuliren.
2. Die Congruenzen
E) x™ — x = 0, X"-1 — 1=0 (mod n)
haben, wenn n eine Primzahl ist, so viele Wurzeln
als ihr Grad beträgt, nämlich n und n— 1.
Beide Behauptungen sind nicht wesentlich verschieden, denn
die erste der Congruenzen E) hat alle Wurzeln der zweiten und
ausserdem die Wurzel 0, die der zweiten nicht genügt. Ebenso
hat die zweite alle Wurzeln der ersten, mit Ausnahme der
Wurzel 0.
Da es nun für den Modul n überhaupt nur n verschiedene
Zahlen giebt, so ist also zu beweisen, dass für jede ganze Zahl
a die Congruenz besteht
F) an = a (mod n).
Diese Congruenz ist richtig für u = 0 und a = 1. Wir
beweisen sie also wieder durch vollständige Induction, indem wir
aus der als richtig vorausgesetzten Congruenz F) die Richtig-
Richtigkeit von
G) (« + 1)" = « + 1 (mod n)
ableiten. Dies ist aber aus dem binomischen Satz zu schliessen,
wenn man beachtet, dass alle Binomialcoefficienten, mit Aus-
Ausnahme des ersten und des letzten, die gleich 1 sind, nämlich
n(n — 1) n(n — 1) (n — 2)
W' Hl ' 1.2.3 ' ' * -
durch n theilbare ganze Zahlen sind (§. 12). Demnach ist
(« -f !)" = «" +1 (mod n%
also folgt die Formel G) aus der Formel F).
Die Differenz
x(x — 1) (x — 2) . . . (x — n -\- 1) — xn ~\- x

§• 143. Primitive Congruenzwurzeln. 469
ist eine Function, höchstens vom n — 1*™ Grade. Sie ist aber
für n Werthe von x, nämlich für x = 0, 1, 2, . . ., n — 1 con-
gruent mit Null, und daher haben wir identisch
x(x — 1) (x — 2) . . . (x — n + 1) = x» — x (mod n).
Daraus ergiebt sich der Wilson'sche Lehrsatz:
1 . 2 . 3 . . . (w — 1) = — 1 (mod n),
wenn man die Coefficienten der ersten Potenz von x beiderseits
vergleicht.
Wir beschränken uns jetzt auf die zweite der Congruenzen E)
(8) xn~x = 1 (mod n)
und beweisen zunächst den Satz:
3. Ist a ein Theiler von n — 1, so hat die Congruenz
(9) xa = 1 (mod n)
genau a verschiedene Wurzeln.
Denn es ist, wenn n — I=a5 ist,
xn-l _ l __ (& _ l) (paCi-l) _J_ ^(S-2) _j 1_ ^ _|_ ^
und da jede Wurzel der linken Seite Wurzel entweder des einen
oder des anderen Factors auf der rechten Seite sein muss, so
folgt, dass, wenn xa — 1=0 weniger als a Wurzeln hätte, der
zweite Factor mehr Wurzeln haben müsste, als sein Grad angiebt
entgegen dem Satz 1.
Ist « eine durch n nicht theilbare Zahl, und a die kleinste
positive Zahl, für die ua = 1 (mod n) wird, ist ferner h irgend
eine positive ganze Zahl, für die ah = 1 (mod n) ist, so ist a
nothwendig ein Theiler von h, insbesondere also a ein Theiler
von n — 1.
Denn setzen wir h — qa -)- a\ worin q eine ganze Zahl und
a! < a ist, so ist auch «°' = 1; also muss al = 0 sein, weil a die
kleinste positive Zahl sein sollte, wofür diese Congruenz befriedigt ist.
Eine Wurzel w der Congruenz (9) von der
Eigenschaft, dass keine niedrigere als die ate
Potenz der Einheit congruent wird, heisst eine
primitive Wurzel dieser Congruenz, oder primi-
primitive ate Congruenzwurzel der Primzahl w, und eine
primitive Wurzel g der Congruenz (8) nennen wii-
auch kurz eine primitive Wurzel der Primzahl n.

470 . Zwölfter Abschnitt. §. 143.
Wir wollen beweisen, dass für jede Primzahl n primitive
.Wurzeln existiren und ihre Anzahl bestimmen, und gehen dabei
denselben Weg, wie bei den Einheitswurzeln.
Es seien a und b zwei Theiler von n — 1, die unter sich
relativ prim sind, und « eine ate, ß eine bte primitive Congruenz-
Congruenzwurzel von n. Setzen wir ab ¦= c, so ist y = aß eine primi-
primitive c^ Congruenzwurzel, und umgekehrt lässtsich auch jede
primitive cte Congruenzwurzel in der Form aß darstellen.
Denn es ist erstens: (aßy = cießc=l (mod n), und zweitens:
wenn (aß)h = ahßh = 1 (mod n) ist, so ist auch ahhßhh = 1,
also cchh = 1, also hb durch a theilbar, also auch h durch a
theilbar, und ebenso schliesst man, dass h durch b, also auch
durch ab = c theilbar sein muss, d. h. aß ist primitive cte
Congruenzwurzel.
Ist umgekehrt y eine primitive cte Congruenzwurzel, so
bestimmen wir die positiven ganzen Zahlen x, y so, dass
A0) ' ay -\- bx = 1 (mod e)
wird, indem wir zunächst x aus bx = 1 (mod a), und dann y
aus y = (mod b) bestimmen. Dann ist y relativ prim
Ctf
zu b, und x relativ prim zu a. Hiernach ist
y = yhxyax — aß (modn),
und yhx = k ist primitive aie Congruenzwurzel, ya" = ß primi-
primitive 6te Congruenzwurzel (weil «Ä = ybxh nur dann =1 sein
kann, wenn In, durch a theilbar ist).
Es ist noch zu zeigen, dass die Producte cxß alle von ein-
einander verschieden sind, d. h. dass die Congruenz
A1) cxß eee a'ß' (mod »),
wenn «, w'; ß, ß' primitive ate und bte Congruenzwurzeln sind,
nur befriedigt werden kann, wenn
<x==k', ß = ß' (mod n)
ist. Dies folgt aber nach A0), wenn man A1) in die Potenz
b x = 1 (mod a)
erhebt, woraus sich « = »' ergiebt, und dann auch ß = ß'.
Bezeichnen wir also die Anzahl der primitiven aten Con-
Congruenzwurzeln mit q>(a), so folgt aus dem Bewiesenen
A2) <p(c) = (p(a)cp(b).

§. 148. Primitive Congruenzwurzeln. 471
Es bleibt noch übrig, wenn p eine Primzahl und ppx eine
in n — 1 aufgehende Potenz von p ist, <p (ppi) zu bestimmen.
Ist « eine nicht primitive Congruenzwurzel vom Grade p",
und p7'^1 = pi, so ist, wenn eth die niedrigste nach dem Modul
n mit 1 congruente Potenz von et, ist, h ein Theiler von ppu
d. h. eine Potenz von j); da h aber kleiner als pp^ sein soll, so
ist es auch ein Theiler von p^, und folglich <&?>¦ = 1 (mod ri),
also: eine nicht primitive Gongruenzwurzel des Grades pj>j ist
zugleich eine Congruenzwurzel des Grades px. Umgekehrt ist
jede Congruenzwurzel des Grades p1. zugleich eine imprimitive
Congruenzwurzel des Grades ppi. Da nun die beiden Con-
gruenzen i»' = 1, x^ = 1 so viele Wurzeln haben, als ihr Grad
beträgt, so bleiben pp1 —pt primitive Congruenzwurzeln
der ersten übrig, und es ist also
A3) 9(fft)=J»i(l>-l>
Die Function cp(a) hat also dieselbe Bedeutung, wie im §.140,
und es ist damit zugleich die Anzahl der primitiven Wurzeln
der Primzahl n gleich <p (n — 1) gefunden. Wir sprechen also
noch den Satz aus:
4. Eine Primzahl n hat <p(n — 1) primitive Wurzeln.
Damit ist die Existenz von primitiven Wurzeln für jede
Primzahl nachgewiesen und zugleich ihre Anzahl bestimmt. Zur
Auffindung der primitiven Wurzeln haben wir freilich keine
andere allgemeine Methode als das Probiren, was durch einige
Kunstgriffe etwas abgekürzt werden kann.
Ist g eine primitive Wurzel der Primzahl n, so sind die
Reste der Potenzen
A4) . l,g,g*,g>,.:^g»-*.
alle von einander verschieden, da, wenn g™ = gm+i* wäre, #"= 1
sein müsste, was nicht möglich ist, so lange ft positiv und kleiner
als n — 1 ist. Es muss also unter den Resten der Reihe A4),
unter denen der Rest 0 nicht vorkommt, jede der Zahlen
A5) 1, 2, 3, . . , n - 1
und jede nur einmal enthalten sein, oder mit anderen Worten:
5. Ist a eine durch n nicht theilbare Zahl, so
giebt es eine und nur eine Zahl w aus der Reihe
d,er Zahlen 0, 1, 2, . . ., n — 2, durch die die Con-
gruenz
A6) ga = a (mod ri)

472 Zwölfter Abschnitt. §. 143.
befriedigt wird. Dieselbe Congruenz wird aber
auch befriedigt, wenn als Exponent eine mit cc
nach dem Modul n — 1 congruente Zahl gesetzt
wird, und man findet in jedem vollen Restsystem
nur eine solche Zahl «.
Der Exponent et, heisst der Index von a in Bezug auf die
Basis g, und es wird geschrieben
A7) . « = inda (mod n — 1).
Man hat also für jede durch n nicht theilbare Zahl
A8) #inda = a (mod n).
Aus den beiden Formeln
A9) gmia + mdb = a ^ gmin&a = „m (m0(J n)
ergiebt sich der Satz:
6. Der Index eines Productes ist gleich der
Summe der Indices der Factoren; der Index
der mten Potenz von a ist gleich dem mfachen
des Index von a.
Diese Sätze sind ganz analog den entsprechenden Sätzen,
die sich auf die Rechnung mit Logarithmen beziehen, und die
Analogie lässt sich noch weiter verfolgen. So wird z. B. der
Uebergang von einer Basis g zu einer anderen Basis g' durch
die Formel
g g m g'
B0) inda = mag' inäa (mod n — 1)
vermittelt.
Wir wollen noch den leicht zu beweisenden Satz anführen,
dass unter den durch n nicht theilbaren Zahlen a die und
nur die primitive Wurzeln sind, deren Indices relativ prim zu
n — 1 sind.
Für praktische Rechnungen bedient man sich zweckmässig
sogenannter Indextabellen, die den Logarithmentafeln entsprechen.
Man nennt in der Congruenz A7) « den Index und a den
Numerus, und stellt am besten zwei Tabellen auf, von denen die
eine zu jedem Index den Numerus, die andere zu jedem Numerus
den Index giebt, wo die zweite durch Umstellung aus der ersten
gewonnen wird. Dabei ist zu beachten, dass für die Indices der
Modul n — 1, für die Numeri der Modul n in Betracht kommt
und congruente Zahlen als gleichwerthig gelten. So erhält man
z. B. für n = 13 und die Basis 2

§. 143. Primitive Congruenzwurzeln. 473
1
N
N
I
0
1
1
0
1
2
2
1
2
4
3
4
3
8
4
2
4
3
5
9
5
6
6
5
6
12
7
11
7
11
8
3
8
9
9
8
9
5
10
10
10
10
11
7
11
7
12
6
Im Canon Arithmeticus von Jacobi A839) sind für alle
Primzahlen im ersten Tausend Indextabellen zusammengestellt.
In kleinerem Umfange nach Berechnungen von Ostrogradsky
in der „Theorie der Congruenzen" von Tschebyscheff (deutsch
von Schapira, Berlin 1889).
Es ist noch zu bemerken, dass der Index von 1 immer gleich
0 ist, und dass der Index von — 1 (oder von n — 1) immer gleich
n 1
-—-— ist. Denn da (— lJ den Index 0 oder n — 1 hat, so
muss — 1, da es nicht den Index 0 hat, und das Doppelte seines
Index gleich 0 oder n — 1 ist, den Index —-— haben; in
Formeln:
« i
B1) ind 1 = 0, ind(— 1) = —-— (mod n — 1).
Ist n eine Primzahl, und m nicht durch n — 1 theilbar, so
giebt es immer wenigstens eine durch n nicht theilbare Zahl &,
so dass hm nicht mit 1 congruent ist. Denn ist m' der Rest von
m nach dem Modul ri — 1, so ist hm = hm' (mod ri), und die
Congruenz x™' = 1 hat weniger als n — 1 Wurzeln. Folglich
giebt es eine durch n untheilbare Zahl Je, die nicht Wurzel
dieser Congruenz ist. Nun durchläuft aber Jcx zugleich mit x
ein volles Restsystem nach dem Modul n (§. 123), und wir
haben daher
2xm = S(kx)m (mod ri),
oder
(hm — 1) Zx™ ^ 0 (mod ri).
Daraus er giebt sich für jeden durch n — 1 nicht theilbaren
Exponenten m
B2) Sxm ^ 0 (mod ri), \m nicht ^0 (mod n—1)],
wenn x ein volles Restsystem für den Modul n durchläuft.
Ist aber m durch n — 1 theilbar, so ist xm für jedes durch
n untheilbare x mit 1 congruent, und wir. erhalten direct
B3) Zx™ = — 1 (mod ri), [m = 0 (mod n — 1)].

474 Zwölfter Abschnitt. §. 144.
Diese Sätze lassen sich auch dadurch beweisen, dass man x
durch eine Potenz einer Primitivwurzel g darstellt, und zeigen
eine weitere Analogie der Potenzreste mit den Einheitswurzeln.
§•
Multiplication und Theilung der trigonometrischen
Functionen.
Wir haben schon auf den Zusammenhang hingewiesen, der
zwischen der Theorie der Einheitswurzeln und der geometrischen
Aufgabe der Theilung der Kreisperipherie besteht. Die Ver-
Verallgemeinerung dieser Aufgabe führt auf die Theilung eines
beliebigen Winkels. Auch diese Aufgabe führt auf algebraische
Gleichungen, von denen wir die für die Dreitheilung schon früher
für die allgemeine Auflösung der Gubischen Gleichungen benutzt
haben (§. 120).
Wir beginnen jetzt mit' der Aufstellung der allgemeinen
Formeln. :
Nach dem, Moivre'sehen Satze (§. 36) ist, wenn n eine
beliebige positive ganze Zahl und qp ein beliebiger Winkel ist,
A) ' cos n qp -\- i sin n qp = (cos qp —|— * sin q>)n,
und wenn wir auf der rechten Seite den binomischen Satz an-
anwenden, so folgt durch Trennung des Reellen vom Imaginären
cos nep = cos qp" — B<g> cos"—2 qp sin2 qp
+ BW cos"-* qp sin* qp —
B) . -T i V V
—:—^- = n cos"-1 qp — _B(") cos"—3 qp sin« m
smqp ^ 3 -r -r
+ -BEn) cos"-5 qp sin* cp — • • •,
worin _B$,n) wie früher die Binominalcoefficienten sind, und die
Summen auf der rechten Seite so weit fortzusetzen sind, als keine
negativen Exponenten von cos qp vorkommen. Da nun sin2 qp
= 1 — cos2 qp ist, so lassen sich diese beiden Ausdrücke rational
durch cosqp darstellen; wir setzen
C) 2 cosqp = x,
und führen die Bezeichnung ein
D) 2 cos n qp = An (x), S1°^ y = Bn (x),
sin cp

§. 144. Trigonometrische Functionen. 475
worin also A„(x) und B„(x) ganze Functionen von x sind, A„(x)
vom Grade n, Bn(x) vom Grade n— 1. Wir wollen das allgemeine
Gesetz dieser Functionen ermitteln. Wir stellen sie für die ersten
Werthe n = 1, 2, 3,... auf, und leiten dann eine Recursionsformel
zur Berechnung der höheren Functionen ab. Man findet
A (x) = x, Bx (x) = 1
E) A, (x) = «2 — 2, _B2 (x) = x
A3 (x) = x* — 3 x, B3 (x) = x* — 1.
Nun ist aber nach bekannten Formeln
cos (»4" 1) 9 ~\~ cos (n — 1) 9 = 2 cos cp cos n q>
sin (n -\- 1) tp -\- sin (n — 1) q> = 2 cos (p sin n <jp,
woraus für An und Bn die Recursionsformeln folgen:
, An + i(x) = Z An (X) An-i (X),
{ ) B(x) = xBH(x) — Bn-l(x)
Daraus kann man An, B„ für jedes beliebige n berechnen,
wenn diese Functionen für n = 1 und n = 2 bekannt sind. So
findet man
At (x) == xi — 4«2 -f 2
A6(x) = x"a — 5 x% -\- 5 a;
J^ (*) = «e — 6 x* -j- 9 «2 — 2
_B4O) = a;3_ 2«
^5 (x) — x* — 3 «2 + 1
B6 (x) = «5 _ 4 £3 _(_ 3 ^
und so kann man fortfahren. Man kommt durch Induction zu
folgendem allgemeinen Gesetz:
G) A*(x) = 2{-iy^B<:-<>x*-*% O^v^^,
(8) Bn (x) = 2 (- 1)' Ä—'-1' aj—»'-S 0 ^ v ^ ^=^,
wo die Summen mit v = 0 beginnen, und so lange fortzusetzen
sind, als die Exponenten von x nicht negativ werden.
Da sich diese Formeln in den ersten Fällen als richtig
erweisen, so ist, um sie allgemein zu beweisen, nur noch der
Nachweis nöthig, dass sie die Formeln F) verificiren. Bilden
wir zu diesem Zweck

476 .Zwölfter Abschnitt. §-144-
und setzen v — 1 an Stelle von v, so folgt
V zu 1
(9) .An-1(x) = -Z(-
£
Wenn wir i?^ = 0 annehmen, können wir auch hierin v
von 0 an wachsen lassen.
Die Werthe, die v in der Formel G) annimmt, unterscheiden
sich dann von denen in der Formel (9) nur wenn n ungerade
ist, weil dann der Werth v = (n -\~ 1) : 2 in (9), aber nicht in
G) vorkommt. Wir können aber diesen Werth in G) zufügen,
wenn wir einen Bin omialcoefficienten -BST+i, in dem der untere
Index den oberen übertrifft, gleich 0 annehmen. Dann er-
giebt sich
A0) xÄn(x) — A-i(«)
Nun ist aber, wie sich aus §. 7 (9) ergiebt,
„ B<?~v) + (n — 1) Sfrl? n+1 w—,+«
= : r- J5r ,
w — v n — v -|- 1
auch in den beiden Grenzfällen v = 0, j; = (» -|- 1):2, und
somit stimmt also A0) mit dem überein, was sich aus der
rechten Seite von G) durch Vertauschung von n mit n -\- 1
ergiebt.
Noch einfacher ergiebt die Formel (8)
xBn(x) - -B.-xC») = i (- l)'aj—»' (Ä—'-" + Sti'-"),
und da
ist, so ist damit auch (8) allgemein bewiesen.
Der Uebersicht halber setzen wir die Formeln etwas aus-
ausführlicher her:
A1) -An (x) = xn — nxn~2
. n(n—3) n(n — 4)(w —5) _ . .

§. 144. Theilung des Winkels. 477
A2) Bn (x) = x»-1 — (n — 2) x"~s
i (n-3)(n-A) (n-4)(n-5)(n-6)
Nehmen wir coswqp und sinwqp als gegeben an, so dient
die Gleichung nten Grades
A3) An (x) — 2 cos n qp = 0
zur Bestimmung der Unbekannten x = 2 cos qp. Die Bedeutung
der n Wurzeln dieser Gleichung ergiebt sich daraus, dass der
Cosinus sich nicht ändert, wenn der Winkel um ein Vielfaches
von 2 % wächst. Demnach genügt der Gleichung A3) jeder
Werth
A4) :r = 2co
wenn v eine beliebige ganze positive oder negative Zahl bedeutet.
Man erhält aber alle von einander verschiedenen Werthe von
A4), wenn man v ein volles Restsystem in Bezug auf n durch-
durchlaufen lässt, also z. B. v = 0, 1, 2, . . ., n — 1 setzt, und man
sieht auch leicht, dass diese n Werthe alle von einander ver-
verschieden sind, wenn man von dem besonderen Falle absieht,
dass qp ein Vielfaches von %:n ist. Denn zwei Cosinus sind nur
dann einander gleich, wenn die Summe oder die Differenz der
Winkel ein Vielfaches von 2sr ist.
Die Gleichung
A5) sin n q> = sin qp Bn (x)
bestimmt, wenn Bn (x) nicht gleich Null ist, sin qp eindeutig
durch x.
Suchen wir in der Gleichung A3) das von x unabhängige
Glied, so ergiebt sich mit Benutzung von F) für ein gerades n
n
2 (— 1)^ — 2coswqp,
und für ein ungerades n
— 2 cos n qp,
und wenn man dies dem positiven oder negativen Product der
Wurzeln gleichsetzt, so erhält man für ein gerades n
A6) 2"-1 Ilcos(q) -| -J = (— l)ä — cosntp,
und für ein ungerades n

478 Zwölfter Abschnitt. §.. 144.
A7) 2»-1 n cos(q> -f =-^\ = cosw<p,
und diese Formeln gelten, da rechts und links stetige Functionen
von qp stehen, auch noch für den zunächst ausgeschlossenen Fall,
wo qp ein Vielfaches von % : n ist.
Hierin können wir unter dem Productzeichen vm fürv setzen,
wenn -m irgend eine zu n theilerfremde Zahl ist, weil dann vm
zugleich mit v ein volles Bestsystem nach dem Modul n durch-
durchläuft. Sondern wir den Werth v = 0 ab, und lassen dann v
sowohl die positiven als die negativen Zahlen durchlaufen, die
absolut kleiner als n : 2 sind, so erhalten wir aus A7) die für
jedes ungerade n gültige Formel
,1O. _„ , -L f . 1vm%\ / 2vm%\ coswqp
A8) 2"-1 II cos ( qp H ) cos ( qp ) = -¦
K ' „_! V~ n ) V n ) cosqp
Setzen wir hierin qp = 0 und ziehen die Quadratwurzel, so
ergiebt sich
A9) 2-^h cos^^ = ±l,
n—i n
worin einstweilen das Vorzeichen noch unbestimmt bleibt.
Wenn wir aber in A8) qp in %: 2 übergehen lassen, so erhält
die rechte Seite, die sich unter der unbestimmten Form 0 : 0
darstellt, den Grenzwerth (—1) 2 n, und wir erhalten wieder
die Formel, die wir im §. 142 für eine Primzahl n abgeleitet
haben, allgemein für jedes ungerade n
n~1 v 2vm% . -,/—
B0) 22 n sin—;— = ± V»,
«-1
11 2
und für m = 1 ist das positive Zeichen zu nehmen.
Die Function _B„, die in Bezug auf x vom (n — l)ten Grade
ist, verschwindet nach D), wenn wqp, aber nicht qp ein Vielfaches
von % ist, also für
B1) # = 2 cos—,
worin h eine ganze, nicht durch n theilbare Zahl ist. Nehmen
wir zunächst n gerade an, so erhalten wir alle in B1) enthaltenen
verschiedenen Werthe, wenn wir für m eine beliebige zu »
theilerfremde Zahl setzen und

§. 144. Theilüng des Winkels. 479.
B2) h = m, 2 m, 3 m, . . ., (n — 1) m
annehmen; denn es ist nur dann
cos — = cos ,
n n
wenn entweder h -\- h' oder h — h' ein Vielfaches von 2 n ist,
was nicht eintreten kann, wenn h und h' beide aus der Reihe
B2) genommen sind.
Unter den Werthen B1) ist einer, nämlich der dem Werth
h = nm : 2 entsprechende, gleich Null und die übrigen sind paar-
paarweise entgegengesetzt. Hiernach ergiebt sich für ein gerades n
B3) Bn(x) = x h (& —
x x n /
Wenn n ungerade ist, so ist B„(x) nur von x2 abhängig;
also sind je zwei der Werthe B1) entgegengesetzt gleich (für h
und h -|- n). Wenn man, indem man wieder m zu n relativ prim
voraussetzt,
h = 2m, im, 6m, . . ., {n — l)w»
annimmt, so erhält man in B1) weder zwei gleiche, noch zwei
entgegengesetzte Wertbe, und es ergeben sich alle von einander
verschiedenen Werthe von x\
Es wird also für ein ungerades n
B4) Bn(x)= n_iV .... n J
ly 2
Setzen wir in dieser Formel
2vm7t
w. • „ n „2vmjc , . o
x = 2 cos qp, x2 = 4 A — sm2 <p), cos2 =1 — sm2
so können wir sie so darstellen:
v } smqp v > ,^LlV n P
woraus wieder für 95 = 0 die Formel B0) folgt.
Da cos n q> bei ungeradem n verschwindet, wenn
, . 2vm7t
cos qp = ¦+- sm
ist, so haben wir damit für diesen Fall auch die Factoren-
zerlegung der Function A„(x) gefunden. Es ist für ungerades n

480 Zwölfter Abschnitt. §. 145.
B6) An(x) = X A (x* —
ri7C\
»-1V" n )
h 2
Die Grossen
.._, . „ 2 vm%
B7) « = sin2
sind also die Wurzeln einer algebraischen Gleichung vom Grade
(n — 1) : 2
<X>n(x) = 0,
und wir erhalten die Function <bn(x), wenn wir an Stelle der
Variablen x*- in der Function An(x) : x eine neue Variable 4«
setzen und durch 2"-1 dividiren. Es wird daher [Formel A1)]
B8) <X>n(x) = II(x- «)
"~x n "~3 |^ w (n — 3) 1 "~5
— * 2 "T^2 "" 1.2 16^ 2 '
und für B5) können wir schreiben
B9) ^^ = (— lfir1 2»-1 JT
§. 145.
Vorzeichenbestimmung. Quadratische Reste.
Wir haben im vorigen Paragraphen zwei Formeln abgeleitet,
in denen noch Vorzeichen zu bestimmen waren, nämlich
A) 2 2 TZ cos = ± 1,
B) 2 V TT sin ^1^ = 4-
worin w» relativ prim zu der ungeraden Zahl n ist, und v die
Reihe der Zahlen
•durchläuft. Wir wollen das Zeichen v für die Zahlen dieser
Reihe hier festhalten.
Jede beliebige ganze Zahl giebt bei der Theilung durch n
als Rest eine der Zahlen v öder 0 oder n — v. Statt n — v
können wir, wenn wir auch negative Reste zulassen, —v wählen,
und wenn wir also von den durch n theilbaren Zahlen absehen,

§. 145. Quadratische Reste. ' 481
so bleibt eine der Zahlen +v als Rest. Wir nennen diese den
absolut kleinsten Rest (zum Unterschied von dem kleinsten
Rest im gewöhnlichen Sinne, der aus den Zahlen 1, 2, ..., n — 1
genommen ist).
Es sei nun also m eine zu n theilerfremde Zahl; wir be-
betrachten die Reihe der Zahlen
(mv) m, 2m, 3m, . . ., ~~ m,
und bilden zu jeder den absolut kleinsten Rest q:
(q) ±t>i, ±v2, ±v3, ¦ ¦ ¦, ±vi(;
2
unter diesen Zahlen q kommen nicht zwei gleiche und auch
nicht zwei entgegengesetzte vor; denn wenn die Summe oder die
Differenz zweier Zahlen (p), also q ~\- q' oder q — q' gleich Null
wäre, so müsste für zwei verschiedene Zahlen v, v' aus (v )
m (v i v')
durch n theilbar sein, also müsste auch v + v' durch n theilbar
sein, was unmöglich ist, da jede der Zahlen v, v' kleiner als
n : 2 ist.
Die Gesammtheit der Zahlen (q) stimmt also, vom
Vorzeichen und von der Reihenfolge abgesehen, mit
der Gesammtheit der Zahlen (v) überein.
In den Formeln A) und B) können wir aber, wegen der
Periodicität von Sinus und Cosinus, vm durch q ersetzen, und da
cos(—qp) = cos<jp ist, so können wir in der Formel A) mv
auch durch v ersetzen, d. h. das Vorzeichen ist von m nicht
abhängig. Um es zu bestimmen, berücksichtigen wir, dass der
Cosinus eines Winkels im ersten Quadranten positiv, im zweiten
Quadranten negativ ist, dass also das Vorzeichen in A) positiv
oder negativ ist, je nachdem von den Winkeln
2vtc
n
«ine gerade oder eine ungerade Anzahl im zweiten Quadranten
liegt, oder je nachdem eine gerade oder eine ungerade Anzahl
von Zahlen v zwischen — und — liegt.
Wir bezeichnen, wenn x irgend eine nicht ganze Zahl ist,
mit E(x) die grösste ganze Zahl, die kleiner als x ist, so dass
x zwischen E(x) und E(x) -\- 1 liegt. Die Anzahl der ganzen
Weber, Algebra. I. 32

482 ' Zwölfter Abschnitt. §-145.
Zahlen, die zwischen zwei Zahlen x und y liegt, ist dann gleich
— E{x), und wir haben also zu untersuchen, ob
eine gerade oder eine ungerade Zahl ist. Wir müssen vier Fälle
unterscheiden, wie sich aus der folgenden Zusammenstellung
ergiebt, worin h eine nicht negative ganze Zahl bedeutet:
Es ist also in A) das positive Zeichen zu nehmen, wenn n
von der Form 8 h -\- 1 oder 8 7c —(— 7, das negative, wenn n von
der Form 8A -j- 3 oder 8 ~k -\- 5 ist. In den ersten Fällen ist
jj2. 1 ' ¦ •
—-— eine gerade, in den beiden letzten eine ungerade Zahl,
o .
und demnach erhalten wir die genaue Formel A):
C) 2T- 71 cos ^^ = ('- l)— •
In der Formel B) hängt das Vorzeichen von m ab; es ist
positiv oder negativ, je nachdem unter den Zahlen (q) eine
gerade oder eine ungerade Anzahl negativer vorkommt.
Wir setzen nun, um die Abhängigkeit des Vorzeichens von
m und n in der Bezeichnung auszudrücken, für B)
D) 2 2 II sm = (-- \ V»,
' 2
worin
ist.
Das Symbol (— J ist von einer anderen Seite her und in
speciellerer Fassung von Legrendre in die Zahlentheorie ein-
eingeführt und von Jacobi verallgemeinert worden. Wir wollen

§. 145. Quadratische Reste. 483
es das Legendre'sche Symbol nennen. Seine Bedeutung für
die Zahlentheorie wird sich gleich ergeben; zunächst haben wir
den Satz:
1. Es ist (—) gleich -j-1 oder gleich —1, je nach-
\n /
dem die Anzahl der negativen unter den absolut
kleinsten Resten von mv eine gerade oder eine
ungerade ist.
Für m = 1 gilt, wie wir schon gesehen haben, das positive
Zeichen in der Formel B);. also haben wir, wie auch die
Formel D) direct zeigt,
Verwandeln wir m in —m, so ändert sich in allen Factoren
des Productes auf der linken Seite von D) das Vorzeichen; da
^, j
die Anzahl der Factoren —-— beträgt, so ergiebt sich
3.
und für m = 1
Setzen wir 2 m für m und benutzen die Formel
. ivftiit „ . Ivmit Ivmit
sm = 2 sm cos ,
n n n
so folgt aus C)
und für m = 1
Aendert man »w um ein Vielfaches von w, so bleiben alle
Factoren des Productes D) ungeändert, und daraus folgt:
7. Es ist
wenn m = m' (mod w).
Wir setzen jetzt nicht nur n, sondern auch m als ungerade
und positiv voraus und wenden die Formel B9) des §. 144 an,
in der wir n durch m ersetzen:
31*

484 Zwölfter Abschnitt. .§. 145.
E)
worin ß die sämmtlichen Wurzeln der Gleichung Q>m(x) = 0
durchläuft, die den Ausdruck
/,.\ o • » 2 II 71
F) ß = sin2 ——
v J m
haben. Ist nun m' eine zu n theilerfremde Zahl, so durchläuft
. . " . 2vmr7C
G) k = sin2
die sämmtlichen Wurzeln der Gleichung #„ (x) = 0, und wenn
wir in E)
setzen und das Product in Bezug auf alle v nehmen, so folgt:
* . 2vmm'7t
Sm n (m — i) (n — i) (m—i) (n-l) a ß
(9) ?-^1— = (— 1) 1 2 a JTJT (« — ß).
JTsin
w
Die rechte Seite dieser Formel ist aber von m' ganz unab-
unabhängig. Der Werth der linken Seite ist also derselbe, als ob
m' = 1 wäre, und wenn man für die Producte die Werthe aus
D) setzt, so folgt
/m m'\ fm'\ /m\ /1 \
( I • ( ) z= ( — 1 • ( I
\ n ) \n / \nj '\nj
oder
Hier war zunächst vorausgesetzt, dass m und m' positiv und
ungerade seien. Nach 3. und 5. aber bleibt 8. auch noch richtig,
wenn m oder m' negativ oder gerade ist, wenn nur m und m'
relativ prim zu n sind.
Nehmen wir wieder in ungerade und positiv an, so folgt
jetzt aus D) und (9)
fm\ , (m-i)(n-i) (ot-1)(«-1) « ß
Wenn wir hierin m mit n vertauschen, so ändert in dem
Doppelproduct auf der rechten Seite jeder Factor sein Vorzeichen;
alles Andere bleibt ungeändert. Die Anzahl dieser Factoren ist aber

§. 145. Quadratische Reste. 485
n — 1 m — 1
2 2
und daraus folgt
9. (a) = (- .f^v^ (*\
\nj v ' \m)
oder (—) ist gleich (—), wenn von den beiden
ungeraden Zahlen m, n wenigstens eine von
der Form 4 fc -f- 1 ist, und ( —) ist entgegen-
gesetzt zu (—-), wenn beide Zahlen von der
Form 4fc -f- 3 sind.
Dieser berühmte Satz ist unter dem Namen des Iieciproci-
tätsgesetzes bekannt. Der hier gegebene Beweis rührt von
Eisenstein her. Man kann mit seiner Hülfe und nach 5. und 6.
den Werth des Symbols (—) sehr schnell ermitteln, indem man
\n /
so verfährt, als ob es sich um die Bestimmung des grössten
gemeinschaftlichen Theilers von m und n handelte.
Aus 8. und 9. ergiebt sich noch ein letzter Satz, der gilt, wenn
n und n' zwei positive ungerade zu m theilerfremde Zahlen sind:
() (
\n'J \nn'
Seine Richtigkeit ergiebt sich, wenn m ungerade und positiv
ist auf Grund der Congruenz
A1) (» - 1) (n' - 1)
= (nn' — 1) — (n — 1) — (ri — 1) = 0 (mod 4),
wenn man auf beide Seiten von 10. die Formel 9. und dann 8.
anwendet, und wenn m gerade oder negativ ist, aus 4. und 6.
Nach diesen Sätzen kann man (—) auf ein Product von
Werthen (—) zurückführen, worin w, q Primzahlen sind. Die
Berechnung von (— j geschieht aber leichter nach 9. ohne diese
Zerlegung.
Wir wollen nun noch eine andere Bedeutung des Symbols
(— j kennen lernen, für den Fall, dass jp eine ungerade Prim-

486 Zwölfter Abschnitt. §. 145.
zahl ist, durch die ursprünglich das Symbol von Legendre ein-
eingeführt ist.
"Wenn wir alle durch p nicht theilbaren ganzen Zahlen x
ins Quadrat erheben, und die Reste der Division durch p auf-
suchen, so erhalten wir im Ganzen nur *—^— verschiedene
Reste, denn erstens geben die Quadrate congruenter Zahlen die-
dieselben Reste, und zweitens geben die Quadrate entgegengesetzter
Zahlen auch dieselben Reste. Wir bekommen also gewiss alle
n \
Reste, wenn wir die ±—-— Zahlen v
(v) 1, 2, S, • • -, *^±
ins Quadrat erheben. Auf der anderen Seite ergeben auch die
Quadrate dieser Zahlen v lauter verschiedene Reste; denn es
kann, wenn v und v' verschiedene von ihnen sind, niemals
va __ v'2 — (v — i/) (V _|_ i/)
durch p theilbar sein, weil sowohl v — v' als v -f- v' kleiner als
p ist. Von den Zahlen
(s) 1, 2, 3, . . ., p - 1
kommt also die Hälfte unter den Resten von x% vor, die Hälfte
nicht. Die ersteren Zahlen und alle mit ihnen nach p con-
gruenten heissen die quadratischen Reste von p, die anderen
die quadratischen Nichtreste von p.
Wenn nun m quadratischer Rest ist, so ist die Congruenz
A2) a;2 = m (mod p)
möglich, und aus 7. und 8. folgt
(?)=(!*)=(§)"=+¦¦
Es ist also (— J :=: -\~ 1, wenn m quadratischer Rest von
p ist.
Es ist aber in §. 142, 1. der Satz ausgesprochen, dass, wenn
— )
ebenso oft das positive wie das negative Zeichen hat, und daraus
ersieht man, dass das negative Zeichen gilt, wenn m quadratischer
Nichtrest ist, es folgt also:

§. 145. Quadratische Reste. , 487
11. Ist p eine ungerade Primzahl, und m durch p
nicht theilbar, so ist (— ) = 4-1 oder = — 1,
je nachdem m quadratischer Rest oder qua-
quadratischer Nichtrest von p ist.
Darin sind alle Hauptsätze über die quadratischen Reste
enthalten, z. B. nach 8. der Satz:
12. Das Product zweier quadratischer Reste oder
zweier Nichtreste ist ein Rest; das Product aus
einem Rest und einem Nichtrest ist ein Nicht-
Nichtrest.
Nach dem Fermat'schen Satze (§. 143) ist für jede durch
p nicht theilbare Zahl m
mP-1 — 1 = \m 2 — l)\m 2 4- \) = 0 (mod m).
Es muss also einer der beiden Factoren
p — i p—i
m 2 — 1, m 2 4- 1
durch p theilbar sein, und es kann auch nur einer von ihnen
sein, weil sonst auch ihre Differenz, die gleich 2 ist, durch p
theilbar sein müsste. Wenn nun die Congruenz A2) möglich
ist, so ist
p — i
m 2 = xp — 1 = 1 (modjp),
woraus folgt, dass alle quadratischen Reste, deren Anzahl
\{p — 1) ist, Wurzeln der Congruenz
x 2 =1 (modjp)
sind. Da aber diese Congruenz nach §. 143 nicht mehr als
| (» — 1) Wurzeln haben kann, so sind die quadratischen Nicht-
Nichtreste Wurzeln der Congruenz
p — i
x 2 = — 1 (mod p),
und hieraus folgt der für jede durch p nicht theilbare Zahl m
gültige Satz von Euler
p i {<wi\
A3) m 2 =(j)(moäp),
oder in Worten:

488 Zwölfter Abschnitt. §. 145.
13. Die durch p nicht theilbare Zahl m ist quadrati-
quadratischer Rest oder Nichtrest von p, je nachdem
p—i . p—i
m 2 — 1 oder m 2 -\- 1
durch p theilbar ist.
Wir können noch hinzufügen, dass die quadratischen ßeste
in jedem Indexsysteme gerade Indices haben, die Nichtreste
ungerade.
Hieraus lassen sich noch einige weitere bemerkenswerthe
Folgerungen ziehen. Wir bezeichnen mit a die quadratischen
Reste, mit b die Nichtreste der ungeraden Primzahl j), so dass
die Anzahl der a und der & je \{p — 1) beträgt. Mit II(a)
und II(p) bezeichnen wir die Producte der sämmtlichen a und
der sämmtlichen b. Die a und b zusammen enthalten alle
Zahlen 1, 2, . . ., p — 1, und es ist daher nach dem Wilson'-
schen Satze (§. 143)
A4) n(a) n(b) = — 1 (mod p).
Ist &0 ein fester Nichtrest, so durchläuft boa nach 12. die
sämmtlichen Nichtreste &, wenn a die sämmtlichen Reste durch-
durchläuft und daraus ergiebt sich nach 13.
A5) n(b) = 60~ n(a) = — JI(o) (mod p).
Ferner ist, da jedes a dem Quadrate einer der Zahlen
1, 2, . . ., ±(p — 1) congruent ist
A6) U(O). = (l, 2, 3, • • ., t^J (mod p).
Die in dem Wilson'schen Satze vorkommenden Zahlen
1, 2, . . ., p — 1 kann man aber auch durch die Zahlen
±1» ±2, . . ., ±|(p — 1) ersetzen, und daraus ergiebt sich
n 1\ 2 p +1
2, • • -, L^) = (_ j)— (mod p)t
und es folgen also aus A5) und A6) die Formeln
p+i p—i
A7) Il(a) = (-1) * ,, n(b) = (- 1) 2 (modi>).

DEITTES BUCH.
ALGEBRAISCHE GROSSEN.

Dreizehnter Abschnitt.
Die Galois'sche Theorie.
§. 146.
Der Körperbegriff.
Ein System von Zahlen wird ein Zahl kör per genannt,
wenn es so in sich vollendet und abgeschlossen ist, dass die vier
fundamentalen Rechenoperationen (die vier Species), die Addi-
Addition, die Subtraction, die Multiplication und die Divi-
Division, ausgeführt mit irgend welchen Zahlen des Systems, aus-
ausgenommen die Division durch Null, immer auf Zahlen führen, die
demselben System angehören. Dieser Begriff, der eine Eintheilung
der Zahlenarten nach einem natürlichen Gesichtspunkte giebt, ist
von Dedekind eingeführt (Dirichlet-Dedekind, Vorlesungen
über Zahlentheorie, 2. Aufl. 1871, §. 159). Er ist für die Algebra
von der grössten Bedeutung, und es ist nicht gleichgültig, dafür
einen bezeichnenden und ausdrucksvollen Namen zu haben. Das
Wort Zahlkörper ist von Dedekind nach zahlreichen Ana-
Analogien gebildet, in denen das Wort Körper (corpus, corps) in ähn-
ähnlicher Weise eine Vereinigung von zusammengehörigen Dingen,
der eine gewisse Vollständigkeit zukommt, bedeutet.
Der Begriff des Zahlkörpers kann erweitert und auf alle
Grossen übertragen werden, mit denen nach den Regeln der vier
Species gerechnet werden kann, insbesondere also auf rationale
Functionen irgend welcher Veränderlichen.
Wir nennen also einen Functionenkörper ein System von
Functionen von einer oder mehreren Veränderlichen von der
Beschaffenheit, dass in diesem System die Rechnungen mit den
vier Species unbegrenzt ausgeführt werden können und immer

492 Dreizehnter Abschnitt. §. 146.
auf eine bestimmte Function desselben Systems führen (immer
mit Ausnahme der Division durch Null). Die Veränderlichen
können ganz von einander unabhängig sein; es ist aber auch
der Fall nicht ausgeschlossen, dass gewisse Beziehungen zwischen
ihnen festgesetzt sind, die beim Rechnen zu berücksichtigen sind.
Eine Function eines Functionenkörpers gilt nur dann als
Null, wenn sie identisch, d. h. für alle in Betracht kommenden
Werthe der Veränderlichen versehwindet.
Da wir vorläufig unsere Betrachtungen nicht einschränken
wollen, so werden wir jetzt von Körpern schlechtweg sprechen,
und die Objecte, mit denen die Rechnungen auszuführen sind,
die sowohl Zahlen als Functionen sein können, als Grossen
oder auch als die Elemente des Körpers bezeichnen1).
Ein Körper ist dann also ein System von Grossen von der
Vollständigkeit, dass in ihm die Grossen addirt, subtrahirt, multi-
plicirt und dividirt werden können.
Wenn alle Grossen eines Körpers in einem zweiten Körper
enthalten sind, so heisst der erste Körper ein Theiler des
zweiten.
Ist ein Körper & ein Theiler eines Körpers &', so werden
wir auch sagen, Sl' ist ein Körper über ß.
Streng genommen, bildet die einzige Zahl „Null" für sich
einen Körper. Diesen wollen wir aber der Kürze wegen ein- für
allemal ausnehmen.
Dann ist das nächstliegende Beispiel eines Körpers der In-
Inbegriff aller rationalen Zahlen.
Dieser Körper ist ein Theiler von jedem anderen Körper;
denn jeder Körper enthält wenigstens eine von Null verschiedene
Grosse k>, also auch den Quotienten e> : k> = 1, d. h. die Zahl 1,
also auch, da alle ganzen Zahlen durch Addition und Subtraction
von Einern entstehen, alle ganzen Zahlen; und aus den ganzen
Zahlen kann man wieder durch Division alle Brüche ableiten.
Andere Beispiele von Zahlkörpern sind: der Inbegriff aller
complexen Zahlen von der Form x ~\- yi-, worin i = v — 1, x
und y alle rationalen Zahlen bedeuten; ferner der Inbegriff aller
(rationalen und irrationalen) reellen Zahlen, oder der In-
Inbegriff aller überhaupt existirenden complexen Zahlen x -\- y i.
x) Vergl. des Verfassers Abhandlung: „Die allgemeinen Grundlagen
der Galois'schen Gleichungstheorie". Mathematische Annalen, Bd. 43.

§. 147. Adjunotion. 493
Als Beispiel eines Functionenkörpers mag der Inbegriff aller
ganzen und gebrochenen rationalen Functionen einer Veränder-
Veränderlichen (mit Einschluss der Constanten) dienen, wobei man die
constanten Coefficienten auf einen beliebigen Zahlkörper, etwa
auf den der rationalen Zahlen beschränken oder auch ganz un-
unbeschränkt annehmen kann.
Wir wollen hier nicht weiter die Beispiele häufen, da die
genaue Untersuchung von Körpern besonderer Art eine der
Hauptaufgaben unserer späteren Ausführungen sein wird.
§• 147.
Adj unction.
Wenn einem Körper irgend welcher Grossen, den wir mit £1
bezeichnen wollen, irgend eine Grosse « hinzugefügt wird, die
nicht in ihm enthalten ist, so entsteht ein neues Grössensystem
£1, «,
das aber kein Körper sein wird; um daraus einen Körper abzu-
abzuleiten, muss man alle Grossen hinzufügen, die sich durch die
Verbindung von « mit den Grossen von £1 mittelst der Grund-
Grundrechnungsarten ableiten lassen. So erhält man einen erweiterten
Körper £l\ der zugleich a und £1 enthält, und der durch « und
Si völlig bestimmt ist. Wir wollen ihn den Körper £1, a nennen.
Dies Hinzufügen einer neuen Grosse « zu einem Körper &l
heisst Adjungiren, und man sagt, der Körper £1' entsteht aus
£1 durch Adj unction von «.
Zu £1' kann man wieder eine Grosse «' adjungiren, und
erhält einen dritten Körper £1", der dann £1, « und «' ent-
enthält u. s. f. Man kann aber auch gleichzeitig zwei oder mehrere
Zahlen zu £1 adjungiren, und erhält so denselben Körper £1",
wenn man gleichzeitig « und a! dem £1 adjungirt. Man kann
auch einem Körper einen zweiten Körper adjungiren und erhält
so einen Körper, der zugleich die Zahlen der beiden Körper
enthält. In dem obigen Beispiel würde man durch Adjunction
des Körpers £1, «' zu dem Körper £1' = £1, « wieder denselben
Körper £1" erhalten.
Adjungirt man einem Körper einen seiner Theile, so entsteht
kein neuer Körper.
So erhält man z. B., wenn man zum Körper der rationalen

494 Dreizehnter Abschnitt. §. 148.
Zahlen, der mit 3t bezeichnet sein mag, die Zahl i == V—1
adjungirt, den Körper der complexen Zahlen x-\- yi, mit ratio-
rationalen %, y, den wir 3 nennen wollen. Durch Adjunction einer
Variablen u zum Körper 3t erhält man den Körper, der aus allen
ganzen und gebrochenen rationalen Functionen von u mit ratio-
rationalen Coefficienten besteht, durch Adjunction von u und i zu 3t
den Körper der rationalen Functionen von u, deren Coefficienten
Zahlen in 3S sind u. s. f.
Es sei schliesslich noch bemerkt, dass ein Körper von
Grossen vielfach auch, nach Kronecker's Vorgang, ein Ratio-
Rationalitätsbereich genannt wird. Es ist bisweilen nützlich, den
Ausdruck Rationalitätsbereich für einen Körper dann zu brauchen,
wenn damit ausgedrückt werden soll, dass bei einer bestimmten
Aufgabe die Grossen dieses Körpers als bekannt oder rational
betrachtet werden sollen.
§. 148.
Functionen in einem Körper.
Wir haben oft Veranlassung, ganze Functionen einer Ver-
Veränderlichen x
A) f(x) = a0 xm + «j xm—1 + • • • + ow-i* + am
zu betrachten, deren Coefficienten einem bestimmten Körper £1
angehören, und die wir in £1 enthaltene Functionen, oder
kurz Functionen in £1 nennen wollen. Sie sind nicht zu ver-
verwechseln rtiit Functionen, die etwa dem Körper £1 angehören,
wenn £1 ein Functionenkörper ist.
Im dritten Abschnitt haben wir gesehen, dass, wenn die
Coefficienten a0, au . . ., am bestimmte Zahlenwerthe haben, in
Wurzeln «x, «2, . . ., «m von f(x) existiren, die gleichfalls be-
bestimmte Zahlenwerthe haben, unter denen aber mehrere einander
gleiche vorkommen, wenn die Discriminante d (a) derFunction(l)
verschwindet. Sind die Coefficienten a von f(x) unabhängige
Variable, so giebt es für jedes bestimmte Werthsystem der a ein
bestimmtes Werthsystem der «, und die « ändern sich stetig mit
den a (§. 44). So lange wir also die Veränderung der a auf ein
hinlänglich enges Gebiet beschränken, in dem solche Werthe nicht
vorkommen, für welche die Discriminante A (a) verschwindet, so

§. 148. Funotiönen in einem Körper. 495
sind die m Grossen « als Functionen der a vollständig bestimmt
und von einander unterschieden, wenn der Werth einer jeden von
ihnen für irgend ein bestimmtes Werthsystem der a gegeben ist.
Sind die a nicht unabhängige Veränderliche, sondern selbst
wieder Functionen von anderen Veränderlichen, so bleibt alles
dies gültig, so lange nur die Aenderungen der a nach der
Stetigkeit erfolgen.
Wir können also hiernach in allen diesen Fällen von den m
Wurzeln einer Gleichung mten Grades sprechen, die als Zahlen
oder als algebraische Functionen ihrer Coefficienten aufzu-
aufzufassen sind.
Wenn nun £1 ein beliebiger Körper, und fix) eine Function
in £1 ist, so sind zwei Fälle möglich.
Die Function f(x) ist entweder zerlegbar oder nicht zerlegbar
in Factoren niedrigeren Grades, deren Coefficienten dem Körper
£1 angehören. Im ersten Falle heisst die Function f{x) redu-
cibel, im zweiten irreducibel in £1. Man spricht bisweilen
auch, wenn der Körper £1 als bekannt und feststehend betrachtet
werden kann, wenn es z. B. der Körper der rationalen Zahlen
ist, schlechtweg von reduciblen oder irreducibeln Functionen,
ohne die Bezeichnung „im Körper £1" ausdrücklich hinzuzufügen.
Dass aber an sich die genaue Präcisirung des Körpers, auf den
sich die Reducibilität bezieht, oder der als Rationalitätsbereich
betrachtet wird, sehr wesentlich ist, ergiebt sich aus folgenden
Bemerkungen.
Eine lineare Function ist selbstverständlich in jedem Körper
irreducibel. Multiplicirt man mehrere Functionen der Form A)
mit einander, so entsteht eine Function derselben Form, die aber
dann natürlich reducibel ist, da sie wieder in die Factoren zer-
zerlegt werden kann, aus denen sie entstanden ist.
Eine Function fix), die in £1 irreducibel ist, kann in einem
erweiterten Körper £1', der aus £1 durch irgend eine Adjunction
entsteht, reducibel werden; so wird jede Function f(x) reducibel
in dem Körper £1', der aus £1 durch Adjunction einer Wurzel «
von f(x) = 0 entsteht; denn es kann von f(x) ein linearer
Factor x — « abgesondert werden. In dem Körper, der aus
allen Zahlen besteht, ist jede Function mit Zahlencoefficienten
reducibel.
I. Eine irreducible Function fix)' kann mit einer
anderen Function F(x), deren Coefficienten

496 Dreizehnter Abschnitt. §. 148.
demselben Körper £1 angehören, keinen gemein-
gemeinsamen Theiler haben, wenn nicht F(x) durch
f(x) theilbar ist.
Dieser Satz, der uns in der Folge noch sehr wichtige Dienste
leisten wird, ist fast selbstverständlich; denn der grösste gemein-
gemeinschaftliche Theiler zweier Functionen F(x) und f(x) lässt sich
durch rationale Rechnung finden, und ist daher auch in £1 ent-
enthalten. Da nun aber/(#) keinen in £1 enthaltenen Theiler hat
als sich selbst oder eine Constante (d. h. eine in £1 enthaltene
Grosse), so muss also dieser grösste gemeinschaftliche Theiler
entweder eine Constante oder f(x) selbst sein.
Es folgt aus diesem Satze, dass eine irreducible Function
niemals mehrfache Factoren haben kann; denn sie müsste sonst
mit ihrer Ableitung f'(x) einen gemeinsamen Theiler haben;
also müsste fix) durch f(x) theilbar sein, was unmöglich ist,
da der Grad von f'(x) niedriger ist als der von f(x).
Wir können dem Satze I. auch den folgenden Ausdruck
geben:
II. Ist f(x) irreducibel, und verschwindet F(x) für
eine Wurzel von f(x) = 0, so verschwindet es
auch für alle anderen Wurzeln von f(x) = 0.
Insbesondere können wir daraus schliessen:
III. Ist F(x) von niedrigerem Grade, als die irre-
irreducible Function f(x), und verschwindet F(x)
für eine Wurzel von f(x), so muss F(x) identisch
verschwinden, d. h. alle Coefficienten von F(x)
müssen Null sein.
Auch ganze rationale Functionen von mehreren Variablen,
fix, y, s, . . .), deren Coefficienten dem Körper £1 angehören,
heissen Functionen in £1. Auch diese werden als reducible
und irreducible Functionen bezeichnet, je nachdem sie zer-
zerlegbar oder nicht zerlegbar sind in mehrere Factoren, die selbst
Functionen in £1 sind, und wenigstens einige der Variablen
x, y, z, . . . wirklich enthalten.
Hier ist aber auf einen Unterschied aufmerksam zu machen.
Unter den Functionen von mehr als einer unabhängigen
Veränderlichen giebt es solche, die überhaupt nicht in Factoren
niedrigeren Grades; die rational von den Veränderlichen ab-
abhängen, zerlegbar sind, die also in dem aus allen Zahlen be-

§. 149. Algebraische Körper. 497
stehenden Körper irreducibel sind, und wieder andere, die zwar
zerlegbar sind, aber nur in solche Factoren, deren Coefficienten
nicht in il enthalten sind, und endlich drittens Functionen, die
in mehrere Functionen in il zerlegbar sind; nur die letztere
Art werden wir reducibel in il nennen, während die der zweiten
Art als zerlegbare} die der ersten Art als unzerlegbare
Functionen bezeichnet werden. Ist z. B. il der Körper der
rationalen Zahlen, so ist x2 — «/2 = (x — y) (x ~f- y) reducibel
in Sl. Die Function x — 2«/2 ist zwar in die Factoren
x -j- yV%, x — yV% zerlegbar, aber diese Factoren sind nicht
Functionen in il. Die Function x% -j- «/2 -\- 1 endlich ist über-
überhaupt nicht zerlegbar. Eine in einem Körper il irreducible, aber
zerlegbare Function wird in einem erweiterten Körper reducibel.
Die fundamentalen Sätze über irreducible Functionen haben
wir in §. 20 kennen gelernt. Bei jenen Ausführungen war zwar
zunächst, dem dortigen Standpunkte entsprechend, der Körper
aller Zahlen als Rationalitätsbereich vorausgesetzt, in dem der
Unterschied zwischen unzerlegbaren und irreduciblen Functionen
wegfällt. * Benutzt ist aber immer nur die Reducibilität oder
Irreducibilität einer Function, und die besondere Natur des Kör-
Körpers il kommt nicht in Betracht. So ist also darin der Beweis
des Satzes enthalten:
IV. Eine reducible Function in il kann nur auf
eine Art in irreducible Factoren zerlegt werden,
wenn man rationale Functionen, die sich nur
durch einen constanten Factor unterscheiden,
als nicht verschieden betrachtet.
§. 149.
Algebraische Körper.
Ist H ein beliebiger Körper, und F(x) eine Function in il,
so heisst die Gleichung
A) F{x) = 0
eine Gleichung in il. Diese Gleichung heisst reducibel oder
irreducibel, je nachdem die Function F(x) reducibel oder irre-
irreducibel ist. Durch Adjunction einer Wurzel « einer solchen
Gleichung zu il entsteht (wenn « nicht selbst schon zu il gehört)
Weber, Algebra. I. 32

498 Dreizehnter Abschnitt. §. 149.
ein neuer Körper £1', den wir einen algebraischen Körper
„über" £1 oder auch, wenn Zweifel über die Bedeutung aus-
ausgeschlossen sind, kurz, einen algebraischen Körper nennen
wollen. Wir brauchen für einen solchen Körper das Zeichen
Sind ß, y, . . , Wurzeln von anderen Gleichungen in £1 oder
auch andere Wurzeln derselben Gleichung, so erhalten wir durch
gleichzeitige Adjunction von «, ß, y, . . . gleichfalls algebraische
Körper über £1, die wir mit
. ß(«, ß,y,-. •)]
bezeichnen. Wir werden gleich sehen, dass diese Erweiterung
des Begriffes algebraischer Körper nur eine scheinbare ist, und
bleiben also zunächst bei der Adjunction einer Grosse «, also
bei der Betrachtung von £l(a) stehen.
Die Gleichung A), deren Wurzel « ist, kann reducibel sein.
Unter den irreducibeln Factoren von F(x) ist aber wenigstens
einer, der für x = « verschwindet, den wir mit f(x) bezeichnen
wollen; diese Function f(x) ist, wenn wir den Coefficienten der
höchsten Potenz von x gleich 1 annehmen, völlig bestimmt, weil
nach dem vorigen Paragraphen x = « nicht die Wurzel von zwei
verschiedenen irreducibeln Gleichungen sein kann.
Die Gleichung f(x) = 0 hat also die Form
B) xn -\- cixX"-1 + a2xn~2 -j- -. • • + an-xx -\- an == 0,
worin «j, a2, . . ., an Grossen in £1 sind. Ist n der Grad dieser
Gleichung, so nennen wir n auch den Grad des Körpers £l(a).
Alle Grossen & des Körpers £l(a) lassen sich ableiten durch
Addition, Subtraction, Multiplicatioh und Division aus « und aus
Zahlen in £1; sie lassen sich also darstellen als rationale Func-
tionen von « mit Coefficienten in £1, oder in der Form
worin %(x) und ip(x) Functionen in £1 sind. Da aber ip(a) von
Null verschieden sein muss, so ist ty(x) nicht durch f(x) theilbar,
und da f(x) irreducibel angenommen ist, so ist il>(x) relativ
prim zu fix).
Danach können wir nach §. 6, Satz II. die Functionen Q (x),
(p (x) in £1, und zwar cp (x) höchstens vom Grade n — 1, so
bestimmen, dass
D) Q (x) f(x) + (jp (x) i>(x) =

§. 150. Mehrfache Adjunotion. 499
wird, und wenn wir also hierin x = « setzen, so dass /(«) = 0
wird, so folgt
Bezeichnen wir die Coefficienten von <p (x), die, wie wir ge-
gesehen haben, Grossen in £1 sind, mit c0, cu . . ., c„—n so kann
also jede Grosse 0 in £i(a) in der Form dargestellt werden:
® = c0 -\- d cc -j- c2«2 -f- ••--{- c»-!«»-1.
Diese Darstellung ist nur auf eine Art möglich; denn ist
gleichzeitig
F) ® = ei + d« -f- C2«2 4 h 4-i«»-1,
so verschwindet die Function (n — l)ten Grades
für a; = «. Das ist aber nach dem Satze III. des vorigen Para-
Paragraphen nur möglich, wenn
Co = Co, Ci = Ci, . . ., £«_i = Cm_j
ist.
Wenn wir den Körper £1 als den gegebenen, seine Grossen
als rational, den Körper Sl(a) als den daraus abgeleiteten
betrachten, so bezeichnen wir eine rationale Function in £1 auch
kurz als eine rationale Function, und können demnach auch
sagen:
Der Körper £l(a) besteht aus allen rationalen
Functionen von «.
§. 150.
Gleichzeitige Adjunction mehrerer algebraischer
Grossen.
Es soll jetzt zunächst nachgewiesen werden, dass man die
gleichzeitige Adjunction mehrerer algebraischen Grossen durch
die Adjunction einer einzigen ersetzen kann, mit anderen
Worten, dass jeder Körper ß(«, ß, y, . . .) angesehen werden
kann als ein Körper £l(a).
Es seien also «, ß, y, . . . algebraische Grossen in beliebiger
Anzahl und
A) Ä(x) = 0, ß(x) = 0, C(x) = 0,...
Gleichungen in £1, deren Wurzeln # = «, x = ß-, x = y, . . .
sind. Keine dieser Gleichungen soll eine mehrfache Wurzel
32*

500 Dreizehnter Abschnitt. §. 150.
haben, eine Voraussetzung, durch die die Allgemeinheit nicht
beschränkt wird. Dagegen ist nicht ausgeschlossen, dass unter
diesen Gleichungen dieselbe mehrmals .vorkommt, wenn etwa «, ß
verschiedene Wurzeln einer Gleichung sind.
Wir haben im vorigen Paragraphen gesehen, dass sich jede
Grosse eines Körpers S2(a) als ganze rationale Function
in Sl von « darstellen lässt. Setzen wir in diesem Satze an
Stelle des Körpers £2 den Körper ß(/3, y, . . .), so folgt, dass jede
Zahl in £1(m, ß, y, . . .) als ganze rationale Function von « mit
Coefficienten aus fi(j3, y, . . .) dargestellt werden kann; und
wenn wir dieselbe Schlussweise in Beziehung auf die Coefficienten
wiederholen, so ergiebt sich:
Jede Grosse des Körpers Sl(a, ß, y, . . .) kann als
ganze rationale Function in £1 von «, ß, y, . . . dar-
dargestellt werden.
Wir bilden eine lineare Function der «, ß, y, . . .
f = «« -f yß + ey -j ,
und beachten, dass jede der Gleichungen A) nicht nur eine,
sondern mehrere Wurzeln hat, deren Zahl gleich dem Grade der
Gleichung ist. Ist also «', ß', y', . . . irgend eine von a, ß, y, . . .
verschiedene Cpmbination von je einer Wurzel von jeder der
Gleichungen A), so setzen wir:
g = x«! + yß' + zy' + -..,
und bilden auf die gleiche Weise f", f", . . . Die Anzahl der so
gebildeten Grossen f ist, wenn a der Grad von A(x), b der
Grad von B(x), c der Grad von C(x) ist u. s. f.,
m = aic ...
Die Differenzen f — f, f — f", f' — f", . . . sind lineare
Functionen von x, y, e, . . . und keine von ihnen ist identisch
Null, da wir angenommen haben, dass keine der Gleichungen A)
gleiche Wurzeln habe. Wir können also nach dem in §. 43
bewiesenen Satze für x, y, s, . . . solche rationale Zahlen
setzen, dass keine von diesen Differenzen verschwindet, dass also
die m Werthe f, f, f", . . . alle von einander verschieden sind. .
Nun ist jede rationale Function, die in Bezug auf die Wurzeln
jeder der Gleichungen A) symmetrisch ist, rational durch die
Coefficienten dieser Gleichungen ausdrückbar, d. h. es ist eine
Zahl in £1. Dazu gehören auch die Coefficienten der Function
wten Grades von t:

§. 151. Primitive und imprimitive Körper. 501
B) F(t) = (t — |) (t — |0 (t - |") • • .,
und F(t) = 0 ist also eine Gleichung in £1, die keine gleichen
Wurzeln hat, und deren eine Wurzel § ist.
Ist ferner © eine Grosse in £1 («, ß, y, . . .), also eine ganze
rationale Function von «, ß, y, . . ., und bezeichnen wir mit
©', ©", ... die Grossen, die aus dieser rationalen Function
hervorgehen, wenn die Variablen durch «', ß', y', ... oder
«", /3", y" . . . u. s. f. ersetzt werden, so ist
© ©' ©"
+ + +
als symmetrische Function der « und der ß, . . . eine ganze
rationale Function (m — l)ten Grades von t in Sl, und wenn
man t = f setzt, so folgt
und © ist also in £1 (f) enthalten. Da umgekehrt auch jede
Grosse in ß(f) zugleich in £l{a, ß, y, . . .) enthalten ist, so sind
beide Körper identisch, d. h. es ist
Damit ist aber unsere Behauptung erwiesen.
§. 151.
Primitive und imprimitive Körper.
Nach dem zuletzt bewiesenen Satze beschränken wir uns
jetzt auf die Betrachtung algebraischer Körper £l(a), worin «
die Wurzel einer Gleichung in £1 ist. Die Gleichung möge, von
mehrfachen Factoren befreit, mit
A) Fix) = 0
bezeichnet und vom Grade m sein. Ihre Wurzeln seien
B) «, «!, «2, ¦ • -, «m-1-
Es kann Fix) in £1 reducibel sein; dann wird es einen und
nur einen irreducibeln Factor fix) von Fix) geben, so
dass « eine Wurzel der Gleichung
C) fix) = 0
ist. Der Grad von /(#) sei n und die Wurzeln von C), die alle
unter den Wurzeln B) enthalten sind, seien
D) «, «!, «2, . . ., «M_!.

502 Dreizehnter Abschnitt. §. 151.
Der Grad des Körpers £2(<x) ist dann nach der in §. 149
gemachten Festsetzung gleichfalls n.
Jede der Grossen D) giebt zu einem algebraischen Körper
Anlass, und so entstehen die Körper
E) &(«), ß(Wl), .., Ä(«n-a),
die wir die mit £i(a) conjugirten Körper nennen. Es kann
sein, dass diese Körper alle oder theilweise identisch sind, sie
können aber auch alle von einander verschieden sein, wovon
später Näheres.
Nach §. 149 erhalten wir jede Grosse © in ß(«), wenn wir
in einer ganzen rationalen Function % (f) in £1, höchstens vom
Grade (n — 1), für die Variable t die Zahl « setzen.
Setzen wir für t in % (t) die verschiedenen Grossen D), so
erhalten wir n Grossen, eine aus jedem der conjugirten Körper
F) © = % («), ©! = % («i), • • -, ®»-i = IM
und diese heissen die mit © conjugirten Grossen.
Jede symmetrische Function dieser Grossen ist zugleich eine
symmetrische Function der Wurzeln der Gleichung C), und
mithin in £1 enthalten.
Unter diesen symmetrischen Functionen wollen wir zwei, die
häufig vorkommen, durch besondere Namen und Bezeichnungen
hervorheben; es ist die Summe
G) 8@) = © + ©! + ©2 ~\ h ®»-I.
die wir die Spur von © nennen, und das Product
(8) N@) = 0 010a...0n-1,
das die Norm von © heisst. Conjugirte Zahlen haben hiernach
dieselben Spuren und Normen.
Das Product
(9) (t —#)(«-#a)-••(*¦—®»-i) = *(9
ist eine ganze rationale Function »ten Grades von i in fl und
ihre Wurzeln sind © und die mit © conjugirten Grossen. Daraus
ergiebt sich der Satz:
1. Jede Grosse in £l(a) ist Wurzel einer Gleichung
nteu Grades in £1, deren übrige Wurzeln die mit
© conjugirten Grossen sind.
Die Berechnung der Function <&(£) aus f(x) ist nichts
Anderes, als die von einem anderen Gesichtspunkte im vierten

§. 151. Primitive und imprimitive Körper. r Qtf6
und sechsten Abschnitt betrachtete Tschirnhausen-Trans-
Tschirnhausen-Transformation.
Wir haben nun die Function <$(£) auf ihre Irreducibilität
zu untersuchen.
Wenn die Function <J>(t) reducibel ist, so hat sie einen irre-
ducibeln Factor y> (t), in dem wir den Coefficienten der höchsten
Potenz von t gleich 1 annehmen können, und jeder solche Factor
verschwindet wenigstens für einen der Werthe &, 0U . . ., ®TC_i.
Es sei also
d. h. die Gleichungen tp [% (x)~\ = 0 und f(x) = 0 haben eine
gemeinsame Wurzel. Da aber f(x) irreducibel vorausgesetzt ist,
so muss tp [% {xj\ nach dem Theorem II., §. 148 für alle Wurzeln
os, %, os2, . . ., a,n—\ von f(x) = 0 verschwinden, d. h. es ist
9(8) = 0, 9(80=0, 9(80 = 0, ... tp (®n-i) = 0.
Wenn also die mit @ conjugirten Werthe alle von einander
verschieden sind, so ist (p(t) mit &(£) identisch, d. h. <&(f) ist
irreducibel. Sind aber unter den mit @ conjugirten Werthen nur
nx von einander verschiedene vorhanden, etwa @, @l5 ®2,..., ®ni-i,
so ist
A0) cp (t) = (t — &) (t — ®,) . . . (t — 0^-0,
und jeder andere irreducibele Factor von <&(£) ist, da er wenig-
wenigstens für einen der conjugirten Werthe &, und folglich für alle
verschwinden muss, mit q>(t) identisch. Es ist also &(£) eine
Potenz von tp (f), etwa
A1)
und
A2)
Daraus ergiebt sich also der Satz:
2. Die Function <&(t) ist entweder irreducibel
oder sie ist eine Potenz einer irreducibeln
Function. Die n mit einer Zahl in ß(«) conju-
conjugirten Zahlen sind entweder alle von einander
verschieden, oder sie zerfallen in % Systeme
von je w2 unter einander gleichen Zahlen. Im
ersten Falle ist <J>(t) irreducibel, im zweiten
die n2te Potenz einer irreducibeln Function
wxten Grades in Sl.

504 Dreizehnter Abschnitt. §. 151.
Eine Grosse 0 in ¦£(«), die von. allen ihren conjugirten
Zahlen verschieden ist, und die also einer irreducibeln Gleichung
wten Grades genügt, heisst eine primitive Grosse des
Körpers. Nach dem Satze §. 43, 1. lassen sich unendlich viele
solche primitive Grossen bestimmen, sogar so, dass die Coeffi-
cienten von @ = % (a) rationale Zahlen sind. Man braucht nur
über die Coefficienten von % so zu verfügen, dass unter den con-
conjugirten Grossen %{a) keine gleichen vorkommen.
3. Jede Grosse ra des Körpers £l(oc) kann rational
durch eine beliebige primitive Grosse ® des
Körpers ausgedrückt werden.
Denn sind ca, ajj, ca2, . . ., caM_i die zu m conjugirten Zahlen,
ebenso ®, @t, ®2, . . ., ®„_i die zu & conjugirten und
*(*) = (* - ®) (t — ®i) • • • (* - ®—0i
so ist
eine ganze rationale Function n — lten Grades von t, deren
Coefficienten Zahlen in Sl sind, und daraus ergiebt sich, wenn
man t = & setzt,
worin <P'(@) von Null verschieden ist.
Es ist hiernach der Körper Sl(@) mit dem Körper
£l(a) identisch.
4. Ist & nicht primitiv, so kann nicht jede Grosse
in £l(oc) rational durch & ausgedrückt werden.
Der Körper £l(&) ist ein Theiler des Körpers
£l(a) und der Grad von Sl(@) ist ein Theiler
des Grades von £l(cc).
Denn jede Zahl des Körpers £l(@) genügt einer Gleichung
in £1 vom Grade w15 wenn % ein Theiler von n und kleiner als
n ist. Also kann eine primitive Grosse des Körpers Sl(cc), die
einer irreducibeln Gleichung wten Grades genügt, nicht in £l(@)
enthalten sein.
Der Körper £l(oc) heisst primitiv, wenn er ausser
den Grossen in Sl keine imprimitiven Grossen ent-
enthält, imprimitiv, wenn er noch andere imprimitive
Grossen enthält.

§. 152. Normalkörper. 505
Aus dieser Definition ergiebt sich zunächst, dass ein Körper
dessen Grad eine Primzahl ist, nothwendig primitiv ist; denn
eine imprimitive Grosse ® in fl («) genügt einer Gleichung,
deren Grad ein von n verschiedener Theiler des Grades n von
Sl(a>) ist. Wenn dieser Theiler gleich 1 ist, so ist ® in ß ent-
enthalten.
Wir wollen jetzt noch einige der wichtigsten Eigenschaften
der imprimitiven Körper kennen lernen.
Hat Sl(cc) einen von Sl verschiedenen Theiler Sl', der seiner-
seinerseits Sl als Theiler enthält (ist also Sl' ein Körper über Sl), und
ist ß eine Grosse, die dem Körper Sl', aber nicht Sl angehört, so
ist der Körper Sl (ß) ein algebraischer Körper über Sl und zugleich
ein Theiler von Sl' und von Sl («). und nach dem, was wir vorhin
bewiesen haben, ist der Grad nx des Körpers Sl (ß) ein Theiler von
n. Ist nun durch Sl (ß) der Körper Sl' nicht erschöpft, so nehmen
wir eine Grosse y in Sl', aber nicht in Sl(ß); dann ist der Körper
Sl(ß, y) ein Theiler von Sl' und von Sl(a) und hat seinerseits
Sl(ß) zum Theiler. Der Grad von Sl(ß, y) ist also grösser als
der von Sl(ß) und kleiner als der von Sl(a). Ist damit Sl' noch
nicht erschöpft, so fahren wir so.fort, müssen aber endlich zum
Abschluss kommen, da die Grade der Körper Sl (ß), Sl (ß, y), . . .
immer wachsen und doch kleiner als n bleiben. Daraus folgt:
5. Jeder Theiler von Sl(cc), der den Körper Sl ent-
enthält, ist ein algebraischer Körper Sl(ß) über Sl.
Der Grad von Sl(ß) ist ein Theiler des Gradjes
von Sl(oc), und wenn beide Körper den gleichen
Grad haben, so sind sie identisch.
Wir können daher unsere Definition auch so fassen:
6. Ein algebraischer Körper über Sl ist primitiv,
wenn er aussei- Sl und sich selbst keinen Kör-
Körper über Sl zum Theiler hat.
§• 152.
Normalkörper. G"alois'sche Resolvente.
Ist Sl(cc) ein algebraischer Körper, so sind die conjugirten
Körper
Ä()

506 Dreizehnter Abschnitt. §. 152.
alle von gleichem Grade, und wenn also einer von ihnen im
anderen enthalten ist, so sind beide identisch.
Ein Körper, der mit allen seinen conjugirten Körpern iden-
identisch ist, heisst ein Normalkörper. In den Normalkörpern
herrschen viel einfachere Gesetze, und der grosse Fortschritt, den
die Algebra Galois verdankt, beruht im Wesentlichen darauf,
dass beliebige Körper auf Normalkörper zurückgeführt werden.
Die Normalkörper heissen daher auch Galois'sche Körper.
Wenn ein Körper fiten Grades &(ß) die Eigenschaft hat,
dass die zu q conjugirten Zahlen pl5 p2> • • ¦¦, Qp-i alle in &(p)
enthalten sind, so ist SI(q) ein Normalkörper; denn dann sind
die Körper &(Qi), ü(p2)i • • •> ¦&(&»—1) auch alle in £1(q) ent-
enthalten und also alle mit £1(q) identisch.
Wir wollen eine Gleichung eine Normalgleichung oder
auch eine Galois'sche Gleichung nennen, wenn sie
irreducibel ist, und die Eigenschaft hat, dass alle
ihre Wurzeln rational (in £1) durch eine von ihnen
ausgedrückt werden können. Dann ist ein primitives Ele-
Element eines Normalkörpers ftten Grades Wurzel einer Normal-
Normalgleichung ftten Grades. Aber es gilt auch das Umgekehrte,
dass nämlich, wenn p eine Wurzel einer Normalgleichung ist,
ü(p) ein Normalkörper gleichen Grades ist. Denn ist g0 die
Wurzel der Normalgleichung, durch die alle anderen rational
ausgedrückt sind, so ist sicher SI(q0) ein Normalkörper. Mit
diesem ist aber &(ß) conjugirt und also identisch. Es folgt
daraus noch, dass bei einer Normalgleichung jede Wurzel nicht
nur durch eine bestimmte unter ihnen, sondern durch jede
beliebige rational ausdrückbar ist.
Man kann nun auf folgendem Wege beliebige algebraische
Körper auf Normalkörper zurückführen.
Es sei
A) F(x) = 0
eine beliebige reducible oder irreducible Gleichung in Sl vom
wten Grade, von der wir nur voraussetzen wollen, dass sie
keine mehrfachen Wurzeln habe. Ihre Wurzeln seien
B) a, «i, . . ., «m_L
Man erhält daraus m algebraische Körper
C) ß(«), £«>, ..., Sl(«._,),
und man kann offenbar die Function F(x) so wählen, dass unter
den Körpern C) irgend welche gegebene algebraische Körper

§. 152. Normalkörper. 507
über Sl vorkommen. Wir nennen den aus allen Grossen B),
d. h. aus allen Wurzeln der Gleichung A) abgeleiteten Körper
über Sl
D) N = Si (cc, «!,..., am_i)
den Galois'schen Körper der Gleichung F(x) = 0.
Ist F(x) irreducibel, so sind die Körper C) die mit £l(cc)
conjugirten Körper. In diesem Falle soll der Körper N die
Norm eines jeden der Körper £l(cc), Slfoij), . . ., Sl(um^i)
heissen.
Ist H (cc) ein Normalkörper, so ist er mit seiner Norm iden-
identisch. Im allgemeinen Falle ist nachzuweisen, dass jV ein
Normalkörper ist. Wir wählen ein primitives Element q des
Körpers N (nach §. 150, 151) und können dann den Körper N
auch durch SI(q) bezeichnen. Ist ft der Grad von N, so genügt
p einer irreducibeln Gleichung fiten Grades
E) g(t) = o,
von der zu zeigen ist, dass es eine Normalgleichung ist. Zu
diesem Zweck bemerken wir zunächst, dass die eine Wurzel p
dieser Gleichung eine rationale Function der a, «1} . . ., am_x ist,
weil sie in N enthalten war. Setzen wir, um dies anzudeuten,
Q = Q («, «i, • • ., «m-l),
und bilden nun alle verschiedenen Anordnungen der Ziffern
0, 1, 2, . . ., m — 1,
deren Anzahl H(m) beträgt:
F) @, 1, 2, . . ., i» - 1), @', 1', 2', . . ., (m - 1)'),
@", 1", 2", . . , (m - 1)"), . . ,
worin die Ziffern mit einem, zwei etc. Accenten dieselben sind,
wie die ohne Accent, nur in anderer Reihenfolge, und bilden
hieraus die Function en
G) Q = Q («0, «i, . . ., am_!), p' = q (a0,, «!-, . . ., a(m_iy),
p" = p («0"i «1") • • •, «(m —l)")j • • •)
unbekümmert darum, ob darunter etwa unter einander gleiche
vorkommen oder nicht.
Wenn wir in allen den Anordnungen F) ein und dieselbe
Vertauschung vornehmen, z. B. 0 mit 1, so ändert sich die
Gesammtheit -dieser Anordnungen nicht, sondern nur ihre Reihen-
Reihenfolge wird eine andere. Denn erstens kann durch eine solche
Vertauschung nichts Anderes entstehen, als Anordnungen der

508 Dreizehnter Abschnitt. §. 153.
Ziffern, und zweitens können nicht zwei verschiedene Anordnungen
durch eine und dieselbe Vertauschung in dieselbe Anordnung
übergehen.
Es werden also auch durch jede solche Vertauschung die
Functionen G) nur unter einander permutirt werden. Bilden
wir also das Product
für eine Veränderliche t, so bleiben seine Coefficienten, die
gewiss Functionen von cc, au . . ., am_j sind, ungeändert, wenn
diese Grossen irgendwie permutirt werden (§. 21); d. h. es sind
symmetrische Functionen der Wurzeln der Function F(x), und
also ist G(t) eine Function von t in Sl. Alle Wurzeln von G(f)
sind Grossen in N, da sie durch die a rational ausgedrückt sind.
Nun haben G(t) und g(t) eine Wurzel gemein. Da aber
g(t) irreducibel ist, so muss G(t) durch g(t) theilbar sein; also
sind auch alle Wurzeln von g(t) in N enthalten, d. h. N ist ein
Normalkörper, w. z. b. w.
Jede Gleichung g(t) — 0 heisst eine Galois'sche Resol-
Resolvente der Gleichung F(x) = 0, und eine Galois'sche Resol-
Resolvente ist also durch folgende Bestimmung definirt:
Eine Gleichung ~'g(t) = 0 ist eine Galois'-
Galois'sche Resolvente einer gegebenen Gleichung
F(x) = 0 in Sl, wenn 1) g(t) irreducibel ist,
wenn 2) alle Wurzeln von F(x) rational durch
eine Wurzel p von g(t) ausdrückbar sind, und
3) eine Wurzel von g (t) rational durch die
Wurzeln von F(x) ausdrückbar ist.
Denn nach 2) ist JV^ in &(q) enthalten, und nach 3) ist
einer der mit SI(q) conjugirten Körper, &(pi), in N enthalten.
Die Grade von N und £1(q) können also nicht verschieden sein
und folglich ist N — Sl (p).
Jede Galois'sche. Resolvente ist eine Nor-
Normalgleichung, und eine Normalgleichung ist
ihre eigene Galois'sche Resolvente.
§. 153.
Die Substitutionen eines Normalkörpers.
Es sei jetzt SI(q) ein Normalkörper ftten Grades und p eine
seiner primitiven Zahlen, ferner

§. 153. Substitutionen eines Normalkörpers. 509
A) g(t) = 0
die irreducible Gleichung ftten Grades, deren eine Wurzel t = p
ist. Die zu p conjugirten Elemente seien
B) p, Qi, p2, . . ., Qft-1-
Da nach der Definition des Normalkörpers die Grossen B)
alle in &(p) enthalten sind, so können wir 0x0), &$(£),..., ©p—ify)
als ganze rationale Functionen in Si, höchstens vom Grade ja — 1,
so bestimmen, dass
C) Ql = ®l(Q), p2 = &2 (p), • • •, Qfl-l = %-l(Q)
wird. Ist ca eine beliebige Grosse in £1 (p), so kann man die
mit ca conjugirten Grossen so darstellen:
D) a> = cp(o), O3i = <p (pj), . . ., 03«-! = g)(p,(_i),
worin q> (t) eine rationale Function in Sl ist.
Da nun g(f) irreducibel ist, so gilt der Satz §. 148, II., den
wir jetzt so aussprechen:
1. Wenn eine rationale Function &(f) in Sl eine
Wurzel mit g(t) gemeinsam hat, so verschwin-
verschwinden alle conjugirten Grossen
Wenn in einer der Functionen ®u(q), durch die nach C)
die Wurzeln von A) ausgedrückt sind, p durch eine andere
Wurzel pft ersetzt wird, so entsteht daraus wieder eine der
Wurzeln; denn ist
so ist nach 1. auch
9 [©*(?*)] = °>
und die Reihe der Grossen
E) Qh, ®i(pft), ®2(Pä), -.., ®^-i (Qh)
stimmt, von der Anordnung abgesehen, mit der Reihe
F) Q, ®!(p), ®2(p), . ... ®„-i(q)
überein. Dies wird erwiesen sein, w.enn wir zeigen, dass in E)
keine zwei gleichen Werthe vorkommen. Bezeichnen wir der
Uebereinstimmung halber mit @0 (q) oder @ (p) die Wurzel q
selbst, so folgt aus der Gleichheit zweier der Grossen E)
G) ®i(Qh)=®,(QH)
nach dem Satze 1.
(8) 0t(Q) = e^g),

510 Dreizehnter Abschnitt. §. 153.
was aber, wenn i von Je verschieden ist, nicht möglich ist. Also
sind zugleich mit den Grossen F) auch die Grossen E) unter
einander verschieden.
Wir können dies als Satz zusammenfassen:
2. Vertauscht man p mit pft, so geht zugleich jede
mit p conjugirte Grosse in eine bestimmte andere
über, und niemals zwei verschiedene in dieselbe.
Wenn wir in allen Functionen von p statt p eine andere
Wurzel pa setzen, so führen wir eine Substitution aus. Wir
bezeichnen diese Substitution mit
'<*<» = O> Qa), a = 0, 1, 2, . . ., ft — 1,
wobei unter <J0 oder <J die sogenannte identische Substitution
(#, p) verstanden wird, die darin besteht, dass p durch sich
selbst ersetzt wird, also alle Zahlen in ü(p) ungeändert bleiben.
Wenn wir in einer beliebigen der Wurzeln C)
(fh = &h(o)
die Substitution da ausführen, so geht pft in eine andere Wurzel
pjt über, die bestimmt ist durch
(9) p* = @h (Qa) = ®U ®a (p) = ®fc <»
Es ist also Qic dieselbe Function von ga, wie pft von p.
Eine beliebige Grosse co = cp (p) des Körpers Sl (p) geht
durch die Substitution 6a in <aa = tp (pa) über. Drücken wir ra
durch pft, und coa durch p* aus:
so sieht man, dass ra in coa übergeht durch die Substitution
A0) «a=(Qh,Qld = [Q*,@h@a(Q)],
und dies ist nur ein anderer Ausdruck für die Substitution (p, pa).
Hierin ist p^ eine beliebige Wurzel von g(t) und das zu-
zugehörige pfc ist nach (9) durch 6a bestimmt. Man kann aber bei
gegebenem 6a auch pjt beliebig annehmen, und das zugehörige p&
bestimmen, indem man in %(pa) den Index h die Werthe
0, 1, 2, . . ., ft — 1 durchlaufen lässt, wobei jede Wurzel p* ein-
einmal zum Vorschein kommt. Also:
3. Jede Substitution <Ja kann in der Form (pft, p^)
dargestellt werden, worin entweder q% oder pjj
eine beliebig gegebene der (i Wurzeln p ist,
während die andere durch 6a völlig bestimmt ist.

§. 154. Zusammensetzung von Substitutionen. 5H
Die Anzahl aller von einander verschiedenen Substitutionen
6a ist also, die identische Substitution mit gerechnet, gleich dem
Grade des Körpers £&(q), den wir oben schon mit ft bezeichnet
haben. Jede dieser Substitutionen führt die Gesammtheit der
Grossen des Körpers &(p) in sich selbst über, so dass jede in
eine bestimmte andere übergeht, und niemals zwei verschiedene
Grossen in die gleiche [Formel G), (8)].
Wir nennen daher die 6a die Substitutionen des Kör-
Körpers &((>)•
Wenn ra = <p (p) im Körper £1 (p) ungeändert bleibt, wenn
p durch Qa ersetzt wird, wenn also
ist, so sagen wir, co erlaubt oder gestattet die Substitution
(p, Qa) oder 6a.
Die Grossen ra, die ausser der identischen Substitution keine
Substitution 6a gestatten, sind die primitiven Elemente des Kör-
Körpers &(p).
4. Eine Grosse, die alle Substitutionen 6a gestattet,
ist nothwendig ein Element von Sl.
Denn eine solche Grosse ist mit allen ihren conjugirten
Grossen identisch, und genügt also nach §. 151 einer Gleichung
ersten Grades in £1.
§. 154.
Zusammensetzung der Substitutionen.
Wenn wir in irgend einer Function von p die Wurzel p
zuerst durch pa und dann pa durch Qb ersetzen, so ist der Erfolg
derselbe, als ob wir gleich von vornherein p mit Qh vertauscht
hätten. Setzen wir also
A) <J = (p, Qa), <J' = (Qa, Q»), ö" = (p, Qh),
so ist es für das Ergebniss gleichgültig, ob wir in allen Zahlen
des Körpers £1(q) zuerst die Substitution <J und dann die Substi-
Substitution <J' ausführen, oder ob wir für einmal die Substitution <J"
machen.
1. Wir nennen daher <J" aus <J und <J' componirt
oder zusammengesetzt, und bezeichnen diese
Beziehung durch die symbolische Gleichung
B) 66' = 6".

512 Dreizehnter Abschnitt. §. 154.
Da wir nach dem Satz 3. des vorigen Paragraphen in der
Bezeichnung einer Substitution (gh, q*) das erste oder das zweite
Element beliebig wählen können, so lassen sich pa, pj so aus-
auswählen, dass <J, ö' zwei beliebig gegebene unter den (i Substi-
Substitutionen des Körpers Si (p) sind; <J" ist aber dadurch völlig
bestimmt. Ebenso ist aber auch, wenn 6 und <J" gegeben sind,
tf' eindeutig bestimmt. Denn wählen wir p beliebig, so ist po
durch <J völlig bestimmt und p6 durch ß", womit auch <J' = (pa, pj)
gegeben ist. Ist endlich <J' und 6" gegeben, so ist <J eindeutig
bestimmt, da zunächst p6 durch 6" und dann p« durch <J' be-
bestimmt ist. Wir haben daher:
2. Von den durch die symbolische Gleichung <?<?' = <?"
verbundenen drei Substitutionen des Körpers
ß(p) können irgend zwei beliebig gegeben sein,
während die dritte dadurch eindeutig be-
bestimmt ist.
Wir haben die Composition der Substitutionen symbolisch
durch das Zeichen der Multiplication ausgedrückt. Es ist hier
aber wohl auf die Reihenfolge der Factoren oder Componenten
zu achten, weil <J <J' von <J' <J verschieden sein kann, d. h. bei der
die Composition ausdrückenden symbolischen Multiplication gilt
nicht das commutative Gesetz der gewöhnlichen Multiplication;
wohl aber gilt das associative Gesetz, das sich in folgendem
Satz ausspricht:
3. Sind <J, <J', <J" irgend drei der ft Substitutionen des
Körpers <ß(p), so ist
C) (<Jö')ö" = tf(tf'ö").
Der Beweis ist sehr einfach; denn nach dem Satze 3., §. 153
können wir pa, pj, pe so bestimmen, dass
D) <J = (p, Qa), <J' = (pa, Qh), <J" = (&, pc),
und dann ist
tftf' = (p, Qb), F 6') 6" = (p, Qi)(Qi, Qc) = (q, pc),
<J'<J" = (pa, pc), <J(<J'0") r= (p, pa)(pa, pc) = (p, pc).
Wir bezeichnen daher kurz die aus den drei Substitutionen
<J, ö', <J" zusammengesetzte Substitution mit
tftf'tf",
und können überhaupt aus beliebig vielen Componenten eine
bestimmte Substitution
tftfW" . . .

§. 155. Permutationsgruppen. 513
dadurch zusammensetzen, dass wir nach einander immer zwei
benachbarte unter den Componenten zu einer Substitution ver-
vereinigen, bis das ganze symbolische Product sich auf eine ein-
einzige Substitution zusammengezogen hat. Denn wir können nach
§. 153, 3. setzen
ö = (?, Qa), ö' = (?o, Qb), ö" = (?6, ?c), ö'" = (?c, ?«),
und erhalten immer
was offenbar auf eine beliebige Anzahl von Componenten aus-
ausgedehnt werden kann.
Auf Grund der Eigenschaften 1., 2., 3. nennen wir die Ge-
sammtheit der (i Substitutionen des Normalkörpers H(q) eine
Gruppe, und zwar eine endliche Gruppe vom Grade [i. Sie
heisst auch die Gruppe der Substitutionen des Körpers
)
Mit der allgemeinen Theorie der Gruppen werden wir uns
in späteren Abschnitten eingehend beschäftigen.
§. 155.
Permutationsgruppen.
Im §. 152 haben wir gesehen, wie man zu einer beliebigen
Gleichung in il vom Grade m
A) F(x) = 0,
von der nur vorausgesetzt wird, dass sie keine gleichen Wurzeln
hat, einen Normalkörper Sl (p) bestimmen kann, dem alle Wurzeln
von A) angehören. Wenn also die Wurzeln von A) mit
B) «, «!, «2, . . ., am_!
bezeichnet werden, so. ist
C) U = X(Q), <*!=%! 0), • • ., «m_! = Xm-l(Q),
und die % sind rationale Functionen in Sl.
Setzen wir aber für q eine mit q conjugirte Grosse qu
führen wir also eine Substitution ö = (q, q-,) aus, so geht jede
Wurzel et, in eine bestimmte andere über, und niemals zwei ver-
verschiedene in dieselbe; denn wenn
ist, so ist nach §. 153, 1.:
Weber, Algebra. I. 33

514 Dreizehnter Abschnitt. §. 155.
d. h. x(Qi) ist aucn eine Wurzel der Gleichung A). Dass aber
nicht zwei verschiedene Grossen des Körpers Q(q) durch eine
Substitution ö in die gleiche Grosse übergehen können, haben
wir im §. 153 schon allgemein gezeigt.
1. Eine Substitution 6 ruft also unter den Wurzeln
<x eine gewisse Permutation hervor, indem jeder
der Indices 0, 1, 2, . . ., m — 1 durch einen be-
bestimmten anderen ersetzt wird.
Dies führt uns also darauf, die Permutationen von m Ziffern
0, 1, 2, . . ., m — 1
und ihre Eigenschaften im Allgemeinen genauer zu studiren.
Geht die Ziffer 0 in a0, 1 in al5 2 in a2 u- s- £» m — 1 in
am_i über, so muss
D) «o, Ox, a2) • • •> «m-i
irgend eine andere Anordnung der Ziffern 0, 1, 2, . . ., m—1 sein.
Den Uebergang von der einen zu der anderen Anordnung be-
bezeichnen wir durch ein Symbol, wie
/0, 1, 2, . . ., m — 1\
E) *« = (''''
und nennen diesen Uebergang eine Permutation.
Die Anzahl aller möglichen Permutationen von m Ele-
Elementen ist
FL(m) = 1.2.3...«»,
worunter auch die identische Permutation
/O, 1, 2, . . ., m - 1\
Vo, 1, 2, . . , m - 1/
die jedes Element an seiner Stelle lässt, mitgezählt ist.
Das Symbol E) ändert seine Bedeutung nicht, wenn man
die einzelnen Paare
0, 1, 2, . . ., m — 1
Oo, <*i, «2, . . ., am—i
anders anordnet. Ist also
&0i ^11 hi • • •) &m-l
irgend eine Anordnung der Ziffern 0, 1, 2, . . ., m— 1, so können
wir für E) auch setzen:

§. 155. Permutationen. . 515
F) *„ = (K 6l' ^ • • •' 6—1 \
was mit E) völlig gleichbedeutend ist.
Hieraus lässt sich der sehr wichtige Begriff der Zusammen-
Zusammensetzung von Permutationen ableiten. Ersetzen wir einen
Index a durch einen Index b, dann b durch c, so ist der Erfolg
derselbe, als wenn sogleich ä durch c ersetzt wird. Wenn wir
also zwei Permutationen nach einander ausführen, so ist das
Ergebniss eine bestimmte Permutation, die wir in folgender
Weise darstellen können. Sind
/0, 1, . . ., m - 1\ /0, 1, . . ., m — 1\
\a0, %, . . ., äW-i / V>o> t>ii ¦ ¦ •) o»-i /
irgend zwei Permutationen, so können wir nach F) die zweite
auch so schreiben:
% =
*0' ßl' ' ' ¦' a'm-1 \
bam bai, . . ., bam_1/
und wenn wir also beide nach einander ausführen, zuerst aa,
sodann »6, so entsteht eine dritte Permutation, die wir aus na
und %i zusammengesetzt (componirt) nennen, und die wir als
symbolisches Product von %a und %j, darstellen:
».»,
Es ist bei dieser Zusammensetzung meist nicht die Ver-
Vertauschung gestattet, da %a%i im Allgemeinen nicht mit %-baa.
übereinstimmt. Aber es gilt das associative Princip, was sich in
der symbolischen Gleichung
(8) (%a 31s) %c = 3Ta fab ^c) = ^a ^i ^c
ausspricht. Davon überzeugt man sich durch folgende einfache
Ueberlegung.
Wird irgend ein Index p durch %a in q, dieser durch %i in
r, und r durch jte in s verwandelt, so geht p durch %a%-b in r,
und q durch nhnc in s über; mithin wirdjp sowohl durch (%a%^)%<.
als durch %a(ni%^) in s verwandelt. Nichts anderes aber besagt
die Formel (8).
Zu jeder Permution %a giebt es eine bestimmte entgegen-
entgegengesetzte (inverse) Permutation, die darin besteht, dass die durch
%a hervorgerufene Veränderung wieder rückgängig gemacht wird,
die also, mit %a zusammengesetzt, die identische Permutation
33*

516 - Dreizehnter Abschnitt. §. 155.
hervorbringt. Wir bezeichnen diese Permutation mit n~1 und
wir haben, wenn %a den Ausdruck E) hat,
Denn nach der Vorschrift der Zusammensetzung in G) ist
„ %^ _ /0, 1, ...,»— 1
*»*« ~Vo, i,...,m-
Ebenso ist aber auch
a \a0, «!, . . ., am-.J
was wieder die identische Permutätion ist. Es ist also die zu
%—x entgegengesetzte Permutation wieder die ursprüng-
ursprüngliche Permutation %a.
Ist Ttattb == #ci so i^
denn es ist srjsrjjr-'sr die identische Permutation.
Bezeichnen wir die identische Permutation mit 3r0, so ist also
A0) %a%7X = %7~1%a == ^05
und 3r0 ist sich selbst entgegengesetzt (wodurch nicht aus-
ausgeschlossen ist, dass es noch andere sich selbst entgegengesetzte
Permutationen giebt). Durch die Composition mit der identischen
Permutation wird keine andere Permutation geändert, also
2. Ist %c aus %a und %i zusammengesetzt, also
so ist nicht nur %c aus %a lind :%, sondern auch
%a aus %i und %e, und ^6 aus %a und n;,, völlig und
eindeutig bestimmt.
Denn es folgt aus A2)
\ / Ott
3. Ein aus der Gesammtheit aller J2(m) Permu-
Permutationen von m Elementen herausgegriffenes
System
Q = %, % , % , 3T . . .,
das so in sich abgeschlossen und vollendet ist,
dass je zwei und folglich auch beliebig viele
Permutationen von Q durch Zusammensetzung

§. 156. Galois'sche Gruppe. 517
immer wieder eine Permutation desselben Systems
ergeben, heisst eine Permutationsgruppe. Unter
dem Grad einer Permutationsgruppe verstehen
wir die Anzahl der Permutationen, die sie ent-
enthält.
Die Gesammtheit aller II(in) Permutationen bildet eine
solche Gruppe. Ebenso ist die einzige identische Permutation
eine Gruppe für sich. Was zwischen diesen beiden extremen
Fällen von Gruppen noch liegen kann, das wird uns in den
folgenden Abschnitten beschäftigen.
Als einfaches Beispiel möge hier nur noch die Gruppe der
cyklischen Permutationen, kurz die cyklische Gruppe,
angeführt werden, die man erhält, wenn man in irgend einer
Anordnung von Ziffern A, 2, 3, . . ., w) jede Ziffer durch die
folgende und die letzte durch die erste ersetzt, und wenn man
diese Permutation so oft wiederholt, bis man zu der ursprüng-
ursprünglichen Anordnung zurückkommt. Der Grad der cyklischen Gruppe
ist gleich der Anzahl der Ziffern; z. B. bei den drei Ziffern:
/l, 2, 3\ /l, 2, 3\ /l, 2, 3\
V2, 3, 1/ \3, 1, 2/ \1, 2, 3/
Es giebt besondere Gruppen, die uns später noch mehr
beschäftigen werden, die nur aus solchen Permutationen bestehen,
bei deren Zusammensetzung ausser den oben erwähnten auch
noch das commutative Gesetz gilt, bei denen also immer %x%%
= %%%!_ ist, und in Folge dessen die Analogie mit der Multi-
plication eine viel vollständigere ist. Solche Gruppen, zu denen
die cyklischen Gruppen gehören, heissen commutative oder
Abel'sehe Gruppen.
Wenn die sämmtlichen Elemente einer Permutationsgruppe
Qx in einer Gruppe Q enthalten sind, so heisst Qx ein Theiler
von Q, und Q durch Qx theilbar.
§. 156.
Galois'sche Gruppe.
Wenn wir in den Wurzeln cc, a,^ a2, ...,«„,_! einer Gleichung
F(x) = 0, wie sie durch §. 155, C) als Grossen des Normal-
körpers £1 (q) vom ftten Grade ausgedrückt sind, eine der (i Substi-

518 Dreizehnter Abschnitt. §. 156.
tutionen 6 des Normalkörpers ausfuhren, so vollzieht sich unter
diesen Wurzeln eine gewisse Permutation, wie schon oben gezeigt
ist. Es entspricht also jeder Substitution ö eine gewisse Permu-
Permutation % der m Ziffern 0, 1, 2, . . ., m — 1. Zwei verschiedene
Substitutionen öft, öfc führen auch zu zwei verschiedenen
Permutationen ith, 3%
Denn nach §. 152 ist q eine rationale Function von «, ccu ...,
«TO_1, die wir durch
q = 0 («, «!, . . ., am_i)
bezeichnen wollen. Wenn wir hierin
«s = X>(Q)
setzen, so folgt
A) ? = *[*(?), Zi (?).•• Z»-i(?)],
und nach §. 153, 1. ist also für jeden Index fc
B) Qk = Q\x(jtt), Xi(Qk) ¦ • ¦ Zm-ifoi)].
Wenn nun die Substitutionen 6h, 6h dieselbe Permutation
unter den a hervorrufen, so ist für jeden Index s = 0, 1,..., m — 1
Xs(Qh) = Xs(Qk),
und daraus folgt nach B), dass auch 6h = 6* sein muss.
Wird durch die Substitution 6h die Permutation %h unter
den Wurzeln von F(x) = 0 hervorgerufen, so sagen wir, dass
die Permutation %% der Substitution 6h entspricht.
Jeder Substitution entspricht eine bestimmte Permutation,
und die Anzahl dieser Permutationen ist also, die identische
Permutation mitgerechnet, die der identischen Substitution ent-
entspricht, gleich [i.
Wenn den Substitutionen 6h und öjt die Permutationen %h und
jrfc entsprechen, so entspricht der zusammengesetzten Substitution
öfcöfc die zusammengesetzte Permutation %h%u- Denn die Permu-
Permutationen sind das Ergebniss der entsprechenden Substitutionen
auf gewisse Grossen des Körpers &(q), und dabei ist es gleich-
gleichgültig, ob wir zwei Substitutionen nach einander oder mit einem
Male die aus beiden zusammengesetzte Substitution ausführen
(nach §. 154). Wir haben also den Satz:
I. Es entsprechen den jt Substitutionen des Kör-
Körpers £1 (q)
C) ¦ Ö, Ö!, ö2, . . ., 6fl_1,
[i Permutationen von m Ziffern
D) 3t, 3t!, 3T2, . . ., 3t,»_i

§. 156. Galois'sche Gruppe. 519
in der Weise, dass der aus zwei Substitutionen
zusammengesetzten Substitution die aus den ent-
entsprechenden Permutationen zusammengesetzte
Permutation entspricht
Daraus folgt aber, dass die Permutationen D) eine Gruppe
bilden. Wir bezeichnen diese Gruppe mit P und nennen sie die
Galois'sche Gruppe der Gleichung F(x) = 0, oder auch
die Galois'sche Gruppe eines jeden der Körper &(«),
Diese Gruppe steht zu der Gruppe der Substitutionen des
Körpers &(q) in der durch den Satz I. ausgedrückten Beziehung,
weshalb die beiden Gruppen isomorph genannt werden.
Um die charakteristischen Eigenschaften der Galois'sehen
Gruppe zu. finden, haben wir nur die Sätze §. 153, 1. bis 4. etwas
anders auszudrücken. Wir sagen von einer Function der m
Wurzeln, die bei irgend einer Permutation ungeändert bleibt, sie
gestatte diese Permutation, und erhalten so:
xa) Jede rationale Gleichung in £1, die zwischen den
m Wurzeln von F(x) besteht, bleibt richtig, wenn
die Wurzeln irgend einer Permutation der
Galois'schen Gruppe unterworfen werden.
b) Jede rationale Function in Si von den m Wurzeln
von F(x), die sämmtliche Permutationen der
Galois'schen Gruppe gestattet, ist eine Zahl in £1.
Denn drücken wir die Wurzeln von F(x) als rationale Func-
tionen von q aus, so geht eine Function der Wurzeln u in eine
Function 9(9) über. Hat man zuvor eine Permutation der Ga-
Galois'schen Gruppe ausgeführt, so erhält man eine der conjugirten
Zahlen <p (Qa), die aus (p (q) durch eine Substitution 6a = (9, Qa)
entsteht. Ist nun q> (q) = 0, so sind nach dem Satz §. 153, 1.
auch alle conjugirten q> (ga) = 0, womit a) bewiesen ist; und
sind die conjugirten Grossen 9 (Qa) alle einander gleich, so ist ihr
gemeinsamer Werth nach §. 153, 4. in Sl enthalten, wodurch b)
bewiesen ist.
Zu a), b) kommt noch als Drittes:
c) Wenn irgend eine Permutation % der Wurzeln
von F(x) auf alle rationalen Gleichungen in il,
die zwischen den Wurzeln bestehen, anwendbar
ist, so gehört % der Galois'schen Gruppe an, und

520 Dreizehnter Abschnitt. §. 156.
die Galois'sche Gruppe kann daher auch erklärt
werden als der Inbegriff aller Permutationen,
die auf sämmtliche rationale Gleichungen zwi-
zwischen den Wurzeln anwendbar sind.
Denn nach §. 43 kann man q als rationale (z. B. lineare)
Function der m Grossen «, ax, «2, . . ., «m_i so annehmen, dass
alle II(m) Werthe, die man durch die U (m) Permutationen
der et, daraus erhält, von einander verschieden sind. Ist dann
g(t) = 0 die Galois'sche Resolvente von F(x) = 0, deren
Wurzel dieses q ist, so ist
9(9) = 0.
Hierauf können wir, wenn q durch die Wurzeln et, aus-
ausgedrückt ist, nach Voraussetzung die Permutation % anwenden
und erhalten also, wenn dadurch q in Qa übergeht, g(Qa) = 0;
d. h. Qa ist auch eine Wurzel der Eesolvente, und die Permutation
% entspricht also einer Substitution (p, Qa) des Körpers &{q),
d. h. % gehört zur Galois'sehen Gruppe.
Daraus schliessen wir noch auf folgenden wichtigen Satz:
d) Ist P eine Gruppe von Permutationen der mWur-
zeln «, der die Eigenschaften a) und b) zukommen,
so ist P die Galois'sche Gruppe der Gleichung
F(x) = 0.
Denn zunächst gehört nach c) jede Permutation von P der
Galois'sehen Gruppe an, und P ist also gewiss ein Theiler von
dieser.
Wenn aber P nur v Permutationen umfasst, so mögen
diese mit
E) »x, 3T2, . . ., Ttv
bezeichnet sein. Wenden wir diese Permutationen auf q an, so
möge sich ergeben:
F) qu p2, . . ., qv.
Wenden wir eine der Permutationen E), etwa itk, auf eine
der Grossen F), etwa auf Qt an, so ist der Erfolg derselbe, als
ob %i%it auf q angewandt worden sei; das Ergebniss dieser Per-
Permutation soll Qi sein. Nun liegt aber in der Voraussetzung, dass
P eine Gruppe sei, dass auch die componirte Permutation jtiJtk
zu P gehört, dass also & unter den Grossen F) enthalten sei.
Zugleich ist g'i nach §. 153, 2. von Q'h verschieden, sobald p» von
Qh verschieden ist. Daraus folgt, dass die Grossen

§. 156. Galois'sche Gruppe. 521
G) q'v 9'2, . . ., q'v
mit den Grossen F), von der Ordnung abgesehen, übereinstimmen.
Das Product
gf(t) = (t — Ql) (t — Q2)...(t- Qt)
bleibt also durch die Permutationen der Gruppe P ungeändert,
und ist folglich, da wir die Eigenschaft b) von P voraussetzen,
eine rationale Function von t in Sl. Zugleich ist g'(t) ein Theiler
von g(t) und muss daher, da g(i) irreducibel ist, mit g{t) über-
übereinstimmen, also ist v nicht kleiner als der Grad der Galois'-
sehen Gruppe und P ist mit der Galois'sehen Gruppe identisch.
Wählen wir, wie oben, die Grosse q als rationale Function
der a so, dass die II(m) durch die Permutationen der u sich
ergebenden Grossen
9, 9', 9" ¦•'
alle von einander verschieden sind, so ist
G(t) = (t-Q) (t-Q') (t-Q")...
eine Function in iß. Nun ist jede von den Grossen q, q', q" . . .
eine primitive Grosse des Normalkörpers N = Sl(<x, mu ..., am_i),
und jede von ihnen ist also die Wurzel einer Galois'sehen
Eesolvente (iten Grades. Je (i von diesen Grossen sind die Wur-
Wurzeln von einer solchen Gleichung. Es muss also G(t), was keine
gleichen Wurzeln hat, in lauter irreducible Factoren (iten Grades
zerfallen, und daraus ergiebt sich noch, dass (i ein Theiler
von II(m) ist. Zugleich ist ft der Grad der Galois'schen
Gruppe von F(x).
Hat der Grad der Galois'schen Eesolvente einer Gleichung
mten Gra(Jes den grössten Werth J7(m), so sagen wir, mit einem
von Kronecker herrührenden Ausdruck, die Gleichung hat
keinen Affe ct. Sie hat einen um so höheren Affect, je niedriger
der Grad (i der Galois'schen Eesolvente ist. Den Quotienten
J7(m):(t, der immer eine ganze Zahl, höchstens gleich n(m)
und mindestens gleich 1 sein muss, wollen wir den Grad des
Affe et es nennen, der also bei einer Gleichung ohne Affect den
Werth 1 hat. Wenn der Affect den möglichst hohen Grad II(m)
hat, dann sind die Wurzeln der Gleichung selbst im Eationalitäts-
bereich Sl enthalten, die Gleichling also gelöst.
Wenn durch Adjunction einer algebraischen Grosse zu £1
die Galois'sche Eesolvente reducibel wird, so entsteht eine neue
Eesolvente niedrigeren Grades, und der Grad des Affects der

522 Dreizehnter Abschnitt. §. 156.
Gleichung F(x) = 0 vergrössert sich. Man nähert sich also
dadurch der Lösung der Gleichung.
Die Galois'sehe Auffassung der Aufgabe, eine Gleichung
F(x) = 0 zu lösen, besteht darin, dass durch auf einander
folgende Adjunction von algebraischen Grossen möglichst einfacher
Art die Gruppe allmählich verkleinert, oder der Affect erhöht
werden soll, bis er seinen höchsten Grad erreicht hat.
Die allgemeine Gleichung mten Grades hat in
dem Körper £1, der aus den rationalen Func-
tionen der Coefficenten al5 a2, . . ., am besteht,
keinen Affect.
Denn die als unabhängige Variable betrachteten Coefficienten
«!, a2, ¦ . ., am können auch dargestellt werden als die symme-
symmetrischen Grundfunctionen der Wurzeln «, a1( a2, . . ., aOT_i. Ist
dann g(t) ein rational durch die a ausgedrückter, irreducibler
Factor von G(t), der für t ¦= q verschwindet, so erhält man,
wenn man a* und q durch die et, darstellt, in g(g) = O eine
identische Gleichung. In dieser können aber die a beliebig per-
mutirt werden, wodurch sich die a nicht ändern, während q in
jede der Wurzeln g, q', q" . . . von G(t) übergehen kann. Es
verschwindet also g (t) für alle Wurzeln von O (t) und muss
folglich mit G(t) übereinstimmen1).
x) fivariste Galois ist im Jahre 1832, kaum 20jährig, im Duell ge-
gefallen. Die erste Andeutung über die Theorie, die heute seinen Namen
trägt, findet sich in einer 1830 im „Bulletin des sciences mathem." von
Ferussac erschienenen Abhandlung „Analyse d'un memoire sur la resolu-
tion algebrique des equations". Ausführlichere Mittheilungen enthält der
berühmte, am Yorabend seines Todes geschriebene Brief an Auguste
Chevalier, der in der „Kevue encyclopedique" vom September 1832
veröffentlicht ist. Erst im Jahre 1846 hat Liouville die sämmtlichen
schon veröffentlichten Arbeiten von Galois nebst einigen Untersuchungen
aus dem Nachlass, darunter die wichtigste: „Mem. sur les conditions de
resolubilite des equations par radicaux" in Bd. XI seines Journals ab-
abdrucken lassen. Eine deutsche Ausgabe von Maser ist 1889 erschienen
(BerlinJ bei Springer). Interessante biographische Mittheilungen finden
sich in der „Revue encyclopedique" vom September 1832, die Liouville
nicht mit abgedruckt hat und die auch in der deutschen Ausgabe fehlen.
Eine ausführliche Biographie von M. P. Dupuy findet sich in den „Annales
de l'ecole normale superieure". Ton weiteren Schriften, die zum Verständ-
niss oder zur Weiterbildung der Galois'schen Theorie beigetragen haben,
seien noch erwähnt: J. A. Serret („Cours d'algebre superieure", II. Aus-
Ausgabe, 1854, IT. 1879); Betti („Annali di scienze fisiche e matematiche")
A853); C. Jordan, „Traite des substitutions" A870). E. Netto, „Sub-
stitutiönentheorie" (Leipzig 1882).

§. 157. Transitive und intransitive Gruppen. 523
§. 157.
Transitive und intransitive Gruppen.
Aus der Galois'sehen Gruppe P können wir ein sehr ein-
einfaches Kennzeichen dafür herleiten, ob die Gleichung F(x) = 0
reducibel oder irreducibel ist.
Nehmen wir an, es sei F (x) vom Grade m reducibel und
f(x) ein Factor von F(x) in £1 vom Grade n, und n sei kleiner
als m. Es mögen die Wurzeln von f(x)
A) es, «j, «a, . . ., «M_i
sein, die übrigen Wurzeln von F(x)
B) On, «n + i, . . ., «m_i.
Ist es' irgend eine der Grossen A), es" eine der Grossen B),
so kann in der Gruppe P keine Permutation vorkommen, durch
die es' in es" übergeführt wird; denn nach Voraussetzung ist
/O') = o,
und wenn nun in P eine Permutation vorkäme, durch die es'
durch es" ersetzt würde, so müsste wegen der Eigenschaft §.156, a)
auch / (es") — 0 sein, was unserer Annahme widerspricht.
Es werden also durch die Permutationen von P die
Wurzeln A) vonf(x) nur unter einander permutirt.
Wenn umgekehrt die Gruppe P die Eigenschaft hat, dass
ihre Permutationen einen Theil der m Wurzeln a wie das System
A) nur unter einander vertauschen, so gestattet das Product
(x — es) (x — esj) . . . (sc — es„_i) =f(x)
alle Permutationen von P, und ist also nach §. 156, b) in £1 ent-
enthalten; d. h. F(x) ist reducibel.
Man nennt eine Permutationsgruppe transitiv, wenn sie
wenigstens eine Permutation enthält, die ein beliebiges Element
in ein beliebiges anderes überführt; im entgegengesetzten Falle,
wenn also die Elemente so in zwei oder mehr Partien zerlegt
werden können, dass durch keine Permutation der Gruppe ein
Element der einen Partie in ein Element der anderen übergeht,
heisst die Gruppe intransitiv. Demnach können wir das Be-
Bewiesene in dem Satze zusammenfassen:
1. Die Gleichung F(x) = 0 ist reducibel oder irre-
irreducibel, je nachdem die Galois'sche Gruppe in-
intransitiv oder transitiv ist.

524 Dreizehnter Abschnitt. §. 158.
Wenn ein Theil der Elemente so zusammenhängt, dass durch
Permutationen aus P jedes Element dieses Theiles in jedes
andere übergehent kann, so nennen wir die Elemente dieses
Theiles transitiv verbunden. Die verschiedenen transitiv ver-
verbundenen Systeme, die durch alle Permutationen von P nur
unter einander permutirt werden, heissen die Systeme der
Intransitivität.
§. 158.
Primitive und imprimitive Gruppen.
Es sei jetzt f(x) = 0 eine irreducible Gleichung nten Grades,
also ihre Galois'sche Gruppe P transitiv. Die "Wurzeln von
f(x) seien
A) «, «i, «2, • • ••> «n-l-
Wenn der Körper £l(a) imprimitiv ist (§. 151), und © = %(«)
ein imprimitives Element, dessen conjugirte Werthe in s Systeme
von je r unter einander gleichen zerfallen, so dass
n = r s
und i1 > 1, s < « ist, so lassen sich die Werthe A) in s Reihen
von je r Elementen zerlegen, die wir mit
A = «,«!,.. ., ar_x
/¦2-\ B = ß, ßl, ¦ ¦ ., ßr-X
bezeichnen wollen, so dass
0 =z(a)
die conjugirten Werthe von 0 sind. Nach §. 151 ist dann
(t —0)(t—01)...(t- e._0 = tp(t)
eine irreducible Function in Si, vom Grade s in Bezug auf t,
deren Wurzeln die Werthe C) sind.
Es ergiebt sich nun aus C), dass die Gruppe P so beschaffen
sein muss, dass alle ihre Permutationen die Elemente der ein-
einzelnen Reihen A, B, . . . S nur unter einander vertauschen und
ausserdem die ganzen Reihen A, B, . . . S mit einander ver-

§. 158. Primitive und imprimitive Gruppen. 525
tauschen, so dass niemals an Stelle von zwei Elementen derselben
Reihe zwei Elemente verschiedener Reihen treten. Denn wenn
etwa durch eine Permutation n von P, « und e^ in ß und ö
übergeführt würden, so würde folgen, da man die Permutation %
[nach a), §. 156] in der Gleichung %(a) = %(a1) ausführen darf,
dass auch % (ß) = % (ö) sein müsste, was der Annahme wider-
widerspricht, dass die Werthe C) von einander verschieden sind.
Permutationsgruppen P, die diese Eigenschaft haben, dass näm-
nämlich die permutirten Elemente sich so in Reihen A, B, ... S
von gleich vielen Elementen zerlegen lassen, dass durch keine
Permutation von P zwei Elemente derselben Reihe in Elemente
verschiedener Reihen übergehen, heissen imprimitiv. Die ein-
einzelnen Reihen A, B . . . S heissen die Systeme der Im-
primitivität. Permutationsgruppen, bei denen eine solche
Zerlegung der Elemente nicht möglich ist, heissen primitive
Gruppen.
Es kann sehr wohl vorkommen, dass eine Gruppe in mehr-
mehrfacher Art imprimitiv ist, dass sie ganz verschiedene Systeme
der Imprimitivität besitzt. So ist z. ß. die Gruppe der cyklischen
Permutationen von sechs Elementen A, 2, 3, 4, 5, 6) in doppelter
Weise imprimitiv und hat die Systeme der Imprimitivität
A = 1, 3, 5, B = 2, 4, 6
und
A = 1, 4, B=2,5, C = 3, 6.
Nachdem also der Begriff der primitiven und imprimitiven
Gruppen festgestellt ist, können wir dem oben Bewiesenen den
Ausdruck geben:
1. Ein imprimitiver Körper hat eine imprimitive
Gruppe.
Es ergiebt sich aus der Imprimitivität der Gruppe für die
imprimitiven Körper ein wichtiges Resultat.
Wir wollen mit
1> (x, «!,..., av-i)
eine rationale symmetrische Function der r Veränderlichen
x, Xi, . . ., äv_i bezeichnen und setzen
ra = ip («, «!, . . ., a,._i)
D) «1 = * 05, ßi, • ¦ ; ßr-l)
ras_i = $ (ö, öj, . . ., 6r-i);

526 Dreizehnter Abschnitt. §. 158.
dann ist zu beweisen, dass ra rational durch & ausgedrückt
werden kann, d. h. im Körper £1 (©) enthalten ist. Es ist
nämlich
eine ganze rationale Function von t, deren Coefficienten rationale
Functionen der «, «!,..., a„—1 sind, die ungeändert bleiben,
wenn irgend eine Permutation der Gruppe P vorgenommen wird,
weil durch diese Permutationen die m entweder ungeändert
bleiben, oder in derselben Weise wie die ® mit einander permu-
tirt werden. Nach §. 156, b) sind diese Coefficienten also in £1
enthalten. Setzen wir dann in E) für das unbestimmte t den
Werth ® ein, so folgt, da cp' (©) von Null verschieden ist,
Wenden wir dies an auf die Coefficienten des Productes
G) (w — «) (w — «,)...(« — a,._i) = <jP (u, ©),
wo u eine Variable bedeutet, so ergiebt sich, dass diese Function
rten Grades, deren Wurzeln die «, «j, . . ., «r_! sind, rational
durch ® ausgedrückt werden kann.
Es ist also die Grosse a, die ursprünglich Wurzel einer
Gleichung wteI1 Grades in £1 ist, zugleich Wurzel einer Gleichung
rten (Grades, deren Coefficienten rational von der Wurzel einer
Gleichung sten Grades abhängen. Eine Gleichung f(x) — 0, deren
Wurzel a diese Eigenschaft hat, nennt man eine imprimitive
Gleichung.
Wir können das Bewiesene auch so ausdrücken:
2. Der imprimitive Körper £1(k) vom nten Grade geht
durch Adjunction des Körpers sten Grades £1'
= £l{®) zu £1 in einen Körper £1'(a) vom rten Grade
über.
Wir wollen noch untersuchen, ob die Imprimitivität der
Gruppe ein ausreichendes Kennzeichen für die Imprimitivität des
Körpers ist, ob man also in einem Körper £l{a) mit imprimitiver
Gruppe immer imprimitive Elemente finden kann.
Sei also jetzt f (x) = 0 eine irreducible Gleichung wten
Grades mit imprimitiver Gruppe, und seien A) die Wurzeln
dieser Gleichung, die so in die Reihen B) zerlegt sind, dass die

§. 158. Imprimitive Körper. 527
Elemente dieser Reihen durch die Permutationen der Gruppe
nicht von einander getrennt werden.
Wir wählen irgend eine symmetrische Function ty (x, a^,..., «V-i)
so, dass die Werthe
y =ip(a, «j, . . ., «r_i)
(g) Vx = * (/5, ßl, • • -, ßr-l)
ya-! = ^ (Ö, <*!, . . ., Ör-1)
alle von einander verschieden sind.
Um die Möglichkeit hiervon einzusehen, können wir z. B.
4, («, 29 = (* -/*)(*-
setzen, und dann lässt sich (nach §. 43, 1.) für t ein solcher
rationaler Werth finden, dass diese Grossen alle von einander
verschieden ausfallen. Diese Werthe können also für die y in (8)
genommen werden.
Wenn wir nun unter u eine unabhängige Variable ver-
verstehen und
A0) 9»(«) = (« —y) (« — Vi)" • («—y.-i)
setzen, so ist g> (m), da seine Coefficienten durch die Permutationen
der Gruppe ungeändert bleiben, eine Function in iß, deren Wur-
Wurzeln die Grossen y sind. Sie ist überdies irreducibel, denn
aus der vorausgesetzten Transitivität der Gruppe folgt, dass,
wenn eine rationale Function von y für einen der Werthe (8)
verschwindet, sie auch für alle anderen verschwinden muss.
Ist m irgend eine symmetrische Function der «,«!,..., «,._i,
so schliessen wir aus der Betrachtung des Ausdruckes
der eine ganze rationale Function von m in ß ist, ganz wie oben,
indem wir u = y setzen, dass m rational durch y dargestellt
werden kann, und demnach kann auch die Function
A1) Tp(t,Ä) = ip(t,y),
deren Wurzeln die Grossen «, «x, ,..,«,._! sind, rational durch
y ausgedrückt werden.
Auch die Gleichung ip (t, Ä) = 0 ist irrreducibel in

528 Dreizehnter Abschnitt. §. 158.
dem Körper &(y); denn ist il>l (t,y) ein rationaler Theiler von
ip (t, y), und ist
i>i («, y) = 0,
so können wir wegen der Transitivität der Gruppe auf diese
Gleichung eine Permutation anwenden, durch die « in eine
beliebige Grosse der Reihe A übergeht, wodurch y ungeändert
bleibt; es ist also jede Wurzel von ty (t,y) zugleich Wurzel von
rpi (t, y) und also sind beide Functionen identisch.
Es ist also die Gleichung nten Grades / (x) = 0 imprimitiv
in dem oben festgesetzten Sinne, d. h. eine Wurzel a dieser
Gleichung kann betrachtet werden als Wurzel einer Gleichung
rten Grades, deren Coefficienten von der Wurzel y einer Glei-
Gleichung sten Grades abhängen.
Um zu beweisen, dass dann auch der Körper £1 («) (in dem
Sinne des §. 151) imprimitiv ist, haben wir noch nachzuweisen,
dass es in Sl («) Grossen giebt, die einer irreducibeln Gleichung
sten Grades genügen.
Wir werden nachweisen, dass y selbst eine solche Grosse
ist, dass also y rational durch a allein darstellbar ist.
Dies ist aber sehr einfach zu schliessen. Nach A1) ist
A2) i, («, y) = 0,
während ^(a,2/i), ..., ^(a,i/s_i) von Null verschieden sind. Denn
wäre etwa tp (a, yi) = 0, so wäre a eine Wurzel der Gleichung
y*™ Grades i\> (t, y^) = 0, deren Wurzeln ja die von « verschie-
verschiedenen Grossen ß, ßu . . ., ßr-\ sind. Es haben also die beiden
Gleichungen
A3) ip («, w) — 0, <p (u) = 0
eine und nur eine gemeinsame Wurzel u = y. Der grösste
gemeinschaftliche Theiler dieser beiden Functionen ist daher in
Bezug auf u linear, und er giebt y rational durch die Coeffi-
Coefficienten von cp(u) und i\>(a,u), also rational durch «. Damit
ist die Umkehrung von 1. bewiesen:
3. Ein primitiver Körper hat eine primitive
Gruppe.

Vierzehnter Abschnitt.
Anwendung der Permutationsgruppen auf
Gleichungen.
§. 159.
Wirkung der Permutationsgruppen auf Functionen von
unabhängigen Veränderlichen.
Für ein tieferes Eindringen in die Algebra ist nach den
Ergebnissen des vorigen Abschnittes ein genaueres Studium der
Permutationsgruppen erforderlich. "Wir stellen zunächst einige
allgemeine Sätze darüber auf, die für das Folgende die Grund-
Grundlage bilden!).
Es sei
A) «i, u2, . . ., um
ein System von einander unabhängiger Zeichen (Veränderliche) und
B) ip («i, w2, . . ., um)
eine ganze rationale Function von ihnen mit Coefficienten aus
einem beliebigen Körper.
Als gleich sind zwei solche Functionen ip nur dann zu
betrachten, wenn in den nach Potenzen und Producten der u
geordneten Ausdrücken entsprechende Glieder die gleichen Coeffi-
Coefficienten haben.
*) Für die Theorie der Permutationen sind besonders hervorzuheben:
Cauchy, „Journal de l'Ecole polytechn. X. cah. A815)" (mehrere Abhand-
Abhandlungen). C. Jordan, „Traite des substitutions et des equations alge-
briques", Paris 1870. Netto, „Substitutionentheorie und ihre Anwendung
auf die Algebra." Leipzig 1882.
Weber, Algebra. I. 34

530 Vierzehnter Abschnitt. §. 159.
Wenn wir die Indices der Variablen w, oder was damit
gleichbedeutend ist, die u selbst einer Permutation % unterwerfen,
so kann die Function tp sich ändern oder sie kann ungeändert
bleiben. Bleibt sie ungeändert, so sagen wir, sie gestatte die
Permutation %. Gestattet sie alle II(m) überhaupt möglichen
Permutationen, so ist sie symmetrisch und kann durch die sym-
symmetrischen Grundfunctionen ausgedrückt werden (§. 48). Der
andere extreme Fall ist der, dass die Function für alle TL(m)
Anordnungen lauter verschiedene Werthe annimmt. Im All-
Allgemeinen werden gewisse Permutationen die Function ip unge-
ungeändert lassen, andere werden sie ändern. Wir stellen nun den
Satz auf:
1. Der Inbegriff aller der Permutationen der
uu wä,..., Mm, die eine ganze Function ^(u^ %>••¦, ««)
ungeändert lassen, ist eine Gruppe von Per-
Permutationen.
Um ihn zu beweisen, nehmen wir an, es sei % eine der Per-
Permutationen, die tp ungeändert lässt, was wir durch
i> = 4>7t
ausdrücken. Da nun die u unabhängige Variable sind, so muss
diese identische Gleichung richtig bleiben, wenn die Variablen
irgend einer Permutation %' unterworfen werden. Wenn aber %'
auf ip„ angewandt wird, so ist das Ergebniss dasselbe, als wenn
die zusammengesetzte Permutation %%' auf ip angewandt wird.
Es folgt also:
und wenn nun
ip = ip„,
ist, so folgt:
d. h. wenn die Function ip durch die Permutationen % und %'
ungeändert bleibt, so bleibt sie auch durch %%' ungeändert,
wodurch nach der Definition der Gruppe der Satz, den wir aus-
ausgesprochen haben, bewiesen ist.
Wir haben darin ein Mittel, um Permutationsgruppen zu
bilden, indem wir irgend eine Function von m Variablen nehmen,
und alle Permutationen aufsuchen, die eine solche Function un-
ungeändert lassen. Dass man auf diese Weise alle Permutations-
Permutationsgruppen bilden kann, wird sich nachher ergeben.

§. 159. Permutationen. 531
2. Ist
P = n, 7t', 7t", id", . . .
eine Gruppe von Permutationen von m Ele-
Elementen und % eine beliebige unter ihnen, so
stimmt das System
Pj = »»!, 7t'it^ «"ätj, mf'iCi, . . .,
von der Reihenfolge abgesehen, vollständig mit
P überein.
Denn die in Px enthaltenen Permutationen, deren Anzahl
ebenso gross ist, wie die der Permutationen P, sind wegen der
Gruppeneigenschaft von P (§. 155, 3.) jedenfalls alle unter den
Permutationen von P enthalten. Ausserdem sind die Permu-
Permutationen von P1 (nach §. 155, 2.) alle von einander verschieden,
und also ist P mit Pj, von der Reihenfolge abgesehen, identisch.
Ebenso kann man auch zeigen, dass
P. =^= Jl± 7t, Tt-^ 7t , Tt-y 7t , Tty 7t , . . .
mit P identisch ist.
Hieraus ergeben sich die folgenden Sätze:
3. Jede Permutationsgruppe enthält die identische
Permutation.
Denn unter den Permutationen von P, müss auch % selbst
vorkommen und wenn 7t0 nx = 7t1 ist, so ist (nach §. 155, 2.) jr0
die identische Permutation.
4. Eine Permutationsgruppe P enthält zu jeder
Permutation auch die entgegengesetzte.
Denn in Pj muss nach 3. die identische Permutation vor-
vorkommen. Ist aber »% die identische Permutation, so ist
3t = 7t~^. Hierin kann % jede Permutation aus P sein.
"Wenn an Stelle der Variablen «j, w2, . . ., um bestimmte
Grossen e^, «j, . . ., am, seien es Zahlenwerthe oder Grossen
irgend eines Körpers, gesetzt werden, so verliert der Satz 1.
seine allgemeine Gültigkeit. Nehmen wir z. B. m = 3 und
setzen zwischen den drei Grossen ax, w2 > «s die Relation 2 a3
= «: -|- «2 fest, indem wir sie sonst nicht weiter beschränken,
so bleibt die Function «2 — «3 umgeändert nur durch die iden-
identische Permutation und durch die Permutation
i, 2, 3\
l, 3, 1/
34*

532 Vierzehnter Abschnitt. §. 159.
Diese beiden Permutationen aber bilden keine Gruppe, weil
die "Wiederholung der letzteren
/l, 2, 3\
\3, 1, V
nicht darunter vorkommt.
Für diese Functionen gilt nun der folgende Satz:
5. Ist P eine Permutationsgruppe von m Ziffern,
und sind alt «2, . . ., «m beliebige von einander
verschiedene Grossen, so giebt es rationale Func-
Functionen der «, sogar mit rationalen Coefficienten,
die sich nicht ändern, wenn auf die Indices von
a eine Permutation der Gruppe P angewandt
wird, und die sich ändern, wenn eine nicht zu P
gehörige Permutation angewandt wird.
Um ihn zu beweisen, nehmen wir eine Function
Q = 0(Ul, «2, . . ., Um),
wie wir sie schon im §. 156 betrachtet haben, die II (m) ver-
verschiedene Werthe erhält, wenn die a auf alle mögliche Arten
vertauscht werden.
Bezeichnen wir die Werthe, die q durch Anwendung der
Permutationen einer Gruppe erhält, mit
A) Q, ,pi, • ..., Qii-i,
so werden nach dem Satze 2. diese Grossen nur unter einander
vertauscht, wenn auf alle zugleich eine Permutation % aus der
Gruppe P ausgeübt wird. Denn die Anwendung der Permutation
%x auf die sämmtlichen Functionen A) hat denselben Erfolg, wie
die Anwendung der in Pt enthaltenen Permutationen auf q.
Nach 2. ist aber Py mit. P, von der Reihenfolge abgesehen,
identisch.
Bedeutet also t eine Variable, so bleibt die Function
B) i, = (t - q) (t - 9l) . . . (* - Pm_0
ungeändert, wenn irgend eine Permutation aus P angewandt
wird. Wenn nun durch eine nicht in P enthaltene Permutation
die Grossen A) in
C) p', q'v ¦ ¦ ., Q'p-i
übergehen, so kommt wenigstens q' sicher nicht unter den
Grossen A) vor, und folglich ist

§. 160. Transpositionen und Cyklen. 533
mit ip nicht identisch. Man kann daher dem t einen solchen
rationalen Werth geben, dass tp von allen nach Art von ip^ ge-
gebildeten Functionen verschieden ist.
Selbstverständlich gelten diese Betrachtungen auch, wenn an
Stelle der cc unabhängige Variable treten.
Eine Function, die alle Permutionen einer Gruppe P ge-
gestattet, während sie sich bei allen nicht zu P gehörigen Permu-
Permutationen ändert, heisst eine zur Gruppe P gehörige Function.
Zu der Gruppe Po, die alle Permutationen von m Ziffern
umfasst, gehören die symmetrischen Functionen. Man nennt
diese Gruppe daher auch die symmetrische Gruppe.
Eine Function q, die zu der aus der einzigen identischen
Permutation bestehenden Gruppe gehört, kann zu einer ein-
eindeutigen Bezeichnungsweise der Permutationen dienen; denn es
giebt nur eine Permutation je', durch die q in p' übergeht. Wir
können also für diese Permutation das Symbol
* = (9, Q')
benutzen, so dass durch
0, q), 0, q'), 0, q") . . .
alle Permutationen der m Ziffern eindeutig bezeichnet sind.
§. 160.
Zerlegung von Permutationen in Transpositionen
und in Cyklen.
Wir haben schon im zweiten Abschnitt bei Gelegenheit der
Determinanten die Zusammensetzung beliebiger Permutationen
aus einer Reihe von Transpositionen, d. h. Vertauschung nur
zweier Ziffern, erwähnt. Solche Transpositionen bezeichnen wir
durch Nebeneinanderstellen der betreffenden Ziffern, z. B. durch
A, 2) die Vertauschung der Ziffern 1 und 2.
Eine Transposition, zweimal wiederholt, führt zur Identität,
so dass jede Transposition sich selbst entgegengesetzt ist. Ist nun
a = /l, 2, ...,m\
\au a3, . . ., amj
eine beliebige Permutation von m Ziffern, so ist
x(m, am) = äj

534 Vierzehnter Abschnitt. §. 160.
eine Permutation, die m — 1 ungeändert lässt, die also durch
/l, 2, . . ., m - 1\
VA, &2, • • •, 6m-l /
dargestellt werden kann und also eine Permutation von höchstens
m — 1 Ziffern ist. Da nun auch
% = %x (m, am)
ist, so folgt hieraus durch vollständige Induction
1. dass man jede Permutation (und zwar auf un-
unendlich viele verschiedene Arten) in Transposi-
Transpositionen zerlegen kann.
Und daraus folgt weiter:
2. Wenn eine Permutationsgruppe von m Ziffern
alle Transpositionen mit einer festen Ziffer, z.B.:
A, 2), A, 3), . . ., A, m)
enthält, so ist sie mit der symmetrischen Gruppe
identisch.
Denn eine solche Gruppe enthält, wie man aus der Zu-
Zusammensetzung
B, 3) = A, 2) A, 3) A, 2)
erkennt, auch alle anderen Transpositionen, und nach 1. lassen
sich daraus alle Permutationen der symmetrischen Gruppe zu-
zusammensetzen.
Eine Permutation % heisst cyklisch, wenn sich die Ziffern
so in eine Reihe ordnen lassen, dass durch n jede Ziffer in die
folgende und die letzte wieder in die erste übergeht, also z. B.
/l, 2, . . ., m — 1, m\
\2, 3, . . ., m1 r
solche cyklische Permutationen bezeichnet man einfacher, indem
man die Ziffern des Cyklus neben einander setzt, durch
A, 2, 3, .. ., m).
Dabei ist es gleichgültig, mit welcher Ziffer man anfängt;
man könnte also auch
B, 3, . . ., m, 1)
dafür setzen. Es gilt nun der folgende Satz:
3. Jede Permutation % lässt sich, und zwar nur
auf eine Weise, in eine Reihe von cyklischen
Permutationen zerlegen, so dass keine zwei
dieser Cyklen eine Ziffer gemeinschaftlich haben.

§. 160. Transpositionen und Cyklen. 535
Ist nämlich
A) »
so fange man mit einer beliebigen Ziffer, etwa mit 1 au, und
setze die Reihe
B) 1, «! = 5, «j = c . . .
so lange fort, bis man auf eine Ziffer zum zweiten Male stösst.
Die zuerst wiederkehrende Ziffer muss 1 sein, da zu jeder Ziffer
die in der Reihe B) vorangehende durch A) eindeutig bestimmt
ist. Dann bilden die Ziffern
C) A, 6, c . . .)
einen ersten Cyklus. Sind dadurch noch nicht alle m Ziffern
von A) erschöpft, so greift man aus den übrigen eine heraus
und verfährt ebenso, bis alle m Ziffern von A) in den Cyklen
untergebracht sind. Da in jedem solchen Cyklus zu jeder Ziffer,
die vorangehende sowohl als die nachfolgende, durch A) völlig
bestimmt ist, so sind auch die Cyklen selbst eindeutig bestimmt.
Bei der Bezeichnung von % durch die Cyklen können aber nicht
nur die verschiedenen Cyklen beliebig angeordnet, sondern man
kann auch in jedem Cyklus mit einer beliebigen seiner Ziffern
anfangen. Eine Ziffer, die nicht geändert wird, bildet für sich
einen eingliedrigen Cyklus.
Wir wählen ein ganz beliebiges Beispiel, wodurch das Ver-
Verfahren sofort klar wird:
l, 2, 3, 4, 5, 6, 7, 8\
) = <*' 3'
5' 7' 6) ^' 2)
4' 5) A' 2' 3'
6, 7, 8\
6, 7, 1, 4, 5, 8, 2) = <*' 3' 7' 8' 2' 6' 5'
/l, 2, 3, 4, 5, 6, 7, 8\
U 1, 3, 5, 7, 8, 6, i) - <8
l, 2, 3, 4, 5, 6, 7, 8\ ,
b 3, 6, 5, 8, 1, 4, ?J = (8
Das Nebeneinandersetzen der Cyklen ist mit einer Compo-
sition in dem bisherigen Sinne gleichbedeutend, nur ist zu be-
bemerken, dass Permutationen, die gar keine gemeinschaftliche
Ziffer enthalten, bei der Composition immer vertauscht werden
können.
Eingliedrige Cyklen, die nichts ändern, werden in der Be-
Bezeichnung auch oft weggelassen.

536 Vierzehnter Abschnitt. §. 160.
Da im Allgemeinen, wenn % und % irgend zwei Permutationen
von m Ziffern sind, % % von % % verschieden ist, so ist auch
von % verschieden. Ist % in seine Cyklen zerlegt, so kann man
%' nach dem folgenden Satze sehr einfach aus x ableiten.
4. Man erhält die Permutation %~x%% dadurch,
dass man in den Cyklen von % die Permutation
% ausführt.
Um diese Regel zu beweisen, sei, in Cyklen zerlegt
x = («, ß, y . . .) («', ß\ y' ...)...
und es sei
% _ /«, ß, r,
V
y„,. . ., cc'„, ß'„, y'„, . . J
Durch 7t—1 geht cc„ in cc über, durch x geht cc in ß über
und durch % wird ß in ß„ übergeführt. Durch ai-'xjs geht also
Kn in CÄ über. Da dieselbe Betrachtung auf ß„, ya,.. . . u. s. f.
anwendbar ist, so folgt:
n~lxn = (a„, ß„, ym . . .) (u'a, ß'„, y'„, ...).. .,
und dies ist der Inhalt des Satzes 4.
Aus der gleichzeitigen Betrachtung der Zerlegung der Per-
Permutationen in Cyklen und in Transpositionen ergiebt sich ein
Beweis für die Eintheilung der Permutationen in zwei Classen,
die wir schon im zweiten Abschnitt bei den Determinanten
kennen gelernt haben.
Bedeutet t eine Transposition und % eine beliebige Permu-
Permutation , so ist in der zusammengesetzten Permutation t % die
Anzahl der Cyklen um eins grösser oder um eins kleiner als in
%. Die beiden Ziffern, die durch tr mit einander vertauscht
werden, können entweder in demselben Cyklus von % vorkommen
oder in zwei verschiedenen Cyklen. Nehmen wir an, es sei ein
in % vorkommender Cyklus y = A, 2, .. . a, a ~\- 1 . . . b) und
es enthalte t zwei Ziffern, die in y vorkommen, etwa t = A, a),
dann ist
¦*y = (l, a+1, ...5) B, 3, . . . a),
d. h. y wird durch Zusammensetzung mit t in zwei Cyklen
zerlegt, während die übrigen Cyklen durch t nicht berührt
werden.

§. 160. Permutationen erster und zweiter Art. 537
Wenn aber die beiden Ziffern von t in zwei verschiedenen
Cyklen von % vorkommen, so mögen diese beiden Cyklen
y = A, 2, 3 . . . a), y' = A', 2', 3' ... a>)
sein und t = A, 1'). Es ist dann
*y/ = (l, 2', 3'...o',l',2, d...a),
d. h. die beiden Cyklen y, y' werden durch r zu einem einzigen
Cyklus vereinigt, während wieder die übrigen Gyklen ungeändert
bleiben.
Wenn wir also eine Permutation % von m Ziffern, die aus
v Cyklen besteht (wobei die eingliedrigen Cyklen mitgezählt
werden), durch ft Transpositionen dargestellt haben, so kann
sie durch Zusammensetzung mit diesen ft Transpositionen in
umgekehrter Reihenfolge in die identische Perinutation verwandelt
werden, die aus m eingliedrigen Cyklen besteht. Es sind daher
im Ganzen m — v Cyklen gewonnen, und da jeder Transposition
ein gewonnener oder ein verlorener Cyklus entspricht, so muss
ft = m — v (mod. 2) sein, d. h. (i ist eine gerade oder eine
ungerade Zahl, je nachdem m — v gerade oder ungerade ist.
Die letzte Zahl ist aber nur von der Permutation %, nicht von
der Art der Zerlegung in Transpositionen abhängig. Wir haben
damit den Satz:
5. Die Permutationen von m Ziffern zerfallen in
zwei Arten, von denen die erste in eine gerade,
die zweite in eine ungerade Anzahl von Trans-
Transpositionen zerlegbar ist.
Jede dieser beiden Arten umfasst gleich viel Permutationen,
nämlich \ II (m); denn durch Hinzufügung einer festen Transposi-
Transposition geht jede Permutation der ersten Art in eine der zweiten
Art über und umgekehrt.
Die Zusammensetzung zweier Permutationen von gleicher
Art giebt stets eine Permutation der ersten Art, während eine
Permutation erster und zweiter Art, zusammengesetzt, eine Permu-
Permutation zweiter Art ergeben, wie aus der Zerlegung in Transposi-
Transpositionen sofort zu ersehen ist. Daraus folgt:
6. Die Permutationen der ersten Art bilden eine
Gruppe.
Nennen wir eine Function von m Veränderlichen %, u2, ¦ ¦ .,um
oder auch von m von einander verschiedenen Grossen uL, «2, • •., «m,

538 Vierzehnter Abschnitt. §. 160.
die ihr Zeichen ändert, wenn zwei der Variablen mit einander
vertauscht werden, wie z. B. das Product aller Differenzen:
(% — u2) (% — %) . . . (Ui — um)
(u2 — u%) . . . (u2 — um)
eine alternirende Function, so wird durch die Permu-
Permutationen der ersten Art eine solche Function nicht verändert,
während sie durch eine Permutation der zweiten Art geändert,
nämlich in den entgegengesetzten Werth verwandelt wird. Die
alternirenden Functionen gehören also zu der Gruppe der
Permutationen der ersten Art.
Wie wir früher die Gruppe, zu der die symmetrischen Func-
Functionen gehören, symmetrische Gruppe genannt haben, so nennen
wir die Gruppe der Permutationen der ersten Art, zu der die
alternirenden Functionen gehören, alternirende Gruppe.
Die Gruppe, die aus der einzigen identischen Permutation be-
besteht, nennen wir die identische Gruppe oder auch die
Einheitsgruppe.
Eine cyklische Permutation von n Gliedern lässt sich in
n — 1 Transpositionen zerlegen, wie man aus der Zusammen-
Zusammensetzung
A, 2, 3 ... n) = A, 2) A, 3) ... A, n)
erkennt, und daraus folgt, dass eine cyklische Permutation zur
ersten oder zur zweiten Art gehört, je nachdem die Anzahl der
Ziffern eine ungerade oder eine gerade ist.
Wie man jede Permutation aus Transpositionen zusammen-
zusammensetzen kann, ebenso kann man jede Permutation der ersten Art
aus dreigliedrigen Cyklen zusammensetzen. Es genügt, wenn
dies für jedes Paar von Transpositionen bewiesen ist, da jede
Permutation der ersten Art sich aus solchen Paaren componiren
lässt. Es ist aber
A, 2) A, 3) = A, 2, 3)
A, 4) B, 3) = A, 2, 3) A, 2, 4),
woraus die Richtigkeit der Behauptung zu ersehen ist, da die
beiden Transpositionen eines Paares entweder eine oder keine
Ziffer gemein haben. Also:
7. Alle Permutationen der ersten Art lassen sich
(auf unendlich viele Weisen) in cyklische Per-
Permutationen von drei Elementen zerlegen.

§. 160. Alternirende Gruppe. 539
Aus 7. folgt weiter
8. Eine Permutationsgruppe von m Ziffern, die
alle dreigliedrigen cyklischen Permutationen
mit zwei festen Ziffern enthält, muss die ganze
alternirende Gruppe enthalten.
Denn aus den Cyklen A, 2, 3), A, 2, 4), . . ., A, 2, m) lassen
sich alle dreigliedrigen Cyklen und also nach 7. alle Permu-
tationen der ersten Art componiren, wie man aus den Zusammen-
Zusammensetzungen
B, 1, 3) = A, 2, 3) A, 2, 3),
A, 3, 4) = A, 2, 3) B, 1, 4) B, 1, 3),
B, 4, 5) = B, 1, 4) A, 2, 5) A, 2, 4)
C, 4, 5) = B, 1, 3) C, 4, 5) A, 2, 3)
ersieht.
9. Ist m grösser als 4, so ist eine Permutations-
Permutationsgruppe von m Ziffern, die alle aus je zwei
Transpositionen ohne gemeinsame Ziffer zu-
zusammengesetzten Permutationen A,2) C,4) ent-
enthält, durch die alternirende Gruppe theilbar.
Denn es ist
A, 2, 3) = A, 2) D, 5) D, 5) A, 3)
und man kann also, wenn ausser den vier Ziffern 1, 2, 3, 4 noch
eine fünfte, 5, vorhanden ist, alle dreigliedrigen Cyklen aus Trans-
Transpositionspaaren von der Form A, 2) D, 5) zusammensetzen.
Ist dagegen m = 4, so bilden die vier Permutationen
1; A,2) C, 4); A, 3) B, 4); A, 4) B, 3)
eine Gruppe, die kleiner ist als die alternirende Gruppe, in der
ausserdem noch die acht dreigliedrigen Cyklen vorkommen.
Hieran schliessen wir die Beweise von zwei weiteren wich-
wichtigen Sätzen, die sich auf transitive Permutationsgruppen be-
beziehen :
10. Wenn eine transitive Permutationsgruppe von
m Ziffern eine einzelne Transposition enthält,
so ist sie entweder die symmetrische Gruppe
oder sie ist imprimitiv.
Die vorgelegte Gruppe sei P, die m Ziffern, die durch sie
permutirt werden, 1, 2, . . ., m, und es komme darin die Trans-
Transposition A, 2) vor. Sie möge überhaupt die Transpositionen

540 Vierzehnter Abschnitt. §. 160.
A, 2), A, 3), A, 4), . . ., A, (t),
aber keine andere Transposition mit der Ziffer 1 enthalten. Ist
nun (t = m, so ist P nach 2. die symmetrische Grnppe. Ist
aber (t < m, so enthält P nach demselben Satze alle Permu-
Permutationen der Ziffern
M= 1, 2, . .., (t.
Daraus folgt, dass P keine Transposition von einer der Ziffern
1, 2, 3, . . ., (t mit einer anderen Ziffer, etwa mit f* —[— 1, enthalten
kann. Denn wenn B. ft + 1) in P vorkommt, so kommt auch
(l,(t + l) = A,2) A,A+1) A,2) darin vor, gegen die Voraus-
Voraussetzung.
Wenn nun P transitiv ist, so giebt es darin eine Permu-
Permutation jz, durch die die Ziffer 1 in eine nicht in dem System M
enthaltene Ziffer, etwa in (t + 1, übergeht, und dann kann durch
% keine der Ziffern von M in eine Ziffer von M übergehen; denn
wenn z. B. 2 in r übergeht, so ist
*-i(l, 2)* = Q* + l,r)
und ((t + 1, r) kann, wenn r zu M gehört, wie wir gesehen haben,
nicht in P vorkommen. Durch jede Permutation von P werden
also die Ziffern des Systems M entweder nur unter sich ver-
vertauscht, oder sie werden in die Ziffern eines ganz davon ver-
verschiedenen Systems M' übergeführt, und in P kommen auch alle
Permutationen der Ziffern M' vor.
Wenn mit M und M' noch nicht alle Ziffern erschöpft sind,
so giebt es eine Permutation in P, durch die M in ein drittes
System M" übergeführt wird, was wieder mit M und mit M'
keine Ziffer gemein haben kann.
Denn sind k, ß zwei Elemente von M (die auch identisch
sein könnten), die durch % und %' in dasselbe sowohl in W als
in M" enthaltene Element y übergehen, so wird ß durch die
Permutation 3Z0 = n'x—1 in cc übergehen. Folglich kann jt0 die
Ziffern von M nur unter sich permutiren, und da %' = jcojc ist,
so ist M' mit M" identisch.
Es zerfällt also die Gesammtheit der Ziffern 1, 2, . . ., in in
Systeme M, M\ M" . . . von je (t Ziffern, die durch P impri-
imprimitiv permutirt werden, d. h. die Gruppe P ist imprimitiv.
Wenn m eine Primzahl ist, so giebt es keine imprimitiven
Permutationsgruppen; also ist in diesem Falle eine transitive
Gruppe, die eine Transposition enthält, nur die symmetrische
Gruppe.

§. 160. Permutationsgruppen. 541
Ganz auf dieselbe Weise schliessen wir aus dem Satze 8:
11. Wenn eine transitive Permutationsgruppe von
m Ziffern einen dreigliedrigen Cyklus enthält,
so enthält sie die ganze alternirende Gruppe,
oder sie ist imprimitiv.
Denn enthält die Gruppe P die dreigliedrigen Cyklen
A, 2, 3), A, 2, 4), ... A, 2, p),
aber keinen anderen mit den Ziffern 1, 2, so enthält sie nach 8.
die ganze alternirende Gruppe der Ziffern M = 1, 2, 3, .. ., m.
Ist nun ft < m, so kann in P kein dreigliedriger Cyklus vor-
vorkommen, der eine oder zwei der Ziffern von M mit anderen Ziffern
verbindet. Denn enthält P eine Permutation A, r, s) von der
Art, dass von den Ziffern r, s wenigstens eine nicht in M vor-
vorkommt, so wähle man k, ß aus M so, dass keines von ihnen mit
1, r, s übereinstimmt, und man findet dann aus der Zusammen-
Zusammensetzung (nach 4.)
A, ß, «) A, r, s) A, «, ß) = («, r, s),
dass alle («, r, s), und mithin nach 7. die ganze alternirende
Gruppe der Ziffern
1, 2, 3, . . .,>, r,s
in P enthalten ist, was der Voraussetzung widerspricht. Es zer-
zerfallen also die m Ziffern von P, wie vorhin, in mehrere Systeme
M, M', M" . . . der Imprimitivität. Wir können noch hinzufügen,
12. dass, wenn der Fall der Imprimitivität ein-
eintritt, die GruppeP im Falle 10. die ganze sym-
symmetrische Gruppe, im Falle 11. die ganz^e alter-
alternirende Gruppe für jedes einzelne System der
Imprimitivität enthält.
Die wiederholte Zusammensetzung einer und derselben Per-
Permutation mit sich selbst bezeichnet man wie Potenzen. Wenn
also % irgend eine Permutation ist, so muss unter den auf ein-
einander folgenden Potenzen
3Z°, 3Z1, 3t2, 3Z3, . . .,
worin %" = 1 die identische Permutation bedeutet, nothwendig
dieselbe Permutation wiederkehren. Aus %p = itß+e folgt aber
%" = 1. Ist e der kleinste positive Exponent, für den %e = 1
wird, so sind die Permutationen
D) 1, st, %\ . .,, »•-*

542 Vierzehnter Abschnitt. §. 161.
alle von einander verschieden, während sie sich bei der Fort-
Fortsetzung ne, ne + 1,..., 7tie-\ ... in derselben Reihenfolge periodisch
wiederholen. Die Reihe D) heisst die Periode der Permu-
Permutation nt, und e wird der Grad von % genannt. Die Periode
von % bildet eine Gruppe, da durch Zusammensetzung zweier
ihrer Elemente ein Element derselben Periode entsteht.
Ist % eine cyklische Permutation
* = A, 2, 3, . . ., n),
so ist bei geradem n
x* == A, 3, . . ., n — 1) B, 4, . . ., n),
und bei ungeradem n
%* = A, 3, .... w, 2, 4, . . ., n — 1),
und der Grad von n ist in beiden Fällen gleich n.
Ist n in mehrere Cyklen zerlegt, so ist der Grad von %
gleich dem kleinsten gemeinschaftlichen Vielfachen der Glieder-
Gliederzahl der einzelnen Cyklen, z. B.
% = A, 2) C, 4, 5), *« = A) B) C, 5, 4), "»» = A, 2) C) D) E),
fr = A) B) C, 4, 5), »* = A,^2) C,]5, 4), »« = 1.
Wenn w in irgend einer Permutationsgruppe P vorkommt,
so enthält P die ganze Periode von %.
§¦ 161.
Divisoren der Gruppen. Nebengruppen und
conjugirte Gruppen.
Wir haben im §. 159 gesehen, dass eine Function von m
unabhängigen Veränderlichen immer eine Permutationsgruppe
von m Ziffern bestimmt, dass aber dies nicht immer zutrifft,
wenn an Stelle der unabhängigen Veränderlichen bestimmte
Grossen gesetzt werden. Durch die Galois'sche Theorie wird
aber dieser Unterschied ausgeglichen, oder wenigstens auf seinen
Kern zurückgeführt. Es sei jetzt F(x) = 0 irgend eine Glei-
Gleichung jwten Grades in einem gegebenen Körper £1 mit den von
einander verschiedenen Wurzeln «j, «2, . . ., am.
Den Normalkörper
Si, (Q) = Si, (¦«!, «2, . . ., Um)
wollen wir mit N bezeichnen.

§. 161. Nebengruppen. 543
Unter der Galois'schen Gruppe P des Körpers N oder der
Gleichung F(x) = 0 können wir (nach §. 156) entweder die
Gruppe der Substitutionen des Körpers N oder auch die damit
isomorphe Permutationsgruppe der Indices der et verstehen.
Es sei p der Grad von P und wir wollen die Operationen
von P (seien es nun Substitutionen von N oder Permutationen
der et) mit
A) P = ff, ff[, ffa, . . ., ffp_!
bezeichnen. Wenn das System Q der in P enthaltenen Permutationen
B) X, *1, X.2, • . ., 3C«_l
für sich eine Gruppe ausmacht, wenn also je zwei der Elemente
von Q, mit einander componirt, wieder ein Element aus Q er-
ergeben, so heisst die Gruppe Q ein Theiler oder Divisor von P1).
Wir leiten zunächst einen wichtigen allgemeinen Satz über
die Theiler einer Gruppe her.
Wenn der Grad q des Theilers kleiner ist als der Grad p
von P, so nehmen wir ein nicht in Q enthaltenes Element %x
in P und bilden das System
C) Qxx = x%x, xxxx, . . ., 3cä_iffj,
das wir als symbolisches Product Q%x darstellen. Die Elemente
von C) sind sowohl unter einander als von den Elementen von
Q verschieden, denn aus xx ffi = x3 %x würde xx = xa, und aus
% = %x %j würde % = x-~x % folgen, was nicht möglich ist, wenn
ff: nicht zu Q gehört. Die Elemente von Qxx bilden keine
Gruppe, denn sonst müsste xx %x x2%x = x3 %x oder %x = x—1 x% ti—1
sein, was wieder erfordern würde, dass %x in Q enthalten ist.
Wir nennen das System Qnx eine Nebengruppe zu Q
(innerhalb P). Die Nebengruppe bleibt in ihrer Gesammtheit
ungeändert, wenn %x durch irgend ein Element x%x von Qn-^
ersetzt wird, weil Q% mit Q identisch ist.
Nennen wir überhaupt jedes System Qit eine Nebengruppe,
so dass Q selbst darunter mitgerechnet ist, so können wir zeigen,
dass zwei Nebengruppen entweder ganz identisch sind, oder
kein gemeinsames Element enthalten. Denn sind Qitx,
Qtc2 zwei Nebengruppen, und ist xl%1 = x.27t2, worin xx, x2 zwei
Elemente aus Q sind, so folgt, wenn x = x^1x1 gesetzt wird,
Auch Untergruppe genannt.

544 Vierzehnter Abschnitt. §. 161.
it^ = %jix. Da aber % zu Q gehört, und folglich Q% = Q ist,
so folgt:
Q7t.2 = Q%Ttx = QjTj.
Ist durch B) und C) die Gruppe P noch nicht völlig er-
erschöpft, so können wir eine weitere Nebengruppe Qtc2 bilden
uud können in der Bildung der Nebengruppen so lange fort-
fortfahren, bis P in lauter Nebengruppen zerlegt ist. Da jede dieser
Nebengruppen q Elemente enthält, so folgt der wichtige Funda-
Fundamentalsatz von Cauchy:
1. Der Grad eines Theilers einer Gruppe P ist
ein Theiler des Grades von P.
Als specieller Fall ist darin enthalten, dass der Grad
eines Elementes der Gruppe (§.160) immer ein Theiler
des Grades der Gruppe ist.
Die Zerlegung von P in seine Nebengruppen können wir
(nach Galois) sehr bezeichnend durch die symbolische Gleichung
ausdrücken:
D) p= Q+ 0% + 0^^ \-Q«j-i,
wenn
E) i>=i2
ist. Den Quotienten j nennen wir den Index des Theilers
Q. Diese Zahl drückt keine Eigenthümlichkeit der Gruppe Q
an sich aus, sondern nur eine Beziehung von Q zu P.
Da, wie wir oben schon gesehen haben, zwei Nebengruppen
zu Q entweder ganz identisch sind, oder kein gemeinschaftliches
Element enthalten, so können wir noch den Satz aussprechen:
2. Ist % eine beliebige Permutation aus P, so ist
das System der Nebengruppen
Q%, Qnx%, Qn%%, . . ., Q%j-x7i
von dem System
Q, Q%x, Qtc.2, . . ., Qtcj-x
nur durch die Anordnung unterschieden.
Wir dehnen die Bezeichnung Nebengruppen auch auf Systeme
von der Form % Q aus, und können P auch in solche Systeme
zerlegen. Es folgt speciell aus der Zerlegung D) die zweite
P = Q + arj-i Q+jc^-Q-\ %j±x Q.
Denn wenn %x nicht in Q vorkommt, so kommt auch %-x nicht
darin vor, und wir erhalten eine erste Nebengruppe %—J Q.

§. 161. Nebengruppen. 545
Wenn dann ti% nicht in Q7t1 vorkommt, so kommt auch %—x
nicht in 7t—1 Q vor; denn aus 7t—1 ¦= 7t—1 % würde 3r2 = x~'lxl
folgen u. s. f.
Wir geben hier der Zerlegung D) den Vorzug wegen der
Bedeutung, die sie, wie wir sogleich sehen werden, für das
algebraische Problem hat.
Wir nennen eine Grosse -ip des Körpers N zu der Gruppe
Q gehörig (wenn nöthig mit dem Zusatz „innerhalb P"), wenn
-ip sich nicht ändert, falls eine der Operationen von Q darauf
angewandt wird, dagegen sich ändert, wenn irgend eine andere
Operation aus P angewandt wird. Wie man sieht, ist dieser
Begriff der Zugehörigkeit gegen den im §.159 festgesetzten etwas
erweitert, insofern die Permutationen, die ausserhalb P liegen,
hier gar nicht in Betracht kommen. Für den Fall, dass P die
symmetrische Gruppe ist, fallen aber beide Begriffsbestimmungen
zusammen.
Bei dieser Definition der Zugehörigkeit gelten nun die fol-
folgenden Sätze allgemein.
3. Zu jedem Theiler Q von P gehören Grossen in
N, und jede Grosse in N gehört zu einem be-
bestimmten Theiler Q von P.
Der erste Theil des Satzes ist bereits im §. 159, 5. bewiesen.
Denn wenn eine Function der Grossen a innerhalb der symme-
symmetrischen Gruppe zu einer Gruppe Q gehört, so gehört sie auch
innerhalb jeder anderen Gruppe P, von der Q ein Theiler ist, zu Q.
Der zweite Theil aber folgt aus den Grundeigenschaften der
Galois'sehen Gruppe.
Um dies einzusehen, wollen wir folgende Bezeichnung ein-
einführen. Wird auf eine Function tp des Körpers N irgend eine
Permutation 7t der Gruppe P ausgeübt, so möge -ip in tp j 7t
übergehen; wird auf ip | % eine Permutation %' ausgeübt, so ist
der Erfolg derselbe, als ob auf -ip die zusammengesetzte Permu-
Permutation 7t 7t' ausgeübt wäre, d. h. es ist
F) (ip | 7t) | %' = tp | 7t 7t'.
Bleibt nun tp ungeändert durch die Permutation x, so ist
1p — tp | je,
und hierin kann nach §. 156$ a) jede Permutation % aus der
Gruppe P angewandt werden. Dadurch ergiebt sich
1p j 7t = Tp | %7t.
Weber, Algebra. I. 35

546 Vierzehnter Abschnitt. §. 161.
Wenn daher -ip | % auch gleich ip ist, so ist auch ip \ % % = ip,
d. h. die Permutationen, die ty ungeändert lassen, bilden eine
Gruppe, w, z. b. w.
Ist tp eine zur Gruppe Q gehörige Function in N, ist also
G) i,\% = i,\%1 = -.. = ii,\ xa-i — n>,
und it-y irgend eine nicht zu Q gehörige Permutation von P, so
können wir jc± auf die Gleichungen G) anwenden und erhalten
und tp-L ist von tp verscbieden. Wenn umgekehrt für irgend ein it
• (8) tp-, = tp 1 it = ^> | x%l
ist, so muss 7t unter der Reihe der Substitutionen
(9) Q%1 =xjeu %x %u . . ., 5cä_i3ri
enthalten sein; denn durch Anwendung von %—1 auf (8) folgt,
dass %%1 n—x in Q enthalten, etwa gleich % sein muss; daraus
aber folgt
Tt = X—1 X 7tt,
was in der That in (9) enthalten ist.
Wir können demnach folgenden Satz aussprechen:
4. Eine zu Q gehörige Function tp geht durch
alle Permutationen einer Nebengruppe Q%,
und durch keine andere Operation aus P in
eine bestimmte von tp verschiedene Grosse -ipx
über.
Demnach entsprechen den j Nebengruppen ebenso viele
Functionen ip, nämlich
A0) 1>, *!, *j, . . ., ti-1,
und aus dem Theorem 2. ergiebt sich der Satz:
5. Die Grossen A0) erleiden eine Permutation,
wenn auf alle gleichzeitig eine und dieselbe
Operation it aus P angewandt wird.
Denn wir können die Grossen A0) so darstellen
ip\x, tp \ xtc^ tp | xn2, . . ., tp | x:*}_!,
und wenn also % darauf angewandt wird,
1p \XJC, 1p | JCJCjJT, 1p | X7C27C, . . ., ty | XJCj — iTt,
worin x und % beliebige Permutationen aus Q und P sind. In
jeder der beiden Reihen

§. 161. Conjugirte Gruppen. 547
X, %7tu
X7t, X7t17t, XJC27t, . . ., X7tj_17t
kommt aber aus jeder der Nebengruppen D) eine und nur eine
Permutation vor.
Die Functionen A0), die, wie wir gesehen haben, alle von
einander verschieden sind, heissen conjugirte Functionen.
Wir können nach dem Vorhergehenden leicht die Gruppen
bilden, zu denen die einzelnen Functionen A0) gehören. Es ist
z. B. ipt = ip | 3Tj, und wenn nun % eine Permutation aus P ist,
durch die fa ungeändert bleibt, so muss
sein. Auf diese Gleichung können wir aber die in P enthaltene
Permutation Tt\~x anwenden, wodurch sich
ty | 7t17t 7t—1 = X[>
ergiebt, d. h. es muss Tt-^TtTt—1 zu Q gehören. Setzen wir es
gleich x, so folgt
A1) % = n—x%%x.
Wenn umgekehrt % diese Form hat, so ist
und tl>1 gestattet also diese Permutation. Demnach können wir
die Gruppe, zu der i^ gehört, durch das Symbol
darstellen, was in der That eine Gruppe ist, wie aus der Zu-
Zusammensetzung
A2) 7t—1 XTt-y n—1 v.^ jt± = 7t—1 % % %x
zu ersehen ist.
Die Gruppen, zu denen die conjugirten Functionen A0)
gehören, nämlich
A3) Q, x-iQx!, n-^Q^, . . ., Ttr-^QTtj-!,
nennen wir conjugirte Theiler von P oder kurz conjugirte
Gruppen1).
Wenn die Elemente zweier Gruppen
Q = x, x1,xi, ...
Q' = x', x\, »4 . . .
J) Auch der Name „gleichberechtigte Untergruppe" ist dafür im
Gebrauch.
35*

548 Vierzehnter Abschnitt. §. 162.
in der Weise eindeutig auf einander bezogen werden können,
dass, wenn x, x' und xu x[ zwei Paare entsprechender Elemente
sind, auch die Zusammensetzungen xxx und x'x[ entsprechende
Elemente sind, so heissen die beiden Gruppen isomorph.
Die in A2) ausgedrückte Regel der Zusammensetzung in der
Gruppe %~1Qn1 zeigt also, dass alle conjugirten Gruppen mit
einander isomorph sind.
Wenn tc eine beliebige Permutation aus P, also von der
Form x%r ist, so ist die Gruppe 7t~1Q7t immer unter den conju-
conjugirten GruppenA3) enthalten, nämlich = n~1x~1 Qx%r =it—1Qicr.
Die Ableitung von %—x Qit aus Q heisst auch eine Trans-
Transformation der Gruppe Q durch % und %~x Q% eine aus
Q transformirte Gruppe.
§. 162.
Reduction der Galois'schen Resolvente durch Ad-
junction. Normaltheiler einer Gruppe.
Wir haben nun die allmähliche Reduction der Gruppe einer
gegebenen Gleichung zu betrachten, die durch die Adjunction
von gewissen algebraischen Grossen eintreten kann.
Es sei, wie im vorigen Paragraphen, P die Galois'sche
Gruppe vom Grade f>, und Q einer ihrer Theiler vom Grade q
und vom Index j, ferner ty eine zu Q gehörige Function der
Wurzeln, und
A) *, 1I>1, 1I>2, ¦ ¦ -, tj-l
seien die conjugirten Grossen. Wir stellen den folgenden Satz
an die Spitze.
1. Die conjugirten Grossen A) sind die Wurzeln
einer irreducibeln Gleichung vom Grade j
in £i.
Denn bedeutet t eine Veränderliche, so bleibt
B) cp (t) = (t — iP)(t-ti).--(t — ty-i)
(nach §. 161, 5.) ungeändert, wenn eine Permutation aus P ange-
angewandt wird; also sind die Coefficienten der Function (p(t), deren
Wurzeln die Grossen A) sind, in £1 enthalten [§. 156, b)].
Um die Irreducibilität von cp(t) nachzuweisen, nehmen wir-
an, es sei <&(t) irgend eine Function in £1, die für t — -ip ver-
verschwindet, also 3> (ip) = 0. Da auf diese Gleichung alle Permu-

§. 162. Reduction der Galois'schen Gruppe. 549
tationen von P angewandt werden dürfen, so folgt, dass auch
0(ti), ^(^2M • • -i ^(^i—1) Null sein müssen, dass also <&(t)
durch 9 (t) theilbar sein muss. Darin aber ist die Irreducibilität
enthalten.
Hieran schliesst sich der Satz von Lagrange1):
2. Jede Grosse des Körpers N, die die Permu-
Permutationen der Gruppe Q gestattet, ist in dem
Körper £l(ip) enthalten, wenn -fy eine zu Q ge-
gehörige Function ist.
Eine die Permutationen von Q gestattende Function o geht
durch die Permutationen einer Nebengruppe Qnx in ein und
dieselbe Function über. Es entsprechen also den conjugirten
Werthen
C) ., 1j>, tl) *2, • • • tj-1
die Werthe
D) a>, o-t, »2, . . ., ©,-_!,
die jedoch nicht nothwendig alle von einander verschieden sind.
Wendet man auf die Grössenreihen C), D) eine der Permu-
Permutationen von P an, so tritt eine gewisse Permutation ein, und
zwar in beiden Reihen die gleiche, da, wenn z. B. tl>l in tp2 über-
übergeht, auch (»j in a>2 übergehen muss (§. 161, 5.).
Betrachten wir nun die Summe
die eine ganze Function (j — l)ten Grades von t ist, so finden
wir, dass sie durch alle Permutationen P ungeändert bleibt und
folglich in £1 enthalten ist. Setzt man dann t = ip und be-
beachtet, dass <jp (t) keine gleichen Wurzeln hat, so folgt
Es ist also es rational durch ¦$ ausgedrückt, und dies ist der
Inhalt des Satzes 2.
3. Wenn wir eine zu Q gehörige Function ip dem
Körper £1 adjungiren, so reducirt sich die
Gruppe des Körpers N auf Q.
!) Lagrange, Reflexions sur la resolution algebrique des equations.
Memoires de l'Academie de BerliB, annees 1770, 1771. Oeuvres de Lagrange.
Tome III. Der Satz ist von Lagrange allerdings nur in einer specielleren
Fassung gegeben. Die allgemeine Formulirang rührt von Galois her.

550 Vierzehnter Abschnitt. §. 162.
Denn bezeichnen wir den Körper £l(ij>) mit &', so gestattet
erstens jede Gleichung in £1' zwischen den Wurzeln der Grund-
Grundgleichung «, «!, . . ., am_i die Permutationen von Q, weil Q in P
enthalten ist, und weil ty durch Q ungeändert bleibt; und zwei-
zweitens ist jede Function, die durch Q ungeändert bleibt, nach
dem Lagrange'sehen Satze in Sl' enthalten. Dies sind aber
[nach §. 156, a), b)] die charakteristischen Merkmale der
Galois'schen Gruppe im Körper SU. Um also die Galois'sche
Gruppe vom Grade p auf den Grad q zu reduciren, muss eine
Wurzel einer Hülfsgieichung jten Grades in Sl adjungirt werden.
Den Satz 3. können wir auch so ausdrücken:
Der Normalkörper N = £i(K,K1,...,um—i) ist ein Körper
f>ten Grades über £1 und qten Grades über Sl' = <ß(^).
Der Erniedrigung der Gruppe durch Adjunction von tp ent-
entspricht, wie schon aus den allgemeinen Grundsätzen hervorgeht,
eine Zerfällung der Galois'schen Resolvente. Nehmen wir an,
es sei (wie im §. 152) g(t) = 0 die Galois'sche Resolvente und
q eine ihrer Wurzeln, und durch die Permutationen von Q gehe
q über in
F) 0, Q1} 02, . . . 03_j,
so dass, wenn xh irgend eine Permutation aus Q ist, nach der
im §. 161 gebrauchten Bezeichnung 0Ä = p | xh ist.
Wendet man auf diese Grossen eine Permutation der Gruppe
Q an, so werden sie nur unter einander permutirt, und ihre sym-
symmetrischen Functionen, und folglich auch die Function der Va-
Variablen (
G) g(t, *) = (*— q) (t—9l)...(t- (fa_i)
sind in <ß(^) enthalten. Zugleich ist g(t, ip) ein Theüer von
g (f). Wendet man auf q die Substitutionen der Nebengruppe
7ti Q an, so geht 0 in
(8) 0o,», 01,<> • • •, Qq-l,i
über, worin
0 9
und zwei der Reihen (8) sind entweder identisch, oder sie ent-
enthalten kein gemeinschaftliches Element. Denn ist 0Äjf = 0r>s, so ist
¦jtt %h = %s %r und ars ist folglich in der Nebengruppe %i Q enthalten.
Aber auch die Grossen (8) vertauschen sich nur unter einander,
wenn man darauf eine Substitution von Q anwendet (weil, wenn
% eine Permutation in Q ist, %t Qx = %{ Q). Demnach ist auch
(9) gt(t, *) = (*— 0o,O (* — 0i,O ...(* — 03_!,i)

§. 162. Reduction der Galois'schen Resolvente. 551
in £l(ip) enthalten und es wird g(t) durch Adjunction von ip in
j Factoren zerlegt:
A0) g (t) = g0 (t, i>) g± (t, *)... gj-i (t, t).
Man kann die Zerlegung aber noch in einer anderen Weise
ausführen, wobei man jedoch Factoren erhält, die nicht alle in
sondern in den conjugirten Körpern &l(ip), "ß(^j), • •
enthalten sind. Setzen wir nämlich
so gehen die Grossen F) durch Anwendung der Permutation
%i in
A1) 00, i, Ql,i, ¦ ¦ •) Qq-l,i
über, und die Gesammtheit dieser Grossen bleibt ungeändert
durch die Permutationen der Gruppe itr-1 Q jc{. Ist nun wie früher
P = <3 + <M + <3% H h Q«j-x,
so geht il> durch »,• in ^ über, und aus G) ergiebt sich
A2) g(t, i>i) = (t — Q'0,i) (t - <,{,{) ...(*- Qt^d.
Dies ist gleichfalls ein Theiler von g(t), und weil zwei von
den Grossen - Reihen A1) entweder identisch sind, oder kein
gemeinschaftliches Element haben, so haben je zwei der Func-
tionen g (t, tt) keinen gemeinsamen Theiler. Daraus ergiebt sich
die Zerlegung
A3) g(t) = g(t, i,) g(t, fy) . . . g(t, t,_0,
die im Allgemeinen von der Zerlegung A0) verschieden ist.
Uebereinstimmung findet nur dann statt, wenn man zu jeder
Permutation % aus P eine zugehörige %' so finden kann, dass
n Q = Q %' ist.
Sind Q und Q' zwei verschiedene Theiler der Gruppe P, so
werden Q und Q' gewisse Permutationen gemein haben, unter
denen sich immer die identische Permutation findet. Es ist
möglich, dass dies die einzige gemeinsame Permutation von Q
und Q' ist, und dann heissen diese beiden Gruppen theilerfremd.
Es können aber noch mehr gemeinsame Elemente vorhanden
sein. Den Inbegriff R aller gemeinsamen Permutationen von Q
und Q' nennen wir den grössten gemeinschaftlichen
Theiler, oder auch den Durchschnitt von Q und Q'1).
*) Der kürzere Ausdruck „Durchschnitt" statt „gemeinschaftlicher
Theiler" ist von Study vorgeschlagen.

552 Vierzehnter Abschnitt. §. 162.
Dies R ist immer eine Gruppe, denn wenn nx und n2 beide
sowohl in Q als in Q' vorkommen, so muss auch %% in Q
und in Q\ also auch in R vorkommen. Der Begriff ist sofort
übertragbar auf mehrere Gruppen Q, Q\ Q" . . .
Ist tp eine zu Q und -ip' eine zu Q' gehörige Function, so
können wir die rationalen Zahlen x, x' (nach §. 43, 1.) so be-
bestimmen, dass <ö = x-ip -f- x'il>' eine zu R gehörige Function
wird. Denn jedenfalls gestattet a> die Permutationen von R, da
ty und tp' sie gestatten. Ist dann % eine nicht in R enthaltene
Permutation aus P, so ist sicher nicht zugleich ip = tp \ % und
i}>' = ip \ n; also können wir x, x' so bestimmen, dass auch nicht
co — m | n wird. Wenn wir also gleichzeitig -ip und -ip', und folg-
liab a> adjungiren, so reducirt sich die Gruppe des Körpers N
nach 3. auf R. Ebenso können wir bei mehr als zwei Gruppen
Q schliessen, und erhalten den Satz:
4. Sind Q, Q\ Q" . . . Theiler von P, R ihr Durch-
Durchschnitt, ^,^',^" ... Functionen, die zu Q, Q', Q"...
gehören, so reducirt sich die Gruppe des Kör-
Körpers N durch gleichzeitige Adjunction von
$, $', i>" ¦ • ¦ auf R.
Wenn wir nicht bloss eine Wurzel tp der Hülfsgieichung
cp(t) = O adjungiren, sondern alle mit tp conjugirten Grossen
ty, t^j, tpz, . . ., tyj—\, wenn wir also aus £1 den Körper
0
ableiten, so ist nach diesem Satze der Erfolg der, dass die
Gruppe von N in £1" der grösste gemeinschaftliche Theiler R
aller mit Q conjugirten Gruppen wird, so dass (nach §. 161)
R der grösste gemeinschaftliche Theiler aller Gruppen %—J Q %
ist, wenn tc die Permutationen von P durchläuft.
Von besonderem Interesse ist nun der Fall, dass
alle conjugirten Gruppen ji—1Qtc mit einander identisch
sind. In diesem Falle ist nach dem Theorem 2. jede der con-
conjugirten Grossen ip, ip±, t^2, . . ., ty—i in £i(tp) enthalten, die
Körper £l(ip), Si^), ..., <ß(#y_i) und £l(tp, ipu . . ., %_!) sind
identisch, und £1 (ip) ist ein Normalkörper über Si. In
diesem Falle sind die Zerlegungen A0) und A3) mit einander
identisch.
Wir nennen daher einen Theiler Q der Gruppe P, der

§. 163. Gruppe der Resolventen. 553
diese Eigenschaft hat,* einen Normaltheiler (oder normalen
Theiler) 1).
Ist aber Q ein Normaltheiler, so ist die Adjunction einer
einzigen Wurzel t\> der Hülfsgieichung gleichbedeutend mit der
gleichzeitigen Adjunction aller dieser Wurzeln.
5. Ist Q selbst nicht normal, so ist der grösste
gemeinschaftliche Theiler B aller conjugirten
Theiler %—YQ% gewiss normal.
Denn ist eine Permutation % in B, also in allen Gruppen
71~1Qti enthalten, so gilt das Gleiche auch von jedem % — 1%ji,
d. h. %—1B% ist Theiler von B, und folglich, da es von gleichem
Grade ist, = B.
Eine Gruppe, die ausser sich selbst und der identischen
Gruppe keinen Normaltheiler hat, heisst eine einfache Gruppe.
Der Durchschnitt aller mit einer einfachen Gruppe conjugirten
Gruppen ist entweder die Gruppe selbst oder die identische
Gruppe, je nachdem diese einfache Gruppe Normaltheiler von P
ist oder nicht.
Ist Q ein Normaltheiler von P, und B ein Normaltheiler
von Q, so ist zwar B ein Theiler von P, aber keineswegs immer
normal; Dagegen ist, wenn B ein Normaltheiler von ¦ P ist,
B auch Normaltheiler von jedem Theiler Q von P, von dem B
Theiler ist.
§. 163.
Die Gruppe der Resolventen.
Die Hülfsgieichung <p (t) = 0, von der die Bestimmung der
Function ty abhängt, geht in die Galois'sche Resolvente über,
wenn der Theiler Q, zu dem ip gehört, die identische Gruppe
ist. Denn dann kann nach dem Satze von Lagrange (§.162, 2.)
jede Function des Körpers N, also auch die Wurzeln et selbst
rational durch i\> ausgedrückt werden, und N ist mit £1 (tl>) identisch.
Wir wollen diese Gleichungen g? (i) = 0 daher in einem all-
allgemeineren Sinne Resolventen nennen. Es sind aber hier zwei
Fälle zu unterscheiden.
J) Galois spricht, von der eigentlichen Zerlegung (decomposition
propre) einer Gruppe; daher der Ausdruck „eigentliche Theiler". der auch
im Gebrauch ist; neuere Schriftsteller bezeichnen die Normaltheiler als
„ausgezeichnete oder invariante Untergruppen".

554 Vierzehnter Abschnitt. §. 163.
1. Wenn die conjugirten Gjpippen jr~a Qit theilerfremd sind,
so ist die gleichzeitige Adjunction sämmtlicher Wurzeln der
Resolvente <p(i) = 0 (nach Satz 4., §. 162) gleichbedeutend mit
der Adjunction einer zur Einheitsgruppe gehörigen Function,
und die Lösung der gegebenen Gleichung ist auf die vollständige
Lösung der Resolvente zurückgeführt. Es ist
und eine Galois'sche Resolvente der Gleichung q>(t) = 0 ist
zugleich eine Galois'sche Resolvente der ursprünglichen Gleichung.
In diesem Falle nennen wir cp(t) = O eine Totalresolvente
der gegebenen Gleichung.
2. Haben die conjugirten Gruppen ji~% Q % einen von der
Einheitsgruppe verschiedenen Theiler B, vom Grade r, der dann
ein Normaltheiler von P ist, so ist* die gleichzeitige Adjunction
von sämmtlichen zu ty conjugirten Functionen gleichbedeutend
mit der Adjunction einer zu B gehörigen Grosse. Die Galois'sche
Resolvente der gegebenen Gleichung ist durch diese Adjunction
noch nicht vollständig gelöst, sondern sie ist nur in Factoren
vom Grade r zerlegt. In diesem Falle heisst q>(ß) = 0 eine
Partialresolvente.
Ist P eine einfache Gruppe, so existiren nur Total-
resolventen, während, wenn P Normaltheiler hat, zu jedem
solchen Normaltheiler eine Partialresolvente gefunden werden
kann.
Derselbe Unterschied tritt auch hervor, wenn wir die
Galois'sche Gruppe der Resolvente <p(t) untersuchen. Diese
Gruppe besteht aus allen Vertauschnngen, die in der Reihe der
Grossen
A) *, #1, *2, • • •, *j-l
durch Anwendung der sämmtlichen Operationen % von P hervor-
hervorgerufen werden; denn jede Gleichung in £1 zwischen den Grossen A)
bleibt richtig, wenn eine dieser Permutationen vorgenommen wird,
da man die Operationen % auf jede Gleichung zwischen den «,
also auch zwischen den i/>, anwenden kann; und wenn eine Func-
Function in £1 der Grossen A) alle diese Permutationen gestattet, so
gestattet sie auch alle Permutationen % und ist also gleich einer
Grosse in £1.
Es ist nun .der Grad dieser Gruppe zu bestimmen. Unter
den Operationen von P werden die und nur die unter den

§. 164. Adjunction beliebiger Irrationalitäten. 555
Grossen A) keine Veränderung hervorrufen, die gleichzeitig in
den Gruppen x—x Qit aller dieser Functionen, also auch in ihrem
grössten gemeinsamen Theiler B vorkommen. Die Operationen
von JR mögen mit 6 bezeichnet sein. Sind dann % und %' zwei
Operationen, die unter den Grossen A) dieselbe Permutation
hervorrufen, so wird %' %~x die ursprüngliche Anordnung der ty
wieder herstellen, also gleich einer der Grossen tf sein, oder
%' = 6%.
Wir haben daher das Ergebniss:
Die Permutationen der Nebengruppe B% und nur
diese rufen unter den Grossen A) eine und dieselbe
Permutation hervor.
Der Grad der Galois'sehen Gruppe der Resolvente <p (t) = 0
ist also gleich der Anzahl dieser Nebengruppen, d. h. gleich dem
Quotienten p : r oder dem Index des Theilers B von P.
Ist B die identische Gruppe, also r = 1, und folglich q> (t) = 0
eine Totalresolvente, so ist der Grad ihrer Gruppe ebenso hoch,
wie der Grad der Gruppe der ursprünglichen Gleichung, und beide
Gruppen sind überdies isomorph. In Bezug auf die Gruppe ist
also nichts gewonnen. Die gegebene Gleichung ist mit der Re-
Resolvente, so verschieden auch ihre Grade sein mögen, äquivalent.
Ist auf der anderen Seite Q ein Normaltheiler, also B mit Q
identisch, so ist q> (t) = 0 eine Partialresolvente und der Grad
ihrer Gruppe ist gleich dem Index j des Theilers Q von P.
Nach der Adjunction einer Wurzel dieser Resolvente reducirt
sich die Gruppe der ursprünglichen Gleichung auf Q, also auf
den Grad q. Es ist also eine Spaltung der Gruppe erfolgt.
Wenn man Resolventen bilden will von möglichst niedrigem
Grade, so hat man Theiler der Gruppe P aufzusuchen von mög-
möglichst kleinem Index, also von möglichst hohem Grade. Will man
aber eine Reduction der Gruppe herbeiführen, so hat man einen
Normaltheiler von P aufzusuchen.
§. 164.
Reduction der Galois'schen Gruppe durch Adjunction
beliebiger Irrationalitäten.
Die Aufgabe der Lösung einer algebraischen Gleichung wird
nach der Galois'schen Auffassung durch eine andere ersetzt,

556 Vierzehnter Abschnitt. §. 164.
nämlich durch Adjunction von algebraischen Grossen möglichst
einfacher Natur eine Zerfällung der Galois'sehen Kesolvente,
also eine Erniedrigung des Grades der Gruppe herbeizuführen.
Wir stellen jetzt die Frage so. In dem ursprünglichen
Körper £1 ist die Galois'sche Resolvente gif) irreducibel. Der
Körper £1 soll zu einem anderen Körper £1' so erweitert werden,
dass g(t) reducibel wird. £1' soll dabei ein algebraischer Körper
über £1 sein, und es muss also nach §. 150 eine algebraische
Grosse s geben, so dass £1' = £l(s) wird. Die Grosse s wird
Wurzel einer gewissen irreducibeln Gleichung in £1 sein, die
wir mit
A) Z(«) = 0
bezeichnen wollen.
Nehmen wir an, in dem Körper £l(s) sondere sich von g(t)
der irreducible Factor
B) 9i® = 9x(t,e)
ab, der die Wurzel t = q hat. Den Grad von gt (t, e) wollen wir
mit q bezeichnen und die Wurzeln mit
C) q, p!, Qt, . . ., p2_i,
so dass
D) 9l (t, «) = (*- Q) (t - Ql) . . . (t - (.9_0.
Zunächst ist nun nachzuweisen, dass die in der Gruppe P
enthaltenen Substitutionen
(q, q), (q, ¦ pi), (q, Qz) . . . (Q, p2-i)
eine Gruppe Q bilden. Um dies zu zeigen, setzen wir wie früher
(§. 153)
und bedenken, dass dann die Gleichung
eine Wurzel, nämlich t = p, mit gt(t), gemein hat, und mithin,
da gt (t) in £1 (s) irreducibel ist, durch gx (t) theilbar ist. Daraus
folgt, dass, wenn p! und p2 irgend zwei der Wurzeln C) sind,
auch &t (q2) = Qs unter diesen Wurzeln enthalten ist. Es ist aber
die Substitution (p, p3) aus (q, q%) und (p, p2) zusammengesetzt,
und damit ist die Gruppeneigenschaft von Q nachgewiesen. Wir
bezeichnen den Index von Q mit j und setzen
E) P=H-

•§. 164. AdjunctioH beliebiger Irrationalitäten. 557
DasProduct D) gestattet nun die Substitutionen der Gruppe Q,
und wenn also ¦ty wie oben eine zu dieser Gruppe gehörige Func-
Function in N bedeutet, so lässt sich nach §. 162, 2. die Function
g1 (t, s) rational durch -ty ausdrücken, d.h. g1(t, s) ist eine Function
von t im Körper jtea Grades Sl(ty), und soll demnach durch
g(t, ty) bezeichnet werden.
Die Grosse -ty ist eine der Wurzeln einer irreducibeln Glei-
Gleichung vom Grade j
<6) cp («) = 0,
deren übrige Wurzeln ty, -ty2, ..., ty—i sind, und nach §. 162, A3)
ist g(t) in die Factoren zerlegbar
G) g(t) = g(t, ty) g(t, ty). .. g(t, %_0.
Nun ist
und aus G) folgt, dass diese Gleichung nicht bestehen bleibt,
wenn auf der linken Seite für ¦ty eine der anderen Wurzeln von
F) gesetzt wird. Denn sonst müsste g(t, ty) mit einem der
übrigen Factoren auf der rechten Seite von G) identisch sein.
Man kann also für t einen solchen rationalen Werth setzen,
dass die Gleichung
(8) g(t, u) - gi(t, s) = 0
nur die eine Wurzel u = i\> mit der Gleichung F) gemein hat.
Der grösste gemeinschaftliche Theiler von F) und (8) ist dann
in Bezug auf m linear, und wenn man darin u =.i\> setzt, so
ergiebt sich, dass ty rational durch s ausdrückbar ist.
Der Körper ß (ty) ist also sicher ein Theiler des Körpers ß (s).
Der Grad des Körpers ß(s), d. h. der Grad der Hülfsgieichung
1 (e) = 0, ist daher ein Vielfaches von j und niemals niedriger
als j. Wenn der Grad der Hülfsgieichung gleich j ist, was z. B.
dann immer eintritt, wenn der Grad von % eine Primzahl ist,
so ist £l(s) mit £l(ty) identisch, d. h. s ist auch rational durch
¦ty ausdrückbar. In diesem Falle sind die conjugirten Werthe
a, a1: . . ., £,_! die sämmtlichen Wurzeln von % = 0, und man
erhält sie, wenn man in dem rationalen Ausdruck von s durch ¦ty
die Function ty durch jede der conjugirten Functionen ¦ty, -ty±,..., ¦tyj—x
ersetzt. Es kann also e selbst für ¦ty genommen werden, und
man findet eine Zerlegung
g (t) = g (t, s) g (t, e{) ...g (t, £,-_!>

558 Vierzehnter Abschnitt. §. 165.
Die Grossen s, a15 £2> • • •> %—1 gehören sämmtlich dem Körper
ß(p) an.
Diese Resultate sind von grosser Wichtigkeit und verdienen
besonders hervorgehoben zu werden.
Nach Kronecker heissen, wenn F(x) = 0 die gegebene
Gleichung ist, und N der zugehörige Galois'sche Körper, die
Grossen von N die der Gleichung F(x) = 0 natürlichen
Irrationalitäten.
Wir haben dann den Satz:
Jede mögliche Reduction der Galois'schen
Gruppe wird herbeigeführt durch Adjunction
einer natürlichen Irrationalität. Ist j der Index
der r§ducirten Gruppe in Bezug auf die ur-
ursprüngliche, so kann die Reduction nicht ein-
eintreten durch Adjunction eines Körpers von
niedrigerem als dem jtea Grade. Der Grad kann
aber gleich j sein, und dann ist die adjungirte
Irrationalität eine natürliche. Ist der Grad
des adjungirten Körpers grösser als j, so ist
er ein Vielfaches von j.
§. 165.
Imprimitive Gruppen.
Wir machen von unseren allgemeinen Sätzen Anwendung
auf Gruppen von besonderer Natur. Zunächst nehmen wir die
imprimitiven Gruppen. Wir haben im §. 158 gesehen, dass,
wenn f(x) ¦== 0 eine irreducibele Gleichung nten Grades mit im-
imprimitiver Gruppe ist, sich n so in zwei Factoren r, s zerlegen
lässt, dass die Wurzeln in s Reihen von je r Gliedern zerfallen:
A = cc, «15 . . ., «,._!,
A) -B = ß-> ßl, • • •) ßr- li
8 = ö, <jx, . . ., ör_1?
und dass durch die Permutationen der Gruppe P die Grossen
der einzelnen Reihen nicht von einander getrennt, sondern nur
unter einander permutirt werden, während andererseits die Reihen
wieder unter sich permutirt werden.

§. 165. Imprimitive Gruppen. 559
Unter den Permutationen der Galois'schen Gruppe P von
f(x) wird es nun gewisse geben, deren Inbegriff wir mit Q
bezeichnen, die die einzelnen Keinen A, B, . . ., S an ihrer Stelle
lassen, und nur die Indices in jeder Reihe permutiren. Diese
Permutationen bilden für sich eine Gruppe, da durch die Zu-
Zusammensetzung von zweien unter ihnen die Reihen A, B, . . ., 8
nicht vertauscht werden können. Diese Gruppe Q ist ein Norm al-
altheiler von P. Denn ist % eine Permutation von Q, und % eine
aus P, so gehört die zusammengesetzte Permutation jc~1xji
wieder zu Q, weil die Permutation unter den A, B, . . ., 8, die
durch jc~1 hervorgerufen ist, durch % nicht geändert und durch
jr wieder rückgängig gemacht wird. Die Gruppe Q ist intransitiv,
und durch Adjunction einer zu Q gehörigen Function i\> wird
nicht nur die Galois'sche Resolvente reducibel, sondern die
Function f(x) selbst zerfällt in s Factoren vom rten Grade,
B) f{X) = fa (X, *) /,, (X, i>)...fa (X, *).
Die Wurzeln von fa (x, i\>) = 0 sind die Grossen «, und die
Galois'sche Gruppe dieser Gleichung besteht aus allen Permu-
Permutationen, die durch Q unter den a hervorgerufen werden.
Denn das Product
fa = (x — k) (x — «0 i . . (x — av_x)
gestattet die [Permutationen von Q, und kann daher rational
durch i\> ausgedrückt werden. In j eder in £1 {ty) rationalen
Gleichung zwischen den Grossen A können die a so permutirt
werden, wie es die Gruppe Q verlangt, und wenn eine Function
der oc diese Permutationen gestattet, so ist sie in &(il>) enthalten.
Die Grosse ijj ist, wenn j der Index des Theilers Q von P
ist, Wurzel einer Partialresolvente j^n Grades %{u) = 0, die eine
Normalgleichung und also ihre eigene Galois'sche Resolvente
ist (§. 162). Bezeichnen wir ihre Wurzeln mit
C) *, *i, ^2, • • o fy-u
so besteht die Galois'sche Gruppe dieser Resolvente aus den
Substitutionen
D) (</>, </>),. w, <M, «>, *2)... (</>, ^),
die durch die Permutationen der Nebengruppen
E) Q, Qxu Qn2,.. ., Qjij-!
hervorgerufen werden. Jede dieser Nebengruppen bringt eine
gewisse Permutation unter den Reihen A, B, . . ., S hervor, und

560 Vierzehnter Abschnitt. §. 165.
zwar sind diese Permutationen alle von einander verschieden;
denn wenn etwa durch nx und n2 dieselbe Permutation unter
den Reihen hervorgerufen wird, so gehört j^^F1 zu Qi nn& Q^v
Qjt2 sind nicht verschiedene Nebengruppen. Die Permutations-
Permutationsgruppe der Partialresolvente % (w) = 0 ist also mit der Gruppe
der Permutationen, die durch P unter den Reihen A, B, . . ., S
hervorgerufen werden, isomorph.
Verstehen wir unter Qa den Inbegriff der Permutationen
von P, durch die die Reihe A nicht verschoben wird, so ist Qa
gewiss eine Gruppe. Ist Tip eine Permutation, durch die die
Reihe A in die Reihe B übergeht, die nach der Voraussetzung
der Transitivität in P existiren muss, so ist Qanp eine Neben-
Nebengruppe zu Qa, durch die A in B übergeht. jiJ 1 Qa%p = Qp ist
eine zu Qa conjugirte Gruppe, und zwar die, durch deren Permu-
Permutation die Reihe B nicht verschoben wird. Auf diese Weise
erhalten wir die conjugirten Gruppen
Qa, Qp, ¦ ¦ ., Qa,
•deren grösster gemeinschaftlicher Theiler die vorhin betrachtete
Gruppe Q vom Index j ist.
Eine zu Qa gehörige Function ya ist die Wurzel einer Glei-
Gleichung vom steu Grade in ß, <p (y) — 0, und die übrigen Wurzeln
yp, . . ., ya gehen aus ya hervor durch Anwendung der Permu-
Permutationen der Nebengruppen QaJtp, . . ., Qtt%a. Die vorhin gefun-
gefundene Gleichung %{u) =0 vom Grade j ist die Galois'sche
Resolvente der Gleichung <p (y) = 0. Wir haben oben bemerkt,
dass die Gruppe der Gleichung % (w) = 0 vom Grade j isomorph
ist mit der Gruppe der Permutationen, die durch P unter den
Systemen der A, B, ..., S hervorgerufen werden. Da aber wegen
der Transitivität von P auch diese Systeme transitiv in einander
übergehen, und da den Vertauschungen der A, B, . . ., S die
Vertauschnngen der ya, yp, . . ., ya entsprechen, so ist <p (y) in £1
irreducibel.
Die gleichzeitige Adjunction sämmtlicher Wurzeln von <p (y)
hat denselben Erfolg wie die Adjunction der Function ty, näm-
nämlich den, die Gruppe der Gleichung f(x) = 0 von P auf Q zu
reduciren.
Durch Adjunction von ytt sondert sich von f(x) ein rationaler
Factor f(x, ya) ab, dessen Wurzeln die Grossen der Reihe A
sind, und durch Adjunction der übrigen y erhält man die Zerlegung
<6) f{x) = f{x, ya) f{x, y?) ... fix, ya),

§. 165. Imprimitive Gruppen. 561
und diese Functionen f{x, ya), f(x, yfi, . . ., f(x, ya) stimmen
überein mit den Factoren in B), fa (x, $), fp (x, ty), . . .,fa (x, ty).
Zu bemerken ist hierbei noch, dass f(x, ya) im Körper £1 (ya)
irreducibel ist. Denn wegen der vorausgesetzten Irreducibilität
von f{x) giebt es in P Permutationen, durch die et in jedes cti
übergeführt wird, und diese Permutationen gehören zu Qa. Wenn
also eine rationale Function <p (x, ya) für x = et verschwindet,
so muss jedes <p(a.i,ya) gleich Null sein, d. h. cp(x,ya) muss
durch f(x, ya) theilbar sein. Es folgt aber hieraus nicht, dass
f(x, ya) = fa(x, tl>) auch im Körper ß(i/>) irreducibel ist.
Dies sind dieselben Sätze, wie im §. 158. Es ist dort noch
gezeigt, dass man für ya eine Function von a allein nehmen kann,
worauf wir nicht nochmals eingehen wollen.
Von Interesse ist es aber, den Zusammenhang der Galois'-
schen Gruppen der einzelnen Factoren f(x, ya), f(x, y^),..., f(x, ya)
zu verfolgen. Wir haben schon oben gesehen, dass man die
Gruppe des Factors/(a;, ya) im Körper S&ty) erhält, wenn man
alle Permutationen der cc aufsucht, die durch Q hervorgerufen
werden. Wir wollen diese Gruppe mit Pa bezeichnen, und ebenso
für die anderen Factoren die Zeichen Pß, . . . , Pff gebrauchen.
Wir greifen aus P irgend s — 1 Permutationen jiß, . . ., jia
von der Art heraus, dass durch itp die Reihe A in JB etc., durch
na die Reihe A in S übergeht, und wir wollen nun der Einfach-
Einfachheit halber, was offenbar noch vollkommen freistellt, die Bezeich-
Bezeichnung der ß, . . ., ö so gewählt annehmen, dass itp, . . ., na fol-
folgende Vertauschungen hervorrufen:
«„, «!, • • ., «,—A /«oi Ki-> • ¦ •» «r
\ßo, ßu . . ., ßr-J' ' ' ' \Ö0, Öl, • • -, «r
Es sei nun % irgend ein Element von Q, das unter den cc
die Vertauschung
bewirkt, dann ist
ebenfalls in Q enthalten, und es wird durch %p unter den ß die
Vertauschung
/on fßo, ßl, ¦ • o ßr-l\
W ~ \K, ßa, ¦ ¦ -, ßar_/
also unter den Indices der ß genau dieselbe Permutation her-
hervorgerufen, wie durch % unter den Indices von a. Nehmen wir
Weber, Algebra. I. 36

562 Vierzehnter Abschnitt. §. 165.
(ß) und ein zugehöriges xp als gegeben an, so ergiebt jißXßitf1
wieder x, so dass also die durch Q hervorgerufenen Permu-
Permutationen der ß genau übereinstimmen mit denen, die unter den
oc hervorgerufen werden; und dasselbe gilt für die übrigen Reihen.
Damit ist aber der folgende Satz bewiesen:
1. Bei einer irreducibeln imprimitiven Gleichnng
können in den einzelnen Reihen die Wurzeln
so bezeichnet werden, dass die Theilgleichungen
fix, ya) = 0, f(x, y?) = 0, . . .fix, ya) — 0 im Körper
ß($) alle dieselbe Gruppe bekommen.
Will man die Bezeichnung der Wurzeln nicht in der an-
angegebenen Weise wählen, so werden die Gruppen wenigstens
isomorph.
Wir stellen noch die Frage, die gewissermaassen dnrch die
Umkehrung dieses Satzes beantwortet wird: Wann hat eine
transitive Gruppe einen intransitiven Normaltheiler?
Ist P eine transitive Permutationsgruppe, und Q ein intran-
intransitiver Normaltheiler von P, so möge
A = «. «1, • • •» «r-l
eines der Systeme sein, deren Elemente durch Q nur unter ein-
einander vertauscht werden, so jedoch, dass die Elemente von A
durch Q transitiv verbunden sind, d. h. dass durch Permutationen
aus Q jedes oc in jedes andere <x übergehen kann. Wenn nun
durch ein Element % aus P die Grossen A in
S = ß, ßi, . . ., ßr-l
übergehen, so müssen diese Elemente entweder alle mit den oc
übereinstimmen, oder alle von den oc verschieden sein; denn
durch die Gruppe %~~ 1Qit, die nach Voraussetzung mit Q iden-
identisch ist, werden die ß nur unter einander vertauscht, und zwar
ebenso wie die m, also transitiv. Wenn also in B nur ein Theil
der « vorkäme, so würden gegen die Voraussetzung durch Q
diese a mit anderen nicht in A vorkommenden Grossen ver-
vertauscht werden.
Sind durch die A nicht alle Elemente erschöpft, auf die
sich die Permutationen von P erstrecken, so giebt es, da P
transitiv ist, eine Permutation %, durch die A in ein ganz davon
verschiedenes System JB übergeführt wird. Ist x eine Permu-
Permutation aus Q, so wird durch die gleichfalls zu Q gehörige Per-
Permutation %~~xx% dieselbe Vertauschung unter den Indices der ß

§. 165. Imprimitive Gruppen. 563
hervorgerufen, wie durch x unter den Indices der «. Daraus
folgt, dass durch Q auch die ß nur unter einander permutirt
werden. Wenn mit A und B die Elemente noch nicht erschöpft
sind, so kann man in derselben Weise ein drittes System C
bilden, das durch %' aus A und durch %~ 1n' aus B entsteht,
und das weder mit A noch mit B ein Element gemein hat. So
fährt man fort, bis alle Elemente erschöpft sind, und kommt zu
folgendem Satze:
2. Eine transitive Gruppe hat nur, wenn sie im-
imprimitiv ist, einen von der identischen Gruppe
verschiedenen intransitiven Normaltheiler. Die
Systeme der Intransitivität des Normaltheilers
sind Systeme der Imprimitivität der gegebenen
Gruppe.
In Bezug auf die Gleichungen können wir mit Kücksicht auf
1. den Satz 2. auch so aussprechen:
3. Eine irreducible Gleichung /(*)= 0 zerfällt,
wenn sie durch Adjunction aller Wurzeln einer
Kesolvente reducibel wird, in mehrere irredu-
irreducible Factoren von gleichem Grade und von
gleicher Gruppe.
Wenn also eine irreducible primitive Gleichung durch Ad-
Adjunction der Wurzeln einer Kesolvente reducirt wird, so zerfällt
sie in lineare Factoren, d. h. sie ist vollständig gelöst. Dieser
Fall tritt immer ein, wenn der Grad der Gleichung f(x) = 0
eine Primzahl ist, weil eine solche Gleichung nicht imprimitiv
sein kann.
36*

Fünfzehnter Abschnitt.
Oyklische Gleichungen.
§. 166.
Cubische Gleichungen.
Wir wollen von dem jetzt gewonnenen Standpunkte aus zu-
zunächst die Auflösung der Gleichungen dritten und vierten Grades
betrachten.
Die Gruppe der Permutationen von drei Ziffern besteht aus
sechs Elementen, nämlich aus der identischen Permutation 1, aus
zwei dreigliedrigen Cyklen und drei Transpositionen:
m 1 @, 1, 2) @, 2, 1)
w A, 2) B, 0) @, 1).
Die drei ersten
1, @, 1, 2) @, 2, 1)
bilden die alternirende Gruppe, sie besteht aus den Potenzen der
cyklischen Permutation it = @, 1, 2):
B) xo = 1, 3t, 3t",
und ist also eine cyklische Gruppe.
Es seien nun a, a1, «2 die drei Wurzeln der cubischen
Gleichung:
C) fix) = x* — ax* -\- hx — c = 0.
Legen wir den Körper ß zu Grunde, der aus allen rationalen
Functionen der unabhängigen Veränderlichen a, b, c besteht, so
ist A) die Gruppe dieser Gleichung; wenn wir aber
D) Vl) = (« — «j) (« — os2) («! — os2)

§. 166. Cubische Gleichungen. 565
adjungiren, worin
E) B = a*b* -\- 18abc — iaH — 4fr* — 27c2
die Discriminante der Gleichung C) ist, so reducirt sich die
Gruppe auf B).
In dem Körper ß', der durch diese Adjunction aus ß ent-
entsteht, kann jede Wurzel rational durch jede andere ausgedrückt
werden, denn es ist
aj -)- «3 = a — k
also
2W « « +
2 «2 = a — cc — jj
und hierin können die Vertauschungen jc, sz2 ausgeführt werden.
Die cubische Gleichung ist also nach Adjunction von YD ihre
eigene Galois'sche Resolvente.
Alles dies bleibt gültig, wenn der Rationalitätsbereich irgend
ein specieller Körper ß ist, in dem a, b, c und VT) enthalten
sind, wenn nicht f(x) selbst in ß reducibel ist, also eine ratio-
rationale Wurzel hat. Denn ausser sich selbst und der cyklischen
Gruppe B) hat die Gruppe A) nur noch intransitive Theiler,
nämlich die Einheitsgruppe und drei Gruppen vom Typus 1,A,2).
Wollen wir die cubische Gleichung nun auflösen, d. h. auf
eine reine cubische Gleichung zurückführen, so müssen wir eine
Function v der Wurzeln suchen, die zwar nicht selbst, deren
Cubus aber die cyklische Permutation n gestattet. Eine solche
Function kann aber nur existiren, wenn die dritten Einheits-
Einheitswurzeln, oder, was dasselbe ist, V—3, dem Körper ß adjungirt
wird; denn v muss durch Anwendung von % eine dritte Einheits-
wurzel als Factor erhalten.
Durch diese Adjunction kann eine Reduction der Gruppe
nicht eintreten, weil die Gruppe B) ausser der Einheitsgruppe
keinen Theiler hat und die Reduction auf die Einheitsgruppe
nicht durch eine quadratische, sondern nur durch eine cubische
Gleichung geschehen kann (§. 164). Wir setzen also
£— 2 ' — 2

566 Fünfzehnter Abschnitt. §. 167.
und
. . v = a t-{- £0«! -J- £2os2
^ ' v' = a -\-£2a,x -j- £os2;
dann ist der Erfolg von n der, dass v in s2v, v' in sv' über-
übergeht, während v3, v'3 und vv' ungeändert bleiben, also in dem
Körper ii' enthalten sind. Es hat keine Schwierigkeit, diese
Grossen zu berechnen. Setzen wir zur Abkürzung
A = K2^ -\- O5j2O!2 -j- OS^OS,
so ist
a- A' = Yd,
und für v3 erhält man
1K — «3 _|_ aZ _j_ a9 _j_ 6 0! 05! 0S2 -\- 3 £ A -\- 3 £2 A',
also
und ebenso
Es ist aber auch
A0) W' = OS2 -\- O5j2 -|- O!22 «05! OSOS2 OSx 0S2 = a2 — 3&,
und aus (8), (9), A0) erhält man in Uebereinstimmung mit einer
früheren Formel [§. 52, (8)]
27D = 4(«2 _ 36K — Ba3 — 9ab + 27cJ.
Fügt man zu G) noch die Gleichung
a = 0! -f~ 0«! -{- O62,
so findet man in Uebereinstimmung mit der Cardanischen
Formel:
3a=a-\-v-\-v'
3 osj = a -(- £2v -|- £v'
3os2= a -j- ev-f- £2^'.
§. 167.
Permutationsgruppen von vier Elementen.
Ein gutes Beispiel für die Galois'sche Theorie bieten die
Gleichungen vierten Grades, wo die Verhältnisse so einfach

§. 167. Permutationsgruppen von vier Elementen. 567
liegen, dass sich Alles leicht übersehen lässt, und doch die wich-
wichtigsten Erscheinungen der Gruppenbildung zu Tage treten.
Aus vier Ziffern, 0, 1, 2, 3, lassen sich 24 Permutationen
bilden, und so hoch ist also der Grad der Galois'schen Gruppe
der allgemeinen Gleichung vierten Grades im Körper der
rationalen Functionen der Coefficienten (vgl. den Schluss von
§. 156). Wir stellen diese Permutationen durch ihre Cyklen in
folgender Weise dar, wobei 1 die identische Permutation bedeutet:
A) P = 1, @, 1), @, 2), @, 3), A, 2), A, 3), B, 3)
@,1) B, 3), @,2) A,3), @,3) A,2)
@, 1, 2), @, 1, 3), @, 2, 3), A, 2, 3)
@, 2, 1), @, 3, 1), @, 3, 2), A, 3, 2)
@, 1, 2, 3), @, 1, 3, 2), @, 2, 3, 1)
@, 2, 1, 3), @, 3, 1, 2), @, 3, 2, 1).
Wir haben also in P ausser der identischen Permutation
sechs Transpositionen, acht dreigliedrige, sechs viergliedrige Cyklen
und drei Permutationen von der Form @, 1) B, 3), die wir
Transpositionspaare nennen wollen.
In P ist die alternirende Gruppe vom Grade 12 als Normal-
theiler enthalten. Diese Gruppe kann keine einzelne Transposi-
Transposition und keine viergliedrige cyklische Permutation enthalten, und
es bleiben also folgende übrig:
B) Q=l, @,1)B, 3), @,2)A,3), @,-3) A, 2)
@, 1, 2), @, 1, 3), @, 2, 3), A, 2, 3)
@, 2, 1), @, 3, 1), @, 3, 2), A, 3, 2).
Wir wollen nun alle vorhandenen Tlieiler der Gruppe P
aufsuchen. Dabei lassen wir die intransitiven Qruppen beiseite,
die alle entweder aus drei oder aus sechs Permutationen von
nur drei Elementen, oder aus den Permutationen von zwei Paaren
von zwei Elementen bestehen. Wir suchen also nur die transi-
transitiven Theiler von P auf. Ausserdem beschränken wir uns bei
einem System conjugirter Theiler auf einen Repräsentanten, aus
dem die anderen ja durch Ziffemvertauschung hergeleitet werden
können (§. 160, 4.).
Eine wesentliche Vereinfachung wird durch folgende beiden
Sätze herbeigeführt:
1. Wenn eine transitive Permutationsgruppe von
vier Ziffern einen dreigliedrigen Cyklus enthält,

568 Fünfzehnter Abschnitt. §. 176.
so ist sie die symmetrische oder die alternirende
Gruppe, und
2. wenn sie zwei Transpositionen mit einem gemein-
gemeinsamen Element enthält, so ist sie die symme-
symmetrische Gruppe.
Wenn nämlich in einer Gruppe des Cyklus @, 1, 2) vor-
vorkommt, und die Gruppe ausserdem transitiv ist, so enthält sie
eine Permutation st, durch die 0 in 3 übergeführt wird. In dem
dreigliedrigen Cyklus 3r~1@, 1, 2)n kommt also gewiss die Ziffer 3
vor; er ist also etwa @, 1, 3), und demnach haben wir in der
Gruppe
@, 1, 2), @, 1, 2J = @, 2, 1)
@, 1, 3), @, 1, 3J = @, 3, 1)
@,1, 2) @,3, 1) =A,2,3)
A, 2, 3J = A, 3, 2)
@, 3, l)@, 1, 2) = @, 3, 2)
@, 3, 2J = @, 2, 3),
d. h. alle überhaupt vorhandenen dreigliedrigen Cyklen. Dem-
Demnach kommen alle Permutationen der, alternirenden Gruppe in
der fraglichen Gruppe vor (§. 160), und sie ist also entweder
damit erschöpft, oder sie enthält noch eine Permutation der
zweiten Art und ist dann die symmetrische Gruppe.
Enthält aber eine transitive Gruppe die beiden Transposi-
Transpositionen @, 1), @, 2), so enthält sie auch
@, 1) @, 2) = @, 1, 2),
und damit die ganze alternirende Gruppe, und da sie auch eine
Transposition enthält, so ist es die symmetrische Gruppe.
Wenn also nun eine von P und Q verschiedene Gruppe
zunächst eine Transposition @, 1) enthält, so muss sie, wenn sie
transitiv ist, auch B, 3) enthalten, und demnach die ganze in-
intransitive Gruppe vierten Grades:
C) 1, @,1), B,3), @,1) B, 3).
Soll also die Gruppe transitiv sein, so müssen noch weitere
Permutationen dazu kommen. Diese können nach 1. und 2. nur
unter den viergliedrigen Cyklen oder unter den Transpositionspaaren
gesucht werden. Ein viergliedriger Cyklus aber, in dem 0 und 1
cyklisch an einander stossen, kann nicht vorkommen, weil er, mit
@, 1) combinirt, einen dreigliedrigen Cyklus geben würde, wie:
@,1, 2, 3) @,1) = A,2, 3).

§. 167. Permutationsgruppen von vier Elementen. 569
Ebenso können nicht 2 und 3 cyklisch an einander stossen,
und es bleiben also nur folgende übrig:
D) @, 2, 1, 3), @, 3, 1, 2), @, 3) A, 2), @, 2) A, 3).
Wenn aber von diesen Permutationen eine zu C) hinzu-
hinzutritt, so müssen auch alle anderen aufgenommen werden, denn
es ist
@, 1) @, 2, 1, 3) = @, 3) A, 2)
B, 3) @, 2, 1, 3) = @, 2) A, 3)
@, 1) B, 3) @, 2, 1, 3) = @, 3, 1, 2),
und man kann also durch Vermittelung der Transpositionen @,1)
und B, 3) jede der Permutationen D) aus jeder anderen her-
herleiten. Aus der Voraussetzung also, dass überhaupt in einem
von P und Q verschiedenen transitiven Theiler von P eine Trans-
Transposition vorkommt, folgt, dass dies die Gruppe achten Grades
E) Px = 1, @, 1), B, 3), @, 2)A, 3), @, 1)B, 3), @, 3)A, 2)
@, 2, 1, 3), @, 3, 1, 2)
oder wenigstens eine damit conjugirte sein muss.
Dass Pj wirklich eine Gruppe ist, erkennt man leicht, wenn
man je zwei seiner Permutationen zusammensetzt.
Es giebt drei verschiedene mit Px conjugirte Gruppen, die
man erhält, wenn man statt von @, 1), B, 3) von den Trans-
Transpositionen @, 2), A, 3) oder @, 3), A, 2) ausgeht. Der Durch-
Durchschnitt dieser drei Gruppen ist ein Normaltheiler von P und
zugleich von Q, nämlich
F) & = 1, @,2) A,3), @,1) B, 3), @,3) A,2).
Wenn eine transitive, von P und Q verschiedene Gruppe
keine Transposition enthält, so enthält sie entweder keinen vier-
gliedrigen Cyklus, und ist dann mit F) identisch, oder sie ent-
enthält einen viergliedrigen Cyklus und enthält dann auch die
ganze cyklische Gruppe, wie
G) P3 = 1, @, 1, 2, 3), @, 2) A, 3), @, 3, 2, 1).
Enthält eine solche Gruppe noch einen zweiten viergliedrigen
Cyklus, etwa @, 1, 3, 2), so ist sie wegen @, 1, 2, 3) @, 1, 3, 2)
= @, 3, 1) die symmetrische Gruppe. Enthält sie aber ausser
P2 noch eine der Permutationen von F), etwa @, 1) B, 3), so
ist wegen
@, 1, 2, 3) @, 1) B, 3) = A, 3)
Pj in ihr enthalten.

570 Fünfzehnter Abschnitt. §. 168.
Aus P2 gehen ebenfalls drei conjugirte Gruppen -hervor, die
aber ausser 1 keinen gemeinschaftlichen Theiler haben.
Es giebt also ausser P, Q, Px, Qlt P2 und den mit Px
und P2 conjugirten Theilern von P keine transitiven
Permutationsgruppen von vier Elementen.
Unter den intransitiven Gruppen verdient noch die Gruppe C):
P3 = 1, @, 1), B, 3), @, 1) B, 3),
hervorgehoben zu werden, die gleichfalls zu einem System von
drei conjugirten Gruppen Anlass giebt. Ausserdem giebt es von
intransitiven Gruppen nur noch die Permutationsgruppen von
nur zwei oder drei Elementen.
§• 168.
Auflösung der biquadratischen Gleichungen.
Die verschiedenen Methoden der Auflösung der biquadratischen
Gleichungen unterscheiden sich von einander durch die Reihenfolge,
in der die verschiedenen Divisoren der Gruppe P benutzt werden.
Es seien «, %, «2, «3 die Wurzeln der biquadratischen
Gleichung
A) f(x) = x4- — öj xs -\- a2 x2 — a3 * -}- «4 = 0.
Wir bezeichnen mit D die Discriminante und setzen
B) 1/5 = (a — Kj) (« — os2) (« — «3) («i — «2) (oj, — a3) («a — a3).
Ausserdem erinnern wir noch an die Ausdrücke für die In-
Invarianten (§. 77) :•
C) A = al — 3 «iös + 12 ttt
D) B = 27 al % -j- 27 a| -}- 2a| — 72 a2a4 — 9^^^,
durch die man D in der Form ausdrückt:
E) 27D = 4 J.3 — ^2.
Adjungirt man zunächst ]/D, so reducirt sich die Gruppe der
Gleichung auf Q, und wenn man weiter eine zu Qx gehörige
Function sucht, so wird durch diese die Gruppe auf Qx reducirt.
Da <2X innerhalb Q den Index 3 hat, so wird eine solche Func-
Function von einer cubischen Gleichung abhängen, und zwar, da Qx
ein Normaltheiler von Q ist, von einer Normalgleichung. Nehmen
wir z. B.
F) y = (« — «j) («2 — a3)

§. 168. Biquadratische Gleichungen. 571
als eine zu Q± gehörige Function, so sind die beiden dazu con-
jugirten Werthe
y1 = (a — O («3 — Kj)
K }- 2/2 = (« — «3) («1 — «2)-
Diese drei Grossen sind die Wurzeln einer cubischen Partial-
resolvente, deren Coefficienteri als Invarianten von / leicht zu
bilden sind (vergl. §.70, 71, wo die Grossen y, yu y% mit U, V, W
bezeichnet waren). Die Gleichung wird [§. 70, G)]
(8) y* — Ay+VD = 0.
Ihre Discriminante ist i?2, und für das Product der Wurzel-
Wurzeldifferenzen kann man das Vorzeichen leicht (durch Vergleichung
der Glieder höchster Ordnung nach der Gauss'sehen Definition,
§. 49, oder auch aus §. 70) bestimmen. So erhält man:
(9) (y — 2/i) (y ~ 2/2) B/1 — 2/2) = B.
Die Gleichung (8) ist, wie schon bemerkt, eine Normal-
Normalgleichung, und es ist leicht, yu y2 durch y wirklich darzustellen.
Wenn man (9) mit (y^ — y2) multiplicirt, so findet man durch
Benutzung der Formeln
Ü/-2/i)B/-2/2) = 31/3_^, (y1-y2y = y2
A0) = 6J.t/3 + 92/ V-D — 4J.2
2/i + 2/2 = - 2/,
wodurch y1, y% bestimmt sind. Adjungirt man also ferner-
fernerhin y, so reducirt sich die Gruppe der biquadratischen Glei-
Gleichung auf
& = 1, @,2) A,3), @,1) B, 3), @,3) A,2).
Diese Gruppe ist imprimitiv (und zwar nach drei Arten), und
die Gleichung kann jetzt durch zwei Quadratwurzeln gelöst
werden. Am besten gelangt man dazu auf folgendem Wege. Die
drei Grossen
Vl = (« + «i — «2 — u3y
A1) v% = (a — «j -)- os2 — «3J
«3 = (« — «1 — «2 + «sJ
gestatten alle die Permutationen der Gruppe $1 und sind daher
rational durch y darstellbar. Man erhält diese Darstellung
folgendermaassen: Es ist

572 Fünfzehnter Abschnitt. §. 168.
vi — «i2 — 4 (os -f- «i) («2 -(- os3)
2/l — 2/2 = (« + «l) («2 + «3) — 2@50! + «2«3)
«2 .= (« + «l) («2 + W3) + ««1 + «2«3,
also, wenn man v2, i>3 ebenso bildet:
31»! = 3af — 8a2 — ^Vi ~\- ^y%
A2) 3v2 = 3«^ — 8% — 4y, +4«/
3v3 = 3a/ — 8a2 — 4y + 4^.
Es kommt aber noch eine Relation hinzu, die sich daraus
ergiebt, dass das Product
(o! -f- «! — «2 — Kg)(a — «! + «2 — «3)(« «1 W2 + ai)
eine symmetrische Function der « ist, die man leicht gleich
— ai ~\~ 4= «1 «2 — ^ «3
findet. Wir machen also die Vorzeichen der drei Wurzelgrössen
durch die Relation
A3) — VvlVv^Vvl = af — 4ai«2 + 8a3
von einander abhängig und setzen:
05-1-0!! —- 0S2 0S3
Vv^ = 05 — 05! + O52 — O53
Vv3 = 05 — 06! — O62 -f- O63
a1=a-fai + a2-l- O53.
Daraus ergiebt sich dann:
4 os =«!-{- Vv, -|- Vv2 -f-
A5) 405! = % + l/vT—Vv2—
4 O52 = «i ]/v1 -\-
4os3 = «i — ]/v1 —
Wenn man der VD in (8) das entgegengesetzte Zeichen
giebt, und y durch —y ersetzt, so muss man nach A0) yu y2
mit — y%, — y1 vertauschen. Es bleibt also vt ungeändert und
v2 und v3 werden mit einander vertauscht. Nimmt man für y
eine andere Wurzel der Gleichung (8), etwa y1: so muss wegen
(9)' Vn 2/2 durch j/2, y ersetzt werden und die Grossen vlt v2, v3
erleiden eine cyklische Permutation, wodurch auch die Grossen
osi, os2, oh, in A5) cyklisch vertauscht werden. Wenn man endlich
die Vorzeichen von Vi^, vv%, Vv3 anders wählt, aber so, dass

§. 168. Biquadratische Gleichungen. 573
immer A3) erfüllt bleibt, so treten unter den Grossen A5) gleich-
gleichfalls gewisse Permutationen ein.
Welche Werthe man den mehrwerthigen algebrai-
algebraischen Grossen, die bei der Auflösung auftreten, auch
beilegen mag, die Ausdrücke A5) stellen also immer die
Wurzeln unserer biquadratischen Gleichung in irgend
einer Reihenfolge dar.
In Bezug auf die übrigen Wege zur Auflösung der biquadra-
biquadratischen Gleichung können wir uns kürzer fassen.
Wenn wir zunächst nicht ]/D adjungiren, sondern eine zu
der Gruppe Px gehörige Function, so erhalten wir eine cubische
Resolvente, die nicht Normalgleichung ist. Wir können für diese
Function etwa y2 wählen, was der cubischen Gleichung
A6) 2/6 — 2 Ay* -+- A*y* — D = 0
genügt. Besser noch nimmt man als Wurzeln der cubischen
Resolvente
A7) g = yx — y2, 0l=y2—y, 02= V — Vv
Es gehört dann g zur Gruppe Pv wie schon aus der zweiten
Gleichung A0) hervorgeht. Aus (8) und (9) erhält man für g die
cubische Gleichung
A8) ^ — 3 Ag + .5 = 0.
Man erhält ferner, wenn man
A9) u = aa1 -\- a2a3
setzt,
g = a2 — 3 u,
und daraus die Resolvente für u:
B0) u* — a2u2 -)- (%% — Aa^u -)- 4a2«4, — «i2«* — a>l = 0.
Wenn man aber von der Gleichung A8) oder B0) nicht
eine, sondern alle Wurzeln ädjungirt, so gelangt man wieder zu
der Gruppe Qt. Die Grossen vu v2, vz sind nach A2) unmittelbar
durch g, gu g2 ausgedrückt, und man kann also die Formeln A5)
zur Darstellung der u auch nach diesem Verfahren anwenden.
Man kann ferner zur Lösung der biquadratischen Gleichung
dadurch gelangen, dass man zuerst eine zu der cyklischen Gruppe
P2 gehörige (eine cyklische) Function der Wurzeln ädjungirt,
wie z. B.
B1) w = aal ~f" aia23 ~f" a2a32 -+- a3a-.

574 Fünfzehnter Abschnitt. §. 168.
Diese Function ist sechswerthig und ist also die Wurzel
einer Gleichung sechsten Grades. Diese Gleichung sechsten
Grades ist aber, wie man leicht sieht, imprimitiv, und kann auf
eine Gleichung dritten Grades und auf zwei Quadratwurzeln
zurückgeführt werden. Diese Gleichung sechsten Grades ist eine
Totalresolvente, und zwei ihrer Wurzeln genügen zur rationalen
Darstellung der Wurzeln u. Die Form dieser Resolventen wird
nicht einfach.
Man kann endlich noch darauf ausgehen, durch Adjunctiön
einer zur Gruppe P3 gehörigen Function § die Function f(x)
direct reducibel zu machen und in zwei quadratische Factoren
zu zerlegen. Eine solche Function § ist gleichfalls die Wurzel
einer Gleichung sechsten Grades, die sich aber auch durch Im-
primitivität auf den dritten und zweiten Grad reducirt. Nimmt
man z. B.
B2) ! = « + «!-lax =1V^T,
so sind von den sechs Wurzeln je zwei entgegengesetzt gleich,
so dass eine cubische Gleichung für g2 resultirt. Durch eine
dieser Grossen | la,ssen sich dann die quadratischen Factoren
von f(x) rational darstellen.
Nehmen wir zur Vereinfachung der Formeln at = 0 an und
B3) f(x) = x* -f- ax* -f- bx + c,
so wird
««1 -\~ «2«3 = I2
also
B4) |
ss die beiden quadratischen
~ + I» + a) = 0
! J
so dass die beiden quadratischen Factoren von/(#) folgende werden
B5)
und für £2 ergiebt sich aus B4) durch Multiplication die cubische
Gleichung
oder
B6) |e + 2a|* + {aP- — 4c)g« — b>- — 0.

§. 169. Abel'sohe Gleichungen. 575
Nimmt man für § irgend eine Wurzel dieser Gleichung
sechsten Grades, so giebt jede der Gleichungen B5) ein Paar
Wurzeln von f(x) = 0.
§• 169.
Abel'sche Gleichungen.
Der Grad einer transitiven Permutationsgruppe von m Ziffern
ist immer durch m theilbar und also niemals kleiner als m.
Denn ist P eine solche Gruppe, und Qo der Inbegriff der Per-
Permutationen von P, die die Ziffer 0 ungeändert lassen, so ist auch
Qo eine Gruppe und also ein Theiler von P. Nun kann man
wegen der vorausgesetzten Transitivität in P ein System von
Permutationen 3tu 3t2, . . ., %m—x finden, die 0 in 1, 0 in 2, ...
0 in m — 1 überführen, und dann ist Qo nrx das System aller der
Permutationen von P, die 0 in 1 verwandeln. Danach ist
A) P = Qo + Go*i + öo*. H h Go*»-i,
also der Grad von P gleich dem Producte aus m und dem Grade
von Qo.
Die Galois'sche Gruppe einer irreducibeln Gleichung
ist also niemals von niedrigerem Grade, als die Gleichung
selbst.
Eine Normalgleichung haben wir früher durch die Be-
Bestimmung erklärt, dass sie irreducibel sei, und dass jede ihrer
Wurzeln rational durch jede andere ausdrückbar sein sollte
(§. 152). Daraus ergiebt sich, dass die Gruppe einer Normal-
Normalgleichung sich auf die identische Gruppe reduciren muss, wenn
man eine Wurzel adjungirt; und umgekehrt ist eine Gleichung,
deren Gruppe so beschaffen ist, wenn sie zugleich irreducibel
ist, immer eine Normalgleichung.
Nun reducirt sich P durch Adjunction der Wurzel a0 auf
Qo, durch ax auf jcj1 $03Ti etc. und wenn also P die Gruppe
einer Normalgleichung sein soll, so ist nothwendig und hin-
hinreichend, dass Qo die Einheitsgruppe ist, dass also durch
x, 3tly 3t2, . . ., 3tm—i die Gruppe erschöpft sei. Wir haben also:
Damit eine irreducible Gleichung eine Normal-
Normalgleichung sei, ist nothwendig und hinreichend, dass
der Grad der Gruppe mit dem Grade der Gleichung
übereinstimme.

576 Fünfzehnter Abschnitt. §. 169.
Wir betrachten hier zunächst die specielle Art von Gleichun-
Gleichungen, zu denen die von Gauss zuerst aufgelösten Kreistheilungs-
gleichungen gehören, die Abel allgemein auflösen gelehrt hat,
und die wir also nach ihm Abel'sche Gleichungen nennen
wollenx).
Eine Gleichung mien Grades F(x) = 0 mit den
Wurzeln a, av a2, . . ., «OT—i heisst eine Abel'sche
Gleichung, wenn jede Wurzel, rational durch
eine von ihnen, a, ausdrückbar ist, und wenn,
falls
B) «l=@l(«), «2 = ®2 («).-. «m-l = @m-l(«)
diese rationalen Ausdrücke sind, die Bedingung
C) @Ä@fc(«) = ®k®h(<x)
für je zwei dieser Functionen besteht.
Es bedeutet hierin das Zeichen ©/.©^(a), dass die Function
®h(%) für das Argument x = ®k(u) gebildet werden soll. Selbst-
Selbstverständlich bezieht sich diese ganze Definition auf einen be-
bestimmten als rational angenommenen Körper Sl. Zu diesen
Gleichungen gehören gewiss, wenn Sl der Körper der rationalen
Zahlen ist, die Gleichungen, durch die die Einheitswurzeln be-
bestimmt sind. Denn jede mte Einheitswurzel ist, wenn r eine
primitive unter ihnen ist, in der Form ®h(r) = ** enthalten, und
es ist
Ebenso gehört, wenn der Körper Sl die mten Einheitswurzeln
r enthält, die reine Gleichung
x™ — a = 0,
in der a dem Körper Sl angehört, zu den Abel'schen Gleichungen.
Denn ist u eine ihrer Wurzeln, so sind alle Wurzeln in der Form
ah = rh u
enthalten; es ist also @h(x) = rhx und daher
®h®h(x) = @fc@ft(a;) = r*+*x.
Wenn die Function F(x) nicht irreducibel ist, so hat sie
einen bestimmten irreducibeln Factor q> (x), der die Wurzel es
hat, und unter den Wurzeln von <p(x) = 0 bestehen gleichfalls
x) Abel, Memoire sur une classe d'equations resolubles algebriquement.
Crelle's Journal f. Mathematik, Bd. 4, 1829. Oeuvres completes, nouvelle
edition, 1881, Bd. 1, S. 418.

§. 169. Abel'sche Gleichungen. 577
die durch B) und C) ausgesprochenen Relationen. Es ist
daher q>(x) = 0 nach §. 15.2 eine Galois'sche Resolvente Ton
F(x) = 0, und wenn <p(x) = 0 gelöst ist, so sind damit alle
Wurzeln von F(x) bekannt. Es genügt also, wenn wir uns auf
die Betrachtung irreducibler Abel'scher Gleichungen
beschränken.
Die Galois'sche Gruppe einer Abel'schen Gleichung, sei
sie irreducibel oder nicht (wenn nur ihre Wurzeln von einander
verschieden sind), hat die Eigenschaft, dass bei der Zusammen-
Zusammensetzung ihrer Permutationen das commutative Gesetz gilt; sie
ist also eine commutative Gruppe.
Es seien nämlich
D) «, «j = 0J («), «2 = @2 («), . . ., «„_! ==: @m_! («)
die Wurzeln von F(x) und
E) «, «' = @», «" = @"(«), . . .
die darunter enthaltenen Wurzeln des irreducibeln Factors cp(x)
von F(x).
Da, wie schon bemerkt, <jp(#) = 0 eine Galois'sche Resol-
Resolvente ist, so besteht die Gruppe der Gleichung aus den Substitu-
Substitutionen des Körpers £l(cc), also aus den Substitutionen
F) ö = («, «), ö' = («, «'), ö" = («, «")...
Diese Gruppe befolgt aber das commutative Gesetz; denn es sei
«' = («,«') = [«,©'(«)]
6"= («,«") = [«.«»];
dann ist nach §. 154
ö' ö" = [«, @' («)] [©' («), @' @"(«)] = [«, @' @"(«)]
6"ö' = [«,©"(«)] [®"(«), @"@'(a)] = [«,©"©' («)].
Wegen C) ist daher ö'ö" = ö"ö', worin ö', 6" zwei beliebige der
Substitutionen 6 sein können. Folglich ist die Gruppe der
Substitutionen des Körpers Sl(u) und damit auch die isomorphe
Permutationsgruppe der Gleichung F(x) = 0 commutativ.
Es gilt nun auch das Umgekehrte, wobei aber die Irre-,
ducibilität vorausgesetzt sein muss.
Eine irreducible Gleichung cp(x) = 0 mit commu-
tativer Gruppe ist eine Abel'sche Gleichung.
Es seien a, csj, a2, ..., «OT—i die Wurzeln von q>(x) = 0, und
P die Gruppe dieser Gleichung, die wegen der Irreducibilität von
Weber, Algebra. I. 37

578 Fünfzehnter Abschnitt. §. 169.
<p{%) transitiv ist, und die wir jetzt ausserdem als commutativ
annehmen. Es sei Q der Theiler Tori P, der das Element 0 in
Ruhe lässt. Ist dann sr» eine Permutation, die die Ziffer 0 in *
überführt, so ist nr1 Q it{ die Gruppe der Permutation in P,
die die Ziffer * nicht ändern. Da nun aber in jeder Zusammen-
Zusammensetzung von Permutationen aus P die Componenten vertauscht
werden können, so ist
d. h. die Gruppe Q lässt auch die Ziffer * ungeändert. "Wegen
der Transitivität vonP kann aber * jede der Ziffern 1, 2,..., m— 1
bedeuten, folglich besteht Q aus der einzigen identischen Permu-
Permutation, und es giebt in P ausser der identischen keine Permu-
Permutation, die eine Ziffer ungeändert lässt. Adjungirt man aber
eine Wurzel u, so reducirt sich die Gruppe P auf eine Gruppe,
die a ungeändert lässt, also auf die Einheitsgruppe, und die
Gleichung ist gelöst, d. h. jede Wurzel von q>(%) kann durch
eine beliebige unter ihnen, «, rational ausgedrückt werden.
Demnach ist cp (x) = 0 eine Normalgleichung und somit ihre
eigene Galois'sche Eesolvente. Ist cck = ®fc(a), so besteht die
Galois'sche Gruppe dieser Gleichung aus den Substitutionen
und es ist
Da die Gruppe commutativ sein soll, so muss
@ft@&(«) = @&@Ä(«)
sein, d. h. <p (%) = 0 ist eine Abel'sche Gleichung. Dies ist
der Grund, weshalb die commutativen Gruppen auch Abel'sche
Gruppen genannt werden (§. 155). Es folgt also noch aus dem
oben gegebenen Satze über die Gruppe von Normalgleichungen,
dass bei einer transitiven Abel'sehen Permutationsgruppe die
Zahl der Permutationen mit der Zahl der vertauschten Ziffern
übereinstimmt.
Hier haben wir die Irreducibilität der gegebenen Gleichung
. vorausgesetzt. Wollen wir auch reducible Gleichungen F(x) = 0
mit commutativer Gruppe P berücksichtigen, so betrachten wir
einen irreduciblen Theiler cp (x) von F(x). Die Gruppe P' der
Gleichung q>(%) = 0 erhält man, wenn man die Permutationen
von P auf die Wurzeln von q>{x) anwendet, und wenn daher P
commutativ ist, so ist es auch P'.. Daraus ergiebt sich:

§.. 170. Cyklische Gleichungen. 579
Hat eine reducible Gleichung .F(a;) = 0 eine com-
mutative Gruppe, so giebt jeder irreducible Thei-
ler q> von F eine Abel'sche Gleichung <p = 0.
Es ist aber nicht nothwendig, dass die Wurzeln' des einen
Theilers q> rational durch die eines anderen ausdrückbar sind,
und daher können wir, im Hinblick auf unsere Definition, die
GleichungF(x) = 0 nicht immer als eine Abel'sche bezeichnen.
Es ist endlich noch zu bemerken, dass bei einer commuta-
commutativen Gruppe jeder Theiler normal ist, da ja immer Jt-1%jt = %isk,
wenn it und % beliebige Elemente einer commutativen Gruppe sind.
•§. 170.
ßeduction der Abel'schen Gleichungen auf cyklische.
Wir haben schon vorhin gesehen, dass in einer transitiven
Abel'schen Gruppe ausser der identischen keine Permutation vor-
vorkommt, die eine Ziffer ungeändert lässt. Daraus aber folgt noch
ein anderer Satz. Nehmen wir an, eine Permutation % einer solchen
Gruppe sei in ihre Cyklen zerlegt, und der Cyklus, der die wenig-
wenigsten Glieder enthält, sei ein r-gliedriger. Dann wird jcr die
Glieder dieses Cyklus ungeändert lassen und muss also die iden-
identische Permutation sein. Daraus folgt aber, dass auch alle
übrigen Cyklen von sr, wenn noch andere vorhanden sind, aus
r Gliedern bestehen müssen, also:
1. Eine Permutation einer transitiven Abel'schen
Gruppe enthält nur Cyklen von gleicherGliederzahl.
Die Anzahl r der Glieder eines Cyklus muss ein Theiler von
m sein, wenn m der Grad der Gruppe ist, und wenn m = r s ist,
so ist s die Anzahl der r-gliedrigen Cyklen, aus denen % besteht.
Ist nun P die Gruppe einer Abel'schen Gleichung F(x) = 0,
so nehmen wir irgend eine nicht identische Permutation it aus
P heraus und zerlegen sie in ihre Cykeln
worin jeder der Cyklen y sich auf r Wurzeln der Gleichung
F(x) = 0 bezieht. Wir wollen diese Wurzeln so anordnen, dass
y = («, al5 «a, . . ., ccr-i)
ysl (, i, 25 1 rl)
wird.
37

580 Fünfzehnter Abschnitt. §. 170.
Ist nx irgend eine Permutation von P, so ist wegen der
Vertauschbarkeit
C) 1C^l1tTCl = lt.
Nach dem Satze über die Bildung der Permutationen sr^sTsr,
(§. 160, 4.) darf also ic nicht geändert werden, wenn die Permu-
Permutationen tcx in den Cyklen von % ausgeführt werden. Da aber
die Cyklen vollständig bestimmt sind, abgesehen von ihrer An-
Anordnung und von ihrem Änfangselement, so ergiebt sich, dass
durch Anwendung irgend einer Permutation % aus P die Ele-
Elemente der einzelnen Cyklen y nicht von einander getrennt,
sondern nur unter einander (cyklisch) vertauscht und ausserdem
die Cyklen mit einander vertauscht werden können. Die Gruppe
ist also, wenn s > 1 ist, imprimitiv.
Eine rationale Function der Argumente a, au . . ., ar—i, die
ihren Werth nicht ändert, wenn die u der cyklischen Permu-
Permutation y und ihren Wiederholungen unterworfen werden, heisst
eine cyklische Function der a. Bezeichnet man mit
D) ca = ij> («, «!, . . ., ar-i)
eine solche cyklische Function und mit
E) ca, cax, ra2, . . ., ras_!
die conjugirten Werthe von oo, setzt also z. B.
F) cal = ^(ß,ß1,...,ßr_1),
so sind diese Grossen nach §.165 die Wurzeln einer irreducibeln
Gleichung sten Grades:
#(*) = 0,
deren Gruppe man erhält, wenn man die durch P hervorgerufenen
Permutationen der Grossen E) aufsucht.
Man erhält aber die durch «x «2 unter den Grossen E)
bewirkte Permutation, wenn man die beiden durch nx und sr2
einzeln hervorgerufenen Permutationen zusammensetzt, und die
Gruppe der Permutationen von E) ist daher auch commutativ.
Daher ist <&(t) = 0 eine Abel'sehe Gleichung sten Grades.
Adjungirt man ca, so zerfällt F{x) in s Factoren rte? Grades:
F(x) = F(x,co)F(x,(ol) . . . *>,(»,_!),
von denen der erste, F(x,ca), die Wurzeln a, a1? . . ., u.r-\ hat,
und die Gruppe der Gleichung F(x, ca) = 0 besteht allein aus
der Periode der cyklischen Permutation y.
Wir wollen eine Gleichung, deren Gruppe aus einem einzigen
Cyklus und seinen Wiederholungen besteht, eine cyklische

§. 170. Cyklische Gleichungen. 581
Gleichung nennen, so dass die cyklischen Gleichungen der
einfachste Specialfall der Abel'sehen Gleichungen sind. "Wir
haben dann also bewiesen, dass die Lösung jeder Abel'sehen
Gleichung zurückgeführt wird auf die Lösung einer Abel'sehen
Gleichung niedrigeren Grades und auf die Lösung einer Reihe
cyklischer Gleichungen. Diesen Satz kann man wieder auf die
Hülfsgieichung stm Grades anwenden, und damit so lange fort-
fortfahren, bis diese Hülfsgieichung sich auf den ersten Grad redu-
cirt. Damit erhält man also das Resultat:
Die Lösung einer Abel'schen Gleichung lässt sich
immer auf die Lösung einer Reihe von cyklischen
Gleichungen zurückführen, deren Grade Theiler des
Grades der gegebenen Gleichung sind.
Es ist nicht nothwendig, in die Definition der cyklischen
Gleichungen die Irreducibilität mit aufzunehmen. Wir können
daher allgemein die Definition so fassen:
Eine Gleichung mten Grades F(x) = 0 mit m
verschiedenen Wurzeln heisst eine cyklische
Gleichung im Körper £1, wenn ihre Wurzeln a, ax,
a2) • • -1 «m-1 nicht rational sind, aber sich so
anordnen lassen, dass die cyklischen Functionen
der Wurzeln in £1 rational sind.
Wenn also
G) n = (cc, ax, a2, . . ., Km_x)
ist, so muss jede Function in Sl enthalten sein, die die Permu-
Permutationen der cyklischen Gruppe
(8) C = 1, n, 3r2, n\ . . ., rf"-1
gestattet. Die Galois'sche Gruppe einer cyklischen Gleichung
ist entweder die Periode C selbst und dann ist die Gleichung
irreducibel, oder sie ist ein Theiler von C; sie besteht dann,
wenn e und / zwei ganzzahlige Factoren von m sind und
m = ef
ist, aus den Permutationen
(9) Ce = 1, tc% tc*°, . . ., n(f-»e,
und die cyklische Gleichung zerfällt in e Factoren ften Grades.
Denn nehmen wir eine zu der Gruppe C gehörige Function
t(>(tt, ccu ..., «m_i), so ist diese nach Voraussetzung gleich einer
Grosse in ß, die wir mit a bezeichnen. Auf die rationale
Gleichung -ip = a ist dann keine nicht in C enthaltene Permu-

582 Fünfzehnter Abschnitt. §. 170.
tation anwendbar, und folglich kann die Gruppe der Gleichung
keine. anderen Substitutionen enthalten als solche, die in C vor-
vorkommen. Wenn nun tt in der Gruppe der Gleichung vorkommt,,
so ist sie mit C identisch, und da C transitiv ist, ist die
Gleichung irreducibel. Ist aber ne die niedrigste Potenz von «,
die in der Gruppe der Gleichung vorkommt, so ist Ce diese
Gruppe. Ce ist aber, wenn e > 1 ist, intransitiv, und die
Gleichung ist reducibel.
Die cyklischen Gleichungen haben, wie alle Abel'schen
Gleichungen, die Eigenschaft, dass jede Wurzel rational durch
jede andere ausdrückbar ist. Hier lassen sich diese Ausdrücke
folgendermaassen cyklisch anordnen. Sind u, ot^, cc2, ..., «„,_! die
Wurzeln der cyklischen Gleichung F(x) = 0, so ist die ganze
Function (m — l.)ten Grades von x
F{X) (J^ + _^_ _| 1 « J) =
W \X « ' X «i1 [ X — «m —1/
ungeändert durch die Permutation it und also in Sl enthalten.
Wenn wir .darin x = cc, ax, . . ., am—x setzen und das Zeichen
einführen, so folgt
A0) a1 = @(a), a2
und dies gilt, mag F(x) reducibel oder irreducibel sein, wenn
nur F(x) und F'(x) keinen gemeinsamen Theiler haben.
Wenn der Grad der cyklischen Gleichung keine Primzahl
ist, so lässt sie sich durch das oben auf Abel'sehe Gleichungen
im Allgemeinen angewandte Verfahren noch weiter reduciren.
Wenn nämlich m = ef irgend eine Zerlegung von m in,
zwei Factoren ist, so zerfällt die Permutation sre in e Cyklen y
von je / Gliedern:
y ==. («, cce, aie, . . .. «(/-De),
Yi = («1, «e + l, «2C + 1» • • •> a(f—l)e + l),
Ye — 1 =; \ae—1, a2e —1, a3e —1, • • •, am—l)-
Nun bestimmen wir eine zu dem ersten dieser Cyklen ge-
gehörige Function tp und setzen
rj = 4>(u, cce, cc.2e, . . ., a(/_i) e),
e + l, «2C + 1, • • •, «(/-l)e + l),'
i, «2e-i, «3e-l, • • ., «m—l)-

§. 170. Cyklische Gleichungen. 583
Diese Grossen sind alle von einander verschieden, aber bei
einer cyklischen Permutation ihrer Argumente bleiben sie un-
geändert. Durch Anwendung der Permutation % gehen die Grossen
¦>?, ¦%,¦%) • • ••, Ve-i
cyklisch in einander über, und nach der Voraussetzung sind also
ihre cyklischen Functionen, und folglich auch ihre symmetrischen
Functionen rational. Sie sind also die Wurzeln einer cyklischen
Gleichung eten Grades, während F(x) in e Factoren ftea Grades
F(x) = F(x, rj)F(x, tIi)... F(x, ne-i)
zerfällt, deren jeder eine cyklische Gleichung /ten Grades für die
Wurzeln eines der Cyklen y ergiebt.
Denn setzen wir etwa
F1 = (X — a) (x — O . . -. (x — M(/_i)e),
so gestattet diese Function die Permutationen der Periode von y.
Also gestattet sie auch die Permutationen der Gruppe, die nach
Adjunction von rj zur Galois' sehen Gruppe unserer Gleichung
wird, die ja nur aus Potenzen von y, y^ . . ., ye—i bestehen kann.
Es ist daher nach dem Satze von Lagrange (§. 162, 2.) I1
rational durch rj darstellbar, also Fr = F(x, rj). Die Gleichung
F(x, rj) = 0 ist aber wieder cyklisch in £1 (¦»?), da die cyklischen
Functionen ihrer Wurzeln diesem Körper angehören.
Die Auflösung der cyklischen Gleichungen mten Grades ist
hierdurch abhängig gemacht von der Lösung cyklischer Glei-
Gleichungen, deren Grade die Primfactoren von m sind. Ist also z. B.
m eine Potenz von 2, so wird die Lösung durch eine Reihe von
Quadratwurzeln bewerkstelligt. Auf diesem Wege hat Gauss
zuerst die Kreistheilungsgleichungen behandelt1).
Wir knüpfen endlich noch die für die Folge wichtige Be-
Bemerkung hier an, dass für einen Primzahlgrad die Begriffe der
Normalgleichung und der cyklischen Gleichung zu-
zusammenfallen. Denn jedenfalls ist eine cyklische Gleichung vom
Primzahlgrad, da sie irreducibel ist, eine Normalgleichung. Und
wenn umgekehrt der Grad n einer Normalgleichung, der zu-
zugleich der Grad der Gruppe dieser Gleichung ist, eine Primzahl
ist, und % eine nicht identische Permutation dieser Gruppe, so
ist der Grad von je, der ja ein Theiler von n sein muss, gleich n,
und die Gruppe der Gleichung ist 1, ä, sz2, . . ., je"—1, also
cyklisch.
Gauss, Disquisitiones arithmeticae, Sectio VII.

584 Fünfzehnter Abschnitt. §. 171.
"§• 171.
Resolventen von Lagrange.
Die Methode der Auflösung cyklischer Gleichungen, die wir
jetzt kennen lernen wollen, ist gleichmässig auf Primzahlgrade
und zusammengesetzte Grade anwendbar. Man bedient sich dazu
gewisser Ausdrücke, die unter dem Namen der Resolventen
von Lagrange bekannt sind1), die bei allen Untersuchungen
über die algebraische Auflösung von Gleichungen von grossem
Nutzen sind.
Es sei F(x) = 0 eine Gleichung mit den Wurzeln a, «1?
«2, • • •, «M-i. Wir bezeichnen mit £ irgend eine mte Einheits-
Einheitswurzel und -führen die Bezeichnung ein
A) (£,«) = « + £«! + £2«2 -| 1- £"i-1am_j.
Die so definirten Summen sind es, die man die Lagrange'-
schen Resolventen nennt. Wenn diese Functionen für alle
mtea Einheitswurzeln £ bekannt sind, so ist auch die Gleichung
selbst gelöst, denn es ist nach §. 141 F)
B) 2sk = m oder = 0,
je nachdem k durch m theilbar ist oder nicht, und daraus folgt
C)
worin sich die Summen über alle m1™ Einheitswurzeln s er-
erstrecken. Man kann auch die anderen Wurzeln in gleicher Weise
ausdrücken:
D) maK=S £-*(£,«),
so dass in der That Alles auf die Kenntniss von £ und der
Functionen (£, «) zurückgeführt ist.
Die Summen B) und C) lassen sich noch in etwas anderer
Weise darstellen, da die sämmtlichen mieu Einheitswurzeln Potenzen
einer primitiven unter ihnen sind. Versteht man also unter s
eine festgehaltene primitive mte Einheitswurzel und unter X einen
Index, der ein volles Restsystem nach dem Modul m, etwa die
a) Lagrange, Reflexions etc., s. S. 508. Früher haben wir unter
Resolventen auflösende Gleichungen verstanden, hier sind es auflösende
Functionen.

§. 171. Resolventen von Lagrange. 585
Zahlenreihe 0, 1, . . ., m — 1 durchläuft, so können wir für die
Gleichungen B), C) setzen
ma
Wir untersuchen diese Resolventen (£, «) zunächst als
Functionen der m unabhängigen Veränderlichen «, und
wollen wegen der einfacheren Darstellungsweise der Formeln
übereinkommen, dass ccm = «0 = a, und überhaupt cch = ak sein
soll, wenn h = Je (mod m) ist. Wir erhalten dann das ganze
System der Variablen «, wenn wir in Kh den Index ein volles
Restsystem nach dem Modul m durchlaufen lassen.
Für diese Resolventen gelten nun die folgenden Sätze.
1. Wenn man auf die Indices der cc die cyklische
Permutation ¦% = @, 1, . . ., m — 1) anwendet, so
geht (£, a) in e~ 1(e,a) über, und durch die Permu-
Permutation sr* geht (£, «) in e~k(e, «) über.
Dies zeigt die Definition A) der Resolventen unmittelbar.
Wir verstehen ferner unter v einen beliebigen positiven
Exponenten und bilden nach dem polynomischen Lehrsatze (£,«)".
In der entwickelten Potenz setzen wir sm = 1 und ordnen dann
nach Potenzen von e. Es ergiebt sich dann ein Ausdruck von
der Form
E) (s, *y = Ap + £ A{» + s'A? H -h £«-i A^_x
= i £ä4">,
0,tn—1
worin die JW, A^, . . .^-A^^^ Formen vtea Grades mit ganz-
ganzzahligen Coefficienten und den Variablen et sind, aber von £ un-
unabhängig. Auch hier möge Ah = A1c sein, so oft h = 7c (mod m).
Danach beweisen wir den Satz:
2. Wenn man auf die Indices der a die cyklische
Permutation ¦% anwendet, so erleiden die Indices
der Coefficienten von (e,a)v die cyklische Permu-
Permutation Jtr, d. h. JLW geht in A^+v über.
Um dies nachzuweisen, bemerken wir, dass die Formel E)
für jede beliebige mte Einheitswurzel s, einschliesslich 1, richtig
bleibt, und hiernach folgt aus B)
F)

586 Fünfzehnter Abschnitt. §. 171.
Macht man auf der rechten Seite dieser Formel in den
Indices der « die Permutation ä, so ergiebt sich nach 1.
d. h. A!jp geht in ^\v über, wie im Satz 2. behauptet ist.
Der Satz 2. ist ein specieller Fall eines allgemeinen Theo-
Theorems. Entwickeln wir ein Product von beliebig vielen Factoren
(«, k)v (e\ «)ri (s\ «)V2 . . .,
worin v, vx, v2 ... positive, Xt, lt . . . beliebige ganze Zahlen
sind, und ordnen es, wie vorher («, «)r, nach Potenzen von s, so
mag sich ergeben
G) (£, «)• (e\ «)n (eV, «y* •••=it»B»,
0,m —1
worin die Bj,- von £ unabhängige Formen von der Variablen «
sind. Da auch diese Entwickelung für alle mten Einheitswurzeln s
gilt, so kann man die Formel B) anwenden und erhält
= 27 £-*(£, ct)v (e\ «)vi (s% a)r« . . .,
woraus man nach 1. schliessen kann, dass B^ durch die Sub-
Substitution % in
übergeht. Wir haben also:
3. Die Permutation ä, auf die Indices der cc an-
angewandt, ruft unter den Indices der Coeffi-
cienten des nach e geordneten Productes
(8) 0, ct)v (a^i, «)"i (s\ «)'s . . .
die Permutation nv + xivi + h*2--- hervor.
In diesen Theoremen kann die Permutation ¦% wiederholt
werden; sie bleiben richtig, wenn ¦n, durch irgend eine Potenz
von n ersetzt wird und sie gelten, was auch £ für eine mte Ein-
Einheitswurzel sein mag. Ist aber e eine imprimitive Einheitswurzel,
so treten gewisse Vereinfachungen ein, die wir noch kennen
lernen müssen. Ist e ein Theiler von m,
m — ef,
und £ irgend eine ete Einheitswurzel, so wird der Ausdruck A)
(£,«) = « -\~ £«! +-"''-l- £e-1«e-l '
-\~(Xe

§. 171. Resolventen von Lagrange. 587
Wir führen nun die Bezeichnung ein:
V == « + K« + «2e + • * • + «</-l)e
¦J?e-1 = «e-1 + «Se-l + «3e-l + • • • + «m-U
und nennen diese Grossen, .wie es Gauss in dem speciellen Falle
der Kreistheilung gethan hat, , die /- gliedrigen Perioden der
Grossen «. Es wird dann
A0) . (£, a) = n +•£% + £2%H h«6^-!,
wofür wir auch (£, vf) schreiben können.
Die Anwendung der Permutation % auf die Indices von «
bringt unter den nach dem Modul e zu nehmenden Indices der
Grossen rj die cyklische Permutation
A1) y = @, 1, 2, . . ., e — 1)
hervor.
Entsprechend der Formel A0) können wir die Formeln E)
und G) nun auch so schreiben:
(e, nY =
worin dann
EW = J.W _|_ J.W 4- . U J.W
(r& = JBjt -f~ -Be + ü ~f" " • " ~|- -^(/-De + S
ist, und JSjW und G^ ganze homogene Functionen der « sind, die
sich auch als Functionen der rj darstellen lassen.
Die Grossen ¦»?&, E^\ Gk bleiben ungeändert, wenn die Permu-
Permutation 3re auf ihre Indices angewandt wird, d. h. wenn, der Index
um ein Vielfaches von e verändert wird, und wir können also
jetzt.die Sätze 2. uud 3. so vervollständigen:
4. Ist e eine beliebige ete Einheitswurzel, und e ein
Theiler von m, so erleiden, wenn auf die Indices
von « die Permutation ¦% ausgeübt wird, die
Indices k der Coefficienten E]p von (s, i])v. .die
Permutation yr; und die Indices der Coeffi-
Coefficienten G des Productes (s, rj)v (e\ rj)vi (e\ ij)r2 . . .
die Permutation y + h^+k^--- . ,. ; .

588 ¦ Fünfzehnter Abschnitt. §. 172.
§. 172.
Auflösung der cyklischen Gleichungen.
Die Lagrange'sehen Resolventen führen durch Anwendung
der jetzt bewiesenen Sätze zu der Auflösung der cyklischen
Gleichungen, genauer gesagt, zur Reduction auf reine Glei-
Gleichungen.
Wir verstehen jetzt unter den a nicht mehr beliebige
Variable, sondern die Wurzeln einer cyklischen Gleichung, so
dass die cyklischen Functionen der cc als bekannte Grossen zu
betrachten sind.
Nach dem Theorem §. 171, 2. sind die Coefficienten von {s,cc)m
cyklische Functionen der cc.
Verstehen wir unter a0, aL, . . ., am_a Grossen in £1 und
setzen
A) ^a = o, + Ol 6* + a, c" H 1- a..! «*»-»*,
so folgt aus diesem Theorem
Bezeichnet darin s eine primitive mte Einheitswurzel, so sind
in der Form (e\ cc) alle Resolventen enthalten.
Bemerken wir noch, dass A, «) = a als die Summe der
Wurzeln zu den bekannten Grossen gehört, so haben wir nach
§• 171 C)
w m m
C) ma = a + Vti + V*. H h
und damit also u durch Radicale mten Grades ausgedrückt, die
unter den Wurzelzeichen aussei* den Grossen, die von Hause aus
in £1 vorkommen, noch mto Einheitswurzeln enthalten.
Jedes dieser Radicale hat, für sich betrachtet, m verschie-
verschiedene Werthe, die sich um mte Einheitswurzeln als Factoren von
einander unterscheiden. Geben wir jeder mtea Wurzel alle ihre
Werthe, so erhalten wir aus C) viele verschiedene Werthe von «,
unter deuen nach §. 171, D) die sämmtlichen Wurzeln «, «15
«2, . . ., «OT_i vorkommen. Aber die Zahl der so aus C) abgelei-
abgeleiteten Ausdrücke ist viel grösser, und es handelt sich noch darum,
die beizubehaltenden von den abzusondernden zu unterscheiden.
Am einfachsten führt dazu folgender Weg.

§. 172. Auflösung cyklischer Gleichungen. 589
Wenden wir das Theorem §. 171, 3. auf nur zwei Factoren
an, so ergiebt sich, dass
(£, «)' (£*, «>«
eine Function in £1 (e) ist, wenn v -\- l (i = 0 (mod m). Setzen
wir also fi ¦= 1, v = m — A, so folgt, wenn
eine Grosse in £&(e) bedeutet,
also nach B):
D)
l—l
und dadurch sind, wenn e eine festgehaltene primitive mte Ein-
Einheitswurzel bedeutet, die sämmtlichen in C) vorkommenden Kadi-
m
cale rational durch eines von ihnen, Vih, ausgedrückt.
Giebt man diesem einen seine m verschiedenen Werthe, so
erhält man aus C) gerade die m verschiedenen Werthe «.
Es ist nur ein Ausnahmefall, in dem dieses Verfahren nicht
anwendbar ist, das ist der, wenn tf»a = 0 ist. Wir können aber
durch eine kleine Modification des Verfahrens uns von einem
solchen Ausnahmefall frei machen. Dem schicken wir Folgendes
voraus.
Es sei p eine in in aufgehende Primzahl und m=pn;
wie oben sei £ irgend eine festgehaltene primitive mte Einheits-
Einheitswurzel. Dann giebt es immer ein durch p nicht theilbares A., so
dass (e\ a) von Null verschieden ist. Denn bilden wir nach der
Formel §. 171, D) die Differenz ccn — «0, so erhalten wir
m («„ — O = V (£-">¦ — 1) (e\ «).
0, m — 1
Nun ist aber s~nX — 1 immer = 0, so oft k durch p theilbar
ist, uud wenn (e\ «) in allen anderen Fällen, wo also l nicht
durch p theilbar ist, verschwindet, so ist «„ = «„, gegen die
Voraussetzung, dass die « alle verschieden sein sollen. Es giebt
also wenigstens ein durch p nicht theilbares A, so dass (V, «)
von Null verschieden ist.
Nun zerlegen wir m in seine Primfactoren und setzen
m = "

, 590 Fünfzehnter Abschnitt. §. 172.
worin 2>i, jpa •¦'• • Potenzen von verschiedenen Primzahleu sind.
Wir setzen noch
m = p1m1 = p2m2 . . .,
und wählen, was nach dem soeben Bewiesenen stets möglich ist,
/tj relativ' prim zu pu X2 relativ prim zu p2 etc., so dass
0*1, «), (e\ a) . . .
von Null verschieden sind. Dann ist nach dem Theorem §. 171, 3.:
E) (s\ k) (s\ «)mir 0^, a)™** • ¦ • == %i
eine in £l(e) enthaltene Grosse, wenn
F) l = — v (^ mi -\- /l2 m2 -\- • ¦ •) (mod m).
Es ist aber (e\ «)"i eine Wurzel p^ Grades einer Func-
tion 9Dj in ß(£), und wir setzen also
G) (£\ «)«i = V<Pi, (e\ «)"• = V<
Dann wird nach E)
(8) '
Nun ist X1m1 -f- /t2m2 -|- • •• relativ prim zu m, da m2 . . .
durch 2>i theilbar, Aj»«! zu j)j relativ prim ist, und also erhält
man aus F) für jedes X eine nach dem Modul m völlig bestimmte
Zahl v.
Wenn wir also die Ausdrücke (8) in C) einsetzen und den
p\ pj
Radicalen Vfi, V<Pü • • • alle ihre Werthe beilegen, so erhalten
wir für « genau m verschiedene Werthe und nicht mehr.
Die letzten Resultate können wir benutzen, um eine Form
der Darstellung der Wurzeln « in etwas verallgemeinerter Gestalt
abzuleiten, die Abel an der angeführten Stelle mittheilt, und die
sich auf den Fall bezieht, wo der Körper Sl reell ist, d. h. aus
lauter reellen Zahlen besteht. Die Functionen cp, il>, %, wie wir
sie oben benutzt haben, sind dann zusammengesetzt aus reellen
Zahlen und aus der Einheitswurzel e, die man durch die Theilung
der Kreisperipherie in m gleiche Theile findet; man kann etwa
^ 1% . . . 2%
s ¦= e m = cos \- t sin —
m ' m
setzen.
Die Function g)t geht, wenn £ in £—1 verwandelt wird, in
den conjugirt imaginären Werth über, den wir mit <pi bezeichnen.

§. 172. Auflösung cyklischer Gleichungen. 591
Wir wollen eine positive Grosse ^ und einen Winkel ®x so
annehmen, dass
(9) K = ?! &\ <p[ = Pl e-*ei,
oder
¦q>1 = Qt (cos ©! + * sin 0t)
<pi = qx (cos ®! — » sin ©!),
woraus noch folgt:
A1) tf. = Vl qpj.
Nun ist
A2) (e*, «) (£~S «) = ± o,
eine Grosse des Körpers ß(a_) (nach §. 171, 3.), und zwar ist es,
da sie sich beim Uebergang zum conjugirt imaginären Werth,
d. h. bei der Vertauschung von s mit s~l nicht ändert, eine
reelle Grosse. Das Vorzeichen wollen wir so bestimmen, dass %
positiv ist. Es ist also nach A1), da q? positiv ist,
und es ergiebt sich daraus, dass bei ungeradem m jedenfalls das
obere Zeichen gilt; bei geradem m kann auch das untere ein-
eintreten. Es ist also
A3) ?! = V^r,
wo die Quadratwurzel positiv zu nehmen ist.
Ferner sind
reelle Grossen in -ß(f), und es ergiebt sich aus A0)
b r ¦
A5) 008®!=-^, sin@!= l
woraus noch die Relation folgt:
«T = 1>? + c>.
Demnach ergiebt sich
und nun verfährt man mit den Functionen q>2 u. s. f. ebenso.
Man bestimmt also ®2 • • • aus einem System von Gleichungen
wie A5) und erhält, wenn man noch
A6) mt ©! + ot2 ®2 -| = ®
setzt, nach (8)

592 Fünfzehnter Abschnitt. §. 172.
A7) Viin = vV«?1 a%* .. .) e ~™v %i.
Nach A5) können wir setzen
und wenn wir also durch Zerlegung in den reellen und imagi-
imaginären Bestandtheil
A8) F, -f id)"! (&2 -f ict)* • • - = B -\-iC
erhalten und
A9) a^a^ ¦ • • ¦= A
setzen, so folgt nach A6)
_ B + iC
also
B0) V1m cos® — B, VÄm sin© = G,
und
B1) Wi = V^^ (cos ^ - ,• sin ^) X,.
Der Winkel ® ist durch B0) nur bis auf ein Vielfaches von
2% bestimmt, und wenn man also & -f- 2hn für @ setzt und h
von 0 bis m — 1 gehen lässt, so erhält man aus B1) die m ver-
&v
schiedenen Werthe der Wurzelgrösse. Die Functionen cos —
, . ®v ... , ,. , , , 0.0
und sin — können noch rational durch cos —, sin — aus-
m mm
gedrückt werden. Die Auflösung der cyklischen Gleichungen in
dem reellen Körper £1 ist also auf Folgendes zurückgeführt.
Man adjungirt zunächst dem Körper £1 die mte Ein-
Einheitswurzel e (Theilung der Kreisperipherie in m gleiche
Theile). Hierauf sind A, B, G bekannt. Man adjungirt
ferner die positive Quadratwurzel "VA, dann sind cos®
und sin® durch B0) bekannt. Endlich adjungirt man
cos —, sin — (Theilung des Winkels ® in m Theile).
m . m
Dann ist die cyklische Gleichung durch B1) gelöst.
Diese Betrachtungen führen noch zu einem interessanten
Resultat über die Realitätsverhältnisse der Wurzeln cyklischer
Gleichungen.

§. 173. Theilung des Winkels. 593
Stellen wir, wie in §. 170, A0), in der Reihe der Wurzeln
«, «u . . ., «m—i jede rational durch die vorangehende dar:
worin, da hier £1 reell vorausgesetzt ist, ®{x) eine reelle ratio-
rationale Function von x bedeutet, so folgt zunächst, dass, wenn
eine der Wurzeln reell ist, auch alle übrigen reell sein müssen.
Dies findet immer bei ungeradem m statt, da eine reelle Glei-
Gleichung ungeraden Grades immer wenigstens eine reelle Wurzel
haben muss.
Bei geradem m können auch imaginäre Wurzeln vorhanden
sein, und wenn eine Wurzel imaginär ist, so müssen es alle sein,
da, wenn eine reelle Wurzel vorkommt, alle anderen auch reell
sind. Bezeichnen wir mit ©v(x) die v malige Wiederholung der
Function @, so ist
Ist also a = a0 mit a* conjugirt imaginär, so sind auch für
jedes v die Functionen &r(u0) und @r(alc), d. h. «„ und av + lc
conjugirt imaginär.
Daraus folgt, dass 2k = m sein muss, und wir schliessen,
dass im Falle imaginärer Wurzeln
«fc und « ,»
*+T
für jeden Index h ein Paar conjugirt imaginärer Wurzeln bilden.
Die cubischen Gleichungen werden diirch Adjunction der
Quadratwurzel aus der Discriminante cyklische Gleichungen.
Wenn die Discriminante positiv ist, so sind die Wurzeln in
Uebereinstimmung mit diesem Satze reell.
Theilung des Winkels.
Zu den cyklischen Gleichungen gehören auch die Gleichungen,
von denen die Theilung eines Winkels in m gleiche Theile ab-
abhängt, auf die wir die allgemeinen cyklischen Gleichungen in
einem reellen Körper zurückgeführt haben.
Die Aufgabe kann so formulirt werden:
Wenn cosmqo und sinmq) gegeben sind, so sollen
daraus coscp und sin<p gefunden werden.
Weber, Algebra. I. gg

594 ' Fünfzehnter Abschnitt. §. 173.
Die Werthe von cos m <p und sin m <p denken wir uns kleiner
als 1 und so, dass ihre Quadratsumme = 1 ist, gegeben.
Wir adjungiren noch wte Einheitswurzeln, mit denen wir uns
im nächsten Abschnitte noch eingehender beschäftigen werden,
die aber jedenfalls von Gleichungen abhängen, deren Grad nie-
niedriger als m ist. Um aber den Körper reell zu behalten, wollen
wir nicht die Einheitswurzeln selbst, sondern
.... . 2sr 2jt
A) sm —, cos —
v ' mm
adjungiren.
Es möge also der Körper £1 aus allen rationalen Zahlen und
aus den rationalen Functionen von cos«.<p, sinmw, cos—, sin —
x m m
bestehen.
Die Gleichung mien Grades, von der x = 2 cos q> abhängt,
haben wir in §. 144 aufgestellt in der Form
B) 2 cos»» <p = Am(x),
worin Am(x) eine ganze Function mten Grades von x ist; wir
haben aber dort auch noch die Gleichung
sin mm
gefunden, durch die sin<p rational durch x ausgedrückt ist. In
diesen .Formeln sind die Einheitswurzeln noch nicht enthalten.
Die m Wurzeln von B) haben nun folgende Bedeutung:
x0 = 2 cos?, Xi = 2 cos (cp + ~\ . . .,
xm-i = 2 cos [y + m )'
und mit Hülfe von B) und C) und unter Adjunction der
Grossen A) kann jede von ihnen als rationale Function einer
anderen dargestellt werden, und zwar so:
x1=f(x0), xi=f(x1), . . ., xo=f(xm-{).
Irgend eine Function der x0, xt, . . ., a;m_j kann also dar-
dargestellt werden als rationale Function F(x0), und bei einer cykli-
schen Permutation geht
F(x0) in Fix,), F(x,) in F(x2), . . ., F(xm^) in Fix,)
über. Für eine cyklische Function ist also

§. 173. Theilung des "Winkels. 595
F(x0) = F(xJ ¦¦¦= F{xm I
und es ist folglich F(x0) rational, da es als symmetrische Func-
tion der Wurzeln dargestellt ist.
Die Theilung des Winkels hängt also von einer
cyklischen Gleichung ab.
Diese cyklische Gleichung ist irreducibel; denn ersetzt man,
in irgend einer rationalen Gleichung <& (x0, cos m <p, sin m q>) = 0,
, , . 2srfc , . .
a> durch a> -\ , so geht sie in
' m
® (ajft, cos m cp, sin m <p) = 0
über, und ist also für alle Wurzeln von B) befriedigt.
Wollten wir nur cos m cp adjungiren, nicht zugleich sin m 90,
dann würde die Gleichung keine cyklische mehr sein, was man
leicht an dem Beispiel der Drei theilung bestätigt, wo eben
sin m 90 die Quadratwurzel aus der Discriminante wird (§. 120).
38*

Sechzehnter Abschnitt.
Kreistheilung.
Irreducibilität der Kr eistheilungsgleichung.
Die wichtigsten unter den Abel'schen Gleichungen sind die,
von denen die Bestimmung der Einheitswurzeln abhängt, deren
elementare Eigenschaften wir schon im zwölften Abschnitt kennen
gelernt haben. Wegen der Beziehung zu der geometrischen Auf-
Aufgabe, die Kreisperipherie in eine bestimmte Anzahl gleicher Theile
zu theilen, heissen alle damit zusammenhängenden Gleichungen
auch die Kreistheilungsgleichungen.
Der Körper £1, der die als bekannt angesehenen Grossen
enthält, ist hier nur der Körper der rationalen Zahlen,
den wir den Körper B nennen wollen.
Ist n eine beliebige natürliche Zahl, Primzahl oder zusammen-
zusammengesetzte, so giebt es, wie wir in §. 140,141 gesehen haben, cp (n) = v
primitive wte Einheitswurzeln, die einer ganzzahligen Gleichung
A) Xn = x" -f «j a;*-i _|_ . . . 4- a, = 0
genügen. Die nächste Frage, die nun zu beantworten ist, ist die
nach der Irreducibilität dieser Gleichung.
Die Irreducibilität von Xn ist, für den Fall, dass n eine
Primzahl ist, zuerst von Gauss bewiesen (Disq. arithmeticae
art. 341). Später sind noch viele andere Beweise gegeben worden
(von Kronecker, Schönemann, Eisenstein, Arndt, Dede-
kind), die sich zum Theil auf denselben einfachen Fall oder den
ebenso zu behandelnden Fall, wo n eine Potenz einer Primzahl

§. 174. Irreducibilität der Kreistheilungsgleichung. 597
ist, beziehen, zum Theil den allgemeinen Fall eines beliebig zu-
zusammengesetzten n behandeln. Wir wollen hier einem besonders
einfachen Beweise für die Irreducibilität von Xn folgen, den
Dedekind gegeben hat, der sich gleich auf den allgemeinen
Fall eines ganz beliebigen n bezieht.
Wir haben schon im §. 12 gezeigt, dass die Polynomial-
coefficienten für einen Primzahlexponenten p alle durch p theilbar
sind, mit Ausnahme derer, die den pten Potenzen entsprechen
und die bei der Theilung durch p den Rest 1 lassen. Diesem
Satze können wir, wenn u, v, w, . . . Variable bedeuten, und
wenn sich die Gongruenz nur auf die Coefficienten der Potenzen
und Producte der Variablen bezieht, den Ausdruck geben:
B) (u -f- v -j- w -j- • • -)p = up -\- vp -\- w* -f- ¦ ¦ • (mod p).
Hieraus ergiebt sich nun ein Hülfssatz, auf den wir unseren
Beweis stützen wollen. Es sei
C)- f(x) = xm + alxm~1 + a2xm~2 -| [- am
irgend eine ganze Function von x mit ganzzahligen rationalen
Coefficienten au a2, . . ., am und die Wurzeln dieser Gleichung
seien a, ß, y, . . ., so dass (§. 7)
D) — % = 2 «, a2 = U u ß, — a3 = 2 u ß y, . . .
Wir setzen nun, wenn p eine beliebige Primzahl ist,
E) F{x) = (x- O (x - ß») (x — /)...
= x™ -\- Ax xm~1 -f Ä2 xm~2 + • • • + Am,
worin die Coefficienten Ax, A^, . . ., Am als ganzzahlige sym-
symmetrische Functionen der u, ß, y, . . . nach dem Fundamental-
Fundamentalsatz von den symmetrischen Functionen (§. 48) ganze^ganzzahlige
Functionen der al5 Oa, . . ., am und also auch ganze rationale
Zahlen sind. Zugleich ist
und folglich nach dem Satze B)
Ax = af, Ai = aP,...,Am = a? (mod p),
und nach dem Fermat'schen Satze (§. 143)
F) A1 = a1, A2 = %, . . ., Am = am (mod p),
was wir auch so ausdrücken können, wenn wir wieder die Con-
gruenz nur auf die Coefficienten entsprechender Potenzen von x
beziehen:
G) f{x) = F{x) (mod p).

598 Sechzehnter Abschnitt. §. 174.
Die Ableitung der Function F(x) aus f{x) ist ein specieller
Fall der Tschirnhausen-Transformation; denn man erhält die
Gleichung F(y) = 0, wenn man x aus 1/ = ^ und f(x) = 0
eliminirt.
Zur Berechnung von F(x) kann auch die Darstellung dienen:
(8) F(x) = nf(eVx),
worin das Product über alle pteu Einheitswurzeln a zu nehmen
ist. Wir fügen noch hinzu, dass, wenn f(x) im Körper B irre-
ducibel ist, und wenn die ap, ßp, y9,... von einander verschieden
sind, auch F(x) irreducibel ist. Denn ist F1(x) ein irreducibler
Factor von F, der für o,p verschwindet, so hat JFj (xp) eine Wurzel
mit f(x) gemein, und ist daher wegen der vorausgesetzten
Irreducibilität von f(x) durch/(a;) theilbar, es ist also
F1 («*) = 0, F, (ß*) = 0, F1 (yp) = 0, . . .,
d. h. JFi (x) verschwindet für alle Wurzeln von F(x), woraus die
Irreducibilität von F(x) folgt.
Hieraus ergiebt sich nun der Beweis der Irreducibilität von
Xn auf folgende Weise:
Es sei u eine primitive nte Einheitswurzel, und f(x) der im
Körper B irreducible Factor von Xn, der für x = u verschwindet.
Hat die höchste in f(x) vorkommende Potenz von x den Coeffi-
cienten 1, so müssen auch die übrigen Coefficienten %, a2,..., om,
nach dem Satze von Gauss (§. 2) ganze Zahlen sein.
Wenn ft eine zu n theilerfremde Zahl ist, so ist o? eben-
ebenfalls primitive wte Einheitswurzel, und jede primitive wte Einheits-
Einheitswurzel, also jede Wurzel der Gleichung X„ = 0 ist in dieser
Form enthalten. Wenn also bewiesen werden kann, dass für alle
Exponenten ft, die mit n keinen gemeinsamen Theiler haben,
/(««) = 0 ist, so folgt, dass f(x) durch Xn theilbar und folg-
folglich mit Xn identisch ist, wodurch dann bewiesen ist, dass Xn
in B irreducibel ist.
Es genügt aber hierzu, nachzuweisen, dass für jede Prim-
Primzahl p, die in n nicht aufgeht, /(«?) = 0 ist. Denn ist f(otP)
= 0, so hat f(%v) mit/(a;) eine gemeinsame Wurzel u und folg-
folglich ist f(%v) wegen der vorausgesetzten Irreducibilität von f(x)
durch f(x) theilbar. Wenn also für eine zweite in n nicht auf-
aufgehende Primzahl q, die auch mit p identisch sein kann, /(«*)
= 0 ist, so folgt, dass auch /(«p«) =0 ist, und wenn man
diesen Schluss wiederholt, so erkennt man, dass, wenn f(otP) für

§ 174. Irreducibilität der Kreistheiltmgsgleichung. 599
jede nicht in n aufgehende Primzahl verschwindet, auch /(«")
verschwinden muss, wenn ft irgend ein Product von Primzahlen
ist, die in n nicht aufgehen.
Ist nun p eine in n nicht aufgehende Primzahl, und sind «
und ß zwei von einander verschiedene Wurzeln von X„, so sind
auch o? und ßp von einander verschiedene primitive nte Einheits-
Einheitswurzeln, denn bestimmt man p' aus der Congruenz p'p = 1
(mod »), so folgt aus aP = ßp durch Erhebung und die Potenz
p', dass « = ß sein muss.
Sind nun a, ß, y, . . . die Wurzeln von fix), so bilden wir
nach (8) die Function F(x), deren Wurzeln ap, ßp, yp, . . . sind,
und die also nach dem oben Bewiesenen gleichfalls irfedu-
cibel ist.
Wenn nun f(x) von F(x) verschieden ist, so haben diese
beiden Functionen auch keinen gemeinschaftlichen Theiler, und
beide sind Theiler der Function Xn und folglich auch Theiler
von xn — 1. Wir setzen
x» — 1 = f(x) F(x) <p (x),
worin <p(x) eine ganzzahlige Function ist. Hierfür können war
aber wegen des Satzes G) auch setzen:
X» — 1 = f(xy cp(x)+pi> (x),
und durch Bildung der abgeleiteten Functionen:
n x"-1 =f(x)%(x)-\-p@ (x),
worin <p, i>, %, & ganze ganzzahlige Functionen sind. Wenn wir
die erste dieser Gleichungen mit —n, die zweite mit x multi-
pliciren und addiren, so ergiebt sich eine Gleichung, die wir als
Congruenz so darstellen können:
(9) n =/(*)*(«), (modp),
worin 0 (x) wieder eine ganzzahlige Function ist. Da n nicht
durch p theilbar ist, so können hier auch nicht alle Coefficienten
von 0 (x) durch p theilbar sein, und wir können annehmen, dass
der Coefficient der höchsten Potenz von <& nicht durch p theilbar
ist. Dann aber ist die Congruenz (9) offenbar unmöglich, da auf
der rechten Seite gewiss ein von x abhängiges Glied mit nicht
durch p theilbarem Coefficienten vorkommt, was auf der linken
Seite nicht der Fall ist.
Es muss also F(x) mit f(x) identisch sein, und es ist daher
f(u») — 0. W. z. b. w.

600 Sechzehnter Abschnitt. §. 174.
Hiermit ist bewiesen:
L Die Function Xn, deren Wurzeln die primitiven
wten Einheitswurzeln sind, ist im Körper der ra-
rationalen Zahlen irreducibel.
Die Irreducibilität von Xn gilt aber, wie hieraus sofort folgt,
in einem noch weiteren Sinne.
II. Die Function Xn ist auch dann noch irreducibel,
wenn dem Körper B beliebige Einheitswurzeln
adjungirt werden, deren Grad relativ prim zu
n ist.
Es sei nämlich a zu n theilerfremd, r eine primitive wte und
et, eine primitive aie Einheitswurzel, also nach §. 140
q = ru
eine primitive wate Einheitswurzel. Bestimmen wir die ganzen
Zahlen x, y so, dass
ax -f- ny = 1
wird, so ist
A0) r = Qax, a = Qnv,
und wenn nun q> (x, <x) ein Theiler von Xn im Körper It («) ist,
§o giebt es wenigstens ein r, für welches
<p (r, k) — 0
ist. Daraus ergiebt sich aber nach A0)
<11) <p(Qax, 9ny) = 0.
Nun aber haben wir die Irreducibilität der Gleichung für
die primitiven naUu Einheitswurzeln im Körper It bewiesen. Es
folgt daher aus A1) für jede zu awtheilerfremde Zahl h
A2) <p(Qhax, Qhnv) = 0,
und wenn nun s eine beliebige zu n theilerfremde Zahl ist, so
können wir h so bestimmen, dass
h = s (mod n), h = 1 (mod a).
Dann folgt aber aus A2)
q> (r8, a) = 0,
und folglich ist q> (x, a) durch Xn theilbar. Darin liegt aber
die Irreducibilität von Xn im Körper R(a).
Dieser Satz rührt von Kronecker her, der gewissermaassen
den umgekehrten Weg geht, indem er zunächst die Irreduci-

§. 175. Kreistheilung. 601
bilität von Xn in R(a) unter der Voraussetzung beweist, dass
n nur durch eine Primzahl theilbar ist, und daraus dann die
Irreducibilität von Xn allgemein ableitet1).
§. 175.
Die Kreistheilungs-Perioden und die Perioden-
Periodengleichungen.
Wir beschäftigen uns nun zunächst mit den wten Einheits-
Einheitswurzeln, unter der Voraussetzung, dass n eine ungerade Prim-
Primzahl ist (die Primzahl 2 bietet zu keinen weiteren Fragen Anlass,
da die einzigen zweiten Einheitswurzeln, +1, in B enthalten sind).
Aüsser der rationalen nieu Einheitswurzel 1 existiren noch
n — 1 primitive, die durch die transcendenten Ausdrücke
2 7t i ±7ti 6 7ti 2 (n — VjTti
p n p n p n p n
dargestellt werden können. Wenn wir eine von ihnen mit r
bezeichnen, so ist das ganze System auch durch
darzustellen. Im Exponenten von r kommt es nur auf den Rest
nach dem Modul n an, da immer und nur dann rh = t* ist,
wenn h = fc (mod n) ist.
Die Grossen A) sind, wie wir schon im §. 140 gesehen haben,
die Wurzeln der Gleichung (n — l)ten Grades
B) X = x»-1 -f- x»-* + xn~3 -| 1- x + 1 = 0,
deren Irreducibilität im vorigen Paragraphen bewiesen ist. Wir
wollen jetzt zunächst nachweisen, dass diese Gleichung cyklisch ist.
Diese Eigenschaft ergiebt sich aus der Existenz primitiver Wur-
Wurzeln der Primzahl n, mit denen wir uns im §. 143 beschäftigt
haben. Es wurde dort nachgewiesen, dass es für jede Primzahl
n gewisse Zahlen g giebt, die man primitive Wurzeln von n
nennt, die durch die Eigenschaft charakterisirt sind, dass unter
den Resten der Potenzen
x; g-i g i g > • • •> g >
x) Kronecker, Mem. sur les facteurs irreducibles de l'expression
x» — 1). LioQville's Journal, Bd. 19 A854).

602 Sechzehnter Abschnitt. §. 175.
bei der Theilung durch n jede der Zahlen
1, 2, . . ., n — 1
ein und nur einmal vorkommt. Der Rest einer Potenz g11 bleibt
derselbe, wenn h um ein Vielfaches von n — 1 verändert wird. Ist
ga = a (mod w),
so heisst a der Index von a (a = ind a) und a die Zahl oder
der Numerus. Der Index wird nach dem Modul n — 1 genom-
genommen, der Numerus nach dem Modul n (§. 143).
Nehmen wir also eine solche primitive Wurzel von n an, so
können wir, von der Reihenfolge abgesehen, die Grossen A) so
darstellen:
™ n*a [ftp ^ ^ ^gn ^,
oder, wenn wir
C)
setzen,
D)
r, t
r<>h = rh
Jede Zahl des Körpers B(r), d. h. jede rationale Function
von r lässt sich in die Form bringen:
E) <p (r) = b0 + hxr + b.2r* + • • • + &„_2r"-2,
oder, da nach B)
1 _|_ r -f r2 -| h *""~1 = 0
ist,
F) 9(r) = (&x - ft,) r + F4 — &0) ^2 H
+ F„_2 — &0)r«-2 — Urn~\
oder da die Potenzen r, r2, . . ., r**~a, von der Reihenfolge ab-
abgesehen, mit r, ru r2, . . ., r„_2 übereinstimmen, in die Form
G) q>(r) = ar + a^ + a2r2 -| • -+- a„_2r„_2,
worin die Coefficienten b und a rationale Zahlen sind. Wenn
von den Zahlensystemen a, b das eine ganzzahlig ist, so
ist es auch das andere.
I. Eine, solche Function <p (r) kann nur dann
gleich Null sein, wenn alle ihre Coefficienten
a, au . . ., a„_2 verschwinden;
denn der Ausdruck E) zeigt, dass cp (r) nicht anders verschwinden
kann, als wenn die &0, bx, ¦ . ., &„_2 Null sind. Sind aber diese
Null, so zeigt F), dass auch die Coefficienten a alle Null sein
müssen. Es kann also q> (r) nur auf eine Weise in die Form G)
gebracht werden.

§. 175. Kreistheilungsperioden. 603
Treffen wir die Festsetzung, dass sich ah und r% nicht ändern
sollen, wenn der Index h um ein Vielfaches von n — 1 wächst,
so können wir auch
. (8) cp (r) = 2 ahrh
setzen, und darin h ein volles Restsystem nach dem Modul n — 1
durchlaufen lassen.
Wir haben nun nachzuweisen, dass die Gruppe der Glei-
Gleichung X = 0 keine andere ist, als die Periode der cyklischen
Permutation
% = (r, ru r2, . . ., r„_2).
Diese Periode oder cyklische Gruppe bezeichnen wir mit
(9) C — 1, 3T, 3T2, . . ., 3T»-2.
Die Gleichung X=0 ist jedenfalls eine Normalgleichung,
weil sie irreducibel ist, und weil alle ihre Wurzeln nach C)
rational durch eine unter ihnen ausdrückbar sind; sie ist also
ihre eigene Galois'sche Resolvente (§. 152). Ihre Substitutionen
sind
A0) (r, r), (r, rj, (r, r2), . . ., (r, rB_2),
und nach C) ist
(r, rk) = (n-, rk+h).
Daraus folgt, dass (r, rx) unter den Wurzeln D) die cyklische
Permutation % hervorruft, und dass also die Substitutionsgruppe
A0) mit der Permutationsgruppe C isomorph ist. Also ist C
die G a 1 o i s' sehe Gruppe von X = 0.
Nach §. 170 lässt sich die Gleichung X = 0 auf eine Reihe
von cyklischen Gleichungen niedrigeren Grades zurückführen,
wenn man Functionen aufsucht, die zu den Theilern der Gruppe C
gehören. Die Theiler von C sind aber, wenn n — 1 in zwei
Factoren e, f zerlegt, also
n — 1 = ef
gesetzt wird, die cyklischen Gruppen
A1) Ce = 1, »•, Jt2e, . . ., «</-»«,
und die Permutation ne ist darin gleichbedeutend mit der Sub-
Substitution (r, re).
Um zu einer zu Ce gehörigen Function der Wurzeln von
möglichst einfacher Form zu gelangen, betrachten wir nach Gauss
die/-gliedrigen Perioden

604 Sechzehnter Abschnitt. §. 175.
n = r + re + r2e H (- r(/_1)(j
A2) ^1 = rl +re + l + r2« + l H \~ r(f-l)° + l
ije_i = re_i + r^.i + r3e_! -| • -j- rB_2,
die aus der ersten von ihnen durch die Substitutionen (r, r),
(r, rj), (r, r2), . . ., (r, re—i) hervorgehen. Wir bezeichnen die
Grossen A2) auch als ein System conjugirter Perioden.
Jede dieser Functionen bleibt durch die Substitution (r, re)
ungeändert, und sie sind alle von einander verschieden, da sich
eine Gleichung ijh — ijfc = 0, wenn h und h verschieden ist, in
der Form
ar -\- c^ri -j- •••-)- a„_2rM_2 = 0
schreiben Hesse, wo die a, a^ . . ., a„_2 nicht alle zugleich ver-
verschwindende ganze Zahlen sind (-|- 1, 0 oder — 1), was nach
dem Theorem I. nicht möglich ist. Jede der Perioden A2) ist
also eine zu der Gruppe Ce gehörige Function, und diese
Grossen sind daher die Wurzeln einer irreducibeln ganzzahligen
Gleichung eten Grades. Adjungirt man eine dieser Grossen, so
hängt die Bestimmung von r noch von einer Gleichung vom
Grade / ab.
Nach den allgemeinen Sätzen des vierzehnten Abschnittes
kann jede Function der r, die die Substitutionen der Gruppe O
gestattet, rational durch jede der Grossen y\ dargestellt werden.
Hier können wir aber noch den folgenden Satz aufstellen:
II. Jede Zahl in B(r), die die Substitution (r, re)
gestattet, also auch jede Zahl des Körpers 2?(ij),
lässt sich als homogene lineare Function der
Perioden ij, %, . . ., ije_x darstellen.
Denn nach I. könneu wir jede Zahl von B(r) auf eine Weise
in die Form
A3) y(r) = Zahrh
setzen, wo die Coefficienten au rationale Zahlen sind, und h ein
volles Restsystem nach dem Modul n—1 durchläuft. Es ist aber
<p(rt) = 2ahrh+e = lah-erh,
und daher muss, wenn tp(r) = •pO'e) sein soll, au—e = au sein
für jedes h; also auch ah = aÄ+e = ah+ie . . . Danach lässt
sich A3) in die Form setzen
h h h
cp(r) = X a%v% + 2 «ft^Ä+e + • • • +
0, e—1 0, e—1 0, e—1

§. 175. Kreistheilungsperioden. 605
oder
A4) cp (r) = a n -\- a, ^ -| (- ae_1ije_1,
was zu beweisen war. Zu bemerken ist dabei noch, dass, wenn
<p ganzzahlige Coefficienten hat, auch die Coefficienten der t]h
ganze Zahlen werden.
Da jede Zahl des Körpers -R(ij) auf eine und nur auf eine
Art in der linearen Form A4) dargestellt werden kann, so nennen
wir das Grössensystem ij, ijl5 ija, . . ., ije_a eine Basis des Kör-
Körpers B(t)).
Wenn man die Darstellung des Productes je zweier Perioden
¦jjkijfc in der Form A4) kennt, so kann man daraus durch eine
wiederholte Anwendung alle rationalen Functionen der Perioden
t\ in derselben Form darstellen. Ebenso kann man auch leicht
die Gleichung bilden, deren Wurzeln die e Grossen r\ sind, wenn
man das Verfahren auf das Product
A5) Fe (x) = (x — rj) (x — rii) . . . (x — ije-i)
anwendet. Diese Gleichung lässt sich auch in Determinanten-
Determinantenform darstellen.
Man setze nämlich
A6) rjfjh = aO,hn -j- «LÄfl + • • • + «e-I.ÄlJe-l,
worin die aOth, a^h, • . •, ae—\,% ganze Zahlen sind, über deren
Berechnung später das Nähere folgen wird. Stellt man diese
Gleichung für h = 0, 1, . . ., e — 1 in der Form auf:
(«0,0 — n)n + «1,0 »h + + «e-l»?e-l = 0
«o,i n + («i,i — n)n\ + + «e-1%-1 = o
ao,e-in + «l,e-l% + • • • («e-l,e-l — 1j)ije-l = 0,
so sieht man, da die rj, rj^ . . ., ije_! nicht verschwinden, dass die
Determinante dieses Systems Null sein muss, also
A7)
«0,0 V, «1,0» • • •) «e —1,0 !
«0,1, «1,1 — 1?, . . ., «e-1,1
«0,e — 1, «l,e —1» • • •» «e—l,e—1
was, wenn man x für r\ schreibt, vom Vorzeichen abgesehen, mit
Fe(x) übereinstimmen muss.
Die Function Fe(x) hat also nicht bloss rationale,
sondern ganzzahlige Coefficienten.

606 Sechzehnter Abschnitt. §. 176.
Man kann nun auch die Gleichung /ten Grades bilden, deren
Wurzeln r, re, r2e, . . ., *¦(/-» e sind; denn es ist für ein unbe-
unbestimmtes x
A8) ®e(x) = (x — r)(x — re)...(x — r(/_1)e)
eine Function im Körper M(rj). Ihre Coefficienten sind in der
Form cp(r), E), mit ganzzahligen b enthalten und lassen sich also
in der Form A4) mit ganzzahligen a darstellen. Sie lassen
sich leicht aus den Newton'schen Formeln berechnen, durch
die die Coefficienten einer Gleichung mittelst der Potenzsummen
der Wurzeln ausgedrückt werden (§. 46). Denn es ist nach A2)
und C)
?**+*? + ••• + ?#_„.=%
also geradezu einer der Potenzsummen gleich, und jede Potenz-
Potenzsumme ist einer der Perioden gleich. Man sieht daher aus den
Newton'schen Formeln zwar unmittelbar, dass die Coefficienten a
rational sind, nicht aber, dass es ganze Zahlen sind.
Die Gleichung A8) lässt sich aber ebenso behandeln, wie
die Gleichung B); denn die Gruppe von <be{%) = 0 ist eben Ce,
und wenn e' ein Theiler von / ist, etwa f = e'f, so ist Cee> ein
Theiler von Ce. Zu Cee> gehört aber die Periode
n' = r -j- ree' -\- r2ee' + f" «V'-D«*
die also von einer Gleichung des Grades e' im Körper 2? (ij) abhängt.
Wenn man die Zahlen e, e' . . . als Primzahlen annimmt,
so besteht die Reihe der Resolventen aus einer Reihe von Glei-
Gleichungen, deren Grade die Primfactoren von n — 1 sind.
Was die Gruppe der Gleichung eten Grades betrifft, deren
Wurzeln die e Grossen y\ sind, so finden wir diese sehr einfach
aus der Bemerkung, dass die Substitution (r, r%) unter den %
die Substitution (ijfc, r{ic+h) hervorruft, wenn der Index von r\
nach dem Modul e genommen wird. Die Gruppe von Fe(x) = 0
besteht daher aus den Potenzen der cyklischen Permutation
§. 176.
Die Gauss'sche Methode zur Berechnung der
Resolventen.
Um in concreten Fällen die Auflösung der Kreistheilungs-
gleichung wirklich durchzuführen, kommt es nach dem, was wir

§. 176. Producte von Perioden. 607
im vorigen Paragraphen entwickelt hahen, nur darauf an, die
Producte je zweier conjugirter Perioden als lineare Functionen
derselben Perioden darzustellen. Dafür hat Gauss ein einfaches
Verfahren angegeben, das wir jetzt kennen lernen wollen. Wir
müssen dazu die Bezeichnung der Perioden ein wenig verändern.
Wir schreiben zwei beliebige der Perioden §. 175, A2) in
der Weise
,(D = ri + ry _j_ ri».]
^ ' ijC«) = rfl -4- r"' -|- r'"" -[-...
so dass, wenn X ^ gh (mod n) ist, ijW = rjh oder auch
qß) _ ^.ndi; es ist dann
B) • (modw);
lassen wir also die Zeichen s und t je ein volles Restsystem
nach dem Modul / durchlaufen, so ist
Das Product davon ist
Halten wir bei der Bildung dieser Summe zunächst s fest,
und summiren in Bezug auf t, so dürfen wir t durch t -j- s er-
ersetzen, weil beide gleichzeitig ein volles Restsystem nach dem
Modul / durchlaufen. Demnach wird
Hierin aber darf die Reihenfolge der Summation vertauscht
werden, so dass auch
C) ij0) ijW = 11
ist. Die nach s genommene Summe
ist aber selbst eine der Perioden, nämlich nach der Bezeich-
Bezeichnung A) die Periode
Es ergiebt sich also aus B) und C)
D) ij(*> ijc«) = ^a+M) _j_ tf-+!>¦') -\
Die rechte Seite dieses Ausdruckes.enthält / Glieder; dar-
darunter kann natürlich auch dieselbe Periode mehrmals auftreten;

608 Sechzehnter Abschnitt. §. 176.
auch. kann darunter die uneigentliche Periode ij(°) vorkommen,
die gleich der ganzen Zahl / zu setzen ist. Will man die homo-
homogene Form des Ausdruckes wieder herstellen, so benutzt man
die Relation
n + % + Vz H + Ve-i — — 1,
die ja nur eine andere Schreibweise der Gleichung §. 175, B) ist.
Wenn man nach D) den Ausdruck für ein Product ij v\%
berechnet hat, dem wir oben schon die Form gegeben haben,
E) r\rjh = aOlhr) + «i.ä^i + ' * • + ae-i,hVe-i,
so erhält man das Product von zwei beliebigen der Perioden
durch die Substitution (ij, ijfc),
F) VtcVh+ic = «o,ä% + ai,ft%+i + • • • + a«-i,Ä»7*-i-
Um an einem einfachen Beispiele diese Regeln zu erläutern,
nehmen wir n = 13. Für 13 ist 2 eine primitive Wurzel, und
wir können die im §. 143 gegebene Indextabelle anwenden:
I
N
0,
1,
1,
2,
2,
4,
3,
8,
4,
3,
5,
6,
6,
12,
7,
11,
8,
9,
9,
5,
10,
10,
11
7
Wenn wir zuerst e = 3, / = 4 annehmen, so erhalten wir
eine cubische Resolvente, deren Wurzeln
n =r + rs -f r6 + r9
(8) . »?i = n -f r4 -f r7 -f r10
% = ra -\- r5 -f r8 -f rn
sind. Aus der Tabelle G) ergiebt sich dafür auch
•q = r -\- r~5 -(- r-1 + r5 = ijW
(9) ij, = r* + rs -j- r~2 + r-3 = ij«
ij2 = r* -|- r6 -f r~4 4- r~e = ijW.
Wendet man die Formel D) an, so erhält man z. B.:
rjrj = ijB) 4- ?j(-4) 4- ,j(o) 4- ^(e) = 4 4- ij(» 4-
und so ergeben sich die Formeln:
f}2= — 4i? — 3ij, — 2%,
^ 1J, = 1J 4- 2 1Jj 4- 1J2,
tj %= 2ij 4- ij! 4- ij2,
•woraus nach §. 175, A7), die Gleichung für 17

§. 176. Kreistheilungsperioden. 609
— 4 — ij, — 3, — 2
1, 2 — rj, 1=0,
2, i, i - n
oder
A0) ij3 -f- ij2 — 4ij -f 1 = 0
folgt. Die Discriminante dieser Gleichung ergiebt sich gleich
169 = 132, also positiv. Die Gleichung hat folglich drei reelle,
und zwar, da das letzte Glied positiv und das vorletzte negativ
ist, zwei positive und eine negative Wurzel.
Setzen wir r = e 1Z , so wird
. 2st . . 10 % . / 2% 3a\
n = 2cos — + 2cos _ = 2^^ - cos _),
„ 4* , . 6ar „ / 4ar. 6jc\
^ = 2COS 13 + 2C°S TF = 2(C°S 13 + C°S 13>
% = 2cos ^ + 2cos -ir = _ 2(cos— + cos -j,
oder auch
. 4 jt 6a; . % bit
n = 4 cos — cos —, fll = 4cos ^ cos ^,
2x 3a
%=-4cos —cos--
Es ist also ij2 die negative, % die grössere, r\ die kleinere der
beiden positiven Wurzeln.
Die Gleichung 4ten Grades, deren Wurzeln r, r~l, r5, r~6
sind, lässt sich nun leicht bilden, wenn man
g = r + r-i = 2cos^|, f = r* + r~ß = 2 cos ^
setzt. Es ist nämlich
also
A1) I2 —^l + % = 0
die quadratische Gleichung für £, aus der man die biquadratische
Gleichung für r erhält,
A2) r* — ijrs -f- (ij2 -f 2) r2 — nr -f 1 = 0.
Die quadratische Gleichung A1) hat eine positive und eine
Q, IT"
negative Wurzel. Die positive Wurzel ist 2 cos -=— • Anstatt r
Weber Algebra. I. 39

610 Sechzehnter Abschnitt. §. 177.
selbst zu berechnen, berechnet man noch 2 sin —> was man als
13
die positive Quadratwurzel V4 — §2 erhält.
An Stelle der drei viergliedrigen Perioden r\ hätte man auch
zuerst zwei Perioden von sechs Gliedern betrachten können:
A3) l = r + r3 + r4 + f + r~3 + ?¦-*
' lx = r» -f- r* -f r« -f r~2 + r~5 -f- r~6.
Für das Product tti findet man nach der Formel D) den
Werth 3 (£ -\- ti) oder — 3, so dass g, ^ die Wurzeln der qua-
quadratischen Gleichung
A4) & + t — 3 = 0
sind, woraus, da aus dem Ausdruck durch die Cosinus leicht zu
sehen ist, dass £ positiv ist:
nn , _ - 1 + Vl3 -l-VIä
A5) £ = g ' ?1 = 2
Nach Adjunction der Werthe £, ^ kann man eine cubische
Gleichung für die zweigliedrigen Perioden bilden. Setzt man
nämlich
| = r + r-1, |x == ^ + r-2,
+ ^ = - i,
also sind g, g2, g4 die Wurzeln der cubischen Gleichung
A6) x* — gas» — x — 1 + t = 0.
§. 177.
Zurückführung der Kreistheilungsgleichung auf
reine Gleichungen.
Gauss hat schon in seiner ersten Darstellung in den disq.
arithm. die Kreistheilungsgleichungen durch Benutzung der Resol-
so folgt
ferner
62 =
it =
: r* + r-\
T3 _j_ r-3?
63
&
^5 _L_
y6 _L
+ &, i

§. 177. ZurüokfüLirung auf reine Gleichungen.
venten direct auf reine Gleichungen zurückgeführt1). Um
dies durchzuführen, setzen wir
n — 1 = m,
und bezeichnen, wie im vorigen Abschnitt, mit e eine primitive
Einheitswurzel mten Grades, mit r, ru r2,..., rm_! die wten Einheits-
Einheitswurzeln in der oben festgesetzten Reihenfolge. Die Lagrange'-
sehen Resolventen sind dann
(s*, r) = I slhrh = v s^t**,
0, n—2 0, n—2
worin X ein beliebiger, nach dem Modul m genommener Expo-
Exponent ist.
Setzen wir gh = s, also h = inds (mod m), so können wir
auch setzen
A) (e\ r) = 2 sn^srs.
l,n — l
Als Grundlage für die weitere Reduction dieser Ausdrücke
dient die Berechnung des Productes zweier solcher Resolventen.
Wir bezeichnen mit (i eine zweite Zahl wie X und verstehen
unter s und t zwei Zeichen, die von einander unabhängig je
ein Restsystem nach dem Modul n durchlaufen, mit Ausschluss
der Null.
Dann ist
Wenn die Summation in Bezug auf t zuerst ausgeführt wird
so kann st an Stelle von t gesetzt werden, da s von Null ver-
verschieden ist, und also st und t zugleich ein volles Restsystem
nach dem Modul n durchlaufen. Also wird
s t
B) (s\ r) («'S r) = 2 2rs(* + 1)£^+^inds£'uind*.
Wir erledigen zuerst den speciellen Fall [i = — X, den
:) Gauss, disq. arithm. art. 359, 360; disq. circa aequationes puras
ulterior evolutio, "Werke Bd. II. Lagrange, res. des equations nume-
riques. Jacobi, „Ueber die Kreistheilung und ihre Anwendung in der
Zahlentheorie". Werke Bd. 6. Kummer, Crelle's Journal, Bd. 35 und
Abhandl. d. Berl. Akademie 1856. Zu erwähnen sind noch Eisenstein
und Cauchy. Die Lehre von der Kreistheilung ist im Zusammenhange
dargestellt und von den historischen Nachweisen begleitet in dem Buche
von Bachmann, „Die Lehre von der Kreistheilung". Leipzig 1872.
39*

612 Sechzehnter Abschnitt. §. 177.
wir aus B) erhalten, wenn wir die Summation nach s zuerst
ausführen:
(e\ r) (s~\ r) = £ £-w<|
Hierin ist
= _^. i} wenn *= 1, 2, ...,» — 2 .
= w — 1, wenn t = n — 1,
also, da (nach §. 143) ind (n — 1) = 7a (n — 1) und
s 2 = — 1
ist,
(s*, r) (s~\ r) = — S £-«ndt _j_ (_ !JW.
1, n—1
In der nach £ genommenen Summe durchläuft ind t ein volles
Restsystem nach dem Modul n — 1, und also ist, wenn X durch
n — 1 nicht theilbar angenommen wird,
1, n— 1
und daher
C) (s\ r) {e-\ r) = (- l)*w,
während, wenn X durch n — 1 theilbar ist, (s\ r) = A, r) = — 1 wird.
Wir behandeln also nun die Summe B.) weiter unter der
Voraussetzung, dass X -\- (t nicht durch (n— 1) theilbar ist.
s
Dann ist 2 £(;i+rt™ds = 0, und es können in der Summe auf der
rechten Seite von B) die dem Werthe t = n — 1 entsprechenden
Glieder weggelassen werden. Man erhält so '
t s
D) (a\ r) (f, r) = 2 £flüld' 2
1, n—2 l, n—1
t
l,n—2
Nun durchläuft s(t -\- 1) bei feststehendem £ zugleich mit s
ein volles Restsystem nach dem Modul n, und e"s ist also
und die Formel D) ergiebt
E) =
wenn zur Abkürzung
F) 2 ^todt-
1,»—2

§. 177. Auflösung durch die Resolventen. 613
gesetzt und X -\- ji durch n — 1 = m nicht theilbar angenommen
wird. Diese Functionen ip sind dann aus den (w — l)ten Einheits-
Einheitswurzeln £ mit ganzzahligen Coefficienten zusammengesetzt, und
sind also bekannt, wenn die (n — l)ten Einheitswurzeln als be-
bekannt vorausgesetzt werden. Es sind Zahlen des Körpers B(e).
Wir nehmen jetzt X durch ji theilbar an, ersetzen also X
durch pX und setzen
G) et, = £¦»,
so dass a auch eine nicht primitive (w — l)te Einheitswurzel,
z. B. eine eie Einheitswurzel sein kann (wenn, wie oben, m = ef
ist und p durch / theilbar, etwa =/ genommen wird), wobei
jedoch der Fall « = 1, also e = 1 auszuschliessen ist.
Dann setzen wir
(8) 2 CcM«-a + l)md(* + l) _ ^(«);
1, n—2
darin ist ^(w) eine Zahl des Körpers -R(ec), die mit Hülfe einer
Indextabelle leicht berechnet werden kann; X kann dabei nach
dem Modul e genommen werden. Die Formel E) giebt für diese
Annahme
(9) (tf,r)(a,r) = (<* + \r)fl>i(«),
und diese Formel gilt, so lange (i (X -\- 1) nicht durch n — 1
theilbar ist, also, wenn ji und m theilerfremd, und daher « eine
primitive mte Einheitswurzel ist, für A = 1, 2, . . ., n — 3, und
wenn f der grösste gemeinschaftliche Theiler von ft und m und
m = ef ist, für X = 1, 2, . . ., e — 2.
Die Formel C) giebt jetzt, wenn ax nicht = 1 ist,
A0) « r) (a~\ r) = (— 1)«*».
Die Formeln (9), A0) genügen, um nicht nur die r selbst,
sondern auch die sämmtlichen Perioden r) durch Kadicale zu
bestimmen, deren Grade die in m aufgehenden Primzahlen sind,
und unter denen die Functionen ^ als die bekannten Grossen
vorkommen.
Da die /-gliedrigen Perioden (für / = 1) die Grossen r mit
umfassen, so wollen wir gleich zur Bestimmung dieser Perioden
übergehen.
Wir wollen also unter u eine primitive eie Einheitswurzel
verstehen und ji = f setzen.
Dann ist
(«*, r) = r -\- Kxri -\- a2Xr2 -(- • • • + a<-n-V*rn-2,

614 Sechzehnter Abschnitt. §. 177.
oder nach §. 175, A2)
A1) (a\ r) = (a\ rj) — n + «^, -\- a"ij2 \- «<«-»* *}«,_!,
und die Formeln (9) und A0) ergeben
A2) («V?) («,*?) = («*+S i?) «*(«) . _19 , «,,
A3) «,)(«-*,,) = (-1>*«. *-i.4-.-.t« ^
Die Gleichung A3) zeigt, dass keine der Zahlen («*, r\) ver-
verschwindet, und nach A2) sind auch die i>z(u) von Null verschie-
verschieden, und wenn wir die Gleichung A2) für A = 1, 2, . . ., A — 1
bilden, so folgt
(«. V)(«, n) = («a,
(«», i?) («, i?) =(«»,
(a*-1, 1?) («, 1?) = (a
Daraus erhalten wir durch Multiplication und Wegheben des
Factors (a2, rj) . . . («il-1, ij)
A4) (et, itf = (a\ rf) ^ («) ^», («)... ^^_! («).
Dadurch ist («^, ij) rational durch («, ¦»?) ausgedrückt. Setzen
wir aber in A4) X — e — 1, so ergiebt sich
(«, 1?)«-1 = (ar\ ^)^i(«)^2(«) • • • ^e-a(«),
und durch Multiplication mit («, ij), wenn A3) in der Form
(«, q) («-S q) = (- l)/n
benutzt wird,
A5) («, t2)e = (— l)/w ^ («) if»2 («)... ^e_2 («),
wodurch die Bildung von («, ij) auf eine eie Wurzel zurückgeführt
ist. Setzen wir e = m, so erhalten wir (a, r).
Wir wollen dies Verfahren auf den interessanten Fall n = 17
anwenden, der zu dem geometrisch merkwürdigen, vcn Gauss
gefundenen Resultat führt, dass die Theilung der Kreisperipherie
in 17 Theile von einer Reihe quadratischer Gleichungen abhängt,
und dass daher das reguläre Siebzehneck mit Zirkel und Lineal
construirt werden kann.
Für die Primzahl 17 ist 3 eine primitive Wurzel, und man
findet die Indextabelle
1
N
0
1
1
3
2
9
3
10
4
13
5
5
6
15
7
11
8
16
9
14
10
8
11
7
12
4
13
12
14
2
15
6

§. 177. Siebzehn-Theilung. 615
Die zweigliedrigen Perioden sind, wenn wir r = e17 setzen,
18ar % _ 10% . 3a;
2 2= — 2cos—,
p^ ^y =- = — 2cos—
A6)
263r 8jt n 10a; _ 7a;
= 2cos —, ^5=2 2
-jy-= 2cos —, ^7 = 2cos^- = —2cos—•
Zur Berechnung der Functionen ip wendet man am ein-
einfachsten folgende Tabelle an:
ind
(*
t
ind t
+ 1)
1
0
14
2
14
1
3
1
12
4
12
5
5
5
15
6
15
11
7
11
10
8
10
2
9
2
3
10
3
7
11
7
13
12
13
4
13
4
9
14
9
6
15
6,
8
woraus man, wenn a eine 8te Einheitswurzel bedeutet, nach der
Formel (8) findet:
A7) ^a(a) = ^5(a) = 2 +3«+ a3+ «4 —j-3os^-j-4«e_j_
il>s(«) = ^4(«) = 3 -f-3« -f-2«2_|_3a3 4_ a
Nimmt man
l-M
«=-—L^, «3 = 4, «* — — 1,
so ergiebt sich
^ («) = if»6 («) = — 3 — * V8
ft (es) = ft (es) = • 1 — 4i
also nach A5)
A9) («, 1?)8 = 17 C + 4 V8I A —¦ 4 *)«.
Aus A3) und A4) aber erhält man
(- 1, ij)* = 17,
B0) (inJ =(-1, »2) (-1 + 44),
ausserdem hat man (l,ij) = — 1,

616 Sechzehnter Abschnitt. §. 177.
(i, q)(—«, ij) = 17,
B1) (a, q)(«-i, q)= 17,
(a»,ij)(a-«, 12)= 17,
und nach (9)
B2) («, ^) («3, ,) = (_ i, ,) C +
wodurch A, 12), (— 1, 12), (± *, v), («, «?), («-1, »2), («3, »2), («~3, *?)
durch Quadratwurzeln bestimmt sind.
Bei der Bestimmung, die wir über r und a, getroffen haben,
ergiebt sich leicht aus der Betrachtung der Werthe der Cosinus
A6), dass (— 1, rj) positiv, also gleich der positiven Quadrat-
Quadratwurzel Vl7 ist, und dass ferner (i, rj) und (a, r[) positive reelle
Theile haben, wodurch auch diese Grossen völlig bestimmt sind.
Es ist also
wenn alle Wurzeln positiv genommen werden, und nach der
letzten Gleichung B0) lässt sich durch eine, wenn auch etwas
lange Formel («, rj) durch Quadratwurzeln aus reellen Grossen
darstellen. Auf die geometrischen Constructionen, die sich hier
anknüpfen, gehen wir nicht ein1).
Die benutzte Vorzeichenbestimmung erhält man einfach,
wenn man nach A6) setzt
1 . , . 2ar % , 8» . ix
2 (— X' n) = COS — — COS _ -[- COS ^r + COS rff
— COS — + COS _ + COS ^- + COS -pp
Nach einer bekannten trigonometrischen Formel ist aber
jc
- cos— +. cos — = 2sm — sin
grösser ist als sin 7^7-, so is
o4
beiden Ausdrücke und damit die ganze Summe (— 1, rf) positiv.
und da sin —— grösser ist als sin 7^7-, so ist die Summe dieser
34 o4
*) Vgl. hierüber v. Staudt, Construction des regulären Siebzehnecks.
Crelle's Journ. Bd. 24, 1842.

§. 178. Die Zahlen tfi. 617
Es ergiebt sich ferner für den reellen Theil von (i, rj)
^ — ¦»22 + ^4—% = 2cosyy + 2cos^y+ 2cosyj-— 2cos—,
was unmittelbar als positiv erkannt wird; endlich für den reellen
Theil von («, ij)
»2 — % + y^- Oh — n% — % + j?7)
= 2cos —— 2cosjy+V2^cos^- + cos—+ cos——
was sich gleichfalls als positiv erweist.
§. 178.
Eigenschaften der Zahlen ip.
Die im vorigen Paragraphen abgeleiteten Formeln für die
Kesolventen gestatten eine Fülle von Anwendungen, auch ohne
eine nähere Bestimmung der Primzahl n, für specielle Annahmen
über die Zahl e; sie geben also zahlentheoretische Sätze für
ganze Kategorien von Primzahlen.
Für die Algebra liefern sie uns die Lösungen cyklischer
Gleichungen von vorgeschriebenem Grade in beliebiger Menge.
Der Ableitung der für die Algebra wichtigsten dieser An-
Anwendungen schicken wir einige allgemeine Betrachtungen über
die im vorigen Paragraphen definirten Functionen if> voraus.
Zur Berechnung der Zahlen ^,« (s) [§. 177, E)] bedient man
sich, wie wir im Falle n = 17 gesehen haben, einer Indextabelle.
Es bestehen aber zwischen diesen Functionen Relationen, durch
die sie sich auf eine geringere Zahl zurückführen lassen, worüber
Jacobi merkwürdige Untersuchungen angestellt hat1).
Die Function ^^(f) ändert sich nach ihrer Definition
nicht, wenn A, ji vertauscht werden, obwohl ihr Ausdruck
[§. 177, F)] dadurch eine andere Gestalt erhält. Wir bekommen
also dieselbe Function ^(«), wenn wir A, ft durch A/,/ oder
durch /, If ersetzen, also [§. 177, (8)]
J) Vergl. Kronecker, Zur Theorie der Abel'sehen Gleichungen.
Journ. f. Mathem. ßd. 93.

618 Sechzehnter Abschnitt. §. 178.
Hängen also zwei Zahlen X, X' durch die Congruenz
A) Xl' = 1 (mod e)
mit einander zusammen, so ergiebt sich
t t
also die Formel
B)
Wenn wir sodann in §. 177, E) für X setzen — X — (i und
also — X für X -\- p (wobei dann vorausgesetzt sein muss, dass
X durch m nicht theilbar ist), so folgt
(*-*-*, r) (£", r) _
(FVr) "" *-*-"•*(8)-
Die linke Seite multipliciren wir mit
und wenden im Zähler und Nenner die Formel
(»i,r)(«-i,r) = (-l)in
[§. 177, C)] an, dann folgt
oder
und wenn wir X, ji durch A/, / ersetzen und X" aus der Congruenz
C) X -f A" -f 1 = 0 (mod e)
bestimmen,
Diese Formel kann man dann wieder mit der Formel B)
verbinden, und so die Anzahl der für ein bestimmtes e zu
berechnenden Functionen auf eine geringere zurückführen. Ist e
eine ungerade Primzahl, so ist nach Jacobi die Zahl der Func-
Functionen ipi, durch die sämmtliche e — 2 auf diese Weise aus-
ausgedrückt werden können, gleich der zunächst über \e gelegenen
ganzen Zahl.
Eine dritte Formel ergiebt sich, wenn man in §. 177, E) für
£ setzt £—1 und dann multiplicirt, also
-¦«, r)

§. 178. Die Zahlen if>. 619
bildet. Und mit Hülfe von §. 177, C) findet man so die Formel
E) ti,ll(B)il>x,ll(£~1) = n^
die nun wieder durch die Substitution Xf,f für A, ji specialisirt wird:
F) 4>x(aL>x(ct,-i) = n.
Schliesslich wollen wir noch eine Eigenschaft der Func-
tionen i\> erwähnen, die sich auch unmittelbar aus ihrer Defini-
Definition §. 177, E) ablesen lässt. Danach ist nämlich, wenn A, p, v
drei solche Zahlen sind, dass X -\- [i, X -\- (i -\- v nicht durch m
theilbar ist
G) *,
d. h. das Product 4>itll(s)il>i+lltr(s) bleibt ungeändert, wenn die
drei Zahlen X, ji, v beliebig vertauscht werden (falls auch X -\- v
und (t-\-v durch m nicht theilbar sind). Danach ergiebt sich z. B
und wenn man darin X, (i, v durch 2A/,/,/ ersetzt, und beachtet,
dass ip2f,2Zf(z) = ifu(«2) ist,
(8) ^ai(«)^2i + i(a) = Tl>i(<«I>x(?fl),
vorausgesetzt, dass 2, 2 A -j- 1, 2A-|-2 nicht durch e theilbar sind.
Jacobi hat den Versuch gemacht, mit Hülfe dieser Formeln
für ein gegebenes, als Primzahl vorausgesetztes e die sämmtlichen
e — 2 Functionen tyxif*) durch die conjugirten Werthe einer
einzigen, d. h. durch ^ («), ^ (a2), ^>t (a3), . . . auszudrücken, und
hat die Kechnung bis e = 23 durchgeführt.
Dass eine solche Darstellung allgemein möglich sei, wie
Jacobi vermuthet zu haben scheint, ist jedoch nach den Unter-
Untersuchungen von Kronecker nicht wahrscheinlich.
Wir wollen als Beispiel den Fall e = 7 durchführen. Für
diesen Fall ist
l = 1, 2, 3, 4, 5
A' = 1, 4, 5, 2, 3
A" = 5, 4, 3, 2, 1,
also ergeben die Formeln B) und D)
und daraus noch

620 Sechzehnter Abschnitt. §. 178.
und wenn man in (8) A = 1 setzt
ii>t 0) *3 («) = *i 0)
endlich nach F)
Berechnet man hiernach die Formel §. 177, A5)
(«, nI = n xl>x («) ^2 («) 4>3 («) 4>i («) #5 («),
so ergiebt sich
(9) («, ^O = ^ («L ^ (a2J ^ («*).
Durch diese Formel lässt sich unmittelbar die Kelation aus
§• 177, A4) 14 _ 2 7
verificiren.
Wir wollen diese Betrachtungen über die Functionen ip mit
dem Beweise eines Satzes beschliessen, der uns später nützlich
sein wird.
Bestimmen wir eine positive ganze Zahl v < m aus der
Congruenz
A0) l -+- [i -\- v = 0 (mod m),
so können wir die Function ^^ (e), wie sie durch §. 177, F)
definirt ist, so darstellen
t
A1) ^,<t(£) == 2 £'lln
1, n— 2
Hierin wollen wir nun die mte Einheitswurzel £ durch die
primitive Congruenzwurzel g der Primzahl w, die dem Index-
Indexsystem zu Grunde liegt, ersetzen, d. h. wir wollen die ganze Zahl
* *
A2) ip).,fi(g) = 2 ^ind*+v'üid(t+i) = v ta (t -f- l)v (mod n)
1, n — 2 l, n—2
bilden. Betrachten wir diese Zahl nach dem Modul n, so können
wir die Summation bis t = n — 1 ausdehnen, da für diesen Werth
(t ~\- 1) congruent mit Null ist. Wir erhalten also
A3) 4m,,«(#) = 2 ta(t -f- l)r (mod n).
1, n—1
Auf die Potenz (t -f- 1)" können wir den binomischen Lehr-
Lehrsatz anwenden und erhalten, wenn, wie früher, _B£° die Binomial-
coefficienten bedeuten,
h t
A4) 1>*,!>¦&) = 2 B^p y, P-+h (mod n).
O.r l.n—1 v

§. 179. Die Gauss'schen Summen. 621
Setzen wir t = g* (mod n), so durchläuft s ein Kestsystein
nach dem Modul m, und wir erhalten
1, n —1 0, m—1
Es ist aber nach der Summenformel für die geometrische
Eeihe
— 1) f gsiu + h) — gmiu+h) _ i = o (mod »),
0, m — 1
und folglich ist
A5) 2 0»C"+*> == 0 (mod w),
o,»t—i
ausser wenn f* -\- h ^ 0 (mod m) ist, und in diesem Falle ist
A6) 2 ^C«+ä) =TO = _ ! (m0(Jw).
O,OT — 1
Nehmen wir A, ;* zwischen 0 und w an, so ist
1) wenn A -\- fi < »» ist, v = w — A — ft,
2) „ A -j- (i > m ist, v = 2m — X — ft.
Der Exponent (i -\- h in der Summe A4) durchläuft also
im Falle 1) die Werthe p -\- h = f*, p -\- 1, . . ., w — A,
„ 2) „ „ F, ^ + 1, . . ., 2m — X.
Im Falle 1) kommt also der in A6) vorausgesetzte Fall
ji -f- h = 0 (mod w) gar nicht vor, im Falle 2) kommt er ein-
einmal vor, für h = m — (i.
Demnach haben wir aus A4) mit Kücksicht auf A5) und
A6), wenn für den Binomialcoefficienten JBj? der Werth
ll-h) gesetzt wird'
„« (ß) = 0) A + f* < w
§. 179.
Die Gauss'schen Summen.
Im §. 175 ist gezeigt, dass, wenn n — 1 = ef ist, die
Perioden rj, %, ..., ^e—i einer ganzzahligen Gleichung eten Grades

622 'Sechzehnter Abschnitt. §. 179.
genügen. Diese Gleichung hat nur reelle Wurzeln, wenn/ gerade
ist, weil dann y2(n — 1) ein Vielfaches von e ist, und folglich
r und r~x in derselben Periode vorkommen. Ist aber / ungerade,
so sind alle Wurzeln imaginär.
Es ist nun vom höchsten Interesse, diese Gleichung eUsa
Grades für einzelne besondere Werthe von e ohne eine specielle
Annahme über die Primzahl n, ausser der, dass n — 1 durch e
theilbar sein soll, zu untersuchen.
Wir betrachten die ersten speciellen Fälle und nehmen zu-
zunächst e = 2 an, was bei jeder ungeraden Primzahl n zulässig
ist; rj, rjx sind hier also die zwei Perioden von J/2 (w — 1) Glie-
Gliedern, die wir jetzt mit A, B bezeichnen wollen, so dass
A = r + r2 -f r4 H 1- rn-B
B = rx + r3 + rb -| j- r„_2.
Die r, r2, r4, .. . haben die Exponenten g°, g2, . . ., gn~B, d. h.
die Exponenten von g sind gerade Zahlen. Die Exponenten von
r sind also die quadratischen Beste von n (§. 145). Ebenso
sind die Exponenten von r in der Summe B die Nichtreste.
Bezeichnen wir also die Beste mit a, die Nichtreste mit b, so ist
A) A = 2r", B = 2r\
und es ist (— 1, r) = A — B. Diese Ausdrücke A, B, werden
die Gauss'sehen Summen genannt.
Machen wir in der Formel §. 177, A0) die Annahme
so ergiebt sich
B) ^-B =
während andererseits
A + B = - 1,
also
C) 2A = — 1 ±K(— 1)~», 2B = -l + K(-l)"r».
Das Vorzeichen, das man der Wurzel zu geben hat, hängt
von der Wahl von r ab. Ist aber über r verfügt, so ist das
Vorzeichen völlig bestimmt. Seine Ermittelung bietet eigen-
thümliche Schwierigkeiten, die zu einer eigenen Abhandlung von
Gauss Anlass gegeben haben1).
J) Summatio quarundam serierum singularium. Gauss Werke, Bd.II.
Auf andere Weise, mit Anwendung der höheren Analysis, ist das Zeichen

§. 179. Die Gauss'schen Summeu. 623
Setzen wir
1,71%
D) r = e~'¦>
so wird das Zeichen in den Formeln B) und C) ein bestimmtes,
und die Formel B) lässt sich mit Benutzung des Legrendre'-
schen Zeichens (§. 145) so darstellen:
(ö) 2
l,u—1 '
Nach §. 145 ist abfer, wenn v die Reihe der Zahlen 1,2,...,
i/s (n — 1) durchläuft,
F) n(f — rrv) = Bi) 2 n sin tUL — { 2 yW)
worin \/n positiv zu nehmen ist. Vergleichen wir dies mit E),
so ergiebt sich, wenn j = ±1 gesetzt wird
G) |
und hieraus soll das Vorzeichen £ bestimmt werden.
Die ganze Function der Variablen x
(8) s
verschwindet für x = r, und ist also, wegen der Irreducibilität
der Kreistheilungsgleichung durch X„ = (xn — 1) : (x — 1) theil-
bar. Da die Function (8) aber auch für x = 1 verschwindet,
weil es ebenso viel quadratische Reste wie Nichtreste giebt, so
ist sie auch durch (x — 1) und folglich durch (xn — 1) theilbar,
und wenn wir also mit f(x) eine ganze und ganzzahlige Function
von x bezeichnen, so ist identisch
(9) s II(x* — xn~*) = i ß^jx* + (xn — 1) f(x).
von Diriohlet, Cauchy, Kronecker bestimmt worden. Der Weg, den
Gauss einschlägt, benutzt nur algebraische Hülfsmittel. Kronecker hat
iu Liouville's Journal Ser. 2, Bd. 1 einen Weg für die Vorzeichenbestim-
Vorzeichenbestimmung angegeben, der mit Benutzung einer Bemerkung von Dedekind
(Schlömilch's Ztschr. Bd. 15, Literaturzeitung S. 21) gleichfalls zu einem
rein algebraischen wird. Einen Weg, der durch sehr einfache Hülfsmittel,
durch Benutzung elementarer goniometrischer Formeln zum Ziele führt,
hat neuerdings Mertens eingeschlagen (Sitzungsber. d. Berliner Akademie,
27. Febr. 1896). Wir folgen im Text dem durch Dedekind vereinfachten
Kronecker'schen Weg.

624 Sechzehnter Abschnitt. §. 179.
Wenn wir in dieser identischen Gleichung x = 1 -\- y setzen,
und nach Potenzen von y ordnen, so giebt ein Factor der
linken Seite
A + yy — A + yy-" = Bv — n)y
n—l
und die linke Seite fängt also mit der Potenz y 2 an, deren
Coefficienten
A0) eIIBv — n) = s2 2 . 1. 2 —^ (mod n).
n — l
Der Coefficient von y 2 auf der rechten Seite von (9) muss
nun diesem Ausdrucke gleich sein, und wir setzen die Reste nach
dem Modul n einander gleich. In der Entwicklung von
xn — 1 = A -\~ y)n — 1
sind aber alle Coefficienten, mit Ausnahme des letzten, durch n
theilbar, also ist in dem Product (xu —1)/(#) der Coefficient von
n — l
y 2 ganz durch n theilbar, da/(#) ganzzahlige Coefficienten hat.
l
n—l
Der Coefficient von y 2 in x* ist aber nach dem binomischen
Satze
A1)
und ist gleich Null, wenn h < \ (n — 1) ist. Da aber der Aus-
Ausdruck A1) für diese Werthe von Tc gleichfalls verschwindet, so
können wir die kleineren Werthe von h trotzdem stehen lassen
und erhalten durch Multiplication mit
.1. 2. ... ?=± = (-1)^ (n-l)(»-2) • •
nach A0) und A1) (mod w)'
n—l n—l
A2) (—l)" 2 2 . 1. 2. . . . (W —1) . £
-^) (mod»),
worin "k ein beliebiges volles Restsystem nach dem Modul n
durchlaufen kann. Nach dem Euler'schen Satze [§. 145, A3), 6.]
ist aber
(modn),

§. 179. Die Gauss'schen Summen. 625
und nach dem Wilson'sehen Satze (§. 143)
1. 2 ...(»— 1) = — 1 (mod «),
und da
^1 + ^^(^-1)^-3) (mod2)
ist, so ergiebt sich aus A2)
(H-l)(»»-3) » + 1
A3) —£ = (-i) 8 2ft 2 (fc
(mod w).
Ordnen wir den unter dem Summenzeichen stehenden Aus-
Ausdruck nach Potenzen von ft, so erhält die Summe die Gestalt
2
worin die Coefficienten a^, a2, . . ., a„_3 ganze Zahlen sind. Nach
den Sätzen §. 143, B2), B3) ist dies aber nach dem Modul n
mit — 1 congruent und wir erhalten aus A2)
(»—1) (»—3)
£ = (— 1) 8 (mod ri).
Daraus ergiebt sich, da £ nur = ± 1 sein kann, und n nicht
= 2 ist,
(u — l) (» — 3)
A4) £ = (— 1) <• .
Setzen wir diesen Werth in G) ein, so folgt nach F)
A5) 2( — )»*= A 2 ^ Vw.
Ist s irgend eine durch n nicht theilbare Zahl, so durch-
durchläuft sie gleichzeitig mit Tc ein volles Restsystem nach dem
Modul n, und wir können daher in der Summe A5) den
Summationsbuchstaben h durch sie ersetzen. Dadurch ergiebt
sich die allgemeinere Formel
wodurch das Vorzeichen in B) und C) allgemein bestimmt ist,
2 ais
nämlich, wenn r = e " gesetzt wird
Weber, Algebra. I. 40

626 Sechzehnter Abschnitt. §. 179.
A — B = f—\ Vn, n = 1 (mod 4)
A — B=i(£\]/n, n = 3 (mod 4).
Nach §.175, A8) sind nun die 1/2(n—1) Grossen ra und die
i/2(m — 1) Grossen rh die Wurzeln je einer Gleichung 1/a(n—l)ten
Grades, deren Coefficienten ganz und ganzzahlig, und zwar linear,
durch A und B ausdrückbar sind. Wenn wir also mit T(x), Z{x)
zwei ganze Functionen von x mit ganzen rationalen Coefficienten
bezeichnen, von denen die erste den Grad 1/2 (n — 1), die zweite
den Grad 1/2 (n — 1O1 hat, so haben wir
2 A(x) = 2 n(x — ra) = Y(x) — Z(x) 2 f—\rk,
)l\
2B(x)= 2n(x — r») = Y(x) + Z(x) 2 \—\rh,
und die Coefficienten der Functionen Y(x), Z(x) können nach
§. 175 berechnet werden, und ergeben sich als rationale ganze
Zahlen.
Multiplicirt man die beiden Formeln A8) mit einander, und
gebraucht X in derselben Bedeutung wie in §. 175, B), so folgt
die Identität
A9) 4 X = Y(x)* — (— l)~ nZ(xf.
Es lässt sich nun noch zeigen, dass die beiden in A8) ent-
enthaltenen Functionen
0\x, V(— 1)~») = Y(x) qp Z(x)
1 / "-1
in dem Körper R, y (— 1) 2 w, der aus dem Körper der ratio-
rationalen Zahlen durch Adjunction von V+ n entsteht, irreducibel
sind. Denn ist #x ein Theiler von <&, so erhalten wir, wenn wir
das Product <&x #i bilden, wo <3>i aus #i durch Aenderung des
Vorzeichens der Wurzel V± n entsteht, eine ganze Function
von x mit rationalen Coefficienten, die mit X eine Wurzel
gemein hat, und folglich durch X theilbar ist Der Grad dieses
Productes kann also nicht kleiner als n — 1 sein, und folglich
kann der Grad von &r nicht kleiner als 1/2(n — 1), d. h. nicht

§. 179. Die Gauss'schen Summen. 627
kleiner als der Grad von <3> sein, und folglich ist <&j, von einem
etwaigen constanten Factor abgesehen, mit <3> identisch. D. h. <3>
ist irreducibel.
Nehmen wir an, es seien die Functionen Y, Z irgendwie mit
ganzzahligen Coefficienten so bestimmt, dass die Gleichung A9)
1/ »n.1
befriedigt ist, so hat T — Z \ (— 1) 2 n bei passender Ver-
Verfügung über das Vorzeichen der Quadratwurzel mit A(x) einen
Theiler gemein und ist also, da der Grad derselbe ist, mit A(x)
bis auf einen Zahlenfactor identisch. Dieser Zahlenfactor ist
aber dann bestimmt, wenn wir annehmen, dass Y von höherem
Grade ist als Z, und dass der Coefficient von x1^"—« in Y
gleich -)- 2 ist. Dann können bei geeigneter Vorzeichenbestim-
Vorzeichenbestimmung für Z diese Functionen in A8) eingesetzt werden, und
es folgt
2A(x) = Y(x) - Z(x) ß
B0)
Das Vorzeichen von Z lässt sich aber in folgender Weise
bestimmen. Setzen wir x = 1, so folgt
_ r«) = Z{\) 2 !
uud es ergiebt sich also wie oben, dass die ganze Function von x
B1) iT(l — a*) — iT(l — x") — Z(l) £ f—) a;fc = (*"
durch x11 — 1 theilbar ist, so dass f(x) eine ganze Function von
x mit ganzzahligen Coefficienten bedeutet. Setzt man hierin
wieder x = 1 -)- y und vergleicht beiderseits die Coefficienten
von ylM«—1M so folgt wie vorhin
woraus nach §. 145, A7)
B2) Z(l) = — 2. 1. 2 • • • ^^ (mod n)
entsteht, und hierdurch ist von zwei entgegengesetzten Func-
Functionen Z(x) eine bestimmte gekennzeichnetl).
l) Nach eiDer briellichen Mittheilung von Dedekind.
40*

628 Sechzehnter Abschnitt. §. 180.
So findet man z. B. für n = 13, wenn man Y, Z zunächst
mit unbestimmten Coefficienten ansetzt, durch einige Versuche
die nachträglich leicht zu verificirende Lösung der Gleichung A9)
4 X = J2 — 13 Z2
r= 2x* -\- x° 4- 4a;* — x°* + 4#2 + x + 2
Z = #5 -j- #3 -j- #,
also Z A) = 3, und da
3 = — 2. 1. 2. 3. 4. 5. 6 (mod 13)
ist, so ist das Zeichen von Z nach B2) richtig gewählt.
Hieraus erhält man nach A5) die Gleichung, deren Wur-
Wurzeln sind:
,2ni ,6ni ,8ai
r° = e~ lB , e~^~, e~ 1B ,
in der Gestalt
2 x« + (l — Vl3) x> + 4 x* — (l +Vl3) & + 4 x*
_ -J- A —V13)-^ -1-2=0,
worin Vl3 positiv zu nehmen ist.
Nehmen wir die Wurzel mit entgegengesetzten Zeichen, so
ergie*bt sich eine Gleichung, deren Wurzeln sind:
r» = e~ 13 ,
13 />— 13
§. 180.
Die Perioden von 1/B(n — 1) und 1/i(n — 1) Gliedern..
Wir gehen jetzt zu dem Falle e = 3 über, wobei n — 1
durch 3 theilbar angenommen werden muss, also n = 7, 13, 19,
31, 37, 43 ... Wir bezeichnen mit q eine imaginäre dritte
Einheitswurzel :
und bestimmen die drei Perioden r), rj1, t]2 von je 1/s(n — 1)
Gliedern, die, wie wir in §. 175 gesehen haben, die Wurzeln
einer cyklischen cubischen Gleichung sind. Nach §. 177 ist
^(p) p
1,»—2
wofür, da — 2 = 1 (mod 3), auch

§. 180.
Specielle Perioden.
629
1,«—2
gesetzt werden kann. Diese Zahl tpi (q) kann in einer der beiden
Formen
B)
dargestellt werden, worin a, b, A ganze Zahlen sind und
A = 2 a — & ist
Es ist dann
C) ^(p«) = a + 6p» = ^
und die Formeln A0), A5) des §. 177 ergeben
D) v\ -f- nx + n2 = — 1
F) (p, vi) (p2, vi) = n, f! (p) f! (p2) = n,
worin
Beispielsweise erhält man für n = 7, 13, wenn man die
primitiven Wurzeln 3, 2 zu Grunde legt und die Indextabellen
anwendet:
n = 7 w = 13
1
0
2
2
3
1
4
4
5
5
6 1
T T
2
1
3
4
4
T
5
9
6
5
7
11
8
T
9
8
10
10
11
7
12
für n = 7, a + & p = — A + 3 q),
für w = 13, a + b q = — D + 3 p).
Aus diesen Formeln können wir leicht die cubische Glei-
Gleichung herleiten, deren Wurzeln die ¦»?, %, 172 sind. Sie hat wegen
D) die Form
(8) i' + ^ + ^ + ^O,
und die ganzen Zahlen ß, y sind zu bestimmen.
Führen wir die Multiplication in F) aus, so ergiebt sich
also
(9)
-(n—1).

630 Sechzehnter Abschnitt. §. 180.
Die Ausführung der Cuben in E) ergiebt, wenn wir für den
Augenblick
ss = n* 4- ni + ni, s = n*-ni + nlv» + nin,
s' = nlri + nhi + rfn-i
setzen
«i^j (p) = s3 — 6 y -f- 3 s p -j- 3 s' p2.
Aus (8) und (9) erhält man aber s3 = — w — 3 y
[§. 46, (9)], also
A0) »[tfi
und ebenso
A1) «[^i(
wozu noch, wenn man D) in den Cubus erhebt,
n — 1 = — 9y + 3s -f- 3s'
kommt. Addirt man die drei letzten Gleichungen, so folgt
»[tfifa) + ^i(?2)] + 3» — 1 = — 27y,
oder endlich nach B) und C)
A2) — 27y = «J. + 3,« — 1.
Aus dieser Relation folgt, da y eine ganze Zahl ist,
A3) Ä = l (mod 3).
Nun ist nach B), C) und F)
A4) n = a2 — ab-\-b\
oder
A5) 4w = J.24- U\
und wenn wir diesen Werth in A2) substituiren,
— 4 . 27y = ^3 _j_ 3 J.J2 _j_ 3^3 _|_ 952 _ 4.
Setzen wir nach A3) für den Augenblick J. = 1 -|- 3 m, so folgt
J.s -\- 3 J.2 — 4 = 0 (mod 27) und mithin
3&3(J.-j- 3) = 0 (mod 27),
und daraus
3&2 = 0 (mod 27),
Es ist also b durch 3 theilbar, und wenn wir b = 3 B setzen,
so folgt aus A5)
A6) 4« = i2 _j_ 27B*.
Wir können auch leicht die Quadratwurzel aus der Dis-
criminante bilden, nämlich
A7) Vd = {n - ni) (n - ijO (Vl - %) = ¦* - s',

§. 180. Periodengleichungen. 631
wenn wir A0) und A1) von einander subtrahiren. Man erhält
daraus
A8) Vl) = nB.
Die cubische Gleichung, deren Wurzeln die drei Grossen v\
sind, hat also, was übrigens schon aus dem am Anfang von
§. 179 Bemerkten folgt, drei reelle Wurzeln. Sie vereinfacht
sich, wenn man
setzt, und ergiebt dann
A9) g3 — 3«£ — nA = 0.
Substituirt man auf der linken Seite für § der Reihe nach
B0) — 2 Vn, — Vn, + Vn, + 2 Vn,
so ergeben sich die Werthe
— »B V» + A), + »B Vn — A), — »B Vn + A),
+ nBVn — A),
die, weil nach A6) A absolut kleiner als 2Vn ist, abwechselnde
Vorzeichen haben. Es liegt also in jedem der drei durch die
Werthe B0) begrenzten Intervalle eine Wurzel der Gleichling A9).
Ueber die Frage, welche der drei Wurzeln der cubischen
Gleichung A9) für g = 3 rj -f- 1, welche für 3 ijx + 1 oder für
3172 -j- 1 zu setzen ist, lässt sich allgemein so viel sagen, dass
das Vorzeichen des Productes A7) mit dem Vorzeichen von A8),
das durch die Definition A), B) bestimmt ist, freilich aber noch
von der Wahl der primitiven Wurzel g abhängt, übereinstimmen
muss. Dadurch sind von den sechs möglichen Zuordnungen drei
ausgeschlossen. Welche Zuordnung unter den drei übrigen zu
treffen ist, hängt vou der Wahl von r ab, und würde zu ähnlichen
Untersuchungen Anlass geben, wie sie im vorigen Paragraphen
zur Bestimmung des Zeichens der Quadratwurzel durchgeführt
sindx).
Wir heben noch den durch die Formeln A4), A6) bewiesenen
Satz hervor:
Ist n eine Primzahl von der Form 3ft-)-l, so ist n
durch die Form a2 — ab -\- 62 und in durch die Form
J.2 -j- 27 JB2 darstellbar, wo a, &, A, B ganze Zahlen sind.
*) Kummer, Journ. f. Mathematik, Bd. 32.

632 Sechzehnter Abschnitt. §. 180.
.Daraus ergiebt sich noch, dass n auch in der Form #2-f- 3«/2
darstellbar ist. Denn wenn von den beiden Zahlen a, b eine,
etwa a, gerade ist, so ist
W==(f-iJ + 1*2'
und wenn a und b beide ungerade sind, so ist
Auch die zweigliedrigen Perioden der 9ten Einheitswurzeln
genügen einer cubischen Gleichung, und weil diese Gleichung
bei der später zu behandelnden allgemeinen Theorie der cubi-
cubischen Kreistheilungskörper eine wichtige Rolle spielt, wollen wir
sie der Vollständigkeit halber hier betrachten, obwohl sie eigent-
eigentlich in ein allgemeineres Gebiet gehört, in dem die Grade der
Einheitswurzeln keine Primzahlen mehr sind.
Eine 9te Einheitswurzel r genügt der Gleichung 6ten Grades:
B1) r« _|_ rs _|_ i — o,
und wir haben drei conjugirte zweigliedrige Perioden
B2) n = r-Jrr-1, <>}' = r3 -\--r~*, n" = ^ + r~\
die die Wurzeln der cubischen Gleichung
B3) y* — 3fj + 1 = 0
sind. Ist p eine dritte Einheitswurzel, so können wir p = rs
setzen, und erhalten die Resolventen
B4) (p, rj) = rj -\- q rj' -\- p2ij", {q~\ rf) = r) -\- q~1 r\' -f- p~2 r)",
für die man nach B2) mit Benutzung von B1) erhält
(p, rf) =: 3r, (p—1, f}) = 3*™1,
also
B5) (p, n)z = 27 p,
B6) (p, rj) (q~\ t]) = 9, :
was den Formeln E) und F) ganz analog ist.
Wir gehen noch in der Kürze auf den Fall e = 4 ein, der
bei den Primzahlen n von der Form 4/ -\- 1 (/ eine ganze Zahl)
eintritt, also bei n =± 5, 13, 17, 29, 37, 41 ...
Die vier Perioden von je / Gliedern seien wieder t], t]u

§. 180. Periodengleichungen. 633
Für « in §. 177 haben wir i zu setzen, erhalten also
(i, t)) = ri -\- irj! — ^2 — i^3,
B7) (—l,rf) = ri— ^ -f n-2 — ya,
(—i, t)) = n — i Vl — V2 -\- iy-i,
und nach §. 177 (8), da — 2 = -f- 2 (mod 4) ist,
#! (l) = j;iind«+2ind(« + l)
t/>2 (*) = 2:iind«2+*» = a + 6«,
worin a und b ganze Zahlen sind. ipl (i) hat dieselbe Form
wie i/>2 (i). Wir werden aber sogleich die eine Function auf die
andere zurückführen.
Da nun tj -j- ij2, ^! -j~ ^3 die beiden 2/-gliedrigen Perioden
sind, so ist nach den Resultaten von §.179
B9) (-hv) = V+Vt—Vi-V» = V»,
und also, da r) -j- ijj -j- ^2 -j- ij3 = — 1 ist,
C0) 2(t2 + t22) = -1 + Vw, 2A?l+%) = -l-Vw,
wo das Vorzeichen von Vw nach §. 179 zu bestimmen ist und
bei passender Annahme über r positiv genommen werden darf.
Wir haben ferner nach §. 177, A0), A4)
C1) (*, n) (— i v) = (— l)fn
1 (*, nY = (- i, n) *i @.
also nach B9) und §. 177, A5):
C2) (*' n) = ^ (i) ^' (~ *» ^J = ^x (~ ^
(», 1?)* = (- 1)/» ^i (») rl>2 (*) = n ^i @2,
woraus folgt:
C3) ^ (*) = (— 1)/^ (») = (— l)/(a + 6 *),
und hieraus nach C1):
C4) i>! (*) ^ (— 0 = rl>.2 (t) ^2 (— «) = aa + 62 _ „.
Um die biquadratische Gleichung zu bilden, deren Wurzeln q,
Vn ^21 Vz sind, suchen wir zunächst die quadratische Gleichung
mit den Wurzeln rj, rjt und erhalten sie aus
Quadriren wir diese beiden Gleichungen und subtrahiren die
zweite von der ersten, so folgt wegen C1) und C2)
C5) 16 n rj2 = 1 + n — 2 Vn — 2 n (— 1)/ — 2 a{— iyVn.

634 Sechzehnter Abschnitt. ¦§. 180.
Durch C0) und C5) sind aber die Coefficienten der ge-
gesuchten quadratischen Gleichung bestimmt. Sie lautet:
V + 2H16
und die biquadratische Gleichung für die vier Perioden erhält
man, wenn man beiderseits quadrirt:
C6)
Suchen wir den Coefficienten der ersten Potenz von 17, der
eine ganze Zahl sein muss, so finden wir dafür
l+„-2n(-l)/ a(-iy+ 1.
C7) ^ » g ,
/ ist gerade, wenn » = 1, ungerade, wenn n = 5 (mod 8) ist,
demnach ist
1 4- n — 2 » (— 1)/ = 0 (mod 8).
Daraus aber folgt wegen C7), dass a(— iy ~\- 1 durch 4
theilbar sein muss, also
C8) a = — (— 1)/ (mod 4),
und, daraus ist nach C4) weiter zu schliessen, dass b gerade
sein muss, also
C9) 6 = 0 (mod 2).
Die biquadratische Gleichung nimmt eine einfachere Gestalt
an, wenn wir
D0) 4 ij + 1 = %
setzen. Sie erhält dann nach C6) die Gestalt:
D1) [g« + »A — 2(— 1)/)]« — 4w[g + (— l)/ap = 0,
oder wenn wir die beiden Fälle «=1 oder =5 (mod8) trennen:
(g»)
V J (£2f 3wJ — 4w(g — af = 0.
Wir wollen auch hier den in der Formel C4) ausgedrückten
Satz hervorheben:
Jede Primzahl von der Form 4/ -\- 1 lässt sich in
die Summe zweier Quadrate zerlegen.

§. 181. Complexe Zahlen. 635
§. 181.
Die complexen Zahlen von Gauss.
Der zuletzt bewiesene Satz bildet die Grundlage für die
Theorie des Zahlkörpers, der durch Adjunction der imaginären
Einheit i = V— 1 aus dem Körper der rationalen Zahlen ent-
entsteht, den wir nach unserer Festsetzung mit B (i) zu bezeichnen
haben!).
Wir haben hier die Primzahlen von der Form 4/ -\- 1 zu
unterscheiden von denen der Form 4/ -f- 3, und wir wollen der
Kürze wegen die ersten mit der Primzahl 2 zusammenfassen und
mit p, die zweiten mit q bezeichnen, also
j> = 4/+1,2; g = 4/+3
setzen. Es gelten dann folgende Sätze:
1. Für jedes p giebt es zwei ganze Zahlen a und b,
so dass
p = cfi + 62
ist.
Dies ist für die Primzahlen von der Form 4/-)-1 im Schluss-
Schlusssatze des letzten Paragraphen ausgesprochen und ist für p = 2
aus 2 = l2 -j- l2 unmittelbar ersichtlich.
Dem steht ein zweiter Satz gegenüber:
2. Eine Primzahl q ist niemals in der Form a2 -)- 6*
darstellbar, oder der noch allgemeinere:
3. Die Summe zweier Quadrate ganzer Zahlen a2-\-b2
ist nur dann durch eine Primzahl q theilbar,
wenn a und b durch q theilbar sind.
Der Satz 2. ergiebt sich einfach daraus, dass, wenn a2 -\- 62
ungerade ist, die eine der beiden Zahlen a, b gerade, also- ihr
Quadrat durch 4 theilbar, die andere ungerade, also ihr Quadrat
— 1 (mod 4), also a2 -f- b2 = 1 (mod 4) sein muss. Der Satz 3.,
der übrigens den zweiten in sich schliesst, wird so bewiesen.
Angenommen, es sei a2 -\- b2, aber nicht b, durch q theilbar,
so bestimmen wir b' aus der Congruenz bb' = 1 (mod q) und
erhalten aus a2 -f- 62 = 0 (mod q)
(ab1J = — 1 (mod q).
:) Gauss, Theoria residuorum biquadraticorum, commentatio secunda.
Werke, Bd. II.

636 Sechzehnter Abschnitt. §. 181.
Dies ist aber urlmöglich, da nach §. 145, 4. für jede Primzahl q
die Zahl — 1 quadratischer Nichtrest ist.
Der Körper B (i) ist der Inbegriff aller Zahlen von der
Form x -f- yi, wenn x, y ganze oder gebrochene rationale Zahlen
sind.
Die Zahlen a -(- bi, in denen a und b ganze Zahlen
in B sind, heissen die ganzen Zahlen desKörpers B(i).
Das Product zweier conjugirter Zahlen
£ = x 4- yi, |' = x — yi,
also
£r = *2 + 2/2
heisst die Norm von £ und wird mit N(£) bezeichnet. Die Norm
einer nicht verschwindenden Zahl £ ist eine positive rationale
Zahl und die Norm einer ganzen Zahl ist eine ganze Zahl. Die
Norm eines Productes oder eines Quotienten ist gleich dem Pro-
Product oder dem Quotienten der Normen.
Eine ganze Zahl, deren Norm gleich 1 ist, heisst
eine Einheit.
Da a2 -\- b'2 (für ganzzahlige a, b) nur dann = 1 sein kann,
wenn a = ± 1, b = 0 oder a = 0, b = ± 1 ist, so giebt es in
B{i) nur die vier Einheiten
+ 1, -1, +.', -.-.
Der reciproke Werth einer Einheit ist auch eine Einheit.
Zwei Zahlen, von denen die eine aus der anderen durch
Multiplication mit einer Einheit entsteht, heissen associirte
Zahlen.
Jede complexe Zahl gehört zu einem System von vier asso-
ciirten Zahlen
a -\- bi, — a — bi, — b -f- ai, b — ai.
Summe, Differenz und Product zweier ganzer Zahlen sind
wieder ganze Zahlen.
Eine ganze Zahl « heisst durch eine ganze Zahl ß
theilbär, wenn eine dritte ganze Zahl y existirt, so
dass a = ßy ist.
Ist a durch ß theilbär, so ist N(a) durch N(ß) theilbär.
Denn aus « = ßy folgt N(u) = N(ß)N(y).
Sind «, ß, y ganze Zahlen in B(i) und ist a durch y theil-
theilbär, so ist auch aß durch yß theilbär, und ist « und ß durch y
theilbär, so ist auch « ± ß durch y theilbär.
Jede ganze Zahl ist durch jede Einheit theilbär.

§. 181. Complexe Zahlen. 637
Die Einheiten sind aber nur durch Einheiten theilbar; denn
ist a/3 eine Einheit, so ist N(u)N(ß) = 1, also N(a) und
N(ß) = 1, d. h. a und ß sind Einheiten.
Associirte Zahlen sind gegenseitig durch einander theilbar,
und wenn zwei Zahlen gegenseitig theilbar sind, so sind sie
associirt. Denn sind a : ß und ß : et beides ganze Zahlen, so ist
das Product dieser beiden Zahlen = 1; also sind beides Ein-
Einheiten.
Für die Zahlen des Körpers B (i) gelten dieselben Gesetze
über die Zerlegung in Primfactoren, wie bei den reellen ganzen
Zahlen:
Eine ganze Zahl a des Körpers B(i), die keine
Einheit ist, heisst zusammengesetzt, wenn sie sich
in mehrere ganzzahlige Factoren, deren keiner eine
Einheit ist, zerlegen lässt.
Lässt sie sich nicht so zerlegen, so soll sie eine
Primzahl im Körper B(i) heissen.
Ist § = x -\- yi eine gebrochene Zahl des Körpers B(i), so
lässt sich eine ganze Zahl [i = m -\- ni so bestimmen, dass die
Norm der Differenz § — ji, also (x — mJ -f- (y — wJ, kleiner
¦oder wenigstens nicht grösser als 1/2 ist; denn man braucht die
ganzen rationalen Zahlen-m, n nur so zu wählen, dass x — m
und y — n absolut genommen nicht grösser als Väi ihre Quadrate
also nicht grösser als 1/i sind.
Sind also a und a1 zwei ganze Zahlen in B(t), und av von
Null verschieden, so kann man hiernach die ganzen Zahlen ji
und «2 so bestimmen, dass
! ! (,) = 2
also
« = ji «! -f- «2, N(a2) < N(al).
Ist «2 nicht Null, so kann man ebenso mit den Zahlen
«!, «2 verfahren und erhält
und so bestimmt man eine Reihe ganzer Zahlen a, uu a2, 03 . . .
mit stets abnehmender Norm, die sich fortsetzen lässt, so lange
die Null nicht darunter vorkommt. Da diese Normen ganze ratio-
rationale positive Zahlen sind, die immer abnehmen, so muss nach
einer endlichen Zahl von Schritten die Null auftreten und man
¦erhält also ein Gleichungssystem:

638 Sechzehnter Abschnitt. §. 181;
«1 = f*l «2 + «3.
A) . -
«A-2 = f*Ä — 2 «7s— 1 -j~ «Ä»
«Ä_i = (tÄ_i au. ¦
Daraus schliesst man, dass die ganze Reihe der Zahlen
«, «j, «2, . . ., also insbesondere auch « und «1) durch «Ä theilbar
sind, und umgekehrt, dass jeder gemeinsame Theiler von a
und «! Theiler von allen folgenden «, also auch von ah ist.
Jede andere Zahl, die diese beiden Eigenschaften hat, muss
mit ah associirt sein, und man nennt also ah (und jede mit ah
associirte Zahl) den grössten gemeinschaftlichen Theiler von
« und «j.
Wenn wir aus dem Algorithmus A) die zwischenliegenden a
eliminiren, indem wir «2 aus der ersten in die zweite, dann o%
aus der zweiten in die dritte Gleichung substituiren u. s. f., so
ergiebt sich ein Resultat von der Form ux -\- a^k = w^, und wir
können also, wenn wir statt «, o^, ah setzen «, ß, 8, den Satz
aussprechen:
4. Wenn «, ß irgend zwei ganze Zahlen in H(i)
sind, und 8 ihr grösster gemeinschaftlicher
Theiler, so kann man die ganzen Zahlen x, X
so bestimmen, dass
B) kx + ßX = 8
wird.
Ist der grösste gemeinschaftliche Theiler 8 zweier Zahlen
a, ß eine Einheit, so heissen a und ß relativ prim, und wir
können in diesem Falle der Gleichung
C) «3t 4- ßl = 1
durch ganzzahlige x, X genügen.
Ist ß eine Primzahl, so ist entweder a durch ß theilbar,
oder « und ß sind relativ prim. Im letzteren Fall besteht die
Gleichung C). Ist dann y eine andere Zahl in H («'), so folgt aus C)
uyx -\- ßyX = y.
Es muss demnach, wenn ay durch ß theilbar ist, auch y
durch ß theilbar sein. Also haben wir folgenden Fundamentalsatz:
5. Ein Product aus zwei oder mehr ganzen Zahlen
in B(i) ist nur dann durch eine Primzahl in B(i)

§. 181. Complexe Zahlen. 639
theilbar, wenn wenigstens einer seiner Factoren
durch diese Primzahl theilbar ist.
Mächt man nun noch die Bemerkung, dass eine Primzahl nur
dann durch eine andere theilbar sein kann, wenn der Quotient
eine Einheit ist, wenn also beide associirt sind, und betrachtet
associirte Primzahlen als nicht wesentlich verschieden, so folgt:
6. Eine ganze Zahl des Körpers JR(i) kann immer
und nur auf eine Art in ein Product von Prim-
Primzahlen zerlegt werden.
Denn sei « irgend eine ganze Zahl in B(i). Ist a nicht
selbst eine Primzahl, so ist sie zerlegbar, etwa in yß; die Normen
von y und von ß sind aber kleiner als die Norm von a. Ist ß
noch keine Primzahl, so ist es wieder zerlegbar, etwa in de; die
Normen dieser Factoren, die alle positive ganze rationale Zahlen
sind, nehmen immer ab, und man muss also nothwendig einmal auf
einen Factor stossen, der eine Primzahl ist. Also ist jede Zahl «
gewiss durch ,eine Primzahl % theilbar. Ist demnach a = %«',
so gilt von «' dasselbe und es ist etwa a' = %' a" . . . Da die
Normen von «, «', «" . . . wieder alle abnehmen, so muss man
bei der Fortsetzung dieser Reihe schliesslich auf eine Einheit
stossen. Es ist daher « in eine endliche Anzahl von Primfactoren
zerlegbar, also
« = % %' %" . . .,
wobei ein zuletzt übrig bleibender Einheitsfactor mit einer der
Primzahlen % vereinigt werden kann. Sind nun x, %', x" ...
gleichfalls Primzahlen und ist a = x x' x" . . ., so folgt aus
x%'%"... = %%'n" ...
nach 5., dass eine der Primzahlen sr, z. B. die erste durch % theil-
theilbar, also von % nicht wesentlich verschieden ist. Hebt man
beiderseits mit jc = sr, so kann man denselben Schluss mit %'
wiederholen u. s. f., und findet also, dass jede der Primzahlen x
auch unter den % vorkommen muss, und wenn unter den x eine
Primzahl mehrmals vorkommt, so muss sie mindestens ebenso
oft unter den % vorkommen. Derselbe Schluss lässt sich aber
auch umgekehrt machen, und daraus folgt, dass die Gesammtheit
der x, von Einheitsfactoren- abgesehen, mit der Gesammtheit
der % übereinstimmen muss.
Es handelt sich nun noch darum, die Primzahlen des
Körpers B(i) wirklich zu ermitteln.

640 Sechzehnter Abschnitt. §. 181.
Jede Primzahl ist Theiler von unendlich vielen rationalen
ganzen Zahlen, z. ß. von der Norm und allen ihren Vielfachen,
unter den rationalen positiven ganzen Zahlen, die durch eine Prim-
Primzahl % theilbar sind, ist eine, die wir mit n bezeichnen wollen,
die kleinste, und diese muss eine Primzahl im Körper H sein.
Denn wäre sie in H zerlegbar, so müsste nach 5. einer ihrer Fac-
Factoren, also eine noch kleinere Zahl, durch % theilbar sein. Ebenso
ist auch umgekehrt jede reelle Primzahl n wenigstens durch eine
Primzahl % theilbar. Es sei also n = im, woraus durch Bildung
der Norm w2 = N(it) N.(a) folgt. Da n eine Primzahl ist und
N(jc)N(a) ganze Zahlen, so sind zwei Fälle möglich:
1. N(x) = n, N(a) = n,
2. N(n) = n2, N(u) = l.
Im ersten Falle ist, wenn %' die zu % conjugirte Zahl be-
bedeutet und % = a -\- bi gesetzt wird, n = nn' = a2 -f- b2,
a = «', und man sieht, dass dieser Fall nur dann eintritt, wenn
n zu den Primzahlen p gehört, die in die Summe von zwei
Quadraten zerlegbar sind. Umgekehrt kann jede solche Zahl p
in zwei conjugirte Factoren ac, %' zerlegt werden, deren keine
eine Einheit ist. Die Primzahlen p sind also im Körper
B(i) nicht Primzahlen.
Im zweiten Falle, der hiernach bei den Primzahlen q ein-
eintritt, ist « eine Einheit, also n mit % associirt, d. h. die reellen
Primzahlen q sind auch im Körper R(i) Primzahlen.
Die Primzahl 2 gehört, wie schon bemerkt, zu der ersten
Art, und es ist 2 = A -f- i) A — i). Aber sie nimmt eine be-
besondere Stellung ein, weil 1 — i = — i A -{-«), also 2 = — i(l-\- *'J
ist. Die reelle Primzahl 2 ist also (von dem Factor — i ab-
abgesehen) im Körper B(i) das Quadrat einer Primzahl. Dieser
Fall tritt, wie man leicht sieht, bei keiner der übrigen Prim-
Primzahlen p ein.
Die Gesammtheit der Primzahlen des Körpers JR(i) besteht
also aus den reellen Primzahlen q und aus den Factoren der Prim-
Primzahlen 2>> Ist p in die Summe zweier Quadrate a2 -f- b2 zerlegt, so
kennt man auch die conjugirten Factoren a i bi von p. Dazu
kommen noch die associirten Zahlen. Aus 5. folgt dann noch,
dass eine Primzahlp nur auf eine Art in die Summe von zwei
Quadraten zerlegt werden kann. Durch diese Zerlegung sind
aber die Zahlen a, b noch nicht völlig bestimmt, sondern sie

§. 182. Körper der dritten Einheitswurzeln. C41
können noch mit einander vertauscht und mit zwei Vorzeichen
versehen werden. Das kommt darauf hinaus, dass man % durch
jede der vier associirten Zahlen a -\-bi, — a — bi, — b -\- ai
b — ai ersetzen kann. Ist ^-ungerade, so muss von den beiden
Zahlen a, b die eine gerade, die andere ungerade sein. Wählen
wir etwa für b die gerade der beiden Zahlen, und bestimmen
das Vorzeichen so, dass a = 1 (mod 4) wird, so ist unter den
vier associirten Zahlen eine bestimmte ausgewählt, die man die
primäre nennen kann1).
Diese Definition der primären Zahlen lässt sich auf alle
ganzen Zahlen des Körpers B(i) übertragen, deren Norm un-
ungerade ist, und man hat dann das Gesetz, dass das Product
zweier primären Zahlen wieder eine primäre Zahl ergiebt.
Das System von vier associirten Zahlen im Körper JR(i) ist
analog dem Paar entgegengesetzter Zahlen im Körper B. In B
betrachtet man die positiven Zahlen als die primären.
Durch die Formel B8) des vorigen Paragraphen ist für
irgend eine gegebene Primzahl p einer der Factoren a + b i aus
der Kreistheilung abgeleitet. Nach den Formeln §. 180, C8), C9)
ist diese Zahl primär, wenn p = 5 (mod 8), dagegen der pri-
primären entgegengesetzt, wenn p = 1 (mod 8) ist. Darüber aber,
welche von den beiden conjugirten Zahlen a ± b i durch diese
Formeln dargestellt ist, haben wir kein allgemeines Kennzeichen.
Beispielsweise sind die complexen Primzahlen in B(f), deren
Normen kleiner als 200 sind:
1 + {, 1 -f 2*, 3 -f 2«, 1 -f 4», 5 -f 2«, 1 + 6», 5 + 4»,
7 + 2», 5 + 6«, 3 + 8», 5 + 8«, 9 + 4», 1 + 10«, 3 + 10«,
7 + 8», 11 + 4i, 7 + 10«, 11 + 6«, 13 + 2«, 9 + 10*, 7 + 12»,
1 + 14».
§. 182.
Der Körper der dritten Einheitswurzeln.
Der Hauptsatz des vorigen Paragraphen, dass jede ganze
Zahl des Körpers B(i) sich nur auf eine Art in unzerlegbare
Factoren zerlegen lässt, demzufolge der Begriff der unzerlegbaren
2) Gauss giebt an der erwähnten Stelle zwei verschiedene Bestim-
Bestimmungen für die primären Zahlen zur Auswahl, von denen dies die erste
ist. Er behält weiterhin die zweite bei.
Weber, Algebra. I. 41

642 Sechzehnter Abschnitt. §.182.
Zahl mit dem der Primzahl zusammenfällt, beruht, wie'man sieht,
in der Hauptsache auf dem Algorithmus des grössten gemein-
gemeinschaftlichen Theilers, der in den Formeln §. 181, A) enthalten ist,
und wenn man also in einem anderen Körper einen solchen, im
Endlichen abbrechenden Algorithmus hat, so lassen sich dieselben
Schlüsse ziehen.
Dies findet statt bei dem Körper, der sich aus B mittelst
der dritten Einheitswurzel q = -^ ableiten lässt und
mit B(q) oder auch mit J?(V— 3) bezeichnet werden kann.
Dieser Körper besteht aus dem Inbegriff aller Zählen der Form
£ = x -f- $y, worin x, y rationale Zahlen sind, und die Norm
einer solchen Zahl ist
x + Q*y) = oft — xy_-\- y*
,= 2x—y + yV^3 2x — y—yV-B _ Ba—y)«-f 3y»
2 ' 2 4
Eine Zahl « = a -f- b q heisst eine ganze Zahl in Jt (p),
wenn a, b ganze rationale Zahlen sind. Die Einheiten in diesem
Körper ergeben sich aus
N(u) = ai — ab-\- 6* = 1,
oder
Ba — bf -f 362 = 4,
die nur erfüllt ist für b = 0, « = f 1 oder a = 0, b =t= + 1
oder a = -j-1> ft = —j— 1 oder a = — 1, b = — 1, so dass man
also hier sechs Einheiten hat
± 1, ± Q, ± Q*.
Ein System associirter Zahlen ist hier
±(a + b9), ±(a9 + bg*) ±= ±[—b + (a — b)g]
± (a92 + b) = ± (b — a - a9).
Ist | eine beliebige gebrochene Zahl in R(q), so kann man die
ganze Zahl ji so bestimmen, dass in £ — ii = x-\-(>y die Compo-
nenten x und y absolut nicht grösser als 1/i sind und dass also
JV(| — (i) = x* — xy + 2/2 ^ |.
Auf Grund dieser Eigenschaft lässt sich, ganz wie im vorigen
Paragraphen, der grösste gemeinschaftliche Theiler zweier Zahlen
«, ß bestimmen und damit beweisen, dass sich jede ganze Zahl
in R(q) nur auf eine Weise in Primzahlen dieses Körpers zer-
zerlegen lässt, wenn associirte Zahlen nicht als wesentlich verschieden
betrachtet werden.

§. 182. Körper der dritten Einheitswurzeln. 643
Wie im vorigen Paragraphen schliesst man, dass man alle
Primzahlen des Körpers B (q) erhält, wenn man alle reellen Prim-
Primzahlen zerlegt, und dass eine reelle Primzahl entweder in zwei
conjugirte Primfactoren in B(q) zerfällt, p = nn\ oder dass sie
auch im Körper B(q) eine Primzahl ist.
Die Primzahl 3 zerfällt in die beiden Factoren A — q),
A — 02); diese sind aber associirt und also ist 3 = — 02A — pJ
mit dem Quadrat einer Primzahl in B(q) associirt. Man kann
V— 3 für diese Primzahl wählen. Alle Primzahlen von der
Form 3/-)- 1 lassen sich nach §. 180 in zwei conjugirte Factoren
in B(q) zerlegen, während die Primzahlen von der Form 3/-)-2
niemals zerlegbar sind, weil ein Ausdruck von der Form a2 — a b + &2
nicht = 2 (mod 3) sein kann. Also erhält man alle Primzahlen
in B(q), wenn man die reellen Primzahlen der Form 3/-f .2
und die conjugirten Factoren der übrigen reellen Primzahlen
aufsucht.
Ist a + b q eine complexe ganze Zahl, deren Norm a2 — a b + b2
nicht durch 3 theilbar ist, so muss von den beiden Zahlen a, b
entweder eine durch 3 theilbar sein, die andere nicht, oder es
muss a = b und folglich a2 — a b + &2 = 1 (mod 3) sein. Es
ist also unter den associirten Zahlen
a + b 0, b + a 02, b — (a — b) q,
immer eine und nur eine, in der derCoefficient.von q (oder von q2)
durch 3 theilbar ist. Nehmen wir an, es sei b = 3B durch 3
theilbar, und setzen N(a -\- b q) = p, so folgt, wenn noch
2 a — b = A gesetzt wird,"
±p = £> + 27 B\
in Uebereinstimmung mit §. 180. Ist p eine reelle Primzahl, und
hat man 4p in dieser Form dargestellt, so erhält man daraus
die complexen Factoren von p
(A + ZB \(A — SB \
* = V 2 h 3 qB) V 2 3qB) "
Die complexen Primzahlen, deren Norm unter 200 ist, sind hier
1 — q, 1 + 3 p, 4+ 3 p, 5 + 39, 5 +9, 7 + 39, 7 + 6 q,
5 + 90, 7 + 9p, 8 + 90, 10 + 39, 11 + 30, 11 + 90,
7 + 120, 13 + 60, 13 + 30, 14 + 90, 13+120, 14 + 30,
11 + 15 0, 16+9 0, 13 + 15 0.
41*

Siebzehnter Abschnitt.
Algebraische Auflösungen von Gleichungen.
§. 183.
Reduction der Gruppe durch reine Gleichungen.
Eine der ältesten Fragen, an der sich vorzugsweise die
neuere Algebra entwickelt hat, ist die nach der sogenannten
algebraischen Auflösung der Gleichungen, worunter man eine
Darstellung der Wurzeln einer Gleichung durch eine Reihe von
Radicalen, oder die Berechnung durch eine endliche Kette von
Wurzelziehungen versteht. Auf diese Frage fällt von der Gruppen-
Gruppentheorie das hellste Licht.
Präcisiren wir zunächst die Frage, um die es sich handelt,
so ist es offenbar die, ob und wie man den Körper £1 durch
successive Adjunction von Wurzelgrössen (Radicalen) so erweitern
kann, dass entweder alle oder wenigstens ein Theil der Wurzeln
im erweiterten Körper enthalten sind. Eine Wurzelgrösse ist
aber eine solche, die zwar nicht selbst, von der aber irgend eine
ganze Potenz in Sl enthalten ist, also, wenn a eine Grosse in Sl
ist, die Wurzel einer Gleichung von der Form
y» — a = 0,
d. h. einer reinen Gleichung.
Soll eine irreducible Gleichung algebraisch auflösbar sein,
oder wenigstens eine oder einige algebraisch darstellbare Wurzeln
haben, so muss nach einer successiven Adjunction von Wurzeln
reiner Gleichungen in endlicher Anzahl die gegebene Gleichung
reducibel werden, da ein Theil ihrer Wurzeln in dem erweiterten
Körper enthalten sein soll. Da die anfängliche Gruppe P transitiv
ist, so muss diese Gruppe schliesslich intransitiv werden, oder

§. 183. Keduction der Gruppe durch reine Gleichungen. 645
sich auf die Einheitsgruppe reduciren. Es muss also jedenfalls
einmal der Fall eintreten, dass die Gruppe P durch Adjunction
einer Wurzel einer reinen Gleichung reducirt wird.
Die Untersuchung dieser Frage wird ausserordentlich ver-
vereinfacht, wenn man sie noch etwas umformt1).
Wir haben im §. 169 gesehen, dass die reinen Gleichungen
zu den Abel'schen gehören, dass alle Abel'schen Gleichungen
durch eine Kette von cyklischen Gleichungen vom Primzahlgrad
und diese letzteren durch Radicale lösbar sind.
Wir ersetzen also die Frage nach der Lösbarkeit durch Radi-
Radicale durch die damit gleichbedeutende der Lösbarkeit durch
Wurzeln Abel'scher Gleichungen. Ersetzen wir die Abel'sche
Gleichung durch eine Kette von cyklischen Gleichungen von
Primzahlgrad, so wird die erste Reduction der Gruppe durch
Adjunction der Wurzel einer solchen Gleichung eintreten, und
wir stehen also zunächst vor der Frage:
Unter welchen Bedingungen wird die Gruppe P
einer Gleichung »ten Grades f{x) = 0 durch Adjunction
einer Wurzel einer cyklischen Gleichung von Prim-
Primzahlgrad m reducirt?
Wir beschränken uns hierbei nicht auf irreducible Gleichungen
f(x) = 0, sondern erörtern die Frage allgemein, immer unter
der selbstverständlichen Voraussetzung, dass f(x) keine mehr-
mehrfachen Wurzeln hat.
Es ist denkbar, dass es nöthig ist, dem Körper £1 zunächst
verschiedene Wurzeln cyklischer Gleichungen (z. B. Einheits-
Einheitswurzeln) zu adjungiren, die die Gruppe P nicht verändern. Da
es sich aber jetzt nur um die Ermittelung der nothwendigen
Eigenschaften der Gruppe P handelt, so nehmen wir an, es seien
alle nöthigen Vorbereitungen getroffen und der Körper Sl so
beschaffen, dass durch Adjunction einer Wurzel der cyklischen
Gleichung q> (x) = 0, vom Primzahlgrad m, die Gruppe P sich
auf einen ihrer Theiler, Q, reducirt.
Bezeichnen wir die Wurzeln von q> (%) = 0 mit
so sind alle diese Grossen rational (in £1) durch eine beliebige
unter ihnen ausdrückbar, und wenn P die Gruppe von f(x) == 0
x) Auf diese Form der Fragestellung hat zuerst C. Jordan hin-
hingewiesen (Traite des substitutions p. 386).

646 Siebzehnter Abschnitt. §. 184.
in £1 ist, so ist Q die Gruppe derselben Gleichung in Sl (s), oder
was dasselbe ist, in £1 (£j), Sl (s2), . . ., £1 (em—i). Nun können wir
aber den Schlusssatz in §.164 anwenden. Nach diesem Satze muss
der Index j des Theilers Q von P ein Theiler von m sein, und
da m als Primzahl vorausgesetzt ist, so ist m=:j. Ausserdem ist
nach demselben Satze s rational durch die Wurzeln der Gleichung
f(x) = 0 darstellbar:
e = if> (x0, ajj, . . ., xm-i).
Diese Function gehört zur Gruppe Q, und wenn wir darauf
sämmtliche Permutationen der Gruppe P anwenden, so erhalten
wir die Functionen e, £x, £2, . . ., em—i und keine anderen. Diese
Functionen gehören zu den conjugirten Gruppen n~1Qn. Da
aber jede dieser Functionen rational durch jede andere aus-
ausdrückbar ist, so müssen sie alle zu derselben Gruppe gehören,
d. h. Q ist ein Normaltheiler von P.
Wir haben also hiermit den ersten Satz bewiesen:
I. Wenn die Gruppe einer Gleichung P durch
Adjunction der Wurzeln einer Abel'schen Glei-
Gleichung reducirt wird, so hat P einen Normal-
Normaltheiler Q von Primzahlindex.
Dieser Satz lässt sich auch umkehren.
Wenn nämlich die Gruppe P einen Normaltheiler Q vom
Index in hat, so können wir eine zu Q gehörige Function il>
wählen, und die damit conjugirten Functionen 4>,ij>i,il>2, ¦ ¦ ¦¦, i>m—i
gehören alle zu derselben Gruppe. Der Körper £l(il>) ist ein
Normalkörper, und ^ die Wurzel einer Normalgleichung. Im
Körper Sl (ip) ist Q die Gruppe von f(x) = 0 (§. 162). Wenn
aber m eine Primzahl ist, so ist ip nach §. 170 die Wurzel einer
cyklischen Gleichung, und damit ist also bewiesen:
II. Wenn die Gruppe P von f(x) = 0 einen Normal-
Normaltheiler Q von Primzahlindex m besitzt, so wird
durch Adjunction der Wurzel einer cyklischen
Gleichung wten Grades die Gruppe P auf Q
reducirt.
§. 184.
Metacyklische Gleichungen.
Wir wollen eine Gleichung, deren vollständige Lösung sich
auf eine Kette von cyklischen Gleichungen zurückführen lässt,

§. 184. - Metacyklische Gleichungen. 647
eine metacyklische Gleichung nennen. Die cyklischen
Gleichungen selbst sind als specieller Fall darunter mit enthalten,
und nach dem im §. 183 Bemerkten sind die metacykliscjien
Gleichungen dieselben, wie die durch Radicale lösbaren Glei-
Gleichungen. Ist P die Gruppe einer solchen Gleichung, so muss sie
nach dem vorigen Paragraphen einen Normaltheiler von Prim-
Primzahlindex h, den wir jetzt mit P1 bezeichnen wollen, besitzen.
Besteht Pt aus der einzigen identischen Permutation, so ist P
selbst cyklisch und von Primzahlgrad. Ist P1 nicht die Einheits-
Einheitsgruppe, so muss Pl wieder einen Normaltheiler P2 von Prim-
Primzahlindex j2 enthalten u. s. f., bis wir endlich zur Einheitsgruppe
gelangen.
Dass es auch die für eine metacyklische Gleichung aus-
ausreichende Bedingung ist, wenn ihre Gruppe P diese Zusammen-
Zusammensetzung hat, ergiebt sich aus dem vorigen Paragraphen. Wir
sprechen also den Satz aus:
III. Die nothwendige und hinreichende Bedingung
für eine metacyklische Gleichung ist die, dass
es eine Reihe von Gruppen
P) Pi> P21 P3 • • •
giebt, deren erste die Galois'sche Gruppe der
Gleichung, deren letzte die Einheitsgruppe ist,
von denen jede folgende ein normaler Theiler
der nächst vorangehenden von Primzahlindex ist.
Hiernach nennen wir eine Permutationsgruppe P, die diese
Eigenschaft hat, zu der sich also eine Kette von Gruppen
P, Pl5 P2, . . ., Pu_!, 1
so bestimmen lässt, dass jedes Glied Normaltheiler des voran-
vorangehenden von Primzahlindex ist, eine metacyklische Gruppe1).
Wir haben hier die Bedingung für die vollständige Auf-
Auflösbarkeit einer Gleichung durch eine Kette von cyklischen
Gleichungen erhalten. Es handelt sich aber noch um die Frage,
ob eine oder einige der Wurzeln auf diese Weise dargestellt
werden können, während andere eine solche Darstellung nicht
') Der Ausdruck „metacyklische Gruppen" ist zuerst von Kronecker,
wenn auch in beschränkterem Sinne, gebraucht. Ich möchte hier diese
leichte Verallgemeinerung eines schon bekannten Ausdruckes an Stelle des
von Frobenius und Holder benutzten Ausdruckes „auflösbare Gruppen"
vorschlagen.

648 Siebzehnter Abschnitt. , §. 181.
gestatten. Diese Frage ist nur berechtigt bei irreduciblen Glei-
Gleichungen, da bei reduciblen Gleichungen alle denkbaren Com-
binationen vorkommen können, und hier gilt nun der Satz:
IV. Wenn eine W'urzel einer irreduciblen Glei-
Gleichung durch Lösung cyklischer Gleichungen be-
bestimmbar ist, so ist die Gleichung metacyklisch1).
Wenn eine irreducible Gleichung nien Grades f(x) = 0 auch
nur eine Wurzel hat, die durch successive Adjunction von Wurzeln
cyklischer Gleichungen rational wird, so muss sie nothwendig
durch diese Adjunction reducibel werden, da sich ja schliesslich
eiii linearer Factor absondern muss. Es sei also P die Gruppe
unserer Gleichung., nachdem alles Nöthige so weit adjungirt ist,
dass zwar f(x) noch nicht reducibel ist, aber durch die nächste
Adjunction der Wurzel s einer cyklischen Gleichung von Prim-
Primzahlgrad m in Factoren zerfällt. Es muss dann P nach §. 183
einen Normaltheiler Q vom Index m haben, auf den sich die
Gruppe der Gleichung nach Adjunction von a reducirt, und die
Permutationsgruppe Q muss intransitiv sein. Wenn Q die Ein-
Einheitsgruppe ist, so ist/(#) = () durch Adjunction von s voll-
vollständig gelöst. Ist aber Q noch von der Einheitsgruppe ver-
verschieden, so treten die Sätze des §. 165 in Kraft. Danach zerfällt
/(#) nach Adjunction von s, da ja hier der Index m von Q eine
Primzahl ist, in m Factoren, <p(x, a), <Pi(x, s), . . ., <pm_1(x, s),
vom gleichen Grade (i und es ist pm = n.
Ist z. B. n eine Primzahl, so muss ft = 1 sein; die Func-
tionen <p sind linear, und die Gleichung f(x)= 0 ist vollständig
gelöst; also ist der Satz IV. für Gleichungen von Primzahlgrad
richtig. Im allgemeinen Falle muss einer der Factoren (iten
Grades cp(x, e), q>x (x, s), . . ., cpm—i(x, s) etwa cp(x, s) eine
Wurzel haben, die durch Adjunction der Wurzeln cyklischer
Gleichungen rational wird, und wenn wir also annehmen, dass
unser Satz für Gleichungen ft1*11 Grades schon bewiesen sei, so
folgt, dass <p(x, s) = 0 selbst und also auch ihre Gruppe meta-
metacyklisch ist.
Da aber nach §. 165 die verschiedenen Gleichungen <p = 0,
q>1 = 0, . . ., (pm—i = 0 dieselbe Gruppe haben, so sind sie alle
und mithin auch f(x) = 0 metacyklisch.
x) Dieser Satz rührt von Abel her. Neuerdings ist ein Beweis von
Seiivanoff gegeben (Acta mathematica, Bd. 19, 1895).

§. 185. Einfachheit der alternirenden Gruppe. 649
Unter der Voraussetzung also, dass der Satz IV. für Glei-
Gleichungen (tten Grades richtig ist, folgt seine Richtigkeit für Glei-
Gleichungen (imten Grades; und da er für Gleichungen von Prim-
Primzahlgrad gilt, so ist er allgemein nachgewiesen.
§. 185.
Einfachheit der alternirenden Gruppe.
Wir haben früher gesehen (§. 156), dass, wenn wir die
Coefficienten einer Gleichung nten Grades als unabhängige Variable
und den Körper aller rationalen Functionen dieser Coefficienten
als Rationalitätsbereich betrachten, die Galois'sche Gruppe der
Gleichung die symmetrische Gruppe ist. In der symmetrischen
Gruppe ist immer ein Nonnaltheiler vom Index 2 enthalten, die
alternirende Gruppe, auf die sich die Gruppe der Gleichung
reducirt, wenn die Quadratwurzel aus der Discriminante adjun-
girt wird. Bei vier Ziffern hat die alternirende Gruppe, die aus
der identischen Permutation, acht dreigliedrigen Cyklen und
drei Paaren von Transpositionen besteht,' den Normaltheiler vom
Index 3:
1, @,1) B, 3), @,2) A,3), @,3) A,2).
Diese Gruppe hat drei verschiedene Normaltheiler vom
Index 2, von denen wir einen 1, @, 1) B, 3) bevorzugen, von
dem wieder die Einheitsgruppe ein Normaltheiler vom Index 2
ist. Die Gruppe der 24 Permutationen von vier Ziffern ist also
metacyklisch, und darauf beruht jede Auflösungsmethode der
biquadratischen Gleichung (§. 167, 168).
Wir wollen nun nachweisen, dass, wenn n grösser als 4 ist,
die alternirende Gruppe ausser der Einheitsgruppe überhaupt
keine normalen Theiler hat, oder nach der früher eingeführten
Bezeichnung einfach ist. Daraus folgt dann, dass die Bedingung,
die wir für die algebraische Auflösbarkeit einer Gleichung als
nothwendig gefunden haben, für die Gleichungen von höherem
als dem vierten Grade, deren Gruppe die symmetrische oder die
alternirende ist, nicht erfüllt ist, und dass also Gleichungen
von höherem als dem vierten Grade, so lange die Coeffi-
Coefficienten unabhängige Variable sind, nicht mehr alge-
algebraisch lösbar sind.

650 Siebzehnter Abschnitt. §.185.
Der Beweis, dass die alternirende Gruppe einfach ist, lässt
sich so führen:
Sei A die altemirende Gruppe der Permutationen von n
Ziffern 1, 2, 3, . . ., n und Q ein normaler Theiler von A. Wir
haben im §. 160, 7. und 4. gesehen, dass sich alle Permuta-
Permutationen von A aus dreigliedrigen Cyklen zusammensetzen lassen,
und dass man, wenn x und n irgend welche Permutationen
sind, die transformirte Permutation zu x, n~x xn erhält, wenn
man in den Cyklen von x die Vertauschungen n vornimmt. Ist
nun x ein dreigliedriger Cyklus, etwa A, 2, 3), so kann man %
aus A so wählen, dass n—^xn jeden beliebigen dreigliedrigen
Cyklus der n Ziffern darstellt; denn man kann in
/l, 2 3, ..„*x
Vöti, «a, a3, . . ., aj
die drei ersten Ziffern ax, a2, a% beliebig wählen, und, wenn es
nöthig ist, damit n zu A gehöre, noch % und a2 vertauschen.
Dadurch geht aus x einer der beiden Cyklen (ax, Oj, aB), (a2, ax, aB)
hervor, von denen jeder die zweite Potenz des anderen ist.
Wenn nun Q ein Normaltheiler von A ist, und x eine Permu-
Permutation aus Q, so ist %-~ 1xn auch in Q enthalten, wenn n in
A enthalten ist, und daraus folgt, dass, wenn in Q ein drei-
dreigliedriger- Cyklus vorkommt, Q mit A identisch ist.
Unser Beweis beruht nun darauf, dass, wenn x irgend eine
Permutation in Q ist, auch n~x x n und folglich auch
A) . X = x~1 n—xxn
in Q vorkommen muss, und es ist dann zu zeigen, dass man,
wenn x irgend eine nicht identische Permutation ist, n immer so
aus A wählen kann, dass die Permutation l ein dreigliedriger
Cyklus, und folglich Q mit A identisch wird.
Wir nehmen zu diesem Zwecke sowohl x als n in ihre Cyklen
zerlegt an und bemerken, dass man bei der Bildung von l solche
Cyklen von x gar nicht zu berücksichtigen braucht, deren Ziffern
durch % ungeändert bleiben, weil sie sich in x~1 und x gegen-
gegenseitig aufheben. Wir müssen nun die verschiedenen möglichen
Formen von x einzeln betrachten.
1. Es enthalte x einen Cyklus von mehr als drei Ziffern etwa
A, 2, 3, ..., m), wir nehmen n = A,2,3) an und erhalten,
indem wir x~ 1n~1x zuerst (nach §. 160, 4.) bilden,
1 = x-^n^xn = B, 4, 3)A, 2, 3) = A, 2, 4).

§. 185. Einfachheit der alternii'enden Gruppe. 651
In Q kommt also ein dreigliedriger Cyklus vor.
2. Es enthalte % zwei dreigliedrige Cyklen A, 2, 3) D, 5, 6).
Wir nehmen n = A, 3, 4) an und erhalten
"* = B, 5, 1)A, 3, 4) = A, 2, 5, 3, 4).
Diese Permutation l, die in Q enthalten ist, fällt aber unter
den Fall 1.
3. Es enthalte % einen dreigliedrigen und einen zwei-
zweigliedrigen Cyklus A, 2, 3) D, 5). (Dass in %, wenn es zu
A gehört, noch ein zweiter Cyklus von gerader Gliederzahl
vorkommen muss, ist hier gleichgültig.) Für «•= A,2,4)
ergiebt sich
A = B, 5, 3)A, 2, 4) = A, 2, 5, 3, 4),
was wieder unter den Fall 1. fällt.
4. Es enthalte % drei Transpositionen, A, 2) C, 4) E, 6).
Für n =. A, 3, 5) folgt
A = B, 6, 4)A, 3, 5),
was unter den Fall 2. fällt.
5. Es enthalte % zwei Transpositionen und ein unverändertes
Element A, 2) C, 4) E). Man setzt n = A, 2, 5) und
erhält
A = (l, 2, 5)A,2, 5) = A,5, 2).
Damit sind alle Fälle erschöpft, wenn n > 4 ist. Für
n = 4 bleibt der eine Fall noch übrig, dass n aus zwei Trans-
Transpositionen besteht, der eben das besondere Verhalten bei n = 4
herbeiführt, wodurch die algebraische Auflösung der Gleichung
4ten Grades ermöglicht wirdv).
Es folgt aus diesem Satze weiter, dass die symmetrische
Gruppe keine anderen normalen Theiler hat, als sich selbst, die
alternirende Gruppe und die Einheitsgruppe. Denn ist 8 die
symmetrische, A die alternirende Gruppe, und Q ein normaler
Theiler von S, so ist der grösste gemeinschaftliche Theiler Q'
von A und Q ein normaler Theiler von A, ist also gleich A
J) Dei" erste vollständige Beweis, dass die allgemeine Gleichung von
höherem als dem 4ten Grade durch Radicale nicht lösbar ist, rührt von
Abel her (Crelle's Journal, Bd. I, 1826). Ueber die älteren Beweisversuche
von Ruffini A799 bis 1806) und ihr Verhältniss zum Abel'schen Beweis
vergleiche man die Abhandlung von Burkhardt, „Die Anfänge der
Gruppentheorie und Paolo Euffini" (Abhandlungen zur Geschichte der
Mathematik VI. Supplement zu Schlömilch's Zeitschrift. Leipzig 1892).

652 Siebzehnter Abschnitt. §. 186.
oder gleich 1. Denn ist %' ein Element in Q' also auch in A,
% ein beliebiges Element in S, so ist n—^vJic zunächst in Q ent-
enthalten, weil Q Normaltheiler von 8 ist. Es ist aber zugleich
n-1%'n in A, also auch in Q' enthalten.
Ist Q' gleich A, so ist Q entweder auch gleich A oder
gleich 8. Ist Q' aber = 1, so enthält Q ausser der Einheit keine
Permutation der ersten Art. Sind also % und A zwei verschiedene
und von der Einheit verschiedene Permutationen von Q, so
müssen %** und % X als von der ersten Art = 1 sein, d. h. l muss
= % sein. Es kann also Q höchstens eine von der identischen
verschiedene Permutation % enthalten. Da aber Q ein Normal-
Normaltheiler von 8 sein soll, so muss für jede Permutation % aus der
symmetrischen Gruppe 71—1%tc = % sein, d. h. % darf sich nicht
ändern, wenn in seinen Cyklen irgend eine Permutation ausgeführt
wird. Dies ist aber nur dann möglieb, wenn überhaupt nur zwei
Ziffern 1, 2 vorhanden sind und % = A, 2) ist. Dann aber ist
1, A, 2) die ganze Gruppe S.
§. 186.
Nicht metaeyklische Gleichungen im Körper der
rationalen Zahlen.
Durch den Satz des vorigen Paragraphen ist der Nachweis
geführt, dass eine Gleichung nien Grades, wenn n grösser als 4
ist, nicht mehr algebraisch gelöst werden kann, wenn die Coeffi-
cienten als unabhängige Veränderliche betrachtet werden. Von
grösserem Interesse noch ist aber die Frage, ob es in dem Körper
der rationalen Zahlen Gleichungen nten Grades giebt, die nicht
algebraisch lösbar sind. Die Frage lässt sich noch etwas all-
allgemeiner stellen, nämlich so, ob es ganzzahlige Gleichungen giebt,
deren Gruppe die symmetrische Gruppe ist, die also nach einer
früher erklärten Ausdrucksweise keinen Affect haben.
Bildet man die Galois'sche Resolvente G(t) — 0 vom Grade
n (n) einer allgemeinen Gleichung nten Grades f(x) = 0 mit un-
unbestimmten Coefficienten a, so ist G(f) eine ganze Function der
Veränderlichen t und a, welche sich nicht in Factören zerlegen
lässt, die wieder rationale Functionen von t und a sind. Sub-
stituirt man für die Variablen a Grossen irgend eines Körpers £1,
und wird dann G(t) in diesem Körper reducibel, so hat die

§. 186. Nicht metacyklische Gleichungen. 653
Gleichung f(x) = 0 im Rationalitätsbereich £1 einen Affect.
Unsere Frage kommt also darauf hinaus, ob man in Q(f) für
die Variablen a solche rationale Zahlen setzen kann, dass G(t)
im Körper der rationalen Zahlen irreducibel bleibt.
Diese Frage hat eine ganz allgemeine Beantwortung ge-
gefunden in einer Abhandlung von Hubert1), wo der allgemeine
Satz bewiesen ist, dass man in einer irreduciblen Function beliebig
vieler Variablen für einen beliebigen Theil der Variablen solche
rationale Zahlen setzen kann, dass eine irreducible Function der
übrigen Variablen entsteht. Auf diesen allgemeinen Satz können
wir hier nicht eingehen.
Wir werden aber die gestellte Frage viel einfacher, wenn
auch bei Weitem nicht so allgemein beantworten, indem wir zeigen,
dass sich für jeden Primzahlgrad Gleichungen ohne Affect finden
lassen.
Wir haben in §. 160, 10. bewiesen, dass eine transitive
Permutationsgruppe von n Ziffern, die nicht die symmetrische
Gruppe ist, wenn n eine Primzahl ist, keine einzelne Transposition
enthalten kann.
Unter einer Gleichung mit einem Affect haben wir eine solche
verstanden, deren Gruppe nicht die symmetrische ist. Hat also
die irreducible Gleichung f(x) = 0 einen Affect und ist ihr Grad
eine Primzahl, so muss ihre Gruppe P transitiv sein, und sie
kann keine Transposition zweier Wurzeln enthalten. Wenn wir
also irgend n — 2 der Wurzeln dem Rationalitätsbereich adjun-
giren, so muss sie sich auf die Einheitsgruppe reduciren, da ja
ausserdem nur noch die Vertauschung der beiden letzten Wurzeln
übrig bleiben könnte, die in P nicht vorkommt. Daraus folgt
also, dass die beiden letzten Wurzeln in dem erweiterten Körper
Sl enthalten sind, oder der Satz:
1. Wenn eine irreducible Gleichung, deren Grad n
eine Primzahl ist, einen Affect hat, so können
zwei beliebige von ihren Wurzeln rational durch
die übrigen ausgedrückt werden.
Daraus folgt als Corollar:
2. Wenn der Körper Sl nur reelle Zahlen enthält,
so kann eine irreducible Gleichung von Prim-
!) Ueber die Irreducibilität ganzer rationaler Functionen mit ganz-
zahligen Coefficienten. Journal für Mathematik, Bd. HO.

654 Siebzehnter Abschnitt. §. 186.
zahlgrad n mit einem Affect in Sl nicht zwei
imaginäre und n — 2 reelle Wurzeln haben.
Nun giebt es aber unzählige Gleichungen von jedem be-
beliebigen Grade », mit reellen Coefficienten, die zwei conjugirt
imaginäre und n — 2 reelle Wurzeln haben; man kann ja in
f(x) — {x— «J (x — a2) . , . (x — a„)
= xn -\- axxn-x -\- a2xn~2 + ••• + «„
«!, a2 beliebig conjugirt imaginär und die übrigen a reell an-
annehmen. Die Anzahl der reellen und imaginären Wurzeln von
f(x) ändert sich aber nicht, wenn die Coefficienten innerhalb
gewisser endlicher Grenzen stetig verändert werden (vergl. den
siebenten Abschnitt), und folglich giebt es auch solche Gleichungen,
deren Coefficienten rationale Zahlen sind, da man in beliebiger
Nähe von irgend welchen gegebenen reellen Zahlen immer ratio-
rationale Zahlen finden kann.
Es ist also nur noch nachzuweisen, dass man diese rationalen
Coefficienten so wählen kann, dass f(x) irreducibel wird. Dies
ergiebt sich aber aus folgendem Satze:
3. Ist p eine Primzahl, c0, cx, <?2> • • ., cn eine Reihe
ganzer Zahlen, von denen c0 durch p nicht theil-
bar, cl5 c2) • ••>£» durch p theilbar, aber c„ nicht
durch p2 theilbar ist, so ist die Function
. <p (x) = Co Xn -f- Cj X»-1 + • • • + C„
irreducibel1).
Denn wenn <p(x) in zwei Factoren mit rationalen Coeffi-
Coefficienten zerfällt, so können (nach §. 2) die Factoren auch ganz-
ganzzahlig angenommen werden. Sei also
tp(x) = («!*!* + «!*»-! -\ \-ax) (ßox* + ft«*-» H h ß*),
h und h beide grösser als Null und ihre Summe gleich n.
Da Mhßic = cn ist, so muss einer der beiden Factoren a^, ßy,
durch p theilbar sein, der andere nicht. Es möge ßk durch p
theilbar, a^ nicht theilbar sein, und da nicht alle ß durch p
theilbar sein können, weil sonst auch c0 durch p theilbar wäre,
so sei ßv nicht durch p theilbar, ßv+i, ßv + n, ¦ • ., ß* durch p
theilbar. Der Coefficient von xk~r in dem Product der beiden
!) Auf diesen Satz hat Eisenstein den Beweis der Irreducibilität
der Kreistheilungsgleichung und noch höherer Gleichungen gegründet.
Crelle's Journal, Bd. 39 A850).

§. 187. Reelle Radicale. 655
Factoren ist danii ahßv -\- ah—i~ßv + 1 -\- • • -, also durch p nicht
theilbar. Es müsste also h — v = n sein, was nicht möglich
ist, da schon h < n sein muss.
Setzt man also für die Coefficienten von f(x):
so ist f(x) irreducibel, und man hat in der Wahl der ganzen
Zahlen c noch Freiheit genug, um die rationalen Brüche at
a2, . . ., an einem beliebig gegebenen Werthsystem beliebig nahe
zu bringen.
Damit ist aber der Satz bewiesen:
4. Es giebt von jedem beliebigen Primzahlgrade un-
unendlich viele Gleichungen mit rationalen Coeffi-
Coefficienten ohne Affect.
Der Beweis, der hier geführt ist, zeigt, dass solche affect-
freie Gleichungen gefunden werden können, deren Coefficienten
ein endliches Gebiet überall dicht erfüllen, das Gebiet nämlich,
in dem die reellen Coefficienten der Gleichungen mit nur zwei
conjugirt imaginären Wurzeln liegen. Der Beweis ist also, ab-
abgesehen davon, dass er sich nur auf Primzahlgrade beschränkt,
auch insofern nicht erschöpfend, als er uns keinen Aufschluss
giebt über die übrigen Gebiete, in denen aller Wahrscheinlichkeit
nach die Sache sich ebenso verhält.
§. 187. •
'¦ Auflösung durch reelle Radicale.
Bei der Auflösung der cubischen Gleichungen mit reellen
Coefficienten hat man von Alters her die zwei Fälle unterschieden,
in denen die Discriminante negativ oder positiv ist. Im zweiten
Falle hat man, obwohl die Gleichung dann gerade drei reelle
Wurzeln hat, bei der Anwendung der Cardanischen Formel die
dritte Wurzel aus einem imaginären Ausdruck zu ziehen, und der
Versuch, die Wurzeln in reeller Form darzustellen, führt immer
wieder auf eine cubische Gleichung von derselben Beschaffenheit.
Darum hat man diesen Fall den casus irreducibilis genannt.
Die cubischen Gleichungen des casus irreducibilis sind ein
specieller Fall der cyklischen Gleichungen mit reellen
Wurzeln, die wir im §. 172 kennen gelernt haben, bei deren

656 Siebzehnter Abschnitt. §. 187.
Lösung gleichfalls Wurzeln aus imaginären Grossen, oder was
auf dasselbe hinauskommt, Winkeltheilungen, vorkommen. Dass
diese Wurzeln aus imaginären Grossen oder Winkeltheilungen
auf keine Weise zu vermeiden sind, können wir jetzt beweisen1).
Wir setzen einen reellen ßationalitätsbereich il vor-
voraus, und nehmen in ihm eine Normalgleichung g(f) = 0 an,
d. h. eine irreducible Gleichung, deren Wurzeln alle rational
durch eine beliebige von ihnen, q, ausdrückbar sind. Wenn eine
von den Wurzeln reell ist, so müssen auch alle anderen reell
sein, und g (t) hat also entweder lauter reelle oder lauter paarweise
conjugirte imaginäre Wurzeln. g(t) = 0 kann die Galois'sche
Resolvente irgend einer gegebenen, sei es irreduciblen, sei es
reduciblen Gleichung F(x) = 0 sein, und wenn also g(f) nur
reelle Wurzeln hat, so kann auch F(x) nur reelle Wurzeln haben,
weil die Wurzeln von F(%) rational durch eine Wurzel von g(t)
darstellbar sind. Wenn unter den Wurzeln von F(x) imaginäre
sind, so hat g(f) nur imaginäre Wurzeln. Hat aber F(x) lauter
reelle Wurzeln, so sind auch die Wurzeln von g(t) reell, weil
sie ja rational durch die Wurzeln von F(x) ausgedrückt werden
können.
Wenn nun g(f) durch Adjunction einer Wurzel s einer
irreduciblen Gleichung % = 0, deren Grad eine Primzahl ist,
reducirt wird, so sind, wie wir im §. 164 gesehen haben, die
sämmtlichen Wurzeln von % in ß(@) enthalten, und wenn also
q reell ist, so sind alle Wurzeln von % reell.
1. Eine Normalgleichung mit reellen Wurzeln kann
also nur durch solche irreducible Gleichungen
von Primzahlgrad reducirt werden, die lauter
reelle Wurzeln haben.
Wir fragen nun, ob eine Reduction der Normalgleichung
durch Adjunction eines reellen Radicales Va bewirkt werden
kann. Wir dürfen dabei annehmen, dass der Grad p des Radicales
eine Primzahl sei, weil jedes Radical sich auf eine Reihe von
Wurzelziehungen von Primzahlgrad reduciren lässt. Auch können
wir voraussetzen, dass a nicht die pte Potenz einer rationalen
p
Grosse sei, weil sonst die reelle Wurzel Va rational wäre.
!) Vergl. Holder, Mathematische Annalen, Bd.38; Kneser, ebendas.,
Bd. 41.

§. 187. . Reelle Radieale. 657
Unter dieser Voraussetzung ist, wie wir jetzt beweisenjwollen,
x* — a irreducibel. Denn bezeichnen wir einen, z.B. den.reellen
p
Werth Va mit a und eine imaginäre pte Einheitswurzel mit s,
so sind
A) oc, sa, s2a, . , ., «*—1 a
die Wurzeln der Gleichung
B) xp — a = 0.
Ist diese Gleichung reducibel, so ist - .
C) x* — a ¦= A(x)ft(x),
und/j,/2 sind Functionen in Sl von niedrigerem als dem p^n
Grade. Ein Theil der Wurzel A) wird auf fx = 0, ein anderer
Theil auf/2 = 0 fallen. Ist also jt der Grad von /,, so muss
für irgend einen Exponenten A
£*«." = h
eine Grosse in Sl sein [das von x unabhängige Glied in /i (#)],
also, wenn man in die pte Potenz erhebt,
D) aa = bP.
Nun ist 0 < ft < p, und daher jt unäp relativ prim, so dass
sich zwei ganze Zahlen h und k aus der Gleichung
bestimmen lassen. Es ist dann also nach D)
a = auh aPu = (&* a*)*;
also wäre, gegen die Voraussetzung, a die ßte Potenz einer Grosse
in fl.
Dieser Satz ist, wie man sieht, unabhängig von der Voraus-
Voraussetzung, dass ß ein reeller Körper sei. Nehmen wir ihn aber
reell an, so hat die Gleichung B), wenn p nicht gleich 2 ist, ima-
imaginäre Wurzeln, und kann nach 1. eine Normal gleichung <?(£),= 0
nicht reduciren. Wenn aber p ==2 ist, so kann g(f) nur dann
durch die Gleichung B) reducirt werden, wenn a positjiv und
der Grad von g(t) eine gerade Zahl.ist (§. 164); also:, . .• ,,.
2. Eine Normalgleichung ungeraden Grades kann
nicht durch Adjunction eines reellen Radicals
reducirt werden.
Adjungirt man im Falle einer reellen cubischen Gleichung
mit positiver Discriminante die Quadratwurzel aus dieser Discri-
minante, so geht die Gleichung in eine Normalgleichung über
und der Rätionalitätsbereich bleibt reell; er bleibt auch reell,
Weber, Algebra. I. 42

658 Siebzehnter Abschnitt. §. 188.
wenn man noch so viele reelle Kadicale adjungirt. Soll die
Gleichung also durch reelle Kadicale lösbar sein, so muss sie bei
solchen Adjunctionen endlich zerfallen, was nach 2. unmöglich
ist. Dies ist der casus irreducibilis der cubischen Gleichungen.
In demselben Falle finden sich die cyklischen und überhaupt
alle irreduciblen Abel'schen Gleichungen von ungeradem Grade,
die also niemals durch reelle Radicale lösbar sind.
Hiernach können wir z. B. die cubischen Gleichungen im
Körper der rationalen Zahlen in drei oder vier Arten unter-
unterscheiden, die alle in gewissen von Alters her berühmten geo-
geometrischen Problemen auftreten. Wir sehen dabei von den
reduciblen Gleichungen ab. Der Grad der Galois'schen Gruppe
muss dann immer durch 3 theilbar sein (§. 169) und ist also
entweder gleich 3 oder gleich 6. Die Gruppe kann also nach
§. 164 niemals durch Adjunction von blossen Quadratwurzeln auf
einen niedrigeren als den dritten Grad reducirt werden; also kann
auch die Gleichung nicht durch Quadratwurzeln gelöst werden.
Die entsprechenden geometrischen Probleme sind nicht mit Zirkel
und Lineal zu lösen.
Ist die Gruppe vom Grade 3, so haben wir eine cyklische
Gleichung. Hierher gehören die aus der Kreistheilung stammen-
stammenden Gleichungen, z. B. die, von der die Construction des regel-
mässigen Siebenecks abhängt. Die drei Wurzeln einer solchen
Gleichung sind reell und können nicht durch reelle Radicale
ausgedrückt werden. Unter den cubischen Gleichungen mit einer
Gruppe 6terL Grades sind zu unterscheiden die mit positiver und
mit negativer Discriminante.
Die ersten gehören zum casus irreducibilis und lassen sich
zurückführen auf die Gleichung, von der die Dreitheilung eines
beliebigen Winkels abhängt. Zu den Gleichungen mit negativer
Discriminante gehören als specielle Fälle auch die reinen cubischen
Gleichungen x% = a, wenn a keine Cubikzahl ist. Für a = 2
ergiebt sich die Gleichung, von der das Delische Problem der
Würfel Verdoppelung abhängt.
§. 188.
Metacyklische Gleichungen von Primzahlgrad.
Die allgemeinen Bedingungen, die wir im §. 184 gefunden
haben, sind noch nicht einfach genug, um eine unmittelbare An-

.§. 188. Gleichungen von Primzahlgrad. 659
wendung auf die Ermittelung von metacyklischen Gleichungen
oder auf die Entscheidung über die Löslichkeit einer vorgelegten
Gleichung durch Radicale zu gestatten. Wir leiten also, zunächst
unter der Voraussetzung, dass der Grad n der Gleichung eine
Primzahl sei, ein anderes von Galois aufgestelltes Kriterium her.
Es sei jetzt f{x) = 0 eine irreducible Gleichung Yom Grade
n, und n eine Primzahl und grösser als 2. Soll /(a;) = 0 alge-
algebraisch lösbar sein, so muss ihre Gruppe P nach §. 184 meta-
cyklisch sein, d. h. es muss eine Kette von Gruppen
A) P, Pl, P» ¦ • ; Pp-i, 1
geben, deren jede ein Normaltheiler der nächst vorangehenden
mit Primzahlindex ist. Durch successive Adjunction von Wur-
Wurzeln cyklischer Gleichungen von Primzahlgrad wird die Gruppe
der Gleichung von P auf Px, P2, . . ., P^—i, 1 reducirt.
Die Function f(x) selbst kann, wie schon im §. 184 gezeigt
ist, nicht reducirt werden, ehe die letzte Adjunction gemacht ist,
worauf sie in n lineare Factoren zerfällt. Der Grad der letzten
cyklischen Gleichung und mithin der Grad der vorletzten Gruppe
Pfi—i muss also nach §. 165, 3. gleich n sein.
Der Grad eines Elementes einer Gruppe ist immer ein
Theiler vom Grade der Gruppe und daher kann Pfi—i ausser
der identischen nur Permutationen von der Ordnung n enthalten.
Sie ist also mit der Periode 1, sr, sr2,..., sr"-1 eines ihrer Elemente
identisch. Daraus folgt nach §. 160, dass it eine cyklische Permu-
Permutation von sämmtlichen n Ziffern sein muss, und wir können die
Bezeichnung der Wurzeln von f(x) so wählen, dass
* = @, 1, 2, ..., n— 1)
wird. Bezeichnen wir die Wurzeln mit xt, und setzen fest, dass
x\ = xz< sein soll, wenn z = z* (mod n) ist, so geht durch sr
jedes z in z -\- 1 über, durch sr2 in z -f- 2 u. s. f., und
wir können also sagen, dass die Gruppe P^—x aus den Sub-
Substitutionen für s
B) 0, s + b), l = 0, 1, 2, . . ., n - 1
besteht. Jede irreducible metacyklische Gleichung von Primzahl-
Primzahlgrad kann also durch Adjunction von Radicalen in eine cyklische
Gleichung verwandelt werden.
Die Substitutionen (z, z -\- V) bilden einen speciellen Fall
der allgemeineren linearen Substitution
C) (*,<** + &),
42*

660 . Siebzehnter Abschnitt. §. 188.
worin «und b feste Zahlen sind, die auch nach dem Modul n
reducirt werden können, wo aber für a der Werth 0 natürlich
auszuschliessen ist, weil sonst ja durch C) alle verschiedenen s
in dasselbe b übergehen, also gar keine Permutation der Grossen xz
ausgedrückt wäre. Ist aber a von 0 verschieden (mod «•), so
-wird durch C) immer eine Permutation dargestellt sein, weil
dann nur, wenn 3 = 3' ist, as -\- b = as' -\- b sein kann. Wir
nennen C) eine Substitution für z, die unter den x eine Permu-
Permutation hervorbringt. Die Anzahl der verschiedenen linearen Sub-
Substitutionen von der Form C) ist n(n — 1). Ihnen entsprechen
ebenso viele verschiedene Permutationen unter den x; denn es
kann nur dann für jedes s
az -\-b = a's -f~ b' (mod n)
sein, wenn b = &' (aus z = 0 zu schliessen) und a = a! (aus
z = 1 zu schliessen).
Die Gesammtheit der Permutationen, die durch C) dar-
dargestellt sind, bildet eine Gruppe; denn es seien
A = O, an.-\-b), X'= (z, a'z-\- V)
zwei von diesen Permutationen, so ist
also
D) X X' = X" = (*, a a'z + a' b + V),
was -wieder von der Form (g, a" s -j- b") ist.
Die durch alle Substitutionen von der Form C) gebildete
Gruppe, die eine Verallgemeinerung der cyklischen Gruppe B)
ist, wollen wir eine lineare Gruppe nennen1); die in ihr ent-
enthaltenen Permutationen sollen lineare, Permutationen heissen.
In der, linearen Gruppe sind verschiedene Divisoren ent-
enthalten. Wir finden darunter eine Gruppe vom Grade n '¦—. 1,
nämlich C, as\ die selbst wieder Divisoren haben kann.
Die Compositionsregel D) zeigt, wie wir. alle Divisoren der
linearen Gruppe bilden können. Ist X = (#, a s -\- b) eine lineare
Substitution, so ergiebt sich nach D) durch Wiederholung für
jeden Exponenten h
E) A* = •[*, a** -f A 4- a + 1- a»-i)b],
Kronecker nennt nur diese Gruppe metacyklisch.

§. 188. Gleichungen von Primzahlgrad. 661
und für a = 1
X» = (g, 0 + hb).
Wenn also in einer Gruppe ij eine Substitution X vorkommt,
in der a = 1 und b von Null verschieden ist, so enthält hiernach
L die ganze cyklische Gruppe (z, z-\-V) (b = 0, 1, . . ., n — 1).
Ist a nicht gleich 1, so setzen wir
und schliessen daraus, dass, wenn e der kleinste positive Expo-
Exponent ist, für den ae = 1 (mod n) ist, A vom Grade e ist.
Die Periode der Substitution X giebt, wenn nicht a = 1 ist,
eine intransitive Permutationsgruppe. Es giebt eine Ziffer s, die
durch X und seine Wiederholungen nicht geändert wird, die aus
der Congruenz z = as -\- b (mod n) bestimmt wird, und mit
#0 = ^7 (mod n)
bezeichnet werden kann, wenn unter — oder jt : v (mod n) eine
ganze Zahl verstanden wird, die durch Multiplication mit dem
Factor v nach dem Modul n mit p congruent wird.
Die cyklische Gruppe (z, z -\- i) ist transitiv und vom
Grade n. Wir beweisen zunächst den Satz:
I. Jede transitive lineare Gruppe (mod n) enthält
die cyklische Gruppe.
Es sei g eine primitive Wurzel von n, und a der Index von
a, d. h. ga = a (mod n) (§. 143). Der Kürze wegen nennen wir
für den Augenblick a zugleich den Index der Substitution
X ¦= (z, az -\- b). Der Index kann kleiner als n — 1 und gleich
oder grösser als Null angenommen werden. Ist er gleich Null,
so ist X entweder die identische Substitution, oder sie gehört
der cyklischen Gruppe an. Nach D) gilt die Regel, dass der
Index einer zusammengesetzten Substitution gleich der Summe
der Indices der Componenten ist.
Daraus folgt, dass alle Indices der Substitutionen einer
linearen Gruppe L Vielfache des kleinsten positiven unter ihnen
sind, und dass folglich, wenn a0 dieser kleinste positive Index
ist, und gat> = a0 gesetzt wird, alle Substitutionen von L in der
Form
X = (z,ahoz-\- b)

662 • Siebzehnter Abschnitt. §. 188.
dargestellt werden können, worin a0 festgehalten wird, und nur
h und b gewisse Zahlenreihen durchlaufen. Eine Substitution
von der Form
Ao = 0, a0 s -f- &0)
xnuss in der Gruppe L vorkommen.
Wenn nun in der Gruppe L eine Substitution X vorkommt,
in der mit h = 0 ein von Null verschiedenes b verbunden ist,
so gehört dieses 1 der cyklischen Gruppe an, und L enthält die
ganze cyklische Gruppe.
Wenn aber h von Null verschieden ist, so bilden wir nach
D) und E) die Zusammensetzung
^Ex 60) •
Diese giebt dann und nur dann die identische Substitution, wenn
—^ =¦ ~h r (m0" n)-
aQ — 1 a\ — 1 v '
Wenn diese Congruenz für alle von Null verschiedenen h
befriedigt ist, und wenn dem Index h = 0 nur die identische
Substitution entspricht, so bleibt das Element — b0 : (a0 — 1)
durch die ganze Gruppe ungeändert, und L ist intransitiv. Folg-
Folglich giebt es in einer transitiven Gruppe L immer ein Ele-
Element A, für das AA^Ä nicht die identische Substitution ist, ob-
obwohl der Index Null ist, und L enthält also die ganze cyklische
Gruppe.
Bildet man die verschiedenen Eotenzen von Ao, so ergiebt
sich, dass der Exponent h in den Substitutionen X der Gruppe L
jeden Werth annehmen kann. Ist e der kleinste positive
Exponent, der der Bedingung a% = 1 (mod n) genügt, so
kommen also die Werthe h = 0, 1, 2, . . ., e — 1 vor, und darin
ist e ein Theiler von n — 1. Aus der zusammengesetzten Sub-
Substitution
0, a\g + 6) 0, e+l) = (e,a*e+-b + 1),
die nach I. in einer transitiven Gruppe L ja auch vorkommen
muss, sieht man weiter, dass mit jedem Werthe von h jeder
der Werthe b = 0, 1, 2, . . ., n — 1 verbunden vorkommt, und
die ganze Gruppe L besteht daher aus den Substitutionen

§. 188. Gleichungeu von Primzahlgrad. 663
und ist vom Grade en. Umgekehrt bildet jedes System von
Substitutionen dieser Form eine Gruppe.
Von den linearen Gruppen gilt nun der folgende Satz:
II. Ist eine transitive lineare Gruppe L Normal-
theiler einer anderen Permutationsgruppe P
derselben n Ziffern, so ist auch P eine lineare
Gruppe.
Der Satz lässt sich so beweisen:
Wenn % eine beliebige Permutation ist:
Tt
\o0, al5 a2,
die auch durch {z, az) dargestellt werden kann, so kann man
eine ganze Function <p (z) von z mit rationalen Coefficienten,
deren Grad nicht höher als n— 1 ist, so bestimmen, dass az=<p{z)
gesetzt werden kann. Man braucht nur die n Coefficienten in
<p (z) aus den n linearen Gleichungen
a0 = <p@), ax = <pA), . . ., aM_! = <p(n—\)
zu bestimmen. Man kann dazu die im §. 15 abgeleitete
Lagrange'sche Interpolationsformel verwenden, der man aber
noch eine einfachere Gestalt geben kann, da es hier nur aut
Congruenzen nach dem Modul n ankommt. Setzt man nämlich
¦4,0) = z(z — 1) 0 — 2) . . . (z — n -j- 1),
so giebt die erwähnte Interpolationsformel
Nun ist, wie wir im §. 143 gesehen haben, die Congruenz
ip (z) = sn — z (mod n)
identisch; also ist auch
ip'(z) eee nz*-1 — 1 ^ — 1 (mod ri),
und daher können wir (p (z) mit ganzzahligen Coefficienten so
darstellen:
Wenn, wie in unserer Aufgabe, die Zahlen a0, %, . . ., aM_i,
von der Ordnung abgesehen, mit den Zahlen 0, 1, 2, . . ., n — 1
übereinstimmen, so ist, wenn n > 2 ist, ao-\- ax-\ 1- a„_i ^ 0

664 ¦ Siebzehnter Abschnitt. §.188.
(mod n) und also <p(z) höchstens vom Grade n — 2, was aber
für unseren Beweis nicht von Bedeutung ist.
Hiernach lässt sich also jede beliebige Permutation »durch
eine Substitution [z, <p(z)] darstellen.
Ist nun L eine transitive lineare Gruppe und zugleich
Normaltheiler von einer anderen Gruppe P, ist X eine beliebige
Permutation von L, % eine gleichfalls beliebige Permutation
von P, so ist %—1X% = V in L enthalten, und X% = %V.
Setzen wir nach dem, was eben bewiesen ist, % = \z, q> (#)] und
wählen für X die cyklische Substitution (z, s ~\- 1), die nach der
Voraussetzung der Transitivität in L vorkommt, so muss sich a'
und a so bestimmen lassen, dass
(*, * + 1) [*, q> (*)] — [*, tp (*)] (*, a! e + o),
oder, wenn man die Zusammensetzung ausführt,
G) <p {s -(- 1) = a' <p (g)\ + a (mod n)
für jedes ganzzahlige z. t)a (f>(s), den Grad' n nicht erreicht, so
müssen (§. 143) in G) die Coefficienten der einzelnen Potenzen
von s auf beiden Seiten congruent sein, und aus der Ver-
Vergleichung der Coefficienten der höchsten Potenzen von s ergiebt
sich a' =. 1 (inod «), also ¦¦ '
> ip {z -j- 1) ^ <p (?) -\- a (mod n).
Setzt man hier z -\- 1, g--\- 2'.-;-. « -j- ä — 1 für z, so folgt
q>(s -\- h) = (p (z)'-{- ah (mod n),
wo h mit jeder beliebigen ganzen Zahl nach dem Modul w con-
congruent sein kann. Darin kann man nun z = 0 setzen und erhält,
wenn man wieder z für h schreibt und; (p(ß) = b setzt,
(8) ... ¦ 9>0O— as -{-b.
Es besteht also , die¦* Gruppe P aus lauter linearen Permu-
Permutationen und unser Satz ist bewiesen.
Wir fügen noch die Bemerkung hinzu, die sich unmittelbar
aus dem Anblick der Formeln ergiebt, dass die cyklische
Gruppe @, z-\^ b) ein normaler Theiler einer jeden
linearen Gruppe ist, in der sie überhaupt enthalten ist.
Wenn wir von dem bewiesenen Satze die Anwendung auf
die Gruppe der metacyklisehen Gleichung machen, so erhalten
wir den.Satz von Galois: . '.
III. Die Gruppe einer irreduciblen metacyklisehen
Gleichujig von Primzahlgrad ist linear.

§. 188. Lineare Gruppen. • 665
Denn kehren wir zu der Kette der Gruppen A) zurück, so
haben wir gesehen, dass P^—x die cyklische Gruppe ist. Ist P«_i
nicht mit P identisch, so ist Pp—X ein Normaltheiler von P^—a
und also P,,_2 linear. P^_2 ist wieder Normaltheiler von P^_8,
also ist auch P^s linear u. s. f., bis wir zu dem Schluss ge-
gelangen, dass auch P selbst linear sein muss. Zugleich ergiebt
sich, dass Pp.—\ Normaltheiler- aller vorangehenden Gruppen,
also auch von P selbst ist..
Es gilt auch der umgekehrte Satz:
IV. Jede irreducible Gleichung von Primzahlgrad,
deren Gruppe linear ist, ist metäcyklisch.
Um ihn zu beweisen, genügt es, zu zeigen, dass jede transi-
transitive lineare Gruppe L einen Normaltheiler U hat, dessen Index
eine Primzahl, und der selbst, wenn er nicht die Einheitsgruppe
ist, eine transitive lineare Gruppe ist.
Dies zeigt" aber unmittelbar die Darstellung der Substitu-
Substitutionen der Gruppe L durch die Formel F).
Wenn darin e = 1 ist, so ist L die cyklische Gruppe vom
Grade n mit dem Normaltheiler 1. Ist aber e> 1, so sei p
eine in e aufgehend« Primzahl, und e = pd. Die lineare Gruppe
L' vom Grade ne', die aus den Substitutionen besteht:
t, r „* , ia * = 0, .1, 2, . . ., e'. — 1
X = (,, «,», + 6), h=0]h2]^^n_v ,
ist gewiss ein Theiler von L vom Index p. Dieser Theiler ist
aber auch normal, wie man aus der Compositionsregel D) ohne
Mühe erkennt.
Die Begrifie der transitiven linearen und der metacyklischen
Gruppen decken sich also bei den Gleichungen von Primzahl-
Primzahlgrad vollständig, und wir können daher auch in der Folge beide
Ausdrücke synonym gebrauchen.
Wenn wir von einer Gruppe jp zu einer conjugirten Gruppe
P' = jt-1Pjt übergehen wollen, so geschieht dieser Uebergang
dadurch, dass bei allen Permutationen von P in den Cyklen die
Vertauschung % vorgenommen wird. P' wird also mit P bis auf
die Bezeichnung der Wurzeln übereinstimmen, und ist daher, wenn
P linear ist, auch als linear zu bezeichnen, wenn auch eine
Aenderung in der Numerirung der Wurzeln nöthig ist, -um sie
durch lineare Substitutionen darzustellen. '

666 Siebzehnter Abschnitt. §. 188.
Zur Vereinfachung der Anwendung bemerke man noch, dass
man die volle lineare Gruppe durch Wiederholung und
Zusammensetzung der beiden Substitutionen
(9) ä = («, * + l), t = (g,gg)t
und jeden transitiven Theiler L der vollen linearen Gruppe
ebenso aus
A0) s = (*, * + 1), t°° = (*, a„ *)
ableiten kann. Man nennt daher die beiden Substitutionen (9)
oder A0) die erzeugenden Substitutionen dieser Gruppen.
Setzen wir a0 = g2, so erhalten wir eine häufig vorkommende
lineare Gruppe (#, az -\- b), in der a nur die quadratischen
Reste von n durchläuft, die von Kronecker die halbmeta-
cyklische Gruppe genannt worden ist.
Diese Darstellung durch die erzeugenden Substitutionen
gestattet einen einfachen Schluss auf die Beziehung der meta-
cyklischen Gruppen zu der symmetrischen und der alternirenden
Gruppe.
Die aus s hervorgehende Permutation besteht aus einem
einzigen Cyklus mit einer ungeraden Gliederzahl @,1,2,..., n — 1),
und gehört daher zu der alternirenden Gruppe. Die Substitu-
Substitution t lässt den Index 0 ungeändert und liefert für die übrigen
Ziffern wieder einen einzigen Cyklus. Denn durch t geht 1 in g.
g in g2, g2 in g3 etc. über und da die Potenzen 1, g, </2, . . ., gn~2,
von der Reihenfolge abgesehen, mit den Ziffern 1, 2, .. ., n — 1
übereinstimmen, so entspricht t dem Cyklus A, g, g% . . ., gn~2),
der aus einer geraden Gliederzahl besteht und folglich zu den
Permutationen zweiter Art gehört, also nicht in der alternirenden
Gruppe enthalten ist. Dagegen ist t2 wieder darin enthalten.
Daraus ergiebt sich das Resultat:
V. Die volle lineare Gruppe ist kein Theiler der
alternirenden Gruppe. Der grösste gemeinschaft-
gemeinschaftliche Theiler beider Gruppen ist die halbmeta-
cyklische Gruppe.
Man kann der Bedingung für die metacyklischen Gleichungen
verschiedene Formen geben, die sich aus dem Bisherigen ableiten
lassen.
Die volle lineare Gruppe ist als Theiler vom Index
v = 1 . 2 . 3 . . . (n — 2) in der symmetrischen Gruppe ent-
enthalten. Eine zu der vollen linearen Gruppe gehörige Function y

§. 188. Metacyklische Gruppen. 667
der n Variablen x0, xL, . . ., #„_i, die wir eine metacyklische
Function nennen können, genügt daher einer Resolvente F(y)=0
vom Grade v, deren Coefficienten symmetrische Functionen der
x sind.
Substituirt man nun für x die Wurzeln einer metacyklischen
Gleichung f(x) = 0, so wird y rational.
Wenn umgekehrt die Function y durch die Substitution der
Wurzeln einer irreduciblen Gleichung/(#)=: 0 für die x rational
wird, während F'(y) von Null verschieden bleibt, so ist f(x)
metacyklisch; denn dann ist die Gruppe von f{x) — 0 gewiss
ein Theiler der vollen linearen Gruppe, und daher selbst linear;
und da/(x) irreducibel ist, so ist die Gleichungf(x) = 0 meta-
metacyklisch. Es genügt aber auch für die algebraische Auflösbar-
Auflösbarkeit von f(x) = 0, wenn die Resolvente F(y) = 0 nur über-
überhaupt eine rationale Wurzel hat, die nicht Doppelwurzel ist.
Denn die verschiedenen Wurzeln dieser Resolvente gehören zu
conjugirten Gruppen, und wenn daher eine von diesen Wurzeln
rational ist, so ist eine der conjugirten Gruppen metacyklisch.
Wir haben also den Satz:
VI. Die nothwendige und hinreichende Bedingung
für die Lösbarkeit der Gleichung f(x) = 0 durch
Radicale ist die, dass die Resolvente vUn Grades
F(y) = 0, die man durch passende Wahl der Func-
Function y so eingerichtet hat, dass sie keine Doppel-
Doppelwurzeln erhält, eine rationale Wurzel hat.
Eine andere Form dieser Bedingung ergiebt sich auf folgende
Weise.
Unter den Permutationen einer linearen Gruppe ist nur die
identische, die irgend zwei Ziffern ungeändert lässt. Denn wenn
(z,ag-\- b) zwei Ziffern nicht ändert, so muss die Congruenz
az -j- b = s (mod n) zwei verschiedene Lösungen haben. Das
ist aber nur möglich, wenn a = 1, b = 0 (mod n) ist
Ist also die Gruppe P von f(x) linear, so reducirt sie sich
durch Adjunction von zwei beliebigen Wurzeln auf die Einheit,
und folglich sind alle Wurzeln rational durch zwei beliebige
unter ihnen ausdrückbar. Also:
VII. Ist eine irreducible Gleichung von Primzahlgrad
metacyklisch, so sind alle Wurzeln rational durch
zwei beliebige unter ihnen ausdrückbar.

668 Siebzehnter Abschnitt. §. 188.
Aber dieser Satz gilt auch umgekehrt, was wir folgender-
maassen einfach beweisen können.
. Es habe eine irreducible Gleichung vom Primzahlgrad n die
Eigenschaft, dass alle Wurzeln rational durch zwei beliebige
unter ihnen ausdrückbar sind. Ist etwa xv = ^{x^^x^} eine
solche Darstellung, so können auf diese Relation alle Permu-
Permutationen der Gruppe P unserer Gleichung angewandt werden,
und wenn also eine von diesen Permutationen x0 und x1 un-
ungeändert lässt, so lässt sie auch alle xv ungeändert, d. h. es ist
die identische Permutation. Also enthält P ausser der
identischen Permutation keine, die zwei Ziffern nicht
änderte
Enthält nun eine der Permutationen % = ccx ... von P zwei
oder mehr verschiedene Cyklen c, Cx ... und ist c vom Grade \ cx
aber von einem höheren Grade, so ist nh = c\ . . ., und jch lässt
die Ziffern von c ungeändert, während sie doch nicht die iden-
identische Substitution ist, weil c\ nicht alle Ziffern ungeändert lässt.
Dies ist aber nicht möglich, wenn h'> 1 ist. Es muss also ent-
entweder % eine Ziffer ungeändert lassen, oder es muss aus Cyklen
von gleichem Grade bestehen. Da aber n Primzahl ist, so kann
% in diesem Falle nur einen Cyklus vom nim Grade bilden.
Es enthält also P ausser der identischen nur cyklische
Permutationen nten Grades, die wir mit y bezeichnen wollen, und
Permutationen %, die eine Ziffer ungeändert lassen und ausser-
dem aus Cyklen von gleichem Grade bestehen.
Jede der Permutationen %, durch die die Ziffer 0 ungeändert
bleibt, wollen wir mit %0 bezeichnen. Ebenso bedeuten %, %.M..., %n—i
die Permutationen %, die die Ziffern 1, 2, . . ., n — 1 ungeändert
lassen. Da P transitiv ist, so müssen ebensoviel %0, wie jq, wie
%-i etc. vorhanden sein.
Denn ist n eine Permutation, die 0 in 1 überführt, so ist
jedes 7T-1%(j% ein %, und umgekehrt jedes nxl7C~1 ein x0, und
ebenso für die übrigen Ziffern. Ist also (i die Anzahl der sc0,
v die Anzahl der y,,m der Grad von P, so ist, da noch die
identische Permutation hinzukommt,
A1) m = [in -j- v,+ 1-
Nun bilden die x0 mit der identischen Permutation zusammen
eine Gruppe Q vom Grade (t -\- 1, und zwar einen .Theiler von P,
nämlich den Inbegriff aller Permutationen von P, die 0 un-

§. 188. Metacyklische Gruppen. 669
geändert lassen. Sind also x1} 7i2, . . ., tt„_1 Permutationen in P,
die 0 in 1, 2, ...,» — 1 überführen, so ist Qnx der Inbegriff
aller der Permutationen von P, die 0 in 1 überführen u. s. f.
Wir erhalten also die Zerlegung von P in die Nebengruppen
P=Q+Qx1+Qx1-\ [- Qxn-i,
woraus folgt
A2) 'w===n((t+l),
also aus A1) und A2) v = n — 1.
Es giebt also n — 1 und nicht mehr cyklische Permutationen
wten Grades in P und diese bilden folglich wieder mit der Ein-
Einheit zusammen eine cyklische Gruppe
C = l, y, y\ ¦ •., r"-1,
da mit y zugleich alle Potenzen von y in P vorkommen.
Wenn nun y eine cyklische Permutation nUn Grades ist, so
ist auch jedes %— 1yhic zyklisch und muss also, wenn it zu P
gehört, auch in C enthalten sein. C ist also ein Normaltheiler
von P, und folglich muss nach dem Theorem II. die Gruppe P
linear sein.
VIII. Eine irreducible Gleichung von Primzahlgrad,
bei der alle Wurzeln rational durch zwei be-
beliebige von ihnen ausdrückbar sind,, ist meta-
cyklisch.
Wir schliessen aus diesen Sätzen noch auf eine merkwürdige,
zuerst von Kronecker bemerkte Eigenschaft der metacyklischen
Gleichungen für den Fall eines reellen Rationalitätsbereichs1).
Wenn bei einer solchen Gleichung zwei Wurzeln reell sind, so
folgt aus VII., dass alle ihre Wurzeln reell sind. Eine reelle
Wurzel muss aber eine solche Gleichung, da sie ungeraden
Grades ist, immer haben. Also folgt
IX. Eine irreducible metacyklische Gleichung von un-
ungeradem Primzahlgrad mit reellen Coefficienten
hat entweder lauter reelle Wurzeln oder nur eine.
Sind alle Wurzeln reell, so ist die Discriminante als Product
von lauter Quadraten reeller Grossen (xh — a;&J positiv. Ist nur
eine Wurzel reell, so entspricht jedem complexen Factor der
Discriminante (xh — #&J ein conjugirter, und deren Product ist
x) Ueber algebraisch auflösbare Gleichungen. Monatsbericht der Ber-
Berliner Akademie, 14. April, 1856.

670 Siebzehnter Abschnitt. §. 189.
positiv. Nur wenn xh und Xy, conjugirt imaginär, also xh — xk
rein imaginär ist, so ist (% — x^J negativ und die Discriminante
erhält also für jedes Paar conjugirt imaginärer Wurzeln den
n—l
Factor — 1. Das Vorzeichen der Discriminante ist also (— 1) 2 ..
Daraus folgt:
X. Wenn n = 1 (mod 4) ist, so ist die Discriminante
immer positiv, ist aber w= 3 (mod 4), so ent-
entscheidet das Vorzeichen der Discriminante, wel-
welcher der beiden Fälle des Theorems IX. eintritt.
§. 189.
Anwendung auf die metacyklischen Gleichungen
5ten Grades.
Wir machen noch eine Anwendung der allgemeinen Sätze
auf die Gleichungen 5ten Grades. Ist n = 5, so hat die cyklische
Gruppe 5, die halbmetacyklische 10 und die volle lineare
Gruppe 20 Permutationen. Eine metacyklische Function genügt
bei einer allgemeinen Gleichung Ö*"*1 Grades einer Resolvente
gten Grades, und wenn diese Gleichung 6ten Grades eine rationale
Wurzel hat, so ist die gegebene Gleichung 5ten Grades meta-
cyklisch. Die halbmetacyklischen Functionen, d. h. die Func-
Function en, die die Permutationen der halbmetacyklischen Gruppe
gestatten, genügen einer Kesolvente 12ten Grades, die aber nach
Adjunction der Quadratwurzel aus der Discriminante in zwei
Factoren 6ten Grades zerfällt.
Wenn man die erzeugenden Substitutionen für den Modul 5
s = 0, * + 1), * = 0, 2 4 P = 0, 4 0)
auf die Ziffern 0, 1, 2, 3, 4 anwendet, so ergeben sich die Ver-
Vertauschungen
A) (S>
(P)
und es ist also, durch Cyklen dargestellt,
. s = @, 1, 2, 3, 4), ' * = A, 2, 4, 3), P = A, 4) B, 3).
Wenden wir die Substitutionen s, P, t auf die Paare von
Ziffern @, 1), A, 2% B, 3), C, 4), D, 0) an, so folgt
o,
1,
o,
o,
1,
2,
2,
4,
2,
3,
4,
3,
3,
'4,
1,
2,
4
0
3
1,

§. 189. Gleichungen 5*«n Grades. 671
@,1), A,2), B,3), C,4), D,0)
B) (s) A,2), B, 3), C, 4), D,0), @,1)
(P) @,4), D,3), C,2), B,1), A,0);
diese Paare bleiben also in ihrer Gesammtheit durch s und
durch P, und folglich durch die halbmetacyklische Gruppe un-
geändert, und eine symmetrische Function der entsprechenden
Wurzelpaare ist halbmetacyklisch. Die Substitution t bewirkt
die Vertauschungen . .
,„. @,1), A,2), B,3), C,4), D,0)'
() (Q @, 2), B, 4), D, 1), A, 3), C, 0),
führt also die fünf Paare in fünf andere über; und da es nur
zehn Paare von fünf Dingen giebt, so kommen in den beiden
Reihen C) alle Paare vor.
Man kann nun auf sehr verschiedene Arten halbmeta-
halbmetacyklische Functionen bilden. Die einfachste ist
D) U = Xo Xx -f Xj, #2 + X2 X3 -f" Xs X4 -\- XiX,,,
die durch t in
E) u' = XoX?, -{- x2Xi + xtxx + xtx3 -{- xsx0
übergeht, und u' gehört selbst zu den halbmetacyklischen Func-
Functionen.
Ist
F) f{x) = x'3 — ax* -\- bx* — ex2 -f- dx — e = 0
die Gleichung, deren Wurzeln x0, x^, x2, x3, xi sind, so ist also
G) u + u' = b.
Die Function . .
(8) y = u — u'
ist gleichfalls halbmetacyklisch, das Quadrat y2 aber ist voll-
metacyklisch und also die Wurzel einer Resolvente 6ten Grades,
wie schon Lagrange gefunden hat.
Ist V^7 das Product der zehn Wurzeldifferenzen (x0 — xt),
(x0 — x2) ¦ ¦ ., also z/ die Discriminante von f(x), so ist
ebenfalls vollmetacyklisch und Wurzel einer Gleichung 6ten Gradesx).
J) Jacobi, „observatiuncnlae ad theoriam aequationum pertinentes",
Crelle's Journ. Bd. 13. Jaoobi's Werke, Bd. 3. Cayley, philos. transao-
tions 1861, Collected math. papers, Vol. IV, p. 309.

672 Siebzehnter Abschnitt. . §. 189.
Um die conjugirten Functionen zu u zu bilden, bezeichnen
wir mit M die vollmetacyklische, mit N die halbmetacyklische,
mit A die . alternirende Gruppe und zerlegen A in die Neben-
Nebengruppen:
A0) A = N + N A, 2) C, 4) -f Nt @, 1) -+- Nt @, 2)
+ Nt @, 3) + Nt @, 4). '¦
Diese Nebengruppen sind in der Thät alle von einander
verschieden. Denn wäre z. B. N = JSf A, 2) C, 4), so müsste
A, 2) C, 4) in N, also
A, 2) C, A)t - A, 2) C, 4) A, 2, 4, 3) ¦= A, 4)
in M vorkommen und dies ist nicht möglich, weil in M keine
Permutation auftritt, die zwei Ziffern ungeändert lässt; und in
ähnlicher Weise zeigt man, dass keine zwei anderen dieser
Nebengruppen einander gleich sind.
Hiernach ergeben sich für' u die innerhalb A conjugirten
Werthe durch Anwendung der Permutationen
A, 2) C, 4), t@, 1) = @, 1, 2, 4, 3), *(Ö, 2) = @, 2, 4, 3, 1)
*@, 3) = @, 3, 1, 2, 4), *@, 4) = @, 4, 3, 1, 2):
\- X1Xi + XiXs -\- XSXO, . .
rm Us ~ XlX2 "*~ x*Xi ^ XiX° ~^~X(>Xz ~*~ XbX"
^ ' -Ut = X2X0 -(- X0X4, + XiXy + %lx3 + ^3^S)
, % =-XBXi + X1X4, -\- XiX1 -\- XtX0 + XOXZ,
u6 = xtx2 -{- xaxa -\- x^Xi -{- x1xs -\- xsxM
und die entsprechenden 1^, u^, u'3, u'i, u's, u'6 findet man, wenn
man auf % die Permutation t anwendet, und dann mit ¦wl
ebenso verfährt, wie eben mit %, oder auch einfach, indem man
die in jedem u fehlenden Paare zu dem entsprechenden u' ver-
vereinigt, so dass für alle diese u die Bedingung-G) befriedigt ist.
,. . . Uri = XqXz 4" %(>%% + XXX3 ,-f- X1Xi -f-'
Uz = XqX-l -\- X6Xi-\- XxXt -\- X2XS +
U'3 = x°Xl + + +
fl2)
' u'i = X0Xir{- XOXS -\- XXX% -\- X2Xt -f-
U'6 = X0X2¦-{- XoXt -\- X1X2 -(
U'6 = XOXS -\- X0Xi -\- XXX2 -
Die sechs Grossen (8): y^y^ytty^y-^y^, sind die Wurzeln eine?
Gleichung 6teii Grades, deren Coefficienten rational von a, 5, c, d, e

§. 189. Gleichungen 5*en Grades. 673
und V^ abhängen. Da die y alle ihr Vorzeichen ändern, wenn
V'd das Vorzeichen ändert, so hat diese Gleichung die Form
+ «6
worin die a rationale Functionen der Coefficienten von f(x) sind.
Es müssen aber auch ganze Functionen dieser Coefficienten sein;
denn a2, a4, as, at V<d, a3 V^, as Vd sind ganze Functionen der
x, die ja hier als unabhängige Variable gelten können, und es
müssen also die drei letzteren durch das Differenzenprodnct ~\f2
theilbar sein, und dann müssen sich «2, a4, a6, at, a3, ab als ganze
symmetrische Functionen der x erweisen. Bestimmt man die
Grade in Bezug auf die x, so ergeben sich, da die y vom zweiten
Grade sind, für
a2, OzV^, a4,
die Grade 2 4 6 ' 8 10 12.
ist aber vom 10ten Grade in den x, und folglich muss at = 0,
as = 0 und a5 eine Zahl sein.
Die Functionen a2, a4, a6 sind in Bezug auf die Variablen x
homogen, und wenn wir daher den Coefficienten a, b, c, d, e die
Gewichte 1, 2, 3, 4, 5 beilegen, so sind die a2, at, a6 isobarische
Functionen dieser Grossen mit den Gewichten 4, 8, 12 (§. 53).
Man kann die Coefficienten a2, a4, a5, a6 durch wirkliche
Bildung der Ausdrücke nach den Vorschriften über die Darstel-
Darstellung der symmetrischen Functionen berechnen, was von Cayley
geschehen ist. Rechnung und Formeln sind aber sehr weitläufig.
Wir wollen uns hier damit begnügen, die Resolvente für
einen besonderen Fall zu bilden. Der dabei gefundene Werth
für die Zahl a5 ist dann natürlich allgemein gültig.
Die Gleichung 5t(m Grades habe die Bring-Jerrard'sche
Form i)
A3) x° + ax + ß = 0.
Dann sind o^i aii a& ganze rationale Functionen von « und ß.
Von den Coefficienten der allgemeinen Gleichung F) ist d vom
Gewicht 4, e vom Gewicht 5, und daraus folgt, dass der Coeffi-
cient e in a2 gar nicht, in a4, a6 aber nur mit einem der Coeffi-
Coefficienten a, b, c multiplicirt vorkommen kann, und dass also, wenn
a, b, c Null gesetzt werden, e aus diesen Ausdrücken herausgehen
') Bunge, Aota mathematica, Bd. 7.
Weber, Algebra. I. ' 43

674 Siebzehnter Abschnitt. §. 189.
muss. Für die Gleichung A3) können also a2, a4, as nicht von
ß abhängen, und man erhält mit Rücksicht auf das Gewicht,
wenn m, mu m2, m% Zahlen bedeuten
A4) a3 = mi«, a4 = m2 k2, a6 = mg a3, a6 = in.
Die Zahlen m, «%, m2, m3 lassen sich aus einer speciellen
Annahme bestimmen. Setzen wir ß = 0, so wird
A5) • xQ = 0, xx = "^— a, #3 = * "^— a,
und daraus ergiebt sich
= (*o — #i) («o — «2) («o — «s) («0 — «4) («i — «2)
^ ~~ ^^ ^ ~~ X^ ^ ~~ ^^ ^ ~~ X^ ^3 ~" '^
= 16« V^ä5 = — 16 V«5
^ = 256 «5.
Da hier 6 = 0 ist, so wird nach G) und (8) y = 2m, und
aus A1) und A5) ergeben sich die Werthe der y:
. . 2/4 — D — üi) V«, 2/ä = D + 2») Vä.
Danach erhält man für ß = 0 die folgende in «/ identische
Gleichung:
A7) 2/6 _|_ a2a4 + «4«/3 + «6 — % V^«/
. ={y + 2 V«)* & — Sy Vä + 20a)
= y* — 20ay* -\- 240«22/2 + 512 Vas«/ + 32O«3;
Daraus findet man aber die allgemeine Resolvente für die
Gleichung A3), wenn man nach A6) für —16 V«5 setzt V^ also
A8) «/e _ 20 ay* -f 240«»^ _ 32 y~jy _(_ 320 a3 = 0.
Die Discriminante J hat hier, wie sich aus der Formel C)
im §.80 ergiebt, den Ausdruck
A9) 4 = 55/3* + 28«5.
Einfacher noch wird die Gleichung für u, nämlich
B0) ms_ 5KM4 _|_ 15K2M2 _ YJu + 5a3 = 0,
und wenn man w2 = v setzt, so ergiebt sich für v die rationale
Gleichung 6ten Grades
B1) (v3 — 5«v2 -f- 15 ofiv -\- 5«3J =

§. 189. Gleichungen 5*™ Grades. 675
Eine andere Form dieser Gleichung erhält man aus A7),
wenn man den zweiten der drei Ausdrücke mit dem multiplicirt,
den man daraus erhält, wenn man V« in — V<% verwandelt.
Dadurch bekommt man
(v — «)* (v2 — 6 av -\- 25 a2) = 0,
und in diesen muss B1) übergehen, wenn ß = 0 gesetzt wird.
Da aber in B1) der von ß abhängige Theil durch A9) bestimmt
ist, so folgt die gesuchte Form der Resolvente
B2) (v — «)* (v2 — %kv -f 25 a2) = 55/3*v.
Man kann noch die Frage aufwerfen, ob die hier eingeführte
Function v immer wirklich metacyklisch ist, ob sie nicht viel-
vielleicht bei besonderen Gleichungen noch andere Permutationen
. gestattet.
Wenn dieser Fall eintreten sollte, so müsste die Gleichung
B1) oder B2) gleiche Wurzeln oder B0) gleiche oder entgegen-
entgegengesetzte Wurzeln haben.
Der Werth u = 0 oder v = 0 tritt nur dann ein, wenn
a = 0 ist. Dann haben wir in der That in A3) die wohl-
wohlbekannte metacyklische Gleichung xb -j- ß = 0; diesen Fall also
lassen wir jetzt bei Seite. Die Gleichung B0) kann nur dann
zwei entgegengesetzte Wurzeln haben, wenn J = 0 ist, wenn
also die Gleichung A3) gleiche Wurzeln hat. Auch dies ist
auszuschliessen, da wir A3) als irreducibel vorausgesetzt haben.
Es bleibt also nur die Frage übrig, ob B0) gleiche Wurzeln
haben kann. Es müsste dann mit B0) zugleich die abgeleitete
Gleichung
6m5 — 20«m3 + 30«2m — Vd = 0
befriedigt sein, und wenn wir Vd aus dieser und aus B0)
eliminiren,
5 m6 — 15 «tt* + 15 «2m2 — 5«3 = 5(w2 — aK = 0.
Es müsste also v = a sein und also nach B2) ß = 0.
Dann wäre aber die Gleichung 5ten Grades wieder reducibel, da
sie den Factor x hat.
• Will man also eine gegebene Gleichung von der Form A3)
in Bezug auf ihre Auflösbarkeit prüfen, so hat man zuerst die
Irreducibilität festzustellen, und dann zu untersuchen, ob B1)
oder B2) eine rationale Wurzel hat.
Sind a und ß ganze Zahlen, so muss auch ein rationales v eine
ganze Zahl sein, die unter den Factoren von 25 a6 zu suchen ist.
43*

676 Siebzehnter Abschnitt. §.. 190.
Ist z. B. k = 5, ß = ht, so ist, wenn t eine durch 5 nicht
theilbare ganze Zahl ist, x -\- ax -j- ß nach §. 186, 3. irredu-
cibel. Für v hat man Potenzen von 5, mit positivem oder
negativem Vorzeichen einzusetzen, aber für keine solche Zahl
kann B2) erfüllt sein, weil auf der linken Seite die Potenz von
5 nicht hoch genug wird.
Es ist also keine Gleichung von der Form
x3 •*¦)- 5x -\- 51 = 0 metacyklisch.
Will man metacyklische Gleichungen ermitteln, so setze man
in B2)
ß = «fi, v = aX,
wodurch man erhält:
( }
P A — iyß2 — 6A + 25)'
und wenn man hierin für X und fi rationale Grossen setzt (aus
einem beliebigen Rationalitätsbereich, z. B. auch aus dem Körper
der rationalen Functionen von X und fi), so ist die Gleichung
5ten Grades
B4) x= -\-ax -)- ß = Ö
algebraisch lösbar, da ja der Fall, dass diese Gleichung redu-
cibel Wird, auch auf algebraisch lösbare Gleichungen führt.
Umgekehrt können wir sagen, dass keine irreducible Glei-
Gleichung 5ten Grades von der Form B4) algebraisch lösbar ist, in
der die Coefficienten «, ß nicht in der Form B3) darstellbar sind.
Setzen wir z. B. X = 3, fi = 1, so erhalten wir 28a = 3.55,
28/3 = 3.55. Die Gleichung B4) vereinfacht sich, wenn wir für x
eine neue Unbekannte £ einführen, durch die Gleichung 4#=5£.
"Wir erhalten so die Gleichung
fs-|- 15|* -f 12 =0
als Beispiel einer algebraisch lösbaren Gleichung, die über-
überdies nach dem vorhin erwähnten Satze (§.186,3.) irreducibel ist.
§. 190.
Die Gruppe der Eesolvente.
Die Sätze, die wir im vorigen Paragraphen abgeleitet haben,
gestatten einen merkwürdigen Schluss über die Gleichungen

§. 190. Gruppe der Resolvente. 677
Wir nehmen jetzt wieder die x0, xt, x2, xs, xt des vorigen
Paragraphen als unabhängige Variable an. Dann sind die sechs
Grossen
Vi = («i — MiJ, V2 = (Mg — «4J, V3 = (U3 — U3K
v4 = (ut — u\y, vh = («5 — «ya, v6 = (m6 — MgJ
die Wurzeln einer Gleichung 6ten Grades, F{v) = 0, deren
Coefficienten rational durch die symmetrischen Grundfunctionen
a, b, c, d, e der x ausdrückbar sind, und die in dem Körper
der rationalen Functionen dieser Grossen irreducibel ist. Diese
Gleichung ist eine Resolvente der Gleichung 5ten Grades f(z) = 0,
deren Wurzeln die x sind.
Ist M die volle lineare Gruppe der x, so haben die zu
M conjugirten Gruppen %~x M n keinen anderen gemeinschaft-
gemeinschaftlichen Theiler, als die identische Permutation. Denn jeder
gemeinsame Theiler aller dieser Gruppen müsste ein Normal-
theiler der symmetrischen und folglich auch der alternirenden
Gruppe sein; da er aber nicht die alternirende Gruppe selbst
sein kann, so muss er sich nach §. 185 auf die Einheitsgruppe
reduciren.
Die Resolvente F(v) = 0 ist also nach der in §. 163 ein-
eingeführten Bezeichnung eine Totalresolvente von f(x) = 0,
und ihre Gruppe muss von gleichem Grade sein, wie die Gruppe
von f(x) = 0, deren Grad 1 . 2 . 3 . 4 . 5 = 120 ist. Da F(e)
auch irreducibel ist, so ist die Permutationsgruppe unter den
Indices der sechs Grossen v transitiv. Sie ist vom Grade 120,
während der Grad der symmetrischen Gruppe der Permutationen
von sechs Ziffern 6 . 120 ist. Damit haben wir den Satz:
Die symmetrische Permutationsgruppe von sechs
Ziffern hat einen transitiven Divisor vom Index 6.
Um diese merkwürdige Gruppe, die wir mit C bezeichnen
wollen, zu finden, haben wir nur den Einfluss zu untersuchen,
den die sämmtlichen 120 Permutationen der x auf die v oder
auf die Grossen A1) des vorigen Paragraphen ausüben.
Wir haben nun früher gesehen (§. 160, 2.), dass die Trans-
Transpositionen @, 1), @, 2), @, 3), @, 4) durch wiederholte Zusammen-
Zusammensetzung die ganze symmetrische Gruppe der Permutationen von
fünf Ziffern erzeugen. Es genügt also, den Einfluss dieser vier
Transpositionen auf die Indices der v zu ermitteln. Durch An-
Anwendung einer Transposition @, 1) geht jeder der Ausdrücke

678 Siebzehnter Abschnitt. . §. 190.
A1), §. 189 in einen der Ausdrücke A2) über und umgekehrt,
und wenn man für die vier genannten Transpositionen diese
Aenderung ermittelt, so erhält man die folgenden vier erzeugen-
erzeugenden Permutationen %, 3i2, n3, ici der Gruppe G
@,1): »1 = A,3) B, 5) D, 6)
@, 2): », = A, 4) B, 3) E, 6)
@, 3): *, = A, 5) B, 6) C, 4)
@,4): »4=A, 6) B, 4) C, 5),
wo sich die in den n vorkommenden Transpositionen A, 3) ...
auf die Indices der u und der v beziehen.
Unter den 120 Permutationen der Gruppe C kommen unter
anderen auch vor
^s», = A, 2, 6) C, 4, 5)
%t 3T2 3T3 = A, 6, 5, 4)
Tlx 3T2 1t.6 3T4 = B, 4, 6, 3, 5)
Crl3r23r33r4K= B, 3, 4, 5, 6).
Hiernach lässt sich leicht eine zur Gruppe G gehörige Func-
tion der sechs Grossen v bilden.
Eine Function, wie
vxvB + ^4 + v-av6, .,;
bleibt durch nx und durch %x%i ungeändert; wenden wir darauf
aber die Potenzen der cyklischen Permutation B, 3, 4, 5, 6)
an, so gehen daraus fünf Functionen hervor, die wir so be-
bezeichnen wollen:
Wo = Vx V.2 + Vi V; + V3 Ve
Wx =VlVi -\- V2 V6 -j- V3 v$
B) w.2 =vtv6-f- v2 v$ -\- v3 v4
Wenn wir auf die Functionen B) die Permutationen %, n2,
3T8, %i anwenden, so gehen diese Functionen nur in einander
über, und zwar in folgender Weise:
Jlx = (Wo, Wi), 3T2 = (Wo, Wa), ns = (WQ, Wz), %i == (WO, Wi),
d. h. die nx, n2, n3, 3r4 entsprechen den Transpositionen @, 1),
@, 2), @, 3), @, 4) unter den Indices der w, und also entspricht
nach §. 160, 2. der ganzen Gruppe G die symmetrische Gruppe

§. 190. Permutationsgruppe von sechs Ziffern. 679
der Indices der w. Eine symmetrische Function der fünf Grossen w,
die nicht zugleich eine symmetrische Function der v ist, wie die
Summe der w, ist also eine zu C gehörige Function.
Man kann z. B. die Summe der Quadrate dafür nehmen
W = w02 -f- wl -f- wl -\- wf -f- w42,
oder eine Function
(l — w0) (* — wi) Q- — w2) (i. — w8) (l — Wi)
für ein beliebiges rationales k
Eine solche Grosse W ist die Wurzel einer irreduciblen
Gleichung 6ten Grades, deren Coefficienten symmetrische Func-
tionen der sechs Grossen v sind.

Achtzehnter Abschnitt.
Wurzeln metacyklischer Gleichungen.
§. 191.
Stellung der Aufgabe. Hülfssatz.
Wir haben im vorigen Abschnitte allgemeine Kennzeichen
gefunden, durch die man entscheiden kann, ob eine vorgelegte
Gleichung von Primzahlgrad metacyklisch ist oder nicht. Damit
ist aber der Gegenstand noch bei Weitem nicht erschöpft. Es
handelt sich vielmehr nach der Form der Problemstellung, wie
sie von Abel herrührt, darum, ein Verfahren anzugeben, nach
dem man alle metacyklischen Gleichungen finden kann. In
dieser Form ist das Problem, über das Abel nur kurze Andeu-
Andeutungen ohne Beweise hinterlassen hat, von Kronecker auf-
aufgenommen worden, und in der Weise vollständig gelöst, dass zu-
zunächst nicht die Gleichungen selbst, sondern ihre Wurzeln
gefunden werden i). So hat Kronecker für jede Primzahl n einen
Ausdruck angegeben, der aus einem gegebenen Körper Sl durch
wiederholtes Wurzelziehen abgeleitet ist, und der die doppelte
l) Abel, Sur la resolution algebrique des equations (Oeuvres completes,
ed. Sylow, tome II, p. 217), Brief an Crelle am 14. März 1826 (Oeuvres
tome II, p. 266). — Kronecker, Ueber die algebraisch auflösbaren Glei-
Gleichungen. Monatsberichte der Berl. Akademie 1853, 1856. — Cayley, on
a theorem of Abel's etc. A880, Math, papers t. XI, p. 132). — H. Weber,
lieber algebraisch auflösbare Gleichungen von Primzahlgrad. Sitzungs-
Sitzungsberichte der Gesellschaft zur Beförderung der Naturwissenschaften zu Mar-
Marburg 1892. Die folgende Darstellung ist gegen die dort gegebene verein-
vereinfacht und in einem Punkte berichtigt.

§. 191. Die Resolventen. 681
Eigenschaft hat, dass jede-Wurzel einer irreduciblen meta-
cyklischen Gleichung wten Grades in Sl in diesem Ausdruck ent-
enthalten ist, und dass auch umgekehrt jeder solche Ausdruck einer
irreduciblen Gleichung wten Grades in Sl genügt.
Die Grundlage für diese Untersuchung liefern uns die Resol-
Resolventen von Lagrange.
Es sei jetzt n eine Primzahl, x0, x±, x2, . . ., xn—x sei ein
System unabhängiger Variablen, und die Bezeichnung so gewählt,
dass xn = x0, xn+i = xx . . . ist. Endlich sei s eine nte Ein-
Einheitswurzel. Wir setzen dann
A) (£, X) = X0 + EXX + £*X2 + •'•• + f1—1^-! ,= 2 ShXh-
0,n—l
Diese Ausdrücke haben wir schon im vierzehnten Abschnitte
unter dem Namen der Resolventen von Lagrange kennen
gelernt, und wir haben dort (§. 171) ihr Verhalten gegenüber
den cyklischen Permutationen untersucht.
Es kommt jetzt darauf an, den Einftuss linearer Permu-
Permutationen von der im §. 188 betrachteten Art auf diese Functionen
festzustellen.
Wir schicken einen Hülfssatz voraus, den wir eigentlich nur
aus dem Früheren zu reproduciren brauchen. Die imaginären
nten Einheitswurzeln e sind die Wurzeln einer Gleichung X= 0,
wenn
B) x = g"-1 + r~2 h h t +1
gesetzt ist, und £ eine Variable bedeutet.
Die Function X ist, wie wir früher gesehen haben (§. 174),
irreducibel im Körper B der rationalen Zahlen.
Legen wir irgend einen Körper Sl zu Grunde, in dem X
irreducibel ist, und leiten daraus den Körper Sl(s) ab, der aus
allen rationalen Functionen von s mit Coefficienten in Sl besteht,
so ergiebt sich nach §. 149, dass jede Grosse dieses Körpers auf
eine und nur auf eine Weise in die Form
C) c0 -f d s + e, £2 H h c»-2 £"~2
gesetzt werden kann, worin die c Grossen in Sl sind.
Der Kürze wegen wollen wir diese Form der Grossen in
Sl(s) die Normalform nennen und wollen also den Satz aus-
aussprechen :
1. Ist Sl ein Körper, in dem die Kreistheilungs-
gleichung X = 0 irreducibel ist, so kann jede

682 Achtzehnter Abschnitt. §.191.
Grosse des Körpers Sl(s) nur auf eine Weise in
die Normalform
O>(» = c0 + Cl s + c2 £2 _| 1- c„_2£»-2
gebracht werden, worin die Coefficienten c in
ß enthalten sind.
Wir können in diesem Satze für Sl den Körper nehmen, der
aus B durch Adjunction von n unabhängigen Variablen xQ, xu
%2, . . ., x„-i entsteht; denn wäre X" in diesem Körper redu-
cibel. also
wo Xlt X2 ganze Functionen von e und rationale Functionen
der x sind, so könnte man für die Variablen x0, xu . . ., #„—1
solche rationale Zahlen setzen, dass Xu X2, ohne ihren Grad in
Bezug auf e zu ändern, in Functionen in B übergehen (§. 43),
und dieses widerspricht der Irreducibilität von X in B.
Dieser Körper £1 hat verschiedene Divisoren, in denen X
gleichfalls irreducibel ist, und die also alle im Theorem 1. für
Sl genommen werden können. Solche Divisoren erhält man,
wenn man irgend eine Permutationsgruppe P der n Ziffern
0, 1, 2, . . ., n — 1 festsetzt und den Inbegriff aller rationalen
Functionen der xQ, xv . . ., #„_i in B betrachtet, die die Permu-
Permutationen dieser Gruppe gestatten.
Der Inbegriff aller dieser Functionen bildet offenbar einen
Körper, und so bekommt man zu jeder Permutationsgruppe der
n Ziffern einen bestimmten zugehörigen Körper Sl. Man kann
die Grossen eines solchen Körpers rational darstellen durch die
symmetrischen Functionen der x und durch eine zu der
Gruppe P gehörige Function.
Wir nennen den so bestimmten Körper Sl den zu der
Gruppe P gehörigen Körper. Jeder solche Körper kann
in 1. die Stelle von Sl vertreten (vergl. §. 159).
Wir können also den zweiten Satz aufstellen:
2. Wenn eine rationale Function d>(xo, xu ..., #B_i, s)
des Körpers Sl(e) ungeändert bleibt, wenn auf die
Indices der x die Permutationen einer Gruppe P
angewandt werden, so gestatten auch die Coeffi-
Coefficienten c0, cu c2, . . ., e„_2 der Normalform von 9
die Permutationen von P.

§. 192. • Sätze über die Kesolventen. 683
Ist <&(e) irgend ein Element des Körpers &(f), so erhält
man die conjugirten Grossen, wenn man für s irgend eine andere
Wurzel von X = 0 setzt, also die Substitution («, sh) für
h = 1, 2, . . ., n — 1 ausführt. Alle diese Körper sind wieder
in £l(e) enthalten; sie sind also mit einander identisch, d. h.
£l(s) ist ein Normalkörper über £1 (§§. 149, 152). Wenn eine
Grosse <5(Y) die Eigenschaft hat, ungeändert zu bleiben, wenn s
durch alle sh ersetzt wird, so ist sie selbst in £1 enthalten. Dies
folgt schon aus den allgemeinen Sätzen des §. 151. Wir sehen
aber die Richtigkeit sofort ein, wenn wir unter der Voraussetzung
setzen, woraus dann nach 1. zu schliessen ist, dass clf c2, ..., cn_2
gleich Null sind. Also:
3. WTenn eine Grosse in £l(s) die sämmtlichen Sub-
Substitutionen (£, sh) gestattet, so ist sie in Sl ent-
enthalten.
§. 192.
Sätze über die Resolventen.
Wir betrachten jetzt die Lagrange'schen Resolventen (s,x)
unter der Voraussetzung, dass s eine imaginäre nte Einheits-
Einheitswurzel und die x unabhängige Variable sind, und wenden darauf
die Sätze des vorigen Paragraphen an.
Wir untersuchen zunächst den Einfluss der linearen Per-
mutationen auf (s, x); dazu genügt es, wenn wir den Einfluss
der beiden erzeugenden Substitutionen
A) s = (Ä,Ä + l), t = (h,gh)
feststellen, worin das nach dem Modul n genommene h dielndices
von x durchläuft und g eine primitive Wurzel der Primzahl n
bedeutet (§. 188).
Wenden wir aber auf
B) 0, x) = xo + sxt + e*x2 -| (- En~1xn--L
die Substitution s an, so geht diese Function über in
X,. + EXz -\- £2% -f • (- En—1X0 = £-!(£, x).
Der Einfluss der Substitution s ist also, dass
... , , (s, x) in s~1(s, x)
übergeht. v ' ' y"'

684 Achtzehnter Abschnitt. ' §. 192.
Gehen wir nun zur Substitution t über und setzen in
h
(£, x) = Xo + 2 £hXh
l,n—1
^a für #Ä, so geht diese Function über in
C) • x0 + | e»*,*
' l,n — 1
In dieser Summe kann h ein beliebiges Kestsystem nach
dem Modul n durchlaufen mit Ausschluss von 0, und wir können
also h durch g~1h ersetzen; dadurch wird die Summe C)
#a + 2 £g~lh xh = (so-1, x).
Wendet man die Permutationen s und t wiederholt an, so
ergiebt sich der Einfluss von s\ t\ der in den Vertauschungen
(s,x), s-*(s,z)
(s, x), (so-\ x)
besteht, speciell also für A = — 1
0, x), s(s, x)
(s, x), (ss, x),
und wir bekommen den folgenden Satz:
4. Die erzeugenden Permutationen s, t der line-
linearen Gruppe bewirken die Vertauschungen
(s): (a,x), s~l(s,x); (s-1): 0, x), s(s, x)
(*): (s,x), (e9-\x); (t~l): (e, *), (e», x).
Aus 2. und 4. aber ergiebt sich, weil s die erzeugende Per-
Permutation der cyklischen Gruppe ist, die Folgerung:
5. Stellt man die Functionen
D) (s,x)» = 0(e), (s\x)(s,x)-* = F(s)
in der Normalform [§. 191, C)]. dar, so sind die
Coefficienten cyklische Functionen jvon x0,
XU . . ., Xn-t (§. 170).
Hierin kann A jede beliebige ganze Zahl, die nicht durch n
theilbar ist, bedeuten.
Aus der Function F(s) entspringen, wenn wir A = </ an-
annehmen und für s seine n — 1 verschiedenen Werthe setzen, n — 1
Functionen, die alle durch s ungeändert bleiben, und die wir
folgendermaassen bezeichnen wollen:

§. 192. Metacyklische Functionen. 685
(S>, X) F, X)-' = f0
so dass also, wenn (£», x)(s, x)~s = /(£) gesetzt wird,
F) /»=/(**)
ist. Wendet man auf E) die Permutation t~1 an, so erleiden,
wie nach dem Theorem 4. zu sehen ist, die Functionen
JOi fli / 8i • • •) fn—ü
eine cyklische Permutation @, 1, 2, . . ., n — 2).
Ausserdem sind die Functionen /„, so lange die x variabel
sind, wie man aus E) ersieht, alle von einander verschieden,
da sie in verschiedene lineare Factoren zerlegt sind.
Bilden wir also eine cyklische Function dieser n — 1 Grossen
G) • <?(/„, U /„ • . ., /B-2),
so bleibt diese sowohl durch s als durch t~\ also durch t und
folglich durch die ganze lineare Gruppe ungeändert, und wir
erhalten das Theorem:
6. Stellt man eine cyklische Function der Grossen
/(b/ii • • o/n—2 in der Normalform dar, so sind die
Coefficienten metacyklische Functionen der
Variablen x0, xu . . ., #„_!.
Hierbei ist unter einer metacyklischen Function jede Func-
Function zu verstehen, die durch die Permutationen der linearen
Gruppe ungeändert bleibt.
Die Functionen /0, /i, . . ., /n—2 gehen aber auch cyklisch in
einander über, wenn man die x ungeändert lässt, und für s die
Substitution (s, ss) macht. Wenn also die cyklische Function G
der Grossen / in ihren Coefficienten s nicht enthält, so bleibt 0
durch sämmtliche Substitutionen (e, sh) ungeändert, und wir er-
erhalten aus 3. das Theorem:
7. Ist O(/0, /i, . . ., /„_2) eine cyklische Function der
Grossen /0, fu . . ., /„_2 mit rationalen Coeffi-
Coefficienten, so ist C eine metacyklische Function
der Variablen x0, xu . . ., xn_1 mit rationalen
Coefficienten.
Wenn wir die Functionen /0, fu . . ., fn-^ wie sie durch E)
gegeben sind, der Reihe nach zu den Potenzen gn~2, gn~3 . . . 1

686 Achtzehnter Abschnitt. §. 192.
erheben und dann alles multipliciren, und wenn wir noch be-
beachten, dass ssn~1 = s ist, so heben sich im Product der linken
Seite der Gleichungen E) alle Kesolventen mit Ausnahme von
(s, x) heraus, und es folgt
(8) (£,^-.»-^=/f-vr3.../„-,
Bezeichnen wir nun mit A einen noch unbestimmten ganz-
ganzzahligen Exponenten, so leiten wir aus (8) die folgende Kela-
tion her:
(9) (s\ x)- = [(e, ar~*~~V, x)] ff" ff'" . . . fn-2.
Verstehen wir unter g1 irgend eine feste primitive Wurzel
von n, so können wir g = g1 -\- Z».setzen, worin l eine beliebige
ganze Zahl bedeutet, da ja die primitiven Wurzeln nur bis auf
Vielfache von n definirt sind. Dann ist
gn-\ = gn-i _j_ «(» — 1Igt~* (mod n%
woraus
g"~1 ~ l = g"-1 "~ l — Im-* (mod n),
und l lässt sich so bestimmen, dass
— ^ = 1 (mod»)
wird.
In (9) setzen wir nun unter dieser Voraussetzung
A0) A = — g"~1~ X = 1 (mod n\
und wie in D)
A1) F(s) = (s\ x) («„*)-* = (e, x)"\
worin sl = s und 1 — A, was durch n theilbar ist, = »ft gesetzt
ist. Daraus erhalten wir
A2) (s, xf = [FWfT'fT' ¦ . • /„-*
Diese Formeln lassen sich verallgemeinern, wenn man be-
beachtet, dass die Functionen f0, /1? . . ., fn—i eine cyklische Permu-
Permutation erleiden, wenn die Substitution (e, £«) ausgeführt wird.
Setzen wir also fest, dass f% = fk sein soll, wenn h = Ti (mod n — 1)
ist, und setzen
A3) >(*¦)=>, = (e»>)"*,
so ergiebt die Substitution (e, £»") in A2)

§. 192. Die Darstellung der Kesolventen. 687
Diese Formeln gelten für jedes v, wenn -wir auch noch in
Bezug auf die Fv festsetzen, dass F% = F* sein soll, wenn
h = Je (mod n — 1) ist. Es ergiebt sich dann aus 4., dass die
Functionen .Fo, Ft, . . ., Fn—i durch die Substitution s ungeändert
bleiben, und durch t~1 eine cyklische Permutation erfahren.
Wenn wir hier die Exponenten auf ihre kleinsten positiven
Reste nach dem Modul n reduciren wollen, so setzen wir
A5) gv = nqv -\- rv, 0 < rv < n, r0 = 1,
und die Zahlen r„ fallen in irgend einer Reihenfolge mit den
Zahlen 1, 2, . . ., n — 1 zusammen, so dass r0 immer = 1 ist.
Dann wird nach E)
A6) /,_! = (?\ x) (sr'-\ x)~g,
und wir setzen noch
V-'J vv MfJv jv + 1 •¦¦Jv + n — 3,
und erhalten aus A4)
Die Exponenten rv bleiben ungeändert, wenn g durch g — In
ersetzt wird, sind also von der Bedingung A0) unabhängig und
können aus einer beliebigen primitiven Wurzel g abgeleitet
werden.
Die charakteristischen Eigenschaften der in diesen Formeln
vorkommenden Functionen /„, Fv, 3>„, deren Gesammtheit wir
mit av bezeichnen wollen, sind, um es nochmals zu wiederholen,
folgende:
a) Durch die cyklische Permutation s = (h,h-{~l)
unter den Indices von x ändern sich die Func-
Functionen a, nicht.
ß) Durch die lineare Permutation t-1 — (h, g^h)
unter den Indices der x wird unter den Indices
der a die cyklische Permutation @, 1, 2,..., n—2)
hervorgerufen.
y) Durch die Substitution ö = (£, ss) wird unter den
Indices von co dieselbe cyklische Permutation
@, 1, 2, ...,» — 2) bewirkt.
d) Die cyklischen Functionen von cor sind meta-
cyklische Functionen der x und von s frei.

688 Achtzehnter Abschnitt. §. 193.
Nach dem Satze von Lagrange (§. 162) kann man jede
Function ©„, der die vier Eigenschaften a), ß), y), d) zukommen,
rational im Körper £1 der metacyklischen Functionen von x durch
eine von ihnen, av, ausdrücken, wenn nur die a0, cd^ ..., c3n-2 von
einander verschieden sind; man kann also für diese Functionen
die fv wählen.
Denn bedeutet u eine Variable, und ist
A9) (m — C3O) (w — coj) . . . (u — ra„_2) = 9(m),
so gestattet die Function <p (u) die Permutationen s, t und auch
die Substitution 6 = (e, a»), und ist also nach dem Satze 3. des
§. 191 eine ganze Function von u mit in Bezug auf x meta-
metacyklischen Coefficienten und unabhängig von s.
Ist nun also 6>0, ®u . . ., @„_2 ein Functionensystein, dem
die Eigenschaften «), ß), y), d) zukommen, so ist die Summe
B0)
0,« —2
eine ganze Function (n — 2)ten Grades von u, die gleichfalls die
Substitutionen s, t, 6 gestattet und die also Coefficienten in £1 hat.
Setzt man
B1) 4§^r = ®(«)
J qp' (m)
und setzt dann in B0) u = <x>v, so folgt
®v = ® (c3v),
worin ® eine rationale Function bedeutet, deren Coefficienten
metacyklische Functionen der x sind, und s nicht mehr enthalten.
§. 193.
Wurzeln metacyklischer Gleichungen.
Es sollen jetzt in den Formeln des vorigen Paragraphen für
die Variablen x0, xu . . ., #»_i die Wurzeln §0, &, . . ., |n_a einer
in irgend einem Körper ß irreduciblen metacyklischen Gleichung
vom Grade n eingeführt werden, und zwar in der Reihenfolge,
dass die metacyklischen Functionen der % rational (in 5?) sind,
was nach den Sätzen des vorigen Abschnittes immer möglich ist.
Wir machen aber dabei zunächst noch zwei beschränkende Vor-

§. 193. Wurzeln metacyklischer Gleichungen. 689
aussetzungen, von denen wir nachträglich das Resultat wieder
befreien werden. Diese Voraussetzungen sind:
1. dass durch diese Substitution der § für die x keine der
Resolventen (s, §), in der s eine imaginäre wte Einheits-
Einheitswurzel ist, verschwindet.
Nach A3), A6), A7), §. 192 bekommen dann die Functionen
/„, F.,, <&v bestimmte von Null verschiedene Werthe und wir
machen die zweite Voraussetzung,
2. dass durch dieselbe Substitution nicht zwei der Func-
Functionen /0, /1} . . ., /„_2 einander gleich werden.
Wir nehmen an, es gehe durch die Substitution der £ für
die x
/0] /l) • • •! Jn—2
in
über, so dass also die fc0, Ttu ..., fc„_2 von einander verschieden sind,
und
0>o, #15 . . ., <Z>„_2
in
wo aber unter den .ST auch gleiche vorkommen können.
Wegen der Eigenschaft d) der Functionen /, sind die Grossen
Jen, \, ..., Ä„_2 die Wurzeln einer cyklischen Gleichung (n — l)ten
(also geraden) Grades ^ (u) = 0, so dass, wenn u eine Variable
bedeutet,
A) q(u) = (u — fc0) («* —Jh) . • • (m — fc„_2)
eine Function (n — l)ten Grades von u mit rationalen Coeffi-
cienten ist. Die Grossen ho, &i, . . ., kn—2 können rational durch
einander ausgedrückt werden in der Form
B) \ = @(k0), \ = ©(*,), • • -, fcn-2 = ®(*»-«), fco = ®(fe»-a)
(§• 170).
Ebenso können die Grossen Z"v nach dem Schlusssatze des
§. 192 durch die fc„ ausgedrückt werden, und zwar in der Form
C) K0 = <&(fc0), JKi = *(fci), • . -, -K«-2 = CP(fcn-2),
worin 9 eine rationale Function (in ß) bedeutet.
Danach liefert uns die Formel A8), §. 192 folgendes Resultat:
Wir setzen zur Abkürzung
D) • zv = i/fcv,
Weber, Algebra. I. 44

690 Achtzehnter Abschnitt. §. 193.
und erhalten
und wenn man diese Formeln alle addirt, und noch die rationale
Grosse A, x) = A setzt:
F) n& = A -f i_Kv<"-«<«+-3 .'. . <<>+ b_2.
Nach §. 192, A6) und A7) sind die Grossen Kv und Ttv alle
von Null verschieden.
Durch F) ist eine der Wurzeln £ dargestellt.
Setzen -wir zur Abkürzung
-«r — t»r Kv + 1 ¦ • ¦ «-r + „_2
und schreiben F) in der Form
G) »|0 = A-j-KoVB'o + K.Vlt, + •.. + Kn^VB^,
so ist also |0 durch % — 1 Eadicale wten Grades ausgedrückt,
von denen jedes an sich n verschiedene Werthe haben kann.
Diese Werthe können aber nicht von einander unabhängig sein,
•weil sonst die Anzahl der Werthe von |, die sich aus G) er-
ergeben, zu gross wäre. Man erhält in der That aus E), wenn
man nach §. 192, A6)
setzt,
(8) Z", Vl"v = K9v-i Jfc,_i(Vü,_i)'
und kann also hiernach alle diese Eadicale rational durch eines
von ihnen und durch % ausdrücken.
Der Ausdruck F) hat aber vor G) den grossen Vorzug,
n
dass er, wie man auch die n — 1 Radicale Vfc„ be-
bestimmen mag, doch nur n verschiedene Werthe, näm-
nämlich die n Wurzeln |, darstellt.
Um dies nachzuweisen, bezeichnen wir mit s0, su . . ., £n_2
irgend ein beliebiges System ntet Einheitswurzeln, und ersetzen
in E)
n n n
durch

§• 194. Verallgemeinerung des Kesultates. 691
Dann geht F) in eine andere Form über, die wir so dar-
darstellen:
worin Ev eine nte Einheitswurzel ist, die durch s so ausgedrückt
wird:
^ / v v-f-i***c-|- ti 2 *
Nun ist nach der Definition von rv [§. 192, A5)]
A1) rv =grv-.1 (mod n),
und nach A0), da der Index von r nach dem Modul n — 1 zu
nehmen ist,
7? — frn~2 /»i —8 Ero
_g» __ £»n-2 r»"» —8 /o
V—1 V V -\-1 • * * V — 1'
also
\lä) Mjy =^ J!/^ 1 ^=^ Mi o •
Sind also die £ irgendwie bestimmt, so ergiebt sich
und dadurch sind nach A2) die übrigen Ev vollkommen bestimmt.
Also ergeben sich in der That nur n Werthe aus F), die man
z. B. dadurch erhalten kann, dass man einem der Radicale xv
seine verschiedenen Werthe beilegt. (Man vergleiche hiermit die
Cayley'sche Auflösung der cubischen Gleichungen §. 39.)
Will man die Grossen £0, |l5 ...,£„_! in der Reihenfolge
bestimmen, die der Bildung der cyklischen und metacyklischen
Gruppe zu Grunde liegt, so muss man in E) vor derSummation
mit s-hrv multipliciren und findet (§. 171)
A4) nl-n = A + 1 «-»'..KX—«t;»-« . . . <°+K_.2,
worin eine veränderte Bestimmung der Radicale nur eine cyklische
Vertauschung der |h bedingt.
§• 194.
Befreiung von den beschränkenden Voraussetzungen.
Es wäre eine wesentliche Beschränkung dieser Unter-
Untersuchungen über auflösbare Gleichungen, wenn die Voraussetzungen
1., 2. des vorigen Paragrapheu aufrecht erhalten werden müssten.
44*

692 Achtzehnter Abschnitt. §. 194.
Das ist aber nicht nothwendig, -wie -wir jetzt nachweisen
wollen.
Es seien jetzt ij0, rju . . ., rjn_1 die n Wurzeln irgend einer
irreduciblen metacyklischen Gleichung nten Grades.
Wir führen die neuen Unbekannten §0, |15 . . ., |„_i durch
ein System von Gleichungen
ein, worin il>(y) eine ganze Function (w — l)ten Grades
B) ii>{y) = «o + «i2/ + «s^ H h ««-i^-1
mit unbestimmten Coefficienten aus dem Körper ß bedeuten soll.
Wir nehmen aber an, dass die n Grossen £Oi In • • •> !»—i von
einander verschieden sind; dann sind auch die £ die Wurzeln
einer irreduciblen metacyklischen Gleichung, und durch A) ist
eine Tsc hirnhaus e n - Transformation ausgedrückt (§. 58); g0
ist ein primitives Element des Körpers ß(%); folglich sind die
Körper ß(|0) und ß(^0) und ebenso die conjugirten Körper
$(£r) und Ä(ijr) mit einander identisch. Es ist also auch, wenn
C) X(^) = ^o + ^i^ + ^2^2 -^ (- ä«-!*"
gesetzt wird, worin die Coefficienten b gleichfalls Grossen in &
sind,
Es ist nun leicht einzusehen, dass man über die Coeffi-
Coefficienten «0, «!,... a„_i in A) so verfügen kann, dass die Voraus-
Voraussetzungen 1. und 2. des vorigen Paragraphen für die £ erfüllt sind.
Denn betrachten wir die a als unabhängige Variable, so
werden die durch A) bestimmten £ gleichfalls Variable, die mit
den a durch eine lineare Substitution mit nicht verschwindender
Determinante zusammenhängen. Die Determinante dieser Sub-
Substitution ist nämlich
nh
d. h. gleich dem Differenzproduct der ij, das nach der Voraus-
Voraussetzung von Null verschieden ist.
Die Functionen (s, x) und die Differenzen fa —fo, die
nach §. 192 nicht verschwindende Functionen der Variablen

§. 194. Verallgemeinerung des Resultates. 693
Xo, #,, ..., xn-i sind, gehen also, wenn für die x die Substitution
Xu = ip (rjh) gemacht wird, in Functionen der Variablen a über,
die auch nicht identisch verschwinden können. Nach dem Satze
§. 43, 1. kann man also für die Grossen a0, au . . ., a„_i solche
rationale Zahlen setzen, dass die Functionen (g, x) und die
Differenzen fa — fy, die dann also in (g, f) und in ~ka — fe? über-
übergehen, von Null verschieden werden, und dass auch die £& von
einander verschieden bleiben, was zu beweisen war.
Nachdem also dies festgestellt ist, führen wir das System
der Variablen x0, x-y, . . ., #„_i und ein davon abhängiges System
von Variablen y
E) Vo = %(%o), Vl = %Ol), • • •, Vn-l = %(Xn-l)
ein, worin % die Function C) bedeutet, und setzen
(G) fc = &v.
Wird auf die Indices der x irgend eine Permutation an-
angewandt, so erleiden die Indices der y die gleiche Permutation.
Wenn wir also auf F) die cyklische Permutation s anwenden,
so ändert sich ®v nicht (nach §. 192, 4.).
Wenn wir also ®v in der Normalform des §.191 darstellen,
so sind seine Coefficienten cyklische Functionen von xfnxl,...,xn—i.
Wendet man auf ©r die Permutation t—1 =(h,g-1h) an,
so geht @r nach §. 192, 4. in ©r + 1 über, und die &v erleiden
also eine cyklische Permutation.
Denselben Erfolg hat aber auch die Substitution ß — (g, a»),
und also hat das System der Functionen @0, ©,, . . ., @„_2 die
Eigenschaften «) ß) y) d) (§. 192).
Nach dem am Ende-des §. 192 bewiesenen Satze geht also,
wenn wir die x durch die £ und folglich die y durch die y\
ersetzen, ©v in eine rationale Function von hv
G) Q,.= Q(kr)
über, und aus F) ergiebt sich
(8) Fr», q) = «,(s", g).
Wenn man hierin für (gr», |) den Ausdruck E), §. 193 substi-
tuirt, so erhält man für (g'v, rf) einen Ausdruck von ganz der-
derselben Form, nur mit dem Unterschiede, dass an Stelle von Kv
getreten ist Qv Kv. Die Functionen Qv Kv haben im Wesentlichen
dieselben Eigenschaften, wie die Function Kv, nur dass sie auch

694 Achtzehnter Abschnitt. §. 194.
zum Theil Null sein können. Durch dieselbe Veränderung er-
giebt dann §. 193 F) den Werth von ij0.
Damit sind also die beschränkenden Voraussetzungen des
§. 190 beseitigt, und wir haben das allgemeine Theorem:
I. Jede Wurzel £ einer metacyklischen Gleichung
vom Primzahlgrad n kann in der Form dargestellt
werden
(9) 1 = ^+2 z;<-»<;-«... <;„_„,
0) n — 2 ¦
worin A eine rationale Grosse, jfc0, fcx, . . ., ftM_2 die
von einander und von Null verschiedenen Wur-
Wurzeln einer cyklischen Gleichung (n — l)ten Grades,
Kv eine rationale Function von Ttv ist, deren Form
für alle v dieselbe ist. Die Exponenten r0,
*x, . . ., r„_2 sind die kleinsten positiven Reste der
Zahlen 1, g, g2, . . ., gn~2, wenn g eine primitive
Wurzel von n ist. Die n Werthe, die man aus (9)
erhält, wenn man den Radicalen rv=y]cr ihre ver-
; schiedenen Werthe beilegt, sind die n Wurzeln
einer und derselben rationalen Gleichung.
Die Formel (9) ergiebt sich aus §. 193 F), wenn A und 2T»
durch nA und itl, ersetzt wird, was zur Vereinfachung ge-
geschehen ist.
Das Theorem I. lässt sich nun aber auch umkehren.
Um das nachzuweisen, bezeichnen wir mit s irgend eine
imaginäre nte Einheitswurzel und setzen
V
A0) & = Ä +0J_fl ^"<"~2<+~78 • • • <V«-2
h = 0, 1, 2, . . . n — 1,
oder abgekürzt
v n
0, n — 2
worin wie früher
gesetzt ist. Wir haben nun die Aenderungen zu untersuchen,
die sich für £Ä ergeben, wenn wir
n
1. eines der Radicale tv = Ykv anders bestimmen und
2. die Jc0, Äj, . . ., fc„_2 cyklisch vertauschen.

§. 194. Wurzeln metacyklischer Gleichungen. 695
Wir wollen einem der Radicale, etwa dem ra, ein anderes
Vorzeichen geben, also die Vertauschung
A3) (ro, st>Ta)
machen, wo ß ein beliebiger Exponent sein kann, und a einer
der Indices 0, 1, . . ., n — 2 ist.
In A2) hat, da der Index von r nach dem Modul n — 1
zu nehmen ist, das Radical xa den Exponenten rM+r_a_2 = rr_a_,,
und also entspricht der Vertauschung A3) die Vertauschung
A4) \VBv, S^v-a-l
Nun ist nach der Bedeutung der Zahlen r allgemein r„+/J
= rarp (mod n), und wenn man also die Vertauschung A3) in
A1) einführt, so geht h in h -f- ßr^a—i über.
1. Es ruft also die Vertauschung A3) unter den Indices
von f die cyklische Permutation
(Ä, Ä -f ßr-^,^)
hervor.
Machen wir zweitens die cyklische Permutation
A5) (r0, t15 . . ., rn_2),
so entspricht diese den Vertauschungen
A6) (\fK, VB^J, (K„ Kr+i), v = 0, 1, 2, ...,« — 2,
und |Ä geht über in
A -f- v e*r, Kv+1
= Ä
2. Demnach erleiden die Indices von f durch die Permu-
Permutation A5) die Permutation
Betrachten wir nun irgend eine rationale symmetrische (oder
auch nur metacyklische) Function der f:
so erhalten wir, wenn wir die Werthe A0) einführen, daraus eine
rationale Function der Radicale
Diese Function ändert sich aber nicht, wenn man einem
dieser Radicale einen anderen seiner n Werthe giebt, und folglich
muss die Function rational von fc0, hu ..., hn_2 abhäügen. Wegen

696 Achtzehnter Abschnitt. §. 194.
2. ändert sich diese Function aber auch nicht, wenn unter den \
die cyklische Permutation (jfc0, 1cl: . . ., Ä„_2) vorgenommen wird,
und weil nun die Grossen Jcv die Wurzeln einer cyklischen Glei-
Gleichung im Körper $ sind, so ist die Function S(£o> £i> • . •, In—i)
eine Grosse in $, d. h. rational. Wendet man dies auf die
Coefficienten der Gleichung an, deren Wurzeln die Grossen A0)
sind, so folgt, dass diese Grossen die Wurzeln einer Gleichung
nten Grades in $ sind.
Was die Irreducibilität dieser Gleichung betrifft, so ist dar-
darüber Folgendes zu bemerken:
n
Wenn das Radical VBo nicht rational durch ]c0 ausdrückbar
ist, so ist nach §. 187 die Function
A7) x» — Bo
im Körper $(jfco), der aus $ durch Adjunction von Tc0 entsteht,
irreducibel. Nach §. 193 (8) kann man jede der Wurzeln f,
I»
etwa f0, rational durch eine der Wurzeln dieser Function, vB0,
ausdrücken, und die übrigen Wurzeln f erhält man, wenn man
. n
für y_ß0 die verschiedenen Wurzeln von A7) setzt. Wenn also
0 (f 0) = 0 eine in $ (ft0) rationale Gleichung ist, der eine der
Wurzeln f genügt, so folgt aus der Irreducibilität von A7), dass
dieser Gleichung auch alle anderen f genügen müssen, und
dass folglich die Gleichung nten Grades, deren Wurzeln die f
sind, im Körper $(&0), und um so mehr also im Körper $ irre-
irreducibel ist.
n
Wenn aber V_B0 in $Gc0) enthalten ist, so sind auch die
n
sämmtlichen Vi?r in diesem Körper enthalten, wie aus §. 193, (8)
hervorgeht. Es sind also zunächst alle £ in dem Körper $(ft0, e)
enthalten.
Durch die Substitution (fc0, ^) geht Bv—j in Bv über, und
folglich Vi?r_i in svVBv, wenn ar eine nte Einheitswurzel ist.
Es ergiebt sich aber, wenn man auf die Gleichung §. 193, (8)
die Substitution (fc0, ftj) anwendet,
A8) e, = «»_, = ef
Hier muss nun £0 dem Körper StQc0) angehören, und die

§. 195. Realitätaverhältnisse. 697
gehören gleichfalls dem Körper $(ft0) an; zugleich geht Sv durch
die Substitution (k0, ftj) in $,. + ! über.
Die Summe
A + KoSo + K^-i K,-a S,_s
ist daher eine Grosse in dem ursprünglichen Rationalitäts-
Rationalitätsbereich $, und nach A1) ist diese gleich einer der Grossen f.
Wir können also das Theorem I. so umkehren:
II. Jede in der Form (9) enthaltene Grosse f ist die
Wurzel einer Gleichung nten Grades in $, und
diese Gleichung ist irreducibel, wenn nicht eine
der n conjugirten Grossen f selbst in St ent-
enthalten ist.
§. 195.
Realitätsverhältnisse.
Wenn der Körper S ein reeller ist, so giebt es, wie wir
im §. 188 gesehen haben, zwei Arten von metacyklischen Glei-
Gleichungen von Primzahlgrad n, solche mit einer reellen und
n — 1 imaginären Wurzeln und solche mit lauter reellen Wurzeln.
Ebenso haben wir im §. 172 gesehen, dass es zwei Arten von
cyklischen Gleichungen eines geraden Grades giebt, nämlich solche
mit lauter reellen und solche mit lauter imaginären Wurzeln.
Wenn nun die cyklische Gleichung, deren Wurzeln die
Grossen ft0, &i, • ¦ ., &»—2 sind, zur ersten Art gehört, wenn also
&o, K, • ¦ •, &«—2 reell sind, und die Radicale r0, tx, . . ., t„_2 auch
reell genommen werden, so zeigt die Formel A0) §. 194, dass
f0 reell, £& und f_Ä conjugirt imaginär sind.
Wenn andererseits die ~k imaginär sind, so ist nach §. 172
hy und Tc n—i conjugirt imaginär, und nach der Formel (8) in
§. 193 können wir setzen, wenn 0 eine rationale Function be-
bedeutet,
n — l
2
oder auch
n—l
3 +1

698 Achtzehnter. Abschnitt. §. 196.
n — l
Weil nun g eine primitive Wurzel von n ist, so ist g 3 +1
durch n theilbar, und die rechte Seite wird daher rational. Be-
Bedeutet also W eine rationale Function, so ist
VB n-lVBv = W(JCV),
und diese Formel zeigt, dass
also dass W(lcr) reell ist. Daraus folgt, dass
r+„_i und
conjugirt imaginär sind; denn erstens sind ihre nten Potenzen
conjugirt imaginär, sie selbst also zunächst bis auf eine nte Ein-
Einheitswurzel als Factor. Da aber ihr Product reell ist, so muss
diese nte Einheitswurzel = 1 sein. Da nun ausserdem
rv = — r n—i (mod n)
ist, so zeigt die Formel A1), dass in diesem Falle die Wurzeln £„
alle reell sind.
Damit ist also der Satz für einen reellen Körper $ be-
bewiesen :
Hat die cyklische Gleichung, deren Wurzeln die
&o, 'kl,"-, kn—2 sind, reelle Wurzeln, so ist von den Wurzeln £
eine reell, die übrigen imaginär; hat diese cyklische
Gleichung imaginäre Wurzeln, so sind alle f reell.
§. 196.
Metacyklische Gleichungen fünften Grades.
Durch die Sätze der vorangehenden Paragraphen sind die
Wurzeln einer metacyklischen Gleichung von Primzahlgrad in
eine allgemein gültige Form gebracht, die es gestattet, alle diese
Grossen wirklich zu bilden, wenn man die Kenntniss der Wurzeln
cyklischer Gleichungen voraussetzt. Ganze Systeme cyklischer
Gleichungen jeden Grades liefert uns z. ß. die Kreistheilungs-
theorie, deren Wurzeln die Kreistheilungsperioden sind. So

§. 196. Metacyklische Gleichungen 5»en Grades. 699
können wir also beispielsweise für den Körper der rationalen
Zahlen beliebig viele metacyklische Gleichungen bilden. Dass
darin alle diese Gleichungen im Körper der rationalen Zahlen
enthalten sind, ist ein sehr merkwürdiger, von Kronecker her-
herrührender Satz, den wir irn zweiten Bande kennen lernen werden.
Hier wollen wir als Anwendung und Veranschaulichung des Vor-
Vorhergehenden noch die specielle Aufgabe behandeln, in einem be-
beliebigen Körper $ die Wurzeln aller metacyklischen Gleichungen
fünften Grades zu finden.
Dazu ist erforderlich und hinreichend, dass wir die Wurzeln
jfco, &i, &2> \ einer cyklischen Gleichung vierten Grades allgemein
bestimmen, und zwar unter der Voraussetzung, dass ft0, &i, &21 ^s
unter einander verschieden und keine von ihnen
Null sei.
Als Grundlage dient uns dabei die Function
A) w = Qh — h) Oh — h),
die von Null verschieden sein muss, und die für einen reellen
Körper $ immer reell ist, da entweder fc0, j^, Tc2, hs reell sind
oder ft0, Ti2 und Tci, ftf zwei conjugirt imaginäre Paare bilden.
Bei der cyklischen Permutation @, 1, 2, 3) ändert w sein
Vorzeichen. Also ist das Quadrat von w eine cyklische Function,
die nach Voraussetzung bekannt sein soll. Wir setzen daher,
indem wir durch die kleinen lateinischen Buchstaben a, b, c . . .
Grossen in $, also rationale Grossen bezeichnen,
B) w = 4 Vc,
und bemerken noch, dass jede Function der jfc, die durch die
cyklische Permutation @, 1, 2, 3) ihr Vorzeichen ändert, das
Product einer rationalen Grosse mit Vc ist.
Es handelt sich dann nur darum, cyklische Functionen in
genügender Anzahl zu bilden, so dass man die vier Grossen jfc0, hu
ft3, jfcj daraus berechnen und durch von einander unabhängige
rationale Grossen algebraisch ausdrücken kann.
Nun sind zwei weitere cyklische Functionen
Oo — «ar -j- Oi —
w
{h0 — tv2) (f»i — 1»$)
und wir bekommen also, wenn a, b rationale Grossen sind,

700 Achtzehnter Abschnitt. §. 196.
. Die drei rationalen Grossen a, b, c sind aber nicht von ein-
einander unabhängig, sondern es besteht nach B) und C) zwischen
ihnen die Relation
D) 62 = c A -f- a*).
Aus C) ergiebt sich ferner
h0 - lc2 = 2 Vb + a Vc
\ — \ = <lVb — aVc,
und zwischen den beiden Quadratwurzeln besteht die Relation
F) Ve = Vb + aVc Vb — a Vc.
Bezeichnen wir ferner mit C und B wieder zwei rationale
Grossen, so ist
k0 -f- 7cj -f- 7i2 + ^ = 4 C,
(J 7c0 -/^-f-fc, — fc,
also
wodurch nach E) folgt:
fc„ = C + BV7+V& + aVc
\ = C - BV^ + Vb -aV7
lc2 = C + BVc -Vb+_aVc_
lcs= C — BVc—Vb — aVc.
Es ist auch umgekehrt leicht, zu zeigen, dass diese Grossen
die Wurzeln einer biquadratischen cyklischen Gleichung sind.
Denn setzen wir zur Abkürzung
A0) r = Vc, q = Vb + a Vc, q' = Vb.~ a V7,
also nach F)
r = q q', q2 = b -\- ar, q'* = b — ar,
so können wir jede rationale Function der fc0, fea, 1c2, ^ als lineare
Function mit rationalen Coefficienten von den sechs Radicalen
1, r, Q, Q1, tq, tq'
darstellen. Die cyklische Permutation (k0, \, fc2, hä) entspricht
der Vertauschung
r, Q, Q1,
— r, q', — Q,
und wenn man diese Vertanschung wiederholt, so sieht man,

§. 196. Cyklische Gleichungen 4terL Grades. 701
dass eine cyklische Function der ft sich nicht ändern kann, wenn
in der linearen Darstellung durch diese sechs Grossen folgende
Vertauschungen gemacht werden:
1, r, o, o', ro, r o'
1, — r, q', — q, — ro', ro
1, r, — q, — q'. — ro, — ro'
1, — r, — q', q, ro', — ro,
und wenn man die vier sich so ergebenden Ausdrücke addirt,
so erhält man für die cyklische Function der Tc einen rationalen
Ausdruck.
Will man die biquadratische Gleichung bilden, deren Wurzeln
die h sind, so führt man am besten h — C = x als Unbekannte
ein. Man bekommt so durch einfache Rechnung die Gleichung
-f- b)x% — iBacx -|
Die Darstellung der ~k durch die Formeln (9) ist aber noch
nicht vollständig befriedigend, weil zwischen den darin vor-
vorkommenden rationalen Grossen a, b, c noch die Relation D)
stattfindet, und wir suchen eine Darstellung durch unabhängige
Grossen.
Einen besonderen Fall müssen wir zunächst abmachen,
nämlich b =¦ 0, was o = i zur Folge hat. Dann geben die
Formeln (9)
Äb = C- BVc-^—J
und die biquadratische Gleichung A1) wird
Xi _ 2B*cx* — iiBcx -\- Bitf -f- c = 0.
Dieser Fall gehört aber nur dann hierher, wenn * im Körper $
-enthalten ist, also niemals bei reellen Körpern.
Wenn aber b nicht verschwindet, so führen wir eine neue
rationale Grosse h ein, indem wir
f a3), c = ¥A + a2)

702 Achtzehnter Abschnitt. §. 196.
setzen, wodurch dann die Relation D) identisch befriedigt ist,
und es geben die Formeln (9), wenn man Bh durch B ersetzt,
0 = C + J5 Vl 4- «
h = C — B Vl -f «2 — Vä (l + a2 — a
Dieser Ausdruck für jfc0 hat noch den Vorzug, dass er, wie
man auch die Vorzeichen der darin vorkommenden Quadrat-
Quadratwurzeln bestimmen mag, nur vier verschiedene Werthe darstellt.
Bei Abel findet sich für jfc0 ein etwas anderer Ausdruck,
nämlich
fco = G -f B Vl 4-e3 4- Vh (l + e2 + Vl 4" e2),
der aus A2) hervorgeht, wenn man a = 1 : e setzt und dann B
und ä durch J5e und he2 ersetzt. Der Ausdruck A2) ist also
insofern allgemeiner, als er auch den besonderen Fall a = 0
umfasst, in dem die biquadratische GleichuDg in zwei quadratische
Gleichungen zerfällt.
Um nun die Wurzel einer metacyklischen Gleichung 5ten Grades
darzustellen, sind diese Ausdrücke für ft0, jfcj, A;2, ft3 in die Formel
(9) des §. 194 zu substituiren. Nehmen wir g = 2 an, so werden
die Exponenten r^rur^r% der Reihe nach congruent mit 1,2,4,8,
also gleich 1, 2, 4, 3, und es ergiebt sich, wenn, wie in §. 193
gesetzt wird,
A3) | = A + Z"o r08 r* r.|r3 + ^ t•' r3* r| r0
+ Z, r| r * r02 r, + Z3 r»t* %* xv
Die Coefficienten in diesem Ausdruck, Ko, Ku K2, Kz, sind
rationale Functionen der Tc0, Ttu Tc2, ks, die durch cyklische Permu-
Permutation der Ti selbst cyklisch permutirt werden. Nach Abel ist
Ko = Ä1 4- J-2 Jc0 4- J-3 h2 4- J.4 jfco fc2
zu setzen, worin Ax, A2, As, A± rational sind, und dieselben
Ausdrücke legt auch Cayley zu Grunde. Diese Annahme ist
aber nicht allgemein genug, weil zwischen ifcoifca, To0 und Tc2 eine
aus A2) leicht abzuleitende lineare Relation besteht. Am ein-
einfachsten drückt man die ~k durch die drei Radicale

§. 196. Metaoyklisolie Gleichungen ö4«1 Grades. 703
r = Vl + a% q = Vh (l + a2 + a VT
q' = Vh (l + a2 — a Vl + a2), qq' = hr
aus.
Man kann das Radical q' linear ausdrücken durch r q und
q, wie man aus der Formel
hr2 q' = r p p'2
ersieht, wenn man rechts für p'2 seinen Ausdruck durch r ein-
einsetzt und bedenkt, dass r2 rational ist. So erhält man, wenn man
statt der cyklischen Permutation der h die Vertauschung
/ r, p, p'\
\— r, q', — q)
anwendet, und mit A^ J.2, As, A4 rationale Grossen bezeichnet:
Ko = Ay -\- Ai r -j- A3 q -f Ai r q
Ki = Ai — A2 r 4- A% p' — A, r o'
A4) /
i = ^lj — j42 r — A$ q' -\- A± r q'.
Diese Grossen K, K, K^ Ks sind selbst wieder die Wurzeln
einer cyklischen biquadratischen Gleichung. Sie haben nur
scheinbar eine allgemeinere Form, als die h; denn setzt man Kq
in die Form
so erkennt man die Form von l;0 in (9) wieder, natürlich mit
veränderten a, 6, c.

Berichtigungen.
Seite 151, Zeile 7 von unten ist zu lesen kleiner statt grösser.
Seite 151, Formel A9), B0) ;? statt <f.
Seite 278, Die Bedingungen (8), (9) für die Existenz von zwei Paaren gleicher
Wurzeln sind zwar nothwendig, aber, wenigstens in dem Falle
imaginärer Wurzeln, nicht hinreichend. Die nothwendigen und
hinreichenden Bedingungen für diesen Fall erhält man am ein-
einfachsten, wenn man die Forderung stellt, dass xl-\-ax*-\- bx-\- c
ein Quadrat sein soll, in der Form
& = o, os2 — 4e = o
und für a<Co sind die Wurzeln reell, für a > o imaginär.