Текст
Gilbert Strang
Lineare Algebra
Übersetzt aus dem Englischen von der djs^ GmbH,
unter Mitarbeit von Michael Dellnitz
Springer
Springer
Berlin
Heidelberg
New York
Hongkong
London
Mailand
Paris
Tokio
Professor Gilbert Strang
Massachusetts Institute of Technology
Department of Mathematics
Cambridge, MA 02139-4307
USA
e-mail: gs@math.mit.edu
URL: http://ocw.mit.edu
http://web.mit.edu/i8.o6/www
Übersetzer
djs2 GmbH
Technologiepark 32
33100 Paderborn
Deutschland
Titel der englischen Originalausgabe: Introduction to Linear Algebra, erschienen bei Wellesley-
Cambridge Press, 1998
Mathematics Subject Classification B000): 15
Bibliografische Information Der Deutschen Bibliothek
Die Deutsche Bibliothek verzeichnet diese Publikation in der Deutschen Nationalbibliografie;
detaillierte bibliografische Daten sind im Internet über <http://dnb.ddb.de> abrufbar.
ISBN 3-540-43949-8 Springer-Verlag Berlin Heidelberg New York
Dieses Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere die der Übersetzung, des
Nachdrucks, des Vortrags, der Entnahme von Abbildungen und Tabellen, der Funksendung, der Mikroverfilmung oder
der Vervielfältigung auf anderen Wegen und der Speicherung in Datenverarbeitungsanlagen, bleiben, auch bei nur
auszugsweiser Verwertung, vorbehalten. Eine Vervielfältigung dieses Werkes oder von Teilen dieses Werkes ist auch
im Einzelfall nur in den Grenzen der gesetzlichen Bestimmungen des Urheberrechtsgesetzes der Bundesrepublik
Deutschland vom 9. September 1965 in der jeweils geltenden Fassung zulässig. Sie ist grundsätzlich
vergütungspflichtig. Zuwiderhandlungen unterliegen den Strafbestimmungen des Urheberrechtsgesetzes.
Springer-Verlag Berlin Heidelberg New York
ein Unternehmen der Springer Science+Business Media
http://www.springer.de
© Springer-Verlag BerUn Heidelberg 2003
Printed in Germany
Die Medergabe von Gebrauchsnamen, Handelsnamen, Warenbezeichnungen usw. in diesem Werk berechtigt auch
ohne besondere Kennzeichnung nicht zu der Annahme, daß solche Namen im Sinne der Warenzeichen- und
Markenschutz-Gesetzgebung als frei zu betrachten wären und daher von jedermann benutzt werden dürften.
Satz: Datenerstellung durch den Übersetzer unter Verwendung eines Springer TßX-Makropakets
Einbandgestaltung: design & production GmbH, Heidelberg
Gedruckt auf säurefreiem Papier 46/3iiick - 5 4 3 2 1 SPiN 11319801
Vorwort
Dies ist ein einführendes Lehrbuch zur linearen Algebra, in dem deren Theorie
gemeinsam mit Anwendungen dargestellt wird. Die zentralen Gegenstände
sind lineare Gleichungssysteme Ax = b und das Eigenwertproblem Ax = Xx.
Es ist einfach verblüffend, wie viel es zu diesen beiden Gleichungen zu sagen
(und zu lernen) gibt. Dieses Buch ist als das Resultat jahrelangen Lehrens,
Organisierens und Nachdenkens über den Kurs zur linearen Algebra zu sehen
— und doch kommt mir das Thema immer wieder neu und sehr lebendig vor.
Ich bin wirklich froh darüber, dass die lineare Algebra weithin als wichtige
Disziplin anerkannt ist. Sie ist definitiv ebenso wichtig wie die
Differentialrechnung. Hier werde ich um nichts nachgeben, insbesondere wenn ich mir
ansehe, wie Mathematik tatsächlich angewendet wird. So viele der
aktuellen Anwendungen sind diskreter statt kontinuierlicher Natur, digital anstatt
analog, linearisierbar anstatt erratisch und chaotisch. In diesen Fällen sind
Vektoren und Matrizen die mathematische Beschreibung der Wahl.
In der Gleichung Ax = b werden diese Begriffe direkt verwendet. Auf
der linken Seite finden wir eine Matrix A und einen unbekannten Vektor
X. Ihr Produkt Ax ist eine Kombination der Spalten von A. Hierin
besteht die beste Sichtweise, die Multiplikation zu betrachten; die Gleichung
fragt nach derjenigen Kombination, die den Vektor b erzeugt. Wir können
die Lösung auf drei Beschreibungsebenen finden, die alle sehr wichtig sind:
1. Direkte Lösung durch Vorwärtseliminieren und Rücksubstitution.
2. Matrix-Lösung durch x = A~^h unter Verwendung der inversen
Matrix A~'^.
3. Vektorraum-Lösung durch Bestimmung aller Linearkombinationen
der Spalten von A und aller Lösungen der Gleichung Ax = 0. Wir
betrachten hierbei den Spaltenraum und den Kern.
Es gibt noch eine weitere Möglichkeit: Es könnte sein, dass die Gleichung
Ax = h keine Lösung hat Der direkte Weg über das Eliminationsverfahren
kann auf eine Gleichung der Form 0 == 1 führen. Der Weg über die Matrix A~^
kann fehlschlagen, weil diese Matrix nicht bestimmt werden kann. Auf dem
Weg über die Vektorräume betrachtet man alle Kombinationen der Spalten.
Es kann aber sein, dass b nicht in diesem Spaltenraum liegt. Ein Teil der
Mathematik wird helfen zu verstehen, unter welchen Umständen eine Gleichung
lösbar ist und wann nicht.
VI Vorwort
Ein weiterer Teil besteht darin, Vektoren zu visualisieren. Bei einem
Vektor V mit zwei Komponenten ist das nicht schwierig. Dessen Komponenten vi
und V2 geben an, wie weit man zur Seite und nach oben gehen muss — damit
können wir einen Pfeil zeichnen. Ein zweiter Vektor w könnte zum Beispiel
rechtwinklig zu v sein (in Kapitel 1 lernen Sie, wann genau). Haben die
Vektoren jedoch sechs Komponenten, so können wir sie nicht länger zeichnen,
obwohl wir in unserer Vorstellung genau dies weiter versuchen. Wir können
uns sogar im sechsdimensionalen Raum einen rechten Winkel vorstellen. Wir
können auch 2v (doppelt so lang) und — w (in die w entgegengesetzte
Richtung) sehen. Wir können uns beinahe Kombinationen wie 2v—w vorstellen.
Am Wichtigsten ist das Bemühen, sich alle Kombinationen von cv
und dw vorzustellen. Diese Kombinationen erzeugen eine Art
„zweidimensionaler Ebene" innerhalb des sechsdimensionalen Raums. Während ich diese
Worte schreibe, bin ich mir überhaupt nicht sicher, ob ich diesen Unterraum
sehen kann. Die lineare Algebra bietet aber eine einfache Möglichkeit, mit
Vektoren und Matrizen jeglicher Größe zu arbeiten. Haben wir es mit sechs
Strömen in einem Netzwerk oder mit sechs Kräften auf eine Struktur zu tun,
oder mit sechs Preisen für unsere Produkte, so befinden wir uns sicherlich in
einem sechsdimensionalen Raum. Für die lineare Algebra ist ein sechsdimen-
sionaler Raum noch verhältnismäßig klein.
Sie erkennen an diesem Vorwort bereits den Stil dieses Buches und seine
Zielsetzung. Es ist im Stil informell, in seiner Zielsetzung aber absolut
ernsthaft. Bei der linearen Algebra handelt es sich um großartige Mathematik, die
ich so klar wie möglich zu erklären versuche. Ich hoffe, dass der Professor,
der diesen Kurs unterrichtet, dabei etwas Neues lernt. Der Autor tut dies
jedes mal. Studierende werden bemerken, dass in den Anwendungen die Ideen
nochmals verdeutlicht werden. Dies ist der Hauptpunkt für uns alle: zu
Lernen, wie man denkt. Ich hoffe, sie erkennen, wie dieses Buch voranschreitet,
schrittweise^ aber unaufhaltsam.
In der Mathematik wird man ständig dazu angehalten, über den Einzelfall
hinauszublicken und das allgemeine Prinzip zu erkennen. Ob wir es mit Pixel-
Intensitäten auf einem Fernsehschirm zu tun haben oder mit Kräften auf ein
Flugzeug, oder auch mit den Flugplänen für die Piloten, immer haben wir
es mit Vektoren zu tun, die mit Matrizen multipliziert werden. Es lohnt sich
also, die lineare Algebra gut zu studieren.
Die Struktur des Lehrbuchs
Ich möchte fünf Anmerkungen zum Aufbau dieses Buchs machen:
1. Kapitel 1 bietet eine kurze Einführung in die wesentlichen Ideen hinter
Vektoren, Matrizen und Skalarprodukten. Wenn der Kurs mit diesen
Begriffen bereits vertraut ist, stellt es kein Problem dar, direkt mit Kapitel 2
zu beginnen, in dem die Lösung eines n x n-Gleichungssystems ^x = b
behandelt wird.
Vorwort VII
2. Ich verwende die reduzierte Zeilen-Treppenform für rechteckige Matrizen
nun häufiger als zuvor. In MATLAB erhält man sie über das
Kommando i? = rref (A). Durch die Reduktion von A auf R erhält man Basen
des Zeilen- und des Spaltenraums. Darüber hinaus liefert die Reduktion
der erweiterten Matrix [AI] die vollständige Information über alle vier
fundamentalen Unterräume.
3. Diese vier Unterräume bieten eine wunderbare Möglichkeit, die Begriffe
lineare Unabhängigkeit, Dimension und Basis zu verstehen. Diese Beispiele
sind so natürlich und ganz ungezwungen der Schlüssel zu den
Anwendungen. Ich möchte mir keine Vektorräume ausdenken, wo es doch so viele
wichtige gibt, die man wirklich braucht. Hat der Kurs erst zahlreiche
Beispiele zur Unabhängigkeit und Abhängigkeit von Vektoren gesehen,
so wird die Definition praktisch im Voraus verstanden. Die Spalten einer
Matrix A sind unabhängig, wenn x = 0 die einzige Lösung der Gleichung
Ax = 0 ist.
4. In Abschnitt 6.1 werden Eigenwerte für 2 x 2-Matrizen eingeführt. Oft
besteht der Wunsch, Eigenwerte früh zu behandeln (um sie für andere
Fächer verfügbar zu machen, oder um zu vermeiden, dass sie ganz
ausgelassen werden). Deshalb ist es kein Problem, von Kapitel 3 direkt in den
Abschnitt 6.1 zu springen. Für eine 2 x 2-Matrix ist die Determinante
sehr einfach, und das Konzept der Eigenwerte wird klar erkennbar.
5. Jeder Abschnitt der Kapitel 1 bis 7 endet mit einer hervorgehobenen
Wiederholung der Wesentlichen Punkte. Der Leser erhält damit die
Möglichkeit, den Inhalt des Textes zu rekapitulieren, indem er diese Wiederholung
sorgfältig durchgeht.
Ein einsemestriger Kurs, der ununterbrochen voranschreitet, kann bis zu den
Eigenwerten gelangen. Die Hauptidee besteht darin, eine Matrix zu diagona-
lisieren. Für die meisten quadratischen Matrizen erhält man dabei die Fakto-
risierung S~^AS mit der Eigenvektormatrix S. Für symmetrische Matrizen
erhält man Q^AQ. Ist A eine allgemeine rechteckige Matrix, so benötigen
wir die Form JJ-^AV. Ich versuche, die Singulärwertzerlegung so gut ich kann
zu erklären, weil sie extrem nützlich geworden ist. Ich habe bei diesem Kurs
und seiner Aufnahme durch die Studierenden ein sehr gutes Gefühl.
Struktur des Kurses
Die Kapitel 1-6 enthalten das Herzstück eines einführenden Kurses zur
linearen Algebra — die Theorie sowie auch Anwendungen. Die Schönheit äußert
sich in der Weise, in der diese beiden Teile ineinander verzahnt sind. Die
Theorie wird benötigt und Anwendungen finden sich überall.
Mittlerweile verwende ich eine Webseite, um den Inhalt, Hausaufgaben
und Lösungen zu Klausuren zu veröffentlichen:
http://web.init.edu/18.06/www
VIII Vorwort
Ich hoffe, Sie finden diese Seite nützlich. Sie hat fast 30.000 Besucher gehabt.
Machen Sie regen Gebrauch davon, und geben Sie mir Anregungen, aufweiche
Weise man sie noch verbessern und erweitern kann.
In Kapitel 7 wird erklärt, wie Matrizen mit linearen Abbildungen
zusammenhängen. Die Matrix hängt von der Wahl einer Basis ab! Wir zeigen, wie
sich Vektoren und Matrizen ändern, wenn die Basis gewechselt wird, und wir
zeigen auch die lineare Abbildung, die hinter der Matrix steht. Ich beginne
den Kurs nicht mit dieser (tiefer liegenden) Idee, weil es besser ist, zunächst
Unterräume zu verstehen.
In Kapitel 8 werden wichtige Anwendungen präsentiert — ich wähle oft
die Markov-Matrizen für eine Vorlesung ohne Klausur. In Kapitel 9 wenden
wir die Aufmerksamkeit wieder der numerischen linearen Algebra zu, und
erklären, wie die Gleichungen Ax = b und Ax = Ax tatsächlich gelöst
werden. In Kapitel 10 machen wir den Schritt von reellen zu komplexen Zahlen
als Einträge in Matrizen und Vektoren. Das ganze Buch ist für einen zweise-
mestrigen Kurs angemessen — es beginnt schrittweise und geht immer weiter
voran.
Berechnungen in der linearen Algebra
Der Text räumt dem wunderbaren Softwaresystem MATLAB den ersten Rang
ein, das speziell für die lineare Algebra entwickelt wurde. Es stellt die
Programmiersprache bereit, in der unsere Unterrichts codes von Cleve Moler für
die erste und von Steven Lee für diese [zweite amerikanische, Anm. d. Übers.]
Ausgabe geschrieben wurden. Die Unterrichtscodes befinden sich auf der
Webseite, zusammen mit den Hausaufgaben für MATLAB, Referenzmaterial
und einer kurzen Einführung. Die beste Art, hiermit zu beginnen, besteht
darin, Aufgaben zu lösen!
Wir bieten auch eine ähnliche Sammlung von Unterrichtscodes für Maple
und für Mathematica an. Am Ende des Buches befindet sich eine Liste dieser
Codes. Sie führen genau die Schritte aus, die wir im Text beschreiben. Der
Leser kann die Matrix-Theorie damit auf zwei Weisen kennenlernen — die
Algebra, und auch die Algorithmen. Sie fügen sich wunderbar zusammen.
Dieses Buch kann einem Kurs, der algorithmische Aspekte einschließt, ebenso
als Grundlage dienen wie einem Kurs, der dies nicht tut.
Es gibt so viel gute Mathematik zu lernen und zu betreiben.
Vorwort IX
Danksagungen
Ich habe viel Hilfe bei der Entstehung dieses Buches erfahren. Eine große
Anzahl von Lesern hat mir Vorschläge per E-Mail geschickt; ich danke Ihnen
dafür!
Steven Lee kam dreimal vom Oak Rigde National Laboratory an das
MIT zu Besuch, um den Kurs 18.06 Lineare Algebra nach diesem Buch zu
unterrichten. Er entwarf die Webseite http://web.init.edu/18.06/www,
und er fügte den MATLAB Unterrichtscodes, die von Cleve Moler für die erste
Ausgabe geschrieben worden waren, weitere hinzu. (Alle Unterrichtscodes
sind am Schluss des Buches aufgeführt.) Ich finde, diese kurzen Programme
illustrieren die wesentlichen Schritte der lineare Algebra auf eine sehr klare
Weise. Wenn Sie Hilfe irgendwelcher Art benötigen, schauen Sie bitte auf der
Webseite nach.
Ich möchte meinen tiefsten Dank für das Entstehen dieses Buches fünf
Freunden aussprechen. Die erste Ausgabe von 1993 wurde von Kai Borre und
Frank Jensen in Dänemark in das I^T^2e-Format gebracht. Es folgte die
hervorragende Arbeit von Sueli Rocha an der neuen Ausgabe. Zunächst am MIT,
und dann in Hong Kong, hat sie all die Aufregung, das Beinahe-Herzversagen
und schließlich das Triumphgefühl mitgemacht, die zur Veröffentlichung eines
Buches dazugehören. Vasily Strela war erfolgreich damit, die Abbildungen in
einen druckfertigen Zustand zu bringen (irgendwie, indem er die PostScript-
Dateien gelesen hat). Im entscheidenden letzten Schritt hat Amy Hendrickson
alles getan, was nötig war, um die Gestaltung zu vollenden. Sie ist ein
Profi ebenso sehr wie ein Freund. Ich hoffe, Sie werden die Wiederholung der
Wesentlichen Punkte am Ende eines jeden Abschnitts mögen, und die
deutlichen Kästchen in den Definitionen und Sätzen. Durch die Wiederholungen
und die Kästchen wird das Wichtigste herausgehoben, und meine Studenten
erinnerten sich gut daran.
Es gibt noch einen anderen besonderen Teil an diesem Buch: Den vorderen
Buchdeckel^. Vor etwa einem Monat erhielt ich eine seltsame Email von Ed
Curtis an der University of Washington. Er bestand darauf, dass ich das
Buch Great American Quilts: Book 5 kaufe, ohne zu sagen, warum. Es ist
vielleicht überflüssig zuzugeben, dass ich noch nicht besonders viele Quilts^
hergestellt habe. Auf Seite 131 dieses Buches fand ich einen erstaunlichen
Quilt, hergestellt von Chris Curtis. Sie hatte die erste Ausgabe dieses Buches
gesehen, auf dessen Einband geneigte Häuser zu sehen waren. Sie illustrieren,
was lineare Transformationen bewirken können, siehe Abschnitt 7.1. Chris
Anm. d. Übers.: Dies bezieht sich auf die zweite amerikanische Ausgabe. Der
Bucheinband ist im Internet abgebildet, zum Beispiel auf der Homepage des
Autors.
Anm. d. Übers.: Eine Art Flickendecke; bei der Verwendung des Wortes so wie
hier wird allerdings mehr Gewicht auf dessen künstlerische Gestaltung gelegt,
als man es mit dem deutschen Wort ausdrücken könnte.
X Vorwort
Curtis mochte diese Häuser, und sie machte sie schön. Möglicherweise sind
sie jetzt nichtlinear — aber das ist Kunst.
Ich bin dankbar dafür, dass Oxmoor House der Verwendung des Quilts auf
diesem Buch zugestimmt hat. Die Farbe wurde einhellig von zwei Personen
ausgewählt. Ich bin glücklich, Tracy Baldwin für die Gestaltung ihres dritten
Einbands für Wellesley-Cambridge Press danken zu können.
Ich möchte dieses Buch meinen Enkeln widmen. Es ist mir eine Freude,
die Namen derer zu nennen, die ich bislang kenne: Roger, Sophie, Kathryn,
Alexander, Scott, Jack, William und Caroline. Ich hoffe, dass Ihr alle eines
Tages diesen Kurs über lineare Algebra besuchen werdet. Bitte besteht ihn,
wie auch immer. Der Autor ist stolz auf Euch.
Februar 2003 Gilbert Strang
Inhaltsverzeichnis
Einführung in die Vektorrechnung 1
1.1 Vektoren und Linearkombinationen 1
1.2 Längen und Skalarprodukte 11
Das Lösen linearer Gleichungen 25
2.1 Vektoren und lineare Gleichungen 25
2.2 Die Idee der Elimination 40
2.3 Elimination mit Hilfe von Matrizen 51
2.4 Regeln für Matrixoperationen 62
2.5 Inverse Matrizen 75
2.6 Elimination = Faktorisierung: A=:LU 88
2.7 Transponierte und Permutationen 102
Vektorräume und Untervektorräume 117
3.1 Räume von Vektoren 117
3.2 Der Kern von A: Lösung von Ax = 0 129
3.3 Die Rang und die reduzierte Treppenform 142
3.4 Die vollständige Lösung von ^x = b 153
3.5 Unabhängigkeit, Basis und Dimension 164
3.6 Dimensionen der vier Unterräume 181
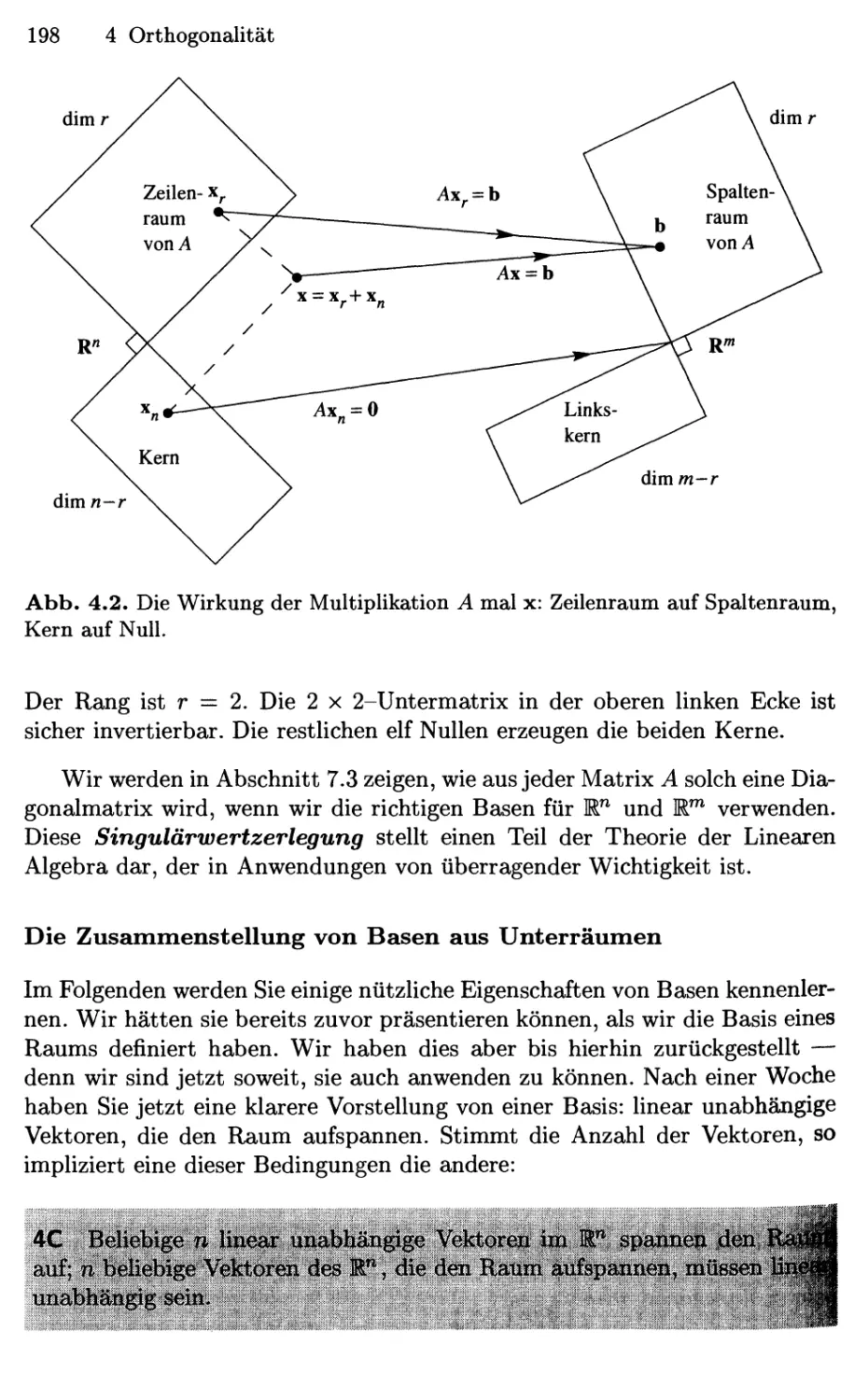
Orthogonalität 193
4.1 Orthogonalität der vier Unterräume 193
4.2 Projektionen 203
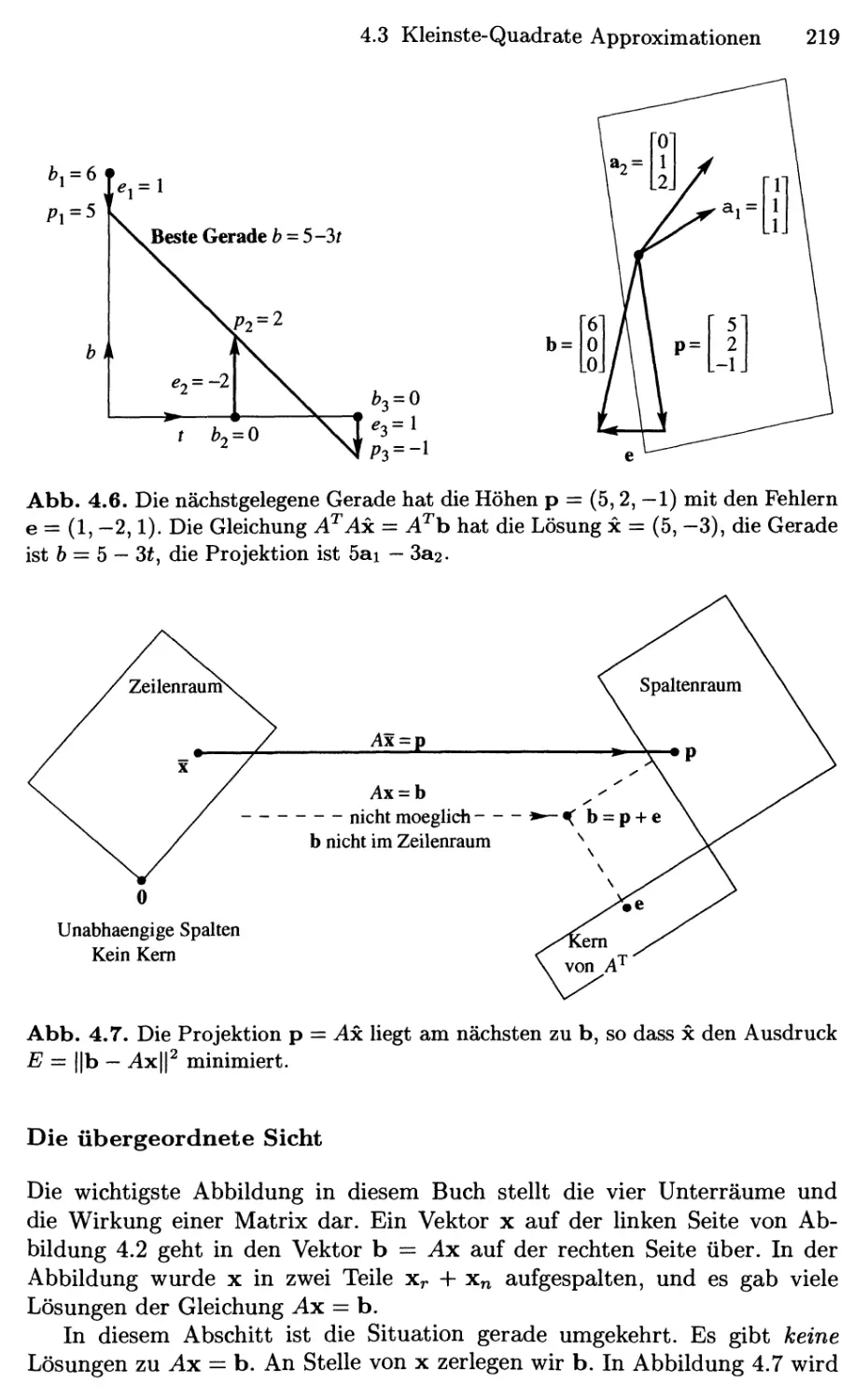
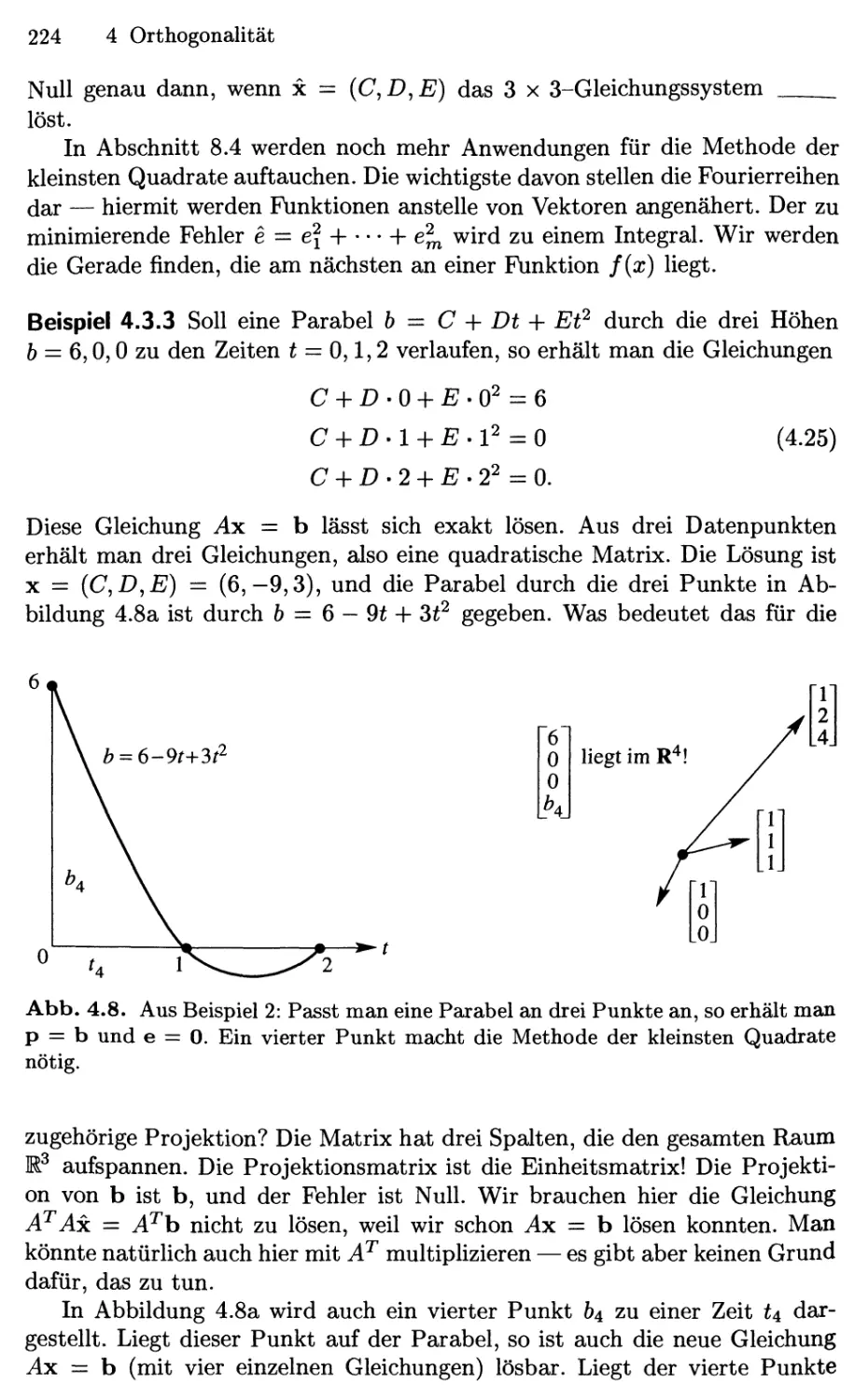
4.3 Kleinste-Quadrate Approximationen 215
4.4 Orthogonale Basen und Gram-Schmidt 229
Determinanten 245
5.1 Die Eigenschaften von Determinanten 245
5.2 Permutationen und Kofaktoren 256
5.3 Cramer'sehe Regel, Inverse und Volumen 272
Eigenwerte und Eigenvektoren 289
6.1 Eigenwerte: Einführung 289
6.2 Diagonalisierung einer Matrix 304
XII Inhaltsverzeichnis
6.3 Anwendungen bei Differentialgleichungen 319
6.4 Symmetrische Matrizen 333
6.5 Positiv definite Matrizen 346
6.6 ÄhnUche Matrizen 360
6.7 Singulärwertzerlegung 368
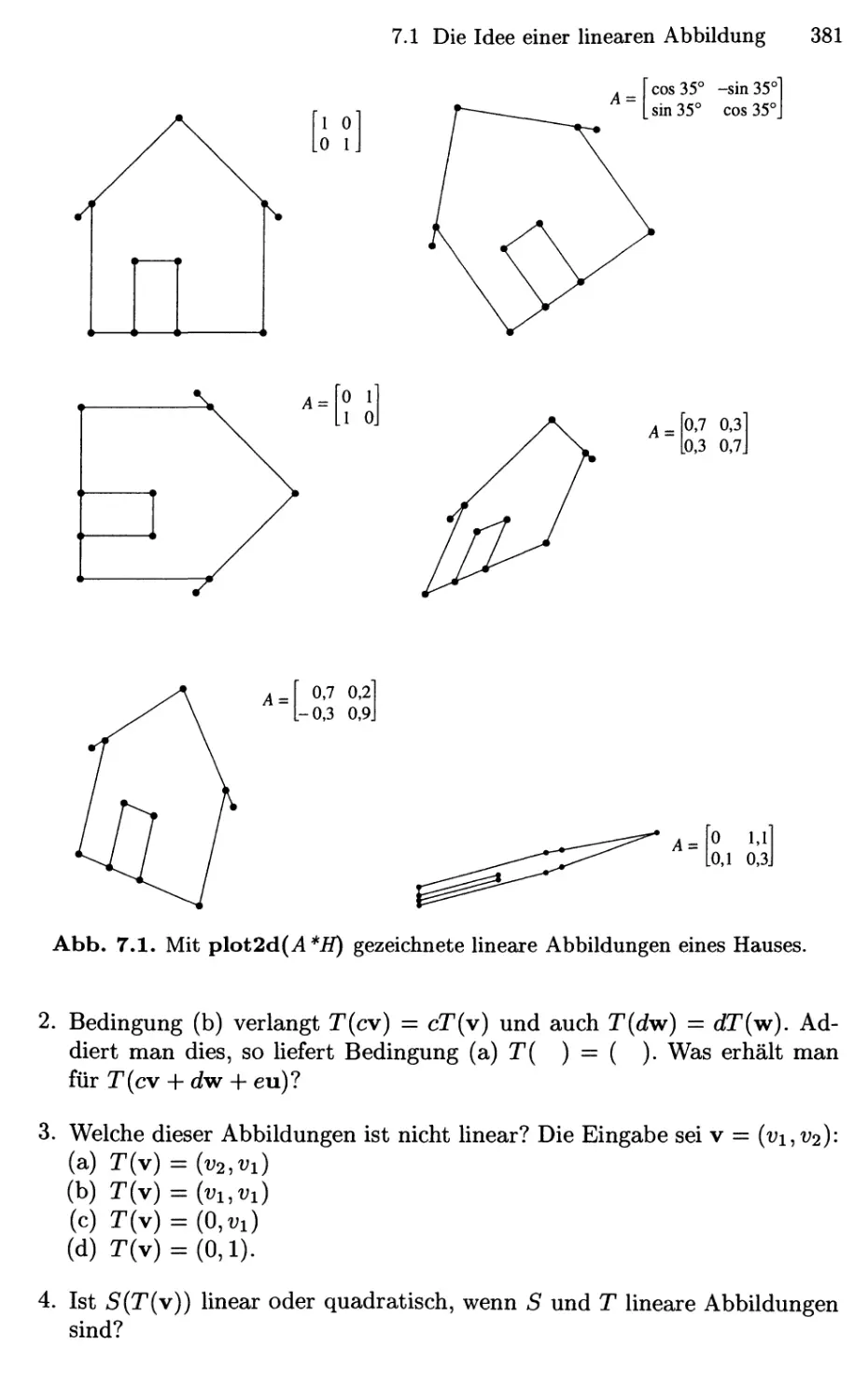
7 Lineare Abbildungen 377
7.1 Die Idee einer linearen Abbildung 377
7.2 Die Matrix einer linearen Abbildung 385
7.3 Basiswechsel 399
7.4 Diagonalisierung und Pseudoinverse 406
8 Anwendungen 419
8.1 Graphen und Netzwerke 419
8.2 Markov-Matrizen und Wirtschaftsmodelle 432
8.3 Lineare Programmierung 441
8.4 Fourier reihen: Lineare Algebra für Funktionen 449
8.5 Computergrafik 457
9 Numerische lineare Algebra 465
9.1 Gauß'sche Elimination in der Praxis 465
9.2 Normen und Konditionszahlen 476
9.3 Iterative Methoden für lineare Algebra 484
10 Komplexe Vektoren und Matrizen 497
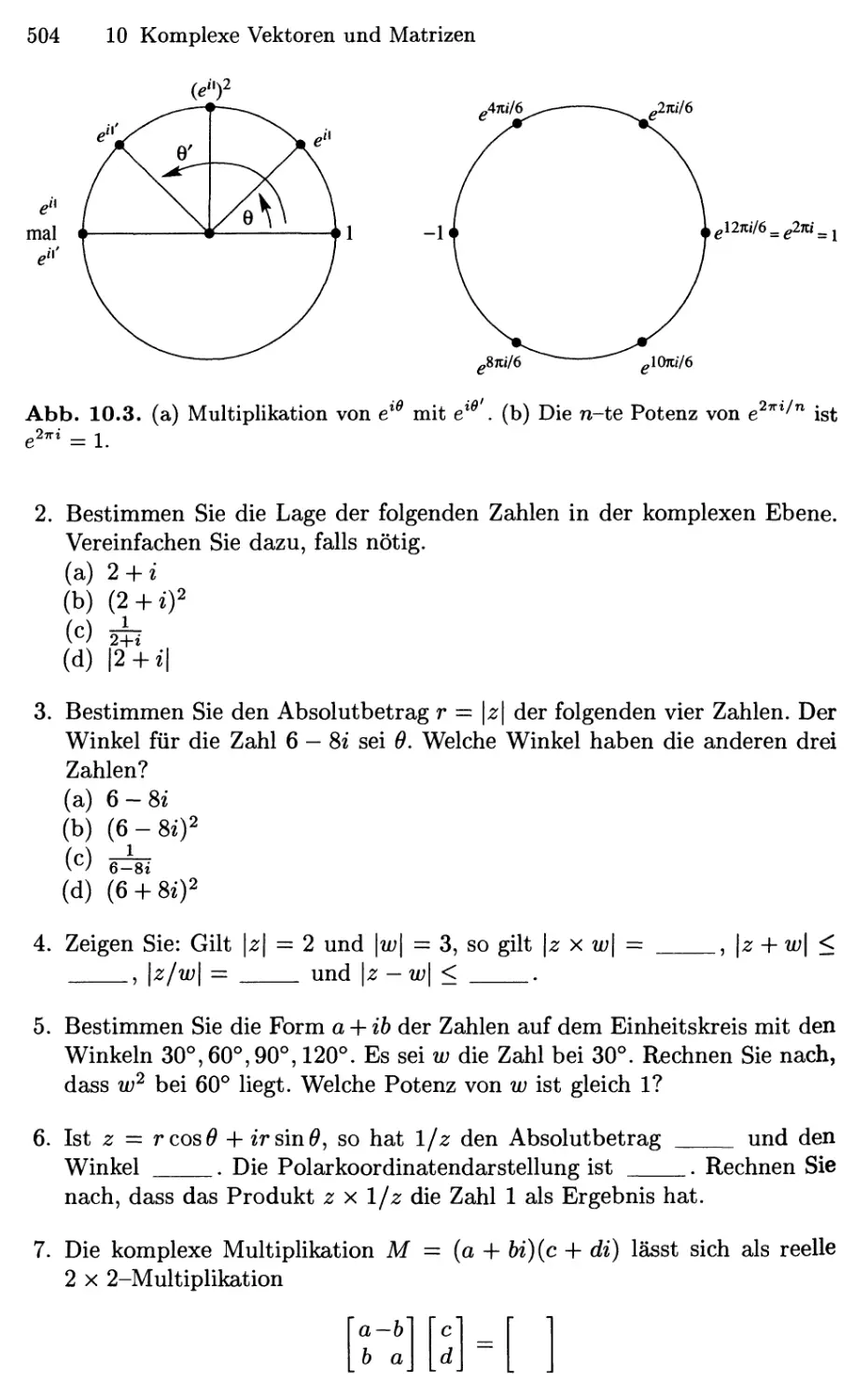
10.1 Komplexe Zahlen 497
10.2 Hermitesche und unitäre Matrizen 507
10.3 Die schnelle Fouriertransformation 517
Lösungen zu ausgewählten Aufgaben 527
Eine Abschlussklausur 587
Matrix-Faktorisierungen 591
Durchgerechnete Aufgaben 595
Index 649
Unterrichtscodes 655
1 Einführung in die Vektorrechnung
Im Zentrum der linearen Algebra stehen zwei Operationen — beide werden
mit Vektoren ausgeführt. Wir addieren Vektoren v, w, um v + w zu erhalten.
Wir multiplizieren sie mit Zahlen c und d, um cv und dw zu erhalten. Die
Kombination dieser Operationen ergibt die Linearkombination cv + dw.
Im ersten Kapitel werden diese beiden zentralen Ideen erläutert, auf
denen anschließend alles weitere aufbaut. Wir beginnen zunächst mit zwei- und
dreidimensionalen Vektoren, denn diese sind auch zeichnerisch gut
darstellbar. Danach gehen wir zu höheren Dimensionen über. Das wirklich
Beeindruckende an der Linearen Algebra besteht darin, dass dieser Schritt in den
n-dimensionalen Raum problemlos durchführbar ist. Die geometrische
Vorstellung aus zwei und drei Dimensionen bleibt hierbei völlig korrekt, auch
wenn man einen zehndimensionalen Vektor nicht mehr zeichnen kann.
Dorthin wird das Buch uns führen (in den n-dimensionalen Raum), und
als erste Schritte betrachten wir die beiden Operationen, die in den
Abschnitten 1.1 und 1.2 eingeführt werden:
1.1 Vektoraddition v + w und Linearkombinationen cv + dw.
1.2 Das Skalarprodukt vw und die Länge ||v|| — y^v • v.
1.1 Vektoren und Linearkombinationen
„Man kann Äpfel nicht mit Birnen vergleichen." Das mag nichts Neues sein,
doch der Satz enthält für uns einen wesentlichen Inhalt. Seltsamerweise
besteht hierin der Grund dafür, dass es Vektoren gibt! Wenn man nämHch die
Anzahl der Äpfel getrennt von der Anzahl der Birnen betrachtet, so erhält
man ein Paar von Zahlen. Dieses Paar ist ein zweidimensionaler Vektor v:
Vi = Anzahl der Äpfel
V2 = Anzahl der Birnen.
Hierbei haben wir v als einen Spaltenvektor geschrieben. Die Zahlen vi
und V2 sind seine „Komponenten." Ein wesentlicher Aspekt liegt darin, dass
wir einen einzigen Buchstaben v (fett gedruckt) für das Zahlenpaar vi und V2
(kursiv gedruckt) schreiben. Selbst wenn wir vi nicht zu V2 addieren können,
2 1 Einführung in die Vektorrechnung
so können wir doch Vektoren addieren. Die ersten Komponenten von v und
w werden dabei getrennt von den zweiten Komponenten behandelt:
V =
und w
Wi
W2
addieren sich zu v -f w =
Vi -\-Wi
V2 -\-W2
Diese Vorgehens weise ist berechtigt und man erkennt leicht den Grund.
Die Gesamtzahl der Äpfel ist Vi-\-wi, die Gesamtzahl der Birnen ist V2+W2.
Die auf diese Weise erklärte Vektoraddition ist grundlegend und wichtig. Die
Subtraktion von Vektoren wird analog durchgeführt: Die Komponenten von
V — w sind Vi — wi und .
Vektoren können mit 2 oder -1 oder mit einer beliebigen Zahl c
multipliziert werden. Es gibt zwei Möglichkeiten, einen Vektor zu verdoppeln. Die
eine besteht in der Addition v + v. Die andere Möglichkeit (der übUche Weg)
ist, jede Komponente von v mit 2 zu multiplizieren:
2v
2i;i
2i;2
-V =
-Vi
-V2
Die Komponenten von cv sind cvi und cv2' Die Zahl c wird ein „Skalar"
genannt.
Man beachte, dass die Summe von -v und v den Nullvektor ergibt. Für
diesen Vektor schreiben wir 0, was nicht der Zahl Null entspricht. Vielmehr
hat der Vektor 0 die zwei Komponenten 0 und 0. Man möge mir verzeihen,
dass ich derart auf dem Unterschied zwischen einem Vektor und seinen
Komponenten herumreite. Die lineare Algebra ist auf diesen Operationen v -+- w
und cv aufgebaut — Addition von Vektoren und Multiplikation mit
Skalaren.
Es gibt noch eine andere Möglichkeit, einen Vektor zu veranschaulichen,
wodurch alle seine Komponeneten gleichzeitig erkennbar werden. Der Vektor
V kann nämlich durch einen Pfeil dargestellt werden. Wenn v zwei
Komponenten hat, so liegt der Pfeil im zweidimensionalen Raum (einer Ebene). Sind
^—► V,
ly^
Abb. 1.1. Der Pfeil beginnt normalerweise im Ursprung @,0); cv ist immer parallel
zu v.
1.1 Vektoren und Linearkombinationen
v =
2
+
-1
2
=
3'
4
v + w =
Abb. 1.2. Die Vektoraddition v + w bildet die Diagonale des Parallelogramms.
Man addiert die ersten und die zweiten Komponenten getrennt voneinander.
Vi und V2 die Komponenten des Vektors, so zeigt der Pfeil vi Einheiten nach
rechts und V2 Einheiten nach oben. Ein solcher Vektor ist in Abbildung 1.1 auf
zwei verschiedene Weisen gezeichnet. Einmal beginnt er im Ursprung (dort,
wo sich die Achsen treffen) — und dies ist die übliche Darstellungsweise. Nur
in Ausnahmefallen werden unsere Vektoren nicht im Ursprung @,0)
beginnen. Im zweiten Fall ist der Anfangspunkt des Pfeils nach A verschoben. Die
Pfeile OP und äS repräsentieren jedoch denselben Vektor. Ein Grund dafür,
prinzipiell alle Startpunkte für Vektoren zu erlauben, besteht darin, dass sich
dadurch die Summe v -+- w zweier Vektoren grafisch darstellen lässt.
Vektoraddition (Spitze zum Anfang) Setze den Anfang von w an die
Spitze von v.
Wir folgen zunächst v vom Anfang bis zur Spitze und gehen dann längs w.
Oder aber wir nehmen die Abkürzung entlang v -+- w. Das gleiche Ergebnis
ergibt sich, wenn man zunächst w folgt und anschließend längs v geht. Anders
gesagt, W-+-V ergibt dasselbe wie v-+-w. All dies sind verschiedene Wege durch
das Parallelogramm (das im gewählten Beispiel speziell ein Rechteck ist). Der
Endpunkt in Abbildung 1.2 ist der diagonal zum Urpsrung liegende Punkt
V -f w, was wiederum dasselbe ist wie w -+- v.
Überprüfen wir unser Vorgehen durch Nachrechnen: die erste Komponente
von V -f w ist i;i -f it;i, und dies ist identisch zu wi-^vi. Die Reihenfolge der
Addition macht somit keinen Unterschied:
V + W :
1
5
+
3
3
—
4
8
—
3
3
-f
[l]
5,
= W -f V.
Der Nullvektor besitzt die Koordinaten i;i = 0 und V2 = 0. Er ist zu kurz,
um ihn durch einen Pfeil darzustellen, aber wir wissen, dass v + 0 = v gilt.
Um 2v zu zeichnen, verdoppeln wir die Länge des Pfeils. Wir kehren seine
4 1 Einführung in die Vektorrechnung
Richtung um, um —v zu erhalten. Diese Umkehrung liefert eine geometrische
Möglichkeit, Vektoren zu subtrahieren.
Vektorsubtraktion Um v - w zu zeichnen, geht man vorwärts
längs V und dann rückwärts längs w (Abbildung 1.3). Die
Komponenten von V — w sind vi — wi und V2 —102-
Bald werden wir das „Skalarprodukt" von Vektoren kennenlernen. Es handelt
sich hierbei jedoch nicht um den Vektor mit den Komponenten viWi und
V2W2'
Linearkombinationen
Bislang haben wir Vektoren addiert, subtrahiert und mit Skalaren
multipliziert. Die Ergebnisse v + w, v — w, und cv werden komponentenweise
berechnet. Indem wir diese Operationen kombinieren, bilden wir jetzt
„Linearkombinationen" von Vektoren v und w. Äpfel bleiben immer noch von
Birnen getrennt — die Linearkombination in Abbildung 1.3 liefert vielmehr
einen neuen Vektor cv + dw.
DEANlTtOiyi; BiiSumme t«m cv tit^#«r ifot^
8] ^^wr
' ,,f./^;/V. '-^;.<r ^,^'/ 3v -f 2w = 3
4-2
Hierin besteht die grundlegende Konstruktion der Linearen Algebra:
Multipliziere und addiere. In diesem Sinne stellt die Summe v + w lediglich eine
spezielle Kombination mit c = c? = 1 dar. Das Vielfache 2v ist der Spezialfall
mit c = 2 und d = 0. Schon bald werden wir sämtliche Linearkombinationen
von V und w betrachten — also gleichzeitig eine ganze Familie von Vektoren.
Auf diesen grundlegenden Gedanken, nämlich den Übergang von zwei
Vektoren zu einer ganzen „Ebene von Vektoren", baut die ganze lineare Algebra
auf.
Die Konstruktion einer Linearkombination von v und w ist sehr einfach.
Sind die Faktoren c = 3 und d = 2 gegeben, so multiplizieren wir und addieren
anschließend um 3v + 2w zu erhalten. Ein Problem ergibt sich jedoch in der
umgekehrten Richtung, wenn c und d „Unbekannte" sind. In diesem Fall
liegt uns nur das Ergebnis vor: cv + dw hat die Komponenten 8 und —1.
Gesucht sind dann die richtigen Faktoren c und d. Die beiden Komponenten
der Vektoren liefern zwei Gleichungen für die beiden Unbekannten c und d.
Die beste Art, 100 Unbekannte zu finden, die die Faktoren vor 100
Vektoren mit je 100 Komponenten sind, wird in Kapitel 2 erläutert werden.
1.1 Vektoren und Linearkombinationen
3v + 2w =
-IJ
Abb. 1.3. Vektorsubtraktion v—w (links). Die Linearkombination 3v+2w (rechts).
Vektoren in drei Dimensionen
Jeder Vektor v mit zwei Komponenten korrespondiert mit einem Punkt in der
xy-Ehene. Die Komponenten von v sind die Koordinaten des Punktes: x = vi
und y = V2. Der Pfeil endet im Punkt (i;i,i;2M wenn er in @,0) beginnt. Von
nun an wollen wir auch Vektoren mit drei Komponenten betrachten. Dabei
wird die xy-Ehene durch den dreidimensionalen Raum ersetzt.
Hier sind einige typische Vektoren (immer noch Spaltenvektoren, aber mit
drei Komponenten):
V =
rii
2
[2
, w =
2]
3
-ij
und V -f w =
Der Vektor v korrespondiert mit einem Pfeil im dreidimensionalen Raum.
Normalerweise startet der Pfeil im Ursprung, also an dem Ort, wo sich die
X-, die y- und die .2;-Achse treffen und dessen Koordinaten @,0,0) sind.
Der Pfeil des Vektors v endet im Punkt mit den Koordinaten x = 1,
y = 2, z — 2. Also gibt es eine völlige Übereinstimmung zwischen einem
Spaltenvektor, dem Pfeil vom, Ursprung und dem Punkt, in dem, der
Pfeil endet Dies sind drei äquivalente MögUchkeiten, denselben Vektor zu
beschreiben.
..ir
^f^^ms
i
V
"H^\:, ,.^.„^#':{
Der Grund für die Spaltenschreibweise (in eckigen Klammern) besteht darin,
dass Vektoren mit Matrizen verträglich sein sollen. Der Grund für die
Zeilenschreibweise (in runden Klammern) besteht darin, Platz zu sparen. Dies
wird insbesondere bei langen Vektoren wichtig. Den Vektor A,2,2,4,4,6) in
einer Spalte zu schreiben, wäre sicherlich Platzverschwendung.
Wichtiger Hinweis: v = A,2,2) ist kein Zeilenvektor. Der Zeilenvektor
[1 2 2] ist etwas völlig anderes, auch wenn er dieselben drei Komponenten
besitzt. Vielmehr ist dies der zu v „transponierte" Vektor.
6 1 Einführung in die Vektorrechnung
Ein Spaltenvektor kann somit auch horizontal (mit Kommata und runden
Klammern) geschrieben werden. Daher ist A,2,2) tatsächUch ein
Spaltenvektor — er hat sich nur zeitweise hingelegt.
C,2)
A,-2,2)
1 \-y
Abb. 1.4. Vektoren [y] und y korrespondieren mit den Punkten (x^y) und
Auch in drei Dimensionen werden Vektoren Komponente für Komponente
addiert. Die Summe v + w hat die Komponenten vi + wi und V2 + W2 und
Vs -\-ws — die Komponenten könnten nun etwa Äpfel, Birnen und Orangen
entsprechen. Man erkennt jetzt, wie man Vektoren in 4, 5 oder n Dimensionen
addiert. Damit ist das Ende der Linearen Algebra für Gemüsehändler erreicht!
Die Addition v + w wird durch Pfeile im Raum dargestellt. Beginnt w
am Ende von v, so ist die dritte Seite durch v + w gegeben. Folgt v auf w,
so erhalten wir die anderen Seiten eines Parallelogramms. Frage: Liegen alle
vier Seiten in derselben Ebene? Ja. Und die Summe v + w — v — w beschreibt
einen Rundgang um das Parallelogramm und ergibt .
Eine typische Linearkombination dreier Vektoren in drei Dimension ist
u + 4v - 2w:
Linearkombination
Wir beenden diesen Abschnitt mit der Frage: Welche Fläche im
dreidimensionalen Raum erhält man aus allen Linearkombinationen von u und v? Die
Fläche enthält die Gerade durch u und die Gerade durch v. Sie enthält den
Nullvektor (die Linearkombination Ou + Ov). Die Fläche enthält auch die
diagonale Gerade durch u + v — und jede andere Kombination cu + dv (ohne
w zu benutzen.) Diese gesamte Fläche ist eine Ebene (es sei denn, u
ist parallel zu v).
Eine Bemerkung zum Rechnen mit dem Computer: Angenommen, die
Komponenten des zehndimensionalen Vektors v sind v{l), ..., v{N), und eben-
1
0
3
+ 4
1
2
1
-2
2
3
-1
=
1
2
9
LI Vektoren und Linearkombinationen 7
so für w. In einer Programmiersprache wie FORTRAN verwendet man eine
Schleife, um die Komponenten einzeln zu addieren:
DO 10 I = 1,N
10 VPLUSW(I) = v(I)+w(I)
MATLAB hingegen arbeitet direkt mit Vektoren und Matrizen. Sind v
und w definiert, dann wird v + w sofort verstanden. Das Ergebnis wird
ausgegeben, falls die Zeile nicht mit einem Semikolon endet. Wir können
Vektoren als Zeilen eingeben — das anschließende Hochkomma ' verwandelt
sie in Spalten. Dann lassen wir v + w und eine andere Linearkombination
ausgeben:
v=[2 3 4]';w=[l 1 l]';u = v + w
2*v - 3*w
Die Summe wird als u = ausgegeben. Die unbenannte Linearkombination
wird mit ans = ausgegeben^:
u = ans =
3 1
4 3
5 5
Die wesentlichen Punkte
l.Ein Vektor v im zweidimensionalen Raum hat zwei Komponenten vi und
2. Vektoren werden Komponente für Komponente addiert und subtrahiert.
3.Das skalare Vielfache ist cv = {cvi,cv2)- Eine Linearkombination von v
und w ist cv -f dw.
4. Sämtliche Linearkombinationen zweier nicht paralleler Vektoren v und w
bilden eine Ebene.
Aufgaben 1.1
Die Aufgaben 1—9 betreffen die Addition von Vektoren und
Linear kombinationen.
1. Zeichnen Sie die Vektoren v= [f] ,w = [2]?^ + ^ ^^^ v — w
gemeinsam in der xy-Ehene.
2. Berechnen und zeichnen Sie die Vektoren v und w, für die gilt v -f w —
[f] und v-w= [l].
3. Bestimmen Sie die Komponenten von 3v -h w, v - 3w und cv + dw für
die Vektoren v = [ J] und w = [l].
^ für engl, „answer" = „Antwort", Anm. d. Ubers.
8 1 Einführung in die Vektorrechnung
4. Berechnen Sie u + v, u + v + w und 2u + 2v + w für die Vektoren
u =
ri"
2
I3
, v =
"-3"
1
-2
, W=:
2]
-3
-ij
5. Die Komponenten jeder Linearkombination von v = A, —2,1) und w =
@,1,-1) addieren sich zu auf. Bestimmen Sie c und d, so dass
cv-\-dw = D, 2, -6) gilt.
6. Zeichnen Sie die folgenden neun Linear kombinat ionen in der x^z-Ebene:
+ d
mit c = 0,l,2 und d = 0,1,2.
7. (a) Die Subtraktion v — w geht vorwärts längs v und rückwärts längs w.
In der Abbildung 1.3 ist auch ein zweiter Weg zu v — w aufgezeigt.
Welcher ist es?
(b) Wenn Sie alle Kombinationen von v und w betrachten, welche
„Vektorenfläche" erhalten Sie?
8. Das Parallelogramm in Abbildung 1.2 hat die Diagonale v -h w. Wie
ist seine andere Diagonale darstellbar? Was ergibt die Summe beider
Diagonalen? Zeichnen Sie diese Vektorsumme.
9. Wenn ein Parallelogramm die drei Ecken A,1), D,2), und A,3) besitzt,
welche möglichen vierten Ecken gibt es? Zeichnen Sie zwei davon.
In den Aufgaben 10—13 geht es um die Länge von Vektoren.
Rechnen Sie mit der Formel (Länge von v)^ = i;^ _^ i;|.
10. Das Parallelogramm mit den Seiten v = D,2) und w = (—1,2) ist ein
Rechteck (vgl. Abbildung 1.2). Überprüfen Sie den Satz des Pythagoras
a^ + &2 _ ^2^ ^gj. yj^^ yr^^ Dreiecke mit rechtem Winkel gilt:
{hBägß Von y)^ ^ (h^ge von w)^ Ä (Linge YpE vf^;w)^*
11. Im rechtwinkligen Fall funktioniert die Formel a^-\-P = (? auch für v—w.
Überprüfen Sie in Abbildung 1.2, dass
(Länge von v)^ + (Länge von w)^ = (Länge von v — w)^
gilt. Finden Sie ein Beispiel für v und w (nicht rechtwinklig) für die diese
Formel falsch ist.
12. Um zu betonen, dass rechtwinklige Dreiecke besondere Dreiecke
darstellen, bestimmen Sie Vektoren v und w, die keinen Winkel von 90°
miteinander bilden. Vergleichen Sie nun (Länge von v)^ -h (Länge von w)^
mit (Länge von v -}- w)^.
1.1 Vektoren und Linearkombinationen 9
13. Überprüfen Sie in Abbildung 1.2 dass (Länge von v) + (Länge von w)
größer ist als (Länge von v + w). Diese „Dreiecksungleichung" ist für
jedes Dreieck richtig, ausgenommen das absolut dünne Dreieck, in dem v
und w sind. Beachten Sie, dass die Längen hier nicht quadriert
werden.
@,0,1)
7 @,1,0)
A,0,0)
4:00
In den Aufgaben 14—18 geht es um spezielle Vektoren in Würfeln
und Uhren.
14. Zeichnen Sie den Würfel ab, und bestimmen Sie die Vektorsumme von
i = A,0,0), j = @,1,0) und k = @,0,1) grafisch. Die Summe i-fj ergibt
die Diagonale von .
15. Drei Kanten des Einheitswürfels sind i,j und k. Drei Ecken sind @,0,0),
A,0,0) und @,1,0). Welches sind die anderen fünf Ecken, und was sind
die Koordinaten des Mittelpunktes? Die Mittelpunkte der sechs Flächen
des Würfels sind .
16. Wie viele Ecken hat ein Würfel in 4 Dimensionen? Wie viele Flächen?
Wie viele Kanten? Eine typische Ecke ist @,0,1,0).
17. (a) Was ist die Summe V der zwölf Vektoren, die vom Mittelpunkt einer
Uhr zu den Zeiten 1:00 Uhr, 2:00 Uhr, ..., 12:00 Uhr zeigen?
(b) Bestimmen Sie die Summe der verbleibenden elf Vektoren, wenn der
Vektor zu 4:00 Uhr herausgenommen wird.
(c) Nehmen Sie an, der 1:00-Uhr-Vektor sei halbiert. Addieren Sie ihn zu
den anderen elf Vektoren.
18. Nehmen Sie an, die zwölf Vektoren beginnen nicht in der Mitte bei @,0),
sondern in @, -1) am unteren Ende der Uhr. Dann ist der Vektor zu 6:00
Uhr der Nullvektor, und der Vektor zu 12:00 Uhr wird zu Bj) verdoppelt.
Summieren Sie die zwölf auf diese Weise konstruierten Vektoren auf.
10 1 Einführung in die Vektorrechnung
Aufgaben 19—22 in einer Ebene Aufgaben 23—27 im dreidimensionalen Raun
Die Aufgaben 19—22 behandeln Linearkombinationen von v und w
(siehe Abbildung).
19. Die Abbildung zeigt den Vektor u =
|v + ^w, ^v + |w und V + w ein.
|v + |w. Zeichnen Sie die Punkte
20. Markieren Sie die Punkte — v + 2w und einer weiteren Linearkombination
cv + dw mit c+d= 1. Zeichnen Sie die Gerade aller Linearkombinationen
mit c -h d = 1.
21. Bestimmen Sie |v + ^w und |v -f- |w. Auf welcher Geraden liegen die
Kombinationen cv -h cw? Welchen Strahl erzeugen die Kombinationen für
c = d mit der Einschränkung c > 0?
22. (a) Zeichnen Sie die Vektoren |v + w und v + |w. Schraffieren Sie den
Bereich, den die Vektoren cv -h dw mit 0 < c < 1 und 0 < d < 1
ausfüllen,
(b) Zeichnen Sie den „Kegel" aller Kombinationen cv + dw mit 0 < c
und 0 < d.
In den Aufgaben 23 — 27 geht es um Vektoren u, v und w im
dreidimensionalen Raum (siehe Abbildung).
23. (a) Wo liegen |u -h |v -h |w und |u + |w in der Abbildung?
(b) Eine kleine Herausforderung: Unter welchen Bedingungen an c, d und
e stellen die Vektoren cu + dv -h ew die Ebene dar, in der die Spitzen
von u, V und w liegen?
24. Die drei Seiten des gestrichelten Dreiecks sind v—u, w—v und u—w. Ihre
Summe ist . Zeichnen Sie die Spitze-Anfang-Summe des ebenen
Dreiecks C,1) plus (-1,1) plus (-2, -2).
1.2 Längen und Skalaxprodukte 11
25. Schraffieren Sie die Pyramide aus den Linear kombinationen cu + dv + e w
mit c > 0, d > 0, e > 0 und c + d + e < 1. Liegt der Vektor |(u + v +w)
innerhalb oder außerhalb der Pyramide?
26. Gibt es einen Vektor, der nicht als Linearkombination cu + dv + ew
dargestellt werden kann, wenn man alle Kombinationen von u, v und w
zulässt?
27. Welche Vektoren liegen gleichzeitig in der u-v-Ebene und in der v-w-
Ebene?
28. (a) Zeichnen Sie Vektoren u, v und w so, dass ihre Linearkombinationen
cu + dv + ew auf nur einer Geraden liegen,
(b) Zeichnen Sie Vektoren u, v und w so, dass ihre Linearkombinationen
cu + dv + ew lediglich eine Ebene ausfüllen.
29. Welche Kombination der Vektoren
1
2
und
3
1
erzeugt
14"
8j
?
Formulieren Sie diese Frage in Form von zwei Gleichungen für die Koeffizienten
c und d in der Linearkombination.
1.2 Längen und Skalarprodukte
Im ersten Abschnitt wurde die Multiplikation von Vektoren zwar erwähnt,
jedoch nicht weiter verfolgt. Wir werden jetzt hierauf genauer eingehen und
das „Skalarprodukt" von Vektoren v und w definieren. In dieser
Multiplikation tauchen wohl die beiden einzelnen Produkte der Komponenten viWi
und V2W2 auf, damit ist aber noch nicht Schluss. Denn diese beiden Zahlen
werden zudem addiert und ergeben eine einzige Zahl v-w.
Beispiel 1.2.1 Das Skalarprodukt der Vektoren v - D,2) und w = (-1,2)
ist Null:
-1
2
= -4-h4 = 0.
Null ist in der Mathematik stets eine besondere Zahl. Bei Skalarprodukten
bedeutet das Auftreten der Null, dass die beiden Vektoren senkrecht
zueinander stehen. Der Winkel zwischen ihnen ist 90°. Als wir die Vektoren in
12 1 Einführung in die Vektorrechnung
Abbildung 1.2 gezeichnet haben, sahen wir ein Rechteck — nicht nur
irgendein Parallelogramm. Das einfachste Beispiel rechtwinkliger Vektoren ist das
Paar i = (i, 0) längs der x-Achse und j = @,1) längs der ^/-Achse. Auch hier
ist das Skalarprodukt i-j =: 0 + 0 = 0 und die Vektoren i und j bilden einen
rechten Winkel.
Die Vektoren v = A,2) und w = B,1) stehen nicht senkrecht
aufeinander. Ihr Skalarprodukt ist 4. Bald wird es uns dieser Wert ermöglichen, den
Winkel zwischen ihnen anzugeben (der nicht 90° ist).
Beispiel 1.2.2 Wir legen ein Gewicht 4 an den Punkt x = —1 und das
Gewicht 2 an den Punkt x = 2. Wäre die x-Achse eine Wippe mit Mittelpunkt
X = 0, würden sich die Gewichte ausbalancieren, denn das Skalarprodukt ist
D)(-l) + B)B) = 0.
Dies ist ein typisches Beispiel aus den Ingenieur- und
Naturwissenschaften. Der Gewichts-Vektor ist {wi,W2) = D,2), der Abstandsvektor (^1,^2) =
(—1,2). Kraft mal Abstand, Wi mal vi, ergibt das „Drehmoment" des ersten
Gewichtes. Die Gleichung, die das Gleichgewicht der Wippe beschreibt, ist
durch wivi -i- W2V2 = 0 gegeben.
Das Skalarprodukt wv ist gleich vw.
Die Reihenfolge von v und w ist somit unwichtig.
Beispiel 1.2.3 Man begegnet Skalarprodukten auch in den
Wirtschaftswissenschaften und im Geschäftsalltag. Stellen wir uns vor, wir hätten fünf
Produkte, die wir kaufen oder verkaufen. Die Preise seien {pi,P2,P3,P4,P5) für
jeweils eine Einheit des jeweiligen Produktes — dies ergibt den „Preisvektor"
p. Die Mengen, die wir ein- oder verkaufen, seien (^1 ,q2,Q3,Q4,Qb) — positiv
für den Verkauf, negativ im Falle des Einkaufs. Wenn wir qi Einheiten des
ersten Produktes zum Preis pi verkaufen, bringt das Einnahmen in Höhe von
qiPi. Die Gesamteinnahmen ergeben sich dann aus dem Skalarprodukt q-p:
Einnahmen = (^1, ^2, • • •, ^5)-(pi,P2, • • • ,^5) = qiPi + ^2^2 + • • • + q^Pb-
Ist das Skalarprodukt Null, so bedeutet dies, dass die Bilanz ausgeghchen
ist — die Gesamteinnahmen sind gleich den Gesamtausgaben, falls q-p = 0
gilt. In diesem Falle steht der Vektor p senkrecht auf dem Vektor q (und zwar
im fünfdimensionalen Raum). Für fünf Produkte sind die Vektoren fünf-
dimensional. Durch Beispiele dieser Art wird man in der linearen Algebra
sehr schnell in hohe Dimensionen geführt.
Noch ein kleiner Hinweis: Tabellenkalkulationen sind im Geschäftsleben
zu unverzichtbaren Hilfsmitteln geworden. Was ist eine Tabellenkalkulation
eigentlich? In ihr werden Linearkombinationen und Skalarprodukte
berechnet, und was man auf dem Computerbildschirm sieht, ist nichts anderes als
eine Matrix.
1.2 Längen und Skalaxprodukte 13
Merkregel: Um das Skalarprodukt auszurechnen, multipliziert man jedes Vi
mit Wi, und addiert die Einzelprodukte auf.
Längen und Einheitsvektoren
Ein wichtiger Fall ist das Skalarprodukt eines Vektors mit sich selbst, wenn
V = w gilt. Das Skalarprodukt des Vektors v = A,2,3) mit sich selbst ist
vv = 14:
v-v =
rr
2
[_3
•
"
2
3j
= 1 + 4 + 9 = 14.
Das Ergebnis ist nicht Null, weil v nicht senkrecht zu sich selbst steht.
Anstelle eines 90°-Winkels haben wir einen 0°-Winkel. In diesem Spezialfall
ergibt das Skalarprodukt v-v das Quadrat der Länge.
iiSfö^^Sevonv = ||v|| =
Im Zweidimensionalen ist die Länge durch Vv^ + v^ gegeben, in drei
Dimensionen durch Vvf +V2+ v^. Entsprechend der Rechnung oben hat v =
A,2,3) die Länge ||v|| = >/l4.
@,2)
1,2,3) hat Länge \/l4
@,2,0)
A,0,0)^ ^^'^A,2,0) hat Länge y/E
Abb. 1.5. Die Länge y/v-yr zwei- und dreidimensionaler Vektoren.
Diese Definition lässt sich plausibel machen. ||v|| ist einfach die ganz
normale Länge eines Pfeiles, der den Vektor darstellt. Im Zweidimensionalen
liegt der Pfeil in einer Ebene und ist dort die dritte Seite eines
rechtwinkligen Dreiecks, dessen andere Seitenlängen durch die Komponenten des Vektors
14
1 Einführung in die Vektorrechnung
gegeben sind, zum Beispiel 1 und 2 für den Vektor v — A,2). Die drei
Seitenlängen sind über die Formel a^ + fe^ = (? miteinander verbunden, d.h., es
giltl2 + 22 = ||v|p.
Um die Länge von v = A,2,3) zu bestimmen, benutzen wir den Satz
des Phythagoras zweimal. Zunächst hat der Vektor in der x — ^/-Ebene die
Komponenten 1,2,0 und die Länge \/5. Dieser Vektor steht senkrecht auf
dem Vektor @,0,3), der gerade nach oben zeigt. Deswegen hat die Diagonale
des gestrichelten Quaders die Länge ||v|| = \/5 + 9 = \f\Ä.
Die Länge eines vierdimensionalen Vektors wäre \/v\ -^ v\ -\- v\ -\' v\. So
hat zum Beispiel A,1,1,1) die Länge \/\^ -f P -f 1^ + 1^ — 2, gerade die
Länge der Diagonalen durch einen Einheitswürfel im vierdimensionalen Raum.
Die Diagonale in n Dimensionen hat die Länge yjn.
Das Wort „Einheits-" bedeutet immer, dass irgendein Maß gleich eins ist.
Der Einheitswürfel hat zum Beispiel Seiten der Länge eins. Ein Einheitskreis
hat den Radius eins. Nun können wir auch die Idee eines „Einheitsvektors"
einführen.
;A ... f i. ^<'^.^yy^ ,
Ein vierdimensionales Beispiel ist u = (|, |, |, ^), dessen Skalarprodukt u-u
gerade ^ + ^ + ^ + ^ = 1 ist. Wir haben den Vektor v = A,1,1,1) durch
seine Länge ||v|| = 2 dividiert, um diesen Vektor zu erhalten.
Beispiel 1.2.4 Die Standardeinheitsvektoren längs der x- und der ^/-Achse
werden mit i und j bezeichnet. Der Einheitsvektor in der x^/—Ebene, der mit
der X-Achse einen Winkel d bildet, ist durch (cos ö, sin ö) gegeben:
1 =
und j
und u =
cos^
sinö
Für ^ = 0 wird der Vektor u gerade zu i. Falls d — 90° (oder | im Bogenmaß),
ist u derselbe Vektor wie j. Aber für jeden Winkel ergeben die Komponenten
cos^ und sinö gerade u-u = 1, weil cos^^ + sin^^ = 1 gilt. Diese Vektoren
zeigen zu den Punkten auf dem Einheitskreis in Abbildung 1.6. Also sind cosö
und sin Q ganz einfach die Koordinaten des Punktes auf dem Einheitskreis mit
zugehörigem Winkel d.
In drei Dimensionen sind i, j und k die Einheitsvektoren längs der drei
Koordinatenachsen. Ihre Komponenten sind A,0,0), @,1,0) und @,0,1).
Beachten Sie, dass jeder dreidimensionale Vektor eine Linearkombination von i,
j und k ist. Der Vektor v — B,2,1) ist zum Beispiel gleich 2i + 2j + k, seine
Länge ist \/22-h22-hl2, also ||v|| = 3.
1.2 Längen und Skalarprodukte 15
i+j = (l,l) J
u=A,1)/n/2
= A,0)
Abb. 1.6. Die Koordinatenvektoren i und j. Der Einheitsvektor u im Winkel von
45° (links) und der Einheitsvektor (cos ^, sin ^) im Winkel 0.
Da B,2,1) die Länge 3 hat, hat der Vektor (|, |, |) die Länge 1. Um
einen Einheitsvektor zu erzeugen, dividiert man einfach v durch seine Länge
Im Dreidimensionalen haben wir so u = (|, |, |) gefunden. Rechnen Sie
nach, dass u-u =|-j~|-j~| = l gilt. Es zeigt also u auf einen Punkt der „Ein-
heitskugel" mit Mittelpunkt im Ursprung. Einheitsvektoren korrespondieren
generell mit Punkten auf der Kugel mit Radius eins.
Der Winkel zwischen zwei Vektoren
Wir haben schon erwähnt, dass für rechtwinklige Vektoren vw = 0 gilt.
Das Skalarprodukt ist null, wenn der Winkel zwischen den Vektoren 90° ist.
Um dies zu begründen, müssen wir rechte Winkel mit Skalarprodukten in
Verbindung bringen. Das wird uns darauf bringen, wie uns v-w den Winkel
zwischen zwei beliebigen Vektoren (ungleich dem Nullvektor) liefert.
%i^^.):.. :f' \:;A- ''X'' ';i/'';'r:h;-/'^ '^'':ä;'- '-<''}-;"". "f;"' y^f'by'i^^i^" 1^f''''.i'=
Beweis. Wenn v und w zueinander rechtwinklig stehen, bilden sie zwei
Seiten eines rechtwinkligen Dreiecks. Die dritte Seite (die Hypotenuse, die in
Abbildung 1.7 von links nach rechts geht) ist dann v — w. Damit wird aus
der Gleichung a^ + 6^ = c^ für die Seitenlängen
16
1 Einführung in die Vektorrechnung
||v|p + ||w|p = ||v - w|p (für senkrechte Vektoren).
A.2)
Schreibt man die Formeln für die Längen in zwei Dimensionen aus, wird
daraus
vl^V2+wf + wl
{Vi -WiY + {V2 - W2Y
A.3)
Nach Ausmultiplikation fängt die rechte Seite mit v\ — 2viWi + w\ an.
Deswegen kann man auf beiden Seiten der Gleichung vi und w\ subtrahieren.
Genauso enthält {v2 —^2)^ die Terme v^ und w^ sowie —2v2W2' Subtrahiert
man wieder auf beiden Seiten, bleiben nur noch —2viWi und —2v2W2 übrig.
(In drei Dimensionen hätte man außerdem noch —2vsw^.) Im letzten Schritt
dividiert man durch -2 und erhält:
0 = —2viWi — 2V2W2 und daher viwi -\-v2W2 = 0.
A.4)
Schlussfolgerung Rechte Winkel ergeben ein Skalarprodukt v-w = 0. Wir
haben damit Satz IB bewiesen. Das Skalarprodukt wird null, wenn der
Winkel 0 = 90° ist. Dann gilt cosO = 0. Der Nullvektor v = 0 steht senkrecht
auf jedem Vektor w, weil 0-w immer Null ergibt.
•=[1,
V25
VsN
V • W=:0
V2Ö
-0
^—I—I-
WinM;
kleiner als 90° in dieser Hälfte
Abb. 1.7. Für senkrechte Vektoren gilt vw = 0. Der Winkel ist geringer als 90°
wenn vw > 0 gilt.
Nehmen wir nun an, dass v-w ungleich null ist. Das Skalarprodukt kann
positiv, aber auch negativ sein. Das Vorzeichen von v-w sagt uns sofort, ob
der Winkel größer oder kleiner als ein rechter Winkel ist. Der Winkel ist
kleiner als 90°, wenn v-w positiv ist. Er ist größer, wenn v-w negativ ist.
Abbildung 1.7 zeigt einen typischen Vektor w = A,3) in der rechten
Halbebene, mit v-w > 0. Für den Vektor W = (-2,0) in der linken Halbebene
gilt V-W = -8.
Die Grenzlinie bilden die Vektoren, die senkrecht zu v stehen. Auf dieser
Geraden zwischen positivem und negativen Vorzeichen ist das Skalarprodukt
null.
Auf der nächsten Seite werden wir einen weiteren Einbhck in die
Geometrie des Skalarprodukts erhalten. Wir werden mit seiner Hilfe den genauen
1.2 Längen und Skalaxprodukte 17
Winkel 6 bestimmen. Dies ist eigentlich nicht notwendig für die lineare
Algebra, Sie könnten hier aufhören zu lesen! Denn haben wir erst einmal Matrizen
und lineare Gleichungen erreicht, so werden wir dem 9 den Rücken kehren.
Aber da es in diesem Abschnitt noch um Winkel geht, ist dies die richtige
Stelle, um die Formel einzuführen, Sie wird uns zeigen, dass der Winkel 6
zwischen v = D,2) und w = A,3) in Abbildung 1.7 genau 45° ist.
Wir beginnen mit Einheitsvektoren u und U. Das Vorzeichen von u-U
gibt an, ob ö < 90° ist oder 6 > 90°. Da die Vektoren die Länge eins haben,
können wir aber noch mehr erfahren. Das Skalarprodukt u-U ist der
Kosinus von 6, Dies gilt sogar in beliebig vielen Dimensionen!
IC (a) Wetiia mmli^^lJ BiBfa'dtsV^toreB'siBÄ^ u-U = cosö .
(b) Weciii 11' lind tF EinheiiÄvefeöireii s&wi, so;^li |u^'U| < 1. ^
Die Aussage (b) folgt direkt aus der Aussage (a). Erinnern Sie sich lediglich
daran, dass cosö niemals größer als 1 ist und niemals kleiner als —1. Das
Skalarprodukt zweier Einheitsvektoren liegt zwischen —1 und 1.
In Abbildung 1.8 erkennt man die obige Aussage deutlich an den Vektoren
u = (cosöjSinö) und i — A,0). Ihr Skalarprodukt ist u-i — cosO, also der
Kosinus des Winkels zwischen ihnen.
Dreht man diese um irgendeinen Winkel a, so sind es immer noch
Einheitsvektoren, und der Winkel zwischen ihnen ist immer noch 0. Die neuen
Vektoren sind u = (cos a, sin a) und U = (cos ^, sin ^). Ihr Skalarprodukt ist
cos a cos ^ + sin a sin ß. Nach den Additionstheoremen für trigonometrische
Funktionen ist dies dasselbe wie cos(^ — a), und da. ß — a = 0 gilt, sind wir
bei der Formel u-U = cosö angelangt.
u =
cosG
sinG.
e = ß-a
Abb. 1.8. Das Skalarprodukt von Einheitsvektoren ist der Kosinus des Winkels 6.
In Aufgabe 24 wird die Ungleichung |u-U| < 1 direkt ohne Bezugnahme
auf Winkel gezeigt. In Aufgabe 22 wird eine andere trigonometrische Formel
angewendet, nämlich der Kosinussatz, Die Ungleichung und die Kosinusfor-
18 1 Einführung in die Vektorrechnung
mel u-U = cos^ gelten für beUebige Dimensionen. Das Skalarprodukt ändert
sich nicht, wenn die Vektoren gedreht werden, weil 0 dabei unverändert bleibt.
Wie stellt sich die Situation dar, wenn v und w keine Einheitsvektoren
sind? Dann ist ihr Skalarprodukt im Allgemeinen nicht mehr cos^. Dividieren
wir sie aber durch ihre Längen, um Einheitsvektoren u = v/||v|| und U =
w/||w|| zu erhalten, so ist das Skalarprodukt dieser skalierten Vektoren wieder
cos^.
Unabhängig vom Winkel wird das Skalarprodukt von v/||v|| mit w/||w||
niemals größer als eins. Das ist die „Schwarz'sche Ungleichung" für Skalarpro-
dukte — oder richtiger die Cauchy-Schwarz-Buniakowsky'sche Ungleichung.
Sie wurde in Frankreich, in Deutschland und in Russland entdeckt (und
womöglich noch andernorts — es handelt sich hier um die wichtigste
Ungleichung der Mathematik). Mit dem zusätzlichen Faktor ||v|| ||w|| aus der
Umskalierung in Einheitsvektoren erhalten wir jetzt für cos^:
ID (a) Kostnusformel Siad v uiid w VekfcoreB tmglei^ nuH^ d^
= cos 6 .. j . ^ ^v ;^ ^ ■ V';"'' -;: - -- >''^#
^ . . i|v||||w|| '-;' ^ ■ ^.^J^^^. /'- '^-v;::';:':, V- ;-r<;. ^r' ::'":,[
(b) Sckwarz^sche Xlngleichiiiij^ Siiia v und/w pel|Bm]ge y^0yen^ Bö
:-,^U |v-w|<||v||||w||.^,^ >;,
Beispiel 1.2.5 Bestimmen Sie den Winkel zwischen v = [3] und w = [J] in
Abbildung 1.7b) .
Lösung Das Skalarprodukt ist v-w = 4 + 6 = 10. Die Länge von v ist
||v|| = \/20- Die Länge von w ist ||w|| = y/TÖ, Also ist der Kosinus des
Winkels
VW 10 1
cos^ = ,, ,,,,—TT = , ,— = —;=, und damit ist 0 = 45°.
||v||||w|| V2ÖVIÖ v^'
Der Winkel mit diesem Kosinus ist also gerade 45°. Er ist kleiner als 90°, weil
VW =: 10 positiv ist. Nach der Schwarz'schen Ungleichung ist ||v|| ||w|| =
V^ÖÖ größer als v-w = 10.
Beispiel 1.2.6 Das Skalarprodukt von v = (a, &) und w = {b,a) ist 2ab. Die
Schwarz'sche Ungleichung liefert 2ab < a^ + b^, zum Beispiel ist 2C)D) =
24 < 32 + 42 := 25.
Begründung Die Längen sind ||v|| = ||w|| = x/a^ + b^. Dann wird v-w = 2ab
niemals ||v|| ||w|| = a^ -\- b^ überschreiten, da die Differenz zwischen a^ + 6^
und 2ab niemals negativ werden kann:
a^ + ^2 _ 2ab ={a- bf > 0.
1.2 Längen und Skalaxprodukte 19
Diese Beziehung ist besser bekannt, wenn man x — c? und y — }? setzt, denn
dann heißt sie: Das „geometrische Mittel" ist nicht größer als das
„arithmetische Mittel", also der Mittelwert von x und y\
c? ^\? . x^y
ab < —-— wird zu ^yxy < —-—.
Die Berechnung von Skalarprodukten und Winkeln Die Zeit ist
reif für einen Augenblick der Wahrheit. Dem Skalarprodukt v-w begegnet
man normalerweise in der Form Zeile mal Spalte:
An Stelle von | ^
debt maB häufiger {1 2]
In FORTRAN benutzt man eine Schleife, um die Komponenten miteinander
zu multiplizieren und aufzuaddieren:
DO 10 I = 1,N
10 VMALW = VMALW + V(I) * W(I)
MATLAB arbeitet mit ganzen Vektoren, nicht mit ihren einzelnen
Komponenten. Sind V und w Spaltenvektoren, so ist v' eine Zeile wie oben:
skpr = v' * w
Die Länge von v ist in MATLAB schon als norni(v) bekannt. Wir könnten
sie aber auch selbst definieren als sqrt (v' * v), indem wir die ebenfalls
bekannte Wurzelfunktion benutzen. Kosinus und Winkel müssen wir uns selbst
berechnen:
cos = v' * w/(norni(v) * norni(w));
Winkel = acos(cos)
Wir haben dabei die Arcuscosinus-Funktion (acos) benutzt, um den Winkel
aus seinem Kosinus zu berechnen. Wir haben keine neue Funktion cos(v, w)
für den zukünftigen Gebrauch geschrieben. Dafür hätten wir eine M-Datei
erzeugen müssen, dessen Format in Kapitel 2 beschrieben werden wird.
(Speziell für dieses Buch sind einige M-Dateien geschrieben worden. Man findet
sie am Ende des Buches.) Die obigen Anweisungen führen dazu, dass die
Zahlen skpr und winkel ausgegeben werden. Der Kosinus wird wegen des
Semikolons am Ende der Zeile nicht ausgegeben.
Die wesentlichen Punkte
1. Das Skalarprodukt v-w wird durch Multiplizieren der Komponenten Vi mit
Wi und anschließendes Auf summieren berechnet.
2. Die Länge ||v|| ist die Quadratwurzel aus v-v.
3. Der Vektor v/||v|| ist ein Einheitsvektor, seine Länge ist eins.
20
1 Einführung in die Vektorrechnung
4. Es gilt v-w = 0, wenn v und w senkrecht zueinander stehen.
5. Der Kosinus von 6 (des Winkels zwischen v und w) überschreitet nie den
Wert 1:
cos 6 —
VW
und deshalb gilt |v-w| < ||v|| ||w||.
Aufgaben 1.2
1. Berechnen Sie die Skalarprodukte u-v, u-w, v-w und w-v:
u =
-0,6
0,8
v =
w
2. Berechnen Sie die Längen ||u||, ||v|| und ||w|| dieser Vektoren. Überprüfen
Sie, dass die Schwarz'schen Ungleichungen |u-v| < ||u|| ||v|| und |v-w| <
||v|| ||w|| erfüllt sind.
3. Geben sie Einheitsvektoren in Richtung der Vektoren v und w aus
Aufgabe 1 an. Berechnen Sie den Kosinus des Winkels zwischen ihnen.
4. Bestimmen Sie Einheitsvektoren ui und U2 in Richtung der Vektoren
V = C,1) und w = B,1,2). Bestimmen Sie weiter Einheitsvektoren Ui
und U2, die senkrecht auf v bzw. w stehen.
5. Zeigen Sie, dass für beliebige Einheitsvektoren v und w der Winkel
zwischen den Vektoren
(a) V und v (b) w und -w (c) v -f- w und v-w
entweder 0° oder 90° oder 180° ist.
6. Bestimmen Sie (über den Kosinus) den Winkel 6 zwischen
2
(b) V = ■
(a) v =
(c) v =
1
1
x/3
und w =
und w =
-1
(d) V
und w =
und w =
2
-1
2
1"
7. (a) Bestimmen Sie alle Vektoren {wi^W2) die senkrecht auf v = B,-1)
stehen,
(b) Beschreiben Sie in Worten alle Vektoren, die senkrecht auf V =
A,1,1) stehen.
8. Wahr oder falsch? Geben Sie eine Begründung an, wenn eine Behauptung
wahr ist, oder ein Gegenbeispiel, wenn sie falsch ist.
1.2 Längen und Skalarprodukte 21
(a) Steht der dreidimensionale Vektor u senkrecht auf v und w, so sind
V und w parallel.
(b) Steht u senkrecht auf v und w, dann auch auf v + 2w.
(c) Es gibt immer eine Linearkombination v + cu die senkrecht auf u
steht.
9. Die Steigungen der Pfeile von @,0) nach (i;i,i;2) und {wi,W2) sind i;2/^'i
und W2/W1. Zeigen Sie, dass v-w = 0 gilt und die Vektoren senkrecht
zueinander sind, wenn das Produkt der Steigungen V2W2/V1W1 = —1 ist.
10. Zeichnen Sie Pfeile von @,0) zu den Punkten v = A,2) und w = (-2,1).
Berechnen Sie die beiden Steigungen und multiplizieren Sie sie. Die
Antwort bedeutet, dass v-w = 0 und dass die Pfeile .
11. Was bedeutet es für den Winkel zwischen v und w, wenn v-w negativ
ist? Zeichnen Sie einen dreidimensionalen Vektor v (als Pfeil) und geben
sie den Bereich aller Vektoren w mit v-w < 0 an.
12. Wählen Sie eine Zahl c so, dass für die Vektoren v = A,1) und w = A,5)
die Kombination w — cv senkrecht auf v steht. Geben Sie dann eine
Formel an, die diese Zahl c für beliebige v und w bestimmt.
13. Bestimmen Sie Vektoren v und w, die zueinander und zu A,1,1)
senkrecht sind.
14. Bestimmen Sie drei Vektoren u, v und w, die zueinander und zu A,1,1,1)
senkrecht stehen.
15. Das geometrische Mittel von x = 2 und ?/ = 8 ist ^/xy — 4. Das
arithmetische Mittel ist größer: \{x -\-y) = . In Beispiel 1.2.6 hatten wir
gesehen, dass dies mit der Schwarz'sehen Ungleichung für v = (\/2, VS)
und w = (v^, \/2) zusammenhängt. Bestimmen Sie cosö für diese
Vektoren V und w.
16. Wie lang ist der neundimensionale Vektor v = A,1,...,1)? Bestimmen
Sie einen Einheitsvektor u in derselben Richtung wie v und einen Vektor
w senkrecht zu v.
17. Wie groß ist der Kosinus der Winkel a^ß und 9 zwischen dem Vektor
A,0, —1) und den Einheitsvektoren i, j und k in Richtung der
Koordinatenachsen? Weisen Sie nach, dass cos^ a -f- cos^ ß -h cos^ 6 =\ gilt.
22 1 Einführung in die Vektorrechnung
Die Aufgaben 18—24 behandeln die wichtigsten Eigenschaften von
Längen und Winkeln. Mehrere Beweise nacheinander werden nicht
wieder vorkommen.
18. (Rechenregeln für Skalarprodukte) Diese Gleichungen sind einfach, aber
nützlich:
A) v-w = w-v B) u-(v + w) = u-v + u-w C) (cv)-w = c(v-w)
Verwenden Sie die Regeln A) und B) mit u = v + w und zeigen Sie,
dass ||v + w|p = v-v + 2v-w + w-w gilt.
19. Die Dreiecksungleichung lautet {Länge von v + w) < {Länge von v)
+ {Länge von w). In Aufgabe 18 wurde ||v + w|p = ||v|p+ 2v-w +||w|p
gezeigt. Benutzen Sie die Schwarz'sehe Ungleichung für v-w und zeigen
Sie, dass
||v + w||2<(||v|| + ||w||J oder ||v + w|| < ||v|| + ||w||
gilt.
20. Auch für ein dreidimensionales rechtwinkliges Dreieck gilt ||v|p + ||w|p =
||v + w|p. Zeigen Sie, wie dies in Aufgabe 18 auf viWi + V2W2 + v^ws = 0
führt.
W = (Wp W2)
V = (Vi,V2)
21. Die Abbildung illustriert, dass cos a = i;i/||v|| und sina = i;2/||v|| gelten.
Analog dazu gilt cos ß = und sin ß = . Der Winkel 0 ist die
Differenz ß — a. Beweisen Sie damit die Formel cosö = cos/? cos a +
sin/?sina = v-w/||v|| ||w||.
22. Schliessen v und w den Winkel 6 ein, so lässt sich nach dem Kosinussatz
die Länge der dritten Seite des entstehenden Dreiecks bestimmen:
||v-w|p = ||v||2-2||v|||H|cosö+||w||2.
Vergleichen Sie dies mit (v — w)-(v — w) =
ein weiteres Mal die Formel für cos 0 her.
., und leiten Sie damit
1.2 Längen und Skalarprodukte 23
23. Die Schwarz'sche Ungleichung lässt sich auch algebraisch statt
trigonometrisch beweisen:
(a) Multiplizieren Sie beide Seiten der Ungleichung {viWi + V2W2)^ <
{vi + V2){wl -h W2) aus.
(b) Zeigen Sie, dass die Differenz beider Seiten gleich {viW2 - V2Wi)^ ist.
Da dies nicht negativ sein kann, muss die Ungleichung immer erfüllt
sein.
24. Ein einzeiliger Beweis der Schwarz'schen Ungleichung |u • U| < 1:
Sind (wi,W2) und {Ui,U2) Einheitsvektoren, wende den Schritt aus
Beispiel 1.2.6 an:
lu.u|<Kr.| + H|f/.l<^ + ^ = i^ = i.
Setzen Sie (^1,^2) = @,6, 0,8) und {Ui,U2) = @,8, 0,6) in dieser Zeile
und bestimmen Sie 0.
25. Warum ist | cosö| überhaupt niemals größer als 1?
26. Wählen Sie beliebige Zahlen x,y, und z mit x -{- y -{- z = 0.
Bestimmen Sie den Winkel zwischen dem Vektor v = {x,y,z) und dem Vektor
w = {z,x,y). Noch eine Herausforderung: Erklären Sie, warum immer
vw/||v||||w|| = -i gilt.
27. Es sei ||v|| = 5 und ||w|| = 3. Bestimmen Sie die kleinsten und die größten
möglichen Werte von ||v — w|| und v • w.
2 Das Lösen linearer Gleichungen
2.1 Vektoren und lineare Gleichungen
Die zentrale Problemstellung der linearen Algebra besteht in der Lösung eines
Systems von Gleichungen. Diese Gleichungen sind linear, was bedeutet, dass
die Unbekannten nur mit Zahlen multipliziert werden — es taucht niemals
ein Produkt x mal y auf. Unser erstes Beispiel für ein lineares System ist
sicherlich nicht groß. Es enthält zwei Gleichungen mit zwei Unbekannten.
Doch wir werden sehen, wie weit uns das führt:
X -2y = 1
Sx + 2y = 11
B.1)
Eine Möglichkeit, diese Gleichungen zu lösen, besteht darin, Zeile für Zeile
vorzugehen. Die erste Zeile ist x — 2^/ = 1. Diese Gleichung entspricht einer
Geraden in der x-y-Ebene. Der Punkt x = 1, y = 0 Hegt auf dieser Geraden,
weil er die Gleichung löst. Der Punkt x = 3, y = 1 liegt ebenso auf der
Geraden, weil 3 — 2 == 1 ist. Wählen wir x = 101, so erhalten wir y = 50. Die
Steigung dieser speziellen Geraden ist |. Steigungen kommen aber doch in
der Analysis vor, hier geht es jedoch um lineare Algebra!
Abb. 2.1. Das Zeilenbild: Der Punkt, an dem sich die Geraden schneiden, stellt
die Lösung dar.
In Abbildung 2.1 ist die Gerade x-2y = 1 dargestellt. Die andere Gerade
in der Abbildung gehört zur Gleichung 3x -\-2y = 11. Man sieht sofort, dass
26
2 Das Lösen linearer Gleichungen
sich die beiden Geraden schneiden. Der Punkt x = S, y = l hegt auf beiden
Geraden. Dieser Punkt löst beide Gleichungen simultan. Er entspricht der
Lösung unseres Systems linearer Gleichungen.
Wir bezeichnen Abbildung 2.1 als das „Zeilenbild" der beiden Gleichungen
mit zwei Unbekannten:
Z Das Zeiienbild Btellt zwei Geraden mit genau einem Schnitt^
punJst dar^
Wenden wir uns nun dem Spaltenbild zu. Ich möchte hierzu das lineare
Gleichungssystem als „Vektorengleichung" begreifen, und hierzu müssen wir
uns an Stelle der Zahlen Vektoren vorstellen. Zerlegt man das ursprüngliche
System in seine Spalten statt in Zeilen, so erhält man
1
:3
+ y
-2
2
=
1
llj
B.2)
Nun stehen zwei Spaltenvektoren auf der linken Seite. Das Problem ist,
diejenige Kombination dieser Vektoren zu finden, die den Vektor auf der rechten
Seite ergibt. Man bildet die Summe des x-fachen des ersten Spaltenvektors
und des ^/-fachen des zweiten Spaltenvektors. Mit der richtigen Wahl x = S
und y = 1 erzeugt diese Linearkombination gerade den Vektor mit den
Komponenten 1 und 11.
S Im SpalfenbUd mcht man diejßn^e LifhbokvfipmlJ^
VfUomn mf dßf linkten Seiie^ 4te den V^Mor^^ ^^a^k r^phieti;
Seite ergibt^;.; ., ; ^ ^=;. ' ^ ' ^^ '/';-': ,.;.-''}/\; -:;/^ c~./^■''x:'i /'> \^-''
Abbildung 2.2 ist das „Spaltenbild" der beiden Gleichungen mit zwei
Unbekannten. Der erste Teil zeigt die beiden einzelnen Spalten
und
-2
2
Er zeigt auch das 3-fache der ersten Spalte. Diese Multiplikation mit einem
Skalar (einer Zahl) ist eine der beiden Grundoperationen der Linearen
Algebra:
Skalarmultiplikation
Sind die Komponenten eines Vektors v die Zahlen vi und V2, so sind die
Komponenten von cv die Zahlen cvi und cv2' Wie zuvor werden Vektoren im
Fettdruck und Zahlen normal dargestellt.
Die andere Grundoperation ist die Addition von Vektoren. Algebraisch
gesehen werden die ersten und die zweiten Komponenten getrennt addiert:
2.1 Vektoren und lineare Gleichungen
27
Abb. 2.2. Das Spaltenbild: Eine Lineaxkombination von Spalten ergibt die rechte
Seite A, 11).
Vektoraddition
Die Zeichnung in Abbildung 2.2 zeigt ein Parallelogramm. Die beiden
Vektoren werden dabei nach der Regel „Spitze an den Anfang" aneinander gehängt.
Ihre Summe ist eine Diagonale des Parallelogramms:
3'
9
+
■-2'
2
=
r
11
Die beiden Seiten sind
und
-2
2
Die Diagonale ist
Wir haben die Spalten des Gleichungssystems mit x = S und y = 1
multipliziert und sie dann addiert, um den Vektor auf der rechten Seite der linearen
Gleichungen zu erhalten.
Rekapitulieren wir noch einmal: Die Hnke Seite der Vektorgleichung ist
eine Linearkomhination der Spalten. Das Problem ist es, die richtigen
Koeffizienten x = 3 und y = 1 zu finden. In dieser Betrachtungsweise werden
SkalarmultipHkation und Vektoraddition zu einem Schritt kombiniert. Dieser
Schritt ist von grundlegender Bedeutung, weil er beide Grundoperationen
enthält:
\1.
'^J'
«i,.;
"•:i;l
Mnm^rkomMntjkiim 3
Die Lösung x = 3, y = 1 ist natürlich dieselbe wie im Zeilenbild. Ich weiss
nicht, welche Betrachtungsweise Sie vorziehen. Die beiden sich schneidenden
Geraden mögen Ihnen zunächst vielleicht vertrauter vorkommen, und sie
entscheiden sich für das Zeilenbild. Morgen kann es aber schon anders sein. Ich
ziehe es vor, Spaltenvektoren zu kombinieren. Man kann sich viel leichter eine
28
2 Das Lösen linearer Gleichungen
Linearkombination von vier Vektoren im vierdimensionalen Raum vorstellen
als vier Hyperebenen, die sich in diesem Raum möglicherweise in einem Punkt
schneiden.
Die Koeffizientenmatrix auf der linken Seite der Gleichungen ist die
2 X 2-Matrix A:
A =
1 -2
3 2
Es ist charakteristisch für die lineare Algebra, eine Matrix sowohl zeilenweise
als auch spaltenweise zu betrachten. Aus den Zeilen erhält man das
Zeilenbild, aus den Spalten das Spaltenbild — dieselben Zahlen, verschiedene
Betrachtungsweisen, aber dieselben Gleichungen. Man kann diese Gleichungen
in Form einer Matrizengleichung Ax = b schreiben:
Matrizengleichung
Im Zeilenbild wird auf der linken Seite zeilenweise multipliziert, im
Spaltenbild hingegen kombiniert man die Spalten. Der Lösungsvektor x besteht aus
den Zahlen x = S und y = l. Damit wird aus Ax = b die Gleichung
-2"
3 2
X
y.
=
r
11
'1 -2'
3 2
"
1
=
r
11
In der ersten Zeile steht 1 • 3 — 2 • 1 und dies ergibt 1. Die zweite Zeile lautet
3-3 + 2-l = ll. Im Spaltenbild liest man stattdessen 3 • A. Spalte ) -f- B.
Spalte), und dies ergibt den Vektor auf der rechten Seite. Beide Wege führen
zur Lösung dieses sehr kleinen Systems!
Drei Gleichungen mit drei Unbekannten
Betrachten wir lineare Gleichungen in den Unbekannten x,y und z:
X -\-2y -\-Sz = 6
2x + by -\-2z = 4
dx - Sy + z = 2
B.3)
Jetzt suchen wir Zahlen x,y und z, die alle drei Gleichungen simultan lösen.
Solche Zahlen können existieren oder auch nicht. Für dieses System existieren
sie. Wenn die Zahl der Unbekannten gleich der Zahl der Gleichungen ist, gibt
es normalerweise genau eine Lösung. Bevor wir das Problem lösen, versuchen
wir wiederum, es uns auf zwei Arten vorzustellen:
Z Im Zeilenbild sieht man drei Ebenen, die sich in genau einem.
Punkte schneiden.
2.1 Vektoren und lineare Gleichungen
29
S Im Spaltenbild werden drei Spalten kombiniert, um, die vierte
Spalte zu erzeugen.
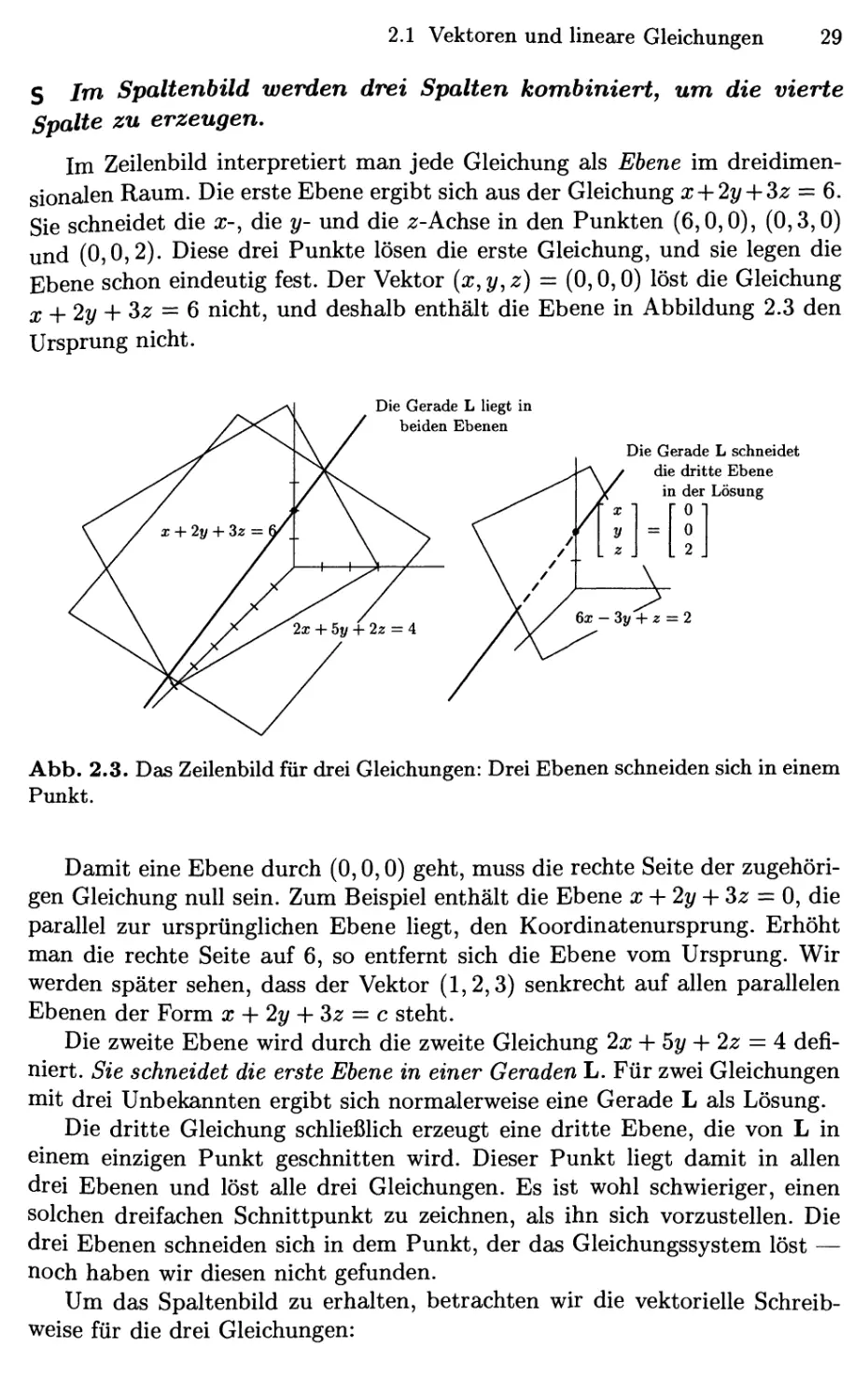
Im Zeilenbild interpretiert man jede Gleichung als Ebene im
dreidimensionalen Raum. Die erste Ebene ergibt sich aus der Gleichung x-\-2y-\-^z =^ Qt.
Sie schneidet die x-, die y- und die 2:-Achse in den Punkten F,0,0), @,3,0)
und @,0,2). Diese drei Punkte lösen die erste Gleichung, und sie legen die
Ebene schon eindeutig fest. Der Vektor {x,y,z) = @,0,0) löst die Gleichung
j, ^2y -\-Sz = 6 nicht, und deshalb enthält die Ebene in Abbildung 2.3 den
Ursprung nicht.
Die Gerade L liegt in
beiden Ebenen
Die Gerade L schneidet
die dritte Ebene
in der Lösung
0
= I 0
6x-3y + z = 2
Abb. 2.3. Das Zeilenbild für drei Gleichungen: Drei Ebenen schneiden sich in einem
Punkt.
Damit eine Ebene durch @,0,0) geht, muss die rechte Seite der
zugehörigen Gleichung null sein. Zum Beispiel enthält die Ebene x-{-2y-\-Sz = 0, die
parallel zur ursprünglichen Ebene liegt, den Koordinatenursprung. Erhöht
man die rechte Seite auf 6, so entfernt sich die Ebene vom Ursprung. Wir
werden später sehen, dass der Vektor A,2,3) senkrecht auf allen parallelen
Ebenen der Form x -\- 2y -\- Sz = c steht.
Die zweite Ebene wird durch die zweite Gleichung 2x -\- 5y + 2z = 4
definiert. Sie schneidet die erste Ebene in einer Geraden L. Für zwei Gleichungen
mit drei Unbekannten ergibt sich normalerweise eine Gerade L als Lösung.
Die dritte Gleichung schUeßHch erzeugt eine dritte Ebene, die von L in
einem einzigen Punkt geschnitten wird. Dieser Punkt Hegt damit in allen
drei Ebenen und löst alle drei Gleichungen. Es ist wohl schwieriger, einen
solchen dreifachen Schnittpunkt zu zeichnen, als ihn sich vorzustellen. Die
drei Ebenen schneiden sich in dem Punkt, der das Gleichungssystem löst —
noch haben wir diesen nicht gefunden.
Um das Spaltenbild zu erhalten, betrachten wir die vektorielle
Schreibweise für die drei Gleichungen:
30
2 Das Lösen linearer Gleichungen
1
2
6
+ y
2
5
-3
-\-z
3
2
1
=
6
4
2
B.4)
Die Unbekannten x,^/, und z sind die Koeffizienten in dieser Linearkombina-
tion. Wir suchen die richtigen Vielfachen der drei Spaltenvektoren, so dass
deren Summe b = F,4,2) ergibt.
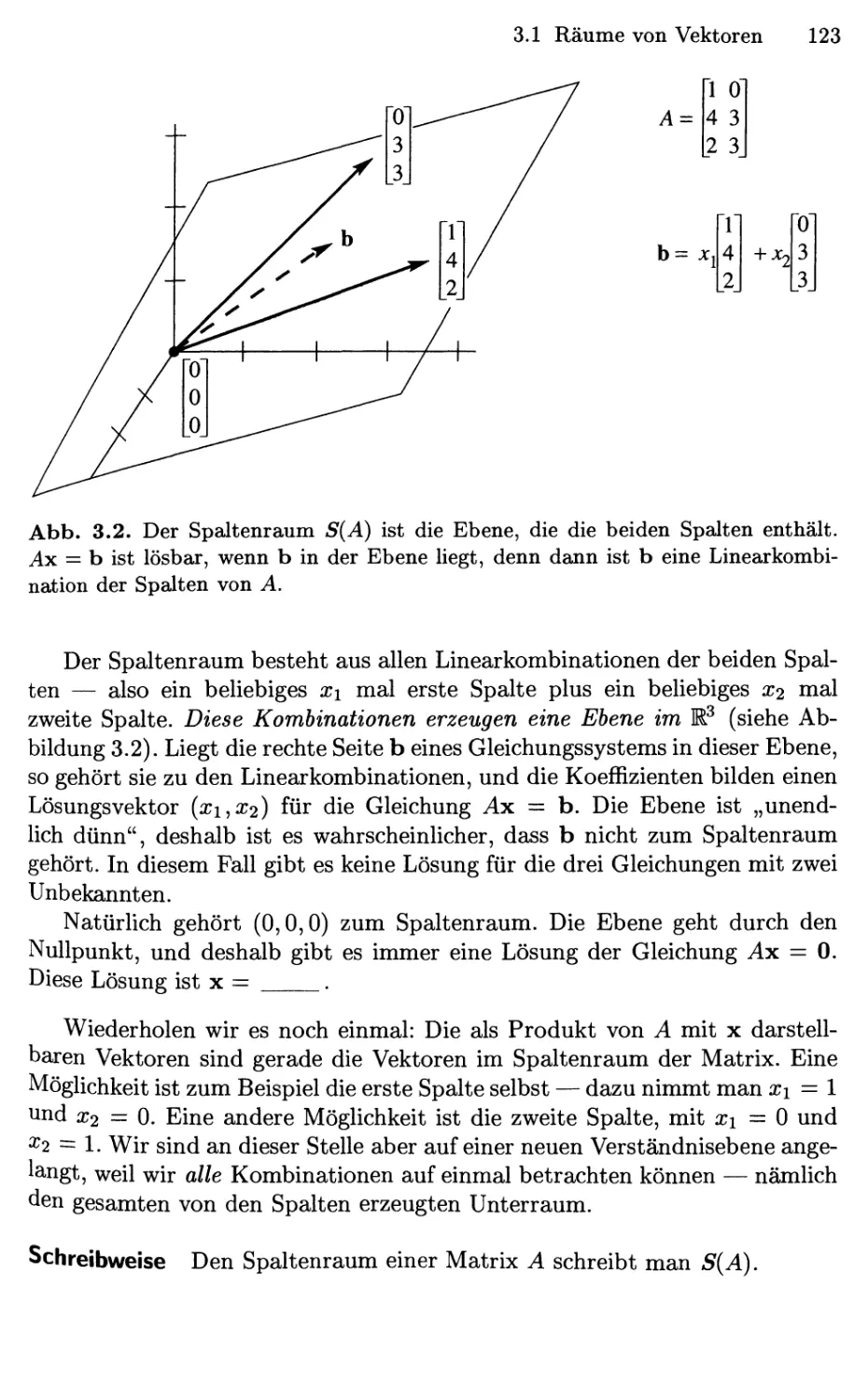
Abb. 2.4. Das Spaltenbild: Die Lösung ist (x,y,z)
doppelte der dritten Spalte ist.
@,0,2), da b gerade das
Abbildung 2.4 zeigt das Spaltenbild. Linearkombinationen dieser Spalten
können alle möglichen rechten Seiten erzeugen, und die Kombination, die b =
F,4,2) ergibt, ist einfach 2-C. Spalte). Wir benötigen also die Koeffizienten
X = 0, y = 0, und z = 2.
Dies ist gleichzeitig der Schnittpunkt der drei Ebenen aus dem Zeilenbild.
Es ist die Lösung des linearen Gleichungssystems:
1
2
6
+ 0
2
5
-3
+ 2
3
2
1
=
6
4
2
Die Matrixform der Gleichungen
Im Zeilenbild betrachten wir drei Zeilen, im Spaltenbild drei Spalten (und
zusätzlich noch die rechte Seite). Die drei Zeilen oder Spalten enthalten
zusammen neun ZahlÄi. Diese neun Zahlen erzeugen eine 3 x 3-Matrix. Diese
„KoefBzientematrix" enthält die Zeilen bzw. Spalten, die wir bislang getrennt
betrachtet haben:
Die Koeffizientenmatrix ist A =
1 23
2 52
6-3 1
2.1 Vektoren und lineare Gleichungen 31
Hier steht der Großbuchstabe A für alle neun Koeffizienten (in der
quadratischen Anordnung). Der Buchstabe b bezeichnet den Spaltenvektor mit
den Einträgen 6,4,2, und die Unbekannte x ist ebenfalls ein Spaltenvektor
mit den Komponenten x, y und z. (Wir stellen ihn im Fettdruck dar, weil
es sich um einen Vektor handelt, und nennen ihn x, weil er eine Unbekannte
bezeichnet.)
In Zeilenform sehen die Gleichungen aus wie in B.3), in Spaltenform wie
in B.4). Gleichung B.5) schließlich ist die Matrixform derselben Gleichungen.
Wir schreiben kurz Ax = b für die
Matrixgleichung:
^1 23"
2 52
6-3 1
X
y
z
=
'61
4
2
B.5)
Man multipliziert also A mit der Unbekannten x, um die rechte Seite b zu
erhalten.
Damit stellt sich die grundlegende Frage: Was bedeutet es, „A mit x zu
multiplizieren"? Wieder kann man spaltenweise oder zeilenweise vorgehen. In
beiden Fällen muss ^x = b eine korrekte Darstellung der drei Gleichungen
liefern. Die Multiplikation einer Matrix A mit einem Vektor x lässt sich also
auf zwei Weisen erklären:
Zeilenweises Multiplizieren Ax entsteht aus Skalarprodukten, nämlich
Zeile mal Spalte:
Ax =
( Zeile i) * X
( Zeile 2) * X
( Zeile 3) * X
B.6)
Spaltenweises Multiplizieren Ax ist eine Linearkombination der
Spaltenvektoren:
Ax:=X' {Spalte 1) -\-y' [Spalte 2) -\-z - {Spalte 3).
B.7)
Unabhängig davon, wie man es durchführt, beide Möglichkeiten beschreiben
A mal X.
Setzen wir für x die Lösung x — @,0,2) ein, so ergibt die Multiplikation
Ax den Vektor b:
23"
2 52
[6-3 1
"
0
2
-
1
4
2
In diesem Fall bedeutet die spaltenweise Multiplikation also schlicht die
Verdoppelung der dritten Spalte. Die rechte Seite b — F,4,2) ist ein Vielfaches
der dritten Spalte C,2,1).
In diesem Buch wird der Ausdruck Ax als Linearkombination
der Spalten von A aufgefasst.
32
2 Das Lösen linearer Gleichungen
10 0"
100
100
"
5
6
=
■
4
4
/x =
00'
010
001
5
6
=
5
6
Man kann zwar auch zeilenweise rechnen, sollte aber die spaltenweise
Multiplikation im Hinterkopf behalten.
Beispiel 2.1.1 Betrachten wir Matrizen A und / mit je drei Einträgen 1 und
sechs Einträgen 0:
Ax =
Im ersten Beispiel ergibt sich Ax = D,4,4). Wenn man sich die Multiplikation
zeilenweise vorstellt, so erhält man jeweils als Produkt jeder Zeile A,0,0) mit
dem Vektor D,5,6) das Ergebnis 4. Geht man spaltenweise vor, so erhält man
die Linearkombination „4 mal die erste Spalte A,1,1)". Denn in der Matrix
A sind die zweite und dritte Spalte Nullvektoren.
Das Beispiel Ix verdient eine genauere Betrachtung, weil es sich bei / um
eine sehr spezielle Matrix handelt. Sie hat Einsen auf der
„Hauptdiagonalen", und abseits dieser Diagonalen sind alle Einträge Null. Jeder Vektor, der
mit dieser Matrix multipliziert wird, bleibt unverändert. Das entspricht der
Multiplikation mit der Zahl 1, nun aber für Matrizen und Vektoren. Diese
außergewöhnliche Matrix heißt 3 x 3-Einheitsinatrix:
1 =
100
010
001
ergibt in der Multiplikation immer /x = x.
Matrix-Notation
Die erste Zeile einer 2 x 2-Matrix enthält die Elemente an und ai2, die zweite
Zeile die Elemente 021 und 022- In dieser Schreibweise gibt der erste Index
die Zeile an (zum Beispiel ist aij ein Eintrag in der i.-ten Zeile), der zweite
Index die Spalte. Solche tiefgestellten Indizes sind mit einer Rechnertastatur
nicht unbedingt praktisch zu verwenden. Statt aij ist es zum Beispiel viel
einfacher, A{i^j) zu tippen. So befindet sich der Eintrag 012 = ^A>2) in
Zeile 1, Spalte 2:
A =
Oll ai2
021 «22
oder
A =
AA,1)AA,2)
AB,1)AB,2)
Der Zeilenindex i einer m x n-Matrix nimmt Werte von 1 bis m an, der
Spaltenindex j läuft von 1 bis n. Es gibt insgesamt mn Werte in einer solchen
Matrix.
Multiplikation mit MATLAB
Ich möchte im Folgenden zeigen, wie A, x und ihr Produkt Ax mit Hilfe von
MATLAB-Kommandos ausgedrückt werden können. Hierbei handelt es sich
2.1 Vektoren und lineare Gleichungen 33
um die ersten Schritte in der Programmiersprache von MATLAB. Ich beginne
mit der Definition der Matrix A und des Vektors x. Dabei wird der Vektor
als 3 X 1-Matrix aufgefasst, besteht also aus drei Zeilen und einer Spalte.
Man gibt eine Matrix zeilenweise ein, und signalisiert das Ende einer Zeile
mit einem Semikolon:
A = [l 2 3; 2 5 2; 6-3 1]
x = [0;0;2]
Im Folgenden stelle ich drei Methoden vor, um in MATLAB das Produkt Ax
zu berechnen:
Mßpti^-MitiÜipUkation h =; 4 * x
Dies ist die Methode, die man normalerweise benutzt. MATLAB ist eine
Hochsprache, und sie arbeitet mit Matrizen als Objekten. Dabei bezeichnet das
Symbol * die Multiplikation.
Wir könnten aber ebenso gut die erste Zeile von A (als kleinere Matrix)
betrachten. Als Notation für derartige Untermatrizen verwendet man A(l,:),
um alle Einträge der ersten Zeile zu erhalten. Multipliziert man diese Zeile
mit dem Spaltenvektor x, so erhält man die erste Komponente 6i = 6:
Zeilenweise: b = [A(l,:) *x; AB,:) *x; AC,:) *x]
Es handelt sich dabei jeweils um das Skalarprodukt einer Zeile mit einer
Spalte.
Eine andere Möglichkeit zu multiplizieren besteht darin, die Spalten von
A zu verwenden. Man erhält die erste Spalte als die 3 x 1-Untermatrix A{:, 1).
In diesem Falle steht der Doppelpunkt für alle Einträge der Spalte 1. Man
erhält das Ergebnis der Matrixmultiplikation, indem man diese Spalte mit
x(l) und die anderen beiden Spalten mit x{2) und x{3) multipliziert:
Spaltenweise: b = A(:, 1) * x{l) + A(:, 2) * x{2) + A(:, 3) * x{3)
Ich glaube, Matrizen werden in MATLAB spaltenweise gespeichert, und
deswegen ist die spaltenweise Multiplikation etwas schneller. Aus diesem Grunde
wird A*x auch intern spaltenweise berechnet.
Man hat dieselbe Wahl bei FORTRAN-ähnlichen Sprachstrukturen, die
mit einzelnen Einträgen von A und x arbeiten. Auf dieser niedrigen
Sprachebene benötigt man eine äußere und eine innere Schleife. Durchläuft die äußere
Schleife den Zeilenindex i, so handelt es sich um zeilenweises Multiplizieren:
FORTRAN zeilenweise MATLAB zeilenweise
DO 10 7 = 1,3 for 2 = 1:3
DOlO J = l,3 forj = l:3
10 Bil) = B{I) + A(/, J) * X{J) h(i) = b{i) + A{i, j) * x{j)
34 2 Das Lösen linearer Gleichungen
Man beachte an dieser Stelle, dass MATLAB Groß- und Kleinbuchstaben
unterscheidet. Die Einträge einer Matrix A heißen A{i,j) und nicht a{i,j).
Gibt die äußere Schleife den Spaltenindex j an, so wird die Multiplikation
spaltenweise durchgeführt, und die innere Schleife durchläuft die einzelne
Spalte:
FORTRAN spaltenweise MATLAB spaltenweise
DO20 J:=l,3 for j = 1:3
DO 20 7=1,3 for i = 1:3
20 B{I) = B{I) + A(/, J) * X{J) b{i) = b{i) + A{iJ) * x{j)
Ich hoffe, Sie ziehen diesen Darstellungen den hochsprachlichen Ausdruck
A * X vor. FORTRAN wird in diesem Buch nicht wieder vorkommen. Maple
und Mathematica sowie symbol verarbeitende Taschenrechner arbeiten auch
auf dieser höheren Ebene. In Mathematica wird die Multiplikation durch "A.
x" ausgedrückt, in Maple durch "niultiply(A,a:); " oder durch den
äquivalenten Ausdruck "evalni(A&; * x);". Diese Sprachen erlauben neben reellen
Zahlen auch symbolische Einträge a, ö, c,..., und berechnen in diesem Fall
(wie auch die Symbolic Toolbox in MATLAB) das korrekte symbolisch
ausgedrückte Ergebnis.
Die wesentlichen Punkte
1. Die grundlegenden Vektoroperationen sind die Skalarmultiplikation cv und
die Vektoraddition v + w.
2. Kombiniert erzeugen diese Operationen Linearkombinationen der Form
cv + w oder cv + dw.
3. Mit der Gleichung Ax = b sucht man die Linearkombination der Spalten
der Matrix A, die b ergibt.
4. Die Multiplikation Ax einer Matrix mit einem Vektor lässt sich zeilen- oder
spaltenweise ausführen.
5. Jede einzelne Gleichung des Systems Ax = b entspricht einer Geraden (im
Falle n = 2), einer Ebene (n = 3) oder einer „Hyperebene" (n > 3). Deren
Schnittmenge bestimmt die Lösung (oder die Lösungen).
Aufgaben 2.1
In den Aufgaben 1-8 geht es um das Zeilen- und das Spaltenbild
der Gleichung Ax = b.
1. Zeichnen Sie die Ebenen des Zeilenbildes für den Fall A — I (die
Einheitsmatrix). Im Schnittpunkt schneiden sich drei Seitenflächen eines Quaders:
Ix + Ot/ + O2; := 2
Ox + It/ + O2; = 3 oder
Ox + O2/ + I2; = 4
"lOO"
0 10
[001
X
y
z
-
"
3
4
2.1 Vektoren und lineare Gleichungen
35
2. Zeichnen Sie die Vektoren des Spaltenbildes von Aufgabe 1: zwei mal
Spalte 1 plus drei mal Spalte 2 plus vier mal Spalte 3 ergibt die rechte
Seite b.
3. Multipliziert man die Gleichungen in Aufgabe 1 mit den Zahlen 1,2, bzw.
3, so erhält man
lx-\-0y-\-0z = 2
0x-h2y-h0z = 6
Ox-h Oy-h Sz = 12
oder
rioo"
' 020
003
X
y
z
=
2"
6
12
Warum bleibt das Zeilenbild unverändert? Ändert sich die Lösung? Das
Spaltenbild bleibt nicht gleich — zeichnen Sie es.
4. Was ändert sich, wenn man Gleichung 1 zu Gleichung 2 addiert: das
Zeilenbild, das Spaltenbild, die Koeffizientenmatrix, die Lösung? In
Aufgabe 1 ergäben sich die neuen Gleichungen x = 2, x-\-y = 5 und z = A,
5. Finden Sie einen Punkt der Schnittgeraden der beiden Ebenen x -\- y -\-
Sz = 6 und X — y -h z = 4. Versuchen Sie noch einen weiteren Punkt der
Geraden durch geschicktes Probieren zu finden.
6. Addiert man die erste dieser Gleichungen zur zweiten, so ergibt sich die
dritte Gleichung:
X + y -\- z — 2
X + 22/+ 2; = 3
2x-\-Zy\2z^ 5.
Die ersten beiden Ebenen schneiden sich in einer Geraden. Auch die dritte
Ebene enthält diese Gerade, da . Deshalb hat dieses
Gleichungssystem unendlich viele Lösungen (nämlich die ganze Schnittgerade). Finden
Sie drei dieser Lösungen.
7. Tauschen Sie die dritte Ebene aus Aufgabe 6 durch die parallele Ebene
2x-\-Zy-V 2z — ^ aus. Das Gleichungssystem hat nun keine Lösung mehr
— warum? Weil sich die ersten beiden Ebenen in einer Geraden
schneiden, die von der dritten Ebene nicht geschnitten wird. (Die künstlerisch
Begabten mögen dies bitte zeichnen!)
8. In Aufgabe 6 sind die Spalten der Matrix durch A,1,2), A,2,3) und
A,1,2) gegeben. Dies ist ein „singulärer Fall", da die dritte Spalte .
Finden Sie zwei verschiedene Linearkombinationen der drei Spalten, die
die rechte Seite B,3,5) darstellen.
36
2 Das Lösen linearer Gleichungen
In den Aufgaben 9-14 geht es um die Multiplikation von Matrizen
und Vektoren.
9. Berechnen Sie jedes Produkt Ax aus den Skalarprodukten der Zeilen mit
dem Spaltenvektor x:
(a)
[124]
-2 3 1
-4 1 2
"
2
3J
(b)
[2 10 0]
1210
012 1
0012
'1'
1
1
2J
10. Berechnen Sie jedes Produkt Ax aus Aufgabe 9 als Linearkombination
der Spalten: Aus 9(a) wird Ax = 2
1
-2
-4
+ 2
2
3
1
+ 3
4
1
2
=
Wie viele einzelne Multiplikationen sind zur Berechnung des Produktes
Ax nötig, wenn A eine 3 x 3-Matrix ist?
11. Bestimmen Sie die Komponenten von Ax zeilen- oder spaltenweise:
3"
5 1
■4"
2
und
■3 6
6 12
2
-1
und
124"
201
"
1
ij
12. Berechnen Sie die Komponenten der Produkte:
rooi"
010
100
X
y
z
und
[2 13]
123
336
r
1
-1
und
[2 1"
12
33
r
1
13. (a) Das Produkt einer Matrix mit m Zeilen und n Spalten mit einem
Vektor mit Komponenten ist ein Vektor mit
Komponenten,
(b) Zu den m Gleichungen in Ax = b gehören Ebenen im -
dimensionalen Raum. Die Linearkombination der Spalten ist im
-dimensionalen Raum.
14. (a) Wie würden Sie einen lineare Gleichung mit drei Unbekannten x,y,z
definieren?
(b) Falls vo = (xo.yo^^o) und vi = {xi,yi,zi) diese Gleichung lösen, so
ist auch cvo + d\i eine Lösung, falls c-\- d = gilt.
(c) Falls die rechte Seite der Gleichung ist, lösen sogar alle
Linearkombinationen von Vo und vi die Gleichung aus (a).
2.1 Vektoren und lineare Gleichungen 37
In den Aufgaben 15-22 geht es um Matrizen, die in besonderer
Weise auf Vektoren wirken.
15 (a) Wie sieht die 2 x 2-Einheitsmatrix aus, d.h. die Matrix / mit / [^] =
(b) Wie sieht die 2 x 2-„Vertauschungsmatrix" aus, d.h. die Matrix P mit
16. (a) Welche 2 x 2-Matrix R dreht jeden Vektor um 90°? Es muss gelten
(b) Welche 2 x 2-Matrix dreht jeden Vektor um 180°?
17. Wie sieht die 3 x 3-Matrix P aus, die die Einträge eines Vektors {x,y, z)
zu {y^z^x) permutiert? Welche Matrix P~^ macht diese Permutation
rückgängig?
18. Welche 2 x 2-Matrix E bewirkt die Subtraktion der ersten
Komponente eines Vektors von der zweiten? Welche 3 x 3-Matrix hat die gleiche
Wirkung?
E
19. Für welche 3 x 3-Matrix E gilt E{x^y,z) = {x,y,z + x)? Wie sieht die
Matrix E~^ aus, für die E~^{x,y,z) = {x,y,z — x) gilt? Multipliziert
man C,4, 5) erst mit E und das Ergebnis dann mit E~^, so erhält man
die Ergebnisse ( ) und ( ).
20. Wie sieht die 2 x 2-Matrix Pi aus, die den Vektor {x,y) auf die x-Achse
projiziert, d.h. für die Pi{x,y) = {x,0) gilt? Welche Matrix P2 projiziert
{x,y) auf die 2/-Achse? Bildet man die Produkte PiE,7) und P2^iE,7),
so ergeben sich ( ) und ( ).
21. Welche 2 x 2-Matrix R dreht jeden Vektor um 45°? Es muss der Vektor
A,0) in den Vektor (\/2/2, \/2/2) überführt werden und der Vektor @,1)
in den Vektor (—\/2/2, \/2/2). Diese beiden Bedingungen beschreiben die
Matrix vollständig. Zeichnen Sie die beiden Vektoren in der xy-Ebene und
bestimmen Sie R.
22. Schreiben Sie das Skalarprodukt von A,4,5) und {x,y,z) als
Matrixgleichung ^x. Die Matrix A hat eine Zeile, und die Lösungen der Gleichung
Ax = 0 bilden eine . Die Spalten von A sind Elemente des lediglich
-dimensionalen Raums.
23. Die beiden folgenden Fragmente Programmcode berechnen beide das
Produkt einer Matrix mit Einträgen A{iJ) mit einem Vektor V mit Ein-
^3
_5
=
2
und E
"
5
7
=
l
2
7\
38 2 Das Lösen linearer Gleichungen
trägen 1^A) und V{2). Welcher Code berechnet die Skalarprodukte der
beiden Zeilen von A mit V?
Welcher Code bestimmt die Linearkombination „F(l) mal Spalte Nr. 1 +
V{2) mal Spalte Nr. 2"? Welche Änderungen sind nötig für eine Matrix
A mit 4 Zeilen und 3 Spalten ?
DO 10 I = 1,2 DO 10 J = 1,2
DO 10 J = 1,2 DO 10 I = 1,2
10 B(I) = B(I)+A(I,J)*V(J) lOB(I) = B(I)+A(I,J)*V(J)
24. Für beide Versionen des Programmcodes in Aufgabe 23 lautet der erste
Schritt ^A) = A{1,1) * V{1). Geben Sie die weiteren Schritte in der
Reihenfolge an, in der die beiden Versionen sie ausführen.
25. Geben Sie in MATLAB eine Matrix und einen Spaltenvektor ein, und
multiplizieren Sie sie miteinander.
In den Aufgaben 26-28 beschäftigen Sie sich noch einmal mit dem
Zeilen- und dem Spaltenbild eines linearen Gleichungssystems.
26. Zeichnen Sie beide Bilder für das Gleichungssystem x — 2y = 0,x-\-y = 6>
27. Besteht das Zeilenbild für ein Gleichungssystem mit zwei Gleichungen in
drei Unbekannten x, y, und z aus 2 oder 3 Geraden oder Ebenen? Liegen
diese im zwei- oder im dreidimensionalen Raum? Wie ist es mit dem
Spaltenbild?
28. Das Zeilenbild eines Gleichungssystems aus vier Gleichungen mit zwei
Unbekannten x und y enthält vier , und das Spaltenbild ist -
dimensional. Das System hat keine Lösung, falls der Vektor auf der
rechten Seite keine Linearkombination von ist.
29. (Markov-Matrix) Wir beginnen mit dem Vektor uq = A,0).
Multiplizieren Sie diesen mehrmals mit derselben Matrix A. Dadurch ergeben sich
die Vektoren ui, U2, U3:
ro,8o,3i rii ro,8i . .
^1 = n o n ^ n = L o U2 = Aui = U3 = Au2 = .
Welche Eigenschaft ist allen vier Vektoren uq, ui,U2 und U3 gemein?
30. Setzen Sie die Rechnung in Aufgabe 29 bis zum Vektor U7 fort (z.B.
unter Zuhilfenahme eines Computers). Berechnen Sie dann, mit vq = @,1)
startend, die Vektoren vi = Avq und V2 = Avi bis hin zu V7.
Bestimmen Sie schließlich noch die Vektoren wi bis W7 für den Startvektor
Wo = @,5, 0,5). Was beobachten Sie bei allen drei Folgen? Zeichnen Sie
2.1 Vektoren und lineare Gleichungen 39
die Folgen von Hand oder mit dem Computer, dazu können Sie die
folgenden MATLAB-Anweisungen benutzen (aber natürlich auch jede andere
geeignete Programmiersprache):
u = [1; 0]; A = [0,8 0,3; 0,2 0,7];
X = u; k = [0:1:7];
while length(x) <= 7
u = A*u; X = [x u];
end
plot(k, x)
31. Die Folgen von u's, v's und w's streben gegen einen stationären Vektor s.
Erraten Sie diesen Vektor und zeigen Sie, dass As = s gilt. Dieser Vektor
heißt „stationär", weil man immer in s bleibt, wenn man in s startet.
32. Das folgende MATLAB-Programm ermöghcht es, einen Startvektor uq =
[a; 6; 1 — a — b] auf dem Bildschirm per Mausklick zu bestimmen.
Hierbei sollten die drei Komponenten positiv sein. Klicken Sie dazu mit der
linken Maustaste auf den gewünschten Punkt (a, 6), oder auch auf
mehrere Punkte. Mit der rechten Maustaste können Sie die Schleife beenden.
Wenn Sie die Anweisung disp(u') nach dem ersten end einfügen, wird
der stationäre Vektor im Textfenster ausgegeben. Beachten Sie, dass die
Matrix A zeilenweise im Programmtext steht — die Summe der
Spalteneinträge ist immer eins.
A = [0,8 0,2 0,1; 0,1 0,7 0,3; 0,1 0,1 0,6]
axis([0 1 0 1]); axis('square')
plot@, 0); hold on
titleCMarkov-Ihr Name'); xlabel('a'); ylabel('b'); grid
but = 1;
while but == 1
[a,b,but] = ginput(l)
u = [a; b; 1-a-b];
X = u; k = [0:1:7];
while length(x) <= 7
u = A*u; X = [x u] ;
end;
plot(x(l,:), xB,:), x(l,:), x B,:), 'o');
end
hold off
33. Denken Sie sich ein magisches Quadrat Ms mit 3x3 Einträgen
1,2,..., 9 aus. Dabei müssen alle Zeilen-, Spalten- und Diagonalsummen
15 ergeben — die erste Spalte könnte z.B. 8,3,4 sein. Welcher Vektor
ergibt sich als Produkt Ms{l, 1,1)? Was ergibt sich für M4(l, 1,1,1), wenn
das magische Quadrat M4 die Zahlen 1,... ,16 enthält?
40 2 Das Lösen linearer Gleichungen
2.2 Die Idee der Elimination
In diesem Kapitel wird ein systematisches Verfahren zur Lösung linearer
Gleichungssysteme vorgestellt. Es wird „Eliminationsverfahren'' genannt,
und man kann es schon an unserem 2 x 2-Beispiel darstellen. Vor der
Elimination sind beide Variablen x und y in beiden Gleichungen enthalten.
Nach der Elimination ist die erste Unbekannte x aus der zweiten Gleichung
verschwunden.
Vorher:
x-2y = l
3a: + 22/ = 11
Nachher:
x-2y = l
Sy = S.
Aus der letzten Gleichung 8y = 8 erhält man sofort y = l, und setzt man
dies in die erste Gleichung ein, erhält man x - 2 = 1. Es ist also x = 3, und
wir haben die vollständige Lösung {x,y) = C,1).
Das Eliminationsverfahren versucht, ein oberes Dreieckssystem zu
erzeugen, also ein Gleichungssystem, in dem die von Null verschiedenen
Koeffizienten ein Dreieck bilden — so wie 1, -2 und 8 in dem Beispiel oben.
Ein solches System kann gelöst werden, indem man von unten nach oben
vorgeht und aus der letzten Gleichung {Sy = 8) die letzte Unbekannte (y)
bestimmt. Diese setzt man in die Gleichung darüber ein, und erhält so x.
Dieses Vorgehen nennt man „Rücksubstitution", und es kann auf obere
Dreieckssysteme jeder Größe angewandt werden, die durch Vorwärtselimination
erzeugt wurden.
Die wichtige Beobachtung ist dabei, dass die ursprünglichen Gleichungen
dieselbe Lösung x = 3 und y = 1 besitzen. In Abbildung 2.5 wird das
ursprüngliche System durch zwei Geraden dargestellt, die sich in der Lösung
C,1) schneiden. Nach der Elimination schneiden sich die Geraden immer
noch in demselben Punkt! Eine Gerade verläuft horizontal, weil die
zugehörige Gleichung 8y = 8 die Variable x nicht mehr enthält.
Wichtig ist natürlich die Frage: Wie haben wir das zweite
Geradenpaar aus dem. ersten erhalten ? Dazu haben wir das dreifache der ersten
Vor der Elimination
y
Nach der Elimination
Abb. 2.5. Die beiden Geraden schneiden sich in der Lösung. Dies gilt auch für die
neue Gerade Sy = S.
2.2 Die Idee der Elimination 41
Gleichung von der zweiten Gleichung subtrahiert. Dieser Schritt, der x aus
der zweiten Gleichung eliminiert, stellt die für dieses Kapitel grundlegende
Operation dar. Wir werden sie sehr oft anwenden und sehen sie uns deshalb
näher an:
Um X zu eliminieren, subtrahiere ein Vielfaches der ersten von
der zweiten Gleichung.
Das Dreifache der Gleichung x — 2y = 1 ist 3x — 6y = 3. Subtrahiert
man dies von der Gleichung 3x-{-2y = 11, so wird die rechte Seite zu 8. Das
Wesentliche ist aber, dass sich auf der linken Seite die Summanden 3a: und
3a: auslöschen, und nur noch 2y - {-6y) = 8y übrig bleibt. Man erhält also
Sy = y, und X wurde eliminiert.
Wie haben wir den Multiplikator 3 gefunden? In der ersten Gleichung
steht la:, d.h. das erste Pivotelement (der Koeffizient vor x) ist 1. Die
zweite Gleichung enthält 3a:, also wird die erste Gleichung mit 3 multipliziert,
so das bei der Subtraktion 3a: - 3a: null ergibt.
Man erkennt die generelle Funktionsweise dieser Regel, wenn man die erste
Gleichung in die Form 5x - lOy = 5 bringt. Dadurch wird dieselbe Gerade im
Zeilenbild beschrieben. Das erste Pivotelement ist jetzt 5, und damit ergibt
sich der Multiplikator ' = f- Man bestimmt den Multiplikator, indem man
den zu eliminierenden Koeffizienten durch das Pivotelement dividiert.
Multipliziere Gleichung 1 mit | 5a: - lO^/ = 5 ., 5a: - lO^/ = 5
Subtraktion von Gleichung 2 3a: + 2^/ = 11 ^^^ 8y = 8.
Hier entsteht ein Dreieckssystem, und aus der letzten Gleichung ergibt
sich wiederum y = 1. Die Rücksubstitution ergibt 5a: — 10 =: 5, also 5a: = 15
und a: = 3. Dass wir die erste Gleichung mit 5 multiplizierten, hat zwar die
Koeffizienten des Gleichungssystems verändert, nicht aber die Geraden im
Zeilenbild oder die Lösung des Systems.
Nach dieser Regel lassen sich Koeffizienten eliminieren:
Pivotelement = erster Koeffizient (ungleich Null) der eliminierenden Zeile
Multiplikator = (zu eliminierender Eintrag) / (Pivotelement)
In der neuen zweiten Gleichung steht das zweite Pivotelement, nämlich
die 8, der Koeffizient von y. Gäbe es noch eine dritte Gleichung, so würde man
dies Pivotelement verwenden, um y aus ihr zu eliminieren. Um ein System aus
n Gleichungen auf diese Weise zu lösen, benötigen wir somit n Pivotelemente.
Sie hätten die beiden Gleichungen für x und y sicher lösen können,
ohne dieses Buch zu lesen. Es ist eigentlich ein sehr einfaches Problem, aber
wir halten uns trotzdem noch ein wenig länger damit auf. Das
Eliminationsverfahren kann nämlich in manchen Fällen fehlschlagen, und wir müssen
noch verstehen, wieso. Wenn wir das mögliche Versagen verstehen (wenn es
nämlich nicht genug Pivotelemente gibt), verstehen wir gleichzeitig auch den
gesamten Eliminationsprozess.
42 2 Das Lösen linearer Gleichungen
Versagen des Eliminations Verfahrens
Normalerweise entstehen im Verlaufe des Eliminationsverfahrens die
Pivotelemente, die wir auf dem Weg zu einer Lösung benötigen. Es kann aber
fehlschlagen. Es kann nämlich sein, dass das Verfahren bis zu einem gewissen
Punkt funktioniert, wir dann aber durch Null dividieren müssten. Das geht
natürlich nicht, und an dieser Stelle muss das Verfahren stoppen.
Anschließend könnte es möglich sein, die Situation zu retten und weiterzumachen. Es
kann aber auch sein, dass das Verfahren endgültig fehlgeschlagen ist. Beispiel
2.2.1 stellt einen solchen Fehlschlag dar, bei dem es keine Lösung gibt; in
Beispiel 2.2.2 gibt es zu viele Lösungen. Beispiel 2.2.3 schließlich erlaubt es
uns, durch Vertauschen von Gleichungen erfolgreich weiterzuarbeiten.
Beispiel 2.2.1 Echtes Versagen ohne Lösung. EUmination ergibt:
X — 2y =^ 1 Subtraktion des Dreifachen x — 2y = 1
Sx - 6y = 11 der 1. Gleichung von der 2. Oy = S.
In der letzten Gleichung steht jetzt Oy = 8. Dafür gibt es keine Lösung.
Wir wollen jetzt die rechte Seite 8 durch das zweite Pivotelement dividieren
— es gibt aber kein zweites Pivotelement. (Null kann niemals als Pivot-
element verwendet werden!) Im Zeilen- wie im Spaltenbild sieht man,
das dies unvermeidbar war. Wenn es keine Lösung gibt, gerät das
Eliminationsverfahren sicher in Schwierigkeiten.
Das Zeilenbild ist in Abbildung 2.6 dargestellt: zwei parallele Geraden, die
sich nicht schneiden. Eine Lösung des Systems müsste auf beiden Geraden
liegen, und da es keinen Schnittpunkt gibt, gibt es auch keine Lösung.
Im Spaltenbild erkennt man, dass die beiden Spalten A,3) und (—2, —6)
auf derselben Geraden liegen. Deshalb liegen auch alle Linearkombinationen
auf dieser Geraden. Nun zeigt die Spalte A,11) für die rechte Seite in
eine andere Richtung, und deshalb kann keine Linearkombination der Spalten
links diese rechte Seite erzeugen — deshalb gibt es keine Lösung.
Ändern wir die rechte Seite zu A,3), so äußert sich das Scheitern in der
Existenz einer ganzen Geraden aus Lösungen — statt keiner, gibt es unendlich
viele Lösungen:
Beispiel 2.2.2 Echtes Versagen mit unendlich vielen Lösungen:
X — 2y — 1 Subtraktion des Dreifachen x — 2y — 1
3a: - 62/ = 3 der 1. Gleichung von der 2. 0^/ = 0.
Die letzte Gleichung lautet nun 0^/ = 0 — jedes y erfüllt diese Gleichung.
Es gibt nur eine echte Bedingung, nämlich x — 2y= 1, und die Unbekannte y
ist „frei". Hat man y beliebig gewählt, so ist x durch x = l + 2y bestimmt.
2.2 Die Idee der Elimination 43
Abb. 2.6.
scheitert.
3jc-6>'=11
Zeilenbild und Spaltenbild für Beispiel 1: Das Eliminations verfahren
Eine Kombination der Spalten erzeugt keine Ebene
Im Zeilenbild stellt sich dies dadurch dar, dass die beiden Parallelen in
einer Geraden zusammenfallen, und jeder Punkt auf dieser Geraden beide
Gleichungen erfüllt. Dadurch gibt es also eine ganze Gerade aus Lösungen.
Im Spaltenbild bedeutet dies, dass die rechte Seite ebenfalls auf einer
Geraden mit den beiden Spalten der linken Seite liegt. Wir können zum
Beispiel x = 1 und y = 0 wählen — die erste Spalte ist gleich der rechten
Seite A,3). Wir könnten ebenso gut auch x = 0 und y = -\ wählen, da
die rechte Seite gleich dem -^-fachen der zweiten Spalte ist. Es gibt noch
unendlich viele weitere Lösungen, und jedes Paar (x, y), das sich im Zeilenbild
als Lösung ergibt, ist auch eine Lösung im Spaltenbild.
Es gibt noch eine dritte Situation, in der das Eliminations verfahren
stecken bleibt. In diesem Fall kann man sich jedoch helfen. Nehmen wir an,
das erste Pivotelement wäre Null. Null können wir aber nicht als
Pivotelement zulassen. In diesem Fall, in dem die erste Gleichung keinen Term mit
X enthält, können wir sie aber mit einer anderen Gleichung vertauschen, die
X enthält, und das Verfahren kann dann mit einem geeigneten Pivot element
fortgesetzt werden:
Beispiel 2.2.3 Vorübergehendes Scheitern bei dem ein Zeilentausch das
nötige Pivotelement liefert:
Ox 4- 2?/ = 4 Vertauschen
3a: - 2?/ = 5 der Gleichungen
Das neue System ist hier bereits in Dreiecksform, und in diesem kleinen
Beispiel sind wir demnach bereit für die Rücksubstitution. Aus der letzten
Gleichung ergibt sich y = 2, und damit liefert die erste Gleichung x = 3,
Das Zeilenbild sieht hier ganz normal aus (zwei sich schneidende Geraden),
und auch das Spaltenbild ist wie üblich — die Spaltenvektoren weisen nicht in
dieselbe Richtung. Auch die beiden Pivotelemente 3 und 2 sind wie gewünscht
— lediglich der Zeilentausch war nötig geworden.
44
2 Das Lösen linearer Gleichungen
3;c-6>' = 3
Dieselbe Gerade aus beiden Gleichungen,
Loesungen sind alle Punkte auf dieser Geraden.
Die rechte Seite ^
liegt auf der Geraden der Spalten.
Abb. 2.7. Zeilen- und Spaltenbild für Beispiel 2: unendlich viele Lösungen.
Die Beispiele 1 und 2 stellen einen singulären Fall dar, in dem es
kein zweites Pivotelement gibt. Das Beispiel 3 ist nichtsingulär — es gibt
genügend Pivotelemente. Singulare Gleichungssysteme haben entweder
keine oder unendlich viele Lösungen. Nichtsinguläre Systeme hingegen haben
genau eine Lösung.
Pivotelemente dürfen nicht Null sein, weil man durch sie dividieren muss.
Drei Gleichungen mit drei Unbekannten
Um das Gauß'sche Eliminationsverfahren wirklich zu durchschauen, muss
man größere als die bisher betrachteten 2 x 2-Systeme ansehen — 3x3-
Systeme sind jedoch ausreichend. Im Augenblick betrachten wir nur
quadratische Matrizen mit ebenso vielen Zeilen wie Spalten, zum Beispiel das
folgende 3 x 3-System, das speziell so konstruiert wurde, dass sich im
Eliminationsverfahren nur ganzzahlige Koeffizienten und keine Brüche ergeben:
2x-{-4y-2z = 2
4x-{-9y-Sz = S
-2x -3y-{-7z = 10
B.8)
Wie sehen nun die einzelnen Schritte aus? Das erste Pivotelement ist die 2
in der linken oberen Ecke. Unter ihm wollen wir Nullen erzeugen. Als erster
Multiplikator ergibt sich das Verhältnis / = 4/2 = 2, mit dem die erste Zeile
multipliziert und das Ergebnis von der zweiten Zeile subtrahiert wird. Diese
Subtraktion entfernt dann 4x aus der zweiten Gleichung.
1 Subtrahiere das 2-fache von Gleichung 1 von Gleichung 2.
Ebenfalls über das erste Pivotelement eliminieren wir x aus Gleichung 3.
Der einfache Weg bestünde darin, die erste zur dritten Gleichung zu addieren,
2.2 Die Idee der Elimination 45
so dass sich 2x und —2x aufheben. Genau das tun wir auch — allerdings
wollen wir in diesem Buch Gleichungen stets subtrahieren, statt zu addieren.
Die systematische Vorgehens weise verwendet also den Multiplikator — 2/2 =:
— 1 und subtrahiert das — 1-fache der ersten Gleichung von der dritten, was
einer Addition der beiden gleichkommt:
2 Subtrahiere das —1-fache von Gleichung 1 von Gleichung 3.
Sehen wir uns die Situation jetzt an. In den beiden neuen Gleichungen
kommen nur die Variablen y und z vor:
ly + lz^A
12/ + 5z = 12
Wir erhalten ein 2 x 2-System. Im letzten Schritt wird y aus einer Gleichung
eliminiert, was zu einem 1 x 1-System führt:
3 Subtrahiere Gleichung 2neu von Gleichung 3neu- Damit ergibt sich Ox 4-
Oy-j-4z = 8.
Insgesamt haben wir das ursprüngliche 3 x 3-System in ein oberes
Dreieckssystem umgeformt:
2x-{-4y-2z = 2 2x-{-4y - 2z = 2
4x-{-9y-Sz = 8 wird zu ly-{-lz = 4 B.9)
-2x-Sy-h7z = 10 4z = 8.
Damit ist das Ziel erreicht, die Vorwärtselimination ist vollständig
durchgeführt. Beachten Sie die Pivotelemente 2, 1 und 4 auf der
Hauptdiagonalen. Die Zahlen 1 und 4 waren in der ursprünglichen Matrix verborgen
und sind vom Eliminationsverfahren hervorgebracht worden.
Unterhalb der Pivotelemente stehen nur noch drei Nullen, die durch die
drei Eliminationsschritte erzeugt worden sind. Damit ist das System bereit
für die Rücksubstitution, die sich schnell durchführen lässt:
4z = 8 liefert z = 2, aus y -{■ z = 4 folgt& y = 2,
und Gleichung 1 führt zu&; x = -1.
Die Lösung ist somit {x,y,z) = (-1,2,2).
Im Zeilenbild stellt sich diese Tatsache durch Ebenen dar, die alle den
Punkt (-1,2,2) enthalten. Alle drei ursprünglichen Ebenen sind geneigt,
doch die letzte Gleichung 4z = 8 stellt eine „horizontale" Ebene parallel zur
x^z-Ebene dar.
46
2 Das Lösen linearer Gleichungen
Das Spaltenbild besteht jeweils aus einer Linearkombination von
Spaltenvektoren, die die rechte Seite ergeben. Dabei stimmen die Koeffizienten —1,
2 und 2 für das ursprüngliche System und das Dreieckssystem überein:
(-1)
r 2"
4
[-2
+ 2
4"
9
-3
+ 2
' -2
-3
7
ergibt
2"
8
10^
B.10)
Für ein 4 x 4-System oder auch ein n x n-System funktioniert das
Eliminationsverfahren ganz genauso. Das Prinzip der Vorwärtselimination ist
einfach:
1. Erzeuge mit Hilfe der ersten Gleichung Nullen unterhalb des
ersten Pivotelem,ents.
2. Verwende die neue zweite Gleichung, um, Nullen unterhalb des
zweiten Pivotelem^ents zu erzeugen.
3. Fahre fort bis zum, n-ten Pivotelem^ent.
Es ergibt sich schließlich ein oberes Dreieckssystem, das nichtsingulär ist,
falls es n Pivotelemente ungleich Null gibt. Sehen wir uns an einem letzten
Beispiel noch einmal das Originalsystem, das obere Dreieckssystem und die
Lösung durch Rücksubstitution an:
x-\- y -{■ z = 6
x-{-2y-{-2z = 9
x-{-2y-{-Sz = 10
x-hy -{- z = 6
y-{-z = 3
z = l
X = 3
y = 2
z=l.
Als Multiplikator ergibt sich immer die Zahl 1, und auch alle
Pivotelemente sind 1. Alle zu den Gleichungen gehörenden Ebenen enthalten die
Lösung C,2,1); die Linearkombination der drei ursprünglichen Spalten mit
den Koeffizienten 3,2,1 ergibt die rechte Spalte F,9,10).
Die wesentlichen Punkte
l.Mit Hilfe des Eliminationsverfahrens wird aus einem linearen
Gleichungssystem ein oberes Dreieckssystem.
2. Das obere Dreieckssystem löst m.an durch Rücksubstitution beginnend in
der letzten Zeile.
3. Zur Elimination des Eintrags {i,j) subtrahiert man ein £ij-faches der
Gleichung j von Gleichung i.
4. Als Multiplikator verwendet man t^j = '^:^^^:!::^^Tf ■ Aus diesem
Grund darf ein Pivotelement nie Null sein!
5. Eine Null auf der Pivot-Position kann durch Vertauschung von Zeilen
umgangen werden, wenn es von Null verschiedene Elemente darunter gibt.
6. Andernfalls scheitert das Verfahren, und es gibt entweder keine oder
unendlich viele Lösungen für das Gleichungssystem.
2.2 Die Idee der Elimination 47
Aufgaben 2.2
Die Aufgaben 1-10 behandeln das Eliminations verfahren für 2x2-
Systeme.
1. Welches Vielfache / der Gleichung 1 subtrahiert man von Gleichung 2?
2x-{-Sy = l
10x-{-9y = 11.
Schreiben Sie das obere Dreieckssystem nieder, das sich nach dem
Eliminationsschritt ergibt, und markieren Sie die beiden Pivotelemente. Die
Zahlen 1 und 11 auf der rechten Seite haben keinen Einfluss auf diese
Pivot demente.
2. Lösen Sie das Dreieckssystem aus Aufgabe 1 durch Rücksubstitution,
erst nach y, dann nach x. Prüfen Sie nach, dass x mal B,10) plus y mal
C,9) den Vektor A,11) ergibt. Welche neue Lösung erhält man, wenn
die rechte Seite durch den Vektor D,44) ausgetauscht wird?
3. Welches Vielfache der Gleichung 1 subtrahiert man von Gleichung 2?
2x - 4y = 6
-X -{-3y = 0.
Lösen Sie das Dreieckssystem, dass sich nach dem Eliminationsschritt
ergibt. Welche Lösung ergibt sich für die rechte Seite (-6,0)?
4. Welches Vielfache / der Gleichung 1 subtrahiert man von Gleichung 2?
ax -hby = f
ex -\- dy = g.
Nehmen Sie an, dass das erste Pivotelement a ungleich Null ist. Welcher
Ausdruck für das zweite Pivotelement ergibt sich durch das
Eliminationsverfahren? Es gibt kein zweites Pivotelement, falls ad = bc gilt.
5. Wählen Sie eine rechte Seite, für die sich keine Lösung ergibt, und eine
andere mit unendlich vielen Lösungen. Benennen Sie zwei dieser
Lösungen.
3x-{-2y = 7
dx -{-4y =
6. Wählen Sie einen Koeffizienten &, so dass das System singular wird.
Wählen Sie dann ein g für die rechte Seite, für das Lösungen existieren.
2x-hby = 13
4x-{-Sy = g.
48 2 Das Lösen linearer Gleichungen
7. Für welche Zahlen a versagt das Eliminationsverfahren a) endgültig oder
b) vorübergehend?
ax -{-3y = -3
4x -h^y = 6.
Lösen Sie das System, nachdem sie den zweiten Fall durch einen
Zeilentausch behoben haben.
8. Für welche drei Zahlen k scheitert das Eliminationsverfahren? Gibt es
jeweils keine, eine oder unendlich viele Lösungen?
kx -{-Sy = 6
3x -{- ky = -6.
9. Wie lässt sich anhand der Zahlen bi und &2 feststellen, ob das
Gleichungssystem eine Lösung besitzt? Wie viele Lösungen gibt es?
Sx-2y = bi
6x - 4y = &2-
10. Zeichnen Sie die Geraden zu den Gleichungen x -hy = 5 und x -{-2y = 6,
und zu der Gleichung y = , die man durch Elimination erhält. Die
Gerade zu 3x - 4y = c geht durch die Lösung dieser Gleichungen, falls
c = gilt.
In den Aufgaben 11-20 wird das Eliminations verfahren auf 3x3-
Systemen und sein mögliches Versagen behandelt.
11. Formen Sie dieses System in obere Dreiecksform um:
2x-{-Sy-{-z =1
4x -h7y -hSz = 7
-2y-h2z = 6.
Markieren Sie die Pivotelemente, und lösen Sie das System durch
Rücksubstitution. Unter welchen Bedingungen genügen zwei Zeilenoperationen
zur Lösung des Systems?
12. Lösen Sie durch Vorwärtselimination und Rücksubstitution das System
2x-3y =3
4x -3y -{■ z = 7
2x- y-3z = 3.
Markieren Sie die Pivotelemente. Durch welche Zeilenoperationen
erzeugen Sie das Dreieckssystem?
2.2 Die Idee der Elimination 49
13. Durch welche Zahl d wird man zum Zeilentausch gezwungen, und wie
sieht das Dreieckssystem dann aus?
Ax -]- dy + z — 2
y- z = S.
Durch welche Zahl d wird das System singular, so dass es kein drittes
Pivotelement gibt?
14. Welcher Wert für b erzwingt einen Zeilentausch? Durch welches b wird
das System singular? Finden Sie für diesen Fall eine nichttriviale Lösung
{x,y,z).
X -\-by = 0
X -2y - z = 0
y-hz = 0.
15. (a) Konstruieren Sie ein 3 x 3-System, zu dessen Lösung zwei Zeilenver-
tauschungen nötig sind,
(b) Konstruieren Sie ein 3 x 3-System, für das das Eliminationsverfahren
durch eine Zeilenvertauschung einen Schritt weiterkommt, schließlich
aber mangels Lösbarkeit scheitert.
16. Wie weit lässt sich das Eliminationsverfahren für eine Matrix mit
identischer erster und zweiter Zeile durchführen? Welches Pivotelement fehlt,
wenn die Spalten 1 und 2 identisch sind?
2x-y-{-z = 0 2x-^2y-j-z = 0
2x - y -^ z = 0 4:X + 4y -^ z = 0
Ax-]-y + z = 2 6a: + 62/ + 2; = 2.
17. Konstruieren Sie ein 3 x 3-System mit 9 verschiedenen Koeffizienten auf
der linken Seite, dessen zweite und dritte Zeile im Verlauf des
Eliminationsverfahrens vollständig verschwinden.
18. Durch welche Zahl q wird dieses System singular, und durch welches
t erhält man in diesem Fall unendlich viele Lösungen? Finden Sie die
Lösung mit z = \.
X -h 4y - 2z = 1
x -{-7y - ßz = 6
Sy -hqz = t
50 2 Das Lösen linearer Gleichungen
19. (Besonders empfohlen) Es ist unmöglich, dass ein lineares
Gleichungssystem genau zwei Lösungen besitzt. Erklären Sie, warum.
(a) Welche Lösungen lassen sich aus zwei Lösungen {x, y, z) und (X, F, Z)
noch konstruieren?
(b) Wo schneiden sich drei Ebenen, die sich in zwei Punkten schneiden,
außerdem noch?
20. Wie kann es passieren, dass sich drei Ebenen nicht in einem Punkte
schneiden, wenn keine zwei von ihnen parallel zueinander sind?
Zeichnen Sie die Situation, so gut es geht. Finden Sie zu den Gleichungen
X -\- y -\- z = ^ und x — y — z = ^ eine dritte, so dass diese Situation
entsteht.
In den Aufgaben 21—23 kommen wir zu 4 X 4- und n X n-Systemen.
21. Bestimmen Sie die Pivotelemente und die Lösung dieser vier Gleichungen:
2x-\- y =0
x-\-2y-\- z =0
y -\-2z-\- t = 0
z +2t = 5
22. Das folgende System hat dieselben Pivotelemente und dieselbe rechte
Seite wie in Aufgabe 21. Wie unterscheiden sich die Lösungen (falls sie
sich überhaupt unterscheiden)?
2x- y =0
-x + 2y- z =0
- y + 2z- t = 0
- z + 2t = 5.
23. Erweitern Sie die Systeme in Aufgabe 21 und 22, indem Sie mit dem
A,2,1)- oder (—1,2, -1)-Muster fortfahren. Was ergibt sich als fünftes
Pivotelement, was als n-tes?
24. Finden Sie drei mögliche Systeme, aus denen dieses Dreieckssystem durch
das Eliminations verfahren entstanden ist:
X + y + z = 0
y + z = 0
Sz = 0.
2.3 Elimination mit Hilfe von Matrizen
51
25. Für welche drei Zahlen a ergeben sich bei der folgenden Matrix keine drei
Pivotelemente?
A =
a2 3
a a 4
a a a
26. Bestimmen Sie eine Matrix, die die Zeilensummen 4 und 8 hat und die
Spaltensummen 2 und s:
Matrix =
a b
c d
a + 6 = 4 a-\-c^ 2
c + d = 8' h-\-d = s'
_. Finden sie zwei
Die vier Gleichungen sind lösbar nur für 5 =
verschiedene Matrizen, die für diesen Fall eine Lösung darstellen.
2.3 Elimination mit Hilfe von Matrizen
Wir werden jetzt zwei Ideen zusammenführen — das Eliminationsprinzip und
die Matrizenrechnung. Wir wollen hiermit versuchen, die einzelnen Schritte
des Eliminationsverfahrens (und dessen Ergebnis) in der klarstmöglichen Art
und Weise darzustellen. Bei unseren 3 x 3-Beispielen konnten wir die Schritte
noch in Worten beschreiben. Für größere Systeme wäre es zwecklos, eine lange
Liste von Schritten aufzuschreiben. Wir werden sehen, wie die Subtraktion
des Vielfachen einer Zeile von einer anderen Zeile durch Matrizen ausgedrückt
werden kann.
Die Matrixform eines Unearen Gleichungssystems ist ^x = b, wobei b,x,
und A folgendes bedeuten:
1 Der Vektor b enthält die rechten Seiten der Gleichungen.
2 Der Vektor x enthält die Unbekannten. (Wir verwenden jetzt die
Bezeichnungen xi, X2, x^, ... statt a:,?/,z,..., weil uns eher die Buchstaben als
die Zahlen ausgehen.)
3 A ist die Matrix, die die Koeffizienten des Systems enthält.
Beispielsweise lässt sich das System aus dem letzten Abschnitt in der
wunderbar kurzen Form ^x = b schreiben:
B.11)
Dabei werden die neun Zahlen der linken Seite in der Matrix A zusammen-
gefasst. Diese Matrix wird nicht einfach links neben den Vektor x geschrieben,
sondern der Vektor wird mit ihr multipliziert. Die Regel, nach der der Vektor
55A mal x" definiert ist, wurde gerade so gewählt, dass sich aus dem Produkt
die drei Gleichungen ergeben.
2a:i + 4a:2 - 2x^ -
4a:i + 9a:2 - 80:3 ■-
2xi - 3x2 + 7xz ■-
= 2
= 8 entspricht
= 10
2 4-2"
4 9-3
-2-3 7
'xi'
X2
.^3.
=
2
8
10
52
2 Das Lösen linearer Gleichungen
Wiederholung: A mal x. Das Produkt „Matrix mal Vektor" ergibt einen
Vektor. Es liegt eine quadratische Matrix vor, wenn die Zahl der Gleichungen
(hier: drei) mit der Anzahl der Unbekannten übereinstimmt (hier ebenfalls
drei). Deshalb erhalten wir in unserem Beispiel eine 3 x 3-Matrix. Eine
allgemeine quadratische Matrix ist eine n x n-Matrix, für die der Vektor x im
n-dimensionalen Raum liegt. In unserem Beispiel liegt x also im
dreidimensionalen Raum.
Die Unbekannte ist x =
Xi
und die Lösung ist x =
Die Schlüsselidee ist die folgende: In der Form ^x = b werden
gleichzeitig die Zeilenform und die Spaltenform der Gleichungen ausgedrückt. Das
Produkt ^x lässt sich zeilenweise, aber auch spaltenweise berechnen:
^x = (-l)
2
4
-2
+ 2
4
9
-3
+ 2
-2
-3
7
=
2
8
10
B.12)
Wir werden diese Regel so oft benötigen, dass sie noch einmal hervorgehoben
werden soll:
2A Das Produkt Ax ist eine Linearkombinaiion der Spcdten von A:
Die Spalten werden mit den Komponenten von x multipliziert, d.li, .4x ist
der Vektor xi - (Spalte 1) -f ^.. + ar^ • (Spalte n).
Noch etwas zur Matrix-Notation: Der Eintrag in Zeile 1, Spalte 1 (also in
der linken oberen Ecke) wird an genannt. Der Eintrag in Zeile 1, Spalte 3
ist ai3, und der Eintrag in der 3. Zeile, 1. Spalte ist asi. (Für die Reihenfolge
der Indizes gilt also: Zeile vor Spalte.) Das Wort „Eintrag" für eine Matrix
entspricht dem Wort „Komponente" für einen Vektor. Die allgemeine Regel
ist also: Der Eintrag in Zeile z, Spalte j einer Matrix A heißt aij.
Beispiel 2.3.1 Für die folgende Matrix gilt üij = 2i+j, Damit ist also an =
3, ai2 = 4 und a2i = 5. So sieht das Produkt ^x mit Zahlen und mit
allgemeinen Variablen aus:
34
56
3-2 + 41
5-2 + 61
an ai2
Ö21 Ö22
Xi
=
aiiXi + ai2a:2
0'2lXi + a22X2
Zur Abwechslung haben wir diesmal zeilenweise multipliziert. Die erste
Komponente von ^x ist 6 + 4 = 10, also das Skalarprodukt der Zeile [3 4] mit
der Spalte B,1). Mit allgemeinen Variablen ist es das Produkt von [an ai2]
mit @:1,0:2).
2.3 Elimination mit Hilfe von Matrizen
53
Zur Berechnung der i-ten Komponente von ^x wird die Zeile i
herangezogen, also [an ai2 . ♦ • ain]- Mit der „Sigma-Notation" lässt sich dies kürzer
fassen:
2B Die «-te Komponente von ^x ist ömxj -jr 0^23^2 4. >.* 4^ »m^^n =
Das Symbol Yl steht für die Addition der Glieder hinter dem Symbol,
startend mit i = 1 und endend mit j = n, also startend mit anXi und endend
mit ainXji-
Die Matrix-Form eines Eliminationsschrittes
Die Schreibweise ^x = b ist eine handliche Form für die Originalgleichung.
Wie sieht es nun mit den Eliminationsschritten aus? In unserem Beispiel
wurde im ersten Schritt das zweifache der ersten Gleichung von der zweiten
subtrahiert; auf der rechten Seite wird das zweifache der ersten Komponente
von b von dessen zweiter Komponente subtrahiert:
Aus b =
10
wird b'
2
4
10
Wir wollen diese Subtraktion mit Hilfe von Matrizen ausdrücken! Wir
können dieses Resultat nämlich auch durch Multiplikation von b mit einer
geeigneten Eliminationsmatrix E erhalten:
Die Eliminationsmatrix ist E =
1 0 0
-2 1 0
0 0 1
1 0 0'
2 1 0
0 0 1
2"
8
10
=
" 2"
4
10
1 0 0"
2 1 0
0 0 1
'h'
62
h
=
Die Multiplikation mit E bewirkt, dass 2 mal Zeile 1 von Zeile 2 subtrahiert
wird, wie man auch an der allgemeinen Variablenform sieht:
bi
62 - 2 61
bs
Beachten Sie, dass 2 und 10 (also 61 und 63) unverändert bleiben. Das
liegt daran, dass die erste und die dritte Zeile der Eliminationsmatrix die
Einstein hat dies noch kürzer gefasst, indem er das Summenzeichen Yl wegließ.
Das wiederholt auftretende j bedeutete automatisch, dass über j summiert wird.
Außerdem schrieb er die Summe als a^Xj. Weil wir aber nicht Einstein sind,
schreiben wir das ^^-Zeichen hin.
54
2 Das Lösen linearer Gleichungen
entsprechenden Zeilen der Einheitsmatrix sind, die alle Vektoren unverändert
lässt. Die neue zweite Komponente ist die 4 = 62 -^ 26i, die nach dem ersten
Eliminationsschritt auf der rechten Seite entstand.
Diese „Eliminationsmatrizen" oder „Elementarmatrizen" wie E lassen
sich leicht beschreiben. Man nehme die Einheitsmatrix / und tausche eine
der Nullen durch den Multiphkator —l aus:
2C Dm MnheiUmmtrix hat Einträge 1 auf der Hanptdiagopalen und
Btetege O'übarätKröiiitVßas^flSbrt da^u, daas Ib ^n'b.;lär ^äIl#'VeKorÄ'
b 0t DieMlmmenMrfnatrim odar MimimMdnm^atrm Bij'^^di0das fti
fache der j-teix Zeile von Zeile % siibtrahiert, hat statt Aet Null an der StelÄ
(ij-^*): den Eintrag-t
Beispiel 2.3.2
/ =
1 00
0 10
001
und -£^31 =
r 1
0
-/
0
1
0
Ol
0
ij
Berechnet man / mal b, so erhält man wieder b. Berechnet man aber ^31 mal
b, so wird das /-fache der ersten Komponente von der dritten Komponente
subtrahiert. Im folgenden Beispiel erhalten wir auf diese Weise 9 — 4 = 5:
rioo"
010
001
"i"
3
9
=
"
3
9
und
1 0 0'
0 10
4 0 1
"r
3
9
=:
'll
3
5j
Dies alles passiert auf der rechten Seite der Gleichung ^x = b. Wie sieht
es auf der linken Seite aus? Wir hatten den Multiplikator Z = 4 so gewählt,
dass durch Subtraktion von 4 • (Pivotelement) eine Null entsteht. Sinn und
Zweck von E^i ist es, eine Null auf Position C,1) zu erzeugen —
daher die Notation.
Wir beginnen mit A und verwenden E's, um Nullen unterhalb der
Pivotelemente zu erzeugen (das erste E ist -£^21M und erhalten schließlich ein
Dreieckssystem. Wir wollen uns jetzt genauer die Vorgänge auf der linken
Seite betrachten — nämlich wie der Eliminationsprozess auf den Ausdruck
^x wirkt.
Zunächst ein kleiner Hinweis. Der Lösungsvektor bleibt während dieses
Prozesses derselbe; die Lösung wird durch die Elimination nicht verändert.
(Dies mag mehr als ein kleiner Hinweis sein.) Stattdessen wird die
Koeffizientenmatrix verändert. Wir beginnen mit ^x = b, multiplizieren diese
Gleichung mit E und erhalten EAx = Eh. Jetzt müssen wir die Matrix EA
bestimmen — das Ergebnis der Multiplikation E mal A.
2.3 Elimination mit Hilfe von Matrizen
55
Matrixmultiplikation
Die Frage ist also: Wie multipliziert man zwei Matrizen? Wenn die erste
dieser beiden eine Eliminationsmatrix (^21) ist, haben wir schon einen wichtigen
Hinweis. Wir kennen A, und wir wissen, wie sie nach dem Eliminationsschritt
aussieht. Damit alles zusammenpasst, hoffen und erwarten wir, dass
E =
mal
A^
gleich EA
r 2 4-2'
4 9-3
[-2-3 7
2 4-2"
0 1 1
-2-3 7]
ist.
In diesem Schritt werden die Zeilen 1 und 3 unverändert in EA
übernommen, nur Zeile 2 ändert sich. Das Doppelte der ersten Zeile wurde von der
zweiten Zeile subtrahiert. Die Matrixmultiplikation liefert hier dasselbe
Ergebnis wie das Eliminations verfahren, und das neue Gleichungssystem lautet
EA^ = Eh.
Das sieht alles einfach aus, aber es verbirgt sich eine subtile Idee dahinter.
Multipliziert man beide Seiten der Gleichung mit E, so erhält man E{Ax) =
Eh. Wir möchten nämlich die Matrixmultiplikation so gestalten, dass dies
mit {EA)x. = Eh übereinstimmt. Das eine ist E mal Ax, das andere EA mal
x — und sie stimmen überein! Wir benötigen keine Klammern und schreiben
einfach EAx = b.
Multipliziert man drei Matrizen ABC, so kann man zunächst BC oder AB
ausrechnen. Darum geht es im „Assoziativgesetz", analog zu 3-D-5) = C-4)-5.
Einmal erhalten wir 3 mal 20, das andere mal 12 mal 5, aber beides ergibt 60.
Diese Regel scheint so offensichtlich zu gelten, dass man sich schwer vorstellen
kann, sie könnte nicht erfüllt sein. Aber das „Kommutativgesetz" 3 • 4 = 4 • 3
scheint noch offensichtlicher zu gelten. Für Matrizen ist aber oft das Produkt
EA verschieden von dem Produkt AE.
2D Assoziativgesetig: A(B0^ ä [(ÄB)ß
KEIN KommntBiW^met^: Oft gätÄB^BÄ.
Es gibt noch eine weitere Bedingung, die wir an die Matrixmultiplikation
stellen müssen. Wir wissen, wie wir A mal x oder E mal b zu berechnen
haben. Die Regel zur Berechnung von Matrix-mal-Matrix sollte mit der
alten Matrix-mal-Vektor Regel zusammenpassen. Angenommen, die Matrix B
habe nur eine Spalte b. Dann sollte das Matrix-Matrix-Produkt EB gleich
dem Matrix-Vektor-Produkt^Jb sein. Es soll weiterhin möglich sein, Matrizen
spaltenweise zu multiplizieren:
Hat die Matrix B die Spalten bi, b2, b^, so sollte EB
die Spalten Ebi, Eb2, Eb^ haben.
56
2 Das Lösen linearer Gleichungen
1 0 0"
2 10
0 0 1
2"
4
-2
=
2"
0
-2]
Diese Bedingung wird von der oben eingeführten Matrixmultiplikation
erfüllt (nur dass dort A steht statt B). MultipUziert man die erste Spalte mit
E, so erhält man die erste Spalte des Ergebnisses:
und ebenso für die Spalten 2 und 3.
Dies ist eine Bedingung an die Spalten, wohingegen das Eliminations
verfahren mit Zeilen arbeitet. Bei einer dritten Herangehens weise (siehe nächster
Abschitt) beschreibt man jeden einzelnen Eintrag des Produktes zweier
Matrizen. Das Schöne an der Matrixmultiplikation ist, dass alle drei Ansätze
(über die Zeilen, die Spalten oder ganze Matrizen) das richtige Ergebnis
liefern.
Die Matrix Pij für einen Zeilentausch
Um die Zeile j von der Zeile i zu subtrahieren, benutzen wir Eij. Um Zeilen
zu vertauschen oder zu „permutieren", verwenden wir eine andere Matrix
Pij. Erinnern wir uns, wofür ein Zeilentausch nötig war: Wenn eine Null auf
der Pivotposition auftaucht, weiter unten aber noch Elemente ungleich Null
vorhanden sind. Indem man zwei Zeilen vertauscht, erhält man damit ein
Pivot element und kann mit dem Eliminations verfahren fortfahren.
Wie sieht die Matrix P23 zur Vertauschung von Zeile 2 mit Zeile 3 aus?
Man erhält sie, indem man die Zeilen der Einheitsmatrix / vertauscht:
P23 —
100
001
010
Dies ist eine Zeilenvertauschungsmatrix. Die Multiplikation mit P23
bewirkt eine Vertauschung der zweiten und dritten Komponente jedes
Spaltenvektors. Deshalb vertauscht sie auch die zweite und dritte Zeile jeder Matrix.
00"
001
010
"
3
5
=
T
5
3
rioo'
001
^010
4 1'
003
065
=
41'
065
0 0 3J
und
Rechts sieht man, dass P23 seinen Zweck erfüllt: Wo eine Null auf der zweiten
Pivotposition steht und eine 6 darunter, setzt ein Zeilentausch die 6 in die
Pivotposition.
Beachten Sie, wie diese Matrizen wirken. Sie stehen nicht einfach nur so
da. Bald werden wir auf Permutationsmatrizen treffen, die die Reihenfolge
mehrerer Zeilen vertauschen. Die Zeilen 1, 2 und 3 können auf die Positionen
2.3 Elimination mit Hilfe von Matrizen
57
3 1, 2 umgesetzt werden. Unser P23 ist eine spezielle Permutationsmatrix,
die nur auf die Zeilen 2 und 3 wirkt.
2E Die Permutationsmatrix Pij vertauscht die Zeilen i und j der
Matrix, mit der sie multipliziert wird* Pi^ entsteht aus d^ Einheit^Bätrix
durch Vertauschen der Zeilen i und j.
Um die Gleichungen 1 und 3 zu vertauschen,
multipliziere mit P13 = 010.
Normalerweise wird kein Zeilentausch benötigt. Die Chancen stehen gut,
dass das Eliminations verfahren nur mit Matrizen Eij durchführbar ist. Falb
benötigt, stehen die Pij aber bereit.
Die erweiterte Matrix A'
Dieses Buch wird uns weit über das Eliminationsverfahren hinausführen. Es
gibt unüberschaubar viele praktische Anwendungen für die
Matrizenmultiplikation. Unser bester Ausgangspunkt war das Produkt einer quadratischen
Matrix E mit einer quadratischen Matrix A^ einfach deshalb, weil wir im
Zusammenhang mit dem Eliminations verfahren darauf gestoßen sind, und weil
wir wissen, welches Ergebnis EA wir erwarten sollten. Der nächste Schritt
wird darin bestehen, rechteckige Matrizen A zuzulassen. Auch dies hängt mit
unserem Gleichungssystem zusammen, denn wir fügen die rechte Seite b zu
einer Matrix A hinzu.
Die Kernidee ist, dass das Eliminationsverfahren sowohl auf ^ als auch auf
b wirkt, und zwar in derselben Weise. Wir können h einfach der Matrix
A als zusätzliche Spalte hinzufügen und das Eliminationsverfahren
durchführen. Die Matrix A wird um b erweitert:
Erweiterte Matrix A' — [Ä ^ b] =
2 4-2 2
4 9--3 8
-2-3 7 10
Die Matrix A' stellt jetzt das ganze Gleichungssystem dar: die rechte wie
die linke Seite. Das Eliminationsverfahren arbeitet mit ganzen Zeilen von A'.
Die Unke wie die rechte Seite werden mit E multipliziert, um das zweifache der
ersten Gleichung von Gleichung 2 zu subtrahieren. Mit A' = [A h] geschieht
dies in einem Schritt:
EA' =
1 0 0"
2 1 0
0 0 1
'2 4-2 2"
4 9-38
-2-3 7 10
=
2 4-2 2
0 114
-2-3 7 10
58 2 Deis Lösen linearer Gleichungen
Die neue zweite Zeile enthält die Einträge 0,1,1,4, d.h. die neue zweite
Gleichung lautet X2+X3 = 4. Beide Bedingungen an die Matrixmultiplikation
werden beachtet:
Z (zeilenweise): Jede Zeile von E wirkt auf A' und Hefert eine Zeile von EA'.
S (spaltenweise): E wirkt auf jede Spalte von A' und Hefert so die Spalten
von EA',
Beachten Sie das Wort „wirkt" — es drückt etwas Wesentliches aus:
Matrizen „handeln"! Die Matrix A wirkt auf x, um b zu liefern. Die Matrix E
wirkt auf A^ um zu EA liefern. Der gesamte Eliminationsprozess ist eine
Folge von Zeilenoperation, Operationen, die Matrizen durch Multiphkation an
dem System durchführen. A geht über in E21A, was seinerseits in £^31 £^21^
verwandelt wird. Schließlich ist £^32^31 £21^ eine Dreiecksmatrix.
Wenn wir mit A' arbeiten, so ist die rechte Seite immer eingeschlossen.
Dann wird aus A' erst E21A', dann ES1E21A' und schließlich das dreieckige
Gleichungssystem £32 £31^21^'•
Nun aber erst einmal ein paar Übungsaufgaben zur Multiplikation mit E,
bevor wir die allgemeine Regel für die Matrixmultiplikation aufstellen.
Die wesentlichen Punkte
l.^x bedeutet xi mal (Spalte 1) H h Xn mal (Spalte n).
2. Multipliziert man ^x = b mit E21, so subtrahiert man das ^21-fache der
ersten Zeile von der zweiten Zeile. Dabei ist -^21 der Eintrag B,1) der
Matrix E21.
3. Führt man ihn mit der erweiterten Matrix [A b] aus, so ergibt dieser
Schritt [E21A E2ih].
4. Bei der Multiplikation AB kann man jede Spalte von B für sich mit A
multiplizieren.
Aufgaben 2.3
Die Aufgaben 1—14 beschäftigen sich mit Eliminationsmatrizen.
1. Welche 3 x 3-Matrizen erzeugen diese Eliminationsschritte?
(a) E21 subtrahiert 5 mal Zeile 1 von Zeile 2.
(b) £^32 subtrahiert -7 mal Zeile 2 von Zeile 3.
(c) P12 vertauscht die Zeilen 1 und 2.
2. Wendet man zunächst E21 und dann £^32 (aus Aufgabe 1) auf die Spalte
b = A,0,0) an, so ergibt sich £32£2ib = . Wendet man £32 vor
£21 an, so erhält man E2iEs2h = . £21^32 unterscheidet sich also
dadurch von £32^215 dass Zeile keinen Einfluss auf Zeile
hat, wenn £32 zuerst angewendet wird.
2.3 Elimination mit Hilfe von Matrizen
59
3. Welche drei Matrizen ^21,^31 und E32 bringen A in eine Dreiecksform
[/? , .
[110
A := 4 6 1 I und ^32^31^21^ = U,
[-2 2 0
Mulitplizieren Sie die E's zu einer Matrix M aus, die das ganze
Eliminationsverfahren darstellt: MA = U.
4. Fügen Sie in der Rechnung aus Aufgabe 3 die Spalte b = A,0,0) als vierte
Spalte hinzu. Führen Sie das Eliminationsverfahren auf der erweiterten
Matrix A' durch und lösen Sie Ax. = b.
5. Nehmen Sie an, dass eine 3 x 3-Matrix mit a33 = 7 als drittes Pivotelement
die Zahl 2 hat. Ändert man nun a33 zu 11, so ergibt sich als Pivotelement
, und ändert man a33 zu , so wird die Matrix singular.
6. Falls jede Spalte einer Matrix A ein Vielfaches von A,1,1) ist, so ist auch
^x immer ein Vielfaches von A,1,1). Zeigen Sie dies an einem 3x3-
Beispiel. Wie viele Pivotelemente erzeugt das Eliminations verfahren?
7. Nehmen wir an, eine Matrix E^\ subtrahiert das 7-fache der ersten Zeile
von Zeile 3. Um diesen Schritt rückgängig zu machen, müsste man 7 mal
Zeile zu Zeile ieren. Welche Matrix i?3i (das ist die
inverse Matrix zu E'n) führt diesen Schritt aus?
8. Betrachten wir noch einmal E^i aus der vorherigen Aufgabe. Welche
Matrix R^i wird durch sie in die Einheitsmatrix / umgeformt? Für dieses
i?3i gilt also EsiRsi = /, wohingegen wir in Aufgabe 7 i^3i^3i = /
hatten. Die Matrizen Esi und Rsi kommutieren also.
9. (a) Eine Matrix E21 subtrahiere Zeile 1 von Zeile 2, dann vertausche eine
Matrix P23 die Zeilen 2 und 3. Welche Matrix M = P23E21 erledigt
beide Schritte in einem?
(b) Nun vertausche zunächst P23 die Zeilen 2 und 3, und dann subtrahiere
E31 Zeile 1 von Zeile 3. Welche Matrix M = E31P23 erledigt dies in
einem? Erklären Sie, warum beide Matrizen M gleich sind, die E's
aber verschieden.
10. Erzeugen Sie eine Matrix mit an = a22 = a33 = 1, für die das
Eliminationsverfahren zwei negative Pivotelemente erzeugt. (Das erste ist ja
bereits 1.)
11. Führen Sie die folgenden Matrixmultiplikationen durch:
10
5 1
22
00
1
1
1
0 0
1 0
0 1
1 23
1 31
140
60
2 Das Lösen linearer Gleichungen
12. Erklären Sie das Folgende: Besteht die dritte Spalte einer Matrix B nur
aus Nullen, so ist auch die dritte Spalte von EB eine Nullspalte, und
zwar für jedes E. Ist aber die dritte Zeile von B eine Nullzeile, so muss
die dritte Zeile von EB nicht liull sein.
13. Für diese 4 x 4-Matrix benötigt man Eliminationsmatrizen ^21, -£32 und
^43. Welche Matrizen sind dies genau?
A =
2-1 0 0
-1 2-1 0
0-1 2-1
0 0-1 2
14. Notieren Sie die 3 x 3-Matrix mit aij = 2i — 3j. Für diese Matrix gilt
032 = O5 ciber während des Eliminations Verfahrens wird trotzdem eine
Matrix £2 zur Erzeugung einer Null an dieser Stelle benötigt. Welcher
vorherige Schritt entfernt die Null, und wie sieht E32 aus?
In den Aufgaben 15—22 geht es um das Erstellen und Multiplizieren
von Matrizen.
15. Bringen Sie diese wohlbekannten Aufgaben in eine Matrixform Ax = b:
(a) X ist doppelt so alt wie Y, und die Summe ihrer Alterszahlen ist 33.
(b) Eine Gerade y = ma: + c verlaufe durch die Punkte (a:, y) = B,5) und
C,7). Bestimmen Sie m und c.
16. Die Parabel y = a+bx+cx'^ verlaufe durch die Punke {x, y) = A,4), B,8)
und C,14). Bestimmen Sie eine Matrixgleichung für die drei Unbekannten
a, b und c. Lösen Sie diese mit dem Eliminationsverfahren.
17. Berechnen Sie die Produkte EF und FE:
E =
100
alO
601
F =
100
010
Ocl
Berechnen Sie auch E'^ = EE und F^ = FF.
18. Multiplizieren Sie diese Zeilenvertauschungsmatrizen in beiden
Reihenfolgen PQ und QP:
P =
0 10
100
001
und Q =
001
010
100
Berechnen Sie auch P^ = PP und (PQ)'^ = PQPQ.
2.3 Elimination mit Hilfe von Matrizen
61
19. (a) Angenommen, alle Spalten einer Matrix B sind identisch. Dann sind
alle Spalten von EB identisch, da jede einzelne gleich E mal
ist.
(b) Nehmen wir nun an, alle Zeilen von B seien identisch. Zeigen Sie mit
einem Beispiel, dass die Zeilen von EB nicht identisch sein müssen.
20. Falls E die erste zur zweiten Zeile addiert und F die zweite zur ersten,
stimmen dann EF und FE überein?
21. Die Einträge einer Matrix A seien a^j, die des Vektors x seien Xj. Die
Matrix £1 subtrahiere die erste von der zweiten Zeile. Geben Sie Formeln
an für
(a) die dritte Komponente von Ax;
(b) den Eintrag B,1) von EA\
(c) die Komponente B,1) von E'x und
(d) die erste Komponente von EAx..
22. Die Eliminationsmatrix E = \__\ J] subtrahiert das 2-fache der ersten
Zeile von A von seiner zweiten Zeile. Dies ergibt das Produkt EA, In der
umgekehrten Reihenfolge AE subtrahiert man 2 mal von A von
. (Sehen Sie sich das anhand eines Beispiels an.)
In den Aufgaben 23-26 wird die um die Spalte h erweiterte
Matrix A' betrachtet.
23. Führen Sie das Eliminations verfahren auf der erweiterten 2 x 3-Matrix
A' durch. Wie sieht das Dreieckssystem t/x = c aus, was ist die Lösung
X?
'2 31
Ax =
41
1
17
24. Führen Sie das Eliminations verfahren für die erweiterte 3 x 4-Matrix A'
durch. Woran erkennt man, dass dieses System keine Lösung hat?
[1 23"
234
357
X
y
z
=
"ll
2
ej
Ax =
Ändern Sie die letzte Zahl 6 so ab, dass eine Lösung existiert.
25. Die Gleichungen Ax = b und Ax* = b* enthalten dieselbe Matrix A.
(a) Welche zweifach erweiterte Matrix A" kann man verwenden, um beide
Gleichungen gleichzeitig zu lösen?
(b) Lösen Sie diese beiden Gleichungen, indem Sie das Eliminations
verfahren auf eine 2 x 4-Matrix A" anwenden:
'14"
2 7
X
y.
=
1"
0
und
14'
2 7
X
y.
=
"
i_
62
2 Das Lösen linearer Gleichungen
26. Wählen Sie die Einträge a, b, c und d der folgenden erweiterten Matrix
so, dass es (a) keine und (b) unendlich viele Lösungen gibt.
A'
123a
045b
OOdc
Welcher dieser Einträge hat keinen Einfluss auf die Lösbarkeit?
27. Eine Herausforderung: Es sei Eij die 4 x 4-Einheitsmatrix mit einer
zusätzlichen 1 an Position {i,j), wobei i > j gelte. Beschreiben Sie die
Matrix EijEkh In welchem Fall ist sie gleich EkiEij? (Betrachten Sie
zunächst einige Beispiele.)
'12'
34
00
+
2"
44
99
=
'3 41
78
99
ri2i
34
00
=
4"
68
00
2.4 Regeln für Matrixoperationen
Lassen Sie uns mit den Grundlagen beginnen. Eine Matrix ist eine rechteckige
Anordnung von Zahlen oder „Einträgen". Besteht A aus m Zeilen und n
Spalten, so ist A eine m x n-Matrix. Matrizen lassen sich addieren, wenn
sie dieselbe Gestalt (d.h. dieselbe Anzahl Zeilen und Spalten) haben, und
sie lassen sich mit Konstanten c multiplizieren. Es folgen einige Beispiele für
Ausdrücke wie A + B oder 2A, jeweils mit 3 x 2-Matrizen:
und 2
Man addiert Matrizen ganz so wie Vektoren — jeden Eintrag für sich.
Man könnte sogar einen Spaltenvektor als einspaltige (d.h. n = 1) Matrix
auffassen. Durch Multiplikation mit -1 (also durch Vorzeichenumkehr in
jedem Eintrag) erhält man die Matrix - A; und addiert man A zu - A, so erhält
man die Nullmatrix, bei der alle Einträge Null sind.
Achtung! Die 3 x 2-Nullmatrix ist von der 2 x 3-Nullmatrix zu
unterscheiden! Bei Matrizen hat sogar die Null (viele) verschiedene Formen. Dies ist
aber alles beinahe selbstverständlich.
Der Eintrag in Zeile i und Spalte j heißt aij oder A(i, j). Der
Eintrag 032 befindet sich also in der dritten Zeile und der zweiten Spalte, und
die n Einträge der ersten Zeile sind an, 012, • • •, ^in, der untere linke Eintrag
der Matrix wird mit ümi bezeichnet, und der untere rechte mit amn-
Noch einmal: der Zeilenindex i läuft von 1 bis m, und der Spaltenindex j
von 1 bis n.
Die Addition von Matrizen ist noch ziemlich leicht nach zu vollziehen.
Interessanter wird es mit der Matrixmultiplikation, Wann kann man A
mit B multiplizieren, und wie sieht das Produkt AB dann aus? Die beiden
Matrizen oben (jeweils 3x2) lassen sich nicht miteinander multiplizieren,
denn sie erfüllen die folgende wichtige Bedingung nicht:
2.4 Regeln für Matrixoperationen 63
*
*
CLi6
yl ist 4 X 5
* * bli * * *
b2y
hj
J5 ist 5 X 6
* 1
* * {AB)ij * * *
*
* J
AB ist 4 X 6
Abb. 2.8. In der Gleichung sind i
(Spalte 3) = Ua2kbk3-
2 und j = 3. {ABJ3 ist dann (Zeile 2) •
Das Produkt AB existiert, falls die Anzahl der Spalten
von A der Anzahl der Zeilen von B entspricht.
Hat A also zwei Spalten, so muss B zwei Zeilen haben. Für eine 3x2-
Matrix A kann B beispielsweise von der Form 2x1 (ein Spaltenvektor) oder
2x2 (eine quadratische Matrix) oder 2 x 20 sein. In allen diesen Fällen lässt
sich jede Spalte von B mit A multiplizieren. Das Ergebnis AB ist dann, je
nachdem, eine 3 x 1-, eine 3x2- oder eine 3 x 20-Matrix.
Nehmen wir an, A sei eine m x n-Matrix und B eine n x p-Matrix. In
diesem Fall lässt sich A mit B multiplizieren, und das Produkt ist eine mxp-
Matrix.
m Zeile^i
n Spalten
n Zeilen
p Spalten
m Zeilen
p Spalten
Einen Extremfall stellt der Fall „Zeile mal Spalte" dar. Hier wird eine
1 X n-Matrix mit einer n x 1-Matrix multipliziert, was eine 1 x 1-Matrix
ergibt. Diese Zahl ist aber gerade das „Skalarprodukt".
Tatsächlich ist das Produkt AB in jedem Fall eine Matrix, deren Einträge
lauter Skalarprodukte sind. Der obere linke Eintrag A,1) von AB
beispielsweise ist gerade (Zeile 1 von A) • (Spalte 1 von B). Man multipliziert also zwei
Matrizen, indem man alle diese Skalarprodukte „Zeile mal Spalte" berechnet.
2F Der Eintrag in Zeile i und Spalte j von AB ist
(Zeile f von-4)' (Spalte jf von B). . "" ' '
In Abbildung 2.8 betrachten wir die zweite Zeile (i = 2) einer 4 x 5-Matrix
A sowie die dritte Spalte {j = 3) einer 5 x 6-Matrix B. Das Skalarprodukt
dieser beiden bildet den Eintrag in Zeile 2, Spalte 3 von AB. Die Matrix AB
hat so viele Zeilen wie A (vier Zeilen) und so viele Spalten wie B.
64
2 Das Lösen linearer Gleichungen
Beispiel 2.4.1 Quadratische Matrizen lassen sich dann und nur dann
miteinander multiplizieren, wenn sie dieselbe Größe haben:
^1 r
2-1
22'
34
=
6"
lOj
Das erste Skalarprodukt ist l-2+l'3 = 5. Die anderen drei Skalarprodukte
ergeben 6, 1 und 0. Für jedes Skalarprodukt benötigt man zwei
Multiplikationen und damit insgesamt 8 Multiplikationen zur Berechnung des Produktes
der Matrizen.
Das Produkt AB zweier n x n-Matrizen A und B ist wieder eine n x n-
Matrix. Diese enthält n^ Skalarprodukte, zu deren Berechnung man je n
Multiplikationen benötigt. Die Berechnung von AB umfasst n^ ein-
zelne Multiplikationen. Für n = 100 hat man also schon eine Million
Multiplikationen durchzuführen, und für n = 2 immerhin n^ = 8.
Bis vor kurzem gingen die Mathematiker davon aus, dass die
Multiplikation AB notwendigerweise 2^ = 8 einzelne Multiplikationen erfordert. Dann
fand jemand eine Möglichkeit, zwei 2 x 2-Matrizen mit 7 einzelnen
Multiplikationen (und zusätzlichen Additionen) zu multiplizieren. Indem man nxn-
Matrizen in 2 x 2-Blöcke zerlegt, lässt sich diese Idee dazu nutzen, auch für
große Matrizen mit weniger Operationen auszukommen. Statt n^ kommt man
damit auf unter n^'^, und dieser Exponent lässt sich noch weiter senken^. Die
beste Methode erreicht im Augenblick n^'^^^, aber dieser Algorithmus ist so
kompliziert, dass man im wissenschaftlichen Rechnen ganz normal vorgeht
— mit n^ Skalarprodukten und je n Multiplikationen pro Skalarprodukt.
Beispiel 2.4.2 Sei A ein 1 x 3-Zeilenvektor und ^ ein 3 x l-Spaltenvektor. In
dem Fall ist AB eine 1 x 1-Matrix: das Skalarprodukt. Das Produkt B mal
A hingegen {Spalte mal Zeile) ist eine „richtige" Matrix:
Spalte mal Zeile:
[12 3] =
000
123
246
Ein „Zeile mal Spalte"-Produkt heißt auch „inneres Produkt" — das ist
nur ein anderer Name für das Skalarprodukt. Im Gegensatz dazu nennt man
das Produkt „Spalte mal Zeile" auch „äußeres Produkt". Diese beiden Fälle
sind die Extremfälle der Matrixmultiplikation, mit sehr „schlanken"
Matrizen. Aber auch diese Fälle folgen der allgemeinen Regel: (n x 1) mal A x n)
ergibt {nx n).
^ Vielleicht lässt sich der Exponent sogar bis auf 2 drücken. Keiner größeren Zahl
scheint eine besondere Bedeutung zuzukommen.
2.4 Regeln für Matrixoperationen 65
Zeilen und Spalten von AB
Im Ergebnis wird A mit jeder Spalte von B multipliziert, was eine Spalte des
Produkts AB ergibt. Diese Spalte ist eine Kombination der Spalten von A.
Jede Spalte von AB ist eine Linearkombination der Spalten von A.
Das ist das Spaltenbild der Matrixmultiplikation.
Eine Spalte von AB ist A • {Spalte von B).
Im Zeilenbild sind die Rollen vertauscht. Jede Zeile von A wird mit der
ganzen Matrix B multipliziert, um eine Zeile von AB zu ergeben. Diese ist
eine Kombination der Zeilen von B.
23"
Zeile i von A ]
456
789
= [ Zeile i von AB].
Wir sind den Zeilenoperationen {E mal A) im Eliminationsverfahren
begegnet, und wir erkennen eine Kombination von Spalten in dem Ausdruck
^x. Jetzt sehen wir in der Matrixmultiplikation das „Zeilen-Spalten-Bild"
mit den Produkten von Zeilen mit Spalten als Matrixeinträgen. Glauben Sie
es, oder glauben Sie es nicht: Es gibt auch ein „Spalten-Zeilen-Bild''
der Matrixmultiplikation. Dass Spalten von A multipliziert mit den
Zeilen von B ebenfalls das Produkt AB ergeben, ist nicht jedem geläufig. Wir
werden mehr davon im nächsten Beispiel (S. 67) sehen.
Die Gesetze der Matrixoperationen
Erlauben Sie mir, sechs Regeln, denen Matrizen gehorchen, nur kurz zu
erwähnen, und hingegen mehr Gewicht auf eine Gleichung zu legen, die sie
nicht erfüllen. Im folgenden können die Matrizen quadratisch oder rechteckig
sein, ihre Summe A + B genügt in jedem Fall diesen drei Additionsgesetzen:
A-\- B = B + A (Kommutativgesetz)
c{A + B) = cA + cB (Distributivgesetz)
A + {B + C) = {A + B) + C (Assoziativgesetz).
Die richtigen Dimensionen für das Produkt AB sind uns bekannt: mx n
kann mit n x p multipliziert werden und ergibt m x p. Die Multiplikation
gehorcht ebenfalls drei Gesetzen, zu denen aber nicht das Kommutativgesetz
AB = BA zählt:
AB :^ BA (Das Kommutativgesetz wird in der Regel verletzt.)
C{A -h B) = CA + CB (linksseitiges Distributivgesetz )
{A + B)C = AC + BC (rechtsseitiges Distributivgesetz )
A{BC) = {AB)C (Assoziativgesetz)(üT/ammern sind unnötig).
66
2 Das Lösen linearer Gleichungen
Sind A und B nicht quadratisch, so hat AB eine andere Gestalt als BA, die
Matrizen können also nicht gleich sein — selbst wenn beide Multiplikationen
möglich sind. Auch für quadratische Matrizen zeigt fast jedes Beispiel, dass
AB nicht dasselbe ist wie BA:
AB =
^0 0'
10
Ol'
0 0
=
0 0'
Ol
aber BA =
roi"
00
0 0'
10
=
10'
0 0
Andererseits gilt immer AI = lA. Alle quadratischen Matrizen
kommutieren also mit /, und auch mit den Vielfachen cl. Umgekehrt kommutieren
auch genau die Matrizen cl mit allen anderen quadratischen Matrizen.
Das Gesetz A{B + C) = AB + AC lässt sich Spalte für Spalte beweisen,
fangen Sie einfach mit A{h + c) = ^b + Ac für die jeweils ersten Spalten b
und c an. Dieses Gesetz ist der Schlüssel für alles weitere — Linearität der
Matrixmultiplikation.
Die Regel A{BC) = {AB)C besagt, dass man entweder BC oder
AB zuerst ausrechnen kann. Der direkte Beweis dieser Regel ist ziemlich
kompliziert (s. Aufgabe 16), aber dieses Gesetz ist enorm nützlich. Wir haben
es oben schon betont, es ist der Schlüssel zur Matrixmultiplikation.
Für den Spezialfall, dass A = B = C = einer quadratischen Matrix ist,
wird aus dieser Regel die Gleichung A • A^ = A^ - A. Egal in welcher
Reihenfolge, wir erhalten A^. Diese Potenzen von Matrizen gehorchen denselben
Regeln wie die Potenzen von Zahlen:
A^ ^ AAA^^^A (p Faktoren) (A^)(^^) ^4?^^ (A^)^ = A^^.
Dies sind die uns bekannten Potenzrechenregeln. A^ mal A'^ ist A^ (d.h.
sieben Faktoren A hintereinander), und A^ hoch vier ist A^^ (also zwölf A's
hintereinander). Für 0 und negative p und q gelten diese Regeln immer noch,
falls es eine „ — 1. Potenz" von A gibt — also die inverse Matrix A~^. In
diesem Fall ist A^ = I die Einheitsmatrix (sozusagen Null Faktoren A).
Für eine Zahl a gilt a~^ = ^. Die Inverse einer Matrix schreibt man
A~^. (Sie ist niemals I/A, mit der Ausnahme, dass genau die Schreibweise
in MATLAB erlaubt ist.) Jede Zahl außer der Null hat ein Inverses, aber bei
Matrizen ist es ein zentrales Problem der Linearen Algebra, herauszufinden,
ob eine Matrix eine Inverse besitzt. In Abschnitt 2.5 werden wir anfangen,
darauf eine Antwort zu geben.
Dieser Abschnitt besteht im Wesentlichen aus einer Liste von Regeln, die
besagen, wann und wie man A und B multiplizieren kann.
Blockmatrizen und blockweises Multiplizieren
Wir müssen einen weiteren Punkt über Matrizen ansprechen. Matrizen
können in Blöcke zerlegt werden, die ihrerseits kleinere Matrizen sind. Dies
2.4 Regeln für Matrixoperationen
67
ergibt sich oft ganz natürlich, wie zum Beispiel bei dieser 4 x 6-Matrix, die
sich in 2 X 2-Blöcke, die alle Einheitsmatrizen sind, zerlegen lässt.
A =
" 1
0
1
. 0
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0
0 ■
1
0
1.
///
///
Eine weitere 4 x 6-Matrix B mit zu A passenden Blockgrößen lässt sich
zu A blockweise zu A-\- B addieren.
Wir sind den Blockmatrizen schon einmal begegnet, als wir den Vektor
b der rechten Seiten eines Gleichungssystems rechts neben die
Koeffizientenmatrix setzten und damit die „erweiterte Matrix" erhielten. Diese Matrix
A' = [A b] bestand aus zwei Blöcken unterschiedlicher Größe, und als wir
sie mit einer Eliminationsmatrix E multiplizierten, erhielten wir [EA Eh]
— es ist also kein Problem, blockweise zu multiplizieren, solange die Größen
zueinander passen:
2G Blockweise Mtiltipiakation Pa^st die Auffeüung te S^^^
zu der der;Zeiteii yptt B; Sb^kanii man ÄS BIodfc#llse atiäMi£öpli^li^Ät;\^
^11 Ai2
A21 A22
Bn
B21
^11^11 + A12B21
A21B11 + A22B21
: ßM)
Dieselbe Gleichung gilt für Zahlen, die wir ja auch als 1 x 1-Blöcke auffassen
können. Wir müssen darauf achten, die Blöcke von A vor denen von B stehen
zu lassen, weil das umgekehrte Produkt BA etwas anderes sein kann (und
meistens sein wird). Die Aufteilung der Zeilen von A (also die Blöcke, die eine
Spalte bilden) bestimmt die Aufteilung der Zeilen von AB, und die Aufteilung
der Spalten von B finden wir ebenfalls in derjenigen von AB wieder.
Das Wesentliche: Teilt man Matrizen in Blöcke auf, so sieht man oft
leichter, wie sie wirken. Das Beispiel der Blockmatrix aus lauter /'s oben ist viel
leichter durchschaubar als die 4 x 6-Matrix A, aus der sie entstand.
Beispiel 2.4.3 (Wichtig!) Betrachten wir die einzelnen Spalten von A als
Blöcke, und die Zeilen einer Matrix B. Die Blockmultiplikation von AB
besteht dann aus einzelnen Multiplikationen der Form Spalte mal Zeile:
AB =
ai
I
bi
— bn —
aibi H h a.nhn
B.14)
Hier erkennen wir eine weitere Möglichkeit, Matrizen zu multiplizieren.
Vergleichen wir sie mit der üblichen Methode „Zeile mal Spalte". Dabei ergab
68
2 Das Lösen linearer Gleichungen
sich der Eintrag A,1) von AB als Zeile 1 von A mal Spalte 1 von B. Jetzt
erhalten wir aus dem Produkt „Spalte 1 von A mal Zeile 1 von ß" eine volle
Matrix, nicht nur eine Zahl. Sehen Sie sich dieses Beispiel an:
14
15
32
10
1
1
3 2
32
[S2j +
[10]
+
40
50
B.15)
Wir brechen hier die Rechnung ab, damit man sieht, wie hier Spalten mit
Zeilen multipliziert werden. Eine 2 x 1-Matrix (eine Spalte) multipliziert mit
einer 1 x 2-Matrix (also einer Zeile) ergibt, wie wir gesehen haben, eine 2x2-
Matrix — das äußere Produkt.
Addiert man nun die beiden Matrizen in B.15), so erhält man die richtige
Antwort AB — für den Eintrag oben links zum Beispiel 3-1-4 = 7, was mit
dem Skalarprodukt von A,4) mit C,1) übereinstimmt.
Zusammenfassung: Multipliziert man auf die übliche Art, so berechnet man 4
Skalarprodukte mit insgesamt 8 Multiplikationen. Bei der „Spalten mal Zei-
len"-Methode, erhält man zwei volle Matrizen, zu deren Berechnung jeweils 4
Multiplikationen nötig waren — also insgesamt wieder 8 Multiplikationen. In
beiden Fällen sind es sogar genau dieselben Multiplikationen und Additionen,
sie werden lediglich in verschiedenen Reihenfolgen ausgeführt.
Beispiel 2.4.4 (Blockweise Elimination) Angenommen, die erste Spalte von
A enthalte die Zahlen 2,6,8. Um an Stelle der 6 und der 8 Nullen zu erzeugen,
multiplizieren wir die Pivot-Zeile mit 3 bzw. 4 und subtrahieren Sie von
den anderen beiden Zeilen. Diese Schritte entsprechen Multiplikationen mit
Eliminationsmatrizen E21 und jE'31:
E'
21
1 0 0
-3 1 0
0 0 1
und E'31
1 0 0
0 1 0
-4 0 1
Die Idee der blockweisen Elimination besteht darin, beide Schritte mit
einer einzigen Matrix E zu erledigen, die sofort die gesamte Spalte unterhalb
des Pivotelements a = 2 zu Null macht:
E =
1 0 0
-3 1 0
-4 0 1
mal A ergibt EA =
2 X X
0 X X
0 X X
Wir erhalten dabei eine Formel für die x in EA aus der Regel für die
Blockmultiplikation. Dazu unterteilen wir A in vier Blöcke: einen (a), der nur
das Pivotelement enthält, einen weiteren (b), der die Spalte unterhalb des
2.4 Regeln für Matrixoperationen 69
Pivotelements aufnimmt, einen Zeilenblock c, der die Zeile rechts vom
Pivotelement umfasst, und einen Block D mit dem Rest der Matrix. Dies ergibt
in der blockweisen Multiplikation von E mit A:
[-c/a I j ] [44^1 = [ü I oXhla] ■ B-^^^
Es wird —c/a mit a multipliziert und zu c addiert: Damit werden Nullen
in der ersten Spalte unterhalb von a erzeugt. An der Stelle daneben wird der
Spaltenvektor —c/a mit der Zeile b multipliziert und die entstehende (n —
1) X (n — 1)-Matrix zu D addiert, was D — ch/a ergibt. Dies ist nichts anderes
als das normale Eliminations verfahren, lediglich mit Hilfe von Blockmatrizen
aufgeschrieben.
Die wesentlichen Punkte
l.Der Eintrag (z,i) der Matrix AB ist (Zeile i von A) • (Spalte j von B).
2. Die Berechnung von m x n mal n x p erfordert mnp einzelne
Multiplikationen.
3.^ mal BC ist gleich AB mal C (überraschend wichtig).
4. AB lässt sich auch als Summe der Produkte (Spalte i von Ä) mal (Zeile j
von B) auffassen.
5. Blockweises Multiplizieren ist möglich, falls die Größen der Blöcke
zueinander passen.
Aufgaben 2.4
In den Aufgaben 1-17 geht es um die Regeln der Matrixmultipli-
kation
1. Nehmen Sie an, A sei eine 3x5-, B eine 5 x 3-, C eine 5x1- und D eine
3 X 1-Matrix. Welche der folgenden Operationen sind erlaubt, und welche
Form hat das Ergebnis, falls es existiert?
(a) BA;
(b) AiB + C);
(c) ABD;
(d) AC + BD;
(e) ABABD.
2. Welche Zeilen oder Spalten welcher Matrizen müssen Sie miteinander
multiplizieren, um
(a) die dritte Spalte von AB,
(b) die erste Zeile von AB,
(c) den Eintrag in der dritten Zeile und der vierten Spalte von AB,
(d) den Eintrag in Zeile 1, Spalte 1 von CDE zu erhalten?
70
2 Das Lösen linearer Gleichungen
3. Berechnen Sie AB-hAC und A{B-hC) und vergleichen Sie die Ergebnisse
für:
A =
15
23
B =
02
Ol
und C=^
3 1
00
4. Berechnen Sie für die Matrizen aus Aufgabe 3 das Produkt aus A und
BC (in der Reihenfolge). Bestimmen Sie dann AB und multiplizieren Sie
dies mit C.
5. Berechnen Sie jeweils A'^ und A^. Wie werden A^ und A"^ aussehen?
A =
16
Ol
und A =
6. Zeigen Sie, dass für die Matrizen
12"
00
A =
und B =^
22
00
10
30
das Quadrat (A-hB)'^ von A^-\-2AB-\-B'^ verschieden ist. Vervollständigen
Sie die richtige Regel: {A -\-B){A-\-B) =^ A^ -\-AB-\- + B'^.
7. Wahr oder falsch? Geben Sie ein Gegenbeispiel an, wenn eine Aussage
falsch ist.
(a) Sind die Spalten 1 und 3 der Matrix B gleich, so auch die Spalten 1
und 3 von AB.
(b) Sind die Zeilen 1 und 3 der Matrix B gleich, so auch die Zeilen 1 und
3 von AB.
(c) Sind die Zeilen 1 und 3 der Matrix A gleich, so auch die Zeilen 1 und
3 von AB.
(d) {ABf = ^2^2
8. Welcher Zusammenhang besteht zwischen den Zeilen von DA und EA
und denen von AI
D =
30
05
und E =
Ol
00
und A -
a b
c d
Welcher Zusammenhang besteht zwischen den Spalten von AD und AE
und denen von AI
9. Addiert man zunächst Zeile 1 von A zu Zeile 2, so ergibt sich EA wie
unten. Wird dann noch die Spalte 1 von EA zur 2. Spalte von EA addiert,
so ergibt sich {EA)F:
10
1 1
EA=:
und {EA)F = {EA)
a b
c d
1 1
0 1
a b
a-i- cb-i- d
a a + b
a-i- c a-i-c-i-b-i- d
2.4 Regeln für Matrixoperationen 71
(a) Führen Sie diese Rechnungen in der umgekehrten Reihenfolge aus:
addieren Sie zuerst die erste Spalte von A zur zweiten (das ergibt
AF), und berechnen Sie dann E{AF), indem Sie die erste Zeile von
AF zur zweiten Zeile addieren.
(b) Vergleichen Sie das Ergebnis mit {EA)F. Welchem Gesetz gehorcht
die Matrixmultiplikation (nicht)?
10. Wir addieren wieder Zeile 1 von A zu Zeile 2 und erhalten EA. Dann
multiplizieren wir von links mit F und addieren so Zeile 2 zu Zeile 1 von
EA. Insgesamt ergibt sich F{EA):
F{EA) =
1 1
Ol
a b
a-j- c b-h d
2a + c26 + d
a-]-c b-hd
(a) Kehren Sie wieder die Reihenfolge um: Addieren Sie zunächst Zeile 2
zu Zeile 1 von A (und erhalten Sie also FA), und addieren Sie dann
Zeile 1 von FA zu Zeile 2.
(b) Vergleichen Sie wieder die Ergebnisse. Wie sieht es hier mit der
„Gesetzestreue" der Matrixmultiplikation aus?
11. Betrachten wir 3 x 3-Matrizen. Wählen Sie jeweils eine Matrix B so, dass,
falls möglich, für jede Matrix A gilt:
(a) BA = 4A;
(b) BA = AB.
(c) In BA sind die Zeilen 1 und 3 von A vertauscht.
(d) Alle Zeilen von BA sind mit Zeile 1 von A identisch.
12. Nehmen Sie an, dass AB = BA und AC = CA für die folgenden Matrizen
B und C gelte:
A =
a b
c d
kommutiert mit B
10
00
und C
Ol
00
Beweisen Sie, dass dann a = d und b = c = 0 gilt. Dann ist also A
ein Vielfaches von /. Tatsächlich sind die Vielfachen von / die einzigen
Matrizen, die mit diesen Matrizen B und C (und außerdem noch mit
allen anderen 2 x 2-Matrizen) kommutieren.
13. Welche der folgenden Matrizen sind auf jeden Fall mit (A-B)'^ identisch?
A^-B\ {B-A)\ A''-2AB-^B\ A{A - B) - B{A - B), A^-
AB-BA-V B'^1
14. Wahr oder Falsch?
(a) Ist A^ definiert, so ist A notwendigerweise eine quadratische Matrix.
(b) Sind sowohl AB als auch BA definiert, so sind A und B notwendig
quadratisch.
72 2 Das Lösen linearer Gleichungen
(c) Sind sowohl AB als auch BA definiert, so sind AB und BA notwendig
quadratisch.
(d) Gilt AB = B, so gilt A = /.
15. Es sei A eine m x n-Matrix. Wie viele Einzelmultiplikationen benötigt
man, um
(a) A mit einem Vektor x mit n Komponenten zu multiplizieren?
(b) A mit einer n x p-Matrix B zu multiplizieren?
(c) A mit sich selbst zu multiplizieren (falls m — n)l
16. Beweisen Sie, dass {AB)C — A{BC) gilt. Betrachten Sie dazu die
Spaltenvektoren bi,...,bn von B. Nehmen wir zunächst an, dass C nur
aus einer Spalte c mit den Einträgen Ci,...,Cn besteht. Dann enthält
AB die Spalten Abi,...,Abn, wohingegen Bc nur aus einer Spalte
cibiH hCnbn besteht. Insgesamt gilt also {AB)c — ciAhi-\ \-CnAhn
und A{Bc) = A{cihi H hCnb^i). Die Linearität der
Matrixmultiplikation bewirkt, dass diese Ausdrücke gleich sind: {AB)c = . Weiter
gilt dasselbe für alle von C, und deshalb gilt {AB)C - A{BC).
17. Berechnen Sie für A = [Izl] und B = [i o e] ^^'^ ^i^ gefragten
Elemente:
(a) Spalte 2 von AB;
(b) Zeile 2 von AB;
(c) Zeile 2 von AA = Ä^]
(d) Zeile 2 von AAA = A^
In den Aufgaben 18—20 betrachten wir den Eintrag aij in Zeile i,
Spalte j einer Matrix A.
18. Geben Sie jeweils die 3 x 3-Matrix mit den Einträgen
(a) aij =i-hj;
(b) aij = (-1)^+^-;
(c) aij ^ i/j
an.
19. Beschreiben Sie in Worten die durch die folgenden Bedingungen
definierten Matrizen. Geben Sie für jede Gruppe ein Beispiel an. Welche Matrix
erfüllt alle Bedingungen?
(a) aij = 0 falls i ^ j;
(b) aij = 0 falls i < j;
\C) aij = aji'y
(d) aij = aij.
20. Die Einträge einer Matrix A seien aij. Nehmen Sie an, dass beim
Eliminationsverfahren keine zusätzlichen Nullen auftauchen. Bestimmen Sie
dann
2.4 Regeln für Matrixoperationen
73
(a) das erste Pivotelement,
(b) das Vielfache von Zeile 1, das von Zeile 3 subtrahiert wird und
(c) den neuen Eintrag an Stelle von 032 nach dieser Subtraktion, sowie
(d) das zweite Pivotelement.
In den Aufgaben 21—25 betrachten wir Potenzen von A.
21. Berechnen Sie die Matrizen A^, A^, A^ sowie die Vektoren A\, A^v, A^v,
A^y für
A =
0 100
0010
0001
0000
und V =
22. Berechnen Sie die Potenzen A^, A^,... und AB, {ABY,. .. für
A =
0,5 0,5
0,5 0,5
und B
1 0
0-1
23. Suchen Sie 2 x 2-Matrizen (mit echten Zahlen), so dass
(a) A? = -I\
(b) BC = -CB (ohne dass BC = 0)
gelten.
24. (a) Suchen Sie eine Matrix A ungleich der Nullmatrix, für die A'^ = 0
gilt,
(b) Finden Sie jetzt eine Matrix mit A'^ ^^ 0, aber A^ - 0.
25. Betrachten Sie die Fälle n = 2 und n = 3, und bestimmen Sie so A^ für
die Matrizen
Ai
2 1
Ol
1 1
1 1
und As =
a b
00
In den Aufgaben 26-34 kommen wir schließlich zur „Spalte-mal-
Zeile-Multiplikation" und zur Blockmultiplikation.
26. Berechnen sie AB mit der „Spalte-mal-Zeile"-Methode:
AB =
0"
24
2 1
'3 30"
1 2 1
=
*" -'
T
2
2
[330] +
^'- Das Produkt von oberen Dreiecksmatrizen ergibt wiederum eine obere
Dreiecksmatrix:
AB =
\ X X X
\{) X X
[0 Ox
XXX
^ X X
0 Ox_
=
0
00
74
2 Das Lösen linearer Gleichungen
„Zeile mal Spalte^^ ist ein Skalarprodukt. (Z. 2 von Ä) • (Sp. 1 von B) = 0.
Welche anderen Skalarprodukte sind ebenso 0?
„Spalte-mal-Zeile" ergibt eine komplette Matrix. Bestimmen Sie die
x'e und Nullen in der Matrix (Spalte 2 von A) (Zeile 2 von B) und in
(Spalte 3 von A) (Zeile 3 von B).
28. Geben Sie Einteilungen einer 2 x 3-Matrix A und einer 3 x 4-Matrix B
sowie der Matrix AB derart an, dass alle folgenden Multiplikationsregeln
Blockmultiplikationen darstellen:
(a) Matrix A mal Spalten von B]
(b) Zeilen von A mal Matrix B;
(c) Zeilen von A mal Spalten von B;
(d) Spalten von A mal Zeilen von B.
29. Teilen Sie A und x so ein, dass Ax spaltenweise berechnet wird: xi mal
Spalte IH .
30. Welche Matrizen £1 und £31 braucht man, um Nullen an den Positionen
B,1) und C,1) von E21A und E31A zu erzeugen?
2 10
-2 0 1
8 5 3
Bestimmen Sie die Matrix E = ES1E21, die beide Nullen in einer
Matrixmultiplikation EA erzeugt.
31. In Beispiel 2.4.4 erhielten wir mit den Regeln der Blockmultiplikation
EA =
32.
1 0
-c/a I
a b
cD
a b
OD- ch/a
Wie sehen c und D in Aufgabe 30 aus, und was ergibt sich für D - cb/a?
Sei i die imaginäre Einheit mit z^ = -1. Als Produkt von {A H- iB) und
(x -h iy) ergibt sich damit Ax -h iBx -h iAy - By. Verwenden Sie die
Blockmultiplikation, um Real- und Imaginärteil zu trennen:
A-B
? ?
Ax- By
?
Realteil
Imaginärteil
33. Für jede komplexe Multiplikation (a -h ib){c -h id) scheint man die vier
Terme ac, bd, ad und bc zu benötigen. Es gilt aber ad-]-bc = {a-h b){c +
d) — ac — bd; 3 Multiplikationen sind also ausreichend. Wendet man diese
Idee auf Matrizen A, B, C, D an, so genügen für die M Methode" 3n^
statt normalerweise 4n^ Multiplikationen. Betrachten Sie die benötigten
Additionen:
2.5 Inverse Matrizen
75
(a) Wie viele Additionen braucht man, um ein Skalarprodukt
auszurechnen? Wie viele Additionen, um eine n x n-Matrixmultiplikation
auszuführen?
(b) (Nach der alten Methode) Wie viele Additionen werden jeweils für
R = AC-BD und S = AD-h BC benötigt?
(c) CM Methode) Wie viele Additionen braucht man insgesamt, um
die Matrizen R (wie oben) und S = {A + B){C + D) - AC ~ BD
zu berechnen? Im Falle n = 2 hat man 24 gegen 32 Multiplikationen,
für n > 2 ist die 3M-Methode klar im Vorteil.
34. Nehmen Sie an, Sie lösen das Gleichungssystem Ax = h für drei spezielle
rechte Seiten b:
b =
Betrachtet man die Lösungen Xi, X2, X3 jetzt als Spalten einer Matrix
X, was ergibt sich für AX?
35. Die drei Lösungen in Aufgabe 34 seien durch Xi = A,1,1), X2 = @,1,1)
und X3 — @,0,1) gegeben. Lösen Sie dann Ax = h mit b = C,5,8).
Zum Abschluss noch etwas zum Knobeln: Wie sieht dann A aus?
ri"
0
[o
5
"
1
0
und
'Ol
0
IJ
2.5 Inverse Matrizen
A sei eine quadratische Matrix. Wir wollen eine Matrix A~^ von gleicher
Größe bestimmen, so dass A~^ mal A gleich I ist. Was immer also A
bewirkt, wird von A~^ rückgängig gemacht — denn das Produkt der beiden
Matrizen ergibt die Einheitsmatrix, die ja nichts bewirkt. Es könnte aber
sein, dass diese inverse Matrix gar nicht erst existiert.
Matrizen werden hauptsächlich dazu benutzt, um sie mit Vektoren x zu
multiplizieren. Multipliziert man die Gleichung Ax = h mit A~^, so erhält
man A~'^Ax = A~^h. Auf der linken Seite steht aber einfach x! Denn eine
Multiplikation mit A~'^A ist dasselbe, wie mit einer Zahl zu multiplizieren
und dann wieder durch sie zu dividieren. Nun haben übliche Zahlen schon
ein Inverses, wenn sie ungleich Null sind. Bei den Matrizen ist das etwas
komplizierter — und deshalb auch etwas interessanter. Die Matrix A~'^ heißt
55die Inverse von A."
Nicht alle Matrizen haben eine Inverse, Die erste Frage, die wir bei
einer quadratischen Matrix stellen können, ist also: Ist A invertierbar? Das
soll nicht heißen, dass wir sofort losrechnen, um A~'^ zu bestimmen. In den
meisten Fällen wird A~^ nie berechnet! Eine Inverse existiert dann und nur
dann, wenn während des Eliminationsverfahrens n Pivotelemente auftreten.
76 2 Das Lösen linearer Gleichungen
(Das wird weiter unten bewiesen. Man muss allerdings Zeilenvertauschun-
gen zulassen.) Das Eliminationsverfahren löst die Gleichung Ax = b, ohne
A~^ zu berechnen oder zu benutzen. Die Idee der Invertierbarkeit ist aber
fundamental.
DEFINITION Eine quadratische Matrix A heißt invertißfbar^ f^lfe esix
ä^^äWi ^ und ÄÄ-^^^m^ ^: ' ^' — -' ^^,
eineMAixllA / gib^^^^
^^r.
''-j
Bemerkung 1. Eine Matrix A kann keine zwei verschiedenen Inversen
haben. Angenommen, es gilt BA = I und außerdem AC — I. Dann gilt schon
B = C, wie man an diesem "Beweis durch Klammern" sieht:
B{AC) = {BA)C bedeutet BI = IC oder B = C. B.18)
Es müssen also eine Linksinverse B (Multiplikation von links) und eine
Rechtsinverse C (Multiplikation von rechts, also AC = I) von A auf jeden
Fall gleich sein.
Bemerkung 2. Ist A invertierbar, so ist die einzige Lösung der Gleichung
Ax — b durch x = A~^b gegeben:
Ax — \y multipliziert mit A ^ ergibt x = A ^Ax = A ^h.
Bemerkung 3. (Wichtig!) Angenommen, es gibt einen von Null
verschiedenen Vektor x mit Ax = 0. Dann kann A keine Inverse besitzen! Denn
keine Matrix kann 0 wieder in x überführen. Andersherum: Ist A invertierbar,
so ist die einzige Lösung von Ax = 0 der Nullvektor x = 0.
Bemerkung 4. Eine 2 x 2-Matrix ist invertierbar genau dann, wenn ad-bc ^
0 gilt:
a b
c d
1
ad — bc
d-b
—c a
B.19)
Die Zahl ad-bc heißt die "Determinante"von A. Eine Matrix ist invertierbar
genau dann, wenn ihre Determinante von 0 verschieden ist (siehe Kapitel 5).
Allerdings weiß man meist, ob es n Pivotelemente gibt, bevor man die
Determinante bestimmt hat.
2.5 Inverse Matrizen 77
Bemerkung 5. Eine Diagonalmatrix ist invertierbar, falls keines der
Diagonalelemente Null ist:
Für A-
dl
gilt A-^ =
1/di
l/d„
Bemerkung 6. Die 2 x 2-Matrix ^ = [J i] ist nicht invertierbar. Sie fällt
durch den Test in Bemerkung 4, denn es gilt od - 6c = 0. Außerdem fällt sie
durch den Test in Bemerkung 3, denn es gilt ^x = 0 für x = B,-1). Die
Matrix hat auch keine zwei Pivotelemente, da der erste Eliminatiönsschritt
in der zweiten Zeile eine Nullzeile erzeugt.
Die Inverse eines Produktes
Betrachtet man zwei Zahlen a 7^ 0 und 6 ^ 0, so kann ihre Summe o + b
invertierbar sein oder auch nicht. Die Zahlen a = 3 und 6 = -3 beispielsweise
haben jeweils die Inversen | und -i, ihre Summe a + b = 0 aber hat keine
Inverse. Das Produkt ab = -9 aber hat eine Inverse, nämlich i mal ^.
Bei zwei Matrizen A und B sieht es ähnlich aus. Es ist nicht leicht viel
über die Invertierbarkeit von A+B zu sagen, aber das Produkt AB hat immer
dann eme Inverse, wenn beide Faktoren A und B invertierbar (und
quadratisch von derselben Größe) sind. Das wichtige dabei ist, dass die Inversen
A und B m umgekehHer Reihenfolge stehen:
2H Smd ^ und S invertierbar, so auch AB. Die Invose von AB ist
iAB)-^=B-'A-K ■ ■ ; :B.20)
Wie sieht man nun ein, warum die Reihenfolge umgedreht werden muss?
Beginnen wir mit AB. Multiplizieren wir dann von links A'^so bleibt B übrig,
viult^phziert man dann noch B'^ von links, so erhält man die Einheitsma-
B ^A ^AB ist gleich B'^IB = B'^B = I.
^Ähnlich verhält es sich^ wenn man von rechts multipliziert: AB mal
reffPl ^ T, J^ ^ AA ' = I . Hier haben wir es mit einer "Grund-
AbPr T ^^^^^^^ti*^" zu tun: Inverse stehen in umgekehrter Reihenfolge
zupr f !-^ o ""^^ ^"*^*' ""'* "^^^ gesunden Menschenverstand: Wenn man
wst die Socken und dann die Schuhe anzieht, muss man auch zuerst die
wieder ausziehen.
78 2 Das Lösen linearer Gleichungen
Ganz analog verhält es sich mit drei oder mehr Matrizen:
B.21)
1 0 0
5 1 0
0 0 1
und E"'^ =
'100
510
001
Beispiel 2.5.1 Es sei E die Elementarmatrix, die das fünffache der ersten
Zeile von der zweiten Zeile subtrahiert. Dann addiert E~^ 5 mal Zeile 1 zu
Zeile 2:
E =
Das Produkt EE~^ ergibt die Einheitsmatrix /, ebenso wie E~^E. Jedesmal
addieren oder subtrahieren wir dasselbe: das fünffache von Zeile 1. Ob man
zuerst addiert und dann subtrahiert, oder erst subtrahiert und dann addiert,
man erhält stets die Matrix, mit der man anfing.
Bei quadratischen Matrizen ist eine Inverse von einer Seite
automatisch auch eine Inverse von der anderen Seite, Wenn also AB = I
gilt, dann mit Sicherheit auch BA = /, und es ist B — A~^. Wir können dies
zwar noch nicht beweisen, es wird aber nützlich werden.
Beispiel 2.5.2 Es sei F eine Matrix, die das vierfache von Zeile 2 von Zeile
3 subtrahiert. Dann addiert F~^ genau das vierfache von Zeile 2 wieder zu
Zeile 3 hinzu:
F=:
n 0
0 1
[O-A
0]
0
ij
und F-i =
100
010
041
Wieder hat man FF~^ = / und auch F~^F = /. Multiplizieren wir nun F
mit E (aus Beispiel 2.5.1) zu FE, und ebenso E'^ mit F''^ zu (FS)"^ —
beachten Sie die umgekehrte Reihenfolge!
FE =
1 0
-5 1
20-4
0"
0
1
ergibt invertiert
£1-1^.-1 _
" 1 00
5 10
0 4 1
B.22)
Es erscheint seltsam, ist aber richtig: im Produkt FE ist ein Eintrag 20
enthalten, in der Inversen E~^F~^ aber nicht. Sie können selbst überprüfen,
ob FE mal E-'^F''^ in der Tat / ergibt.
Es gibt einen Grund dafür, warum die Zahl 20 in FE, jedoch nicht in der
Inversen auftaucht. Die Matrix E subtrahiert 5 mal Zeile 1 von Zeile 2. F
subtrahiert dann das vierfache der neuen Zeile 2 (die —5 mal Zeile 1 enthält)
von Zeile 3. In der Reihenfolge FE wirkt sich Zeile 1 auf Zeile 3 aus.
2.5 Inverse Matrizen 79
In der umgekehrten Reihenfolge E~^F~^ tritt dieser Effekt nicht auf,
denn zuerst addiert F~^ 4 mal Zeile 2 zu Zeile 3. Dann erst wird durch E~^
5 mal Zeile 1 zu Zeile 2 addiert, so dass keine Doppelbeeinflussung vorkommt.
An diesem Beispiel erkennt man zwei Dinge:
1 Normalerweise sieht man einer Matrix A ihre Inverse A~^ nicht unmittelbar
an.
2 Zu Elementarmatrizen in der üblichen Anordnung FE lässt sich die
Inverse E^^F'^ schnell bestimmen. Die Mulitplikatoren nehmen ihren Platz
unterhalb der Diagonalen ein.
Wir werden diese besondere Eigenschaft der Matrizen E~^F'~^ und
^-i^-igi-i in den kommenden Abschnitten noch nutzen können. Sie wird
dann noch einmal ausführlicher besprochen werden. Jetzt geht es uns um die
inverse Matrix A~^, und wir dürfen ein gutes Stück Arbeit bei der
Berechnung dieser Matrix erwarten. Im Folgenden werden wir sehen, wie sich diese
Arbeit organisieren lässt.
Die Berechnung der inversen Matrix A~^ durch Gauß-Jordan
Elimination
Ich habe schon einmal angedeutet, dass es Fälle gibt, in denen die Matrix
A~^ nicht explizit benötigt wird. Zwar ist die Lösung der Gleichung Ax = b
durch den Vektor x = A~^h gegeben, es ist aber nicht unbedingt nötig oder
gar effizient, A~^ zu berechnen und mit b zu multiplizieren. Das
Eliminationsverfahren berechnet x direkt. Wie wir jetzt sehen werden, ermöglicht es
aber gleichzeitig, A~^ zu bestimmen.
Die Idee ist dabei, die Gleichung AA~^ = / spaltenweise zu lösen. Das
Produkt von A mit der ersten Spalte von A~^ (nennen wir sie Xi) soll also die
erste Spalte von / ergeben. Dies ergibt also die Gleichung Axi — ei. Genauso
ist es mit den anderen Spalten von A"^: Mit A multipliziert, ergeben sie
Spalten von /.
AA^^ - A[xi X2 X3] = [ei e2 es] = L B.23)
Um eine 3 x 3-Matrix A zu invertieren, müssen wir also 3 Gleichungssysteme
lösen: Axi ~ ei, Ax2 = e2 und Ax^ — e^. Die Vektoren Xi,X2 und X3 sind
dann die Spalten von A~^.
Bemerkung: Hier sieht man bereits, warum es aufwändig ist, A~'^ zu
berechnen. Dazu müssen wir n Gleichungssysteme für die n Spalten lösen, statt
lediglich eines Gleichungsystems, wenn man Ax = b direkt löst.
Zur Verteidigung der inversen Matrix A~^ ist anzuführen, dass die
Berechnung nicht wirklich n mal so teuer ist wie das Lösen eines Gleichungssys-
tiems Ax = h. Überraschenderweise ist der Aufwand bei n Spalten lediglich
80
2 Das Lösen linearer Gleichungen
verdreifacht. Das liegt daran, dass in den n Gleichungen Axi — e^ immer
dieselbe Matrix A steht. Auch wenn man viele verschiedene rechte Seiten hat,
muss man das Eliminations verfahren nur einmal auf A anwenden. Mit den
rechten Seiten ei kann man dabei relativ leicht umgehen. Zur Berechnung
der vollständigen Matrix A~^ bedarf es v? Eliminationsschritten gegenüber
n^/3 Schritten, wenn man nur ein einzelnes x berechnen will. Im nächsten
Abschnitt werden wir uns genauer mit diesen Kosten befassen.
Mit der Gauß-Jordan Methode berechnet man A~^ durch simultanes
Lösen aller n Gleichungen. Normalerweise besitzt die erweiterte Matrix nur
eine zusätzliche Spalte b von der rechten Seite der Gleichung. Nun sind es
3 rechte Seiten (im Falle einer 3 x 3-Matrix), nämlich die Spalten von /, so
dass die erweiterte Matrix jetzt [AI] ist.
Betrachten wir ein ausführliches Beispiel: Die Matrix A habe auf der
Hauptdiagonalen die Einträge 2 und auf den Nebendiagonalen die Einträge
-1. Dann ergibt sich:
[Aei 62 es] =
->■
->■
2 -1
-1 2
0 -1
2-1 0
0 1-1
0-1 2
2-1 0
0 1-1
0 0 1
1
1
2
0
1
1
2
1
3
0
-1
2
0
1
0
0
1
2
3
1
0
0 1
0 0
o'
0
1
o'
0
1
0
0
1
(| Zeile 1 + Zeile 2)
(| Zeile 2 + Zeile 3)
An dieser Stelle sind wir halbwegs fertig. Die Matrix aus den ersten drei
Spalten ist nur eine obere Dreiecksmatrix U, auf deren Diagonale die
Pivotelemente 2, |, I stehen. Gauß hätte hier mit Rücksubstitution weitergearbeitet.
Jordans Idee war es, mit der Elimination bis zu einer ^'reduzierten Trep-
penform" fortzufahren. Jetzt werden Zeilen zu darüber stehenden Zeilen
addiert, um Nullen oberhalb der Pivotelemente zu erzeugen:
r 2-1
0 1
[ 0 0
0
0
4
3
1
3
4
1
3
0
3
2
2
3
01
3
4
l\
2
0
0 0
^ 0
2 ^
0 0 I
1 i
3 3
2 4
o 3 -L
(| Zeile 3 + Zeile 2)
(I Zeile 2-^ Zeile 1)
2.5 Inverse Matrizen
81
Anschließend wird jede Zeile durch ihr Pivotelement dividiert. So erhält
man als neue Pivotelemente immer die 1, und als Resultat hat man in der
ersten Hälfte der Matrix die Einheitsmatrix /. (Diese reduzierte Treppenform
hat hier die Form R = I, weil A invertierbar ist.) In der zweiten Hälfte
stehen die Spalten von A~^,
(Division durch 2)
(Division durch |)
(Division durch |)
1 0 0
0 1 0
0 0 1
3
4
1
2
1
4
1,
4
1
2
i
4
[/X1X2X3].
Ausgehend von der 3 x 6-Matrix [AI] sind wir also bei [lA ^] angelangt. Der
ganze Gauß-Jordan-Eliminationsprozess lässt sich in einer Zeile schreiben:
Multipliziere [AI] mit A~^ und erhalte [IA~^].
Stück für Stück erzeugen die Eliminationsschritte die inverse Matrix. Um es
noch einmal zu sagen, oftmals wird die Matrix A"'^ gar nicht benötigt. Für
kleine Matrizen A kann es aber sehr lohnend sein, die Inverse zu kennen.
Dieses Beispiel ist sehr wichtig, und wir fügen noch drei Bemerkungen an. Es
geht um die Begriffe symmetrisch, tridiagonal und Determinante.
1 A ist symmetrisch bezüglich einer "Spiegelung" an der Haupt diagonalen.
Dies gilt dann auch für A~^.
2 Die Matrix A ist eine Tridiagonalmatrix (d. h. sie hat drei von Null
verschiedene Diagonalen). A~^ ist voll besetzt und enthält keine Null mehr.
Ein Grund mehr, warum man Inverse oft nicht explizit berechnet.
3 Das Produkt der Pivotelemente ergibt 2 • | • | = 4. Diese Zahl heißt die
Determinante von A. Im fünften Kapitel werden wir sehen, warum bei
der Berechnung der Inversen immer eine Division durch 4 vorkommt:
Die Inverse oben ist A ^ =
32 1
242
1 23
B.24)
Beispiel 2.5.3 Wir berechnen die Inverse der Matrix A= [^ f ] durch Gauß-
Jordan-Elimination.
[AI] =
-^
2 3 10'
4 7 0 1
2 0 7-3'
0 1-2 1
->
->•
2
0
1
0
3 1
1-2
0 i-
1-2
0"
1
3"
2
1
[lA-^].
Die reduzierte Treppenform von [AI] ist gerade die Matrix [/^~^].
Während der Berechnung tauchte wieder eine Division durch die
Determinante 2.7-3-4 = 2 auf.
82 2 Das Lösen linearer Gleichungen
Der MATLAB-Code für X — inverse(>l) enthält drei wichtige Zeilen^:
/ = eye(n,n);
R^TTef{[AI]y,
X = R{:,n + l \n + n)
In der letzten Zeile werden die Spalten 1 bin n vernachlässigt, also die linke
Hälfte von R. Übrig bleibt die rechte Hälfte, die X = A~^ enthält. Dazu
muss A natürlich erst einmal invertierbar sein; andernfalls steht links in R
nicht die Einheitsmatrix /.
Singular oder invertierbar?
Kehren wir zur zentralen Frage zurück: Welche Matrizen haben eine
Inverse? Am Anfang dieses Abschnitts haben wir den Pivot-Test vorgestellt: A~^
existiert genau dann, wenn A n von Null verschiedene Pivotelemen-
te hat, (Dabei sind Zeilenvertauschungen natürlich erlaubt.) Dies können wir
jetzt mittels des Gauß-Jordan-Eliminationsverfahrens beweisen:
1. Sind alle n Pivotelemente von Null verschieden, so können mit dem
Eliminationsverfahren alle Gleichungen Axi — ei gelöst werden. Die Spalten
Xi bilden dann die Matrix A~^ und es gilt AA~^ — I, so dass A~^
wenigstens eine Rechtsinverse ist.
2. Das Eliminations verfahren ist eigentlich nichts anderes als eine lange
Kette von Matrixmultiplikationen
{D-^'"E'"P"E)A = L
Dabei stellt D~^ die Division durch die Pivotelemente dar, die Matrizen E
erzeugen Nullen ober- und unterhalb des Pivotelementes, und die Matrizen
P führen Zeilenvertauschungen durch — mehr dazu in Abschnitt 2.7. Das
in Klammern gefasste Produkt ist dann offensichtlich eine Linksinverse mit
A~^A = /. Nach Hinweis 1 in diesem Abschnitt sind Links- und Rechtsinverse
aber gleich. Wir haben also insgesamt gezeigt: Sind alle Pivot-Elemente von
Null verschieden, so ist A in vertier bar.
Die Umkehrung dieser Aussage ist ebenfalls wahr. Falls A~^ existiert^ so
muss A n von Null verschiedene Pivotelemente haben. Der Beweis erfolgt
wieder in zwei Schritten:
1. Enthält A eine Nullzeile, so kann keine Inverse existieren, denn dann
hätte jedes Matrixprodukt AB eine Nullzeile, und könnte daher nicht /
ergeben.
^ Anm. d. Übers.:Der Befehl eye steht für die Einheitsmatrix und schließt an den
Klang von "I" im Englischen an. rref steht für "reduced row echelon form", also
"reduzierte Zeilen-Treppenform".
2.5 Inverse Matrizen
83
2. Ist aber das Pivotelement für eine Spalte gleich Null, so ergibt sich
schließlich eine Nullzeile
dl X X
0 Ox
0 Ox
wird zu
dl X X
0 Ox
0 00
und wir sind bei einer nicht invertierbaren Matrix angelangt. Da aber jeder
einzelne Eliminationsschritt invertierbar ist, kann die ursprüngliche Matrix
A nicht invertierbar gewesen sein. Fehlen Pivotelemente, lässt sich A~^
nicht bilden.
21 Das Eliminatioiisverfahreii stellt einea vollständigen Test auf Invertier-
barkeit dar. Es muss n Pivötelemente ungleich Null geben.
Beispiel 2.5.4 Ist L eine untere Dreiecksmatrix mit Einsen auf der
Hauptdiagonalen, so gilt dies auch für L~^.
Wir benutzen wieder die Gauß-Jordan-Methode, um L~^ zu bestimmen.
Wir beginnen, indem wir Vielfache der Pivot-Zeilen von Zeilen darunter
subtrahieren. Auf diese Weise gelangen wir normalerweise nur bis zu einer oberen
Dreiecksmatrix, aber in diesem Fall sind wir hier schon fertig. Dies ist ein
typisches Beispiel:
\LI]^
-^
10 0 10 0
3 10 0 10
4 5 10 0 1
10 0 10 0
0 1 0-3 1 0
0 5 1-4 0 1
10 0 10 0
0 1 0-3 1 0
0 0 1 11-5 1
C mal Zeile 1 von Zeile 2 subtrahiert)
D mal Zeile 1 von Zeile3 subtrahiert)
= \IL-
So wie L durch das Eliminationsverfahren in / überführt wird, wird aus
I die inverse Matrix L"^ Mit anderen Worten: L~^ ist gerade das Produkt
der Eliminationsmatrizen E32E31E21. Hier sind alle Pivotelemente 1. L~Mst
eine untere Dreiecksmatrix.
Die wesentlichen Punkte
1-Die Inverse A~^ einer Matrix ist durch die Gleichungen AA~'^ = I und
A~^A = /bestimmt.
2. Die Inverse eines Produkts AB ist das Produkt B~^A~^.
84 2 Das Lösen linearer Gleichungen
3. Gilt Ax = 0 für einen Vektor x ^ 0, so hat A keine Inverse.
4. Mit dem Gauß-Jordan-Verfahren löst man die Gleichung AA~^ = I nach
A~^ auf. Dabei wird die erweiterte Matrix [AI] durch Zeilenoperationen
in [/ A~^ ] überführt.
5. A ist invertier bar genau dann, wenn A n Pivotelemente ungleich Null hat.
Dabei sind Zeilenvertauschungen erlaubt.
Aufgaben 2.5
1. Bestimmen Sie mittels der Formel für 2 x 2-Matrizen die Inversen der
Matrizen A, B und C:
03
40
und B
20
42
und C
34
5 7
2. Versuchen Sie, durch Ausprobieren die Inversen P ^ dieser
"Permutationsmatrizen" zu finden
P =
00 1
0 1 0
100
und P =
010
001
100
3. Lösen Sie dieses Gleichungssystem nach den Spalten von ^ ^ = [cd]
auf:
^10 20"
20 50
a
c
=
"l"
0
und
10 20'
20 50
b
d
-
'0'
Ij
4. Zeigen Sie, dass [ J §] keine Inverse hat, indem Sie versuchen, die
Gleichungssysteme für die Spalten (a, c) und (ö, d) zu lösen:
2"
36
o h
c d
=
0"
5. Bestimmen Sie drei 2 x 2-Matrizen (nicht die Einheitsmatrix), die invers
zu sich selbst sind, d.h. für die A^ = I gilt.
6. (a) Zeigen Sie in einer Zeile, dass aus AB — AC sofort B = C folgt, falls
A invertierbar ist.
(b) Zeigen Sie für A = [\\]i dass es zwei Matrizen B ^ C gibt, für die
AB = AC gilt.
7. (Wichtig) Zeigen Sie, dass eine 3x3 Matrix A, für die "Zeile 1 + Zeile 2
= Zeile 3" gilt, nicht invertierbar ist:
(a) Erklären Sie, warum die Gleichung Ax = A,0,0) keine Lösung haben
kann.
2.5 Inverse Matrizen
85
(b) Für welche rechten Seiten {bi,b2,bs) gibt es Lösungen der Gleichung
Ax = h?
(c) Was passiert während des Eliminationsverfahrens mit Zeile 3 ?
8. Die Matrix B entstehe aus der invertierbaren Matrix A, indem die
ersten beiden Zeilen vertauscht werden. Ist B ebenfalls invertierbar? Wie
bestimmt man B~^ aus A~^?
9. Finden Sie die Inversen dieser beiden Matrizen:
0002
0030
0400
5000
und B
3 2 00
4300
0065
0076
10. (a) Finden Sie invertierbare Matrizen A und B, deren Summe A -\- B
nicht invertierbar ist.
(b) Finden Sie zwei singulare Matrizen A und B, deren Summe A -\- B
invertierbar ist.
11. Zeigen Sie: Ist das Produkt C = AB zweier Matrizen invertierbar, dann
ist auch A invertierbar. Bestimmen Sie eine Formel für A~^ in
Abhängigkeit von C~^ und B.
12. Zeigen Sie: Ist das Produkt M = ABC dreier quadratischer Matrizen
invertierbar, so ist auch B invertierbar (wie auch A und C). Bestimmen
Sie eine Formel im B~^ in Abhängigkeit von M~^, A und C.
13. Die Matrix B entstehe aus der Matrix A, indem Zeile 1 zu Zeile 2
hinzuaddiert wird. Wie bestimmt man B~^ aus A~^?
Die Inverse von B =
10
1 1
ist
14. Beweisen Sie, dass eine Matrix mit einer Nullspalte keine Inverse haben
kann.
15. Mulitplizieren Sie die Matrix [^^] mit der Matrix [_c ~a]- ^^^ sehen
die Inversen dieser beiden Matrizen aus, falls ad ^ bc gilt ?
16. (a) Welche einzelne Matrix E führt die folgenden drei Schritte auf einmal
aus?
- Zeile 1 wird von Zeile 2 subtrahiert;
- Zeile 1 wird von Zeile 3 subtrahiert;
- Zeile 2 wird von Zeile 3 subtrahiert.
(b) Welche Matrix L führt die folgenden 3 Schritte auf einmal aus?
- Zeile 2 wird zu Zeile 3 addiert;
86
2 Das Lösen linearer Gleichungen
- Zeile 1 wird zu Zeile 3 addiert;
- Zeile 1 wird zu Zeile 2 addiert.
17. Zeigen Sie, dass eine 3 x 3-Matrix A, für die "Spalte 1 + Spalte 2 = Spalte
3" gilt, nicht invertierbar sein kann:
(a) Finden Sie eine nicht-triviale Lösung der Gleichung Ax = 0.
(b) Gilt auch für die einzelnen Matrizen während des
Eliminationsverfahrens "Spalte 1 + Spalte 2 = Spalte 3"? Erklären Sie, wieso das
dritte Pivotelement gleich Null ist.
18. Zeigen Sie, dass AB die Inverse zu A ist, falls B die Inverse zu A^ ist.
19. Bestimmen Sie zwei Zahlen a und b, so dass die folgende Gleichung erfüllt
ist:
4-1-1-1"
1 4-1-1
1-1 4-1
1-1-1 4
-1
a b b b
b a b b \
b b a b \
b b b a\
20. Es gibt sechzehn 2 x 2-Matrizen mit den Einträgen 1 und 0. Wie viele
von ihnen sind invertierbar?
In den Aufgaben 21-27 geht es um die Gauß-Jordan-Methode zur
Berechnung von A~^.
21. Erzeugen Sie aus / die Matrix A~^, indem Sie durch Zeilenoperationen
die Matrix A in die Matrix / überführen:
[AI] =
1310
2701
und [AI] =
1310
3801
22. Tauschen Sie im Beispiel im Text auf Seite 80 die Minuszeichen durch
Pluszeichen aus und rechnen Sie es noch einmal durch. Eliminieren Sie
dazu die Einträge oberhalb und unterhalb des Pivotelements und führen
Sie dadurch [A /] in [/ A"^ ] über:
[AI] =
2 10 100
12 1010
0 12001
23. Verwenden Sie das Gauß-Jordan'sche Eliminations verfahren, um die
Gleichung AA~^ = I nach A~^ aufzulösen:
lab
0 1 c
00 1
Xl
X2
"
X3
—
"lOOl
010
OOlJ
2.5 Inverse Matrizen
87
24. Bestimmen Sie mit dem Gauß-Jordan'schen Eliminationsverfahren
angewendet auf [AI] die Matrix A~^, falls sie existiert:
[21 r
12 1
1 12
und A =
2-1-1
-1 2-1
-1-1 2
25. Durch welche Elementarmatrizen E21, E12 und D ^ wird A = [le] ^^
die Einheitsmatrix überführt? Berechnen Sie dann D~^Ei2E2i = A~^.
26. Invertieren Sie diese Matrizen mit Hilfe des Gauß-Jordan'schen
Eliminationsverfahrens:
A =
100
2 1 3
001
und A
1 1 1
12 2
123
27. Hier müssen Sie eine Zeilenvertauschung vornehmen, bevor Sie mit dem
Gauß-Jordan-Verfahren die Inverse berechnen können:
[AI] =
02 10
220 1
28. Wahr oder falsch? Geben Sie ein Gegenbeispiel an, falls die Aussage falsch
ist.
(a) Eine 4 x 4-Matrix mit Nullen ist nicht invertierbar.
(b) Jede Matrix mit Einsen auf der Hauptdiagonalen ist invertierbar.
(c) Ist A invertierbar, so ist auch A~^ invertierbar.
(d) Ist A invertierbar, so auch A'^.
29. Für welche Zahlen c ist diese Matrix nicht invertierbar? Warum nicht?
A =
2 cc
c c c
87 c
30. Beweisen Sie, dass diese Matrix invertierbar ist, falls a ^ 0 und a ^ b
gelten:
abb
a ab
a a a
^^' Die folgende Matrix hat eine bemerkenswerte Inverse. Berechnen Sie A"^,
erraten sie die Inverse im 5-dimensionalen Fall, und berechnen Sie dafür
, um ihr Rateergebnis zu überprüfen:
2 Das Lösen linearer Gleichungen
A =
1-1 1-1
0 1-1 1
0 0 1-1
0 0 0 1
32. Benutzen sie die Inversen aus Aufgabe 31, um Ax — A,1,1,1) und Ax =
A,1,1,1,1) zu lösen.
33. Die Matrizen mit den Einträgen aij — l/(z-h j - 1) heißen Hilbert-
Matrizen. Berechnen Sie die Inverse der sechsdimensionalen Hilbert-
Matrix mit dem MATLAB-Befehl invhilbF). Vergleichen Sie das
Ergebnis mit dem Ergebnis des Befehls inv(hilbF)). Wie erklären Sie
sich den Unterschied?
34. Bestimmen Sie die Inversen dieser Blockmatrizen:
' I 0"
C I
'A 0"
CD
/]
ID
2.6 Elimination = Faktorisierung: A=LU
Studenten beklagen sich oft darüber, dass Mathematik-Vorlesungen zu
theoretisch seien. Das gilt sicher nicht für diesen Abschnitt. Er wendet sich fast
nur praktischen Fragestellungen zu. Unser Ziel wird es sein, das Gauß'sche
Eliminationsverfahren in einer praktisch nützlichen Form zu beschreiben.
Viele der Schlüsselideen der Linearen Algebra lassen sich, wenn man sie genau
anschaut, als Matrix-Faktorisierungen auffassen. Dabei wird eine Matrix A
als Produkt von 2 oder 3 besonderen Matrizen beschrieben. Die erste dieser
Faktorisierungen — praktisch auch die wichtigste — erhält man aus dem
Eliminationsverfahren. Die Faktoren sind dabei Dreiecksmatrizen. Man nennt
diese Faktorisierung auch A=LU.
Beginnen wir mit einem 2 x 2-Beispiel. Die Matrix A enthalte die Zahlen
2,1,6 und 8. Die erste Zahl, die wir zu eliminieren haben, ist also die 6. Dazu
subtrahieren wir das dreifache der ersten Zeile von Zeile 2. In
"Vorwärtsrichtung" drücken wir diesen Schritt durch die Elementar mat rix E21 aus. In
"Rückrichtung" von U nach A hätten wir dann E21 (eine Addition zweier
Zeilen):
Vorwärts nach U : E21A =
Zurück von U nach A
E^,'U
10]
-3lJ
f 1 Ol
[nl
[21
[es
[211
\PM
■ 1
i- 1
[21]
[05J
2i]
.6 8 J
= u
A.
In der zweiten Zeile steht aber schon die Faktorisierung. Anstelle von
A = E21U schreiben wir A - LU. Betrachten wir nun größere Matrizen mit
2.6 Elimination — Faktorisierung: A=LU 89
vielen Elementarmatrizen E. Die untere Dreiecksmatrix L ergibt sich in dem
Fall gerade als Produkt der Inversen dieser Elementarmatrizen.
In jedem Schritt von A nach U wird mit einer Matrix Ey multipliziert,
um in Position (ij) eine Null zu erzeugen. Möglicherweise sind dabei auch
Zeilenvertauschungen durch Matrizen Pij nötig, um Elemente ungleich Null
in die jeweilige Pivotposition zu bringen. Schließlich erhält man eine lange
Folge von E- und P- Matrizen, deren Produkt mit A die Matrix U ergibt
Bringen wir alle diese Matrizen auf die rechte Seite, so erhalten wir A zurück:
A = iE~'...p-K..E-^)U. B.25)
In dieser Faktorisierung stehen sehr viele Faktoren. Deswegen kombinieren
wir die einfachen Faktoren E~^ und p-i in eine einzige Matrix L, die alle
Elhninationsschritte auf einmal rückgängig macht. Möglicherweise ist eine
weitere Matrix P nötig, die alle Zeilenvertauschungen enthält (mehr dazu im
nächsten Abschnitt). Die Matrix A ist dann aus den Matrizen L, P und U
aufgebaut.
Betrachten wir zunächst den einfachsten Fall, in dem keine
Zeilenvertauschungen nötig sind. Eine 3 x 3-Matrix A muss mit Matrizen E21, E31 und
E32 multipliziert werden, um Nullen an den Positionen B,1), C,1) und C,2)
unterhalb der Diagonalen zu erzeugen. Dadurch erhalten wir schließlich die
obere Dreiecksmatrix U. Bringen wir diese Matrizen auf die andere Seite der
Gleichung, so erhalten wir die Faktorisierung von A:
{BnEsiBzi)A:=U wird zu 4 = (£S%^i*ß^i)£f ^
bzw. .A'='LU: B.26)
Die Inversen stehen dabei in der umgekehrten Reihenfolge, wie wir schon
gesehen haben. Das Produkt dieser drei Inversen ist die untere Dreiecksmatrix
J^- Wir erhalten also A = LU. Sehen wir uns dies etwas näher an.
H.r Tfr"u'' if^^ "^^^ '"''^'''^'' Matrizen E^' ist eine untere Dreiecksmatrix,
HnrK ^;::^*-J^iagonal-Eintrag £,^ ist, der die durch den Eintrag -% in £,,
du chgefuhrte Subtraktion rückgängig macht. Auf den Hauptdiagonden von
^undE 1 stehen nur Einsen.
^»ertens; Das Produkt dieser Matrizen E ist ebenfalls eine untere Dreiecks-
matrix_ Einerseits ergibt die Multiplikation der Matrizen E mit A die Matrix
Dietfp'^'f f f ^'^ ''"^ ^ ^'' ^^ P'^^^"^* d^^ I^^«r««'i dieser E's mit U.
leses Produkt der Inversen ist die untere Dreiecksmatrix L
ist H«f -^"^f ff ^ ^'"'''^^' "^^"^ "^^"^ ^'^"^ '"i* den Inversen arbeiten. Einer
darin H ^'' faktorisieren wollen, und nicht U. Der zweite Grund besteht
Haus^rhu'^""/'''! sehr nützliche Eigenschaft der Matrix L praktisch frei
«aus erhalten: der folgende Punkt zeigt, dass die Wahl von L gerade richtig
90
2 Das Lösen linearer Gleichungen
Drittens: Die Multikplikatoren lij stehen unverändert an ihren Positionen
(z, j) in der Matrix L. Normalerweise werden bei einer Matrixmultiplikation
alle Einträge "durcheinandergewürfelt". Bei dieser Multiplikation passiert das
gerade nicht. Die Reihenfolge ist bei den inversen Matrizen gerade so, dass
alle Multiplikatoren unverändert bleiben. Wir werden weiter unten sehen,
woran das liegt.
Als letzten Punkt kann man noch festhalten, dass die Matrix L auf ihrer
Hauptdiagonalen nur Einträge 1 hat, da dies schon für die Matrizen E~^ gilt.
^"
2J (A = hV) Das ElimmatioBsvepaJhxen ohne ZeileÄertauschung, Die
obere Örei^cksmMtix t7 enthält a^if Ä HatiptdiagoBali^die Pivoteiemen*
te. Die uatefB Draecksmatiix L bat Etesen auf der HÄiptdiagoöialeii. Um-^i
terhalb d^r Di^onalen stehen die Älultipllkatoreii liji. "
Beispiel 2.6.1 Ist A die Matrix mit Einträgen 2 auf der Hauptdiagonalen und
1 auf den beiden Nebendiagonalen, wird man beim Eliminationsverfahren
zunächst |mal Zeile 1 von Zeile 2 subtrahieren. Es ist also /21
Schritt subtrahiert das |-fache von Zeile 2 von Zeile 3:
^. Der letzte
A-
'210"
121
012
—
0 0'
1 0'
0| 1
.oo|.
= LU.
Der Multiplikator ^34 ist Null, weil der Eintrag an Position C,1) von A
Null ist, weswegen hier keine weitere Operation nötig ist.
Beispiel 2.6.2 Ändern wir den oberen linken Eintrag von 2 nach 1. Dann
werden alle Multiplikatoren zu 1, und auch alle Pivotelemente sind 1. Dieses
Muster wiederholt sich für 4x4- oder n x n-Matrizen.
riioo"
1210
0121
[0012
'1
11
Ol 1
0011
1100]
110
11
ij
LU.
An diesen Beispielen für Faktorisierungen A = LU lässt sich noch eine
zusätzliche Eigenschaft erkennen, die in praktischen Anwendungen sehr wichtig ist.
Nehmen wir an, es seien keine Zeilenvertauschungen nötig. In welchen Fällen
können wir dann Nullen in L und in U vorhersagen?
Beginnt eine Zeile von A mit Nullen, so gilt dies auch für die
entsprechende Zeile von L,
Beginnt eine Spalte von A mit Nullen, so auch die entsprechende
Spalte von U.
2.6 Elimination = Faktorisierung: A=LU
91
Steht am Anfang einer Zeile eine Null, so brauchen wir für diese Zeile
keinen Eliminationsschritt. Nullen unterhalb der Diagonalen von A ergeben also
Nullen in L, da der entsprechende Multiplikator lij Null ist. Diese
Erkenntnis spart Rechenzeit! Ähnlich lassen sich Nullen am Anfang einer Zeile direkt
nach U übertragen. Bedenken Sie aber bitte: Nullen mitten in einer Matrix
werden sehr wahrscheinlich überschrieben, während das
Eliminationsverfahren über sie hinwegschreitet.
Wir wollen jetzt sehen, warum in der Matrix L gerade die Multiplikatoren
l^j stehen.
Der Schlüssel zum Verständnis der Faktorisierung A = LU.
Welche Zeilen werden während des Eliminationsverfahrens von den darunter
liegenden Zeilen subtrahiert? Es sind nicht mehr die ursprünglichen Zeilen von
A, denn diese sind sehr wahrscheinlich bereits verändert worden. Stattdessen
sind es die Zeilen von C/, denn Pivotzeilen werden vom Eliminationsverfahren
nicht mehr weiter verändert. So subtrahieren wir beispielsweise Vielfache der
Zeilen 1 und 2 von U {nicht der Zeilen von A!), um die dritte Zeile von U
zu erhalten:
Zeile 3 von C/ = Zeile 3 von A - /31 (Zeile 1 von U)
Schreiben wir dies um:
/32(Zeile2 von U).
B.27)
Zeile 3 von A = 23x (Zeile 1 von U) -f Z32 (Zeile 2 von U) + 1 (Zeile 3 von U)..
B.28)
Rechts steht aber gerade [/31 ls2 1] multipliziert mit U, und dies ist Zeile
3 der Faktorisierung A = LU. So sehen alle Zeilen aus, unabhängig von
der Größe von A. Treten keine Zeilenvertauschungen auf, erhalten wir so die
Faktorisierung A = LU.
Bemerkung Die LU Faktorisierung ist in einer Hinsicht "unsymmetrisch":
in U stehen auf der Hauptdiagonalen die Pivotelemente, während dort in
L Einsen stehen. Dies lässt sich aber leicht ändern: wir dividieren einfach
U durch eine Diagonalmatrix D, die die Pivotelemente enthält. Dann ist U
gleich D mal eine Matrix mit Einsen auf der Hauptdiagonalen.
U =
dl
dn
1 ui2/di uis/di
1 U23/d2
Der Einfachheit halber (wenn es auch etwas verwirrend ist) wollen wir
für diese neue Matrix ebenfalls den Buchstaben U verwenden. Gerade wie
L enthält sie Einsen auf der Haupt diagonalen. Anstelle des normalen LU
92
2 Das Lösen linearer Gleichungen
'lO'
3 1
'2 8'
0 5
=
lO'
3 1
5
'14'
Ol
erhalten wir jetzt LDU: Untere Dreiecksmatrix mal Diagonalmatrix
mal obere Dreiecksmatrix.
Die DTeiecksfaktojisierumg lässt sieh sehreiben als A = LU oder
A^LDU.
Immer wenn der Ausdruck LDU auftritt, ist gemeint, dass U Einsen auf
der Hauptdiagonalen hat. Jede Zeile ist also durch ihren Diagonaleintrag —
das Pivotelement — dividiert worden. Dann werden L und U genau gleich
behandelt. Hier sind noch einmal LU und LDU:
B.29)
Die beiden Pivotelemente 2 und 5 stehen in der Matrix J9, und die Division
der Zeilen durch 2 bzw. 5 liefert [14] und [0 1] in der neuen Matrix U. L
enthält in beiden Fällen den Multiplikator 3.
Ein quadratisches System = zwei Dreieckssysteme
Wir haben schon daraufhingewiesen, dass L sozusagen das "Gedächtnis" des
Eliminations Verfahrens darstellt. Sie enthält die Vielfachen der Pivot Zeilen,
die von den darunterliegenden Zeilen subtrahiert wurden. Wozu brauchen wir
dieses Gedächtnis? Wie können wir es nutzen? Wir brauchen L, sobald es ein
Gleichungssystem Ax = b zu lösen gilt. Die beiden Faktoren L und U sind
ganz von der linken Seite A der Gleichung bestimmt. Betrachten wir jetzt die
rechte Seite. Die meisten Computerprogramme, die lineare
Gleichungssysteme lösen, teilen das Problem Ax = b in zwei Teile auf:
1 Faktorisiere A (m L und U)
2 Löse nach x (mittels L, U und b).
..f
Bis jetzt haben wir die rechte Seite b immer gleich mitbearbeitet, während
wir die rechte Seite A in Dreiecksform brachten. Dies lies sich einfach lösen:
man erweiterte die Matrix A einfach durch eine zusätzliche Spalte. Beim
Gauß-Jordan-Verfahren zur Berechnung von A~^ haben wir sogar mit n
rechten Seiten auf einmal gearbeitet.
Die meisten Computerprogramme hingegen halten die beiden Seiten der
Gleichung auseinander. Die linke Seite wird in L und U faktorisiert, ohne
dass zusätzlicher Speicherbedarf anfällt. Das Ergebnis kann man auf eine
rechte Seite b anwenden, wann immer es nötig wird. Die Benutzerhinweise
zum Programmpaket LINPACK drücken das so aus: „Diese Situation tritt so
häufig auf, und die Einsparungen sind so bedeutend, dass keine Routine für das
Lösen eines einzelnen Systems vorgesehen wurde."
2.6 Elimination = Faktorisierung: A=LU
93
Wie gehen wir nun mit b vor? Zunächst müssen die in L gespeicherten
Schritte der Vorwärtselimination auf b angewendet werden. Dadurch erhalten
wir eine neue rechte Seite c. Dies läuft auf die Lösung eines Systems Lc = b
hinaus. Danach wird die Gleichung [/x = c durch Rücksubstitution gelöst.
Das Originalsystem Ax = b ist also in zwei Dreieckssysteme faktorisiert
worden:
Lose zunächst Lc
und dmnn Ux
B.30)
Man sieht, dass auf diese Art und Weise das richtige x berechnet wird,
indem man die Gleichung Ux = c mit L multipliziert. Man erhält dann LU
gleich A und Lc gleich b, also Ax = b.
Es sei noch einmal betont: nichts daran ist neu. Dies ist genau das, was wir
schon die ganze Zeit getan haben. Die Vorwärtselimination führte die rechte
Seite b in eine neue rechte Seite c über, wir haben also sozusagen das
Dreieckssystem Lc = h durch "Vorwärtssubstitution" gelöst. Rücksubstitution
erzeugt dann x. Man sieht dies alles am besten an einem Beispiel:
Beispiel 2.6.3 Die Vorwärtselimination führt zu Ux = c:
2u + 2v = S . , 2u-{-2v = S
Ax = h
Au-\-9v = 21
wird zu
5v = 5.
Der Multiplikator ist 2. Auf der linken Seite der Gleichung wurde dabei L
erzeugt, auf der rechten Seite hingegen die Lösung der Gleichung Lc = h:
jLc = b Das obere Dreieckssystem
Ux^^
Das untere Dreieckssystem
'loi r
2lJ [
[2 2]
[osj
c =
8^
21J
[8]
ergibt c =
ergibt x
Besonders schön an dieser Faktorisierung ist, dass sich A durch L und U ohne
zusätzlichen Speicherbedarf ersetzen lässt — die beiden Dreiecksmatrizen
lassen sich in den n^ Speicherplätzen unterbringen, in denen ursprünglich A
stand. Die vorangehende Diskussion war nur dazu da, uns klarzumachen, was
das Eliminations verfahren eigentlich bewirkt.
Der Aufwand des Eliminations Verfahrens
Eine sehr praktische Frage ist die nach den Kosten — also der Rechenzeit.
Lassen sich 1000 Gleichungen auf einem PC lösen? Was passiert, wenn n =
10,000 ist? Im wissenschaftlichen Rechnen, wo dreidimensionale Modelle sehr
leicht zu einer Million Unbekannten führen können, hat man ständig mit sehr
großen Gleichungssystemen zu tun. Derartige Rechnungen kann man zwar
über Nacht laufen lassen, nicht aber über 100 Jahre.
94
2 Das Lösen linearer Gleichungen
nmaln
Fläche n^
r
I
n-\ mal n-\
n
Fläche (n-lJ
+ . . . =
^ n-2 ^
,
P- \
1^
L-
n-\
— —n— —
\
Volumen -n^
Abb. 2.9. Das Eliminationsverfahren braucht etwa je \r? Multiplikationen und
Subtraktionen. Genau sind es (n^ — n)H + A^ — 1)
Es ist nicht besonders schwierig abzuschätzen, wie viele einzelne
Multiplikationen während des Eliminationsverfahrens auftreten. Konzentrieren
wir uns auf die aufwändige Unke Seite, wo A in C/ überführt wird. Im ersten
Schritt werden Nullen unterhalb des ersten Pivotelements erzeugt. Dazu
werden pro Eintrag von A eine Multiphkation und eine Subtraktion durchgeführt.
In diesem. Schritt zählen wir (grob) n^ Multiplikationen und n^
Subtraktionen. Tatsächlich sind es etwas weniger, nämlich jeweils n^ — n, da die erste
Zeile unverändert bleibt. Spalte 1 ist jetzt abgeschlossen.
Im nächsten Schritt wird die zweite Spalte unterhalb des Pivotelementes
gelöscht. Dazu wird eine Matrix mit n — 1 Zeilen und Spalten verändert. Den
Aufwand dazu können wir mit je (n — 1)^ Multiplikationen und
Subtraktionen abschätzen. Je weiter jetzt das Eliminationsverfahren fortschreitet, desto
kleiner werden die Matrizen, auf denen effektiv gearbeitet wird. In unserer
groben Abschätzung sind es insgesamt n^ + (n —1)^H f-2^ + 1^ Operationen,
bis U erreicht ist.
Die Summe dieser Quadratzahlen ist genau |n(n + |)(n + 1). Für große
n werden die Summanden 1 und | vernachlässigbar, und wir haben es im
Wesentlichen mit |n^ Operationen zu tun. Man findet diese Zahl sofort im
Bild mit der "Pyramide" in Abbildung 2.9 wieder. Die Grundfläche steht
dabei für die n^ Operationen im ersten Schritt, und die Höhe der Pyramide
entspricht den n Schritten, während derer die zu bearbeitende Matrix kleiner
und kleiner wird. Das Volumen dieser Pyramide ist also ein guter Schätzwert
für den Gesamtaufwands. Eine Pyramide mit Länge, Breite und Höhe n hat
aber gerade das Volumen |n^.
Wie sieht es mit der rechten Seite b aus? Im ersten Schritt werden
Vielfache von h\ von den Komponenten 62,...,^n darunter subtrahiert, wozu
2.6 Elimination = Faktorisierung: A=LU 95
insgesamt je n — 1 Operationen nötig sind. Im zweiten Schritt treten je
n - 2 Operationen auf, weil öi nicht beteiligt ist. Im letzten Schritt der
Vöriüärt5elimination wird schließlich noch eine Operation benötigt, um die
Berechnung von c abzuschließen.
Weiter geht es mit der Rücksubstitution. Die Berechnung von Xn
erfordert nur eine Division (durch das letzte Pivotelement). Für die nächste
Unbekannte sind 2 Operationen nötig, und für Xi schließlich n Operationen (n — 1
Substitutionen der übrigen Unbekannten, und eine Division durch das erste
Pivotelement). Insgesamt — in Vorwärts- und Rückwärtsrichtung - werden
genau n^ Operationen benötigt:
(n - 1) + (n - 2) + • • • + 1 + 1 + 2 + . • • + (n - 1) + n = n^ B.31)
Man sieht, dass dies stimmt, indem man (n —1) mit 1 zusammenfasst, (n —2)
mit 2 und so weiter. Jedes Paar liefert einen Beitrag zur Gesamtsumme von
genau n. Mit n Paaren ergibt sich also n^. Es ist also viel weniger aufwändig,
die rechte Seite eines Gleichungssystems zu bearbeiten, als die linke!
Für eine rechte Seite (von b über c zu x) werden n^ MultipUkaUonen
und n^ Subtraktionen benötigt.
Im Folgenden stelle ich noch zwei MATLAB-Funktionen vor, die die
Faktorisierung A = LU einer Matrix berechnen bzw. ein Gleichungssystem Ax = b
zu lösen erlauben. Die Funktion slu hält noch an, falls als Pivotelement eine
Null auftaucht, und bringt eine entsprechende Meldung auf den Bildschirm.
Dieses Problem wird später von der Funktion plu umgangen werden, die
die ganze Spalte nach einem passeden Pivotelement absucht und dann einen
Zeilentausch ausführt. Sie finden diese .m-Dateien auch im Internet.
function [L, U] = slu(A)
y. slu: Quadratische LU-Faktorisierung ohne Zeilentausch
[n,n] = size(A);
toi =l.e-6;
for k = l:n
if abs(A(k,k)) < toi
disp(['Pivotelement zu klein! Spalte \ int2str(k)])
end 7, Ohne Zeilentausch kein Fortgang möglich!
L(k,k) = 1;
for i = k+l:n 7, A(k,k) ist das k-te Pivotelement
L(i,k) = A(i,k)/A(k,k);
for j = k+l:n
A(i,j) = A(i,j) - L(i,k)*A(k,j);
end
end
for j = k:n
96 2 Das Lösen linearer Gleichungen
U(k,j) = A(k,j); % Benenne A in U um.
end
end
function x = slv(A,b)
'/o Löst Ax = b unter Verwendung von L und U aus slu(A) .
% Es werden keine Zeilenvertauschungen ausgeführt!
[L,U] = slu(A);
% Vorwärtselimination löst Lc = b.
% L ist eine untere Dreicksmatrix mit len auf der Diagonalen.
[n,n] = size(A);
for k = l:n
for j = l:k-l
s = s + L(k,j)*c(j);
end
c(k) = b(k) - s;
end
7o Rücksubstitution löst Ux = c.
for k = n:-l:l % Rückwärts durch x(n),...,x(l)
for j = k+l:n
t = t + U(k,j)*x(j);
end
x(k) = (c(k) - t)/U(k,k);
end
X = x' ;
Wie lange benötigen diese Funktionen für die Faktorisierung? Wir haben
die Zeit, die für eine Matrix mit zufälligen Einträgen und n = 100 gebraucht
wird, mittels der MATLAB-Kommandost = clock; lu(A); time(clock,t)
bestimmt. Auf einer SUN Sparestation 1 verging dabei 1 Sekunde, für n = 200
schon 8 Sekunden. Man erkennt die Abhängigkeit von n^ wieder —
verdoppelt sich n, so verachtfacht sich die Rechenzeit!
Aufgrund der n^-Abhängigkeit beträgt der Aufwand für 10 mal größere
Matrizen (also n = 1000) schon 1000 Sekunden. Matrizen der Größe 10.000
schlagen mit A00)^ Sekunden zu Buche. Das ist einerseits schon sehr lang.
Man muss aber bedenken, dass es sich hier um vollständig besetzte Matrizen
(also mit sehr wenigen Nullen) handelt. In der Praxis sind die auftretenden
Matrizen aber sehr dünn besetzt, haben also sehr viele Nullen. In solchen
Fällen lässt sich die Faktorisierung A = LU viel schneller erreichen. Die
Lösung der Gleichung Ax = b mit einer 10000 x 10000-Tridiagonalmatrix
kann innerhalb eines Augenblicks berechnet werden.
Die wesentlichen Punkte
l.Das Gauß'sche EUminationsverfahren (ohne Zeilenvertauschung) liefert
eine Faktorisierung einer Matrix A in L mal U.
2.6 Elimination = Faktorisierung: A=LU
97
2. In der unteren Dreiecksmatrix L stehen die Vielfachen der Pivotzeilen,
die von den darunterliegenden Zeilen subtrahiert werden. Berechnet man
das Produkt LU, wird dies wieder rückgängig gemacht, so dass wieder A
entsteht.
3. Auf der rechten Seite löst man zunächst Lc = b (in Vorwärtsrichtung) und
dann Ux = c (rückwärts).
4. Zur Faktorisierung der linken Seite werden je |(n^ — n) Multiplikationen
und Subtraktionen benötigt.
5. Die Lösung eines Gleichungssystems mit rechter Seite erfordert dann noch
je n^ Multiplikationen und Subtraktionen.
Aufgaben 2.6
In den Aufgaben 1-8 wird die Faktorisierung A = LU (und auch
A = LDU) berechnet.
1. Welche Matrix E bringt A in obere Dreiecksform EA = U? Multiplikation
mit E~^ = L liefert die Faktorisierung A = LU:
A
2 10
042
635
2. Welche Elementarmatrizen £^21 und £^32 bringen A in obere Dreiecksform
ES2E21A = Ul Multiplizieren Sie dann mit E^^ ^^^ ^21 ^^^ faktorisie-
ren Sie A so in
A^
1 1 1
245
040
3. Welche drei Elementarmatrizen E2i,Esi und £^32 bringen A in obere
Dreiecksform ES2E31E21A = U? Multiplikation mit E^^^, E^^^ und E^i^
liefert die Faktorisierung von A in LU mit L = E^iE^^E^^ - Bestimmen
Sie L und U:
101"
A =
222
345
4. Falls A selbst eine untere Dreiecksmatrix mit Einsen auf der
Hauptdiagonalen ist, so erhält man U = I:
A =
100
a 1 0
bei
Die Elementarmatrizen £^215^315^32 enthalten -a bzw. -b und -c.
98
2 Das Lösen linearer Gleichungen
(a) Bestimmen sie durch Ausmultiplizieren von E32E31E21 die Matrix E
mit EA = I.
(b) Berechnen Sie dann L = ^2l^^3l^^32^ so dass A = LU (or LI).
5. Steht an einer Pivot posit ion eine Null, so ist keine Faktorisiserung A =
LU möglich, denn in U erlauben wir nur Pivotelemente ungleich Null.
Zeigen Sie in den folgenden Fällen direkt, dass A = LC/-Faktorisierungen
unmöglich sind.
'Ol'
2 3
=
10'
J 1.
d e
.0/.
'110'
112
121
=
'1
/ 1
m n 1
'de g'.
fh\
i \
Durch Zeilenvertauschungen liesse sich dieses Problem umgehen.
6. Durch welches c entsteht an der zweiten Pivotposition eine Null? Hier
wird ein Zeilentausch nötig, es gibt keine Faktorisierung A = LU. Durch
welches c entsteht eine Null an der dritten Pivotposition? In diesem Fall
hilft nicht einmal ein Zeilentausch und das Eliminationsverfahren
scheitert.
A =
241
351
7. Wie sehen L und D für diese Matrix A aus? Geben Sie die Matrix U der
Faktorisierung A = LU und das "neue" U in A — LDU an.
^248^
039
007
8. A und B sind bezüglich "Spiegelung" an der Diagonalen symmetrisch.
Bestimmen Sie die Faktorisierung in LDU und geben Sie an, wie U mit
L zusammenhängt.
2 4
4 11
9. (Empfohlen) Berechnen Sie L und U für die symmetrische Matrix
und B =
40"
4 12 4
0 40
A=^
a a a a
ah h h
a b c c
abed
Bestimmen Sie vier Bedingungen an a, 6, c und d, so dass eine
Faktorisierung A = LU mit vier Pivot element en möglich ist.
2.6 Elimination = Faktorisierung: A=LU 99
10. Bestimmen Sie L und U für die nicht symmetrische Matrix
a r r r
ah s s
ah c t
ah c d
Bestimmen Sie auch hier vier Bedingungen an a, ö, c, d, r, s und t, die eine
Faktorisierung A = LU mit vier Pivotelementen garantieren.
In den Aufgaben 11-12 lösen wir Ax = b mittels L und U (ohne A
zu benötigen)
11. Lösen Sie das Dreieckssystem Lc = b, um c zu bestimmen. Lösen Sie
dann Ux = c und bestimmen Sie so x:
10
41
und U =
2 4
Ol
und b =
Zur Kontrolle können Sie A = LU ausrechnen und Ax = b auf dem
üblichen Wege lösen. Achten Sie darauf, wo im Verlaufe der Rechnung c
auftritt.
12. Lösen Sie Lc = b nach c und dann Ux
faktorisiert worden?
L =
c nach x. Welches A ist hier
10 0'
110
111
und U =
1 1 1
011
001
und b =
4
5
6
" 1 0
kl 1
Jsi ^32
Ol
0
1
13. (a) Was passiert, wenn Sie das Eliminations verfahren noch einmal auf L
anwenden?
L =
(b) Was erhalten Sie, wenn sie dieselben Schritte auf / anwenden?
(c) Was erhalten Sie, wenn sie diese Schritte auf LU anwenden?
14. Hat man A = LDU und außerdem A = LiDiUi (wobei alle Faktoren als
invertierbar angenommen werden), so gilt L = Li, D = Di und U = Ui.
Die Faktoren sind also eindeutig bestimmt.
(a) Leiten Sie die Gleichung Li^LD = DiUiU~^ her. Handelt es sich
bei dieser Matrix um eine untere oder obere Dreiecksmatrix, oder
um eine Diagonalmatrix?
(b) Zeigen Sie, dass die Einträge der Haupt diagonalen in dieser Gleichung
D — Dl liefern. Warum gilt L — Lil
100
2 Das Lösen linearer Gleichungen
15. Tridiagonalmatrizen enthalten außerhalb der Haupt- und den ersten
beiden Nebendiagonalen nur Nullen. Berechnen Sie Faktorisierungen A =
LU und A = LDL^:
A =
16. Die Faktoren L und U einer Tridiagonalmatrix T haben nur je zwei
Diagonalen mit Einträgen ungleich Null. Wie könnte man die Nullen in T in
einem Computerprogramm nutzen? Bestimmen Sie L und C/.
1 10"
121
0 1 2
und A =
a a 0
a a-\-b b
0 b b-\-c
T =
1200
2310
0123
0034
17. An den mit x markierten Stellen der Matrizen A und B seien Einträge
ungleich Null vorhanden. Welche Nullen bleiben in den Faktoren L und
U erhalten?
A =
X X X X
X X X 0
0 X X X
0 0 xx
und B =
X X X 0
X X 0 X
X 0 X X
0 X X X
18. Geben sie (durch Markierung mit x) an, welche Einträge der Matrizen L
und U nach dem ersten Eliminationsschritt bereits bekannt sind.
XXX
XXX
XXX
=
00"
10
1
0
0 J
19. Angenommen, wir wollen in Aufwärtsrichtung eliminieren. Dann
verwenden wir die letzte Zeile, um in der letzten Spalte Nullen zu erzeugen
(das Pivotelement wäre also die 1), und dann die zweite Zeile, um eine
Null über dem zweiten Pivotelement zu erhalten. Bestimmen Sie so die
Faktorisierung A = UL (!):
A =
53 1
331
1 1 1
20. Das Verfahren von Collins verwendet die Elimination in beiden
Richtungen gleichzeitig. Das Eliminationsverfahren endet also in der Mitte, von
wo die Rücksubstitution wieder in beide Richtungen fortschreitet. Welche
Matrix erhalten Sie, nachdem Sie die beiden Einträge 2 in A (einen von
2.6 Elimination = Faktorisierung: A=LU 101
oben, einen von unten) eliminiert haben? Lösen sie die Gleichung Ax = b
auf diesem Weg.
1100
2110
0132
001 1
und b =
21. (Wichtig) A habe die Pivotelemente 2,7 und 6 (keine Zeilenvertauschun-
gen nötig). Welche Pivotelemente hat die obere linke 2 x 2-Untermatrix
B (also A ohne die dritte Zeile und die dritte Spalte)? Begründen Sie ihre
Antwort!
22. Fügen Sie je eine Zeile und eine Spalte hinzu, um aus der Matrix A in
Aufgabe 21 eine 4 x4-Matrix M zu erzeugen. Welches sind ihre ersten drei
Pivotelemente? (Warum?) Wie können Sie die hinzuzufügenden Elemente
so wählen, dass sich als viertes Pivot element garantiert eine 9 ergibt?
23. MATLAB kennt die n x n-Matrix pascal(n). Bestimmen Sie die
zugehörigen Faktoren L und U, und beschreiben Sie das sich ergebende Schema.
Dazu können Sie die Funktionen chol(pascal(n)) oder slu(A) (aus dem
Text) verwenden, oder einfach von Hand rechnen. MATLAB's Funktion
lu führt Zeilenvertauschungen durch, die das Schema zerstören. Dies
passiert nicht, wenn man chol verwendet:
A = pascalD) =
1111
12 3 4
13 610
1 4 10 20
24. (Ein bisschen Wiederholung) Für welche Zahlen c gibt es keine
Faktorisierung A = LU, obwohl es drei Pivotelemente ungleich Null gibt?
A =
120
3cl
Ol 1
25. Schreiben Sie das Programm slu(A) zu sldu(A) um, so dass es die
Matrizen L,D, und U berechnet.
26. Schreiben Sie slu(A) so um, dass die Faktoren L und U keinen
zusätzlichen Speicher mehr verwenden, sondern in den n^ Speicherplätzen von
A untergebracht werden. Man benötigt keinen zusätzlichen Speicher für
-L/.
27. Erklären Sie, warum am Ende von sW{A,b) x{k) auf {c{k) - t)/U{k,k)
gesetzt wird.
102 2 Das Lösen linearer Gleichungen
28. Schreiben Sie ein Programm zur Multiplikation von Dreiecksmatrizen L
mal U. Vermeiden Sie dabei Schleifen von 1 bis n, wo sie wegen der Nullen
in den Matrizen unnötig sind. Das Programm sollte also die Operationen
in slu rückgängig machen.
2.7 Transponierte und Permutationen
Wir müssen uns jetzt noch mit einer weiteren Operation auf Matrizen
beschäftigen, die glücklicherweise viel einfacher ist als das Invertieren. Es
geht um die transponierte'^ Matrix zu einer Matrix A, die mit A^
bezeichnet wird. Ist A eine m x n-Matrix, so ist Ä^ eine n x m-Matrix:
Ist A =
123
004
so ist
1 0
2 0
3 4
Es werden also die Zeilen von A zu den Spalten von A^, oder auch die
Spalten von A zu den Zeilen von A^. Die Matrix wird gewissermaßen an
ihrer Haupt diagonalen gespiegelt. Der Eintrag in Zeile i, Spalte j von A^ ist
gerade der Eintrag aus Zeile j, Spalte i von A:
(A )ij ^ -Aji,
Die transponierte Matrix einer unteren Dreiecksmatrix ist eine obere
Dreiecksmatrix. Die transponierte von Ä^ ist .
Hinweis MATLAB's Schreibweise für die Transponierte einer Matrix A ist
A'. Um einen Spaltenvektor einzugeben, kann man eine Zeile eingeben und
sie dann transponieren: v =[123]'. Wollen Sie eine Matrix mit der zweiten
Spalte w =[456]' eingeben, so könnten Sie M = [v w] setzen. Es ist aber
schneller, Zeilen einzugeben und dann die ganze Matrix zu transponieren:
M =[1 2 3; 4 5 6]'.
Die Regeln für das Rechnen mit Transponierten sind sehr einfach.
Transponiert man A+B zu {A-\-B)'^, so erhält man die Summe der Transponierten
Ä^ _l_ ßT Interessanter ist, wie es sich mit Produkten AB und Inversen A~^
verhält:
Die transponierte Matrix zu A-{- B ist A^ + B^. B.32)
Die zu AB transponierte Matrix ist {ASf^ — B'^Ä^, B.33)
Die transponierte Matrix zu A~^ ist (A~^)^ = (^^)~^- B.34)
Beachten Sie, dass die Transponierten B^A^ gegenüber dem Produkt
AB in umgekehrter Reihenfolge stehen, gerade so, wie es bei den Inversen
j^-i^-i (jgj, p^Yl war. Für Inverse lässt sich die Formel schnell beweisen:
B~^A~^ mal AB ergibt /. Um sie auch für transponierte Produkte zu
beweisen, beginnen wir mit (Ax)^:
2.7 Transponierte und Permutationen 103
Ax stelle eine Linearkombination der Spalten von A dar,
x^A^ hingegen eine Kombination der Zeilen von A^.
Es handelt sich aber um dieselbe Linearkombination derselben Vektoren,
die lediglich einmal als Spalten und einmal als Zeilen gelesen werden. Die
Transponierte der Spalte Ax ist also die Zeile x^A^. Dies passt mit unserer
Formel {Ax)'^ = x^A^ zusammen. Damit können wir die Formeln für (AB)'^
und für (^~^)^ beweisen.
Hat B = [xi X2] zwei Spalten, so wenden wir dazu die Idee aus dem
letzten Absatz auf jede Spalte an. Die Spalten der Matrix AB sind Axi und
Ax2, und ihre Transponierten also xfA^ und xjA^. Dies sind aber gerade
die Zeilen von B^A^:
AB =
Axi Ax2
transponiert ist
= B'^Ä^. B.35)
Wir haben hier die Lösung B^Ä^ zeilenweise erhalten. Vielleicht gefällt Ihnen
auch unser "durchsichtiger Beweis" am Ende des nächsten Aufgabenblocks.
Vielleicht versteht man alles am besten an einem Zahlenbeispiel:
AB =
'lO'
11
■50"
41
=
0"
91
und B^A^ =
'5 4'
Ol
1 r
Ol
=
■59"
Ol
Die Rechenregel für transponierte Produkte lässt sich auch auf drei oder
mehr Faktoren anwenden: (A^C)^ equals C^B^A^.
Hat man A = LDU, so gilt Ä^ =z U^D^L^. Die Matrix
D = D^ mit den Pivotelementen bleibt unverändert.
Jetzt wollen wir diese Produktregel auf die beiden Seiten der Gleichung
A~^A = I anwenden. Auf der rechten Seite erhalten wir I^ — I. Auf der
anderen Seite der Gleichung können wir aber eine Entdeckung machen. Es
ist nämlich (A~^)^ die Inverse zu A^:
A ^A = I transponiert ergibt A^(A ^)^ = ^-
B.36)
Genauso führt uns die Gleichung AA~^ = I zu (A~^)^A^ = /. Insbesondere
gilt natürlich: A^ ist invertierbar genau dann, wenn A invertierbar ist. Ob wir
also eine Matrix zuerst invertieren und dann transponieren oder umgekehrt,
spielt keine Rolle.
Beispiel 2.7.1 Die Inverse von A =
nierte Matrix dazu ist A^ = [J ?]•
{A~^)'^ ist gleich
[j;] ist A-i = [_6?]- Die transpo
gleich (A'^y
104 2 Das Lösen linearer Gleichungen
Bevor wir weitergehen, wollen wir noch einmal an das Skalarprodukt
erinnern. Die folgende Regel sieht sehr einfach aus, aber sie enthält tatsächlich
den tieferfliegenden Grund dafür, dass man transponierte Matrizen
betrachtet. Für zwei beliebige Vektoren x und y gilt
{Axfy ist gleich x^i4^y gleich x^{A^y). B.37)
Man kann also Klammern setzen oder weglassen. Wir wollen noch schnell
einen Blick auf drei Anwendungen im Ingenieurwesen und der
Betriebswirtschaftslehre werfen.
Sei X ein Vektor, der die Potentiale (Spannungen an den Knoten) eines
elektrischen Netzwerks enthält, sei y der Vektor der Ströme. Dann beschreibt
man mittels einer bestimmten Matrix A durch Ax die Potentialdifferenzen
und durch A^y den Gesamtstrom durch jeden Knoten. Jeder Vektor hat also
seine Bedeutung, und das Skalarprodukt beschreibt den Wärmeverlust beim
Energietransport durch dieses Netzwerk.
Diese wichtige Anwendung der Linearen Algebra auf elektrische
Netzwerke wird in Kapitel 8 noch detailliert beschrieben werden. Hier soll nur soviel
verraten werden: Die Natur verhält sich extrem symmetrisch, was sich hier
in einer Symmetrie zwischen A und Ä^ ausdrückt.
In der Physik und im Ingenieurswesen beschreibt man die Deformation
einer Struktur unter einer Last durch einen Vektor x. Als Ax erhält man
dann die Streckung (bzw. Dehnung), und ist y die interne Spannung, so
erhält man aus Ä^y die äußere Kraft. Diese Gleichung stellt eine Aussage
über ein Skalarprodukt dar, und ebenso eine Gleichgewichtsbeschreibung:
Interne Arbeit (Dehnung • Spannung) =
externe Arbeit (Deformation • Kraft).
In der Betriebswirtschaftslehre kann man durch einen Vektor x die
Produktionsmengen von n Produkten beschreiben. Die m verschiedenen
Rohstoffe, die zu deren Herstellung nötig sind, ergeben sich über eine Input-Output-
Matrix A als Ax, Fasst man nun in y die Kosten pro Rohstoff zusammen, so
erhält man in A^y den Wert pro Produkt:
Die Gesamtkosten für die Rohstoffe sind Ax • y (Rohstoff-
menge mal Kosten pro Rohstoff)
Der Gesamtwert ist x • A^y (Produktmengen mal Wert pro
Produkt)
Wechselt eine Matrix A von einer Seite eines Skalarproduktes auf die
andere, so wird daraus Ä^.
Symmetrische Matrizen
Für symmetrische Matrizen, die die wichtigste Klasse von Matrizen
darstellen, besteht kein Unterschied zwischen einer Matrix und der zu ihr
transponierten Matrix, es gilt A^ = A. Solche Matrizen sind also symmetrisch
2.7 Transponierte und Permutationen 105
bezüglich der Hauptdiagonalen — jeder Eintrag an der Stelle {j, i) stimmt
jjiit dem an der Stelle (i, j) überein. Eine symmetrische Matrix ist
insbesondere notwendigerweise quadratisch.
DEFINITION Für eine symmetrische Matrix gilt Ä^ = A. Dies he-
deutet aji = üij . ;
Beispiel 2.7.2
A =
12
25
- AT
und D
1 0
0 10
= D'
A ist symmetrisch aufgrund der beiden Einträge 2 auf beiden Seiten der
Diagonalen. In D steht an ihrer Stelle 0. Allgemein ist jede Diagonalmatrix
automatisch symmetrisch.
Die Inverse einer symmetrischen Matrix A ist ebenfalls
symmetrisch. (Wobei man hinzufügen muss: Falls A = A^ überhaupt invertierbar
ist.) Denn wird A~^ transponiert, so erhält man {A'^)~^ gleich A~^. Die
Transponierte zu A~^ ist für eine symmetrischen Matrix A also A~^:
A-' =
5-2
-2 1
und D-^ =
10
0 0.1
Als nächstes zeigen wir, dass das Produkt einer Matrix mit ihrer
Transponierten immer eine symmetrische Matrix ist.
Symmetrische Produkte R^R, RR^ und LDL^
Nehmen wir irgendeine nicht unbedingt quadratische Matrix R und
betrachten wir das Produkt R^ mal R. Dieses Produkt ist automatisch symmetrisch:
Die transponierte Matrix zu R^R ist R^{R^)^ = R^R. B.38)
Anstelle dieses sehr kurzen Beweises, dass R^R symmetrisch ist, hätten
wir auch die einzelnen Einträge betrachten können. An Position {i,j) von
R R steht das Skalarprodukt von Zeile i von R'^ (also Spalte i von R) mit
Spalte j von R; die Position {j,i) von R'-'^R enthält hingegen das
Skalarprodukt von Zeile j von R'^ mit Spalte z von i^ — Zeile j von i^^ ist aber Spalte
J von R: es sind also beide Einträge gleich dem Skalarprodukt der Spalten i
^nd j. Also ist R'^R symmetrisch.
Auch die Matrix RR'^ ist symmetrisch. (Die Formen von R und R'^ erlau-
t>en die Multiplikation dieser Matrizen.) Sie ist aber von R'^R verschieden,
'unserer Erfahrung nach wird man, wenn man bei einer wissenschaftlichen
Fragestellung mit einer rechteckigen Matrix R zu tun hat, meistens auf R^R
oder RRT (oder auch beide) geführt.
12
27
—
10
21
10
21
12
03
10
03
12
Ol
106 2 Das Lösen linearer Gleichungen
Beispiel 2.7.3 R=[12] und R^R = [l l] und RR'^ = [5].
Ist R eine m x n-Matrix, so ist R^R eine n x n-Matrix und RR^ eine mxm-
Matrix. Selbst im Fall m = n muss nicht R'^R = RR^ gelten. Es kann
passieren, dass hier Gleichheit auftritt, es ist aber normalerweise nicht der
Fall.
Wir können hoffen, dass die Symmetrie Ä^ — A bei der Anwendung des
Eliminationsverfahrens einen Vorteil bietet. Dies hängt natürlich davon ab,
ob die im Verlaufe des Verfahrens entstehenden Unter mat rizen auch wieder
symmetrisch sind. Dies ist der Fall. Natürlich kann nun die obere
Dreiecksmatrix U allein nicht immer symmetrisch sein — die Symmetrie findet sich
vielmehr im Produkt LDU wieder. Erinnern wir uns daran, dass man eine
Diagonalmatrix D von Pivotelementen aus U herausziehen kann, so dass auf
der Diagonalen sowohl von L als auch von U nur Einsen stehen:
{LU zerstört die Symmetrie)
{LDU spiegelt die Symmetrie wider)
U ist transponiert zu L.
Ist A symmetrisch, so wird aus der üblichen Form A = LDU also die
Gleichung A — LDL^, die Matrix U mit Einsen auf der Diagonalen ist die
zu L transponierte Matrix. Die Diagonalmatrix D, die die Pivotelemente
erhält, ist natürlich sowieso schon symmetrisch.
2K Lässt sich A — A?' ohne ZeilenvertauschuBgen m LDU faktorisiereBy:
so gilt U = L^. Die symmetrische Faktorisierung ist A = LDL'^. :i..
Beachten Sie, dass die Transponierte zu LDL^ automatisch (L^)^D^L^ =
LDL^ ist. Wir erhalten eine symmetrische Faktorisierung einer
symmetrischen Matrix. Der Aufwand für das Eliminationsverfahren wird dadurch
halbiert, von n^/3 Multiplikation zu n^/6. Auch der Speicherbedarf wird im
Wesentlichen halbiert, da wir lediglich L und D, nicht aber U speichern
müssen.
Permutations-Matrizen
Das Transponieren hat eine besondere Bedeutung für Permutationsmatrizen.
Eine solche Matrix P hat genau einen Eintrag, nämlich eine ", in jeder
Zeile und in jeder Spalte. Dann ist auch P^ eine Permutationsmatrix —
vielleicht dieselbe, vielleicht eine andere. Jedes Produkt P1P2 zweier
Permutationsmatrizen ist wieder eine. Wir wollen jetzt jede Permutationsmatrix P
durch Umordnen der Zeilen von / erzeugen.
2.7 Transponierte und Permutationen 107
Die einfachste Permutationsmatrix ist P = / {keine Veränderung). Die
nächst einfachen sind die Zeilenvertauschungen Pij, die durch Vertauschen
der beiden Zeilen i und j von / entstehen. Wieder andere Permutationen
vertauschen 3 Zeilen. Indem wir alle möglichen Zeilenvertauschungen auf /
anwenden, erhalten wir auch alle möglichen Permutationsmatrizen:
DEFINITION Eine nxn-Perym^tationBmatrim P enü^tt d$en Zeir
len nofi I in beliebiger Eeihenfi^t^e^: }
Beispiel 2.7.4 Es gibt sechs 3 x 3-Permutationsmatrizen (die Nulleinträge
wurden leer gelassen):
/ =
^31 =
P21 =
P32 —
-^32-^21 =
^21-^32 —
Es gibt n\ Permutationsmatrizen der Ordnung n. Das Symbol n\ bedeutet
„n Fakultät", also das Produkt der Zahlen A)B) • • • (n). Es ist also 3! =
A)B)C) = 6. Ebenso gibt es 24 Permutationsmatrizen der Ordnung 4.
Es gibt nur 2 Permutationsmatrizen der Ordnung 2, nämlich [J 5] ^^^
Wichtig: P~^ ist ebenfalls eine Permutationsmatrix. Im Beispiel oben sind
die linken vier Matrizen alle ihre eigenen Inversen. Die beiden rechten
Matrizen sind zueinander in vers. In allen Fällen ist eine einfache Zeilenvertauschung
ihre eigene Inverse, da zweifache Anwendung einer Zeilenvertauschung wieder
/ ergibt. Bildet man aber das Produkt ^32^21? so ist die dazu inverse Matrix
Ai-P32- die einzelnen Inversen in der Reihenfolge vertauscht.
Wichtiger noch: P~^ ist immer gleich P^. Die vier Matrizen links
sind ihre eigenen Transponierten und Inversen. Die beiden Matrizen rechts
sind die Transponierte (und Inverse) der jeweils anderen. Dies sieht man
folgendermaßen. Im Produkt PP^ trifft die " der ersten Zeile von P genau
auf die " der ersten Spalte von P^, in den anderen Spalten trifft sie aber
immer nur auf Nullen. Dasselbe gilt für alle Zeilen von P. Deshalb gilt PP^ =
L
Man könnte dies auch anders beweisen. Betrachten wir P als Produkt
von Zeilenvertauschungen. Eine Zeilenvertauschung ist nun sowohl zu sich
selbst invers wie auch zu sich selbst transponiert. P^ ist aber das Produkt
der Vertauschungen in umgekehrter Reihenfolge, wie auch P~^. P^ und P
sind also die gleichen Matrizen.
108 2 Das Lösen linearer Gleichungen
Symmetrische Matrizen führten zu der Gleichung A = LDL^^
Permutationen führen uns jetzt zu PA = LU,
Die LU Faktorisierung mit Zeilenvertauschungen
Ich hoffe, sie können sich noch an die Gleichung A = LU erinnern. Wir
erhielten sie aus der Gleichung A = {E^i • • • E^'^ '")U, indem die Inversen der
Eliminationsmatrizen Eij in der unteren Dreiecksmatrix L zusammengefasst
wurden. Das Ergebnis war dann A = LU mit einer oberen Dreiecksmatrix U
und Einsen auf der Haupt diagonalen der Matrix L.
Leider kann man diese großartige Faktorisierung nicht in jedem Fall
erreichen! Manchmal werden Zeilenvertauschungen nötig, um geeignete
Pivotelemente an die nötige Stelle zu bringen. In diesem Fall erhält man eine
Gleichung A = {E''^ • • • p-^ • • • E'^ • • • p-^ '•')U, wobei jede Zeilenvertau-
schung durch Multiplikation mit einer Matrix Pij bewirkt wird, die dann (als
ihre eigene Inverse) auch auf der anderen Seite auftaucht. Die
Zeilenvertauschungen werden jetzt in einer Permutationsmatrix P zusammengefasst. So
erhält man eine Faktorisierung für jede invertierbare Matrix A— was wir
natürlich erreichen wollen.
Die Hauptfrage ist nun, wo die Pij 's gesammelt werden. Es gibt zwei
naheliegende Möglichkeiten — alle Vertauschungen vor dem
Eliminationsverfahren durchzuführen, oder die Vertauschungen hinter den Eij zu platzieren.
Im ersten Fall erhält man die Faktorisierung PA = LU, im zweiten Falle
steht die Permutationsmatrix in der Mitte der Faktorisierung.
1. Die Zeilenvertauschungen können auf die linke Seite gebracht werden, vor
A. Wir können uns dies so vorstellen, als brächten wir A vor dem
Eliminationsverfahren in eine Form PA, für die keine Zeilenvertauschungen
mehr nötig sind. Man hat dann also die Gleichung PA = LU.
2. Wir können die Zeilenvertauschungen auch im Anschluss an das
Eliminationsverfahren durchführen, so dass die Pivotzeilen zunächst in einer
falschen Reihenfolge stehen und die reduzierte Matrix erst durch die
Zeilenvertauschungen in einer Matrix Pi in obere Dreiecksform gebracht
werden. Dann hat man A = LiPiUi.
In fast allen Anwendungen (und stets in MATLAB) wird die Form PA =
LU verwendet. Wir werden uns deshalb auf sie konzentrieren. Die
Faktorisierung A = LiPiUi ist eher für die theoretische lineare Algebra geeignet, da
sie eleganter ist. Ich erwähne nur deshalb beide Formen, weil der Unterschied
zwischen ihnen nicht besonders bekannt ist. Wahrscheinlich werden Sie sich
kaum mit beiden Formen beschäftigen müssen, da der Fall P = I, wenn keine
Zeilenvertauschungen nötig sind, bei weitem der wichtigste ist.
Bei der folgenden Matrix A müssen wir zuerst die Zeilen 1 und 2
vertauschen, so dass an der ersten Pivotposition keine Null steht. Wenden wir dann
das Eliminations verfahren an:
2.7 Transponierte und Permutationen 109
Ol 1
121
279
A
-^
121
Ol 1
279
PA
-^
21"
011
037
4i =
-^
2
211
011
0 0 4]
42 = 3
Die Zeilen der Matrix PA sind jetzt in einer Reihenfolge, in der sich die
Matrix problemlos faktorisieren lässt:
PA =
00"
010
231
21"
Ol 1
OO4J
= LU,
B.39)
Hier konnten wir also wie üblich mit A beginnen und bei U aufhören. Die
einzige Bedingung ist, dass A invertierbar ist.
2L (PA—LU) Ist Ä invertierbar, so lassen sich die Zeilen durch eine
Permutation P so anordnen^ da^ PA in die Form LU faktorlsiert worden kann.
Alle Pivotelemente sind von Null verschieden, und die Gleichung Äx — b
hat eine eindeutige Lösung,
Im MAT LAB-Code für die Faktorisierung vertauschen diese Zeilen die k-te
Zeile der Matrix A mit der r-ten Zeile darunter, in der ein fc-tes Pivotelement
gefunden wurde. Der Ausdruck A{[r fc],l : n) Uefert die aus diesen beiden
Zeilen und allen Spalten 1 bis n bestehende Matrix zurück.
A([r k],l:n) = A([k r],l:n);
L([r k],l:k-l) = L([k r],l:k-l);
P([r k],l:n) = P([k r],l:n);
sign = -sign
Das Vorzeichen sign der Matrix P gibt an, ob die Anzahl Zeilenvertau-
schungen bis hierher gerade (sign = 1) oder ungerade (sign = — 1) ist. Zu
Beginn der Faktorisierung gilt P = I und sign = 1. Jedesmal, wenn eine Zei-
lenvertauschung auftritt, wechselt sign das Vorzeichen. Der Wert von sign
am Ende der Faktorisierung ist gerade die Determinante von P, Sie hängt
nicht von der Reihenfolge der Vertauschungen ab.
Für die Matrix PA erhalten wir also die bekannte Faktorisierung LU. Der
Computer verwendet allerdings nicht immer das erste mögliche Pivotelement.
Für den Algebraiker mag ein kleines Pivotelement akzeptabel sein, jeder Wert
außer der Null ist gleich brauchbar. Der Computer hingegen sucht die ganze
Spalte abwärts nach dem größten Pivotelement. (In Kapitel 9.1 wird erklärt,
^ieso dies die Rundungsfehler reduziert. Diese Strategie wird partielle oder
Spaltenpivotierung genannt.) Die Matrix P kann also Zeilenvertauschungen
enthalten, die im algebraischen Sinne nicht notwendig sind. Man hat trotzdem
noch die Faktorisierung PA = LU.
110 2 Das Lösen linearer Gleichungen
Unser Rat ist, Permutationen zu verstehen, das Rechnen aber MATLAB
zu überlassen. Man hat schon genug Mühe mit der Faktorisierung A = LU,
ohne dass ein P auftritt. Der Programmcode für splu(A) berechnet die
Faktorisierung PA = LU, und splv(yl,6) löst die Gleichung Ax = b für eine
beliebige quadratische invertierbare Matrix A. Kann in einer Spalte k
überhaupt kein Pivotelement gefunden werden (ist A also nicht invertierbar), so
hält die Prozedur splu an und gibt eine entsprechende Meldung aus.
Die wesentlichen Punkte
l.Beim Transponieren werden die Zeilen von A zu den Spalten von Ä^. Es
gilt daher {A'^)ij = Aji.
2. Die Transponierte zu AB ist B^Ä^, und die Transponierte zu A~^ ist die
Inverse von Ä^,
3.Das Skalarprodukt (Ax)^y ist gleich dem Skalarprodukt x^(A^y).
4. Zu einer symmetrischen Matrix {A^ = A) gibt es eine symmetrische
Faktorisierung A = LDL^.
5. Eine Permutationsmatrix hat in jeder Zeile und jeder Spalte nur jeweils
einen Eintrag mit dem Wert 1. Es gilt P^ = P~^.
6. Ist A invertierbar, so gibt es eine Permutation P, so dass PA = LU fakto-
risierbar ist.
Aufgaben 2.7
In den Aufgaben 1-7 geht es um die Rechenregeln für
transponierte Matrizen.
1. Bestimmen Sie A^, A-\ {A'^)'^ und {Ä^)~^ für
A-
10
82
und auch A
1 1
10
2. Überprüfen Sie, dass (AB)'^ ^ B'^Ä^ gilt, nicht aber (AB)'^ = A^B^:
10
2 1
B =
13
Ol
AB^
13
27
Wie beweisen Sie, falls AB — BA gilt (dies ist im Allgemeinen nicht
richtig!), dass auch B"^A^ = A^B^ gilt?
3. (a) Die Matrix {{AB)~'^)^ besteht aus dem Produkt von (A~^)^ und
{B~^)^. In welcher Reihenfolge!
(b) Ist U eine obere Dreiecksmatrix, so ist {U~^)^ eine
Dreiecksmatrix.
4. Zeigen Sie, dass für eine Matrix A ^ 0 A^ = 0 möglich, aber A^A — 0
unmöglich ist.
2.7 Transponierte und Permutationen 111
5. (a) Welche Zahl ergibt das Produkt Zeilenvektor x^ mal A mal
Spaltenvektor y?
'0"
x^Ay-[01]
1 23
456
(b) Dies ist dasselbe wie x^A =
(c) ebenso wie x^ = [0 1] mal Ay =
mal y-@,1,0),
6. Transponiert man eine Blockmatrix M = [c Bj' ^^ ergibt sich M^ =
. Probieren Sie dies aus. Welche Bedingungen müssen die Matrizen
A, B, C und D erfüllen, damit M symmetrisch ist?
7. Wahr oder falsch?
(a) Eine Blockmatrix [ a ^ ] ^^^ automatisch symmetrisch.
(b) Sind A und B symmetrisch, so ist es auch ihr Produkt AB.
(c) Ist A nicht symmetrisch, dann ist auch die Inverse A~^ nicht
symmetrisch.
(d) Sind A,B und C symmetrisch, so gilt (ABC)'^ = CBA.
Die Aufgaben 8-14 beschäftigen sich mit Permutationsmatrizen.
8. Warum gibt es n! Permutationsmatrizen der Ordnung n?
9. Sind Pi und P2 Permutationsmatrizen, so auch P1P2. Finden Sie zwei
Beispiele mit P1P2 # P2P1 und P3P4 = PaPs-
10. Es gibt 12 Permutationen der Zahlen A,2,3,4) mit einer geraden Anzahl
von Vertauschungen. Zwei davon sind A,2,3,4) mit keiner Vertauschung
und D,3,2,1) mit 2 Vertauschungen. Bestimmen Sie die anderen zehn,
wobei Sie die Zahlen 1 bis 4 in unterschiedliche Reihenfolgen bringen,
statt jedesmal eine 4 x 4-Matrix aufzuschreiben.
11. Mittels welcher Permutation P wird aus A eine obere Dreiecksmatrix
PA? Welche Permutationen erzeugen eine untere Dreiecksmatrix P1AP2?
Multiplikation mit einer Matrix P2 von rechts vertauscht die von
A.
0 6"
A =
1 23
045
12. (a) Erklären Sie, warum das Skalarprodukt von x und y gleich dem von
Px und Py für eine beliebige Permutationsmatrix P ist.
(b) Zeigen Sie für x = A,2,3) und y = A,1,2), dass Px • y nicht immer
gleich X • Py ist.
^^' (a) Warum befindet sich unter den Potenzen P*^ einer Permutationmatrix
immer die Einheitsmatrix /?
112 2 Das Lösen linearer Gleichungen
(b) Bestimmen Sie eine 5 x 5-Permutationsmatrix, für die P^ die kleinste
Potenz gleich / ist. (Tip: Kombinieren Sie einen 2 x 2-Block mit einem
3 X 3-Block.)
14. Manche Permutationsmatrizen sind symmetrisch: P^ ~ P. Dann erhält
man aus P^P = / die Gleichung P^ = /.
(a) Wird mittels P aus Zeile 1 die Zeile 4, so führt P^ Zeile in
über. Gilt P^ = P, so besteht P aus paarweisen Zeilenvertau-
schungen, die sich nicht überlappen.
(b) Finden Sie eine symmetrische 4 x 4-Permutation, die keine Zeile
unverändert lässt.
In den Aufgaben 15-20 geht es um symmetrische Matrizen und
ihre Faktorisierungen.
15. Geben Sie symmetrische 2 x 2-Matrizen A = A^ mit den folgenden
Eigenschaften an:
(a) A ist nicht invertierbar.
(b) A ist invertierbar, kann aber nicht in der Form A ~ LU faktorisiert
werden.
(c) A lässt in der Form LU faktorisieren, aber nicht in der Form LL^.
16. Welche der folgenden Matrizen sind symmetrisch, wenn A = A^ und
B = B^ gilt?
(a) A2 - B^
(b) {A + B){A-B)
(c) ABA
(d) ABAB.
17. (a) Wie viele Einträge einer symmetrischen 5 x 5-Matrix können
unabhängig voneinander gewählt werden?
(b) In welcher Weise hat man für die Matrizen die L und D dieselbe
Anzahl Wahlmöglichkeiten?
(c) Wie viele Einträge kann man für eine schief symmetrische Matrix mit
A^ = -A wählen?
18. R sei eine rechteckige m x n-Matrix, A sei eine symmetrische m x m-
Matrix.
(a) Beweisen Sie, dass R^AR symmetrisch ist. Welche Dimensionen hat
diese Matrix?
(b) Beweisen Sie, dass auf der Diagonalen von R^R keine negativen
Elemente stehen.
19. Faktorisieren Sie diese Matrizen in der Form A — LDL^.
2.7 Transponierte und Permutationen 113
A =
13
32
A =
16
bc
und A =
2-1 0
-1 2-1
0-1 2
20. Bestimmen Sie die symmetrische 2 x 2-Matrix, die entsteht, nachdem das
Eliminations verfahren mit der ersten Spalte fertig ist:
A =
248
439
890
und A —
1 h c
b d e
Cef
In den Aufgabe 21-29 geht es um Faktorisierungen der Formen
PA = LU und A = LiPiUi.
21. Bestimmen Sie die Faktorisierung PA — LU für die Matrizen
Ol 1
101
234
Machen Sie auch die Probe.
und A —
120
24 1
1 1 1
22. Geben Sie eine 3 x 3-Permutationsmatrix an, bei der das
Eliminationsverfahren zwei Zeilen vertauschungen vornehmen muss. Wie sehen die
Faktoren P, L und U für diese Matrix aus?
23. Faktorisieren Sie die folgende Matrix nach PA — LU. Bestimmen Sie
dann auch eine Faktorisierung nach A = LiPiUi. Warten Sie dazu mit
dem Zeilentausch, bis das Dreifache von Zeile 1 von Zeile 2 subtrahiert
wurde:
A =
012
038
2 1 1
24. Wie würde P nach jedem Schritt der M ATLAB-Prozedur splu angewandt
auf A aussehen?
A =
Ol
23
und A -
001
234
056
25. Wie sehen P und L nach jedem Schritt von splu für
"Ol 2"
1 10
254
aus?
114 2 Das Lösen linearer Gleichungen
26. Erweitern Sie splu zu einer Prozedur spldu, die die Faktorisierung PA
LDU liefert.
ri 1 r
113
258
-^
1 1^
002
osej
rioo"
001
010
11"
036
OO2J
27. Wie sieht die Matrix Li der Faktorisierung A — L\P\IJ\ aus?
-^PiUi =
28. Sei A eine Permutationsmatrix. Dann gilt L = U = I. Erklären Sie,
warum in der Faktorisierung PA — LU P = A^ gilt. Die Zeilen von A
werden also durch Multiplikation mit in die richtige Reihenfolge
gebracht.
29. Beweisen Sie, dass man die Einheitsmatrix niemals als Produkt von drei
oder fünf Zeilenvertauschungen erhalten kann, wohl aber als Produkt von
zwei oder vier Vertauschungen.
30. (a) Bestimmen Sie eine Matrix E21, die die 3 unterhalb des ersten
Pivotelements entfernt. Das Produkt E21AE21 entfernt dann beide
Einträge 3:
A =
'1
3 0'
3 114
0
4 9_
wird
D^
100
020
001
(b) Bestimmen Sie dann noch E32, um an Stelle der 4 unter dem zweiten
Pivotelement eine Null entstehen zu lassen. Damit lässt sich A auf
E32E21AE21E22 ~
Faktorisierung A
D reduzieren. Bestimmen Sie die Inversen für die
-- LDL^.
Die nächsten Aufgaben behandeln Anwendungen der Gleichung
(Ax)^y = x^(A^y).
31. Wir betrachten Überlandleitungen zwischen Boston, Chicago und Seattle.
Die Spannungen in den jeweiligen Städten seien durch xb, xc und xs
gegeben. Wird der Ohm'sche Widerstand der Leitungen als jeweils gleich
angenommen, so enthält y die Ströme zwischen den Städten:
y = Ax ist
(a) Bestimmen Sie die Gesamtströme in A^y, die aus den Städten her-
ausfiiessen.
(b) Überprüfen Sie, dass (Ax)^y mit x^{A^y) übereinstimmt — beide
Ausdrücke müssen sechs Summanden enthalten.
Vbc
ycs
IVBS _
—
-1 0"
0 1-1
1 0-1
'xb]
Xc
.^s,
2.7 Transponierte und Permutationen 115
32. Zur Herstellung von xi Lastkraftwagen und X2 Flugzeugen benötigt man
xi +50x2 Tonnen Stahl, 40xi + 1000x2 Kilogramm Gummi und 2xi +50x2
Mannmonate Arbeit. Die Kosten pro Einheit seien 2/1 = 700 Euro pro
Tonne Stahl, 2/2=3 Euro pro Kilogramm Gummi und 2/3 = 3000 Euro
pro Monat. Welchen Wert haben dann ein LKW und ein Flugzeug? Dies
sind gerade die Komponenten von Ä^y.
33. Bestimmen Sie eine Matrix A, so dass Ax die Mengen an Stahl, Gummi
und Arbeitsmonaten angibt, die zur Herstellung von x LKW's und
Flugzeugen nötig sind. Dann gibt Ax • y die der Eingangsgrößen an,
während x • Ä^y den Wert von ausdrückt.
34. Die Permutationsmatrix, die (x, 2/, z) in (z, x, 2/)überführt, stellt auch eine
Drehmatrix dar. Bestimmen Sie P und P^. Die Drehachse a = A,1,1)
ist gleich Pa. Um welchen Winkel wird v = B,3,-5) in den Vektor
Pv = (-5,2,3) gedreht?
35. Beschreiben Sie A = [1 2 j ^\^ Produkt EH einer Elementarmatrix mit
einer symmetrischen Matrix H.
36. Wir beenden dieses Kapitel mit einer neuen Faktorisierung: A = EH.
Dazu beginnen wir mit der Faktorisierung A = LDU. Fügen Sie Matrizen
C und U^ ein, um E und H zu bestimmen.
A = {LC){U^DU) = (untere Dreiecksmatrix E)(symmetrische Matrix H)
Hierbei sollen auf der Diagonalen von E = LC Einsen stehen. Wie
erhalten Sie C? Warum ist LC eine untere Dreiecksmatrix?
*
Durchsichtiger Beweis für (AB)'^ = B^A^. Betrachtet man eine
Matrix, indem man von der anderen Seite durch das Papier schaut, so
sieht man die Transponierte. Halten Sie diese Seite ins Licht und sehen
Sie sich die Matrix B unten an. Die Spalte wird zu einer Zeile von B^.
Vielleicht können Sie sie besser sehen, wenn Sie die Zeichnung auf dünnes
Papier abzeichnen und dann umdrehen, so dass das Symbol B^ aufrecht
steht.
Die drei Matrizen lassen sich multiplizieren: Die Zeile von A mal der
Spalte von B ergibt einen Eintrag in AB. Betrachtet man dies von der
anderen Seite, so erhält man denselben Eintrag in B^Ä^ - {^BY als
Produkt einer Zeile von B^ und einer Spalte von A^.
116 2 Das Lösen linearer Gleichungen
CD
m
AB
OD
©
3 Vektorräume und Untervektorräume
3.1 Räume von Vektoren
Für einen Anfänger scheinen Rechnungen mit Matrizen viele Zahlen zu
enthalten. Für Sie hat die Matrizenrechnung mit Vektoren zu tun, da die Spalten
von Ax und von AB Linearkombinationen von n Vektoren sind — den
Spalten von A. In diesem Kapitel werden wir zu einer dritten (der höchsten)
Ebene des Verständnisses gelangen. An Stelle einzelner Spalten betrachten
wir nun „Räume" von Vektoren. Ohne Vektorräume und im Besonderen ihre
Unterräume gesehen zu haben, hat man die Gleichung Ax = b noch nicht
vollständig verstanden.
Da dieses Kapitel ein wenig tiefer eintaucht, könnte es auch ein wenig
schwieriger erscheinen. Das ist nur natürlich. Es ist deshalb die Aufgabe des
Autors, verständlich zu machen, wo sich hinter den Rechnungen die
Mathematik verbirgt. Immerhin werden die folgenden Seiten uns bis zum Kern der
Linearen Algebra führen.
Wir fangen mit den wichtigsten Vektorräumen an. Sie werden mit M^, M^,
M^, M^ usw. beschrieben. Jeder dieser Räume W besteht aus einer ganzen
Ansammlung von Vektoren. Der M^ besteht aus allen Spaltenvektoren mit
fünf Komponenten. Man nennt ihn einen „fünfdimensionalen Raum".
DEFINITION Der Raum W^ besteht ans allen Spaltenvektoren v
rnit n Komponenten.
Die Komponenten von v sind reelle Zahlen, daher der Buchstabe M.
Entsprechend gehört ein Vektor, dessen n Komponenten komplexe Zahlen
sind, zum Raum C^.
Der Vektorraum M^ wird durch die normale x-y-Ehene dargestellt. Jeder
Vektor im M^ hat zwei Komponenten. Das Wort „Raum" soll bedeuten, dass
^lle diese Vektoren gemeint sind — die ganze Ebene. Jeder Vektor enthält
^ie X- und die ^/-Koordinate eines Punktes der Ebene.
Ganz ähnlich gehören die Vektorem im E^ zu den Punkten {x,y,z) des
^J^eidimensionalen Raumes. Der eindimensionale Raum M^ ist eine Gerade
V^ie die x-Achse). Wie im vorherigen Kapitel schreiben wir Vektoren als
118 3 Vektorräume und Unter vektorräume
Spalte zwischen eckigen Klammern, oder in einer Zeile in runden Klammern.
ist imM^ A,1,0,1,1) ist im
1+2
1-z
ist im C^.
Das Tolle an der linearen Algebra ist, dass sie es ermöglicht, bequem mit
dem fünfdimensionalen Raum zu arbeiten. Anstatt einen Vektor zeichnen zu
müssen, braucht man nur seine 5 (oder n) Komponenten, und um v mit 7
zu multiplizieren, multipliziert man lediglich seine Komponenten mit 7. Die
Zahl 7 heißt hier auch ein „Skalar". Will man zwei Vektoren im M^ addieren,
so addiert man sie ebenfalls komponentenweise. Beide Operation geschehen
also „innerhalb" des Vektorraums:
Wir können zwei beliebige Vektoren im W^ addieren, und wir
können jeden beliebigen Vektor im W^ mit jedem beliebigen Skalar
multiplizieren.
„Innerhalb des Vektorraums" heißt hier, dass das Ergebnis zu
demselben Raum gehört, Ist v der Vektor im M^ mit den Komponenten 1,0,0,1,
so ist 2v der Vektor im M^ mit den Komponenten 2,0,0,2. (Hier ist 2 der
Skalar.) Für die Räume M^ lässt sich eine ganze Reihe von Eigenschaften
zeigen. Das Kommutativgesetz beispielsweise lautet v + w = w + v; das
Distributivgesetz besagt, dass c(v + w) = cv + cw ist, und es gibt einen einzigen
„Nullvektor" 0 mit der Eigenschaft 0 + v = v. Dies sind schon drei der acht
Bedingungen, die am Anfang des nächsten Aufgabenblocks angegeben sind.
Diese acht Bedingungen stellt man an einen Vektorraum. Es gibt noch
andere Vektoren als die bekannten Spaltenvektoren, und andere Vektorräume
als die Räume M^; sie alle genügen diesen Bedingungen.
Ein reeller Vektorraum ist eine Menge von „Vektoren'' mit Regeln für
die Addition von Vektoren und für die Multiplikation mit reellen Zahlen.
Sowohl die Addition wie auch diese Multiplikation müssen wieder Vektoren in
diesem Vektorraum ergeben, und die Operationen müssen die acht
Bedingungen erfüllen (was normalerweise kein Problem ist). Einige Beispiele für
andere Vektorräume als die Räume M^ sind:
M Der Vektorraum aller reellen 2 x 2-Matrizen.
F Der Vektörraum aller reuen Funktionen /(a?)« /,
N Der Vektorraum, der nur einen NuÜmktor eniUWlt
Die Vektoren in M sind „in Wirklichkeit" Matrizen, und die Vektoren von
F sind Funktionen. In N gibt es nur eine einzige Addition: 0 + 0 = 0. Aber
in jedem Fall ist die Möglichkeit der Addition gegeben: Matrizen lassen sich
zu Matrizen addieren, Funktionen zu Funktionen, und der Nullvektor zum
Nullvektor. Eine Matrix lässt sich mit 4 multiplizieren, ebenso eine Funktion
3.1 Räume von Vektoren
119
0 0"
P 1.
a b
c d
v^^
/^
1 0
P
0
0 0
1 0
0 1
P 0
der kleinste Vektorraum
Abb. 3.1. Der vierdimensionale Matrizenraum M. Der nulldimensionale Raum N.
und auch der Nullvektor. In jedem Fall gehört das Resultat wieder zu M, F
oder N. Dass die acht Bedingungen erfüllt sind, sieht man leicht.
Der Raum N ist nuUdimensional (für jede sinnvolle Definition der
Dimension), deshalb stellt er den kleinstmöglichen Vektorraum dar. Wir wollen
ihn nicht M^ nennen, weil dies zu der Idee verleiten könnte, es gäbe in
diesem Raum keinen Vektor (keine Komponenten — kein Vektor!). Tatsächlich
enthält der Vektorraum N genau einen Vektor (den Nullvektor). Ohne einen
Nullvektor kommt kein Vektorraum aus. Natürlich hat jeder Vektorraum
seinen eigenen Nullvektor: die Nullmatrix, die Funktion, die überall den Wert
null hat, oder den Vektor @,0,0) im M^.
Unterräume
Hin und wieder wird es vorkommen, dass wir Matrizen oder Funktionen als
Vektoren betrachten. Weitaus am meisten werden wir aber Räume benötigen,
die ganz normale Spaltenvektoren mit n Komponenten enthalten — aber
nicht unbedingt alle Vektoren mit n Komponenten. Es gibt nämlich wichtige
Vektorräume innerhalb der Räume W.
Beginnen wir mit dem normalen dreidimensionalen Raum M^. Wir wählen
eine Ebene durch den Koordinatenursprung @,0,0). Nun ist diese Ebene
ebenfalls ein Vektorraum, denn die Summe zweier Vektoren dieser Ebene
liegt wieder in der Ebene, und multipliziert man einen Vektor der Ebene mit
Zahlen wie 2 oder —5, so liegt das Ergebnis ebenfalls in der Ebene. Die Ebene
ist aber nicht der Raum M^, obwohl sie „so aussieht", denn die Vektoren haben
arei Komponenten, und sie gehören zum Raum M^. Wir haben es mit einem
Vektorraum innerhalb des M^ zu tun.
Dieses Beispiel illustriert eine der wichtigsten Ideen der linearen Algebra.
Die Ebene ist ein Unterraum des Vektorraums M^.
120 3 Vektorräume und Untervektorräume
DEFINITION Ein Unterraum eines Vektorrauma ist eine Menge 'raE
Vektoren (ixu den^ auch Ogehcört), die zwei Bedingungen erftillt: Sin^ '^
undw zwei Vektoren avs dem ünterrauw.^ und ist c ein heliebige^^
Skalar^ so miisaen (i) v 4- w und (ii) cv ebenfalls zum Unterrautifiß
gehören* '^%
Man sagt auch, die Menge von Vektoren sei „abgeschlossen" unter der
Addition v+w und der Skalarmultiplikation cv (und natürlich auch cw). Man
muss bei Anwendung dieser Operationen innerhalb des Unterraums bleiben.
Wenn die beiden Bedingungen erfüllt sind, bedeutet das, dass man auch
innerhalb des Unterraums subtrahieren kann, denn mit w ist auch (—l)w
im Unterraum, und also auch die Summe v + (—l)w = v—w. Kurz gesagt,
mit V und w gehören alle Linearkombinationen von v und w zum
Unterraum.
Die Operationen im Unterraum erfüllen natürlich die Gesetze des „großen"
Vektorraumes, zu dem der Unterraum gehört. Deshalb sind die acht
Bedingungen für die Vektorraumoperationen automatisch erfüllt. Um zu zeigen,
dass eine Menge ein Unterraum eines Vektorraums ist, müssen also nur die
Bedingungen (i) und (ii) erfüllt sein.
Stellen wir einige Eigenschaften von Unterräumen zusammen. Erstens:
Jeder Unterraum eines Vektorraums enthält dessen Nullvektor.
Beispielsweise muss eine Ebene im E^ den Ursprung @,0,0) enthalten, um
ein Unterraum zu sein. Diese Eigenschaft folgt sofort aus der Bedingung (ii):
Für c = 0 besagt sie nichts anderes, als dass Ov = 0 im Vektorraum enthalten
sein muss.
Ebenen, die den Ursprung nicht enthalten, erfüllen diese Bedingungen
nicht. Liegt beispielsweise v in einer solchen Ebene, so gehören — v und Ov
nicht zur Ebene. Eine Ebene, die den Ursprung nicht enthält, ist kein
Unterraum.
Geraden durch den Ursprung sind hingegen Unterräume. Man bleibt auf
einer Geraden, wenn man einen Vektor mit 5 multipliziert, oder zwei Vektoren
der Geraden addiert. Dies gilt aber nur für die Geraden, die durch @,0,0)
gehen.
Der Raum E^ ist natürlich ebenfalls ein Unterraum. Jeder Vektorraum
ist ein Unterraum seiner selbst. Betrachten wir eine Liste aller möglichen
Unterräume des E^:
(L): Alle Geraden durch @,0,0) (R^) als Ganzes
(E): Alle Ebenen durch @,0,0) (N): Nur der Nullvektor @,0,0)
Versuchen wir, nur Teile einer Geraden oder einer Ebenen zu verwenden,
so werden die Bedingungen für einen Unterraum nicht erfüllt. Betrachten wir
einige Beispiele im E'^:
3.1 Räume von Vektoren 121
Beispiel 3.1.1 Die Menge, die nur solche Vektoren (x, y) enthält, deren
Komponenten nicht negativ sind (also eine „Viertelebene", der erste Quadrant) ist
kein Unterraum. Sie enthält nämlich den Vektor B,3), nicht aber (—2,-3),
und verletzt deshalb die zweite Bedingung mit c= —1.
Beispiel 3.1.2 Fügen wir zu der Menge aus dem letzten Beispiel die
Vektoren hinzu, deren beide Komponenten negativ oder Null sind, (also zwei
Quadranten), so ist die zweite Bedingung erfüllt, da man mit beliebigen
Zahlen c multiplizieren kann, ohne die beiden Quadranten zu verlassen. Die erste
Bedingung ist jedoch immer noch nicht erfüllt: Zum Beispiel ist der Vektor
(-1,1) die Summe von v = B,3) und w = (-3,-2), liegt aber außerhalb
der beiden Quadranten. Diese bilden also zusammen keinen Unterraum.
Die Bedingungen (i) und (ii) über die Abgeschlossenheit von Addition
und Skalarmultiplikation lassen sich zu einer einzigen Bedingung
zusammenfassen — der Unterraumhedingung:
Enthält ein Unterraum die Vektoren v und w, so mu$s er auch
oUe Zinearkombinationen cv -hdw enthalten.
Beispiel 3.1.3 Zwei Beispiele für Unterräume des Vektorraums M aller 2x2-
Matrizen:
a b]
(O) Alle oberen Dreiecksmatrizen
(D) Alle Diagonalmatrizen
Od
aO
Od
Addieren Sie zwei Matrizen aus O, und sie erhalten wieder eine Matrix
in O. Addiert man zwei Diagonalmatrizen, so ist auch die Summe eine
Diagonalmatrix. Bei diesen Beispielen ist D sogar wieder ein Unterraum von
O! In beiden Mengen liegt natürlich auch die Nullmatrix, die man nämlich
füT a = b = d = 0 erhält. Wir würden beispielsweise einen (noch kleineren)
Unterraum von D erhalten, wenn wir a = d forderten. Diese Matrizen sind
Vielfache der Einheitsmatrix /. Dazu gehört zum Beispiel die Summe 2/-h3/,
oder auch 3 mal 41. Dieser Unterraum ist sozusagen eine „Matrizengerade"
innerhalb von M, O und D.
Ist die Menge, die nur die Einheitsmatrix / enthält, ein Unterraum?
Natürlich nicht. Nur die Nullmatrix bildet für sich einen Unterraum. Sie
haben sicher keine Schwierigkeiten, noch weitere Unterräume von M zu finden—
in Aufgabe 5 sollen Sie einige davon angeben.
Der Spaltenraum einer Matrix A
Die wichtigsten Unterräume hängen eng mit Matrizen zusammen. Wir wollen
wieder einmal das Gleichungssystem Ak = h lösen. Ist A nicht invertierbar,
122 3 Vektorräume und Untervektorräume
so ist das System für manche Vektoren b lösbar, für andere nicht. Wir wollen
deshalb eine Beschreibung für die „guten" Vektoren finden, mit denen das
System lösbar ist — für solche Vektoren b also, die als Produkt von A mit
einem Vektor x darstellbar sind.
Erinnern wir uns daran, dass das Produkt Ax eine Linearkombination der
Spalten von A ist. Um alle guten rechten Seiten b zu bestimmen, nehmen wir
alle möglichen Vektoren x. Wir erzeugen also alle Linearkombinationen
der Spalten von A. Auf diese Weise erhält man den Spaltenraum der Matrix
A. Dies ist ein Vektorraum, der aus Spaltenvektoren besteht — und zwar nicht
nur aus den Spalten von A, sondern aus allen ihren Linearkombinationen Ax.
Indem wir alle Kombinationen erfassen, erzeugen wir einen Vektorraum.
DEFINITION Der Spattenraum einer Matrix A b^teht aus allen Jtir;
nearkombinationen der Spalten von A. Diese sind durch alle mÖgücheÄj
Vektoren i4x gegeben.-*^ -^
Das Gleichungssystem Ax = b zu lösen, bedeutet, b als
Linearkombination der Spalten von A auszudrücken. Der Vektor b auf der rechten Seite muss
also im Spaltenraum der Matrix A liegen.
-•^^
3A Ein Gleichungssystem Ax = b ist lösbar genau dann, wenn b im SpalHI
tenraum von A liegt. 4
Liegt b im Spaltenraum, so ist dieser Vektor eine Linear kombination der
Spalten. Die Koeffizienten dieser Kombination bilden einen Lösungsvektor x
für das Gleichungssystem Ax = b.
Nehmen wir an, A sei eine m x n-Matrix. Die Spalten haben also m
Komponenten, und gehören damit zu E"^. Der Spaltenraum ist ein Un-
terraum von W^, da die Menge aller Linearkombinationen die Bedingungen
(i) und (ii) erfüllt: Ob wir Linearkombinationen addieren, oder sie mit
Skalaren multiplizieren, wir erzeugen wieder Linear kombinationen der Spalten
von A. Es ist also gerechtfertigt, von einem Unterraum zu sprechen.
Betrachten wir eine 3 x 2-Matrix, deren Spaltenraum ein Unterraum von
E^ ist. Es handelt sich in diesem Fall um eine Ebene.
Beispiel 3.1.4
Ax ist
10"
43
23
Xi
X2
also xi
"
i ^
[2
-\-X2
"Ol
3 1
3
^ Anm. d. Übers.: Im deutschen Sprachraum wird der Spaltenraum auch oft das
Bild einer Matrix genannt.
3.1 Räume von Vektoren
123
A =
1 0
4 3
2 3
b= Xi
r
4
_2_
+ •^7
ro"
3
3_
Abb. 3.2. Der Spaltenraum 5(A) ist die Ebene, die die beiden Spalten enthält.
Ax = b ist lösbar, wenn b in der Ebene liegt, denn dann ist b eine
Linearkombination der Spalten von A.
Der Spaltenraum besteht aus allen Linearkombinationen der beiden
Spalten — also ein beliebiges xi mal erste Spalte plus ein beliebiges X2 mal
zweite Spalte. Diese Kombinationen erzeugen eine Ebene im W (siehe
Abbildung 3.2). Liegt die rechte Seite b eines Gleichungssystems in dieser Ebene,
so gehört sie zu den Linear kombinationen, und die Koeffizienten bilden einen
Lösungsvektor {xi.x^) für die Gleichung Ax = b. Die Ebene ist
„unendlich dünn", deshalb ist es wahrscheinlicher, dass b nicht zum Spaltenraum
gehört. In diesem Fall gibt es keine Lösung für die drei Gleichungen mit zwei
Unbekannten.
Natürlich gehört @,0,0) zum Spaltenraum. Die Ebene geht durch den
Nullpunkt, und deshalb gibt es immer eine Lösung der Gleichung Ax = 0.
Diese Lösung ist x = .
Wiederholen wir es noch einmal: Die als Produkt von A mit x
darstellbaren Vektoren sind gerade die Vektoren im Spaltenraum der Matrix. Eine
Möglichkeit ist zum Beispiel die erste Spalte selbst — dazu nimmt man xi = 1
und X2 — 0. Eine andere Möglichkeit ist die zweite Spalte, mit xi = 0 und
2^2 = 1. Wir sind an dieser Stelle aber auf einer neuen Verständnisebene
angelangt, weil wir alle Kombinationen auf einmal betrachten können — nämlich
den gesamten von den Spalten erzeugten Unterraum.
Schreibweise Den Spaltenraum einer Matrix A schreibt man S[^A).
124 3 Vektorräume und Unter vektorräume
Beispiel 3.1.5 Beschreiben Sie die Spaltenräume der Matrizen
/ =
10
Ol
A =
12
24
und B
1 23
004
Es handelt sich jeweils um Unterräume des Vektorraums M^.
Lösung Der Spaltenraum der Matrix / ist der gesamte Raum E^, da jeder
Vektor im E^ eine Linearkombination der Spalten von / ist; es ist also 5G) =
R\
Der Spaltenraum der Matrix A ist eine Gerade, da die zweite Spalte B,4)
ein Vielfaches der ersten Spalte A, 2) ist. Die Vektoren sind zwar verschieden,
aber wir interessieren uns ja für Vektorröitme. Der Spaltenraum enthält die
Vektoren A,2) und B,4) sowie alle weiteren Vektoren (c, 2c) auf dieser
Geraden. Die Gleichung Ax = h ist also nur lösbar, wenn b auf dieser Geraden
liegt.
Die dritte Matrix (mit den drei Spalten) lässt alle rechten Seiten b zu, der
Spaltenraum S{B) ist wieder der gesamte Raum E^ — jeder Vektor b ist als
Linearkombination der Spalten darstellbar. So ist zum Beispiel b = E,4) die
Summe von Spalte 2 und Spalte 3, eine Möglichkeit wäre also x = @,1,1).
Derselbe Vektor lässt sich aber auch als Summe des Zweifachen von Spalte
1 und von Spalte 3 darstellen, eine andere Lösung wäre also x = B,0,1).
Diese Matrix hat also denselben Spaltenraum wie / — jedes b ist erlaubt.
Die Lösungen x haben aber mehr Komponenten, und es gibt offenbar jeweils
mehrere Lösungen.
Im folgenden Abschnitt werden wir uns mit einem weiteren Vektorraum
beschäftigen, der es uns erlauben wird, alle möglichen Lösungen einer
Gleichung Ax = 0 zu beschreiben. In diesem Abschnitt hatten wir den
Spaltenraum eingeführt, der uns eine Beschreibung aller erlaubten rechten Seiten
lieferte.
Die wesentlichen Punkte
l.M^, C", M (Matrizen), F (Funktionen) und N (nur ein Nullvektor) sind
Vektorräume.
2. Ein Vektorraum muss mit v und w auch deren Linearkombinationen cv -H
dw enthalten.
3. Die Linear kombinationen der Spalten einer Matrix A bilden den
Spaltenraum von A.
4. Das Gleichungssystem Ax = h ist genau dann lösbar, wenn b dem
Spaltenraum von A angehört.
3.1 Räume von Vektoren 125
Aufgaben 3.1
Die ersten Aufgaben behandeln allgemeine Vektorräume. Die
Vektoren in diesen Räumen müssen nicht unbedingt Spaltenvektoren
sein.
Die Definition eines Vektorraums verlangt, dass die Vektoraddition x + y
und die Skalarmultiplikation ex die folgenden acht Bedingungen erfüllen:
1. x + y = y + x
2. X + (y + z) = (x + y) + z
3. Es gibt einen eindeutigen Nullvektor 0 mit der Eigenschaft
X + 0 = X für alle x
4. Für jeden Vektor x gibt es einen eindeutigen Vektor — x, so dass
X + (-x) = 0 gilt.
5. 1 mal X ist gleich x
6. (ciC2)x = Ci(c2x)
7. c(x + y) = ex + cy
8. (Ci + C2)x = CiX + C2X.
1. Wir definieren die Addition von Vektoren um, so dass {xi, X2) + B/1,2/2) =
{xi +2/2, ^2 +2/1)• Die Skalarmultiplikation sei wie üblich. Welche der acht
Bedingungen werden nicht erfüllt?
2. Als nächstes definieren wir die Skalarmultiplikation um zu c{xi,X2) :=
(cxi,0) anstatt {0x1,0x2) und belassen es bei der gewöhnlichen Addition
im E^. Welche Bedingungen werden jetzt verletzt?
3. (a) Eine Halbgerade ist kein Vektorraum. Welche Bedingungen an einen
Vektorraum werden verletzt, wenn man nur die positiven Zahlen
X > 0 in E betrachtet? Die Skalarmultiplikation muss für jedes 0
definiert sein!
(b) Betrachtet man die positiven reellen Zahlen und definiert darauf eine
neue Addition x^y := xy und eine neue Skalarmultiplikation oCDx :=
x^, so erfüllen diese alle acht Bedingungen. Überprüfen Sie dies an
Bedingung 7 mit 0 = 3, x = 2 und y = 1 {es ist also x 0 2/ = 2 und
c 0 X = 8). Welche Zahl spielt hier die Rolle des Nullvektors? Der
Vektor -2 ist gleich .
4. Die Matrix A= [2 I2] ist ein Vektor im Raum M aller 2 x 2-Matrizen.
Benennen Sie den Nullvektor dieses Raums, sowie die Vektoren ^A und
—A. Welche Matrizen bilden den kleinsten Unterraum von M, dem auch
A angehört?
^- (a) Beschreiben Sie einen Unterraum von M, der die Matrix A = [ J g]
enthält, nicht aber die Matrix B = [S -?]•
126 3 Vektorräume und Untervektorräume
(b) Muss ein Unterraum von M, der A und B enthält, automatisch auch
/ enthalten?
(c) Beschreiben Sie einen Unterraum von M, der keine Diagonalmatrix
(außer der Nullmatrix) enthält.
6. Es sei F der Raum aller Funktionen E -^ E. Dann sind durch f{x) = x^
und g{x) = bx zwei Vektoren / und g aus F gegeben. Bestimmen Sie die
Linearkombination h = Zf — Ag: h{x) = .
7. Welche Bedingungen werden verletzt, wenn man die übliche Addition
auf F beibehält und die Skalarmultiplikation folgendermaßen definiert:
c-fix):=f{cx)?
8. Würde man als Summe zweier Funktionen f{x) und g{x) die Funktion
f{g{x)) definieren, so ergäbe sich als Nullvektor die Funktion g{x) = x.
Untersuchen Sie, welche Bedingungen verletzt werden, wenn man diese
„Addition" zusammen mit der üblichen Skalarmultiplikation verwendet.
Die Aufgaben 9-18 behandeln die Unterraumbedingungen: x + y
und ex müssen im Unterraum liegen.
9. Es ist möglich, dass eine Bedingung erfüllt ist und die andere verletzt
wird. Zeigen Sie dies an diesen beiden Beispielen:
(a) Finden Sie eine Teilmenge von E^, die mit x und y auch x+y enthält,
aber einen Vektor x besitzt, für den ^x nicht zur Menge gehört.
(b) Finden Sie eine Teilmenge von E^ (nicht die beiden Quadranten aus
dem Beispiel im Text), die unter Skalarmultiplikation abgeschlossen
ist, nicht aber unter der Addition. Es soll also für jeden Vektor x aus
der Menge und jede Zahl c auch ex in der Menge liegen, aber es gibt
zwei Vektoren x und y in der Menge, deren Summe x + y nicht darin
liegt.
10. Welche dieser Teilmengen von E^ sind Unterräume?
(a) Die Ebene der Vektoren F1,62,^3) mit bi = 0.
(b) Die Ebene der Vektoren mit bi = 1.
(c) Die Vektoren, die die Gleichung 6162^3 = 0 erfüllen.
(d) Alle Linearkombinationen der Vektoren v = A,4,0) und w =
B,2,2).
(e) Alle Vektoren F1,62, bs), die die Gleichung bi -{-b2 -^ bs = 0 erfüllen.
(f) Alle Vektoren, für die 61 < 62 < ^3 gilt.
11. Beschreiben Sie den kleinsten Unterraum des Matrizenraums M, der die
folgenden Matrizen enthält:
(a)
10
00
und
"Oll
00
(b)
1 1 ]
00
(c)
0
100
und
;io
101
3.1 Räume von Vektoren
127
12. Sei E die durch die Gleichung x + y - 2z = A beschriebene Ebene im
R^. Bestimmen Sie zwei Vektoren in E und verifizieren Sie, dass deren
Summe nicht zu E gehört.
13. Sei Eo die Ebene im R^, die parallel zu E durch @,0,0) geht. Wie sieht die
zugehörige Ebenengleichung aus? Bestimmen Sie auch hier zwei Vektoren
in Eo und zeigen Sie, dass ihre Summe in Eo liegt.
14. Die Unterräume von R^ sind Ebenen, Geraden, der M^ selbst, oder der
Raum N, der nur den Nullvektor @,0,0) enthält.
(a) Beschreiben Sie die drei Typen von Unterräumen des Raums M^.
(b) Beschreiben Sie die fünf Typen von Unterräumen des Raums R^.
15. (a) Die Schnittmenge zweier Ebenen durch @,0,0) ist wahrscheinlich eine
(b) Die Schnittmenge einer Ebenen durch @,0,0) mit einer Geraden
durch @,0,0) ist wahrscheinlich ein .
(c) Es seien S und T Unterräume von R^. Beweisen Sie, dass die Menge
S r\T (also die Menge aller Vektoren, die in S und in T liegen) ein
Unterraum von E^ ist. Überprüfen Sie dazu die Forderungen on x + y
und an ex.
16. Sei E eine Ebene durch @,0,0) und G eine Gerade durch @,0,0). Der
kleinste Vektorraum, der sowohl E als auch G enthält, ist entweder
oder .
17. (a) Zeigen Sie, dass die Menge der invertierbaren Matrizen keinen
Unterraum von M bildet,
(b) Zeigen Sie, dass die Menge der singulären Matrizen ebenfalls kein
Unterraum von M ist.
18. Wahr oder falsch? Überprüfen Sie die Addition jeweils an einem Beispiel.
(a) Die symmetrischen Matrizen in M (also jene mit A^ = A) bilden
einen Unterraum.
(b) Die schief symmetrischen Matrizen in M (also jene mit A^ = -■^)
bilden einen Unterraum.
(c) Die unsymmetrischen Matrizen in M (also jene mit A-^ ^ A) bilden
einen Unterraum.
In den Aufgaben 19-27 geht es um Spaltenvektoren S{A) und
Gleichungssysteme Ax = b.
19. Beschreiben Sie die Spaltenräume (Geraden oder Ebenen) dieser drei
Matrizen:
[121
00
00
, B^
rio]
02
ooj
und C
10
20
00
128
3 Vektorräume und Untervektorräume
20. Für welche rechten Seiten b existieren Lösungen dieser
Gleichungssysteme?
(a)
r 1 4
2
2 8 4
[-1-4-2
" 1 4"
2 9
-1-4
[
Xi
X2
'xil
X2
_x^\
=
■=
[öl]
02
ösj
(b)
21. B entsteht aus A, indem Zeile 1 zu Zeile 2 addiert wird. C entsteht aus
A, indem Spalte 1 zu Spalte 2 addiert wird. Vervollständigen Sie: Eine
Linearkombination der Spalten von ist also auch eine Kombination
der Spalten von A, und deshalb haben diese beiden Matrizen denselben
A =
12
24
B
12
36
und C =
13
26
22. Für welche Vektoren {bi, 62, ''s) besitzen die folgenden Gleichungssysteme
Lösungen?
111
Ol 1
001
Xi
X2
X3
=
bi
b2
hz
5
1 1 1
Ol 1
000
Xi
X2
X3
=
bi
Ö2
bs
ri 11"
001
001
'xi'
X2
.^3.
=
\bi]
02
[bsj
und
23. Vervollständigen Sie: Fügt man einer Matrix A eine zusätzliche Spalte b
hinzu, so wird der Spaltenraum größer, falls nicht . Geben Sie für
beide Fälle Beispiele an. Warum ist das Gleichungssystem Ak = b lösbar
genau dann, wenn die Spaltenräume für A und [A h] gleich sind?
24. Vervollständigen Sie: Die Spalten von AB sind Linearkombinationen der
Spalten von A, und deshalb ist der Spaltenraum von AB enthalten im
Spaltenraum von . Möglicherweise sind beide Spaltenräume gleich.
Geben Sie ein Beispiel an, bei dem sie nicht gleich sind.
25. Zeigen Sie: Sind die Gleichungssysteme Ak = h und Ay = b* beide
lösbar, so ist auch das System Az = b + b* lösbar. Wie erhält man z?
Dies lässt sich auch so sagen: Gehören b und b* zum Spaltenraum 5(A),
so auch .
26. Ist A eine invertierbare 5 x 5-Matrix, so ist der Spalteraum
ist das so?
.. Warum
3.2 Der Kern von A: Lösung von Ax. = 0 129
27. Wahr oder falsch? Geben Sie ein Gegenbeispiel an, falls die Behauptung
falsch ist.
(a) Die Vektoren b, die nicht zum Spaltenraum S{A) gehören, bilden
einen Unterraum.
(b) Enthält S{A) nur den Nullvektor, so ist A die Nullmatrix.
(c) Der Spaltenraum der Matrix 2A ist gleich dem Spaltenraum der
Matrix A.
(d) Der Spaltenraum von A — I ist gleich dem Spaltenraum von A,
28. Konstruieren Sie eine 3 x 3-Matrix, deren Spaltenraum die Vektoren
A,1,0) und A,0,1) enthält, aber nicht den Vektor A,1,1).
3.2 Der Kern von A: Lösung von Ax = 0
In diesem Abschnitt betrachten wir die Menge der Lösungen eines
Gleichungssystems Ax = 0. Dabei kann die Matrix A quadratisch oder rechteckig sein.
In jedem Fall existiert die Lösung x = 0, und für invertierbare Matrizen
ist dies auch die einzige Lösung. Für andere, nicht-invertierbare Matrizen
gibt es weitere Lösungen dieser Gleichung. Jede dieser Lösungen gehört zum
Kern der Matrix A. Wir wollen im Folgenden alle Lösungen finden und damit
diesen wichtigen Unterraum beschreiben.
DEFINITION Der Kern van A besteht ans allen Lösungen der Gleichting
Ax =^ 0. Die Vektoren x liegen im W. Man bezeichnet den Kern auch mit
Wir überprüfen zunächst, ob die Lösungsvektoren überhaupt einen
Unterraum bilden. Seien dazu x und y aus dem Kern, es gelte also Ax = 0
und Ay = 0. Aus den Gesetzen der Matrizenmultiplikation folgt dann
A{x + y) = 0 -h 0. Ebenso folgt A{cx) = cO. Es ergibt sich also in beiden
Fällen auf der rechten Seite der Nullvektor, und deshalb gehören auch die
Vektoren x-hy und ex zum Kern. Der Kern ist also ein Unterraum, und zwar
ein Unterraum des Raums W, da die Lösungsvektoren x n Komponenten
besitzen. Der Spaltenraum S{A) hingegen ist ein Unterraum von W^.
Ist die rechte Seite b eines Gleichungssystems Ax = b ungleich Null, so
bilden die Lösungen des Systems keinen Unterraum, denn der Vektor x = 0
ist nur dann eine Lösung, wenn auch b = 0 gilt. Umfasst die Lösungsmenge
^ber nicht den Nullvektor, so kann sie kein Unterraum sein. In Abschnitt
3-4 wird erklärt werden, dass die Lösungen eines Systems Ax = h (wenn es
Anm. d. Übers.: N(A) steht für engl, nullspace, etwa „Nullraum". Im Deutschen
besteht bei diesem Wort Verwechslungsgefahr mit dem Raum, der nur aus einem
Null Vektor besteht.
130 3 Vektorräume und Unter vektorräume
überhaupt welche gibt) eine Menge bilden, die aus einem Unterraum entsteht,
der durch eine spezielle Lösung vom Nullvektor weg „verschoben" wird.
Beispiel 3.2.1 Die Gleichung x -\-2y -\-3z = 0 beschreibt eine Ebene durch
den Koordinatenursprung. Diese Ebene ist also ein Unterraum des E^, und
zwar der Kern der zugehörigen Matrix A = [1 2 3 ].
Die Lösungen der Gleichung x-\-2y-\-Sz = 6 bilden zwar auch eine Ebene,
aber keinen Unterraum des E^.
Beispiel 3.2.2 Wir beschreiben den Kern der Matrix A
12
36
Dazu bestimmen wir die Lösungen des Gleichungssystems Ax = 0 mit
Hilfe des Eliminations Verfahrens:
Xi 4- 2a:2 = 0
3a:i 4- 60:2 = 0
->
xi + 20:2 = 0
0 = 0
Wir haben es also „eigentlich" nur mit einer Gleichung zu tun, da die zweite
Gleichung einfach das dreifache der ersten ist. Dies sieht man auch im
Zeilenbild des Gleichungssystems: Die Gleichungen Xi +2x2 = 0 und 3a:i +6x2 = 0
beschreiben dieselbe Gerade, nämUch den Kern N(A).
Wie beschreibt man diese Gerade? Die beste Methode besteht darin, nur
einen einzigen Punkt darauf anzugeben (eine spezielle Lösung); die Gerade
erhält man dann als Menge der Vielfachen dieses Punktes. Welchen Punkt
wir wählen, ist dabei egal, deshalb wählen wir den Punkt einfach so, dass
2:2 == 1 ist. Aus der Gleichung Xi + 2a:2 = 0 erhält man dann, dass die erste
Komponente Xi = -2 sein muss. Auf diese Weise erhält man den gesamten
Kern:
Der Kern N(A) besteht aus den Vielfachen von s =
Die beste Art, den Kern zu beschreiben, ist also, spezielle Lösungen der
Gleichung Ax = 0 zu berechnen. Der Kern ergibt sich dann als Menge der
Linearkombinationen dieser speziellen Lösungen, Im letzten Beispiel gab es
eine spezielle Lösung, und der Kern war eine Gerade. Im Beispiel 3.2.1 gab
es hingegen zwei spezielle Lösungen:
:i23]
0 hat die Lösungen si =
2"
1
0
und S2 =
■-3
0
1
Die Vektoren si und S2 liegen beide in der Ebenen x + 2y -\- Sz = 0, dem
Kern der Matrix A = [1 2 3]. Alle anderen Vektoren in dieser Ebenen sind
Linear kombinationen von si und S2.
3.2 Der Kern von A: Lösung von Ay: = 0 131
Was ist so „speziell" an diesen Lösungen? In den letzten beiden
Komponenten stehen nur die Einträge Null oder Eins. Das liegt daran, dass diese
Komponenten „frei" sind, und wir ihre Werte speziell wählen. Die erste
Komponente -2 bzw —3 ergibt sich dann aus der Gleichung Ax = 0.
In der ersten Spalte von A = [12 3] steht das Pivotelement, deshalb
ist die erste Komponente von x nicht frei wählbar. In den Spalten ohne
Pivotelement können wir hingegen die Einträge (Eins oder Null) frei wählen.
Betrachten wir ein weiteres Beispiel, um die speziellen Lösungen vollständig
zu verstehen.
Beispiel 3.2.3 Wir beschreiben den Kern dieser drei Matrizen:
undC = [A2A]
12
38
B =
A'
2 A
2
3 8
2 4
616
122 4
3 86 16
Die Gleichung Ax — 0 hat nur eine Lösung, den Nullvektor x = 0.
Deshalb ist der Kern der Unterraum N, der nur den Nullvektor enthält. Dies
sieht man anhand des Eliminations Verfahrens:
12'
38
Xi
=
'Ol
0
wird zu
12
02
Xi
.^2.
=
0
0
und deshalb ist
xi = 0
a:2 = 0
Die quadratische Matrix A ist also invertierbar, und deshalb gibt es keine
speziellen Lösungen. Der Kern besteht nur aus dem Vektor x = 0.
Auch die rechteckige Matrix B hat den Kern N, denn schon die ersten
beiden Gleichungen des Systems Bx = 0 für sich haben nur die Lösung
X = 0. Auch die letzten beiden Gleichungen lassen nur diese Lösung zu. Wenn
wir weitere Gleichungen hinzufügen, so wird der Lösungsraum sicher nicht
größer, da zusätzliche Zeilen in der Matrix auch zusätzliche Bedingungen an
die Vektoren des Kerns bedeuten.
Mit der rechteckigen Matrix C verhält es sich anders. Sie besitzt mehr
Spalten als Zeilen, und jeder Lösungsvektor x muss vier Komponenten haben.
Hier erzeugt das Eliminationsverfahren Pivotelemente in den ersten beiden
Spalten, aber die letzten beiden bleiben natürlich „frei".
C
122 4
386 16
wird zuU =
12 24
0204
Für die freien Variablen xs und X4 können wir jetzt Eins und Null als
Einträge wählen, um dann die Pivot variablen aus der Gleichung Ux = 0 zu
bestimmen. Auf diese Weise erhalten wir zwei spezielle Lösungen im Kern
von C (der auch der Kern von U ist). Diese sind:
132 3 Vektorräume und Unter vektorräume
2"
0
1
0
und S2 =
0"
-2
0
1
<r- PivOt-
<r- Variablen
<r- freie
<— Variablen
Sl
Wir wollen noch auf eine Idee hinweisen, die im nächsten Abschnitt
beschrieben wird. Beim Eliminationsverfahren muss man nicht mit der oberen
Dreiecksmatrix U aufhören. Stattdessen kann man die Matrix noch weiter
vereinfachen, nämlich auf zwei Weisen:
l.Man erzeugt Nullen oberhalb der Pivotelemente, durch
„Aufwärtselimination" .
2. Man erzeugt Einsen anstelle der Pivotelemente, indem man eine
ganze Zeile durch ihr Pivotelement dividiert.
Beide Schritte ändern nichts am Nullvektor auf der rechten Seite, der Kern
bleibt derselbe. Man kann ihn leicht ablesen, wenn man bei der reduzierten
Zeilen-Treppenform, R angekommen ist:
U
1224] . , ^ ri020l
0204] ^^^^"^ ^^[0102j
tt
Die Pivotspalten enthalten /
Hier wurde die zweite Zeile von U von ihrer ersten Zeile subtrahiert, und
dann noch mit | multipliziert. Auf diese Weise wurden die Gleichungen zu
xi -\- 2x3 = 0 und X2 + 2x4 — 0 vereinfacht, nämlich zu dem System i^x = 0,
das in den Pivotspalten einfach die Einheitsmatrix enthält.
Die speziellen Lösungen dieses Systems sind dieselben wie am Anfang,
man kann sie aber viel einfacher am reduzierten System Rk — 0 ablesen.
Lassen Sie mich, bevor wir mit mxn-Matrizen und ihren Kernen
weitermachen, noch eine Bemerkung anbringen. Für viele Matrizen A ist die einzige
Lösung des Gleichungssystems Ax = 0 der Nullvektor x == 0. Ihr Kern enthält
also nur diesen einen Vektor. Das heißt, die einzige Kombination der Spalten
von A, die den Nullvektor erzeugt, ist die „Null-Kombination" oder auch die
„triviale Lösung". Diese Lösung mag trivial sein (nämlich einfach x = 0),
aber die Idee dahinter ist es sicher nicht.
Der Fall eines trivialen Kerns ist von höchster Wichtigkeit. In diesem Fall
sind die Spalten von A alle unabhängig. Es gibt keine Linearkombination,
die den Nullvektor erzeugt, außer der Kombination, in der alle Koeffizienten
Null sind. Dann gibt es für jede Spalte ein Pivotelement ungleich Null, und
deshalb ist keine Spalte „frei". Dieser Idee — Unabhängigkeit von Vektoren
— werden wir noch mehrmals begegnen ...
Die Lösung von Ax = 0
Dieser Abschnitt ist besonders wichtig. Wir werden sehen, wie man m
Gleichungen in n Unbekannten löst, wenn auf der rechten Seite nur Nullen stehen.
3.2 Der Kern von A: Lösung von i4x = 0
133
Dazu vereinfachen wir die linken Seiten durch Zeilenoperationen, bis man die
Lösungen einfach ablesen kann. Erinnern wir uns an die beiden Schritte beim
Lösen eines Gleichungssystems Ax = 0:
1, Vorwärtselimination führt von A zu einer oberen Dreiecksmatrix U (oder
sogar zur reduzierten Treppenform R).
2. Rücksubstitution von C/x — 0 oder Rx = 0 erzeugt die Lösung x.
In diesem Kapitel werden Sie bei der Rücksubstitution einen Unterschied
gegenüber früher feststellen, und zwar für den Fall, dass die Matrizen A und
U weniger als n Pivotelemente besitzen. Im Folgenden lassen wir nämlich alle
Matrizen zu, nicht nur die einfachen Fälle (nämlich quadratische Matrizen,
die zudem noch invertierbar sind).
Als Pivotelemente sind weiterhin nur Einträge ungleich Null erlaubt.
Unterhalb der Pivotelemente stehen weiterhin nur Nullen. Tritt jetzt aber der
Fall ein, dass für eine Spalte kein Pivotelement zur Verfügung steht, so hören
wir nicht einfach auf, sondern machen mit der nächsten Spalte weiter. Sehen
wir uns einmal als Beispiel eine 3 x 4-Matrix an:
A=:
112 3
22 8 10
3 3 10 13
Der Eintrag an = l ist zugleich das erste Pivotelement. Eliminieren wir also
die Einträge darunter:
1 123
0044
0044
(subtrahiere 2x Zeile 1)
(subtrahiere 3x Zeile 1)
Jetzt steht in der zweiten Spalte aber eine Null auf der Pivotposition. Wir
könnten eine Zeilenvertauschung probieren, aber auch die Zeilen darunter
enthalten kein geeignetes Pivotelement — dies deutet auf ein Problem hin.
Andererseits müssen wir dies für eine solche Matrix (mehr Spalten als Zeilen)
auch so erwarten. Machen wir also einfach mit der dritten Spalte weiter.
Als zweites Pivotelement erhalten wir jetzt die 4 in der dritten Spalte.
Wir erzeugen darunter eine Null, indem wir Zeile 2 von Zeile 3 subtrahieren.
Dann erhält man
U^
1123
0 0 44
0000
{Nur zwei PivoteUmente)
{Die letzte Gleiehnng
wird mt 0 ^i^)r' ] - '/
Auch in der vierten Spalte steht jetzt eine Null an der Pivotposition — hier
können wir nichts mehr machen. Es gibt keine Zeile mehr, mit der man
tauschen könnte, und mit der Elimination sind wir auch am Ende angelangt.
Diese Matrix hat also drei Zeilen, vier Spalten, aber nur zwei Pivotelemente.
134 3 Vektorräume und Unter vektorräume
Das ursprüngliche System Ax = 0 schien aus drei Gleichungen zu bestehen,
aber die dritte war die Summe der ersten beiden, und deshalb ist sie
automatisch erfüllt (nichts anderes sagt die Gleichung 0 = 0), wenn die ersten
beiden erfüllt sind. Diese Tatsache wurde durch das Eliminations verfahren
ans Licht gebracht.
Jetzt käme die Rücksubstitution zur Bestimmung der Lösungen von Ux =
0 an die Reihe. Hat man aber vier Unbekannte und nur zwei Pivotelemente,
so wird es viele Lösungen geben. Die Frage ist also, wie man sie am besten
angibt. Eine gute Idee ist es hierbei, die Pivot-Variablen von den freien
Variablen zu trennen.
P Als Pivot-Variablen haben wir xi und 2:3, da in den Spalten 1 und
3 die Pivotelemente stehen.
F Als freie Variablen haben wir X2 und 2:4, denn in den Spalten 2
und 4 stehen keine Pivotelemente.
Den freien Variablen kann man nun beliebige Werte geben. Dann erhält man
durch die Rücksubstitution die zugehörigen Werte für die Pivot-Variablen.
(In Kapitel 2 gab es keine freien Variablen. Ist A invertierbar, so ist jede
Variable auch eine Pivot-Variable.) Die einfachste Möglichkeit ist es nun, für
die freien Variablen Einsen oder Nullen zu wählen. Auf diese Weise erhält
man die speziellen Lösungen.
Spezielle Lösungen
— Wir setzen 2:2 = 1 und X4 = 0. Durch Rücksubstitution erhält man 2:3 = 0
und xi = —1.
— Wir setzen 2:2 = 0 und X4 =^ 1. Dann erhält man 2:3 = —1 und xi = —1.
Diese speziellen Lösungen lösen die Gleichung Ux = 0, und deshalb auch die
Gleichung Ax = 0. Sie liegen also im Kern von A. Das besondere an ihnen
ist, dass jede Lösung eine Linearkombination der speziellen Lösungen ist.
■-X2
spes
"-1"
1
0
0
5iell
-\-X4
spe
-1"
0
-1
1
ziel
—
,
—X2 — X4
^2
— X4
X4
allgemein
Allgemeine Lösung
C.1)
Bitte sehen Sie sich diese Lösung genau an. Hiermit haben wir das
Hauptziel dieses Abschnitts erreicht: alle Lösungen der Gleichung Ax = 0 sind
Linearkombinationen der beiden speziellen Lösungen si = (-1,1,0,0) (die
man aus 2:2 =^ 1 und 2:4 = 0 erhält) und S2 — (-1,0, -1,1) (mit 2:2 = 0 und
X4 = 1). Die speziellen Lösungen liegen also nicht nur im Kern, sie erzeugen
ihn sogar, das heißt, deren Linearkombinationen füllen ihn ganz aus.
3.2 Der Kern von A: Lösung von Ajc = 0
135
Das MATLAB-Programm nulbasis berechnet diese speziellen Lösungen.
Es liefert eine Matrix N zurück, deren Spalten die speziellen Lösungen sind.
Man erhält dann also jede Lösung zu Ax = 0 als Linearkombination dieser
Spalten, und sobald man diese kennt, kennt man auch den ganzen Kern.
Für jede freie Variable gibt es genau eine spezielle Lösung. Gibt es keine
freien Variablen, gibt es also n Pivotelemente, so ist die einzige Lösung der
Gleichungen Ux = 0 und Ax = 0 die „triviale Lösung" x = 0. In diesem
Fall enthält der Kern von A und U nur den Nullvektor, und die Funktion
nulbasis gibt eine leere Matrix zurück.
Beispiel 3.2.4 Wir bestimmen den Kern der Matrix U —
157
009
In der zweiten Spalte von U steht kein Pivotelement, X2 ist also eine freie
Variable, und man erhält eine spezielle Lösung, wenn man x^ — ^ setzt. Die
Gleichung 9x3 = 0 liefert 0:3 — 0, und aus x\ 4- 5x2 — 0 folgt x\ — -5. Die
Lösungen der Gleichung Ux — 0 sind also Vielfache dieser einen Lösung:
X2
-5
1
0
Der Kern von JJ ist eine Gerade im M^, die die
Vielfachen der speziellen Lösung enthält. Es gibt
eine freie Variable, und N — nulbasis ([/)
besitzt eine Spalte.
Wir fahren mit dem Eliminationsverfahren fort und erzeugen Nullen oberhalb
der Pivotelemente, und Einsen auf den Pivotpositionen. Dabei wird die 7 zu
0, und die 9 zu 1. Die reduzierte Treppenform R sieht dann so aus:
V
1 57
009
wird zu i^ =
150
001
Hier erkennt man deutlich die spezielle Lösung s — (-5,1,0).
Trepp enmatrizen
Ausgehend von einer beliebigen mxn-Matrix A wendet das Eliminations
verfahren Zeilenoperationen (einschließlich Zeilenvertauschungen) an, um Spalte
für Spalte Nullen unterhalb des Pivotelements zu erzeugen. Ist in einer Spalte
kein Pivotelement verfügbar, schreitet es zur nächsten fort, und erzeugt so
schließhch die „Treppenmatrix" IJ.
Dies ist ein Beispiel für eine solche Matrix. Die drei Pivotelemente sind
hervorgehoben.
U
Xrp rn rp rn qn rp
JU JU JU JU JU JU
^ X X X X X X
0 0 0 0 0 xx
0 0 0 0 0 0 0
Drei Pivot-Variablen Xi, 2:2, Xß
Vier freie Variablen 2:3,0:4,2:5, xj
und vier spezielle Lösungen in N(t/)
136 3 Vektorräume und Unter vektorräume
Frage Wie sehen der Kern und der Spaltenraum dieser Matrix aus?
Antwort Die Spalten haben vier Komponenten, und sind deshalb Elemente
des Raums E'* (nicht des E^). Die vierte Komponente jeder Spalte ist aber
Null, und deshalb auch die jeder Linear kombinat ion dieser Spalten, also aller
Vektoren im Spaltenraum. Der Spaltenraum S{U) besteht aus allen Vektoren
der Form F1,62, ^3,0), denn für solche Vektoren b können wir die Gleichung
t/x = b durch Rücksubstitution lösen. Diese Vektoren bilden also alle
möglichen Linear kombinat ionen der Spalten von U.
Der Kern N(t/) ist ein Unterraum des M^. Alle Kombinationen der vier
speziellen Lösungen (eine für jede freie Variable) sind Lösungen der Gleichung
Ux = 0.
1. In den Spalten 3,4,5 und 7 stehen keine Pivotelemente, die freien Variablen
sind deshalb 2:3,2:4,2:5 und X7.
2. Man gibt jeweils einer dieser Variablen den Wert Eins und den anderen
den Wert Null.
3. Damit löst man jeweils die Gleichung Ux = 0 nach den Pivot variablen Xi,
X2 und xq auf,
4. und erhält so die vier speziellen Lösungen im Kern von U.
Die oberen Zeilen einer Treppenmatrix enthalten von Null verschiedene
Einträge, und ein Pivotelement ist jeweils der erste von Null verschiedene
Eintrag in seiner Zeile; sie bilden deshalb (von oben nach unten) eine Art
Treppe. Die üblichen Zeilenoperationen (zum Beispiel im Programm plu)
erzeugen Nullspalten unterhalb eines Pivotelements.
Zählt man die Pivotelemente einer Matrix, so gelangt man zu einem sehr
wichtigen Satz. Angenommen, A habe mehr Spalten als Zeilen. Gilt n >
m, so gibt es mindestens eine freie Variable, und deshalb hat das
Gleichungssystem Ax = 0 mindestens eine (von Null verschiedene) spezielle
Lösung.
3B Enthält ein Gleichlingssystem ^x = 0 mehr Unbekannte als Oleic
gen (besitzt also Ä mehr Spalten als Zeilen)^ so existiert eine von NÄ
verschiedene Lösung: f^m
Mit anderen Worten, der Kern einer flachen breiten Matrix (also n > m)
enthält immer nichttriviale Vektoren. Es muss mindestens n — m freie
Variablen geben, denn die Matrix kann höchstens m Pivotelemente besitzen, da in
jeder Zeile maximal ein Pivotelement steht. Fehlt dann in einer Zeile noch ein
Pivotelement, so hat man eine weitere freie Variable. Das ist der springende
Punkt: Hat man eine freie Variable, kann man sie zu Eins setzen, und erhält
hiermit eine nichttriviale Lösung.
3.2 Der Kern von A: Lösung von Ax = 0 137
Noch einmal: Es gibt höchstens m Pivotelemente. Ist n > m, so besitzt
das System Ax = 0 mindestens eine freie Variable und damit auch eine
nichttriviale Lösung. Es sind natürlich sogar unendlich viele Lösungen, denn jedes
Vielfache ex einer Lösung ist ebenfalls eine. Der Kern enthält also mindestens
eine ganze Gerade aus Lösungen. Gibt es zwei freie Variablen, so gibt es auch
zwei spezielle Lösungen, und der Kern ist noch größer.
Der Kern ist ein Unterraum, dessen „Dimension" durch die Anzahl der
freien Variablen gegeben ist Hier taucht eine weitere wesentliche Idee auf —
die Dimension — die wir später in diesem Kapitel noch genauer definieren
und erklären werden.
Die reduzierte Treppenform R
Von der Treppenmatrix U aus kann man noch einen Schritt weitergehen und
in
U =
1123
0044
0000
die zweite Zeile durch 4 dividieren, so dass auf beiden Pivotpositionen eine
Eins steht. Subtrahiert man das Doppelte der so entstehenden Zeile von der
ersten, so erzeugt man eine Null oberhalb des Pivotelements, ebenso wie
darunter bereits eine Null steht. Auf diese Weise erhält man die reduzierte
Zeilen- Treppenform
R =
110 1
0011
0000
R enthält auf den Pivotpositionen nur Einsen, und in den Pivot-Spalten
ansonsten nur Nullen. Die Nullen oberhalb des Pivotelements stammen dabei
aus der Aufwärts elimination. Ist A eine invertierbare Matrix, so ist die
zugehörige reduzierte Treppenform die Einheitsmatrix I. Weiter lässt sich eine
Matrix nicht vereinfachen.
Die Nullen in R machen es einfach, die speziellen Lösungen zu finden.
1. Setze a:2 = 1 und X4 = 0. Löse Rx = 0. Dann erhält man xi = -1 und
X3 = 0.
2. Setze 2:2 = 0 und X4 = 1. Löse i^x = 0 und erhalte xi = -1 und xs = -1.
Die Zahlen —1 und 0 entstammen der zweiten Spalte von R, allerdings mit
vertauschten Vorzeichen. Ebenso findet man die Zahlen -1 und -1 der
zweiten Lösung mit anderen Vorzeichen in der vierten Spalte von R wieder. Man
kann also die speziellen Lösungen einfach aus R ablesen, wenn man nur die
Vorzeichen der Einträge ändert. Die allgemeine Lösung der Gleichung Ax = 0
138
3 Vektorräume und Untervektorräume
oder auch Ux = 0 oder Rx = 0 ist dann eine Linearkombination dieser beiden
speziellen Lösungen: Der Kern N(A) = N(t/) = N(i^) enthält die Vektoren
X2
\-l'
1
0
0
+ X4
■-1]
0
-1
ij
= {allgemeine Lösung von Ax = 0).
Im nächsten Abschnitt werden wir beherzt den Schritt von U zu R tun.
Mit dem MATLAB-Befehl [R^pivsp] = rref{A) bestimmt man die Matrix
R sowie eine Liste, die die Pivot spalten enthält.
Die wesentlichen Punkte
l.Der Kern N{A) enthält alle Lösungen der Gleichung Ax = 0.
2. Mit dem Eliminations verfahren erzeugt man eine Treppenmatrix U, oder
auch die reduzierte Zeilen-Treppenform R, aus denen man Pivotspalten
und „freie Spalten" ablesen kann.
3. Zu jeder freien Spalte gehört eine spezielle Lösung der Gleichung Ax = 0.
Dabei setzt man die zugehörige freie Variable auf 1 und alle anderen freien
Variablen auf 0.
4. Jede Lösung von Ax = 0 kann man dann als Linear kombinat ion der
speziellen Lösungen schreiben.
5.1st n > m, so hat A mindestens eine Spalte ohne Pivotelement, also auch
eine spezielle Lösung. Der Kern von A enthält also nichttriviale Vektoren.
Aufgaben 3.2
In den Aufgaben 1—8 sind jeweils die Matrizen in Aufgabe 1 bzw.
in Aufgabe 5 zu betrachten.
1. Bringen Sie diese Matrizen in ihre Treppenform U:
(a) A
12246
12369
00123
(b) A
242
044
088
Welches sind jeweils die freien und welches die Pivotvariablen?
2. Bestimmen Sie für die Matrizen aus Aufgabe 1 eine spezielle Lösung für
jede freie Variable.
3. Beschreiben Sie die allgemeine Form einer Lösung von Ax = 0. Der Kern
von A besteht nur aus dem Vektor x = 0, falls .
4. Bestimmen Sie zu jeder Matrix U aus Aufgabe 1 auch die reduzierte
Treppenform R. Der Kern von R ist Kern von U.
3.2 Der Kern von A: Lösung von Ax = 0 139
5. Bringen Sie A durch Zeilenoperationen in seine Treppenform U, und
bestimmen Sie eine untere Dreiecksmatrix L mit A = LU.
(a) A =
-13 5
-2 6 10
(b) A =
-13 5
-2 6 7
6. Bestimmen Sie für die Matrizen in Aufgabe 5 spezielle Lösungen. Für
eine m x n-Matrix gilt: Addiert man die Anzahl der Pivot variablen zur
Anzahl der freien Variablen, so erhält man .
7. Beschreiben sie die Kerne der Matrizen auf zwei Weisen. Geben Sie
Gleichungen für die Ebene oder Gerade N(A) an und beschreiben Sie alle
Vektoren x, die diese Gleichungen erfüllen. (Es handelt sich um die
Linearkombinationen der speziellen Lösungen.)
8. Bestimmen Sie auch die reduzierten Treppenformen R für die Matrizen
aus Aufgabe 5. Kennzeichnen Sie in beiden die in den Pivotspalten (und
-Zeilen) enthaltene Einheitsmatrix.
In den Aufgaben 9-17 geht es um freie und Pivot variablen.
9. Wahr oder falsch? Ist eine Aussage falsch, so geben Sie ein Gegenbeispiel,
sonst eine Begründung an:
(a) Eine quadratische Matrix kann keine freien Variablen haben.
(b) Eine invertierbare Matrix kann keine freien Variablen haben.
(c) Eine m x n-Matrix hat höchstens n Pivot variablen.
(d) Eine m x n-Matrix hat höchstens m Pivotvariablen.
10. Konstruieren Sie 3 x 3-Matrizen, die (falls möglich) jeweils die folgende
Eigenschaft haben:
(a) A hat keinen Null-Eintrag, und es gilt U = I.
(b) A hat keinen Null-Eintrag, und es gilt R — I.
(c) A hat keinen Null-Eintrag, und es gilt R — U.
(d) A^U = 2R.
11. Setzen Sie in eine 4 x 7-Treppenmatrix U Einträge 0 und x (für
„NichtNull") ein, so dass die Pivot variablen
(a) 2, 4, 5
(b) 1, 3, 6, 7
(c) 4 und 6 sind.
12. Konstruieren Sie eine Matrix in reduzierter Treppenform mit Einträgen
0, 1 und X, deren zugehörige freie Variablen
(a) X2, X4, ^5, Xq
(b) a:i,a:3,X6,a:7,a:8 sind.
13. Die vierte Spalte einer 3x5-Matrix sei eine Nullspalte. Dann ist X4 sicher
eine und die zugehörige spezielle Lösung ist x = .
140
3 Vektorräume und Untervektorräume
14. Es seien die erste und die letzte Spalte einer 3x5-Matrix identisch (aber
keine Nullspalten). Dann ist eine freie Variable mit zugehöriger
spezieller Lösung x = .
15. Eine mxn-Matrix habe r Pivotelemente. Die Anzahl spezieller Lösungen
ist dann . Der Kern enthält nur den Nullvektor, falls r =
gilt. Der Spaltenraum ist ganz M'^, falls r = gilt.
16. Der Kern einer 5x5-Matrix ist trivial, wenn die Matrix
Pivotelemente hat. Der Spaltenraum ist M^, wenn r = ist. Begründen Sie
dies.
17. Die Gleichung x-32/-^ = 0 definiert eine Ebene im M^. Schreiben Sie die
Gleichung mit Hilfe einer Matrix A. Welches sind ihre freien Variablen?
Die speziellen Lösungen sind C,1,0) und .
18. Die durch die Gleichung a: - 3^/— ^ = 12 bestimmte Ebene liegt parallel zu
der in Aufgabe 17. Ein Punkt dieser Ebene ist A2,0,0), und alle Punkte
der Ebene haben die Form (setzen Sie die ersten Komponenten ein):
X
y
z
—
0
0
+ 2/
1
0
^z
0
1
19. Zeigen Sie, dass x im Kern von AB liegt, wenn x im Kern von B liegt. Das
heißt: falls 5x = 0, dann auch . Geben Sie Beispiele für Matrizen
A und B, so dass die Kerne von B und AB verschieden sind.
20. Falls A invertierbar ist, so gilt N(A^) - N(^). Die erste Hälfte dieser
Aussage ist in Aufgabe 19 gezeigt worden. Beweisen Sie die zweite Hälfte:
falls AByi = 0, so auch 5x = 0.
Diese Tatsache bedeutet auch, dass C/x — 0 gilt, wenn LC/x — 0 gilt. Die
Matrizen C/ und LU haben also identische Kerne. Der Schlüssel dabei ist
nicht, dass L eine Dreiecksmatrix, sondern dctss L ist.
In den Aufgaben 21—28 sollen Sie Matrizen mit speziellen
Eigenschaften bestimmen, falls es diese gibt.
21. Konstruieren Sie eine Matrix, deren Kern aus den Linearkombinationen
der Vektoren B,2,1,0) und C,1,0,1) besteht.
22. Konstruieren Sie eine Matrix, deren Kern aus den Vielfachen des Vektors
D,3,2,1) besteht.
23. Konstruieren Sie eine Matrix, deren Spaltenraum die Vektoren A,1,5)
und @,3,1) und deren Kern den Vektor A,1,2) enthält.
3.2 Der Kern von A: Lösung von Ax = 0 141
24. Konstruieren Sie eine Matrix, deren Spaltenraum die Vektoren A,1,0)
und @,1,1) und deren Kern die Vektoren A,0,1) und @,0,1) enthält.
25. Konstruieren Sie eine Matrix, deren Spaltenraum den Vektor A,1,1)
enthält, und deren Kern aus den Vielfachen von A,1,1,1) besteht.
26. Konstruieren Sie eine 2 x 2-Matrix, deren Kern und Spaltenraum
identisch sind. Dies ist möglich.
27. Warum kann es keine 3 x 3-Matrix mit dieser Eigenschaft geben?
28. Falls AB = 0 gilt, so ist der Spaltenraum von B im von A
enthalten. Geben Sie ein Beispiel dafür an.
29. Die reduzierte Treppenform einer 3 x 3-Matrix mit zufällig gewählten
Einträgen ist beinahe sicher . Wie sieht die reduzierte Treppenform
einer zufälligen 4 x 3-Matrix wahrscheinlich aus?
30. Zeigen Sie durch Beispiele, dass die folgenden Aussagen im Allgemeinen
falsch sind.
(a) A und A^ haben den gleichen Kern.
(b) A und Ä^ haben die gleichen freien Variablen.
(c) A und A^ haben (eventuell nach einem Zeilentausch) die gleichen
Pivotelemente. A und A^ haben allerdings immer dieselbe Anzahl an
Pivotelementen. Das wird noch wichtig werden.
31. Bestimmen Sie Matrizen N, deren Spalten jeweils durch die speziellen
Lösungen für die Matrizen A, B und C gegeben sind.
A = [II], B =
II
00
und C = I.
32. Wie viele Pivotelemente hat die Treppenform U einer Matrix A, deren
Kern aus den Vielfachen von x = B,1,0,1) besteht?
33. Die Matrix A^ enthalte jeweils die speziellen Lösungen der Gleichung
i?x = 0. Welche Zeilen von R sind dann keine Nullzeilen?
N
3"
10
Ol
, N =
"O"
0
1
und N
34. (a) Es gibt fünf 2 x 2-Matrizen in reduzierter Treppenform, die nur die
Einträge 0 oder 1 haben. Geben Sie diese an.
(b) Geben Sie die acht Ix3-Matrizen an, die nur die Einträge 0 oder 1
besitzen. Ist jede von ihnen in reduzierter Treppenform?
142 3 Vektorräume und Untervektorräume
3.3 Die Rang und die reduzierte Treppenform
In diesem Abschnitt werden wir den Übergang von der Matrix A zu ihrer
reduzierten Zeilen-Treppenform R vollenden. Wir betrachten ganz
allgemeine m x n-Matrizen A und deren reduzierte Treppenformen R. Diese sind
ebenfalls m x n-Matrizen, deren Pivot spalten nur einen einzigen von Null
verschiedenen Eintrag haben — nämlich das Pivotelement, das in der
reduzierten Treppenform immer 1 ist:
R
130 2-1
00 14-3
0000 0
Oberhalb wie unterhalb der Pivotelemente stehen Nullen. Eine solche Matrix
stellt das Endresultat des Eliminationsverfahrens dar. In MATLAB wird es
mit dem Befehl rref berechnet, und auch der Unterrichtscode elim verwendet
rref:
MATLAB [R,pivsp]= rref{A) Unterrichtscode: [E,R]= elim(A)
Die zusätzliche Ausgabe pivsp gibt an, welche Spalten Pivotspalten sind.
Diese stimmen in A und R überein. Die Ausgabe E enthält die m x m-
Eliminationsmatrix, die A in die reduzierte Zeilen-Treppenform bringt:
EA = R. C.2)
Die Matrix E ist das Produkt der Elementarmatrizen Eij, Pij und D~^, die
die Eliminationsschritte enthalten. Die Matrizen Eij subtrahieren jeweils ein
Vielfaches der j-ten Zeile von der i-ten Zeile. Die Matrizen Pij vertauschen
jene beiden Zeilen, und die Matrix D~^ dividiert jede Pivotzeile durch ihr
Pivotelement, so dass jedes Pivotelement zu 1 wird.
Man berechnet E, indem man das Eliminationsverfahren auf die
erweiterte Matrix [AI] anwendet. Jede einzelne Elementarmatrix wird dann sowohl
mit A als auch mit / multipliziert. Das Produkt mit A ergibt R, das mit /
aber einfach das Produkt der Elementarmatrizen: E.
E[A I] = [R E]
t t t t C.3)
n Spalten m Spalten n m
Wir erkennen hier dieselbe Idee wie beim Gauß-Jordan-Verfahren, das
in Kapitel 2 zur Berechnung von A~^ verwendet wurde. Ist A eine
quadratische invertierbare Matrix, so ist seine reduzierte Treppenform
gerade R — I. Dann wird aus EA = R die Gleichung EA = /, und E ist
einfach die inverse Matrix A~^. In diesem Kapitel verallgemeinern wir diese
3.3 Die Rang und die reduzierte Treppenform 143
Beziehung auf allgemeine rechteckige Matrizen A, und deren reduzierte
Treppenform R. Die Matrix E bleibt dabei eine quadratische invertierbare Matrix,
deren Produkt mit A aber nicht mehr /, sondern „nur noch" R ergibt.
Nehmen wir an, datss wir eine solche Matrix R berechnet haben. Das
Eliminations verfahren ist beendet, und wir wollen nun die wesentlichen
Informationen nutzen, die R enthält.
Wir können aus R entnehmen, welche der Spalten von A die Pivot spalten
sind, und wir können an R die speziellen Lösungen der Gleichung Ax = 0
ablesen, aus denen man wiederum den Kern von A bilden kann. In A sind
diese Informationen verborgen, in U immer noch teilweise. Am deutlichsten
erkennt man sie in R, in der die Pivotspalten auf Nullen und Einsen reduziert
sind.
Der Rang einer Matrix
Die beiden Zahlen m und n bestimmen die Größe einer Matrix — jedoch nicht
unbedingt die „wirkliche Größe" eines linearen Gleichungssystems. In einem
solchen System sollte zum Beispiel eine Gleichung wie 0 = 0 nicht mitzählen.
Auch von zwei identischen Gleichungen kann man eine vernachlässigen.
Identische Gleichungen werden durch identische Zeilen in der zugehörigen Matrix
repräsentiert. Von solchen identischen Zeilen wird in der reduzierten
Treppenform R eine Zeile durch eine Nullzeile ersetzt. Weiterhin würde zum Beispiel
die dritte Zeile einer Matrix zu einer Nullzeile, wenn sie eine
Linearkombination der ersten beiden Zeilen ist. Solche Nullzeilen interessieren nicht
besonders, weswegen man sie nicht beachtet, wenn man den Rang einer Matrix
bestimmt:
DEFINITION Der Rtm^ einer Matrix A ist die Anzahl r ihrer
Pivotetemente.
Die Matrix R am Beginn dieses Abschnitts hat den Rang r = 2, da
sie zwei Pivotspalten enthält. Dasselbe gilt für eine Matrix A, aus der R
als Treppenform entstanden sein könnte. Der Rang r einer Matrix spielt
in der Theorie eine wichtige Rolle, obwohl unsere erste Definition für diese
Zahl auf einer Rechnung beruht: soll ein Computer dcts Kommando r =
rank(A) ausführen, so berechnet er die Treppenform der Matrix und zählt
die Pivotelemente. Stellt pivsp eine Liste der Pivotspalten dar, so ist r einfach
die Länge dieser Liste.
Man sieht sofort, dass r < m und r < n gelten muss, da die Anzahl
der Pivotelemente weder größer als die Anzahl der Spalten, noch als die der
Zeilen sein kann. Die beiden Fälle r = m und r = n des „vollen Zeilenrangs"
Anm. d. Übers.: Der englische Begriff lautet rank. Dieses Wort wird auch
normalerweise als Name des entsprechenden Kommandos in Softwarepaketen benutzt.
144 3 Vektorräume und Untervektorräume
bzw. des „vollen Spaltenrangs" sind dabei besonders wichtig. Wir erwähnen
sie hier nur kurz, kommen jedoch schon bald darauf zurück:
— A hat vollen Zeilenrang, wenn jede Zeile ein Pivotelemente enthält
r = m, In diesem Fall enthält R keine Nullzeilen.
— A hat vollen Spaltenrang, wenn jede Spalte eine Pivotspalte ist:
r — n, und es gibt keine freien Variablen.
Für eine invertierbare quadratische Matrix gilt r — m — n. Die reduzierte
Zeilen-Treppenform R ist in diesem Fall gleich der Einheitsmatrix /.
Für einen Computer ist es schwierig, zu entscheiden, wann eine sehr kleine
Zahl tatsächHch Null ist. Subtrahiert man 3 mal 0,33 • • • 3 von 1, erhält man
dann 0? Der Unterrichtscode behandelt Zahlen, deren Betrag kleiner ist als
10~^, als Null. Diese Methode ist aber nicht völlig sicher.
Wir werden bald eine zweite, auf einer höheren Ebene angesiedelte
Definition des Rangs kennen lernen. Sie geht von ganzen Zeilen oder Spalten
aus — von Vektoren also, nicht nur von Zahlen. Die Matrizen A, U und R
haben unabhängige Zeilen (die Pivotzeilen) und unabhängige Spalten (die
Pivotspalten). Um dies richtig formulieren zu können, müssen wir genau
definieren, was es heißen soll, dass Spalten oder Zeilen unabhängig sind. Die
entscheidende Idee dazu werden wir in Abschnitt 3.5 vorstellen.
Eine dritte Definition, auf der höchsten Beschreibungsebene der Linearen
Algebra, geht schließlich von ganzen Vektorräumen aus. Der Rang r wird
die „Dimension" des Bildes (des Spaltenraums) einer Matrix sein, aber auch
die Dimension des „Zeilenraums" der Matrix. Das Besondere daran ist, dass
man daraus auch die Dimensionen aller anderen wichtigen Unterräume erhält,
einschließlich des Kerns.
Beispiel 3.3.1
134
268
7
03
06
5
5
2
und [6] haben alle den Rang 1.
Die reduzierten Zeilen-Treppenformen dieser Matrizen enthalten alle nur eine
Zeile, die keine Nullzeile ist:
134
000
7
Ol
00
5
1
0
und [1].
Alle Zeilen einer Matrix mit Rang 1 sind Vielfache einer Zeile (nicht einer
Nullzeile!), und deshalb hat i? jeweils nur ein Pivotelement. Bitte überprüfen
Sie das an jedem dieser Beispiele.
Die Pivot spalten
In den Pivotspalten steht auf der Pivotposition eine Eins, und überall sonst
stehen Nullen. Deshalb bilden die r Pivotspalten zusammen die r x r-
Einheitsmatrix, die oberhalb von m - r Nullzeilen steht. Wir hatten die
Nummern der Pivotspalten in der Liste pivsp zusammengefaisst.
3.3 Die Rang und die reduzierte Treppenform 145
Man sieht einer Matrix A normalerweise nicht sofort an, welche ihre
Pivotspalten sind. Sie sind aber durch dieselbe Liste pivsp gegeben, die man
aus der reduzierten Treppenform R von A erhält. Sie gibt ja gerade jene r
Spalten von A an, die schließlich (in R) ein Pivotelement enthalten, auch die
pivotspalten von A sind.
Die erste Matrix R dieses Abschnitts ist die reduzierte Treppenform von
A:
A =
1302-1
00 14-3
13 16-4
wird zu R •
13 0 2-1
0 0 1 4-3
0 0 0 0 0
Die letzte Zeile von A ist schlicht die Summe der ersten und der zweiten
Zeile. Diese Tatsache wird beim Eliminationsverfahren aufgedeckt, das die
dritte Zeile durch eine Nullzeile ersetzt. Man erhält als Pivotspalten die erste
und die dritte Spalte, welche auch die Pivotspalten von A sind. Natürlich
sind die Pivotspalten von A von denen von R verschieden, da sie in den
„unteren" Positionen auch andere Werte als Null haben können. Unsere
Unterrichtsprogramme greifen sich die Pivotspalten von A durch den Ausdruck
A{:,pivsp) heraus. Das Symbol : bedeutet hier, dass alle Zeilen der durch
pivsp angegebenen Spalten gemeint sind.
In diesem Beispiel subtrahiert eine Matrix E die erste und die zweite Zeile
von der dritten Zeile, und erzeugt so die Nullzeile in R. Die
Eliminationsmatrix E und ihre Inverse sind also
E
1
0
-1-
0 0]
10
-11
und E
-1
100
010
111
Wir finden die r Pivotspalten von A in den ersten r Spalten von E~^
wieder! Die Spalten 1 und 3 von A sind gerade die ersten beiden Spalten von
E~^. Der Grund dafür ist, dass A = E~^R gelten muss, jede Spalte von A
erhalten wir also (spaltenweise Matrixmultiplikation!) als Produkt von E"^
mit einer Spalte von R. In den Pivotspalten von R greifen nun die Einsen
gerade eine der ersten r Spalten von E~^ heraus.
Wir wollen noch eine weitere wichtige Tatsache über die Pivotspalten
kennenlernen. Die Definition, die wir bis jetzt kennen, beruht auf einer Rechnung:
Man liest die Pivotspalten an der Treppenform R einer Matrix ab. Sehen wir
uns eine etwas mathematischere Beschreibung dieser Pivotspalten an:
3C Eine Piyotspalte von A kann nieht als Lineatkombmationv<?3i; davor
'stehek4#'S|>äItien'feechri^ben w^^
^^r die Matrix R ist dies einfach zu sehen. Die zweite Pivotspalte hat eine
Eins in Zeile 2, alle Spalten davor enthalten in Zeile 2 aber nur Nullen. Die
146 3 Vektorräume und Unter vektorräume
zweite Pivotspalte kann also nicht als Linearkombination von davor
stehenden Spalten geschrieben werden. Dasselbe gilt auch für A. Der Grund dafür
ist, dass Ax = 0 genau dann gilt, wenn auch Rx = 0 gilt. (Die
Lösungen dieser Gleichung blieben während des gesamten Eliminationsverfahrens
unverändert.) Der Ausdruck Ax ist aber nichts anderes als eine
Linearkombination der Spalten von A, und ebenso ist Rx dieselbe Kombination der
entsprechenden Spalten von R. Ist nun eine Spalte von A eine Linearkombi-
nation von davor stehenden Spalten, so gilt dasselbe für die entsprechenden
Spalten von R.
Die Pivotspalten von R sind nun eben keine Linearkombinationen von
davor stehenden Spalten, und deshalb können die entsprechenden Spalten
von A dies auch nicht sein.
Die „freien" Spalten sind aber Linearkombinationen davor stehender
Spalten. Die entsprechenden Kombinationen werden durch die speziellen
Lösungen der Gleichung Ax = 0 geliefert. Das wollen wir uns als nächstes näher
ansehen.
Die speziellen Lösungen
In jeder speziellen Lösung der Gleichungen Ax = 0 und Rx = 0 wird eine
der freien Variablen auf 1, die anderen auf 0 gesetzt. Die Lösungen, die sich
so ergeben, kann man direkt aus der Treppenform R ablesen:
Rx
1302-1
00 14-3
0000 0
Xi
X2
X3
X4
X5_
=
"Ol
0
oj
C.4)
Setzen wir die erste freie Variable X2 = 1 und X4 = x^ = 0, so erhält man
aus dem Gleichungssystem für die Pivot variablen die Lösungen xi = — 3 und
X3 = 0. Wir erhalten also die spezielle Lösung si = (-3,1,0,0,0). Daran
können wir erkennen, dass die (freie) zweite Spalte eine Linearkombination
davor stehender Spalten ist, nämlich 3 mal Spalte 1: Denn (—3) mal Spalte
1 plus Spalte 2 ergibt den Nullvektor.
Die nächste spezielle Lösung erhält man, indem man X4 = 1 und X2 = 0
und X5 = 0 setzt. Als Lösung ergibt sich dann S2 = (—2,0,-4,1,0).
Beachten Sie, dctss wiederum die Einträge aus R mit vertauschtem Vorzeichen
auftauchen.
Die dritte spezielle Lösung (aus x^ = 1 und X2 = X4 = 0) ist schließlich
S3 = A,0,3,0,1). Die Zahlen xi = 1 und X3 = 3 stammen diesmal aus der
fünften Spalte von R, wie immer mit vertauschtem Vorzeichen. Man erkennt
hier eine allgemeine Regel, die wir bald beweisen werden.
Wir fassen diese drei speziellen Lösungen in der Matrix N zusammen:
3.3 Die Rang und die reduzierte Treppenform 147
3-
1
0-
0
0
-2 1"
00
-4 3
10
Ol
nicht frei
frei
nicht frei
frei
frei
N =
Die Linearkombinationen dieser drei Spalten liefern alle Vektoren des Kerns,
also die komplette Lösungsmenge der Gleichungen Ax = 0 und Rx = 0.
Ebenso wie E die 2 x 2-Einheitsmatrix an den Positionen der Pivotspalten
enthält, enthält N die 3 x 3-Einheitsmatrix in den freien Zeilen.
Für jede freie Variable gibt es eine spezielle Lösung, Gibt es nun
r Pivotelemente, so bleiben n — r freie Variablen. Das ist der Schlüssel zum
Verständnis der Gleichung Ax = 0.
3D Für ein Gleichuegs^ystem Ax ^. 0 gibt e^n^- r sp^ielle Löstmgeu^ die
die Spalten der JTeimmalnaJ iV^ bilden.
Wenn wir später das Konzept „linear unabhängiger" Vektoren
kennenlernen, werden wir zeigen, dass diese speziellen Lösungen linear unabhängig
sind. Vielleicht können Sie aber auch hier schon sehen, dass keine Spalte der
Matrix N eine Linearkombination der anderen Spalten ist. Das Schöne ist,
dass man mit der folgenden intuitiven Argumentation vöUig richtig liegt:
l.Im Gleichungssystem Ax = 0 sind n Unbekannte enthalten.
2. Es gibt nur r wirkHch unabhängige Gleichungen.
3. Also muss es n — r unabhängige Lösungen geben.
Zum Abschluss dieses Abschnitts wollen wir uns noch einmal der oben
entdeckten Regel für spezielle Lösungen zuwenden. Der Einfachheit halber
wollen wir annehmen, dass die ersten r Spalten der Matrix die
Pivotspalten sind, und die letzten n - r Spalten freie Spalten. Die reduzierte Zeilen-
Treppenform der Matrix ist also von der Form
r Pivotspalten
/ F
0 0
r Pivotzeilen
m — r Nullzeilen
C.5)
n — r freie Spalten
3E '- Bie EBS'äen-n'^^r ape2^Men;I^stliigen'besleteMe;K^^^
feW:
"n:"^ T" freie :VariaMen''
mi
Multipliziert man R mit N, so erhält man die Nullmatrix, denn in der
oberen Hälfte erhält man / • {-F) + F • / = 0. Die Spalten von N lösen also
148 3 Vektorräume und Untervektorräume
die Gleichungen Rx = 0 und Ax = 0. Sie folgen genau dem oben entdeckten
Muster: Die Pivotvariablen entstehen durch Vorzeichenwechsel (F wird zu
—F) in den freien Spalten von R. Der Grund dafür besteht darin, dass das
Gleichungssystem Rx = 0 von so einfacher Form ist. Bringt man die zu
den freien Spalten gehörenden Terme auf die rechte Seite jeder Gleichung, so
bleibt auf der linken Seite einfach die Einheitsmatrix übrig:
Pivotvariablen
-F
freie
Variablen
C.7)
Die speziellen Lösungen bestehen nun aus je einer Spalte von / (die freien
Variablen) und der zugehörigen Spalte von -F (Pivotvariablen). Zusammen
ergeben diese beiden Matrizen die Matrix N.
Diese Überlegungen bleiben richtig, wenn die Pivotspalten nicht alle
gemeinsam die ersten Spalten der Matrix bilden. Stehen die Pivotspalten am
Anfang der Matrix, so hat man einfach / vor F wie in Gleichung C.6).
Stehen aber Pivotspalten und freie Spalten vermischt, so sind natürlich auch die
Spalten von / und F ineinander vermischt. Man kann aber immer noch eine
Matrix / und eine Matrix F erkennen.
Betrachten wir noch ein Beispiel mit / = [1] am Anfang und F = [2 3]
dahinter:
Beispiel 3.3.2 Die speziellen Lösungen der Gleichung xi +2x2 + 30:3 = 0 sind
in den Spalten von
N^
-2-3
1 0
0 1
enthalten. Wir schreiben die Koefßzientennmatrix als [1 2 3] = [/ F], ihr
Rang ist Eins. Der Kern wird also durch n - r = 3 — 1 spezielle Lösungen
aufgespannt, deren erste Komponente jeweils durch — F = [—2 — 3] bestimmt
wird. Die anderen beiden Komponenten (die freien Variablen) stammen aus
der Einheitsmatrix /.
Hinweis zum Ahschluss Wieso kann ich hier so bestimmt etwas über die
Matrix R sagen, wenn ich gar nicht weiss, wie zum Beispiel MATLAB sie
berechnet? Es gibt sicher verschiedene Wege, eine Matrix A auf eine reduzierte
Treppenform R zu bringen. Es ist gar nicht unwahrscheinlich, dass Sie oder
ich, oder MATLAB oder Maple jeweils etwas anders bei der Elimination
vorgehen. Der springende Punkt ist aber, dass das Endresultat R immer gleich
ist. Warum?
Durch die Matrix A sind die Matrizen /, F und die Nullzeilen in R schon
komplett bestimmt:
1. Welche Spalten Pivotspalten sind (und / enthalten), entscheidet sich durch
Eigenschaft 3C: die Spalten, die keine Linearkombinationen davor
stehender Spalten sind.
3.3 Die Rang und die reduzierte Treppenform 149
2. Welche Spalten freie Spalten sind (und F enthalten), wird durch
Eigenschaft 3D bestimmt: jene Spalten, die Linearkombinationen davor
stehender Spalten sind. Die Matrix F enthält die Information, welche
Kombinationen dies sind.
Die Lösungen der Gleichung Rx = 0 stimmen mit denen der Gleichung
Ax = 0 überein, und auch die speziellen Lösungen sind identisch. An
einem kleinen Beispiel mit Rang 1 können wir sehen, dass zwei verschiedene
Eliminationsmatrizen E dieselbe Matrix R erzeugen können:
22
1 1
wird zu R =
1 1
00
Man könnte nun die erste Zeile mit | multiplizieren, und sie von der zweiten
Zeile subtrahieren:
E.
Man kann aber auch erst die Zeilen von A vertauschen und anschließend das
Doppelte der neuen ersten Zeile von der zweiten subtrahieren:
\ 10]
[1/2 0'
[ 0 1.
=
1/2 0'
-1/2 1
10'
_-2 1
Ol'
10
=
0 1'
1-2
En
Wir erhalten also EA = R, aber auch E^euA = R. Obwohl die beiden
Eliminationsmatrizen verschieden sind, erzeugen sie dasselbe R. Eines kann sich
bei den E^s allerdings nicht ändern: Die erste Spalte von
E
-1 _
20
1 1
und
21
10
ist immer durch die erste Pivotspalte von A = E~^R gegeben. Die zweite
Spalte von E~^ wird aber nur mit den Nullen in R multipliziert, und deshalb
kann man sie ändern, ohne dass sich das Ergebnis der Multiplikation ändert.
Die Matrix R und die r Pivotspalten von E~^ sind jedoch durch die Matrix
A völlig festgelegt.
Die wesentlichen Punkte
l.Man erhält die reduzierte Treppenform aus der Matrix A als EA = R.
2. Der Rang von A ist die Anzahl der Pivotelemente in der zugehörigen
Treppenform R.
3. Wir fassen die übereinstimmenden Nummern der Pivotspalten von A und
von R in der Liste pivsp zusammen.
4- Die Pivot spalten können nicht als Linerakombination davor stehender
Spalten aufgefasst werden.
150 3 Vektorräume und Untervektorräume
5. Zu einem Gleichungssystem Ax = 0 gehören n — r spezielle Lösungen, die
in den Spalten der Matrix A^ zusammengefasst sind.
Aufgaben 3.3
1. Durch welche Formulierungen wird der Rang einer Matrix A richtig
beschrieben?
(a) Die Anzahl der Nicht-Nullzeilen in R.
(b) Gesamtzahl der Spalten minus Gesamtzahl der Zeilen.
(c) Gesamtzahl der Spalten inklusive Anzahl der freien Spalten.
(d) Anzahl der Einträge 'V in R.
2. Vergisst man die letzten n — r Nullzeilen in R und auch die letzten n — r
Spalten von E~^, so liest sich die Faktorisierung A = E~^R so:
A — (erste r Spalten von E~^) (erste r Zeilen von R).
Schreiben Sie die 3 x 5-Matrix A vom Beginn dieses Abschnitts als ein
solches Produkt einer 3 x 2-Matrix (bestehend aus den Spalten von E~^)
und einer 2x5 Matrix mit den Nicht-Nullzeilen von R,
Sie erhalten so eine Faktorisierung A = (Spalten)(Zeilen)'^. Jede m x n-
Matrix lässt sich also als Produkt einer m x r-Matrix mit einer r x n-
Matrix schreiben.
3. Bestimmen Sie die reduzierte Treppenform R der folgenden Matrizen:
(a) Die 3x4-Matrix, in der jeder Eintrag T ist.
(b) Die 3 x 4-Matrix, für die aij = i-i- j - 1 gilt.
(c) Die 3 X 4-Matrix mit aij = (-1)-^.
4. Bestimmen Sie R für die folgenden Blockmatrizen:
A= I 0031 B= [AA] C =
000
003
246
AA
A 0
5. Nehmen Sie an, die hinteren Spalten einer Matrix wären ihre Pivot
spalten. Beschreiben Sie alle vier Blöcke der sich ergebenden reduzierten
Treppenform
R =
AB
CD
B ist hierbei ein r x r-Block. Wie sieht die Matrix A^ mit den speziellen
Lösungen aus?
3.3 Die Rang und die reduzierte Treppenform 151
6. (Nicht ganz ernst gemeint!) Beschreiben Sie alle 2x3 Matrizen Ai und
A2 und ihre Zeilen-Treppenformen Ri und R2, für die i?i +-R2 die Zeilen-
Treppenform von Ai + A2 ist. Gilt in einem solchen Fall Ri = Ai und
R2 = A2I
7. Wie können Sie schließen, dass Ä^ r Pivotelemente besitzt, wenn A r
Pivotelemente hat? Finden Sie ein Beispiel einer 3 x 3-Matrix, in der
jeweils unterschiedliche Spalten die Pivotspalten sind.
8. Bestimmen Sie die speziellen Lösungen der Gleichungen Rx = 0 und
IL
y^R = 0 für die folgenden Matrizen R:
R =
1023
0145
0000
R =
Ol 2
000
000
In den Aufgaben 9—11 geht es um invertierbare r x r—Matrizen
innerhalb einer Matrix A.
Hat A den Rang r, so gibt es eine invertierbare r x r-Untermatrix S von
R. Um sie zu finden, streichen Sie m — r Zeilen und n — r Spalten von A.
A =
10. P sei die mxr-Untermatrix von A, die nur aus den Pivotspalten besteht.
Erklären Sie, warum P den Rang r hat.
23'
124
A =
■123'
246
A =
10]
001
oooj
Welchen Rang hat die Transponierte P^ der Matrix in Aufgabe 10? Fasst
man dann in S die Pivotspalten von P^ zusammen, so besitzt auch S
den Rang r. Die Matrix S ist also eine invertierbare r x r-Untermatrix
von A. Führen Sie diese Konstruktion (von A über P, P^, S^ bis hin zu
S) für die folgende Matrix aus:
Bestimmen Sie für A =
123
246
247
die invertierbare Untermatrix S.
In den Aufgaben 12—15 stellen wir eine Beziehung zwischen dem
Rang von AB und den Rängen von A und B her,
12. (a) Es sei die j-te Spalte von B eine Linearkombination davor stehender
Spalten von B. Zeigen Sie, dass man die j-te Spalte von AB durch
dieselbe Kombination der entsprechenden Spalten von AB erhält.
(b) Aus Teil (a) folgt, dass Rang(^5) < RangE) gilt, da in AB keine
neuen Pivotspalten auftauchen können. Finden Sie Matrizen Ai und
152 3 Vektorräume und Untervektorräume
A2 so, dass Rang(AiJ5) = Rang(J5) und Rang(A2J5) < Rang(J5) gilt,
wobei
B =
12
36
13. In Aufgabe 12 wurde gezeigt, dass Rang(AJ5) < Rang(J5) gilt. Mit
demselben Argument folgt auch, dass Rang(J5^A'^) < Rang(A^) ist. Wie
kann man daraus folgern, dass Rang(AJ5) < Rang(A) gilt?
14. Wichtig! Es seien A und B nx n-Matrizen mit AB = I. Zeigen Sie mit
der Ungleichung Rang(A5) < Rang(A), dass Rang(A) = n sein muss.
Die Matrix A ist also invertierbar, und B daher ihre beidseitige Inverse
(siehe Abschnitt 2.5). Es gilt also sogar BA = I (was nicht offensichtlich
ist!).
15. Es sei nun A eine 2 x 3-Matrix und B eine 3 x 2-Matrix mit AB = I,
Zeigen Sie mit Hilfe der Ränge der Matrizen, dass BA ^ I gilt. Geben
Sie ein Beispiel für diesen Fall an.
16. Es seien A und B zwei Matrizen mit derselben reduzierten Zeilen-
Treppenform R.
(a) Zeigen Sie, dass A und B denselben Kern und denselben Zeilenraum
besitzen.
(b) Es gilt EiA = R und E2B = R, deshalb muss A das Produkt einer
Matrix mit B sein.
17. Durch die Faktorisierung A = (Spalten) (Zeilen)'^ aus Aufgabe 2 kann
man jede Matrix mit dem Rang r als Summe aus Matrizen mit Rang 1
beschreiben, indem man die Multiplikation als „Spalte mal Zeile" auffasst.
Schreiben Sie die Matrizen A und B auf diese Weise als Summe von zwei
Matrizen vom Rang 1:
A =
1 10
1 14
1 18
B= [AA]
18. Es sei A eine mxn-Matrix mit Rang r, die zugehörige reduzierte
Treppenform sei R. Z sei die Transponierte der Treppenform von R^. (In
MATLAB wird eine transponierte Matrix durch ein Hochkomma
gekennzeichnet: R^ = R'.) Beschreiben Sie die Form und die Einträge der Matrix
Z.
R= rref(A) und Z = (rref(i^'))'•
19. Vergleichen Sie die Matrix Z aus Aufgabe 18 mit der Matrix, die man
erhält, wenn man mit der Treppenform von A^ beginnt (das ist nicht
3.4 Die vollständige Lösung von Ax = b 153
einfach R'^l):
S= rref{A') and Y= rrefE').
Erklären Sie in einer Zeile, warum Z gleich (oder ungleich) Y ist.
20. In Aufgabe 18 könnten wir auch die Matrizen E und A bestimmen, die
A und R' auf Zeilen-Treppenform bringen (wie in EA = R):
[RE]=TTef{[AI]) und [S F] = rTef{[R' I]) und Z = S'.
Welche Form haben die Matrizen E und F? Wie hängt Z über E und F
mit dem ursprünglichen R zusammen?
3.4 Die vollständige Lösung von Ax = b
Im letzten Abschnitt haben wir die vollständige Lösung der Gleichung Ax = 0
untersucht. Das Problem konnte mit Hilfe des Eliminationsverfahrens auf die
Gleichung Rx = 0 reduziert werden, in der man den freien Variablen
spezielle Werte zuweisen kann (Einsen und Nullen nämlich). Die Pivotvariablen
ergeben sich dann durch Rücksubstitution.
Bislang haben wir allerdings eine allgemeine die rechte Seite b noch nicht
betrachtet — dort stand immer der Nullvektor, und die Lösungen x, die wir
erhielten, gehörten zum Kern von A.
Im Folgenden wird b ungleich Null sein. Deshalb müssen wir die
Zeilenoperationen, die wir links auf die Matrix anwenden, auch auf die rechte
Seite wirken lassen. Eine Möglichkeit, dies zu erreichen, ist es, den Vektor b
als zusätzliche Spalte der Matrix hinzuzufügen. Betrachten wir dazu
dieselbe Matrix A wie zuvor, die wir durch die rechte Seite F1,62,63) = A,6,7)
ergänzen.
[1302"
0014
1316
'xi'
^2
^3
X4
=
]
6
7}
führt zu der
erweiterten
Matrix
1302 1
00146
13167
= [Ab].
Die erweiterte Matrix ist also einfach [ ^ b ]. Wenden wir nun einen
Eliminationsschritt auf A an, so wirkt dieser direkt auch auf b. Im Beispiel
subtrahieren wir die erste von der dritten Zeile, und dann die zweite von der dritten
Zeile. Damit erzeugen wir eine komplette Nullzeile:
302"
0014
0000
'xi'
X2
2^3
X4
=
"
6
0
hat die
erweiterte
Matrix
1302 1
00146
00000
= [Rdl
154 3 Vektorräume und Unter vektorräume
Die allerletzte Null ist dabei entscheidend. Dass in der hinzugefügten
Spalte ebenfalls eine Null entsteht, bedeutet nämlich, dass die Gleichung gelöst
werden kann. Da in der Matrix A die dritte Zeile die Summe aus der ersten
und der zweiten Zeile ist, muss das gleiche für die rechte Seite gelten, wenn
die Gleichungen konsistent sein sollen (also eine Lösung besitzen sollen). Ist
dies der Fall, so entsteht durch die Eliminationsschritte die Gleichung 0 = 0.
Die entscheidende Eigenschaft des Vektors auf der rechten Seite ist also, dass
der dritte Eintrag 1 + 6 = 7 ist.
Betrachten wir dieselbe Matrix, erweitert um einen allgemeinen Vektor
b = F1,62,63):
1302bi
0 0 1 4 b2
1 3 1 6 bs
130 2bi
0 0 1 4 b2
0 0 0 0 bs - bi
Man erhält als dritte Gleichung also 0 = 0 genau dann, wenn 63 — 61 — 62 = 0
ist, oder gleichbedeutend 61 + 62 = 63.
Im obigen Beispiel sind die freien Variablen ^2=^4= 0, und die
Pivotvariablen sind xi = 1 und X3 = 6 aus der letzten Spalte der auf Treppenform
reduzierten erweiterten Matrix. Mit dem Befehl x = partic(A, b) erhält man
in MATLAB diese „partikuläre" Lösung der Gleichung Ax = b. Dazu werden
zunächst A und h zu R und d reduziert. Dann kann man die r Pivot variablen
direkt dem Vektor d entnehmen, da in den Pivotspalten von R die
Einheitsmatrix steht. Nachdem die Matrix auf Treppenform reduziert wurde, muss
man also nur noch die Gleichung /x = d lösen, um die Pivot variablen zu
erhalten.
Beachten Sie, dass wir die freien Variablen wählen und dann nach den
Pivotvariablen lösen. Dies geht sehr schnell, wenn man die Matrix vorher in
ihre Treppenform R gebracht hat. Man sieht dann sofort, welche Variablen
frei sind, nämUch jene, die zu den Spalten ohne Pivotelemente gehören. Setzt
man diese Variablen zu Null, findet man die Pivot variablen von Xp in der
hinzugefügten Spalte.
Die partikuläre Lösung löst die Gleichung Axp = b
Die n — r speziellen Lösungen lösen die Gleichung Axn — 0.
Frage Wie sehen Xp und x^ aus, wenn A eine quadratische invertier bare
Matrix ist?
Antwort Die partikuläre Lösung A~^h ist dann die einzige Lösung. Es
gibt keine speziellen Lösungen, weil es keine freien Variablen gibt, und der
Kern der Matrix besteht lediglich aus x^ = 0. Die vollständige Lösung ist
also X = Xp + Xn = A~^h + 0.
Wir kennen diese Situation bereits aus Kapitel 2. Dort wurde der Kern
nicht erwähnt, weil er immer nur den Nullvektor enthielt. In der zusätzlichen
Spalte stand die Lösung A~^b, weil die Treppenform von A die
Einheitsmatrix / ist, und das Eliminationsverfahren aus der Matrix [Ab] die Matrix
3.4 Die vollständige Lösung von Ak — b 155
[/ yl~^b] generiert. Das ursprüngliche Gleichungssystem ylx — b wird in
diesem Fall also bis zur Lösung x = A~^b umgeformt.
In diesem Kapitel bedeutet dieser Fall, dass m — n — r gilt. Es handelt
sich um einen Spezialfall, in der Praxis sind aber invertierbare Matrizen der
Fall, der einem am häufigsten begegnet. Deshalb haben wir sie in einem
eigenen Kapitel am Anfang des Buches behandelt.
Für kleine Beispiele können wir die Matrix \Ah\ noch von Hand in die
reduzierte Treppenform bringen. Bei größeren Matrizen ist aber MATLAB die
bessere Wahl. Betrachten wir zunächst ein weiteres kleines Beispiel, in dem
die Matrix vollen Spaltenrang hat. In beiden Spalten steht also ein
Pivotelement.
Beispiel 3.4,1 Unter welchen Bedingungen an F1,62,63) ist das
Gleichungssystem Ax = b mit der Matrix
A^
1 1
1 2
-2-3
und b =
lösbar? Wenn diese Bedingung erfüllt ist, liegt b also im Spaltenraum von A.
Bestimmen Sie dann die vollständige Lösung x = Xp -h Xn-
Lösung Wir verwenden die um die zusätzliche Spalte b erweiterte Matrix.
Während des Eliminationsverfahrens wird zunächst Zeile 1 von Zeile 2
subtrahiert, und dann das Doppelte von Zeile 1 zu Zeile 3 addiert:
r 1 löi'
1 202
-2-363
—)■
161
162 - 61
-163 + 261
->
10261 -62
0 1 62 - 61
0 0 63 + 61 -h 62
In der letzten Zeile steht nun 0 = 0 genau dann, wenn 63 -h 61 -h 62 = 0 ist.
Dies ist somit die Bedingung, die dafür sorgt, dass b zum Spaltenraum von A
gehört, ist sie erfüllt, so ist die Gleichung lösbar. Die Zeilen von A addieren
sich zu einer Nullzeile. Aus Gründen der Konsistenz (es handelt sich um eine
Gleichung!) müssen sich die Komponenten von b ebenfalls zu Null addieren.
In diesem Beispiel haben wir keine freien Variablen, und keine
speziellen Lösungen. Der Kern besteht aus dem Vektor x^ = 0, und die (einzige)
partikuläre Lösung Xp steht in den oberen Einträgen der zusätzlichen Spalte:
X — Xp -r Xyj —
26i - 62
62 - 61
+
Ist die Bedingung 63 -h 61 + 62 = 0 nicht erfüllt, so gibt es keine Lösung für
die Gleichung Ax = b, und Xp existiert nicht.
Dieses Beispiel ist typisch für den wichtigen Fall, dass A vollen
Spaltenrang hat. Dann gibt es für jede Spalte ein Pivotelement und der Rang der
Matrix ist r = n. Man kann sich eine solche Matrix als „hoch und schlank"
156 3 Vektorräume und Untervektorräume
vorstellen {m>n). Beim Eliminationsverfahren wird dann A zu einer Matrix
R reduziert, die aus einer Einheitsmatrix in den oberen Zeilen und Nullzeilen
darunter besteht:
R =
nxn Einheitsmatrix
m - n Nullzeilen
C.8)
Es gibt hier also keine freien Spalten, oder freie Variablen, und die Matrix F
ist leer.
Im Folgenden wollen wir verschiedene Möglichkeiten zusammenstellen,
diese Art von Matrizen zu erkennen.
3F 3ede Matrix A mit vollem Spaltenrang (r = n) hatdie folge|i|
Eigeßschafteiir '''^' \ :^ . ^ 'r--
l^AUe. Spalten .von-^ sind Pivotspalten,' ^ '- <';-; \^ ' i ' " ' '^'^
2. Es gibt keilte freien VariableB imd keine speziellen ^Löspngeii,, \
3.Der Kern enthält nur den Nnllvektor'x == 0, ^ , , - ,^^^..^
4. Die Gleichung Ax = b blitzt höchstem eine Lösung. Es mn^ aber i ^^
nnbedingt;ane LdsiiBg geben,. ';/',;'./ ^L:„,^^ , >;
Mit den im folgenden Abschnittes eingeführten Begriffen ausgedrückt: Die
Spalten von A sind linear unabhängig, wenn r = n gilt. In Kapitel 4 werden
wir dieser Liste noch einen Punkt hinzufügen, nämlich: Die quadratische
Matrix A^A ist invertierbar.
In diesem Fall ist der Kern von A (der auch der Kern von R ist) auf den
Nullvektor zusammengeschrumpft. Deshalb ist eine Lösung der Gleichung
Ak = b, wenn sie überhaupt existiert, immer eindeutig. Die Treppenmatrix
R enthält m — n Nullzeilen, und somit gibt es auch m — n Bedingungen an b,
die erfüllt sein müssen, damit die Gleichungen in den Nullzeilen 0 = 0 lauten.
In dem Beispiel hatten wir m = 3 und r = n = 2, es gab also nur die eine
Bedingung 63 + 6i + 62 = 0 an den Vektor auf der rechten Seite der Gleichung.
Ist diese Bedingung erfüllt, so besitzt die Gleichung genau eine Lösung.
Im anderen Extremfall hat die Matrix vollen Zeilenrank. In diesem Fall
schrumpft der Kern der transponierten Matrix A^ auf den Nullvektor
zusammen. Man kann sich solche Matrizen als „breit und kurz" vorstellen, es
gilt m < n: Es gibt also mindestens so viele Unbekannte, wie es Gleichungen
gibt. Eine Matrix hat vollen Zeilenrank, wenn r =m gilt, also in jeder Zeile
ein Pivotelement steht. Betrachten wir wiederum ein Beispiel:
Beispiel 3.4,2 Wir haben n = 3 Unbekannte, aber nur 2 Gleichungen. Der
Rang der Matrix ist r = m = 2:
X -\- y -\- z = 3
X -\- 2y — z = 4:
3.4 Die vollständige Lösung von Ak = h 157
jVlan kann sich diese Situation durch zwei Ebenen im dreidimensionalen Raum
veranschaulichen. Die beiden Ebenen sind nicht parallel, und schneiden sich
deshalb in einer Geraden. Diese Lösungsgerade ist genau das, was man mit
dem Eliminations verfahren bestimmen kann: Die partikuläre Lösung
entspricht einem Punkt auf der Geraden. Addiert man die Vektoren x^ des Kerns
hinzu, so erhält man die anderen Punkte der Geraden. Durch x = Xp + x^
wird also die gesamte Lösungsgerade beschrieben.
Man bestimmt die Vektoren Xp und Xn mit Hilfe des
Eliminationsverfahrens. Subtrahieren wir zunächst die erste von der zweiten Gleichung, und
dann noch einmal die neue zweite Gleichung von der ersten Gleichung:
1 1
12
13
-14
->
1113
0 1-2 1
->
10
01-
32
2 1
Wir erhalten x^ als freie Variable. Wir können also die partikuläre Lösung
bestimmen, indem wir X3 = 0 setzen, und die spezielle Lösung, indem wir
0:3 = 1 setzen.
Xpartikuiär entstammt der rechten Seite: Xp = B,1,0)
Xspezieii entstammt der dritten Spalte, der freien Spalte F: s = (—3,2,1)
Es ist immer sinnvoll, zu überprüfen, ob die Lösungen Xp und s die
Gleichungen Axp = b und As = 0 erfüllen:
2-hl = 3
2-h2 = 4
-3 -h 2 -h 1 = 0
-3-h4-l =0
Die Vektoren x^ im Kern sind beliebige Vielfache von s. Addiert man sie zu
Xpartikuiär, SO ergibt sich eine ganze Lösungsgerade:
Vollständige Lösung:
X — Xp -r Xt^
[2"
1
0
+ X3
"-31
2
IJ
Diese Gerade wird in Abbildung 3.3 dargestellt. Man hätte auch jeden
anderen Punkt auf der Geraden als partikuläre Lösung wählen können, wir haben
einfach den Punkt mit X3 = 0 gewählt. Die partikuläre Lösung darf nicht mit
einer beliebigen Konstanten multipliziert werden! Die spezielle Lösung sehr
wohl; weswegen das so ist, haben wir schon gesehen.
Fassen wir den Fall einer Matrix mit vollem Zeilenrang noch einmal
zusammen:
158 3 Vektorräume und Unter vektorräume
X ^^^ Xp -\- X72
Lösungsgerade
Ax=:h
insbesondere
Axp = b
Kern
Axn = 0
Abb. 3.3. Die vollständige Lösung ergibt sich, wenn sämtliche Vektoren des Kerns
zu einer partikulären Lösung addiert werden.
3G Jede Matrix A mit vMem Zeilenrang (r —tu) hat die folgGin
Elgensclhafteii: ^ :',//'.'' ^/^'^^'
2. Die Gleichuag A:sc ^ b besitzt för Jede iJechte Seite b eine jLi^üng* ;|
3.DerSpall^nraiim ist der grämte Raimil?^. ; ?4
4. Der Kern von A wird durch n — r == n t-<m spemeEe Lösungen eri
In diesem Fall, in dem es m Pivotelemente gibt, sind die Zeilen „linear
unabhängig". Anders ausgedrückt, die Spalten von A'^ sind linear unabhängig.
Es ist jetzt höchste Zeit für die Definition der linearen Unabhängigkeit, wir
wollen vorher nur noch die vier Möglichkeiten für die Struktur der
Lösungsmenge linearer Gleichungssysteme zusammenfassen. Beachten Sie hierbei, wie
alles von den 'kritischen Zahlen' r, m, und n abhängt!
Welcher der vier möglichen Fälle auf ein Gleichungssystem
zutrifft, hängt vom Rang r der Matrix ab:
r = m, r = n : quadratisch und invertierbar, Ax = b besitzt 1 Lösung
r = m, r < n : breit und kurz, Ax = b besitzt cxd viele Lösungen
r < m, r = n : hoch und schlank, Ax = h besitzt keine oder 1 Lösung
r < m, r < n : unbestimmte Gestalt, Ax — b besitzt keine oder
cxD viele Lösungen
Die reduzierte Treppenform R gehört jeweils in dieselbe Klasse wie die Matrix
A. Nehmen wir an, dass die Pivotspalten zuvorderst stehen, dann können wir
die entsprechenden Treppenmatrizen folgendermaßen beschreiben:
R=[I]
[IF]
I F
0 0
rn = n r = m<n r = n<m r < m,r < n
3.4 Die vollständige Lösung von Ak = h 159
Die Fälle 1 und 2 haben jeweils vollen Zeilenrang, und die Fälle 1 und 3
vollen Spaltenrang. Der vierte Fall ist der theoretisch allgemeinste Fall, der
allerdings in der Praxis am seltensten auftritt.
Hinweis In der ersten (amerikanischen) Ausgabe dieses Buches wurde das
Eliminationsverfahren normalerweise bei der oberen Dreiecksmatrix U
abgebrochen, anstatt bis zur reduzierten Treppenform R fortzuschreiten. In
diesem Fall kann man die Lösung nicht aus der Gleichung Rx = d ablesen,
sie muss stattdessen durch Rücksubstitution aus der Gleichung C/x = c
bestimmt werden. Diese Methode ist zwar ein wenig schneller, wir ziehen jetzt
aber trotzdem die vollständige Reduktion vor, bei der in jeder Pivotspalte
nur ein Eintrag 'V übrig ist. Wir sind der Meinung, dass man an der
Matrix R alles viel einfacher erklären kann — und die harte Rechenarbeit sollte
sowieso von einem Computer übernommen werden. Deshalb haben wir die
Reduktion in dieser Ausgabe vollständig durchgeführt.
Die wesentlichen Punkte
l.Mit dem Rang r einer Matrix bezeichnen wir die Anzahl ihrer
Pivotelemente.
2. Die Gleichung Ax = b ist genau dann lösbar, wenn sich die letzten m — r
Gleichungen zu 0 = 0 reduzieren.
3. Dann erhält man ein partikuläre Lösung, indem man alle freien Variablen
auf 0 setzt.
4. Die Werte der Pivot variablen ergeben sich in Abhängigkeit von den Werten,
die man für die freien Variablen wählt.
5. Hat eine Matrix vollen Spaltenrang r = n, so gibt es keine freien Variablen:
es existiert genau eine Lösung oder keine.
6. Hat eine Matrix vollen Zeilenrang r = m, so gibt es genau eine oder
unendlich viele Lösungen.
Aufgaben 3.4
Die Aufgaben 1—12 behandeln die Gleichung Ax = b. Gehen Sie wie
im Text beschrieben vor, um Xp und x^ zu bestimmen. Verwenden
Sie die um die letzte Spalte b erweiterte Matrix.
1. Schreiben Sie die vollständige Lösung als Xp plus ein Vielfaches von s:
x-{-3y-{-Sz = l
2x-\-6y-\-9z = 5
-x-Sy + Sz^ 5.
2. Bestimmen Sie die vollständige Lösung (man nennt sie auch die
allgemeine Lösung) der Gleichung
160 3 Vektorräume und Untervektorräume
^131 2"
2648
^00 2 4
X
y
z
_t _
—
T
3
1
3. Unter welcher Bedingung an öi,Ö2,&3 ist das folgende System lösbar?
Fügen Sie b der Matrix als vierte Spalte hinzu, und bestimmen Sie alle
Lösungen mit Hilfe des Eliminations Verfahrens.
x^-2y -2z = hi
2x -\-5y - Az = 02
4x-\-9y-Sz = Ö3.
4. Unter welchen Bedingungen an öi, Ö2, ^s, &4 sind die folgenden
Gleichungssysteme lösbar? Bestimmen Sie die Lösungen.
12
24
25
39
Xi
X2
und
'1 2 3"
2 4 6
2 5 7
3 9 12
_
Xi
X2
.^3.
—
'W
02
h
h
5. Zeigen Sie mit dem Eliminations verfahren, dass F1,62, ^s) im
Spaltenraum von A liegt, wenn 63 - 2Ö2 -1- 4öi = 0 gilt. Hierbei sei
A =
131
382
240
Welche Linearkombination der Spalten von A ergibt den Nullvektor?
6. Welche Vektoren F1,02,63) bilden den Spaltenraum von AI Welche
Linearkombinationen der Spalten von A ergeben den Nullvektor?
(a) A^
121
263
025
(b) A^
1 1 1
124
248
7. Konstruieren Sie ein 2 x 3-System Ax = b mit der partikulären Lösung
Xp = B,4,0) und Lösungen der homogenen Gleichung Ak — 0, die
Vielfache von A,1,1) sind.
8. Warum kann man die Situation der letzten Aufgabe nicht mit einem 1x3-
System erreichen?
9. (a) Das Gleichungssystem Ak — b habe die beiden Lösungen xi und X2.
Bestimmen Sie zwei Lösungen der Gleichung Ax = 0.
(b) Bestimmen Sie dann noch eine Lösung für die Gleichung Ak — 0,
und eine weitere Lösung der Gleichung Ax = b.
3.4 Die vollständige Lösung von Ax = h 161
10. Begründen Sie, warum die folgenden Behauptungen falsch sind:
(a) Die allgemeine Lösung ist eine Linearkombination von Xp und x^.
(b) Ein Gleichungssystem Ax = b besitzt höchstens eine spezielle Lösung.
(c) Die Lösung Xp, in der alle freien Variablen den Wert 0 haben, stellt
den kürzesten Lösungsvektor dar. (Das heißt, die Länge ||x|| ist
minimal.) Finden Sie ein 2 x 2-Gegenbeispiel.
(d) Ist A invertierbar, so gibt es keine Lösung Xn für das homogene
Gleichungssystem.
11. In der fünften Spalte von U stehe kein Pivotelement. Dann ist x^ eine
Variable, und der Nullvektor ist die einzige Lösung der
Gleichung Ax = 0. Hat die Gleichung Ax — b eine Lösung, so hat sie
Lösungen.
12. Die dritte Zeile von [/ habe kein Pivot element. Dann ist diese Zeile
und die Gleichung JJx — c ist nur dann lösbar, wenn gilt. Die
Gleichung Ax = b (ist) (ist nicht) (ist möglicherweise) lösbar.
In den Aufgaben 13-18 geht es um Matrizen mit vollem Rang
r = m oder r = n.
13. Was ist der höchstmögliche Rang einer 3 x 5-Matrix? In dem Falle steht
ein Pivot element in jeder von U. Gibt es immer eine Lösung
der Gleichung Ax = b? Ist sie eindeutig? Welchen Spaltenraum hat A?
Geben Sie ein Beispiel für diesen Fall an.
14. Was ist der höchstmögliche Rang einer 6 x 4-Matrix? In dem Falle steht
ein Pivotelement in jeder von U. Gibt es immer eine Lösung der
Gleichung Ax = b? Ist sie eindeutig? Welchen Kern hat A? Geben Sie
auch für diesen Fall ein Beispiel an.
15. Bestimmen Sie die Ränge von A und von
01
A = I 2 11 5 I und ^ = I 1 1 2
1
4
2 11
-1
Ol
5
2 10j
llq
. (Der Rang hängt von g^ ab.)
16. Bestimmen Sie die Ränge von A, von A^ und von AA^:
A =
1 15
101
und A =
2 0
1 1
1 2
17. Bringen Sie A auf Treppenform U. Bestimmen Sie dann eine obere
Dreiecksmatrix L, so dass A = LU gilt.
34 10
6521
und A =
10 10"
2203
0654
162 3 Vektorräume und Unter vektorräume
18. Die folgenden Gleichungssysteme haben jeweils vollen Rang. Bestimmen
Sie ihre allgemeinen Lösungen in der Form Xp -|- Xn-
X -\-y -\- z = 4
(a) x-\-y-\-z = 4 (b)
X - y -\- z = 4.
19. Die Gleichung Ax = b habe unendlich viele Lösungen. Ist es möglich,
dass die Gleichung Ax = B mit einer anderen rechten Seite B nur eine
einzige Lösung hat? Kann es sein, dass Ax = B keine Lösung besitzt?
20. Wählen Sie für q Werte so, dass (falls möglich) A und B den Rang (a) 1,
(b) 2, (c) 3 haben.
A =
6 4 2
-3-2-1
9 6^
und B
3 1 3
q2q
In den Aufgaben 21—26 geht es um Matrizen vom Rang r = 1.
21. Tragen Sie in die leeren Felder Werte so ein, dass die Matrizen den Rang
Eins haben:
124
2
4
und B
2
1
2 6-3
und M
a b
c
22. Ist A eine mxn-Matrix mit Rang r = 1, so sind alle Spalten Vielfache
einer Spalte und alle Zeilen Vielfache einer Zeile. Der Spaltenraum ist
dann eine im Raum M^, und der Kern ist eine im Raum
l^. Der Spaltenraum von A^ schließlich ist eine
im Raum E^.
23. Wählen Sie Vektoren u und v so, dass A = uv^ — Spalte mal Zeile:
A^
366
1 22
488
und A
2 2 6 4
-1-1-3-2
A — uv^ ist eine „natürliche" Darstellung für jede Matrix vom Rang
r = 1.
24. Ist A eine Matrix vom Rang 1, so ist die zweite Zeile von U eine .
Rechnen Sie ein Beispiel durch.
25. Die Matrizen AB und AM sind Produkte von Matrizen vom Rang r = 1.
Bestimmen Sie ihre Ränge.
A =
12
24
und B^
2 1 4
3 1,5 6
und M =
1 h
c hc
3.4 Die vollständige Lösung von Ax = h 163
26. Das Produkt der beiden Matrizen uv^ und wz^ vom Rang 1 ist die
Matrix -(iiz^)? die ebenfalls den Rang 1 hat, solange nicht =
0 gilt.
27. Geben Sie Beispiele für Matrizen A an, so dass die Gleichung Ax. — b
(a) 0 oder 1, je nach b,
(b) 00 viele, unabhängig von b,
(c) 0 oder oo viele, je nach b,
(d) genau 1, unabhängig von b
Lösungen hat.
28. Was wissen Sie über die Beziehungen zwischen r, m und n, wenn Sie
wissen, dass die Gleichung Ax — b
(a) für manche Vektoren b keine Lösung,
(b) für jedes b unendlich viele Lösungen,
(c) für manche b genau eine, für andere aber keine Lösung,
(d) genau eine Lösung für jedes b besitzt?
Die Aufgaben 29—33 behandeln das Gauß-Jordan-Eliminations-
verfahren (abwärts und aufwärts) sowie die reduzierte Treppen-
form R,
29. Bringen Sie die Matrizen U auf die reduzierte Treppenform R.
Dividieren Sie dazu jede Zeile durch das zugehörige Pivotelement, so dass alle
Pivotelemente zu 1 werden, und erzeugen Sie dann Nullen oberhalb der
Pivotelemente, bis sie R erhalten:
U
244
036
000
undCZ
244
036
005
30. Sei U eine quadratische Matrix mit n Pivotelementen {U sei also
invertierbar). Erklären Sie, warum dann R — I gilt.
31. Wenden Sie das Gauß-Jordan-Verfahren auf die Gleichungen C7x = 0 und
C/x = c an, so dass Sie Gleichungen i?x — 0 und i?x — d erhalten:
[C70] =
123 0
004 0
und[C/c] =
123 5
004 8
Lösen Sie dann die Gleichung J?x = 0, und bestimmen Sie so Xn (die
freie Variable ist X2 = 1). Lösen Sie dann auch die Gleichung Äx = d,
um Xp zu bestimmen; setzen Sie dazu die freie Variable auf X2 — 0.
32. Mit dem Gauß-Jordan-Eliminationsverfahren erzeugt man die reduzierte
Treppenform R. Bestimmen Sie die Gleichungen Rx — 0 und Rx — d:
164 3 Vektorräume und Unter vektorräume
\u 0
=
06 0'
002 0
000 0
und
U c
=
'3 0 6 9]
002 4
000 öj
Ax =
023"
1320
2049
'xi'
^2
X4
=
' 2'
5
10
Lösen Sie die Gleichung Ux = 0 oder Rx — 0, um x^ zu bestimmen.
Welche Lösungen hat die Gleichung Rx — d?
33. Reduzieren Sie Ax = b zu Ux — c (Gauß'sche Elimination) und dann zu
Rx — d (Gauß-Jordan'sche Elimination):
= b.
Bestimmen Sie eine partikuläre Lösung Xp und alle Lösungen Xn der
homogenen Gleichung.
34. Bestimmen sie Matrizen A und B mit der gewünschten Eigenschaft, oder
erklären Sie, warum es solche Matrizen nicht gibt: Die einzige Lösung von
Ax — 2 ist X = [5]. Die einzige Lösung der Gleichung Bx — [5] ist
"[if-
35. Bestimmen Sie die LC7-Faktorisierung von A und die allgemeine Lösung
der Gleichung Ax — b:
131
1 23
246
1 1 5
und b
und dann b —
36. Die vollständige Lösung der Gleichung Ax — [^] sei durch x = [o] "^
c[5] gegeben. Bestimmen Sie A.
3.5 Unabhängigkeit, Basis und Dimension
In diesem wichtigen Abschnitt geht es um die wahre Größe eines Unterraums.
Eine m x n-Matrix hat n Spalten und jede dieser Spalten m Komponenten,
doch die tatsächliche „Dimension" des Spaltenraums muss nicht unbedingt m
oder n sein. Man bestimmt die Dimension, indem man unabhängige
Spalten zählt — wir werden jetzt erklären, was das bedeutet. Für den
Spaltenraum im Besonderen werden wir feststellen, dass seine tatsächliche Dimension
durch den Rang r gegeben ist.
Man kann die Idee der Unabhängigkeit auf eine beliebige Menge vi,... , v^
von Vektoren eines beliebigen Vektorraums anwenden. Wir werden uns aber
3.5 Unabhängigkeit, Basis und Dimension 165
meistens auf diejenigen Unterräume beschränken, die wir kennen und
verwenden — besonders den Kern und den Spaltenraum einer Matrix. Im letzten
Teil werden wir jedoch auch „Vektoren" betrachten, die keine
Spaltenvektoren sind. Das können Matrizen sein oder auch Funktionen, sie können linear
unabhängig sein oder auch nicht. Zunächst werden wir jedoch die wichtigen
Beispiele mit Spaltenvektoren betrachten, bevor wir zu den Beispielen mit
Matrizen und Funktionen kommen.
Das Ziel wird es sein, zu verstehen, worum es sich bei einer Basis eines
Vektorraums handelt. Wir sind damit zum inhaltlichen Kern vorgestoßen,
und kommen nicht mehr länger ohne eine Basis aus. Dies sind die vier
wesentlichen Ideen dieses Abschnitts:
1. Unabhängige Vektoren.
2. Einen Raum aufspannen.
3. Eine Basis eines Raums.
4. Die Dimension eines Raums.
Lineare Unabhängigkeit
Unsere erste Definition für lineare Unabhängigkeit fällt nicht so
umgangssprachlich aus wie bisher, aber Sie sind sicher bereit dafür.
DEFINITION BieSpalten einer Matrix A heißeii linßürunaifjSngig^meim
der Nii|l|räctt[^r''x/==r;0'd^^^^ einzige Lösüngl-ciar öföchuiig'^ Jk -.ä
ne andere Linearkombiüation Ak der Spalten wri A darf den^ N^
ergaben. , '-.-', ^, - , \ , -', , ,>■,';' ^^^ -^ -^ ir - ^ -
Sind die Spalten linear unabhängig, so enthält der Kern N(A) nur den
Nullvektor. Wir wollen die lineare Unabhängigkeit (oder Abhängigkeit) am
Beispiel dreier Vektoren im M^ illustrieren:
I.Abbildung 3.4 (links) stellt drei Vektoren dar, die nicht in einer Ebene
liegen. Sie sind linear unabhängig.
2, Abbildung 3.4 (rechts) stellt drei Vektoren dar, die in einer Ebene liegen.
Sie sind linear abhängig.
Man kann denselben Begriff von linearer Abhängigkeit natürlich auch auf
7 Vektoren im 12-dimensionalen Raum anwenden. Sind die Vektoren linear
unabhängig, so enthält der Kern der aus ihnen gebildeten Matrix nur den
Nullvektor. Wir wollen jetzt dieselbe Idee noch einmal mit anderen Worten
ausdrücken. Die folgende Definition kann nicht nur auf die Spalten einer
Matrix angewendet werden, sondern auf jede Folge von Vektoren eines beliebigen
Vektorraums. Bilden diese Vektoren aber die Spalten einer Matrix, so sagen
beide Definitionen exakt dasselbe aus.
166 3 Vektorräume und Unter vektorräume
iV3
Abb. 3.4. Unabhängige Vektoren vi, V2,V3. Abhängige Vektoren wi,W2,W3. Die
Linearkombination wi — W2 + W3 ergibt den Nullvektor @,0, 0).
DEFINITION Eine Folge vi,.,, ^y^ vob Yektoren heifit^l^^^
abhängig^ weim die einzige LinearkomMnatioii aua iS'^$m,.'N^O]:^f^
den MnäYßktot pt^t^ die-triviale Kom'bin^
Lineare üöabhEixgigMt bedeutet also, dass
alle Xi NuU sindv
Gibt es jedoch eine Kombination, die 0 ergibt, in der nicht alle Xi Null sind,
so sind die Vektoren linear abhängig.
Vollständig korrekt lautet die Formulierung: „Die Folge von Vektoren ist
linear unabhängig." Eine akzeptable Abkürzung ist aber: „Die Vektoren sind
unabhängig."
Eine Menge von Vektoren ist entweder abhängig, oder sie ist unabhängig.
Entweder können sie nicht-trivial zum Nullvektor kombiniert werden, oder
eben nicht. Die entscheidende Frage lautet also: Welche
Linearkombinationen der Vektoren ergeben den Nullvektor? Beginnen wir mit einigen kleinen
Beispielen im M^:
1. Die Vektoren A,0) und @,1) sind unabhängig.
2. Die Vektoren A,1) und A, 1,001) sind unabhängig.
3. Die Vektoren A,1) und B,2) sind abhängig,
4. Die Vektoren A,1) und @,0) sind abhängig.
In der geometrischen Betrachtungsweise liegen die Vektoren A,1) und B,2)
auf einer Geraden durch den Ursprung. Deshalb sind sie nicht unabhängig.
Wollen wir die Definition verwenden, um dies formal zu zeigen, so müssen
wir Zahlen xi und X2 finden, so dass xi(l,l) -|-X2B,2) = @,0) gilt. Das
bedeutet, wir müssen das folgende Gleichungssystem lösen:
2"
1 2
Xi'
X2
=
0"
0
gilt für xi = 2 und X2 = — 1.
3.5 Unabhängigkeit, Basis und Dimension 167
Die Spalten sind genau dann unabhängig, wenn es einen nichttrivialen Vektor
im Kern gibt.
Ist einer der Vektoren selbst der Nullvektor, so kann die Menge nicht
linear unabhängig sein. Warum nicht?
Betrachten wir nun drei Vektoren im E^. Sie sind sicher linear abhängig,
wenn ein Vektor ein Vielfaches eines der anderen Vektoren ist. Um lineare
Unabhängigkeit zu überprüfen, müssen wir aber alle drei Vektoren
gleichzeitig betrachten. Wir schreiben Sie darum in eine Matrix und versuchen, die
Gleichung Ax = 0 zu lösen.
Beispiel 3.5.1 Die Spalten dieser Matrix sind linear abhängig:
Ax
rio3'
215
' 103
r-3'
1
ij
ist
1
2
' 1
+ 1
0
1
0
+ 1
3
5
3
=
0
0
0
Der Rang von A ist nur r = 2. Unabhängige Spalten würden einen vollen
Spaltenrang von n = r = S ergeben.
Die Zeilen dieser Matrix sind ebenfalls linear abhängig. Man kann eine die
Nullzeile ergebende Linearkombination der Zeilen direkt sehen, nämlich Zeile
1 minus Zeile 3. Wir werden zeigen, dass die Spalten einer quadratischen
Matrix genau dann linear unabhängig sind, wenn ihre Zeilen linear unabhängig
sind.
Frage Wie findet man Lösungen der Gleichung Ax — 0? Man findet solche
Lösungen systematisch, indem man das Eliminationsverfahren anwendet.
103
215
103
wird zu i? =
10 3
01-1
00 0
Die Lösung x — (-3,1,1) ist eine spezielle Lösung dieses Gleichungssystems.
Man sieht daran, dass die freie Spalte (Spalte 3) eine Kombination der beiden
Pivotspalten ist. Das schließt aus, dass die Spalten linear unabhängig sind.
Wir erhalten so eine allgemeine Regel:
3H Die Spalten einer Matrix A sind genau dann linear unabhängig, w^nn
der Rang d^r Matrix r ^^n ist. Dann gibt es n Piyotspalten tmd keine freien
Spalten, so dass der Kern nur aus dem NuUvektor besteht.' " '
Ein Spezialfall, der besonders wichtig ist, ist sofort klar. Angenommen, wir
haben sieben Spaltenvektoren mit je 5 Komponenten. Da m = 5 kleiner ist als
n ~7y müssen die Spalten linear abhängig sein. Sieben beliebige Vektoren im
ft^ müssen linear abhängig sein, da der Rang der Matrix nicht größer als fünf
168 3 Vektorräume und Unter vektorräume
sein kann. In fünf Zeilen kann es nicht mehr als fünf Pivotelemente geben,
und deshalb hat das zugehörige Gleichungssystem mindestens 7-5 = 2 freie
Variablen, also auch nicht-triviale Lösungen. Deshalb sind die Spalten linear
abhängig.
3] Eine beliebige Menge von n Vektoren im W^ ist linear abhängig.
n>ni gilt.
Die Matrix hat mehr Spalten als Zeilen — sie ist „breit und kurz". Die
Spalten sind dann sicher linear abhängig, weil die Gleichung Ax = 0 nicht triviale
Lösungen hat. Gilt hingegen n < m, so können die Spalten linear unabhängig
oder auch abhängig sein. In diesem Fall ermittelt man mit dem
Eliminationsverfahren die Pivotspalten. Die Pivotspalten sind untereinander immer
unabhängig.
Hinweis Eine weitere Möglichkeit, lineare Abhängigkeit zu beschreiben,
besteht in der folgenden Formulierung: „Einer der Vektoren ist eine
Linearkombination der übrigen Vektoren." Das klingt sehr verständlich, warum haben
wir es so nicht von Anfang an ausgedrückt? Unsere Definition war länger: „Es
gibt eine nichttriviale Linearkombination, die den Nullvektor ergibt." Man
muss immer den einfachsten Weg, den Nullvektor zu erzeugen, ausschließen.
Diese triviale Kombination ist es, die jedem Autor Kopfzerbrechen bereitet.
In der ersten Formulierung hat der Vektor, der eine Linearkombination der
anderen ist, den Koeffizienten x = 1.
Der Grund, weswegen wir unsere Definition der obigen vorgezogen haben,
besteht darin, dass sie nicht einen bestimmten Vektor als „Schuldigen" auf-
fasst. Wir behandeln alle Spalten von A gleich, und fragen lediglich, ob die
Gleichung Ax. = 0 eine nichttriviale Lösung hat oder nicht. Im Endeffekt ist
das besser, als zu fragen, ob die letzte, oder die erste, oder eine der mittleren
Spalten eine Kombination der anderen ist.
Vektoren, die einen Unterraum aufspannen
Der erste Unterraum, der uns in diesem Buch begegnete, war der
Spaltenraum einer Matrix. Wir begannen mit den n Spalten vi, • • • , Vn, fügten dann
alle Linearkombinationen xi vi H \- Xn^n hinzu und erzeugten so den
Unterraum. Um dies zu beschreiben, führen wir jetzt das Wort „Erzeugnis" ein.
Der Spaltenraum wird von den Spalten der Matrix erzeugt.'^
^ Anm. d. Übers.: Man nennt den von den Spalten erzeugten Unterraum auch
die „lineare Hülle" der Spalten, und spricht auch davon, dass die Spalten sie
„aufspannen".
3.5 Unabhängigkeit, Basis und Dimension 169
DJEFIISHTIÖISI ptoe Menge von Vektoren erzeugt einen IRiinm^ weim die
Menge detÖhearkombinationea der Vektoren denRatim genistu atisfüllt:
Beispiel 3.5.2 vi
nalen Raum E^.
Beispiel 3.5.3 vi
und V2
V2
erzeugen den ganzen zweidimensio-
V3
ebenfalls den Raum M^.
Beispiel 3.5.4 wi =
und W2
erzeugen nur eine Gerade im
Dieselbe Gerade wird auch von wi und von W2 einzeln erzeugt.
Stellen sie sich zwei Vektoren am Ursprung @,0,0) des dreidimensionalen
Raums M^ vor. Normalerweise spannen sie eine Ebene auf, die aus allen
Linearkombinationen der beiden Vektoren entsteht. Wir wissen aber, dass es noch
weitere Möglichkeiten gibt: Zwei Vektoren, die nur eine Gerade erzeugen, drei
Vektoren, die den ganzen M^ erzeugen, oder drei Vektoren, die nur eine Ebene
aufspannen. Natürlich ist es sogar möglich, dass drei Vektoren lediglich eine
Gerade aufspannen, oder zehn Vektoren nur eine Ebene. Derartige Vektoren
sind sicher nicht unabhängig.
Die Spalten einer Matrix erzeugen ihren Spaltenraum. Wir wollen noch
einen anderen Raum betrachten: Die Zeilen einer Matrix erzeugen ihren
„Zeilenraum".
DEFINITION Der Zeilenraum einer Matrix Ist der Unterranm von W^^
der von ihren Zeilen ausgespannt wird.
Die Zeilen einer m x n-Matrix haben n Komponenten, sie sind also
Vektoren im E^ — jedenfalls wären sie das, wenn man sie als Spaltenvektoren
schriebe. Es gibt eine einfache Möglichkeit, das zu tun: die Matrix
transponieren. Anstelle der Zeilen von A betrachtet man einfach die Spalten von Ä^
— das sind dieselben Einträge, lediglich als Spalten angeordnet.
Der Zeilenraum von A ist also der Spaltenraum S{A^) von A^. Er ist
ein Unterraum von W, der von den Spalten von A^, also den Zeilen von A,
aufgespannt wird.
Beispiel 3.5.5
A =
14
27
35
und A^
123
475
Hier sind m = 3 und n = 2.
170 3 Vektorräume und Untervektorräume
Der Spaltenraum von A wird durch die beiden Spalten von A aufgespannt
und stellt eine Ebene im R^ dar. Der Zeilenraum von A wird durch die drei
Zeilen von A (also die Spalten von A^) aufgespannt. Hier ist es der gesamte
Raum R^. Wir merken uns: die Zeilen sind Elemente von R^, die Spalten von
R^. Dieselben Zahlen einer Matrix bilden verschiedene Vektoren in
verschiedenen Räumen.
Eine Basis für einen Vektorraum
Eine Menge linear unabhängiger Vektoren in der xy-Ehene kann sehr klein
sein, sie kann zum Beispiel aus nur einem einzigen Vektor bestehen. Eine
Menge, die die xy-Ehene aufspannt, kann hingegen sehr groß sein — drei,
vier, oder unendlich viele Vektoren. Ein Vektor allein kann jedoch die Ebene
nicht aufspannen, und drei Vektoren können nicht linear unabhängig sein.
Eine „Basis" der Ebene ist gerade richtig:
DEFINITION Eine Baaia eines Vektorraums ist eiae Menge you Vi?
ren,.die gleichzeitig zwei Eigenschaften besitzt:
l»Die Vektoren sind Enear unabhängig und
2-die Vektoren er^ieugen den Vektorraum/
Diese Kombination zweier Eigenschaften ist grundlegend für die gesamte
lineare Algebra. Jeder Vektor v eines Raums lässt sich als Kombination von
Basiselementen schreiben, da diese den Raum aufspannen. Weiterhin ist
diese Kombination eindeutig, da die Basisvektoren vi,... , v^ linear unabhängig
sind:
Es gibt genau eine Möglichkeit, einen Vektor v als
Linearkombination von Basisvektoren zu schreiben.
Begründung: Angenommen, es gilt v = aivi H h a^v^ und ebenso v =
biVi + • • • bn^^n- Subtrahiert man die eine Gleichung von der anderen, erhält
dass (ai — 6i)vi H h (a^ — bn)y^n = 0. Da die v^ linear unabhängig sind, gilt
also immer ai — bi = 0, und daher ai — bi. Die beiden Linearkombinationen
sind also tatsächlich gleich.
Beispiel 3.5.6 Die Spalten der Matrix / —
Man nennt sie die „Standardbasis".
10
Ol
bilden eine Basis des M^.
Die Vektoren i —
und j =
sind unabhängig. Sie spannen E^ auf.
3.5 Unabhängigkeit, Basis und Dimension 171
An diese Basis denkt jedermann zuerst. Der Vektor i liegt horizontal, der
Vektor j vertikal. Ganz ähnlich bilden die Spalten der 3 x 3-Einheitsmatrix
die Standardbasis i, j, k, und die Spalten der nxn-Einheitsmatrix die
Standardbasis des W. Wir betrachten jetzt andere Basen.
Beispiel 3.5.7 (Wichtig) Die Spalten jeder invertierbaren Matrix bilden eine
Basis des W.
1 2
25
und A
100
1 10
1 1 1
aber nicht A =
12
24
Ist A invertierbar, so sind die Spalten unabhängig, da die einzige Lösung
der Gleichung Ax = 0 der Nullvektor x == 0 ist. Die Spalten spannen den
ganzen Raum W^ auf, da jeder Vektor b eine Linearkombination der Spalten
ist — denn die Gleichung Ax = b kann für jedes b durch x = A~^h gelöst
werden. Erkennen Sie, wie die Dinge zusammenpassen, wenn die die Matrix
invertierbar ist? Wir fassen alles noch einmal in einem Satz zusammen:
3J Die. Viktoren;V|^j.-,,„y^ hMm^ eme-Baaiä d^^^R^^.gen^ai ^aaa/i^^W,
si6 4i^ Spalten einer mvertiei^bareii nxw-MBimx mnd. JD^r R^^tÄ Bf^fcresitijsl,
also tineiidlich viele Basen. ; .
Sind die Spalten einer Matrix unabhängig, bilden sie eine Basis des
Spaltenraums. Sind sie aber linear abhängig, dann bilden die r Pivot spalten eine
Basis von, denn sie sind linear unabhängig und spannen den Spaltenraum
auf.
3K Bie BiP0ti^pmUen einer Mutffix A Mtäem eine Bmu 4eä iSpät-
tenraums. 'M4Vhr<^Tmim <tegegeii .b|ldm;eko giaäi^.das^ ZBÜmixkmsiB^ 0^
auch die PivotzeEeii ä^t radtiderten lireppenforjßi Ä; . . ' ( -
Beispiel 3.5.8 Diese Matrix ist nicht invertierbar, und deswegen bilden ihre
Spalten keine Basis irgendeines Raums!
A =
24
36
wird zu i^ =
12
00
Die erste Spalte von A ist die Pivotspalte. Diese Spalte allein bildet schon
eine Basis des Spaltenraums. Die zweite Spalte allein würde eine andere Basis
darstellen, wie auch jedes andere nichttriviale Vielfache dieser Spalte. Es
gibt also wirklich nicht zu wenige Basen! Deswegen wählen wir oft eine ganz
spezielle Basis aus: jene, die aus den Pivotspalten besteht.
172 3 Vektorräume und Unter vektorräume
Beachten Sie, dass die Pivotspalten von R sich deutlich von denen von A
unterscheiden, da die Spalten von R mit Nullen enden. Diese Spalten bilden
eine Basis des Spaltenraums von R, sie müssen aber nicht einmal zum
Spaltenraum von A gehören. Die Spaltenräume von A und von R können also
verschieden sein, wie auch deren Basen.
Der Zeilenraum von A ist hingegen identisch mit dem Zeilenraum von R,
Im Beispiel enthält er die Vektoren B,4) und A,2) und alle weiteren
Vielfachen dieser Vektoren. Wie immer können wir für diesen Raum aus unendlich
vielen Basen auswählen. Ich glaube, die naheliegendste Wahl besteht in den
Pivotzeilen von R. Eine Basis des Zeilenraums dieser Matrix vom Rang 1
besteht also aus nur einem Vektor:
Basis des Spaltenraums:
Basis des Zeilenraums:
Im nächsten Kapitel werden wir auf diese Basen zurückkommen. Für's erste
wollen wir uns mit Beispielen zufrieden geben, in denen die Situation relativ
klar ist — immerhin ist der Begriff der Basis noch neu für Sie. Im
nächsten Beispiel ist die Matrix zwar größer, aber die Situation ist trotzdem gut
durchschaubar.
Beispiel 3.5.9 Bestimmen Sie Basen für den Spalten- und den Zeilenraum
der Matrix
R =
1203
0014
0000
Die Spalten 1 und 3 sind die Pivotspalten, die eine Basis des Spaltenraums
(von R\) bilden. Die Vektoren dieses Raums haben also alle die Form b =
(a;,?/,0), der Spaltenraum von R ist somit die xy-Ehene innerhalb des vollen
dreidimensionalen xyz-RaMins. Diese Ebene ist nicht der Raum E^, sie ist
ein Unterraum des Raums E?. Die Spalten 2 und 3 wären auch eine Basis für
denselben Spaltenraum, ebenso wie die Spalten 2 und 4. Welche Spalten von
R bilden keine Basis des Spaltenraums?
Der Zeilenraum von R ist ein Unterraum des E^. Seine einfachste Basis ist
durch Nicht-Nullzeilen von R gegeben. Die dritte Zeile (die Nullzeile) gehört
zwar auch zum Zeilenraum, sie darf aber nicht zur Basis hinzufgenommen
werden, da die Basisvektoren linear unabhängig sein müssen.
frage; Qeg^hßu BümfiXpiVeHot^^ Wie^ßriMp'Mjm^e^^
d^älM^it^i^ ' /^'''^:.4fi:ri^n0i^^
Erste Antwort: Man schreibt die Vektoren als Zeilen einer Matrix A und
verwendet das Eliminations verfahren, um eine Basis des Zeilenraums von R
(und damit von A) zu finden.
3.5 Unabhängigkeit, Basis und Dimension 173
Zweite Antwort: Man schreibt die Vektoren als Spalten einer Matrix A, und
verwendet das Eliminations verfahren, um die Pivotspalten zu bestimmen. Die
entsprechenden Spalten von A stellen eine Basis des Spaltenraums dar. Das
Programm colbasis verwendet die Spaltennummer der Liste pivsp in dieser
Weise.
Der Spaltenraum von R hatte r = 2 Basisvektoren. Könnte eine andere
Basis aus mehr (oder weniger) Vektoren bestehen? Dies ist eine
entscheidende Präge, und es gibt eine zufriedenstellende Antwort. Jede Basis eines
Vektorraums besteht aus derselben Anzahl Vektoren. Diese Anzahl
ist die „Dimension^' des Raums.
Die Dimension eines Vektorraums
Was gerade gesagt wurde, müssen wir noch beweisen: Es gibt zwar eine große
Auswahl an Basisvektoren, aber die Anzahl Vektoren in einer Basis ändert
sich nie.
3L Sind Vi,... ,v^ imd wi,,..^w« zwei Basen desselben Vektorratims,
Beweis, Angenommen, es gibt mehr w's als v's. Dann wollen wir aus der
Annahme n > m einen Widerspruch konstruieren. Die Vektoren v^ bilden eine
Basis, also muss sich wi als Linearkombination an vi H homiVm aus ihnen
darstellen lassen. Dies entspricht der ersten Spalte eines Matrixprodukts VA:
W =
WiW2...Wn
Vi
an
Öml
= VA.
Wir kennen zwar nicht jedes einzelne aij, wohl aber die Gestalt der m x n-
Matrix A. Der zweite Vektor W2 lässt sich ebenfalls als Kombination der
Vj darstellen, und diese Linearkombination bestimmt die zweite Spalte von
A. Die Matrix A hat also eine Zeile für jedes Vj, und eine Spalte für jedes
w^. Da n > m ist, gibt es eine nichttriviale Lösung der Gleichung Ax = 0.
Aber dann gilt auch VAx = 0 und daher Wx = 0. Das heißt aber: es gibt
eine nichttriviale Linearkombination der w^, die den Nullvektor ergibt. Dann
können diese Vektoren aber keine Basis bilden — und das ist der Widerspruch
zu den Annahmen, den wir konstruieren wollten!
Gilt nun m > n, so vertauschen wir einfach die Rollen der beiden Basen
und benutzen dasselbe Argument noch einmal. Die einzige Möglichkeit, einen
Widerspruch zu vermeiden, besteht also darin, m — n anzunehmen. Damit
ist der Beweis beendet.
Die Anzahl der Vektoren in einer Basis hängt also nur von dem
Vektorraum ab, aber nicht von einer speziellen Basis. Diese Zahl ist für alle Basen
174 3 Vektorräume und Untervektorräume
des Raums gleich, und sie gibt an, wieviele „Preiheitsgrade" der Vektorraum
besitzt. Für die Räume E"^ ist diese Zahl gleich n — dies ist die
„Dimension" des Raums W. Diesen wichtigen Begriff führen wir jetzt auch für andere
Vektor räume ein.
DEFINITtON Die Dimension eines Vektormums iBt durcH die
zaU der Vektoren in jeder Öaiäis des Raums ddpmart.
Diese Definition stimmt genau mit unserer Intuition überein. Eine Gerade
durch den Vektor v = A,5,2) hat die Dimension Eins, da sie einen Unterraum
mit einem Basisvektor darstellt. Senkrecht zu dieser Geraden liegt die durch
die Gleichung x-^5y-^2z = 0 definierte Ebene. Diese Ebene hat die Dimension
Zwei. Um das zu beweisen, konstruieren wir eine Basis aus zwei Vektoren,
nämlich (—5,1,0) und (-2,0,1). Die Dimension ist dann Zwei, weil die Basis
zwei Vektoren enthält.
Die Ebene stellt den Kern der Matrix A = [15 2] dar, die zwei freie
Variablen hat. Die beiden Basisvektoren (-5,1,0) und (—2,0,1) sind gerade
die speziellen Lösungen der Gleichung Ax == 0. Im nächsten Abschnitt
werden wir noch weitere Kerne betrachten, um zu beweisen, dass die speziellen
Lösungen immer eine Basis des Kerns definieren. An dieser Stelle wollen wir
nur eins betonen: Alle Basen eines Raums enthalten dieselbe Anzahl
Vektoren.
Zur „Sprache der linearen Algebra" Man sagt nicht „Der Rang eines Raums",
oder „die Dimension einer Basis", oder „die Basis einer Matrix" — solche
Ausdrücke haben keinerlei Bedeutung. Stattdessen ist es die Dimension
eines Raums, die dem Rang einer Matrix gleicht.
Basen für Matrizen—Räume und Funktionen—Räume
Die Anwendbarkeit der Begriffe „lineare Unabhängigkeit", „Basis" und
„Dimension" ist nicht im geringsten auf Spaltenvektoren beschränkt. Wir können
ebenso gut fragen, ob drei 3x4-Matrizen Ai,A2, As unabhängig voneinander
sind. Sie gehören zum Vektorraum der 3 x 4-Matrizen, und eine
bestimmte Linearkombination dieser Matrizen könnte die Nullmatrix ergeben. Wir
können auch nach der Dimension dieses Raumes fragen (sie ist 12).
In der Theorie der gewöhnlichen Differentialgleichungen bestimmt man
eine Basis des Lösungsraums der Gleichung (Py/dx^ = y. Eine solche Basis
enthält Funktionen, typischerweise die beiden Funktionen y — e^ und y =
e~^. Zählt man die Basisfunktionen, so erhält man die Dimension 2 für den
Raum aller Lösungen dieser Differentialgleichung.
Wir betrachten diese Matrizenräume und Funktionenräume als
zusätzlichen Stoff, über den man in diesem Kurs hinweggehen kann. Sie haben die
Ideen der linearen Algebra aber nicht richtig verstanden, wenn Sie sie nicht
auch auf andere Vektoren als Spaltenvektoren anwenden können.
3.5 Unabhängigkeit, Basis und Dimension 175
Matrizenräume Der Vektorraum M enthält alle 2x2-Matrizen. Es handelt
sich damit um einen vierdimensionaler Raum mit der Basis
^1,^2, A3, A4 =
Diese Matrizen sind linear unabhängig. Es geht dabei nicht um einzelne
Spalten, sondern um die ganze Matrix. Durch Linearkombinationen dieser vier
Matrizen kann man jede beliebige Matrix in M erzeugen, also spannen sie
den Raum auf:
0'
00
J
"Ol"
00
J
00'
10
J
"oo"
Ol
CiAi 4- C2A2 4- C3A3 4- C4A4
Cl C2
C3 C4
Die Nullmatrix entsteht nur, wenn alle c's Null sind — damit ist die lineare
Unabhängigkeit bewiesen.
Die Matrizen ^1,^2, A4 bilden die Basis eines Unterraums — des drei-
dimensinalen Unterraums der oberen Dreiecksmatrizen. Ai und A4 sind eine
Basis für die Diagonalmatrizen. Wie sieht eine Basis für die symmetrischen
Matrizen aus? Nehmen Sie zu Ai und A4 noch A2 H- A3 hinzu.
Wir gehen noch weiter und betrachten den Raum aller n x n-Matrizen.
Als Basis wählen wir die Menge der Matrizen, die nur einen von Null
verschiedenen Eintrag, nämlich eine Eins, haben. Da es n^ Positionen für diese
Eins gibt, gibt es auch n^ Basismatrizen:
- Die Dimension des gesamten Matrixraums ist n^.
- Die Dimension des Unterraums, der aus den oberen Dreiecksmatrizen
besteht, ist |(n^ 4- n).
- Die Dimension des Unterraums der Diagonalmatrizen ist n.
~ Die Dimension des Unterraums der symmetrischen Matrizen ist |(n^ 4-n).
Funktionenräume Die Gleichungen d'^y/dx^ = 0, d'^y/dx^ 4- 2/ = 0 und
d'^y/dx'^ —y = 0 sind Differentialgleichungen zweiter Ordnung, für die in der
Analysis Lösungsfunktionen y{x) gesucht werden:
2/" = 0 wird durch lineare Funktionen y — ex + d gelöst,
2/" = ~y wird durch Funktionen der Form ?/ = csinx 4- dcosx gelöst, und
y'''' ~y wird durch Funktionen der Form y — ce^ -\- de~^ gelöst.
Der zweite Lösungsraum enthält zwei Basisfunktionen: sinx und cosx.
Der dritte Lösungsraum hat die Basisfunktionen e^ und e~^ und der erste
Raum die Funktionen x und 1. Diese bilden den „Kern" der zweiten
Ableitung! In allen Fällen ist die Dimension Zwei, da es sich um
Differentialgleichungen zweiter Ordnung handelt.
176
3 Vektorräume und Untervektorräume
Wie steht es mit der Gleichung ?/" = 2? Ihre Lösungen bilden keinen
Vektor räum, da sie eine nichttriviale rechte Seite b= 2 hat. Eine partikuläre
Lösung ist y{x) — x^, und die allgemeine Lösung ist y{x) = x^ + ex + d.
Beachten Sie, dass hier wieder das Schema „partikuläre Lösung plus ein
Element des Kerns" auftritt. Eine lineare Differentialgleichung verhält sich also
wie eine lineare Matrixgleichung Ax = b. Im Gegensatz zu linearen
Matrizengleichungen löst man lineare Differentialgleichungen jedoch mit Methoden
der Analysis.
Wir schließen diesen Abschnitt mit dem Raum N ab, der nur den NuUvek-
tor enthält. Die Dimension dieses Raums ist Null, und die leere Menge (die
keinen Vektor enthält) ist eine Basis. Eine Basis kann niemals den Nullvektor
enthalten, da sie dann nicht linear unabhängig ist.
Die wesentlichen Punkte
l.Die Spalten einer Matrix A sind linear unabhängig, wenn der Nullvektor
X == 0 die einzige Lösung der Gleichung Ax = 0 darstellt.
2.Vektoren vi,... ,Vr erzeugen einen Raum, wenn dieser gleich der Menge
ihrer Linearkombinationen ist.
3. Eine Basis eines Vektorraums ist eine Menge linear unabhängiger Vektoren,
die den Raum erzeugen.
4. Alle Basen eines Vektorraums enthalten die gleiche Anzahl Vektoren. Diese
Anzahl ist die Dimension des Raums.
5. Die Pivotspalten bilden eine Basis des Spaltenraums einer Matrix, dessen
Dimension daher der Rang r ist.
Aufgaben 3.5
In den Aufgaben 1-10 geht es um lineare Abhängigkeit und
Unabhängigkeit .
1. Zeigen Sie, dass die Vektoren vi,V2 und vs linear unabhängig sind, die
Vektoren vi, V2, V3 und V4 aber linear abhängig sind:
"l"
0
0
V2 ==
"
1
0
V3 =
"
1
1
V4 =
"
3
4J
Vi
Lösen Sie dazu die Gleichung ciVi 4- C2V2 4- C3V3 = 0, oder betrachten
Sie direkt die Gleichung Ax =^ 0 (wobei die Vektoren v die Spalten von
A bilden).
2. (Empfohlen) Bestimmen Sie die größtmögliche Anzahl linear
unabhängiger Vektoren aus der Menge
3.5 Unabhängigkeit, Basis und Dimension 177
Vi
r 1"
-1
0
0
V2 =
r
0
-1
0
V3 =
r
0
0
-1
V4 =
0"
1
-1
0
V5 =
r Ol
1
0
-1
V6 =
r Ol
0
1
-1
3. Beweisen Sie, dass die Spalten von U linear abhängig sind, wenn a
d = 0 oder / = 0 gilt:
a h c
U= I Ode
00/
4. Zeigen Sie, dass in dem Fall, dass a,d und / sämtlich nicht null sind,
die Gleichung Ux = 0 nur die Lösung x == 0 hat. U hat dann linear
abhängige Spalten.
5. Sind die folgenden Vektoren linear abhängig oder unabhängig?
(a) A,3,2), B,1,3) und C,2,1)
(b) A,-3,2), B,1,-3) und (-3,2,1).
6. Wählen Sie drei verschiedene Tripel linear unabhängiger Spalten von U
aus. Finden Sie dann drei solcher Tripel von Spalten von A.
U =
234 1
0670
0009
0000
und A ■■
234 1
0670
0009
4682
7. Die Vektoren wi, W2 und W3 seien linear unabhängig. Zeigen Sie, dass
die Differenzen vi = W2 — W3, V2 = wi - W3 und V3 == Wi - W2
linear abhängig sind. Bestimmen Sie dazu eine Linearkombination dieser
Vektoren, die den Nullvektor erzeugt.
8. Wi,W2 und W3 seien wieder linear unabhängige Vektoren. Zeigen Sie,
dass die Summen vi = W2 4- W3, V2 = Wi 4- W3 und V3 == wi 4- W2 linear
unabhängig sind. Schreiben Sie dazu die Gleichung ci vi 4-C2V2 4-C3V3 == 0
mit Hilfe der Vektoren w^, und lösen Sie die entsprechende Gleichung für
die Koeffizienten q.
9. Es seien vi, V2,V3 und V4 Vektoren im Raum E^.
(a) Diese vier Vektoren sind linear abhängig, da
(b) Die beiden Vektoren vi und V2 sind abhängig, falls
(c) Die Vektoren vi und @,0,0) sind linear abhängig, da
10. Bestimmen Sie zwei Unear unabhängige Vektoren innerhalb der durch die
Gleichung x + 2y — 3z — t = 0 beschriebenen Hyperebene im E^. Finden
Sie dann drei unabhängige Vektoren in dieser Hyperebene. Warum ist
178 3 Vektorräume und Unter vektorräume
es nicht möglich, vier linear unabhängige Vektoren zu finden? Den Kern
welcher Matrix stellt die Hyperebene dar?
In den Aufgaben 11-15 geht es um das Erzeugnis einer Menge
von Vektoren. Dabei handelt es sich um die Menge aller
Linearkombinationen der Vektoren.
11. Beschreiben Sie die Unterräume des M?, die durch
(a) die Vektoren A,1, -1) und (-1, -1,1),
(b) die drei Vektoren @,1,1), A,1,0) und @,0,0),
(c) die Spalten einer 3 x 5-Treppenmatrix mit Rang 2,
(d) alle Vektoren mit ausschließlich positiven Komponenten
erzeugt werden. Handelt es sich jeweils um eine Gerade, eine Ebene, oder
den ganzen Raum?
12. Ein Vektor b gehört zu dem Unterraum, der durch die Spalten einer
Matrix A aufgespannt wird, wenn die Gleichung eine Lösung hat. Ein
Vektor c liegt im Zeilenraum von A, wenn es eine Lösung der Gleichung
gibt. Ist diese Behauptung wahr oder falsch? „Liegt der Nullvektor
im Zeilenraum, so sind die Zeilen linear abhängig."
13. Bestimmen Sie die Dimensionen der folgenden vier Räume. Welche von
ihnen sind identisch? (a) der Spaltenraum von A, (b) der Spaltenraum
von [/, (c) der Zeilenraum von A, (d) der Zeilenraum von U:
A^
1
3
1 Ol
3 1
1-1
undU
1 10
02 1
000
14. Zu einem Vektor x = {xi,X2,X3,X4) im R^ gibt es 24 Umordnungen, zum
Beispiel {x2,xi,X3,X4) und {x4,Xs,xi,X2)- Diese 24 Vektoren
(einschließlich x) erzeugen einen Unterraum S. Finden Sie Vektoren x, so dass die
Dimension von S (a) Null, (b) Eins, (c) Drei, (d) Vier ist.
15. V + w und V - w sind Linearkombinationen der Vektoren v und w.
Schreiben Sie umgekehrt v und w als Kombinationen von v + w und
V — w. Die beiden Paare also denselben Raum. Unter welcher
Bedingung sind sie Basen desselben Raums?
Die Aufgaben 16-26 behandeln die Bedingungen für eine Basis.
16. Sind die Vektoren Vi,. •., v^ linear unabhängig, so hat der von ihnen
aufgespannte Raum die Dimension . Die Vektoren sind dann eine
des Raums. Sind die Vektoren die Spalten einer m x n-Matrix, so
ist m als n.
17. Bestimmen Sie für jeden dieser Unterräume von E'* eine Basis:
3.5 Unabhängigkeit, Basis und Dimension 179
(a) alle Vektoren mit identischen Komponenten,
(b) alle Vektoren, deren Komponenten die Summe 0 bilden,
(c) alle Vektoren, die senkrecht auf A,1,0,0) und A,0,1,1) stehen,
(d) Spaltenraum und Kern der Matrix U = [ o i o i o ] •
18. Bestimmen Sie drei verschiedene Basen des Spaltenraums der Matrix U
in der letzten Aufgabe. Finden Sie dann zwei verschiedene Basen des
Zeilenraums von U.
19. Es seien vi, V2,..., ve Vektoren im Raum M^.
(a) Diese Vektoren erzeugen den M^ (sicher) (sicher nicht) (möglicherweise
nicht).
(b) Sie sind (sicher) (sicher nicht) (möglicherweise) linear unabhängig.
(c) Jede beliebige Auswahl von vier dieser Vektoren bildet (sicher) (sicher
nicht) (möglicherweise) eine Basis des M^.
20. Die Spalten einer m x n-Matrix A stellen n Vektoren aus dem W^ dar.
Welchen Rang hat A, wenn die Spalten linear unabhängig sind? Welchen
Rang hat A, wenn sie den W^ aufspannen? Was können Sie folgern, wenn
die Spalten eine Basis des W^ bilden?
21. Bestimmen Sie eine Basis der durch die Gleichung x-2y-\-Zz = ^
dargestellten Ebene im W, und ebenso eine Basis für die Schnittmenge dieser
Ebenen mit der a;-?/-Ebene. Bestimmen Sie dann eine Basis für den
Unterraum der Vektoren, die senkrecht auf der Ebene stehen.
22. Die Spalten einer 5 x 5-Matrix seien eine Basis des E^.
(a) Die Gleichung Ax = 0 hat nur die triviale Lösung x = 0, da .
(b) Für einen beliebigen Vektor b aus dem E^ ist die Gleichung Ax = b
lösbar, da .
Folgerung: A ist invertierbar und ihr Rang ist 5.
23. Es sei S ein fünfdimensionaler Unterraum des E^. Sind die folgenden
Behauptungen wahr oder falsch?
(a) Jede Basis von S kann durch Hinzufügen eines Vektors zu einer Basis
des E^ erweitert werden.
(b) Jede Basis des E^ kann durch Entfernen eines Vektors auf eine Basis
von S eingeschränkt werden.
24. U entsteht aus A, indem Zeile 1 von Zeile 3 subtrahiert wird:
A =
1 32
Ol 1
1 32
und U
132
Ol 1
000
Bestimmen Sie Basen für die beiden Spaltenräume. Bestimmen Sie ebenso
Basen für die beiden Zeilenräume und die Kerne der Matrizen.
180 3 Vektorräume und Untervektorräume
25. Wahr oder falsch? Begründen Sie:
(a) Sind die Spalten einer Matrix linear abhängig, dann sind auch die
Zeilen linear abhängig.
(b) Der Spaltenraum einer 2 x 2-Matrix ist gleich dem Zeilenraum.
(c) Der Spaltenraum einer 2 x 2-Matrix hat die gleiche Dimension wie
der Zeilenraum.
(d) Die Spalten einer Matrix bilden eine Basis des Spaltenraums.
26. Für welche Werte von c und d haben diese Matrizen den Rang 2?
A =
12505
00c22
000d2
undB
c d
d c
In den Aufgaben 27-32 geht es um Vektorräume, deren
Elemente Matrizen sind.
27. Bestimmen Sie Basen für die folgenden Unterräume des Raums der 3x3-
Matrizen:
(a) Die Diagonalmatrizen.
(b) Die symmetrischen Matrizen {Ä^ = A).
(c) Die schief-symmetrischen Matrizen {A^ — —A).
28. Konstruieren Sie sechs linear unabhängige 3 x 3-Treppenmatrizen Gi,
29. Bestimmen Sie eine Basis für den Raum der 2 x 3-Matrizen, deren
Spalten als Summe den Nullvektor ergeben. Bestimmen Sie auch eine Basis
für den Unterraum der Matrizen, deren Zeilen als Summe ebenfalls den
Nullvektor ergeben.
30. Zeigen Sie, dass die sechs 3x3-Permutationsmatrizen (siehe Abschnitt 2.6)
linear abhängig sind.
31. Welchen Unterraum des Raums der 3 x 3-Matrizen erzeugen
(a) die invertierbaren Matrizen,
(b) die Treppenmatrizen,
(c) die Einheitsmatrix?
32. Bestimmen Sie eine Basis für den Vektorraum der 2 x 3-Matrizen, deren
Kern den Vektor B,1,1) enthält.
In den Aufgaben 33—37 geht es um Funktionenräume.
33. (a) Bestimmen Sie alle Funktionen, die die Gleichung ^ = 0 lösen.
(b) Finden Sie eine Funktion, die die Gleichung j^ = S löst.
(c) Bestimmen Sie alle Funktionen, die die Gleichung ^ = 3 lösen.
3.6 Dimensionen der vier Unterräume 181
34. Der Raum F3 enthalte alle Funktionen der Form y{x) — Acosx -h
Bcos2x + Ccos3x. Bestimmen Sie eine Basis für den Unterraum der
Funktionen mit 2/@) — 0.
35. Bestimmen Sie eine Basis für den Raum der Funktionen, die die Gleichung
(a) £-2j/ = 0
(b) £-1 = 0
erfüllen.
36. Es seien yi{x)^y2{x) und 2/3(^) drei verschiedene Funktionen. Der von
ihnen aufgespannte Vektorraum könnte ein-, zwei- oder dreidimensional
sein. Geben Sie für jede dieser Möglichkeiten ein Beispiel an.
37. Bestimmen Sie eine Basis für den Raum der Polynomfunktionen p{x) vom
Grade < 3. Bestimmen Sie eine Basis für den Unterraum der Funktionen
mit p(l) = 0.
38. Bestimmen Sie eine Basis des Raums S der Vektoren (a, 6, c, d) mit a +
c + d = 0, und eine Basis des Raums T der Vektoren mit a-\-b — ^ und
c = 2d. Welche Dimension hat die Schnittmenge S fl T?
3.6 Dimensionen der vier Unterräume
Der Hauptsatz dieses Kapitels verbindet die Begriffe Rang und Dimension.
Der Rang einer Matrix ist die Anzahl ihrer Pivotelemente. Die Dimension
eines Unterraums ist die Anzahl der Vektoren in einer Basis des Unterraums.
Wir zählen hier also einerseits Pivotelemente und andererseits Basisvektoren.
Der Rang einer Matrix A offenbart die Dimensionen der vier wesentlichen
mit der Matrix zusammenhängenden Unterräume. Die folgenden Unterräume
sind gemeint, unter denen einer ist, den wir noch nicht kennen gelernt haben.
Zwei von ihnen gehören direkt zu A, die anderen beiden eher zu Ä^:
l.Der Zeilenraum S(A^) ist ein Unterraum von W.
2. Der Spaltenraum S[A) ist ein Unterraum von W^.
3. Der Kern N(A) ist ein Unterraum von W.
4. Der Linkskern N(A"^) ist ein Unterraum des W^. Diesem Raum begegnen
wir hier das erste Mal.
Der Kern und der Spaltenraum einer Matrix sind in diesem Buch bereits
behandelt worden, und wir wissen über beide bereits ziemlich gut Bescheid.
Jetzt wenden wir uns den anderen beiden Unterräumen zu.
Der Zeilenraum besteht aus allen Linearkombinationen der Zeilen einer
Matrix, man kann ihn auch als Spaltenraum der transponierten Matrix A^
auffassen. Der Linkskern besteht aus den Lösungen der Gleichung A^y — 0
182 3 Vektorräume und Unter vektorräume
(also eines nxm-Systems) und ist deshalb der Kern der Matrix Ä^.
Transponiert man diese Gleichung, so erhält man y^A = 0-^, in der die Vektoren
y^ auf der linken Seite stehen. Die Matrizen A und A^ sind normalerweise
sehr verschieden, wie auch ihre Spaltenräume und ihre Kerne. Diese Räume
hängen aber in einer faszinierenden Weise zusammen.
Der erste Teil des Hauptsatzes bestimmt die Dimensionen der vier
Unterräume. Eine Tatsache ist dabei besonders wichtig: Der Zeilenraum und der
Spaltenraum haben dieselbe Dimension, nämlich den Rang r der Matrix. Die
anderen beiden wichtigen Tatsachen sind Aussagen über die beiden Kerne:
Deren Dimensionen sind n — r und m — r, so dass sich in der Summe die
Dimensionen n und m ergeben.
Der zweite Teil des Satzes beschreibt, auf welche Weise die vier
Unterräume zusammengehören — zwei von ihnen im M^ und zwei im W^. Mit
diesem Wissen werden Sie die Gleichung Ax = h „richtig" verstanden haben.
Bleiben Sie dabei — wir betreiben hier richtige Mathematik.
Die vier Unterräume zur Treppenmatrix R
Angenommen, eine Matrix A wird auf die Zeilen-Treppenform R reduziert. In
dieser speziellen Form sind die vier Unterräume sehr leicht zu bestimmen. Wir
werden eine Basis für jeden Raum bestimmen, und damit seine Dimension.
Dann werden wir untersuchen, ob und wie sich die Räume ändern, wenn man
statt R die ursprüngliche Matrix A betrachtet. Der Hauptpunkt ist dabei,
dass die Dimensionen für A und R übereinstimmen.
Sehen wir uns als Beispiel eine 3x5-Treppenform R und ihre Unterräume
an:
m = 3
n = 5
r = 2
13509
00018
00000
Die Pivotzeilen sind 1 und 2
Die Pivotspalten sind 1 und 4
Der Rang ist also r == 2. Betrachten wir die Unterräume:
1. Der Zeilenraum von R hat die Dimension 2, übereinstimmend mit dem
Rang.
Begründung: Die ersten beiden Zeilen bilden eine Basis des Zeilenraums,
der aus den Linearkombinationen der Zeilen besteht. Die dritte Zeile, die
Nullzeile, gehört zwar auch dazu, fügt aber gegenüber dem von den ersten
beiden Zeilen erzeugten Raum nichts hinzu. Die ersten beiden Zeilen spannen
also den gesamten Zeilenraum auf.
Die Pivotzeilen 1 und 2 sind auch linear unabhängig. In diesem Beispiel
ist das offensichtlich, es gilt aber für alle Matrizen. Sieht man sich die Pi-
votzeilen der reduzierten Treppenform gesondert an, so erhält man die ry<r-
Einheitsmatrix und deshalb gibt es keine andere Möglichkeit, aus ihren Zeilen
eine Nullzeile zu erzeugen, als die triviale Kombination. Deshalb sind die r
3.6 Dimensionen der vier Unterräume
183
Pivotzeilen linear unabhängig, was wiederum bedeutet, dass die Dimension
des Zeilenraums r ist.
Die Dimension des Zeilenraums ist r. Die von Null verschiedenen
Zeilen von R bilden eine Basis,
2. Der Spaltenraum von R hat ebenfalls die Dimension r = 2.
Begründung: Die Pivotspalten bilden eine Basis. Sie sind linear unabhängig,
weil sie die r x r-Einheitsmatrix enthalten, und es deshalb keine
nichttriviale Linearkombination der Pivotspalten gibt, die den Nullvektor erzeugt. Da
jede andere (freie) Spalte ihrerseits als Linearkombination der Pivotspalten
geschrieben werden kann, spannen die Pivotspalten den Spaltenraum auch
auf. Dies erkennt man auch an den speziellen Lösungen:
Spalte 2 ist 3 mal Spalte 1. Die zugehörige spezielle Lösung ist (—3,1,0,0,0).
Spalte 3 ist 5 mal Spalte 1, die spezielle Lösung ist (-5,0,1,0,0).
Spalte 5 ist 9 mal Spalte 1 + 8 mal Spalte 4, wie man an der speziellen
Lösung (-9,0,0, -8,1) sieht.
Da die Pivotspalten einerseits linear unabhängig sind, andererseits den
Spaltenraum aufspannen, bilden sie eine Basis des Spaltenraums.
Die Dimension des Spaltenraums ist r, und die Pivotspalten
bilden eine Basis.
3. Der Kern von R hat die Dimension n — r = 5 — 2, daesn — r==3 freie
Variablen gibt, und daher 3 spezielle Lösungen der Gleichung fix = 0. Um
sie zu bestimmmen, setzen wir jeweils eine der freien Variablen X2, X3, X5 auf
1, und lösen nach Xi und X4 auf:
S2 =
r-3"
1
0
1 0
0
S3 =
■-5"
0
1
0
0
S5 ==
"-9"
0
0
-8
ij
fix = 0 hat die
allgemeine Lösung
X - X2S2 -f X3S3 +X5S5
Zu jeder freien Variablen gibt es eine spezielle Lösung. Da wir insgesamt
n Variablen und r Pivotvariablen haben, bleiben n - r freie Variablen und
ebenso viele spezielle Lösungen:
Der Kern hat die Dimension n — r, und die speziellen Lösungen
bilden eine Basis.
Die speziellen Lösungen sind linear unabhängig, weil sie gemeinsam in den
Zeilen 2, 3 und 5 die Einheitsmatrix enthalten. Weiter ist jede andere Lösung
X eine Linearkombination der speziellen Lösungen, da durch die Kombination
X = a:^2S2 + X3S3 + X5S5 die Komponenten X2, Xs und x^ gesetzt werden und
184 3 Vektorräume und Unter vektorräume
damit die Pivotvariablen xi und X4 durch die Gleichung Rx = 0 festgelegt
sind.
4. Der Kern von R^ hat die Dimension m - r = 3 — 2.
Begründung: Durch die Gleichung R^y = 0 werden Linearkombinationen
der Spalten von R^ {also der Zeilen von R) bestimmt, die den Nullvektor
ergeben. Ausgeschrieben sieht dies folgendermaßen aus:
2/i(l,3,5,0,9) + 2/2@,0,0,l,8) + 2/3@,0,0,0,0) = @,0,0,0,0). C.10)
Die Lösungen für t/i, 2/2 und 2/3 sind offenbar: Es muss t/i = 0 und auch 2/2=0
gelten. Die Variable 2/3 kann hingegen jeden Wert annehmen. Der Kern von
R^ enthält also alle Vektoren der Form y = @,0,2/3), und stellt daher die
Gerade dar, die aus den Vielfachen des Basisvektors @,0,1) besteht.
Eine reduzierte Treppenmatrix R enthält immer m — r Nullzeilen. Jede
beliebige Kombination dieser Nullzeilen ergibt wieder die Nullzeile.
Andersherum sind dies aber auch die einzigen nichttrivialen Kombinationen der
Zeilen von ß, die die Nullzeile erzeugen, da die Pivotzeilen linear unabhängig
sind. Mit diesem Argument erhalten wir den Linkskern von ß, also den Kern
von R^:
jyT _ n • ^^^ Linkskem hat die Dimension m — r.
~ ' Die Lösungen sind y = @,... ,0,2/r+i,- • • 5 2/m)-
Die ersten r Zeilen von R sind linear unabhängig, die restlichen Zeilen sind
Nullzeilen. Um aus ihnen eine Nullzeile zu kombinieren, müssen die ersten r
Komponenten von y Null sein, die restlichen m — r Komponenten sind frei
wählbar. Daher ist die Dimension des Linkskerns m — r.
Warum heißt dieser Raum „Linkskern"? Der Grund dafür wird ersichtlich,
wenn man die Gleichung R^y = 0 transponiert, sie lautet dann y^R =
0^. Hier steht der Zeilenvektor y^ links neben der Matrix R. In Gleichung
C.10) sehen Sie, wie die Komponenten dieses Vektors mit den Zeilen von R
multipliziert werden.
Wir betrachteten diesen Unterraum als vierten Raum. Manche
Lehrbücher zur linearen Algebra lassen ihn ganz aus — und versäumen es damit,
die Eleganz dieses Themas wiederzugeben.
Der Zeilenraum und der Kern im EP haben die Dimensionen r und
n — r — die Summe der Dimensionen ist n.
Der Spaltenraum und der Linkskern im W^ haben die Dimensionen
r und m — r — die Summe der Dimensionen ist also m.
Bis jetzt haben wir alles nur für Treppenmatrizen R bewiesen. In
Abbildung 3.5 erkennt man jedoch bereits dasselbe für A.
3.6 Dimensionen der vier Unterräume 185
S(AT)
dim r
N{A)
Dimension n
Dimension m-r
Abb. 3.5. Die Dimensionen der vier fundamentalen Unterräume für R und für A.
Die vier Unterräume für A
Wir haben noch eine Kleinigkeit zu erledigen. Die Dimensionen der
Unterräume zu A sind dieselben wie die zu R. Wir müssen noch erklären, warum
das so ist. Erinnern Sie sich, dass die beiden Matrizen über eine invertierbare
Matrix E (das Produkt der Eliminationsmatrizen) zusammenhängen:
EA^R und A^ E'^R.
C.11)
1. A hat denselben Zeilenraum wie R, Die Zeilenräume von A und von
R haben also auch die gleiche Dimension und identische Basen.
Begründung: Jede Zeile von A lässt sich als Kombination der Zeilen von R
darstellen. Andererseits ist aber auch jede Zeile von R eine Linearkombination
der Zeilen von A. Diese Kombinationen werden in der einen Richtung durch
die Matrix E~^ ^ in der anderen Richtung durch die Matrix E ausgedrückt.
Beim Eliminieren verwandeln sich zwar die Zeilen von A in die Zeilen von i?,
die Zeilenräi/me bleiben aber unverändert.
Da A denselben Zeilenraum wie R hat, können wir einfach die ersten r
Zeilen von R als Basis wählen. Es ist jedoch ebenso möglich, geeignete r
Zeilen der Matrix A auszuwählen. Es kann aber sein, dass die ersten r Zeilen
von A nicht geeignet sind, weil sie linear abhängig sind. Die Zeilen von A,
die schließlich zu Pivotzeilen werden, sind aber sicher wählbar.
2. Der Spaltenraum von A hat die Dimension r. Dahinter verbirgt sich
eine grundlegende, für alle Matrizen geltende Tatsache: Die Anzahl linear
unabhängiger Spalten ist gleich der Anzahl linear unabhängiger Zeilen.
Falsche Begründung: „A und R haben denselben Spaltenraum". Diese
Behauptung ist falsch, was man schon daran sehen kann, dass die Spalten von
186 3 Vektorräume und Unter vektorräume
R mit Nullen aufhören, war für die Spalten von A nicht zutreffen muss. Die
Spaltenräume sind zwar verschieden, lediglich ihre Dimensionen sind gleich,
nämlich gleich r.
Richtige Begründung: Eine Kombination der Spalten von A ergibt den
Nullvektor genau dann, wenn dieselbe Kombination der Spalten von R den
Nullvektor ergibt. Anders gesagt: Ax = 0 gilt dann und nur dann, wenn
Rx = 0 gilt.
Folgerung: Die r Pivot spalten von R bilden eine Basis des Spaltenraums
von R. Also bilden auch die r Pivot spalten von A eine Basis des zugehörigen
Spaltenraums.
3. A hat denselben Kern wie R. Die beiden Kerne haben also auch
dieselbe Dimension, und dieselben Basen.
Begründung: Im Laufe des Eliminationsverfahren verändern sich die
Lösungen nicht. Die speziellen Lösungen bilden eine Basis des Kerns. Es gibt n — r
freie Variablen, seine Dimension ist also n — r. Beachten Sie, dass r-\-{n — r)
gleich n ist:
(Dimension des Spaltenraums) 4- (Dimension des Kerns)
= Dimension des M^.
4. Der Linkskern von A (also der Kern von A^) hat die
Dimension m — r.
Begründung: Was wir über Matrizen A wissen, können wir natürlich
auch auf A^ anwenden. Wir haben bereits bewiesen, dass der Spaltenraum
von A^ die Dimension r hat. Da A^ eine n x m-Matrix ist, übernimmt der
Raum W^ jetzt die Rolle des „ganzen Raums", die der Raum W^ für m xn-
Matrizen hat. Für solche Matrizen gilt die Aufspaltung r 4- (n - r) = n und
deshalb haben wir für A^ die Aufspaltung r 4- (m — r) = m. Der Kern von
A^ hat also die Dimension m — r.
Damit haben wir alle Einzelheiten des wichtigsten Satzes dieses Kapitels
zusammengestellt:
Fundamentalsatz der Line£iren Algebra, Teil 1
Der Spaltenraum und der Zeilenraum einer Matrix
haben beide die Dimension r. Der Kern hat die
Dimension n~r^ und der Linkskern hat die Dimension m — r.
Wir haben diese einfachen Regeln herausgefunden, indem wir uns auf
Vektorräume konzentriert haben, statt auf einzelne Zahlen oder Vektoren
zu achten. Sie werden sie schon bald für selbstverständlich halten — und
schließlich werden sie Ihnen offensichtlich erscheinen. Schreiben Sie aber zum
Beispiel eine 11 x 17-Matrix mit 187 verschiedenen Einträgen auf, so werden
die wenigsten Leute unserer Einschätzung nach erkennen können, warum
diese Aussagen wahr sind:
3.6 Dimensionen der vier Unterräume 187
Dimension von S{A) = Dimension von S{Ä^)
Dimension von S{A) + Dimension von N{A) = 17.
Beispiel 3.6.1 Für ^ = [123] gilt m = 1, n = 3, und der Rang ist r = 1.
Der Zeilenraum ist eine Gerade im M^, der Kern die durch die Gleichung
Ax z=z xi -\- 2x2 + 3x3 = 0 beschriebene Ebene im M^. Diese Ebene hat
die Dimension 2 (nämlich 3 — 1), also summieren sich die Dimensionen zu
1 + 2 = 3.
Die Spalten dieser 1 x 3-Matrix sind Elemente des M^, und der
Spaltenraum ist einfach ganz M^. Der Linkskern enthält nur den Nullvektor, da die
einzige Lösung zu Ä^y = 0 durch y = 0 gegeben ist. Dies ist nämlich die
einzige „Linearkombination" der Zeile, die die Nullzeile ergibt. N{A'^) ist also
N, der Nullraum mit Dimension 0. Wieder ist die Summe der Dimensionen
1 + 0 = 1 die Dimension des W.
Beispiel 3.6.2 Für A =
123
123
gilt m = 2, n = 3 und r = 1.
Der Zeilenraum besteht wieder aus der Geraden durch A,2,3). Auch der Kern
ist durch dieselbe Ebene xi + 2x2 + 3x3 = 0 gegeben und ihre Dimensionen
1 + 2 = 3 summieren sich immer noch zu 3 auf.
Alle Spalten sind Vielfache der ersten Spalte A,1). Im Linkskern gibt es
aber mehr als nur den Nullvektor, da die erste minus die zweite Zeile die
Nullzeile ergibt. Deshalb hat die Gleichung A^y = 0 beispielsweise die Lösung
y = A, — 1). Der Spaltenraum und der Linkskern sind also durch zueinander
senkrechte Geraden im M^ gegeben. Sie haben jeweils die Dimension 1, und
die Summe der Dimensionen ist daher 2:
Spaltenraum = Gerade durch
Linkskern == Gerade durch
1
-1
Hat die Matrix A drei gleiche Zeilen, so ist der Rang
Welche zwei
Vektoren y liegen im Linkskern? Sie entsprechen Linearkombinationen der
Zeilen, die die Nullzeile ergeben.
Matrizen vom Rang Eins
Die Matrix im gerade betrachteten Beispiel hatte den Rang r = 1 — und
Matrizen vom Rang Eins sind besondere Matrizen. Wir können Sie vollständig
beschreiben. Man erkennt wiederum, dass die Beziehung „Dimension des
Spaltenraums" =„Dimension des Zeilenraums" gilt. Haben wir r == 1, so ist
jede Zeile das Vielfache einer bestimmten Zeile, und auch jede Spalte das
Vielfache einer Spalte der Matrix:
188 3 Vektorräume und Untervektorräume
A =
r 1
2
-3-
0
2
4
-6-
0
3"
6
-9
oj
ist gleich
mal [12 3].
Das Produkt einer Spalte mit einer Zeile Dx1 mal 1x3) erzeugt eine
4X 3-Matrix. Alle Zeilen sind hier Vielfache der Zeile A,2,3), und alle Spalten
sind Vielfache der Spalte A,2, -3,0). Der Zeilenraum ist eine Gerade im E^,
und der Spaltenraum eine Gerade im W^.
Jede Matrix vom Rang 1 hat die Form
A = uv^ =::: (Spalte) mal (Zeile).
Die Spalten sind Vielfache von u, und die Zeilen von v^. Der Kern ist
durch eine Ebene gegeben, die senkrecht zu v steht, da Ax = 0 einfach
u(v^x) = 0 bedeutet, also v^x = 0. Diese Beziehung der Unterräume
untereinander wird der Gegenstand des zweiten Teils des Fundamentalsatzes
sein.
Die wesentlichen Punkte
l.Die r Pivotzeilen von R bilden eine Basis der Zeilenräume von R und A,
2. Die r Pivotspalten von A (!) bilden eine Basis des Spaltenraums von A.
3. Die n — r speziellen Lösungen bilden eine Basis der Kerne von A und R.
4. Die letzten m — r Zeilen von I bilden eine Basis des Linkskerns von R.
5. Die letzten m — r Zeilen von E bilden eine Basis des Linkskerns von A.
Aufgaben 3.6
1. (a) Geben Sie die Dimensionen der vier Unterrräume zu einer 7x9-
Matrix vom Rang 5 an.
(b) Bestimmen Sie den Spaltenraum und den Linkskern einer 3x4-
Matrix vom Rang 3.
2. Bestimmen Sie Basen für die vier Unterräume zu den Matrizen A und B:
A =
124
248
und B^
1 24
258
3. Bestimmen Sie eine Basis für jeden der vier zu der Matrix
A^
[0 1234"
01246
[000 12
=
'100"
1 10
Ol 1
'0 12341
00012
oooooj
gehörenden Unterräume.
3.6 Dimensionen der vier Unterräume
189
4. Konstruieren Sie jeweils eine Matrix mit der gegebenen Eigenschaft, oder
erklären Sie, warum es keine solche Matrix gibt.
(a) Der Spaltenraum enthält die Vektoren i , o , der Zeilenraum
enthält die Vektoren [ 2 ] ? [ i ] •
(b) Der Vektor 1 bildet eine Basis des Spaltenraums, der Vektor 1
eine Basis des Kerns.
(c) Dimension des Kerns = 1 + Dimension des Linkskerns.
(d) Der Linkskern enhält den Vektor [J], der Zeilenraum enthält den
Vektor [?].
(e) Zeilenraum und Spaltenraum sind identisch. Kern und Linkskern aber
nicht.
5. Sei V das Erzeugnis der Vektoren A,1,1) und B,1,0). Konstruieren Sie
eine Matrix A, deren Zeilenraum V ist, und eine Matrix B, deren Kern
Vist.
6. Bestimmen sie je eine Basis und die Dimension der vier Unterräume zu
den Matrizen
0333
0000
0101
und B =
ohne das Eliminationsverfahren anzuwenden.
7. Es sei A eine invertierbare 3 x 3-Matrix. Geben Sie Basen der zu A und
der zu B = [A A] gehörenden Unterräume an.
8. Es sei 7 die 3 X 3-Einheitsmatrix und 0 die 3 x 2-Nullmatrix. Welche
Dimensionen haben die zu den folgenden Matrizen A, B und C gehörenden
Unterräume?
A=:[IO], B
I I
0^0^
undC- [0].
9. Welche Unterräume der beiden Matrizen stimmen jeweils überein? Zeigen
Sie, dass alle drei Matrizen denselben Rang haben.
'AI
(a) [A] und
(b)
und
A A
AA
10. Welche Dimensionen haben die zu einer 3 x 3-Matrix mit zufällig zwischen
0 und 1 gewählten Einträgen gehörenden Unterräume wahrscheinlich?
Wie sieht es aus, wenn es sich um eine 3 x 5-Matrix handelt?
190
3 Vektorräume und Untervektorräume
11. (Wichtig) A sei eine m x n-Matrix vom Rang r. Nehmen Sie an, dass es
Vektoren b gibt, für die die Gleichung Ax — b keine Lösung hat.
(a) Welche Ungleichungen (< oder < ?) mit den Größen Tn,n und r
gelten?
(b) Wie können Sie schließen, dass die Gleichung A^y — 0 nichttriviale
Lösungen y 7^ 0 hat?
12. Konstruieren Sie eine Matrix, deren Zeilen- und Spaltenraum beide durch
die Vektoren A,0,1) und A,2,0) aufgespannt werden. Warum ist diese
Konstruktion nicht mit Zeilenraum und Kern möglich?
13. Wahr oder falsch? Begründen Sie!
(a) Gilt m = n, so sind Zeilen- und Spaltenraum einer Matrix identisch.
(b) Die zu den Matrizen A und -A gehörenden Unterräume stimmen
überein.
(c) Stimmen die zu A und B gehörenden Räume sämtlich überein, so ist
A ein Vielfaches von B.
14. Bestimmen Sie Basen für die vier zu A gehörenden Unterräume, ohne die
Matrix auszurechnen:
A =
100
610
981
1234
0123
0012
15. Welche der vier Unterräume bleiben unverändert, wenn die ersten beiden
Zeilen einer Matrix A vertauscht werden? Der Vektor v = A,2,3,4)
sei ein Element des Spaltenraums von A. Geben Sie einen Vektor des
Spaltenraums der neuen Matrix an.
16. Erklären Sie, warum der Vektor v = A,2,3) nicht gleichzeitig eine Zeile
von A und ein Element des Kerns von A sein kann.
17. Beschreiben Sie die vier zu den Matrizen
A =
0 10
001
000
und / -h A =
1 10
Ol 1
001
gehörenden Unter räume.
18. (Linkskern) Wir fügen einer Matrix A eine zusätzliche Spalte b hinzu,
und bringen sie dann auf Treppenform:
[Ah] =
12 36i
456^2
78 9 63
1 2 3 6i
0-3-6 62-461
0 0 0 63-262 + 61
3.6 Dimensionen der vier Unterräume
191
Eine gewisse Kombination der Zeilen von A erzeugt also eine Nullzeile in
[A b]. Welche Kombination ist dies? (Sehen Sie sich die letzte Spalte an.)
Welche Vektoren gehören also dem Kern von A^ an, welche dem von A?
19. Wenden Sie die Methode aus Aufgabe 18 noch einmal an: Reduzieren Sie
eine erweiterte Matrix A auf Treppenform und sehen Sie sich die
Nullzeilen an. Die letzte Spalte gibt jeweils an, welche Kombinationen der
anderen Zeilen erzeugt wurden. Aus dieser Spalte können Sie also
Vektoren im Linkskern von A ablesen. Bestimmen Sie m — r Basisvektoren
von NA'^.
(a)
(b)
1 2 bi
3 4 62
4 6 bs
12 bi
2 3 62
2 4 63
2 5 64
20. (a) Beschreiben Sie die Lösungen der Gleichung Ax = 0 mit
A =
100
210
341
420 1
0013
0000
(b) Wie viele linear unabhängige Lösungen der Gleichung A^y — 0 gibt
es?
(c) Bestimmen Sie eine Basis des Spaltenraums von A.
21. Es sei A die Summe zweier Matrizen vom Rang eins: A — uv^ -f wz^.
(a) Welche Vektoren spannen den Spaltenraum von A auf?
(b) Welche Vektoren spannen den Zeilenraum von A auf?
(c) Der Rang von A ist geringer als 2, falls oder falls .
(d) Es seien u = z = A,0,0) und v = w = @,0,1). Berechnen Sie A.
22. Konstruieren Sie eine Matrix, deren Spaltenraum durch die Vektoren
A,2,4) und B,2,1), und deren Zeilenraum durch die Vektoren A,0,0)
und @,1,1) aufgespannt wird.
23. Bestimmen Sie Basen für den Spalten- und den Zeilenraum von A, ohne
die Matrix auszurechnen:
A^
12
45
27
303
112
192 3 Vektorräume und Unter vektorräume
Wieso kann man aus der Gestalt der beiden Matrizen schließen, dass A
nicht invertierbar ist?
24. Zu welchem Unterraum gehört d, wenn die Gleichung Ä^y = d lösbar
ist? Welcher Raum muss trivial sein, damit die Lösung eindeutig ist?
25. Wahr oder falsch? Geben Sie Begründungen oder Gegenbeispiele an.
(a) A und A^ haben dieselbe Anzahl Pivotelemente.
(b) A und A^ haben denselben Linkskern.
(c) Ist der Zeilenraum einer Matrix A mit ihrem Spaltenraum identisch,
so gilt A^ = A.
(d) Gilt A^ — -A, so stimmen Zeilen- und Spaltenraum von A überein.
26. Gilt AB = C, so sind die Zeilen von C Kombinationen der Zeilen von
, weshalb der Rang von C nicht größer sein kann als der Rang von
. Da auch B^A^ = C^ gilt, ist der Rang von C ebenfalls nicht
größer als .
27. Es seien a, 6, c mit a^ 0 gegeben. Wie muss man den Wert von d wählen,
damit die Matrix A = [^ d] ^^^ Rang Eins hat? Bestimmen Sie jeweils
eine Basis für den Zeilenraum und den Kern.
28. Bestimmen Sie die Ränge der 8 x 8-Schachbrett-Matrix B und der
Schachfeld-Matrix C
B =
1010 10 10
0 10 10 101
1010 10 10
01010101
und C =
t sl dkl s t
bbbbbbbb
vier Nullzeilen
bbbbbbbb
tsldklst
wobei die Zahlen b,t,s,l,d und k paarweise verschieden seien.
Bestimmen Sie Basen der Zeilenräume und der Linkskerne von B und C. Eine
Herausforderung: Bestimmen Sie eine Basis des Kerns von C.
4 Orthogonalität
4.1 Orthogonalität der vier Unterräume
Zwei Vektoren heißen orthogonal, wenn ihr Skalarprodukt Null ist: v • w = 0,
oder v-^w = 0. In diesem Kapitel gehen wir einen Schritt weiter, von
orthogonalen Vektoren zu orthogonalen Unterräumen. Der Begriff „Orthogonal"
heißt einfach „senkrecht".
In Kapitel 3 haben wir Unterräume zu einem ganz bestimmten Zweck
betrachtet — um die Gleichung Ax = b zu erhellen. Dazu benötigten wir
zunächst den Spaltenraum (für b) und den Kern (für x) von A. Dann haben
wir unsere Aufmerksamkeit den entsprechenden Räumen der transponierten
Matrix A^ zugewendet. Diese vier Unterräume gemeinsam enthüllen die
eigentliche Wirkung einer Matrix.
Eine Matrix wird mit einem Vektor multipUziert: A mal x. Auf unterster
Ebene betrachtet handelt es sich nur um Zahlen. Auf der nächsthöheren
Ebene sieht man eine Kombination von Spaltenvektoren. Auf der dritten Ebene
sieht man schließlich Unterräume. Ich glaube aber, Sie haben noch nicht alles
gesehen, solange sie nicht Abbildung 4.1 betrachtet haben. Dort werden die
Unterräume so zusammengefügt, dass man die verborgene Wirkung der
Multiplikation A mal X erkennt. Die rechten Winkel zwischen den Unterräumen
sind dabei neu — wir müssen noch erklären, was sie bedeuten sollen.
Der Zeilenraum steht senkrecht auf dem Kern. Jede Zeile von A steht
senkrecht auf jeder Lösung der Gleichung Ax = 0. Ebenso steht jede
Spalte von A senkrecht auf den Lösungen der Gleichung A^y = 0, daher der
rechte Winkel in der rechten Hälfte des Bildes. Diese Rechtwinkligkeit der
Unterräume ist der Gegenstand des zweiten Teils des Fundamentalsatzes der
Linearen Algebra.
Wir wollen noch eine Bemerkung über den Kern der transponierten
Matrix hinzufügen. Man könnte ihn zunächst als unnütz betrachten, da keiner
der Vektoren Ax in ihm liegt. Aber für den Fall, dass wir eine Gleichung
Ax = b lösen wollen und daran scheitern, weil b außerhalb des Spaltenraums
liegt, wird der Kern der transponierten Matrix benötigt. Er enthält dann den
„Fehler", den man mit einer Näherung für die Lösung nach der „Methode
der kleinsten Quadrate" macht. Dies wird die wesentliche Anwendung der
linearen Algebra sein, die wir in diesem Kapitel besprechen.
194 4 Orthogonalität
Dimension
Dimension
Dimension
= n
Dimension
m-r
Abb. 4.1. Zwei Paare orthogonaler Unterräume. Die Summe der Dimensionen ist
n beziehungsweise m.
Der erste Teil des Fundamentalsatzes gibt über die Dimensionen der
Unterräume Auskunft: Zeilen- und Spaltenraum sind r-dimensional (deshalb
haben sie in der Abbildung dieselbe Größe), und die beiden Kerne haben
die Dimensionen n — r und m — r. Im Folgenden werden wir zeigen, dass
Zeilenraum und Kern sogar senkrecht aufeinander stehen.
DEFINITION Zwei Unterräume V und W eines Vektorraums heißen
orthogonal^ wenn jeder Vektor v in V senkrecht auf jedem Vektor w in W
steht:
Beispiel 4.1.1 Betrachten Sie eine Fußbodenecke ihres Zimmers als
Koordinatenursprung @,0,0), den Fußboden (ins Unendliche erweitert) als einen
Unterraum V, und die Gerade, in der sich die zwei (ebenfalls unendlich
erweiterte) Wände schneiden, als einen anderen (eindimensionalen) Unterraum
W. Diese beiden Unterräume sind orthogonal, da jeder Vektor in der
Schnittgeraden der Wände senkrecht auf jedem Vektor im Fußboden steht. Dabei
nehmen wir natürlich an, dass sie nicht in einem Zelt leben.
Beispiel 4.1,2 Sei V wieder der Fußboden ihres Zimmers, aber sei jetzt W
eine der Wände, also ein zweidimensionaler Raum. Fußboden und
Zimmerwand sehen immer noch orthogonal aus, sind es aber nicht! Es lassen sich in
4.1 Orthogonalität der vier Unterräume 195
V und W Vektoren finden, die nicht senkrecht aufeinander stehen. Ein
Vektor entlang des unteren Endes der Wand gehört ja sogar sowohl zur Wand als
auch zum Boden, also gleichzeitig zu V und W, und diese Vektoren stehen
nicht senkrecht auf sich selbst.
Beispiel 4.1.3 Liegt ein Vektor v in zwei orthogonalen Räumen, so muss er
senkrecht auf sich selbst stehen. Es muss also v^v = 0 gelten: Dies trifft
nur auf den Nullvektor zu. Kern und Zeilenraum schneiden sich also nur im
Nullvektor.
Die wesentlichen Beispiele in der linearen Algebra hängen mit den vier
Unterräumen zusammen.
4A -, Jeder yektor-K deä Kariis von i4'steM^,seiilar^cM;;i8ltlf jaäet''&^ mn'A^
Kern Bild 'MMdt^nm söxd ako orthogonale tliitterräutaie;
Um zu verstehen, wieso ein Vektor x aus dem Kern senkrecht auf den
Zeilen steht, sehen wir uns die Gleichung Ax = 0 an. Jede Zeile wird mit x
multipliziert:
Ax =
Zeile 1
Zeile m
0
0
D.1)
Die erste Zeile besagt, dass Zeile 1 senkrecht auf x steht. Die letzte
Zeile schließlich besagt, dass Zeile m senkrecht auf x steht. Das Skalarprodukt
jeder Zeile mit x ist Null. Dann steht x aber auch senkrecht auf jeder
Linearkombination der Zeilen. Der gesamte Zeilenraum S{A'^) steht senkrecht
auf dem gesamten Kern N{A).
Für diejenigen Leser, die die kürzere Matrizennotation schätzen, hier noch
ein zweiter Beweis. Die Vektoren des Zeilenraums sind Linearkombinationen
der Zeilen, die man durch den Ausdruck A^y beschreiben kann. Betrachten
wir das Skalarprodukt einer solchen Linearkombination mit einem Vektor x
des Kerns von A:
x^(A^y) = {Axfy = O^y - 0.
D.2)
Die Vektoren x und A^y sind also orthogonal.
Wir ziehen den ersten Beweis vor, weil man in D.1) erkennt, wie jede
Zeile von A mit x multipliziert wird und Null ergibt. Der zweite Beweis lässt
aber erkennen, warum im Fundamentalsatz sowohl die Matrix A als auch A'^
auftreten. A'^ gehört zu y und A zu x, so dass wir im Beweis schließlich
Ax = 0 verwenden können.
Im nächsten Beispiel sehen wir Zeilen, die senkrecht auf dem Vektor
A,1, —1) aus dem Kern stehen:
196 4 Orthogonalität
Ax =
134'
52 7
1"
1
-1
=
"
0_
erzeugt die Skalarprodukte
1+3-4-0
5 + 2-7 = 0*
Wenden wir uns nun den anderen beiden Unterräumen zu. Auch sie sind
orthogonal, aber im Raum E^.
4B Jeder Vi^kior y im Kern von 4^ steht serifcteqbtaöf Jeder Spalte Yo^^i
A. Der Sfialtenraiiln von 4 und der Mem von Ä^ sMd also or^^^'^-^^
gonale Vnte^rämne*
Wir wenden den Beweis von 4A auf Ä^ an. Der Kern von Ä^ steht senkrecht
auf dem Zeilenraum von Ä^ — das ist aber der Spaltenraum von A. Q.E.D.
Um einen anschaulichen Beweis zu erhalten, sehen Sie sich die Gleichung
y^A = 0 an. Der Zeilenvektor y^ wird mit jeder Spalte von A multipliziert:
y^A = [
rs
p
a
1
t
e
_1
Sl
P
a
1
t
e
n\
= [0...0].
D.3)
Das Skalarprodukt mit jeder einzelnen Spalte ist also Null, y steht senkrecht
auf jeder Spalte und damit auf dem ganzen Spaltenraum.
Besonders wichtig Die vier Unterräume sind nicht nur zu ihrem
jeweiligen Partner orthogonal. Auch die Dimensionen passen genau zusammen. Im
dreidimensionalen Raum könnten zwei Geraden senkrecht aufeinander
stehen, sie könnten aber nicht Zeilenraum und Kern einer Matrix sein. Das
liegt daran, dass die Summe der Dimensionen der Geraden 2 wäre, die
Dimensionen n — r und r von Kern und Zeilenraum sich aber zu n = 3 addieren
müssen. Solche Unterräume müssen also die Dimensionen 2 und 1, oder 0 und
3, haben. Die Unterräume sind nicht nur orthogonal, sie bilden orthogonale
Komplemente,
DEFINITION Das orthogonale Komplement eines Unterraums V
enthält jeden auf V senkrecht stehenden Vektor. Dieser orthogonale
Unterraum wird V-^ geschrieben (gesprochen „V senkrecht").
Nach dieser Definition ist der Kern einer Matrix das orthogonale
Komplement des Zeilenraums. Jeder Vektor x, der senkrecht auf allen Zeilen steht,
erfüllt auch die Gleichung Ax = 0 und gehört daher zum Kern.
4.1 Orthogonalität der vier Unterräume 197
Auch die Umkehrung trifft (automatisch) zu. Ist v ein zum Kern
orthogonaler Vektor, so muss er zum Zeilenraum gehören. Andernfalls könnte man v
als zusätzliche Zeile der Matrix hinzufügen, ohne den Kern zu verändern. Der
Zeilenraum (und dessen Dimension) würde größer, was einen Verstoß gegen
die Summenregel r + {n - r) = n für die Dimensionen bedeutete. Deshalb
schließen wir, dass N{A)^ genau der Zeilenraum S{Ä^) sein muss.
Der Spaltenraum und der Kern der transponierten Matrix sind nicht nur
orthogonale Unterräume von E^, sondern orthogonale Komplemente.
Beachten sie die 90°-Winkel in Abbildung 4.2. Die Dimensionen addieren sich zu
m, der Dimension des gesamten Raums.
Fundamentalsatz der Linearen Algebra, Teil 2
Der Kern und der Zeilenraum einer Matrix sind
orthogonale Komplemente im E*^. Der Kern der
transponierten Matrix ist das orthogonale Komiplemient des
Spaltenraums im E'^.
Teil 1 gab die Dimensionen der Unterräume an, Teil 2 besagt nun etwas
über ihre Orientierung: Die beiden Räume eines Paares stehen senkrecht
aufeinander. Das Wesentliche bei der Aufspaltung des gesamten Raums in
„Komplemente" ist, dass jeder Vektor x in eine Zeilenraum-Komponente Xz und
eine Kern-Komponente x^ zerlegt werden kann. An Abbildung 4.2 können
wir erkennen, was passiert, wenn A mit x = x^ -f x^ multipliziert wird:
Die Kern-Komponente wird zu Null: Axn = 0.
Die Zeilenraum-Komponente erzeugt einen Vektor des Spaltenraums:
Axz — Ax.
Jeder Vektor x wird in den Spaltenraum abgebildet! Bei einer Multiplikation
mit A kann nichts anderes passieren. Mehr noch: Jeder Vektor im
Spaltenraum wird von einem und nur einem Vektor aus dem Zeilenraum erzeugt.
Beweis: Gilt Axz = Ax'^, so muss die Differenz Xz — x!^ zum Kern gehören.
Sie gehört aber auch zum Zeilenraum, da Xz und x!^ aus dem Zeilenraum sind.
Der Differenzvektor muss also der Nullvektor sein, da Kern und Zeilenraum
orthogonale Unterräume sind. Es gilt somit Xz = x^.
Lassen wir die beiden Kerne außer Acht, so taucht eine in A verborgene
invertierbare Matrix auf: Betrachtet man A als Matrix "vom Zeilenraum in
den Spaltenraum", so ist A invertierbar. In Abschnitt 7.4 werden wir diese
Abbildung mit der „Pseudoinversen" invertieren.
Beispiel 4.1.4 Jede Diagonalmatrix enthält eine invertierbare r Y.r-
Untermatrix:
A^
30000
05000
00000
enthält
30
05
198 4 Orthogonalität
dim r
dim m-r
dim w-r
Abb. 4.2. Die Wirkung der Multiplikation A mal x: Zeilenraum auf Spaltenraum,
Kern auf Null.
Der Rang ist r = 2. Die 2 x 2-Untermatrix in der oberen linken Ecke ist
sicher invertierbar. Die restlichen elf Nullen erzeugen die beiden Kerne.
Wir werden in Abschnitt 7.3 zeigen, wie aus jeder Matrix A solch eine
Diagonalmatrix wird, wenn wir die richtigen Basen für W' und W^ verwenden.
Diese Singulärwertzerlegung stellt einen Teil der Theorie der Linearen
Algebra dar, der in Anwendungen von überragender Wichtigkeit ist.
Die Zusammenstellung von Basen aus Unterräumen
Im Folgenden werden Sie einige nützliche Eigenschaften von Basen
kennenlernen. Wir hätten sie bereits zuvor präsentieren können, als wir die Basis eines
Raums definiert haben. Wir haben dies aber bis hierhin zurückgestellt —
denn wir sind jetzt soweit, sie auch anwenden zu können. Nach einer Woche
haben Sie jetzt eine klarere Vorstellung von einer Basis: linear unabhängige
Vektoren, die den Raum aufspannen. Stimmt die Anzahl der Vektoren, so
impliziert eine dieser Bedingungen die andere:
i^:4ii;&
4.1 Orthogonalität der vier Unterräume 199
Normalerweise müssen wir beide Eigenschaften überprüfen — ob die
Vektoren linear unabhängig sind, und ob sie den Raum aufspannen. Für n
Vektoren im MP' genügt es aber schon, wenn sie unabhängig sind oder den Raum
erzeugen. Liegt allerdings die richtige Anzahl von Vektoren vor, so bedingt
eine Eigenschaft die andere.
Diese Tatsache gilt für jeden Vektorraum, uns interessiert jedoch
insbesondere der W^ aber am meisten. FormuUeren wir die obigen Aussagen also
für die Spalten einem x n-Matrix A. Bedenken Sie hierbei, dass A quadratisch
ist.
Ein quadratisches Gleichungssystem Ax = b besitzt genau dann für alle
Vektoren b eine Lösung, wenn es niemals zwei verschiedene Lösungen hat. Die
Eindeutigkeit von Lösungen impUziert deren Existenz, und die Existenz zieht
schon die Eindeutigkeit nach sich. Die quadratische Matrix A ist invertierbar
und ihre Spalten bilden eine Basis des R^.
Unsere übUche Beweismethode basiert auf dem Eliminationsverfahren.
Gibt es keine freien Variablen (Eindeutigkeit), so muss es n Pivotelemente
geben, und durch Rücksubstitution lässt sich jede Gleichung Ax = h lösen
(Existenz). Nehmen wir umgekehrt an, dass die Gleichung immer gelöst
werden kann (Existenz), dann bedeutet dies, dass bei der Elimination keine
Nullzeilen entstehen. Es gibt also n Pivotelemente und keine freien Variablen. Der
Kern enthält nur den Nullvektor x = 0 (Eindeutigkeit der Lösung).
Für den Zeilenraum und den Kern einer Matrix A zusammen ergibt sich
immer die die richtige Anzahl, da sie die Dimensionen t und n — r haben.
Eine Basis des Zeilenraums zusammen mit einer Basis des Kerns umfasst also
r -h (n — r) = n Vektoren — genau die richtige Anzalil. Diese n Vektoren sind
Unear unabhängig,^ also erzeugen sie den W^, Sie bilden also eine Basis:
Jeder Vektor x im R^ lässt sich als Summe Xz + x^^ eines Vektors Xz aus
dem Zeilenraum und eines Vektors x^ aus dem Kern schreiben.
Dies bestätigt die in Abbildung 4.2 illustrierte Zerlegung. Hierin besteht
der Kernpunkt des orthogonalen Komplements — die Summe der
Dimensionen ist n, und bei der Kombination geht kein Vektor verloren.
Ergibt eine Kombination von Vektoren der beiden Räume den Nullvektor x^ -h
Xn = 0, so folgt Xz = —Xn, SO dass dieser Vektor in beiden Unterräumen liegt —
es muss sich also um den Nullvektor handeln. Dann müssen die Koeffizienten für
die Basis Vektoren des Kerns und des Zeilenraums alle Null sein — was beweist,
dass auch alle n Vektoren zusammen linear unabhängig sind.
200 4 Orthogonalität
Beispiel 4.1.5 Sei A =[//] = [J J J J]. Zerlegen Sie jeden Vektor x in eine
Summe x^. 4- x^.
A,0,1,0) und @,1,0,1) bilden eine Basis des Zeilenraums, und A,0, -1,0)
und @,1,0, —1) eine Basis des Kerns. Zusammen bilden die vier Vektoren eine
Basis des E"^. Jeder Vektor x = (a, b, c, d) lässt sich in x^. + x^ aufspalten:
a-{- c
+
h^-d
+
b-d
Die wesentlichen Punkte
1. Zwei Unterräume V und W sind orthogonal, wenn jeder Vektor v in V
orthogonal zu jedem Vektor w in W ist.
2. V und W sind „orthogonale Komplemente", wenn jeder Raum jeweils
alle zu dem anderen Raum senkrechten Vektoren enthält.
3. Der Kern N{Ä) und der Zeilenraum S{A^) einer Matrix A sind
orthogonale Komplemente.
4. Je n linear unabhängige Vektoren im E^ spannen den Raum auf.
5. Jeder Vektor x im W- hat kann in einen Vektor aus dem Kern und einen
Vektor aus dem Zeilenraum zerlegt werden.
Aufgaben 4.1
Die Aufgaben 1—10 beschäftigen sich mit den Abbildungen 4.1
und 4.2.
1. Sei A eine 2 x 3-Matrix vom Rang 1. Passen Sie Abbildung 4.1 an die
Dimensionen der Unterräume an.
2. Passen Sie Abbildung 4.2 für eine 3 x 2-Matrix vom Rang r =:= 2 an. Wo
finden sich die Teile x^. und x^?
3. Konstruieren Sie eine Matrix mit der verlangten Eigenschaft, oder
begründen Sie, warum dies nicht möglich ist:
(a) Der Spaltenraum enthält die Vektoren 2 und -3 , der Kern den
Vektor [i].
(b) Der Zeilenraum enthält die Vektoren 2 und -3 , der Kern den
Vektor [1].
(c) Der Spaltenraum ist orthogonal zum Kern.
(d) Es gelte (Zeile 1 -h Zeile 2 -h Zeile 3) = 0, und der Spaltenraum
enthalte den Vektor A,2,3).
4.1 Orthogonalität der vier Unterräume 201
(e) Die Summe der Spalten ergibt den Nullvektor, die Summe der Zeilen
eine Zeile von Einsen.
4. Es ist möglich, dass der Zeilenraum den Kern enthält. Geben Sie ein
Beispiel an.
5. (a) Hat Ax = b eine Lösung und gilt Ä^y = 0, so steht y senkrecht auf
(b) Erklären Sie, warum y nicht senkrecht auf steht, wenn Ax = b
keine Lösung hat und Ä^y — 0 gilt.
6. Woher wissen wir in Abbildung 4.2, dass Ax^. gleich Ax ist? Woher wissen
wir, dass dieser Vektor im Spaltenraum liegt?
7. Gehört Ax zum Kern von Ä^, so muss Ax Null sein. Warum? In
welchem anderen Unterraum liegt Ax außerdem ? Dies ist wichtig: A^A hat
denselben Kern wie A.
8. Es sei A eine symmetrische Matrix (d. h. A^ = A),
(a) Warum steht der Spaltenraum senkrecht auf dem Kern?
(b) Warum steht x senkrecht auf z, wenn Ax = 0 und Az = 5z gilt? Es
handelt sich hier um „Eigenvektoren".
9. (Empfohlen) Zeichnen Sie Abbildung 4.2 passend zu den Matrizen
A =
12
36
undB =
10
30
nach.
10. Bestimmen Sie die Zerlegung in x^. und Xn, und passen Sie Abbildung
4.2 an:
A =
ri-
0
[0
-1'
0
0
und
Aufgaben 11—19 behandeln die orthogonalen Unterräume.
11. Beweisen Sie, dass jedes y in N{A'^) senkrecht auf jedem Vektor ^x
im Spaltenraum steht. Benutzen Sie dazu, ausgehend von der Gleichung
Ä^y = 0, die kurze Matrixschreibweise wie in Gleichung D.2).
12. Man kann den Fundamentalsatz auch in der Form der Fredholm'sehen
Alternative formulieren: Für jede Matrix A und jeden Vektor b hat genau
eine dieser beiden Gleichungen eine Lösung:
(a) Ax = h
(b) A^y = 0 mit b^y ^ 0.
202 4 Orthogonalität
Entweder liegt b im Spaltenraum von A, oder b ist nicht orthogonal
zum Kern von Ä^. Wählen Sie A und B so, dass für Alternative (a)
keine Lösung existiert, und bestimmen Sie anschließend eine Lösung von
Alternative (b).
13. Was ist S-^, wenn S derjenige Unterraum von E^ ist, der nur den
Nullvektor enthält? Wie sieht S-^ aus, wenn S durch den Vektor A,1,1)
aufgespannt wird? Wie, wenn S durch die Vektoren B,0,0) und @,0,3)
aufgespannt wird?
14. Die Menge S enthalte lediglich die Vektoren A,5,1) und B,2,2) (S ist
also kein Unterraum). Dann ist S"^ der Kern der Matrix A = .
Deshalb ist S"^ ein sogar dann, wenn S keiner ist.
15. Sei L ein eindimensionaler Unterraum (also eine Gerade) von E^. Das
orthogonale Komplement ist die senkrecht zu L. Dann ist (L-^)-^
eine senkrecht zu L-^. Tatsächlich ist (L-^)-^ dasselbe wie .
16. Sei V der ganze Raum M^. Dann ist V-^ = , und (V-^)-^ = .
(V-^)-^ ist also dasselbe wie .
17. Es sei S der von den Vektoren A,2,2,3) und A,3,3,2) aufgespannte
Raum. Bestimmen Sie zwei Vektoren, die S-^ aufspannen.
18. Es sei P die durch Xi + X2 + xs + X4 =0 definierte Hyperebene von
Vektoren im R^. Bestimmen Sie eine Basis für P-^, und konstruieren Sie
eine Matrix, deren Kern P ist.
19. Zeigen Sie, dass der Unterraum S"^ den Unterraum V-^ enthält, wenn S
in V enthalten ist.
In den Aufgaben 20—26 geht es um orthogonale Spalten und Zeilen.
20. Sei A eine invertierbare n x n-Matrix: AA~^ = I. Dann ist die erste
Spalte von A~^ orthogonal zu dem von den aufgespannten Raum.
21. Die Spalten von A seien paarweise orthogonale Einheitsvektoren. Was ist
dann A^A?
22. Konstruieren Sie eine 3 x 3-Matrix ohne Nulleinträge, deren Spalten
paarweise orthogonal sind. Berechnen Sie A^A. Warum erhalten Sie eine
Diagonalmatrix?
23. Die durch 3x + y = bi und 6x + 2y = 62 definierten Geraden sind _>
und sie sind identisch, falls . In diesem Fall ist F1,62) senkrecht zu
dem Vektor . Der Kern der Matrix ist die durch 3x + y =
definierte Gerade, und ein Vektor dieses Kerns ist .
4.2 Projektionen 203
24. Warum ist jede einzelne dieser Behauptungen falsch?
(a) A,1,1) steht senkrecht auf A,1, -2), deshalb definieren x-\-y-\-z = 0
und X -\-y — 2z = 0 orthogonale Unterräume.
(b) Die Geraden von @,0,0) durch B,4,5) und A, -3,2) sind orthogonale
Komplemente.
(c) Schneiden sich zwei Unterräume nur im Nullvektor, so sind sie
orthogonal.
25. Bestimmen Sie eine Matrix, deren Zeilen- und deren Spaltenraum den
Vektor v = A,2,3) enthalten. Bestimmen Sie weiter eine Matrix,
deren Kern und deren Spaltenraum v enthalten. Mit welchem Paar von
Unterräumen ist diese Konstruktion nicht möglich?
26. Der MATLAB-Befehl N = nu\\{A) erzeugt eine Basis des Kerns von A.
Eine Basis welchen Raumes erzeugt dann der Befehl B = null(A^')?
4.2 Projektionen
Erlauben Sie, dass wir diesen Abschnitt mit zwei Fragen beginnen?
(Zusätzlich zu dieser hier.) Die erste Frage soll zeigen, dass man sich Projektionen
leicht vorstellen kann. In der zweiten Frage geht es um Matrizen:
1 Wie sehen die Projektionen des Vektors b = B,3,4) auf die z-Achse und
auf die xy-Ehene aus?
2 Durch welche Matrizen werden diese Projektionen auf eine Gerade und
eine Ebene erzeugt?
Projiziert man einen Vektor b auf eine Gerade, so ist die Projektion p der
Teil von b längs dieser Geraden. Projiziert man ihn auf eine Ebene, so ist p
der Teil von b, der in der Ebene liegt.
Man erhält p aus b durch Multiplikation mit einer Matrix P: Die Projektion
p ist Pb.
Sie können sich Projektionen wie in Abbildung 4.3 vorstellen. Die eine
verläuft horizontal zur z-Achse, die andere fällt senkrecht in die xy-Ehene.
Beginnt man mit dem Vektor b = B,3,4), so erhält man einerseits die
Projektion pi — @,0,4) und andererseits p2 = B,3,0). Dies sind die Anteile
von b längs der z-Achse und in der xy-Ehene.
Die zugehörigen Projektionsmatrizen Pi und P2 sind 3 x 3-Matrizen: Sie
werden mit Vektoren multipliziert, die aus drei Komponenten bestehen, und
das Ergebnis ist wieder ein Vektor mit drei Komponenten. Die Projektion
auf eine Gerade wird durch eine Matrix vom Rang Eins dargestellt, eine
Projektion auf eine Ebene durch eine Matrix vom Rang Zwei.
Auf die z-Achse: Pi
000
000
001
Auf die xy-Ehene: P2
1 00
0 10
000
204 4 Orthogonalität
Abb. 4.3. Die Projektionen von b auf die ^-Achse und die xy-Ehene.
Pi greift gerade die z-Komponente eines Vektors heraus, P2 die x- und die
^/-Komponente. Man erhält pi und p2, wenn b mit Pi beziehungsweise mit
P2 multipliziert wird. (Kleinbuchstaben für die Vektoren, Großbuchstaben
für die Matrizen.)
Pi - Pih -
rooo"
000
001
X
y
z
=
^
0
z\
P2 = P2b
rioo"
010
lOOO
X
y
z
—
x^
y
_oJ
In diesem Fall sind die beiden Projektionen Pi und P2 zueinander senkrecht,
und die xy-Ehene und die z-Achse sind orthogonale Unterräume, genau wie
der Fußboden und eine Gerade in der Ecke zwischen zwei Wänden. Mehr
noch, die Gerade und die Ebene bilden orthogonale Komplemente. Die
Dimensionen addieren sich zu 1 + 2 = 3 — jeder Vektor b im dreidimensionalen
Raum ist also die Summe seiner Teile in den beiden Unterräumen. Die
Projektionen pi und p2 sind genau diese Teile:
Für die Vektoren gilt pi + P2 = b, für die Matrizen Pi -\- P2 = L D.4)
Das ist ausgezeichnet. Wir haben unser Ziel erreicht — wenigstens für
dieses eine Beispiel. Dasselbe Ziel haben wir uns für eine beliebige Gerade, eine
beliebige Ebene, oder für beliebige n-dimensionale Unterräume gesteckt.
Unsere Aufgabe besteht darin, für jeden Unterraum den Teil p eines Vektors b in
diesem Unterraum zu finden, sowie die Projektionsmatrix P, für die p = Ph
gilt. Zu jedem Unterraum des W^ gibt es eine m x m-Projektionsmatrix. Um
dieses P berechnen zu können, benötigen wir unbedingt eine gute
Beschreibung des Unterraums, auf den projiziert werden soll.
Die beste Beschreibung eines Unterraums ist durch eine Basis gegeben.
Die Basisvektoren bilden die Spalten einer Matrix A, und wir projizieren
auf den Spaltenraum von A. Der Spaltenraum der folgenden Matrix Ai ist
offenbar die z-Achse, und der Spaltenraum von A2 die xy-Ehene. Dieser
Unterraum wird auch von den Spalten von A3 erzeugt — ein Unterraum
besitzt viele verschiedene Basen:
0"
0
1
und A2 =
"lO"
Ol
00
4.2 Projektionen
und As =
2"
23
00
205
Ai
Das grundlegende Problem ist es also, auf den Spaltenraum einer beliebigen
m X n-Matrix zu projizieren. Wir beginnen mit Geraden. Es gilt also n = 1,
und die Matrix A hat nur eine Spalte.
Projektion auf eine Gerade
Gegeben seien ein Punkt b = F1,..., hm) im m-dimensionalen Raum, und
eine Gerade durch den Ursprung in Richtung des Vektors a = (ai,... ,am)-
Auf dieser Geraden suchen wir denjenigen Punkt p, der b am nächsten liegt.
OrthogonaUtät ist dabei der Schlüssel: Die Gerade, die b mit p verbindet,
muss senkrecht auf dem Vektor a stehen. In Abbildung 4.4 ist sie als
gestrichelte Linie e dargestellt. Wir wollen sie jetzt algebraisch bestimmen.
Die Projektion p von b muss ein Vielfaches von a sein, also schreiben
wir p = fa = „x Dach" mal a. Als erstes müssen wir die Unbekannte x
berechnen. Auf diese Weise werden wir p erhalten, und aus der Formel für
p die Projektionsmatrix P. Mittels dieser drei Schritte werden wir alle
Projektionsmatrizen bestimmen: Berechne zuerst x, dann p, und anschließend
P.
Die gestrichelte Linie b — p = b — f a steht senkrecht auf a. Aus dieser
Beziehung bestimmen wir x, indem wir verwenden, dass zwei Vektoren genau
dann senkrecht sind, wenn ihr Skalarprodukt Null ist:
(b — xa) = 0 oder a • b — f a • a = 0 oder st -
>h a^b
a*a
D.5)
Für Vektoren ist a-^b dasselbe wie a-b. Die Schreibweise mit dem
transponierten Vektor ist hier angebracht, weil sie sich auch auf Matrizen anwenden
lässt. (Schon bald wird uns der Ausdruck A^h begegnen.) Aus der Formel
für X erhält man sofort eine Formel für p:
4E Die Projektion eines Vektor b auf eine Gerade entlapg dem Vektor a
ist 4er y^pT;!>;=='^a = gj^a;-^-' , ^,','/, ■ ''/■- /^.i , r -,- "^'^-iil'''
Speii^öB;!: Gilt,b =' a, so folgt ^ = 1. ;bie'Projektipk;vob a^atifa^^lst^a
p'=0.'/:'/"' ' ';,,^ \ '','■' 'i' ■'. '. ' ', ;/" ',"';''"
206 4 Orthogonalität
Abb. 4.4. Die Projektion von b auf eine Gerade hat die Länge ||p|| = ||b|| cosO.
Beispiel 4.2.1 Projizieren Sie den Vektor b = i auf den Vektor a— 2 ,
und bestimmen Sie so p = xa aus Abbildung 4.4.
Lösung Die Zahl x ist das Verhältnis von a^b= 5 zu a^a = 9. Die
Projektion ist also p — |a. Der Fehlervekt«
Summe der Vektoren p und e ist b:
tion ist also p — |a. Der Fehlervektor zwischen b und p ist e = b — p. Die
p == -a = -, -TT-» -^r) und e = b — p= -,—-,—-).
^9 ^999^ *^ ^9 9' 9^
Der Fehler e sollte orthogonal zu a sein, und er ist es auch: e-^a = |
0.
2 _
'9 ~
Betrachten Sie das rechtwinklige Dreieck zwischen b, p und e. Der
Vektor b wird in zwei Teile aufgespalten — in seine Komponente p entlang
der Geraden, und die dazu senkrechte Komponente e. Die beiden Seiten des
rechtwinkligen Dreiecks haben die Längen ||b|| cosö und ||b|| sinö. Neben der
Trigonometrie liefert auch das Skalarprodukt dieses Ergebnis:
P =
a^b
a^ a
a, die Länge ist also ||p]|
||a||||b|| cosl9
l|a|P
l|a|| = llblleoa^
D.6)
Mit dem Skalarprodukt lässt sich viel leichter umgehen als mit cos 6 und
der Länge von b. Im Beispiel tauchen in cos e = 5/3\/3 und in ||b|| = VS
Quadratwurzeln auf, die im Ausdruck für die Projektion p = |a nicht benötigt
werden.
Wir kommen jetzt zur Projektionsmatrix. Wie lässt sich die Formel für
p als Produkt einer Matrix mit b schreiben? Man erkennt dies besser, wenn
man x rechts von a platziert:
a^b
p = ax = a—^fT-
a^ a
= Ph mit der Matrix P
aa^
4.2 Projektionen 207
P ist also das Produkt eines Spaltenvektors mit einem Zeilenvektor. Die
Spalte ist a, die Zeile a^. Hat man diese Matrix ausgerechnet, muss nur noch
durch die Zahl a^a dividiert werden. P ist eine m x m-Matrix vom Rang
Eins. Wir projizieren auf einen eindimensionalen Unterraum, nämlich die
Gerade durch a.
Beispiel 4.2.2 Bestimmen Sie die Projektionsmatrix F == ffi^ für eine
Projektion auf die Gerade durch a = 2 .
Lösung Wir bilden das „Spalte-mal-Zeile"-Produkt und dividieren durch
a^a = 9:
P =
aa"
1
9
"l"
2
2}
[122] = -
122
244
244
Diese Matrix projiziert jeden Vektor b auf a. Überprüfen wir die Beziehung
p = Pb an dem Vektor b = A,1,1) aus Beispiel 4.2.1:
^^=9
[1 22"
244
244
"
1
1
_ 1
~ 9
■ 5 1
10
loj
stimmt.
Verdoppelt man a, so bleibt P unverändert und projiziert immer noch auf
dieselbe Gerade. Das Quadrat P^ ist genau gleich F. Ein zweites Mal zu
projizieren bringt keine Veränderung, deshalb gilt P^ = P. Die Summe der
Diagonaleinträge von P ist |A + 4 + 4) = 1.
Die Matrix I - P sollte ebenfalls eine Projektion sein. Sie erzeugt die
andere Seite e des Dreiecks — den Teil von b senkrecht zur Geraden. Beachten
Sie, dass (/ - P)b = b - p = e ist. Projiziert P auf einen Unterraum, so
projiziert I — P auf den dazu orthogonalen Unterraum. In unserem Beispiel
ist das die Ebene senkrecht zu a.
Im Folgenden projizieren wir nicht mehr nur auf Geraden. Die Projektion
auf einen n-dimensionalen Unterraum von W^ zu berechnen, wird etwas mehr
Aufwand erfordern. Die entscheidenden Formeln stehen in den Gleichungen
D.8), D.9) und D.10). Sie müssen sich im Wesentlichen diese Formeln
merken.
Projektion auf einen Unterraum
Wir beginnen mit n Vektoren ai,..., an im E"^, von denen wir annehmen,
dass sie linear unabhängig sind. Die Aufgabe ist, diejenige Linearkombination
Xiai + • • • + XnSt.n zu finden, die am nächsten an einem gegebenen Vektor h
liegt. Auf diese Weise projizieren wir jeden Vektor aus E^ auf den von den
a's aufgespannten Unterraum.
208 4 Orthogonalität
Für n = 1 (also nur einen Vektor ai) handelt es sich dabei genau um die
Projektion auf eine Gerade, die den Spaltenraum einer einspaltigen Matrix
A darstellt. Im allgemeinen Fall hat A die n Spalten ai,...,a^, deren
Linearkombinationen Ax in M^ den Spaltenraum bilden. In diesem Fall suchen
wir nach einer speziellen Linearkombination p = A5t (die Projektion von b),
die am nächsten an b liegt. Das „Dach" auf x soll andeuten, dass es sich um
die beste Wahl, den nächsten Vektor im Spaltenraum handelt. Für n = 1 ist
diese Wahl gerade a^b/a^a, und für n > 1 erhalten wir als bestes x einen
Vektor (xi,... ,Xn).
Wir lösen diese Aufgabe auch für n-dimensionale Unterräume in drei
Schritten: Bestimme den Vektor x, dann die zugehörige Projektion p = Ax,
und dann die Matrix P.
Der Schlüssel zur Lösung hegt wiederum in der Geometrie! Die gestrichelte
Linie in Abbildung 4.5 geht von b zum nächsten Punkt im Unterraum. Dieser
Fehlervektor b — Ak steht senkrecht auf dem Unterraum. Der Vektor b —
Ak bildet also einen rechten Winkel mit allen Vektoren b.\.,... ,b^. Daraus
erhalten wir n Gleichungen, aus denen sich x bestimmen lässt:
a^b - ylx) = 0
a^(b - Ax) = 0
oder
b-Ax
D.7)
Die Matrix in der letzten Gleichung ist Ä^. Die n Gleichungen sind genau
die Gleichungen des Systems Ä^{b — Ak) = 0.
Wir bringen dies durch Ausmultiplizieren in die bekannte Form A^Ak =
um, und erhalten eine Gleichung für x mit der Koeffizientenmatrix A^A.
Damit lassen sich x, p und P bestimmen:
4F Die Linearkombination ^lai +;--!- Xn^n — Ax^ die am iiächstiei)L.^m;|
Hegt, erhält man aus der Gleichung , , ^ ^'^
Ä^{h -^ Ax) - Ö^, oder / A^A±'— A*^h;' \.;'- \
Die Matrix A^A ist eine symmetrische n x n-Matrix, djie inyertierb^j
wenn;die,a^s linear unabhängig sind. Die Lösuag ist x ^ {A^'ä)'^^ä'^^
Projektion von b auf den Unterraum ist dann der Vektor,
Die2sug(
p == Ax = Ä{A^A)^''^A?'h,^ '
Projektionsmatrix P ist äaiso gi^g^lbeii döbelt
P-
-^A^V'
Vergleichen wir dies mit der Projektion auf eine Gerade, bei der die Matrix
A nur aus der einen Spalte a besteht:
4.2 Projektionen
209
a|e = 0
aTe = 0
Ä^e=Ä^(h-Ait)=0
Spalte a 2
Abb. 4.5. Die Projektion p ist der zu b nächste Punkt im Spaltenraum von A.
Der dazu senkrechte Fehlervektor e muss im Kern von A^ liegen.
a^b
X =
a^b
und p = a-^^7-
und P =
aa"
a^ a
Diese Formeln stimmen mit D.8), D.9) und D.10) überein. Die Zahl a^a wird
zu der Matrix A^A. Anstatt durch a^a zu dividieren, invertieren wir, weshalb
in der neuen Formel (A^A)"^ anstelle von 1/a^a steht. Dass diese Inverse
existiert, wird durch die lineare Unabhängigkeit der Spalten ai,...,an
garantiert.
Der wesentliche Schritt wurde mit der Gleichung yl^(b — Ax) = 0 getan.
Um sie zu begründen, haben wir geometrische Überlegungen angestellt — e
soll senkrecht zu allen a's sein. Mit unserem Wissen aus der linearen Algebra
können wir diese „Normalengleichung" ebenso sehr schnell erhalten:
l.Der Unterraum, auf den projiziert wird, ist der Spaltenraum von A.
2, Der Fehlervektor b — Ait steht senkrecht auf diesem Spaltenraum.
3, Deshalb muss b — Ait im Kern der transponierten Matrix liegen. Das
bedeutet aber A^(b - Ax) = 0.
Der Kern der transponierten Matrix ist für Projektionen sehr wichtig. In
ihm liegt der Fehlervektor e = b — Ax, der Vektor b wird in die Projektion p
und den Fehler e = b —p aufgespalten. In Abbildung 4.5 ist das rechtwinklige
Dreieck mit den Seiten p, e und b dargestellt.
Beispiel 4.2,3 Bestimmen Sie für A
und p sowie die Matrix P.
11 und b = 0 die Vektoren x
Lösung Man berechnet die quadratische Matrix A^A und den Vektor A^h:
Ä'A
111"
Ol 2
0"
1 1
1 2
=
33"
35
und Ä^b=
11"
012
'6"
0
0
=
"
0
210 4 Orthogonalität
Als nächstes löst man die Normalengleichung A^Ax — A^h und bestimmt
so x:
3'
35
=
6'
0_
ergibt x
Xi
X2
5
-3
D.11)
Die Linearkombination p = Ax ist dann die Projektion von b auf den
Spaltenraum von A:
p-5
1
1
1
-3
0
1
2
=
5
2
-1
. Der Fehler ist e = b — p =
D.12)
Auf diese Weise löst man das Problem für ein bestimmtes b. Um
Lösungen für alle b gleichzeitig zu bestimmen, berechnet man die Matrix P =
A{Ä^A)~^Ä^. Die Determinante von Ä^A ist 15-9 = 6; die Inverse
[Ä^A)~^ ist einfach zu bestimmen. Man multipliziert dann A mal (^4^^)"^
mal Ä^ und erhält P:
{A^Ä)-^ = l
53
-3 3
und P =
5 2-1
2 2 2
-12 5
D.13)
Man kann das Ergebnis folgendermaßen überprüfen. Zum einen muss der
Fehler e - A, -2,1) senkrecht auf den beiden Spalten A,1,1) und @,1,2)
stehen. Zum anderen muss P mal b = F,0,0) das richtige Ergebnis @,1,2)
liefern. Außerdem muss P'^ — P gelten, weil ein nochmaliges Projizieren
nichts mehr ändert.
Warnung Der Ausdruck P = A{A'^A)~^A'^ ist trügerisch. Man ist versucht,
die Inverse {A'^A)~'^ in das Produkt A~^ mal (^^)~^ aufzuspalten. Macht
man diesen Fehler und setzt das Produkt in die Gleichung für P ein, so erhält
man P = 74^4"^ (^4^)"^^^, und augenscheinlich heben sich je zwei Terme so
auf, dass man P ~ I erhält. Warum ist dies falsch?
Die Matrix A ist rechteckig, Sie besitzt keine Inverse, Man kann
(^4^74)"^ nicht in A~^ mal (^^)~^ aufspalten, da A~^ nicht existiert.
Nach unserer Erfahrung führt ein Problem, in dem eine rechteckige Matrix
A vorkommt, fast immer auf die Matrix ^4^74. Deren Inverse kann man nicht
in ein Produkt wie oben aufspalten, weil es ^4"^ und {A'^)~^ nicht gibt. Nur
die Inverse der Matrix ^4^74 existiert. Diese Tatsache ist so entscheidend, dass
wir sie ausdrücklich formulieren und beweisen wollen.
von;
M iiatertierbär dato tind OT dtonyl^enii ii^Sp-
4.2 Projektionen 211
Beweis A^A ist eine quadratische n x n-Matrix. Wir werden zeigen, dass
für eine beliebige Matrix A der Kern von A^A mit dem Kern von A
übereinstimmt. Sind die Spalten von A linear unabhängig, so enthält der Kern
von A nur den Nullvektor. Deswegen ist die quadratische Matrix A^A (mit
demselben Kern) invertierbar.
Sei A eine beliebige Matrix und x ein Vektor aus dem Kern, so dass
Ax = 0 gilt. Multiplikation mit A^ liefert A^Ax = 0; deshalb liegt x auch
im Kern von A^A.
Betrachten wir nun den Kern von A^A. Wir müssen zeigen, dass aus
A^Ax = 0 folgt, dass Ax = 0 gilt. Wir können dazu nicht einfach mit (^^)~^
multiplizieren, da diese Matrix im Allgemeinen nicht existiert. Stattdessen
multiplizieren wir mit x^:
(x^)^^^x = 0 oder (^x)^(^x) = 0 oder \\Ax\\
0.
Der Vektor Ax hat also die Länge Null. Deshalb gilt Ax = 0.
Jeder Vektor im Kern der einen Matrix ist also auch im Kern der anderen
Matrix. Hat A linear abhängige Spalten, so auch A^A. Besitzt aber A linear
unabhängige Spalten, so gilt auch dies für A^A. Damit ist die
unproblematische Situation gegeben:
Hat A linear unabhängige Spalten, so ist A^A eine quadratische,
symmetrische und invertierhare Matrix.
Zur Betonung sei es noch einmal wiederholt: Das Produkt A^A ist ein
(n X m)-mal-(m x n)-Produkt. Das Ergebnis ist also eine quadratische nxn-
Matrix. Sie ist immer symmetrisch, denn für die Transponierte gilt (^4^^)^ =
AT(^j[T^t^ und das ist gleich A^A.
Wir haben gerade bewiesen, dass A^A invertierbar ist, wenn A linear
unabhängige Spalten hat. Beachten Sie den Unterschied, der sich ergibt, wenn
A linear abhängige Spalten hat.
1 0'
2 2 0
A
2"
1 2
00
=
A'^A
4"
4 8
1 0'
2 2 1
A
'1 2"
1 2
0 1
=
A^A
'2 4"
49
abhängig singular
unabh. invertierbar
Kurze Zusammenfassung Man bestimmt die Projektion p = xisli H h
XnS^n, indem man die Gleichung A^Ax = A^h löst. Die Projektion ist p =
Ax und der Fehler iste = b — p = b — Ax, Aus der Projektionsmatrix
P = A{A'^A)-'^A'^ erhält man direkt p = Pb. Für diese Matrix gilt P^ = P.
Der Abstand von b zum Spaltenraum von A ist ||e||.
Die wesentlichen Punkte
l.Die Projektion von b auf die Gerade durch den Nullpunkt und a ist p =
ax = a(a^b/a^a).
212 4 Orthogonalität
2. Die Projektionsmatrix P — aa^/a^a hat den Rang Eins. Man multipliziert
sie mit b, um p zu erhalten.
3. Die Differenz e = b — p zwischen b und seiner Projektion p auf einen
Unterraum steht senkrecht auf dem Unterraum.
4. Bilden die Spalten von A eine Basis des Spaltenraums, so führt die
Normalengleichung A^Ax = A^h auf p = Ax.
5. Für die Projektionsmatrix P = ^(^^^)-M^ gilt P^ ^ P und P^ = P,
Eine zweite Projektion lässt p also unverändert.
Aufgaben 4.2
In den Aufgaben 1—9 geht es um Projektionen auf eine Gerade, die
zugehörigen Matrizen P sowie um den Fehlervektor e = b — p.
1. Projizieren Sie den Vektor b auf die Gerade durch a. Überprüfen Sie, ob
e senkrecht auf a steht.
(a) b^
(b) b =
a =
a =
"
1
1
?
'-1"
-3
-ij
2. Zeichnen Sie die Projektion von b auf a. Berechnen Sie sie auch als
p = xa:
(a) b^
(b) b =
cosö
sinö
1
und a =
und a =
1
-1
3. Bestimmen Sie die Projektionsmatrizen P — aa-^/a^a aus Aufgabe 1,
und überprüfen Sie jedesmal, ob P^ = P gilt. Berechnen Sie auch für
jeden Fall p = Pb.
4. Bestimmen Sie die Projektionsmatrizen auf die Geraden aus Aufgabe 2.
Erklären Sie, warum P^ gleich P sein muss.
5. Berechnen Sie die Projektionsmatrizen aa^/a^a auf die Geraden durch
ai = (-1,2,2) und a2 = B,2,-1). Multiplizieren Sie diese Matrizen.
Erklären Sie das Ergebnis.
6. Projizieren Sie den Vektor b = A,0,0) auf die Geraden durch ai und a2
aus Aufgabe 5 und auch auf as = B,-1,2). Bilden Sie die Summe der
drei Projektionen pi + P2 + Ps-
4.2 Projektionen 213
7. Bestimmen Sie (im Anschluss an die Aufgaben 5 und 6) die
Projektionsmatrix P3 auf den Vektor as = B,-1,2). Überprüfen Sie, dass
Pi + P2 + P3 = / gilt.
a2 =
Aufgaben 5, 6, und 7
P2ai
b =
^SLi =
P1P2SL
Aufgaben 8,9 und 10
8. Projizieren Sie den Vektor b = A,1) auf die Geraden durch die Vektoren
ai = A,0) und a2 = A,2). Zeichnen Sie die Projektionen pi und p2
und addieren Sie sie zu pi + P2. Die Summe ist nicht b, weil die beiden
Vektoren ai und a2 nicht orthogonal sind.
9. Die Projektion von b auf die von den Vektoren ai und a2 aus Aufgabe 8
aufgespannte Ebene ist gleich b. Die Projektionsmatrix ist also P =
. Überprüfen Sie dies über die Gleichung P = A{A'^A)~^Ä^ mit
^ = [aia2]=[äi].
10. Projizieren Sie ai = A,0) auf a2 = A,2), und projizieren Sie das
Ergebnis wieder auf ai. Zeichnen Sie diese Projektion und berechnen Sie
auch das Produkt P1P2 der Projektionsmatrizen. Handelt es sich dabei
um eine Projektion?
In den Aufgabe 11—20 geht es um Projektionen auf Unterräume,
und um die zugehörigen Projektionsmatrizen.
11. Projizieren Sie b auf den Spaltenraum von A^ indem Sie die Gleichung
A^Ax = A^h und p = Ait lösen:
(a)
(b)
A =
A =
1]
Ol
ooj
'1 ll
11
OlJ
undb =
undb =
12.
Bestimmen Sie e = b — p. Dieser Vektor muss senkrecht auf den Spalten
von A stehen.
Berechnen Sie die Projektionsmatrizen Pi und P2 auf die Spaltenräume
aus Aufgabe 11. Überprüfen Sie, ob Pib die erste Projektion pi ergibt
und ob P2^ = P2 gilt.
214 4 Orthogonalität
13. Es sei ^4 die 4 X 3-Matrix, die aus der 4 x 4-Einheitsmatrix entsteht, wenn
man die letzte Spalte entfernt. Projizieren Sie den Vektor b = A,2,3,4)
auf den Spaltenraum von A. Welche Form hat die Projektionsmatrix P?
Bestimmen Sie P.
14. Es sei b das Doppelte der ersten Spalte von A. Welchen Vektor erhält man
als Projektion von b auf den Spaltenraum von A? Gilt P = I ? Berechnen
Sie p und F für b = @,2,4) und A bestehend aus den Spalten @,1,2)
und A,2,0).
15. Verdoppelt man A zu 2^4, so erhält man die Projektionsmatrix P =
2^D^^^)-^2^^. Dies ist dieselbe Matrix wie A{A'^A)'^A'^. Der
Spaltenraum von 2^4 ist also derselbe wie der von . Ist auch x für A
und 2^4 gleich?
16. Welche Linearkombination der Vektoren A,2, -1) und A,0,1) reicht am
nächsten an den Vektor b = B,1,1) heran?
17. (Wichtig) Zeigen Sie, dass {I - Pf = I - P folgt, wenn P'^ = P gilt.
Projiziert P auf den Spaltenraum einer Matrix A, so projiziert I - P auf
den .
18. (a) Es sei P die 2 x 2-Projektionsmatrix auf die Gerade durch A,1).
/ - P ist dann die Projektionsmatrix auf .
(b) Es sei P die 3 x 3-Projektionsmatrix auf die Gerade durch A,1,1).
/ — P ist dann die Projektionsmatrix auf .
19. Bestimmen Sie die Projektionsmatrix auf die durch x — y - 2z = 0
beschriebene Ebene, indem Sie zwei Vektoren aus der Ebene auswählen und
als Spalten einer Matrix A auffassen. Die Ebene sollte der Spaltenraum
von A sein. Berechnen Sie dann P = A{A^A)~^A^.
20. Sie können die Projektionsmatrix auf die Ebene x — y — 2z = 0 auch
bestimmen, indem Sie einen zu der Ebene senkrechten Vektor e
betrachten, erst die Projektion Q — ee^/e^e bestimmen und dann P = I — Q
berechnen.
In den Aufgaben 21-26 wird gezeigt, dass für Projektionsmatrizen
stets P^ = P und P^ = P gilt.
21. Multiplizieren Sie die Matrix P = A{A'^A)~'^A^ mit sich selbst, und
beweisen Sie, dass P'^ = P gilt, indem sie zeigen, welche Terme sich
aufheben. Erklären Sie, warum P(Pb) immer gleich Pb sein muss: Der
Vektor Pb liegt im Spaltenraum, deshalb ist seine Projektion .
4.3 Kleinste-Quadrate Approximationen 215
22. Berechnen Sie zu P = A{Ä^A)~'^Ä^ die Matrix P^ und beweisen Sie so,
dass P symmetrisch ist. Erinnern Sie sich daran, dass die Inverse einer
symmetrischen Matrix symmetrisch ist.
23. Ist A eine quadratische und invertierbare Matrix, so spielt die im Text
gegebene Warnung, den Ausdruck (A'^A)'^ aufzuspalten, keine Rolle; es
gilt P = AA~^{A'^)~^A'^ = I. Warum ist P = I, wenn A invertierbar
ist? Wie verhält es sich mit dem bei einer Projektion auf den Spaltenraum
von A gemachten Fehler e ?
24. Der Kern von A^ ist zum Spaltenraum S{A). Gilt also A^h = 0,
so sollte die Projektion eines Vektors b auf S{A) durch den Vektor p =
gegeben sein. Überprüfen Sie, ob man dieses Ergebnis auch über
die Projektionsmatrix P = A{A'^A)~^A'^ erhält.
25. Die Projektionsmatrix P auf einen n-dimensionalen Unterraum hat den
Rang r = n. Begründung: Die Projektionen Ph erzeugen einen
Unterraum 5. 5 ist also der von P.
26. Beweisen Sie, dass eine m x m-Matrix A mit Rang m, für die A? = A
gilt, automatisch die Einheitsmatrix A = / ist.
27. Das Wichtige an Satz 4G ist das Folgende: Gilt A^Ax = 0, so gilt
Ax = 0. Dazu ein neuer Beweis: Der Vektor Ai^ liegt im Kern von .
Außerdem liegt Ak immer im Spaltenraum von . Damit er in diesen
zueinander senkrechten Räumen gleichzeitig enthalten sein kann, muss
der Vektor Ai^ Null sein.
28. Benutzen Sie die beiden Eigenschaften P^ = P und P^ = P, um
zu zeigen, dass das Quadrat der Länge der zweiten Spalte einer
Projektionsmatrix P gleich dem Diagonaleintrag P22 ist. Beispielsweise gilt
P22 = I = ^ + ^ + ^ für die Matrix
--1
5 2-1
22 2
-12 5
4.3 Kleinste-Quadrate Approximationen
Es passiert häufig, dass eine Gleichung Ax = b keine Lösung besitzt.
Üblicherweise besteht der Grund einfach darin, dass das Gleichungssystem zu viele
Gleichungen enthält. Das passiert, wenn es mehr Gleichungen als
Unbekannte gibt, wenn also die Matrix mehr Zeilen als Spalten hat, also m größer als n
ist. Die n Spalten spannen dann nur einen kleinen Teil des m-dimensionalen
Raums auf.
216 4 Orthogonalität
Wenn nicht alle Messungen fehlerlos sind, liegt b außerhalb des
Spaltenraums. Mit dem Eliminations verfahren gelangt man also irgendwann zu einer
unmöglichen Gleichung und muss abbrechen. Bei dem Gleichungssystem
handelt es sich aber um ein reales Problem, das gelöst werden muss.
Um es noch einmal zu wiederholen: Es gelingt nicht immer, den Fehler
e = b — Ax zu Null zu machen. Ist e Null, so ist x eine exakte Lösung der
Gleichung Ax = b. Ist die Länge von e so klein wie möglich, so nennt
man x eine Lösung mit kleinstem Fehlerquadrat, In diesem Abschnitt
wird es unser Ziel sein, x zu berechnen und zu verwenden.
Im letzten Abschnitt haben wir uns vorrangig mit der Projektion p
beschäftigt. Jetzt steht x (die Lösung mit kleinstem Fehlerquadrat) im
Vordergrund. Diese beiden Vektoren hängen über die Gleichung p = Ax
zusammen. Die grundlegende Gleichung ist immer noch A^Ax = A^h. Man könnte
sie ad hoc so herleiten:
Hat die Gleichung Ax = b keine Lösung, so multipliziert man
sie mit Ä^ und löst stattdessen Ä^Ax = A^h.
Beispiel 4.3.1 Bestimmen Sie die Gerade, die den drei Punkten @,6), A,0)
und B,0) am nächsten liegt.
Es gibt keine Gerade, die durch alle drei Punkte verläuft. Drücken wir die
Gerade durch b = C -\- Dt aus, so suchen wir zwei Zahlen C und D, die drei
Gleichungen erfüllen sollen, so dass sich für t = 0,1,2 die Werte ö = 6,0,0
ergeben.
Der erste Punkte liegt auf der Geraden b = C -\- Dt, falls C -\- D -0 = 6 gilt.
Der zweite Punkte liegt auf der Geraden b = C -\- Dt, falls C -\- D -1 = 0 gilt.
Der dritte Punkte liegt auf der Geraden b = C -{-Dt, falls C -{-D »2 = 0 gilt.
Dieses 3 x 2-System hat keine Lösung, da der Vektor b = F,0,0) keine
Linearkombination der Spalten von A ist:
[101 r^n [6]
^4=11, x=K^, b=0, Ax = h ist nicht lösbar.
0'
11
12
, x =
c
D
, b =
'6"
0
0
In Beispiel 4.2.3 im letzten Abschnitt haben wir dieselben Zahlen
verwendet. In praktischen Anwendungen liegen die Datenpunkte relativ nahe an
einer Geraden. Sie lassen sich aber durch keinen Ausdruck C -\- Dt exakt
beschreiben, und es kann leicht m = 100 (statt m = 3) Punkte geben. Mit den
Zahlen 6,0,0 übertreiben wir den Fehler, so dass Sie ihn deutlich erkennen
können.
4.3 Kleinste-Quadrate Approximationen 217
Minimierung des Fehlers
Wie kann man den Fehler e = b — Ax so klein wie möglich machen? Das ist
eine wichtige Frage mit einer wunderbaren Antwort. Das beste x (genannt
x) lässt sich geometrisch, algebraisch oder analytisch bestimmen:
Geometrisch: Jeder Vektor Ax liegt in der durch die Geraden A,1,1) und
@,1,2) aufgespannten Ebene. Wir suchen den Punkt dieser Ebene, der am
nächsten an b liegt. Es handelt sich um die Projektion p von b.
Die beste Wahl für Ax ist p. Dann gilt x = x, und der kleinstmögliche
Fehler ist e = b — p.
Algebraisch: Jeder Vektor b besteht aus einem Teil innerhalb des
Spaltenraums von A und einem Teil senkrecht dazu. Der Teil im Spaltenraum ist p.
Der Teil im Kern der transponierten Matrix ist e. Wir haben eine Gleichung
{Ax = b), die wir nicht lösen können. Daraus erzeugen wir eine Gleichung,
die eine Lösung besitzt, indem wir e entfernen:
^x = b = p + e ist unlösbar; Ax = p ist lösbar. D-14)
Für die Lösung x von Ax = p erhält man den kleinsten Fehler, weil für
jedes X gilt:
\\AK-hf = \\A^-pf + \\e\\\ D.15)
Das ist nichts anderes als c^ = a^ -\- h'^ in einem rechtwinkligen Dreieck — der
Satz des Pythagoras. Der Vektor Ax — p im Spaltenraum ist senkrecht zu e
im Kern der transponierten Matrix. Wählen wir für x den Vektor x, so wird
^x — p zu Null und wir erhalten also den kleinst möglichen Fehler, nämlich
e.
Beachten Sie, was hier „kleinster" bedeutet. Das Quadrat der Länge von
Ax — b wird minimiert:
Für die Lösung x mit kleinstem Fehlerquadrat ist E = \\Ax — b|p so
klein wie möglich.
Analytisch: Die meisten Funktionen lassen sich mit Hilfe der
Differentialrechnung minimieren! In einem Minimum sind die Ableitungen Null, da der
Graph dort einen „Talboden" hat und die Steigung in jede Richtung Null ist.
In unserem Fall müssen wir als Fehlerfunktion eine Summe von Quadraten
(das Quadrat des Fehlers in jeder Gleichung) minimieren:
E = \\Ax - b|p = (C + L) . 0 - 6J + (C + L). 1J + (C + L). 2J. D.16)
Die Unbekannten sind C und D, die Komponenten von x, die die Gerade
bestimmen. Für zwei Unbekannte gibt es zwei Ableitungen, die am Minimum
218 4 Orthogonalität
beide den Wert Null annnehmen. Es handelt sich um „partielle Ableitungen",
weil in dem Ausdruck dE/dC die Variable D als konstant angesehen wird,
wie auch C im Ausdruck dE/dD:
dE/dC = 2{C-{-D'0-6) -\-2{C-\-D -1) -\-2{C-\-D-2) =0
dE/dD = 2{C-\-D'0- 6)@) -\-2{C-{-D' 1)A) -{-2{C-{-D' 2)B) = 0.
Der Ausdruck dE/dD enthält die Faktoren 0,1 und 2. Es sind dies die
Faktoren, die in der Gleichung für E vor D stehen. Nach der Kettenregel
gehen sie als „innere Ableitung" auch in die Ableitung von E nach D ein.
(Die Ableitung von D + 5x)^ ist zum Beispiel 2 mal 4 + 5x mal 5.)
Die zugehörigen Faktoren in der Ableitung nach C sind immer 1, weil C
jedesmal mit 1 multipliziert wird. Es ist hier kein Zufall, dass 1, 1, 1 und 0,
1, 2 gerade die Spalten von A sind.
Fassen wir die Gleichungen zusammen und dividieren durch 2:
Die Ableitung fg nach C ist Null: 3C + 3i^ = 6
Die Ableitung |g nach D ist Null: 3C -{-5D = 0.
D.17)
Diese Gleichungen sind mit Ä^Ax = A^h identisch. Die besten Werte
für C und D sind die Komponenten von x. Die Gleichungen D.17) aus der
Differentialrechnung sind schlicht die Normalengleichungen aus der linearen
Algebra:
Die partiellen Ableitungen von || Ax - b|p sind genau dann Null,
wenn A^Ax = A^b gilt.
Die Lösung ist also C = 5 und D = —3. Deshalb wird durch b = 5 - 3t
die beste Gerade beschrieben. Sie kommt den drei gegebenen Punkten am
nächsten. Für t = 0,1,2 geht sie durch p = 5, 2, —1. Sie kann nicht durch
b = 6, 0, 0 gehen, und die Fehler sind 1, -2, 1. Das ist gerade der Vektor e!
In Abbildung 4.6a wird diese Gerade dargestellt. Sie verfehlt die Punkte
mit den vertikalen Abständen ei,62,63. Die Gerade mit den kleinsten
Fehlerquadraten ist so gewählt worden, dass der Ausdruck ^ = ef + 63 + 63 minimal
ist.
In Abbildung 4.6b wird dasselbe Problem etwas anders, im
dreidimensionalen Raum, dargestellt. Der Vektor b liegt nicht im Spaltenraum von A. Das
ist der Grund dafür, dass sich Ax — h nicht lösen lässt, weswegen sich also
keine Gerade durch die drei Punkte legen lässt. Der kleinstmögliche Fehler
ist der zur Ebene senkrechte Vektor e = b — Ax, der Fehlervektor A, —2,1)
mit den Fehlern in den drei Gleichungen. Diese sind durch die Abstände der
Punkte von der besten Geraden gegeben. Hinter beiden Darstellungen steht
die grundlegende Gleichung Ä^Ax = A^h.
Beachten Sie, dass die Summe der Fehler 1, -2,1 Null ergibt. Der Fehler
e = F1,62,63) ist senkrecht zur ersten Spalte A,1,1) von A, das Skalarpro-
dukt muss also 61 + 62 + 63 = 0 ergeben.
4.3 Kleinste-Quadrate Approximationen 219
Beste Gerade/? = 5-3/
[6]
0
LOj
/\ \ ^"
\ 5]
2
L-lJ
Abb. 4.6. Die nächstgelegene Gerade hat die Höhen p = E, 2, —1) mit den Fehlern
e = A, -2,1). Die Gleichung A^Ak = A^h hat die Lösung x = E, -3), die Gerade
ist b = 5 — 3t, die Projektion ist 5ai — 3a2.
Ax = p
Ax = b
nicht moeglich - -
b nicht im Zeilenraum
Unabhaengige Spalten
Kein Kern
Abb. 4.7. Die Projektion p = Ait liegt am nächsten zu b, so dass x den Ausdruck
E = \\h- Ax||^ minimiert.
Die übergeordnete Sicht
Die wichtigste Abbildung in diesem Buch stellt die vier Unterräume und
die Wirkung einer Matrix dar. Ein Vektor x auf der linken Seite von
Abbildung 4.2 geht in den Vektor b = Ax auf der rechten Seite über. In der
Abbildung wurde x in zwei Teile x^ + x^ aufgespalten, und es gab viele
Lösungen der Gleichung Ax = b.
In diesem Abschitt ist die Situation gerade umgekehrt. Es gibt keine
Lösungen zu Ax = b. An Stelle von x zerlegen wir b. In Abbildung 4.7 wird
220 4 Orthogonalität
die Situation, bei der die Methode der kleinsten Quadrate zur Anwendung
kommt, dargestellt. Wir lösen die Gleichung Ax = p anstelle von Ax = b.
Dabei ist ein Fehler e == b — p unvermeidbar.
Beachten Sie, dass der Kern N{A) sehr klein ist — er besteht nur aus
einem Element. Hat man linear unabhängige Spalten, so ist die einzige Lösung
der Gleichung Ax = 0 der Nullvektor x = 0. In diesem Fall ist A^A
invertierbar, und deswegen wird der Vektor x durch die Gleichung A^Ait = Ä^h
eindeutig bestimmt.
In Kapitel 7 werden wir einen vollständigen Überblick über alle vier
Unterräume gewinnen. Jedes x wird in Xr + x^ zerlegt und jedes b in p + e.
Die beste Lösung wird weiterhin x (oder x^) im Zeilenraum sein. Um e
kommen wir nicht herum, und an Xn sind wir nicht interessiert — es bleibt also
Ax = p.
Eine Gerade anpassen
Wir präsentieren jetzt das einleuchtendste Beispiel für die Anwendung der
Methode der kleinsten Quadrate. Man beginnt mit m Punkten in einer Ebene
— hoffentlich in der Nähe einer Geraden. Zu den Zeiten ti,,.. ,tm befinden
sich diese Punkte in den Höhen &i,..., 6^. In Abbildung 4.6a ist die beste
Gerade h = C -\- Dt dargestellt, die die Punkte jedoch mit den Abständen
ei,..., e^ verpasst. Es handelt sich um vertikale Abstände. Keine Gerade ist
perfekt, und mit der Methode der kleinsten Quadrate wählt man jene Gerade
aus, für die E — e\-\- " • -\- el^ minimal wird.
Im ersten Beispiel in diesem Abschnitt betrachteten wir drei Punkte. Im
Folgenden wollen wir m Punkte zulassen, wobei m sehr groß sein kann. Wir
werden dann weiterhin auf dieselben zwei linearen Gleichungen in Ä^Ak =
A^h geführt, wobei x die Komponenten C und D enthält.
Dieses Problem wird in Abbildung 4.6b auf andere Art verdeutlicht,
nämlich im m-dimensionalen Raum. Eine Gerade geht genau dann exakt
durch die m Punkte, wenn die Gleichung Ax = b eine Lösung besitzt. Das
ist im Allgemeinen nicht der Fall, da es nur die beiden Unbekannten C und
D gibt, A also nur 2 Spalten hat:
C + Dti=^ bi
Ä . . ^ C-\-Dt2 = b2 , .
Ax = h ist . und A =
C-[-Dtm = hm
1 h
1 t2
lU
D.18)
Der Spaltenraum ist so dünn, dass b fast sicher außerhalb liegt. Die m Punkte
(ti, hi) liegen also fast sicher nicht auf einer Geraden. Die Komponenten von
e sind dann deren Abstände ei,..., Cm zur am nächsten liegenden Geraden.
Sollte b doch im Spaltenraum liegen, so bedeutet das, dass die Punkte
gerade doch auf einer Geraden liegen. In diesem Fall gilt b = p, und Ax = b
ist lösbar, so dass sich die Fehler e == @,..., 0) ergeben.
4.3 Kleinste-Quadrate Approximationen 221
Die nächste Gerade hat die Höhen pi,... ,Pm mit den Fehlern ei,..., e^.
Aus der Gleichung Ä^Ax = A^h erhält man x = (C, D) und die Fehler
ei = bi-C- Dti.
Das Problem, eine Gerade an vorgegebene Punkte anzupassen, ist so
wichtig, dass wir die beiden entsprechenden Gleichungen explizit angeben wollen.
Erinnern wir uns, dass die Gerade b — C -\- Dt genau zu den Datenpunkten
passt, wenn
C ^-Dti= hl
C + Dim = K
oder
ri h'
c
p
=
'bi'\
D.19)
gilt. Hierdurch ist die Gleichung Ax = b gegeben. Sie ist für m > 2 im
Allgemeinen unlösbar. Es gibt aber einen Lichtblick. Die Spalten von A sind
linear unabhängig (falls nicht alle Zeiten ti identisch sind). Wir benutzen
dann die Methode der kleinsten Fehlerquadrate, und lösen dazu die Gleichung
A'^Ait - A^h. Die „Skalarprodukt-Matrix" A'^A ist eine 2 x 2-Matrix:
A^A =
\1 ■
.*1 •
• 1'
^771
<r
_ 1 tm _
m J2ti
D.20)
Auf der rechten Seite der Gleichung steht der zweielementige Vektor Ä^h:
A'h =
1
D.21)
Bei einer konkreten Aufgabe sind diese Zahlen alle gegeben. Die m
Gleichungen in Ax — b werden auf die zwei Gleichungen A^Ax = A^h reduziert.
In Gleichung D.23) geben wir eine Formel für C und D an.
4H Die; Gerade 'C'-^Di^ die die Summe 6f 4- - * * H-e^ mmimiert^ wird durch
die Gteiffiim§A^^x=:= ^'^b:bestimmt --^ / ' -'-i'-'
m X)*i
EtiEtl
C
D
'Eh]
E*ih\
D.22)^
Die vertikalen Abweichungen an den m Punkten der Geraden bilden die
Komponenten von e = b — p.
Wie immer kann man diese Gleichungen entweder mit geometrischen
Methoden, mit Hilfe der Differentialrechnung oder mit Mitteln der Unearen
Algebra herleiten. Der Fehlervektor b — Ax steht senkrecht auf den Spalten von
222 4 Orthogonalität
A (die geometrische Methode). Er liegt im Kern von A^ (lineare Algebra).
Die beste Näherung x = (C, D) minimiert den Gesamtfehler E, die Summe
der Quadrate der Abweichungen:
E{x) = \\Ax - b|p = {C-\- Dti - hif + ... + (C + Dt^ - hmf^
In der Differentialrechnung setzt man die Ableitungen dE/dC und öE/dD
gleich Null, um ein Minimum zu finden. Daraus erhält man die beiden
Gleichungen in D.22).
In anderen Problemen, die man mit der Methode der kleinsten Quadrate
lösen kann, tauchen mehr als zwei Unbekannte auf. Will man eine Parabel an
Messpunkte anpassen, so erhält man n = 3 Unbekannte C, D und E (siehe
unten). Ganz allgemein passt man n Parameter xi,..., x^ an m Datenpunkte
an. Entsprechend besitzt die Matrix A dann n Spalten, wobei n < m gilt.
Der Gesamtfehler ist eine Funktion ^(x) = \\Ax - b|p, die von n Variablen
abhängt. Aus ihren Ableitungen erhält man die n Gleichungen A^Ax = A^h.
Die Ableitung einer quadratischen Funktion ist schlicht linear — das ist der
Grund dafür, dass die Methode der kleinsten Quadrate so populär ist.
Beispiel 4.3.2 In einem Spezialfall sind die Spalten von A orthogonal, nämlich
dann, wenn sich die Zeiten ti der Messungen zu Null addieren. Nehmen wir
an, es gilt b = 1,2,4 zu den Zeiten t = -2,0,2. Die Summe dieser Zeiten ist
Null. Das Skalarprodukt mit 1,1,1 ist Null, und A hat orthogonale Spalten:
C-\-D{-2) = l
C + D{0) = 2
C + D{2) = 4
oder
Ax =
ri-2"
1 0
[l 2
c
D
=
1
2
4j
Die Messungen 1,2,4 liegen nicht auf einer Geraden, es gibt also keine exakten
Werte für C, D und x. Sehen Sie sich die Matrix A^A in der Gleichung für
X an:
A' Ax = A'h
ist
'3 0'
0 8
C'
ß
=
"
6
Das Wichtige: Die Matrix Ä^A ist diagonal. Sie lässt sich einzeln nach C =
I und ^ = I auflösen. Die Nulleinträge in A^A sind Skalarprodukte von
zueinander senkrechten Spalten von A. Die Nenner 3 und 8 sind ungleich 1,
weil die Spalten keine Einheitsvektoren sind. Aber eine Diagonalmatrix ist
genauso gut wie die Einheitsmatrix.
Es ist so hilfreich, wenn die Spalten orthogonal sind, dass es sich lohnt,
den Zeitursprung so zu verschieben, dass sich orthogonale Spalten ergeben.
Um dies zu erreichen, subtrahiert man von allen Zeiten die durchschnittliche
Zeit i= (tl^ \-tm)lm. Die verschobenen Messzeitpunkte Ti — ti-tbilden
dann die Summe Null. Da dann die Spalten orthogonal sind, ist Ä^A eine
Diagonalmatrix. Für die Werte C und D ergeben sich damit direkte Formeln:
4.3 Kleinste-Quadrate Approximationen 223
m T^ + ...+Tl ^ '
Die am besten angepasste Gerade wird dann durch C + DT oder C +
D{t — i) erzeugt. Die Zeitverschiebung, durch die Ä^A eine Diagonalmatrix
wird, ist ein Beispiel für das Gram-Schmidt-Verfahren, durch das Spalten im
Voraus orthogonalisiert werden.
Eine Parabel anpassen
Es wäre irrsinnig, einen Ballwurf durch eine Gerade anpassen zu wollen.
Eine Parabel h = C -\- Dt-\- Et"^ jedoch erlaubt es dem Ball, aufzusteigen und
wieder herunterzufallen. Die Variable b beschreibt dabei die Höhe zur Zeit
t. Der tatsächliche Verlauf ist zwar keine perfekte Parabel, aber mit dieser
Näherung beginnt die gesamte Theorie der Flugbahnen von Projektilen.
Als Galileo Galilei einen Stein vom schiefen Turm von Pisa warf, wurde
dieser beschleunigt. Der Abstand vom Boden enthält einen quadratischen
Term ^gt"^. (Es war Galilei's Erkenntnis, dass die Masse des Steins keine
Rolle spielt.) Ohne diesen Term könnten wir niemals einen Satelliten auf die
richtige Flugbahn schicken. Aber sogar mit einem nichtlinearen Ausdruck
wie t^ tauchen die Unbekannten C, D und E nur als lineare Vorfaktoren auf.
Deshalb gehört das Problem, die beste Parabel ausfindig zu machen, immer
noch zur linearen Algebra.
Aufgabe Passen Sie eine Parabel b — C + Dt + Et"^ an die Werte 6i,..., b^n
zu Zeiten ti,...,tm an.
Mit m > 3 Punkten gibt es normalerweise keine exakte Lösung für die
Gleichungen:
C + Dti + Etl = bi
: hat die m x 3-Matrix A =
C-\-Dtm+ Etl, = hm
Iti t? 1
. D.24)
1 / /2
Methode der kleinsten Quadrate Die beste Parabel ist jene, für die x =
{C,D,E) die drei Normalengleichungen A'^Ait = A^h erfüllt.
Darf ich Sie bitten, dies in eine Projektionsaufgabe umzuformulieren?
Der Spaltenraum von A hat die Dimension . Die Projektion von b ist
p = Ait, also eine Linearkombination der drei Spalten mit den Koeffizienten
C, D, und E.
Der Fehler im ersten Datenpunkt ist ei = bi—C-Dti-Etl. Der gesamte
quadratische Fehler ist e = el + . Wenn Sie es vorziehen, die
Minimierung per Differentialrechnung durchzuführen, so müssen Sie die Ableitungen
von e nach , , bestimmen. Diese drei Ableitungen werden
224 4 Orthogonalität
Null genau dann, wenn x = {C,D,E) das 3 x 3-Gleichungssystem .
löst.
In Abschnitt 8.4 werden noch mehr Anwendungen für die Methode der
kleinsten Quadrate auftauchen. Die wichtigste davon stellen die Fourierreihen
dar — hiermit werden Funktionen anstelle von Vektoren angenähert. Der zu
minimierende Fehler e = e^ + • • • + e^ wird zu einem Integral. Wir werden
die Gerade finden, die am nächsten an einer Funktion f{x) liegt.
Beispiel 4.3.3 Soll eine Parabel b =^ C -\- Dt -\- Et^ durch die drei Höhen
^ = 6,0,0 zu den Zeiten t = 0,1,2 verlaufen, so erhält man die Gleichungen
D.25)
Diese Gleichung Ax = b lässt sich exakt lösen. Aus drei Datenpunkten
erhält man drei Gleichungen, also eine quadratische Matrix. Die Lösung ist
X == {C,D,E) — F,-9,3), und die Parabel durch die drei Punkte in
Abbildung 4.8a ist durch b = 6 — 9t -{- St"^ gegeben. Was bedeutet das für die
b = 6-9t-h3fl
liegt im R"^!
Abb. 4.8. Aus Beispiel 2: Passt man eine Parabel an drei Punkte an, so erhält man
p = b und e = 0. Ein vierter Punkt macht die Methode der kleinsten Quadrate
nötig.
zugehörige Projektion? Die Matrix hat drei Spalten, die den gesamten Raum
E^ aufspannen. Die Projektionsmatrix ist die Einheitsmatrix! Die
Projektion von b ist b, und der Fehler ist Null. Wir brauchen hier die Gleichung
Ä^Ait = Ä^h nicht zu lösen, weil wir schon Ax = b lösen konnten. Man
könnte natürlich auch hier mit A^ multiplizieren — es gibt aber keinen Grund
dafür, das zu tun.
In Abbildung 4.8a wird auch ein vierter Punkt b^ zu einer Zeit t^
dargestellt. Liegt dieser Punkt auf der Parabel, so ist auch die neue Gleichung
Ax = b (mit vier einzelnen Gleichungen) lösbar. Liegt der vierte Punkte
4.3 Kleinste-Quadrate Approximationen 225
nicht auf der Parabel, so lösen wir stattdessen Ä^Ak = A^h. Wird dabei
die nach der Methode der kleinsten Quadrate bestimmte Parabel
gleichbleiben, so dass sich der gesamte Fehler im vierten Datenpunkt konzentriert?
Wahrscheinlich nicht!
Ein Fehlervektor @,0,0,64) wäre nicht senkrecht zur Spalte A,1,1,1) von
A, Die Methode der kleinsten Quadrate gleicht die Fehler so aus, dass ihre
Summe immer Null ist.
Die wesentlichen Punkte
l.Die Methode der kleinsten Fehlerquadrate liefert eine Lösung x, die den
Gesamtfehler E = ||Ax —b|p minimiert, also die Summe der Quadrate der
in den m Gleichungen auftretenden Fehler.
2. Man erhält x aus den Normalengleichungen A^Ait = A^h.
3. Passt man eine Gerade b = C -{- Dt an m Punkte an, so ergeben sich aus
den Normalengleichungen die Werte für C und D.
4.Die Höhen der am besten angepassten Gerade sind p = (pi,... ,Pm)-
Die vertikalen Abstände von den Datenpunkten stehen im Vektor e =
(ei,... , CttiJ«
5. Passt man eine Linearkombination von n Funktionen an m Punkte an, so
sind die m Gleichungen ^Xjyj(ti) = bi im Allgemeinen unlösbar. Die n
Normalengleichungen liefern dann die beste Näherung x = (xi,... Xn)-
Aufgaben 4.3
In den Aufgaben 1—10 stellen wir die wesentlichen Ideen an 4
Datenpunkten dar.
1. (Gerade b = C -\- Dt durch vier Punkte) Zu den Zeiten t = 0,1,3,4 sei
6 = 0,8,8,20. Bestimmen Sie das (unlösbare) Gleichungssystem Ax = b.
Ändern Sie dann die Messwerte zu p = 1,5,13,17 und bestimmen Sie
eine exakte Lösung der Gleichung Ax = p.
2. Es sei b = 0,S, 8,20 zu den Zeiten t = 0,1,3,4. Bestimmen Sie die
Normalengleichungen A^Ax = A^h. Bestimmen Sie die Höhen und zugehörigen
Fehler der am besten angepassten Gerade (in Abbildung 4.9a). Welchen
Minimalwert nimmt E = el -\- 62-\- e^-\- el an?
3. Berechnen Sie p = Ait für den Vektor b und die Matrix A aus der vor-
hergehenen Aufgabe. Verwenden Sie dazu die Gleichung A'^Ax = A^h,
und überprüfen Sie, ob e = b - p senkrecht zu beiden Spalten von A ist.
Bestimmen Sie den kürzesten Abstand ||e|| von b zum Spaltenraum.
4. (Verwenden Sie hier die Differentialrechnung) Schreiben Sie E = \\Ax —
b|p als Summe von vier Quadraten, in denen jeweils C und D vorkom-
226 4 Orthogonalität
men. Bestimmen Sie die Gleichungen dE/dC = 0 und dE/dD = 0 und
daraus die Normalengleichungen, indem Sie durch 2 dividieren.
5. Bestimmen Sie die Höhe der am besten an die Messungen b = @,8,8,20)
angepassten horizontalen Gerade. Eine exakte Anpassung wäre eine
Lösung des unlösbaren Gleichungssystems C = 0, C = 8, C = 8, C = 20.
Bestimmen Sie die zu diesen Gleichungen gehörende 4 x 1-Matrix A, und
lösen Sie die Gleichung Ä^Ax = A^h. Zeichnen Sie die Höhe x = C und
die Fehler in Abbildung 4.9a ein.
b = @,8, 8, 20)
► p = Caj+Daj
32^@, 1,3,4)
ai = (l, 1, 1, 1)
Abb. 4.9. Aufgaben 1—11: Die am besten angepasste Gerade C + Dt gehört zur
Projektion in R^.
6. Projizieren Sie den Vektor b = @,8,8,20) auf die Gerade durch den
Vektor a = A,1,1,1). Bestimmen Sie x = a^b/a^a und die Projektion
p = XR. Passen Sie Abbildung 4.9b entsprechend an, und überprüfen Sie,
ob e = b — p senkrecht zu a steht. Bestimmen Sie auch den kürzesten
Abstand ||e|| von b zu der neu gezeichneten Geraden.
7. Bestimmen Sie die zu den vier Punkten aus der vorhergehenden Aufgabe
am nächsten gelegene Gerade h — Dt durch den Ursprung. Eine exakt
passende Gerade würde das Gleichungssystem Z)-0 = 0,Z)-1 = 8,Z)-3 =
8, D • 4 = 20 lösen. Tragen Sie wie in Abbildung 4.9a die beste Steigung
X = D und die vier Fehler ein.
8. Projizieren Sie den Vektor b = @,8,8,20) auf die Gerade durch a =
@,1,3,4). Bestimmen Sie x und p = xr. Die jeweils am besten
angepassten Werte für C aus den Aufgaben 5 und 6 sowie für D aus den
Aufgaben 7 und 8 stimmen nicht mit den besten Werten (C, D) aus den
Aufgaben 1-4 überein. Der Grund dafür ist, dass A,1,1,1) und @,1,3,4)
senkrecht sind.
4.3 Kleinste-Quadrate Approximationen 227
9. Bestimmen Sie die unlösbaren Gleichungen Ax = b, die sich für die
Anpassung einer Parabel b = C-\-Dt-\-Et^ an dieselben vier
Datenpunkte ergibt. Bestimmen Sie die drei Normalengleichungen A^Ax = A^h.
(Lösung nicht nötig.) In Abbildung 4.9a wird jetzt also eine Parabel an-
gepasst. Was passiert in Abbildung 4.9b?
10. Bestimmen Sie die Gleichung Ax = b, die sich aus der Anpassung einer
kubischen Parabel b = C-\-Dt-\-Et^ -\-Ft^ an dieselben vier Datenpunkte
ergibt. Lösen Sie sie mit dem Eliminations verfahren. Der Graph in
Abbildung 4.9a geht nun genau durch die vier Punkte. Bestimmen Sie ohne
Rechnung p und e in Abbildung 4.9b.
11. Der Durchschnittswert der vier Zeiten ist f = |@ + 1 + 3 + 4) = 2. Der
Durchschnittswert der vier ^)'s ist S = ^@ + 8 + 8 + 20) = 9.
(a) Verifizieren Sie, dass die beste Gerade durch den „Mittelpunkt"
(U) = B,9) geht.
(b) Erklären Sie, wie sich C -\- Dt = b aus der ersten Normalengleichung
ergibt.
In den Aufgaben 12—16 werden grundlegende Konzepte der
Statistik eingeführt — die Basis für die Methode der kleinsten
Fehlerquadrate.
12. (Empfohlen) In dieser Aufgabe wird der Vektor b = Fi,..., bm) auf die
Gerade durch a = A,..., 1) projiziert.
(a) Lösen Sie die Gleichung a^ax = a^b und zeigen Sie, dass x der
Mittelwert der b's ist.
(b) Bestimmen Sie den Fehlervektor e, die Varianz ||e|p und die Stan-
dardabweichung ||e||.
(c) Zeichnen Sie eine an die Werte b = A,2,6) angepasste horizontale
Gerade. Wo finden Sie in der Zeichnung p und e? Überprüfen Sie, ob
p senkrecht auf e steht, und bestimmen Sie die Matrix P.
13. Die erste Annahme hinter der Methode der kleinsten Quadrate: Jeder
Messfehler hat den Er wart ungs wert Null. Multiplizieren Sie die acht
Fehlervektoren b — Ax = (d=l,d=l,d=l) mit {Ä^A)~^A'^ und zeigen Sie so,
dass die acht Vektoren x - x ebenfalls den Mittelwert Null bilden. Der
Er wart ungs wert von x ist die richtige Wahl für x.
14. Die zweite Annahme: Die Messfehler sind statistisch unabhängig mit
gleicher Varianz a^. Der Mittelwert von (b - Ax)(h - Ax)'^ ist a'^I.
MultipUzieren Sie den Ausdruck {A'^A)~'^A'^ von links, und den
Ausdruck A{A'^A)~'^ von rechts. Zeigen Sie so, dass der Mittelwert von
(x — x)(x - x)^ gleich a^{Ä^A)~^ ist. Dies ist die Kovarianzmatrix des
Fehlers in x.
228 4 Orthogonalität
15. Ein Arzt ermittelt m Messwerte &i,...,&^ für Ihre Herzfrequenz. Die
Kleinste-Quadrate-Lösung der m Gleichungen x = bi,x = 62?•••,2: =
bm ist der Durchschnittswert x = F1 + • • • + hm)lm. In diesem Fall
ist die Matrix A schlicht eine Spalte mit Einsen. In Aufgabe 14 wird
als erwartetes Fehlerquadrat {x — x)^ der Wert g'^{Ä^Ä)~^ =
angegeben. Führt man m Messungen durch, so fällt die Varianz von a^
auf a^/m.
16. Der Mittelwert xqq von 99 Zahlen &i,..., 699 sei Ihnen bekannt. Wie lässt
sich der Mittelwert xioo, der sich durch Hinzunahme einer weiteren Zahl
bioo ergibt, schnell bestimmen? Die Idee hinter der rekursiven Methode
der kleinsten Quadrate ist es, die Addition von 100 Zahlen zu vermeiden.
Für welche Koeffizienten ergibt sich xioo richtig aus 6100 and X99?
löö^ioo + ^99 = I5ö(^i "• ^ ^100).
In den Aufgaben 17—25 üben Sie den Umgang mit den Größen x,
p und e.
17. Bestimmen Sie die drei Gleichungen, die ausdrücken, dass die Gerade
h = C -\- Dt durch fe = 7 für t = -1, durch h = 1 hei t = l und durch
b = 21 bei t = 2 gehen soll. Bestimmen Sie die Kleinste-Quadrate-Lösung
X = {C,D)^ und zeichnen Sie die am besten angepasste Gerade.
18. Bestimmen Sie die Projektion p = Ax für die Werte in Aufgabe 17. So
erhalten Sie die drei der am besten angepassten Gerade. Zeigen
Sie, dass der Fehlervektor durch e = B, -6,4) gegeben ist.
19. Angenommen, wir betrachten die Fehler 2, -6,4 aus Aufgabe 18 als
Messwerte zu den Zeiten t = -1,1,2. Berechnen Sie wieder x und die
nächstgelegene Gerade. Erklären Sie das Ergebnis: b = B, —6,4) steht senkrecht
auf , also ist die Projektion p = 0.
20. Die Messwerte zu t = -1,1,2 seien b = E,13,17). Berechnen Sie x und
die nächste Gerade, sowie e. Der Fehler ist e = 0, weil dieses b
ist.
21. Welcher der vier Unterräume enthält den Fehlervektor e? Welcher
Unterraum enthält p? Wo findet man x? Welchen Kern hat A?
22. Bestimmen Sie die am besten angepasste Gerade C + Dt zu den Werten
ö = 4,2, -1,0,0 und den Zeiten t = -2, -1,0,1,2.
23. (Abstand zwischen Geraden) Die Punkte P = {x, x, x) Hegen auf der
Geraden durch A,1,1), die Punkte Q = {y,Sy,-l) liegen auf einer anderen
Geraden. Wählen Sie x und y, so dass das Abstandsquadrat ||P - QlP
minimal wird.
4.4 Orthogonale Basen und Gram-Schmidt 229
24. Ist der Fehlervektor e orthogonal zu b, p, e oder x? Zeigen Sie, dass ||e|p
gleich e^b gleich b^b — b^p ist. Dies ist genau der kleinste quadratische
Gesamtfehler E.
25. Die Ableitungen des Ausdrucks mx|p nach den Variablen xi,...,Xn
bilden den Vektor 2Ä^Ax. Die Ableitungen von 2h^Ax bilden den Vektor
2A^b. Die Ableitungen von H^x — b|p sind also Null, wenn .
4.4 Orthogonale Basen und Gram-Schmidt
In diesem Abschnitt verfolgen wir zwei Ziele. Erstens wollen wir erklären, dass
orthogonale Vektoren viele Rechnungen vereinfachen. Viele Skalarprodukte
sind Null, und Ä^A wird zu einer diagonalen Matrix.
Das zweite Ziel wird sein, orthogonale Vektoren zu konstruieren. Wir
werden geeignete Linearkombinationen der gegebenen Vektoren auswählen,
die jeweils rechtwinklig aufeinander stehen. Die gegebenen Vektoren sind die
Spalten von A. Die orthogonalen Vektoren werden die Spalten einer neuen
Matrix Q bilden.
Aus Kapitel 3 wissen wir, woraus eine Basis besteht — aus linear
unabhängigen Vektoren, die den Raum aufspannen. Eine Basis definiert einen
Satz Koordinatenachsen. Solche Achsen können sich im Prinzip in beliebigen
Winkeln schneiden (mit Ausnahme von 0° und 180°). Doch wann immer wir
Koordinatenachsen darstellen, stehen sie senkrecht aufeinander. In unserer
Vorstellung sind Koordinatenachsen fast immer orthogonal. Dadurch werden
die Darstellungen einfacher, und auch alle Rechnungen.
Die Vektoren qi,..., Qn sind orthogonal, wenn die Skalarprodukte q^ • q^-
Null sind. Genauer gesagt muss qf qj = 0 dann gelten, wenn i ^ j ist. Nur
einen Schritt weiter — man dividiert einfach jeden Vektor durch seine Länge
— werden aus den Vektoren orthogonale Einheitsvektoren mit der Länge 1.
Eine solche Basis nennt man orthonormal.
DEFINITION Vektoren qi,. * *, q« heissen oHhonorrntilMh
T , _ / 0 falls i 5?^ i (örtÄogonafe Vektoren)
' ^^^ ^;tl'falls ^='j' {BmheiUmktomm\\^^^^^^ -
Eine MÄix mit; brihonormaleu Spalten wird^dtircK d^n Buchstaben Q
dargestellt';"'' '' 'V'' ; '' " \'' , "",'": "'"'''' "'" ' \ ^
Mit einer Matrix Q lässt sich leicht arbeiten, weil Q^Q — I gilt. Das
beschreibt in Matrixschreibweise nichts anderes, als dass die Spalten qi,..., qn
orthonormal sind. Wir sehen das in Gleichung D.26) weiter unten. Q muss
dabei nicht quadratisch sein. Ist Q aber quadratisch, so bedeutet Q^Q — I
230 4 Orthogonalität
automatisch Q^ — Q~^: Es gilt in diesem Fall also „Transponierte gleich
Inverse."
41 Eine Matrix: Qtm%: oiÄonormalen Spalten erfüllt die
Q^Q
—Mi — -.
— <ln —
pJ V'':l''
Li » *, *
, aryi
J< * , ^ > . f ^ * J
_Q 0 ■..- ij
Wird Zeile i von Q^ mit Spalte j von Q multipliziert, so ist das dasselbe
wie das Skalarprodukt qfqj. Außerhalb der Diagonalen {i ^ j) ergibt sich
also Null, weil die Vektoren orthogonal zueinander sind. Auf der Diagonalen
(i — j) liefern die Einheitsvektoren qf q^ = ||qi|P = 1.
Sind die Spalten nur orthogonal (also keine Einheitsvektoren), so ist Q^Q
eine Diagonalmatrix, aber nicht die Einheitsmatrix. Dafür wollen wir den
Buchstaben Q nicht verwenden. Eine solche Matrix ist aber beinahe ebenso
gut. Das Wichtige ist die Orthogonalität — Einheitsvektoren erzeugt man
dann sehr einfach.
Noch einmal gesagt: Es gilt Q^Q = I sogar dann, wenn Q eine rechteckige
Matrix ist. In einem solchen Fall ist Q^ nur eine Linksinverse. Für
quadratische Matrizen gilt zusätzlich QQ'^ = 7, die Matrix Q^ ist also die beidseitige
Inverse von Q. Die Zeilen einer quadratischen Matrix Q sind somit ebenso or-
thonormal wie die Spalten. Um eine solche Matrix zu invertieren, müssen wir
sie nur transponieren. In diesem Fall nennen wir Q eine orthogonale Matrix^,
Es folgen drei Beispiele für orthogonale Matrizen — eine Drehmatrix, eine
Permutation und eine Spiegelung.
Beispiel 4.4.1 (Drehmatrix) Q dreht jeden Vektor in der Ebene um den
Winkel 0:
Q =
cos 0 — sinO
sin 0 cos 0
und Q' = Q-^ =
cosO sin 6
- sin 0 cos 0
Die Spalten von Q sind orthogonal (berechnen Sie das Skalarprodukt). Es
sind Einheitsvektoren, weil sin^ 6 + cos^ 0 = 1 gilt. Die Spalten stellen eine
Orthonormalhasis für die Ebene M^ dar, nämlich die beiden
Standardbasisvektoren i und j um den Winkel 6 gedreht (siehe Abbildung 4.10a).
^ „Orthonormale Matrix" wäre ein angemessenerer Name für Q, er ist aber nicht
gebräuchlich. Jede Matrix mit orthonormalen Spalten wird durch den
Buchstaben Q bezeichnet, wir nennen sie aber nur eine orthogonale Matrix^ wenn es sich
um eine quadratische Matrix handelt.
4.4 Orthogonale Basen und Gram-Schmidt 231
Q~^ dreht jeden Vektor wieder um -0 zurück. Diese Matrix stimmt mit
Q^ überein, weil cos -0 = cosO und sin -0 = - sinO gilt. Es gilt also Q^Q =
I und QQ'^ = I.
Beispiel 4.4.2 (Permutation) Diese Matrizen ändern die Reihenfolge der
Komponenten eines Vektors:
[0 10'
001
100
X
y
z
—
y
z
X
und
0 1
1 0
X
y.
y'
X
Alle Spalten dieser Matrizen Q sind Einheitsvektoren (die Länge ist
offensichtlich 1), und sie sind auch orthogonal zueinander, da die Einsen an
verschiedenen Stellen stehen. Die Inverse einer Permutationsmatrix ist ihre
Transponierte. Die Inverse bringt die Elemente wieder in ihre ursprüngliche
Reihenfolge:
^001"
100
010
'y'
z
X
=
X
y
z
und
"Ol"
10
y
X
=
Inverse = Transponierte:
Jede Permutationsmatrix üt eine orthogonale Matrix.
ßj =
ßi=j
Spiegelung
>^ßj = i
Abb. 4.10. Drehung durch Q = [^ j] ^^^ Spiegelung durch Q = [? J].
Beispiel 4.4.3 (Spiegelung) Es sei u ein beliebiger Einheitsvektor, und es
sei E = / - 2uu^. (Beachten Sie, dass uu^ eine Matrix ist, wohingegen u^u
die Zahl ||u|p = 1 ist.) Dann sind Q^ und Q~^ beide gleich Q:
Q^=^J-2mX^ :^Q und Q^Q = / - 4uu^ + 4uu^uu^ =/. D.27)
Die Spiegelungsmatrizen I — 2uu^ sind symmetrisch und orthogonal.
Quadriert man sie, so erhält man die Einheitsmatrix — eine zweifache Spiegelung
an einem Spiegel erzeugt wieder das Original und es gilt Q^ = Q^Q = I.
Beachten Sie, dass u^u = 1 gilt (am Ende von Gleichung D.27)).
232 4 Orthogonalität
Als Beispiel wählen wir die Einheitsvektoren ui = A,0) und U2 =
(l/\/2,-l/\/2). Wir berechnen 2uu^ (Spalte mal Zeile) und subtrahieren
das Ergebnis von I:
Qx=I-2
[10]
-10
Ol
und Q2= I -2
0,5-0,5
-0,5 0,5
Ol
10
^-1 0"
0 1
X
y.
=
—X
y.
Qi spiegelt den Vektor ui = A,0) an der y-kchse nach (-1,0). Genauso
wird jeder andere Vektor {x^y) in sein Spiegelbild {—x^y) an der y-kchse
gespiegelt:
Spiegelung durch Q\:
Q2 bewirkt eine Spiegelung an der 45°-Geraden. Jeder Vektor (x, y) wird
zu B/, x) — das ist gerade die Permutation aus Beispiel 4.4.2. Ein Vektor wie
C,3) bleibt unverändert, wenn 3 und 3 vertauscht werden — er liegt auf der
Spiegelachse. In Abbildung 4.10b wird die Spiegelung dargestellt.
Durch eine Drehung ändert sich die Länge eines Vektors nicht, auch nicht
durch Spiegelungen oder Permutationen. Die Multiplikation mit irgendeiner
orthogonalen Matrix erhält Längen und Winkel.
4J Hat Q orthonormale Spalten {Q'^Q = /), so lässt Q £äfi0^:
unverändert:
\\Qx\\ = ||x|| für jeden Vektor x. , ,;D'
Q erhält aaadx Skalarprodukte: {Qx)^{Qy) = x^Q'^Qy == x^y. Man;
wende eiBfaeh Q^Q = J!
Beweis HQxlp ist gleich ||x||2, da (Q^fiQx) = x'^Q^Qx = x^/x = x^x.
Orthogonale Matrizen sind hervorragend für Rechnungen geeignet: Die
auftretenden Zahlen können nie zu groß werden, wenn die Längen unverändert
bleiben. Gute Computerprogramme verwenden soviele Q's wie möglich. So
laufen die Programme numerisch stabil.
Projektionen mit Orthonormalbasen: Q ersetzt A
In diesem Kapitel geht es um Projektionen auf Unterräume. Wir haben
bereits Gleichungen für x, p und P hergeleitet. Bilden die Spalten einer Matrix
A eine Basis des Unterraums, so haben alle Formeln den Ausdruck A^A
verwendet. Die Einträge von Ä^A sind gerade die Skalarprodukte a^'aj.
Nehmen wir an, die Basisvektoren seien orthonormal, wir schreiben also q
statt a. Der Ausdruck A^A vereinfacht sich dann zu Q^Q = L Beachten Sie
4.4 Orthogonale Basen und Gram-Schmidt
233
die Vereinfachungen in den Ausdrücken für x, p und P. Anstelle von Q^Q
setzen wir einen Leerraum für die Einheitsmatrix:
.x = C^b und p = Qx. und P = Q_
.Q^-
D.29)
Die Kleinste-Quadrate-Lösung der Gleichung Qx = b ist einfach x = Q^h.
Die Projektionsmatrix ist P = QQ^.
Es muss in diesem Fall nicht eine einzige Matrix invertiert werden. Das
ist das Entscheidende bei einer Orthonormalbasis. Für die Berechnung der
besten Approximation x — Q^h benötigt man lediglich die Skalarprodukte
von b mit den Zeilen von Q^, also mit den q's:
r-qf--
.-ql-.
b
=
-qfb"
.q^b.
(Skalarprodukte)
Wir erkennen in dieser Gleichung n einzelne eindimensionale Projektionen.
Die „Kopplungsmatrix" oder „Korrelationsmatrix" A^A wird einfach zu
Q^Q = I. Es gibt keine Kopplung. Wir berechnen jetzt p — Q:k:
P -'
1 1 ]
ll ••• Qn
J- f J
r^b|
1 *
1 T-L^
^ qi(qfb) + -.. + q^(q^b).
D.30)
Wichtiger Fall: Ist Q quadratisch und m = n, so ist der Unterraum der
gesamte Raum. Dann gilt Q^ — Q~^ und x = Q^h ist gleich x = Q~^h.
Diese Lösung ist exakt! Die Projektion von b auf den gesamten Raum ist
einfach b selbst. In diesem Fall ist P — QQ^ = I.
Sie sind eventuell der Meinung, dass eine Projektion auf den gesamten
Raum nicht besonders erwähnenswert ist. Aber wenn wir p = b haben, ergibt
unsere Formel, dass b aus seinen eindimensionalen Projektionen
zusammensetzt werden kann. Bilden die Vektoren qi,..., Qn eine Orthonormalbasis für
den gesamten Raum, so ist Q eine quadratische Matrix, und dann ist jedes
b die Summe seiner Komponenten längs der Vektoren q^:
b - qi(qf b) + q2(qi^b) + - • + ^niqilh).
D.31)
Dies entspricht der Gleichung QQ^ = I. Sie bildet die Grundlage für die
Theorie der Fourierreihen und alle wichtigen „Transformationen" der
Angewandten Mathematik. Sie alle zerlegen Vektoren oder Funktionen in
zueinander rechtwinklige Teile. Durch Aufaddieren dieser Teile baut die inverse
Transformation die Funktion wieder zusammen.
Beispiel 4.4.4 Die Spalten dieser Matrix Q sind orthonormale Vektoren
qi5q2,q3:
234 4 Orthogonalität
Q
-12 2
2-1 2
2 2-1
hat die erste Spalte qi
3
2
3
2
3 J
Die einzelnen Projektionen von b = @,0,1) auf qi, q2 und qs sind
qi(qfb) = |qi und q2(qjb) = |q2 und q3(qjb) =-^qs.
Die Summe der ersten beiden bildet die Projektion von b auf die Ebene aus
qi und q2. Die Summe aller drei ist die Projektion von b auf den gesamten
Raum — also b selbst:
fqi +1^2
3^3 - 9
2 + 4-2'
4-2-2
4 + 4+1
=
"
0
Ij
= b.
Das Gram—Schmidt—Verfahren
Der Hintergrund dieses Abschnittes ist: „Orthogonale Vektoren sind gute
Vektoren". Projektionen und die Methode der kleinsten Quadrate verwenden
immer den Ausdruck Ä^A. Wird aus dieser Matrix Q^Q = I, so bereitet
die Inverse keine Probleme mehr. Die eindimensionalen Projektionen sind
alle entkoppelt, und die beste Approximation x ist schlicht Q^h, bestehend
aus n einzelnen Skalarprodukten. Damit dies klappt, mussten wir bis jetzt
formulieren ,,Falls die Vektoren orthonormal sind, ... ". Wir werden jetzt
einen Weg beschreiben, orthonormale zu Vektoren erzeugen.
Wir beginnen mit drei linear unabhängigen Vektoren a, b,c. Daraus
wollen wir drei orthogonale Vektoren A,B,C konstruieren. Schließlich (am
einfachstem am Schluss) dividieren wir A, B, C durch ihre Längen und erhalten
orthonormale Vektoren qi - A/||A||, q2 - B/||B|| und qs = C/||C||.
B
IIBII
Abb. 4.11. Bestimme als erstes B, dann C. Dividiere dann durch ||A||, ||B||
und IICII.
4.4 Orthogonale Basen und Gram-Schmidt 235
Gram-Schmidt Am Anfang wählen wir A = a. Das liefert uns die erste
Richtung. Die nächste Richtung muss dazu senkrecht sein. Wir nehmen dazu
h und subtrahieren davon die Projektion auf A. Es bleibt der zu A senkrechte
Teil, also der zu A orthogonale Vektor B übrig:
B = b
A7b
A^A^
D.32)
In Abbildung 4.11 sieht man, dass A und B orthogonal sind. Berechnen Sie
das Skalarprodukt von B mit A und überprüfen Sie, dass A^B = A^b -
A-^b = 0 gilt. Den Vektor B haben wir zuvor den „Fehlervektor" genannt,
der senkrecht auf A steht. Beachten Sie, dass B nicht Null sein kann, denn
sonst wären a und b linear abhängig. Von nun an halten wir die Richtungen
A und B fest.
Um die dritte Richtung zu erhalten, betrachten wir c. Dieser Vektor ist
keine Linearkombination von A und B, da c keine Linearkombination von a
und b ist. Aber höchstwahrscheinlich steht c nicht senkrecht auf A und B.
Deshalb subtrahieren wir die Komponenten in diese beiden Richtungen und
nennen das Resultat C:
C = c
A^c
a^a'
B^c
B^B
B.
D.33)
Das ist schon die ganze Idee des Gram-Schmidt-Verfahrens. Man subtrahiere
von jedem neuen Vektor die Projektionen auf die bereits gesetzten
Richtungen. Diese Idee wird in jedem Schritt wiederholt. ^
Hätten wir noch einen vierten Vektor d, so würden wir seine
Projektionen auf A, B und C davon subtrahieren und so D erhalten. Zum Schluss
dividieren wir die orthogonalen Vektoren A, B, C, D durch ihre Längen. Die
Vektoren qi,q2,q3,q4, die wir daraus erhalten, sind orthonormal.
Beispiel 4.4.5 Die linear unabhängigen Vektoren a, b, c seien
a =
1
-1
0
und b =
und c =
3
-3
3
Mit A = a erhalten wir A^ A = 2. Subtrahiere von b die Projektion auf A:
B = b-^5^A = b-|A
Probe: Es gilt A^B = 0 wie verlangt. Als nächstes subtrahiere zwei
Projektionen von c:
^ Ich glaube, die Idee stammt von Gram. Ich weiss nicht wirklich, was Schmidt
damit zu tun hat.
236 4 OrthogonaJität
c —
B=c
|A +
|B
Probe: C steht senkrecht auf A und B. Zum Schluss skaliere die Vektoren
A,B,C zu Einheitsvektoren (also Länge 1) und damit zu orthonormalen
Vektoren. Die Längen von A, B und C sind \/2, \/6 und \/3. Dividiere durch
diese Zahlen, um eine Orthonormalbasis zu erhalten:
qi
7!
und q2
_1_
und q3 =
^/3
Normalerweise enthalten die Vektoren A, B,C Brüche, und fast immer
enthalten die Vektoren qi,q2,q3 Quadratwurzeln.
Die Faktorisierung A = QR
Wir hatten das Gram-Schmidt-Verfahren mit einer Matrix A mit den
Spalten a, b,c begonnen. Wir erhielten schließlich eine Matrix Q, deren
Spalten qi, q2, qs sind. Wie hängen diese Matrizen zusammen? Da die Vektoren
a, b, c Linearkombinationen der q's sind (und auch umgekehrt), muss es eine
dritte Matrix geben, die A mit Q verbindet. Wir nennen sie R.
Der erste Schritt war qi = a/||a|| — neben a kein Einfluss anderer
Vektoren. Die zweite Gleichung war Gleichung D.32), in der b als
Linearkombination von A und B ausgedrückt wird. In diesem Schritt hatten C und qs
keinen Einfluss. Diese „Einflusslosigkeit" der später behandelten Vektoren ist
der Schlüssel zum ganzen Verfahren:
- Die Vektoren a, A und qi liegen alle auf einer Geraden.
- Die Vektoren a,b, A,B und qi,q2 liegen alle in derselben Ebene.
- Die Vektoren a, b, c und A, B, C und qi, q2, qs gehören alle zu demselben
dreidimensionalen Unter räum.
In jedem Schritt lassen sich die Vektoren ai,... ,a.k als
Linearkombinationen der qi,..., qik schreiben. Später hinzukommende q's haben keinen
Einfluss. Die verbindende Matrix R ist eine Dreiecksmatrix, es gilt A = QR-
-
ab c
L '
/;:=;,
qi q2 qa
"qfaqfbqfcl
' -qfb-qi'c 1
' ^'^]
oder;;: A = QR, D.34)
Die Gleichung A = QR ist also eine Kurzfassung des Gram-Schmidt-
Verfahrens.
4.4 Orthogonale Basen und Gram-Schmidt 237
4K, (Gram-Schmidt) Aus linear unabhängigen, Vektoren a*;»,. s %*
konstruiert das Gram-Schxxüdt-Verfahren ortJionarmale Vektoren qit\;,, q^
Die Maträe^n njit diesen Spalten genügen der filei$hung A = QR* Deshalb
ist Ä = QTA eine Dreiecksmatrix, denn spätoe q'sörtnpgohäl zu früheren
a's> weswegen qf a* W 0 für i > i gilt. ; :
Hier noch einmal die a's und q's aus dem Beispiel. Der Eintrag i,j der
Matrix R = QTA ist das Skalarprodukt von q^ mit a^-:
A= -
[12 3"
-1 0-3
0-2 3
=
1/V5 1/V6 1/V5
-l/v^ 1/V6 i/V5
0 -2/V6 1/V5J
\/2\/2 vT8
o Vß-Vß
o o 73
= <2#.
Die Längen der Vektoren A, B, C sind die Zahlen \/2, Vö, \/3 auf der
Diagonalen von R. Wegen dieser Quadratwurzeln erscheint die Faktorisierung
weniger schön als die L[/-Faktorisierung. Beide Faktorisierungen sind aber
unabdingbar für Berechnungen in der linearen Algebra.
Jede ra x n-Matrix A mit linear unabhängigen Spalten kann in ein
Produkt QR faktorisiert werden. Die ra x n-Matrix Q hat dann orthogonale
Spalten, und die quadratische Matrix R ist eine obere Dreiecksmatrix mit
positiven Diagonaleinträgen. Vergessen wir nicht, warum dies für die
Methode der kleinsten Quadrate wichtig ist: ATA ist gleich RTQTQR = RTR.
Deshalb vereinfacht sich die Gleichung ATAk = ATb zu
ßTßx = RTQTb oder ßx = QTb.
D.35)
Anstatt Ax = b zu lösen (was unmöglich ist), lösen wir also ßx = QTb durch
Rücksubstitution. Dies geht sehr schnell. Der eigentliche Aufwand liegt in den
ran2 Multiplikationen für das Gram-Schmidt-Verfahren, das gebraucht wird,
um Q und R zu bestimmen.
Es folgt ein formloser Computercode. In ihm werden die Gleichungen
D.36) und D.37) für k = 1, dann für k = 2, schließlich für k = n als
Anweisungen ausgeführt. In Gleichung D.36) werden die Vektoren auf Einheitslänge
normiert: Für k = 1,..., n setze
Tkk
1/2
und qik = -^— für alle i = 1,..., ra. D.36)
Thk
Gleichung D.37) subtrahiert die Projektionen auf qi<: Für j = k + 1,... ,n
setze
m
rkj = ^2 Qikaij und aij = aij - Qikrkj für alle i — 1,..., ra. D.37)
Beginnend mit a,b,c = ai,a2,a3 erzeugt dieser Code qi, B, q2, C, q3:
238 4 Orthogonalität
1 qi z=ai/||ai|| wie in D.36)
2 B = a2 - (qf a2)qi und C* = as - (qf a3)qi wie in D.37)
3 q2 = B/||B|| wie in D.36)
4 C = C* - (q^C*)q2 wie in D.37)
5 qs zz: C/||C|| wie in D.36)
Gleichung D.37) subtrahiert die Projektionen, sobald ein neuer Vektor qj^
bestimmt wurde. Diese Änderung (jede Projektion für sich) wird auch
modifiziertes Gram-Schmidt-Verfahren genannt. Es ist numerisch stabiler als
Gleichung D.33), in der alle Projektionen auf einmal subtrahiert werden.
Die wesentlichen Punkte
1. Bilden die orthonormalen Vektoren qi,... qn die Spalten einer Matrix Q,
so übersetzen sich die Eigenschaften qf q^ — 0 und qf q^ = 1 zu Q^Q = I.
2.Ist Q quadratisch (also eine orthogonale Matrix), so gilt Q^ = Q~^.
3.Die Länge von Qx ist gleich der Länge von x: ||Cx|| = ||x||.
4. Die Projektion auf den von den q's aufgespannten Spaltenraum ist P =
5.1st Q quadratisch, so gilt P = I, und jedes b ist gleich qi(qf b) + ... -h
qn(qnb).
6.Das Gram-Schmidt-Verfahren erzeugt orthonormale Vektoren qi,q2,q3
aus unabhängigen Vektoren a, b, c. In Matrixschreibweise ergibt sich
daraus die Faktorisierung A = QR,
Aufgaben 4.4
In den Aufgaben 1—12 geht es um orthogonale Vektoren und
Matrizen.
1. Sind diese Paare von Vektoren orthonormal, orthogonal oder nur linear
unabhängig ?
(a)
(b)
(c)
1
0
0,6
0,8
und
und
0,4
-0,3
cosO
sinO
und
-sinö
cosO
Wo nötig, ändern Sie den zweiten Vektor so, dass jedes Paar orthonormal
wird.
2. Die Vektoren B,2,-1) und (-1,2,2) sind orthogonal. Dividieren Sie
durch die Längen und bestimmen sie so orthonormale Vektoren qi und
q2. Schreiben Sie sie als Spalten einer Matrix Q und berechnen Sie Q^Q
und 00^.
4.4 Orthogonale Basen und Gram-Schmidt 239
3. (a) Die Matrix A habe drei orthogonale Spalten der Länge 4. Bestimmen
Sie A'^A.
(b) Die Matrix A habe drei orthogonale Spalten der Längen 1,2 und 3.
Bestimmen Sie A^A.
4. Geben Sie für jeden Unterpunkt ein Beispiel an:
(a) Eine Matrix Q mit orthonormalen Spalten und QQ^ 7^ /.
(b) Zwei orthogonale Vektoren, die nicht linear unabhängig sind.
(c) Eine Orthonormalbasis des M^, in der jede Komponente | oder -|
ist.
5. Bestimmen Sie zwei zueinander orthogonale Vektoren in der Ebene x +
y -{-2z = 0. Erzeugen Sie daraus orthonormale Vektoren.
6. Zeigen Sie, dass das Produkt Q1Q2 zweier orthogonaler Matrizen Qi und
Q2 wieder orthogonal ist. (Verwenden Sie die Beziehung Q^Q = /.)
7. Bestimmen Sie die Kleinste-Quadrate-Lösung der Gleichung Qx = b für
eine Matrix Q mit orthonormalen Spalten. Geben Sie ein Beispiel an mit
b 7«^ 0, aber x = 0.
8. (a) Berechnen Sie P = QQ^ für qi = @,8, 0,6, 0) und q2 = (-0,6, 0,8, 0)
Überprüfen Sie, ob P^ = P gilt,
(b) Beweisen Sie die Gleichung {QQ^){QQ^) = QQ^ für Matrizen Q mit
Q^Q = I. P = QQ^ ist die Projektionsmatrix auf den Spaltenraum
von Q.
9. Orthonormale Vektoren sind automatisch linear unabhängig.
(a) Beweis mit Vektoren: Durch welches Skalarprodukt erhält man aus
ciqi + C2q_2 + csqs = 0 die Gleichung ci = 0? Analog erhält man
C2 = 0 und cs = 0, und deshalb sind die q's linear unabhängig.
(b) Beweis mit Matrizen: Zeigen Sie, dass aus Q-x. = 0 die Gleichung
X = 0 folgt. Da Q rechteckig sein kann, dürfen Sie Q^ benutzen,
nicht aber Q~~^.
10. (a) Bestimmen Sie orthonormale Vektoren qi und q2 in der durch a =
A,3,4,5,7) und b = (-6,6,8,0,8) aufgespannten Ebene,
(b) Welcher Vektor in dieser Ebene liegt am nächsten an A,0,0,0,0)?
11. Es seien qi und q2 orthonormale Vektoren im M^. Welche
Linearkombination qi + q2 Hegt einem gegebenen Vektor b am nächsten?
12. Ist ai, a2, as eine Basis für den M^, so kann jeder Vektor b als
Xi
b = xiai + X2a2 + xssls oder | ai a2 as | | X2
= h
240 4 Orthogonalität
geschrieben werden.
(a) Angenommen, die a's sind orthonormal. Zeigen Sie, dass dann xi =
af b gilt.
(b) Nehmen Sie an, die a's seien orthogonal. Zeigen Sie, dass dann xi =
af b/af ai gilt.
(c) Sind die a's linear unabhängig, so ist xi die erste Komponente von
mal b.
In den Aufgaben 13-24 geht es um das Gram-Schmidt-Verfahren
und die Faktorisierung A = QR.
13. Welches Vielfache von a = [J] muss von b = [^] subtrahiert werden,
damit das Ergebnis B orthogonal zu a ist? Fertigen Sie eine Skizze mit
den Vektoren a, b und B an.
14. Beenden Sie das Gram-Schmidt-Verfahren aus Aufgabe 13, indem Sie
qi = a/||a|| und q2 = B/||B|| berechnen. Bestimmen Sie auch die
Faktorisierung QR:
'14
10
=
qi q2
"INI ? 1
. 0 ||B||_
15. (a) Bestimmen Sie orthonormale Vektoren qi,q2 und qa so, dass qi und
q2 den Spaltenraum von
r 1
2-
[-2
1]
-1
4j
aufspannen.
(b) Welcher der vier Unterräume enthält qa?
(c) Bestimmen Sie die beste Näherung an eine Lösung der Gleichung
^x = A,2,7) nach der Methode der kleinsten Quadrate.
16. Welches Vielfache von a = D,5,2,2) liegt am nächsten an b = A,2,0,0)?
Bestimmen Sie orthonormale Vektoren qi und q2 in der von a und b
aufgespannten Ebene.
17. Bestimmen Sie die Projektion von b auf die Gerade durch a:
"r
1
1
, b =
T
3
5
p = ? und e =: b - p
Berechnen Sie orthonormale Vektoren qi = a/||a|| und q2 = e/||e||
18. Ist ^ = Qi^ so ist Ä^A = R^R
Dreiecksmatrix mal
Dreiecksmatrix. Das Gram-Schmidt-Verfahren für A entspricht somit dem
4.4 Orthogonale Basen und Gram-Schmidt 241
Eliminationsverfahren für Ä^A. Vergleichen Sie die Pivotelemente von
A^A mit ||a|p = 3 und ||e||2 = 8 aus Aufgabe 17:
A =
1 1
13
15
und
A^A
3 9
9 35
19. Wahr oder falsch? Geben Sie jeweils ein Beispiel an:
(a) Die Inverse einer orthogonalen Matrix ist eine orthogonale Matrix.
(b) Hat die 3 x 2-Matrix Q orthonormale Spalten, so gilt ||Qx|| = ||x||
für alle x.
20. Bestimmen Sie eine Orthonormalbasis des Spaltenraums von A:
A =
1-2
1 0
1 1
1 3
und b =
Berechnen Sie die Projektion von b auf den Spaltenraum.
21. Bestimmen Sie mit dem Gram-Schmidt-Verfahren orthogonale Vektoren
A, B und C aus
a =
r
1
2
und b =
r
-1
0
und c =
0
4
22. Schreiben Sie die orthonormalen Vektoren qi,q2 und qa als
Linearkombinationen der linear unabhängigen Vektoren a, b und c. Schreiben Sie
damit A in der Form QR:
A =
1 24
005
036
23. (a) Bestimmen Sie eine Basis des durch die Lösungen der Gleichung
^1 + ^2 + ^3 - ^4 = 0
aufgespannten Unterraums S in M^.
(b) Bestimmen Sie auch eine Basis für das orthogonale Komplement S-^.
(c) Bestimmen Sie bi in S und b2 in S-^ so, dass bi +b2 = b = A,1,1,1)
gilt.
24. Gilt ad-ho 0, so haben die Einträge der Faktorisierung A = QR die
Form
242 4 Orthogonahtät
a b
c d
a—c
c a
y/a? -f c^
a^ -\- c^ ab-{- cd
0 ad- bc
Va?T^
Bestimmen Sie die Faktorisierung A = QR für a,b,c,d= 2,1,1,1 und für
1,1,1,1. Welcher Eintrag wird Null, wenn das Gram-Schmidt-Verfahren
versagt?
Die Aufgaben 25-28 verwenden den QR-Code der Gleichungen
D.11-4.12). Er fuhrt das Gram-Schmidt-Verfahren aus.
25. Erklären Sie, warum das C, das man aus C* in den Schritten nach
Gleichung D.37) erhält, gleich dem C in Gleichung D.33) ist.
26. In Gleichung D.33) werden die Komponenten längs A und B von c
subtrahiert. Warum subtrahiert man nicht die Komponenten längs a und
b?
27. Schreiben Sie ein funktionstüchtiges Computerprogramm und wenden Sie
es auf a = B,2, -1), b = @, -3,3) und c = A,0,0) an. Welche Vektoren
q^ erhalten Sie?
28. Wo in den Gleichungen D.36) und D.37) stecken die mn^
Multiplikationen?
In den Aufgaben 29—32 geht es um besondere orthogonale
Matrizen.
29. (a) Wählen Sie c so, dass Q eine orthogonale Matrix ist:
Q = c
1 -1-1-1
-1 1-1-1
-1-1 1-1
-1-1-1 1
(b) Ersetzen Sie die erste Zeile und die erste Spalte vollständig durch
Einsen, und ändern sie den Rest der Matrix so ab, dass sich wieder
eine orthogonale Matrix ergibt.
30. Projizieren Sie b = A,1,1,1) auf die erste Spalte aus Aufgabe 29(a).
Projizieren Sie dann b auf die von den ersten beiden Spalten aufgespannte
Ebene.
31. Ist u ein Einheitsvektor, so ist Q = I~-2uu^ eine Spiegelungsmatrix
(Beispiel 4.4.3). Berechnen Sie Q für u = @,1) und für u = @, \/2/2, V^/2).
Fertigen Sie Skizzen an, in denen Sie die Spiegelung beliebiger Vektoren
(x,2/) und {x,y,z) darstellen.
32. Q = I - 2uu^ ist eine Spiegelungsmatrix, falls u^u = 1 gilt.
4.4 Orthogonale Basen und Gram-Schmidt 243
(a) Zeigen Sie, dass Qu = -u gilt. Der Spiegel liegt also senkrecht zu u.
(b) Bestimmen Sie Qv für ein v mit u-^v = 0. Der Spiegel enthält v also.
33. Die ersten vier Wavelets stehen in den Spalten dieser Wavelet-Matrix
W:
w = -
1 1 v^ 0
1 1-v^ 0
1-1 0 \/2
1-1 0-v^.
Was ist an den Spalten von W besonders? Bestimmen Sie die inverse
Wavelet-Transformation W~^. Wie verhält sich W~^ zu W?
5 Determinanten
5.1 Die Eigenschaften von Determinanten
Die Determinante einer quadratischen Matrix ist eine Zahl. In dieser Zahl
ist eine erstaunliche Menge an Information über die Matrix enthalten. Man
sieht ihr beispielsweise sofort an, ob die Matrix invertierbar ist. Hat eine
Matrix keine Inverse, so ist die Determinante Null Ist A invertierbar, so ist
die Determinante von A~^ gleich l/{detA); ist beispielsweise detA = 2, so
gilt detA~^ = |. Mit Hilfe der Determinante kann man sogar eine Formel
für jeden einzelnen Eintrag von A~^ entwickeln.
Hierin besteht eine der Anwendungen von Determinanten — die
Entwicklung von Formeln für inverse Matrizen, für Pivotelemente und für
Lösungen von Gleichungen wie A~^h. Für Matrizen, deren Einträge Zahlen sind,
benötigen wir aber nur selten Formeln. Stattdessen verwenden wir häufig das
Eliminations verfahren als schnellste Möglichkeit, eine Lösung zu gewinnen.
Für eine Matrix mit Einträgen wie a,b,c und d aber zeigt uns die
Determinante, wie sich A"^ ändert, wenn sich A ändert.:
A =
a b
c d
hat die Inverse A ^ =
ad— bc
d-b
—c a
E.1)
Das Produkt dieser Matrizen ist die Einheitsmatrix /. Die Determinante
von A ist ad — bc. Gilt detA = 0, so müssten wir durch Null dividieren,
was unmöglich ist. A ist dann nicht invertierbar. (Die Zeilen von A stellen
parallele Vektoren dar, wenn a/c = b/d, also ad = bc gilt. In diesem Fall ist
die Determinante Null.) Linear abhängige Zeilen ziehen det A = 0 nach sich.
Es gibt auch eine Verbindung zu den Pivotelementen, hier a und d—{c/a)b.
Die Determinante ist gerade das Produkt der beiden Pivotelemente:
a(d b\ = ad — bc ist gleich detA.
Führt man zuerst einen Zeilentausch durch, so ergeben sich die
Pivotelemente c und b — {a/c)d. Ihr Produkt ist minus die Determinante von A. Der
Zeilentausch führte also zu einem Vorzeichenwechsel von det A.
246 5 Determinanten
Ein Blich voraus Die Determinante einer n x n-Matrix lässt sich auf ;4f||
Weisen berechnen: ***.*'* ' d$ft
1 Mm mütiplfeiert alte n Pivotelemente (mal 1 oder -1) — die Rl^J|j
forme!* ; .,',**/* - - ,/1;^
2 Mw addiert ^! Summanden,;{iaal 1 oder -1) — die „große" Eorn^|S
3 MM-komMmert^'Weinere^Determmanten-Cmal 1 oder -1) -f'^p
KÖfaktor^FormeL ' " |§||
Sie können hier schon erkennen, dass Plus- und Minus-Zeichen — also die
Entscheidung zwischen 1 und — 1 — eine wichtige Rolle für die Determinante
spielen. Das liegt an der folgenden Regel für n x n-Matrizen:
Die Determiiiaiite wechselt ihr Vorzeichen, wenn sswei ZeUje^Q
(oder zwei Spalten) der Matrix vertauscht werden* ; vgl
Die Einheitsmatrix hat die Determinante +1. Vertauscht man zwei Zeilen,
so ergibt sich eine Permutation mit det P = — 1. Vertauscht man zwei weitere
Zeilen, so ergibt sich eine neue Permutation mit detP = +1. Die Hälfte
aller Permutationen sind gerade (mit detP = +1), die andere Hälfte heißt
ungerade (mit detP = — 1). Beginnt man mit /, so entsteht die eine Hälfte
aus einer geraden Anzahl von Vertauschungen, die andere aus einer ungeraden
Anzahl. Im folgenden 2 x 2-Beispiel hat der Term ad ein positives Vorzeichen
und der Term be ein negatives — das liegt an einem Zeilentausch:
det =1 und det L n — — 1.
Die andere wesentliche Regel ist die „Linearität" der Determinante. Doch
zuerst eine Warnung: „Linearität" bedeutet hier nicht det(^4 + B) = det A +
deti?. Dies ist schlicht falsch. Diese Gleichung gilt nicht einmal für A = I
und B = I. Aus der falschen Regel würde det 21 = 1 + 1 = 2 folgen. Richtig
ist aber det 21 = 2n. Determinanten müssen also mit tn multipliziert werden,
wenn die Matrix mit t multipliziert wird. Aber greifen wir nicht zu weit vor.
Vor die Wahl gestellt, ob wir die Determinante durch Formeln oder durch
ihre Eigenschaften definieren wollen, entscheiden wir uns für die
Eigenschaften — Vorzeichentausch und Linearität Die Eigenschaften sind sehr einfach
(Abschnitt 5.1), und sie bereiten die Formeln vor (Abschnitt 5.2). Danach
kommen Anwendungen, darunter die folgenden drei:
A) Determinanten liefern A~l und A~xb (nach der Cramer'schen Regel).
B) Das Volumen eines n-dimensionalen Quaders ist |det^4|, wenn man mit
den Zeilen von A die Kanten des Quaders beschreibt.
5.1 Die Eigenschaften von Determinanten 247
C) Jene Zahlen A, für die det(^ — XI) = 0 gilt, heißen die Eigenwerte von
A. Diese Anwendung ist die wichtigste, sie ist Gegenstand des gesamten
Kapitels 6.
Die Eigenschaften der Determinante
Es gibt drei grundlegende Eigenschaften (Regeln 1, 2 und 3). Durch
Anwendung dieser Regeln lässt sich die Determinante jeder quadratischen Matrix A
berechnen. Man schreibt diese Zahl auf zwei Weisen, det A oder \A\. (Beachte:
Eckige Klammern stehen für Matrizen, gerade Linien für deren
Determinanten.) Ist A eine 2 x 2-Matrix, so führen uns die drei Regeln auf die erwartete
Antwort:
Die Determinante von
a b
c d
ist
a b
c d
= ad— bc.
Wir werden jede Regel anhand dieser Formel für 2 x 2-Determinanten
überprüfen. Dabei dürfen wir aber nicht vergessen, dass die Regeln für jede nxn-
Matrix gelten. Wollen wir beweisen, dass die Eigenschaften 4-10 aus den
Regeln 1-3 folgen, so muss der Beweis auf alle quadratischen Matrizen
anwendbar sein.
Eigenschaft 1 (die einfachste Regel) bringt die Determinante der
Einheitsmatrix / mit dem Volumen eines Einheitswürfeis in Verbindung.
1. Die Determinante der n x n-Einheitsmatrix ist 1.
10
Ol
1 und
1
1
=: 1.
2. Die Determinante ändert ihr Vorzeichen, wenn zwei Zeilen der Matrix
vertauscht werden (Vorzeichenwechsel):
Probe:
c d
a b
a b
c d
(beide Seiten sind gleich bc — ad).
Mit dieser Regel lässt sich det P für jede Permutationsmatrix bestimmen.
Man muss lediglich Zeilen von / vertauschen, bis man P erzeugt hat. Dann
gilt detP = +1, falls eine gerade Anzahl Vertauschungen nötig war und
detP = — 1 bei einer ungeraden Anzahl.
Mit der dritten Regel machen wir den Sprung, der es uns erlaubt, die
Determinante für jede quadratische Matrix zu berechnen.
3. Die Determinante als Funktion in Abhängigkeit einer einzelnen Zeile
(alle bis auf eine bleiben unverändert) ist eine lineare Funktion. Multipliziert
man die erste Spalte mit t, so multipliziert sich die Determinante mit t.
Addiert man zwei erste Zeilen, so addieren sich auch die Determinanten.
248
5 Determinanten
Diese Regel gilt nur, wenn die anderen Zeilen unverändert bleiben. Beachten
Sie, dass c und d stets gleich bleiben:
multipliziere Zeile 1 mit t:
addiere Zeile 1 von A zu Zeile 1 von A*:
tatb
c d
= t
e d
Im ersten Fall erhält man auf beiden Seiten tad — the, und t lässt sich
ausklammern. Im zweiten Fall erhält man auf beiden Seiten ad-{-a'd—bc — b'c.
Diese Regeln gelten auch, wenn A eine n x n-Matrix ist und die letzten n — 1
Zeilen unverändert bleiben. Wir wollen das an einem Zahlenbeispiel betonen:
500
010
001
= 5
100
010
001
und
1 23
010
00 1
100
010
001
+
023
010
001
Regel 3 für sich erlaubt es nicht, irgendeine dieser Determinanten zu
bestimmen. Sie verlangt lediglich, dass die Determinanten die Linearitätsbedingung
erfüllen müssen.
Durch die Kombination von Multiplikation und Addition erhalten wir jede
Linearkombination in der ersten Zeile: ^(Zeile 1 von A) + ^'(Zeile 1 von A').
Die Determinante einer Matrix mit dieser kombinierten Zeile ist t mal det A
plus t' mal det^'. Das bedeutet aber nicht det2/ = 2det/.
Um 2/ zu erhalten, müssen wir beide Zeilen mit 2 multiplizieren, so dass
zwei mal ein Faktor 2 herauskommt:
20
02
= 2^ = 4 und
t
= t'
Das ist genau so wie bei Flächeninhalten und Volumina. Vergrößert man ein
Rechteck um den Faktor 2, so wächst der Flächeninhalt um den Faktor 4.
Vergrößert man einen n-dimensionalen Quader um den Faktor t, so wächst
sein Volumen um den Faktor f^. Dieser Zusammenhang ist kein Zufall. Wir
werden noch sehen, dass Determinanten gleich Volumina sind.
Bitte beachten Sie besonders die Regeln 1-3. Durch sie wird die Zahl det A
völlig festgelegt. Für große Matrizen ist das aber nicht offensichtlich. Wir
könnten hier verharren und versuchen, eine Formel für n x n-Determinanten
zu bestimmen. Das wäre aber ein wenig kompliziert, weswegen wir es
vorziehen, schrittweise vorzugehen. Wir geben zuerst ein paar weitere Regeln an,
die direkt aus den Regeln 1-3 folgen. Diese zusätzlichen Regeln machen es
viel einfacher, mit Determinanten umzugehen.
4. Sind zwei Zeilen von A identisch, so gilt det ^ = 0.
Probe am 2 x 2-Beispiel:
a b
a b
0.
5.1 Die Eigenschaften von Determinanten 249
Regel 4 folgt aus Regel 2. (Sie erinnern sich, wir müssen die Regeln
verwenden, nicht die Formel für den 2 x 2-Fall.) Dazu vertauschen wir die beiden
identischen Zeilen. Dann muss die Determinante D ihr Vorzeichen wechseln.
D muss aber auch gleich bleiben, da die Matrix gleich bleibt. Die einzige
Zahl aber mit -D = D ist D = 0 — dies muss also die Determinante sein.
(Hinweis: In einer Bool'schen Algebra ist dieses Argument nicht anwendbar,
da dort -1 = 1 gilt. In diesem Fall definiert man die Determinante durch die
Regeln 1, 3 und 4.)
Eine Matrix mit zwei gleichen Zeilen hat keine Inverse. Nach Regel 4 gilt
in diesem Fall det^ == 0. Es ist aber auch möglich, dass Matrizen singular
sind und eine Determinante Null haben, ohne dass sie zwei identische Zeilen
besitzen. Der Schlüssel für diese Feststellung liegt in Regel 5. Sie besagt, dass
man Zeilenoperationen durchführen kann, ohne det A zu ändern.
5. Subtrahiert man ein Vielfaches einer Zeile von einer anderen Zeile, so
bleibt det A unverändert.
a b
c-lad-lb
a h
cd
Wegen der Linearität kann man die linke Seite aufspalten in den Term
auf der rechten Seite plus -^[a b]* Wegen Regel 4 ist dieser Summand aber
Null. Deshalb gilt Regel 5. Beachten Sie, dass sich nur eine Zeile ändert, alle
anderen bleiben gleich, wie es für Regel 3 verlangt wird.
Folgerung Die Determinante ändert sich hei der Anwendung der üblichen
Eliminationsschritte nicht: det A ist gleich det U. Wenn wir also die
Determinanten von Dreiecksmatrizen U berechnen können, so können wir die
Determinanten aller Matrizen bestimmen. Jeder Zeilentausch kehrt dabei das
Vorzeichen um, es gilt also immer det^ == ±detC/. Damit haben wir das
Problem der Determinantenberechnung auf Dreiecksmatrizen reduziert.
6. Eine Matrix mit einer Nullzeile hat die Determinante Null.
00
c d
Ound
a b
00
-0.
Man erhält einen einfachen Beweis, indem man irgendeine andere Zeile auf
die Nullzeile addiert. Dabei ändert sich die Determinante nicht (Regel 5). Die
Matrix hat dann aber zwei identische Zeilen und deshalb ist die Determinante
Null (Regel 4).
7. Ist A eine Dreiecksmatrix, so ist det A — aiia22 " • cinn — das Produkt
der Diagonaleinträge.
a b
Od
= ad
und ebenso
aO
c d
= ad.
Angenommen, alle Diagonaleinträge von A wären von Null verschieden.
Dann eliminiere die Einträge abseits der Diagonalen wie üblich. (Ist A eine
250
5 Determinanten
untere Dreiecksmatrix, subtrahiere Vielfache jeder Zeile von den darunter
liegenden Zeilen. Ist A eine obere Dreiecksmatrix, subtrahiere von den Zeilen
darüber.) Dieses Verfahren lässt die Determinante nach Regel 5 unverändert
— die resultierende Matrix ist jetzt aber eine Diagonalmatrix. Wir müssen
noch beweisen, dass
an
0
022
0
011022 • • 'O^nn
gilt. Dazu wenden wir die Regeln 1 und 3 an. Nach Regel drei können wir den
Faktor an aus der ersten Zeile gewinnen, es bleibt dort eine Eins. Ebenso
können wir aus der zweiten Zeile den Faktor a22 gewinnen und so weiter.
Schließlich erhält man einen Faktor
(^nn 3,US der letzten Zeile. Die
Determinante ist dann an mal a22 mal • • • mal ünn mal det 7. Nach Regel 1 ist aber
det 7= 1.
Was passiert, wenn einer der Diagonaleinträge einer Dreiecksmatrix Null
ist? Dann ist die Matrix singular, und das Eliminationsverfahren erzeugt eine
Nullzeile. Nach Regel 5 verändert sich dabei die Determinante nicht, nach
Regel 6 bedeutet eine Nullzeile aber det A = 0. Damit haben wir Regel 7
bewiesen — die Determinanten von Dreiecksmatrizen lassen sich direkt von
der Hauptdiagonalen ablesen.
8. Ist A singular, so gilt det A = 0. 1st A invertierbar, so folgt det A^^O.
a b
c d
ist singular dann und nur dann, wenn ad — hc = {).
Beweis. Mit dem Eliminationsverfahren gelangt man von A nach U. Ist A
singular, so hat U eine Nullzeile. Damit folgt det A = det U = 0. Ist A
invertierbar, so stehen auf der Diagonalen von U von Null verschiedene
Pivotelemente stehen. Deren Produkt (nach Regel 7) liefert eine von Null verschiedene
Determinante:
det A = ±detf/ = ± {Produkt der Pivotelemente).
Damit haben wir die erste Formel für die Determinante erhalten. MAT-
LAB verwendet sie, um det A aus den Pivotelementen zu berechnen. Das
Vorzeichen hängt davon ab, ob die Anzahl an Zeilen vertauschungen gerade oder
ungerade ist. Mit anderen Worten, das Vorzeichen ist die Determinante -hl
oder —1 der Permutationsmatrix P, die die Zeilenvertauschungen durchführt.
Müssen keine Zeilen vertauscht werden, so gilt P = I und det A = det U. Auf
jeden Fall gilt immer det L = 1, da L eine Dreiecksmatrix mit Einsen auf der
Diagonalen ist. Wir haben also folgendes:
Aus PA = LU folgt det P detA = det L det U.
E.2)
5.1 Die Eigenschaften von Determinanten 251
Wieder haben wir detP = ±1 und det^ = ±detU. Gleichung E.2) ist das
erste Beispiel für Regel 9.
9. Die Determinante des Produktes AB ist das Produkt det A mal det B
der Determinanten: \AB\ = \A\ \B\.
Insbesondere ist
1/det^.-
a b
c d
pq
r s
ap + br aq + bs
cp + dr cq + ds
für B = A-'^
die Determinante von A ^ gleich
AA^^ = / also gilt (det A) (det A'^) = det / = 1
Diese Produktregel ist bis jetzt die schwierigste überhaupt. Den 2 x 2-Fall
könnten wir direkt durch Nachrechnen überprüfen:
{ad — bc){ps — qr) = {ap 4- br){cq 4- ds) — {aq 4- bs){cp 4- dr).
Jetzt beweisen wir die Gleichung \AB\ — \A\\B\ für den n x n-Fall. Die
Idee ist dabei, das Verhältnis D{Ä) — \AB\I\B\ zu betrachten. Hat dieser
Ausdruck die Eigenschaften 1-3, was wir im Folgenden überprüfen, so muss
es sich um die Determinante von A handeln. (Der Fall |B| = 0 muss gesondert
behandelt werden. Das ist aber einfach: Ist \B\ = 0, so ist B singular und
daher auch AB. Dann gilt aber \AB\ =^ = \A\\B\.) Überprüfen wir also die
drei Determinanteneigenschaften für das Verhältnis |^B|/|B|:
Eigenschaft 1 (Determinante von /): Gilt ^ = 7, so wird das Verhältnis zu
\B\I\B\ = 1.
Eigenschaft 2 (Vorzeichenwechsel): Werden zwei Zeilen von A vertauscht,
trifft dies auch auf die entsprechenden Zeilen von AB zu. Deshalb wechselt
das Vorzeichen von \AB\ und auch des Verhältnisses |^5|/|B|.
Eigenschaft 3 (Linearität): Multipliziert man die erste Zeile von A mit ^,
so passiert dasselbe mit der ersten Zeile von AB. Also werden auch — wie
gewünscht — \AB\ und damit das Verhältnis mit t multipliziert.
Nehmen wir nun an, die erste Zeile von A werde zur ersten Zeile von A'
addiert, wobei die beiden Matrizen in allen anderen Zeilen übereinstimmen.
Dann wird auch die erste Zeile von AB zur ersten Zeile von A'B addiert. Nach
Regel 3 ist die Determinante dann die Summe der beiden Determinanten, und
nach Division durch \B\ gilt dies auch für das Verhältnis.
Folgerung Das Verhältnis |AB|/|B| hat die drei definierenden Eigenschaften
für \A\. Deshalb ist es gleich \A\. Damit ist die Produktregel \AB\ = \A\ \B\
bewiesen.
10. Die transponierte Matrix A^ hat die gleiche Determinante wie A.
Probe:
a b
c d
a c
bd
da beide Seiten gleich ad — bc sind.
252 5 Determinanten
Falls A Singular ist, wird aus der Gleichung \Ä^\ = \A\ schlicht 0 = 0, da Ä^
dann ebenfalls singular ist. Im anderen Fall betrachten wir die Faktorisierung
PA — LU und transponieren beide Seiten, um die Gleichung Ä^P^ — U^L^
zu erhalten. Es folgt
det PdetA = det L det U und det A^ det P^ = det U^ det L^.
Unter Anwendung von Regel 9 haben wir dann Regel 10 bewiesen, denn
erstens gilt deti = detL^. Zweitens haben wir detf/ = detf/^, da die
Transposition die Diagonale unverändert lässt, und in die Determinante
einer Dreiecksmatrix nur die Diagonale eingeht. Drittens gilt schließlich noch
det P = det P^, da für Permutationen P^ = P'^ gilt und daher |P| \P^\ = 1
nach Regel 9. Deshalb müssen |P| und |P^| beide gleich 1 oder gleich —1 sein.
Zusammen bedeutet dies durch Vergleich der beiden Gleichungen, dass det A
gleich det A^ ist.
Ein wichtiger Hinweis Durch Regel 10 wird unsere Liste von
Eigenschaften praktisch verdoppelt. Jede Regel, die für die Zeilen gilt, kann auch auf
Spalten angewendet werden, einfach, indem man die gesamte Situation
transponiert. Die Determinante wechselt also ihr Vorzeichen, wenn zwei Spalten
vertauscht werden. Multipliziert man eine Spalte mit einem Faktor t, so
geschieht dasselbe mit der Determinante. Auf die einzelnen Spalten wirkt die
Determinante als lineare Funktion.
Es ist an der Zeit inne zu halten. Unsere Liste der Eigenschaften ist lang
genug. Als nächstes werden wir eine explizite Formel für die Determinante
bestimmen, und sie auch anwenden.
Die wesentlichen Punkte
l.Die Determinante wird definiert durch die Eigenschaft der Linearität, den
Vorzeichenwechsel und die Gleichung det/ = 1.
2. Nach der Elimination ist det A gleich ± (Produkt der Pivotelemente).
3. Die Determinante hat den Wert Null genau dann, wenn A nicht invertierbar
ist.
4. Zwei bemerkenswerte Eigenschaften sind det AB — (det ^) (det B) und
det Ä^ = det A.
Aufgaben 5.1
Die Aufgaben 1-12 behandeln die Rechenregeln für
Determinanten.
1. Bestimmen Sie für eine 4 x 4-Matrix A mit Determinante det^ = 2 die
Determinanten detBA), det(-A), det(A^) und det{A~^).
2. Die 3 X 3-Matrix A habe die Determinante det A = -3. Bestimmen Sie
det(l^), det(-^) sowie det{A^) und det{A-^).
5.1 Die Eigenschaften von Determinanten 253
Wahr oder falsch? Geben Sie eine Begründung oder ein Gegenbeispiel an:
(a) Die Determinante von 7 4- A ist 1 4- det A.
(b) Die Determinante von ABC ist \A\ \B\ \C\.
(c) Die Determinante von A^ ist \A\^.
(d) Die Determinante von 4A ist 4|A|.
Durch welche Zeilenvertauschungen lässt sich zeigen, dass die folgenden
„umgekehrten Einheitsmatrizen" J3 und J4 die Determinanten \Js\ = —1
und IJ4I = +1 besitzen?
det
00 1
010
100
= -1,
aber
det
000 1
00 10
0100
1000
= 4-1.
5. Bestimmen Sie die Anzahl der für n = 5,6, 7 nötigen
Zeilenvertauschungen, um von Jn zur Einheitsmatrix In zu gelangen. Bestimmen Sie eine
Regel für alle n, und geben Sie an, ob die Anzahl für Jioi gerade oder
ungerade ist.
6. Zeigen Sie, wie sich Regel 6 (Determinante ist Null, falls eine Nullzeile
vorhanden ist) aus Regel 3 ergibt.
7. Beweisen Sie mittels der Produktregel \AB\ = \A\ \B\, dass eine
orthogonale Matrix Q Determinante 1 oder —1 hat. Beweisen Sie weiter die
Gleichung |Q| = |Q-i| = |Q^|.
8. Bestimmen Sie die Determinanten dieser Rotations- und
Spiegelungsmatrizen:
Q =
COS O—sinO
sin 6 cos 6
und Q =
l-2cos2|9-2cosl9sinl9
-2cosösinö l-2sin^ö
9. Zeigen Sie, dass \Ä^\ = \A\ gilt, indem sie die Faktorisierung A = QR
transponieren. {R ist eine Dreiecksmatrix, Q ist eine orthogonale Matrix,
beachten Sie Aufgabe 7.) Warum gilt |i?^| = |i?|?
10. Sei A eine Matrix, deren Einträge in jeder Zeile die Summe Null ergeben.
Zeigen Sie, dass det A = 0 gilt. Zeigen Sie auch, dass det{A — I) = Q gilt,
falls jede Zeilensumme den Wert eins hat. Folgt daraus, dass det A = 1
gilt?
11. Es seien C und D Matrizen mit der Eigenschaft CD — —DC. Wo liegt
der Fehler in der folgenden Argumentation? Aus CD = —DC folgt für
die Determinanten \C\\D\ = -\D\\C\. Deshalb muss entweder |C| = 0
254
5 Determinanten
oder \D\ = 0 sein. Mindestens eine der Matrizen muss deshalb singular
sein. (Das ist nicht richtig!)
12. Die Determinante der Inversen einer 2 x 2-Matrix scheint stets den Wert
Eins zu haben. Was ist an der folgenden Rechnung falsch?
detA'^ =det
ad — bc
d-b
—c a
ad— bc
ad — bc
= 1.
In den Aufgaben 13—26 verwenden Sie die Rechenregeln zur
Berechnung von Determinanten.
13. Berechnen Sie
det
indem Sie die Matrizen durch Zeilenoperationen in obere
Dreiecksmatrizen überführen.
14. Bestimmen Sie mittels Zeilenoperationen die Determinante der Vander-
monde'schen 3 x 3-Matrix
1230
2661
-1003
0205
und det
2-1 0 0
-1 2-1 0
0-1 2-1
0 0-1 2
det
1 a a^
Ibb''
lcc2
= {b — a){c - a){c — b).
15. Bestimmen Sie die Determinante einer Matrix mit Rang Eins, sowie einer
schief symmetrischen Matrix:
A =
[1-4 5] und K =
0 1 3
-10 4
-3-4 0
16. Für eine schiefsymmetrische Matrix gilt K^ = —K. Schreiben Sie a,b,c
anstelle von 1,3,4 in Aufgabe 15, und zeigen Sie so, dass \K\ — 0 gilt.
Geben Sie auch ein Beispiel einer schiefsymmetrischen 4 x 4-Matrix K
mit \K\ — 1 an.
17. Vereinfachen Sie diese Matrizen durch Zeilenoperationen und bestimmen
Sie ihre Determinanten:
det
101201301"
102 202 302
103 203 303
und det
'\te
t 1 t
e t 1
5.1 Die Eigenschaften von Determinanten
18. Berechnen Sie die Determinanten von U, U~^ und U^:
255
U =
123
045
006
und U =
a b
Od
19. Zwei verschiedene Zeilenoperationen führen von
nach
a b
c d
a - Leb- Ld
c — la d — lb
Bestimmen Sie die Determinante der zweiten Matrix. Ist sie gleich ad—bei
20. Addieren Sie Zeile 1 von A zu Zeile 2, subtrahieren Sie dann Zeile 2
von Zeile 1. Addieren Sie weiter Zeile 1 zu Zeile 2 und multiplizieren Sie
schließlich Zeile 1 mit —1. Sie erhalten B. Durch Anwendung welcher
Regeln lässt sich zeigen, dass für
A =
a b
c d
und B =
c d
a b
die Beziehung det B = — det A gilt?
Durch diese Regeln ließe sich Regel 2 in der Definition der Determinante
ersetzen.
21. Bestimmen Sie aus ad — bc die Determinanten von A, A~^ und A — XI:
1
A =
2 1
12
und A'^ =
2-1
-1 2
und A- XI =
2-X 1
1 2-A
Für welche zwei Zahlen A gilt det{A — XI) = 0? Bestimmen Sie die
Matrizen A — XI für diese beiden Werte — sie sollten nicht invertierbar
sein.
22. Berechnen Sie für A = [^ ^] die Matrizen A^, A"'^ und A ~ XI sowie
deren Determinanten. Für welche beiden Zahlen A folgt |A — A7| =0?
23. Mit dem Eliminationsverfahren gelangt man von A zu U. Dann hat man
A = LU:
A =
3 3 4"
6 8 7
3 5-9
=
10 0'
2 1 0
-14 1
3 4'
0 2-1
0 0-1
= LU.
Bestimmen Sie die Determinanten der Matrizen L, C/, A, U ^L~^ und
U-^L-^A.
24. Sei A eine n x n-Matrix, deren Eintrag an der Stelle ij gleich i • j ist.
Zeigen Sie, dass (außer iüv A = [1]) det A = 0 gilt.
256
5 Determinanten
25. Sei A nun eine n x n-Matrix, deren Eintrag an der Stelle z,j gleich i+ j
ist. Zeigen Sie, dass (außer für n = 1 oder 2) det A = 0 gilt.
26. Berechnen Sie mittels Zeilenumformungen die Determinanten der
Matrizen:
'OaO"
A =
00b
cOO
und B =
OaOO
00 60
000c
dOOO
undC =
a a a
abb
ab c
27. Wahr oder falsch? Ist eine Aussage wahr, so geben Sie eine Begründung
an, ist sie falsch, so nennen Sie ein 2 x 2-Gegenbeispiel:
(a) Ist A nicht invertierbar, so ist AB ebenfalls nicht invertierbar.
(b) Die Determinante von A ist das Produkt ihrer Pivotelemente.
(c) Die Determinante von A — B ist gleich det A — det B.
(d) AB und BA haben identische Determinanten.
28. (Eine Aufgabe aus der Analysis) Zeigen Sie, dass die partiellen
Ableitungen von f{Ä) — ln(det A) die Matrix A"^ ergeben!
/(a, 6, c, d) — ln(ad — bc) führt auf
djida df/dc
df/db df/dd
= A-
5.2 Permutationen und Kofaktoren
Ein Computer berechnet die Determinante aus den Pivotelementen einer
Matrix. In diesem Abschnitt werden wir noch andere Möglichkeiten zur
Berechnung von Determinanten beschreiben: mittels Permutationen und mittels
Kofaktoren. Wir werden eine weitere Formel für die Determinante angeben —
nachdem wir uns die Pivot-Formel noch einmal angesehen haben.
Darf ich das beste Beispiel gleich zu Anfang präsentieren? Es handelt sich
um meine Lieblings-4 x 4-Matrix:
A =
2-10 0
-1 2-1 0
0-1 2-1
0 0-1 2
Die Determinante dieser Matrix ist 5. Sie lässt sich auf drei Arten bestimmen:
l.Das Produkt der Pivotelemente ist 2 • | • | • |. Insgesamt also 5.
2. Die „große Formel" aus der noch folgenden Gleichung E.9) beinhaltet 4! =
24 Summanden. Aber nur 5 davon sind von Null verschieden:
det A = 16 - 4 - 4 - 4 + 1 = 5.
5.2 Permutationen und Kofaktoren 257
Die Zahl 16 ergibt sich aus den Zahlen 2 • 2 • 2 • 2 auf der Diagonalen. Woher
kommt die 4-1? Wenn Sie sich diese fünf Ter me erklären können, so haben
Sie Formel E.7) verstanden.
3. Die Zahlen 2,-1,0,0 aus der ersten Zeile werden mit ihren Kofaktoren
4,3,2,1 aus den anderen Zeilen multipliziert. So erhält man 2 • 4 — 1 • 3 = 5.
Diese Kofaktoren sind 3 x 3-Determinanten aus jenen Zeilen und Spalten,
die nicht den entsprechenden Eintrag der ersten Zeile enthalten. Jeder
Term in einer Determinante verwendet jede Zeile und jede Spalte genau
einmal
Die Pivot—Formel
Das Eliminationsverfahren liefert die Pivotelemente di, ..., dn auf der
Diagonalen der oberen Dreiecksmatrix U. Waren keine Zeilenvertauschungen nötig,
so muss man lediglich die Pivotelemente multiplizieren, um die Determinante
zu erhalten.
detA = (detL)(det[/) = (l)(did2 • •-dn). E.3)
Das ist unsere erste Formel für det A. Beim Übergang von A zu U bleibt
die Determinante unverändert. Die Matrix L besitzt auf der Diagonalen nur
Einsen, daher erhält man det L = 1. Formel E.3) stammt aus dem vorherigen
Abschnitt, wo wir zusätzlich die Möglichkeit von Zeilenvertauschungen
hinzugenommen hatten. Die Permutationsmatrix in der Faktorisierung PA = LU
hat als Determinante —1 oder 4-1. Dieser Faktor ±1 geht noch in die
Determinante von A ein:
(detP)(detA) = {detL)(det[/) liefert det A = ±{did2"-dn), (^-4)
Hat A weniger als n von Null verschiedene Pivotelemente, so gilt nach Regel 8
det A = 0, die Matrix ist also singular.
Beispiel 5.2.1 Durch eine Zeilenvertauschung erhalten wir die Pivotelemente
4, 2, 1 sowie das wichtige Minuszeichen:
A =
001
023
456
PA =
456
023
001
detA= -D)B)A) = -S.
Die ungerade Anzahl Zeilenvertauschungen (nämlich eine) führt zu detP =
-1.
Im nächsten Beispiel tritt keine Zeilenvertauschung auf. Es ist eine der
ersten Matrizen, die wir in Abschnitt 2.6 faktorisierten (als 3 x 3-Matrix). Es
ist hierbei bemerkenswert, dass wir direkt die n x n-Determinante behandeln
können. Große Determinanten sind also sehr leicht zu berechnen, wenn man
die Pivotelemente kennt.
258
5 Determinanten
Beispiel 5.2,2 {Die —1, 2, —1 Tridiagonal-Matrix) Die ersten drei
Pivotelemente sind 2, I und ~. Als nächstes erhält man | und | und schließlich
n+l.
2 -1
-1 2-1
-1 2
• -1
-1 2
wird zerlegt in
1
-I 1
2-1
^-1
^ 4
-1
= Lf/.
Die Pivotelemente sind auf der Diagonalen von U (der letzten Matrix) zu
finden. Multipliziert man 2, |, | und |, so heben sich alle Brüche auf, und
die Determinante der 4 x 4-Matrix ist 5. Im allgemeinen Fall erhalten wir
die Determinate n 4- 1:
detA=B)(|)(|)..-(^)=n4-l.
Die Determinante einer entsprechenden 3 x 3-Matrix ist 4. Wichtig: Die
Pivotelemente hängen nur von der oberen linken Ecke der Matrix ab. Diese
Feststellung gilt für alle Matrizen, für die keine Zeilenvertauschungen nötig
sind. Das wollen wir erklären, solange das Beispiel noch ganz frisch ist:
Die ersten k Pivotelemente ergeben sich aus einer k x fc-Matrix in
der oberen linken Ecke von A. Das Produkt did2" -dk ist die
Determinante von Ak.
Die 1 X 1-Matrix Ai enthält das allererste Pivotelement di = det Ai. Für
die 2 X 2-Matrix in der oberen linken Ecke gilt det A2 = ^1^2- Die n x n-
Determinante det An = det A schließlich verwendet alle n Pivotelemente.
Beim Eliminationsverfahren für ganz A wird die Matrix Ak zu Beginn
behandelt. Wir nehmen an, dass keine Zeilenvertauschungen nötig sind — dann
gilt A = LU und Ak = LkUk- Dividiert man immer eine Determinante durch
die vorherige {det Ak dividiert durch detAk-i), so heben sich alle Faktoren
bis auf das letzte Pivotelement dk auf. Die Pivotelemente sind Verhältnisse
von Determinanten:
jyäß^ki^PivoiplBÜx^nti^^^ dj^ =^
4idr-i.d]^.
detAk
di;da.;,4fei^i":V detAk-i
Im Beispiel der ( — 1, 2, — 1)-Bandmatrix liefern diese Verhältnisse die
korrekten Pivotelemente {k -{- l)/k.
5.2 Permutationen und Kofaktoren 259
Es werden keine Zeilenvertauschungen benötigt, wenn für alle
Eckmatrizen det Ak ^ 0 gilt
Die große Formel für Determinanten
Pivotelemente eignen sich gut zum Rechnen. In ihnen ist eine Menge
Information zusammengefasst — genug, um daraus die Determinante zu berechnen.
Auf diese Weise ist es aber unmöglich zu sehen, wie ein einzelner Eintrag üij
zur Determinante beiträgt. Das wird deutlicher, wenn wir zu den Regeln 1, 2
und 3 zurückkehren — Linearität, Vorzeichenumkehr und det/ = 1. Daraus
wollen wir eine einzige explizite Formel für die Determinante herleiten, in die
nur die Einträge üij eingehen.
Die Formel besteht aus n! Termen. Sie wird daher sehr schnell sehr groß,
da die Fakultät wie n! = 1,2,6,24,120,... wächst. Für n = 11 gibt es zum
Beispiel schon knapp vierzig Millionen Terme. Für n = 2 hingegen haben wir
nur die beiden Terme ad und bc. Der Hälfte aller Summanden geht ein
Minuszeichen voraus (wie zum Beispiel —bc), die andere Hälfte hat ein positives
Vorzeichen (wie ad). Für n = 3 sind es also 3! = 3 • 2 • 1 = 6 Summanden,
nämlich die folgenden:
<?u %3 <^U
%l ß22 Ö5231
%1 %2 ^m
_ +011022033 + 012023^31 + 013^21032 /r c\
— 011023032 — 012021033 — Oi3022Ö31-
Erkennen Sie das Muster? Jedes einzelne Produkt (wie 011O23O32) enthält
einen Eintrag aus jeder Zeile, und auch einen Eintrag aus jeder Spalte. Ist
die Reihenfolge der Spalten zum Beispiel 1, 3, 2, so hat der Term ein
negatives Vorzeichen, eine Reihenfolge 3, 1, 2 wie in 013O21O32 ergibt ein positives
Vorzeichen. Anhand dieser „Permutationen" werden wir das Vorzeichen
bestimmen.
Im nächsten Schritt (n = 4) haben wir schon 4! = 24 Terme in der Formel.
Es gibt 24 Möglichkeiten, je einen Eintrag aus jeder Zeile und jeder Spalte
auszuwählen. Der „Diagonalsummand" 011022^33044 mit der
Spaltenreihenfolge 1, 2, 3, 4 besitzt immer ein positives Vorzeichen.
Um die große Formel herzuleiten, beginne ich mit n = 2. Mein Ziel ist es,
den Ausdruck ad - bc auf systematische Weise zu erzeugen. Dazu zerlege ich
jede Zeile in zwei einfachere Zeilen:
[o b] = [o 0] -h [0 b] und [c d] = [c 0] -h [0 d].
Jetzt verwende ich die Linearität der Determinante — zuerst für die erste
Zeile (mit unveränderter zweiter Zeile), dann für die zweite Zeile (mit
festgehaltener erster Zeile):
260
5 Determinanten
a b
c d
=
=
aO
c d
aO
cO
+
+
Oh
c d
aO
Od
+
Oh
cO
+
Oh
Od
E.6)
In der letzten Zeile stehen 2^ = 4 Determinanten. Die erste und die vierte
haben aber den Wert Null, weil die Zeilen linear abhängig sind — die eine Zeile
ist ein Vielfaches der anderen. Es bleiben 2! = 2 Determinaten zu berechnen:
aO
Od
+
Oh
cO
ad
10
Ol
+ hc
Ol
10
ad — hc.
Ich will nicht darauf herumreiten — Sie sehen es schon selbst. Die Anwendung
der Regeln führt uns offenbar auf Permutationsmatrizen, die nur die Einträge
1 und 0 haben und uns die Vorzeichen liefern. Die Einsen in den
Permutationsmatrizen werden mit den Einträgen aus A multipliziert. Die Permutation
legt dabei die Reihenfolge der Spalten fest, in unserem Fall A,2) oder B,1).
Versuchen wir uns jetzt am Fall n = 3. Jede Zeile wird in 3 einfache
Zeilen (wie zum Beispiel [an 0 0]) zerlegt. Indem wir die Linearität für jede
Zeile anwenden, zerlegen wir det A in eine Summe aus 3^ = 27 einfacheren
Determinanten. Wird dabei eine Spalte zweimal gewählt, zum Beispiel wenn
wir mit der obigen Zeile auch die Zeile [a2i 0 0] betrachten, so ist diese
einfache Determinante schlicht Null. Wir müssen also nur auf die Summanden
achten, deren Einträge aus verschiedenen Spalten stammen. Damit bleiben
uns 3! = 6 Determinanten:
eJii ai2 ats
(i%l <H'^ %3
<^31 (^S2 f3l33
an
^22
^33
+
012
023
^31
+
013
021
^32
+
an
023
^32
+
Ö12
021
Ö33
+
013
022
aai
Zusätzlich wird ein Eintrag aus der ersten Zeile gewählt. Wir wollen ihn
aioc nennen, wobei die Spaltennummer a eine der Zahlen 1, 2 oder 3 ist.
Der Eintrag aus der zweiten Zeile ist dann a2/5, wobei uns noch zwei
Auswahlmöglichkeiten für ß bleiben (Spalte a können wir nicht mehr wählen, sie
ist schon „verbraucht"). Für die letzte Zeile bleibt dann nur noch eine Spalte
übrig.
Es gibt also 3! = 6 Möglichkeiten, die Spalten in eine Reihenfolge zu
bringen. Die sechs Permutationen von A,2,3) schUeßen die identische
Permutation A,2,3) ein, die sich aus P = I ergibt:
(a,/?,üj) - A,2,3), B,3,1), C,1,2), A,3,2), B,1,3), C,2,1). E.7)
5.2 Permutationen und Kofaktoren 261
Die letzten drei sind ungerade Permutationen (eine Vertauschung), die ersten
drei sind gerade Permutationen (mit keiner oder zwei Vertauschungen). Für
jede Spaltenabfolge {a,ß,(jü) wählen wir die Einträge aiaCi2ß(^3uj, wobei jede
der Reihenfolgen ihr eigenes Vorzeichen mitbringt. Die Determinante wird
also in sechs einfache Terme zerlegt, aus denen wir die Einträge der Matrix
nacheinander herausziehen dürfen:
detA = 011022^33
1
1
+ 011023^32
+ 012023^31
+ 012021033
+ 013^21032
1
1
+ 013022031
1
E.8)
Die ersten drei (geraden) Permutationen haben das Vorzeichen detP == +1,
die letzten drei (ungeraden) Permutationen das Vorzeichen detP == -1.
Damit haben wir die 3 x 3-Formel auf systematische Weise bewiesen.
Denselben Weg kann man auch im Fall einer n x n-Determinante
gehen. Dann gibt es n! Anordnungen der Spaltennummern. Für die Anordnung
(a, ^,..., üü) der Spaltennummern A,2,..., n) erhalten wir als Determinante
das Produkt aiaa2ß • • • ünuj mal plus oder minus eins. Das Vorzeichen hängt
von der Parität (gerade oder ungerade) der Reihenfolge der Spaltennummern
ab. Die Determinante der ganzen Matrix ist dann die Summe von n! einfachen
Determinanten mal 1 oder mal -1. Damit haben wir unsere große Formel:
Determinantenformel
det A — Summe über alle n! Permutationen ,P '— {a^ /3,..., o;)
= ^(det P)aiaa2ß • • • anuj
E.9)
Im 2 X 2-Fall erhält man so -\-a11a22 —0,12(^21 (das ist dasselbe wie ad—bc).
P ist hier entweder A,2) oder B,1). Für den 3 x 3-Fall erhält man drei „links
oben nach rechts unten "-Produkte und drei „rechts oben nach links unten"-
Produkte. Eine Warnung: Viele Leute glauben, dass man diesem Muster auch
im 4 X 4-Fall folgen kann und erhalten nur 8 Produkte statt der 24, die sie
eigentlich brauchen.
Beispiel 5.2.3 (Determinante von U) Ist U eine obere Dreiecksmatrix, so
kann nur eines der n! Produkte von Null verschieden sein, nämlich der Diago-
nalterm: det U = +U11U22 • • • Unn- In allen anderen Spaltenanordnungen wird
mindestens ein Eintrag unterhalb der Diagonalen ausgewählt, wo jedoch nur
Nullen stehen. Sobald wir aber einen Eintrag wie zum Beispiel 1*21 = 0 im
Produkt haben, ist dieser Summand in E.9) sicher Null.
Man erhält natürUch det/ = 1. Der einzige nicht verschwindende Term
ist der Diagonalterm +(!)(!) • • • A).
262
5 Determinanten
Beispiel 5.2.4 Sei Z die Einheitsmatrix, mit Ausnahme von Spalte 3. Dann
gilt
Determinante von Z
lOaO
Ol h^
OOcO
00dl
== c.
E.10)
Der Term A)A) (c)A) ist der Diagonal term mit positivem Vorzeichen. In
E.9) stehen noch 23 anderen Summanden mit einem Faktor aus jeder Zeile
und jeder Spalte. Sie sind aber alle Null, denn sobald wir eine der drei Zahlen
a, ö, oder d aus Spalte 3 auswählen, ist diese Spalte verbraucht. Als einzige
mögliche Auswahl für die dritte Zeile bleibt dann eine Null.
Wir können auch eine andere Begründung angeben. Ist c = 0, so enthält
Z eine Nullzeile, und det Z == c == 0 ist richtig. Ist c ungleich Null, wende das
Eliminationsverfahren an. Man subtrahiert dann ein Vielfaches von Zeile 3
von den anderen Zeilen, und löscht so die Einträge a, h und d aus. Es bleibt
eine Diagonalmatrix mit det Z = c.
Dieses Beispiel werden wir bald auch für die „Cramer'sehe Regel"
verwenden. Setzen wir die Zahlen a,b,c,d in die erste Spalte um, so erhalten
wir die Determinante det Z — a. Warum? Wenn man nur eine Spalte von
/ verändert, dann bleibt die Determinante von Z einfach zu berechnen —
nämlich als Produkt ihrer Diagonaleinträge.
Beispiel 5.2.5 Sei A eine Matrix, in der nur Einsen direkt oberhalb und
unterhalb der Haupt diagonalen stehen, wie hier für n == 4:
^4
0100
1010
0101
0010
und P4
0 100
1000
0001
0010
In der ersten Zeile ist die einzige Wahl ungleich Null die zweite Spalte. In
Zeile 4 haben wir dann als einzige Möglichkeit ungleich Null die dritte Spalte.
Dann müssen wir in den Zeilen 2 und 3 aber die Spalten 1 und 4 auswählen.
Anders gesagt: P4 ist die einzige mögliche Permutation, die von A\ nur
Einträge ungleich Null auswählt. Die Determinante von P4 ist +1 (es sind zwei
Vertauschungen nötig, um die Reihenfolge 1, 2, 3, 4 zu erreichen). Also gilt
det A4 == +1.
Determinantenberechnung über Kofaktoren
In Formel E.9) haben wir eine direkte Definition der Determinante. Sie liefert
alles auf einmal — das muss man erst einmal verdauen. Irgendwie muss diese
Summe von n! Produkten die Regeln 1, 2 und 3 für Determinanten erfüllen
(damit folgt ja schon alles weitere). Die einfachste davon ist det/ = 1, und
5.2 Permutationen und Kofaktoren
263
diese haben wir schon überprüft. Dass die Summe die Regel über die Li-
nearität erfüllt, sieht man, wenn man jeden Faktor an oder ai2 oder aia
herausgreift, der aus der ersten Zeile stammt. Für n = 3 zerlegen wie die
Determinante so in die Teile
dBtA = an @22^33 - 023032) -f a^^ @23031 - a2ia33) ,-f E.11)
+ ^13 (Ö2IÖ32 — Ö22Ö3l)-
Die drei Größen in Klammern heissen Kofaktoren. Es handelt sich jeweils
um 2 X 2-Determinanten aus Matrizen in den Zeilen 2 und 3. Aus der ersten
Zeile stammen die Faktoren an,ai2 und ai3, und aus den unteren Zeilen
kommen die Kofaktoren Cn, C12 und C13 hinzu. Man sieht hier, dass die
Determinante sicher linear von den Einträgen 011,012,013 abhängt — das ist
gerade Regel 3.
Der Kofaktor zu an ist Cn = ^22^33 - 023032- Sie können dies auch in
der folgenden Aufteilung erkennen:
an ai2 «13
Ö21 0,22 0,23
031 032 033
an
Ö22 Ö23
Ö32 Ö33
+
012
Ö21 0,23
O3I Ö33
+
Ol3
O21 O22
O3I O32
Hier wählen wir wiederum einen Eintrag aus jeder Zeile und jeder
Spalte. Da an die erste Zeile und die erste Spalte belegt, bleibt eine 2x2-
Determinante als Kofaktor.
Wie immer müssen wir dabei die Vorzeichen beachten. Die zu ai2
gehörende Determinante sieht aus wie a2ia33 — a23a3i, doch im zugehörigen Kofaktor
C12 sind die Vorzeichen vertauscht. Die Vorzeichen der Kofaktoren der
ersten Zeile sind plus — minus — plus — minus, allgemein ist das Vorzeichen
(_lji+j für den zu aij gehörenden Kofaktor Cij. Man streicht also Zeile
1 und Spalte j, und erhält so eine Untermatrix Mij. Deren Determinante
berechnet man, multipliziert sie mit (-1)^+-^ und erhält so den Kofaktor.
Die Kofaktoren sind Cij = (-1)^"^-^ detMij.
Dann gilt detA = onCn + ai2Ci2 H h ainCin-
E.12)
Man nennt dies die „Kofaktor—Entwicklung nach der ersten Zeile".
Alle Terme aus der großen Formel E.9), die mit an multipliziert werden,
lassen sich zu detMn zusammenfassen. Das Vorzeichen dafür ist (-1)^+^,
also positiv. Gleichung E.12) ist eine andere Form von Gleichung E.9), in
der die Faktoren aus der ersten Zeile zusammen mit ihren Kofaktoren aus
den Zeilen 2, 3, ..., n auftreten.
Hinweis Was für die erste Zeile funktioniert, funktioniert auch für Zeile i.
Auch zu den Einträgen aij gibt es Kofaktoren dj, also (n - 1) x (n - 1)-
Determinanten, die mit (-1)*"^-^ multipliziert werden. Da aij in Zeile i und
264
5 Determinanten
Spalte j steht, und jede Zeile und jede Spalte genau einmal verwendet werden
darf, entsteht die Matrix Mij durch Streichen von Zeile i und Spalte j. Unten
sehen wir als Beispiel 043 und die Matrix M43 (entstanden durch Streichen
von Zeile 4 und Spalte 3), deren Determinante zusammen mit dem Vorzeichen
(_ 1L+3 jgj^ Kofaktor C43 ergibt. In der Vorzeichen-Matrix erkennt man das
Muster aus positiven und negativen Vorzeichen:
A =
X '
• M43 X '
X '
X X a43 X
(-1)
i-\-3
+ - + -
- + - +
+ - + -
- + - +
5A Kofaktor-Fortnel Die D^terinmante einer Malarix A ist das Skalarpryd^;
dtikt einer Zeile i nait den zugehörigen Kofaktorent , ;;i|'|
det A — ÜiiCii + ai2Ci2 H h CHnCin' , ; .,i%8
In jedem Kofaktor Ci^ (einer 71 — 1 x n — l-Determinante ohne Zelle ii
Spalte i) ist das richtige Vorzeichen schon enthalten:
Ci, = (-l)^+^'detMi,-. '
Eine n x n-Determinante ist also eine Linearkombination von n— 1 x n— 1-
Determinanten. Eine rekursiv veranlagte Person würde damit einfach
weitermachen: Jede der Unterdeterminanten wird in Determinanten der Dimension
n — 2 zerlegt, und so weiter. Man könnte jede Determinante durch Gleichung
E.13) definieren. So gelangt man von Dimension n zu Dimension n — 1, von
dort zu Dimension n — 2, und schUeßlich bis zur Dimension 1. Definiert man
dann die 1 x 1-Determinante \a\ als die Zahl a, so erhält man eine vollständige
Definition der Determinante.
Wir haben es vorgezogen, det A von den Eigenschaften (Linearität,
Vorzeichenwechsel und det / == 1) ausgehend zu definieren. Die explizite Formel
E.9) und die Kofaktor-Formeln E.9)-E.13) folgen aus diesen Eigenschaften.
Sie erlauben es uns, A in eine einfachere Matrix wie U umzuformen, wenn
wir die Determinante berechnen wollen.
Eine letzte Formel folgt aus der Regel det A = detA'^. Wir können
nämlich eine Determinante auch nach einer Spalte in Kofaktoren entwickeln.
Entlang der Spalte j stehen die Einträge aij bis ünj- Die zugehörigen
Kofaktoren sind Cij bis Cnj, und die Determinante erhält man wieder als Skalar-
produkt.
Kofaktor-Entwicklung nach Spalte j:
det A = üijCij + a2jC2j +
I ^nj ^ nj'
E.14)
5.2 Permutationen und Kofaktoren 265
Kofaktoren sind besonders nützlich, wenn eine Matrix viele Nullen enthält.
Dies wird in den nächsten Beispielen ersichtlich:
Beispiel 5.2.6 Die (-1, 2, -1)-Bandmatrix enthält in der ersten Zeile nur
zwei Einträge ungleich Null. Die Determinante besteht also nur aus zwei
Kofaktoren:
2-1
1 2 -1
-1 2-1
-1 2
==2
2-1
-1 2-1
-1 2
(-1)
-1 -1
2-1
-1 2
E.15)
Rechts steht 2 mal Cn. Dieser Kofaktor entsteht aus genau demselben (—1,
2, -1)-Muster wie in der Matrix A, nur um eins kleiner. Der andere Kofaktor
Ci2 entstand durch Streichen von Zeile 1 und Spalte 2. Er wird mit ai2 = —1
und dem Vorzeichen (-1)^+^ = -1 multipliziert.
Um Ci2 zu berechnen, entwickeln wir nach den Kofaktoren der ersten
Spalte. Ganz oben steht der einzige von Null verschiedene Eintrag, der einen
weiteren Faktor —1 beiträgt. (Wir sind jetzt also bei —1.) Der zugehörige
Kofaktor ist wiederum eine (—1,2, — 1)-Matrix, allerdings zwei Dimensionen
kleiner als A.
Zusammenfassung Es sei Dn die Determinante der (—1,2, — 1)-Matrix der
Dimension n. Nach Gleichung E.15) erhält man die 4 x 4-Determinante D4
aus einem 3 x 3-Kofaktor D3 und einem 2 x 2-Kofaktor D2:
D4 = 2Ds — D2 und allgemein ö^ = 2JP„_i -^ Dn-2'
E.16)
Durch direktes Ausrechnen erhält man D2 = ^ und D-^ = 4. Deshalb gilt
D4 = 2D) - 3 == 5 und weiter D^ = 10 — A = 6. Alle diese Determinanten 3,
4, 5, 6 passen zu der Formel Dn = n + 1, die wir in Beispiel 5.2.2 bereits aus
den Pivotelementen hergeleitet hatten.
Die Idee hinter den Kofaktoren ist es, schrittweise die Dimension zu
reduzieren. In diesem Beispiel folgen die Determinanten Dn = n + 1 der
Rekursionsformel n+l=2n— (n — 1), wie es sein muss.
Beispiel 5.2.7 Wir betrachten dieselbe Matrix, bis auf den ersten (oberen
linken) Eintrag, der nun 1 ist:
B4 =
1 -1
-1 2-1
-1 2-1
-1 2
Es ergibt sich, dass alle Pivotelemente dieser Matrix 1 sind, weswegen die
Determinante auch 1 sein muss. Wie erhält man dieses Ergebnis aus den
Kofaktoren? Bei der Entwicklung nach der ersten Zeile stimmen alle Kofaktoren
mit Beispiel 5.2.6 überein. Wir ändern nur an = 2 zu 611 = 1:
266 5 Determinanten
det B4 = D3- D2 an Stelle von det A4 = 2D3 - D2.
Die Determinante von B4 ist 4 — 3 == 1, die Determinante jedes Bn ist n ~
(n - 1) == 1. In Aufgabe 13 sollen Sie die Determinante nach den Kofaktoren
der letzten Zeile entwickeln. Sie erhalten dann immer noch det J5n = 1.
Die wesentlichen Punkte
l.Ohne Zeilenvertauschungen gilt det^l = {Produkt der Pivotelemente). Die
Determinante der oberen linken Ecke ist detAk = {Produkt der ersten k
Pivotelemente).
2. Jeder Term in Formel E.9) verwendet jede Zeile und jede Spalte genau
einmal. Die Hälfte dieser n! Summanden hat ein positives Vorzeichen, nämlich
wenn det P = +1 gilt.
3.Der Kofaktor dj ist gleich (-l)*"*"-^, multipHziert mit der kleineren
Determinante, aus der Zeile i und Spalte j gestrichen wurden (weil diese schon
von üij besetzt sind).
4. Eine Determinante ist ein Skalarprodukt einer Zeile von A mit den
entsprechenden Kofaktoren.
Aufgaben 5.2
In den Aufgaben 1—10 wird die Formel mit n! Termen verwendet:
1. Berechnen Sie die Determinanten von A und B aus den sechs
Summanden. Sind die Spalten linear unabhängig?
123
101
1 10
und B =
1 23
444
567
2. Berechnen Sie die Determinanten von A und B. Sind die Spalten linear
unabhängig?
A =
1 10
101
Ol 1
und B =
123
456
789
3. Zeigen Sie, dass det A = 0 unabhängig von den fünf Einträgen ungleich
Null (markiert durch x) gilt.
A =
XXX
0 Ox
0 Ox
(Welchen Rang hat AI)
5.2 Permutationen und Kofaktoren 267
4. Hier sieht man auf zwei Weisen, dass det A = 0 gilt. Die Einträge x stehen
für beliebige Zahlen.
T* T* T* T* T*
»ty JU Uj JU JU
nf* qf* /TT» /TT» /TT»
*L/ *L/ tJU »Aj »Aj
0 0 Oxx
0 0 Oxx
0 0 Oxx
(a) Woran kann man erkennen, dass die Zeilen linear abhängig sind?
(b) Erklären Sie, warum jeder Term in Formel E.9) für det A gleich Null
ist.
5. Finden Sie zwei Möglichkeiten, aus jeder Zeile und Spalte Einträge
ungleich Null auszuwählen.
A =
1001
Olli
110 1
1001
B =
1 002
0345
5403
2001
{B hat die gleichen Nullen wie A).
Ist det A gleich 1 + 1 oder gleich 1 — 1 oder gleich —1
hat det El
1? Welchen Wert
6. Setzen Sie in eine 4 x 4-Matrix so wenige Nullen wie möglich so ein, dass
die Determinante Null wird. Setzen Sie auch so viele Nullen wie möglich
ein, ohne dass die Determinante Null wird.
7. (a) Es seien an — 022 = 033 = 0. Wie viele der sechs Summanden von
det A sind dann Null?
(b) Es seien an = 022 = ^33 = 044 = 0. Wie viele der 24 Produkte
aija2kO'3i(^4m sind sicher Null?
8. Für wie viele 5 x 5-Permutationsmatrizen gilt detP == +1? Dieses sind
die geraden Permutationen. Geben Sie eine Permutation an, die durch
vier Vertauschungen aus der Identität entsteht.
9. Ist det A ungleich Null, so ist mindestens einer der Terme in E.9)
ungleich Null. Folgern Sie daraus, dass für mindestens eine Anordnung der
Zeilen von A keine Null auf der Diagonalen steht. (Verwenden Sie nicht
die Permutation P aus dem Eliminations verfahren; die Matrix PA kann
Nullen auf der Diagonale haben.)
10. (a) Wie viele gerade Permutationen von A,2,3,4) gibt es? Wie lauten
sie?
(b) Eine ungerade Permutationsmatrix mal eine ungerade
Permutationsmatrix ergibt eine Permutationsmatrix.
268
5 Determinanten
In den Aufgaben 11-20 werden Kofaktoren dj = (-1)*+^ det Af^^
verwendet. Entfernen Sie dazu Zeile i und Spalte j.
11. Bestimmen Sie alle Kofaktoren und schreiben Sie sie in eine Kofaktorma-
trix C. Berechnen Sie daraus det B:
A
21
36
B =
1 23
456
700
12. Bestimmen Sie die Kofakt or matrix C und berechnen Sie A mal C^. Was
ist A-i?
2-1 0
-1 2-1
0-1 2
13. Die Matrix Bn sei gleich der (-1,2, — 1)-Bandmatrix An mit dem
Unterschied, dass bii = 1 statt an = 2 gilt Zeigen Sie unter Verwendung der
Kofaktoren der letzten Zeile von B4, dass |J54| = 2|J53| - |J52| gilt, und
bestimmen Sie |J54|:
^4-
Die Rekursionsgleichung \Bn\ = 2\Bn-i \ - |^n-2| wird erfüllt, wenn jedes
\Bn\ = 1 ist. Für die Matrizen A ergibt sich dieselbe Rekursionsgleichung.
Der Unterschied liegt lediglich in den Startwerten 1,1,1 für n = 1,2,3.
14. Die n X n Determinanten Cn haben Einsen oberhalb und unterhalb der
Diagonalen:
1-1
-1 2-1
-1 2-1
-1 2
B3 =
1-1
-1 2-1
-1 2
Ci-|0| C2 =
Ol
10
010
101
010
C4
0100
1010
0101
0010
(a) Worum handelt es sich bei den Determinanten Ci,C2,C3,C4?
(b) Bestimmen Sie den Zusammenhang zwischen Cn, Cn-i und C„-2 mit
Hilfe von Kofaktoren. Bestimmen Sie Cio-
15. Die Matrizen in Aufgabe 14 enthalten direkt ober- und unterhalb der
Diagonalen Einsen. Welche Anordnung der Spalten liefert beim
Abwärtsgehen immer Einsen? Entscheiden Sie, ob die Anordnung gerade oder
ungerade ist, und zeigen Sie damit
C„ = 0 (ungerade n) C„ = 1 (n = 4,8,-• •) C„ =-1 (n = 2,6,-••)•
5.2 Permutationen und Kofaktoren 269
16. Die A,1, l)-Tridiagonalmatrix der Dimension n hat die Determinante
El — |1| E2 =
1 1
1 1
£
1 10
1 1 1
Ol 1
E4
1 100
1110
Olli
001 1
En-
(a) Zeigen Sie über eine Kofaktorentwicklung, dass En = En-i
gilt.
(b) Beginnen Sie mit £ == 1 und E2 = 0, und bestimmen Sie £3, £4, • • •, £"8
(c) Finden Sie eine Wiederholung in der Folge der Zahlen, und
bestimmen Sie so EioQ.
17. Fn sei die Determinante der A,1, -l)-Tridiagonalmatrix der Dimension
n:
1-1
II — INI I
1-1
Fo =
1 1
= 2 F,
1-
1
0
-1
1-
1
0
-1
1
==3 F4
1 1-1
1 1-1
1 1
/4.
Benutzen Sie eine Kofaktorentwicklung, um Fn = Fn-i -\-Fn-2 zu zeigen.
Die Determinanten sind also die Fibonacci-Zahlen 1,2,3,5,8,13, — Da
die Folge normalerweise mit 1,1,2,3 beginnt, also mit zwei Einsen am
Anfang, stimmt unser Fn mit dem üblichen Fn^i überein.
18. Betrachten Sie noch einmal die Matrix Bn aus Aufgabe 13. Es ist dieselbe
Matrix wie A^ außer dass hu = 1 gilt. Verwenden Sie zur Berechnung
der Determinante die Linearität in der ersten Zeile: Es gilt [1—10] ==
[2 -1 0] - [1 0 0]. Daraus erhält man \Bn\:
1 -1
-1
0
0
■^n-
2-1
-1
0
0
in-l
10
-1
0
0
■^n-
Aus der Linearität erhält man also |5n| = |An| — |^n-i| = •
19. Erklären Sie, warum die Vandermonde'sche 4 x 4-Determinante Terme
x^, aber nicht x^ oder x^ enthält:
l a a^ a^\
\lhh^ h^
V4
l X x'^ X^
., und
.. Der
Die Determinante wird Null für x = ,
Kofaktor zu x^ is V3 = {b-a){c-a){c-b). Deshalb gilt V4 = {b-a){c-
a){c - b){x - a){x - b){x - c).
270
5 Determinanten
20. Erzeugen Sie durch Zeilenumformungen zusätzliche Nulleinträge und
berechnen Sie die Determinante von
G4 =
Olli
1011
1101
1110
Bestimmen Sie auch detG2 und detGs. Dies sind alles Matrizen mit
Nullen auf der Hauptdiagonale und Einsen überall sonst. Können Sie
det Gn angeben?
In den Aufgaben 21—24 geht es um Blockmatrizen und
Blockdeterminanten.
21. Die Determinante einer 4 x 4-Matrix lässt sich nicht immer in die
Determinanten von vier 2 x 2-Blocken zerlegen:
AB
OD
= \A\ \D\ aber
AB
CD
^|^||Z)|-|G||5|.
(a) Warum ist die erste Aussage richtig? Offenbar geht B nicht in das
Ergebnis ein.
(b) Geben Sie ein Beispiel an, um zu zeigen, dass (wie angedeutet) die
Gleichheit verloren geht, wenn C in das Ergebnis eingeht.
(c) Geben Sie auch ein Beispiel an, das zeigt, dass das Ergebnis det{AD-
CB) ebenfalls nicht richtig ist.
22. Per blockweisem Multiplizieren sieht man, dass die Faktorisierung A =
LU in der oberen linken Ecke die Form Ak = L^Uk hat:
'Ak *"
* *
=
* *
0 *
(a) A habe die Pivotelemente 2,3, —1. Bestimmen Sie die Determinanten
von I/i,L2 und L3, von U\, U2 und t/3, und von ^1,^2 und A3.
(b) Die Matrizen ^1,^2 und A3 haben die Determinanten 2,3 und —1.
Bestimmen Sie die drei Pivotelemente.
23. Beim blockweisen Eliminationsverfahren subtrahiert man das Produkt
von CA"^ mit der ersten Zeile [^5] von der zweiten Zeile. Es bleibt
das Schur-Komplement D — CA~^B in der Ecke stehen:
/ 0
-CA-^ I
AB
CD
A
0 D
B
CA-^B
Berechnen Sie die Determinanten dieser Blockmatrizen, und beweisen Sie
damit diese (korrekten) Regeln für quadratische Blöcke:
5.2 Permutationen und Kofaktoren 271
AB
CD
\A\\D-CA-^B\
falls A~^ existiert
\AD - CB\
falls AC = CA.
OA'
-B I
AB A'
0 /
7 0"
-B I
24. Ist A eine m x n-Matrix und B eine n x m-Matrix, so erhält man per
Blockmultiplikation detM = det^^:
M
Ist A eine einzelne Zeile und B eine Spalte, was erhält man für det M?
Welche Determinante erhält man, wenn A eine Spalte und B eine Zeile
ist? Geben Sie für jeden Fall ein 3 x 3-Beispiel an.
25. (Eine Frage aus der Differentialrechnung über die Kofaktorentwicklung)
(a) Bestimmen Sie die Ableitung von det^ nach au. Die anderen
Einträge seien alle festgehalten — in Gleichung E.12) werde nur an
variiert.
(b) Bestimmen Sie die Ableitung von In(det^) nach an. Nach der
Kettenregel ist sie 1/ det ^ mal das Ergebnis von (a), das ist der Eintrag
an der Position A,1) der Matrix.
26. Eine 3 x 3-Determinante besteht aus drei „links oben nach rechts unten"-
Produkten und drei mit einem negativen Vorzeichen versehenen „rechts
oben nach links unten"-Produkten. Berechnen Sie diese sechs Terme und
bestimmen Sie so D. Erklären Sie dann ohne die Verwendung von
Determinanten, warum diese Matrix invertierbar oder nicht invertierbar ist.
27. Fünf der 4! = 24 Terme aus der großen Formel E.9) für die Determinante
E4 aus Aufgabe 16 sind ungleich Null. Bestimmen Sie diese fünf Terme,
und zeigen Sie, dass E4 = —1 ist.
28. Bestimmen Sie die fünf Terme der großen Formel für die 4 x 4-Matrix
am Anfang dieses Abschnitts, aus denen man det^ = 16-4-4-4 + 1
erhält.
29. Berechnen Sie die Determinanten |5i|, |52| und |53| dieser A,3,1)-
Tridiagonalmat rizen:
272
5 Determinanten
5i = [3], 52 =
31
13
3 10
131
013
Raten Sie eine Fibonacci-Zahl für |54| und zeigen Sie, dass Sie damit
richtig liegen.
30. Die Kofaktoren der A,3,1)-Bandmatrizen liefern eine Rekursion ähnlich
der für die (-1,2, —1)-Matrizen, mit einer 3 an Stelle der 2:
\Sn\ = 3|5n-l| — |5n-2|-
Die Herausforderung: Zeigen Sie, dass die Fibonacci-Zahlen \Sn\ =
-^2n+2 diese Rekursionsgleichung erfüllen. Benutzen Sie auch dafür die
Fibonacci-Regel Fk = Fk-i + Fjk-2-
31. Ändern Sie die 3 in der oberen linken Ecke von Sn in eine 2. Zeigen Sie,
dass die Determinanten dann von den Fibonacci-Zahlen -F2n+2 auf F2n+i
fallen.
5.3 Cramer'sche Regel, Inverse und Volumen
In diesem Abschnitt geht es um Anwendungen von Determinanten, zunächst
auf die Gleichung ^x = b, und dann auf die Inverse A~^. Jeder Eintrag von
A~^ enthält det^ als Nenner — bei der Berechnung dividiert man durch
detA. (Ist die Determinante Null, so existiert A~^ nicht.) Jeder Eintrag von
A~^ ist sogar als Quotient zweier Determinanten darstellbar, ebenso wie jede
Komponente von x = A~^h.
Beginnen wir mit der Cramer'schen Regel zur Berechnung von x. Mit
einer raffinierten Idee erhält man diese Lösung sofort. Wir schreiben x in die
erste Spalte von /. Multipliziert man mit A, wird aus der ersten Spalte Ax,
also b:
xi 0 0"
X2 10
^3 Ol
=
^1 CL\2 ai3
62 022 Ö23
63 032 033
= 51.
E.17)
Hier haben wir spaltenweise multipliziert. Die erste Spalte von Bi ist ^x, die
anderen sind einfach Kopien der entsprechenden Spalten von A. Berechnen
wir jetzt die Determinanten. Die Produktregel liefert
(det^) • xi = det^i oder xi =
detBi
detA '
E.18)
Das ist die erste Komponente von x, gefunden mit der Cramer'schen Regel.
Man erhält Bi durch Austauschen einer Spalte von A.
5.3 Cramer'sehe Regel, Inverse und Volumen 273
Um X2 zu bestimmen, schreibt man den Vektor x in die zweite Spalte der
Einheitsmatrix:
ai a2 as
'Ixi 0"
0X2 0
0X3 1_
=
ai b as
Bo
E.19)
Aus den Determinanten erhält man dann (det Ä) • X2 = det B2, nach der
Cramer'sehen Regel also X2:
58 (Cramar-sche Regat) Ist det^ ungleich NuU^ so hat die Gleichung
Ax — h did eiiideutige Lösung
Xi
det^i
X2 =
detB2
det Bn
det A ' " det A ' *••' "^ det A '
Man erhält die Matrix Bj^ indem man die Spalte j von A durch b ersetzt*
Ein Computerprogramm für die Cramer'sehe Regel braucht nur eine Zeile:
x{j)=det{[A{:,l:j-l) b A{:,j-^l:n)])/det{A)
Um ein n x n-System zu lösen, muss man dabei n +1 Determinanten (von
A und den verschiedenen 5's) berechnen. Da jede Determinante eine Summe
aus n\ Termen ist (nach der „großen Formel" mit allen Permutationen) erhält
man insgesamt (n + 1)! verschiedene Terme. Es wäre wahnsinnig, auf diese
Weise Gleichungen lösen zu wollen. Aber wir haben endlich eine explizite
Formel für die Lösung x.
Beispiel 5.3.1 Wir verwenden die Cramer'sehe Regel (wofür wir hier vier
Determinanten benötigen), um das Gleichungssystem
xi+0:2+3:3 = 1
-2x1+0:2 :=0
-4x1 +2:3 = 0
zu lösen.
Die erste Determinante ist |^|. Sie sollte nicht Null sein. Dann schreiben
wir nacheinander die rechte Seite A,0,0) in die erste, zweite und dritte Spalte,
und erhalten so die Matrizen Bi, B2 und ^3:
1^1
IBo
1 1 1
-2 10
-4 0 1
1 1 1
-2 0 0
-4 0 1
= 7 und 1^11
2 und l^sl
1 1 1
010
001
111
-2 10
-4 0 0
= 1
274
5 Determinanten
Die Cramer'sche Regel drückt die Komponenten von x als Verhältnis von
Determinanten aus. Wir dividieren also immer durch \A\:
\Bi\ 1 . \B2\
2 . 1^31 4
= -unda:3 = ^ = ^.
Ich setze die Xi immer noch einmal in die Gleichungen ein und mache eine
Probe.
Eine Formel für A ^
In Beispiel 1 hatten wir als rechte Seite b = A,0,0), die erste Spalte von /.
Die Lösung x muss dann die erste Spalte der Inversen sein. Dann ergibt sich
nämlich richtig die erste Spalte auf beiden Seiten von AA"^ = I.
Daneben gibt es noch eine weitere wichtige Beobachtung: tauscht man eine
Spalte von A durch b = A,0,0) aus, um eine der Matrizen Bi zu erhalten, so
ergeben sich als Determinanten einfach 1 mal Kofaktor. Sehen wir uns noch
einmal an, dass jede Determinante \B\ ein Kofaktor ist:
l^il = 1 ist der Kofaktor Cu =
1^21 = 2 ist der Kofaktor C12 =
1^31=4 ist der Kofaktor C13 =
10
Ol
-2 0
-4 1
-2 1
-4 0
Der springende Punkt ist: Die Zähler in A"^ sind Kofaktoren, die
durch det A dividiert werden.
Um die zweite Spalte von A~^ zu erhalten, müssen wir für b den Vektor
@,1,0) einsetzen. Beobachten Sie, dass die Determinanten von ^1,^2 und
^3 jetzt die Kofaktoren der zweiten Zeile sind — inklusive der Vorzeichen
(-)(+)(-):
Ol 1
1 10
001
= -1 und
1 0 1
-2 1 0
-4 0 1
= 5 und
1 1 0
-2 1 1
-4 0 0
= -4.
Dividiert man die Zahlen -1,5 und - durch \A\ = 7, so erhält man die zweite
Spalte von A~^.
Die dritte Spalte von A~^ erhalten wir durch b = @,0,1). Die
Determinanten der 5's sind dann die Kofaktoren der dritten Zeile, nämlich —1,2 und
3. Wir dividieren wieder durch |^| = 7. Jetzt haben wir alle Spalten von A~^
berechnet:
A =
1 1 1
-2 10
mal A ^ =
1/7-1/7-1/7"
2/7 5/7-2/7
ist gleich /.
5.3 Cramer'sche Regel, Inverse und Volumen 275
Zusammenfassung Man kann A~^ berechnen, indem man die Gleichung
AA~^ = I löst. Die Spalten von / führen dann auf die Spalten von A~^.
Wir werden jetzt eine kurze Formel für A~^ mit einem direkten Beweis dafür
angeben. Dann haben Sie zwei Methoden zur Berechnung der Inversen —
indem Sie die Cramer'sche Regel auf die Spalten von / anwenden (wie oben),
oder über Kofaktoren (der schnellere Weg über Gleichung E.23) unten).
SC IFormii für .4 •^) Der Eintrag {i,j} der Matrix -Ä^^ ist !glei<^h dem
(A-'h
yjl
detA
und
-1 _
detA'
E*20)
Die Kofaktoren bilden die „Kofaktormatrix" C. Diese Matrix wird
transponiert. Um den Eintrag (z, j) von A~^ zu bestimmen, streicht man also Zeile
j und Spalte i von A, multipliziert die Determinante mit (—l)*"*"-^ (um den
Kofaktor zu erhalten), und dividiert durch det A.
Beispiel 5.3.2 Die Matrix A= [^^] hat die Kofaktormatrix C = [_b ~a]-
Betrachten wir das Produkt von A mit der Transponierten von C:
AC^ =
a b
c d
d-h
-c a
ad —he 0
0 ad—he
E.21)
Auf der rechten Seite steht det A mal /. Deshalb dividiert man durch det A
und erhält AC^/det A = /, und damit A~^:
ist
det A
gleich
1
ad — he
d-h
—e a
E.22)
In diesem 2 x 2-Beispiel verwenden wir einfach Buchstaben, im 3 x 3-
Beispiel hatten wir Zahlen. Um eine 4 x 4-Matrix zu invertieren, würden wir
16 Kofaktoren benötigen, von denen jeder eine 3 x 3-Determinante ist. Da
ist das Eliminationsverfahren schneller — aber wir kennen jetzt eine explizite
Formel für A~^.
Direkter Beweis für die Formel A"^ — C^/ det A Die Idee ist, A mit C^
zu multiplizieren:
^Zl %2 «33
Ctt C21 Csi
C?13 C23 C^33
det4 Q P '
0 ; det>t 0
0 0 detJ.
E.23)
Zeile 1 von A mal Spalte 1 der transponierten Kofaktormatrix Uefert auf der
276 5 Determinanten
Die Kofaktoren von Zeile 1: auCn H- ai2Ci2 + clisCis = detA.
Ebenso ergibt Zeile 2 von A mal Spalte 2 von C^ detA. Die Einträge a2j
werden ganz einfach mit den zugehörigen Kofaktoren C2J multipliziert.
Warum sind die Einträge in Gleichung E.23) abseits der Diagonalen
Null? Abseits der Diagonalen kombiniert man Zeilen von A mit den
Kofaktoren von anderen Zeilen. Zeile 2 von A mal Spalte 1 von C^ ergibt Null,
aber warum?
021^11 + 022^12 + Ci23Ci3 = 0.
E.24)
Die Antwort ist: dies ist die Determinante einer Matrix A* mit zwei
identischen Zeilen. A* ist gleich A, außer dass die erste Zeile eine Kopie der zweiten
Zeile ist. Deshalb gilt det ^* = 0. Genau dieser Sachverhalt wird in Gleichung
E.24) ausgedrückt. Dort steht die Entwicklung von det^* nach der ersten
Zeile, in der A* dieselben Kofaktoren Cu, C12, C13 hat wie A — weil nach der
ersten Zeile alle Zeilen übereinstimmen. Deshalb ist Gleichung E.23) korrekt.
Auf der rechten Seite steht det A mal /:
AC'^ = {det A)I oder A'^
detA'
Beispiel 5.3.3 Eine Dreiecksmatrix aus Einsen hat die Determinante 1. Die
inverse Matrix enthält dann die Kofaktoren:
A^
1000
1100
1110
1111
hat die Inverse A ^ =
10 0 0
-110 0
0-1 1 0
0 0-1 1
Wenn man Zeile 1 und Spalte 1 streicht, erhält man den Kofaktor Cu = 1.
Streicht man Zeile 1 und Spalte 2, so ist die 3 x 3-Untermatrix immer noch
eine Dreiecksmatrix mit Determinante 1. Der Kofaktor C12 ist aber -1 wegen
des Vorzeichens (—1)^"*"^. Der Eintrag B,1) (vergessen Sie das Transponieren
nicht!) von A~^ ist also —1.
Die Inverse einer Dreiecksmatrix ist also eine Dreiecksmatrix. An den
Kofaktoren sieht man, warum das so ist.
Beispiel 5.3.4 Ist A sicher invertierbar, wenn alle Kofaktoren ungleich Null
sind? Garantiert nicht.
Beispiel 5.3.5 Ein Teil der direkten Berechnung von A~^ über Kofaktoren:
0 13"
10 1
2 10
1^1 = 5
und C12 = -(-2) und A~
C22 = —6
1
5
X X
2-6
X X
x1
X
X \
5.3 Cramer'sche Regel, Inverse und Volumen 277
Der Flächeninhalt eines Dreiecks
Jeder kennt den Flächeninhalt eines Rechtecks — Grundlinie mal Höhe. Der
Flächeninhalt eines Dreiecks ist einhalb mal Grundlinie mal Höhe. Diese
Formeln geben aber keine Antwort auf diese Frage: Gegeben die Ecken (a:i,?/i),
(a^2j2/2) und (xs^ys) eines Dreiecks — wie berechnet man seinen
Flächeninhalt?
Aus den Ecken die Länge einer Grundlinie und die Höhe zu bestimmen
wäre keine gute Idee. Mit Determinanten geht es viel besser. In der Grundlinie
und der Höhe kommen zwar Quadratwurzeln vor, die sich in der Formel
aber gegenseitig aufheben. Der Flächeninhalt eines Dreiecks ist die Hälfte
einer 3 x 3-Determinante. Liegt eine der Ecken im Ursprung, zum Beispiel
{xs,ys) = @,0), so benötigt man nur eine 2 x 2-Determinante.
5p {Flächeninhatl eiiie$ Dreiecks) Das Dreieck mit den Ecken (wuyi)^
@^2,1/2) Bad (xs^ps) hat den Flächeninhalt ^ | (Determmante):
Fläche =
1
2
xi 2/1 1
X2 2/2 1
xs 2/3 1
oder
Fläche =
1
2
xi 2/1
X2 2/2
falls (^3,2/3) = @,0).
Setzt man in der 3 x 3-Determinante xs = ys = 0, so erhält man die 2x2-
Determinante. In diesen Formeln tauchen keine Wurzeln auf — es ist
sinnvoll, sie auswendig zu lernen. Die 3 x 3-Determinante zerfällt in drei 2x2-
Determinanten, ganz so, wie das dritte Dreieck in Abbildung 5.1 in drei von
@,0) ausgehende Dreiecke zerfällt.
xi 2/1 1
X2 2/2 1
Xs 2/3 1
+ |(a:i2/2 -
= +|(a:22/3 -
+ |(a:32/i -
-X2yi)
- 2:32/2)
- 2:12/3)
E.25)
Hier wird der Flächeninhalt eines allgemeinen Dreiecks als Summe von
drei speziellen Dreiecken dargestellt. Liegt @,0) außerhalb des Dreiecks, so
können zwei der drei Flächeninhalte negativ sein — es ergibt sich aber
trotzdem die richtige Summe.
Warum erhält man auf diese Weise den Flächeninhalt eines Dreiecks?
Wir können den Faktor ^ fallen lassen, wenn wir zu einem doppelt so großen
Parallelogramm aus zwei gleichen Dreiecken übergehen. Wir wollen jetzt
beweisen, dass der Flächeninhalt des Parallelogramms gleich der Determinante
2:12/2 -2:22/1 ist. In Abbildung 5.2 ist dieser Flächeninhalt 11, das Dreieck hat
daher den Flächeninhalt 5|.
Beweis, dass der Flächeninhalt eines Parallelogramms mit Ecke
@,0) als 2 X 2-Determinante darstellbar ist.
278
5 Determinanten
(iP2,2/2)
(^2,2/2)
{xi,yi)
(^1,2/1)
B:3,2/3)
Abb. 5.1. Allgemeines Dreieck; spezielles Dreieck an @,0); ein allgemeines aus
drei speziellen Dreiecken.
@,0)
@,0)
4 1
1 3
= 11
Flaeche des Dreiecks 5~
2
Abb. 5.2. Ein Dreieck als Hälfte eines Parallelogramms.
Es gibt viele Beweise, aber dieser passt in dieses Buch. Wir zeigen, dass der
Flächeninhalt die Eigenschaften 1, 2 und 3 der Determinante hat. Dann gilt
„Flächeninhalt = Determinante"! Erinnern Sie sich, dass die Determinante
über diese drei Eigenschaften definiert ist, aus denen alle weiteren
Eigenschaften folgen.
Gestrichelte Flaeche = Gefiiellte Flaeche =A+A'
Gesamtflaeche =^tA '
(•^2'3^2)
(tx^, O'i)
(^p>'l)
@,0)
{x^+x\,y^+y[)
@,0)
Abb. 5.3. Die Flächen tA und A-\- A' (eine Seite wird festgehalten) erfüllen die
Linearitätsbedingung.
1 Gilt A = I, wird das Parallelogramm zum Einheitsquadrat. Der
Flächeninhalt ist deti = 1.
2 Vertauscht man die Zeilen, so wechselt die Determinante das Vorzeichen.
Der Absolutbetrag (der positive Flächeninhalt) bleibt derselbe — es handelt
sich um dasselbe Parallelogramm.
5.3 Cramer'sehe Regel, Inverse und Volumen 279
3 In Abbildung 5.3a erkennt man, dass der Flächeninhalt mit t
multipliziert werden muss, wenn eine Zeile mit t multipliziert wird. Addiert man
Zeile 1 von A zu Zeile 1 von A' (bei gleicher Zeile 2), so ist die neue
Determinante |A| + |A'|. Abbildung 5.3b zeigt, dass die Summe der Flächeninhalte
der beiden mit durchgezogenen Linien gezeichneten Parallelogramme gleich
dem Flächeninhalt des gestrichelt gezeichneten Parallelogramms ist — da die
beiden Dreiecke, deren längste Seite gestrichelt ist, kongruent sind.
Dies ist ein exotischer Beweis, wir könnten doch einfach geometrisch
argumentieren. Dieser Beweis hat aber einen großen Pluspunkt — er ist in n
Dimensionen anwendbar. Die n vom Nullpunkt ausgehenden Kanten sind die
Zeilen einer n x n-Matrix — gerade so wie das Dreieck mit zwei Kanten vom
Nullpunkt aus. Durch weitere Kanten wird ein Kasten vervollständigt, so wie
das Parallelogramm aus dem Dreieck entstand. In Abbildung 5.4 wird ein
solcher dreidimensionaler Kasten dargestellt, dessen Kanten nicht rechtwinklig
zueinander sind.
Das Volumen des Kastens in Abbildung 5.4 ist gleich dem Absolutbetrag
von detA. Wir beweisen dies, indem wir zeigen, dass das Volumen die
Eigenschaften 1-3 der Determinante hat. Wird eine Kante um den Faktor
t gestreckt, so wird das Volumen mit t multipliziert. Wird zu Kante 1 eine
Kante 1' addiert, so hat der neue Kasten eine Kante 1 + 1', und sein
Volumen ist die Summe der beiden anderen Volumina. Dies ist die Situation
von Abbildung 5.3b, lediglich in drei (oder n) Dimensionen. Ich würde ja
dreidimensionale Kästen zeichnen, aber das Papier ist nur zweidimensional.
Der EinheitsWürfel hat das Volumen 1, also det/. Es bleibt also nur noch
Eigenschaft 2 zu überprüfen. Zeilenvertauschungen — Vertauschungen von
Kanten also — lassen den Kasten unverändert, ebenso wie sein absolutes
Volumen. Die Determinante wechselt ihr Vorzeichen, und zeigt so an, ob die
Kanten ein rechtshändiges System (det A > 0) oder ein linkshändiges System
(det A<0) bilden.
Das Volumen eines Kastens gehorcht den Gesetzen für eine Determinante,
und deshalb ist das Volumen gleich der Determinante.
(aii,ai2,ai3
Abb. 5.4. Dreidimensionaler, durch die Zeilen von A beschriebener Kasten.
280 5 Determinanten
Beispiel 5.3.6 Ein rechteckiger Kasten (90°-Winkel) habe die Seitenlängen
r, s und t. Sein Volumen ist dann r mal s mal t. Eine Matrix, die diese Kanten
beschreibt, wäre A = . Damit gilt auch detA = rst.
Beispiel 5.3.7 (Doppel- und Dreifachintegrale) In der Infinitesimalrechnung
betrachtet man infinitesimal kleine Kästchen! Sind die Koordinaten x, y und
z, so ist das Kästchenvolumen dV = dxdydz. Um über einen Kreis zu
integrieren, wollen wir von den kartesischen Koordinaten x und y vielleicht auf
Polarkoordinaten r und 9 übergehen: x = r cos 6» und j/ = r sin 9. Der
Flächeninhalt eines „Polarkoordinatenkästchens" ergibt sich als eine Determinante J
mal dr dß:
j ^ I dx/dr dx/dO
I dy/dr dy/de
cos 6 -r sin 9
sin 9 r cos 9
= r.
Die Determinante ist J = r cos ^9 + r sin^ 9 = r.Es handelt sich um das r aus
den Polarkoordinaten. Ein kleines Flächenstück ist also dA = rdrdß. Dieser
Streckungsfaktor J bewirkt in Doppelintegralen genau das, was der Faktor
dx/du m einem gewöhnUchen Integral J dx = J{dx/du) du bewirkt.
Das Kreuzprodukt
Hierbei handelt es sich um eine zusätzliche (und optionale) Anwendung,
speziell für drei Dimensionen. Betrachten wir zwei Vektoren u={ui,U2, ws) und
V = {vi,V2,V3). Auf dem folgenden Seiten geht es um deren Kreuzprodukt.
Anders als das Skalarprodukt, das eine Zahl ist, ist das Kreuzprodukt
zweier dreidimensionaler Vektoren ebenfalls ein dreidimensionaler Vektor. Man
schreibt es u X V und spricht „u kreuz v". Wir geben kurz die Komponenten
dieses Vektors an, sowie seine Eigenschaften, die ihn in Geometrie und Physik
nützlich machen.
Dieses Mal beißen wir in den sauren Apfel und führen die Formel ein
bevor die Eigenschaften besprechen.
Pfr'^IJ!^'^ Dasifne««|wd«Ät voixu = («i,W2,«3) und v = (vt,Vim)
ist der Vektor ';-"
U X V =
i j k
Ui U2 Us
Vi V2 Vs
- iu2V^ - u^'Ö2)i 4 (u^vi ^ uiv^)^^4^ (tiit/a -:'t*2^^i^
Dieö^r Vektor steht senkrecht auf u und vr Das Kreuzprochittt^ll
ist -(uxv), ," ' '-
^^M
5.3 Cramer'sche Regel, Inverse und Volumen 281
Bemerkung Am einfachsten merkt man sich u x v über eine 3x3-
Determinante. Das ist nicht ganz legal, weil die erste Zeile der Matrix die
Vektoren i, j, k und die anderen beiden Zeilen Zahlen enthalten. In der
Determinante tritt dann der Vektor i = A,0,0) multipliziert mit U2V3 und -U3V2
auf, also als Vektor {U2V3 — usV2,0,0), entsprechend der ersten Komponente
des Kreuzprodukts.
Beachten Sie das zyklische Muster der Indizes: 2 und 3 liefern die erste
Komponente, 3 und 1 die zweite Komponente, und schließlich gewinnt man
die dritte Komponente aus 1 und 2. Damit wollen wir die Definition von u x v
abschließen. Als nächstes führen wir die Eigenschaften des Kreuzprodukts
auf.
Eigenschaft 1 In v x u wird jedes Vorzeichen umgekehrt, so dass dieses
Produkt gleich -(u x v) ist. Das erwartet man auch, da ja die Zeilen 2 und
3 in der Determinantendarstellung vertauscht werden, wenn man u und v
vertauscht.
Eigenschaft 2 Das Kreuzprodukt steht senkrecht auf u und auf v. Der
einfachste Beweis dafür ist, das Skalarprodukt auszurechnen und festzustellen,
dass sich alle Terme aufheben.
U ■ (u X V) = Ui{u2Vs - U3V2) + U2{u3Vi - U1V3) + U3{UiV2 - U2V1) = 0.
E.27)
Das entspricht einem Austausch von i, j, k in der ersten Zeile gegen ui, U2,
U3. Die Determinante enthält dann zwei identische Zeilen und ist deswegen
Null.
Eigenschaft 3 Das Kreuzprodukt eines beliebigen Vektors mit sich selbst
ist u X u = 0. (In der Determinante stehen zwei gleich Zeilen.)
Auch wenn u und v parallel sind, ist das Kreuzprodukt Null. Stehen u
und V hingegen senkrecht aufeinander, so ist das Skalarprodukt Null. In dem
einen Produkt kommt sinö vor, in dem anderen cosö:
||u x^vll ^ ||u|| tMI |smÖ| und |ü vv| = t|p|l llv|| | cob0\. E.28)
Beispiel 5.3.8 Da u = C,2,0) und v = A,4,0) beide in der xy-Ebene liegen,
ist u X V parallel zur z-Achse:
U X V =
ijk
32 0
140
= 10k. Das Kreuzprodukt ist @,0,10).
Die Länge von u x v ist gleich dem Flächeninhalt des Parallelogramms mit
den Kanten u und v. Hier ist der Flächeninhalt also 10. Dies wird noch
wichtig werden.
282 5 Determinanten
Beispiel 5.3.9 Das Kreuzprodukt von u = A,1,1) und v = A 1 2) ist
A,-1,0): ' ' ' '
i jk
11 1
11 2
= 1
11
12
1 1
12
+ k
1 1
1 1
i-J
Der Vektor A, -1,0) steht senkrecht auf A,1,1) und A,1,2), wie
vorhergesagt. Der Flächeninhalt ist \/2.
Beispiel 5.3.10 Das Kreuzprodukt von A,0,0) und @,1,0) gehorcht der
Rechte-Hand-Regel und zeigt aufwärts, nicht abwärts.
ijk
100
010
ix j = k
= k
U =1
Regel u x v zeigt in Richtung
des rechten Daumens, wenn die
Finger von u nach v zeigen.
y=j
Es gut also i X j = k. Aus der Rechte-Hand-Regel folgt auch j x k = i und
k X i = j. Beachten Sie die zyklische Reihenfolge. In der anderen
Reihenfolge wird der Daumen umgedreht, und das Kreuzprodukt zeigt in die andere
Richtung: k X j = -i und i X k = -j und j X i = -k. Wir sehen hier jene
drei Pluszeichen und die drei Minuszeichen, die wir schon von der 3x3-
Determinante her kennen.
Man kann das Kreuzprodukt u x v auch über Vektoren statt über
Komponenten definieren:
DEFINITION T>e&Kr&u2^ßwauMUem^e^kkmitL^<&\\u\\
der senkredit auf u und v steht «ii«J gemäß d^ Rßchle-ffaod-Itei*ils^''
„oben" odarnach^tmt^" zeigt. ' ,- ■ ■ .,■.:.;/,. r/'-.v-uv-/
Diese Definition ist interessant für Physiker, die es nicht mögen, Achsen und
Koordinaten wählen zu müssen. Für sie ist {u,,U2,us) die Position einer
Masse und (F^, F„, F,) eine Kraft, die darauf wirkt. Ist F parallel zu u, dann
ist u X F - 0 — es gibt keine Drehung, die Masse wird gestoßen oder gezogen.
Das Kreuzprodukt uxF ist die drehende Kraft, oder besser das Drehmoment
i^s zeigt längs der Drehachse, senkrecht zu u und F. Die Länge llull HFII sinö
gibt den Betrag des Drehmoments an.
5.3 Cramer'sche Regel, Inverse und Volumen 283
Spatprodukt = Determinante = Volumen
Da u X V ein Vektor ist, kann man dessen Skalarprodukt mit einem dritten
Vektor w betrachten. Man erhält so das Spatprodukt (u x v) • w.
Dabei handelt es sich um eine Determinante:
(ti X v) • w =
Wi W2 Ws
Ui U2 Us
Vi V2 VS
=
Ui U2 Us
Vi V2 Vs
Wi W2 Ws
E.29)
Dabei können wir w in in die obere oder die untere Zeile schreiben — die
Determinanten sind gleich, weil Vertauschungen nötig sind, um von
der einen zur anderen zu gelangen. Beachten Sie, in welchem Fall die
Determinante Null ist:
(u X v) • w = 0 genau dann, wenn die Vektoren u, v, w in derselben
Ebene liegen.
- Erste Begründung u x v steht senkrecht auf der Ebene, so dass das
Skalarprodukt mit w Null ergibt.
- Zweite Begründung Drei Vektoren in einer Ebene sind notwendigerweise
linear abhängig. Die Matrix ist also singular, und die Determinante ist
Null.
- Dritte Begründung Die Determinante stellt ein Volumen dar. Dcts Volumen
muss Null sein, wenn der durch u, v und w aufgespannte Kasten sich in
einer Ebene befindet.
Es ist sehr bemerkenswert, dctss (u x v) ■ w gleich dem Volumen des Kastens
mit den Kanten u, v, w ist.
Beide Werte sind durch die 3 x 3-Determinante gegeben — die eine Menge
an Information enthält. Analog dem Ausdruck ad — bc für eine 2 x 2-Matrix
trennt sie invertierbar von singular. Kapitel 6 wird sich mit dem singulären
Fall beschäftigen.
Die wesentlichen Punkte
1. Mit der Cramer'sehen Regel erhält man eine Lösung der Gleichung ^x = b
durch Ausdrücke wie Xi = |ba2 ... a„|/m.
2. Die Formel für die inverse Matrix ist A~^ = C^/(det ^).
3. Dcts Volumen eines Kastens, dessen Seiten durch die Zeilen von A gegeben
sind, ist | det^|.
4. Dieses Volumen wird zum Beispiel für einen Koordinatenwechsel bei Doppel-
und Dreifachintegralen benötigt.
5. Das Kreuzprodukt u x v steht senkrecht auf u und v.
Aufgaben 5.3
In den Aufgaben 1-5 geht es um die Cramer'sche Regel für die
Lösungen der Gleichung x = A~^h.
284 5 Determinanten
1. Lösen Sie die folgenden linearen Gleichungssysteme mit Hilfe der
Cramer'sehen Regel Xj = det Bj / detA:
. . 2xi + 3x2 = 1
^^^ xi + 4x2 = -2
2xi + X2 =1
(b) xi + 2x2 + 2:3 = 0
X2 + 2X3 = 0.
2. Bestimmen Sie mit der Cramer'sehen Regel eine Lösung für y. Nennen
Sie die 3 x 3-Determinante dabei D:
ax + by + cz = 1
(a)
ax + by = 1
ex + dy = 0
(b) dx + ey + fz = 0
gx + hy + iz = 0.
Die Cramer'sche Regel versagt im Falle det ^ = 0. Im Beispiel (a) gibt
es keine Lösung, im Beispiel (b) unendlich viele. Was ergibt sich für die
Ausdrücke Xj = det Bj/ det A in diesen beiden Fällen?
2xi + 3x2 = 1 ^^^ 2xi + 3x2 = 1
(a)
4x1 + 6x2 = 1
(b)
4xi + 6x2 = 2.
4. Ein kurzer Beweis für die Cramer'sche Regel Die Determinante ist eine
lineare Funktion in der ersten Spalte. Sie hat den Wert Null, wenn zwei
Spalten gleich sind. Schreibt man b = ^x = ^sljXj als erste Spalte von
A, so ergibt sich für die Determinante dieser Matrix Bi
|b a2 a3| = l^ajXj a2 a3| = xi|ai a2 a3| = Xi det^.
(a) Welche Formel für xi kann man aus dieser Gleichung herleiten?
(b) Warum ist die mittlere Determinante gleich der rechten Seite?
5. Die erste Spalte von A sei gleich der rechten Seite b. Lösen Sie das
3 X 3-System ^x = b. Wie tragen die einzelnen Determinanten der
Cramer'sehen Regel zur Lösung bei?
In den Aufgaben 6-16 geht es um die Formel A~^ = C^/det A.
Vergessen Sie nicht, C zu transponieren.
6. Bestimmen Sie A~^ mit Hilfe der Kofaktor-Formel C^/ det A. Verwenden
Sie in Teil (b) die Symmetrie von A.
(a) A =
(b) A =
20"
030
04 1
2-1 Ol
-1 2-1
0-1
2_
5.3 Cramer'sche Regel, Inverse und Volumen 285
7. Wieso hat A sicher keine Inverse, wenn alle Kofaktoren Null sind? Kann
man sicher sein, dass A invertierbar ist, wenn alle Kofaktoren ungleich
Null sind?
8. Bestimmen Sie die Kofaktoren von A und berechnen Sie AC^ zur
Bestimmung von det A:
A =
1 1 1
122
1 25
undC =
6-3 0
9. Angenommen, Sie kennen alle Kofaktoren einer Matrix A, und wissen
außerdem, dctss det A = 1 gilt. Wie können Sie A bestimmen?
10. Beweisen Sie mit Hilfe der Formel AC^ = (det A)I die Gleichung det C =
(detA)"-^
11. (Nur für Professoren) Wie bestimmt man eine invertierbare 4 x 4-Matrix
A aus ihren 16 Kofaktoren?
12. Zeigen Sie, dass alle Einträge von A"^ ganze Zahlen sind, wenn alle
Einträge von A ganzzahlig sind, und det A = 1 oder det A = — 1 gilt. Geben
Sie als Beispiel eine 2 x 2-Matrix an.
13. Es seien umgekehrt alle Einträge von A und A"^ ganzzahlig. Beweisen
Sie, dctss det^ = 1 oder det^ = -1 gilt. Hinweis: Was erhält man für
det A mal detA'^?
14. Beenden Sie die Berechnung von A~^ in Beispiel 5.3.5 mit Hilfe von
Kofaktoren.
15. Es seien L eine invertierbare untere Dreiecksmatrix und S eine
symmetrische invertierbare Matrix.
L =
aO 0
bcO
def
S =
ab d
b c e
def
(a) L ^ ist ebenfalls eine untere Dreiecksmatrix. Welche Kofaktoren sind
Null?
(b) S"^ ist ebenfalls symmetrisch. Welche Kofaktoren stimmen überein?
16. Für n = 5 besteht die Matrix C aus Kofaktoren, jeder dieser
4 X 4-Kofaktoren besteht aus Termen, die zur Berechnung jeweils
Multiplikationen erfordern. Vergleichen Sie dies mit den 5^ = 125
Multiplikationen, die das Gauß-Jordan-Verfahren in Abschnitt 2.4 zur
Berechnung von A"'^ benötigt.
286 5 Determinanten
In den Aufgaben 17—26 geht es um Flächeninhalte und Volumina,
die als Determinanten ausgedrückt werden.
17. (a) Bestimmen Sie den Flächeninhalt eines Parallelogramms mit den
Kanten v = C,2) und w = A,4).
(b) Bestimmen Sie den Flächeninhalt eines Dreiecks mit den Seiten v, w
und V + w. (Skizze.)
(c) Bestimmen Sie den Flächeninhalt eines Dreiecks mit den Seiten v, w
und w - V. (Skizze.)
18. Ein Kasten habe Kanten von @,0,0) nach C,1,1), nach A,3,1) und
nach A,1,3). Bestimmen Sie sein Volumen sowie den Flächeninhalt jeder
Seitenfläche (Parallelogramme) mittels des Kreuzprodukts ||u x v||.
19. (a) Als Ecken eines Dreiecks seien B,1), C,4) und @,5) gegeben.
Bestimmen Sie den Flächeninhalt,
(b) Bestimmen Sie den Flächeninhalt des Vierecks, das durch Hinzufügen
eines Eckpunkts (—1,0) entsteht.
20. Das Parallelogramm mit den Kanten B,1) und B,3) hat denselben
Flächeninhalt wie dcts Parallelogramm mit den Kanten B,2) und A,3).
Bestimmen Sie die Flächeninhalte aus einer 2 x 2-Determinante, und
erklären Sie, warum diese gleich sein müssen. (Ich kann mir die Gleichheit
nicht an einem Bild erklären. Wenn Sie eine Erklärung finden, schreiben
Sie mir bitte.)
21. (a) Die Spaltenvektoren einer 3 x 3—Matrix mögen die Längen Li, L2
und Ls haben. Welchen größtmöglichen Wert kann die Determinante
annehmen?
(b) Kann die Determinante einer 3 x 3-Matrix mit \aij\ = 1 den Wert 6
annehmen?
22. Zeigen Sie anhand einer Skizze, wie der Flächeninhalt unseres
Parallelogramms durch ein Rechteck mit Flächeninhalt Xiy2 minus ein Rechteck
mit Flächeninhalt X2yi dargestellt werden kann.
23. Sind die Kanten a, b und c eines Kastens rechtwinklig zueinander, so
hat der Kasten das Volumen ||a|| mal ||b|| mal ||c||. Die Matrix Ä^A ist
. Bestimmen Sie die Determinanten von Ä^A und A.
24. Der Kasten mit den Kanten i, j und w = 2i + 3j + 4k hat die Höhe
. Bestimmen Sie sein Volumen. Wie sieht die Matrix aus, deren
Determinante das Volumen darstellt? Weis erhält man für i x j und für
das Skalarprodukt davon mit w?
5.3 Cramer'sehe Regel, Inverse und Volumen 287
25. Wie viele Ecken und wie viele Kanten hat ein n-dimensionaler Würfel?
Wie viele (n - l)-dimensionale Seitenflächen hat er? Welches Volumen
hat der Würfel, dessen Kanten die Zeilen von 27 sind? Ein Parallelrechner
mit der Architektur eines solchen Hyperwürfels besitzt für
jede Ecke des Würfels einen Prozessor und Kommunikationsverbindungen
zwischen je zwei Ecken, die durch eine Kante des Hyperwürfels verbunden
sind.
26. Das Dreieck mit den Ecken @,0), A,0), @,1) hat den Flächeninhalt |.
Die Pyramide mit den vier Ecken @,0,0), A,0,0), @,1,0), @,0,1) hat
da^ Volumen . Welches Volumen hat eine vierdimensionale
Pyramide mit @,0,0,0) und den Spalten von 7 als Ecken?
In den Aufgaben 27—30 geht es um Flächenelemente dA und Volu-
menelemente dV in der Infinitesimalrechnung.
27. Die Polarkoordinaten r,ö sind durch x = rcosO und y = rsinO definiert.
Die Darstellung eines Flächenelements in Polarkoordinaten enthält J:
J =
dx/dr dx/de
dy/dr dy/dO
cos 6—r sin 6
sin 0 r cos 0
Die beiden Spalten sind orthogonal mit den Längen
J= .
.. Deshalb gilt
28. Die Kugelkoordinaten p,(f),0 sind durch x = psin(/)COSÖ, y = psin(/)sinö
und z = pcos(j) definiert. Berechnen Sie die 3 x 3-Matrix der partiellen
Ableitungen mit dxjdp, dx/dcj)^ dxld0 in der ersten Zeile. Vereinfachen
Sie die Determinante tm J — fp' sin 0. Ein Volumenelement ÖV wird dann
in Kugelkoordinaten durch p^ sin (p dp d(j)d0 ausgedrückt.
29. In Aufgabe 27 steht die Matrix, die r, ö mit x,y verbindet. Invertieren
Sie sie:
J-' =
dr/dx dr/dy
80/dx 00/dy
cosö ?
? ?
— ?
überraschenderweise ergibt sich dr/dx = dx/dr (siehe Calculus,
Gilbert Strang, S. 501). Aus dem Produkt der Matrizen in Aufgabe 27 und
in Aufgabe 29 erhält man die Kettenregel ff = |^f^ + ff|f = l.
30. Das Dreieck mit den Ecken @,0), F,0), und A,4) hat den Flächeninhalt
. Dreht man es um 0 = 60°, so ist der Flächeninhalt . Die
Determinante der Drehmatrix ist
J =
cos ö — sin ö
sin 0 cos 0
1 ?
2 •
? ?
288 5 Determinanten
In den Aufgaben 31—37 geht es um Spatprodukte (u X v) • w in drei
Dimensionen.
31. Ein Kasten habe die Grundfläche ||u x v||. Die dazu senkrechte Höhe sei
||w|| cosö. Das Volumen berechnet man aus Grundfläche mal Höhe, es ist
also ||ux v|| ||w|| cosö gleich (ux v)-w. Berechnen Sie die Grundfläche, die
Höhe und das Volumen für u = B,4,0), v = (-1,3,0) und w = A,2,2).
32. Das Volumen des gleichen Kastens lässt sich auch als 3 x 3-Determinante
ausdrücken. Berechnen Sie diese Determinante.
33. Entwickeln Sie die 3 x 3-Determinante in Gleichung A3) aus den Kofak-
toren der Zeile ui,U2,U3, Sie erhalten das Skalarprodukt von u mit dem
Vektor .
34. Welches der Spatprodukte (u x w) • v, (w x u) • v und (v x w) • u hat
denselben Wert wie (u x v) • w? Für welche Reihenfolgen der Zeilen u,
V und w erhält man die richtige Determinante?
35. Es seien P = A,0,-1), Q = A,1,1) und R = B,2,1). Wählen Sie S
so, dass PQRS ein Parallelogramm ist, und berechnen Sie seine Fläche.
Wählen Sie Punkte T, U und V so, dass OPQRSTUV ein Parallelepiped
ist, und berechnen Sie sein Volumen.
36. Angenommen, die Punkte {x,y,z), A,1,0) und A,2,1) liegen in einer
Ebene durch den Ursprung. Welche Determinante ist dann Null? Welche
Ebenengleichung erhält man daraus?
37. Es sei {x,y,z) eine Linearkombination von B,3,1) und A,2,3). Welche
Determinante ist dann Null? Welche Gleichung für die Ebene erhält man
daraus?
38. (a) Erklären Sie anhand der Volumeninterpretation, warum det2^ =
2" det ^ für n X n-Matrizen gilt,
(b) Für Matrizen welcher Größe gilt det ^ + det ^ = det(^ -\- A) ?
6 Eigenwerte und Eigenvektoren
6.1 Eigenwerte: Einführung
Lineare Gleichungen Ax = b rühren von Gleichgewichtsproblemen her.
Eigenwerte sind am wichtigsten bei dynamischen Problemen. Deren Lösungen
ändern sich mit der Zeit — sie wachsen, sie klingen ab, oder sie oszillieren.
Solche Lösungen lassen sich mit dem Eliminations verfahren nicht bestimmen.
In diesem Kapitel begegnen wir einem ganz neuen Teil der linearen Algebra.
Dabei werden alle Matrizen quadratische Matrizen sein.
Als gutes Beispiel kann man die Potenzen A,A'^,A^,... einer Matrix
heranziehen. Angenommen, wir suchen die hundertste Potenz A^^^. Schon nach
ein paar Schritten kann man die ursprüngliche Matrix A überhaupt nicht
mehr erkennen:
0,8 0,3
0,2 0,7
0,70 0,45
0,30 0,55
A^
0,650 0,525
0,350 0,475
A^
0,6000 0,6000
0,4000 0,4000
y^ioo wurde hier mit Hilfe der Eigenwerte von A bestimmt, nicht, indem
100 Matrizen miteinander multipliziert wurden. Diese Eigenwerte können wir
als neue Möglichkeit auffassen, ins Innerste einer Matrix zu blicken.
Um Eigenwerte zu erklären, erklären wir zunächst Eigenvektoren. Fast alle
Vektoren ändern ihre Richtung, wenn sie mit A multipliziert werden. Einige
„Ausnahme-"Vektoren x aber liegen in derselben Richtung wie ^x. Solche
Vektoren nennt man „Eigenvektoren". Multipliziert man einen Eigenvektor
mit A, so ist das Ergebnis ^x gleich einer Zahl A, multipliziert mit dem
Anfangsvektor x.
Die grundlegende Gleichung ist also ^x = Ax. Die Zahl A ist dabei der
„Eigenwert". Ihr Wert entscheidet darüber, ob der spezielle Vektor x
gestreckt, gestaucht oder umgedreht wird, oder ob er unverändert bleibt, wenn
er mit A multipliziert wird. Man könnte A = 2, A=:|,A = -1 oder A = 1
vorfinden. Der Eigenwert A kann auch Null sein. Die Gleichung ^x = Ox
bedeutet schlicht, dass dieser Eigenvektor x im Kern von A liegt.
Ist A die Einheitsmatrix, so gilt für jeden Vektor Ax = x, so dass alle
Vektoren Eigenvektoren sind, nämlich zum Eigenwert A = 1. Dies ist, vorsichtig
290 6 Eigenwerte und Eigenvektoren
gesagt, unüblich. Die meisten 2 x 2-Matrizen haben zwei
Eigenvektorrichtungen und zwei Eigenwerte. In diesem Abschnitt werden wir erklären, wie
man die Eigenvektoren x und die Eigenwerte A bestimmt. Dies kann deshalb
so früh im Kurs kommen, weil man dazu lediglich die Determinante einer
2 X 2-Matrix benötigt.
Hier sehen Sie die Eigenvektoren xi und X2 der Matrix A in unserem
Beispiel. Multipliziert man diese Vektoren mit A, so erhält man xi und ^X2.
Die Eigenwerte A sind also 1 und ^:
xi =
X2 =
■0,6"
ll
-ij
und Axi =
und Ax2 —
[0,8 0,3]
[o,2 0,7j
[0,8 0,3]
•0,2 0,7j
[0,6'
[0,4
r ll
[-ij
Xl {u
0,5"
-0,5
(= |x2, also A2 = \).
Multiplizieren wir xi noch einmal mit A^ so erhalten wir wieder xi. Für
jede Potenz von A gilt A^yi\ — xi. Wenn man X2 mit A multipliziert, erhält
man |x2, und multipliziert man das Ergebnis noch einmal mit A, hat man
A)^X2. Quadriert man A, so bleiben die Eigenvektoren xi und X2
unverändert. Die Eigenwerte sind hingegen 1^ und (|)^ — sie werden
quadriert! Dieses Muster wiederholt sich für höhere Potenzen, weil die
Eigenvektoren immer in ihrer Richtung bleiben, und nie vermischt werden (siehe
Abbildung 6.1). Die Eigenvektoren von A^^^ sind genau dieselben Vektoren
Xl und X2. Die Eigenwerte von A^^^ sind 1^^^ = 1 und (|)^^^, also eine sehr
kleine Zahl.
0,6
0,4
^^xi = AJx1
A'^2 = @,5)^X2 :
ylX2 = A2X2 =
0,5
-0,5
0,25
-0,25
X2 =
1
-1
Abb. 6.1. Die Eigenvektoren behalten ihre Richtung. Die Eigenwerte von A^ sind
die Zahlen A^.
Andere Vektoren ändern ihre Richtung. Andere Vektoren sind aber auch
Linearkombinationen der beiden Eigenvektoren. Die erste Spalte von A ist
xi-f @,2)X2:
F.1)
'0,8'
0,2
=
'0,6'
0,4
+
■ 0,2"
-0,2
6.1 Eigenwerte: Einführung 291
Multipliziert man mit A, so erhält man die erste Spalte von A^, Wir schreiben
dieses einzeln für xi und @,2)x2 auf. Natürlich gilt Axi = xi, und der
zweite Vektor wird bei der Multiplikation mit A mit seinem Eigenwert |
multipliziert:
0,7
0,3
0,6
0,4
+
0,1
-0,1
Jeder Eigenvektor wird mit seinem Eigenwert multipliziert, wenn man A
darauf anwendet. Um A^ zu berechnen, brauchen wir die Eigenvektoren nicht,
aber sie stellen eine gute Methode dar, 99 Multiplikationen auf einmal
durchzuführen. In jedem Schritt bleibt xi unverändert, wohingegen X2 mit |
multipliziert wird, so dass wir am Schluss auf einen Faktor (|)^^ kommen:
4 99
0,8
0,2
ist eigentlich xi -f @,2)(-)^^X2 =
0,6
0,4
-f
sehr
kleiner
Vektor
Hier sehen wir die erste Spalte von A^^^. Die Zahl, die wir am Anfang
als 0,6000 geschrieben haben, war nicht ganz genau. Wir haben den Teil
@,2)(|)^^ ausgelassen, der erst nach der 30. Dezimalstelle auftauchen würde.
Der Eigenvektor xi ist ein „stationärer Zustand", der sich (wegen Ai = 1)
nicht verändert. Der Eigenvektor X2 dagegen ist eine „abklingende Mode",
die (wegen A2 = 0,5) praktisch verschwindet. Je höher die Potenz von A,
desto weiter nähern sich die Spalten dem stabilen Zustand an.
Wir wollen noch erwähnen, dass diese spezielle Matrix A eine Markov-
Matrix ist. Ihre Einträge sind positiv, und die Summe der Einträge in
jeder Spalte ist 1. Diese Eigenschaften garantieren, dass der größte
Eigenwert A = 1 ist (was wir auch gefunden haben). Der zugehörige
Eigenvektor xi = @,6, 0,4) ist der stationäre Zustand, dem sich alle Spalten von
A^ nähern. In Abschnitt 8.2 werden wir Markov-Matrizen in Anwendungen
kennenlernen.
Beispiel 6.1.1 Die Projektionsmatrix P = [0^0^] hat die Eigenwerte 0
und 1.
Die Eigenvektoren sind xi = A,1) und X2 = A,-1). Für diese Vektoren gilt
Pxi = xi und Px2 = 0. Diese Projektionsmatrix illustriert drei Dinge auf
einmal:
1 Die Einträge jeder Spalte von P bilden die Summe 1, also ist A = 1 ein
Eigenwert.
2 P ist eine singulare Matrix, also ist A = 0 ein Eigenwert.
3 P ist eine symmetrische Matrix, weswegen xi und X2 zueinander senkrecht
sind.
Die einzigen möglichen Eigenwerte einer Projektionsmatrix sind 0 und 1.
Die Eigenvektoren zu A = 0, für die also Px = Ox gilt, bilden den Kern.
292 6 Eigenwerte und Eigenvektoren
Die Eigenvektoren zu A = 1 (mit Px = x) bilden den Spaltenraum. Der
Kern wird auf die Null projiziert, und der Spaltenraum bleibt fest, da jene
Vektoren auf sich selbst projiziert werden.
Ein Vektor, der „zwischen" diesen beiden Fällen liegt, wie v = C,1)
verschwindet zum Teil, zum Teil bleibt er:
Für V =
-h
ist Pv
-h
Die Projektion erhält jenen Teil von v, der im Spaltenraum liegt, und
löscht den Teil, der im Kern liegt. Um es zu betonen: Spezielle
Eigenschaften der Matrix ziehen spezielle Eigenwerte und Eigenvektoren nach sich. Dies
ist eines der wichtigeren Themen in diesem Kapitel. Projektionen haben die
Eigenwerte A = 0 und 1. Die nächste Matrix (eine Spiegelung und eine
Permutation) ist ebenfalls ein Spezialfall.
Beispiel 6.1.2 Die Spiegelungsmatrix R = [iJ] hat die Eigenwerte 1
und —1.
Der Eigenvektor A,1) bleibt von R unverändert. Der zweite Eigenvektor ist
A,-1), Multiplikation mit R bewirkt eine Vorzeichenumkehr. Eine Matrix
ohne negative Einträge kann trotzdem einen negativen Eigenwert haben! Die
rechtwinkligen Eigenvektoren sind dieselben Vektoren xi und X2, wie wir
sie auch für die Projektion gefunden haben. Dahinter steckt eine Beziehung
zwischen R und P:
2P-I = R
oder
,5 0,5'
0,5 0,5
-
IG'
Ol
=
Ol'
10
F.2)
Das ist der Punkt. Gilt Px = Ax, so gilt auch 2Px = 2Ax, die Eigenwerte
verdoppeln sich, wenn die Matrix verdoppelt wird. Subtrahiert man dann
/x = X, so erhält man BP - /)x = BA - l)x. Wird eine Matrix um I
„verschoben", so wird jeder Eigenwert A um 1 verschoben, die Eigenvektoren
bleiben aber gleich.
Die Eigenwerte verhalten sich also zueinander genauso wie die Matrizen:
2P — I = R die Eigenwerte von R sind also
2A)-1 = 1
2@) - 1 = -1.
Analog hat R'^ die Eigenwerte A^. In diesem Fall gilt R"^ = I, da 1^
und (-1J = 1 ist.
Die Eigenwertgleichung
Für kleine Beispiele könnten wir versuchen, die Gleichung Ax = Ax durch
Probieren zu lösen. Jetzt wollen wir dafür die lineare Algebra, insbesondere
6.1 Eigenwerte: Einführung 293
\
\
\ Xpx2 =
y/Projektion
^x
0X2
/ auf die Gerade
.PXj
= ^1
V
\
\
Spiegelung
an der Gerat
\
\
\
ien
•
X '\^
\
\
\
\
\
/?X2 =
\
\
-X2\
/?Xj = Xj
Rx.
Abb. 6.2. Für Projektionen gilt A = 1 und 0. Spiegelungen haben die Eigenwerte
A = 1 und —1 und senkrechte Eigenvektoren.
Determinanten, verwenden. Dieses Vorgehen wird die wichtigste Rechnung
des ganzen Kapitels darstellen — die Bestimmung der Eigenwerte A und der
Eigenvektoren x.
Als erstes bringen wir den Ausdruck Ax auf die linke Seite und schreiben
die Gleichung Ax = Ax als {A - A/)x = 0. Das Produkt der Matrix A- XI
mit dem Eigenvektor x ergibt also den Nullvektor. Die Eigenvektoren bilden
den Kern von A — XI\ Kennen wir also einen Eigenwert A, so können wir
einen Eigenvektor bestimmen, indem wir die Gleichung {A — A/)x = 0 lösen.
Zunächst zu den Eigenwerten. Hat die Gleichung [A — A/)x = 0 eine
nichttriviale Lösung, so ist A- XI nicht invertierbar. Die Determinante von
A — XI muss also Null sein. Daran erkennt man einen Eigenwert A:
6A Eine Zahl A ist pln Eigenwert von A dann miä nur dmn^ wenn. .
, . . det{A -XI) = 0 [^ \^ - ;? : -, {6J)
gilt; ^ ' ' " ' ^ '^ '- , ^ ^' ^ • ^ '< '"''^';' /^ ;■-•
In dieser „charakteristischen Gleichung" taucht nur A auf, nicht x. Zu jedem
Eigenwert A erhält man dann die zugehörigen Eigenvektoren x:
Löse dazu {A — A/)x = 0
oder
Ax = Ax.
F.4)
Da auf der linken Seite det{A — XI) — 0 ein Polynom n-ten Grades steht,
hat die Matrix n Eigenwerte.
Beispiel 6.1.3 Die Matrix A = [^^] ist singular (hat also Determinante
Null). Bestimmen Sie ihre Eigenwerte A und Eigenvektoren x.
Ist A singular, so ist A = 0 bereits einer der Eigenwerte, da für die
Gleichung Ax = Ox Lösungen existieren, die die Eigenvektoren zu A = 0
darstellen. Um aber alle Eigenwerte und Eigenvektoren zu finden, subtrahiert man
294 6 Eigenwerte und Eigenvektoren
als erstes \I von A:
Subtrahiere A von der Diagonalen: A — \I —
1-A 2
2 4-A
Dann berechnet man die Determinante dieser Matrix. Aus A — A) • D - A)
erhält man den Term A^ — 5A + 4, der andere Term ist 2 • 2 = 4. Wie in ad — bc
subtrahiert man den einen vom anderen:
1-A 2
2 4-A
A-A)D-A)-B)B)=:A2-5A.
F.5)
2"
2 4
y
z
y
z
=
"
0
2]
-l!
Die Determinante A^ — 5A ist Null, wenn A ein Eigenwert ist. Faktorisiert
man den Term in A • (A — 5), erhält man direkt die beiden Nullstellen A = 0
und A = 5:
det{A ~ XI) = A^ - SA = 0 ergibt die Eigenwerte Ai = 0 und . X^= 5*
Als nächstes bestimmt man die Eigen vekt or en. Dazu löst man die Gleichung
{A — A/)x = 0 für jedes A einzeln:
{A — 0/)x =|^^||^|=:|^| liefert einen Eigenvektor
für Ai = 0,
I /i j j — ± j
r_4 2irvl [ol
{A — 5/)x =1 ^ ill-y|~lnl l^^f^^^ einen Eigenvektor
für A2 = 5.
Die Matrizen A — Ol und A — 51 sind singular (weil 0 und 5 Eigenwerte
sind). Die Eigenvektoren liegen jeweils im Kern der Matrizen: {A — A/)x = 0
bedeutet Ax = Ax.
Es ist zu betonen, dass der Eigenwert X = 0 kein Ausnahmefall ist Wie
jede andere Zahl kann Null ein Eigenwert sein oder auch nicht. Ist A singular,
so ist Null ein Eigenwert, dessen Eigenvektoren den Kern bilden: Ax = Ox =
0. Ist A invertier bar, so ist Null kein Eigenwert. Dann „verschiebt" man um
ein Vielfaches von /, um die Matrix singular zu machen. Im Beispiel war die
verschobene Matrix A - 51 singular, so dass der andere Eigenwert 5 war.
Zusammenfassung Um das Eigenwertproblem für eine n x n-Matrix zu
lösen, folge man diesen Schritten:
"-4 2"
2-1
y'
z
y'
z
'0"
Oj
"ll
2\
6.1 Eigenwerte: Einführung 295
l.Beredbm die Determinante von Ä:- AI. Du. A läiigs der Diagonato
siibtxahieri wWv beglmit die Determmaixtemit: A^ oder -A^* Sie ist eto
2. Be^imme die ISTttQ Palynoms^mdBSs detD^AI) =Ö
^t* pie;?^.]?WPfetelieii: ^iiifdidlß^.m.pge^werte vom ^4.-. :v\' ^'; =;
3. Lose das' Gleidbu^ngss^^stem (iL7- AJ)x ^ 0 für jeden Eigenwert;
Da die Determinante Null ist, gibt es im letzten Schritt andere Lösungen
als X = 0. Diese Lösungen sind die Eigenvektoren.
Ist A eine 2 x 2-Matrix, so ist die Determinante von A — XI ein quadratischer
Ausdruck, der mit A^ beginnt. Durch Faktorisieren oder durch quadratische
Ergänzung bestimmt man die beiden Nullstellen (die Eigenwerte). Die
Eigenvektoren erhält man dann direkt aus A — XI: Die Matrix ist singular, also
sind beide Zeilen Vielfache eines Vektors (a, b). Dann sind beliebige Vielfache
von F, —a) Eigenvektoren. Im Beispiel hatten wir A = 0 und A = 5:
A = 0 : Zeilen von A - 0/ in Richtung A,2); Eigenvektor in Richtung B, -1)
A = 5 : Zeilen von A - 5/ in Richtung (-4,2); Eigenvektor in Richtung B,4)
Weiter oben haben wir den letzten Eigenvektor als A,2) geschrieben. Beide
Vektoren, A,2) und B,4), stellen korrekte Lösungen dar. Es gibt eine ganze
Gerade aus Eigenvektoren — jedes nichttriviale Vielfache von x geht genauso
gut wie X. Deshalb dividiert man oft durch die Länge, so dass man einen
Einheitsvektor erhält.
Wir beenden den Abschnitt mit einer Warnung. Einige 2 x 2-Matrizen
besitzen nur eine Gerade aus Eigenvektoren. Dies kann nur passieren, wenn die
beiden Eigenwerte gleich sind. (Andererseits hat A = I nur gleiche
Eigenwerte, und jede Menge Eigenvektoren.) Analog gibt es n x n-Matrizen, die keine
n linear unabhängigen Eigenvektoren besitzen. Ohne n solcher Eigenvektoren
bilden diese aber keine Basis, weswegen nicht jeder Vektor v als
Linearkombination von Eigenvektoren geschrieben werden kann. Mit der Sprechweise
des nächsten Kapitels: Die Matrix lässt sich nicht diagonalisieren.
Eine gute Nachricht, eine schlechte
Die schlechte Nachricht zuerst: Addiert man eine Zeile von A zu einer anderen
Zeile, so verändern sich die Eigenwerte für gewöhnlich. Beim
Eliminationsverfahren bleiben die A's also nicht erhalten. Am Ende des
Eliminationsverfahrens stehen auf der Diagonalen der Dreiecksmatrix U deren Eigenwerte: die
Pivotelemente. Diese sind aber keine Eigenwerte von A\ Eigenwerte ändern
sich, wenn man Zeile 1 zu Zeile 2 addiert:
u =
A =
1 1'
0 0_
1 r
_i ij
296 6 Eigenwerte und Eigenvektoren
hat die Eigenwerte A = 0 und A = 1;
hat die Eigenwerte A = 0 und A = 2.
Jetzt aber die gute Nachricht: das Produkt Ai • A2 und die Summe Ai -f A2
der Eigenwerte lassen sich schnell aus A bestimmen. In unserem Beispiel ist
das Produkt gleich 0-2, was genau mit der Determinante von A
übereinstimmt. Die Summe der Eigenwerte ist 0 + 2, was wir als Summe der
Diagonalelemente von A{l-\-\) wiederfinden. Diese schnellen Proben funktionieren
immer:
6B Das Produkt der n Eigenwerte ist gleich der Determmante yon A.
6C Die Summe der n EigeEwerte Ist gleich der Summe der n BiagaBaJem'-::
träge. Mannennt di^e Zahl die Spur von A: ^
Ai -f A2 H 1- An = Spur = an -f a22 H h ann- F»6)
Diese Proben sind sehr nützlich. Sie werden in den Aufgaben 15 und 16
bewiesen, und noch einmal im nächsten Abschnitt. Sie erleichtern es zwar
nicht, die Eigenwerte zu berechnen. Ist die Rechnung aber falsch, so sieht
man dies an der Probe. Um dann die richtigen A's zu berechnen, muss man
noch einmal mit det(A - \I) = 0 anfangen.
Der Determinantentest besagt, dass das Produkt der A's gleich dem
Produkt der Pivotelemente ist (falls keine Zeilenvertauschungen nötig sind). Aber
die Summe der A's ist nicht gleich der Summe der Pivotelemente — wie wir
im Beispiel gesehen haben. Die einzelnen A's haben fast nichts mit den
einzelnen Pivotelementen zu tun. Die wesentliche Gleichung dieses neuen Teils
der linearen Algebra ist eigentlich nichtlinear: A wird mit x multipliziert.
Imaginäre Eigenwerte
Noch eine Nachricht (nicht allzu schlimm). Es kann sein, dass die Eigenwerte
keine reellen Zahlen sind.
Beispiel 6.1.4 Die QO'^-Drehmatrix Q = [ _? j] hat keine reellen
Eigenvektoren oder Eigenwerte.
Kein Vektor Qx liegt in derselben Richtung wie x (außer dem Nullvektor,
aber das ändert nichts). Es kann keinen Eigenvektor geben, es sei denn, wir
verwenden imaginäre Zahlen. Tun wir das also.
6.1 Eigenwerte: Einführung 297
Um zu verstehen, warum die Verwendung von i eine Hilfe sein kann,
betrachten Sie Q^ = -/. Ist Q eine Drehung um 90°, so stellt (J^ eine Drehung
um 180° dar, deren Eigenwerte 1 und -1 sind (da -/x = -Ix gilt). Quadriert
man aber Q, so müssten auch die Eigenwerte A quadriert werden, so dass
A^ = — 1 gilt. Die Eigenwerte der 90°-Drehmatrix sind also -\-i und —i.
Man erhält diese A's wie üblich aus der Gleichung det{Q — XI) — 0, die
hier A^ -f 1 = 0 ergibt. Ihre Nullstellen sind Ai = i und A2 = -i. Ihre Summe
ist 0 (die Spur von Q) und ihr Produkt ist 1 (die Determinante).
Dann finden wir die imaginäre Einheit i (mit i^ = -1) auch in den
Eigenvektoren von Q:
Ol"
-10
r
i
— i
r
i
und
Ol"
-10
i
1
= -i
i
Ij
Irgendwie behalten diese komplexwertigen Vektoren ihre Richtung, wenn
sie gedreht werden. Fragen Sie mich nicht, wie. An diesem Beispiel kann
man die wichtige Erfahrung klar machen, dass reelle Matrizen leicht
komplexe Eigenwerte haben können. Daran kann man auch zwei Eigenschaften
illustrieren, die wir bis Kapitel 10 nicht vollständig behandeln werden.
1 Q ist eine schiefsymmetrische Matrix, so dass jeder Eigenwert A rein
imaginär ist.
2 Q ist eine orthogonale Matrix, so dass der Absolutbetrag jedes Eigenwerts
1 ist.
Eine symmetrische Matrix (Ä^ = A) kann mit einer rellen Zahl verglichen
werden, eine schiefsymmetrische Matrix {Ä^ = -A) mit einer rein
imaginären Zahl, und eine orthogonale Matrix mit einer komplexen Zahl A mit
|A| = 1.
Für Eigenwerte sind diese Beziehungen mehr als Analogien — es sind
Sätze, die bewiesen werden können. Die Eigenvektoren aller dieser speziellen
Matrizen stehen senkrecht aufeinander.^
Eigshow
Es gibt ein MATLAB-Demo mit dem Namen eigshow, das das
Eigenwertproblem für eine 2 x 2-Matrix darstellt. Es beginnt mit einem Einheitsvektor
X = A,0). Mittels der Maus kann man den Vektor auf dem Einheitskreis
bewegen. Gleichzeitig zeigt der Graph den Vektor Ax an, farbig und
ebenfalls bewegt. Manchmal ist Ax dem Vektor x voraus, manchmal hängt er
hinterher. Manchmal ist Ax parallel zu x. Dann gilt Ax = Ax, und x ist ein
Eigenvektor.
Der Eigenwert A hängt mit Länge und Richtung von Ax zusammen. Die
im Demo eingebauten Wahlmöglichkeiten für A illustrieren verschiedene
Situationen:
^ In Kapitel 10 wird definiert, was „rechtwinklig" für komplexe Vektoren bedeutet.
In einem gewissen Sinne sind (z, 1) und (l,i) zueinander rechtwinklig.
298 6 Eigenwerte und Eigenvektoren
1. Es gibt keine (reellen) Eigenvektoren. Die Richtungen von x und Ax
stimmen nie überein. Dann sind die Eigenwerte und Eigenvektoren komplex.
2. Es gibt nur eine Eigenvektorgerade. Die sich ändernden Richtungen von
Ax und X treffen sich, überholen sich aber nicht.
3. Es gibt Eigenvektoren in zwei voneinander unabhängigen Richtungen.
Diese ist die typische Situation. Ax überholt x beim ersten Eigenvektor, und
wird beim zweiten Eigenvektor wieder überholt.
Sie finden die Datei in der Studentenversion und in MATLAB 5.2. Sie
gehört auch zu unserem „Unterrichtscode" und kann aus dem WWW
heruntergeladen werden:
web.init.edu/18.06/www oder ocw.mit.edu
Angenommen, A ist singular (hat den Rang Eins). Der Spaltenraum ist
dann eine Gerade. Der Vektor Ax kann sich deshalb nicht frei bewegen,
sondern muss auf dieser Geraden bleiben. Einer der Eigenvektoren liegt auf dieser
Geraden. Der andere ist jener Vektor x, für den Ax2 = 0 ist. Null ist immer
ein Eigenwert einer singulären Matrix.
Können Sie sich im Kopf vorstellen, wie das Bild mit x und Ax für die
folgenden sechs Matrizen aussieht? Wie viele Eigenvektoren gibt es, und wo
liegen sie? Unter welchen Umständen läuft Ax im Gegenuhrzeigersinn, wann
im Uhrzeigersinn?
A =
20
Ol
2 0
0-1
Ol
10
0 1
-10
1 1
Ol
1 1
1 1
Die wesentlichen Punkte
1. Ax = Ax bedeutet, dass der Vektor x die Richtung beibehält, wenn er mit
A multipliziert wird.
2.Ax = Ax bedeutet auch, dass det{A — XI) = 0. Durch diese Gleichung
werden n Eigenwerte festgelegt.
3. Die Eigenwerte von A'^ und A~^ sind A^ und A""\ mit denselben
Eigenvektoren.
4. Summe und Produkt der Eigenwerte sind gleich der Spur und der
Determinante der Matrix.
0,8 0,3
0,2 0,7
A\x = @,8, 0,2)
J
x = (l,0)
6.1 Eigenwerte: Einführung 299
5. Spezielle Matrizen, wie Projektionen und Drehmatrizen, haben auch
spezielle Eigenwerte.
Aufgaben 6.1
1. Für das Beispiel am Anfang dieses Abschnitts gilt
0,8 0,3
0,2 0,7
und Ä'^
0,70 0,45
0,30 0,55
und A^ =
0,6 0,6
0,4 0,4
Die Matrix A^ liegt auf halbem Wege zwischen A und A^. Erklären Sie
mit Hilfe der Eigenvektoren und Eigenwerte dieser drei Matrizen, warum
A^ = \{A^-A^)gi\t.
(a) Zeigen Sie am Beispiel A^ dass ein Zeilentausch zu anderen
Eigenwerten führen kann.
(b) Warum wird der Eigenwert Null nicht von den Eliminationsschritten
beeinträchtigt?
2. Bestimmen Sie die Eigenwerte und Eigenvektoren dieser beiden Matrizen:
A =
14
23
und A-\-I
24
24
A-\-I hat die
denen von A
Eigenvektoren wie A^ die Eigenwerte sind gegenüber
3. Berechnen Sie die Eigenvektoren und Eigenwerte von A und A
02
23
und A-^ =
-3/4 1/2
1/2 0
hat
Eigenvektoren wie A. Hat A die Eigenwerte Ai und A2,
so hat die Inverse die Eigenwerte
4. Berechnen Sie die Eigenvektoren und Eigenwerte von A und A'^:
-13
20
7-3
-2 6
A^ hat dieselben
A'^ die Eigenwerte
und A^ =
wie A. Hat A die Eigenwerte Ai und A2, so hat
5. Bestimmen Sie die Eigenwerte von A, B und A-\- B:
A =
10
1 1
1 1
Ol
und A-\- B
2 1
1 2
Sind Eigenwerte von A + B gleich oder verschieden von den Eigenwerten
von A plus den Eigenwerten von B?
300 6 Eigenwerte und Eigenvektoren
6. Bestimmen Sie die Eigenwerte von A, B, AB und BA:
A =
'10"
1 ij
.B =
1 r
[u ij
,AB =
'1 1 1
1 2J
und BA =
2 1
1 1
Sind Eigenwerte von AB gleich oder verschieden von Eigenwerten von A
mal Eigenwerten von B? Sind Eigenwerte von AB gleich oder verschieden
von Eigenwerten von BA?
7. Das Eliminations verfahren liefert eine Faktorisierung A = LU. Die
Eigenwerte von U stehen auf der Diagonalen, es sind die . Die Eigenwerte
von L stehen ebenfalls auf der Diagonalen, alle Eigenwerte sind .
Die Eigenwerte von A sind nicht dieselben wie .
8. (a) Wie kann man, wenn man weiß, dass x ein Eigenvektor ist, den
zugehörigen Eigenwert A finden?
(b) Wie bestimmt man umgekehrt x, wenn man weiß, dass A ein
Eigenwert ist?
9. Wie formen Sie die Gleichung Ax = Ax um, um (a), (b), und (c) zu
beweisen?
(a) A^ ist ein Eigenwert von A^, wie in Aufgabe 4.
(b) A~^ ist ein Eigenwert von A~^, wie in Aufgabe 3.
(c) A -h 1 ist ein Eigenwert von A-\-1, wie in Aufgabe 2.
10. Bestimmen Sie die Eigenvektoren und Eigenwerte der folgenden Markov-
Matrizen A und A"^. Erklären Sie, warum A^^^ nahe bei A"^ ist:
A =
0,6 0,2
0,4 0,8
und A^ =
1/3 1/3
2/3 2/3
11. Bestimmen Sie die Eigenwerte und Eigenvektoren der
Projektionsmatrizen P und P^^^:
P =
0,2 0,4 0
0,4 0,8 0
0 0 1
Gehören zwei Eigenvektoren zu demselben Eigenwert A, so sind auch
alle ihre Linearkombinationen Eigenvektoren zu A. Bestimmen Sie einen
Eigen Vektor von P, der keine Komponente Null enthält.
12. Konstruieren Sie aus dem Einheitsvektor u = (^, |, |, |) eine Projektion
P = uu^ mit Rang 1.
(a) Zeigen Sie, dass Pu = u gilt, und u ein Eigenvektor zum Eigenwert
A = 1 ist.
(b) Zeigen Sie, dass Pv = 0 gilt, wenn der Vektor v senkrecht auf u
steht. Der zugehörige Eigenwert ist A = 0.
6.1 Eigenwerte: Einführung 301
(c) Bestimmen Sie drei linear unabhängige Eigenvektoren von P zum
Eigenwert A = 0.
13. Lösen Sie die Gleichung det{Q — XI) = 0 (z. B. mit quadratischer
Ergänzung), um die Eigenwerte A = cosö ± isinO zu erhalten:
Q =
COS ö - sin ö
sin 6 cos 6
dreht die xy-Ehene um den Winkel 6.
Bestimmen Sie die Eigenvektoren von Q, indem sie {Q — A/)x = 0 lösen.
Beachten Sie i^ = —1.
14. Jede Permutationsmatrix lässt den Vektor x = A,1,..., 1) unverändert.
Dies ist also ein Eigenvektor zum Eigenwert A = 1. Bestimmen Sie für
die folgenden Permutationen je zwei weitere Eigenwerte:
P =
0 10
001
100
und P =
001
010
100
15. Beweisen Sie, dass die Determinante von A gleich dem Produkt Ai A2 • • • An
ist. Beginnen Sie dazu mit det{A — XI), geschrieben als Produkt von n
Linearfaktoren. Setzen Sie dann A = :
det{A-XI) = (Ai-A)(A2-A) • • • (A„-A) und deshalb detA= .
16. Die Summe der Diagonaleinträge (die Spur) ist gleich der Summe der
Eigenwerte:
A =
a b
c d
hat die Determinante dei{A-XI) = X^-{a+d)X-\-ad—bc = 0.
Hat A die Eigenwerte Ai = 3 und A2 = 4, so gilt det{A — XI) = .
Aus der Lösungsformel für quadratische Gleichungen erhält man die
Eigenwerte X = {a -\- d-\- a/ )/2 und A = . Sie bilden die Summe
17. Hat A die Eigenwerte Ai = 4 und A2 = 5, so gilt det{A-XI) = (A-4)(A-
5) = A^ — 9A -h 20. Bestimmen Sie drei Matrizen, die die Spur a -h d = 9,
die Determinante 20 und Eigenwerte 4 und 5 gemeinsam haben.
18. Eine 3 x 3-Matrix B habe die Eigenwerte 0,1,2. Diese Information reicht
aus, um drei der folgenden Größen zu bestimmen:
(a) Den Rang von B
(b) Die Determinanten von B^B
(c) Die Eigenwerte von B^B
(d) Die Eigenwerte von {B -\-1)~'^.
302 6 Eigenwerte und Eigenvektoren
19. Wählen Sie die zweite Zeile der Matrix A = [^l] so, dass A die
Eigenwerte 4 und 7 hat.
20. Wählen Sie Zahlen a, b und c so, dass det{A - XI) = 9A - A^. Die
Eigenwerte sind dann -3,0,3:
A =
010
001
ab c
21. Die Eigenwerte von A sind gleich den Eigenwerten von A^. Das liegt
einfach daran, dass det(A - \I) gleich det(A^ - \I) ist, weil .
Zeigen Sie anhand eines Beispiel, dass die Eigenvektoren von A nicht mit
denen von A^ übereinstimmen.
22. Konstruieren Sie eine beliebige Markov-Matrix M: sie enthält nur
positive Einträge, die sich in jeder Spalte zu 1 aufsummieren. Überprüfen
Sie, dass für e = (l,!,!) die Gleichung M^e = e gilt. Nach Aufgabe
21 ist A = 1 ebenfalls ein Eigenwert von M. Eine Herausforderung: Eine
singulare 3 x 3-Markov-Matrix mit Spur | hat die Eigenwerte A = .
23. Suchen Sie drei 2 x 2-Matrizen mit den Eigenwerten Ai = A2 = 0. Dann
sind sowohl die Spur als auch die Determinante Null. Die Matrix A muss
nicht Null sein, aber es gilt A^ = 0. (Überprüfen Sie das!)
24. Die folgende Matrix ist singular und hat den Rang eins. Bestimmen Sie
drei Eigenwerte und drei Eigenvektoren:
A =
[2 12]
2 1 2
424
2 12
25. Seien A und B Matrizen mit denselben Eigenwerten Ai,..., A„ und
denselben linear unabhängigen Eigenvektoren xi,... ,x„. Dann gilt A = B.
Der Grund: Jeder Vektor x lässt sich als Linearkombination ciXi H h
Cn'x.n schreiben. Welchen Ausdruck erhält man dann für Ax, welchen für
Bx?
26. Der Block B hat die Eigenwerte 1 und 2, C hat die Eigenwerte 3 und
4, und D hat die Eigenwerte 5 und 7. Bestimmen Sie die Eigenwerte der
4 X 4-Matrix A:
B C'
0 D
0 130^
-2 30 4
0061
0016
6.1 Eigenwerte: Einführung
27. Bestimmen Sie den Rang und die vier Eigenwerte der Matrizen
303
A =
1111
1111
1111
1111
und C =
1010
0101
1010
0101
28. Subtrahieren Sie / von der Matrix A aus der letzten Aufgabe. Bestimmen
Sie die Eigenwerte und die Determinante:
B=A-I=
Olli
1011
1 101
1110
Ist jeder Eintrag einer 5 x 5-Matrix A gleich 1, so haben A und B = A-I
die Eigenwerte und .
29. (Wiederholung) Bestimmen Sie die Eigenwerte der Matrizen A, B, und
C:
[1231
045
006
, B =
01]
020
300
undC =
222
222
222
30. Es gelte a + b — c-\-d. Zeigen Sie, dass A,1) ein Eigenvektor der Matrix
A
a b
c d
ist, und bestimmen Sie beide Eigenwerte.
31. Vertauscht man mit einer Permutationsmatrix P die Zeilen 1 und 2 und
die Spalten 1 und 2, so ändern sich die Eigenwerte nicht. Bestimmen Sie
die Eigenvektoren von A und PAP für A = 11:
121
363
484
und PAP ■■
633
21 1
844
32. Es sei A eine Matrix mit den Eigenwerten 0,3,5 und linear unabhängigen
Eigenvektoren u, v, w.
(a) Nennen Sie eine Basis für den Kern und eine Basis für den
Spaltenraum.
(b) Finden Sie eine spezielle Lösung für das Gleichungssystem Ax = v -h
w. Bestimmen Sie alle Lösungen.
(c) Zeigen Sie, dass die Gleichung A^ — u keine Lösung hat. (Andernfalls
läge im Spaltenraum.)
304 6 Eigenwerte und Eigenvektoren
6.2 Diagonalisierung einer Matrix
Ist X ein Eigenvektor, so bewirkt die Multiplikation mit A einfach die
Multiplikation mit einer einzigen Zahl: Ax = Ax. Alles, was Matrizen schwierig
zu handhaben macht, verschwindet einfach. An Stelle eines gekoppelten
Systems können wir jedem Eigenvektor einzeln folgen. Das ist so wie bei einer
Diagonalmatrix, ohne Kopplungen abseits der Diagonalen. Dann lässt sich
die 100. Potenz einer Matrix einfach berechnen.
Der Hauptpunkt in diesem Abschnitt ist einfach zu nennen. Eine Matrix
A wird zu einer Diagonalmatrix A, wenn wir die Eigenvektoren richtig
verwenden. Das ist die Hauptidee (sozusagen in Matrixform). Wir fangen gleich
an mit der wichtigsten Rechnung dazu.
6D DiagonaHsieruiig Angenommen, die nxn Matrix A hat n linear
unabhängige Eigehvsektoren. Wir schreiben sie als Spalten einer Mgenvekfor-
Matrix S. Damit erhalten wir die Eigenwerimatrix A:
S^'^AS^A=^
Ai
^n
iß^
Die Matrix A ist dadurch „diagonalisiert" worden. Wir verwenden den
Großbuchstaben Lambda für diese Matrix, um auf die „kleinen" A's (die
Eigenwerte) auf der Diagonalen hinzuweisen.
Beweis. Multipliziere A mit seinen Eigenvektoren, also den Spalten von S.
Die erste Spalte von AS ist Axi, und das ist AiXi:
AS=-A
Xi • • • Xr,
AiXi • • • ÄnX.n
Der Trick ist nun, die Matrix AS als S mal A zu schreiben
"Ai
AiXi • • • AnX„
xi • • • x^
An
= SA.
Passen Sie auf, dass Sie diese Matrizen in der richtigen Reihenfolge
behalten, so dass Ai mit der ersten Spalte xi multipliziert wird, wie gezeigt.
Die Matrix wird vollständig diagonalisiert, und wir können die Gleichung
AS = SA auf zwei Weisen aufschreiben:
6.2 Diagonalisierung einer Matrix 305
AS = SA^ bedeutet auch S-'^AS = A oder A = SAS-K
F.8)
Die Matrix S besitzt eine Inverse, weil die Spalten (die Eigenvektoren von
A) als linear unabhängig angenommen wurden. Ohne n linear unabhängige
Eigenvektoren ist eine Diagonalisierung unmöglich.
Die Matrizen A und A besitzen dieselben Eigenwerte Ai,..., An. Die
Eigenvektoren sind verschieden. Die originalen Eigenvektoren wurden dazu
verwendet, A zu diagonalisieren — sie bildeten die Matrix 5. Die neuen
Eigenvektoren der Matrix A sind einfach die Spalten von /. Indem wir A verwenden,
können wir Differentialgleichungen oder Differenzengleichungen oder sogar
Gleichungen wie Ax = b lösen.
Beispiel 6.2,1 Die Projektionsmatrix P = [o^S^] hat die Eigenwerte A =
1 und A = 0 mit den Eigenvektoren A,1) und (-1,1). Schreiben Sie die
Eigenwerte als Einträge von A und die Eigenvektoren als Spalten von S.
Dann gilt 5-1 P5 = ^:
0,5 0,5'
-0,5 0,5
0,5 0,5'
0,5 0,5
'1-1'
1 1
=
'lO'
00
5-1 P S = A
Für die ursprüngliche Projektion galt P^ = P. Die neue Projektion
gehorcht der Gleichung A^ — A. Der Spaltenraum hat sich von A,1) nach A,0)
gedreht, und der Kern von (-1,1) nach @,1). Die Diagonlisierung bringt also
die Eigenvektoren mit den Koordinatenachsen in Übereinstimmung.
Zunächst noch vier kurze Bemerkungen zur Diagonalisierung, bevor wir
zu den Anwendungen kommen.
Bemerkung 1 Angenommen, die Zahlen Ai,..., An sind alle verschieden.
Dann sind die Eigenvektoren xi,..., x^ automatisch linear unabhängig.
(Siehe 6E unten.) Deshalb kann jede n x n-Matrix, die n verschiedene Eigenwerte
hat, diagonalisiert werden.
Bemerkung 2 Die Eigenvektormatrix 5 ist nicht eindeutig. Man kann jede
Spalte mit beliebigen Konstanten (außer Null) multiplizieren. Angenommen,
wir multiplizieren die Spalten mit 5 und -1. Dann dividiert man die Zeilen
von 5-1 durch 5 und -1, um die neue Inverse zu bestimmen.
»-'n*»!!-' *-5neu —
,1 0,1'
0,5-0,5
'0,5 0,5'
0,5 0,5
■5 r
5-1
=
'lOi
00
= dasselbe A.
Der Extremfall ist A — I, wenn also jeder Vektor ein Eigenvektor ist. Dann
kann jede invertierbare Matrix 5 die Eigenvektormatrix sein. Man erhält
dann S'^IS = I = A.
306 6 Eigenwerte und Eigenvektoren
Bemerkung 3 Zur Diagonalisierung muss man eine Eigenvektormatrix
verwenden. Aus S~^AS = A erhält man AS = SA. Die erste Spalte von S sei y.
Dann sind die ersten Spalten von AS und von SA gleich Ay und Xiy. Damit
diese beiden gleich sind, muss y ein Eigenvektor sein.
Die Eigenvektoren in S müssen in derselben Reihenfolge wie die
Eigenwerte in A stehen. Um die Reihen in S und A zum Beispiel umzudrehen,
setzen wir (-1,1) vor A,1):
= neues A.
■-0,5 0,5"
0,5 0,5
0,5 0,5'
0,5 0,5
-1 r
1 1
=
0 0'
0 1_
Bemerkung 4 (Warnung vor mehrfachen Eigenwerten) Manche Matrizen
haben zu wenige Eigenvektoren. Diese Matrizen sind nicht diagonalisierbar.
Zwei Beispiele:
A =
1-1
1-1
und A =
Ol
00
Ol'
0 0
X
=
0'
0
Die Eigenwerte sind zufällig 0 und 0. An der Null ist nichts besonderes. Dass
sie zweimal auftritt, zählt. Suchen wir nun die Eigenvektoren der zweiten
Matrix
Ax = Ox bedeutet
Der Eigenvektor x ist ein Vielfaches von A,0). Es gibt keinen zweiten
Eigenvektor, und deshalb kann A nicht diagonalisiert werden. Diese Matrix ist das
beste Testbeispiel für Aussagen über Eigenvektoren. Bei vielen „Wahr oder
Falsch?"-Fragen führt dieses Beispiel zur Antwort falsch.
Beachten Sie, dass es keine Verbindung zwischen der Diagonalisierbarkeit
einer Matrix und ihrer In vertierbar keit gibt:
— Bei der Invertierharkeit geht es um die Eigenwerte (Null oder nicht Null).
— Bei der Diagonalisierbarkeit geht es um die Eigenvektoren (zu wenige oder
genug).
Zu jedem Eigenwert gehört mindestens ein Eigenvektor. Führt die Gleichung
{A - A/)x = 0 auf X = 0, dann ist A kein Eigenwert. Suchen Sie dann lieber
einen Fehler beim Lösen der Gleichung det{A - XI) = 0. Haben Sie aber
n verschiedene Eigen vektoren für n verschiedene Eigenwerte, so sind diese
Eigenvektoren also linear unabhängig, und A ist diagonalisierbar.
6E (Bnabt&igtj^ Eigenrektoren fi^
m^ktf^mMism^ wtms:<hh0:ä^^^(^^
6.2 Diagonalisierung einer Matrix 307
Beweis. Es sei ciXi + C2X2 = 0. Durch Multiplikation mit A erhält man
ciAiXi + C2A2X2 = 0. Durch Multiplikation mit A2 erhält man C1A2X1 +
C2A2X2 = 0. Subtrahiert man beide Gleichungen voneinander, so bleibt
(Ai - A2)cixi = 0.
Da die A's verschieden sind und xi 7^ 0, bleibt nur ci = 0. Analog erhält man
C2 = 0. Keine andere Linearkombination liefert cixi +C2X2 = 0, also müssen
die Eigenvektoren xi und X2 linear unabhängig sein.
Diesen Beweis kann man sofort auf j Eigenvektoren ausdehnen.
Angenommen, es gilt ciXi H h CjXj = 0. Durch Multiplikation mit A einerseits
und mit dem Eigenwert Xj andererseits erhält man Gleichungen, die
voneinander substrahiert werden. Dadurch wird Xj aus der Gleichung entfernt. Als
nächstes multipliziert man mit A und mit Aj_i, und subtrahiert die
Ergebnisse wieder voneinander. Der Vektor Xj_i fällt weg. Schließlich bleibt nur
noch ein Vielfaches von xi übrig:
(Ai - A2) • • • (Ai - Aj)ciXi = 0 also ci = 0.
F.9)
Analog erhält man Ci = 0 für alle anderen Indizes i. Wenn die Eigenwerte
verschieden sind, sind die Eigenvektoren linear unabhängig.
Hat man n verschiedene Eigenwerte, so bildet ein vollständiger Satz
Eigenvektoren die Spalten von S. Dann ist A diagonalisiert.
Beispiel 6,2,2 Die Markov-Matrix A = [Sfof] ™ letzten Abschnitt hatte
die Eigenwerte Ai = 1 und A2 = 0,5. Es folgt die Faktorisierung A = SAS~^:
= SAS-
Die Eigenvektoren @,6,0,4) und A,-1) stehen in den Spalten von S. Wir
wissen, dass sie auch Eigenvektoren von A^ sind. Daher hat A^ dieselbe
Matrix 5, und die Eigenwerte in A sind schlicht quadriert:
Macht man einfach weiter, sieht man schnell, warum die hohen Potenzen A^
sich einem stationären Zustand nähern:
,8 0,3'
0,2 0,7
=
0,6 ll
0,4-lJ
ri Ol
[00,5]
r 1 1'
[0,4-0,6
A" = SA^S-^ =
0,6 1
0,4-1
0
0
@,5)*
1 1
0,4-0,6
Wird k größer, so wird @,5)* kleiner, und verschwindet im Grenzwert völlig.
Der Grenzwert ist
A°° =
Der Grenzwert enthält den Eigenvektor xi in beiden Spalten. Diesem
stationären Zustand sind wir schon im letzten Abschnitt begegnet. Aus den
Potenzen wie A^°° = SA^°°S~^ erhält man ihn aber viel schneller.
,6 1'
_0,4-l
lO'
00
1 1"
0,4-0,6
=
0,6 0,6'
.0,4 0,4 1
308 6 Eigenwerte und Eigenvektoren
Eigenwerte von AB und A-\- B
Die erste Vermutung über die Eigenwerte von AB trifft nicht zu. Ein
Eigenwert A von A mal ein Eigenwert ß von B ergibt normalerweise keinen
Eigenwert von AB. Der Gedanke ist allerdings sehr verführerisch. Hier ein
falscher Beweis:
AByi = Aßx = ßAx = /3Ax. F.10)
Es scheint, als sei ßX ein Eigenwert. Ist x ein Eigenvektor mit Eigenwert A
für A und mit Eigenwert ß für J9, so ist der Beweis auch korrekt. Der Fehler
liegt darin, zu erwarten, dass A und B automatisch denselben Eigenvektor x
haben. Das ist für gewöhnlich nicht der Fall. Die Eigenvektoren von A sind
im Allgemeinen keine Eigenvektoren von B.
Es gibt Matrizen A und J9, deren Produkt AB den Eigenwert 1 hat,
obwohl A und B jeweils nur die Eigenwerte 0 haben:
A =
Ol
00
und B =
00
10
dann ist AB =
10
00
und A + B
Ol
10
Aus den gleichen Gründen sind die Eigenwerte von A-\-B normalerweise nicht
von der Form A -h /?. Im Beispiel gilt A -h /? = 0, obwohl A-\-B die Eigenwerte
1 und -1 hat. (Wenigstens ist deren Summe Null.)
Am falschen Beweis sieht man, was stattdessen wahr ist. Wenn x tatsächlicl
ein gemeinsamer Eigenvektor von A und B ist, so gilt ABx = A/3x. In
manchen Fällen haben zwei Matrizen alle n Eigenvektoren gemeinsam, so dass
man die Eigenwerte multiplizieren kann. Ob A und B gemeinsame
Eigenvektoren haben, ist sehr wichtig für die Quantenmechanik — wir machen einen
kleinen Ausflug, um diese Anwendung der linearen Algebra zu erwähnen:
6F KommnUerende Muirizen haben gemeinsame BigenveHoren
Abgenommen, A und B lassen sich beide dlagonalisi^ren* Dann haben sie
eine gemeii^ame Eigenvektor-Matrix S dann nrid nur dann^ wenn AB =
BÄ^lt. '^'''''
Die Unschärferelation Die Positionsmatrix P und die Impulsmatrix Q in
der Quantenmechanik kommutieren nicht. Es gilt sogar QP — PQ = I. (Es
handelt sich hierbei um unendliche Matrizen.) Dann kann es nicht eintreten,
dass Px = 0 gleichzeitig mit Qx = 0 gilt (außer für x = 0). Wüssten wir die
Position exakt, so könnten wir den Impuls nicht ebenfalls exakt kennen. In
Aufgabe 32 wird die Heisenberg'sche Unschärferelation aus der Schwarz'schen
Ungleichung hergeleitet.
6.2 Diagonalisierung einer Matrix
309
Fibonacci—Zahlen
Wir wollen hier ein berühmtes Beispiel darstellen, das uns auf die Potenzen
einer Matrix führt. Die Fibonacci-Zahlen beginnen mit Fq = 0 und Fi = 1.
Danach ist jedes neue F die Summe der beiden vorhergehenden F's:
Die Folge 0,1,1,2,3,5,8,13,... resultiert aus Fk+i = Fk+i + Fk.
Diese Zahlen tauchen in einer unglaublichen Menge von Anwendungen auf.
Pflanzen und Bäume wachsen in einem spiralförmigen Muster, und ein
Birnbaum zum Beispiel weist 8 Triebe auf je drei Umdrehungen auf. Für eine
Weide finden sich die Zahlen 13 und 5. Der Rekordhalter ist aber eine
Sonnenblume von Daniel O'Connell, die 233 Samenkörner in 144 Spiralumdrehungen
aufweist. Dies sind gerade die Fibonacci-Zahlen F13 und F12. Die Probleme,
mit denen wir uns beschäftigen, werden aber etwas einfacherer Natur sein.
Problem: Man bestimme die Fibonacci-Zahl Fioo- Langsam geht es,
indem man die Regel Fk-\-2 = F^+i + Fk Schritt für Schritt anwendet, also
Fe = 8 zu F7 = 13 addiert, um Fs = 21 zu berechnen. Auf die Weise gelangt
man schließlich zu Fioo- Mit der linearen Algebra geht es aber schneller.
Der Schlüssel liegt darin, mit einer Matrix-Gleichung u^+i = Auk zu
beginnen. Dies ist eine Ein-Schritt-Regel für Vektoren, im Gegensatz zu den
Fibonacci-Zahlen, die über eine Zwei-Schritt-Regel für Zahlen definiert sind.
Um die beiden Regeln zur Übereinstimmung zu bringen, schreiben wir je zwei
Fibonacci-Zahlen in einen Vektor:
Sei Uk =
Fk+i
Fk
. Aus
Fk+2-^Fk^i^Fk
wird dann u^+i =
1 1
10
Ufc.
F.11)
In jedem Schritt wird der Vektor mit A = [J J] multipliziert. Nach 100
Schritten erreicht man also uioo = A^^^uq:
'1'
0
, ui =
1'
1
, U2 =
'
1
, U3 =
■3
2
, U4 =
"
3
Uo =
Die Fibonacci-Zahlen erhalten wir also aus den Potenzen von A — und A^°°
können wir berechnen, ohne 100 Matrizenmultiplikationen durchzuführen.
Dieses Problem ist daher hervorragend zur Lösung mit Hilfe von
Eigenwerten geeignet. Wir subtrahieren A von der Diagonalen von A:
A-XI =
1-A 1
1 -A
führt auf det{A - A/) = A^ - A - 1.
Die Eigenwerte sind die Lösungen der Gleichung A^ - A - 1 = 0, die wir mit
Hilfe der Lösungsformel [-b± Vb'^ — 4ac)/2a bestimmen:
310 6 Eigenwerte und Eigenvektoren
Ai =
1 + a/5
lßl8 und A2
1-1/5
-0,618.
Die Eigenwerte Ai und A2 gehören zu den Eigenvektoren xi und X2. Damit
ist Schritt 1 beendet:
ri-Ai 1 ■
[ 1 -Aij
[I-A2 1 ■
1 -A2
Xl
X2
=
=
Q
0
'Ol
_oJ
falls Xl
falls X2
Ai
1
A2
1
Im zweiten Schritt bestimmen wir die Kombination der Eigenvektoren, die
uo = A,0) ergibt:
1 f\Xi] \X2]\
1-A2UIJ [iJ/
oder
Uo =
Xl -X2
Ai — A2
F.12)
Im letzten Schritt multiplizieren wir uq mit A^^^, um uioo zu bestimmen.
Dabei bleiben die Eigenvektoren getrennt. Sie werden mit (Ai)^^^
beziehungsweise mit (A2)^^^ multipliziert.
uioo —
(A,I00xi-^(A2)^^^:X2
Ai — A2
F.13)
Die gesuchte Zahl Fioo ist die zweite Komponente von uioo- Die zweiten
Komponenten von xi und X2 sind 1. Setzt man die Zahlen Ai und A2 in
Gleichung G) ein, erhält man Ai — A2 = \/5 und damit Fioo-
^100 =
V5
{^r-{^)
100
3,54.10
20
F.14)
Handelt es sich hierbei um eine ganze Zahl? Ja. Alle Brüche und Wurzeln
müssen verschwinden, weil nach Fibonacci's Regel Fk^2 = Fk^i + Fk aus
ganzen Zahlen immer nur wieder ganze Zahlen erzeugt werden. Der zweite
Term in Gleichung F.14) ist kleiner als |, er bringt also den ersten Term auf
die nächste ganze Zahl:
k-te Fibonacci-Zahl = die ganze Zahl am nächsten an —z=z f —-— J .
F.15)
Das Verhältnis von Fe zu F5 ist 8/5 = 1,6. Das Verhältnis Fioi/Fioo muss
sehr nahe an (l +v^)/2 sein. Die Griechen nannten diese Zahl den Goldenen
Schnitt Aus irgendeinem Grund sieht ein Rechteck mit Seitenlängen lßl8
und 1 besonders wohlproportioniert aus.
6.2 Diagonalisierung einer Matrix 311
Potenzen von Matrizen: A^
Fibonacci's Zahlenreihe ist ein typisches Beispiel für eine
Differenzengleichung der Form Wk-^ti — Auk. In jedem Schritt wird dabei mit A
multipliziert. Die Lösung ist Uk = A^uq, Wir wollen noch einmal klarmachen, wie
die Diagonalisierung einer Matrix einen schnellen Weg zur Berechnung von
A^ liefert.
Die Eigenvektor-Matrix S liefert uns die Faktorisierung A — SAS~^,
ähnlich wie A = LU oder A = QR. Diese Faktorisierung ist nun perfekt
dafür geeignet, Potenzen einer Matrix zu berechnen, da bei jeder Potenz ein
Faktor S'^S = I herausfällt:
A^ = SAS-^SAS-^ = SA'^S-^
A^ = (SAS-^)'' • {SAS-') = SA'^S'K
Die Eigenvektor-Matrix für A ist also immer noch 5, und die Eigenwert-
Matrix ist A^. Das wussten wir bereits. Die Eigenvektoren ändern sich nicht,
und die Eigenwerte werden in die k-te Potenz erhoben. Hat man A diagona-
lisiert, so ist A^uq leicht zu berechnen:
1. Man bestimmt die Eigenwerte von A und n linear unabhängige
Eigenvektoren.
2. Man schreibt Uo als Linearkombination CiXi H + Cny^n der
Eigenvektoren.
3. Man multipliziert jeden Eigenvektor x^ mit (A^)^. Dann gilt
Ujk - A^no - Ci(Ai)^Xi -h ^ • * -f CniXnf^n*
F.16)
In Matrizenschreibweise ausgedrückt, ist A^ gleich {SAS~^)^, und das ist
gleich S mal A^ mal 5~^. In Vektorenschreibweise erhält man die
Koeffizienten Ci aus den Eigenvektoren in S:
Uo = CiXiH hCnXn =
Xl
Cl
. Dies besagt, dass uq = Sc ist.
Die Koeffizienten ci,...,Cn aus Schritt 2 sind in c = 5~^uo zusammenge-
fasst. In Schritt 3 wird mit A^ multipliziert. Die Linearkombination Uk =
Z^Q(Ai)^Xi wird durch die Matrizen 5, A^ und 5~^ ausgedrückt:
A*uo = 5yl*5-iuo = 5yl*c
Xl • • • X„
(A„)*
F.17)
Das Ergebnis ist genau U/t = ci(Ai)*xi + \- c„(A„)*x„, eine Lösung der
Gleichung Ufc+i = ^u^.
312 6 Eigenwerte und Eigenvektoren
Beispiel 6.2.3 Berechne A^ für 5, A und S~^ mit ganzzahligen Einträgen:
Für A =
1 1
02
sind Ai = 1 und xi
A2 = 2 und X2
A ist eine Dreiecksmatrix mit Diagonaleinträgen 1 und 2. Auch A'^ ist eine
Dreiecksmatrix, mit Diagonaleinträgen 1 und 2^. In A'^ bleiben diese Zahlen
für sich, in A^ gibt es aber auch einen Eintrag, in dem beide Teile auftauchen.
A;c-i
r
Ol
* "
2*
1 -1"
0 1
=
'1 2*-l"
0 2* j
A" = SA^S
Für k = 1 erhält man A. Für k = 0 erhält man I, und für k — —1 schließlich
A-\
Hinweis Die Nullte Potenz einer nichtsingulären Matrix ist A^ = I. Aus
dem Produkt SA^S~^ wird dann SIS~^, also /. Die Nullte Potenz eines
jeden Eigenwerts A ist 1. Dieses Argument ist nicht mehr anwendbar, wenn
A = 0 ist. In diesem Fall ist 0^ nicht definiert. Wir kennen A^ nicht, wenn A
singular ist.
Nicht diagonalisierbare Matrizen (optional)
Angenommen, A ist ein Eigenwert von A. Diese Tatsache kann man auf zwei
Weisen feststellen:
l.Über die Eigenvektoren (geometrisch) Es gibt nichttriviale Lösungen der
Gleichung Ax = Ax.
2. Über die Eigenwerte (algebraisch) Die Determinante von A — \I ist Null.
Die Zahl A kann ein einfacher oder ein mehrfacher Eigenwert sein.
Deswegen wollen wir ihre Vielfachheit bestimmen. Die meisten Eigenwerte haben
die Vielfachheit M = 1 (einfache Eigenwerte). In diesem Fall gibt es eine
einzelne Gerade von Eigenvektoren, und det{A - XI) enthält keinen
Linearfaktor doppelt. In Ausnahmefällen kann ein Eigenwert allerdings mehrfach
vorkommen. Dann gibt es zwei Möglichkeiten, die Vielfachheit zu zählen:
1. (Die Geometrische Vielfachheit — GM)
gibt die Anzahl linear unabhängiger Eigenvektoren zum Eigenwert A an,
also die Dimension des Kerns von A - XL
2. (Die Algebraische Vielfachheit = AM)
gibt an, wie oft A unter den n Nullstellen von det{A — XI) = 0 vorkommt.
6.2 Diagonalisierung einer Matrix 313
Die folgende Matrix A ist der Standard-Problemfall. Der Eigenwert 0
tritt mehrfach auf. Es handelt sich um einen doppelten Eigenwert (AM = 2)
mit nur einem Eigenvektor (GM = 1). Die geometrische Vielfachheit kann
kleiner sein als die algebraische Vielfachheit, aber sie ist niemals größer.
Ol
00
hat die Determinante det{A — XI)
-X 1
0-X
= X^
Es „sollte" zwei Eigenvektoren geben, weil die Gleichung A^ = 0 eine doppelte
Nullstelle hat. Dass der Faktor A doppelt auftritt, bedeutet AM = 2. Es gibt
aber nur den einen Eigenvektor x = A,0). Dieser Mangel an Eigenvektoren
(GM < AM) bedeutet, dass A nicht diagonalisierbar ist.
Der Vektor mit dem Namen "repeats^^ im Unterrichtscode eigval gibt die
algebraische Vielfachheit AM für jeden Eigenwert an. Ist
repeats = [l 1... 1], so wissen wir, dass die n Eigenwerte sämtlich
verschieden sind. In diesem Fall ist A sicher diagonalisierbar. Die Summe der
Komponenten von repeats ist immer n, weil eine Polynomgleichung n-ten
Grades immer n Nullstellen hat (nach Vielfachheit gezählt).
Die Diagonalmatrix D im Unterrichtscode eigvec gibt die geometrische
Vielfachheit GM eines jeden Eigenwerts an, also die Zahl linear unabhängiger
Vektoren. Die Gesamtzahl linear unabhängiger Eigenvektoren kann kleiner
sein als n. Eine n x n-Matrix A ist genau dann diagonalisierbar, wenn diese
Gesamtzahl ebenfalls n is.
Um es nochmals zu betonen: am Eigenwert A = 0 ist nichts besonderes. Er
führt zu leicht durchführbaren Rechnungen, aber zum Beispiel die folgenden
drei Matrizen weisen genau denselben Mangel an Eigenvektoren auf. Der
mehrfache Eigenwert ist hier A = 5:
A =
5 1
05
6-1
1 4
und A =
72
-2 3
Für alle diese Matrizen gilt det{A — XI) = (A — 5)^. Die algebraische
Vielfachheit ist in jedem Fall AM = 2. Die Matrix A — 51 hat jedoch den
Rang r = 1. Die geometrische Vielfachheit ist also GM = 1. Da es nur einen
Eigenvektor gibt, sind diese Matrizen nicht diagonalisierbar.
Die wesentlichen Punkte
l.Hat A n linear unabhängige Eigenvektoren (geschrieben als Spalten von
5), so ist S~'^AS eine Diagonalmatrix: S~'^AS = A und A - SAS~^.
2. Die Potenzen von A sind A^ = SA'^S'^.
3. Die Eigenwerte von A^ sind (Ai)^,... , (An)^ •
4. Die Lösung der Gleichung u/t+i = Auk mit Startwert uo ist Uk = A^uq =
SA^S-^uo:
Uk = Ci(Ai)^Xi H h Cn(An)^Xn falls Uq = CiXi H h Cn:Sin
314 6 Eigenwerte und Eigenvektoren
5. A ist diagonalisierbar, falls zu jedem Eigenwert genügend Eigenvektoren
existieren (so dass GM = AM gilt).
Aufgaben 6.2
Die Aufgaben 1-8 behandeln Eigenvektor- und Eigenwertmatrizen.
1. Faktorisieren Sie diese beiden Matrizen in die Form A = SAS~^:
A =
1 2
03
und A =
1 1
22
2. Für A = SAS-^ gilt A^ = { )( )( ) und A-^ = { )( )( ).
3. Die Matrix A habe den Eigenwert Ai = 2 mit dem Eigenvektor
xi = [J] und den Eigenwert A2 = 5 mit zugehörigem Eigenvektor
X2 = [1]. Bestimmen Sie A über das Produkt SAS'^. Keine andere
Matrix hat dieselben Eigenwerte und Eigenvektoren.
4. Es gelte A = SAS~^. Bestimmen Sie die Eigenwertmatrix zu A -\-
21. Bestimmen Sie auch die Eigenvektormatrix. Überprüfen Sie, dass
A + 2I = i )( )( )-igilt.
5. Wahr oder falsch: Sind die Spalten von S (also die Eigenvektoren von A)
linear unabhängig, so gilt
(a) A ist invertierbar.
(b) A ist diagonalisierbar.
(c) S ist invertierbar.
(d) S ist diagonalisierbar.
6. Sind die Spalten von / die Eigenvektoren einer Matrix A, so ist A eine
. Ist die Eigenvektormatrix 5 eine Dreiecksmatrix, so ist auch S~^
eine Dreiecksmatrix. Beweisen Sie, dass auch A eine Dreiecksmatrix ist.
7. Beschreiben Sie alle Matrizen 5, durch die diese Matrix A diagonalisiert
wird:
Mol
1 2
Beschreiben Sie außerdem alle Matrizen 5, durch die A'^ diagonalisiert
wird.
8. Geben Sie die allgemeine Form einer Matrix mit den Eigenvektoren [\]
und [_\] an.
6.2 Diagonalisierung einer Matrix 315
In den Aufgaben 9-14 geht es um Fibonacci- und Gibonacci-
Zahlen.
9. Berechnen Sie für die Fibonacci-Matrix A = [Iq] die Potenzen A^, A^
und A^. Berechnen Sie dann mit Hilfe eines Taschenrechners (und des
Verfahrens im Text) die Zahl F20.
10. Es sei jede Zahl Gk-^2 der Mittelwert der zwei vorhergehenden Zahlen
Gk+i und Gk, es gelte also Gk+2 = ^{Gk+i -^Gk):
Gjfe-f 1 = Gk-\-i
ist
[ Gk-\-2
=
A
Gk-\-i
Gk \
(a) Bestimmen Sie die Eigenwerte und Eigenvektoren von A.
(b) Bestimmen Sie den Grenzwert der Matrizen A^ = SA'^S~^
für n —>• 00.
(c) Zeigen Sie, dass für Go = 0 und Gi = 1 die Gibonacci-Zahlen gegen
den Wert | streben.
11. Diagonalisieren Sie die Fibonacci-Matrix, indem Sie 5~^
vervollständigen:
1 r
10
=
Ai A2
1 1
Ai 0"
OA2
Berechnen Sie das Produkt SA^S ^[0], um die zweite Komponente zu
bestimmen, also die k-te Fibonacci-Zahl Fk — (Af — A2)/(Ai — A2).
12. Die Zahlen Af und A2 erfüllen die Fibonacci-Regel FkJf-2 = Fk^i + Fk'.
Af+2 = A^i + Aj und A^+2 - A^^ + A^
Beweisen Sie dies mit Hilfe der ursprünglichen Gleichung für die A's.
Dann genügt auch jede Linearkombination von Af und A2 der Regel. Die
Kombination Fk = (Af — A2)/(Ai — A2) liefert die richtigen Startwerte
Fo = 0 und Fl = 1.
13. Angenommen, Fibonacci hätte mit den Startwerten Fo = 2 und Fi = 1
begonnen. Die Regel Fk^2 = Fk-^i + Fk bleibt gleich, also bleibt auch die
Matrix A unverändert. Die Summe der Eigenvektoren ist
Xl +X2
|A + V^)
1
+
1
Fl
Fo
Nach 20 Schritten ist die zweite Komponente von ^^^(xi + X2) gleich
( )^^ + ( )^^- Berechnen Sie die Zahl F20.
316 6 Eigenwerte und Eigenvektoren
14. Beweisen Sie, dass jede dritte Fibonacci-Zahl in der Folge 0,1,1,2,3,...
gerade ist.
In den Fragen 15-18 geht es um Diagonalisierbarkeit.
15. Wahr oder falsch: Sind die Zahlen 2, 2 und 5 die Eigenwerte von A, so
ist die Matrix sicher
(a) invertierbar
(b) diagonalisierbar
(c) nicht diagonalisierbar.
16. Wahr oder falsch: Sind die einzigen Eigenvektoren von A die Vielfachen
von A,4), so besitzt A
(a) keine Inverse
(b) einen mehrfachen Eigenwert
(c) keine Diagonalisierung der Form SAS~^.
17. Vervollständigen Sie die folgenden Matrizen so, dass detA = 25 gilt.
Überprüfen Sie, dass dann A = 5 ein mehrfacher Eigenwert, die
Determinante von A — \I also (A — 5)^ ist. Finden Sie einen Eigenvektor mit
Ax = 5x. Diese Matrizen sind nicht diagonalisierbar, weil ihnen ein
zweiter Eigenwert fehlt.
A =
8
,A =
94
1
und A =
10 5
-5
18.
Die Matrix A = [03] ist nicht diagonalisierbar, da der Rang von A
gleich ist. Ändern Sie den Wert eines Eintrags um 0,01
3/
um A
diagonalisierbar zu machen. Welche Einträge könnten Sie ändern?
Die Aufgaben 19-23 behandeln Potenzen von Matrizen.
19. A^ = SA^S~^ geht für A; -> 00 gegen die Nullmatrix genau dann, wenn
jedes A einen Absolutbetrag kleiner als
Matrizen gilt A^
hat. Für welche dieser
0?
0,6 0,4
0,4 0,6
und 5 =
0,6 0,9
0,1 0,6
20. (Empfohlen) Bestimmen Sie A und S für die Diagonalisierung von A
in Aufgabe 19. Gegen welchen Grenzwert streben die Matrizen A'^ für
k -> 00? Gegen welchen Grenzwert strebt dann SA^S~^? In den Spalten
dieser Grenzwert-Matrix findet man den .
21. Bestimmen Sie A und 5, um B in Aufgabe 19 zu diagonalisieren. Welcher
Vektor B^^uq ergibt sich für die folgenden uo?
uo
und Uo =
und Uo =
6.2 Diagonalisierung einer Matrix 317
22. Diagonalisieren Sie A und berechnen Sie SA^S ^, um die folgende Formel
für A^ zu beweisen:
21
12
hat die Potenzen
^ - 2
1+3^-3^
1 - 3M + 3^
23. Diagonalisieren Sie B und berechnen Sie 5^1^5 ^, um die folgende Formel
für B'^ zu beweisen:
B
31
02
hat die Potenzen B
3^ ^k _2kl
0 2^
Die Aufgaben 24—29 behandeln neue Anwendungen der Faktorisie-
rung A = SAS-^.
24. Es gelte A = SAS~^. Berechnen Sie die Determinanten und zeigen Sie,
dass detA = AiA2---An = (Produkt der A's) ist. Dieser kurze Beweis
funktioniert nur, wenn A ist.
25. Zeigen Sie, dass die Spur von AB gleich der Spur von BA ist, indem Sie
die Diagonaleinträge von AB und BA addieren:
A =
a b
c d
und B
q r
s t
Wählen Sie A als S und B als AS ^. Dann hat SAS ^ dieselbe Spur wie
AS'^S. Die Spur von A ist gleich der Spur von A, also gleich .
26. Es ist unmöglich, dass AB — BA = / gilt, da die linke Seite die Spur
hat. Finden Sie stattdessen eine Eliminationsmatrix A = E und
B =^ E^ so, dass
AB-BA =
-10
Ol
(mit der Spur Null) gilt.
27. Diagonalisieren Sie für A - SAS~'^ die Blockmatrix B = [^ 2a]- ^^"
stimmen Sie die Eigenwert- und Eigenvektor-Matrizen.
28. Betrachten Sie alle 4 x 4-Matrizen, die durch dieselbe Matix S diagonali-
siert werden. Zeigen Sie, dass diese Matrizen A einen Unterraum bilden,
dass also mit Ai und A2 auch cAi und Ai + A2 durch S diagonalisiert
werden. Welchen Unterraum erhalten Sie für S = I? Welche Dimension
hat er?
29. Es gelte Ä^ = A. Auf der linken Seite der Gleichung wird jede Spalte
von A mit A multipliziert. In welchem unserer vier Unterräume finden
Sie einen Eigenvektor mit A = 1? Welcher der Unterräume enthält
Eigenvektoren zu A = 0? An den Dimensionen dieser Unterräume kann man
318 6 Eigenwerte und Eigenvektoren
erkennen, dass A einen vollen Satz linear unabhängiger Eigenvektoren
besitzt und diagonalisiert werden kann.
30. (Empfohlen) Es gelte Ax = Ax. Ist A = 0, so liegt x im Kern von A. Gilt
A ^ 0, so liegt X im Spaltenraum. Die Dimensionen dieser Räume
addieren sich zu {n — r) + r = n auf. Warum hat dann nicht jede quadratische
Matrix n linear unabhängige Eigenvektoren?
31. Die Eigenwerte von A sind 1 und 9, die Eigenwerte von B sind —1 und
9:
54
45
und B =
45
54
Bestimmen Sie eine „Wurzel aus A" aus der Gleichung W = Sy/ÄS ^.
Warum gibt es keine reelle Matrix, die eine Wurzel aus B wäre?
32. (Heisenbergsche Unschärferelation) Für unendliche Matrizen A und
B mit A = Ä^ und B ^ -B^ kann die Gleichung AB - BA = I erfüllt
sein. Dann gilt
x^x = x^ABx - x^BAx < 2\\Ax\\ \\Bx\\,
Erklären Sie mit Hilfe der Schwarz'schen Ungleichung den letzten Schritt.
Diese Ungleichung besagt, dass ||ylx||/||x|| mal ||5x||/||x|| mindestens den
Wert \ hat. Es ist unmöglich, den Messfehler für die Position und den
Fehler für den Impuls gleichzeitig beliebig klein zu machen.
33. Haben A und B dieselben Eigenwerte mit denselben linear unabhängigen
Eigenvektoren, so sind auch ihre Faktorisierungen der Form gleich.
Deshalb gilt A = B.
34. Zeigen Sie, dass AB = BA gilt, wenn die Matrizen A und B durch
dieselbe Matrix S diagonalisiert werden, so dass A = SAiS~^ und B =
SA2S-' gilt.
35. Zeigen Sie, dass für A = SAS'^ das Produkt {A - \iI){A - X2I) • • • (A -
An/) die Nullmatrix ergibt. Der Satz von Gay ley-Hamilton besagt, dass
dieses Produkt immer Null ist. Man setzt A anstelle von A in das Polynom
det{A - XI) ein.
36. Die Matrix A = [zlt] hat die Determinante det{A - XI) = A^ - 1.
Zeigen Sie mit Hilfe von Aufgabe 35, dass A^ — I = 0 gilt, folgern Sie, dass
A~^ = A gilt, und überprüfen Sie diese Beziehung durch Nachrechnen.
37. (a) Unter welchen Umständen erzeugen die Eigenvektoren zum Eigenwert
A = 0 den Kern N{A)?
(b) Unter welchen Umständen erzeugen die Eigenvektoren zu
Eigenwerten A / 0 den Spaltenraum S{A)?
= Xu besitzt die Lösungen u{t) = Ge^^ F.18)
6.3 Anwendungen bei Differentialgleichungen 319
6,3 Anwendungen bei Differentialgleichungen
Eigenwerte, Eigenvektoren und die Faktorisierung A = SAS''^ eignen sich
perfekt zur Berechnung von Potenzen A^ von Matrizen. Sie sind ebenso
hervorragend zur Behandlung von Differentialgleichungen geeignet. In diesem
Abschnitt geht es hauptsächlich um lineare Algebra, aber um ihn zu lesen,
müssen Sie eine Tatsache aus der Differentialrechnung mitbringen: Die
Ableitung von e^^ ist Ae^^ Es macht die Sache leichter, wenn Sie wissen, was e
ist, aber ich bin mir nicht einmal sicher, ob das nötig ist. Alles, worum es in
diesem Abschnitt geht, ist: die Lösung von Differentialgleichungen zu
einem Problem der linearen Algebra zu machen.
Die Gleichung du/dt = u wird durch die Funktion u = e^ gelöst. Die
Gleichung du/dt = 4u wird durch die Funktion u = e^^ gelöst. Die einfachsten
Gleichungen werden also durch Exponentialfunktionen gelöst.
du
Die Zahl C tritt dabei auf beiden Seiten der Gleichung du/dt = Xu auf, und
kann deswegen hinausdividiert werden.
Für ^ = 0 hat die Lösung den Wert C (wegen e^ = 1). Durch Wahl
von C = u{0) erfüllt man also eine „Anfangsbedingung". Die Lösung der
Gleichung, die mit dem Wert u{0) bei ^ = 0 beginnt, ist u{0)e^^.
Wir haben gerade ein 1 x 1-Problem gelöst. Mit Hilfe der linearen Algebra
kann man auch n x n-Probleme betrachten. Die unbekannte Funktion ist
dann ein Vektor u (in Fettdruck), der bei einem gegebenen Anfangsvektor
u@) beginnt. In den n Gleichungen ist eine quadratische Matrix A enthalten:
Problem
Löse die Gleichung — = Au mit der Anfengsbedinguag^ u@) bei ti= 0.
F.19)
Dies ist ein lineares Differentialgleichungssystem. Sind u(^) und v(^) zwei
Lösungen, so ist auch jede Linearkombination Cu(^) + Dv{t) eine Lösung.
Wir werden n freie Konstanten benötigen, um die n Komponenten von u@)
zu erhalten. Unsere erste Aufgabe ist aber, „reine Exponentiallösungen" für
die Gleichung du/dt = Au zu bestimmen.
Beachten Sie, dass A eine konstante Matrix ist. Bei anderen linearen
Differentialgleichungen kann A von t abhängig sein. In einer nicht linearen
Gleichung kann A sogar von u abhängig sein. Mit keiner von diesen
Schwierigkeiten wollen wir uns befassen. Die Gleichung F.19) ist eine „lineare
Differentialgleichung mit konstanten Koeffizienten". Die Lösung solcher (und nur
solcher) Differentialgleichungen kann man direkt in ein Problem der linearen
Algebra umwandeln. Die wesentliche Idee ist: Man löst lineare
Differentialgleichungen mit konstanten Koeffizienten durch Exponentialfunktionen e^^x.
320 6 Eigenwerte und Eigenvektoren
Die Lösung der Gleichung du/dt = Au
Unsere reine Exponentiallösung wird von der Form eines Produktes aus der
Zahl e^^ und einem festen Vektor x sein. Vielleicht ahnen Sie schon, dass dabei
A ein Eigenwert und x ein Eigenvektor von A ist. Setzt man u(^) - e^^x in
die Gleichung du/dt = Au ein, so sieht man, dass dies richtig ist (der Faktor
e^^ kann hinausgekürzt werden):
Au = Ae^^x und -p = Ae^^x stimmen überein, falls Ax = Ax. F.20)
dt
Alle Komponenten dieser speziellen Lösung u = e-^^x haben einen
gemeinsamen Faktor e^^. Die Lösung wächst also, wenn A > 0 ist, und sie klingt
ab, wenn A < 0 ist. Im allgemeinen Fall kann A eine komplexe Zahl sein. In
diesem Fall entscheidet der Realteil von A über Wachstum oder Abklingen,
während der Imaginärteil zu einer Schwingung ähnlich der einer Sinuskurve
führt.
Beispiel 6.3.1 Man löse die Gleichung ^ = Au= [J J]u mit dem
Anfangswert u@) = [i].
Hierbei handelt es sich um eine Vektorgleichung für u, die zwei skalare
Gleichungen für die Komponenten x und y enthält. Es sind „gekoppelte"
Gleichungen, weil die Matrix keine Diagonalmatrix ist:
dt
y'
z
=
Ol"
10
'y'
Z i
dy
bedeutet, dass ^-
dt
und
dz
'dt
Die Idee hinter der Verwendung von Eigenvektoren ist, diese Gleichungen
so zu kombinieren, dass man wieder zu eindimensionalen Problemen gelangt.
Die Kombinationen y -^ z und y — z leisten dies:
— {y + z) = z + y und —{y - z) ^ -{y - z).
Die Kombination y -^ z wächst proportional zu e*, weil sie A := 1 enthält. Die
Kombination y — z hingegen klingt wie e~* ab, weil sie A = -1 enthält. Der
springende Punkt ist nun, dass wir nicht mit den ursprünglichen Gleichungen
du/dt = Au hantieren müssen, um solche Kombinationen zu finden. Diese
Aufgabe wird von den Eigenvektoren und Eigenwerten erledigt.
Die Matrix A hat die Eigenwerte 1 und -1 mit den Eigenvektoren
"Ol"
10
r
1
=
1"
1
und
"Ol"
10
r
-1
=
-1"
1
xt^.
Die reinen Exponentiallösungen Ui und U2 haben also die Form e'^^x:
tix(t) = e^^%x-e^
undu2{t) -e^^^X2
=-[-iJ:
F.21)
6.3 Anwendungen bei Differentialgleichungen 321
Hinweis: Diese u's sind Eigenvektoren. Sie erfüllen die Gleichungen ^ui =
ui und Au2 = -U2, ebenso wie xi und X2. Die Faktoren e* und e~^ ändern
sich mit der Zeit. Diese Faktoren führen dazu, dass die Gleichungen dui/dt =
ui und du2/dt = -U2 erfüllt sind. Damit haben wir zwei Lösungen der
Differentialgleichung du/dt = Au. Um alle anderen Lösungen zu bestimmen,
bilden wir Linearkombinationen dieser beiden:
Allgemeine Lösung
u{t) = Ce^
+ 06"
F.22)
Mit diesen Konstanten C und D können wir die Lösung an jeden
Anfangsvektor u@) anpassen. Dazu setzen wir ^ := 0 (und erhalten e^ = 1). Die
Aufgabe war, eine Lösung mit u@) — D,2) zu finden:
C
+ D
liefert C := 3 und L) = 1.
Setzt man also C — ^ und i^ = 1 in die Lösung F.22) ein, erhält man eine
Lösung des Anfangswertproblems.
Fassen wir dies noch einmal zusammen. Durch dieselben Schritte, mit
denen wir die Differenzengleichung u^+i — A\ik im letzten Abschnitt lösen
konnten, gelangen wir jetzt zu einer Lösung der Differentialgleichung du/dt =
Au. Die Potenzen A'^ der Matrix führten auf A^. Die Differentialgleichung
hingegen führt zu e^^:
1. Man bestimmt die Eigenwerte und n linear unabhängige Eigenvektoren
von A.
2. Man schreibt u@) als Kombination ciXi H h Cn^n der Eigenvektoren.
3. Man multipliziert jeden Eigenvektor x^ mit e^'^. Dann ist die Lösung u(^)
durch die Kombination
u{t) - eie^^*xi -h
t Cj^G X^
F.23)
gegeben.
Beispiel 6.3.2 Man löse die Gleichung du/dt = ^u {A hat die Eigenwerte
A = 1,2 und 3):
du
~dt
1 1 1
02 1
003
u mit der Anfangsbedingung u@)
Schritt 1 Die Eigenvektoren sind xi = A,0,0), X2 = A,1,0) und X3 =
A,1,1).
Schritt 2 Der Vektor u@) = F,5,4) ist gleich Xi 4- X2 4- 4x3. Es gilt also
(Cl,C2,C3) = A,1,4).
'
Xi X2 X3
Cl
C2
.^3_
=
1
5
ej
322 6 Eigenwerte und Eigenvektoren
Schritt 3 Die reinen Exponentiallösungen sind e^xi, e^*X2 und e^^xs.
Die Kombination, die den Anfangswert u@) liefert, ist u(^) =
e^xi +e^*X2 + 4e^*X3.
Die Koeffizienten 1, 1 und 4 erhält man als Lösung des linearen
Gleichungssystems ciXi + C2X2 + C3X3 := u@):
hat die Lösung 5c := u@). F.24)
Sie kennen jetzt die grundlegende Idee, wie man eine Differentialgleichung
du/dt = Au löst. Im weiteren Verlauf dieses Abschnitts werden wir noch
weitergehen. Wir werden Differentialgleichungen lösen, die zweite Ableitungen
enthalten, weil sie sehr oft in Anwendungen auftreten. Wir werden auch
entscheiden, ob deren Lösungen u(^) gegen Null gehen, ob sie „explodieren"
oder einfach oszillieren. Zum Schluss lernen wir die Exponentialfunktion e"^^
für Matrizen kennen. Mit ihrer Hilfe erhalten wir die Lösung e'^*u@) für die
Differentialgleichung du/dt = Au in genau der Weise, wie ^^uo eine Lösung
von U)fe+i = Auk ist.
Bei allen diesen weiteren Schritten werden wir Eigenwerte A und
Eigenvektoren X verwenden. Mit der zusätzlich hinzukommenden Zeit t stellt dieser
Abschnitt eine enge Verbindung zur Theorie der Differentialgleichungen her.
Wir stellen die Lösung der Probleme mit konstanten Koeffizienten dar, die
sich vollständig in Probleme der linearen Algebra verwandeln. Verwenden Sie
diesen Abschnitt, um sich Klarheit über diese einfachsten, aber äußerst
wichtigen Differentialgleichungen zu verschaffen, deren Lösung komplett auf e^^
basiert.
Gleichungen zweiter Ordnung
Wir beginnen mit der Gleichung y" + hy' ^-ky = 0, wobei die Unbekannte y{t)
eine skalare Funktion ist, keine Vektorfunktion. Die Schreibweisen y" und y'
stehen für d'^y/dt'^ und dy/dt. Es handelt sich hier um eine Gleichung zweiter
Ordnung, weil sie die zweite Ableitung y" enthält. Sie ist aber immer noch
eine lineare Gleichung mit konstanten Koeffizienten h und k.
In einer Vorlesung über Differentialgleichungen löst man solche
Gleichungen, indem man y = e^^ einsetzt. Durch jede Ableitung wird dann ein Faktor
A erzeugt. Die Funktion y — e^^ soll die folgende Gleichung lösen:
^ + b^ + ky = {\' + bX + k)e^' = 0 F.25)
at"^ dt
Ob y eine Lösung ist, hängt also davon ab, ob X"^ + bX + k =^ 0 gilt. Diese
Gleichung für A hat zwei Nullstellen Ai und A2. Dann hat also die
Differentialgleichung für y zwei reine Exponentialfunktionen 1/1 = e^^^ und 1/2 = e^'^^
6.3 Anwendungen bei Differentialgleichungen 323
als Lösung. Durch die Linearkombinationen ciyi -\-C2y2 erhält man alle
anderen Lösungen. In der allgemeinen Lösung sind zwei freie Konstanten ci und
C2 enthalten, weil die Differentialgleichung eine zweite Ableitung enthält.
In einer Vorlesung über lineare Algebra erwarten wir aber Matrizen und
Eigenwerte. Deshalb schreiben wir die skalare Gleichung in eine
Vektorgleichung um. Der unbekannte Vektor u hat dabei die Komponenten y und y',
für den man eine Gleichung der Form du/dt = Au erhält:
F.26)
Die erste Gleichung dy/dt = y' ist trivial (aber wahr). Durch die zweite
Gleichung wird y" mit y' und y in Beziehung gesetzt. Zusammen setzen die
Gleichungen u' mit u in Verbindung. Diese Vektorgleichung können wir mit
Hilfe von Eigenwerten lösen:
dy ,
di^y
%^-^y-W
wird zu --
dt
' y'
y'.
0 1"
-k-b
' y'
y'.
A~XI =
-\ 1
-k^b-X
liat die Deteriainaate >? ^hX-^h = 0;
Es ergibt sich dieselbe Bedingung für die Eigenwerte Aj. Sie müssen wieder
die Gleichung A^ + 6A + fe = 0 erfüllen. Deren Nullstellen Ai und A2 erhalten
wir diesmal als Eigenwerte von A. Die Eigenvektoren und die vollständige
Lösung sind
Xl
1
Ai
X2
1
A2
Ali
u(^) =cie^^
1
Ai
+ C2e^2*
1
A2
In der ersten Komponente von u(^) haben wir dieselbe Lösung y = ae^ +
c^e^^^ wie zuvor. Was hätte es auch sonst sein sollen? In der zweiten
Komponente haben wie die Ableitung dy/dt. Die Formulierung mit Hilfe von
Vektoren ist also völlig konsistent mit dem ursprünglichen skalaren Problem.
Bemerkung 1 In der linearen Algebra stellt ein möglicher Mangel an
Eigenvektoren eine ernste Gefahr dar. Unsere Eigenvektoren A, Ai) und A, A2)
fallen zusammen, wenn Ai = A2 gilt. In diesem Fall lässt sich A nicht diagonali-
sieren, und wir erhalten keine vollständige Lösung der Gleichung du/dt = Au.
Auch in der Theorie der Differentialgleichungen stellt ein mehrfacher
Eigenwert A ein Problem dar. Die beiden reinen Exponentiallösungen sind
gleich, wenn die Eigenwerte gleich sind, und deshalb ist das Problem
wieder nicht vollständig gelöst. Man muss noch eine zweite Lösung finden, die,
wie sich herausstellt, durch y = te^^ gegeben ist.
Diese „unreine" Lösung (mit einem zusätzlichen Faktor t) erhält man auch
in der Formulierung über Vektoren. Hier können wir keine Diagonalmatrix A
verwenden, wenn es nur einen Eigenvektor gibt. In diesem Fall wird A durch
324 6 Eigenwerte und Eigenvektoren
eine Jordanmatrix J ersetzt. Diese Matrix wird im letzten Abschnitt dieses
Kapitels beschrieben. Die Exponentialfunktion angewendet auf J liefert dann
das zusätzliche t.
Bemerkung 2 In den Ingenieurwissenschaften und in der Physik kommen
zweite Ableitungen durch Newtons Gesetz F = ma ins Spiel. Die
Beschleunigung a = y" wird mit der Masse m multipliziert. Die Gleichung lautet
eigentlich my" + by' -^ ky — f. (Die Kraft F in Newtons Gesetz besteht aus
drei Teilen, einer externen Kraft /, einer Dämpfungskraft hy' und einer
internen Kraft ky.) Hier haben wir durch m dividiert, so dass die linke Seite in
ihrer Standardform (mit y" am Anfang) erscheint.
Bemerkung 3 Physiker und Ingenieure haben es in der Realität mit
Systemen (nicht nur einzelnen Massenpui^ten) zu tun. Eigentlich ist die
Unbekannte y ein Vektor, der KoefRzient m eine Massenmatrix M statt einer
Zahl, und der KoefRzient k eine Elastizitätsmatrix K. Der KoefRzient von y'
ist eine Dämpfungsmatrix, die Null sein kann. In dem Fall ist die eigentliche
Differentialgleichung My" -^Ky — f. Um sie in die Standardform zu bringen,
multipliziert man beide Seiten mit M"^. Die Lösung enthält dann die
Eigenwerte von M~^K, die zu bestimmen einen wesentlichen Teil der Rechnungen
in der Mechanik ausmacht.
Beispiel 6.3.3 Lösen Sie die Gleichung y" + 4y' -\- 3y = 0 durch Einsetzen
von e^^ sowie mit den Methoden aus der linearen Algebra.
Lösung Durch Einsetzen von y = e^^ erhält man (A^ + 4A + 3N-^* = 0.
Die quadratische Gleichung ist also A^ +4A + 3 = 0, die in die Faktorisierung
(A+l)(A+3) = 0 zerfällt. Sie hat daher die Nullstellen Ai = -1 und A2 := -3.
Die reinen Lösungen sind also yi = e""* und 1/2 = e""^*. Als vollständige
Lösung erhält man die Linearkombination ciyi + C21/2, die für wachsendes t
gegen Null geht.
Um die lineare Algebra anwenden zu können, setzen wir u = {y,y'), was
uns auf eine Vektorgleichung führt:
dy dt — y . . du
^ ' /jj. o At wird zu -r-
dy /dt = -Sy- Ay' dt
0 1
-3-4
u;
Als nächstes bestimmen wir die Eigenwerte über die Determinante A — \I:
\A-\I\
-A 1
-3-4-A
= A^ + 4A + 3 - 0.
Wir erhalten dieselbe Gleichung mit denselben Nullstellen, und daher
dieselben Lösungen. Im Fall von konstanten Koeffizienten und reinen Expo-
nentiallösungen lässt sich die Differentialrechnung vollständig auf die lineare
Algebra zurückführen.
6.3 Anwendungen bei Differentialgleichungen 325
Stabilität von 2 X 2-Matrizen
Es gibt eine fundamentale Frage über die Lösung einer Differentialgleichung
du/dt = Au, Geht die Lösung für t ^ oo gegen u = 0 ? Ist das Problem
stabin Beispiel 6.3.3 war sicher stabil, da beide reinen Lösungen e"* und
g-3t gegen Null gehen. Die Stabilität hängt von den Eigenwerten ab, und die
Eigenwerte hängen von A ab.
Die vollständige Lösung u(^) ist aus den reinen Exponentiallösungen e^*x
aufgebaut. Ist der Eigenwert A reell, so wissen wir genau, wann e^* gegen
Null geht: die Zahl A muss negativ sein. Ist der Eigenwert eine komplexe Zahl
A := a-\-ibj so kann man e^* in die Faktoren e^*e*^* zerlegen. Der Absolutbetrag
des zweiten Faktors ist konstant 1:
e'^* := cos bt + i sin bt hat den Betrag |e'^*p := cos^ bt + sin^ bt = 1.
Der andere Faktor e^* entscheidet über Wachstum (Instabilität) oder
Abklingen (Stabilität). Für eine stabile Lösung muss der Realteil von A negativ
sein, denn dann geht der Ausdruck e^* gegen Null.
Die Frage ist also: Welche Matrizen haben negative Eigenwerte? Genauer
gesagt, unter welchen Umständen sind die Realteile der Eigenwerte sämtlich
negativ? Für 2 x 2-Matrizen gibt es eine eindeutige Antwort.
6G Stabilität Die Matrix^ = [^^] ist stabil, n(t) geht gegen NttU, wenn
zwei Bedingungen arfüUt sind:
Die Spur T = a-\- d muss negativ sein.
Die Determinante D = ad-bc muss positiv sein.
Begründung Sind die A's reell und negativ, so ist ihre Summe, also die
Spur, ebenfalls negativ. Ihr Produkt, die Determinante, ist dann positiv. Das
Argument lässt sich auch in der umgekehrten Richtung verwenden. Ist D =
Ai A2 positiv, so müssen Ai und A2 dasselbe Vorzeichen haben. Ist T = Ai + A2
aber negativ, so muss dieses Vorzeichen negativ sein.
Sind die A's komplexe Zahlen, so müssen sie von der Form a-\-ib und a — ib
sein, andernfalls wären T und D keine reellen Zahlen. Die Determinante ist
dann automatisch positiv, da (a + ib){a — ib) = a^ -\- h^ gilt. Die Spur ist
a + ib -\- a — ib = 2a, eine negative Spur impliziert also, dass der Realteil a
negativ ist, und die Matrix daher stabil. Q.E.D.
In Abbildung 6.3 wird die Parabel T^ := 4D dargestellt, die reelle von
komplexen Eigenwerten trennt. In der Lösung der Gleichung A^ -TA + i^ = 0
kommt der Term y/T"^ - 4D vor, der reell oberhalb der Parabel und darunter
imaginär ist. Die stabile Region ist das obere linke Viertel der Abbildung, wo
T < 0 und JD > 0 gilt.
326 6 Eigenwerte und Eigenvektoren
Determinante D
A
""x beide Re^KO
^^ stabil
beide Re>.>0 /
instabil ^ ^
'ji ^ r^ ^ Jl x''beide >.>0
stabil -'^^2^ndT^^t^- ^"^tabil
^ 0|JU1 l
X^<0 und >.2 > 0 : instabil
Abb. 6.3. Eine 2 x 2-Matrix is stabil (u@ -^ 0), wenn T < 0 und D > 0 gilt.
Beispiel 6.3.4 Welche dieser Matrizen ist stabil?
Ai
0-1
-2-3
A2
4 5
-6-7
A.^
Die Exponentialfunktion für Matrizen
Wir wollen uns noch einmal kurz den Lösungen u(^) einer linearen
Differentialgleichung zuwenden, und sie in einer neuen Form e'^*u@) angeben.
Durch diese Schreibweise ziehen wir eine perfekte Parallele zu den Lösungen
^^uo des vorherigen Abschnitts. Dazu müssen wir aber zuerst sagen, was e"^*
bedeuten soll.
Bei der Matrix e"^* steht eine Matrix im Exponenten. Um den Ausdruck
e-^^ zu definieren, halten wir uns an e^. Dessen direkte Definition geschieht
über die unendliche Reihe l + a:+|a:^ + |a:^ + -
At an Stelle von x ein, erhält man e^*:
. Setzt man hier die Matrix
Definition der ExponeniialfunMion für eine Matrix
Die Zahl, durch die {At)'' dividiert wird, ist „n Fakultät", also
n! := (l)B).-.(n - l)(n). Die Fakultäten nach 1, 2 und 6 sind 4! := 24
und 5! = 120. Sie wachsen sehr schnell an. Die Reihe konvergiert immer,
ihre Ableitung ist immer Ae^^ (s. Aufgabe 17). Aus diesem Grund löst der
Ausdruck e^*u@) die Differentialgleichung mit einer kurzen Formel — sogar,
wenn es nicht genug Eigenvektoren gibt.
In diesem Kapitel wollen wir besonders herausstellen, wie man über
die Diagonalisierung an eine Lösung kommt. Wir nehmen an, dass A dia-
gonalisierbar ist, und setzen in die Reihe A — SAS~^ ein. Überall, wo
6.3 Anwendungen bei Differentialgleichungen 327
SAS ^SAS ^ auftaucht, kann man das Produkt S~^S = I in der Mitte
weglassen:
e^^ := / + SAS-H + ^{SAS-H){SAS-h) +
F.28)
Diese Gleichung besagt, dass e"^^ gleich Se^^S~^ ist. Um also e^^ zu
berechnen, berechnet man die Eigenwerte wie üblich. Für die Diagonalmatrix A ist
auch e^^ eine Diagonalmatrix, auf deren Diagonale die Zahlen e^*^ stehen.
Berechnen wir den Ausdruck 5e'^*5~^u@), um die neue Lösung u(^) — e^*u@)
darzustellen. Es ergibt sich die alte Lösung, durch Eigenvektoren und
Eigenwerte ausgedrückt.
e^*u@) = Se^'S-^u{0)
xi ... x^
rgAit
o^n*
c\
F.29)
5 enthält die Eigenvektoren x^. Das Produkt 5c stellt eine Linearkombination
der Spalten von 5 dar. Diese Linear kombination passt zum Startwert, wenn
u@) — Sc gilt. Durch den Ausdruck c = 5~^u@) am Ende von Gleichung
F.29) erhalten wir wieder die beste Form der Lösung:
u{t) =
Xl
cie^i*""
CfiC
Xnt
.Ali
cie-'^'xi + hcne
Ant,
F.30)
Dies ist also e'^*u@). Es ist dieselbe Lösung, wie wir sie aus unseren drei
Schritten erhalten haben:
1. Man bestimmt die Eigenwerte A und die Eigenvektoren x.
2. Man schreibt u@) = cixi H h Cn^X-n^
3. Man multipliziert jeden Eigenvektor x^ mit e^'^. Die Lösung ist dann
U(^) = Cie^^^Xi + • • • + CnC^^^Xn
F.31)
Beispiel 6.3.5 Man bestimme e^* für A = [ _? ä] • Beachten Sie, dass A"^ = I
gilt:
A =
Die Matrizen A^, A^, Ä^, A? sind also einfach eine Wiederholung dieser
vier Matrizen. In der oberen rechten Ecke wiederholen sich die Einträge 1,
0,-1 und 0 immer wieder. Die unendliche Reihe für e^* hat an dieser Stelle
1"
-1
A^^
-1
-1
A^^
-1
1
A^^
1
1_
328 6 Eigenwerte und Eigenvektoren
also die Einträge ^11,0, -^^/3!,0; anders gesagt, ist t - t^/6 der Beginn der
Reihe für diesen Eintrag:
I + At+UAt)^ + l{^if + --- =
t-U^ +
Die Reihe links ist e^^. Die oberste Zeile der Matrix enthält die Reihen für
cos t und sin t. Damit haben wir e^^ direkt ausgerechnet:
.M .
COBt Bint
'Bint COBt
F.32)
Für ^ = 0 ergibt sich e^ = I. Viel wichtiger ist aber, dass die Ableitung von
^At (jurch Ae"^^ gegeben ist:
_1
dt
cost sint
— sin t cos t
- sin t cos t
cos ^ — sin ^
Ol
-10
cos^ sin^
- sin t cos t
A ist eine schief-symmetrische Matrix {A'^ = —A) mit den Eigenwerten 1
und -1. Die Exponentialfunktion e^* ergibt dann eine orthogonale Matrix,
deren Eigenwerte e** und e~** sind. Dies ist ein Beispiel für zwei allgemein
gültige Regeln:
1. Die Eigenwerte von e^* sind e^*.
2. Ist A eine schief-symmetrische Matrix, so ist e^^ orthogonal.
Beispiel 6.3.6 Man löse die Differentialgleichung ^ = Au = [02]" ™^
dem Anfangswert u@) — [?] für ^ = 0.
Lösung Die Eigenwerte von A sind die Diagonaleinträge 1 und 2 (da A eine
Dreiecksmatrix ist). Die Eigenvektoren sind A,0) und A,1):
Es gilt
Im zweiten Schritt schreibt man u@) als Linearkombination xi + X2 der
Eigen Vektoren. Erinnern Sie sich: Diese Kombination ist im allgemeinen Fall
durch 5c = u@) gegeben, in unserem Fall mit ci = C2 = 1. ie Lösung ist
dann dieselbe Kombination der reinen Exponentiallösungen:
r
02
r
0
=
T
0
und
1 1"
02
1"
1
= 2
"
1
u(^) = e'
-\-e
2t
Dies ist die Lösung in ihrer klarsten Form e^^^^Xi + e^^^:x.2. In der
Matrizenschreibweise sind die Eigenvektoren in S enthalten:
u{t) = Se'^'S~'u{0)is
1'
0 1
g2f
1 r
0 1
1 -1
u@) =
o2i
u@).
6.3 Anwendungen bei Differentialgleichungen 329
Die letzte Matrix ist e"^^. Es ist ganz nett, einmal das Ergebnis der
Exponentialfunktion für eine Matrix explizit zu sehen, und dieses ist ganz besonders
hübsch. Es ist ganz ähnlich wie mit der Gleichung ^x = b und inversen
Matrizen. Wir müssen nicht wirklich die Matrix A~^ berechnen, um x zu
bestimmen, und genauso wenig brauchen wir die Matrix e^^, um die Gleichung
du/dt = Au zu lösen. Aber als kurze Lösungsformel sind ^""^b und e'^*u@)
unschlagbar.
Die wesentlichen Punkte
1. Die Gleichung u' := ^u ist eine lineare Differentialgleichung mit konstanten
Koeffizienten.
2. Die Lösung lässt sich gewöhlich als Linearkombination von
Exponentialfunktionen schreiben, die die Eigenwerte A und Eigenvektoren x enthalten:
u{t) = cie^'^xi + • • • + Cne^-^Xn.
3. Die Konstanten ci,..., c^ sind durch die Linearkombination u@) = C1X1 +
h Cn:x.n festgelegt.
4. Die Lösung geht gegen Null (Stabilität), wenn der Realteil aller Eigenwerte
A kleiner als 0 ist.
5. Die Lösung lässt sich immer als u(^) := e'^*u@) schreiben, wobei e^^ die
Exponentialfunktion für Matrizen ist.
6. Gleichungen, die y" enthalten, können in ein System u' = ^u
umgeschrieben werden, indem y' und y in einem Vektor u = {y',y) zusammengefasst
werden.
Aufgaben 6.3
1. Bestimmen Sie die Eigenwerte A und Eigenvektoren x so, dass u = e^^x
die Differentialgleichung
du
It
43
Ol
u
löst. Welche Kombination u = cie^^^Xi +C2e^^^X2 erfüllt die
Anfangsbedingung u@) = E, -2)?
2. Lösen Sie Aufgabe 1 mit der Anfangsbedingung u = {y,z) durch
Rücksubstitution:
dz
Lösen Sie zunächst — = z mit der Anfangsbedingung z{0) = —2
dy
und dann — = 4y + 3z mit der Anfangsbedingung y{0) = 5.
Die Lösung für y ist eine Kombination von e'^* und e*.
330
3.
6 Eigenwerte und Eigenvektoren
Bestimmen Sie die Matrix A, mit der die skalare Gleichung y" = 5y' -\-4y
in eine Vektorgleichung für u = {y, y') umgeschrieben werden kann:
du
'y''
y".
=
y
y'.
= Am,
Welche Eigenwerte hat AI Bestimmen Sie die Eigenwerte auch durch
Einsetzen von y — e^^ in die Gleichung t/" = 5^/' + 4y.
Die Kaninchenpopulation A: nimmt schnell zu (Summand 6A:), es gibt aber
einen Verlust proportional zur Wolfspopulation w {—2w):
dk ^, ^ , dw
-— = ^k — 2w und ——
dt dt
2k-\-w.
Bestimmen Sie die Eigenwerte und Eigenvektoren dieses Systems. Welche
Populationen erhält man für die Zeit t bei den Anfangswerten A:@) =
w{0) = 30 ? Ist das Verhältnis der Populationen von Kaninchen zu Wölfen
nach einer langen Zeit 1 zu 2 oder 2 zu 1?
5. Zwischen zwei Räumen, die v{0) = 30 und w{0) = 10 Personen
enthalten, wird eine Tür geöffnet. Die Bewegung zwischen den Räumen sei
proportional zur Differenz v — w:
dv . dw
—-= w — V und -;— = V — w.
dt dt
Beweisen Sie, dass die Gesamtzahl v -\-w konstant bei 40 Personen liegt.
Bestimmen Sie die Matrix in du/dt = Au sowie ihre Eigenwerte und
Eigenvektoren. Welche Werte für v und w ergeben sich für t = 1?
6. Wir kehren die Diffusion von Personen aus Aufgabe 5 um, und betrachten
das System du/dt = -Au:
dv . dw
-—= V — w und —— = w — V.
dt dt
Wiederum bleibt die Summe v -\- w konstant. Wie ändern sich die
Eigenwerte, wenn A mit -A vertauscht wird? Zeigen Sie, dass v{t) vom
Startwert v{0) = 30 gegen unendlich geht.
7. Die Lösung der Differentialgleichung t/" = 0 ist die Gerade y = C -\- Dt.
Schreiben Sie die Gleichung in eine Matrixgleichung um:
dt
' y'
=
0 1"
0 0
y
y.
hat die Lösung
r,At
2/@)
J/'@)
Diese Matrix A kann nicht diagonalisiert werden. Bestimmen Sie ^^, und
berechnen Sie e^^ = I + At -\- ^A^t"^ + • • •. Berechnen Sie das Produkt
von e^* mit [y{G),y'{G)), um die Lösung y{t) = y{0) -h y'{0)t nochmals
zu erhalten.
6.3 Anwendungen bei Differentialgleichungen 331
8. Setzen Sie den Ansatz y = e^^ in die Gleichung y'' = 6y' — 9y ein, und
zeigen Sie, dass A = 3 eine doppelte Nullstelle ist. Das bedeutet Ärger,
wir brauchen eine zweite Lösung. Die Matrixgleichung lautet
d_
dt
Zeigen Sie, dass die Eigenvektoren der Matrix nur eine Gerade bilden
— also wieder ein Problem. Zeigen Sie, dass die zweite Lösung durch
y = te^^ gegeben ist.
9. Die Matrix in dieser Aufgabe ist schiefsymmetrisch:
=
Ol'
-9 6
y
y'\
du
[" 0
—c
L ^■
c-
0
-a
-6"
a
Oj
u'y = CU2 — bUs
u oder U2 = au^ — cui
Uo = bui — au2.
(a) Die Ableitung von ul+u^+ul ist 2iiiiii+21/2^*2+21/31/3. Setzen Sie
die Ausdrücke für u[, 1*2 und u'^ ein, und zeigen Sie, dass die Summe
dann Null ist. Das bedeutet, dass der Ausdruck ||u(^)|p konstant ist.
(b) Für welche Matrizen gilt immer ||e^^u@)|| = ||u@)||? Ist A
schiefsymmetrisch, so ist Q = e^^ eine
Matrix.
10. (a) Schreiben Sie A,0) als Linearkombination ciXi + C2X2 dieser beiden
Eigenvektoren von A:
12.
Ol'
-10
1
i
-i
l"
l
Ol'
-10
■ r
—i
=-i
—i
(b) Die Lösung der Gleichung du/dt = Au mit dem Anfangswert A,0)
ist cie^^xi + C2e~*^X2. Setzen Sie e*^ = cos^ + zsin^ und e~*^ =
cos^ — isint ein, und bestimmen sie daraus einen Ausdruck für u(^).
11. (a) Geben Sie zwei bekannte Funktionen an, die die Gleichung d'^y/dt^ =
—y lösen. Welche hat die Anfangswerte y{G) = 1 und y'{0) = 0?
(b) Die Gleichung zweiter Ordnung y" = —y führt auf eine
Vektorgleichung u' = Au:
u
y
du
~dt
'y''
y".
=
Ol'
-10
y
y'.
= Au.
Setzen Sie die Funktion y(t) aus Teil (a) in den Vektor u(t) — {y,y')
ein. Dadurch erhalten sie ein weiteres Mal die Lösung zu Aufgabe 10.
Welcher konstante Vektor löst die Gleichung du/dt = Au-h mit einer
invertierbaren Matrix A? Dieser Vektor ist Upartikuiär, die Lösungen der
Gleichung du/dt = Au bilden Uhomogen- Bestimmen Sie die vollständige
Lösung Up -h Uh der Gleichung
332 6 Eigenwerte und Eigenvektoren
. ^ du
<^)f =
'2 0'
03
B
u —
'8
6
13. Die Zahl c sei kein Eigenwert von A. Bestimmen Sie einen Vektor v, so
dass u = e^^v eine Lösung der Gleichung du/dt = Au — e^^h ist. Dieses
u = e^^w ist eine partikuläre Lösung. Wieso versagt dieses Verfahren,
wenn c ein Eigenwert ist?
14. Geben Sie für jede der Regionen in Abbildung 6.3 eine Matrix A als
Beispiel an:
(a) Ai < 0 und A2 > 0
(b) Ai > 0 und A2 > 0
(c) Komplexe A's mit Realteil a > 0.
In den Aufgaben 17—25 geht es um die Exponentialfunktion e"^* für
Matrizen.
15. Geben Sie fünf Terme der unendlichen Reihe für e^^ an. Leiten Sie jeden
Term nach t ab, und zeigen Sie, dass sie so vier Terme des Produkts Ae^^
erhalten. Folgerung: die Matrix e^^ löst die Differentialgleichung.
16. Für die Matrix B ■= [S "ä] S^^^ ^^ = 0- Bestimmen Sie e^^ aus der
(kurzen) unendlichen Reihe. Rechnen Sie nach, dass die Ableitung von
^Bt duj^ch Be^^ gegeben ist.
17. Von der Anfangsbedingung u@) aus erreicht man zur Zeit T die Lösung
e^^u(O). Nach einer weiteren Zeit t hat die Lösung dann den Wert
e^^(e^^u@)). Diese Lösung zur Zeit t -\-T lässt sich ebenso als
schreiben. Folgerung: e^^ mal e^^ ist gleich
18. Bringen Sie die Matrix A = [J J] in die Form SAS~'^, und bestimmen
Sie aus der Faktorisierung Se'^^S~'^ die Matrix e^^
19. Zeigen Sie, dass man aus der unendlichen Reihe die Gleichung e^^ =
/ + (e^ - l)A folgern kann, wenn A'^ = A gilt. Für die Matrix A- [ J J]
aus Aufgabe 20 impliziert dies e^^ = .
20. Im Allgemeinen sind e^e^, e^e^ und e^+^ drei verschiedene Matrizen.
Rechnen Sie dies mit Hilfe der Aufgaben 18, 20 und 21 nach:
A-
1 1
00
B
0-1
0 0
A-\-B =
10
00
21. Schreiben Sie A = [H] als SAS-\ Berechnen Sie Se'^^S-^ also die
Matrix e^^. Überprüfen Sie das Ergebnis von e^* für t = 0.
6.4 Symmetrische Matrizen 333
22. Setzen Sie A = [Jo] i^ die unendliche Reihe ein, und berechnen Sie e^^
Bestimmen Sie als erstes Ä^l
a^^ —
10
Ol
+
^3^
0 0
+
+ ... =
0
23. Geben Sie zwei Gründe an, warum eine Matrix e^^ niemals singular sein
kann:
(a) Geben Sie die Inverse an.
(b) Betrachten Sie die Eigenwerte. Gilt Ax — Ax, so folgt e^^x —
X.
24. Bestimmen Sie eine Lösung x{t),y{t) des linken der beiden folgenden
Gleichungssysteme, die für ^ ^ oo sehr groß wird. Um diese Instabilität
zu vermeiden, vertauschte ein Wissenschaftler die beiden Gleichungen:
dx/dt = Ox — 4y
dy/dt = -2x + 2y
wird zu
dy/dt =
dx/dt =
-2x + 2y
Ox — 4y.
Die Matrix [ 0-4] i^^ stabil, sie hat negative Eigenwerte. Kommentieren
Sie dieses Vorgehen.
6.4 Symmetrische Matrizen
Die Eigenwerte von Projektionsmatrizen sind 1 und 0. Die Eigenwerte von
Spiegelungsmatrizen sind 1 und —1. Wir dehnen unseren Blick nun auf alle
anderen symmetrischen Matrizen aus. Es ist nicht übertrieben zu sagen, dass
diese Matrizen die wichtigsten sind, die überhaupt vorkommen — sowohl in
der Theorie der linearen Algebra, als auch in den Anwendungen. Wir kommen
sofort zu den grundlegenden Fragen zu diesem Thema — aber nicht nur zu
den Fragen, sondern auch zu Antworten.
Sie erraten die Fragen sicher. Die erste Frage ist die nach den Eigenwerten.
Die zweite Frage ist die nach den Eigenvektoren. Was ist besonders an der
Gleichung Ax = Ax, wenn A eine symmetrische Matrix ist? In der Sprache
der Matrizen fragen wir nach speziellen Eigenschaften von A und S für den
Fall, dass A = A^ gilt.
In der Diagonalisierung A = SAS~^ sollte sich die Tatsache, dass A
symmetrisch ist, wieder spiegeln. Einen Hinweis darauf erhalten wir, wenn wir die
Diagonalisierung transponieren: E~^)^yl5^ sollte wegen A = A^ dasselbe
sein wie SÄS~^. Möglicherweise ist die Matrix S~^ der ersten Form gleich
5^ in der transponierten Form. Dann würde S^S = I gelten. Damit sind wir
den Antworten schon ganz nahe gekommen. Hier sind sie:
1. Eine S3rmmetme& Matrix hat aur reelle Eigenwerte.
2, BleMgenm^otenk^mi^R orthoiiormal gewählt werdem.
334 6 Eigenwerte und Eigenvektoren
Diese orthonormalen Eigenvektoren bilden die Spalten von 5. Es gibt n
Eigenvektoren (linear unabhängig, da orthonormal). Jede symmetrische Matrix
kann mit einer orthogonalen Eigenvektormatrix S diagonalisiert werden. Für
orthogonale Matrizen gilt Q~^ = Q^ — was wir über S vermutet hatten, ist
wahr. Um uns daran zu erinnern, schreiben wir Q statt 5, wenn wir
orthonormale Eigen Vektoren wählen.
Warum gebrauchen wir hier das Wort „wählen"? Weil die Eigenvektoren
keine Einheitsvektoren sein müssen. Ihre Längen können wir frei wählen. Wir
wählen Einheitsvektoren, also Vektoren der Länge eins, die orthonormal sind
und nicht nur orthogonal. Damit haben wir die Diagonalisierung A = SÄS~^
in ihrer besonderen Form für symmetrische Matrizen.
6H (Spektralsatz) Jede i&ymmetris€l^ Matrix A.- A^ b^it^t eiE^.FÄo-
nsimnngQÄQ'^ mit einer reallen Diagonalmatrix A tmd einer orthogonalen
Matrix Q:- ^ •''.'' - -/' /' ^■' :' ^
A = QAQ-^=QAQ^ mit Q-^=Q^,
Es ist leicht zu sehen, dass QAQ^ symmetrisch ist. Transponiert man die
Matrix, so erhält man {Q^)^A^Q^, also wieder QAQ^, Es ist also jede
Matrix dieser Form symmetrisch. Der schwierigere Teil ist es, zu beweisen, dass
jede symmetrische Matrix reelle Eigenwerte und orthonormale Eigenvektoren
hat. Dies ist die Aussage des „Spektralsatzes" in der Mathematik, und des
„Hauptachsensatzes" in Geometrie und Physik. Wir gehen den Beweis in drei
Schritten an:
1. Mit einem Beispiel (durch das nichts bewiesen wird, außer, dass der Satz
wahr sein könnte),
2. indem wir den 2 x 2-Fall durchrechnen (und damit die meisten
unvoreingenommenen Zeitgenossen überzeugen),
3. durch einen Beweis für den Fall, dass keine mehrfachen Eigenwerte
auftreten (der nur wirklich sture Köpfe skeptisch lässt).
Die Sturköpfe haben Bauchschmerzen im Falle mehrfacher Eigenwerte. Gibt
es in diesem Fall immer noch n orthonormale Eigenvektoren? Ja, es gibt sie.
Sie bilden die Spalten von S (das jetzt Q heisst). Auf der letzten Seite vor
den Aufgaben werden wir diesen vierten und letzten Schritt skizzieren.
Wir wollen jetzt die Schritte 1 und 2 durchführen. Sie sind gewissermassen
optional. Den 2 x 2-Fall besprechen wir hauptsächlich spaßeshalber, da er ja
im allgemeinen n x n-Fall enthalten ist.
Beispiel 6.4.1 Bestimmen Sie die Eigenwerte A und Eigenvektoren x für A =
1 2
24
und A- \I =
1-A 2
2 4-A
6.4 Symmetrische Matrizen 335
Lösung Die Gleichung det{A - \I) = 0 ergibt A^ - 5A — 0. Die Eigenwerte
sind 0 und 5 {beide reell). Wir können sie auch direkt sehen: A = 0 ist ein
Eigenwert, weil A singular ist, und A = 5 ist der andere Eigenwert, so dass
0 + 5 gleich der Spur 1 + 4 ist.
Die Eigenvektoren sind B,-1) und A,2)—orthogonal, aber noch nicht
orthonormal. Der Eigenvektor für A = 0 liegt im Kern von A. Der Eigenvektor
für A = 5 liegt im Spaltenraum. Fragen wir uns, warum Kern und Spaltenraum
senkrecht aufeinander stehen. Der Fundamentalsatz besagt, dass der Kern
senkrecht auf dem Zeilenraum steht, nicht auf dem Spaltenraum. Aber unsere
Matrix ist symmetrischl Spaltenraum und Zeilenraum sind identisch. Deshalb
stehen die Eigenvektoren B, —1) und A,2) senkrecht aufeinander — was man
sowieso am Skalarprodukt sehen kann.
Diese Eigenvektoren haben die Länge y/b. Dividieren wie sie durch \/b, so
erhalten wir Einheitsvektoren, die wir in die Spalten von S (also Q) schreiben.
Damit ist A diagonalisiert.
Q-'AQ =
-1'
1 2
"TT
12"
2 4
21'
-12
"TT
00'
05
= A.
Der nächste Schritt ist die Rechnung für eine beliebige symmetrische 2x2-
Matrix. Erstens: reelle Eigenwerte. Zweitens: senkrechte Eigenvektoren. Die
Eigenwerte ergeben sich aus
det
a — A b
b c-X
A^ - (a + c)A + {ac - fc^) = 0.
F.33)
Den Ausdruck auf der linken Seite kann man in seine Linearfaktoren
(A — Ai)(A — A2) zerlegen. Das Produkt A1A2 ist dabei die Determinante
D = ac—b'^. Die Summe Ai + A2 ist die Spur T — a-\- c.
Ob die Nullstellen einer Gleichung Ax^ + Bx + C = 0 reell sind, erkennt
man am Wert des Ausdrucks B'^ - 4AC. Er darf nicht negativ sein, denn
dann ergibt sich eine imaginäre Quadratwurzel in der Lösungsformel. In der
Determinantengleichung A^ - TA + D = 0 haben wir andere Buchstaben
verwendet, wir müssen uns also den Ausdruck T^ - 4D ansehen:
Reelle Eigenwerte: T^ - 4D = (a + c)^ - 4(ac - fc^) darf nicht negativ
sein. Wir schreiben den Ausdruck zu a^ + 2ac + c^ - 4ac + 4fc^ um, und dann
zu (a - c)^ + 4fc^. Dies ist nicht negativ! Deshalb sind die Nullstellen Ai und
A2 (die Eigenwerte) sicherlich reell.
Senkrechte Eigenvektoren: Wir berechnen xi und X2 sowie ihr
Skalarprodukt:
336 6 Eigenwerte und Eigenvektoren
{A-XJ)xi =
{A - A2/)X2 =
a — Xi b
b c - Ai
a — X2 b
b c- X2
Xl
X2
= 0 also Xl =
= 0 also X2 =
b
Xl — a
X2 - c
b
aus der
ersten
Zeile
aus der
zweiten
Zeile
Hat b den Wert Null, so hat A die senkrechten Eigenvektoren A,0) und
@,1). Andernfalls berechnen wir das Skalarprodukt und beweisen so, dass
sie senkrecht auf einander stehen:
Xl • X2 = fc(A2 - c) + (Ai - a)b = fc(Ai + A2 - a - c) = 0.
F.34)
Dies ist Null, da Ai + A2 gleich der Spur a-\- c ist. Es gilt also xi ■ X2 = 0.
Betrachten wir jetzt den allgemeinen n x n-Fall mit reellen Eigenwerten und
senkrechten Eigenvektoren.
61 Reelle Eigenwerte
scheu Matrix sind reell.
Die Eigenwerte einer symmetrischen quadrati-
Beweis. Es gelte Ax = Ax. Bis wir uns vom Gegenteil überzeugt haben,
könnte A eine komplexe Zahl sein. Dann hat A die Form a + ib, wobei a und
b reelle Zahlen sind. Die komplex konjugierte Zahl ist dann Ä = a — ib. Ganz
analog können auch die Komponenten von x komplexe Zahlen sein; dreht man
das Vorzeichen der Imaginärteile um, erhält man x. Nun ist glücklicherweise
Ä mal X der zu A mal x komplex konjugierte Ausdruck. Konjugieren wir die
Gleichung Ax — Ax, erhalten wir also (da A — A^ reell ist):
Ax — Ax führt auf Ax — Xx. Transponieren ergibt x^A = x^Ä.
F.35)
Wir berechnen jetzt das Skalarprodukt der ersten Gleichung mit x und das
Skalarprodukt der zweiten Gleichung mit x:
Es gilt
X Ax — X Xx
sowie
x^ Ax
-JXx.
F.36)
Die Ausdrücke auf den linken Seiten der Gleichungen sind gleich, also müssen
auch die Ausdrücke rechts gleich sein. In der einen Gleichung steht A, in der
anderen Ä; sie werden jeweils mit x^x multipliziert, was das Quadrat der
Länge des Eigenvektors ergibt und daher nicht Null ist. Deshalb muss A
gleich Ä sein, also a -\- ib gleich a — ib. Dann ist aber der Imaginärteil b = 0
und die Zahl X = a reell. Q.E.D.
Die Eigenvektoren x sind Lösungen der rein reellen Gleichung {A — XI)x —
0, also auch reell. Das Wichtige ist, dass die Eigenvektoren zueinander
senkrecht stehen.
6.4 Symmetrische Matrizen 337
6 J Orthogonafe Etgenvektoreti Zu verschiedenen Eigenwertea gehörende
Eigenvektoren einer reeEen symmetrischen Matrix stehen senkrecht aufelfii-
ander.
Eine Matrix A besitzt reelle Eigenwerte und orthogonale Eigenvektoren dann
und nur dann, wenn A = A^ gilt.
Beweis. Es gelte Ax = Aix, Ay = A2y und A = A^. Betrachtet man das
Skalarprodukt der ersten Gleichung mit y und das der zweiten Gleichung mit
X, so erhält man
(Aix)^ y = {Axyy = x^A^y = x^Ay = x^A2y
F.37)
Ganz hnks steht x^Aiy, ganz rechts steht x^A2y. Setzt man Ai ^ A2 voraus,
so muss x^y = 0 gelten. Die Eigenvektoren sind also senkrecht.
Beispiel 6.4,2 Man bestimme die Eigenwerte und Eigenvektoren dieser
symmetrischen Matrix mit Spur 0:
A =
-3 4
43
hat det{A - XI) =:
-3-A 4
4 3-A
= A^ - 25.
Die Nullstellen der Gleichung A^ - 25 = 0 sind Ai = 5 und A2 = — 5, sie
sind beide reell. Die Eigenvektoren xi = (I52) und X2 = (—2,1) stehen
senkrecht aufeinander. Um daraus Einheitsvektoren zu erzeugen, dividiert
man durch ihre Länge \/5. Die resultierenden neuen Vektoren xi und X2
bilden die Spalten der Matrix Q, für die Q"^ =: Q^ gilt:
A = QAQ^
Dieses Beispiel illustriert unser Hauptziel in diesem Abschnitt —
symmetrische Matrizen A mittels orthogonaler Eigenvektormatrizen S = Q zu
diagonalisieren.
ri-2'
[2 1
n/s
0"
0-5
12"
-21J
v^
"j|iffllijij||j
IIIIB^ A = SAS'^ wird zu A = QAQ'^. I
Hat A — Ä^ einen doppelten Eigenwert A, so gehören zu diesem zwei
linear unabhängige Eigenvektoren, auf die wir das Gram-Schmidt-Verfahren zur
Orthogonalisierung anwenden können. Der Unterrichtscode führt es für jeden
338 6 Eigenwerte und Eigenvektoren
Eigenraum von A aus, unabhängig von seiner Dimension. Die Eigenvektoren
bilden die Spalten von Q.
Noch ein Schritt: Jede symmetrische 2 x 2-Matrix hat die Form
A = QAQ^ =
Xi X2
^2.
T
Xi
T
^2 J
F.38)
Das Produkt der Zeilen xi und X2 mit den Zeilen Aixf und A2X2^ ergibt A:
A — AiXixf -f A2X2X2'. F.39)
Dies ist nichts anderes als die Faktorisierung QAQ^ durch Eigenvektoren und
Eigenwerte ausgedrückt. Handelt es sich um eine symmetrische n x n-Matrix,
so enthält Q n Spalten, die mit den n Zeilen von Q^ multipliziert werden.
Die n Summanden haben die Form A^x^xf. Dies sind Matrizen! Gleichung
F.39) lautet für unser Beispiel
-3 4
43
1/5 2/5
2/5 4/5
4/5-2/5
-2/5 1/5
F.40)
Die Ausdrücke x^xf auf der rechten Seite stellen Projektionsmatrizen dar,
ebenso wie die Matrizen uu^ aus Kapitel 4. Der Spektralsatz für
symmetrische Matrizen sagt also aus, dass A eine Linearkombination aus
Projektionsmatrizen ist:
A = XiPi-\ \-XnPn,^i = Eigenwert, Pi = Projektion auf den Eigenraum.
Komplexe Eigenwerte reeller Matrizen
Wir haben die Gleichung F.35) von Ak = Ax zu Ax = Ax umgeformt. Das
Ergebnis war schließlich, dass A und x beide reell sein mussten, die beiden
Gleichungen also identisch sind. Eine nic/it-symmetrische Matrix kann aber
leicht komplexe Eigenwerte A und Eigenvektoren x besitzen. In diesem Fall
ist die Gleichung Ax = Ax von der Gleichung Ax = Ax verschieden. Sie liefert
uns einen neuen Eigenwert A mit einem neuen Eigenvektor x:
Die Eigenwerte und Eigenvektoren reeller Matrizen A treten in
„komplex konjugierten Paaren" auf.
Gilt Ax = Ax, so gilt auch Ax = Ax.
Beispiel 6.4.3 A = [^°^| '^l^t] ^^^ ^^^ Eigenwerte Ai = cos9 + isme und
A2 — cosO - i sinO. Diese Eigenwerte sind zueinander komplex konjugiert, sie
sind also A und A, da das Vorzeichen des Imaginärteils sinö wechselt. Da A
reell ist, müssen die Eigenvektoren x und x sein:
COS O — sinO
sin 6 cos 0
COS O — sinO
sin 6 cos 6
■ 1'
—i
■ 1"
i
6.4 Symmetrische Matrizen 339
= (cos 6 -\-i sin 0)
= (cos Ö — 2 sin 6)
' 1
-i
' 1"
i
F.41)
Eine Gleichung ist Ax = Ax, die andere ist Ax = Äx. Die Eigenvektoren sind
X = A, -i) und X = (l,i). Die Eigenvektoren und Eigenwerte dieser reellen
Matrix bilden ein komplex konjugiertes Paar.
Nach der Euler'schen Formel ist cos6-\-ism6 dasselbe wir e*^, der
Absolutbetrag ist |A| = 1, da cos^ 0 + sin^ 0 = 1 gilt. Alle orthogonalen Matrizen
haben Eigenwerte mit |A| = 1 — auch diese Drehmatrix.
Wir entschuldigen uns dafür, dass wir ein wenig die komplexen Zahlen
streifen mussten. Sie sind unvermeidbar, sogar bei reellen Matrizen. In
Kapitel 10 betrachten wir über komplexe Zahlen A und komplexe Vektoren x
hinausgehend auch komplexe Matrizen A. Dann werden Sie die gesamte
Situation überblicken.
Wir wollen diesen Abschnitt mit zwei optionalen Betrachtungen beenden.
Eigenwerte und Pivotelemente
Die Eigenwerte einer Matrix A sind etwas ganz anderes als die Pivotelemente.
Um die Eigenwerte zu berechnen, lösen wir die Gleichung det{A — XI) = 0.
Um Pivotelemente zu berechnen, verwendet man das Eliminations verfahren.
Die bislang einzige Verbindung ist diese:
(Produkt der Pivotelemente) = (Determinante) = (Produkt der Eigenwerte)
Nehmen wir A = A^ = LU an. Es gebe einen vollen Satz Pivotelemente
dl,..., dn- Dann gibt es auch n reelle Eigenwerte Ai,..., A^. Bei den d's und
A's handelt es sich nicht dieselben Zahlen, sie rühren jedoch von derselben
Matrix her. In diesem Abschnitt geht es um eine versteckte Beziehung, die
für symmetrische Matrizen gilt: Die Pivotelemente und die Eigenwerte haben
dieselben Vorzeichen.
6K Ist A eine symmetrisclie Matrix, so ist die Anzahl positiver (hegati^r)
Eigenwerte gleich der Anzahl positiver (negativer) Pivotelemente, h '--'
Beispiel 6.4,4 Die folgende symmetrische Matrix A hat einen positiven
Eigenwert und ein positives Pivotelement:
1 3
3-1
besitzt die Pivotelemente 1 und —10
und die Eigenwerte y/lÖ und -x/TÖ.
340 6 Eigenwerte und Eigenvektoren
Die Vorzeichen der Pivotelemente stimmen mit den Vorzeichen der
Eigenwerte überein, jeweils ein positives und ein negatives Zeichen. Dies kann für
nicht symmetrische Matrizen falsch sein:
5 =
1 6
-1-4
besitzt die Pivotelemente 1 und 2
und die Eigenwerte —1 und —2.
'1 3'
3-1
10'
31
'lO'
31
3]
0-ioJ
'l 1
-loj
[13"
[Ol,
Die Pivotelemente sind positiv, die Eigenwerte dagegen negativ. Auf der
Diagonalen von B stehen beide Vorzeichen! Die Diagonaleinträge bilden noch eine
dritte Menge, über die wir nichts aussagen.
Es folgt ein Beweis, dass die Pivotelemente und die Eigenwerte im Falle
A = Ä^ = LU übereinstimmende Vorzeichen haben. Man sieht dies am
besten, wenn man die Pivotelemente aus den Zeilen von U herausdividiert
und gesondert in einer Diagonalmatrix D aufschreibt. Die Pivotmatrix D
steht dann zwischen den Dreicksmatrizen L und L^, deren Diagonaleinträge
sämtlich 1 sind:
A — LU: ziehe —10 aus U heraus.
Die symmetrische Form A =■ LDL^.
Das Besondere ist, dass L^ in der Faktorisierung steht. Dies geschieht nur für
symmetrische Matrizen, da eine Matrix der Form LDL^ immer symmetrisch
ist. (Transponiert man sie, erhält man wieder LDL^.) Für symmetrische
Matrizen geht die Faktorisierung A = LU in die Form LDL^ über, wenn
man die Pivotelemente herausdividiert.
Betrachten wir die Eigenwerte, während wir L und L-^ in die
Einheitsmatrix verwandeln. Am Anfang sind \/lÜ und — \/lÜ die Eigenwerte von LDL^.
Nachher sind die Eigenwerte von IDI^ aber 1 und -10 — die Pivotelemente.
Während die 3 in L sich in eine 0 verwandelt, wandern die Eigenwerte also.
Um aber das Vorzeichen zu wechseln, müsste ein Eigenwert die Null
passieren. In diesem Augenblick wäre die Matrix singular. Die Matrix besitzt aber
während der gesamten Verwandlung die Pivotelemente 1 und -10, ist also
niemals singular. Die Vorzeichen können also nicht wechseln, während sich
die A's zu den d's hin bewegen.
Wiederholen wir den Beweis für eine beliebige Matrix der Form A ~
LDL^. Man verwandelt L in /, indem man die Einträge abseits der
Diagonalen gegen Null gehen lässt. Die Pivotelemente bleiben konstant und ungleich
Null. Dagegen wandern die Eigenwerte A von LDL^ zu den Eigenwerten d
von IDI^. Da die Eigenwerte während des Übergangs den Wert Null nicht
überschreiten können, können sie auch ihr Vorzeichen nicht ändern. Q.E.D.
So sind also die beiden Hälften der angewandten linearen Algebra —
Pivotelemente und Eigenwerte — miteinander verknüpft.
6.4 Symmetrische Matrizen 341
Alle symmetrischen Matrizen sind diagonalisierbar
Kommt keiner der Eigenwerte von A mehrfach vor, so sind die Eigenvektoren
sicher linear unabhängig. In diesem Fall kann A diagonalisiert werden. Ein
mehrfacher Eigenwert kann aber fehlende Eigenvektoren nach sich ziehen.
Dies passiert manchmal bei nichtsymmetrischen Matrizen. Es geschieht nie
bei symmetrischen Matrizen. Es gibt immer genügend Eigenvektoren, um
eine Matrix A = Ä^ zu diagonalisieren.
Betrachten wir drei Matrizen mit den Eigenwerten A = -1, 1 und 1 (ein
mehrfacher Eigenwert):
010
100
001
5 =
r-i 01"
010
001
c =
■-10 0'
011
001
A ist symmetrisch. Wir garantieren Ihnen, dass die Matrix diagonalisiert
werden kann. Die nicht symmetrische Matrix B kann ebenfalls diagonalisiert
werden. Die nicht symmetrische Matrix C hingegen hat nur zwei
Eigenvektoren, und kann nicht diagonalisiert werden.
Eine Möglichkeit, mit mehrfachen Eigenwerten umzugehen, ist, sie ein
wenig voneinander zu trennen. Ändern wir die untere rechte Ecke der Matrizen
A, B und C von 1 zu d. Die Eigenwerte sind dann -1, 1 und d, und die
drei Eigenvektoren sind linear unabhängig. Geht aber d gegen 1, fallen die
Eigenvektoren von C in einem Eigenvektor zusammen. Die Matrix S verliert
so ihre Invertierbarkeit:
5 =
10 0
Ol 1
OOd-1
geht gegen
100
011
000
= schlecht.
Dies kann im Fall A ~ Ä^ nicht passieren. Der Grund: Die Eigenvektoren
bleiben immer senkrecht zueinander, weswegen sie nicht für d -> 1
zusammenfallen können. In unserem Beispiel ändern sich die Eigenvektoren nicht
einmal:
0 10'
100
OOd
hat orthogonale Eigenvektoren = Spalten von S
110
-110
001
Hinweis zum Schluss Die Eigenvektoren einer schiefsymmetrischen Matrix
{A^ ~ -Ä) sind orthogonal. Die Eigenvektoren einer orthogonalen Matrix
{Q^ = Q-i) sind ebenfalls orthogonal. Die besten Matrizen haben
orthogonale Eigenvektoren, und sind alle diagonalisierbar. Hier möchte ich zunächst
inne halten.
Der Grund dafür ist, dass die Eigenvektoren komplexe Zahlen enthalten
könnten. Wir erklären erst in Kapitel 10, was dann „senkrecht" bedeutet.
Sind X und y komplexe Vektoren, so überprüft man diese Eigenschaft nicht
342 6 Eigenwerte und Eigenvektoren
mehr mit Hilfe des Kriteriums x^y = 0. Deshalb können wir jetzt noch nichts
beweisen — wir können aber schon einmal die Antwort verraten. Eine reelle
Matrix hat orthogonale Eigenvektoren dann und nur dann, wenn A^A ~ AA^
gilt. Zu diesen „normalen" Matrizen zählen die symmetrischen, die
schiefsymmetrischen und die orthogonalen Matrizen. Sie heissen vielleicht normal, sie
sind aber etwas Besonderes. Die besten von ihnen sind die symmetrischen.
Die wesentlichen Punkte
l.Eine symmetrische Matrix hat reelle Eigenwerte und senkrechte
Eigenvektoren.
2. Die Diagonalisierung wird dann zu A = QAQ^ mit einer orthogonalen
Matrix Q.
3. Alle symmetrischen Matrizen sind diagonalisierbar.
4. Die Vorzeichen der Eigenwerte stimmen mit den Vorzeichen der Pivotele-
mente überein.
Aufgaben 6.4
1. Schreiben Sie A in der Form M -\- N, als Summe einer symmetrischen
und einer schiefsymmetrischen Matrix:
A =
124
430
865
= M -h iV {M^ =:M,N^ = -N).
Für eine beliebige quadratische Matrix bilden M — ^^^ und N ~
die Summe A.
2. Beweisen Sie, dass A^CA symmetrisch ist, wenn C symmetrisch ist.
(Transponieren!) Welche Form haben C und A^CA, wenn A eine 6x3-
Matrix ist?
3. Zeigen Sie, dass das Skalarprodukt von Ax mit y gleich dem Skalarpro-
dukt von X mit Ay ist, wenn A symmetrisch ist. Ist A nicht symmetrisch,
so gilt (Ax)'^y = x'^( ).
4. Bestimmen Sie eine orthogonale Matrix Q, durch die A = ["^ 7] diago-
nalisiert wird.
5. Bestimmen Sie eine orthogonale Matrix Q, durch die die folgende
symmetrische Matrix diagonalisiert wird:
A =
1 0 2
0-1-2
2-2 0
6.4 Symmetrische Matrizen
6. Beschreiben Sie alle orthogonalen Matrizen, durch die A =
gonalisiert wird.
9 12
12 16
343
dia-
7. (a) Bestimmen Sie eine symmetrische 2 x 2-Matrix mit Einträgen 1 auf
der Diagonalen, die aber einen negativen Eigenwert hat.
(b) Wieso muss diese Matrix ein negatives Pivotelement besitzen?
(c) Wieso kann sie keine zwei negativen Diagonaleinträge haben?
8. Gilt A^ = 0, so müssen die Eigenwerte von A sein. Geben Sie ein
Beispiel A^O an. Verwenden Sie die Diagonalisierung, um zu beweisen,
dass eine solche Matrix Null sein muss, wenn sie symmetrisch ist.
9. Ist \ = a-\-ib ein Eigenwert einer reellen Matrix A, so ist auch das komplex
konjugierte X = a — ib ein Eigenwert. (Gilt Ax = Ax, so auch Ax = Ax.)
Beweisen Sie, dass jede reelle 3 x 3-Matrix einen reellen Eigenwert hat.
10. Ein kurzer „Beweis", dass die Eigenwerte aller reellen Matrizen reell sind:
Ax = Ax liefert x^Ax = Xx^x also ist A = —
^Ax
reell.
Finden Sie den Fehler in dieser Argumentation — eine versteckte
Annahme muss nicht erfüllt sein.
11. Schreiben Sie die Matrizen A und B in der Form Aixixf -h A2X2X2^ aus
dem Spektralsatz QAQ^:
A =
31
13
B =
9 12
12 16
(wählen Sie ||xi|| = ||x2|| = 1).
12. Welche Eigenwerte hat A = [_bo]'^ Konstruieren Sie eine
schiefsymmetrische {Ä^ = —A) 3 X 3-Matrix und verifizieren Sie, dass alle ihre
Eigenwerte imaginär sind.
13. Die folgende Matrix ist
und
.. Deshalb sind die Eigenwerte
rein imaginär und haben den Betrag |A| = 1. (Grund: Es gilt ||Mx|| = ||x||
für jedes x, also ||Ax|| = ||x|| für Eigenvektoren.) Bestimmen Sie alle vier
Eigenwerte von
M =
^/3
Olli
-1 0-1 1
-1 1 0-1
-1-1 1 0
14. Zeigen Sie, dass die folgende Matrix A (symmetrisch, aber komplex) keine
zwei linear unabhängigen Eigenvektoren hat:
344 6 Eigenwerte und Eigenvektoren
2i 1
10
ist nicht diagonalisierbar; det(A — XI) = (A — i)^.
Die Eigenschaft Ä^ = A ist für komplexe Matrizen keine besondere Ei-
—T
genschaft mehr. Eine gute Eigenschaft ist stattdessen A ~ A. Ist sie
erfüllt, so hat A reelle Eigenwerte und ist diagonalisierbar.
15. Die Blockmatrix B = [^t ^] ist sogar für rechteckige Matrizen A
symmetrisch:
5x = Ax ist gleich
r OA'
A^ 0
"y
z
- A
y'
Z j
gleich
Az = Xy
A^y = Az.
(a) Zeigen Sie, dass A^Az = A^z gilt, so dass A^ ein Eigenwert von A^A
ist.
(b) Bestimmen Sie alle vier Eigenwerte von B, wenn A die 2x2-
Einheitsmatrix ist.
16. Bestimmen Sie die drei Eigenwerte und Eigenvektoren von B aus Aufgabe
15 für A = [l].
17. Jede symmetrische 2 x 2-Matrix hat die Form AiXiXi^-|-A2X2X2^ = AiPi -h
A2-P2- Erklären Sie, warum
(a) Pi-^P2 = I und
(b) PiP2-0gilt.
18. (Ein weiterer Beweis, dass Eigenvektoren orthogonal sind, wenn
gilt.) Es gelte Ax = Ax, Ay = Oy und A / 0. Dann liegt y im Kern und
X im Spaltenraum. Warum sind sie zueinander senkrecht? Seien Sie
vorsichtig — warum sind die Unterräume orthogonal? Wenden Sie dasselbe
Argument auf A — ßl für den zweiten, von Null verschiedenen
Eigenwert ß an. Der Eigenwert wird in die Null verschoben, die Eigenvektoren
bleiben identisch — deshalb sind sie senkrecht.
19. Bestimmen Sie die Eigenvektormatrix S für die folgende Matrix B. Zeigen
Sie, dass sie für d = 1 nicht singular wird, obwohl der Eigenwert A == 1
mehrfach auftritt. Sind die Eigenvektoren senkrecht?
B =
-10 1
010
OOd
hat die Eigenwerte A = — 1, l,(i.
20. Bestimmen Sie die Eigenwerte aus Spur und Determinante der Matrix
A:
-3 4
43
Vergleichen Sie die Vorzeichen der A's mit den Vorzeichen der
Pivotelemente.
6.4 Symmetrische Matrizen 345
21. Wahr oder falsch? Geben Sie Begründungen oder Gegenbeispiele an.
(a) Eine Matrix mit reellen Eigenwerten und Eigenvektoren ist
symmetrisch.
(b) Das Produkt zweier symmetrischer Matrizen ist symmetrisch.
(c) Die Inverse einer symmetrischen Matrix ist symmetrisch.
(d) Die Eigenvektormatrix S einer symmetrischen Matrix ist
symmetrisch.
22. Für eine normale Matrix gilt A^A =■ AÄ^. Warum ist jede
schiefsymmetrische Matrix normal? Warum ist jede orthogonale Matrix normal?
Unter welchen Bedingungen ist [ _i a ] normal?
23. (Ein Paradoxon für Lehrende) Gilt AA'^ = A^A, so besitzen A und A'^
dieselben Eigenvektoren (wahr). Sie haben auch gemeinsame Eigenwerte
(wahr). Wo liegt der Fehler in dieser Folgerung: Sie müssen dann auch
die Matrizen S und Ä gemeinsam haben. Deshalb ist A gleich A^.
24. Zu welcher dieser Klassen von Matrizen gehören die folgenden
Matrizen A und B: Invertierbare Matrizen, orthogonale Matrizen,
Projektionsmatrizen, Permutationsmatrizen, diagonalierbare Matrizen, Markov-
Matrizen?
A =
001"
010
100
B = k
I 1 1
II 1
1 1 1
Welche dieser Faktorisierungen sind für A und B möglich: LU, QR,
SAS-\QAQ^1
25. Welche Zahl b in der Matrix [lo] erlaubt eine Faktorisierung A —
QAQ^l Bei welchem Wert wird eine Diagonalisierung A — SAS~^
unmöglich?
26. Diese Matrix A ist beinahe symmetrisch. Die Eigenvektoren sind aber
ganz und gar nicht orthogonal:
A =
1 10-1^
0 1-hlO-i^
hat die Eigenvektoren
und [?]
Bestimmen Sie den Winkel zwischen den Eigenvektoren.
27. Wenn man mit MATLAB das Produkt Ä^A berechnet, so ist das
Ergebnis symmetrisch. Die berechnete Projektionsmatrix P ~ A{Ä^A)~^Ä^
ist vielleicht nicht genau symmetrisch. Konstruieren Sie P aus A =
[11111;1234 5], und verwenden Sie [S, LAMBDA] =eig(P). Zeigen
Sie über die Matrix S' * 5, dass das Skalarprodukt von zwei der
berechneten Eigenvektoren 0,9999 ist.
346 6 Eigenwerte und Eigenvektoren
6.5 Positiv definite Matrizen
Dieser Abschnitt beschäftigt sich mit symmetrischen Matrizen mit positiven
Eigenwerten. Symmetrie allein macht eine Matrix schon wichtig, diese
zusätzliche Eigenschaft macht sie wirklich besonders. Wenn wir „besonders" sagen,
meinen wir nicht „selten". Symmetrische Matrizen mit positiven
Eigenwerten tauchen in allen möglichen Anwendungen der linearen Algebra auf. Man
nennt sie positiv definit
Das erste Problem ist, diese Matrizen zu erkennen. Sie werden vielleicht
sagen, man bestimmt einfach die Eigenwerte und ermittelt, ob immer A > 0
gilt. Das ist aber genau das, was wir vermeiden wollen. Eigenwerte zu
berechnen ist Arbeit. Wenn wir sie wirklich benötigen, können wir sie berechnen.
Wenn wir aber nur wissen wollen, ob sie positiv sind, gibt es schnellere
Methoden. Dies sind die zwei Ziele dieses Abschnitts:
1. Schnelle Tests zu finden, die garantieren, dass eine symmetrische Matrix
positive Eigenwerte hat.
2. Anwendungen positiv definiter Matrizen zu erklären.
Da die Matrizen symmetrisch sind, sind die Eigenwerte automatisch reelle
Zahlen. Ein wichtiger Fall ist der der 2 x 2-Matrizen. Wann hat die Matrix
A= [ll] Eigenwerte Ai > 0 und A2 > 0?
6L Die Eigenmerte von A — A^ sind positiv dann und nur dann,
wenn a > 0 und ac — 6^ > 0 gilt>
Die Matrix A = [57] besteht diesen Test zum Beispiel. Die Matrizen [5 1]
und [ ~J „7] bestehen ihn nicht. Einmal liegt es daran, dass die Determinante
gleich 24 — 25 < 0 ist, das andere mal daran, dass a = —1 ist. Es ist nicht
genug, dass im zweiten Fall die Determinante -1-7 ist, da der Test aus zwei
Teilen besteht.
Wir können a auch als 1 x 1-Determinante und ac — l? als 2x2-
Determinante betrachten.
Beweis ohne Berechnung der Eigenwerte Es seien Ai > 0 und A2 > 0. Das
Produkt Ai A2 ist gleich der Determinante ac—b'^, die positiv sein muss. Daher
muss auch ac positiv sein, was bedeutet, dass a und c dasselbe Vorzeichen
haben. Dieses Vorzeichen muss positiv sein, da Ai -h A2 gleich der Spur a-\-c
sein muss. Bis hierher haben wir bewiesen: Positive Eigenwerte bedingen
notwendig ac - 6^ > 0 und a > 0.
Die Aussage ist eine „dann und nur dann"-Aussage, es gibt also noch eine
andere Hälfte zu beweisen. Wir beginnen mit a > 0 und ac — h'^ > 0. Dann
ist auch c > 0 garantiert. Da A1A2 gleich der Determinante ac — }? ist, sind
beide Eigenwerte entweder positiv oder negativ. Da deren Summe Ai -h A2
gleich der Spur a -h c > 0 ist, müssen sie positiv sein. Ende des Beweises.
6.5 Positiv definite Matrizen 347
Es folgt ein weiterer Test. An Stelle der Determinanten überprüft er, ob
die Matrix positive Pivotelemente hat.
6M Bie IJig^werte ^iner symmetrischen Matrix A ^ A^ sind pc^tiv dann
und nijjr;damin,\.wäim.alle Pivptelemente tJosMv sind:;,,^ ^:; ^^; ^ ^^.., ; \\J,: ^
: a > 0 und > 0.
Ein neuer Beweis ist unnötig. Der Quotient zweier positiver Zahlen ist
sicherlich positiv:
a > 0 und ac — 6^ > 0 gilt dann und nur dann, wenn
flc — b
a> 0 und > Ogilt.
a
Das Wichtige ist, den zweiten Term als zweites Pivot element von A zu
identifizieren:
,-, Das erste Pivotelement ist a r , -, Das zweite Pivotelement ist
a 0 \ I ^ *. I
bc
->
Das Vielfache ist b/a ^ « -^ ^ a
62 ac-62
So werden zwei große Teile der linearen Algebra miteinander verbunden.
Positive Eigenwerte (symmetrischer Matrizen!) implizieren positive
Pivotelemente und umgekehrt. Gilt dies auch für symmetrische n x n-Matrizen (das ist
so), so haben wir dadurch einen schnellen Test, ob A > 0 gilt. Pivotelemente
sind viel schneller zu berechnen als Eigenwerte. Es ist sehr aufschlussreich,
die Verbindungen zwischen Pivotelementen, Determinanten, Eigenwerten und
sogar der Methode der kleinsten Quadrate zu erkennen.
Beispiel 6.5.1 Für die folgende Matrix gilt a = 1 (positiv). Aber ac — b'^ =
3 - 2^ ist negativ:
12
23
hat einen negativen Eigenwert und ein negatives Pivotelement.
Die Pivotelemente sind 1 und -1. Das Produkt der Eigenwerte ist ebenfalls
-1. Ein Eigenwert ist negativ. (Wir brauchen die Formel nicht, nur das
Vorzeichen.)
Es gibt noch eine andere Möglichkeit, symmetrische Matrizen mit
positiven Eigenwerten zu betrachten. Die Gleichung Ax = Ax multipliziert man
von links mit den Vektor x^ und erhält x^ Ax = Ax^x. Auf der rechten Seite
348 6 Eigenwerte und Eigenvektoren
steht ein positives A, multipliziert mit einem positiven x^x = ||x|p. Deshalb
muss auch die linke Seite x^Ax positiv sein, wenn x ein Eigenvektor ist. Die
neue Idee ist, dass diese Zahl x^Ax für alle Vektoren x positiv sein
muss, nicht nur für die Eigenvektoren. (Natürlich gilt x^Ax = 0 für den
trivialen Vektor x = 0.)
Es gibt einen Namen für Matrizen mit dieser Eigenschaft x^Ax > 0.
Sie heißen positiv definit Wir werden beweisen, dass genau diese Matrizen
positive Eigenwerte und Pivotelemente haben.
^x^Axr-^l^ßi^^
^P]
;:i=^ ax"^ 4- 2bxy 4- q/'' > 0. :
x^Ax ist eine Zahl (eine 1 x 1-Matrix). Die vier Einträge a, 6, b und c erzeugen
die vier Terme von x^Ax. Von den Diagonaleinträgen a und c stammen die
rein quadratischen Terme ax'^ und ci/^. Von den Einträgen b und b abseits
der Diagonalen stammen die gemischten Terme bxy und byx (die gleich sind).
Die Summe dieser vier Terme ist x^Ax = ax'^ -h 2bxy 4- cy^. Dies ist eine
quadratische Funktion in x und y:
fi^^y) = <^^^ + 26x2/ + C2/^ ist eine Funktion „zweiten Grades".
Der übrige Teil dieses Buches hat sich mit Unearen Funktionen beschäftigt
(meistens Ax). Soeben hat der Grad von 1 auf 2 gewechselt. Die zweiten
Ableitungen von ax^ + 2bxy + q/^ sind konstant. Sie bilden die Matrix der
zweiten Ableitungen 2A:
dx
2ax -h 2by
df
-^ =2bx-\- 2cy
dy
und
0X2
d'f
dydx
dxdy dy'^
ÖV
2a 2b
2b 2c
Dies ist die 2 x 2-Version dessen, was jeder im 1 x 1-Fall kennt. Die Funktion
ist dort ax^, mit der Steigung 2ax und der zweiten Ableitung 2a. Hier ist die
Punktion x^Ax, die ersten Ableitungen sind durch den Vektor 2Ax gegeben,
und die zweiten Ableitungen durch die Matrix 2A. Die dritten Ableitungen
sind alle Null.
Wofür verwendet man in der Differentialrechnung zweite Ableitungen?
Um die Krümmung des Graphen zu bestimmen. Ist /" positiv, krümmt er
sich von der Tangente aus nach oben. Die Parabel y = ax^ ist aufwärts oder
abwärts konkav, je nachdem a > 0 oder a < 0 ist. Die Stelle x = 0 ist
eine Minimalstelle von y = x^ und eine Maximalstelle von y = —x^. Um
6.5 Positiv definite Matrizen 349
also zu entscheiden, ob es sich um ein Minimum oder ein Maximum handelt,
ermittelt man die zweite Ableitung.
Für eine Funktion f{x,y), die von zwei Variablen abhängt, liegt der
Schlüssel in der Matrix der zweiten Ableitungen. Eine Zahl ist nicht genug, um
zwischen Minimum, Maximum (oder Sattelstelle) zu entscheiden. Die
Funktion / = x^Ax hat ein Minimum hei x = y = 0 dann und nur dann, wenn
A positiv definit ist. Die Aussage „A ist eine positiv definite Matrix" ist die
2 X 2-Version von „a ist eine positive Zahl".
Beispiel 6.5.2 In diesem Beispiel ist die Matrix positiv definit. Die Funktion
f{x, y) ist positiv:
12
27
hat die Pivotelemente 1 und 3.
Die Funktion ist x^Ax — x'^ + Axy -h 7y'^. Sie ist positiv, da sie als Summe
von Quadraten darstellbar ist:
x'^ -h ^xy + 72/^ = {x + 2yf -h Zy'^.
Die Pivotelemente sind die Vorfaktoren vor den quadratischen Termen. Das
ist kein Zufall! Wir beweisen unten durch „quadratische Ergänzung", dass
dies immer passiert. Sind also die Pivotelemente positiv, so ist auch die
Summe f{x,y) garantiert positiv.
Im Vergleich von Beispiel 6.5.1 und 6.5.2 ist der einzige Unterschied, dass
a22 von 3 zu 7 geändert wurde. Die Grenze liegt bei 022 = 4. Oberhalb von
4 ist die Matrix positiv definit. Bei 022 = 4 ist die Matrix nur semidefinit
Dann geht es von (> 0) zu (> 0):
12
24
hat die Pivotelemente 1 und
Die Matrix hat die Eigenwerte 5 und 0. Es gilt a > 0, aber nur ac-b^ = 0.
Nicht ganz positiv definit.
Fassen wir diesen Abschnitt bis hierhin zusammen. Wir kennen vier
Möglichkeiten, eine positiv definite Matrix zu erkennen, bislang allerdings
nur für 2 x 2-Matrizen.
:,-<^;', ' ••;; j-f "'« '?' ' ^'']"'' ">i^ "■ <' '"'^'' ;.;> j^H^' ^'^^^',1''^^'"■^'h'"'', i'^il fl "^'>'^hiS'X''f<^\}fJ>fi^
350 6 Eigenwerte und Eigenvektoren
Hat A eine (und daher alle) der vier Eigenschaften, so ist sie positiv definit.
Hinweis Wir behandeln nur symmetrische Matrizen. Die gemischte
Ableitung d'^f/dxdy ist immer gleich d'^f jdydx. Für eine Funktion /(x, y, z) bilden
die neun zweiten Ableitungen eine symmetrische 3 x 3-Matrix, die positiv
definit ist, wenn die drei Pivotelemente (und die drei Eigenwerte, und die drei
Determinanten) positiv sind.
Beispiel 6.5.3 Ist f{x,y) =x^ -\- Sxy + 3y^ überall außer bei @,0) positiv?
Lösung Die zweiten Ableitungen sind fxx = 2, fxy = fyx = 8 und fyy = 6,
also alle positiv. Es geht aber nicht darum, ob die Ableitungen positiv sind,
sondern darum, ob die Matrix positiv definit ist. Die Antwort ist nein, diese
Funktion ist nicht immer positiv. Durch Probieren findet man einen Punkt
X = 1, y = -1 mit /(l, -1) = 1 - 8 + 3 = -4. Es jedoch ist günstiger,
die lineare Algebra zu verwenden und die Tests auf die Matrix, die f{x,y)
erzeugt, anzuwenden:
x^ + Sxy + 32/^
Für die Matrix gilt ac — b^ = 3 — 16. Die Pivotelemente sind 1 und —13.
Die Eigenwerte sind (benötigen wir nicht). Daher ist die Matrix nicht
positiv definit.
Beachten Sie, dass der Term Sxy von den Einträgen ai2 = 4 oberhalb
der Diagonalen und 021 = 4 darunter stammt. Die Matrixmultiplikation im
Ausdruck x^Ax erzeugt diesen Term.
Wichtig Das Vorzeichen von b ist nicht wichtig. Die gemischte Ableitung
d^f/dxdy kann positiv oder negativ sein — der Test hängt von 6^ ab.
Stattdessen entscheidet die Größe von b im Vergleich zu a und c darüber, ob A
positiv definit ist, und die Funktion ein Minimum hat.
Beispiel 6.5.4 Für welche Zahlen c ist x^ + Sxy + cy^ immer positiv (oder
Null)?
Lösung Es geht um die Matrix A = [Ic]- ^^^ Eintrag a = 1 besteht den
ersten Test. Der zweite Test lautet ac — b'^=c— 16, für eine positiv definite
Matrix muss also c > 16 gelten.
Der „semidefinite" Grenzfall tritt für c = 16 ein. Für diesen Wert hat die
Matrix [41!] die Eigenwerte A = 17 und 0, die Determinanten 1 und 0, und
die Pivotelemente 1 und . Der Term x^-\-Sxy + 16y^ ist gleich {x-\-4y)^.
Die dadurch definierte Funktion nimmt keine Werte unter Null an, hat aber
den Wert Null auf der Geraden x + Ay — 0. Sie ist also fast positiv definit,
besteht jeden Test aber nur beinahe: x^Ax ist gleich Null für x = D, -1).
6.5 Positiv definite Matrizen 351
Beispiel 6.5.5 Schreiben Sie die Funktion f{x^y) als Summe zweier
Quadrate, wenn A positiv definit ist.
Lösung Man nennt dies „quadratische Ergänzung". Man fasst den Term
ax^ -h 2bxy als die ersten beiden Summanden des Quadrats a{x -{- ^y) auf.
Dieses Quadrat hat aber als letzten Summanden ci{^y) • Um diesen
auszugleichen, muss b'^y^/a von cy^ subtrahiert werden:
ax^
-{-2bxy-\-cy'^ = a (x-\--yj -\- (— jy'^. F.42)
Nach diesem kleinen Ausflug in die Algebra erscheint die Situation etwas
klarer. Die Funktion enthält zwei quadratische Terme, die niemals Null
werden. Die Vorfaktoren dieser Terme können positiv oder negativ sein. Bei den
Faktoren a und {ac — b'^)/a handelt es sich um die Pivotelemente! Deshalb
führen positive Pivotelemente zu einer positiven Summe quadratischer Terme
und zu einer positiv definiten Matrix. Erinnern Sie sich an die Faktorisierung
A = LDL^:
a b
bc
1 0
b/al
a
{ac -b'^)/a
Ib/a
0 1
(Faktorisierung in LDL^).
F.43)
Bei der quadratischen Ergänzung haben wir uns zuerst um die Terme mit
a und b gekümmert, und erst später um den Teil mit c. Beim
Eliminationsverfahren passiert exakt dasselbe. Zuerst wird die erste Spalte bearbeitet,
der Rest später angepasst. Die Zahlen, die man als Ergebnis erhält, sind in
beiden Fällen identisch.
Als Vorfaktoren vor den quadratischen Termen stehen die Pivotelemente.
Innerhalb des Terms [x + ^y) hingegen stehen die beiden Zahlen 1 und
I aus der Matrix L. Jede symmetrische positiv definite Matrix besitzt eine
Faktorisierung A — LDL^ mit positiven Pivotelementen.
Es ist interessant, A = LDL^ mit A = QAQ^ zu vergleichen. Die eine
Faktorisierung basiert auf den Pivotelementen (in D)^ die andere auf den
Eigenwerten (in A). Bitte verwechseln Sie die Pivotelemente nicht mit den
Eigenwerten. Die Vorzeichen sind zwar identisch, die Zahlen aber völlig
verschieden.
Positiv definite Matrizen: der n X n-Fall
Die Tests auf positive Definitheit einer 2 x 2-Matrix verwenden die
Eigenwerte, die Determinanten oder die Pivotelemente der Matrix. Alle diese Zahlen
müssen positiv sein. Wir erhoffen und erwarten, dass man diese Tests auch
für größere Matrizen verwenden kann. Man kann.
352 6 Eigenwerte und Eigen Vektoren
60 Besitzt eine symmetrische n x n-Matrix eine dieser vier ßig^nschafteB^
so besitzt sie alle:
1,'Die'Äi§feifitit?eÄ-sind,p.c^
4. Der Ausdruck x^i4k ist pösitir ^dBer fiir x = 0. Die Matrix yt Mso
positiv defihii
Die oberen Unken Determinanten sind A x 1)-, B x 2)-, ... , (n x n)-
Determinanten. Die letzte ist die Determinante von A. In diesem
bemerkenswerten Satz wird unser gesamter Kurs über lineare Algebra zusammengeführt
— jedenfalls für symmetrische Matrizen. Wir glauben, dass zwei Beispiele für
das Verständnis hilfreicher sind als ein Beweis. Danach nennen wir zwei
Anwendungen.
Beispiel 6.5.6 Wir testen die Matrizen A und A* auf positive Definitheit:
A =
2-1 0
1 2-1
0-12
und A* =
2-1 b
-1 2-1
6-1 2
Lösung Diese Matrix ist ein alter Bekannter (oder Feind). Ihre
Pivotelemente sind 2, I und |, also alle positiv. Die oberen linken Determinanten
sind 2, 3 und 4, ebenfalls alle positiv. Die Eigenwerte sind 2 — v^, 2 und
2-h V^ (also positiv). Damit fallen die Tests 1, 2, und 3 sämtUch positiv aus.
Wir können den Ausdruck k^Ak als Summe dreier (wegen n = 3)
quadratischer Terme schreiben. Wir verwenden die Faktorisierung A = LDL^, die
Pivotelemente 2, | und | bilden die Vorfaktoren der quadratischen Terme,
die Multiplikatoren in der Matrix L stehen innerhalb der Terme.
Jc^Ax = 2{xl — a;iX2 -\- x\— X2Xs + x^)
= 2(a:i - ^X2f + |(a:2 - fxs)^ + H > 0-
Betrachten wir die zweite Matrix A*. Hier ist der Determinanten-Test am
einfachsten. Die 1 x 1-Determinante hat den Wert 2, die 2 x 2-Determinante
den Wert 3. Die 3 x 3-Determinante ist die Determinante von A:
det A* = 4 + 26 — 26^ muss positiv sein.
Wir erhalten detA* = 0 für 6 = -1 und 6 = 2. In diesen Fällen ist A*
positiv 5emzdefinit (keine Inverse, ein Eigenwert ist Null, es gilt x^A*x > 0).
Im ersten Beispiel hatte der Eckeintrag b = 0 einen ungefährUchen Wert
dazwischen.
6.5 Positiv definite Matrizen 353
Abb. 6.4. Die geneigte Ellipse 5ir^ + Sxy + 5y^ = 1. Die gedrehte Version genügt
der Gleichung 9X'^ -\-Y^ = 1.
Zweite Anwendung: Die Ellipse ax^ + 2bxy + cy^ = 1
Stellen Sie sich eine geneigte EUipse mit Mittelpunkt @,0) wie in Abbildung
6.4a vor, und drehen Sie sie, so dass ihre Hauptachsen auf den
Koordinatenachsen zu liegen kommen. Das ist die Situation von Abbildung 6.4b. In diesen
beiden Bildern erkennt man die geometrische Bedeutung der Faktorisierung
A = QAQ-^:
1. Die geneigte EUipse gehört zu A, sie wird durch die Gleichung k^Ax = 1
beschrieben.
2. Die mit den Koordinatenachsen in Übereinstimmung gebrachte Ellipse
gehört zu A, sie wird durch die Gleichung X^AX = 1 beschrieben.
3. Die Drehmatrix, durch die x in X überführt wird und durch die die
Hauptachsen mit den Koordinatenachsen in Deckung gebracht werden,
ist Q.
Beispiel 6.5.7 Bestimmen Sie die Hauptachsen der geneigten Ellipse 5a;^ -h
8xy -h 5y^ = 1.
Lösung Wir beginnen mit der positiv definiten Matrix, die diesen
quadratischen Term erzeugt:
[xy]
54
45
Die zugehörige Matrix ist A ^l
Die Eigenwerte von A sind Ai = 9 und A2 = 1. Die Eigenvektoren sind [\]
und [_i]. Wir erhalten Einheitsvektoren, indem wir durch y/2 dividieren.
Die Faktorisierung A = QAQ^ ist dann
354 6 Eigenwerte und Eigenvektoren
54
45
1 1
90
Ol
_1_
Vi
1 1
1-1
Multipliziert man jetzt [x y] von links und [y ] von rechts, so erhält man
wieder den Ausdruck x-^^x:
5x^ + 8xy + 5y' = 9 {^-^^ ' + 1 {^^ ' . F.44)
Es handelt sich also wieder um die Summe zweier quadratischer Terme. Dies
ist aber nicht dasselbe wie bei der quadratischen Ergänzung. Die
Koeffizienten sind nicht die Pivotelemente 5 und 9/5 aus der Matrix D^ sondern die
Eigenwerte 9 und 1 aus A. Innerhalb der quadrierten Terme erkennt man die
Eigenvektoren A,1)/V5 und A, -l)/v^.
Die Achsen der geneigten Ellipse befinden sich in Richtung der
Eigenvektoren. Diese Tatsache erklärt, warum die Zerlegung A = QAQ^ auch
„Hauptachsensatz" genannt wird — sie offenbart die Hauptachsen der
Ellipse. Man erhält nicht nur die Richtungen der Achsen (aus den Eigenvektoren),
sondern auch deren Längen aus den Eigenwerten. Um dies zu sehen,
verwenden wir Großbuchstaben für die neuen Koordinaten, deren Achsen auf den
Hauptachsen der EUipse liegen:
^/2
= Xund
x-y
V2
Y.
Die EUipsengleichung erhält dann die Form 9X^ -h F^ = 1. Der größte Wert,
den X^ annehmen kann, ist |, da der Punkt am Ende der kurzen Hauptachse
die Koordinaten X = ^ und Y = 0 hat. Beachten Sie: der größere Eigenwert
Ai korrespondiert mit der kürzeren Achse, deren Halbachsenlänge l/y/Xi = |
ist. Der Punkt am Ende der größeren Halbachse hat die Koordinaten X = 0
und Y = 1. Der kleinere Eigenwert A2 = 1 liefert also die größere Achsenlänge
l/x/Ä^=l.
Im ^^/-Koordinatensystem liegen die Hauptachsen entlang der
Eigenvektoren von A, im XF-System entlang der Eigenvektoren von A — also den
Koordinatenachsen. Es hängt also alles mit der Diagonalisierung A = QAQ^
zusammen.
::n^y]QÄQ^
[XY]A
= XiX^ + X2Y^ = 1.
Di6 fc&igöa der großen und kleinen Halbachse sind l/s/Xi und 1/v^
6.5 Positiv definite Matrizen 355
Damit es sich bei der Lösungsmenge um eine Ellipse handelt, muss A
positiv definit sein. Ist einer der Eigenwerte negativ (wechselt man zum Beispiel
die Einträge 4 in A gegen Einträge 5 aus), erhält man keine Ellipse mehr.
Aus der Summe quadratischer Terme wird dann eine Differenz 9X^ — F^ = 1.
Die Lösungsmenge dieser Gleichung ist eine Hyperbel
Die wesentlichen Punkte
I.Positiv definite Matrizen haben positive Eigenwerte und positive
Pivotelemente.
2. Aus den oberen linken Determinanten erhält man einen schnellen Test: Gilt
a > 0 und ac-P > 0?
3. Die quadratische Funktion / = x-^Ax hat ein Minimum in x = 0:
x^Ax = ax^ -h 2bxy -h cy^ ist außer in (x, y) = @,0) positiv.
4. Die Hauptachsen der Ellipse x-^Ax = 1 liegen entlang der Eigenvektoren
von A.
5.Ä^A ist automatisch positiv definit, wenn A linear unabhängige Spalten
hat (r = n).
Aufgaben 6.5
In den Aufgaben 1-13 geht es um Tests auf positive Definitheit.
1. Welche der Matrizen Ai, A2, A3 und A4 hat zwei positive Eigenwerte?
Berechnen Sie diese nicht, sondern verwenden Sie einen der Tests.
Ai =
Erklären Sie, warum c > 0 (an Stelle von a > 0) zusammen mit ac—l? > 0
ebenfalls garantiert, dass [5 c] positive Eigenwerte hat.
2. Für welche Zahlen b und c sind diese Matrizen positiv definit?
'5 6'
6 7
A2 =
-1 -2'
-2 -5
^3 =
1 10'
10 100
^4 =
1 10"
10 101
A =
16
69
und A =
24
4c
Bestimmen Sie für jedes A die Faktorisierungen LU und LDL^.
3. Wie lautet die quadratische Funktion / = ax'^ -\- 2bxy -\- cy^ für jede der
folgenden beiden Matrizen? Wenden Sie die quadratische Ergänzung an,
um / als Quadrat oder als Summe zweier quadratischer Terme di{ )^ -h
d2{ )^ zu schreiben.
A =
12]
27
und A =
2
24
356 6 Eigenwerte und Eigenvektoren
4. Zeigen Sie, dass die Funktion f{x,y) = x^ + ^xy -\- Sy^ in @,0) kein
Minimum annimmt, obwohl nur positive Koeffizienten auftreten. Schreiben
sie / als Differenz von quadratischen Ausdrücken, und bestimmen Sie
einen Punkt {x,y), an dem / negativ ist.
5. Die Funktion f{x,y) = 2xy hat in @,0) sicher einen Sattelpunkt und
kein Minimum. Welche symmetrische Matrix erzeugt dieses /? Welche
Eigenwerte hat sie?
6. Überprüfen Sie, ob A^A positiv definit ist:
A =
12
03
und A =
1 1
12
21
und A
1 1 2
12 1
7. (Wichtig) Hat A Unear unabhängige Spalten, so ist A^A eine
quadratische symmetrische invertierbare Matrix (s. Abschnitt 4.2). Erklären Sie,
warum der Ausdruck x^A^Ax außer in x = 0 immer positiv ist. Die
Matrix A^A ist also mehr als nur invertierbar, sie ist positiv definit.
8. Die Funktion f{x,y) = 3{x -h 2y)^ -h 4y'^ ist außer in @,0) positiv. Für
welche Matrix A gilt f = [x y]A[x y]'^? Rechnen Sie nach, dass die
Zahlen 3 und 4 die Pivotelemente von A sind.
9. Bestimmen Sie die 3 x 3-Matrix A und ihre Pivotelemente, ihren Rang,
ihre Eigenwerte sowie ihre Determinante:
[Xi X2 Xs]
Xl
X2
X3
4{xi -X2-\- 2x3^
10. Durch welche symmetrischen 3 x 3-Matrizen A werden diese Funktionen
/ = x-^Ax erzeugt? Warum ist die erste Matrix positiv definit, die zweite
aber nicht?
(a) f = 2[xi-{-xl-{-xl - xiX2 - X2X3)
(b) f -2 {x\ -^-x\+x\- 0:1X2 - X1X3- X2X3).
11. Berechnen Sie die drei Determinanten der oberen linken Untermatrizen,
und zeigen Sie so, dass A positiv definit ist. Rechnen Sie nach, dass die
Quotienten der Determinanten das zweite und dritte Pivotelement liefern.
A =
2 20
253
038
12. Für welche Zahlen c und d sind A und B positiv definit? Bestimmen Sie
ihre Antwort mit Hilfe der drei Determinanten:
A =
c 1 1
Icl
1 Ic
6.5 Positiv definite Matrizen 357
und B =
123
345
13. Bestimmen Sie eine Matrix mit a > 0, c > 0 und a-\-c> 2b, die negative
Eigenwerte hat.
In den Aufgaben 14-20 geht es um Anwendungen der Tests.
14. Ist A positiv definit, so ist auch A~^ positiv definit. Erster Beweis: Die
Eigenwerte von A~^ sind positiv, da . Zweiter Beweis B x 2-Fall):
Die Einträge von
-1 _
1
ac — IP"
c-b
—b a
bestehen den Test
15. Zeigen Sie, dass A-{- B positiv definit ist, wenn A und B beide positiv
definit sind. Pivotelemente und Eigenwerte sind dazu nicht besonders
gut geeignet; besser zeigt man x^(A -h ^)x > 0 mit Hilfe der positiven
Definitheit von A und von B.
16. Damit eine Blockmatrix positiv definit ist, muss der obere linke Block A
positiv definit sein:
[x^y^]
A B
B^ C
wird zu x^Ax für y
Der vollständige Test verlangt, dass A und C — B^A ^B positiv definit
sein müssen.
17. Auf der Diagonalen einer positiv definiten Matrix kann kein Eintrag Null
(oder, schlimmer noch, negativ) sein. Beweisen Sie, dass diese Matrix
nicht positiv definit ist:
[Xi X2 Xs]
[41 r
102
[125
"xil
X2
_X3\
ist nicht positiv für (xi,0:2,0:3) = (
18. Der erste Eintrag an einer symmetrischen Matrix A kann nicht kleiner
als der kleinste Eigenwert sein. Wäre an kleiner, so hätte die Matrix
A - Ulli Eigenwerte, aber eine auf der Diagonalen. Nach
einem ähnlichen Argument kann kein Diagonaleintrag größer sein als der
größte Eigenwert.
19. Ist X ein Eigenvektor von A, so gilt x^Ak =
X positiv ist, wenn A positiv definit ist.
Beweisen Sie, dass
358 6 Eigenwerte und Eigenvektoren
20. Begründen Sie mit einem kurzen Argument, warum die folgenden
Aussagen wahr sind:
(a) Jede positiv definite Matrix ist invertierbar.
(b) Die einzige positiv definite Permutationsmatrix ist P = I.
(c) Die einzige positiv definite Projektionsmatrix ist P = I.
(d) Eine Diagonalmatrix mit positiven Diagonaleinträgen ist positiv de-
finit.
(e) Eine symmetrische Matrix mit positiver Determinante muss nicht
positiv definit sein!
In den Aufgaben 21—24 verwenden Sie die Eigenwerte; die
Aufgaben 25—27 basieren auf den Pivot element en.
21. Für welche Zahlen s und t haben diese Matrizen positive Eigenwerte (und
sind daher positiv definit)?
A^ \-
r s-
-4
[-4-
-4-
5-
-4
-4]
-4
s\
und B =
^30
3^ 4
04 t
22. Berechnen Sie aus der Diagonalisierung A — QAQ^ die positiv definite
symmetrische Quadratwurzel W = QA^^^Q^ jeder der Matrizen.
Rechnen Sie nach, dass W^ = A gilt.
A =
54
45
und A =
10 6
6 10
23. Vielleicht kennen Sie die Gleichung (|) -h (f) = 1 als Ellipsengleichung.
Bestimmen Sie a und 6, wenn man die Gleichung als XiX^ + X2y^ = 1
schreibt. Die Ellipse 9x^ -h Idy^ = 1 hat die Halbachsenlängen a =
und b = .
24. Zeichnen Sie die geneigte Ellipse x^ -{-xy-\-y^ = 1 und bestimmen sie die
Halbachsenlängen aus den Eigenwerten der zugehörigen Matrix A.
25. Sind die Pivotelemente in D positiv, so kann man die Faktorisierung A =
LDL^ als Ly/D\fDL^ schreiben. (Aus den Wurzeln der Pivotelemente
erzeugt man D = y/D\/D.) Mit C = Ly/ü erhält man die Cholesky-
Faktorisierung A = CC^:
Bestimmen Sie aus C
30
12
die Matrix A.
Bestimmen Sie aus A =
4 8
8 25
die Matrix C.
6.5 Positiv definite Matrizen 359
26. Bei der Cholesky-Faktorisierung A = CC^ (mit C — Ly/D) stehen auf
der Diagonalen von C die der Pivot demente. Bestimmen Sie die
untere Dreiecksmatrix C für
A =
9 00
012
028
und A =
1 1 1
122
127
27. Die symmetrische Faktorisierung A = LDL^ impliziert k^Ak = k^LDL^x
also
[xy]
a b
bc
[xyl
1 0
b/al
a 0
0 {ac - b^)/a
Ib/a
0 1
Durch Ausmultiplizieren erhält man ax^ -h 2bxy -h cy^ = a{x -{- ^y) -\-
y^. Das zweite Pivotelement vervollständigt die quadratische
Ergänzung. Überprüfen Sie dies mit a = 2, 6 = 4, c = 10.
28. Bestimmen Sie (ohne Ausmultiplizieren) von
A =
cos 6 —sin 6
sin 6 cos 9
20
05
cos 6 sin 6
— sin 6 cos 6
(a) die Determinante von A
(b) die Eigenwerte von A
(c) die Eigenvektoren von A
(d) eine Begründung, warum A positiv definit ist.
29. Bestimmen Sie die Matrizen der zweiten Ableitungen für /i {x, y) — \x^ -\-
x'^y -h 2/^ und f2{x, y) = x^ -{-xy - x:
A =
d^f/dx^ d^f/dxdy
d^f/dydx d^f/dy^
Ai ist positiv definit, deshalb ist /i konvex. Bestimmen sie die
Minimalstelle von /i und die Sattelstelle von /2 (wo also die ersten Ableitungen
Null sind.)
30. Der Graph von z = x^ -{-y^ ist eine nach oben oflFene Schüssel. Der Graph
von z = x^ —y^ ist ein Sattel. Der Graph von z — —x^ — y^ ist eine nach
unten geöflFnete Schüssel. Wie überprüft man, ob 2: = ax^ -\- 2bxy -\- cy^ in
@,0) einen Sattelpunkt hat?
31. Für welche Werte von c erhält man eine Schüssel, für welche einen Sattel
als Graph der Funktion z = Ax"^ 4- I2xy + ci/^? Beschreiben Sie den
Graphen, der sich für das c an der Grenze zwischen diesen Bereichen
ergibt.
360 6 Eigenwerte und Eigenvektoren
6.6 Ähnliche Matrizen
Der große Schritt, den wir in diesem Kapitel getan haben, war die Diagona-
lisierung einer Matrix. Sie wurde mit Hilfe der Eigenvektor matrix S erreicht.
Die Diagonalmatrix S~^AS nennen wir die Eigenwertmatrix A. Die Diagona-
lisierung ist aber nicht für jede Matrix A möglich — einige Matrizen
„widersetzten" sich ihr, und wir konnten nichts weiter tun. Diese Matrizen haben
schlicht zu wenige Eigenvektoren, um eine Eigenvektormatrix S zu bilden. In
diesem Abschnitt bleibt S die beste Wahl, wo möglich, wir erlauben aber alle
invertierbaren Matrizen M.
Von A gehen wir zu der Matrix M~^AM über. Diese Matrix kann unter
Umständen eine Diagonalmatrix sein — eher aber nicht. Sie hat aber
wichtige Eigenschaften mit A gemein. Unabhängig davon, welche Matrix M wir
wählen, die Eigenwerte bleiben dieselben. Die Matrizen A und M~^AM
werden „ähnlich" genannt. Eine typische Matrix A ist ähnlich zu einer großen
Menge anderer Matrizen, da es so viele Möglichkeiten für M gibt.
DEFINITION Sei M eine iövertierbareMatrix. Dana heißt B ^ M'^^ÄM-
ähnlich' miA, ' /' ^ ' - - •' ^ V ^
Hat man B = M~^AM, so erhält man sofort A = MBM~^. Das bedeutet:
Ist B ähnlich zu A, so ist auch A ähnlich zu B. In umgekehrter Richtung
wird die Matrix M~^ verwendet, ganz so wie M.
Eine diagonalisierbare Matrix ist ähnlich zu A, In diesem Spezialfall ist S
die Ähnlichkeitsmatrix M. Es gilt A = SAS''^ und A = S~'^AS. Diese
Matrizen haben sicherlich dieselben Eigenwerte! In diesem Abschnitt erweitern
wir unsere Betrachtungen auf andere ähnliche Matrizen B = M~^AM.
Der Ausdruck M~^AM taucht bei einer Variablensubstitution auf.
Betrachten Sie eine Differentialgleichung für u, und setzen Sie u = Mv:
-— = Au wird zu M-— = AMw gleich —- = M~^AMw.
dt dt ^ dt
Die ursprüngliche Koeffizientenmatrix war A, die neue Matrix auf der rechten
Seite ist M~^AM. Eine Variablensubstitution führt also auf eine ähnliche
Koeffizientenmatrix. Gilt M = 5, so ist das neue System ein Diagonalsystem
— einfacher geht es nicht. Es gibt aber auch andere Möglichkeiten für M, die
zu einfacher zu lösenden System führen. Da wir immer zu den ursprünglichen
Koordinaten u zurückkehren können, müssen ähnliche Matrizen auf dieselben
Wachstums- oder Abklingeigenschaften führen. Genauer gesagt, sie haben
immer dieselben Eigenwerte.
6.6 Ähnliche Matrizen
361
6Q .(Ideiitische Eigenweite) Zwei ähnliche Matrizen A und M-ÄM har
ben identische Eigenwerte. Ist x ein Eigenvektor von A, so ist M'^^x ein
Eigenvektor von B = M'^^AM.
Der Beweis dafür ist sehr kurz, da, B = M ^AM auf A = MBM ^ führt.
Es sei Ax = Ax:
MBM~^x = Ax impliziert BM~^x = XM~^x.
Der Eigenwert von B ist dasselbe A, der zugehörige Eigenvektor ist M~^x.
Im folgenden Beispiel entdecken wir drei Matrizen, die alle ähnlich zu
einer Projektionsmatrix sind.
Beispiel 6.6.1
Die Projektion A =
Wähle M =
Wähle M =
0,5 0,5
0,5 0,5
10
1 1
0-1
1 0
ist ähnlich zu ^4 = S~^AS =
: eine ähnliche Matrix M~^AM ist
: eine ähnhche Matrix ist M~^AM gleich
10
00
10,5
0 0
0,5-0,5
-0,5 0,5
Diese Matrizen M~^AM haben alle die Eigenwerte 1 und 0. Jede 2x2-
Matrix mit diesen Eigenwerten ist ähnlich zu A. Die Eigenvektoren verändern
sich mit M.
In diesem Beispiel sind die Eigenwerte 1 und 0, beide Eigenwerte sind
einfach. Das macht die Situation einfach. Mehrfache Eigenwerte machen sie
kompHzierter. Im nächsten Beispiel haben die Matrizen die Eigenwerte 0 und
0. Die Nullmatrix hat zwar auch diese Eigenwerte, sie ist aber nur zu sich
selbst ähnhch: M'^OM = 0.
Die folgende Matrix A hingegen ist zu allen von der Nullmatrix
verschiedenen Matrizen mit den Eigenwerten 0 und 0 ähnlich.
Beispiel 6.6.2
A =
Ol
00
ist ähnlich zu jeder Matrix B
cd-d[^
c^ -cd
außer zu 5 = 0.
Diese Matrizen B sind (wie A) alle singular. Sie haben alle (wie A) den Rang
eins, und ihre Spur ist cd - cd — 0. Ihre Eigenwerte sind (wie die von A) 0
und 0. Dabei haben wir eine beliebige Matrix M — [^ ^j mit ad - bc = 1
gewählt.
Diese Matrizen B können nicht diagonalisiert werden. Die Matrix A ist
sogar so nah an einer Diagonalmatrix wie möglich. Man nennt sie die
Jordanische Normalform für diese Familie von Matrizen. Sie sticht aus allen
362 6 Eigenwerte und Eigenvektoren
Matrizen dieser Familie hervor. Die Jordan'sche Normalform kommt einer
Diagonalmatrix so nah, wie es möglich ist, wenn es nur einen Eigenvektor
gibt.
In Kapitel 7 werden wir noch eine andere Herangehensweise an ähnliche
Matrizen kennenlernen. Anstatt von einem Variablen Wechsel durch u = Mv
sprechen wir von einem Basiswechsel In dieser Sicht weise stellen ähnliche
Matrizen dieselbe Abbildung im n-dimensionalen Raum dar. Wählen wir
eine Basis für diesen Raum, so erhalten wir eine Matrix. Die üblichen
Basisvektoren in M = / führen zur Darstellungsmatrix I~^AI, also zu A. Andere
Basen hingegen führen zu anderen Matrizen B = M~^AM.
Bei dieser „Ähnlichkeitstransformation" von A zu B ändern sich einige
Dinge, andere ändern sich nicht. Die folgende Tabelle listet einige
Beziehungen zwischen A und B auf:
Unverändert
Eigenwerte
Spur und Determinante
Rang
Anzahl linear unabhängiger
Eigenvektoren
Jordan'sche Normalform
Verändert
Eigenvektoren
Kern
Spaltenraum
Zeilenraum
Kern der Transponierten
Singulärwerte
Die Eigenwerte ändern sich zwischen ähnlichen Matrizen nicht, die
Eigenvektoren schon. Die Spur ist die Summe der Eigenwerte, daher unverändert.
Die Determinante ist das Produkt der Eigenwerte.^ Der Kern besteht aus
den Eigenvektoren zum Eigenwert A == 0 (falls es sie gibt), er kann sich also
ändern. Seine Dimension n — r ändert sich nicht! Die Anzahl der
Eigenvektoren bleibt für jedes A unverändert, die Vektoren selbst werden hingegen mit
M~^ multipliziert.
Die Singulärwerte hängen von der Matrix A^A ab, die sich auf jeden
Fall ändert. Wir werden sie im nächsten Abschnitt besprechen. Anhand der
Tabelle lassen sich gut Übungen zur linearen Algebra erstellen. Der letzte
Eintrag in der Spalte mit unveränderten Eigenschaften — die Jordan'sche
Normalform — stellt jedoch mehr als nur eine Übung dar. Wir nähern uns
ihr mit einem weiteren Beispiel für ähnliche Matrizen.
Beispiel 6.6.3 Diese Jordan-Matrix J hat den dreifachen Eigenwert 5. Die
einzigen Eigenvektoren sind aber die Vielfachen von A,0,0):
Für
J.= :■
rs-iöi
m-r\
'•ö'ösj
hat J -51 =
010
001
000
den Rang 2.
^ Hier ein direkter Beweis, dass die Determinante unverändert bleibt: detB
(detM-^)(det A)(detM) = det A
6.6 Ähnliche Matrizen 363
Jede dazu ähnliche Matrix B = M~^JM hat denselben dreifachen Eigenwert
5, und jedes B — 51 muss ebenfalls den Rang 2 haben. Der Kern hat also die
Dimension 3 — 2 = 1, weswegen auch jede ähnliche Matrix B nur einen linear
unabhängigen Eigenvektor besitzt.
Die transponierte Matrix J^ hat dieselben Eigenwerte 5,5,5, und J^ — 51
hat denselben Rang 2. Die Jordan'sche Theorie besagt, dass J^ zur Matrix
J ähnlich ist. Die Matrix, die die Ähnlichkeit erzeugt, ist die umgekehrte
Einheitsmatrix M:
J^ = M~^JM ist gleich
röoo"
150
015
=
1"
1
1
1
5 1
5
r
1
1 \
Alle nichtbesetzten Einträge sind Null. Der einzige Eigenvektor von J^
ist M~^A,0,0) = @,0,1). Genauer gesagt gibt es eine Gerade (a:i,0,0) aus
Eigenvektoren von J und eine andere Gerade @,0,0:3) für J^.
Die wichtigste Eigenschaft dieser Matrix J ist, dass sie zu jeder Matrix
mit einem dreifachen Eigenwert 5 und nur einer Eigenvektorgerade ähnlich
ist.
Beispiel 6.6.4 Da J einer Diagonalmatrix so nah wie möglich kommt, kann
man die Gleichung du/dt — Ju nicht mehr durch Variablensubstitution
vereinfachen. Wir müssen sie so lösen, wie sie dasteht:
du
= Ju =
[5 10"
051
[005
xl
y
z\
dx/dt = 5a: -f 2/
ist dy/dt = 5y -\- z
dz/dt = 5z.
Das letzte System ist ein Dreieckssystem, wie denken deshalb automatisch
an eine Rücksubstitution: Man löse die letzte Gleichung zuerst, und arbeite
sich dann nach oben durch. Das wichtige: Alle Lösungen enthalten e^*:
dz
dt
dx
~di
liefert z = z{0)e^*
= 5y-\-z liefert y = {y{0) -f tz{0))e^^
= 5x-hy liefert x = {x{0) -f ty{0) -f lt'^z{0))e^K
Die beiden fehlenden Eigenvektoren verursachen die Terme te^^ und t'^e^^ in
dieser Lösung. Sie tauchen auf, weil A = 5 ein dreifacher Eigenwert ist.
Die Jordan'sche Normalform
Wir wollen jetzt für jede Matrix A eine Matrix M so wählen, dass M~^AM
einer Diagonalmatrix so nahe kommt wie möglich. Hat A einen vollständigen
364 6 Eigenwerte und Eigenvektoren
Satz von n Eigenvektoren, so schreibt man diese in die Spalten von M — S^
und erhält eine Diagonalmatrix S~^AS. Fertig. Diese Matrix ist die
Jordanform für A — wenn A diagonalisiert werden kann. Im allgemeinen Fall fehlen
uns aber Eigenvektoren, und eine Diagonalmatrix A kann nicht erreicht
werden.
Angenommen, A hat s linear unabhängige Eigenvektoren. Dann ist diese
Matrix ähnlich zu einer Matrix mit s Blöcken, von denen jeder wie die Matrix
J in Beispiel 3 aufgebaut ist. Der Eigenwert steht auf der Diagonalen, die
Einträge auf der Nebendiagonalen darüber sind eins. Dieser Block steht für
einen Eigenvektor von A. Gibt es n Eigenvektoren und daher n Blöcke, so
sind sie alle 1 x 1-Blöcke. In diesem Fall ist J die Diagonalmatrix A.
6R (Jordaififortii) HHät diie Makix As Itoear uiiabMägigb ligÄTOteöttoj
so ^ sfe älmiteh izrii'^^ Matrix /mit b Jördanbl^ieenatrf^^r Di^^^
es gibt'$fe6emeMÄirix:M'mit ^ ^ -' v, : : ^ ^ -_'^}^y::^<^'^: -^'fv\ff-'Ss'^;;r/r
;;:.; r: m-^am
Ji
j.
"A^'^v::
Ja<ier'B|oc&\M''J ii^t>aneii "Eigenwert Äi, emen BigeriireKia^* ,mmv^;J^M
oberJämD der'Jp^iag0|ial6B: <- > r-^--.^^^ ";>=!; r ^ v-i^^^=?crv .>.;.
^^.ä;.-,;'>,5< ^^sV^f,'*; vf
Ji =
Ail
1
Ai
Mne1|^^^-^?fertm -B, '-wHili;:*!!^!!
foiÄ;3[;:Ka&^i;:^3^:i5|^ ';':,
^-fe
Dies ist der zentrale Satz über Ähnlichkeit von Matrizen. In jeder Familie
ähnlicher Matrizen greifen wir eine Matrix heraus, die wir J nennen. Sie ist
beinahe eine Diagonalmatrix, oder, falls möglich, eine echte Diagonalmatrix.
Für eine solche Matrix können wir das Gleichungssystem du/dt = J\i wie
in Beispiel 6.6.4 lösen. Wir können auch die Potenzen J^ berechnen, wie in
den Aufgaben 9 und 10. Jede andere Matrix in dieser Familie lässt sich aber
in der Form A — MJM~^ schreiben. Über die Verbindung durch M können
wir dann auch die Gleichung du/dt = Au lösen.
Was man dazu sehen muss, ist schlicht die Beziehung MJM~^MJM~^ =
MPM~^. Wir haben das Herausfallen von M~^M in der Mitte bereits im
ganzen Kapitel benutzt (mit 5 statt M). Wir haben A^^^ aus SA^^^S'^
berechnet, also über die Diagonalisierung der Matrix. Nun lässt sich A nicht
ganz diagonalisieren, also verwenden wir MJ^^^M~^ stattdessen.
6.6 Ähnliche Matrizen
365
Der Jordan'sche Satz 6R wird in meinem Lehrbuch Linear Algebra and Its
Applications im Verlag HBJ/Saunders bewiesen. Entnehmen Sie den Beweis
bitte diesem Buch (oder fortgeschritteneren Büchern). Die Argumente sind
ziemlich kompliziert; und für reale Rechnungen wird die Jordanform nicht
oft herangezogen, weil ihre Berechnung nicht stabil ist. Eine kleine
Veränderung in A separiert mehrfache Eigenwerte, und entfernt so die Einsen auf
der Nebendiagonalen — es bleibt nur die Diagonalmatrix A. Ob mit Beweis
oder ohne, sie kennen jetzt die wesentliche Idee hinter der Ähnlichkeit von
Matrizen — die Matrix A so einfach wie nur möglich zu machen, ohne dabei
wichtige Eigenschaften zu verändern.
Die wesentlichen Punkte
l.Eine Matrix B ist ähnlich zu A, wenn B = M~^AM gilt.
2. Ähnliche Matrizen haben dieselben Eigenwerte.
3. Hat eine Matrix A n linear unabhängige Eigenvektoren A, so ist sie ähnlich
zu A (mit M = S).
4. Jede Matrix ist zu einer Jordanmatrix J ähnlich, die als Diagonalteil A
hat. In J steht für jeden fehlenden Eigenvektor eine „1" direkt oberhalb
der Diagonalen.
Aufgaben 6.6
1. Es gelte B = M'^AM und auch C = N'^BN. Mit welcher Matrix T
gilt C = T-^ATl Folgerung: Ist B ähnlich zu A und C ähnlich zu B, so
2. Welche Matrix liefert B := M-^AM, wenn C = P-^AF und C - G-^BG
gelten? Folgerung: Ist C zu A und auch zu B ähnlich, so .
3. Beweisen Sie, dass A und B ähnliche Matrizen sind, indem Sie M
angeben:
A^
A =
A =
4. Warum ist eine 2 x 2-Matrix mit den Eigenwerten 0 und 1 ähnlich zu
^ - [o o]^ Folgern Sie aus Aufgabe 2, dass alle 2 x 2-Matrizen mit diesen
Eigenwerten ähnlich sind.
5. Welche dieser Matrizen sind einander ähnlich? Überprüfen Sie die
Eigenwerte:
"lO"
10
1"
11
2"
3 4
und 5:=
und 5 =
und 5 =
"Ol"
Ol
1-1"
-1 1
3
2 1
366 6 Eigenwerte und Eigenvektoren
10
Ol
Ol
10
11
0 0
00
11
10
10
Ol
Ol
6. Es gibt 16 2 X 2-Matrizen, die nur Einträge 0 und 1 haben. Ähnliche
Matrizen werden in derselben Familie zusammengefasst. Wie viele Familien
gibt es? Wie viele Matrizen in jeder Familie? (Gesamtzahl 16)
7. (a) Zeigen Sie, dass M~^x im Kern von M~^AM liegt, wenn x im Kern
von A ist.
(b) Die Kerne von A und M~^AM besitzen dieselben (Vektoren) (Basen)
(Dimensionen).
8. Gilt A = B, wenn A und B genau dieselben Eigenvektoren und
Eigenwerte haben? Gibt es n linear unabhängige Eigenvektoren, so ist A = J5
wahr. Was ist, wenn A die Eigenwerte 0 und 0 hat, aber nur eine Gerade
von Eigenvektoren (xi,0)?
9. Bestimmen Sie durch Ausrechnen die Matrizen A^ und A^ für
A =
1 1
Ol
Erraten Sie die Form von A^, und überprüfen Sie Ihre Vermutung für
k = 6. Setzen Sie dann A: = 0 ein, um A^ zu bestimmen, und A; = — 1 zur
Bestimmung von A~^.
In den Aufgaben 10—14 geht es um die Jordanform.
10. Bestimmen Sie durch direktes Ausrechnen die Matrizen J^ und J^^ür
cl^
Oc
Erraten Sie die Form von J^, setzen Sie A; == 0 ein, um J^ zu bestimmen,
und A; = — 1, um J~^ zu bestimmen.
11. Im Text wurde die Differentialgleichung du/dt = J\i für einen 3x3-
Jordanblock J gelöst. Fügen Sie eine vierte Gleichung dw/dt = 5w -h x
hinzu, und folgen Sie dem Muster der Lösungen für z, y und x, um w zu
bestimmen.
12. Die folgenden Jordanmatrizen haben die Eigenwerte 0,0,0,0 und jeweils
zwei Eigenvektoren (einen für jeden Block). Die Blockgrößen passen aber
nicht zusammen, und daher sind die Matrizen nicht ähnlich.
J =
"Ol
00
0 0
00
00
Ol
00
und K
10
00 1
0 00
6.6 Ähnliche Matrizen
367
Vergleichen Sie die Matrizen JM und MK für eine beliebige Matrix M.
Zeigen Sie, dass M nicht invertierbar ist, wenn die beiden Matrizen gleich
sind. Deswegen ist eine Ähnlichkeit M~^JM = K unmöghch.
13. J^ in Beispiel 6.6.3 war ähnhch zu J. Beweisen Sie in drei Schritten, dass
die Transponierte A^ immer ähnlich zu A ist:
Erstens: Sei A ein Jordanblock Ji. Bestimmen Sie eine Matrix M^, so dass
Mr^JiMi^jJ gilt.
Zweitens: Sei A eine Jordanmatrix J: Setzen Sie eine Matrix Mq so aus
den Blöcken zusammen, dass Mq^JMq = J^ gilt.
Drittens: Sei A eine beliebige Matrix MJM~^: Beweisen Sie, dass A^
ähnlich zu J^, deswegen zu J und zu A ist.
14. Bestimmen Sie noch zwei weitere Matrizen, die zu J aus Beispiel 6.6.3
ähnlich sind.
15. Beweisen Sie, dass det(A - XI) = det{M~^AM - XI) gilt. Schreiben
Sie dazu / = M~^M, und klammern Sie detM~^ und detM aus. Dies
bedeutet, dass M~^AM dasselbe charakteristische Polynom hat wie A.
Deshalb sind seine Nullstellen dieselben Eigenwerte.
16. Welche Paare sind einander ähnlich? Wählen Sie Werte für a, b, c und d,
um zu zeigen, dass die anderen es nicht sind.
a b
c d
b a
d c
c d
a b
d c
b a
17. Wahr oder falsch? Geben Sie eine gute Begründung an.
(a) Eine invertierbare Matrix kann nicht ähnlich zu einer singulären
Matrix sein.
(b) Eine symmetrische Matrix kann nicht zu einer nicht symmetrischen
Matrix ähnlich sein.
(c) A kann (außer für A = 0) nicht ähnlich zu — A sein.
(d) A kann nicht ähnlich zu A -f / sein.
18. Beweisen Sie, dass AB dieselben Eigenwerte hat wie BA, wenn B eine
invertierbare Matrix ist.
19. Ist A eine m x n-Matrix und B eine n x m-Matrix, so können die Matrizen
AB und BA von unterschiedlicher Größe sein. Es gilt aber trotzdem
I-A
0 /
ABO'
BO
I A
0 /
=
■ 0 0'
B BA
(a) Welche Größen haben die Blöcke? (Sie sind in beiden Matrizen
gleich.)
368 6 Eigenwerte und Eigenvektoren
(b) Diese Blockgleichung ist M~^FM = G, F und G haben also dieselben
Eigenwerte. F hat die Eigenwerte von AB zuzüglich n Nullen, G hat
die Eigenwerte von BA zuzüglich m Nullen. Folgerung für m > n:
AB hat dieselben Eigenwerte wie BA zuzüglich Nullen.
20. Warum sind alle diese Aussagen wahr?
(a) Ist A ähnlich zu J5, so ist A^ ähnlich zu B^.
(b) A^ und B^ können ähnlich sein, obwohl A und B es nicht sind.
(c) [g2] ist ähnlich zu [l\].
(d) [os] ^^^ nicht ähnlich zu [q 3]-
(e) Vertauscht man erst die Zeilen 1 und 2 von A, und dann die Spalten
1 und 2, so bleiben die Eigenwerte unverändert.
6.7 Singulärwertzerlegung
Die Singulärwertzerlegung stellt einen der Höhepunkte der linearen Algebra
dar. Es sei A eine beliebige m x n-Matrix. Unabhängig davon, ob es eine
quadratische oder eine rechteckige Matrix ist, werden wir sie diagonalisieren.
Ihr Zeilenraum ist r-dimensional (innerhalb von W^) ebenso wie ihr
Spaltenraum, der in W^ liegt. Wir werden orthonormale Basen vi,...,Vr für den
Zeilenraum und ui,..., u^. für den Spaltenraum wählen.
Beginnen wir mit einer 2 x 2-Matrix: Es gilt m = n = 2. Der Rang
sei ebenfalls r = 2, so dass die Matrix invertierbar ist. Der Zeilenraum ist
also die Ebene M^. Wir wollen dann orthogonale Einheitsvektoren vi und V2
finden, also eine orthonormale Basis. Dabei wollen wir auch, dass die Vektoren
Avi und Av2 senkrecht zueinander stehen. Das ist der schwierige Teil dabei.
Dann sind auch die Einheitsvektoren ui = ^vi/||Avi|| und U2 =^ Av2/||Av2||
orthogonal. Als ein Beispiel betrachten wir die unsymmetrische Matrix
A =
22
-1 1
F.47)
Erstens Warum nicht nur eine orthogonale Basis an Stelle von zweien
wählen? Weil keine orthogonale Matrix Q den Ausdruck Q~^AQ zu einer
Diagonalmatrix macht.
Zweitens Warum wählt man nicht die Eigenvektoren von A als Basis? Weil
diese Basis nicht orthonormal ist. A ist nicht symmetrisch, deshalb brauchen
wir zwei verschiedene orthogonale Matrizen, um A zu diagonalisieren.
Wir suchen orthonormale Basen, bezüglich derer A diagonalisiert ist. Die
beiden Basen werden verschieden sein — mit einer allein geht es nicht. Fängt
man mit vi und V2 an, so erhält man Avi und Av2. Wir möchten, dass
diese Vektoren parallel zu den Vektoren ui und U2 sind. Es soll also Avi =
6.7 Singulärwertzerlegung 369
ö^iUi und Av2 = cr2U2 für die Basisvektoren gelten. Die Zahlen ai und a2
sind dabei schlicht die Längen ||Avi|| und mv2||. Wenn wir vi und V2 als
Spaltenvektoren schreiben, so erkennen Sie, was wir verlangen:
Vi V2
(Tltli cr2U2
ttl U2
(Tl
<J2
F.48)
In Matrizenschreibweise wollen wir also AV = UE erreichen. Die
Diagonalmatrix E ist analog zu A (großes Sigma und großes Lambda), sie enthält
die Singulärwerte cri,cr2, so wie A die Eigenwerte enthält.
Der Unterschied liegt in U und V, Sind sie beide gleich 5, so erhalten wir
die Gleichung AS — SA^ also S~^AS = A, und die Matrix ist diagonalisiert.
Die Eigenvektoren in S sind aber im Allgemeinen nicht orthonormal. Die
neue Bedingung ist, dass U und V orthogonale Matrizen sein sollen. Die
Basisvektoren, die ihre Spalten bilden, müssen orthonormal sein:
F^F =
v^ —
Vi V2
10
Ol
F.49)
Es gilt also V^V = I beziehungsweise V^ := F i, und ähnlich U^U = /
sowie U^ = U~^.
6S Die SingulärwerizBriegung (SVD^ $mi^ular <Mue ämmposttion)
:, v.,,^, AV = UE ^<^Pl,^A=: UEV-' - UEV"^, r:X,i^;^,,^^,
Dies ist,liiHseri^.p<sue Faktorister^ der Matrix 4^ oii^Äa§^<>fiiötf |
Es gibt eine hübsche Methode, die Matrix U aus der Darstellung
herauszuhalten, und nur V stehen zu lassen: Man multipliziert A^ mit A.
A^A = {USV^)'^{UEV^) - VE'^U'^USV^'.
F.51)
Die Matrix U^U verschwindet dabei, weil sie gleich / ist. Dann steht E'^
direkt neben E. Im Produkt der beiden Diagonalmatrizen erhält man aj
und crf. Es bleibt also die übliche Faktorisierung der symmetrischen Matrix
A^A:
Ä'A = V
0 G?
V'
F.52)
370 6 Eigenwerte und Eigenvektoren
Dies ist genau dasselbe wie A = QAQ^. Die symmetrische Matrix ist aber
nicht A selbst, sondern Ä^A\ Die Spalten von V sind die Eigenvektoren dieser
Matrix.
Daran erkennen wir, wie man V bestimmen kann. Wir sind jetzt soweit,
dass wir das Beispiel zu Ende führen können.
Beispiel 6.7.1 Man bestimme die Singulärwertzerlegung von A= [_i i]-
Lösung: Man berechnet A^ A und die Eigen vektoren dieser Matrix. Daraus
macht man Einheitsvektoren:
Ä'A =
Vi
53
35
hat die Einheits-Eigenvektoren
l/v^
und V2 =
-1/V2
1/v^J
Die Eigenwerte von A^A sind 8 und 2. Die Eigen vektoren v stehen
senkrecht aufeinander, weil die Eigen vektoren einer jeden symmetrischen Matrix
senkrecht aufeinander stehen, und A^A automatisch symmetrisch ist.
Was machen wir mit ui und U2? Diese Vektoren können schnell bestimmt
werden, da Avi in der Richtung von ui und Av2 in Richtung von U2 liegt:
Avi =
22]
=
■2v^"
0^
Der Einheitsvektor ist ui =
Avi ist dasselbe wie 2\/^ui. Der erste Singulärwert ist also ai = 2v^. Damit
gilt
.2 _
8; diese Zahl ist ein Eigenwert von A^A. Es gilt Avi = criUi,
genauso, wie wir es haben wollten. Analog gilt
Avo =
22]
-1 ij
r-i/v^'
[ 1/V2.
=
0'
Der Einheitsvektor ist U2
Diesmal ist Av2 gleich \/^U2. Der zweite Singulärwert ist 0*2 = v^, und crf
stimmt mit dem anderen Eigenwert 2 von A^A überein. Damit haben wir
die vollständige Singulärwertzerlegung von A bestimmt:
Ä = usy^ ist
22"
-11
=
10]
OlJ
[2^2
[ ^/2.
I/V2 l/v/2
-I/V2I/V2J
. F.53)
Diese Matrix (und auch jede andere invertierbare 2 x 2-Matrix)
transformiert den Einheitskreis in eine Ellipse. Dies ist in der Abbildung dargestellt,
die von ClifF Long und Tom Hern gestaltet wurde.
Noch eine letzte Bemerkung zu diesem Beispiel. Wir haben die u's aus
den v's bestimmt. Könnten wir nicht auch die u's direkt bestimmen? Ja,
indem man AÄ^ an Stelle von Ä^A betrachtet:
6.7 Singulärwertzerlegung 371
Abb. 6.5. [7 und V bewirken Drehungen und Spiegelungen. U ist eine
Streckmatrix.
-TttT
AA' = {UUV ){VZ:' U') = UEE' U
F.54)
Dieses Mal verschwindet V^V = I. Aus Z'Z'^ erhält man wieder aj und crl-
Dies ist also die übliche Faktorisierung der symmetrischen Matrix AA^. Die
Spalten von U sind dann die Eigenvektoren von AA^:
2 2"
_-ll
-1"
2 1
=
"8 0"
02J
AA'
Diese Matrix ist eine Diagonalmatrix, deren Eigenvektoren A,0) und @,1)
sind. Sie stimmen mit den Vektoren Ui und U2 überein, die wir zuvor
bestimmt hatten. Warum müssen wir als ersten Eigenvektor A,0) und nicht
@,1) wählen? Weil wir die Reihenfolge der Eigenwerte beachten müssen.
Beachten Sie, dass AA^ dieselben Eigenwerte (8 und 2) besitzt wie A^A. Die
Singulärwerte sind y/S und y/2.
Beispiel 6.7.2 Bestimmen Sie die Singulärwertzerlegung der singulären
Matrix A = [11]. Ihr Rang ist r = 1. Der Zeilenraum hat also nur einen
Basisvektor Vi, und der Spaltenraum nur einen Basisvektor ui. Diese Vektoren
kann man in A durch Hinsehen finden und zu Einheitsvektoren machen:
Vi = Vielfaches der Zeile
ui = Vielfaches der Spalte
1
V2
_ _1_
~ VE
Dann muss Avi gleich criUi sein. Das ist mit dem Singulärwert ai = \/lÖ
der Fall. Hier könnte man mit der SVD aufhören (dies geschieht aber
normalerweise nicht):
372 6 Eigenwerte und Eigenvektoren
Avi = VlÖ u
Spaltenraum
Kern von Ä^
Abb. 6.6. Bei der Singular wert Zerlegung wählt man Basen mit Avi = aiUi.
22
1 1
[2/x/5
l/x/5j
[VTÖ][1/V2 1/V2].
Üblicherweise sollen U und V quadratische Matrizen sein. Die Matrizen
brauchen also eine zweite Spalte. Der Vektor V2 muss zu vi orthogonal sein,
und U2 muss zu ui orthogonal sein.
^2 = 72
und U2 = ^
1
-2
Der Vektor V2 stam,m,t aus dem, Kern, Er steht senkrecht auf vi aus
dem Zeilenraum. Multipliziert man mit A^ erhält man Av2 — 0. Man
könnte deshalb sagen, dass der zweite Singulärwert 0*2 = 0 ist, aber mit den
Singulärwerten ist es wie mit den Pivotelementen: nur die r von Null
verschiedenen Werte werden gezählt.
Ist A eine 2x2-Matrix, so sind in der vollständigen SVD alle drei Matrizen
C/, r und y 2 X 2-Matrizen:
22
1 1
= u^y^ = -k
2 1
1-2
00
1
V2
1 1
1-1
F.55)
6S Die MMfitmU nndy Basen der
vier Unterränme: ■■ - i-- ■- - . .^—'s a
Erste , r j Spalten von F ;
Letzte" j^ ^ r SfpaJten von-'F :
■ M^;':':" '-^, Spälbeft -tod Ü ;
Zeilenraum vonA
Kern von A
Spaltenraum von A
IMzi^fn-'-'t Spalten von £/ : Kern von A^,
Die ersten Spalten vi,..., v^ und ui,..., u^ sind am schwersten
auszuwählen, weil Avi in Richtung der u^ liegen muss. Die letzten v's und u's
6.7 Singulärwertzerlegung 373
(die in den Kernen liegen) sind viel einfacher zu wählen. Solange sie orthonor-
mal sind, wird sich eine korrekte Singulärwertzerlegung ergeben. Die v's sind
Eigenvektoren der Matrix A^A und die u's sind Eigenvektoren von AA^. In
Beispiel 2 haben wir dafür die Matrizen
A^A
55
55
und AA'^
84
42
mit den identischen Eigenwerten 10 und 0. Die erste Matrix hat die
Eigenvektoren Vi und V2, die zweite die Eigenvektoren ui und U2. Durch Ausrechnen
sieht man, dass Avi = a/1Öui und Av2 = 0 gilt. Diese Beziehung Avi — cr^u^
ist immer erfüllt; den Grund erklären wir jetzt:
Beweis zur SVD: Ausgehend von A^Avi = afwi multipliziert man mit vf
und mit A:
wjA^Awi = (jf^J^i liefert \\Awif = af so dass \\Avi\\ = ai F.56)
AÄ^Avi = a^Avi liefert u^ = Avi/ai als Einheits-Eigenvektor von AA^.
F.57)
In Gleichung F.56) haben wir als Trick Klammern im Ausdruck {vTA^){Avi)
verwendet. So liest man „Vektor mal transponierter Vektor" und erhält
ll^lvilp. In Gleichung F.57) wurden die Klammern {AA'^){Avi) gesetzt, was
beweist, dass Avi ein Eigenvektor von AA^ ist. Dividiert man durch die
Länge cr^, so erhält man den Einheitsvektor u^ = Avi/ai. Es ergibt sich
die Gleichung Avi — cr^u^, die besagt, dass A durch die besonderen Basen
diagonalisiert wird.
Wir wollen Ihnen unsere Meinung ganz offen sagen. Die
Singulärwertzerlegung stellt den Höhepunkt dieses Kurses über lineare Algebra dar. Wir
halten sie für den letzten Schritt des Fundamentalsatzes. Zunächst hatten
wir nur die Dimensionen der vier Unterräume. Es folgte deren Orthogona-
lität Schließlich konnten wir sogar noch Basen finden, die A diagonalisieren.
All das steckt in der Formel A = UUV^. Jetzt folgen noch Anwendungen
— die sicherlich wichtig sind! — aber an diesem Punkt haben Sie den Gipfel
erklommen.
Eigshow (Teil 2)
In Abschnitt 6.1 haben wir die MATLAB-Routine namens eigshow
vorgestellt, und die zugehörige Internetadresse genannt (die Routine ist auch in
MATLAB 5.2 enthalten). Ihre erste Option ist eig, bei der man x auf einem
Kreis bewegen kann, und ylx auf einer Ellipse folgt. Die zweite Option ist svd,
bei der zwei orthogonale Vektoren x und y auf einem Kreis bewegt werden.
Auch in diesem Fall sieht man, wie Ax und Ay sich mit den Vektoren ändern.
Man sieht also vier Vektoren auf dem Bildschirm.
374 6 Eigenwerte und Eigenvektoren
Man erkennt die Singulärwertzerlegung graphisch daran, dass Ax
senkrecht auf Ay steht. Deren Richtungen in diesem Moment liefern die Ortho-
normalbasis ui, U2, und die Längen die Singulärwerte cri, cr2. Die Vektoren x
und y bilden dann die Orthonormalbasis vi, V2.
Auf dem Bildschirm sieht man Basen, für die Avi = criui und Av2 —
cr2U2 gilt. In der Matrizenschreibweise ist dies einfach AV — UE. Dies ist die
Singulärwertzerlegung.
Ax = B, -1)
Ay = v^U2
A
y = V2 X = Vi
Ax = 2v^ui
Die wesentlichen Punkte
l.Die Singulärwertzerlegung liefert eine Faktorisierung von A in UEV^ mit
den Singular wer ten cri > • • • > cr^. > 0.
2.Bei den Zahlen ctj, ... ,cr^ handelt es sich um die von Null verschiedenen
Eigenwerte von AÄ^ und Ä^ A,
3. Die orthogonalen Spalten von U und V sind die Eigenvektoren von AÄ^
und Ä^A.
4. Diese Spalten liefern orthogonale Basen der vier fundamentalen zu A
gehörenden Unterräume. Durch sie wird die Matrix diagonalisiert: Es gilt
A\i — GiWi für i <r.
Aufgaben 6.7
In den Aufgaben 1—3 berechnen Sie die Singulärwerte einer
singular en quadratischen Matrix A,
1. Berechnen Sie A^A und die Eigenwerte cri,0 dieser Matrix, sowie
zugehörige Eigenvektoren vi, V2 mit Einheitslänge:
14
28
2. (a) Berechnen Sie AA^^ die Eigenwerte cr^,0 und Eigenvektoren ui,U2
mit Länge eins,
(b) Rechnen Sie nach, dass in Aufgabe 1 Avi — criui gilt. Bestimmen
Sie alle Einträge der Singulärwertzerlegung:
14
28
= [^^^^][^'o]h^^l^-
6.7 Singulärwertzerlegung 375
3. Geben Sie Orthonormalbasen für die vier Unterräume zu dieser Matrix
A an.
In den Aufgaben 4—7 geht es um die Singulärwertzerlegung von
Matrizen mit Rang 2.
4. (a) Bestimmen Sie die Eigenwerte und Eigenvektoren mit Länge eins zu
den Matrizen A^A und AA^ für die Fibonacci-Matrix
A =
1 1
10
(b) Bestimmen Sie die Singulärwertzerlegung von A.
5. Zeigen Sie, dass für die Vektoren in Aufgabe 4 Avi = criUi und Av2 =
0-2U2 gilt.
6. Verwenden Sie die Option svd der MATLAB-Routine eigshow, um
dieselben Vektoren vi und V2 graphisch zu bestimmen.
7. Berechnen Sie für
A =
110
Ol 1
die Matrizen A^A und AA^ sowie deren Eigenwerte und Eigenvektoren
mit Länge eins. Zeigen Sie auch, dass das Produkt der drei Matrizen
UUV^ wieder A ergibt.
In den Aufgaben 8-15 werden die der SVD zu Grunde liegenden
Ideen herausgestellt.
8. Es seien ui,... , u^ und vi,... , v^^ Orthonormalbasen für den M".
Bestimmen Sie die Matrix A, die jeden Vektor v^ in Uj überführt: es soll
also Avi = ui,... , Avn — u^ gelten.
9. Konstruieren Sie die Matrix mit Rang eins, die für den Vektor v =
1A,1,1,1) das Produkt A\ = 12u mit u = |B,2,1) liefert. Ihr
einziger Singulärwert ist ai = .
10. Die Matrix A bestehe aus orthogonalen Spalten wi,W2,... ,Wn der
Längen cri,cr2,... ,an- Wie sehen die Matrizen C/, U und V in der
Singulärwertzerlegung aus?
11. Erklären Sie, wieso die Singulärwertzerlegung eine Matrix A als Summe
von r Matrizen vom Rang eins darstellt:
A = (TiUivJ + • • • + cr^u^v^.
376 6 Eigenwerte und Eigenvektoren
12. Es sei yl eine symmetrische 2 x 2-Matrix mit den Eigenvektoren ui und
U2 (mit Länge eins). Welche Matrizen C/, E und V^ erhalten Sie in der
Singulärwertzerlegung, wenn die Eigenwerte von yl Ai = 3 und A2 = —2
sind?
13. Gilt A = QR mit einer orthonormalen Matrix Q, so stimmt die SVD von
A beinahe mit der von R überein. Welche der drei Matrizen ändert sich,
wenn man R die Matrix Q voranstellt?
14. Die Matrix A sei invertierbar (mit Singulärwerten cri > cr2 > 0). Ändern
Sie A durch eine möglichst kleine Matrix so ab, dass eine singulare Matrix
Aq entsteht. Hinweis: U und V ändern sich nicht:
= ["^"^lha2][''^'^^l
15. (a) Wie äußert es sich in der Singulärwertzerlegung, wenn man A durch
AA austauscht?
(b) Bestimmen Sie die Singulärwertzerlegung der Matrizen A^ und A~^.
16. Warum steht in der SVD von A + I nicht einfach T 4- /?
7 Lineare Abbildungen
7.1 Die Idee einer linearen Abbildung
Multipliziert man einen Vektor v mit einer Matrix A, so wird v in einen
anderen Vektor Av „abgebildet". Aus einer „Eingabe" v erhält man eine
„Ausgabe" Av. Eine solche Abbildung basiert auf derselben Idee wie eine
Funktion. Dort wird aus einer Eingabe x die Ausgabe f{x). Für jeden Vektor
V oder jede Zahl x multipliziert man mit einer Matrix, oder wertet die
Funktion aus. Das eigentliche Ziel ist aber, alle v's gleichzeitig zu betrachten. Man
bildet den gesamten Raum ab, wenn man jeden Vektor v mit A multipliziert.
Betrachten wir eine Matrix A. Durch sie wird ein Vektor v auf einem
Vektor Av abgebildet, und ein Vektor w zu Aw. Damit wissen wir bereits,
was mit u = v4-w geschieht: ohne Zweifel muss Au gleich Av + Aw sein. Die
Matrixmultiplikation stellt also eine lineare Abbildung (oder lineare
Transformation) dar.
(a) r(v 4- w) = r(v) 4- T(w) (b) T{cv) = cT(y) für alle c. ^Jj^
Ist die Eingabe v = 0, so muss die Ausgabe T(v) = 0 sein. Wir kombinieren
(a) und (b) in eine Bedingung:
Lineariiät: T{cv 4- dw) - cT{y) 4- dt{vf).
Eine lineare Abbildung unterliegt starken Beschränkungen. Angenommen,
wir würden zu jedem Vektor einen anderen Vektor uq hinzuaddieren, so dass
r(v) = V 4- uo und T(w) = w + uq gilt. Dies wäre nicht gut, oder zumindest
nicht linear. Wendet man nämlich T auf v + w an, so erhält man v + w + uq,
was nicht dasselbe ist wie T(v) + T(w):
T(v) + T(w) = V + Uo + w + Uo
378 7 Lineare Abbildungen
ist ungleich
T(v + w) =^ V + w + uq.
Die Ausnahme ist der Fall uq =^ 0. Die Abbildung ist dann T(v) = v. Hierbei
handelt es sich um die identische Abbildung (nichts ändert sich, wie bei einer
Multiplikation mit /). Sie ist sicherlich linear. In diesem Fall stimmen der
„Eingaberaum" V und der „Ausgaberaum" W überein.
Abbildungen T(v) = Av + uq der Form „linear plus Verschiebung" nennt
man affin. Geraden bleiben bei Anwendung solcher Abbildungen Geraden.
Man benötigt sie in der Computergrafik, wir werden dies in Abschnitt 8.5
beschreiben.
Beispiel 7.1.1 Wählen Sie einen festen Vektor a = A,3,4), und definieren
Sie T(v) durch das Skalarprodukt a ■ v:
Die Eingabe ist v = A^1,^2,^3)- Die Ausgabe ist T(v) = a-v = i;i+3i;2+4i;3.
Diese Abbildung ist linear. Die Eingaben v stammen aus dem
dreidimensionalen Raum V = M^. Die Ausgaben sind Zahlen, der Ausgaberaum ist also
W = E^. Wir multiplizieren mit der Zeilenmatrix yl = [1 3 4], es gilt also
T(v) = Av.
Sie werden bald gut erkennen können, welche Abbildungen linear sind.
Enthält die Ausgabe quadratische Terme, Produkte oder Längen, also Terme
wie Vi, i;ii;2 oder ||v||, so ist T nicht linear.
Beispiel 7.1.2 T(v) = ||v|| ist nicht linear. Bedingung (a) für Linearität wäre
hier ||v4-w|| = ||v|| 4-||w||, und Bedingung (b) wäre ||cv|| = c||v||. Beide sind
falsch! (a): Die Seiten eines Dreiecks gehorchen einer Ungleichung ||v4-w|| <
||v|| 4- ||w||. (b): Die Länge von || - v|| ist nicht -||v||.
Beispiel 7.1.3 (Wichtig) T sei die Abbildung, die jeden Vektor um 30° dreht.
Der Definitionsbereich (aus dem der Eingabevektor v stammt) ist die xy-
Ebene, der Bildbereich (in dem der gedrehte Vektor T(v) liegt) ist ebenfalls
die xy~Ehene. Wir haben hier T ohne Erwähnung einer Matrix beschrieben:
einfach als Drehung in der Ebene.
Ist dieser Drehung linear? Ja. Wir können zwei Vektoren drehen und sie
dann addieren. Die Summe der gedrehten Vektoren T(v) + ^(w) ist derselbe
Vektor wie der Vektor T(v + w), den man erhält, wenn man die Summe
dreht. Bei dieser linearen Abbildung dreht sich die gesamte Ebene.
Hinweis Für Abbildungen verwendet man spezielle Begriffe. Wo es keine
Matrix gibt, kann man auch nicht vom Spaltenraum reden. Man kann aber
die Idee dahinter weiter verwenden. Der Spaltenraum besteht aus der Menge
aller Ausgabevektoren Av. Der Kern besteht aus allen Eingaben, für die
7.1 Die Idee einer lineaxen Abbildung 379
Av = 0 gilt. Dafür verwendet man den Begriff „Bild" und wiederum den
Begriff „Kern":
Bild von T = Menge aller Ausgaben T(v): Analogon zum Spaltenraum.
Kern von T = Menge alle Eingaben v mit T(v) = 0: Wie bei einer
Matrix.
Das Bild liegt im Ausgaberaum W. Der Kern liegt im Eingaberaum V.
Ist T durch Multiplikation mit einer Matrix gegeben, also T(v) = Av, kann
man ebensogut wieder Spaltenraum und Kern sagen.
Der Kern einer m x n-Matrix ist ein Unterraum von V = M^. Der
Spaltenraum ist ein Unterraum des . Das Bild kann, muss aber nicht den
ganzen Ausgaberaum W ausmachen.
Beispiele für Abbildungen (meistens linear)
Beispiel 7.1.4 Betrachten Sie die Projektion eines dreidimensionalen Vektors
in die xy-Ehene, Das Bild ist die gesamte Ebene, die jeden Vektor T(v)
enthält. Der Kern ist die z-Achse (die auf den Nullvektor projiziert wird).
Diese Projektion ist linear.
Beispiel 7.1.5 Betrachten Sie nun die Projektion eines dreidimensionalen
Vektors in die horizontale Ebene bei z = 1. Der Vektor v = (^,2/, 10) zum
Beispiel wird auf den Vektor T(v) = {x,y,l) abgebildet. Diese Abbildung
ist nicht linear. Warum nicht? Weil nicht einmal der Vektor v = 0 auf den
Vektor T(v) = 0 abgebildet wird.
Das Bächate Befepid sei die Mttltiplikation mm dreidiiöeiisionaieiii;
Vektors mit^ etiler 3;'x, 3r*Matri:x:,:Es liaiidelt/^iph äeSmp.^{^i^^0im^
bildimg, , :'^ \;,; ; . ,'^. \?;/-^/ '';'!': ^ VV-''^^^'^^t^'-t^
^''^'»r ■■
T(v 4- w) = A{v 4- w) ' ist'glelÄ Av + Aw = T(v) 4- T(w). ;' ^y-^ ,
Beispiel 7.1.6 Es sei yl eine invertierbare Matrix. Der Kern von T ist dann
der Nullvektor; das Bild W ist gleich dem Definitionsbereich V. Durch
Multiplikation mit A~^ wird eine andere lineare Abbildung definiert. Es handelt
sich um die inverse Abbildung T~^, durch die jeder Vektor T(v) wieder zurück
auf V abgebildet wird.
r~^(T(v)) = V analog zur Matrixmultiplikation A~^{Av) = v.
Wir gelangen zu einer unvermeidbaren Frage. Werden alle linearen
Abbildungen von Matrizen erzeugt? Jede m x n-Matrix erzeugt eine lineare
Abbildung von W nach M^, nämlich gemäß der Regel T(v) = Av. Wir
stellen die umgekehrte Frage: Gibt es hinter einer linearen Abbildung T, die als
„Drehung", „Projektion" oder „ ... " definiert ist, immer eine Matrix?
380 7 Lineare Abbildungen
Die Antwort ist ja. Es gibt eine Herangehensweise an die lineare Algebra,
bei der man nicht mit Matrizen beginnt. Im nächsten Abschnitt werden wir
zeigen, dass man doch wieder bei ihnen landet.
Lineare Abbildungen der Ebene
Es ist interessanter, eine Abbildung zu sehen, als sie zu definieren. Man kann
sich anschauen, wie die Multiplikation eines Vektors aus dem E^ mit einer
2 X 2-Matrix wirkt. Beginnen wir mit einem „Haus" in der xy-Ehene, das
aus elf Endpunkten besteht. Diese elf Vektoren v werden auf elf Vektoren Av
abgebildet. Geraden zwischen zwei Vektoren v werden dabei zu Geraden
zwischen den transformierten Vektoren Av, (Die Abbildung ist linear!) Wendet
man A auf ein Haus an, erhält man so ein neues Haus — das möglicherweise
gestreckt, oder gedreht, oder sonstwie unbewohnbar ist.
Der nun folgende Teil dieses Buches ist visuell gehalten, nicht theoretisch.
Wir werden Ihnen sechs Häuser zeigen, und die Matrizen, mit denen die
Häuser erzeugt wurden. Die Spalten einer Matrix H stellen die elf Punkte des
ersten Hauses dar. {H ist eine 2 x 12-Matrix, damit plot2d den elften Punkt
mit dem ersten verbindet.) Die elf Punkte in der Hausmatrix H werden dann
mit A multipliziert und erzeugen so die anderen Häuser. Auf diese Weise
entstanden die Häuser auf dem Bucheinband [der zweiten amerikanischen
Ausgabe; Anm. d. Übers.] (bevor Christine Curtis daraus einen Quilt^ für
Professor Curtis machte).
H
-6-6-7 0 7 6 6-3-3 0 0-6
-72181 2-7-7-2-2-7-7
Die wesentlichen Punkte
l.Eine Abbildung T bildet jedes v im Eingaberaum auf r(v) im
Ausgaberaum ab.
2. Linearität bedeutet, dass r(civi H h CnV„) = cir(vi) H h CnT{vn)
gilt.
3. Eine Abbildung T(v) = Av + vq ist nur für vq = 0 linear !
4. Der Quilt auf dem Einband [der amerikanischen Ausgabe] stellt T(Haus) =
AH für neun Matrizen A dar.
Aufgaben 7.1
1. Eine lineare Abbildung muss den Nullvektor unverändert lassen (r@) =
0). Beweisen Sie dies aus der Bedingung T{v + w) = T{v) + r(w),
indem Sie w = wählen, und beweisen sie es ein zweites Mal aus
Bedingung (b), indem Sie c = wählen.
^ Anm. d. Übers.: siehe Danksagung.
7.1 Die Idee einer linearen Abbildung 381
1 0
0 1
cos 35° -sin 35°
sin 35° cos 35°
0 1
1 0.
A =0,7 0,3
L0,3 0,7.
A = | 0,7 0,2
-0,3 0,9
1,1
.0,1 0,3j
Abb. 7.1. Mit plot2d(i4 *i/) gezeichnete lineare Abbildungen eines Hauses.
2. Bedingung (b) verlangt T{cv) = cT{v) und auch T{dw) = dr(w).
Addiert man dies, so liefert Bedingung (a) T( ) = ( ). Was erhält man
für T{cv + dw + eu)?
3. Welche dieser Abbildungen ist nicht linear? Die Eingabe sei v = (^1,^2):
(a) T{y) = {v2,vi)
(b) Tiy) = iv,,v,)
(c) r(v) = @,t;i)
(d) T(v) = @,l).
4. Ist S{T{v)) linear oder quadratisch, wenn S und T lineare Abbildungen
sind?
382 7 Lineare Abbildungen
(a) (Spezialfall) Gilt 5(v) = v und r(v) = v, ist dann 5(r(v)) = v oder
(b) (allgemeiner Fall) 5(wi + W2) = 5(wi) + S(w2) und r(vi + V2) =
r(vi) + T{v2) ergeben zusammen
5(r(vi + V2)) - 5( ) = + .
5. Es gelte r(v) = v, aber r@,'y2) = @,0). Zeigen Sie, dass diese
Abbildung zwar die Bedingung T{cv) = cT{v), aber nicht die Bedingung
r(v + w) = r(v) + r(w) erfüllt.
6. Welche dieser Abbildungen erfüllen die Bedingung T(v + w) = T(v) +
r(w), und welche erfüllen die Bedingung T{cv) = cT{v)?
(a)r(v)=v/||v||
(b) r(v) = Vi + V2 + V3
(c) T{v) = {vu2v2,Sv3)
(d) r(v) = letzte Komponente von v.
7. Bestimmen Sie einen Ausdruck für r(r(v)) für die folgenden
Abbildungen von V = M^ nach W = E^. Ist die Abbildung T^ jeweils linear?
(a) r(v) = -V
(b) r(v)=v + (i,i)
(c) r(v) = 90°-Drehung = (-^2,^1)
(d) r(v) = Projektion = (^^, ^^).
8. Bestimmen Sie Bild und Kern von T:
(a) T{vi,V2) = (v2,vi)
(b) T{vi,V2,V3) = (^1,^2)
(c) T{vi,V2) = @,0)
(d) T{vi,V2) = {VuVl).
9. Die „zyklische" Abbildung T ist definiert durch r(vi, ^2, V3) = {v2,V3,vi).
Was erhält man für T{T{v)), für T^{v) und für T^^^{v)? Wenden Sie T
also dreimal beziehungsweise einhundertmal auf v an.
10. Eine lineare Abbildung von V nach W besitzt eine Inverse von W nach
V, wenn das Bild ganz W ausmacht, und der Kern nur den Nullvektor
V = 0 enthält. Warum sind die folgenden Abbildungen nicht invertierbar?
(a) T{VI,V2) = {V2,V2) W-E2
(b) T{Vi,V2) = {VuV2,Vl+V2) W = E3
(c) T{vi,V2) =vi W = Ei
11. Gilt r(v) = Av für eine m x n-Matrix A, so ist T die Abbildung
„Multiplikation mit A".
(a) Geben Sie den Eingaberaum V und den Ausgaberaum W an.
(b) Warum ist der Spaltenraum von A das Bild von T?
7.1 Die Idee einer linearen Abbildung 383
(c) Warum ist der Kern von A der Kern von T?
12. Eine lineare Abbildung T bildet den Vektor A,1) auf den Vektor B,2)
und den Vektor B,0) auf den Vektor @,0) ab. Bestimmen Sie T(v) für
(a) v = B,2)
(b) v = C,l)
(c) v = (-l,l)
(d) v = (a,6).
Die Aufgaben 13-20 sind vielleicht etwas schwieriger. Der Ein-
gaberaum V sei der Raum aller 2 X 2-Matrizen M.
13. M sei eine beliebige 2 x 2-Matrix, und es sei A = [34]- E)i6
Abbildung T sei definiert durch T{M) = AM. Mit Hilfe welcher Gesetze der
Matrixmultiplikation kann man zeigen, dass T linear ist?
14. Es sei A = [35]- Zeigen Sie, dass das Bild von T der ganze Matrixraum
V ist, und dass der Kern nur aus der Nullmatrix besteht.
A) Beweisen Sie, dass M die Nullmatrix sein muss, wenn AM = 0 gilt.
B) Bestimmen Sie eine Lösung der Gleichung AM = B für eine beliebige
2 X 2-Matrix B.
15. Es sei A = [si]- Zeigen Sie, dass die Einheitsmatrix / nicht im Bild von
T liegt. Bestimmen Sie eine Matrix M ungleich Null so, dass T{M) =
AM = 0 ist.
16. Angenommen, eine Abbildung T transponiert jede Matrix M. Versuchen
Sie, eine Matrix A zu finden, für die AM = M^ für jedes M gilt. Zeigen
Sie, dass es keine solche Matrix A gibt. Für Professoren: Ist dies eine
lineare Abbildung, die nicht als Matrixmultiplikation darstellbar ist?
17. Die Abbildung T, die jede Matrix transponiert, ist auf jeden Fall linear.
Welche zusätzlichen Eigenschaften sind noch gegeben?
(a) r^ = Identität.
(b) Der Kern von T ist die Nullmatrix.
(c) Jede Matrix liegt im Bild von T.
(d) T{M) = -M ist unmöglich.
18. Es sei T{M) = [oo][^][oi]- Bestimmen Sie eine Matrix M mit
T{M) ^ 0. Beschreiben Sie alle Matrizen mit T{M) = 0 (Kern von
T) sowie alle Ausgaben T{M) (das Bild von T).
19. Gilt A^O und B ^ 0, so gibt es eine Matrix M, für die AMB ^ 0 ist.
Zeigen Sie anhand eines Beispiels, dass dies nicht unbedingt für M = /
gelten muss. Bestimmen Sie auch ein für Ihr Beispiel passendes M.
384 7 Lineare Abbildungen
20. Bestimmen Sie die inverse Abbildung T~^{M) in der Form ( )M( )
für T{M) — AMB mit invertierbaren Matrizen A und B,
Die Aufgaben 21-27 behandeln die Abbildungen von „Häusern"
durch eine Multiplikation AH. Die Ausgabe ist T (Haus).
21. Wie kann man anhand des Bildes von T (Haus) erkennen, ob A
(a) eine Diagonalmatrix,
(b) eine Matrix mit Rang eins,
(c) eine untere Dreiecksmatrix ist?
22. Zeichnen Sie für die folgenden Matrizen das Bild T (Haus):
D
20
Ol
und A
0,7 0,7
0,3 0,3
undU =
1 1
0 1
23. Welche Bedingungen muss A= [^^] erfüllen, damit T (Haus)
(a) aufrecht steht?
(b) das Haus in alle Richtungen um den Faktor 3 vergrößert?
(c) das Haus ohne Änderung der Form dreht?
24. Welche Bedingungen muss det A = ad - bc erfüllen, damit T (Haus)
(a) auf eine Gerade gequetscht wird?
(b) die Endpunkte im Uhrzeigersinn behält, also nicht gespiegelt wird.
(c) denselben Flächeninhalt hat wie das originale Haus?
Wieso gilt A = I, wenn auch nur eine Seite des Hauses unverändert
bleibt?
25. Beschreiben Sie T (Haus) für r(v) = -v+(l, 0). Dieses T ist eine „affine"
Abbildung.
26. Ergänzen Sie die Matrix H so, dass das Haus noch einen Schornstein
erhält.
27. Das folgende MATLAB-Programm erzeugt einen Vektor namens theta, der
50 Winkelgrößen enthält, und zeichnet damit einen Einheitskreis sowie
die Ellipse T(Kreis). Man kann A variieren.
A = [2 1;1 2]
theta = [0:2*pi/50:2*pi];
circle = [cos(theta); sin(theta)];
ellipse = A*circle;
axis([-4 4 -4 4]); axis('square')
plot (circled, :) »circle B, :) , ellipse A, :) »ellipse B,:))
28. Fügen Sie dem Kreis in Aufgabe 27 zwei Augen und einen (lächelnden)
Mund hinzu. (Wenn Sie das eine Auge hell und das andere dunkel
zeichnen, so können Sie erkennen, ob der Kreis an der ^/-Achse gespiegelt
7.2 Die Matrix einer linearen Abbildung 385
wird.) Multiplizieren Sie das Gesicht mit Matrizen A, um neue Gesichter
zu erzeugen.
29. Das erste Haus wurde mit Hilfe dieses Programms plot2d(H) gezeichnet.
Die Kreise erhält man durch das Zeichen o und die Geraden durch das
Zeichen -:
X = HCl,:)'; y = HB,:)';
axis([-10 10 -10 10]), axis('square')
plot(x,y,'o',x,y,'-');
Testen Sie plot2d(A'*H) und plot2d(A'*A*H) mit den Matrizen aus
Abbildung 7.1 .
30. Beschreiben Sie mit Hilfe eines Computers die Häuser A ^ H für die
folgenden Matrizen A:
1 0
0 0,1
und
0,5 0,5
0,5 0,5
und
0,5 0,5
-0,5 0,5
und
1 1
10
7.2 Die Matrix einer linearen Abbildung
Auf den nächsten Seiten werden wir jeder linearen Abbildung eine Matrix
zuweisen. Bei gewöhnlichen Spaltenvektoren mit Eingabe v in V= W und
Ausgabe r(v) in W= W^ erhalten wir eine m x n-Matrix.
Die Vektoren der Standardbasis für W und W^ führen auf eine
Standardmatrix für r, für die wie gewöhnlich r(v) = Av gilt. Diese Räume haben
aber auch andere Basen, bei deren Verwendung T durch andere Matrizen
dargestellt wird. Ein Hauptaugenmerk der linearen Algebra liegt darin, solche
Basen zu wählen, die die beste Matrix liefern.
Sind die Räume V und W nicht W und W^, so haben sie doch immer
noch Basen. Jede Wahl einer Basis führt zu einer Matrix für T. Ist die Basis
des Eingaberaums verschieden von der des Ausgaberaums, so ist die Matrix
für die Abbildung r(v) = v nicht die Identität /. Stattdessen wird es die
„BasisWechselmatrix" sein.
Schlüsselidee in diesem Abschnitt
Wenn man T(vi),..., T(vn) für Basisvektoren vi,..., v^, kennte
dann kann man über die Linearität T(v) für jeden beliebigen
Vektor v bestimmen.
Begründung Jede mögliche Eingabe v lässt sich als eindeutige
Linearkombination civi + ••• + Cn'Vn der Basisvektoren darstellen. Da T eine linare
Abbildung ist (hier kommt die Linearität ins Spiel), muss die Ausgabe T(v)
dieselbe Linearkombination der bekannten Ausgaben T(vi),... ,T(vn) sein:
386 7 Lineare Abbildungen
Die Linearität fordert dann T(v) = ciT(vi) 4- . *. + ertT{vn).
G.1)
Die Linearität dehnt sich also von cv + dw auf alle Kombinationen ciVi +
1- Cn^n aus.
Beispiel 7.2.1 Angenommen, T bildet den Vektor vi = A,0) auf den Vektor
r(vi) = B,3,4) und den zweiten Basisvektor V2 = @,1) auf den Vektor
r(v2) = E,5,5) ab. Ist T dann eine lineare Abbildung von E^ nach E^, so
ist die zugehörige Standardmatrix eine 3 x 2-Matrix:
A =
25
35
45
Wegen der Linearität gilt r(vi + V2)
'25'
35
45
1"
1
=
■7]
8
9J
Beispiel 7.2.2 Die Ableitungen der Funktionen l,x,x'^,x^ sind 0, l,2a:,3a:^.
Dies sind vier Eigenschaften der Abbildung T, die „die Ableitung berechnet".
Jetzt fügen wir die entscheidende Tatsache hinzu, dass T linear ist:
^ (v) = T" ~ genügt.! der tmeäiritatsbedmgiiiig; ^ tc^ -+ öf#)' = >c-f- :'H§ äi~-^,
Man braucht nur diese Eigenschaften, um alle anderen Ableitungen zu
bestimmen. Anhand der Ableitung der einzelnen Potenzen 1 , X, X , X ^ (dies sind
die Basisvektoren Vi, V2, V3, V4) bestimmt man die Ableitung eines jeden
Polynoms wie zum Beispiel 4-\- x -\- x"^ -\- x^:
-—{4 + X + x'^ -\- x^) = 1 + 2x + Sx'^ (wegen der Linearität!) G.2)
dx
Der Eingaberaum V enthält hier alle Linearkombinationen der Ausdrücke
l,x,x'^,x^. Ich nenne sie hier Vektoren, Sie werden sie vielleicht
Funktionen nennen wollen. Diese vier Vektoren bilden eine Basis des Raums V der
kubischen Polynome (vom Grad < 3).
Um den Kern einer Matrix A zu berechnen, haben wir das
Gleichungssystem Av = 0 gelöst. Um den Kern dieser Ableitung T zu bestimmen, lösen
wir die Gleichung dv/dx = 0. Die Lösung ist v = konstant. Der Kern von
T ist also eindimensional und besteht aus allen konstanten Funktionen wie
t;i = 1 (die erste Basisfunktion).
Um das Bild (oder den Spaltenraum) zu bestimmen, sehen wir uns alle
Ausgaben von r(v) = dv/dx an. Die Eingaben sind kubische Polynome
a -\- bx -\- cx^ + dx^, die Ausgaben sind daher quadratische Polynome vom
Grad < 2. Für den Bildraum W haben wir daher die Wahl. Wählen wir W =
7.2 Die Matrix einer linearen Abbildung 387
kubische Polynome, so ist das Bild von T (die quadratischen Polynome) ein
Unter räum davon. Wählen wir hingegen gleich W = quadratische Polynome,
so ist das Bild gleich dem ganzen Raum W.
Diese zweite Wahl betont den Unterschied zwischen dem
Definitionsbereich oder Eingaberaum (V = kubische Polynome) und dem Bildbereich oder
Ausgaberaum (W = quadratische Polynome). V hat die Dimension n — A
und W hat die Dimension m = 3. Die Matrix für T ist dann eine 3 x 4-Matrix.
Das Bild von T ist ein dreidimensionaler Unterraum. Die Matrix wird also
den Rang r — Z haben, und der Kern ist eindimensional. Die Summe 3+1 = 4
ist gleich der Dimensiona des Eingaberaums. Diese Beziehung kennen wir aus
der Formel r -{-{n — r) = n im Fundamentalsatz der linearen Algebra. Es gilt
immer (Dimension des Bildes) + (Dimension des Kerns)=(Dimension von V).
Beispiel 7.2.3 Das Integral ist die Inverse zur Ableitung. Dies ist die
Aussage des Hauptsatzes der Integral- und Differentialrechnung. Hier finden wir
diesen Sachverhalt in der linearen Algebra wieder. Die Abbildung T~^, die
„das Integral von 0 bis x berechnet", ist linear! Wenden wir T~^ auf 1, x und
x^ an:
nX nX nX
l ldx = x, / xdx = ^x'^, / x'^
Jo Jo Jo
dx = ^x^.
Wegen der Linearität ist das Integral von w = B + Cx + Dx"^ dann gleich
T~^(w) = Bx + ^Cx'^ + ^Dx^. Das Integral eines quadratischen Polynoms
ist ein kubisches Polynom. Der Eingaberaum von T~^ ist also der Raum
der quadratischen Polynome, und der Ausgaberaum der Raum der kubischen
Polynome. Bei der Integration geht man also von W zurück nach V. Die
zugehörige Matrix ist eine 4 x 3-Matrix.
Bild von T~^ Die Ausgaben Bx + ^Cx'^ + ^Dx^ sind kubische Polynome
ohne konstanten Term.
Kern von T~^ Die Ausgabe ist dann und nur dann gleich Null, wenn B =
C = D = 0 gilt. Der Kern besteht also aus dem Nullvektor. Die Dimension
des Eingaberaums W für T~^ ist also 3 + 0 = 3.
Matrizen für Ableitung und Integral
Wir werden zeigen, wie die Matrizen A und A~'^ mit der Ableitung T und dem
Integral T~^ zusammenhängen. Dies ist ein hervorragendes Beispiel aus der
Differentialrechnung. Danach folgt die allgemeine Regel, wie eine beliebige
lineare Abbildung T durch eine Matrix A ausdrückt werden kann.
Die Ableitung bildet den Raum V der kubischen Polynome in den Raum
W der quadratischen Polynome ab. Die Basis für V wird durch die Polynome
1, a:, x^ und x^ gebildet, und die Basis für W ist durch die Polynome 1, x und
^ gegeben. Die Matrix, die „die Ableitung berechnet", ist eine 3 x 4-Matrix:
388
7 Lineare Abbildungen
A^
oiöa'
100 20
0003
=; MatrixdarstelluHg Von TJ
Warum ist A die richtige Matrix? Weil die Multiplikation mit A dasselbe
bewirkt wie die Abbildung durch T. Die Ableitung von v = a + bx + cx^ +
dx^ ist T(v) = 6 + 2cx + 3dx^. Dieselben Koeffizienten erhält man durch
Multiplikation mit der Matrix:
G.3)
Betrachten wir auch T~^. Die „Integrationsmatrix" muss eine 4 x 3-Matrix
sein. Beobachten Sie, wie die folgende Matrix aus w = 5 + Cx + Dx"^ das
Integral Bx + |Cx^ + \Dx^ erzeugt:
[0 10 0"
0020
0003
a
b
c
d
■=L
■ fe"
2c
U\
Integration:
fooo"
10 0
0| 0
c
D
■=
' 0'
r jB:i
G.4)
Ich möchte diese Matrix A~^ nennen, und ich werde es auch. Seien Sie sich
aber im Klaren darüber, dass rechteckige Matrizen keine Inverse haben,
jedenfalls keine beidseitige Inverse. Diese rechteckige Matrix A jedoch hat eine
einseitige Inverse. Das Integral ist eine einseitige Inverse der Ableitung!
AA
-1 _
100
010
001
aber
A-^A =
0000
0100
00 10
0001
Integriert man erst eine Funktion und leitet sie dann ab, so erhält man die
Funktion, mit der man begonnen hat. Deshalb gilt AA~^ = I. Leitet man
aber zuerst ab und integriert dann, so verliert man den konstanten Term.
Das Integral der Ableitung von 1 ist Null:
r-^r(l) = Integral der Nullfunktion = 0.
Wir finden diese Eigenschaft in der Matrix A~^A wieder, deren erste Spalte
die Nullspalte ist. Die Ableitung T hat einen Kern (die konstanten
Funktionen), ihre Matrix A hat ebenfalls einen Kern. Wir erkennen wieder einmal:
Die Multiplikation Av hat dieselben Eigenschaften wie die Abbildung T{v).
7.2 Die Matrix einer linearen Abbildung 389
Konstruktion der Matrix
Jetzt zur allgemeinen Regel. Angenommen, T bildet den n-dimensionalen
Raum V in den m-dimensionalen Raum W ab. Wir wählen dann eine Basis
Vi,..., Vn für V und eine Basis wi,..., w^ für W. Die Matrix A ist dann
eine m x n-Matrix. Um ihre erste Spalte zu bestimmen, wenden wir T auf
den ersten Basisvektor vi an:
r(vi) liegt in W. Der Vektor ist eine Linearkombination
öiiWi + h cimi^m der Elemente der Basis von W .
Diese Zahlen ßii,..., ßmi bilden die erste Spalte von A. Den Vektor Vi auf
den Vektor T(vi) abzubilden bewirkt dasselbe, wie den Vektor A,0,... ,0)
mit A zu multiplizieren. Denn dadurch erhält man die erste Spalte der Matrix.
Ist T zum Beispiel die Ableitung und die konstante Funktion 1 der erste
Basisvektor, so ist die Ableitung T(vi) = 0. Deshalb war die erste Spalte der
Matrix A eine Nullspalte.
Beim Integral erhält man aus der ersten Basisfunktion 1 die Funktion x,
also die zweite Basisfunktion. Entsprechend ist @,1,0,0) die erste Spalte von
A-\
7A Jede Une^g-e Abbildiiifcg T von Vtnalch W wird jttodij dße. M^
dargestellt (nachdmn maB<^Öaieii'^fÖir. ¥;iiiid;SV^vg0i;rSfttfeliij^);i^
von A erhät löaiiycmdemt^aa'T^tf 4*^ Saii^yö^ t / '^^^;"'
Ti^'^y^^ Ltoear|coiiibma;tioii^d€r Bäsis^^ekte^^.^^
Diese Zahlen aij,... ,amj bilden die Spalte j von A. Die Matrix wird also
so konstruiert, dass man für Basisvektoren die richtigen Ergebnisse erhält.
Wegen der Linearität erhält man dann auch für alle anderen Vektoren
die richtigen Ergebnisse. Jeder Vektor v lässt sich als Linearkombination
civi H \- Cn^n schreiben, und r(v) als Linearkombination der w's.
Multipliziert man dann A mit dem Koeffizientenvektor c = (ci,... ,c„) der
Kombination für V, so erhält man in Ac die Koeffizienten der Linearkombination
für T(v). Das liegt daran, dass die Matrixmultiplikation (also das Erzeugen
von Linearkombinationen der Spalten) linear ist, ebenso wie T.
An A erkennt man, wie T wirkt. Jede lineare Abbildung kann als Matrix
geschrieben werden, die allerdings von den gewählten Basen abhängt.
Beispiel 7.2.4 Wechselt man die Basen, so bleibt zwar T unverändert, aber
die Matrix A ändert sich.
Angenommen, wir verwenden eine andere Reihenfolge "^, 1 für die
Basis der kubischen Polynome, und behalten die ursprüngliche Reihenfolge
390 7 Lineare Abbildungen
l^x^x^ für die quadratischen Polynome in W. Jetzt wenden wir T auf den
ersten Basisvektor an: die Ableitung von x ist 1, also der erste Basisvektor
von W. Die erste Spalte von A sieht daher jetzt anders aus:
A =
1000
0200
0030
Matrix für die Ableitung T
= für die Basen
x,x^,x^, 1 und l,x,x^.
Ordnen wir also die Basiselemente von V um, so entspricht dem eine Um-
ordnung der Spalten von A. Der Eingabe-Basisvektor Vj bestimmt die
entsprechende Spalte j. Jeder Ausgabe-Basisvektor w^ bestimmt hingegen die
Zeile i der Matrix. Schon bald werden wir andere Basiswechsel als nur
Permutationen betrachten.
Produkte AB gehören zu Abbildungen TS
Am Beispiel der Ableitung und des Integrals konnten wir drei Dinge sehen.
Erstens, lineare Abbildungen finden sich überall — in der
Differentialrechnung, in Differentialgleichungen, und natürlich in der linearen Algebra.
Zweitens, auch andere Räume als die Räume W^ sind wichtig — wir haben die der
kubischen und quadratischen Polynome gesehen. Drittens, eine Abbildung T
lässt sich immer noch auf eine Matrix reduzieren. Jetzt kümmern wir uns
darum, wie wir diese Matrix bestimmen können.
In den nächsten Beispielen gilt V = W, und wir wählen für beide Räume
dieselbe Basis. Dann lassen sich die Matrizen A^ und AB mit den
Abbildungen T^ und TS vergleichen.
Beispiel 7.2.5 Die Abbildung T drehe jeden Vektor in der Ebene um
denselben Winkel 9. In diesem Fall ist also V = W = R^. Bestimmen Sie die
Drehmatrix A. Die Antwort hängt von der verwendeten Basis ab!
Lösung Die Standardbasis ist durch die Vektoren vi = A,0) und V2 = @,1)
gegeben. Um A zu bestimmen, wende man T auf diese Basisvektoren an. In
Abbildung 7.2a werden sie um den Winkel 9 gedreht dargestellt. Der erste
Vektor A,0) landet auf dem Vektor (cosö,sinö), also cos9 mal A,0) plus
sinö mal @,1). Die Zahlen cosö und sin 9 bilden deshalb die erste Spalte von
A:
cos 9
sin 9
Spalte 1 A
cos 9—sin 9
sin 9 cos 9
beide Spalten.
Um die zweite Spalte zu bestimmen, transformiere man den zweiten Vektor
@,1). In der Abbildung erkennt man, dass er in den Vektor (—sinö,cosö)
gedreht wird. Diese Zahlen bilden also die zweite Spalte. Multipliziert man
dann A mit @,1), so erhält man wieder genau diese Spalte, so dass A mit T
übereinstimmt.
1^2
^^^2)=| cos I \
COS I ^ Q
7.2 Die Matrix einer linearen Abbildung 391
A-72
":''{'>" 1
LlA
L1/2J
Abb. 7.2. Drehung um 6 und Projektion auf die 45°-Gerade.
Beispiel 7.2.6 {Projektion) Die Abbildung T projiziert jeden Vektor in der
Ebene auf die 45°-Gerade. Bestimmen Sie die Matrix für zwei verschiedene
Basen.
Lösung Wir beginnen mit einer speziell gewählten Basis. Der Basisvektor
Vi liege entlang der 45°-Geraden. Er wird auf sich selbst projiziert. Deshalb
enthält die erste Spalte von A die Zahlen 1 und 0. Der zweite Basisvektor
liege auf der dazu senkrechten 135°-Geraden. Dieser Vektor wird dann auf
die Null projiziert. Die zweite Spalte enthält also die Einträge 0 und 0:
Projektion A =
10
00
wenn man V und W in einer 45°-135°-Basis betrachtet.
Stellt man die Basis in der umgekehrten Reihenfolge auf (erst 135° und dann
45°), so erhält man die Matrix .
Wir betrachten als nächstes die Standardbasis A,0) und @,1). In
Abbildung 7.2b sieht man, dass der Vektor A,0) auf den Vektor (|, |) projiziert
wird. So erhält man die erste Spalte von A. Der andere Basisvektor @,1)
wird ebenfalls auf (|, |) projiziert. Die Matrix ist also
Projektion A =
r 1
2
1
L 2
11
2
1
2 J
für dasselbe T und die Standardbasis.
Beide Matrizen A sind Projektionsmatrizen, wenn man sie quadriert, so
ändern sie sich nicht. Zweimal zu projizieren bewirkt dasselbe wie nur einmal
zu projizieren. Es ist T^ = T, deshalb gilt A^ = A. Beachten Sie, was sich
hinter dieser Aussage verbirgt: Die Matrix für die Abbildung T^ ist A^.
Wir sind hier bei etwas Wichtigem angelangt — dem wahren Grund für
die Art, wie man Matrizen multipliziert. Zwei Abbildungen S und T seien
durch die Matrizen B und A dargestellt. Wendet man T auf die Ausgabe
von S an, so erhält man die „Komposition" oder „Verkettung" TS. Wendet
man A nach B an, so erhält man das Matrixprodukt AB. Die Regeln für
die Matrizenmultiplikation ergeben genau die richtige Matrix AB, um TS
darzustellen.
392 7 Lineare Abbildungen
Die Abbildung S bilde einen Raum U auf einen Raum V ab, für ihre nxj9-
Matrix verwenden wir eine Basis ui,..., u^ für U und eine Basis vi,..., v^
für V. Die Abbildung T bilde wie zuvor V auf W ab, und für ihre Matrix
A verwenden wir dieselbe Basis vi,..., v^ für V — dieser Raum ist der
Ausgaberaum für S und der Eingaberaum für T. Dann passt die Matrix AB
mit der Abbildung TS zusammen:
7B Multiplikation Die Imeare Äbbüdung TS nimmt einen beliebigen Vekr
tot.u in 0, bildet ihn auf d^B Vektor 5(u) in V ab nn^ daanabf da»; Vektor
r(iS?Cii)Ji:^'^ W- Pi^M^tim-AB mmmt eiaen^Vekt^ir :^^iE;K^)■;g^t dwift
zu 53t lu i:^ über und dmu zu ÄBx in W .Die Matrix AB stellt tS also
korrekt dar:
TS: U ^ V ^ W
AB : (m x n){n x p) = {m x p).
Die Eingabe ist u = xiUi H h XpUp. Die Ausgabe TE(u)) entspricht der
Ausgabe A^x. Verkettungen von Abbildungen entsprechen also Produkten
von Matrizen. Die wichtigsten Fälle sind die, in denen die Räume U, V und
W und deren Basen alle gleich sind. Da dann m = n = p gilt, haben wir es
in diesen Fällen mit quadratischen Matrizen zu tun.
Beispiel 7.2.7 5 drehe die Ebene um den Winkel 6, und T drehe sie noch
einmal um 9. Dann dreht TS um den Winkel 29. Diese Abbildung T^ entspricht
der Drehmatrix A^:
T = S A = B
J^ = Drehung um 29 =
cos2ö-sin2ö
sin 29 cos 29
Wenn wir (Abbildung)^ mit (Matrix)^ vergleichen, können wir Formeln für
cos 29 und sin 29 erhalten. Berechnen wir also A mal A:
cos 9—sin 9
sin 9 cos 9
cos9-
sin9
-sin 9
cos 9
cos^ 9 - sin^ 9 -2 sinö cos 9
2 sin 9 cos 9 cos^ 9 - sin^ 9
Nach Vergleich mit der Matrix oben gilt also cos 29 = cos^ 9 — sin^ 9 und
sin2ö = 2 sin ö cos ö. Die Trigonometrie kommt aus der linearen Algebra.
Beispiel 7,2.8 5 drehe um 9 und T drehe um -9. Dann gilt TS = I und
AB = 1.
In diesem Fall ist T{S{u)) gleich u. Wir drehen erst vorwärts, dann
zurück. Damit sich dieser Sachverhalt in den Matrizen wiederspiegelt, muss
ABx gleich x sein. Die beiden Matrizen sind also zueinander invers. Wir
überprüfen dies, indem wir cos{—9) = cos9 und sin(—ö) = —sinö in A
einsetzen:
7.2 Die Matrix einer linearen Abbildung 393
AB =
cosö sinö
— sin 6 cos 6
cos ö — sin ö
sin 0 cos 6
cos^ e + sin^ e 0
0 cos^ ö + sin^ e
Wegen der berühmten Gleichung cos^ 6 + sin^ ö = 1 ist dies /.
Zuvor beschrieb T die Ableitung und S das Integral. In dem Fall ist TS
die Identität, nicht aber ST. Deshalb ist AB die Einheitsmatrix, aber BA
nicht.
AB =
0 100
0020
0003
00 0
1 0 0
0| 0
00|j
= 1
aber
BA
0000
0100
0010
0001
Die Identitäts—Abbildung und ihre Matrizen
Wir benötigen die Matrix für die besondere und langweilige Abbildung
T{y) = V. Diese Identitäts-Abbildung bewirkt überhaupt nichts an v. Auch
die zugehörige Matrix bewirkt nichts, wenn Eingabe-Basis und Ausgabe-
Basis übereinstimmen. Die Ausgabe T(vi) ist vi. Sind die Basen gleich, so
ist dieser Vektor auch wi, und die erste Spalte von A ist A,0,..., 0).
Ist jede Ausgabe T{vj) = v^* gleich w^, so ist die Matrix einfach I
Das hört sich vernünftig an: die Identitäts-Abbildung wird durch die
Einheitsmatrix dargestellt. Aber stellen Sie sich vor, die Basen wären
verschieden. Dann ist T(vi) = vi eine Linearkombination der w's. Diese
Linearkombination miiwi H h mniWn liefert uns dann die erste Spalte der Matrix
M. Wir werden den Buchstaben M (anstelle von A) für solche Matrizen
verwenden, die die Identität darstellen.
Sind die Ausgaben T(v^) = Vj durch Linearkombinationen
SiLi tUij^Wi^ gegebeny so istt die „Baäismechseimatri^^^ M.
Die Basis ändert sich, aber die Vektoren selbst ändern sich nicht: T(v) = v.
Benutzt man für die Eingabe eine andere Basis als für die Ausgabe, so ist die
Darstellungsmatrix nicht /.
Beispiel 7.2.9 Die Eingabe-Basis sei durch vi = C,7) und V2 = B,5), und
die Ausgabe-Basis durch wi = A,0) und W2 = @,1) gegeben. Dann ist die
Matrix M einfach zu berechnen:
Die Matrix für T(v) =^ v ist M =
32
75
394 7 Lineare Abbildungen
Begründung Die erste Eingabe ist vi = C,7). Die Ausgabe, die ebenfalls
C,7) ist, drücken wir aber als 3wi -f7w2 aus. Die erste Spalte von M enthält
also die Einträge 3 und 7.
Es scheint, dies ist zu einfach, um wichtig zu sein. Es wird ein wenig
komplizierter, wenn der Basiswechsel in die andere Richtung geht. Wir erhalten
dann die inverse Matrix.
Beispiel 7.2,10 Die Eingabe-Basis ist vi = A,0) und V2 — @,1). Die
Ausgabe-Basis ist wi = C,7) und W2 = B,5).
Die Matrix für T(v) = v ist
32
75
1 -1
5-2
-7 3
Begründung Die erste Eingabe ist vi = A,0). Die Ausgabe vi drücken wir
aber als 5wi — 7w2 aus. Rechnen Sie nach, dass 5C,7) — 7B,5) den Vektor
A,0) ergibt. Wir kombinieren also die Spalten der vorherigen Matrix M, um
die Spalten von / zu erhalten. Die Matrix, die dies leistet, ist M~^:
is MM-^ = L
Ein Mathematiker würde sagen, dass MM~^ dem Produkt zweier Identitäts-
Abbildungen entspricht. Man beginnt und endet mit derselben Basis A,0)
und @,1). Die Matrixmultiplikation muss / ergeben, deshalb müssen die
beiden Basiswechselmatrizen zueinander invers sein.
Wi
W2
5-2"
-7 3
Vi
V2
Warnung Man erliegt leicht dem folgenden Fehlschluss über die Matrix M.
Sie steht für den Basiswechsel von den v's zur Standardbasis aus den Spalten
von /. Die Matrixmultiplikation geht aber anders herum. Multipliziert man
M mit den Spalten von /, so erhält man die v's. Das scheint die
Rückwärtsrichtung zu sein, aber es schon richtig so.
Eines ist sicher. Multipliziert man A mit A,0,...,0), so erhält man
die erste Spalte der Matrix. In diesem Abschnitt ist neu, dass der Vektor
A,0,..., 0) als Schreibweise für den ersten Vektor vi der Basis aus v's steht.
Dann ist die erste Spalte der Matrix eben dieser Vektor vi, ausgedrückt in
der Standardbasis. Dies gilt für den Fall T = /, in dem aber die Basis
gewechselt wird. Im Rest dieses Buchs werden wir die Basis festhalten und T
als Multiplikation mit A betrachten.
Die wesentlichen Punkte
1, Kennen wir T'(vi),... T(\n) für die Vektoren einer Basis, so sind alle
anderen r(v) bereits durch die Forderung der Linearität festgelegt.
{Lineare AbbildungT Matrix A (m x n) "j
Eingabe-Basis vi,..., Vn die T >
Ausgabe-Basiswi,..., w^ bezüglich dieser Basen darstellt. J
7.2 Die Matrix einer linearen Abbildung 395
3. Die Matrizen für die Ableitung und das Integral sind einseitige Inverse:
d(Konstante)/c?x = 0:
(Ableitung) (Integral) = I
= Hauptsatz der Integral- und Differentialrechnung !
4. Die Basiswechselmatrix M stellt T = I dar. Ihre Spalten enthalten die
Koeffizienten der durch die Eingabe-Basisvektoren ausgedrückten Ausgabe-
BasisVektoren: Wj = mijVi + h mnj^n-
Aufgaben 7.2
In den Aufgaben 1—4 wird das Beispiel mit der ersten Ableitung
auf höhere Ableitungen erweitert.
1. Die Abbildung S besrechne die zweite Ableitung. Verwenden Sie als
Eingabe-Basis vi, V2, V3, V4 und auch als Ausgabe-Basis wi, W2, W3, W4
weiterhin die Funktionen 1, x, x^ und x^. Schreiben Sie 5vi, 5v2,5v3,5v4
als Linearkombination der w's, und bestimmen Sie so eine 4 x 4-Matrix
B für S.
2. Für welche Funktionen gilt v" = 0? Sie bilden den Kern der zweiten
Ableitung S. Welche Vektoren liegen im Kern der zugehörigen Matrix B
in Aufgabe 1?
3. Die Matrix B aus Aufgabe 2 ist nicht das Quadrat der 4 x 3-Matrix
0 100
0020
0003
für die erste Ableitung. Fügen Sie der Matrix A eine Nullzeile hinzu,
so dass der Eingaberaum gleich dem Ausgaberaum wird. Vergleichen Sie
dann A^ mit B. Folgerung: Um B = A^ zu erhalten, müssen wir die
Ausgabe-Basis gleich setzen, so dass m — n gilt.
4. (a) Das Produkt TS erzeugt die dritte Ableitung. Fügen Sie Nullzeilen
ein, um 4 x 4-Matrizen zu erhalten, und berechnen Sie dann AB.
(b) Die Matrix B'^ entspricht der vierten Ableitung 5^. Warum ist sie
gleich Null?
In den Aufgaben 5-10 geht es um eine bestimmte Abbildung T und
die zugehörige Matrix A.
5. Für die Basen vi,V2,V3 und wi,W2,W3 sei die lineare Abbildung T
gegeben durch T(vi) = W2 und T(v2) = T(v3) = wi + W3. Bestimmen Sie
die Darstellungsmatrix A.
396 7 Lineare Abbildungen
6. (a) Welche Ausgabe liefert die Abbildung T aus Aufgabe 5 für die
Eingabe Vi + V2 + V3?
(b) Multiplizieren Sie A mit dem Vektor A,1,1).
7. Da T(v2) = T{y^) gilt, sind die Lösungen der Gleichung T(v) = 0 durch
v = gegeben. Welche Vektoren gehören zum Kern von AI
Bestimmen Sie auch alle Lösungen der Gleichung T(v) = W2.
8. Bestimmen Sie einen Vektor, der nicht im Spaltenraum von A liegt, und
eine Linearkombination der w's, die nicht im Bild von T liegt.
9. Sie haben nicht genügend Informationen, um T^ zu bestimmen. Warum
nicht? Warum muss die zugehörige Matrix nicht unbedingt A^ sein?
10. Bestimmen Sie den Rang von A. Diese Zahl gibt nicht die Dimension des
Ausgaberaums W an, sondern die Dimension des von T.
In den Aufgaben 11—14 geht es um invertierbare lineare
Abbildungen.
11. Es gelte T(vi) = wi -f W2 + W3, T(v2) = W2 + W3 und T(v3) = W3.
Bestimmen Sie die Matrix für T bezüglich dieser Vektoren. Welcher
Eingabe-Vektor v liefert T(v) = wi?
12. Invertieren Sie die Matrix A aus Aufgabe 11. Invertieren Sie auch die
Abbildung T — wie erhält man T-^wi), T-^{^2) und T-i(w3)?
Bestimmen Sie alle Lösungen der Gleichung T(v) = 0.
13. Welche dieser Aussagen sind wahr, und warum ist die andere unsinnig?
(a) T-^T = I
(b) T-\T{v^))=v,
(c) T-HT(wO)-wi.
14. Nehmen Sie an, dass die Räume V und W eine gemeinsame Basis vi, V2
besitzen.
(a) Beschreiben Sie eine Abbildung T (nicht /) die ihre eigene Inverse
ist.
(b) Geben Sie eine Abbildung T (nicht /) an, die gleich T^ ist.
(c) Warum kann man nicht für (a) und (b) dasselbe T verwenden?
Die Aufgaben 15-20 behandeln den Basis Wechsel.
15. (a) Welche Matrix bildet den Vektor A,0) auf den Vektor B,5) und den
Vektor @,1) auf den Vektor A,3) ab?
(b) Welche Matrix bildet den Vektor B,5) auf den Vektor A,0) und den
Vektor A,3) auf den Vektor @,1) ab?
(c) Warum kann keine Matrix den Vektor B,6) auf den Vektor A,0) und
den Vektor A,3) auf den Vektor @,1) abbilden?
7.2 Die Matrix einer linearen Abbildung 397
16. (a) Welche Matrix M bildet die Vektoren A,0) und @,1) auf die
Vektoren (r, ^) und (s,u) ab?
(b) Welche Matrix N bildet die Vektoren (a, c) und (&, d) auf die Vektoren
A,0) und @,1) ab?
(c) Welche Bedingung an die Zahlen a, &, c und d macht Teil (b) unmöglich?
17. (a) Wie erhält man aus M und N in Aufgabe 16 die Matrix, die (a, c)
auf (r, ^) und F, c?) auf (s,u) abbildet?
(b) Welche Matrix bildet den Vektor B,5) auf den Vektor A,1) und den
Vektor A,3) auf den Vektor @,2) ab?
18. Verwendet man nach einem Basiswechsel dieselbe Basis in einer
anderen Reihenfolge, so ist die zugehörige Basiswechselmatrix M eine .
Lässt man die Reihenfolge unverändert, ändert aber die Längen der
Vektoren, so ist M eine Matrix.
19. Q sei die Matrix, die die beiden Achsenvektoren A,0) und @,1) um einen
Winkel 6 dreht. Welche Koordinaten (a, b) hat der ursprüngliche Vektor
A, 0), wenn man ihn durch die neuen (gedrehten) Achsen ausdrückt?
Diese Frage ist vielleicht etwas kompliziert. Zeichnen Sie eine Skizze, oder
lösen Sie die folgende Gleichung für a und b:
cos 6—sin 6
sin 6 cos 6
rii
0
= a
cos 9
sinö
+ &
— sin 9
cosöj
Q
20. Die Matrix, die die Vektoren A,0) und @,1) auf die Vektoren A,4) und
A,5) abbildet, ist M = . Die Kombination a(l,4) + &A,5), die
den Vektor A,0) ergibt, ist (a, &) = ( , ). Wie hängen diese neuen
Koordinaten für den Vektor A,0) mit M oder M~^ zusammen?
In den Aufgaben 21-24 geht es um den Raum der quadratischen
Polynome A + Bx + Cx^.
21. Die Parabel wi = |(a:^ + x) nimmt bei x = 1 den Wert Eins, und bei
X = 0 und x = — 1 den Wert Null an. Bestimmen Sie Parabeln W2,W3,
und y{x):
(a) W2 hat bei x = 0 den Wert Eins, und den Wert Null bei x = 1 und
x = -1.
(b) W3 hat bei x = -1 den Wert Eins, und den Wert Null bei x = 0 und
x = l,
(c) y{x) hat bei x = 1 den Wert vier, den Wert fünf bei x = 0 und den
Wert 6 bei x = —1. Verwenden Sie zur Bestimmung dieser Parabel
die Parabeln wi,W2 und W3.
22. Eine Basis für den Raum der Polynome zweiten Grades ist durch vi = 1,
V2 = X und V3 = x'^ gegeben. Eine andere Basis wird durch die Pa-
398 7 Lineare Abbildungen
rabeln wi,W2,W3 aus Aufgabe 21 gebildet. Bestimmen sie die beiden
Basiswechselmatrizen (von den w's zu den v's und umgekehrt).
23. Bestimmen Sie die drei Gleichungen für A, B und C, so dass die Parabel
Y = A-\- Bx + Cx^ hei X = a den Wert vier, den Wert fünf bei x = &
und den Wert 6 bei x = c hat. Bestimmen Sie die Determinante der
zugehörigen 3 x 3-Matrix. Für welche Zahlen a, b und c ist es unmöglich,
eine solche Parabel Y zu bestimmen?
24. Unter welchen Bedingungen an die Zahlen mi, m2,..., mg bilden die
folgenden Parabeln eine Basis für den Raum aller Parabeln?
Vi {x) =m\-\- m2X + msx^ und V2(a:) = m4 + m^x + rriex'^ und
V3(a:) = my + rrisx + rrigx^,
25. Das Gram-Schmidt-Verfahren stellt den Wechsel von einer Basis ai, a2, as
zu einer orthonormalen Basis qi, q2, Qs dar. Diese Vektoren findet man
in den Spalten der Faktorisierung A = QR. Beweisen Sie, dass R die
Basiswechselmatrix von den a's zu den q's ist. (Aus welcher Kombination
der q's erhält man a2, wenn A = QR gilt?)
26. Das Eliminationsverfahren verändert die Zeilen von A so, dass die
Zeilen der Matrix U in der Faktorisierung A — LU entstehen. Durch
welche Kombination der Zeilen von U erhält man die zweite Zeile von AI
Schreibt man Al^ — U^L^, um mit Spalten zu arbeiten, so erhält man als
Basiswechselmatrix M = L^. (Es handelt sich um Basen, falls .)
27. Angenommen, die Vektoren vi,V2,V3 sind Eigenvektoren für T, das
heißt, es gilt T{vi) = A^v^ für i = 1,2,3. Welche Matrix beschreibt T
bezüglich der Eingabe- und Ausgabe-Basis aus den Eigenvektoren v^?
28. Jede invertierbare lineare Abbildung kann durch die Matrix /
beschrieben werden. Dazu wähle man eine beliebige Eingabe-Basis vi,...,Vn,
und als Ausgabe-Basis die Vektoren w^ = T{vi). Warum muss dazu T
invertierbar sein?
Die Aufgaben 29-32 wiederholen einige grundlegende lineare
Abbildungen.
29. Bestimmen Sie für die Vektoren vi — wi und V2 = W2 die
Standardmatrix für die folgenden Abbildungen T:
(a) T(vi) = 0 und T(v2) = 3vi
(b) T(vi) = Vi und T(vi + V2) = vi.
30. Die Abbildung T sei die Spiegelung an der x-Achse, und S sei die
Spiegelung an der ^/-Achse. Der Definitionsbereich V sei die x^z-Ebene. Welchen
7.3 Basiswechsel 399
Vektor S{T{v)) erhält man für v = (x^y)? Finden Sie eine einfachere
Beschreibung für die Verkettung ST.
31. Die Abbildung T sei die Spiegelung an der 45°-Geraden, und S sei die
Spiegelung an der ^/-Achse. Ist v = B,1), so gilt T(v) = A,2).
Bestimmen Sie 5(T(v)) und T{S{v)). Im Allgemeinen gilt also ST ^ TS,
32. Zeigen Sie, dass die Verkettung ST zweier Spiegelungen eine Rotation ist.
Berechnen Sie das Produkt der Spiegelungsmatrizen, um den Drehwinkel
zu bestimmen:
cos 29 sin 29
sin2ö-cos2ö
cos 2a sin 2a
sin 2a — cos 2a
33. Wahr oder falsch? Kennt man das Bild T(v) von n verschiedenen von
Null verschiedenen Vektoren im W^, so kennt man schon T(v) für jeden
Vektor im E^.
7.3 Basiswechsel
In diesem Abschnitt kehren wir zu einer der fundamentalen Ideen der
linearen Algebra zurück — einer Basis für den W. Wir wollen an der Idee nichts
ändern, aber wir wollen die Basis wechseln. Es passiert häufig (dafür werden
wir Beispiele liefern), dass eine bestimmte Basis für ein spezielles Problem
besonders gut geeignet ist. Wenn wir zu dieser Basis wechseln, enthüllen
uns die Vektoren und Matrizen genau die Informationen, die wir haben
wollen. Die ganze Idee hinter einer Transformation (in diesem Buch werden wir
die Fourier-Transformation und die Wavelet-Transformation erklären) ist im
Grunde nichts anderes als ein Basiswechsel.
Erinnern wir uns, was es bedeutete, dass die Vektoren wi,..., w^ eine
Basis des W bilden:
1, Die w's sind linear unabhängig.
2, Die n x n-Matrix W aus diesen Spalten ist invertierbar.
3, Jeder Vektor v im W kann auf genau eine Weise als Linearkombination
der w's geschrieben werden:
V = Ci Wi + C2W2 H h CnWn. G.6)
Dies ist die Grundidee: Hat man sich für eine Basis entschieden, so
beschreiben die Koeffizienten ci,..., Cn einen Vektor v vollständig. Anfangs besteht
ein Spaltenvektor einfach aus seinen Komponenten vi,... ^Vn- In der neuen
Basis der w's wird derselbe Vektor durch einen anderen Satz von Zahlen
ci,... Cn dargestellt. Man braucht immer n Zahlen und eine festgewählte
Basis, um einen Vektor zu beschreiben. Die n Zahlen nennt man die Koordinaten
des Vektors in der jeweiligen Basis:
400 7 Lineare Abbildungen
Vi
und auch
ci
G.7)
I Standardbasis L^" J Basis aus w's
Eine Basis bestimmt einen Satz Koordinatenachsen für den E", die
Koordinaten Ci,..., Cn bestimmen, wie weit man entlang jeder Achse zu gehen
hat, um den Vektor zu erreichen. Es sind rechtwinklige Achsen, wenn die w's
orthogonal sind.
Eine Bemerkung am Rande: Was ist die Standardbasis? Sie besteht aus
den Spalten ei,..., en der n x n-Einheitsmatrix /. Schreibe ich einen Vektor
im E^ als v = B,4,5), so meine ich dies (und sie erwarten es auch so)
bezüglich der Standardbasis — bezüglich der üblichen x-, y- und ;2;-Achse
also entlang derer die Koordinaten 2, 4 und 5 sind:
V =: 2ei + 4e2 + öes = 2
Die neue Frage ist nun: Welche Koordinaten ci, C2, C3 hat ein Vektor bezüglich
einer neuen Basis wi,W2,W3? Wie üblich schreiben wir die Basisvektoren
als Spalten einer Matrix, der Basismatrix W, Dann hat die grundlegende
Gleichung v = ciWi-\ h c^w^ in Matrizenschreibweise die Form v =: Wc.
Damit kennen wir aber den Vektor c sofort.
7C. Die Koordinaten c = (cx, - ■ ^, On) eines Vektors v ip der B^sis Wi, 1.. ^ Wh
sind durch den Vektor c ^ W^ gegeben. Die BäsiswecisehHatrixJi^
J5t damit die Inverse der Basismatrix W. \ ,. -
1
0
0
+ 4
0
1
0
+ 5
0
0
1
=
2
4
5
Die Standardbasis ei,..., e^ hat die Basismatrix W = I. Die Koordinaten
bezüglich dieser Matrix sind die üblichen Komponenten vi,...,Vn' Unser
erstes neues Beispiel ist die Wavelet-Basis für M^.
Beispiel 7.3.1 [Wavelet-Basis] Wavelets^ sind kleine Wellen. Sie haben
unterschiedliche Längen, und befinden sich an unterschiedlichen Orten. Der
erste Basisvektor ist eigentlich kein Wavelet, es handelt sich um den sehr
nützlichen „flachen" Vektor aus Einsen:
wi =
"
1
1
[l
W2 =
1"
1
-1
-1
W3 =
1"
-1
0
0
W4 =
Ol
0
1
-1
G.8)
^ Anm. d. Übers.: Bei diesem Wort handelt es sich um ein englisches Kunstwort,
das formal ein Diminutiv des Wortes wave= Welle ist. Da dieser im Deutschen
ebenso unüblich ist wie im Englischen, hat sich auch in der deutschsprachigen
Literatur die Verwendung des englischen Begriffs eingebürgert.
7.3 Basis Wechsel
401
Diese Vektoren sind orthogonal, was schon einmal gut ist. Wie sie sehen,
ist W3 in der ersten Hälfte und W4 in der zweiten Hälfte „lokaHsiert". Die
Koeffizienten C3 und C4 geben daher Details in der ersten und der letzten Hälfte
von V an. Die Standarbasis stellt sozusagen das Extrem an Lokalisierung dar.
Warum sollte man zu dieser Basis wechseln wollen? Ich stelle mir die
Komponenten vi, V2, vs und V4 als Intensitäten eines Signals vor. Es könnte
sich um ein Audiosignal handeln, zum Beispiel um Musik auf einer CD, oder
ein medizinisches Signal wie ein Elektrokardiogramm. Natürlich ist n = 4
ein sehr kurzes Signal, n = 10.000 ist realistischer. Ein so langes Signal muss
man vielleicht komprimieren, indem man nur die größten 5% der Koeffizienten
behält. Dies wäre ein Beispiel für eine 20:1-Kompression, die (um nur eine
der Anwendungen zu nennen) moderne Videokonferenzen möglich macht.
Wenn wir nur 5% der Koeffizienten der Standardbasis behalten, so
verlieren wir schlicht 95% des Signals. Bei der Bildbearbeitung würde der größte
Teil des Bildes verschwinden; bei einem Audiosignal wären 95% des
Aufnahmebands leer. Wählen wir aber eine bessere Basis, so können 5% der
Basisvektoren dem originalen Signal schon sehr nahe kommen. Bei der
Bildbearbeitung oder bei der Audiocodierung sieht oder hört man den
Unterschied nicht. Ein guter Basisvektor ist ein flacher Vektor wie wi = A,1,1,1).
Dieser Teil kann allein schon den gesamten konstanten Hintergrund unseres
Bildes beschreiben. Eine kurze Welle wie W4 = @,0,1, —1), oder in höheren
Dimensionen wg = @,0,0,0,0,0,1,-1), stellt dann ein Detail am Ende des
Signals dar.
Die drei Schritte aus Abbildung, Kompression und Rückabbildung sind
Eingabe v —^ Koeffizienten c -^ komprimiertes c -^ komprimiertes v
[verlustfrei] [verlu^tbehußet] lrek0n$irpier0n}
In der linearen Algebra, wo alles perfekt ist, lassen wir den
Kompressionsschritt aus. Die Ausgabe v ist genau derselbe Vektor wie die Eingabe v,
die Abbildung ist c = W~^v, die Rekonstruktion ist v = Wc. Bei der realen
Signal Verarbeitung, bei der nichts perfekt ist, aber alles schnell gehen muss,
sind die (verlustfreie) Abbildung und die Kompression, bei der nur unnötige
Informationen verloren gehen, der Schlüssel zum Erfolg.
Ich werde diese Schritte für einen typischen Vektor wie v = F,4,5,1)
demonstrieren. Seine Koeffizienten in der Wavelet-Basis sind c = D,1,1,2).
Das heisst, dass der Vektor v aus c mit Hilfe der w's rekonstruiert werden
kann. In Matrizenschreibweise lautet die Rekonstruktion v = Wc:
6
4
5
1
= 4
1
1
1
1
+
1
1
-1
-1
+
1
-1
0
0
+ 2
0
0
1
-1
—
1110
1 1-1 0
1-1 0 1
1-1 0-1
G.9)
Diese Koeffizienten c = D,1,1,2) erhält man als W~^v. Die Matrix W zu
invertieren ist einfach, da die w's in den Spalten orthogonal sind. Die Inverse
402 7 Lineare Abbildungen
ist also die transponierte Matrix, deren Spalten durch das Quadrat ihrer
Länge dividiert wurden: W~^ = {W^W)~^W^,
w-^ =
1111
1 1-1-1
1-1 0 0
0 0 1-1
Beachten Sie, dass wegen der Einsen in der ersten Zeile von c = W~^y der
Koeffizient Ci den arithmetischen Mittelwert der Komponenten t;i, t;2, ^3 ? ^4
angibt:
6+4+5+1 ,
ci = = 4.
Beispiel 7.3.2 (Dieselbe Wavelet-Basis, rekursiv betrachtet) Ich kann
der Versuchung nicht widerstehen, Ihnen eine schnellere Möglichkeit zur
Bestimmung der Koeffizienten Ci zu zeigen. Das besondere an der Wavelet-Basis
ist, dass man die Details in cs und C4 bestimmen kann, bevor man die
gröberen Details in C2 und das Gesamt-Mittel in ci berechnet. Ein Bild wird
Ihnen diese „Multiskalen-Methode" klarmachen, die ich in Kapitel 1 meines
zusammen mit Nguyen verfassten Lehrbuchs über Wavelets and Filter Banks
erkläre:
Man teilt v = F,4,5,1) in Mittelwerte und Wellen auf kleinen
und später größeren Skalen auf:
6
1
4
i
Mittelwei
5 5
1 1
5
3
Mittelwert
1 4 4 4
1
N
3
Differenzen/2
plus 1| 1
Differenz/2
4
plus 1|
2. .
—^1 L
C3 =1
C4 = 2
—^2
Ci = 4
C2 = l
1 -.
Beispiel 7.3.3 (Die Fourier-Basis) Ein Elektrotechniker berechnet als
allererstes zu jedem Signal die Fouriertransformation. Es handelt sich hierbei
7.3 Basiswechsel 403
um ein diskretes Signal (einen Vektor v), und wir sprechen von der diskreten
Fouriertransformation (DFT). Bei DFT kommen komplexwertige Zahlen vor.
Wenn wir aber n — A wählen, so sind die Matrizen klein, und die einzigen
komplexen Zahlen sind i und i^.
Beachten Sie, dass i^ — —i gilt, weil P = —1 ist. Ein echter
Elektrotechniker würde hier j statt i schreiben, aber irgendwo müssen wir eine Grenze
ziehen. (Immerhin fängt das Wort „imaginär" mit i an!) Dies sind die vier
Basisvektoren, die Spalten der Fouriermatrix F:
F = :
Kl;i:i;l-';1
,il«%iö'i«j
In der ersten Spalte steht der nützUche „flache" Basisvektor A,1,1,1), der das
durchschnittliche Signal (oder den Gleichstromanteil) darstellt. Man kann ihn
auch als Welle mit der Frequenz Null auffassen. Die dritte Spalte hingegen
ist A, —1,1,—1), alterniert also mit der höchsten Frequenz. Bei der
Fouriertransformation wird ein Signal in Wellen mit äquidistanten Frequenzen
zerlegt.
Die Fouriermatrix F ist definitiv die wichtigste komplexe Matrix in der
Mathematik, und in den Natur- und Ingenieurwissenschaften. Der letzte
Abschnitt dieses Buchs wird ihnen die schnelle Fouriertransformation (FFT)
erklären: eine Faktorisierung dieser Matrix F in Matrizen, die viele
Nulleinträge enthalten. Die FFT hat ganze Industriezweige revolutioniert, weil sie
die Fouriertransformation beschleunigt. Das Schöne an der
Fouriertransformation ist, dass F~^ wie F aussieht, wenn man nur i mit ~i vertauscht:
W~^ wird zu F~^ = -
4
1111
1 (-Z) (-ZJ (-ZK
1 (_,-J (_^L (_,.N
1 (-ZK (-zr i-i)'
Das MATLAB-Kommando c = fft(v) liefert die Fourierkoeffizienten Ci,..., c^
eines Vektors v. Es multipliziert also v auf sehr schnelle Weise mit der Matrix
F~\
Die duale Basis
Die Spalten von W enthalten die Basisvektoren wi,..., w^. Um die
Koeffizienten Ci,..., Cn eines Vektors bezüglich dieser Basis zu bestimmen,
verwenden wir die Matrix W~^. In diesem Abschnitt wollen wir nur eine Schreibweise
^nd einen neuen Begriff für die Zeilen von W~^ einführen. Die Vektoren in
diesen Zeilen (nennen wir sie uf,..., u^) bilden die sogenannte duale Basis.
Die Eigenschaften der dualen Basis erschließen sich aus den Beziehungen
W~^W = I und WW-^ = I. Das Produkt W'^W besteht aus Zeilen von
404 7 Lineare Abbildungen
W~^ multipliziert mit den Spalten von VT, also Skalarprodukte der u's mit
den w's. Die zwei Basen sind „biorthogonal", weil man nur Einsen und Nullen
erhält:
w-^w ^
VC.
wi • • • w^
= /
also
T
u, w
_ rifü
^' ~ \ 0 fü
für % = jf
für % 7^ j
Bei einer Orthonormalhasis sind die u '5 mit den w 's identisch. Die Basis
ist also biorthogonal zu sich selbst! Die Zeilen von W~^ sind dieselben wie die
Spalten von W. Mit anderen Worten gilt W~^ = W^. Dies ist der besonders
wichtige Fall einer orthogonalen Matrix W.
Es gibt andere, nicht orthonormale Basen. Die Achsen müssen nicht
zueinander senkrecht sein. Eine Basismatrix W kann invertierbar sein, ohne
dabei orthogonale Spalten zu besitzen.
Wenn wir die inversen Matrizen in der umgekehrten Reihenfolge WW~^ =
/ betrachten, so lernen wir etwas Neues. Die Produkte der Spalten Wj und
der Zeilen uf sind Matrizen vom Rang Eins. Es handelt sich um die
Multiplikation von Spalten mit Zeilen:
wi • • • w„
T
u;^
= Wiuf + --- + WnuJ
In dieser Reihenfolge verwenden wir die Matrizen beim Basis Wechsel. Die
Koeffizienten sind durch den Vektor c = W~^\ gegeben, und daraus
rekonstruieren wir V als Wc, Wir schreiben die Beziehungen c = W~^y und
V = Wc =: WW~^\ in der neuen Notation auf:
Die Koeffizienten sind Ci — ufv , der Vektor ist v — y^w^(ufv).
G.10)
Im Analyse-Schritt werden also Skalarprodukte mit der dualen Basis
berechnet, um die Koeffizienten zu bestimmen. Im Synthese-Schritt werden die
Teile QWi dann wieder addiert und ergeben den Vektor v.
Die wesentlichen Punkte
l.Die neuen Basisvektoren w^ bilden die Spalten einer invertierbaren Matrix
W.
2. Die Koeffizienten eines Vektors v bezüglich der neuen Basis sind durch
c = W~^Y gegeben (der Analyse-Schritt).
3. Der Vektor v wird durch den Ausdruck Wc = ciWi + • • • + c^w^
rekonstruiert (der Synthese-Schritt).
7.3 Basis Wechsel
405
4. Wird eine Kompression durchgeführt, so erzeugt man aus c den Vektor c,
und man rekonstruiert v = ci wi H h c^w^.
5. Die Zeilen von W~^ bilden die duale Basis, für die q = ufv gilt. Dann
folgt ufwj- =Sij.
Aufgaben 7.3
1. Drücken Sie die Vektoren e = A,0,0,0) und v = A, -1,1, -1) durch die
Wavelet-Basis wie in Gleichung G.14) aus. Die Koeffizienten ci,C2,C3,C4
bilden die Lösung der Gleichungen Wc = e und Wc = v.
2. Drücken Sie wie in Beispiel 7.3.2 den Vektor v = G,5,3,1) mit Hilfe der
Wavelet-Basis aus. Der erste Schritt ist
Mittelwerte + Differenzen =
-1 -1
Im letzten Schritt wird F,6,2, 2) unter Verwendung von A,1,1,1) und
A,1, —1, —1) als Gesamtmittelwert plus eine Differenz dargestellt.
3. Welche acht Vektoren bilden die Wavelet-Basis für E^? Zu ihnen gehört
das lange Wavelet A,1,1,1, -1, -1, -1, -1) und das kurze Wavelet
A,-1,0,0,0,0,0,0).
4. Die Wavelet-Basismatrix W kann in einfachere Matrizen Wi und W2
faktorisiert werden:
1110"
1 1-1 0
1-1 0 1
1-1 0-1
10 1 Ol
10-1 0
Ol 0 1
Ol 0-1
100]
1-100
0 010
0 OOlJ
Damit lässt sich wegen W~^ = W2^W^^ der Vektor c in zwei Schritten
berechnen. Die erste Aufspaltung in Beispiel 2 illustriert W^^v. Die
zweite Aufspaltung stellt dann die Anwendung von W^^ dar. Bestimmen Sie
die inversen Matrizen VTf ^ und W^^ direkt aus Wi und W2, und wenden
Sie sie auf v = F,4,5,1) an.
5. Die 4 X b-Hadamard-Matrix ist ähnlich der Wavelet-Matrix, besitzt aber
nur die Einträge +1 und —1:
406 7 Lineare Abbildungen
H ^
1111
1-1 1-1
1 1-1-1
1-1-1 1
Bestimmen Sie die Matrix H ^ und schreiben Sie v = G,5,3,1) als
Linearkombination der Spalten von H.
6. Es seien Vi,..., v„ und wi,..., w„ zwei Basen des E"^. Die Zahlen hi
seien die Koeffizienten eines Vektors bezüglich der ersten, die Zahlen Ci
bezüglich der zweiten Basis. Bestimmen Sie die Basiswechselmatrix M in
der Gleichung b = Mc. Beginnen Sie dazu mit
ftlVi H h hnVn = Vh- CiWi H h CnW„ = Wc.
Mit ihrer Antwort drücken Sie T(v) = v mit den v's als Eingabe-Basis
und den w's als Ausgabe-Basis aus. Die zugehörige Matrix ist ungleich
/, weil verschiedene Basen verwendet werden.
7. Die Vektoren w*,..., w* der dualen Basis bilden die Spalten der
Matrix W* = {W~^)^. Zeigen Sie, dass die ursprüngliche Basis wi,..., w„
„das Dual des Duals" ist. Mit anderen Worten, zeigen Sie, dass die w's
die Zeilen von {W*)~^ sind. Hinweis: Transponieren Sie die Gleichung
ww-^ = I.
7,4 Diagonalisierung und Pseudoinverse
In diesem kurzen Abschnitt werden wir Ideen aus Abschnitt 7.2 (Matrix einer
linearen Abbildung) und Abschnitt 7.3 (Basiswechsel) miteinander
kombinieren. Aus der Kombination erwächst ein wichtiges Resultat: Die Änderung der
Darstellungsmatrix auf Grund eines Basiswechsels. Die Matrix hängt von der
Eingabe-Basis und der Ausgabe-Basis ab. Wir wollen eine bessere Matrix als
A erzeugen, indem wir eine bessere Basis als die Standardbasis verwenden.
In Wahrheit können alle unsere wichtigen Faktorisierungen einer Matrix
A als Basiswechsel betrachtet werden. Der folgende soll aber ein kurzer
Abschnitt werden, und deshalb werden wir uns auf zwei herausragende Beispiele
konzentrieren. In beiden Fällen handelt es sich bei der guten Matrix um eine
Diagonalmatrix, entweder A oder U:
l.Es ist S~^AS = A, wenn man als Eingabe- und Ausgabe-Basis
Eigenvektoren von A verwendet.
2, Es ist U~^AV = U, wenn die Eingabe-Basis aus Eigenvektoren von A^A
und die Ausgabe-Basis aus Eigenvektoren von AÄ^ besteht.
7.4 Diagonalisierung und Pseudoinverse 407
Man sieht den Unterschied zwischen A und U sofort. Für A sind beide Basen
identisch, dazu muss A eine quadratische Matrix sein. Auch manche
quadratische Matrix kann durch kein S diagonaUsiert werden, weil sie keine n linear
unabhängigen Eigenvektoren hat.
Bei der Singulärwertzerlegung mit U ist die Eingabe-Basis von der
Ausgabe-Basis verschieden. Die Matrix A kann daher rechteckig sein. Es
handelt sich um orthonormale Basen, weil A^A und AÄ^ symmetrische
Matrizen sind. Deshalb gilt auch U~^ - U^ und V~^ = V^. Hier wird jede
Matrix A zugelassen, und jede Matrix kann diagonaUsiert werden.
Ich will nur kurz darauf hinweisen, dass bei der Gram-Schmidt-Faktori-
sierung A = QR nur eine neue Basis gewählt wird, nämlich die orthogonale
Ausgabe-Basis, die durch die Spalten von Q gegeben ist. Für die Eingabe
wird die durch / gegebene Standardbasis verwendet. Man erreicht so keine
Diagonalmatrix, aber eine Dreiecksmatrix R. Beachten Sie, dass die
Ausgabematrix links von R steht und die Eingabematrix rechts.
Wir beginnen mit dem Fall, dass die Eingabe-Basis gleich der Ausgabe-
Basis ist.
Ähnliche Matrizen: A, SAS-^^ und WAW^^
Wir beginnen mit einer quadratischen Matrix und nur einer Basis. Der
Eingabe-Raum V ist der Raum M", und der Ausgabe-Raum W ist eben-
faUs der M". Als Basis verwenden wir die Spalten von /. Wir betrachten eine
n X n-Matrix A bezüglich dieser Basis, und als Abbildung wollen wir die
zugehörige lineare Abbildung „Multiplikation mit A" betrachten.
Der größte Teil dieses Buches war mit einem grundlegenden Problem
beschäftigt — Matrizen zu vereinfachen. In Kapitel 2 konnten wir durch
das Eliminationsverfahren eine Dreiecksmatrix erreichen, und in Kapitel 6
mit Hilfe von Eigenvektoren eine Diagonalgestalt der Matrix. Hier rührt die
Änderung der Matrix nun von einem Wechsel der Basis her.
Hier zunächst die wichtigsten Fakten. Wenn man zu der Basis V
wechselt, ändert sich die Matrix von A zu AM. Weil V der Eingabe-Raum ist,
steht die Matrix M auf der rechten Seite (um zuerst angewendet zu
werden). Wechseln wir dann die Basis von W, dann ist die neue Matrix M~^A,
denn wir arbeiten mit dem Ausgabe-Raum, weswegen M~^ auf der linken
Seite steht (und zuletzt angewendet wird ). Wenn man beide Basen
gleichermaßen ändert, dann ist die neue Matrix M~^AM. Die guten
Basisvektoren sind die Eigenvektoren, die in den Spalten von M = S stehen.
Die Matrix wird dann zu S'^^AS = A.
408
7 Lineare Abbildungen
Begründung Um die Spalte 1 der Matrix zu bestimmen, wenden wir die
Abbildung auf den ersten Basisvektor an. Die Abbildung multipliziert aber
schlicht mit A, und deshalb erhalten wir Axi = AiXi, also Ai mal erster
Basisvektor plus Null mal andere Basisvektoren. Deshalb ist die erste Spalte
der Darstellungsmatrix (Ai,0,... ,0). Bezüglich der Eigenvektorbasis ist die
Matrix diagonal.
1350x3' = -^ '♦
Projektion
i\
Ä^'l
f>S*''' ^.5
H
-[;]
Projektion '
Abb. 7.3. Projektion auf die 135°-Gerade y
torbasis.
projiziert auf Xj
-X. Standardbasis und Eigenvek-
Beispiel 7.4.1 Man bestimme die Diagonalmatrix, die auf die 135°-Gerade
y = —X projiziert. Die Standardvektoren A,0) und @,1) werden in
Abbildung 7.3 auf die Gerade projiziert. Bezüglich der Standardbasis erhält man
die Matrix
A =
0,5-0,5
-0,5 0,5
Lösung Die Eigenvektoren dieser Projektion sind xi = A,-1) und X2 =
A,1). Der erste Eigenvektor liegt auf der Projektionsgeraden, der zweite
senkrecht dazu (siehe Abbildung 7.3). Ihre Projektionen sind xi und 0, die
Eigenwerte sind also Ai = 1 und A2 = 0. Bezüglich der Eigenvektorbasis hat
die Projektionsmatrix also die Gestalt
yl =
10
00
Was geschieht, wenn man eine andere Basis, zum Beispiel vi = wi = B,0)
und V2 = W2 = A,1) wählt? Da wi kein Eigenvektor ist, wird die
Darstellungsmatrix B bezüglich dieser Basis nicht diagonal sein. Die erste
Möglichkeit, B zu berechnen, ist die aus dem Abschnitt 7.2: Man bestimmt die
Spalten der Matrix, indem man die Vektoren Avj als Linearkombination der w's
schreibt.
Wenden wir die Projektion T also auf den Vektor B,0) an. Das Ergebnis
ist A,-1) = wi — W2. Die erste Spalte von B enthält also die Einträge 1
7.4 Diagonalisierung und Pseudoinverse 409
und -1. Der zweite Vektor W2 == A,1) wird auf den Nullvektor projiziert,
die zweite Spalte von B enthält also die Einträge 0 und 0.
B=^
10
-10
bezüglich der Basis wi, W2.
G.11)
Die zweite Möglichkeit, dieselbe Matrix B zu bestimmen, ist ein wenig
aufschlussreicher. Wir verwenden die Matrizen W~^ und VT, um von der
Standardbasis zu der Basis aus den w's zu wechseln. Diese Basis wechselmatrizen
stellen die Identitäts-Abbildung dar. Wir beschreiben also die Verkettung
der Abbildungen ITI durch das Produkt der Matrizen B = W~^AW. Diese
Matrix ist also ähnlich zu A.
7E Man ^<beis,tir|ij^ B -bearüglieh-.^r %mm.^^ :Wi> ^^^ '^m^^:^;;^€i
Schritten* TiXjk^;p^^M md^-^:m%.^''M^^
Eingabe-Ba3i%.^e?^üglid|'4i^^4i^ ÄbbUdtog;^^
wird, und scMIeßlidi wechselt ißan die Ausga:be-^Basis ^^'W^^'mi^A^t izur
Be^Is' der ^\iMm^ Pi^fikt; 'B-i=^ W'^^^ St^lt-die Ablpld^»g':J2?l^<4^ '
B
w's zu w's — ^Standard zu w's "^Standard
W.
w's zu Standard
Beispiel 7.4.2 (Fortsetzung der Projektion) Wir wenden die W~^AW-
Regel an, um B bezüglich der aus den Vektoren B,0) und A,1) bestehenden
Basis zu bestimmen:
W-^AW =
Die W-^AW-Rege\ liefert dieselbe Matrix B wie in Gleichung G.11). Ein
Basiswechsel erzeugt also eine Ähnlichkeitstransformation der
Darstellungsmatrix. Die Matrizen A und B sind einander ähnlich, und sie haben dieselben
Eigenwerte A und 0).
r 1 1 ■
2 2
0 1
■ 1 1 ■
! !
.2 2.
21
Ol
=
10|
-loj
Die Singulärwertzerlegung
Nun wollen wir verschiedene Eingabe- und Ausgabe-Basen erlauben. Es darf
sogar der Eingabe-Raum W vom Ausgabe-Raum W^ verschieden sein. Für
diesen Fall wollen wir eine m x n-Matrix bestimmen. Wir werden die Eingabe-
Basis mit Vi,..., v„ und die Ausgabe-Basis mit ui,...,u^ bezeichnen.
Wieder ist die beste Matrix eine (jetzt m x n-)Diagonalmatrix. Um diese
Diagonalmatrix U zu erzeugen, muss jeder Eingabe-Basisvektor v^ auf ein
Vielfaches des Ausgabe-Basisvektors u^- abgebildet werden. Bei dem
Vielfachen handelt es sich um den Singulärwert gj auf der Hauptdiagonalen von
2^ I
410 7 Lineare Abbildungen
_ra,u, füri<r
^ [0 für j > r ^ ^
Die Singular werte sind in der Reihenfolge ai > a2 > " • > (Tr gegeben.
Der Grund, warum der Rang r hier eingeht, ist, dass (nach Definition) Sin-
gulärwerte nicht null sein dürfen. Der zweite Teil der obigen Gleichung besagt,
dass Vj für j* = r + 1,... ,n im Kern liegt. Auf diese Weise erhält man die
korrekte Anzahl von n — r Basisvektoren für den Kern.
Lassen Sie mich eine Verbindung zwischen den Matrizen A^ E, V und U
und den durch sie dargestellten linearen Abbildungen ziehen. Die Matrizen
A und E stellen dieselbe Abbildung dar, die Matrix A bezüglich der
Standardbasen für W und W^, die Matrix E bezüglich einer Eingabe-Basis aus
v's und einer Ausgabe-Basis aus u's. Die Matrizen V und U stehen für die
Basiswechsel, sie stellen die Identitäts-Abbildung in W und im E^ dar. Als
Verkettung der Abbildungen erhält man wieder /T/, sie wird bezüglich der
V- und u-Basen durch die Matrix U~^AV dargestellt:
7F Die Matrix I? jbezüglkli der peiien BäBiä hängt mit def 5|iatrbc 41
bezüglich der Standardbaßeß über die Gleichung : / ;;
^v's zu u's — ^Standard zu u's "^Standard ^v's zu Standard ('-M)-
zusammen. Die Singulirwertizerleguntg wählt OrthönoxmiähaseniU^^^^^fJ^^
und y^.^= F^)i bezüglich derer A =-^1
Die beiden Orthonormalbasen in der Singulärwertzerlegung sind die
Eigenvektorbasen für die Matrizen A^A (die v's) und AA^ (die u's). Da diese
Matrizen symmetrisch sind, sind ihre Einheits-Eigenvektoren orthonormal.
Ihre Eigenwerte sind die Zahlen a'j. Um zu verstehen, warum diese Basen die
Matrix diagonalisieren, verwenden wir einen „Beweis durch Klammerung".
Ist Vj ein Einheits-Eigenvektor von A^A, so zeigt die erste Zeile, dass Avj
die Länge aj hat. In der zweiten Zeile wird die Richtung Uj bestimmt. Dazu
beginnt man mit der Eigenwertgleichung A^Avj = cr^j^j'-
\^A^Avj — (r'j'vjvj liefert ||^Vj||^ — ^j' ^^ ^^^^ II^Vj|| = aj ist.
G.15)
AA^Avj = ^j^v^- liefert u^- = Awj/aj G.16)
als einen Einheits-Eigenvektor von AÄ^.
Der Eigenvektor Uj der Matrix AÄ^ hat wegen Gleichung G.15) die Länge 1.
Die Gleichung Avj = ajUj besagt dann, dass diese Basen die Matrix A
diagonalisieren.
7.4 Diagonalisierung und Pseudoinverse 411
Polarzerlegung
Zu jeder komplexen Zahl gibt es eine Polarkoordinatendarstellung re*^. Dabei
wird eine nichtnegative Zahl r mit einer Zahl auf dem Einheitskreis
multipliziert. (Denken Sie daran, dass |e*^| = \cos6 -\- ism6\ = 1 gilt.) Stellt
man sich diese Zahlen als 1 x 1-Matrizen vor, so entspricht die Bedingung
r > 0 einer positiv semidefiniten Matrix (nennen wir sie H) und der
Ausdruck e*^ einer orthogonalen Matrix Q. Die Singularwertzerlegung erweitert
diese Faktorisierung re*^ auf Matrizen, für rechteckige Matrizen Q sogar auf
m X n-Matrizen
7G Jede^^ealfequadraJispMe^Matrix feaäinAm<4^Jf\^^Ö^'^;^^ ,^,-QÄ.;l^ktbrir'
Als Beweis fügen wir einfach die Matrix V^V = / in der Mitte der Sin-
gulärwertzerlegung ein:
A = UUV = {UV ){VUV') = {Q){H).
G.17)
Der erste Faktor UV^ ist Q. Das Produkt orthogonaler Matrizen ist
orthogonal. Der zweite Faktor VEV^ ist H. Er ist positiv semidefinit, weil seine
Eigenwerte in S stehen. Ist A invertier bar, so muss auch H invertier bar sein,
also positiv definit. Die Matrix H ist die Quadratwurzel der Matrix A-^A.
Gleichung G) besagt, dass H'^ = VS'^V^ = Ä^A ist.
Es gibt auch eine Polarzerlegung A — KQ in der umgekehrten
Reihenfolge. Die Matrix Q bleibt dieselbe, aber K = UEU^. In dem Fall ist K die
Quadratwurzel der Matrix AÄ^.
Beispiel 7.4.3 Man bestimme die Polarzerlegung A = QH aus der Sin-
gulärwertzerlegung:
A^
\ 2 2'
=r
Ol'
10
\V2 ]
2^f2
lly/2 1/v^
UEV'^.
Lösung Der orthogonale Teil ist Q = UV'^. Der positiv definite Teil ist
Q
H =
Ol
10
-1/v^ 1/v^
1/v^1/v^
1/^-1/v^
1/^ 1/v^
22
-1 1
1/v^ 1/v^
l/V2 1/v^
Z/s/2 l/x/2
l/x/2 3/%/2j ■
In der Mechanik trennt die Polarzerlegung eine Drehung (in Q) von einer
Streckung (in H). Die Eigenwerte von H sind die Singulärwerte von A, die
412 7 Lineare Abbildungen
Streckfaktoren. Die Eigenvektoren von A sind die Eigenvektoren von A^A,
an ihnen erkennt man die Streckrichtungen (die Hauptachsen).
Mit Hilfe der Polar Zerlegung kann man sich die Gleichung Avi — aiUi in
zwei Schritte zerlegt denken. Der if-Teil multipliziert den Vektor v^ mit dem
Singulärwert cr^, und der Q-Teil dreht die v-Richtung in die u-Richtung. In
der anderen Reihenfolge A = KQ werden zunächst (durch dieselbe Matrix Q)
die v's in die u's gedreht, und dann werden die u^ von K mit ai multipHziert,
so dass sich die Wirkung von A ergibt.
Die Pseudoinverse
Durch die Wahl geeigneter Basen ist uns die Wirkung einer Matrix A klar
geworden. Sie multipliziert einen Vektor v^ im Zeilenraum und liefert daraus
einen Vektor aiUi im Spaltenraum. Die inverse Matrix muss genau umgekehrt
wirken! Gilt Av = au, so muss ^~^u = v/a sein. Die Singulärwerte von
A~^ sind I/o-, gerade so, wie die Eigenwerte von A~^ durch die Zahlen 1/A
gegeben sind. Die Basen müssen dabei vertauscht werden. Die u's liegen im
Zeilenraum von A~^, die v's sind Elemente des Spaltenraums.
Bis zu diesem Punkt hätten wir immer die Worte ''wenn A~^ existiert,''
hinzufügen müssen. Im Folgenden werden wir das nicht mehr müssen. Es
existiert eine Matrix, die, mit u^ multipliziert, den Vektor Vi/ai erzeugt.
Man bezeichnet sie als A+:
r^-i
A-^^VS-^U^ =
Vi •• • Vr • • •
n mal n
n mal m
Ui • • • Ur • • • U^
m mal m
G.18)
A'^ ist die Pseudoinverse von A. Es handelt sich um eine n x m-Matrix.
Wenn A~^ existiert (sagen wir es noch einmal), so ist A+ dieselbe Matrix
wie A~^, In diesem Fall gilt m = n = r, und wir invertieren das Produkt
UUV^, um VU~^U^ zu erhalten. Man braucht das neue Symbol A'^ nur für
den Fall, dass r < m oder r < n gilt. Dann hat nämlich A keine beidseitige
Inverse, aber eine Pseudoinverse A'^ mit den folgenden Eigenschaften:
A'^Ui = —Vi für i < r
und A'^Mi — 0 für i> r.
Wissen wir, wie die Matrix A'^ auf jeden Basisvektor wirkt, so kennen wir
bereits die gesamte Matrix. Die Vektoren ui,..., Ur im Spaltenraum von
A werden zurück in den Zeilenraum abgebildet. Die restlichen Vektoren
Ur+i,...,Um liegen im Kern der transponierten Matrix, und A'^ bildet sie
auf den Nullvektor ab.
7.4 Diagonalisierung und Pseudoinverse 413
Abb. 7.4. A ist invertierbar als Abbildung vom Zeilenraum in den Spaltenraum,
sie wird durch A'^ invertiert.
Betrachten Sie die Pseudoinverse U~^ der Diagonalmatrix U, Jeder Sin-
gulärwert a wird einfach durch a~^ ersetzt. Das Produkt U~^U liegt damit
so nahe an der Einheitsmatrix wie möglich. An den Nullzeilen und -spalten
kann man nichts ändern, aber man erhält eine r x r-Einheitsmatrix. In diesem
Beispiel gilt 0-1=2 und 02 =3:
U"^U =
1/2 0 0"
0 1/3 0
0 0 0
0 0"
030
000
=
'lOOl
010
oooj
Beispiel 7.4.4 Bestimmen Sie die Pseudoinverse der Matrix A =
22
1 1
.Diese Matrix ist nicht invertierbar. Ihr Rang ist 1, der Singulärwert ist VTÖ- In
^~^ wird diese Zahl invertiert:
^+ = VE^U^ :
^
1 1
1-1
1/v^O
0 0
71
2 1
1-2
10
2 1
2 1
A'^ hat ebenfalls den Rang 1. Der Spaltenraum dieser Matrix ist der
Zeilenraum von A. Bildet A den Vektor A,1) aus dem Zeilenraum auf den Vektor
D,2) im Spaltenraum ab, so bewirkt A'^ gerade das Umgekehrte. Jede Matrix
vom Rang Eins lässt sich als Zeile-mal-Spalte-Produkt darstellen.
Verwendet man Einheitsvektoren u und v, ist dies die Darstellung A = cruv^. Die
beste Inverse, die sich dazu finden lässt, ist A'^ = vu^/a.
414 7 Lineare Abbildungen
Das Produkt AA^ ist dann uu-^, also die Projektion auf die Gerade durch
u, und das Produkt A'^A ist durch vv^ gegeben, also durch die Projektion
auf die Gerade durch v. Für allgemeine Matrizen A sind AA'^ und A'^A
Projektionen auf den Spaltenraum und den Zeilenraum.
Die kürzeste „Kleinste-Quadrate-Lösung" der Gleichung ^x = b ist
daher x+ = ^+b (siehe Aufgabe 18), und jeder andere Vektor, der die
Normalengleichung A^ASi = A^h löst, ist länger als x+.
Die wesentlichen Punkte
l.Die Diagonalisierung S~^AS = A ist nichts anderes als der Wechsel zur
Eigenvektorbasis.
2. Bei der Singulärwertzerlegung wird eine Eingabe-Basis aus v's und eine
Ausgabe-Basis aus u's gewählt. Bezüglich dieser beiden orthogonalen
Basen ist A diagonal.
3. Bei der Polarzerlegung wird eine Matrix A in ein Produkt einer positiv
definiten Matrix und einer orthogonalen Matrix zerlegt.
4. Die Pseudoinverse A'^ = VE^U^ bildet den Spaltenraum von A wieder auf
den Zeilenraum ab. Damit ist A'^A gleich der Identität auf dem Zeilenraum
(und Null auf dem Kern).
Aufgaben 7.4
In den Aufgaben 1—6 berechnen und verwenden Sie die
Singulärwertzerlegung einer nicht invertierbaren Matrix A.
1. Berechnen Sie die Matrix Ä^ A und ihre Eigenwerte sowie Eigenvektoren
Vi und V2 mit der Länge Eins:
A^
12
36
Welchen Wert erhalten Sie für den einzigen Singulärwert ^i? Der Rang
von ^ ist r = 1.
2. (a) Berechnen Sie die Matrix AÄ^ und ihre Eigenwerte sowie Eigen
Vektoren ui und U2 mit der Länge Eins,
(b) Rechnen Sie nach, dass (nach Aufgabe 1) ^vi = aiui gilt. Setzen
Sie in die Singulärwertzerlegung die tatsächlichen Zahlen ein:
1 2
36
Ui U2
Ol
0
Vi V2
3. Berechnen Sie aus den u's und v's Orthonormalbasen für die vier
Unterräume dieser Matrix A.
4. Beschreiben Sie alle Matrizen mit denselben vier Unterräumen.
7.4 Diagonalisierung und Pseudoinverse 415
5. Bestimmen Sie aus U, V, und U eine orthogonale Matrix Q = UV^ und
eine symmetrische Matrix H = VUV^. Rechnen Sie die Polarzerlegung
A — QH nach. Warum ist dieses H nur semidefinit ?
6. Berechnen Sie die Pseudoinverse A^ — VE^U^. Die Diagonalmatrix
E'^ enthält die Zahlen 1/ai. Andern Sie die Benennungen der vier
Unterräume für A in Abbildung 7.4 so, dass sie die Unterräume zu A+
darstellt. Berechnen Sie A'^A und AA'^.
Die Aufgaben 7-11 behandeln die Singulärwertzerlegung einer
invertierbaren Matrix.
7. Berechnen Sie die Matrix Ä^ A und ihre Eigenwerte sowie Eigenvektoren
Vi und V2 mit der Länge Eins. Welche Singulärwerte oi und G2 erhalten
Sie?
A =
33
-1 1
33"
-1 1
=
Ui U2
^2_
Vi V2
Die Matrix AA^ besitzt dieselben Eigenwerte al und a^ wie Ä^A.
Bestimmen Sie ihre Eigenvektoren mit Länge Eins. Setzen Sie die fehlenden
Zahlen ein:
A^
9. Multiplizieren Sie in Aufgabe 8 Spalten mit Zeilen, und zeigen Sie, dass
A — GiWiwJ + a-2U2V2^ gilt. Beweisen Sie ausgehend von A = UEV^,
dass jede Matrix vom Rang r als Summe von r Matrizen mit Rang Eins
darstellbar ist.
10. Bestimmen Sie aus den Matrizen U, V und E die orthogonale Matrix
Q — UV^ und die symmetrische Matrix K = UEU^. Rechnen Sie nach,
dass die Polarzerlegung in der umgekehrten Richtung A — KQ korrekt
ist.
11. Die Pseudoinverse dieser Matrix A stimmt mit
überein, da_
In den Aufgaben 12-13 berechnen und verwenden Sie die
Singulärwertzerlegung einer 1 x 3-Matrix.
12. Berechnen Sie für ^ = [3 4 0] die Matrizen Ä^A und AÄ^, ihre
Eigenwerte und Eigenvektoren mit der Länge Eins. Welche Singulärwerte hat
AI
13. Setzen Sie die tatsächhchen Zahlwerte in die Singulärwertzerlegung von
A ein.
416 7 Lineare Abbildungen
^= [3 4 0] =[ui][ai 0 0] [vi V2 va]^.
Setzen Sie die fehlenden Zahlen in die Pseudoinverse von A ein. Berechnen
Sie die Matrizen AA'^ und A'^A:
^+-
=
Vi V2 V3
'1M|
0
0 J
[uiP
14. Geben Sie die einzige 2 x 3-Matrix ohne Pivotelemente und ohne Sin-
gulärwerte an. Wie sieht U für diese Matrix aus? Welche Form hat die
Nullmatrix ^+?
15. Wieso muss det A'^ = 0 gelten, wenn det ^ = 0 gilt?
16. In welchem Fall stimmt die Faktorisierung UEV^ mit der Faktorisierung
QAQ^ überein? Die Eigenwerte A^ müssen positiv sein, damit sie gleich
den Gi sind. Dann muss A sein.
Die Aufgaben 17—20 stellen die Haupteigenschaften von A+ und
x~^ = A+b heraus.
17. Die folgenden Matrizen haben alle den Rang Eins. Der Vektor b sei
einfach {hl, 1J).
A =
22
1 1
Ä'^
0,2 0,1
0,2 0,1
AÄ' =
0,8 0,4
0,4 0,2
Ä'A =
0,5 0,5
0,5 0,5
(a) Die Gleichung A^A'k = A^h hat viele Lösungen, weil A^A
ist.
(b) Rechnen Sie nach, dass x+ = A^h = @,2fti +0,1^2,0,201 +0,1^2) die
Gleichung A'^Ax^ = A'^h löst.
(c) Die Matrix AA'^ projiziert auf den Spaltenraum von A. Deshalb
projiziert auf den Kern von A^. Dann gilt A^{AA'^ — I)h = 0,
und deshalb A^Ax.^ = A^h, so dass x = x+ sein kann.
18. Der Vektor x~^ ist die kürzeste mögliche Lösung der Gleichung A^ASi =
A^h. Der Grund: Die Differenz x — x+ liegt im Kern von A^A. Dies ist
auch der Kern von A. Erklären Sie, wie daraus die Gleichung
IxlP =
|X+||2 + ||X-X+||2
folgt. Jede andere Lösung hat eine x größere Länge als x+.
19. Jeder Vektor b im W^ lässt sich in der Formp + e zerlegen, also in einen
Teil im Spaltenraum und einen Teil im Kern der transponierten Matrix.
Jeder Vektor x im W^ lässt sich in der Form x^ + Xn = (Zeilenraum) +
(Kern) zerlegen. Damit folgt
AA-^p = AA-^e = A-^Axr = A-^Axn =
7.4 Diagonalisierung und Pseudoinverse 417
20. Bestimmen Sie die Matrizen ^+, A'^A und AA'^ für die 2 x 1-Matrix A,
deren Singulärwertzerlegung durch
A =
4
=
,6-0,8]
0,8 0,6 J
[5"
[oj
[1]
gegeben ist.
21. Eine allgemeine 2 x 2-Matrix A wird durch vier Zahlen beschrieben. Ist
sie eine Dreiecksmatrix, so genügen drei Zahlen, handelt es sich um eine
Diagonalmatrix, sogar nur zwei. Eine Drehmatrix wird durch eine einzige
Zahl beschrieben. Rechnen Sie nach, dass sich für jede Faktorisierung von
A immer vier Zahlen ergeben:
LU LDU QR UEV^ SAS'^,
22. Rechnen Sie (wie in Aufgabe 21) nach, dass die Faktorisierungen LDL^
und QAQ^ jeweils durch drei Zahlen bestimmt sind. Dies ist richtig, weil
die Matrix A sein muss.
23. Eine neue Faktorisierung! Zerlegen Sie die Matrix
a b
c d
in ein Produkt
A — EH, wobei E eine untere Dreiecksmatrix mit Einsen auf der
Diagonalen, und H eine symmetrische Matrix ist. In welchem Fall ist diese
Zerlegung nicht möglich?
24. Durch die Vektoren vi,... Vr und ui,..., u,. seien Basen des Zeilenraums
und des Spaltenraums von A gegeben. Beschreiben Sie alle möglichen
Matrizen A.
25. Ein Paar v und u singulärer Vektoren erfüllt die Gleichungen Av = au
und ^^u = av. Dies bedeutet, dass der doppelte Vektor x =
em
Eigenvektor einer symmetrischen Matrix ist. Um welche Matrix handelt
es sich? Was ist der zugehörige Eigenwert?
8 Anwendungen
8.1 Graphen und Netzwerke
In diesem Kapitel stellen wir fünf ausgewählte Anwendungen der linearen
Algebra vor. Dazu konnten wir aus sehr vielen Anwendungen auswählen,
denn immer, wenn man ein zusammenhängendes System hat, bei dem jedes
Teil von anderen Teilen abhängt, hat man auch eine Matrix. Interagierende
Systeme lassen sich mit den Methoden der linearen Algebra behandeln, falls
nur die Gesetze, denen sie gehorchen, linearer Natur sind. Im Verlauf der
Jahre habe ich ein Modell so oft gesehen, und es als so grundlegend und
nützlich kennen gelernt, dass ich es immer als erstes nenne. Dieses Modell
besteht aus durch Kanten verbundene Knoten. So etwas nennt man einen
Graphen.
Graphen, wie Sie sie kennen, stellen Funktionen f{x) dar. Graphen dieser
Art (m Kanten, die n Knoten verbinden) führen hingegen auf Matrizen. In
diesem Abschnitt geht es um die Inzidenzmatrix A eines Graphen — und
besonders um die vier Unterräume, die man daraus erhält.
Für jede m x n-Matrix gibt es zwei Unterräume des W und zwei
Unterräume des W^. Es handelt sich um die Spaltenräume und die Kerne von
A und A^. Ihre Dimensionen hängen über den wichtigsten Satz der
gesamten linearen Algebra zusammen. Der zweite Teil dieses Satzes besagt, dass
die Unterräume orthogonal sind. Unser Ziel ist zu zeigen, in welcher Weise
Beispiele aus der Graphentheorie den Fundamentalsatz der linearen Algebra
illustrieren.
Wir werden noch einmal die vier Unterräume (für eine beliebige
Matrix) wiederholen. Dann werden wir einen gerichteten Graphen und seine
Inzidenzmatrix konstruieren. Es wird leicht sein, ihre Dimensionen zu
bestimmen, wir wollen aber die Unterräume selbst beschreiben. Hier hilft die
Orthogonalität. Dabei ist es wesentlich, die Unterräume mit den Graphen
m Verbindung zu bringen, von denen sie stammen. Indem wir uns auf In-
zidenzmatrizen spezialisieren, werden aus den Regeln der linearen Algebra
die KirchhofF'schen Regeln. Bitte lassen Sie sich von den Worten „Strom",
»Potential" und „Kirchhof?' nicht abschrecken. Diese rechteckigen Matrizen
sind die besten.
Jeder Eintrag einer Inzidenzmatrix ist entweder 0, 1 oder —1. Während
des Eliminationsverfahrens bleibt diese Eigenschaft immer erhalten. Alle Mul-
420 8 Anwendungen
tiplikatoren sind ±1. Deshalb enthalten die beiden Faktoren A = LU
ebenfalls nur die Einträge 0,1 und -1, wie auch die Kernmatrizen. Alle vier
Unterräume besitzen Basisvektoren mit diesen besonders einfachen
Komponenten. Wir haben uns die Matrizen nicht einfach für dieses Lehrbuch
ausgedacht, sie stammen von einem Modell, das in der reinen wie der angewandten
Mathematik absolut essentiell ist.
Wiederholung der vier Unterräume
Wir beginnen mit einer m x n-Matrix A. Ihre Spalten sind Vektoren im
M^, deren Linearkombinationen den Spaltenraum S{A) erzeugen, einen
Unterraum des M^. Diese Linearkombinationen sind genau durch die Matrix-
Vektor-Produkte ^x gegeben.
Die Zeilen von A sind Vektoren im M"^ (oder sie wären es, wenn sie
Spaltenvektoren wären). Ihre Linearkombinationen erzeugen den Zeilenraum. Um
jegliche Unannehmlichkeiten wegen der Zeilen zu vermeiden, transponieren
wir die Matrix. Aus dem Zeilenraum wird dann der Spaltenraum S(A^).
Die wichtigsten Fragen der linearen Algebra rühren von diesen beiden
Möglichkeiten her, dieselben Zahlen zu betrachten, als Spalten oder als Zeilen.
Der Kern N(^) von A enthält jeden Vektor x, für den ^x = 0 gilt —
es ist ein Unterraum des M"^. Der Kern der transponierten Matrix enthält
alle Lösungen der Gleichung A^y = 0. Die Vektoren y bestehen aus m
Komponenten, so dass N(^^) ein Unterraum von M^ ist. Schreiben wir die
Gleichung oben als y^A = 0-^, so sieht man, wie Zeilen zu einer Nullzeile
kombiniert werden. Die vier Unterräume werden in Abbildung 8.1 dargestellt.
Auf der einen Seite der Abbildung befindet sich der Raum M"^ und auf der
anderen Seite der Raum W^. Die Verbindung zwischen ihnen wird durch die
Matrix A hergestellt.
Die Information, die diese Abbildung vermittelt, ist entscheidend. Zuerst
geht es um die Dimensionen, die den beiden zentralen Gesetzen der linearen
Algebra gehorchen:
dim S{A) ~ dim S{A^) und dim S(^) + dim ND) = n.
Hat der Zeilenraum die Dimension r, so hat der Kern die Dimension n — r.
Beim Eliminationsverfahren bleiben diese Räume unverändert, und an der
Treppenform U erkennt man die Dimensionen. Sie enthält r Zeilen und
Spalten, die Pivotelemente enthalten. Damit gibt es n — r freie Spalten ohne
Pivotelemente, an denen man Vektoren im Kern ablesen kann.
Die folgende Inzidenzmatrix A stammt von einem Graphen. Ihre
Treppenform ist die Matrix U:
8.1 Graphen und Netzwerke 421
dim r
dim m-r
Abb. 8.1. Die vier Unterräume mit ihren Dimensionen und der Orthogonalität.
A =
-110 0
-10 10
0-1 1 0
-10 0 1
0-1 0 1
0 0-1 1
wird zu U =
-110 0
0-1 1 0
0 0-1 1
0 0 0 0
0 0 0 0
0 0 0 0
Der Kern von A und U ist eine Gerade durch den Vektor x = A,1,1,1).
Die Spaltenräume von A und U haben die Dimension r = 3. Die Pivotzeilen
bilden eine Basis des Zeilenraums.
In Abbildung 8.1 wird noch mehr dargestellt — die Unterräume sind
orthogonal. Jeder Vektor im Kern steht senkrecht auf jedem Vektor im
Zeilenraum. Dies sieht man direkt an den m Gleichungen Ax — 0. Für die Matrizen
A und U wie oben steht also der Vektor x = A,1,1,1) senkrecht auf allen
Zeilen, und daher auf dem gesamten Raum.
Was in dieser Wiederholung über die Unterräume gesagt wurde, kann
man auf alle Matrizen anwenden — lediglich das Beispiel war ein
besonderes. Wir wollen uns jetzt auf dieses Beispiel konzentrieren. Es handelt sich
um die Inzidenzmatrix eines speziellen Graphen, und um die Bedeutung der
Unterräume zu erfassen, sehen wir uns den Graphen an.
Gerichtete Graphen und Inzidenzmatrizen
In Abbildung 8.2 wird ein Graph mit m = 6 Kanten und n = 4 Knoten
dargestellt, die zugehörige Matrix ist deshalb eine 6 x 4-Matrix. Die Matrix
422 8 Anwendungen
gibt an, welche Knoten durch welche Kanten miteinander verbunden sind.
Durch die Einträge -1 und 1 wird auch die Richtung eines jeden Pfeils (es
handelt sich um einen gerichteten Graphen) beschrieben. Die erste Zeile von
A beschreibt die erste Kante:
Die erste Kante verlaeuft von
Knoten 1 zu Knoten 2.
Die erste 2^ile hat -1 in
Spalte 1 and +1 in Spalte 2.
Knoten
® ©CD®
A =
-1 10 0"
-10 10
0-110
-10 0 1
0-101
_0 0 -1 1_
1
2
3
4
5
6
Kante
Abb. 8.2a. Vollständiger Graph mit m = 6 Kanten und n = 4 Knoten.
Zeilennummern sind also Kantennummern, Spaltennummern sind
Knotennummern.
Ein Blick auf den Graphen genügt, um die Matrix A aufzuschreiben. Der
zweite Graph hat dieselben vier Knoten, aber nur drei Kanten. Seine Inzi-
denzmatrix ist also eine 3 x 4-Matrix:
Knoten
0 (D C) @
B =
-110 0
0-110
0 0-11
1
2 Kante
3
Abb. 8.2b. Baum mit 3 Kanten und 4 Knoten und ohne Zyklen.
Der erste Graph ist vollständig — Jedes Paar von Knoten ist durch eine
Kante verbunden. Der zweite Graph ist ein Baum — der Graph enthält
keine geschlossenen Zyklen. Diese Graphen stellen zwei Extreme dar, mit der
Maximalzahl Kanten m — \n{n — 1) und der Minimalzahl m = n — 1. Wir
nehmen dabei an, dass der Graph zusammenhängend ist, es macht dabei
keinen wesentlichen Unterschied, in welche Richtung die Pfeile zeigen. An
jeder Kante ist ein Fluss „mit dem Pfeil" positiv, ein Fluss in Gegenrichtung
8.1 Graphen und Netzwerke 423
zählt negativ. Der Fluss könnte dabei ein Strom sein, oder ein Signal oder
eine Kraft — oder sogar Öl, oder Gas, oder Wasser.
Die Zeilen von B stimmen mit den von Null verschiedenen Zeilen von
JJ überein — der Treppenform, die wir bereits zuvor bestimmt hatten. Das
Eliminationsverfahren reduziert jeden Graphen auf einen Baum. Alle Zyklen
erzeugen Nullzeilen in U. Beachten Sie den Zyklus entlang der Kanten 1, 2
und 3, der zu einer Nullzeile führt:
-110 0
0-110
0 0 0 0
Diese Schritte sind typisch. Wenn zwei Kanten einen gemeinsamen
Knoten haben, erzeugt das Eliminationsverfahren eine „Abkürzung" ohne diesen
Knoten. Enthält der Graph bereits diese Kante, so entsteht bei der
Elimination eine Nullzeile. Wenn sich dann der Nebel lichtet, erkennt man einen
Baum.
Die folgende Idee drängt sich auf: Zeilen sind abhängig, wenn die
zugehörigen Kanten einen Zyklus bilden. Unabhängige Zeilen stammen also von einem
Baum. Diese Idee ist der Schlüssel zur Bestimmung des Zeilenraums.
Für den Spaltenraum betrachten wir den Vektor Ax, der Vektor aus
Differenzen besteht:
110 0'
10 10
0-1 1 0
—)■
110 0'
0-110
0-110
—)■
>*JnÄ. "
1 1 0 0"
1 0 1 0
0-^1 1 0
1 ö ;o 1^
0^1 öl
0 0-1 1
^^i:
^2
^S
;^4-<
^ \.
^2 — ^1 1
^3 - Xi
X^-X2\
X^ — Xi
X4 — X2
_X4 - Xsj
(8.1)
Die Unbekannten a:i,a:2,X3 und x^ stellen Potentiale an den Knoten dar.
Die Matrix Ax liefert die Potentialdifferenzen entlang der Kanten. Diese
Differenzen verursachen Flüsse. Im Folgenden untersuchen wir die Bedeutung
eines jeden der vier Unter räume.
1 Der Kern enthält die Lösungen der Gleichung Ax = 0. Für solche
Vektoren sind alle sechs Potentialdifferenzen Null. Das bedeutet:a//e vier Potentiale
sind gleich. Jedes x im Kern ist ein konstanter Vektor {c,c,c,c). Der Kern
von A ist eine Gerade im Raum M"^ — seine Dimension ist n - r = 1.
Die zweite Inzidenzmatrix B besitzt denselben Kern. Er enthält den Vek-
^^r A,1,1,1):
Bx =
-110 0
0-1 1 0
0 0-1 1
"
1
1
1
^
ü
0
0
424 8 Anwendungen
Wir können alle Potentiale um denselben Betrag c erhöhen oder erniedrigen,
ohne die Potent ialdifFerenzen zu ändern. Es gibt also eine „frei wählbare
Konstante" in den Potentialen. Vergleichen Sie dies mit derselben Aussage
für Funktionen. Man kann eine Funktion f{x) um eine Konstante C erhöhen
oder erniedrigen, ohne die Ableitung zu ändern. Im Integral gibt es eine frei
wählbare Konstante C.
In der Integralrechnung wird eine Konstante „+C" zu unbestimmten
Integralen addiert. In der Graphentheorie kann man einen Vektor (c, c, c, c) zu
jedem Potential vektor x addieren. In der linearen Algebra kann man jeden
Vektor Xn im Kern zu einer speziellen Lösung der Gleichung Ax = b
addieren.
Die Konstante in der Integralrechnung verschwindet, wenn man das
Integral an einer bestimmten Stelle x = a beginnt. Ganz analog verschwindet der
Kern, wenn man X4 = 0 setzt. Die Unbekannte X4 verschwindet, die vierte
Spalte von A und B verschwinden ebenso. Ein Elektrotechniker würde sagen,
dass Knoten 4 „geerdet" wurde.
2 Der Zeilenraum enthält alle Linearkombinationen der sechs Zeilen. Seine
Dimension ist mit Sicherheit nicht sechs. Die Gleichung r-\-{n — r) —n muss
in diesem Fall die Werte 3 + 1 = 4 enthalten. Der Rang ist also r = 3, wie
wir auch beim Eliminations verfahren gesehen haben. Treten mehr als drei
Kanten auf, bilden sich Zyklen. Die neuen Zeilen sind nicht unabhängig.
Wie kann man entscheiden, ob der Vektor v = {vi,V2,v^,V4) im
Zeilenraum liegt? Die langsame Methode wäre, Zeilen zu kombinieren. Der schnelle
Weg geht über die Orthogonalität.
Ein Vektor v liegt im Zeilenraum dann und nur dann, wenn er
senkrecht zum Vektor A,1,1,1) im Kern ist.
Der Vektor v = @,1,2,3) besteht diesen Test nicht — die Summe der
Komponenten ist 6. Der Vektor (-6,1,2,3) hingegen besteht den Test. Er
liegt im Zeilenraum, weil seine Komponenten die Summe 0 bilden. Es handelt
sich um die Kombination 6 • (Zeile 1) + 5 • (Zeile 3) + 3 • (Zeile 6).
Die Einträge jeder Zeile von A bilden die Summe 0. Dies muss dann für
jeden Vektor im Zeilenraum gelten.
3 Der Spaltenraum enthält alle Linearkombinationen der vier Spalten. Wir
erwarten drei linear unabhängige Spalten, da es ja auch drei linear
unabhängige Zeilen gegeben hat. Die ersten drei Spalten sind linear unabhängig, drei
beliebige Spalten sind linear unabhängig. Aber die Summe der vier Spalten
bildet den Nullvektor, was noch einmal besagt, dass der Vektor A,1,1,1)
zum Kern gehört. Wie kann man entscheiden, oh ein gewisser Vektor b zum
Spaltenraum gehört?
Erste Antwort Man versucht, die Gleichung Ax = b zu lösen. Wie zuvor
erhalten wir über die Orthogonalität eine bessere Antwort. Damit kommen wir
8.1 Graphen und Netzwerke 425
zu den beiden berühmten Kirchhoff'sehen Regeln der Schaltkreistheorie, der
Maschenregel und der Knotenregel. Durch sie äußern sich auf eine natürliche
Weise „Gesetze" der Unearen Algebra. Es ist besonders erfreulich zu sehen,
welche Schlüsselrolle der Kern der transponierten Matrix dabei spielt.
Zweite Antwort ^x ist der Vektor der Differenzen in Gleichung (8.1).
Addiert man die Differenzen entlang eines geschlossenen Zyklus, so heben sich
alle Terme zu null auf. Entlang des großen Dreiecks aus den Kanten 1, 3 und
-2 (an Kante zwei geht man entgegen der Pfeilrichtung) sind die Differenzen
zum Beispiel
{X2 - Xi) + {Xs - X2) - {Xs - Xi) = 0.
Dies ist die Maschenregel: Die Komponenten von Ax bilden entlang eines
Zyklus die Summe null. Liegt b im Spaltenraum, muss dies auch für den
Vektor gelten:
Kirchhoff ^s Maschenregel: &i + 63 - ^2 = 0.
Indem man dies an jedem Zyklus überprüft, lässt sich entscheiden, ob ein
Vektor b im Spaltenraum liegt, ^x = h hat genau dann eine Lösung, wenn
die Komponenten von b genau denselben Abhängigkeiten unterliegen wie die
Zeilen von A. Dann führt die Elimination zu der Gleichung 0 = 0, und das
System ^x = b ist konsistent.
4 Der Kern der transponierten Matrix enthält die Lösungen der Gleichung
A'^y — 0 und hat die Dimension m - r = 6 - 3:
A^y^
-1-1 0-1 0 0
1 0-1 0-1 0
0 110 0-1
0 0 0 111
'y\
Vi
2/3
2/4
2/5
.2/6.
Ol
0
0
0
(8.2)
Die wahre Anzahl an Gleichungen ist r = 3 und nicht n = 4, weil die Summe
der vier Gleichungen 0 = 0 ist. Die vierte Gleichung folgt also automatisch
aus den ersten drei Gleichungen.
Was bedeuten diese Gleichungen? Die erste Gleichung besagt, dass —y\ —
2/2—2/4 =0 gilt. Der Nettofluss in den ersten Knoten hinein ist null. Die
vierte Gleichung besagt, dass 2/4+2/5 + 2/6 = 0 ist. Fluss in den Knoten minus
Fluss aus dem Knoten ergibt null. Die Gleichungen A^y — 0 sind berühmt
und grundlegend:
Die Kirchhoff ^sche Knotenregel: Der Fluss in einen Knoten
' V hinßin ist gleich dem Flüss hinausi
426 8 Anwendungen
Dieser Regel gebührt der erste Platz unter den Gleichungen der
angewandten Mathematik. Sie drückt „Erhaltung", „Kontinuität" oder
„Gleichgewicht" aus. Nichts geht verloren, nichts wird hinzugewonnen. Wenn Ströme
oder Kräfte im Gleichgewicht sind, muss man die Gleichung A^y = 0 lösen.
Beachten Sie die hübsche Tatsache, dass die Matrix in der
Gleichgewichtsgleichung die transponierte Inzidenzmatrix ist.
Wie bestimmt man die Lösungen der Gleichung A^y = 0? Die Ströme
müssen sich ausgleichen. Die einfachste Möglichkeit dazu ist, entlang der
Kanten eines Zyklus zu fließen. Der Vektor, der einen Strom der Stärke eins
entlang des großen Dreiecks (vorwärts entlang Kante 1, vorwärts entlang
Kante 3, rückwärts entlang Kante 2) beschreibt, ist y = A, -1,1,0,0,0). Er
erfüllt die Gleichung A-^y = 0. Jeder Kreisstrom führt auf eine Lösung y,
weil bei Kreisströmen der Fluss hinein in jeden Knoten gleich dem Fluss aus
dem Knoten heraus ist. Ein kleinerer Zyklus wäre vorwärts entlang Kante
1, vorwärts entlang Kante 4, zurück über Kante 4. Der zugehörige Vektor
y = A,0,0, —1,1,0) liegt also im Kern der transponierten Matrix.
Wir erwarten drei linear unabhängige y's, da 6—3 = 3 gilt. Die drei kleinen
Zyklen im Graphen sind linear unabhängig. Das grosse Dreieck scheint auf
einen vierten Vektor y hinzuweisen, der aber die Summe der Flüsse entlang
der kleinen Zyklen ist. Diese bilden also eine Basis des Kerns der
transponierten Matrix.
Zusartiinerifassutig Die Inzidenzjmatrix A gehört zu eiBem za:töamm€
hängeiici^i örapheii mit n Knotm mid m Käntea, Der ^eileijraTiim.padjÄ
Spaltenraum haben die Dimension n — 1, die Kerne haimi die Diöiet^iot
Inndm — n-^li' ' ' "; '' ^ -^ ^-^ -'^"' ^ ''
1 Die kOBStaafeii Vektoren (c, c,;.,, c) bilden den Kern von A,
2 Es gibt r =^ n — 1 nnabhängige Zeilen^ dije ij^änteii-eines b<qHebi^
Batmis. H: ' ' , ^< ^ ' ^ ■ -,:', S ' ^^ ' " \" -^''^'^ '■'
3 Määchenregeli Bie.Kompbnenteri des Vektors Mx bifö^eii/entlängri
Zyk^n die'Sirfeiii^'NMl. ='' "\ ^' ''^--'^^ ^' - .: ^^' 'f;;^'-'"'" - - .„^
, 4 'J^i«öi|^jfe*TC5#ir^^ der; QlmSmmi' A^y'^ Ji^Äe&-icÄl.
^tA^T^lÄmm^k^< 'Diei^-Ketn der t^^3[iWi^ßxmi^^r3^'M^%t^
die Diinension m—r» Es gibt m—r = m-Tn^k-^ tpmbitogig#;&
Für jeden Graphen in der Ebene liefert die lineare Algebra damit die
Euler'sehe Formel:
(Anzahl Knoten)— (Anzahl Kanten)+ (Anzahl kleiner Zyklen) =1.
Dies ist einfach n — m + (rn — n + 1) = 1. Beim Graphen in unserem
Beispiel ist dies 4 - 6 + 3 = 1.
8.1 Graphen und Netzwerke 427
1
0
0
-1
1
0
+
0
0
1
0
-1
1
+
0
-1
0
1
0
-1
=
1
-1
1
0
0
0
kleiner Zyklus
grosser Zyklus
Ein einfaches Dreieck hat C Knoten)-C Kanten)+A kleiner Zyklus)=1.
Bei einem zehn-knotigen Baum mit 9 Kanten und ohne Zyklen ergibt die
Euler'sche Formel 10-9 + 0. Alle planaren Graphen führen auf die Antwort 1.
Netze und A^CA
In einem realen Netzwerk ergibt sich der Strom y entlang einer Kante als
das Produkt zweier Zahlen. Die eine Zahl ist die Differenz zwischen den
Potentialen X an den Enden der Kante. Man erhält sie als Ax, sie erzeugt den
Fluss. Die andere Zahl ist die ,,Leitfähigkeit^' c, die angibt, wie leicht dieser
Fluss durch die Kante fließt.
In der Physik und in den Ingenieurwissenschaften wird c durch das
Material bestimmt. Für elektrische Ströme ist c groß für Metalle und klein für
Plastik. Bei einem Supraleiter ist c beinahe unendlich. Betrachten wir
hingegen elastische Streckungen, so ist c klein für Metalle und größer für Plastik.
In den Wirtschaftswissenschaften beschreibt c die Kapazität oder die Kosten
einer Kante.
Zusammenfassend gesagt, erhält man den Graphen aus seiner
„Verbindungsmatrix" A. Sie beschreibt die Verbindungen zwischen Knoten und
Kanten. Ein Netzwerk geht noch weiter und schreibt jeder Kante eine
Leitfähigkeit c zu. Die Zahlen ci,... ,Cm bilden zusammen die diagonale
„Leitfähigkeitsmatrix" C.
Für ein Netzwerk aus Widerständen ist die Leitfähigkeit c — 1/(Widerstand)
Zusätzlich zur Kirchhoff'sehen Regel für das gesamte System aus Strömen
gibt es das Ohm'sche Gesetz für jeden einzelnen Strom. Das Ohm'sche
Gesetz stellt eine Verbindung zwischen dem Strom y\ in der Kante 1 und der
Potentialdifferenz x^ — X\ zwischen den Knoten her:
Für alle m Ströme gleichzeitig liest sich das Ohm'sche Gesetz y —
-CAx. Der Vektor Ax liefert die Potentialdifferenzen, C multipliziert mit
428 8 Anwendungen
den Leitfähigkeiten. Kombiniert man das Ohm'sche Gesetz mit der Kirch-
hoff'schen Knotenregel, so erhält man A^CAx = 0. Dies ist beinahe die
zentrale Gleichung für Flüsse in Netzwerken. Der einzige Fehler dabei ist die
Null auf der rechten Seite. Das Netzwerk benötigt Leistung von außerhalb —
eine Spannungsquelle oder eine Stromquelle — damit etwas passiert.
Hinweis zu den Vorzeichen In der Schaltkreistheorie wechseln wir von Ax
zu -^x. Der Fluss fließt vom höheren zum niedrigeren Potential. Der Strom
von Knoten 1 zu Knoten 2 ist positiv, wenn xi - X2 positiv ist — wohingegen
die Matrix ^x nach Konstruktion X2 — Xi liefert. Anstelle des Minuszeichens
in der Physik und in der Elektrotechnik findet man ein Pluszeichen im
Maschinenbau oder den Wirtschaftswissenschaften. Der Streit um ^x oder —Ax
ist ein generelles, aber unvermeidbares Problem.
Ein Hinweis zur angewandten Mathematik Jede neue Anwendung hat ihre
eigene Form des Ohm'schen Gesetzes. Bei elastischen Strukturen beschreibt
y = CAx das Hooke'sche Gesetz. Die Belastung y ist (Elastizität C) mal
(Dehnung ^x).
Bei der Hitzeleitung beschreibt Ax einen Temperaturgradienten. Bei
Ölflüssen ist es ein Druckgradient. Es gibt ein ähnliches Gesetz für das
Regressionverfahren nach der Methode der kleinsten Quadrate in der Statistik.
Mein Lehrbuch Introduction to Applied Mathematics (Wellesley-Cambridge
Press) basiert im Wesentlichen nur auf ,,A^CA'\ Dieser Ausdruck ist der
Schlüssel zu Gleichgewichten in Matrixgleichungen und auch in
Differentialgleichungen.
Die angewandte Mathematik ist besser organisiert, als es scheint. Ich habe
gelernt, nach Ausdrücken der Form A^CA Ausschau zu halten.
Wir wollen jetzt ein Beispiel mit einer Stromquelle besprechen. Die
Kirchhoff'sehe Knotenregel wird dann von Ä^y = 0 zu Ä^y = f, um den Strom
f aus der Quelle außerhalb zu beschreiben. Der Fluss in jeden Knoten ist
immer noch gleich dem Fluss aus jedem Knoten. In Abbildung 8.3 wird ein
Netzwerk mit den Leitfähigkeiten Ci,..., ce und einer Stromquelle dargestellt,
die Strom in den Knoten 1 einspeist. Damit das Gleichgewicht erhalten bleibt
(einfließender Strom = ausfließender Strom) fließt dieser Strom an Knoten 4
wieder heraus. Die Aufgabe ist nun, die Ströme 2/1,.. •, 2/6 in den sechs Kanten
zu bestimmen.
Beispiel 8.1.1 Alle Leitfähigkeiten seien c = 1, so dass C = I gilt. Ein Strom
2/4 geht direkt von Knoten 1 zu Knoten 4. Ein anderer Strom fließt den
längeren Weg von Knoten 1 über Knoten 2 zu Knoten 4. Für diesen Strom
muss 2/1 = Vb gelten. Schließlich fließt noch Strom von Knoten 1 über Knoten
3 zu Knoten 4, es gilt also 2/2 =2/6- Wir können die sechs Ströme bestimmen,
indem wir bestimmte Symmetrieregeln beachten, oder indem wir sofort die
Matrix A^CA verwenden. Da C = / gilt, ist diese Matrix gleich A^A:
8.1 Graphen und Netzwerke 429
Abb. 8.3. Die Ströme in einem Netzwerk mit einer Quelle S in Knoten 1.
-1-1 0-1 0 0
1 0-1 0-1 0
0 110 0-1
0 0 0 111
-110 0
-1 0 1
0-1 1
-10 0
0-1 0
0 0-1
■'■S-rl-l-l'
Die letzte Matrix ist nicht invertierbar! Man kann die Gleichung nicht nach
den Potentialen lösen, weil der Vektor A,1,1,1) im Kern liegt. Ein Knoten
muss geerdet werden. Setzt man X4 = 0, so entfernt man die vierte Zeile und
die vierte Spalte, übrig bleibt eine invertierbare 3 x 3-Matrix. Lösen wir jetzt
die Gleichung A^CAx = f nach den unbekannten Potentialen a;i, a;2, X3 bei
einem Quellstrom S in Knoten 1:
3-1-1
1 3-1
1-1 3
Xi
X2
xz
=
S
0
0
ergibt
Xi
X2
X3
=
'S/2
5/4
.5/4
Über das Ohm'sche Gesetz y = -CAx erhält man hieraus die sechs Ströme.
Es gilt C = Iundx4= 0:
J/l"
J/2
2/3
2/4
2/5
2/6.
'-1 1 0
-1 0 1
0-1 1
-10 0
0-1 0
0 0-1
0"
0
0
1
1
1
/2"
5/4
5/4
0
[5/4
5/4
0
5/2
5/4
_5/4
Die Hälfte des Stroms fließt also direkt in Kante 4: 2/4 = 5/2. Es fließt kein
Strom von Knoten 2 zu Knoten 3. Wegen der Symmetrie hatten wir ys = 0
erwartet, die Lösung beweist dies nun.
430 8 Anwendungen
Dieselbe Matrix Ä^A wird bei der Methode der kleinsten Quadrate
verwendet. Die Natur verteilt die Ströme so, dass der Wärmeverlust minimiert
wird, gerade so, wie man in der Statistik x wählt, um den Fehler zu
minimieren.
Aufgaben 8.1
In den Aufgaben 1-7 und 8-14 geht es um die Inzidenzmatrizen
der folgenden Graphen:
Kante 1/ \ Kante 2
1. Geben Sie die 3 x 3-Inzidenzmatrix A für den dreieckigen Graphen an.
Die erste Zeile enthält eine -1 in Spalte 1 und eine 1 in Spalte 2.
Welche Vektoren (xi,X2,X3) liegen im Kern? Wieso liegt A,0,0) nicht im
Zeilenraum?
2. Geben Sie Ä^ für den dreieckigen Graphen an. Bestimmen Sie einen
Vektor y im Kern der Matrix. Die Komponenten von y beschreiben Ströme
in den Kanten — wie viel Strom fließt in dem Dreieck herum?
3. Eliminieren Sie Xi und X2 aus der dritten Gleichung, und bestimmen Sie
so die Treppenmatrix U. Welcher Baum entspricht den beiden von Null
verschiedenen Zeilen von U?
-Xi + X2 = bi
-Xi +X3 -b2
-X2 + Xs =bs
4. Wählen Sie einen Vektor (öi, 62, ^3), für den die Gleichung Ax = b gelöst
werden kann, und einen anderen Vektor, der keine Lösung darstellt. In
welcher Beziehung stehen diese b's zu y = A, -1,1)?
5. Wählen Sie einen Vektor (/i, /2, /s), für den die Gleichung A'^y = f gelöst
werden kann, und einen Vektor, der keine Lösung darstellt. In welcher
Beziehung stehen diese f's zu x = A,1,1)? Die Gleichung A'^y = f
beschreibt die Kirchhoff'sehe .
8.1 Graphen und Netzwerke 431
6. Berechnen Sie Ä^A. Wählen Sie einen Vektor f, für den die Gleichung
Ä^Ax — f gelöst werden kann, und lösen Sie sie nach x. Tragen Sie die
Potentiale in x, die Ströme in y = -Ax und die Stromquelle in f in den
dreieckigen Graphen ein. Die Leitfähigkeiten haben hier alle den Wert 1,
weil C = I angenommen wurde.
7. Berechnen Sie die Matrix Ä^CA für die Leitfähigkeiten Ci = 1 und C2 =
cs = 2. Bestimmen Sie eine Lösung der Gleichung A^CAx = f für f =
A,0, -1). Tragen Sie die Potentiale in x und die Ströme in y = -CAk
in den dreieckigen Graphen ein, wobei der Strom f in den Knoten 1
hineinfließe und aus Knoten 3 heraus. ^
8. Geben Sie die 5 x 4-Inzidenzmatrix A für den quadratischen Graphen
mit zwei Zyklen an. Bestimmen Sie eine Lösung der Gleichung Ax = 0
und zwei Lösungen der Gleichung A^y = 0.
9. Bestimmen sie die Bedingungen an einen Vektor b\ so dass sich die
Einträge öi, ^2, ^3, ^4, ^5 als Differenzen X2—a:i,X3—Xi,X3—X2,X4—X2,X4—X3
darstellen lassen. Damit haben Sie die Kirchhoff'sehe für die
beiden im Graphen gefunden.
10. Reduzieren Sie die Matrix A auf ihre Treppenform U, Für welchen
Graphen stellen die drei von Null verschiedenen Zeilen eine Inzidenzmatrix
dar? Damit haben Sie einen Baum in dem quadratischen Graphen
gefunden — finden Sie auch die anderen sieben Bäume.
11. Berechnen Sie die Matrix A^A und erraten Sie, wie die Einträge mit dem
Graphen zusammenhängen.
(a) Was gibt die Diagonale von Ä^A für jeden Knoten an?
(b) Was geben die Einträge —1 oder 0 über Paare von Knoten an?
12. Warum stimmen die folgenden Aussagen über Ä^A? Geben Sie ihre
Antworten für Ä^A, nicht für A.
(a) Der Kern enthält den Vektor A,1,1,1). Der Rang ist n - 1.
(b) Die Matrix ist positiv semidefinit, aber nicht positiv definit.
(c) Die vier Eigenwerte sind reell, ihre Vorzeichen sind .
13. Berechnen Sie die Matrix A^CA für die Leitfähigkeiten ci—C2=2 und
C3 = C4 =: C5 = 3. Löseu Sie die Gleichung Ä^CAx = f = A,0,0, -1).
Tragen Sie die Potentiale in x und die Ströme in y = -CAx an den
Knoten und Kanten des quadratischen Graphen ein.
14. Die Matrix Ä^CA ist nicht invertierbar. Welche Vektoren x bilden ihren
Kern? Warum hat die Gleichung A^CAx = f dann und nur dann eine
Lösung, wenn /i + /2 + /s + A = 0 gilt?
432 8 Anwendungen
15. Wie viele Zyklen enthält ein zusammenhängender Graph mit 7 Knoten
und 7 Kanten ?
16. Fügen Sie einem Graphen mit 4 Knoten, 6 Kanten und 3 Zyklen einen
neuen Knoten hinzu. Verbindet man diesen mit einem der alten Knoten,
so ergibt sich die Euler'sehe Formel zu ( ) - ( ) + ( ) = 1. Verbindet
man den neuen mit zwei alten Knoten, so erhält man ( ) - ( ) + ( ) =
1.
17. Die Matrix A sei die 12 x 9-Inzidenzmatrix eines unbekannten
zusammenhängenden Graphen.
(a) Wie viele Spalten von A sind linear unabhängig?
(b) Welche Bedingung an f erlaubt es, die Gleichung Ä^y = f zu lösen?
(c) Die Diagonaleinträge von A^A geben die Anzahl Kanten an jedem
Knoten an. Welche Bedeutung hat die Summe der Diagonaleinträge?
18. Warum hat ein vollständiger Graph mit n = 6 Knoten m = 15 Kanten?
Wie viele Kanten hat ein Baum mit 6 Knoten?
8.2 Markov-Matrizen und Wirtschaftsmodelle
Zu Anfang dieses Buchs hatten wir Ihnen ein Experiment vorgeschlagen. Man
beginne mit einem beliebigen Vektor uq = (x, 1 — x) und multipliziere ihn
wieder und wieder mit der „Übergangsmatrix" A:
A =
0,8 0,3
0,2 0,7
Bei diesem Experiment werden also die Vektoren ui = Auq und dann U2 =
Awi usw. erzeugt. Nach k Schritten erhält man den Vektor A^uq. Die
Vektoren uo, ui, U2, U3,... nähern sich einem stationären Zustand an (außer falls
MATLAB völlig durcheinander ist). Der Grenzzustand ist Uqo = @,6, 0,4);
und dieses Ergebnis hängt nicht vom Startvektor ab. Die Vektoren
konvergieren für jeden Startvektor gegen @,6, 0,4). Man fragt sich, warum?
Als wir das Experiment vorschlugen, hatten wir keine gute Möglichkeit,
diese Frage zu beantworten. Wir wussten noch nichts über Eigenwerte. Wir
konnten lediglich anhand der Gleichung Auqq = Uqo überprüfen, dass es sich
um einen stationären Zustand handelt:
'0,8 0,3]
0,2 0,7]
[,6'
[0,4
=
'0,6'
Jetzt würden Sie wohl sagen, dass Uoo ein Eigenvektor zum Eigenwert 1 ist.
Deshalb ist dieser Vektor stationär. Die Multiplikation mit A ändert nichts.
Die Gleichung Auoo = Uqo erklärt nicht, warum man von allen Vektoren
8.2 Markov-Matrizen und Wirtschaftsmodelle 433
Uo zu Uoo gelangt. Auch andere Beispiele können einen stationären Zustand
besitzen, ohne dass dieser besonders attraktiv wäre:
B =
10
02
besitzt den stationären Zustand B
In diesem Fall führt der Startvektor uo = @,1) auf ui — @,2) und U2 =
@,4). Die zweiten Komponenten werden von der 2 in B verdoppelt. B hat
den Eigenwert A = 1, aber die Matrix hat ebenfalls den Eigenwert A = 2 —
und ein Eigenwert größer als eins erzeugt Instabilität. Die Komponente von
u entlang des instabilen Eigenvektors wird mit A multipliziert, und |A| > 1
bedeutet deshalb, dass der Eigenvektor „explodiert".
In diesem Abschnitt geht es um zwei besondere Eigenschaften einer Matrix
A^ die einen stationären Zustand Uqo garantieren. Durch diese Eigenschaften
werden Markov-Matrizen definiert, von denen jene oben ein spezielles
Beispiel ist.
1 Kein Eintrug von A tat negativ.
2 Die Sufkrne der Einträge in jeder Spalte mn Ä ist 1.
Die Matrix B besitzt Eigenschaft 2 nicht. Für eine Markov-Matrix A kann
man sofort zwei Eigenschaften folgern:
Multipliziert man einen nichtnegativen Vektor uq mit A, so erhält man
einen nichtnegativen Vektor ui = Auq.
Ist die Summe der Komponenten von uq gleich 1, so gilt dies auch für die
Komponenten von ui = Auq.
Begründung: Die Summe der Komponenten von uq ist 1, wenn [1 • • • l]uo ==
1 gilt. Wegen Eigenschaft 2 gilt dies für jede Spalte von A. Nach den Regeln
der Matrixmultiplikation bleibt die Eigenschaft für Auq erhalten:
[l--- l]Auo = [l"' l]uo-l.
Auch die Vektoren U2 = Aui und U3 = Au2 haben diese Eigenschaft. Jeder
Vektor Uk = A^uq hat nur nichtnegative Komponenten mit der Summe 1.
Alle diese Vektoren sind „Wahrscheinlichkeitsvektoren". Auch der Grenzwert
^00 ist ein Wahrscheinlichkeitsvektor — dazu müssen wir aber beweisen, dass
6s diesen Grenzwert gibt. Auch die Existenz eines stationären Zustands folgt
^us den Eigenschaften 1 und 2, dies ist aber nicht so schnell zu zeigen. Wir
ßiüssen zeigen, dass A = 1 ein Eigenwert von A ist, und wir müssen die
anderen Eigenwerte abschätzen.
Beispiel 8.2.1 Der Bruchteil aller Mietwagen, die sich in Denver befinden, sei
^m Anfang ^ = 0,02, und der Anteil außerhalb von Denver sei 0,98. Diese
434 8 Anwendungen
Anteile (deren Summe 1 ist) werden jeden Monat mit einer Markov-Matrix
A multipliziert:
A =
0,80 0,05
0,20 0,95
führt auf ui = Auq = A
0,02
0,98
0,065
0,935
Nach einem Monat ist der Anteil Mietwagen in Denver auf 0,065 gestiegen.
Hier sehen wir einen Schritt einer Markov-Kette. Als Kette fassen wir die
Vektoren uq, ui, U2,..., auf, die in jedem Schritt mit A multipliziert wurden:
Ui = Auo, U2 = A Uo,
liefert u^ = A uq.
Alle diese Vektoren haben nichtnegative Einträge, weil A nichtnegativ ist.
Außerdem gilt 0,065 + 0,935 = 1,000. In jedem Vektor u^ bilden die
Komponenten die Summe 1. Als Vektor U2 = Aui hat man @,09875,0,90125). Die
erste Komponente ist von 0,02 über 0,065 auf beinahe 0,099 angewachsen. Es
fahren also Wagen nach Denver hinein. Was passiert auf lange Sicht?
In diesem Abschnitt tauchen Potenzen von Matrizen auf. Die
Beschreibung solcher Potenzen A^ war unsere erste und beste Anwendung der Diago-
nalisierung. Auch wenn eine Matrix A'^ kompliziert ist, ist die Diagonalmatrix
A^ leicht zu bestimmen. Die beiden Matrizen hängen über die
Eigenvektormatrix S zusammen: A^ ist gleich SA'^S'^. Unsere neue Anwendung auf
Markov-Matrizen wird auf diese Idee — die Eigenwerte (in A) und die
Eigenvektoren (in S) zu verwenden — aufbauen. Wir werden zeigen, dass Uqo
ein Eigenvektor zum Eigenwert A = 1 ist.
Da jede Spalte von A die Summe 1 hat, geht nichts verloren, und nichts
kommt hinzu. Mietwagen oder Populationen werden bewegt, aber weder
tauchen Autos oder Personen plötzlich auf, noch verschwinden sie. Die Summe
der Bruchteile ist 1, und A ändert daran nichts. Die Frage ist, wie sie nach A;
Zeitabschnitten verteilt sind — was auf die Potenzen A^ führt.
Lösung zu Beispiel 8.2.1 Die Bruchteile an Mietwagen innerhalb und
außerhalb Denvers nach k Schritten bilden die Komponenten des Vektors A^uo-
Um die Potenzen von A zu untersuchen, diagonalisieren wir die Matrix.
Der erste Eigenvektor, dessen Komponenten die Summe eins bilden, ist
XI = @,2,0,8):
\A-XI\ =
0,80 - A 0,05
0,20 0,95 - A
0,2
= A^ - 1,75A + 0,75 - (A - 1)(A - 0,75)
0,8
= 1
0,2
0,8
und A
-1
1
0,75
Die Eigenvektoren sind die Vektoren xi und X2, die die Spalten der Matrix
S bilden. Der Startvektor uq lässt sich als Linearkombination der Vektoren
xi und X2 mit den Koeffizienten 1 und 0,18 schreiben:
8.2 Maxkov-Matrizen und Wirtschaftsmodelle 435
uo
0,02
0,98
0,2
0,8
+ 0,18
Um ui zu bestimmen, multipliziert man mit A. Die Eigen vektoren werden
daher mit Ai = 1 und A2 = 0,75 multipliziert:
ui
0,2
0,8
+ @,75)@,18)
Jedes Mal, wenn mit A multipliziert wird, kommt ein weiterer Faktor 0,75
zum zweiten Vektor hinzu. Der Eigenvektor Xi hingegen bleibt unverändert.
Uk = A^Uo =
0,2
0,8
+ @,75)^^@,18)
Diese Gleichung zeigt uns, was passiert. Der Eigenvektor Xi mit dem
Eigenwert A = 1 ist der stationäre Zustand Uoo- Der andere Eigenvektor X2
verschwindet schrittweise, da |A| < 1 ist. Je mehr Schritte man betrachtet,
desto näher kommt man dem Vektor Uqo = @,2,0,8). Im Grenzfall befinden
sich also ^ der Mietwagen in Denver und ^ außerhalb. Dieses Verhalten
beobachtet man bei Markov-Matrizen immer:
8A fot A eim positive Markov-Matri^ (mit Eihtrageii aif> 0^ deren SgSl-
tensumme 1 ist),^ ist A = 1 gröSer & jöder mäme Eig&w^t: Der Eigen-
vektoTKl ist der Btütionäre ZMstmä^: ' \'? '/' /''\= ^ :r''-''\ .':-,.-..
Ufc = xi + C2(A2)''x2 H h Cn{Xn)'^Xn geht gegen Uoo = xi.
Nehmen wir an, dass die Summe der Komponenten von uq gleich 1 ist.
Dann gilt dasselbe für ui,U2, Das wichtige ist, dass man sich von
jedem Startvektor aus an ein Vielfaches von xi annähert. Unabhängig davon,
ob man mit allen Mietwagen außerhalb von Denver beginnt, oder mit allen
Wagen in Denver, der Grenzwert ist trotzdem Uqo = xi = @,2,0,8).
Das erste, was man dazu beweisen muss, ist, dass A = 1 ein Eigenwert
von A ist. Begründung: Jede Spaltensumme von A - / ist 1 - 1 = 0. Dann
ist die Summe aller Zeilen von A- I gleich der Nullzeile, die Zeilen sind also
linear abhängig, und A- I ist singular. Ihre Determinante ist also Null, und
deshalb ist A = 1 ein Eigenwert. Da die Spur von A gleich 1,75 ist, muss der
andere Eigenwert A2 = 0,75 sein.
Der nächste Punkt ist, dass kein Eigenwert einen Betrag |A| > 1 haben
l^nn. Gäbe es einen solchen Eigenwert, so würden die Potenzen A'^ wachsen,
^ber auch A^ ist eine Markov-Matrix mit nichtnegativen Einträgen, deren
^Paltensummen 1 ist — da bleibt kein Platz zum Wachsen.
Der Möglichkeit, dass ein weiterer Eigenwert den Betrag |A| = 1 haben
l^önnte, wird viel Aufmerksamkeit geschenkt. Nehmen wir dazu an, dass die
436 8 Anwendungen
Einträge von A oder einer beliebigen Potenz A^ sämtlich positiv sind — Null
ist nicht erlaubt. In diesem „regulären" Fall ist A = 1 echt größer als jeder
andere Eigenwert. Besitzen A und alle Potenzen auch Nulleinträge, so kann
es auch einen anderen Eigenwert mit Betrag 1 geben.
Beispiel 8.2.2 Die Matrix A= [J J] besitzt keinen stationären Zustand, da
A2 = -1 ist.
Diese Matrix schickt alle Wagen innerhalb Denvers nach außerhalb, und
umgekehrt. Die Potenzen A^ wechseln zwischen A und /. Der zweite
Eigenvektor X2 = (—I5I) wird in jedem Schritt mit A2 = — 1 multipliziert, und
wird nicht kleiner. Bei einer regulären Markov-Matrix nähern sich die
Potenzen einer Matrix mit Rang eins an, die in allen Spalten den stationären
Zustand xi enthält.
Beispiel 8.2.3 („Jeder bewegt sich") Wir beginnen mit drei Gruppen. In
jedem Schritt geht die eine Hälfte von Gruppe 1 in Gruppe 2 und die andere
Hälfte in Gruppe 3. Auch die anderen beiden Gruppen halbieren und verteilen
sich. Sind die Startpopulationen durch die Zahlen pi,p2 und ps gegeben, so
sind die Populationen nach einem Schritt gleich
Ui = ^Uo =
A ist eine Markov-Matrix. Niemand wird hinzugeboren, niemand geht
verloren. Zwar enthält die Matrix A Nulleinträge, die in Beispiel 2 die Probleme
bereitet hatten. Aber nach zwei Schritten verschwinden die Nullen aus A'^:
ro i ^1
U 0 i
2^2
_ 2 2 ^-
'pi'
P2
.^3_
=
'^P2+^P3'
hpi + ^3
,^1 + ^2]
r 1 1 1 -
2 4 4
111
4 2 4
111
L 4 4 2 .
"Pll
P2
_P3j
U2 = ^ Uo =
Welches ist der stationäre Zustand? Die Eigenwerte von A sind Ai = 1 (weil A
eine Markov-Matrix ist) und A2 = A3 = -^. Der Eigenvektor xi = (|, |, |)
zu A = 1 ist der stationäre Zustand. Wenn sich drei gleich große Populationen
aufspalten und mischen, so sind die Endpopulationen wieder gleich groß.
Auch wenn man mit den Populationen uq = (8,16,32) beginnt, nähert sich
die Markov-Kette ihrem stationären Zustand an:
uo
Es lässt sich nicht vermeiden, dass beim Schritt zu U4 einige Leute halbiert
werden müssen. Die Gesamtpopulation ist 8 -f 16 -f 32 = 56 (auch später ist
die Summe 20+19 + 17 = 56). Die Populationen des stationären Zustands Uqo
sind also (|, |, |). Sie sehen, wie die drei Populationen sich ihren Grenzwerten
8
16
32
Ui =
24
20
12
U2 =
16
18
22
=
20
19
17
Kall
oöT-n CMn O KöT» niö c\^r^rc\^
,i/-»V>c
8.2 Maxkov-Matrizen und Wirtschaftsmodelle 437
LineEire Algebra in den Wirtschaftswissenschaften:
Die Verbrauchsmatrix
Ein langer Aufsatz über lineare Algebra in den Wirtschaftswissenschaften
wäre hier fehl am Platze. Ein kurze Bemerkung über eine spezielle Matrix
scheint aber angebracht. Die Verbrauchsmatrix gibt an, wieviel Input für
eine Einheit an Output gebraucht wird. Wir betrachten n Produkte, zum
Beispiel Chemikalien, Nahrungsmittel und Öl. Um eine Einheit Chemikalien
zu produzieren, braucht man vielleicht 0,2 Einheiten an Chemikalien, 0,3
Einheiten Nahrungsmittel und 0,4 Einheiten Öl. Diese Zahlen bilden die erste
Spalte der Verbrauchsmatrix A:
Chemikalien-Output
Nahrungsmittel-Output
Öl-Output
0,2 0,3 0,4
0,4 0,4 0,1
0,5 0,1 0,3
Chemikalien-Input
Nahrungsmittel-Input
Öl-Input
Zeile 2 gibt die nötigen Inputs für die Nahrungsmittelproduktion an — viele
Chemikalien und Nahrungsmittel, nicht so viel Öl. Die echte
Verbrauchsmatrix für die Vereinigten Staaten von 1958 umfasste 83 Industriezweige. In den
1990er Jahren sind die Modelle viel größer und präziser. Wir haben hier eine
Verbrauchsmatrix mit einem einfachen Eigenvektor gewählt.
Die Frage ist nun: Kann diese Wirtschaft die Nachfrage nach 2/1,2/2
beziehungsweise 2/3 Einheiten von Chemikalien, Nahrungsmitteln beziehungsweise
Öl befriedigen? Damit dies möglich ist, werden die Inputs pi,P2,P3 sicher
größer sein müssen — weil ein Teil von p während der Produktion von y
verbraucht wird. Der Input ist p, der Verbrauch ist Ap; übrig bleibt also die
Nettoproduktion p - Ap, mit der die Nachfrage y bedient wird.
Aufgabe Bestimmen Sie einen Vektor p, so dass p — Ap = y oder (/ —
A)p — y oder p = (I - A)~V gilt.
Es scheint, die Frage, die die lineare Algebra betrifft, ist schlicht, oh I -A
invertierbar ist. Es steckt aber noch mehr dahinter. Der Nachfragevektor y ist
nichtnegativ, ebenso wie A. Auch die Produktionsmengen in p = (/ - A)~^y
müssen nichtnegativ sein. Die wirkliche Frage ist also:
Wann ist {I — A)~^ eine nichtnegative Matrix?
So kann man an (/-A)~^ überprüfen, ob durch A eine produktive Wirtschaft
beschrieben wird, die jede positive Nachfrage bedienen kann. Ist A klein im
Vergleich zu /, so ist auch Ap klein im Vergleich zu p, und es gibt viel Output.
Ist aber A zu groß, so verbraucht die Produktion mehr, als sie erzeugt. In
einem solchen Fall kann die externe Nachfrage y nicht befriedigt werden.
Ob A „klein" oder „groß" ist, hängt vom größten Eigenwert Ai von A ab
ist r»rkGifixr^'
438 8 Anwendungen
Falls Ai > 1, so hat {I - A)~^ negative Einträge;
Falls Ai = 1, so existiert {I — A)~^ nicht;
Falls Ai < 1, so hat {I — A)"^ (wie gewünscht) nur nichtnegative Einträge.
Der wichtigste Punkt ist der letzte. Die Begründung dafür verwendet eine
nette Formel für die Matrix (/ — A)~^, die wir jetzt nennen wollen. Die
wichtigste unendliche Reihe in der Mathematik ist die geometrische Reihe
1 + X -i- x^ + "'. Der Wert dieser Reihe ist 1/A — x) , falls x zwischen 1
und -1 liegt. (Für x = 1 hat die Reihe den Wert 1 + 1 + 1 + "- = cxd.
Für |a;| > 1 bilden die Summanden keine Nullfolge, und daher kann die Reihe
nicht konvergieren.) Die nette Formel für {I — A)~^ ist die geometrische Reihe
für Matrizen:
Multipliziert man diese Reihe mit A, so erhält man dieselbe Reihe 5, vom
ersten Term / abgesehen. Deshalb gilt S - AS = /, also {I — A)S = I. Die
Reihe S hat also den Wert S = {I — A)~^, falls sie konvergiert. Sie konvergiert
für |Amax| < 1.
In unserem Fall gilt A > 0. Alle Summanden sind nichtnegativ, und die
Summe ist {I - A)'^ > 0.
rO;2 03 0,4l
Beispiel 8.2.4 A= o,4 o,4 oa hat den Eigenwert Ai = 0,9, und (/ - A)~^ =
1 [41 25 27]
ö^ 33 36 24 .
93 [34 23 36 J
Die Wirtschaft ist produktiv. A ist im Vergleich zu / klein, weil Amax gleich
0,9 ist. Um die Nachfrage y zu bedienen, benötigt man p = {I — A)~^y.
Davon wird während der Produktion Ap verbraucht, übrig bleibt p — Ap =
(/ — A)p = y, was der Nachfrage entspricht.
Beispiel 8.2.5 A= [? g] hat den Eigenwert Ai = 2, es gilt also (/ - A)~'^ =
Die Verbrauchsmatrix A ist zu groß. Eine Nachfrage kann nicht bedient
werden, weil die Produktion mehr verbraucht, als sie liefert. Die Reihe
I + A-^ A^ + ... konvergiert nicht gegen {I — A)~^, ihr Wert wird immer
größer, obwohl {I - A)~^ eigentlich negativ ist.
Aufgaben 8.2
In den Aufgaben 1-14 geht es um Markov-Matrizen, ihre
Eigenwerte und ihre Potenzen.
1. Bestimmen Sie die Eigenwerte der folgenden Markov-Matrix. Die Summe
der Eigenwerte ist die Spur:
8.2 Markov-Matrizen und Wirt Schaftsmodelle 439
A
0,90 0,15
0,10 0,85
Geben Sie den Eigenvektor zum stationären Zustand an.
Diagonalisieren Sie die Markov-Matrix in Aufgabe 1 in der Form A
SAS~^, indem Sie auch den anderen Eigenvektor bestimmen:
A=:
Welchen Grenzwert hat die Folge A'^ = SA'^S ^, wenn A'^ = [oors*']
gegen [Jg] geht?
3. Bestimmen Sie die Eigenwerte und die stationären Zustände der
folgenden Markov-Matrizen:
1
0,75
[10,2'
_0 0,8
A =
,2 1"
0,8 0
A =
-1 1 1 -
2 4 4
1 1 1
4 2 4
1 1 1
. 4 4 2 J
4. Welcher Eigen vekt or von Ä^ für eine 4 x 4-Markov-Matrix A gehört zum
Eigenwert A = 1?
5. In jedem Jahr werden 2% der jungen Leute alt, und 3% der alten Leute
sterben. Es gibt keine Geburten. Bestimmen Sie den stationären Zustand
des Systems
jung"
alt
- tot _
fc+i 1
0,98 0,00 0
0,02 0,97 0
0,00 0,03 1
jung
alt
tot
6. Die Summe der Komponenten von x sei gleich der Summe der
Komponenten von Ax. Beweisen Sie, dass die Komponenten eines nicht-stationären
Eigen Vektors Ax — Ax mit A 7«^ 1 die Summe null bilden müssen.
7. Bestimmen Sie die Eigenwerte und Eigenvektoren von A. Faktorisieren
Sie A in der Form SAS'^:
A^
0,8 0,3
0,2 0,7
Diese Matrix diente als Beispiel für die Verwendung von MATLAB in
Kapitel 1. Dort hatten wir die Matrix A^^ durch viermaliges Quadrieren
berechnet. Wie sehen die Faktoren in A^^ — S/^^S'^ aus?
8. Erklären Sie, warum die Potenzen A!^ in Aufgabe 7 gegen die Matrix A"^
gehen:
440 8 Anwendungen
0,6 0,6
0,4 0,4
Herausforderung: Welche Markov-Matrizen erzeugen den stationären
Zustand @,6,0,4)?
9. Die Permutationsmatrix ist ebenfalls eine Markov-Matrix:
0100
0010
000 1
1000
Der stationäre Eigenvektor für A = 1 ist (|^, |^, |^, |). Für uq = @,0,0,1)
nähern sich die Zustände diesem Eigenvektor nicht an. Bestimmen Sie
die Vektoren ui, U2, U3 und U4. Welche Eigenwerte von P lösen die
charakteristische Gleichung A^ = 1?
10. Beweisen Sie, dass das Quadrat einer Markov-Matrix ebenfalls eine
Markov-Matrix ist.
11. Ist die Matrix A = [^^] eine Markov-Matrix, so sind ihre Eigenwerte 1
und , und der stationäre Eigenvektor ist xi = .
12. Vervollständigen Sie die letzte Zeile so, dass A eine Markov-Matrix wird,
und bestimmen Sie den stationären Zustand.
A^
0,7 0,10,2
0,1 0,6 0,3
Warum ist xi = A,..., 1) der stationäre Zustand, wenn A eine
symmetrische Markov-Matrix ist?
13. Eine Markov-Differentialgleichung ist eine Gleichung der Form du/dt =
{A — I)u (nicht du/dt — A\i). Bestimmen Sie die Eigenwerte von
B=A-I=
-0,2 0,3
0,2-0,3
Welcher stationäre Zustand ergibt sich für ^ —> 00, wenn die Lösungen
durch e^i* mal xi plus e^^* mal X2 gegeben sind?
14. In der Matrix B — A — I einer Markov-Differentialgleichung bilden die
Einträge in jeder Spalte die Summe . Der stationäre Zustand ist
derselbe wie für A, aber hier gilt Ai = und e^^^ = .
8.3 Lineare Programmierung 441
Bei den Aufgaben 15-18 geht es um die lineare Algebra in den
Wirtschaftswissenschaften.
15. Jede Zeile in der Verbrauchsmatrix in Beispiel 4 hat die Summe 0,9.
Warum ist dann A = 0,9 ein Eigenwert, und zu welchem Eigenvektor?
16. MultipHzieren Sie die Reihe I -\-A-\- A'^ -\- A^ -\ mit I - A, und zeigen
Sie, dass der Wert der Reihe gleich ist. Bestimmen Sie für A =
[° 2 ] die Matrizen A^ und A^, und verwenden Sie dieses Muster, um
den Grenzwert der Reihe auszurechnen.
17. Für welche der folgenden Matrizen ergibt I-\-A-{-A'^-\ eine
nichtnegative Matrix (I- A)~^? In diesem Fall kann die Wirtschaft jede Nachfrage
befriedigen:
101
0 0
A =
4
0,2 0
A =
'0,5 1'
0,5 Oj
A=:
18. Die Nachfrage sei in Aufgabe 17 durch den Vektor y = B,6) gegeben.
Welcher zugehörige Vektor p = (I — A)~^y ergibt sich daraus?
19. (Noch einmal Markov-Matrizen) Die folgende Matrix hat die
Determinante null. Bestimmen Sie ihre Eigenwerte:
0,4 0,2 0,3
0,2 0,4 0,3
0,4 0,4 0,4
Bestimmen Sie die Grenzwerte für A^uq mit uq = A,0,0) und mit uq =
A00,0,0).
20. Ist der Grenzwert der Reihe I + A + A'^ -\ gleich (/ - A)~^, wenn A
eine Markov-Matrix ist?
8.3 Lineare Programmierung
Lineare Programmierung ist lineare Algebra mit zwei neuen Zutaten:
Ungleichungen und Minimierung. Der Startpunkt ist wieder eine Matrixgleichung
^x = b. Aber unsere einzigen akzeptablen Lösungen sollen die nichtnegativen
Lösungen sein. Wir verlangen also x > 0 (das soll bedeuten, dass keine der
Komponenten von x negativ sein darf). Für die Matrix gilt n > m, es gibt
^Iso mehr Unbekannte als Gleichungen. Wenn es dann überhaupt
nichtnegative Lösungen einer Gleichung Ax — b gibt, so gibt es derer wahrscheinlich
viele. Bei der linearen Programmierung wählt man eine Lösung x* > 0 aus,
die die Kosten minimiert:
442 8 Anwendungen
Die Kosten sind CtXi + . • • -f c^Xn* D^t beste Vektor x* ist
die nichtnegative Lösung von Ail = b mit den geringsten Kosten*
Ein Problem der linearen Programmierung besteht also aus einer Matrix A
und zwei Vektoren b und c:
i) Für A gilt n > m: zum Beispiel A = [1 1 2]
ii) b hat m Komponenten: zum Beispiel b = [4]
iii) Der Kostenvektor c hat n Komponenten: zum Beispiel c = [5 3 8].
Die Aufgabe ist es, den Ausdruck c • x unter den Bedingungen Ax — b und
X > 0 zu minimieren:
Minimiere 5aJi + 3aj2 + ^Xs unter den Bedingungen
a^i + ^2 + 2aj3 = 4 und aJi, aj2, Xs > 0.
Wir haben hier sofort das Problem beschrieben, ohne zu erklären, woher es
stammt. Bei der linearen Programmierung handelt es sich eigentlich um die
wichtigste Anwendung der Mathematik auf betriebswirtschaftliche Probleme.
Es besteht ein lebhafter Wettbewerb, den schnellsten Algorithmus und die
schnellsten Programme zu entwickeln. Wir werden sehen, dass es schwieriger
ist, den Vektor x* zu finden, als die Gleichung Ax = b zu lösen. Der Grund
hierfür liegt in den zusätzlichen Bedingungen der Kostenminimierung und
der Nichtnegativität. Nachdem wir für das Beispiel die Lösung bestimmt
haben, werden wir den Hintergrund dieses Problems erklären, und auch den
berühmten Simplex-Algorithmus.
Sehen wir uns zunächst die „Nebenbedingungen" an: Ax = b und x > 0.
Die Gleichung xi + X2 + 2x3 — 4 beschreibt eine Ebene im dreidimensionalen
Raum. Die Bedingung der Nichtnegativität xi > 0,X2 > 0,X3 > 0 schneidet
aus der Ebene ein Dreieck (Dreieck PQR in Abbildung 8.4) heraus, in dem
die Lösung x* liegen muss. Außerhalb des Dreiecks ist mindestens eine der
Komponenten von x negativ. Auf den Kanten des Dreiecks ist eine
Komponente Null, an den Ecken sind zwei Komponenten Null. Die Lösung x* ist
eine dieser Ecken! Wir zeigen jetzt, warum dies so ist.
Das Dreieck enthält alle Vektoren x, die die Bedingungen Ax — b und
X > 0 erfüllen. Man nennt diese Vektoren x zulässige Punkte^ und das Dreieck
nennt man den zulässigen Bereich, Die Punkte im zulässigen Bereich sind die
Kandidaten bei der Minimierung von c • x, dem letzten Schritt:
Man bestimme x* in dem Dreieck so,
dass 5a3i + 3aj2 + Sica minimiert wird.
Die Vektoren mit Kosten Null liegen in der durch die Gleichung 5xi + 3x2 +
8x3 = 0 beschriebenen Ebene. Diese Ebene schneidet das Dreieck nicht. Es
lassen sich also keine Kosten vom Wert Null erreichen, wenn man gleichzeitig
die Bedingungen an x erfüllen will. Stattdessen erhöht man die Kosten C
8.3 Lineare Programmierung 443
R = @, 0, 2)
(Computer: 2 Stunden)/^J^,^^-^v^^^ ^ Ax = b ist die Ebene x^+X2 +2x^ = 4
. Das Dreieck hat jCj> 0, JC2 ^ 0, JC3 > 0
ß = @,4, 0) (Student: 4 Stunden)
P = D, 0, 0) (Promovierter: 4 Stunden)
Abb. 8.4. Das Dreieck aus nichtnegativen Lösungen von Ax = b und x > 0. Die
Lösung X* mit geringsten Kosten ist eine der Ecken P, Q oder R.
solange, bis die Bedingungen erfüllt sind, bis also die Ebene 5x1+3x2 +8x3 =
C das Dreieck berührt. Hier haben wir eine Familie paralleler Ebenen, eine
für jedes C. Wächst C, so bewegt sich die Ebene in Richtung des Dreiecks.
Die erste Ebene, die das Dreieck berührt, hat die minimalen Kosten C.
Der Punkt, in dem sie das Dreieck berührt, ist die Lösung x*. Dieser
Berührpunkt muss aber einer der Eckpunkte P, Q oder R sein. Eine sich bewegende
Ebene kann das Dreieck nicht im Inneren schneiden, bevor sie es in einem
der Eckpunkte berührt. Deshalb berechnen wir die Kosten an jeder Ecke:
P = D,0,0) Kosten 20 Q = @,4,0) Kosten 12 R =:: @,0,2) Kelten 16.
Der Sieger ist Q. Deshalb löst x* == @,4,0) dieses Problem der linearen
Programmierung.
Ändert man den Kostenvektor c, so werden die parallelen Ebenen alle
gleich geneigt. Bei kleinen Änderungen ist daher Q immer noch der beste
Vektor. Für die Kostenfunktion c • x == 5x1 + 4x2 + 7x3 verändert sich das
Optimum x* aber zum Punkt R = @,0,2). Die minimalen Kosten sind dann
7 . 2 = 14.
Bemerkung 1 Bei einigen linearen Programmen wird der Gewinn maxi-
'n^iert, anstatt die Kosten zu minimieren. Die Mathematik bleibt aber
beinahe unverändert. Man beginnt mit einem großen Wert für C, anstatt mit
einem kleinen, und bewegt die parallelen Ebenen in Richtung des Ursprungs
(statt von ihm weg), wenn C kleiner wird. Der erste Berührpunkt ist dann
weiterhin eine Ecke.
Bemerkung 2 Es kann vorkommen, dass die Bedingungen Ax = b und
^ ^ 0 unmöglich zu erfüllen sind. Die Gleichung xi + X2 + X3 = —1 zum
Beispiel kann unter der Bedingung x > 0 nicht gelöst werden. Der zulässige
Bereich ist hier leer.
444 8 Anwendungen
Bemerkung 3 Es kann auch passieren, dass der zulässige Bereich eine
unbeschränkte Menge ist. Ändere ich die Bedingung auf Xi + X2 — 2x3 = 4, so
ist der große positive Vektor A00,100,98) ein Kandidat, und auch der noch
größere Vektor A000,1000,998). Aus der Ebene Ax = h wird kein
Dreieck mehr herausgeschnitten. Die beiden Ecken P und Q sind nach wie vor
Kandidaten für x*, aber die dritte Ecke ist in die Unendlichkeit gewandert.
Bemerkung 4 Hat man einen unbeschränkten zulässigen Bereich, so können
die minimalen Kosten den Wert — oo (minus unendlich) annehmen.
Angenommen, die Kostenfunktion wäre —xi — X2 + ^3. Dann führt der Vektor
A00,100,98) auf die Kosten C = -102, und der Vektor A000,1000,998) auf
die Kosten C = -1002. Wir werden hier für die Komponenten xi und X2
bezahlt, anstatt dafür zu bezahlen. In reaUstischen Situationen tritt dieser
Fall nicht ein. Es ist aber theoretisch möglich, dass Änderungen an A, b und
c unerwartete Dreiecke oder Kosten erzeugen.
Der Hintergrund der linearen Programmierung
Ich habe dieses erste Beispiel so gestaltet, dass es zum vorherigen Beispiel
passt. Die Unbekannten a;i,a;2,a;3 sollen die Arbeitsstunden eines
Promovierten, eines Studenten und einer Maschine darstellen. Die Kosten pro
Stunde sind $5, $3 und $8. {Ich muss für die Niedriglöhne um
Entschuldigung bitten.) Die Arbeitsstunden können nicht negativ sein, es gilt also
xi > 0,a;2 > 0,xs > 0. Der Promovierte und der Student können beide
pro Stunde eine Übungsaufgabe lösen, die Maschine schafft pro Stunde zwei
Aufgaben. Im Prinzip können Sie sich die gesamte Hausaufgabe, die aus vier
Aufgaben besteht, aufteilen: xi -f- 0:2 + 2xs = 4.
Das Problem ist es nun, die vier Aufgaben mit minimalen
Kosten lösen zu lassen.
Arbeiten alle drei gleichzeitig, so wird nur eine Stunde benötigt: xi == 0:2 =
xs = 1. Die Kosten sind 5 -f- 3 -f- 8 = 16. Der Promovierte wird aber sicher
durch den Studenten arbeitslos (der genauso schnell ist und weniger kostet
— das Problem wird realistisch). Arbeitet der Student zwei Stunden und die
Maschine eine Stunde, werden alle Aufgaben zu den Kosten 6 -f- 8 gelöst.
Wir befinden uns hier auf der Kante QR des Dreiecks, weil der Promovierte
arbeitslos ist: xi — 0. Die beste Lösung findet sich aber auf einer Ecke: alle
Arbeit dem Studenten (bei Q), oder alle Arbeit der Maschine (bei R). In
diesem Beispiel löst der Student die vier Aufgaben in vier Stunden für $12
— den minimalen Kosten.
Besteht das Gleichungssystem Ax = b nur aus einer Gleichung, so haben
die Ecken (wie @,4,0)) nur eine von Null verschiedene Komponente. Besteht
Ax — b aus m Gleichungen, so haben die Ecken m von Null verschiedene
Einträge. Wie in Kapitel 3 werden n — m freie Variablen auf null gesetzt und
dann die Gleichung Ax = b nach den Basisvariablen (Pivotvariablen) gelöst.
8.3 Lineare Programmierung 445
Aber anders als in Kapitel 3 wissen wir hier nicht, welche m Variablen wir als
Basis variablen wählen müssen. Unsere Wahl muss die Kosten minimieren.
Die Anzahl möglicher Ecken ist gleich der Anzahl Möglichkeiten, m
Komponenten aus n Komponenten auszuwählen. Diese Zahl „n über m" hängt eng
mit Glückspielen und der Wahrscheinlichkeitsrechnung zusammen. Bei n =
20 Unbekannten und m — S Gleichungen (das sind immer noch kleine
Zahlen!) kann der zulässige Bereich 20!/8!12! = B0)A9) • • • A3) = 5079110400
Ecken besitzen!
Drei Ecken auf minimale Kosten hin zu überprüfen mag ja noch möglich
sein. Fünf Milliarden Ecken zu überprüfen wäre aber der falsche Weg. Der
Simplex-Algorithmus, der unten beschrieben wird, ist viel schneller.
Das duale Problem Bei der linearen Programmierung treten die Probleme
immer paarweise auf — ein ursprüngliches und sein „duales" Problem. Das
ursprüngliche Problem wird durch die Matrix A und die beiden Vektoren b
und c beschrieben. Das duale Problem verwendet dieselben Daten, die Matrix
A wird aber transponiert, und b und c werden vertauscht. Betrachten wir zu
unserem Beispiel das duale Problem:
Ein Betrüger bietet an, die Aufgaben durch Nachschauen der
Antworten zu lösen. Sein Preis ist y Dollar pro Aufgabe, oder 4y
zusammen. (Hier sehen sie, wie b = 4 in die Kostenfunktion eingeht.)
Der Betrüger muss ebenso billig sein wie der Promovierte, oder wie
der Student, oder wie die Maschine; es muss y < 5 und y < S und
2y < S gelten. (Hier sehen Sie, wie der Vektor c = E,3,8) in die
Ungleichungs-Bedingungen eingeht.) Der Betrüger maximiert sein
Einkommen 4y.
Daa äuäie PMkteifn: Muximiere h - y unter der Bedingwtiß:
Das Maximum tritt für y = 3 auf, der Gewinn ist dann 4y = 12. Das
Maximum des dualen Problems ($12) ist gleich dem Minimum im
Originalproblem ($12). Diese Beziehung gilt immer:
Dualitä^BailZ:' L,E3äh|ferl'för' em(^',der Probleme -iem;,pptii3|d€3r';Yfk^^^
Nehmen Sie bitte zur Kenntnis, dass ich oft selbst die Lösungen
nachschlage. Es handelt sich dabei nicht um Betrug.
446 8 Anwendungen
Dieses Buch begann mit einem Zeilenbild und einem Spaltenbild. Der
erste „Dualitätssatz" machte eine Aussage über den Rang: Die Anzahl linear
unabhängiger Zeilen ist gleich der Anzahl linear unabhängiger Spalten. Jener
Satz war, ebenso wie dieser, einfach für kleine Matrizen. Den Beweis für die
Behauptung, dass die minimalen Kosten mit dem maximalen Gewinn beim
dualen Problem übereinstimmen, finden Sie in unserem Lehrbuch Linear
Algebra und Its Applications. Hier wollen wir nur die einfache Hälfte zeigen:
Der Gewinn des Betrügers kann nicht größer sein als die wirklichen Kosten:
Gilt Ax = b, X > 0, A'^y < c,
so folgt b^y = (Ax)^y = x^(A^y) < x^c.
Der Dualitätssatz besagt, dass das Maximum des Ausdrucks b^y und das
Minimum des Ausdrucks x^c gleich sind: b • y* = c • x*.
Der Simplex-Algorithmus
Das Eliminationsverfahren ist das Arbeitspferd für lineare Gleichungen.
Entsprechend ist der Simplex-Algorithmus das Arbeitspferd für lineare
Ungleichungen. Wir können ihm hier nicht soviel Platz einräumen wie dem
Eliminationsverfahren, aber wir wollen die Idee kurz beschreiben. Das Simplex-
Verfahren geht von einer Ecke zu einer benachbarten Ecke mit geringeren
Kosten. Schließlich (in der Praxis auch recht schnell) gelangt es an eine Ecke
minimaler Kosten. Dort befindet sich die Lösung x*.
Eine Ecke ist ein Vektor x > 0 mit höchstens m positiven Komponenten,
der die m Gleichungen ^x = h erfüllt. Die anderen n — m Komponenten
sind null. (Diese n — m Komponenten stehen für die freien Variablen. Durch
Rücksubstitution erhält man die Basisvariablen. Keine der Komponenten darf
negativ sein, sonst handelt es sich um eine falsche Ecke.) Bei einer
benachbarten Ecke wird eine positive Komponente zu null, und eine Nullkomponente
wird positiv.
Der Simplex-Algorithmus muss entscheiden, welche Komponente
„hinzukommt", indem sie positiv wird, und welche Komponente den Vektor
„verlassen" muss, indem sie zu null wird. Man führt diesen Austausch so durch,
dass die Gesamtkosten geringer werden. Dies ist ein Schritt des Simplex-
Algorithmus.
Die Gesamtstrategie ist wie folgt: Man betrachtet jede Nullkomponente
der aktuellen Ecke. Wenn sie ihren Wert von null zu eins ändert, so müssen
sich die übrigen Nicht-Null-Komponenten anpassen, damit die Gleichung
Ax — b erhalten bleibt. Man findet den neuen Vektor x durch
Rücksubstitution, und berechnet die Änderung der Gesamtkosten c • x. Diese Änderung
nennt man die „reduzierten Kosten" r der neuen Komponente. Man wählt
die freie Variable aus, zu der das „negativste" r gehört, denn dabei handelt
es sich um die größte Kostenreduktion pro Einheit der neuen Variable.
8.3 Lineare Programmierung 447
Beispiel 8.3.1 Angenommen, die aktuelle Ecke wäre D,0,0), bei der der
Promovierte alle Arbeit tut — zu den Kosten von $20. Arbeitet stattdessen der
Student eine Stunde, so sinken die Kosten für den Vektor x = C,1,0) auf
$18. Die reduzierten Kosten sind also r — -2. Arbeitet die Maschine
eine Stunde, so fallen für den Vektor x = B,0,1) ebenfalls $18 Kosten an,
die reduzierten Kosten sind also ebenfalls r = -2. In diesem Fall kann der
Simplex-Algorithmus entweder den Studenten oder die Maschine als
hinzukommende Variable auswählen.
Sogar in diesem kleinen Beispiel muss der erste Schritt nicht sofort zum
besten x* gelangen. Der Algorithmus wählt die hinzukommende Variable
aus, ohne zu wissen, welchen Wert die Variable erhält. Wir haben r für einen
Wechsel der hinzukommenden Variable von 0 auf 1 berechnet; eine Einheit
kann aber zu viel oder zu wenig sein. Als nächstes wählt der Algorithmus die
herausfallende Variable aus (den Promovierten).
Je höher der Wert der hinzukommenden Variablen ist, desto geringer sind
die Kosten. Man kann diesen Wert nicht weiter erhöhen, wenn eine der
anderen positiven Komponenten (die sich ständig anpassen, um Ax = b zu
erhalten) zu null wird. Die herausfallende Variable ist jenes x^, das beim
Erhöhen des Wertes der hinzukommenden Variable zuerst den Wert null
erreicht. Wenn dies passiert, ist man an einer benachbarten Ecke angelangt.
Würde der Wert der hinzukommenden Variablen noch weiter erhöht, so würde
die herausfallende Variable negativ, was nicht passieren darf.
Wir sind gerade entlang einer Kante des zulässigen Bereichs gewandert,
von einer alten Ecke zu einer neuen Ecke. Vor dort beginnen wir erneut, die
nächste hinzukommende und herausfallende Variable zu bestimmen.
Erst wenn alle reduzierten Kosten positiv sind, ist man an einer
optimalen Ecke X* angelangt. Dort kann keine der Nullkomponenten positiv werden,
ohne die Kosten c • x zu erhöhen. Es sollte also keine neue Variable
hinzukommen, das Problem ist gelöst.
Hinweis Im Allgemeinen wird x* nach an Schritten erreicht, wobei a
nicht groß ist. Man hat aber Beispiele gefunden, bei denen der Simplex-
Algorithmus eine exponentielle Anzahl von Schritten benötigt. Es wurde
schließlich ein anderer Ansatz entwickelt, bei dem die Lösung x* garantiert
in weniger (aber komplizierteren) Schritten erreicht wird. Bei der neuen
Methode geht man durch das Innere des zulässigen Bereichs und findet x* so in
polynomieller Zeit. Khachian bewies, dass ein solches Verfahren funktioniert,
und Karmarkar machte es eflSzient. Es herrscht heute ein lebhafter
Wettbewerb zwischen Dantzig's Simplex-Algorithmus (der an den Kanten entlang
wandert) und Karmarkars Weg durch das Innere.
Beispiel 8.3.2 Man minimiere die Kosten c • x = 3x1 -\-X2+ 9x3 + 0:4, wobei
die Bedingungen durch x > 0 und zwei Gleichungen in Ak = b gegeben seien:
448 8 Anwendungen
xi + 2x3 + a;4 = 4 m — 2 Gleichungen
X2 + x^ — X4, — 2 n = 4 Unbekannte.
Als Startecke wählen wir x = D,2,0,0) mit den Kosten c • x = 14. Hier
sind m — 2 von Null verschiedene und n — m = 2 Nulleinträge {x^ und x^)
gegeben. Die Frage ist nun, ob Xs oder x^, hinzukommen sollte (also einen
Wert ungleich null annehmen sollte).
Bei xs = 1 und 0:4 = 0 verursacht der Vektor x = B,1,1,0) die Kosten 16.
Bei 0:4 = 1 und xs = 0 verursacht der Vektor x = C,3,0,1) die Kosten 13.
Man vergleiche diese Kosten mit der Zahl 14. Die reduzierten Kosten von x^
sind dann r = 2, also positiv und daher nutzlos. Die reduzierten Kosten für X4,
sind r = — 1, also negativ und hilfreich. Es wird die Variable X4 hinzukommen.
Welchen Wert darf X4 annehmen? Bei einer Einheit X4 fällt xi von 4 auf 3.
Bei vier Einheiten X4 fällt xi also von 4 auf 0, während sich X2 auf 6 erhöht.
Die herausfallende Variable ist also xi, und die neue Ecke ist x = @,6,0,4)
mit den Kosten c • x = 10. Hierbei handelt es sich um das optimale x*,
aber um dies sicher zu wissen, müssen wir noch probieren, von @,6,0,4)
einen weiteren Simplex-Schritt zu gehen. Angenommen, eine der Variablen
xi oder X3 wollte hinzukommen:
Bei xi = 1 und 0:3 = 0 kostet x = A,5,0,3) 11 Einheiten.
Bei xs = 1 und xi == 0 kostet x = @,3,1,2) 14 Einheiten.
Diese Kosten sind beide höher als 10. Beide r's sind positiv — es zahlt sich
nicht aus, sich zu bewegen. Die aktuelle Ecke @,6,0,4) stellt also wirklich
die Lösung x* dar.
Man kann diese Rechnungen noch beschleunigen. Es stellt sich heraus,
dass in jedem Simplex-Schritt drei Gleichungssysteme mit derselben Matrix
B gelöst werden, nämlich mit der m x m-Matrix, die aus den m Basisspalten
von A besteht. Es gibt eine schnelle Methode, die Inverse B~^ zu
aktualisieren, wenn eine neue Spalte hinzukommt und eine andere herausfällt. Die
meisten Computerprogramme organisieren die Schritte des Simplex-Algorithmus
auf diese Weise.
Noch ein letzter Hinweis. Wir haben beschrieben, wie man von einer Ecke
zu einem besseren Nachbarn gelangt. Wir haben aber nicht beschrieben, wie
man die erste Ecke wählt — was zwar in den Beispielen, aber nicht immer
einfach ist. Eine Möglichkeit ist, neue Variablen X5 und xq mit den
anfänglichen Werten 4 und 2 einzuführen, so dass alle eigentlichen Variablen den
Wert null haben. Dann beginnt man den Simplex-Algorithmus mit der
Kostenfunktion X5 + xq. Man schaltet auf das Originalproblem um, sobald x^
und xq den Wert null angenommen haben, denn dann wurde eine Startecke
für das eigentliche Problem gefunden.
8.4 Fourierreihen: Lineare Algebra für Funktionen 449
Aufgaben 8.3
1. Zeichnen Sie den Bereich in der xy-Ehene, in dem x + 2y = ß, x > 0
und y > 0 gilt. Welcher Punkt in dieser „zulässigen Menge" minimiert
die Kosten c = x + 3y, welcher Punkt maximiert sie?
2. Zeichnen Sie den Bereich in der xy-Ehene, in dem x + 2y < 6, 2x + y <
6, X > 0 und y > 0 gilt. Er hat vier Ecken. Welche Ecke minimiert die
Kostenfunktion c — 2x — yl
3. Bestimmen Sie die Ecken der Menge, für die xi + 2x2 — x^ — A mit
nichtnegativen Werten für xi,X2,X3 gilt. Zeigen Sie, dass die Funktion
xi + 2x3 auf der Lösungsmenge der Gleichung sehr negativ sein kann.
4. Beginnen Sie das Beispiel aus dem Text mit dem Vektor x = @,0,2),
bei dem die Maschine für 16 Dollar die gesamte Arbeit verrichtet.
Gehen Sie von dort zu x = @,1, ), und bestimmen Sie die zugehörigen
reduzierten Kosten r, also die Ersparnis pro Stunde, wenn der Student
Arbeit übernimmt. Bestimmen Sie auch die reduzierten Kosten r für den
Promovierten, indem Sie zum Vektor x = A,0, ) übergehen. Beachten
Sie, dass r nichts über die Anzahl der Stunden oder die Gesamtersparnis
aussagt.
5. Beginnen Sie mit dem Vektor D,0,0) und einem geänderten
Kostenvektor c = [ 5 3 7 ]. Zeigen Sie, dass die reduzierten Kosten r für die Maschine
besser sind, dass aber die Gesamtkosten beim Studenten geringer sind.
In diesem Fall geht der Simplex-Algorithmus zwei Schritte, erst zur
Maschine, dann zum Studenten.
6. Wählen Sie einen Kostenvektor c so, dass der Promovierte den Job erhält.
Schreiben Sie auch das duale Problem entsprechend um.
8.4 Fourierreihen: Lineare Algebra für Funktionen
In diesem Abschnitt machen wir einen Schritt von endlich vielen zu
unendlich vielen Dimensionen. Ich möchte Ihnen die lineare Algebra in unendlich-
dimensionalen Räumen vorstellen und zeigen, dass sie immer noch
funktioniert. Der erste Schritt dazu: ein Blick zurück. Wir haben in diesem Buch mit
Vektoren, mit Skalarprodukten und Linearkombinationen begonnen. Jetzt
fangen wir damit an, diese Ideen auf den unendlich-dimensionalen Fall
anzuwenden. Der Rest wird dann daraus folgen.
Was soll es bedeuten, dass ein Vektor unendlich viele Komponenten hat?
Es gibt zwei verschiedene, gute Antworten:
1 Der Vektor wird zu einer Folge -v = {vi.v^.v^,...), zum Beispiel A, |, ^,...
450 8 Anwendungen
2 Der Vektor wird zu einer Funktion /(x), zum Beispiel sinx.
Wir werden beide Möglichkeiten nutzen — sie sind über die Idee der Fourier-
reihen miteinander verbunden.
Nach den Vektoren folgte das Skalarprodukt Das natürliche Skalarprodukt
zweier unendlicher Vektoren (vi, ^2, • • •) und {wi, i(;2,...) ist eine unendliche
Reihe:
V • w = viwi + V2W2 H . (8.3)
Dies führt uns auf eine neue Frage, die bei Vektoren im W^ nie vorgekommen
war. Ergibt diese unendliche Reihe eine endliche Zahl? Konvergiert die Reihe?
Dies ist der erste und größte Unterschied zwischen endlich und unendlich.
Ist V = w = A,1,1,...), so konvergiert die Reihe sicher nicht, für diese
Vektoren istv«w = 1 + 1 + 1 + --- unendlich. Da v gleich w ist, ist der
obige Ausdruck eigentUch v • v =: ||v|p = Quadrat der Länge. Der Vektor
A,1,1,...) hat also eine unendliche Länge. Einen solchen Vektor wollen wir
nicht betrachten. Und da wir die Regeln aufstellen, müssen wir solche
Vektoren nicht berücksichtigen. Die einzigen erlaubten Vektoren sind jene mit
endlicher Länge:
DEFINITION Ein Vektor (vi, ^2, • • •) gehört zu unserem unendlich-dimen-
sionalen Hilhertraum dann und nur dann, wenn er endliche Länge hat:
||v|P = V • V =: V? + Vo + '^q + • • • muss einen endlichen Wert haben.
Beispiel 8.4.1 Der Vektor v = A, |, ^,...) gehört zum Hilbertraum, da
seine Länge 2/\/3 ist. Das Skalarprodukt ist eine geometrische Reihe mit dem
Wert 4/3. Die Länge von v ist die Quadratwurzel daraus:
-•- A
_ 4
3'
4
Frage Wie groß kann das Skalarprodukt von v und w werden, wenn beide
Vektoren endliche Länge haben?
Antwort Die Reihe \»vf = viwi +V2W2 H hat dann auch einen endlichen
Wert. Die Schwarz'sehe Ungleichung ist immer noch richtig:
|v.w|<|iv|||H|. (8.4)
Der Verhältnis von v«w zu ||v|| ||w|| ist immer noch der Kosinus des Winkels
9 zwischen v und w. Sogar in undlichdimensionalen Räumen ist |cosö| nicht
größer als 1.
Betrachten wir jetzt Funktionen als Vektoren. Der Raum von Funktionen
f{x),g{x), h{x),..., die für 0 < X < 27r definiert sind, muss in gewisser Weise
8.4 Fourierreihen: Lineare Algebra für Funktionen 451
größer sein als W. Welches Skalarprodukt haben zwei Funktionen f{x) und
Im kontinuierlichen Fall ist die Grundidee, Summen durch Integrale zu
ersetzen. Anstelle einer Summe über Vj mal Wj ist das Skalarprodukt ein
Integral über f{x) mal g{x). Wir ändern in der Notation den „Punkt" zu runden
Klammern mit einem Komma in der Mitte, und anstelle von „Skalarprodukt"
spricht man auch von einem inneren Produkt.
DEHI^(!tiOlSI'';, t>Bä"inn^]^n>d^ X(^Xj^^^.^^(f).w4 ä)||\|CiiftM|J
<i€^€JSrfg^,:Mh4';::^":h[]-': ^, ''::'r; ?';/lr"j^ ;-;' 7:;MX'''''^''^r:^]i^
' {f,9)= rf{x)9{x)dx 'tÄ^: ||/|p= f\f{x))'dx, ^'"-Öi?
Man könnte das Intervall [0,27r], auf dem die Funktionen definiert sind, durch
ein anderes Intervall wie [0,1] ersetzen. Wir haben 27r gewählt, weil wir als
erste Beispiele sin x und cos x betrachten wollen.
Beispiel 8.4.2 Die Länge von j{x) — sin x erhält man aus dem Skalarprodukt
des Vektors mit sich selbst:
/•27r
(/,/) — / (sinx)^ dx — TT. Die Länge von sinx ist \pK.
Jo
Dies ist eines der Standardintegrale in der Integralrechnung — es gehört nicht
zur linearen Algebra. Wenn wir sin^ x als | - | cos2x schreiben, sehen wir,
wie die Funktion um ihren Mittelwert | schwingt. Multipliziert man diesen
Mittelwert mit der Intervalllänge 27r, so erhält man das Ergebnis tt.
Viel wichtiger: Die Funktionen sinx und cosx sind orthogonal Das
innere Produkt ist null:
f^^ f^^ 27r
/ sinx cosx dx—j | sin 2x dx =: [-1 cos 2x] ^ =0. (8.6)
JQ Jo
Diese Null ist kein Zufall. Sie ist für die Wissenschaft extrem wichtig. Die
Orthogonalität erstreckt sich über die beiden Funktionen sin x und cos x
hinaus auf eine unendliche Liste von Kosinus- und Sinusfunktionen. Diese Liste
enthält die Funktionen cosOx (also konstant 1), sinx, cosx, sin2x, cos2x,
sin3x, cos3x,
Jede Funktion dieser Liste ist orthogonal zu jeder anderen
Funktion in der Liste.
Der nächste Schritt ist, sich die Linearkombinationen dieser Funktionen
anzusehen.
452 8 Anwendungen
Fourierreihen
Die Fourierreihe einer Funktion y{x) ist die Entwicklung dieser Funktion nach
Kosinus- und Sinusfunktionen:
y{x) =ao "j-äicosx-^bisinx -^a2Cos2x + b2sm2x ^ ■•' . (8.7)
Wir haben eine Orthogonalbasis! Die Vektoren in diesem Funktionenraum
sind Linearkombinationen der Sinus- und Kosinusfunktionen. Auf dem
Intervall von X =: 27r bis X == 47r wiederholen alle unsere Funktionen ihre Werte
vom Intervall 0 bis 27r. Sie sind periodisch. Der Abstand zwischen zwei
Wiederholungen, die Periode, ist 27r.
Denken Sie daran, dass unsere Liste unendlich ist. Die Fourierreihe ist
eine unendliche Reihe. Genauso, wie wir den Vektor v = A,1,1,...) wegen
seiner unendlichen Länge ausschließen mussten, schließen wir auch
Funktionen wie I + cos X + cos 2x + cos 3x + • • • aus. {Hinweis: Hierbei handelt es
sich um das 7r-fache der berühmten Deltafunktion. Diese Funktion ist eine
„unendlich hohe Spitze" über einem einzigen Punkt. Bei x = 0 ist die Höhe
I + 1 + 1 + • • • unendlich. An allen anderen Stellen 0 < x < 27r geht die
Reihe in einem gewissen gemittelten Sinn gegen Null.) Die Deltafunktion
hat eine unendliche Länge, und ist deshalb bedauerlicherweise aus unserem
Funktionenraum ausgeschlossen.
Wir berechnen die Länge einer typischen Summe /(x):
/•27r
(/j f) — (^0 + öl cos X -I- Öl sin X -I- a2 cos 2x -|- • • • )^ dx
r27r
{al + al cos^ X -\-bl sin^ x + al cos^ 2x H ) dx
0
= 27ra^ + 7r(a? -\-bj-\-al + "-). (8.8)
Im Schritt von Zeile 1 auf Zeile 2 haben wir die Orthogonalität
verwendet. Das Integral aller Produkte wie cosxcos2x und sinxcosSx ist null. In
Zeile 2 steht, was dann noch übrig bleibt — die Integrale der quadrierten
Kosinus- und Sinusfunktionen. In Zeile 3 wurden diese Integrale
ausgerechnet. Unglücklicherweise ist das Integral von 1^ gleich 27r, wohingegen alle
anderen Integrale den Wert n haben. Dividieren wir durch die Längen, so
erhalten wir orthonormale Funktionen:
1 cosx sinx cos2x . , . ^ ., „ •
ist eine ürthonormalbasis
L
unseres Funktionenraums.
Diese Vektoren sind Einheitsvektoren. Bilden wir aus ihnen
Linearkombinationen mit Koeffizienten ^0,^1,^1,^2,... und erzeugen so eine Funktion
F(x), so fallen die Faktoren mit tt aus der Formel für die Länge heraus. Aus
Gleichung (8.8) wird dann schlicht Länge der Funktion^Länge des Vektors:
8.4 Fourierreihen: Lineare Algebra für Funktionen 453
||F|P = {F,F)^Al+Al + Bl + Al + .... (89)
Dies ist ein wichtiger Punkt, für f{x) ebenso wie für F{x). Die Funktion hat
genau dann eine endliche Länge, wenn der Koeffizientenvektor eine endliche
Länge hat. Das Integral von {F{x)f stimmt genau mit der Summe der
Quadrate der Koeffizienten überein. Durch die Fourierreihen haben wir also eine
perfekte Übereinstimmung zwischen dem Funktionenraum und dem unend-
lichdimensionalen Hilbertraum. Auf der einen Seite steht eine Funktion auf
der anderen Seite ihre FourierkoefRzienten. '
8B Der Funktioö^arauiii enth^t eine FusktioÄ /(ar) gßte dato w^ö
der Hilberttarjm den Vektpr y = (%;4A,/^.yd^ Ppijj|ä|q^^i^'
enthält. JÖaim h&l^m. sowohI../{a;) als au^h v eins enälÄ t^^^ä^^f^y'^-T,
Beispiel 8.4.3 Angenommen, die Funktion f{x) sehe aus wie eine
„Rechteckkurve", das heißt gleich -1 für negative x und gleich +1 für positive x Bis
hierhier sieht es nach einer Treppenfunktion aus, aber nicht nach einer
Rechteckkurve. Bedenken Sie aber, dass sich die Funktionswerte f{x) nach jedem
Intervall der Länge 2n wiederholen müssen. Wir hätten also sagen sollen:
(-1 für -TT < X <0
[+1 für 0<a;<7r.
Die Punktion nimmt dann für tt < x < 27r wieder den Wert -1 an, und so
weiter. Bei dieser Funktion handelt es sich um eine ungerade Funktion, wie
alle Smusfunktionen. Die Kosinus-Koeffizienten sind deshalb null. Wir werden
die Fourierreihe dieser Punktion bestimmen; sie besteht nur aus Sinustermen:
,, V 4 rsinaj _ sinSo; sinBa; - i
/(.) = -.[_ + __ + __ + ....]. (8.10)
Die Rechteckkurve hat die Länge v^, weil das Quadrat (f(x)? an jeder
Stelle gleich (-1J oder (+1J ist: ^ '
II/IP=/ {f{x)fdx= ldx = 2iT.
Jo Jo
ei X = 0 sind die Sinusterme alle null, und die Fourierreihe (8.10) ergibt
oen Wert null. Dieser Wert liegt in der Mitte des Sprungs von -1 zu +1. Der
wert der Fourierreihe ist auch für x = f interessant. Das Quadrat der Recht-
cKkurve an dieser Stelle hat den Wert eins, aber die Sinusterme alternieren
zwischen -1-1 und -1:
1 4/ 1 1 1 V
(8.11)
454 8 Anwendungen
Multiplizieren Sie die Gleichung mit tt, und Sie erhalten eine magische Formel
4A - I + I - 7 + • • •) für diese berühmte Zahl.
Die Fourierkoeffizienten
Wie bestimmt man die Koeffizienten ak und bk vor den Kosinus- und Sinus-
termen? Wir suchen die Fourierkoeffizienten einer gegebenen Funktion /(x),
so dass gilt:
f{x) = ao + ai cos x + &i sin x + a2 cos 2x + • • • .
Eine Möglichkeit, ai zu bestimmen, ist, beide Seiten der Gleichung mit cosx
zu multiplizieren, und dann von 0 bis 27r zu integrieren. Der Schlüssel dabei
ist die Orthogonalität. Auf der rechten Seite sind alle Integrale bis auf das
Integral über ai cos^ x null:
/»27r /»27r
/ f{x)cosxdx= / aicos^ xdx = nai. (8.12)
Jo Jo
Dividiert man dann noch durch tt, so erhält man ai. Um ein anderes ak zu
bestimmen, multipliziert man einfach die Fourierreihe mit coskx und
integriert von 0 bis 27r. Wegen der Orthogonalität bleibt nur das Integral von
ak cos^ kx mit dem Wert nak übrig. Nach Division durch n erhält man also
Uk = — I f{w)coshü5dx und analog &^ =: - / . /(a:)sitiA;^(to,
(8.13)
Eine Ausnahme stellt ao dar, hier multipliziert man mit cosOx = 1. Das
Integral von 1 ist 27r:
1 f^^
ao = —- / f{x) 'ldx = Mittelwert von f{x). (8.14)
27r Jo
Ich habe diese Formeln verwendet, um die Koeffizienten in Gleichung (8.10)
für die Rechteckkurve zu bestimmen. Das Integral von f{x)coskx ist null.
Das Integral von f{x) sin kx ist A/k für ungerade k.
Es soll hier betont werden, wie sehr der unendlich-dimensionale Fall dem
n-dimensionalen ähnelt. Nehmen wir an, die von Null verschiedenen Vektoren
Vi,..., Vn sind orthogonal. Wir wollen dann den Vektor b als Kombination
der v's schreiben:
b = CiVi + C2V2 H h Cn-^n- (8.15)
Multipliziert man beide Seiten mit vf und verwendet die Orthogonalität, so
erhält man vf V2 = 0, und nur der Term mit ci bleibt übrig:
8.4 Fourierreihen: Lineare Algebra für Funktionen 455
vf b = civf Vi + 0 H h 0. Deshalb gilt ci =
vfb
T
Vi Vi
(8.16)
Im Nenner steht das Quadrat der Länge, vf vi, wie n in Gleichung (8.13). Der
Zähler vfh ist das innere Produkt analog f f{x) cos kxdx. Die Koeffizienten
sind also leicht zu bestimmen, wenn die Basisvektoren orthogonal sind. Wir
führen einfach eindimensionale Projektionen durch, um die Komponenten
längs eines jeden Basisvektors zu bestimmen.
Die Formeln werden sogar noch besser, wenn die Vektoren orthonormal,
also Einheitsvektoren sind. Dann sind die Nenner yjvk alle gleich Eins. In
diesem orthonormalen Fall gilt
Ci = vf b und C2 = v^b und Cn — v^b. (8.17)
In anderer Form kennen Sie dies bereits. Die Gleichung für die c's ist
civi H h Cn^n — b oder
Vi
ci
= b.
Dies ist eine orthogonale Matrix Q\ Ihre Inverse ist Q^^ und daraus erhält
man dieselben c's wie in Gleichung (8.17):
Qc — h liefert c = Q^h, Zeilenweise gelesen ist dies q = vf b.
Mit den Fourierreihen ist es wie mit einer Matrix mit unendlich vielen
orthogonalen Spalten. Diese Spalten sind die Basisfunktionen 1, cos x, sin x,
Dividiert man sie durch ihre Längen, so erhält man eine „unendliche
orthogonale Matrix", deren Inverse ihre Transponierte ist. Die Formeln für die
Fourierkoeffizienten sind analog zu (8.17) für Einheitsvektoren und zu (8.16)
für andere orthonormale Vektoren. Die Orthogonalität ist es also, die eine
unendliche Reihe auf einen einzigen Term reduziert.
Aufgaben 8.4
1- Integrieren Sie die Gleichung 2cos jxcoste = cos(j -h k)x -}- cos(j - k)x
und zeigen Sie so, dass cosjx orthogonal zu coskx ist, wenn j ^ k gilt.
Welches Ergebnis erhalten Sie für j — kl
2. Zeigen Sie, dass die drei Funktionen l,x, und x'^ - \ orthogonal sind,
wenn man von x = -1 bis x = 1 integriert. Schreiben Sie f{x) = 2x^ als
Linearkombination dieser orthogonalen Funktionen.
3. Bestimmen Sie einen Vektor {wi,W2,W3,...), der orthogonal zu v =
A, |, |,...) ist, und berechnen Sie seine Länge ||w||.
456 8 Anwendungen
4. Die ersten drei Legendre-Polynome sind l,x und x'^ - ^, Bestimmen Sie
eine Zahl c so, dass das vierte Polynom x^ — ex orthogonal zu den ersten
drei Polynomen ist. Die Integrale werden wieder von —1 bis 1 berechnet.
5. Zeigen Sie, dass für die Rechteckkurve f{x) in Beispiel 8.4.3 die
Gleichungen
/»27r /»27r /»27r
/ f{x)cosxdx = 0 / f{x)sinxdx = 4 / f{x)sin2xdx = 0
Jo Jo Jo
gelten. Welche Fourierkoeffizienten erhält man über diese Integrale?
6. Den Wert welcher bemerkenswerten Reihe stellt die Länge ||/|p = 27r der
Rechteckkurve nach Gleichung (8.8) dar?
7. Zeichnen sie den Graphen der Rechteckkurve, und dann (von Hand) den
Graphen der Summe von zweien der Sinusterme in der Fourierreihe, oder
(mit Hilfe eines Rechners) die Summe von zwei, drei und vier Termen.
8. Bestimmen Sie die Länge der folgenden Vektoren im Hilbertraum:
(b) v = (l,a,a2,...)
(c) f{x) = 1 + sinx.
9. Berechnen Sie die Fourierkoeffizienten a^ und bk für die folgenden von 0
bis 27r definierten Funktionen f{x):
(a) f{x) = 1 für 0 < X < TT, f{x) = 0 für tt < x < 27r
(b) fix) = X.
10. Warum ist das Integral einer 27r-periodischen Funktion f{x) von —tt bis
TT gleich dem Integral von 0 bis 27r? Zeigen Sie, dass Jq ^ f{x) dx gleich
Null ist, wenn f{x) eine ungerade Funktion ist (wenn also f{—x) — —f{x)
gilt).
11. Bestimmen Sie mit Hilfe der Additionstheoreme zwei Terme der
Fourierreihe zu f{x):
(a) f{x) — cos^ X
(b) fix) =:cos(x+f)
12. Die Funktionen 1, cos x, sin x, cos 2x, sin 2x,... bilden eine Basis des Hil-
bertraums. Geben Sie die Ableitungen der ersten fünf Funktionen als
Linearkombinationen derselben fünf Funktionen an, und bestimmen Sie
die 5 X 5-„Ableitungsmatrix" für diese Funktionen.
13. Bestimmen Sie die vollständige Lösung der Differentialgleichung dy/dx =
cos x als Summe aus einer speziellen Lösung und den Lösungen der Glei-
rVinnoc Hii IHnr =z 0
8.5 Computergrafik 457
8.5 Computergrafik
pie Computergrafik behandelt dreidimensionale Bilder. Diese Bilder werden
bewegt, skaliert oder auf eine zweidimensionale Ebene projiziert. Alle
wesentlichen Operationen werden mit Hilfe von Matrizen durchgeführt — deren
Gestalt aber etwas überraschend ist.
Die Transformationen des dreidimensionalen Raums werden mit Hilfe von
4 X 4-Matrizen durchgeführt, statt der 3 x 3-Matrizen, die man erwarten
würde. Der Grund für diese Änderung ist, dass eine der vier
Grundoperationen nicht durch eine 3 x 3-Matrixmultiplikation dargestellt werden kann.
Dies sind die vier Operationen:
- Translation (man bewegt den Ursprung zu einem anderen Punkt Pq =
- Skalierung (um einen Faktor c in alle Richtungen, oder um verschiedene
Faktoren ci, 02,03)
- Drehung (um eine Achse durch den Ursprung, oder eine Achse durch Fo)
- Projektion (auf eine Ebene durch den Ursprung, oder eine Ebene durch
Po).
Die einfachste Operation ist die Translation — man addiert einfach (xo, 2/0, zq)
zu jedem Punkt. Diese Operation ist aber nicht linear! Keine 3 x 3-Matrix
kann den Ursprung verschieben. Deshalb schreiben wir die Koordinaten des
Ursprungs als @,0,0,1). Deshalb tauchen 4 x 4-Matrizen auf. Die
„homogenen Koordinaten" eines Punktes {x,y,z) sind {x,y,z, 1). Wir werden jetzt
beschreiben, welchen Effekt diese Änderung hat.
1. Translation Wir wollen den gesamten dreidimensionalen Raum um einen
Vektor vq verschieben. Der Ursprung wird also zu (xo^yo^zo), und dieser
Vektor wird zu jedem Punkt im M^ hinzuaddiert. In homogenen Koordinaten
wird die Translation um einen Vektor vo durch die folgende 4 x 4-Matrix T
beschrieben:
Transtationsmatrix T —
10 0 0'
0 100
0 0 1 ö
^0 yo ^l
Wichtig: In der Computergrafik arbeitet man mit Zeilenvektoren. Hier wird
^Iso die „Zeile-mal-Matrix"-Multiplikation verwendet. Es lässt sich leicht
überprüfen, dass [0 0 0 1] T = [xq yo zq 1] gilt.
Um also die Punkte @,0,0) und {x,y,z) um vq zu bewegen, wechselt
nian zuerst zu den homogenen Koordinaten @,0,0,1) und {x,y,z,l) und
Multipliziert dann mit T. Das Produkt eines Zeilenvektors mit T ist wieder ein
Zeilenvektor: Jedes V wird zuv+vq: [x y z 1]T = [x+xo y-^yo z+zq 1]
458 8 Anwendungen
Aus dem Ergebnis der Multiplikation ergibt sich also, wohin ein beliebiges
V bewegt wird. (Nämlich zu v + vq.) Damit wird die Translation durch eine
Matrixmultiplikation beschrieben, was im M^ unmöglich war.
2. Skalierung Um ein Bild an die Seitengröße anzupassen, ändert man seine
Breite und seine Höhe. Ein Kopiergerät kann eine Grafik zum Beispiel auf
90% skaUeren. In der linearen Algebra bedeutet dies, ein Bild mit 0,9 mal
Einheitsmatrix zu multiplizieren, wobei die Matrix normalerweise eine 2x2-
Matrix für eine Ebene und eine 3 x 3-Matrix für dreidimensionale Körper
ist. Für die homogenen Koordinaten in der Computergrafik muss die Matrix
um eins größer sein:
Skalierung der Ebene: S =
%9
Skalierung eines Körpers: S
0,9
cOOO
OcOO
OOcO
0001
Wichtig: S ist nicht cl. Wir behalten die 1 in der unteren rechten Ecke. Dann
bleibt [x,y, 1] mal S ein richtiges Ergebnis in homogenen Koordinaten. Der
Ursprung bleibt in seiner Position, da [0 0 1]5 = [0 01] gilt.
Würde man die 1 zu einem c ändern, so ergäbe sich ein seltsames Ergebnis.
Der Punkt {cx,cy,cz,c) ist derselbe Punkt wie {x,y,z,l). Die besondere
Eigenschaft der homogenen Koordinaten ist, dass eine Multiplikation mit
cl einen Punkt nicht verändert. Der Ursprung des M^ hat die homogenen
Koordinaten @,0,0,1) oder @,0,0, c) für jedes von Null verschiedene c. Dies
ist die Idee hinter dem Begriff „homogen".
Man kann in verschiedene Richtungen verschieden stark skalieren. Um
ein ganzseitiges Bild auf eine halbe Seite zu bringen, skaliert man die y-
Richtung um einen Faktor |. Um noch einen Seitenrand zu erlauben, kann
man in x-Richtung um einen Faktor | skalieren. In der Computergrafik
werden Skalierungen durch eine diagonale Matrix vorgenommen, die allerdings
keine 2 x 2-Matrix ist, sondern eine 3 x 3-Matrix für ebene und eine 4x4-
Matrix für räumliche Skalierungen:
Skalierungsmatrix S =
und 5 =
Cl
C2
C3
Die letzte Matrix S skaliert die x-, die y- und die ^-Richtung um
positive Zahlen ci,C2,C3. Der Ursprung bewegt sich nicht, weil [O 0 0 l] 5 =
[0 0 0 1] ist.
8.5 Computergrafik 459
Zusammenfassung Die Skalierungsmatrix S hat dieselbe Größe wie die
Translationsmatrix T. Man kann sie also miteinander multiplizieren. Um
erst eine Translation und dann eine Skalierung durchzuführen, berechnet
man vTS, und um umgekehrt erst zu skalieren und dann die Translation
auszuführen, berechnet man vST. (Gibt es da einen Unterschied? Ja.) Die
zusätzliche Spalte in allen Matrizen sorgt dafür, dass die zusätzliche 1 am
Ende der Vektoren bei der Multiplikation erhalten bleibt.
Ein Punkt {x,y,z) im M? hat die homogenen Koordinaten {x,y,z,l) in
P^. Dieser „projektive Raum" ist nicht dasselbe wie der M^. Er ist nach wie
vor dreidimensional. Damit dies gilt, muss man {cx,cy,cz,c) als denselben
Punkt ansehen wie {x,y,z, 1). Die Punkte in P^ sind also eigentlich Geraden
durch den Ursprung im IR;*.
In der Computergrafik werden affine Abbildungen verwendet, lineare
Abbildung plus Verschiebung. Eine affine Abbildung T wirkt im P^ durch eine
4 X 4-Matrix mit einer speziellen vierten Spalte:
A=:
«11 0,12 0,13 0
«21 Ö22 «23 0
^31 Os2 a33 0
«41 042 «43 1_
TA,0,0H
T@,1,0H
no, 0,1H
no, 0,0I
Die üblichen 3x3-Matrizen liefern drei Ergebniskomponenten, diese Matrizen
liefern vier. Die übUchen drei Ergebnisse stammen von den Eingaben A,0,0),
@,1,0) und @,0,1). Ist die Abbildung eine lineare Abbildung, so wird durch
die Ergebnisse für diese drei Vektoren die gesamte Abbildung bestimmt. Bei
einer affinen Abbildung kommt noch das Ergebnis für @,0,0) hinzu — die
Verschiebung.
3. Drehung Eine Drehung im M^ oder E^ wird durch eine orthogonale
Matrix Q dargestellt, deren Determinante +1 ist. (Ist die Determinante -1, so
ist noch eine Spiegelung enthalten.) Wenn wir homogene Koordinaten
verwenden, müssen wir noch eine zusätzliche Spalte hinzufügen!
Die ebene Drehung Q —
cos ö — sin ö
sin 6 cos 6
wird zu -S ^
COS ^V sin ^ 0
Diese Matrix dreht eine Ebene um den Ursprung. Wie würde man um
^inen anderen Punkt drehen^ zum Beispiel D,5)? In der Antwort erkennt
^an die Eleganz der homogenen Koordinaten. Man verschiebt den Punkt
D,5) nach @,0), dreht dann um einen Winkel 9, und verschiebt dann den
Ursprung zurück zu D,5):
vT_RT^ = [xyl]
1 0 0
0 10
-4-5 1
cos^-
sin^
0
-sinö 0"
cos (9 0
0 1
001
0 10
45 ij
460 8 Anwendungen
Ich werde dies jetzt nicht ausrechnen. Der Punkt ist gerade, dass man die
Matrizen eine nach der anderen anwendet: v wird zu vT« verschoben, dann
in den Punkt vT-R gedreht und dann zurück zu vT-RT^ verschoben. Weil
jeder Punkt [a: 2/ 1] durch einen Zeilenvektor dargestellt wird, wirkt T-
zuerst. Der Drehmittelpunkt D,5) — wir schreiben D,5,1) — wird dann zu
@,0,1). Dieser Vektor wird bei der Drehung nicht verändert. Schließlich wird
er durch 7+ zurück zu D,5,1) verschoben — so sollte es sein. Der Punkt
D,6,1) beispielsweise wird in den Punkt @,1,1) verschoben, gedreht und
zurückverschoben.
In drei Dimensionen dreht jede Drehung Q um eine Achse. Die Achse
bewegt sich dabei nicht — es handelt sich um die Eigenvektorgerade zum
Eigenwert A = 1. Nehmen wir an, die Achse läge in .^-Richtung. Die 1 in Q
sorgt dafür, dass die z-Achse unverändert bleibt, die zusätzliche 1 in i? sorgt
dafür, dass der Ursprung unverändert bleibt.
Q
cos ö - sin ö 0
sin 9 cos ö 0
0 0 1
und R =
0
0
0
0 001
Q
Nehmen wir nun an, die Drehung soll um eine Achse in Richtung des
Einheitsvektors a = @1,02,03) herum stattfinden. Dann besteht die Drehmatrix
Q (innerhalb von R) aus drei Teilen:
Q = (cosi9)/ + (l-cos(9)
2
of O1O2 O1O3
0102 02 0203
0103 0203 03
— sin ö
0 03 —02
—03 0 Ol
02 —Ol 0
(8.18)
Die Achse wird nicht verändert, weil aQ = a gilt. Für a = @,0,1) erhälf
man gerade die z-Richtung und daher dasselbe Q wie zuvor.
Die lineare Abbildung Q bildet immer den oberen linken Block von Rp
Darunter liegen Nulleinträge, weil eine Drehung den Ursprung unverändert
lässt. Sind diese Einträge von Null verschieden, so handelt es sich um eine
affine Abbildung, die den Ursprung bewegt.
4. Projektion In einer Vorlesung über lineare Algebra enthalten die meisten
Ebenen den Ursprung. Im wirklichen Leben enthalten sie ihn meist nicht. Eine
Ebene durch den Ursprung ist ein Vektorraum, und die anderen Ebenen sind
aflftne Räume. Man erhält einen aflänen Raum, wenn man einen Vektorraum
verschiebt.
Wir wollen jetzt dreidimensionale Vektoren auf Ebenen projizieren. Dazu
beginnen wir mit einer Ebene durch den Ursprung mit
Einheitsnormalenvektor n. (Wir schreiben n weiterhin als Spaltenvektor.) Die Vektoren der
Ebene erfüllen die Gleichung n^v = 0. Die übliche Projektion auf die Ebene
ist durch die Matrix / — nn^ gegeben, die den Vektor n auf Null projiziert
und die Vektoren in der Ebene auf sich selbst:
8.5 Computergrafik 461
(/ — nn^)n = n — n(n^n) = 0 und (/ — nn^)v = v — n(n^v) = v.
In homogenen Koordinaten erhalten wir eine 4 x 4-Projektionsmatrix (die
den Ursprung nicht bewegt):
.^.'^--'<rA;-k. a;%
i'ih^^lC:- 'l<^'fi'i
hu
^Iv^
Jetzt wollen wir auf eine Ebene der Form n-^(v—vo) =0 projizieren, die nicht
durch den Ursprung verläuft. Ein Punkt der Ebene sei vq. Es handelt sich
hierbei um einen affinen Raum, wie bei den Lösungen der Gleichung Av = b,
wenn die rechte Seite nicht null ist. Dabei wird eine spezielle Lösung vo zum
Kern addiert, und so ergibt sich ein affiner Raum.
Die Projektion auf eine affine Ebene geschieht wieder in drei Schritten.
Zuerst wird durch eine Translation TL der Vektor vo in den Ursprung
verschoben. Dann projiziert man entlang der Richtung des Vektors n, und schUeßlich
verschiebt man den Ursprung wieder zurück nach vq:
Projektion auf eine affine Ebene
T-PT^ =
/ 0
-Vo 1
- nn
0
^0
1
/ 0
Vo 1
Ich kann nicht anders, als kurz zu bemerken, dass T- und 7+ zueinander
inverse Matrizen sind: Translation hin und zurück. Sie sind vergleichbar den
Elementarmatrizen aus Kapitel 2.
In den Aufgaben werden auch Spiegelungsmatrizen auftreten, die als
fünfter Typ von Operationen in der Computergrafik verwendet werden. Eine
Spiegelung bewegt jeden Punkt doppelt so weit wie die Projektion — sie verläuft
durch die Ebene hindurch auf die andere Seite. Um eine Spiegelungsmatrix
zu beschreiben, ändert man also einfach die Projektionsmatrix von / — nn^
zu / - 2nn^ ab.
Die Matrix P beschreibt eine Para//e/projektion. Alle Punkte bewegen
sich parallel zu n, bis sie die Ebene erreichen. Eine andere Möglichkeit in
der Computergraphik ist die perspektivische Projektion. Sie wird öfter
verwendet, weil sie die Längenverkürzung darstellt. Bei einer perspektivischen
Darstellung sieht ein Objekt größer aus, wenn es sich näher heranbewegt.
Anstatt parallel zu n (und daher parallel zueinander) zu liegen, laufen die
Projektionsgeraden auf das Auge zu — das Projektionszentrum. Auf diese
Weise nehmen wir Tiefe in einem zweidimensionalen Foto wahr.
Die grundlegende Fragestellung der Computergrafik beginnt mit einer
Szene und einem Betrachterstandpunkt. Idealerweise sieht man als Bild auf dem
Bildschirm genau das, was der Betrachter sehen würde. Das einfachste Bild
ordnet jedem kleinem Element des Bildes ein Bit zu — man nennt dies ein
462 8 Anwendungen
Pixel Dieses Pixel ist entweder hell oder dunkel. Auf diese Weise erhält man
ein Schwarz-Weiß-Bild ohne Graustufen. Das würde Ihnen wohl kaum
gefallen. In der Praxis weist man jeder der drei Farben Rot, Grün und Blau einen
Helligkeitswert zwischen 0 und 2^ zu. Dann braucht man aber für jedes Pixel
8 X 3 = 24 Bit. Multipliziert man dies mit der Anzahl der Pixel, so erhält
man einen immensen Speicherbedarf!
Physikalisch wird ein Elektronenstrahl durch einen Raster-Bildspeicher
gesteuert, der den Strahl wie bei einem Fernsehgerät lenkt. Die Bildqualität
wird durch die Anzahl der Pixel und die Anzahl Bits pro Pixel festgelegt. Ein
Standardlehrbuch für dieses Gebiet ist Computer Graphics: Principles and
Practices von Foley, Van Dam, Feiner und Hughes (Addison-Wesley, 1990).
Meine besten Referenzunterlagen dazu sind Vorlesungsskripte von Ronald
Goldman von der Rice University und von Tony DeRose von der University
of Washington (mittlerweile bei Pixar).
Die wesentlichen Punkte
l.In der Computergrafik werden Verschiebungen der Form T'(v) = v + vq
und lineare Operationen T'(v) = Av verwendet.
2. Eine Verschiebung in E"^ kann bei Verwendung homogener Koordinaten
durch eine (n + 1) x (n + 1)-Matrix ausgedrückt werden.
3. Die zusätzliche Komponente 1 in[xyzl] bleibt erhalten, wenn alle
Matrizen die Zahlen 0,0,0,1 als letzte Spalte haben.
Aufgaben 8.5
1. Ein allgemeiner Punkt im E^ hat die Form xi + yj-{- zk, wobei die
Koordinatenvektoren i, j und k durch A,0,0), @,1,0) und @,0,1) gegeben
sind. Die Koordinaten des Punktes sind dann {x^y^z).
In der Computergrafik beschreibt man diesen Punkt als xi + yj -{■ zk -t
Ursprung. Seine homogenen Koordinaten sind (,,,), oder auch
(,,,).
2. Eine lineare Abbildung T wird durch die Vektoren T(i),T(j) und r(k)
festgelegt. Bei einer affinen Abbildung muss man außerdem noch T{ _)
angeben. Ein Punkt (a:, y, z, 1) wird dann auf den Punkt ^^^(i) + yT{j) -f
zT{k) + abgebildet.
3. Multiplizieren Sie die 4 x 4-Matrizen T für eine Translation um A,4,3)
und Ti für eine Translation um @,2,5). Das Produkt TTi ist eine
Translation um .
4. Multiplizieren Sie die 4 x 4-Matrix S für eine Skalierung um den Faktor
c und die Translationsmatrix T für eine Translation um A,4,3). Würden
8.5 Computergrafik 463
Sie vST oder vTS verwenden, wenn Sie ein Bild um den Mittelpunkt
A,4,3) herum vergrößern wollen?
5. Durch welche 3 x 3-Skalierungsmatrix S (in homogenen Koordinaten)
würde diese Seite quadratisch werden?
6. Welche 4 x 4-Matrix verwendet man, um die Ecke eines Würfels von
A,1,2) in den Ursprung zu bewegen und dann alle Längen mit 2 zu
multiplizieren?
7. Zeigen Sie, dass das Produkt der drei Matrizen in Gleichung (8.18) mit
dem Einheitsvektor a die Vektoren (cosö)a, A -cosö)a und 0 ergibt. Die
Addition ergibt dann aQ = a, so dass die Drehachse unverändert bleibt.
8. Zeigen Sie, dass das Produkt eines Vektors b (senkrecht zur Drehachse a)
mit den drei Matrizen in Gleichung (8.18) die Vektoren (cosö)b, 0 sowie
einen Vektor senkrecht zu b liefert. Deshalb bildet Qb mit b einen Winkel
0. Dies ist eine Drehung.
9. Bestimmen Sie die 3 x 3-Projektionsmatrix / - nn^ auf die Ebene ^x +
ly -\- ^z = 0. Fügen Sie 0,0,0,1 als zusätzliche Zeile und Spalte an, um
zu homogenen Koordinaten überzugehen.
10. Bestimmen Sie eine Translation T-, die einen beliebigen Punkt der Ebene
|a:+|2/+|z = lin den Ursprung verschiebt. Die inverse Matrix T^
verschiebt ihn wieder zurück. Bestimmen Sie schließlich aus dem Produkt
T-PT^ die Projektionsmatrix auf die Ebene ^x -\- ^y -\- ^z = 1.
11. Projizieren Sie den Vektor C,3,3) mit der Matrix P aus Aufgabe 9 und
der Matrix T-PT^ aus Aufgabe 10 auf die beiden Ebenen.
12. Welche Form hat die Projektion eines Quadrats auf eine Ebene?
13. Welchen Umriss ergibt die Projektion eines Würfels auf eine Ebene, wenn
die Projektionsebene senkrecht zu einer Diagonalen des Würfels steht?
14. Die 3 X 3-Spiegelungsmatrix, die einen Punkt an einer Ebene n^v = 0
spiegelt, ist durch M = I — 2nn^ gegeben. Bestimmen Sie den zu C,3,3)
an der Ebene ^x -\- ^y -\- ^z = 0 gespiegelten Punkt.
15. Bestimmen Sie die Spiegelung von C,3,3) an der Ebene ^x+^y+^z = 1
durch 4 x 4-Matrizen mit Hilfe der drei Schritte T-MTy. Verschieben
Sie die Ebene mittels r_ in den Ursprung, spiegeln Sie den verschobenen
Punkt C,3,3, l)!"- an dieser Ebene und verschieben Sie das Ergebnis
mit T^ zurück.
464 8 Anwendungen
16. Der Vektor zwischen dem Ursprung @,0,0,1) und dem Punkt {x, y, z, 1)
ist die Differenz v = . In homogenen Koordinaten enden Vektoren
auf . Man addiert also einen zu einem Punkt, nicht einen
Punkt zu einem Punkt.
17. Multipliziert man nur die letzte homogene Koordinate eines Punktes und
erhält {x,y,z,c), so skaliert man eigentlich den gesamten Raum um den
Faktor , weil {x,y,z,c) dasselbe ist wie ( , , ,1).
9 Numerische lineare Algebra
9.1 Gauß'sche Elimination in der Praxis
Die numerische lineare Algebra ist ein Ringen um schnelle und präzise
Lösungsverfahren. Man braucht effiziente Verfahren, aber man muss
Instabilität vermeiden. Bei der Gauß'schen Elimination liegt die größte Freiheit
(die man immer hat) in der Möglichkeit, Gleichungen zu vertauschen. In
diesem Abschnitt werden wir erklären, wann man Zeilen aus Gründen der
Geschwindigkeit vertauschen sollte, und wann, um eine höhere Genauigkeit
zu erreichen.
Der Schlüssel zur Genauigkeit liegt darin, unnötig große Zahlen zu
vermeiden. Oft verlangt dies, dass wir kleine Zahlen vermeiden! Ein kleines
Pivotelement führt zu großen Multiplikatoren (da wir durch das Pivotelement
dividieren). Außerdem zieht ein kleines Pivotelement jetzt ein großes später
nach sich — das Produkt der Pivotelemente ist (bis auf das Vorzeichen) durch
die Determinante festgelegt.
Es ist daher eine gute Idee, in jeder Spalte den größten Kandidaten als
Pivotelement zu verwenden. Man nennt dies ,,partielle Pivotierung^\ Die
Kandidaten sind die Einträge der aktuellen Spalte in der Pivotposition und in den
Zeilen darunter. Sie werden sehen, warum man diese Strategie in
Computerprogrammen implementiert.
Man kann auch Zeilenvertauschungen vornehmen, um
Eliminationsschritte einzusparen. In der Praxis haben die meisten großen Matrizen nur einen
kleinen Prozentsatz von null verschiedener Einträge, und der Anwender weiß
wahrscheinlich, wo sich diese befinden. Das Eliminationsverfahren ist im
Allgemeinen dann am schnellsten, wenn man die Gleichungen so anordnet, dass
sich die von null verschiedenen Einträge nahe der Diagonalen befinden, wenn
die Matrix also eine „Bandmatrix" mit kleinstmöglichen Bändern darstellt.
Für Parallelrechner tauchen neue Fragen auf. In Vektorrechnern wie der
Cray arbeiten 4, 8 oder 16 Prozessoren auf einmal. In der „Connection
Machine" sind schon 1024 Prozessoren tätig, und die CM-5 wird für 2^^ = 16.384
parallele Prozessoren entworfen. In solchen Maschinen ist das Problem die
Kommunikation — also die Aufgabe, den Prozessoren die nötigen Daten zur
richtigen Zeit zukommen zu lassen. Dies ist im Augenblick ein Feld
ausgedehnter Forschungstätigkeit. Mit den kurzen Hinweisen in diesem Abschnitt
möchte ich versuchen, Sie an das parallele Denken zu gewöhnen.
466 9 Numerische lineare Algebra
In Abschnitt 9.2 geht es um unvermeidbare Instabilitäten, die sich direkt
aus der Matrix ergeben. Man misst die Sensitivität einer Matrix durch die
Konditionszahl Abschnitt 9.3 beschreibt, wie man eine Gleichung Ax = b
iterativ lösen kann. Anstatt direkt das Eliminationsverfahren anzuwenden,
löst der Rechner eine einfachere Gleichung viele Male, wobei jedes Ergebnis
Xk wieder in die Gleichung einfließt, um die nächste Näherung Xk-\-i zu
bestimmen. Bei guten Iterationen konvergieren die x^ schnell gegen x = A~^h.
Rundungsfehler und partielle Pivotierung
Bis zu diesem Punkt haben wir jedes von null verschiedene Pivotelement
akzeptiert. In der Praxis ist ein kleines Pivotelement aber gefährlich. Eine
Katastrophe kann geschehen, wenn Zahlen sehr unterschiedlicher Größe
addiert werden. Ein Rechner arbeitet mit einer festen Anzahl Stellen, sagen
wir: 3 Dezimalstellen (bei einem sehr leistungsschwachen Rechner). Bei
diesem Rechner wird die Summe 10000+1 zu 10000 gerundet. Dabei geht die „1"
verloren. Beachten Sie, wie sehr dieser Unterschied die Lösung der folgenden
Aufgabe ändert:
0, OOOlit + v = l
-u + v = 0
startet mit der KoefRzientenmatrix A =
0,00011
■1 1
Wenn wir 0,0001 als Pivotelement akzeptieren, wird beim
Eliminationsverfahren 10.000 mal Zeile 1 zu Zeile 2 addiert. Nach der Rundung bleibt die
Zeile
lO.OOOt^ = 10.000 an Stelle von lO.OOlt^ = 10.000.
Das Ergebnis t' = 1, das der Rechner bestimmt hat, liegt nahe an dem wahren
Wert V = 0,9999. Die Rücksubstitution führt dann aber zu
0, OOOlit + 1 = 1 an Stelle von 0, OOOlit + 0,9999 = 1.
Aus der ersten Gleichung erhält man u = 0. Das korrekte Ergebnis wäre aber
u = 1 (siehe zweite Gleichung). Weil uns in der Matrix also die „1" verloren
gegangen ist, haben wir auch die Lösung verloren. Eine Veränderung von
10001 zu 10000 hat die Lösung von u = 1 zu u = 0 verfälscht — ein Fehler
von 100 % !
Vertauschen wir aber die Zeilen, so kann selbst unser leistungsschwacher
Rechner die Lösung bis auf drei Dezimalstellen genau bestimmen:
—u -\-v = 0 —u -\-v = 0 u = 1
0, OOOlit +1; = 1 ^ v = l ^ v = l.
Die ursprünglichen Pivotelemente waren 0,0001 und 10000 — sehr schlecht
skaliert. Nach einer Zeilenvertauschung erhält man die Pivotelemente -1 und
9.1 Gauß'sche Elimination in der Praxis 467
1,0001 — gut skaliert. Die berechneten Pivotelemente -1 und 1 kommen den
exakten Werten sehr nahe. Kleine Pivotelemente führen also zu numerischen
Instabilitäten; die Problemlösung liegt in der partiellen Pivotierung. Das
Verfahren entscheidet sich für ein k-tes Pivotelement, wenn es die k-te Spalte
erreicht und durchsucht hat:
Wähle die größte Zahl aus den Zeilen k und darunter, und
vertausche deren Zeile mit Zeile k.
Bei der Strategie der vollständigen Pivotierung durchsucht man auch noch
die später folgenden Zeilen nach dem größten Pivotelement, und muss dann
sowohl Zeilen als auch Spalten vertauschen. Dieser Aufwand ist nur selten
gerechtfertigt, weswegen alle wichtigen Programme die partielle Pivotierung
verwenden. Es kann auch lohnend sein, eine Zeile oder eine Spalte mit einer
Skalierungskonstante zu multiplizieren. Wäre die erste Gleichung im Beispiel
oben it+10000t; = 10000, so würden wir ein Pivotelement 1 erhalten, aber wir
wären wieder in Schwierigkeiten, wenn wir die Gleichung nicht umskalierten.
Für positiv definite Matrizen benötigt man keine Zeilenvertauschungen,
man kann die Pivotelemente problemlos so verwenden, wie sie während der
Rechnung erzeugt werden. Es kann passieren, dass kleine Pivotelemente
auftreten, in diesem Fall kann die Matrix aber nicht durch Zeilenvertauschungen
verbessert werden. Ist die Konditionszahl groß, so liegt das Problem in der
Matrix, nicht in der Reihenfolge der Eliminationsschritte. In diesem Fall ist
das Ergebnis unvermeidbar sensitiv gegenüber den Eingangsgrößen.
Der Leser versteht nun, wie ein Computer die Gleichung Ax = b
tatsächlich löst — durch das Eliminationsverfahren mit partieller
Pivotierung. Verglichen mit der theoretischen Beschreibung — man berechne A~^
und damit A~^b — sind die Details etwas zeit auf wändiger. Aber im Hinblick
auf die Rechenzeit ist Elimination viel schneller. Ich denke, dass dieser
Algorithmus auch die beste Herangehensweise an die Theorie von Zeilenräumen
und Kernen darstellt.
Aufwandsbetrachtungen: Vollbesetzte Matrizen und
Bandmatrizen
Eine praktische Frage nach dem Aufwand: Wie viele einzele Rechenoperatio-
^en werden benötigt, um ein Gleichungssystem Ax = h mit Hilfe des Eli-
f^inationsverfahrens zu lösen? Von der Antwort hängt es ab, wie groß die
Probleme sein dürfen, die wir lösen können.
Sehen wir uns zuerst die Matrix A an, die Stück für Stück in die Matrix U
verwandelt wird. Subtrahieren wir ein Vielfaches der ersten Zeile von der
zweiten Zeile, so führen wir n Operationen aus. Die erste ist die Division durch
das Pivotelement, um den MultipUkator l zu bestimmen. Bei den anderen
^ — 1 Einträgen handelt es sich um kombinierte Multiplikation-Subtraktion-
Operationen, die wir der Einfachheit halber jeweils als eine Operation zählen
468 9 Numerische lineare Algebra
wollen. Betrachten Sie stattdessen die Multiplikation mit / und die
Subtraktion vom bestehenden Eintrag als zwei einzelne Operationen, so müssen sie
alle Operationsanzahlen verdoppeln.
A ist eine n x n-Matrix. Für alle n - 1 Zeilen unterhalb der ersten Zeile
benötigt man die oben bestimmte Anzahl Schritte. Um also die Nullen
unterhalb des ersten Pivotelements zu erzeugen, benötigt man insgesamt n mal
n — 1, also n^ —n Operationen. Probe: Von den n^ Einträgen werden alle bis
auf die n Einträge der ersten Zeile verändert.
Ist das Eliminations verfahren schon so weit fortgeschritten, dass nur noch
k Zeilen zu bearbeiten sind, so sind auch die zu bearbeitenden Zeilen kürzer.
An Stelle der n^ —n Operationen benötigt man nur noch k"^ — k Operationen,
um die Spalte unterhalb des Pivotelements zu löschen. Diese Beziehung gilt
für alle 1 < k < n. Im letzten Schritt wird keine Operation mehr benötigt
A^ -1 = 0), weil das Pivotelement stehen bleibt und die Vorwärtselimination
beendet ist. Die Gesamtzahl an Operationen zur Erzeugung von U ist die
Summe von k^ — k im alle Werte von k zwischen 1 und n:
/.2 2^ /-. X n(n + l)Bn + l) n(n +1) n^-mi
Dies sind altbekannte Formeln für die Summe der ersten n Zahlen und die
Summe der ersten n Quadratzahlen. Setzt man n = 1 ein, so erhält man 0.
Setzt man aber n = 100 ein, so erhält man ein Drittel von einer Million minus
100 Operationen. (Auf einem Arbeitsplatzrechner ist das etwa eine Sekunde).
Wir ignorieren — im Vergleich mit dem größeren Term n^ — den Term n
und erhalten so unsere wichtigste Folgerung:
Der Rechenaufwand für die Vorwärtselimination (von A nach U)
beträgt |n^ Operationen.
Das bedeutet, dass |n^ Multiplikationen und |n^ Subtraktionen nötig
sind. Verdoppelt man n, so erhöht dies die Kosten um den Faktor acht (weil
n zur dritten Potenz erhoben wird). Ein System aus 100 Gleichungen ist
völlig unproblematisch, ein System mit 1000 Gleichungen schon teuer, und
ein System mit 10000 Gleichungen ist unmöglich zu lösen. Dafür brauchen
wir einen schnelleren Computer, oder viele Nullen, oder eine neue Idee.
Auf der rechten Seite der Gleichungen lassen sich die Schritte viel schneller
durchführen. Hier arbeiten wir immer nur mit einzelnen Zahlen, nicht mit
ganzen Zeilen. Für jede rechte Seite benötigt man genau n^ Operationen.
Sie erinnern sich, man löst dabei zwei Dreieckssysteme, nämlich Lc = b in
Vorwärtsrichtung und f/x = c rückwärts. Bei der Rücksubstitution benötigt
man für die letzte Unbekannte nur eine Operation, die Division durch das
letzte Pivotelement. Die Zeile darüber benötigt zur Lösung zwei Operationen
— das Einsetzen von x^ und die Division durch das Pivotelement dieser
Zeile. Im fc-ten Schritt benötigt man k Operationen, die Gesamtsumme für
die Rücksubstitution ist also
9.1 Gauß'sche Elimination in der Praxis
469
A =
Abb. 9.1. Die Faktorisierung A
finden sich in L und U wieder.
= LU
LU für eine Bandmatrix. Gute Nullen in A
l + 2+--- + n =
n{n + 1)
hn'
Operationen.
In Vorwärtsrichtung fallen ebenso viele Schritte an. Die Gesamtzahl von n^
Schritten ist genau gleich der Anzahl, die nötig wäre, um A~^ mit b zu
multiplizieren! Das Gauß'sche Eliminationsverfahren hat aber gegenüber der
Berechnung von A~^h zwei große Vorteile:
1 Das Eliminationsverfahren benötigt |n^ Rechenschritte, wohingegen die
Berechnung von A~^ n^ Schritte benötigt.
2 Ist A eine Bandmatrix, so sind auch L und U Bandmatrizen. Die Matrix
A~^ hingegen ist voll besetzt.
Bandmatrizen
Der Rechenaufwand, den wir oben bestimmt haben, wird verringert, wenn die
Matrix A ,,gute Nullen'' besitzt. Eine gute Null ist ein Nulleintrag, der auch
in L und U Null bleibt. Die wichtigsten guten Nullen sind jene am Anfang
einer Zeile. Für solche Einträge werden keine Eliminationsschritte benötigt
— die Multiplikatoren sind Null. Deshalb tauchen diese Nullen in L wieder
auf. Dies wird besonders deutlich für die folgende Tridiagonalmatrix A:
1-1
1 2-1
-1 2-1
-1 2
1
-1 1
-1 1
-1 1
1-1
1-1
1-1
1
Die Zeilen 3 und 4 von A beginnen mit Nullen. Für diese Zahlen braucht
nian keinen Multiplikator, deshalb stehen auch in L an diesen Stellen Nullen.
Weiterhin enden die Zeilen 1 und 2 mit Nullen. Subtrahiert man also ein
Vielfaches der Zeile 1 von Zeile 2, so braucht man jenseits der zweiten Spalte
nichts mehr zu berechnen. Die Zeilen sind also kurz, und sie bleiben kurz! In
Abbildung 9.1 erkennt man, dass die Faktoren L und U einer Bandmatrix A
ebenfalls Bandmatrizen sind.
Diese Nullen führen zu einer einschneidenden Änderung in der
Aufwandsbetrachtung.
470 9 Numerische lineare Algebra
Eine Matrix A ist eine Bandmatrix mit „Halbbandbreite" w^
wenn gilt: üij = 0 für \i — j\ > w.
Für eine Diagonalmatrix ist also w = 1, für eine Tridiagonalmatrix w = 2.
Die Länge einer Pivotzeile ist höchstens w. Es gibt nicht mehr als it; — 1 von
null verschiedene Einträge unterhalt eines jeden Pivotelements. Damit ist
jeder Eliminationsschritt nach w{w — l) Schritten vollendet, wobei die
Bandstruktur erhalten bleibt. Es müssen insgesamt n Spalten bearbeitet werden,
woraus sich der Gesamtaufwand ergibt:
Die Vorwärtselimination auf einer Bandmatrix benötigt weniger
als w'^n Operationen.
Der Aufwand für eine Bandmatrix ist also proportional zu n und nicht
mehr zu n^. Er ist allerdings auch zu w^ proportional, so dass sich für eine
volle Matrix mit w — n wieder n^ ergibt. Um den Aufwand genauer zu
analysieren, muss man bedenken, dass die Breite des Bandes in der unteren
rechten Ecke geringer als w ist (die Matrix bietet nicht genug Platz). Der
exakte Aufwand für die Berechnung von L und U ist
w{w-l){Zn-2w-^l) ... . ^ , , .
lur eme Bandmatrix
3
n(n — l)(n 4-1) n^ — n
für w — n.
Der Aufwand zur Bestimmung einer Lösung x aus einem Vektor b auf der
rechten Seite beträgt etwa 2wn Rechenoperationen. Entscheidend ist hier,
dass bei einer Bandmatrix der Aufwand proportional zu n ist. Dies ist extrem
schnell. Es ist sehr leicht, eine Tridiagonalmatrix der Größenordnung 10.000
zu bearbeiten, solange man nicht A~^ berechnen muss. Die Inverse enthält
oft überhaupt keine Nullen:
A^
1-1 0 0
-1 2-1 0
0-1 2-1
0 0-1 2
hat die Inverse A ^ —U ^L ^ =
4321
3321
222 1
1111
Die Kenntnis von A~^ ist sogar weniger nützlich als die von L und U. Eine
Multiplikation mit A~^ benötigt die vollen n^ Operationen. Um die beiden
Gleichungen Lc — h und i7x — c zu lösen, bedarf es aber nur 2wn
Operationen. In diesem Fall bedeutet das An. In der Praxis tritt eine Bandstruktur
sehr häufig auf, wenn eine Matrix Abhängigkeiten zwischen nahe
benachbarten Punkten ausdrückt. Man hat dann zum Beispiel ais = 0 und ai4 = 0,
weil 1 kein Nachbar von 3 oder 4 ist.
Wir schließen diesen Abschnitt mit zwei weiteren
Aufwandsbetrachtungen:
9.1 Gauß'sche Elimination in der Praxis 471
1 A"^ kostet n^ Operationea. = ; 2QR kostet ^n^ Operationen.
1 Wir beginnen mit AA~^ = /. Spalte j von A~^ ist dann die Lösung
der Gleichung Axj = (Spalte j von /). Normalerweise brauchte man für jede
der n rechten Seiten n^ Operationen, also insgesamt n^ Operationen. Der
Aufwand für die Faktorisierung der linken Seite beträgt wie üblich |n^. Sie
fällt nur einmal an, da die Berechnung von L und U nicht für jede rechte
Seite neu geschehen muss. Zusammen erhält man so |n^ Operationen — es
ist aber möglich, diese Zahl auf n^ zu reduzieren.
Der Grund dafür liegt in den ersten j — l Nullen in Spalte j von /.
Auf der rechten Seite ist keine Arbeit nötig, bis die Elimination bei Zeile j
angelangt ist. Der Aufwand für die Elimination in Vorwärtsrichtung beträgt
hier also ^{n — j)^ statt |n^. Summiert man über j, so erhält man einen
Gesamtaufwand von ^n^ für die n rechten Seiten. Daher ist n^ die Gesamtzahl
nötiger Multiplikationen (und ebenso Subtraktionen) für die Berechnung von
A-':
Tl 71 / 71 \
—- (L und U) -{■ -— (vorwärts) + 7i( —- ) (Rücksubstitutionen) — n^.
3 6 \ 2 /
(9.1)
2 Beim Gram-Schmidt-Verfahren arbeitet man mit Spalten, nicht mit
Zeilen. Dieser Unterschied ist für den Aufwand nicht entscheidend. Der
wesentliche Unterschied zum Eliminations verfahren ist, dass der Multiplikator
durch ein Skalarprodukt gegeben ist Hier braucht man also n Operationen,
um einen Multiplikator zu bestimmen, wo beim Eliminations verfahren
einfach durch das Pivot element dividiert wird. Weiterhin werden n
kombinierte „Multiplikation-Subtraktion"-Operationen benötigt, um von Spalte 2 die
Projektion auf Spalte 1 zu subtrahieren. (Siehe Abschnittt 4.4 und Aufgabe
4.4.28.) Beim Gram-Schmidt-Verfahren fallen also 2n Operationen an, wo
das Eliminationsverfahren nur n Operationen benötigt. Dieser Faktor 2 ist
der Preis, den man für die Orthogonalität zu zahlen hat — wir müssen ja ein
Skalarprodukt Null werden lassen, und nicht nur einen Eintrag.
Vorsicht Zur Beurteilung eines numerischen Algorithmus' reicht es nicht
aus, die Anzahl nötiger Operationen zu bestimmen. Über das „Flop^-Zählen"
hinaus gibt es noch die Stabilität des Algorithmus' und den Datenfluss zu
beachten. Van Loan unterscheidet drei Ebenen der linearen Algebra:
Linearkombinationen cu -h V von Vektoren A. Ebene), Matrix-Vektor-Kombinationen
^u-h V (Ebene 2) und Matrix-Matrix-Operationen AB + C (Ebene 3).
Paralleles Rechnen funktioniert auf der dritten Ebene am besten. Zur Berechnung
eines Produkts AB sind 2n^ Flops (Additionen und Multiplikationen) und
472 9 Numerische lineare Algebra
nur 2n^ Daten nötig — ein gutes Verhältnis von Rechenarbeit zu
Kommunikationsaufwand. Die Lösung einer Gleichung UX — B mit Matrizen ist
effizienter als die einer Gleichung i7x — b mit Vektoren. Schließlich ist das
Gauß-Jordan-Verfahren in gewisser Hinsicht überlegen!
Drehungen einer Ebene
Es gibt zwei Möglichkeiten, die wichtige Faktorisierung A — QR zu
bestimmen. Die eine ist, erst die Matrix Q zu bestimmen, die andere wäre, zunächst
R zu berechnen. Mit dem Gram-Schmidt-Verfahren wählt man die erste
Möglichkeit, die Spalten von A werden orthonormalisiert und bilden dann
die Spalten von Q. Die Matrix R ergab sich dabei als Nebeneffekt. Dass sie
eine obere Dreiecksmatrix ist, liegt an der Reihenfolge der einzelnen
Schritte im Gram-Schmidt-Verfahren. Im folgenden wollen wir uns eine Methode
ansehen, die aus A direkt die Matrix R berechnet.
Bei der Elimination erhält man die Faktorisierung A — LU^ bei der Or-
thogonalisierung die Faktorisierung A = QR, In beiden Fällen sind R
beziehungsweise U obere Dreiecksmatrizen. Worin Hegt der Unterschied? Beim
Eliminations verfahren ergibt sich die untere Dreiecksmatrix L als Produkt
von Elementarmatrizen E, sie enthält Einsen auf der Hauptdiagonalen und
die Multiplikatoren Uj darunter. Für die Faktorisierung QR hingegen
verwenden wir orthogonale Matrizen. Hier sind keine „E's" erlaubt, weil wir keine
Dreiecksmatrix L erhalten wollen, sondern eine orthogonale Matrix Q.
Es gibt zwei einfache orthogonale Matrizen, die die Rolle der „E's"
übernehmen können. Die Spiegelungsmatrizen I — 2uu^ sind nach Householder
benannt, und die ebenen Rotationsmatrizen (Drehmatrizen) nach Givens.
Eine Drehung der xy-Ehene um einen Winkel 6, die die z-Richtung unverändert
lässt, wird durch die Matrix
Givens—Rotation Q21 =
cos6 -sin6 0
sin 9 cos 6 0
0 Ol
beschrieben. Man kann durch Wahl von 9 die Matrix Q21 ähnlich wie eine
Matrix E21 benutzen, um eine Null an der Position B,1) zu erzeugen. Das
folgende Beispiel wird von Bill Hager in Applied Numerical Linear Algebra
(Prentice-Hall, 1988) beschrieben:
0,6 0,8 0'
-0,8 Ö;8 0
0 0 1
90
120
200
-153 114'
-79 -223
-40 395
=
'150-155-110
0 75 -225
200 -40 395
Q2lA =
^ Anm. d. Übers.: Ein „Flop" = „floating point operation" = „Fließkommaoperar
tion" ist ein Grundrechenschritt im Computermodell der reilen Zahlen.
9.1 Gauß'sche Elimination in der Praxis 473
Die 0 ergibt sich aus -0,8 • 90 4- 0,6 • 120. Es ist nicht nötig, 0 selbst zu
bestimmen, wir verwenden ledigHch
cos 6 —
90
\/902 + 1202
und sin 6
-120
\/902 + 1202
(9.2)
Als nächstes geht es um den Eintrag C,1), die Drehung soll also in den Zeilen
und Spalten 3 und 1 wirken. Man bestimmt die Zahlen cosö und sinö aus
den Werten 150 und 200, anstatt 90 und 120. In diesem Fall handelt es sich
wieder um 0,6 und -0,8:
0,6 0 0,8 1
0 1 0
-0,8 0 0,6
r 150 ••]
0 ••
. 200 • •.
=
250-
0
0
-125
75
100
250
-225
325
1
0
0
0 0 1
0,6 0,8
-0^8 0,6
0-125 •"
0 75 •
0 100 •
=
250-125
0 125
0 0
250
125
375
^31^21^ -
Wir brauchen noch einen Schritt bis zur Matrix R, wir müssen noch den
Eintrag C,2) eliminieren. Die Werte für cos 9 und sinö erhält man jetzt aus
den Zahlen 75 und 100, die Drehung wirkt in Zeile und Spalte 2 und 3:
032031^21^
Damit haben wir die obere Dreiecksmatrix R erzeugt. Wie erhält man Ql Man
bringt die Drehungen Qij auf die andere Seite und erhält so eine Gleichung
A = QR — gerade so, wie wir die Eliminationsmatrizen Eij ami die rechte
Seite gebracht und A = LU erhalten haben:
Q32Q31Q21A - R bedeutet A = {Q2iQsiQsi)R = QR. (9.3)
Die Inverse jeder Matrix Qij ist schlicht Qj- (Drehung um -6). Hierin liegt
ein Unterschied zu den Inversen von Eij^ die keine orthogonalen Matrizen
sind. E^^ addiert zu Zeile i das Vielfache Uj von Zeile j wieder hinzu, das
von Eij subtrahiert worden war. Ich hoffe, Sie erkennen, dass diese wichtigen
Rechnungen in der linearen Algebra — LU und QR — ähnlich, aber nicht
gleich sind.
Es gibt noch eine dritte wesentliche Rechnung — Eigenwerte und
Eigenvektoren.
Wenn wir die Matrix A auf Dreiecksform bringen, können wir ihre
Eigenwerte auf der Diagonalen ablesen. Dafür können wir aber weder die Matrix
^ noch die Matrix R verwenden. Die Eigenwerte bleiben bei einem Schritt
von der Form Q21AQ21 unverändert, nicht aber bei Q21A. Der zusätzliche
Faktor Q~^ zerstört aber die Null, die gerade erst von Q21 erzeugt wurde!
Es gibt hier zwei Möglichkeiten. Keine von beiden liefert die Eigenwerte
nach einer festen Anzahl von Schritten. (Dies ist auch unmöglich. Die Ter-
me für cos 6 und sinO enthielten nur Quadratwurzeln, die Polynomgleichung
474 9 Numerische lineare Algebra
det{A — XI) — 0 vom Grad n kann aber nicht nur durch Quadratwurzeln
gelöst werden.) Die Drehungen Qij sind aber trotzdem nützlich:
Methode 1 Man erzeugt eine Null an der Stelle C,1) der Matrix Q2\A,
nicht an der Stelle B,1). Eine solche Null wird durch Q21 nicht wieder
gelöscht. Bei dieser Methode bleibt eine Nebendiagonale aus von Null
verschiedenen Elementen unterhalb der Haupt diagonalen stehen, so dass man
die Eigenwerte nicht einfach ablesen kann. Diese „Hessenberg-Matrix" hat
aber trotz der zusätzlichen Diagonale viele „gute Nullen".
Methode 2 Man wählt Q21 so, dass an Position B,1) der Matrix Q2\AQ2i
eine Null entsteht. Hierbei handelt es sich um ein 2 x 2-Eigenwertproblem für
die Matrix in der oberen linken Ecke von A. Die Spalte (cosö, — sinö) ist ein
Eigenvektor dieser Matrix. Dieses ist der erste Schritt des Jacobi-Verfahrens.
Bei diesem Verfahren hat man ebenfalls das Problem, dass erzeugte
Nullen wieder verschwinden. Beim zweiten Schritt wird Qsi so gewählt, dass an
der Position C,1) von Q^iQ2i AQ21 Q^i eine Null steht. Dabei geht aber die
Null an der Position B,1) verloren. Beim Jacobi-Verfahren bestimmt man
die Matrizen Qij aus 2 x 2-Eigenwertproblemen, jedoch werden ehemalige
Einträge ungleich Null wieder auftauchen. Im Allgemeinen sind die neuen
Einträge dabei kleiner als die vorherigen, und nach mehreren Durchgängen
durch die Matrix ist der Teil unterhalb der Diagonalen deutlich kleiner
geworden. Dabei entstehen auf der Hauptdiagonalen langsam die Eigenwerte.
Sie sollten hiervon das Folgende im Gedächtnis behalten. Die Q's sind
orthogonale Matrizen, ihre Spalten mit den Einträgen (cos ö, sin ö) und
(—sinö,cosö) sind orthogonale Einheitsvektoren. Berechnungen mit solchen
Q's sind sehr stabil. Man kann den Winkel 6 so wählen, dass ein spezieller
Eintrag null wird — ein Schritt in Richtung einer Dreiecksmatrix. Dies war
das Ziel unserer Bemühungen am Anfang des Buches, und das ist es immer
noch.
Aufgaben 9.1
1. Bestimmen Sie mit und ohne partielle Pivotierung die beiden
Pivotelemente der Matrix
0,001 0
1 1000
Warum ist keiner der Einträge von L größer als 1, wenn Sie die partielle
Pivotierung anwenden? Geben Sie ein Beispiel einer 3 x 3-Matrix A an,
für die \aij\ < 1 und \lij\ < 1 gilt, deren drittes Pivotelement aber gleich
4 ist.
2. Berechnen Sie mit dem Eliminationsverfahren die exakte Inverse der
Hilbert-Matrix A. Berechnen Sie dann A~'^ noch einmal, wobei sie
alle Zahlen auf drei Stellen runden:
9.1 Gauß'sche Elimination in der Praxis
475
ri
1
2
1
- 3
1
2
1
3
1
4
1 "
3
1
4
1
5 J
A^hilbO)
3. Berechnen Sie für dieselbe Matrix A den Vektor b = Ax für x — A,1,1)
und X = @,6, —3,6). Eine kleine Änderung Äh erzeugt also einen großen
Unterschied Äx.
4. Bestimmen Sie (mit Hilfe eines Computers) die Eigenwerte der 8x8-
Hilbert-Matrix mit den Einträgen aij — l/(z + j — 1). Wie groß kann ||x||
in einer Gleichung Ax = b mit ||b|| — 1 werden? Der Rundungsfehler in
b sei kleiner als 10"^^, wie groß kann dann der Fehler in x werden?
5. Zeigen Sie, dass die Anzahl an Multiplikationen für die Rücksubstitution
Ux = c bei einer Bandmatrix (mit Breite w) etwa wn ist.
6. Kann man die Gleichung LUx = b oder die Gleichung QRx
lösen, wenn man L und U sowie Q und R kennt?
b schneller
Zeigen Sie, dass eine obere n x n-Dreiecksmatrix mit etwa |n^
Multiplikationen invertiert werden kann. Wenden Sie dazu die Rücksubstitution
auf die Spalten von / an, jeweils von der 1 aufwärts gehend.
Faktorisieren Sie die folgenden Matrizen A in der Form PA — LU, indem
Sie in jeder Spalte das größtmögliche Pivotelement auswählen (partielle
Pivotierung):
A-
10
22
und A —
101
220
020
9. Füllen Sie die drei mittleren Diagonalen einer 4 x 4-Tridiagonalmatrix mit
Einsen, und bestimmen Sie dann die Kofaktoren der sechs Nulleinträge.
Diese Einträge in A~^ sind also von null verschieden.
10. (Vorgeschlagen von C. Van Loan.) Bestimmen Sie die Li7-Faktorisierung
der Matrix A = [f J]. Lösen Sie mit einem Computer die Gleichung
'e l
1 1
=
"l + e"
2
für e = 10-^10-^10-^ 10-12,10-15 mit dem Eliminationsverfahren
(ohne Pivotierung). Die richtige Lösung ist x - A,1). Legen Sie eine
Tabelle der Fehler für jedes e an. Vertauschen Sie jetzt die beiden Zeilen,
und lösen Sie das System noch einmal — die Fehler sollten fast
verschwinden.
476 9 Numerische lineare Algebra
11. Wählen Sie sinö und cos 6 so, dass A zu einer Dreiecksmatrix wird, und
bestimmen Sie R:
Q2lA =
cos 6—sin 6
sin 9 cos 6
l-l"
3 5
* *
0 *
R.
12. Wählen Sie sin 9 und cos 6 so, dass Q21AQ21 (für dasselbe A) eine
Dreiecksmatrix ist. Welche Eigenwerte hat A?
13. Welche der n^ Einträge von A ändern sich, wenn die Matrix von links
mit Qij multipliziert wird? Welche Einträge ändern sich, wenn QijA von
rechts mit Q^j^ multipliziert wird?
14. Wie viele Multiplikationen, wie viele Additionen sind nötig, um die
Matrix QijA zu berechnen? (Ordnet man die Folge der Drehungen geschickt
an, so sind |n^ Multiplikationen und |n^ Additionen nötig —
dieselbe Anzahl wie für die Berechnung von QR durch Spiegelungsmatrizen,
doppelt so viele wie für die Li7-Zerlegung.)
15. (Drehen einer Roboterhand) Ein Roboter erzeugt sämtliche 3x3-
Drehungen A aus ebenen Drehungen um die x-, y- und die z-Achse.
Da A orthogonal ist, ist in der Zerlegung Q32Q31Q21A — R die Matrix
i? = /. Die drei Drehungen des Roboters sind also in den Matrizen A =
Q21Q31Q32 enthalten. Man nennt die drei Winkel „Euler'sche Winkel",
und es gilt detQ = 1, um Spiegelungen auszuschließen. Beginnen Sie,
indem Sie cos9 und sin9 so wählen, dass die Matrix
Q21A
an Position B,1) eine Null enthält.
cos9-
sin9
0
-sinl9 0"
cos 9 0
0 1
1
3
-1 2 2
2-1 2
2 2-1
9.2 Normen und Konditionszahlen
Wie misst man die Größe einer Matrix? Die Länge eines Vektors ist durch
||x|| gegeben. Analog gibt es für eine Matrix die Norm \\A\\. Man verwendet
das Wort „Norm" manchmal auch an Stelle von „Länge" für einen Vektor.
Bei Matrizen verwendet man es immer, und es gibt viele Möglichkeiten, ||i4||
zu definieren.
Wir schauen uns zunächst die Bedingungen an, die an alle Matrixnormen
gestellt werden, und wählen dann eine aus. Frobenius zum Beispiel quadrierte
alle Einträge von A und bildete die Summe, seine Norm \\A\\f ist die Wurzel
aus dieser Summe. Er behandelt Matrizen also wie lange Vektoren. Es ist
aber günstiger, Matrizen auch als Matrizen zu behandeln.
9.2 Normen und Konditionszahlen 477
Beginnen wir mit einer Vektornorm: ||x4-y|| ist nicht größer als die Summe
||x|| 4- ||y||. Dies ist die Dreiecksungleichung: x + y ist die dritte Seite des
Dreiecks. Für Vektoren gilt auch, dass die Länge von 2x oder —2x gleich
2||x|| ist. Dieselben Regeln fordert man auch für Matrixnormen:
\\A + B\\ < \\A\\ + \\B\\ und ||c^|| - \c\ \\A\\. (9.4)
Die zweite Bedingung an eine Norm für Matrizen ist neu — weil man
Matrizen multiplizieren kann. Die Größe von Ax und die Größe von AB
sollen unter Kontrolle bleiben. Deshalb verlangt man, dass für alle Matrizen
und Vektoren
||Ax||<||A||||x||und||Aß||<||A||||ß|| (9.5)
gilt. Dies führt auf eine natürliche Definition für \\A\\. Außer für die
Nullmatrix ist die Norm eine positive Zahl. Die folgende Wahl erfüllt alle
Bedingungen:
DEFINITION Die Norm ainer Matrix Ä ist das Maximüni
des;Verhältnisses |'|4xti/|xj|:; ^';-r _ ' ';\''' ^.r \^^'^ ^y':/]:''r^:,:!::X'':
Dann ist ||Ax||/||x|| nie größer als \\A\\ (das Maximum), und deshalb gilt
||Ax|| < \\A\\ j|x|| wie verlangt.
Beispiel 9.2.1 Ist A die Einheitsmatrix /, so ist das Verhältnis immer
||x||/||x||, es gilt also ||/|| = 1. Ist A eine orthogonale Matrix Q, so
bleiben die Längen ebenfalls erhalten: es gilt ||Qx|| = ||x|| für jeden Vektor x.
Man erhält also wieder ||Q|| = 1.
Beispiel 9.2.2 Die Norm einer Diagonalmatrix ist durch den (nach
Absolutbeträgen) größten Eintrag gegeben:
Die Norm von A
20
03
ist
Das Verhältnis ist hier px|| = ^2^x\ + '^^x\ dividiert durch ||x|| ^ \/^f+ -^
6s wird maximal für x\—^ und X2 — 1. Dieser Vektor x = @,1) ist ein
Eigenvektor mit Ax - @,3), also zum Eigenwert 3. Diese Zahl ist der betragsgrößte
Eigenwert von A, sie ist gleich der Norm.
Die Norm einer positiv definiten symmetrischen Matrix ist
11-^11 == '^max*
2»
478 9 Numerische lineare Algebra
Wähle für x einen Eigen vektor zum größten Eigenwert, so dass Ax =
AmaxX gilt. Das Entscheidende ist, dass für keinen anderen Vektor x ein
größeres Längenverhältnis erzeugt werden kann. Die Matrix kann als A — QAQ^
geschrieben werden, wobei die orthogonalen Matrizen Q und Q^ die Längen
unverändert lassen. Das zu maximierende Längenverhältnis ist also eigent-
Uch ||ylx||/||x||, und die Norm der Diagonalmatrix A ist der größte Eigenwert
'^max*
Symmetrische Matrizen Sei A eine symmetrische, aber nicht positiv
definite Matrix — einige der Eigenwerte seien negativ oder null. Dann ist die Norm
die größte der Zahlen |Ai|, IA2I, ..., |An|. Wir betrachten die Absolutbeträge
der A's, weil es bei einer Norm nur um die Länge geht. Für einen Eigen vektor
gilt mx|| = ||Ax||, also |A| mal ||x||. Dividiert man dies durch ||x||, so bleibt
|A|. Das maximale Längenverhältnis ergibt sich, wenn ein Eigenvektor zum
größten |A| als x gewählt wird.
Unsymmetrische Matrizen Ist A nicht symmetrisch, so geben die
Eigenwerte nicht die wahre Größe der Matrix wieder. Die Norm kann groß sein,
obwohl die Eigenwerte klein sind. Die Norm ist im allgemeinen größer als
|A|max- Für das folgende sehr unsymmetrische Beispiel gilt Ai = A2 = 0,
wohingegen die Norm nicht Null ist:
02
00
\\Ax.\\
hat die Norm lUII = max Vrr = 2.
x^O X
Der Vektor x = @,1) liefert Ax — B,0), das Verhältnis der Längen ist also
2/1. Dieser Wert ist auch der Maximalwert, obwohl x kein Eigenvektor ist.
Die symmetrische Matrix Ä^A^ nicht die unsymmetrische Matrix A^ hat
den Eigenvektor x — @,1). Die Norm ist tatsächlich durch den größten
Eigenwert von A^A gegeben, wie wir jetzt beweisen werden.
§A Die' ffqicsd'-'femA Hilatrfac A (symm^tnisch Mär^^Ä^S&aelSsc^)/^^^^^
/ ~ ;. ; .' ' ^'; '' " "" .'""' ;;,"; ';^, ^ v -'„ -, - -" -:; '■■■' ---''"\ " ;' - - '; /' - ^\''\"^^,,
Beweis. Sei x ein Eigenvektor von A^A zum größten Eigenwert Amax- Das
Verhältnis in Gleichung (9.4) ist dann x^A^Ax — x^(Amax)x geteilt durch
x^x. Für dieses x ist das Längenverhältnis also gleich Amax-
Es kann sich für kein anderes x ein größerer Wert ergeben. Die
symmetrische Matrix A^A besitzt orthonormale Eigenvektoren qi, q2, • • •, Qn? jeder
Vektor x ist eine Linearkombination dieser Vektoren. Setzt man also die
Linearkombination in das Längenverhältnis ein (und benutzt qfqj =: 0), so
erhält man
9.2 Normen und Konditionszahlen 479
X^Ä^Ax ^ (ciqi + • • • + Cnqn)^(ciAiqi 4- • • • + CnA^qn) ^ cf Ai 4- • • • + c^Xn
""Ic^b^ (Ciqi + • • • + Cnqn)^(ciqi + • • • + Cn^n) cf + ' ' ' + ^
(9.8)
Das letzte Verhältnis kann nicht größer sein als Amax? das maximale Verhältnis
tritt auf, wenn alle Koeffizienten bis auf jenen vor Amax null sind.
Bemerkung 1 Das Verhältnis in Gleichung (9.8) ist auch als Rayleigh-
Quotient der Matrix A^A bekannt. Sein Maximum ist der größte Eigenwert
Amax(^^^)) sein Minimum ist Amin(^^^)- Setzt man also einen beliebigen
Vektor x in den Rayleigh-Quotienten x^A^Ax/x^x ein, so erhält man
garantiert eine Zahl zwischen Amin und Amax-
Bemerkung 2 Die Norm \\A\\ ist gleich dem größten Singulärwert cTmax von
A, Die Singulärwerte cri,..., cr^. sind die Wurzeln der positiven Eigenwerte
von A^A. Deshalb ist sicherlich cTmax = (Amax)^'^^ gleich der Norm von A.
Bemerkung 3 Rechnen Sie nach, dass die unsymmetrische Matrix in
Gleichung (9.6) als größten Eigenwert Amax(^^^) = 4 hat:
02
00
führt auf Ä^A -
Die Norm ist also \\A\\ — >/4.
00
04
mit Amax - 4.
Die Konditionszahl von A
In Abschnitt 9.1 haben wir gesehen, dass Rundungsfehler ernsthaft
Probleme bereiten können. Einige Systeme sind sehr empfindlich, andere weniger.
Man misst die Empfindlichkeit gegenüber Fehlern mit der Konditionszahl. In
diesem Kapitel führen wir zum ersten Mal bewusst Fehler ein. Wir wollen
abschätzen, wie sehr sie eine Lösung x verändern.
Betrachten wir eine Gleichung Ax — b. Nehmen wir an, die rechte Seite
würde aufgrund von Rundungs- oder Messfehlern zu b + ^b abgeändert.
Dann ändert sich die Lösung zu x + Ax. Unser Ziel ist, die Änderung Ax
der Lösung aus der Änderung Ah in der Gleichung abschätzen zu können.
Durch Subtraktion erhält man die Fehlergleichung A{Ax) — Ah:
Man subtrahiert Ax^h von A{x + Ax) = b + Z\b (9.9)
und erhält -0^^:^,,^
Der Fehler ist also Ax = A~Mb, er wird groß, wenn A~^ groß ist, wenn
also A beinahe singular ist. Der Fehler Z\x ist besonders groß, wenn Ah in
die Richtung zeigt, in der A~^ am meisten vergrößert. Der größtmögliche
Ausgabefehler ist also ||zAx|| = \\A-^ \\Ah\\.
480 9 Numerische lineare Algebra
Die Fehlerschranke ||^~^|| hat einen wesentlichen Nachteil. Multipliziert
man A mit 1000, so wird A~^ durch 1000 dividiert, und die Matrix sieht
tausendmal besser aus. Durch eine einfache Umskalierung kann man aber
nicht das real vorhandene Problem beheben. Es ist zwar richtig, dass auch
Zix durch den Faktor 1000 dividiert wird. Dies gilt aber auch für die exakte
Lösung X = A~^h. Der relative Fehler ||zix||/||x|| bleibt also gleich. Man
sollte also die relative Änderung von x mit der relativen Änderung von b
vergleichen.
Dieser Vergleich der relativen Fehler führt uns auf die „Konditionszahl"
c = \\A\\ ||^~^||. Multipliziert man A mit 1000, so ändert sich nichts, weil
A~^ durch 1000 dividiert wird, und das Produkt c also unverändert bleibt.
9B Der Fehler in der tösmig i$i Heiner aU c = |J4I( ll^'^^jl t^^l;
Eifigabefehleri
\: /. „ , , ;■■■ 11^ pb|| . 'i ■„;,::■■
... \; ■:...:::<■::]■'::?: M - INI • "=.":: vis,
M der Emgai>efehler jfikÄ (ein FeWer in der Matrix slä^lf öl;b)^'sd^ wird M^B
Abschätzung 2;u^ ' ^^ ', „ :/ \ r\"]
"■■■■'■ '"'"" <c^. ■■ ::'V:,':'i9ä
||x + zlx||- \\A\\
Beweis. Die ursprüngliche Gleichung ist b = Ax, und die Fehlergleichung
(9.10) ist Zlx = A'^Ah. Wenden wir die Eigenschaft (9.5) einer Matrixnorm
an:
||b||<M||||x|| und ||zlx||<p-i||||zib||.
Multiplizieren Sie nun die beiden Ungleichungen, auf der linken Seite steht
||b|| ||zix||. Dividieren Sie beide Seiten durch ||b|| ||x||. Auf der linken
Seite steht nun der relative Fehler ||zix||/||x||, und auf der rechten die obere
Schranke aus Gleichung (9.10).
Die Konditionszahl c = ||^|| ||^~^|| spielt auch eine Rolle, wenn ein Fehler
in der Matrix vorliegt, und wir ein AA anstelle von Ah haben:
Man subtrahiert ^x = b von {A + AA){x + Ax) = h
und erhält A{Ax) = -(zi^)(x 4- Ax).
Multipliziert man die letzte Gleichung mit A~^^ und betrachtet von beiden
Seiten die Norm, so erhält man
||zix||<p-i||||zlA||||x + Zix|| oder „J'f ^^y < Mil M"Ml^-
9.2 Normen und Konditionszahlen 481
Folgerung Eine Rechnung kann auf zwei Weisen fehlerhaft werden, durch
einen Fehler AA oder einen Fehler Ah — wir verwenden eine falsche Matrix,
oder einen falschen Vektor b. Dieser Eingabefehler findet sich (stark oder
weniger stark) verstärkt im Lösungsfehler Ax wieder. Dieser Fehler ist (relativ
zu X selbst) durch die Konditionszahl c beschränkt.
Der Fehler Ah rührt von Rundungsfehlern her, die der Computer macht,
oder von Messfehlern in der Bestimmung des Vektors b. Der Fehler AA kann
auch durch die Eliminationsschritte bedingt sein. Kleine Pivotelemente ziehen
große Fehler in L und U nach sich, und aus (L + AL){U + AU) wird A + AA.
Sind AA oder die Konditionszahl sehr groß, kann es sein, dass der Fehler Ax
untolerierbar wird.
Beispiel 9.2.3 Sind A und A~^ symmetrisch, so erhält man c = \\A\\ ||^~^||
aus den Eigenwerten:
A =
60
02
hat die Norm 6.
A-' =
0^
hat die Norm ^.
Diese Matrix A ist symmetrisch positiv definit, ihre Norm ist Amax = 6-
Die Norm von A~^ ist l/Amin = ^- Das Produkt dieser Normen liefert die
Konditionszahl:
_ ^max _ 6 _ Q
Beispiel 9.2.4 Wir betrachten dieselbe Matrix A mit den Eigenwerten 6 und
2. Um einen kleinen Vektor x zu erhalten, wählen wir b in Richtung des ersten
Eigenvektors A,0), und um ein großes Ax zu erzeugen, wählen wir Ah in
Richtung des zweiten Eigenvektors @,1). Dann gilt x = |b und Ax = |b.
Das Verhältnis ||zAx||/||x|| ist genau c = 3 mal dem Verhältnis ||zAb||/||b||.
Dieses Beispiel zeigt, dass der größte durch die Konditionszahl erlaubte
Fehler in der Tat auftreten kann. Es gibt eine nützliche Daumenregel, die
für das Gauß'sche Eliminationsverfahren experimentell überprüft wurde: Ein
Rechner kann aufgrund von Rundungsfehlern log c Dezimalstellen verlieren.
Aufgaben 9.2
1. Bestimmen Sie die Normen Amax und die Konditionszahlen Amax/Amin
der folgenden positiv definiten Matrizen:
•0,50'
[O 2
■2 1'
12
31'
11
2. Bestimmen Sie die Normen und die Konditionszahlen aus den Wurzeln
von Xma.A^'^^) ^^^ Xm\n{A'^A):
482 9 Numerische lineare Algebra
r-2 0"
0 2
1 1"
0 0
1 1"
-11
3. Beweisen Sie die folgenden Ungleichungen aus den Definitionen von ||^||
und \\B\\:
PBx||<m||Px||<|H|||B||||x||.
Folgern Sie aus dem Bruch (siehe 9A) für \\AB\\, dass \\AB\\ < \\A\\ \\B\\
gilt. Diese Ungleichung ist entscheidend für Matrixnormen.
4. Folgern Sie aus \\AB\\ < \\A\\ \\B\\, dass die Konditionszahl einer Matrix
mindestens 1 ist.
5. Warum ist / die einzige symmetrische positiv definite Matrix mit Amax =
Amin = 1? Deshalb sind die einzigen Matrizen mit ||^|| = 1 und ||^~^|| =
1 jene, für die A^A = / gilt. Dies sind Matrizen.
6. Orthogonale Matrizen haben die Norm \\Q\\ = 1. Zeigen Sie, dass für eine
Matrix A = QR die Ungleichungen \\A\\ < \\R\\ und \\R\\ < \\A\\ gelten.
Es folgt ll^ll = ||i^||. Geben Sie ein Beispiel einer Zerlegung A = LU mit
\\A\\ < \\L\\\\U\\ an.
7. (a) Aus welcher berühmten Ungleichung erhält man ||(^ + B)x\\ <
mx|| + ||^x|| für jedes X?
(b) Warum folgt aus der Definition (9.7) der Matrixnorm die Ungleichung
11^+ßii< 11^11 +iißii?
8. Zeigen Sie ausgehend von ^x = Ax, dass |A| < ||^|| für jeden Eigenwert
A von A gilt.
9. Der Spektralradius p{A) = |Aniax| ist der Absolutbetrag des größten
Eigenwerts. Zeigen Sie anhand eines 2 x 2-Beispiels, dass die Ungleichungen
p{A + B) < p{A) + p{B) und p{AB) < p{A)p{B) beide verletzt werden.
Der Spektralradius ist daher nicht als Norm verwendbar.
10. (a) Erklären Sie, warum A und A~^ dieselbe Konditionszahl besitzen,
(b) Erklären Sie, warum A und A^ dieselbe Norm haben.
11. Schätzen Sie die Konditionszahl der (schlecht konditionierten) Matrix
^ — [l 1,0001 J ^b.
12. Warum lässt sich die Determinante einer Matrix weder als Konditionszahl
noch als Norm verwenden?
13. (Vorgeschlagen von C. Moler und C. Van Loan.) Berechnen Sie b — Ay
und h — Az für
b =
0,217
0,254
0,780 0,563
0,913 0,659
9.2 Normen und Konditionszalilen
[ 0,341]
483
0,999
1,0
Ist y eine bessere Lösung der Gleichung ^x = b als z? Antworten Sie
auf zwei Weisen: Vergleichen Sie das Residuum b — Ay mit h — Az, und
vergleichen Sie y und z mit der richtigen Lösung x = A,-1). Beide
Antworten können richtig sein — manchmal braucht man ein kleines
Residuum, manchmal ein kleines Zix.
14. (a) Berechnen Sie die Determinante der Matrix A in Aufgabe 13, und
berechnen Sie A~^.
(b) Berechnen Sie, wenn möglich, ||^|| und m~^||, und zeigen Sie, dass
c > 10^ gilt.
Die Aufgaben 15—19 behandeln andere Vektornormen als die
übliche Norm ||x|| = V^Töc.
15. Die „1^ Norm" und die „1°° Norm" von x = (xi,... ,Xn) sind durch
||x||i = |xi|+ ••• +|xn| und ||x||oo = max |xi|
l<i<n
definiert. Berechnen Sie die Normen ||x||, ||x||i und ||x||oo der folgenden
beiden Vektoren im E^:
X = A,1,1,1,1) x = @,1, 0,7, 0,3, 0,4, 0,5).
16. Beweisen Sie, dass ||x||oo < ||x|| < ||x||i gilt. Zeigen Sie mit Hilfe
der Schwarz'schen Ungleichung, dass die Verhältnisse ||x||/||x||oo und
||x||i/||x|| niemals größer als ^/n werden. Für welchen Vektor erhält man
als Verhältnis der Normen genau ^/n?
17. Alle Vektornormen müssen der Dreiecksungleichung genügen. Beweisen
Sie, dass
l|x + ylloo < ||x||oo + llylloo und ||x + y||i < ||x||i + ||y||i
gilt.
18. Vektornormen müssen auch die Gleichung ||cx|| = \c\ ||x|| erfüllen, und sie
müssen positiv (außer für x = 0) sein. Welche der folgenden Ausdrücke
definieren eine Norm für (a:i,X2)?
|x|U = ki|+2|x2|
1x||c-||x|| + ||x||oo
||x||b = min|xi|
W^Wd = ||^x|| (Antwort hängt von A ab).
484 9 Numerische lineare Algebra
9.3 Iterative Methoden für lineare Algebra
Bis jetzt sind wir eher „direkt" an die Gleichung ^x = b herangegangen. Wir
haben die Matrix A so akzeptiert, wie sie vorlag, und haben das Gauß'sche
Eliminations verfahren verwendet. In diesem Abschnitt geht es um iterative
Methoden, in denen A durch eine einfachere Matrix S ersetzt wird. Die
Differenz T = S — A wird auf die rechte Seite der Gleichung gebracht. Mit S
an der Stelle von A wird das Problem einfacher lösbar. Dafür muss ein Preis
gezahlt werden — das einfache System muss wiederholt gelöst werden.
Es ist leicht, eine iterative Methode zu erfinden. Man schreibt einfach
A = S — T. Dann wird die Gleichung ^x = b zu
5x = Tx + b. (9.12)
Das Neue ist nun, dass man Gleichung (9.12) iterativ löst. Jede
Approximation Xjfc führt über die Gleichung
zur nächsten Approximation Xj^+i. Man beginnt diesen Prozess mit einem
beliebigen Vektor xo, und löst dann die Gleichung 5xi = Txo+b, danach die
Gleichung 5x2 = Txi -h b, und so weiter. Einhundert Iterationen sind nicht
ungewöhnlich, vielleicht sogar mehr. Man beendet die Rechnung, wenn der
neue Vektor Xjfc^_i hinreichend nahe an Xjt, oder das Residuum Axk — b nahe
bei Null liegt. Die Abbruchbedingung können wir selbst wählen. Man hofft
bei diesem Verfahren, dass man der richtigen Lösung nahe kommt, und zwar
schneller als durch das Eliminations verfahren. Wenn die Folge Xk konvergiert,
so ist X = Xoo eine Lösung für Gleichung (9.12). Dies beweist man, indem
man in Gleichung (9.13) k gegen unendlich gehen lässt.
Die beiden Ziele der Zerlegung A = S — T sind einerseits eine
schnelle Ausführung eines Iterationsschrittes und andererseits schnelle Konvergenz
der Xjfc. Die Dauer eines Schrittes hängt von 5 ab, die
Konvergenzgeschwindigkeit hingegen von S~^T:
1 Gleichung (9.13) sollte leicht nach Xj^+i auflösbar sein. Der ,,Präkondi-
tionierer'^ S könnte zum Beispiel eine Diagonalmatrix, oder eine
Dreiecksmatrix sein. Kennt man seine Lt/-Faktorisierung, so lässt sich jeder
Iterationsschritt schnell durchführen.
2 Die Differenz x — Xjk (also der Fehler ek) sollte schnell gegen null gehen.
Subtrahiert man Gleichung (9.13) von Gleichung (9.12), so fällt b heraus,
und es bleibt die Fehlergleichung:
Sek+i = Tek oder e^+i = S'^Tsk. (9.14)
In jedem Schritt wird also der Approximationsfehler mit der Matrix S~^T
multipliziert. Ist S~^T klein, so konvergieren die Potenzen dieser Matrix
schnell gegen null. Was aber heißt hier „klein"?
9.3 Iterative Methoden für lineare Algebra 485
Ein Extremfall der Zerlegung wäre S — A und T = 0. In diesem Fall ist
der erste Schritt der Iteration die ursprüngliche Gleichung Ax — b. Dann
ist die Konvergenz perfekt, da S~^T Null ist. Die Kosten für die Lösung
des Gleichungssystems sind allerdings genau das, was wir vermeiden wollten.
Bei der Wahl von S wägt man also zwischen schnellen Einzelschritten
(einfaches S) und schneller Konvergenz E nahe an A) ab. Einige oft verwendete
Möglichkeiten sind:
J S = Diagonalanteil von A (Man nennt die Iteration Jacobi-
Verfahren)
GS S = unterer Dreiecksteil von A (das Gauß-Seidel-Verfahren)
SOR S — Kombination des Jacobi- und des Gauß-Seidel-
Verfahrens {successive overrelaxation)
ILU S = approximiertes L mal approximiertes U {unvollständiges
LU-Verfahren)
Die erste Frage ist reine Hneare Algebra: Wann konvergieren die Xk gegen
X ? Bei der Antwort darauf taucht als die die Konvergenz bestimmende Größe
die Zahl |A|max auf. Wir werden in Beispielen für J, GS und SOR diesen
Spektralradius berechnen. Es handelt sich um den betragsgrößten Eigenwert
der Iterationsmatrix S~^T.
Der Spektralradius bestimmt die Konvergenz
Gleichung (9.14) ist ej^+i = S'^Tek- In jedem Iterationsschritt wird der
Fehler mit derselben Matrix B = S~^T multipliziert. Nach k Schritten ist
der Fehler daher ek = B'^bq, Die Fehlervektoren gehen gegen Null, wenn
die Potenzen der Matrix B = S~^T gegen Null gehen. Es ist interessant zu
sehen, wie die Eigenwerte von B, insbesondere der betragsgrößte Eigenwert,
die Potenzen J5* bestimmen.
Das Konvergenzkriterium ist also |A|max < 1- Reelle Eigenwerte müssen
zwischen -1 und 1 liegen, komplexe Eigenwerte X = a -\- ib innerhalb des
Einheitskreises in der komplexen Ebene. In diesem Fall ist der Absolutbetrag
|A| die Wurzel aus a^ + fe^. Wir werden komplexe Zahlen in Kapitel 10
behandeln. Auf jeden Fall ist der Spektralradius der größte Abstand eines der
Eigenwerte Ai,..., An der Iterationsmatrix B = S~^T zur 0.
Um zu verstehen, warum |A|niax < 1 eine notwendige Bedingung ist,
nehmen wir an, der erste Fehler eo sei ein Eigenvektor von B. Nach einem
Schritt ist dieser Fehler dann Beo = Aeo, und nach k Schritten ist der Fehler
-ö'^eo = A^eo. Beginnen wir mit einem Eigenvektor, so setzt sich die Iteration
486 9 Numerische lineare Algebra
immer mit diesem Eigenvektor fort. Dieser Vektor wächst oder schrumpft mit
den Potenzen A*. Der Faktor A* geht gegen Null, wenn |A| < 1 ist. Dies muss
für jeden Eigenwert gelten, und deshalb benötigt man |A|max < 1-
Um zu verstehen, warum |A|max < 1 eine hinreichende Bedingung dafür
ist, dass der Fehler gegen Null geht, nehmen wir an, dass eo sich als
Linearkombination von Eigenvektoren schreiben lässt:
eo = CiXi -\ h Cn^X^n führt auf ek = Ci(Ai)*Xi -\ h Cn(An)*Xn.
(9.15)
Das ist das Entscheidende bei den Eigenvektoren. Sie wachsen unabhängig
voneinander, je nach Eigenwert. Multiplizieren wir mit B, so wird der
Eigenvektor Xi mit Xi multipliziert. Wenn aber alle \Xi\ < 1, so garantiert
Gleichung (9.15), dass ek gegen Null geht.
Beispiel 9.3.1 Für die Matrix B = [o\lo\l] gilt A^ax = 1,1, für B' =
[^'ooiö] gilt Amax = 0,6. B^ ist 1,1 mal B, und B^ ist A,1)^ mal B, Die
Potenzen von B explodieren. Betrachten wir im Gegensatz dazu die
Potenzen von B\ Auf der Diagonalen der Matrix (J5')* stehen die Werte @,6)*
und @,5)*. Auch die Einträge abseits der Diagonalen enthalten einen Faktor
0,6*, der die Konvergenzgeschwindigkeit bestimmt.
Bemerkung Es gibt hier eine technische Schwierigkeit, wenn B keine n
linear unabhängigen Eigenvektoren hat. (Sie erzeugen diesen Effekt in J5', wenn
sie 0,5 in 0,6 ändern.) In diesem Fall kann es sein, dass der Startvektor eo
keine Linearkombination der Eigenvektoren ist — es gibt zu wenige für eine
Basis. Dann ist eine Diagonalisierung unmöglich, und Gleichung (9.15) ist
nicht mehr richtig. Für diesen Fall betrachten wir die Jordansche Normal-
form:
B = SJS-^ und J5* - SJ'^S-K (9.16)
In Abschnitt 6.6 wird beschrieben, wie J und J* aus Blöcken mit mehrfachen
Eigenwerten zusammengesetzt sind.
Die Potenzen eines 2 x 2-Blocks sind
A 1
0 A
A* kX^-^
0 A*
Gilt |A| < 1, so gehen die Potenzen gegen Null. Der Faktor k für einen
doppelten Eigenwert wird von dem stark abnehmenden Faktor A*"^ wirkungslos
gemacht. Dies gilt für alle Jordanblöcke. Bei einem größeren Block stehen in
J* Einträge der Form A;^A*~^, die ebenfalls gegen Null gehen, wenn |A| < 1
ist.
Gilt für alle Eigenwerte |A| < 1, so folgt also J^ -> 0. Damit ist Satz 9C
bewiesen: Für Konvergenz ist |A|max < 1 notwendig.
9.3 Iterative Methoden für lineare Algebra 487
Jacobi gegen Seidel
Im Folgenden lösen wir ein spezielles 2x2-Problem. Die Theorie der iterativen
Verfahren sagt uns, dass die entscheidende Größe der Spektralradius von
ß — S~^T ist. Achten Sie auf diese Zahl |A|inax- Man schreibt sie auch als
pfB) — der griechische Buchstabe „rho" steht für den Spektralradius:
2u — V = 4
-u + 2v = -2
hat die Lösung
(9.17)
Die erste Zerlegung stellt das Jacobi-Verfahren dar. Wir behalten die Dia-
gonalterme auf der linken Seite (in 5), und verlegen die Terme jenseits der
Diagonalen auf die rechte Seite (in T). Dann iterieren wir:
2uk+i = f jfc + 4
2?;ifc+i =Uk-2.
Wir beginnen die Iteration mit uq = vq
2, Vi = -1. So geht es weiter:
0. Der erste Schritt liefert ui =
'0"
0
2"
-1
'3/2'
0
2
.-1/4.
5/8"
0
2"
-1/16
geht gegen
Man erkennt die Konvergenz. In den Schritten 1, 3 und 5 ist die zweite
Komponente —1, —1/4 und —1/16. Der Fehler wird also alle zwei Schritte mit
\ multipliziert. Dasselbe gilt für den Fehler der ersten Komponente. Zu den
Werten 0, 3/2, 15/8 gehören die Fehler 2, i, |. Auch diese Fehler schrumpfen
alle zwei Schritte um einen Faktor 4. Die Fehlergleichung ist Sek-^i = Tek'.
20
02
ejfc+i
Ol
10
ek oder eu^i =
ejfc.
(9.18)
Die letzte Matrix ist 5 ^T. Die Eigenwerte dieser Matrix sind | und -|, so
dass ihr Spektralradius ^ ist:
B = S-^T
hat |A|,
= I und
L 2
Ol
10
In diesem speziellen Beispiel wird der Fehler in zwei Schritten genau mit \
multipliziert. Es illustriert den folgenden Sachverhalt: Das Jacobi-Verfahren
funktioniert gut, wenn die Haupt diagonale von A im Vergleich zum Rest
groß ist. Der Diagonalteil ist 5, der Rest ist -T. Wir möchten, dass der
Diagonalteil dominant ist, und S~^T klein.
Der Eigenwert A = | ist ungewöhnlich klein. Zehn Iterationen
reduzieren den Fehler um den Faktor 2^^ = 1024, und 20 Iterationen um A024)^.
Typischer (und teurer) sind Werte wie |A|max = 0,99 oder 0,999.
488 9 Numerische lineare Algebra
Das Gauß-Seidel-Verfahren verwendet die gesamte untere Dreiecksmatrix
von ^ als 5:
oder
Vk-^i = huk-^i - 1.
(9.19)
Beachten Sie den Unterschied. Das neue Uk-^i aus der ersten Gleichung wird in
der zweiten Gleichung sofort verwendet. Beim Jacobi-Verfahren behielten wir
den alten Wert Uk, bis der gesamte Schritt vollendet war. Beim Gauß-Seidel-
Verfahren gehen die neuen Werte in die Rechnung ein, die alten Uk fallen
weg. Auf diese Weise wird der Speicherbedarf halbiert, und normalerweise
wird dadurch auch die Iteration beschleunigt. Das Verfahren bringt keinen
höheren Aufwand mit sich als das Jacobi-Verfahren.
Beginnt man mit @,0), so erreicht man nach zwei Schritten die exakte
Lösung B,0). Diese Tatsache ist ein Zufall, den ich nicht erwartet hatte. Wir
führen die Iteration mit einem anderen Startvektor uo = 0 und ijq = — 1
durch:
^ o'
-1
3/2'
.-1/4.
15/8"
-1/16
■ 63/32"
-1/64
geht gegen
Die Fehler in der ersten Komponente sind 2, 1/2, 1/8, 1/32, und die Fehler
der zweiten Komponente sind —1, —1/4, —1/16, —1/32. Sie werden also in
jedem Schritt, nicht in zwei Schritten, um einen Faktor vier verringert. Das
Gauß-Seidel-Verfahren ist doppelt so schnell wie das Jacobi-Verfahren.
Dies gilt für alle positiv definiten Tridiagonalmatrizen; der Spektralradius
|A|max des Gauß—Seidel-Verfahrens ist das Doppelte des Spektralradius für
das Jacobi-Verfahren. Dies gilt für viele weitere Anwendungen, aber nicht
für jede Matrix. Wenn A stark nichtsymmetrisch ist, gibt es viele
Möglichkeiten — machmal ist das Jacobi-Verfahren schneller, manchmal können beide
Verfahren versagen. Unser Beispiel dafür ist klein:
20
-12
und T
Ol
00
und S-^T =
Die Eigenwerte beim Gauß-Seidel-Verfahren sind 0 und \. Vergleichen Sie
dies mit den Werten ^ und — ^ für das Jacobi-Verfahren.
Mit einer kleinen Anstrengung können wir auch das SOR-Verfahren
{successive overrelaxation) erklären. Die neue Idee ist dabei, einen Parameter UJ
(omega) in die Iterations Vorschrift einzuführen. Dieser Parameter cj wird so
gewählt, dass der Spektralradius von S~^T so klein wie möglich wird.
Wir schreiben dazu ^x = b als üjAx = ujh. Die Diagonale der Matrix 5
im SOR-Verfahren ist die Diagonale von A, aber unterhalb der Diagonalen
verwenden wir üjA. Die Matrix T auf der rechten Seite ist 5 — ujA:
2uk-^i = B - 2üj)uk + üJVk + 4a;
-üJUk-^i + 2vk-^i — B - 2üj)vk - 2(jj.
(9.20)
9.3 Iterative Methoden für lineare Algebra 489
Für uns sieht dies komplizierter aus, aber ein Computer arbeitet damit so
schnell wie immer. Jedes neue Uk-^i aus der ersten Gleichung wird sofort
für die Berechnung von vj^^i in der zweiten Gleichung verwendet. Dieses
Vorgehen entspricht dem Gauß-Seidel-Verfahren, mit einer anpassbaren Zahl
(jj. Die wichtigste Matrix ist immer S~^T:
S-'T =
1 -uj ^üj
(9.21)
Die Determinante ist A -o;)^. Beim optimalen u haben beide Eigenwerte den
Wert 7 — 4\/3, nahe bei (|)^. Deshalb ist das SOR-Verfahren in diesem
Beispiel doppelt so schnell wie das Gauß-Seidel-Verfahren. In anderen Beispielen
kann das SOR-Verfahren zehnmal oder hundertmal so schnell konvergieren.
Ich werde ihnen noch die wichtigste n x n-Testmatrix nennen. Es ist
unsere Lieblings-Tridiagonalmatrix mit den Diagonal werten -1, 2 und —1.
Die Hauptdiagonale ist 2/, darunter und darüber stehen die Einträge —1.
In unserem Beispiel hatten wir n = 2 mit dem Eigenwert cos f = | beim
Jacobi-Verfahren. (Diesen Wert hatten wir schon zuvor bestimmt.) Beachten
Sie, dass dieser Eigenwert beim Gauß-Seidel-Verfahren quadriert wird:
9D Die Zerlegtmgea der(—15 2, --l)-T>idiagonalmatrix der Dimension: n
Uefem dietolgea^^^^Elgenwertefär S: - - > -:'
Jacobi ^' '^ '^: ^ 1^^^^ @,2,^Ö)-Matrix):: S^^S \m% y>^^^ cos ^
^ ^ n + 1
Gauß-Seictei (ä^ ^ ^' (--1,2,0)^Matrix)^=^ ^S^^^ %at' '^ jAjma^ ^' ^ =
r ' .,r,\- ' cos " ^. . } \, ^r:. ^ ^ ^'^^ .
(cos -) /(l + sin -)
V 72 + 1/ / V 72 + 1/
Lassen Sie mich Folgendes klarstellen: Für die (—1, 2, — l)-Tridiagonal-
matrix sollte man keines dieser Verfahren anwenden! Für diese Matrix
funktioniert das Eliminationsverfahren (exakte Lt/-Zerlegung) sehr schnell.
Iterative Verfahren sind für große dünnbesetzte Matrizen gedacht, bei denen
ein großer Teil der Nulleinträge „nicht gut" ist. Die schlechten Nullen liegen
innerhalb eines sehr großen Bandes. Bei der exakten Berechnung von L und
U verschwinden diese Nullen, mit der Folge, dass die Elimination aufwändig
wird.
Lassen Sie uns noch eine weitere Zerlegung besprechen. Man verbindet
sie mit den Worten „ unvollständige LU-Faktorisierung''. Die Idee ist, kleine
von Null verschiedene Einträge in den Matrizen L und U zu Null zu setzen,
490 9 Numerische lineare Algebra
so dass man dünnbesetzte Dreiecksmatrizen Lq und Uo erhält, die schnelle
Berechnungen erlauben.
Auf der linken Seite der Zerlegung steht S = LqUo- Hier lässt sich jeder
Schritt schnell durchführen:
LoUoXk-^i ={A- LoUo)xk + b.
Auf der rechten Seite werden dünnbesetzte Matrizen mit Vektoren
multipliziert. Man multipliziert nicht die beiden Matrizen Lq und Uo miteinander,
sondern Xk mit Uo, und das Ergebnis mit Lq. Auf der linken Seite arbeitet
man mit Vorwärts- und Rückwärtssubstitution. Liegt LoUo nahe bei A, so
ist |A|inax klein, und wenige Iterationen führen zu einer guten Lösung.
Das Problem bei allen vier Zerlegungen ist, dass ein einziger großer
Eigenwert in S~^T alles zunichte macht. Es gibt eine sicherere Iteration, das
Verfahren der konjugierten Gradienten, bei der dieses Problem vermieden
wird. Kombiniert man es mit einem guten Präkonditionierer S (aus der
Zerlegung ^ = 5 — T), so erhält man einen der mächtigsten und Verbreitetesten
Algorithmen der numerischen linearen Algebra.^
Iterative Verfahren für Eigenwerte
Wir gehen von der Gleichung Ax = b zur Gleichung Ax = \x über. Für
lineare Gleichungssysteme sind iterative Verfahren eine Möglichkeit der Lösung,
bei Eigenwertproblemen sind sie notwendig. Die Eigenwerte einer n x n-
Matrix sind die Nullstellen eines Polynoms n-ten Grades, da die
Determinante von A- \I mit dem Term (-A)" beginnt. Dieses Buch sollte nicht den
Eindruck hinterlassen, dass man die Eigenwerte aus dem Polynom berechnet.
Außer für kleine n ist die Determinante von A — XI nur schlecht geeignet.
Es gibt für n > 4 keine exakte Formel für die Lösungen der Gleichung
det{A - \I) = 0. Schlimmer noch ist, dass die A's sehr instabil und
empfindlich gegenüber Rechenfehlern sein können. Es ist viel besser, mit der
Matrix A direkt zu arbeiten und sie in eine Diagonal- oder Dreiecksmatrix
umzuformen, so dass auf der Diagonalen die Eigenwerte erscheinen. Gute
Computerroutinen dafür stehen in der LAPACK-Bibliothek zur Verfügung
— man bekommt einzelne Routinen kostenfrei unter www.netlib.org. In
dieser Bibliothek sind die früheren Sammlungen LINPACK und EISPACK
(mit Verbesserungen) zusammengefasst. Es handelt sich um eine Sammlung
von Fortran 77-Programmen für lineare Algebra auf Hochleistungsrechnern.
Auf Rechnern wie sie oder ich sie besitzen, erhält man dieselbe Effizienz durch
hochwertige Matrix-Pakete wie MATLAB.
Wir werden hier kurz die Vektoriteration und das QÄ-Verfahren zur
Berechnung von Eigenwerten vorstellen. Es ist hier nicht sinnvoll, die
dazugehörigen Computerprogramme detailliert zu besprechen.
^ Das Verfahren der konjugierten Gradienten wird in dem Buch Introduction to
Applied Mathematics des Autors und detailierter von Golub-Van Loan und
Trefethen-Bau beschrieben.
9.3 Iterative Methoden für lineare Algebra 491
1 Vektoriteration und inverse Vektoriteration. Man beginnt mit einem
beliebigen Vektor uo, multipliziert ihn mit A und erhält so ui. Erneute
Multiplikation mit A liefert U2. Wenn uq eine Linearkombination von
Eigenvektoren ist, dann multipUziert A jede Eigen vektorkomponente x^ mit A^. Nach
k Schritten erhält man (A«)^:
Uk = yl^uo = ci(Ai)^xi + --- + Cn(An)*
(9.22)
Setzt man das Verfahren fort, so beginnt der größte Eigenwert, den Vektor zu
dominieren. Die Vektoren Uk zeigen in Richtung des dominanten Eigen
Vektors. Für Markov-Matrizen haben wir diesen Effekt in Kapitel 8 beobachtet:
0,9 0,3
0,1 0,7
hat An
1 mit dem Eigenvektor
Man beginnt mit uo und multipliziert in jedem Schritt mit A:
geht gegen Uoo =
Uo
ui
0,9
0,1
U2
0,84
0,16
0,75
0,25
0,75
0,25
Die Konvergenzgeschwindigkeit hängt vom Verhältnis des zweitgrößten
Eigenwerts A2 zum betragsgrößten Eigenwert Ai ab. Wir wollen nicht, dass Ai
klein ist, aber wir wünschen uns, dass A2/Ai klein ist. In unserem Fall ist
A2/A1 = 0,6/1, was zu einer akzeptablen Konvergenzgeschwindigkeit führt.
Bei großen Matrizen geschieht es oft, dass das Verhältnis |A2/Ai| sehr nahe
bei 1 hegt. In diesem Fall ist die Vektoriteration zu langsam.
Gibt es eine Möglichkeit, den kleinsten Eigenwert, der in Anwendungen
oft der wichtigste Eigenwert ist, zu bestimmen? Ja, durch die inverse
Vektoriteration: Man multipliziert Uq mit A~^ anstatt mit A, Da man A"^ nicht
berechnen will, löst man in der ReaUtät die Gleichung Aui = uq. Wenn man
die Faktoren L und U abspeichert, lässt sich der nächste Schritt Au2 = ui
sehr schnell durchführen. SchUeßUch erhält man
Uk = A ^uo =
(Ai)^
+ ••• +
(9.23)
In diesem Fall gewinnt der kleinste Eigenwert Amin die Oberhand. Ist er
sehr klein, so ist der Faktor l/X^i^ sehr groß. Um die Geschwindigkeit noch
zu erhöhen, verkleinert man Amin noch weiter, indem man die Matrix zu
A — X*I verschiebt. Liegt A* nahe bei Amin, so hat A — X*I den sehr kleinen
Eigenwert Amin - A*. In jedem Schritt mit der verschobenen Inversen wird
der Eigenvektor durch diese Zahl dividiert, so dass er sehr schnell die anderen
Komponenten dominiert.
2 Das Q/^-Verfahren Dieses Verfahren stellt einen der wichtigsten Erfolge
in der numerischen linearen Algebra dar. Vor fünfzig Jahren waren
Eigenwertberechnungen langsam und ungenau. Man hatte damals noch nicht einmal
492 9 Numerische lineare Algebra
erkannt, dass das Lösen der Gleichung det(A—XI) = 0 eine unbrauchbare
Methode darstellt. Jacobi hatte schon vorher vorgeschlagen, die Matrix A Schritt
für Schritt in eine Dreiecksmatrix umzuformen — so dass die Eigenwerte
automatisch auf der Diagonalen erscheinen. Er verwendete 2 x 2-Drehungen, um
Nullen abseits der Diagonalen zu erzeugen. (Unglücklicherweise kommt es vor,
das bereits erzeugte Nullen wieder verschwinden. Das Jacobi-Verfahren hat
aber im Zusammenhang mit Parallelrechnern ein kleines Comeback erlebt.)
Im Moment stellt das Qi?-Verfahren die wichtigste Methode zur Berechnung
von Eigenwerten dar, weswegen wir es kurz beschreiben.
Der wesentliche Schritt ist, die Matrix A, deren Eigenwerte wir
bestimmen wollen, in der Form QR zu faktorisieren. Erinnern Sie sich daran, dass
(wie beim Gram-Schmidt-Verfahren in Abschnitt 4.4) die Matrix Q ortho-
normale Spalten hat, und jR eine obere Dreiecksmatrix ist. Die Schlüsselidee
für Eigenwert berechnungen ist, die Matrizen Q und jR zu vertauschen. Man
betrachtet die neue Matrix Ai = RQ, die zu ^ = QR ähnlich ist und deshalb
dieselben Eigenwerte hat.
QRx = Xx liefert RQ{Q-^x) = X{Q~^x).
(9.24)
Man setzt den Prozess fort, indem man Ai in QiRi faktorisiert und wieder
die Faktoren vertauscht. So erhält man die Matrix A2 = RiQi, die wiederum
dieselben Eigenwerte wie A hat. Oft enthält der letzte Eintrag von A4 bereits
einen genauen Eigenwert. In diesem Fall entfernt man die letzte Zeile und
Spalte und fährt mit einer kleineren Matrix fort, um weitere Eigenwerte zu
bestimmen.
Zwei zusätzliche Ideen führen diese Methode zum Erfolg. Die eine ist,
die Matrix um ein Vielfaches von / zu verschieben, bevor man sie in QR
faktorisiert, und dann RQ zurück zu verschieben:
Man faktorisiert Ak - Ckl in QkRk- Die nächste Matrix der Iteration ist
Ak+i = RkQk + Ckl.
Ak+i besitzt dieselben Eigenwerte wie Ak und die ursprüngliche Matrix Aq —
A. Am besten wählt man c nahe einem der (unbekannten) Eigenwerte. Dieser
Eigenwert erscheint dann präziser auf der Diagonalen Ak^^i — und liefert so
ein besseres c für den nächsten Schritt zur Matrix AkJ^2 •
Die andere Idee ist, schon vor dem QÄ-Verfahren Nullen abseits der
Diagonalen zu erzeugen. Dazu wechselt man (ohne Änderung der Eigenwerte)
von A zur ähnlichen Matrix L~^ AL
1
-1 1
23"
145
167
1
1 1
-
531
195
O42J
L-^AL
L~^ subtrahiert Zeile 2 von Zeile 3 und erzeugt so die Null in Spalte 1. L
addiert Spalte 3 zu Spalte 2, und lässt die Null unverändert. Versucht man,
auf diese Weise eine weitere Null zu erzeugen, so scheitert man. Zwar erzeugt
9.3 Iterative Methoden für lineare Algebra 493
die Subtraktion von Zeile 1 von Zeile 2 eine Null, aber durch Anwendung von
L wird Spalte 2 zu Spalte 1 addiert, und dabei geht diese Null verloren.
Wir müssen also die von null verschiedenen Einträge A und 4) entlang
der Nebendiagonalen stehen lassen. Bei dieser Matrix handelt es sich um eine
Hessenherg-Matrix, die sich in einer festen Anzahl von Schritten berechnen
lässt. Die Nullen in der unteren linken Ecke bleiben während des gesamten
Ei^-Verfahrens Null. Der Rechenaufwand für jede Qi^-Faktorisierung sinkt
dadurch von O(n^) auf O(n^).
Golub und Van Loan geben das folgende Beispiel für einen verschobenen
(Ji^-Schritt auf einer Hessenberg-Matrix A an. Die Matrix wird um cl = 71
verschoben:
A =
1 2 3
45 6
0 0,001 7
führt auf Ai
-0,54 1,69 0835
0,31 6,53 -6,656
0 0,00002 7,012
Die Faktorisierung von ^ - 7/ in die Faktoren QR Uefert Ai = RQ + 71.
Beachten Sie die sehr kleine Zahl 0P0002. Der Diagonaleintrag 7,012 ist ein
beinahe exakter Eigenwert von Ai, und daher von A. Ein weiterer Qi^-Schritt
mit einem Shift um 7,012 würde zu einer hervorragenden Genauigkeit führen.
Aufgaben 9.3
In den Aufgaben 1—12 geht es um iterative Verfahren zur Lösung
von Ax = b.
1. Schreiben Sie die Gleichung Ax = b als x = (/ - A)x + b. Welche
Matrizen S und T verwenden Sie in dieser Zerlegung? Bestimmen Sie die
Matrix S~^T, die über die Konvergenz der Folge Xjk+i = {I - A)xk + b
bestimmt.
2. Ist A ein Eigenwert von A, so ist ein Eigenwert von B = I — A.
Die reellen Eigenwerte von B haben also einen Absolutbetrag kleiner als
1, falls die reellen Eigenwerte von A zwischen und liegen.
3. Zeigen Sie, dass die Iteration Xk+i = {^ — A)xk + b für die Matrix A =
[-12] nicht konvergiert.
4. Warum ist die Norm von B^ niemals größer als ||jB||^? Dann garantiert
IIB II < 1 dass die Potenzen B^ gegen Null gehen (daraus folgt die
Konvergenz). Dies ist keine Überraschung, da |A|inax kleiner als oder gleich
||ß|| ist.
5. Ist A eine singulare Matrix, so müssen alle Zerlegungen A = S - T
versagen. Zeigen Sie aus Ax = 0, dass S~^Tx = x gilt. Die Matrix
J5 = ^"^T hat also einen Eigenwert A = 1, weswegen das Verfahren
nicht funktionieren kann.
494 9 Numerische lineare Algebra
6. Ändern Sie die Einträge 2 in 3, und bestimmen Sie die Eigenwerte von
S~^T für das Jacobi-Verfahren:
12.
5xfc+i = Txk + b ist
30
03
Xfc+l
Ol
10
Xfc +b.
Bestimmen Sie die Eigenwerte von S ^T für das Gauß-Seidel-Verfahren
angewandt auf Aufgabe 6:
3 0
-1 3
Xfc+l
Ol
00
Xfc +b.
Ist |A|max für das Gauß-Seidel-Verfahren gleich |A|
Verfahren?
^ax für das Jacobi-
8. Zeigen Sie, dass für eine beliebige 2 x 2-Matrix [ ^ J] der Eigenwert |A|max
gleich \bc/ad\ beim Gauß-Seidel-Verfahren, und gleich \bc/ad\^^^ beim
Jacobi-Verfahren ist. Es muss ad ^ 0 gelten, damit die Matrix S
invertierbar ist.
9. Beim SOR-Verfahren erzeugt das optimale oü zwei gleiche Eigenwerte von
S~^T. Als Eigenwert hat man dann o; - 1, da die Determinante {üü — 1)^
ist. Setzen Sie die Spur in Gleichung (9.21) mit {üü — 1) + {üü — 1) gleich,
und bestimmen Sie so das optimale üü.
10. Schreiben Sie ein Computerprogramm (in MATLAB oder einer anderen
Sprache) für das Gauß-Seidel-Verfahren. Sie können entweder
Matrizen S und T aus A definieren, oder die Iterationsschleife direkt auf
den üij arbeiten lassen. Testen Sie ihr Programm mit der (—1,2,-1)-
Tridiagonalmatrix für n = 10, n = 20 und n = 50 und mit dem Vektor
b=(l,0,...,0).
11. Die Gauß-Seidel-Iteration für die Komponente i ist
3=1 3=1
Wieso folgt aus x^^^ = xf^ für jede Komponente, dass x die richtige
Lösung ist? Wie ändert sich die Formel für das Jacobi-Verfahren? Für
das SOR-Verfahren müssen Sie üü außerhalb der Klammern hinzufügen.
Beim SOR-Verfahren ist die Matrix S dieselbe Matrix wie beim Gauß-
Seidel-Verfahren, außer dass die Diagonale durch üü dividiert wird.
Schreiben Sie ein Programm für das SOR-Verfahren auf einem xn-Matrix, und
wenden Sie es mit üü = 1,1,4,18, 2^ auf die (-1,2, -l)-Tridiagonalmatrix
für n = 10 an.
9.3 Iterative Methoden für lineare Algebra 495
13. Dividieren Sie Gleichung (9.22) durch Af und erklären Sie, warum das
Verhältnis IA2/A1I über die Konvergenz der Vektoriteration entscheidet.
Konstruieren Sie eine Matrix A, bei der das Verfahren nicht konvergiert.
14. Die Markov-Matrix A = [0^ 07] ^^^ ^^^ Eigenwerte A =: 1 und 0,6, und
die Vektoriteration Uk = A^uq konvergiert gegen [o'^s]- Bestimmen Sie
die Eigen Vektoren von A~^. Gegen welchen Vektor konvergiert die
inverse Vektoriteration u-k = A~^uo (nachdem Sie mit @,6)^ multipliziert
haben)?
15. Zeigen Sie, dass die (-1,2, -l)-Tridiagonalmatrix der Dimension n den
Eigenvektor xi = (sin ^^,sin ^^,... ,sin ^^) besitzt. Bestimmen Sie
den zugehörigen Eigenwert, indem sie Axi berechnen. Hinweis: Um die
anderen Eigenvektoren und Eigenwerte der Matrix zu bestimmen, müssen
Sie den Wert n in xi und in Ai in den Wert jn ändern.
16. Berechnen Sie drei Schritte der Vektoriteration Uj^-f-i = Auk für die
Matrix A = [_l~l] mit dem Startvektor uq = [J] an. Gegen welchen
Eigenvektor konvergiert das Verfahren?
17. Berechnen Sie drei Schritte der inversen Vektoriteration Uj^-^i = A~^Uk
für die Matrix aus Aufgabe 11 mit demselben Startvektor uq. Gegen
welchen Eigen vektor konvergieren die Vektoren Ujk?
18. Zeigen Sie, dass beim Qi^-Verfahren für Eigenwerte der Eintrag an der
Stelle B,1) von sinö in A = QR auf - sin^ 9 in RQ fällt. Berechnen Sie
dazu die Matrizen R und RQ. Wegen dieser „kubischen Konvergenz" ist
das Verfahren so erfolgreich.
A =
cos 6 sin 6
sin 9 0
= QR
cos 9 —sin 9
sin 9 cos 9
1?
0?
19. Ist A eine orthogonale Matrix, so besteht die Qi^-Faktorisierung aus den
Faktoren Q — und R = . Deshalb gilt RQ = . Dies
ist eines der wenigen Beispiele, bei denen das Qi^-Verfahren versagt.
20. Beim verschobenen Qi^-Verfahren faktorisiert man eine Matrix A - cl
in die Form QR. Zeigen Sie, dass die nächste Matrix der Iteration Ai =
RQ + cl gleich Q~^AQ ist. Deshalb hat Ai dieselben Eigenwerte wie A,
liegt aber näher an der Dreicksform.
21. Gilt A = A^, so bestimmt man mit dem „Lanczos-Verfahren"' Zahlen üj
und bj und orthonormale Vektoren q^, so dass Aq^ = bj-ic^-i -\- ajqj +
bjqj^i (mit qo = 0) gilt. Multiplizieren Sie dies mit qj und bestimmen
Sie eine Formel für die üj. Die Gleichung besagt, dass AQ = QT mit
einer -Matrix T gilt.
496 9 Numerische lineare Algebra
22. Die Gleichung in Aufgabe 21 entwickelt sich aus der folgenden Schleife
mit bo = 1 und tq = ein beliebiges qi:
üj =qj^q^-;
^3
-4q,
bj-icij-i - ajC\j]
23.
Schreiben Sie dafür ein Computerprogramm, und testen Sie es an der
(-1,2, -l)-Tridiagonalmatrix A. Es sollte Q^Q gleich / sein.
A sei eine symmetrische Tridiagonalmatrix. Zeigen Sie, dass die Matrix
Ai = Q~^AQ beim Qi^-Verfahren ebenfalls symmetrisch ist. Zeigen Sie
dann aus Ai = RAR~^, dass Ai ebenfalls eine Tridiagonalmatrix ist.
(Hat man dies für die untere Hälfte bewiesen, so gilt es wegen der
Symmetrie auch für die obere Hälfte.) Symmetrische Tridiagonalmatrizen bilden
den Kern des Qi^-Verfahr ens.
In den Fragen 24—26 geht es um schnelle Methoden, die Lage von
Eigenwerten abzuschätzen.
24. Zeigen Sie, dass |A| < 1 gilt, falls die Summe der Beträge \aij\ in jeder
Zeile kleiner als 1 ist. (Warum ist \UaijXj\ kleiner als \xi\, wenn \xi\
größer als die anderen Komponenten von x ist? Daraus folgt \Xxi\ < \xi\
und deshalb |A| < 1.)
(Gerschgorin-Kreise) Jeder Eigenwert von A liegt in einem Kreis,
dessen Mittelpunkt ein Diagonaleintrag au und dessen Radius n = Uj^i\aij\
ist. Dies folgt aus (A — aii)xi = Uj^iüijXj.
Ist \xi\ größer als die anderen Komponenten von x, so hat diese Summe
höchstens den Wert ri\xi\. Die Division durch \xi\ liefert |A - a^l < n.
25. Welche Schranke für |A|max liefert Aufgabe 24 für die folgenden Matrizen?
Welche drei Gerschgorin-Kreise enthalten alle Eigenwerte?
0,3 0,3 0,2"
0,3 0,2 0,4
0,2 0,4 0,1
A =
2-1 0"
-1 2-1
0-1 2J
26.
Die folgenden Matrizen sind diagonaldominant, weil jeder
Diagonaleintrag au größer als die Summe r^ der Absolutbeträge der restlichen
Einträge in Zeile i ist. Zeigen Sie mit Hilfe der Gerschgorin-Kreise, in denen
alle Eigenwerte enthalten sind, dass diagonaldominante Matrizen
invertierbar sind.
10,3 0,4
0,3 1 0,5
0,4 0,5 1
A =
421
13 1
225
10 Komplexe Vektoren und Matrizen
10.1 Komplexe Zahlen
In einer vollständigen Darstellung der linearen Algebra kann man komplexe
Zahlen nicht auslassen. Selbst wenn eine reelle Matrix vorliegt, sind ihre
Eigenvektoren und Eigenwerte häufig komplex. Ein Beispiel: Eine 2x2-
Drehmatrix besitzt keine reellen Eigenvektoren, denn jeder Vektor wird um
einen Winkel 0 gedreht — seine Richtung ändert sich also. Sie hat aber die
komplexen Eigenvektoren (l,i) und A,—i). Die Eigenwerte sind ebenfalls
komplexe Zahlen, nämlich e*^ und e~*^. Wollten wir darauf bestehen, nur
reelle Zahlen zu betrachten, so müssten wir die Eigen Werttheorie auf halbem
Wege verlassen.
Der zweite Grund, komplexe Zahlen zuzulassen, geht über Eigenwerte
und Eigenvektoren einer Matrix A hinaus. Die Matrix selbst kann komplex
sein. Wir werden einen ganzen Abschnitt dem wichtigsten Beispiel widmen —
der Fouriermatrix. Die Ingenieurwissenschaften, die Naturwissenschaften, die
Musik und die Wirtschaftswissenschaften — sie alle verwenden Fourierreihen.
In der Realität sind die Reihen endlich, nicht unendlich. Die Berechnung der
Koeffizienten in Cie*^ + C2e*^^ H \-Cne^'^^ ist daher ein Problem der linearen
Algebra.
Im folgenden Abschnitt werden wir die wichtigsten Eigenschaften der
komplexen Zahlen vorstellen. Für einige Studierende mag es eine
Wiederholung sein, für alle ist er eine Referenz. Wir werden bis zu der erstaunlichen
Formel e^^^ = 1 gelangen.
Addition und Multiplikation komplexer Zahlen
Wir beginnen mit der komplexen Zahl i. Es ist allgemein bekannt, dass die
Gleichung x^ = —1 keine reelle Lösung hat — wenn man eine reelle Zahl
quadriert, so ist das Ergebnis niemals negativ. Deshalb haben sich alle
Wissenschaftler auf eine Lösung names i geeinigt (mit Ausnahme der
Elektrotechniker, die sie j nennen). Imaginäre Zahlen unterliegen den normalen Regeln
der Addition und der Multiplikation, mit nur einem Unterschied: Überall, wo
^ steht, ersetzt man —1.
498 10 Komplexe Vektoren und Matrizen
lOA Eim komplexe Zahl {zum Beispiel 3+21) ist die Summe atis einer j
elUu !^a||l'C)\ijua<i einer^rein imaginärm^ Zahl (%i).3ei dey Adäitiofl l>Jä;b|
der r^0j|e ^ind der iikagiBäre Teil voneinander getrennt* Bei der MiiltipÖi'
tioii verwendet rnan i^ =-^1:
Addition: C + 2i) -1- C + 2i) - 6 + 4i
Multiplikation: C + 2i)(I - i) = 3 + 2i -- 3^ -r 2i^ = 5 -- L
Addiere ich 3 + 2i zu 1 - i, so ist das Ergebnis 4 + 2. Die reellen Zahlen 3 + 1
bleiben von den imaginären Zahlen 2i — i getrennt. Wir addieren letztlich die
Vektoren C,2) und A,-1).
Die Zahl A - i)^ ist 1 - i mal 1 - i. Aus den Regeln folgt
überraschenderweise, dass das Ergebnis —2i ist:
A - z)(l -i) = l-i-i-\-i^ = -2L
Die Zahl 1-i befindet sich in der komplexen Ebene beim Winkel -45°. Wenn
wir sie quadrieren, so erhalten wir —2i und verdoppeln damit den Winkel.
Wenn wir das Ergebnis noch einmal quadrieren, so erhalten wir {—2i)^ = —4,
aus dem Winkel —90° wird also —180°, also die Richtung der negativen reellen
Zahlen.
Eine reelle Zahl ist einfach eine komplexe Zahl z — a + bi mit Imaginärteil
Null: ö = 0. Bei einer rein imaginären Zahl ist a =: 0:
Der Realteil ist a = Re(a + bi). Der Imaginärteil ist b — Im(a + bi).
Die komplexe Ebene
Komplexe Zahlen entsprechen Punkten der Ebene. Die reellen Zahlen liegen
auf der a:-Achse dieser Ebene, die rein imaginären Zahlen auf der y-Achse.
Die komplexe Zahl 3 + 2z entspricht dem Punkt mit den Koordinaten C,2).
Die Zahl Null, also 0 + Oz, liegt im Ursprung.
Die Addition und Subtraktion komplexer Zahlen entspricht der
Addition und Subtraktion von Vektoren in der Ebene. Der Realteil bleibt dabei
vom Imaginärteil getrennt. Wie üblich kann man die Addition also
darstellen, indem man den Anfang des einen Vektors an die Spitze des anderen
anhängt. Die komplexe Ebene C^ stimmt mit der gewöhnlichen
zweidimensionalen Ebene überein, außer, dass man komplexe Zahlen multiplizieren kann,
Vektoren aber nicht.
Es folgt eine wichtige Idee. Die komplex konjugierte Zahl zu 3+2z ist 3—2i.
Die komplex konjugierte Zahl zw z = a + bi ist 'z = a — bi, (Beachten Sie den
Querstrich auf der Zahl, der die Konjugation darstellt.) Der Imaginärteil von
z und „z quer" haben entgegengesetzte Vorzeichen. In der komplexen Ebene
ist J das Bild von z unter Spiegelung an der a:-Achse.
10.1 Komplexe Zahlen 499
Komplexe
Ebene
2i +
I Imaginaere
Achse
z = 3 + 2/
Relle Achse
1 2 3
Abb. 10.1. z = a + bi korrespondiert mit dem Punkt (a,&) und dem Vektor [j].
Zwei weitere nützliche Eigenschaften: multipliziert man konjugierte
Zahlen ^1 und 'Z2y so erhält man die komplex Konjugierte zu ziZ2. Addiert man
zi und ^2, so erhält man die komplex Konjugierte zu zi +2^2-
'zi -\-Z2 = {S-2i) -\- {l-\-i) = 4-i = Konjugierte zu zi + Z2.
zi X Z2 = {S - 21) X {1 -\- i) = b -\- i = Konjugierte zu zi x Z2.
Addition und Multiplikation sind genau die beiden Operationen, die man in
der linearen Algebra benötigt. Wenn man die Gleichung Ax = Ax (mit_einer
reellen Matrix A) konjugiert, so erhält man einen weiteren Eigenwert A und
seinen Eigenvektor x:
Falls Ax = Ax gilt und A reell ist, so folgt Ax = Ax.
A0.1)
Etwas Besonderes passiert, wenn man z = 3 -\- 2i mit der eigenen komplex
Konjugierten ^ = 3 - 2i kombiniert. Das Ergebnis einer Addition z -\-'z oder
einer Multiplikation z^ ist immer reell:
C + 2i) + C - 20 = 6 (reell)
C + 2i) x{3-2i) = 9 + 6i-6i- 4i^ = 13 (reell).
Die Summe einer Zahl z = a -\- bi und ihrer Konjugierten J = a - bi ist die
reelle Zahl 2a. Das Produkt von z mit z ist die reelle Zahl a^ + 6^:
'zz:^^,(a4-ln){a r-bi) ^ f^^J^;
A0.2)
Der nächste Schritt mit den komplexen Zahlen ist die Division. Die beste
Idee dafür ist, einen Nenner mit der komplex Konjugierten zu multiplizieren,
so dass die reelle Zahl a^ + 6^ entsteht:
1 a — ib a — ib
a-\-ib a^iba-ib a^ ^b'^ 3 4- 2i 3 4- 2i 3 - 22
1 3-22 3-22
500 10 Komplexe Vektoren und Matrizen
\ ► Reelle Achse
-2/-L
Jiomplex Konjugierte von z
z = 3-2i
Abb. 10.2. Die Konjugation ergibt das Spiegelbild. Die Zahl z -{- z ist reell.
Falls a^ -\- b^ = 1 gilt, bedeutet dies, dass die inverse Zahl (a + ib)~^ gleich
a — ib ist. Auf dem Einheitskreis gilt 1/z = 'z. Später werden wir sagen: 1/e*^
ist gleich der Konjugierten e~*^. Die Polarkoordinatendarstellung mit einem
Abstand r und einem Winkel 6 stellt eine einfache Möglichkeit dar, komplexe
Zahlen zu multiplizieren und zu dividieren.
Die Polarkoordinatendarstellung
Die Wurzel aus a^+b^ ist \z\. Diese Zahl nennt man den (Absolut-)betrag (oder
auch Modul^) der Zahl z = a-\-ib. Man bezeichnet diese Wurzel auch mit dem
Buchstaben r, weil sie den Abstand der komplexen Zahl zu 0 angibt. Diese
Zahl r gibt in der Polarkoordinatendarstellung die Größe einer komplexen
Zahl z an:
Der Absolutbetrag von z = a + ib ist \z\ = v^^^^?
er wird auch mit r bezeichnet.
Der Absolutbetrag von z = 3-\-2i ist \z\ = v 3^ -\- 2^, also r = vlS.
Der andere Teil der Polarkoordinatendarstellung ist der Winkel 6. Für z = 5
ist der Winkel 6 = 0, weil z reell und positiv ist. Für z = 3z ist der (im
Bogenmaß gemessene) Winkel 7r/2, und für z — —9 ist der Winkel tt. Der
Winkel verdoppelt sich, wenn eine Zahl quadriert wird. Dies ist einer der
Gründe, warum die Polarkoordinatendarstellung gut für die Multiplikation
komplexer Zahlen geeignet ist (aber nicht so gut für die Addition).
Sind Abstand r und Winkel 6 festgelegt, so erhält man aus der
Trigonometrie die anderen beiden Seiten des Dreiecks. Der Realteil (also die Grundlinie)
^ Anm. d. Übers.: Der zweite Name wird zwar verwendet, ist im deutschen
Sprachraum aber veraltet.
10.1 Komplexe Zahlen 501
ist durch a = rcosö, der Imaginärteil („hoch oder runter") durch h — rsmO
gegeben. Setzt man diese zusammen, so wird aus der kartesischen Darstellung
die PolarkoordinatendarStellung:
Die Zahl z = a + i& ist gleich z = r cos Ö Hh ^"^ ^sm Q.
Hinweis: cosö + isinO hat immer den Absolutbetrag r = 1, da
cos^ 6 + sin^ 6=1. Deshalb liegt cos6 + isinO auf dem Kreis mit
Radius 1 — dem Einheitskreis.
Beispiel 10.1.1 Man bestimme r und 6 für z = 1 -\- i und für die komplex
Konjugierte 'z = 1 — i.
Lösung Die Absolutbeträge von z und von ^ sind gleich, in diesem Fall gilt
z
= V-\-V =2 sowie \z\^ = r + {-ly = 2.
Der Abstand vom Mittelpunkt ist also y/2. Wie erhält man den Winkel? Die
Zahl l + i liegt im Punkt A,1) der komplexen Ebene. Der Winkel zu diesem
Punkt ist 7r/4 (oder 45°). Der Kosinus ist also 1/v^, und der Sinus ebenfalls
l/\/2. Kombiniert man r und 6, erhält man z = 1 -\-i zurück:
rcosö + zrsinö = \/2 ( —P j +z\/2 ( — j =
1 + z.
Der Winkel zur komplex konjugierten Zahl 1 — i kann positiv oder negativ
sein. Wir könnten einerseits den Winkel 77r/4 (also 315°) verwenden, oder
auch (rückwärts) den negativen Winkel -7r/4 (-45°). Hat eine Zahl z den
Winkel 6, so hat die komplex konjugierte Zahl 'z den Winkel 27r — 6 und auch
den Winkel -6.
Zu einem Winkel kann man beliebig 27r oder 47r oder — 27r hinzuaddieren,
ohne ihn zu ändern. Diese Winkel beschreiben volle Kreise, der Endpunkt ist
also derselbe. Aus diesem Grund gibt es unendlich viele Möglichkeiten für 6.
Oft wählt man einen Winkel zwischen 0 und 27r, aber die Form —6 ist für die
Konjugation J sehr nützlich.
Potenzen und Produkte: die Polarkoordinatendarstellung
öie Berechnung von Potenzen (l + i)^ und A+i)^ geschieht am schnellsten in
der Polarkoordinatendarstellung. Hier gilt r = y/2 und 6 = 7r/4 (oder 45°).
Man quadriert den Absolutbetrag zu r^ = 2 und verdoppelt den Winkel
auf 26 = TT 12 (oder 90°). Damit erhalten wir A + z)^. Für die achte Potenz
benötigt man r^ und 8Ö:
r^ = 2 • 2 • 2 • 2 = 16 und 8(9 == 8 • - = 27r.
4
502 10 Komplexe Vektoren und Matrizen
Dies bedeutet: Die Zahl A + i)^ hat den Absolutbetrag 16 und den Winkel
27r. Die achte Potenz von 1 + z ist also die reelle Zahl 16.
Potenzen lassen sich in Polarkoordinaten leicht berechnen. Das gilt auch
für die Multiplikation komplexer Zahlen:
i)ien-te.Potenz vpn ': z'^'ri^mB + iätoff) Ut AÖ*|
In diesem Fall wird z mit sich selbst multipliziert. In allen Fällen
multipliziert man die r 's und addiert die Winkel:
r(cos(9 + zsinö) mal r'(cos(9' + isinö') = rr'(cos((9 + (9') + zsin((9 + (9')).
A0.4)
Die Trigonometrie bietet eine Möglichkeit, dies zu verstehen. Betrachten wir
die Winkel. Warum erhält man den doppelten Winkel 26 für z^?
(cos 6 + i sin 6) x (cos 6 + i sin 6) = cos^ 6 + z^ sin^ 6 + 2z sin 6 cos 6.
Der Realteil cos^ö - sin^ö ist gleich cos2ö. Der Imaginärteil 2 sin ö cos ö ist
sin2ö. Man nennt diese Formeln die „Doppelwinkelformeln". Sie beweisen,
dass aus dem Winkel 6 in z der Winkel 26 in z^ wird.
Sind die Winkel 6 und 6' verschieden, so verwendet man stattdessen die
„ Additionstheoreme"
(cosö + isinö)(cosö' + isinö') =
[cos 6 cos 6' - sin 6 sin 6'] + i [sin 6 cos ö' + cos 6 sin 6'].
In den eckigen Klammern steht der Kosinus und der Sinus von 6 + 6'. Damit
wird die Aussage von Gleichung A0.4) bestätigt, dass die Winkel addiert
werden, wenn man komplexe Zahlen multipliziert.
Es gibt eine zweite Möglichkeit, die Regel für Potenzen z" zu verstehen.
Sie verwendet die einzige erstaunliche Formel dieses Abschnitts. Wir erinnern
uns daran, dass eine Zahl cosö + z sinö den Absolutbetrag 1 hat. Der Kosinus
besteht aus geraden Potenzen, beginnend mit 1 — |ö^, der Sinus hingegen
besteht aus ungeraden Potenzen; seine Reihe beginnt mit 6 — ^6^. Das Schöne
ist, dass der Ausdruck e*^ diese beiden Reihen in der Form cos 6 -\- i sin 6
zusammenfasst:
e^ = l+x-\-lx'^ + lx^-{-'-' implizierte*^ = 1 + i6> + h'^6^ + li^6^ + • • •
2 6 2 6
10.1 Komplexe Zahlen 503
Schreibt man -1 für z^, so sieht man, dass der Realteil 1 - |ö^ + • • • genau
cosö ist. Der Imaginärteil 6 — \6^ H ist sinö. Die Summe auf der rechten
Seite ist also insgesamt cosö + z sinö:
Euler^Bche Formel e'^ = cos6 -\-i sin6. A0.5)
Für 6 = 27r erhält man cos 27r + i sin 27r, diese Zahl hat den Wert 1. Auf eine
gewisse Weise summiert sich die unendliche Reihe e^^* = 1 + 27rz + |B7rz)^ +
• • • zu 1.
Wir wollen nun e*^ mit e*^ multiplizieren. Winkel werden aus demselben
Grund addiert, aus dem auch Potenzen addiert werden:
e^ mal e^ ist e^, weil (e)(e) x (e)(e)(e) = (e)(e)(e)(e)(e)
e'' mal e'' ist e''', e'' mal e''' ist e^(^+^'). ^^^'^^
Jede komplexe Zahl a-\-ib = r cos6+ ir sin6 können wir nun in der
bestmöglichen Form re*^ schreiben.
Die Potenzen (re*^)" sind gleich r"e*"^. Sie bleiben also auf dem
Einheit skr eis, wenn r = 1 (und daher r" = 1) gilt. In diesem Fall gibt es n
verschiedene Zahlen, deren n-te Potenz gleich 1 ist:
Sei w = e27ri/n j)jg n-ten Potenzen der Zahlen l,w;,w;^,..., w;"~^
sind alle gleich 1.
Man nennt diese Zahlen die „n-ten Einheitswurzeln". Es handelt sich um die
Lösungen der Gleichung z'^ = 1. Sie sind gleichmäßig auf dem Einheitskreis
verteilt, wie man in Abbildung 10.3b sehen kann, wo der volle Winkel 27r
in n gleiche Teile geteilt wurde. Um die n-ten Potenzen zu erhalten, muss
man einfach den Winkel mit n multiplizieren. Dies liefert w'^ = e^^* gleich 1.
Weiter gilt (w;^)" = e^^* = 1. Die n-te Potenz aller dieser Zahlen ist 1.
Diese Einheitswurzeln sind die wichtigsten Zahlen bei der
Signalverarbeitung. Ein realer Computer verwendet nur die Ziffern 1 und 0. Bei der
komplexen Fouriertransformation verwendet man die Zahl w und ihre Potenzen. Im
letzten Abschnitt dieses Buches werden wir zeigen, wie man einen Vektor (ein
Signal) mittels der schnellen Fouriertransformation in n Frequenzen zerlegt.
Aufgaben 10.1
In den Aufgaben 1-8 geht es um das Rechnen mit komplexen
Zahlen.
1. Addieren und multiplizieren Sie die folgenden Paare komplexer Zahlen:
(a) 2-\-i,2-i
(b) -l-hz,-l + i
(c) cos6 -\-ism6,cos6 -isinO
504 10 Komplexe Vektoren und Matrizen
^4ni/6
^2Ki/6
^127cj/6^^27ci^j
Abb. 10.3. (a) Multiplikation von e'^ mit e'^'. (b) Die n-te Potenz von e^'''/'' ist
= 1.
2. Bestimmen Sie die Lage der folgenden Zahlen in der komplexen Ebene.
Vereinfachen Sie dazu, falls nötig.
(a) 2 + z
(b) B + iJ
(d) |2 + z|
3. Bestimmen Sie den Absolutbetrag r = |^| der folgenden vier Zahlen. Der
Winkel für die Zahl 6 - Si sei 6. Welche Winkel haben die anderen drei
Zahlen?
(a) 6-Si
(b) {6-Si)'
(d) {6 + Si)^
4. Zeigen Sie: Gilt \z\ = 2 und \w\ = 3, so gilt \z x w\ =
, \z/w\ = und 1^ - w^l < .
+ w\ <
5. Bestimmen Sie die Form a-\-ib der Zahlen auf dem Einheitskreis mit den
Winkeln 30°, 60°, 90°, 120°. Es sei w die Zahl bei 30°. Rechnen Sie nach,
dass w^ bei 60° liegt. Welche Potenz von w ist gleich 1?
6. Ist z = rcosO + irsinO, so hat 1/z den Absolutbetrag und den
Winkel . Die Polarkoordinatendarstellung ist . Rechnen Sie
nach, dass das Produkt z x 1/z die Zahl 1 als Ergebnis hat.
7. Die komplexe Multiplikation M = {a + hi){c + di) lässt sich als reelle
2 X 2-Multiplikation
a—b
b a
c
d
=
10.1 Komplexe Zahlen 505
darstellen. Die rechte Seite enthält den Real- und den Imaginärteil von
M. Rechnen Sie dies am Beispiel M = {1 + Si){l — 3i) nach.
^. A = Ai + iA2 sei eine komplexe n x n-Matrix, und b = bi + ib2 sei
ein komplexer Vektor. Die Lösung zu A-x. = b sei xi + 2x2. Schreiben Sie
Ax = b als ein reelles 2n x 2n-System:
Xl
=
>2.
In den Aufgaben 9-16 geht es um die komplex Konjugierte z =
a — 10 = re
-iS
der Zahl z = a -{- ib = re
«r»ö*ö
9. Geben Sie die komplex Konjugierte aller folgenden Zahlen an, indem Sie
i durch —i ersetzen:
(a) 2-z
(b) B-0A-0
(c) e'^/2 (gleich i)
(d) e^^ = -1
(^) i^ (ebenfajls gleich i)
(f) 2^03^
10. Eine Summe z -\-^ ist immer , und eine Differenz z — ^ ist immer
. Es sei z ^ 0. Das Produkt z x ;2 ist immer , und der Bruch
z/z hat immer den Absolutbetrag
11. Für eine reelle 3 x 3-Matrix sind die Zahlen a2, ai, ao in der Determinante
det(A - \I) = -A^ + a2\^ + aiA + ao = 0
immer reell. Jede Nullstelle A ist ein Eigenwert. Durch Konjugation erhält
3 2
man die Gleichung -A + a2A + aiA + ao = 0, also ist A ebenfalls ein
Eigenwert. Bestimmen Sie det{A — XI) und die drei Eigenwerte für die
Matrix mit den Komponenten üij = i — j.
Bemerkung Die komplex konjugierte Gleichung zu Ax = Ax ist Ax = Ax.
Daran erkennt man zwei Tatsachen: A ist ein Eigenwert, und x ist der
zugehörige Eigenvektor. In Aufgabe 11 wird lediglich bewiesen, dass A
ein Eigenwert ist.
12. Man erhält die Eigenwerte einer 2 x 2-Matrix aus der Lösungsformel für
quadratische Gleichungen:
a — A b
c d — X
= A^ - (a + d)X + {ad - bc) = 0
liefert die beiden Eigenwerte (beachten Sie das =b-Zeichen):
506
10 Komplexe Vektoren und Matrizen
A =
_ a~\-d± v^(a + dJ - 4{ad - bc)
(a) Ist a = ö =: c? — 1, so sind die Eigenwerte komplex, wenn c ist.
(b) Welche Eigenwerte erhält man für ad = bc?
(c) Die beiden Eigenwerte müssen nicht immer komplex konjugiert
zueinander sein. Warum nicht?
13. Die Eigenwerte in Aufgabe 12 sind nicht reell, wenn (Spur)^ - (a + d)^
kleiner als ist. Beweisen Sie, dass die A's reell sind, wenn bc > Q
gilt.
14. Bestimmen Sie die Eigenwerte und Eigenvektoren der folgenden
Permutationsmatrix:
Pa =
0001
1000
0100
0010
hat das charakterischtische Polynom det(P4 - XI) = .
15. Erweitern Sie die obige Matrix P4 so zu einer Matrix Pq, dass fünf
Einträge 1 unterhalb der Diagonalen und einer in der Ecke stehen.
Bestimmen Sie det(P6 - A/) und die sechs Eigenwerte in der komplexen Ebene.
16. Eine reelle schiefsymmetrische Matrix {Ä^ = -A) hat rein imaginäre
Eigenwerte. Erster Beweis: Gilt Ax = Ax, so erhält man mit blockweisem
Multiplizieren
1 OA'
-A 0
X
zx
= iX
X
ix
Diese Blockmatrix ist symmetrisch, ihre Eigenwerte müssen
Deshalb ist A gleich .
sein!
In den Aufgaben 17-24 geht es um die Darstellung re^^ einer
komplexen Zahl r cos 6 + ir sin 6,
17. Schreiben Sie die folgenden Zahlen in der Euler'schen Form re'^, und
quadrieren Sie sie:
(a) 1 + y/Si
(b) cos 2(9+ i sin 2(9
(c) -7z
(d) 5-5i.
18. Bestimmen Sie den Absolutbetrag und den Winkel der Zahl z = sinö -h
icosO (Vorsicht!), und bestimmen Sie ihre Lage in der komplexen Ebene.
Multiplizieren Sie z mit cos 9 -\- isinO.
10.2 Hermitesche und unitäre Matrizen 507
19. Zeichnen Sie die acht Lösungen der Gleichung z^ = 1 in der komplexen
Ebene. Bestimmen Sie die kartesische Darstellung a + ib dieser Zahlen.
20. Bestimmen Sie die Lage der dritten Wurzeln aus 1 in der komplexen
Ebene, und bestimmen Sie die Lage der dritten Wurzeln aus —1. Zusammen
bilden Sie die sechsten Wurzeln aus .
21. Vergleichen Sie e^'^ = cos 3(9 + z sin3(9 mit {e'^)^ = (cos(9 + zsin(9)^ und
drücken Sie so cos3ö und sin3ö durch cos 6 und sin 6 aus.
22. Die komplex Konjugierte ^ einer Zahl sei gleich 1/z. Welche Möglichkeiten
gibt es für z?
23. (a) Warum hat sowohl e* als auch i^ den Absolutbetrag 1?
(b) Markieren Sie die Punkte e* und i^ in der komplexen Ebene.
(c) Die Zahl i^ kann man sich als {e^^^^y oder als (e^^^/^)^ denken. Sind
diese Zahlen gleich?
24. Zeichnen Sie die Pfade der komplexen Zahlen von t = 0 bis ^ = 27r in der
komplexen Eben3 nach:
(a) e''
(b) e(-i+^)* = e-*e^*
(c) (-1)* = e*^\
10.2 Hermitesche und unitäre Matrizen
Die Haupt aussage dieses Abschnitts kann im ersten Satz dargestellt werden:
Wenn man einen komplexen Vektor z oder eine Matrix A transponiert, muss
man sie auch konjugieren. Bleiben Sie nicht bei z^ oder Ä^ stehen, sondern
kehren Sie die Vorzeichen aller Imaginärteile um. Der zu einem Spaltenvektor
mit den Komponenten Zj = üj + ibj gehörende Zeilenvektor ist der konjugiert
transponierte Vektor mit den Komponenten üj — ibji
z'^ = ['zi " ' Jn] = [dl - ibi " ' ün -ibn]' A0-7)
Einer der Gründe dafür, z zu verwenden, ist der folgende. Das Quadrat der
Länge eines reellen Vektors ist x? + • • • + x^. Das Quadrat der Länge eines
komplexen Vektors ist nicht z\-\ 1-2;^, da mit dieser (falschen) Definition
die Länge des Vektors A, i) zum Beispiel 1^ + z^ zz: 0 wäre. Dies wäre ein von
Null verschiedener Vektor mit der Länge Null. Deswegen verwenden wir an
Stelle von (a + bi)'^ das Quadrat des Absolutbetrags a^ + b^. Diesen Ausdruck
erhält man aus (a + bi) mal (a - bi).
Für jede Komponente möchten wir also Zj mal Zj bilden, also \zj\^ =
a^ -\-b^. Wenn man die Komponenten von z mit denen von z multipliziert,
erhält man genau dies:
508 10 Komplexe Vektoren und Matrizen
\Zi • " Zn
kir + --- + kn|. Dies ist z^z = ||z|p. A0.8)
Hiermit ist das Quadrat der Länge von (l,z) gleich 1^ + |ip — 2, und die
Länge daher V^, nicht null. Das Längenquadrat von A + i, 1 - i) ist 4. Der
einzige Vektor mit der Länge null ist der Nullvektor.
Bevor wir forfahren, wollen wir noch zwei Symbole durch eines ersetzen.
An Stelle eines Querstrichs für die Konjugation und eines T für die
Transponierte schreiben wir das Superskript H. Damit gilt z^ = z^. Dies ist
„z-Hermitesch" die „konjugiert Transponierte" zu z. Man kann dieses
Symbol auch auf Matrizen anwenden: die konjugiert Transponierte einer Matrix
A ist A^.
-irT
Notation Der Vektor z^ ist gleich z^, und die Matrix A^ ist A
konjugiert Transponierte von A:
die
Falls A =
1 i
Ol+ 2
dann A^ =
1 0
-i 1 — i
= ,,A hermitesch.''
Komplexe Skalarprodukte
Für reelle Vektoren erhält man das Quadrat der Länge aus dem Skalarpro-
dukt x-^x des Vektors mit sich selbst. Für komplexe Vektoren ist das
Längenquadrat durch z^z gegeben. Es ist sehr wünschenswert, dass dieser Ausdruck
das Skalarprodukt von z mit sich selbst ist. Deshalb verwendet man für das
komplexe Skalarprodukt nicht einfach die Transponierte, sondern die
konjugierte Transponierte. Wenn die Vektoren reell sind, hat dies keinen Effekt. Es
hat aber definitiv einen Effekt, wenn es sich um komplexe Vektoren handelt:
f," K
10.2 Hermitesche und unitäre Matrizen
509
Bei komplexen Vektoren ist dann aber u^v verschieden von v^u. Die
Reihenfolge der Vektoren wird nun wichtig. Tatsächlich ist v^u = ViUi + • • • +
VniJ'n die komplex konjugierte Zahl zu u^v. Wir müssen also ein paar
Unannehmlichkeiten in Kauf nehmen.
Beispiel 10.2.1 Das Skalarprodukt von u :
[1
0. Nicht 2i.
\1'
i
mit V =
i
ll
ist
Beispiel 10.2.2 Das Skalarprodukt von u =
u^v = 2- 2z.
l + i
0
mit V =
ist
Beispiel 10.2.1 ist überraschend. Die Vektoren (l,z) und (i, 1) erwecken nicht
den Eindruck, orthogonal zu sein, sie sind es aber. Dass das Skalarprodukt
Null ist, bedeutet weiterhin^ dass die (komplexen) Vektoren orthogonal sind.
Ebenso ist (l,i) orthogonal zu A,—i), da ihr Skalarprodukt 1 — 1 = 0 ist.
Wir erhalten den korrekten Wert Null für das Skalarprodukt, wo wir den
inkorrekten Wert Null für die Länge von (l,i) erhalten würden, wenn wir zu
konjugieren vergäßen.
Bemerkung Wir haben uns dafür entschieden, den ersten Vektor u zu
konjugieren. Einige Autoren ziehen es vor, den zweiten Vektor v zu konjugieren.
Das Skalarprodukt dieser Autoren wäre dann u^v. Man kann hier frei wählen,
solange man sich an eine Wahl hält. Wir wollen aber auch in der nächsten
Formel das Symbol ^ verwenden:
Das Skalarprodukt von Au mit v ist gleich dem Skalarprodukt
von u mit A^v:
{An)^^r^n^iA'^y).
A0.10)
Der konjugierte Vektor zu Au ist Au. Durch Transponieren erhält man ü^A ,
wie üblich. Dies ist aber nichts anderes als u^A^. Alles, was funktionieren
sollte, funktioniert also auch. Die Regel für ^ rührt von der Regel für ^ her.
Dies gilt auch für Produkte von Matrizen:
iidÄ'/iitJiÄ
t „'S''^^'V\'''''' '<"'''':^i^'i^"'-\'ih''''''if:.''V\'rf'/'?;^'.^i 'h"\ 1 r^;' -;/'.-^'^^ \'^fi<V 'J'^''^'-'^''-',% '-:;;'f;'r/-;'"w ';"-:^:fl^i
Wir verwenden hier ständig die Tatsache, dass a—ih mal c—id das Konjugierte
von a + ih mal c + id ist.
Unter den reellen Matrizen bilden die symmetrischen Matrizen mit A =
Ä^ die wichtigste Klasse. Sie haben reelle Eigenwerte und einen vollen Satz
510 10 Komplexe Vektoren und Matrizen
orthogonaler Eigenvektoren. Die Diagonalisierungsmatrix S ist eine
orthogonale Matrix Q, jede symmetrische Matrix A kann also als A = QAQ~^ und
auch als A — QAQ^ geschrieben werden (weil Q~^ — Q^ gilt). Alles dies
folgt aus der Gleichung aij = üji, wenn A reell ist.
Unter den komplexen Matrizen wird die spezielle Klasse von den hermi-
teschen Matrizen mit A = A^ gebildet. Die Bedingung an die Einträge ist
nun also aij = äji. Man sagt in diesem Fall, dass A hermitesch ist. Jede reelle
symmetrische Matrix ist hermitesch, weil die Konjugation keinen Effekt hat.
Die folgende Matrix ist ebenfalls hermitesch:
A =
2 3-32
3 + 32 5
Die Hauptdiagonale ist reell, da gelten muss
Quer stehen konjugierte Einträge 3 + 32 und 3 - 3z.
An diesem Beispiel werden wir die drei entscheidenden Eigenschaften aller
hermiteschen Matrizen illustrieren.
WD m A
z^Az reelt
2=r A^ imd z ein M^hijgBr Vektat/ sü'^isf die Zt
AM
Ein schneller Beweis: z^Az ist sicher eine 1 x 1-Matrix. Berechnen wir die
konjugiert transponierte Matrix:
(z^Az)^ = z"A^(z")" dies ist wieder z"Az ist.
Durch eine Umkehrung der Reihenfolge haben wir (unter Ausnutzung von
A — A^) dieselbe 1 x 1-Matrix erzeugt. Für solche Matrizen ist aber die
konjugiert Transponierte einfach gleich der konjugierten Zahl. Deshalb ist die
Zahl z^Az gleich ihrer komplex Konjugierten, und daher reell. In unserem
Beispiel ist dies z^Az:
\Zl Z2\
2 3-3z
3 +3z 5
= 22^1^1 + 52^2^2 + C - Si)ziZ2 + C + 3i)ziZ2'
Die Terme 2|zip und 5|z2p auf der Diagonalen sind beide reell. Die Terme
abseits der Diagonalen bilden ein komplex konjugiertes Paar, so dass ihre
Summe reell ist. (Die Imaginärteile heben sich bei der Addition auf.) Der
gesamte Ausdruck z^ Az ist also reell.
icHg,;,iife
Beweis. Es gelte Az = Az. Multiplizieren Sie beide Seiten mit z^, Sie
erhalten z^Az = Az^z. Der Ausdruck z^Az links ist nach lOD reell. Der
Ausdruck z^z auf der rechten Seite ist das Quadrat der Länge, also reell und
positiv. Deshalb ist das Verhältnis A = z^Azjz^z eine reelle Zahl. Q.E.D.
10.2 Hermitesche und unitäre Matrizen
511
Im obigen Beispiel sind die Eigenwerte A = 8 und A = -1. Die
Determinante von A- XI ist (rf - 8)(rf + 1):
2-A 3-
3 + 3z 5
32
A
= A^ - 7A + 10 - |3 + 32f
= A^ - 7A + 10 - 18 = (A - 8)(A + 1).
lOf; ßie Bigenrnkformt einer hemmi^achßnM^tri^ vemehier
dei^en;Jßweß^ertm)/smä orfifti^oi^al^LÖÜt 4a& = Ay^. =:,^y^ sp
gilt aiicte^'^Ä;= 0» '/^; ' , \-^''' '-\ ; .-v . -(''' -v "" l>'^ ^ ' - ' -:
Beweis. Multiplizieren Sie Az = Az von links mit y^, und multiplizieren Sie
yH j^H _ ßyH ^Qj^ rechts mit z:
,i?
H^if„
,i^.
y^ Az = Ay^ z und y^ A^ z = ^y^ z.
A0.11)
Die linken Seiten sind gleich, da, A = A^ gilt. Deshalb sind auch die rechten
Seiten gleich. Da ß und A verschieden sind, muss der andere Faktor y^z
gleich Null sein. Die Eigenvektoren sind also orthogonal, wie im folgenden
Beispiel mit A = 8 und ß = -1:
{A - SI)z =
{A + I)y =
-6 3-3z
3 + 3z -3
3 3-3z
3 +3z 6
.2/2.
—
0
'0'
0
und z =
und y =
1 1
_l + i\
[ -1 _
Berechnen wir das Skalarprodukt der Eigenvektoren y und z:
y^z = [l + z-l]
1
1 + z
0 (orthogonale Eigen vektoren).
Das Längenquadrat dieser Eigenvektoren ist 1^ + 1^ + 1^ = 3, nach einer
Division durch \/3 ergeben sich also Einheitsvektoren. Waren sie vorher nur
orthogonal, so sind sie jetzt orthonormal Diese Vektoren bilden die Spalten
der Eigenvektormatrix 5, durch die A diagonalisiert wird.
Ist A reell und symmetrisch, so hat die Matrix orthogonale Eigen vektoren.
In diesem Fall ist 5 eine orthogonale Matrix Q, Hier ist A eine komplexe
hermitesche Matrix, deren Eigenvektoren komplex sind, aber orthonormal.
Die Eigenvektormatrix S ist wie Q, aber komplex. Wir wollen den komplexen
orthogonalen Matrizen jetzt einen neuen Namen und einen neuen Buchstaben
zuweisen.
512 10 Komplexe Vektoren und Matrizen
Unitäre Matrizen
Eine unitäre Matrix ist eine (komplexe) Matrix mit orthonormalen Spalten.
Sie wird mit U bezeichnet — das komplexe Äquivalent zu Q. Die
Eigenvektoren im Beispiel oben, durch ^/S dividiert und daher Einheitsvektoren, stellen
ein perfektes Beispiel dar:
U =
Vs
1 1-2
1 + Z -1
ist eine unitäre Matrix.
Dieses U ist außerdem noch eine hermitesche Matrix. Das hatte ich nicht
erwartet! Das Beispiel ist beinahe zu perfekt. Wir könnten die zweite
Spalte mit —1 oder sogar mit i multiplizieren, und die Eigenvektormatrix wäre
immer noch unitär:
U =
Vs
1
l + z
-1 + z
1
ist ebenfalls eine unitäre Matrix.
Man überprüft, ob eine reelle Matrix orthonormale Spalten hat, indem
man die Beziehung Q^Q = I nachrechnet. Multipliziert man Q^ mit Q, so
müssen abseits der Diagonalen Nullen erscheinen. Im komplexen Fall wird Q
zu U und das Symbol ^ zu ^. Es stellt sich heraus, ob die Spalten orthonormal
sind, wenn man U^ mit U multipliziert. Die Skalarprodukte der Spalten
müssen dann wieder 1 oder 0 sein, so dass sich U^U = I ergibt:
lOG Eine Mutrik Ü Hat oHhonormate Spalten, wenn Vf^-H. =i|
güU Ist U ^iae, quadratische Matrix, ^o iB% eßeiuß unUär^ Matrim.JJ^4
giltU^^tj-K , / v^ / ; /;, ^.,; ^ W'/ >' ' ^"
c/^c/ = 4=
Vs
1 l-z
1 + z -1
_1_
73
1 1-z
1 + z -1
10
Ol
A0.12)
Angenommen, eine Matrix U mit orthogonalen Spalten wird mit einem
Vektor z multipliziert. Die Länge des Vektors bleibt dabei unverändert, weil
z^U^Uz = z^z gilt. Ist z ein Eigenvektor, so erfahren wir noch mehr: Die
Eigenwerte von unitären (und von orthogonalen) Matrizen haben alle den
Absolutbetrag |A| = 1.
lOrt'' ,fet''K.tinitär," «ö'-pt \\Uzl\ /-; ||z|i; D6sMb'^fol^'''&^^ W^^M/M
Die Matrix in unserem 2 x 2-Beispiel ist sowohl hermitesch {U = C/^),
als auch unitär {U~^ = U^). Sie hat also reelle Eigenwerte (A = A) vom
10.2 Hermitesche und unitäre Matrizen 513
Fourier _i_
Matrix ~ VT
1 1 1
l ^4to/3 ^2Ki/3
Abb. 10.4. Die dritten Wurzeln aus 1 bilden die Fouriermatrix F = F3.
Absolutbetrag eins (A~^ = A). Dafür gibt es nur zwei Möglichkeiten: Die
Eigenwerte sind 1 oder —1.
Noch etwas zu diesem Beispiel: Die Diagonaleinträge von U bilden die
Summe null, die Spur ist null. Daher muss der eine Eigenwert 1 sein und der
andere -1, und die Determinante muss gleich 1 mal -1 sein — dem Produkt
der Eigenwerte.
Beispiel 10.2.3 In Abbildung 10.4 wird die 3 x 3-Fouriermatrix dargestellt.
Ist sie hermitesch? Ist sie unitär?
Die Fouriermatrix ist definitiv symmetrisch, sie ist gleich ihrer
Transponierten. Sie ist aber nicht gleich der konjugiert Transponierten, und deshalb ist
sie nicht hermitesch. Ändert man hier z zu -i, so erhält man eine andere
Matrix.
Ist F unitär? Ja. Das Quadrat der Länge jeder Spalte ist |A + 1 + 1), die
Spalten sind also Einheitsvektoren. Die erste Spalte ist zur zweiten
orthogonal, da 1 + e^^^/^ + e^""'/^ = 0 ist. Diese drei Zahlen sind in Abbildung 10.4
markiert.
Beachten Sie die Symmetrie der Abbildung. Dreht man sie um 120°, so
befinden sich die drei Punkte wiederum an derselben Position. Damit bleibt
auch ihre Summe S unverändert. Der einzige mögliche Wert für die Summe
ist 5 = 0, weil dies der einzige Punkt ist, der unter einer 120°-Drehung
unverändert bleibt.
Ist Spalte 2 von F orthogonal zu Spalte 3? Das Skalarprodukt scheint
1A + e^"^/^ + e^"^/^) = 1A + 1 + 1)
zu sein. Dies ist nicht null — aber das liegt daran, dass wir zu konjugieren
vergessen haben! Das komplexe Skalarprodukt verwendet ^, nicht ^:
(Spalte 2)^(Spalte 3) = ^A • 1 + e'^^^/^e^^^/^ + e-4^V3g2^V3)
= Ui^^2ni/3_^^-2ni/3^^Q
Damit ist die Orthogonalität bewiesen. Folgerung: F ist eine unitäre
Matrix.
514 10 Komplexe Vektoren und Matrizen
Im nächsten Abschnitt werden wir n x n-Fouriermatrizen studieren.
Unter allen komplexen unitären Matrizen sind diese die wichtigsten.
Multipliziert man einen Vektor mit F, so berechnet man die diskrete Fourier-
Transformierte^ und wenn man mit F~^ multipliziert, so berechnet man die
inverse Transformation. Die spezielle Eigenschaft unitärer Matrizen ist, dass
F~^ = F^ gilt. Die inverse Transformation unterscheidet sich also nur durch
-z an Stelle von i:
jP-i =fH ^
_1_
1 1 1
-j^ g-27ri/3 g-47ri/3
Jeder, der mit der Matrix F arbeitet, kennt ihren Nutzen. Im letzten
Abschnitt dieses Buches werden wir die Fourieranalyse mit der linearen Algebra
in Verbindung bringen.
Wir beenden diesen Abschnitt mit einer „Übersetzungstabelle" zwischen
dem reellen und dem komplexen Fall, für Matrizen und für Vektoren:
Reell gegenüber Komplex
ET". Vektoren mit n reellen Kom- f-^
ponenten
Länge: ||x|p = xj-[- [-x^
[A )ij — Aji
(AB)^ = B^A^
Skalarprodukt: x^y = xiyi-\
{Ax)^y = K^{Ä^y)
Orthogonalität: x^y = 0
symmetrische Matrizen: A = A^
A = QAQ-^ = QAQ^ (reelles .1)
schiefsymmetrische
C": Vektoren mit n komplexen
Komponenten
Länge: ||z|i2_= 1^1 |2 + ... + |z„|2
[A )ij = Aji
{AB)^ = B^A^
Skalarprodukt: u^v = iliVi-\ h
Orthogonalität:u^v = 0
hermitesche Matrizen: A = A^
A = UAU-^ = UAU" (reelles A)
Matrizen: ^' schiefhermitesche Matrizen: K" =
~K
f^
unitäre Matrizen: U^ — U^
orthonormale Spalten: U^U = I
(C/x)^(C/y) = x^y und \\Uz\\ =
llzll
orthogonale Matrizen: Q^ = Q ^
orthonormale Spalten : Q^Q = I
(Q^ViQy) = x^y und IIQxll =
l|x||
Die Spalten und die Eigenvektoren von Q und U sind orthonormal. Jeder
Eigenwert hat den Betrag |A| = 1.
Aufgaben 10.2
1. Bestimmen Sie die Längen der Vektoren u=(l + z,l-z,l + 2i) und
V = (i,i,z). Berechnen Sie auch u^v und v^u.
10.2 Hermitesche und unitäxe Matrizen 515
2. Berechnen Sie A^A und AA^. Beide Matrizen sind :
A =
i 1 i
1 i i
3. Lösen Sie die Gleichung Az = 0, um einen Vektor im Kern der Matrix
A aus Aufgabe 2 zu finden. Zeigen Sie, dass z orthogonal zu den Spalten
von A^, aber nicht zu den Spalten von A^ ist.
4. Aufgabe 3 legt nahe, dass die vier fundamentalen Unterräume durch
S{A), N{A) sowie und gegeben sind. Die Dimensionen sind
weiterhin r und n—r sowie r und m—r, und sie sind weiterhin orthogonale
Unterräume. Das Symbol ^ nimmt den Platz von ^ ein.
5. (a) Beweisen Sie, dass A^A immer eine hermitesche Matrix ist.
(b) Ist Az = 0, so ist auch A^Az = O.Es gelte umgekehrt A^Az = 0.
Multiplizieren Sie dies mit z^ und beweisen Sie so, dass Az = 0
sein muss. Die Kerne von A und A^A sind . Deshalb ist A^A
eine invertierbare hermitesche Matrix, wenn der Kern von A nur z =
enthält.
6. Wahr oder falsch? Geben Sie eine Begründung oder ein Gegenbeispiel an:
(a) Wenn A eine reelle Matrix ist, so ist A + il invertierbar.
(b) Wenn A eine hermitesche Matrix ist, so ist A + il invertierbar.
(c) Wenn U eine unitäre Matrix ist, so ist A + il invertierbar.
7. Ist cA hermitesch, wenn c eine reelle Zahl und A eine hermitesche Matrix
ist? Zeigen Sie, dass cA für c = i eine schief-hermitesche Matrix ist.
Die hermiteschen 3 x 3-Matrizen bilden also einen Unterraum, wenn die
Skalare reelle Zahlen sind.
8. Zu welchen Klassen von Matrizen gehört P: orthogonal, invertierbar, her-
mitesch, unitär, in LU faktorisierbar, in QR faktorisierbar?
P =
010
001
100
9. Berechnen Sie P'^.P^ und P^°° für die Matrix in Aufgabe 8. Welche
Eigenwerte hat P?
10. Bestimmen Sie Eigenvektoren der Länge eins für P aus Aufgabe 8, und
schreiben Sie sie als die Spalten einer unitären Matrix F. Wegen welcher
Eigenschaft von P sind diese Eigenvektoren orthogonal?
516 10 Komplexe Vektoren und Matrizen
11. Berechnen Sie die zyklische 3x3 Matrix C = 2/ + 5P + 4P^. Sie hat
dieselben Eigenvektoren wie die Matrix P in Aufgabe 8. Bestimmen Sie
ihre Eigenwerte.
12. Es seien U und V unitäre Matrizen. Zeigen Sie, dass U~^ und UV
ebenfalls unitäre Matrizen sind. Beginnen Sie dazu mit U^U = I und
V^V = I.
13. Wieso ist die Determinante jeder hermiteschen Matrix reell?
14. Die Matrix A^A ist nicht nur hermitesch, sondern sogar positiv definit,
wenn die Spalten von A linear unabhängig sind. Beweis: z^A^Az ist
positiv für z ungleich Null, da .
15. Diagonalisieren Sie die folgende hermitesche Matrix in der Form A =
UAU":
A =
0 1-z
z + 1 1
16. Diagonalisieren Sie die folgende schiefhermitesche Matrix in der Form
K = UAU^. Alle Eigenwerte sind .
K =
0 -1 + i
1 + z i
17. Diagonalisieren Sie die folgende orthogonale Matrix in der Form Q =
UAU^. Jetzt sind alle Eigenwerte .
Q =
COS ö — sin ö
sin 0 cos 0
18. Diagonalisieren Sie die folgende unitäre Matrix V in der Form V =
UAU^. Wieder sind die Eigenwerte :
V =
x/3
1 1-z
1 + 2 -1
19. Ist Vi,..., Vn eine orthogonale Basis des C"^, so ist die Matrix mit
diesen Spalten eine Matrix. Zeigen Sie, dass jeder Vektor z gleich
(vf Z)V1 + . • • + (vf z)Vn ist.
20. Die Funktionen e~*^ und e^^ sind auf dem Intervall 0 < x < 27r
orthogonal, da ihr Skalarprodukt /^ ^ = 0 ist.
21. Die Vektoren v = A, z, 1), w = (z, 1,0) und z =
gonale Basis des .
bilden eine ortho-
10.3 Die schnelle Fouriertransformation 517
22. Sind der Real- und der Imaginärteil einer hermiteschen Matrix A = R-\-
iS symmetrisch?
23. Die (komplexe) Dimension von C" ist . Finden Sie eine nicht-reelle
Basis für C.
24. Beschreiben Sie alle hermiteschen und unitären 1 x l~Matrizen und 2x2-
Matrizen.
25. Wie hängen die Eigenwerte von A^ mit den Eigenwerten einer
quadratischen komplexen Matrix A zusammen?
26. Zeigen Sie, dass / - 2uu^ eine hermitesche und unitäre Matrix ist, wenn
u^u = 1 gilt. Welche Projektion im C^ wird durch die Matrix uu^
dargestellt?
27. Zeigen Sie, dass Q = [b~'a] ^^^^ orthogonale Matrix ist, wenn A + iB
unitär ist und A und B reell sind.
28. Zeigen Sie, dass Q = [b~'a] ^^^^ symmetrische Matrix ist, wenn A + iB
hermitesch ist und A und B reell sind.
29. Beweisen Sie, dass die Inverse einer hermiteschen Matrix hermitesch ist.
30. Diagonalisieren Sie die folgende Matrix, indem Sie die Eigenwertmatrix
A und die Eigenvektormatrix S bestimmen:
A =
2 1-z
1 + z 3
= A
H
31. Eine Matrix mit orthonormalen Eigenvektoren hat die Form A = UAU~^ =
UAU^. Beweisen Sie, dass dann AA^ = A^A gilt. Diese Matrizen sind
genau die normalen Matrizen.
10,3 Die schnelle Fouriertransformation
Für viele Anwendungen der linearen Algebra braucht es eine gewisse Zeit, um
sie darzustellen. Es ist nicht leicht, sie innerhalb von einer Stunde zu erklären.
Ein Lehrer oder Autor muss daher wählen, ob er die Theorie
vervollständigen will, oder neue Anwendungen hinzufügen möchte. Normalerweise obsiegt
dabei die Theorie, weil man auf diese Weise die größte Chance hat, die Dinge
verständlich zu machen — und weil die Wichtigkeit beinahe jeder einzelnen
Anwendung beschränkt scheint. Dieser Abschnitt ist beinahe eine Ausnahme,
weil die Wichtigkeit der Fouriertransformation beinahe unbeschränkt ist.
518 10 Komplexe Vektoren und Matrizen
Darüber hinaus sind die notwendigen Rechnungen sehr einfach. Wir
wollen schnell mit den Matrizen F und F~\ der Fouriermatrix und ihrer In-
Versen, multiplizieren können. Dies erreicht man durch die schnelle Fourier-
transformation (FFT^) — den wertvollsten numerischen Algorithmus unseres
Lebens.
Die FFT hat die Signal Verarbeitung revolutioniert. Durch diese eine Idee
wurden ganze Industrien beschleunigt. Elektrotechniker würden als erstes
Ihre Fouriertransformierte berechnen, wenn Sie ihnen begegneten (und Sie eine
Funktion wären). Fourier's Idee war es, eine Funktion als Summe
harmonischer Funktionen c^e*^^ darzustellen. Durch die Koeffizienten Ck sieht man
die Funktion im Frequenzraum anstatt durch die Werte f{x) im
physikalischen Raum. Der Wechsel zwischen den c's und den /'s geschieht durch die
Fouriertransformation. Ein schneller Wechsel geschieht durch die FFT.
Für ein gewöhnliches Produkt der Form Fe werden n^ Multiplikationen
benötigt, wenn die Matrix n^ von Null verschiedene Einträge hat. Für die
FFT braucht man nur n mal \ log2 n Multiplikationen. Wir werden erkennen,
warum das so ist.
Einheitswurzeln und die Fouriermatrix
Quadratische Gleichungen haben zwei Nullstellen (oder eine doppelte).
Gleichungen vom Grad n haben n Nullstellen (nach Vielfachheit gezählt). Dies
ist der Fundamentalsatz der Algebra — man muss komplexe Nullstellen
zulassen, damit er wahr ist. In diesem Abschnitt geht es um die sehr spezielle
Gleichung z" = 1. Man nennt die Lösungen z die n-ten Einheitswurzeln. Es
handelt sich um n gleichmäßig auf dem Einheitskreis der komplexen Ebene
verteilte Punkte.
In Abbildung 10.5 werden die acht Lösungen der Gleichung z^ = 1
dargestellt. Ihr Abstand ist |C60°) = 45°. Die erste Wurzel liegt also bei 45°
oder e = 27r/8 im Bogenmaß. Sie ist die komplexe Zahl w = e''^ - e*^""/^. Sie
könnten sie auch mit cos ^ und sin ^ schreiben — tun Sie das aber nicht.
Die sieben anderen achten Wurzeln sind die Zahlen uP" ,w'^,... ,w^ entlang
des Kreises. Potenzen von w schreibt man am besten in der Polarkoordina-
tendarstellung, weil es uns nur um den Winkel geht.
Die vierten Einheitswurzeln sind ebenfalls in der Abbildung dargestellt.
Es handelt sich um die Zahlen z, -1, -z, 1. Hier ist der Winkel 27r/4 oder 90°.
Die erste dieser Wurzeln 1^4 = e^^*/^ ist nichts anderes als i. Die Abbildung
enthält auch die Quadratwurzeln von 1, nämlich W2 = e*^^/^ = -1. Verachten
Sie die Quadratwurzeln -1 und 1 nicht. Die Idee hinter der FFT ist, von einer
8 X 8-Fouriermatrix (mit den Potenzen von ws) zu einer 4 x 4-Fouriermatrix
(mit den Potenzen von W4 = i) überzugehen. Mit derselben Idee gelangt man
von 4 zu 2. Indem sie die Verbindungen zwi'schen Fg und F4 und Fi6 (und
^ Anm. d. Übers.: FFT = Fast Fourier Transform = schnelle Fouriertransformation
10.3 Die schnelle Fouriertransformation 519
w = ^2K//8^cos^+/sin^
Reelle Achse
w' = w = cos-T- -1 sin-7-
Abb. 10.5. Die acht Lösungen der Gleichung z^
«; = A + 0/\/2.
1 sind 1,1/;, t/;^,... ,t/;^ mit
darüber hinaus) ausnutzt, macht die FFT eine sehr schnelle Multiplikation
mit Fio24 möglich.
Wir beschreiben die Fouriermatrix zunächst für n = 4. Ihre Zeilen
enthalten die Potenzen von 1, w, w^ und w^, also der vierten Einheitswurzeln.
Die Potenzen stehen in einer besonderen Reihenfolge:
F4 =
Die Matrix ist symmetrisch {F — F^), aber nicht hermitesch. Ihre
Hauptdiagonale ist nicht reell. Die Matrix \F ist aber unitär, das heißt, es gilt
1111]
1 w w^ w^
1 w'^ w"^ w^
1 w^ w^ w^
—
ri 1 111
1 i «^ i^
1 i2 i* i«
liUU^j
Die Spalten von F liefern F^JP = 4J. Die iiwerseÄyqn; F ist älsQ;
Bei der Inversen ist also w — i durch w — —i ausgetauscht. So gelangt
man von F zu F. Wenn wir durch die FFT also eine Möglichkeit zur schnellen
Multiplikation mit F4 erlangen, so gilt dasselbe für die Inverse.
Die unitäre Matrix ist U = F/y/n. Wir ziehen es vor, den Faktor y/n zu
vermeiden und einfach ^ vor die Matrix F~^ zu schreiben. Das Wesentliche
ist die Multiplikation der Matrix F mit den Koeffizienten der Fourierreihe
520
10 Komplexe Vektoren und Matrizen
^1111
Fe-
1 W W'^ W^
1 w'^ w^ w^
1 w^ w^ w^
Co
Cl
C2
C3
+ Ci + C2 + C3
,2
Co
Co + ciit; + C2W^ + cait;^
Co + ciw'^ + C2w;^ + C3?i;^
[co + ciw^ + C2i(;^ + C3?i;^ J
A0.13)
Als Eingabe verwenden wir vier komplexe Koeffizienten co,ci,C2,C3, als
Ausgabe erhalten wir vier Funktionswerte yo,yi,y2iy3' Der erste Ausgabewert
^Q — Co + ci + C2 + C3 ist der Wert der Fourierreihe bei x = 0. Der zweite
Ausgabewert ist der Wert der Reihe ^Cke'^^^ bei x — 27r/4:
yi
- Co + cie^2./^ + C2e^^"/^ + C3e^ö"/^ = co + c^w + C2^' + C3^^
Der dritte und der vierte Wert 2/2 und ^3 geben die Werte von Y^Cke^^^
für X — 47r/4 und x — ^-k/A an. Hierbei handelt es sich um endliche Fou-
rierreihen! Sie bestehen aus n — A Termen und werden an n == 4 Punkten
ausgewertet. Diese Punkte x — 0,27r/4,47r/4,67r/4 sind gleichmäßig verteilt.
Der nächste Punkt wäre x — 87r/4, also 27r. Damit gelangt die Reihe
wieder bei yo an, weil e^^* dasselbe ist wie e^ = 1. Alles wiederholt sich also
mit der Periode 4. In dieser Welt ist 2 + 2 = 0, weil {w^){w'^) == it;^ == 1 ist.
Kurzgefasst liefert F mal c einen Spaltenvektor y. Die vier Komponenten
enthalten die Werte der Reihe an den vier Stellen Xi mit Abstand 27r/4:
y = Fe erzeugt yj - ^ c^e'*'^^''-^/^^ = Wert der Reihe bei x -
27rj
k=0
Wir folgen der Konvention, dass j und k von 0 bis n - 1 (anstatt von 1 bis
n) laufen. Die nullte Zeile und die nullte Spalte von F enthalten nur Einsen.
Die n x n-Fouriermatrix enthält die Potenzen von w — e^'^*/"^:
FnC-
1 1
1 VJ
1 ^2
1
w^
1
lt;2(n-l)
1 ?i;^-^ it»2(n-i) . it»(^-i)
Co
Cl
C2
_Cn-l_
-
2/0
2/1
2/2
.2/n-lj
A0.14)
Fn ist symmetrisch, aber nicht hermitesch. Ihre Spalten sind orthogonal, und
FnFn = n/, weswegen F~^ — Fn/n gilt. Die Inverse enthält die Potenzen
von Wn — e"^^*/^. Beachten Sie das Muster in F:
Der .Emtirag li^ Zeile j^ Spalte k isi tt;^^» SpÜte ntill mid Zeile':
Der nullte Ausgabewert ist 2/0 = Co 4- Ci 4- • • • + Cn-i, also der Wert der
Reihe Yl Cke^^^ bei x = 0. Multipliziert man c mit Fn, so berechnet man den
10.3 Die schnelle Fouriertransformation 521
Wert der Reihe an n Punkten. Multipliziert man y mit F~^, so bestimmt
man die Koeffizienten c aus den Funktionswerten y. Die Matrix F bildet aus
dem „Frequenzraum" in den „physikalischen Raum" ab. F~^ kehrt von den
Funktionswerten y zu den Fourierkoeffizienten c zurück.
Ein Schritt der schnellen Fouriertransformation
Wir möchten F so schnell wie möglich mit c multiplizieren. Normalerweise
benötigt man für das Produkt einer Matrix mit einem Vektor n^ einzelne
Multiplikationen, da die Matrix n^ Einträge hat. Sie denken vielleicht, dass
dies nicht besser geht. (Wenn die Matrix Nulleinträge hat, so kann man
Multiplikationen weglassen. Die Fouriermatrix hat aber keine Nulleinträge!) Indem
man die spezielle Form w^^ der Einträge ausnutzt, kann man F so faktori-
sieren, dass die Faktoren viele Nulleinträge haben. Dies ist die FFT.
Die Haupt idee ist es, die Matrix Fn mit der halb so großen
Fouriermatrix F^/2 in Verbindung zu bringen. Es sei n eine Potenz
von 2 (sagen wir, n = 2^^ = 1024). Wir werden dann F1024 mit F512 in
Verbindung bringen, oder eher mit zwei Kopien von F512. Für n = 4 liegt
der Schlüssel in der Beziehung zwischen den beiden Matrizen
^4 =
Links steht F4, ohne Nulleinträge. Rechts steht eine Matrix, die zur Hälfte
aus Nulleinträgen besteht. Damit spart man die Hälfte der Rechenarbeit.
Aber halt! Diese Matrizen sind nicht gleich. Die Blockmatrix mit den beiden
Kopien der halb so großen Matrix ist ein Teil der Idee, aber nicht der einzige
Teil. Die „nullenreiche" Faktorisierung von F4 lautet:
ri 1 1 1"
1 j2 i* i6
lliUU\
und
F2
F2
=
1 1
U2
1 1
li^\
F4
1 1
1 i
1 -1
1 -i
1 1
1^2
1 1
li2
A0.15)
Die Matrix auf der rechten Seite ist eine Permutation, die die geraden c's (co
und C2) vor die ungeraden c's (ci und C3) stellt. Die Matrix auf der linken
Seite kombiniert die beiden halb so großen Ergebnisse so, dass das richtige
Gesamtergebnis y = F4C entsteht. Wenn Sie die drei Matrizen multipUzieren,
werden Sie sehen, dass das Produkt F4 ist.
Dieselbe Idee lässt sich auf n = 1024 und m=|n = 512 anwenden. Die
Zahl w ist 62^^^1024 g^^ i^^gt in Richtung des Winkels 0 = 27r/1024 auf dem
Einheitskreis. Die Fouriermatrix F1024 besteht nur aus Potenzen von w. Der
erste Schritt der FFT ist diese Faktorisierung, die von Cooley und Tukey
entdeckt (und 1805 von Gauß vorausgeahnt) wurde:
522 10 Komplexe Vektoren und Matrizen
F1024 =,
J512 D^i2
^'Bl^
gerade-tingerade
Permutation
A0.16)
/512 ist die Einheitsmatrix. 1^512 ist die Diagonalmatrix mit den Einträgen
{l,w,...,w^'^^), und die beiden Kopien von F512 sind genau das, was Sie
erwarten. Erinnern Sie sich, dass diese Matrizen die 512. Einheitswurzel
verwenden, die nichts anderes als nP" ist. Die Permutationsmatrix zerlegt den
Eingabevektor c in die Komponenten mit geradem und ungeradem Index
C' = (Co,C2,...,Ci022) und C" == (Ci,C3,...,Ci023)-
An den folgenden Formeln kann man erkennen, dass das Produkt oben
eine Faktorisierung von Fi024 ist:
10t (FFT) ,Sam =.\n* Diepx^immund diektzteamKomponeiitea'
y == F^e sind KomW^tatioMn der haih;sagro ^i-
uixd y^' ^ FrJ''^ Gleichung A016) stellt Jy^+ Dy[ undTy';^4>y":'"
2/i = Vj + ^n^i ,
j = 0,..., m -1
i = 0,...,m- 1.
Die drei Schritte sind also: c in c' und c^' m zerlegen, diese Vektoren;i
Em in y' und y'' zju transformieren, und y aus Gleichung A0.17) zu rel?!
struieren.
Vielleicht ziehen Sie das Flussdiagramm in Abbildung 10.6 diesen Formeln
vor. Das Diagramm für n — 4 zeigt, wie die Vektoren c' und c" durch die halb
so große Matrix F2 transformiert werden. Wegen der Form des Diagramms
nennt man diese Schritte „Schmetterlinge". Die Ergebnisse der Multiplikation
mit F2 werden dann über die Matrizen / und D so kombiniert, dass sich
y = F4C ergibt:
00
10
Ol
11
0 •^
2 •"'"^
1 •^
^1 •"^
-1
y' N.
^ X
y\
y\i
2^
>'o
3^1
y2
y-i
00
Ol
10
11
-1 -i
Abb. 10.6. Flussdiagramm für die schnelle Fouriertransformation mit n = 4.
10.3 Die schnelle Fouriertransformation 523
purch diese Reduktion von F^ auf zwei Kopien von Fm wird der Aufwand
beinahe halbiert — wie Sie an den Nullen in der Matrixfaktorisierung sehen
können. Diese Reduktion ist zwar gut, aber nicht hervorragend. Die Idee
hinter der FFT geht noch weiter, und man spart viel mehr als die Hafte der
Zeit.
Die vollständige FFT durch Rekursion
Wenn Sie bis hierhin gelesen haben, werden Sie vermutlich raten können, was
als nächstes kommt. Wir haben die Multiplikation von Fn auf Fn/2 reduziert.
Damit machen wir weiter und reduzieren auf Fn/4. Die beiden Matrizen F512
führen auf vier Kopien von F256. Von 256 gelangt man zu 128. Das ist die
Rekursion. Sie ist ein Grundprinzip vieler schneller Algorithmen. Betrachten
wir den zweiten Schritt mit vier Kopien von F = F256 und D = i^256-
^512
12
I D
I-D
D
D
wähle 0,4,8,- •
wähle 2,6,10,-
wähle 1,5,9, • •
wähle 3,7,11,-
Zählen wir die Anzahl einzelner Multiplikationen, um zu sehen, wie viel
wir gespart haben. Bevor die FFT erfunden wurde, benötigte man die
üblichen n^ — A024)^, also etwa eine Million Multiplikationen. Ich will nicht
sagen, dass diese Multiplikationen viel Zeit in Anspruch nehmen. Die
Kosten werden aber groß, wenn man viele Transformationen auszuführen hat —
was typischerweise der Fall ist. Dann ist auch die Ersparnis durch die FFT
besonders groß:
Die Anzahl an Operationen bei einer Größe von n — 2^ wird von
n^ auf ^nl reduziert.
Die Zahl 1024 ist 2^^, wir haben also / = 10. Der ursprüngliche Aufwand
von A024J wird auf 5 • 1024 reduziert, also um einen Faktor 200. Eine
Million wird auf fünftausend reduziert. Dies ist der Grund, warum die FFT die
Signal Verarbeitung revolutioniert hat.
Der Gedanke hinter dem Aufwand \nl verläuft wie folgt. Man reduziert
das Problem in / Schritten von n — 2^ auf n == 1. In jedem Schritt werden
2^ Multiplikationen in den Diagonalen i^'s nötig, um die Ergebnisse des
vorausgegangenen Schrittes zusammenzusetzen. Auf diese Weise erhält man
den Gesamtaufwand \nl — |nlog2n.
Noch einen letzten Hinweis zu diesem bemerkenswerten Algorithmus. Es
gibt eine erstaunliche Regel für die Reihenfolge, in der die Koeffizienten c
schließlich nach all den Gerade-Ungerade-Vertauschungen bei der FFT
auftauchen. Man schreibt die Zahlen 0 bis n - 1 als Binärzahlen (also zur Basis
2), und kehrt die Reihenfolge der Ziffern (der Bits) um. In einer vollständigen
Darstellung steht die durch diese Umkehrung gegebene Ordnung am Anfang,
524 10 Komplexe Vektoren und Matrizen
dann folgen die / = log2n Schritte der Rekursion, woraus man am Ende
das Ergebnis 2/0, • • • ? Vn-i, also Fn mal c erhält. Das Buch endet mit diesem
fundamentalen Konzept: Ein Vektor wird mit einer Matrix multipliziert.
Vielen Dank, dass Sie die lineare Algebra studieren. Ich hoffe, sie hatten
Freude daran, und ich hoffe sehr, dass Sie sie gebrauchen werden. Aus diesem
Grunde wurde dieses Buch nämlich geschrieben. Es war mir ein Vergnügen.
Aufgaben 10.3
1. Multiplizieren Sie die drei Matrizen in Gleichung A0.15), und vergleichen
Sie das Ergebnis mit F. Für welche sechs Einträge verwenden Sie i^ =
-1?
2. Invertieren Sie die drei Faktoren in Gleichung A0.15), und bestimmen
Sie so eine schnelle Faktorisierung von F~^.
3. F ist symmetrisch. Transponieren Sie also Gleichung A0.15), und finden
Sie eine neue schnelle Fouriertransformation!
4. Alle Einträge in der Faktorisierung von Fq enthalten Potenzen von w =
sechste Einheitswurzel
Fe =
Geben Sie die drei Faktoren mit l,w,w'^ in D und Potenzen von w'^ in
Fs an. Berechnen Sie das Produkt!
5. Es sei V = A,0,0,0) und w = A,1,1,1). Zeigen Sie, dass Fv = w und
Fw = 4v gilt. Deshalb gilt auch F~^w = v und F~^v = .
6. Bestimmen Sie F^ und F"^ für die 4 x 4-Fouriermatrix.
7. Wenden Sie die drei Schritte der FFT auf den Vektor c = A,0,1,0) an,
und bestimmen Sie so y = Fe. Führen Sie dasselbe mit c = @,1,0,1)
durch.
8. Berechnen Sie über die drei FFT-Schritte den Vektor y = Fgc für c =
A,0,1,0,1,0,1,0) und für c = @,1,0,1,0,1,0,1).
9. Für w — e^^*/^"* sind iv^ und y/w unter den und den
Einheit s wurzeln.
10. (a) Zeichnen Sie die sechsten Einheitswurzeln, und beweisen Sie, dass
ihre Summe Null ist.
\I D'
I-D
"i=3
P
10.3 Die schnelle Fouriertransformation 525
(b) Welches sind die drei dritten Einheitswurzeln? Ist ihre Summe ebenso
Null?
11. Die Spalten der Fouriermatrix F sind die Eigenvektoren der zyklischen
Permutation P. Berechnen Sie PF und bestimmen Sie so die Eigenwerte
Ai bis A4:
Ai
roioo"
0010
0001
[1000
111"
1 2 i^ i^
1 2-2 i^ z6
_\i''iU\
111"
1 i i^ i^
1 z2 i^ i^
_liUU\
Hier steht die Zerlegung PF = FA oder P
matrix (normalerweise 5) ist F.
FAF~^. Die Eigenvektor-
12. Die Gleichung det(P ■
Eigenwertmatrix A _
XI) = 0 ist A^ = 1. Dies zeigt wiederum, dass die
ist. Welche Permutation P hat als Eigenwerte
die dritten Einheitswurzeln?
13. (a) Zwei Eigenvektoren von C sind A,1,1,1) und A, i, i^, i^). Bestimmen
Sie die Eigenwerte.
"
1
1
1
= ei
"
1
1
1
undC
"
i
f_
= e2
I
i
y\
Co Ci C2 Cs
C3 Co Ci C2
C2 Cs Co Ci
Cl C2 Cs Co
(b) P = FAF-^ liefert sofort P^ :::. FA^p-^ und P^ = FA^P-^. Es folgt
C = coI + ciP + C2P2 + csP^ = F{coI + ciA + cs^l^ + csA^)F-'^ =
FEF~^, Die Matrix E in Klammern ist eine Diagonalmatrix. Sie
enthält die von C.
14. Bestimmen Sie die Eigenwerte der „periodischen" (—1,2, -1)-Matrix aus
E — 21 — A — A^ ^ mit den Eigenwerten von P in A. Die Einträge —1 in
den Ecken machen die Matrix periodisch:
C =
2-1 0-1
-1 2-1 0
0-1 2-1
-1 0-1 2
hat Co = 2,ci = ~1,C2 = 0,C3 = — 1.
15. Um C mit einem Vektor x zu multiplizieren, können wir stattdessen das
Produkt F(-E(F~^x)) berechnen. Für die direkte Methode braucht man
in? einzelne Multiplikationen. Kennt man E und F, so braucht man für
die zweite Methode nur noch n log2 n 4- n MultipUkationen. Wie viele
davon rühren von E her, wie viele von F, und wie viele von F"^?
526 10 Komplexe Vektoren und Matrizen
16. Wie würden Sie die vier Komponenten von Fe schnell berechnen, wenn
Sie von co + C2, co — C2, ci + C3, ci - C3 ausgehen? Sie erhalten die schnelle
Fouriertransformation!
Fc =
C0 + C1+C2+ CS
Co + ici + i^C2 + i^cs
Co + i^ci + i^C2 + i^cs
Co + i^ci + i^C2 + i^cs
Lösungen zu ausgewählten Aufgaben
Aufgaben 1.1, Seite 7
3 3v + w == G,5), v-3w = (-1,-5) und cv + dw == {2c +d,c-\-2d).
5 (a) Die Komponenten cv bilden die Summe Null
(b) Die Komponenten aller Vektoren cv + dw bilden die Summe Null
(c) Man wählt c = 4 und d = 10.
7 (a) Rückwärts entlang w, vorwärts entlang v
(b) Die Kombinationen erzeugen die Ebene, die v und w enthält.
9 Die vierte Ecke kann D,4), D,0) oder (-2,2) sein.
10 Es gilt (Länge von v)^ + (Länge von w)^ ==42+2^ + (-1)^ + 2^ == 25
und auch (Länge von v + w)^ =z 32 + 42 — 25.
12 Man wähle v = B,1) und w = A,2). Dann gilt (Länge von v)^ = (Länge
von w)^ = 5, aber (Länge von v + w)^ == 3^ + 3^.
15 Fünf weitere Ecken @,0,1), A,1,0), A,0,1), @,1,1), A,1,1). Der
Mittelpunkt ist (|,|,|)- Die Mittelpunkte der Seitenflächen sind (|,|,0),
(|,|,1) und @,|,i), A,|,|) und A,0, i), (|,l,i).
16 Ein vierdimensionaler Würfel hat 2^ = 16 Ecken und 2-4 =^ 8
dreidimensionale Seiten sowie 4B)^ = 32 zweidimensionale Kanten.
17 (a) Die Summe ergibt den Nullvektor (b) Die Summe ergibt den
Vektor bei -4:00 Uhr (c) Die Summe ergibt den Vektor bei -|A:00
Uhr).
19 Es gilt V - u = V - (|v -h |w) = |(v - w). Der Punkt |v -h |w liegt
bei drei Vierteln der Strecke von w nach v. Der Punkt |v -h ^w ist ^u.
20 Alle Kombinationen mit c-\- d = 1 liegen auf der Geraden durch v und
w. Der Punkt V = -v -h 2w liegt auf dieser Geraden hinter w.
528 Lösungen zu ausgewählten Aufgaben
21 Die Vektoren cv + cw erzeugen die Gerade zwischen @,0) und u == |v -f
|w. Sie geht über den Punkt v + w hinaus. Durch c > 0 wird die Hälfte
der Geraden entfernt, der resultierende Strahl beginnt bei @,0).
22 (a) Die Kombinationen mit 0 < c < 1 und 0 < d < 1 füllen das
Parallelogramm mit den Seiten v und w und einer Ecke in @,0) aus. (b) Mit
0 < c und 0 < d wird aus dem Parallelogramm ein „unendlicher Keil".
23 (a) Der Punkt |u + |v + |w bildet den Mittelpunkt des Dreiecks
zwischen u, V und w; der Punkt ^u+ |w bildet den Mittelpunkt der Kante
zwischen u und w (b) Um das Dreieck auszufüllen, setzt man c > 0,
d > 0, e > 0 und c-\-d + e = l.
25 Der Vektor |(u + v -h w) liegt außerhalb der Pyramide, da c + d + e =
1 + i + i > 1 ist.
26 Alle Vektoren sind Kombinationen von u, v und w.
27 Die Vektoren cv liegen in beiden Ebenen.
29 Die Lösung ist s =^ 2 und d =^ 4. Dann gilt 2A,2) + 4C,1) = A4,8).
Aufgaben 1.2, Seite 20
2 Es gilt ||u|| = 1 und ||v|| - 5 = ||w|| und 1,4 < A)E) und 24 < E)E).
4 Es gilt ui - v/||v|| - ^C,1) und U2 - w/||w|| = |B,1,2). Ui =
^A,-3) oder -^(-1,3) ist möglich. U2 könnte ;^(l,-2,0) sein.
5 (a) Winkel Null (b) 180° (oder n) (c) (v + w) • (v - w) := v • v +
w.v-v.w-w.w==l + ( )-( )-l = 0, so dass 9 = 90° (oder f
im Bogenmaß).
6 (a) Es gilt cos 9 = B7A)' deshalb ist 9 - 60° oder | im Bogenmaß (b)
Es gilt cosö = 0, deshalb ist 9 — 90° oder | im Bogenmaß (c) Es gilt
^ösÖ = ^^ =: |, deshalb gilt 9 = 60° oder f (d) Es gilt cos 9 =
-1/v^, deshalb gilt Ö = 135° oder ^.
8 (a) Falsch (b) Wahr: u • (cv + dw) = cu • v + du • w = 0 (c) Wahr:
für cu • V + du • w — 0 wählt man c = u • w und d = —u • v.
12 Der Vektor A,1) ist senkrecht zu A,5) - c(l, 1) wenn 6 - 2c =: 0 oder
c = 3 gilt; es gilt v • (w - cv) = 0 wenn c = v • w/v • v.
Lösungen zu ausgewählten Aufgaben 529
16 Es gilt ||v|p = 9 und daher ||v|| = 3; weiter u -r iy und w =
A,-1,0,...,0).
18 Es gilt (v+w).(v+w) = (v+w).v+(v+w).w = v.(v+w)+w.(v+w) =
vv + v-w + w-v + w.w==v-v + 2vw'hw-w.
19 Aus 2v . w < 2||v||||w|| folgt ||v + w|p = vv + 2v.w + w.w<
||v|p + 2||v||||w|| + ||w|p = (||v|| + ||w||)^
21 Es gilt cos/? = w;i/||w|| und sin/? =^ w;2/||w||. Daraus folgt cos(/? - a) =
cos/?cosa + sin/?sina = ^iw;i/||v||||w||+V2^^2/l|v||||w||=::v.w/||v||||w||.
22 Wir wissen, dass (v - w) • (v - w) =^ v • v - 2v • w + w • w gilt.
Vergleichen Sie dies mit dem Kosinussatz, und dividieren Sie durch -2, um
||v||||w|| cosö = V • w zu erhalten.
24 Beispiel 1.2.6 liefert \ui\\Ui\ < \{ul + Ul) und 1^211^^21 < \{ul + Ul). Aus
der Zeile wird 0,96 < @,6)@,8) + @,8)@,6) < ^@,6^ + 0,8^) + 1@,8^ +
0,62) = 1.
26 Für den Winkel zwischen v = A,2, -3) und w ^ (-3,1,2) gilt cos l9 = f|^
und e = 120°. Schreiben Sie w - ^ ^ xz + yz + xy als \{x + y + zf -
\[x^ + 2/^ + z^), also -\{x^ +y'^ + z^)'
27 Die Länge ||v - w|| liegt zwischen 2 und 8. Das Skalarprodukt v • w liegt
zwischen —15 und 15.
Aufgaben 2.1, Seite 34
4 Die Lösung ändert sich nicht, die zweite Ebene und die zweite Zeile der
Matrix, sowie alle Zeilen werden geändert.
5 Setzt man x == 0, so erhält man y = -3/2 und z = 5/2. Aus ^ = 0 folgt
X = 3 und z — l.
6 Wenn x,y,z die ersten beiden Gleichungen erfüllen, so auch die dritte.
Die Lösungsgerade enthält die Vektoren v = (l,l,0),w = B,l,2) ^^^
u = ^v + |w, sowie alle Linearkombinationen cv + dw mit c + d == 1.
7 Gleichung 1 + Gleichung 2 - Gleichung 3 ergibt 0 ^ -4. Eine Lösung ist
daher unmöglich.
9 Es gilt ^x - A8, 5,0), ^x - C,4, 5, 5).
10 Es sind neun Multiplikationen für Ax := A8, 5, 0) nötig.
530 Lösungen zu ausgewählten Aufgaben
12 iz,y,x) und @,0,0) und C,3,6).
13 (a) Der Vektor x hat n Komponenten, Ax hat m Komponenten (b) Die
Ebenen liegen im n-dimensionalen Raum, die Spalten im m-dimensiona-
len Raum.
14 (a) Lineare Gleichungen in den Unbekannten x,y,z haben die Form ax +
by + CZ = d (b) cvq H- dvi ist ebenfalls eine Lösung, falls c H- d = 1 gilt,
(c) Ist die rechte Seite der Gleichung konstant null, so sind beliebige c
und d erlaubt.
16 R =
17 P =
Ol
-10
0 10
001
100
180°-Drehung aus i?^ =
und P~^ =
001
100
010
-1 0
0-1
= -L
19 E =
00'
010
101
,E-' =
" 100]
010
-lOlJ
, Ev = C,4,8), E-^Ev = C,4,5).
23 Das erste Programm berechnet die Skalarprodukte für / = 1,2; das zweite
Programm kombiniert die Spalten J = 1,2. Für eine 4 x 3-Matrix A muss
man die entsprechenden Zeilen zu / = 1,4 und J = 1,3 ändern.
24 B{1) = BA)+A{1,2)*V{2),B{2) = A{2,1)*V{1),B{2) = J5B)H-AB,2)*
VB). Im zweiten Programm sind die ersten beiden Schritte vertauscht.
29 U2 =
0,7
0,3
, U3 =
0,65
0,35
. Die Summe der Komponenten ist immer eins.
30 U7, V7,W7 liegen alle nahe bei @,6,0,4). Die Komponenten bilden immer
noch die Summe eins.
31
'0,8 0,3]
.0,2 0,7j
[0,6'
[0,4
=
0,6"
0,4 _
= stationärer Zustand s.
32 Die Vektoren gehen von allen Startpunkten aus gegen @,45,0,35,0,20).
33 M =
834
159
672
b -hu 5 — u + v 5 — V
5 — u — V 5 5 + u + V
5 + V 5 + u — V 5 — u
die 16 Zahlen in M4
bilden die Summe 136, eine Zeilensumme ist daher = 136/4 = 34.
Lösungen zu ausgewählten Aufgaben 531
Aufgaben 2.2, Seite 47
1 Multiplizieren Sie mit / = ^ = 5 und subtrahieren Sie, um 2x-\-3y = 14
und —6y = 6 zu erhalten.
3 Man subtrahiert — | mal Gleichung 1 (oder addiert | mal Gleichung 1),
so dass die neue zweite Gleichung 3y = 3 ist. Daraus folgt y = 1 und
X = 5. Ändert man das Vorzeichen der rechten Seite, so auch der Lösung:
(x,y) = i-5,-l).
4 Man subtrahiert / = ^ mal Gleichung 1. Als neues zweites Pivotelement
vor y ergibt sich d — (cb/a) oder {ad — bc)/a.
6 Für 6 = 4 ist das System singular, weil 4x-\-Sy gleich 2 mal 2x-\-4y ist. In
dem Fall wird das System für ^ = 2 • 13 = 26 lösbar. Die beiden Geraden
fallen zusammen — es gibt unendlich viele Lösungen.
7 Für a = 2 versagt das Eliminations verfahren, da die Gleichungen keine
Lösung besitzen. Für a = 0 wird eine Zeilenvertauschung nötig. Aus
3y = —3 erhält man dann y = —l und aus 4x -\-6y = 6 schließlich x = 3.
8 Für A; = 3 versagt das Eliminations verfahren: es gibt keine Lösung. Für
A; = — 3 erhält man 0 = 0 in Gleichung 2: unendlich viele Lösungen. Für
k = 0 wird eine Zeilenvertauschung nötig, die dann eine Lösung liefert.
11 2x + 3y -\- z = 1 X — 1 Steht eine Null am Anfang
y -^ 3z = 5 ergibt y — —l von Zeile 2 oder 3, vermeidet
8z = 16 z = 2 man eine Zeilenoperation.
12 2a: - 3i/ =3 2x-3y =3 x = 3 2 x Z. 1 von Z. 2
y + z = 1 => y + z = 1 ^ y =1 IxZ. 1 von Z. 3
2y - 3z =2 - 5z =0 z = 0 2 x Z. 2 von Z. 3
13 Man subtrahiert 2 mal Zeile 1 von Zeile 2 und erhält {d — 10)y — z —
2. Gleichung B.10) ist i/ — z = 3. Falls d = 10 gilt, vertauscht man
Zeilen 2 und 3. Für d = 11 ist das System singular; es fehlt ein drittes
Pivotelement.
14 Auf der zweiten Pivotposition steht —2 — h. Für h — —2 muss man mit
Zeile 3 tauschen. Für h — —\ wird die zweite Gleichung zu —y — z — 0,
eine Lösung \^\. x — \, y — \, z — -1.
16 Ist Zeile 1 = Zeile 2, so wird Zeile 2 nach dem ersten Schritt zu einer
Nullzeile. Dann vertauscht man mit Zeile 3, so dass das dritte Pivotelement
fehlt. Ist Spalte 1 = Spalte 2, so fehlt das zweite Pivotelement.
17 X + 22/ + 3z = 0, 4x + 82/ + 12z = 0, 5j: + \^y + 15z = 0.
532 Lösungen zu ausgewählten Aufgaben
18 Aus Zeile 2 wird Sy - 4z = 5, dann wird Zeile 3 zu (^ H- 4)z = ^ - 5. Für
g = — 4 ist das System singular — es fehlt das dritte Pivotelement. Für
^ = 5 erhält man als dritte Gleichung 0 = 0. Wählt man dann z = 1, so
liefert die Gleichung 3y — 4z = 5 y = 3, und aus Gleichung 1 erhält man
x = -9.
20 „Von hinten gesehen" bilden die drei Ebenen ein Dreieck. Dies geschieht,
wenn die Summe von Zeile 1 und Zeile 2 auf der linken Seite gleich Zeile
3 ist, auf der rechten Seite aber nicht; zum Beispiel für x + y + z =^ 0^
X — y — z = 0, 2x + Oy + Oz = 1. Die Ebenen sind nicht parallel, es gibt
aber trotzdem keine Lösung.
22 Die Lösung ist A,2,3,4) anstelle von (-1,2,-3,4).
23 Das fünfte Pivotelement ist |. Das n-te Pivotelement ist ^^~^^K
5 n
24 A
1 1 1
a a+ 1 a+1
b b + c b + c + 3
25 o = 2 (gleiche Spalten), o = 4 (gleiche Zeilen), o = 0 (Nullspalte).
26 Lösbar für s = 10 (Gleichungen addieren);
13
17
und
04
26
Aufgaben 2.3, Seite 58
1 £^21
100
-5 10
001
, £^32 —
100
010
071
Pl2 =
010
100
001
'100'
-4 10
001_
1 0
J
0]
-4 10
10-2
ij
rioo'
010
[201
J
'1 0 0]
0 1 0
0-2 ij
sind E2i,E^i,E^2- ^ — E22E21E21 ist
4 Elimination von Spalte 4: b =
Rücksubstitution in Ux = A,-4,10) liefert z =
Dies ist eine Lösung von ^x = A,0,0).
ri"
0
0
-)-
r
-4
0
-)-
r
-4
2
-)-
" 1]
-4
10
-5, y
_ i
~ 2'
X =
Lösungen zu ausgewählten Aufgaben 533
5 Ändert man 033 von 7 zu 11, so ändert sich das dritte Pivotelement von
2 zu 6. Ändert man 033 von 7 zu 5, so ändert sich das Pivotelement von
2 zu „kein Pivotelement".
7 Um £^31 rückgängig zu machen, addiert man 7 mal Zeile 1 zu Zeile 3. Die
'100"
Matrix ist R31
010
701
9 M
100
001
-110
. Nach dem Austausch muss E auf die neue Zeile 3 wirken.
\ 2 2]
^loioj
5
2 3l
0 1-2
0 2-3J
11
12 (a) E mal dritte Spalte von B ergibt die dritte Spalte von EB (b) E
kann Zeile 2 zu Zeile 3 addieren, um von Null verschiedene Einträge zu
erzeugen.
14 A
-1-4-7
1-2-5
3 0-3
->
1 -4 -7"
0 -6-12
0-12-24
. Es2 =
0 Ol
0 1 0
0-2 ij
EF =
F^ =
[100]
alO
[bc ij
0 Ol
0 10
0 2clJ
FE
1 00
a 10
b-^ ac c 1
, E^ =
[100]
2ol0
26 0 1
19 (a) Jede Spalte ist E mal eine Spalte von B
(b)
'10'
21
1'
1 1
=
1'
33
21 (a) Yl cisjXj
23 A' =
(b) 021-an (c) Xa-Xi (d) {Ax)i ^Yl^^ij^j
23 1
4 1 17
->
2 3 1
0-5 15
2x1 + 3^2 =1 xi = 5
—5x2 = 15 X2 = —3.
24 Aus der letzten Gleichung wird 0 = 3. Man muss die ursprüngliche 6 zu
3 ändern. Dann ist Zeile 1 -h Zeile 2 = Zeile 3.
534 Lösungen zu ausgewählten Aufgaben
25 (a) A" hat zwei zusätzliche Spalten:
-7 4
2-1*
1410
270 1
->
14 10
0-1-2 1
26 (a) Es gibt keine Lösung, wenn d = 0 und c 7«^ 0 ist (b) Es gibt
unendlich viele Lösungen für d = 0 und c = 0. Keinen Effekt haben a
und b.
Aufgaben 2.4, Seite 69
2 (a) A (Spalte 3 von B) (b) (Zeile 1 von A) B (c) (Zeile 3 von
A) (Spalte 4 von B) (d) (Zeile 1 von C)i^(Spalte 1 von E).
5 A" =
Ibn
0 1
und A"
2n 2"
0 0
7 (a) Wahr (b) Falsch (c) Wahr (d) Falsch.
8 Die Zeilen von DA sind 3-(Zeile 1 von A) und 5-(Zeile 2 von A). Die
Zeilen von EA sind Zeile 2 von A und die Nullzeile. Die Spalten von AD
sind 3-(Spalte 1 von A) und 5-(Spalte 2 von A). Die Spalten von AE sind
eine Nullspalte und Spalte 1 von A.
9 AF =
\a a-\-b
c c-\- d
assoziativ ist.
E{AF) ist gleich {EA)F, weil die Matrixmultiplikation
10 FA
a-\- cb + d
c d
und daher E(FA) =
a-\- c b-\- d
a-\-2cb-\-2d
E{FA) ist
ungleich F{EA), weil die Multiplikation nicht kommutativ ist.
11 (a) B = 4I (h) B = 0 (c) B =
001
010
100
(d) B muss gleiche
Zeilen haben.
12 AB =
= BA
aO
cO
AC = CA, also A = al.
a b
00
liefert b = c = 0. Dann folgt a = ci aus
13 {A - BJ = {B- AJ = A{A -B)- B{A - B) = A'^ - AB - BA + ß^.
15 (a) mn (Jeder Eintrag)
te).
(b) mnp (c) n^ (also n^ Skalarproduk-
Lösungen zu ausgewählten Aufgaben 535
16 Wegen der Linearität stimmt {AB)c mit A{Bc) überein. Dies gilt auch
für alle anderen Spalten von C.
17 (a) Man verwendet nur Spalte 2 von B (b) Man verwendet nur Zeile
2 von A (c)-(d) Man verwendet Zeile 2 der ersten Matrix A.
19 Diagonalmatrix, untere Dreiecksmatrix, symmetrische Matrix, alle Zeilen
gleich. Nullmatrix.
20 (a) an (b) an/an (c) a^ - (f^)ai2 (d) 022 - {^)an-
23 Für A =
Ol
-10
gilt A^
-/; BC
Ol
10
Ol
-10
-10
Ol
= -<7ß.
25 A^
2" 2" - 1
0 1
A^ =2"-i
1 1
1 1
A^ =
0 0
27 (a) (Zeile 3 von A)-(Spalte 1 von B) = (Zeile 3 v. A)-(Spalte 2 v. ß) = 0
(b)
[Ox x]
[0 X X
0 X X
_000_
und
xl
X
x\
[00a:] =
OOx
OOx
OOx
28 A
- [ ]
31 In Aufgabe 30 gilt c =
B,
-2"
8
—i
, D =
("Oll
[53J
5
, D — cb/o =
1 ]
1'
13
[=1
33 (a) n — 1 Additionen für ein Skalarprodukt; 'n?{n — 1) für m? Skalar-
produkte (b) 4n^(n - 1) H- 2n^ Additionen für R und S (c)
2n^(n — 1) H- n^ für R und weitere 4n^ H- n^(n — 1) für 5, wenn man
AC und BZ) kennt. Insgesamt: 3n^(n — 1) H- 5n^ Additionen mit der
3M-Methode.
34 A mal X ist die Einheitsmatrix /.
35 Die Lösung von b = C,5,8) ist 3xi + 5x2 + 8x3 = C,8,16).
Aufgaben 2.5, Seite 84
1 A-
0
\i
B-
2 J
c-
7-4
-5 3
536 Lösungen zu ausgewählten Aufgaben
2 P
-1 _
P; P-
001
100
010
. Die Matrix P ist immer die Transponierte
von P.
4 a + 2c= 1, 3a + 6c — 0: unmöglich.
5 A =
-1 0
0-1
und
-10
Ol
und jede Matrix
a b
c d
-10"
Ol
a b
c d
-1
7 (a) Für Ax = A,0,0) ergibt Gleichung 1 + Gleichung 2 - Gleichung 3
die Gleichung 0=1 (b) Die rechten Seiten müssen die Gleichung
bi-^b2 — bs erfüllen (c) Zeile 3 wird zu einer Nullzeile — es gibt kein
drittes Pivotelement.
8 Vertauscht man Zeilen 1 und 2 von A, so vertauscht man Spalten 1 und
2 von A-^.
11 C = AB liefert C"^ = B-^A-\ deshalb gilt A'^ = BC'^.
12 M-i = C-^B-^A-^ und deshalb B-^ = CM'^A.
13 B-^ = A-^
von Spalte 1.
16
10
1 1
- j-i
10
-11
: man subtrahiert Spalte 2 von A
-1
ri
1
L -1 1
1
1
-1 1
1
-11
1
=
1
1 1
0-1 1
^E-
'l
1 1
1 1 1
L =
E ^ nachdem die Reihenfolge umgedreht und —1 mit H-1 vertauscht
wurde.
18 A'^B = / kann man A{AB) - I schreiben. Deshalb gilt A~^ = AB,
19 Der Eintrag A,1) verlangt 4a-Sb = 1. Der Eintrag A,2) verlangt 2b-a =
0. Daher gilt ^ — | und a = |.
20 6 von den 16 Matrizen sind invertierbar, einschließlich der vier mit drei
Einsen.
21
1310'
2701
1310'
3801
—>
—>
13 10
0 1-21
1 0-8 3
0 1 3-1
-^
1 0 7-3
0 1-2 1
= \I A-
= [IA-'].
Lösungen zu ausgewählten Aufgaben 537
23
lab 100
0 1 cOlO
001001
1aO 1 0-b
0 1001-c
00100 1
24 A
26 A
-1
3-1-1"
1 3-1
1-1 3
; A
"
1
1
=
'Ol
0
oj
1001-aac-b
0 100 1 -c
0010 0 1
deshalb existiert A ^ nicht.
-1 _
1 0 0
-2 1-3
0 0 1
(man achte auf das Muster); A
-1
2-1 0
-1 2-1
0-1 1
28 (a) Falsch mit 4 Nullen; Wahr mit 13 Nullen (b) Falsch (alle
Matrixeinträge gleich 1) (c) Wahr (d) Wahr.
29 Nicht invertierbar für c = 7 (gleiche Spalten), c = 2 (gleiche Zeilen), c = 0
(Nullspalte).
30 Das Ehminationsverfahren erzeugt die Pivotelemente a, a — b und a — b.
31 A-^ =
1 100
0110
0011
0001
32 X = B,2,2,1) und x = B,2,2,2,1).
33 hilb{6) ist nicht die exakte Hilbertmatrix, weil Brüche gerundet werden.
34
10
-C I
A-^ 0
und
-DI
10
Aufgaben 2.6, Seite 97
1 EA =
r 1
Ol
[-3 0 1
10"
042
635
=
lOl
042
005
^21 ■E'32 U
LU.
U; A = LU
0 1
0-2 1
1
-2 1
00 1
A =
1 1]
0 2 3
0 0-6
1
Ol
301
U.
U. Damit ist A
100
210
021
U
538 Lösungen zu ausgewählten Aufgaben
4 E = E22E31E21
ist A ^, und es ist L = A.
ri
1
L -^1
1
1
-b 1
1
-al
1
=
ri 10"
112
[121
=
' 1
i 1
■mn 1
'd e g'
fh\
i J
1
-a 1
ac — b—c 1
d= 1, e = 1 in Zeile 1
damit / = 1, und f = 0 :
kein Pivotelement in Zeile 2
Dies
6 c = 2 führt zu einer Null in der zweiten Pivotposition. Vertauscht man
die Zeilen 2 und 3, so ist die Matrix in Ordnung. c = 1 führt zu einer
Null in der dritten Pivotposition => die Matrix ist singular.
0'
2 1
■24'
0 3
=
lO'
2 1
■2 0'
03
■12"
Ol
8 A =
die Transponierte ist.
'1
4 1
0-1 1
4 0"
0-4 4
0 0 4
=
4 1
0-1 1
-4
4
4 Ol
0 1-1
0 0 1
= LDU; beachten Sie, dass U
= LDL'^.
10
12
\ a r r r
a b s s
übet
ab c d
1 1
1 1 1
1111
a r r r
b — rs — rs — r
c — s t — s
d-t
Man braucht
a#0
c^ s'
d^t
100
1 10
1 1 1
liefert c =
Damit ergibt
1 r
Ol 1
001
X =
1
1
Ij
den
Vektor x =
13 (a) L wird zu / (b) / wird zu L
-1
(c) LU wird zu U.
14 (a) Multiplizieren Sie die Gleichung LDU — LiDiUi mit den Inversen
und erhalten Sie L^^LD = DiUiU~^. Die linke Seite ist eine untere
Dreiecksmatrix, die rechte Seite eine obere Dreiecksmatrix => es stehen auf
beiden Seiten Diagonalmatrizen (b) Da die Diagonalen der
Matrizen L,U,Li,Ui aus Einsen bestehen, erhält man D = Di. Dann müssen
L^^L und UiU~^ gleich / sein.
15
[1
11
[0 1 1
ches U)
10"
1 1
1
= LU;
a a 0
a a-^ b b
0 b b-^c
= (gleiches L)
a 1
b
c
(glei-
Lösungen zu ausgewählten Aufgaben 539
16 Ist T eine Tridiagonalmatrix, so hat jede Pivotzeile nur 2 von Null
verschiedene Einträge. Jeder Eliminationsschritt wirkt nur auf die nächste
Zeile, nicht aber auf spätere Zeilen. Die Matrizen U und L haben also
abseits der Haupt- und der ersten Nebendiagonalen nur Nulleinträge.
17 Die Matrix L besitzt die 3 unteren Nullen von A, U kann die obere Null
aber verloren haben. L besitzt die untere linke Null aus B, und U die
obere rechte Null. Eine Null in A und zwei Nullen in B werden also
„ausgefüllt".
18
\ X X X
\ X X X
IX X X
=
00"
X 10
X 1
X X xl
0
0 J
(Die x'e sind nach der Bestimmung des
ersten Pivotelements bekannt.)
21 Die obere 2 x 2-Untermatrix B besitzt die Pivotlemente 2,7. Der Grund:
das Eliminationverfahren für A beginnt mit der Elimination auf B.
23
1111"
12 3 4
13 6 10
1 4 10 20
1 1
1 2 1
1331
111"
123
13
ij
. PascaVsches Dreieck in L und U.
24 Die Werte c — ^ und c = 7 lassen eine Faktorisierung LU nicht zu. (Für
c — ^ wird eine Permutation benötigt).
Aufgaben 2.7, Seite 110
1 A^
'18]
02J
-1 _
, A-'
[0 1'
[1-1
=
=
1 0'
-4 1/2
{A-'r.
, (A-^v = (An
T\-l
1 -4
0 1/2
; Ä^ = A
4 Für yl =
Ol
00
gilt A'^ = 0. Die Diagonaleinträge von Ä^A sind die
Skalarprodukte der Spalten von A mit sich selbst. Gilt A^A = 0, sind
also die Skalarprodukte Null => Nullspalten.
6 üij wird mit Xj und y, multipliziert: (Ax)^y = K^{A^y).
7 MT =
8 (a) Falsch (b) Falsch (c) Wahr (d) Falsch.
540 Lösungen zu ausgewählten Aufgaben
13 (a) Es gibt n\ n x n-Permutationsmatrizen. Es müssen also schließlich
zwei Potenzen von P identisch sein: P^ = P^. Multipliziert man dies mit
{P~^y, so erhält man P*—« = /. Dabei gilt sicher r - s < n\ (b)
'0 10'
mit P2
Ol
10
und F3
14 (a) P
15 (a) A
E 0
0 E
1 1
11
P^ mit E =
Ol
10
001
100
(b) P^(Zeile 4) = Zeile 1.
(b)^:
Ol
11
19
13
32
=
10
31
1 0
0-7
13
Ol
7
16
bc
ic)A =
10
6 1
11
10
1 0
Oc-62
16
Ol
20 Die 2 x 2-Matrix unten rechts ist
1
012
23 I 1 I I 0 3 8
21 1
tausch: A — LiPiUi
1
0 1
0 1/3 1
1
31
-5 -7
-7-32
2 1 1
3 8
-2/3
1
1
1
d — 6^ e -bc
e-bc f - (?
. Wartet man mit dem Aus-
211
012
002
24 Es gilt a6s(^(l, 1)) = 0, man muss also abs{A{2,1)) > toi finden; A
23
Ol
und P
Ol
10
; kein Austausch in L; keine weitere Elimination
nötig, deshalb ist L = / und U = neues A. Bei der zweiten Matrix gilt
^2 3 4'
wieder abs{A{l, 1)) - 0, aber abs{A{2,1)) > toi; also A-i^ | 0 0 1 I und
056
[0 10]
100
[ooi_
[2341
056
[ooij
; weiter ist abs{A{2,2)) - 0 aber a&s(AC,2)) > toi, daher
und L = /, P ->
010
001
100
27 Die Matrix Li
1
1 1
20 1
beschreibt die EUminationsschritte, wie sie
tatsächlich geschehen — L wird durch P beeinflusst.
Lösungen zu ausgewählten Aufgaben 541
30 Es gilt E21
1
-3 1
; die Matrix E^iAE'^^ -
100
024
049
ist
symmetrisch; mit £2 =
1
-4 1
gilt Es2E2iAEj^Ej^ = D. Durch
Elimination von beiden Seiten erhält man die symmetrische Zerlegung LDL^
direkt.
31 Die Gesamtströme sind Ä^y
1 0 1] \yBc
-1 1 Ollycs
0-1-lJ [yBS
Für beide Ausdrücke erhält man (Ax)^y = x^{Ä^y) = xbvbc +
XBVBS - XcVbC + Xcycs - Xsycs - XSVBS-
Vbc + Vbs
-Vbc + ycs
-ycs - Vbs
32 Rohstoffe
6820
188000
1 50
40 1000
2 50
ILKW
1 Flugzeug
Xi
X2
Ax; Ä^y =
1 40 2
50 1000 50
700
3
3000
34 Es gilt P^ = /, also drei Drehungen für 360°; P dreht um 120° um die
Achse durch A,1,1).
Aufgaben 3.1, Seite 125
1 x + y/y + x und x + (y + z) / (x + y) + z und (ci + C2)x / CiX + C2X.
2 Als einzige Regel wird Ix = x verletzt.
3 (a) Es kommt vor, dass ex nicht in der Menge liegt: sie ist unter Skalar-
multiplikation nicht „abgeschlossen". Weiterhin gibt es keine 0 und kein
-X. (b) c(x + y) ist das übliche {xyy, und ex + cy ist das übliche
{x^){y^). Beide sind gleich. Mit c = 3^ x = 2 und 2/ = 1 ist der Wert 8.
Der Nullvektor ist die Zahl 1. Der Vektor -2 ist die Zahl +\.
7 Regel 8 wird verletzt: Definiert man cf{x) als das übliche f{cx), so ist
(ci + C2)f = /((ci + C2)x) von cif + C2f = f{cix) + f{c2x) (übliche
Notation) verschieden.
8 Ist (f + g){x) gleich dem üblichen f{g{x)), so ist dies von (g + f)x =
gifix)) verschieden. Beide Seiten von Regel 2 sind f{g{h{x))). Regel 4
wird verletzt, weil es keine inverse Funktion mit f{f~^{x)) = x geben
muss. Wenn f~^ existiert, so ist es der Vektor -f.
542 Lösungen zu ausgewählten Aufgaben
9 (a) Die Vektoren mit ganzzahligen Komponenten lassen eine Addition
zu, aber nicht die Multiplikation mit | (b) Entfernt man die a;-Achse
(bis auf den Ursprung) aus der xy-Ehene, so ist die Multiplikation mit
jedem c möglich, aber nicht alle Vektoradditionen.
a b
00
(b) Alle Matrizen
a a
00
(c) Alle Dia-
11 (a) Alle Matrizen
gonalmatrizen.
12 Die Summe von D,0,0) und @,4,0) liegt nicht in der Ebene.
14 (a) Die Unterräume von M^ sind M^ selbst, die Geraden durch @,0), und
@,0) selbst, (b) Die Unterräume von M^ sind M^ selbst, dreidimensionale
Ebenen der Form n • v = 0, zweidimensionale Unterräume der Form
m • V = 0 und n2 • V = 0, Geraden durch den Ursprung @,0,0,0), und
@,0,0,0) selbst.
15 (a) Zwei Ebenen durch @,0,0) schneiden sich wahrscheinUch in einer
Geraden durch @,0,0) (b) Die Ebene und die Gerade schneiden
sich wahrscheinlich im Punkt @,0,0) (c) Der Vektor x sei in S H T
und y in SflT. Beide Vektoren liegen in beiden Unterräumen, und deshalb
liegen auch x + y und ex in beiden Unterräumen.
19 Der Spaltenraum von A ist die a;-Achse, also alle Vektoren der Form
{x, 0,0). Der Spaltenraum von B ist die xy-Ehene, also alle Vektoren der
Form (a:,2/,0). Der Spaltenraum von C ist die Gerade {x,2x,0).
20 (a) Eine Lösung existiert nur, wenn &2 = 2&i und bs = —bi gilt (b)
Eine Lösung existiert nur für bs = —bi.
22 (a) Jedes b (b) Lösbar nur für bs = 0 (c) Lösbar nur für 63 = 62-
23 Die zusätzliche Spalte b macht den Spaltenraum größer, es sei denn, b
101"
liegt bereits im Spaltenraum von A: [Ah] =
001
(größerer
Spaltenraum) ,
101
Ol 1
(gleicher Spaltenraum).
24 Der Spaltenraum von AB ist im Spaltenraum von A enthalten,
möglicherweise gleich. Ist ^ = 0 und A / 0 so hat AB = 0 einen kleineren
Spaltenraum als A.
26 Der Spaltenraum einer beliebigen invertierbaren 5 x 5-Matrix ist M^. Die
Gleichung Ax = b ist immer lösbar (durch x = A~^b), also liegt jedes b
im Spaltenraum.
27 (a) Falsch (b) Wahr (c) Wahr (d) Falsch.
Lösungen zu ausgewählten Aufgaben 543
28 A
\1 10'
100
010
oder
12"
101
Ol ij
Aufgaben 3.2, Seite 138
2 (a) Freie Variablen a;2,a;4,a;5 und Lösungen (-2,1,0,0,0), @,0, -2,1,0),
@,0, -3,0,1) (b) Freie Variable xs: Lösung A, -1,1).
3 Die vollständige Lösung ist (-2a;2,a;2,-2a;4 — 3x5^x4^x5). Der Kern
enthält nur die 0, wenn es keine freien Variablen gibt.
4 R
ri2 000'
!00123
00000
, R =
0-1"
Olli
0 0 oj
, gleicher Kern wie U und A.
-13 5'
-2 6 10
=
10'
2 1
-13 5'
000
)
-13 5
-2 6 7
=
10'
2 1
-1 3 5|
0 0-3J
6 (a) Spezielle Lösungen C,1,0) und E,0,1)
me von Pivot- und freien Variablen n.
(b) C,1,0). Gesamtsum-
7 (a) Der Kern ist die Ebene -x + Sy + 5z = 0; sie enthält alle Vektoren
C2/ + 5z, 2/, z) (b) -X + 3y + bz = 0 und -2x + 62/ + 7z = 0; die
Gerade enthält alle Punkte (82/, 2/» 0).
9 (a) Falsch (b) Wahr (c) Wahr (d) Wahr.
10 (a) Unmöglich (b) A =
1 1 1
1 1 1
1 1 1
1 1 1
1 2 1
1 12
(d) A = 2I,U=^2I,R = L
ist invertierbar
(c) A =
12
la;Oa;a;a;00
001a;a;a;00
0000 0 0 10
00000 001
01a;00a;a;a;
000 1 Oa;a;a;
0000 la;a:a;
00000000
14 Ist Spalte 1 = Spalte 5, so ist x^ eine freie Variable. Die zugehörige
spezielle Lösung ist (-1,0,0,0,1).
15 Es gibt n — r spezielle Lösungen. Der Kern enthält nur x = 0, wenn r = n
gilt. Der Spaltenraum ist W^ wenn r = m gilt.
544 Lösungen zu ausgewählten Aufgaben
17 A = [1-3-1]; 2/ und z sind freie Variablen mit speziellen Lösungen
C,1,0) und A,0,1).
20 Ist A invertierbar, so kann man ABjl — 0 mit A~^ multiplizieren, und
erhält so ^x = 0. Der Grund, warum JJ und LU denselben Kern haben,
liegt darin, dass L invertier bar ist.
23 A =
24 A
25 A
26 A
1
1
[5
0-1/2
3 -2
1 -3
[ 10 0"
0101
[0001
[-1 0 0
1 0-1 0
[1 0 0-1
"Ol
0 0
27 Ist der Kern gleich dem Spaltenraum, so gilt n — r
3 = 2r unmöglich.
r. Für n = 3 ist
29 R ist höchstwahrscheinlich gleich /; R wahrscheinhch gleich / mit einer
Nullzeile als vierte Zeile.
30 (a) A =
Ol
00
31 N =
I
-I
N
ib)A =
I
-I
Ol
00
(c)^ =
010
Ol 1
100
(Schwierig!)
N = leer.
32 Drei Pivotelemente.
33 Die von Null verschiedenen Zeilen sind i? = [l-2—3], R
R^I.
100
010
34 (a)
10
^01
)
10
0 0
J
11
0 0
J
Ol
0 0
7
00
0 0
(b) Ja!
Lösungen zu ausgewählten Aufgaben 545
Aufgaben 3.3, Seite 150
1 (a) und (c) sind wahr; (d) ist falsch, weil R Einsen an Nicht-Pivotpositionen
haben kann.
3 {&) R =
1111
0000
0000
ih)R =
1 0-1-2
0 12 3
0 0 0 0
ic)R.
1-1 1-1
0 0 0 0
0 0 0 0
5 Wenn die Pivot variablen als letzte kommen, muss R aus den vier Blöcken
R
Ol
00
bestehen. Die Kernmatrix ist dann N
7 Die Matrizen A und Ä^ haben denselben Rang r. Aber pivsp (die
Spaltenzahl) ist 2 für A und 1 für Ä^:
A =
9 S
13
14
und5 = [l] und S ■
010
000
000
10
Ol
11 Der Rang von R^ ist ebenfalls r, und im Beispiel ist der Rang 2:
P =
13
26
27
P' =
122
367
S^ =
12
37
13
27
13 Aus Rang(ß^A^) < RangGl^), erhält man Rang{AB) < RangGl), weil
der Rang bei der Transposition erhalten bleibt.
15 A und B haben höchstens den Rang 2, also hat auch das Produkt
höchstens den Rang 2. Da BA eine 3 x 3-Matrix ist, kann die Matrix nicht /
sein, selbst wenn AB = I gilt:
A =
17 A =
10
14
18
100
010
110
001
ß =
1 10
110
1 10
10
Ol
00
Aß = / und BA 7^ /.
+
10
14
18
110110
001001
000
004
008
110110
110110
110110
+
000000
004004
008008
546 Lösungen zu ausgewählten Aufgaben
19 Y ist gleich Z, weil die Form vollständig vom Rang bestimmt wird, der
für A und A^ übereinstimmt.
Aufgaben 3.4, Seite 159
1 Xvollst
r-2"
0
[ 1
+ X2
■-3]
1
oj
3 Das System ist lösbar, wenn 2&1+&2 = &3 gilt. Dann ist x —
die allgemeine Lösung.
5&1 — 2&2
&2 - 2&1
0
xs
4 (a) Lösbar für &2 = 2&i und 3&i - 3&3 + 64 = 0. Eine Lösung ist x
bi
2bi
(keine freien Variablen). (b) Lösbar für &2 = 2&i und 3&i -
3&3 + &4 = 0. Eine Lösung ist x =
461-2&3"
h - 26i
0
+ 2:3
"-1"
-1
ij
1 3 1 &1
38 2&2
24 0&3
1 3 1 &2
0-1-1 &2-3&1
0-2-2 &3-2&1
Zeile 3-2 Zeile 2 + 4 Zeile 1
ergibt die Nullzeile
0 0 0 &3 - 2&2 + 4&1
6 Jedes b liegt im Spaltenraum: linear unabhängige Zeilen.
braucht 63 == 2&2. Zeile 3-2 Zeile 2 = 0.
9 (a) xi -X2 und 0 lösen das System Ax = 0
2xi - X2 löst Ax = b.
(b) Man
(b) 2x1-2x2 löst Ax = 0;
10 (a) Die partikuläre Lösung Xp hat immer den Vorfaktor 1.
(b) Jede Lösung kann als partikuläre Lösung verwendet werden.
(c)
3 3'
33
X
y.
=
'6'
6
. Dann ist
kürzer als
(d) Die homogene Lösung ist x^ = 0.
12 Hat Zeile 3 von U kein Pivotelement, so ist es eine Nullzeile. Ux = c
ist lösbar, wenn C3 == 0 gilt. Ax = h kann unlösbar sein, weil U andere
Nullzeilen haben kann.
Lösungen zu ausgewählten Aufgaben 547
18 (a)
X
y
z
—
4
0
0
+ 2/
-1
1
0
+ z
-1
0
1
(b)
X
y
z
—
4
0
0
+ z
-1
0
1
19 Gilt Ax\ — b und Ax2 — b, so kann man xi — X2 zu jeder Lösung
Ax — B addieren. Es gibt keine Lösung von Ax — B, wenn B nicht im
Spaltenraum liegt.
23 u-C,1,4), v = A,2,2); u=B,-l), v-A,1,3,2).
24 Eine Matrix mit Rang Eins hat ein Pivotelement. Die zweite Zeile von JJ
ist Null.
26 (uv^)(wz^) = (uz^) mal v^w. Der Rang ist Eins, außer wenn v^w — 0.
28 (a) r < m, es gilt immer r < n (b) r = m, r < n (c) r < m,
r = n (d) r = m = n.
31
1230
0040
-^
1200
00 10
1235
0048
-^
1 2 0-1
0 0 12
und
Xn —
. Die Pivotspalten enthalten die Einheitsmatrix /, deshalb
tauchen —1 und 2 im Vektor Xp auf.
32 ß ==
1000
00 1 0
0000
und Xn
0
1
0
7
1 0 0-1
0 0 12
0 0 0 5
: wegen Zeile 3 keine
Lösung.
34 A=:
1 1
02
03
; B kann nicht existieren, da 2 Gleichungen in 3 Unbekannten
keine eindeutige Lösung haben können.
35 LU =
Lösung.
36 A
'lOOOl
1 100
22 10
Ll201
[1 3 ll
0-1 2
0 0 0
0 0 0
und X =
1'
-2
[ 0
+ x^
■-7]
2
ij
13
00
und keine
548 Lösungen zu ausgewählten Aufgaben
Aufgaben 3.5, Seite 176
111
Ol 1
001
0 liefert C3 = C2 = ci = 0. Es ist aber -2vi - 3v2 --
4v3 + V4 = 0 (linear abhängig).
2 Vi, V2, V3 sind linear unabhängig. Alle sechs Vektoren liegen in der Ebene
A,1,1,1) «v — 0, so dass keine vier dieser Vektoren linear unabhängig
sein können.
3 Für a == 0 ist Spalte 1 = 0; für d == 0 ist &(Spalte 1) - «(Spalte 2) = 0;
für / = 0 haben alle drei Vektoren Null als letzte Komponente, sind also
senkrecht zu @,0,1). Die Vektoren liegen in der xy-Ebene und sind daher
linear abhängig.
6 Die Spalten 1, 2, 4 von U sind linear unabhängig. Dasselbe gilt für die
Spalten 1, 3, 4 und die Spalten 2, 3, 4 und weitere (aber nicht 1, 2, 3).
Dieselbe Antwort auch für A (obwohl die Spalten nicht identisch sind).
8 Aus Ci(W2 + Ws) + C2(Wi + W3) + C3(Wi + W2) = 0 folgt (C2 + C3)Wi +
(ci + C3)w2 + (ci + C2)w3 = 0. Da die Wj linear unabhängig sind, folgt
daraus C2 + C3 = 0, ci + C3 = 0, ci + C2 = 0. Die einzige Lösung ist
Ci = C2 = C3 = 0.
9 (a) Die vier Vektoren bilden die Spalten einer 3 x 4-Matrix A. Es gibt
eine nichttriviale Lösung zu Ac = 0, weil es mindestens eine freie Variable
gibt. (c) Ovi +3@,0,0) ==0.
11 (a) Gerade (b) Ebene (c) Ebene im M^ (d) Der gesamte
Raum M^.
12 Ein Vektor b liegt im Spaltenraum, wenn es eine Lösung der Gleichung
Ax = b gibt; c liegt im Zeilenraum, wenn es eine Lösung zu A^y — c gibt.
Die Behauptung ist falsch. Der Nullvektor gehört immer zum Zeilenraum.
14 Die Dimension von S ist (a) null für x = 0 (b) eins für x =
A,1,1,1) (c) drei, wenn x = A,1,-1,-1) gilt, weil alle Umord-
nungen dieses Vektors senkrecht auf A,1,1,1) stehen (d) vier, wenn
die x'e nicht gleich sind und ihre Summe nicht null ist. Kein x ergibt
dimS = 2.
16 Die n linear unabhängigen Vektoren spannen einen Raum der Dimension
n auf. Sie bilden eine Basis für diesen Raum. Handelt es sich um die
Spalten von A, so ist m nicht kleiner als n {m > n).
Lösungen zu ausgewählten Aufgaben 549
19 (a) Die 6 Vektoren erzeugen den E* möglicherweise nicht, (b) Die
Vektoren sind nicht lineax unabhängig, (c) Vier beliebige Vektoren bilden
möglicherweise eine Basis.
22 (a) Die einzige Lösung ist x = 0, weil die Spalten linear unabhängig sind.
(b) Ali. = b ist lösbar, weil die Spalten den E^ aufspannen.
25 (a) Falsch für [11] (b) Falsch (c) Wahr: Beide Dimensionen
sind 2, wenn A invertierbar ist, die Dimensionen sind 0, wenn ^ = 0
ist, andernfalls sind die Dimensionen gleich 1 (d) Falsch, die Spalten
können Hnear abhängig sein.
27 (a)
100
000
000
(b) Addiere
0 00
010
000
0 10^
100
000
00 0
000
001
oor
000
100
000
001
010
31 (a) Alle 3 x 3-Matrizen
fachen cl.
32
(b) Obere Dreiecksmatrizen (c) Alle Viel-
"-1 2 0'
0 0 0
J
-1 0 2'
0 0 0
)
0 0 0'
-1 2 0
)
■ 0 0 Oj
-1 0 2j
35 (a) y{x) = e^^ {h) y = x (in jedem Fall ein Basisvektor).
37 Basis l^x^x'^^x^; Basis x - l^x"^ - l^x^ - 1.
38 Basis für S: A,0,-1,0), @,1,0,0), A,0,0,-1); Basis für T: A,-1,0,0)
und @,0,2,1); S n T hat die Dimension 1.
Aufgaben 3.6, Seite 188
2 A: Zeilenraum A,2,4); Kern (-2,1,0) und (-4,0,1); Spaltenraum A,2);
Kern der Transponierten (-2,1). B: Zeilenraum A,2,4) und B,5,8);
Spaltenraum A,2) und B,5); Kern (-4,0,1); Die Basis für den Kern der
Transponierten ist die leere Menge;
(b) Unmöglich: r + {n - r) muss 3 sein (c) [0 0]
(e) Unmöglich: Zeilenraum = Spaltenraum setzt m = n
4 (a)
(d) [
fio'
10
[oi_
-9-3'
3 1
voraus. Dann muss auch m, — r = n — r gelten.
550 Lösungen zu ausgewählten Aufgaben
6 A: Zeilenraum @,3,3,3) und @,1,0,1); Spaltenraum C,0,1) und C,0,0);
Kern A,0,0,0) und @,-1,0,1); Kern der Transponierten @,1,0). B:
Zeilenraum A), Spaltenraum A,4,5), Kern: leere Basis, Kern der
Transponierten (-4,1,0) und (-5,0,1).
7 A ist invertierbar: Basis des Zeilenraums = Basis des Spaltenraums =
A,0,0), @,1,0), @,0,1); die Basen von Kern und Kern der
Transponierten sind leer. Matrix B: Basis des Zeilenraums A,0,0,1,0,0),
@,1,0,0,1,0) und @,0,1,0,0,1); Basis des Spaltenraums A,0,0), @,1,0),
@,0,1); Basis des Kerns (-1,0,0,1,0,0), @, -1,0,0,1,0), @,0, -1,0,0,1);
Der Kern der Transponierten ist der Nullraum.
8 Zeilenraumdimensionen 3,3,0; Spaltenraumdimensionen 3,3,0;
Dimensionen des Kerns 2,3,2; Dimensionen des Kerns der Transponierten
0,2,3.
11 (a) Dass es keine Lösungen gibt, bedeutet r < m. Es gilt immer r < n.
Die Werte für m und n lassen sich nicht vergleichen (b) Ist m — r > 0,
so enthält der Kern der Transponierten einen nichttrivialen Vektor.
12 02 lon^^^^h r + (n-r)=n = 3 aber 2 + 2 ist 4.
[11"
02
[10
lor
120
=
211
240
101
13 (a) Falsch (b) Wahr (c) Falsch (man wähle A und B von gleicher
Größe und invertierbar).
14 Basis des Zeilenraums A,2,3,4), @,1,2,3), @,0,1,2); Basis des Kerns
@,1,-2,1); Basis des Spaltenraums A,0,0), @,1,0), @,0,1); der Kern
der Transponierten ist der Nullraum.
16 Gilt einerseits Av — 0 und ist v andererseits eine Zeile von A, so gilt
V . V = 0.
18 Es gilt Zeile 3-2 Zeile 2 + Zeile 1 = 0, so dass die Vektoren c(l, -2,1)
im Kern der Transponierten liegen. Dieselben Vektoren liegen auch im
Kern.
19 Das Eliminationsverfahren führt auf 0 = Ö3 — Ö2 — ^i, so dass (—1, —1,1)
im Kern der Transponierten liegt. Das Eliminations verfahren führt auf
Ö3 -2Ö1 = 0 und Ö4 + Ö2 -4Ö1 = 0, so dass (-2,0,1,0) und (-4,1,0,1)
im Kern der Transponierten liegen.
20 (a) Alle Linearkombinationen von (—1,2,0,0) und (—|, 0, —3,1) (b) 1
(c) A,2,3), @,1,4).
[2'
22
41
00'
Ol 1
=
'1221
222
4 1 ij
Lösungen zu ausgewählten Aufgaben 551
21 (a)uundw (b)vundz (c) Der Rang ist kleiner als 2, wenn u und
w oder v und z linear abhängig sind. (d) Der Rang von uv^ + wz-^
ist 2.
22
25 (a) Wahr (gleicher Rang) (b) Falsch A = [1 0] (c) Falsch {A kann
invertierbar und unsymmetrisch sein) (d) Wahr.
27 Man wählt d = bc/a. Dann hat der Zeilenraum die Basis (a, b) und der
Kern die Basis (—ö, a).
28 Beide Ränge sind 2; Zeilen 1 und 2 bilden eine Basis; N{B^) besteht
aus sechs Vektoren mit 1 und —1 durch eine Null voneinander getrennt;
iV(C^) besteht aus (-1,0,0,0,0,0,0,1), @,-1,0,0,0,0,1,0) und den
Spalten 3,4,5,6 von /; N{C) bleibt eine Herausforderung.
Aufgaben 4.1, Seite 200
3 (a)
(c) A =
1 2-3
2-3 1
3 5-2
1 1
(b)
steht nicht senkrecht auf
1 1
(d) Zeile 1+ Zeile 2+ Zeile 3 = F, , ) ist von
Null verschieden; es gibt keine solche Matrix (e) A,1,1) liegt in Kern
und Zeilenraum — es gibt keine solche Matrix.
5 (a) Hat die Gleichung Ax = h eine Lösung und gilt A^y = 0, so steht y
senkrecht auf b. (Ax)^y = b^y = 0 (b) Hat die Gleichung Ax = b
keine Lösung, so liegt b nicht im Spaltenraum und steht nicht senkrecht
auf y.
6 Es gilt X = Xr + Xn, wobei x^. im Zeilenraum und x^ im Kern liegt.
Daher gilt Axn = 0 und Ax = Axr + Axn = Axr- Alle Vektoren Ax sind
Linearkombinationen der Spalten von A.
7 Liegt Ax im Kern von A^, so muss Ax gleich Null sein, da der Vektor
außerdem im Spaltenraum liegt und daher senkrecht auf sich selbst steht.
8 (a) Spaltenraum und Zeilenraum einer symmetrischen Matrix stimmen
überein (b) x liegt im Kern, und z liegt im Spaltenraum =
Zeilenraum, da A = A^.
552 Lösungen zu ausgewählten Aufgaben
10 X = X, + Xn = A, -1) + A, 1) = B, 0).
11 Ä^y = 0=^ x^Ä^y = (Ax)^y = 0 ::^ y i. Ax.
13 Ist S der Unterraum des E^, der nur den Nullvektor enthält, so ist S-^
gleich E^. Wird S durch den Vektor A,1,1) erzeugt, so wird S-^ durch die
Vektoren A, —1,0) und A,0, —1) aufgespannt. Wird S durch die Vektoren
B,0,0) und @,0,3) erzeugt, so wird S-^ durch @,1,0) aufgespannt.
151
222
Deshalb ist S"^ ein Unterraum,
14 S-^ ist der Kern der Matrix A —
obwohl S keiner ist.
17 Die Vektoren (-5,0,1,1) und @,1, -1,0) spannen S-^ auf.
19 Ein Vektor x in V-^ steht senkrecht auf jedem Vektor in V. Da V alle
Vektoren in S enthält, steht x auch senkrecht auf jedem Vektor in S.
Deshalb ist jeder Vektor x in V-^ ebenfalls in S-^ enthalten.
20 Spalte 1 von A~^ ist orthogonal zu dem Raum, der von den Zeilen 2,..., n
von A aufgespannt wird.
24 (a) Der Vektor A,-1,0) liegt in beiden Ebenen. Die Normalenvektoren
stehen senkrecht aufeinander, aber die Ebenen schneiden sich, (b) Der
Vektor B,-1,0) steht senkrecht auf der ersten, aber nicht auf der zweiten
Geraden. (c) Geraden können sich schneiden, ohne orthogonal zu
sein.
Aufgaben 4.2, Seite 212
1 (l)p^(|,|,|); e-(-|,|,|) B) p = A,3,1); e-@,0,0).
3 Pi-^
5i^i = l
*.3' 3' S-*
11 1
1 1 1
1 1 1
EsgiltF2 = Pj.p.2 = i
131
393
131
1-2-2
-2 4 4
-2 4 4
F2 = i
4 4-2
4 4-2
-2-2 1
. Es gilt P1P2 - 0, da ai ± a2.
6 Es gilt PI = (|, -|, -I), P2 = (|, |, -§) und PS = (|, -|, I). Daher
P1+P2+P3- A,0,0) =b.
8 Es gilt pi ^ A,0) und p2 = @,6, 1,2). Daher pi -I- P2 7^ b.
Lösungen zu ausgewählten Aufgaben 553
10 Es gilt P = 7. Ist A invertierbar, so ist P = A{A'^A)''^ A'^ = AA-^ (A^)-^^
= 1,
11 A) p = A(A^A)-iA^b = B,3,0) und e = @,0,4)
und e = 0.
B)p = D,4,6)
14 Die Projektion von b auf den Spaltenraum von A ist b selbst, aber P
5 8-4'
muss nicht unbedingt / sein. P
21
8 17 2
-4 2 20
undp=: @,2,4).
16 Es gilt 1A,2, -1) + 1A,0,1) = B,1,1). Deshalb liegt b in der Ebene.
17 Es gilt P^=^P und deshalb (/-P)^ = {I-P){I-P) = I-PI-IP+P'^ =
I — P. Ist P die Projektion auf den Spaltenraum von A, so ist 7 — P die
Projektion auf den Kern der Transponierten von A.
20 e-A,-1,-2), Q
1/6-1/6-1/3'
-1/6 1/6 1/3
-1/3 1/3 2/3
' ^^
5/6 1/6 1/3
1/6 5/6-1/3
1/3-1/3 1/3
21 {A{A^A)-^A^)^ = A{A^A)-\A^A){A^A)-^A^ = A{A^A)-^A^, Es
gilt also P^ = P. Pb liegt immer im Spaltenraum (auf den P projiziert).
Deshalb ist P(Pb) gleich Pb.
24 Der Kern von A^ ist orthogonal zum Zeilenraum Z{A), Gilt also A^b =
0, so sollte die Projektion von b auf Z{A) der Vektor p = 0 sein. Rechnen
Sie Pb = A(A^A)-iA^b = A(A^A)-iO = 0 nach.
26 A~^ existiert wegen r = m. Multipliziert man A'^ = A mit A~^, so erhält
man A = 7.
27 Ax liegt im Kern von A. Aber Ax liegt immer im Spaltenraum von A.
Damit der Vektor in beiden orthogonalen Unterräumen liegen kann, muss
Ax der Nullvektor sein. Daher haben A und A^A denselben Kern.
Aufgaben 4.3, Seite 225
rio"
11
13
[14
c
p
' ^1
8
8
20
. Mit p
1
5
13
17
ist X = A,4) die exakte Lösung.
554 Lösungen zu ausgewählten Aufgaben
2 Ä^A =
,A'^h =
■4 8
J8 26
5, 13, 17. Die Fehler sind
36
112
. Es gilt X = A,4). Die vier Höhen sind 1,
-1,3, -5,3. Der minimale Fehler ist E = 44.
4 Esgilt£? = (C+0£>J + (C+£>-8J + (C+3£>-8J + (G+4Z)-20Jund
damitö£;/öC = 2C + 2(C + £>-8) + 2(C+3£>-8) + 2(C+4Z)-20) = 0
undö£;/ö£> = l-2(C+£>-8) + 3-2(C+3Z)-8) + 4-2(C+4£>-20) = 0.
Die Gleichungen sind
5 E = (G-0J + (G-8J + (C-8J + (C-20J. A^ = [1 1 1 1],Ä^A = [4],
Ä^h = [36] und C = 9. e = (-9, -1, -1,11).
7 A = [0 1 3 4]^, A'^A = [26], A'^h = [112] und D = 112/26 = 56/13.
■4 8'
8 26
C
D
=
■ 36'
II2J
[10 0"
111
13 9
[14 16
'C
D
E
=
' 0"
8
8
20
■ 4 8 26"
8 26 92
26 92 338
'C
D
E
=z
' 36]
112
400 J
10
rio 0 0'
1111
13 9 27
[14 16 64
'C
D
E
F
=
' 0"
8
8
20
. Also
'C
D
E
F
_ 1
~ 3
0'
47
-28
5
p = b und e = 0.
11 (a) Die bestangepasste Gerade ist a; = 1 + 4^ durch den Punkt B,9)
(b) Aus der ersten Gleichung: C - m + D - X^Hi ^i — Y^iLi ^i- Division
durch m liefert C + Dt = h.
12 (a) Es gilt a^a = m und a^b = bi-\ höm- Deshalb ist x der Mittelwert
''--ET=iibi-xy (c)p-C,3,3),
1 r
der ö's (b) e = b - xa.. ||e|
e=: (-2,-1,3), p^e=:0. P
1 1 1
1 1 1
13 (A^A)-M^(Ax - b) = X - X. Die Fehlervektoren (±1,±1,±1) bilden
die Summe 0, so dass x — x ebenfalls 0 ergibt.
14 Es gilt (x - x)(x - x)^ = (A^A)-M^(b - Ax){h - Ax)^A(A^A)-^
Aus den Mittelwerten erhält man die „Kovarianz-Matrix" {A'^A)~^A
a^A(A^A)~\ oder einfacher a^(A^A)~^
16 T^öioo + ^^99 = Toö(^i + • • • + ^loo)-
Lösungen zu ausgewählten Aufgaben 555
IS p = Ax = E,13,17) gibt die Höhen der bestangepassten Geraden an.
Die Fehler sind b - p = B, -6,4).
20 X = (9,4). p = Ax = E,13,17) = b. Der Fehler ist e = 0, da b im
Zeilenraum von A liegt.
21 e liegt in iV(A^); p liegt in Z{A); x liegt in Z{A'^); N{A) = {0}.
23 Das Quadrat des Abstandes zwischen Punkten auf zwei Geraden ist E =
{y - a;J + {Sy - xf + A + x)\ Es gilt ^dE/dx = -{y - o;) ~ {3y -
a;) + (a; + 1) = 0 und ^dE/dy = {y - x) + S{3y - x) = 0. Die Lösung ist
a;=:-|,2/ = -f;£^=f, und der geringste Abstand ist A/y.
24 e ist orthogonal zu p; ||e|p = e^{h - p) = e'^b = b^b - b'^p.
25 Die Ableitungen von ||Ax - b|p sind Null, wenn x = (A^A)~^ A^b.
Aufgaben 4.4, Seite 238
3 (a) A^A = 16/
1, 4, 9.
(b) A^A ist eine Diagonalmatrix mit den Einträgen
4 (a) Q -
10
Ol
00
T _
QQ' =
1 00
010
000
gonal, aber nicht linear unabhängig
V2 ' 2' 2 ' 2/' V 2 ' 2 ' 2 ' 2/'
(b) A,0) und @,0) sind ortho-
\^J V2'2'2'2>'' V2'2' 2' 2/'
6 Sind Qi und Q2 orthogonale Matrizen, so gilt {QiQ2)^QiQ2 — QJQTQ1Q2
= Q2Q2 — I- Dies impHziert, dass Q\Q2 ebenfalls orthogonal ist.
7 Die Kleinste-Quadrate-Lösung ist x = Q^h. Die Lösung ist 0 für Q =
und b =
9 (a) Sind qi, ^2 und qs orthonormal^ so erhält man durch das Skalarpro-
dukt von qi mit der Gleichung ciqi + C2q2 + Csqa = 0 die Gleichung
ci = 0. Analog erhält man 02=03= 0. (b) Qx = 0 => Q^Qx =
10 (a) Zwei or^/ionorma/e Vektoren sind 3^A,3,4,5,7) und j^G,-3,-4,5,-1)
(b) Der nächste Vektor in der Ebene ist die Projektion QQ^(l, 0,0,0,0) =
@,5, -0,18, -0,24, 0,4, 0).
556 Lösungen zu ausgewählten Aufgaben
11 Sind qi und q2 orthonormale Vektoren im M^, so ist (qfb)qi 4- (q2^b)q2
am nächsten zu b.
12 (a) Es gilt afb — af (a;iai + a;2a2 + ajaas) = a;i(af ai) = Xi, (b) Es gilt
af b = af (a;iai +a;2a2 +a;3a3) = a;i(af ai) und deshalb Xi = af b/af ai.
(c) xi ist die erste Komponente von A~^ mal b.
14 Esgiltqi = (^,^), q2 = (-i^,--^)und
14
10
= [qi 02]
Tul
l|a||q/b
0 IIBII
15 (a) qi = i(l,2,-2), q^ = iB,l,2), qg = |B,-2,-l) (b) Der
Kern von A"^ enthält qs (c) x = {Ä^A)-^A^{1,2,7) = A,2).
16 Das Vielfache p = fr^a = i|a = |a ist am nächsten. Es gilt qi =
a/||a|| = ia und q^ = B/||B|| = ^F, -3,10,10).
18 Für A = QR ist A^A = R^R = untere multipliziert mit einer oberen
Dreiecksmatrix. Die Pivotelemente von A^A sind 3 und 8.
19 (a) Wahr (b) Wahr. Qx = a;iqi+a;2q2- ||Qx|p = xj+x^, daqi-q2 =
0.
20 Die orthonormalen Vektoren sind (|,|,|,|) und (-5/\/52,-l/>/52,
l/\/52,5/\/52). Damit wird b auf den Vektor p = (-3,5, -1,5, -0,5, 1,5)
projiziert. Rechnen Sie nach, dass b — p orthogonal zu beiden Vektoren
ist.
21 A = A,1,2), B = A,-1,0), C = (-1,-1,1). Noch nicht orthonormal.
23 (a) Eine Basis für den Unterraum ist Vi = A,-1,0,0), V2 = A,0,-1,0),
V3 = A,0,0,1) (b) A,1,1,-1) (c) b2 = (|,|,|,-|) und bi =
V2 ' 2 ' 2 ' 2^'
25 (q2^C*)q2 ist dasselbe wie §t§B, weil q2 = tt^ und die zusätzliche
Spalte qi in C* orthogonal zu q2 ist.
28 In Gleichung D.36) fallen mn Multiplikationen an, und ^rn^n
Multiplikationen in jedem Teil von Gleichung D.37).
32 (a) Es gilt Qu = (/-2uu^)u = u-2uu^u. Dies ist -u wenn u^u gleich
1 ist. (b) Qv = {I - 2uu^)v = u - 2uu^v = u, u^v = 0 vorausgesetzt.
33 Die Spalten der Wavelet-Matrix W sind orthonormal. Daher gilt W~^ —
W^. In Abschnitt 7.3 erfahren Sie mehr über Wavelets.
Lösungen zu ausgewählten Aufgaben 557
Aufgaben 5.1, Seite 252
2 Es gilt det(|A) - i^fdetA = -|, det(-A) = {-ifdetA = 3,
det{A^) = 9 und det{A-^) = -|.
3 (a) Falsch (b) Wahr (c) Wahr (d) Falsch.
4 Vertauschen Sie Zeilen 1 und 3. Vertauschen Sie Zeilen 1 und 4, dann 2
und 3.
5 IJ5I = 1, iJel — -1, |JV| == -1- Die Determinanten sind 1, 1, -1, -1, 1,
1, ... es gilt also | Jioi| = 1.
6 Man multipliziert die Nullzeile mit t. Dann wird auch die Determinante
mit t multipliziert — die Matrix bleibt aber unverändert =^ det = 0.
7 Q^ = Q-^ und Q^Q = 1^ \Q\^ = 1 ^ |Q| ^ ±1.
10 Bilden die Einträge jeder Zeile die Summe null, so liegt A,1,..., 1) im
Kern: die singulare Matrix A hat det == 0. Bilden die Einträge jeder Zeile
die Summe eins, so bilden die Einträge der Zeilen der Matrix A - / die
Summe null (nicht notwendigerweise det A = 1).
11 Es gilt CD = -DC ^ \CD\ = (-1)^|DC| und nicht -\DC\. Ist n
gerade, so ist \CD\ ^ 0 mögUch.
-b
12 det(A-^)=det
ad—bc ad—bc
—c a
. ad—bc ad—bc
13 det(A) = 24 und det(A) =^ 5.
15 det Abound d(
3t K = 0.
ad—bc 1
{ad—bc)^ ad—bc'
16 Für eine beliebige schiefsymmetrische 3 x 3-Matrix K gilt det{K'^)
det{-K) = {-lfdet{K), also -det{K). Es gilt aber auch det{K'^)
det{K)j daher muss det{K) — 0 gelten.
19 det
a — Leb — Ld
c — la d — lh
= {ad-bc){l-Ll).
20 Regel 2 folgt aus den Regeln 5 und 1.
21 Es gilt det(A) = 3, det(A-i) =: |, det(A-A/) = A^-4A + 3. Aus A = 1
und A = 3 folgt dann det(A - XI) = 0.
24 Zeile 2 = 2 mal Zeile 1, daher det A = 0.
25 Zeile 3 - Zeile 2 = Zeile 2 - Zeile 1, daher ist A singular.
558 Lösungen zu ausgewählten Aufgaben
28
dfidadfidc
df/db df/dd
d -b 1
ad—bc ad—bc
— c a
ad—bc ad—bc .
_ 1
ad—bc
■ d-b'i
—c a\
- J-1
Aufgaben 5.2, Seite 266
1 Es gilt det A = 4, die Spalten sind linear unabhängig; weiter ist det B = 0,
die Spalten sind linear abhängig.
3 Jeder der sechs Terme in det A ist null, der Rang ist höchstens 2; Spalte
2 besitzt kein Pivotelement.
5 011023032^44 ergibt —1, 014023032^41 ergibt +1, daher ist det A = 0;
detB = 2-4-4-2-l-4.41=:48.
7 (a) Mit an = 022 = CL33 = 0 haben vier Summanden garantiert den Wert
null. (b) 15 Summanden sind null.
8 Für 5!/2 = 60 Permutationsmatrizen gilt det(P) = +1. Man setze Zeile
5 von / als erste Zeile.
9 Es sei aiaa2ß • • • anu ^ 0. Man setze dann die Zeilen 1, 2, ... , n an die
Stellen a, ß, ... ,0;. Dann erscheinen die von Null verschiedenen Einträge
auf der Haupt diagonalen.
11 C =
6-3
-1 2
12 Es gilt C =
13 IB4I = 2 det
2IB3I-IB2I.
C =
32 1
242
1 23
0 42-35
0-21 14
-3 6 -3
und AC^ =
. \B\ - 1@) + 2D2) + 3(-35) = -21.
4 0 0"
040
004
Daher ist A'^ = \C'^.
1-1
-1 2-1
-1 2
+ det
r 1-1 1
-1 2
-1-lJ
= 2|B3|-det
1-1
-1 2
15 Man setzt zuerst Spalte 2, dann Spalte 1, dann Spalte 4, dann Spalte 3,
und so weiter. Deshalb muss n gerade sein, damit det An ^ 0 gilt. Die
Anzahl der Zeilenvertauschungen ist f, es gilt also Cn = (—1)"/^.
16 Der Kofaktor in Position A,1) ist En-i- Der Kofaktor in Position A,2)
hat eine einzelne Eins in der ersten Spalte mit zugehörigem Kofaktor
En-2' Aus den Vorzeichen ergibt sich En = En-i — ^n-2- Daher
wiederholt sich ein Muster 1, 0, —1, -1, 0, 1; es gilt Eiqq = -1.
Lösungen zu ausgewählten Aufgaben 559
17 Der Kofaktor in Position A,1) ist Fn-i- Der Kofaktor in Position A,2)
hat eine Eins in der ersten Spalte mit zugehörigem Kofaktor Fn-2- Nach
Multiplikation mit den Vorzeichen (-1)^"^^ und der (-1) vom Eintrag
A,2) erhält man Fn — i^n—i + -^n—2-
20 Es gilt 02 = -1, Gz = 2, G4 = -3, und G« = (-l)"-i(n - 1).
21 (a) Für jeden Eintrag aus B muss man auch einen Eintrag aus dem
Nullblock wählen, diese Siunmanden sind also null. Es bleiben die Einträge
0
aus A und D, die zu \A\\D\ führen, (b) und (c) Man nehme A =
00
B =
00
10
C =
Ol
00
£> =
00
Ol
22 (a) Für alle L's gilt det = 1; weiter detUk = det Aj; = 2, dann 6, dann
-6 (b) die Pivotelemente sind 2, |, -|.
23 Aus Aufgabe 21 hat man det
I 0
-CA-i I
= 1 und det
AB
CD
= \A\
mal \D-CA-^B\. Für AC = CA ist dies \AD-CAA-^B\ = \AD-CB\.
24 Ist A eine Zeile und B eine Spalte, so gilt det M = det AB = Skalarpro-
dukt von A und B. Ist A eine Spalte und B eine Zeile, so hat AB den
Rang 1, und det M — det AB = 0 (außer für m = n = 1).
25 (a) Es gilt det A = auAu + Oi2j4i2 + • • • + Oi„Ai„. Die Ableitung nach
Oll ist der Kofaktor An (b) dln{detA)/daii = An/det A ist der
Eintrag A,1) der inversen Matrix A~^.
27 Die fünf von Null verschiedenen Produkte sind alle ±1:
+ A,1)B,2)C,3)D,4) + A,2)B,1)C,4)D,3) - A,2)B,1)C,3)D,4)
- A,1)B,2)C,4)D,3) - A,1)B,3)C,2)D,4).
Insgesamt 1 + 1 — 1 — 1 — 1 = —1.
29 Es gilt |5i| ^ 3, |52| = 8, l^sl = 21. Die Reihe scheint jede zweite der
Fibonacci-Zahlen ...3, 5, 8, 13, 21, 34, 55, ... zu enthalten, man rät
daher |54| = 55. Wie in der Lösung zu Aufgabe 28 (mit 3 an Stelle von
2) erhält man \S^\ = 81 + 1 - 9 - 9 - 9 = 55.
31 Die Änderung von 3 zu 2 in der Ecke ändert die Determinante um 1 mal
den Kofaktor des Eckeintrags. Dieser Kofaktor ist die Determinante von
Sn-i, also F2n- Ändert man also 3 in 2, so ändert man die Determinante
von F2n+2 zu F2n+2 " -^2n, also F2n+l.
560 Lösungen zu ausgewählten Aufgaben
Aufgaben 5.3, Seite 283
1 (a) Es gilt detA = 5, detJ5i = 10, detJ52 = —5, die Lösung ist daher
xi = 2 und X2 = -1 (b) Es gilt \A\ = 4, \Bi\ = 3, \B2\ = -2,
IJ^sl = 1 und damit xi = ^, X2 = —\ und X3 = \.
3 (a) xi = 3/0 und X2 = —2/0: keine Lösung
X2 = 0/0: unbestimmt.
(b) xi = 0/0 und
4 (a) Es gilt det([ba2 a3])/detA, falls detA 7^ 0 (b) Die
Determinante ist eine lineare Funktion in der ersten Spalte, daher gilt
xilai SL2 asi + X2\sL2 a2 asi + Xslas a2 asl- Die letzten beiden
Determinanten sind null.
5 Ist die erste Spalte von A gleich der rechten Seite b, so gilt det A = det J5i.
Sowohl B2 als auch ^3 sind singular, da eine Spalte doppelt vorkommt.
Daher gilt xi — \Bi\/\A\ = 1 und 0:2 = 0:3 := 0.
6 (a)
[1-1 0-
0 1 0
Lo-I 1.
(b)
r3 1 1 -|
4 2 4
i 1 i
2-^2
113
.4 2 4 J
. Die Inverse einer symmetrischen
Matrix ist symmetrisch.
7 Sind alle Kofaktoren Null, so wäre A ^ gleich der Nullmatrix, falls sie
existierte: sie
kann also nicht existieren. Die Matrix A =
11'
1 1
hat keinen
Kofaktor Null, ist aber nicht invertierbar.
8 Es gilt C =
6-3 0"
-3 4-1
0-1 1
und AC^ =
0 0"
030
003
und daher det A = S.
10 Berechnen Sie auf beiden Seiten die Determinante. Auf der linken Seite
erhält man detAC^ = (det^)(detC), auf der rechten Seite (detA)".
Dividieren Sie dann noch durch det A.
11 Man bestimmt zunächst detA = (detC)"^=^ mit n = A und daraus
det A~^ = 1/ det A. Dann konstruiert man A~^ mit Hilfe der Kofaktoren,
und invertiert die Matrix, um A zu bestimmen.
13 Sowohl detA als auch detA~^ sind ganze Zahlen, da die Matrizen nur
ganze Zahlen enthalten. Es gilt aber detA"^ = 1/detA, also muss
detA = 1 oder -1 sein.
15 (a) C21 = C31 = C32 = 0 (b) C12 = C2i,C3i = Ci3,C32 = 6*23-
Lösungen zu ausgewählten Aufgaben 561
16 Für n = 5 besteht die Matrix C aus 25 Kofaktoren, jeder 4 x 4-Kofaktor
besteht aus 24 Termen, die jeweils 3 Multiplikationen erfordern:
insgesamt 1800 gegenüber 125 für das Gauss-Jordan-Verfahren.
17 (a) Flächeninhalt | f 1| = 10 (b) 5 (c) 5.
3 11
18 Volumen = U 3 i = 20. Flächeninhalt der Seitenfläche = Länge des
i i k
Kreuzprodukts 311= 6\/2.
19 (a) I
5 + 7=12.
211
3 4 1
0 5 1
= 5
(b) 5 + zusätzlicher Flächeninhalt |
211
0 5 1
-1 0 1
21 (a) Es gilt V — L1L2L3, wenn die Seiten rechtwinklig sind. (b) \aij\ <
1 liefert jeweils L < y/S. Das Volumen ist daher < (\/3)^ < 6.
Herausforderung: Ist das Volumen 5 möglich?
24 Der Kasten hat die Höhe 4, und das Volumen ist 4. Die Matrix ist
100]
0 1 0 ; es gilt i x j = k und (k • w) = 4.
234J
25 Ein n-dimensionaler Würfel hat 2^ Ecken, n2^~^ Kanten und 2n{n -
l)-dimensionale Seitenflächen. Der Würfel mit den Spalten von 2/ als
Kanten hat das Volumen 2^.
26 Die Pyramide hat das Volumen |. Die vierdimensionale Pyramide hat
das Volumen ^.
— ^2
I sin (p cos 9 p cos ip cos 9 —p sin (p sin 9
28 Es gilt J ^= sin(/?sinö pcosipsm9 p sin (p cos 9
I cos(p —ps'iTKp 0
sen Ausdruck für Dreifachintegrale über Kugeln
p^ sin if, man benötigt die-
2Q Po rrilf I ^f/^^ dr/dy 1 _ 1 cos ö sin ö
^ ^S gur ^^^^^ ^^^^^ _ \_l.sm9 i cosö
_ 1
30 Das Dreieck mit den Ecken @,0), F,0), A,4) hat einen Flächeninhalt
von 24. Eine Drehung um 6 = 60^ lässt den Flächeninhalt unverändert.
Die Determinante der Drehmatrix ist J =
cos 9 — sin 6
sin 6 cos 9
1
2
vi
2
V3
~-T
1
2
= 1.
32 Es gilt V = det
2 40
-13 0
122
= 20.
562 Lösungen zu ausgewählten Aufgaben
34 Es gilt (w X u) • V = (v X w) • u = (u X v) • w: Zyklische Vertauschungen \
= gerade Permutationen von (u, v, w).
35 Es gilt 5 = B,1,-1). Der Flächeninhalt ist ||PQxP5|| = ||(-2,-2,-1)|| :=;^
3. Die anderen vier Ecken könnten @,0,0), @,0,2), A,2,2), A,1,0) sein.
Das Volumen des Parallelepipeds ist 1.
36 Sind A,1,0), A,2,1) und {x,y,z) koplanar, so ist das Volumen
det
X y z
1 10
1 21
z={)z= X -y -\- z.
37 Es gilt det
X y z
3 2 1
1 23
= 0 = 7a:-52/+2:; die Ebene mit den beiden Vektoren.
Aufgaben 6.1, Seite 299
1 A, A^ und A^ besitzen alle dieselben Eigenvektoren. Die Eigenwerte
sind 1 und 0,5 für A, 1 und 0,25 für A^, 1 und 0 für A°°. Daher liegt A^
halbwegs zwischen A und A^.
Vertauscht man die Zeilen von A, so ändern sich die Eigenwerte zu 1
und —0,5, weil es sich weiterhin um eine Markov-Matrix mit Eigenwert
1 handelt, die Spur jetzt aber 0,2 + 0,3 ist, so dass der andere Eigenwert
gleich -0,5 sein muss. Die Eigenwerte können sich also völlig ändern,
wenn man Zeilen vertauscht.
Singulare Matrizen bleiben während des Elmininationsverfahrens
singular.
2 Die Eigenwerte sind Ai = — 1 und A2 = 5 mit den Eigenvektoren xi =
(-2,1) und X2 = A,1). Die Matrix A-\-1 hat dieselben Eigenvektoren
mit den Eigenwerten 0 und 6.
4 A hat die Eigenwerte Ai = — 3 und A2 = 2 mit den Eigenvektoren xi =
C, -2) und X2 — A,1). A^ hat dieselben Eigenvektoren wie A mit den
Eigenwerten Af = 9 und \\ — ^.
6 A und B haben die Eigenwerte Ai = 1 und A2 = 1. AB und BA haben die
Eigenwerte A = |Cdi\/5). Die Eigenwerte von AB sind nicht Eigenwerte
von A mal Eigenwerte von B. Die Eigenwerte von AB sind gleich den
Eigenwerten von BA.
8 (a) Man berechnet Ax, erhält Ax und damit A.
A/)x = 0, um X zu bestimmen.
(b) Man löst {A -
Lösungen zu ausgewählten Aufgaben 563
10 A hat die Eigenwerte Ai = 1 und A2 = 0,4 zu den Eigenvektoren Xi =
A,2) und X2 = (Ij-l)- A^ hat die Eigenwerte Ai = 1 und A2 = 0
zu denselben Eigenvektoren. A^^^ hat die Eigenwerte Ai = 1 und A2 =
@,4I0°, g^lgQ beinahe null. Deshalb ist A^^^ nahe bei A°°.
12 (a) Es gilt Pu = (uu^)u = u(u^u) = u und daher A = 1. (b) Es gilt
Pv = (uu^)v = u(u^v) = 0. (c) Die Vektoren xi = (-1,1,0,0),
X2 = (-3,0,1,0) und X3 = (-5,0,0,1) sind Eigenvektoren mit A = 0.
14 Es gilt A = |(-1 ± iV^); A = -1 und 1 (mehrfacher Eigenwert 1).
15 Man setzt A = 0 und erhält det A = (Ai)(A2) • • • (An).
16 Hat A die Eigenwerte Ai = 3 und A2 = 4, so gilt det(A - XI) = (A -
3)(A _ 4) = A2 - 7A -f 12. Es gilt immer Ai = |(a -f d -f y/{a - dJ -f Abc)
und A2 = ^(a -\- d — ^ ). Die Summe ist a -f d.
19 A =
0 1
-28 11
22 A = 1 (für eine Markov-Matrix), 0 (für eine singulare Matrix), -| (so
dass die Summe gleich der Spur | ist).
26 A = 1, 2, 5, 7.
27 Rang(A) := 1 mit A = 0, 0, 0, 4; Rang(C) = 2 mit A = 0, 0, 2, 2.
28 B hat die Eigenwerte A = -l, -1, -1, 3, es gilt also det5 — -3. Die
5 X 5-Matrix A hat die Eigenwerte A = 0, 0, 0, 0, 5, und 5 = A - / hat
die Eigenwerte A — -1, -1, -1, -1, 4.
30 Es gilt
a b
c d
a + 6
X2 = d — b, damit sich die
= {a + b)
I t. -r u/j
Spur a -\- d ergibt.
32 (a) u ist eine Basis für den Kern, v und w bilden eine Basis für den
Spaltenraum. (b) x = @, |, |) ist eine spezielle Lösung. Man kann
jedes (c, 0,0) addieren. (c) Hätte die Gleichung Ax = u eine Lösung,
so läge u im Spaltenraum, der die Dimension 3 haben müsste.
Aufgaben 6.2, Seite 314
1 Es gilt
2'
103
=
1'
Ol
10"
03
1-1"
0 1
und
1 1"
22
=
1 1"
-1 2
00"
0 3
1 1
3 3
1 1
3 3 J
564 Lösungen zu ausgewählten Aufgaben
4 Gilt A = 5^15 ^ so ist die Eigenwertmatrix für A+ 21 gleich A + 2/,
und die Eigenvektormatrix ist weiterhin S. Daher gilt A + 2I = S{A +
2I)S-^ = SAS-'^ + S{2I)S-^ =A + 2I.
5 (a) Falsch (b) Wahr
9 Es gilt A^ =
21
1 1
, A^ =
(c) Wahr
, A'^
32
2 1
53
32
(d) Falsch.
^20 = 6765.
10 (a) A =
0,5 0,5
1 0
hat die Eigenwerte Ai = 1, A2 = -| mit den Eigenvek-
1 1
1 -2
1" 0
0 (-0,5)"
2 ll
3 3
1 1
.3 Sj
toren Xi = A,1), X2 = A, -2) (b) A" =
A°^
(c)
13 Es gilt A20(xi + X2) = A^Oxi + ^20x2 = Af^xi + \fy.2. Die zweite
Komponente ist Af + \f. Es gilt F20 = 15127.
'21'
3 3
2 1
-33.
. Gk
= A^
Gl
Gn
-^
L - j
1"
3 3
2 1
.33.
r
0
=
^ ""
■ 2"
3
2
. 3 j
15 (a) Wahr (b) Falsch (c) Falsch.
16 (a) Falsch (b) Wahr (c) Wahr.
20 Es gilt A =
5^1*5-1
1
0"
00,2
r 1 1"
2 2
1
L 2
1
2.
und 5 —
1 1
1-1
weiter A^
10
00
und
21 Esgiltyl =
@,3I0
3
-1
0,9 0
0 0,3
,5-
3-3
1 1
; B
10
= @,9)
10
B
10
3
-1
, B
10
= Summe der beiden.
23 Es gilt B^ =
1 1"
0-1
'3 0'
0 2
k
1"
0-1
-
3^ 3^ - 2^
0 2^
24 Es gilt detA = (det5)(det^)(det5-i) := det^ = Ai---An. Dies ist
möglich, wenn A diagonalisierbar ist.
Lösungen zu ausgewählten Aufgaben 565
26 Unmöglich, weil die Spur von AB - BA gleich Spur AB - Spur BA — 0
ist. E =
1 1
29 Hat A die Spalten (xi,... ,Xn), so bedeutet A^ = A, dass (Axi,..., Ax^) -
(xi,..., Xn) gilt. Alle Vektoren des Spaltenraums sind Eigenvektoren mit
Eigenwert A = 1. Der Kern hat immer den Eigenwert A = 0. Die Summe
der Dimensionen ist n => A ist diagonalisierbar.
30 Zwei Probleme: Kern und Spaltenraum können eine nichttriviale
Schnittmenge haben, und es muss nicht r linear unabhängige Eigenvektoren im
Spaltenraum geben.
31 Es gilt R = S\/ÄS-^ =
2 1
12
; die Quadratwurzel von B hätte die
Eigenwerte X = y/9 (reell) und A = y/^ (imaginär), so dass die Spur
nicht reell ist.
-1 0
0-1
hat eine reelle Quadratwurzel
Ol
-10
35 Gilt A = SAS-\ so ist das Produkt (A - Ai/) • • • (A - A^/) gleich 5(^1 -
Ai/) '-• {A — XnI)S~^. Zeile j des Faktors A — Xjl ist null, es sind also
alle Zeilen des Produktes Null, es ergibt sich die Nullmatrix.
36 A^ — 1 kann in (A — 1)(A -f 1) zerlegt werden, so dass nach Aufgabe 35
{A-I){A-\-I) die Nullmatrix ist. Dann gilt A"^ = I und A = A~^. Hinweis:
Es ist nicht nötig, p{X) = det{A — XI) in der Form (A — Ai) • • • (A - A^) zu
faktorisieren. Der Satz von Cayley-Hamilton besagt schlicht, dass p{A)
die Nullmatrix ist.
37 (a) Die Eigenvektoren zu A = 0 spannen immer den Kern auf. (b) Die
Eigenvektoren zu Eigenwerten X ^ 0 spannen den Spaltenraum auf, wenn
es r linear unabhängige Eigenvektoren gibt. Dann ist die algebraische
gleich der geometrischen Vielfachheit eines jeden von Null verschiedenen
Eigenwerts A.
Aufgaben 6.3, Seite 329
1 Es gilt Ui = e
- ^3t
a^t
-f e"
und U2 = e
- o-t
. Mit u@) = D,0) ist u(^) :=
566 Lösungen zu ausgewählten Aufgaben
2 Es gilt d'^y/dt'^ = 2dy/dt + 3y. Für y = e^^ wird die Gleichung zu A^e^* =
2Ae^* + 3e^* oder A^ - 2A - 3 = 0. Dies ist det(A - XI) = 0. Es löst also
y = e^^ die Gleichung, wenn A ein Eigenwert ist.
4 Es gilt z{t) — —2eS dann liefert dy/dt — 4y — 6e^ mit 2/@) = 5 die Lösung
y{t) = 3e^^ + 2e* wie in Aufgabe 3.
5 Es gilt
Ol
45
. Dann ist A = |E±v^).
6-2
2 1
hat die Eigenwerte Ai = 5 zu xi = B,1), A2 = 2 zu X2 = A,2);
Es gilt r{t) = 20e^* + lOe^^ w{t) = lOe^* + 206^^ Das Verhältnis von
Kaninchen zu Wölfen geht gegen 2 zu 1.
9 Es gilt e"^^ = I + t
Ol
00
+ Nullen =
1 t
Ol
11 Ist A eine schiefsymmetrische Matrix, so ist Q = e^* eine Orthogonalma-
trix, und es gilt ||e^*u@)|| = ||u@)||.
Ip-it
» gilt
■ 1"
—i
1
0
=
cost
sin^
1
2
1
i
+ 1
1
. Damit folgt u{t) = \e'^
+
14 Es gilt \ip = A ^b, Mp — A und u{t) — ce^^ + 4; weiter Up =
und
- ^, ^2f
u(^) = cie'
0
+ C2e3'
0'
1
+
■4'
2
15 Einsetzen von u = e'^'v liefert ce'^'v = Ae'^'v — e'^'b oder {A — cl)\ = b
oder V = {A — cl)~^h = partikuläre Lösung.
19 Die Lösung zur Zeit i + T ist ebenfalls e^('+^)u@). Es gilt also e^' mal
e^^ gleich e^('+^).
20 Es gilt A =
[e'e'-ll
Ol
1 1
00
1 1
0-1
10
00
1 1
0-1
und e"*' =
1'
[0-1
'e'O'
0 1
[1 1]
0-1]
Lösungen zu ausgewählten Aufgaben 567
22 Es gilt e^ =
eO
Ol
e e — 1
0 1
e^ =
1-1
0 1
, e^e^^e^e^ =
e e
Ol
oA-\-B
23 (a) Die Inverse von e"^^ ist e "^^
und e^^ 7«^ 0.
(b) Gilt Ax = Ax, so gilt e^^x = e-^^x
24 a:(t) = e^* und t/(t) = —e^* ist eine wachsende Lösung. Die Matrix für
das vertauschte System ist
ursprüngHche Matrix.
2-2
-4 0
die dieselben Eigenwerte hat wie die
Aufgaben 6.4, Seite 342
4 Es gilt Q = ^
1 2
2-1
5 Es gilt Q=^
2 1 2
2-2-1
-1-2 2
7(a)
1 2
21
(b) Die Pivotelemente haben dieselben Vorzeichen wie die
Eigenwerte (c) Es gilt Spur = Ai -f A2 = 2, deshalb kann A keine
zwei negativen Eigenwerte haben.
8 Gilt A^ = 0, so sind alle A^ = 0, und deshalb alle A = 0 wie in A
Ol
00
Ist A symmetrisch, so ergibt sich aus A^ = QA^Q^ = 0 die Matrix A = 0
und damit A = 0.
9 Ist A komplex, so ist A ebenfalls ein Eigenwert, und A -f A is reell. Die
Spur is reell, deshalb muss der dritte Eigenwert reell sein.
10 Ist X nicht reell, so ist A = x^Ax/x^x nicht notwendigerweise reell.
12 Die Eigenwerte sind X = ib und -ib; Für die Matrix A =
0 3 0
3 0 4
0-4 0
gilt det(A - XI) = -X^ - 25A = 0, die Eigenwerte sind A = 0, 5i, -6i.
13 Schiefsymmetrisch und orthogonal; A = z, z, -i, -i, damit sich die Spur
Null ergibt.
568 Lösungen zu ausgewählten Aufgaben
15 (a) Es gilt Az = Ay und A^y = Az, damit A'^Az = A^(Ay) = AA^y =
A^z. Die Eigenwerte von A^A sind > 0 (b) Die Eigenwerte von B sind
— 1, —1, 1, 1 mit den Eigenvektoren xi = A,0,-1,0), X2 = @,1,0,—1),
X3 = A,0,1,0), X4- @,1,0,1).
16 Die Eigenwerte von B sind 0, \/2, —y/2 mit den Eigenvektoren xi =
A,-1,0), X2 = A,1, v^), X3 - A,1,-\/2).
17 (a) [xi X2] ist eine Orthogonalmatrix, deshalb gilt Pi -\- P2 = xixf 4-
X2X|^ = [Xi X2]
= 1.
(b) Es gilt P1P2 ^ xi{x[x2)xj = 0.
18 Der Vektor y liegt im Kern von A, und x liegt im Spaltenraum. Aber
für A = A^ stimmt der Spaltenraum mit dem Zeilenraum überein, der
senkrecht auf dem Kern steht. Wenn Ax = Ax und Ay = ßy gelten, so
muss {A — ßl)x = (A — ß)x und {A — ßl)y = 0 sein — wieder gilt x J_ y.
21 (a) Falsch. A =
1 2
Ol
(b) Falsch.
■l2'
2 3
5 4'
46
=
13 16'
22 26
(c) Wahr.
Es gilt A = QAQ~^, A~^ = QA~^Q~^ ist ebenfalls symmetrisch (d)
'1 1 1"
Falsch für A —
1 1 1
1 1 1
22 Gilt Ä^ = -A, so ist A'^A = AÄ^ = -ß?. Ist A orthogonal, so gilt
a 1^
A^A = AA^ = LA =
-Id
ist normal nur für a = d.
23 A und A^ haben dieselben Eigenwerte, aber die Reihenfolge der Eigen-
[ Ol'
-101
hat die Eigenwerte X = i und —i
Vektoren kann sich ändern. A
mit xi := (l,z) für A aber xi = A, —i) für A^.
25 Symmetrische Matrix für 6 = 1; mehrfacher Eigenwert für b = —1.
Aufgaben 6.5, Seite 355
10
bl
2 -3 < & < 3, LU =
^^ - [21J [Oc-oj
A x^ + Axy -f Zy'^ = {x-\- 2y)'^
1 b
0 9-&2
1 0
2 1
2 0
Oc-.
10
b 1
1 2
Ol
1 0
0 9-&2
1 b
Ol
c>
ist negativ für x = 2^ y = —1.
Lösungen zu ausgewählten Aufgaben 569
7 x^Ä^Ax = (Ax)^(Ax) = 0 nur dann, wenn Ax = 0 gilt. Da A linear
unabhängige Spalten hat, ist dies nur für x = 0 der Fall.
r 4-4 8"
9 A= -4 4-8
[ SS 16_
werte sind 24, 0, 0, und die Determinante ist 0.
hat nur das Pivotelement 4, den Rang eins, die Eigen-
11 Es gilt |Ai| = 2, IA2I = 6, IA3I = 30. Die Pivotelemente sind 2/1,
6/2, 30/6.
12 A ist positiv definit für c > 1; J5 ist nie positiv definit (die Determinanten
d — 4 und -Ad + 12 sind niemals beide positiv).
18 Wäre an kleiner als alle Eigenwerte, so würde A — anl positive
Eigenwerte haben (und daher positiv definit sein). An Position A,1) steht aber
eine Null.
19 Aus Ax = Ax folgt x^Ax = Ax^x. Falls A positiv definit ist, führt dies
auf A = x^Ax/x^x > 0 (Verhältnis positiver Zahlen).
22^=;^
31
13
1-1
1 1
^/9
v/T
1
y/2
1 1
-1 1
2 1
1 2
; R = Q
40
02
Q^ =
23 Es gilt Ai - l/a^ und A2 = l/b^ und daher a = l/x/ÄT und b = l/y/M-
Die Ellipse 9a:^ -I- 16t/^ — 1 hat die Halbachsenlängen a = ^ und b= j.
27 Es gilt aa:2 + 26a:t/ + ct/^ = a{x + f y)^ + ^^t/^.
28 Es gilt det ^ = 10; A = 2 und 5; xi = (cos ö, - sinö), X2 = (sin ö, cosö);
die Eigenwerte sind positiv.
29 Ai =
6x2 2a:
2x 2
ist positiv definit, falls x ^ 0 ist; /i = (^x^ + t/)^ = 0
auf der Kurve ^x^ + t/ = 0; A2 =
Sattelpunkt.
61
10
ist indefinit und @,1) ist ein
31 Für c > 9 ist der Graph von z eine Schüssel, für c < 9 hat der Graph
einen Sattelpunkt. Für c = 9 ist der Graph von z = {2x + Sy)'^ eine Rinne
mit dem Wert null auf der Geraden 2x + 3y = 0.
570 Lösungen zu ausgewählten Aufgaben
Aufgaben 6.6, Seite 365
1 Es gilt C = {MN)-^A{MN), ist also B ähnlich zu A und C ähnlich zu
B, dann ist A ähnlich zu C.
6 Es gibt acht Familien ähnlicher Matrizen. Sechs Matrizen haben die
Eigenwerte A = 0, 1; drei Matrizen haben die Eigenwerte A = 1, 1 und drei
haben die Eigenwerte A = 0, 0 (je zwei Familien!); eine hat die Eigenwerte
A = 1, -1; eine hat die Eigenwerte A = 2, 0; zwei haben die Eigenwerte
A = |(l±v^).
(b) Die Kerne von
"cl"
_0c
0'
Ol
cl
Oc
=
' '^~' =
[c^ 2c"
[O c2
, J' =
"c-l-C-2"
0 c-\
"c3 3c2"
0 c\
, J* =
c* A;c* ^ ]
0 c* _
7 (a) {M-^AM){M-^x) = M-^{Ax) = M-^O = 0
A und von M~^AM haben dieselbe Dimension.
10 J2 =
13 Man wähle als Mi eine umgekehrte Diagonalmatrix, so dass in jedem
Block M^^JiMi = Ml gilt; Mo hat die Blöcke Mj auf der
Hauptdiagonalen; damit gilt A^ = {M'^J'^M'^ = {M-'^YM^^JM^M^ =
(MMoM^)-M(MMoM^), und A^ ist ähnlich zu A.
15 Esgiltdet(M-MM-AJ) = Aet{M-'^AM-M-'^\IM) = det(M-H^-
\I)M) = det(^ - \I).
17 (a) Wahr: Die eine hat den Eigenwert A = 0, die andere nicht. (b) Falsch
Diagonalisiert man eine nichtsymmetrische Matrix, so ist A symmetrisch.
(c) Falsch:
Ol
-10
und
0-1
1 0
sind ähnlich. (d) Wahr: Alle
Eigenwerte von A + I sind um 1 erhöht.
19 (b) AB hat dieselben Eigenwerte wie BA zuzüglich n -m Nullen.
Aufgaben 6.7, Seite 374
1 A'^A =
5 20
20 80
hat (Tj = 85, Vi
i/%/i7
4/v/l7
, V2 =
4/^/I7
-1/v^J"
3 ui =
U2
l/^/5
2/^/5
2/\/5
-l/\/5
Lösungen zu ausgewählten Aufgaben 571
für den Spaltenraum, vi = \ J r— für den Zeilenraum,
für den Kern, V2 = | -. / /tt:; I für den Kern der Trans-
L-i/\/i7
ponierten
7 AA^^ =
21
12
hat cTi = 3 mit Ui =
1/V2]
und ^2 = 1 mit U2
.A^A
110
121
Ol 1
hat cTj = 3 mit vi =
1/n/6
2/^/6
l/^/6,
, (T2 = 1 mit
V2 =
■I/V2
0
-1/v^J
Damit gilt
1 10
011
; und V3
[ui U2]
■ 1/V3
-1/v^
1
0
[Vi V2 Vs]^.
9 Es gilt A = 12 f/y^.
11 Multiplizieren Sie USV"^ nach den Spalten (von U) und den Zeilen
(von SV^) aus.
13 Die Singulärwertzerlegung von fi sei i? = UEV^. Multiplizieren Sie mit
Q. Dann ist die Singulärwertzerlegung dieser Matrix A gleich (QU)SV^.
15 (a) Wenn man A zu 4A ändert, wird aus S die Matrix 4. (b) Es
gilt Ä^ = VE'^U'^. Falls A~^ existiert, ist es die quadratische Matrix
Aufgaben 7.1, Seite 380
4 (a) 5(T(v)) = V (b) 5(T(vi) + T(v2)) = 5(T(vi)) + 5(T(v2)).
5 Man wähle v = A,1) und w = (-1,0). Damit gilt T(v) + T(w) = v + w
aber T(v4-w) = @,0).
7 (a) TiTiv)) = V (b) T(r(v)) = v + B,2) (c) T(Tiv)) = -v
(d) T{T{yr)) = T(v).
10 (a) T(l, 0) = 0 (b) @,0,1) liegt nicht im Bild (c) T@,1) = 0.
12 T(v) = D,4); B,2); B,2); für v = (o,b) = 6A,1) +^^6 B,0) gilt T(v) =
6B,2)+ @,0).
572 Lösungen zu ausgewählten Aufgaben
15 A ist nicht invertierbar. AM = I ist also unmöglich. A
2 2
-1-1
0 0
00
16 Keine Matrix A liefert A
00
10
Ol
00
Für Professoren: Der
Matrizenraum hat die Dimension 4. Lineare Abbildungen werden also durch
4 X 4-Matrizen dargestellt. Die Matrizen in den Aufgaben 13-15 sind
Spezialfälle.
17 (a) Wahr (b) Wahr (c) Wahr (d) Falsch.
18 Es gilt T(/) = 0, aber M =
Ob
00
= T{M); diese Matrizen erzeugen das
Bild. M
aO
c d
liegt im Kern.
-1
20 Es gilt T(T-^{M)) = M und daher T-^{M) = A'^MB
21 (a) Horizontale Geraden bleiben horizontal, vertikale Geraden bleiben
vertikal. (b) Das Haus wird auf eine Gerade gequetscht. (c)
Vertikale Geraden bleiben vertikal.
24 (a) ad-bc = 0 (b) ad-boO (c) \ad - bc\ = 1.
25 Werden zwei linear unabhängige Vektoren auf sich selbst abgebildet, so
gilt wegen der Linear it ät T = I.
28 Hier wird noch einmal betont, dass Kreise auf Ellipsen abgebildet werden.
Siehe auch Abbildung 7.7.
Aufgaben 7.2, Seite 395
1 5vi = 5v2 = 0, 5v3 = 2vi, 5v4 = 6v2; B
00 20
0006
0000
0000
4 Die dritte Ableitung hat eine 6 auf der Position A,4); die vierte Ableitung
eines kubischen Polynoms ist null.
5 A =
Ol 1
100
Ol 1
6 EsgiltT(vi+V2 + V3) = 2wi + W2 + 2w3; A mal A,1,1) ergibt B,1,2).
Lösungen zu ausgewählten Aufgaben 573
7 Für V = c(v2 — V3) ergibt sich T(v) = 0; der Kern ist @,c, —c); die
Lösungen sind A,0,0) + ein beliebiges @,c,-c).
9 Sie kennen die Vektoren T(w) nicht, es sei denn, die w's sind dieselben
Vektoren wie die v's. Nur in dem Fall ist die Matrix A^.
12 Es gilt A
-1
, damit T-i(wi) = vi - V2, T'^^iw^) =
1 0 0'
-1 1 0
0-1 Ij
V2 - V3, T~'^{ws) = V3; die einzige Lösung für T(v) = 0 ist v = 0.
15 (a)
2A
21
53
1
3
(b)
3-1
-5 2
= Inverse von (a) (c) A
sem.
muss gleich
16 (a) M =
r s
t u
(bOV =
a b
c d
(c) ad = bc.
17 MN =
10
12
2 1
53
3-1
-7 3
21 W2(x) = 1 - x^; W3(x) = |(x^ - x); y = 4wi + 5w2 + 6W3.
22 Von den w's zu den v's:
0 1 0
0,5 0-0,5
0,5-1 0,5
. Von den v's zu den w's: die
inverse Matrix
1 1 1
1 0 0
1-1 1
25 a2 = ri2qi + ^22^2 ergibt a2 als Linearkombination der q's. Die
Basiswechselmatrix ist also R.
26 Zeile 2 von A ist /21 (Zeile 1 von U) + /22 (Zeile 2 von U). Eine
Basiswechselmatrix ist immer invertierbar.
30 Es gilt T(x,y) = {x,-y) und damit S{x,-y) = {-x,-y). Daher gilt
ST = -I.
32
cos2((9-a)-sin2((9-a)
sin2((9-a) cos2((9-a)
rotiert um den Winkel 2{6 — a).
33 Falsch, weil die v's nicht linear unabhängig sein müssen.
574 Lösungen zu ausgewählten Aufgaben
Aufgaben 7.3, Seite 405
1 Die inverse Matrix ist W ^
i i i i
4 4 4 4
4 4 4 4
l-l 0 0
0 0 l-i.
Damit folgt e = :jWi -f
\w2 + |w3 und V = W3 + W4.
3 Die acht Vektoren sind A,1,1,1,1,1,1,1), das lange Wavelet, zwei „mit-
tellange" Wavelets A,1,-1,-1,0,0,0,0) und @,0,0,0,1,1,-1,-1)
sowie vier kurze Wavelets mit den Einträgen 1,-1 jeweils versetzt.
5 Die Hadamard-Matrix H hat orthogonale Spalten der Länge 2. Die
Inverse ist also H^/4: = H/4:.
7 Die Transponierte von WW'^ = I ist {W-'^)^W^ = I. Daher ist die
Matrix W^ (mit den w's als Zeilen) die Inverse der Matrix mit den w*'s
in den Spalten.
Aufgaben 7.4, Seite 414
1 Die Matrix A^A = | r,^ /in I ^^^ ^^^ Eigenwerte A = 50 und 0 mit den
r o 1
Eigenvektoren vi = 4g | ^ | und V2 = 77^ | ^ |; cri = y/EÖ.
2 AA^ =
Ui
_ 1
5 15
15 45
1
3
ist.
hat die Eigenwerte A = 50 und 0 mit den Eigenvektoren
undu2=.^m.
'in onl
. H ist semidefinit, weil A singular
7-1
1 7
1
\/50
10 20
20 40
6 A+ = V
0,1 0,3
0,3 0,9
l/>/5Ö0
0 0
^ 50
13
26
A+A =
0,2 0,4
0,4 0,8
AA+ =
9 [aiUi cr2U2]
Lösungen zu ausgewählten Aufgaben 575
= cTiUivf + cr2U2V^. Im allgemeinen Fall ist dies
aiUivJ H h CTrUrvJT.
13 Es gilt A = [1] [5 0 0]V^ und A^ = V
[1]',A^A =
ro,2"
0
0
[1] =
,12'
0,16
0 J
AA+ =
0,36 0,48 0
0,48 0,64 0
0 0 0
17 (a) A^A ist singular (b) A^Ax+ = Ä^h (c) (/ - AA+)
projiziert auf A/'(A^).
18 x"^ im Zeilenraum von A steht senkrecht auf x - x"^ im Kern von Ä^A =
Kern von A. Für das Dreieck gilt c^ = a^ -{-P.
20 Es gilt A+ = |[0,6 0,8] = [0,12 0,16] und A+A = [1] und AA+ =
[0,36 0,48]
0,48 0,64
21 L wird durch eine Zahl unterhalb der Diagonalen bestimmt. Die
Eigenvektoren in S werden jeweils durch eine Zahl bestimmt. Damit ergibt sich
1 + 3 für LC/, 1 + 2 + 1 für LDU, 1 + 3 für Qß, 1+2 + 1 für UUV^,
1 + 2+1 für 5.15-1.
23 Die Zerlegung
a b
b {ad-bc-{-b'^)/a
setzt a ^ 0
a61 _ r 1 Ol
c d\ ~ [{c — b)/a 1
voraus. Ändern Sie A = LDU in {LU~'^){U^DU) =
(Dreiecksmatrix) (symmetrische Matrix). Ich habe bislang noch keine gute Anwendung
dafür gefunden.
Aufgaben 8.1, Seite 430
1 Es gilt A =
[-1 1 0
-1 0 1
0-1 1
gonal zu diesem Kern.
der Kern enthält
c
c
c
)
T
0
0
ist nicht ortho-
2 Es gilt A^y = 0 für y = A,-1,1); Strom = 1 an Kante 1, Kante 3,
zurück über Kante 2 (geschlossener Kreis).
576 Lösungen zu ausgewählten Aufgaben
5 Die KirchhofF'sche Knotenregel Ä^y = f ist lösbar für f = A, —1,0) und
nicht lösbar für f = A,0,0); f muss orthogonal zum Vektor A,1,1) im
Kern sein.
6 Ä^Ax =
2-1-1
-1 2-1
-1-1 2
X =
3
-3
0
= f erzeugt x =
r r
!-l
0
+
c
c
c
;
Potentiale 1, -1, 0 und Ströme -Ax. = 2, 1, -1; f schickt 3 Einheiten in
Knoten 1 hinein und aus Knoten 2 hinaus.
7 Es gilt Ä^
1
A =
3-1-2"
-1 3-2
-2-2 4
;f =
r
0
-1
liefert x =
5/4"
1
7/8
+
; die Potientiale sind |, 1, | und die Ströme —CAx = ^, |, ^•
9 Das Eliminationsverfahren auf Ax = b führt immer auf y^b = 0, also
-&i + &2 - ^3 = 0 und &3 - &4 + &5 = 0 (y's aus Aufgabe 8 im Linkskern).
Dies ist die Kirchhoff'sehe Maschenregel entlang einer Schleife.
11 Es gilt AM
TA _
2-1-1 0
-1 3-1-1
-1-1 3-1
0-1-1 2
Diagonaleintrag = Anzahl
Kanten in den Knoten
andere Einträge = -1
wenn die Knoten verbunden sind.
13 A^CAx=
4-2-2 0'
2 8-3-3
2-3 8-3
0-3-3 6
X =
1]
0
0
-ij
ergibt die Potentiale x = (^, ^, |, 0)
(x4 = 0 geerdet und 3 Gleichungen gelöst); y = -CAx = (|, |,0, |, |).
17 (a) 8 linear unabhängige Spalten (b) f muss orthogonal zum Kern
sein, daher /i + • • • + /g = 0 (c) Jede Kante verbindet zwei Knoten,
aus 12 Kanten folgt daher als Summe der Diagonaleinträge 24.
Aufgaben 8.2, Seite 438
A —
/% —
A* g«
0,6-1"
0,4 1
iht gege
n
1 1
0,75 J
[0,6-1]
[0,4-lJ
r 1
1
[-0,4 0,6
[10]
[0 0
-0
5
1 1"
,4 0,6
=
'0,6 0,6"
0,4 0,4
Lösungen zu ausgewählten Aufgaben 577
3 A = 1 und 0,8, X = A,0); A = 1 und -0,8, x = (|, f). a = 1, i und
4' ^ V3' 3' 3>'*
5 Der stationäre Zustand ist @,0,1) = alle tot.
6 Gilt Ax = Ax, so ist die Summe auf beiden Seiten 5 = Xs. Für A 7^ 1
muss die Summe 5 = 0 sein.
8 @,5)^ -> 0 ergibt A^ -> A"^; ein beliebiges A =
0,6 + 0,4a 0,6 - 0,6a
0,4 - 0,4a 0,4 + 0,6a
mit -| < a < 1.
10 M^ ist ebenfalls nichtnegativ; es gilt [1"-1]M = [1---1],
multipliziert man dies mit M, so erhält man [ 1 • • • 1 ]M^ = [ 1 • • • 1 ] =:^ Spalten
von M^ bilden die Summe 1.
11 Es gilt A = 1 und a + d - 1 wegen der Spur; der stationäre Zustand ist
ein Vielfaches von xi = (&, 1 - a).
13 B hat die Eigenwerte A = 0 und -0,5 mit den Eigenvektoren xi =
@,3, 0,2) und X2 = (-I5I); e~^^* geht gegen Null, die Lösung geht
gegen cie^^xi = CiXi.
15 Der Eigenvektor ist x = A,1,1), es gilt Ax = @,9,0,9,0,9).
18 Es gilt p = und ; -^ — n'c; n ^^^ keine Inverse.
19 A = 1 (Markov), 0 (singular), 0,2 (wegen der Spur). Stationäre Zustände
@,3,0,3,0,4) und C0,30,40).
20 Nein, A hat einen Eigenwert A = 1, und {I - A)~^ existiert nicht.
Aufgaben 8.3, Seite 449
1 Der zulässige Bereich ist die Strecke von F,0) bis @,3); die Kosten sind
minimal bei F,0) und maximal bei @,3).
2 Der zulässige Bereich ist das Viereck mit den Ecken @,0), F,0), B,2), @,6).
2x — 2/ wird minimal bei F,0).
3 Es gibt nur die beiden Ecken D,0,0) und @,2,0); man wähle xi „sehr
negativ", X2 =^ 0, und xs = xi - 4.
4 Von @,0,2) geht man zu x = @, 1, 1,5) mit der Bedingung xi + X2 +
2x3 = 4, Die neuen Kosten sind 3A) + 8A,5) = $15, so dass sich r = -1
578 Lösungen zu ausgewählten Aufgaben
für die reduzierten Kosten ergibt. Der Simplex-Algorithmus überprüft
auch X = A, 0, 1,5) mit den Kosten 5A) + 8A,5) = $17, also r = l
(teurer).
5 Die Kosten sind 20 beim Startvektor D,0,0); unter Einhaltung von xi -f
X2 + 2x3 = 4 bewegt man sich zu C,1,0) mit den Kosten 18 und r = —2;
oder nach B,0,1) mit den Kosten 17 und r = -3. Man wählt xs als
hinzukommende Variable und bewegt sich zu @,0,2) mit den Kosten 14.
Nach einem weiteren Schritt wird @,4,0) mit den minimalen Kosten 12
erreicht.
6 Für c = [3 5 7] ergeben sich als minimale Kosten 12 durch den
Promovierten mit X = D,0,0). Beim dualen Problem wird 4^/ unter den
Bedingungen y<S, y<^, y<7 maximiert. Maximum = 12.
Aufgaben 8.4, Seite 455
1 Es gilt /o^"cos(j + k)xdx = p^"(J+^)^J^'' = 0 und analog /o^" cos(j ~
k)x dx = 0 (beachten Sie, dass im Nenner j — k ^ 0 steht). Für j = k gilt
Jq^ COS^ jxdx = TT.
4 Es gilt /_i(l)(x^ - ex) dx = 0 und /_i(x^ - |)(x^ - ex) dx = 0 für alle
c (Integral einer ungeraden Funktion). Man wähle c so, dass J_^ x{x^ —
ex) dx - [\x^ - f x^]l_i = I - c| = 0 ist. Dann gilt c = |.
5 Die Integrale führen auf ai =0, 6i = 4/7r, 62 = 0.
6 Wegen Gleichung (8.10) sind die ak gleich Null und die hk = 4/7rA:.
Für die Rechteckkurve gilt ||/|p = 27r. Gleichung (8.8) ist dann 27r =
7rA6/7r^)(p- + p- + ^ H ), diese unendliche Reihe ergibt also 7r^/8.
8 Es gilt ||v|p = l + | + ^ + | + "- = 2und damit ||v|| = a/2; weiter
||v||2 = 1 + a2 _^ ^4 _^ ... ^ 1/A _ ^2) ^nd damit ||v|| = l/v^iT^;
/q^''A + 2 sinx + sin^ x) dx = 27r + 0 + tt und damit ||/|| = y/Zir.
9 (a) Es gilt /(x) = 1 + 1 (Rechteckkurve), die a's sind also ^, 0, 0, ... , und
die h's sind 2/7r, 0, -2/37r, 0, 2/57r, ... (b) Es ist üq = f^"" x dx/27r =
TT, die anderen ak =0, bk = -2/k.
11 Es gilt cos^x = I + |cos2x; cos(x + f) = cosxcos| - sinxsin| =
h cosx - ^sinx.
Lösungen zu ausgewählten Aufgaben 579
13 Für dy/dx = cosx gilt y = yp -{- y^ = sinx + C.
Aufgaben 8.5, Seite 462
1 Der Punkt {x,y,z) hat die homogenen Koordinaten {x,y,z,l) und ebenso
(ex, cy,cz,c) für jedes von Null verschiedene c.
3 TTi =
A,6,8).
4 Es gilt S ■■
Sie vTS.
/8,5
ri
1
1
143 1
1
1
0251
=
1
1
168lJ
ist eine Translation längs
[ c
c
1
, ST =
c
c
c
1431_
, TS =
c
c
c
_c4c3clj
Verwenden
5 S ■
1/11
1
für ein 1 x 1-Quadrat.
9 Der Vektor n = (|, |, ^) hat die Länge ||n|| = 1. Es gilt P = I - nn^ =
5-4-2'
-4 5-2
-2-2 8
10 Man wähle @,0,3) auf der Ebene und berechne T^PT^ = ^
5-4-2 0
-4 5-2 0
-2-2 8 0
6 6 3 9
11 C,3,3) wird auf |(-1,-1,4) projiziert, und C,3,3,1) auf (i, ^, |, 1).
13 Die Projektion des Würfels ist ein Sechseck.
14 EsgiltC,3,3)(/-2nn^) = (i,i,|)
15 C,3,3,1)-^ C,3,0,1)-^(-|,
1-8-4
-8 1-4 I =(-U,_U,_i).
-4-4 7
3' 3' 3'1) "^ V 3) ~3) 35 !)•
7 7 8
17 Mit 1/c umskaliert, weil {x,y,z,c) derselbe Punkt wie {xjc.yjc.zIc.X)
ist.
580 Lösungen zu ausgewählten Aufgaben
Aufgaben 9.1, Seite 474
1 Ohne Zeilenvertauschung erhält man die Pivot element e 0,001 und 1000;
mit einem Austausch die Pivotelemente 1 und —1. Ist das
Pivotelement größer als die Einträge darunter, so hat das Verhältnis Uj = Ein-
1 1 1'
trag/Pivotelement einen Betrag \lij\ <1. A = \ 0 1—1
-1 1 1
3 A =
\\Ah\
[1'
1
1_
<
=
0,04
1/16"
13/12
47/60_
aber \\A
=
^x||>
,833]
1,083
_ 0,783 J
>6.
r 0
6
[-3,6
=
,801
1,10
0,78 J
im Vergleich zu A
4 Das größte ||x|| = ||A~^b|| ist l/Amin; der größte Fehler ist lO-^^/Amin-
5 Jede Zeile von U enthält höchstens w Einträge. Daher sind w Mulitplika-
tionen nötig, um die bereits von unterhalb bekannten Komponenten von
X einzusetzen, und eine Division durch das Pivotelement. Die
Gesamtkosten für n Zeilen betragen daher weniger als wn Operationen.
6 Zur Lösung einer linearen Gleichung mit L, U, oder R benötigt man |n^
Multiplikationen. Um die rechte Seite einer Gleichung mit Q~^ = Q^ zu
multiplizieren, werden n^ Multiplikationen benötigt. Von QR ausgehend
benötigt man also 1,5 mal so lange wie von LU ausgehend, um x zu
berechnen.
7 Die Rücksubstitution für Spalte j von / benötigt | j^ Multiplikationen,
weil nur der obere linke j x j-Block betrachtet wird. Es fallen also
Gesamtkosten von |A^ 4- 2^ H hn'^) ^ |(|^^) Multiplikationen an.
10 Mit einer 16-stelligen Fließkommaarithmetik sind die Fehler ||x-yberechnet|
für e = 10-^ 10-^ 10-^ 10-12^ 10-^^ von der Größenordnung 10-^^
10-i\ 10-^ 10-^ 10-^
11 Es gilt cos i9 = l/\/TÜ, sin i9 =
-3/v/IÖ, R=-^^
1 3
-3 1
1-1
3 5
1
\/rö
10 14
0 8
14 Die Berechnung von QijA benötigt 4n Multiplikationen B für jeden
Eintrag in den Zeilen i und j). Klammert man cosö aus, benötigen die
Einträge 1 und zbtan^ nur jeweils 2n Multiplikationen, also insgesamt |n^
für QR.
Lösungen zu ausgewählten Aufgaben 581
Aufgaben 9.2, Seite 481
1 \\A\\ = 2, c = 2/0,5 = 4; \\A\\ = 3, c = 3/1 = 3; \\A\\ = 2 + >/2,
c = B + v^)/B - v^) = 5,83.
3 Für die erste Ungleichung ersetze man x durch ßx in ||^x|| < |m|||x||;
die zweite Ungleichung ist schlicht ||ßx|| < ||ß||||x||. Damit gilt \\AB\\ =
max(mßx||/||x||)<||^||||ß||.
7 Die Dreiecksungleichung liefert mx+Bx|| < ||Ax|| + ||Bx||. Dividiert man
durch ||x|| und berechnet das Maximum über alle von Null verschiedenen
Vektoren, so erhält man \\A + B\\ < \\A\\ + \\B\\.
8 Aus Ax = Ax folgt mx||/||x|| = |A| für diesen speziellen Vektor x. Ma-
ximiert man das Verhältnis über alle Vektoren, erhält man ||A|| > |A|.
13 Das Residuum b - Ay = A0~^,0) ist viel kleiner als h — Az =
@,0013, 0,0016). Aber z ist viel näher an der Lösung als y.
14 Es gilt detA = 10"^ und daher A'^ =
Pli>i, p-l||>lo^ oio^
659,000-563,000
-913,000 780,000
. Es folgt
16 xf H h x^ ist nicht kleiner als max(a:f) und nicht größer als xf H h
x^ -h 2|a:i||a:2| H = ||x||i. Sicher gilt xj -\ h x^ < n max(a:f) und
daher ||x|| < \/n||x||oo- Man wähle y = (signxi,sign0:2,... ,signa:n),
um X • y = ||x||i zu erhalten. Nach der Schwarz'schen Ungleichung ist
dieses höchstens ||x||||y|| = v^||x||. Mit x = A,1,..., 1) erhält man das
maximale Verhältnis ^yn.
Aufgaben 9.3, Seite 493
2 Aus Ax = Ax folgt (/ - A)x = A — A)x. Für reelle Eigenwerte von
B = I ~ A gilt |1 - A| < 1, falls A zwischen 0 und 2 liegt.
6 Es ist S-'T = I
Ol
10
mit |A|
_ j_
max — 3 •
7 Beim Gauß-Seidel-Verfahren ist S-'^T
(|A|max für das Jacobi-Verfahren)^.
Oh
mit |A|r,
9 Setzt man die Spur 2 - 2uj + \üü^ mit {u - 1) + {oj - 1) gleich, so erhält
man c^opt = 4B - VS) « 1,07. Die Eigenwerte üj - 1 liegen bei 0,07.
582 Lösungen zu ausgewählten Aufgaben
15 Die Komponente j von Axi ist 2 sin ;^ - sin ^^~^{ - sin ^^^^{ . Unter
Verwendung von sin(a + b) = sin a cos fe 4- cos a sin fe erhält man aus den
letzten beiden Termen -2 sin-^ cos-^r- Der Eigenwert ist Ai = 2 -
n+l
2 COS
n+l •
17 Aus A-^ = h
2 1
12
27
14
13
18 Es gilt R = Q^A =
Ai=RQ =
folgt uo
1 cos ö sin ö
0 -sin^ö
n+l"
Ui =
u, = h
U3 =
und
cosö(l4-sin2ö) -sin^ö
-sin^ö -cosösin^ö
20 Aus A-cI = QR folgt Ai=RQ-hcI = Q-^{QR-hcI)Q = Q-^AQ, Die
Eigenwerte ändern sich von A zu Ai nicht.
21 Multipliziert man Aq^ = bj-iqj-i +ajqj +&jqj+i mit qj, so erhält man
qjAqj = üj (weil die q's orthonormal sind). In Matrizenschreibweise
(spaltenweise Multiplikation) ist dies AQ = QT, wobei T eine Tridiago-
nalmatrix ist. Die Einträge sind die a's und 6's.
23 Ist A symmetrisch, so ist Ai = Q~^AQ — Q^AQ ebenfalls symmetrisch.
In Ai=RQ = R{QR)R-^ = RAR'^ sind R und R'^ obere
Dreiecksmatrizen, deshalb kann Ai keine von Null verschiedenen Einträge auf einer
Diagonalen unter der von A haben. Ist A eine symmetrische Tridiago-
nalmatrix, so ist (wegen der Symmetrie für die obere Hälfte von Ai) die
Matrix Ai = RAR~^ ebenfalls eine Tridiagonalmatrix.
Aufgaben 10.1, Seite 503
2 In Polarkoordinatendarstellung: v^e*^, 5e^*^, -j^^~^^^ V^-
4 \z X w\ =6, \z + 101 < 5, Iz/w] = |, \z -w] < 5.
5 a-hib=^ + U, ^ + ^2,2, -| + #*; w^^ = l.
2 ' 2 ' 2 ' 2 ' ' 2 ' 2
9 2 + i; B + i)(l + i) = 1 + 3«; e''''/^ = -i; e~''' = -1; i^ =
-»;
Lösungen zu ausgewählten Aufgaben 583
10 z -\r^ ist reell ; z —^ ist rein imaginär; zz ist positiv; z/z hat den
Absolutbetrag 1.
12 (a) Mit a = b = d = 1 wird die Quadratwurzel zu \/4c; A ist komplex
für c < 0. (b) Es gilt A = 0 und X = a-\-d im ad = bc. (c) Die
A's können reell und verschieden sein.
13 Es ergeben sich komplexe A's für (a + c?)^ < 4(ac? - fee); man schreibe
(a + c?)^ — 4{ad — bc) als (a — d)'^ + 4fec, dies ist positiv für fee > 0.
14 det(P - A/) = A^ - 1 = 0 hat die Nullstellen A = 1, -1, i, -i mit den
Eigenvektoren A,1,1,1), A, -1,1, -1), (l,i, —1, —i) und A, —z,—l,i) =
Spalten der Fouriermatrix.
16 Die Blockmatrix hat reelle Eigenwerte; daher ist i\ reell und A rein
imaginär.
18 Es gilt r = 1, der Winkel ist f - ö; nach Multiplikation mit e^^ erhält
man e*^/^ = i.
21 cos 3Ö = Re(cos ö + z sin Of = cos^ ö - 3 cos ö sin^ ö; sin 3Ö = Im(cos ö +
z sinö)^ = 3 cos^ ö sin ö - sin^ 6.
23 (a) e* liegt beim Winkel ö = 1 auf dem Einheitskreis; es gilt |z^| = P = 1
(c) Es gibt unendlich viele Kandidaten von der Form i^ = giGr/2+27rn)e
24 (a) Einheitskreis (b) Einwärts-Spirale bis e"^'^ (c) mehrfacher
Kreis bis 6 = 27v'^.
Aufgaben 10.2, Seite 514
3 z ist ein Vielfaches von A + z, 1 + z, -2); Az = 0 ergibt z^A^ = 0^, z
(nicht z!) ist daher orthogonal zu allen Spalten von A^ (unter
Verwendung des komplexen Skalarprodukts z^ mal Spalte).
4 Die vier fundamentalen Unterräume sind Z{A), N{A), Z{A^), N{A^).
5 (a) Es ist (A^A)^ = A^A^^ = A^A (b) Aus A^Az = 0 folgt
{z^A^){Az) = 0. Dies ist \\Az\\^ = 0, und daher gilt Az = 0. Die Kerne
von A und A^A sind identisch. A^A ist invertierbar, wenn N{A) = {0}
gilt.
6 (a) Falsch: A
(c) Falsch.
0 1
-1 0
(b) Wahr: -i ist kein Eigenwert, falls A = A^
584 Lösungen zu ausgewählten Aufgaben
10 Die Vektoren A,1,1), (l,e2^^/^e^^^/3), (l,e^^^/^e2^^/^) sind orthogonal
(mit dem komplexen Skalarprodukt!) weil P eine orthogonale Matrix ist
— und daher unitär.
11 Die Matrix C
254
425
542
= 2 4- 5P 4- 4P2 hat die Eigenwerte A =
2 + 5 + 4 = 11,2 + 5e2^^/2 + 4e^^^/^ 2 + 56^^^/^ + 4e«^^/^
13 Die Determinante ist das Produkt der Eigenwerte (alle reell).
1^^ = 73
1 -1 + 2
1 + Z 1
2 0
0-1
1
73
1 1-i
-\-i 1
18 YiiiV = ^
1 +V^ -1 + f
1 + 2 l + \/3
1 0
0-1
1 + V^ 1-2
-1-2 1 + v^
mit L"^ = ^^
2yß gilt |A| = 1. V = V^ bedingt reelles A, die Spur null bedingt
A = l, -1.
19 Die v's sind die Spalten einer unitären Matrix U. Damit ist z = UU^z =
(spaltenweise Multiplikation) = vi(vf^z) + • • • + v„(v^z).
20 Multiplizieren Sie nicht e~*^ mit e*^; der erste Faktor muss konjugiert
werden, dann ergibt sich /^ ^ e^*^ dx = [e"^^^/2i]l^ = 0.
22 Es gilt R + iS = (R-h iS)" = R^ - iS^\ R ist symmetrisch, aber 5 ist
schiefsymmetrisch.
24 [l]und[-l]; jedes [e^^];
1.
a b-{- ic
b — ic d
—z e^^w
mit |i/;P + |2;P =
27 Unitär bedeutet U^U = I oder {A^ - iB^){A + 2^) = (A'^A + B^B) +
iiA'^B - B'^A) = I. Damit ist A'^A + B'^B = I und A'^B - B'^A = 0,
weswegen die Blockmatrix orthogonal ist.
30 A
1-21-2
-1 2
10
04
2 + 22-2
1+2 2
= SAS
-1
Lösungen zu ausgewählten Aufgaben 585
Aufgaben 10.3, Seite 524
Ol
1
0
11
1 ^ 1
0
1
|o|
-^
-^
lol
0
1
111
1 ^ 1
1
0
|o|
->■
->•
lol
0
2
{o|
1 ^1
p
p
|o|
->■
-^
1 ^
0
-2
1 0
2
0
2
0
= Fc;
8 c -)^ A,1,1,1,0,0,0,0) -)^ D,0,0,0,0,0,0,0) -^ D,0,0,0,4,0,0,0) gleich
Fgc. Aus dem zweiten Vektor wird @,0,0,0,1,1,1,1) -^ @,0,0,0,4,0,0,0)
^D,0,0,0,-4,0,0,0).
9 Ist w^^ = 1, so ist w'^ eine 32. Einheitswurzel, und y/w ist eine 128.
Einheitswurzel.
13 Es gilt ei = Co 4- ci 4- C2 4- Cs und 62 = co 4- Cii 4- C22^ 4- csz^; E enthält
die vier Eigenwerte C
14 Eigenwerteei = 2-1-1 = 0, 62 = 2-i-i^ = 2, 63 = 2-(-l)-(-l) = 4,
64 = 2 - i^ - i^ = 2. Rechnen Sie die Spur 04-24-44-2 = 8 nach.
15 Für die Diagonalmatrix E werden n Multiplikationen, für die Fourierma-
trix F und F~^ jeweils |nlog2 n Multiplikationen für die FFT benötigt.
Insgesamt viel weniger als die üblichen n^.
16 (co4-C2L-(ci 4-Ca); dann (cq -C2L-2(ci -C3); dann (co4-C2) - (ci 4-C3);
dann (co - C2) — i{ci — C3). Diese Schritte sind genau die FFT!
Eine Abschlussklausur
Diese Abschlussklausur wurde am 18. Mai 1998 dem Kurs 18.06 „Lineare
Algebra" am MIT gestellt.
1. Es sei A eine 5 x 4-Matrix mit linear unabhängigen Spalten. Bestimmen
Sie explizit
(a) den Kern von A;
(b) die Dimension des Kerns der transponierten Matrix, N(A^);
(c) eine spezielle Lösung Xp der Gleichung Axp = Spalte 2 von A;
(d) die allgemeine Lösung der Gleichung Axp = Spalte 2 von A]
(e) die reduzierte Treppenform R von A.
2. (a) Bestimmen sie die allgemeine (vollständige) Lösung der Gleichung
Ax = b:
ri 12"
1 12
[2 2 2
'xi'
X2
.^3.
=
'21
2
4
(b) Bestimmen sie eine Basis des Spaltenraums für die 3 x 9-BIockmatrix
[A2AA'^].
3. (a) Das Kommando N = null{A) erzeugt eine Matrix, deren Spalten
eine Basis für den Kern von A bilden. Welche Matrix (beschreiben Sie
ihre Eigenschaften) wird dann durch das Kommando B — null(Ar')
erzeugt? Achten Sie darauf, dass es N\ nicht A' heißt,
(b) Welche Form (wieviele Zeilen und Spalten) haben diese Matrizen N
und B, wenn A eine m x n-Matrix vom Rang r ist?
4. Bestimmen Sie die Determinanten dieser drei Matrizen:
=
00 1'
0020
0300
1234
, B =
'0-A'
I -I
, c =
A-A
I -I
588
Eine Abschlussklausur
Falls möglich, konstruieren Sie 3 x 3-Matrizen A, B, C und D mit den
folgenden Eigenschaften:
(a) A sei eine symmetrische Matrix, deren Zeilenraum durch den
Vektor A,1,2) und deren Spaltenraum durch B,2,4) aufgespannt werde.
(b) Die folgenden drei Gleichungen besitzen keine Lösung, es ist aber
B^O:
Bx
(c) C sei eine reelle quadratische Matrix mit nichtreellen Eigenwerten.
(d) Der Vektor A,1,1) liege im Zeilenraum von D, aber der Vektor
A,-1,0) liege nicht im Kern.
Die Vektoren ui, U2, U3 seien eine Orthonormalbasis für tf, und vi, V2
seien eine Orthonormalbasis für R^.
(a) Es sei B = ui(vi 4- V2)^. Bestimmen Sie den Rang von B, alle
Vektoren im Spaltenraum und eine Basis des Kerns.
1
0
0
Bx =
0
1
0
Bx =
0
0
1
(b)
Es sei A = uivf 4- U2vJ. Berechnen Sie das Produkt AA^ und
vereinfachen Sie das Ergebnis. Zeigen Sie, dass es sich um eine
Projektionsmatrix handelt, indem Sie die dafür verlangten Eigenschaften
nachrechnen.
(c) Berechnen Sie A^A und vereinfachen Sie das Ergebnis. Es handelt
sich um die Einheitsmatrix! Beweisen Sie dies (indem Sie zum Beispiel
A^Avi berechnen und das Argument vollenden).
7. (a) Welches Gleichungssystem Ax = b aus drei Gleichungen in zwei
Unbekannten X = (C, D) wäre lösbar, wenn die folgenden drei Punkte
auf einer Geraden y = C + Dt lägen?
y = 0 bei ^ = — 1, y = l bei ^ = 0, y = B bei ^ = 1.
Für welchen Wert von B liegt der Vektor b = @,1,B) im
Spaltenraum von A?
(b) Bestimmen sie für jedes B die Zahlen C und D, die die beste Gerade
y = C + Dt (im Sinne der Methode der kleinsten Quadrate) liefern.
(c) Bestimmen Sie die Projektion von b auf den Spaltenraum von A.
(d) Welche Matrix Q mit orthonormalen Spalten erhalten Sie, wenn Sie
das Gram-Schmidt-Verfahren auf die Matrix A anwenden?
8. (a) Bestimmen Sie einen vollständigen Satz Eigenwerte und
Eigenvektoren für die Matrix
A =
21 1
1 2 1
1 1 2
Eine Abschlussklausur 589
(b) Markieren Sie alle Eigenschaften, die auf A zutreffen:
] A ist eine Projektionsmatrix;
] Die Determinante von A ist größer als die Spur;
] A ist eine positiv definite Matrix;
] A hat drei orthonormale Eigenvektoren;
] A ist eine Markov-Matrix;
] A kann in die Form A = LU faktorisiert werden.
(c) Schreiben Sie Uo = o als Linearkombination der Eigenvektoren von
A, und berechnen Sie uioo = A^^^uq.
Matrix-Faktorisierungen
1. A = LU =
/untere Dreiecksmatrix L\ /" obere Dreiecksmatrix U \
\^Einsen auf der Diagonaley \^Pivotelemente auf der Diagonale/
Voraussetzungen: keine Zeilenvertauschungen beim Gauß'schen
Eliminationsverfahren von A nach U nötig. Abschnitt 2.6
2. A = LDU =
(untere Dreiecksmatrix L\ /" Pivotmatrix \ / obere Dreiecksmatrix U \
Einsen auf der Diagonaley y Diagonalmatrix DJ ^Einsen auf der Diagonaley
Voraussetzungen: Keine Zeilenvertauschungen. Es wird durch die
Pivotelemente in der Matrix D dividiert, um Einsen in U zu erzeugen. Ist
A symmetrisch, so ist U — L^ und A — LDL^. Abschnitte 2.6 und 2.7
3. PA = LU (Permutationsmatrix P, um Nullen in den Pivotpositionen zu
vermeiden).
Voraussetzungen: A invertierbar. Dann sind P, L und U invertierbar. P
führt Zeilenvertauschungen im Voraus durch. Alternative: A — L\P\U\.
Abschnitt 2.1
4. EA = R (£^ invertierbare m x m-Matrix) (beliebiges Al) — rref(A).
Voraussetzungen: Keine! Die reduzierte Treppenform R besitzt r
Pivotzeilen und Pivot spalten. Der einzige von Null verschiedene Eintrag in
einer Pivotspalte ist das Pivotelement 1. Die letzten m-r Zeilen von E
bilden eine Basis des Kerns von A^, und die ersten r Spalten von E~^
bilden eine Basis des Spaltenraums von A. Abschnitte 3.2 und 3.3
5. A = CC"^ = (Untere Dreiecksmatrix C) (Die Transponierte ist eine obere
Dreiecksmatrix)
592 Matrix-Faktorisierungen
Voraussetzungen: A ist symmetrisch und positiv definit (d.h. alle n
Pivotelemente in D sind positiv). Diese Cholesky-Faktorisierung hat die
Form C = LVD. Abschnitt 6.5
6. A == QR = (orthonormale Spalten in Q) (obere Dreiecksmatrix R)
Voraussetzungen: A hat linear unabhängige Spalten. Diese Spalten
werden durch das Gram-Schmidt-Verfahren orthogonalisiert und liefern
Q.Ist A eine quadratische Matrix, so gilt Q~^ = Q^. Abschnitt 4-4
7. A = SytS"-^ = (Eigenvektoren in 5) (Eigenwerte in ^l) (Linkseigenvektoren
in 5-1).
Voraussetzungen: A muss n linear unabhängige Eigenvektoren haben.
Abschnitt 6.2
8. A = QylQ"^ == (orthogonale Matrix E)(reelle Eigenvektormatrix A){Q^
ist g-i).
Voraussetzungen: A ist symmetrisch. Dies ist der Spektralsatz.
Abschnitt 6.4
9. A = MJM"-^ = (verallgemeinerte Eigenvektoren in M)(Jordanblöcke in
J)(M-i).
Voraussetzungen: A ist eine beliebige quadratische Matrix. Die
Jordanform J besteht aus einem Block für jeden linear unabhängigen
Eigenvektor von A. Jedem Block ist ein Eigenwert zugeordnet. Abschnitt 6.6
in A —TT rvT — ( orthogonale \ f mx n-Singulärwertmatrix \
\m X m-Matrix Uj \ai,... ,ar auf der Hauptdiagonaley
/ orthogonale \
\n X n-Matrix Vj'
Voraussetzungen: Keine. Die Singulärwertzerlegung (SVD) besteht aus
den Eigenvektoren von AÄ^ in U und von Ä^A in V; ai — y/\i{A^A) =
y/\i{AA^). Abschnitte 6.7 and 7.4
^^ A+—A/r+TTT—/^ orthogonale \ / n x m-Pseudoinverse von U \
~ ~ \n X n-Matrixy \l/ai,..., 1/ar auf der Diagonalen/
(orthogonale \
m X m-Matrixy *
Matrix-Fakt or isierungen 593
Voraussetzungen: Keine. Mit der Pseudoinversen ist A'^A eine
Projektion auf den Zeilenraum von A und AA'^ = eine Projektion auf den
Spaltenraum. Die kürzeste Lösung (im Sinne der Methode der
kleinsten Quadrate) der Gleichung Ax = b ist x = A^h. Dieser Vektor löst
Ä^Ax = A'^h. Abschnitt 74
12. A = QH = (orthogonale Matrix Q) (symmetrisch positiv definite Matrix
H).
Voraussetzungen: A ist invertierbar. Bei dieser Polarzerlegung gilt
i/2 _ j\Tj^ j)gj. pgii^tor H is semidefinit, wenn A singular ist. Für die
umgekehrte Polarzerlegung A = KQ gilt K'^ = AA^. Für beide gilt
Q = UV^ aus der Singulärwertzerlegung. Abschnitt 7.4
13. A = U^U~^ = (unitäre Matrix C/)(Eigenwertmatrix Ä){U~'^ mit U~^ =
Voraussetzungen: A ist normal: A^A = AA^. Die orthonormalen
(und möglicherweise komplexen) Eigenvektoren sind die Spalten von U.
Die Eigenwerte sind komplex, falls nicht A = A^ gilt. Abschnitt 10,2
14. A = UTU~^ = (unitäre Matrix C/) (Dreiecksmatrix T mit Eigenwerten
auf der Diagonalen) {U~^ ~ U^).
Voraussetzungen: Schur-Zerlegung einer beliebigen quadratischen
Matrix A. Es gibt eine Matrix U mit orthonormalen Spalten, so dass U~^AU
eine Dreiecksmatrix ist. Abschnitt 10.2
15. F„ -
/ D
I-D
Fn/2
Fn/2
gerade-ungerade
Permutation
= ein Schritt der FFT.
Voraussetzungen: Fn — Fouriermatrix mit den Einträgen w^^ ^ wobei
w'^ — l gilt. Dann gilt FnFn = nl. D hat die Einträge l.w.iiP ^... auf der
Haupt diagonalen. Für n = 2^ benötigt die schnelle Fouriertransformation
\nl Multiplikationen. Abschnitt 10.3
Durchgerechnete Aufgaben
ri"
1
0
+ d
"o"
1
1
=
c 1
c + d
d \
1.1 A Beschreiben Sie alle Linearkombinationen der Vektoren v = A,1,0)
und w = @,1,1). Bestimmen Sie einen Vektor, der keine Linearkombination
von V und w ist.
Lösung Es handelt sich um Vektoren im dreidimensionalen Raum M^.
Ihre Linearkombinationen cv + dw bilden eine Ebene im B?. Beliebige Werte
für c und d ergeben Vektoren in dieser Ebene:
cv + dw = c
Vier konkrete Vektoren in dieser Ebene sind zum Beispiel @,0,0), B,3,1),
E,7,2) und (v^, 0, —V^). Die zweite Komponente muss immer gleich der
Summe der ersten und der dritten Komponente sein. Der Vektor A,1,1)
gehört nicht zu dieser Ebene.
Eine andere Möglichkeit, diese Ebene zu beschreiben, ist, einen Vektor
anzugeben, der senkrecht auf der Ebene steht. In unserem Fall ist n = A,-1,1)
senkrecht, wie in Abschnitt 1.2 über die Skalarprodukte nachgewiesen wird.
Es gilt V • n = 0 und w • n = 0.
1.1 B Beschreiben Sie für die Vektoren v = A,0) und w = @,1) alle
Punkte der Form cv und alle Linearkombinationen cv + dw mit beliebigem
d und A) ganzen Zahlen c, B) nicht negativen Zahlen c > 0.
Lösung
1. Die Vektoren cv = (c,0) mit ganzzahligen c sind Punkte im Abstand
eins auf der x-Achse (der Richtung von v). Zu ihnen gehören die
Punkte (-2,0), (-1,0), @,0), A,0), B,0). Addiert man alle Vektoren dw =
@, d), so fügt man an jeden dieser Punkte eine ganze Gerade in Richtung
der 2/-Achse an.
Damit ergeben sich unendlich viele parallele Geraden aus den Punkten
der Form cv + dw = (ganze Zahl, behebige Zahl). Es handelt sich um
vertikale Geraden in der xy-Ehene, die durch im Abstand eins festgelegte
Punkte auf der x-Achse verlaufen.
596 Durchgerechnete Aufgaben
2. Die Vektoren der Form cv mit c > 0 bilden eine Halbgerade. Es handelt
sich um die positive x-Achse, beginnend mit @, 0) (für c = 0): Zu ihr
gehört zum Beispiel (tt, 0), nicht aber (—tt, 0). Addiert man alle Vektoren
der Form dw, so fügt man eine ganze Gerade in Richtung der ?/-Achse
an jeden Punkt der Halbgeraden an. Damit erhält man eine Halbebene,
nämlich die rechte Hälfte der xy-Ehene, in der x > 0 gilt.
1.2 A Überprüfen Sie an den Vektoren v = C,4) und w = D,3) die
Schwarz'sche Ungleichung für v-w und die Dreiecksungleichung für ||v + w||.
Bestimmen Sie cos 6 für den Winkel zwischen v und w. Unter welchen
Umständen tritt die Gleichheit |v • w| = ||v|| ||w|| und ||v + w|| = ||v|| + ||w||
ein?
Lösung Das Skalarprodukt ist v • w = 3 • 4 + 4 • 3 = 24. Die Länge von v
ist ||v|| = \/9 + 16 = 5, es gilt ebenso ||w|| = 5. Die Summe v + w = G,7)
hat die Länge ||v + w|| = 7\/2 « 9.9.
Schwarz'sche Ungleichung |v • w| < ||v|| ||w||, hier: 24 < 25.
Dreiecksungleichung ||v -h w|| < ||v|| + ||w||, hier: 7\/2 < 10.
Kosinus des Winkels cos^ = || (spitzer Winkel!)
Ist ein Vektor ein Vielfaches eines anderen, wie in w = -2v, so ist der Winkel
zwischen ihnen 0° oder 180°, und es gilt |cosö| = 1, so dass |v • w| gleich
||v|| ||w|| ist. Ist der Winkel 0°, wie in w = 2v, so gilt ||v + w|| = ||v|| + ||w||:
Das Dreieck wird zu einer Strecke.
1.2 B Bestimmen Sie einen Einheitsvektor u in Richtung von v = C,4).
Bestimmen Sie einen Einheitsvektor U senkrecht zu u. Wie viele
Möglichkeiten gibt es für die Wahl von U?
Lösung Um einen Einheitsvektor u zu erhalten, dividiert man den Vektor
V durch seine Länge ||v|| = 5. Als senkrechten Vektor V kann man (-4,3)
wählen, da das Skalarprodukt v • V = 3 • (-4) + 4-3 = 0 ist. Um einen
Einheitsvektor U zu bestimmen, dividiert man den Vektor V durch seine
Länge ||V||:
j^ ^ C^ ^ /3 4\ TT = -^ = (-4,3) ^ /_4 3
INI 5 U'S^' ^ ||V|| 5 V 5'5
Der einzige andere senkrechte Einheitsvektor ist -U = (|, -|).
2.1 A Beschreiben Sie das Spaltenbild der folgenden drei Gleichungen.
Lösen Sie sie durch „aufmerksames Betrachten" der Spalten (anstatt das
Gleichungssystem umzuformen):
Durchgerechnete Aufgaben 597
2x-\-2y-^2z = -2
Sx + 5y-\-4z= -5
gleich Ax = b :
[132'
222
^354
X
y
z
=
■-3]
-2
-öj
Lösung Im Spaltenbild wird nach einer Linearkombination gefragt, die
den Vektor b aus den drei Spalten von A erzeugt. In unserem Beispiel ist
b gleich minus zweite Spalte. Die Lösung ist also x = 0,y = -l,z = 0.
Um zu zeigen, dass @,-1,0) die einzige Lösung ist, müssen wir wissen, dass
A „invertierbar" ist und die Spalten „linear unabhängig" sind, so dass die
„Determinante ungleich null" ist. Wir kennen die Bedeutung dieser Worte
noch nicht, können aber mit Hilfe des Eliminations Verfahrens das Ergebnis
verifizieren: Wir brauchen (und finden!) einen vollen Satz aus drei von Null
verschiedenen Pivotelementen.
Ändert man die rechte Seite zu b = D,4,8) = Summe der ersten beiden
Spalten, so ist die richtige Linearkombination durch x = l,y = l,z = 0
gegeben, der Lösungsvektor ist x = A,1,0).
2.1 B Das folgende System hat keine Lösung, weil die drei Ebenen im
Zeilenbild sich in keinem Punkt schneiden. Durch keine Kombination der drei
Spalten kann der Vektor b erzeugt werden:
x + 3y + 5z = 4
x-\-2y -3z = 5
2x-\-5y-\-2z = S
[13 5"
1 2 -3
25 2
X
y
z
=
1
5
s\
= h
1. Multiplizieren Sie die Gleichungen mit 1, 1 beziehungsweise —1 und
addieren Sie sie, um zu zeigen, dass sich die Ebenen in keinem Punkt
schneiden. Sind zwei der drei Ebenen parallel? Welche Gleichungen beschreiben
Ebenen, die parallel zu x -\- 3y + 5z = 4 sind?
2. Berechnen Sie das Skalarprodukt jeder Spalte (und auch von b) mit dem
Vektor y = A,1, —1). Wie kann man anhand dieser Skalarprodukte
erkennen, dass das System keine Lösung hat?
3. Bestimmen Sie drei Vektoren b*, b** und b*** für die rechte Seite, für
die es Lösungen gibt.
Lösung
1. Multipliziert man die Gleichungen mit 1,1 beziehungsweise —1 und
addiert man sie, so erhält man
x-h3y-h5z = 4
x-h2y-Sz = 5
-[2x -h5y-h2z = 8]
Ox -h Oy -h Oz = 1 keine Lösung
598 Durchgerechnete Aufgaben
Die Ebenen schneiden sich in keinem Punkt, aber keine zwei Ebenen
sind parallel. Um eine Ebene parallel zu x -\- Sy -\- 5z = 4 zu erzeugen,
muss man nur die „4" ändern. Die parallele Ebene x -\- 3y + 5z = 0
enthält den Ursprung @,0,0). Multipliziert man die Gleichung mit einer
beliebigen (von Null verschiedenen) Konstanten, so erhält man wieder
dieselbe Ebene, wie zum Beispiel durch 2x -\- 6y -\- 10z = S.
2. Das Skalarprodukt aller Spalten auf der linken Seite mit y = A,1,—1)
ist null. Auf der rechten Seite ist y • b = A,1, — 1) • D,5,8) = 1 aber
nicht null. Daher ist eine Lösung unmöglich. (Würde eine Kombination
der Spalten den Vektor b ergeben, so wäre das Skalarprodukt mit y eine
Kombination von Nullen, die nicht 1 ergeben kann.)
3. Es gibt eine Lösung, wenn b eine Linearkombination der Spalten ist. Die
folgenden Beispiele b*,b** und b*** haben die Lösungen x* = A,0,0),
X** = A,1,1) undx*** = @,0,0):
b* =
= 1. Spalte, b** =
= Summe d. Spalten, b*** =
2.2 A Wenn man das Eliminationsverfahren auf die folgende Matrix A
anwendet, was ergibt sich für das erste und das zweite Pivotelement? Welchen
Multiplikator /21 erhalten sie für den ersten Schritt (in dem /21 mal Zeile 1 von
Zeile 2 subtrahiert wird) ? Welcher Eintrag (an Stelle der 9) in der Position
B,2) würde eine Vertauschung der Zeilen 2 und 3 nötig machen? Warum ist
der Multiplikator /31 = 0, so dass 0 mal Zeile 1 von Zeile 3 subtrahiert wird?
A =
3 10
692
0 1 5
Lösung Das erste Pivotelement ist 3. Der Multiplikator /21 ist | = 2.
Subtrahiert man 2 mal Zeile 1 von Zeile 2, so erhält man das zweite Pivot
element 7. Ändert man den Eintrag „9" auf „2", so würde diese Reduktion um
7 in der Position B, 2) einen Zeilenwechsel nötig machen. (Die zweite Zeile
würde mit den Einträgen 6,2 beginnen, also Vielfachen der Einträge 3,1 in
der ersten Zeile. Daher erzeugt man eine Null auf der zweiten Pivotposition.)
Der Multiplikator /31 ist null, weil 031 = 0 ist. Eine Null am Anfang einer
Zeile bedarf keiner Elimination.
2.2 B Verwenden Sie das Eliminations verfahren, um obere
Dreiecksmatrizen U zu erzeugen, und lösen Sie die Gleichungen durch Rücksubstitution,
Durchgerechnete Aufgaben 599
oder erklären Sie, warum dies unmöglich ist. Welche Pivotelemente (ungleich
Null!) erhalten Sie? Vertauschen Sie Zeilen, falls nötig. Der einzige
Unterschied zwischen beiden Gleichungssystemen liegt im Term — x in der dritten
Gleichung:
X -\-y -\- z = 7 X -\-y + z = 7
X -\-y - z = 5 X -\-y - z = 5
X - y + z = S -X - y -\- z = 3
Lösung Man subtrahiert für das erste System Gleichung 1 von den
Gleichungen 2 und 3 (die Multiplikatoren sind /21 = 1 und /31 = 1). Der Eintrag
B,2) wird null, daher müssen zwei Gleichungen vertauscht werden:
x-\-y-\-z= 7 x + y + z= 7
Oy — 2z = —2 wird vertauscht zu —2y-\-0z = —4
-2y-\-0z = -4 -2z = -2
Rücksubstitution liefert dann z = 1^ y = 2 und x = 4. Die Pivotelemente
sind 1, —2 und —2.
Beim zweiten System muss wie zuvor Gleichung 1 von Gleichung 2 subtrahiert
werden, aber zu Gleichung 3 addiert werden. Damit erhält man eine Null an
der Stelle B, 2) und darunter:
x-\-y -\- z — 7 Es gibt kein Pivotelement in Spalte 2.
Oy — 2z = —2 Der nächste Eliminationsschritt liefert Oz = S
Oy -\-2z = 10 Die drei Ebenen schneiden sich nicht!
Ebene 1 schneidet sich mit Ebene 2 in einer Geraden, und mit Ebene 3 in
einer Geraden parallel dazu. Es gibt keine Lösung.
Ändert man die „3" in der ursprünglichen dritten Gleichung auf „—5" ab,
so erhält man 22: = 2 anstelle von 2z — 10. Diese Gleichung 2: = 1 wäre
konsistent — wir haben die dritte Ebene verschoben. Setzt man 2: = 1 in
die erste Gleichung ein, so erhält man x + 2/ = 6. Es gibt unendlich viele
Lösungen! Die drei Ebenen schneiden sich jetzt in einer Geraden.
2.3 A Welche 3 x 3-Matrix E21 subtrahiert 4 mal Zeile 1 von Zeile 2?
Welche Matrix P32 vertauscht die Zeilen 2 und 3? Beschreiben Sie die
Ergebnisse AE2\ und ^P32, die man erhält, wenn man A von rechts statt von links
multipliziert.
Lösung Wendet man die Operationen auf die Einheitsmatrix an, so erhält
man
^21 —
100
-4 10
00 1
und P32 =
100
00 1
0 10
600
Durchgerechnete Aufgaben
Multipliziert man E21 von rechts, so wird 4 mal Spalte 2 von Spalte 1
subtrahiert. Multipliziert man P32 von rechts, so werden die Spalten 2 und 3
vertauscht.
2.3 B
te an:
Geben Sie die erweiterte Matrix [A b] mit einer zusätzlichen Spal-
x + 2y-h2z = l
4x + 8y-^9z = 3
3y-^2z = l
Wenden Sie E21 und dann P32 an, um ein Dreieckssystem zu erhalten,
und lösen Sie es durch Rücksubstitution. Durch welche kombinierte Matrix
-P32 E21 werden beide Schritte gleichzeitig ausgeführt?
Lösung
sind
Die erweiterte Matrix und das Ergebnis der Anwendung von £^21
[A h] =
1221
4893
0321
und E2i[A b] =
122 1
001 -1
032 1
P32 vertauscht die Gleichungen 2 und 3. Durch Rücksubstitution erhält man
ix,y,z):
P32E2l[A b] =
122 1
032 1
00 1-1
und
X
y
z
=
r
1
-1
Um die Matrix P32 E21 zu bestimmen, die beide Schritte gleichzeitig ausführt,
wendet man P32 auf E21 an:
P32 E21 = Vertausche Zeilen von E21 =
100
001
-4 10
2.3 C Multiplizieren Sie die folgenden Matrizen auf zwei Arten: zunächst
die Zeilen von A mit den Spalten von B, um die Einträge von AB zu
bestimmen, danach die Spalten von A mit den Zeilen von jB, so dass sich Matrizen
ergeben, deren Summe AB ist. Wie viele verschiedene gewöhnliche
Multiplikationen werden benötigt?
AB =
34
15
20
24
1 1
= C X 2)B X 2)
Durchgerechnete Aufgaben 601
Lösung Die Produkte der Zeilen von A mit den Spalten von B sind Ska-
larprodukte von Vektoren:
(Zeile 1). (Spalte 1)
_[34]
= 10 ergibt den Eintrag A,1) von AB
(Zeile 2) • (Spalte 1)
[15]
= 7 ergibt den Eintrag B,1) von AB
Die ersten Spalten von AB sind A0,7,4) und A6,9,8). Wir benötigen 6
Skalarprodukte mit jeweils 2, also insgesamt 12 Multiplikationen C • 2 • 2).
Man erhält dieselbe Matrix AB wie über die Produkte der Spalten von A
mit den Zeilen von B:
AB =
[3'
1
2
[24]
+
"
5
Oj
[11]
[6 12'
2 4
4 8
+
4"
55
00
=
'10 161
7 9
4 8]
2.4 A Stellen Sie sich vor, Sie seien der Autor! Ich möchte Ihnen besondere
Matrixmultiplikationen zeigen, aber meistens bleibe ich bei kleinen Matrizen
hängen. Es gibt eine wunderbare Familie von Pascal'schen Matrizen, die
es in allen Größen gibt, und die vor allem wirkliche Bedeutung haben. Ich
denke, 4 x 4 ist eine gute Größe, um einige der faszinierenden Eigenschaften
zu demonstrieren.
Die folgende Matrix ist die Pascal'sche untere Dreiecksmatrix L. Ihre
Einträge stammen aus dem Pascal'schen Dreieck. Ich multipliziere L mit dem
„Einsen-Vektor" und mit dem „Potenzen-Vektor":
Pascal'sche
Matrix
1 1
121
1331
1'
1
1
1
1'
2
4
8
1 1
121
1331
" 1 '
X
x2
x^
1
1+x
(l+x)V
(l+xK
Jede Zeile von L führt auf die nächste Zeile: Man addiert zu einem Eintrag
den linken Nachbarn, um den Eintrag darunter zu erhalten. Symbolisch
geschrieben also £ij -\- iij-i = ^i-f-i j. Die auf 1,3,3,1 folgenden Zahlen wären
1,4,6,4,1. Pascal lebte im 17. Jahrhundert, lange bevor es Matrizen gab,
aber sein Dreieck passt perfekt in die Matrix L.
Mit Einsen zu multiplizieren bewirkt dasselbe, wie jede Zeile aufzuaddieren,
so dass man die Potenzen von 2 erhält. Es gilt ja auch Potenzen = Einsen,
wenn x = l ist. Bildet man das Skalarprodukt der letzten Zeile von L mit
dem Potenzen-Vektor, so erhält man als Einträge von L die „Binomialkoef-
fizienten", die so entscheidend für die Glücksspieler sind:
1 -h 2x -h la:^ = A + xJ
1 -h 3x -h 3x2 -h Ix^ = A + x)^
602 Durchgerechnete Aufgaben
Die Zahl „3" gibt die Anzahl an Möglichkeiten an, bei drei Münzwürfen
einmal „Kopf und zweimal „Zahl" zu erhalten: KZZ, ZKZ oder ZZK. Die
andere „3" gibt die Anzahl an Möglichkeiten an, zweimal „Kopf" zu erhalten:
ZKK, KZK oder KKZ. Dies sind Beispiele für den Ausdruck „i über j", also
die Anzahl Möglichkeiten, in i Münzwürfen j „Köpfe" zu erhalten. Diese Zahl
ist genau lij, wenn man die Zeilen- und die Spaltenzählung bei i = 0 und
j = 0 beginnt:
Hj —
= i über j =
ß{i-j)r
4!
2!2!
= 6.
Es gibt sechs Möglichkeiten, zwei aus vier Assen auszuwählen. Wir werden
dem Pascal'schen Dreieck und diesen Matrizen in Zukunft noch begegnen.
Jetzt möchte ich Ihnen die folgenden Fragen stellen:
1. Was ist H = L2? Dies ist die "Hyperkubus^-Matrix".
2. Berechnen Sie H mal Einsen und Potenzen.
3. Die letzte Zeile von H ist 8,12,6,1. Ein Würfel hat 8 Ecken, 12 Kanten, 6
Seitenflächen, 1 Würfel. Welche Daten eines vierdimensionalen Hyperkubus
gibt die nächste Zeile von H an?
Lösung Multiplizieren wir L mit L, um die Hyperkubus-Matrix H — L'^
zu berechnen:
1
1 1
1 2 1
1331
1
1 1
121
133 1
1
2 1
4 4 1
8 12 6 1
= H.
Als nächstes multiplizieren wir H mit dem Vektor aus Einsen und
Potenzen:
[1
2 1
4 4 1
8 12 6 1
"r
1
1
1
" 1
3
9
27
2 1
4 4 1
8 12 6 1
" 1 ■
X
x^
_x\
1 ]
2 + x
B + xJ
B+xKj
Mit X — 1 erhalten wir die Potenzen von 3. Für x = 0 erhalten wir die
Potenzen von 2 (wo tauchen 1,2,4,8 in H auf?). So, wie L aus x A + x)
gemacht hat, erzeugt die erneute Anwendung von L aus {l + x) die Matrix
B + x).
Wie können die Zeilen von H die Ecken, Kanten und Seitenflächen
eines Würfels zählen? Ein Quadrat in zwei Dimensionen hat 4 Ecken, 4
Seiten, 1 Fläche. Fügen wir eine Dimension nach der anderen hinzu:
Anm. d. Übers,: etwa: „hochdimensionaler Würfel"
Durchgerechnete Aufgaben 603
Man verbindet zwei Quadrate und erhält einen Würfel in 3 Dimensionen.
Man verbindet zwei Würfel und erhält einen Hyperkubus in 4 Dimensionen.
Der Würfel hat 8 Ecken und 12 Kanten: 4 Kanten in jedem Quadrat, und
4 Kanten zwischen den Quadraten. Der Würfel hat 6 Seiten: eine in jedem
Quadrat, und vier Flächen zwischen den Quadraten. Die Zeile 8,12,6,1 von
H führt über 2hij-\-hij-i = ^i+i j zur nächsten Zeile (eine Dimension höher).
Können Sie dies vierdimensional sehen? Der Hyperkubus hat 16 Ecken, kein
Problem. Er hat 12 Kanten vom einen Würfel, 12 Kanten vom anderen, 8
Kanten, die die Ecken zwischen den Würfeln verbinden: insgesamt 2 x 12+8 =
32 Kanten. Er hat 6 Seitenflächen aus jedem einzelnen Würfel und 12 Flächen
von den verbindenden Kanten: insgesamt 2 x 6 + 12 = 24 Seitenflächen.
Von jedem Würfel erhält er einen Würfel, und weitere 6 Würfel aus Paaren
verbindender Seitenflächen: insgesamt 2x1+6 = 8 Würfel. Und, Tatsache,
die nächste Zeile von H enthält die Einträge 16,32,24,8,1.
2.4 B Wann gilt für die folgenden Matrizen AB = BAI Wann gilt BC =
CB? Wann ist A mal BC gleich AB mal C? Geben Sie Bedingungen an die
Einträge p, q, r und z an:
A =
pO
q r
B =
1 1
Ol
C =
Oz
00
Ändern sich die Antworten, wenn p, q, r, 1 und 2; 4 x 4-Blöcke anstelle von
Zahlen sind?
Lösung Zunächst: A mal BC ist immer gleich AB mal C. Man braucht
die Klammern in A{BC) = {AB)C = ABC nicht. Man muss aber die
Matrizen in der Reihenfolge A, B, C belassen. Vergleichen wir AB mit BA:
AB =
p p
q q-\-r
BA =
p + qr
q r
Es gilt nur AB = BA, falls q = 0 und p = r. Vergleichen wir BC mit CB:
BC =
Oz
00
CB
Oz
00
B und C kommutieren zufällig. Eine Erklärung ist, dass der Diagonalteil von
B gleich der Matrix / ist, die mit allen anderen 2 x 2-Matrizen kommutiert.
Der Teil abseits der Diagonalen von B ist mit dem entsprechenden Teil von
C (bis auf einen skalaren Faktor z) identisch, und jede Matrix kommutiert
mit sich selbst.
Sind p,q,r und 2; 4 x 4-Blöcke, und ändert man die 1 zu einer 4x4-
Einheitsmatrix, so bleiben alle Produkte korrekt. Die Antworten bleiben also
unverändert. (Ändert man die /'s in B in Blockmatrizen t, t, t, so enthält BC
604 Durchgerechnete Aufgaben
den Block tz und CB den Block zt. Diese sind normalerweise verschieden —
bei der Blockmultiplikation ist die Reihenfolge wichtig.)
2.4 C Ein gerichteter Graph beginnt mit n Knoten. Zwischen ihnen gibt
es n^ mögliche Kanten — jede Kante verläuft von einem der n Knoten zu
einem (möglicherweise demselben) der n Knoten. Die n x n-Adjazenzmatrix
hat einen Eintrag üij = 1, wenn es eine Kante von Knoten i zu Knoten j
gibt, gibt es keine solche Kante, so ist aij = 0. Die folgende Abbildung zeigt
zwei gerichtete Graphen mit ihren Adjazenzmatrizen:
Kante 1 nach 1^
Kante 2 nach 1
111
100
100
Der Eintrag (i,j) von A^ ist anaijH hainanj. Wieso gibt Ä^ die Anzahl
der Pfade mit zwei Kanten von einem Knoten i zu einem Knoten j an? Der
Eintrag (z, j) von A^ gibt die Anzahl der Pfade mit k Kanten an:
1 1
10
2 1
1 1
zählt die Pfade
mit zwei Kanten
l->2->l, 1->1->1 l->l->2
2 -> 1 -> 1 2 -> 1 -> 2
Geben Sie alle Pfade mit drei Kanten zwischen je zwei Knoten an, und
vergleichen Sie ihre Liste mit A^.
Lösung Die Zahl üikükj ist „1", wenn es eine Kante von i nach k und eine
Kante von k nach j gibt. Diese Kanten machen den Pfad mit zwei Kanten
aus. Die Zahl aikakj ist „0", wenn eine der beiden Kanten fehlt. Daher ist die
Summe über aikühj gleich der Zahl der Pfade von i nach j mit zwei Kanten.
Die Matrixmultiplikation ist für diese Zählung gerade passend!
Die Pfade mit drei Kanten werden von A^ gezählt, wir sehen uns die Pfade
zu Knoten 2 an:
A^ =
32
2 1
zählt die Pfade
mit drei Kanten
•• l->l->l->2, l->2->l->2
• • • 2 -> 1 -> 1 -> 2
Diese Matrizen A^ enthalten die Fibonacci-Zahlen 0,1,1,2,3,5,8,13,...,
die uns in Abschnitt 6.2 noch begegnen werden. Fibonacci's Regel Fk-\-2 =
Ffc-f-i +Fk (zum Beispiel 13 = 8 + 5) taucht in der Beziehung {Ä){A^) = ^^+^
auf:
1 1
10
Fk+i
Fk
Fk
Fk-i
Fk+2 Fk-{-i
Fk-{-i Fk
= A^^\
Durchgerechnete Aufgaben 605
Es gibt 13 Pfade mit sechs Kanten von Knoten 1 nach Knoten 1, aber ich
kann sie nicht alle finden.
Mit A^ kann man auch Wörter zahlen. Ein Pfad wie 1 nach 1 nach 2 nach
1 kann man mit der Zahl 1121 oder mit dem Wort aaba beschreiben. Die
Ziffer 2 (der Buchstabe b) darf sich dabei nicht wiederholen, weil der Graph
keine Kante von Knoten 2 nach Knoten 2 hat. Der Eintrag (z, j) von A^ gibt
die Anzahl erlaubter Zahlen (oder Worte) der Länge A: + 1 an, die mit dem
z-ten Buchstaben beginnen und auf den j-ten Buchstaben enden.
2.5 A Drei der folgenden Matrizen sind invertierbar, drei sind singular.
Bestimmen Sie die Inverse, wenn sie existiert. Geben Sie Gründe für die
Nichtinvertierbarkeit (Determinante null, zu wenige Pivotelemente,
nichttriviale Lösung zu Ax = 0) der anderen drei Matrizen an, und zwar in dieser
Reihenfolge. Die Matrizen A, B, C, D, E, F sind
43'
86
43
87
66
60
66
66
00"
1 10
111
'11 r
110
111\
Lösung
B-' =
7-3
-8 4
C
-1 _
36
0 6
6-6
E-' =
r 1
-1
0-
ool
10
-1 ij
A ist nicht invertierbar, weil die Determinante 4-6 — 3-8 = 24 — 24 = 0 ist.
D ist nicht invertierbar, weil es nur ein Pivotelement gibt; die zweite Zeile
wird zu einer Nullzeile, wenn man die erste Zeile davon subtrahiert. F ist
nicht invertierbar, weil es eine Kombination der Spalten gibt (zweite minus
erste Spalte), die den Nullvektor darstellt — anders gesagt, Fx = 0 hat die
Lösung X = (—1,1,0).
Man kann natürlich alle drei Begründungen für die Nichtinvertierbarkeit auf
jede der Matrizen A,D,F anwenden.
2.5 B Verwenden Sie das Gauß-Jordan-Verfahren, um die Inverse der
folgenden dreieckigen Pascal'schen Matrix A = abs(pascal D,1)) zu
bestimmen. Sie erkennen darin das Pascal'sche Dreieck — die Summe eines
Eintrags mit dem Eintrag links daneben ergibt den Eintrag darunter. Die
Einträge sind die „Binomialkoeffizienten":
Dreieckige Pascal'sche Matrix A
10 00"
110 0
12 10
1331
606 Durchgerechnete Aufgaben
Lösung Das Gauß-Jordan-Verfahren beginnt mit [A I] und erzeugt
Nullen, indem es Zeile 1 subtrahiert:
[A /] =
1000
1100
12 10
133 1
1000
0100
0010
0001
1000
0100
0210
0331
1000
-1 100
-10 10
-100 1
Im nächsten Schritt werden Nullen unterhalb des zweiten Pivotelements
erzeugt, die Multiplikatoren sind 2 und 3. Im letzten Schritt wird das dreifache
der neuen Zeile 3 von der neuen Zeile 4 subtrahiert:
1000
0100
0010
0031
1 000
-1 100
1-210
2-301
1000
0100
0010
0001
10 00
-1100
1-2 10
1 3-3 1
= [I A-^].
Alle Pivotelemente sind 1! Wir brauchten also keine Zeilen durch ein
Pivotelement zu dividieren, um / zu bestimmen. Die inverse Matrix A~^ sieht wie
A aus, außer dass die Diagonalen mit einer ungeraden Nummer mit —1
multipliziert werden. Prägen Sie sich diese 4 x 4-Matrix A~^ ein — wir werden
den Pascal'schen Matrizen noch begegnen. Dasselbe Muster findet sich in den
n X n-Pascal-Matrizen: die Inverse hat „alternierende Diagonalen".
2.6 A Die Pascal'sche untere Dreiecksmatrix Pl wurde im
durchgerechneten Beispiel 2.5 B vorgestellt. (Sie enthält das Pascal'sche Dreieck; mit dem
Gauß-Jordan-Verfahren wurde die Inverse bestimmt.) Die folgende Aufgabe
liefert eine Verbindung von Pl mit der symmetrischen Pascal'schen Matrix
Ps und der Pascal'schen oberen Dreiecksmatrix Pc/. In der symmetrischen
Matrix Ps steht das Pascal'sche Dreieck geneigt, so dass jeder Eintrag sich als
Summe aus dem darüberstehenden und dem links danebenstehenden ergibt.
In MATLAB erhält man die symmetrische n x n-Matrix Ps durch pascal (n).
Aufgabe: Beweisen Sie die faszinierende Faktorisierung Ps = PlPu'
pascalD) =
1111
12 3 4
13 6 10
1 4 10 20
1000
1 100
12 10
1331
1111
0123
0013
0001
= PlPu-
Machen Sie dann eine Vorhersage für die letzte Zeile und Spalte der 5x5-
Pascal-Matrix, und überprüfen Sie sie.
Lösung Man könnte einfach PlPu ausrechnen und Ps erhalten. Es ist
aber eleganter, mit Ps zu beginnen und die obere Dreiecksmatrix Pu über
das Eliminations verfahren zu erhalten:
Durchgerechnete Aufgaben 607
Ps =
1111'
12 3 4
13 610
1 4 10 20
—y
111"
012 3
025 9
039 19
—y
111"
012 3
001 3
003 10
—y
'1111]
0123
0013
OOOlJ
= Pu-
Die Multiplikatoren, die wir in diesen Schritten verwendeten, passen perfekt
in die Matrix Pl- Damit ist die Ps = PlPu ein besonders schönes Beispiel
für A = LU. Beachten Sie, dass jedes Pivotelement 1 ist. Die Pivotelemente
stehen auf der Diagonalen von Pu- Im nächsten Abschnitt werden wir sehen,
wie durch die Symmetrie eine spezielle Beziehung zwischen den
Dreiecksmatrizen L und U entsteht. Man sieht dann Pu als die „Transponierte" von
Sie erwarten vielleicht, dass das MATLAB-Kommando lu(pascalD))
diese Faktorisierung in Pl und Pu ausgibt. Dies ist deswegen nicht der Fall,
weil die Routine in lu jeweils das größtmögliche Pivotelement in einer Spalte
auswählt (in unserem Fall werden zum Beispiel die Zeilen so vertauscht, dass
als zweites Pivotelement 3 auftritt). Ein anderes Kommando, chol, führt eine
Faktorisierung ohne Zeilenvertauschung durch. Deswegen erhält man durch
[L , U] = Chol (pascal D)) die Pascal'schen Dreiecksmatrizen in L und
U. Probieren Sie es aus!
Auch im 5 X 5-Fall bleibt die Faktorisierung Ps = PlPu erhalten:
Nächste Zeile:
1 5 15 35 70 vonPs, 14 6 4 1 von P^
Ich überprüfe nur, ob das Produkt dieser fünften Zeile von Ps mit der
(identischen) fünften Spalte von Pu den Eintrag 1^ + 4^ + 6^ + 4^ + 1^ = 70 in der
fünften Zeile von Ps ergibt. Der volle Beweis dafür, dass immer Ps = PlPu
gilt, ist sehr interessant — man kann die Faktorisierung auf mindestens vier
verschiedene Arten erlangen. Ich werde diese Beweise auf den Webseiten
(web.mit.edu/18.06/www) für den Kurs veröffentlichen, die man auch
durch die OpenCourseWare des MIT unter ocw.mit.edu erreichen kann.
Die Pascal'schen Matrizen Ps,Pl,Pu haben viele bemerkenswerte
Eigenschaften — wir werden ihnen aber noch einmal begegnen. Sie können sie mit
Hilfe des Stichwortverzeichnisses am Ende des Buches ausfindig machen.
2.6 B Die Aufgabe ist: Lösen Sie die Gleichung P^x = b = A,0,0,0).
Für diese spezielle rechte Seite ist x die erste Spalte von P^^ — genau wie
beim Gauß-Jordan-Verfahren, wo PsPs^ = ^ spaltenweise gelöst wird. Wir
kennen die Dreiecksmatrizen Pl und Pu bereits von 2.6 A, deswegen lösen
wir
Plc = b (Vorwärtssubstitution) Pc/ x = c (Rücksubstitution).
Um die volle Inverse P^^ zu bestimmen, verwenden Sie am besten MATLAB.
Lösung
unten:
Das untere Dreieckssystem P^c = b löst man von oben nach
608
Durchgerechnete Aufgaben
ci =1
Ci + C2 =0
Ci -h 2C2 -h C3 =0
Ci + 3C2 + 3C3 + C4 =0
ergibt
ci = +1
C3 = +1
C4 = — 1
Die Vorwärtselimination entspricht der Multiplikation mit P^^- Es entsteht
das obere Dreieckssystem Pux = c, aus dem man die Lösung x durch
Rücksubstitution von unten nach oben erhält:
^1 + ^2 + ^3 + ^4 = 1
X2 + 2X3 +3^4 = -1
Xs + 3^4 = 1
X4 = -1
ergibt
xi = +4
X2 = -6
Xs = +4
X4 = —1
In der vollständigen inversen Matrix P^ ^ steht dieses x tatsächlich in der
ersten Spalte:
inv(pascalD))
4-6 4-1
-6 14 -11 3
4 -11 10 -3
-1 3-3 1
2.7 A Wendet man eine Permutation P auf die Zeilen von A an, so wird
die Symmetrie zerstört:
P =
0 10
001
100
145
426
563
PA =
426
563
145
Welche Permutationsmatrix Q wendet man auf die Spalten von PA an, damit
man eine symmetrische Matrix zurückerhält? Die Zahlen 1,2,3 müssen dazu
wieder auf die Haupt diagonale gebracht werden — wenn auch nicht in dieser
Reihenfolge. Wie hängt Q mit P zusammen, wenn das Produkt PAQ die
Symmetrie erhält?
Lösung Um die Symmetrie wiederzuerlangen und auf die Diagonale die
Zahl „2" zu setzen, muss Spalte 2 von PA die neue Spalte 1 werden. Spalte
3 von PA (mit der „3") muss die neue Spalte 2 werden, so dass die „1" in
die Position C,3) gelangt. Im folgenden wird diese Permutation der Spalten
durch die Matrix Q vorgenommen:
PA =
426
563
145
Q =
001
100
0 10
PAQ =
264
635
45 1
ist symmetrisch.
Durchgerechnete Aufgaben 609
Die Matrix Q ist P^. Mit dieser Wahl erhält man immer die Symmetrie
zurück, weil PAP^ garantiert symmetrisch ist — die Transponierte ist
wieder PAP^. Die Matrix Q ist auch gleich P~^, weil die Inverse jeder
Permutationsmatrix gleich der Transponierten ist
Betrachten wir nur die Hauptdiagonale D von A, so sehen wir, dass PDP
garantiert diagonal ist. Verschiebt P Zeile 1 nach Zeile 3, so bewegt P^ von
rechts Spalte 1 nach Spalte 3. Der Eintrag A,1) wird erst zu C,1) und dann
C,3).
2.7 B Bestimmen Sie die symmetrische Faktorisierung A = LDL^ der
Matrix A von oben. Ist A invertierbar? Bestimmen Sie auch die
Faktorisierung PQ = LU von E, bei der Zeilenvertauschungen nötig sind.
Lösung Um A in der Form LDL^ zu faktorisieren, führen wir das
Eliminationsverfahren unterhalb der Pivotelemente durch:
A =
145"
426
563
—y
4 5 ■
0-14-14
0-14-22
—y
4 5
0-14-14
0 0-8
= u.
Die Multiplikatoren sind ^21 = 4, £31 = 5 und ^2 = 1- Die Pivotelemente
1,-14, —8 bilden die Matrix D. Teilt man die Zeilen von U durch das jeweilige
Pivotelement, so erscheint L^:
A = LDL^
00"
410
51 1
-14
-8
45]
Ol 1
001
Diese Matrix A ist invertierbar, weil sie drei Pivotelemente hat. Die Inverse
ist die ebenfalls symmetrische Matrix (L^)"^i^"^L"^ Die Zahlen 14 und
8 tauchen in den Nennern in A~^ auf. Die „Determinante" von A ist das
Produkt der Pivotelemente (l)(-14)(-8) = 112.
Die Matrix Q ist garantiert invertierbar. Das Eliminationsverfahren benötigt
aber zwei Zeilenvertauschungen:
Q =
01"
100
0 10
Zeilen
—y
1 ^2
00"
001
010
Zeilen
—y
2^3
00]
010
OOlJ
= /.
Hier sind L — I und t/ = / die Faktoren LU. Wir brauchen lediglich eine
Permutation P, die die Zeilen von Q in die richtige Reihenfolge (nämlich die
der Zeilen von /) bringt. Nun, dazu muss P gleich Q~^ sein. Es handelt sich
um dasselbe P wie zuvor! Wir konnten es als Produkt von zwei
Zeilenvertauschungen bestimmen, nämlich 1 o 2 und 2 o 3:
610 Durchgerechnete Aufgaben
P = P23P12 —
rioo"
001
010
'0 10"
100
001
r=
10"
001
looj
ordnet Q in I um.
3.1 A Gegeben seien drei verschiedene Vektoren bi, b2, bs. Man
konstruiere eine Matrix A, so dass die Gleichungen ^x = bi und ^x = b2 lösbar
sind, nicht aber die Gleichung ^x = bs. Wie können Sie entscheiden, ob dies
möglich ist? Wie könnten Sie A konstruieren?
Lösung Wir möchten, dass bi und b2 im Spaltenraum von A liegen.
Dann sind die Gleichungen ^x = bi und ^x = b2 lösbar. Die schnellste
Möglichkeit dazu ist, bi und b2 als einzige Spalten von A zu verwenden. Die
Lösungen sind dann x = A,0) und x = @,1).
Zusätzlich wollen wir noch, dass ^x = bs nicht lösbar ist. Deswegen darf der
Spaltenraum nicht größer werden! Verwendet man nur die Spalten bi und
b2, so bleiben die Fragen:
Ist ^x
bi b2
X2
bs lösbar?
Ist bs eine Linearkombination der Spalten bi und b2?
Ist die Antwort nein, so haben wir eine Matrix wie gewünscht. Ist die
Antwort ja, so ist es unmöglich, eine solche Matrix A zu konstruieren. Enthält
der Spaltenraum die Vektoren bi und b2, so muss er auch alle ihre
Linearkombinationen enthalten. Deshalb wäre bs notwendigerweise in diesem
Spaltenraum, und ^x = bs ist ebenso notwendig lösbar.
3.1 B Beschreiben Sie einen Unterraum S eines jeden der folgenden
Vektorräume V, und dann einen Unterraum SS von S.
Vi = alle Linearkombinationen von A,1,0,0) und A,1,1,0) und A,1,1,1)
V2 = alle Vektoren, die senkrecht auf u = A,2,2,1) stehen
Vs = alle symmetrischen 2 x 2-Matrizen
V4 = alle Lösungen der Gleichung dt^y/dx"^ = 0.
Beschreiben Sie jeden Raum V auf zwei Weisen: Alle Linearkombinationen
von ...., Alle Lösungen der Gleichungen
Lösung Ein Unterraum S von Vi besteht aus allen Linearkombinationen
der ersten beiden Vektoren A,1,0,0) und A,1,1,0). Ein Unterraum SS von
S wäre durch alle Vielfachen (c, c, 0,0) des ersten Vektors gegeben.
Einen Unterraum S von V2 erhält man durch alle Linearkombinationen von
zwei Vektoren A,0,0, -1) und @,1, -1,0) senkrecht zu u. Der Vektor x =
A,1, -1, -1) liegt in S, und seine Vielfachen ex liefern einen Unterraum SS.
Durchgerechnete Aufgaben 611
Die Diagonalmatrizen bilden einen Unterraum S der symmetrischen
Matrizen. Die Vielfachen cl wiederum bilden einen Unterraum SS der
Diagonalmatrizen.
V4 enthält alle kubischen Polynome y =^ a-\-bx -\- cx^ -h dx^. Die
quadratischen Polynome bilden einen Unterraum S, die linearen Polynome wären ein
möglicher Unterraum SS. Die Konstanten könnte man als Unterraum SSS
darin wählen.
In allen vier Fällen hätten wir S = V selbst und SS = Z (Nullraum) wählen
können.
Jeden Raum V kann man als Menge der Linearkombinationen von und
als Menge der Lösungen von beschreiben:
Vi = alle Linearkombinationen der 3 Vektoren
=: alle Lösungen von t;i — '^2 = 0
V2 = alle Linearkombinationen von A,0,0,—1), @,1,-1,0), B,—1,0,0)
= alle Lösungen von u^v = 0
V3 = alle Linearkombinationen von [oo]'[io]'[oi]
= alle Lösungen [^ ^] von b = c
V4 — alle Linearkombinationen von l,a:,a:^,a:^
= alle Lösungen von d^y/dx^ = 0.
3.2 A Geben Sie eine 3 x 4-Matrix an, deren spezielle Lösungen der
Gleichung ^x = 0 durch si und S2 gegeben sind:
si
r-3'
1
0
0
und S2 =
'-2'
0
-6
1
Pivotspalten 1 und 3
freie Variablen X2 und X4
Sie könnten die Matrix A in reduzierter Treppenform R konstruieren, und
dann alle möglichen Matrizen A angeben, deren Kern wie verlangt von si
und S2 erzeugt wird.
Lösung Die reduzierte Matrix R hat die Pivotelemente 1 in den Spalten
1 und 3. Es gibt kein drittes Pivot element, deshalb ist die dritte Zeile von
R eine Nullzeile. Die freien Spalten 2 und 4 sind Linearkombinationen der
Pivotspalten:
Für R =
1302
00 16
0000
gilt Rsi = 0 und Rs2 = 0.
612 Durchgerechnete Aufgaben
Die Einträge 3,2,6 sind die mit -1 multiplizierten Einträge -3,-2,-6 in
den speziellen Lösungen!
R ist nur eine Matrix (ein mögliches A) mit dem verlangten Kern. Wir
könnten beliebige Elementaroperationen (Zeilenvertauschungen, Zeilen mit
beliebigem c^ 0 multiplizieren, ein Vielfaches einer Zeile von einer anderen
subtrahieren) auf R anwenden, ohne den Kern zu verändern. Alle Matrizen A
mit einem Kern wie oben verlangt lassen sich so erzeugen. (Sie haben alle
denselben Zeilenraum.)
Jede 3 x 4-Matrix hat mindestens eine spezielle Lösung. Diese A''s haben
zwei.
3.2 B Bestimmen Sie die speziellen Lösungen, und beschreiben Sie die
vollständige Lösung der Gleichungen ^x = 0 mit
Ai = 3 X i-Nullmatrix
36
12
As = [A2 A2]
Geben Sie die Pivotspalten und die freien Variablen an, und bestimmen Sie
R in jedem Fall.
Lösung Die Gleichung ^ix = 0 hat vier spezielle Lösungen. Es handelt
sich um die Spalten 81,82,83,34 der 4 x 4-Einheitsmatrix. Der Kern ist der
gesamte R^. Als vollständige Lösung erhält man einen beliebigen Vektor x =
C181 +C282 + C383 -I-C484 in R^. Es gibt keine Pivotspalten, alle Variablen sind
frei, die reduzierte Treppenform R ist die Nullmatrix Ai.
Die Gleichung A2X = 0 hat nur die eine spezielle Lösung s = (-2,1). Die
Vielfachen x = C8 liefern die vollständige Lösung. Die erste Spalte von A2 ist
die Pivotspalte, und X2 ist die freie Variable. Die reduzierten Treppenformen
R2 für A2 und Rs für ^3 = [^2 ^2] haben die Pivotelemente 1:
R2 =
1 2
00
Rs
12 12
0000
Beachten Sie, dass -R3 nur eine Pivotspalte hat (die erste Spalte). Die
Variablen 0:2,3:3, a;4 sind alle frei, und es gibt drei spezielle Lösungen der Gleichung
^3X = 0 (und auch der Gleichung R^x^ 0):
81 = (-2,1,0,0), 82 = (-1,0,1,0), 83-(-2,0,0,1),
voll8tändig x = Ci8i -h C282 + C383.
Mit r Pivotelementen hat An — r freie Variablen, und die Gleichung ^x = 0
hat n — r spezielle Lösungen.
3.3 A Man faktorisiere die folgenden Matrizen vom Rang eins in der Form
A = uv^ = Spalte mal Zeile:
A =
123
246
369
a b
c d
Durchgerechnete Aufgaben 613
(bestimmen Sie d aus a"^, &, c)
Zerlegen Sie diese Matrix vom Rang 2 in der Form uivf + vl^m^
mal B X 4) unter Verwendung von E~^ und R:
E-^R.
Cx 2)
Fl 102'
1203
[2305
=
'1 10'
120
231
'1001'
0101
000 oj
Lösung Alle Zeilen der 3 x 3-Matrix A sind Vielfache von v^ = [1 2 3].
Alle Spalten sind Vielfache der Spalte u = A,2,3). Für diese symmetrische
Matrix gilt also u = v, so dass A = uu-^ ist. Jede symmetrische Matrix vom
Rang eins hat entweder diese Form, oder die Form — uu-^.
Hat eine 2 x 2-Matrix [^ ^] den Rang eins, so muss sie singular sein. In
Kapitel 5 werden wir sehen, dass ihre Determinante ad — bc = 0 ist. In
diesem Kapitel sehen wir, dass Zeile 2 ein Vielfaches von Zeile 1 ist, nämlich
das --fache (unter der Voraussetzung a ^ 0). Ist der Rang eins, hat man
immer ein Produkt einer Spalte mit einer Zeile:
a b
c d
1
c/a
[a h] ^
a b
c bc/a
Also d =
bc
Die 3 X 4-Matrix vom Rang zwei ist die Summe zweier Matrizen vom Rang
eins. Alle Spalten von A sind Linearkombinationen der Pivotspalten 1 und
2. Alle Zeilen sind Linearkombinationen der beiden von Null verschiedenen
Zeilen in R. Die Pivotspalten sind Ui und U2, und die von Null verschiedenen
Zeilen sind vf und v^. Dann ist A gleich Uiv^^ + U2V2^, wobei die Spalten
von E~^ mit den Zeilen von R multipliziert werden:
102"
1203
2305
=
"l"
1
2
[10 0 1]
[0 10 1]
3.3 B Bestimmen Sie die reduzierte Treppenform R und den Rang r von
A — sie hängen von c ab. Welche Spalten sind die Pivotspalten von A?
Welche Variablen sind frei? Geben Sie auch die speziellen Lösungen und die
Kernmatrix N (immer in Abhängigkeit von c) an.
A =
12 1
363
48c
und A =
c c
c c
614 Durchgerechnete Aufgaben
Lösung Die 3 x 3-Matrix A hat den Rang r = 2 außer für 0 = 4. Die
Pivotelemente stehen in den Spalten 1 und 3. Die zweite Variable X2 ist frei.
Beachten Sie die Form von R:
c^A R
1 20
001
000
4 R =
121
000
000
Für c = 4 steht das einzige Pivotelement in Spalte 1 (eine Pivotspalte). Die
Spalten 2 und 3 sind Vielfache von Spalte 1, der Rang ist also eins. Damit sind
die zweite und die dritte Variable frei und liefern zwei spezielle Lösungen.
c 7^ 4 Spezielle Lösung mit X2 = 1 ergibt N =
-2
1
0_
[-2
1
0
-1
0
1
c = 4 Eine weitere spezielle Lösung ergibt N
Die 2 X 2-Matrix [^ c] hat den Rang r = 1 außer für c = 0, in diesem Fall
ist der Rang null.
c:^0 R =
1 1
00
c = 0 R =
00
00
Die erste Spalte ist die Pivotspalte, falls c ^ 0 gilt, und die zweite Variable
ist frei (also eine spezielle Lösung in AT). Die Matrix hat keine Pivotspalten
für c = 0, so dass beide Variablen frei sind:
c:^0 N =
c = 0 N =
10
Ol
3.4 A In dieser Aufgabe geht es um die Verbindung zwischen der
Elimination, den Pivotspalten und der Rücksubstitution einerseits und dem
Spaltenraum, dem Kern, dem Rang und der Lösbarkeit andererseits — also um
das große Ganze. Die 3 x 4-Matrix A hat den Rang zwei:
xi + 2a:2 + 3a:3 + 5x4 = bi
^x = b ist 2a:i + 4:X2 + 80:3 + 12a:4 = 62
Sxi + 60:2 + 7a:3 + 13a:4 = 63
1. Reduzieren Sie [^ b] auf [C/ c], so dass Ak = b zu einem Dreieckssystem
C/x = c wird.
Durchgerechnete Aufgaben 615
2. Finden Sie eine Bedingung an 61,62? ^s? die sicherstellt, dass ^x = b eine
Lösung hat.
3. Beschreiben Sie den Spaltenraum von A. Um welche Ebene in R^ handelt
es sich?
4. Beschreiben Sie den Kern von A. Welche Vektoren in R^ sind spezielle
Lösungen?
5. Bestimmen Sie eine partikuläre Lösung der Gleichung ^x = @,6, —6)
und damit die vollständige Lösung.
6. Reduzieren Sie [U c] zu [i^d]: spezielle Lösungen aus R, partikuläre
Lösung aus d.
Lösung
1. Die Multiplikatoren beim EHminationsverfahren sind 2, 3 und -1. Aus
[^b] wird [U c].
123 5bi
2 4 8 12 b2
3 6 7 13 bs
12 3 5
00 2 2
0 0-2-2
bi
b2-
bs-
-2bi
-3bi
->
'1235
0022
0000
bi
b2 — 2bi
bs + b2 - 5bi
2. In der letzten Zeile steht die Bedingung für die Lösbarkeit: 63 + 62-561 =
0. Dann gilt 0 = 0.
3. Erste Beschreibung: Der Spaltenraum ist die Ebene, die alle
Linearkombinationen der Pivotspalten A,2,3) und C,8,7) enthält, da die
Pivotelemente in den Spalten 1 und 3 stehen. Zweite Beschreibung:
Der Spaltenraum enthält alle Vektoren, für die 63 + 62 — 561 = 0 gilt.
Diese Bedingung macht Ax = h lösbar, b liegt im Spaltenraum. Alle
Spalten von A geniigen der Bedingung 63 + 62 — 56i = 0. Dies ist die
Ebenengleichung der ersten Beschreibung.
4. Die speziellen Lösungen haben die freien Variablen 0:2 = 1,^:4 = 0 und
damit 0:2 = 0,0:4 = 1:
Spezielle Lösungen für ^x = 0
Rücksubstitution in Ux = 0
si
-2'
1
0
0
S2 =
"-2
0
-1
1
Der Kern N(A) in E^ enthält alle Xn = ciSi + C2S2 = (-2ci -
2C2,C1, -C2,C2).
616 Durchgerechnete Aufgaben
5. Man erhält eine partikuläre Lösung Xp, wenn man alle freien Variablen
zu Null setzt. Rücksubstitution in Ux = c liefert dann:
Partikuläre Lösung für Axp = @,6, -6)
Der Vektor b erfüllt 63 + &2 - 56i = 0
Xr> —
Die vollständige Lösung der Gleichung ^x = @,6,-6) ist also x = Xp +
alle Xn-
6. In der reduzierten Treppenform R ändert sich die dritte Zeile von C,2,0)
in U zu @,1,0). Die rechte Seite c = @,6,0) wird zu d = (-9,3,0), mit
-9 und 3 aus x^:
[Uc]
12350
00226
00000
\Rd] =
1202-9
00 11 3
0000 0
3.4 B Was können Sie aus den folgenden Informationen über die
Lösungen der Gleichung ^x = b für ein festes b über die Gestalt von A, A selbst,
und womöglich über b schließen?
1. Es gibt genau eine Lösung.
2. Alle Lösungen der Gleichung ^x = h haben die Form x = [^] + c[J].
3. Es gibt keine Lösung.
4. Alle Lösungen von ^x = h haben die Form x = 1 + c 0 .
5. Es gibt unendlich viele Lösungen.
Lösung Im Fall 1 mit genau einer Lösung muss A vollen Spaltenrang
r — n haben. Der Kern von A enthält nur den Nullvektor, und es muss
notwendigerweise m > n gelten.
Im Fall 2 muss A n~2 Spalten (bei beliebigem m) haben. Da [\] im Kern
von A liegt, muss Spalte 2 gleich minus Spalte 1 sein. Da a: = [ ^ ] eine Lösung
ist, gilt b = (Spalte 1) + 2 (Spalte 2) = Spalte 2. Die Spalten können keine
Null Vektoren sein.
Im Fall 3 wissen wir nur, dass b nicht im Spaltenraum von A liegt. Der Rang
von A muss kleiner als m sein. Ich schätze, wir wissen, dass b 7^ 0 ist, denn
andernfalls wäre x = 0 eine Lösung.
Durchgerechnete Aufgaben 617
Im Fall 4 muss An = S Spalten haben. Da A,0,1) im Kern liegt, ist Spalte 3
gleich minus Spalte 1. Spalte 2 kann kein Vielfaches von Spalte 1 sein, denn
dann gäbe es noch eine weitere spezielle Lösung im Kern. Der Rang von A
ist also 3 — 1 = 2. Damit hat Am>2 Zeilen. Die rechte Seite b ist Spalte 1
+ Spalte 2.
Im Fall 5 mit unendlich vielen Lösungen muss der Kern von Null verschiedene
Vektoren enthalten. Der Rang r muss dazu kleiner als n sein (kein voller
Spaltenrang), und b muss im Spaltenraum von A liegen. Wir wissen nicht,
ob jedes h im Spaltenraum liegt, wir wissen also nicht, ob r = m gilt.
3.4 C Bestimmen Sie die vollständige Lösung x — Xp+Xn durch
Vorwärtselimination auf [A b]:
[12 10"
2448
l4868
'xi~
^2
^3
X4
=
' 4'
2
10 j
Bestimmen Sie Zahlenyi,y2,y3 so, dass yi (Zeile l)+y2 (Zeile 2)+y3 (Zeile 3) =
Nullzeile. Überprüfen Sie, dass b = D,2,10) die Bedingung yibi + ^2^2 +
y^bs =0 erfüllt. Warum ist dies die Bedingung dafür, dass das
Gleichungssystem lösbar ist und b im Spaltenraum liegt?
Lösung Durch Vorwärtselimination auf [A h] erzeugt man eine Nullzeile
in [U c]. Die dritte Gleichung wird also 0 = 0, so dass das Gleichungssystem
konsistent und damit lösbar ist:
12 10 4
2448 2
48 68 10
12 10 4
00 28-6
002 8-6
12 10 4
002 8-6
0000 0
Die Spalten 1 und 3 enthalten die Pivotelemente. Die Variablen X2 und X4
sind die freien Variablen. Setzt man sie zu Null, lässt sich das System per
Rücksubstitution mit einer partikulären Lösung Xp = G,0, —3,0) lösen. Man
findet 7 und -3 wieder, wenn man die Elimination bis zu [R d] weiterführt:
12 10
0028
0000
1210
0014
0000
1 20
001
000
Um die Kernvektoren Xn mit b = 0 zu bestimmen, setzt man die freien
Variablen X2,X4 auf 1,0 und auch auf 0,1:
Spezielle Lösungen si = (-2,1,0,0) und S2 — D,0, -4,1)
Die vollständige Lösung der Gleichungen Ax = h und -Rx = d ist damit
durch Xvoiist = Xp + CiSi + C2S2 gegeben.
618 Durchgerechnete Aufgaben
Aus den Zeilen von A erzeugt man die Nullzeile durch 2(Zeile 1) + (Zeile 2) -
(Zeile 3) = @,0,0,0). Dieselbe Kombination für b = D,2,10) ergibt 2D) -f
B) - A0) = 0. Ergibt eine Linearkombination der Zeilen auf der linken Seite
die Nullzeile, so muss dieselbe Kombination auf der rechten Seite Null ergeben
— natürlich! Denn sonst gäbe es keine Lösung.
Später werden wir dies mit anderen Begriffen ausdrücken: Ist jede Spalte von
A senkrecht zu y = B,1,-1), so ist auch jede Linearkombination b dieser
Spalten senkrecht zu y. Gilt dies für ein b nicht, so liegt der Vektor nicht im
Spaltenraum, so dass ^x = b nicht lösbar ist.
Und noch einmal: Ist y im Kern von SO muss y senkrecht auf jedem
Vektor b im Kern stehen. Nur eine kleine Vorschau ...
3.5 A Gegeben seien die Vektoren vi = A,2,0) und V2 = B,3,0). (a)
Sind sie linear unabhängig? (b) Bilden sie die Basis irgendeines Vektorraums?
(c) Welchen Raum V erzeugen sie? (d) Welche Dimension hat dieser Raum?
(e) Zu welchen Matrizen ist V der Spaltenraum? (f) Zu welchen Matrizen
ist V der Kern? (g) Beschreiben Sie alle Vektoren V3, so dass vi, V2, V3 eine
Basis des E^ ist.
Lösung
1. Vi und V2 sind linear unabhängig — die einzige Linearkombination, die
0 erzeugt, ist Ovi + 0v2.
2. Ja, sie bilden eine Basis für den von ihnen aufgespannten Raum V.
3. Dieser Raum V enthält alle Vektoren der Form (a:,y,0). Es handelt sich
um die xy-Ehene in R^.
4. Die Dimension von V ist 2, da die Basis aus zwei Vektoren besteht.
5. Dieser Raum V ist der Spaltenraum einer jeden 3 x n-Matrix A vom Rang
2, deren Spalten Linearkombinationen von vi und V2 sind. Insbesondere
könnte A einfach aus den Spalten vi und V2 bestehen.
6. Dieser Raum V ist der Kern einer jeden m x 3-Matrix B mit Rang
1, deren Zeilen Vielfache von @,0,1) sind. Als Beispiel betrachte man
B = [0 0 1]. Für diese Matrix gilt Bvi = 0 und Bv2 = 0.
7. Mit einem beliebigen Vektor V3 = {a,b,c) mit c ^ 0 ergibt sich eine
vollständige Basis des R^.
3.5 B Gegeben seien drei linear unabhängige Vektoren wi,W2,W3. Die
Vektoren vi,V2,V3 seien Linearkombinationen dieser Vektoren. Stellen Sie
diesen Sachverhalt als Matrizengleichung V = WM dar:
Vi V2 V3
=
Wi W2 W3
'1 10
121
01c
Durchgerechnete Aufgaben 619
Vi = Wi + W2
V2 = Wi + 2w2 + W3 bzw.
V3 = W2 + CW3
Wie überprüft man für die Matrix V, ob ihre Spalten linear unabhängig sind?
Zeigen Sie, das vi,V2,V3 für c 7^ 1 linear unabhängig und für c = 1 linear
abhängig sind.
Lösung Wir können unserer ersten Definition entnehmen, wie man die
lineare Unabhängigkeit der Spalten einer Matrix V überprüft: Der Kern von
V darf nur den Nullvektor enthalten. Dann ist x = @,0,0) die einzige
Linearkombination der Spalten, für die Fx den Nullvektor ergibt.
Für c = 1 können wir die lineare Abhängigkeit auf zwei Arten feststellen.
Erstens ist vi + V3 dasselbe wie V2. (Addiert man wi + W2 zu W2 + W3, so
erhält man wi + 2w2 + W3 gleich V2.) Anders gesagt, gilt vi — V2 + V3 = 0
— die v's sind also nicht linear unabhängig.
Die andere Möglichkeit ist, den Kern von M zu betrachten. Für c = 1 liegt
der Vektor x = A, —1,1) in diesem Kern, es gilt Mx = 0. Dann gilt sicher
auch WMx = 0, also Vx = 0. Daher sind die v's linear abhängig. Dieser
Vektor x = A,-1,1) im Kern liefert uns wieder, dass vi — V2 + V3 = 0 gilt.
Sei nun c ^ 1. Dann ist die Matrix M invertierbar. Ist also x ein beliebiger
von Null verschiedener Vektor, so ist auch Mx von Null verschieden. Da wir
vorausgesetzt haben, dass die w's linear unabhängig sind, muss auch T^Mx
von Null verschieden sein. Aus V — WM folgt damit, dass x nicht im Kern
von V liegt. Anders gesagt: die Vektoren vi, V2,V3 sind linear unabhängig.
Die allgemeine Regel ist: „Man erhält unabhängige v's aus unabhängigen w's,
wenn M invertierbar ist." Liegen diese Vektoren in W, so sind sie nicht nur
linear unabhängig, sondern sie bilden auch eine Basis des M^: „Man erhält
eine Basis aus v's aus einer Basis aus w's, wenn die Basiswechselmatrix M
invertierbar ist."
3.5 C Es sei Vi,... ,Vn eine Basis des M"^, und die n x n-Matrix A sei
invertierbar. Zeigen Sie, dass Awi,... , Awn ebenfalls eine Basis des W^ bildet.
Lösung Durch Matrizen ausgedrückt: Die Basisvektoren vi,... ,Vn
bilden die Spalten einer invertierbaren Matrix V. Dann bilden ^vi,... ,Av„
die Spalten der Matrix AV. Da A invertierbar ist, ist auch AV invertierbar,
und die Spalten bilden eine Basis.
Durch Vektoren ausgedrückt: Es sei ciAvi H h CnAwn = 0. Dies lässt sich
mit V = ciVi H h CnVn auch als A\ = 0 schreiben. Multipliziert man mit
A~'^, so erhält man v = 0. Da die v's linear unabhängig sind, müssen alle
Koeffizienten ci = 0 sein. Es sind also auch die ^v's linear unabhängig.
Um zu zeigen, dass die ^v's den W erzeugen, löst man die Gleichung ci Avi +
h CnAvn = b. Dies ist äquivalent zu civi H h Cnyrn = A~^h. Da die
v's eine Basis bilden, muss diese Gleichung lösbar sein.
620 Durchgerechnete Aufgaben
3.6 A Bestimmen Sie Basen und die Dimensionen der vier fundamentalen
Unterräume von
A= 210 0016 ^E-^R.
rioo'
210
[öOl
'13051
0016
ooooj
Ändern Sie nur eine Zahl so, dass sich die Dimensionen aller vier Unterräume
ändern.
Lösung Diese Matrix hat ihre Pivotelemente in den Spalten 1 und 3, und
ihr Rang ist r = 2.
Zeilenraum: Basis A,3,0,5) und @,0,1,6) aus R. Dimension 2.
Spaltenraum: Basis A,2,5) und @,1,0) aus E~^. Dimension 2.
Kern: Basis (—3,1,0,0) und (—5,0, —6,1) aus R. Dimension 2.
Kern von Ä^: Basis (—5,0,1) aus Zeile 3 von E. Dimension 3 — 2 = 1.
Über den Kern N(A-^) müssen wir noch eine Bemerkung machen. Die
Gleichung EA = R besagt, dass die letzte Zeile von E ein Basisvektor des Kerns
der Transponierten ist. Hätte R zwei Nullzeilen, dann wären die letzten beiden
Zeilen von E eine Basis des Kerns der Transponierten (der die Kombinationen
der Zeilen von A enthält, die die Nullzeile ergeben).
Um diese Dimensionen zu ändern, müssen wir den Rang r verändern. Man
erreicht dies, indem man einen (beliebigen) Eintrag in der letzten Zeile von
R ändert.
3.6 B Stellen Sie sich vor, sie sollen vier Einsen in einer 5 x 6-Matrix
platzieren, deren restUche Einträge Nullen sind. Beschreiben Sie alle
Möglichkeiten, die Dimension des Zeilenraums so klein wie möglich zu machen.
Beschreiben Sie auch alle Möglichkeiten, die Dimension des Spaltenraums so
klein wie möglich zu machen. Beschreiben Sie schließlich alle Möglichkeiten,
die Dimension des Kerns so klein wie mögUch zu machen. Geben Sie die
minimalen Dimensionen an. Welche Möglichkeiten haben Sie, wenn Sie die
Summe der Dimensionen aller vier Unterräume so klein wie möglich machen
wollen?
Lösung Der Rang ist 1, wenn man die vier Einsen in eine Zeile oder in eine
Spalte setzt, oder in zwei Zeilen und zwei Spalten (so dass au = aij = üji =
üjj — 1 gilt). Da Spaltenraum und Zeilenraum immer dieselbe Dimension
haben, beantwortet dies die ersten beiden Fragen: die Dimension ist 1.
Der Kern hat die kleinst mögliche Dimension 6 — 4 = 2, wenn der Rang r = 4
ist. Um Rang vier zu erreichen, müssen die vier Einsen in vier
unterschiedlichen Zeilen und Spalten stehen. Bei der Summe r-\-{n—r)-\-r-{-{Tfi—r) = n-Vvfi
kann man nichts erreichen — sie wird immer 6 + 5 = 11 sein, unabhängig
davon, wie die Einsen platziert werden. Die Summe ist sogar 11, wenn es gar
keine Einsen gibt ...
Durchgerechnete Aufgaben 621
Wie ändern sich die Antworten, wenn alle übrigen Einträge von A „2" statt
„0" sind?
4.1 A Es sei S ein sechsdimensionaler Unterraum des E^. Welche
Dimensionen können Unterräume orthogonal zu S haben? Welche Möglichkeiten
bestehen für die Dimension des orthogonalen Komplements S"*- von S?
Bestimmen Sie die kleinst mögliche Größe einer Matrix A, deren Zeilenraum S
ist. Welche Gestalt hat ihre Kernmatrix N? Wie könnten Sie eine Matrix B
mit zusätzlichen Zeilen, aber identischem Zeilenraum erzeugen? Vergleichen
Sie die Kernmatrix für B mit der Kernmatrix für A.
Lösung Unterräume von M^, die orthogonal zu dem sechsdimensionalen
Unterraum S sind, können die Dimensionen 0, 1, 2 und 3 haben. Das
orthogonale Komplement ist der größte orthogonale Unterraum mit der Dimension
3. Die kleinste Matrix A muss aus 9 Spalten und 6 Zeilen bestehen, die eine
Basis des sechsdimensionalen Zeilenraums S bilden. Die Kernmatrix ist eine
9 X 3-Matrix, da ihre Spalten eine Basis für S-*- enthalten.
Setzt man als Zeile 7 von B eine Linearkombination der sechs Zeilen von A,
so hat B denselben Zeilenraum wie A. Sie hat auch dieselbe Kernmatrix iV,
da die speziellen Lösungen gleich bleiben — das Eliminationsverfahren macht
aus Zeile 7 eine Nullzeile.
4.1 B Die Gleichung x — 4y — 5z = 0 beschreibt eine Ebene E in M^. Den
Kern welcher 1 x 3-Matrix stellt diese Ebene dar? Bestimmen Sie eine Basis
si, S2 aus speziellen Lösungen von x — Sy-4:Z = 0 — sie bilden die Spalten der
Kernmatrix N. Bestimmen Sie auch eine Basis für die Gerade E-*- senkrecht
zu E. Zerlegen Sie den Vektor v = F,4,5) in seine Kernkomponente Vn in
E und seine Zeilenraumkomponente v^. in E-*-.
Lösung Die Gleichung x - 3y — iz = 0 lässt sich als Ax = 0 mit der
1 X 3-Matrix A = [1 - 3 - 4] schreiben. Die Spalten 2 und 3 sind frei (keine
Pivotelemente), und die speziellen Lösungen, bei denen die freien Variablen
auf 1 beziehungsweise 0 gesetzt werden, sind si = C,1,0) und S2 = D,0,1).
Der Zeilenraum von A (die Gerade E-*-) hat die Basis z = A, —3, —4). Dieser
Vektor steht senkrecht auf si und S2, und auf der ganzen Ebene E.
Um V in Vfi ~l~ Vy. — (ciSi -l~ C2S2) -l- C3Z zu zerlegen, löst man diese Gleichung
nach ci, C2, C3 auf:
führt auf ci = 1^ C2 = 1, C3 = —1
Vn = si+S2 = G,1,1) liegt in E = N(A)
v^ =-S3 = (-1,3,4) liegtauf E^ = S(A^).
4.2 A Projizieren Sie den Vektor b = C,4,4) auf die Gerade durch a =
B,2,1) und dann auf die Ebene, die auch a* = A,0,0) enthält. Rechnen
[34 1"
10-3
[01 -4
"ci"
C2
.^3_
=
1
4
5J
622 Durchgerechnete Aufgaben
Sie nach, dass der erste Fehlervektor b — p senkrecht auf a steht und der
zweite Fehlervektor b — p* außerdem noch senkrecht auf a*. Bestimmen Sie
die 3 X 3-Projektionsmatrix auf diese Ebene. Bestimmen Sie einen Vektor e*,
dessen Projektion auf die Ebene von a und a* der Nullvektor ist.
Lösung
ist 2a:
Die Projektion von b = C,4,4) auf die Gerade durch a = B,2,1)
p=^a=HB,2,l) = D,4,2).
a^ a
9
Der Fehlervektor e = b-p = (-l,0,2) steht senkrecht auf a. Der Vektor p
ist also richtig berechnet worden.
Die Ebene, die die Vektoren a = B,2,1) und a* = A,0,0) enthält, ist der
Spaltenraum von A:
A =
2 1
20
10
A^A =
92
21
{Ä'A)-^ -
1-2
-2 9
10 0
0 0,8 0,4
0 0,4 0,2
Damit gilt p* = Pb = C, 4,8, 2,4), und e* = b - p* = @, -0,8, 1,6) steht
senkrecht auf a und a*. Dieser Vektor e* liegt im Kern von P, seine Projektion
ist null! Beachten Sie P^ ::^ p
4.2 B Stellen Sie sich vor, ihr Puls wird einmal mit a: = 70 Schlägen pro
Minute gemessen, dann mit a: = 80 und dann mit x — 120 Schlägen. Diese drei
Gleichungen Ax = b in einer Unbekannten lassen sich mit A^ = [111] und
b = G0,80,120) schreiben. Der beste Wert x ist der von 70,80,120.
Verwenden Sie dazu einerseits die Differentialrechnung, andererseits
Projektionen:
1. Minimieren Sie E = {x-l{)f^-{x-mf^-{x-l20Y, indem Sie dE/dx = 0
lösen.
2. Projizieren Sie den Vektor b = G0,80,120) auf a = A,1,1) und
bestimmen Sie X — a^b/a^a.
Verwendet man die Methode der kleinsten Quadrate rekursiv, so bestimmt
man bei einer weiteren Messung 130 aus Jait einen neuen Wert Jneu-
Berechnen Sie Xneu und verifizieren Sie die „Aktualisierungs-Formel" x^eu =
^ait + ^A30 - Salt)- Vom 999. zum 1000. Messwert erhält man den
aktualisierten Wert durch Jneu = ^ait + 1^(^1000 — ^ait)- Man benötigt also nur
Salt und den letzten Messwert 61000, und muss nicht den Mittelwert aller 1000
Zahlen bestimmen!
Lösung Die nächste horizontale Gerade zu den Höhen 70,80,120 ist der
Mittelwert x = 90:
DifF'rechnung :
Projektion :
Durchgerechnete Aufgaben 623
dE
-— = 2{x- 70) + 2(x - 80) + 2{x - 120) = 0
,. - ^ ^ 70 + 80 + 120
liefert x =
3
^ a^b A,1,1)^G0,80,120) 70 + 80 + 120
"^-a^a- A,1,1)^A,1,1) - 3
Ä^Ax = Ä^h ist eine 1 x 1-Matrix, weil A nur eine Spalte A,1,1) hat. Die
neue Messung 64 = 130 fügt eine vierte Gleichung hinzu, und x wird entweder
dadurch auf den Wert 100 aktualisiert, dass man den neuen Mittelwert aus
^1) ^2, ^3, ^4 berechnet, oder rekursiv unter Verwendung des alten Mittelwerts
aus 61,62,63:
70 + 80 + 120 + 130 ^^^ ^ ^ru - ^ nn . '^ rAf^\
a:neu = ^ = 100 = x^it + 4(^4 - a:ait) = 90 + |D0).
Die Aktualisierung von 999 auf 1000 Messungen weist die „Verstärkungs-
Matrix" Y^ in einem Kaiman-Filter auf, die mit dem Fehlerschätzer 6neu —
Xait multipliziert wird. Beachten Sie, dass j^ = ^ - Qöiööö Sil^'
61 H h 61000 61 H h 6999 , 1 A 61 H h 6999 ^
^neu = TTTT^T; — 7^7^ ^ TT^TTT^ ^1000
^('
1000 999 1000 V 999
4.3 A Gegeben seien neun Messungen 61 bis 69, alle mit dem Wert null,
zu den Zeiten ^ = 1,... , 9. Die zehnte Messung 610 = 40 ist ein Ausreißer.
Bestimmen Sie die am besten an die zehn Punkte A,0), B,0),... , (9,0), A0,40)
angepasste horizontale Gerade y — C. Verwenden Sie dazu drei verschiedene
Fehlermaße: A) Kleinste Quadrate e\-\ he^o B) Kleinster Maximalfehler
kmaxl C) Kleinste Fehlersumme |ei| + • • • + |eio|.
Bestimmen Sie dann nach der Methode der kleinsten Quadrate die beste
Gerade C -\- Dt durch diese zehn Punkte. Was geschieht mit C und D, wenn
man die bi mit 3 multipliziert und 30 addiert, und bneu = C0,30,. •. , 150)
betrachtet? Welche beste Gerade erhält man, wenn man die Zeitpunkte ti =
1,... ,10 mit 2 multipliziert und 10 addiert, so dass sich ^„eu = 12,14,... ,30
ergibt?
Lösung A) Nach der Methode der kleinsten Quadrate passt man an die
Werte 0,0,... , 0,40 eine horizontale Gerade mit dem Mittelwert C = f^ == 4
an. B) Der kleinste Maximalfehler entsteht für C = 20, in der Mitte zwischen
0 und 40. C) Die kleinste Fehlersumme erhält man für C = 0 (ü). Die
Fehlersumme 9|C| + |40 - C\ würde wachsen, wenn man C erhöhte.
Das Fehlermaß der kleinsten Fehlersumme stammt von einer Medianmessung
— der Median von 0,... ,0,40 ist Null. Ändert man den besten Wert y =
624 Durchgerechnete Aufgaben
C = ^median? SO erhöht man die eine Hälfte der Fehler und verringert die
andere Hälfte. Viele Statistiker sind der Meinung, dass bei der Methode der
kleinsten Quadrate Ausreißer wie 610 = 40 das Ergebnis zu stark beeinflussen,
und ziehen die Methode der kleinsten Fehlersumme vor. Bei dieser Methode
werden die Gleichungen aber nichtlinear.
Um die beste Gerade C -{- Dt nach der Methode der kleinsten Quadrate zu
bestimmen, benötigt man Ä^A und A^h mit ^ = 1,... , 10:
A^A
10 Eti'
EtiEtl
0 55'
55 385
A^h =
' Eti '
. Z) tibi
■55
400
Diese Matrizen erhält man aus Gleichung (9). Mit ihnen ergibt sich A^Ax =
A^h, also C = —1 und D = 13/11. Wegen der Linearität dürfen wir die
Messungen b = @,0,... ,40) umskalieren. Multipliziert man b mit 3, so
werden auch C und D mit 3 multipliziert. Addiert man 30 zu allen bi, so
wird auch 30 zu C addiert.
MultipHziert man die Zeiten ti mit 2, so wird D durch 2 dividiert, so dass
die Gerade zu den neuen Zeiten dieselben Höhen erreicht. Addiert man zu
allen Zeiten 10 hinzu, so muss man t gegen ^ — 10 austauschen. Die neue
Gerade C-\-D{^^y^) erreicht die Höhen (mit denselben Fehlern) zu den Zeiten
^ = 12,14,... , 30, die sie vorher zu den Zeiten ^ = 1,2,... , 10 erreicht hatte.
In der Sprechweise der linearen Algebra haben die Matrizen Aalt und Aneu
denselben Spaltenraum (warum?), so dass keine Änderung der Projektion
nötig ist:
111111111 1
1 23456789 10
iT
1111111111
12 14 16 18 20 22 24 26 28 30
4.3 B Bestimmen Sie die Parabel C-\-Dt-\-Et^, die (im Sinne der Methode
der kleinsten Quadrate) den Werten b = @,0,1,0,0) zu den Zeiten t =
-2,-1,0,1,2 am nächsten kommt. Geben Sie zuerst die fünf Gleichungen
in drei Unbekannten dafür an, dass die Parabel durch die Punkte verläuft.
Es gibt dazu keine Lösung, weil keine solche Parabel existiert. Lösen Sie das
Gleichungssystem Ax = b dann im Kleinste-Quadrate-Sinn, indem Sie die
Gleichung A^Ax = Ä^h lösen.
Meine Vorhersage wäre D = 0. Warum sollte die beste Parabel symmetrisch
um ^ = 0 sein? In dem System A^Ax = A^h sollte Gleichung 2 von den
Gleichungen 1 und 3 entkoppelt sein.
Durchgerechnete Aufgaben 625
Lösung Die fünf Gleichungen in Ax = b und die 3 x 3-Matrix A^A sind
C + D (-2) + E (-2J
C + £>(-!) + E(-lJ
C + D @) + E @J
C + D A) + E AJ
C + D B) + E BJ
= 0
- 0
= 0 A^
= 0
= 0
'1 -24"
1 -1 1
1 00
1 1 1
1 24
Ä^A =
'5 0 10
0 10 0
10 0 34
Die Nullen in A^A besagen, dass Spalte 2 von A orthogonal zu den Spalten
1 und 3 ist. Dies sieht man auch direkt in A (weil die Zeiten —2,-1,0,1,2
symmetrisch sind). Die optimalen Werte für C, D und E in der Parabel C +
Dt + Et"^ erhält man aus der Gleichung Ä^A9. = A^h, in der Gleichung 2
für D entkoppelt ist:
70 35
führt auf -D = 0 wie vorhergesagt
E^-'-^ = -l
70 7
Die Symmetrie der t's ist der Grund dafür, dass Gleichung 2 entkoppelt
ist. Die Symmetrie des Vektors b = @,0,1,0,0) lässt die rechte Seite zu
Null werden. Die symmetrischen Ausgangs werte erzeugten eine symmetrische
Parabel || - y^^
Man kann Spalte 3 orthogonalisieren, indem man die Projektion B,2,2,2,2)
auf Spalte 1 subtrahiert:
0 10"
0 10 0
10 0 34
"C"
D
E
=
"
0
0
^neu ^neu
= b ist
'1-2 2"
1 -1 -1
1 0-2
1 1-1
[l 2 2
'C + 2E'
D
E
=
^
0
1
0
0
Beachten Sie die
neue 3. Spalte
{A
neu ^neuj Xneu — ^neu" ^^^
'5 0 0"
0 10 0
0 0 14
'C + 2E'
D
E
=
1]
Ol
-2
Jetzt sind alle Gleichungen entkoppelt, und Aneu hat orthogonale Spalten.
Man erhält sofort UE = -2, daraus E = -\, und D = {). kus C + 2E = \
erhält man dann C' = | + f = |f wie zuvor. Die Matrix A^A wird
leicht zugänglich, wenn die Arbeit der Orthogonalisierung (also das Gram-
Schmidt-Verfahren) vorher getan wird.
4.4 A Füllen Sie die beiden Spalten mit Einträgen 1 oder -1 aus, so dass
die Spalten der entstehenden 4 x 4-„Hadamard-Matrix" orthogonal sind. Wie
erzeugen Sie aus H eine orthogonale Matrix Q?
626 Durchgerechnete Aufgaben
H
1 \ X X
1 1 X X
l—\ X X
l—\ X X
und
Q =
Warum kann eine 5 x 5-Matrix mit Einträgen 1 und —1 keine orthogonalen
Spalten haben? Tatsächlich ist die nächstmögliche Größe erst ^xS^ aus vier
Blöcken bestehend:
Die Blockmatrix Hs
H H
H-H
ist eine Hadamard-Matrix mit
orthogonalen Spalten. Was ist Hq^Hs?
Die Projektion von b = F,0,0,2) auf die erste Spalte von H ist pi =
B,2,2,2), und die Projektion auf die zweite Spalte ist p2 — A,1,-1,-1).
Bestimmen Sie die Projektion pi,2 von b auf den zweidimensionalen Raum,
der von den ersten beiden Spalten aufgespannt wird.
Lösung Die Spalten 3 und 4 dieser Matrix H könnten auch mit
tipliziert oder vertauscht werden:
-1 mul-
H =^
1111
1 1-1-1
1-1 1-1
1-1-1 1
hat orthogonale Spalten,
H
H^ H^'
H^-H^
H H'
H-H
—
'2H'^H 0
0 2if^if
"8/ 0
0 8/
Q = — hat orthonormale Spalten.
Dividiert man durch 2, so erhält man die Einheitsvektoren in der Matrix Q.
Orthogonalität ist für eine 5 x 5-Matrix dieser Art unmöglich, weil in den
Skalarprodukten jeweils fünf Summanden 1 oder —1 stehen, die nicht die
Summe Null ergeben können. Die 8 x 8-Matrix Hs hat orthogonale Spalten
der Länge \/8. Damit ist Qs gleich Hg/VS:
Hg Hs
Weil die Spalten orthogonal sind, können wir einfach den Vektor F,0,0,2) auf
die Vektoren A,1,1,1) und A,1, —1, -1) projizieren, und die Projektionen
addieren:
Projektion pi,2 = Pi + P2 - B, 2,2,2) + A,1, -1, -1) = C,3,1,1).
Dies ist der Grund, warum orthogonale Spalten so wertvoll sind. Man kann
schnell beweisen, dass pi,2 = Pi +P2 gilt, indem man überprüft, ob die
Spalten 1 und 2 (nennen wir sie ai und a2) senkrecht auf dem Fehlervektor
e = b — pi — p2 stehen:
Durchgerechnete Aufgaben 627
e = b-
afb aj^b
T
a^ai
ai -
T
a^a2
»2,
ii b ^—a( ai
T
a^ai
0, ebenso a^e
Der Vektor pi + p2 hegt also in dem von ai und a2 erzeugten Raum, und
der Fehler e steht senkrecht auf diesen Raum.
Beim Gram-Schmidt-Verfahren würde an den Richtungen von ai und a2
nichts geändert, es würden nur die Vektoren durch ihre Länge dividiert
werden. Sind aber ai und sl2 nicht orthogonal^ so ist die Projektion pi,2 im
Allgemeinen nicht gleich pi + P2 • Ist zum Beispiel b = ai, so folgt Pi = b
und pi,2 = b aber p2 ^ 0.
5.1 A Wenden Sie die folgenden Operationen auf A an und bestimmen
Sie die Determinanten von Mi, M2, M3, M4:
In Ml wird jeder Eintrag aij mit (—1)*+-^ multipliziert, so dass eine Matrix
mit Vorzeichen wie unten entsteht. In M2 werden die Zeilen 1,2,3 von A von
den Zeilen 2,3,1 subtrahiert. In M3 werden die Zeilen 1,2,3 von A zu den
Zeilen 2,3,1 addiert. Der Eintrag {i,j) von M4 ist das Skalarprodukt (Zeile
i von A)-(Zeile j von A).
Wie hängen die Determinanten von Mi,M2,M3,M4 mit der Determinante
von A zusammen?
Ml
M3 =
Oll—O12 «13 1
—«21 O22 —«23
031—032 033]
Zeile 1 + Zeile 3
Zeile 2 + Zeile 1
Zeile 3 + Zeile 2
M2 =
L
M4 =
Zeile 1 -
Zeile 2 -
Zeile 3 -
Zeile
Zeile
Zeile
Zeile 1.
Zeile 2«
Zeile 3 • Zeile 1
Zeile 1
Zeile 1
Lösung Die vier Determinanten sind detA, 0, 2detA und (det A)^. Hier
die Gründe:
Ml =
1
-1
Oll «12 «13
«21 «22 «23
«31 O32 0,33 _
1
-1
1
detMi = (-l)(detA)(-l).
Die Matrix M2 ist singular, weil die Summe der Zeilen die Nullzeile ergibt.
Daher gilt det M2 = 0.
Die Determinante der Matrix M3 kann nach Regel 3 (Linearität in jeder Zeile)
in acht Matrizen zerlegt werden:
det M3 =
Zeile 1
Zeile 2
Zeile 3
+
Zeile 3
Zeile 2
Zeile 3
+
Zeile 1
Zeile 1
Zeile 3
+ •
• +
Zeile 3
Zeile 1
Zeile 2
628 Durchgerechnete Aufgaben
Alle Matrizen bis auf die erste und die letzte haben mehrfach auftretende
Zeilen, so dass deren Determinanten den Wert Null haben. Die erste Matrix
ist A, und die letzte Matrix entsteht durch zwei Zeilenvertauschungen aus
A. Daher gilt det M3 = det A H- det A. (Zur Verdeutlichung versuchen Sie es
mit A = /.)
Die Matrix M4 ist genau AA^. Ihre Determinante ist daher (det A){det A'^) =
(detAJ.
5.1 B Bestimmen Sie die Determinante von A, indem Sie Zeile 1 von Zeile
2 subtrahieren, dann Spalte 3 von Spalte 2, und dann Zeilen oder Spalten so
vertauschen, dass eine untere Dreiecksmatrix entsteht:
Für welche a und 6 ist A =
1 1 1
al 1
06 1
Singular?
Lösung Subtrahieren Sie Zeile 1 von Zeile 2, und dann Spalte 3 von Spalte
2. Durch zwei Vertauschungen wird die Matrix auf Dreiecksgestalt gebracht.
Damit gilt det A = {a-l){b-l).
1 0 1
a-1 0 0
0 6-11
Zeilen 1^2
Spalten 2^3
a-1 0 0
1 1 0
0 16-1
Beachten Sie, dass sich für a = 1 in A identische Zeilen ergeben, und für
6=1 identische Spalten. Es ist also nicht überraschend, dass (a — 1) und
F — 1) die Faktoren von det A sind.
5.2 A Eine Hessenberg-Matrix ist eine Dreiecksmatrix mit einer
zusätzlichen Nebendiagonale. Verwenden Sie die Kofaktoren der ersten Zeile, um zu
zeigen, dass die 4 x 4-Determinante der Fibonacci-Regel |/f4| = |/f3| -h |//|
genügt. Dieselbe Regel gilt für alle Größen, es gilt \Hn\ = |^n-i| + |^n-2|-
Welche Fibonacci-Zahl ist also \Hn\^
Ho =
2 1
12
Hs =
2 1
121
1 1 2
H^ =
2 1
121
1121
1112
Lösung Der Kofaktor Cn für H4 ist die Determinante {Hsl. Wir brauchen
auch C12 (fett gedruckt):
Cr
110
12 1
112
= —
2 10
1 21
1 12
+
100
1 2 1
1 12
Durchgerechnete Aufgaben 629
Zeilen 2 und 3 bleiben gleich, in Zeile 1 haben wir die Linearität
verwendet. Die beiden Determinanten rechts sind -|i^3| und H-|i^2|- Die 4x4-
Determinante ist dann
\H4\ = 2Cn + lCi2 = 2\Hs\ - \Hs\ + IF2I = I//3I + |i^2|.
Die tatsächUchen Werte sind |ür2| = 3 und \Hs\ = 5 (und natürlich lifil = 2).
Da die Werte für \Hn\ der Fibonacci-Regel genügend gleich \Hn-i\ + \Hn-2\
sind, muss \Hn\ = i^n+2 sein.
5.2 B Bei diesen Fragen geht es um die Vorzeichen (also gerade und
ungerade Permutationen) in der großen Formel für die Determinante:
1. Es sei A die 10 x 10-Matrix, deren Einträge sämtlich 1 sind. Wie erhält
man det A = 0 aus der großen Formel?
2. Ist das Ergebnis gerade oder ungerade, wenn Sie alle n! Permutationen
miteinander zu einer einzigen Permutation P multiplizieren?
3. Warum bleibt det A unverändert, wenn Sie jeden Eintrag aij mit dem
Bruch ^ multiplizieren ?
Lösung Zu Frage 1: Alle Produkte in Formel E.9) haben den Wert 1, da
für alle Einträge aij — 1 gilt. Die Hälfte dieser Produkte hat ein positives
Vorzeichen, die andere Hälfte hat ein negatives Vorzeichen. Sie heben sich
also alle auf und liefern det A = 0. (Natürlich, weil diese Matrix singular ist.)
Zu Frage 2: Das Produkt [0 ?] [0 1 ] ergibt eine ungerade Permutation. Für
den 3 x 3-Fall ergibt das Produkt der drei ungeraden Permutationen (in
beliebiger Reihenfolge) wieder eine ungerade Permutation. Für n > 3 ist das
Produkt aller Permutationen gerade, denn es gibt n!/2 ungerade
Permutationen, also eine gerade Anzahl, solange in der Fakultät ein Faktor 4 enthalten
ist.
Zu Frage 3: Jeder Eintrag a^ wird mit ijj multipliziert. Es wird also jedes
der Produkte aiaa2ß • • • anu in der großen Formel mit allen Zeilennummern
i — 1,2,... , n multipliziert und durch alle Spaltennummern j — 1,2,... , n
dividiert (wobei die Spaltennummern in einer permutierten Reihenfolge
auftreten). Damit bleibt aber tatsächlich jedes Produkt unverändert, so dass
auch det A gleich bleibt.
Man kann dies auch anders erklären: Multipliziert man jede Zeile mit z, so
ist dies dasselbe, wie A von links mit der Diagonalmatrix D = diag(l : n) zu
multiplizieren. Die Division jeder Spalte durch j entspricht der MultipUkation
von rechts mit der Matrix D~^. Die Determinante von DAD~^ ist aber nach
der Produktregel gleich det A.
630 Durchgerechnete Aufgaben
5.3 A Verwenden Sie die Cramer'sehe Regel mit den Quotienten det Bj/ det A,
um die Gleichung Ax == b zu lösen. Bestimmen Sie auch die inverse Matrix
A~^ = C^/detA. Warum stimmt die Lösung x für den ersten Teil mit der
dritten Spalte von A~^ überein? Welche Kofaktoren gehen in die Berechnung
dieser Spalte x ein?
Ax = b ist
Bestimmen Sie die Volumina der beiden Parallelepipeds, deren Kanten die
Spalten von A beziehungsweise die Zeilen von A~^ sind.
[2 6 2"
142
590
X
y
z
=
'Ol
0
ij
Lösung
sind
Die Determinanten der Bj (rechte Seite b an Stelle von Spalte j)
\Bi\ =
062
042
190
= 4
\B2\ =
202
1 02
510
= -2
l^3| =
260
140
591
= 2.
Dies sind die Kofaktoren C31, C32, C33 in Zeile 3. Ihr Skalarprodukt mit Zeile
3 ergibt det A:
detA = asiCsi + a32Cs2 + assCss = E,9,0) • D,-2,2) = 2.
Die drei Verhältnisse det Bj/ det A Hefern die drei Komponenten von x =
B, -1,1). Dieser Vektor ist die dritte Spalte von A~^, weil b = @,0,1) die
dritte Spalte von / ist. Die Kofaktoren entlang der anderen Zeilen von A,
dividiert durch det A = 2, ergeben die anderen Spalten von A~^:
A-' =
C'
det A
-18 18 4
10-10-2
-11 12 2
Überprüfen Sie, ob AA ^ = I gilt.
Das Parallelepiped aus den Spalten von A hat das Volumen det A = 2 (dies ist
dasselbe Volumen, wie es sich aus den Spalten ergeben würde, da |A^| = \A\
gilt). Das Parallelepiped aus den Zeilen von A~^ hat das Volumen \A~^\ =
i/i^i
_ 1.
2"
5.3 B Ist A singular, so wird aus der Gleichung AC^ = {det A)I die
Gleichung AC^ = Nullmatrix. Das bedeutet, dass jede Spalte von C^ im
Kern von A liegt. Diese Spalten enthalten die Kofaktoren längs der Zeilen
von A. Auf diese Weise gelangt man über die Kofaktoren also schnell zum
Kern einer 3 x 3-Matrix — ich bitte um Entschuldigung, dass ich dies erst
so spät erwähne!
Durchgerechnete Aufgaben 631
Lösen Sie die Gleichung Ak = 0 für die folgende singulare Matrix mit Rang
2, indem Sie x aus den Kofaktoren entlang einer Zeile bestimmen:
A =
147
239
228
A =
1 1 2
1 1 1
1 1 1
Jede von Null verschiedene Spalte von C^ liefert die gewünschte Lösung der
Gleichung Ak = 0 (da der Rang 2 ist, hat A mindestens einen von Null
verschiedenen Kofaktor). Hätte A den Rang 1, so erhielte man immer x = 0,
so dass die Idee nicht funktioniert.
Lösung Für die erste Matrix ergeben sich die Kofaktoren (beachten Sie
die Vorzeichen!) der obersten Zeile zu
39
28
= 6
29
28
= 2
23
22
= -2
Damit ist der Vektor x = F,2, -2) eine Lösung von Ak = 0. Die Kofaktoren
der zweiten Zeile sind (-18, -6,6), also -3x. Dieser Vektor liegt ebenfalls im
eindimensionalen Kern von A.
Die zweite Matrix hat entlang der ersten Zeile nur Kofaktoren Null. Der
Nullvektor x = @,0,0) ist nicht interessant. Die Kofaktoren von Zeile 2
liefern x = A, —1,0), so dass dieser Vektor eine Lösung der Gleichung Ak = 0
darstellt.
Jede n x n-Matrix vom Rang n-1 hat (nach Aufgabe 3.3.9) mindestens einen
von null verschiedenen Kofaktor. Ab Rang n — 2 sind aber alle Kofaktoren
null. In dem Fall findet man durch die Kofaktoren nur die Lösung x = 0.
6.1 A Bestimmen Sie die Eigenwerte und Eigenvektoren der Matrizen A,
A^,A-^ und A+ 4/:
A =
2-1
-1 2
und A' =
5-4
-4 5
Überprüfen Sie für A und für A^, dass die Spur gleich Ai + A2 ist und die
Determinante gleich A1A2.
Lösung Man erhält die Eigenwerte von A als Lösungen der Gleichung
det{A - XI) = 0:
det{A - XI) =
2-A -1
-1 2-A
= A^ - 4A + 3 = 0.
Diese Gleichung lässt sich als (A - 1)(A - 3) =0 faktorisieren, so dass man
als Eigenwerte von A die Zahlen Ai = 1 und A2 = 3 erhält. Deren Summe
632 Durchgerechnete Aufgaben
1 + 3 stimmt mit der Spur 2 + 2 überein, und die Determinante 3 mit dem
Produkt A1A2 = 3. Man erhält die Eigenvektoren als Lösungen der Gleichung
{A — A/)x = 0, was nichts anderes ist als Ax = Ax:
A = l: {A-I)k =
A = 3: {A- 3/)x =
r 1-1"
-1 1
L
[-1-1"
-1-1
X
y.
X
y.
=
'0'
"Ol
oj
Eigenvektor Xi =
Eigenvektor X2 =
A'^, A ^ und A + 41 haben dieselben Eigenvektoren wie A. Ihre Eigenwerte
sind A^, A~^ und A + 4:
A^ hat die Eigenwerte 1^ = 1 und 3^ = 9,
A~^ hat die Eigenwerte - und -,
A+ 41 hat die Eigenwerte 1 + 4 = 5 und 3 + 4 = 7.
Die Spur von A^ ist 5 + 5 = 1 + 9 = 10. Die Determinante ist 25 - 16 = 9.
Hinweise auf spätere Abschnitte: A hat orthogonale Eigenvektoren (s.
Abschnitt 6.4 über symmetrische Matrizen). A kann diagonalisiert werden
(Abschnitt 6.2). A ist zu jeder 2 x 2-Matrix mit den Eigenwerten 1 und 3 ähnlich
(Abschnitt 6,6). A ist eine positiv definite Matrix (Abschnitt 6.5), da A = A^
gilt, und die A's positiv sind.
6.1 B Für welche reellen Zahlen c hat die folgende Matrix A (a) zwei
relle Eigenwerte und Eigenvektoren (b) einen doppelten Eigenwert mit nur
einem Eigenvektor (c) zwei komplexe Eigenwerte und Eigenvektoren?
A =
2-c
-1 2
A^A =
5 -2c-2
-2c-2 4 + c2
Bestimmen Sie über die Produktregel die Determinante von A^A, und
bestimmen Sie auch die Spur. Warum hat A^A keinen negativen Eigenwert?
Lösung
ist
Die Determinante von A ist 4 - c. Die Determinante von A — XI
det
2-A -c
-1 2-A
= A^ - 4A + D - c) = 0.
Die Lösungsformel für quadratische Gleichungen lautet
A
-b±Vb^ -4ac 4 ± v^l6 - 16 + 4c
= 2±y/c.
Durchgerechnete Aufgaben 633
Rechnen Sie die Spur D) und die Determinante B + >/c)B —>/c) = 4 —c nach.
Die Eigenwerte sind reell und für c > 0 voneinander verschieden. In diesem
Fall gibt es zwei linear unabhängige Eigenvektoren (>/c, 1) und {—y/c, 1). Für
c = 0 werden beide Nullstellen zu A = 2, und in dem Fall gibt es nur den
einen Eigenvektor @,1). Für c < 0 sind beide Eigenwerte komplex, und damit
werden auch die Eigenvektoren (-y/c, 1) und {—y/c, 1) komplex.
Die Determinante von A^A ist det(A^) det{A) = D-c)^. Die Spur von A^A
ist 5 + 4 + c^. Wäre einer der Eigenwerte negativ, so muss der andere positiv
sein, damit sich die Spur Ai + A2 = 9 + c^ ergibt. Dann hätte man aber aus
„negativ mal positiv" eine negative Determinante.
In der Tat hat jede Matrix A^ A reelle, nichtnegative Eigenwerte (s. Abschnitt
6.2 A Die Lucaszahlen sind wie die Fibonaccizahlen, mit dem
Unterschied, dass sie mit Li = 1 und L2 = 3 beginnen. Gemäß der Regel
Lfc+2 = ^fc+i + Lk sind die nächsten Lucaszahlen 4,7,11,18. Zeigen Sie,
dass die Lucaszahl Lioo = Aj^^ + \^^ ist.
Lösung Die Gleichung ua;+i = [1 o]^^ ^^^ ^^ jener für die
Fibonaccizahlen identisch, weil die Lucaszahlen derselben Regel Lfc+2 = ^fc+i + Lk
(mit unterschiedlichen Startwerten) genügen. Deshalb können wir Gleichung
F.11) abschreiben:
Sei Ufc =
Lk+\
Lk
Die Regel wird zu u^+i
Lh+i ^ Lk-^i
1 1
10
Ufc.
Die Eigenwerte und Eigenvektoren von A = [ J J ] gehorchen weiterhin der
Regel A^ = A+1:
Ai = —-— und xi =
Ai
1
A2 = —-— und X2 =
A2
1
Lösen wir nun CiXi + C2X2 = Ui = C,1). Die Koeffizienten sind ci = Ai und
C2 = A2! Rechnen Sie es nach:
Aixi + A2X2 =
Ai A2
1 1 J
[A2.
=
"Af + Ai"
A1+A2
=
Spur von A^
Spur von A
= ui
Der Lösung uioo = A^^Ui können wir die Lucaszahlen (Lioi,I/ioo)
entnehmen. Die zweiten Komponenten von xi und X2 sind 1, deshalb ist die zweite
Komponente von uioo gleich
i^ioo - ciAf+c2Af = Ar+Ar«
634 Durchgerechnete Aufgaben
Jede Zahl L^ = Af + Af ist ganzzahlig (warum?). Da A2 sehr klein ist, muss
Lk nahe bei \\ liegen. Die Lucaszahlen wachsen also schneller als die Fibo-
naccizahlen, und sind später um einen Faktor nahe bei \/5 größer.
6.2 B Bestimmen Sie alle Eigenvektormatrizen 5, die die Matrix A (mit
Rang 1) zu S~^AS — A diagonalisieren:
A^
\\ 1 r
111
111
=
"ii
1
ij
[111]
Bestimmen Sie A^. Welche Matrizen B kommutieren mit A (so dass AB —
BA gilt)?
Lösung Da A den Rang 1 hat, ist der Kern eine zweidimensionale Ebene.
Jeder Vektor mit x + 2/ + ^ = 0 (Summe der Komponenten ist null) löst die
Gleichung Ax = 0. Daher ist A = 0 ein Eigenwert mit Vielfachheit 2. Es gibt
zwei linear unabhängige Eigenvektoren (GM = 2). Der andere Eigenwert
muss A = 3 sein, weil die Spur von A gleich 1 + 1 + 1 = 3 ist. Rechnen Sie es
nach:
det{A - XI) =
1-A 1 1
1 1-A 1
1 1 1-A
= A - AK + 2 - 3A - A) = -A^ + 3A2.
Die Determinante ist also A^C - A) = 0 und die Eigenwerte sind Ai = 0,
A2 = 0 und A3 = 3. Die Eigenvektoren zu A = 3 sind die Vielfachen von
X3 = A,1,1). Die Eigenvektoren zu Ai = A2 = 0 sind zwei beliebige linear
unabhängige Vektoren in der Ebene x -\-y -^z =^ 0. Diese Vektoren bilden die
Spalten aller möglichen Eigenvektormatrizen:
S =
X X c
y y c
-X - y -X -Yc
und S-^AS = A =
000
000
003
wobei c ^ 0 und xY ^ yX. Man erhält die Potenzen A^ schnell durch
Multiplikation:
Es gilt A^ =
333
333
333
= SA und A"=3"-^A.
Um die Matrizen B zu bestimmen, die mit A kommutieren, betrachten wir
AB und BA. Die Einträge 1 in A erzeugen die Spaltensummen Ci,C2,C3
und die Zeilensummen i^i,i?2,^3 von B:
Durchgerechnete Aufgaben 635
AB = Spaltensummen =
BA = Zeilensummen =
Ci C2 Cs
Ci C2 Cs
Ci C2 Cs
Ri R\ R\
R2 R2 R2
Rs Rs R3
Gilt AB = BA, so müssen alle sechs Spalten- und Zeilensummen von B
identisch sein. Ein mögliches B ist A selbst, da A A = A A gilt. B ist eine
beliebige Linearkombination von Permutationsmatrizen!
Es handelt sich hier um einen fünfdimensionalen (Aufgabe 3.5.39) Raum von
Matrizen, die mit A kommutieren. Alle B's haben den Eigenvektor A,1,1)
gemein. Ihre anderen Eigenvektoren liegen in der Ebene x -^y -^ z — {). Wir
haben drei Preiheitsgrade in den Eigenwerten und zwei in den Eigenvektoren.
6.3 A Bestimmen Sie die Eigenwerte und Eigenvektoren von A, und
schreiben Sie u@) = B,0,2) als Linearkombination cixi + C2X2 + C3X3 der
Eigenvektoren. Lösen Sie dann beide Gleichungen:
d\i
~dt
= Au =
-2 1 0
1-2 1
0 1-2
u sowie ——- = Au mit —riO) = 0.
dt^ dt^ '
Wegen der A,—2,1)-Diagonalen berechnet die Matrix A die zweiten
Differenzen (ähnlich einer zweiten Ableitung) des Vektors. Daher ist die erste
Gleichung u' = A\i ähnlich der Wärmeleitungsgleichung du/dt = d^u/dx^.
Ihre Lösung u{t) klingt ab, weil die Wärme abfließt. Die zweite Gleichung
= Au ist ähnlich der Wellengleichung d^u/dt^ = d^u/dx^. Ihre Lösung
u
oszilliert, wie eine Saite einer Geige.
Lösung Man erhält die Eigenwerte und Eigenvektoren aus det{A — XI) =
0:
det{A - XI) =
-2-A 1 0
1 -2-A 1
0 1 -2 - A
= (-2-A)'-2(-2-A) = 0.
Ein Eigenwert ist A = —2, so dass —2-A null ist. Klammert man -2—A aus, so
bleibt (-2-A)^-2 = 0 oder A^+4A+2 = 0. Die anderen (ebenfalls negativen)
Eigenwerte sind also A = -2 ± \/2. Man bestimmt die Eigenvektoren jeweils
für sich:
A = -2 :
{A + 2/)x =
[0 10"
101
[0 10
X
y
z
=
"Ol
0
0
für xi =
V2-
0
636 Durchgerechnete Aufgaben
A= -2-a/2 :
(A - XI)x =
A = -2 + V^ :
{A - \I)x =
\/2 1 0
1 V2 1
0 1 v^
-V2 1 0
1 -V2 1
0 1 -V2
X
y
z
=
'0]
0
0
für X2 =
X
y
z
=
"Ol
0
oj
für X3 =
1
1
1
1
Alle diese Eigenvektoren haben die Länge 2, daher sind |xi, |x2, |x3
Einheitsvektoren. Diese Eigenvektoren sind orthogonal (dies wird in Abschnitt 6.4
für jede reelle symmetrische Matrix A bewiesen). Entwickeln wir u@) als
Linearkombination CiXi + C2X2 + C3X3 (mit ci = 0 und C2 = C3 = 1):
Xi X2 X3
= u@)
ist
^/2 1 1
0 -v/2v^
-V2 1 1
[Ol
1
1
=
1
0
2J
Wegen u@) = X2 + X3 klingt die Lösung auf u(^) = e ^^*X2 + e '^^*X3 ab.
Da alle A's negativ sind, geht u(^) gegen Null {Stabilität). Der am wenigsten
negative Eigenwert A = 2 - \/2 bestimmt die Abklingrate. Dies ist
genauso wie in Aufgabe 6.3.5, außer dass die Leute sich in drei Räumen befinden
(bei der Wärmeleitungsgleichung betrachten wir anstelle von Personen
Temperaturen). Die Bewegungsrate u' von Personen zwischen den Zimmern ist
die Temperaturdifferenz, oder die Differenz der Personenzahlen. Der
Gesamtstrom in den ersten Raum ist U2 — 2ui, wie von Au verlangt. Schließlich gilt
u(^) -> 0, und die Räume werden leerer.
Bewegung
-Ui
ui{t)
Bewegung
U2 — Ui
U2[t)
Beweeung
Uz -U2
Mt)
Bewegung
^^3
Betrachten wir jetzt die „Wellengleichung" cfu/dt'^ = Au (sie wurde im
Haupttext nicht betrachtet). Dieselben Eigenvektoren führen auf
Oszillationen e*^*x und e~*^*x mit Frequenzen aus üü^ = -A:
dt^
(e^^^x) = ^(e^'^^x) wird zu {iuj)^e''''y: = Ae^^^x und lü' = -A.
Es gibt zwei Quadratwurzeln zu — A, deshalb erhalten wir die Lösungen e*^*x
und e~*^*x. Zusammen mit den drei Eigenvektoren liefert dies sechs
Lösungen. Durch eine geeignete Linearkombination kann man die sechs
Komponenten von u@) (Position) und u'@) (Geschwindigkeit) anpassen. Da wir in
Durchgerechnete Aufgaben 637
unserem Fall u'@) = 0 haben wollen, kombinieren wir e*'^*x mit e~*'^*x zu
2cosci;^x. Unser spezielles u@) ist wieder X2 + X3, so dass wir eine
oszillierende Lösung erhalten:
u(^) = 2{cosuj2t)x2 + 2(cosa;3^)x3 mit (cj2)^ = 2 + \/2, (cjs)^ = 2 - \/2.
Jedes A ist negativ, und deshalb ergeben sich aus u^ = -X zwei reelle
Frequenzen. Eine symmetrische Matrix wie A mit negativen Eigenwerten ist eine
negativ definite Matrix. (In Abschnitt 6.5 betrachten wir dies von der
positiven Seite, das heißt, positiv definite Matrizen.) Matrizen wie A und —A
stellen den Schlüssel für alle Anwendungen im Ingenieurwesen dar, die wir in
Kapitel 8 darstellen wollen.
6.3 B Lösen Sie die vier Gleichungen da/dt = O^db/dt = a^dc/dt =
2&, dz/dt = Sc in dieser Reihenfolge, mit dem Anfangswert u@) = (a@), &@),
c@),^@)). Bestimmen Sie die Matrix für u' = Au, und lösen Sie diese
Gleichungen mit Hilfe der Exponentialfunktion für Matrizen durch u(^) =
e^*u@):
d
dt
a
b
c
z
0 0 0"
1000
0200
0030
a
b
c
z
ist
du
It
= Au.
Bestimmen Sie zunächst A'^,A^,A'^ und dann e^* = I-\-At-^^{At)'^-\-^{At)^.
Warum bricht die Reihe hier ab? Rechnen Sie nach, dass e^ für ^ = 1 die
PascaPsche Dreiecksmatrix ist, und verifizieren Sie die Gleichung {e^){e'^) =
(e^^^). Warum gilt dies für jedes A?
Lösung Man integriert zunächst da/dt = 0, dann db/dt
dc/dt = 2b und schließlich dz/dt = Sc:
a, dann
a{t) = a{0)
b{t)= ta{0)+ b{0)
c{t) = t'^a{0) + 2^&@) + c@)
z{t) = t^a{0) + 3^2^@) + 3^c@) + ^@)
muss gleich e u@) sein
Die Potenzen von A nach A^ sind alle null Daher bricht die Reihe für e"^^
nach vier Termen ab:
A =
0000
1000
0200
0030
A^ =
0000
0000
2000
0600
A^ =
0000
0000
0000
6000
638 Durchgerechnete Aufgaben
In jedem Schritt werden die Diagonalen nach unten verschoben, so dass sie für
A'^ ganz verschwinden. (Es müsste eigenthch auch eine Diagonale-Diagonale-
Regel für die Matrizenmultiplikation geben, genauso wie die Zeile-Spalte-
Regel und die Spalte-Zeile-Regel.) Die Exponentialfunktion für diese Matrix
ergibt dieselbe Matrix wie die, mit der (a@),&@),c@),^@)) oben
multipliziert wurde:
At r A. (^0' {Atf
e"^^ = I -i- At-i- ^^—^ + ^Hr^
1
t 1
t^ 2t 1
t^ St^ St 1
Für ^ = 1 ist e"^ die PascaVsche Dreiecksmatrix Pl- Die Ableitung von e^*'
bei ^ = 0 ist A:
oAt .
lim
= lim
t-^o
[0 0 00"
1 0 00
N 2 00
[^2 3^3 0
"ooool
1000
0200
003 oj
= A.
A ist der Matrix-Logarithmus der Pascal'schen Matrix e^\ Die Inverse der
Pascal'schen Matrix ist e~^ mit zwei negativen Diagonalen. Das Quadrat
von e^ ist immer e^^ (so wie auch e^^e^*' = e"^^^"^*^ ist), und dies hat viele
Gründe:
Löst man mit e^ erst von ^ = 0 bis 1 und dann von 1 bis 2, so ist dies dasselbe
wie mit e^^ von 0 bis 2 zu gehen.
Die quadrierte Reihe (/+A+ ^ + • • • )^ stimmt mit /+2A+ i^^^ +... = e^^
überein.
Wenn A diagonalisiert werden kann (dieses A nicht!), so gilt {Se^S~^)
6.4 A Bestimmen Sie die Eigenwerte von A^ und ^4, und überprüfen
Sie, dass die ersten beiden Eigenvektoren orthogonal sind. Stellen Sie die
Eigenvektoren graphisch dar, es ergeben sich diskrete Darstellungen des Sinus
und des Kosinus:
A.=
2-1 0
-1 2 -1
0-12
B^ =
1 -1
-1 2 -1
-1 2 -1
-1 1
Das (-1,2, -1)-Muster in den beiden Matrizen ist eine „zweite Differenz".
In Abschnitt 8.1 werden wir erklären, inwieweit dies einer zweiten Ableitung
ähnelt. Damit ähneln nämlich die Gleichungen Ax = Ax und ^x = Ax den
Durchgerechnete Aufgaben 639
Differentialgleichungen (Px/dt^ = Xx. Diese Matrizen haben die
Eigenvektoren X = sin kt und x = cos kt, die die Grundlage der Fourierreihen bilden. Die
Matrizen führen auf „diskrete Sinus-" und „diskrete Kosinusfunktionen" die
die Grundlage für die Diskrete Fouriertransformation darstellen. Diese nimmt
eine zentrale Stellung in allen Bereichen der Signalverarbeitung ein. Eine
beliebte Wahl für das JPEG-Format in der Bildverarbeitung sind beispielsweise
A7 und ^8-
Lösung Die Eigenwerte von As sind A = 2 - ^/2, 2 und 2 + \/2. Ihre
Summe ist 6 (dies ist die Spur von As) und ihr Produkt ist 4 (Die
Determinante). Die Eigenvektormatrix S liefert die „Diskrete Sinus-Transformation" am
Graphen erkennt man, wie sich die Komponenten der ersten beiden
Eigenvektoren in die Sinuskurven einfügen. Zeichnen Sie bitte den dritten Eigenvektor
in die dritte Sinuskurve!
S =
1 1/2 1 ■
V2 0 -V2
1 -V2 1
sin^
sin 2^ \
Die Eigenwerte von B4 sind A = 2 - v^, 2, 2 + v^ und 0 (also dieselben
Eigenwerte wie die von As zuzüglich eines Eigenwerts 0). Die Spur ist weiterhin
6, aber die Determinante hat den Wert null. Die Eigenvektormatrix C liefert
die 4-punktige „Diskrete Kosinus-Transformation", man sieht am Graphen,
dass sich die Eigenvektoren diesmal in Kosinuskurven einfügen. (Zeichnen Sie
bitte wieder den dritten Eigenvektor!) Diese Eigenvektoren stimmen mit den
Kosinuskurven in den Zwischenpunkten ?, ^, ^, ^ überein.
8 ' 8
c =
1111
1 \/2-l -1 I-V2
1 l-\/2 -1 1/2-1
1-11-1
^~~K
H I-Ar-H H
IZLTT
8
Sowohl S als auch C haben orthogonale Spalten (es handelt sich um
Eigenvektoren der symmetrischen Matrizen As und ^4). Multiphziert man also
640 Durchgerechnete Aufgaben
ein Eingangssignal mit S oder mit C, so zerlegt man dieses Signal in reine
Frequenzen — ganz so, als ob man in der Musik einen Akkord in seine
einzelnen Noten zerlegt. Die diskrete Fouriertransformation ist die nützlichste
und aufschlussreichste Transformation in der gesamten Signalverarbeitung.
Hier sehen wir die Sinus- und Kosinuskomponenten (DST und DKT), die
zusammen die DFT bilden. Dieses wunderbare Muster bleibt natürlich auch
für größere Matrizen erhalten. Der folgende MATLAB-Code erzeugt Bs und
die Eigenvektormatrix Cs, und zeichnet die ersten vier Eigenvektoren auf
Kosinuskurven auf:
n = 8;e= ones(n - 1,1); 5 = 2* eye(n)-diag(e,-l)-diag(e, 1); B{1,1) =
1; B{n,n) = l;
[C, yl] = eig(ß);plot(C(:,l:4)/-o')
6.5 A Die bedeutenden Faktorisierungen einer symmetrischen Matrix
sind A = LDL^ (aus den Pivotelementen und den Multiplikatoren) und
A = QAQ^ (aus den Eigenwerten und Eigenvektoren). Zeigen Sie, dass die
Ungleichung x^Ax > 0 für alle von null verschiedenen Vektoren x genau dann
gilt, wenn die Pivotelemente und die Eigenwerte positiv sind. Probieren Sie
dieses Kriterium für n x n-Matrizen an pascal F), ones F) und hilbF)
und anderen Matrizen in MATLAB's gallery aus.
Lösung Um die Ungleichung x^Ax > 0 zu beweisen, setzt man geeignet
Klammern in die Formeln x^LDL^x und x^QAQ^x ein:
x^Ax = (L^x)^D(L^x) und x^Ax = (Q^xfAiQ^'x).
Ist X von Null verschieden, so sind auch y = L^x und z = Q^x von Null
verschieden (die Matrizen sind invertierbar). Aus x^Ax = y^Dy = z'^Az
wird daher eine Summe von Quadraten — A ist positiv definit:
x^Ax = y^Dy = d^yl + • • • + dnvl > 0
x^Ax = z^Az = Xizf + • • • + Xnzl > 0
Aber ich will ehrlich bleiben, und deshalb muss ich diesem schnellen und
eleganten Beweis noch einen kleinen Kommentar nachschieben. Eine Null in
einer Pivotposition würde eine Zeilenvertauschung erzwingen, und damit
eine Permutationmatrix P. Die Faktorisierung wäre dann PAP^ = LDL^
(um die Symmetrie zu erhalten, vertauschen wir auch Spalten mit P^)-
Man kann unseren schnellen Beweis aber auch ohne Probleme auf A —
{P-^L)D{P-^L)^ anwenden.
MATLAB enthält eine „Galerie" ungewöhnlicher Matrizen (mehr unter help
gallery), hier sind vier davon:
pascal F) ist positiv definit, weil alle Pivotelemente 1 sind (siehe das
durchgerechnete Beispiel 2.6A).
Durchgerechnete Aufgaben 641
ones F) ist positiv semidefinit, weil die Eigenwerte 0,0,0,0,0,6 sind.
hilbF) ist positiv definit, obwohl eig(hilbF)) zwei Eigenwerte sehr nahe
bei Null hat. Es gilt aber tatsächlich x^ hilbF) x = /^ (xi + X2S H h
Xqs^)^ ds > 0.
randF)+randF) ' kann positiv definit sein, oder auch nicht (experimentell
aber nur 1 mal in 10000 Versuchen)yi = 20000;p = 0; for k = l:n,A =
randF);p = p+ all(eig{A + A') > 0); end, p/n
6.5 B Geben Sie Bedingungen an die Blöcke A — Ä^, C = C^ und B
der folgenden Matrix M an:
Unter welchen Bedingungen ist die symmetrische Blockmatrix
A B]
M =
B^ C
positiv definit?
Lösung Überprüfen Sie M auf positive Pivotelemente, beginnend in der
oberen linken Ecke. Die ersten Pivotelemente von M sind die Pivotelemente
von A\
Erste Bedingung Der Block A muss positiv definit sein.
MultipUzieren Sie die erste Zeile von M mit B^A~^ ^ und subtrahieren Sie
dies von der zweiten Zeile. Sie erhalten einen Nullblock. In der Ecke erscheint
das Schur-Komplement S = C - B^A~^B:
I 0
-B^A-' I
A B
B^ C
A B
0 C-B^A-^B
AB
0 5
Die letzten Pivotelemente von M sind jene von 5!
Zweite Bedingung 5 muss positiv definit sein.
Diese beiden Bedingungen stimmen genau mit den Bedingungen a > 0 und
c > b'^/a überein, außer dass sie auf Blockmatrizen angewandt werden.
6.6 A Die Pascal'sche 4 x 4-Dreiecksmatrix Pl und ihre Inverse
(alternierende Diagonalen) sind
Pl-
1000
1 100
12 10
1331
und Pr =
1 0 00
-1100
1-2 10
-1 3-3 1
Rechnen Sie nach, dass Pl und P£^ dieselben Eigenwerte haben. Bestimmen
Sie eine Diagonalmatrix D mit alternierenden Vorzeichen, für die P^ =
D-^PlD gilt, so dass Pl ähnlich zu P~^ ist. Berechnen Sie die Matrix PlD
642 Durchgerechnete Aufgaben
mit alternierenden Spalten, und zeigen Sie, dass diese Matrix ihre eigene
Inverse ist.
Da Pl und P£^ ähnUch sind, haben sie dieselbe Jordanform J. Bestimmen
Sie J, indem Sie die Anzahl linear unabhängiger Eigenvektoren von Pl mit
A = 1 ausrechnen.
Lösung Die Eigenwerte der beiden Dreiecksmatrizen Pl und P^^ sind
die Einträge 1 auf den Hauptdiagonalen. Wählen Sie D mit alternierenden
Einträgen 1 und -1 auf der Diagonalen. Diese Matrix ist gleich D~^\
D-'PlD =
1
1000
1 100
12 10
1331
-1
-1
= p;
Probe: Wir multiplizieren die Zeilen 1 und 3 sowie die Spalten 1 und 3 mit
— 1. Dadurch werden vier negative Einträge in P£"^ erzeugt. Allgemein
multiplizieren wir Zeile i mit (-1)* und Spalte j mit (-l)-^. Jeder Eintrag wird
also mit (-l)^*^-^ = (-l)^""-^ multipliziert, was die alternierenden Diagonalen
erzeugt. Die Matrix PlD hat Spalten mit alternierenden Vorzeichen und ist
ihre eigene Inverse!
{PlD){PlD) = PlD-'PlD - PlPl' = /•
Die Matrix Pl hat nur den einen Eigenvektor x = @,0,0,1) mit A = 1. Der
Rang von Pl — -^ ist 3. Die Jordanform J besteht also nur aus einem Block
(mit A = 1):
Pl and also Pr ^ sind ähnlich zu J =
1 100
0110
001 1
0001
6.6 B Erklären Sie, warum die Eigenwerte einer Matrix A in reziproken
Paaren X = a und X = 1/a auftreten, wenn A ähnlich zu A~^ ist. Die
symmetrische 3x3 Pascal'sche Matrix Ps hat die Eigenwerte 4 + VT5,4 - \/l5,1-
Verwenden Sie P£"^ = D~^PlD (mit D = D~^ = D^) und die symmetrische
Faktorisierung Ps = PlPl ^^ 2.6 A, um zu zeigen, dass Ps ähnlich zu Pg^
ist.
Lösung Hat A von Null verschiedenen Eigenwerte Ai,... , An, so hat die
Inverse die Eigenwerte Af ^,... , A~^. Der Grund: Multipliziert man die
Gleichung Ax = Ax mit A~^ und A~^, so erhält man A~^k = A~^x.
Durchgerechnete Aufgaben 643
Sind A und A~^ ähnUch, so müssen sie dieselben Eigenwerte haben. Eine
gerade Anzahl von Eigenwerten muss also Paare der Form a und 1/a bilden.
Das Produkt D + \/l5)D - \/l5) = 16 - 15 = 1 zeigt, dass die Eigenwerte
4 + vTs, 4 — \/l5,1 solche Paare bilden.
Die symmetrischen Pascal'schen Matrizen haben paarweise Eigenwerte, weil
Ps ähnlich zu Pg^ ist. Um die Ähnlichkeit zu beweisen, beginnen wir mit
Ps = PlPl und verwenden D = D'^ = D^.
Ps' - {PD'^Pl') = {D-'PLDf{D-'PLD) = D-'pIPlD
= {PlD)-\PlPI){PlD).
Dies ist die Beziehung P^^ — M'^PsM (ähnhche Matrizen!) mit M — PlD.
Für die Eigenwerte größerer Pascal'scher Matrizen Ps gibt es keine schönen
Formeln. Sie können aber mit Hilfe von eig(P5) überprüfen, dass auch
deren Eigenwerte in reziproken Paaren a und 1/a auftreten. Die Jordan'sche
Normalform von Ps ist die Diagonalmatrix yl, weil symmetrische Matrizen
immer einen vollständigen Satz Eigenvektoren besitzen.
6.7 A Geben Sie die Namen der folgenden Zerlegungen A = ciTi-\ h
CnVn einer n x n-Matrix in n Matrizen vom Rang eins (Spalte c mal Zeile r)
an:
1. Orthogonale Spalten ci,... ,Cn und orthogonale Zeilen ri,... ,rn
2. Orthogonale Spalten ci,... ^Cn und Zeilen ri,... .Vn in Dreiecksform
3. Spalten ci,... , Cn und Zeilen ri,... ,rn in Dreiecksform
„Dreiecksform" bedeutet hier, dass c^ und r^ vor der Komponente i nur Nullen
enthalten, so dass die Matrix C mit den Spalten c^ eine untere Dreiecksmatrix
und die Matrix R mit den Zeilen r^ eine obere Dreiecksmatrix ist.
Wie kommen der Rang, die Pivotelemente und die Singulärwerte ins Spiel?
Warum gehört die Diagonalisierung A = SAS~^ hier nicht dazu?
Lösung Die folgenden drei Zerlegungen A — CR sind grundlegend für die
gesamte lineare Algebra, sei sie rein oder angewandt:
1. Singulärwertzerlegung A — UEV^ {orthogonales [/, orthogonales EV-^)
2. Gram-Schmidt-Orthogonalisierung A = QR {orthogonales Q,
Dreiecksmatrix R)
3. Gauß'sche EUmination A = LU {Dreiecksmatrix L, Dreiecksmatrix U)
644 Durchgerechnete Aufgaben
Hat die (möglicherweise rechteckige) Matrix A den Rang r, so braucht man
nur r (nicht n) Matrizen vom Rang eins.
Die CT's in E kommen über die orthonormalen Zeilen in V^ ins Spiel: A =
aiCiTi -\ h anCnTn- Wegen der Einträge 1 auf den Diagonalen von L und
U sind die Pivotelemente di die Koeffizienten in der Gleichung: A = LDU =
diCiTi H hdnCnTn- Setzt man die Diagonaleinträge R in eine Matrix H, so
erhält man die Zerlegung QR mit QHR = hiCiTi -\ h hnCnTn- Für diese
Zahlen hi gibt es keinen Standardnamen, ich schlage „Höhen" vor. Jedes hi
gibt die Höhe der Spalte i über der Grundfläche aus den ersten i — 1 Spalten
an. Das Volumem eines vollen n-dimensionalen Parallelepipeds ist:
I det A| = {Produkt der cr's| = \Produkt der d^s | = {Produkt der h^s |.
Man erhält diese Produkte aus den Determinanten von A = UEV^ =
QHR = LDU.
Auch die Diagonalisierung A = SAS~^ ist eine Summe von n Matrizen vom
Rang eins (Spalten mal Zeilen). Die Spalten von S sind die Eigenvektoren
von A. Die Zeilen erhält man aus ^15"^ (dies sind die Eigenvektoren von
Ä^, wie man sieht, wenn man A = SAS~^ transponiert). Diese Zeilen sind
nicht orthogonal zu sich selbst, und die Spalten sind nicht orthogonal zu den
anderen Spalten. Es ist aber Zeile i orthogonal zu Spalte j (falls i ^ j), weil
AS~^ mal S gleich der Diagonalmatrix A ist.
Ist A symmetrisch, so ist man durch die orthogonalen Eigenvektoren im
Wesentlichen wieder im Fall 1: es gilt S — U und S~^ = V^.
7.1 A Die Eliminationsmatrix [li] liefert eine Scher-Abbildung
T(x, y) = (x, 3x-\-y). Zeichnen Sie die x^y-Ebene, und zeigen Sie, was mit den
Vektoren A,0) und B,0) auf der x-Achse unter Anwendung dieser Abbildung
geschieht. Was passiert mit den Punkten auf den vertikalen Geraden x = 0
und X = a? Zeichnen Sie auch das Bild des Einheitsquadrats 0 < x < 1, 0 <
2/<l-
Lösung Die Punkte A,0) und B,0) auf der x-Achse werden durch T zu
A,3) und B,6) transformiert. Die horizontale x-Achse wird zu einer
Geraden mit Steigung 3 (die natürlich durch @,0) geht). Die Punkte auf der
?/-Achse bleiben unverändert, weil T{0,y) = @,2/) gilt. Die ?/-Achse ist die
Eigenvektorgerade von T zum Eigenwert A = 1.
Die vertikale Gerade x = a wird um 3a nach oben bewegt, da zur y-
Komponente die Zahl 3a addiert wird. Dies ist die „Scherung" — vertikale
Geraden werden von links nach rechts höher und höher nach oben geschoben.
Eine Seite des Einheitsquadrats ist die ^/-Achse, die unverändert bleibt, die
gegenüberliegende Seite von A,0) nach A,1) wird nach oben verschoben und
geht von A,3) nach A,4). Die untere Seite des transformierten Quadrats
geht von @,0) nach A,3), und die parallele obere Seite von @,1) nach A,4).
Durchgerechnete Aufgaben 645
Es handelt sich also um ein Parallelogramm. Die Multiplikation mit einem
beliebigen A macht aus Quadraten Parallelogramme!
7.1 B Eine nichtlineare Abbildung T ist invertierbar, wenn jeder
Vektor b im Ausgaberaum das Bild genau eines Vektors x im Eingaberaum ist:
wenn also die Gleichung T(x) = b immer genau eine Lösung hat. Welche der
folgenden Abbildung (auf den reellen Zahlen x) ist invertierbar? Was ist im
Fall T~^? Keine der Abbildungen ist linear, nicht einmal T3. Löst man die
Gleichung T(x) = b, so invertiert man T:
Ti(x) = x^ T2{x) = x^ Tsix) =x + 9 T^{x) = e" T^{x) = - für x 7^ 0.
X
Lösung Ti ist nicht invertierbar, weil x^ = 1 zwei Lösungen hat (und
x^ = — 1 keine). T4 ist nicht in vertierbar, weil e^ = — 1 keine Lösung hat.
(Betrachtet man als Ausgaberaum die Menge der positiven Zahlen, so ist die
inverse Abbildung zu e^ = b durch x = \nh gegeben.) Beachten Sie, dass T5
die Identität ist, aber T3 (x) = x + 18. Geben Sie auch T^ (x) und T4 an.
T2,T3,T5 sind invertierbar. Die Lösungen zu x^ = h, zu x -\- 9 = b und zu
- = b sind eindeutig:
= T^\b) = &^/^ X = T^\b) = b-9
T,-\b) =
7.2 A Bestimmen Sie bezüglich der Standardbasis eine 4 x 4-Permuta-
tionsmatrix P, die eine zyklische Permutation von x = (xi,X2,X3,X4) zu
T(x) = (^4,xi,X2,X3) repräsentiert. Bestimmen Sie auch die Matrix für T^.
Was erhält man für die dreifache Anwendung T^(x), und warum ist T^ =
T~^? Bestimmen Sie zwei linear unabhängige reelle Eigenvektoren von P,
und bestimmen Sie alle Eigenwerte.
Lösung Der erste Vektor A,0,0,0) der Standardbasis wird in den zweiten
Basisvektor @,1,0,0) abgebildet. Die erste Spalte von P ist also @,1,0,0).
Die anderen drei Spalten erhält man aus den Bildern der restlichen
Basisvektoren:
P =
0001
1000
0100
0010
Dann beschreibt P
"xi"
X2
X3
L^4
X4I
Xi
X2
_X3j
die Abbildung T.
Da wir die Standardbasis verwenden, entspricht die Anwendung von T der
gewöhnlichen Multiplikation mit P. Die Matrix für T^ ist die „zweifache
zyklische Verschiebung" P^, die den Vektor (x3,X4,Xi,X2) erzeugt.
646 Durchgerechnete Aufgaben
Die dreifache Verschiebung T^ bildet den Vektor x = {xi,X2,Xs,x^) auf den
Vektor T^(x) = (x2,X3,X4,xi) ab. Wendet man T dann noch einmal an, so
erhält man das ursprüngliche x zurück —'■ deshalb ist T^ die
Identitätsabbildung, oder, durch Matrizen ausgedrückt, es ist P"^ — I. Dies bedeutet, dass
T^T die Identität ist, also T^ = T'^.
Zwei reelle Eigenvektoren von P sind A,1,1,1) mit dem Eigenwert A = 1 und
A, —1,1, —1) mit dem Eigenwert A = — 1. Die Verschiebung lässt den Vektor
A,1,1,1) unverändert, und sie kehrt die Vorzeichen im Vektor A,-1,1,-1)
um. Die anderen beiden Eigenwerte sind A3 = i und A4 — —i. Die
Determinante von P ist A1A2A3A4 = -1 wie in Aufgabe 5.2, wo die Kofaktoren der
ersten Zeile verwendet wurden.
Bitte beachten Sie, dass die Summe der Eigenwerte 1,—1,2,-z gleich Null
ist (wie die Spur von P). Es handelt sich um die vierten Einheitswurzeln,
da det(P — XI) = A^ — 1 ist. Sie sind in gleichmäßigen Abständen auf dem
Einheitskreis in der komplexen Ebene angeordnet. Ich glaube, P ist eine 90°-
Drehung zusammen mit einer Spiegelung im R^.
7.2 B Der Raum der 2 x 2-Matrizen wird von den folgenden vier Basis-
„Vektoren" erzeugt:
ui
10'
00
U2 =
Ol'
00
=
'00'
10
U4 =
'0 0
Ol
T sei die lineare Abbildung, die jede 2 x 2-Matrix transponiert. Durch welche
Matrix A wird T bezüglich dieser Basis (Ausgabebasis = Eingabebasis)
dargestellt? Was ist die inverse Matrix A~^? Welche Abbildung T~^ invertiert
die Transpositions-Abbildung?
Weiterhin sei T2 die Abbildung, die jede Matrix mit M = [^a] multipliziert.
Durch welche 4 x 4-Matrix A2 wird T2 dargestellt?
Lösung Die Transposition permutiert die Basismatrizen in die
Reihenfolge Ui,U3,U2,U4
T(ui)-ui
T(U2) - U3
T{us) = U2
T(U4) - U4
ergibt die vier Spalten von A =
1000
00 10
0100
0001
Die inverse Matrix A~^ ist mit A identisch. Die inverse Abbildung T~^ ist
also mit T identisch — transponiert man einmal und dann noch einmal, so
erhält man die Matrix, mit der man begonnen hat.
Um die Matrix A2 zu bestimmen, wenden wir T2 auf die Basismatrizen
ui,U2,U3,U4 an. Multiplizieren wir also mit M:
\ a bl
a b\
a b
a b\
.c d\
ri 0]
lo 0.
1 0 1
Vol-
Lo 1.
=
a 0"
■^°-
0 a
.0 c.
b 0
.d Oj
0 6
.0 dJ
= aui + CU3
= aU2 + CU4
= &Ui + dU3
= &U2 + C/U4
Durchgerechnete Aufgaben 647
liefert die Spalten von A
[a 0 6 Ol
Oa06
cOdO
[OcOdJ
Diese Matrix A ist das „Kronecker-Produkt" oder „Tensorprodukt" von M
mit 7, geschrieben M ^ I.
7.3 A Vergleichen Sie ao + aix + a2X^ mit bo + &i(x +1) + b2(x + 1J^ um
eine 3 x 3-Matrix Mi zu bestimmen, die die KoefBzienten durch a = Mib
miteinander verbindet. Mi wird der Pascal'schen Matrix ähnlich sein!
Die Matrix, die diesen Wechsel umkehrt, ist Mf ^, und es gilt b = M~^a.
Sie verlegt den Entwicklungspunkt der Reihe zurück, so dass öq + ai(x —
1) + a2{x - 1)^ gleich &o + hx + b2x'^ ist. Vergleichen Sie die quadratischen
Polynome, um M_i, die Inverse der Pascal'schen Matrix, zu bestimmmen.
Bestimmen Sie dann Mt aus ao -\- aix + a2X^ = bo + bi{x -\-1) -\- 62(x -f t)^,
und verifizieren Sie, dass MgMt — Ms-^t gilt.
Lösung Man findet Mi, indem man ao + aix + a2X mit &o + 6i(x + 1) +
b2{x + 1)'^ vergleicht:
Konstanter Term
Koeffizient von x
Koeffizient von x^
ao = bo + bi + &2
öl = &1 + 2&2
02 = &2
«0
öl
[02
=
11"
12
1
0I
61
h2\
Schreibt man (x + 1)^ = 1 + 2x + x^, so erkennt man die Zahlen 1,2,1 aus
dieser Basiswechselmatrix.
Die Matrix Mi ist die obere Pascal'sche Dreiecksmatrix Pu- Man erhält die
Inverse Mf^ durch Vergleich von ao+ai(x-l)+a2(x-l)^ mit bo+biX+b2X^.
Die konstanten Terme sind gleich, wenn ao - ai +02 = ^0 gut- Dadurch erhält
man die alternierenden Vorzeichen in Mf ^ = M_i.
Inverse von Mi = M_i =
Verschiebung um t M^ =
1 -1 1
1 -2
1
tt^
1 2t
1
Es gilt MsMt = Ms+t und MiM_i = Mo = /. Fans der Pascal'schen
Matrizen fragen sich vielleicht, ob auch die symmetrische Matrix Ps als^^^^^
wechselmatrix auftritt. Das ist der Fall, und zwar, wenn die neue Basis auc
negative Potenzen (x + 1)"^ enthält. Mehr darüber auf der Kurs-Webseite
web.init.edu/18.06/www.
7.4 A Sei A eine m x n-Matrix. Hat sie den vollen Spaltenrang r = n, so
hat A eine Linksinverse C = {A'^A)~^A'^. Für diese Matrix C gilt CA — I.
Erklären Sie, warum in diesem Fall die Pseudoinverse A'^ = C ist. Hat A
den vollen Zeilenrang r = m, so hat die Matrix eine Rechtsinverse B =
A^{AÄ^)~^ mit der Eigenschaft AB = I. Erklären Sie, warum in diesem
Fall A^ = B gilt.
Bestimmen Sie, falls möglich, die Matrizen B und C, und bestimmen Sie A+
für alle drei Matrizen:
Ai =
A2 = [2 2] As
22
22
Lösung Hat A den Rang n (unabhängige Spalten), so ist A^A
invertierbar — dies ist einer der wesentlichen Punkte in Abschnitt 4.2. Damit ist
das Produkt von C = {Ä^A)~^A'^ mit A sicherUch CA — I. In der
umgekehrten Reihenfolge ist AC = A{Ä^A)~^A'^ die Projektionsmatrix (siehe
Abschnitt 4.2) auf den Spaltenraum. Die Matrix C genügt also den
Bedingungen 7H an die Pseudoinverse A+.
Hat A den vollen Zeilenrang, so ist AA^ invertierbar, und das Produkt
von A mit B = A^{AÄ^)~^ ist AB = I. Umgekehrt, wiederum, ist
BA = A'^{AA'^)~^A die Projektionsmatrix auf den Zeilenraum, und
deshalb ist B die Pseudoinverse A+.
Das Beispiel Ai hat vollen Spaltenrang (für C), und A2 hat vollen Zeilenrang
(für B):
At = {AUir'Al= ^[2 2]
At = AUA^Alr'= ±
Beachten Sie, dass AtAi = [1] und A2At = [1] gilt. Die Matrix A3 hat aber
keine Rechts- oder Linksinverse. Ihre Pseudoinverse ist At = crf^viuf =
[ri]/4.
Index
-1,2, -1 Matrix, 80, 90, 112, 254, 352 blockweise Multiplikation, 67
A = LDL^, 105, 351
A = LDU, 92, 98, 99
A = LU, 90, 98
QAQ'^, 354
QR, 236, 240
-1
A
A
A = 5yl5-S304, 317
A = UIJV'^, 369
AA'^, 370
A^A, 211, 356
Abbildung
- affine, 459
Abbruchbedingung, 484
Absolutbetrag
- einer komplexen Zahl, 500
Abstand, 211
Achsen, 354
äußeres Produkt, 64
affine Abbildung, 459
Anzahl Operationen
- bei der Bestimmung der inversen
Matrix, 79
- bei der Multiplikation von Matrizen,
64
- bei der Rücksubstitution, 95
- beim Eliminationsverfahren, 94
Assoziativgesetz, 55, 65, 72
Aufwandsbetrachtungen, 467
Basiswechsel, 406
Baum, 422
Betrag
- einer komplexen Zahl, 500
Bild, 379, 382
- einer Matrix, 122
Blockmatrix, 66
Gay ley-Hamilton, 318
charakteristische Gleichung, 293
Gholesky, 358
Gramer'sche Regel, 272, 273
Deltafunktion, 452
Determinante, 76, 245, 293, 296
- der Inversen, 251
- der Transponierten, 251
- eines Produktes, 251
diagonalisierbar, 306
Diagonalisierung, 304
Diagonalmatrix, 407
Distributivgesetz, 65
Drehmatrix, 230, 296, 472
Drehung, 457
- einer Ebene, 472
Dreiecksmatrix, 249
Dreiecksungleichung, 22
duales Programm, 445
Dualitätssatz, 445
Eigenvektor, 289, 294
Eigenwert, 289, 293
- komplexer, 338
- mehrfacher, 305
- positiver, 346
- reeller, 333, 335
Eigenwerte
- Berechnung, 473
- Produkt der, 296, 301
- Summe der, 296, 301
- Eigenwerte
-- von A^ 290
eindeutige Lösung, 161
Eingabefehler, 481
Einheitskreis, 14, 501
650
Index
Einheitsmatrix, 54
Einheitsvektor, 14, 15
Einheitswurzel, 503
Einnahmen, 12
Einstein, 53
EISPACK, 490
Elementarmatrix, 54
Elimination, 94
Eliminationsmatrix, 53, 58
Eliminations verfahren, 40
Ellipse, 353, 354
erweiterte Matrix, 61, 80
Erzeugnis, 178
Euler'sche Formel, 426, 503
Euler'sche Winkel, 476
Fast Fourier Transform, 518
Fehler
- relativer, 480
Fehlergleichung, 479, 484
FFT, 518, 522
Fibonacci, 309, 315
Fließkommaoperation, 472
floating point operation, 472
Flop, 471
Flussdiagramm
- für die FFT, 522
Formel für A~\ 275
FORTRAN , 7, 19
Fourierkoeffizient, 453
Fouriermatrix, 513, 519
Fourierreihe, 233, 449, 452
Fouriertransformation, 517
- schnelle, 517
Fredholm, 201
freie Variable, 42
Frobenius-Norm, 476
Pundamentalsatz, 186, 197, 201
- der Algebra, 518
Funktionenraum, 118, 180, 452
Gauß'sches Eliminations verfahren, 44,
465
Gauß-Seidel-Verfahren, 485, 488
Gauß-Jordan, 79, 80, 86, 163
geometrische Reihe, 438
geometrisches Mittel, 19, 21
gerade Permutation, 111, 246
Gerschgorin-Kreise, 496
Givens-Rotation, 472
Gram-Schmidt, 234, 235
Graph
- gerichteter, 419
- vollständiger, 422
- zusammenhängender, 422
Graphen, 419
Hadamard-Matrix, 405
Hauptachse, 334, 354
Haus, 384
Heisenberg, 308, 318
hermitesche Matrix, 507
Hessenberg-Matrix, 474, 493
Hilbert-Matrix, 474
Hilbertraum, 450
homogene Koordinaten, 457
Hooke'sches Gesetz, 428
Householder-Matrix, 472
imaginäre Zahl, 497
Imaginärteil
- einer komplexen Zahl, 498
inneres Produkt, 11, 451
inverse Matrix, 75
inverse Vektoriteration, 491
Inverse von AB, 77, 86
invertierbar, 76, 82
Inzidenzmatrix
- eines Graphen, 419
Iterationsmatrix, 485
iterative Methode, 484
iteratives Verfahren, 484
- für Eigenwerte, 490
Jacobi-Verfahren, 474, 485, 487
Jordansche Normalform, 486
Kante
- eines Graphen, 421
kartesische Darstellung
- einer komplexen Zahl, 501
Kern, 129, 379, 383
Kern von A'^A, 211
KirchhofF'sche Knotenregel, 425
KirchhofF'sche Regeln, 425
kleinstes Fehler quadrat, 216
Knoten
- eines Graphen, 421
Index 651
Knotenregel, 425
Kofaktormatrix, 275
Kommutativgesetz, 55, 65, 72
komplex konjugiert, 338
komplex konjugierte Zahl, 498
komplex Konjugiertes, 336
komplexe Ebene, 498
komplexe Eigenwerte, 338
komplexe Matrix, 74
komplexe Zahl, 497
Komponenten, 1
Konditionszahl
- einer Matrix, 466, 476, 479
konjugiert Transponierte, 508
Konvergenz, 484
- kubische, 495
Konvergenzgeschwindigkeit, 484, 485
- der Vektoriteration, 491
Konvergenzkriterium, 485
Kosinus, 18, 22
Kosinussatz, 22
Kostenfunktion
- eines linearen Programms, 443
kubische Konvergenz, 495
Länge, 232
- eines Vektors, 13
lösbar, 122
Lösungsfehler, 481
Lanczos-Verfahren, 495
LAPACK, 490
Legendre-Polynom, 456
Leitfähigkeitsmatrix, 427
linear unabhängige Spalten, 199
lineare Abbildung, 377, 379
Lineare Programmierung, 441
lineare Transformation, 377
Lineaxkombination, 4, 10, 122
- von Spalten, 52, 65
Linksinverse, 76
Linkskern, 186, 190
LINPACK, 92, 490
Lt/-Faktorisierung, 91
- unvollständige, 489
Lt/-Verfahren, 485
Magisches Quadrat, 39
Markov-Differentialgleichung, 440
Maxkov-Kette, 434, 436
Markov-Matrix, 38, 291, 302, 307, 432,
433, 491
Maschenregel, 425
MATLAB , 7, 19, 95
Matrix, 30, 62
- -1,2,-1, 80, 112, 254, 352
- ähnliche, 407
- Block, 66
- dünnbesetzte, 489
- diagonaldominante, 496
- Dreh-, 230, 296
- Dreiecks-, 249
- Einheits-, 54
- Elementar-, 54
- Eliminations-, 53, 58
- erweiterte, 57, 61, 80
- Hadamard-, 405
- hermitesche, 507, 510
- inverse, 75, 81
- Kofaktor-, 275
- komplexe, 74
- Markov-, 38, 291, 302, 307, 432,
433, 491
- normale, 517
- orthogonale, 230, 297, 334, 369, 514
- Permutations-, 57, 106, 111
- positiv definit, 348, 349, 352, 358
- Projektions-, 207, 208, 214, 291,
338
- Schachbrett, 192
- schiefhermitesche, 514
- schiefsymmetrische, 112, 127, 254,
297, 514
- semidefinit, 349, 350
- singular, 250
- Spiegelungs-, 231, 242, 292, 461
- symmetrische, 104, 297, 333
- TridiagonaJ-, 81, 96, 100
- umgekehrte Einheits-, 253
- unitäxe, 507, 512, 514
- Vandermonde'sche, 254
- Wurzel aus, 358
Matrix mal Vektor, 36
Matrixmultiplikation, 62
Matrixnorm, 476
Matrixraum, 383
Matrizenraum, 119, 126, 180
mehrfache Eigenwerte, 305
652
Index
Messfehler, 479
Methode der kleinsten Quadrate, 217
- rekursives Verfahren, 228
Minimum, 349
Mittelwert, 227
Multiplikation
- blockweise, 67
Multiplikator, 41
nächstgelegene Gerade, 216, 219, 220
Nebenbedingungen
- eines linearen Programms, 442
Netzwerk, 419, 427
nicht diagonalisierbar, 312
Nichtdiagonalisierbarkeit, 306
nichtsingulär, 44
Norm
- einer Diagonlmatrix, 477
- einer Matrix, 476, 478
- einer positiv definiten
symmetrischen Matrix, 477
- eines Vektors, 13
- Probenius-, 476
Normalengleichung, 209, 218
Nullmatrix, 62
oberes Dreieckssystem, 40
Ohm'sches Gesetz, 427
orthogonale Matrix, 230, 297, 334, 369,
514
orthogonaler Unterraum, 193, 195, 196
orthogonales Komplement, 196, 203
orthonormal, 229
Orthonormalbasis, 368
orthonormale Spalten, 230, 232, 238
PA = LU, 108-110
Parabel, 223, 224
Parallelogramm, 3, 6
Parallelprojektion, 461
Parallelrechner, 465
partielle Pivotierung, 465
Pascal, 101
Permutation
- gerade, 246
- ungerade, 246
Permutationsmatrix, 57, 106, 111
perspektivische Projektion, 461
Pivotelement, 42
Pivotierung
- partielle, 465
- vollständige, 467
Polarkoordinatendarstellung
- einer komplexen Zahl, 500
Polarzerlegung, 411
positiv definite Matrix, 348, 349, 352,
358
positive Eigenwerte, 346, 352
Potentialdifferenz, 423
Potenz
- einer komplexen Zahl, 501
Potenzen einer Matrix, 289, 307, 311,
316
Präkonditionierer, 484, 490
Produkt von Determinanten, 251
Projektion, 203, 204, 208, 457
- Parallel-, 461
- perspektivische, 461
Projektion auf einen Unterraum, 207
Projektionsmatrix, 207, 208, 214, 291,
338
projektiver Raum, 459
Pseudoinverse, 406, 412
Pythagoras, 8
QR-Verfahren, 490, 491
Quadratwurzel (einer Matrix), 358
Rücksubstitution, 93, 96
Rang, 186, 207
Rayleigh-Quotient, 479
Realteil
- einer komplexen Zahl, 498
Rechenaufwand
- für die (JÄ-Zerlegung, 471
- für die Bestimmung der Inversen,
471
- für die FFT, 523
- für die Vorwärtselimination, 468
-- bei Bandmatrizen, 470
Rechteckkurve, 453
rechter Winkel, 15
Rechtsinverse, 76
rechwinklig, 15
reduzierte Treppenform, 80, 81
Rekursion
- bei der FFT, 523
Index 653
relativer Fehler, 480
Residuum, 483
Roboterhand, 476
Rotation
- einer Ebene, 472
Rotationsmatrizen, 472
Rundungsfehler, 466
5-^^5 = ^,304
Schachbrett-Matrix, 192
Schaltkreistheorie, 425
schiefhermitesche Matrix, 514
schiefsymmetrisch, 127
schiefsymmetrische Matrix, 112, 254,
297, 514
Schur-Komplement, 270
Schwarz'sche Ungleichung, 18, 20, 23,
450
semidefinite Matrix, 350
senkrecht, 20
senkrechte Eigenvektoren, 293, 335
senkrechte Vektoren, 334
Sensitivität
- einer Matrix, 466
Sigma-Notation, 53
Simplex-Algorithmus, 442, 446
singular, 44
singulare Matrix, 250
Singulärwert, 409, 479
SingulärwertZerlegung, 409
Skalar, 2, 118
Skalarprodukt, 11, 16, 17, 450
- komplexes, 508
Skalierung, 457
SOR-Verfahren, 485, 488
Spalte-mal-Zeile, 67, 74
Spaltenbild, 43
Spaltenraum, 122
Spaltenvektor, 5
Spektralradius, 482, 485
Spektralsatz, 334
Spiegelung, 461
Spiegelungsmatrix, 231, 242, 292, 461,
472
Spur, 296, 301, 317
Standardabweichung, 227
stationärer Zustand, 432
successive overrelaxation, 485
SVD, 369
symmetrische Matrix, 104, 297, 333
symmetrisches Produkt, 105
Tabellenkalkulation, 12
Transformation, 399
Translation, 457
transponierte Matrix, 102
Tridiagonalmatrix, 81, 96, 100
Uhr, 9
umgekehrte Einheitsmatrix, 253
umgekehrte Reihenfolge, 77, 102
unabhängige Spalten, 185
unabhängige Zeilen, 185
unendliche Reihe
- geometrische, 438
ungerade Permutation, 246
unitäre Matrix, 507, 512, 514
Unschärferelation, 308, 318
Unterraum, 119, 126
unvollständige LC/-Faktorisierung, 489
Vandermonde-Matrix, 254
Varianz, 227
Vektor
- Länge, 13
- Norm, 13
Vektoraddition, 2, 3, 118
Vektoriteration, 490
- inverse, 491
Vektorraum, 117, 125
Verbrauchsmatrix, 437
Verfahren der konjugierten Gradienten,
490
Versagen des Eliminations Verfahrens,
48
Vielfachheit, 312
vier fundamentale Unterräume, 185
voller Rang, 161
vollständige Lösung, 159
vollständige Pivotierung, 467
Volumen, 248
Vorwärtselimination, 93, 96
Vor zeichen Wechsel, 247
Würfel, 9
Wavelets, 243
Winkel, 15
- einer komplexen Zahl, 500
654 Index
- Euler'sche, 476 zulässiger Bereich
- eines linearen Programms, 442
Zeilenbild, 43 zulässiger Punkt
Zeilentausch, 57 - eines linearen Programms, 442
Zeilenvektor, 5 Zyklus
Zeilenvertauschung, 107 - eines Graphen, 422
MATLAB Unterrichtscodes
cofactor Berechnet die n x n-Matrix der Kofaktoren
Cramer Löst das System Ax = b mit Hilfe der Cramer'schen Regel.
deter Matrix-Determinante, berechnet aus den Pivotelementen in
PA = LU.
eigen2 Eigenwerte, Eigenvektoren und det(A ~ \I) für 2 x 2-Matrizen.
eigshow Grafische Veranschaulichung von Eigenwerten und Eigenvektoren.
eigval Eigenwerte und ihre Vielfachheit als Lösungen der Gleichung
det(A - \I) = 0.
eigvec Berechnet so viele linear unabhängige Eigenvektoren wie möglich.
elim Reduktion der Matrix A auf Zeilen-Treppenform R mit Hilfe einer
invertierbaren Matrix E.
findpiv Bestimmt ein Pivotelement für das Gauß'sche
Eliminationsverfahren (wird von plu verwendet).
fourbase Konstruiert Basen für die vier fundamentalen Unterräume.
grams Gram-Schmidt-OrthogonaUsierung der Spalten von A.
house 2 X 12-Matrix mit den Koordinaten der Ecken eines Hauses.
inverse Inverse einer Matrix (falls existent), berechnet mit dem Gauß-
Jordan-Verfahren.
leftnuU Berechnet eine Basis des Linkskerns.
linefit Zeichnet die Kleinste-Quadrate-Approximation von m gegebenen
Punkten durch eine Gerade.
Isq Kleinste-Quadrate-Approximation von Ax = b, berechnet mit
Hilfe von A'^Ax = A^h.
normal Eigenwerte und orthonormale Eigenvektoren für den Fall A'^A =
AA^.
nulbasis Matrix von speziellen Lösungen der Gleichung Ax = 0 (Basis des
Kerns).
orthcomp Findet eine Basis für das orthogonale Komplement eines
Unterraums.
partic Partikuläre Lösung der Gleichung Ax = b, wobei alle freien
Variablen zu Null gesetzt werden.
plot2d Zweidimensionaler Plot für die Haus-Abbildungen (Einband [der
zweiten amerikanischen Ausgabe, Anm. d. Übers.] und
Abschnitt 7.1).
plu Rechteckige PA = LCZ-Faktorisierung mit Zeilentausch.
poly2str Wandelt ein Polynom in eine Zeichenkette um.
project Projiziert einen Vektor b auf den Spaltenraum von A,
projmat Konstruiert die Projektionsmatrix auf den Spaltenraum von A.
randperm Konstruiert eine zufällige Permutation.
656 MATLAB Unterrichtscodes
rowbasis Berechnet eine Basis für den Zeilenraum aus den Pivotzeilen von
R.
samespan Überprüft, ob zwei Matrizen denselben Spaltenraum besitzen.
Signperm Determinante der Permutationsmatrix, deren Zeilenordnung
durch den Vektor p gegeben ist.
slu LCZ-Faktorisierung einer quadratischen Matrix ohne
Zeilentausch.
slv Wendet slu an, um das Gleichungssystem Ax = h ohne
Zeilentausch zu lösen.
splu Quadratische PA = LC/-Faktorisierung mit Zeilentausch.
splv Berechnet die Lösung eines quadratischen Gleichungssystems
Ax = b mit invertierbarer Matrix A.
symmeig Berechnet die Eigenwerte und Eigenvektoren einer symmetrischen
Matrix.
tridiag Konstruiert eine Tridiagonalmatrix mit konstanten Diagonalen a,
ö, c.
Diese Unterrichtscodes sind direkt erhältlich auf der Homepage zur linearen
Algebra
http://web.mit.edu/18.06/www
Sie sind in MATLAB geschrieben, wurden aber auch in Maple und Mathema-
tica übersetzt.