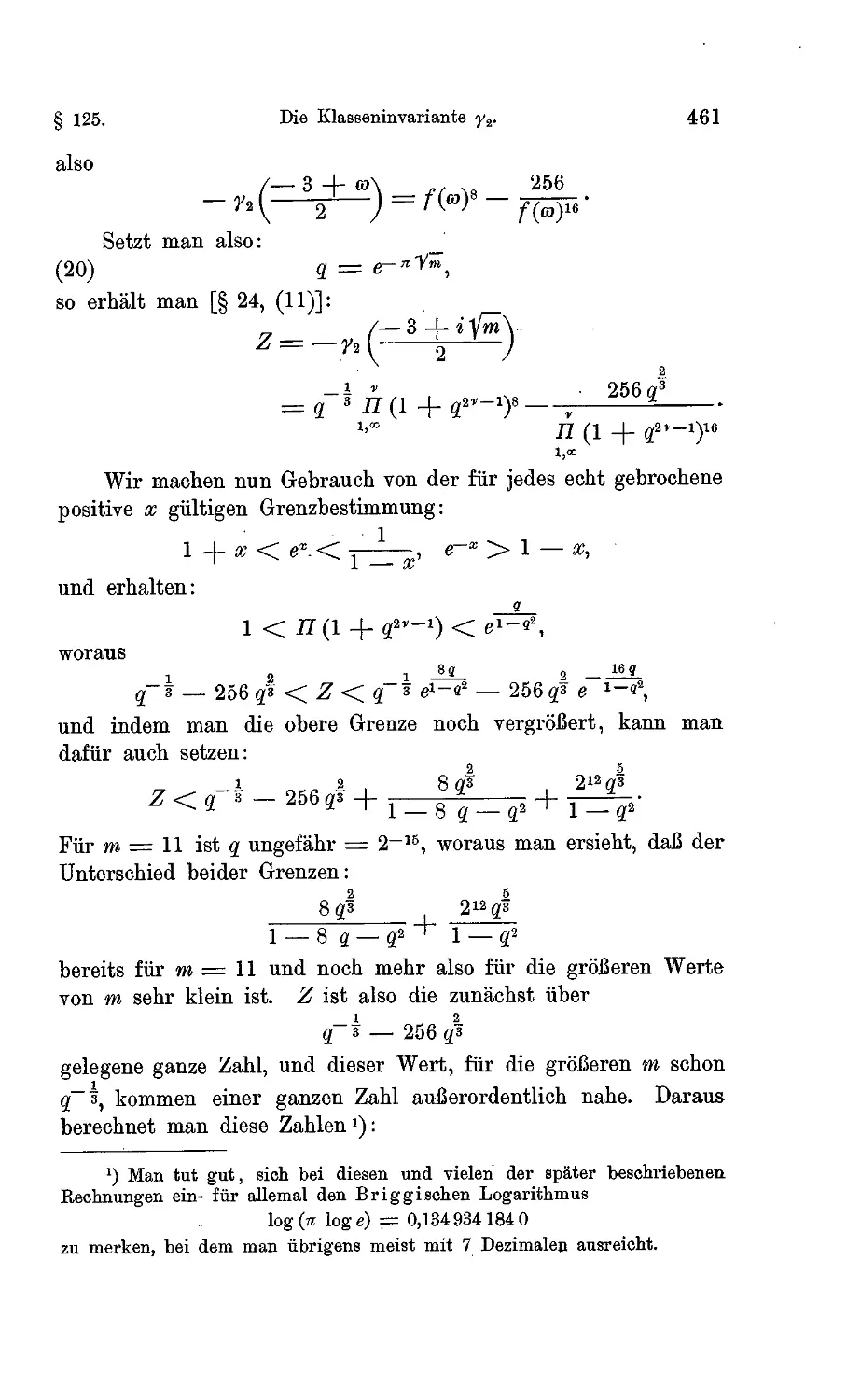Текст
Cornell University Library
reformatted this volume
to digital files to preserve
the informational content
of the deteriorated original.
The original volume was scanned
bitonally at 600 dots per inch
and compressed prior to storage
using ITU Group 4 compression.
1997
®onwll Unwersitf Jitaig
BOUGHT WITH THE INCOME
FROM THE
SAGE ENDOWMENT FUND
THE GIFT OF
Sage
1891 j
LEHRBUCH
Ü
DER
VON
HEINRICH WEBER
PROFESSOR DER MATHEMATIK AN DER UNIVERSITÄT STRASSBURG
ZWEITE AUFLAGE
DRITTER BAND
MIT ZWEI ABBILDUNGEN IM TEXT
BRAUNSCHWEIG
DRUCK UND VERLAG VON FRIEDRICH VIEWEG UND SOHN
19 0 8
ELLIPTISCHE
FUNKTIONEN
UND
ALGEBRAISCHE ZAHLEN
VON
HEINRICH WEBER
PROFESSOR DER MATHEMATIK AN DER UNIVERSITÄT STRASSBURG
ZWEITE AUFLAGE
MIT ZWEI ABBILDUNGEN IM TEXT
BRAUNSCHWEIG
DRUCK UND VERLAG VON FRIEDRICH VIEWEG UND SOHN
19 0 8
tÜ,
Alle Rechte,
namentlich dasjenige der Übersetzung in fremde Sprachen, vorbehalten.
Published May 24, 1908.
Privilege of Copyright in the United States reserved ander the Act
approved March 3, 1905 by Friedr. Vieweg & Sohn, Braunschweig,
Germany.
RICHARD DEDEKIND,
DAVID HILBERT, HERMANN MINKOWSKI
IN HERZLICHER FREUNDSCHAFT
GEWIDMET.
VORWORT.
Es ist mir vergönnt, den Plan einer Weiterführung meines
Lehrbuches der Algebra, den ich vor zwölf Jahren in der Vor-
rede zur ersten Auflage des zweiten Bandes angekündigt habe,
nach mannigfaltigen Abhaltungen noch auszuführen. Durch das
Entgegenkommen der Verlagsfirma erscheint dieser dritte Band
der Algebra zugleich als zweite Auflage der im Jahre 1891 zum
erstenmal gedruckten „Elliptischen Funktionen und algebraischen
Zahlen“.
Er beschäftigt sich hauptsächlich mit dem weiteren Ausbau
der mannigfaltigen Anwendungen der Algebra und besonders der
Theorie der quadratischen Körper auf die aus den elliptischen
Funktionen hervorgegangenen Probleme, die uns das erste über
die Kreisteilung hinausgehende Beispiel von algebraischen Zahlen
liefern, deren Gesetze einigermaßen bekannt sind. Als Grund-
lage dazu dient eine eingehendere Behandlung der quadratischen
Körper mit negativer Diskriminante. Freilich ist auch hier nicht
alles erreicht, was ich mir als letztes Ziel gesteckt hatte. So
mußte die Ausführung der Theorie der relativ zyklischen Körper
noch zurückgestellt werden — hoffentlich nur einstweilen.
Dagegen habe ich, einem mehrfach an mich herangetretenen
Wunsche entsprechend, einen Abriß der Theorie der algebrai-
schen Funktionen auf arithmetischer Grundlage beigefügt, der
vin
V orwort.
sich im wesentlichen an die Abhandlung von Dedekind und mir
im 92. Bande von Grelles Journal anschließt, aber durch An-
wendung der Theorie der Funktionale, auf die ich im zweiten
Bande die Theorie der algebraischen Zahlen gegründet habe, wie
mir scheint, eine Vereinfachung erreicht.
Straßburg, im Mai 1908.
H. Weber.
INHALTSVERZEICHNIS.
Erstes Buch.
Analytischer Teil.
Erster Abschnitt.
Die elliptischen Integrale.
Seite
§ 1. Definition der elliptischen Integrale......................... 3
§ 2. Doppelverhältnisse............................................ 5
§ 3. Lineare Transformation des elliptischen Differentials......... 8
§ 4. Die Legendresche Normalform ..................................11
§ 5. Die Weierstrasssche Normalform................................13
§ 6. Elliptische Kurven............................................18
§ 7. Elliptische Raumkurven vierter Ordnung........................23
§ 8. Das Jaeobisehe Transformationsprinzip.........................30
§ 9. Die Transformation zweiten Grades.............................32
§ 10. Die Transformation dritten Grades ............................35
§ 11. Die drei Gattungen elliptischer Integrale.....................38
§ 12. Darstellung der elliptischen Integrale dnrch die einfachsten
Grundintegrale.......................................................40
§ 13. Das Additionstheorem..........................................43
§ 14. Ursprung der elliptischen Funktionen..........................49
Zweiter Abschnitt.
Theta Funktionen.
§ 15. Voraussetzungen aus der Funktionentheorie.....................53
§16. Periodizität..................................................56
§ 17. Die Funktionen T..............................................60
§ 18. Relationen zwischen verwandten T-Funktionen...................65
§19. T-Funktionen erster Ordnung...................................67
§ 20. Die O-Funktion................................................69
§ 21. Die Theta - Funktionen verschiedener Charakteristiken. Haupt-
eharakteristiken.................................................... 71
§ 22. Das Additionstheorem..........................................76
§ 23. Die Derivierten der O-Funktionen .............................81
§ 24. Darstellung der O-Funktionen durch unendliche Produkte .... 83
X
Inhaltsverzeichnis.
Seite
§ 25. Darstellung der .9-Funktionen durch unendliche Reihen .... 86
§ 26. Entwickelung von »-Quotienten.................................... 88
Dritter Abschnitt.
Transformation der Theta - Funktionen.
§ 27. Das Transformationsprinzip ...................................... 93
§ 28. Zusammensetzung der Transformationen ............................ 96
§ 29. Zusammensetzung der Transformationen aus einfacheren .... 99
§ 30. Die linearen Fundamentaltransformationen ........................101
§ 31. Die linearen Fundamentaltransformationen der »-Funktionen . . 103
§ 32. Die Haupttransformationen zweiter Ordnung der »-Funktionen . 105
§ 33. Die Haupttransformationen ungerader Ordnung.............110
§ 34. Die Funktionen i/ (<o), (®),'(w) .............................112
§ 35. Die Weierstrasssche o-Funktion..........................116
§ 36. Die Funktionen o00, <r01, ff10..........................119
§ 37. Darstellung der <r-Funktionen dnrch »-Funktionen........122
§ 38. Lineare Transformationen der Funktion T](a>)............124
§ 39. Lineare Transformation der »-Funktionen.................130
§ 40. Lineare Transformation der Funktionen /'(«>), 132
Vierter Abschnitt.
Die elliptischen Funktionen.
§ 41. Zusammenhang der »-Funktionen mit den elliptischen Integralen 135
§ 42. Jacobis elliptische Funktionen.........'.........................137
§ 43. Die Jaeobisehen Funktionen @(v), H(v)............................141
§ 44. Additionstheorem der elliptischen Funktionen.....................142
§ 45. Die lineare Transformation der elliptischen Funktionen .... 147
§ 46. Die Weierstrasssche p-Funktion..................................150
§ 47. Die elliptischen Transzendenten zweiter Gattung.................153
§ 48. Die elliptischen Transzendenten dritter Gattung.................156
§ 49. Die Transzendenten zweiter und dritter Gattung von Weier strass 160
§ 50. Entwickelungen der elliptischen Funktionen.......................162
Fünfter Abschnitt.
Die Modulfunktionen.
§ 51. Die elliptischen Differentialgleichungen........................166
§ 52. Die unabhängige Variable z2. Lineare Differentialgleichung für K 167
§ 53. Die Lösungen der Gleichung j (<o) = j («/)......................174
§ 54. Die Modulfunktionen.............................................176
§ 55. Darstellung der elliptischen Funktionen durch v und z2 . . . . 181
§ 56. Potenzreihen für die Weierstrassschen Funktionen p (w), a(u) 185
Sechster Abschnitt.
Multiplikation und Teilung der elliptischen Funktionen.
§ 57. Multiplikation der elliptischen Funktionen ......................190
§ 58. Multiplikation der Funktion p («/.)............................. 196
Inhaltsverzeichnis. XI
Seite
§ 59. Die Teilung durch 2........................................200
§ 60. Die Teilung durch eine ungerade Zahl......................202
§ 61. Die Teilung der Perioden...................................204
§ 62. Die Abel sehen Relationen..................................205
§ 63. Die Galoissehe Gruppe der Teilungsgleichung................208
§ 64. Die irreduzibeln Faktoren der Teilungsgleiehung............216
§ 65. Zurüekführung der Teilungsgleichung auf Transformations-
gleichungen.......................................................217
Siebenter Abschnitt.
Theorie der Transformationsgleichungen.
§ 66. Bildung von Transformationsgleichungen.................... 225
§ 67. Besondere Transformationsgleichungen........................228
§ 68. Zweite Darstellung der Wurzeln der Transformationsgleichungen 231
§ 69. Die Invariantengleichung...................................237
§ 70. Transformationsgleichungen erster Stufe....................245
§ 71. Die Transformationsgleichungen für y2 und y3...............247
§ 72. Multiplikatorgleichungen erster Stufe.......................248
§ 73. Die Sehlaeflisehen Modulargleiehungen......................256
'§ 74. Die Form der Sehlaeflisehen Modulargleiehungen.............265
§ 75. Die irrationalen Formen der Modulargleiehungen..............269
§ 76. Zusammengesetzte Transformationsgrade.......................274
§ 77. Geometrische Deutung der irrationalen Modulargleiehungen als
Korrespondenzen..........................................280
Achter Abschnitt.
Die Gruppe der Transformationsgleichungen und die Gleichung
5ten Grades.
§ 78. Die Galoissehe Gruppe der Transformationsgleichungen für
einen Primzahlgrad................................................284
§ 79. Untersuchung der Gruppe ...................................290
§ 80. Normalteiler der Gruppe So.................................294
§ 81. Niehtnormale Teiler von ...................................299
§ 82. Teiler von ß0.vom Index p für p = 5, 7, 11 . . . ..........305
§ 83. Verschiedene Resolventen 5ten Grades für den 5ten Trans-
formationsgrad ...................................................309
Zweites Buch.
Quadratische Körper.
Neunter Abschnitt.
Diskriminante.
§ 84. Definition der Diskriminanten..............................321
§ 85. Das erweiterte Legendre-Jacobi sehe Symbol.................322
§ 86. Die Gaussschen Summen..................................... 328
XII
Inhaltsverzeichnis.
Zehntel- Abschnitt.
Algebraische Zahlen und Formen.
X. Seite
§ 87. Ideale und Formen in algebraischen Körpern....................................................................................................330
§ 88. Idealklassen und Formenklassen.333
§ 89. Komposition der Formen und Multiplikation der Ideale .... 335
Elfter Abschnitt.
Ideale in quadratischen Körpern.
§ 90. Diskriminante des quadratischen Körpers...............338
§ 91. Ideale und Formen in quadratischen Körpern...............340
§ 92. Primideale im quadratischen Körper...............342
§ 93. Darstellung von Zahlen als Idealnormen...................................................................344
§ 94. Das quadratische Reziprozitätsgesetz...............345
§ 95. Äquivalente Formen und Ideale im quadratischen Körper . . . 347
Zwölfter Abschnitt.
Ordnungen im quadratischen Körper.
§ 96. Diskriminanten der Ordnungen..................................................................................................................351
§ 97. Ordnungen und Ideale..........................................................................................................................353
Dreizehnter Abschnitt.
Äquivalenz nach Zahlgruppen.
§ 98. Zahlgruppen in den Ordnungen..................................................................................................................358
§ 99. Äquivalenz in den Ordnungen...................................................................................................................361
§ 100. Idealklassen nach den Ordnungen.................... . . . 362
Vierzehnter Abschnitt.
Komposition der Formen und Ideale.
'• § 101. Komposition in den Ordnungen..................................................................................................................368
§ 102. Komposition der Ordnungen.....................................................................................................................373
Fünfzehnter Abschnitt.
Geschlechter der quadratischen Formen.
§ 103. Darstellung von Zahlen durch quadratische Formen.........376
§ 104. Charaktere und Geschlechter der quadratischen Formen .... 380
§ 105. Anwendung des Legendreschen Symbols...........................................................................................................385
106. Die Geschlechter der Idealklassen.............................................................................................................388
§ 107. Zusammensetzung der Normenrestgruppen....................................................................................................... 389
§ 108. Normenreste der Primzahlpotenzen .............................................................................................................390
§ 109. Die Geschlechter der Ideale..............................395
Inhaltsverzeichnis. XIII
Sechzehnter Abschnitt.
Klassenzahl in quadratischen Körpern. g
§ 110. Fundamentale Einheiten in den Ordnungen ...................398
§ 111. Die Diriehletsche Grenzformel .............................402
§ 112. Klassenzahl ...............................................405
§ 113. Die Anzahl der Geschlechter................................409
Drittes Buch.
Komplexe Multiplikation.
Siebzehnter Abschnitt.
Elliptische Funktionen und quadratische Formen.
§ 114. Singuläre Perioden der doppelt periodischen Funktionen . . . 413
§ 115. Die singulären Werte der Invariante j (<o).................418
§ 116. Klassenzahlrelationen......................................423
§ 117. Arithmetische Natur der Klassenfunktion Hrn(u') ....... 426
§ 118. Komposition der quadratischen Formen.......................428
§ 119. Die Diskriminante der Invariantengleichung.................431
Achtzehnter Abschnitt.
Galoissehe Gruppe der Klassengleichung.
§ 120. Relationen zwischen den Klasseninvarianten derselben Diskri-
minante ..........................................................435
§ 121. Trennung der entgegengesetzten Klassen.....................437
§ 122. Irredueibilität............................................442
§ 123. Beziehungen zwischen den Klasseninvarianten in den verschie-
denen Ordnungen...................................................450
§ 124. Klassenkörper und Ordnungskörper...........................455
Neunzehnter Abschnitt.
Berechnung der Klasseninvarianten.
§ 125. Die Klasseninvariante ys...................................457
§ 126. Die Klasseninvarianten ..................... 462
§ 127. Die Potenzen von /'(oi) als Klasseninvarianten.............467
§ 128. Die ersten Fälle der Berechnung von f(V—m).................474
§ 129. Anwendung der Transformation zweiter Ordnung zur Berechnung
von Klasseninvarianten............................................476
§ 130. Berechnung von Klasseninvarianten aus den Sehlaeflisehen
Modulargleiehungen................................................477
§ 131. Berechnung von Klasseninvarianten aus den irrationalen Formen
der Modulargleiehungen............................................485
XIV Inhaltsverzeichnis.
Seite
§ 132. Die Schlaeflische Modulargleichung für den 23sten Trans-
formationsgrad..................................................489
§ 133. Die Resolventen 7ten und Ilten Grades für den7ten und Ilten
Transformationsgrad.............................................491
Zwanzigster Abschnitt.
Die Multiplikatorgleichung in der komplexen Multiplikation.
§ 134. Die Klasseninvariante 73'(«j)............................500
§ 135. Die Klasseninvarianten z2 und x..........................505
§ 136. Quadratische Transformationsgrade........................507
§ 137. Zurückführung ungerader Diskriminanten auf gerade........512
§ 138. Zerfällung der Klassengleichung nach den Geschlechtern . . . 513
§ 139. Beispiele................................................521
Einundzwanzigster Abschnitt.
Die Normen der Klasseninvarianten /'(<»).
§ 140. Konvergenz einer unendlichen Reihe.......................525
§ 141. Die Kroneckersche Grenzformel............................526
§ 142. Die Normen der Klasseninvarianten f(oi)..................533
§ 143. Partialnormen von .......................................541
§ 144. Berechnung einiger weiterer Klassen invarianten..........545
Zweiundzwanzigster Abschnitt.
Cayleys Entwickelung der Modulfunktionen.
§ 145. Grenzwerte für s = 1.....................................548
§ 146. Ein Satz über Reihenkonvergenz...........................551
§ 147. Entwickelung von f, fv f.2 ..............................553
§ 148. Elementare Ableitung der Entwickelungen .......... 557
§ 149. Entwickelungen für die Funktion log tj (<o)..............559
Viertes Buch.
Klassenkörper.
Dreiundzwanzigser Abschnitt.
Der Teilungskörper.
§ 150. Die homogenen Weierstrasssehen Funktionen ....... 563
§ 151. Die komplexe Multiplikation der Funktion p (u)..........566
§ 152. Die Pole der Funktion p (u u)...........................568
§ 153. Die Funktion r(w).......................................571
§ 154. Der Teilungskörper......................................573
§ 155. Multiplikation der elliptischen Funktionen für einen ungeraden
MultipHkator....................................................576
§ 156. Übergang zu den singulären Moduln........................581
Inhaltsverzeichnis. XV
Seite
§ 157. Komplexe Multiplikatoren..................................583
§ 158. Zerlegung der Funktion A(%y..............................590
§ 159. Primideale................................................592
§ 160. Primideale ersten Grades in 2m............................594
§ 161. Zahlgruppen und Idealgruppen..............................596
§ 162. Die durch ein Ideal teilbaren Ideale der Hauptklassen .... 599
§ 163. Die Dirichletschen Summen.................................602
§ 164. Der Klassenkörper.........................................607
§ 165. Primideale in den Klassen.................................611
§ 166. Primideale in den Idealklassen............................612
§ 167. Primzahlen in Linearformen................................613
§ 168. Reduktion der Klassengleichung in den Kreisteilungskörpern. . 616
§ 169. Beziehung der Teilungskörper zu dem Klassenkörper.........619
Fünftes Buch.
Algebraische Funktionen.
Vierundzwanzigster Abschnitt.
Algebraische Funktionen einer Variablen.
§ 170. Einleitendes..............................................623
§ 171. Definition der algebraischen Funktionen...................624
§ 172. Normen und Spuren.........................................627
§ 173. Diskriminanten............................................631
§ 174. Die Potenzsummen..........................................632
§ 175. Ganze Funktionen von z....................................635
§ 176. Minimalbasis und Körperdiskriminante......................637
Fünfundzwanzigster Abschnitt.
Funktionale.
§ 177. Rationale Funktionale . ._................................640
§ 178. Funktionale des Körpers 12 . . ...........................642
§ 179. Ganze Funktionale des Körpers 12 .... •...................643
§ 180. Teilbarkeit von Funktionalen. Einheiten...................644
§ 181. Größter gemeinschaftlicher Teiler.........................645
§ 182. Primfunktionale in 12.....................................646
§ 183. Basen und Basisformen der Funktionale.....................651
§ 184. Basisform und Verzweigungsfunktional......................654
§ 185. Die gebrochenen Funktionen in 12 und die Taylorsche Ent-
wickelung .......................................................658
§ 186. Birationale Transformation.............................. 660
Seehsundzwanzigster Abschnitt.
Zahlenwerte der algebraischen Funktionen.
§ 187. Der Punkt.................................................663
§ 188. Ordnungszahlen............................................666
XVI
Inhaltsverzeichnis.
Seite
§ 189. Polygone....................................................667
§ 190. Verzweigungspunkte und Verzweigungszahlen...................669
§ 191. Polygonquotienten und Polygonklassen........................670
§ 192. Polygonscharen..............................................672
§ 193. Normalbasen.................................................676
§ 194. Differentialquotienten......................................679
§ 195. Darstellung der Differentialquotienten durch Polygonquotienten 682
§ 196. Geschlecht des Körpers £1...................................685
Siebenundzwanzigster Abschnitt.
Algebraische und Abelsche Differentiale.
§ 197. Differentiale in fi.........................................688
§ 198. Die Polygonschar erster Gattung.............................690
§ 199. Der Riemann-Roehsehe Satz...................................695
§ 200. Differentiale zweiter und dritter Gattung...................699
§ 201. Die Residuen................................................702
Tabellen.
I. Entwickelungen der sechzehn 3-Quotienten (S. 88).........711
II. Zweite Form dei’ Entwickelung der sechzehn ^-Quotienten (S. 91) 713
III. Entwickelung der 3 -Quotienten in trigonometrischen Reihen (S. 92) 716
IV. Entwickelungen der elliptischen Funktionen (S. 163)......718
V. Entwickelung der Transzendenten zweiter Gattung (S. 164) .... 720
VI. Verzeichnis von Klasseninvarianten (zum neunzehnten Abschnitt) . 721
Alphabetisches Register.......................................727
ERSTES BUCH.
ANALYTISCHER TEIL.
*
Weber, Algebra. III.
1
Erster Abschnitt.
Die elliptischen Integrale.
§ 1. Definition der elliptischen Integrale.
Wenn die systematische Darstellung der Integralrechnung bis
zu dem Punkte gelangt ist, wo algebraische Integrale mit der
Quadratwurzel aus einer Funktion ersten oder zweiten Grades
auf Integrale rationaler Funktionen zurückgeführt werden, so tritt
an dieser Stelle dem Lernenden eine Schranke entgegen, die er
mit den ihm bis dahin zu Gebote stehenden Hilfsmitteln nicht
zu übersteigen imstande ist. Das Streben nach einer Erweiterung
der Hilfsmittel, um auch noch die nächste Klasse von Integralen
der Forschung zugänglich zu machen, ist, wie es historisch der
Anlaß gewesen, zu einem eingehenderen Studium der elliptischen
Integrale und zur Einführung der elliptischen Funktionen, auch
der naturgemäßeste und verständlichste Ausgangspunkt für den,
der in die Theorie dieser Funktionen zuerst eingeführt werden
soll. Es soll daher auch unsere nächste Aufgabe sein, uns mit
den elliptischen Integralen und ihren wichtigsten Eigenschaften
bekannt zu machen.
Die Definition eines elliptischen Integrals, von der wir aus-
gehen wollen, ist die folgende: Es bedeute f(x) eine ganze
rationale Funktion dritten oder vierten Grades mit vier verschie-
denen Wurzeln
(1) f(x) = a0a;4 -|- lojs;3 a4,
worin a0 und ax nicht beide zugleich verschwinden; es sei ferner
<D(x, y) eine beliebige ganze oder gebrochene rationale Funktion
der beiden Argumente x, y. Dann ist
\f(x))dx
das allgemeine elliptische Integral und
<5 («, y f(x)) d x
1*
4
Erster Abschnitt.
das allgemeine elliptische Differential. Es läßt sich nun
aber dies allgemeine Integral und Differential auf wesentlich ein-
fachere zurückführen. Zunächst läßt sich in die Form setzen:
worin A, B, C, D ganze rationale Funktionen von x sind, und
indem man diesen Bruch mit C — D ]/ f(x) erweitert, in die Form
V/GO
worin IP- (x). und (a;) ganze oder gebrochene rationale Funk-
tionen von x sind, nämlich
. AC — BDf(x)
w — C2 — D2f(x) '
(BC-AD)f(x)
W ~ G'2 — D2f(x)
Wir lassen nun das rationale Integral
j ’9f(x)dx,
das auf Logarithmen und algebraische Funktionen führt, außer
Betracht, und befassen uns nur noch mit dem elliptischen Integral
(2)
\f(x)
oder dem entsprechenden elliptischen Differential
(3)
W)
Es ist bisweilen nützlich, dies Differential in der homogenen
Form zu betrachten; zu diesem Ende setzen wir für x das Ver-
hältnis zweier Variablen x:y, und demnach für dx
ydx — xdy
y~2
Ist dann
/(a;, y) = aüx> -|- ka^y Qa^y* -|- <La3xy3 -|- <a4«/4,
und &(a>, y) eine homogene Funktion Oter Ordnung, so erhält
unser elliptisches Differential die Gestalt
ydx — xdy
y)
GO
§ 2. Doppelverhältnisse. 5
Die Aufgabe, die uns nun zunächst beschäftigen wird, ist
eine doppelte: Es soll durch Einführung neuer Veränderlicher
das Differential
dx , ydx — xdy
(5) ~== oder -—,
\f(x) if&y)
in ein anderes von derselben Form transformiert werden, worin
aber die Funktion unter dem Quadratwurzelzeichen möglichst
vereinfacht und besonders von einer möglichst kleinen Zahl von
Parametern abhängig gemacht wird (§ 3, 4, 5). Es soll zweitens
das allgemeine Differential (3) oder (4) in andere ähnliche zerlegt
werden, in welchen die Funktion <f>(x) oder <5(.r,«/) möglichst
einfach ist (§ 12).
Die Funktion f(x) läßt sich in lineare Faktoren zerlegen
(Bd. I, § 33). Wir setzen demnach auch
f(x) = a0(x — a,1)(a; — x2~)(x —• x3)(x — x4).
Denken wir uns die Größen x, xlt x2, ... als Abszissen von
Punkten auf eine gerade Linie von einem beliebigen Nullpunkte
aus aufgetragen, die positiven nach der einen, die negativen nach
der anderen Seite (z. B. positiv nach rechts, negativ nach links),
so stellen die Differenzen x — x4, x — x2, x — x3, x — xt die
Entfernungen des Punktes x von xlt x2, x3, x4 dar, und zwar
positiv gerechnet, wenn x nach der positiven Seite von x4, x2, ...
liegt. In demselben Sinne ist x2 — x\ die Entfernung des Punktes
x2 von usf.
Wir bezeichnen die Differenzen auch kürzer durch (xx4),
(xx2), ... (x2x4), ... Wir benutzen diese Darstellungsweise aber
nur zur leichteren Übersicht und schließen auch imaginäre Punkte
der Geraden, nicht aus.
§ 2. Doppelverhältnisse.
Das einfachste Mittel zur Vereinfachung des elliptischen
Differentials stützt sich auf die lineare Transformation der Funk-
tion f(x) (Bd. I, § 67). Es mögen a, ß, y, d vier beliebige Kon-
stanten bedeuten, deren Determinante
(1) aS — ßy = r
von Null verschieden ist. Wir setzen
ax' -L ß
x ~ —>T x’
yx -L d
6 Erster Abschnitt. § 2.
und nennen dies eine lineare Substitution. Deuten wir x
und x' wie im § 1 als Punkte auf zwei geraden Linien L und L',
so ist durch (2) eine gegenseitig eindeutige Beziehung der
Punkte von L und L', eine Abbildung, festgelegt. Den Werten
x — <x> und x' = <x> entsprechen die unendlich fernen Teile
der Geraden, die wir ebenfalls als bestimmte Punkte betrachten.
Es entspricht dann der Punkt x' = co dem Punkt x = a: 7 und
der Punkt x = co dem Punkt x' = — ö: y, und nur wenn y = 0,
die Substitution (2) also ganz ist, entsprechen sich die unendlich
fernen Punkte auf L und L' gegenseitig.
Die Substitution (2) ändert sich nicht, wenn die vier Trans-
formationszahlen mit demselben Faktor multipliziert werden. Die
Determinante v vervielfältigt sich mit dem Quadrate dieses
Faktors, und man kann daher diesen Faktor so bestimmen, daß
die Determinante einen beliebig gegebenen Wert, z. B. den Wert 1
erhält.
Wendet man die Substitution (2) auf irgend zwei Punkte xu x2
und die zugehörigen x{, x2 an, so ergibt sich
. rCxix'i)
und wenn man ein zweites Punktepaar x-s, x4 und das ent-
sprechende x'3, x4 hinzunimmt:
/ w x r2(x'1X2')(x'sx'i)
k A + $)(yx2 + b)(yx3 + ä)(yxt ä)
Vertauscht man hierin x2 mit x3 und bildet den Quotienten,
So folgt
, . • (XjX2) (x3x4) _ (xjx2)(x3x4)
W (x1x3)(x2x4) ~ (x[Xs) (x2x4)
Der Ausdruck auf der linken Seite wird das Doppelver-
hältnis des Punktepaares x4x4 zu dem Punktepaar a;2a;3 genannt,
und es ist also in dieser Formel der Satz enthalten:
Das Doppelverhältnis zweier Punktepaare ist bei
gleichzeitiger linearer Transformation der vier Punkte
invariant.
Vier Punkte lassen sich auf sechs Arten in zwei Paare zer-
legen. Setzen wir aber
a = (a;äa:3)
b =
c —
§ 2.
Doppelverhältnisse.
7
so besteht die Identität:
(4) a e = 0
und wir erhalten die sechs Doppelverhältnisse
c a b
b ’ c ’ a ’
(5) Ä
v > b c a .
c ' a' b ’
setzen wir das erste von ihnen —c:b = x2, so erhält man
nach (4) die sechs:
1 1 1 x2
(6) x2, 1 — —2, T _ x2, ~2, k2—p 1 — jc2.
Es sind also die sechs Doppelverhältnisse aus den vier Punkten
linear durch eines unter ihnen ausgedrückt.
Wenn die xlt x2, x3, xt untereinander permutiert werden, so
werden die a, b, c untereinander permutiert und ändern ihre
Vorzeichen, jedoch so, daß entweder alle drei Vorzeichen gleich-
zeitig geändert werden oder ungeändert bleiben. Beispielsweise
geben die Transpositionen
(U) „na (23) (_“ J J)
(24) „„a (31) (_“ J
(34) und (12) f z &
v 7 v \—b —a —cj
Wenn xlt x2, xs, xit reell sind, so wird %2 dann und nur
dann ein positiver echter Bruch, wenn %2 und 1 — z2 positiv,
also entweder a und c positiv und b negativ oder a und c negativ,
b positiv ist. Dies findet statt, wenn xlt x2, xs, xi in dieser
Reihenfolge der Größe nach aufsteigend einander folgen und bei
allen den Anordnungen, die daraus durch solche Permutationen
entstehen, die b ungeändert lassen. Dies sind die folgenden acht:
12 3 4
2 3 4 1
3 4 12
4 12 3
14 3 2
4 3 2 1
3 2 14
2 14 3
8 Erster Abschnitt. § 3.
Denkt man sich also x4, x2, x3, x4 in dieser Reihenfolge auf
eine Kreisperipherie gesetzt, so erhält man immer dann ein posi-
tives echt gebrochenes z2, wenn die x{ so der Größe nach auf-
einander folgen, daß man mit einem beliebigen als kleinstem an-
fängt und dann auf dem Kreise entweder nach rechts oder nach
links weiter zählt. Wir drücken dies so aus:
Damit z2 ein positiver echter Bruch sei, müssen die
Größen a?15 x2, x3, x4 der Größe nach zyklisch aufeinander
folgen.
§ 3. Lineare Transformation des elliptischen Differentials.
Wenn sich die beiden Punkte x3 und x4 einem und demselben
Punkte x annähern, so nähern sich x'3 und x\ dem entsprechenden
Punkte x' an. Wir setzen dann (x3x^-.(x'3x'i) = dx'.dx' und
erhalten aus (3), § 2, die Beziehung zwischen den Differentialen
dXi dx':
. . (x-iX^dx (x^x’^dx'
' ' (x1x'){x.ix') (x^x^^x1)
Ebenso ergibt sich, wenn man an Stelle von a?15 x2 zwei
andere Punkte x3, xt setzt:
(x3xi)dx ____ (x’sx^dod
} (x3X~) (X4X) (X3X')(X4X')’
und wenn man multipliziert und die Wurzel zieht:
y(.£ia:2)(a;3.r4)da; _ Y(x’Jxsl)(x3x’i)dx'
)/(a\a:) (x2x) (x3 x) (x4x) y (x'jx') (x'2x’) (x3x') (x^x') ’
also eine Transformation des elliptischen Differentials
durch eine lineare Substitution:
o' 4- ß
x — —r-j—ä*
yx ö
Diese Substitution ist vollkommen bestimmt, wenn zu drei
beliebigen Punkten x4, a:2, x3 die zugehörigen Werte x4, a4, x3
willkürlich gegeben sind, und man erhält sie aus der Gleichheit
des Doppelverhältnisses:
(a?xa;2)(a;3a;) _ (x^^x^)
' (_X1Xi')(x2x) (XiX'sj^X1) ’
durch Auflösung nach x, und den vierten zu x4 gehörigen Wert
x'4 erhält man aus
§ 3. Lineare Transformation des elliptischen Differentials.
(5)
{x3Xj) __ (x'1x'<i')(x!ix'i')
(X-iX^^Xi) (^)(;W)
Wenn die Funktion f(x) in dem elliptischen Differential
, dx
du = _
VfW
gegeben ist, so sind damit auch die xit x2, xs, x4 gegeben, und
durch die lineare Transformation (3) kann man das Differential
auf eine andere Form bringen, bei der drei der Größe x^, x2,
x'3, x'i beliebig gegebene Werte haben. Man erhält die Normal-
form, wenn man
x' Xi = 0, a?2 = 1, x's = \, x'i = oo
z2
annimmt. Die Größe z heißt bei Legendre der Modul des
elliptischen Differentials und ]/1 — z2 — das Komplement
des Moduls. Ordnet man also die Punkte in folgender Weise
einander zu:
n , 1
0, 0, 1, -5, 00,
z2
zy> zy> zy zy> zy
«Xz J «Xzg ? ^41
so ergeben sich aus der Gleichheit der Doppelverhältnisse leicht
die Relationen:
__ (xxj) (x2x4)
(xx4)(x2x1)’
zfix 1 _«—
) (xx^(x4xi)'>
1 —
(xXi) (x4x3) ’
, _ (xix1)(xixi') dx
1 } — (x2xt) (xx^'
J£ä __ (x3xi)(x-tx2') k,2 _ (x2x3) (Xj Xj)
' <x1x3)(x2xi')'
und aus (3):
(xtx^fxjx^dx _ _____________________dz___________
V — (xr x) (x2 x) (x3 x) (x4 x) y«(l — z)(l — v^z)
Nach § 2 wird x2 ein positiver echter Bruch, wenn die xv
reell sind und der Größe nach zyklisch aufeinander
folgen. Dies gibt also acht verschiedene solche Transformationen,
10
Erster Abschnitt.
§ 3.
und man kann darunter je zwei auswählen, bei denen das Intervall
s = 0 bis s = 1 einem gegebenen der Intervalle (x1x2), (x2Xg),
(xgXi), (a;4a’i) entspricht; dem wachsenden 3 entsprechen bei der
einen dieser Transformationen die wachsenden x, bei der anderen
die abnehmenden x (mit dem Durchgänge von -|-oo zu —co).
Im ersten Falle haben die Quadratwurzeln in (9) beiderseits das
gleiche, im zweiten das entgegengesetzte Zeichen.
Wenn man nicht darauf besteht, daß z2 3 ein positiver echter
Bruch ist, so kann man die Punkte xlf x2, xs, x± auf alle Arten
permutieren und erhält 24 verschiedene lineare Transformationen
in die Normalform, von denen je vier dasselbe z2 ergeben; man
erhält im ganzen sechs verschiedene Modulen, die nach § 2, (6)
auseinander abgeleitet werden.
Man übersieht am leichtesten die Gesamtheit dieser Trans-
formationen, wenn man annimmt, das zu transformierende Integral
habe bereits die Normalform:
dx
\ x (1 — x) (1 — Z2 x) ’
man hat dann in den Formeln (6) bis (9) die xlt x2, x3, x±
auf alle möglichen Arten durch 0, 1, 1:Z2, co zu ersetzen. Wir
nehmen als Beispiel die folgenden Zuordnungen:
/yi /y> zy» /y>
9 ^3 9
1) 0, «>, 1, 1,
A,
2) 0, 1, 1,
A,
3) 1, 0, 4-
Man erhält dann aus (6) und (8)
1) 3 = , X2 = 1 — Z2 = Z'2,
' 1 — X '
2) 3 - Z2a;, x2 - i,
3) z = -1^-, z2 = Z2
7 1 — k2x
und für das Differential
dz
y 3(1 3)(1 — X23)
§ 4. Die Legendresche Normalform. 11
ergibt sich in den drei Fällen:
dx
— x (1 — a;) (1 — Z2x) ’
'kdx
^x(\ — «)(1 — Z2«)’
3) clx •
l/ic (1 — a;)(l — Z2oj)
§ 4. Die Leg en dresche Normalform.
Wenn, die Funktion f(x), die in dem elliptischen Differential
unter dem Wurzelzeichen steht, reelle Koeffizienten hat, so sind
drei Fälle möglich:
. 1. f(x) hat vier reelle Wurzeln xlt x2, x3, a?4;
2. f(x') hat zwei reelle Wurzeln xly x2 und ein paar kon-
jugiert imaginäre Wurzeln xs, a;4;
3. f(x) hat zwei Paare konjugiert imaginärer Wurzeln xr, x2
und x3, a;4.
In allen drei Fällen läßt sich das elliptische Differential durch
eine reelle lineare Transformation auf die Form bringen:
y> — a) (z2 — ß) ’
worin a und ß reelle (positive oder negative) Konstanten sind.
Wir bestimmen die lineare Abhängigkeit zwischen den
Variablen x und z so, daß sich folgende .Werte entsprechen:
z2) x, x^ x2^ z, y«, —ya, und erhalten eine Substitution der \ß, -w, Form:
/o. 7 x — xr (3) n = \ / /y . /y z — y« z -|- y«
Um In, zu bestimmen, setzen wir x = x,. x = a;4 und ent-
sprechend z = ]/ß, z = —y/3, und erhalten
Ä (^s^i) _ ~ V« (x^) = Vß + V« .
(^3^2) \ß + yä’ Guo yß — y«'
Daraus durch Multiplikation und Division
(4} _ 1/(^3^2)(^4^2) ypt — y^ _ 1/(^1) (^4 4)
} I (a^i) (^4^1)’ y<x 4-yjs F
12 Erster Abschnitt. § 4.
Setzen wir, wie in § 2
a = (.r2 a;3) (xr x^,
& = (^i)
' c = (a?! a;2) (ap a;4),
a -|- & + c — 0,
so könnnen wir, da es nur auf das Verhältnis von a zu ß an-
kommt, die letzte der Gleichungen (4) dadurch befriedigen, daß
wir setzen:
(6) y« = y±ä + y^r, y? = y±ä — yq=&,
und aus (3) ergibt sich für z der Ausdruck
g _ + (xx^\{x3x^(XjX^
(a;a;2)y(a’3a;1)(a;4a:1) — (xxß)\(x3xiß(xix2ß
Stellt man neben (3) noch die daraus folgende Gleichung:
-^x — x3 __ s — y!ß
X — Xi g Yß
auf, so ergibt sich durch logarithmische Differentiation:
(x-iX^dx %1/adz (x3Xi)dx Z^ßdz
(xx^)(xx^) . ^2 — a ’ (xx3)(xx4) z2 — ß ’
und daraus durch Multiplikation mit Rücksicht auf (5) und (6):
dx ___ '2dz
J ^±(xx1)(xx2)(xxs)(xxi) y(^2 — a)(z2 — ß")
Wenn nun die vier Wurzeln von f(x) reell sind, so gibt es,
wie wir im § 2 gesehen haben, acht Arten, diese Wurzeln den
Zeichen xlt x2, x3, a;4 so zuzuordnen, daß a und b entgegen-
gesetzte Zeichen haben, und wenn also +«, positiv sind, so
werden ]/«, \ß reell,'also a, ß positiv, und nach (7) wird dann
auch z reell.
Sind zweitens a?j, x2 reell, «3, a;4 konjugiert imaginär, so sind
a und —b konjugiert imaginär, also wird, wenn die Vorzeichen
der Quadratwurzeln y + a, y^p b passend bestimmt werden, ’fä
reell, ]/ß rein imaginär, also oc positiv, ß negativ und z reell [weil
(XiXßj^XiX-^ und (a'3«2)(«4«2) als Produkte konjugiert imaginärer
Größen positiv sind].
Sind endlich x2 und x3, xt zwei konjugiert imaginäre
Paare, so sind a und —b beide positiv. Nehmen wir also in (6)
die unteren Zeichen, so werden ]/«, \ß rein imaginär, also a
und ß negativ, und aus (7) ergibt sich für z ein reeller Ausdruck.
Die Weierstrasssche Normalform.
13
§ 5.
Setzt man dann
(9) — y,
so ergibt sich
(io) 2de = dy
#2 — a) — ß) l/y (y — a) (t/ — ß)
und man hat also durch die quadratische Substitution (9)
ein elliptisches Differential erhalten, bei dem unter dem Wurzel-
zeichen eine Funktion dritten Grades mit reellen Wurzeln steht,
das man nach § 3 durch lineare Substitution auf die Normalform
_________rfg______
y g(i — g)(i — %2g)
bringen kann, und darin können g und x als positive echte
Brüche angenommen werden.
Die Legen dresche Normalform ergibt sich daraus, wenn man
g = sin2<p, d£ = 2 sin qp cos qp qp
setzt:
(11) , dt — = , .
y?(l — S) (1 — *2g) yi —%2sin2gp
§ 5. Die Weierstrasssche Normalform.
Eine andere Normalform des elliptischen Differentials hat
Weier st rass seinen Untersuchungen zugrunde gelegt, nämlich
die Form
dz
y4^3 _ — gz'
in der g2, g3 Konstanten sind, die die erste und zweite In-
variante des Differentials genannt werden. Das allgemeine
elliptische Differential
(1) du =
worin
(3) = a0 x* -|- «ixS + a2+ «sx + ai
ist, kann durch eine lineare Transformation auf die Weier-
strasssche Normalform gebracht werden, wenn die Wurzeln
xr, x2, xs, x± von f(x) bekannt sind. Am einfachsten geschieht
dies auf folgende Weise.
14
Erster Abschnitt.
§ 5.
Die Wurzeln der kubischen Funktion
(p(z) — 4 — g2z — gs
mögen mit e15 e2, es bezeichnet sein. Dann ist
<p(z) = 4(> — eL)(z — e2)(£ — e3)
und e2 e3 = 0.
Wir lassen die Werte von x und z einander folgendermaßen
entsprechen:
zy» zy» zy» zy» zy»
<Xz «X/j , ‘^-'2 ? *^31 ?
CO, er, e2, es,
und es ergibt sich, wenn wir mit m einen konstanten Faktor
bezeichnen, der willkürlich angenommen werden kann:
m(xx2) / 1 1 \
Z — ei = 7----\ , = «» ( 7--x — 7-----x )
(X^X^IXXl) \(^1X2) (g^X)/
. m(xx3) / 1 1 \
v 7 (XlX3)(XXi) Y^x^) (XXX)J
m(xx.) / 1 1 \
Z --- = 7---\. — m ,------------r — ------)
(XiXJfXX-J fax)/
Der Faktor m muß in allen drei Gleichungen derselbe sein,
damit die Differenzen (z — e3) — (z — e2) = — e3 usw. von x
unabhängig werden.
Bildet man diese Differenzen und setzt wie in Algebra
Bd. 1,' § 70
(a?! x2) (xs xt) —U,-
^XgjfXiXi) = 7,
(xr a?4) (.r2 a?3) == W, ‘ .
so folgt
^mU
. z X *
(^X2) (X-iX^)
Führt man einen neuen willkürlichen Faktor g ein, indem
man
(5) m = 3 ga^^x^^x^iXyX^)
setzt, so folgt
e2—es =—3fia07, e3—er = —3ga0V, e2 — e2 ——3ga0W
und daraus wegen eT —j— —|—. es = 0,
= ga0(V— W),
e2 = ga0( W — ü),
es = ga0(U— V).
§ 5. Die Weierstrasssche Normalform. 15
Die in Algebra I, § 70 eingefiihrten Größen yt, y2, y3 sind
also gleich e1:y, e.2:g, und man erhält nach der dortigen
Formel (11) für die e2, e2, e3 die kubische Gleichung:
zs — 3A(i2z 4“ = 0-
Es wird also, wenn <p(z) = — g2z — g3,
<p(z) = 4(ä — — e2)(^ — e3) = 4^ _ _ g3
sein soll,
(6) g2 = 12 g2A, g3 = — 4y3B.
Hierin sind
, A = al — ßdiCtj 4~ 12a0a4
' B = 27a2a4 4“ 27aoag 2a28 — 72aou2a4 — 9a1a2as
die erste und zweite Invariante der biquadratischen Form f(x).
Die logarithmische Differentiation der beiden ersten Glei-
chungen (4) ergibt
dz2 _________ dx2(x1x2)(x1x3)
(z — Ci) (z — e2) ~ (xx^x^xx^
und mit Hilfe der letzten Gleichung (4) nach (5):
. . dz __________ dx
faz3 ~ g2z — g3
Wollen wir diese Resultate auf den Fall an wenden, wo f(x)
die Normalform
— x(l — a:)(l — h2x~) = x — a?2 (1 —j— x2) —x2x3
hat, und der Punkt z = co dem Punkte x = 0 entspricht, so
lassen wir a0 in Null, xt in Unendlich übergehen, aber das
Produkt a0a?4 in einen endlichen Wert, den wir = 1 annehmen
können.
Es wird dann
aQXi = 1, «o = 0, ai = «2,
<Z2 = (1 —4 ---I? U4 ~ 0
und folglich
A = (1 + x2)2 — 3 7.2 = 1 — x2 — x4 = 1 —• x2 v!2
B = —(1 + x2)[2(1 4- x2)2 — 9x2]
— _(1 4- X2)(2 — x2)(l — 2x2)
= (14-xi) (1 + —5C'2)
= (2 4- x2x'2)(x2 — x'2),
wenn x'2 = 1 — x2 gesetzt ist.
16
Erster Abschnitt.
§ 5.
Es wird also, wenn wir noch die Diskriminante
z/ = 16.27^(4A3 — 1?2)
beifügen
g2 = 12ft2(l — z2x'2),
(9) g3 = — 4fts (2 —}— x2x'2)(x2 — x'2),
zf = g% — 27 g* = 272.16(^x4x'4,
und man erhält aus (6) die Transformation
_______ds________ _ ______________dx____________
j/4^3 — g2z— g3 yi2fia:(l —x) (1— h2x)’
um die Substitution zu finden, setzen wir x, = 0, x2 = 1,
x3 = 1: x2, Xi = oo, aQ = 1 und erhalten
__1 v'2
a0U=l, a0V — ——, a0W = —,
folglich
x2 —2 1 — 2x2 1 4- x2
z2 ’
(11)
3 /%2 + 1 1 \
x2 \ 3 x)'
Bei dieser Transformation des elliptischen Differentials in der
Weierstrassschen Normalform wird die Zerlegung der Funk-
tion f(x) in ihre linearen Faktoren, also die Auflösung der bi-
quadratischen Gleichung f(x) = 0, vorausgesetzt. Eine andere,
freilich nicht lineare Transformation, die ohne diese Voraussetzung
den gleichen Zweck erreicht, hat Hermite gegeben (Grelles
Journal, Bd. 52). Um sie darzustellen, benutzen wir die homogene
Form des elliptischen Differentials
ydx — xdy
worin
(13) f(xy) = + a-iX^y a2x2y2 -f- a3xy3 aty\
Diese biquadratische Form hat außer den beiden Invarianten
A,JB noch zwei Kovarianten:
i p2/1 gy _ / gy yi
3 c>y2 J
(14) T ’
12 kdo; dy dy dx )
§ 5. Die Weierstrasssche Normalform. 17
wo H und T Formen vierten und sechsten Grades sind, deren
Koeffizienten sich rational und mit ganzzahligen Zahlenkoeffizienten
aus den Koeffizienten von f zusammensetzen. Zwischen diesen
Formen besteht dann noch die Relation
(15) Hs — 48 AHf2 — 64 Bf3 = — 27
(Bd. I, § 70, 72).
Es ist aber nach dem Eulerschen Satz über homogene
Funktionen
4f = -+-X^-4y, df = ^4-dx^-dy,
dx dy dx dy
„ dH dH j tt cH- i . dH
4 H = tt- x + -z—y-, dH = -—m+—m,
dx dyv dx 1 dy v
woraus
fdH — Hdf — — 3T(gdx — xdy),
und wenn also nach (15)
(16) 3 yä T — V—Zfs 48Af2H -f- 64_Bp
gesetzt wird:
ydx— xdy_____ —^3(fdH—Hdf)
Vf ~ ^—(H3 — 48Af2H—64Bf3)f
Macht man nun die Substitution
mit einem unbestimmten Faktor y, so ergibt sich
ydx — xdy dz
(18) :=-------- = , ,
^4z3 — g2z — gs
wenn wie früher
(19) g2 = 12y2A, gs = — 4y3B.
Man kann diese Transformation auf ein Differential anwenden,
das schon die Normalform hat. Setzt man
/“(a;, y) = 4x3y — g2xy3 — g3y*,
so hat man
a0 ax a2 as a±
durch
0 4 0 —g2 —gs
zu ersetzen, und es ergibt sich aus (7)
^=12^2, B=— 27.16<zs.
Weber, Algebra. III. 2
18 Erster Abschnitt. § 6.
Wenn man also ft = setzt, so gehen die Gleichungen (19)
in die Identitäten g2 = g2, gs = </s über.
Wenn man dann y — 1 setzt, so ergibt die Transformation (18)
(20) ^dx = ds
\4;xi — g2x — gs ^4:^ — g2s — g3
Diese Transformation wird nach (16) durch
vermittelt. Es ergibt sich aber aus (14):
H = — 48 [(a?2 + |&)2 + 2&oT|,
und folglich erhalten wir
(21) z = O2 + i-^)2 + 2g8a:
' ’ 4=x» — g2x — gs
Weiter ergibt sich noch aus (14)
T — 64a;e — 80g2a;4 — 320p3as —20p22a;2— \§g2g3x -\-g}— 32^.,2
und dann nach (16)
(22) • 4|/4a:3 — g2x — gs fas* — g2z — gs = T.
Durch (20), (21), (22) ist die Multiplikation des ellipti-
schen Differentials mit 2 geleistet. Es ist dadurch nicht nur
z als eindeutige (rationale) Funktion von x dargestellt, sondern
auch die eine Quadratwurzel eindeutig durch die andere, d. h. es
ist einem Punkte x eindeutig ein Punkt z zugeordnet.
§ 6. Elliptische Kurven.
Jede algebraische Abhängigkeit zwischen zwei Veränderlichen
x, y wird ausgedrückt durch eine Gleichung der Form
(1) F{x,y) = 0,
worin F(x,y) eine ganze Funktion der beiden Veränderlichen x, y
bezeichnet. Betrachtet man x und y als Cartesische Koordinaten
eines Punktes in der Ebene, so ist (1) die Gleichung einer Kurve
«ten Grades, wenn F in bezug auf x und y zusammengenommen
von der nten Dimension ist. Diese Kurve ist dann das geome-
trische Bild der algebraischen Abhängigkeit, wobei indessen auch
imaginäre Punkte mit berücksichtigt werden müssen.
§ 6.
Elliptische Kurven.
19
Ist dann <I>(x,y) eine ganze oder gebrochene rationale Funk-
tion von x und «/, und y von x durch die Gleichung (1) abhängig,
so sind
(2) O (x, y) d x, fG>(x,y')dx
die zu der Kurve F gehörigen algebraischen Differentiale
und Integrale.
Beispielsweise ist, wenn f(F) eine Funktion dritten oder
vierten Grades von x ist,
— f(x) - 0
die Gleichung einer Kurve dritten oder vierten Grades, zu der
die mit der Irrationalität f(x) behafteten elliptischen Diffe-
rentiale und Integrale gehören.
Wir wollen hier alle Kurven, deren Differentiale und Inte-
grale auf elliptische reduzierbar sind, elliptische Kurven
nennen. Wie das Beispiel zeigt, kommen darunter Kurven dritten
und vierten Grades vor.
Kegelschnitte gehören nicht zu den elliptischen Kurven, weil,
wenn zwischen x und y eine Gleichung zweiten Grades besteht,
x und y als rationale Funktionen eines Parameters t dargestellt
werden können, wodurch das algebraische Differential auf ein
rationales nach t zurückgeführt werden kann. Solche Kurven
heißen rationale Kurven.
Wir werden sehen, daß alle Kurven dritten Grades ohne
Doppel- oder Rückkehrpunkt zu den elliptischen gehören. Kurven
höheren Grades können nur dann dazu gehören, wenn sie eine
gewisse Anzahl singulärer Punkte haben. Dies ist ein fundamen-
tales Kapitel in der allgemeinen Theorie der algebraischen Funk-
tionen, das nicht in den Plan dieses Werkes gehört1).
’) Die wichtigsten diesen Gegenstand betreffenden Arbeiten sind:
Riemann, Theorie der Abelschen Funktionen [Grelles Journal,
Bd. 54 (1857)]. Mathematische Werke, 2. Aufl., S. 88, 487. Nachträge,
herausgegeben von Noethei’ und Wirtinger (1902).
Aronhold, Monatsberichte der Berliner Akademie vom 25. April
1861.
Clebsch, Uber die Anwendung der Abelschen Funktionen in
der Geometrie (Grelles Journal, Bd. 63).
Clebsch, Uber diejenigen ebenen Kurven, deren Koordinaten
rationale Funktionen eines Parameters sind (ibid., Bd. 64).
Clebsch, Über diejenigen Kurven, deren Koordinaten sich als
elliptische Funktionen eines Parameters darstellen lassen (ibid., Bd. 64).
2*
20
Erster Abschnitt.
§ 6.
Für die Untersuchung algebraischer Differentiale von diesem
Gesichtspunkte ist die Einführung homogener Variablen zweck-
mäßig. Wir setzen x = xx: a:s, y = x2:x3, x3‘F(x,y) = f(x2,x2,x3);
dann ist f(x^ x2, xz) eine homogene Funktion wter Ordnung
der drei Veränderlichen x2, x3 und
(3) flx-^x^ = 0
die Gleichung einer Kurve nter Ordnung in homogenen Koordi-
naten. Es wird
, x3 dx, — x,dx3
dx = — —
zy» 2
und
(4) dSl = 0(x,y)dx = ®(—,— 'j (XgdXj^— x1dx3).
^3 \#3 *^3 /
Nun ist aber nach dem Eulerschen Satz über homogene
Funktionen, wenn wir mit f2, f3 die partiellen Ableitungen
von f nach
5 ^2 ? ^3 bezeichnen,
4-/2^ 4-/3^ = 0,
f1dx1 4- f2dx2 4- f3dx3 = 0,
daher, wenn p einen Proportionalitätsfaktor bedeutet,
/i — p (x2 d x3 — x3d x2),
f2 = p^jda?! — x1dx3),
f3 = Q(x1dx2 — x2dXi),
und wenn man mit c2, c3 ganz willkürliche Größen, z. B. Kon-
stanten, bezeichnet:
C1 fl 4- fi 4“ C3 /s == Q E ^.c2x2dx3,
wenn + cTx2dx3 in üblicher Weise die Determinante
#1 £3
zy» zy» zy»
<X/J «Az2 «Azg
OCy (l 00^ d iS/fJ
bedeutet. Es folgt also:
x (1 r _ x /I r _
x3 a,xt xxax3 — L j? L . j? ,
11 ~T~ 12 ~r 1-3 13
und wenn man
A 0 (= ’F
zy» 2 \ zy> ’ zy» /
^3 \‘<z4 *^3'
Brill, Über diejenigen Kurven, deren Koordinaten sich als hyper-
elliptische Funktionen eines Parameters darstellen lassen (ibid., Bd. 65).
Clebsch und Gordan, Theorie der Abelschen Funktionen
(Teubner, Leipzig 1866).
Elliptische Kurven.
21
setzt, so ergibt sich aus (4) der Ausdruck für das allgemeinste
zu der Kurve f gehörige algebraische Differential:
S +
Clfl cs/ä + czfz ’
worin eine ganze oder gebrochene homogene Funktion der
(n — 3)ten Ordnung ist. Die willkürlichen Größen cx, c2, cs
kommen nur scheinbar in diesem Ausdruck vor. In Wirklichkeit
ist er davon ganz unabhängig.
Wir betrachten wieder den Fall n == 3. Dann ist der ein-
fachste Fall der, daß IP1 eine Konstante ist, und (5) geht dann
in das elliptische Differential erster Gattung über:
2? + CyX2dx3
clfl + cs
Dieses wollen wir nun mit Hilfe der Kovarianten der ternären
Form dritten Grades auf die Weierstrasssche Form trans-
formieren.
Wir haben Bd. II, § 107 die fundamentalen Kovarianten der
kubischen Form kennen gelernt. Es waren dies, außer f selbst:
wobei die
63 £21’
/sn
63
Indizes
fiz-l
ft2l
fl3
/j,,
1, 2, 3 die
fii
fzi
1
36
fl2> fltl
fll, f221 fit. ^2
fsi, ft2l fttl ^2
A, ^21 ^Z > 0
2
Differentiation
nach
den Variablen
*^3 bedeuten.
Es folgt aus dem Multiplikationssatz der Determinanten, da
f und df — 0 sind:
1
£
9
fz, ft
42, ^3
Jj, J3
8 >
C11 C21 cs
Xy , X.y, X3
dx-y, dx2, dx3
Sxi^i, dzJ
2JXiJi, dJ
und daraus
(?)
== 3Sctfi(.4dJ — 2Jdd),
du — 3
ddJ—2Jdd
K
22 Erster Abschnitt. § 6.
Mit Hilfe der Kovarianten haben -wir die Form f(x) auf die
kanonische Form
<p(.y) = y* + y? 4- y* + h 3/23/3
reduziert.
Wir haben,' wenn r die Substitutionsdeterminante bedeutet:
p____ (2 —m3)m3f2 + (2 — 5 m3)mr2/’z/ 3>«2r4z/4 — r3J
~ (1 -f- 8 m3)2 : ’
„ (1 + — 6mr2z/
V — 1 -j- 8 m3 ’
r m2 f r2J
1 -|- 8 m3
gesetzt und erhielten y3, yl, yf als Wurzeln der kubischen
Gleichung
u3 — Qu2 Pw — R« — 0,
und die Diskriminante dieser kubischen Gleichung ist
~~ (1 4. 8 m3)3 ’
Drückt man diese Diskriminante durch P, Q, R aus, so erhält
man K2 rational durch f, J dargestellt. Wir haben an der
erwähnten Stelle der Algebra diesen Ausdruck nicht explizite an-
gegeben. Jetzt müssen wir ihn aber bilden, wenn auch nur untei;
der Voraussetzung f = 0, d. h. nur für die Punkte der Kurve.
Es ist aber [nach Bd. I, § 50, (10)]
— pi(p 1SPQR3 — 4P3 — 4 23Ps — 27R3.
Darin hat man zu setzen:
n ___ 3»i2r4J2 — r3J n _______ —fimr-d p ________ r2d
— (1 8 m8)2 ’ V — 1_L8«8 ’ — 1 '4- 8 m3’
und man erhält durch eine nicht schwierige Rechnung, wenn man
mit S und T die beiden Invarianten der Kurve dritter Ordnung
bezeichnet (Bd. II, § 108),
(1 + 8 m3)3 D1 — r™(±J3 4- 108SJzP — 27 Td3),
und folglich
(8) K2 = 4 J3 4- 108 S JzP — 27 Td3.
Diese Gleichung ist aber nicht identisch, sondern nur unter
der Voraussetzung f — 0 befriedigt. Der vollständige Ausdruck
von K2 durch J, zf, f wird sehr viel komplizierter.
§ 7. Elliptische Raumkui'ven vierter Ordnung. 23
Setzt man
J - , 1 ddJ — 2Jdd
(9) = 3*> dz = T--------------’
so ergibt sich aus (8)
K2 = 27^(4^ 4- 12 — T)
und aus (7)
(10) dw = -7= -======,
v 7 1/3 1/4^3 _|_ 12 Sz — T -
und dies ist die Weierstrasssche Normalform für — —12 S,
03 — T.
§ 7. Elliptische Raumkurven vierter Ordnung.
Man kann algebraische Funktionen einer Veränderlichen auch
durch Gleichungen zwischen mehreren Variablen darstellen, wenn
man die Anzahl der Gleichungen entsprechend vergrößert. Nimmt
man z. B. drei Variable x, y, z und läßt zwischen ihnen zwei
Gleichungen
(1) <?(«,«/,4 = 0, tp(x,y,z) = 0
bestehen, so kann man aus diesen beiden Gleichungen z. B. x
eliminieren und erhält eine Gleichung zwischen y und z, durch
die y als algebraische Funktion von z definiert ist. Es kann
dann, wenn man gewisse Ausnahmefälle ausschließt, x und jede
rationale Funktion von x, y, £ rational durch y und z dargestellt
werden. Die Integrale der Form
(2) j F (x, y, z) dz,
in denen F eine rationale Funktion bedeutet, gehören dann zu
dem durch (1) dargestellten algebraischen Gebilde. Nimmt man
x, y, z als Cartesische Koordinaten im Raume an, so stellt (1)
eine Raumkurve als den Durchschnitt zweier Flächen = 0,
= 0 dar, und die Integrale (2) gehören zu dieser Raumkurve.
Die Kurve heißt wieder elliptisch, wenn diese Integrale ellip-
tisch sind.
Wir wollen diese Betrachtungen auf die Raumkurven vierter
Ordnung erster' Spezies anwenden, d. h. auf die Kurven vierter
Ordnung, die sich als vollständiger Durchschnitt zweier Flächen
zweiten Grades darstellen lassen.
24 Erster Abschnitt. § 7.
Wir führen wieder homogene Koordinaten sc1, x2, xs, ein
und nehmen die Gleichungen zweier gegebenen Flächen zweiten
Grades in der Form an:
z^x , ^25 ^3, ^4) -
4^ j ^21 ^3 5 ^4) - QCfc' /
Die beiden Flächen bestimmen ein Flächenbüschel zweiter
Ordnung g<jo = tjip. Alle Flächen des Büschels schneiden sich
in einer Raumkurve vierter Ordnung, die wir die Grundkurve
nennen. Man erhält dieselbe Kurve und dasselbe Büschel, wenn
man die Funktionen q> und durch q>', 1p' ersetzt, die aus <p,
(fl'l 'M* \
), also durch
P <1/
z4x <JP' = + nt[>,
' ip' = pq> qty
abgeleitet wird, deren Determinante r = mq — np von Null
verschieden ist. Dadurch ergibt sich die Identität
(5) 190 4-
worin
(6x i + pv',
i] = n^' 4" qrf
eine lineare Transformation der Variablen |, 1/ darstellt. Außer
dieser binären Substitution kommt noch eine lineare quater-
näre Substitution der Variablen
^3J "^4 (Koordinatentrans-
formation) in Betracht, deren Determinante wir = 1 annehmen
können.
Jede quadratische Form besitzt diesen letzteren Transforma-
tionen gegenüber eine Invariante, nämlich die Hesse sehe
Determinante (Bd. I, § 62, 63, 66), und wir erhalten also als
Invariante der Form (5):
(7) fW =
J S + (iail+’iM(ia22+’?M(ia33+’i^3).(ia44 + ’?W
Dies ist eine binäre biquadratische Form der Variablen |, q,
die wir, entwickelt, so darstellen:
(8) f(&f) = «0S4 4* (h^3n 4- aal2-»/2 + <h£n3 4“
Die Koeffizienten dieser biquadratischen Form a0, cq, a2, a3,
ändern sich nicht bei einer Koordinatentransformation. Sie heißen
daher simultane Invarianten des Formenpaares g>, 1p (a0 und
a4 sind die Determinanten von q> und von V).
§ 7.
Elliptische Raumkurven vierter Ordnung.
Die at ändern sich, wenn man die |, ?/ einer Substitution (6)
unterwirft. Bildet man aber die Invarianten der Form (8) (nach
Algebra, Bd. I, § 70), so erhält man Funktionen der Koeffizienten,
die auch diesen Substitutionen gegenüber invariant sind, die also
nicht zu den individuellen Formen <p, tp, sondern zu dem ganzen
Büschel und also auch zu ihrem Durchschnitt, dei’ Grundkurve,
gehören. Wir nennen sie Invarianten der Grundkurve. In
bezug auf das Formensystem <p, ip werden sie auch Kombinanten
genannt. Die Grundkurve hat also zwei Invarianten:
. . A = al — 3 a, «3 4- 12a0a4,
' 2? = 27 afa4 + 27 a0a32 2 a3 — 72 <70a2«4 — 9ai«2a3,
aus denen man die Diskriminante D nach der Formel
(10)
27 D = 4A3 — B*
ableitet. In bezug auf die Koeffizienten von <p und ip sind die
Invarianten A, B, D von den Graden 8, 12, 24.
Das Formensystem cp, ip hat zwei simultane quadratische
Kovarianten, die man ebenso wie die Kovariante G (in Algebra I,
§ 65) ableitet. Die erste von, ihnen ist, wenn wir = -i- ..
Ai 0
setzen:
GO
«111 «12 1
«21, «22,
«31, «32,
«41, «42,
«4, «4,
«13 ,
«23,
«33 ,
«43 ,
«4,
«14 ,
«24,
a341
«44,
«4.
«l-i
«4
«/’s
^4
0
$ =
und die zweite erhält man daraus, indem man ailc mit
und ip mit q> vertauscht.
Die Gleichung 0 = 0 drückt eine Fläche zweiten Grades
aus (die nicht zum Büschel gehört), die der geometrische Ort
der Punkte x ist, deren Polaren in bezug auf ip die Fläche cp
berühren.
Wir nehmen jetzt an, daß die Diskriminante B von Null
verschieden ist. Dann lassen sich die beiden Funktionen <p, ip
simultan in die Summe von vier Quadraten transformieren:
(12)
q = «i?/i + ^yl: + «3?/82 4- «4?/42,
= ßiy? + ß^ + ßsyl + ßAjt,
worin die yt lineare Funktionen der x4 sind. Dies ist die
kanonische Form des Funktionenpaares. Es wird dann:
(13) /’(!,’/) = (^l+’?Ä)(ia2 + ’?/J2)(i«3 4-’?Ä)(ia4 4-’iÄ),
26
Erstei’ Abschnitt.
§ 7.
und die Funktionen <P, ’F erhalten die kanonische Form:
/, 4.x ®
Die Determinante des Systems (12), (14), als lineare Gleichun-
gen für y*, yf, yg, y% betrachtet, ist
Ki ßzßaßn ^ßißaßti K?ß1ßißi, K^ßißißa
715x ßi^l^^i, A?ala2«4, ß^l^S
' 1 «!, 0C2, CC3, «.
ßl 1 ßil ß.3 1 ßi
Sie verschwindet, wenn d1:d2 =. ßi'ßz wird, weil dann die
beiden ersten Kolonnen miteinander proportional werden, und
ebenso wenn df-.d^ = ßp.ßk wird. Es ist daher (15) als ganze
Funktion der a, ß betrachtet, teilbar durch
(16) d{ ßk — dk ßi (P"ißk)‘i
und folglich auch durch das Produkt aller dieser Faktoren
(17) (W1 ßi) (K1 ßs) (K1 ßi) (tt-2 ßs) (K2 ßi) (w3 ßi) =
Aus der Vergleichung der Grade ergibt sich, daß sich die beiden
Funktionen (15), (17) nur durch einen Zahlenfaktor unterscheiden
können, und dieser ergibt sich aus der Annahme ßy = 0, a2 = 0,
<z4 = 0 gleich 1. Die Determinante (15) ist also dem Produkt z7
gleich, und das Quadrat von A ist die Diskriminante D der
Funktion f(J-,y), also gleich der Funktion D, von der wir an-
genommen haben, daß sie von Null verschieden sei. Es lassen
sich also die y%, y%, y%, yf linear durch <p, iß, <P, ’F darstellen.
Die Kovarianten ’F ändern sich, wenn <p und iß nach (4)
durch <p', iß' ersetzt werden. Sie gehören also nicht zu der Grund-
kurve, sondern zu dem Formenpaar <p, iß. Aber es gehen bei
dieser Substitution und ’F als lineare Funktionen von y*, yf,
yl, yl in lineare Funktionen von <p, <&, W über. Diese Aus-
drücke sind ziemlich kompliziert. Wir brauchen sie hier aber
nur für die Punkte der Grundkurve, also für <p = 0, iß — 0,
und unter dieser Voraussetzung werden sie sehr einfach. Es ist
da nämlich
— ^(pccj +qß1)\md2 + nß2)(md3^nßs)(mdi-irnßi)yf,
W = Z? (m«! 4- m ßi)a ( pa2 + g- ß.2) (p ds 4- q ß3) (pa4 -j- q ß4) yf,
§ 7. Elliptische Raumkurven vierter Ordnung. 27
und daraus ist nach (12) und (14) abzuleiten:
» 4- NW,
«F' = P0 4-
worin die Koeffizienten M, N, P, Q noch zu bestimmen sind.
Wir können dies durch Rechnung ausführen. Ohne Rechnung
ergibt sich das Resultat auf folgendem Wege:
Die HI, N sind ganze Funktionen zweiten Grades von p, q
und dritten Grades von m, n. Nimmt man p:q = m:n, also
r = mq — np = 0, so gehen 0' und nach (18) in lineare
Verbindungen von <p und über und verschwinden also. Daraus
folgt, daß HI und N durch r2 teilbar sind, und die Quotienten
sind lineare Funktionen von m und n. Da aber für die beiden
Fälle = (o 1)’ (1 o) un(^ übergehen muß,
und da man dieselbe Betrachtung auf ’F' an wenden kann, so folgt:
. . = r2(m0 nW),
qr> — r2(p<j> q-qry
Es werden also (von dem Faktor r2 abgesehen) die Funk-
tionen 0, ’F mit den cp, kongredient transformiert. (Über
die strenge Begründung dieser Schlüsse sehe man Bd. I, § 20.)
Aus diesen Ergebnissen können wir auf einfache Weise, immer
unter der Voraussetzung <p = 0, = 0, die y* durch 0 und ’F
ausdrücken, also die linearen Gleichungen (12), (14) auflösen.
Wenn wir nämlich die Formeln (19) auf die Substitution
('m, n\ _ /ft, — «A
\p, q) \0, 1 /
anwenden, so ist r = ft, die Funktion bleibt ungeändert =
und q>' geht aus q> hervor, wenn
durch
0, (a2Ä)i («3 ft), (aift)
ersetzt werden. Es wird also nach (14)
0' = ft2(a2ft)(asft)(a4ft)^
und folglich nach (19):
(a2ft)(aäft)(«4ft)ft2 = 0^0 — ft ?F,
z20x («i ßi) («3 ßt) (“< ßt) Vl — a2 0 — ft
k J («lft)(aäft)<Kft)?/32 == «3^ ” ft
(«1 ft) («2 ft) (a3 ft) y2 = <z4 0 — ft ’F.
28 ’ Erster Abschnitt. § 7.
Das Produkt des konstanten Faktors auf der linken Seite ist
die Diskriminante D, und man erhält also nach (13)
z2n
v ’ = a0^ — a1®3’P’+a2®2?p-2_a8$?p-3_|_a4?p-45
und die y* sind also die linearen Faktoren dieser biquadratischen
Form.
Es gibt noch eine weitere simultane Kovariante der Form <p, V,
nämlich die Jacobische Funktionaldeterminante der vier Funk-
tionen <jp, (P-. Wir bezeichnen sie so:
9>i, ?2, Ts, 9>4
(22) K = Vi, 4>2, ®2, tl’s, ®3, <l>4
&2, ^3,
Bildet man sie für die kanonische Form, so ergibt sich nach
(12), (14), (15)
K = — Ay^y^,
und da 42 = D ist:
= Dy?yly%yl,
also haben wir nach (21)
(23) — W).
Die biquadratische F die wir wie in Bd.I, § 70 H = ^ (24) T = — 12 orm /?(^&, — ’P’) hat so bezeichnen: d*f d*f zwei Kovarianten, 5
g$2’ gOg’P' dZf g’P’g®’ g’P's /'(- W)
Sie sind vom vierten und sechsten Grade in der tP, ’-P-, also
vom achten und zwölften Grade in den xt. Es sind Kovarianten
der Grund kurve (Kombinanten vön <jo und V’), und es besteht
zwischen ihnen die Relation:
(25) Hs — 48AHp — — — 271*.
§ 7.
Elliptische Raumkurven vierter Ordnung.
29
Das allgemeinste zu der Grundkurve gehörige Integral (2)
geht durch Einführung homogener Variabler z = xz-.x4 in fol-
gende Form über:
xz dx4 — x4dxz
/y 2
oder wenn man
n, s OF(X,, X«,X3, X4}
F(x,y,z) = x4 .3.2 v
v 1 4 qpi’/’s — <3P2^i
setzt, in
C-r,, ,xzdx4—x4dxz
\ Fix,, x2, x3, xÄ ——,
J 11 3,v
worin F eine homogene Funktion Oten Grades ist. Der einfachste
Fall ist F — 1, und wir betrachten also das Integral erster
Gattung:
(26)
f xzdx4 — x4dx3
u — I -
J <P1^2 — <P2^1
Nun bilden wir nach dem Multiplikationssatze der Determi-
nanten das Produkt K(x3dx4 — x2dx4), also wegen <p — 0, ip = 0:
S>3, Vi 1, o, o, 0 Sh, T2, o, 0
’/’i, ^2, ^3, o, 1, o, 0 ^2, o, 0
®2, #i, ^2» ^35 x4 ®2, d®
’F2, ?jr4 dx4, dx2, dx3, dx4 ’P’x, ^2, ap1 dW
= (<M2 — - ’FdO),
und folglich ergibt sich aus (26) und (23)
fodip-— f ®d’P’—«Fd®
J K J V/w — ^)
Wendet man hierauf die Transformation des § 5 an, indem
man x, y durch d>, — ersetzt, so folgt
fdH—Hdf
und wenn man in § 5, (17) p = 3, also
3ZZ
Ä — ±f
setzt:
dz
^±zs—g2z — g3'
<72=12.9M, p8 = —4.27Ä
30
Erster Abschnitt.
§ 8. Das Jaeobisehe Transformationsprinzip.
Die Jaeobisehe Transformationstheorie stellt sich im all-
gemeinen die Aufgabe, ein elliptisches Differential durch eine
algebraische Substitution auf ein anderes elliptisches Differential
zurückzuführen. Indem wir hier die Grundlagen dieser Theorie
auseinandersetzen, bedienen wir uns der Darstellung des ellipti-
schen Differentials in homogenen Variablen [§ 1, (4-)]:
, . xdy — ydx
und substituieren darin für x, y zwei teilerfremde ganze homo-
gene Funktionen gleichen, aber beliebigen Grades n zweier neuer
y =
ITT 7 > 8 | J 8 U
au =ai^+a^~,
ar^as^ + ü^
var-rau = mta? — ^asi,
Funktionaldeterminante
h— 1 87 dV dU\
geht das elliptische Differential (1) in das folgende
über:
(5) H^drl —
Damit nun dieses Differential wieder die Form eines ellipti-
schen erhält, ist erforderlich, daß von der Funktion f(U, V),
deren Grad der 4wte ist, sich ein quadratischer Faktor T2 vom
Grade 4n — 4 absondern lasse, also, wenn <p(|, ?/) eine Funktion
vierten Grades bedeutet, daß
(6) f(U,V) = T*<p&y)
werde, wodurch, wenn
T
co 4 = M
Variablen '
(2) x=ü&y),
Aus den Gleichungen
TT . 8t?
„ .ar , ar
"r= +’s?’
folgt sodann
(3)
wenn H die
(<)
bedeutet.
Danach
§ 8.
Das Jacobische Transformationspriuzip.
31
gesetzt wird, das Differential (5) in
1 ^dri —
übergeht. Es läßt sich nun nachweisen, daß, sobald die Bedin-
gung (6) erfüllt ist, H durch T teilbar, und also, da der Grad
beider Funktionen derselbe ist, Jf eine Konstante wird. Diese
Konstante heißt der Multiplikator der Transformation.
Bemerken wir nämlich, daß, da f{x,y) keinen quadratischen
Faktor enthält, die beiden Funktionen
cf 8f
8x’ 8y
keinen gemeinschaftlichen Teiler haben, und daß infolgedessen,
weil U und V teilerfremd sind, auch
8D’ bf
keinen gemeinschaftlichen Teiler (in Beziehung auf |, ?/) haben,
so lassen sich zwei Funktionen a, ß von 17 so bestimmen, daß
cVtPcV
zu einer beliebig gegebenen Funktion T teilerfremd ist. Man
kann z. B. a teilerfremd zu I und ß durch die in nicht
aufgehenden Teiler von T teilbar, dagegen durch die gemein-
schaffliehen Teiler von T und unteilbar annehmen. Wenn
8U
wir nun die Gleichung (6), die wir als erfüllt voraussetzen, nach
g, t] differentiieren, so folgt:
— TY
8U 8£ + 8V 0g- — ’
8U 8jf8V_ __
8U 8t) 8V 8t] — ’
C "f cf
und daraus durch Auflösung in bezug auf 7-X,
worin X, Y, Z ganze homogene Funktionen von £, 1/ sind. Aus
der letzten Gleichung aber schließt man, daß II durch T teilbar
sein muß.
32 Erster Abschnitt. § 9.
Demnach ist unser ganzes Problem enthalten in der Glei-
chung (6), die nichts anderes besagt, als daß die Funktion tuten
Grades 2 m — 2 quadratische Faktoren enthalten soll.
Zur Befriedigung der hieraus folgenden (2 n — 2) Bedingungen hat
man die 2n 2 in U, F enthaltenen Koeffizienten zur Verfügung,
so daß vier von diesen unbestimmt bleiben. Dies war vorauszu-
sehen, da für £, y beliebige homogene lineare Funktionen von £, y
eingeführt werden können. Man kann diese vier überzähligen
Konstanten dazu verwenden, um das Differential (8) in eine
Normalform zu bringen. Da aber die Bedingungsgleichungen für
die Koeffizienten von U, V nicht linear sind, so gibt es für einen
gegebenen Transformationsgrad mehrere Transformationen.
Wir werden diesem Transformationsproblem später von einer
ganz anderen Seite her wieder begegnen und weit tiefer darauf
eingehen müssen. Es soll daher auf die Einzelheiten des alge-
braischen Problems hier' nicht näher eingegangen werden; dagegen
wollen wir durch zwei Beispiele das Gesagte veranschaulichen.
§ 9. Die Transformation zweiten Grades.
Wir setzen, um die elliptischen Differentiale in der Normal-
form zu erhalten:
f&,y) = xy(x — y)(x — Vy),
= £>](£ — if)(£ —
und es seien ü, V vom zweiten Grade.
Die Gleichung (6), § 8, wird jetzt, da T vom zweiten Grade ist
CTF(17-F)(17-A2F)
' } = («i + — ä«2»j),
und es müssen zwei der vier Faktoren zweiten Grades auf der
linken Seite dieser Gleichung Quadrate sein. Die große Zahl
der hierin liegenden Möglichkeiten wollen wir dadurch noch
beschränken, daß wir voraussetzen, und y sollen gleichzeitig
verschwinden, also V durch y teilbar sein. Dies gibt (von einem
konstanten Faktor abgesehen) für V die folgenden drei Möglich-
keiten :
1. V = ^y, . 2. V = q(J; — y), 3. F = — x^y).
Jeder dieser drei Fälle umfaßt nun wieder drei ünterfälle, indem
von den drei übrigen Faktoren ü, U — F, U — Z2F irgend zwei
als Quadrate angenommen werden können. Von diesen letzteren
§ 9-
Die Transformation zweiten Grades.
33
drei Fällen gehen zwei ineinander über durch Vertauschung von
V, Z2 mit F:Z2, 1:Z2.
Wir wollen zwei für die Folge besonders wichtige unter diesen
Transformationen vollständig durchführen.
1. Die Gausssche Transformation.
V = (a£ 4- &17)2.
Wenn nun noch V — Z2F ein Quadrat sein soll, so ist
Z2 — ±ab
zu setzen, und es wird
U—Z2F = (al-— bq)2.
Da U — F sodann durch g — r] und durch g — teilbar sein
muß, so ergeben sich, wenn man g = 17, g = z2/; setzt, aus
U — F die Bedingungen
a b = +1, ax2 b — + x-,
woraus, wenn die oberen Zeichen genommen werden,
«= ' (,= « i =
i 4~ z i -G x i x
U— F= Ö-
T _ & — n2f}2
(i +4T’
jf =
Setzt man also wieder
\ 1 —j— Ä /
-q)(g — x2q)
(1 + ")2 ’
_ g2 — x2q2
(i 4- x)2 ’
1
i 4- x
so haben wir das Resultat, daß durch die Substitution
' (1 + W~ (1 4- «)2
die Transformation
fs) dz = C1 +
*} y^(i — *)(i — z2^) yg(i — :)(i — x2£)
geleistet wird.
Weber, Algebra. III. £j
34
Erster Abschnitt.
§ 9-
2. Die Landensche Transformation.
7= aqtf — t].), U = — x2j/).
Die Bedingungen, daß U — 7, U — Z2 7 Quadrate sind, lauten
4a = (x2 a)2, 4aZ2 = (x2 -|- aZ2)2,
woraus
Z(x2 a) = x2-|- aZ2,
oder durch Z — 1 dividiert
aZ = %2;
dies in eine der obigen Gleichungen eingesetzt, gibt
4Z = x2(l + Z)2,
und durch Auflösung dieser quadratischen Gleichung, wenn
x' = yi — x2 gesetzt ist:
] _ v'
Z = —,, a = fl 4- x')2
U — V = [| — (1 + x')q]?,
U — W = [| — (1 — x')^,
H = (1 + x')2[g - (1 + O<|[£ - (1 - x')^],
T = (1 -|- x')[(| — y)2 — x'2ij2],
M =
also durch die Substitution
z4) z _ (i + - S) z _ 1 - X'
w z — i -x2r ’ k - i + x'’
die Umformung:.
z5) _____________________ (1 +
y^(i —^)(i —z2^) y§(i — g)(i — x2^)*
Wendet man auf die linke Seite dieser Gleichung wieder die
Gausssche Transformation an, indem man in den Formeln (2), (3)
?, x durch z, Z und z durch eine Variable ij ersetzt, so ist, wie
aus (2) und (4) folgt, Z in (3) durch x zu ersetzen, und durch
Kombination von (5) und (3) findet man:
_________drj_________ _ ______ 2d^_______
1 ' ^(1 -^(1 -x2^) “ V£(l -g)(l -x2£)’
und die Verbindung von (2) und (4) ergibt zwischen den
Variablen und den Zusammenhang:
G)
4g(l-g)(l-x2g)
(1 — x2£2)2
Die Transformation dritten Grades.
35
§ 10.
Die Kombination der beiden Transformationen zweiten Grades
gibt also die Multiplikation mit 2.
§ 10. Die Transformation dritten Grades.
Als zweites Beispiel betrachten wir die Transformation dritten
Grades. Die Gleichung
(1) UV(U— V)(U— PF) = — —
fordert, daß jeder der vier Faktoren dritten Grades U, V, U — F,
U — PF durch einen der Linearfaktoren |, ij, | —• tj, l- —
teilbar und daß der Quotient ein Quadrat sei. Wir setzen also
(2) U= +
und verlangen noch, daß
TJ — V
£ — '
V — 7j(a'^ ö'»/)2,
ü— &V
g —
(3)
die Quadrate linearer Funktionen werden.
Von den beiden letzten Forderungen folgt die eine aus der
anderen, wenn wir U, V so einrichten, daß, von konstanten
Faktoren abgesehen, ü und V ineinander übergehen durch die
Vertauschung von |, ij mit z2»;, |. Durch diese Vertauschung
geht aber
£(«£ + »/(a't -4- b'^y
über in
z2j^(6| <zx2ij)2, -4- ct'z2»?)2,
und unsere Forderung ist erfüllt, wenn
ist. Wenn dann
(5)
P = x2
ist, so geht durch diese Vertauschung
Ü — V . b'2 U— PF
(6) | — t] 111 a2 — x2t]
über. Nachdem dies festgesetzt, ist nur noch die Bedingung zu
erfüllen, daß die erste der beiden Größen (3) das Quadrat einer
linearen Fünktion wird, die wir mit (a2| — ß2/r[) bezeichnen, also:
(7) U— K = (| — »?) (a2£—ß2^)2
oder
jj — — ß2^2 = v— — ß2v)2i
3*
36
Erster Abschnitt.
§ 10.
und da U durch |, V durch q teilbar ist, so muß diese Funktion
durch 11] teilbar sein; setzen wir sie = | q (ml- n17), so ergibt
sich aus (2)
(ag — /D>?)2 _j_
(a'l; -j- ö'»/)2 = (cc2| — ß2i])2 f (>n| n>]).
Die Vergleichung der Koeffizienten ergibt
a — a2, b — —ß2 4- b2 = ß* n,
1 1 2 cc2
b' = ß2, a' = — a2 a'2 — + mi
und aus den beiden letzten Gleichungen jeder Reihe:
m2 = 4a2 (na2 mß2),
n2 = 4=ß2(na2 -|- mß2).
Wenn man also
m — ha, n — hß
setzt, so wird
h — 4a ß (a ß).
Hiernach lassen sich a, b, a', b' durch die beiden Größen a, ß
ausdriicken in der Weise:
a = a2, b — ß2 + 2aß,
w a'=a2-\-2aß, b' = ß2,
und danach aus (4), (5)
zq'. 2 __ ß “ ß 2a
k ~ a* a+2ß' H ß a-]-2ß’
oder durch Multiplikation und Division dieser beiden Gleichungen:
(I0) = «• t
v 7 ’ a a 2 ß Z ai
Durch Elimination von ß: a erhält man eine Gleichung zwi-
schen x, Z, die man die Modulargleichung nennt, deren Grad
die Anzahl der verschiedenen Transformationen dritten Grades
angibt. Sie nimmt die einfachste Gestalt an, wenn man setzt:
(11) = u, = v.
Dann werden die Gleichungen (10)
o» ß ß 4~ 2 a u3 ß
a a 2 p v a
also durch Einsetzen des Wertes von ß: a in die erste Gleichung
und Beseitigung des Faktors u2:
(12) — w4 2tt3i’3 — 2wv = 0,
eine Gleichung vom vierten Grade.
§ io-
Die Transformation dritten Grades.
37
Man erhält ferner [ohne weitläufige Rechnung durch Ver-
gleichung der Koeffizienten der höchsten Potenz von | in (1)]
T = + bV) (a'l + ö'|) (a^ - /^) (04 -
„____ £ /8 U dV_____ dV 8 U\ _____ q' _
~ 3 . 8g 8y) ~ a '
woraus man leicht nach (8) findet:
4/ _ r. — ” _ v .
a' a -J- 2 ß v 2 u3
Setzt man den hieraus sich ergebenden Ausdruck
2w3>
V ~ 1—M
in die Gleichung (12) ein, so ergibt sich für M eine Gleichung
vierten Grades, die Multiplikatorgleichung, die die Modular-
gleichung ersetzen kann. Man erhält aber diese Gleichung ein-
facher auf folgendem Wege. Nach (13) ist
1 _ , _ 2 ß l,o_ 2(/3 + 2«)
M « ’ AI+ a
also nach (9):
a
und folglich nach (13)
16^ _ ZA iVZ1 ln \
M ~ \M ) \M^
oder geordnet
(14) J_ _ A + SO - 2»’) _3-o
' > « Jl< + M
Drücken wir also unsere Formeln durch m, v aus, so ist das Er-
gebnis dieser Betrachtung das folgende:
Durch die Substitution
__ t; [(r2 4- 2 v u3) 4- ue g]2
0 “ — [r2 4- (w« 4- 2vw3)g]2
wird die Transformation bewirkt
dz _ v 4~ 2u3 d£
V>(i — ^) (i — ^7) ~ f£(i — o (i -
falls zwischen u, v die Modulargleichung (12) besteht.
Zu einem gegebenen u ergibt die Modulargleichung vierWerte
von v, also vier verschiedene Transformationen dritten Grades.
38
Erster Abschnitt.
§ 11.
§ 11. Die drei Gattungen elliptischer Integrale.
Es sei jetzt
(1) ($) <Zq XA —!“ <7j XA -j— (Zq X% -j- CEg X “j“
eine ganze Funktion dritten oder vierten Grades, und
(2) &(«:) = \ ^^-=\R(x)dx,
j yf(?) J
wenn zur Abkürzung
(3) H(x) =
VfO)
gesetzt ist, ein elliptisches Integral. Es bedeutet darin x eine
unbeschränkt veränderliche (auch komplexe) Größe, und V/’(#)
hat für jeden Wert von x, für den f(x) nicht verschwindet, zwei
entgegengesetzte Werte. Wir verstehen unter einem Punkt
nicht einen Wert von x allein, sondern ein zusammengehöriges
Wertepaar von x und also einen Wert von x mit einem
bestimmten Vorzeichen von ^f(x). Ist daher jr0 irgend ein Wert
von x, so gibt es zwei Punkte a?0, wenn f(xü) von Null ver-
schieden ist, aber nur einen, wenn f(x^) = 0 ist. Für x — oo
bestimmen wir die Punkte nach dem Vorzeichen von yf(x:):xA,
und wir haben also zwei Punkte x = <x>, wenn f(x) vom vierten,
und nur einen, wenn f(x) vom dritten Grade ist.
Nach bekannten Sätzen der Funktionentheorie gibt es, wenn
von Null verschieden ist, eine in einem gewissen Bereich
konvergente Entwickelung nach dem Taylorscheu Lehrsatz:
(4) R(x') = j4m(x—Xo)m-^-Am^-i(x—Xo)m'^1 -j— Am + %(x—X()')m +2-j—•••,
worin m eine positive oder negative ganze Zahl oder auch Null
ist, während Am Am+1, Am+z, ... Konstanten bedeuten, von denen
Am nicht verschwindet. Dies ist eine Entwickelung nach steigen-
den Potenzen. Ergänzend tritt hinzu, falls f(x) vom vierten
(nicht vom dritten) Grade ist, die Entwickelung nach fallenden
Potenzen
(5) R(x) = GmX-m-‘1 + Cm + lX-m-Z + + -j-------,
von der wir sagen, daß sie in der Umgebung eines unendlich
fernen Punktes gilt.
§ 11. Die drei Gattungen elliptischer Integrale. 39
Wenn aber verschwindet, so erhält die Entwickelung
von R(x) die Form:
(6) R(x) = Am(x — x^-1^ 4- An+1(x — xQ)m~^+l
4" + — ^o)m—*fe + 2 4- •••,
und wenn f(x) vom dritten Grade ist, so gilt in der Umgebung
des unendlich fernen Punktes die Entwickelung
(7) R(x) = Cmx~m~^ 4- Cm+lx~m-% 4- Cm + 2x~m~% 4----
Aus den Entwickelungen (4) bis (7) können wir die Ent-
wickelungen von Q ableiten, wobei eine additive Konstante un-
bestimmt bleibt.
Die Entwickelung von £i ist dann ebenfalls eine Potenzreihe,
wozu, wenn m negativ ist, in den Fällen (4) oder (5) noch ein
Glied A-tiogtx — x0), C^Aogx tritt.
Wir nennen nun xa einen Punkt erster Gattung von
ü, wenn m in diesen Entwickelungen nicht negativ ist.
Dann ist £1 im Punkte xü endlich (auch im Falle x0 = oo).
Der Punkt x0 heißt ein Punkt zweiter Gattung von £Z,
wenn in den Entwickelungen (4), (5) m negativ und = 0,
C—i = 0 ist, und in dem Falle der Entwickelung (6), (7) mit
negativem m.
Endlich heißt x0 ein Punkt dritter Gattung, wenn in
den Entwickelungen (4) oder (5) oder CLj von Null .ver-
schieden ist, wenn also in der Entwickelung von.ß ein logarith-
misches Glied vorkommt.
Die Nullpunkte von f(x) können bei dem Integral (2) nicht
von der dritten Gattung sein; sie können aber von der dritten
Gattung werden, wenn wir das elliptische Integral in der all-
gemeinen Form j f(x))dx betrachten.
Das Integral ß heißt ein Integral erster Gattung, wenn
es nur Punkte erster Gattung hat. Ein solches Integral hat
dann für alle endlichen und unendlichen Werte von x einen
endlichen Wert.
£1 heißt ein Integral zweiter Gattung, wenn es nur
Punkte erster und zweiter Gattung hat, und
£1 heißt ein Integral dritter Gattung, wenn es neben
Punkten erster und zweiter Gattung auch Punkte dritter Gat-
tung hat.
40
Erster Abschnitt.
§ 12.
§ 12. Darstellung der elliptischen Integrale durch die
einfachsten Grundintegrale.
Um das Integral £i(x) durch Integrale von möglichst ein-
fachem Typus darzustellen, zerlegen wir die rationale Funktion
0(jc) in eine ganze Funktion und in eine Summe von Partial-
briichen, d. h. wir stellen <I>(x) dar als eine Summe von Aus-
drücken der Form
zzn ___________
’ (x — «)«
mit konstanten Koeffizienten, worin n eine ganze positive Zahl
(auch Null) und a einen konstanten Wert bedeutet, für den $>(x)
unendlich wird.
Setzen wir dann für positive und für negative oder ver-
schwindende n
\ o z \ 1* (^ cc)whx
(1) ’ = J V7W ’
so wird £i(x) eine Summe der Form
M Sn (a),
wo sich die Summe auf mehrere verschiedene Werte von n und
von a erstrecken kann und die M Konstanten sind.
Die Funktionen Sn lassen sich durch Vermittelung algebrai-
scher Funktionen auf eine geringe Anzahl zurückführen. Zu dem
Ende bilden wir
n . n . V/»
und wenn wir dann setzen
= /(«) + (* - «)f(«) («)
+ /'"(«) +
t\x) = f W + (x-a)^(a) + (±ZLfO2r(a) +
Ai O
so folgt
(x — a)« y f(x) = »/(«) Sn-i + + -|) f (W) Sn
(2) + n-^f"^Sn+1 + /"'(«) Sn+,
+ (£ + ^)r"(«)sn+3.
§ 12. Die einfachsten Grundintegrale. 41
Wir unterscheiden vier Fälle:
1. f""(a) und f(a) nicht = 0 [d. h. f(x') vom vierten Grade
und a keine Wurzel von f(x)].
In diesem Falle läßt sich durch die Formel (2) für n = 0
S8 durch So, S2 ausdrücken, und daher Sn für jedes positive n
durch So, <S\, S>. Setzt man aber n = —1, —2, ..., so erhält
man S_2, S_3, ... ausgedrückt durch S—i, So, S15 S2. Also
bleiben in diesem Falle die vier Grundintegrale
S^, So, slf s2.
2. f"" («) nicht = 0, f(a) = 0. In diesem Falle kann man
noch S-i durch So, S,, S2 ausdrücken und erhält als Grund-
integrale
s0, s15 s2.
3. /'""(«) = 0, f(a) nicht = 0. Hier sind die Grund-
integrale
S_1, s0, sr
4. f"" («) = 0, f(a) = 0. Hier sind die Grundintegrale
So, Sj.
Das Resultat hiervon ist also:
I. Ist f(x) vom vierten Grade (a0 = 1), so lassen sich alle
Integrale £2,(x) ausdrücken durch Integrale der Form
Q ___ f dx „ f xdx „ f x*dx
O-Jw 1-J77W’ 2-Jwr .
$ _____ f dx
J (x — a) y f(x) ’
worin S_i noch von dem Parameter a abhängig ist.
II. Ist aber f(x) vom dritten Grade, so genügen die drei
Integrale
o C dx Q f xdx Q _______________________ f dx
J V f(.x) J V f(x) J (X — a) y f(x)
In beiden Fällen ist So von der ersten Gattung. Ist f(x)
vom dritten Grade, so ist Sj von der zweiten und S_j von der
dritten Gattung. Ist dagegen f(x) vom vierten Grade, so sind
Si, S2 und S-i von der dritten Gattung. Man kann aber aus
S, und ein Integral zweiter Gattung zusammensetzen. Denn
es ist
42
Erster Abschnitt.
§ 12.
= (jc4 4~ jc3 4“ a2 + a3 a?2 -|- a4)_I/2
V/»
= x~2 —• ^x~3 4- ••,
2
und in der Entwickelung von ^a?2 + : j/ f(x) nach fallenden
Potenzen kommt kein Glied mit a?-1 vor. Folglich ist S2 4- tt 4
2
ein Integral zweiter Gattung.
Durch Vermittelung einer logarithmischen Funktion kann
man aber auch noch die vier Integrale des Falles I auf drei
reduzieren. Zu dem Ende bringe man f(x) auf die Form
a.4 —x3 4” a'2 4“ O3 x 4- 664. jP2 4- <x x 4“
worin P — x2-{-px-]-q eine quadratische Funktion und a
und b Konstanten sind. Es ergibt sich:
Nun ist:
(3) (ilog£=A = £W^VfeWi_£=,
VF+p f—p‘ m«)
f — P2 = ax 4- b,
f'(x) = 2PP' 4- a
und folglich
f' (x)P — 2f(x)P'(x) = a(P — 2xP') — 2bP' = Q
eine quadratische Funktion von x, und demnach ergibt sich aus (3)
z.x ' 1 V7— P ______ f Q dx
°SV7+ p ~~ J ax + b V7W'
Die rechte Seite ist aber eine lineare Funktion von So, Sx
und S_i (für a — —b/a). In dem besonderen Falle, wo a = 0
ist, wird Q vom ersten Grade, und man kann eine lineare Ver-
bindung von SQ und durch eine logarithmische Funktion
ausdrücken.
Nehmen wir a2 und as = 0 an, worauf wir den allgemeinen
Fall nach § 4 durch lineare Transformation zurückführen können,
so erhalten wir als die Grundintegrale
Das Additionstheorem.
43
§ 13-
o ( dx Q _______________ C x*dx „ f dx
w j V7W 1 j (.*-*) yw
/* $
während & = -?= durch die Substitution = 11 auf das
JV7H
nicht elliptische Integral
1 f dy
2 J + a2V + «4
zurückgeführt -wird. Hier ist So von der ersten, Ss von der
zweiten, S—i von der dritten Gattung. Für die Legendresche
Normalform setzen wir f(x) — (1 — x-) (1 — %2^2) und nehmen
als Normalintegral der zweiten Gattung nicht $2 selbst, sondern
So — Sr Dadurch ergeben sich die Normalintegrale der drei
Gattungen :
f________dx_______ /}_^2^2^^ f___________ dx
J y(l — a;2)(l—%2a?2)’J l' 1—x- ^’Jc#—«) V(1 — a;2)(l—%2a?2)
und wenn man x = sing? setzt:
f <p f i---------------------- f dcp
„ . ===> vl — x2 sin2 a> d a>, ~ x„ '.~T~‘
Jyl—%2sin2g> J ~r ~ri J(slng> — a)yl — 5C2Sin2gp
Dasselbe erhält man, wenn man das elliptische Differential
in der Normalform
d z
y#(l — z) (1 — %2£)
annimmt und nach dem Falle H verfährt.
§ 13. Das Additionstheorem.
Das von Euler entdeckte Additionstheorem der elliptischen
Integrale besteht in dem Satze, der für die ganze weitere Theorie
von fundamentaler Bedeutung ist, daß, wenn von den drei Wert-
paaren
®i, y/XO; ^2, Vf«); y/xo
zwei als gegeben vorausgesetzt werden, man auf algebraischem
Wege das dritte so bestimmen kann, daß die Differentialgleichung
dxt . dx2 dx3 _ 0
yxc^i) y/x%) y/x^s)
befriedigt ist. Darin ist f(x) eine gegebene Funktion vom dritten
oder vierten Grade. Es ist dies ein spezieller Fall des großen
44 Erster Abschnitt. § 13.
Abelschen Theorems und soll auch in dieser Weise hier auf-
gefaßt und abgeleitet werden J). Dem Beweise schicken wir fol-
genden elementaren algebraischen Satz voraus:
Ist F(x) eine ganze rationale Funktion nten Grades
ohne mehrfache Faktoren, F'(x) ihre Derivierte, sind
ferner x1, xt, ..., xn die Wurzeln der Gleichung F(x) — 0
und <p(x) eine ganze Funktion von’ x, deren Grad höch-
stens = n — 2, so ist
, <jp(a?2) . _
F' (^) “T F' O2) ' F' (^) ~
Der Beweis dieses Satzes ergibt sich unmittelbar aus der
Zerlegung des rationalen Bruches
x <p (x)
in Partialbrüche
. xt <p (x2~) ______ xn<p(Xn)
F'(x1)(x — x^ ‘ jF'(a?2)(a? — ‘ F’(x„)(x — a?«)1
wenn darin x = 0 gesetzt wird [Bd. I, § 1.5 (9)].
Es sollen nun _P, Q ganze Funktionen von x von den Graden
m und m — 2 bedeuten, und wir fragen nach den Werten von
x, V für die die Funktion
(3) P +, Q ff(x)
verschwindet. Solcher Wertpaare (Punkte) gibt es 2»n, und zwar
findet man die Werte von x als Wurzeln der Gleichung 2mten
Grades:
(4) F (x) = Pä — Q'2 f(x) = 0,
und die zugehörigen Werte von ]/ f(x) aus
(5) P' + Q V7ÖÖ = 0.
Wir nehmen nun an, die Koeffizienten in den Funktionen
P, Q seien veränderlich, entweder unabhängige Veränderliche
oder in irgend einer Weise von anderen Veränderlichen abhängig.
*) Dieses weltumfassende Theorem findet sich iu großartiger Einfachheit
abgeleitet in einem kaum zwei Seiten umfassenden Aufsatze im vierten Bande
von Grelles Journal „Demonstration d’une propriete generale d’une certaine
classe de fonctions transcendentes“; Oeuvres completes de N. H. Abel.
Nouvelle edition, T. I, p. 515. Ausführliche Darstellung und Anwendungen
in der nachgelassenen großen Abhandlung: „Memoire sur une propriete
generale d’une classe tres etendue de fonctions transcendentes“.
§.13.
Das Additionstheorem.
45
Es werden dann auch die durch (4), (5) bestimmten Werte x
und V f(x) Funktionen dieser Veränderlichen, und (ö) läßt sich
differentiieren.
Bezeichnen wir mit 5 die Differentiation nach den in den
Koeffizienten von P, Q vorkommenden Veränderlichen, wobei x
als konstant gilt, mit dx das entsprechende Differential vou x,
wenn x durch (4) oder (5) als Funktion dieser Koeffizienten
bestimmt ist, so ergibt die Differentiation von (4)
2PdP — 2 QSQf(x) + F'(x)dx = 0,
(6)
woraus mit Benutzung von (5):
QSP — PS Q _ dx
i'W — 2y7öö’
und da der Zähler auf der linken Seite vom Grade 2»i — 2,
F(x) vom Grade 2 m ist, so läßt sich die Formel (2) anwenden,
und es folgt
(?)
Ai_ = o,
V/l»)
wenn die Summe auf sämtliche Wurzeln der Gleichung (5) er-
streckt ist.
Wir wenden dieses Theorem auf den einfachsten Fall, näm-
lich m = 2, an uud erhalten dann folgenden Satz:
Wenn
(8) «i, y^i); y^); *3, yf(O; mo
vier Wertepaare sind, für die irgend eine Funktion der
Form
(9) a bx cx- y f(x)
verschwindet, so sind diese Wertepaare nicht gänzlich
voneinander unabhängig, sondern es besteht zwischen
ihnen die Differentialgleichung
z'10') dX1 I । dxg i dXi _ 0
y/w y/’w y/’c^) v/cgi
Die Abhängigkeit dieser vier Wertepaare, also eine Inte-
gration der Differentialgleichung (10), kann aber auch in alge-
braischer Weise ausgedrückt werden, indem man die Funktion
(9) für x — xx, x%, xs, Xi gleich Null setzt und dann a, b, c
eliminiert. Man erhält so die Determinantengleichung:
46
Erster Abschnitt.
§ 13-
(11)
i 1, Xu X2, V/(«!)
1, x2, x£,
1, ^3,
xl ^f(x2)
xl, V/'(«s)
= 0.
1, x^ a%, if(x^)
Aus dieser Gleichung kann man xx und ^fix^ rational
durch a?2, f(x^)\ xs, ]/f(xs); x4, V f(xt) ausdrücken; denn
x± ist die Wurzel einer biquadratischen Gleichung, deren drei
andere Wurzeln a?2, x3, xt sind, und deren Koeffizienten rational
von x2, y f(rc2); x3, y f(a?3); xu y /,(a?4) abhängen, und \ f(xt) ist
mittels (11) rational durch xT darstellbar. Setzt man <r4 einer
beliebigen Konstanten gleich, so geht die Differentialgleichung
(10) in (1) über und (11) ergibt ihr Integral.
Wir wenden dies Theorem zunächst auf die Normalform an
und setzen
f(x) = x(l — x)(l — x2x).
Nehmen wir in (11) a?4 = 0 an, so reduziert sich diese
Gleichung durch Division mit ^x1x2x3 auf:
(12)
y^, xi y^n y (i — — %2®i)
y^, a?2 y^, y(i — ®2)(i — ^2®a) = o,
y^, x3 ya?3, y(i — a?3)(i —
oder wenn wir die Determinante nach den Elementen der ersten
Zeile entwickeln:
(13) y^ (a -]- b x^ c y (1 — x^ (1 — %a aq) = 0,
worin zur Abkürzung gesetzt ist:
a = x2 ^Xi y(l — a?3) (1 — %2a?3) — x3 ^x3 y(l — x2) (1 — x2jr2),
(14) & =—y^ y(i—a?3)(i—«%) + y^s v(i—^((i—x^’äh
c=—(x2 — xs) y^ y«3.
Wenn wir (13) rational machen, so erhalten wir die kubische
Gleichung:
x(a -]- bx)- — c2(l — x)(l — xsx) = 0,
deren drei. Wurzeln a?,, a?2, x3 sind. Es ist demnach identisch
(15) bs(x—x^(x—x2) (x —- xs) — x (a -|- b x)2—c2 (1 — x) (1—x2a:),
Das Additionstheorem.
47
§ 13.
und indem wir in dieser identischen Gleichung x — 0, 1, 1: %2
setzen, so folgt:
V x1x2x$ — —
(16) V(1 -0(1-0(1-0 =
)/(l — %2O(1 — %2O(1 — x2O — •
Zur Bestimmung der Vorzeichen in diesen Gleichungen er-
halten wir noch aus (13), wenn wir durch x2 und xs ersetzen
und die Ergebnisse multiplizieren:
a?ix2x3(a bx^ia bx^) (a bxs) = — c3 ^f(x,) ^f(x^) ^f(Xs)
und (15) ergibt für x = —a:b
c2
(a -j- bxi)(a -|- bx2)(a bx3) — — (b a)(b O x*a)-
Benutzt man noch das Quadrat der ersten Gleichung (16),
so folgt hieraus
V7(O V/(O W(O = — + a)(b + %2a).
Dasselbe Resultat ergibt aber die Multiplikation der drei
Gleichungen (16), und die Vorzeichen sind also in diesen Formeln
so gewählt, daß das Produkt der linken Seiten den durch die
Differentialgleichung (1) geforderten Wert von f (O ergibt.
Eine weitere Bestimmung der Vorzeichen ist in (16) der Natur
der Sache nach nicht möglich, und diese Gleichungen dienen zur
eindeutigen Definition von \x1, ]/l — xr, ]/l — %2O wenn die
}'x2, ]/l — x2, yi — »c2O ]/a?8, )/l — a?3, V1 — z2^ als gegeben
vorausgesetzt werden.
Um die Gleichungen (16) in die gebräuchliche Form zu
bringen, machen wir zunächst in (14) den Zähler von b rational
und erhalten
b ____________________(x2 — a?3)(l — h2x2x3")____________
y(l — a?3)(l — %2O + V(1 — 0(1 — «2O’
ferner nach (14):
b a =
— y(i—o(i ~«s) {^(i-O Vi — h2xs — (1 — x8) yi — x2x2 ;
b n2a =
— V(1 -%2O (1- %2O ! ix2(l-‘X2x2)^l-xs-^xs(l—H2xs) yi~Or
48 Erster Abschnitt. § 13.
wodurch die Gleichungen (16) leicht in die Form gebracht werden:
V(I—a?8) (1 — %2a;8) 4~ ^xs |/(I — a?2) (I — -/Jx,)
1 — %2a:2a?3 ’
Vi — x2 (1 — x3 — ^x2xs ]/(l — %2a:2)(l —• x2a?s)
1 — y.-X2X!1 ’
1Ä-_V1 — V1 — — %2 V«2xs y(l—a:2)(l —a?3)
y 1 —— zt Jty-I - ------------------------------------------------•
' 1 — H2X2XS
und unsere Betrachtung lehrt, daß, wenn x4 und die Wurzeln
y^!, yi—x2, (1— x2^ durch diese Gleichungen als Funktionen
von x2, xs bestimmt werden, die Differentialgleichung (1) identisch
befriedigt ist.
Um auch für die Weierstrasssche Normalform das Additions-
theorem in möglichst einfacher Gestalt zu erhalten, setze man
f(x) — 4x« — ff2X — ffs,
und lasse in der Gleichung (11) (nach Division mit xf) x4 un-
endlich groß werden. Es ergibt sich alsdann das Integral der
Differentialgleichung (1)
in der Form dx2 . 1, Xi, ^f(xC) dxs _ 0
(18) oder 1, ®2, )//’(a:2) 1,^3, y^) = 0,
(19) wenn a -|~ bx4 = 0, a = x2 ^f(x3) — xs ^f(x2)
(20) b c = W'W — —— . X 2 • y^^s)
Es werden Gleichung dann (a xlt ®2, xs die Wurzeln der kubischen -|- bx)^ — &f(x\ — 0,
und wenn man hierin den Koeffizienten .von a:2, geteilt durch
den von x" gleich der negativen Summe der Wurzeln setzt, so erhält man
Ursprung der elliptischen Funktionen.
49
§ 14.
ii — if(x3y\2
(21) + x. + xs = - V ’
und aus (19)
(22) vife)=i (i7® - v/(-»y - fe+~ ^(s)
*^3 ' *^2 *^3
X3 ~ ^2 17(^)
zy» zy>
iVq vl/g
§ 14. Ursprung der elliptischen Funktionen.
Wenn in dem elliptischen Differential erster Gattung in der
Leg en dreschen Normalform
1 dz
2 y^(i _^)(i _
die Substitution
(1) z = sin2<p
gemacht und sodann die Integration von <p = 0 an ausgeführt
wird, so entsteht das elliptische Integral erster Gattung
v
f d<p
(2) - —- . ' = w.
7 J yl — x2sin2 (p
0
Jacobi nennt die obere Grenze (p dieses Integrals seine
Amplitude und schreibt
(3) <p = am«.
Die trigonometrischen Funktionen dieses Bogens
(4) sinqp, cosg>, ]/l — x2sin2<p = z/g>
sind es nun, die, als Funktionen von w betrachtet, elliptische
Funktionen genannt und von Jacobi mit
sinamw, cosam u, z/amu,
oder, nach Gudermann, kürzer mit
(ö) sn«, cnit, dnw
bezeichnet werden. Diese Funktionen hängen von den zwei
Argumenten u und x2 ab, und wenn eine genauere Bezeichnung
notwendig ist, wird dafür auch
sn (u, x2), cn (u, x2), dn (w, x2)
gesetzt.
Weber, Algebra. III. 4.
50
Erster Abschnitt.
§ U.
Wenn in der Formel (1) cp in —<p verwandelt wird, so geht
u in —u über, es ist also am(—u) = —amu und folglich
sn(—u) = —snu, cn(—-u) — cnu, dn(—u) = dnu,
d. h. es ist snu eine ungerade, cnu, dnu sin gerade Funktionen.
Setzt man also
d cpn .. dtp, , dtp. ,
—= du, = dv, = — d(u + v),
^<}>2 4<f>g VI/’
so lassen sich die Formeln (17), § 13 anwenden, und man erhält
die Additionstheoreme:
, , . sn u cn v dn v -4- sn v cn u dn u
Sn<M + = --------1 — %2'sn2usn2P--------
cn (u -|- v) =
(6)
cnu cnu — snu snu dnu dnu
1 — %2 sn2u sn2v
dn(u -|" f) =
dnudnt? — z2snusnvcnucnv
1 — %asn2usn2v
Man kann daraus die drei elliptischen Funktionen für beliebige
Werte des Arguments eindeutig berechnen, wenn sie für irgend
ein noch so kleines Gebiet um den Nullpunkt bestimmt sind.
Diesen Satz nimmt Weierstrass zum Ausgangspunkt der Theorie
der elliptischen Funktionen.
Setzt man
2
f = jr,
J z/ <p
o
so ist snW = 1, cnK = 0, dnAT = |/1 — x2 = v!, und es
ergeben also die Formeln (6), indem man v = K setzt:
. —%'snu
cn (u 4- K) = —i-,
1 7 dnu
dn(ul£)=
' 1 7 dnu
und wenn man diese Formel noch einmal anwendet:
sn (u -|- 2 IC) = — sn u,
(8) cn (u 2 AT) = — cn u,
dn (u 2 K) = dn u,
§ 14.
Ursprung der elliptischen Funktionen.
51
und abermals angewandt:
sn (u -]- 4 K) = sn w,
(9) cn (n 4 K) — cn u,
dn(u 4 Jv) = dnw.
Es haben also die elliptischen Funktionen die Eigenschaft der
Periodizität mit den trigonometrischen Funktionen gemein. Sie
haben die Periode iK (dnw auch die Periode ‘IK').
In § 3 haben wir als Beispiel die Transformation, die
Formel (1), abgeleitet:
z . dz dx
(10) -===== = —. ... ,
~\jz (1 — z) (1 — x2z~) i yx (1 — x) (1 — x'2a?)
wenn
war. Setzt man also
dx . ,
-—===== = idu,
yx (1 — x) (1 — x'2 a?)
also
so ist, wenn x und w zugleich verschwinden, x = sn2(iw, x'),
1 — x = cna(iw, x'), und aus (10) folgt:
dz 7
^=== = du,
y z(i — z)(i — %az~)
z = sn2(u, x).
Demnach ergibt (11)
. z \ —isn(w, x')
(12) sn(w,x) =-------z.v \ 7
v 7 v 7 cn(?w, x')
(worin das Vorzeichen aus dem speziellen Wert w = 0 zu be-
stimmen ist).
Setzt man nun
2
f d(P — VI
J "|/1 — x'2 sh2 <p
0
so ergibt sich aus (8)
sn (iu 2 K', x') = — sn (iu, x'),
cn (iw 2 K.', x') = — cn (iu,
und folglich aus (12)
sn (u — 2 i K', x) — sn (u, x)
4.*
52 Erster Abschnitt. § 14.
oder auch, indem man u in u -|- 2tl£' verwandelt und die Be-
zeichnung x wieder wegläßt:
(13) sn (u 2fÄ') = snu.
Es hat also die Funktion snu eine doppelte Periodizität.
Die eine dieser Perioden, 4K, ist reell die andere, 2iK, rein
imaginär (wenigstens wenn der Modul % ein positiver echter
Bruch ist). Diese doppelte Periodizität ist eine Eigenschaft, die
in dem Gebiete der elementaren Funktionen nirgends vorkommt,
und so am deutlichsten zeigte, daß man es hier mit einer neuen
Funktionenart zu tun hat. Die aus der doppelten Periodizität
abgeleiteten Folgerungen sind es zugleich, die, wie die Erfahrung
gezeigt hat, weitaus am schnellsten mit befriedigender Strenge
in das Innere der Theorie einführen, so daß hier der zweck-
mäßigste Ausgangspunkt für eine methodische Entwickelung zu
suchen ist. Unsere nächsten Betrachtungen werden daher den
doppelt periodischen Funktionen im allgemeinen gewidmet sein
Zweiter Abschnitt.
Theta - Funktionen.
§ 15. Voraussetzungen aus der Funktionentheorie.
Der Begriff der doppelt periodischen Funktionen kann nur
dann richtig aufgefaßt werden, wenn man sie als Funktionen
eines komplexen Arguments u = v iw betrachtet, worin i wie
gewöhnlich die Bedeutung von \— 1 hat. Die Variable u gilt
uns als unabhängige und unbeschränkt veränderliche Größe, die
nach dem Vorgänge von Gauss durch die Punkte einer Ebene in
der Weise geometrisch verauschaulicht wird, daß der Punkt,
dessen Koordinaten in einem rechtwinkeligen System v, w sind,
als Träger des Wertes u — v iw angesehen und kurz als der
Punkt u bezeichnet wird.
Wir beschränken unsere Betrachtung hier auf eindeutige
analytische Funktionen <p(u), die im Endlichen keine wesent-
lich singulären Stellen haben. Was im Unendlichen geschieht,
lassen wir dahingestellt. Wir setzen also von den betrachteten
Funktionen folgendes voraus:
1. In jedem endlichen Flächenstück liegt eine endliche An-
zahl von Punkten, in denen die Funktion <p(w) unendlich wird;
diese Punkte heißen Unstetigkeitspunkte.
Die Anzahl der Unstetigkeitspunkte überhaupt, d. h. in der
ganzen unendlichen Ebene, kann natürlich auch unendlich groß
sein.
2. Ist w0 ein nicht zu den Unstetigkeitspunkten gehöriger
Punkt, so ist die Funktion entwickelbar in eine nach ganzen auf-
steigenden positiven Potenzen von w — m0 fortschreitende Reihe,
die konvergent ist in einem Kreise, der den Punkt m0 znm Mittel-
punkte hat und bis zum nächstgelegenen Unstetigkeitspunkte
reicht. Man sagt, die Funktion habe in der Umgebung des
Punktes m0 den Charakter einer ganzen Funktion.
54
Zweiter Abschnitt.
§ 15.
3. Ist u0 ein Unstetigkeitspunkt, so gibt es eine ganze
positive Zahl m von der Art, daß (u— M0)m<jp(u) in dem
Punkte u0 endlich, stetig und von Null verschieden bleibt und
daher nach ganzen positiven Potenzen von u — u0 entwickelbar
ist. Der Unstetigkeitspunkt wird in diesem Falle von der mten
Ordnung genannt. Es ergibt sich daraus eine Entwickelung
von <p(u) nach steigendenPotenzen von w—w0, die mit (u—u0)-m
anfängt und in einem um u0 beschriebenen Kreise, der bis zum
nächstgelegenen Unstetigkeitspunkte reicht, konvergiert. Der
Koeffizient von (w — u0)—1 in dieser Entwickelung heißt das
Residuum dieser Funktion für den Punkt u0.
4. Der Cauchysche Satz. Das Integral
1 f / \ 7
H--r «> (u)du,
2 m J v
in positivem Sinne über die Begrenzung eines endlichen Flächen-
stückes erstreckt, das auf der Randlinie keine Unstetigkeitspunkte
enthält, ist gleich der Summe der Residuen für die im Inneren
des Flächenstückes liegenden Unstetigkeitspunkte. Als positive
Integrationsrichtung ist dabei diejenige anzusehen, die gegen das
Innere des Flächenstückes so liegt, wie die »-Achse zur w-Achse,
so daß bei der üblichen Bestimmungsweise dieser Achsen beim
positiven Durchlaufen des Randes das Innere der Fläche zur
Linken bleibt.
5. Die Funktion
= dlogy(u) = 1 d<p(u)
' ' du <p(u) du
hat nur Unstetigkeitspunkte erster Ordnung, und weun in einem
Punkte u0 das Produkt (w — endlich und von Null
verschieden ist, so ist m das Residuum von ^(w) für diesen
Punkt. Ist m positiv, so heißt w0 ein Nullpunkt mter Ordnung
von <p (u).
Hiernach ist eine unmittelbare Folgerung des Cauchyschen
Theorems:
6. Das Integral
^plog^M),
ausgedehnt in positiver Richtung über die Begrenzung eines
Flächenstückes, ist gleich der Anzahl der Nullpunkte, vermindert
um die Anzahl der Unstetigkeitspunkte, die im Inneren dieses
§ 15. Voraussetzungen aus der Funktionentheorie. 55
Flächenstückes liegen, wobei Nullpunkte und Unstetigkeitspunkte
mter Ordnung wie m solche Punkte erster Ordnung zu zählen sind.
Hieraus folgt, daß im Inneren eines endlichen Flächenstückes auch
nur eine endliche Anzahl von Nullpunkten liegt.
In gleichem Sinne ergibt sich
7. Das Integral
2^7 pcnog<p(u)
ist gleich der Summe der Werte von w, für die <p(w) verschwindet,
vermindert um die Summe der Werte von u, für die cp(u) un-
endlich wird.
8. Eine Funktion, die im Endlichen gar keine Unstetigkeits-
punkte besitzt, heißt eine ganze Funktion. Eine ganze
Funktion, die auch im Unendlichen endlich bleibt,
ist eine Konstante. Eine ganze Funktion, die auch im Un-
endlichen keine wesentlich singuläre Stelle hat, für die es also
einen Exponenten m derart gibt, daß u~m <p (u) für u = co nicht
unendlich wird, ist eine rationale Funktion.
9. Eine ganze Funktion, deren Reziproke gleichfalls ganz
ist, heißt eine Einheitsfunktion. Eine solche Funktion wird
im Endlichen weder Unendlich noch Null. Ihr Logarithmus ist
daher ebenfalls eine ganze Funktion, und es folgt daraus, daß
jede Einheitsfunktion in der Form dargestellt werden kann,
worin </(«) eine ganze Funktion ist. Umgekehrt ist jeder Aus-
druck von dieser Form- eine Einheitsfunktion.
10. Nach den grundlegenden Untersuchungen von Weier-
strass über die eindeutigen analytischen Funktionen (Abhand-
lungen der Berliner Akademie von 1876) gibt es immer eine
ganze Funktion G-(w), die in den Unstetigkeitspunkten einer
Funktion <p (u) und nur in diesen verschwindet, und diese
Funktion G (w) ist durch die Unstetigkeitspunkte von <p (u) bis
auf eine Einheitsfunktion als Faktor bestimmt. Es ist dann
cp(u)G(ii) = Uj (m) gleichfalls eine ganze Funktion, und man
kann also jede Funktion (p (u) als Quotienten zweier ganzen
Funktionen
<p(u) =
darstellen, worin G(u) und G1 (w) keine gemeinschaftlichen Null-
punkte haben.
56
Zweiter Abschnitt.
§ 16-
11. Zähler und Nenner dieser Darstellung sind
durch <p(u) selbst, abgesehen von Einheitsfaktoren, ein-
deutig bestimmt.
Die Funktionen G(w), ^(w) können in Primfaktoren, d. h.
in Faktoren zerlegt werden, die nur in einem Punkte Null
werden. Verfolgt man diesen Weg bei den doppelt periodischen
Funktionen, so gelangt man zu den Weierstrassschen ö-Funk-
tionen. Wir werden aber einen anderen Weg gehen, auf dem
wir den ö-Funktionen erst an einer späteren Stelle begegnen.
§ 16. Periodizität.
Eine Funktion <p (w) von w, welche die Eigenschaft hat, daß
für ein konstantes <a und für jeden Wert von w
(1) <p (w -j- G>) = <p (w)
ist, heißt periodisch und co heißt die Periode.
Der Gegenstand unserer Untersuchung sind Funktionen <p (w)
mit zwei Perioden <»2, von denen wir ein für allemal voraus-
setzen wollen, daß ihr Verhältnis <»2: <o1 nicht reell und daß der
imaginäre Teil dieses Verhältnisses positiv sei. In der letzteren
Annahme liegt nur eine Festsetzung über die Bezeichnung
<»!, 63%. Denn wenn <o2:(o1 einen negativen imaginären Teil hat,
so ist der von »j: cj2 positiv.
Jede Kombination- m2cj2 ist, wenn m1, m2 ganze
Zahlen sind, gleichfalls eine Periode.
Wir nehmen in der Ebene u einen beliebigen Punkt w0 an
und bezeichnen die vier Punkte
Wo, Wo G>!, Wo -j- ß>2, Wo G52;
verbinden wir diese vier Punkte der Reihe nach durch gerade
Linien, indem wir vom letzten zum ersten zurückkehren, so er-
halten wir ein Parallelogramm, welches das Periodenparallelo-
gramm genannt wird. Es können die geradlinigen Seiten des
Periodenparallelogramms auch durch krummlinige Züge ersetzt
werden, wenn nur die gegenüberliegenden durch Parallelver-
schiebung zur Deckung gelangen und die einzelnen Züge keine
Schleifen bilden.
Ist cjj — w, ßLi, cj2 — w2 ßai und o^, cc2, ßlt ß3 reell,
so ist nach der Voraussetzung (ax ß2 — oc2 ß,) positiv, und die
geometrische Bedeutung dieser Größe ist (nach bekannten Sätzen
§16. Periodizität. 57
der analytischen Geometrie) der Flächeninhalt des Perioden-
parallelogramms.
Durch Aneinanderreihen kongruenter Periodenparallelogramme
läßt sich die ganze u-Ebene einfach und lückenlos überdecken.
Entsprechende Punkte zweier verschiedener dieser Parallelogramme
sind die Repräsentanten von «-Werten, die sich um ganzzahlige
Vielfache der Perioden unterscheiden, und die nach dem Modul
(<»!, w2) kongruent oder, wenn kein Zweifel möglich ist, kurzweg
kongruent genannt werden. Das Zeichen der Kongruenz ist
u = u' (mod <»!, <»2),
und besagt, daß u' die Form u -|- m,± <o1 wi2 hat, wenn m2
ganze Zahlen sind.
So stellt die Fig. 1 vier aneinander gelagerte Periodenparal-
lelogramme dar; die Punkte u2, us, u4 sind kongruent:
«2 = “I- ^1) «3 —|— <Z>2, «4 «1 —,
und Wj, «2, w3, w4 bilden ebenfalls die Ecken eines Perioden-
parallelogramms.
Die doppelt periodische Funktion <p(u) hat in allen
kongruenten Punkten denselben Wert, und der ganze Wert-
vorrat dieser Funktion erschöpft sich also in einem Perioden-
parallelogramm, wenn von zwei gegenüberliegenden Seiten nur
die eine mit zum Parallelogramm gerechnet wird.
Wir ziehen aus unseren allgemeinen Voraussetzungen die
Folgerung:
1. Es existiert (außer der Konstanten) keine doppelt
periodische Funktion, die im Periodenparallelogramm
frei von Unstetigkeitspunkten ist; denn eine solche Funk-
58
Zweiter Abschnitt.
§ 16.
tion wäre in der ganzen u-Ebene endlich und müßte also nach
§ 15, 8 eine Konstante sein.
Ist cp(w) eine doppeltperiodische Funktion mit den Perioden
<»£, so ist das über die Begrenzung des Periodenparallelo-
gramms genommene Integral [wegen (1)]
Wo + «1
j d log <p (u) = j [cZ log (p (w) — d log <p (u <»2)]
«o
«0 + w2
— j \d log <p (u) — d log <p(u «,)] = 0.
M0
Daraus folgt nach § 15, 6. der Satz:
2. Eine doppeltperiodische Funktion wird in einem
Periodenparallelogramm in ebenso vielen Punkten Null
wie unendlich. Ist m diese Zahl, so heißt m die Ordnung
der doppeltperiodischen Funktion. Nach 1. gibt es keine
doppeltperiodischen Funktionen von der Ordnung Null.
Ersetzt man in dem Beweise die Funktion (u) durch <p (w) — c,
so folgt, daß eine doppeltperiodische Funktion witer Ordnung
jeden beliebigen Wert c in gleich vielen Punkten annimmt.
Wenn wir das Integral der Formel in 7., § 15 über die Be-
grenzung des Periodenparallelogramms nehmen, so ergibt sich:
Wo 4" wi
j U^log(p(u) = j [udlogqp(u) — (u <ö2)dlog<p(u ^2)]
«o *
Wo +
— j [udlog <p(u) —• (u 4“ ö>i)dlogqp(u -|- G^)]
Wo
Wo + w2 Wo +
= <»£ j d log <p (u) — <»2 j d log <p (w).
Wo Wo
Nun ist wegen der Mehrdeutigkeit des Logarithmus
Wo + w2
jdlog cp(u) — log<p(u -|- gj2) — logqp(u) =
Wo
Wo +
j dlog <p (w) = log <p(u -|- cjj) — log <p(u) = — 2
M«
worin und unbestimmte ganze Zahlen sind.
Wenn daher die Funktion <p(ü) in den Punkten a2, ..., am
unendlich, in den Punkten /3X, j32, ..., ßm Null wird, so ist nach
§ 15, 7.:
= Sßi (modcjj, ra2).
Periodizität.
59
§ 16.
Ersetzt man <p(u) durch <p(u) — c, worin c einen beliebigen
Wert bedeutet, so folgt der wichtige Satz:
3. Die Summe der Argumentwerte, in denen eine
doppeltperiodische Funktion im Inneren eines Perioden-
parallelogramms einen und denselben Wert c annimmt,
ist von c unabhängig oder ändert sich bei stetiger Ver-
änderung von c höchstens sprungweise um eine Periode.
4. Hieraus folgt, daß es auch keine doppeltperiodi-
sche Funktion erster Ordnung gibt.
Denn eine solche Funktion müßte jeden Wert c in einem
Punkte u annehmen. Ist sie also gleich c' in einem Punkte u'
und gleich c" in einem davon verschiedenen Punkte u", so würde
aus 3. u' = u" folgen, gegen die Voraussetzung.
Unter einer doppeltperiodischen Funktion der zweiten
Art versteht man nach Hermite eine Funktion ilAu), die den
Perioden Oj, ot>2 gegenüber sich den Gleichungen gemäß verhält:
^(w 4- »i) = ajV'Cw), ty(u -|- <»2) = a2^(u),
worin alf a2 Konstanten sind.
5. Auch für eine doppeltperiodische Funktion der
zweiten Art gilt der Satz, daß sie in gleich vielen
Punkten des Periodenparallelogramms Null .und unend-
lich wird. Ist die Zahl dieser Punkte m, so heißt auch hier die
Funktion von der mten Ordnung.
Der Beweis ist derselbe wie der des Satzes 2. Es gilt aber
hier nicht mehr die Erweiterung, daß die Funktion 4>(u) jeden
Wert gleich oft annimmt, weil ^(u) — c jetzt nicht mehr perio-
disch ist.
6. Eine doppeltperiodische Funktion ri(M) von der
zweiten Art und der Ordnung Null ist notwendig eine
Konstante oder eine Exponentialfunktion. Denn wenn V'(w)
nicht Null wird, so ist
= W)
eine doppeltperiodische Funktion von der ersten Art, die nicht
unendlich wird, also nach 1. eine Konstante a. Daraus folgt:
= Ae““,
worin A eine neue Konstante ist.
60 Zweiter Abschnitt. § 17.
§ 17. Die Funktionen T.
Wenn doppeltperiodische Funktionen <p(w) von der wzten
Ordnung existieren, so müssen es gebrochene Funktionen sein.
Setzen wir sie also nach § 15, 10. in der Form
(jr (U)
wenn Cr^u) und G(u) ganze Funktionen ohne gemeinsamen Null-
punkt sind, so ist
Cri(u -|- cjj) G^u -f- <»2) G1(u')
G(u -j- cjj) G(u -j- öj) G(u) '
und darin haben die drei Funktionen 6r(«), G(u-\-a>^, 6r(w-j-<u2)
dieselben m Nullpunkte, nämlich die Unstetigkeitspunkte von qp(w).
Ihre Quotienten sind also Einheitsfunktionen, nnd nach § 15, 9.
ist also, wenn ^(w), </2(m) ganze Funktionen sind:
.„x G(u cjj) = G(u),
G(u <»2) = <“) G(u),
und die Funktion G1 (u) genügt den nämlichen Gleichungen.
Ist
(3) = TW
eine zweite Darstellung von <p(u) von der Form (1), so ist
(4) T(u) = es'<“) G(w),
worin g(u) wieder eine ganze Funktion ist, und wenn also nach (2)
(5) T(u + <»,) = e'i(«>7’(u),
T(m —cj,) — e'*MT(u)
ist, so ist
0i(M) = l^u) 4- .?(«) -</(« + O,
g2(u) = Z2(t0 + g(u) — g(u <»2).
Es kommt also alles darauf an, daß wir unter irgend einer
passenden Annahme über die ganzen Funktionen /,(«), Z2(w) ganze
Funktionen T(w) bilden können, die den Bedingungen (5) genügen
und iu m beliebig gegebenen Punkten des Periodenparallelogramms
verschwinden. Durch die Quotienten zweier solcher Funktionen
mit denselben Z,(u), Z2(m) können wir dann alle doppeltperiodi-
schen Funktionen <jp(m) darstellen, und die allgemeineren Funk-
tionen 6t(m), die dasselbe leisten, erhält man nach (4) durch Hinzu-
fügung eines willkürlichen Einheitsfaktors.
Die Funktionen T.
61
§ 17.
Wollten wir ?,(«), Z2(w) als Konstanten annehmen, so wäre
T (u) eine ganze doppeltperiodische Funktion der zweiten Art
und folglich nach § 16, 6. eine Exponentialfunktion, aus der sich
keine doppeltperiodischen Funktionen bilden lassen. Die ein-
fachste Annahme, die uns hiernach bleibt, ist die, daß ^(m), 72(w)
lineare Funktionen von u sind, worunter als Spezialfall auch
der enthalten ist, daß eine der beiden Funktionen , Z2 kon-
stant ist.
Wir stellen also die folgende Definition auf:
1. Eine T-Funktion, T(m), ist eine ganze Funktion
von u, die den folgenden beiden Gleichungen genügt:
T(u -|- cjj) = +Wi) + I'ii T(u),
( ) T(u -j- <»2) = e— ««CM2« + "2) + T(u).
Hierin sind bly «ä, &2 Konstanten, d. h. von u unabhängige
Größen. Die Perioden <»2 gelten hier durchweg als ein für
allemal gegebene Konstanten, deren Verhältnis <»2:<»1 einen posi-
tiven imaginären Teil hat.
Die Faktoren
e, = ßi(w) = e— ««[«1(2«+ wi) + 6i] 5
----- £?2 (ju) 6—7?«[a2 (2 a-J-w2) 4-&2]
heißen die beiden Periodizitätsfaktoren der Funktion T.
Die Periodizitätsfaktoren ändern sich nicht, wenn Z>2 um
gerade ganze Zahlen verändert werden. Daß es Funktionen
dieser Art wirklich gibt, wird sich erst im weiteren Verlaufe der
Untersuchung ergeben.
2. Wenn die Funktion T(u) in irgend einem Punkte
verschwindet, so verschwindet sie auch in allen kon-
gruenten Punkten. Verschwindet sie in m Punkten des
Periodenparallelogramms, so heißt sie von der witen
Ordnung.
Aus dieser Definition ergibt sich sofort:
3. Durch Multiplikation zweier T-Funktionen T, Tr
der Ordnung m, m' erhält man eine T-Funktion der
Ordnung m -j- m'. Die Periodizitätsfaktoren des Pro-
duktes T, T' sind die Produkte der Periodizitätsfaktoren
von T und T'.
62 • Zweiter Abschnitt. § 17.
Wir fragen zunächst nach der Möglichkeit von T-Funktionen
nullter Ordnung: Ist L(u) eine solche und L'(u) ihre Ableitung,
so folgt durch zweimalige Differentiation von (6)
d L'(u + <»i) d L'(u)
du L(u -j- <»,) du L(u) ’
und entsprechend aus der zweiten Gleichung (6). Danach ist
d2logZ(u)/du2 als ganze doppeltperiodische Funktion eine Kon-
stante, und folglich logi(tt) eine ganze Funktion zweiten Grades
von u. Wir erhalten also:
4. Eine T-Funktion nullter Ordnung ist von der Form
(7) L(u) = C'fc~7ri('l«2 +
worin A, ft, C Konstanten sind.
Daß jede Funktion dieser Form eine T- Funktion nullter
Ordnung ist, ersieht man ohne weiteres.
Das Produkt
(8) T'(u)' = L(u)T(u)
ist ebenso wie T(u) eine T- Funktion mter Ordnung und ver-
schwindet in denselben Punkten.
Die Periodizitätsfaktoren von T' erhält man aus denen von T,
wenn man die Exponenten 04, a3, b15 b2 durch
aj — ax -|- Aoj, bj = bx -j- ft«»!
0&2 = ft2 —Ag>2, &2 "f“ fto2
ersetzt, worin die b, b' jedoch nur bis auf additive gerade ganze
Zahlen bestimmt sind.
5. Nach (9) kann man ft immer und nur auf eine
Weise so bestimmen, daß bj, bl reell werden.
Denn setzt man die imaginären Teile von bj, bl gleich Null,
so erhält man für den imaginären und reellen Teil von ft zwei
lineare Gleichungen, deren Determinante nach § 16 der Flächen-
inhalt des Periodenparallelogramms, also von Null verschieden ist.
Die Periodizitätsfaktoren und die Nullpunkte einer T- Funk-
tion mter Ordnung stehen in einer gewissen Abhängigkeit von-
einander, die wir leicht aus den Sätzen des § 15 erhalten. Zu-
nächst ergibt sich die Ordnung m, wenn man das Integral
i plogT(u) = m
Jl v I
Die Funktionen T.
63
§ 17-
über die Begrenzung des Periodenparallelogramms ausdehnt. Legt
man der Einfachheit halber die Ecke m0 (Fig. 1) in den Koor-
dinatenanfangspunkt, so kann man dieses Integral so zerlegen:
‘Inim = Jd[logT(w) — logT(w -|- co2)]
o
— j d [log T(u) — log T(u -|- ©j)]
o
und nach (6) ist
d[logT(tt) — logT(w ra2)] = 2?tia2.
<2[logT(w) — logT(w + ®i)] = 25r/aP
Daraus ergibt sich
(10) — «i<»2 — m-
Bezeichnen wir weiter mit a15 «2, ..., ctm die Nullpunkte einer
T-Funktion im Innern eines Periodenparallelogramms, so erhalten
wir aus § 15, 7.
2niS«. = judlogTw,
wenn das Integral wieder über die Begrenzung des Parallelo-
gramms erstreckt wird. Es ist aber
“i
JwdlogTw = j[ud log Tu — (w + a^dlog T(u ra2)]
o
— j [wdlog Tu — (w + ca^dlog T(u Oj)],
o
und das erste dieser beiden Integrale ist nach (6)
Wj a»j
— <a2 jdlog T(u) -|- 2aia2\(u ra2)dw
o o
= — <o2[logT(<a1) — logl’(O)] 3tia2eo1((o1 2co2)
= 31/0)2(0!eDi 4- &x) 4~ 3t ia2(a>! 2 2 3tiN2ea2,
worin N2 (wegen der Vieldeutigkeit des Logarithmus) eine nicht
näher bestimmte ganze Zahl ist. Ebenso ergibt sich für das
zweite der Integrale:
— 3tiö2) — 3rfa1(ra22 4- 2co1g)2) -|- 23tiN1a1,
und folglich (als Kongruenz geschrieben)
1 IW,
(11) Set = 4- y(»i + ra2).
64 Zweiter Abschnitt. § 17.
Diese Summe oder vielmehr die Gesamtheit der damit nach
dem Modul (oj, co2) kongruenten Zahlen heißt der Charakter
der T- Funktion.
Der Charakter der Funktion T ändert sich nicht, wenn man T
durch eine der Funktionen LT ersetzt (nach 8.). Man kann also
nach 5. den Charakter auch in der Form darstellen:
(12) = ^(^raa — + y (oj + ra2),
worin «ft, g2 reell sind. Diese reellen Zahlen sind durch den
Charakter bis auf Vielfache von 2 bestimmt und können jeden
Wert zwischen 0 und 2 haben. Das Symbol (g^ g^) heißt die
Charakteristik dei’ Z-Funktion. Aus der Charakteristik wird
der Charakter der T- Funktion nach (12) bestimmt.
Ist 7 der Charakter einer Funktion Z(m) von der Ordnung m
und v eine beliebige Konstante, so hat Z(w v) den Charakter
/ = 7 — vm.
Hiernach lassen sich, wenn m 0 ist, die ver-
schiedenen Charaktere aufeinander zurückführen.
Mit Hilfe der Gleichung (10) kann man die beiden Glei-
chungen (6) in eine allgemeine zusammenfassen:
Wenn man in der ersten Gleichung (6) wiederholt w in
w -]- Wj verwandelt, so erhält man das System:
T(w «() = e~ + + T(u),
T(u -|- 2 Oj) — e~+ sa.j + 61] Z(w -j- Oj),
T(u -|- n1to1) = er-»»l«i(2« + (2«i—i)«0 + »i] Z[w -|- (nT — l)»i],
und durch Multiplikation aller dieser Formeln:
(13) Z(w OT^j) — e—»»[Ol(2»l1u + n12Wi)+»li»i] Z(w).
Diese Formel ist zunächst für ein positives ganzzahliges
abgeleitet. Ersetzt man aber darin w durch u — so ergibt
sich ihre Richtigkeit auch für negative «].
Ebenso ergibt sich:
(14) T(u t?2<»2) = + T(ti),
und wenn man in dieser Formel w in w -|- verwandelt und
wieder (13) anwendet:
T(u + Mi»! m2o2)
' ' e—»«’[2(ui«i + a5«2)«+ 2a2«i»i?w1 + a,n^wi + + m»!+«562] Z(u).
Relationen zwischen verwandten T- Funktionen.
65
§ 18.
Es ist aber nach (10)
2«2w1w2w1 = a1n1n2tol a2n1n2co2 mn^,
und demnach wird diese letzte Formel:
T(u + MjOi 4- n2ra2)
--- g— xi[(n1a1 + n2a2) (2u + n1ml + n.2 w2) + rt-1(1^1-^ + 62h2 + »iHin2)] X^U).
Und hierin sind und n2 beliebige ganze positive oder
negative Zahlen.
Wenn man zwei T-Funktionen der Ordnung m und m' von
den Charakteren y, y' miteinander multipliziert, so entsteht eine
neue T-Funktion, deren Ordnung m m' und deren Charakter
7 + / ist. Sind (glt g2) und (g'i, g'2) die Charakteristiken der
beiden Faktoren, so ist (g± g'i, <72 + g'z) die Charakteristik des
Produktes.
§ 18. Relationen zwischen verwandten T- Funktionen.
Zwei T-Funktionen von den gleichen Perioden, derselben
Ordnung und demselben Charakter wollen wir verwandt nennen.
Ist T'(u) eine mit T(u) verwandte T-Funktion und haben a], a2,
&J, &2 dieselbe Bedeutung für T', wie a2> &n ^2 für T, so ist
infolge der vorausgesetzten Verwandtschaft [§ 17, (10), (11)]:
(1) U1K>2 • «2®1 = «1W2 «2®1»
(2) &]<»2 &2®1 = &1®2 4~ SWjOs 2^2 0!,
worin n1} na ganze Zahlen sind.
Daher lassen sich Z und g nach § 17, (9) so bestimmen, daß
die Periodizitätsfaktoren der Funktion
g—ni(lu^ + fiu) T(U)
dieselben werden wie die der Funktion T'(u), und daher haben
wir den Satz:
1. Verwandten T-Funktionen können durch Hinzu-
fügung einer T-Funktion nullter Ordnung:
T — ®j(iu2 + ,uu)
als Faktor dieselben Periodizitätsfaktoren gegeben
werden.
Ferner folgt unmittelbar aus der Gleichheit der Charaktere;
2. Wenn verwandte T-Funktionen mter Ordnung
m — 1 gemeinsame Nullpunkte im Periodenparallelo-
gramm haben, so haben sie auch den mten gemeinsam;
und hieraus:
Weber, Algebra. III. 5
66
Zweiter Abschnitt.
§ 18.
3. Zwischen höchstens m -j- 1 verwandten T-Funk-
tionen mter Ordnung T, Tn ..., Tm besteht eine identische
Gleichung von der Form
L T • • • 4- Lm Tm == 0.
Denn besteht diese Relation nicht bereits für L = 0, so kann
man von den in L2, ..., Lm verfügbaren Konstanten zunächst
..., ..., so bestimmen, daß die sämtlichen
Produkte ZjTj, L2T2, ..., LmTm dieselben Periodizitätsfaktoren
erhalten, und dann die Gr, C2, ..., Cm so, daß m — 1 und folglich
alle Nullpunkte der Funktion L± Tr -|- L2 T2 -LmTm mit den
Nullpunkten der Funktion T zusammenfallen. Daraus aber folgt,
daß das Verhältnis von L1T1 -|- L2T2 LmTm zu T gleich
einer T°-Funktion —-L ist, was zu beweisen ist.
4. Die Quotienten verwandter T-Funktionen können
durch Hinzufügung eines Faktors L in doppeltperiodische
Funktionen verwandelt werden.
5. Setzen wir die Existenz einer T-Funktion erster
Ordnung t(w) voraus, so läßt sich daraus jede T-Funktion
mter Ordnung ableiten.
Es sei nämlich y der Charakter von t(w) und o^, a2, ..., am
beliebig gegebene Werte. Es verschwindet dann die Funktion
t(w --- Cti ~j- 7) = ti(u), i = 1, 2 ...m
in dem Punkte a; und allen mit at kongruenten Punkten, aber
in keinem anderen.
Das Produkt
T(w) = t1(w)t2(w) ... tm(u)
ist also eine T-Funktion mter Ordnung mit den beliebig ge-
gebenen Nullpunkten 0^, a2, am.
6. Hieraus läßt sich leicht beweisen, daß jede
doppeltperiodische Funktion, die in einem Perioden-
parallelogramm nui’ eine endliche Anzahl von Unstetig-
keitspunkten hat, als* Quotient zweier T-Funktionen
darstellbar ist.
Es sei nämlich <p (rt) eine doppeltperiodische Funktion mit
den Perioden g>1, ra2 und den Unstetigkeitspunkten 0^, <x2, ..., am,
die auch teilweise in Ünstetigkeitspunkte höherer Ordnung zu-
sammenfallen können.
§ 19. 2’-Funktionen erster Ordnung. 67
Bestimmt man nach 5. eine Funktion T(u) mit den Null-
punkten an a2, ..., am so ist:
T(.u)<p(u) = T^u)
eine T-Funktion mter Ordnung, und
/ X 1 GO T
Cp (u) = W. 8, b. w.
2 (U)
Die Funktionen T(u), T1(u') sind verwandt, da sie die-
selben Periodizitätsfaktoren und also auch dieselbe Charakteristik
haben.
Die Nullpunkte von Tj(tt) sind zugleich die Nullpunkte von
<p(u), und die Summe dieser Nullwerte ist also kongruent mit
der Summe der Unstetigkeitswerte.
§ 19. T-Funktionen erster Ordnung.
Wir gehen nun dazu über, die T-Funktionen erster Ord-
nung, die wir mit t(u) bezeichnen, aus denen sich die übrigen
T-Funktionen, wie wir gesehen haben, ableiten lassen, näher zu
bestimmen.
Aus 3. des vorigen Paragraphen folgt, daß zwei t-Funktionen
derselben Charakteristik sich nm- durch einen Faktor von der
Form 4- pu)
voneinander unterscheiden, und wir wollen nun durch eine Er-
weiterung der Definition diesen Faktor noch näher bestimmen.
Dies soll, was nach § 17, (9) ohne Beschränkung der All-
gemeinheit möglich ist, so geschehen, daß in den Periodizitäts-
faktoren
«i' — 0, bt = gt, b2 = g2
wird, wenn (^, p2) die Charakteristik ist; wegen der Relation
a2 op — at co2 = 1
ist dann
1
a» = —,
und die Bedingungen für diese t-Funktion lauten alsdann (§ 17,1.):
t(u -|- <aj =
(!)
t(u <a2) = e 011 e~xi9*t(u).,
und hierdurch ist die Funktion t(u) bis auf einen von u unab-
hängigen Faktor bestimmt. Um diesen Faktor noch näher zu
5*
68
Zweiter Abschnitt.
§ 19-
bestimmen, fassen wir die Abhängigkeit der Funktion t auch
von Oj, ra2 ins Auge und bezeichnen sie, indem wir gt, g2 als
gegebene von »j, m2 unabhängige Zahlen betrachten, mit
t(u, coj, co2). Es zeigt sich dann, daß, wenn h ein willkürlicher
Faktor ist,
t(hu, hco2)
gleichfalls den Bedingungen (1) genügt, und daß demnach
(2) t(hu, hco,, heo2) . -A—2 ——±2 = f(a o ) t(M, <»!, C02) ' v ’ z
von u unabhängig ist.
Die Funktion /’(ra1, ®2) kann aber immer in die Form ge-
setzt werden: / ( ^2) ~ / \ 5
man hat nur, wenn t(u) für m = 0 nicht verschwindet: 9>(®i, ®2) = O»
und wenn t(0) = 0 ist, etwa
<jp(o15 <»2) = tM’(0, »i, ra2)
zu setzen, wenn t' die Derivierte’von t nach u bezeichnet. Indem
man also jetzt
/3x t(u, g>!, <a2)
' } 9>(®i, ®2)
wieder mit t(u, cou <n2) bezeichnet, kann man den Bedingungen (1)
noch die hinzufügen, daß für ein beliebiges h
(4) t(w, Oj, ra2) = t(hu, hco2).
Die Funktion t hängt also jetzt nur noch von zwei Veränder-
lichen, nämlich den Verhältnissen :w2, ab. Wir setzen in (4)
, I m <»9
h = —, — — v, — = CO,
Oj COj ®1
und erhalten
(5) t(M, Oj, o2) = t(—, 1, —= & (%£□),
\®1 ®1/
worin ft ein neues Funktionszeichen ist.
Hierdurch ist also eine neue Funktion ü(-y) definiert von nur
zwei Variablen v, w, deren erste unbeschränkt veränderlich ist,
während eo nach der im § 16 gemachten Voraussetzung einen
positiven imaginären Bestandteil hat; v heißt das Argument,
co der Modul der Funktion.
U 0»2
O»! ’ tOj
§ 20. Die 9-Funktion. 69
§ 20. Die ft-Funktion.
Die Funktion 4>(F) ist eine ganze Funktion von v, die den
Bedingungen genügt:
. . &(y 1) = e~
fff); -|- ») = g— »i(2« + m)
und ist dadurch bis auf einen von v unabhängigen Faktor
bestimmt. Sie ist also unter den t-Funktionen als Spezialfall
enthalten, während andererseits die allgemeine f-Funktion durch
die h-Funktion ausgedrückt werden kann in der Weise:
t(u) =
worin C, 1, jz. beliebige konstante oder von eoi, ea2 abhängige
Größen sind.
Die Funktion 9' ist noch von den in der Charakteristik vor-
kommenden Zahlen gu g2 abhängig, und wenn eine Bezeichnung
dieser Abhängigkeit erforderlich ist, so soll für &(v. co):
ö'pl,p2(^ M)
gesetzt werden, es können dabei g}, g2 beliebige Zahlen sein.
Nach dem früheren genügt es, wenn wir sie reell und zwischen 0
und 2 annehmen.
Entsprechend den T-Funktionen höherer Ordnung werden
wir auch ©-Funktionen mter Ordnung einführen und verstehen
darunter eine ganze Funktion von v, die den Bedingungen genügt:
, ®(v 1) = e~ai^®(y) '
®(/V co) = g—“»8(2« + W) g—»802
Auch hierbei kann die Charakteristik gt, g2 in die Bezeich-
nung mit aufgenommen werden:
©pc.PsO,®).
Diese Funktionen sind als spezielle Fälle unter den T-Funk-
tionen enthalten, und man kann allgemeine T-Funktionen in der
Weise bilden:
(3) Q+ !iu) \.
V 7 \®1 «1/
Es ergibt sich also aus § 18, 3. der Fundamentalsatz für
die ©-Funktionen, den wir folgendermaßen aussprechen:
70
Zweiter Abschnitt.
§ 20.
Nennen wir ©-Funktionen mit denselben Perioden gleicher
Ordnung und gleicher Charakteristik verwandt, und bezeichnen
wir ferner ein System von Funktionen als linear abhängig
oder unabhängig, je nachdem eine homogene lineare Relation
mit konstanten (nicht sämtlich verschwindenden) Koeffizienten
zwischen diesen Funktionen besteht oder nicht besteht, so gilt
der Satz:
m -|- 1 verwandte ©-Funktionen mter Ordnung sind
immer linear abhängig;
oder:
Aus m linear unabhängigen verwandten ©-Funktio-
nen »»ter Ordnung läßt sich jede andere verwandte
©-Funktion linear (mit konstanten Koeffizienten)
zus am men setz en.
Dieser Satz ist für unsere folgenden Betrachtungen von der
fundamentalsten Bedeutung; es ergibt sich daraus nach § 18, 3.,
daß jede T-Funktion »der Ordnung mit Anwendung der Formel (3)
aus m linear unabhängigen © - Funktionen zusammengesetzt
werden kann.
Nach § 17, (11) ist die Summe der m Argumentwerte, für
welche die Funktion im Periodenparallelogramm ver-
schwindet, nach dem Modul (1, w) kongruent mit
Die bis jetzt gegebene Definition der Funktion läßt einen
Faktor, der eine Funktion von to sein kann, unbestimmt. Wir
können aber durch einen Zusatz zur Definition diesen Faktor
noch näher bestimmen.
Wenn man die Definitionsgleichungen (1) zweimal nach v
und einmal nach a differentiiert, indem man gr, als konstant
ansieht, so ergibt sich nach einfacher Rechnung, daß die Funktion
d2&(v, a) ,d&(v, ra)
selbst den Bedingungen (1) genügt und also die Form
<f> (®) (v, <a)
hat, worin g>(ra) in bezug auf v konstant, also eine Funktion von w
allein ist. Wenn man jetzt
— —I Cp(w)da»
e ^(v,®)
§ 21.
Hauptcharakteristiken.
71
gleich einem neuen ft setzt, so ergibt sich für dieses die partielle
Differentialgleichung
(4)
82 ff (v, co) , a & (v,»)
—— 4 20——Z = 0,
8 V2 0 K»
und durch (1) und (4) ist jetzt die Funktion ft bis auf
einen von v und ra unabhängigen, also nur noch von g2
abhängigen Faktor definiert.
§ 21. Die Theta - Funktionen verschiedener Charakteristiken.
Hauptcharakteristiken.
Wir wollen jetzt, ehe wir an die Bestimmung des noch
übrigen von v und a unabhängigen Faktors in den ft-Funktionen
gehen, die verschiedenen Charakteristiken aufeinander zurück-
führen, was nach § 17 immer möglich ist. Bezeichnet man mit
•ü(v) die zur Charakteristik (0, 0) gehörige h-Funktion, so ist
&(v — — 9*\
eine den Bedingungen (1) § 20 genügende Funktion. Es ist aber
nun mit Rücksicht auf die Differentialgleichung (4):
82<b , 8 0 „ „ .
—--------420 —----- = -----2r2<7.20,
8«s 8ra '7| ’
und wenn wir also
rtiwg-p
(1)
(»-
2 a-
gl« — g2
2
setzen, so ist die Differentialgleichung (4) § 20 durch alle
diese Funktionen befriedigt. Hierdurch also sind die Funk-
tionen bis auf einen allen gemeinschaftlichen numerischen
Faktor bestimmt.
Aus der Formel (1) läßt sich eine allgemeinere ableiten,
indem man v durch v — —— ersetzt. Man erhält so
,9. — &\
o 2 /
»iW /o . r . > Tti > . , o
--- 6 + ffp 02 V)’
72 . Zweiter Abschnitt. § 21.
Aus (2) ergibt sich noch, mit Benutzung von (1) § 20, wenn
man = 2, g'2 = 0, oder g't = 0, g'2 = 2 setzt:
und durch (2) ist also zugleich die Periodizität der Funktionen
vollständig ausgedrückt. Beispielsweise ergibt sich, wenn
g und v ganze Zahlen sind:
O, (2v —l)o + 2g — 1\
•uoo ( — -----------2-----------)
(4=) ' -„io, 7
» + 1 -------(2r — l)2 ä»(2»—1)«
= (-1) i e 4 e ^nOO-
(5) — va—g) = (-1).“ + ’’ e27lirv&11(y').
Die Formel (2) ist gültig für ganz beliebige, selbst komplexe
Werte von gt, g2.
Wenn man in den Definitionsformeln der fi - Funktionen
[§ 20, (1)] v durch —v— 1, und durch — v—ca, ferner gr, g2 durch
-g1, -02 ersetzt, so zeigt sich, daß v) denselben Be-
dingungen genügt, wie ^(r), und daß sonach
&91,9 s (V) ’ &—91, ~9s W)
bis auf einen konstanten Faktor identisch sind; es ist also ins-
besondere, wie aus v = 0 hervorgeht:
fio.o 0) = fi'o.oC-«),
und danach ergibt die Formel (1), wenn man v, gr, g2 durch
-g-i, -g2 ersetzt:
(6)
Sind die Elemente gt, g2 ganze Zahlen, so heißt (^, g2)
eine Hauptcharakteristik. Es gibt deren vier wesentlich
verschiedene, nämlich:
(0,0), (0,1), (1,0), (1,1),
und demnach auch vier wesentlich verschiedene Haupt-fi-Funk-
tionen:
(7) fi'oo (0, fi'oi^), fi'ioO), fi'nC'f’),
von denen die erste auch mit fi(F) bezeichnet wird.
In der Folge werden unter Charakteristiken und
fi-Funktionen nur noch Hauptcharakteristiken und
Hauptfunktionen verstanden.
§ 21.
Haupteharakteristiken.
73
Die Formel (2), auf dies Funktionensystem angewandt, ergibt
die folgende, häufig benutzte Tabelle:
worin zur Abkürzung
TtlÜi
--------- + 7t iV
s = e 4
gesetzt ist
Nach (3), (4) ist
/qa #oo(~0 = #oo0, #oi(-«) = #oi0,
1 ; #io(-«) = #io 0, = — #n0,
d. h. es sind ftOo0, #oi0, #io0 gerade Funktionen,
•frufV) ist eine ungerade Funktion.
Nach § 17 (12) verschwinden die vier Funktionen (7), bzw.
für die folgenden Werte des Arguments
1 +
2 ’ 2’ 2’ ’
also für gewisse halbe Perioden. Von Wichtigkeit sind die Werte,
welche die sämtlichen Funktionen (7) für diese Argumentwerte an-
nehmen, und diese lassen sich mittels der Tabelle (8) auf die drei
#oo (0) — #oo, #oi (b) — #01, #io (0) — #1
zurückführen. Man erhält so aus (8) das folgende System yon
Formeln:
74
Zweiter Abschnitt.
§ 21.
W011H Ttioj
£0 = e 4
und
(11) 4>n (0) = 0, 4>10 Q) = 0, 4>01 (£) = 0, «’oo (4^) = °-
Die Quadrate der Funktionen (7):
(12) ^(v), ^10, ^(y), 4^0
sind @00 - Funktionen zweiter Ordnung, und folglich bestehen
zwischen ihnen zwei lineare Relationen. Nehmen wir diese Rela-
tionen in der Form an:
9io 0 = -A. (y) + JB (y),
9§o0 = (y) -f- B'Q'lxiy),
so kann man die Koeffizienten auf Grund der Formeln (10), (11)
leicht bestimmen, wenn man v = 0 und v — setzt. Man
erhält so
7131 '9°1 = ^1« ^«0 — 9oo 9h 0,
' 9oi 9020 0 = ^oo 0 — &io 'ö'ii (v),
und daraus noch, indem man v = | setzt:
(14)
9»o — fi’oi + Ufo.
Durch zwei beliebige von den Quadraten (12) können alle
Funktionen @00 der zweiten Ordnung linear dargestellt werden;
aber auch die übrigen ©-Funktionen zweiter Ordnung lassen sich
aus den Funktionen 9-pl>ff2 zusammensetzen, denn man erhält für
jede Charakteristik zwei linear unabhängige Produkte, von denen
das eine eine gerade, das andere eine ungerade Funktion ist,
nämlich:
(15)
900 (y) 901 0» 9-10 (y) ^ii (?) Charakteristik (0,1)
9OO0 91O0, 9ol0^11(u) „ (1,0)
9W0 9O10, 9’oo0«’110 „ (1,1)
Nach demselben Prinzip lassen sich nun alle ©-Funktionen
beliebiger Ordnung und beliebiger Hauptcharakteristik aus den
Funktionen ft bilden. Um dies nachzuweisen, bezeichnen wir mit
@0, irgend zwei der ^--Quadrate (12) und mit (@0, ©Q eine
ganze rationale und homogene Funktion wter Ordnung der beiden
Argumente @0, ®v Man erhält hiernach für die ©-Funktionen
»zter Ordnung ©(^(u) folgende Ausdrücke:
76
§ 21. Hauptoharakteristiken.
m gerade gerade Funktionen
= F® (@0,
(m \
(®0, ®1)
(m \
2 ' (®0, ©i) .
G^«) = fl'01(t>) F<2 ' (®0, @0
(16) ungerade Funktionen
/ m—4\
@(oo«) = «oo«) #io«) #oi «) #11 (y) 2 ' (®0, ®j)
(m \
T-1^ (®0, ®j)
/ m \
= 0-ol (y) (y) F^J (®0, ®j)
/TO \
®(J?«) = 0-oo(t>) £•„(*,) F^~y (®0, ©j)
m ungerade gerade Funktionen
®(^(v) = &00(y) F' 2 > (@0, ®0
/TO —1\
®W(«i) = »01 (y) F< 2 ) (®0, ®i)
/TO —1\
©fo’OO = #10«) F^FJ (®0, ®J
/TO —3\
®(«)(u) = ^oo (u) 0iO(t>) 2 J (®0, ®j)
(17) ungerade Funktionen
/TO—3\
®<’$«) = ^01(i>) ^I0(») &u(y)F^ 2 > (®0, ®j)
—3\
@(O1(») = #00«) #10«) #1i«)F’^~r->' (®o, ®1)
/m — 3\
®(™>«) = #00«) Ö-01(v) »^(y^F^ 2 > (®0, ®i)
/TO —1\
®(m)«) — (®0, ©j).
Daß in dieser Form alle ©-Funktionen darstellbar sind,
ergibt sich auf Grund von § 20 aus folgenden drei Erwägungen.
1. Zwischen geraden und ungeraden Funktionen kann keine
lineare Abhängigkeit bestehen, wenn nicht schon zwischen den
geraden Funktionen für sich oder den ungeraden für sich eine
lineare Abhängigkeit besteht.
76 Zweiter Abschnitt. § 22.
2. Da zwei der 9-Quadrate (12) nicht in konstantem Ver-
hältnis stehen, so besteht auch keine Gleichung von der Form
F® (@0, ©j) = o.
3. Die Gesamtzahl der Konstanten, die nach (16), (17) in
den zu einer und derselben Charakteristik gehörenden geraden
und ungeraden Funktionen auftreten, ist genau gleich der Ord-
nung m.
§ 22. Das AcLditionstlieorem.
Sind u, v zwei Veränderliche, so gehören die Produkte
— V»
zu den ©-Funktionen zweiter Ordnung, mit der Charakteristik
(9i + 9i, 9i + 9$,
und zwar für jede der beiden Variablen u, v, sie sind also als
Funktionen von v linear darstellbar durch die Funktionen (12)
und (15) in § 21, so daß die Variable u in den Koeffizienten
vorkommt. Diese Darstellung ist, wenn die Charakteristik (0, 0)
ist, auf mehrfache Art möglich, da man zwei beliebige der Funk-
tionen (12) wählen kann, in den anderen Fällen nur auf eine
Art. Man erhält so 16 Formeln, von denen aber 6 durch bloße
Vertauschung von v mit —v aus den anderen herzuleiten sind,
so daß nur 10 wesentlich verschiedene bleiben. Man leitet diese
Formeln sehr leicht ab, indem man sie zunächst mit unbestimmten
Koeffizienten ansetzt und diese dann dadurch bestimmt, daß man
für v solche spezielle Werte setzt, für die je eine der Funk-
tionen üfv) verschwindet. So ist z. B.:
S’oo (« + v) 900 (u — v) = (y) + (y),
I ßj
und wenn man v = 0 und v = —~— setzt, so erhält man mit
Benutzung der Formeln des § 21:
•^oo = W- = ®ii (u),
also
(1) ö'o2» ^oo (w + 'V) #oo (u — v) = 9020 (u) (v) 4- 9^ (u) 92x (y),
und wenn man hierin w durch
। 1 । to 1 4- co
M 2’ u u --------------------2~—
ersetzt, so bildet man drei weitere Relationen, die man auf dem-
selben Wege wie (1) auch direkt hätte ableiten können:
Das Additionstheorem.
77
§ 22.
(2) 42i #01 0 4- 4 #01 (u — 4 = 41 (M) #U21 4) — #n (w) #121 (4-
(3) 4o #io (« + 4 #io 0 — 4 = #io W #i20 (4 — #i2i (m) 4h (4-
(4) #<h #n (« 4~ v) #n (w — v) = 4h (u) (v) — (u) (t>).
Diese vier Gleichungen können, wie schon erwähnt, durch
Anwendung der Formeln (13) des vorigen Paragraphen in mannig-
facher Weise umgeformt werden. Die folgenden sechs Formeln
haben nur eine Form. Es ist, um wieder mit einem beliebigen
Beispiel zu beginnen:
#00 + 4 #11 (u — f) = J. #01 (4 #10 (4 + -B #00 (4 #n (4,
und wenn man v = 0 setzt:
•4414o = #00 W #11W,
daraus erhält man B durch Vertauschung von u mit v. So sind
die drei folgenden Formeln abgeleitet:
(5) #oi#io#oo(“ + 4#n(M — v)
= O'oo(4#ii(4#oi(4#io4) — #oi(4#io(M)#oo(4#nH
(6) 4o#oi#ioO 4~ 4#n(M — v)
== 4o(M)#n(M)#oo(4#oi4) — #oo(w)#oi(«)#io(^)#n(i’),
(7) 4o#io#oi(w + 4#n(M — 4
= #oi(«)#uW#oo(4#io(4 — #oo(w)#io(M)#oi (4#n (4>
die sich unmittelbar verifizieren lassen, indem man erst u, dann
v = 0 setzt. Hieraus folgen die drei anderen durch Vermehrung
von u um
1 w 1
2’ 2’ 2'
(8) 4j 4 04i (u + i>)40 (« — 4
= 4i(u)4oO)#oiO)#ioO) + #oo(w)#n(M)#oo(4#ii(®)>
(9) 40#0!#00(w 4- 441 (tt — v)
. = 4o(w)#oi(w)#oo(4#oi(v) — #io(/4#ii(m)#1'4®)#ii4)i
(10) 4o#io#oo(w + 4#io(M — 4
= 4o(w)#ioW#oo(4#ioW + #01 (w)#n (M)#oi (4#U (y)-
Es lassen sich diese Formeln, deren Gesamtheit mit dem
Namen des Additionstheorems bezeichnet wird, in mannigfacher
Weise verallgemeinern, wovon das folgende als Beispiel dienen
möge.
Sind w, v zwei Variable, so sind die vier Produkte
4o(w)#oo(« 4- 4> #oi(M)#oi(M 4- 4>
#io(«)#io(w 4- 4i(u)4i(m + 4,
78
Zweiter Abschnitt.
§ 22.
als Funktionen von u betrachtet, verwandte T-Funktionen zweiter
Ordnung mit den gleichen Periodizitätsfaktoren, und daher sind
je drei von ihnen linear abhängig. Es ist also
.zL'9’oo(M)'®oo(tt 4~ v) 4“ -B#io(M)ffio(w 4~ v) -|~ C'ö'n(u)-ffn (u —|- v)
= 0,
woraus für u = 0, u =
4'9’oo'9’oo(4) -j- B#io#io(,y) == 0
yL'&oi'^’oiÖ’) 4” C#io#ioO) = 0
und daraus:
0^) #io#io(«)#oo(w)#oo(w 4~ 0 ------- #OÜ#Oo(^)#lo(M)#lo(M 4“ ®)
— #01#01O)#llO)#llO + 0 = °-
Ebenso sind nun auch, wenn w eine dritte Variable ist, die
in der Form
#Vi,VS(w + ®)#vi,v2(w + w), #^»s(w)#Wl,p2(w 4- f + w)
enthaltenen Produkte, als Funktionen von u betrachtet, verwandte
T-Funktionen zweiter Ordnung mit den gleichen Periodizitäts-
faktoren, so daß zwischen je dreien unter ihnen eine lineare Ab-
hängigkeit besteht. Die Koeffizienten bestimmt man wie oben
durch spezielle Werte von u. So folgt das Formelsystem:
#OO#Oo(® 0“ W)#OoO -j- v)&qq(u -f- w)
(12) = ff00 (u) »0Q (t>) ff00 (w) ff00 (u + v + w)
— #n(u)#110)#ll(w’)#ll(w + V + w)-
#oi#oi(« *4 wj’S’oiCw 4“ f)#oi(w 0“ ^)
(13) = #oi (w) #oi 0) #oi («’) #oi (« + « + »)
-0 (u) «’n (0 (w) ffn (tt 4- v. -j- w):
#io#io(f 4" w)#i0(w + f)^io(M + w)
(14) = S’io (tt) S’k, (v) S’jo (w) S’k, (u 4- v -j- w)
4- («) (0 #ii (w) #u (» + «’ + W).
Alle diese Formeln können als spezielle Fälle einer all-
gemeinen Formel aufgefaßt werden, die Jacobi aus den Reihen-
entwickelungen abgeleitet und zur Begründung der Theorie der
elliptischen Funktionen verwandt hat1)- Diese Formel läßt sich
auch folgendermaßen aus dem Begriffe der Thetafunktionen ge-
winnen.
*) Theorie der elliptischen Funktionen, aus den Eigenschaften der
Thetareihen abgeleitet. Jacobis gesammelte Werke, Bd. I, S. 497.
Das Additionstheorem.
79
§ 22.
Die vier Funktionen
(15) M2«)’ -9-01(2^), «-11(2«?),
sind @00-Funktionen vierter Ordnung von v, und da sie linear
unabhängig sind, so lassen sich alle @00-Funktionen vierter
Ordnung linear durch sie ausdrücken. Eine solche Funktion ist
aber auch das Produkt
(16) . 6-(t> + ®i) M A a2)^(t> a8)9-(t> a*)’
vorausgesetzt, daß die Größen a der Bedingung
(17) «1 -f- «2 A as A «4 = 0
genügen. Wir erhalten also, wenn wir mit Au A2, As, Ai Kon-
stanten (in bezug auf v) bezeichnen:
ü (y A «4) 9’ (y A «2) 9 (v A «8) 9- (y A a4)
= AM2«) + AM2«) + AM2«) + AM2«),
und daraus erhält man durch Vermehrung von v um A*h>)
vier Formeln:
M2(« + «1)W + «s)M2(« + «8)Mä(« + «%)
= AM2«) + (~i>AM2«) + (—1> AM2«)
A (—i> + ^AAi(2«)-
Wenn man diese'vier Formeln addiert, so folgt:
4 At 9oO (2 v)
/1Q\ ö'ljP'S
= S4A4444’M4J«AMA«M
wo in der Summe für gi und g2 alle Kombinationen von 0 und 1
zu setzen sind.
Wir führen jetzt eine etwas audere Bezeichnung ein, indem
wir setzen:
V A ai = «1> V A a2 — «2, « + a3 — «3! « + a4 ~ «45
also wegen (17)
i» = + + 4
und definieren jetzt die vier Größen v2, v3, durch die
Gleichungen
= | (y'i + 4 A «3 4* «1) 5
(X9) «2 = I(«l A «2 — «8 — «4)5
«3 = 1(«1 — «2 A «3 — «i),
«4 = 1 («1 — «2 — «3 A «!)•
80
Zweiter Abschnitt.
§ 22.
Hieraus erhält man aber:
4 = + v2 4- v3 4- v4), = |( v2 4- vg 4- t>4),
(20) = 2 01 4- «2 — Vg — t>4), «2 = H «2 — Vg — t>4),
k ' 4 = i(^i — v2 4- Vg — v4), a3 = i(-v2 4- Vg — v4),
V4, = |(«1 — v2 — Vg 4- v4), a4 = 1(— Vg — Vg 4- t>4),
und danach ergibt die Formel (18):
= 2^>^0i)^i,v2(4)^1)p2(4)^1,^(4),
worin nun entweder die Vi oder die 4 als unabhängige Variable
angesehen werden können.
Betrachtet man die v, als unabhängige Variable, so ist in
dieser Formel Ä4 von v4 unabhängig, wohl aber noch von v2>
Vg, v4 abhängig. Setzen wir daher 44 = cfrooOa^ooOs^ooOi),
so ergibt sich
c froo (y 1) ö’oo (v 2) #00 (vs) O’oo (y 4)
= 1 ^9l, 9i (^1) &9l, 9l (V^) gg (Vg) ftg,, g^ (4),
und darin ist c jedenfalls von v4 unabhängig. Da nun aber die
rechte Seite dieser Formel bei beliebigen Vertauschungen von
v4, v2, va, v4 ungeändert bleibt, so ist c von allen vt unabhängig,
und man erhält seinen Wert, wenn man alle v4 — 0 setzt:
cO’oo = 'O’oo 4" ^01 + #10,
woraus nach § 21, (14) c — 2 folgt.
Wir haben also die Formel:
2 O’oo Oi) Voo ('c2) ft00 (4) O’oq (v4)
~ ®0l, 9<i 01) ^01> 9i (Vi) ^9l> 9n (4) ^glt g.> (v*).
Wenn man darin jede der Variablen vt, v2, v3, v4 um eine
halbe Periode — | (4 «j — 4) vermehrt, so wird v{ um eine ganze
Periode —(,yi«i — g'2) vermehrt, während v'2, v3, v4 ungeändert
bleiben, und demnach erhält man mit Hilfe von § 21, (2) und (3)
ein System von vier Formeln:
(21) . Sl,92
= S (— lyig'2 + 5,2/1 + M (y'l) &9^ (4) &9l,g, (4)..
Dies sind die Jacobischen Formeln.
Setzt man z. B.
1>1 == 0, . v^ — V 4- w, Vg = U 4- V, v4 — w 4- w,
v't = U 4- V 4" wi v'2 = ---------------------------------W, 4 ~ —w, V4 = ---------------------------------------V,
§ 23. Die Derivierten der F-Funktionen. 81
so ergibt sich aus (21) für g'h g'2 = 1,1:
gl<gg
0 = ]£(— + + « + «'),
und hieraus erhält man dann, wenn man in (21) für #1, g’2 die
drei anderen Charakteristiken setzt, die Formeln (12), (13), (14).
§ 23. Die Derivierten der ff-Funktionen.
Wir bezeichnen im folgenden durch ff^,ffa(f), ^,gi(y) die
nach v genommenen Derivierten der Funktion ff91)9a(f), und mit
ff^IiP , ff".,P2 die Werte dieser Funktion für v — 0. Es ver-
schwinden dann ff«, fflo, &'tx>, weil ffM(y), &10(y), &w(v) gerade
Funktionen von v sind, und ebenso verschwindet ffi'i.
Die sechs Funktionen
• ^g-2 (v) ^'i, p's (») — ^'i, (v) g* 0
sind, wie aus den Fundamentalgleichungen § 20, (1) hervorgeht,
ft-Funktionen zweiter Ordnung mit der Charakteristik
(#i + ^a),
und zugleich entweder gerade oder ungerade Funktionen, wonach
sie sich nach § 21 durch ^-Funktionen darstellen lassen. Ein
konstanter Faktor wird durch einen speziellen Wert von v(y = 0)
bestimmt. So ist
. (1) ffn (y) ff01 (y) — (y) 9n (f) = A ff10 (t>) ff00 (t>).
Dieser Ausdruck für A läßt sich aber noch vereinfachen.
Differentiieren wir (1) zweimal nach v und setzen dann v — 0,
so folgt
ffiiffoi — 9'01'9'11 = Z(ffi'off„o -|- 910ff00),
und wenn man für A den Wert (2) einführt:
9'11 __ 9q! . ff'/p . ffpo
W 90I ff10 ff00
Nun genügen aber [nach § 20, (4)] die vier Funktionen ffii,
9W, 910, ff00 der Differentialgleichung
(4) ff" — 4ir^^,
- J do
und danach läßt sich (3) so schreiben:
log ff ii __ dlogff00ff10 ffOi
do do ’
Weber, Algebra. III.
6
82 Zweiter Abschnitt. § 23.
oder durch Integration:
ttu = C'S’qq •9’10'9’ul,
worin c von co unabhängig ist. Durch § 20, 21 waren die
9-Funktionen bestimmt bis auf einen von v, co unabhängigen,
allen gemeinschaftlichen Faktor. Über diesen Faktor soll nun
so verfügt werden, daß die Konstante c den Wert % erhält,
also die Formel besteht:
(5) ö’li =
und dadurch sind jetzt die 9-Funktionen bis auf das
gemeinschaftliche Vorzeichen + vollständig definiert.
Durch Anwendung von (5) läßt sich der Formel (1) die Gestalt
geben:
(6) . «li(v)'9’oi(^’) — ^oiORnGO = n&oi^io
und ebenso erhält man mit Benutzung von § 21, (8):
(7) «iiH-9’oo(«) — 8ooO),9'ii('y) = 3tO'o2o«’io(®)«’oi('ü)5
(8) •9u«)#io(v> — ^io(«)'ö'ii (w) = ^iVoiO’PooO’),
(9) #io(v) ^oiG) —
(10) &'w(v) ^(v) — '9oi0#oo(V) = —
(11) #oo(<)^io(<) — = srfl&^oiORiiO)-
Differentiieren wir die Gleichungen (9), (10), (11) nach v und
setzen v — 0, so erhalten wir mittels (4) und (5) die Relationen
(!2) 4^10g^ = i«S«.,
<13> 4Ä
(U) 4 A10g|L« =
Wenn man die Fundamentformeln für die 9- -Funktionen
zweimal logarithmisch differentiiert, so erkennt man, daß die
Funktionen
©-Funktionen zweiter Ordnung mit der Charakteristik (0, 0) sind,
und man kann sie daher durch die Funktionen 92(?j) linear aus-
drücken. Auf diese Weise ergibt sich
§ 24. Darstellung der fl -Funktionen durch unendliche Produkte. 83
(15) ff0% = ^00 Oöo 0j) + 0),
(16) »o2!^^)-10^1^ = ffolWo» - «(4
(17) = ^M(v) —
(18) ^pff^^l^M^ = ffppffj'off^) — ff^ff^).
d v*
Hieraus lassen sich noch weitere Relationen herleiten durch
fortgesetzte Differentiation. Wir führen noch eine dieser Formeln
an, die sich ergibt, wenn man (15) noch zweimal nach v diffe-
rentiiert und dann v — 0 setzt. Drückt man die Differentiationen
nach v durch solche nach eo aus mittels der partiellen Differen-
tialgleichung (4), so folgt:
d2logff00 O<dlogff00\2_ i
—j—7,-------\------ü---- I —---------S"'*'lo^oi,
dco2 \ deo / 8
oder
,, d / 1 d ffpp\ ____ ___ ft2 fffp ffpi
(Zm\ffoo dco / 4 ff&
§ 24. Darstellung der ff-Funktionen durch unendliche
Produkte.
Die Theorie der ff-Funktionen ist nun so weit gefördert, daß
sich ihre Darstellung sehr leicht ergibt. Damit wird dann die
Existenz dieser Funktionen nachgewiesen und die bisherigen Be-
trachtungen erhalten erst ihren sicheren Boden. Zwei Wege zu
diesem Ziele stehen uns offen. Der erste geht aus von den uns
schon bekannten Nullpunkten der ff-Funktionen und setzt daraus
unendliche Produkte zusammen.
Die Funktion ffopf«) verschwindet nach § 21, wenn
2v = (2v — l)c? —|— (2 ft — 1)
ist, worin v, ft ganze Zahlen sind, oder wenn
ß+2rtiv ----------------------- --g7tiw(2v—l)
worin wir nun v auf positive Zahlen beschränken können.
Setzen wir also zur Abkürzung
gffio _ q
6*
84 Zweiter Abschnitt. § 24.
so ist q eine Größe, deren absoluter Wert ein echter Bruch ist.
Das konvergente unendliche Produkt
P(y) — 11(1 -|-
1,00
verschwindet also in allen und nur in den Punkten, in denen
0oo(f) verschwindet, und es ist überdies
P(v 1) = P(v)
P(v +<u)= Pfo) = q—1e~27t(vP(v).
Dies ist aber nach § 20, (1) die Periodeneigenschaft der
Funktion HooG), und wir haben daher:
(1) 'ü'ooOO = QH(1 + qiv~1e2
1,<»
worin Q ein von v unabhängiger Faktor ist. Nach den Formeln (8)
des § 21 erhält man hieraus, indem man v durch
। 1 । co . 1 —j— co
^+2’ ^+2’ 2~
ersetzt:
(2) '9’0i(«) = QH(1 — qir-'!-e2aiv')(l—g»’-irUi’),
1,00
(3) öio (f) = C^(eÄ”’H-e_Ä’>)II(l-|-^2’'e2Ä«)(l-|-^2’'e-2Ä«),
1,00
1 v
(4) = —iQqi(eniv——q2veMv)(l—q2*e-27tiv').
l,oo
Setzt man in diesen Formeln v = 0, in der letzten nach
einmaliger Differentiation, so folgt
0OO = QH(i +
1,00
0oi = Qn(i — ^T-1)2,
(5) 1’“1 v
010 = 2^17(1 ga”)2,
1,00
fth = !2,itQqiII(l —q2vy.
1,00
Hiernach läßt sich mittels (5), § 23:
0ii = 310oo 0«i 0io
§ 24. Darstellung der 9-Funktionen durch unendliche Produkte. 85
der Faktor Q bestimmen. Man erhält zunächst
, _ 02 „l1 - 1)2(1 + <z202
1 -- * U (1 __ ’
oder, indem man über das noch unbestimmte Vorzeichen von Q
und damit über die Vorzeichen der 0-Funktionen verfügt:
” ' (1 — qlv)
Im Nenner kann man für 27 (1 —|— g2’j(l -|- q2v~l) setzen
11(1 -|- qr), und der Zähler 11(1 — q2*) läßt sich zerlegen in
17(1 — g”)(l + ^) = 77(1 — g2r)(l — q2r~1')(l 4- qv).
Dadurch ergibt sich endlich
(6) Q = Il(l—q2*).
Die Ausdrücke (1), (2), (3), (4) lassen sich in reeller Form
darstellen, wenn man die Multiplikation der konjugiert imaginären
Faktoren ausführt. Man erhält so:
©oo^) — 11(1 — g2’)(l + 2 g2’'-1 cos2srt> -|- qiv~2),
l.oo
0ol(v) = n(l — g2’)(l — 2 g2’-1 cos2srt> -|- qiv-1),
(7) 3’°° i
&10(y) = 2 qi cosjtvll(l — g2r)(l + 2 q2r cos 2 av -|- qiv),
0U (t>) = 2 qi sin nv II (1 — g2”) (1 — 2 q-v cos 2 sr-w —j— g“j.
l,oo
Führen wir den Ausdruck (6) in die letzte Gleichung (5)
ein, so ergibt sich
0,n = 2srg^ZZ(l — g2”)8,
und wenn wir also
(8) hf03) = g1äIT(l— g2’)
setzen, so wird
(9) ö’n = 2'3rij(»)8.
Indem wir Q mit Hilfe der Relation
Q = q-h<n(a>)
aus (5) eliminieren, setzen wir
000 = !?(») f(cO)\
(10) 0O1 = t] (m) /( (»)2,
01O = v(eo)f2(co)2,
86 Zweiter Abschnitt. § 25.
worin die Funktionen /’(»), AO0), AC*3) folgendermaßen defi-
niert sind:
f(a) = q~iin(\ -|- ^”-1),
1,00
(ii) A(«) =
1,00
AO) = + q^.
l,oo
Die Funktionen f(eo), AO), AO) wel'den in unseren
späteren Betrachtungen eine wichtige Rolle spielen. Aus § 21, (14)
ergibt sich nach (10) die Relation
(12) /'(ro)s = AO)8 H~ AO)8,
und aus § 23 (5) nach (9)
(13) f(ra)AO)AO) = V2.
Die letzte Formel ergibt sich auch aus (11) mit Benutzung
der identischen Relation:
J7(i + £»)(i — S2”-i) = n — = 1-
§ 25. Darstellung der ^-Funktionen durch unendliche Reihen.
Der zweite Weg, um zur Darstellung der ft-Funktionen zu
gelangen, besteht darin, daß man eine den Fundamentalgleichungen
genügende konvergente unendliche Reihe zu bilden sucht.
Bemerken wir zunächst, daß wegen der Bedingung
^ooO + 1) = fi'ooO’)
die Funktion ft00(«) als eindeutige Funktion von e2niv angesehen
werden kann, und setzen demgemäß
«00(t>) = 2? Aye17tivv,
—oo ,oo
so ergibt die Differentialgleichung § 20, (4):
S2«' . .89-
—— — 4«— =0
ov2 fico
für Av die Bedingung
d A
— niv2Ar, Av — cveTlimv'2 = cvqv\
aa>
worin cv in bezug auf ra konstant ist. Es wird also
fr00(t>) = 2?ct
§ 25. Darstellung der ^-Funktionen durch unendliche Reihen. 87
und daraus:
^00(v + ») = 2cvqvi+2v e2niv'’
--- g—1 f>—%niv £ g(v +1)2 ^2 7tiv(y + 1),
Da v von —<x> bis + <x> geht, so ist es gestattet, in dieser
Formel v — 1 an Stelle von v zu setzen, und wenn man dies
tut, so ergibt sich
9-00(F + <»)== q-ie-2rr{v 2?cr_ig’,2e2;!it”'.
Nach der zweiten der Fundamentalgleichungen [§ 20, (1)]
müssen also die beiden Reihen
2? c^e2und e2nivv
miteinander übereinstimmen, d. h. es muß
Cv — i —cv
sein. Die cv sind also alle einander gleich; daß sie den Wert 1
haben, ergibt die Vergleichung der beiden Entwickelungen
2? jtq — q2v)(l + g2”-1 e27r<l,)(l + gsr-ie-a«»»)
—00,00 l,co
für den Wert q — 0.
Der hiermit für D-oo <+) gefundenen Entwickelung kann man
auch die beiden Formeln geben:
(1) #00(t>) =
— 1 + 2 q cos 2nv + 2 q* cos 4 7tv + 2 g9 cos 6 7t v + • • •,
und daraus erhält man nach § 21, (8) durch Vermehrung von v
um vj, vr, -—+— die Entwickelungen für die drei übrigen
ff -Funktionen:
(2) ö’o, (t>) = 2- (— iy e2V7tiv
= 1 — 2 q cos 2 7t v -f- 2 g4 cos 4 av — 2q9 cos 6 nv + • • •
(2> + l)ä
(3) ÖioOO = ^<1 4 +
1 9 25
= 2 g* cos 7t v 2 cos 3 Ttv -j- 2 q 4 cos 5 itv -|- • • •
(2 *+1)2
(4) = —i2?(—l)^ 4 e(2v + i)^v
1 9 25 .
= 2 #4 sin jrt? — 2^4 sm 3 itv 2 q4 sm bitv •• •
Wir ziehen für spätere Anwendungen aus diesen Entwicke-
lungen die Schlüsse:
88
Zweiter Abschnitt.
§ 26.
Wenn der imaginäre Teil von co ins Unendliche wächst, so
daß der absolute Wert von # verschwindet, so wird
öboO) = 1, öbiGO = K HM'-’) = 2cos5tt>,
q 4 ^ii 00 — 2 sm nv.
Nehmen wir co rein imaginär, also q reell, positiv und echt
gebrochen an, so sind für ein reelles v:
1. ftooC«), ü01(h), O'joOO, '’OiOO ree^, und wenn v zwischen 0
und | liegt, positiv [nach § 24 (7)], folglich auch ü00, Ö’O1, -ün
positiv;
2. Ö’oo0v)> 0'oi(««’), 0’io(««’), —^iiO'f) reell, und solange v
zwischen 0 und —-— liegt, positiv; ferner mit Zuziehung der
Formeln § 21, (8)
3. 0oo(| + ««), '0'01(1+««’), «0-io(l + «f), 0’11(1 + ««’)
reell, und solange v zwischen 0 und —liegt, positiv;
i / co
4. q*e"tv&M( —
1 _ /co
qt (—
\ u
+V
+ V
1. / co
— iqi eniv ü’oi (vr + v
\ Ä
. 1 / co
— eniv üu 1— + v
reell, und solange v zwischen 0 und | liegt, positiv.
§ 26. Entwickelung von Quotienten.
Bedeutet v eine Variable und a eine beliebige Konstante, so
sind die Quotienten
0,gi,g8(«’ + «)
doppeltperiodische Funktionen zweiter Art und erster Ordnung
mit den Periodizitätsfaktoren (—Ipi + g'i, (—l)fc+/8e—z*®“, und
wenn man einen Exponentialfaktor e'-v hinzufügt, so kann man 2
und a so bestimmen, daß die Periodizitätsfaktoren beliebig ge-
gebene Größen werden. Indem man die Hauptcharakteristiken
(+,.</2), (.+,.+) auf alle mögliche Arten wählt, erhält man 16 solcher
Funktionen. Wir gehen aus von einer unter ihnen, für die wir
unter Hinzufügung eines konstanten Faktors
m -p_ 0» »ix (v + a)
§ 26. Entwickelung von ^-Quotienten. 89
wählen. Dies ist eine eindeutige Funktion F(z) der Variablen
z — e2aiv,
und wenn wie früher q — enim ist, so hat sie die Perioden-
eigenschaft:
(2) = e-*xiaF(z'),
woraus für jedes ganzzahlige v folgt:
F(q2vz) — e~27tiavF(z).
Die Funktion F’(^) wird für ein endliches z nur dann un-
endlich, wenn einer der Faktoren F'z — 1 verschwindet, und es
ist insbesondere
(3) (z — l)F(F) = 1 (für z = 1).
Nach (2) ist aber
z — 1) F0'2’’£) = e-i7tia'’F(z){qiv z — 1)
und folglich ist nach (3)
(4) F(z)(^vz — 1) — &xiav (für z =
Setzen wir unter der gleich noch näher zu prüfenden Vor-
aussetzung der Konvergenz
(5) S(?) = S g!iv0 _ p
— 00,00
so ergibt sich, indem wir z durch q2z und v durch v — 1 er-
setzen :
(6) S(q2z) — e-sxia8(z),
und die Differenz F(z) — 8(z) wäre also, als Funktion von v
betrachtet, nach (3) und (4) eine ganze doppeltperiodische Funk-
tion zweiter Art. Eine solche muß aber nach § 16, 6. eine Expo-
nentialfunktion sein, und es ist also
F(z) = S(z) Ce-~i7timv,
worin m eine ganze Zahl und G eine Konstante ist. Aus (2) und
(6) aber ergibt sich, wenn nicht G = 0 ist:
g— STZitnw -— ß—Inia»
also a = rnn> -]- n, worin m, n ganze Zahlen sind. Ist aber a
eine Periode, so reduziert sich F(z) auf eine Konstante oder eine
Exponentialfunktion. Anderenfalls muß C = 0 sein, und es folgt
die Entwickelung:
. fr'nfrufo + a) _ -A e2””a _
e27tiv — 1
90
Zweiter Abschnitt.
§ 26.
Wir haben die Konvergenz dieser Reihe für alle Werte von v
vorausgesetzt; um diese zu beurteilen, bemerken wir, daß das all-
gemeine Glied dieser Reihe
für v — -(7 00 gleich —e1"''1
* ry ß—Sitivg—%7tiv(a)— a)
wird. Es wird also Konvergenz stattfinden, wenn der imaginäre
Teil von a und von co— a positiv ist. Setzen wir daher
co = co' -|- i co", a = a' -|- i a", so ist die Bedingung der Kon-
vergenz
(8) 0 < a" < co".
Wenn man in (7) a durch a -|- | ersetzt, so ergibt sich die
Entwickelung für eine zweite der 16 Funktionen:
(9) flii »10 (^ + a) _ y (—l/e2^ar 2sri'9'11(v)-9'10(a) q2ve27Iiv — 1’
und wenn man in (7) und (9) a in a -|- | co verwandelt:
(io) •911 O'oi (v + a) y e27tiav qv e72™ 2 (v)&01(a) q^e27liv — 1’
(11) 9ii»oofo + a) _ y (—e72™ 2 3rifi,11(v)'9'oo(fl) q^v e27liv — 1
wobei jedoch zu bemerken ist, daß in den letzten beiden Formeln
die Konvergenzbedingung geändert ist, nämlich:
rJ1
ÜJ »/ - VJ
— < a < y
Aus den vier Formeln ergeben sich die übrigen zwölf, wenn
wir v durch v -1- |, v -j- |co, v -j- (1 -1- co) ersetzen, wobei die
Konvergenzbereiche nicht weiter geändert werden. Auf diese Weise
sind die Formeln der Tabelle I am Schlüsse des Bandes abgeleitet.
Die so gewonnenen Reihen konvergieren für reelle Werte
von a nicht alle, z. B. tut es nicht die Reihe (7), worin der nach
der Seite der positiven v verlaufende Teil
(12)
____ z>2 n i v a
V—-------------
1,00 *
aufhört zu konvergieren, wenn der imaginäre Teil von a gleich
Null wird, während der andere Teil auch da noch konvergent
Entwickelung von ^-Quotienten.
91
§ 26.
bleibt. Man erhält aber aus (12) einen Ausdruck, der auch für
ein reelles a noch konvergiert, wenn man die Summe
(13)
ß2rcia _. [
hinzufügt. Dadurch geht er nämlich über in
** gSTtiva g2*
l,co *
und diese Reihe bleibt konvergent, solange der imaginäre Teil a"
von a zwischen —a>" und —f— <z>" liegt.
Demnach ergibt sich aus (7), wenn wir das dem Werte v = 0
entsprechende Glied absondern und die negativen v durch —v
ersetzen:
2t
«#ii(O&n(«) e:
v 0— 2rtiva
_L 2 i V'---------------
I 7..1 g—2v ß27tzv 1
l,oo
Es ist aber
2i
ß27tiv_|
2^2 Tria
ß2rtia_|
! 2 iei7tia
I ^7tia _____ 1
^2v ftirtiva g2rti
g2V ß^Ttiv ___ 1
=• cotgsrt? — i,
= cotgsra -j- i,
g— 7TIV
sinav
gTtia
sinsra
und demnach läßt sich diese Entwickelung auch so darstellen:
(14)
u 11 v 11 ™ ) X I r
- o. -7 \ o. r \ = cotgsn? -k cotgrca
(qm, gmTtia qm g—mrtia \
g—2 xiv gm j ’
worin m die Reihe der geraden Zahlen
m = 2, 4, 6, 8, ...
durchläuft. Der Gültigkeitsbereich dieser Entwickelung ist
— ra" <Z a'' <Z a".
In der Tabelle II sind diese 16 Entwickelungen zusammen-
gestellt.
Aus diesen Formeln sind drei andere ableitbar, indem man
v oder a oder beide um | vermehrt. Drei andere aber, die der
Vermehrung von v und a um entsprechen, müssen direkt ab-
geleitet werden. Sie zeigen reelle Form, wenn <7, a, v reell sind.
92
Zweiter Abschnitt.
§ 26.
Eine dritte Art der Entwickelung, in der die Symmetrie der
Funktionen in bezug auf die beiden Variablen a zum Ausdruck
kommt, ergibt sich, wenn man die Brüche, die in den vorigen
Entwickelungen auftraten, nach Potenzen von # entwickelt. So
erhält man
om
_____±______ ___ £ gtn v ß2 n t v v
g— qm * ’
__ gwi v ’
v — 1, 2, 3, ...
und diese Entwickelungen gelten, solange der absolute Wert
von q&mv ejn echter Bruch ist, also, wenn v = v' -|- gesetzt
wird, solange
— co" <Z v <Z
ist. Hiernach ergibt sich aus (14)
- a. z \ o. z ; = cotgsrv -4- cotgjra
»MOM«)
mm'
4 27 g 2 sin(ma -j- m'v)n^
worin m, m! voneinander unabhängig die geraden Zahlen
2, 4, 6, 8, ... durchlaufen. Diese Formel ist gültig für reelle
a und v und gilt darüber hinaus noch, solange der imaginäre
Teil, sowohl von v als von a, absolut kleiner ist als ra".
In der Tabelle HI sind die 16 Formeln dieser Art zusammen-
gestellt 1).
’) Solche Entwickelungen sind von Jacobi (sur la rotation d’un corps)
(ges. Werke Bd. II), hierauf von. Her mite (Annales de l’ecole normale 1885)
und von Kronecker (Berliner Akademie 1885) betrachtet. Vgl. auch die
Straßburger Dissertation von L. Vockerodt (1905).
Dritter Abschnitt.
Transformation der Theta-Funktionen.
§ 27. Das Transformationsprinzip.
Wir kehren zurück zu den in § 17 gegebenen Definitions-
gleichungen der T-Funktionen mter Ordnung und versehen darin
aus einem gleich ersichtlichen Grunde die Buchstaben <o, a, b, m
mit Akzenten, so daß diese Gleichungen lauten:
T(u »1) = e~ T(u),
T(m -|- = e—Äia'a(2w + tl’'2>+!>'2 T(w).
(2) »2 »1 — «4 »2 = wG
Sind u, c irgend welche ganze (positive oder negative) Zahlen,
so ergibt sich, wenn man in § 17, (16) nt, n2 durch —c, a ersetzt:
’ T(u — cea'i. + aaty
-- q——ca'i + aa'8)(2w— + a&'8 —m'ac)
eine Gleichung, die auch aus einer der Gleichungen (1) hervor-
geht, wenn man darin b', »' durch
— caiaa'z, —cbi ob's— m’ac, —c»i -{- aa'i
ersetzt
Hierin ist das Prinzip der Transformation der T-Funktionen
enthalten.
Es seien b, 8 zwei andere ganze Zahlen, für welche die
Determinante
(4) n = a 8 — bc
einen positiven Wert hat. Wir setzen
(5) »1 = +8»; — ba)2,
»2 = —-f- aa>2,
und folglich
neoi — an-i -|- ba>2
’ na2 = ci»! -j- 8»2.
94 Dritter Abschnitt. § 27.
Es hat dann, wie man aus
«2 C ft), 4“ c<uä
cjJ a»! -|- 6»2
durch Trennung des reellen vom imaginären Teil erkennt, der
imaginäre Teil von oj2:a1 dasselbe Vorzeichen, wie der von
«4 <4 (das positive).
Setzen wir
.„Y ay = da'i — ba2
a2 = —ca'i aa’z
zgx 4 = d&i — bb2 — m'bc
} &2 = —cb'j 4- ab2 —• m'act
so schließt man aus (3), daß die Funktion T(u) nicht nur den
Bedingungen (1), sondern auch den aus (1) durch Vertauschung
von coj, »2, a’x, a2, b{, b2 mit cj2, a1, a2, bu b2 hervorgehenden
Gleichungen, d. h. den Gleichungen (1), § 17, genügt. Sie ist
also gleichzeitig eine T-Funktion der Perioden »1, a2 und der
Perioden »2, was wir durch folgende Gleichung andeuten:
(9) T'(w, <4 <4) = T(u, »t, ro2).
Es ist aber nach (5) und (7)
a2rai — = (4 <4 — 4 »2) («8 — bc),
also, wenn m die Ordnung von T ist,
(10) m = m'n.
Nach (8) ist die Charakteristik (^, g2) von T, wenn (4, g2)
die von T' ist (§ 17),
(11) (,9r> 9z) — (^9i — ^9’n — m'b'd, — cg'^ 4- ag'a — m'ac).
Unter der Transformation der T-Funktionen versteht
man die Darstellung der Funktionen T' mit den Perioden
»1, <4 durch T-Funktionen mit den Perioden a2.
Die Zahlen a, b, c, 8 heißen die Transformationszahlen
und n = ad — bc der Transformationsgrad.
Um die Form dieser Darstellung deutlicher zu übersehen,
wollen wir die Bedingungen aufsuchen, unter denen T(w, Oj, ro2)
eine ©-Funktion der mten Ordnung @(w, ») wird (§ 20). Wir
nehmen b't, b2 und folglich auch b2 als ganze Zahlen, so daß
4, b2, b'i, b2 durch gt, g2, g[, g2 ersetzt werden können. Es
ist dann
= 1, »2 = ai = 0, a2 = m
§ 27.
§ 27. Das Transformationsprinzip.
zu setzen, und demnach wird [nach (6), (7), (10)]
, _______________________ a bco , _____________ c -f- da>
a'i = m'b, a'z — m'd.
Die Funktion T'(u, cjJ, »2) genügt a’so den Bedingungen (1):
T(U -f- »]) = (--1)9'1 g-^im'KZu + ^j
T(tt -|- <»2) = (—1)9'26—Ä»m'<!(2w+a’y t(m),
und daraus ergibt sich, daß das Produkt
e "'i T'(u, ro[, »Q
eine ©-Funktion der Ordnung m' ist, mit den Argumenten
u
ro'i’
«2
und der Charakteristik (#], g’^). Wir können dies in der Glei-
chung ausdrücken:
e « + »« @(m0 ( nu .
si>s^ \a -f- bco
worin die Charakteristiken durch (11) bestimmt sind. Die Mittel
zur Darstellung dieser Funktionen sind in § 21 enthalten.
Wir bezeichnen die Transformation von T und T' durch
einen einzelnen Buchstaben S oder durch (I", T), also:
8 = (!', T).
Bedeutet 8' eine zweite Transformation, durch die T' in T"
übergeht, also
8' = (T", I'),
so können wir daraus eine neue Transformation 8" ableiten,
durch die T in T" übergeht. Diese heißt aus 8 und 8' zusammen-
gesetzt und wird so bezeichnet:
oder
8" =8'8
Bei dieser Zusammensetzung gilt im allgemeinen nicht das
kommutative Gesetz; es ist also SS' von 8'S verschieden. Es
gilt aber das assoziative Gesetz, das sich in der Formel aus-
spricht :
(T'", T") [(T", T') (P, T)] = [(T'", T"~) (T", T')] (T', T) = (T'", T).
96
Dritter Abschnitt.
§ 28.
§ 28. Zusammensetzung der Transformationen.
Eine Transformation [§ 27, (9)] ist vollständig bestimmt
durch die Transformationszahlen a, b, c, d, und diese vier ganzen
Zahlen können beliebig gegeben sein, wenn nur ihre Determinante
n = ad — bc positiv ist. Gibt man diesen vier Zahlen das
entgegengesetzte Zeichen, so gehen »1, »a- nach § 27, (6) in
— »i, —»2 über, und ersetzt man a, b,c,d durch ma, mb, mc, md,
worin m eine beliebige natürliche Zahl ist, so gehen coj, »2 in coJ/jot,
a’^/m und n in m2n über. Das Periodenverhältnis co' = co^/mi
bleibt in diesen beiden Fällen ungeändert. Einstweilen wollen
wir aber zwei Transformationen immer als verschieden betrachten,
wenn die Transformationszahlen verschieden sind. Nach dieser
Festsetzung können wir eine Transformation unzweideutig durch
eine Matrix
W « = (“’*)
darstellen. Die Determinante
(2) n = ad — bc
ist der Transformationsgrad.
Nach dieser Bezeichnung stellen wir die Relationen (6), § 27
auch so dar:
(3) »ä) = ^(»1,
0/
Setzt man
8' — f0/ a'^' — Vc' = n' >
so ist
(4) ro£) = Q,’ <»2),
und wenn man in (4) coj, »2 nach (3) durch Oj, co2 ausdrückt,
so erhält man
zz >> >r\ fcc'a —b'c, a!b —f— b’d\ , .
(5) »»'(»„ ».) =
Setzen wir also
(6) S" = 8’8,
so ist
a„ /a'a-|- b’c, a'b b'd\ fa", b"\
\c'a d'c, c'b 4- d'd) \c", &"/’
a"d"— b" c" = n" = nn'.
§ 28. Zusammensetzung der Transformationen. 97
Die Transformationen 8 setzen sich also nach derselben
Regel zusammen wie die linearen Substitutionen und Matrizes,
die wir im sechsten Abschnitte des zweiten Bandes betrachtet
haben. Der Grad einer zusammengesetzten Transformation ist
gleich dem Produkte der Grade der Komponenten. Diese Matrizes
sind hier an die Voraussetzung gebunden, daß ihre Elemente
ganze Zahlen und ihre Determinante positiv ist.
Diese Eigenschaften bleiben bei der Zusammensetzung der
Transformationen erhalten. Trotzdem bildet die Gesamtheit <S
der Transformationen S keine Gruppe, so wenig wie die Gesamt-
heit der natürlichen Zahlen bei der Komposition durch Multi-
plikation eine Gruppe ist; denn es läßt sich bei gegebenem 8', 8”
nicht immer ein 8 bestimmen, das der Bedingung (6) genügt, was
doch (nach Bd. II, § 1, 4.) für eine Gruppe erforderlich wäre.
Durch die spezielle Transformation vom Grade m2:
II = 0 )
\ 0, +m/
gehen die Perioden ro1? m2 in »j = »j/m, m2 = m2/m über, und
das Periodenverhältnis k> = <d2/<d1 bleibt ungeändert. Diese
Transformationen heißen Multiplikationen (Ähnlichkeits-
Transformationen, Bd. II, § 41). Es ist darunter die identische
Substitution
1 - f1’ 0>)
\0, 1/
enthalten, die alles ungeändert läßt und bei der Komposition die
Rolle der Einheit spielt.
Die Multiplikationen sind bei der Zusammensetzung
mit jeder Transformation 8 vertauschbar:
(7) SM = MS.
Hält man in SM oder MS die Transformation 8 fest und
läßt M die Gesamtheit TU der Multiplikationen durchlaufen, so
erhält man ein System DJi 8, das man nach Bd. II, § 46 als eine
Kollineation zu bezeichnen hätte. Gehören 8X und 82 einer
Kollineation C an und 8i und 82 einer Kollineation 0", so ge-
hören auch S'i81 und 8282 derselben Kollineation C" an. Man
kann so, indem man C" = C'C setzt, die Kollineationen zu-
sammensetzen. Bei dieser Zusammensetzung spielt die Kolli-
Weber, Algebra. IIL 7
98
Dritter Abschnitt.
§ 28.
neation 9Ji die Rolle der Einheit. Ist S = Q’ eine beliebige
Transformation, so ist
/a, b\/ 8, —d\ _____ /», 0\
\c, 8/\—c, a ) \0, n)
eine Multiplikation. Die beiden Kollineationen
C = W“’ C“1 = 0’ “
\c, oj \—c, a J
geben also bei der Komposition CC-1 = C~1G = TU und sind
also zueinander reziprok.
Demnach bildet die Gesamtheit der Kollineationen
eine Gruppe.
Die Transformationen vom Grade 1 heißen lineare Trans-
formationen. Wir bezeichnen bei diesen die Transformations-
zahlen zum Unterschiede mit den griechischen Buchstaben a, ß, y, d,
so daß
l = CJ)’
eine lineare Transformation bedeutet. Das System 2 der linearen
Transformationen ist eine in <S enthaltene Gruppe, denn sind
L =
V, d/’ V', d'/
so ist
T„ T.T _ + ß'?, <*'ß + ß'^\ _ /«"> ß"\
gleichfalls linear, und man kann L bei gegebenem Z', L" aus
den Gleichungen
a'a -j- d'y — a", a'ß -f- ß'$ = ß"i
‘y'a d'y = 7", y'ß -f- d'd = d"
eindeutig bestimmen. Die Einheit der Gruppe £ ist die identische
Substitution und jede Substitution L hat ihre Reziproke L~l,
wie aus der Zusammensetzung
hervorgeht. Die Gruppe £ ist unendlich und ist nicht kommu-
tativ.
§ 29. - Zusammensetzung der Transformationen. 99
Aus der Gleichung
(8) ad — ßy = 1
folgt, daß weder a, ß noch a, y, noch d, ß, noch d, 7 einen gemein-
schaftlichen Faktor haben können. Hat man aber a, ß beliebig
ohne gemeinschaftlichen. Teiler angenommen, so kann man 7, d
noch auf unendlich viele Arten aus (8) bestimmen. Ist 7, d eine
dieser Bestimmungen, so sind sie alle in der Form
(9) . 7 4- Aa, . d + Xß
enthalten, worin X eine beliebige ganze Zahl ist (Bd. I, § 126).
§ 29. Zusammensetzung der Transformationen aus einfacheren.
In dem System g aller Transformationen S ist ein System g0
enthalten, das aus allen den Transformationen So besteht, deren
zweite Transformationszahl b — 0 ist, während a und d positiv
sind:
W = (“’")•
Bei der Zusammensetzung zweier 80 entsteht wieder ein S0,
aber doch ist g0 so wenig eine Gruppe wie g.
Man kann jede beliebige Transformation
\r, sj
durch eine Zusammensetzung ZS auf ein So zurückführen. Soll
nämlich
aw=C:")
sein, so muß a, ß der Bedingung genügen:
aq + ßs — 0,
und wenn also 8 der größte gemeinschaftliche Teiler von q und s
ist, so setze man
da = s, dß = —q,
und bestimme, nachdem a und ß hierdurch als relative Primzahlen
ermittelt sind, 7 und d aus der Formel (8), § 28. Dann ist (2),
erfüllt, wenn
ad ~ n, c = 7jp -j- dr
gesetzt wird; a und d sind hierdurch eindeutig bestimmt, c kann
aber bei anderer Wahl von 7 und d durch c Xa ersetzt
werden. Man kann daher über X so verfügen, daß c in der Reihe
7*
100
Dritter Abschnitt.
§ 29.
der Zahlen 0, 1, 2 ... a — 1 enthalten ist, und dadurch ist dann
die Substitution iS0 vollständig bestimmt.
Wenn die vier Transformationszahlen einen gemeinsamen
Faktor haben, so läßt sich dieser mittels der Formel
/m, 0\ /a, b\ /ma, mb\
\0, m) \c, d) \mc, md)
durch Zusammensetzung mit der Multiplikation absondern, und
wir setzen demnach jetzt voraus, daß a, b, c, 8 keinen gemein-
schaftlichen Teiler haben. Man kann dann immer die zwei
ganzen Zahlen |, t) so bestimmen, daß
, aij — = a
w bt] — 8^=ß
ohne gemeinsamen Teiler sind.
Um dies einzusehen, setzen wir zunächst |, relativ prim
voraus. Dann ist jeder gemeinsame Teiler vou «, ß notwendig
Teiler von n, wie man aus den Auflösungen von (3)
, . = ba — aß
' ni) = dtt — cß
erkennt. Nimmt man also | nicht teilbar durch alle in a
und b zugleich aufgehenden Primzahlen, dagegen £ teilbar,
t) unteilbar durch alle anderen in n aufgehenden Primzahlen,
und überdies |, 17 relativ prim, was stets möglich ist, so haben
a und ß keinen gemeinsamen Teiler. Hierauf bestimmt man 7, <5
so, daß
a,8 — ßy — 1.
Es ist dann nach (3) auch
(a8 — by)^ — (c8 — 87)! = 1,
und es ergibt sich die folgende Zusammensetzung, wie leicht mit
Benutzung von (4) erkannt wird:
A _ )a8 — 67, |\ /l, 0\ /«, ß\ .
\c, 8/. \cö — 87,17/ \0, n) \7, 8)
Nennen wir also
(6) (0 °)
7 \0, n)
die Haupttransformation vom Grade n, so ist damit bewiesen,
daß sich alle Transformationen vom Grade n aus einer
Multiplikation, einer Haupttransformation und linearen
Transformationen zusammensetzen lassen.
§ 30. Die linearen Fundamentaltransformationen.
101
Aus der Zusammensetzung
/l, 0\/l, 0 \ = /i, 0 \ /l, 0\ /n, (h /n, 0\
' 1 \0, n) \0, m) \0, mn/’ \0, n) \0, 1/ \0, n'
können wir noch weiter schließen, daß sich jede Transformation
vom Grade n aus solchen zusammensetzen läßt, deren
Grad eine Primzahl ist. Zerlegt man n — pq in zwei Fak-
toren p und q, die zueinander relativ prim sind, so ergibt sich,
indem man die Zahlen ß, 8 aus
p8 — qß = 1
bestimmt, die Zusammensetzung
(P, ß\ A 0\ Zpd, — qß\ _ /p, 0\
kg, 8) ^0, n) 1, 1 ) \0, q/ ’
woraus zu ersehen ist, daß man statt der Haupttransformation
zur Ableitung aller
anderen benutzen kann.
auch jede dieser Transformationen r
§ 30. Die linearen Fundamentaltransformationen.
Die ganze Gruppe £ der linearen Transformationen läßt sich
durch Wiederholung von zweien unter ihnen, die wir die linearen
Fundamentaltransformationen nennen, ableiten.
Ist
L = a8 — ßy = 1.
\y,. 8/
eine beliebige lineare Transformation, so ist
und da die identische Transformation die Einheit in der Gruppe L
ist, so ist
z- = ( ö’
7, /
die zu L reziproke Transformätion.
Wir bezeichnen durch die Potenz L~m das, was durch mmalige
Wiederholung von L oder LT1 entsteht, und wollen nun nach-
weisen, daß sich durch die Potenzen der Fundamentaltrans-
formationen
(2) = b=(-i,ö)
102 Dritter Abschnitt. § 30.
jede Substitution L der Gruppe £ zusammensetzen läßt. Es ist
zunächst
® - = (’:?)
(für jedes ganzzahlige positive oder negative Z)
o) Ht-i)’
Wir setzen noch
® = c,=G:h')’
C ist also aus A und B ableitbar.
Nun sei L = eine beliebige lineare Transformation.
Wir leiten daraus die Reihe ab:
L' = LA*, L" = L'C*', L'" = L"A*", L"" = L"'C*"',
deren erste und zweite Elemente so gebildet sind:
a' = a 4- kß, ß" = ß'— l'a', a'" = a" -j- Z"/3",
ß"" = ß'" — Z'"a"', ...,
und man kann über Z, Z', Z", Z'", ... so verfügen, daß, dem
absoluten Werte nach
a! 1 ß, ß" < a!" 1 ß",, ß"" 1 a"’...,
solange keine dieser Zahlen verschwindet. Die Zahlen
ß, a!,.ß", ß"", ...
bilden daher eine dem absoluten Werte nach abnehmende Zahlen-
reihe, und nach einer endlichen Anzahl von Zusammensetzungen
dieser Art muß eine Zahl dieser Reihe verschwinden.
Ist ß& — 0, so ist
r(r) _ /il, 0 -\ ___ /il, 0 \
~ ±1/ — \ o, ±v
und ist = 0, so ist
W = ( — A^" B^1
8^) — ^ ß ' •,
und da
L = L'A~* = L"C-*'A-*
= L’"A-*"C-*'A-* = L""C-*'''A~*"G-*'A~\ ...
ist, so ist der Satz bewiesen.
§ 31. Die linearen Fundamentaltransformatiönen der ^-Funktionen. 103
§ 31. Die linearen Fundamentaltransformationen
der ft-Funktionen.
Bei der Anwendung auf die Transformation der ©-Funktionen
[§ 27, (12)] kommt zunächst der transformierte Modul
, c dca
a = -------------------------------FT
a -j- ba>
in Betracht. Dieser ändert sich nicht, wenn die vier Trans-
formationszahlen einen gemeinsamen Faktor m bekommen. Die
Transformation heißt eine eigentliche, wenn a, b, c, d keinen
gemeinsamen Faktor haben.
Das transformierte Argument
, nu
u —FF-
a-\- ba
geht über in mu', wenn a, b, c, 8 durch ma, mb, mc, md, also n
(w?« 0\
0 } läßt den
Modul ra ungeändert und verwandelt u in mu.
Nach den Resultaten der beiden vorigen Paragraphen läßt
sich das ganze System der eigentlichen Transformationen her-
leiten durch wiederholte Anwendung der drei Transformationen
/l, 0\ / 0, 1\ /«, 0\
kl, I/ k-i, 0/ ko, V’
und wir betrachten also zunächst die linearen Fundamental-
transformationen der h-Funktionen.
I. oder (a>, ra 1). .
Nach § 27, (11), (12) ist
(1) («, + 1) = ®),
worin A von u unabhängig ist. Ersetzt man u durch
’ 1 ra 1 -4- rä ’
u + 2 ’ 71 + y i u n 2 ’
so ergeben die Formeln § 21, (8)
(2) cj -]- 1) = M4t10(w, ra)
71 i
(3) e4 'O’oo(W) ® + 1) = -4ö-Oi(«, ra)
tt i
(4) 'ß’oi05 "4“ 1) -‘d'^’ooC^ G5)>
104
Dritter Abschnitt.
§ 31.
Zur Bestimmung der Konstanten A wenden wir, wie in der
Folge häufig, das Mittel an, daß wir u = 0 setzen, in (1) nach
der Differentiation, und dann rechts und links von der Formel (5),
§ 23
(5) #n = 3t#Oo Hio^oi
Gebrauch machen; so folgt
7t i 7t i
A2 — e'2, A — e4;
daß bei A das positive Zeichen steht, ergibt sich aus einer der
Formeln (3), (4) nach der Schlußbemerkung von § 25, wenn man
<d unendlich werden läßt.
Sonach erhält man
7t i
ftutu, (o -|- 1) = e4 #u(u)
7t i
(6) #10(w, 03 -4- 1) = e4#10(w)
#oi (u, 03 4- 1) = #00(u)
#Oo('A ® + 1) = #0104
TT / Ö, i\ , / — 1\
II. ( , ’ ) oder 03,----) •
\— 1,0/ \ 03 )
Es ist wieder nach § 27, (12)
(7) e “«•»(-,--) = A^u.,03),
und durch Vermehrung von u um
(8) e “ 0oi ra),
Ttitfi , -| .
(9) e ~ #10 J = iA #01 («, ®),
/u 1\
(10) e w ’8'00(rä’ —rä) ~ ra),
woraus man wie oben erhält:
A = +1 y—io3.
Aus u = 0 und einem rein imaginären ra schließt man, daß,
wenn (/—io3 so genommen wird, daß der reelle Teil positiv
ist, das untere Zeichen stehen muß, und es ergibt sich daher:
§ 32. Haupttransformationen zweiter Ordnung. 105
e “ #Ti ( —, ) \O3 03/ e w O’oif-, ) \03 03/ (11) , e w ü10(-, ) \G3 G3> e “Mm’-mJ = — i )/— i 03 ttn (w), = y- <osfri0(w), = y- 4ü3^01(w), । = y_ ? osfloo (m).
§ 32. Die Haupttransformationen zweiter Ordnung
der ft-Funktionen.
Die beiden Haupttransformationen «ter Ordnung
/l, 0\ /«, 0x
AO, n)' \0, 1/
verwandeln nach § 27, (11) die Charakteristik (^i, g2) in
(wtZi, M (ö'i, ng^,
d. h. bei ungeradem n bleibt die Charakteristik ungeändert, bei
geradem n geht sie über in
(1) (M oder (^,0).
Da sich hiernach die Transformation geraden Grades wesent-
lich anders verhält als die ungeraden Grades, so betrachten wir
zunächst den Fall n = 2. Die erste und. zweite Haupttrans-
formation zweiten Grades werden die Lande.nsche und die
Gausssche Transformation genannt.
Nach § 27, (12) sind
(2) = ®91,o(w, ®)
^.vA2“,2®) = ®o)92(w, »)
©-Funktionen zweiter Ordnung von m, os, die sich nach § 21
darstellen lassen.
Wir erhalten zunächst die zwei Formelpaare, in denen A, B
von u unabhängig sind:
(u, = »n(u, o3)0„(m, cs),
(3) "
, (2m,2») = '9'i0(m, a)&ll(u, 03),
D0o1(2m, 2os) = 0oo(m, ro)^^, os),
106
Dritter Abschnitt.
§ 32.
wovon jedesmal die zweite aus der ersten abgeleitet werden kann
durch Vermehrung des Arguments um eine halbe Periode.
Setzt man in diesen Gleichungen u = 0, so folgt
2 k>) = '9’109ii,
-^^lo^O, — = 'O’oo'O’io, 2 ÜJ) = 9’00'9'01,
woraus durch Division, mit Benutzung der Relation
= Jr'Ooo'O’n'Ooi,
(6) . ^oo (0, 5)^(0, 5) =
(7) 2'9’oo(O, 2to)'9’i0(0, 2 ») = O’io.,
und wenn man in (6) ra durch 2ra, in (7) ra durch a:2 ersetzt:
(8) #ol(O, 2 ra)2 == ö’oo'd’oi,
(9) ^io (O, —== 2'9’00'9’i0.
Nach (8) und (9) ergibt sich aus den zweiten Gleichungen (5):
2A = 9lt(0,^, B = 4tol(O, 2o),
und man erhält also für die Gausssche Transformation:
ölof0, ^) == 2 9-01(u, oj^i^w, o),
(10 } / o\ / o\
^1° (0, -] 'O’iJu, 2) = a^oo^, o)9’10(tt, o),
und für die Landensche Transformation:
(IB ^(°’ 2ra)'9’u(2M’ 2ra) ~ ^ioO rapnOh »),
^(O, 2 69)iT01 (2 u, 2 o) = 9'00(m, oj'ü’o^u, 0).
Es bleiben für jede der beiden Transformationen noch zwei
ü-Funktionen auszudrücken. Man kann diese Ausdrücke aus
(10), (11) herleiten nach § 21, (13), gelangt aber auch direkt dazu
auf folgende Weise. Die Funktionen
(12) 'ü'oi^w, '9’i0(2u, 2o)
verschwinden für
o 1
m=4’ u = r
§ 32. Haupttransformationen zweiter Ordnung. 107
Andererseits ergibt sich ans den Formeln (8) des § 21, wenn
dort v = —und = —gesetzt wird,
(j) = Q)
und demnach sind die beiden Funktionen (12), die linear durch
zwei -it-Quadrate ausdrückbar sind, von konstanten Faktoren ab-
gesehen, übereinstimmend mit
W + («), ^10 W — frfi («)• ;
Die konstanten Faktoren ergeben sich unmittelbar durch u = 0
aus den Relationen (6), (7):
(13) »00 (o, ü0:. (u, (u) + ^(u),
(14) 2 froo(0, 2 cj)ü10(2 w, 2 ßj) = (u) — (u).
Daraus erhält man die beiden letzten Formeln, wenn man u
1 G3
in w -|- -jj und w -f- -5 verwandelt [oder auch auf demselben Wege
wie (13), (14)]:
(15) • ft00 (0, fl,,« (u, (w) + (w),
(16) 2ftoo(O, 2 ro) ü’oo (2 u, 2m) = ^qoW
Hieraus lassen sich mannigfache Relationen zwischen den
Nullwerten der &-Funktionen herleiten, von denen wir nur die
drei folgenden anführen, deren beide ersten aus (8), (9)'fließen,
während sich die letzte aus der ersten Gleichung (11) ergibt,
wenn man co durch w: 2 ersetzt und u = 1/i annimmt und be-
rücksichtigt, daß ftu (V4) = 'd’iotVi)
V’fl'oo fl'oi = fl'oi (0, 2 m),
(17)
V'fl'oi 'fl’io — '2^*
Diese Formeln sind darum von Interesse, weil sie die Quadrat-
wurzeln als eindeutige:Funktionen von m darstellen.
108
Dritter Abschnitt.
-§ 32.
Wir machen von der Transformation zweiter Ordnung noch
eine Anwendung auf den Beweis einer Formel, die für die Trans-
formation ungerader Ordnung notwendig ist.
Wir ersetzen in der zweiten Gleichung (10) ra durch 2 ra, also:
2O00(u, 2ra)ü’]0(w, 2ra) = Ol» Oip («)•
Hiermit multiplizieren wir die zweite Gleichung (11), so daß
wir erhalten
2'9’01(0, 2 ra) ü01 (2 u, 2m)ü'0p(u, 2co)f>l0(u, 2 ro)
= Oi o Oio («) Ooo («) O'oi («)•
Dies dividieren wir durch das Produkt der beiden Gleichungen
(7), (8):
2 ü’oo(0, 2 ra) Ü’jo(0, 2 ra) 9'01 (0, 2 ra)2 = fr*, ö'ooOpi
und erhalten
, . O00(u, 2g>)»10(u, 2ct)»Oi(2w, 2 gj) _ »op (u) O10 (w) »01 (tt)
' Oop(0, 2w jülft(0, 2ra)ü’01(0, 2 w) OppOipOpi
Wenn nun n irgend eine ungerade ganze Zahl bedeutet,
so bleibt die Funktion
wenn v um ein Vielfaches von n wächst, ungeändert, und folg-
lich ist das Produkt '
wenn es über ein volles Restsystem nach dem Modul n genommen
wird, unabhängig von der besonderen Wahl dieses Restsystems.
Daher ist,
läuft,
(19)
da 2 v zugleich mit v ein solches Restsystem durch-
v01
1, n—1
/7 Opi
Wenn wir also in (18) u = v:n setzen, das Produkt bilden
und im letzten Faktor der linken Seite von der Formel (19)
Gebrauch machen, so ergibt sich, daß das Produkt
(20)
ungeändert bleibt, wenn gj durch 2 ra ersetzt wird.
§ 32. Haupttransformationen zweiter Ordnung. 109
Die in (20) vorkommenden Werte von v lassen sich in Paare
anordnen derart:
io n — 1
v, n — v, v = 1, 2, ••• —g—,
und da
so stimmt (20) bis auf das Vorzeichen überein mit dem Quadrat von
(22)
1,
n — 1 n — 1 n — 1
o, 2 2 zy 2
V 00 jo Voi
Der letzte Quotient, der eine stetige, von Null verschiedene
Funktion von <a ist, solange der imaginäre Teil von co positiv
ist, bleibt also gleichfalls ungeändert, wenn co durch 2ra, also
auch durch 4ra, 8ra, ... ersetzt wird. Man kann den Wert dieses
Ausdruckes dadurch bestimmen, daß man den imaginären Teil
von co unendlich, also q = 0 annimmt. Für q = 0 ist aber
(nach § 25):
•ü00(u) = 1, ^(u) == 1, = cossru,
^10
und daher der Wert von (21):
A vn
n cos —
n — 1
F
Da hierin vitjn kleiner als ist, so hat dieses Produkt
einen positiven Wert. Es ist aber
vjc (n — v)sr
cos — = — cos ----------—
n n
und nach Bd. I, § 144 ist
W~1 V
2 2 Ü cos— = 1.
n — 1
' 2
Dadurch ist die Formel bewiesen:
n—1 v zx / s zv n—1 n-1 n—1
(23) 2“ 2 ^o2 ^2 ’
110
Dritter Abschnitt.
§ 33.
(24)
Mit Rücksicht auf die Formel Bd. I, § 145, (3) kann mau
dieser Relation noch die Form geben:
’ 2
n2— 1 n — 1 i
= (-1) 8 Ao 2 Ao
n — 1 n— 1
2 fr 2‘ .
) v01
§ 33. Die Haupttransformationen ungerader Ordnung.
Die zuletzt bewiesene Formel ist uns von Nutzen bei der
Durchführung der Transformation ungerader Ordnung n. Wir
betrachten zunächst die erste Haupttransformation. Nach
§ 27, (12) ist
(1) ü’11(mm, na)
eine ©u-Funktion «ter Ordnung von u und k>, und diese läßt
sich aus ihren Nullpunkten leicht bilden, deren es im Perioden-
parallelogramm n gibt. Die Nullpunkte von (1) sind die Werte
v + um v ,
u =------------------------5---- —-------H ura,
n- '
n
wenn v und ja ganze Zahlen sind, und man erhält alle inkon-
gruenten unter diesen Werten, wenn man {i festhält und v ein
volles Restsystem nach dem Modul n durchlaufen läßt. Wir
wählen das Restsystem
0, +1, +2, ..., +
und erhalten demnach, wenn G einen von u unabhängigen Faktor
bedeutet,
(2) na) — Ai(w) H -j- u \ — u^,
2’ 2
eine Formel, die sich nach § 22, (4) in folgender Weise auch
durch die Funktionen &„(«)> h01(u) ausdrücken läßt:
(7'9’"“1 ü1!! (mm, Mra)
= (u) n Fax ü’oi (m) - Ai Ai (w)l •
n — 1 L \ »«' / \ ^ / J
’ ‘ 2
Wir ersetzen m durch
। 1 । ® । 1 + ®
M + 2’ u + "ä’ --------------------2—
§ 33. Haupttransformationen ungerader Ordnung. Ul
und erhalten aus (8) (§ 21):
O'-9’10(mw, na) = ^a(u) H &l0
n — 1
’ " 2
v (V \ (V
(3) C&01(nu, na) — &01(u) H J — -f- u ) ü-01 (— — u
n — 1 XU / \
’ 2
C&M(nu, na) — &w(u) II &w(— + M) ^oo (~ — “)
n — 1 / \™ /
’ 2
Daraus aber ergibt sich für u ~ 0 nach der Formel
ftjl = n »oo^oi #io •
oder mit Benutzung von (23) des vorigen Paragraphen:
(6)
(7)
(8)
(9)
Das Vorzeichen ergibt sich aus dem Umstande, der aus einer
der Formeln (3) folgt, daß C = 1 wird für q = 0.
Nach dieser Bestimmung von C lassen sich die Formeln (2), (3)
so schreiben:
na)&002 &102 &012
=Q +n) _ uy
’’ 2
n — 1 n — 1 n—1
na)®^2 ü’io2 'ü’oi2
= 2 2 »10(u) n (-) ^01 (- + «)#o1 (-—“)•
n — 1 \^/ / \fi /
' 2
n—1 n—1 n—1
y^^oi ^G5)'^00 ‘fr’lO ^01
= 2~ t>01 (m) n tt01 Q + w) 4t01 •
n — 1 \ 'V \ '«' / /
’ 2
n — 1 n — 1 n—1
yn&w(nu, na)&002 ^1O2 #oi2
r / v\ /V \ /V \.
= 2 2 it00 (m) n_ ^oo (- + m) ^00 •
11 ' 2 ‘
112 Dritter Abschnitt. § 34.
§ 34. Die Funktionen /W AO), A(«)-
Es sind bereits im § 24 die Funktionen g (ra), f(a), /i(ra),
f2(ai) erwähnt, die sich dort als einwertige Funktionen von ra
bei der Darstellung der tt-Funktionen durch unendliche Produkte
fast von selbst einstellten, die sich aber nicht ergaben bei der
zweiten Darstellung durch unendliche Reihen. Damit im Zu-
sammenhänge steht ein bemerkenswerter Umstand, daß viele
unserer Formeln, z. B. die zur Transformation zweiter Ordnung
gehörigen (17), § 32 oder die Formel (23), § 32, leicht verifiziert
werden können durch die unendlichen Produkte, dagegen schwer
oder gar nicht durch die unendlichen Reihen. Darum war es für
uns von Interesse, diese Resultate ohne die Benutzung des einen
oder anderen dieser Ausdrücke aus der Transformationstheorie
herzuleiten, und ebenso sollen nun auch aus dieser Quelle die
Funktionen (ra), /(«), /j (ra), f2 (ra) und ihre Grundeigenschaften
gewonnen werden.
Die Formel (6) des vorigen Paragraphen ergibt für n = 3:
V3^u(3w, ScQfroo^ofl-o! = 2ü’11(|)ü’11(u)ü11(i M)^u(l — M),
und wenn man differentiiert und dann u = 0 setzt nach (4):
S'l/Fö'n^, 3 gj) = 2%ü’11(|)3,
oder indem man ra durch ersetzt,
Ö
31/3^ = 23rhu(|,
L \ö O/J
Setzt man also
(1) =
so folgt in der Bezeichnung übereinstimmend mit § 24 (9):
(2) &'u = = 2 ar >7(40)3
und aus § 25, (4) erhält man für i?(ra) die Reihenentwickelung
(3) rj (ro) = q12 2J (— 1)” g3 + ’.
—co, co
Die Funktion ij(ra) ist für ein rein imaginäres w (reelles q)
reell, und für ein unendlich großes ra (d.h. verschwindendes q) ist
q 12 i?(ra) = 1.
§ 34. Die Funktionen f2(a>). 113
Hiernach findet man, wenn man in (2) die Formeln § 31,
(6), (11) anwendet, für die linearen Fundamentaltransformationen
von i?(ro)
n i
W 1) = e12
(5) = V—
von denen die erste auch unmittelbar aus der Reihendarstellung (3)
folgt, während die zweite nicht so leicht durch direkte Umformung
der Reihen bewiesen werden kann.
Wir gehen über zur Betrachtung der beiden Haupttrans-
formationen zweiter Ordnung der ^-Funktion.
Aus § 32, (11) erhält man durch Differentiation und Null-
setzen von w
2 (0, 2 ro) n (2 ro)8 = fi-10i} (<»)»,
also wenn man ins Quadrat erhebt und § 32, (8) anwendet:
4 fi-io ^oi 1? (2 o)6 = fiiot] (»)6,
und mit Anwendung von (2) und Ausziehen der Kubikwurzel:
(6) 2ij(2o)2 = fi-10ij(<»).
Ersetzt man in (6) o durch , so folgt
2
2 ij (o)2 = ^10 (o, (y) ,
und wenn man quadriert und die Formel § 32 (9) anwendet:
(CJ \ 2
fi'oofi'io-
Multipliziert man beiderseits mit Itoi, 80 folgt nach (2):
/ G>\2
(7)
und durch Verwandlung von o in o + 1 [(4) und § 31, (6)]:
ä i / । i \ 2
(8) e-12?j(—) = fron ??(<»).
\ 2 J
Weber, Algebra. III. g
114 Dritter Abschnitt. § 34.
Hiernach führen wir die drei Funktionen ein:
/c»\
(9)
K 7 q (co)
Dann ist nach (6), (7), (8)
9oo — n(«>)f(<a)2i
(10) ' ^oi = ^(<»)A(<»)25
9-10 — ^(«OAÖ»)2,
und aus (8) und (9) folgt, daß /'(co), /j (“h AF) Fr ein rein
imaginäres k> reell und positiv sind. (10) stimmt überein mit
§ 24, (10), und die dort eingeführten Funktionen f, flt sind
dieselben wie diese. Aus (10) folgen aber leicht die Relationen
[(2) und § 21 (14)]:
nn fW = A(®)8 + A(«>)%
V2 = /(<») A(<»)A(<4
Mit Hilfe dieser Formeln kann man durch Quadratwurzeln
jede der drei Funktionen /'(co)8, /] (co)s, AG3)8 durch jede andere
ausdrücken. Dazu führt die aus (11) fließende Formel:
[fdtoy - Am = /»16-
64
(12) [f («)8 + A («Fl2 = A («F +
64
[f (0)3 + A (<U)S]2 = /2(«p6 + .
Für die linearen Fundamentaltransformationen der
Funktionen f erhält man zunächst aus (4) und (9):
/> + 1) = e 2‘A(<»),
<13) A(« + l) = e“^/>),
A(«> + 1) = ^2(<u).
§ 34. Die Funktionen ?;(w), fs^)-
115
Ferner ergibt sich aus (5) und den beiden letzten Glei-
chungen (9):
(u) a(-^) = =
und wenn man hiervon in der zweiten Gleichung (11) Gebrauch
macht:
(15) r(-^) = /»
Für die Transformation zweiter Ordnung folgt unmittelbar
aus den beiden letzten Gleichungen (9):
(16) A Wäg») = 1/2,
woraus sich noch durch Anwendung von (12) ergibt:
(17) + AM8] = 2[f(<u)8 + f^n
Setzt man in (16) nach (13), (14)
n i
= e"2t/'(2» — 1),
— / 1 \
= /(l — —
so ergibt sich:
= V'2,
und indem man 2 co — 1 gleich einem neuen k> setzt:
08) rt»)f(^) = Vä.
Ersetzt man in (16) <» durch und , so folgt:
2 2
(19)
= V2,
= e^y2.
\ /
Wii' stellen endlich noch für ein ungerades n die Formeln
für die Haupttransformation «ter Ordnung der Funktionen tj, f
auf. Für ij(m(») ergibt sich leicht, wenn man in den Formeln (6),
§ 33 nach der Differentiation u = 0 setzt, und die dritte Wurzel
zieht:
n — 3 v > 20
(20) y«i?(n<»)i2(<») 2 = n
\ / n —1 \ •f'
’ 2
8*
116
Dritter Abschnitt.
§ 35.
Setzt man ferner u = 0 in (7), (8), (9), § 33, benutzt als-
dann die Relationen (10) und (20) und zieht die Quadratwurzel,
so findet sich
/(n<»)i2(<»)~ =/(«) n fi-oo
n — 1 \'*/
’ 2
W~1 v /V\
(21) A 0<5?) O) 2 = A (<5?) ,
2__1 v /v\
AO^M*») 2 = A(<») n
n — 1 \ »*/
Die Vorzeichen ergeben sich hier aus der Annahme eines
unendlich kleinen q.
§ 35. Die Weierstrasssche <J-Funktion.
Durch die allgemeine lineare Substitution
(“:«)• =
angewandt auf die Variablen t»j, k>2, geht jede ^-Funktion wieder
in eine t-Funktion über, wobei die Charakteristik sich geändert
hat. Ist (<7X, g2) die Charakteristik der ursprünglichen, (<4, g'%)
die der transformierten Funktion, so ist nach § 27, (11)
01, 9z) = (ßg'i — ß(j2 — M, —791 + K9i — <*7)-
Löst man die beiden darin enthaltenen linearen Gleichungen
für g\, g'2 auf und beachtet, daß aß (7 ö -|- 1), yö(a -|- ß + 1)
notwendig gerade Zahlen sind, und daß eine Charakteristik sich
nicht ändert, wenn sich ihre Elemente um Vielfache von 2 ändern,
so kann man dafür auch setzen:
(1) (9i, $) = («^ + ß92 + <*ß, 79i + ög2 4- yfi).
Die tt - Funktionen gehen also, abgesehen von Exponential-
faktoren, ineinander über. Von Wichtigkeit ist es aber, eine
Funktion zu bilden, die den linearen Transformationen gegenüber
absolut invariant ist, und eine solche Funktion ist die von
Weierstrass in die Theorie eingeführte ö-Funktion, zu deren
Definition wir jetzt übergehen.
Wenn wir die Formel (1) auf die vier Hauptcharakteristiken
(0, 0), (0, 1), (1, 0), (1, 1) anwenden, so gehen diese der Reihe
§ 35.
Die Weierstrasssche <r-Funktion.
117
nach über in (aß, yd), [(a 4- 1) ß, (y -|-1) d], [oc(/5—1), / (d -|-1)],
[(" + l)(/5 + 1) - 1, (y + l)(d + 1) - 1) = (1,1)]. Es bleibt
also nur die letzte Charakteristik (1, 1) bei allen linearen Trans-
formationen ungeändert, da weder a und ß noch / und d zugleich
gerade Zahlen sein können. Es sei also t(u, k>x, o2) eine f-Funk-
tion von der Charakteristik (1, 1), die nach § 17, (12) für u = 0
verschwinden muß.
so sind nach unserem Transformationsprinzip
/(w, »j, a>2) und t(u, coi, a>2)
verwandte T-Funktionen erster Ordnung, und folglich ist, wenn
C, Z, p von u unabhängige Größen sind,
(2) f(w, <»i, <»2) = Ce'l“2 + *tMf(w, Oj, k>2).
Es ergibt sich hieraus durch logarithmische Differentiation
('31 2 Z u 4- u. == dl°g*(w’ 02) _ dlogf(w, <»!, o2)
du .du
Nun ist, wenn wir nach Potenzen von u nach dem Taylorschen
Lehrsatz entwickeln und mit t', t", f" die erste, zweite, dritte
Derivierte von t nach u für u = 0 bezeichnen,
dlogffu, <»1, <»2) _______ 1 , t" । t"2\ ।
du ~~ w 2? — ’
woraus sich durch Vergleichung mit (3) ergibt, daß Z und p in
die Form gesetzt werden können:
Z----g7(<Z>i, G52) — <p(®i, ®2),
p = <»2) — ^(oj, <»2),
worin
t"' t"2 t"
(4) <;?(<»!, <»2) = = —,
Bestimmt man ferner noch den Faktor C in (2) durch den
speziellen Wert u = 0, so folgt
Hiernach läßt sich die Formel (2) in folgendem Lehrsatz
aussprechen:
Die Funktion
/1’" t,r^ \ tf/ / \
(6) =
* V
118 Drittel- Abschnitt. § 35.
bleibt ungeändert, wenn man ro1( ö2 durch a'2 ersetzt,
d. b. wenn man irgend eine lineare Transformation an-
wendet, oder:
(7) o(w, t»l, k>2) = <5(m, rox, o.2).
Die durch (6) definierte Funktion bleibt, wie eine einfache
Rechnung zeigt, ungeändert, wenn man t durch irgend eine ver-
wandte (-Funktion ersetzt.
Die Funktion t(u) hat nach Voraussetzung die Charakteristik
(1,1) und ihre Nullpunkte sind also kongruent mit 0. Demnach
hat t (— w) dieselben Nullpunkte und daher auch denselben
Charakter wie t(u). Beide Funktionen unterscheiden sich also nur
durch einen Exponentialfaktor voneinander, und es ergibt sich
leicht, wenn man einen konstanten Faktor aus w = 0 bestimmt:
f(—w) = —e2ai‘uut(u),
worin p. eine Konstante ist.
Differentiiert man diese Gleichung zweimal nach u und setzt
dann u = 0, so folgt
o • t"
2 m(i = —-p-,
V
und daraus ergibt sich nach (6), daß die Funktion ö(ti) der
Bedingung
(8) o(—w) — —o(w)
genügt, also eine ungerade Funktion von u ist.
Da <J(w) eine (-Funktion erster Ordnung ist, so genügt es
den beiden Bedingungen:
<>(w -|- <»x) = c1e’ii(2“+lc>)ö(m),
<j(w -|- k>2) = c2e,^<2“+“’2)6(M),
worin cx, c2, ijx, ij2 Konstanten sind. Die Funktion ö(m) ver-
schwindet für m = 0, aber nicht für u = | rox, u = j k>2 , und
wenn man also in den vorstehenden Formeln u = — | g?x,
— | <3j.> setzt, so ergibt sich nach (8) cx — — 1, c2 = — 1, also
die Formeln:
ö(m -(- g?2) = —e'fe(2“ + m2) ö(m).
Die hierdurch eingeführten sind Funktionen von <ux, ro2,
die nach der Relation § 17, (10) (worin ir««2, m durch
—%, —j?2, 1 zu ersetzen ist) die Gleichung befriedigen:
(10) — '’ia05! = ä i.
§ 36. Die Funktionen a^, c01, <rw.
119
Durch wiederholte Anwendung von (9) ergibt sich, wenn a, b
ganze Zahlen sind [vgl. § 17, (16)]:
ö(m + ac»i + &wa)
\ / —— ( 4- ft 4- aft g(a *Ji 4-1) *$) (2u 4* a tot 4- ft w2) & (h).
Wenn man die Funktion 0(u), wie sie durch die Formel (6)
gegeben ist, nach Potenzen von u entwickelt, so findet sich, daß
nicht nur die zweite, sondern auch die dritte Potenz von u in
der Entwickelung nicht vorkommt, und man hat also:
(12) ö(0) = 0, ö'(0) = 1, 0"(O) = 0, 0"'(O) =-- 0.
Wenn auf rox, k>,2 eine lineare Substitution
(15)
und indem
(13) (<»i, <»2) = <»2)
angewendet wird, so erfahren die Größen die entsprechende
Substitution
(14) ^2) = (“’1?2),
wie man unmittelbar aus den Relationen (7) und (11) folgert.
Differentiiert man die Formeln (9) logarithmisch nach u, so
o'(M 4- (»Q _ 0»
0 (u 6 (u) ' ’
0'(w + <n.2) _ g'(w)
<5 (M .4 <a2) ~ 0 (m) “T
man in der ersten w = — ~, in der zweiten
setzt, und beachtet, daß e(w) eine ungerade und
folglich 0'(w) eine gerade Funktion von u ist:
(16)
=
§ 36. Die Funktionen ß00, 601, 610.
Es bleibt uns noch übrig, die analogen Resultate für die
übrigen Charakteristiken zu gewinnen. Wir gehen aus von der
folgenden Bemerkung: Sind x^ x2-, yT, y.2 irgend zwei Paare von
Größen, welche durch dieselbe lineare Substitution S in x[, #2;
yi, y’2 transformiert werden, ist also:
120
Dritter Abschnitt.
§ 36.
(4, x'2) = Q («Jj, x2); (i/i, y’2) = Q’ (2Z1, 2/a),
so ist auch
^i3/a — ^23/i = ^i3/ä — ^23/1,
wie aus der Multiplikation der Determinanten hervorgeht. Dem-
nach ist, was auch xu x2 sei, nach (7), § 35:
(1) ö(u -1-x2»i — xxa2y k>1, k>2) = <5(uXz— x'itOfy co), a>2)-
Diese Funktion ändert sich der Formel (11) des vorigen
Paragraphen gemäß, wenn xlt x2 um ganze Zahlen geändert
werden. Diese Änderung kann man aber vermeiden, wenn man
statt dessen die Funktion
e—2 (>n «2—
0 (x2 (»1 Xi <x>2 )
betrachtet, die wir (für den Augenblick) mit o(u, xlf x2, on ®2)
bezeichnen wollen. Diese Funktion genügt den Bedingungen:
(2)
0(w, X'i, x'z, <»i, <»2) = ö(w, X1, X2, fijj, <»2)5
0(w, Xi -|- 1, x2i <»2) = 6(.u, a?2, <»i> <»2),
0 (w, xly x2 4-1, <»1, <u2) = 0 («, a?!, a;2, <»!, »2)1
0(w 4~ ^i) — —e~2Ä»a:i eii(1 2«+“i) 0(w),
k>2) = —e-2Ä®“-2e>i2(2«+“2) <?(«),
bleibt also ungeändert, wenn xx und x2 um ganze
(3)
(4)
und
Zahlen geändert werden.
Indem wir uns nun wieder auf die Hauptcharakteristiken
beschränken, setzen wir (x^ a:2) — (—(L tA, (o, (—-L 0^)
und erhalten so die folgenden drei Funktionen:
/ 1 1 \ ev
öoo(m) = 0(4, 2’ + --
' 0
T~ ^2
2
1 0
(5) 0lo(w) = 0 (w, 0, <»i> <»2) =
§ 36.
Die Funktionen tr00, crn, er 10.
121
und die Funktion <j(m) selbst kann entsprechend auch mit «„(w)
bezeichnet werden.
Für diese Funktionen ergeben sich nach (4) die charakteristi-
schen Periodengleichungen
•^(w + roi) = (—l)s'1e’il(2u+“1)ö^1,S2(M),
(6) 0 4- «2) = (— e,k(2u+ “2) <^)9s(w)’
<Wä(M + «<»i + &<u2)
= (— l^ia + P26 + a6e(a’<1 + 6’12)(2“ + a“iF6m2)(Jpi 9s,(u).
Durch Anwendung einer linearen Transformation werden die
drei Funktionen o00, öOn öio untereinander permutiert, wie die
Formel (2) lehrt [oder § 35, (1)]. Je nach dieser Permutation
zerfallen die linearen Transformationen in sechs Klassen, deren
erste alle die Transformationen umfaßt, die die Funktionen <J00,
ö01, öio ungeändert lassen. Diese sind dadurch charakterisiert,
daß a, d ungerade, ß, y gerade Zahlen sind, was wir kurz so
schreiben:
C4 s (ö: ?>o<i2)'
Hiernach sind die sechs Klassen der linearen Transforma-
tionen folgendermaßen zu charakterisieren:
h—1 sG* Q? “Cb ti-^O 's' Q P-i bO (00, 01, 10),
II = ( 0’ ” ~ \-l, 0/ (00, 10, 01),
III = ( 1’ 1U> ” ~ \-l, 0) ” (10, 00, 01),
(7) /I 1\
IV- „ = (0, » (10, 01, 00),
v- " s (m) " (01, 00, 10),
VI. , „ (01, 10, 00),
wo in der letzten Kolumne die jedesmalige Permutation der
Charakteristiken 00, 01, 10 auf geführt ist.
Die Transformationen der ersten Klasse bilden eine in der
Gruppe aller linearen Substitutionen enthaltene Gruppe 21, also
einen Teiler der Gruppe 8 (§ 28). Setzen wir
122
Dritter Abschnitt.
§ 37.
/I, 0\ / 0, 1\ / 1, IX
061 — \o, 1?’ “2~\-i, o/’ “8 - V-1, oj’
/l, 1\ zi, o\ . / o, i\
a‘ = ko, i> “6= U “6 = U, 1?’
so sind cCjQl, oc2$I, as91, a49(, a69l, a69l die Nebengruppen zu 91
und es ist
8 = -|- CC29l + «3 21 + «49l +
und 91 ist ein Teiler von 8 vom endlichen Index 6:
(8, 91) = 6 (Bd. II, § 2).
Die Gesamtheit 91 -|- a2 21 ist ebenfalls eine Gruppe 9V,
und es ist
8 = a49V + a8 91' + a49l'
und (8,91') = 3.
So wie sämtliche lineare Transformationen aus den
beiden Fundamentaltransformationen, so lassen sich die
Transformationen der ersten Klasse aus wiederholter
Anwendung von
/l, 0\ /l, 2\ z-1, 0\
\2, 1/’ \0, V’ \ 0, -V
ableiten, was sich auf dem Wege des § 30 beweisen läßt.
§ 37. Darstellung der 6-Funktionen durch ff-Funktionen.
Um die Funktion ö(w) als h-Funktion darzustellen, kann
man einfach die Formel (6) des § 35 auf die Funktion
#(w) =
an wen den, also
(1) ö(w, Oj, k>2) = Oje 6“i2^n
Uli
setzen. Es ist aber infolge der Differentialgleichung § 20, (4):
q.',' a & ^11
da
und also nach der Definition der Funktion in § 34, (2):
(2)
— 12.^3 ^10gl?(<3)
z- , — *T Jl V -J — £ JV J
'O’n ao do
§ 37.
3-Funktionen.
123
Darstellung der <r-Funktionen durch
Durch logarithmische Differentiation
mittels (2):
dlogö(w) ____ 4 st iw dlogrj(o)
d w «a? d co
von (1) erhält man
du
und wenn man
§21 anwendet
, . . g>, <o» , , .
hienn w = setzt und
nach § 35, (16):
___ 2 st i d log y (in')
die Formeln (8) des
(3)
«>! dco ’
___ 2itico2 d log y(co) 7t i
co? dco
Hiernach kann man für 6 setzen:
$n (---j )
(4) 6 (w) = e~---------,
1711
und für die drei Funktionen 600, 601, 610 erhält man nach § 36, (5),
wenn man einen konstanten Faktor aus
(5)
bestimmt:
6oo (0) — 1, 601(0) — 1, 610(0) — 1
ö00(w) =
(6)
®oi (M) —
«er ( ~•
---- \G)v
fr«r
von
von
(7)
Die
wichtige
öooi ö01,
während
sind also 6 , 600 , 60i,
q, / 2 \
. fr>0
Die Funktionen 600(w), 601(w), 610(w) sind gerade Funktionen
w, und durch zweimalige Differentiation der Logarithmen
(6) ergibt sich noch [nach (3) und § 34, (2)]:
6oo (0) -f- 6oi (0) öi'o (0) = 0.
Ausdrücke (4), (6) lassen auf den ersten Blick eine
Eigenschaft der 6-Funktionen erkennen, daß nämlich
610 nur von den Verhältnissen abhängen,
bei 6 dasselbe, abgesehen von dem Faktor co^ gilt. Es
öio homogene Funktionen der drei
Öio (w) —
124
Dritter Abschnitt.
§ 38.
Variablen w, g)j, co2 erstere von der ersten, die drei anderen von
der nullten Ordnung, oder, in Zeichen, wenn 2 einen willkür-
lichen Faktor bedeutet:
ö(2«i, 2«!, 2gj2) = 2ö(«, ©!, g>2),
6qq(2«i, 2g?!, 2gj2) — 6qq(«, a?!, gj2),
601(2«i, 2 g?!, 2g)2) ~ 6q! («, G?!, G)2),
610 (2 «i, 2gj2) - — 610 1«, g?!, g>2).
§ 38. Lineare Transformationen der Funktion jj(gj).
Die Formeln (3), § 37 führen zur linearen Transformation
der Funktion -tj (gj). Wird nämlich
(1) («’n O = (“? ä) <A’ “2)
\/5 u/
gesetzt, so geht (iji, ij2) über in
(2) (’li, (*li,
[§ 35, (14)] und co = g>2:g>! in
, _ 7 + d<a
— a + ßco'
Nun folgt aus (2) mit Rücksicht auf (3) des vorigen Para-
graphen:
, __ 2o dlog-tj(G)') ___________________ 2 «iwi dlog-»;(g>) niß
g>1 dco' co( dco g>! ’
, __ 2 oG)ä dlog-tj(g/) iti_______ 2o<»2 dlog-tj(G)) Jtiö
G?i2 d co' co^ cof dco G>! ’
und diese beiden Relationen geben übereinstimmend
dlog^(Gj') dlog^(G)) . ß
co'i dco' ~ co^dco ' 2g)jgjI ’
oder endlich, da nach (3)
dco' — -—p-%- ro'i’dro' = co^dco
(a -f- ßco)2 1
d log q («') d log n] (co} . ß
dco dco ' 2 (a ßco)
Hieraus folgt durch Integration:
(4) =
worin s eine von co unabhängige, also nur von den Zahlen a, ß,
y, 8 abhängige Größe ist.
Lineare Transformationen der Funktion >; (tu).
125
§ 38.
Die genaue Bestimmung dieser Konstanten e, namentlich
auch mit Rücksicht auf das Vorzeichen ist ein bekanntes wichtiges
Problem, das eigentümliche Schwierigkeiten bietet, dessen Lösung
aber für uns unerläßlich ist. Lösungen haben auf verschiedenen
Wegen Hermite1) und Dedekind2 3 * * *), neuerdings auch Mertens
und Scheibner8) gegeben. Wir wollen hier einen Weg gehen,
der den Vorzug großer Einfachheit hat, dafür freilich nicht eine
Ableitung, sondern nur einen Beweis der fertigen Formel enthält.
Für zwei spezielle Fälle haben wir schon früher [§ 34, (4), (5)]
diese Bestimmung ausgeführt und auf dies Ergebnis werden wir
uns hier stützen. Es sind die Formeln:
worin —iea mit positivem reellem Teil zu.nehmen ist.
Wir setzen nun
Zy —|— ö ß>\
(?) =
»?(«) \y, o )
und haben den Wert dieses Symbols zu bestimmen. Nach (5),
(6), (7) haben wir:
(9) ») = >.
(10) E(±1i:» = Z^,
(ii) o’ = V—
*) Liouvilles Journal, Ser. II, T. III, 1858. Oeuvres de Charles Her-
mite, p. 487.
2) Erläuterungen zu Nr.XXVIII von Riemanns Werken, zweite Auf-
lage und „Über die elliptischen Modulfunktionen“, Grelles Journal, Bd. 83,
S. 265. Vgl. auch des Verfassers Abhandlung- „Zur Theorie der elliptischen
Funktionen“, Acta Mathematica, Bd. 6, S. 341 ff.
3) Mertens, Zur linearen Transformation der 9-Reihen, Transactions
of the American mathematical society. Ju]y 1901. — Scheibner, Zur
linearen Transformation der Theta-Funktionen und elliptischen Modulfunk-
tionen, Berichte der Sachs. Gesellschaft der Wissenschaften. Oktober 1906.
126
Dritter Abschnitt.
§ 38.
Wir betrachten jetzt zwei Substitutionen und die aus beiden
zusammengesetzte, also:
/«"’ ß"\ _ /a', ß'x /a, ß\
V", d’7 ~ V', d'Ay, ö)'
Ist dann , .
, y -4- o <x>
O) = ----!»
a + ßa>
so ergibt sich aus der Definition (7):
und davon zwei besondere Fälle, indem man
/a, 0\ _ / 1, 0\ / 0, 1\
\7, d/ \4-1, 1/’ \—1, 0/
setzt und an Stelle von a', ß', y', 8' wieder a, ß, y, d schreibt, also
/«"’ ß"\ — ± A ß\ u'\.
\y", 8") \y + <5, d/’ \—8, y/
zi f /w i ß, ß \ + — 7-,/c, ß . , \
(13) ± <5, d’ °7 ~ 12 E\y, d’ “ — V ’
(14) E(~ß' ß — )•
X— d, y > ’ \y, d <d /
Es hat sich nun in § 30 gezeigt, daß sich alle linearen Trans-
formationen durch wiederholte Anwendung der beiden Fundamental-
transformationen
/i, 0\ / 0, 1\
V, 1/’ X— 1, o>
und ihrer inversen Transformationen zusammensetzen lassen, und
daraus folgt auf Grund von (12), daß durch die Formeln (8)
bis (14) das Symbol E vollständig definiert ist.
Wenn wir also einen diesen Bedingungen genügenden Aus-
druck kennen, so muß dieser mit E übereinstimmen. Um einen
solchen aufzustellen, unterscheiden wir zwei Fälle. Da a, ß
relative Primzahlen sind, so ist eine von ihnen sicher ungerade.
Wir setzen:
1. a ungerade und positiv:
t,/«, ß \ (ß\ z’)—(“2—;—ö—r
E \y\ d’ a) = +
(15)
2. ß ungerade und positiv:
E \y\ d’ = (jr e y—<(m-/m
§ 38. Lineare Transformationen der Funktion (")• 127
wozu noch folgendes zu bemerken ist: Die Wurzeln ya -J- ß a>,
)/—i(a-\-ßco) sind mit positivem reellem Teil zu nehmen.
Daß eine von ihnen rein imaginär sei, ist durch die Annahme,
daß co einen positiven imaginären Teil hat und « bzw. ß positiv
sei, ausgeschlossen, denn danach kann a ß co oder — i (a ß co)
nicht reell und negativ sein; (^0 und ist das Legendre-
Jacobi sehe Symbol aus der Theorie der quadratischen Reste,
mit der Erweiterung, daß und = 1 kein soll. Wenn
im ersten Falle a oder im zweiten ß negativ ist, so müssen rechts
die sämtlichen Vorzeichen von «, ß, y, ö umgekehrt werden. Wenn
sowohl a als ß ungerade sind, so kann sowohl (15), 1. als (15), 2.
angewandt werden, und beides ergibt, wie man leicht auf Grund
des Reziprozitätsgesetzes der quadratischen Reste nachweist, das-
selbe Resultat. Es ist nämlich, wenn a und ß ungerade sind,
« positiv angenommen wird, und das obere oder untere Zeichen
gilt, je nachdem ß positiv.oder negativ ist:
_____________ _ n i ____________
]/qri(« -j- ßco) = e+ 4 y« + ßco
und die Identität von (15), 1., 2. ergibt sich dann aus den Kon-
gruenzen
— 3aß-\-ß(a-\-8)— (ß2— l)«y = oc(y—ß)—(«a— l)ßö (mod 24),
ay aß = ߧ (mod8),
von denen die zweite, wenn a und ß beide nicht durch 3 teilbar,
also a2 =. ß2 = 1 (mod 3) sind, auch für den Modul 24 besteht.
Daß durch (15) die Formeln (8) bis (11) befriedigt sind, ist
unmittelbar einzusehen, und es bleibt noch zu zeigen, daß (13)
und (14) erfüllt sind. Wir beginnen mit (14), wobei angenommen
werden kann, daß a ungerade (und positiv) sei; denn vertauscht
man in (14) co mit —l:o, so vertauschen sich a und —ß, und
diese können nicht beide gerade sein.
Es ist
y— ia> |/a—£ = y— i(— ß aco)-
denn setzen wir für den Augenblick
128
Dritter Abschnitt.
§ 38.
— ico = re’V a------------------— = Qff-'l'
co
—i(—ß wo) = rpe*tt’+V')J
so ist, da die reellen Teile von — to, —i(— ß 4- a<a) positiv sind,
und der reelle Teil von
____ .7 ß ______________ _____ i(<P + W
y — ico 1/a-------------------— = y—i(—ß 4- ao) = y»" p e 2
positiv. Demnach ergibt sich aus (15)j 1:
•-T- TV
t i e12
Dieselbe Formel aber erhält man,
aus (15), 2. für
,z—ßi a \
und damit ist (14) bewiesen.
Es bleibt noch die Formel (13). Es genügt, die oberen
Zeichen allein zu berücksichtigen, also die Formel
co
zu beweisen, da der andere Fall durch Vertauschung von a, 7, co
mit a -j- ß, 7 4" <» 4“ i auf diesen zurückkommt. Ist zunächst
ß ungerade (und positiv), so ergibt sich (13) aus (15), 2. auf
Grund der Kongruenz
(ß2—1)(1 — ßy — aö — ßö) = — ß(ß2— l)(2y -j-d) = 0(mod 24).
Ist ß gerade, so ist a ungerade. Nehmen wir a positiv, so
kann a ß positiv oder negativ sein. Gelten im ersten Falle die
oberen, im zweiten die unteren Zeichen, so ergibt uns (15), 1:
(16)
/ ß \ .- [1 + aO'-/S)-(«2_i)/?(J] ,-————------------
= \ a A 2 ß2 V« + ß + ß03,
§ 38. Lineare Transformationen der Funktion >] 129
(17) V + M /
Nun ist, wenn die unteren Zeichen
wenn also
— (a + ß + ß —
gelten, ß negativ, und
(p
i (a ß ß co) =
, , • n , <jp ,<jp 3t 3t , । 3t ,
gesetzt wird, so liegt und — — zwischen —— und und
2 2 4 2 2
daraus folgt, daß wir zu setzen haben:
)/— (a ß ß co) = i \a -|- ß ß a>,
ferner nach dem Reziprozitätsgesetz der quadratischen Reste:
(__r----) = (—n * (!-}
\K-[-ßJ 1 \aj'
/ — ß \ — ?(a~iy /ß\
(Z7(4w) = (-')’ (-1) ‘ □)
und daraus folgt die Übereinstimmung der beiden Ausdrücke
(16), (17) und mithin die Richtigkeit der Formel (13) nach der
Kongruenz
ß(3a, — 2y + ß — ö 4- ß*ö + 2a/?d) == 0 (mod24),
die sich, da ß gerade vorausgesetzt ist, aus ad — ßy — 1 ergibt.
Somit sind also die Formeln (15) als richtig erwiesen.
*) Nach dem Reziprozitätsgesetz ist, wenn ß = + 2^ß' gesetzt und ß'
ungerade und positiv angenommen wird, wenn « -J- ß positiv ist
, „2 (« + /* — 1)
= ( ±2i) (fL\ r- ,
Ist 1 > 2, so sind diese beiden Werte einander gleich, ist 1 = 1, so
«4-1
unterscheiden sie sich durch den Faktor (— 1) 2 , in Übereinstimmung
mit der ersten der obigen Formeln. Die Richtigkeit der zweiten Formel
ergibt sich, wenn «4-/3 negativ ist, aus
„z (“+/3 —1)(/3' —1)
i 1
Weber, Algebra. III.
9
130
Dritter Abschnitt.
§ 39.
Setzen wir
(18) E Q’ = e -f- ß co,
so ist s eine 24ste Einheitswurzel, deren Produkt mit -|- ßo
durch (15) vollständig bestimmt ist, und es ergibt sich die Trans-
formation der t]- Funktion
(i9) - y + = £Va +
Für f12 findet man
(20) e'2 = (— l)«|5+r<?+|5r.
§ 39. Lineare Transformation der ft-Funktionen.
Die Transformationsformeln der &-Funktionen sind Folgen
der Grundeigenschaften der ö-Funktion, durch die Substitution
(coi, c^) = Q («a15 o2)
ungeändert zu bleiben. Aus § 37, (4) ergibt sich hiernach, wenn
man ox, «a2, Vi durch oi, <a2, ijl ersetzt:
oder, weil nach § 35, (10), (13), (14)
V'i _
ist, wenn wir:
(2)
, vv
V =
«01
setzen:
v
a -f- ßa> ’
911 («', £□') ____
911 (0, «□') a, -|- ß <d 9-h (0, to)
Es ist ferner
•9’h (0, ta) = 2 n iq (ta)8, 9ij (0, ta') — 2 jr -r] («a')8,
woraus nach § 38, (19):
.---------------------------------------------------------3
(0, ta') = f8 ytx -|- ßw (0, ta),
§ 39. Lineare Transformation der f)-Funktionen. 131
und daraus endlich:
(3) e—^ifivv’ #^0/, m') = £3|/a ßj).
Die Transformationsformeln der drei übrigen Funktionen
»00, ^ou ^10 sind verschieden in den sechs Klassen des § 36 und
können aus den Formeln (5), § 36 in derselben Weise hergeleitet
werden. Man kann die sechs Fälle aber auch in ein einziges
Formelsystem zusammenfassen, das man aus (3) erhält, wenn
man v ersetzt durch
v H--------2-’ + 2 ’ 2 ’
also v' durch
1 o)' , 1 -f- a>'
«'+2’ ^=—2—’
und dann auf der rechten und linken Seite von (3) die Formeln
(2), (3), (8) des § 21 anwendet. So kommt:
e-’rVSvt,''9'10(y, «')
= ffe 4 f8 V« ßw&1+?' i_«(v, w),
e-0')
(5) _ _______
= id—1e 4 f3 |/a ßct)&1 + s, i-y(v, tu),
_. ^+ß—«de 4 ya _|_ ßafr1+ß+^ 1_a_y(y, tu).
Die vierten Potenzen dieser Funktionen lassen sich einfacher
ausdrücken durch
(7) e-4’”7t,t,'ü'4liä,2(«',«') = (—l)s'2“i«+s'ir<J + /’r(aßw)*
worin in den sechs Klassen die zu den Charakteristiken
(ö’i, #2) = (00), (01), (10) gehörigen Charakteristiken (<?;, g2~) aus
der letzten Kolumne der Tabelle in § 36 zu entnehmen sind.
Eine einfachere Transformationsformel erhält man aus den
ö-Funktionen für das Produkt der drei il-Funktionen (4), (5), (6).
Es ist nämlich, wenn man das Produkt der drei Funktionen
§ 37, (6) bildet:
600 (M) öoi (-O öio (w)
/ u co2\ / u a2\ / u ca2\
3>ilM2 «00 (— > — ) ^011—, — I ^10 — 1 — )
__ M1 \M1 «>1/ \M1 «>1/ X03! ^l/
'O'oo'O'oi ’O'io
9*
132
Dritter Abschnitt.
§ 40.
eine Funktion, die nach § 36 bei linearer Transformation völlig
ungeändert bleibt. Macht man noch Gebrauch von der Relation (2):
^1»! — »ii«; = —iciß,
so folgt
»00(«, <a)»oi(«, <a)»10(«, co)
#00 #01 #10
= ^00 O#oi« O#io(>',
#oo(O, co'jd'o^O, co') #10 (0, co') ’
worin man noch nach (19) des vorigen Paragraphen
.______________________________________________3
#oo(O, ®')#oi(0, O#10(0, co') = es^a ßco #oo#oi#io
setzen kann.
Wir ziehen aber aus (8) einen anderen Schluß: Setzt man
nämlich
, h h(a -4- ßco)
n n
Yb 1
und nimmt das Produkt für h = 1, 2, • • •, —x—, so ergibt sich
mittels der bekannten Relation (Bd. I, § 11)
h ™2 -- 1
x>—
wenn man auf der rechten Seite von (8) die Formel (23), § 32
anwendet:
(9)
«-1 h
2 2 n ^oo
, n — 1
n ) 01
h (a ß co)
n
#10(/t(W+-^))
Tti n2 — 1 a, , o . n — 1 n — 1 n —
= e~ 8 n 2 #01 —
worin nun a, ß irgend ein Paar relativer Primzahlen sein kann.
§ 40. Lineare Transformation der Funktionen
/(«), f^co), f2(to).
Die Formeln für die lineare Transformation der /‘-Funktionen
sind nach § 34, (9) eine einfache Folge der Transformation der
-tj-Funktion.
Setzen wir in der linearen Transformation
/% ß\
§ 40. Lineare Transformation der Funktionen /,(«>), AW' 133
zunächst ß als gerade und folglich a, 6 als ungerade voraus,
so ist
zn /1, o\/a, A _/«, |A/1, o\
{ J \o, 2/ V, ÖV — \2y, öj \0, 2/’
d. h.
„ 7 + ößj ____ 2y-|-d.2ßj
a -J- ßßj a -J- iß .2 ßj
Es ist aber nach § 34, (9):
/2(ra) = ]/2^
und wenn wir also die Substitution
y + da
’ a + ß a
machen, so ergibt sich, mit Benutzung der Bezeichnung des § 38
(M
/(«) ’
Hier sind die ^/-Funktionen nach § 38, (15), 1. zu bestimmen,
woraus sich ergibt:
Es ist aber Jj — | — j und
. aß , , „ ßö a(2 y 4- 0) , ,
«Z + + («2 — 1) = ä (m°d 8)
= a(y — ß) — («2 — l)/3d (mod3),
und wenn wir also zur Abkürzung
(3) p =
setzen, so ergibt sich aus (2):
0) = = 0 (mod2)-
\w> —— U> UJ / \ w> /
In derselben Weise lassen sich alle anderen Formeln dieser
Art herleiten; man erhält sie aber einfacher aus (4) selbst mit
Benutzung der Fundamentaltransformationen § 34, (13), (14), (15).
So ergibt sich, wenn man in (4) cs durch — l:ra ersetzt und
dann a, ß, y, ö mit ß, —a, 6, —y vertauscht (wodurch 9 un-
geändert bleibt):
134 Dritter Abschnitt. § 40.
(5) = K = 0 (mod2)>
\OG -f~ p W/ \p /
und ersetzt man hierin co durch co —I— 3 und p, a durch y — 3d,
a — 3 ß, so folgt
(6) = — 9 “>f(ß>), « —^ = °(mod2).
\0G —— p tu J
Setzt man in (4), (5), (6)
f d f (_ « + ß^X
'* \ y-j-dßj/’
und vertauscht dann a, ß, y, ö mit —y, —8, a, ß, so ergibt sich
CO ßm) = (l)96”— r(2“~ä)f^ 8 = 0(mod2),
(8) =(4)9e 8 'W+r)/i(ß’)> / = 0(mod2),
(9) = — pe 8 15(2<?+r)/((□), /—8 = 0 (mod2).
Aus ('9') und (6) erhält man, indem man <a durch —
v 7 v 7 o — ß<D
und dann a, ß, y, 8 durch 8, —ß, —y, u ersetzt:
(10) = —Qe ~a^+Y)fi(^), a—y = 0(mod2),
C11) /"(« jßa) = ß —8 = 0(mod2),
und wenn man endlich in (10) co durch co —j— 9 und y, a durch
y — 9 8, a — 9 ß ersetzt:
(12) f (! + £?) = (. (-?-?)
- 7 \aß co/ \a — ß/ 1 v 7
a + ß -|- 7 — 8 = 0 (mod 2) ’)•
’) Die von Hermite (Sur la theorie des equations modulaires, Paris
1859) eingeführten Funktionen <p(a>), / (co) hängen mit den Funktionen
A(w) durch die Gleichungen
f(<o) = ^, = =
/(«>)’ V /(co) /2V V /(co)
zusammen. Die Transformationsformeln der f- Funktionen lassen sich mit
Benutzung der Relation aä — ßy = 1 auf mannigfaltige Weise umgestalten.
So sind die von Hermite a. a. 0. angegebenen Formeln nicht ohne weiteres
mit den nnserigen als identisch zu erkennen. Eine einfache Rechnung zeigt
aber ihre Übereinstimmung. Die oben gegebenen Formeln haben den Vorzug,
daß sie, ohne an Einfachheit zu verlieren, je zwei der sechs Transformations-,
klassen in einen Ausdruck zusammenfassen.
Vierter Abschnitt.
Die elliptischen Funktionen.
§ 41. Zusammenhang der ft-Funktionen mit den elliptischen
Integralen.
Nach § 21 bestehen zwischen den Quadraten der vier ^-Funk-
tionen zwei voneinander unabhängige lineare Gleichungen, und
man kann also zwei von diesen Quadraten durch die beiden
anderen oder auch alle vier durch zwei unabhängige Variable g, >]
ausdrücken. Indem wir das letztere tun, bezeichnen wir mit
tu ’li; tai ’iai tat Vs'i tu Vt Konstanten und setzen, indem wir
an die Bezeichnungsweise Bd. I, § 67 anknüpfen:
0) = t Vi — V ti = (t m),
zn , 0?i («) = t»Ja — »7 ta = (t^Ji
’ 0?oO) = t’is — its = (t’isli
0-öo(«) = t»h — nh = (Zk)-
Zwischen den Konstanten &, i;,: und den Werten ü01, üm, ü00
bestehen vier Relationen, die sich aus den Gleichungen (13) des § 21
herleiten lassen. Diese Gleichungen können wir nach der Be-
zeichnung (1) in der Form schreiben:
Z<y. (t *h)0ol = (t’lO^lO (t ^2) 0001
(t^i = (t^^o-Ct^^O-
Man kann diesen Relationen, indem man in (2) |, 77 = |15 t]1
und = ij2 setzt, die Form geben:
(ti’ls)^2! = (ta 1?i)0ooi
zo\ (tz’Jä^ol — (ta’?i)0?oi
w (t^Q^i = (tä’?1)02ioi
(ta *?<) 0qi — (ta’?i)0ooi
wozu man noch fügen kann, indem man in (2) |, tj = i?4
setzt und (3) und § 21, (14) benutzt:
(4) (tils) = (ta»7i)-
136 Vierter Abschnitt. § 41.
Aus (3) und (4) folgt für die Doppelverhältnisse:
~ «t»’
v} (UW) ~ «£o‘
Wenn wir nun zwei der Gleichungen (1), etwa die beiden
ersten, differentiieren, so folgt:
2 «01(w) ««(«)(? w = % dl;—^di] = (in dl;),
2&11(u)&'n(u)du = ij2d^ —
und daraus mit Benutzung von (1)
2 «01 (w) «u (u) [ö-qi(w) «’n (w) — «n («) «oi («)] du
= (Vidb&h^u) — (ti2d^&201(u)
= (mdg)(gi]2) — (md^ih) = (Sa’hXH’?)-
Den letzten Ausdruck kann man ohne Rechnung dadurch
ableiten, daß man den vorletzten als lineare Funktion von di;, dy
betrachtet, die für di-:di] — £:>] verschwindet und daher durch
(£di]) teilbar ist. Den Quotienten erhält man, wenn man
dl-:d?] = §2:t]2 setzt. Mit Benutzung von § 23, (6) erhält man
dann
(7) 2®««1«0o(w)«n(w)«lo(w)«o1(w)dw = (|i q2)(gdi]).
Führt man hierin nach (3) (erste und letzte Formel)
(8) (^m Ǥi
ein, und setzt für die «-Funktionen die Ausdrücke (1), so folgt
schließlich
(9) 2 «»>, do = iWWW ,
V(£ *11) (£’h) (£ »h) (i^i)
wodurch du als elliptisches Differential erster Gattung
in homogenen Variablen [§ 1, (5)] dargestellt ist.
Es ist durch (1) das Verhältnis als doppeltperiodische
Funktion von u bestimmt. Desgleichen sind aber auch die
Verhältnisse der Quadratwurzeln
(10) V(£*/i), V(^2), VQ’Js), V(Ud)
als eindeutige doppeltperiodische Funktionen erklärt, und das
Vorzeichen der Quadratwurzeln in (9) ist hierdurch und durch
(8) ebenfalls eindeutig bestimmt.
§ 42.
Jacobis elliptische Funktionen.
137
Ist ß) der Modul der ü-Funktionen, so gehören, wie sich
nach (1) aus dem Verschwinden der vier &-Funktionen ergibt,
die folgenden Werte zusammen:
w = 0, — g2:i?2,
(11) w — |, — g8:i?8,
w = 1 i h '
§ 42. Jacobis elliptische Funktionen.
Da man die Variablen g, q mittels einer linearen Substitution,
in der vier Koeffizienten disponibel sind, durch zwei neue Variable
ersetzen kann, so kann man vier von der Größe &, oder drei
von ihren Verhältnissen beliebige Werte erteilen, ohne die All-
gemeinheit zu beeinträchtigen.
Wir wollen setzen
(1) ti =0. % = 0, = Vb,
und führen noch x2, %'2, £ durch die Gleichungen an:
(2) = %2^, — 1 — %2, y = g.
Aus § 41, (3), (5), (6) ergibt sich dann
ta = (3) _ »io Vb »io Vt ___ »oo »?o ’h ^oi ’li »oi ^00 ^00
und aus (1), (9), § 41 findet sich:
(<). »00 » 11 (M) _ yTf »io fi-Oi(w) ~ V ’ »01 »io(«). »io »oi («) V »oi »ooOt) = yi _ »00 »01 (M)
(5) 25r^°w ~! fga - g)(i- 0
worin der Integrationsweg und die Bedeutung der Wurzelzeichen
durch die Formeln (4) selbst bestimmt ist, wenn der Übergang
(8)
(9)
und nun
138 Vierter Abschnitt. § 42.
von 0 zu u in der u- Ebene gegeben ist. Es darf aber dann
auch der Integrationsweg in (5) geändert werden, wenn dabei nur
keiner der singulären Punkte oo, 1, überschritten wird.
Die Gleichung (5) läßt sich in folgenden drei Formen
schreiben:
d . = 5t f(l —g)(l —%2g) d u,
(6) d yi — i = — jt |/g(1 _ du,
dyjl — x2g = — 5t^o x2 VSC1 — Qdu.
Führen wir eine neue Variable v ein durch die Gleichung
(7) = v,
so werden die Gleichungen (5), (6):
— 1 f
2 J V&(1 — g)(l —
d^ = V(l — g)(l —
d^l — £ = — fg(l - &$)dv,
d\l — = — %2 y?(l —
betrachten wir die drei Größen = x, V1 - ? = y,
yi —• — s durch (4) und (7) als Funktionen der Variablen v
definiert. Nach (4) sind es eindeutige, doppeltperiodische
und, abgesehen von einzelnen Punkten, in denen sie unendlich
werden, stetige Funktionen von v. Sie werden nach Jacobi
sinus amplitudinis, Cosinus amplitudinis, z/ amplitudinis von v
genannt und mit sinamr, cosam», Jam» bezeichnet. Wir wollen
uns hier der schon in § 14 erwähnten kürzeren Gudermann-
schen Bezeichnung snr, cna, dnv bedienen, wonach
0io(M) l/%
X- -H = I/ — cnt>,
— _Ldnt>
§ 42-
Jacobis elliptische Funktionen.
139
Diese Funktionen genügen nach (9) den Differentialgleichungen
dx
— = yz,
av 9
(U)
dz .
t- — —n2xy,
dv J
und den Nebenbedingungen:
(12) snO = 0, cnO = 1, dnO = 1.
Es bestehen zwischen ihnen die Relationen
(13) y2 = 1 — x\ z* — 1 — v?x\
Aus den Fundamentaleigenschaften der ff-Funktionen ergeben
sich die ersten Eigenschaften der elliptischen Funktionen:
sn« = —sn(—«), cn« = cn(—«), dn« = dn(—«),
d. h. sn« ist eine ungerade, cn«, dn« sind gerade Funktionen.
Setzen wir noch
(14) = 2 , srff20ßj = 2i7f',
und folglich
(15) ’t'9'oi = 2x'i, jrff20 = 2%Ä, to = >
so erhält « die Werte Ä, iK', K i K', wenn w = —, —, —
2 2 2
wird, und es folgt aus (4) mit Rücksicht auf (3) und § 21, (10):
sn W = 1, sn(RT + iK') = -,
%
(16) cnW=;0, cn(A:+ iK') = —
dn W = dn(W iK') = 0,
snt.S7, cnt-ZT, dnfAT' = oo.
Nun lassen sich K, K' vermittelst (8) durch bestimmte
Integrale ausdrücken, und man erhält, wenn man « von einem
Eckpunkte des Parallelogramms 0, K, K iK', iK' bis zum
folgenden längs der Peripherie verschiebt, also u längs
1 1 4- o ßj
2’ 2“ ’ 2“
140
Vierter Abschnitt.
§ 42-
(17)
(18)
(19)
(20)
1 f dj
2jyg(i — g)(i —
1
X*
1 f dj
2j y?(i-g)(i-%^)’
00
1 f dj_____________
2J yg(i — g) (i — x»g)’
dt,
0
2 f_______________
2] yg(i- g)(i-^g)
Die Werte von \i, j/l — g, )/l — %1 2g sind bei diesen Inte-
grationen durch die Formeln (4) bestimmt. Wenn aber co rein
imaginär und infolgedessen %2 ein positiver echter Bruch und
K, K' reell und positiv sind, so sind die Wege für v der reellen
und imaginären Achse parallel, und mit Rücksicht auf die Be-
merkungen am Schluß des § 25. zeigen die Formeln (4) folgendes:
In (17) sind yg, yi—g, yi — %2g reell und positiv,
„ (18) „ yt^yr^g; yi-*2? „ „ „
„ (19) „ yi;tyi-g, t-yi-x2? „ „ „
„ (20) „ yi-t, yi-%2g „ „
und yg hat auf keinem der Integrationswege ein Maximum oder
Minimum. Es können daher K, K' durch die vier folgenden
reellen Integrale mit positiver Quadratwurzel erklärt werden:
00
1 f di_______________
2jyg(g_i)(x2g-i)’
1
*2
1
X*
1 f di
2j yg(g_ i)(i- x2g) ‘
1 f dj ,
2J yg(i _ g)(i _x2g)
0
0
1 f_______di______
2j y_g(i_g)(i_xsg)
- 00
§ <3.
Die Jaeobischen Funktionen &(y), H(v).
141
§ 43. Die Jaeobischen Funktionen ®(v), H(v).
Wenn man die ^-Funktionen der Variablen u als Funktionen
von v betrachtet, so erhält man die Jaeobischen ©-Funktionen.
Wir setzen
«oi (2^, = ®(v),
^11 (2^, ra) = H(y).
Es sind dann ®(v), H(y) als Funktionen t(v, 2K. 2K’) zu be-
zeichnen, und nach § 25 ist
®(y) = 1 — 2gcos-=r- -|- 2 g^cos -2q9 cos —=—|--
(2) Ä
H(v) = 2ä4sm^ —22*sm^^-4-234 sm^y---------------
7t Kr
q = e
Nach § 21 (8) ist
__ 7t Kf I Ttiv
H(y) =—ie iK ™ ®(v + iK'),
W itK' Ttiv
®(y) = — ie iK + 2Z H(y + iK').
Ferner:
#00 fö-^’ ~ 4~
(0 (
».. (5^, ») = H{V + K),
wonach, mittels der Formeln (3), (10), (15) des vorigen Para-
graphen und (5), § 23:
^'(0)
_ 0(0)
©(£)’ F — ®(K)'
0(0) = ^(-K) =
_ 0(0) H(^) _ 1/2x/Ä-
© (K) ]/ 3T ’
endlich die Darstellung der elliptischen Funktionen:
142
Vierter Abschnitt.
§ 44.
(6)
®(y)
H(y 4- -K) _
®(y)
®(y 4- K) _
®(y)
fic sn?;,
l/-^- cnv,
1 ,
-7= dnu
y%'
Die Funktionen ®, H haben, wie aus (3) leicht folgt, die
durch die folgenden Gleichungen ausgedrückte Periodizität:
® (y 4- 2 n K) — ® (y),
n-rtK' rtinv
®(y 4- ‘IniK') = (—l)Me E z ®(y),
H(y 4- 2nK) = (—l)«H(t>),
f ö') w2 n K9 Ttinv
H(y + ‘IniK’) = (— s H(y).
Es ist bisweilen nützlich, die Gleichungen (3), (7), (8)
folgendermaßen zusammenzufassen:
Ttinv
(9) 4- niK'} = vp(y),
worin, wenn n gerade, <5 und 3’’ beide gleich ® oder beide
gleich H, wenn n ungerade, 0 = ®, ?P = H oder 0 = 17,
’P’ = ® zu setzen ist.
Aus § 22 (2), (4) ergeben sich die Additionsformeln:
fl 01 @ 4 + 4 ® 4 — f) = ®2 (M) ®2 4) — (w) -ED 4),
1 ) ®2(ff)H(u -j- v)H(u — v) — H2(u)®2(y) — ®2(u)H2(y\
wofür man auch schreiben kann:
(11)
@2 (0) ® (u 4* v) ® (M — f) = ®2 (w) ®2 4) (1 — sn2 u sn2«),
®2(ff)H(u 4- v)H(u — v) = @2(w)@24)%(sn2w — sn2t>).
Wir gehen nun dazu über, die Sätze über die ^Funktionen
auf die elliptischen Funktionen zu übertragen und beginnen mit
dem Additionstheorem.
§ 44. Additionstheorem der elliptischen Funktionen.
Aus den vier & - Funktionen lassen sich im ganzen zwölf
Quotienten bilden, die nach § 42 durch elliptische Funktionen
ausdrückbar sind. Bildet man diese Quotienten für das Argument.
u 4- so kann man diese nach § 22 durch ^--Funktionen von u
und von v einzeln, also auch durch die entsprechenden ellipti-
schen Funktionen darstellen, und zwar immei- so, daß der Nenner
Additionstheorem der elliptischen Funktionen.
143
§ 44.
nur Quadrate von fr enthält, also rational durch sn2u, sn2-y aus-
gedrückt wird. Nehmen wir, um ein Beispiel durchzuführen, die
Formel (5), § 22, und dividieren sie einmal durch (1) und dann
durch (4) (indem wir das erste Mal iu (5) v in —- v verwandeln),
so folgt:
»oi »io »n (w 4- v)
»0 0 »00 ('M “l“ &)
_ »00 («) »11 (U) »01 (y) »! o (y) -4- (w) »10 (w) »00 (y) fru (y)
»00 (M) ^0 0 0) + »11 (w) ^11 0)
»10 »00 (w ~|~ v)
»oi »il(w + f)
_ »oo (m) »h (m) »01 fo) »10 (y) — »01 (y) »10 (u) »oo (y) »11 (t>)
0?i(w)»?i(f)-»o2i(M)0ii0
und wenn man u, v ersetzt durch u:2K, v:‘2K, so kann man
nach § 42 (10) alles durch elliptische Funktionen ausdrücken.
Man erhält so
sn (u v) __ dnusnucnvdnvsnvcnu
dn(w v) dn2udn2v x'2 x'2 sn2 u sn2 v ’
dn(u -|- v) dnusnucnv — dnvsnvcnu
' sn (u + v) sn2M — sn2v
Auf demselben Wege erhält man aus den Formeln (6), (3),
(4); (7), (2), (4); (8), (2), (3); (9), (1), (2); (10), (1), (3) des § 22:
(3) sn (u + v) cnusnudnv 4- cnvsnvdnu
cn(u v) cn2wcn2t> — x'2sn2wsn--y ’
(4) cn (u v) cnusnudnv — cnusnvdnu
sn (u v) sn2u — sn2v ’
(5) sn (u «>) snucnvdnv snvcnwdnw
1 — x2sn2Msn2v ’
(6) 1 snucnvdnv — snvcnudnu
sn (u v) sn2w — sn2v ’
(?) cn(u -|- v) cn u cn v — sn u sn v dn u dn v
1 — %2sn2usn2v ’
(8) 1 cnucnv sn«sn-ydnudn-w
cn(u v) cn2ucn2i> — x'2sn2usn2v ’
(9) dn(u v) dn u dn v — x2 sn u sn v cn u cn v
— 1 — x2sn2usn2v
144 (io) Vierter Abschnitt. § 44.
1 dnttdnv 4~ z2snttsnt>cnticn® dn2udn2v 4~ 5(2 sn2 w sn2 v ’
dn(w + v)
(11) dn(u + v) dnwdnvcnttcnv 4~ *'ssnM8nt>
cn(M + v) cn2Mcn2v — %'2sn2usn2i; ’
(12) cu(m + v) dnwdnvcnucnv — x'2snusnv
dn(M + 4 dn2 u dn2 v 4- ^2 x'2 sn2 u sn2 v
Man kann noch mannigfache andere Formeln auf dieselbe
Weise herleiten, unter denen wir die folgenden drei anführen, die
sich durch Division von § 22 (4), (3), (1) durch (2) ergeben.
(13) sn (u -|- v) sn (u — v)
(14) cn(« 4“ v) cn(u — v)
(15) dn(M -|- v) dn(u — t?)
sn2M — sn2-y
1 — x2ns2usn2v ’
cn2wcn2i-’ — x'2sn2Msn2i;
1 — %2 sn2 w sn2 v ’
dn2udn2-y 4~ x2x'2 sn2usn2v
1 — %2 sn2 m sn2 v
sn (m v) =
(16) cn(w v) =
dn(M -4- v) =
Die wichtigsten unter diesen Formeln sind (5), (7), (9), aus
denen sich, wenn auch durch weitläufige Rechnungen, die übrigen
alle herleiten lassen. Der Übersicht halber setzen wir sie noch
einmal her:
sniicnvdnv snvcnwdnw
1 — x2sn2Msn2v ’
cnwcnt; — snwsnvdnMdnu
1 — x2sn2Msn2v ’
dnudnu — x2snwsnt>cnttcnv
1 — x2sn2Msn2u
Indem man je zwei dieser Gleichungen kombiniert, kann man
ihnen unter anderen die Formen geben:
cn(M v)dnwdnv — dn(w -f- v)cnucnu = —x'2snusnv
dn(w -|- v) snM cnv —sn (m -|- v) dnw = —cn«®,
sn(u ®)cn« — cn(u 4- v)snudnv = dnusnv,
cn(u 4- f)cnu 4~ sn (M f)snMdnv = cnv.
Wir wenden die Formeln (16) zunächst an zur Feststellung
der Periodizität der elliptischen Funktionen, die sich natürlich
auch aus § 21 herleiten läßt. Setzt man in (16) v = +K,
v = K 4- iK', so folgt aus § 42 (16):
§ 44. Additionstheorem der elliptischen Funktionen. 145
/ । । cn u
sn (u + K) = + ,
v — 7 ~ dn «
z1o\ r i — «'snu
(18) cn(M±X) = +-a^-,
dn(u + K) =
' — 7 du«
/ । 7^. । • T7~f\ _ 1 dn u
sn (u 4- K 4- iK') =---------,
- 7 x cnu
(19) Cn(«-(- K-\-iK') =
, , „ । . ix'snu
dn(u + K + 4.87) = ——,
vH w
und wenn man in (19) u in u — K verwandelt:
sn (u 4- i K") = —---—,
' ' 7 x snu
znn. / i i änu
(20) cn(u + iK') = — - —-,
zV oll w
T / | T7‘t\ _____ ‘ 'M
dn(u + iK} — —i-----------♦
v 1 7 snw
Die Formeln (20) zeigen, daß die drei Funktionen snw, cnu,
dnu für u = iK' unendlich werden. Bildet man die Quotienten
je zweier von ihnen, so folgt:
... sn u
hm ----- = i
cnw „ .
(21) für m = iK'.
' 7 ,. sn m
hm — = i
dnu
Mit Hilfe der Relationen (18), (19), (20) kann man aus jeder
Additionsformel drei andere ableiten, indem man u durch u -|- K,
u-\-K-\-iK’, u-\-iK' ersetzt, also die Vertauschungen macht,
die in folgender Tabelle zusammengestellt sind:
snu, CHU, dnu,
cnu — n' snu x'
dnu ’ dnu ’ dnu ’
1 dnu ix' ix' snu
n cnu ’ XCHU ’ cnu ’
1 — tdnu — icnu
xsnu ’ Weber, Algebra. III. xsnu ’ snu ’ 10
146
Vierter Abschnitt.
§ 44.
und dieselben Vertauschungen auch auf sn (u + v), cn (w 4- v),
dn (m + v) anwendet. So ergeben sich z. B. die zwölf Formeln
(1) bis (12) aus den drei Formeln (16).
Wendet man diese Vertauschungen auf die Relationen (18),
(19), (20) selber an, so ergibt sich:
sn (u -|- 2JT) = —snu, sn(u ‘liK') = snu,
(22) cn(w 2.5?) — —cnu, cn(u 2ijß7) = —cnu,
dn(u 2JT) = dnu, dn(u 2iW) = —dnu.
Die gemeinschaftlichen Perioden dieser drei Funktionen sind
also 4=K, außerdem hat aber snu die Periode 2iZC,
dnu die Periode 2ZC, cnu die Periode 2jK’-|- 2tZf'.
Wir geben nur dem Satz über ©-Funktionen (§ 21) einen
anderen Ausdruck, indem wir den folgenden Satz aussprechen:
Jede doppelt periodische Funktion von v mit den
Perioden 2A, c2,iK' (die überall den Charakter einer
rationalen Funktion hat) ist, wenn sie eine gerade
Funktion ist, eine rationale Funktion von sn2v, und
wenn sie eine ungerade Funktion ist, das Produkt von
sn»cn»dnt> mit einer rationalen Funktion von sn2u
So kann man jeden Satz, der sich auf homogene Funktionen
nullter Ordnung von ff-Funktionen bezieht, in einen Satz über
elliptische Funktionen verwandeln,- und erhält daraus wieder ent-
sprechende Sätze über elliptische Integrale. Man erkennt sofort,
daß die Additionsformeln (16) keine anderen sind, als die For-
meln (17) des § 13 im ersten Abschnitt. In derselben Weise liefert
uns die Transformationstheorie der ff-Funktionen eine Lösung des
Jacobischen Transformationsproblems der elliptischen Integrale,
wie wir es im § 8 dargelegt haben.
Wir wollen dies an den beiden Haupttransformationen zweiter
Ordnung nachweisen, die wir im § 32 ebenso wie im § 9 als
Gausssche und Landensche Transformation bezeichnet haben.
Nach § 32 ist für die Gausssche Transformation
,,,, 8,1 (°' 2) *'(*' v) = 2 »„(«)»„(«)
0, ^) ».<(«,-J) 8*"<“) +
0 — Y —
’ 2/ _ 2 0-jo^oo _ 2y%
2 “ ^0 + ~ 1 + *’
§ 45. Die lineare Transformation der elliptischen Funktionen. 147
(25) tf00 (o, + = (1 4- x)
Nach § 42 erhalten wir also eine Beziehung zwischen ellip-
tischen Funktionen mit zwei verschiedenen Moduln, und es ist,
wenn Z, L, L' aus x, K, K' durch die Vertauschung ^co,
hervorgehen, nach (23), (24), (25)
(26) z = L = Z' = (1+x)Z'
(27) sn [(1 x)v, Z] =
v ’ LV I / > J i XSI12V ’
wenn der Deutlichkeit halber der Modul unter dem Funktions-
zeichen sn als zweites Argument mit aufgeführt ist.
Für die Land en sehe Transformation ist
#n (2 u, 2 co) 01O (u) 0n (u)
001 (2 u, 2 co) 0 oo (u) 0oi (t<)
0O1 (o, 2 cop _ 2 000^01 _ 2y'7
0oo(O, 2<d)2 — 0§o+^l ~ l + %”
2 02o(O, 2«) = (l + ^')02o,
daraus, wenn Z, Z', L, L' durch die Vertauschung (co, 2 co) aus
x, x' K, K' entstehen:
(28) r = VÄ =
2L = (1 + x') K, L' = (1 + x') K1,
Zonv r/i I 'V 11 (1 + X')snvcnv
(29) sn [(1 + x') v, Z] = ,
und in (26) bis (29) erkennt man nach § 42 die Formeln (2)
und (4) des § 9.
§ 45. Die lineare Transformation der elliptischen Funktionen.
Die Einwirkung der linearen Transformation auf die ellip-
tischen Funktionen übersieht man am besten aus der Darstellung
durch die ö-Funktionen. Man erhält aus (4) oder (10), § 42 und
den Formeln (4), (6) des § 37:
10*
148
Vierter Abschnitt.
§ 45.
cox 2 Ku 6(u) 2K Sn co1 0ol(u)’
(1) 2 Ku 0io(u) CH — “ \ * G?1 ÖO1 (u) n 2jK"'W ^00 00 COi ~ 0O1(M)’
oder auch, indem man von der Homogeneität der 0-Funktion
Gebrauch, macht [§ 37 (8)]:
0 (t>, 2Ä, 2iK')
en-»------1------------
(2) “ öOi(v, 2K, 2iK')' 0lo(v, 2K, 2iK') nn — *v V ' ' ~ öoi(f, 2Ä, 2iK'Y
,u„ ___ <?oo(% 2iK')
0ol(v, 2K, 2iK')
Die auf der rechten Seite von (2) vorkommenden 0-Funk-
tionen hängen nur von den beiden Variablen v, co ab und es
kommt zunächst darauf an, die Änderung dieser Funktionen bei
Anwendung der Fundamentaltransformationen
(<o, <0 + 1), (g), — P)
zu bestimmen. Wegen
n = 2 K, 2iK' = 2eaK
erhält man aus § 31 (6) und (11) die entsprechenden Änderungen:
<0, 2JF, 2iK', v!,
<0 2k'K, 2n\K-]-iK'), v! ’
1 co ’ 2K', 2iK, X.
Setzt man für den Augenblick:
f(y, co) = 0(% 2Ä, 2iK'),
so ergibt sich:
f(y, co 1) = 0[% 2z'K, 2%'(7f -|- iK')]
= 6(y, 2%'K, 2x'iK') [nach § 35 (7)]
= %'0 Q, 2K, 2iK'^ [nach § 37 (8)],
f (v, — — 0 (i>, 2 K', 2iK)
= 6(y, —2iK, 2K') [nach § 35 (7)]
= —i6(iv. 2K, 2iK') [nach § 37 (8)],
§ 45. Die lineare Transformation der elliptischen Funktionen.
149
und wenn man für die drei übrigen 6-Funktionen das ent-
sprechende macht und § 36 (7) berücksichtigt, so erhält man die
folgenden zusammengehörigen Vertauschungen:
ö(v), öoo(f),
£0,
/v\ /v'
öoo(^7l, ö10 ( 77
— tö(w), ö00(iv),
eio (iv).
öoi(^),
tu ’
worin die Perioden 2 K. 2 iK' sind. Daraus folgen nach (2) die
beiden ersten linearen Transformationen der elliptischen Funk-
tionen :
sn
(4)
cn
dn
sn(tt>, x') =
(5)
cn(tt>, x') =
(6)
, snt;
x' -5—,
dn-y
cn v
dnu ’
1
dn-y
. snt;
t-----,
cn v
1
ent; ’
, . dnt;
dn (t v, x') = ——- •
v 7 cn v
Die erste Formel (5) zeigt nach § 44 (21), daß sn(n,x') = 1
wird, wenn v = K' wird. Daraus ergibt sich nach § 42 (17) die
zweite häufig gebrauchte Darstellung für K':
K' = - f •
2j yg(i-g)(i -x'20
0
Aus (4), (5) erhält man die übrigen Fälle der linearen Trans-
formation durch wiederholte Anwendung. Setzt man in (4) iv, v!
an Stelle von v, x und wendet (5) an, so folgt:
(. i %' X . sn v
sn (t x v, — = t x -j—,
\ x / dn-y
1
dn-y ’
cnu
dnt;
(?)
cn
t x
«x®, —
X
150 Vierter Abschnitt. § 46.
'Z' % 1
Ersetzt man umgekehrt in (5) v, x, x' durch x' v, und
% %
wendet (4) an, so folgt:
/. . 1 \ . ,snt>
sn (v, —T ) = ix'-----,
\ x / cn®
dn ( i x'v, —r ) ------------
\ x J cn v
Ersetzt man hierin wieder v durch iv und x, x' durch x
und wendet (5) an, so findet man:
snj^x-y, =zsn®,
womit die sechs Klassen der linearen Transformationen erschöpft
sind, da eine noch häufigere Wiederholung zu keinen neuen
Formeln Anlaß gibt.
§ 46. Die Weierstrasssche ^-Funktion.
Die linearen Transformationen der elliptischen Funktionen
legen es nahe, eine elliptische Funktion zu suchen, die, wie die
ö-Funktion selbst, den linearen Transformationen gegenüber un-
veränderlich ist. Um eine solche Funktion zu bilden, setzen
wir zunächst die Gleichungen (1) des vorigen Paragraphen in
folgende Form:
01o(m) __ 2K ent;
0(u) ~~ sn® ’
/.x 0QO(u) __ 2K~ dnr
' 0 (u) cü1 sn v’
0oi(u) ‘2K 1
0 (u) co, sn v ’
worin zur Abkürzung
2 Ku
v — --------
«i
gesetzt ist. Hieraus schließt man mit Hilfe der Relationen
(2)
§ 46. Die Weierstrasssche p-Funktion. 151
cn2v = 1 — sn2«;, du2?; = 1 — x2snsv,
ö?>i w 4o W _ 4 A4
ö2(m) ö2(u) — «1 ’
O2! W eoo (M) — —
62 (u) ö2(u)
Es lassen sich daher drei von u unabhängige (also nur von
»j, co2 abhängige) Größen G, ®3 so bestimmen, daß
ZOX ^10 (M) 1 e _ °oo (M) 1 c 62W 1 62W Ö01 (M) 1 Z x > = «"(») +‘, =
worin p (u) eine durch (3) neu definierte, doppelt periodische
Funktion ist. Die Größen elt e2, e3 können irgend welche sein,
wenn sie nur den Bedingungen
(4) e3 -- 1 e2 e3 ----- ^2 x
genügen. Es steht uns also frei, zur völligen Bestimmung der-
selben noch die Bedingung
(5) hinzuzufügen, drücke: g 4~ e2 4~ es — o Dann ergeben sich für et, e2, es folgende Aus- 4Z2 1 4- *'2 ^1 = 9 5 <> C&L 3
(6) 4 K2 v.>2 — z2 C2 r- 2 d » 4W2 1 -4- v2 n2 a
Die Funktion p (w), welche die Perioden co2 besitzt, wird
hiernach durch (1) ausgedrückt:
( ) ^(M) \sn2i> 3 /
Die Funktion p (u) hat die gewünschte Eigenschaft der ün-
veränderlichkeit bei linearen Transformationen, wie man aus dem
Ausdruck
/ox 1 ööo(M) 4- ÖqiW -j- ö|0(u)
(8) pW - 3 ^W
erkennt.
Infolge von (3) vertauschen sich die eu e2, es bei einer linearen
Transformation in derselben Weise wie die ö10, o00, 601 ; eine sym-
metrische Funktion derselben ist daher bei einer linearen Trans-
152
Vierter Abschnitt.
§ 46.
formation ungeändert und wird eine Invariante genannt. Es
gibt deren zwei fundamentale, die wir mit g2, g3 bezeichnen:
(9) Ä = — 4(e2e3 + e3e! + = 2(e,2 + e22-|-e32)
98 jV6
(10) g3 = 4e1e2e3 = -^-(2 + x2x'2)(x'2 _ %2)t
und wir fügen noch die unter dem Namen der Diskriminante
bekannte Funktion bei:
(11) <? = («, — «,)>(«, — «,)•(«, — «,) = Afj,« _ 27;/;)
COj
wofür nach § 43 (3), (15) und § 34 (2) auch gesetzt werden kann:
28jr12^(co)24
fp (w), /73, sind homogene Funktionen, wie folgende Rela-
tionen zeigen, worin Ä ein willkürlicher Faktor ist.
Acoj, Ä coa) = Ä-2^(w, rax, <x>2),
g?'(Au, Äcox, Zra2) — Ä_3^?'(u, cox, co2),
(13) = ^~4f/a(®n «2),
<73(A<Dj, A go2) = A eg3(jx>1,
Cr (A con Ä co2) = 12 G (cox, co2).
Setzen wir, wie in § 45 (2)
cox = 2 K, co2 = 2 i K',
so wird
1 + x'2 x'2 — x2 1 4- x2
ei — 3 , e2 — § , e3 _ g ,
f!41 4 4
k 7 9t = ö(l — 91 = — O(2 + K2*'2),
O ZI
G = x4x'4.
Wenn wir coj aus den allgemeinen Ausdrücken (9), (10), (11)
für g2, g3, G eliminieren, so erhalten wir homogene Funktionen
nullter Ordnung, also Funktionen von co allein, die bei linearen
Transformationen ungeändert bleiben. Solche Funktionen
sind gl :G, g^'-G. Wir heben unter diesen Funktionen, die sich
alle aufeinander zurückführen lassen, eine hervor, die wir mit
§ 47.
Die elliptischen Transzendenten zweiter Gattung.
153
.)(<») bezeichnen und schlechtweg die Invariante nennen und
so definieren:
(15)
J(<») = 2s
woraus wir erhalten:
(1 — X2x'2)3
x4 x'4
(16)
4-27ff/
G
= j(v),
.27.27g2 = _ 27. ß4 = 64.(2+ x2x'2)2(x'2-x2)2
x4x'4
Als Funktion von x2 betrachtet, hat die Funktion j(<x>) die
Eigenschaft, ungeändert zu bleiben, wenn x2 durch einen der
sechs Werte
„ 1 1 x2 x'2
’ ’ x2’ x'2’ x'2 ’ X2
ersetzt wird.
Wenn wir nach (7) den Differentialquotienten der Funktion
(u) bilden, so erhalten wir
//„a _ 16 AS8 cn«dn« _ o ^oo (u) g10 (u) <?01 (u)
( ) ^ ( ) co( sn3« ö(u)3
und daraus nach (3):
(18) p'(u)2 = 4[p(u) - ej][^(u) — e2][^ (u) — <?s]
— 4 P (w)s ^2 p (M) (Jz,
oder endlich
<7 ej
(19) du = -----* ,
V4^3 — g2 p — g3
woraus man ersieht, daß die Funktion p (u) in derselben Be-
ziehung zur Wei er strass sehen Normalform des elliptischen Diffe-
rentials steht, wie die Funktion sn« zu der Legendreschen.
§ 47. Die elliptischen Transzendenten zweiter Gattung.
Jacobi hat als Transzendente zweiter Gattung die Funktion
11 11 @(«) dv
eingeführt. Die Beziehung dieser Funktion zu den elliptischen
Integralen zweiter Gattung ergibt sich aus der Formel (16) des
§ 23, wobei gleich bemerkt sei, daß ganz ähnliche Betrachtungen
an die dortigen Formeln (15), (17), (18) anzuknüpfen wären, die
aber nicht zu wesentlich neuen Resultaten führen.
154
Vierter Abschnitt.
§ 47.
Setzen wir dort v: 2 K an Stelle von v, so ergibt sich aus
§ 42 und 43:
(2) ;
<72log@(«) _ 1
= tU ~ 1 + dn2«-
4 *1/ oi
dv2
9oi
--------x2sn2«
'O’oi
Wir setzen
(3)
, ö’o'l
4j5?t>01
und erhalten durch Integration von (2)
V
d\og&(v) . E , f , „ ,
---§—— Z(v) =------------^v 4- dn2t?<7«
dv ' 7 K ' J
o
oder indem wir
(4) E(v) = j dn2«<7«
0
setzen:
(5) Z(y) = E(y) - = dn2v - Jl-
Die Funktionen @(v) und &(y -|- K) sind gerade Funktionen
und daher ist ®'(0) und ®’(K) == 0. Wenn wir also in (5)
v = K setzen, so folgt:
K
(6) E = | dn2v<Zv.
o
Führt man noch für dv das Differential
1 dt,
2 -|/£(1 - £)(1 - x2g)
ein [§ 42 (8)], so erhält man für E(y) ein elliptisches Integral
zweiter Gattung (§ 11):
(7) E(v) = f —-c?^1-x2g) ,
0.
(8) E = - f_______dg(l — x2g)_______
U 2 J V&(1 — 0(1 — ^0’
0
wo letzteres Integral in demselben Sinne zu nehmen ist, wie
§ 42 (17).
§ 47. Die elliptischen Transzendenten zweiter Gattung. 155
E(v) und Z(y) sind ungerade Funktionen des Arguments.
Aus dem Additionstheorem der ©-Funktion [§ 43 (11)] ergibt
sich durch logarithmische Differentiation:
/n. , . , ' , nr7, x 2x2sn2t:snticntidnti
(9) Z(« + «) + Z(« - ») = 2 Z(«) - .
(10) Z(« + <) - Z(u - <.) = 2 /(<) - 2 .
v ! v 1 7 ' 7 '7 1 — z2sn2u sn2t;
Hierin kann Z auch durch E ersetzt werden und durch
Addition ergibt sich [§ 44 (16)]:
(11) Afw) -|- E(v) — E(u -]-«) = x2sntisnt:sn(ti -|- v).
Hieraus erhält man die Periodeneigenschaften der Funktion
E(u), wenn man v — + 2£, K -|- iE' setzt. Man kommt aber
auch auf folgendem Wege dazu.
Aus der ersten Gleichung § 43 (3) folgt:
= Z(» + iK') + ij,
av ' 71 2jx
und demnach aus § 43 (6) und § 42 (11):
ent: dnt: in
Z(v 4- iK1 = Z(v) -]------- —
v 1 7 v 7 1 snt: 2W
w x x2snt:ent:
Z(, + ^) = Z(t:)—-
man in der ersten dieser Formeln v = K setzt:
z(Ar+tW') = -^J.
(12)
und wenn
(13)
Durch zweimalige Anwendung der Formeln (12) [mit Rück-
sicht auf § 44 (18), (20)]:
(U) Z(t: + 2^') = Z(t:)-^,
Z(t:4-2W) = Z(v).
Überträgt man diese Gleichungen auf die Funktion E(v),
so folgt:
। • tz-m 7->z x , cnvdnt: , iEK' in
E(„ + tK') =£W + _——
(15)
(16)
77Z I n-77A 7-1Z X 1 HER' in
E(y ~[-.2iK) — E(y) ------------
E{v + 2 K) = E(y) + 2E.
156 Vierter Abschnitt. § 48.
Wenn wir in (15) v = K setzen und eine Größe E' durch
die Gleichung definieren:
(17) E(K + iE') == E + i(K' — E'),
so erhält man die unter dem Namen der Legendreschen Rela-
tion bekannte Formel
(18) EK' + KE’ — KK' = %
Die Bedeutung der hier eingeführten Größe E' erkennt man,
wenn man die Legendresche Relation auf einem zweiten Wege
ahleitet, mit Benutzung einer der linearen Transformationen.
Es ergibt sich, wenn man in § 31 (11) setzt:
___________________ v ________________ iK’ u _ v
U ~________________________________~ JT’ ä ~
nach § 43 (1), (4):
n v2
(19) fEe~T™r &(iv, x') = + K),
und daraus durch logarithmische Differentiation
(20) iZ(iv, x') =
oder nach § 43 (6)
(21) iZ(iv, x') =
Es ist aber nach (5)
. <7Z(f«,x') E'
«---j------- = — dn2 G«, x
dv v ’ ' K'
wenn jetzt E' die Bedeutung hat:
K'
(22) E' = J dn2(«,x')^«,
V
also aus E durch Vertauschung von x mit x' hervorgeht. Setzt
man aber in (21) v = 0, nachdem man zuvor differentiiert hat,
so ergibt sich wiederum die Relation (18), woraus folgt, daß E'
beide Male dieselbe Größe ist.
§ '48. Die elliptischen. Transzendenten dritter Gattung.
Wenn wir die Formel (10) des vorigen Paragraphen:
®'(u -|- v) &'(u — v) _____ . 2x2sn2«. snvcnvdnv
& (u -|- v) ®(u — v) ' 1 — x2 sn2 u sn2 v
2KK' + H(y 4- K)
uv , rrr \ i dlogcnv
ÜK' + Z(”> +
§' 48. Die elliptischen Transzendenten dritter Gattung. 157
in bezug auf u integrieren, so folgt:
u
1, ®(u— v) . . f z2sn2iisii»cn»dii» ,
(1) TjlogTv)--;---( 4~ WZ(«) = ----------------du,
k 7 2 ° ®(u 4“ v) v 7 J 1 — x2sn2usn2«
0
und wir können noch die auf gleiche Weise [aus § 43 (11)] her-
zuleitende Formel:
u
1 . H(v — u) , . f sn»cn»dn»(G
(2) — log tt4—;—( 4- uZ(v) = —-------------—
v 7 2 ° R(y u)' 7 J sn2w — sn2«
o
hinzufügen, die übrigens auch aus (1) abgeleitet werden kann.
Wir setzen nun mit Jacobi
u
, ' „ , . f x2 sn2 u sn v cn v dn v ,
(3) H(w, V) = ------5--z----;-- du,
v 7 v 7 J 1 — %2sn2usn2«
0
und. nennen ü(u, v) die Transzendente dritter Gattung mit
dem Argument u und dem Parameter v. Ersetzt man du durch
den Ausdruck:
_________dt,________
2 y^(i — g) (i — %2o
und sn2« durch g, so ergibt sowohl (1) als (2) ein elliptisches
Integral dritter Gattung, wie wir es in § 11 kennen gelernt haben.
Aus (1) folgt zunächst
(4) II (u, «) — uZ(y) = II (y, u) — vZ(u),
oder der Jacobische Satz über die Vertauschung von Argu-
ment und Parameter.
Die Funktion H(u,v) verschwindet, wenn v = K oder
« = ist, weil für den ersteren Wert cn«, für den
zweiten dn« gleich Null ist. Setzen wir daher diese Werte für u
in (4) ein, so folgt
n(K, «) = KZ(y)
(ö) II (K 4- iK', v) = (Ki K')Z(y) 4- [§ 47, (13)],
wodurch die vollständigen Integrale dritter Gattung auf die
zweite Gattung zurückgeführt sind.
Wir wollen noch das Additionstheorem der II-Funktion ab-
leiten, das Jacobi in den Fund, nova art. 53—55‘) in ver-
*) C. G-. J. Jacobis gesammelte Werke, Berlin 1881, Bd.I, S.204.
158 Vierter Abschnitt. § 48.
schiedenen Formen gibt, die nur mühsam aufeinander zurück-
führbar sind. Zunächst erhalten wir aus der Definition (1), wenn
wir den Parameter jetzt mit a bezeichnen:
II (w -j- v, d) — n (u, a) — a)
(6) 1. 0 (u -l- v — a) 0 (u a) 0 (v 4- a)
= 2toeä(u + » + o) C(,. — 4^(4 —4*
und es handelt sich noch darum, den unter dem Logarithmus
stehenden Ausdruck durch elliptische Funktionen darzustellen.
Dies geschieht zunächst leicht, wie an der erwähnten Stelle
der Fundamenta, mittels der Formel [§ 43, (11)]:
O2(0) O(vt v)0(u — v) — 02(u) 02 (v)[ 1 — x2 sn2 u sn21>],
wenn man darin für u, v setzt « i «, v + dann + a, u -|- v + a.
Man erhält so:
<92(0) 0(u v + 2 d) 0(u — v)
= @2(u 4- d)02(v + a)[l — x2sn2(u + a)sn2(v + «)], •
@2(0) @(u -j- « + 2 «.) 0(«, + t:)
= 02(a)02(u v i u)[l — x2sn2asn2(u v + a)],
woraus folgt:
0(u -|~ v — a)0(u d)0(v a)
0 (w -|- v a) 0 (u — a)0(y — a)
[1 — x2 sn2 (u — a) sn2 (y —«)] [1 — x2 sn2« sn2 (u -I- « 4~ «)]
[1 — x2 sn2(u-|- a) sn2 (v-|-«)] [1 — x2 sn2 asn2(u -|- v— «)]
Einen zweiten Ausdruck erhält man aus der Additionsformel
(13), § 22, die mau so darstellen kann:
0(0) 0(u + d)0(v + a) 0(u -|- v)
= 0(u) 0(d) 0(a) 0(u-|- v ± a) [1 + x2 sn a sn usn v sn (u -|- v + «)],
woraus durch Division:
®(u-(-v—d)0(ud)@(^q)_________l-)-x2snasnwsnvsn(u-|-«-|-a)
0(u-1-v-1-a)0(u—d)0(v—a) 1 —x2snasnwsn«sn(u-|-«— a)
Jacobi gibt noch einen dritten Ausdruck für die ©-Quo-
tienten in (6):
§ 48.
Die elliptischen Transzendenten dritter Gattung.
159
Die direkte Überführung der drei Ausdrücke (7), (8), (9) in-
einander gelingt am einfachsten, wenn man von der von Jacobi
zuletzt gegebenen Formel ausgeht:
1 — x2 sn (a u) sn (a — u) sn (a -|- i>) sn (a — v)
(10) ____ (1 — x2sn4a)(l—‘ z2 sn2 u sn2«)
(1 — x2 sn2 a sn2 w) (1 — x2 sn2 a sn2 v)
Die Verifikation dieser Formel ist darum leicht, weil man
mit Hilfe von § 44, (13) rechts und links rationale Funktionen
von sn2«, sn2« erhält, deren Identität unmittelbar ersichtlich ist.
Ersetzt man in dieser Formel
m, «, a
durch
W - V U -I- V . U V
so ergibt sich
1 + z2snwsn«snasn(w v + a)
r o /u- —i— «\i 14 o /w—«i \~|
1 — X2sn*( -\ 1 — x2sn2(—jsn2( —+ aj
1—x2sn2(—-—Isn2—— 1 —%2sn2(—4—)sn2(—)
und wenn man die beiden hierin enthaltenen Formeln durch-
einander dividiert, so ergibt sich die Übereinstimmung von (8)
und (9).
Setzt man in (10) v = w, so ergibt sich:
(11) 1—x2 sn2 (a -|- w) sn2 (a — u)
Ersetzt man hierin
a
zuerst durch
u -4-.v ,
~2 -
sodann durch
w + v
2 -
(1 — x2 sn4 a) (1 — x2 sn4 u)
(1 — x2sn2asn2u)2
u
u 4- v
2“’
u — v
~2~’
so ergeben sich vier Formeln:
1 — x2sn2asn2(u 4“ v i a)
£1 — x2sn4 ± (1 — x2 sn4 M
[1 — x2sn2(U~^V ± a\sn2-+--l
L \ J
160
Vierter Abschnitt.
§ 49.
1 — x2 sn2 (u + a) sn2 (y + a)
1 — x2 sn4 (—+ a \ I ( 1 — x2 sn4 —-— j
r, „ , \ „/«—t>\i2 ’
11 — x2 sn2 ( ~~2— i a)sn2( —2— /
woraus sich die Übereinstimmung von (9) mit (7) ergibt.
§ 49. Die Transzendenten zweiter und dritter Gattung
von Weierstrass.
Es sind nun noch die Transzendenten zweiter und dritter
Gattung in der Wei erstrass sehen Form aufzustellen. Zu der
ersteren gelangen wir ähnlich wie in § 47 durch zweimalige
Differentiation von logö(u). Es ergibt sich so aus
(1)
>11M'2 ^11 ( )
4«)=«,,^ -n)17- [§ 37, (4)],
''n
(ülog
\G>i/
<Z2 log 0 (u) 2
du2 g)1
d w2
7WT [§23’ <18)]
^00
<»! COf ö’oo
frÄ -
\®i/
und also, wenn man den ft-Quotienten nach § 42 durch elliptische
Funktionen und diese nach §46 durch die ^-Funktion ausdrückt:
<72log<5(w) . .
worin A eine Konstante ist. Diese findet man aber, wenn man
die Gleichung nach § 46, (8) so schreibt:
0"(w)0(u) — 0'(w)0'(«) = ^4ö2(w) — 1 [ö0% (u) + 0?J (u) + 0?o («)].
Wenn man hierin zweimal differentiiert und dann u = 0
setzt, so ergibt sich J. = 0 [§ 35, (12), § 37, (5), (7)], und wir
erhalten:
(2) «ö=_pw,
eine Formel, die bei Weierstrass zur Definition der ^-Funktion
dient.
§ 49. Die Transzendenten zweiter u. dritter Gattung v. Weierstrass. 161
Wird also
0^)=
gesetzt, so ist £(w) eine eindeutige Funktion von u, und zwar ein
elliptisches Integral zweiter Gattung:
(4) g(W) = — j^(u)du = -f ....- [§ 46, (19)],
worin die additive Konstante dadurch bestimmt ist, daß £(w)
eine ungerade Funktion sein muß. Die Periodizität der g-Funk-
tion ergibt sich aus den Periodengleichungen der 0-Funktion
[§ 35, (9)]:
/-X £(» 4- Oi) — g(w) = 2^,
''' ' g(u -|- ®2) — £(«) = 2 %•
Es sind also und 2t;2 als vollständige Integrale zweiter
Gattung (analog den E, E1) dargestellt:
w 4- u + w2
(6) 2’ii=—j g)(u)du, 2 = — j fp(u)du
u u
mit der der Legendreschen Relation entsprechenden Gleichung
(7) [§ 35, (10)].
Um die Additionstheoreme für die Weierstrassschen
Transzendenten zu bilden, gehen wir von der 0-Funktion aus.
Für diese erhalten wir aus (1) mit Benutzung der Additions-
formel für ö’n, § 22, (4):
6(u -4- v)6(u —v) . . , .
0(U)2 0(^)2--- = ~ P W’
daraus durch logarithmische Differentiation:
g(M + ,) + g(M _ ,) - 2 g (M) =
—&'(v)
1 ©z(w) — &'(v)
(10) g(M 4-) =:w + + 2 •
Hieraus leitet man durch abermalige Differentiation das
Additionstheorem für die -Funktion her. Man erhält aus (9)
durch Differentiation nach u und v.
Weber, Algebra. III.
162 Vierter Abschnitt. § 50.
g?'z(w) &'(u)2
p(«+.) + p(x-O-2p(«)=-pW_flW+[pW_#)(„)p.
2p'(w) g?'(v)
V TT ) g/k / [g?(w)~g?(0]2
g>"Ü) g/Ü)2
PH-Hpf-Hf(<,) = p(M)_p(„j + [p(o) _ p(„)K
und indem man addiert:
. , . . „ /g/fa)-g>W g/'W—g/'(O
g?(u+«) g?(M) g?(«) g?(u) — g?(«)
Es ist aber
g/(w)2 = 4 (u)3 — g* & (u) — g3,
fp"(u) = 6g?(w)2 — Idz,
p"(u) — g/'<?) = 6[g>2W — g?2(?)l
woraus man erhält:
(11) + i>) + g?W + g><?) = | (^(M) _ ^y) ’
in Übereinstimmung mit der Formel (21), § 13.
Endlich erhält man noch durch Integration der zweiten
Gleichung (9) in bezug auf u:
u
1, . 0(v — u) , 6/ . 1 f p'(v)du
( } 210gö(t> + M) + M?W ~ 2j ^(M)-^(t>)’
0
wodurch ein Integral dritter Gattung vom Argument u
und dem Parameter v durch die 0-Funktion ausgedrückt ist.
Eine andere Form des Integrals dritter Gattung erhält man
durch Integration von (10):
z.aA , «(« + ») pz x 1 f g?'(M) g?'^),,
(13) log \ < — wg(«) = — —au.
v ’ °0(u)0(f) v 7 2J g?(w) —g?(«)‘
§ 50. Entwickelungen der elliptischen Funktionen.
Setzt man in den Entwickelungen der Theta-Quotienten, die
in § 26 abgeleitet und in der Tabelle II zusammengestellt sind,
a = 0, so erhält man, wenn man zunächst die Formeln, die
^•„(a) im Nenner enthalten, wegläßt, die Partialbruchentwicke-
lungen von zwölf elliptischen Funktionen:
§ 50. Entwickelungen der elliptischen Funktionen. 163
sn 2 Ku, cn 2 K u, dn2.Kw,
1 cn 2 Ku dn2.Kw
sn 2 Km ! sn 2 K u ’ sn 2 K u ’
1 sn 2 Ku dn 2 Ku
cn 2 K u ’ cn 2 Ku' cn 2 Ku ’
1 sn 2 Ku cn 2 Ku
dn 2Ku' dn2^w’ dn 2 Ku
So ergibt sich aus der Formel (2), Tabelle II:
&11 -8n>Q) — , _2 iS(— 1)qm ( *____________-____
sr-SuW^io tg * 9 \e-^iu—q.m e^iu—qm)
ni
= cotg itu + 4 sm 2 au >, ---:——,
6 ' 1 — 2</”*cos2%m-|-2
worin m die Reihe der positiven geraden Zahlen 2, 4, 6, 8, ...
durchläuft.
Es ist aber nach § 42, (4)
»io (w) _ #00 cn2Ku
&n(u) ^oi sn27Fii’
und daraus ergibt sich
m
m2Kcn2Ku , , . . o (—l)29m
(1)-----„ = cotg sr u d- 4 sm 2 n u >,,----—-—;—— •
' ’ n sn2 Ku 5 ' 1 — 2 qm cos au -j- g2m
Wenn man in der Formel (2) der Tabelle III das gleiche
Verfahren an wendet, so erhält man:
2tv r» 77 'm! m m!
Ken 2 Ku , . , , vr —5~ •
-------= cotgjrw -4- 4 >,(—l)2 q 2 smsm«.
® sn2Ä« ° 7
Hierin durchlaufen m und w! voneinander unabhängig die
Reihen der positiven geraden Zahlen, und es läßt sich die
Summation in bezug auf m' noch ausführen:
«»' mm’ m
also:
... 2 K cn 2 Ku , . qm
(2)-----------— cotgjru — 4 >.i—r—-snnrfflM.
1 n sn2 Ku ö 1 + 0.
Während aber die beiden, ersten Formeln für alle Werte
von u konvergieren, ist die Konvergenz der dritten auf das
Gebiet beschränkt, in dem der imaginäre Teil von u absolut
kleiner ist als der imaginäre Teil von c?. Die Formel ist also
für reelle u jedenfalls gültig.
n*
164
Vierter Abschnitt.
§ 50.
In der Tabelle IV sind die Entwickelungen für die 12 Funk-
tionen zusammengestellt.
Unter den 16 Formeln der Tabellen II, III finden sich vier,
die den Faktor •9'n(a) im Nenner enthalten, in denen man also
nicht ohne weiteres a = 0 setzen kann. Es sind dies die
Formeln (1), (5), (9), (13). Entwickelt man in diesen Formeln
nach steigenden Potenzen von a, so fangen die Entwickelungen
rechts und links mit a~1 an, und wenn man die von a unab-
hängigen Glieder beiderseits einander gleich setzt, so ergeben
sich die gesuchten Entwickelungen.
Man kann etwa so verfahren, daß man in der Formel (1)
«in —a verwandelt und das arithmetrische Mittel aus beiden
Formeln nimmt. Dann hebt sich rechts das unendliche Glied
1: cotg % a heraus und links erhält man:
frulftnfo + a) — »u(f — «)] _ frufo) fHr „ = 0
2 n 9'11 (v) 9'11 (a) x x (v) ’
auf der rechten Seite von (1) in Tabelle II ergibt sich:
cotgjrw 4?)>|e2niv __________________qmj
, । . x^ omsin2?r??
cogxv+ i _ 2g“cos2?rw-|-g2“’
und auf der rechten Seite der Formel (1) der Tabelle III erhält man
m
q2
6 I 1--qm ’
und wenn man noch die Jaeobisehe H-Funktion einführt,
und u für v schreibt, erhält man
2 log Hf 2 .Km) a . n
(3) ° < = cotg?rw+4sin2?ru » -—ss,
- 7 jt d,2Ku 6 ' '1—22“cos2?ru-)-g“
qm
——, qm
— cotgjru 4 >,-— --------sinmstw.
° 1 1 — q™
Auf der linken Seite steht eine Transzendente zweiter Gattung,
die sich nach § 47, (12) durch die Z-Funktion ausdrücken läßt:
2Ar//n„i 2K cn 2 Ahidn 2 Ku
--------------------------------------^K~u------’
wofür man auch setzen kann:
27f„/r,T. . . dlogsin2Ku
Z(2 Ku) -)-2—j-
n-----------------------71 nau
§ 50. Entwickelungen der elliptischen Funktionen. 165
In der Tabelle V sind die vier Formeln, die sich auf diese
Weise ergeben, zusammengestellt. Subtrahiert man die Formel (3)
dieser Tabelle von den drei übrigen, so ergeben sich Entwicke-
lungen für die logarithmischen Ableitungen der drei elliptischen
Grundfunktionen, von denen wir die eine anführen wollen:
,jXdlogsn2Ä’w dlogsinwM . , . „ (—l)hqh
(4) .— = —----t-4sm2jtu >, ----:—-
v 7 ndu Ttdu 1—2qhcos2nu-\-q2k
__ dlogsin%M qksin2hnu
ndu i _i_ nfe
Entwickelungen für die Transzendenten dritter Gattung
ergeben sich, wenn man die Formeln der fünften Tabelle zwischen
den Grenzen u -|- v, u — v integriert. Man erhält so z. B. aus
der Formel (3) dieser Tabelle:
m
. 1 0[‘2K(u—t?)] y—, , q2
(5) w log —i—vi = — 4 > —y-------------r sm m n u sm m n v.
v 7 2 ®0[2K(w4-t?)] — qm)
Setzt man in den Formeln der Tabelle IV und V u = 0, so
ergeben sich die folgenden Entwickelungen:
m n—1
- 1 + 4^rzpp -1 + 42j ’
n n—1 n
4V = 4V(-l)~gT
n 1 V” 1 — ’
mm n — 1
2^ _ i i p y(~W _ i _ 1V(-l)~y
n ~ 1 + 2“ 1-4-g”
Endlich erhält man eine Entwickelung für das vollständige
Integral zweiter Gattung JE aus der Formel
Setzt man hierin nach der Differentiation v = 0, so folgt:
und mithin nach der Tabelle V, Formel (3):
m
p_____ 2%s y qn ______________ ä2 x-''
— K (1 — g”)2 ~~ K '
Fünfter Abschnitt.
Die Modulfunktionen.
§ 51. Die elliptischen Differentialgleichungen.
Die bisher definierten elliptischen Funktionen sind Funktionen
der beiden Variablen v, a>, und die Moduln %, ferner y(a>),
K, K' sind von dem Periodenverhältnis a>, das einen positiv
imaginären Bestandteil haben muß, abhängig. Ebenso ist die
Funktion £?(«) eine Funktion der drei Variablen «, a^, a>2 und
die Invarianten g2, gs sind von <x>1, a>2 abhängig. Die Aufgabe
der Umkehrung der elliptischen Integrale, wie wir sie in
§ 14 formuliert haben, setzt aber voraus, daß in den elliptischen
Funktionen z2 (oder bei der Weier strasssehen Normalform g^g^)
beliebig gegebene Werte haben, und die vollständige Lösung
dieser Aufgabe verlangt also, daß nicht a>, sondern x2 (bzw. </2, gz)
als zweite unabhängige Variable auf tritt, und daß a> durch diese
ausgedrückt werde. Dieser Aufgabe werden die nächsten Be-
trachtungen gewidmet sein.
Wir gehen aus von der Aufgabe, ein System von Differential-
gleichungen, welches wir das der elliptischen Differential-
gleichungen nennen, zu integrieren:
dx
dv y ’
d g
= —ex,
dv
dz
-j- = —x2xy,
dv
unter den Nebenbedingungen:
(2) für v — 0 soll x — 0, = 1, = 1 sein.
(i)
§ 52.
Die unabhängige Variable
167
Wir haben im vorigen Abschnitt gesehen, daß, wenn
(3) *2 =
9oo
ist, diese Aufgabe durch die elliptischen Funktionen gelöst wird,
und zwar in der Weise, daß x, y, z in der ganzen «-Ebene ein-
deutige und, außer wo sie unendlich sind, stetige Funktionen
von v werden. Ist nun aber %2 gegeben, so entsteht die Frage,
ob es zu jedem Wert von z2 einen der Bedingung (3) genügenden
Wert von to gibt und ob es mehrere solche gibt.
Wir beweisen zunächst, daß durch die Differentialgleichungen (1)
mit den Nebenbedingungen die Funktionen x, y, z eindeutig
bestimmt sind.
Es ergibt sich zunächst aus (1), daß «2 -|- «/2, %2«2 -|- z2
konstant sind, und aus den Nebenbedingungen folgt:
(4) y2 — 1 — x2, z2 = 1 — x2x2.
Angenommen, es existiere ein zweites System denselben Be-
dingungen genügender Funktionen xx, yx, z^ so ist zunächst
y2 = 1 — X*, zf — 1 — %2 xf,
und eine einfache Differentiation ergibt, daß
xy1z1 — xiyz
1 — X2^2«!3
konstant ist. (Das Additionstheorem der elliptischen Integrale,
aus dem man die Form dieses Ausdruckes erhält, wird unmittelbar
durch Differentiation bestätigt.) Aus den Nebenbedingungen folgt
aber, daß diese Konstante verschwindet, also:
^yi^i — x-tyz,
woraus man leicht schließt, indem man beiderseits quadriert:
x — «i, %y = 26, e — zv
§ 52. Die unabhängige Variable z2. Lineare Differential-
gleichung für K.
Wir zeigen nun zunächst, daß und wie man zu einem be-
liebig gegebenen Wert von z2 wenigstens einen der Bedingung
ff4
(1)
voo
genügenden Wert von o finden kann. Diese Frage wird am
vollständigsten beantwortet durch Zurückführung auf eine lineare
Differentialgleichung zweiter Ordnung.
168
Fünfter Abschnitt.
§ 52.
Eine solche Differentialgleichung ist aber in den Formeln
des § 23 bereits enthalten.
Es folgt zunächst aus § 23, (14):
dlogx2 =
oder mit Rücksicht auf
(2) äü20=2.K, 3rff20= = 2x'K [§ 42, (3), (15)]:
(3) ?rd(x2) = 4 i x2 v!i K3 d a>,
und aus § 23, (19):
d dK 4 ,
-j— yö, =----------k3k'2K3.
d (x> K2 d(D n3
Führt man vermittelst (3) für a> die Variable x2 ein, so folgt
d / 2 ,2 dK
y— ( X2X 2 7 , „
und dies ist die gesuchte Differentialgleichung.
Setzen wir weiter
• K'
(5) — = X’
(6) — iK2da = KdK' — K'dK,
so ergibt sich nach (3):
(7)
%2 x'2 (K
dK'
d (x2)
dK \ _ a
Ä Z(^)J — ~ Z’
also durch abermalige Differentiation:
1 d ( „ dK \ 1 . d / ,dK'\
K d(x2)\ d(x2)/ — K' d(x2)\ d(x2)7’
woraus zu ersehen, daß K' das zweite partikulare Integral der
Differentialgleichung (4) ist. . • -
Diese Differentialgleichung läßt sich durch hypergeometrische
Reihen integrieren (Gauss, Disq. circa seriem infinitum Werke,
Bd. in, S. 125).
Setzen wir für den Augenblick x2 =. ar, K = y, so lautet
die Differentialgleichung (4) ,
(8) ar(l — ar) + (1^ 2ar)|^ — = 0,
und sie geht aus der allgemeinen Gaussschen Differentialgleichung
(9) (ar — ar2)^4-[y — (K1)ar]— aßy = 0
§ 52. Lineare Differentialgleichung für K. 169
hervor, wenn man a — ß — y = 1 getzt. Das eine ihrer
partikularen Integrale ist also
(io) i, i,^) = i + i;
und diese Reihe ist konvergent, so lange der absolute Wert von x
kleiner als 1 ist. Als das zweite partikulare Integral kann man
wählen
(11) _F(1, 1, 1, 1-0,
das aber einen anderen Konvergenzbereich hat. Denken wir uns
x als komplexe Variable in einer Ebene dargestellt, so konvergiert
(10) in einem mit dem Radius 1 um den Nullpunkt beschriebenen
Kreise, (11) in einem gleichen Kreise um den Punkt 1 beschrieben,
so daß der gemeinsame Konvergenzbereich aus einem Zweieck
besteht, das den zwischen 0 und 1 gelegenen Teil der reellen
Achse enthält. Man kann aber auch, was für uns wichtig ist,
das zweite partikulare Integral in einer Form auf stellen, die in
demselben Kreise wie die Reihe (10) konvergiert. Dabei ist zu
beachten, daß das zweite partikulare Integral für x = 0 unend-
lich wird.
Dieses zweite partikulare Integral erhält man durch den
folgenden Grenzübergang: Bezeichnen wir die hypergeometrische
Reihe nach Gauss mit
F(^,r,x>=1+^x+^±^±nx.+...
- X* g(« + ^-l)^(^ + ^-l)
- 77(«-1)77(0-1) ^ I7(y + ^-l)D(O
so erhält man im allgemeinen die beiden partikularen Integrale
von (9):
yx = Fx(x) — F(a, ß, y, 0,
y2 = F2(x)=. x1-^ (!'— F(1—a, 1 — ß, 2 — y, x).
Da diese aber für a = ß = %, y = 1 miteinander identisch
werden, so setze man zunächst a = ß = |, y = 1 -|- e, also
?/i =' F& i 1 + ^)<
170
Fünfter Abschnitt.
§ 52.
Es ist aber
•F(|, 4, 1 ± G x) =
77 (±£) n(y-&'
und man kann unter Hinzufügung eines konstanten Faktors als
zweites partikulares Integral auch folgendes annehmen:
±.v w-M -1 i ( x 1 '
2e n(y) L7^(v + £) ' \i — x) n(y — s).
Entwickelt man hier nach Potenzen von s und setzt dann
e — 0, so folgt:
77'(v) 1 . x 1
77(v) — 2 10gl^J’
wofür man mit Benutzung der Gaussschen Formel
n(y — ^n(y) _ ./“2-2V
77(2v) — V 2
mit Abwertung eines konstanten Faktors auch setzen kann:
zi2) v —- io? x
' J \16j LH(i/) 2l gl —d
Es ist aber für ein ganzzahliges positives v:
FA> = ff(o) + ' + i + t + - + i,
und wenn wir also zur Abkürzung setzen:
F(x) = V (JüY
so ergeben sich die beiden partikularen Lösungen der Differential-
gleichung (8), wenn man für das zweite eine lineare Kombination
von (10) und (12) nimmt:
1 1 /r
(14) — F(%),
Um nun aber die partikularen Integrale K und K' durch
diese Funktionen darzustellen, müssen wir das Verhalten von K,K'
für q — 0 untersuchen, wofür zugleich %2 — 0 wird.
Es ist aber für q = 0 nach § 25 und § 42:
g-iX2 — ig, 2K — vt.
/ ^2
Lim (log — — /ttgj
\ 16
§ 52. Lineare Differentialgleichung für K. 171
also:
andererseits ist 2iK' = (§ 42) oder:
21'4- log= (log -f- ^«(1 — #'2O),
woraus:
/ 1 7.2\
(15) Lim —log —) = 0.
x2=o \ * 10/
Da nun K und K' partikulare Integrale von (8) sind (für
x = x2), so haben beide die Form:
S. — aly1 + a2y2, K' — a'^ + a$y2,
worin at, a2, al, a'2 konstant sind. Da K für x — 0 endlich
bleibt und den Wert erhält, so ist a2 — 0, ax = |jr, und
damit K' |logx endlich bleibe und [nach (15)] den Wert log 4
erhalte, muß al = 1 und a'i = 0 sein. Also ergibt sich, wenn
man x = %2, 1 — x = n'2 setzt:
'tt 11
(16) K = jA(x2), K' = A G(x2) - -logl^F(x2)
und
<17) 2 = e * =
16% 2
worin, wie schon bemerkt, die Reihen (z(%2), _F(%2) konvergent
sind, so lange der absolute Wert von x2 ein echter Bruch ist. In
der Differentialgleichung (4) liegen nun freilich die Mittel, die
gefundenen Ausdrücke für A, K\ q über dies Konvergenzbereich
hinaus fortzusetzen. Einfacher gelangt man dazu aber durch die
Anwendung der Landenschen Transformation.
Wir begrenzen die Ebene der komplexen Werte x2, indem
wir längs der reellen Achse zwei Schnitte von 0 bis — <x> und
von 1 bis oo legen. In der so begrenzten Ebene sind dann alle
Wurzeln aus x2, x'2 eindeutig dadurch bestimmt, daß sie für
positive echt gebrochene x2 reell und positiv sein sollen. Es
ist nun nach den Formeln der Landenschen Transformation
[§ 44, (28)], wenn wir mit xn x(, j^, die Funktionen von <o
bezeichnen, die sich aus x, x', Ä] K' ergeben, wenn co durch 2 a>
ersetzt wird: __
__ 1 — x' , 2
(18) Xi — %i ~ n-v’
2 K, = (1 + x') K, K'x ~ (1 -|- *') K.
172 Fünfter Abschnitt. § 52.
Wenn wir also in (17) a> durch 2a> ersetzen und die Quadrat-
wurzel ziehen, so folgt:
(19) * =
Hierin erstreckt sich nun der Konvergenzhereich über den
in der Ebene gelegenen Einheitskreis und dieser entspricht der
ganzen Ebene x2. Denn der reelle Teil vom v! ist in der ganzen
Ebene der x2 positiv mit Ausnahme der beiden Ufer des von
-Q1 nach oo verlaufenden Schnittes, an denen x' rein imaginär
ist. Daraus ergibt sich, daß der absolute Wert von xx kleiner
als 1 ist, und daß die Peripherie des Einheitskreises in der
Ebene x, den beiden Ufern dieses Schnittes entspricht.
Man kann aber die Konvergenz dieser Ausdrücke noch ver-
bessern durch eine abermalige Anwendung der Landenschen
Transformation. Bezeichnen wir das Resultat einer nochmaligen
Verdoppelung von a> durch den Index 2, so folgt:
(20) 4Ä-S = (1.+ Vx'pK; = (1 + y7)2K',
. - A
q = 4fW,.
f 4x2
worin nun der Konvergenzbereich die Ebene der x2 zweimal
(mit einer Verzweigung im Punkte x2 = 1) bedeckt.
Diese Operation kann man fortsetzeh, indem man nach der
Formel (17) aus x2 durch Verdoppelung von co eine neue Größe x3,
daraus ebenso x4 usf. herleitet. Man bekommt dann eine Reihe
von Ausdrücken für q, deren Konvergenz eine immer' bessere
wird. Für ein beliebiges v ist:
21-^- G(**)
<21) 2^(*?).
I 4x1
Die erste Gleichung (18)
x2
zeigt, daß, so lange der absolute Wert von x2 kleiner als 1 ist,
und folglich der absolute Wert von 1 -|- x' größer als 1, der
absolute Wert von x, kleiner ist als der von x2, und folglich
§ 52. Lineare Differentialgleichung für K. 173
nähert sich x,, mit unendlich wachsendem v der Grenze Null.
Daraus erhält man für q die Darstellung:
r-1 >—1
2 l~ 2 /
(22) q = Lim 1/~- = Lim 1/J,
die bei reellen Werten von x zur Berechnung geeignet ist.
Aus jeder der Formeln (21) kann man eine Reihenentwicke-
lung von q nach den steigenden Potenzen von xr herleiten, deren
Konvergenz mit wachsendem v zunimmt. Wendet man ins-
besondere die Formel (20) an, so erhält man eine Entwickelung,
die von Weierstrass in den Monatsberichten der Berliner Aka-
demie vom Jahre 1883 mitgeteilt ist, deren Konvergenzbereich
die Ebene x2 zweimal ausfüllt.
Die Koeffizienten dieser Entwickelung berechnet man am
einfachsten aus:
znox </T - ^o(°’ _ 2« + 2«9 + 2ä26 + •••
} 12 ~ ^oo(O, H - 1 + 2g4 + 2gie + ••• ’
und erhält so nach der Methode der unbestimmten Koeffizienten:
(2D 9 = §+2(.fe)s+i5(fe)’+160(t.)“
+ lT07(ih)"+...
Ebenso läßt sich nach (23) auch umgekehrt j/x2 in eine
nach Potenzen von q fortschreitende Reihe entwickeln:
(25) = q — 2<p + 5^ — 10g« + 18q” ...,
die man auch durch Umkehrung der Reihe (24) erhält.
Damit ist die am Anfang dieses Paragraphen gestellte Frage
vollständig beantwortet.
Bezüglich der Anwendung der hier entwickelten Formeln zu
numerischer Berechnung von q sei noch bemerkt, daß, wenn x2
näher an 1 liegt, man ein besser konvergentes Verfahren erhält,
wenn man x2 mit x'2 vertauscht. Die Rechnung ergibt dann zu-
nächst nicht q, sondern
7t i
q! = e ",
woraus man aber q aus der Formel erhält:
log q log q' = ar2.
174
Fünfter Abschnitt.
§ 53.
§ 53. Die Lösungen der Gleichung j (g>) = j (»').
Die Resultate von § 51 genügen zunächst, um die Beziehungen
der verschiedenen Werte von co festzustellen, die zu demselben
Wert von z2 führen. Sei also:
fr/0(O,Q _ fr*,(O, u>) _
^„(0, o') ' -^o4o(0, ~ '
Setzen wir
(2) v — n ö20 (0, ra) u = it (0, co') u',
so genügen (nach § 42)
sowohl die Funktionen
(3)
»PO (0, o) co) fr01 (0, (q)frl0(w, tu)
Ü’ioCO, cj)#01(w, ra)’ f\0(O, ©)’
»01(Q, 03)^00 (u, co)
#oo (0, ft>) •ü’oi («, ») ’
als auch
(±)
fr00(O, o,)»11(w',o') &01(O,(a')'8'10(u', tu') fr01(O, tu') fr00 (w', o')
&! o (0,»') Ü’oi (u', co') ’ #10 (0, co') Ü’oj («', co')' &00 (0, co') #ol («',«') ’
für x, y, z gesetzt, den Differentialgleichungen (1) des vorigen
Paragraphen, und die entsprechenden dieser Funktionen sind also
identisch. Wenn nun u' = | ist, so verschwindet ra')
und es muß dann auch 9'10(w, co) verschwinden. Demnach folgt
aus (2) mit Rücksicht auf § 21:
(5) & 20 (0, co') = &20 (0, co) (a 4- ß co),
worin <%, ß ganze Zahlen sind, die der Bedingung
(6) a 1, ß = 0 (mod2)
genügen. Ist u' = co': 2, so verschwinden ü'oj (w', cj') und fto, (u, co),
und daher ist wie oben
(7)
worin
'd’ooC0, M')«' = ^o2o(0, co)(y 4- dra),
(8)
(9)
y = 0, ö = 1 (mod 2).
Daraus folgt:
, y 4- d co
co' = ;—3---
CC —j— p 0
Da aber in gleicher Weise geschlossen werden kann:
(0, ») = ^oo (°, «') («' +
^o2o(0, co)co = &20(Q, ra')(/4- 6'co'),
worin <%', ß', y', d' gleichfalls ganze Zahlen sind, so ergibt die
Substitution (5) in diesen Gleichungen:
1 = (a 4~ ß <o) (a' 4- ß' ß>'),
co = (a 4- ß(°)(y' 4" dv co').
§ 53.
Die Lösungen der Gleichung j (a>) = j (<>/).
175
Drückt man in diesen Gleichungen co' nach (9) durch <o aus,
so erhält man
1 = a' (a ß 65) ß'(y -|- d<»),
<a = /(a d'(y d»),
und da co nicht reell ist, so zerfällt jede dieser Gleichungen in
zwei andere:
txa' -f- yß' =1, ßa' -I- d ß' = 0,
a y' y d’ = 0, ß y' d §' = 1.
Mithin ist
(ad — ßy)(a'd' — ß'y') = 1,
und daher, da <», <»' beide einen positiven imaginären Teil haben
müssen, also nach (9) die Determinante ad — ßy positiv sein
muß:
ad — ßy = 1,
a = d', d — a', y = — y', ß = — ß'.
1. Es hängen also co, co' durch eine lineare Trans-
formation, und zwar [nach (6), (8)] durch eine der ersten
Klasse (§ 36) miteinander zusammen. Daß auch um-
gekehrt zwei solche Werte co, co' denselben Wert x2 er-
geben, ist bereits oben nachgewiesen.
Ein ähnlicher Satz ergibt sich als unmittelbare Konsequenz
hieraus, für die Invariante j (co) (§ 46).
2. Die Gleichung:
(10) j(eo') = j(co)
ist dann und nur dann befriedigt, wenn co' mit co durch
irgend eine lineare Transformation
/a, ß'
\7, d
zusammenhängt, wenn also
(11) ist. y -|- d co x a 1 co' = '—t— Kd — ßy — 1 a ß co
Denn bezeichnen wir die zu co' gehörigen Werte von x2, x'2
mit A2, A'2, so kann die Gleichung (10) so geschrieben werden: (1 — A2A'2)3 _ (1 — x2x'2)3 A4A'* x<x'4 ’
und ist in Wurzeln bezug auf A2 eine Gleichung sechsten Grades, deren ,„11 x'2' X2 . . ’ ’ ’ X2’ x'2’ X2’ x'2
176 Fünfter.Abschnitt. § 54.
sind. Es findet daher (mit Rücksicht auf § 45) eine der folgenden
Beziehungen statt:
wonach aus dem ersten Satze die Richtigkeit des zweiten folgt.
Die Variable ct> ist hier immer auf einen positiven imaginären
Teil beschränkt, und wenn wir zwei durch eine Gleichung (11)
zusammenhängende Zahlen co, co' äquivalent nennen, so haben
alle mit w äquivalenten Zahlen einen positiven imaginären Teil.
Wir können unseren Satz 2. auch so aussprechen:
3. Die Funktion j(co) hat für alle äquivalenten Werte w
und nur für diese einen und denselben Wert1 *).
Zu jedem Wert von gehört ein bestimmter Wert von 7(0),
und zu jedem Wert von j((a) ein Wert von ct> und die Gesamt-
heit der äquivalenten Werte g>'. Wenn also eine einwertige
Funktion <b(co) von ea der Bedingung genügt:
so ist d>(cj) eine einwertige Funktion von j (&>'), und wenn wir
also annehmen, daß (co) nur für eine endliche Anzahl von
Werten J (ra) unendlich und nur in endlicher Ordnung unendlich
werde, so folgt, daß <b(w) eine rationale Funktion von j(co) ist.
Die Voraussetzung trifft z. B. immer dann zu, wenn <b(ra)
mit J(co) in einem algebraischen Zusammenhänge steht.
§ 54. Die Modulfunktionen.
Es sei ^(») eine eindeutige Funktion von co. Wendet man
auf <x> eine lineare Transformation S
in eine andere Funktion
(1)
zy 4- dm
über, die wir mit bezeichnen wollen.
l) Dieser Satz ist zuerst von Dedekind bewiesen (Grelle, Bd. 83).
Dedekind nennt danach die Funktion val(<o) = 3~32~8J(<o) die Valenz
von io.
§ 54. Die Modulfunktionen. 177
Die Funktion ^»(u>) kann möglicherweise bei gewissen Trans-
formationen iS ungeändert bleiben (z. B. immer bei der identi-
schen Transformation). Alle Transformationen, die eine Funk-
tion ungeändert lassen, bilden eine Gruppe ®. Denn ist
ty\S = il>,
so ist auch
V | $ Sj = il> ] Sj =
Die Gruppe ® ist ein Teiler der Gruppe ß aller linearen
Transformationen.
Ist S ein Teiler von ß von endlichem Index (ß, S), und
ij>((o) eine Funktion von a> von der Eigenschaft, daß auch
umgekehrt
^(co') = ^(ra)
einen linearen Zusammenhang
~ a ßco
zur Folge hat, in dem eine zu ® gehörige Trans-
formation ist, so heißt ^>(<») eine zur Gruppe ® gehörige
Modulfunktion.
Wir beschränken uns auf die Betrachtung solcher Modul-
funktionen, die mit dem Modul x2, also auch mit J(ö), in einem
algebraischen Zusammenhänge stehen.
Unter dieser Voraussetzung läßt sich der folgende allgemeine
Satz aussprechen:
Wenn t/>(co) zur Gruppe ® gehört und x(<») durch die
Transformationen von ® ungeändert bleibt, so ist z(«)
rational durch ausdrückbar.
Denn zunächst ist x(63) eine algebraische Funktion von ^(w),
und ^(<o) kann als algebraische Funktion von J(w) jeden Wert
annehmen. Zu jedem Wert von ^(o) gehört aber nach Voraus-
setzung nur ein Wert von xC03), und daher ist x(e>) a^s ein-
wertige algebraische Funktion von ^(<o) rational.
Das Studium der in ß enthaltenen Gruppen und der zu ihnen
gehörigen Modulfunktionen bildet den Hauptgegenstand des großen
Werkes von Klein und Fricke: „Vorlesungen über die Theorie
der elliptischen Modulfunktionen“ (2 Bde., Leipzig, Teubner,
1890, 1892). Wir betrachten hier nur einige ganz spezielle Fälle
dieser Gruppen und Funktionen, auf die wir im Verlauf unserer
Untersuchungen gestoßen sind.
Weber, Algebra. III. 12
178
Fünfter Abschnitt.
§ 54.
Eine große Klasse von Teilern der Gruppe 8 mit endlichem
Index bilden die sogenannten Kongruenzgruppen, die, wenn
m irgend eine ganze Zahl ist, durch die vier Kongruenzen
(m)=(ö:
charakterisiert sind. Die zu diesen Gruppen gehörigen Modul-
funktionen heißen Kongruenzmoduln mter Stufe. Für m = 2
ist dies die Gruppe 31 (§ 36). Wir werden von den folgenden
Sätzen Gebrauch machen:
1. Der Modul x2 ist nach § 52 eine zu dieser Gruppe ge-
hörige Modulfunktion; da nach § 36 alle diese Transformationen
aus den beiden
/!, 0\ /l, 2\
\2, 1/’ \O, 1)
zusammensetzbar sind, so können wir den Satz aussprechen:
Jede Modulfunktion, die durch die beiden Ver-
tauschungen
(«,, « + 2), («,,
ungeändert bleibt, ist eine rationale Funktion von x2.
2. Die Funktion x2x'2 gehört zu der aus der ersten und
zweiten Klasse des § 36 gemeinschaftlich gebildeten Gruppe ?l'.
Diese Gruppe läßt sich durch Wiederholung der beiden Trans-
formationen
/!, 0\ / 0, 1\
\2, V’ 1,0?
ableiten, und wir können daher den Satz aussprechen:
Jede Modulfunktion, die durch die beiden Ver-
tauschungen
(ra, © + 2), (a, —
ungeändert bleibt, ist eine rationale Funktion von x2x'2
Hieraus folgt noch:
3. Jede Modulfunktion, die durch (o, ro —j— 2) ungeändert
bleibt und durch (co, —— ) ihr Zeichen ändert, ist das
\ coj
Produkt von (x'2 — x2) mit einer rationalen Funktion
von x2x'2.
§ 54. Die Modulfunktionen. 179
4. Die Invariante 7(0) gehört zur Gruppe S (§ 53) und
daher der Satz:
Jede Modulfunktion, die durch die beiden Ver-
tauschungen
(o, k> 1), (a, —
\ <x> /
ungeändert bleibt, ist eine rationale Funktion von 7(0).
Außer diesen führen wir noch zwei andere Modulfunktionen ein.
Aus der Definition der Funktionen /"(ri), (03)-> AC0’) [§ 34,
(1), (10)] ergibt sich, wenn man die beiden Gleichungen § 42, (3)
miteinander multipliziert:
... ... ]/2 .... -16/77 ,z x Wk17^
(2) /(<»)= AO) = 1/2 I/—, AG») = ]/2 V-;,
]/xx' F z / x
(3) AW = Aö = ri
’ /» f(tö)
Auf Grund von § 46, (15), (16) definieren wir zwei Funk-
tionen y2(o), y3G»):
,2(o) = W) = r281^±^,
zx 8(2 4- %*%'*) (%'* — %*)
7s(o) = 1'7®) — 27.64 = T ,
die nach (2) und (3) als eindeutige Funktionen von 0 folgender-
maßen darstellbar sind:
(5) z^x CAO)24 + 8] [A (»)8 - A (»M
wofür man nach den Grundformeln für die f-Funktionen [§ 34,
(11), (12)] auch setzen kann:
(6) 72 G») = /G»)8AG»)8 + /‘G»)8AG»)8 — AW/jW
(7) 73(0) = + AG»)8][AG»)8-AG»)8]-
Es sind also x = A, —ff, —A8 (^e Wurzeln der kubischen
Gleichung
(8) xz — y2x — 16 — 0,
und 4y32 ist die Diskriminante dieser Gleichung.
12*
180 Fünfter Abschnitt. § 54.
Bemerkenswert sind auch die Differentialgleichungen:
(9) dx2 = —du'2 = :ir/ft40x2x'2<fo [§ 52, (3)],
(10) dx2x'2 =——x'2) x2 x'2 d o,
(11) d f (o)3 = [f2 (0)3 - A (0)3] d O,
o
Q ijy /i
(12) dy2(o) —-— y3 (o) i/ (o)4 d o [nach (5) und §34, (10)],
ö
(13) d)(o) = —2 a i y2 (o)2 y3 (o) i/ (o)4 d o.
Man erhält sodann für die linearen Fundamentaltransforma-
tionen aus § 34, (13), (14),-(15):
y2(o 1) = e 3 y2(o), r2(—-) = Za («4
(14) ( n
n (o + 1) = — ps (o), y3 ( — - J = — y3 (o),
und aus § 40 findet man allgemein:
4^+7^) = 9M<a)’
(15) / Ta x
= (-1)“z+'5y+'s^3(ra)’
worin p wie in § 40, (3) die Bedeutung hat:
— hAl (a / + (? 4 — aß — d)
p = e 3 .
Es sind dies also Modulfunktionen, und die Gruppen, zu
denen sie gehören, sind durch die beiden Kongruenzen charak-
terisiert :
— aß ay -f- ßd — a2ßy = 0 (mod 3),
ay -|- ßy ßd =0 (mod 2).
Wir geben hiernach unserem Satz 4. die folgende Ergänzung,
die sich aus den Formeln (14) ergibt.
5. Eine Modulfunktion, die durch die beiden Sub-
stitutionen
(o, o -]- 1), (o, - 1)
das Zeichen ändert, ist das Produkt von y3(o) mit einer
rationalen Funktion von 7(0).
§ 55. Darstellung der elliptischen Funktionen durch v und z2. 181
6. Eine Modulfunktion, die durch die Substitution
ungeändert bleibt und durch (o>, —|— 1) den
+ — +1
Faktor e 3 annimmt, ist das Produkt von y3 (w) mit
einer rationalen Funktion J(ra).
7. Eine Modulfunktion, die durch die Substitutionen
(g>, — das Zeichen ändert und durch (u>, ct> —(— 1) den
— 2ff» +1
Faktor —e 3 annimmt, ist das Produkt von (co)Zs(co)
mit einer rationalen Funktion von j(co).
Eingehender werden wir uns mit den Modulfunktionen im
zweiten Teil beschäftigen.
§ 55. Darstellung der elliptischen Funktionen durch v und zl 2.
Wenn wir das Umkehrproblem der elliptischen Integrale so
wie in § 51 als die Aufgabe der Integration der elliptischen
Differentialgleichungen fassen, so verlangt es die Darstellung
der drei Funktionen snt;, ent-’, dnt; durch die beiden unabhängigen
Variablen v, x2. Diese Aufgabe ist durch § 42 gelöst, aber be-
züglich der Variablen x2 nur implizite. Man kann aber auch
Darstellungen finden, in denen z2 explizite vorkommt, und zwar
durch Reihen, die nach Potenzen von v fortschreiten, deren
Koeffizienten rationale Funktionen von x2 sind. Die
Koeffizienten dieser Reihen können freilich nicht durch ein all-
gemeines Gesetz dargestellt, sondern nur sukzessive berechnet
werden. Diese Darstellungen verdankt man hauptsächlich Weier-
strass ’)•
Die ö-Funktionen können, da sie durchaus endliche und
stetige Funktionen von w sind, in unbedingt konvergente Potenz-
reihen nach u entwickelt werden, und wenn wir daher die in
§ 45, (2) vorkommenden ö-Funktionen in dieser Weise ent-
wickeln, so bekommen wir eine Lösung unserer Aufgabe. Wir
setzen- daher
l) Über die Weierstrasssche Theorie der elliptischen Funktionen vgl.
man besonders die von H. A. Schwarz herausgegebenen „Formeln und
Lehrsätze zum Gebrauch der elliptischen Funktionen“. Über die Reihen-
entwickelungen vgl. man auchKönigsberger, „Vorlesungen über die Theorie
der elliptischen Funktionen“, 25. Vorlesung.
182
Fünfter Abschnitt.
§ 55.
a(v, 2K, 2iK') = X A, 0,oo 2,2 v-n (2* + 1)!’
(1) 0Oo ('v, 2A7, 2iK') = 22 Bv 0,oo V y2’’ (2v)!’ ^,2r
und öoi (55 2 K, 2 i K ) — 22 Cv , . (, 0,oo " V qA-V 0loO, 2AT, 2iK') = y, 0,«> die A„, Cr, sind die zu bestimmenden Funktionen
von x2 oder von g>. Fassen wir sie zunächst als Funktionen von
o> auf, so ergeben die linearen Transformationen [§ 45, (3)]:
x(-4) = (-iyx(o),
f = ( Ij' -Bdöj,
(2) / iv
A(-4) = (-iyc,(<4
A„ (o> 1) = Av(co),
1) = 6',(w),
x'2^ a(<» +1) = K(o),
x'2,,Dr(cj -4— 1) = />,(<»).
X(ü> + 2) = A(o),
4- 2) = £,(<»),
W 0,0 + 2) = a(«>),
D, (oo -|- 2) = Du (o).
Hieraus schließen wir auf die charakteristischen Eigenschaften
dieser Koeffizienten als Funktionen von x2. Zunächst erhellt aus
der Bedeutung der Koeffizienten, daß für jeden Wert von x2 mit
etwaiger Ausnahme von x2 = 0, 1, oo die Koeffizienten Ar(x2),
£,(x2), C\(x2), D»(x2) endliche und stetige Funktionen von x2 sind.
Aber auch für x2 = 0 bleiben diese Funktionen endlich
und man kann ihre Werte leicht finden, wenn man in den Dar-
stellungen des § 37 q und mithin x2 in Null übergehen läßt.
§ 55. Darstellung der elliptischen Funktionen durch v und z4. 183
Man erhält dann aus. den Entwickelungen in § 25 mit Rücksicht
darauf, daß nach § 34 und § 42 für ein verschwindendes q
1
= ä12, 2Z — %
wird: „ ^r + i
e6 = 21^(0)^,
z5l o.» k?(2V)l
e& = Ja(0)(2^)!’
8,2 v
e6cosv — 2JD„(0) ,n ., •
o,« v 7 (2v)l
Die Formeln (2) ergeben nun:
Jr(x'2) = (—l)Mr(x2),
= (— i/^o2),
(6) a(x'2) = (-iyA(%2),
A(%'2) = (-iy a<z2),
woraus folgt, daß auch für x2 — 1 diese Funktionen endlich
bleiben, nämlich:
X(l) = (—iyx(o),
K(l) = (-W(0),
cr(i) = (-iyA(o),
A(i) = (-iya(o).
Das System (3) läßt sich ferner so schreiben:
/ •—- v 2\
= a<x2)’
(8) \
v 7 / V? x
= A(%2),
woraus für ein. unendliches x2:
X(x2) = x2Mv(0),
j?,(x2) =
C,(x2) = x2*Ä(0),
Bv (x2) = x2 ” Cv (0),
184
Fünfter Abschnitt.
§ 55.
und hieraus wird geschlossen, daß die Koeffizienten Av, Bt, Cr, JD,
ganze rationale Funktionen von x2 vom Grade v sind, und
aus § 54, 2, 3, folgt überdies noch, daß Ar, B„ bei geradem v
rational durch x2x'2 ausgedrückt sind, während sie bei ungeradem
v gleich dem Produkt von (x'2 — x2) mit einer rationalen Funk-
tion von x2x'2 sind.
Aus Bv findet man Cv mittels der Formel:
/__</2\
(10) cv^ = A^BA-AL)
und JDV durch Anwendung von (6) und (8):
(11) A(*2) == (—lyt^x'2) = (—l/x^A
Da man aus (5) die Koeffizienten A(0), Bv(ö), CV(Q'), A(0)
leicht bestimmen kann, so ergeben sich aus dem hier ent-
wickelten Formelsystem die Koeffizienten Ar, Bv, C„, A ohne
weitere Rechnung bis v = 3 einschließlich.
Man findet:
A — 1, A = o, A 0 — w(l — X2x'2), 0
A = 1, A = w(x'2 —X2), o A = 1(1 4“ 2x2x'2) tj
= 1, G = 1(1 + X2), o c2 = 1(^4 _ 2x2), 0
A = i, A = -l(i+ x'2), A = l(x*- 2x'2). 0
Q
A3 = q(k'2 X2)(2 X2x'2),
Bg = l(x'2 — x2)(5 — 2x2x'2),
V
Cg = 1(1 + X2)(5x'< 4- 2x2),
V
A = -1(1 + x'2)(5x4 + 2x'2).
y
Weitere Koeffizienten lassen sich auf demselben Wege, wenn
auch weitläufiger berechnen, indem man die Ausdrücke für die
0-Funktionen in § 32 nach Potenzen von q entwickelt und, wie
hier die niedrigste Potenz von q, so die höheren benutzt. Weier-
strass bedient sich zur rekurrenten Berechnung der Koeffizienten
gewisser partieller Differentialgleichungen, ähnlich der, die wir im
nächsten Paragraphen für die Funktion 0 ableiten werden.
§ 56. Potenzreihen für die Weier st rass sehen Funktionen p (w), a(it'). 185
§ 56. Potenzreihen für die Weierstrasssehen Funktionen
£>(«), 0(«). .
Die Funktion 0(w), als Funktion von u betrachtet, läßt sich,
wie schon bemerkt, in eine in der ganzen «-Ebene konvergierende
Reihe nach Potenzen von w entwickeln, und nach § 35, (8), (12)
hat diese Entwickelung die folgende Form:
(1) 6 (u) = w + a w3 4- aL us a2 4" asu9 + •• ’
Die Funktion
log0 W _ ö'(wp — 00"(w)
(2) («) ----------------------------------------
läßt sich ebenfalls nach steigenden Potenzen von u entwickeln,
aber nicht mehr in eine immer konvergente Reihe, sondern diese
Reihe hat einen Konvergenzkreis. Sie hat die Form:
(3) ß) («) = —|— (t —«2 4” ^3 4- * ’ *
und man kann die Koeffizienten «, a2> ••• der Reihe nach
aus der Differentialgleichung [§ 46, (18)]
(4) £?'(w)2 = < p (w)3 — ,9s p («) —
als Funktionen von g^ t/3 bestimmen.
Es ist zunächst
2
——-------- ~4~ 2 di h —|“ 4 d% 6 d$ u® • • *,
^'W2 = ~ 4? ~ 16“2 + (4a2 — 24«b)m2 +
und da ta'(w)2 kein Glied mit u~i enthält, während in ^?(w)3
das Glied 3«m-4 vorkommt, so muß a = 0 sein. Danach er-
gibt sich:
^>(w)ä = — 4- 3a2 + 3(«3 4- «j2)«2 4- •••
p (M) — m2 + • • •
Und wenn man dies in die Gleichung (4) einsetzt, so folgt
a — — a — 9* -
W U1 — 20’ 2 28’ 3 — 1200
186
Fünfter Abschnitt.
§ 56.
0'
Durch Integration von (2) findet man:
mw3 «2w9 a»w7 \ , x
t-------------------------------5-------V-'r«'
und aus dieser Gleichung folgt:
(6) a = 0, «i = a2 = “3 = 161 280'
Daß a — 0 ist, folgt auch aus dem in § 35 bewiesenen
0"' (w) = 0; indessen war dies dort auf ziemlich umständlichem
Wege bewiesen. Wir haben sonach folgenden Anfang der Ent-
wickelung von 0(w), wobei der Übersicht halber die numerischen
Nenner in ihre Primfaktoren zerlegt sind:
(7) =
Zur rekurrenten Berechnung der Koeffizienten in der Potenz-
reihe für 0(u) dient eine partielle Differentialgleichung, die als
eine Umformung der partiellen Differentialgleichung für die
•^-Funktionen betrachtet werden kann. Wir leiten sie auf fol-
gendem Wege her.
Die Funktion 0(w) war durch die beiden Periodengleichungen
§ 35, (9)
0(w-|- Gij) = —e’n<2M+wi)0(w),
0(w a»2) = —e'fe(2u + wi)0(u),
iji «2 — = ni
bis auf einen von u unabhängigen Faktor bestimmt. Es ergibt
sich aber durch Differentiation der letzten Gleichung (8):
0i/i 0i/2
Ö-T- «2 — ö— <»1 — = °,
0 CO± OG)[
0i/i ' 8i?2 । n
C V ^2
(8)
also:
• / 01/2 I 8i/2\
W1V,hä7r + ^äT?)’
2/ \ v ü
und wir führen also eine Größe r ein, die wir so definieren:
01/1 . 01/1
i/iz-2- + >?2—- = —reo!,
0G11 1 CGIj
01/1 , 01/2
= —rco2-
0ß>2 0<»2
(9)
§ 56. Potenzreihen für die Weier strasssehen Funktionen p(w),a(w). 187
Nun weist man durch Differentiation der Periodengleichungen
(8) nach, daß die Funktion
ar \ ^20 r a ’ ^0 i a
®<“> = 0^ +4’> äs; +4r“°
den Periodengleichungen (8) genügt, und also gleich Cß(u) ist,
worin C von u unabhängig ist. Die Entwickelung von 0(h) nach
Potenzen von w fängt aber mit w3 an, während 0-(w) mit w an-
fängt, und folglich muß C — 0 sein.
Nach (7) beginnt die Entwickelung von go/giOj und g0/gio2
erst mit w5, und die ersten Glieder von g20/gw2 und 4rw20 sind
—g2w3/12, 4rw3, woraus 4r = g2/12 folgt, und demnach erhält
die Differentialgleichung für 0 die Form:
<10) ^ + ^ + 4^+fb2ö = °’
und nebenbei ergeben sich aus (9) die Relationen:
(11)
K 8 । „ =
?18 6o2 ' a>2
--
48 11
— Sir,
48 2’
Nun sollen in der Differentialgleichung (10) statt der Variablen
<»!, io2 die Variablen g2, g3 eingeführt werden, und wenn wir also
g 0 g</2 g0 gg3
gß>! gg2 gcj; ~ dg3 gt»!
g0 _ g0 gff2 g0 gg3
gm2 gg2 ga»2 ' dg3 ga»2
setzen, so erhält (10) die Form:
<12) + g 0 . , g 0 , q 2 . '8»r + s,ä»+i5“'’ = l)
worin
^2 \ 0 GJj 0
Ä3 V^ga»! ^2gta2z
Die Größen 7z2, ä8, durch g2, g3 ausgedrückt, ergeben sich nun
aus der Differentialgleichung selbst, wenn man für 0 die Ent-
wickelung (7) einsetzt. Danach ist bis zur 7ten Potenz von u:
188
Fünfter Abschnitt.
§ 56.
cm2 — i2w3 12ä2‘.3.5 8 23.3.5.7’
002
g,0
003
^«20 _ £2M3
J. a X
2<. 3.5
w7
~ 28.3.5.7’
_ 7 2 w7
249i 23.3.5.7’
und wenn man dies in (12) einsetzt und die Koeffizienten von u5
und w7 gleich Null setzt, so ergibt sich:
Ä2 = —120g,
und wir erhalten die Differentialgleichung:
(131 ___ 12 2 8<? । g-2
, gw2 1J^3ö</2 39'2 dg3 ' 12
Setzt man die Reihenentwickelung für 0 mit unbestimmten
Koeffizienten an:
(14)
0 = 2J A,
u2v + 1
(2^ + 1)!’
so erhält man aus (13) die Rekursionsformel:
(iK\ j __ i9ö d-4r_i । 2 2gjlv_i (2v l)(2i> 2) 2 .
(15) X — 12& +-ör2-^_ ^2X-2,
woraus zu schließen ist, daß die A? ganze rationale Funk-
tionen von g2 und g3 sind, deren Koeffizienten rationale Zahlen
sind, die nur Potenzen von 2 und von 3 im Nenner haben können.
Die Reihe (14) besteht daher aus Gliedern von der Form
» (1 Sd”1 (2 gs)n (Qy | l)~j >
und aus der Homogenität der Funktion 0 [§ 37, (8), § 46, (13)]
folgt:
(16) 2 m 3 n = v,
für die Koeffizienten am>n ergibt sich dann aus (15):
16
(17) dm,n == 3 (7W ~1) dm + 1, n—1 “j- "ö" (w 1) dm—2, n + 1
O
— (2 m 3 n — 1) (4 m 6 n — l)a»i-i,n,
O
worin a00 — 1 und die a, bei denen einer der beiden Indizes
negativ ist, gleich Null zu setzen sind.
§ 56. Potenzreihen für die Weierstrass sehen Funktionen p (w), a(w). 189
Daraus läßt sich «OTjM finden, wenn die früheren am>n, d. h.
die in dem 2 m 3 n kleiner als v ist, schon berechnet sind.
Man sieht daraus, daß die nur Potenzen von 3 im
Nenner enthalten. In den von H. A. Schwarz herausgegebenen
„Formeln und Lehrsätzen zum Gebrauch der elliptischen Funk-
tionen“, nach Vorlesungen von Weierstrass (2. Ausgabe 1893),
sind die am>n bis zu v = 17 berechnet. Es zeigt sich dabei, daß
diese Koeffizienten nicht nur ganze Zahlen sind, sondern daß sie
auch mit v wachsende Potenzen von 3 als Faktoren enthalten.
Einen Beweis hierfür vermag ich nicht zu geben.
Sechster Abschnitt.
Multiplikation und Teilung der elliptischen
Funktionen.
§ 57. Multiplikation der elliptischen Funktionen.
Unter der Multiplikation der elliptischen Funktionen versteht
man die Darstellung der Funktionen sn»?;, cn wi;, dn???; für ein
ganzzahliges n als rationale Funktionen von sn?;, cn?;, dn?;, eine
Aufgabe, die, wie aus dem Additionstheorem ersichtlich ist, immer
gelöst werden kann.
Die Form der- Lösung ergibt sich leicht aus der Betrachtung
der •9-Funktionen.
Es sind, wie aus § 21 unmittelbar zu ersehen, die Funktionen
® - Funktionen der Ordnung n2, deren Charakteristik
bei geradem n gleich (0, 0), bei ungeradem n gleich (^, <j2) ist.
Überdies ist 9,u(nu) eine ungerade, 9,10(nw),
sind gerade Funktionen von w. Es lassen sich also diese Funk-
tionen rational durch die -9-Funktionen darstellen und die Sätze
des § 21 ergeben die Form dieser Ausdrücke. Es wird, wenn wir
wieder mit Fw(x,y) eine ganze, rationale, homogene Funktion
vter Ordnung bezeichnen:
bei geradem n:
n2 — 4
0ii(nw) = •ö'ooW^oi 2 ['®’n(M)».'^oi (M)]»
(1) «2
[^?1 («)>%(«)]> (^1,^2) = (10), (01), (00),
bei ungeradem n:
1
(2) 2 [^11 W? ^0! («)]•
§ 57. Multiplikation der elliptischen Funktionen. 191
Wenn wir diese Formeln durch •froi (M)"2 dividieren, so lassen
sich die rechten Seiten als ganze rationale Funktionen von den
elliptischen Funktionen snt?, cn?;, dnt? darstellen (§ 42). Wenn
wir also
(3) v = snv — x, ent? = y, dnt? = z
setzen, so können wir die Formeln (1), (2), indem wir einen kon-
stanten Faktor passend bestimmen, so schreiben:
I. bei geradem n:
w- - - 1
£4^ = w cm = i ^00
r<0) - ’•
II. bei ungeradem n:
»oo»^-1 »10 »11 (nu) »oi (w)"2 = xAfx2'), J.(0) = n
An2 v 01 »10 »10 (ww) »01 (w)"2 = yB(x*), B^f) = 1
An2 u 01 »00 »ooptu) »01 O)"2 = z (7(a?2), (7(0) = 1
77 01 »01 (nw) »oi («r = X>(«a), 17(0) = 1
worin A, B, C, D ganze rationale Funktionen von x2 sind, deren
Grade sich aus den Formeln (1), (2) folgendermaßen ergeben:
A(x2), B(x-'), C(x2), D(a?2),
~ , n2 „ n2 w2 n2 ,
Grad: — — 2, —, -y »gerade,
n2 — 1 n2 — 1 m2 •— 1 m2 — 2 ,
—2—’ —2—’ —2—’ —2— n unSerade-
Aus den Definitionen I., II. erhält man unmittelbar die Werte
von A (0), B (0), C (0), D (0), d. h. die von n unabhängigen Glieder,
wie sie beigefügt sind.
Mannigfache Beziehungen zwischen diesen Funktionen ergeben
sich noch auf folgendem Wege:
192
Sechster Abschnitt.
§ 57.
Ersetzt man, um ein Beispiel hier ausführlicher durchzuführen,
v durch .v -|- K, also u durch u -|- |, so gehen x, y, z nach § 44,
(18) in yjz^ —x'x/z, x'/s über, und man erhält nach § 21, (8)
aus der ersten Formel II für ein ungerades n:
#oo#oi"2-1 #io(«w) ( y A (V*\
#10 #oi («)"' \#oo(«)/ ? * W
Andererseits ist die linke Seite nach der zweiten Gleichung II
und nach § 42 gleich
und folglich:
\V% / w
Setzt man darin x = 1, y = 0, z = x' oder x = 0, y = 1,
z — 1, so folgt:
J?(l) = (— 1) 2 n^x' , J.(l) = (—1) 2 .
Man kann ein ganzes System solcher Formeln ableiten, indem
man in I und II folgende Substitutionen macht:
w, X, y-.
, 1 y —x'x x'
w + 2’ z ’ z ’ z ’
1 — iz —
w + TT’ — .11
1 2 xx' XX ’ X ’
। 1H- 05 z i x' 1 i x' x
w H s—i . . - •
1 2 ’ *y . X y ' y
So erhält man:
/ z \n2-4 (t?) Ä! (t\ = (- V2/ 1 n M(l) n i n2—4 = (—l)2 nyx'
^w2\ n n .—n*
fc) = <“ l)2 B(x^)y B(l) = (-i)2 ,
W X A/2\ n2
(iF> r y \ C(x2), C(l) = ,
/ Z \«2 1» •D( 5)= D(x^), D(l) n'1
n gerade.
§'57.
Multiplikation der elliptischen Funktionen.
193
/ z v2-1 ( 777 ) AI \yx'/ ' / 2\ M — * = (-l)~£(*a), ^(i)t= (— i) 2 y*'
/ z \”2-1 (y?) L' g?) = (-1)2 A*-2), »—1 n2 — 5(1) = (—1) 2
P) ' (y?) Cl © = ' _«2 — c(i) = y»'
G&r- (5) = 5(1) = y7"2-
n ungerade.
\X2X2 / n = (-l)7-1^2), n \(y7f
(fixf B 6) 0| \x2a;2/ < 1 \ \X2X2) 1 = B(x2), = C(x2), 5(») = 0(») = , n2 - v*, ' /-"2
(yxrr)"2 D| Z 1 \ <z2a;2) n = (-l)2 B(x2), D(W) = (-1)2 pc ,
n gerade.
(yäca;)"2-1 A( < 1 \ {%2X2/ n — 1 = (-1) 2 D(x2\ n — 1 A®) = (-1) 2 n2 — 1 y^ ,
(yöp B{ :?) (fix)”'2-1 0( (, 1 \ \U2X2) 7 1 \ \X2X2) = C(x2\ .= B(xi), B(X) = o(») ==; _n2 — 1 yj« , _«2 — 1 pc ,
(y^)"2-1 d( f 1 \ \k2x2') n — 1- = (-1) 2 A(xt), . n — 1 5(») = (-l) 2. _ n2 - 1 n yu ,
n ungerade.
Hier sind unter J.(co), _B(x), O(oo), D(oo) jedesmal die
Koeffizienten der höchsten Potenz von x in diesen Funk-
tionen zu verstehen. In (7) können die beiden letzten Formeln
aus der ersten durch Vertauschung von x mit 1/xx hergeleitet
werden.
Das dritte System von Formeln, kann man entweder auf
demselben Wege oder auch dadurch erhalten, daß man in den
Formeln (4), (5) x durch 1/xx ersetzt und (6), (7) anwendet.
Weber, Algebra. III. 13
194
Sechster Abschnitt.
§ 57.
V
^O2),
Gy?)
(s7 , , L
L’M cU0= c^)’
Gyi)’ '»(^=
n gerade.
/ \ 2^2
IV.
Bei ungeradem n:
xäi'x2]
snnv ~ ~D(aA) '
y Btx2)
Cnn v ~ D(a?2) ’
, z C(x*)
im - wr
C, D hängen noch von co oder
Nach diesen Formeln kann man für den Fall eines ungeraden
n die vier Polynome A(xi').l B(aA), C(a;2), D(a>2) auf eines von
ihnen, z. B. auf A(x2'), zurückführen.
Wenn man von den Formeln I, II je die drei ersten durch
die letzte dividiert, so erhält man die Multiplikationsformeln für
die elliptischen Funktionen (§ 42).
III. Bei geradem n: ]
xyzA(x2~)
snnv — ,
B(x2)
cnnv ~ DhÄ)'1
dn
D(x2y
Die Koeffizienten von A, B,
von x2 ab. Über die Art dieser Abhängigkeit geben die Rekur-
sionsformeln Aufschluß, die man zur sukzessiven Berechnung von
§ 57. Multiplikation der elliptischen Funktionen. 195
A, B, C, D aus dem Additionstheorem folgert. Wenn wir den
Wert des Multiplikators n, zu dem diese Funktionen gehören,
durch einen Index andeuten, so haben wir zunächst
(10) ferner A = 1, A =1, Q = 1, A = 1; aus den Additionsformeln [§ 44, (16), für u = v\: _ 2snvcnvdnv sn2-y = —-—, 1 — x2sn4u
(11) _ cn2v— sn2wdn2« cn2y = - , 1 — x2sn4v . „ dn2v — x2sn2vcn2v dn2v = — 1 — x2sn4t> A = 2,
(12) A = 1 — 2 o:2 —x2A C2 = 1 — 2x2x2 A ^2A A = 1 — s«2«4.
Wenn wir in (11) v durch nv ersetzen, so folgt:
A‘jn ----- 2AnBnCnDn,
An = BnD% — x2y2z2 A Cn, n gerade, = y2B%D% — x2z2A%Cn, n ungerade,
(13) Can = C’;1A — x2x2y2z2A^B„, n gerade, = #2C|A — x2x2y2A£B%, n ungerade,
An = Dn — x2xiyiziA^, n gerade, = A — x2<r4A> n ungerade,
und wenn man in den Additionsformeln des § 44 w = nv,
v = (n 1) v setzt:
A2n + i = y2Z2AnDnBn + 1Cn + i-[~-^-n+lDn + lCnBn, H gerade,
— AnI)nBn+1Cn+1-[- y2^An+1I)n+1CnBm n ungerade,
(14) B^n+i = BnBn +1DnDn^.1 x2s2AnAn+iCnCn+i,-
Gtl-j-1- CnCn-\-l Dn Dn^-i H2X2y2AnAn-\-iBnBn+l,
Din+1 = DIDI+1 — x2x*y2s2A£A2+1.
Aus diesen Formeln schließt man, daß die A, B, C, D
ganze rationale Funktionen von x2 sind, und daß die
Zahlenkoeffizienten ganze rationale Zahlen sind.
Denn nach (10), (12) hat diese Eigenschaft für n = 1, 2
statt und folglich nach (13), (14) allgemein.
13*
196
Sechster Abschnitt.
§.58.
Über den Grad in bezug auf x2 läßt sich noch schließen,
daß die Koeffizienten von xiv den Grad v in bezug auf x2 nicht
übersteigen. Denn ist diese Regel richtig für n und n 1, so
folgt ihre Richtigkeit für 2 h und 2n 1, und für n = 1, n = 2
trifft sie zu.
Aus den Grundgleichungen' zwischen den drei elliptischen
Funktionen:
1 = cn2® sn2® =.dn2® x2sn2a;
ergeben sich noch die Relationen:
D2 = Ba xayaza J.2 = C2 x2#2?/2#2 J2, n gerade,
(15) ^2^2 _ (jz x2a;2A2, n ungerade,
mit deren Hilfe man nach (14) Bin und C2„ durch und Dn
allein so ausdrücken kann:
Bin = Di — 2xayaza A%D% xaxiyi^Ai 1
(16) Cssn = — 2xaxayazaJ
Bin = Di — 2xaA£Di xaxi Ai 1
' -r.. „ ,, > n ungerade.
C2„ == Di — 2 x*xaAi Di -|- z2.®4Ai J
§ 58. Multiplikation der Funktion (u).
Eine sehr elegante Form erhält die Multiplikationstheorie für
die Weierstrasssche Funktion p (u) mit den beiden Perioden
»!, CO2.
Betrachten wir die doppelt periodische Funktion
(1) (»«) — p (u),
worin n eine beliebige positive ganze Zahl sein mag. Diese
Funktion wird unendlich für u = 0, und zwar so, daß
(2) . (nu) - («) + 1
für u = 0 endlich bleibt. Außerdem wird sie aber unendlich
für alle Werte u* von u, die der Bedingung
nu* = 0 (mod »u co2)
genügen, also von der Form sind:
Hl C?I -|- y2 co2
n ’
worin vlf v2 beliebige ganze Zahlen bedeuten. Wir erhalten alle
in (3) enthaltenen inkongruenten Werte, wenn wir r, und je
ein vollständiges Restsystem nach dem Modul n durchlaufen lassen.
§ 58. Multiplikation der Funktion p (u). 197
Die Funktion (1) verschwindet für alle von Null verschiedenen
Werte von u, die der Bedingung
+ bu° = u° (mod o?!, ca2)
genügen, also für
wenn wieder Vj, v2 beliebige ganze Zahlen sind. Die Nullpunkte
sind von der ersten, die Unendlichkeitspunkte von der zweiten
Ordnung.
Wir führen daher jetzt eine Funktion il>n(u) ein, die wir
folgendermaßen erklären:
(5) p(~lt01 ^y2t°2)],
wobei Vi, v2 je ein vollständiges Restsystem nach dem Modul n,
mit alleinigem Ausschluß des Wertepaares 0,0 durchlaufen, und
fügen noch die Bestimmung hinzu, daß '== 1 sein soll.
Wenn n ungerade ist, so kommt in dem Produkt (5) jeder
Linearfaktor zweimal vor, da die beiden inkongruenten Werte
M _ +^itax -j- u2k>2
— n
den gleichen Wert von (u) ergeben. Ist aber n gerade, so
kommen wieder in (5) alle Linearfaktoren zweimal vor, mit Aus-
nahme der drei
die nur einfach vorkommen. Beachtet man nun, daß nach § 41
^'W2 = 4[^ w- (y)][^ W-
ist, so ergibt sich das Resultat:
» ungerade: i[>n = P«,
n gerade: = p'(u)Pn,
wenn Pn eine ganze rationale Funktion von (u) bedeutet,
die bei ungeradem n vom Grade | (n2 — 1) und bei geradem n
vom Grade |(n2 — 4) ist, und in der das Glied höchster Ordnung
bzw. gleich
— 1 n na — 4
p («0 2, “ 2 ’
198
Sechster Abschnitt.
§ 58.
ist, wodurch zugleich das nach (5) noch unbestimmte Vorzeichen
bestimmt ist. Bei dieser Bestimmung der Vorzeichen ist das
Anfangsglied in der Entwickelung von nach steigenden
Potenzen von u in beiden Fällen (§ 56):
Erwägt man nun, daß die Unendlichkeitspunkte der Funk-
tion (1) mit den Nullpunkten von i/>„(u) zusammenfallen und die
Nullpunkte von (1) mit den Nullpunkten von #„+i(u), daß also
^.(u)2[^(hu) — (u)]
eine überall endliche doppelt periodische Funktion und daher
eine Konstante ist, deren Wert sich aus ü = 0 gleich — 1 er-
gibt, so folgt:
(9) (,«) = ,, («) -
woraus sich die beiden folgenden Formeln ergeben:
(10) (nu) = p (u) — n gerade,
/ X ^'(«)2-P« + lJn-l ,
= (u) — 2-------- ---------, n ungerade.
-tn
Wir bestimmen zunächst die Funktion Pn in den ersten
Fällen n = 1, 2, 3, 4. Dazu bilden wir nach dem Additions-
theorem der ^-Funktion [§ 49, (11)]:
/ & ' (u) &' (v)\ 2
W (f) + + «)] =
indem wir u = v setzen und den Grenzwert rechts durch Differen-
tiation bestimmen:
1 / 1 V
i (&" WV 4 v W2 “ 2 92)
® (2w) 2 (u) — J
oder
3 ff2
3 W4 - W2 — 3ff3 p («) —
(11) = p(«)------------------------
so daß
^1=1, Wz = — £?'(«), ^3 = -P3,
§ 58. Multiplikation der Funktion p (u). 199
(12) -Pj = l, P2 =-l, P3 = 3^(wp-^a^(u)a-3^^(«)-^
wird. Wir erhalten ferner aus der Additionsformel (§ 49):
indem wir v = 2u setzen, nach (9):
^'(«)^'(2b) __ p'(»)5p'(2«)
^( ) ^( ) ~ [p(2«)~p(«)]8~ ^W3 ’
__ _ ^0<)i/aW
l/>3 (u)2 ’
also:
^(») = ^'(u)P4 = — ^'(w)4^'(2u),
und wenn man aus (11) den Wert ^'(2a) bildet:
(13) P± = — 2^(«)6-|- -ffss^(uy + lO08p(«p
+ -g#2 (M)2 + & (M) + 9l — ^2'
Für größere Werte von n leiten wir Rekursionsformeln ab.
Zu diesem Zweck wenden wir die Formel (9) auf zwei verschiedene
Zahlen m, n an und erhalten:
z x z x fe+i(«)Vl(»)
w- '
Z X z X ^ + 1(«)*.-1(b)
(M) - (o) =----------»
woraus zu ersehen ist, daß die rechten Seiten einander gleich
werden für solche Werte w° von «, die von Null verschieden sind
und der Bedingung genügen
mun = +nu° (mod Wj, ca2),
oder
(m + ri)u° = 0 (mod cax, ca2);
für dieselben Werte verschwinden aber auch die Funktionen
i.n ('M) >
so daß die beiden Funktionen:
il>m+i(u) ^m-i(u)^n(u)2 — V>n + i(u)^„_i(u)^m(u)2,
(t^) — n (t^),
die nach (6) ganze rationale Funktionen von (u) sind, für die
nämlichen endlichen Werte von (u) verschwinden. Sie unter-
200 Sechster Abschnitt. § 59.
scheiden sich also nur durch einen konstanten Faktor voneinander,
der sich aus (7) gleich 1 ergibt. Wir haben daher
' — ^m+1(u)^m-1(u)ipn(uy — ^„+i(u)^„_1(u)^,n(u)2.
Diese Formel wenden wir auf zwei spezielle Fälle an, indem
wir n -|- 1, n oder n -|- 1, n —-1 an Stelle von m, n setzen, und
erhalten so;
V’an+iW = ^„+2(u)^„(u)3 —
§}' (w) ^2 n (w) = — Ipn (w) [^„ + 2 (u) 1/^ _ x (u)2 — ?/>„ +1 (u)2 _ 2 («)],
und daraus erhält man nach (6) die Rekursionsformeln für P„:
(15) P2„+x = p'(u)*P„+aP% — -Pä + i-Pn-1, n gerade,
= Pn+2Pl — ^'(u^P^ + iPn-i, w ungerade.
(16) P2„ ==- PM(P„+2P4_X-P^ + XP„_2).
Da sich die Funktionen Pn alle hiernach aus Px, P2, P3, P4
berechnen lassen, so folgt, daß die Koeffizienten von P„
rational aus </2, gs und rationalen Zahlen zusammen-
gesetzt sind.
Unsere ferneren Betrachtungen über die Teilung knüpfen
wir aber an die Multiplikationsformeln der Funktionen sn«, cnu,
dnu, deren Vorzüge erst im vierten Teil vollständig zur Geltung
kommen werden.
§ 59. Die Teilung durch 2.
Indem wir uns zunächst zur Betrachtung des einfachsten
Falles wenden, setzen wir in den Gleichungen (5) des §57 v an
Stelle von 2 v. Dann ist, wenn wir
(1) setzen: V V ' , V <r = sn^, y = cn^-, z = dn — 2 xyz , - sm; — 1 — X2Z‘
(2) «2 a;2^2 cnv = ~ r, 1 — X2 xA , «2 — x2#2«2 ; dm; — -—. I x2Z4
Die beiden letzten dieser Gleichungen sind quadratisch in
bezug auf sie haben aber nur eine gemeinschaftliche
Wurzel,denn die Wurzeln der zweiten der Gleichungen (2) sind
§ 59.
Die Teilung durch 2.
201
sna|, sn2(|j-K+ ȣ'),
und die der dritten
-sn2|,
Man findet nun leicht aus (2):
, . 2«2 1 |
1 + cnu = --------J 1 dnu =
- 1.— x2a;4 . 1 ..
, 2 .u2 s* , j
1 — cnu = -------r—, 1 — dnu =
1 — x2<r4
. . 2//-.S2
dnu -4- cnu = =—-—-—
1 1 - X2iU4
also -
1 — cn u 1
1 -|-dnu x
dnu-]-cnu ______i /dnu -f- cnu,
1 dnu ’ Z ~ f 1 cnu ’
zwischen den Vorzeichen dieser drei Größen besteht nach der
ersten Gleichung (2) noch eine Eelation, so daß man nur vier
verschiedene Wertsysteme erhält, welche folgende Bedeutung haben:
2«2
1 — x2a;4’
2 x2#2?/2
1 — x2<r4’
1 — dnu
202
Sechster Abschnitt.
§60.
Hieraus folgt nun, daß man die Teilung durch 2 und mithin
auch durch jede Potenz von 2 durch eine Kette von Quadrat-
wurzeln ausführen kann. Setzt man daher die Aufgabe der Tei-
lung durch eine ungerade Zahl als gelöst voraus, so ist die Teilung
durch eine gerade Zahl auf Quadratwurzeln zurückgeführt. Im
folgenden beschäftigen wir uns ausschließlich mit der Teilung
durch ungerade Zahlen.
§ 60. Die Teilung durch eine ungerade Zahl.
Setzt man, wenn n eine ungerade Zahl ist,
(1)
V V , V
x = sn—, « = cn —, z = dn —,
n n n
so erhält man aus den Gleichungen IV, § 57:
D(<r2) sn« — xÄ(xl) = 0,
(2) D (a;2) cn v — yB (a;2) = 0,
D (xa~) dn v — zC (x2) = 0.
Die erste dieser Gleichungen ist in bezug auf die Unbekannte
x vom Grade ft2; durch die zweite und dritte werden y und z
rational durch x (und durch cn«, du«) ausgedrückt. Es ergeben
sich also ft2 Wertsysteme für die drei Unbekannten x, y, z, deren
Bedeutung ist:
(v AyK -j- Ay'iK'
xa u, = sn---------------!-------
1 ’ \w 1 n
zox I Ay'iK'
(3) »„ = «»(-+ -----
“u.a’ - tlll I — —I--------------
\ft 1 n
worin y, y' je ein vollständiges Restsystem (mod n) durchlaufen.
Die erste Gleichung (2):
(4) D(x2)sd.v — xA(x2) = 0,
vom Grade ft2 heißt die allgemeine Teilungsgleichung. Sie
ist in dem Sinne irreducibel, daß sie nicht in Faktoren zerlegbar
ist, die in bezug auf sn«, cn«, dn« rational sind und beliebige
von v unabhängige Koeffizienten haben.
Denn zunächst sind die ft2 Werte x^ alle voneinander ver-
schieden, und wenn irgend eine rationale Gleichung:
/ V \
F (sn —, sn v, cn «, dn v ) = 0
§ 60. Die Teilung durch eine ungerade Zahl. 203
besteht, so kann darin die Variable v durch v -|- iiiK -j-
ersetzt werden. Wegen der Periodizität von sn«, ent', dn« folgt
aber daraus, daß die Gleichung
F(x, sn«, cn«, dn«) = 0
für alle Wurzeln der Gleichung (4) erfüllt ist. Um ihre Galois-
sche Gruppe zu ermitteln, setzen wir zunächst den Rationali-
tätsbereich fest. Er soll folgende Größen umfassen:
1. rationale Zahlen,
2. rationale Funktionen von z2,
3. die drei Funktionen sn«, cn«, dn«,
4. die Großen sn —---------1---5-----) •
\ n )
Aus (2) folgt dann, daß auch
cn 4pG~F'\ dn /4pK+ 4p'^K'\
\ n /’ \ n )
zum Rationalitätsbereich gehören.
Wir bemerken nun, daß nach dem Additionstheorem jede der
Größen x^u> durch jede andere unter ihnen rational ausdrückbar
ist. Wenn insbesondere
(5) .Tu,«' ----------- K„u/(^0,0)
ist, so ist
(6) Xfi + + vr Fuyu' (^/»,»') -Fu v, u'4-(^1'0, o)*
Daraus folgt, daß die Galoissche Gruppe unserer Gleichung
aus den w2 Vertauschungen SVyV' besteht, die man erhält, wenn
man in den Wurzeln die Indizes p, p' alle um dasselbe
Zahlenpaar v, v' vermehrt (wobei jeder Index nach dem Modul n
zu nehmen ist).
Denn nach (5) kann jede rationale Funktion der Wurzeln
a?U)U, rational durch a?o,o in der Form
®(a?o,o)
ausgedrückt werden und geht also nach (6) durch die Substitution
S t, in über; bleibt sie also durch diese Substitution
ungeändert, so ist sie rational. Umgekehrt folgt aus der
Irreduzibilität, daß jede rationale Gleichung zwischen den Wurzeln,
da sie in die Form gesetzt werden kann:
^(a?o,o) = 0,
und also
(a?r,t>) = 0
204 Sechster Abschnitt, § 61.
zur Folge hat, die Substitution Sv,v' gestattet. Die Gruppe
der Sv,i> ist aber wegen
Sv,Vr -- Sv -p
eine Abelsche, welche nach der Formel
Ä,,- = 8^8^
durch die Basis <S1)0., So,i darstellbar ist, und also ist die all-
gemeine Teilungsgleichung eiue Abelsche Gleichung und
mithin algebraisch lösbar (Bd. I, § 169f.).
§ 61. Die Teilung der Perioden.
Die weiter noch zu lösende Aufgabe besteht nun darin, auf
algebraischem Wege die Größen
(i) x^, = sn^- r —-J
zu bestimmen. Man erhält alle Werte dieser Größe, wenn man
ft, ft', voneinander unabhängig, je ein vollständiges Restsystem
nach dem Modul n durchlaufen läßt. Diese Werte sind aber
auch alle voneinander verschieden, denn sn« kann nur dann
= sn«' sein, wenn «' kongruent v oder kongruent 2 K — v
modulo 4A, 2«A?', und beides kann für zwei verschiedene der
Argumente von (1) nicht eintreten.
Die n2 Größen (1) sind die Wurzeln der Gleichung
(2) .== 0,
und nach den Formeln ,
- 5(a?2) D(a?2)
y~ B(x*)'' Z ~ C(a?)
können auch
/4ftK4- iu’iK'X
rational durch ausgedrückt werden, wenn der Rationali-
tätsbereich aus rationalen Zahlen und rationalen
Funktionen-vön x2 besteht.
Aus den Wurzeln a?2 der Gleichung A — 0 lassen sich nach
§ 60, (2) und § 44, (18), (19), (20) die Wurzeln von 5 = 0,
C = 0, D — 0 rational ableiten; wenn nämlich x2 eine Wurzel
von A = 0 ist, so sind - .
§62.
Die Abel sehen Relationen.
205
1 — ..'2 1 — x2.<-2 1
1 - X2«2’ X2(l-- X'2)’ X2«2
die Wurzeln von B = 0, C == 0, D = 0. Die Bedeutung dieser
letzteren Wurzel ist aber . _
sn/(4ft+l)K+4^^'y
\ • n- )'
/(4fi + l)K+(4ft'-4-l)iK'\2
öll l -— I«
\ n /
gQ /4fiK + (4fi'+ l)tW'\2
\ n /’ . . . .
und hiernach sind durch Auflösung der Gleichung A = 0 alle
Größen von der; Form
gn + n'iKy
\ n /’
worin [i, fi' beliebige ganze Zahlen sind, rational bestimmt.
§ 62. Die Abel sehen Relationen.
Für eine nähere Untersuchung der algebraischen Natur der
Periodenteilungsgleichung ist ein System von Relationen zwischen
ihren Wurzeln von großer Wichtigkeit, zu dessen Ableitung wir
jetzt übergehen1).
Wir betrachten die Summe:
genommen nach v über ein volles Restsystem für den (ungeraden)
Modul n. v1 ist eine beliebige ganze Zahl und g2 eine der
drei geraden Charakteristiken (0,0), (0,1), (1,0). Diese Summe
ist unabhängig von dem besonderen Restsystem, das man für v
genommen hat.
*) Diese Relationen rühren von Abel her (Oeuvres completes, Bd. I,
8. 523; Bd. II, S. 251 der neuen Ausgabe). Der oben gegebene Beweis
dieser Relationen schließt sich an Hermite an (Grelles Journal, Bd. 32,
8. 283). Zu erwähnen ist noch Sylow, Christiania Videnskabsselskabs
Forhandlinger 1864 und 1871. Kroneeker, Berichte der Berliner Akademie,
19. Juli 1875. Engel, Berichte der Sächsischen Gesellschaft der Wissen-
schaften, 31. Juli 1884.
206
Sechster Abschnitt.
§ 62.
Der Hauptnenner der in (1) verkommenden Brüche:
v / 2 V\ 1 / iA
+ ~) =
\ / \ '*/
ist nach den letzten Formeln des § 33, von einem konstanten
Faktor abgesehen, gleich
W(a)>
und wenn wir also die Summe (1) gleich
(2) ______________
nm)
setzen, so ist O(w) eine ganze transzendente Funktion von u.
Nun ist
M“+^)
q / . 2 V —|- 1\
®'9l,92\U' M-ü-J
und v durchläuft gleichzeitig mit v -|- j (n 1) ein volles Rest-
system nach n. Daraus ergibt sich nach (1) und (2)
(1 \ 4 t' 7ti
u + w = ~e ~
und ähnlich
(4) 0(w -|- co) = —e-«Äi<2“+“>$(w).
Daraus ergibt sich, daß die Funktion ®(w) eine t-Funktion
ist mit den Perioden 1/n, co, die durch die Bedingungen (3), (4)
bis auf einen von u unabhängigen Faktor bestimmt und durch
eine -9-Funktion ausdrückbar ist (§ 19). Man sieht leicht, daß
die Bedingungen (3), (4) durch die Funktion
g—(nu — 4v'gj? nto)
befriedigt sind, so daß sich ergibt:
/ । 2v\
-v Svv'rti d/i! I U -H-I , / \
fö) n' = cc-^'u^(nu — 2v^n<0)
+ n J
Die Bestimmung der Konstanten C kann man leicht aus-
führen, wenn man rechts und links rn.it
multipliziert und dann
u _ (l — 9^ + (1 — ^i)®
§ 62.
Die Abelschen Relationen.
207
setzt. Die Formel (2) des § 21 ergibt dann:
(6) £>_( 1)to + 1Kga + 1)V-ra ^(0,®) »’u(0,na>)
^l.<72(2v'°b W0J) 0ii(O,®)
Die Abelschen Relationen erhält man einfach, indem man
in (5) nu = 2v'<o setzt, wodurch die rechte Seite verschwindet:
. /2v'co 4- 2v\
v 2v'r7ti 47*ii I ----------- I
(7) y \"_____________________________________z o.
’ > /2v'o + 2v\
Wendet man auf die hier vorkommenden ^-Funktionen eine
lineare Transformation
«) »ä - =1
an, so erhält man nach § 39 die allgemeine Formel:
„ /2(va 4- v'v) 4- 2(vß v'd'ja'x
v Svi'xi O’]1 (—------111-------------------------)
Ve " _______________-________________L n
' ‘‘—i /2 (v a -f- v' y) -|- 2 (y ß -|~ v' d) co\
l « )
Diese Gleichungen gehen nun, wenn man glf g2 = 0,1 setzt
und die Bezeichnungen des § 42 einführt, unmittelbar in Rela-
tionen zwischen den Wurzeln (§ 61) über:
v üw’Tti
CO & n #?a-|-Vy, + :-- 0,
und den beiden speziellen Fällen:
/«, A _ Z1, 0\ / 0, 1\
V, <V V0, 1/ \-l, 0/
entsprechend:
v Sv^Tti
(10) = 0,
»' Svy'Tti
(ii) ye n = 0.
Nach (5), (6) kann man auch den Wert dieser Summen be-
stimmen, wenn darin die wte Einheitswurzel
208 Sechster Abschnitt. § 63.
durch eine andere ersetzt wird; indem man . in. (5) v' durch ein
anderes Zeichen, m, ersetzt und dann nu = 2p'gj setzt. Be-
schränken wir uns auf den Fall = (0,1) und multipliziert
(5) noch mit -Ooo^io, so folgt:
V Smvrti
(12) I? " =
&00 (Q, n(o)&11 [2 (y’ — <u]
' •9’10O-ii'9’01(2mGj,WGj)'9’01 (2v'c<j,no) ’
wo die linke Seite dann, aber auch nur dann verschwindet,
wenn m = v' (mod n) ist.
§ 63. Die Galoissche Gruppe der Teilungsgleichung.
Im dreizehnten Abschnitt des ersten Bandes ist gezeigt, wie
die algebraische Natur einer Gleichung ihren einfachsten Aus-
druck in der Galoisschen Gruppe der Gleichung findet.
Es sei hier kürz an die Definition der Galoisschen Gruppe
erinnert.
Nachdem der Rationalitätsbereich £1 festgesetzt war, ist die
Galoissche Gruppe einer Gleichung F(x~) = 0, von der nur
vorausgesetzt wird, daß sie keine gleichen Wurzeln habe, definiert
als die Gruppe G der. Permutationen unter den Wurzeln dieser
Gleichung, der die doppelte Eigenschaft zukommt:
a) Jede rationale Gleichung in £i, die zwischen den Wurzeln
vonF(x) besteht, bleibt richtig, wenn die Wurzeln irgend
einer Permutation dieser Gruppe unterworfen werden.
b) Jede rationale Funktion in £l von den Wurzeln von Ffti),
die sämtliche Permutationen der Gruppe gestattet, ist in
£1 enthalten.
Indem wir nun die Gruppe G der Teilungsgleichung zu be-
stimmen suchen, setzen , wir als Rätionalitätsbereich zunächst deu
Inbegriff aller rationalen Zahlen und rationalen Funk-
tionen von x2 voraus.
Nach dem Additions- und Multiplikationstheorem (vgl. § 57,
61) ist, wenn f und <pm rationale Funktionen bedeuten, die von
fi, fi' v, v' unabhängig sind,
(1) Xu 4- V, flr + 1' - f (^'1U,,U,7 >'),
(2) (^u, ,«')•
§ 63. Die Galoissehe Gruppe der Teilungsgleichung. 209
Ist nun iS irgend eine Substitution der Gruppe ®, durch die,
wenn a, ö, c, c ganze Zahlen bedeuten, die nach dem Modul n
genommen sind,
#o,i in
übergeht, so können wir S auf jede der Formeln (1), (2) an-
wenden. Es ist aber nach (2):
#«,o =
woraus zu schließen, daß durch die Substitution S
#«,o in <pu(«ö,_c) — .-ra,u,-c.u
übergeht. Ebenso findet man, daß durch 8
#0, u' in (#—a) %—
übergeht.
Wenden wir dies auf die aus (1) hervorgehende Gleichung
#u, u' ------------------- / (#u, 01 #0, u'j
an, so folgt, daß durch S
(3) u' ID. — bp',—cit+au'
übergeht.
Hieraus schließen wir zunächst, daß die Zahlen a, b, c, d so
beschaffen sein müssen, daß ihre Determinante
(4) m — ab — bc
mit n keinen Teiler gemein hat. Denn wäre ein solcher Teiler
vorhanden, so würden p, p', ohne daß beide durch n teilbar sind,
so bestimmt werden können, daß
dfi — bp' = 0, — ci.i -f- ap' = 0 (mod w),
und es würden mehrere voneinander verschiedene Wurzeln
durch 8 in ein und dieselbe Wurzel übergehen, was unmöglich
ist. Denn zunächst können weder a und b noch c und c einen
Teiler mit n gemein haben, weil sonst, wenn np', bp' oder cp, 8 p
durch n teilbar genommen werden, alle a?u>i0 oder alle a?0,u in
o übergehen würden. Setzt, man dann ma = n(h a -f- Ä'Z>),
wp' = n(hc -j- 7»'d), und bestimmt h und h' so, daß ha -|- h'b
keine Teiler mit n gemein hat, so brauchen, wenn n und m einen
gemeinsamen Teiler haben, p, p' nicht beide durch n teilbar zu sein,
und es geht nicht nur sondern auch nach (3) in a?o,o über.
Bezeichnen wir abgekürzt die Vertauschung (3) mit
(#u, ,u' , #>', »') 1
so ist
v = du — bu' , .
(mod n),
v' = — c a -|- a p'
Weber, Algebra. III.
14
210 Sechster Abschnitt. § 63.
und daraus, durch Auflösung, mit Benutzung der Bezeichnung
§ 28, (4):
(5) m(jt, n') = (a' b\ (v, v').
\ k, o /
Es ist daher
(6) /«, b\
\d, 0/
ein zweckmäßiges Zeichen für die Vertauschung <S, und aus (5)
ersieht man, daß sich zwei solche Vertauschungen:
genau nach der in § 28 gegebenen Regel:
(?) ss'=s" = °?:+t83
\ c a' 4- c c, c b 8 o J
zusammensetzen, so daß die Vertauschung 8" der Wurzeln ent-
steht, wenn zuerst die Vertauschung 8, sodann die Vertauschung
8' unter den Wurzeln der Teilungsgleichung vorgenommen wird.
Zu beachten ist aber immer, daß hier nur die nach dem Modul
n genommenen Reste der Zahlen a, />, c, c in Betracht kommen,
so daß die Anzahl der Vertauschungen 8 stets endlich ist1).
1. Der Inbegriff aller Substitutionen bildet
eine Gruppe, die wir mit bezeichnen, und in ihr ist,
wie wir bewiesen haben, die Gruppe ® der Teilungs-
gleichung enthalten.
In ist als Teiler eine Gruppe SB enthalten, die aus allen
Substitutionen (5)
besteht, die der Bedingung
(9)_ aö — ßy = 1 (mod ri)
genügen.
’) Wollte man, was auf den ersten Blick näher zu liegen scheint, die
Bezeichnung 8 = ( wählen, so würde die Komposition nach der
Formel 8' S = 8", also umgekehrt wie bei der üblichen Komposition der
Fermentationen, zu bezeichnen sein.
§ 63. Die Galoissche Gruppe der Teilungsgleichung. 211
Jede Substitution S läßt sich durch Zusammensetzung von
m, 0\
o, V
mit einer Substitution T herleiten; man hat, damit
sei, a, ß, y, Ö einfach aus den Kongruenzen
a = am, b = ßm, c = y, d = Ö (mod n)
zu bestimmen.
Wir betrachten nun
2 p -f" 2fi'<D
. /4pK4p'*A?
(10) x^ — sn'-5---*------
n
n
als Funktionen von co, und wenden darauf eine lineare Trans-
formation
(“: s) = (J: ?) 8)
an, indem wir w durch
y öa>
CC —|— ß G)
ersetzen; dann ergibt sich nach den Formeln (3), (5) und (6),
§ 39, daß
ID u + 3u + du'
übergeht, d. h. es erleiden die x^ eine Substitution, die nach
(3), (6) mit
zu bezeichnen ist, während z2 ungeändert bleibt.
Auf diese Weise kann auch umgekehrt jede der Substitutionen
T entstehen; denn wenn irgend eine Substitution T gegeben ist,
so kann man durch Hinzufügen passender Vielfachen der (un-
geraden) Zahl n zu den Zahlen a, ß, y, § den Bedingungen
a = 1, Ö = 1, ß = 0, . y = 0 (mod 8)
immer genügen.
14*
212 Sechster Abschnitt. § 63.
Irgend eine rationale Gleichung zwischen den Wurzeln
und %2 geht, auch wenn beliebige konstante, d. h. von gj unab-
hängige Zahlenkoeffizienten darin Vorkommen, durch (10) in eine
Identität über, und man kann daher für gj
y -f- Ö gj
a ßeo
substituieren, d. h. man kann jede Substitution T auf die rationale
Gleichung zwischen den x^ an wenden. Daraus folgt, daß die
ganze Gruppe SB in ® enthalten ist (Bd. I, § 156) und sogar
in der Gruppe ®', die aus der Gruppe ® der Teilungs-
gleichung durch Adjunktion beliebiger Zahlen entsteht.
Wenn wir den Rationalitätsbereich der rationalen Zahlen
durch Adjunktion von nten Einheitswurzeln erweitern, so gehören
zu den rationalen Gleichungen auch die Abelschen Relationen
des vorigen Paragraphen. Auf diese Relationen, etwa auf
8v ni
Ee ” x^' = 0
ist aber keine der Substitutionen
in der m von 1 verschwindet, anwendbar; denn durch diese Sub-
stitution geht, wenn mm’ = 1 (mod w) ist,
v ------ V ---------------
2Je n x„^> in 2Je ” xr,r>
über, was nach (12), § 62 von Null verschieden ist, wenn nicht
m' und also auch m zi 1 (mod n) ist. Daraus folgt der Satz:
2. Nach Adjunktion der nten Einheitswurzeln (und
beliebiger anderer Konstanten) ist SB die Galoissche Gruppe
der Teilungsgleichung. Es wird :B auch die Monodromie-
gruppe der Teilungsgleichung genannt.
3. Wir beweisen jetzt noch, daß in dem ursprünglichen
Rationalitätsbereich, also ohne Adjunktion der nten Einheits-
wurzeln oder anderer irrationaler Zahlen, die Gruppe der
Teilungsgleichung mit der Gruppe 91 identisch ist.
Es ist in Bd. I, § 174 gezeigt, daß die primitiven nten Ein-
heitswurzeln p Wurzeln einer irreduziblen Gleichung
(12) ®(e) = o
§ 63. Die Galoissche Gruppe der Teilungsgleichung. 213
sind, und diese Gleichung kann auch nicht zerfallen, wenn der
unabhängigen Veränderlichen durch Adjunktion der Rationalitäts-
bereich der rationalen Zahlen erweitert wird.
Der Grad dieser Gleichung ist (f> (m), d. h. gleich der Anzahl
der Modulo n inkongruenten Zahlen m, die relativ prim zu n sind.
Es sei nun
(13) F(f) = 0
eine Galoissche Resolvente vom Grade p der Teilungsgleichung
im ursprünglichen Rationalitätsbereich (so daß alle Wurzeln xv,y
rational durch r darstellbar sind, Bd. I, § 152). Diese Gleichung
muß nach Adjunktion einer Wurzel von (12) zerfallen; denn
wäre dies nicht, so würde jede rationale Relation
(14) ^(Gp) = 0
für alle Wurzeln von (13) befriedigt sein, und ^(f, p) wäre durch
F(t) (für ein variables f) teilbar. Es würde also (14) noch be-
stehen bleiben, wenn p durch eine andere Wurzel p“ von (12)
ersetzt wird. Dies ist aber nach § 62, (12) nicht zutreffend, wenn
man an Stelle von (14) eine der Abelschen Relationen setzt.
Es sei nun nach Adjunktion von p
(15) F^/t, p) = 0
die Galoissche Resolvente vom Grade v der Teilungsgleichung,
so daß v nach 2. gleich dem Grade der Gruppe ® ist. Es ist
dann F(t) durch F(t, p) algebraisch teilbar und also wegen der
Irreduzibilität von (12) auch durch jede der Funktionen F(t, p”1).
Da die Funktionen F(t, om) irreduzibel sind, so können nur dann
zwei von ihnen einen gemeinsamen Teiler haben, wenn sie ganz
identisch sind. Wenn aber
F(f,p) = F(f, p’n)
wäre, dann würde aus jeder Gleichung der Form (14) folgen, daß
p) durch F(t, p) = F(t, p’M) teilbar wäre, und es würde
folgen, daß in (14) die Vertauschung (p, p’M) gestattet ist, was
wieder bei den Abelschen Relationen nicht zutrifft. Mithin sind
die Funktionen F(t,p’n) alle voneinander verschieden, und
F(t) ist durch ihr Produkt teilbar. Der Grad p von F(t') ist
also wenigstens = v <f> (n). Er kann aber auch nicht höher als
v(p(n) sein, da vtp(n) der Grad der Gruppe 'M ist, und die
214 Sechster Abschnitt. § 63.
Gruppe ® vom Grade p gewiß in 21 enthalten ist. Es ergibt
sich hieraus
(16) p — vqp(w)
und zugleich die Identität von ® mit 21.
Daraus folgt aber auch, daß F(t) dem Produkt der sämtlichen
Faktoren F(t, p’M) gleich ist, also
m
(17) F(f) = ÜF(t, r),
und da F(f) = 0 keine gleichen Wurzeln hat, daß zwar F(r, p),
aber keiner von den anderen Faktoren F(r, p’n) verschwindet.
Die Gleichungen
(18) F(r,f) = 0, 0(f) = O
haben daher nur die eine Wurzel t = p miteinander gemein,
und durch Aufsuchen ihres größten gemeinschaftlichen Teilers
findet man p rational ausgedrückt durch r, d. h. durch
die Wurzeln der Teilungsgleichung.
Diese Ausdrücke für p ändern ihren Wert nicht, wenn auf r
eine Substitution der Gruppe 23 angewandt wird, während [nach
(12)] p durch eine Substitution der Gruppe 21 in eine Potenz
von p übergeht.
Abel sehen Relationen zeigen, daß durch die in 2t ent-
Substitution
übergeht; denn setzen wir
8 ni
e n — p\
so lautet eine der Abelschen Relationen
(20) = 0,
worauf, wenn für p der Ausdruck durch r gesetzt wird, alle
Substitutionen von 21, also auch (19), anwendbar sind. Nach § 62,
(12) bleibt aber (20) bei dieser Substitution nur richtig, wenn
p in p”( übergeht.
Da p durch die Substitutionen in 23 nicht geändert wird,
und da die Gruppe 21 aus 23 durch Zusammensetzung mit (19)
entsteht, so folgt, daß durch irgend eine Substitution in 21
Die
haltene
(19)
p in om
§ 63. Die Galoissche Gruppe der Teilungsgleichung. 215
p in <pn übergeht, wenn m der Determinante (ad — bc) nach
dem Modul n kongruent ist.
4. Wir wollen schließlich noch die Zahl v, d. h. den Grad
der Gruppe 29 bestimmen.
<p(n) hat, wie bekannt, den Ausdruck (Bd. I, § 140)
(21) . tp(n) = nü(l —1^,
wenn das Produktzeichen II sich auf alle in n aufgehenden, von-
einander verschiedenen Primzahlen p erstreckt.
Die Zahl v ist gleich der Anzahl der nach n inkongruenten
Zahlensysteme a, ß, y, 8, die der Bedingung
(22) a8 — ßy ~ 1 (mod n)
genügen. Wir fragen zunächst nach der Anzahl der Paare a. ß,
die mit n keinen gemeinschaftlichen Teiler haben, und bezeichnen
diese mit %(«).
Ist n = n' n" und n' relativ prim zu m", so kann man aus
jeder Kombination eines zu n' gehörigen Zahlenpaares ß' mit
einem zu n" gehörigen Zahlenpaar a", ß" ein zu n gehöriges
a = n" a' -|- n' a", ß — n" ß' n' ß"
herleiten, und man erhält auf diese Weise alle Zahlenpaare a, ß
und jedes nur einmal. Daraus folgt:
(23) %(») = z(O %(«")•
Es ist also noch %(p'r), d. h. %(n) für eine Primzahlpotenz
n — pn zu bestimmen.
Setzen wir zunächst für a, ß alle modulo p71 verschiedenen
Zahlen, so ist diese Anzahl p>i7t. Hiervon sind aber alle die
Paare wegzulassen, bei denen «und ß durch p teilbar sind,
deren Anzahl pi7t~2 beträgt, so daß
%(pn) = pi7t — p2Ä—2,
und folglich nach (23) allgemein
(24) z(n) =
folgt, wenn p die in n aufgehenden Primzahlen durchläuft.
Jedes Zahlenpaar a, ß läßt sich durch Vermehrung um Viel-
fache von n in ein solches verwandeln, deren Zahlen unter sich
relativ prim sind, und dann läßt sich y, 8 so bestimmen, daß
a,8 — ßy — 1
216 Sechster Abschnitt. § 64.
wird, darin kann y, ö durch y -j- h a,, ö h ß ersetzt werden,
und indem man h ein volles Restsystem modulo n durchlaufen
läßt, erkennt man, daß zu jedem Zahlenpaar a, ß n der Bedingung
(23) genügende Zahlenpaare y, ö gehören. Demnach ist die Ord-
nung der Gruppe 23:
V = «3 71(4
oder, wenn wir noch die numerische Funktion
(25) ip(-n)' = nH
einführen:
(26) v — n(f>(n)tp («)
und die Ordnung der Gruppe '21:
(27) ft = n tp (n)2(n).
§ 64. Die irreduzibeln Faktoren der Teilungsgleichung.
Ist
v = öji — 6 ft'
v' = — Cft ap'
und «8 — bc relativ prim zu n, so ist der größte gemeinschaft-
liche Teiler von ft, ft', n zugleich der größte gemeinschaftliche
Teiler von v, v', n. Die Wurzeln x^' der Teilungsgleichung
zerfallen also nach dem größten gemeinschaftlichen Teiler von
u, (i', n in Systeme, die durch die Substitutionen der Gruppe 21
immer nur ineinander übergehen, d. h. die Gruppe ® ist in-
transitiv, und die Systeme der Intransitivität sind die
Systeme x^, in denen ft, ft', n einen und denselben größten
gemeinschaftlichen Teiler haben. Die Teilungsgleichung ist also
reduzibel (außer wenn n eine Primzahl ist) und die Wurzeln
eines dieser Systeme der Imprimitivität genügen einer rationalen
Gleichung (Bd. I, § 157).
Nach dem vorhergehenden Paragraphen gibt es y (n) ip (n)
Zahlenpaare ft, ft', deren größter gemeinschaftlicher Teiler mit n
gleich 1 ist, und die diesen Zahlenpaaren entsprechenden Wurzeln
xu^i genügen daher einer rationalen Gleichung des Grades qr?(«)^(w).
Diese Gleichung nennen wir die eigentlicheTeilungsgleichung
für den Divisor n, weil nur dann, wenn ft, ft', n ohne gemein-
samen Teiler sind, x^^ nicht zugleich Wurzel einer Teilungs-
§ 65. Zurückführ. d. Teilungsgleiehung a. Transformationsgleichungeii. 217
gleichung für einen kleineren Divisor ist. Im Gegensatz hierzu
nennen wir die Gleichung, deren Wurzeln die sämtichen
sind, die allgemeine Teilungsgleichung für den Divisor n.
Durch irgend eine Substitution der Gruppe 31
s=C,i)
geht (1,0), (0,1) in (9, —c), (—b, a) über, und wenn also S nicht
die identische Substitution ist, so wird gewiß wenigstens eine der
beiden Wurzeln 0, a?o, i durch S verändert. Daraus ergibt sich,
daß die Galoissche Gruppe der eigentlichen Teilungs-
gleichung genau dieselbe ist, wie die der allgemeinen,
nur angewandt auf den Fall, daß p, p', n keinen gemeinsamen
Teiler haben, nämlich, je nachdem die wten Einheitswurzeln
adjungiert sind oder nicht, 39 oder 31.
Daraus folgt noch, daß die eigentliche Teilungs-
gleichung irreduzibel ist, selbst nach Adjunktion be-
liebiger Konstanten.
Denn sind y, 8 irgend zwei Zahlen ohne gemeinsamen Teiler
mit n, so kann man a, ß der Kongruenz
a8 — ßy = 1 (mod n)
gemäß bestimmen und die in 33 enthaltene Substitution
T =
V, 0/ .
auf jede rationale Gleichung zwischen den Wurzeln anwenden.
Wenn also «li0 einer rationalen Gleichung (mit beliebigen kon-
stanten Koeffizienten)
®(«i,o) = 0
genügt, so genügt derselben Gleichung jede andere Wurzel xn,-r
der eigentlichen Teilungsgleichung, woraus die Irreduzibilität der
letzteren folgt.
§ 65. Zurückführung der Teilungsgleichung
auf Transformationsgleichungen.
Die Wurzeln der eigentlichen Teilungsgleichung lassen sich
in folgender Weise in Reihen anordnen. Man wähle nach Be-
lieben eine der Wurzeln:
/4p1K' 4“ 4pj iK'\
= sn( —-------—--------) = sußp
218 Sechster Abschnitt. § 65.
Unter den Wurzeln der Teilungsgleichung kommen auch die
(m) Größen
(R-j sn h Si1
vor, die, wenn k ein vollständiges System inkongruenter zu
n teilerfremder Zahlen durchläuft, alle voneinander verschieden
sind. Das System (Aj wollen wir die erste Reihe der Wurzeln
nennen.
Ist nun sn Sl2 eine in (_Rj) nicht enthaltene Wurzel, so bilden
die (f> (w) Größen
(_R2) sn h S1.2,
die sowohl untereinander als von den Wurzeln (Aj verschieden
sind, eine zweite Reihe; und auf diese Weise kann man fortfahren,
his sämtliche <p(n) ip (n) Wurzeln der eigentlichen Teilungsgleichung
in ip (m) Reihen von je <p(n) Gliedern verteilt sind.
Nach dem Multiplikationstheorem läßt sich durch eine Wurzel
jede andere Wurzel derselben Reihe rational ausdrücken in der
Form:
(1) snkSl — /h(snß),
worin fh eine nur von dem Multiplikator Ä, nicht von der Wahl
von Si abhängige rationale Funktion ist.
Wenn die beiden Wurzeln in dieselbe Reihe ge-
hören, so muß sich die Zahl ä so bestimmen lassen, daß
(2) h p = i', k p' = v' (mod w),
und umgekehrt, wenn dies der Fall ist, so gehören die beiden
Wurzeln in dieselbe Reihe. Aus (2) aber folgt die Kongruenz
(3) ilv' — vp' = 0 (mod m),
und aus dieser lassen sich auch umgekehrt die Kongruenzen (2)
wieder herleiten.
Denn da p, p', n relativ prim sind, so kann man die Zahlen
a, ß so bestimmen, daß
«p — ßp' = -l (mod m)
wird, und daraus folgt mittels (3):
v ~ (av — (3v')p, v' = (av — ßv')p' (mod ri),
also, wenn u v — ßv' = h gesetzt wird, die Kongruenzen (2).
Die Kongruenz (3) ist also die notwendige und hin-
reichende Bedingung dafür, daß die beiden Wurzeln der
eigentlichen Teilungsgleichung ««„«', xv,v derselben Reihe
angehören.
§ 65. Zurückführ. d. Teilungsgleichung a. Transformationsgleichungen. 219
Hieraus folgt, daß die Einteilung in Reihen gänzlich unab-
hängig ist von der Willkürlichkeit in der Annahme über die
Wurzeln snßj. snß2 ...
Es folgt aber noch weiter daraus, daß durch die Sub-
stitutionen der Gruppe 21 die Reihen nicht auseinander-
gerissen, sondern nur untereinander vertauscht werden.
Die Gruppe der Teilungsgleichung ist also imprimitiv, und die
einzelnen Reihen, sind die Systeme der Imprimitivität (Bd. I, § 158).
Denn wendet man auf (p, p') und (v, v') gleichzeitig die
Substitution
/a, ö\
\.c, d)
an, so bleibt die Kongruenz (3) erhalten.
Sucht man unter den Substitutionen der Gruppe 21 die Sub-
stitutionen aus, welche die Wurzeln einer Reihe nur untereinander
vertauschen, so erhält man eine Gruppe, und zwar einen Teiler
von 21. Zu jeder Reihe gehört also ein solcher Teiler von 21.
Bezeichnen wir mit R^w die Reihe, in der die Wurzel a?UiU- vor-
kommt, und mit den zu dieser Reihe gehörigen Divisor von 21,
so sind nach (3) [vgl. § 63, (3)] die Substitutionen
von 2(„,„- durch die Kongruenz
(4) (dp — 6 p') p' + (c p — a p') p = 0 (mod n)
charakterisiert.
Ebenso erhält man eine Gruppe 23«„u', wenn man die Sub-
stitutionen in 39 auf sucht, die die Wurzeln der Reihe -Ru,«' nur
unter sich vertauschen, deren Substitutionen:
/«,
V, ö)
durch die beiden Kongruenzen:
(5) (öp — /Jp')p'4-(tp — = 0 /mod x
cx,S — ßy 1 v '
charakterisiert sind.
Beispielsweise bestehen die Gruppen 2Ii|0, ®i,o aus den Sub-
stitutionen
(oj)> (o,s)’ «ä = 1 W «)•
220
Sechster Abschnitt.
§ 65-
Die Gruppen 2(UifJ> sind konjugierte Divisoren von 21
(Bd. II, § 3), denn wenn #1)0 durch S in #U)U,, also A,o in -8«,,«'
übergeht, so werden durch die Gruppe
S-12l1)0 S
die Wurzeln von nur unter sich vertauscht, und es ist also
(6) = 9W
Ebenso ist, wenn T eine Substitution in 23 ist, durch die
#1,0 in übergeht:
(7) T~^lt0T=
Der größte gemeinschaftliche Teiler 2(0 aller Gruppen 21g,,u>
wird nach (4) bestimmt durch
b = 0, c = 0, a = d (mod ri)
und besteht also aus den Substitutionen:
/«, 0\
\0, «/’
worin a eine beliebige, zu n teilerfremde Zahl ist. 210 ist identisch
mit dem größten gemeinschaftlichen Teiler dreier der Gruppen
2IU)U-, die verschiedenen Reihen angehören. Denn 2(0 ist dann
der größte gemeinschaftliche Teiler von 2IU)g-, 21»,»', 2fp, wenn
die drei Kongruenzen
cji2 — (g — — gfi'2 = 0
c v2 — (d — a) v v' — bv'2 = 0 (mod n)
c p2 — (ö — a) p p' — b p'2 = 0
nur unter der Voraussetzung
8 = a, b = 0, c = 0 (mod n)
erfüllt sind. Dies findet statt, wenn die Determinante
p-2, p-p,',
v2, W,
p2, pp',
fi'2
v'2
p'2
= — (vp' — pv')(pfl' — f^p')((xv' — Vf?)
relativ prim zu n ist.
Ebenso ist nach (5) der größte gemeinschaftliche Teiler
aller 23UjU> der. Inbegriff der Substitutionen:
mit der Bedingung:
(9) a2 = 1 (mod n).
§ 65. Zurückführ. d. Teilungsgleichung a. Transformationsgleichungen. 221
Die Kongruenz (9) besitzt, wenn Z; die Anzahl der in n auf-
gehenden, voneinander verschiedenen Primzahlen ist, 2* inkon-
gruente Lösungen, und dies ist also der Grad der Gruppe 23O ’)•
Eine rationale Funktion g der Wurzeln einer Reihe, etwa
der Reihe Ri)0, läßt sich nach (1) rational durch eine dieser
Wurzeln dar stellen. Wenn diese Funktion die Eigenschaft hat,
ungeändert zu bleiben, falls diese eine Wurzel durch eine andere
derselben Reihe ersetzt wird, wenn also beispielsweise £ eine
symmetrische Funktion der Wurzeln einer Reihe ist, dann
erhält § durch Anwendung der Substitutionen von 21 (oder auch
von 21) nur
(10) v = il>(n)
verschiedene Werte
(11) £2,
und wenn diese Werte alle voneinander verschieden
sind, so gehört § zu der Gruppe und alle anderen
symmetrischen Funktionen der Wurzeln von R1>0 sind
rational durch £ darstellbar (Bd. I, § 162).
Die v Größen (11) sind die Wurzeln einer irreduzibeln ratio-
nalen Gleichung vten Grades, die wir eine Transformations-
gleichung nennen.
Die Transformationsgleichung hat, wenn in £ nur rationale
Zahlkoeffizienten vorkommen, selbst rationale Zahlkoeffizienten.
Sie 'bleibt aber irreduzibel, wenn auch wte Einheits-
wurzeln oder überhaupt irgend welche Konstanten ad-
jungiert werden, wie sich daraus ergibt, daß durch Substitu-
tionen der Gruppe 23 jede Wurzel der Teilungsgleichung in jede
andere, also auch jede Reihe in jede andere Reihe übergeführt
werden kann.
Durch die Adjunktion einer Wurzel £ der Transformations-
gleichung, etwa der zur Gruppe 9I11O gehörigen, reduziert sich die
Gruppe der Teilungsgleichung auf 2li, 0, die letztere Gruppe ist
aber nicht mehr transitiv, sondern vertauscht die cp (n) Wurzeln
worin h ein vollständiges System inkongruenter, zu n teiler-
fremder Zahlen durchläuft, untereinander. Die Teilungsgleichung
wird also reduzibel und hat einen Faktor <p(w)ten Grades,
') Vgl. Dirichlet-Dedekind, Vorlesungen über Zahlentheorie, 4. Auf].,
§ 37.
222 Sechster Abschnitt. § 65.
dessen Wurzeln die aj,)0 sind. Der Einfluß einer- Substitution
der Gruppe 911,0
/a, 6\
\0, 8/
auf 0 besteht darin, daß x!lt 0 in 0 übergeht, und die Gruppe
dieser Gleichung <p(w)ten Grades besteht daher aus den Ver-
tauschungen
(p-'h, 0, ^ÖÄ,0),
worin 0 jede beliebige zu n teilerfremde Zahl sein kann. Diese
Gruppe ist eine Abelsche und daher sind die Wurzeln a;^0
nach Adjunktion von g algebraisch durch Radikale zu
bestimmen.
Wenn wir aber nicht nur eine, sondern sämtliche Wurzeln £
der Transformationsgleichung adjungieren, oder, was auf dasselbe
hinauskommt, die drei zu 2?ij0, -Ro, 1, -Ri,i gehörigen, so reduziert
sich die Gruppe der Teilungsgleichung auf 9I0, und wenn wir
noch nte, Einheitswurzeln adjungieren, auf 5B0. Die Gruppe
ist eine Abelsche vom Grade 2fc, die nur solche Elemente ent-
hält, deren Grad — 2 ist. Infolgedessen ist die Teilungs-
gleichung durch Quadratwurzeln lösbar.
Um die Form dieser Lösung zu finden, setze man
n = pnp'n'...,
worin p, p', ... voneinander verschiedene Primzahlen, sr, jr', ...
positive Exponenten sind. Man bestimme die Zahlen c, c', ... aus
den Kongruenzen
c = — 1 (mod pÄ), c' = — 1 (mod p'Ä/) ...
c = -j- 1 (mod np—Ä), c' = -j- 1 (mod np'-...
dann erhält man jede Lösung a, der Kongruenz
a2 = 1 (nmd n),
und jede nur einmal, in der Form
(12) a = clc's' ... (mod «),
wenn s, s', ... die Werte 0, 1 annehmen.
Ist nun Sl irgend einer der Werte
4fiA + iii'iK’
---------------__,
n
§ 65. Zurückführ. d. Teilungsgleichung a. Transformationsgleichungen. 223
also snß irgend eine Wurzel der eigentlichen Teilungsgleichung,
so hat die auf alle a auszudehnende Summe
(13) 2?(+1 )s(+ l)6' ... sn«ß — V’(ß),
worin die Ä Vorzeichen von + 1 beliebig gewählt werden können,
die Eigenschaft, daß für jedes nach (12) bestimmte a
(14) ip(a£Z) = (+ 1)£ (± 1)£'. •. (&)
ist, und das Quadrat von ^(ß) bleibt durch die Substitutionen der
Gruppe So ungeändert, ist also durch nte Einheitswurzeln und
die Wurzeln einer Transformationsgleichung rational ausdrückbar.
4>(ß) ist also die Quadratwurzel |C1 aus einem solchen Aus-
druck A. Die Anzahl der Ausdrücke (13) beträgt aber 2Ä, und
es ergibt sich durch Addition aller so gebildeter Gleichungen
(15) 2,;snß = 2?]/A.
Es ist noch zu bemerken, daß von den Größen also auch
von den A, die Hälfte verschwindet. Denn es ist
— 1 = cc'... (mod w),
und wenn man also in (14) a = —1 setzt, so folgt:
ß) = (±1) (±1)... ^(ß);
andererseits ist aber
ip (— iß) = — (iß),
und folglich verschwindet 4 (ß) immer dann, wenn unter den in
(14) vorkommenden k Größen +1 eine gerade Anzahl von nega-
tiven Einheiten enthalten ist.
Die Wurzeln können also linear’ durch 27c-1 Quadrat-
wurzeln ausgedrückt werden.
Wenn n eine Primzahl oder eine Potenz einer Prim-
zahl ist, so sind die Quadrate der Wurzeln der Teilungs-
gleichung rational durch die Wurzeln der Transforma-
tionsgleichung ausdrückbar1).
Ist n eine zusammengesetzte Zahl, so läßt sich die Einteilung
der Wurzeln in Reihen noch weiter treiben. Ist p eine in
) Vgl. über diesen Satz Kronecker, Monatsbericht der Berliner
Akademie, 19. Juli 1875. Kroneeker macht dort auf ein Versehen auf-
merksam, das sich in einer diesen Gegenstand betreffenden Abhandlung
von Jacobi (Grelle, Bd. 47 und Bd. 50) findet.
224
Sechster Abschnitt.
§ 65.
n aufgehende Primzahl, so nehme man zwei Wurzeln
in dieselbe oder in verschiedene Reihen auf, je nachdem
p v' — v (i' = 0 (mod p)
oder nicht; gehören hiernach xv^ und a\, in eine Reihe mit
so gehören sie auch untereinander in dieselbe Reihe. Die
Anzahl der so gebildeten Reihen ist, wie leicht nachzuweisen,
p .1 und man erhält auf diese Weise als erste Resolvente der
Teilungsgleichung eine zum Divisor p gehörige Transformations-
gleichung. Wir werden später auf anderem Wege zeigen, wie die
Transformationsgleichungen für zusammengesetzte Divisoren auf
solche für Primzahldivisoren zurückgeführt werden können.
Siebenter Abschnitt.
Theorie der Transformationsgleichungen.
§ 66. Bildung von Transformationsgleiehungen.
Nachdem nun die Teilungsgleichungen auf Transformations-
gleichungen zurückgeführt sind, gehen wir an ein genaueres
Studium dieser letzteren Gleichungen.
Wir nehmen n ungerade an, verstehen unter p die in 'n auf-
gehenden Primzahlen, setzen
(1) v = ^(n) = nH (1 4- 1),
und bezeichnen die v Reihen der Wurzeln der Teilungsgleichung
mit jRj, jR2, ..., JRV.
Aus jeder dieser Reihen nehmen wir für
(2) a,., =
einen Repräsentanten ß,, ß2, ..., ßr und erhalten die (p(n)
Wurzeln einer Reihe, wenn wir in
snmß
m ein vollständiges System inkongruenter zu n teilerfremder Zahlen
durchlaufen lassen.
Die einfachsten Ausdrücke, die als Wurzeln von Transforma-
tionsgleichungen eingeführt werden können, sind die Produkte
(3) n <Z>(snÄß),
1, n — 1
wenn 0 eine beliebige rationale Funktion ist, und h die. Reihe
der Zahlen 1, 2, ..., n — 1 durchläuft.
Jede solche Funktion ist rational ausdrückbar durch snß
und bleibt offenbar ungeändert, wenn ß durch irgend ein mß
Weber, Algebra. IU. 15
226 Siebenter Abschnitt. § 66.
ersetzt wird; man hat also nur noch dafür zu sorgen, daß die
v Werte von (3), die den v Reihen entsprechen, voneinander
verschieden sind, um (3) zur Wurzel einer (irreduzibeln)
Transformationsgleichung zu machen1).
Wir nehmen an, die Funktion ®(a?) sei entweder eine
gerade oder eine ungerade Funktion von x, und machen
danach folgende Unterscheidung.
Ist <b(.r) eine gerade Funktion, so sind unter den Faktoren
des Produktes (3) je zwei, nämlich
(4) (sn h ß), 0 [sn (n — h) ß]
einander gleich. Setzen wir also
(5) n(ß) — n ®(snÄß),
1 n — 1
so ist, wenn m eine beliebige zu n teilerfremde Zahl ist,
(6) n (mß) =
[weil unter den |(w — 1) Zahlen hm nicht zwei eine durch n
teilbare Summe oder Differenz haben, also, vom Vorzeichen ab-
gesehen, die snAß dieselben sind, wie die snÄmß]. Es ist also
77(ß) die Wurzel einer Transformationsgleichung. Diese Klasse von
Transformationsgleichungen nennen wir Modulargleiehungen.
Ist 0(rr) eine ungerade Funktion, so sind die beiden Größen
(4) entgegengesetzt und (6) ist nicht mehr allgemein richtig,
sondern es ist
(7) 77(mß) = ±H(ß).
Daher ist, wenigstens im allgemeinen, nicht mehr 77 (ß),
sondern erst 77 (ß)2 Wurzel einer Transformationsgleichung. Diese
Art von Transformationsgleichungen nennen wir Multiplikator-
gleichungen. Um die Fälle kennen zu lernen, in denen 77(ß)
selbst Wurzel einer Transformation ist, muß das Vorzeichen in
(7) bestimmt werden.
Dies gelingt auf Grund eines Satzes der Zahlentheorie, dei'
im Bd. I, § 145 abgeleitet ist.
Dei' Satz lautet:
') Ausdrücke wie (3) sind auch dann noch Wurzeln von Transformations-
gleichungen, wenn h nur zu n teilerfremde Werte annimmt. Solche Trans-
formationsgleiehung hat man bisher noch wenig benutzt. Wir werden
weiterhin ein Beispiel kennen lernen.
§ 66. Bildung von Transformationsgleichungen. 227
Sind m, n irgend zwei teilerfremde Zahlen, letztere ungerade,
bedeutet ferner p, die Anzahl derjenigen unter den Zahlen
n — 1
m, 2 m, 3 m • • • —— m,
deren absolut kleinste Reste (mod n) negativ sind, so ist
(8) (-> = ©,
— \ das Legendre-Jaeobisehe Symbol aus der Theorie
der quadratischen Reste ist1).
Dieser Satz führt nun unmittelbar zur Bestimmung des Vor-
zeichens in (7). Denn wenn in (5) die Funktion ®(.r) ungerade
ist, so ändern beim Übergang von ß zu. mß genau g Faktoren
in (5) ihr Vorzeichen und wir schließen
(9) = Q 77(ß).
Ist n keine Quadratzahl, so kann man m immer so annehmen,
— 1 = —1 ist. Ist nämlich n = pln', /. ungerade, n' nicht
durch p teilbar, ß ein quadratischer Nichtrest von p, so braucht
man m nur aus den Kongruenzen
m = ß (mod m = 1 (mod n')
zu bestimmen, um eine solche Zahl m zu finden. Und dann ist
77 (mß) = —77 (ß) und nicht II (ß), sondern erst 77 (ß)2 Wurzel
einer Transformationsgleichung. Ist aber n eine Quadratzahl,-so
ist 77(mß) = n(ß) für jedes m und folglich 77 (ß) selbst Wurzel
einer Transformationsgleichung. Es folgt also der Satz:
Bei ungerader Funktion 0 ist 77(ß)2, und nur
wenn n eine Quadratzahl ist, 17(ß) selbst, Wurzel
einer Transformationsgleichung2).
’) Vgl. über diesen Satz: Sehering und Kronecker im Monats-
bericht der Berliner Akademie vom 22. Juni 1876. Schering, Acta mathe-
• matica I.
2) Diese Vereinfachung der Multiplikatorgleichung in dem Fall, wo n
ein Quadrat ist, hat Joubert entdeckt, aber auf einem von dem unserigen
ganz verschiedenen Wege nachgewiesen. „Sur les equations, qui se ren-
contrent dans la theorie de la transformation des fonctions elliptiques.“
Paris 1876.
15*
228
Siebenter Abschnitt.
§ 67.
§ 67. Besondere Transformationsgleichungen.
Es sollen nun die Wurzeln der Transformationsgleiehungen
durch &- Funktionen dargestellt werden. Wir setzen zu diesem
Zweck:
ß = 4p'tP' iK, _ K
n
~H n/ ® n . T7-
Tä = r -------- ß —
n
und betrachten die Produkte
h h h h
n <9’00(2 7»7n), n -9’01(2 7»tn), II 4t10(2äuj), II -9’11(27»to).
Es empfiehlt sich folgende Bezeichnung:
n — 1 n i ,, . , v n2—1
—*— **7“ #*' Cu + ,u' °>)- h
PoO^OO == e ^00
n — 1
X’ 2
n — 1 fri ,, , —1
—-— —lu/(,a4-(U,<ü)------- h
(2) Pi«Ao2 =e6 n n 4W2M,
7 n— 1
’ —2
n — 1 7ti tr , , n*—1
— ---------jj,f (a 4- ,UrÖ>) - h
PoiV =e6 ” n 4f01(2 7m).
, n — 1
Es ist jetzt die Formel § 39, (9) anzuwenden, die man aber
für den gegenwärtigen Zweck etwas anders darstellt.
Setzt man in § 39, (8) v' = ‘Ih/n, v = 2h(aß co)/n
und nimmt abermals das Produkt über h = 1, 2, ... (n — l)/2,
so folgt mit Anwendung von § 32, (24):
/2 h (cc ß co)\ (2 h(a ßco)\ /2h(a ßco)'
V0Q I ------------- ) 'M 01 ( ------- } Vi o ( ---------
l. \ / \ / \
Demnach erhält man durch Multiplikation der drei Glei-
chungen (2):
(3) (-1)^2^P00P1()P01 = 1.
l) In § 34, (9) der ersten Auflage ist die betreffende Formel gleich in
dieser Form angegeben, die sich auch, wenn auch etwas umständlicher,
aus § 39, (9) ableiten läßt.
Besondere Transformationsgleichungen.
229
§ 67.
Außerdem setzen wir noch:
(*)
n—1 ni . n2—1 h
2 = e6 u M “ n n P-u(2huf).
Diese Größen P lassen sich durch die Wurzeln der Teilungs-
gleichung ausdrücken, wenn man unter Anwendung von (3) die
Quotienten
J oo
^oxÄo’
-Pfll-Poo1 -P10-P(
bildet und vermittelst der Formeln
tionen einführt.
Man
ps
•PooPoi-Pxo
(5)
(6)
>2 P2
10 x 01
oo
des § 42 elliptische Funk-
erhält so
n‘2—X n — 1
(-1) s 2 2 P30
n2—1 n—1
(-1) 8 2 2 P?o
(-1) 8 2 2 P^
h
= n
1 n — 1
h
dn2/iß
cnhSl 1
i,----------
’ 2
Tl
cn2 /iß
dn/iß ’
n2—1 n — 1
(- l)~Ph = (xx')~
sn3/iß
cnAßdnAß
Diese Ausdrücke zeigen nun, daß P030, P^, P^ die Wurzeln
von Transformationsgleichungen (Modulargleiehungen) sind.
Pfj ist die Wurzel einer Multiplikatorgleichung, und wenn n
eine Quadratzahl ist, so ist auch P3j die Wurzel einer Multi-
plikatorgleichung.
Man
einander
erhalten.
(7)
kann in mannigfaltiger Weise die Funktionen P mit-
kombinieren, um neue Transformationsgleichungen zu
Wir führen folgende an:
P cn/iß
i dn/iß’
i, -—-
’ 2
h 1
11
n_i dn/iß
J10
-Poo
-Poo
1
2
h
n — 1
230
Siebenter Abschnitt.
§ 67.
M — 1
«2~1 9 3 p2 p
(__ 1) 8 • O0-Cll
n — 1
"'s”
sn/ißduTzAZ
„_i cn/iß
1,—2
(8)
n—1
«8~1 0—3~ pa p
(_i) s ±__£n>_£’
sn/ißcn/iß
dnfcß
n — 1
3
n — 1
2
n2~1 9 3 pa p h
(-i) 8 --------= n
h’ 3
wichtiges Resultat ergibt sich
snfeß
cn/ißdn/iß
aber noch durch An-
Ein
wendung des Multiplikationstheorems. Wenn man- in der letzten
Formel II des § 57 w = 2 h ts setzt, so findet man
v 7 01 v 7 D(sn2A^i)
worin, wie wir uns erinnern, D eine ganze rationale Funktion ist,
deren Koeffizienten rational aus z2 und ganzen Zahlen gebildet sind.
Nehmen wir das Produkt aus diesen Ausdrücken, für
h = 1,2,..., W \ so
^weil bekanntlich Sh2 =
(10)
1
folgt aus der letzten Gleichung (2)
n(n2 — 1)\
—24 )'
h
01 ^./IiJfsn2/!^)'
’ 2
Wir schließen hieraus, daß auch P”i die Wurzel einer Trans-
formationsgleichung ist. Dies ist nichts Neues, wenn n durch 3
teilbar ist, wohl aber, wenn n nicht durch 3, also n2 — 1 durch
3 teilbar ist. Wir erhalten dann nämlich aus (10) mit Be-
nutzung von (5), (7), (8):
(n — 1) («2 — 1) R
P01 = 2 « n
n — 1
(W —1)(«2—1) h
(11) Poo = 2 3 n
1
’ 2
(W —1)(«2—1) h
-P10 = 2 6 n
ng—1 «g—1
(cn/iß) 3 (dnfeß) 3
D(sn2Aß)
n2—1 - n2+2
fcn/iß) 3 (dn/iß) 3
_D(sn27iß)
n-4-2 «2—1
(cn/iß) 8 (dn/iß) 8
D(sn2Äß)
n— 1
2
§ 68. Zweite Darstellung der Wurzeln der Transformationsgleichungen. 231
«2—1 «2(m— i)
(12) (-1) 8 2 « Pn
--- y/KK 2«2+1 2«2 + 1
’>(cnÄß) 3 (dnAß) 8
Soll als Rationalitätsbereich der der rationalen Zahlen und
rationalen Funktionen von x2 aufrecht erhalten werden, so schreibt
man die letzte Gleichung besser in der Form [vgl. § 54, (4)]:
« —1 «2—i _ («2—<)(« — i) _ n — 1 n — 1
2 =(—1) 8 2 8 (xx') 2 (1 —x2x'2) 2
(13) A. snÄßZ)(sn2Äß)2
X — 2 «2 + l 2«a + l ’
(cnfeß) 8 (dn/iß) 8
und schließt daraus auf den folgenden Satz:
Wenn n nicht durch 3 teilbar ist, so sind Poa, P01,
Pio, Pny2(ra)"-1, und wenn n ein Quadrat ist, auch
n—1
Puy2(<») 2 Wurzeln von Transformationsgleichungen.
§ 68. Zweite Darstellung der Wurzeln der Transformations-
gleiehungen.
Wenn wir zunächst eine der Reihen ins Auge fassen, nämlich
die, zu der die Wurzel gehört, also = 1, fi' = 0 setzen,
so können wir auf (2), (3) des vorigen Paragraphen die Formeln
(20), (21), (10), § 34 anwenden. Setzt man dort, wenn v un-
gerade ist, n — v an Stelle von v und benutzt die Formel
(n — v\ s-Ds-2+1) /v\
n"~) ~~ ( ®9'9i\n)'
dann kommen in diesen Formeln nur die geraden v vor, und
wenn man also v = 2 h setzt, so kann man die dortigen Formeln
(20), (21) auch so schreiben:
___ n—3 h
]/n n] (n«) t] (ra) 2 = 17 — ),
n — 1 X W /
’ 2
n— 1 h /fy Ji\
f(no)i}(p) 2 = f(ro) 17 -9oo( —),
n — 1 \ '*' /
2
n — 1 h
fi (110)11(0) 2 = fr(o) n -9oi(— ),
n —1 \ *^ /
X’ ~~2~ .
n — 1 /O\ h /£>'h\
4 (n o) (o) 2 = ( -) /3 (<d) n 1 (—),
232
Siebenter Abschnitt.
§ 68.
(2\ —i
— \ = (— 1) s , und wenn wir also die dem Falle
ji = 1, jß = 0 entsprechenden Funktionen P mit P° bezeichnen,
so folgt aus § 67, (2) und (4) mit Rücksicht auf § 34, (10):
Po xO0 fßnea) f(.a)n '
(1) = fitnco) A(®)"
po — ( 10 \n > . f2(ne>)
(2) P^ = (/n rj (nra) j?(ra)
Um durch solche Formeln die sämtlichen Wurzeln der Trans-
formationsgleichungen darzustellen, bestimmen wir eine lineare
Transformation folgendermaßen:
<3’ Q«) - G: ?)
(4) a = «, ß = p' (mod ri),
und ersetzen ra in (1), (2) durch
auf die linke Seite lassen sich dann die Formeln (3) bis (6)
§ 39 und (19), § 38 anwenden und ergeben:
p _ fW)
00 ~ />')’» ’
p _ A(W(a')
761 A ’
W p _ /2\ f2(nt0'')
10 - W
worin e die in § 33, (15), (18) genau definierte 24ste Einheits-
wurzel ist.
Nun lassen sich zwei Transformationen
§ 68. Zweite Darstellung der Wurzeln der Transformationsgleichungen. 233
von denen die erste linear, die andere von der nten Ordnung ist,
so bestimmen, daß
z7x /«', ß'\ (a, 0\ _ /l, 0\ Sa, ß\
V, Ö7 V, d) — \0, n/ V, $)'
Denn schreiben wir die Relation (7) so:
/ /l,0\ Za, 0\ / S,—ß\
\—y', a'J \0, n) \c, 0/ \—-y,
so leitet man daraus einfach her:
ö' = aö, y' — dy — cö,
' dß' = ß, na' — da — cß, aa' — a — eß'.
Hierdurch ist zunächst g bestimmt als der größte gemein-
schaftliche Teiler von ß und n oder [wegen (4)] von p' und n.
Denn wäre 0 nicht der größte gemeinschaftliche Teiler von
n = d a und ß — 0 ß', so müßten a und ß' einen gemeinsamen
Teiler haben und folglich auch ß und a — aa' -|- cß, was nicht
sein kann. Dadurch ist zugleich a = n/d bestimmt, und c muß
der Kongruenz
(9) da — cß = 0 (mod ri)
genügen, wodurch jedoch c nicht absolut, sondern nur nach dem
Modul a bestimmt ist. Man kann also c z. B. noch an die Be-
dingung knüpfen, daß es durch irgend eine Potenz von 2, oder
wenn a nicht durch 3 teilbar ist, durch irgend eine Potenz von 3
teilbar sein soll, was wir später bisweilen tun werden.
Die drei Zahlen a, 0, c können keinen gemeinsamen Teiler
haben, denn ein solcher wäre [nach (8)] auch Teiler von a und ß,
was unmöglich ist. Bezeichnen wir also den größten gemeinsamen
Teiler von a und 0 mit e, so muß c relativ prim zu e sein.
Die Zahlen a, d, c, letztere modulo a, sind wegen (4) und (8)
durch die beiden Zahlen p, p' völlig bestimmt und ändern sich
nicht, wenn p, p' mit einem gemeinsamen, zu n teilerfremden
Faktor multipliziert, d.h. durch ein anderes Paar derselben Reihe
ersetzt werden. Zerlegt man n irgendwie in zwei Faktoren a, 0,
so kann man für c noch
a , .
7^(6)
nach dem Modul a verschiedene zu e teilerfremde Werte an-
nehmen. Jede dieser Annahmen führt zu einem Zahlenpaar (i, p'
durch die Kongruenzen
234 . Siebenter Abschnitt. § 68.
0«)
worin ß' eine beliebige, zu a teilerfremde Zahl bedeutet und ot,'
so bestimmt wird, daß «, ß relativ prim werden, und es ist auch
leicht [nach § 65, (3)] einzusehen, daß, so lange a, d, c dieselben
bleiben, die nach (10) bestimmten Zahlenpaare ft, p' derselben
Reihe angehören.
Wir nennen die Zahlen a, c, c (wie in § 27) die Trans-
formationszahlen und n den Transformationsgrad.
Das Zahlensystem a, c, d ist also vollständig charakte-
ristisch für eine Reihe, und die Anzahl der Reihen ist gleich
der Anzahl dieser Zahlensysteme, woraus für die Zahl V’(n),
(§ 63) folgt:
(11) .^(W) = 2|<jp(c>
wenn die Summe auf alle Divisoren a von n erstreckt, wird.
Es ist von Interesse, diese Relation auch direkt zu beweisen,
wobei die Beschränkung auf ein ungerades n wegfallen kann.
Betrachten wir tl>(n) jetzt als Zeichen für die Summe (11), s'o
ergibt sich, wenn n', n'1 relativ prim sind, zunächst
$ (»') (n") — (n1 n,r),
und es bleibt also nur übrig, die Summe ip(n) für den Fall zu
bestimmen, daß n = pn eine Primzahlpotenz ist. In diesem
Falle ist nun e gleich dem kleineren der beiden Divisoren a. c,
und wenn a = d ist, e = a. Wenn wir also das erste und
letzte Glied der Summe.^(m) absondern, so erhalten wir
V(p’1) =!-)-7^ 4- (8)-
KatS-Vn . : ’
Yncacn
Es ist aber
<P(«) = ?(8) —
also
7/)(pÄ) = 1 -f- p71 ----- Sa
. . » : ‘ _ \tp fl<a<n
__ 1 4- (p—1) (1 4-p -j-j44- • • = p’r.fi4_~\
§ 68. Zweite Darstellung der Wurzeln der Transformationsgleichungen. 235
woraus sich für ^(m) der Ausdruck
V’(m) = w77(1 +j)
ergibt, wie in § 63x),
Nach (7) ist nun in den Formeln (6) für na' zu setzen:
§, c±Za
a
a' + ^l+8t0’
a
und es lassen sich die linearen Transformationen der /"-Funk-
tionen [§ 40, (4), (8), (11)] anwenden. Wir nehmen dabei
(12) c = 0 (mod 16),
so daß nach (3) und (8):
/«', ß'
W, s1
) - (;•’’) ->•
Bezeichnen wir mit die dritte Einheitswurzel
— ~ [«'(/'—/J')—(a,a—l“(r—ß)—(«s—i)3<ll
(13) q = e ä e ä
so erhalten wir
gibt nach § 54, (3), wenn man
u(a) —
setzt, die Größen
’) Vgl. Dedekind: Über die elliptischen Modulfunktionen. Journal
f. Mathematik, Bd. 83.
236
Siebenter Abschnitt.
§ 68.
/c + 8 <a\
/ 9 \ u (—-------‘)
<,6> Q ,(;
als Wurzeln einer Modulargleichung, und dies ist die Jacobische
ModulargleichungQ.
Ist n nicht durch 3 teilbar, so nehmen wir
(17) c = 0 (mod 3)
an, wodurch p den Wert 1 erhält.
In gleicher Weise kann man die Transformation der ^-Funk-
tion [§ 38, (15), (18), (19)] auf die letzte der Gleichungen (6)
* anwenden und erhält:
(wobei es schon genügen würde, wenn c durch 8 teilbar ist).
Ist n durch 3 nicht teilbar und c durch 3 teilbar, so ist auch
hierin p = 1 zu setzen.
Die Bestimmung des. Vorzeichens in (18) hat für uns nur
in dem Falle Interesse, wo n ein Quadrat ist. Es ist aber
[nach (8)]
m (A\ = (Aj m = (L\ = \
\a/\a'/ \a J \aa'J \a/\a/ \o/\aj
[letzteres nach dem Reziprozitätsgesetz der quadratischen Reste,
weil a = 1 (mod 4)]. Wenn nun n ein Quadrat ist, so sind
auch a:e, d:e Quadrate und es ergibt sich:
(^\ = (^\ — (£
\8/ \a) \ e / \e
also wird in diesem Fälle
c +
- w
Die zur Charakterisierung einer Reihe aufgestellten Formeln
(10) sind ein spezieller Fall eines allgemeineren Systems, das
man erhält, indem man auf ß' in (10) eine lineare Trans-
formation anwendet. Man erhält dann folgendes:
*) Ist J7 der Jacobische Multiplikator, so ist
n—1 n—1
3
— 4 P2 3 P4
— * -*-11 -roo •
Die Invariantengleichung.
237
Sind a, b, c, 0 vier der Bedingung:
ad — bc = n
genügende ganze Zahlen ohne gemeinsamen Teiler, so erhält man
die einer Reihe entsprechenden Zahlenpaare ft, p', wenn man in
f4 = aa' + cß' r 4 x
<19> = s«- + Dß' <“',d ">
a', ß' alle und nur solche Werte durchlaufen läßt, hei denen
ft, p.' ohne gemeinsamen Teiler mit n sind.
Daß zwei den Kongruenzen (19) entsprechende Wertpaare
ft, ft' wirklich derselben Reihe angehören, ergibt sich unmittelbar
aus § 65 (3), und ebenso ist selbstverständlich, daß alle Zahlen-
paare einer Reihe in dieser Form enthalten sind, da man ß'
durch ha', hß' ersetzen kann, wenn h relativ prim zu n ist. Daß
man sämtliche Reihen auf diesem Wege bekommt, zeigen
die Formeln (10).
§ 60. Die Invariantengleichung.
Unter den Transformationsgleichungen verdient eine ein be-
sonderes Interesse, nämlich die, deren Wurzeln die ^(n) Größen
(1)
a
oder nach der Bestimmung (19), § 68 die damit identischen
Größen
sind, wenn J(ro) die in § 46 definierte Invariante ist.
Diese Gleichung heißt die Invariantengleichung.
Die Funktion J(m) läßt sich nach § 54 rational durch /"(o)24
darstellen, nämlich
(3)
(/(ö)24 — 16p
/(+
J(c>) =
so daß also nach den Resultaten des vorigen Paragraphen die
Größen (1) die Wurzeln einer Gleichung sind, deren Koeffizienten
rationale Funktionen von x2 sind.
Setzt man aber für /"(») in (3) eine der früher gefundenen
Entwickelungen, z. B. § 24, (11):
/•(«,) = 17(1 +g2”-4),
f ...
238
Siebenter Abschnitt.
§ 69.
so erkennt man, daß j(ct>) sich in eine nach Potenzen von q3
fortschreitende Reihe entwickeln läßt, welche die Form hat
(4) — q~3 4- «j -p a2q3 -j- a3g* ---,
worin die ax, a2, a3 ... ganze rationale Zahlen sind, die sich
successive berechnen lassen (es ergibt sich z. B. Oj = 744,
a2 = 196 884). Die Entwickelungen der Größen (1) beginnen
also mit
2 nie 2nit)
Z-\ ------------W
(o) e a e a
und sind daher alle voneinander verschieden. Die
Invariantengleichung ist also nach § 65 irreducibel.
Es gibt aber einen zweiten Weg, um zu dieser wie überhaupt
zu den Transformationsgleiehungen zu gelangen, den wir jetzt
zunächst bei der Invariantengleichung kennen lernen wollen.
Diese Ableitung stützt sich auf die Sätze des § 54 über Modul-
funktionen und gilt auch für ein gerades n. Hier ist es der
Satz 4, § 54, der zur Anwendung kommt:
I. Jede Modulfunktion, die durch die beiden Trans-
formationen
G: '
(7) Ui:»)
ungeändert bleibt, ist eine rationale Funktion von j(ß>).
Wir weisen zunächst nach, daß durch Anwendung der Sub-
stitutionen (6), (7) die v Größen (1) untereinander vertauscht
werden. Wir haben die Zusammensetzung
r . Za, 0\ ZI, 0\ ZI, 0\ Za, 0\
wenn
(9) . q = c 0 — Xa
gesetzt wird, und es geht durch die Transformation (6), da )(w)
durch jede lineare Transformation ungeändert bleibt,
über.
Ferner bestimmen wir a2, d2, c2, so daß
7101 (a' °\ ( °’ 1'\ —
k ; V, 0/ \— 1, oj - V, V U, dj ’
ad — ßy = 1.
§ 69. Die Invariantengleichung. 239
Dazu ist erforderlich
a <x2 —ß c2 0
ya2 +'öc2 = —0,
ßd2 = a
ÖÖ2 = c.
Es ist also 02 bestimmt als der größte gemeinschaftliche
Teiler von a und c, und damit zugleich, wegen «202 = n, auch «2.
Nach den beiden Gleichungen (12) kennt man jetzt ß, d
als relative Primzahlen und kann a, y aus der diophantischen
Gleichung
ad — ßy = 1
bestimmen. Ist dies geschehen, so folgt aus den beiden
Gleichungen (11)
«2 = dß,
c2 = —da,
wodurch auch c2 bestimmt ist, und es zeigt sich zugleich, daß d
der größte gemeinschaftliche Teiler von «2, c2 ist. Ersetzt man
a, y durch eine andere Lösung a hß, y hd, so ändert sich
nur c2 um ein Vielfaches von «2.
Durch die Transformation (7) geht also
c -I- d a> \ . . ( c2 -I- 02 <x>
—•---------------------- m d ——!—-—
a / \ a2
über.
Bilden wir nun eine symmetrische Funktion der sämtlichen
Größen (1), etwa für ein unbestimmtes x das Produkt
so ändert sich diese Funktion nicht durch die Transformationen
(6), (7) und ist also nach dem oben erwähnten Satz eine ratio-
nale Funktion von ;’(<»). Außerdem ist sie eine ganze ratio-
nale Funktion vten Grades von x mit dem Anfangsglied xr, und
wir bezeichnen sie mit Fn [x, j (»)]. Die Gleichung
(14) Fn O, j (<»)] = 0
( I (tj x
—1-----) zu Wurzeln und ist die Inva-
aj
riantengleichung, deren wichtigste Eigenschaften wir nun ab-
leiten wollen.
1. Die Invariantengleichung ist irreducibel, wenn als
Rationalitätsbereich der Inbegriff aller rationalen Funktionen von
240 Siebenter Abschnitt. § 69.
mit beliebigen Zahlenkoeffizienten betrachtet wird. Denn
besteht irgend eine rationale Gleichung
(15) 0[J(mo), J(o)] = 0,
so darf darauf jede beliebige lineare Transformation
/«, A
V, $/
angewandt werden, und nach § 29, (5) lassen sich, wenn
CC)
eine beliebige Transformation nter Ordnung ist, die linearen
Transformationen
/a, ß\ Sa', ß'\
V, s)' W, S')
immer so bestimmen, daß
/1fn /«', ß'\ fa,i\ _ Zl, 0\ /a, ß\
{ > V', 6') d) — ^0, n) ß) '
Daraus folgt aber, daß die Gleichung (9) durch jede der
Größen
/e + deA
J \a -|- bcoj
und mithin auch durch jede der Größen (1) befriedigt ist, woraus
[wegen der Verschiedenheit der Größen (1)] die Irreducibilität
von (14) folgt.
2. Die Funktion
(17) Fn[x, j(»)] = n — j
hat für jeden endlichen Wert von a> mit positiv imaginärem Be-
standteil, also auch für jeden endlichen Wert von einen
endlichen Wert und ist sonach eine ganze rationale Funktion
von J(<o).
Suchen wir ferner nach (3) das Anfangsglied der Entwicke-
lung der Funktion (17) nach Potenzen von q, so ergibt sich
— SitiS— —Zrria S — ®(e)
(— l)»e ae .. e — Cq~2*,
wenn C eine endliche Konstante ist. Es ist daher
7(»)-,'iC.[a:,7(0’)]
für ein unendliches endlich, d. h. der Grad von F„[x, j(a>)]
in bezug auf j (co) ist ebenfalls der vte.
§ 69. Die Invariantengleichung. 241
3. Es ist
= 0
uud wenn wir na durch a> ersetzen:
Da nun j gleichfalls eine Wurzel der Invarianten-
gleichung ist, so folgt, daß die beiden Gleichungen vten Grades
Fn[x, y(m)] = 0, Fn[j(ai), x\ = 0
eine Wurzel gemeinsam haben, und folglich, wegen der Irre-
ducibilität der ersteren und der Gleichheit des Grades, alle. Es
ist daher
Fn(x, y) = CFn(y, x)
für unbestimmte Werte der Variablen x, y und ein konstantes C.
Daher auch, durch Vertauschung von x mit y:
Fityi ^*) - CFn(x. 7/),
also C2 — 1 oder
Fn(x, y) = + Fn(y, x).
Wenn wir nun x = y setzen, so folgt:
Fn (y, y) = ± Fn (?/, t/),
also, wenn das untere Zeichen gilt,
Fn (y, y) = 0.
Dies ist aber nur möglich, wenn n — 1 ist [wo Fx(x, y)
= x — y wird], da sonst Fn(x, y) durch x — y teilbar sein
müßte, was der Irreducibilität widerspricht. Daher ist immer,
sobald n > 1 ist:
(18) Fn(x, y) — Fn(y, x).
4. Es sei
n = n'n", v' = il>(n''), v" = ^(n"),
und n', n" ohne gemeinsamen Teiler, und x^ x2, ... xv» seien
die Wurzeln der Gleichung
(19) Fn»[x, y(ro)] = 0.
Das Produkt
(20) Fn-(x, x^ Fn>(x, ®2) ... Fn>(x, x?n),
dessen Grad in bezug auf x gleich
v = ip(n) = («') ip (n”)
ist, hängt als symmetrische Funktion der Wurzeln von (19),
rational von j(a) ab und verschwindet für
. / a> \
Weber, Algebra. IIT.
16
242 Siebenter Abschnitt. § 69.
d. h. für eine Wurzel der Gleichung Fn[x, )(«)] = 0. Wegen
der Irreducibilität der letzteren Gleichung, der Gleichheit des
Grades und des Koeffizienten von xv ist also
(21) Fa[x, y(ro)] = Fn>(x, Xy)Fn'(x, x^ ... Fnl(x, xt,’).
5. Ist n = p7T- eine Primzahlpotenz, so ist der Grad der
Funktion Fn [x, j (»)] gleich pn~Gp -|- 1), und die Gleichung
(22) Fpx-i [x, j (®)] = 0
ist vom Grade
v' — px—^fj) 1).
Wir bezeichnen ihre Wurzeln mit xly
Das Produkt
P = Fp (x, x-^ Fp (x, a?2)... Fp (x, x,<)
ist in bezug auf x vom Grade v'(p 1) = px~-(p -|- l)2; es
hängt symmetrisch von den Wurzeln von (22), also rational von
y(ro) ab und verschwindet für
Daher ist P durch Fn [x, j (»)] teilbar.
Aber der Grad von P ist höher als der von Fn. Nehmen wir
______________________ . co\
p7*-1 )'
wo c jeden der Werte 0, 1, 2, ... p — 1 haben kann, so ver-
schwindet Fp(x, xx) für
(23) !>,;(<»)]
d. h. es haben p von den Faktoren von P einen bestimmten
Faktor mit Fp«—2 [«,/(»)] gemein; daraus folgt, daß P durch
{Fp^-2[x,
teilbar ist, und mithin, wie die Vergleichung der Grade und
höchsten Glieder lehrt:
Fp(x, x1)Fp(x, x2) ... Fp(x, xtl)
J(co)]f
Diese Formel ist einer Ausnahme unterworfen für ft = 2,
weil in diesem Falle der Grad der Funktion auf der rechten
Seite noch zu hoch ist. Für diesen Fall hat aber jeder der
p -|- 1 Faktoren des Produktes P den Teiler x — j(fF)-> weil eben
•jedes x{ Wurzel der Gleichung Fp[x, y’(<»)] ist, und es tritt an
Stelle von (23) die Formel
/oz. 7? r™ ___________ Pp(.xi ^i)Fp(x, x^j... Fp(x. a^ + i)
§ 69. Die Invariantengleichung. 243
Hierdurch ist die Lösung der Invariantengleichung Fn = 0
auf die successive Lösung solcher Fälle zurückgeführt, in denen
n eine Primzahl ist.
6. W ährend bei der Ableitung der Transformationsgleichungen
aus den Teilungsgleichungen von Haus aus feststeht, daß die
numerischen Koeffizienten in diesen Gleichungen rationale Zahlen
sind, so lehrt uns die zweite Ableitung zunächst nichts über die
Zahlenkoeffizienten. Wir können aber nachträglich beweisen, daß
diese Koeffizienten nicht nur rationale, sondern auch ganze
Zahlen sind und gelangen zugleich zu einem wichtigen Satz über
die Teilbarkeit dieser Koeffizienten.
Wenn wir beweisen können, daß, wenn p eine Primzahl ist,
die Koeffizienten in Fp(x. y) ganze Zahlen sind, so folgt das
Gleiche aus 4. und .5. für jedes zusammengesetzte n.
Nach (4) ist j'(ra) in eine Reihe von der Form entwickelbar
(25) J(o) = q~2 S ahq2h,
0,co
deren Koeffizienten ah ganze Zahlen sind, und zwar a0 = 1.
Bilden wir hiervon, wenn p eine Primzahl ist, die pte Potenz,
und beachten den für jede ganze Zahl gültigen Fermatschen Satz:
ap = a (mod p),
so folgt
h h
(26) = q~2p 2 ahq2hp pq-M.p-»S bhq2h,
0,<® 0,oo
worin bh ebenfalls ganze Zahlen sind. Andererseits ist, wenn man
in (25) a durch pa ersetzt:
h
(27) j(Pra) = %~2p 2
0,<®
und daraus, wenn man
y(») = u, j(pco) = v
setzt:
Ä
— v = pq~ 2<~p~’> 2 bh(^hi
0zco
wofür wir auch schreiben können:
li
•(28) (up — v)(u — vp) = pq—i(p2 + p—1'> 2? chq-\
0,oo
wenn ch ein drittes System ganzer Zahlen bedeutet.
Nun kommen in Fp(x, y) die in bezug auf x, y höchsten
Glieder xp + 1 yp + 1 vor, und wir setzen demnach
h, h
(29) Fp(x, y) = (xp — y)(x — yp) — £ cKltxhy\
O,P
16*
244 Siebenter Abschnitt. § 69.
worin die zu bestimmenden Koeffizienten sind, die nach 3.
der Bedingung
Ck, k —• ^k. h
genügen. Um sie zu bestimmen, setzen wir in (29)
x — u, y = z>,
wodurch Fp verschwindet, und erhalten
h k
(30) (up — v)(u — vp~) = 27 cÄ> uh vk.
Hieraus folgt zunächst, daß
sein muß, da nach (28) bei der Entwickelung (der linken Seite)
nach Potenzen von g die Potenz q~2<r2+r) nicht vorkommen kann,
und wir können (29) jetzt in die Form setzen:
h k
(31) (Up -- v)(u -- Vp) — S s
0,p 0,7i —1
Ä
+ 2) chlhuhv\
o,p —1
Hierin sind die aus (25) und (27) sich ergebenden Ent-
wickelungen von
UhVlc Uk V‘\ tFv11
nach Potenzen von # einzusetzen, deren Anfangsglieder
q— 2(hp+K>, q—ihtp+i)
die Koeffizienten 1 haben.
Auf der rechten Seite von (31) kommen nicht zwei Glieder vor,
deren Entwickelung mit derselben Potenz von q beginnt, denn aus
hp fc = h'p 4- k'
folgt k = k' (mod p) und mithin, da k und k' <Z p sind, k = k',
h = h'.
Ordnet man daher die Reihen, welche die beiden Seiten von
(31) darstellen, nach auf steigenden Potenzen von q, und setzt
dann die Koeffizienten gleich hoher Potenzen einander gleich, so
erhält man eine Reihe linearer Gleichungen für die Unbekannten
Ch,i» von denen jede folgende nur eine neue Unbekannte enthält,
und diese mit dem Koeffizienten 1. Die aus der linken Seite sich-
ergebenden bekannten Glieder dieser Gleichungen sind nach (28)
lauter durch p teilbare ganze Zahlen, und es ergeben sich
also für die ch,k ebenfalls ganzzahlige, durch p teilbare Zahlwerte.
Demnach haben wir
h k
(32) Fp(x, y) = (xp — y)(x — yp) — p s ah>kxhy\
0,_p
§ 70. Transformationsgleichungen erster Stufe. 245
worin aR)R ganze Zahlen sind, die den Bedingungen
uRj R —; uR)R, — 0
genügen.
§ 70. Transformationsgleichungen erster Stufe.
Die Invariantengleichung ist von großer theoretischer Wichtig-
keit teils wegen ihrer allgemeinen Gültigkeit (auch für gerade n),
teils wegen der Leichtigkeit, mit der die linearen Transfonnationen
auf j (tu) angewandt werden können. Die wirkliche Berechnung
dieser Gleichung aber zeigt sich so kompliziert, und die Zahlen-
koeffizienten sind so groß, daß die Berechnung bis jetzt nur in
dem einfachsten Falle p = 2 durchgeführt ist. Dagegen kann
man, indem man andere Modulfunktionen benutzt, weit einfachere
Transformationsgleichungen erhalten.
Über das hierbei anzuwendende Prinzip bemerken wir folgendes:
Wenn irgend ein System von v Funktionen von « vorliegt,
entsprechend den v Systemen von Transformationszahlen a, c, S,
die wir mit
(1)
bezeichnen wollen und die isomorph mit den Funktionen
(2) 7
\ a /
durch die Substitutionen
(3) (<»,<» + 1)
uutereinander permutiert werden, so ist (1) rational durch (2)
und durch j («) ausdrückbar, denn die Funktion
(4)
a, c, ü
Fn[x,j(a)] S
X — j
&a, e, d
’P’D», Ära)]
bleibt durch die Substitutionen (3) ungeändert, und ist daher
(für ein unbestimmtes x) eine rationale Funktion von j(<»)
und überdies eine ganze rationale Funktion von x, höchstens vom
Grade v — 1; Fn[x, j(ra)] hat dieselbe Bedeutung, wie in (17)
des vorigen Paragraphen, und v = ty(n) ist der Grad dieser
Funktion in bezug auf x. Aus (4) aber erhält.man, indem man
. Ze + d ea \
x M---------ä---)
setzt:
246
Siebenter Abschnitt.
§ 70.
Es gehört also 0a,C)a dem algebraischen Körper an, der aus
den rationalen Funktionen von j f und j (ra) besteht, und
\ CI J
wir können die Sätze von Bd. I, § 151 anwenden. Aus diesen folgt,
daß die v Größen die "Wurzeln einer Gleichung vten Grades
sind, deren Koeffizienten rational von j(eo) abhängen. Wenn die
v Größen Ci a voneinander verschieden sind, so ist diese Gleichung
irreducibel. Eine solche Gleichung nennen wir eine zum Trans-
formationsgrad n gehörige Transformationsgleichung
erster Stufe*). Jede andere Größe des Körpers kann durch ein
solches und durch j(gj) rational ausgedriickt werden.
Haben die Funktionen 3>a, c, s die Eigenschaft, für jeden endlichen
Wert von gj mit positivem, imaginärem Teil, also für jedes endliche
J(gj) endlich zu bleiben, so ist die Funktion j’(gj)] in (4) auch
in bezug auf eine ganze Funktion. Die Formel (5) könnte
daher nur für solche besondere Werte von gj versagen, für die
zwei Wurzeln der Invariantengleichung einander gleich werden.
Wenn die v Größen ®a,c,3 nicht alle voneinander verschieden
sind, so zerfallen sie in Reihen von gleich vielen untereinander
gleichen, und die aus (5) abzuleitende Gleichung vten Grades ist
eine Potenz einer irreducibeln Gleichung, die wir gelegentlich
wohl auch als Transformationsgleichung bezeichnen werden (Bd. I,
§ 151, 2).
Sind die Größen Cj d so gewählt, daß sie für kein endliches
ca mit positiv imaginärem Bestandteil unendlich werden, so bleiben
sie für jedes endliche j (gj) endlich, woraus folgt, daß die Koeffi-
zienten in der Funktion des vten Grades
(6) II(x —
ganze rationale Funktionen von j (gj) sind, d. h. die
sind ganze algebraische Funktionen von J(gj).
l) In der ersten Auflage habe ich diese Gleichungen „invariante
Transformationsgleichungen“ genannt. Dieser Ausdruck ist von Klein
beanstandet worden (Vorlesungen über ausgewählte Kapitel der Zahlen-
theorie, autographiertes Heft, Göttingen 1897). Ich schließe mich Kleins
Vorschlag an, indem ich diese Gleichungen jetzt „Transformations-
gleiehungen erster Stufe“ nenne, ohne hier näher auf die Begründung
dieses Ausdruckes einzugehen.
.§ 71. Die Transfoi’mationsgleichuiigen für y2 und y3. 247
Richtet man die Funktionen ®a, e,®, etwa durch geeignete
Bestimmung von Konstanten, die darin noch verfügbar sind, so
ein, daß sie auch für ein unendliches imaginäres gj, d. h. für
2 = 0 endlich bleiben, so sind diese Funktionen auch für ein
unendliches j(to') endlich, und die Koeffizienten in (6) sind kon-
stant. Dies ist aber nur dadurch möglich, daß die ®a,c,s alle
einer und derselben Konstanten C gleich sind. Kennt
man 0«, Cj3 als rationale Funktion einer anderen Größe 0),
so ist c,a = C entweder eine Identität oder eine Trans-
formationsgleichung für
§ 71. Die Transformationsgleiehungen für y2 und y3.
Transformationsgleiehungen erster Stufe erhält man zunächst
aus der Betrachtung der Funktionen § 54, (4), (5):
PaG») = ^'(gj), 7s(ra) = Vj(ra) — 1728.
Wenn n nicht durch 3 teilbar ist, so können wir die Zählen
a, c, d so wählen, daß immer c durch 3 teilbar wird.
Nun übt nach § 54, (15) eine lineare Transformation
auf die Funktion y2(ra) den Einfluß:
y2 a = e 8 y2 (»)•
* \cc —p gj/ x '
In den Zusammensetzungen (8), (10) des § 69 wird
A = n, d = 0 (mod 3),
und dann kann man a noch so bestimmen, daß auch a und
folglich c2 durch 3 teilbar werden.
Daraus ergibt sich, daß durch die beiden. Substitutionen
(gj, gj-I-1), (to, —Y
v \ to j
die v Funktionen
(i) 7^~^^vYYYn
\ Uj y
nur untereinander vertauscht werden und also die .Wurzeln einer
Transformationsgleichung erster Stufe sind.
Ist zweitens n eine ungerade Zahl, so nehme man c
gerade an.
248
Siebenter Abschnitt.
§ 72.
Für die Funktion y3 (gj) ist [nach § 54, (15)]:
^3 1= (—l)“y+/9y + '9<’73(GJ),
16 \a v 7 7
und in den Zusammensetzungen (8), (10), § 69 ist
X = 1, « = d = 0 (mod 2).
Die v Größen
zot (c H- d (0\ r \
(2) ---------J73(gj)
vertauschen sich daher untereinander und sind also gleichfalls
die Wurzeln einer Transformationsgleichung erster Stufe.
Um für den einfachsten Fall n = 2 die erstere dieser
Gleichungen zu bilden, beachte man die Relation [§ 54, (5)]:
m v ~ 16 = AH24 + 16 _ 4- 16 72 /•(gj)s fl(<»)S /2 (gj)8 ’
woraus wegen
folgt: /i (2 gj)/2(gj) = |/2 [§34,(16)]
. 28 + /2(gj)24
w /ra\ _ 28 -|- /] (gj)24 n\2)~ A(gj)» /gj 4- 3\ 28 — /(gj)24 2 )~ /(gj)48 • [§34,(13)]
Bezeichnen wir diese drei Größen mit x, x0, xlt so ergibt
sich aus den Relationen (6), (8), § 54:
x -[- x0 -f- xr — 7, (gj)2
X Xq —| XX^ —j— XqX^ = 495 (gj)
xxax1 — —j(a>) + 24.33.53,
so daß x, X&, xr die Wurzeln der Gleichung sind
(5) x* — p2(Gj)2a>2 5.9.11 .?2(eo)x j(gj) — 24.33.53 = 0.
Die Gleichung, deren Wurzeln die Kuben der Wurzeln von
(5) sind, ist die Invariantengleichung für n = 2, und läßt sich
daraus ohne Schwierigkeit berechnen.
§ 72. Multiplikatorgleichungen erster Stufe.
Unter den Multiplikatorgleichungen sollen hier die betrachtet
werden, deren Wurzeln die verschiedenen Potenzen von Pu sind,
multipliziert mit Potenzen von y2(Gj), ys(Gj), deren Koeffizienten
§ 72.
Multiplikatorgleichungen erster Stufe.
249
rational von j (gj) abhängen. Diese Gleichungen nennen wir
Multiplikatorgleichungen erster Stufe1).
Wir betrachten die Größen [§ 68, (16)]:
/C GJ\
CO p — i/g" a '
und den Einfluß, den die Transformationen
/l, 0\ / 0, 1\
\1, 1/’ 1, 0/
auf sie ausüben. Dieser Einfluß bestimmt sich nach den Formeln
(8) bis (13), § 69, wonach [weil cr = c (mod e)]
n i (Z — 1)
Pc,s,a durch (gj, gj 1) in e 12 PC1,d,a
(2) durch ^gj, —
___ a — a2
• l/L i 2 (C\ (C-£\ 7?/“’ + 82 P
111 r ? 1/ • \e ) W ) Ä’ a )
f 03 y— 1 gj \ o / \O2 / \y, 0 ®2 /
übergeht, worin P die in § 38, (lö) angegebene Bedeutung hat.
Es ist aber [§ 69, (11), (12)]
a ß = V'O ra>
und mithin, wenn wir
\y, 0 «2 / f d
setzen,
Za\ <|«2—
r = \~ßjl e
eine 24ste Einheitswurzel, und durch die Vertauschung
geht
Pc^a in r — ^(^P^
über.
l) Diese Gleichungen sind besonders eingehend von Kiepert unter-
sucht worden, zuerst in mehreren Abhandlungen in Grelles Journal, Bd. 87,
88, 95, am ausführlichsten in den Abhandlungen in den Mathematischen
Annalen, Bd. 26, 33. Vgl. auch F. Klein, Mathematische Annalen, Bd. 14, 15
und die oben erwähnten autographierten Vorlesungen.
250 Siebenter Abschnitt. § 72.
Daraus ergibt sich wie oben der Schluß:
1. Für jedes-beliebige n sind die Größen
P24,
c, ö, a
die Wurzeln einer Transformationsgleichung.
Ist n durch 3 nicht teilbar, so kann man die c, c2, cL durch
3 teilbar voraussetzen. Dann wird
Z = n, a = 0, Ö = 0 (mod 3).
Es ist also, wie aus § 38, (15) hervorgeht, r eine achte
Einheitswurzel, beachtet man daher noch
72(cj 4-1) = e 8 y2(ra), y2(— — y2(©), .[§54,(14)]
so haben wir den Satz:
2. Ist n nicht durch 3 teilbar und c durch 3 teilbar,
so sind die Größen
Pc,z,a?2 (ra)”-1
Wurzeln einer Transformationsgleichung.
Um die Anwendung auf den. einfachsten Fall n = 2 zu
machen, setzen wir
zSA 1ß’?(2ra)8 H 2 )
(3) X = 16 \ <7, Xo = - z / , X1 —-7-^--,
' ,i?(ra)8 ^(to)8. 1 jj(o)8
und dann sind x, xw xx nichts anderes als unsere Funktionen
/•2(ra)8, /,(«X —/(<a)8. [§34,(9)]
Diese sind, wie wir schon früher gesehen haben [§ 54, (8)], die
Wurzeln der kubischen Gleichung
(4) x* — X]>2(a) —|— 16 = 0.
Der Umstand, daß f8, f8, —fs selbst Wurzeln einer Trans-
formationsgleichung für den Transformationsgrad 2 sind, erklärt
die Erscheinung, daß bei Adjunktion dieser Größen, also auch
bei Adjunktion von x2, die zu einem geraden n gehörigen Trans-
formationsgleichungen reducibel werden.
Wenn n eine ungerade Zahl ist, so nehme man c durch 4
teilbar an, dann ist [§ 69, (9), (11), (12)]
Z = n (mod 4),
w = 0, ö = 0, ß . ad2, y = —0a2 (mod 4),
also ergibt sich
' ß—1 n—1 a — «2
VS = (— 1) 2 = (—1) 2 (— 1)“
§72. Multiplikatorgleichungen erster Stufe. 251
und daraus folgt mit Rücksicht auf
z(® + 1) = — ZsG»), — Zs(®): [§ 54, (14)]
3. Ist n ungerade, c durch 4 teilbar, so sind die
Größen n_,
-Pe.a.anC05) 2
Wurzeln einer Multiplikatorgleichung. Ist w = 1 (mod4),
so gilt dasselbe von Pc,<>,a-
Als Beispiel wählen wir n = 3 und setzen
/ /gj\\6
n_ (3 gj)\ < i \ 3 ) ]
/r - 97 I * v ' i t x '
d/ — a I i / \ / i *^0 — \ / \ / i
\ »/(®) /
/ /4-l-(ü\\6 / /8+<»\\6
n-3 ) _ MzjH .
X1 \ ^(ro) /’ \ ’/C®) /
Die Koeffizienten der Gleichung, die diese Größen zu Wurzeln
hat, sind rationale Funktionen von y8(ra), und da keine der
Größen (5) für einen endlichen Wert von y3 unendlich wird, so
sind es ganze Funktionen von y8. Nach 3. können wir diese
Gleichung also in der Form ansetzen:
xi 4- An«3 + A«2 + An« + A = o,
worin Alt A2, Ai A ganze rationale Funktionen von j (gj) sind.
Zunächst erhält man A als das Produkt xx0x1x2, welches für
keinen Wert von J(ra) verschwinden kann und daher konstant
sein muß. Aus den Anfängen der Entwickelung [§ 24]
x — 27 2...,
1
«o = — q 8 •••,
(R\ —
w X1 - — e 3 q 3
2 ni 1
x.t — — e 3 q 8 ...,
y3 = 2-’...
findet man daher
A = — 27.
Es ist ferner
— A y3 = « + «o + «i + «2-
Da die rechte Seite für ein unendliches y3, d. h. für q = 0,
nicht einmal in der ersten Ordnung unendlich wird, so muß Ar
verschwinden.
252 Siebenter Abschnitt. § 72.
Aus
. / 1 , 1 > 1 , 1 \
— J8y8 = + - + -)
\ *Z/Q ^2/
ergibt sich nach (6) für A3 der konstante Wert 1. Um aber A2
zu bestimmen, müssen wir in der Entwickelung noch um ein
Glied weiter gehen. Wir setzen in
+^3^0 — 27 = — A2x^
für x0 die Entwickelung
_____________________________i_ _i_
xo = — 3 3 6 g3 • • •,
und finden A2 — 18, so daß also die gesuchte Gleichung lautet:
(7) X* 4- 18x2 + ?3x — 27 = 0.
Ist n ungerade und nicht durch 3 teilbar, so nehme man c
durch 12 teilbar an.
Es ist alsdann
A = m, a = 0, Ö = 0, ß = ao2, ? = —da2 (mod 12)
und es wird
ff —1 n — 1 a — a'
r2 = (— 1) 2 = (—1) 2 (— 1) 2 ,
also der Satz
4. Ist n relativ prim zu 6, c durch 12 teilbar, so sind
die Größen
Wurzeln einer Multiplikatorgleichung erster Stufe.
Da die Funktionen P2 für keinen endlichen Wert von j'(gj)
unendlich oder Null werden, so schließen wir, daß die Koeffizienten
der Gleichung, deren Wurzeln die P2 sind, ganze rationale
Funktionen von y2, y3 sind und daß der letzte Koeffizient
eine Konstante ist.
Ist n eine Primzahl p, so sind die Wurzeln dieser Gleichung
/. Z12 Ä -f- <a\\2
x = r x" = ) ‘=0.
und die Anfangsglieder der Entwickelungen sind folgende:
jp —1 p — 1 Zrtih p — 1
x = pq 6 ..., x,h — (—1) 2 e p q ei: ...,
r—i
wodurch sich für den letzten Koeffizienten der Wert (—1) 2 p
ergibt. Daraus, daß das erste Glied in der Entwickelung von
§ 72. Multiplikatorgleichungen erster Stufe. 253
j (<a) nach Potenzen von q den Koeffizienten 1 hat, schließt man
leicht, daß die numerischen Koeffizienten in diesen Gleichungen
rationale ganze Zahlen sind.
Für p = 5 hat die fragliche Gleichung die Form:
«6 4- 4~ M2y2a:4 + + A^x 4-5 = 0,
worin die J.15 Aa, A3, A4 ganze rationale Funktionen von j(<A)
und, wie leicht zu sehen, Konstante sind.
Aus den Anfangsgliedern ergibt sich sofort
A1 = 0, Aa = 0, At, = — 1.
Um aber A3 zu bestimmen, geht man in der Entwickelung
von bis zum nächstfolgenden Gliede:
x0 = q 16(1 — 2gs .. .),
woraus man A3 = 10 erhält; also lautet für n = 5 die Multi-
plikatorgleichung
(8) xe 10a:8 — y2x —{—5 = 0.
In gleicher Weise berechnet man die Gleichungen für p = 7,
p = 11, indem man die Entwickelungen von x0 benutzt:
_J_Z 2 4 6 \
p = 7: x0 = —q 7 (1 — 2g7 — g7 4~ 2 g7.../,
p = 11: j;0 = —^33(1 —241—414-2g” 4-414.2414---4
während von y2(c,5)i 7a («®) immer nur die ersten Glieder gebraucht
werden. So findet sich
(9) p = 7: xs 7.2x6 7.9 x4 7.10x2 -j- p3x — 7 = 0,
(10) p = 11: a>12 — 11 • 90a:6 4* H • 7a«4 4* H •
4-11.2y22a:2 4-y2y3a:—11 = 0.
Wenn n eine ungerade Quadratzahl ist, so nehmen wir c
durch 8 teilbar an. Es sind dann a:e und d:e ebenfalls
Quadratzahlen. Es ist ferner
(11) a = d = 0 (mod 8), A = 1 (mod 8)
' 7 c = ö 82, c2 = — «8, a2 = 82 = e2 = 1J
Die Einheitswurzel r in (2) erhält den Wert
, , 1—ß ^(a + J) ——l)ay
254
Siebenter Abschnitt.
§ 72.
Es ist aber nach (12) ß sowohl durch e als auch durch e2
teilbar und ßee2 ein Quadrat; also
also
Durch die Vertauschungen (2) geht also
2 jtj Ä— 1 2tz,3 ß(a±ö) — (ß%—l)ay
(14) PCi^a in e 8 8 Pei,^a und in e 8 -P<-2,a2,«.2
über.
Ist n noch durch 3 unteilbar, so nehme man c durch 3
teilbar an, wodurch
A = 1, a = d = 0 (mod 3)
werden und die in (14) verkommenden dritten Einheitswurzeln den
Wert 1 erhalten.
Hieraus ergeben sich die Sätze:
5. Ist n eine ungerade Quadratzahl, c durch 8 teilbar,
so sind die Größen
P8
J- c,
und ist n eine durch 3 nicht teilbare ungerade Quadrat-
zahl, c durch 24 teilbar, so sind die Größen
p ,
J- c, a
Wurzeln von Multiplikatorgleichungen erster Stufe.
Die ersten Beispiele sind n = 9, n = 25.
, Zur Bildung dieser Gleichungen kann man auf verschiedene
Arten gelangen. Wir wollen hier [nach Kiepert1)] den Weg
gehen, daß wir nach § 69 die Wurzeln einer zum Grade p ge-
') Zur Transformationstheorie der elliptischen Funktionen. Grelles
Journal, Bd. 87, 88, 95.
§ 72.
Multiplikatorgleichungen erster Stufe.
255
hörenden Transformationsgleichung durch die für den Grad p*
rational ausdrücken und diesen Ausdruck in die zu p gehörige
Transformationsgleichung einsetzen.
Nach 3., Formel (7) wird die Gleichung
(15) x* -|- 18 a?2 -|- Vsfp3)® — 27 = 0
von den beiden Funktionen
/ /<U\ \ 6
(16) J44, «my
\ V (p>) / v V (f°) /
befriedigt. Bezeichnen wir den ersten dieser Werte mit x, so
\ ___ 27
o, -5-) in ---- über,
und folglich wird durch x auch die Gleichung
(17) 273 4- 18.27«2 _ _ xi = 0
befriedigt. Setzen wir nun
/ /o\\3 - '
P9
(18) y = ~h
/ ß)\ y2
so geht x durch die Substitution («,—-) in — über, so daß man
auch die Gleichung erhält:
(19) y* -|- 18yixi Vs (^\10xZ — 27 a?4 = 0,
\ ü J
und durch Elimination von y3 (-?) aus (17) und (19) erhält man
\ ü J
nach Weghebung des Faktors t/2 4- 27
(20) x^ — 18 «V — t/2(«ti — 27 t/2 272) == 0.
Löst man diese quadratische Gleichung nach xP auf, so folgt:
(21) a?2 = 3/S + 9 y* 4- 27 y = (y -|- 3)3 — 27,
wo über das Zeichen durch Einsetzen der Anfangsglieder der
Entwickelungen entschieden wird, am einfachsten wohl, da diese.
Gleichung (nach § 69) auch für
erfüllt wird, indem man
x = 27 q 4- •••, ?/ = 27 g2 4- "•
setzt.
256
Siebenter Abschnitt.
§ 73.
Sondert man in (15) die erste Potenz von x ab und erhebt
ins Quadrat, so erhält man durch Einsetzen von (21) die gesuchte
Multiplikatorgleichung für den 9ten Transformationsgrad. Sie
erhält eine einfachere Gestalt, wenn man
(22) (y + 3p = t
setzt:
(23) [J(g>) — 27.64] (t — 27) = (t2 — 361 -|- 27.8)2
oder
(24) J(o) (t — 27) = t(t — 24)3.
Ganz ähnlich kann man beim 25sten Transformationsgrad
verfahren.
Wenn wir
/ /<D\\ 2 /'
PW 12 w
(25) x = I ) ( , y — —4-4
setzen, so haben wir zunächst nach 4. (8):
(26) x3 lOi»8 — 72 (ca)a; —|— 5 = 0,
woraus, wie oben, die beiden Gleichungen
55 lO.ö2«3 — y2 00 & + «:6 = 0,
i/12 10 y3x3 — y2 00 y^xi + 5«6 = 0,
und durch Elimination von
Hf)
x3 — 10«3?/2(5 4- ?/2) — y\ya —5z/6 —|— 52?/4 -|- 53?/2 -|- 54)-
Diese Gleichung nach x3 aufgelöst, ergibt:
(27) x3 = y’: 4- 5 yi -|- 15 y3 4" 25 y2 4- 25 z/,
und wenn wir zur Abkürzung die rechte Seite dieser Gleichung
mit %(«/) bezeichnen, nach (26)
(28) J(o)x(y) = E%(y)2 4- io%(?/) 4- 5]3-
Dies ist die gesuchte Gleichung 30sten Grades für y.
§ 73. Die Schlaeflischen Modulargleichungen.
Zu einfacheren Transformationsgleiehungen gelangt man, wenn
man dem Rationalitätsbereich, der bis jetzt aus den rationalen
Funktionen von j(a') bestand, die Größe /T«)24 adjungiert. Diesem
§•73.
Die S chlaeflisehen Modulargleichungen.
257
Rationalitätsbereich gehören die Funktionen von co an, die durch
die beiden Substitutionen
(1) («b ~ (g>, G> + 2)
ungeändert bleiben (§ 54, 2). Wenn also ein System von v
Funktionen durch die Substitutionen (1) nur unter sich
permutiert wird, so sind diese Funktionen die Wurzeln einer
Transformationsgleichung, deren Koeffizienten rational von /'(co)24
abhängen. Hierzu gehören (wie wir früher schon auf anderem
Wege nachgewiesen haben) für ein ungerades n, das wir jetzt
immer voraussetzen, gewisse Potenzen der Größen
worin, wie ein- für allemal bemerkt sei, c durch 16, und wenn n
nicht durch 3 teilbar ist, durch 48 teilbar angenommen wird.
Die etwas erweiterten Grundsätze des § 70 führen verhältnis-
mäßig einfach zur Berechnung dieser Gleichungen.
Eine Erweiterung ist aber notwendig aus folgendem Grunde:
Bei den bisherigen Betrachtungen konnten wir den Schluß
machen: wenn eine rationale Funktion von j(co) für jedes end-
liche co mit positiv imaginärem Teil endlich bleibt, so ist sie
eine ganze Funktion von j(co~), weil zu jedem endlichen j(co~)
auch ein endliches, nicht reelles co gehört (§ 52). Bei den ratio-
nalen Funktionen von /’(<») können wir aber aus der Endlichkeit
für jedes endliche imaginäre co nur schließen, daß sie ganze
Funktionen von /’(gj) und l:f(co) sind, weil nur zu jedem end-
lichen f(co) mit Ausnahme von f(co~) = 0 ein endliches imaginäres
co gehört.
Es entspricht aber der Substitution
die Vertauschung
r§ 34, (18)]
und wenn also die Funktionen so gewählt sind, daß sie
auch durch die Substitution (2) nur untereinander permutiert
werden, so werden die Koeffizienten der Gleichung, deren Wurzeln
sie sind, rational von
Weber, Algebra. III. 17
258 Siebenter Abschnitt. § 73.
abhängen. Sie sind ganze Funktionen dieser Verbindungen,
wenn die 0ffjC>a für jedes endliche, nicht reelle <0 endlich bleiben,
und sie sind konstant, wenn alle auch für q = 0, d. h.
für /'(gj) = 0 und f(ai) = 00, endlich bleiben. In diesem Falle
sind sämtliche ®a)<,)3 einer und derselben Konstanten
gleich (§ 70).
Daraus ergibt sich der Satz:
Bildet man ganze rationale Funktionen aus
H“ \ 1 1
'\ a J' „./c-j- 8gj\’ />)’
\ a )
welche die Eigenschaft haben:
1. durch die Substitutionen
nur untereinander vertauscht zu werden,
2. für q — 0 nicht unendlich zu werden, so ist
— constans
eine Transformationsgleichung.
Um diese Bedingungen zu befriedigen, ist zunächst der Ein-
fluß der Substitutionen (1) auf die Funktionen f zu untersuchen.
Dieser ergibt sich aus den Zusammensetzungen § 69, (8) bis (13)
und aus den Transformationsformeln für die /-Funktionen § 40.
Zur Abkürzung führen wir die Bezeichnung ein:
Es ergeben sich dann folgende zusammengehörige Ände-
rungen, wenn in der Bezeichnung auf die Verwandlung der
Zahlen a, c, c in a, 0 oder a2, c2, 82, wie sie eben durch die
angeführten Formeln des § 69 charakterisiert ist, keine Rücksicht
genommen wird:
§ 73. Die Schlaeflischen Modulargleichungen. 259
GJ, «1, w2,
1
w2, «1,
co
7t i n i 7t i
GJ —j— 1, C 24 «1, e 24 u, e12 w2,
n i 7t i 7t i
a + 2’ e 12 tl, e 12 ux, ee Ui,
GJ, V, ^1,
1
, Qv, co p^i,
nrti niti n Jti
co —|— 1, öe 24 t>x, öe 24 V, 0e 12 Vn
n ni n?ti nrti
co -|— 2, 02e 12 v, o2e 12 Vj, 02e 6 Vi,
worin
— [«(/-/?) + («-- q — e 3 -1)M 0 = ( (n-Ä)jti —) e 24 a j
zwei dritte Einheitswurzeln sind, die, falls n nicht durch 3 teilbar
ist, den Wert 1 haben.
Um ferner die Wirkung der Substitution (2), die aus der
Transformation zweiten Grades
( 1,
1,1/
hervorgeht, auf die Funktionen w, v zu ermitteln, müssen wir die
Transformationen erster und «ter Ordnung
/'a, ß\ (al, 0\
\y, d/’ \c', 'd'J
so bestimmen, daß
wird. Dieser Ansatz führt zu den Gleichungen
. . a = a'(a — ß) c'(a —|— /?), a = 8'(a-|- ß),
' c — 8 = a’ (y — Ö) -|- c'(y —|— ö), c 8 = 8'(y -j- d).
Hiermit ist zunächst, da a ß und y d zufolge ad — ßy
= 1 relativ prim sind, 8' bestimmt als der größte gemeinschaft-
liche Teiler von a und c —|— ö, und aus n = a’d' ergibt sich al.
Dann ist nach den Gleichungen (6):
, o <1 I v e 8
a + ß — ph 7 + — ßF~ ,
0 ß
17*
260
Siebenter Abschnitt.
§ 73.
und Ö und ß lassen sich so bestimmen, daß
(7) 8(a ß~) — ß(y 8) — a8 — ßy = 1.
Aus den Gleichungen (6) für a und c — c findet sich dann
(8) c' -|- a' = a 8 — (c — 8) ß.
8 und ß können, da a ß und y -]- beide ungerade sind,
nach (7) nicht beide ungerade sein; folglich fällt c' nach (8)
gerade aus. Ersetzt man, was nach (7) gestattet ist, 8, ß durch
Ö h (y -|- Ö), ß h (« + ß), für ein beliebiges h, so ändert
sich c' nach (6) und (8) um 2ha', und über h kann so verfügt
werden, daß c' durch 16 oder 48 teilbar Wird.
Es ist dann nach (6) a -1- ß y — 8 gerade und daher
die Formel (12), § 40 anzuwenden. Darin ist nun zu berück-
sichtigen
a'(a — ß) = a, 8 (a — ß) = 8'
S'(a ß) = a, a! (y — d) = —8
(mod 16),
woraus folgt:
n(a — ß) (a -|- ß -|- y — d) = «2 — 8'2 (mod 16),
also
' 2 \ _ /2\ /2\ /2 \ /2_\ _ /2\
,a— ß) e \a) \a'/ \a/ \8'/ \n/
und
—— c *
Ist n nicht durch 3 teilbar, so ist
2a = a(a' -j- 8'),
2/3 = a(d' — a’),
2d = d(a' + 8'),
2y == 8(8' — «')
(mod 3),
also entweder n und d oder ß und y durch 3 teilbar und also
4» = L
Hieraus ergeben sich folgende zusammengehörige Vertau-
schungen (wobei die Änderung von a, c, 8 in a', c', 8' durch (6)
bestimmt ist):
gj, w, v
Wir wenden die Vertauschungen (4), (5), (9) auf folgende
Funktionen an:
§ 73.
Die Sehlaeflisehen Modulargleiehungen.
261
(10) /2\r + s 2S
v ' ' \n/ (uv)s
worin r, s zwei ganze Zahlen sind, die den Bedingungen
(11) (n — l)r = 0, (n -|- l)s = 0 (mod 12)
Es ergeben sich
tauschungen:
o,
co ’
genügen, die also, wenn n durch 3 teilbar ist, beide durch 3
teilbar sind und
/2\ '
Q“(-1)8
ist.
dann folgende zusammengehörige Ver-
A, B,
Ä, B,
(n—l)r (n + l)s
(-1)“^“ A (—1)~^~B,
(12)
(0 --- 1
G) -4— 1?
Bilden wir nun aus A, B eine ganze rationale Funktion mit
numerischen Koeffizienten
(13) <5^ =
worin, falls in (12) Vorzeichenänderungen auftreten, die Expo-
nenten ä, k so einzurichten sind, daß in allen Gliedern von (13)
die gleichen Vorzeichen Veränderungen stattfinden, so wird das
Funktionensystem oder wenigstens der Forderung 1.
des oben aufgestellten Satzes genügen und wir haben, um auch
die Forderung 2. zu befriedigen und so eine Transformations-
gleichung zu erhalten, die Koeffizienten so zu bestimmen,
daß die sämtlichen v Werte von 0a,Cia für q = 0 endlich bleiben.
Diese Aufgabe vereinfacht sich wesentlich, wenn n keinen quadra-
tischen Teiler hat, und noch mehr, wenn n eine Primzahl ist.
Hat nämlich n keinen quadratischen Teiler, so kann man aus
0a,o,a die sämtlichen Werte herleiten, durch Vermehrung
von o um gewisse ganze Zahlen; wenn also, was unsere Forde-
rung ist, in der Entwickelung von $a,o.s nach steigenden Potenzen
von q keine negativen Potenzen vorkommen, so gilt das Gleiche
von sämtlichen $a,c>a.
262
Siebenter Abschnitt.
§ 73.
Ist aber « eine Primzahl, so genügt der Nachweis, daß d^o, M
keine negativen Potenzen von q enthält, da das Gleiche durch
Vertauschung von co mit co:n für ®n,o,i folgt.
Der konstante Wert, den die Funktion ®a,c,a erhält, bestimmt
sich aus einem Gliede der Entwickelung.
Bei der Ausführung dieser Rechnungen dienen die Ent-
wickelungen § 24, (11),
A = 2
(14)
— r » / 1-4- ö2'*-1 V
I 24 TT I 1 > 'i____________ \
1,00 \1 + 3n(2Ä-17
" + 1. h
B = q 2* n (1 + q™~ 1)s (1 + g«(2Ä-i))«
r +«
0» + D
q 24
h
2s n
],CD
1
Die Formeln werden nicht immer am einfachsten, wenn r, s
möglichst klein angenommen werden, sondern es erweist sich am
zweckmäßigsten, noch die Bedingung
(w— l)r (w + l)s / ,1 nx
(1°) "" 12 = 12 (mod 2)
hinzuzufügen.
Wir erhalten so für die sieben ersten ungeraden Primzahlen
folgende Bestimmung von A und B:
n - 3- Ä - Q + («) -s - (»'’>• („).
«-5, A-(-)+(-), B_(uv)* (w)2
n= 7, A = (-?+(-¥, B = (wv)» + -4^- \v / 1 \uj (wt>)3
n A fU\6 1 fV\e T> 2 n — 11, A = ( —) -4- — ), B = uv ,
\V / \w/
n=13, A = - + B=(uv-)° — -4^ ’ V 1 u ’ J (uv)e
n = 17, A = f-Y 4- (-Y, B = (uvy +
n = 19, A = f-Y + (-Y, B = (uv)^ — \v) 1 \u / v 1 (uv)s
§ 73. Die Schlaeflischen Modulargleichungen. 263
Die Entwickelungen nach Potenzen von q für A und B er-
geben sich aus (14), soweit sie zur Rechnung gebraucht werden,
folgendermaßen:
__i_
n = 3, A = q 2 (1 — 5 q ...),
B = q 2 (1 — 5 q ...),
1
n = 5, A = q 2 (1 — 2g...),
_ 2_
B = q 2 (1 — 2g...),
n = 7, A = q-1 (1 — 4g ...),
B = g—1 (1 + 3g...),
_ 5
n = 11, A = q 2 (1 — 6 21 .
B = S~7(l — 3 + 2g2 ...),
___________________1_
n = 13, A = g 2 (1 + 2g2— 2g3 ...),
__7
B = q 2 (1 + 6g-|-15g2-|-26g3 ...),
n = 17, A = g~2(l —3g-|-6g2 —13g3-|-25g4—39g5-|-76g6...),
B = g-3(14-4g+6g-’+ 8g3-|-17 g4-|-28g5-|-54g«...),
_ £
n = 19, A — q 2 (1 — 2 g -(- 3 g2 — 5 gs —11 g4 — 13g6 + 24g«
— 28g7 ...),
B = q 2 (1 + 3 g + 3 g2 -|- 4 gs + 9 g4 -f- 4 g» + 39 g«
— 27 g7...),
und daraus erhält man durch Elimination der negativen Potenzen
die gesuchten Gleichungen zwischen A und B:
I. n = 3, A — B = 0,
n = 5, A — B = 0,
n = 7, A — B + 7 = 0,
n = 11, A — + -S® + 2 s = 0,
n = 13, >L7 -f- 6 A> + A.s — 20 A — B = 0,
n — 17, ^3 —+ 17 AB — 34^+ 34R-|-116^
4- 440 = 0,
n = 19, A= — Bs 19 ABz —95 A^B -f- 109 A^
+ 128B — 128 A = Oi).
*) Diese Gleichungen sind zuerst von Schlaefli aufgestellt (Journal für
Mathematik, Bd. 72).
264
Siebenter Abschnitt.
§ 73.
Aus diesem System von Gleichungen leitet man ein zweites
und drittes her für die Funktionen fly indem man co durch
co 4- 1 und darauf co durch —• 1: co ersetzt. Diese beiden Systeme
haben die gleiche Form, nur ist das eine Mal
Wi = A(®),
das andere Mal
«i = /•,(©),
zu setzen. Aus den Vertauschungen (4) ergibt sich so:
A -|- Bf — 19 AA + 95 AÄ — 109 A
+ 1281?! — 128 A = 0-
§ 74.
Die Form der Sehlaeflisehen Modulargleiehungen.
265
§ 74. Die Form der Sehlaeflisehen Modulargleiehungen
für einen Primzahlgrad.
Die Form, die wir im vorigen Paragraphen für die zwischen
bestehenden Relationen gefunden haben, läßt sich, wenigstens
wenn der Transformationsgrad eine Primzahl p ist, leicht unter
ein allgemeines Gesetz bringen. Da für die Folge viel auf diese
Form ankommt, gehen wir hier noch etwas genauer darauf ein.
Die Bestimmung der Zahlen r, s nach (11) und (15) des
vorigen Paragraphen hängt von dem Verhalten von p gegen den
Modul 24 ab, und da wir den Fall p = 3 ausschließen können,
so haben wir folgende Fälle: p = 1 (mod 24) r = 1 s = 12
p = 5 r = 3 s = 2
p= 7 r = 4 s = 3
z x P = n r = 6 s = 1
(2) p = 13 r = 1 s = 6
p = 17 r — 3 s = 4
p = 19 r = 2 8=3
p = 23 r = 12 8=1,
so daß r -|- s stets ungerade ist und p 1 durch 2 r, p — 1
durch 2 s teilbar ist. Hiernach wird
Ä=© +©
2S
(uv)s
Nun wissen wir, daß die p -|- 1 Größen v die Wurzeln einer
irreducibeln Transformationsgleichung
(4) ®p(t>, u) = ^ + 1 + Upv* + ••• Up + 1 = 0
sind, in der die Koeffizienten Ui ..., Up+1 rationale Funktionen
von u sind.
Wir schließen sofort, daß es ganze rationale Funktionen
von u sind. Denn erstens werden für u = oo die sämtlichen
Wurzeln von (4) unendlich, wie man erkennt, wenn man ® = ioo,
also q — 0 werden läßt. Zweitens geht nach (9) des vorigen
266
Siebenter Abschnitt.
§ 74.
Paragraphen durch die Vertauschung die Gesamtheit
der Wurzeln v in
m VI
\p/ v
über. Hieraus folgt, daß für u = 0 die sämtlichen Wurzeln v
in Null übergehen, also keine von ihnen unendlich wird, woraus
zu schließen ist, daß nicht nur die U2, • • • Up + 1 ganze
Funktionen von u sind, sondern daß auch jede von ihnen den
Faktor u enthalten muß.
Wir schließen nun zunächst, genau wie bei der Invarianten-
gleichung (§ 69, 2., 3. und 6.), daß
(5) &p(v, u) = ®p(u, v),
und daß
(6) (t>, u) = — u) (y — u?) 4- p E Ch,icUh v11,
1
worin cht]t = ganze Zahlen sind.
Wir wollen diese Funktion in der Weise darstellen
h fc
(7) iPpty, u) = VV + 1 w1>+1 -|- E a^-kuh'vk,
i,p
worin also ah<lc = a^h ebenfalls ganze Zahlen sind, auf deren
Teilbarkeit durch p es nun weiter nicht ankommt, und es ist
insbesondere aPtP — —1. Wenn wir in der Gleichung
/»] = 0
o» durch co —2 ersetzen, so ergibt sich wegen der Irreducibilität
auf Grund der Relation
n i
f(y> 4- 2) = e 12 /'(co),
daß in (7) nicht alle Glieder; sondern nur solche vorkommen,
in denen die Exponenten h, k der Kongruenz
(8) hp 4~ k = p 4- 1 (mod 24)
genügen.
Nun kennen wir noch eine weitere Eigenschaft der Funk-
tionen <hp(y? w), die sich aus der schon benutzten Vertauschung
(9) des vorigen Paragraphen ergibt, wo p = 1 zu setzen ist, und
die, wenn wir zur Abkürzung
/2\ ^=1
§ 74. Die Form der Schlaeflischen Modulargleichungen. 267
setzen, so dargestellt werden kann:
. fuv\p + * /etä l/2\
(9) = y.
Hieraus schließt man auf die Relationen
h + fc—p—1
(10) £h 2 2 — ft, p-f-1—Je - Tc —— ^ICyh*
Wenn wir also in (7) die Glieder mit gleichen Koeffizienten
ah,ic zusammenfassen, so können wir uns auf die Annahme be-
schränken, daß fe > fc. fe -4- fc > n -I- 1 sei, und es ergibt sich
(frp, von den beiden Gliedern «r+i abgesehen, als ein Aggregat
von Gliedern von den folgenden beiden Formen (wenn noch be-
rücksichtigt wird, daß wegen (8) sh = e* ist):
(11)
h-yk—p — 1
2 *—hyP +1— k_+ l— kvp + l—h'j ——
Die Koeffizienten dieser Glieder in <&p sind ganze Zahlen.
Nun ergibt sich aus (8):
(h _ Ä) = (h _ 1) (p + 1)
h k — p — 1 = —h(p — 1)
(mod 24),
und daher ist h — k durch 2 r, 7z —|— Ä; — p — 1 (worin h auch
= k sein kann) durch 2 s teilbar [§ 74, (2)].
Setzen wir daher
h — k h k — p — 1 „
—w— = r«, —!------------ = sß,
so sind a und ß positive ganze Zahlen, die zwischen den Grenzen
(13) o^«<^,
liegen, und überdies ergibt die aus (8) folgende Kongruenz
— Ä(p—1) = 2sß (mod 24), daß wenigstens in den Fällen,
wo s = —1 ist, Ä = ß (mod 2) [§ 74, (2)], also stets eh = eA
268
Siebenter Abschnitt.
§ 74.
und (12)
Demnach wird (11)
p + l
(«») 2
h»)®? 4*
t? 2S?
(«®)’li
Nun gelten die bekannten Formeln, wenn x, y beliebige
Größen sind und
x + v = y
gesetzt wird,
>y2
x2 + = y2 —2 ?'> xi + = yz — 3vy' • • •>
woraus man durch den Schluß von n auf n 1 erkennt, daß
xn 4- i—
' xn
sich für jedes beliebige n als ganze rationale Funktion nten
Grades von y darstellen läßt, die, wenn 7 eine ganze Zahl ist,
ganzzahlige Koeffizienten hat, deren höchster = 1 ist.
Die beiden Größen
/uV“ . /uV“ , . ... ^2®^
— ) + ( — ) und («®W 4- -—r-s
\uj ' \vJ J 1 (u«)5<
können also in dieser Weise als ganze rationale Funktionen von
Ä und B der Grade « und ß dargestellt werden, und wir finden,
n —— 1
wenn wir noch das dem Werte ß = ~— entsprechende Glied,
A s
das den Koeffizienten —1 hat, absondern und mit ca,ß ganzzahlige
Koeffizienten bezeichnen:
® (u P+l ’ 2=1
(14) = .±Sca,?A“B?,
(uv) 2
worin a und ß an die Grenzen
gebunden sind. Dies ist die Form, die wir im vorigen Paragraphen
den Modulargleiehungen bis p = 19 gegeben haben.
§ 75.
Die irrationalen Formen der Modulargleichungen.
269
Es ist noch zu erwähnen, daß die in § 69, 4., 5. für die
Invariantengleichung bei zusammengesetztem Transformationsgrade
durchgeführte Betrachtung unverändert auch für die Schlaefli-
schen Modulargleichungen gilt, woraus wir schließen können, daß
alle diese Gleichungen rationale Zahlenkoeffizienten haben.
§ 75. Die irrationalen Formen der Modulargleichungen.
Den Transformationsgleiehungen lassen sich durch Anwen-
dung desselben Verfahrens weit einfachere Formen geben. Die
Gleichungsformen, mit denen wir uns jetzt beschäftigen werden,
enthalten die drei Funktionen f, fx, zugleich; da man aber
nach § 34, (11), (12) zwei dieser Funktionen durch die dritte
ausdrücken kann, so lassen sich zwei von ihnen eliminieren, und
man kann so zu den Gleichungen des vorigen Paragraphen ge-
langen. Wenn man für /15 die Ausdrücke durch oder für
die drei Funktionen f2 die Ausdrücke durch fc2 einsetzt,
so kommen Wurzelzeichen vor, woraus sich der Name dieser
Gleichungen erklärt.
Wir setzen wie oben
UUjUj = ]/2, VV1V2 = (—) y2,
und erhalten folgende zusammengehörige Vertauschungen:
<2> UV, U,v2, U2V2, QUV, QUfy PMl'yl, (n+l)7Zi +
CO -|- 1, worin p, ß e 24 ßu2vh e 24 ßuv, e 12 ßu2v2, die oben [§ 73, (4)] definierten dritten Einheits-
wurzeln sind.
Wir unterscheiden drei verschiedene Fälle nach dem Ver-
halten von n zum Modul 8.
1. n ~|- 1 = 0, (mod 8).
270
Siebenter Abschnitt.
§ 75.
Wir setzen
(3)
so daß
Jo = uvu2v2 -f- uvu^v^ -f- (— 1) 8
9 O n+1 o
= —4-^-4-(-l)8 —,
Ujl/l 1 U2V.2 1 UV
sich die zusammengehörigen Vertauschungen ergeben
A,
-B,
(±)
prt,
7ti(n +1)
e iä- Ort,
Ein Produkt von
beiden Vertauschungen
e 12
der Form AhBle nimmt
«»(n+l)
62B.
also durch die
ö,
g» ’
?2B,
o»,------
die Faktoren an
— fc g ' 12 6Ä — fc
die — 1 sind, wenn m -|- 1 durch 3 teilbar ist.
jetzt mit numerischen Koeffizienten DB,* 1__________...
. Wir bilden also
Funktionen der Form
(5) ®a,c,a =
worin, wenn n = 0 oder = 1 (mod 3) ist, h und fc nur solche
(ganzzahlige) Werte annehmen dürfen, deren Differenzen h — k
bei der Teilung mit 3 denselben Rest lassen, wenn aber n = — 1
(mod 3) dieser Beschränkung nicht unterworfen sind. Eine solche
Funktion selbst, oder wenigstens ihre dritte Potenz genügt also
einer Transformationsgleichung erster Stufe. Sie bleibt außer-
dem für alle endlichen Werte von ./(o) endlich und ist folglich
eine ganze algebraische Funktion von j(a). [Die Transformation
zweiter Ordnung braucht hier nicht zugezogen zu werden,
da der Inbegriff der schon bei der Substitution (®, co -|- 1),
nicht erst bei (co, co -|- 2) ungeändert bleibt. Vgl. die Bemerkung
am Anfang des § 73.]
Wenn wir also die Konstanten in <Pa,c,a so bestimmen, daß
in den Entwickelungen dieser Funktionen keine negativen Potenzen
von q vorkommen, so müssen die sämtlichen <&«,<.,<) einer und
derselben Konstanten gleich sein.
§ 75. Die irrationalen Formen der Modulargleichungen. 271
Zur Erreichung dieses Zieles genügt es auch hier, wenn n
keinen quadratischen Teiler hat, daß o,a, und wenn n eine
Primzahl ist, wenn d>1]OjK für q = 0 endlich bleibt.
Bei diesen Rechnungen machen wir Gebrauch von den Ent-
wickelungen :
n +1
uv — q 24 17(1 -|- g”<2Ä+i>) (1 —q2h+1'),
n +1
(6) tqtq = q~^ 77(1 — sn(2Ä + D)(l _ 32ä+i),
« + 1
u.v, = 2q™ 17(1 + S2Ä”)(1 + q2Ä),
woraus durch Entwickelung nach Potenzen q:
_ re + 1
uv — q 24 (i 4-q+ss+qi+q:>+qe + q1+2q&...),
_ «+1
(7) u1v1 = q 24 (1 — q — qs-{-qi — qs -f- qe — q7 2 qs .),
n-f-1
w,-y2 = 2q'42” (l-p4 + S4 + 2q« + 2qs-f-...).
Die letzteren Formeln sind richtig für n^> 7 (für n = 3, 5, 7
sind die Glieder von qs, q5, q7 an zu modifizieren). Für n = 7,
n = 23 zeigen diese Ausdrücke, daß A selbst für q = 0 endlich
bleibt, woraus für diese Fälle die Gleichungen folgen:
n = 7, A = 0,
W n = 23, A = 1.
Durch einfache Rechnung .findet man ferner noch:
n — 31, (A2 — B^ — A = 0,
(9) n = 47, A2 — A — B = 2,
n = 71, As — 4 J2 + 2 A — B = 1.
Nicht ganz so einfach gestaltet sich die Rechnung für ein
zusammengesetztes n. So muß man z. B. für n = 15 die Be-
dingung der Endlichkeit für q = 0 nicht nur für sondern
auch für ®Sj0,5 berücksichtigen. Diese beiden aber genügen.
Man erhält so:
(10) n = 15, As — AB + 1 = 0.
2. Ist n = 3 (mod 8), so sind dieselben Schlüsse zu ziehen,,
wenn wir setzen:
AA = u2v2 — u^v^ —
~ B = u^v^u^vf -f- u2v2«2v22 — u^v^u^v^
272
Siebenter Abschnitt.
§ 75.
für die man aus (2) die zusammengehörigen Vertauschungen
erhält: A, -B,
(12) co' (AA,
® + 1, (m + l)ni e 6 e 6 aB
und hieraus leitet man in der gleichen Weise die Gleichungen ab:
(13)
n = 3, A = 0,
n = 11, A = 1,
n = 19, J.6 — 7A2 — B == 0.
3. Ist n = 1 (mod 4), so kann man ebenso verfahren mit
den Funktionen
(14)
8 A = vW — u* vf —•
B — -|- M4t>4u24t>24 — ufvfujvg,
(15)
für die man die zusammengehörigen Vertauschungen erhält:
A B,
. 1 co' pA, q^B,
(n +1) n i
C» + 1, e 3 6A, e 3 &B.
Nur der erste Fall n = 5 führt
Resultat:
hier zu einem einfachen
(16) n = 5, A = 1.
Für n = 5 läßt sich noch eine einfachere Form der Trans-
formationsgleichung gewinnen.
Wenn,wir nämlich auf die drei Funktionen
die Substitutionen (co,---— Y (co,
\ co/
sich unter der Voraussetzung n
gehörigen Vertauschungen:
1) an wenden, so ergeben
= 5 (mod 8) die zusammen-
w, wr, w2,
w, w2,
co' 7t i n i jii
c» + 1, e~^(n-S)w, eü<n~vWi,
§ 75. Die irrationalen Formen der Modulargleiehungen. 273
Setzt man also
A — w2 w2 w|,
JB = w2 w? 4“ W2 4“ W1 W2 ’
C = w Wt w2,
so erhält man
<o, A, JB, C,
A, JB, G,
CO
(O 4-1, e~^(n~&)A, e~^(n~i)B, 0,
so daß zwei dieser Funktionen ebenso wie oben A und JB benutzt
werden können. Für n = 5 zeigt sich aber, daß in den Ent-
wickelungen von w, Wt, w2 nach Potenzen von q keine negativen
Potenzen vorkommen und daß also A, JB, C und mithin auch
w, Wm selbst konstant sind.
Es läßt sich also die Modulargleichung für n = 5 in jeder
der drei Formen auf stellen:
U2 V2 + U2V1 = U V ,
(18) u%v2 — v2u2 = 2«]^,
U2 V2 —• 2 «2 = 2 «2 v2.
Diese Gleichungen lassen sich auch aus der von Jacobi
(Fund. art. 30, gesammelte Werke, Bd. 1, S. 123) gegebenen her-
leiten.
Wir schließen diese Betrachtungen, indem wir in den ein-
fachsten Fällen die Jacobischen Modulargleiehungen aus
diesen irrationalen Formen ableiten.
Wir setzen [vgl. § 54, (3)]:
= x = = x' = ^7,
u v u y
(19)
und eliminieren mittels der Relationen
Xs 4- = 1, xx' — 1—
yy = t
die Größen u und v.
Weber, Algebra. III.
18
274 Siebenter Abschnitt.. ' ; § 76.
Für n = 3 erhält man aus (13): :
(20) a:2 y2 4- x'2 y'2 — 1
eine Form der ModulargLeichung,;die von Legendre herrührt.
Daraus, indem man für x', y' aus (19) die Werte setzt,
a?s 4“ ys — 4 a:2«/2 —- 6xiyi 4 a;6«/6,
oder
(x4 t/4)2 — ^(xy — x3y3~)2
und indem man hieraus die Wurzel zieht und das Vorzeichen
durch q = 0 bestimmt, findet man:
(21) a?4.— y* — ‘Ixy —. %x3y3, , _ . (n = 3),
was, abgesehen von dem dort nicht näher erklärten Vorzeichen
von A, mit § 10,_ (12) übereinstimmt.
Füf n == 5 folgt aus der zweiten Gleichung (18):
(x2 — i/2)3 = 4 x y x'4 y'*,
und daraus durch Quadrieren
(x2 — t/2)6 = 16x2y2(1 —• x3 — y3 -|- x3y3~), .
was leicht in die Form gebracht wird
(x2 — y2)2[(x2 — y2)2 + 8x2y2]2 = lQx2y2(l — x*y*)2.
Zieht man hieraus die Wurzel, so folgt, wie oben:
(22) xe — ye — 4 xy(l — a?4«/4) -|- 5x2y2(x2 —• y2~) — 0 (n = 5).
. Für n =1 erhält man, ohne Wurzelziehen, aus (8):
(23) xy -|- x’ y' — 1,
und daraus:
(24) x3 -f- y3 — 8xy(l -f- xey6) -j- 28a;2«/2(l -|- xiyi)
'— 56 x3y3 (1 -|- x2y2) -|- 70 a?4«/4 = 0 (n = 7).
§ 76. , Zusammengesetzte Transformationsgrade.
Ist der Transformationsgrad eine zusammengesetzte Zahl, so
kann man noch einfachere Transformationsgleichungen aufstellen
als die, die man auf dem Wege des vorigen Paragraphen gewinnt.
Wir führen diese Betrachtungen hier nur in den einfachsten
Fällen durch.
Der ungerade Transformationsgrad n sei in zwei Faktoren
zerlegt
(1) n'='n'n",
die zueinander relativ prim sind.
§ 76. Zusammengesetzte Transformationsgrade. 275
Es lassen sich dann jeder Transformation Uten Grades von
der Form
je eine und nur eine Transformation der Grade h', n":
/a', (a"' o \
W, d')’ \c", d")
zuordnen, die durch folgende Bedingungen bestimmt sind:
. a = a'a", d=d'd",
' 8"c' = c (mod a’), d'c" = c (mod u"),
und umgekehrt folgt aus jedem Paar Transformationen von der
Form (3) nach (4) eine und nur eine Transformation (2). Nach
(4) sind nämlich zunächst 8', 8" bestimmt als die größten gemein-
schaftlichen Teiler von 8 mit n' und n", und darauf wird c' nach
dem Modul a', c" nach dem Modul a" bestimmt aus den beiden
letzten Kongruenzen (4).
Es kommt nun vor allem darauf an, zu zeigen, daß die
Kongruenzen (4) erhalten bleiben, wenn die Transformationen (2)
und (3) nach § 69, (8) bis (12) durch die beiden linearen Trans-
formationen
(<o, o-j- l),
umgeformt werden.
Wir setzen nach den erwähnten Formeln:
1, 0\ / a, 0\
A, V U, 8/
1, 0\ Zu', 0 \
a', i) v;, 87
1, 0\ /a", 0 \
A", 1J U, 8"/
a, ß\ /a2, 0 \
7, 8J \c2, 82/
a', ß'\ /a'i, 0 \
7', 8’)\c2,
a", ß"\ (a'ii 0 \
Y' ,8") \c'i, %)'
18*
276 Siebenter Abschnitt. § 76.
Es folgt zunächst aus § 69, (9):
Cj . c 3 (mod a), c) = d 0' (mod a'), ei' = c" -|- 0" (mod a"),
woraus, nach (4)
d" ci = 0" d 0 = Ci (mod a')
0' cf = 0' c" + 0 = Cj (mod a")
in Übereinstimmung mit den Kongruenzen (4).
Für die Zusammensetzung (6) ergibt sich nach § 69, (12),
daß 02, 02, die größten gemeinschaftlichen Teiler von a, c;
a', d; a", c" sind; weil aber 0" relativ prim zu a', und 0" d = c
(mod a') ist, so ist auch 0ä der größte gemeinschaftliche Teiler
von a! und c und aus den gleichen Gründen %' der größte gemein-
schaftliche Teiler von a" und c, woraus man schließt, da a', a"
relativ prim sind:
02 = 02 02, W2 = «2 a'i-
Ferner ist nach § 69, (11), (12), (13):
02 == a c — y a, c2 = —da,
02 = a' d — y’ a', di — — d' a',
also nach (4):
02d2 — c202 = aa'(dd — co') = 0 (mod 7),
folglich auch
02 d2 — c2 = 0 (mod a'i),
in Übereinstimmung mit (4), und ebenso folgt:
02 c'i — c2 = 0 (mod af),
wodurch also der Beweis geführt ist, daß die durch (4) aus-
gedrückte Zusammengehörigkeit der Transformationen
z'a, 0\ /a', 0\ /a", 0 \
\c, 0/ \c', 07’ \c", 0'7
durch Anwendung irgend einer linearen Transformation auf o
nicht gestört wird. Da wir hier n als ungerade voraussetzen, so
können wir immer c, d, c" durch 16 teilbar annehmen; und wenn n
und folglich auch n-, n" durch 3 unteilbar sind, so können c, d, d'
auch durch 3 teilbar angenommen werden. Ist aber n durch 3
teilbar, so wird von den beiden Faktoren n', n" der eine, etwa n",
durch 3 teilbar sein, der andere, n', nicht. Es kann dann d
noch durch 3 teilbar vorausgesetzt werden, nicht aber c und c".
In diesem Falle soll die Abhängigkeit des c" von c noch näher
bestimmt werden durch die Kongruenz
(7) 0' c" = c (mod 3 a").
§ 76.
Zusammengesetzte Transformationsgrade.
277
Eine Lösung dieser Kongruenz kann man
Lösung der Kongruenz (4) d' c" = c (mod a")
man zu c" ein Vielfaches von a" hinzufiigt.
Die Kongruenz (7) hat dann nach § 69,
Folge:
(8)
immer aus einer
herleiten, indem
(9) bis (13)
zur
(9)
A = n' t." (mod 3),
a ~ a" 0' %, ß = /S"a'02 z
<mod3>
Es mögen nun v', v[, v£; v", vl’, v'£ dieselbe Bedeutung für
die Zahlen n', n1' haben, welche den v, v2 in § 73, (3) für die
Zahl n gegeben war, nämlich:
, .e “4“ 40 \ n f (-|- 8" gj\
v = f (—^-----) ’ v =f (—~ö-------) ’
\ W / \ (Jj /
(10)
, /2\ „ /c' 4- 8'<a\
yCv / \ vt /
, /2\ /c' + 0' gj\
V” - (l\f (cl±^\
1 a" )'
/ 2 \ . (c" + 0" gj'
Wir wenden die Vertauschungstabelle (4), § 73 auf diese
Funktionen an. Da n' unter allen Umständen durch 3 unteilbar
ist, so sind die kubischen Einheitswurzeln 9', 6' = 1 zu setzen,
während infolge der Kongruenzen (8), (9):
(11) q" — 6" = 6n'
wird. Wir erhalten hiernach folgende zusammengehörige Ver- tauschungen :
to, v'2,
1 v', v'2, n' 7t i nf 7t i V'i, nf 7t i
G) ’
(12) co -|- 1, e 24 «j, e 24 U, e 12 v'2,
GJ, w", 4', V'2,
G) ’ 9”'«", Qn''v'i-, n,f7ti n"7ti 9”' fi', n,r7ti
GJ -|- 1, <jn'e 24 Vi, 6n'e 24 v", 6”'e 12 v'z,
die zusammen mit den Vertauschungen (4), § 73 gelten.
Wir unterscheiden jetzt zwei Fälle.
1. Wenn
(13) (n1 -|- 1) («" + 1) = 8 g. = 0 (mod 8)
278 - Siebenter Abschnitt. •§ 76.
ist, so setzen wir
(14) U = üvv'v", Q = ttj Vi A v'{, U2 — UzVzv’z'v'i,
2A= + U2),
(15) B = UU + U Uz + (— 1>“ Vz,
4 4 4
= ^ + -i + (-1>“TT-.
Aus (12) und § 73, (4) erhalten wir dann folgende zusammen-
gehörige Vertauschungen:
o, A, B,
(16) —1, ?»'+U, q-^’ + ^B,
Zf-ini -2
o + 1, Ö^ + ^^A, o-^'+De“ 8 B.
Wir wenden unser Prinzip zur Herleitung von Modular-
gleichungen auf diese Funktionen an und bemerken dazu noch
folgendes:
Die in (16) vorkommenden dritten Einheitswurzeln sind = 1,
wenn entweder n durch 3 unteilbar und p durch 3 teilbar ist,
oder n" durch 3 teilbar ist und n' den Rest 2 läßt. In diesen
Fällen ist jede rationale Funktion von A und B Wurzel einer
Transformationsgleichung. In den anderen Fällen kommt diese
Eigenschaft dem Kubus einer solchen rationalen Funktion von A
und B zu, bei denen die Differenzen der Exponenten sämtlicher
Glieder einander nach dem Modul 3 kongruent sind.
Sind diese rationalen Funktionen ganze Funktionen und
sind außerdem ihre sämtlichen Werte für q — 0 endlich, so
müssen sie einer Konstanten gleich sein, und dadurch gewinnen
wir Transformationsgleiehungen.
Sind n', n" Primzahlen, so genügt es auch hier (vgl. § 72),
wenn die negativen Potenzen von q in der Entwickelung einer
solchen Funktion nach steigenden Potenzen von q in dem einen
Hauptfall wegfallen, nämlich in dem, wo
/a, 0\ /a', 0\ /a", 0 \
\c, 0/ \c', 07’ \c", 0'7
gleich sind
/l, 0\ zl, 0\ ZI, 0 \
\0, n)' \0, n')' \0, n"/’
also
U — f (co) f(n' co) /(n" co) f(n' n" co);
§ 76.
Zusammengesetzte Transformationsgrade.
279
indem man m
denn aus der Entwickelung für diesen einen Fall kann man die
Entwickelungen für die übrigen Fälle herleiten,
ersetzt durch
(17)
<a <a <a
n ’ n' ’ n”
und dann noch <a um ganze Zahlen vermehrt, wodurch keine
negativen Potenzen von q neu eingeführt werden können;
Für die Durchführung der Rechnung bedient man sibh der
Entwickelungen
(»' + l)(n" + D
V = q 24 X
71(1 +<Z2Ä-J)(l »»’)(! +S(2Ä-l)n'')(14-g(2Ä-l)n)
_ in' + 1) («" + 1)
- -Dj = s . 24 X
(18) 77(1 — tf2*“1) (1 — (1 _ g(2Ä-l)n") (1 _ gr(2Ä—1) »)
(n>+ !)(»"+1)
t72 = 4q 12 x '
77(1 4- qih) (1 g2Än') (1 4- (1 4- </2;”’),
die in den einzelnen Fällen die Potenzentwickelungen von A, B
liefern, woraus die negativen Potenzen von q zu eliminieren sind.
Man berechnet auf diese Weise sehr einfach die folgenden
Gleichungen:
n = 15, A = 1,
n == 21, (J2 — B)2 — A = 0,
(19) n = 33, A2 — B — A = 4,
n — 35, -42 — B — A = 2,
n = 55, As — B — 4A2 — A 4~ 4 = 0.
2. W enn
(n' — l)(n" — 1) = 8/x = Ö (mod 8),
so setzen wir
(20)
und erhalten nach (12) die zusammengehörigen Vertauschungen:
(21)
<0, A,
<a 4- 1, 61-"’ e 3 A,
Ön-Tl e 3~&
280
Siebenter Abschnitt.
AB 4-1 = 0,
2(A 4- B) — AB = 5
2 (A -j- B) — AB = 3.
(22)
§ 77.
Wir können daher dasselbe Verfahren anwenden wie oben, wenn
wir noch die Beschränkung hinzufügen, daß nur symmetrische
Funktionen von A und B, d. h. rationale Funktionen von AB,
A 4- B benutzt werden, weil nur unter dieser Voraussetzung
aus einem der Werte einer solchen Funktion durch die Ver-
tauschungen (17) alle übrigen folgen. Man berechnet leicht die
folgenden Beispiele:
n — 15,
n = 35,
n = 39,
Die Rechnung bietet auch in noch komplizierteren Fällen
keine unüberwindlichen Schwierigkeiten. So habe ich in der Ab-
handlung Acta mathematica Bd. II, S. 359 für den Fall n = 105
folgende Formel mitgeteilt:
f(°’)f(15 <a)/’(21 <a)/’(35 <a) ’
7? — V1 ZX15
gj) f gj) y(7 gj) /(105 »)’
424-52- 4(M 4- B)3 4- 10MB(M 4- B)
4- 4(A + B)2 4- 10AB 4- 14(A 4- B) 4- 5 = 0,
wenn sich die Summen S in A und B auf die drei Funktionen
f, fii beziehen.
§ 77. Geometrische Deutung der irrationalen Modular-
gleichungen als Modularkorrespondenzen.
Den Inhalt der irrationalen Formen der Modulargleichungen
machen wir durch eine geometrische Deutung anschaulicher. Be-
trachten wir zunächst den Fall n = — 1 (mod 8) und setzen
(i) « = /(»), y = A(ö), = A(«),
so wird hierdurch, wenn wir x, y, z als Cartesische Koordinaten
eines Punktes B ansehen, eine Raumkurve dargestellt, die wir
auch durch die beiden Gleichungen:
#8 -- y8 - ^8 — 0
x y z =
ausdrücken können, und die wir die Grundkurve nennen wollen.
Diese Kurve ist also von der 24. Ordnung. Mau kann sie auf
(2)
§ 77. Modularkorrespondenzen. 281
eine ebene Kurve 3. Ordnung abbilden, wenn man x8 — X,
y8 — K setzt:
(3) X F(X — T) = 16.
Setzen wir [§ 75, (1)]
so genüge die Größe g, y, £ ebenfalls den Gleichungen (2), da
(IO ~ GD = “b 1 ist, und der Punkt II, dessen Koordi-
naten £, y, g sind, liegt also auch auf der Grundkurve.
Eine Gleichuug
- ® («, y, e, & v, £) = °
bedeutet, wenn der Punkt P festgehalten wird, eine Fläche, auf
der II liegen soll, und der Schnittpunkt dieser Fläche mit der
Grundkurve gibt eine gewisse Anzahl von Punkten II, die dem
Punkt P entsprechen. Ebenso entspricht einem festen Punkt II
eine gewisse Anzahl von Punkten P, und diese Zuordnung heißt
eine Korrespondenz auf der Grundkurve. Fällt der Punkt P
mit einem der ihm entsprechenden Punkte II zusammen, so er-
halten wir einen Doppelpunkt oder Koinzidenz der Korre-
spondenz.
Wenn die Gleichung (5) bei Vertauschung von P mit ü sich
nicht ändert, so ist die Korrespondenz eine wechselseitige.
Solche Korrespondenzen sind durch die Gleichungen (8), (9),
(10), § 75 gegeben.
Es ist dann nach § 75, (3)
2A = x% + (— 1)~ (yy +
k0/ n + 1
B = xl-yy x 1) 8 yyzt,
zu setzen. A ist vom ersten, B vom zweiten Grad in bezug auf
die Koordinaten eines jeden der beiden Punkte P und II.
Wir wollen den Grad von diesen Korrespondenzen, d. h. die
Anzahl der einem Punkte P entsprechenden Punkte II, fest-
stellen. Dabei haben wir den Grad der Gleichung O = 0 in
bezug auf y, £ mit dem Grad der Grundkurve, d. h. mit 24,
zu multiplizieren und es ergibt sich:
-282
Siebenter Abschnitt.
•§ 77.
für n “ 7, m — 24,
5? n = 23, m = 24,
55 n = 31, m = 96,
55 n = 47, m — 48,
55 n = 71, m = 72,
55 n = 15,, tn = 72.
In den Fällen 23, 47, 71 ist also der Grad der Korrespondenz
gleich dem Grad der entsprechenden Modulargleichung, d. h. gleich
der Anzahl der betreffenden Transformationen; in den Fällen
n — 7, 31, 15 ist der Grad das Dreifache des Grades der
Modulargleichungen.
Was ‘ haben diese überzähligen Punkte zu bedeuten? Sie
erklären sich dadurch, daß in diesen Fällen, in denen n = 0, 1
(mod 3) ist, in der Funktion ®a,e,a [§ 75, (5)], die nach der obigen
Gleichung (5) einer Konstanten gleich ist, die Exponenten h 2 k
in allen Gliedern denselben Rest nach dem Modul 3 lassen, und
daß also die Gleichung ® = 0 und ebenso die Gleichungen (2)
erfüllt bleiben, wenn £, 17, g mit einer beliebigen dritten Einheits-
wurzel multipliziert werden. Es geben also je drei Punkte der
Korrespondenz dieselbe Transformation.
Wir hätten auch, wenn x, y, z durch (1) bestimmt sind,
statt (4)
und folglich für A, JB:
(7) 2A = ^§ + (-1)^(2/^ + ^),
B — x^y^x^zi]l)8 yyzt,
setzen können. Die Grundkurve und der Grad der Korrespondenz
wären dann dieselben geblieben, aber die Koinzidenzen hätten
eine andere, und zwar einfachere, Bedeutung bekommen. In
beiden Fällen gehören die Koinzidenzen zu den singulären Werten
der Modulfunktionen, in denen <a eine imaginäre quadratische
Irrationalität ist, wie wir in der Folge noch genauer sehen
werden.
Im Falle n = 3 (mod 8) setzen wir
x = />2(e’), y = s
§ 77.
. Modularkorrespondenzen.
283
und erhalten eine Grundkurve
x* — y* — z* = 0,
' xyz = 2,
die nur vom 12. Grade ist. Wir haben dann weiter nach § 75:
4JL = — yy — zq,
S = x^yv]-\rx^zQ — yyz 9,
und man erhält für den Grad m der Korrespondenz nach
75 (13):
m = 12,
m = 12,
m == 60,
n = 3,
n — 11,
n = 19,
also wieder wie im vorigen Falle, wenn n = 0, 1 (mod 3) ist,
eine dreifach zu große Zahl.
Ist endlich n = 1 (mod 4), so setze man
a: = f*(ß>), y = z = //(»)
und erhält eine Grundkurve vom sechsten Grade.
Für n = 5 ergibt sich die richtige Zahl m = 6.
Achter Abschnitt.
Die Gruppe der Transformationsgleiehungen und die
Gleichung Sten Grades.
§ 78. Die Galoissche Gruppe der Transformationsgleiehungen
für einen Primzahlgrad.
Ein eingehenderes algebraisches Studium der Transformations-
gleichungen erfordert die Kenntnis ihrer Galois sehen Gruppe. Da
wir die Transformationsgleiehungen aus den Teilungsgleichungen
hergeleitet haben, deren Gruppe uns bekannt ist (§ 63), so können
wir die Gruppe der Transformationsgleiehungen gleichfalls bilden.
Die Transformationsgleiehungen ergaben sich (§ 65) dadurch,
daß die Wurzeln der Teilungsgleichungen sich in Reihen ein-
teilen ließen, die durch die Vertauschungen der Gruppe der
Teilungsgleichung nicht auseinandergerissen, sondern nur unter-
einander vertauscht werden.
Jeder dieser Reihen ordnet sich eine bestimmte Wurzel einer
Transformationsgleichung zu, und die Gruppe der letzteren
besteht daher aus dem Inbegriff der Vertauschungen,
die durch die Gruppe der Teilungsgleichung unter den
Reihen hervorgerufen werden.
Ist der Transformationsgrad n eine ungerade Primzahl p,
so gestattet diese Gruppe eine sehr elegante Darstellung, die zu
weiteren Untersuchungen geeignet ist, und wir halten jetzt diese
Voraussetzung fest.
Es wurde im § 65, (3) bereits die notwendige und hinreichende
Bedingung ermittelt, daß zwei Wurzeln der Teilungsgleichung
(1)
in dieselbe Reihe R gehören, nämlich die Kongruenz
(2) [iv1 — vp' = 0 (mod p).
§ 78. Galoissche Gruppe der Transformationsgleiehungen. 285
Wenn wir nun, wie es in der Zahlentheorie üblich ist (Gauss,
Disquisitiones arithmeticae, art. 31), durch das Symbol
(mod p)
eine ganze Zahl [oder Zahlklasse (mod p)] verstehen, die, mit b
multipliziert, bei der Teilung durch p den Rest a läßt, so können
wir, vorausgesetzt, daß p' v' nicht durch p teilbar sind, die eine
Reihe definierende Kongruenz (2) auch so schreiben:
z . P V , , s
(3) = V (mod-P)’
und wir werden also naturgemäß darauf geführt, durch den
Wert des Verhältnisses
(4) = * (mod p),
das jeder der Zahlen 0, 1, ..., p — 1 kongruent sein kann, und
das für eine ganze Reihe unveränderlich ist, diese Reihe R zu
bezeichnen. Es bleibt dabei zunächst die eine Reihe unbezeichnet,
in der p' und folglich alle v' durch p teilbar sind, aber auch
diese Reihe ordnet sich der allgemeinen Bezeichnung sehr gut
unter, wenn wir, falls p' = 0 (mod p)
(5) co (mod p)
setzen, so daß wir also noch eine (p -p l)te Reihe Rx erhalten.
Die Gesamtheit der Reihen, deren Anzahl p 1 beträgt, ist
hiernach zu bezeichnen durch
(6) -Ra,, Ro, ..., Rp—i-
Entsprechend werden die zugehörigen Wurzeln einer Trans-
formationsgleichung mit
(7) . Vl, •••, «’j.-i
zu bezeichnen sein.
Wenn wir beispielsweise die Invariantengleichung (§ 69) zu-
grunde legen, so ist [nach den Bestimmungen des § 68, (10) über
die Zahlen a, c, 8]
, x . (Z -4- O>\
(8) «’» =XPra)> —)
zu setzen, und ebenso, wenn irgend eine andere Transformations-
gleichung gewählt wird.
286
- Achter Abschnitt.
§ 78.
Nach dieser Bezeichnungsweise sind wir imstande, die Gruppe
der Transformationsgleichung aus der der Teilungsgleichung sofort
ahzuleiten.
Wir setzen zunächst als Rationalitätshereich den Inbegriff
der rationalen Funktionen von x2 mit rationalen Zahlen-
koeffizienten fest.
Nach . § 63, 3. besteht in diesem Rationalitätsbereich die
Gruppe der Teilungsgleichung aus allen Substitütionen, durch die
ft, ft' in
öft — &ft'
— Cft -|- «ft'
übergeführt werden, worin a, b, c, 3 beliebige, nach dem Modul p
genommene ganze Zahlen sind, deren Determinante
(9) J = «8 — bc
durch p nicht teilbar ist, und die Anzahl aller dieser Substitu-
tionen beträgt
(10) - p(p- 1) (p2- 1) [§ 63, (27)]
Daraus ergibt sich aber nach der Bezeichnungsweise (4), (5)
die Gruppe „der. Transformationsgleichung als bestehend
aus allen durch das Symbol
(H) (*> JcZz + ba) <m°d
ausgedrückten Vertauschungen.
Wir bezeichnen eine Substitution (z, z'), wenn
Q2) z = ^±^, (mod p)
ist, ähnlich wie früher durch
(13)
und erhalten für die Zusammensetzung zweier solcher Substi-
tutionen, wenn
, c' 4- d'z" . , .
z = (mod
ist, die Regel:
(14) (*, ^') (z< z")
fa. b\ /a', b'\ ./ad 4- 6ab' -+-bd'\ , 3 . .
= G <>) G, <>') - G.’ + a»', ei' + aa) t““3 *>’
§ 78. Galoissche Gruppe der Transformationsgleiehungen. 287
in Übereinstimmung mit der Regel für die Zusammensetzung
zweier Transformationen in § 28. Die Substitution (11) ist hier-
nach zu bezeichnen mit
/8, c\
V', a)
Die durch alle Substitutionen dieser Form [nach (14)] ge-
bildete Gruppe bezeichnen wir mit 8 (Gruppe der linearen Sub-
stitutionen).
Die Funktionen (12) von z’ und also auch die Substitutionen
(13) bleiben ungeändert, wenn die vier Zahlen a, &, c, 8 mit
einem und demselben durch p nicht teilbaren Faktor multipli-
ziert werden, und daraus ergibt sich nach (10) die Anzahl dieser
Funktionen oder der Grad der Gruppe 8
(15) P(p2— 1),
den man auch leicht durch direkte .Abzählung findet.
Werden in einer der Substitutionen (13) die vier Zahlen
a, b, c, 8 mit einem gemeinsamen, durchs unteilbaren Faktor
multipliziert, so wird die Determinante z/ mit dem Quadrat
dieses Faktors multipliziert. Es bleibt daher nicht die Deter-
minante z/, wohl aber ihr quadratischer Charakter, d. h. der
Wert des Symbols . ,
. &
durch diese Multiplikation erhalten.
Setzen wir zwei der Substitutionen (13) zusammen, so multi-
plizieren sich ihre Determinanten und hieraus folgt, daß alle
Substitutionen der Gruppe 8, in denen z/ quadratischer
Rest von p ist, eine.Gruppe unter sich bilden, die wir
mit So bezeichnen wollen.
Die Gruppe 80 ist ein (eigentlicher) Divisor der Gruppe 8
vom Index 2.
Setzt man die Substitutionen von So zusammen mit irgend
einer Substitution (z, ßz)' =
wo ß und also auch ß~1
ein quadratischer Nichttest von p ist, so erhält man die ganze
Gruppe 8.
Ist z/ quadratischer Rest von p, so kann man einen zu
a, b, c, 8 hinzuzufügenden gemeinsamen Faktor so wählen, daß
z/ = 1 (mod p) wird, so daß wir die Gruppe So auch darstellen
können durch ....
288 Achtel’ Abschnitt. § 78.
(16) Q’ aS — ßy = 1 (mod p).
In einer dieser Substitutionen sind die Zahlen a, ß, y, ö
nach dem Modul p bis auf das gemeinsame Vorzeichen bestimmt.
Der Grad der Gruppe So ist
(17) l^^-l).
Ai
Auf die Form (16) kommt man aber direkt, wenn man als
die Gruppe der Teilungsgleichung nicht die Gruppe '21, sondern
die Gruppe 33 des § 63 betrachtet, d. h. wenn man pte Ein-
heitswurzeln dem Rationalitätsbereich adjungiert, woraus
der Satz fließt:
Die Gruppe So ist die Gruppe der Transformations-
gleichung, wenn pte Einheitswurzeln dem Rationalitäts-
bereich adjungiert sind.
Zur Reduktion der Gruppe S auf die Gruppe genügt aber
schon die Adjunktion einer zweiwertigen Funktion und daher ist
mit der Adjunktion der pten Einheitswurzeln zu viel geschehen,
üm zu erkennen, welche Irrationalität notwendig zu adjungieren
ist, dienen die Sätze der §§ 63, 65.
Im § 63, 3. haben wir gesehen, daß die pte Einheitswurzel p
rational darstellbar ist durch die Wurzeln der Teilungsgleichung
und daß durch eine Substitution der Gruppe 31, deren Deter-
minante mit m kongruent ist, p in om übergeht; ferner haben
wir im § 65 nachgewiesen, daß durch Adjunktion sämtlicher
Wurzeln einer Transformationsgleichung die Gruppe der Teilungs-
gleichung auf die Gruppe '210 reduziert wird, die aus sämtlichen
Substitutionen der Form
a, 0\
P, a)
besteht, wo a eine beliebige, durch p nicht teilbare Zahl ist.
Die Determinanten der Substitutionen von 3I0 sind also Quadrate
und sind daher nach dem Modul p kongruent mit je einem der
| (p — 1) quadratischen Reste von p.
Die Summe
(19) A — So",
worin für a die sämtlichen quadratischen Reste von p zu
setzen sind, bleibt daher ungeändert durch die Substitutionen
§ 78. Galoissche Gi'uppe der Transformationsgleichungen. 289
von 2(0 und ist infolgedessen rational durch die Wurzeln der
Transformationsgleichung ausdrückbar. Die Summe A bleibt
ungeändert durch die Substitutionen der Gruppe 23 und also
auch durch So, während sie durch die Substitutionen von 21 und
daher auch von S zwei verschiedene Werte erhält, nämlich,
wenn b die Reihe der Nichtreste durchläuft,
a b
A = S Qa, B = S pb.
A ist daher eine zur Gruppe So gehörige Funktion und
durch ihre Adjunktion wird S auf So reduziert.
Die Werte der Summen A, B sind aber bekannt (Bd. I,
§ 179):
A _ - 1±K- P B _ - l + /(- P
A - , B —
Das Vorzeichen der Wurzel hängt von der Wahl der Wurzel p
ab und läßt sich bestimmen, kommt aber hier nicht in Betracht.
Wir haben daher den Satz:
Die Gruppe der Transformationsgleichung ist So,
i/ r—i
wenn y (— 1) 2 p dem Rationalitätsbereich adjungiert
wird.
Die Gruppe der Invariantengleichung läßt sich auch ohne
die Teilung der elliptischen Funktionen in folgender einfachen
Weise ableiten, wobei man jedoch nur die Monodromie-
gruppe erhält, d. h. die Gruppe in dem Körper der rationalen
Funktionen von j (k>), ohne Rücksicht auf die zu adjungierenden
Konstanten. Wir beschränken uns auf den Fall eines Primzahl-
grades p der Transformation, und setzen
(20) Ve = U=j(G>),
wobei c nach dem Modul p zu nehmen ist.
(cc ß\
s)
7, o/
an, so bleibt j (k>) ungeändert, und vc geht in über. Um c' zu
finden, hat man eine zweite lineare Substitution 8' = ( .)
\M/
zu suchen, so daß
ß’\ (p, 0\ _ (p, 0\ /a, ß\
8') \c', 1) \c, 1/ V, 8j
Weber, Algebra. III. 19
290 Achter Abschnitt. § 79.
oder
pa' d ß' = pa, ß' = pß
py' d 8' — ca y, ö' = cß d\
Hieraus ergibt sich nach der dritten Gleichung: c'ö' = c« p,
und mit Hilfe der vierten:
Ist cß d = 0, so ergibt sich c' = co, und ist c = co, so
folgt c' = a/ß.
Bei der Anwendung auf die Bestimmung von c, c' kann man
die w, ß, y, 8 durch kongruente Zahlen a, b, c, d ersetzen, deren
Determinante ad — bc quadratischer Rest von c ist, und es läßt
sich auch zeigen, daß man auf diese Weise jede Substitution der
Gruppe ß0 erhalten kann. Jede Funktion von ve also, die durch
die Substitutionen der Gruppe ß0 ungeändert bleibt, bleibt daher
auch ungeändert, wenn auf co eine lineare Substitution angewandt
wird, und ist folglich eine rationale Funktion von j(co). Wie
aber die Koeffizienten in dieser Funktion beschaffen sind, darüber
lehrt uns diese Betrachtung nichts, und es ist daher So nur als
die Monodromiegruppe der Invariantengleichung erkannt.
§ 79. Untersuchung der Gruppe £*01).
Wir haben im 10. Abschnitt des II. Bandes die Kongruenz-
gruppe und ihre Teiler ganz allgemein untersucht. Wir führen
hier diese Untersuchung, soweit sie auf das Transformations-
problem Bezug hat, in spezieller Form noch einmal durch.
Die in So enthaltenen Substitutionen
(1) (a' = (z —c + az\
\c, d/ \ ’ 8 — bz )'
in denen
(2) z/ = ad — bc
quadratischer Rest von p ist, können, wie schon oben bemerkt,
auf die Form gebracht werden:
(3) (“ = G, -/ + “A
v \y, 8/ \ o — ßz /
L) Über die Gruppe der linearen Substitutionen 20 ist zu vergleichen:
Galois, Liouvilles. Journal, Bd.XI. Serret, Algebre superieure, SectionIV,
Chapitre IV. C. Jordan, Tratte des Substitutions. Gierster, Gruppe der
Modulargleichungen. Mathematische Annalen, Bd. 18.
§ 79. Untersuchung der Gruppe ß0. 291
worin
(4) aS — ßy = 1 (mod p),
wir haben nur, wenn wir unter (/zT (mod p) eine ganze Zahl
verstehen, deren Quadrat nach dem Modul p kongruent mit z/ ist:
a = ^Vz7, &=d|/z7
(mod2,)
zu setzen. In der Form (3) können noch die Vorzeichen von
a, ß-, 7, 8 gleichzeitig geändert werden.
Wir fragen nach solchen Elementen die durch eine Sub-
stitution von der Form (3) ungeändert bleiben. Diese werden
bestimmt durch die Kongruenz
7 + 8 z ,
oder
(5) ß z* (a — ö) z — y = 0 (mod p)^
eine Kongruenz, die, wenn sie nicht identisch ist, höchstens zwei
inkongruente Wurzeln hat. Um diese zu erhalten, schreiben wir,
zunächst unter der Voraussetzung, daß ß nicht durch p teilbar
ist, die Kongruenz (5) so:
/„ , a — ö\a /a — d\2 . ,
[ß z + —2~) ~ \2/ + ß y (mod i’)>
oder mit Hilfe von (4):
(6) (ßz + = (—3—) — 1 (mod^)-
Demnach sind drei verschiedene Fälle zu unterscheiden:
I. (~2~) ~ 1 — 0 (mod i’)?
dann hat die Kongruenz (5) eine Wurzel; es gibt ein und
nur ein Element z, das ungeändert bleibt.
II. — 1 quadratischer Rest von pt,
die Kongruenz (5) hat zwei verschiedene Wurzeln, es gibt zwei
Elemente z, die ungeändert bleiben.
/K I g\2
HL \ 2 / — 1 quadratischer Nichtrest von p-,
die Kongruenz (5) hat gar keine Wurzel und alle Elemente z
werden umgesetzt.
19*
292
Achter Abschnitt.
§ 79.
Ist ß = 0, so hat (5) immer die eine Wurzel z = oo; ist
dann 8 = <x, und y nicht = 0 (mod p), so gibt es nur diese
eine; in diesem Falle ist aber
/_1— $ \2
<x6 = 1, « = 6, ( / = * (mod p),
und die Bedingung I. erfüllt. Ist aber gleichzeitig y = 0 (mod p),
so ist die Substitution die identische.
Ist ß = 0, aber a — d nicht = 0 (mod p), so hat (5) noch
eine zweite Wurzel; da jetzt ad = 1 (mod p), so ist:
Za-j-dX2 /a — d\2 , .
^“2 J ~ 1 = \“2“) (m°d
also quadratischer Rest, und die Bedingung II. erfüllt. Wir fassen
diese Sätze so zusammen:
Im Falle I. bleibt ein Element oder alle Elemente
ungeändert, im Falle II. bleiben zwei Elemente un-
geändert und im Falle III. werden alle Elemente
geändert.
Wenn wir eine und dieselbe Substitution
(7)
mehrmals wiederholen, so entstehen die Substitutionen
A, A2, A* ...,
in deren Reihe einmal die identische Substitution
auftreten
muß. Ist n die kleinste positive Zahl, für die
ist, so heißt n der Grad von A (Bd. II, § 2).
Setzen wir für ein beliebiges m
so erhalten wir zur. Berechnung der Zahlen a,n, ßm, ym, 8m
folgendes System rekurrenter. Formeln: , >
am —|— ß"yjn, ßm-j-l & ßm "j~ ß dm,
J'm + l = 7wm d^m, dm-f-i = V ßm “j- d 8m-
Besonders einfach lassen sich hieraus die Zahlen ecm, ßm,
ym, dm im Falle I. berechnen.
§ 79.
Untersuchung der Gruppe 20.
293
In diesem Falle können wir, da die Vorzeichen von a, ß,
y, d alle gleichzeitig umgekehrt werden dürfen, annehmen:
a-f-ö = 2, ad — ßy = 1 (mod p),
und so erhalten wir aus (8):
«2 = 1 + 2 a, ßz = 2ß
d2 = - 1 -j- 2d, ?2 = 2 7 (mod
OCg := 2 —j— 3 cij ß3 = 3 ß (m°d P)>
d8 = - 2 + 3d, 7s = 3 7
woraus durch den Schluß von m auf m -|- 1 gefolgert wird:
' = - (m — 1) + ma, ßm = mß
W dm = ~ (m — l) + md, pm = mp ' P)'
Hieraus ersieht man, daß die sämtlichen Am wieder
zum Falle I. gehören, und daß p der Grad von A ist.
Die analoge Betrachtung der beiden anderen Fälle ist von
Serret durchgeführt, erscheint aber für unseren Zweck ent-
behrlich.
Dagegen wollen wir hier noch den Satz hinzufügen, daß
die ganze Gruppe £0 sich zusammensetzen läßt aus den
beiden folgenden speziellen Substitutionen
Der Beweis ergibt sich aus § 30, wenn man beachtet, daß
zu jedem der Bedingung ad — ßp = 1- (mod p) genügenden
Zahlensystem a, ß, p, d sich das Zahlensystem a', ß', p', d' so
wählen läßt, daß
(/,’ d') = Q d) (m0d Und “'d' ~ = 1
wird. Es sind also alle Substitutionen von 20 unter den in § 30
betrachteten enthalten. Wir können hier aber auch leicht die
Zusammensetzung einer beliebigen Substitution in 20 aus A und B
wirklich darstellen, und so unabhängig von § 30 den Beweis
führen.
Denn wenn zunächst c eine beliebige, durch p nicht teilbare
Zahl ist, so ergibt sich durch wirkliche Ausrechnung leicht
<n) a-=C: ?)•c=G:to = a--'ba-ba-^b,
294
Achter Abschnitt.
§ 80.
und sodann, wenn ( ’ *1
\r, o;
ß von 0 verschieden ist:
eine beliebige Substitution in 20
-und
1, 0\
aß-\ V
und wenn ß = 0 ist:
(13)
a, 0 \ __ /a, 0 \ / 1, 0'
.7, oc-1/ \0, a~ y yy, 1,
Es ist aus diesem Satz zu schließen, daß eine in 20 ent-
haltene Gruppe, die die zwei Substitutionen enthält,
notwendig mit 20 identisch sein muß.
§ 80. Normalteiler der Gruppe 20-
Um die etwa möglichen Reduktionen der Transformations-
gleichung kennen zu lernen, ist vor allem erforderlich, die Divi-
soren der Gruppe 20 zu untersuchen. Wir fragen zuerst nach
der Existenz eines Normalteilers ff von 20 (Bd. II, § 3)1)-
Ist
irgend eine von der identischen Substitution verschiedene Substi-
tution in ff, so ist, nach dem Wesen des Normalteilers, jede
Substitution
(2) U = TST-1
gleichfalls in ff enthalten, wenn
eine beliebige Substitution in 20 ist.
Wir stellen uns die Aufgabe, T und £ so zu bestimmen, daß
(<) ^=(-13)
wird. Diese Bedingung kann auch so geschrieben werden:
/«', ß'\ /a, ß\ / 0, 1\ /«', ß'\
V, $') ly, s) ~ V-1, Ü U $7’
*) Nach Galois: „Eigentliche Teiler“.
§ 80.
Normalteiler der 'Gruppe ß0.
295
und führt zu den Kongruenzen:
1. v.' a -|- ß' y = y'
,K. 2. a'ß + ß'8 = $' . , v
4. r>ß ö'd = — ß' 4-
und aus 1. und 2. folgt noch:
... 5. a' = / ö —- §' y , , .
(«) 6. ? = Lyß + (“»a ?)
Setzt man diese Werte in (5) 3. und 4. ein, so folgt:
y'(a d — g) = 0 , , .
d'(« + d — g) = 0 (modl>)’
woraus, da y', d' nicht beide durch p teilbar sein können, folgt:
(7) = a 4- d (mod p);
ist £ so bestimmt, so folgen in (5) die Kongruenzen 3., 4. aus
1., 2. Setzt man aber y', d' aus 1., 2. in
(8) a'd' — ß'y' = 1 (mod p)
ein, so erhält man
(9) a'2ß 4- «' ß' (d — a) — ß'2y = 1 (mod p).
Ist hieraus ß' bestimmt, so sind alle in (5), und also
auch in (2), (4) ausgesprochenen Forderungen befriedigt.
Es handelt sich also noch darum, nachzuweisen, daß die
Kongruenz (9) immer lösbar ist.
Diese Möglichkeit ist evident, wenn ß oder — y quadratischer
Rest von p ist; denn dann genügt
' = ß' = 0 . ,
’ ,----- (mod
oder a' = 0, ß' = \—y~l
der gestellten Forderung.
Im weiteren ist nun zu unterscheiden, ob die Substitution S
zu Klasse I, II, III des vorigen Paragraphen gehört.
Ist zunächst
I- = 1 (mod p),
so geht, wenn wir Sm an Stelle von S setzen, nach § 79, (9),
ß in mß, y in my über, und es läßt sich m immer so bestimmen,
daß mß oder — my quadratischer Rest von p wird.
Hierher gehört auch der Fall, daß ß = 0 oder y = 0 und
a = d (mod p') ist.
296 Achter Abschnitt. § 80.
Ist dagegen ß = 0 und a — d nicht durch p teilbar, so
kann man in (9) ß' beliebig wählen und dann a' aus einer Kon-
gruenz ersten Grades bestimmen.
Ist ß nicht durch p teilbar, so setze man (9) in die Form
(10) [a'/j + ß'(L=-^J= ß + i] (modp),
und wenn nun
(C4 I -
—} — 1 quadratischer Rest von p ist, so bestimme
man ß' aus der Kongruenz:
[FF- *] - (FF
wodurch (10) übergeht in
«'0 + ß' = ± (mod ^)’
und woraus a' bestimmt werden kann, welches Zeichen auch
gewählt wird.
Ist
/ I
III. (—2—j — 1 quadratischer Nichtrest von p und zu-
gleich ß quadratischer Nichtrest, so läßt sich immer ein Nicht-
rest v so bestimmen, daß ß v quadratischer Rest wird; denn
läßt man v in ß v die Reihe der Nichtreste durchlaufen, so
können nicht lauter Nichtreste entstehen, weil unter diesen
auch ß sein müßte.
Dann kann man ß' so bestimmen, daß
F 4"") — — v (mod l’)’
und dann a' aus
<*'ß + ß' 2 “) — i ^ß + v (mod P)-
Hieraus folgt:
In einem Normalteiler $ der Gruppe 20 muß gewiß
eine Substitution U, von der Form
vorkommen.
Es sei zunächst | von Null verschieden (mod p).
§ 80. Normalteiler der Gruppe 20. 29 7
Nach dem Begriff des Normalteilers enthält $ auch die
Substitution
(-) (4444(4;) = 44
und folglich auch
(«) (4 j) (4 = (2 j1: ?) -A,! ß ” o1»
also auch A und alle seine Potenzen. Daher enthält -St auch
co (4(44444,)
für ein beliebiges »7, d. h. die Substitution (11) für jedes
beliebige g und mithin auch
-44J)-
Demnach ist nach dem Satze des vorigen Paragraphen die
Gruppe St mit £0 identisch.
Es bleibt noch die Möglichkeit zu erörtern, daß in (11)
g = 0 ist.
In diesem Falle enthält die Gruppe St also die Substitution
und folglich auch für ein beliebiges, durch p nicht teilbares a
Daraus leitet man, als in St enthalten, noch weiter ab:
/ l,0\/«-M)\/l,0\M0 \ 71, ' 0\
1, 1J \0, «7 \1, 1/ \ 0, a_v W — 1, 1/
Wenn nun p größer ist als 5, so kann man a so annehmen,
daß a4 — 1 nicht durch p teilbar ist; dann enthält also Ä auch
die Substitution A und ihre Potenzen und mithin ist St mit £0
identisch.
Ist p = 5, so ist a4 — 1 immer durch p teilbar, also dieser
Schluß nicht anwendbar.
In diesem Falle folgt aber aus dem Begriff des Normalteilers
als in Ä enthalten:
298
Achter Abschnitt.
.§ 80.
ZI, 1\ / 0, 1\ /— 2, — 1\ / 0, 1\ _ /—2, 0\
\2, — 2? 1, 0/ 2, 1/ \— 1, 0/ \ 0, 2/’
/— 2, 0\Z l,O\/2, 0\ /l, 0\ _ /l, 0\
\ 0, 2/ 1, 1J \0, —2/ \1, 1/ \2, 1/’
d. h. A2 und mithin alle Potenzen von A, woraus wie oben zu
schließen, daß St mit 20 identisch ist. Wir haben also den Satz:
Ist p >> 3, so hat die Gruppe £0 keinen Normal-
teiler.
Im Falle p = 3 enthält $ gleichfalls
/ 0, 1\
\-l, 07’
also auch
und es bilden auch in der Tat die vier Substitutionen
zt-x /l, 0\ / 0, 1\ /— 1, 1\ 71, 1\
(lo) \o, 17’ i, o)’ \ 1,17’ Kl, —1/
einen Normalteiler von 20 im Index 3.
Im Falle p = 3 ist die Gruppe £0 isomorph mit der alter-
nierenden Gruppe der Vertauschungen von vier Elementen. Es
ist dies die Gruppe einer beliebigen Gleichung vierten Grades,
wenn die Quadratwurzel aus der Diskriminante dem Rationalitäts-
bereich adjungiert wird. Der Divisor (15) dieser Gruppe vom
Index 3 liefert dann die in der Algebra bekannte kubische Re-
solvente der biquadratischen Gleichung.
Eine zur Gruppe (15) gehörige Funktion der Wurzeln
4^, der Transformationsgleichung für den dritten Trans-
formationsgrad ist z. B.
«oo «0 + »1 «2
oder
•(«’«, — ^o) («i — ^)-
Der' Unterschied zwischen diesen beiden Funktionen ist der,
daß die erstere durch die Substitution der Determinante — 1
/— 1, o\
\ 0, 17
ungeändert bleibt, während die zweite dabei ihr Zeichen ändert.
Die erstere wird daher zu einer Gleichung dritten Grades mit
rationalen Koeffizienten führen, während in der kubischen
Gleichung für die zweite noch ]/ — 3 auftritt (§ 78).
§ 81.
Nichtnormale Teiler von ß0.
299
§ 81. Nichtnormale Teiler von £0.
Wir fragen nun, indem wir den Fall p = 3 beiseite lassen,
nach den nichtnormalen Teilern der Gruppe 20, deren Index
kleiner als p -|- 1 ist; von der Existenz solcher Teiler hängt
die Möglichkeit der Bildung von Resolventen der Transformations-
gleichung ab, deren Grad niedriger ist als p -|- 1.
Zunächst läßt sich zeigen, daß der Index eines Teilers $
von 20 niemals kleiner als p sein kann.
Es sei
(1) $ = So, ..., &—i
irgend ein Teiler von 20 vom Grade v, und, wenn es möglich ist,
(2)
T =
eine Substitution pten Grades, die in 20, aber nicht in $ vor-
kommt. Es kann dann auch, da p Primzahl ist, keine niedrigere
Potenz von T als die pte in ft' vorkommen. Die Nebengruppen
(3) ft, Tft, T2ft, ..., TP-ift
enthalten lauter voneinander verschiedene Elemente FSic,
und demnach ist vp höchstens gleich dem Grade der Gruppe
20, d. h.:
: v
— p2 — 1
vp P —2----------
Also ist der Index von ft, d. h. der Quotient
p2 — 1
gleich p oder größer als p.
Ein Teiler ft von 20, dessen Index kleiner als p ist, muß
daher sämtliche Substitutionen pten Grades enthalten, also auch
(§ 79, I.) alle Substitutionen T, in
(4) a + 5 = 2
ist.
Demnach enthält eine solche
stitution
denen
(mod p)
Gruppe ft zunächst die Sub-
(5)
A
300
Achter Abschnitt.
§ 81.
und
ihre Potenzen; ebenso die Substitutionen
und
(6)
folglich auch
B :
Wenn aber die Substitutionen A, B in $ enthalten sind, so
muß $ nach § 79 mit 20 identisch sein. Wir haben also den
Satz:
Der Index eines Teilers von 20 kann nicht kleiner
als p sein.
Unser Problem beschränkt sich also
Teilern von 20 vom Index p oder vom Grade —
Es sei $ ein solcher Teiler
seine Elemente, so daß die Zahl v den Wert
p2 — 1
v — —
und
auf die Frage nach den
'2 — 1
2
80, Si, ..., 8,._i seien
(7)
hat.
Da der Grad eines jeden Elementes einer Gruppe immer ein
Teiler des Grades der Gruppe ist, so kann, da v durch p nicht
teilbar ist, in S kein Element vom Grade p vorkommen; nehmen
wir also für T die Substitution vom Grade p:
(8)
so läßt sich die Gruppe 20 in die p Nebengruppen zerlegen:
(9) 20 = A®, J2®...,
Mit S?
Index alle
Es sei
20 = A2$ ...
sind von demselben Grade, also auch von demselben
seine konjugierten Teiler
T$T-\
nun g eine primitive Wurzel der Primzahl p, und
<101 U = v 1
eine Substitution, die offenbar vom Grade ——— ist. Diese muß,
wie jede Substitution von 20, in einer der Reihen (9) vorkommen;
d. h. es gibt eine Substitution 8 in $ und einen Exponenten A,
für den
(11)
C = A*S, S = Ä~'L C.
A
§ 81.
Niehtnormale Teiler von ß0.
301
Es läßt sich, aber y weiter so bestimmen, daß
(12) AY~l CA~Y = C, •
man erhält dafür die Bedingung
Vi.9 ~ 5r-1) = ^9 (mod p),
die, da p >► 3 ist, immer befriedigt werden kann; danach ist
aber wegen (11)
C = AY SA~Y.
Es kommt also C in dem mit £? konjugierten Teiler AY$A~Y
vor, und wir können also, indem diese Gruppe an Stelle von
gesetzt wird, unbeschadet der Allgemeinheit annehmen, $ ent-
halte selbst die Substitution C.
Es kann nun in $ die Substitution
B
_(
~ \-l, oj
entweder vorkommen oder nicht vorkommen. Im ersten Fall ent-
hält $ auch alle aus B und C zusammengesetzten Substitutionen,
die sämtlich von einer der beiden Formen sind:
(13)
= 0, i,...^
r
Im ersten Fall enthält also $
(13) und keine der Form (14).
<14) U/,0 )•
und deren Anzahl p — 1 beträgt.
alle Substitutionen von der Form (13), (14), im zweiten alle Sub-
stitutionen der Form
Es sei nun
(15)
eine in $ enthaltene
noch in der Form (14) enthalten ist, bei der also weder a und d,
noch ß und y zugleich kongruent mit 0 sind. Dann sind die
sämtlichen Substitutionen der Form
V =
Substitution, die weder in der Form (13),
/im __ /(i9r + si ß 9r s \
(16) C VC _
wenn r, s beide die Reihe der Zahlen durchlaufen:
0,l,2,./.^=^
Al
in $ enthalten und alle voneinander verschieden. Denn
sind zwei unter den Substitutionen (16) einander gleich, so muß
302
Achter Abschnitt.
§ 81.
es auch eine unter ihnen geben, die, ohne daß r, s verschwinden,
mit V identisch wird. Dies verlangt aber
a = + agr+s,
7 = +yg-r+s,
ß = ±ßgr-s
8 = +8g~r~s
(mod p),
wo in allen vier Formeln die oberen oder die unteren Zeichen
gelten, also, da weder a und d, noch ß und y gleichzeitig ver-
schwinden,
r s = 0, r — s = 0 (mod p — 1),
oder
r -f- s = —-, r — s = 1 (mod p — 1),
also in beiden Fällen
(p 1\
mod —1, w. z. b. w.
In der Form (16) sind also ( —j verschiedene Sub-
stitutionen enthalten. Ist damit die Gruppe S noch nicht
erschöpft, so wähle man eine nicht in (13), (14), (16) enthaltene
Substitution V und bilde in gleicher Weise die Reihe
(17) CrV'Cs,
deren Substitutionen sowohl unter sich als auch von den in (13),
(14), (16) enthaltenen verschieden sind, und fahre auf diese Weise
fort, bis die ganze Gruppe $ erschöpft ist.
Bezeichnen wir die Anzahl der so gebildeten Reihen (16),
(17), ... mit g, so ergibt sich also der Grad der Gruppe
1. wenn B in S nicht vorkommt:
2. wenn B in S? vorkommt:
und diese Zahl soll also nach der Forderung unserer Aufgabe
= (P — 1) O 4- 1)
2
sein. Hieraus aber ergibt sich, daß der Fall 1. unmöglich ist,
denn es müßte in diesem Falle
/p — 1\
q (-T~) =
§ 81. Nichtnormale Teiler von 20. 303
also
2 = P, p = 8
sein, was wir ausgeschlossen haben.
Im Falle 2. aber folgt für jedes beliebige p:
q = 2.
Daher muß in $ jedenfalls die Substitution B vorkommen,
und die gesuchte Gruppe ist durch (13), (14), (16), (17) erschöpft.
Wir zeigen zunächst, daß in den beiden Substitutionen F, V
der Gruppe $ keine der Zahlen a, ß, y, 8, a', ß', y', 8' kongruent 0
sein kann.
Es kommt nämlich, wie wir schon gesehen haben, in $
nicht vor
A o\
V, v’
wenn 7 von 0 verschieden ist, also auch nicht
Za, 0 \ / 1, 0\ ___ za, 0 \
\0, a-y W, 17 — V, a-y’
wenn a beliebig ist; und folglich auch nicht
za, 0 \ / 0, 1\ __ / 0, a\
V, a-1/ 1, 0/ ~ a-1, 7/
/ 0, 1\ Za, 0 \ _ Z y, a~l\
X— 1, 0/ V, «~V \— «, 0 /
(°, —1 \( 0, ,a\ Za-1, 7\
\1, OA— a-1, — ?/ \0, a/’
worin alle Substitutionen (W' enthalten sind, in denen eine
Vi o/
der vier Zahlen a, ß, y, 8 kongruent mit 0 ist.
Die Substitutionen des Systems (16) bezeichnen wir jetzt mit
W = (K9r+s, ßgr~s A
\7P~ r+*, 8g~ r~s)'
und setzen
(18) £ = <+’, g = ^ßg-^ , d }
(19) a8 = m, ßy = m — 1 P)
m ändert sich nicht, wenn V durch eine beliebige Substitution des
Systems (16) ersetzt wird. Die Zahl m' soll die entsprechende
Bedeutung für das System (17) haben; | kann in jedem dieser
beiden Systeme jeden der Werte
(20) 1, 2, ... p — 1
304
Achter Abschnitt.
§ 81.
(21) W = (
annehmen, und g durchläuft, je nachdem a~ 1ß quadrati-
scher Rest oder Nichtrest ist, in einem System die Reihe
der Reste oder der Nichtreste. Die Änderung des Vor-
zeichens von | gibt keine neue Substitution W. Hiernach können
wir W so darstellen:
t-14>-1 (m — 1), |-1 m)'
Da nun das Quadrat von W
W2 — f t2 + m — 1, (F + m)Q \
\t-2 4>-1 (»» — 1) (£2 + m), [(m — 1) £2 + m2]£-2/
zu Ä gehören muß, so ist es unter einem der Systeme (13), (14),
(16), (17) enthalten, woraus sich folgende vier Möglichkeiten
ergeben:
1. |2 -|- m = 0,
/22x 2. g2 m — 1 = 0, (m — 1)|2 -j- m2 = 0,
' 3. (|2 -|- m — 1) [(m — 1) —|— m2] = mg2,
4. (|2 -|- m — 1) [(»» — 1) |2 -|- m2] = m' |2,
und jeder der p — 1 Werte (20), für £ gesetzt, muß einem
dieser vier Fälle genügen. Wenn eine der Kongruenzen (22), 2.
erfüllt ist, so muß die andere daraus folgen, was nur möglich
ist, wenn
(23) 2m = 1, g2 = m (mod p).
Nun hat eine Kongruenz in bezug auf einen Primzahlmodul
höchstens so viele inkongruente Wurzeln, als der Grad der
Kongruenz beträgt; 1. und 2. können also höchstens für je zwei,
3. und 4. höchstens für je vier Werte von g befriedigt sein; also
gibt es im ganzen höchstens zwölf Werte von g, die einer der
vier Kongruenzen (22) genügen.
Daraus folgt:
p — 1 <! 12, p 13.
Ist aber p = 13, so muß jede der Kongruenzen (22) die
Maximalzahl von Wurzeln haben; es muß also auch 2. für zwei
Werte von g befriedigt sein; dann müßte nach (23) m = 7,
g2 = 7 (mod 13) sein, was unmöglich ist, da 7 quadratischer
Niehtrest von 13 ist.
Ein Teiler von So vom Index p existiert also nicht,
wenn p > 11 ist.
§ 82. Teiler von 20 vom Index p für p — 5, 7, 11. 305
§ 82. Teiler von £0 vom Index p für p = 5, 7, 11.
Es bleibt die Möglichkeit übrig, daß für p = 5, 7, 11 Teiler
von 20 vom Index p existieren.
1. p — 5. Wir untersuchen zunächst den Fall p = 5.
Da m und m — 1 nicht kongruent 0 sein können, so bleiben
für m die Annahmen
m = 2, 3, 4 (mod p).
Ersetzen wir aber die Substitution W § 81, (21) durch
(T) WB = (
wodurch m in 1 — m übergeht, so kommt der Fall m = 4 auf
den Fall m = 2 zurück.
Für m = 2 ist aber (23), § 81 nicht erfüllt, und von den
Kongruenzen (22) ist keine möglich, da + 2 Nichtreste von 5 sind
und die linken Seiten von (22), 3., 4. sich für m = 2 auf — 1
reduzieren, was für jedes von Null verschiedene £ durch 5 teilbar
ist. Es bleibt also nur übrig, daß
(2) m - 3, m' = 3 (mod 5)
und die beiden Systeme W, W' [§ 81, (16), (17)] können sich nur
dadurch voneinander unterscheiden, daß a~ 1ß und also auch p
in dem einen quadratischer Rest, in dem anderen quadratischer
Nichtrest von 5 ist. Die gesuchte Gruppe besteht also, falls sie
existiert, aus den 12 in den drei Formen
<’) (4-d)’ U-U-.)
enthaltenen Substitutionen, worin
|=1, 2, ^ = +1, + 2 (mod 5)
zu setzen ist.
2. p = 7, 11.
Da — 1 für p = 7, 11 unter den quadratischen Nichtresten
zu finden ist, so gehört die zusammengesetzte Substitution WB,
(1), zu den W' [weil der quadratische Charakter der in (18),
§ 81 mit p bezeichneten Größe in W und WB der entgegen-
gesetzte ist]. .Demnach ist nach (1) und §81, (19), (21)
ß'y' = —m = m' — 1, also:
(4) m -|- m' = 1 (mod p).
Weber, Algebra. HI.
20
306 Achter Abschnitt. § 82.
Für p = 7 bleiben also, da die Vertauschung von m mit m'
nichts Neues liefert, die drei folgenden Möglichkeiten:
1. m = 2, m' = 6. 2. m = 3, m' = ö. 3. m = 4, w! = 4.
Im Falle 1. ist von den Kongruenzen § 81, (22), 1. und 2.
unmöglich; also müßte für jedes £ eine der beiden Kongruenzen
.3., 4. erfüllt sein, die hier lauten:
(F + 1) (F + 4) = 2 & 6 ? (mod 7),
deren keine für £ = 1 erfüllt ist.
Im Falle 3. ist (22), 1. nicht erfüllbar und (22), 2. ist für
|2 = 4 erfüllt; daher muß für = 1, 2 die Kongruenz (22)
3. oder 4.:
(i2 + 3) (3 i2 + 2) = 4 (mod 7)
erfüllt sein, was wieder nicht der Fall ist. Es bleibt also für
p — 7 allein übrig:
(5) m = 3, m' = 5 (mod 7).
Für p — 11 ist von vornherein die Möglichkeit auszuschließen,
daß die Kongruenzen (22), 2. erfüllt seien, weil in diesem Falle
infolge von (4) und § 81, (23):
m = m’
sein müßte; dann wären (22), 3., 4. nicht verschieden und die
Kongruenzen (22) könnten zusammen höchstens acht Wurzeln
haben und nicht zehn, wie es doch sein müßte.
Es müssen also die Kongruenzen (22), 1., 3., 4. jede die
Maximalzahl von Wurzeln haben, und es muß, damit 1. erfüllt
sei, m, und aus gleichen Gründen w! quadratischer Nichtrest von
11 sein. Dieser Bedingung und gleichzeitig der Bedingung (4)
genügen aber nur die beiden Zahlen
(6) m, m' = 2, —1 (mod 11).
Die gesuchten Gruppen bestehen also in diesen beiden Fällen,
falls sie existieren, aus folgenden Substitutionen:
p = 7
1' \o, rv’ vt-1, o/ \2ri(>-1,3^-v’ sr1,
= 1, 2, 3 (mod 7),
p = 11
(8) (o, £-0’ (- tL1, o)’ 4»-1, 2U)’ (- 2 r1 p-1)
£ = 1, 2, 3, 4, 5 (mod 11);
§ 82. Teiler von 20 vom Index p für p = 5, 7, 11. 307
g durchläuft in (7) und (8) entweder die Reihe der quadratischen
Reste oder die der Nichtreste, so daß man für p = 7 oder 11
je zwei Gruppen vom Index p erhält.
Daß die in (3), (7), (8) zusammengestellten Substitutions-
systeme wirklich Gruppen konstituieren, läßt sich durch direkte
Zusammensetzung auf verschiedene Arten nachweisen. Einfacher
gelangt man zu diesem Beweise aber dadurch, daß man Funk-
tionen der #z, § 78, (7), bildet, die durch die Substitutionen dieser
Systeme ungeändert bleiben, und durch die Substitutionen von 20
überhaupt nur p verschiedene Werte erhalten.
Die Systeme (3), (7), (8) lassen sich, wie aus ihrer Ent-
stehungsweise hervorgeht, durch wiederholte Anwendung von
B, C, U, U' zusammensetzen, wenn 17, Ü' irgend zwei spezielle
Substitutionen W, W' sind. Für p = 5 gehört U2 und für
p — 7, 11 gehört UB zu den W, so daß U' noch weggelasseu
werden kann. Wählen wir U irgendwie beliebig, und nehmen für
die primitive Wurzel g in C für p == 5, 7, 11 bzw. 2, —2, 2, so
können wir die Gruppe (3) zusammensetzen aus:
die Gruppe (7) aus:
die Gruppe (8) aus:
wo in den beiden letzten Fällen aus den doppelten Vorzeichen
die oben erwähnten zwei verschiedenen Gruppen entspringen.
Wir stellen nun die diesen Substitutionen entsprechenden
Vertauschungen der Indizes z zusammen [§ 79, (3)].
z = OO, 0, 1, 2, 3, 4
0, OO, 4, 2, 3, 1 (B)
oo, 0, 4, 3, 2, 1 (<7)
4, 1, 2, 0, oo, 3 (17).
Es werden also durch B, C, U die Indexpaare
(OT,0), (1,4), (2,3)
20*
308 Achter Abschnitt. § 82.
nicht auseinandergerissen, sondern nur untereinander vertauscht.
Überdies werden jedesmal in zweien dieser Paare die Elemente
vertauscht. Bilden wir daher eine Funktion wie
(9) V = (t>„ — t>0) («i — «4) («2 — «8),
so bleibt diese durch B, C, U und also durch das ganze System
(3) ungeändert, während sie durch wiederholte Anwendung der
zyklischen Vertauschung (0, 1, 2, 3, 4), d. h. der Substitution
fünf verschiedene Werte erhält. Aus A und B läßt sich aber
[§ 79, (10)] die ganze Gruppe So zusammensetzen, und V erhält
daher durch Anwendung von So nicht mehr als fünf Werte.
Die fünf Werte von V sind die Wurzeln einer Gleichung
fünften Grades.
Für p = 7 ist
B = (2, —C = (^, 4/), Ü = (z, •
\ 2 J \ \ 3 -yz /
Zur besseren Übersicht stellen wir noch B, C, V durch die
zyklischen Vertauschungen dar, die durch sie in den acht
Werten von z hervorgerufen werden:
B = (0, 00) (1,-1) (2, 3) (-2,-3),
C = (1, —3, 2) (—1, 3, —2),
ZT = (00, -p 1> ± 1, dz3) (0, -j-3, -j- 2, + 2),
und daraus erhält man die siebenwertige Funktion
(10) F== (^ — ^0) («71 — «73) («±1 — V+t) (Pti — «±2>,
worin das eine oder das andere Zeichen genommen werden kann.
Für p — 11 ist
B = c = P=(e.3y^),
oder durch di$ Zyklen dargestellt:
B = (0, co) (1, -1) (2, 5) (-2,-5) (3, -4) (-3, 4),
C = (1, 4, 5, —2, 3) (—1, —4, —5, 2, —3),
U = (00, 4ZI, +3, +2, +2) (0, +5, +5, +4, ±1),
woraus die beiden 11 wertigen Funktionen
(11) V =
(«„ — «o) («71 — «±5) («±S — «7ä) («72 — «74) («±2 — «±1) («±4 — «73)-
Resolventen 5ten Grades.
309
§ 83.
Hierbei ist noch folgende Bemerkung von Interesse. Die
Resolventen pten Grades, deren Wurzeln die Größen (9), (10),
(11) sind, enthalten nach § 78 in ihren Koeffizienten noch ]/+p.
Die Gruppe So wird aber zur Gruppe S erweitert, wenn wir
eine lineare Substitution von der Form § 78, (13) hinzufügen, in
der ac — bc quadratischer Nichtrest ist, also etwa:
für p = 5 («, 2 z)
für p = 7, 11 (ä, — z).
Durch Anwendung dieser Substitution geht aber der Wert (9)
V = («’„ — «’o) («h «h) («2 — «’s)
in den entgegengesetzten über, und daraus folgt, daß, wenn
p — q ist, V2 einer Gleichung 5ten Grades mit rationalen
Zahlenkoeffizienten genügt. Daraus schließt man, daß in der
Gleichung für V die Koeffizienten der ungeraden Potenzen den
Faktor /ö" haben, während die anderen rational sind, oder daß
man für die Unbekannte /ö” V eine Gleichung mit rationalen
Koeffizienten erhält.
Für p — 7, 11 gehen die den beiden Vorzeichen in (10) oder
(11) entsprechenden Ausdrücke durch die Vertauschung (#, —z)
ineinander über. Die Resolventen 7ten oder Ilten Grades, denen
einer der beiden Ausdrücke (10) bzw. (11) genügt, gehen also
durch Änderung des Vorzeichens von —7, y'—11 ineinander
über.
§ 83. Verschiedene Resolventen 5ten Grades für den
5 ten Transformationsgrad.
Bei der Bildung der Resolventen pten Grades beschränken
wir uns hier auf den Fall p — 5.
Diesen Resolventen kann man sehr mannigfaltige Formen
geben, indem man nicht nur in der Funktion F, (9) des vorigen
Paragraphen für die Größen v die Wurzeln einer beliebigen
Transformationsgleichung wählen, sondern auch Vdurch mancherlei
andere Funktionen ersetzen kann, etwa durch
(«’oo + «’o) («’l + «h) («2 + «’s),
oder durch
«’oo «’o + «’l «’l + «’2 «’s-
310
Achter Abschnitt.
§ 83.
Wir wollen zunächst die Transformationsgleichung § 72, (8)’
in der jetzt in Übereinstimmung mit dem vorigen Paragraphen
v für x gesetzt ist:
(1) . ve 10 -|- 5 = 0
anwenden. Hierin ist, wenn
c = 0 (mod 12), z = c (mod 5)
ist,
Nehmen wir dann
(3) wz = («„ — vz") (^..j — ^_j) (^_2 — i-z+2)
= (+ — (^+12 — ^-12) O’c+SM — ^-2*),
z = 0, 1, 2, 3, 4, c = 0, +12, + 24,
so sind nach der Schlußhemerkung des vorigen Paragraphen die
w0, wn w2, wg, w4 die Wurzeln einer Gleichung 5ten Grades,
deren Koeffizienten rational aus y2 und rationalen Zahlen ge-
bildet sind.
Beachtet man aber die Relationen [§ 54, (14)]:
+ (« 4- 1) = e ~r2(o), 72^— —) — 7z(^),
so folgt aus der Form von (1), daß durch die Vertauschung
(<»,<» -|- 1) die Wurzeln v, abgesehen von einer Umstellung, den
— / 1\
Faktor e 8 annehmen, während sie durch I <», —— \ ungeändert
bleiben. Die w2 vertauschen sich also nur untereinander, und
ihre symmetrischen Funktionen bleiben ungeändert und hängen
daher rational nur von der Invariante y'(ro) ab. Die Koeffizienten
in der Gleichung für w können überdies für kein endliches j (ra)
unendlich werden und sind demnach ganze Funktionen
von j (m).
Ein weiterer Aufschluß über diese Koeffizienten ergibt sich
durch die Entwickelung nach steigenden Potenzen von q. Die
Entwickelungen der v haben nach (2) die Anfänge
2 c 2 71 i 2
— 5g8 4----, + = e12 6 q 16~l------
und daraus folgt mit Benutzung der bekannten Gleichung
. 2 a . 43r 1-
4 sin — • sm — = V 5
0 5 '
§ 83. Resolventen 5ten Grades. 311
der Anfang der Entwickelung für ws:
2 c rti
(4) wz — q 5 e2 6 -|-----
Hieraus folgt, daß die Potenzsummen der bis zur vierten
einschließlich Konstanten sind, da sie nicht einmal die erste
Potenz von j (co) enthalten können, und daß das Produkt der
eine lineare Funktion von j(w) sein muß, in der j(co) den
Koeffizienten 1 hat.
Die Gleichung der w hat daher die Form:
(5) w5 w4 + «s + bs w2 -j- bi w 4- b6 = 3 («),
wenn die b rationale Zahlen sind. Diese Koeffizienten lassen sich
dadurch berechnen, daß man die Entwickelung (4) weiter fort-
setzt. Wir schlagen hier einen anderen Weg ein, der, streng
genommen, zu der im nächsten Teil behandelten komplexen
Multiplikation gehört, bei seiner Einfachheit aber trotzdem ganz
wohl hier seine Stelle finden kann.
Setzen wir co = i = y— 1, so ist
1
co =-------
co
und infolgedessen ist [§ 34, (11), (12), (14)]:
/•10 = AO’)=f/2, f(i) = l/2,
also [§ 54, (5)]:
(6) ?s(i) = 0, y2(i) = 12, j(i) = 12».
Man findet aber ferner aus den Transformationsformeln für
(<»)[§ 34, (4), (5)]:
if / i \ _____
7](CO 4" 1) = ß12 V (®), (---—) = V------i<0 7] (co),
wenn man auf die Zerlegung
5 = (2 4" 0 (2 — 0
Rücksicht nimmt:
also
v2 — 1 4- 2 i, vs- — 1 — 2«,
und man kann jetzt, da für = 12 zwei Wurzeln der Gleichung
(1) bekannt sind, für diesen besonderen Wert von y2 den linken
Teil dieser Gleichung leicht in Faktoren zerlegen:
v6 4- io«8 — 12« 4" 5 = («2 4- 2« 4~ 5) («2 4~ v — i)2’
312
Achter Abschnitt.
§ 83.
woraus zu schließen:
(«o, müssen, da in ihnen q reell ist, positiv sein.)
Aus (3) ergibt sich sodann:
(8) tc0 = 0, wr — wa = —5 — 2 t |/5,
w2 = Wt = —5 -|- 2 t ]/ö.
Dies müssen die Wurzeln von (5) sein für j = 123 und
daraus erhält man die gesuchte Resolvente in der Form:
(9) w(w2 10 w 4- 45)2 = j(co) — 12s —
Diese Gleichung laßt sich auch in die Form bringen:
(10) (w -|- 3)8 (w2 —|— 11m? —|— 64) —
auf die man auch direkt kommt, wenn man, anstatt » = t zu
setzen,
annimmt.
Die gefundene Resolvente vereinfacht sich noch, wenn man
[nach (9)]:
__ i— ___ ys .
g yw iQ w
setzt:
(11) #5 10-|- 45# = 7S,
oder wenn man [nach (10)]
(12) w2 + litt? + 64 = t/8, 2/ = -^
setzt:
(13) t/5 — 40 t/2 — 5 72 y — y2 = 0,
eine Gleichung, die sich auch ergibt, wenn man von vornherein
die Annahme macht:
2 t/ = + Vi-
In der Gleichung (13) fehlen, wie man sieht, die dritte und
die vierte Potenz der Unbekannten. Dieselbe Eigenschaft kommt
auch, wie leicht nachzuweisen ist, der Gleichung zu, deren
Wurzeln
§ 83. Resolventen 5ten Grades. 313
(14) x = y(X + <^) =
sind, wenn A, y beliebige Parameter bedeuten, die für alle fünf
Werte x die gleichen sind.
Setzt man diese Gleichung in die Form
(15) x6 — 5 m3 — 5&y2a; — bcp£ = 0,
so ergeben sich nach einigen Rechnungen mit Benutzung der
besonderen Werte von x für y3 = 0 und y8 = oo für a, b, c
die folgenden Ausdrücke.:
u = 8 A3 — 72 A —j— (Al 2 y — ^t3),
(16) b = 1A 4- 18A2g2 — 27fi* -|- y3l(is,
c = A5 -|- 10 A3 ft2 -|- 45 A ft3 -|- y3
Es soll noch eine Resolvente 5ten Grades mit Benutzung der
Funktion /'(<») gebildet werden.
Wir setzen:
(17) u = /(<»), va = /(öo), vz =
c = 0 (mod 48), c (mod 5),
und haben nach § 73 zwischen w und v die Gleichung 6tenGrades:
(18) w6 -|- — w5®5 -|- 4w® = 0.
Wir untersuchen den Einfluß, den die drei Vertauschungen
(»•“ + A (»’-!)'
auf die Größen vz haben. Durch diese Vertauschungen geht c
über in c15 c2, c', die nach § 69, (9), (11) und § 73, (6) durch
die Kongruenzen
Cj = c + 2, c2 = —1, c' = (mod
bestimmt sind. Abgesehen von dieser Änderung des Index gehen
nach § 73, (4) und (9) die v über in
5 H i \l
(20) e 12 v, v, ——
l) Vgl. Kiepert, Auflösung der Gleichung 5ten Grades. Grelles Journal,
Bd. 87, S. 114.
314
Achter Abschnitt.
§ 83.
§7ti
Man hat also, wenn zur Abkürzung e 12 = e gesetzt wird,
folgende zusammengehörige Vertauschungen:
CO, w, V , 00 5 ®0, ®2, ®3, ®4,
G) + 2, e 12 w, f-y . 00 > st>2, «®4,
(21) - 1 ~ü’ w, V», V , 00 V4, ®2, ®3, ^1,
G) — 1 V2 V2 V2 V2 V2 V2 V2
G) + 1’ u ’ Vt ’ ®2 ’ ®3 ’ <£>
Wir führen nun die fünf Größen we durch die Gleichung ein:
(22) W2 = <^0° ~ O (^ + 1 ~(^+2 —
y& w3
also:
_ K — ^o) (®i — ^4) (^2 —
Wq -- -------------7=-------------,
yo u3
... _ (®=o — ®1) (®2 — ®o) (®8 — ®<)
3
y& w3
... _ (®=o — ®2) (®8 — (®4 — *>«)
W2 -- -------------r=-------------,
y.5 ws
,,, _ (v«> — *3) (®4 — ®2) (f0 — *h)
y& w3
,,, _ (v*, — O foo — M (v< — ^2)
4 yö«8
so daß, wenn man in der letzten Reihe davon Gebrauch macht,
daß nach (18) das Produkt der sechs Größen v2 den Wert w6 hat, sich aus (21) folgende zusammengehörige Vertauschungen
der w ergeben: to, Wo, Wi, w2, ws, w4,
GJ -f- 2, -W2, Ws, — W4, Wo, — w15
(23) 1 to ’ Wo, W2, wn w4, w8,
GJ 1 GJ —p 1 ’ -Wo, — Ws, — w4, — w2, Wp
Die Funktionen w können für keinen von 0 und a> ver-
schiedenen Wert von u unendlich werden. Nehmen wir daher
die Gleichung, deren Wurzeln die fünf Größen we sind, in der
Form an:
w5 + A —|— ^2 “I- -A3 “I- ^4.4 w —.A5 — 0,
§ 83.
Resolventen 5ten Grades.
315
so sind J.2, A2, J.2, At, A? nach den Grundsätzen des § 73
ganze rationale Funktionen von
212
(2*) «” + =;
Die Entwickelung von (24) nach steigenden Potenzen von q
fängt an mit q~\ während der Anfang der Entwickelung von wz
1 tm
q 10 e 60
ist. Die Größen Af, A2, Ag, A4 können daher nicht einmal die
erste Potenz von (24) enthalten und sind also konstant, während
A? die Form hat:
212
J 2 = M24 + ±_ I C,
worin C eine Konstante ist. Die Werte der Konstanten kann
man bestimmen, wenn man die Werte der für to = i kennt.
Es ist aber für « = i [vgl. oben (6), (7)]:
u = f(i) = 1/2,
= VH = + 10) = ‘ )•
107ti _
= e * f(i + 2) = — »1/2,
v2 = »1/2
und folglich nach (18): _
= <>, = 1X2 U-ft
Folglich wird:
Wo = 0, Wj = w2 = »]/K, w8 = w4 = —»j/ö.
Danach wird zunächst C = —27, also
und
/ 64\2
A? = (w>2 - ,
daraus durch Vergleichung der Anfänge der Entwickelung
= —w12
6 ' «12’
und die Gleichung für w bekommt die Form:
(25)
64
W (w2 4- 5)2 = «12 — —
m12
316
Achter Abschnitt.
§ 83.
Man kann ihr aber noch eine andere, sehr bemerkenswerte
Form geben.
Nach den zwischen den Funktionen /(gj), /i(gj), /2(gj)
stehenden Relationen [§ 34, (11), (12)] ist:
/(°j)24 — 64 _ [/x (oj)8 — /g (<a)8]2
/(«)12 /(«)4
Führen wir also für w die neue Unbekannte
y =- yjw =
(26)
/i(°j)8 — /afo)8
/(to)2 (w2 + 5)
ein, so erhalten wir die Form:
(27)
2/5 + 5 y =
fi (gj)8 — fz (®)8
/(gj)2
Auf diese Formeln gründet sich die von Her mite und
Kronecker geschaffene Auflösung der Gleichung fünften Grades
durch elliptische Funktionen, auf die wir im 14. Abschnitt des
IL Bandes hingewiesen haben.
Nach Bd. I, § 60 kann die allgemeine Gleichung fünften
Grades auf die Form reduziert werden:
(28) ^-\-bz = a,
und diese Gleichung wird mit (27) identisch, wenn man setzt:
/i (®)8 — fi («)s = «/2(<»).
Nimmt man hierzu die Gleichungen:
= = =
so erhält man
(29) /34 _ aifn _ 64 — o.
Durch diese quadratische Gleichung ist /12 als Funktion
von a bestimmt.
Dann sind die Wurzeln der Gleichung (28) durch die Quadrat-
wurzeln aus den Ausdrücken (22) dargestellt. Das doppelte Vor-
zeichen dieser Quadratwurzeln erklärt sich daraus, daß zwei ent-
gegengesetzte Werte von a zu derselben Gleichung (29) führen.
Man kann aber auch die Wurzeln eindeutig bestimmen nach der
Formel (26):
(30)
a
w2 —5
z =
§ 83. Resolventen 5ten Grades. 317
In der oben erwähnten Arbeit von Kiepert wird die all-
gemeine Gleichung fünften Grades auf die Form (15) trans-
formiert, wozu nur die Auflösung einer quadratischen Gleichung
erforderlich ist. Sieht man darin a, b, c als beliebig gegeben
an, so dienen die Gleichungen (16) zur Bestimmung von Z, (i, ys.
Dies geschieht ebenfalls mit Hilfe einer quadratischen Gleichung,
was allerdings nicht auf den ersten Blick zu ersehen ist. (Vgl.
F. Klein, Vorlesungen über das Ikosaeder, S. 191 f.)
Auf die Resolventenbildung für den siebenten Transformations-
grad werden wir weiter unten zurückkommen, wenn wir über
die Hilfsmittel verfügen, die uns die komplexe Multiplikation
bietet.
ZWEITES BUCH.
QUADRATISCHE KÖRPER.
Neunter Abschnitt.
Diskriminante.
§ 84. Definition der Diskriminanten.
In der Theorie der quadratischen Körper treten als Diskri-
minanten gewisse ganze rationale (positive oder negative) Zahlen
auf, die, wenn sie gerade sind, durch 4 teilbar sind, und wenn
sie ungerade sind, bei der Teilung durch 4 den Rest 1 lassen.
Kronecker hat solche Zahlen „Zahlen von Diskrimi-
nantenform“ genannt. Wir wollen sie hier kurz Diskrimi-
nanten nennen, und uns nicht daran stoßen, daß dieses Wort
in der Algebra noch mannigfache andere Bedeutungen hat. Wir
definieren daher:
1. Eine positive oder negative, von Null verschiedene
ganze Zahl, die einer der beiden Kongruenzen
(1) D = 0, D = 1 (mod 4)
genügt, heißt eine Diskriminante.
Jede Quadratzahl ist nach dieser Definition eine Diskrimi-
nante. Da diese aber eine gewisse Ausnahmestellung einnehmen,
wollen wir sie, wenn die Unterscheidung nötig ist, uneigent-
liche Diskriminanten nennen.
2. Das Produkt zweier und folglich beliebig vieler
Diskriminanten ist wieder eine Diskriminante.
3. Eine Diskriminante, die (außer 1) keinen quadra-
tischen Teiler enthält, nach dessen Absonderung eine
Diskriminante übrig bleibt, heißt Stammdiskriminante.
Stammdiskriminanten sollen in der Folge zum Unterschied
von anderen mit zi bezeichnet sein. Ist D keine Stammdiskri-
minante, so gibt es eine und nur eine Quadratzahl ()2 und eine
Stammdiskriminante zf, so daß
(2) D = z/ Q2
ist; z7 heißt dann der Stamm von D.
Weber, Algebra. III. 21
322 Neunter Abschnitt. § 85.
Eine Stammdiskriminante ist durch keine ungerade Quadrat-
zahl teilbar. Ist aber zf durch 4 teilbar, so muß
(3) z/ = 8, 12 (mod 16)
sein. Denn wäre z/ = 0,4 (mod 16), so würde nach Forthebung
des Faktors 4 eine Diskriminante übrig bleiben.
Um also zu einem gegebenen D den Stamm zu finden, hat
man zunächst die größte ungerade Quadratzahl und dann noch
eine so hohe Potenz von 4 abzusondern, daß z/ entweder ungerade
und = 1 (mod 4) oder = 8, oder = 12 (mod 16) wird.
4. Eine eigentliche Diskriminante, die nicht in
Faktoren zerlegbar ist, die selbst wieder Diskriminanten
sind, heißt Primdiskriminante.
Ist p eine natürliche ungerade Primzahl, und wird das
Zeichen ± so bestimmt, daß +.P = 1 (mod 4) ist, so gibt es
folgende Primdiskriminanten:
(4) + p, —4, —|—8, —8.
5. Jede Stammdiskriminante läßt sich auf eine und
nur auf eine Weise in Primdiskriminanten zerlegen.
Denn sondert man von z/ zuerst alle Faktoren +p ab, so
bleibt nur eine der Zahlen 1, —4, -4—8, —8 übrig.
§ 85. Das erweiterte Legendre-Jacobische Symbol.
• / \
Das Legendresche Symbol j hat, wenn m eine be-
liebige positive oder negative von Null verschiedene Zahl, p eine
in m nicht auf gehende natürliche Primzahl ist, den Wert —|— 1,
wenn m quadratischer Rest, und den Wert — 1, wenn m quadra-
tischer Nichtrest von p ist (Bd. I, § 145).
Die Bedeutung des Symbols ist von Jacobi so erweitert
worden, daß für p auch eine zusammengesetzte Zahl gesetzt
werden kann. Wenn aber m eine Diskriminante ist, so empfiehlt
sich bisweilen eine noch weitergehende Verallgemeinerung, die
wir jetzt darlegen müssen ’).
l) Kroneeker, Berliner Sitzungsberichte, 30. Juli 1885. Dirichlet-
Dedekind, Vorlesungen über Zahlentheorie, 4. Aufl., § 186. H. Weber,
Göttinger Nachrichten, Januar 1893.
§ 85. Das erweiterte Legendre-Jacobische Symbol. 323
Wenn D eine Diskriminante und n eine ganze rationale Zahl
ist, so definieren wir ein Symbol (D, n) durch folgende Bestim-
mungen :
(1) (Z>, 0) = 0.
(2) (D, 1) = 1.
(3) (D,-l) = +l, D > 0.
= —.1, D < 0.
(4) (D,p) = 0,
wenn p ein Primteiler von D ist.
jü —i
(5) (D, 2) = (— 1) 8 , I) ungerade.
W p,ri = (y),
wenn p eine nicht in D aufgehende ungerade Primzahl ist.
Zerlegt man +n in seine Primfaktoren
n = + p, p', p", .-
so ist
(7) (D, n) = (D, ±1) (D, p) (D, p') (D, p") ...
Durch (1) bis (7) ist offenbar das Symbol (Z>, n) wider-
spruchslos für alle Zahlen n definiert, und kann nur einen der
Werte —1, 0, -|-1 haben. Es ist immer dann und nur dann
= 0, wenn D und n nicht relativ prim zueinander sind. Aus
(7) ergibt sich noch:
(8) (D, n) (D, n') = (D, nn'),
und wenn Q2 eine Quadratzahl ist, die mit n keinen gemeinsamen
Teiler hat,
(9) w) = (D, n).
Die auf das Reziprozitätsgesetz bezüglichen Formeln nehmen
in dieser Bezeichnungsweise eine besondere Form an. Wir be-
trachten zunächst die Primdiskriminanten.
Ist 1 (mo<l 4), so ist nach (3), (5), (6):
p— /—1\
(±P, -1) = (-1) i = (~),
(±P,2) = (-1) 8
(4-^, n). = (=^-\ = (—\
7 \ n / \pj
21*
324
Neunter Abschnitt.
§ 85.
wenn n eine ungerade Primzahl ist (nach dem Reziprozitätsgesetz
und seinen Ergänzungssätzen [Bd. I, § 145, 9.]), und diese Formeln
lassen sich zusammenfassen in
(10) (±P, w) = Q-
Diese Formel gilt aber wegen (7) für jedes beliebige n, das
durch p nicht teilbar ist.
In gleicher Weise findet ihan für ein ungerades n:
n — 1
(—4, n) = (—1)~
>r2—i
(H) (8, n) = (-1) 8 ,
n — 1 n2—1
(_8, n).= (-1)“ ~
Weiter ist allgemein, wenn D, D' zwei Diskriminanten sind:
(12) (D, ri) (D1, n) = {DD1, n).
Diese Formel gilt zunächst, wenn DD' und n nicht relativ
prim sind, weil dann beide Seiten — 0 sind. Sie gilt ferner
für n = — 1 [nach (3)], für n = 2 [nach (5) und der Kon-
1)2 1 D'2—i D^D^ 1
gruenz —5------1-----3— = -------5---- (mod 2)1 und für eine
o o o .
ungerade Primzahl n [nach (6)]. Also gilt sie wegen (7) all-
gemein.
Wir können nun das Reziprozitätsgesetz mit seinen Ergänzungs-
sätzen für Diskriminanten in folgender Weise zusammenfassen:
(13) (D, D') = +(D', D),
worin das obere Zeichen gilt, wenn von den beiden Dis-
kriminanten D, D' wenigstens eine positiv ist, das untere,
wenn beide negativ sind.
Um diese Formel aus der gewöhnlichen Form des Rezi-
prozitätsgesetzes abzuleiten, nehmen wir zunächst an, es gelten
die beiden Formeln:
(D, D'j = +(D', D),
(A,D') = +(D', A).
Dann folgt aus (8) und (12)
(DA, D') = +(D', DA),
worin wieder1 das untere Zeichen nur dann gilt, wenn D'
und D D. beide negativ sind. Durch nochmalige Anwendung
ergibt sich
(DA, D'Dl) = ±(D'Di, DD.)
§ 85. Das erweiterte Legendre-Jacobische Symbol. 325
und folglich ist die Formel (12) erwiesen, wenn sie für irgend
zwei Primdiskriminanten gilt.
Es ist aber nach (10), wennp und p' ungerade Primzahlen sind:
(±P, ±P') = ±(|-)’ = -(f-)’
worin rechts das negative Zeichen nur dann steht, wenn links
beide Zeichen negativ, also p sowohl als p' = 3 (mod 4) sind.
In diesem und nur in diesem Falle ist aber ( — ) = — (),
\PJ \P')
sonst ( —) = ( Also ergibt sich für diesen Fall die Formel
\p) \py
(13) als richtig.
Ferner ist nach (11) und (3), (5)
(—4, ±p) = +1, (+p, —4) - ±1,
(P, ±8) = (p, +2) = (p, 2) =
(±8,P) - (^-) = (-1) * ,
[p = 1 (mod 4)],
(-P, ±8) = (-p, ±2) = ±(-p, 2) = -1,
(+s.-i>) = ±(=^) = -i,
[p = 3 (mod 8)],
woraus für diese Fälle die Formel (13) folgt, die damit allgemein
erwiesen ist.
Aus (13) folgt weiter, da jede Quadratzahl eine positive Dis-
kriminante ist, falls m zu I) relativ prim ist,
(14) (D, »>’) = 1
und folglich nach (8):
(15) (D, m2n) = (D, n),
wenn m und D keinen gemeinschaftlichen Teiler haben.
Wir haben ferner den Satz:
(16) (-D, n) = (2>, n'),
wenn n = n (mod Z>).
Der Satz ist richtig, wenn n und D einen gemeinschaft-
lichen Teiler haben, und nach (12) ist er allgemein erwiesen,
wenn er für jede Primdiskriminante D gilt. Für diese ergibt er
sich aber sofort aus (10), (11).
326 Neunter Abschnitt. § 85.
Nehmen wir an, in (16) seien n, n' selbst Diskriminanten:
n = Du n' = D2, Dy = Z>2 (mod Z>),
so ist
(D, Z>,) = (Z>, Z»2)
und es folgt aus (13):
(D, A) = ±P>, 2>)
(D, D2) = ±(A, 2>),
worin die oberen Zeichen gelten, wenn D positiv ist, die unteren,
wenn D, Dx, D2 alle drei negativ sind, und verschiedene Zeichen,
wenn D negativ und Dlt D2 von verschiedenen Vorzeichen sind.
Es ist also nach (16):
(17) (A, -D) = ±(A, D),
worin das untere Zeichen nur dann gilt, wenn die beiden Zahlen
D und Dj D2 beide negativ sind.
Sind D^ D2 ungerade, so können wir D = 4 »i setzen, worin
m eine beliebige ganze Zahl ist, und wir erhalten aus (17)
(18) (D-i, m) = +(D2, m),
wenn
(19) Di - D2 (mod lm)
ist, und das untere Zeichen nur dann gilt, wenn m und
Di D2 beide negativ sind.
Dieser Satz ist zunächst bewiesen unter der Voraussetzung,
daß Di und D2 ungerade sind. Er gilt aber allgemein. Denn
die Kongruenz (19) verlangt zunächst, daß Di und D2 zugleich
gerade oder zugleich ungerade seien. Sind sie beide gerade und
ist dann m gerade, so ist (18) richtig, weil beide Seiten ver-
schwinden. Ist aber m ungerade, Dy, D2 gerade, so setze man
in (17) D = +»i = 1 (mod 4), worin m eine positive ungerade
Zahl ist. Dann folgt aus Di = D2 (mod Z>) die Kongruenz (19)
und nach (17) ist
(Di, m) = (Z)2, m),
(20) (Di, —m) — +(Z)2> — m),
(Di, -1) = +(D2, -1),
und folglich wieder
(Z>„ m) = (D2, m).
Also gilt diese Formel für jedes positive ungerade m, und
nach (20) ist dann (18) auch für ein negatives m erwiesen. Die
Formeln (16) und (18) können zur Berechnung des Symbols (D, n)
§ 85. Das erweiterte Legrende-Jacobische Symbol. 327
nach dem Algorithmus des größten gemeinschaftlichen Teilers
dienen. Denn man kann aus den Kongruenzen
D = D' (mod 4n),
n = n' (mod D'),
I)' = D" (mod 4n'),
n' = n" (mod D"),
die Reihe der Zahlen
Z>', 2 n', D", 2 n", ...
so bestimmen, daß jede folgende dem absoluten Werte nach kleiner
ist als die vorhergehende, solange keine der Zahlen n', n", ri", ...
gleich 4-1 geworden ist.
Ist D keine Quadratzahl, so läßt sich immer eine Zahl ß so
bestimmen, daß
(21) (D, ß) = — 1.
Ist nämlich zf der Stamm von D und ist ß relativ prim zu
D, so ist (nach 9)
(D, ß) = (4, ß).
Ist zf = &d' und ö eine Primdiskriminante, also relativ
prim zu zf, so kann man ß^ so annehmen, daß
(<WO) = -1
wird [nach (10) und (11)] und man kann ß aus den beiden
Kongruenzen
ß = ßo (mod S),
= 1 (mod zf')
bestimmen. Dann erhält man nach (12)
(D, ß) = (ö, ßQ) = -1.
Läßt man s ein volles Restsystem nach dem Modul I) durch-
laufen und setzt
S = 2?(D, s),
so folgt durch Multiplikation mit (_D, ß)
— 8 = X(D, ßs),
und da ßs zugleich mit s ein Restsystem durchläuft, so folgt
(22) 8=0.
Es folgt hieraus:
328 Neunter Abschnitt. § 86.
In einem vollständigen System inkongruenter, zu D teiler-
fremder Zahlen s gibt es ebensoviele Zahlen a, für die (P, a)
= 1 ist, wie Zahlen ß, für die (P, /3) = — 1 ist, und es ist
(P, n) — 4-1, wenn n = a , ,
= -!, , n = ß <m0<i P>'
§ 86. Die Gaussschen Summen.
Wir haben im ersten Bande die Gaussschen Summen aus
der Theorie der Kreisteilung kennen gelernt. Diese Ausdrücke
lassen sich verallgemeinern und nehmen durch Anwendung des
Symbols (2), n) eine einfache Gestalt an.
Es war [Bd. I, § 179, (16)], wenn n eine ungerade Primzahl,
s eine durch n nicht teilbare Zahl bedeutet und k ein Restsystem
nach dem Modul n durchläuft:
zl.\ . . /•«—!> 2 _
Setzen, wir + n = P = 1 (mod 4), so ist P eine Prim-
diskriminante, und es ist nach § 85, (10)
Q = (J, D, (t!) = (4 +S) = w S)
[letzteres nach § 85, (3), da die oberen Zeichen bei positiven, die
unteren.bei negativen P gelten], ferner:
A 2 ' \n = ]/P,
wenn ]/z/ positiv reell oder positiv imaginär ist, je nachdem n = 1
oder = 3 (mod 4) ist, und wir können (1) in der Form schreiben:
- -fr Zitiks _
W 2?(P, k)e ~ = (P, s)]/P,
wenn wir im Falle, wo P positiv ist, s durch —• s ersetzen. Diese
Formel ist zunächst nur für eine ungerade Primdiskriminante
erwiesen. Sie gilt aber auch, wie die direkte Rechnung zeigt, für
P = — 4, ' 8, — 8,
also für jede Primdiskriminante.
Setzen wir die Richtigkeit der Formel (2) für P = P',
P = P" voraus, so folgt, wenn P' und P" keinen gemeinschaft-
lichen Teiler haben, ihre Richtigkeit für P = P'P".
Es ist nämlich
(3) yp7 yp7' = +yp'p",
Die Gaussschen Summen.
329
§ 86.
wenn das obere Zeichen gilt, falls von den beiden Stammdiskrimi-
nanten z/, z/" wenigstens eine positiv ist, das untere, wenn beide
negativ sind.
Setzen wir
k = k'd" 4- k"d',
und lassen k', k" Restsysteme nach z/', d" durchlaufen, so durch-
läuft k ein Restsystem nach z7 == z/'z/".
Die Multiplikation der beiden Summen
(4) 2? (zf, k') e , S (d", k") e~
ergibt
Wk'f 2s rriTc
(5) S (d’, k') (d", k")
Es ist aber nach § 85, (16)
(zf, k) = (zf, z/") (zf, W),
(d", k) = (d", d') (d", k”),
und folglich nach § 85, (13)
(z/, 7c) = +(z/', 7c') (z/'', 7c"),
und demnach ergibt sich aus (3), (4) und (5) die allgemeine
Gültigkeit der Formel (2) für jede Stammdiskriminante d.
Zehnter Abschnitt.
Algebraische Zahlen und Formen.
§ 87. Ideale und Formen in algebraischen Körpern.
Das Interesse, das die Theorie der elliptischen Funktionen
für den Algebraiker hat, entspringt aus ihrer Anwendung auf
die Theorie der quadratischen Irrationalzahlen, zu denen sie in
einer analogen Beziehung stehen, wie die Einheitswurzeln zu den
rationalen Zahlen. Sie bieten uns das erste und bisher einzige
in seinen Gesetzen genauer bekannte Beispiel eines Gebietes
algebraischer Zahlen, die über die Kreisteilungszahlen hinaus-
gehen. Um die Theorie dieser Zahlen eingehender darstellen zu
können, müssen wir einige Sätze aus der Theorie der Formen
und algebraischen Körper und speziell der quadratischen Formen
vorausschicken.
In Bd. II, § 163, 169 hat sich ein Zusammenhang ergeben
zwischen den Idealen eines algebraischen Körpers £1 vom nten
Grade und gewissen homogenen Funktionen nten Grades von
n Variablen. Ehe wir dies auf quadratische Körper anwenden,
sei kurz an die allgemeinen Sätze erinnert.
Es sei a ein Ideal eines Körpers £1 und a,, a2, ..., aM eine
Basis dieses Ideals. Ferner sei to1, ra2, ..., <»„ eine Minimalbasis
von Sh. Dann ist
(1) («i, «s, «») = (M) (<»!, ra2, ..., ra„),
wenn (M) eine lineare Substitution mit ganzzahligen Koeffi-
zienten bedeutet. Um zu einer anderen Basis al, al, ..., a'n von a
überzugehen, mache man eine lineare Substitution L mit der
Determinante +1,
(2) (al, aä, ..., a;) — (E) (a„ a2, ..., a„),
woraus sich ergibt
(3) (al, a2, ..., «;,) = (L) (J.) (cq, ra, ..., ra„) >)•
’) Uber lineare Substitutionen und ihre Zusammensetzung vergleiche
man den sechsten Abschnitt des zweiten Bandes.
§ 87. Ideale und Formen in algebraischen Körpern. 331
Unter der Norm N(a) des Ideals a verstellt man den
absoluten Wert der Determinante A der Substitution (J.):
A --- 1 i tla, 2 • * • n ,
und nach (3) ist die Norm unabhängig von der Wahl der Basis.
1. Wir wollen die Basis (ar) positiv nennen, wenn
die Determinante A positiv, also der Norm von ci
gleich ist. Ist (ar) positiv, so ist («',) immer dann
positiv, wenn die Substitutionsdeterminante
L = -|-1 ist.
Man kann aus jeder Basis durch eine Substitution mit der
Determinante —1, also z. B. durch-Vertauschung zweier eine
positive Basis ableiten, und wir werden in der Folge meist nur
positive Basen verwenden.
Die in Bd. II, § 163, (3) bestimmte Basis ist positiv.
Bedeutet nun tt, t2, ..., tn ein System unabhängiger Vari-
ablen und
(4) A = 2Jartv
eine Basisform mit positiver Basis, so ergibt sich (Bd. II, § 164)
(5) W(A) = W(a)T,
worin
(6) 1 = Aj ~T~ #i.i #2,2 • • • tn,n
eine primitive ganzzahlige homogene Form nten Grades der
Variablen t„ ist. Die tr.s sind lineare Funktionen der tv.
Wendet man auf (4) die. Substitution (2) an, so ergibt sich
(7) Ä = r = Za;#',,
wenn
(8) (#1, #2, . •., #„) = L (ti, #2, • • •» tn)i
worin L' die transponierte Substitution von L ist, und wenn
(al) gleichfalls eine positive Basis ist, so hat L' die Determinante
-j-1 und die Formel (5) ergibt
(9) ' W) = W(a)T',
worin T' eine homogene Funktion nten Grades der Variablen #'
ist, die durch die Substitution (8) aus T hervorgeht.
Zwei Formen, die durch ganzzahlige lineare Substitution mit
der Determinante 1 auseinander hervorgehen, heißen äqui-
valent. Bisweilen werden die Formen auch dann äquivalent
genannt, wenn die Substitutionsdeterminante — 1 ist, dann aber
mit dem Zusatze „uneigentlich“. Es ist dann durch (8) bewiesen:
332 Zehnter Abschnitt. § 87.
2. Nennen wir die Form T die zu der Basis (av) von ci
gehörige Form, so sind die zu verschiedenen
positiven Basen desselben Ideals gehörigen
Formen äquivalent.
Bezeichnen wir die konjugierten Werte von ras mit
und setzen
(10) «s, ? ~~~ ,
so ergibt sich
(11) (2? + oq,i «2,2 ••• «w,»)2 = W(a)2z7,
wenn d die Grundzahl des Körpers &, nämlich das Determinanten-
quadrat:
Zf = (2? + 01,1 «2,2 ••• «H,»)2
ist (Bd. II, § 162).
Sind Zj, A2, ..., An die konjugierten Werte von A, so ist
nach (4)
(12) Ar = 2JaVirtv
eine lineare Substitution für die Variablen tv mit der Substitutions-
determinante
(13) r = N(a)
und durch diese geht nach (5) die Form T in das Produkt
(14) T' = [^(a)]-1^...^
über, weil W(A) das Produkt der konjugierten Werte von A ist
(Bd. II, § 151). Wir können hierauf die Invariantentheorie (Bd. I,
§ 65) anwenden, und wenn wir die Hessesche Determinante
bilden:
(15) a = i- + ..” AL...Al
— 0ii 8ii ct2 ot2 dtndtn'
so ist
(16) H' = r~2H.
Wenn wir aber H’ nach (14) in den Variablen A, bilden, und
beachten, daß eine n-reihige Determinante, in der die Diagonal-
glieder = 0 und alle anderen Glieder = 1 sind, den Wert
(— 1)M~1 (n — 1) hat!), so folgt:
*) Man kann diesen Satz leicht beweisen, wenn man die Determinante
durch Zufügung einer (n + l)ten Zeile und einer (n -j- l)ten Spalte
erweitert, bei der in der hinzugefügten Zeile nur Einer, in der Spalte mit
Ausnahme des letzten Elementes Nullen stehen.
§ 88. Idealklassen und Formenklassen. 333
H' = (-l)”"1^ — 1) N(a)-"(Ä1 Ä2... ÄH)”-2,
= (— — 1) _N(n)~2 T"-2
und folglich nach (13) und (16)
(17) H = (— l)*-1 (n — 1) Tn~2d.
§ 88. Idealklassen und Formenklassen.
Wir haben in Bd. II, § 170 die Äquivalenz der Ideale
und die Idealklassen erklärt. Danach waren zwei Ideale u, b
äquivalent. Wenn es eine ganze oder gebrochene Zahl des
Körpers ß gibt, die der Quotient von b und u ist, also:
(1) V o = b,
und es hat sich gezeigt, daß danach die Ideale in Klassen ein-
geteilt werden, und daß die Zahl dieser Klassen endlich
ist. In manchen Fällen ist es zweckmäßig, den Äquivalenzbegriff
etwas enger zu fassen und a und b nur dann äquivalent zu
nennen, wenn es eine der Bedingung (1) genügende Zahl q mit
positiver Norm gibt. Dieser Unterschied kommt natürlich
nicht in Betracht, wenn die Normen aller Zahlen positiv sind,
wie z. B. im imaginären quadratischen Körper. Äuch dann kommt
er nicht in Betracht, wenn es Einheiten mit der Norm —1
gibt, weil, wenn s eine solche Einheit ist, entweder NQj) oder
N(si]) positiv ist und s und st; gleichzeitig der Bedingung (1)
genügen.
Gibt es aber keine Einheiten, deren Norm = — 1 ist, wohl
aber andere Zahlen in ß mit negativer Norm, so teilt sich bei
der engeren Definition der Äquivalenz jede Idealklasse noch ein-
mal in zwei Klassen. Wir wollen hier den engeren Äquivalenz-
begriff festhalten, der z. B. bei manchen reellen quadratischen
Körpern in Kraft tritt1).
In (1) kann q gebrochen sein. Ist aber a eine durch u teil-
bare ganze Zahl, so ist 77 eine durch b teilbare ganze Zahl,
und daraus ergibt sich: Wenn
(2) (oq, a2, ..., an)
eine Basis von u ist, so ist
(ßl, ßa, •••> ß») = («1 V, 'M, ..., an1])
eine Basis von b, und wenn die erste Basis positiv ist, so ist es
(bei dem engeren Äquivalenzbegriff) auch die zweite.
') Wenn nämlich die P ellsche Gleichung t2—Dus = — 4 keine Lösung hat.
334 Zehnter Abschnitt. § 88.
Denn die notwendige und hinreichende Bedingung, daß (2)
Basis von a sei, besteht darin, daß jede durch a teilbare ganze
Zahl a und nur solche in der Form:
(3) a = xt oq 4- a:2 a2 + • • • + X„ an
mit ganzzahligen xt, x2, ..., xn enthalten ist. Folglich sind alle
Zahlen
(4) ß = x1a1i] x2a2ri -j---------j- xnani]
durch b teilbar. Ist umgekehrt ß eine durch b teilbare ganze
Zahl, so ist ß/q durch d teilbar und folglich in der Form (3)
darstellbar. Mithin ist ß durch (4) darstellbar.
Ferner ist nach der Bezeichnung von (9) und (10), § 87,
wenn a eine positive Basis ist:
2 *^1,1 w2, 2 N (o) E ®1,1 <«>2,2 ••• <*>»,«,
E i. $1,1 2 ßn,n ----- -N(iy) ± ®^1,1 *^2,2
= N(y) N(a) 2 + rai)1 <»2,2 ... ®n,„,
= +JV(b) 2? + <»2,2
und da nach (1)
(5) N(&) = N(y) N(a)
ist, so muß bei + N(b) das positive Zeichen stehen.
Ist Ä eine Basisform von a, so ist i; Ä eine Basisform von
b, und
!V(A) = N(a)T,
w = N(K)T,
und zu den beiden Idealen u, b gehört also dieselbe Form T.
Vereinigen wir äquivalente Formen T in eine Klasse, so können
wir nach 2. sagen:
3. Zu jeder Idealklasse gehört eine bestimmte
Formenklasse.
Bei der Beantwortung der Frage, ob zu einer und derselben
Formenklasse verschiedene Idealklassen gehören können, machen
wir die Voraussetzung, daß & ein Normalkörper sei: Nehmen wir
also an, zu zwei Idealen a und a' gehören äquivalente Formen T
und T', so ist, wenn Ä eine Basisform von a ist,
(7) IV(Ä) = N(a)T,
und wenn wir T' durch eine lineare Substitution in T überführen,
und unter Ä' eine Basisform von a' (mit denselben Variablen t
wie Ä) verstehen, so ist
(8) N(Ä') = N(a') T.
§ 89. Komposition der Formen und Multiplikation der Ideale. 335
Die linearen Faktoren von N(K) und W(Ä') müssen also, von
einem konstanten Faktor abgesehen, miteinander übereinstimmen,
weil man eine ganze Funktion beliebiger Variablen nur auf eine
Weise in irreducible (hier lineare) Faktoren zerlegen kann (Bd. I,
§ 20, Bd. II, § 152), und da alle diese Faktoren demselben
Körper ß angehören, so gibt es unter den konjugierten Faktoren I'
einen, der der Bedingung genügt:
A = q V,
worin t] eine Zahl in ß ist. Die Funktionale Ä und Z' und dem-
nach die entsprechenden Ideale sind also äquivalent.
4. Gehört in einem Normalkörper zu den zwei
Idealen a und a' dieselbe Formenklasse, so gibt
es unter den mit a' konjugierten Idealen eines,
das mit u äquivalent ist.
§ 89. Komposition der Formen und Multiplikation der Ideale.
Es seien jetzt o und b zwei Ideale in ß und
(1) c = ob
das aus beiden gebildete Produkt. Es seien ferner
Q --- (oq, ’ *1 ^n)i
(2) b = (/?!, ßzi • • -1 ßn),
C = (Zl, Y* • •, Yn)
Basen dieser Ideale. Da jede Zahl ahßk zu c gehört, so gibt
es ein System ganzer ratioualer Zahlen c^, so daß
(3) ßk --
wird, und da jede Zahl in t durch Multiplikation je einer Zahl
aus a und aus b und Addition dieser Produkte entsteht (Bd. II,
§ 169), so ist auch umgekehrt
h k
(4) Ys — ßk ,
worin die gleichfalls ganze rationale Zahlen sind.
Setzt man (3) in (4) ein, so folgt
r h,Tc
(5) 2?
und daraus
h k
(6) . =
worin
(r, r) = 1, (r, s) = 0, r # s.
336 Zehnter Abschnitt. § 89.
Bezeichnen wir also mit xr Variable und setzen
T
(7) £ Xr —•- Hhfr
so folgt:
h, k
(8) xs — 2 yh> k.
Jetzt bedeuten ur, vr, tr drei Systeme von Variablen und
[t — ccr Ur-,
(9) v — Sßrvr,
Z = £yrtr
Basisformen von u, b, c, ferner U, F, T die zu u, b, c gehörigen
Formen, in den Variablen u, v, t geschrieben. Es ist dann
N(p) = N(d)U,
(10) N(v) = N(b) V,
N(k) = N(c)T.
Es ergibt sich also aus (3) durch Multiplikation mit uhvk
und Summation nach (9):
r Ä, &
(11) . [IV = 2yr2 c^'-kUh-Vk,
also, wenn man
h k
(12) . tr = S C$UhVk
setzt:
(13) fi v — Z,
und daraus, da W(a)W(b) = W(c), ist nach (10)
(14) T = UV.
Darin sind aber die tr nicht mehr unabhängige Variable,
sondern sie gehen durch die bilineare Substitution (12) aus
«a, Vk hervor.
5. Die Form T geht durch die bilineare Substitution
(12) in das Produkt der beiden Formen U, V über.
Diese Substitution hat aber noch eine wesentliche Eigen-
tümlichkeit. Wir nennen die durch (12) bestimmten Funktionen tr
nach einem Primzahlmodul p linear unabhängig, wenn
aus der Kongruenz
(15) xrtr = 0 (mod p),
in dem die xr ganze rationale Zahlen sind, folgt, daß diese
Zahlen alle durch p teilbar sind. Findet dies für jede beliebige
Primzahl p statt, so heißen die tr schlechthin linear unab-
hängig.
§ 89. Komposition der Formen und Multiplikation der Ideale. 337
Die Kongruenz (15) ist nach (12) und (7) gleichbedeutend
mit den n2-Kongruenzen
yh,k — = o (rnodp)
und aus (6) folgt alsdann:
xs = 0 (mod p),
und dies besagt, daß die Substitutionen (17) für jeden Modul p
linear’ unabhängig sind.
Nach Gauss (I)isq. aritm. art. 235) heißt eine Form T
aus den beiden Formen V, V komponiert oder zusammen-
gesetzt, wenn T durch eine bilineare Substitution für
die Variable t, deren Gleichungen für jeden Modul linear
unabhängig sind, in das Produkt U V übergeht.
Danach haben wir den Satz:
6. Die Form, die zu dem Produkt zweier Ideale u, b
gehört, ist aus den Formen der Ideale n und b
komponiert1).
*) Die Sätze, die Gauss an der erwähnten Stelle durch sehr weitläufige
Rechnung für binäre quadratische Formen beweist, sind hier in größter
Allgemeinheit durch einfache Betrachtungen abgeleitet. Vgl. Dirichlet-
Dedekind, Vorlesungen über Zahlentheorie, § 182. Für binäre quadratische
Formen: Dedekind, Grelles Journal, Bd. 129; H. Weber, Göttinger Nach-
richten 1907.
Weber, Algebra. III.
22
Elfter Abschnitt.
Ideale in quadratischen Körpern.
§ 90. Diskriminante des quadratischen Körpers.
Ein quadratischer Körper entsteht, wenn_ man dem Körper
der rationalen Zahlen eine Quadratwurzel \d adjungiert, hier
kann d als ganze Zahl ohne quadratischen Teiler an-
genommen werden. Der Körper ist reell oder imaginär, je nach-
dem d positiv oder negativ ist. Bezeichnet man den Körper der
rationalen Zahlen, den absoluten Rationalitätsbereich, mit 91 und
mit 3t (x, x',...) den Körper, der durch Adjunktion von x, x', ...
zu 3i entsteht, so ist der quadratische Körper ß so zu bezeichnen:
(1) ß = 31 (fd).
Jede Zahl des Körpers ß kann in die Form gesetzt werden:
... x + y
(2) ® ,
worin x, y rationale ganze oder’ gebrochene Zahlen sind.
Die zu <a konjugierte Zahl
... •, x — y ^d
(3) ® i
ist gleichfalls in dem Körper ß enthalten, und folglich ist ß ein
Normalkörper.
Damit <a eine ganze Zahl sei, ist notwendig, daß
a> a>' = x, (<» — <»')2 ~ y2 d
ganze rationale Zahlen sind, und da d keinen quadratischen Teiler
haben soll, so müssen x und y ganze Zahlen sein. Damit aber*
auch a wirklich eine ganze Zahl sei, muß auch noch die Norm
1/i (^2 — y2 eine ganze rationale Zahl sein, d. h. es muß
(4) x2 —• y2d = 0 (mod 4)
sein. Ist d = 2 oder = 3 (mod 4), so kann diese Bedingung
nur erfüllt sein, wenn x und y gerade Zahlen sind, und wenn
wir also x, y durch 2 a?, ersetzen, folgt:
§ 80.
Diskriminante des quadratischen Körpers.
339
1. Ist d = 2, 3 (mod 4), so sind alle und nur die
Zahlen des Körpers ß ganz, die in der Form
x + y
mit ganzem rationalen x, y enthalten sind.
Ist aber d ~ 1 (mod 4), so ist (3) befriedigt, wenn x und y
beide gerade oder beide ungerade sind, also wenn x die Form
2 x-l — y hat. Ersetzt man dann wieder xL durch x, so folgt:
2. Ist d = 1 (mod 4), so sind alle und nur die Zahlen
in ß ganz, die in der Form
। — 1 -1- \d
% + y-------
mit ganzen rationalen x, y enthalten sind. __
Es ist also im Falle 1. (1, ]/d), im Falle 2. ^1, —*
eine Minimalbasis des Körpers ß. Die Grundzahl oder Dis-
kriminante des Körpers ß ist also im Falle 1.:
1, 2
(5) = i, — yj — 4d,
im Falle 2.:
i, ~1 + \d 2
(6) 4 = 2 - d.
1 -1- y^
11 2
In beiden Fällen kann man also die ganze Zahl <a in die
Form setzen: _
zr-x x 4- y^zl
mit der Bedingung, daß
(8) 4=N(a>) = x2 — Jy2 = 0 (mod 4)
sek
Die beiden Formen der Minimalbasis, die wir erhalten haben,
nämlich (1, ^~d) und ^1, —~-7^—sind also:
(9) (1, 0) = (1, z/ = 0,
= (!,-' + V^).
Hierin kann das Vorzeichen von in beliebiger Weise be-
stimmt werden, soll aber dann in derselben Betrachtung fest-
gehalten werden. Wir wollen ein für allemal annehmen:
22*
340 Elfter Abschnitt. § 91.
3. Wenn z/ positiv ist, soll gleichfalls positiv
sein, und wenn zf negativ ist, soll —z|/z/ positiv, oder
)/z/ positiv imaginär sein.
Aus (1), (2) ergibt sich noch:
4. Die Grundzahl eines quadratischen Körpers ist
immer = 0 oder = 1 nach dem Modul 4 und hat, außer 4,
keinen quadratischen Teiler. Sie ist also Diskriminante
und zwar Stammdiskriminante.
§ 91. Ideale und Formen in quadratischen Körpern.
Ist a ein Ideal des quadratischen Körpers ß, oq, eine
positive Basis, und
(1) ä — ©6, f, —|— oq f2
eine Basisform von o, so ist
(2) N (Ä) = (oq t1 —|- cq 12) (cq i, -|- cc2 i2) = IV(ci) T,
und W(a) ist der größte gemeinschaftliche Teiler der’ drei ganzen
rationalen Zahlen
06, 06,, 06, Ö62 ~|— Ö62 06,, 062 062.
Setzen wir also
cq a'i = aN(a),
(3) oqa2 062 06, = bN(a),
a2 062 = cN(a),
so ist
(4) T — at? btxt2 -f- c f22
die zur Basis oq, 062 gehörige Form. Wir bezeichnen sie, wenn
es auf die Bezeichnung der Variablen nicht ankommt, mit
(5) <p = (a, b, c).
Es ist eine primitive .quadratische Form, deren Diskriminante
(6) z/ = &2 — 4 a c
gleich der Grundzahl des Körpers ß ist (§ 87). Um die Basis
oq, cq nach Bd. II, § 163 zu bilden, suche man zunächst die kleinste
durch a teilbare natürliche Zahl a,, und hierauf die kleinste
natürliche Zahl a,2, für die sich eine rationale, der Bedingung
(7) <q2 -j- «22 ö = 0 (mod o)
genügende Zahl <q2 bestimmen läßt. Da die Kongruenz (7) für
a22 = a„ befriedigt werden kann, nämlich durch «12 = 0, so
§ 91. Ideale und Formen in quadratischen Körpern. 341
folgt, daß «ii durch a22 teilbar ist, und wir setzen »n — a22 a.
Dann haben wir die Basis von n:
(g) oq — a22a,
«2 — a12 “p a22 6.
Es ist dann nach Bd. II, § 164, (12):
(9) W(a) = a22a,
und wenn wir für (1, Ö) die Basis § 90, (9) nehmen, so ist
Ö —|— 6' = 0 oder = — 1,
(10) n z„ i . , 1 — Z/
7 O = — |z/ oder = —-------------
4 4
Je nachdem z/ = 0, oder = 1 (mod 4) ist, und
(Ö — 0')2 = z/.
Es wird dann in diesen beiden Fällen, wenn man (8) in (3)
substituiert und (9) berücksichtigt:
a22& = 2a12 oder = 2a12 —• a22,
und folglich in beiden Fällen:
(11) «1 = «22«, «2 = «22 ----,
und die Form
T = (a, &, c)
hat hier einen positiven ersten Koeffizienten.
Setzen wir
«2 _____________________________ +
ocj 2a’
so ist co Wurzel der quadratischen Gleichung:
(13) a <»2 -|- b m c = 0
und
(14) A = a22 a (x — coy)
ist ein dem Ideal n entsprechendes Funktional und zugleich eine
Basisform von a. a ist die kleinste positive ganze Zahl, für die
am eine ganze Zahl wird.
Die notwendige und hinreichende Bedingung dafür, daß zwei
ganze Zahlen a2, a2 des Körpers ß die Basis eines Ideals bilden,
besteht darin, daß zunächst oq, os2 eine Basis des Körpers ß ist,
und daß, wenn ron m2 eine Minimalbasis dieses Körpers ist,
cq cot, a2 ß>i, cq m2, cq co2
durch die Linearform
A = oq ty —oc2 t2
342 Elfter Abschnitt. § 92.
mit ganzzahligen i2 darstellbar sind (Bd. II, § 163, 164). Denn
dann ist, wenn a durch A darstellbar ist, auch jedes Produkt a>a
durch Ä darstellbar. Für unseren Fall reduziert sich diese Be-
dingung darauf, daß oq fl, a2 0 durch Ä darstellbar sein müssen. Ist
aber (a, b. c) irgend eine quadratische Form der Diskriminanten z/
mit positivem ersten Koeffizienten a, so können wir für 0 auch
| (b -|- |/z/) nehmen und da
ist, so ist (11) immer die Basis eines Ideals in ß. Dabei kann
die positive Zahl a22 willkürlich angenommen werden. Setzen wir
a22 — 1, so ist
(15) l = a (x — ay)
Basisform eines durch («, b, c) völlig bestimmten Ideals et, dessen
Norm gleich a ist, und eine Basis dieses Ideals ist
(16) (er, aco).
§ 92. Primideale im quadratischen Körper.
Eine Primzahl p ist im quadratischen Körper ß entweder
selbst noch unzerlegbar und ist dann ein Primideal zweiten
Grades oder es zerfällt p in zwei Primideale ersten Grades p, p'.
Wir haben hiernach zwei Fälle zu unterscheiden:
a) p — p in ß unzerlegbar: JV(p) = p2,
b) p = pp' Nty) — W(p') = p,
und im letzten Falle können die beiden Primideale p, p' entweder*
voneinander verschieden oder auch gleich sein, so daß wir noch
einen dritten Fall unterscheiden können:
c) p = p2, N(p) = p.
Es handelt sich nun darum, die Bedingungen zu ermitteln,
unter denen der eine oder der andere dieser Fälle eintritt.
Wenn W(p) = p ist, so ist p die Anzahl der inkongruenten
Zahlen (mod p) in ß und folglich ist in diesem Fall jede Zahl
in ß einer der rationalen Zahlen r:
(1) 0, 1, 2, ...,p — 1
kongruent.
/ Ist dagegen W(p) = p2, so gibt es auch Zahlen, die nach p
nicht mit einer rationalen Zahl kongruent sind.
§ 92. Primideale im quadratischen Körper. 343
Wenn aber (1, 0) eine Basis von ß ist und, um beide Fälle
von § 90, (9) zu umfassen, -
P)
angenommen wird, so ist im Falle a)
6 nicht kongruent mit einer Zahl r,
im Falle b) oder c)
0 = r (mod p),
wenn man also —x = 2r 4~ setzt, so folgt: .
1. Die notwendige und hinreichende Bedingung für
das Eintreten eines der Fälle b), c) ist die, daß es
eine rationale ganze Zahl gibt, die mit zf zugleich
gerade oder ungerade ist, für die
(3) = o (mod p).
Ist p' das mit p konjugierte Ideal, so ist
(4) ~X — 0 (mod P')’
und daraus folgt
(5) a?2 = zf (mod 4 p).
Ist umgekehrt die Kongruenz (5) durch x = r befriedigt, so ist
r 4- V zf —r -4- .
---------y == 0 (mod p),
und folglich genügt entweder x = r oder x = — r der Be-
dingung (3).
Die beiden Ideale p, p' werden daun miteinander identisch
sein, wenu_die beiden Zahlen (3) und (4) und folglich auch ihre
Summe V zf durch p und mithin z/ durch p teilbar ist. Dann ist
x = 0 oder x = p (mod 2p) die einzige Wurzel von (5).
Wir haben also das Resultat:
2. Der Primfaktor p der natürlichen Primzahl p ist
vom zweiten Grad, wenn die Kongruenz (5) keine
Lösung hat, vom ersten Grad, wenn (5) eine Lösung
hat, und p ist das Quadrat von p, wenn (5) nur
eine Lösung hat, wenn also p in zf aufgeht.
Das letztere ist in Übereinstimmung mit dem allgemeinen
Satze Bd. II, § 174.
344
Elfter Abschnitt.
§ 93.
Mit Benutzung des Symbols (zf, p), das wir in § 85 ein-
geführt haben, können wir diesen Sätzen auch die Form geben:
3. Ist (z/, p) — —1, so ist p unzerlegbar in £1.
„ (4.p) = 4-1, so zerfällt p in zwei verschie-
dene konjugierte Primideale.
„ (z7, p) = 0, so ist p das Quadrat eines Prim-
ideals.
§ 93. Darstellung von Zahlen als Idealnormen.
Eine Primzahl p ist nur dann die Norm eines Ideals, wenn
(z/, p) = 1 oder = 0 ist, nicht aber, wenn (z/, p) = — 1 ist.
Im letzten Falle ist erst p2 eine Norm, nämlich die von p. Im
allgemeinen kann eine positive ganze rationale Zahl m auf mehr-
fache Art als Norm dargestellt werden. Wir wollen die Anzahl
dieser Darstellungen für den Augenblick mit t[> (m) bezeichnen
uud näher bestimmen.
Wir nehmen zunächst m als Primzahlpotenz p* an. Ist dann
(zf, p) = 1 und p = . p p', so kann man pF in folgender Weise
darstellen:
(1) p^ = N^), W^p'), W(p*-2p'2), ..., W(p*),
und es ist daher
(2) (z/,p) = 4-1: ^(p4 = + 1.
Ist aber (z/,p) = — 1, so ist, wenn k gerade ist, p1: — .^(p’/s*),
wenn k ungerade ist, p nicht als Norm darstellbar. Es ist also
(3) (zf, p) — — 1: i/> (pZl) = 0 oder = 1,
je nachdem k ungerade oder gerade ist.
Ist endlich (zf, p) = 0, also p in z/ enthalten, so ist p = p2
und pk = N (ps); also:
(4) (zf, p) = 0: ,4>(pk') = 1.
Man kann diese drei Fälle in eine Formel zusammenfassen:
Die Zahl p* hat nämlich die folgenden k -f- 1 Teiler:
(5) 1, p, p2, ..., pk.
Und daher geben die Formeln (2), (3), (4), wenn m = p* ist,
und n die Teiler von m durchläuft,
(6) (ni) = 2j (zf, w).
§ 94. ‘ Das quadratische Reziprozitätsgesetz. 345
Dieser Ausdruck gilt aber allgemein. Denn sind »q und m2
relativ prim und ist
mi — ^(ntj), m2 = W(m2),
so ist
m = nii m2 = N (wr m2).
Man kann also aus einer Darstellung von nq, m2 als Normen
eine Darstellung von m als Norm ableiten.
Ist umgekehrt
m1m2 -= JV(ni) = mm',
wo m, m' konjugierte Ideale sind, so muß, wenn niy und m durch
ein Primideäl p teilbar sind, Wj auch durch p p' teilbar sein, also
ist auch »«! = JV(nii) und ebenso m2 = Nfm^.
Demnach gilt, wenn »Mj und m2 relativ prim sind:
(7) V» ('m,) V» (»?,) = ri m2).
Andererseits ist, wenn «j und n2 die Teiler von und m2
durchlaufen,
S (z/, «i) 27 (z/, «2) = 27 (zf, nt),
und damit ist die Formel (6) allgemein nachgewiesen.. Wir
sprechen dies als Satz aus:
4. Eine natürliche Zahl m kann in dem quadratischen
Körper ß mit der Grundzahl zf auf
27 (zf, n)
verschiedene Arten als Norm eines Ideals dar-
gestellt werden, wenn n die sämtlichen Teiler
von m durchläuft.
§ 94. Das quadratische Reziprozitätsgesetz.
Aus der Zerlegung der Primzahlen im quadratischen Körper
leitet Dedekind einen neuen Beweis des Reziprozitätsgesetzes
der quadratischen Reste her1).
Nach Bd. II, § 167, 3. ist die notwendige und hinreichende
Bedingung dafür, daß das in der Primzahl p aufgehende Prim-
ideal p (in irgend einem Körper ß) vom ersten Grade sei, die,
daß für jede ganze Zahl <a des Körpers ß
(1) <aP = ca (mod p),
’) Dirichlet-Dedekind, Zahlentheorie, 4. Aufl. (S. 636, Anm.).
346 Elfter Abschnitt. § 94.
und dies reduziert sich in unserem Falle des quadratischen
Körpers darauf, daß
(2) 0? = 0 (mod p)
sein muß.
Nehmen wir zf = — 4, so ist 0 = i = |/—1 und die Kon-
gruenz (2) wird
= 1 (mod p).
Da nun (1 i) (1 — i) = 2, also weder 2 noch (1 + i) für
ein ungerades p durch p teilbar sein kann, so muß = 1,
also p — 1 durch 4 teilbar sein.
Demnach folgt aus § 92, 2.:
1) Die Kongruenz
x2 = —4 (mod 4 p),
oder, was dasselbe ist,
xr‘ = — 1 (mod p)
hat dann und nur dann Lösungen, wenn p = 1 (mod 4) ist.
Nehmen wir zweitens z/ = 8, so ist 0 = ^2, oder, wenn
r = |/7 eine 8te Einheitswurzel ist,
0 = r \
und die Bedingung (2) läßt sich nach dem binomischen Satze
so darstellen:
r'p r~P = r r^1 (mod p).
Dies fordert:
(tp — (rp — r— i'j r—p = q (mod p),
also:
rp = r oder r? = (mod p),
p±i
rp±1 = 1, i 2 — 1=0 (mod p),
und daraus folgt wie oben für ein ungerades p:
p = +1 (mod 8).
2) Die Kongruenz
.-r2 = 2 (mod p)
ist also dann und nur dann lösbar, wenn p = 1 oder
p = — 1 (mod 8) ist.
Endlich setzen wir, wenn q eine ungerade Primzahl ist,
(3) . . zf = ±q
§ 95. Äquivalente Formen und Ideale im quadratischen Körper. 347
und bestimmen das Vorzeichen so, daß + q = 1 (mod 4) wird.
Es ist in diesem Falle
n - 1 + ffi
2
und diesen Ausdruck können wir durch </te Einheitswurzeln dar-
stellen. Es bedeute r eine imaginäre </te Einheitswurzel und es
durchlaufe a 'die quadratischen Reste, b die Nichtreste von q.
Wir setzen, wie in Bd. I, § 179
(4) A = B = Sro
und haben nach den dortigen Formeln (3), die ohne Benutzung
des Reziprozitätsgesetzes abgeleitet sind:
(5) 0 = A, 6' = B.
Das Vorzeichen von (/Jz 1 hängt von der Wahl von r ab,
kommt aber hier nicht in Betracht. Nun ist nach dem poly-
nomischen Lehrsatz:
= zrt>a, B» = 2rPb,
also
A# = A, B’p = B, wenn 1,
und
Ap = B, Bp = A, wenn (~\ = — 1.
W
Da A nicht kongruent B ist, wenn p von q verschieden ist,
so folgt hieraus und aus 2. des vorigen Paragraphen:
3) Die Kongruenz
.r2 = +q (mod p)
hat dann und nur dann Lösungen, wenn p quadratischer
Rest von q ist.
Und dies ist das Reziprozitätsgesetz mit seinen Ergänzungs-
sätzen.
‘ § 95. Äquivalente Formen und Ideale im quadratischen Körper.
Wenn die beiden Ideale [§ 91, (16)]
(1) a = (a, ata), a' = (a', a'co')
äquivalent sind, so gibt es eine (ganze oder nicht: ganze) Zahl y
in ß, für die pa1 = a ist, und diese Zahl p ist durch die Ideale
(i, a' selbst bis auf einen Faktor, der eine numerische Einheit
ja, —y j 1, co
j —ß, d I 1, Bq
348 Elfter Abschnitt. § 95.
ist, bestimmt. Es muß also vier ganze rationale Zahlen
a, ß, 7, ö geben, die der Bedingung
t] a' — a(a — y co),
' t] a' co' = a (— ß -|- ö o)
genügen. Bezeichnen wir für den Augenblick mit t]„ cat, co', die
zu t], co, co' konjugierten Zahlen, so ist hiernach
also:
a'2 7] tj, (co' — ’co’i) = a2(ad — ßy) (co — co,),
und da nach § 91, (12):
a (co — Wj) = a' (co' — raj) = —
ist, so folgt hieraus, wenn
£ = ad — ßy
gesetzt wird,
(3) a £ = a’ t] t], •,
wenn also, wie wir schon angenommen haben, «und a' positiv
sind und (nach dem verschärften Äquivalenzbegriff) i]7], positiv
ist, so ist auch £ positiv.
Vertauschen wir aber a mit a', so geht tj in l:iy über und
£ mag in übergehen. Demnach folgt auch
(4) a' e' —
7] Tj,
und folglich ee’ = 1. Da aber s und «' positive ganze rationale
Zahlen sind, so folgt hieraus c = e’ = 1. Also nach (2)
, — ß — d co aco ß
G) -- ”, G) -------------- f . T. ,
oc — yG) y G) + 0
ad — ßy = 1.
Nun sind co und co' die Wurzeln der beiden Formen
(a, b, c), (a', b', c') [§ 91, (13)],
durch (5) ist die Äquivalenz dieser Formen ausgedrückt,
haben daher, übereinstimmend mit der allgemeinen Theorie
(§ 88) den Satz:
5. Die zu äquivalenten Idealen gehörigen quadra-
tischen Formen sind äquivalent.
Man erkennt hieraus die Bedeutung des verschärften Äqui-
valenzbegriffes: Wollte man nämlich auch negative Werte von
N(y) zulassen, so könnten auch £ = — 1 und die entsprechenden
Formen uneigentlich äquivalent sein.
und
Wir
§ 95. Äquivalente Formen und Ideale im quadratischen Körper. 349
Es seien nun umgekehrt <p — (a, b, c), <p' = (a', b', c') zwei
äquivalente Formen mit positiven ersten Koeffizienten
a, a', und .
/p'. __ b + „/ __ 4-
(6) m ---------<n ------------------•
Dann gibt es eine lineare Substitution Q’ mit der Determi-
nante —1, durch die (a, d, c) in (a', b', c') übergeht.
Es ist dann
a' = a a2 b a y -|- c y2,
(7) b' — 2 a u ß b (a d 4- ß y) -|- c y d,
c' = a ß- b ß d -f- c d2,
a co' 4- ß d co — ß
(8) co = -------- । co' =-----------p— ,
v J y co -f- o — yco-f-a
und eine kleine Rechnung zeigt, daß co und co' entsprechende
Wurzeln, d. h. Wurzeln mit dem gleichen Vorzeichen von sind.
Demnach erhalten wir für die zu <p und cp1 gehörigen Ideale
(i, a' zwei Basisformen:
2 = a(x — coy),
2' — a' (x' — co'y'),
und nach (8) ist
_ q [(d a? — 1/) 4~ (y a? — ay) <o']
y cn' 4~ d
Setzt man also
x' = d x — ßy, y' = —• y x 4- « y-,
so folgt
j — a 2'
~ a'(ym'+d) ’
da a: a' (y co' 4- d) eine Zahl in ß ist, so folgt, daß a und a'
äquivalent sind.
Wir haben also wieder in Übereinstimmung mit dem all-
gemeinen Satz § 88, 4. und zugleich in näherer Bestimmung:
6. Sind (q, b, c) (a', b', c') zwei äquivalente Formen
mit positiven ersten Koeffizienten, und sind co, co'
entsprechende Wurzeln dieser Formen, so sind
die Ideale (a, aco) und (a', a' co') äquivalent.
Bei negativer Diskriminante haben die ersten Koeffizienten
äquivalenter Formen immer dasselbe Vorzeichen, und man berück-
sichtigt nur die Formen, in denen dieses Vorzeichen positiv ist.
350
Elfter Abschnitt.
§ 95.
Bei positiver Diskriminante gibt es in jeder Formklasse Formen
mit positiven ersten Koeffizienten, und daher entsprechen sich
Formenklassen und Idealklassen in eindeutiger Weise.
Eine Basis des Hauptideals 17 ist (17, r] 0) und
0 = 02 = T’ A = 0
Sind or, y ganze rationale Zahlen und
t] — x y6,
so ist diese Basis in den beiden Fällen:
(tZj, a2) = (x yOi —£ -|- 0
= (x-{-y0, y + (x — y) ö)
und die Substitutionsdeterminante A [§ 87, (1)] ist
^2—j«/2, ^2 —+
Die Basis (an a2) ist also positiv, wenn die Norm von q positiv
ist (sonst müßte «, mit a2 vertauscht werden). Aus der Basisform
A = tz2 f2 — ij (fj -j- 0 f2)
erhält man
N(k) = N(ri) T,
und danach wird T die Hauptform
(S>) (‘-“’t)’
Wäre N(yi) negativ, so würde man für T die Formen
erhalten haben, und diese sind mit (9) nur dann äquivalent, wenn
die Feilsche Gleichung f2 — z/m2 — —4 lösbar ist.
Zwölfter Abschnitt.
Ordnungen im quadratischen Körper1).
§ 96. Diskriminanten der Ordnungen.
1. Definition. Ist Q eine natürliche Zahl, so heißt
die Gesamtheit der ganzen Zahlen des quadrati-
schen Körpers ß, die nach dem Modul Q mit
einer rationalen Zahl kongruent sind, eine Ord-
nung, und Q heißt der Führer dieser Ordnung.
Die Ordnung mit dem Führer Q wird mit [()] bezeichnet.
Es ergibt sich aus dieser Definition:
1. Alle rationalen ganzen Zahlen gehören jeder Ord-
nung an;
2. Summe, Differenz und Produkt zweier Zahlen der
Ordnung gehören derselben Ordnung an;
d. h. man kann innerhalb der Ordnung Addition, Subtraktion
und Multiplikation unbedingt ausführen, nicht aber allgemein
die Division.
Die Gesamtheit aller ganzen Zahlen des Körpers ß bilde
gleichfalls eine Ordnung (vom Führer 1), die Hauptordnung,
die also’ mit [1] zu bezeichnen wäre.
') Dedekind hat den Ausdruck Ordnung in der allgemeinen Theorie
der algebraischen Zahlen eingeführt, weil sie in dem besonderen Fall des
quadratischen Körpers den Gauss sehen Ordnungen der quadratischen Formen
entsprechen. Hilbert gebraucht dafür den Ausdruck „King“ oder- „Zahl-
ring“. Vgl. Dirichlet-Dedekind, Vorlesungen über Zahlentheorie (§ 172
der dritten, § 170 der vierten Auflage). Dedekind: Übel- die Anzahl der
Idealklassen in den verschiedenen Ordnungen eines endlichen Körpers, Fest-
schrift zur Säkularfeier von Gauss’ Geburtstag, Braunschweig 1877.
Hilbert: Die Theorie der algebraischen Zahlen, Bericht der Deutschen
Mathematischen Vereinigung von 1894/95, Kap. IX. - •
352
Zwölfter Abschnitt.
§ 96.
Wir setzen, wenn zf die Grundzahl des Körpers ß ist, je
nachdem z/ gerade oder ungerade ist:
0O = oder
(1) o _ - 1 +
W° — 2
Dann ist nach § 90 jede ganze Zahl des Körpers ß in der
Form
(2) co = x + y 0O
darstellbar, worin x und y ganze Zahlen sind, und diese Zahl ist
dann und nur dann nach dem Modul Q mit einer rationalen
Zahl a kongruent, wenn y durch Q teilbar ist, weil dann
x — a yf)0
Q
eine ganze Zahl sein muß. Demnach sind alle Zahlen der Ord-
nung [$] in der Form enthalten:
oder in den beiden in
co = x y QOo,
(1) unterschiedenen Fällen, wenn
(3) D = Q2z/
gesetzt wird:
yz>
x — y , z7 gerade,
(4) x — y y z/ ungerade, D gerade,
J 2
2—1 । — 1 + n .
x-------ö— y + y---------, -D ungerade.
Setzen wir also
0 = D = 0 (mod 4)
(6) , -i + Vi>
0 = J D __ T (mod
und ersetzen in den beiden letzten Formeln (4) die willkürlich
ganzen Zahlen
Q 2—i
x — fy, x — —y
durch x, so erhalten wir das Resultat:
§ 97. Ordnungen und Ideale. 353
2. Satz. Jede Zahl der Ordnung [$] und nur diese
sind in der Form enthalten
(6) « = x y 0,
worin x, y beliebige ganze rationale Zahlen sind.
Wir nennen das System
(7) (1, ö)
eine Basis der Ordnung [$].
Durch Einsetzen von (5) kann man die Zahlen (6) auch in
der Form darstellen:
(8) v =
wobei die x, y ganze Zahlen sind, die der Bedingung genügen
(9) x2 — y2D = 0 (mod 4).
Die Zahl D ist eine Diskriminante, deren Stamm z/ ist.
Wir nennen sie die Diskriminante der Ordnung [$].
§ 97. Ordnungen und Ideale.
Es sei m ein Ideal des quadratischen Körpers £1. Wenn alle
durch <i teilbaren ganzen Zahlen durch eine rationale Zahl m
teilbar sind, so ist das Ideal ct = wm durch m teilbar; es ist
2V(a) = m2W(tn),
und die rationale Zahl mN(m), die kleiner ist als N(a), ist
durch a teilbar.
Ist m die größte natürliche Zahl, durch die ct teilbar ist, so
wollen wir m den Teiler von a nennen. Ist der Teiler = 1, so
heißt das Ideal primär, sonst abgeleitet. Man erhält alle aus
einem primären Ideal tu abgeleiteten Ideale, indem man tu mit
beliebigen natürlichen Zahlen multipliziert, und alle aus einem
primären Ideal abgeleiteten Ideale sind untereinander äquivalent.
3. Satz. Ist a ein primäres Ideal, so ist die Norm
von ct zugleich die kleinste durch a teilbare natürliche
Zahl.
Bezeichnen wir nämlich die kleinste durch a teilbare natür-
liche Zahl mit a, so ist die Norm von ct jedenfalls durch a teilbar.
Wir setzen
W(a) = ma.
und wenn a' das zu ct konjugierte Ideal ist, so ergibt sich, da
nach Bd. II, § 164 die Norm eines Ideals gleich dem Produkt
der konjugierten Ideale ist,
(1) N'(a) = a ct' = ma.
Weber, Algebra. III.
23
354 Zwölfter Abschnitt. § 97.
Da a durch n teilbar sein soll, so setzen wir
a = am' = a'm
und erhalten aus (1):
(2) a = mm.
Also geht m im Teiler des Ideals n auf, und damit ist der Satz 3.
bewiesen, da, wenn a primär ist, sein Teiler — 1 sein muß.
4. Satz. Ist m ein primäres Ideal des Körpers ü, so
ist jede ganze Zahl in ü nach dem Modul m mit einer
rationalen Zahl kongruent.
Nach Bd. II, § 165 ist nämlich allgemein N(m) die Anzahl
der nach m inkongruenten Zahlen in Sl. Ist nun 2V(m) = a
zugleich die kleinste durch m teilbare natürliche Zahl, so sind
die a Zahlen
0, 1, 2, ..., a — 1
alle inkongruent, und darunter sind alle Zahlklassen modulo m
vertreten.
Es sei jetzt [(>] eine Ordnung mit dem Führer Q und der
Diskriminante D und (1,0) die Basis dieser Ordnung. Ferner
sei m ein primäres zu Q teilerfremdes Ideal. Nach dem Satz 4.
gibt es dann eine ganze rationale Zahl t, die der Bedingung
d t = 0 (mod m)
genügt. Wir setzen
t — wenn D = 0
(3) T i b (mod 4)
t = ,, D = 1
£
ist, und erhalten nach § 96, (5):
(4) 0 t — = 0 (mod m),
worin b eine ganze rationale Zahl ist, die nach (3) der Bedingung
b = D (mod 2)
genügt. Außerdem sei
(5) IV(m) = a,
also a die kleinste durch m teilbare natürliche Zahl.
Durch die Kongruenz (4) ist die Zahl b nur nach dem
Modul 2a bestimmt. Denn sind d, b' zwei Zahlen, die der
Bedingung (4) genügen, so ist j (b1 — b) durch a teilbar.
Da ferner
Ordnungen und Ideale.
355
§ 97.
eine durch m teilbare ganze rationale Zahl ist, so muß sie durch a
teilbar sein; setzen wir sie = ac, so ist c eine ganze rationale
Zahl und
(6) D = h2 — 4ac,
(7) 52 = D (mod da),
und wenn die Kongruenz (7) erfüllt ist, so genügt auch jede mit b
nach dem Modul 2 a kongruente Zahl b' derselben Kongruenz.
Wir schließen hieraus:
5. Satz. Jedes primäre zu Q teilerfremde Ideal tu,
dessen Norm = a ist, liefert uns durch (4) eine und nur
eine Wurzel b der Kongruenz (7), wenn als Wurzeln
nicht einzelne Zahlen, sondern Zahlklassen nach dem
Modul 2a‘betrachtet werden.
Die beiden Zahlen _
(8) »
können, wenn a relativ prim zu Q ist, nicht beide durch eine
und dieselbe rationale Primzahl teilbar sein; denn sonst müßte
?> +1^ _ b - yp _
2 2 F
durch p teilbar sein; also wäre D durch p2 teilbar und p müßte
ein Teiler von Q sein, gegen die Voraussetzung.
Für ein ungerades p ist dies evident, für p = 2 aber würde
folgen:
b = 0 (mod 2), b2 — D = 0 (mod 16),
und mithin
D = 0, 4 (mod 16).
Es wäre also Z>/4 noch Diskriminante und 2 müßte in Q auf-
gehen. Damit ist bewiesen:
6. Satz. Ist a eine zu Q teilerfremde natürliche Zahl
und b eine Wurzel von (7), so erhält man ein bestimmtes
primäres Ideal tn als größten gemeinschaftlichen Teiler
der beiden Zahlen (8).
Jetzt beweisen wir:
7. Satz. Jede durch das primäre Ideal m teilbare, zu
Q teilerfremde Zahl p der Ordnung [2] ist in der Form
। b ]/D
(9) p = ax ---------L2J— y
einmal und nur einmal darstellbar, wenn x, y ganze
rationale Zahlen sind. Werden x, y als Variable be-
23*
356 Zwölfter Abschnitt. § 97.
trachtet, so heißt eine Basisform des Ideals m in der
Ordnung [$].
Zum Beweis bemerken wir, daß jede Zahl der Ordnung [2]
wegen (4) in der Form enthalten ist
(io) y,
wenn y und z ganze rationale Zahlen sind. Ist nun m primär, so ist
(11) N (m) = a
die kleinste durch m teilbare natürliche Zahl, und wenn also co
durch ni teilbar sein soll, so muß z durch a teilbar sein. Wenn
wir also z = ax setzen, so erhalten wir die Form (9). Um-
gekehrt ist evident, daß jede Zahl dieser Form durch ni teilbar ist.
Daß die Darstellung einer Zahl nur auf eine Art in dieser
Form möglich ist, folgt daraus, daß \D irrational ist.
Die Form p heißt daher eine Basisform des Ideals in in
der Ordnung Q. Man erhält daraus eine Basisform desselben
Ideals im Körper ü:
i । 4-
L = ax -------y,
wenn b' aus der Kongruenz
b' Q = b (mod 2 a)
bestimmt wird, die immer lösbar ist, da Q relativ prim zu a, und
bei geradem Q auch b gerade ist.
Aus (9) ergibt sich
(12) = <*(ax2 -|- bxy -|- ci/2).
Die Zahl die man erhält, wenn man in (9) für x, y be-
stimmte Zahlen setzt., können wir in Idealfaktoren- zerlegen:
p, = am,
wenn
(13) W(a) = ax2 + bxy cy2
ist, und es gilt der Satz:
8. Satz. Ist (i relativ prim zu Q, und haben x, y keine
gemeinschaftlichen Teiler, so ist das Ideal a primär.
Wir beweisen ihn so: Es sei p eine in a aufgehende rationale
Primzahl; dann ist durch p teilbar und daraus folgt zunächst,
daß y durch p teilbar sein muß; denn eine Zahl co von der
Form (10) kann nur dann durch eine in Q nicht auf gehende
Primzahl p teilbar sein, wenn sowohl y als z = ax durch p
teilbar sind. Demnach kann, da nach Voraussetzung x und y
§ 97.
Ordnungen und Ideale.
357
relativ prim sind, x nicht durch p teilbar sein, und es muß a
durch p teilbar sein.
Setzen wir a = pFc^, wo «j nicht mehr durch p teilbar ist,
und bezeichnen mit p ein in p aufgehendes Primideal, so muß
wegen (11) p in tu oder in tu' aufgehen, und da m primär voraus-
gesetzt war, kann p nicht — p sein. Es ist daher W(p) = p = pp',
und wenn tu durch p teilbar ist, kann es nicht zugleich durch p'
teilbar sein. Folglich ist tu durch ps teilbar. Es ist also nach
der Definition von tu (Satz 6) auch - durch ps teilbar,
folglich y mindestens durch p’£ + 1, und ar und folglich p
Ai
genau durch pÄ, während andererseits am = p gleichfalls minde-
stens durch pÄ +1 teilbar ist, worin ein Widerspruch liegt. Ähn-
liches gilt auch, wenn p = p2 ist, also in z/ (aber nicht in Q)
aufgeht. Folglich kann in a keine rationale Primzahl enthalten
sein und a ist primär.
Nach dem, was bisher bewiesen ist, können wir noch folgenden
Satz formulieren:
9. Satz. Sind __
. b + V-D
p = ar -|-------= m0>
, ,. -j- yo, ,
p' — ax —y = ma
zwei zu Q teilerfremde Zahlen, haben weder x und y
noch x' und y' einen gemeinschaftlichen Teiler, ist
W(a) = W(a') = A,
und für eine und dieselbe Zahl B
= 0 (mod a)
= 0 (mod a'),
so sind die beiden Ideale a und a' identisch, und die
Zahlen p, p' unterscheiden sich nur durch einen Ein-
heitsfaktor.
Denn a sowohl als a' sind nach 8. primär und sind nach 6.
definiert als größter gemeinschaftlicher Teiler von
A und -------------
Dreizehnter Abschnitt.
Äquivalenz nach Zahlgruppen.
§ 98. Zahlgruppen in den Ordnungen.
Um die Beziehungen der quadratischen Irrationalzahlen zu
den Ordnungen der quadratischen Formen genauer zu erforschen,
leiten wir aus den Zahlen des Körpers ü Zahlgruppen nach
folgenden Gesichtspunkten ab.
1. Wir nehmen eine beliebige natürliche Zahl Q und schließen
von den ganzen Zahlen in ü zunächst alle die aus, die nicht
teilerfremd zu Q sind. Von den übrigen nehmen wir auch noch
beliebige Quotienten.
Die so erhaltenen ganzen und gebrochenen Zahlen ij nennen
wir fremd gegen Q. Ihre Gesamtheit sei mit 0 bezeichnet. Sie
bilden insofern eine Gruppe, als Multiplikation und Division
zweier dieser Zahlen immer Zahlen desselben Systems liefern.
2. Wir verfahren nun ebenso mit den Zahlen der Ordnung [2],
d. h. wir schließen alle Zahlen dieser Ordnung, die mit Q nicht
relativ prim sind, aus und bilden auch noch die Quotienten
beliebiger zweier der übrig gebliebenen Zahlen. Wir bezeichnen
diese Zahlen in ij' und ihre Gesamtheit mit 0', und nennen sie
ganze und gebrochene Zahlen der Ordnung [$]. Die Zahlen 0'
sind alle in 0 enthalten und bilden gleichfalls der Multiplikation
und Division gegenüber eine Gruppe. Wir nennen sie die
Gruppe der Ordnung [2] oder kurz eine Ordnungsgruppe.
Jede Zahl ij in 0 kann durch Multiplikation mit einer ganzen
rationalen zu Q teilerfremden Zahl n in eine ganze Zahl co
verwandelt werden.
Wenn i/ eine Zahl in 0' ist, so kann man den Nenner
rational machen und findet, daß eine ganze Zahl der Ord-
nung [Q] und folglich mit einer rationalen Zahl nach dem Modul Q
kongruent ist.
§ 98. Zahlgruppen in den Ordnungen. 359
Da n teilerfremd zu Q ist, so kann man diese Zahl = nr
setzen, worin r eine zu Q teilerfremde rationale Zahl ist. Dem-
nach hat jede Zahl rf die Eigenschaft
(1) 1?' = r (mod Q),
worin r eine ganze rationale Zahl und die Kongruenz in dem
Sinne nr/’ = nr zu verstehen ist.
Die Kongruenzen (1) lassen sich multiplizieren und dividieren,
wenn man unter r-1 die der Bedingung r. t—1 = 1 (mod Q)
genügende ganze Zahl versteht.
Umgekehrt gehört eine ganze oder gebrochene Zahl r/, die
einer Bedingung (1) genügt, der Gruppe 0' an. Denn ist
ntf = co = nr eine Zahl in [()], so ist i?' = co : n ein Quotient
zweier solcher Zahlen.
3. In 0' ist nun wieder eine Gruppe O0 enthalten, die aus
allen Zahlen besteht, die der Bedingung
(2) Vo = 1 (mod 2)
genügen, und die Zahlen von O0 ergeben durch Multiplikation
und Division gleichfalls wieder Zahlen von O0.
Wir haben also dreierlei Zahlgruppen, deren jede in der
vorangehenden enthalten ist:
1. 0 enthält alle gegen Q fremden Zahlen in £1.
2. 0' enthält die gegen Q fremden ganzen und ge-
brochenen Zahlen der Ordnung [Q].
3. O0 enthält die Zahlklassen in 0', die nach dem
Modul Q mit der Einheit kongruent sind.
Die Gruppen 0, 0', O0 sind unendliche Abelsche Gruppen.
Nimmt man aber ein volles Restsystem rationaler, zu Q teiler-
fremder Zahlen Fj, r2, ..., ru, so kann jede Zahl in 0' als Produkt
eines dieser r{ mit einer Zahl in O0 dargestellt werden, und man
kann daher nach der in Bd. II, § 2 gebrauchten Ausdrucksweise
setzen:
(3) , 0' = r, 0Q 4- r.2 Oit -I-P O0,
und ist der Index des Teilers O0 von 0:
(4) ft = (0', O0),
also eine endliche Zahl, nämlich:
(5) ft = cp(Q) =
worin <p(Q) das in der Zahlentheorie gebräuchliche Zeichen für
die Anzahl der Zahlklassen nach dem Modul Q mit zu Q teiler-
360 Dreizehnter Abschnitt. § 98.
fremden Zahlen bedeutet und g in dem Produkt TI die vonein-
ander verschieden in Q aufgehenden Primzahlen durchläuft.
Bezeichnen wir mit
Pu p-a, •••» Pl-
ein volles Repräsentantensystem der zu Q teilerfremden Zahlen
in £1, nach dem Modul Q genommen, so ist in gleicher Weise
(6) 0 = Pi O0 -|- p2 O0 • • P»- O0
und
(7) v = = (0, O0)
ist der Index des Teilers O0 io bezug auf 0.
Die Zahl if’(O) haben wir in § 168, (3) des II. Bandes all-
gemein bestimmt, auch für den Fall, daß an Stelle von Q ein
Ideal tritt. Da nun hier N(Q) = Q2 ist, so haben wir:
(8) ^(Q)= 0^(1-^),
wenn q die voneinander verschiedenen idealen Primteiler von Q
durchläuft.
Nun ist (§ 92)
1. -W(q) = q, wenn (z/, g) = 0,
2. JV(q) = q, wenn (z/,g) = —|— 1,
3. N(q) = q2, wenn (zf,g) = —1.
Wir wollen diese dreierlei Primzahlen mit qt, q2, q3 be-
zeichnen und bemerken, daß jede Primzahl q2 die Norm von
zwei verschiedenen Primidealen q ist. Demnach ergibt sich aus (8)
(9) ♦(« =
Nun ist der Index von 0' in bezug auf 0 nach Bd. II, § 2 (4) :
J - - <u,u) - (o;0o) -
und
folglich ergibt sich:
(0,0') = +
\ q-2/ \ <h/
wofür dann auch gesetzt werden kann (nach 1., 2., 3.):
(10) j = (0,0') = q n (i -
§ 99. Äquivalenz in den Ordnungen. 361
Darin bezieht sich das Produkt n auf alle in Q auf gehenden
Primzahlen q.
Wir können also ein Repräsentantensystem
^ii
in 0 so auswählen, daß
(11) 0 = öj 0' ö2 0' -I- • • • öj 0'
wird.
§ 99. Äquivalenz in den Ordnungen.
10. Definition. Wir wollen jetzt zwei Ideale a, (V
äquivalent nach der Ordnung [2] nennen, wenn
(1) a' = »j'a
ist, und ij' eine Zahl in 0' bedeutet. <i und a' werden
dabei immer zu Q teilerfremd vorausgesetzt.
Nimmt man eine durch et teilbare Zahl = atu in [()] so an,
daß m ein primäres Ideal wird, und setzt q' = ij'p, so wird:
(2) = mn;
- 7 (j,' = ma',
und wir können die Äquivalenz von a und a' nach [2] auch
dadurch erklären, daß a und a' durch Multiplikation mit
einem und demselben Ideal m in Zahlen der Ordnung [2]
verwandelt werden.
Durch das Ideal ni ist nach § 97 eine Schar paralleler
quadratischer Formen (a, b, c) bestimmt1), in der a und b aus
(3) a = N(m), = 0 (mod m)
bestimmt wird. Und diese Formenschar ändert sich also nach
(2) nicht, wenn a durch ein äquivalentes Ideal a' ersetzt wird.
Nimmt man aber in (2) an Stelle des Ideals m ein anderes
Ideal tiq und setzt
(4) ft = iiqa,
so ist
u m
— = ----- =7?
Jh mi
eine Zahl in [0'], also nii äquivalent mit m.
l) Unter einer Schar parallelei- Formen versteht man das System
(a, 6 4- 21 a, c -f- Ib -|- Pa),
wenn l alle ganzen rationalen Zahlen durchläuft.
362
Dreizehnter Abschnitt.
§ 100.
Setzt man also
(5) Oj = ^(nij) = mjinJ, = o (mod ntj),
so erhält man eine andere quadratische Form (oq, Zq, Cj), von der
wir nachweisen können, daß sie mit («, 6, c) äquivalent ist.
Wir setzen zur Abkürzung:
= &1 _|_ y
1 2 aT
und bemerken, daß
ijtq = ijnqmi = mni(,
m b2 4- V-D
' ntj 2
durch m teilbare Zahlen in [()] sind [nach (5)]. Demnach lassen
sich nach § 97, 7. die ganzen rationalen Zahlen a, ß, y, Ö so
bestimmen, daß:
. j? a, = a (« — 7 ra),
' t]a1(ol = a (— ß -|- Ö «),
uud man beweist ganz wie in § 95, daß
ab — ßy = 1
sein muß, daß also die beiden Formen
(a, b, c), (Oj, Z>i, Cj)
äquivalent sind. Wir haben also:
11. Satz. Jede durch ein Ideal n repräsentierte Ideal-
klasse nach [2] entspricht einer durch die Form (a, b, c)
repräsentierten Formklasse A und umgekehrt.
Um die Formklasse A zu erhalten, nehme man ein primäres
Ideal m der zu A reziproken Klasse A~1 und setze a = N (m),
= 0 (mod m). Und ist umgekehrt die Form (a, b, c)
A
gegeben, so ist der größte gemeinschaftliche Teiler m von
„ L+J®
2
ein Ideal der Klasse A~\
§ 100. Idealklassen nach den Ordnungen.
Der Begriff der Äquivalenz der Ideale und die Sätze über
Klassenzahlen lassen sich am übersichtlichsten darstellen, wenn.
§ 100. . Idealklassen nach den Ordnungen. 363
man die Ideale nach Bd. II, § 169 durch die in Bd. II, § 153 ff.
besprochenen Funktionale repräsentiert, weil man dabei die
gewöhnlichen Regeln der Multiplikation und Division benutzen
kannx).
Wir beschränken uns hier ein für allemal in dem
Körper Sl auf Zahlen und Ideale, die zu einer beliebig
anzunehmenden ganzen rationalen Zahl Q (dem Führer
einer Ordnung) teilerfremd sind.
Nach dieser Voraussetzung bilden die ganzen und gebrochenen
Zahlen des Körpers die vorher mit 0 bezeichnete Gruppe.
Wir erweitern diese Gruppe durch Hinzufügung der Funktionale
und bezeichnen die so erweiterte Gruppe mit 0. Jedem Element
von 0 entspricht dann ein ganzes oder gebrochenes Ideal, und
solchen Elementen, deren Quotient eine funktionale Einheit ist,
entspricht dasselbe Ideal.
Ist n eine Zahl in 0 und s irgend eine funktionale Einheit,
so entspricht dem Produkt er] ein Hauptideal. Demnach be-
zeichnen wir
mit E die Gruppe der funktionalen Einheiten,
„ E „ „ „ numerischen Einheiten,
und durch
EO die Hauptklasse der Funktionale.
Nehmen wir ein Repräsentantensystem
(1) <Pi, •••, <S>h
nicht äquivalenter ganzer Funktionale in ß, so wird jedes ganze
oder gebrochene Funktional 0 in der Weise darstellbar sein:
0 =
wo m ein Funktional aus EO ist, und die Idealklassen in Sl sind
die Nebengruppen von EO in 0. Demnach ist die Klassen-
zahl h der Index des Teilers E 0 von 0:
(2) h = (Ö, EO).
Hierbei hat man sich bei der schärferen Klasseneinteilung
bei 0 auf die Zahlen mit positiver Norm zu beschränken.
Betrachten wir nun die Klasseneinteilung der Ideale nach
der Ordnung [Q], so haben wir als Hauptklasse die Funktional-
gruppe E 0' zu betrachten und die Klassenzahl ist
h' = (Ö, EO').
') Vgl. auch des Verfassers Abhandlung „Uber Zahlengruppen in alge-
braischen Körpern“, erste Mitteilung, Mathematische Annalen 48, 438.
364
Dreizehnter Abschnitt.
§ 100.
Um hieraus die Beziehung zwischen h und h' herzuleiten,
machen wir von den allgemeinen Gruppensätzen Bd. II, § 2
Gebrauch, die wir folgendermaßen formulieren und ergänzen:
12. Satz. Ist A eine Gruppe und B ein Teiler von A
von endlichem Index (4, Bj, ferner C ein Teiler von B
von endlichem Index (B, C), so ist Bd. II, § 2, (4):
(4) (A, C) = (A, B) (_B, C).
Ist A wieder eine Gruppe mit dem Teiler B vom Index ft,
so setzen wir
(5) A = 04 B —ctg B —• • • —B,
worin öj, a2, ..., «« ein volles Repräsentantensystem von A nach
B ist.
Es sei nun 0 eine Gruppe von Elementen, die mit den Ele-
menten von A zusammensetzbar sind (z. B. in unserem Falle ein-
fach durch Multiplikation), so ergibt sich aus (5):
(6) AC = aiBC-\- a2BC -|--\-auBC.
Nun kann in den beiden Nebengruppen a^BC, a.2B C nur
dann ein und dasselbe Element vorkommen, wenn ax ay1 in B C,
aber nicht in B enthalten ist.
Daraus formulieren wir den Satz:
13. Satz. Ist A eine Gruppe, B ein Teiler von A vom
endlichen Index (A, B), ferner C eine mit A zusammen-
setzbare Gruppe von der Art, daß A und B C außer den
B keine gemeinschaftlichen Elemente enthalten, so ist
(7) (A C,BC)= (4, B).
Die Voraussetzung dieses Satzes läßt sich auch so aussprechen:
B ist der Durchschnitt von A und B C,
und sie ist z. B. erfüllt, wenn C in B enthalten, also B — BC
ist, und auch dann, wenn C mit A kein Element gemein hat.
14. Satz. Ist A eine aus den beiden Gruppen A' und
B zusammengesetzte Gruppe
(8) A = A!B
und B der Durchschnitt von A' und B, so ist
(9) (A B) = (A', B), .
vorausgesetzt, daß diese Indices endlich sind.
Denn nach (8) ist in jeder Nebengruppe aB zu B in A ein
Element a' aus A' enthalten, und man kann also diese Neben-
§ 100. Idealklassen nach den Ordnungen. 365
gruppen auch durch a'B darstellen, wo a' in A! enthalten ist.
Sind dann ChB, a^B verschiedene Nebengruppen zu B in A,
so sind a’iB', a'^B' verschiedene Nebengruppen zu B' in A' und
umgekehrt; denn aiaä-1 ist dann und nur dann in B' enthalten,
wenn es zugleich in B enthalten ist, und daraus folgt die
Formel (9).
Diese Sätze wenden wir nun auf die Ausdrücke (2) und (3)
für h und h' an. Nach (4) ist
(10) (Ö, EO') = (Ö, EO) (EO, EO'),
also
(11) h' = h(EO, EO').
Wir bezeichnen jetzt, wie schon oben, mit E die Gruppe
der numerischen Einheiten in 0. Dann ist EE = E, da die
numerischen Einheiten unter den funktionalen enthalten sind,
und jede Zahl, die in EO' enthalten ist, ist in EO' enthalten.
Folglich ist EO' der Durchschnitt von 0 und EO'. Wenden
wir also (7) an, indem wir 0, EO', E an Stelle von A, B, C
setzen, so ist B der Durchschnitt von A und BC und wir
erhalten:
(12) (EO, EO’) = (EO, EEO') = (0, EO').
Es ist ferner nach (4):
(13) (0, EO') (EO', 0') = (0, 0'),
und wenn wir mit E' die Gruppe der numerischen Einheit in 0',
also den Durchschnitt von E mit 0' bezeichnen, so daß E' 0'
= 0' ist:
(EO', 0') = (EO1, E'O') = (E, E')
(nach 2), denn E' ist der Durchschnitt von E' 0' und E.
Also haben wir nach (13)
(0, EO') (E, E>) = (0, 0')
und nach (12)
(EO, EO') (EE1) = (0, 0’),
also schließlich nach (11):
(14) (E, E')h' = (0, O')h.
15. Satz. Die Formel (14) gilt unverändert, wenn 0'
nicht gerade die Ordnungsgruppe, sondern irgend eine
in 0 enthaltene Zahlgruppe von endlichem Index (0, 0')
bedeutet, wenn wir zwei Ideale a, a’ nach 0' äquivalent
nennen, falls ihr Quotient a'/a = 17' eine Zahl in 0' ist.
366
Dreizehnter Abschnitt.
§ 100.
Ist E' die Gruppe der in 0' enthaltenen Einheiten, und
hat (£, E') einen endlichen Wert, so ist die Klassen-
zahl h' endlich und durch die Formel (12) bestimmt.
Ist z. B. 0 die Gruppe aller Zahlen in £i (außer 0), 0' die
Gruppe der Zahlen mit positiver Norm, so ist, falls es überhaupt
Zahlen mit negativer Norm gibt, (0, 0') = 2. Gibt es dann Ein-
heiten mit negativer Norm, so ist auch (E, E'~) = 2. Haben aber alle
Einheiten positive Norm, so ist (E, E') = 1, und wir erhalten
im ersten Falle h' — h, im zweiten Falle 2 h' = h.
Die Äquivalenz nach 0 ist dann die allgemeine Äqui-
valenz, die nach 0' die verschärfte.
Kehren wir zu den Ordnungen [$] zurück und verstehen
unter 0 die zu Q teilerfremden Zahlen (wenn nötig nur die mit
positiver Norm), so haben wir (0, 0') im vorigen Paragraphen
bestimmt,
Ist die Diskriminante _D und ihr Stamm z/ negativ, so gibt
es im allgemeinen sowohl in E als in E' nur die zwei Einheiten
+ 1. In den beiden Ausnahmefällen z/ = —3, —4 enthält E
sechs und vier Einheiten, E' aber, wenn Q > 1 ist, nur zwei,
und es ist also (E, E') — 1 im allgemeinen, (E. E1) = 3 im
Falle z/ == —3, (E, E') = 2 im Falle z/ — —4. Also haben
wir in diesen Fällen nach § 98, (10):
(15) xh' = Qn(l — ^^h,
worin:
A = 2, für z/ = —4
(16) 1 = 3, „ z/ = — 3
A = 1, „ zf < -4
Dies ist die Beziehung, die zuerst von Gauss abgeleitet und
später von Dirichlet auf anderem Wege bestätigt ist.
Ist z. B. z/ = 1 (mod 4), Q = 2, so ist nach Gaussscher
Bezeichnung h die Klassenzahl für die Formen zweiter, h' die der
Formen erster Art. Es ist
Also
= 1, d~l (mod 8),
— 3, z/ = 5 (mod 8).
Ä' = Ä, z/ = 1 .
= 3h, J = S
und nur in dem Ausnahmefalle zf = —3 kommt h' = h.
§ 100. Idealklassen nach den Ordnungen. 367
Ist D positiv, so ist noch (E, E1) zu bestimmen.
Es sei
t 4- u 11D
£ ~~ 2
die fundamentale Einheit in 0 und Z der kleinste positive Exponent,
für den _
a___V-0
~ 2
in 0' enthalten ist. Dann besteht E aus den Potenzen
und E' aus den Potenzen und es ist
(£, E’) = Z,
und die Formel (15) gibt die Klassenzahl h'. Eine weitere
Bestimmung läßt sich im allgemeinen für k nicht geben.
Ist wieder zf = 1 (mod 4) und Q — 2, so ist Z = 1 oder
= 3; nämlich = 1, wenn in (17) u gerade ist, und = 3, wenn
u ungerade ist. Letzteres kann nur vorkommen, wenn 4=5
(mod 8) ist, und folglich ist für 4=1 (mod 8) immer Z = 1,
während für 4 = 1 (mod 8) k sowohl = 1 als = 3 sein kann.
Vierzehnter Abschnitt.
Komposition der Formen nnd Ideale.
§ 101. Komposition in den Ordnungen.
Es sei zf die Körperdiskriminante und D — Q2 zf die Dis-
kriminante der Ordnung [$]•
Ist T = (a, b, c) eine primitive quadratische Form der
Diskriminanten D mit positivem, zu Q teilerfremdem «, so können
wir daraus eine Basisform 2 in 0 eines zu Q teilerfremden
Ideals o in folgender Weise bestimmen:
Wir setzen _
(1) A = atj ------"~L —t2,
Li
(2) N (A) = a (a ff b t2 -4- c ff).
Bezeichnen wir das durch das Funktional A bestimmte Ideal,
d. h. den größten gemeinschaftlichen Teiler von
mit o, so folgt aus (2)
(4) W(q) = a.
Hierin ist a die kleinste durch a teilbare natürliche Zahl.
Denn ist diese kleinste Zahl so muß (q ein Teiler von a sein,
also etwa a — cq a2. Hierin können au a2, b keinen gemeinsamen
Teiler haben, denn sie können erstens nicht alle drei gerade sein,
weil sonst a — 4 a', b = 2 b', c = c',
D = 4 (Z>'2 — 4 a' c)
wäre, und 4 müßte in Q auf gehen, entgegen der Annahme, daß
a zu Q teilerfremd sei; und ebenso würde ein ungerader ge-
meinschaftlicher Primteiler von a15 b, a2 in Q aufgehen.
§ 101. Komposition in den Ordnungen. 369
Setzen wir also _
& _l_ l/£)
ft -- 0-1 ^1~|----n---- hl
so wird
N(A,) = oq («j b ti t2 a2 c t[),
und («i, b, a2c) ist gleichfalls primitiv. Da nun A, durch a teil-
bar ist, so muß flj durch W(n), d. h. durch a teilbar und mithin
= a sein. Also ist a primär^
Wenn wir in (1) die \J) ein für allemal fest bestimmen,
z. B. positiv reell oder positiv imaginär, so ist die lineare Form A
durch die quadratische Form T eindeutig bestimmt. Die Form
des konjugierten Ideals würde nicht durch Änderung des Vor-
zeichens von yi), sondern von b erhalten.
Es seien a und b irgend zwei zum Führer Q der Ordnung [Q],
die wir jetzt mit 0 bezeichnen wollen, teilerfremde Ideale, und
== a, u, -f- a2 u2,
1 ' v — ßi + ft «2
seien Basisformen von a und b in 0. Aus a und b bilden wir
das Produkt
ab = c
mit der Basisform in 0:
(6) + ?2^2-
Die zu ft, v, A gehörigen quadratischen Formen mögen in
ZT, V, T bezeichnet sein.
1. Wir nennen A aus ft und v, T aus U und V zu-
sammengesetzt oder komponiert.
Wir setzen:
T = (a, 6, c),
(7) U = (cq, ft, Cj),
V = (a2, ft, c2),
und unsere Aufgabe ist gelöst, wenn T aus U und V abgeleitet
werden kann.
a äquivalent mit a',
6 ,, „ 6',
so ist auch
ab „ „ a'b',
also
c » ii c ’
und wenn also ZT, V durch äquivalente Formen 17', V ersetzt
werden, so tritt auch an Stelle von T eine äquivalente Form T'.
Weber, Algebra. III. 24
370
Vierzehnter Abschnitt.
§ 101.
Bezeichnen wir die Klassen in 0, zu denen Z, [i, v gehören,
mit A, B, C und bezeichnen ebenso die Klassen der quadratischen
Formen ü, V, T, so heißt auch C aus A und B komponiert,
und man setzt symbolisch
(8) C = AB.
Diese Komposition der Klassen ist eindeutig bestimmt,
wenn irgend drei Repräsentanten U, V, T derselben gegeben sind,
und es genügt also, wenn wir U, V in ihren Klassen irgendwie
passend wählen.
In jeder Idealklasse gibt es Ideale, die zu einem beliebigen
Ideal relativ prim sind. Wir nehmen also zunächst a in A primär,
sonst beliebig, dann b gleichfalls primär und relativ prim, nicht
nur zu a, sondern zu at. Dann sind aT und a2 relativ prim
(denn der größte gemeinschaftliche Teiler d von (q und a2 wäre
relativ prim zu b, und folglich wäre a2: d durch b teilbar). Daraus
folgt aber d = 1, weil a2 die kleinste durch b teilbare natürliche
Zahl sein sollte.
Hat man <q, a2 so bestimmt, so kann man b den beiden
Kongruenzen s s (mod
= b2 (mod 2a2)
gemäß bestimmen, und dann ist
b- — D = 4 «j a2 c
durch 4 a2 teilbar. Wir setzen also
, . U = (ctj, b, a2 c),
\ V = (a2, b, cij c).
Es ist «i a2 die kleinste durch a b teilbare ganze rationale
Zahl, und ab ist der größte gemeinschaftliche Teiler von
b —
«i «2, ---g2— ;
folglich ist
(10) T — (cij a2, b, c)
die aus U und V komponierte Form, und die den quadratischen
Formen T, ü, V entsprechenden Linearformen 2, p., v sind:
. __ , , b —
a — cq a2 q -----------hi
, b — -\/D
P = aiMi H---------2---M'2’
। b-^D
v — a2v1 ----------s-i— v2.
§ 101. Komposition in den Ordnungen. 371
Daraus folgt, mit Rücksicht auf
A- ypy
—2~) = «i«2c + 6 —2~:
(11) qv = ala2(u1v1 — cu2v2)
,b — \D. . . , .
+ •—2— (fli ui v2 a2u2v1 b u2 v2).
Macht man also die bilineare Substitution:
ZJ2) = cu2v2,
' ’ f2 = “i M-l f 2 + «2 M-2 f 1 + 6 u2 v2,
so ergibt sich
(13) 2 = (tv,
und folglich
(14) T = UV.
In der Forderung, daß a, und a2 relativ prim sein sollen,
liegt bisweilen eine gewisse Unbequemlichkeit, z. B. wenn es sich
um die Komposition einer Form mit sich selbst handelt.
Lassen wir also die Voraussetzung fallen, daß a zu b und
(t, zu a2 relativ prim seien, halten dagegen an der Annahme
fest, daß
(15) A2 — D = Tcqa^c
durch 4(1^2 teilbar sei, so gilt die Relation (11) noch, und es
folgt, daß ab der größte gemeinschaftliche Teiler von
b — Vß b — ylD ^b — fD
«1 «2, «1 --, «2 ---b ----------
ist (Bd. II, § 160, 2).
Haben nun «q, a2, b keinen gemeinschaftlichen Teiler, so
kann man der Gleichung cq fc2 a2 -f- h b = 1 durch ganze
rationale fc genügen, und demnach ist ab auch der größte ge-
meinschaftliche Teiler von
z,„x b — VD
(16) cij a2, - •
2. Es ist zu beweisen, daß axa2 die kleinste durch ab
teilbare natürliche Zahl ist.
Setzen wir nämlich diese kleinste Zahl = a, so ist cqcq
durch a teilbar, etwa
cq a2 = a a'.
2i*
372
V ierzehnter Abschnitt.
§ Ml-
Bilden wir die beiden Formen
A = cq a2 --------2^— ^2,
r = at, + h,
Ai
so folgt:
JN (Z) = d, a« (a, a« t,2 -4- b t, t2 -4- c t!\
N(l') = d(dt2 4- bt^ + a'ct*). ' .
Die beiden Formen (dj d2, b, c), (a, 5, d'c) sind primitiv (weil
ein gemeinsamer Primteiler von a2 a2, b. c wegen (15) in Q auf-
gehen müßte), und es folgt für die absolute Norm:
Na(i.) = «jda = JV(ab),
^a(A') = a;
da aber A' durch a 6 teilbar ist, so muß a durch a, a2 teilbar und
mithin a' = 1 sein.
Hieraus ergibt sich:
3. Sind ci], a2, b ohne gemeinsamen Teiler und
D — b2 —
so ist die Form
T — (t^i Uq, b) c)
aus den beiden Formen
U = (dj, b, ca2), V — (d2, b, caj)
komponiert.
Wendet man dies auf zwei entgegengesetzte Formen
U — (d, b, c), V = (c, b, d)
an, so ergibt sich
T = (d c, b, 1),
und dies ist mit der Hauptform ^1, 0, ) oder ^1, 1, -—
äquivalent.
4. Zwei entgegengesetzte Klassen geben komponiert
die Hauptklasse.
Um eine Klasse A wiederholt mit sich selbst zusammen-
zusetzen, wähle man a in A so, daß es relativ prim zu D ist,
und bezeichne mit (a, b, c) die entsprechende Form. Dann ist
a relativ prim zu b. Denn wäre d ein Teiler von d und 5, so
wäre d auch in D enthalten, also relativ prim zu a. Es wäre
also auch a-.d durch a teilbar, was, wenn d > 1 ist, der De-
finition von d widerspricht.
§ 102. Komposition der Ordnungen. 373
Nun kann man aber b so wählen, daß
(17) b2 = D (mod 4 aM)
ist, für ein beliebig großes n. Denn man kann b um ein be-
liebiges Vielfachem von 2 a verändern. Nehmen wir also (17) als
erfüllt an für einen Exponenten n, und setzen demgemäß
(18) b2 = D-[-4anc,
so folgt:
(b -j- 2han)2 —D = 4an (c hb) (mod 4an + 1),
und wenn man also h aus der Kongruenz c h b = 0 (mod d)
bestimmt, so ergibt sich ein der Kongruenz (17) für n -|- 1
genügendes b.
Da nun b relativ prim zu a ist, so folgt nach 2., daß, wenn
n m ist, am die kleinste durch am teilbare natürliche Zahl ist,
und daraus ergibt sich folgende Kompositionsregel:
5. Genügt die Form (n, b, anc) — U der Bedingung
(18), und ist m n, so ist
Um = (am, b, an~m c).
Hiermit sind die Klassen quadratischer Formen der Dis-
kriminante z/ zu einer Abelschen Gruppe vereinigt, die mit
der Gruppe der Ide al klassen isomorph ist, und es ist zugleich
ein Weg angegeben, wie man durch passend gewählte Repräsen-
tanten die Komposition in diesen Gruppen wirklich ausführen
kann *).
§ 102. Komposition, der Ordnungen.
Eine Ordnung 0 = [0] im Körper £2 ist durch den Führer Q
vollständig bestimmt. Es seien 0,, 02 zwei Ordnungen mit den
Führern Qt, Q2, und der größte gemeinschaftliche Teiler von Oi
und Q2 sei Q. Ist dann M das kleinste gemeinschaftliche Multi-
plum von Qi und Q2, so ist
(1) Qi Qi == QHf.
*) Die Einheit in dei- Gruppe der Klassen bildet die Hauptklasse.
Über die Komposition der quadratischen Formen ist zu erwähnen: Gauss,
„Disquisitiones arithmeticae“, Art. 235 u. f. Dirichlet, De formarum
binariarum secundi gradus compositione (1851), Werke Bd. II, S. 105.
Dirichlet-Dedekind, Vorlesungen über Zahlentheorie,. 4. Auf!., § 145f.
Dedekind, Grelles Journal, Bd. 129. H. Weber, Göttinger Nachrichten,
9. Februai’ 1907.
374 Vierzehnter Abschnitt. § 102.
6. Die zum Führer Q gehörige Ordnung 0 heißt aus
0, und O2 zusammengesetzt oder komponiert.
Wir setzen symbolisch
(2) 0=0, O2.
Die Diskriminanten dieser drei Ordnungen sind
(3) D = Q^, 1), = Q^, D2 = Q^.
Sind Q, und Q2 relativ prim, so ist die aus beiden kom-
ponierte Ordnung die Hauptordnung OQ.
Um die Komposition der Ordnungen auszuführen, kann man
ebenso verfahren, wie im vorigen Paragraphen. Wir setzen
(4) Q, = Qm,, Q2 - Qm2,
und dann sind m„ m2 relativ prim zueinander.
Es mögen dann a und b zwei Ideale bedeuten, die zu Q, Q2
relativ prim sind.
Ist dann
a äquivalent a' nach 0,,
t> « t>' „ o2,
so ist
y = q, eine Zahl in 0,,
b_ _ n
I)/ — Vi » n n Gj,
d. h. t], ist nach dem Modnl Q,, i/2 nach dem Modul Q2 mit
einer rationalen Zahl kongruent.. Also sind beide, und folglich
ihr Produkt, nach dem Modul Q mit einer rationalen Zahl kon-
gruent und gehören in die Ordnung Q. Demnach ist auch
c = a b äquivalent mit c' = a' b' nach 0.
Es sei a, die kleinste durch a teilbare natürliche Zahl und
b relativ prim zu a, (folglich auch zu a), und wenn a2 die
kleinste durch b teilbare natürliche Zahl ist, so sind auch a,
und a2 relativ prim. Man kann dann immer, was auch b„ b2
sein mögen, den Kongruenzen
b, = m,b (mod 2a,j,
b2 = m2b (mod 2a2)
genügen und demnach die Basisformen von a und b in der
Gestalt annehmen:
§ 102.
Komposition der Ordnungen.
375
p, = Uj + ---—! U2,
i & — vd
V = a21>! 4- m2------— t>2,
und es ist
ö2 — D = 4 öj a2 c
durch 4 tq a2 teilbar. Dann ist ar a2 die kleinste durch a t> teil-
bare natürliche Zahl, und es ist
ö — 1<D
A — czj a2 tj ----------t2
eine Basisform von c.
Demnach gibt die Zusammensetzung der entsprechenden
quadratischen Formen der Diskriminanten D1? D2:
U = (a1? wqS,
' V = (a2, m2 b, tq c),
die Form T der Diskriminante D:
(6) T = («j a2, ö, c).
Fünfzehnter Abschnitt.
Geschlechter der quadratischen Formen.
§ 103. Darstellung von Zahlen durch quadratische Formen.
Eine natürliche Zahl m heißt durch die primitive Form (a, b, c)
mit der Diskriminante D eigentlich darstellbar, wenn es
zwei relative Primzahlen x, y gibt, die die Gleichung
(1) ax2 bxy -|- cy2 = m
erfüllen, und man kann eine mit (a, b, c) äquivalente Form (m,n,l)
finden, deren Diskriminante
(2) D = n2 — 4ml
ist. Ist m durch die Form (a, b, c) darstellbar, so ist sie auch
durch jede äquivalente Form, also durch jede Form der Klasse A,
zu der (a, ö, c) gehört, darstellbar. Wir nennen dann m durch
die Klasse A darstellbar. Sind A, A' zwei Klassen, m, m' zwei
zueinander teilerfremde Zahlen, die durch diese Klasse eigentlich
darstellbar sind, so ist das Produkt mm' durch die zusammen-
gesetzte Klasse AA' eigentlich darstellbar. Dies folgt aus den
Kompositionen der Formen (12), (14), § 101.
Aus (2) ergab sich:
(3) n2 = D (mod 4 m).
Ist (m, n, l) imprimitiv, so kann D keine Stammdiskriminante
sein. Wir bezeichnen, wie bisher, den Stamm von D mit A und
setzen
D = Q2A,
und der größte gemeinschaftliche Teiler von m, n, l geht in Q2
auf. Wir nehmen daher im Folgenden an, m sei relativ prim
zu Q, und sind dann sicher, daß die durch (2) bestimmte
Form (m, n, l) primitiv ist.
§ 103. Darstellung von Zahlen durch quadratische Formen. 377
Ist umgekehrt die Kongruenz (3) erfüllt, so kann man
D = u2 — 4 ml setzen und erhält eine Form der Diskrimi-
nante D, (m, w, Z), durch die m eigentlich darstellbar ist.
1. Die notwendige und hinreichende Bedingung dafür,
daß eine zu Q teilerfremde Zahl m durch eine Form der
Diskriminante D eigentlich darstellbar ist, besteht also
darin, daß die Kongruenz
(4) x2 = D (mod 4 m)
lösbar sei.
Aus einer Form (a,b,c) erhält man eine Schar äquivalenter
Formen:
(5) (u, b 2 Au, C),
worin A eine beliebige ganze Zahl und C durch die Gleichung
D = (b 2 Aa)2 — 4a C
bestimmt ist und sich gleich al2 b A c ergibt. Das System (5)
wird eine Schar paralleler Formen genannt.
Wenn die Kongruenz (4) erfüllt ist, so ist auch
(x -|- 2 Am)2 = D (mod 4 m),
und wir wollen die ganze Schar der Wurzeln von (4), die nach
dem Modul 2m kongruent sind, als eine Wurzel betrachten. In
diesem Sinne sei die Anzahl der Wurzeln von (4), die demnach
sicher endlich ist, mit ip (D, m) zu bezeichnen.
2. Jede Wurzel von (4) gibt Anlaß zu einer Schar
paralleler Formen, durch die die Zahl m eigentlich dar-
stellbar ist.
Die Zahl tp (D, ni) läßt sich leicht bestimmen. Sind zunächst
m', m" relativ prim, so ist
(6) tp (D, m'), ip(D, m") — ip(D, m'm").
Denn ist
(7) x'2 = D (mod 4 m'), x"2 = D (mod 4 m"),
und
, , x = x' (mod 2 m'),
= x" (mod 2 m"),
so ist (x2 — D): 4 durch m' und durch m", also auch durch m' m"
teilbar, und die Kongruenz
(9) x2 = D (mod 4m'm")
erfüllt. Umgekehrt gibt jede Wurzel der Kongruenz (9) je eine
Wurzel der beiden Kongruenzen (7). Also erhält man alle
378 Fünfzehnter Abschnitt. § 103.
Wurzeln von (9) und nur diese, wenn man in (8) die Wurzeln
x" von (7) paarweise kombiniert, und daraus folgt (6).
Nach (6) ist nur noch nötig, die Funktion ^(2), m) für den
Fall zu bestimmen, daß m = q* eine Potenz einer in Q nicht
aufgehenden Primzahl q ist. Wir brauchen das Symbol (2), ri) in
dem in § 85 erklärten Sinn und unterscheiden drei Fälle:
1) Wenn q in z/ aufgeht, so ist (2), q) = 0, und die Kon-
gruenz (3) hat nur dann eine Lösung, wenn k = 1 ist, nämlich je
nachdem D gerade oder ungerade, ist x = 0 oder = q (mod 2 g),
dagegen keine Lösung, wenn k > 1 ist, und dies gilt auch für
q — 2. Denn in diesem Falle müßte Q ungerade, A durch 4
teilbar sein, folglich x gerade. Die Kongruenz
(zv> \ 2 A
fJ (mod 2”)
ist aber nur lösbar für k = 1, da A: 4 keine Diskriminante ist.
2) Ist (2), g) = —1, so ist die Kongruenz (3) nicht lösbar,
weil dann D quadratischer Nichtrest von q oder (für q = 2)
von 8 ist.
3) Ist (2), q) = 1, so ist D quadratischer Rest von q
(oder von 8) und die Kongruenz,
x* = D mod 4</fc
hat, wie aus der Zahlentheorie bekannt ist, zwei Wurzeln.
Wir fassen diese Resultate übersichtlich so zusammen:
Ist 1) (2),g) — 0, so ist ^(D,<?) — 1, ^(Z>,q*) = 0 (&>>1),
„ 2) (2),g) = —1, „ „ tf(2>,g*) = 01,
„ 3) (D,q) = +1, „ „ ^(2),^) = 2/^>i;’
wozu noch koinmt:
^(2), 1) = 1.
Nach (5) ist also ^(2), m) immer dann gleich Null, wenn in
m eine Primzahl auf geht, für die (2), q) — — 1 ist, oder wenn
in m ein Primfaktor von D mehr als einmal aufgeht.
In den anderen Fällen ist ^(2), q) eine Potenz von 2, deren
Exponent gleich der Anzahl der in m, aber nicht in 2) auf-
gehenden Primzahlen ist.
Zwischen den Symbolen ty (D, m) und (2), m) besteht die
folgende allgemeine Beziehung immer unter der Voraussetzung,
daß m relativ prim zu Q ist:
§ 103. Darstellung von Zahlen durch quadratische Formen. 379
Es durchlaufe e die sämtlichen Teiler von m (1 und m ein-
geschlossen) und e2 die sämtlichen quadratischen Teiler von nr,
dann ist
e2 / f
(10) sh>(d,-} = s(D, 4
Ist diese Relation richtig für zwei Zahlen m', m", die keinen
gemeinsamen Teiler haben, so folgt sie für m = m'm". Denn
haben e', s' und e", s" dieselbe Bedeutung für m' und m", wie
e, 8 für m, so sind s = s's" die Teiler und e2 = e'2e"2 die
quadratischen Teiler von m = m'm". Es ist aber nach (6) und
§ 85, (8):
S2(D, «") = S(D, t).
Hiernach brauchen wir die Relation (10) nur noch unter der
Voraussetzung zu beweisen, daß m — qk eine Primzahlpotenz ist.
Unter dieser Voraussetzung ist aber:
s = qs, s = 0, 1, 2, ..., k.
Ist nun
1. (D, q) — 0, so ist g*-2’) = 1,
2. (Z), g) = —1, „ „ qk-2,>) = 1 (ä gerade),
= 0 (fc ungerade),
3. (D, q) = 1, „ „ qk~^) = Ä+l,
und ebenso groß ergibt sich in den drei Fällen die Summe
o, fc
denn im Falle 1. hat nur das dem s = 0 entsprechende Glied
dieser Summe den Wert 1, die anderen verschwinden; im Falle 2.
haben die den geraden s entsprechenden Glieder den Wert
4-1, die anderen den Wert —1, und im Falle 3. haben alle
k 1-Glieder den Wert -]-l.
Damit ist also die Relation (10) allgemein bewiesen.
380
Fünfzehnter Abschnitt.
§ 104.
§ 104. Charaktere und Geschlechter der quadratischen Formen.
Unter einem Stammteiler d einer Diskriminante D wollen
wir folgendes verstehen (§ 84):
1. d ist eine in D aufgehende Stammdiskriminante.
2. Der Quotient D : d = D1 ist selbst noch Dis-
kriminante.
Ein ungerader Stammteiler kann keine anderen Primfaktoren
enthalten als solche, die in D auf gehen, und keinen mehr als
einmal; dagegen ist ein beliebiges Produkt aus verschiedenen in
D aufgehenden ungeraden Primzahlen, mit einem solchen Vor-
zeichen versehen, daß' d = 1 (mod 4) wird, immer ein Stammteiler.
Außerdem kommt noch unter den Stammteilern vor:
— 4, wenn D = 0, —4 (mod 16),
(1) ~H 8, „ D = 0, 8 (mod 32),
— 8, „ D = 0, —8 (mod 32),
Bezeichnen wir also mit die ungeraden Stammteiler, so
ergeben sich die sämtlichen Stammteiler d:
1) d = d1? D = 1 4 (mod 4), (mod 16),
2) d = d\, — 4dj, D = — 4 (mod 16),
~=. 16 (mod 32),
3) d = dn 8d„ D = 8 (mod 32),
4) d = dn — 8 d\, D = — 8 (mod 32),
5) d = dlt — 4d„ D = 0 (mod 32).
8dn -8d15
Die Anzahl der Stammteiler (1 als Stammteiler mitgerechnet)
ist hiernach stets eine Potenz von 2.
3. Setzen wir sie gleich 2l, so ist A in den Fällen 1), 2),
3), 4) gleich der Anzahl der in D aufgehenden ver-
schiedenen Primzahlen, in dem Falle 5) um eins größer.
Die Stammteiler von D lassen sich durch Anwendung einer
symbolischen Multiplikation zu einer Abelschen Gruppe machen.
Wenn nämlich dlt d2 zwei Stammteiler von D sind, so ist
das Produkt d, d2 auch eine Diskriminante, aber nicht immer
eine Stammdiskriminante. Wir bezeichnen mit d den Stamm
von d, d2 und setzen symbolisch
(2) d—d.d,.
§ 104. Charaktere und Geschlechter der quadratischen Formen.
381
Haben dj, ö2 keinen gemeinschaftlichen Teiler, so ist diese
symbolische Multiplikation eine wirkliche. Haben sie aber einen
gemeinschaftlichen Teiler, so ist noch ein quadratischer Faktor
aus dem wahren Produkt dj d2 abzuwerfen. Setzen wir in (2)
dj = d2, so ist d = 1, d. h. es ist jedes Element der Gruppe
der d sich selbst reziprok, und es besteht zugleich mit (2):
(3) dj = dd2.
Die Elemente dieser Gruppe lassen sich folgendermaßen
durch eine Basis darstellen (Bd. II, § 11):
(4) d = dX...d?,
worin £1? s2, ... «2 die Werte 0 oder 1 haben, und Ä die oben
angegebene Bedeutung hat. dn d2, ... Sj. sind in dem Falle 1) die
in D aufgeh enden ungeraden Primdiskriminanten + p, im Falle 2)
kommt dazu noch —4, im Falle 3) 8, im Falle 4) —8, im
Falle 5) 8 und —8 (oder —4 und 8 oder —4 und —8).
Mit Hilfe der Stammteiler werden nun die Charaktere der
primitiven quadratischen Formen definiert.
Wir wählen in einer Formenklasse A einen Repräsentanten
(a,ö,c), in dem a positiv und relativ prim zu D ist. Ist dann eine
zu D teilerfremde Zahl m durch A darstellbar, so ist
m = ax* -|- bxy cy*,
(5) 4am — (2ax-j- by)* — Dy*.
Es sei nun d ein Stammteiler von D und m relativ prim
zu d, so ist, zunächst für ein ungerades d, nach § 85, (14), (16):
(6)
(d, m) = (d, a).
Diese Relation gilt aber auch für d == —4dn —|— 8 d1? —8dj.
a und m ungerade und nach (1)
Denn es ist
und (5):
d = — 4dn
d = 8dn
d = —8dn
woraus nach
die danach allgemein bewiesen ist.
in
diesen Fällen
D = 0,
D = 0,
D = 0,
§85 auch
(mod 16),
(mod 32),
(mod 32),
— 4
8
— 8
für diese Fälle
am = 1 (mod 4),
am = +1 (mod 8),
am = 1,3 (mod 8),
die Gleichung (6) folgt,
4. Der Wert des Symbols (d, ni) ist also nicht von
der Zahl m, sondern nur von der Formenklasse A abhängig,
durch die m darstellbar ist. Es wird der zum Stamm-
teiler d gehörige Charakter dieser Klasse genannt und
mit %(d, A) bezeichnet.
382 Fünfzehnter Abschnitt. § 104.
Es gilt zunächst für jede beliebige Klasse A und für beliebige
Stammteiler d, d15 d2:
(7) %(1, A) = 1,
(8) % (dn A) i (d2, A) = x (dj d2, A),
(9) %(d, A) = i,
worin djd2 das oben definierte symbolische Produkt ist und Ao
die Hauptklasse bedeutet, durch die die Zahl 1 darstellbar ist.
Sind für eine Klasse A die Charaktere % (d17 A), % (d2, A) ...
%(§h A.) gegeben, so sind nach (4) und (8) alle %(d, A) bestimmt.
Jeder dieser Charaktere kann aber = -|-1 oder = — 1 sein,
und so ergeben sich 2Z mögliche Bestimmungen über die Charaktere.
Diese sind aber nicht voneinander unabhängig.
Denn es folgt aus (5)
Dy2 = (2ax by)2 (mod im),
und daraus folgt, wenn man m relaliv prim zu a, folglich zu y
annimmt:
(Dy2, m) = (z/, m) = 1.
Daraus ergibt sich, daß für jede Klasse A
(10) X(A,A) = +1.
Nun läßt sich zu jedem Stammteiler d ein bestimmter, von
d verschiedener komplementärer Stammteiler d' so bestimmen,
daß im Sinne der symbolischen Multiplikation
(11) dd' = A
ist. Das Komplement von d' ist wieder d, und jeder Primteiler,
der in d und d' zugleich aufgeht, muß in Q aufgehen.
Daraus folgt nach (10) für jede Klasse A:
(12) Z(d,M) = Z(d',M),
und hiernach ist die Anzahl der möglichen Bestimmungen über
die % (d, A) nur noch 2k~1.
Man vereinigt in ein Geschlecht (Genus) alle Formen-
klassen A, in denen sämtliche Charaktere % (d, A) übereinstimmen,
und gelangt zu dem Resultate:
5. Die Anzahl der existierenden Geschlechter ist
höchstens gleich 2Ä~’.
Ob die Anzahl der existierenden Geschlechter wirklich so
groß ist, ist eine tiefere Frage, auf die wir später zurückkommen.
§ 104. Charaktere und Geschlechter dei- quadratischen Formen. 383
Wenn die Klasse A aus der Klasse A', A" komponiert ist,
so ist symbolisch
A = A' A".
Sei m', m" durch die Klasse A', A" darstellbar, und nehmen
wir m', m" relativ prim, so ist m = m'm'1 durch A darstellbar
(§ 103), und daraus ergibt sich für die Charaktere die Formel:
(13) z(ö,A'A") = A') %(§, A").
Nach 1. ist das Symbol % (d, A) durch irgend eine zu d
teilerfremde, durch A eigentlich darstellbare Zahl m bestimmt,
und wir definieren daher die Charaktere dieser Zahlen m durch
(14) 1 (d, m) = / (d, M).
Es ist aber zweckmäßig, daß man sich noch von der Vor-
aussetzung frei macht, daß m zu d relativ prim sei, und dies
kann auf folgende Weise geschehen. An der Voraussetzung, daß
m relativ prim zu Q sei, soll aber festgehalten werden.
Ist m durch die Klasse A eigentlich darstellbar, so können
wir in A einen Repräsentanten
(15) tp = (m, B, C)
finden. Wir zerlegen m in zwei Faktoren
(16) m = nn',
so daß n und n' teilerfremd sind und n relativ prim zu d, n'
relativ prim zu d' ist.
Dies ist immer möglich, meist auf mehrere Arten, da nach
Voraussetzung m relativ prim zu Q ist, und also m, d, d' keinen
gemeinschaftlichen Teiler haben. Man nehme z. B. in n die in
d' aufgehenden Primzahlen in so hohen Potenzen auf, als sie
in m enthalten sind, und außerdem noch die Primzahlpotenzen,
die zu d teilerfremd sind.
Dann ist die Form <p aus den beiden Formen
(w, j?, Cn') (n', B, Cn)
komponiert, deren Charaktere nach (12) und 4. durch
(d, n), (§' n')
bestimmt sind, und es ist also nach (13):
(17) %(d,M) = (d,n)(d',<).
Hierin kann aber auch noch die Forderung aufgegeben
werden, daß m durch A eigentlich darstellbar sei; denn ein
gemeinsamer Teiler von x, y (relativ prim zu Q) gibt einen
384 Fünfzehnter Abschnitt. § 104.
quadratischen Teiler von m, den man wieder in zwei teilerfremde
quadratische Faktoren zerlegt, von denen der eine zu n. der andere
zu n' genommen wird, und dadurch ändern sich (d, n) und
(d', n') nicht.
Man kann hiernach einen Charakter % (d, n) einer beliebigen
zu Q teilerfremden Zahl folgendermaßen bestimmen.
Man setze:
(18) n = sn’
und verstehe unter s das Produkt der in n aufgehenden Potenzen
solcher Primzahlen, die zugleich in d aufgehen; dann ist « relativ
prim zu d' und n' relativ prim zu d, und man setze:
(19) % (d, ri) = (d', «) (d, n'),
wodurch % (d, n) eindeutig und immer von Null verschieden be-
stimmt ist. Ist dann (a, b, c) ein Repräsentant der Klasse A,
so ist
(20) (A + b xy + c2/2) = % (d, A),
worin a?, y beliebige ganze Zahlen mit oder ohne gemeinsamen
Teiler sind, für die aa?2 bxy cy2 teilerfremd zu Q wird.
Über das so definierte Symbol % (d, ri) gilt eine Reihe von
Sätzen, die wir noch ableiten müssen.
6. Sind ni und n2 irgend zwei zu Q teilerfremde
Zahlen, so ist
(21) Z (d, nj i (d, n2) = % (d, n2).
Denn setzen wir nach (18)
so ist
ntn2 = els2n'1n2,
und dies geht in (18) über, wenn man n = n1n2, s = s1s2,
ri = ri^ setzt. Also folgt (21) aus § 103 (8).
7. Läßt man e die Reihe der Divisoren von n durch-
laufen, und setzt n = ee', so ist
(22) %(d,n)i(D,e) = ^(d,e)(d',e').
Wenn die Formel (22) für n = nY und n = n2 gilt, so gilt
sie, unter der Voraussetzung, daß n2 relativ prim sind, auch
für n = nxn2 [nach (21)]; sie braucht also nur noch für eiue
Primzahlpotenz n — pk bewiesen zu werden, wenn p nicht in Q
§ 105. Anwendung des Legendreschen Symbols. 385
aufgeht. In diesem Falle ist aber (7), ps) = (z/, p8') [§ 85 (9)],
und es ist also zu beweisen:
% (d, pk) E (4, ps) = 2J (d, ps) (d', p1:~s).
0, k 0, k
Geht nun p nicht in d auf, so ist
ZfAP*) = (d,pk),
und wenn man rechts jedes Glied unter dem Summenzeichen mit
(d, p*-8)2 = 1 multipliziert, so erhält man übereinstimmend mit
der linken Seite
(d, pk)£( J, pk~8).
Geht aber p in d und folglich nicht in d' auf, so ist % (d, y?)
= (6', p*), multipliziert man also ebenso mit (d', ps)2, so folgt
das gleiche, wodurch (22) bewiesen ist.
8. Ist y (d, n) von %(d', n) verschieden, so ist
(23) 2? (7), e) = 0, 2?(d, e) (d', e') = 0.
Denn da sich die beiden Summen nicht ändern, wenn d mit
d' vertauscht wird, so folgt dies aus (22).
9. Sind d15 d2 zwei Stammteiler von D und d,d2 ihr
symbolisches Produkt, so ist
(24) i (dn n) % (d2, n) = % (ßi d2, n).
Diese Formel braucht wegen (21) nur für den Fall bewiesen
zu werden, daß n eine Primzahl ist.
Es ist aber symbolisch
(d,d2)' = öid2 = djd2,
und hiernach ergibt sich (24) leicht aus der Definition (19).
§ 105. Anwendung des Legendreschen Symbols.
Will man sich der bekannteren Bezeichnung nach Legendre
und Jacobi bedienen, so gestaltet sich die Sache folgendermaßen.
Bedeutet Z eine ungerade Primzahl und a eine durch Z nicht
teilbare Zahl, so ist nach Legendre:
(!) (t) = +1’
wenn a quadratischer Rest von Z ist,
Weber, Algebra. III.
25
386 Fünfzehnter Abschnitt. § 105.
wenn a quadratischer Nichtrest von Z ist, und nach der von
Jacobi eingeführten erweiterten Definition dieses Symbols ist
Ist ferner a ungerade, so ist
/__a~i /________________o\ a2-1
(3) = 2, (^) = (-l) 8 ,
\ (Jj / \ u /
und daraus, wenn a, b, ... relativ prim zu m sind:
ist D eine Diskriminante und a eine zu 2D teilerfremde Zahl,
die durch eine Form <p der Diskriminante D eigentlich dar-
stellbar ist, ferner 1 eine in D aufgehende ungerade Primzahl,
so ist der Wert des Symbols nicht von der besonderen
Zahl a, sondern nur von der Formenklasse A, zu der cp gehört,
abhängig. Dasselbe gilt von
(—-A mod D = 0, —4 (mod 16),
\ (X /
7) = 0, — 8
Hieraus lassen sich die Charaktere der Formenklassen
zusammensetzen.
Wir werden bei einer späteren Anwendung den Fall be-
sonders zu berücksichtigen haben, daß D durch 4 teilbar ist.
Wir setzen daher:
(6) D = —4 m1),
und erhalten für diesen Fall, wenn 1,1',... die verschiedenen
in m aufgehenden ungeraden Primzahlen sind, die folgenden
Charaktere:
*) Nach der Bezeichnung von Gauss: Formen erster Art der Deter-
minante — m.
§ 105.
Anwendung des Legendreschen Symbols.
387
(^)’ / a\ \T/’ /a \ \T)' / a\ MV’ ' /a\ MV’ •• m = 3 m = 1 (mod 4), (mod 4),
m he 4 (mod 8),
m © MV’ m = 6 (mod 8),
\ a / ( a\ MA /a\ \v)' ’• m — 2 (mod 8),
(=1 \ \ a /’ \a r /a\ W (!) m = 0 (mod 8).
Die Anzahl dieser Grundcharaktere ist, wie man sieht, gleich
der in § 104, 3. näher bestimmten Zahl Ä und die Anzahl der
Vorzeichenkombinationen ist gleich 2 h
Die Abhängigkeit zwischen diesen Charakteren kann man so
darstellen.
Ist
m — n2m', D = Q2d = —4=n2m'
und n2 die größte in m aufgehende Quadratzahl, so ist
, . z/ = —m', wenn m! = 3 (mod 4),
' z/ = —4m' „ m' = 1, 2 (mod 4);
im ersten Fall ist m' ungerade und nicht gleich 1, also gleich
einer der Primzahlen l oder gleich einem Produkt aus mehreren
von ihnen, und aus
worin das Reziprozitätsgesetz der quadratischen Reste angewandt
ist, ergibt sich eine Relation zwischen den Charakteren.
Im zweiten Fall ist bei ungeradem m'
Z-1X Z^\ _
\ a ) \a ) \m') ~ ’
und dies ist wieder ein Produkt mehrerer der Charaktere (7),
und ist endlich m' = 2 m" gerade, so ist
/—m'\ /+2\ / a \
\ a ) \ a / Xm"/’
wo das Zeichen + so bestimmt wird, daß + m" = 1 (mod 4) wird.
Also ist wiederum die Anzahl der Geschlechter höchstens = 2Ä—L
25*
388
Fünfzehnter Abschnitt.
§ 106.
§ 106. Die Geschlechter der Idealklassen.
In § 100 haben wir gesehen, wie wir aus einer Zahlgruppe
im Körper Sl Einteilungen der Ideale in Klassen ableiten können,
und wie für diese Einteilungen die Klassenzahl zu bestimmen ist.
Wir wollen hier auch die Einteilung in Geschlechter aus
diesem Gesichtspunkte betrachten.
Um unsere Betrachtungen gleich auf die Ordnungen aus-
dehnen zu können, scheiden wir von dem Gebiet der natür-
lichen Zahlen zunächst alle Zahlen aus, die mit irgend einer
beliebig angenommenen Zahl S einen gemeinschaftlichen Teiler
haben.
Hierauf nehmen wir einen positiven rationalen Modul m, und
nehmen in S unter anderen alle Primzahlen auf, die in m ent-
halten sind.
Damit sind also alle Zahlen ausgeschieden, die einen gemein-
schaftlichen Teiler mit m haben.
Aus den übrigbleibenden Zahlen und ihren Quotienten
kann man eine Gruppe rationaler Brüche bilden, die wir mit
Z bezeichnen wollen.
Ersetzen wir (nach Gauss) eine Zahl a-1 durch die
ganze Zahl, die, mit a multipliziert, eine der Einheit
kongruente Zahl ergibt, so können wir die Lehre von
der Kongruenz nach dem Modul m ohne weiteres auf
die gebrochenen Zahlen Z übertragen.
Sind dann a/b und Brüche in Z, so ist a/b = äj/öj,
wenn a bt = aT b im gewöhnlichen Sinne ist.
Vereinigen wir also alle untereinander kongruenten Zahlen
in Z in eine Klasse, so zerfällt Z in <p (m)-Zahlklassen, deren
jede durch eine ganze rationale Zahl repräsentiert werden kann.
Ist df die Gruppe der Zahlen a aus Z, die der Bedingung
a = 1 (mod m)
genügen, so sind die Zahlklassen (modulo m) die Nebengruppen
zu Jü, und es ist
(1) (4 = <p(m).
Wir betrachten nun, wie im § 98, die Gruppen 0 der ganzen
und gebrochenen Zahlen des quadratischen Körpers Q, oder
einer Ordnung [Q] dieses Körpers, von denen wir alle
§ 107. Zusammensetzung der Normenrestgruppen. 389
Zahlen ausschließen, die im Zähler oder im Nenner nicht
relativ prim zu S sind. (Im Falle der Ordnungen müssen
die Primfaktoren des Führers Q in S enthalten sein.)
Wir bilden nun aus AL einen Teiler A, in den wir - alle
Zahlen a aufnehmen, die einer Kongruenz
(2) N (k>) = a (mod m)
genügen, d. h. für die eine Zahl ea in 0 existiert, deren Norm
mit a kongruent ist.
1. Diese Zahlen heißen Normenreste für den Modul m.
Aus der Definition der Normenreste ergibt sich, daß die
Nonnenreste der Multiplikation und Division gegenüber eine
Gruppe bilden.
Ferner ergibt sich, daß jedes Quadrat und jeder quadra-
tische Rest (modulo m) zugleich Normenrest ist, daß also
jeder Normennichtrest zugleich quadratischer Nichtrest
ist. Aus der Gruppennatur von A folgt:
Das Produkt aus Normenrest und Normenrest ist
Normenrest.
Das Produkt aus Normenrest und Normennichtrest
ist Normennichtrest.
Die Gruppe der Nonnenreste hat stets einen endlichen Index
(Z, A), denn sie vereinigt in sich ganze Zahlklassen nach dem
Modul tn, deren Anzahl endlich ist.
§ 107. Zusammensetzung der Normenrestgruppen.
Wir wollen zwei Moduln mT, m2 betrachten, die zueinander
relativ prim sind, und bezeichnen die Gruppen der Normenreste
von m1 und m2 mit AT und A2. Setzen wir für den Augenblick
(Z, A) =
und zerlegen
(i) z = ctj A -j- a2 A 4" * +
so können wir die alt a2, ..., au durch beliebige nach dem
Modul m1 kongruente Zahlen ersetzen. Da mT und m2 relativ
prim vorausgesetzt sind, so lassen sich, welches auch die rationalen
Zahlen c( seien, rationale Xt aus den Kongruenzen
ai A Xim-i = ct (mod m2)
bestimmen, und man kann also die cq so wählen, daß sie in A2
enthalten sind. Man kann also jede Zahl z in Z als Produkt
390 Fünfzehnter Abschnitt. § 108.
einer Zahl in AT mit einer Zahl in A2 darstellen, was wir sym-
bolisch durch
(2) Z — A1 M2
ausdrücken.
Der Durchschnitt A der Gruppen Ai und A2 enthält alle
und nur die Zahlen, die zugleich Normenreste von und von
m2 sind, und wir beweisen, daß A die Gruppe der Normenreste m
(3) m = mlm2
ist.
Ist nämlich a eine Zahl, die zugleich in Ay und in vl2 enthalten
ist, so gibt es zwei Zahlen gj,, k>2 in 0, die den Bedingungen
. . ^V(ß>i) = a (mod mj,
) N(co2) = a (mod m2)
genügen. Es lassen sich nun zwei rationale Zahlen xt, x2 so be-
stimmen, daß
a?! = 1 (mod mj, x2 = 0 (mod Wj),
= 0 (mod m2), = 1 (mod m2),
und wenn wir dann also
(9 = Xj 0; ß)2
setzen, so ist
, . -N(gj) = ^(cjj) = a (mod mj,
''} = N (k>2) = a (mod m2),
und da rn, und m2 relativ prim sind, so ist auch
(6) jN(cj) = a (mod m),
also a Normenrest von m. Umgekehrt ist ein Normenrest von
m zugleich Normenrest jedes Teilers von m, also auch von
und m2.
Hieraus ergibt sich nun mit Hilfe der Sätze 13. und 14., § 100:
(4 Ai) = (Aj^ A2, A^ = (A1A2, AiA) = (A2, A),
(Z, A) = (4 A2) (A2, A) = (Z, (Z, A2),
und wir haben die Beziehung:
(7) (4 4) = (Z, (4 A2).
Damit ist die Frage nach den Normenresten auf den Fall
zurückgeführt, daß der Modul eine Primzahlpotenz ist.
§ 108. Normenreste der Primzahlpotenzen.
Es sei 0 eine Ordnungsgruppe im Körper Si (§ 98) und P,
die Gruppen der rationalen Zahlen, die relativ prim zur Diskri-
§ 108. Normenreste der Primzahlpotenzen. 391
minante D dieser Ordnung und zugleich Normenreste einer Prim-
zahl p in bezug auf diese Ordnung sind, d. h. der Zahlen a,
die der Bedingung
(1) N(ß>) = a (mod p)
für eine Zahl co der Ordnung 0 genügen. Es gilt zunächst
der Satz:
1. Wenn]) nicht in D aufgeht, so ist jede Zahl a in
Z Normenrest.
Es braucht dies nur bewiesen zu werden für den Fall, daß
a ein quadratischer Nichtrest ist, da ja jeder quadratischer
Rest zugleich Normenrest ist.
Es sei also p ein in p aufgehendes Primideal des Körpers
Ist dann D quadratischer Rest von p, so ist p vom ersten
Grade (§ 92), und jede Zahl ist nach dem Modul p mit einer
rationalen Zahl kongruent.
Da p nicht in D aufgeht, so ist das zu p konjugierte Ideal p'
von p verschieden, und wir können eine Zahl ß> in 0 finden, die
den Kongruenzen:
oi = a (mod p),
= 1 (mod p') i)
genügt (Bd. II, § 166). Ist dann co1 zu co konjugiert, so ist
= a, co' = 1 (mod p),
und folglich
W(gj) = a (mod p).
Ist aber D quadratischer Nichtrest von p, so ist p = p, und
p~ I __ ___________
D 2 = —1 (mod p), folglich und für jede Zahl
in 0
. . co? = co' (mod p),
N (co) = cop +1 (mod p).
Ist nun 7 eine primitive Wurzel von p im Körper Si, so ist
c = yr + i (mod p) eine primitive Wurzel von p im Körper der
rationalen Zahlen (Bd. II, § 167).
Setzen wir also
(3) a = +0 x, co = (mod p),
so ist nach (2) N(co) = a (modp) und unser Satz somit bewiesen.
*) Setzt man a = a-i-Sn Q, wo n eine durch p, aber nicht durch p'
teilbare Zahl ist, so kann man die Zahl | aus der Kongruenz a-j-ErrQ = 1
(mod p') bestimmen, und a> gehört wegen des Faktors Q zur Ordnung 0.
392
Fünfzehnter Abschnitt.
§ 108.
2. Ist p eine in D aufgehende ungerade Primzahl,
so ist a dann und nur dann Normenrest, wenn a quadra-
tischer Rest von p ist.
Das ergibt sich unmittelbar aus der Bedingung für die
Normenreste:
(4) x2 — Dy2 = ia (mod p),
die sich in diesem Fall auf x2 = 4 a (mod p) reduziert.
Die Primzahl 2 kommt nicht in Betracht, weil x2 = a (mod 2)
immer lösbar ist, wohl aber die Moduln 4 und 8. Ist JD un-
gerade, so ist D = 1 (mod 4), und die Bedingung für einen
Normenrest a ist:
----® (mod 4) oder (mod 8),
und diese Kongruenz ist für jedes ungerade a lösbar (durch
gerade x, y), also:
3. Geht 4 in JD nicht auf, so ist jede ungerade Zahl a
Normenrest von 4 und von 8.
Ist JD durch 4 teilbar, so ist die Bedingung für einen
Normenrest a die Möglichkeit der Kongruenz:
(5) x2 — ~ y2 = a (mod 4) oder (mod 8).
Da a ungerade ist, so können x und Dy214 nicht beide
ungerade sein.
Geht man hiernach die
einzelnen Fälle durch, so ergibt sich
JD _ 4 ~ 0 (mod 8), a ~ 1 (mod 4), a = 1 (mod 8),
JD = 4 — 1 (mod 8), keine Bedingung für a. 1
JD = 4 — 2 (mod 8), a = -j~ 1, — -1 (mod 8),
D = 4 — 3 (mod 8), a = 1 (mod 4), a = —1, 5 (mod 8),
JD = 4 ~ 4 (mod 8), a = 1 (mod 4), a = -j-1, 5 (mod 8),
JD = 4 — 5 (mod 8), keine Bedingung für a,
JD __ 4 ~ 6 (mod 8), a = -f-1, 3 (mod 8),
JD = 4 ~ 7 (mod 8), a = 1 (mod 4), a = 1, 5 (mod 8).
§ 108. Normenreste der Primzahlpotenzen. 393
Danach haben wir:
4. Ist |Z> = 1 (mod 8), so ist jede ungerade Zahl
Normenrest von 4 und von 8.
Ist |Z> = 0 (mod 8), so sind nur die Zahlen von der
Form 4m -|- 1 Normenreste von 4 und die Zahlen der
Form 8m + 1 Normenreste von 8.
Ist = 2 (mod 4), so sind alle ungeraden Zahlen
Normenreste von 4.
Ist |Z> = 2, oder = 6 (mod 8), so sind im ersten Fall
die Zahlen 8» 1, 8m — 1, im zweiten Fall die Zahlen
8m -j“ 4 4“ Normenreste von 8.
Ist jD = 3, 4, 7 (mod 8), so sind alle und nur die
Zahlen der Form 4m -|- 1 Normenreste von 4 und von 8.
5. Ist p eine ungerade Primzahl, und ein durch p
nicht teilbares a Normenrest von p* (für irgend einen
positiven Exponenten fc), so ist a auch Normenrest
von p'c + 1.
Zum Beweis sei
N (cj) = a 4~ p1- b,-
(öj = W (1
worin x rational. Folglich
N (cjj) = (a -j- p11 &) (1 -j- a;^)2,
= a p* (b a x") (mod #Ä+1)>
und wenn x aus der Kongruenz b -|- a x = 0 (mod p) bestimmt
wird, so folgt
N’(cjj) = a (mod p'c + 1)-
6. Ist D ungerade, so gilt dasselbe auch noch für
p — 2.
Denn in diesem Falle ist jedes ungerade a Normenrest von 8.
Man setze also
1V(«) = a + 2Äi, li 3,
w1 = gj ^1 2'ca;
jV (cjj) = (a 4~ 2'CZ>) (1 2'ca;) (mod 2l: + 1))
und wenn man ax 4~ & = 0 (mod 2) annimmt, so folgt
N(gj-l) = a (mod 2fe+1)-
7. Ist D gerade und a Normenrest von 2'c 8, so ist
a auch Normenrest von 2'c + 1.
394
Fünfzehnter Abschnitt.
§ 108.
Denn man setze
JV (ö) = a -|- 2fe b,
Wj = co (1 -|- 21c~1x'),
worin x rational. Dann ist 2 7c — 2 >> k, und folglich
= (a 2'c6) (1 -|- 2lcx') (mod 2/c+1);
= a 2/c (b «> %)’,
wenn also
so ist
ax -|- b = 0 (mod 2),
jV(k>l) = a (mod 2'c + 1).
Aus alledem ergibt sich nun folgender Satz:
8. Ist eine Zahl r in Z
D aufgehenden ungeraden
bei geraden D
r = 1 (mod 8)
a) Ir = —1, —1 (mod 8)
r = 1, 3 (mod 8)
b) r = —1,' — 5 (mod 4)
quadratischer Rest jeder in
Primzahl, und ist außerdem
falls y = 0 (mod 8),
» 7 = 2 (mod 8)>
„ 7 — 6 (mod 8)’
” 7 = 3’ 4’ 7 (mod 8)>
so ist r Normenrest von jedem beliebigen zu r teiler-
fremden Modul m.
Diese Zahlen r bilden eine Gruppe P, die wir die Gruppe
der absoluten Normenreste nennen.
Ist b ein fester quadratischer Nichtrest der ungeraden Prim-
zahl p, und g eine Zahl in Z, so ist entweder g oder b~
in der Gruppe der Normenreste enthalten. Ist also P die Gruppe
der Normenreste von p*, so ist
(Z, P) = 1, wenn p nicht in D auf geht,
(Z, P) = 2, wenn p in D aufgeht,
ferner, wenn L die Gruppe der Normenreste von 2k ist:
(Z, L) = 1, D = 1 (mod 4),
D = 4, 20 (mod 32),
(Z, L) = 2, D = 8, 12, 16, 24, 28 (mod 32),
(Z, L) — 4, D = 0 (mod 32) x).
Es ist nicht zu befürchten, daß das in § 99 und in Bd. II, § 21
erklärte Symbol (Z, P) für den Index eines Teilers einer Gruppe mit dem
in § 85 ähnlich bezeichneten erweiterten Legendre-Jacobischen Symbol
verwechselt werde.
§ 109.
Die Geschlechter der Ideale.
395
9. Bezeichnen wir also mit v die Anzahl der ver-
schiedenen ungeraden in D aufgehenden Primzahlen, so
ist nach § 98, 12.
(Z, 22) = 2”,
(Z, R) = 2”+’,
(Z, 22) = 2-+2,
oder allgemein
D = 1 (mod 4), D = 4 (mod 16),
D = 8, 12, 16, 24, 28 (mod 32),
D = 0 (mod 32),
(Z, R) = 21,
wo A dieselbe Bedeutung hat wie in § 104, 3.
Diese Zahl stimmt, wie man sieht, mit der Anzahl der
Stammteiler von D überein, und aus 8. folgt, daß ein absoluter
Normenrest r diese Eigenschaft behält, wenn r um ein Vielfaches
von D vermehrt wird.
Daraus der Satz:
10. Die absoluten Normenreste sind in einer end-
lichen Anzahl von arithmetischen Progressionen, die
nach Vielfachen von D fortschreiten, enthalten.
Die in D aufgehenden ungeraden Primzahlen und in den
Fällen a) und b) von Nr. 8 die Zahl 8 oder 4 heißen die charak-
teristischen Primzahlen und Primzahlpotenzen der Ord-
nung.
§ 109. Die Geschlechter der Ideale.
Nach dem Vorigen können wir die Gesamtheit der rationalen
Zahlen mit Ausschluß derer, die zu D im Zähler oder Nenner
nicht relativ prim sind, in fi Klassen (Nebengruppen) zerlegen,
wobei
(1) (3 22) = ft
der oben bestimmte Wert ist. Hiernach ist:
(2) Z = 22 ——]— 223 ... —|— 22« _ !•
Wenn eine Zahl z in eine dieser Nebengruppen gehört, so
gehören alle mit z nach dem Modul D kongruenten Zahlen in
dieselbe Nebengruppe.
11. Die Hauptklasse 22 der Normenreste ist bei der
Multiplikation und Division eine Gruppe.
Gehört r in die Hauptklasse 22, so gehören zwei Zahlen z
und rz in ein und dieselbe Klasse.
Die Gesamtheit der zu D teilerfremden ganzen und ge-
brochenen Ideale a des Körpers ß bilden auch eine Gruppe 0.
396
Fünfzehnter Abschnitt.
§ 109.
12. Wir teilen die Ideale a in Geschlechter G, Gj, G2, ...
ein, indem wir alle Ideale or, deren Normen W(a„) in einer
Klasse Bv enthalten sind, in ein Geschlecht G„ vereinigen.
13. Die Ideale, deren Normen zugleich Normenreste r
sind, gehören dem Hauptgeschlecht G an, und das Haupt-
geschlecht ist selbst eine Gruppe.
Wollen wir gleich die Ordnungen berücksichtigen, so müssen
wir auch Äquivalenz nach der Ordnung [$] zulassen (§ 100),
was ja (für Q — 1) die allgemeine Äquivalenz einschließt. Dann
gilt das Folgende:
14. Die Ideale der Hauptklasse gehören dem Haupt-
geschlecht an, und äquivalente Ideale haben dasselbe
Geschlecht.
Denn ist a äquivalent mit cq, so gibt es eine Zahl q in [$],
für die (1=17^ ist; folglich ist W(a) = N(rj) ^(tq) und N(y) ist
eine Zahl in B. Folglich gehören a und cq nach 13. in dasselbe
Geschlecht. Die Geschlechter umfassen daher nicht bloß die
einzelnen Ideale, sondern die Idealklassen.
Damit eine Zahl a aus Z Idealnorm sein kann, ist eine
gewisse Bedingung zu erfüllen. Ist nämlich
(3) a = N(a),
und zunächst 0 ein primäres ganzes Ideal, so ist nach § 91
(4) z/ = b- — 4ac,
worin b, c ganze rationale Zahlen sind, und folglich ist
(5) (z/, a) = +l.
Ist a nicht primär, sondern gleich moo mit primärem c0, und
a0 = W(a0), so ist a = m2a0, und folglich muß nach § 85, (15)
auch hier die Bedingung (5) befriedigt sein, und das gleiche ergibt
sich auch für gebrochene Zahlen, wenn Zähler und Nenner relativ
prim zu D sind, wenn man in (5) a als ganzzahligen Repräsen-
tanten seiner Klasse nach dem Modul D ansieht.
Da es nun Zahlen a gibt, für die (z/, a) = — 1 ist, so
kann nicht jede Zahl in Z Norm eines Ideals sein, und die Anzahl
der Geschlechter ist also kleiner als ft. Sie muß ein Teiler von
fi, d. h. eine Potenz von 2 sein, und folglich haben wir den Satz:
15. DieAnzahl g der Geschlechter ist höchstens gleich
I (4 B),
also der Hälfte der in 9. bestimmten Zahl.
§ 109. Die Geschlechter der Ideale. 397
Daß diese Zahl wirklich die genaue Anzahl der Geschlechter
ist, werden wir später beweisen. Wir bemerken hierzu noch
folgendes:
Die Tatsache, daß es für jedes z/ Zahlen a gibt, für die
(z7, a) = — 1 ist, folgt aus dem Reziprozitätsgesetze der quadra-
tischen Reste. Kann man, ohne dieses Gesetz vorauszusetzen, die
Existenz solcher Zahlen a nachweisen, so läßt sich umgekehrt
dadurch ein Beweis des Reziprozitätsgesetzes ableiten. In dieser
Weise hat Gauss seinen zweiten Beweis dieses Gesetzes her-
geleitet. (Vgl. Dirichlet-Dedekind, § 152ff.)
Ist r ein Normenrest und d irgend ein Stammteiler von Z>,
so ist
(6) W(«) = ~ r (mod d)
und folglich, wenn r relativ prim zu d ist,
(7) ' (d,r) = +l.
Für ungerade d ist dies evident, für die geraden folgt es
leicht in den verschiedenen Fällen von § 108. Wir setzen also
allgemein, wenn z relativ prim zu D ist:
(8) %(^) = (d, 4
Dann ist (d, r) = 1 für jede Zahl r der Gruppe der ab-
soluten Normenreste, und allgemein ist
(9) ZOW = iW
Für alle Ideale a des Hauptgeschlechtes, die zu I) teiler-
fremd sind, ist
Z[W(o)] = +1,
und daraus folgt, daß %[W(u)] für alle Ideale o eines Ge-
schlechtes einen und denselben Wert %(G) hat.
Diese Funktionen sind also die Charaktere der Gruppe
der Geschlechter.
Sechzehnter Abschnitt.
Klassenzahl in quadratischen Körpern.
§ 110. Fundamentale Einheiten in den Ordnungen.
Die Theorie der Einheiten, die wir allgemein in Bd. II, § 191
auseinandergesetzt haben,, nimmt für die quadratischen Körper
eine einfachere Gestalt an, muß aber andererseits erweitert und
für die Ordnungen ausgebildet werden.
Die ganzen Zahlen der Ordnung 0 mit der Diskriminante JD
sind nach § 96, (6) in der Form aq x2f) enthalten, worin
6 = | ]/Z>, wenn D = 0 (mod 4),
0 = „ D = 1 (mod 4),
und scj, x2 ganze rationale Zahlen sind.
Eine solche Zahl s ist eine Einheit, wenn
(1) N («) = (x! x20) (aq a;20') = +1
ist. Hierfür ergibt sich die Bedingung
(2) x% — x£D = +4.
Ist D negativ, so kann hier nur das positive Zeichen stehen,
und es gibt im allgemeinen nur die zwei Lösungen x = + 2,
y = 0 und in den beiden Ausnahmefällen die vier oder sechs
Lösungen:
JD = -4, aq = + 2, x± — 0, x2 — 0, x2 = +1.
D = — 3, aq = + 2, a?i = +1, X2 = 0, ,rä = +1.
§ 110. Fundamentale Einheiten in den Ordnungen. 399
Daraus folgt:
1. Für ein negatives D gibt es im allgemeinen nur
die zwei Einheiten
E = —1, E — ---1,
und für zwei besondere Fälle
D — 4: s = —|— 1, — 1, —|— i, — i,
D = —3: s = +1, —1,
i +1/=3 i — ! i + , i —
2 ’ 2 ’ ' 2 ’ 2 '
Die von Null verschiedenen Zahlen der Ordnung 0 sind
dann zu je zwei oder in den beiden Ausnahmefällen zu je vier
oder zu je sechs assoziiert.
2. Ist D positiv, so gibt es eine Lösung der Feil-
schen Gleichung:
T* 2 — UW = + 4,
in der T und U positive und möglichst kleine Werte
haben. Ist dann _
_ T + U^D
£ ~~ 2
so sind alle Einheiten in der Form +e±’’ enthalten, wo
v die Reihe der Zahlen 0, 1, 2, ... durchläuft.
Ist die Gleichung (2) für das negative Zeichen lösbar, so
ist N(e) — —-1, und es hat + s±’' für gerade v eine positive,
für ungerade v eine negative Norm. Ist aber (2) nur für das
obere Zeichen lösbar, so haben alle Einheiten positive Norm.
Unter den Zahlen y der Ordnung 0, die nicht Einheiten sind,
gibt es aber immer solche mit negativer Norm.
Ist W(s) = — 1, so gibt es zu jeder Zahl y in 0 mit negativer
Norm eine assoziierte mit positiver Norm. Ist aber W(s) =-|-1,
so zerfallen die Zahlen y in zwei Klassen, von denen die eine
positive und die andere negative Norm hat, und keine Zahl der
einen Klasse ist mit einer der anderen Klasse assoziiert.
Demgemäß betrachten wir nur die Zahlen y der Ordnung 0
mit positiver Norm, unter denen y und +s±’,j/ nur dann
assoziiert sind, wenn
_ T + U]ÜD
£ 9
400 Sechzehnter Abschnitt. § 110.
die fundamentale Einheit mit positiver Norm, also T, U die
kleinste positive Lösung von
(3) T* — U*D = +4
ist.
Bei positiver Diskriminante gibt es unendliche Scharen asso-
ziierter Zahlen, und es kommt darauf an, durch eine passende
Bestimmung von jeder dieser Scharen eine bestimmte auszuson-
dern. Dazu bieten uns die allgemeinen Betrachtungen von Bd. II,
§ 195 die Hilfsmittel, die wir jetzt auf unseren speziellen Fall
anwenden.
Es sei nach § 98 __
Ä — atj -j------^2
eine Basisform in der Ordnung [$] eines Ideals a, das wir
primär voraussetzen wollen und
, b + fD
y = axl -j-------
(4) -
, , b — ^D
y = aa?r_|--------
mit ganzen rationalen xx, x2 eine durch a teilbare ganze Zahl y
in [$] mit positiver Norm nebst ihrer Konjugierten y', und da
wir a als primär vorausgesetzt haben, so ist
(5) a = N(a).
Es sei ferner
g = t+ i/yä
(6) 2 ’
v ’ £, _ T — XJ\D
die fundamentale Einheit in 0 mit ihrer Konjugierten, die beide
positiv sind und positive Norm haben.
Wir bestimmen die Zahlen und aus den linearen
Gleichungen:
illogs + = log|2/|,
Ijlogs' + |2 = log|j/'|,
lo§? = lo§\i ’
c I V
& = pog|«/«/'|,
worin |j/| den absoluten Wert von y bedeutet.
§ 110. Fundamentale Einheiten in den Ordnungen. 401
Ersetzt man y durch eine assoziierte Zahl so geht
in £, k über, worin k eine positive oder negative ganze Zahl
ist, und man kann also y unter den Assoziierten immer auf eine
Weise so wählen, daß
(8) 0 < 1
wird. Die so bestimmte Zahl y ist dann die reduzierte
Zahl.
Beachtet inan noch, daß die Gleichungen (7) sich nicht
ändern, wenn y durch —y ersetzt wird, so folgt:
3. In einer Schar assoziierter Zahlen gibt es immer
zwei und nur zwei reduzierte Zahlen, die sich nur im
Vorzeichen unterscheiden.
Aus (7) ergibt sich, wenn g, der Bedingung (8) genügt:
° = 1OS|^I<1OS?’
daraus
(9)
und
(10)
und
umgekehrt folgen aus (10) wieder die Gleichungen (7) mit
der Bedingung (8).
Da wir überdies vorausgesetzt haben, daß y eine positive
Norm haben soll, so haben «/, y' das gleiche Vorzeichen, und dieses
ist positiv, wenn rr, positiv ist. Denn dann ist y — y' = x2
positiv, und da |j/| > \y'\ ist, so müssen y und y' positiv sein.
In dem besonderen Falle x2 — 0 ist y und y' positiv, wenn
wir xY positiv voraussetzen. Damit ist dann die in 3. noch übrig-
gebliebene Zweideutigkeit beseitigt.
Da also y und y' positiv sind, so folgt aus (10):
(11) — ys'>0.
Woraus nach (4) und (6):
(12) 2 a Ux2 — (T — b U) x2 >. 0, x2 0.
Und diese Bedingungen, die wir die Isolierungsbedin-
gungen nennen, schließen bereits in sich, daß y' und folglich
N(y) positiv ist. Denn nach (3) ist
t > ü yz>,
und demnach folgt aus (12):
ü [2 a xr (b — ^Djx^ > 0.
Damit ist bewiesen:
Weber, Algebra. HI. 26
402
Sechzehnter Abschnitt.
§ Hl.
4. Ist a ein ,zu Q teilerfremdes Ideal, so liefert uns
yedes den Bedingungen (12) genügende Zahlenpaar xt, xa
eine durch a teilbare positive Zahl y mit positiver Norm
der Ordnung [$]
/, ___ < & —i— vd
(i3) y = axt -|------L-4 5—a>2,
und unter diesen Zahlen sind keine zwei assoziiert.
§ 111. Die Dirichletsche Grenzformel.
Bedeutet t eine positive Konstante, so ist durch die Be-
dingung :
(1) N(y) = a(axf bxrx2 -f- cxf) f,
und, bei positiver Diskriminante, durch die Isolierungsbedingungen,
in einer Ebene, in der x^, x2 rechtwinkelige Koordinaten sind,
ein Gebiet Ft begrenzt, das bei negativer Diskriminante durch
eine Ellipse, bei positiver Diskriminante durch einen Hyperbel-
bogen und durch gerade Linien begrenzt ist. Die Punkte, deren
Koordinaten x1, x2 ganze rationale Zahlen sind, heißen Gitter-
punkte.
Einem ganzen System von assoziierten Zahlen, deren Norm
positiv und kleiner als t ist, entspricht dann bei positiver Dis-
kriminante ein Gitterpunkt in Ft und bei negativer Diskriminante
zwei und in den beiden Ausnahmefällen vier und sechs Gitter-
punkte.
Bezeichnet Zt di'e Anzahl der Gitterpunkte in dem Gebiete
Ft und V die Fläche des Gebietes Ft,, so ist [Bd. II, § 194, (6)]:
(2) V = ZtC1 +
worin Rf mit unendlich wachsendem t nicht unendlich wird.
Bei negativer Diskriminante erhält man V aus dem bekannten
Flächeninhalt: der Ellipse:
und bei positiver Diskriminante erhält man ihn am einfachsten,
indem man nach § 110, (7j an Stelle von xt, x2 die Integrations-
variablen £2 einführt, deren Grenzen 0,1 und —oo,0 sind:
(4)
a^/D
§ 111.
Die Diriehletsehe Grenzformel.
403
Hiernach ergibt sich aus (2):
(5)
__ 2?r
Nach Bd. H, § 196, 4. ist aber
und es ergibt sich also aus (5):
Hier durchläuft y die Reihe der ganzen Zahlen der Ordnung
[Q], die durch ein zu Q teilerfremdes primäres Ideal a teilbar
sind, wobei jedoch von einer Schar assoziierter Zahlen immer
nur ein Repräsentant, der jetzt beliebig gewählt sein kann, beizu-
behalten ist (bei negativen D zwei oder vier oder sechs).
Hierbei sind unter assoziierten Zahlen (nach der Ordnung
[$]) solche zu verstehen, deren Quotient eine Einheit der
Ordnung Q ist.
Wir wollen jetzt von den Zahlen y noch aUe die ausschließen,
die nicht relativ prim zu Q sind. Dann modifiziert sich die
Summe (6) in folgender Weise: Ist r ein Primfaktor von Q, so
sind alle Zahlen der Ordnung [$], die zu r nicht teilerfremd
sind, durch r teilbar, weil sie ja nach dem Modul r mit einer
rationalen Zahl kongruent sind..
Setzen wir also
(?) y = ryly
so ist yi durch a teilbar, braucht aber nicht der Ordnung [$],
sondern nur der Ordnung = [^x] anzugehören. Ist bei
positiver Diskriminante die fundamentale Einheit der Ordnung
[Ox], so ist
(8) s =
eine Potenz von und es ist Die Zahlen
(9) . y — ryY a*, t = 0, 1, 2, ..., k — 1
26*
404 Sechzehnter Abschnitt. § 111.
haben alle dieselbe Norm; sie sind assoziiert nach [(),], aber
nicht nach [()]. Demnach erhalten wir nach (6):
T. X” s — 1 r log«
Lim > , ---r- = ---T= —2— ;
,=1 (Ny^ a\JD k
um daraus die auf die Zahlen (9) bezügliche Summe zu erhalten,
hat man; da N(«x) — 1, N(r) = r2 ist, mit k zu multiplizieren
und mit r2 zu dividieren. Man erhält so:
Lim $ T log«.
^(Ny)s ra^D 8
Zieht man dies von der Summe (6) ab und verfährt ebenso
mit allen Primfaktoren r von Q, so ergibt sich:
(10) Lim S. X7—'4 = TT (1 — — log «, D >> 0,
und noch einfacher bei negativer Diskriminante:
worin sich die Summe nur auf die Zahlen y erstreckt, die
zu Q teilerfremd sind, und das Produkt 71 sich auf alle
Primfaktoren von r bezieht. Nur in den beiden Ausnahmefällen
JD = —4, JD = —3 ist die rechte Seite der letzten Formel
noch durch 2 oder durch 3 zu dividieren.
Zerlegt man y in Idealfaktoren
(11) y = am,
so durchläuft m alle Ideale einer bestimmten Idealklasse nach
der Ordnung [$], die zu Q teilerfremd sind. Diese Klasse ist,
wenn a in die Klasse A gehört,
JMJ = A~\
und unter den Zahlen
N(t/) = aN(m)
kommt im Falle der positiven Diskriminante jedes N(m') nur ein-
mal, im Falle einer negativen Diskriminante zwei- oder vier- oder
sechsmal vor.
Demnach ergibt sich aus (10):
§ 112. Klassenzahl. 405
und in den beiden Ausnahmefällen D = — 4, JD = — 3 ist der
letzte Ausdruck durch 2 oder durch 3 zu dividieren.
Es durchläuft hierin m die Gesamtheit der Ideale
einer Klasse (nach [$]), und man sieht, daß dieser Grenz-
wert von dieser besonderen Klasse nicht abhängig ist.
Es ist bisweilen zweckmäßig, in der Summe auf der linken
Seite der Formel (12) nicht bloß solche Ideale von tn auszu-
schließen , die mit. Q einen Teiler gemein haben, sondern auch
die, die nicht teilerfremd zu zf sind. Die Formel (12) gilt unter
dieser Voraussetzung unverändert, wenn man unter den r der
rechten Seite nicht nur die Primteiler von Q, sondern alle Prim-
teiler von D versteht.
Ist nämlich r ein in D, aber nicht in Q auf gehendes Prim-
ideal, so ist N(y) = Zj eine in JD, aber nicht in Q aufgehende
natürliche Primzahl, und es ist W(rtn) = IV’(m). Nimmt man
also von der Summe der linken Seite von y die den rtn ent-
sprechenden Glieder noch weg, so kommt rechts der Faktor
A 1 \ k-
(1------) hinzu.
\ rJ
5. Der Grenzwert in der Formel (12) ist nur von der
Diskriminante JD, nicht von der besonderen Klasse JH
abhängig und ist stets von Null verschieden.
§ 112. Klassenzahl.
Wir nehmen nun eine Funktion F(z) an, die übrigens nur
für ganzzahlige Werte von z definiert zu sein braucht, von der
wir voraussetzen, daß die unendliche Reihe
(1) ZF (Na),
in der a die Gesamtheit der Ideale des Körpers (oder nur
einen Teil davon) durchläuft, unbedingt konvergent sei. Wir
wollen, wenn es sich um Ordnungen [Q] handelt, von a alle die
ausschließen, die nicht relativ prim zu Q sind.
Irgend eine natürliche zu Q teilerfremde Zahl m kommt
dann unter den N(a) nach § 93, 4.
n
Z(d,n)
mal vor, wenn n die Teiler von m durchläuft, und wir erhalten
die Formel:
tn n
(2) 2? F(Na) = 2? 2? (zf, ri) F(m),
406
Sechzehnter Abschnitt.
§ 112.
worin m alle positiven ganzen Zahlen, die zu Q relativ prim sind,
und n für jedes m die Teiler von m durchläuft.
Ordnen wir auf der rechten Seite von (2) nach n, so kommen
für ein gegebenes n unter den m alle Vielfachen von n vor, und
wir können auch setzen:
m n
(3) ZF (Na) = SS(d,n)F(mn),
worin jetzt m und n, voneinander unabhängig, alle natürlichen
Zahlenwerte annehmen, die mit Q keinen Teiler gemein haben.
Ist im besonderen F so beschaffen, daß
(4) F(mn) = F(m)F(n)
ist, so können wir (3) auch so darstellen:
a m n
(5) . SF(Na) = 2F(m)2(J,n)F(n).
Bei den Summen - nach m und n sind die Zahlen aus-
geschlossen, die mit Q einen Teiler gemein haben.
Ebenso sind auf der linken Seite die Ideale ausgeschlossen,
die zu Q nicht relativ prim sind.
Die Formel (5) können wir zunächst anwenden, um aus den
Formeln des vorigen Paragraphen die Klassenzahl zu bestimmen.
Man erhält auf diese Weise auch das Verhältnis der Klassenzahl
im Körper zu der Klassenzahl nach der Ordnung [$]. Da wir
dieses Verhältnis aber schon auf anderem Wege bestimmt haben
(§ 100), so wollen wir .uns hier auf die Klassenzahl des Kör-
pers beschränken, d. h. wir wollen Q = 1 setzen.
Setzen wir in (5) F(z) — z~s, so findet die vorausgesetzte
unbedingte Konvergenz statt, solange s > 1 ist. Multiplizieren
wir aber mit s — 1 und lassen s in 1 übergehen, so können wir
von § 111, (12) Gebrauch machen.
Diese Formel wenden wir in der ersten Fassung an, bei
der tu die zu Q teilerfremden Ideale der Klasse M durchläuft
und r die Primfaktoren von Q bedeuten. Diese fallen also für
Q = 1 ganz weg, und m ist in der Summenformel:
z/ > 0
__ TT
- v=^’
keiner Beschränkung in bezug auf
worfen.
z/ 0
Teilbarkeit mehr unter-
§ 112.
Klassenzahl.
407
Jeder Teil der Summe auf der linken Seite der Formel (5),
der sich auf eine Idealklasse bezieht, gibt dann denselben Beitrag
zu der Summe, und wir erhalten:
(7) Lim(s — 1)3\—r zf > 0
' 7 s=iv ’ ms ns '
= h z/ < 0.
y_z/
. Hier ist h die Klassenzahl des Körpers Sl, und um
nicht immer wieder die beiden Ausnahmefälle zf = —4,
zf = —3 anführen zu müssen, wollen wir festsetzen, daß
in diesen beiden Fällen, in denen die Klassenzahl 1 ist,
unter h der Wert | oder | verstanden werden soll.
So oft n ein volles Restsystem nach dem Modul zf durch-
läuft, ist 2?(z/,n).= 0 [§ 85, (22)], und folglich bleibt die Summe
2?(z/,n), wenn die n der Größe nach geordnet sind, wie weit
auch n wächst, immer endlich. Danach ist der Satz Bd. II,
§ 196, 1. anwendbar, nach dem
s = i ns n
ist. Andererseits ist
Lim (s — 1)2?— = 1
(Bd. II, § 196, S. 723), und es ergibt sich aus (7):
Alog« = Vz/ w) zZ > 0
1, 00
(8) . _________________ n Z
A % = l/— z/ z7 <C 0.
r n
1, 00
Die Summe
ö = 2?
n..
läßt sich in endlicher Form darstellen. Es ist nämlich nach
' ____ -fc znkrti
(9) Vzf (z/,n) = 2?(z/,fc)e J ,
worin k ein vollständiges Restsystem nach dem Modul zf durch-
läuft und bei negativer Diskriminante —z/ zu setzen
ist. Danach folgt:
i 7c n t Znkrti
408
Sechzehnter Abschnitt.
§ 112.
und da ö reell ist:
A 4 > 0. ö * Tc sw » j 2nkit cos ——, A
A < o. i A i . mkit
n sm -• — A
Die beiden unendlichen Reihen nach n haben aber bestimmte
Werte, die Abel in der Abhandlung über die Binomialreihe aus
der Potenzwickelung von log (1 — g) abgeleitet hat, und die sich
auch aus der Theorie der Fourierschen Reihen ergeben. Wird
dann k positiv und zwischen 0 und +z7 genommen, so ergibt sich:
x-'i 1 2nkn . / . k?t\
>, — cos —3— = — log 2sm— ,
n A ö \ z/ /’
21.2nkit a /„ 2k \
— sm-------— = -(1---------)•
n —A 2\ —A)
Also ergibt sich aus (8) [mit Rücksicht auf 2 (A, k) = 0]:
* kir
k log s = — 2 (A, k) log sin ,
1
k = ^2?(z/,Ä)Ä,
Für den Fall der negativen Diskriminante
Ausdruck für k so umgestalten, daß er die Form einer ganzen
Zahl annimmt.
Ist zunächst A ungerade (= 1 mod 4), so kann man die
Zahlenreihe k so zerlegen:
— A — v, A
— A — 2v, <''V 2’
z/ > 0,
(10)
z/ < 0.
kann man den
v,
2 v,
und erhält also, da hier (zf,—v) = —(4v) ist (§ 85), zwei
Formen des Ausdrucks k:
Q v v
k = — 2?(z7,v)v 2(A,v),
4 r
k = — 2(A,2v)v -f- 2 (A, v),
woraus, wenn man die erste mit 2, die zweite mit (zf, 2) multi-
pliziert und subtrahiert:
(11) [2 — (z/, 2)] k = 2 (A,v).
Wenn also (z/, 2) = —1 ist, so muß die rechte Seite
durch 3 teilbar sein.
§ 113.
Die Anzahl der Geschlechter.
409
Für den Fall eines geraden zf zerlegt man k in
z/ , • z/
v, —-2+^ 0<v<2-
und wendet die Formel an:
— f + ") = —(^v),
die sich aus den Sätzen des § 85 leicht ergibt.
Dann findet man zunächst:
h = ±S(A,V),
und wenn man die v nochmals zerlegt in
(12)
A = 2?(z7,ft).
Die Formel für positive Diskriminanten läßt sich mit Hilfe
der Kreisteilungstheorie umformen, worauf wir hier nicht eingehen
wollen.
(2)
§ 113. Die Anzahl der Geschlechter.
Die Formel (5) des vorigen Paragraphen gestattet die Be-
stimmung der genauen Anzahl der Geschlechter nach Dirichlet.
Wir verstehen unter d irgend einen Stammteiler von D und setzen:
F(z) = “7^5 wo z relativ prim zu D ist,
F(z) — 0, wenn z und D einen gemeinsamen Teiler haben.
Dann ist (d, Wa) einer der Charaktere des durch u bestimmten
Geschlechtes. Bezeichnen wir diesen Charakter also mit (d,J.),
so folgt aus § 112, (5):
'V (d A} 'V 1 = 'V 'V .
V ’ > (jyms ns
Darin ist d' = dzf und kann, da n relativ prim zu D ist,
auch durch den Stamm von dz/ ersetzt werden (nach der sym-
bolischen Multiplikation in § 104). Ist d = 1, so ist d' = zf,
und ist d = z/, so ist d' = 1.
Von den beiden Fällen d = 1, d = z/ abgesehen, behalten
also die Summen auf der rechten Seite von (2) für s = 1 einen
endlichen Wert (die nach dem vorigen Paragraphen durch Klassen-
zahlen der Diskriminanten d, d' ausdrückbar sind).
Auf der linken Seite von (2) durchläuft in der Summe nach ct
das Zeichen a die Gesamtheit der Ideale der einzelnen Klassen,
410
Sechzehnter Abschnitt.
§ HB.
und die Summe > über eine Klasse A ausgedehnt, hat
für s=l einen bestimmten von Null verschiedenen Grenzwert,
der nach § 111, 5. für alle Klassen der gleiche ist. Daraus folgt
nach 2.:
(3) . i(d,A) = 0,
außer wenn d = 1 oder = A ist,
(4) i(d,-ä)=Ä,
wenn d = 1 oder = A ist [weil (A,A) = 1, § 104, (10)].
Ferner ist für jede Klasse Ao des Hauptgeschlechts (d, Ao) = b
während es für jede Klasse A, die nicht dem Hauptgeschlecht
angehört, wenigstens ein dx. gibt, so daß (d15 A) — —1 ist.
Daraus folgt, wenn 2” die Anzahl der Stammteiler ist,
(5) 2?(d,A) = 2*’,
9 9
(8U A) S (8, A) = 2?(ddx,A),
und da d d, zugleich mit d die Gesamtheit der Stammteiler
durchläuft (wenn man d dx nach der symbolischen Multiplikation
in § 104 reduziert):
d d
(dx, J.) 2? (d, A) - 2(8, A),
und wenn also (d[, A) = — 1 ist:
(6) 2?(d,J.) = 0.
Hiernach können wir die Doppelsumme
A
2?2?(d,^)
auf zwei Arten bestimmen. Es ergibt sich nach (3), (4):
9 A
(7) 2?2?(d,AL) = 2h,
und nach (5), (6):
6 A
(8) 2?2?(dM) = 2^,
wenn g die Anzahl der Klassen des Hauptgeschlechtes (und folg-
lich jedes Geschlechtes) bedeutet. Die Vergleichung gibt:
(9) h = 2”-^,
also den Satz:
6. Die Anzahl der Geschlechter ist genau gleich
21'-x, d. h. gleich |(Z,2?), § 108, 9.
DRITTES BUCH.
KOMPLEXE MULTIPLIKATION.
Siebzehnter Abschnitt.
Elliptische Funktionen und quadratische Formen.
§ 114. Singuläre Perioden der doppelt periodischen Funktionen.
Bezeichnen wir mit (w) eine doppelt periodische Funktion
mit den Perioden ro15 <a2, so besitzt, wenn n eine ganze Zahl be-
deutet, g>(nw) dieselben Perioden, und hierauf beruht die Multi-
plikation der elliptischen Funktionen, die im sechsten Abschnitt
betrachtet wurde. Es entsteht nun die Frage, ob sich nicht noch
auf andere Weise ein Multiplikator (i so bestimmen läßt, daß
cp Qi w) die Perioden cor, co2 besitzt, ob also eine Multiplikation
auch mit nicht ganzzahligem Multiplikator existiert. Dies wird
dann und nur dann der Fall sein, wenn für ein System ganzer
Zahlen a, b, c, 8 die Gleichungen bestehen:
(i oj1 = a coi -|- b <a2,
[i a>2 = c »i -|- 8 gj2.
Setzen wir, um die darin enthaltene Forderung näher zu
ergründen:
: »2
co = —
und nehmen an, daß co einen positiven imaginären Bestandteil
habe, so folgt:
[i = a bco,
Solange co als variabel betrachtet wird, ist diese Gleichung
nur möglich, wenn b — c = 0, a = d und fi also eine ganze
Zahl ist.
414 . Siebzehnter Abschnitt. " § 114.
Ist dagegen die Gleichung (1) nicht eine identische, so ist co
die Wurzel einer ganzzahligen quadratischen Gleichung:
(2) & co2 —|— (« — 8) ca — c = 0,
also, wenn wir
a c — bc = n
m = — 4 b c — (a — 8)2 = 4 n — (a 8)2
setzen, so ist
m =_ 0 oder = — 1 (mod 4),
und es ergibt sich:
— a + 8 |/— m
05 - ~ 26
____ a + 8 -f- — m
“ — 2 ’
.__ a 8 |/—m ad— y—m
ji2 — (a -|- 8) p + « = 0.
Damit co einen positiven imaginären Teil habe, muß m und
umsomehr also n positiv sein, und ist eine komplexe, ganze,
algebraische Zahl. Daher erklärt sich die Bezeichnung komplexe
Multiplikation.
Wenn nun umgekehrt co einer quadratischen Gleichung
(3) J.a>2 _|_ Bä _|_ C = 0
genügt, worin A, B, C ganze Zahlen sind, und die Diskriminante
(4) B = B1-4ÄC
negativ ist, so ist co nicht reell, und in einer der beiden Wurzeln
von (3) ist der imaginäre Teil positiv. Diese soll für co- genommen
werden. Es heißt dann co eine Wurzel der quadratischen Form
(AL, B, C).
Unbeschadet der Allgemeinheit können A, B, C ohne gemein-
samen Teiler und A, C positiv angenommen werden. Es lassen
sich dann für co unendlich viele Relationen von der Form (1) [oder
(2)] aufstellen. Man hat nur,. wenn x eine ganze von Null ver-
schiedene Zahl ist, zu setzen:
b = Ax, '
(5) c = — Cx,
a — 8 — Bi.
§ 114. Singuläre Perioden der doppelt periodischen Funktionen. 415
Setzt man noch
(6) - a -|- 8' = y,
so folgt:
w -4- Bx
a = -----2---’
(7) b = Ax,
c = — C x,
y — Bx
=
woraus sich, wenn
ad — bc = n
gesetzt wird, ergibt:
(8) 4n = y2 — Dx2.
Die Zahl n wird also in die beiden komplexen ganzzahligen
Faktoren __
____ y + xtfD y — x \D
n ~ 2 2
zerlegt. Für co und y findet sich noch:
—-B4-1/D 2C
05 - . 2J. --5-^’
y = a + b co = y_+S^JL.
Die hier eingeführten Zahlen x, y sind nur an die eine Be-
dingung geknüpft, daß y-\-Bx und folglich auch y — Bx
gerade Zahlen seien, damit ä, 8 nach (7) ganze Zahlen werden.
Ist also B gerade, so muß y gerade sein, während x beliebig
ist; ist B ungerade, so sind x und y beide gerade oder beide
ungerade anzunehmen. Nach (4) kann man diese Unterscheidung
auch so aüsdrücken:
1) Ist D = 0 (mod 4), so ist y = 0 (mod 2),
2) Ist D = 1 (mod 4), so ist y = x (mod 2).
Sollen bei gegebenen A, B, C die Zahlen a, b, c, 8 ohne
gemeinsamen Teiler sein, so kommen noch andere Bedingungen
hinzu:
Aus (5), (6) folgt, daß jeder gemeinsame Teiler von a, b,
c; 8 auch Teiler von x und y ist; umgekehrt ist jeder gemein-
same Teiler von x und y auch Teiler von b, c, 2 a, 2 8. Sollen
also a, b, c, 8 ohne gemeinsamen Teiler sein, so können x und y
416
Siebzehnter Abschnitt.
§ 114.
keinen größeren gemeinsamen Teiler haben als 2. Haben x und
y den größten gemeinschaftlichen'Teiler 2, so sind b und c gerade
und a, b, c, d sind dann und nur dann relativ prim, wenn a und c,
also auch n — ad — bc ungerade sind.
Die Gleichung (8) hat, wenn wir von dem iuteresselosen Fall
n — 1 absehen, keine diesen Bedingungen genügende Lösung, in
der x = 0 ist. Ändern wir aber die Vorzeichen von xy y zugleich,
so gehen a, ö, c, 8 nach (10) in — a, — b, — c, — 8 über, und die
(d b\
c' bleibt
also ungeändert.
Wir nennen jetzt der Kürze wegen eine Lösung der Glei-
chung (8) eine eigentliche Lösung und n = | (t/2 — D x2) eine
eigentliche Darstellung von n, wenn x und y den folgenden
Bedingungen genügt:
x ist positiv.
Der größte gemeinschaftliche Teiler von x und y ist
1 oder 2.
Ist er = 2, so ist n ungerade.
Wenn nun a> einer gegebenen Gleichung (3) genügt, so ist
(ci b\
’ „ ) eine eigentliche Lösung von (8) ein-
C, V/
deutig bestimmt. Denn nach (5) ist x der größte gemeinschaft-
liche Teiler von b, c, a — 8, und durch (6) ist y bestimmt, und
andererseits ist aus einer eigentlichen Lösung von (8) durch (7)
das System a, b, c, 8 vollständig bestimmt. Es ist aber noch
die Frage zu entscheiden, ob zwei verschiedene eigentliche
Lösungen x, y und x', y’ zu äquivalentem System Q’ Q’
führen können. Unter äquivalentem System sind hier nach § 28,
§ 53 zwei solche zu verstehen, bei denen
(9)
ist, wenn ( ’ eine lineare Transformation ist, also
\7, oJ
(10) a8 — ßy = 1.
Wenn wir beide Seiten der Gleichung (9) von rechts mit
/ 8, — 6\ ., . ,
I__I zusammensetzen, so ergibt sich:
§ 114. Singuläre Perioden der doppelt periodischen Punktionen. 417
/a'8 — b' c, —a'b b'a\ /na, nß\
\c'8 — 8'c, — c'b + 8' a) \ny, nb)'
oder, wenn wir für a, b, c, 8 die Ausdrücke (7) und für a', V, c', 8'
die entsprechenden
, y' -4- B x' ,, . .
a’ = -—L, b' = Ax',
c' = — Cx', 8' = y' ~Bx'-
setzen:
/ yy' — Dxx'-\-B(x'y— y'x) Ax'y— V'x \
4 ’ 2 /na, nß\
,,x'y — y'x yy' — Dxx'— B(x'y — y'x) \n,y^ n^/
\ 2 ’ 4 /
Daraus folgt:
4 n a = yy' — Dxx' -|- B(x' y — y' x),
2 n ß = A(x’ y — y' x),
2 n 7 — — C(x'y — y' x),
4 n b = yy' — Bxx' — B(x' y — y'x),
2n(a — b) = B(x'y — y' x),
2n(a -|- ö) = yy' — Dxx'.
Da nun A, B, G ohne gemeinsamen Teiler sind, so folgt, daß
2/ — y' x durch 2 n teilbar sein muß, und nach der letzten
Gleichung ist auch yy' — Dxx' durch 2n teilbar. Also setzen wir
x'y — y'x = 2n^,
' ' y y' — Dxx' = 2 ny
und erhalten:
r = -C^, b =
woraus nach (10) folgt:
(12) »ja —Z>^ = 4.
Lösen wir die Gleichungen (11) nach a/ und y' auf, so
folgt:
2a?' = £y -hyx,
2y’==yy-)-D^x.
Ist — D > 4, so hat (12) nur die beiden Lösungen
(14) = 0, y = + 2,
Weber, Algebra. III. 27
418
Siebzehnter Abschnitt.
§ H5.
und daraus ergibt sich, da x und x' positiv sein sollen:
x' = x, y' — y, (q = + 2).
Ist aber — D = 4, so hat (12) außerdem noch die Lösung
g = ± 1, 1? = 0,
und es folgt aus (13):
y' ~ + 2 x,
und das Zeichen von q ist so zu bestimmen, daß. x' positiv wird.
Ist endlich — D = 3, so haben wir außer (14) die Lösungen
£ = ± 1, i? = ± 1,
worin zunächst beide Zeichen beliebig sind.
Dann folgt aber aus (13):
+ 2 x' — x ± y,
+ 2 y' = y zp 3 x,
und man kann die Vorzeichen auf zwei Arten so wählen, daß x'
positiv wird. Wir haben also den Satz:
I. Bei gegebener Gleichung (3) führt jede eigent-
liche Lösung der Gleichung (8) zu einer Trans-
formation (ä’g) von de1’ wten Ordnung. Verschie-
dene Lösungen von (8) führen im allgemeinen zu
(CI &\
’ i. In den beiden
c, 0 J
Ausnahmefällen D = —4 und D — —3 führen je
zwei oder je drei verschiedene Lösungen von (8)
zu äquivalenten Systemen.
Bezeichnen wir mit Ä eine Zahl, die im allgemeinen gleich
der Zahl der eigentlichen Lösungen von (8) ist, für_D = — 4
und D = —3 aber die Hälfte oder ein Drittel der Zahl
dieser Lösungen, so können wir das Theorem I. so fassen:
II. Aus einer Gleichung (3) können wir k nicht äqui-
ableiten, die der Gleichung
(1) genügen.
valente Systeme Q’
§ 115. Die singulären Werte der Invariante j (co).
Die Frage, die zunächst unser Interesse in Anspruch nimmt,
ist die nach den Werten der Modulfunktionen von co für die
§ 115.
Die singulären Werte der Invariante j (<o).
419
besonderen Werte des Arguments gj, die wir im vorigen Para-
graphen betrachtet haben. Von diesen hängen die Moduln der
elliptischen Funktionen ab, die eine komplexe Multiplikation zu-
lassen. Sie heißen nach Kronecker singuläre Moduln. Wir
werden dementsprechend auch von den singulären Werten
der Modulfunktionen, insbesondere von den singulären In-
varianten j(co') sprechen, und verstehen darunter die Werte, die
diese Funktionen annehmen, wenn co die Wurzel (mit positiv
imaginärem Bestandteil) einer quadratischen Form mit nega-
tiver Diskriminante ist.
Wenn co der Gleichung (3), § 114, genügt und a, b, c, 8, n
wie im vorigen Paragraphen bestimmt sind, so folgt zunächst:
und wenn also
(2) Fn (u, v) — 0
die zum Transformationsgrad n gehörige Invariantengleichung ist
(§ 69), so ist (2) befriedigt, wenn a, b, c, 8 ohne gemeinsamen
Teiler sind und
/o • i x • /c “I- 8 °j\
(3) U — 1 (GJ), V = jt ——?— ) = u
' ! J J \a bco)
gesetzt wird. Danach gelangen wir zu dem ersten Hauptsatz
dieser Theorie:
III. Der singuläre Wert
u __= j (»)
ist eine Wurzel der algebraischen Gleichung:
(4) Fn (w, w) = 0.
Ist umgekehrt u eine Wurzel der Gleichung (4), so ist, wenn
co aus der Gleichung j (gj) = w bestimmt wird, einer von den der
Gleichung (2) genügenden Werten von v gleichfalls = w, und es
besteht also eine Gleichung von der Form (1); diese hat nach
C I (i)
§53 zur Folge, daß co mit äquivalent ist, und daraus
ergibt sich eine Gleichung von der Form § 114, (3). Also haben
wir die Ergänzung zu III.:
IV. Jede Wurzel von (4) ist eine singuläre Invariante.
27*
420
Siebzehnter Abschnitt.
§ 115.
Ist r eine Variable mit positiv imaginärem Teil, und v gleich-
falls eine Variable, so zerfällt F„[v, J(t)] nach §69 in die
linearen Faktoren
worin Q’ ein vollständiges Repräsentantensystem nicht äqui-
valenter Transformationen nten Grades durchläuft, und folglich
kann F„ (w, w) in die Faktoren
<5> «-'tw
zerlegt werden, wenn u — j (r) gesetzt wird.
Aus dem Theorem II., § 114, aber folgt, daß, wenn wir r = co
setzen, 1c von den Faktoren (5) verschwinden. Wir können aber
auch noch folgern, daß der Quotient
• z x • /c —1~ 8 r\
<«)
i 0) — i (»)
für j (t) = j (co') endlich und von Null verschieden bleibt. Denn
differentiiert man Zähler und Nenner nach t und setzt dann
t = co, so ergibt sich der Grenzwert:
n ______ 2
(a-^-bco)* y ^x'
der von Null verschieden ist.
Die Invariante j(co') bleibt unverändert, wenn co durch eine
äquivalente Zahl ersetzt wird, hat aber für jede andere Zahl co
einen anderen Wert. Sie gehört also nicht zu der individuellen
Form (rf, B, C), sondern zu der ganzen Klasse äquivalenter
Formen, und wird darum die Klasseninvariante genannt.
Ferner ist die Zahl k nicht von den Koeffizienten rf, B, C,
sondern nur von B und n abhängig, und ist daher für alle primi-
tiven Formen der Diskriminante B dieselbe. Wir führen nun die
folgende Funktion der Variablen u ein: Es bedeute cjj, <n2, ...,
ein vollständiges System nicht äquivalenter Zahlen der Diskrimi-
nante D, also das System der Wurzeln eines Systems nicht
äquivalenter Formen (rf, B, C) der Diskriminante B. Wir setzen
(7) Hm(u) = [w —>(»!)] [w —>(<n2)] ••• [« —j(O],
§ 115. Die singulären Werte der Invariante J (tu). 421
worin, wie wir jetzt öfter tun werden,
(8) m = — D
gesetzt ist, so daß m eine positive ganze Zahl bedeutet.
Diese Funktion, die für die Folge sehr wichtig ist, heißt die
Klassenfunktion. Die Wurzeln der Gleichung
(9) Hm(u) = 0
sind die Klasseninvarianten der Diskriminante D = — m, und
diese Gleichung heißt darum die Klassengleichung.
Der Grad h der Klassengleichung ist gleich der Zahl primi-
tiver Klassen der quadratischen Formen der Diskriminante D.
Wenn man nun die Quotienten (6) betrachtet, so ergibt sich aus
alledem:
V. Die Funktion Fn(u, w) ist durch [Hm(u)]fe teilbar, und
der Quotient ist relativ prim zu
Hiernach läßt sich die Funktion Fn (w, w) in Faktoren zer-
legen, und es ergibt sich, wenn C eine Konstante ist, die gleich
den Koeffizienten der höchsten Potenz wiV von u ist:
(10) K(w,w) = G^(w)^', («)<,(«) ...,
wenn sich das Produkt auf alle die positiven ganzen Zahlen m,
m', m1', ... erstreckt, für die Gleichung § 114, (8)
(11) 4w = 2/2 mx%
eigentliche Lösungen zuläßt, und k, k', k”, ... jedesmal die Anzahl
dieser Lösungen bedeutet (mit der dort angegebenen Modifikation
in den beiden Ausnahmefällen JD = — 4, D = —-3).
Es ist zunächst der Grad N der Gleichung _Fm(m, w) zu be-
stimmen.
Wenn wir die Repräsentanten in (5) wie in § 69 auswählen,
so wird
(12) Fn\j(r), >(t)] = 77p(r) - j(^^)] •
Hierin bedeutete «, 8 alle der Bedingung ad = n genügen-
den Paare positiver ganzer Zahlen, und c durchläuft ein Rest-
system nach dem Modul a, mit Ausschluß solcher Werte, die zu
dem größten gemeinschaftlichen Teiler e von a und 8 nicht relativ
prim sind, so daß die Anzahl der Werte von c, die zu einer Zer-
legung von n in die beiden Faktoren a und d gehören, gleich
a q> (e): e ist. Ist nun N der Grad von Fn (w, w) und C der Koeffi-
zient der höchsten Potenz von u, so beginnt die Entwickelung
422 Siebzehnter Abschnitt. § 115.
von Fn[j(r), j(t)] nach Potenzen von g = eniT mit Cg~2N
[§69, Wl
Wenn wir also die Faktoren der rechten Seite von (12) in
gleicher Weise entwickeln, so können wir sowohl C als N be-
stimmen.
Für einen Faktor der rechten Seite von (1)
— “, 8 > a,
q~2, 8 < a,
(2?n’c\
1 — e a ), d = a.
zunächst an, n sei kein Quadrat, so kommt der
und es ist
N = X-<p( e ) + X - <p (e),
haben wir folgende Anfänge der Entwickelung
2ö 2 nie
1.
2.
3.
Nehmen wir
Fall 3. nicht vor,
oder, was dasselbe ist,
(13) ^=2Z%(e).
6>a
C ist nach 1. jedenfalls eine nte Einheitswurzel, und da es
zugleich eine rationale Zahl ist, so muß es = +1 sein.
Ist sodann n ein Quadrat, so kommen <p (|/m) Faktoren von
der Form 3. vor und es ergibt sich:
(14) N = 2 2? - <p (e) + <jo (^).
C ist hier zwar auch von Null verschieden, aber nicht gleich
+1. Den Wert von C brauchen wir in diesem Falle nicht näher
zu bestimmen. (Er istA wie aus der Kreisteilungstheorie folgt,
immer ein Teiler von |/n).
Wenn im besondern n eine Primzahl ist, so ist
(15) N = 2 n.
Man kann über x und y immer so verfügen, daß unter Ein-
haltung der Bedingungen § 114 n = \(y2 -|- nix2) kein Quadrat
wird. Zu dem Ende nehme man x durch 4, y durch 2, aber nicht
durch 4 teilbar, und überdies y ohne ungeraden gemeinsamen
Teiler mit mx2 an. Ist dann mx2) ein Quadrat M2, so
§ 116. Klassenzahlrelationen. 423
hat es einen ungraden quadratischen Primteiler p2, der nicht
in «/2 aufgeht, und es ist
ty 4Zp)2 mx2 = 4M2 -8Xyp -j- 16Z2p2,
und diese Zahl ist, wenn Z nicht durch p teilbar ist, zwar durch
p, aber nicht durch p2 teilbar, und kann also kein Quadrat sein.
Überdies kann man über Z noch so verfügen, daß y -|- 4Zp mit
x keinen ungeraden gemeinsamen Teiler hat, daß also die Be-
dingungen § 114 erfüllt sind. Demnach genügt j(a>) für jedes m
einer Gleichung Fn(u, u), in der G — + 1 ist, und daraus folgt
nach Bd. II, § 149:
VI. Die Klassenvarianten sind ganze algebraische
Zahlen.
§ 116. Klassenzahlrelationen.
Wenn man den Grad, wie er sich hiernach für beide Teile
der Gleichung (10), § 115 ergibt, gleich setzt, so erhält man die
Formel
(1) N = hk + h'k' 4- h"k" -J- •••,
(2) = 22?|<p(e) + <p(y»),
worin <p (]/«) = 0 zu setzen ist, wenn n kein Quadrat ist, und.
N durch (13), (14) oder (15) des vorigen Paragraphen bestimmt
ist. Dies ist die Kroneckersche Klassenzahlrelation, der
wir noch eine etwas bequemere Form geben wollen Q.
Wir fassen neben n alle Werte n' ins Auge, die aus n durch
Fortheben eines quadratischen Faktors entstehen, bilden für sie
die Gleichung (2) und addieren alle so gewonnenen Resultate.
Dabei ist nur, falls n ein Quadrat ist, der Wert ri = 1 aus-
zuschließen, weil Fx (w, m) = 0 ist.
Es sei also 82 irgend ein von n selbst verschiedener quadra-
tischer Faktor von n und
n = ri ö2.
Zerlegen wir ri in zwei Faktoren ri = a' o' und bezeichnen
mit e' den größten gemeinschaftlichen Teiler von c' und a', so ist
’) Die Klassenzahlrelationen, von denen die hier abgeleitete nur der ein-
fachste Fall ist, sind von Kronecker entdeckt (Grelles Journal, Bd. 57) und
von Gierster (Mathematische Annalen, Bd. 21, 22) und Hurwitz (ebenda
Bd. 25) bedeutend verallgemeinert.
424
Siebzehnter Abschnitt.
§ 116.
(3) SN' =22Z ^<f>(e') + Sy^n'),
wenn ö2 alle quadratischen Faktoren von n (mit etwaiger Aus-
nahme von n selbst) durchläuft.
Setzen wir nun
S'ö = 8, a'8 = a, e' 8 = e,
so ist ad = n, und e ist der größte gemeinschaftliche Teiler von
a und 8; zugleich hat 8' n' zur Folge, daß 8 a ist. Um-
gekehrt erhält man aus jeder Zerlegung ad von n und jedem
Teiler e' von e eine Zerlegung a'd' von n', wobei
x e de' , ae'
e' e e
wird. Demnach ist
n' . ___________________________________________
(4) SN' = 2S -S<p(e') -j- Scptyn').
®>a e
Hierin machen wir nun Gebrauch von der zahlentheoreti-
schen Relation: 2?g>(8) = n, worin sich die Summe auf alle Divi-
soren von n bezieht. Nehmen wir zunächst an, daß n kein Quadrat
sei, so sind auch alle n' keine Quadrate und tp (V«') = 0. Also
erhalten wir wegen Scp(e!) = e
(5) SN' = 2 2?8.
Wenn dagegen n ein Quadrat ist, so durchläuft e' noch
immer die sämtlichen Divisoren von e, j/n7 aber die sämtlichen
Divisoren von j/n, mit Ausnahme von 1; danach ergibt sich für
diesen Fall:
(6) S N' = 2 S 8_-f- V« — 1.
5>V»
In beiden Fällen durchläuft 8 die sämtlichen Divisoren von
n, die größer als ]/n sind.
Wir haben nun noch die Summe der Ausdrücke S Tch für
die verschiedenen Werte von «' oder 8 zu bilden. Setzen wir
aber n = ö2so erhalten wir aus jeder eigentlichen Lösung von
(7) 4n' = y'2 -|- mx'2
durch Multiplikation mit 82 eine (wenn ö 1 ist, uneigentliche)
Lösung von
(8) 4 n = y2 -|- m x2,
nämlich
y = 8y', x = 8 x'.
§ 116. Klassenzahlrelationen. 425
Ist umgekehrt irgend eine Lösung x, y von (8) gegeben, so
ist 4n durch das Quadrat eines jeden gemeinschaftlichen Teilers
von x und y teilbar. Wir bezeichnen mit ö den größten gemein-
schaftlichen Teiler von x, y, dessen Quadrat zugleich Teiler von
n ist, der also entweder gleich dem größten gemeinschaftlichen
Teiler von x, y oder gleich der Hälfte desselben ist, und setzen
y = 8y', n = 8x',
und erhalten so eine eigentliche Lösung von (7).
Wenn wir also für —m alle Diskriminanten setzen, für die
die Gleichung (8) überhaupt Lösungen hat, und mit k die Anzahl
dieser Lösungen (mit positivem x~) verstehen, ferner mit h(m)
die Klassenzahl primitiver Formen der Diskriminante —m, so
ergibt sich die Formel
(9) SkJi(m) = 2 278,
wenn n kein Quadrat ist,
= 2 27 d \n — 1,
wenn n ein Quadrat ist.
Hier ist noch daran zu erinnern, daß in den beiden Aus-
nahmefällen m = 3, m = 4 unter k in § 115 nur der dritte
Teil oder die Hälfte der Zahl der eigentlichen Lösungen von (8)
verstanden war.
Diesem Umstand wollen wir jetzt dadurch gerecht werden,
daß wir unter k die Gesamtzahl der Lösungen von (8) ver-
stehen, aber
Ä(3) = |, Ä(4) = j
setzen [statt Ä(3) = 1, Ä(4) = 1].
Es ist ferner zu bemerken, daß bei der Bildung der Summe
(9) die zu dem Wert n' = 1 gehörigen Lösungen nicht mitgezählt
sind. Dies kommt nur für den Fall in Betracht, daß n ein
Quadrat ist. Es hat dann die Gleichung (7):
4 = y'2 mx'2
nur die folgenden eigentlichen Lösungen:
m = 3: x' = 1, «/' = +1, 7c = 2, h = j,
m = 4: x! — 1, y' = 0, k = 1, h — |,
und es würde also, wenn man diese Ausnahme beseitigen wollte,
zu (9) noch zu addieren sein:
2Jkh, auf n' — 1 bezogen, = | -|- | = |.
426
Siebzehnter Abschnitt.
§ 117.
Demnach lautet jetzt die Formel
(10) 27fcÄ(m) = 2278,
n kein Quadrat,
= 2 27 8 -j- }[n |,
n ein Quadrat.
Die Summe auf der linken Seite von (10) zerlegen wir in
ihre einzelnen Bestandteile, indem wir jede Lösung der Gleichung
(8) besonders nehmen. Dann bekommen wir eine Summe von
Ausdrücken h(m), wo aber dasselbe m so oft vorkommt, als (8)
Lösungen hat. Eine der Lösungen ergibt aber
4n — w2
/VW - -------'__
und diese kommt, wenn y = 0 ist, einmal, wenn y von Null
verschieden ist, zweimal (mit -|- y und — y) vor. Es ist aber
die Anzahl der primitiven Klassen der Diskriminante —m gleich
der Anzahl der nicht primitiven Klassen der Diskriminante —x2m
vom Teiler x, und wenn wir also jetzt (zum Unterschied von der
vorigen Formel) mit h(m) die Gesamtzahl der Klassen von der
Diskriminante — m (primitiven und imprimitiven) verstehen, so
erhalten wir aus (10):
(11) ä(4m) -1- 2ä(4m — 1) 2A(4n — 4) 2Ä(4«— 9) -f- •••
= 2278, (n kein Quadrat),
a>V»
— 2 27 8 -j- (n ein Quadrat).
Darin ist links die Summe der h (4 n — y^) so lange fortzu-
setzen, als 4 n — y'2 positiv bleibt, und rechts durchläuft 8 alle
Divisoren von n, die größer als ]'n sind.
Dabei ist jedoch zu beachten, daß die Formen (x, 0,x)
nur je mit | und (x, x, x) mit | in Rechnung zu setzen
sind, weil sie aus den Darstellungen von 4« durch die Dis-
kriminante m = — 4, — 3 hervorgehen.
§ 117. Arithmetische Natur der Klassenfunktion Hm(u).
Wir kehren jetzt wieder zurück zu der Gleichung (10), § 115,
um daraus die Natur der Koeffizienten der Klassengleichung
Hm(u) = 0 abzuleiten. Zunächst aber betrachten wir die beiden
speziellen Fälle: m = 4 und m = 3.
§ 117. Arithmetische Natur der Klassenfunktion 427
Setzen wir wie in § 54, (4)
7a (®) = (®), 7s (®) = Vj (®) — 1728,
so ergibt sich aus § 54, (14):
7s (0 = — 7s (0, also 7S (i) = 0.
Es ist ferner nach derselben Formel, wenn wir
setzen:
7a(s» + 1) = « ®” 7a(p) = 7a(— -) = 7s(e),
\ Vz
folglich 72(9) = 0, und wir erhalten
H3(u) = w, J(p) = 0,
1 ; H^u) = u — 1728, j(i) = 1728.
Es haben also die beiden Funktionen Hä (w) und Hi (u)
ganze rationale Zahlenkoeffizienten. Diese Eigenschaft können
wir nun durch vollständige Induktion allgemein für alle Hm
nachweisen.
Zunächst bemerken wir, daß, wenn bewiesen ist, daß H,n(u)
rationale Koeffizienten hat, sogleich folgt, daß die Koeffizienten
ganze rationale Zahlen sind (der erste = 1). Denn diese Koeffi-
zienten sind ganze algebraische Zahlen (nach § 115, VI.) und folg-
lich, wenn sie rational sind, ganze rationale Zahlen. Nun
betrachten wir die größten unter den Werten von m, die in der
Gleichung (10), § 115 vorkommen; das sind
m = in, x = 1, y = 0, fc = 1,
m = in—1, x = 1, y = +1, fc = 2.
Es enthält hiernach Fk(u, u) die beiden Faktoren Hin(u'),
und sonst lauter Faktoren Hm(u), in denen
m < 4 n — 1 ist. Nehmen wir an, daß von den letzteren schon
bewiesen sei, daß sie rationale Koeffizienten haben, so folgt, daß
= <2(u)
rationale Koeffizienten hat, und man hat also, um H4„_i(m) zu
finden, den größten gemeinschaftlichen Teiler von <P(u) und ®'(w)
zu suchen, was durch rationale Rechnung geschieht. Damit ist
aber auch Hin (w) auf rationalem Wege gefunden, und da Hs (w)
und H4(u) rationale Koeffizienten haben, so folgt allgemein:
VII. Die Klassenfunktionen Hm(u) haben ganze ratio-
nale Zahlenkoeffizienten.
428
Siebzehnter Abschnitt.
§ 118.
§ 118. Komposition der quadratischen Formen.
Da wir uns in der algebraischen Theorie der Klassengleichung
auf die Theorie der Komposition der quadratischen Formen stützen
müssen, so schicken wir darüber die folgenden Bemerkungen
voraus:
Zwei primitive Formen qq = (an Cj), <p2 — («2> &2> c2)
der Diskriminante — m heißen einhellig (einig, concordantes),
wenn oq, a2, l(b1 -|- &2) ohne gemeinschaftlichen Teiler sind; (p1
und <p2 sind also gewiß einhellig, wenn schon a.2 ohne gemein-
samen Teiler sind, und da man, wenn nur die Klassen 7c2
von qq, <p2 gegeben sind, <p,, <p2 in ihren Klassen immer so wählen
kann, so folgt, daß man in irgend zwei Klassen (die auch identisch
sein können), immer zwei einhellige Formen finden kann. Wenn
also diese Voraussetzung zutrifft, so folgt aus
| (&f — &2) = | (&j — 62). | (b1 -|- &2) = «j Cj — n2 c2,
daß |(&! — b2) durch den größten gemeinschaftlichen Teiler ö
von «j, a2 teilbar ist, und daraus, daß man die beiden Kongruenzen
(1) b' - b± (mod 2 «q), b' = b2 (mod 2 n2)
immer befriedigen kann.
Denn aus der ersten von ihnen folgt b' = b2 2 2,alf und
man hat also Z aus der Kongruenz
| (&i — &2) «j Z = 0 (mod n2)
zu bestimmen, die immer lösbar ist. Ist p das kleinste gemein-
schaftliche Vielfache von a2 und n2, also ^^ = ^,8, so kann
b' nach (1) noch durch b = b' -|- 2ith ersetzt werden, wenn h eine
beliebige ganze Zahl ist. Da nun j(b? -|- m) durch |(&22 -|- m)
durch a2 teilbar ist, so ist | (&'2 m) durch fi teilbar, und wenn
wir h aus der Kongruenz
- + m -\-b'h = 0 (mod ö)
bestimmen, die immer lösbar ist, da b' nach Voraussetzung relativ
prim zu ö ist, so wird b2 m = 4 cq n2 c durch 4 a2 teilbar.
Die zwei Klassen Äq, fc2 sind dann repräsentiert durch
9h = («i, «2 c), <p2 = (a2, b, a, c),
und die Form
T = 9>i 9>2 = («i «2, K c)
§ 118. Komposition der quadratischen Formen. 429
ist aus gq tp2 komponiert. Die Form tp gehört in eine Klasse k,
die aus fcj, fc2 komponiert heißt.
Nehmen wir tp = (a, b, c) so an, daß a relativ prim zu m
ist, so ist auch b relativ prim zu a (wegen m = 4a c— &2). Ist
a = a± a2, so sind auch (an b, c a2), (a2, b, c at) einhellige primi-
tive Formen, und man erhält die Komposition
(a, b, c) = (ßj, b, ca.2), (a2, b, cd),
und durch wiederholte Anwendung dieses Satzes gelangt man zu
dem Resultat:
I. Die Form tp = (a, b, c) läßt sich, wenn a relativ
prim zu m ist, aus solchen Formen zusammen-
setzen, deren erste Koeffizienten Primzahlen,
nämlich die Primfaktoren von a sind.
Eine dieser Komponenten, etwa
(p, b, a c p-1),
läßt sich durch eine äquivalente Form (p, b', c'p«) ersetzen,
deren dritter Koeffizient c'p« durch eine beliebig hohe Potenz
von p teilbar ist.
Um dies zu beweisen, brauchen wir für die Äquivalenz das
Zeichen ~, und haben
(p, b, cps-1) ~ (p,b 2Zp0, c'ps'),
worin c' wegen der Gleichheit der Diskriminanten aus
pc' = c kb k2p0
zu bestimmen ist. Da nun b durch p nicht teilbar ist, so kann
Z aus der Kongruenz c -)- Z b = 0 (mod p) bestimmt werden, und
c' ergibt sich als ganze Zahl. Damit ist mit Rücksicht auf (I.)
bewiesen:
II. Man kann in jeder Klasse fc von primitiven
Formen der Diskriminante D einen Repräsen-
tanten <p finden, der sich aus Formen
P = (p, b, p'Jc),
worin p eine in D nicht aufgehende Primzahl,
und g ein beliebiger Exponent ist, zusammen-
setzen läßt.
Die Form P läßt sich leicht mit sich selbst zusammensetzen,
denn es ist im Sinne der Kompositionen, wenn g >> v ist:
(pr, b, p9~”c) (p, b, p;ic) = (p”+1, b,
und folglich durch den Schluß von v — 1 auf v:
(2) P” = (p”, b, pe—”c).
430
Siebzehnter Abschnitt.
§ U8.
In der Kette der Kompositionen
(3) P, P2, P3, ...
kann eine Form vorkommen, die in die Hauptklasse gehört,
die also mit (1, 0, oder [1, 1, 1)] äquivalent ist.
Wenn dies bei Ps ein tritt, so ist p£ durch die Hauptform dar-
stellbar, und es gibt eine eigentliche Darstellung
(4) 4p£ = y2 — Dx2.
Ist umgekehrt eine solche Darstellung möglich, so gibt es in der
Hauptklasse eine Form (p!, 6, c).
Ist s der kleinste positive Exponent, für den die
Gleichung (4) eigentlich lösbar ist, so heißt s der Index
von p, und p gehört zum Exponenten s.
Ist
(5) P — (p, b, p'-1 c),
so ist
b2 = D (mod 4p£),
und wenn diese Bedingung erfüllt ist, so ist in der Form (p, b, c')
der Diskriminante D der dritte Koeffizient durch ps~1 teilbar.
Die Form (5) bleibt erhalten, wenn wir b durch irgend eine nach
dem Modul 2p£ kongruente Zahl b' ersetzen. Ist also a nicht
durch p teilbar und
<P = («, 0
irgend eine mit P einhellige Form der Diskriminante D, so lassen
sich die beiden Kongruenzen
x = b (mod 2p£), x = B (mod 2 a)
zugleich befriedigen, und wenn man dieses x also an Stelle von
b und B setzt, folgt:
III. Ist l die Klasse von P und k eine beliebige Klasse
der Diskriminante Z>, so kann man in l und k die
Repräsentanten wählen:
(6) (p, b, acpi~1'), (n, &, cp£),
und in der komponierten Klasse Ik erhält man
einen Repräsentanten
(7) (ap, b, p*-1 c).
Ist also ____
_ -& + V— m
co --------„------
2 a
eine Wurzel der Klasse k, so ist co:p eine Wurzel
der Klasse Ik.
§ 119-
Die Diskriminante der Invariantengleichung.
431
§ 119. Die Diskriminante der Invariantengleichung.
Wir stellen uns jetzt die Frage, wann eine Invarianten-
gleichung
(1) FP(v, u) = 0,
worin p eine Primzahl ist, für w=J(co) zwei oder mehrere
gleiche Wurzeln v hat, oder wann unter den p -j- 1 Größen
--L----), C = 0, 1, ...,p— 1
oder mehrere einander gleiche vorkommen. Dies findet
und nur dann statt, wenn unter den p -|- 1 Größen
(2)
zwei
dann
p co, ----1—
* p
äquivalente vorkommen. Es muß also jedenfalls co einer
(3)
zwei'
ganzzahligen quadratischen Gleichung mit negativer Diskrimi-
nante D = —m genügen, die wir in der Form annehmen:
(4) Aco2 * + B<a 4- C= 0, 4 AO — B2 = m > 0,
worin A, B, C ohne gemeinsamen Teiler sind.
Ersetzen wir co durch eine äquivalente Zahl, also (4) durch
eine äquivalente Gleichung, so werden die Größen (2) nur unter-
einander vertauscht. Die Frage nach der Anzahl der gleichen
Wurzeln von (1) wird also davon nicht berührt, und wir können
daher annehmen, daß A durch p nicht teilbar sei. Ist nun zu-
nächst pea äquivalent mit so is^:
a + c 7 + 8pea » „ .
(o) ---1— = ~—, a8 — ßy = 1.
p cc-j-ßpco
Schreiben wir diese Gleichung so:
(6) ßp co2 -|“ (a + ß cp — 8 p2) co -j- ca — yp = 0,
so folgt durch Vergleichung mit (4) (da A durch p unteilbar
sein
daß
(?)
(8)
so folgt:
(9)
sollte), daß a durch p teilbar, also = po! sein muß, und
eine ganze Zahl x existiert, die den Bedingungen genügt:
ß — Ax, a! -|- ßc — 8p = B x, co' — y = Gx.
Setzen wir noch
2 a' = Bx -j- y,
2(ßc — 8 p) = Bx — y,
432
Siebzehnter Abschnitt.
§ 119.
und aus
(10) pa'ö — ßy = 1
folgt sodann
(11) y2 mx2 = 4.
Der Wert x = 0 ist auszuschließen, weil sonst ß = 0 sein
müßte, was der Gleichung (10) widerspricht, und wir können
unbeschadet der Allgemeinheit x positiv annehmen. Da überdies
m nach dem Modul 4 entweder = 0 oder = 3 sein muß, so
bleiben zur Erfüllung von (11) nur folgende zwei Möglichkeiten
übrig:
1. m = 3, x — 1, y = +1.
Da es für die Diskriminante — 3 nur eine Formenklasse
gibt, so können wir A = 1, B = 1, C — 1 annehmen, d. h. für
co die imaginäre dritte Einheitswurzel e 8 setzen, und erhalten
unter den Größen (3) drei äquivalente, indem wir «/ = —]— 1 und
= — 1 annehmen:
wie auch aus den Gleichungen
co __ —1 co —|— 1 _______—1
p p -|- p co’ p ' pco
erkannt wird, aus denen die Äquivalenz der drei Größen (12)
evident ist.
2. m = 4, x = 1, y = 0.
Weil es auch hier nur eine Formenklasse gibt, so können wir
B = 0, A = C = 1, d. h. co = t annehmen, und finden die zwei
äquivalenten Werte:
co
p co, --,
p
wie auch aus der Gleichung
—P
n co = ——
co
folgt.
Es seien ferner zwei der Werte (3)
co —|— c co —|— c'
p ’ p
äquivalent, so daß eine Gleichung besteht:
(13) !L±_’ = n + »(» + «') ,
’ p ap -|“ ß (co 4- c )
§ 119. Die Diskriminante der Invariantengleichung. 433
oder
(14) ß co2 -|- (ß c' -|- ß c + KP — Sp) co -|-
ßcd -|- acp — 8 d p — yp2 = 0,
woraus durch Vergleichung mit (4):
ß = Ax,
(15) ßd ß c ap — 8p — Bx,
ßcd acp — 8 d p — yp2 — Cx,
und wenn man wieder
(16) ßc' — ßc ap 8p = y
setzt:
, 2(ßd + ap) = Bx + y,
2 (ßc — 8 p) = Hx — y.
Daraus
(18) y2 -|- mx2 = Ap2.
Ist x durch p teilbar, so muß auch y durch p teilbar sein,
und wir kommen durch Wegheben des Faktors p2 auf die Glei-
chung (11) zurück, die, wie wir gesehen haben, nur für die Fälle
m = 3 und m = 4 lösbar ist. Wir nehmen also weiter an, x sei
durch p unteilbar.
Ist m durch p teilbar, so ist auch y durch p teilbar, ß ist
nach (15) nicht durch p teilbar. Dann aber folgt aus (16):
c = d (mod p), und beide entsprechen also der nämlichen Wurzel
von (1).
Es gehe jetzt also p weder in x noch in m auf. Dann geht
es auch nicht in y auf, und nach (17) werden c und d aus den
Kongruenzen
a , Bx-\-y a Bx— y . , .
(19)------------------ßc =--------------, ßc ~ ~ (mod p)
bestimmt, und wenn c, c' bestimmt sind, ergeben sich aus (17)
a und d als ganze Zahlen. Damit sind die beiden ersten
Gleichungen (15) befriedigt, und y erhält man aus der letzten
Gleichung (15) gleichfalls als ganze Zahl.
Es ist nämlich
(20) yp2 = ßcd -j- (ac — 8 c') p — Cx = 0 (mod p2).
Denn wir haben aus (17) und (15)
ß2cd -j- ß(ac — 8 c')p — a8p2 — AGx2
= ß [ß c d -|- (a c — 8 c')p — Cx] — a 8p2
___________ y2-]-mx2 __
Weber, Algebra. III.
28
434 Siebzehnter Abschnitt. § 119.
folglich ist das zweite Glied von (20) durch p2 teilbar, und wenn
man yp2 dafür einsetzt, so folgt
ad — ßy = 1.
Wir kommen also zu dem Resultat:
IV. Die Invariantengleichung Fp(v, u) hat immer dann
und nur dann mehrfache Wurzeln, wenn u=j(ca)
ist, worin ca die Wurzel einer quadratischen Glei-
chung ist, deren Diskriminante nicht durch p
teilbar ist, aber eine Lösung der Gleichung (18)
gestattet.
Es gibt für ein gegebenes p nur eine endliche Anzahl von
Werten m, die dieser Forderung entsprechen, da m <Z 4p2 sein
muß. Die Werte m = 3, m = 4 sind darunter als spezielle
Fälle enthalten.
Da nach (18) —m quadratischer Rest von p ist, so ist p
durch eine Form der Diskriminante —m darstellbar; p2 ist aber
durch die Hauptform einer Diskriminante darstellbar. Die
Formenklasse, durch die p darstellbar ist, ist also selbst entweder
die Hauptklasse oder sie gibt, mit sich selbst komponiert, die
Hauptklasse, ist also zweiseitig. Wir können das Theorem IV. also
auch folgendermaßen aussprechen:
V. Die Wurzeln der Diskriminante der Invarianten-
gleichung Fp(v, u) sind die singulären Invarianten
j(ca), worin ca die Wurzel einer quadratischen
Gleichung von negativer Diskriminante D ist, für
die die Primzahl p den Index 1 oder 2 hat.
Achtzehnter Abschnitt.
Galoissche Gruppe der Klassengleichung.
§ 120. Relationen zwischen den Klasseninvarianten derselben
Diskriminante.
Es ist für die Folge eine Bezeichnung zweckmäßig, durch
die die Abhängigkeit der Klasseninvariante von der Formenklasse
einfacher ausgedrückt wird. Wir setzen daher, wenn k eine be-
liebige primitive Klasse der Diskriminante — m bedeutet, die
nach § 118, III. durch (a, b, cps) repräsentiert wird:
(?) = J (~ b
Wenn eine oder mehrere der (k) unter einem Funktions-
zeichen auftreten, so werden wir die Klammern auch weglassen,
also z. B. f(k, k', ...) für /[(fc), (k'), ...] schreiben.
Ist also
(1) (*) =>(»),
und l eine durch (p, b, a cp*-1) repräsentierte Klasse, so ist nach
§ 118, III.:
(2) .
und es genügen also die beiden Größen
u - (fc), v — (lk)
der Invariantengleichung
(3) Fp(v, u) = 0.
Die Größe v — (lk) ist aber außerdem eine Wurzel der
Klassengleichung
(4) Hm(v) = 0,
und es ist zunächst festzustellen, wieviele Wurzeln die Gleichung
(3) mit (4) gemein hat.
28*
436
Achtzehnter Abschnitt.
§ 120.
Die sämtlichen Wurzeln von (3) sind aber nach § 69:
(•’>) 3 (”
wenn A ein Restsystem nach dem Modul p durchläuft. Die erste
von diesen gehört nicht zu den Wurzeln von (4), denn »' == p ca
genügt der Gleichung:
a ca'2 -|- p b gj' pe +2 c = 0,
die primitiv und von der Diskriminante —mp2 ist. Wenn wir aber
p ca' = ca -|- A setzen, so erhalten wir für ca' die Gleichung:
(6) ap2 ca'2 p(b — 2 aA) ca' -|- (« A2 —• b A -f- cp£) = 0,
und diese Gleichungen sind ebenfalls von der Diskriminante
— mp2. Es sind aber zwei darunter, die imprimitiv vom Teiler p
sind, nämlich die den Werten
(7) A = 0, a A — b = 0 (mod p)
entsprechen. Die erste ist die Wurzel der Form (ap, b, cp*-1), die
zweite die der Form
(ap, b — 2 a A, 6’),
und da & — 2 a A = J (mod 2a) und [nach (7)] = — b (mod 2p)
ist, so ist diese Form komponiert aus(a, b, cps) und (p,—&, acpE-1),
die in die zu l reziproke Klasse 1 gehört. Daraus ergibt sich:
I. Die Gleichungen (3) und (4) haben nur zwei Wur-
zeln miteinander gemein, nämlich die Klassen-
invarianten (Ik) und (l~1k), und wenn die Klasse l
zweiseitig ist, so haben sie nur eine Wurzel
gemein.
Setzt man also in (3) u = (/c), so ist der größte gemein-
schaftliche Teiler von (3) und (4) vom zweiten, und wenn l
zweiseitig ist, vom ersten Grade. Im ersteren Falle sind (l fe) und
(/-1fc) die Wurzeln einer quadratischen Gleichung, deren Koeffi-
zienten rational von u abhängen, und deren Form im übrigen
nur von der Klasse ?, nicht von k abhängig ist. Dem hiermit
bewiesenen können wir den Ausdruck geben:
II. Es ist
(8) (zfc) + (r1fc) = /-I(fc),
oder, wenn l zweiseitig ist,
(9) (lk) = ft(k\
worin fi(k) eine rationale Funktion von (k) be-
deutet, deren rationale Zahlenkoeffizienten nur
von der Klasse l, nicht von der Klasse k abhängen.
§ 121. Trennung der entgegengesetzten Klassen. 437
Wir betrachten nun die Reihe der Klasseninvarianten
(10) ..., (F2fc), (T'k), (&), (Ik), (l?k), (fk), ...,
die beliebig nach vorwärts und nach rückwärts fortgesetzt werden
kann. In dieser Reihe ist, wenn l zum Exponenten e gehört,
(l* k) mit (ll +£ k) identisch, während alle zwischenliegenden Glieder
davon und untereinander verschieden sind. Ist l zweiseitig, so
enthält die Reihe (10) nur zwei verschiedene Glieder, von denen
jedes durch das andere rational ausdrückbar ist. Anderenfalls
schließen wir nach (8), daß jedes Glied der Reihe (10) rational
ausdrückbar ist durch die beiden vorhergehenden (oder auch durch
die beiden folgenden) in der Form
(11) (l'+'k) = — (Z’-ifc) + ft(Vk).
Durch eine wiederholte Anwendung dieser Formel gelangt
man zu dem Satze, daß jedes Glied der Reihe (10) rational
ausgedrückt werden kann durch irgend zwei aufein-
anderfolgende Glieder derselben Reihe.
Ist aber l zweiseitig, so sind alle Glieder der Reihe
(10) rational durch eines ausdrückbar.
§ 121. Trennung der entgegengesetzten Klassen.
Es kommt nun darauf an, auch im Falle eines nicht zwei-
seitigen l die beiden Wurzeln der quadratischen Gleichung von-
einander zu trennen, was durch Adjunktion von möglich ist.
Ist die Klasse l nicht zweiseitig, so sind die beiden Klassen-
invarianten (Ik), (Z—17c) voneinander verschieden und daher
(§ ns, in.)
v = (Ik) = j
eine einfache Wurzel der Transformationsgleichung
Fp(u,v) = 0
(§ 119, V.). Setzen wir also
/ /ca\\24
/\
(1) M =
V(<») /’
so folgt nach § 72, daß rational durch
j(ca) und j
438
Achtzehnter Abschnitt.
§ 121
also rational durch (fc) und (lk) ausdrückbar ist, und aus § 72
ergibt sich, daß eine ganze algebraische Zahl ist.
Diesen Satz wenden wir an auf je zwei aufeinanderfolgende
Glieder der Reihe (7) und erhalten, wenn wir
ca ca. »s—i
ca, = —, ca, = —, ..., cat = ---
P P P
setzen, und wenn <p eine durch die Klasse l vollständig bestimmte
rationale Funktion bedeutet:
M =*<!^
W < = (^)“ =
Durch Multiplikation aller dieser Gleichungen folgt:
(3) (^h)24= ••• *)•
Nach § 120 kann aber die rechte Seite dieser Gleichung als
rationale Funktion <Z* (k, l k) von (k) und (l k) (mit rationalen Zahl-
koeffizienten) dargestellt werden.
Andererseits ist, da l zum Exponenten e gehört, P mit der
Hauptform, also ?8 k mit k und ca£ mit ca äquivalent, also besteht
eine Gleichung:
w “ = ^+75’ = 1’
und es ist 17 (ca£) : q (ca) nach § 38 zu bestimmen. Genügt, wie
wir angenommen haben, ca der Gleichung
(5) aca2 -|- bca cpe = 0,
so erhält man aus (4), da ca£ = ca/ps ist:
ß ca2 (a — ps 6) ca -|- yps = 0,
was durch Vergleichung mit (5) gibt
ß — ax, a — pfb -= bx, y = — cx,
und wenn man a -|- ps S — y setzt:
znx y + bx o
(6) a — -—L-----, ß — , ax,
, y — bx
psy = — cx, ps o = -—~-------,
§ 121.
also
Trennung der entgegengesetzten Klassen.
439
ips = y2 -|- mx1.
Daraus sind x und y bis auf die Vorzeichen bestimmt, und
x kann positiv angenommen werden, und das Vorzeichen von y
ergibt sich aus der Kongruenz
(7) y = bx (modp5).
Betrachtet man dagegen die Komposition Z-1 fc, so hat man
die Form (a, b, cp*) mit (p, —b, acp£~1') zu komponieren; man
bestimmt b' aus den beiden Kongruenzen:
b' = b (mod 2 a), b' = —b (mod 2ps),
und es ist alles ebenso durchzuführen, nur daß an Stelle von
(7) der Kongruenz
(8) y = — b x (mod pe)
tritt, d. h. y bekommt das entgegengesetzte Zeichen.
Nach (5) und (6) ist aber
(9) «+
worin, wenn a und x und folglich ß positiv angenommen sind,
Y—m positiv imaginär'zu nehmen ist.
Es ist aber nach § 38, (4)
(«e)\24 / y + y—
\i?(ra)/ — \ 2 / ’
und folglich erhält man nach (3)
(io) ® (&, z fe) = ------)
Auf die gleiche Weise ergibt sich wegen (16):
<H)
_ t— 17. (y — V-—m «\12
0(Ä, Z Zc) = --L-----
und die Gleichung (10) ist daher nicht erfüllt, wenn (Ik) durch
(Z-17c) ersetzt wird, außer wenn
(12) (? + = (s -
ist.
Dies ist aber nicht möglich, wenn, wie wir angenommen
haben, p nicht in m aufgeht. Denn zerlegt man p im Körper
= 31 (yö) in die zwei voneinander verschiedenen konjugierten
Primideale p, p', so geht das eine in j(y -|- y—mx), das andere
440 Achtzehnter Abschnitt. § 121.
in %(y— y—mx) auf, und diese beiden Größen müssen also
relativ prim sein. Folglich kann die Gleichung (12) nicht bestehen.
Die quadratische Gleichung, deren beide Wurzeln (Ik), (Z-1fc)
sind, hat also mit (18) nur eine Wurzel gemein, und daraus
ergibt sich der wichtige Satz:
III. Nach Adjunktion von ist (Zfc) rational aus-
drückbar durch (fc) in der Form:
(13) (?fc) =/i0,i4ö),
wo fi eine rationale Funktion ist, deren Form
durch die Klasse l allein bestimmt ist.
Die Änderung des Zeichens von ]'D hat den Erfolg, daß (Ik)
in (7-1fc) übergeht, also:
ft(k, )/D) = fi-* (k,-^D).
_ Ist l zweiseitig, so gilt nach I. dieselbe Formel, nur daß
\D in fi dann nicht vorkommt.
Ist V eine zweite Klasse von derselben Beschaffenheit wie 7,
so kann man die Formel (13) auf l'k anwenden und erhält:
(ll'k) = fitl'k, \D),
was mit Anwendung von
(l'k) = fv(k,
in eine Gleichung der Form:
(ll'k) = flv(k, yD)
übergeht. Da man auf der linken Seite l mit V vertauschen
kann, so folgt
ftl.(k, ^d) = fvl (k, y5),
so daß fiV nur von der zusammengesetzten Klasse IV abhängt.
Ebenso läßt sich ableiten
(ll'V'k) = flvv,(k, 1/^),
und da nach § 118, II. jede beliebige Klasse s der Diskriminante
D aus solchen Klassen l zusammensetzbar ist, so ist die Formel
(13) nebst den daraus gezogenen Folgerungen nicht mehr an die
über l gemachte besondere Voraussetzung gebunden, daß der
erste Koeffizient eine Primzahl sei.
Wir haben also, wenn s, k zwei beliebige Klassen der
Diskriminante D bedeuten, die Formeln:
(u) (sk) = fs(k, y5),
(15) (s-'k) = f,(k,— yj).
§ 121. Trennung' der entgegengesetzten Klassen. 441
Ist 7c die Hauptklasse, so ist
2 a = oder 2 ca = — 1 -|- ]/D,
und da rein imaginär ist, so ist k = y(ca) nach § 69 (4)
reell. Demnach ergibt sich aus (14) und (15), da jetzt (s7c) = (s)
wird :
Die Invarianten entgegengesetzter Klassen sind kon-
jugiert imaginär, die Invarianten zweiseitiger Klassen
sind reell.
Kehren wir zu einer beliebigen Klasse k zurück und setzen
in der Formel (15) sk an Stelle von k, so folgt:
(iß) (k) = fs(sk, -yp),
oder, indem man sk = k' setzt und f für fs schreibt, nach (21)
fö),
{ (fc) = f(k’,-l/D\
worin nun k, k' irgend zwei Klassen der Determinante D sein
können.
Hiernach sind wir imstande, die Galoissche Gruppe der
Klassengleichung, oder zunächst wenigstens eine Gruppe von
Permutationen zu bestimmen, in der die Gruppe der Klassen-
gleichung als Teiler enthalten ist.
Nehmen wir zunächst an, es sei die \D dem Rationalitäts-
bereich der rationalen Zahlen adjungiert, und wenn (k), (k'), (k")...
die sämtlichen Klasseninvarianten der Diskriminante D bedeuten,
R (k, 7c", . . .)
irgend eine rationale Funktion dieser Größen. Nach unserem
Satze läßt sich diese Funktion rational ausdrücken durch eine
der Größen (Zc), also etwa:
R(k, k', k", ... .) = R'(k).
Bedeutet ferner (s) eine beliebige Klasseninvariante der Dis-
kriminante _D, und hat die Funktion R die Eigenschaft, durch
die sämtlichen h Permutationen
/ k, k', k", . . .\
\s k, s k', s k", . . . /’
deren Gesamtheit wir mit ® bezeichnen wollen, ungeändert zu
bleiben, so ist R!(k) = R'(s7c), und daher rational ausdrückbar.
Die Galoissche^ Gruppe der Klassengleichung nach
Adjunktion von ist also in dem System ® enthalten,
442 Achtzehnter Abschnitt. § J22.
und da ® eine Abelsche Gruppe ist, so ist die Klassen-
gleichung eine Abelsche.
Nehmen wir an, die Funktion R habe reelle (rationale)
Koeffizienten, _so wird gleichwohl ihr rationaler Ausdruck die
Form a -f- b \D haben, worin «, b rationale Zahlen sind. Der
imaginäre Teil wird dann und nur dann wegfallen, wenn R auch
durch die Vertauschung sämtlicher Klassen k, k', k", ... mit ihren
entgegengesetzten ungeändert bleibt. Daraus folgt, daß ohne
Adjunktion von \T) die Galoissche Gruppe der Klassengleichung
enthalten ist in dem System von 2Ä Permutationen, die man
erhält, wenn man in ® jede Klasse in ihre entgegengesetzte ver-
wandelt. Nur in dem besonderen Falle, in dem alle Klassen
zweiseitig sind (der nur für eine endliche Anzahl von Deter-
minanten stattfindet), ist dies letztere System mit ® identisch, und
die Klassengleichung ist ohne Adjunktion von \D eine Abelsche.
Der algebraische Körper, der aus den rationalen Funktionen
einer Klasseninvariante gebildet ist, ist daher, von dem zuletzt
erwähnten Ausnahmefall abgesehen, kein Normalkörper, sondern
ist von seinen konjugierten Körpern verschieden. Dagegen erhält
man einen Normalkörper, wenn man die Quadratwurzel dem
Körper der Klasseninvarianten adjungiert. Denn jede rationale
Funktion sämtlicher Wurzeln der Gleichung kann durch eine von
ihnen und rational ausgedrückt werden.
§ 122. Irreducibilit&t.
Wir betrachten jetzt den algebraischen Zahlkörper
(1) R = ®(k, -fD),
der aus einer Klasseninvariante (fc) der Diskriminante D und \D
zusammengesetzt ist; in diesem Körper sind nach dem vorigen
Paragraphen alle zu derselben Diskriminante gehörenden Klassen-
invarianten (fc), (fc'), (fc"), ... enthalten. Diesen Körper nennen wir
den Klassenkörper der Diskriminante I). Den quadratischen
Körper 3t (yD) bezeichnen wir wie bisher mit ß, der, wenn
D = Q2 zf und zf der Stamm von D ist, mit S<R (Vzf) identisch ist.
h sei die Klassenzahl der Diskriminante D.
1. Es sei (/c) irgend eine der h Klassenvarianten und
(2) <Z>(fc) = [ky ^(fcy-i a2(/c)’’-2 •••-(- 0C„ — 0
die Gleichung niedrigsten Grades in ß, deren Wurzel (k) ist.
Da (fc) eine ganze Zahl ist, so müssen auch die os, ganze Zahlen
§ 122. Irreducibilität. 443
des Körpers £i sein (Bd. II, § 149). Es ist dann, wenn t eine
Variable bedeutet, $(t) ein Divisor der Klassenfunktion
und folglich ist auch die Diskriminante von <&(£) ein Teiler der
Diskriminante von 77m(f).
Ist £ eine beliebige ganze Zahl des Körpers St, so ist die
Belativspur in bezug auf £1 (Bd. II, § 175):
M
eine ganze Funktion von t, höchstens vom Grade v — 1, deren
Koeffizienten ganze Zahlen von Sl sind. Lassen wir also t in (7c)
übergehen, so folgt:
und daraus:
(4) bi = & + + ------(-^(fcy-i,
worin ß0, ßlz ..., ßv—t ganze Zahlen in H sind, und b eine ganze
rationale Zahl bedeutet, für die man die Diskriminante der
Gleichung (2):
b = W [$'(&)]
nehmen kann. Die Körperdiskriminante geht dann in b auf, und
keine der in b nicht aufgehenden Primzahlen ist in £1
oder in 3? durch das Quadrat eines Primideals teilbar
(Bd. II, § 174). Die Zahl b hängt nicht von der besonderen
Zahl i ab.
Eine ganze Zahl i ist nur auf eine Weise in der Form (4)
darstellbar, weil sonst (k) einer Gleichung von niedrigerem als
dem rten Grade genügen würde, was der Voraussetzung wider-
spricht; und daraus folgt, daß i nur dann durch eine
ganze Zahl a des Körpers Sl teilbar ist, wenn alle Koeffi-
zienten &, ß1, ..., ßv—i durch a teilbar sind. Denn stellt
man i/a in der Form (4) dar, so müssen die Koeffizienten in
dieser Darstellung ebenfalls ganze Zahlen sein.
Ersetzen wir (7c) in (3) durch eine andere Wurzel der Glei-
chung (2), so geht i in einen konjugierten Wert über, der eben-
falls eine ganze Zahl ist.
2. Nach dem Fermatschen Satze ist für jede beliebige
Primzahl p, wenn a eine ganze rationale Zahl bedeutet:
(5) = a (mod p).
444
Achtzehnter Abschnitt.
§ 122.
Ferner ist, wenn p nicht in 2 D auf geht, nach § 85
p—i
D 2 = (D, p) (mod p),
also:
(6) ^if = (D, p) (mod p).
Bezeichnet daher a wie oben eine ganze Zahl des Körpers ß;
_ a? + y (/ z7
— 2
also, wenn man mit ‘IQ multipliziert, x für Q x schreibt und mit
a' die zu a konjugierte Zahl bezeichnet:
2 Q a = x -|- y \I), 2Qa' — x — y \I>,
und daraus folgt nach dem Fermatschen Satze und nach (6):
= <*, (D, p) = 4- 1, , . .
(7) , /n \ ~-i (mod p).
x ap = a', (_D, p) = — 1, ' '
Daraus folgt nun, wenn f(k, y—m) irgend eine Zahl von
der Form (4) ist, mit Anwendung des polynomischen Lehrsatzes:
(8) /(*. W =/(f. 1®), (-D,l>) = +1, zmod
(8) f (k, w EH f(y, - V5), (I>, ,) = -!. (mod "
worin kp für (le)# steht, also die Bedeutung einer wirklichen
Potenz hat.
3. Wenn iß ein in p aufgehendes Primideal in ß ist, so ist
die Norm von iß eine Potenz von p:
(9) W('ß) = pf.
Der Exponent f ist der Grad des Primideals iß. Für jede
beliebige ganze Zahl g des Körpers © ist
(10) = C (mod iß),
und wenn umgekehrt pf die niedrigste Potenz von p ist, bei der
die Kongruenz
(11) tpf = ? (mod iß)
durch jede Zahl t, befriedigt wird, so ist f der Grad des Ideals iß
(Bd. II, § 167).
Es sind nun die Grade der Primideale zu ermitteln, die in
der Primzahl p enthalten sind.
Da p nicht in der Grundzahl des Körpers S aufgeht, so ist
p nicht durch das Quadrat eines Primideals teilbar.
§ 122. IrreducibiEtät. 445
4. Bedeuten (k), (k'~), ..(fc**-1)) die sämtlichen Wurzeln der
Gleichung
Hm (w) — 0,
so ist für ein variables t
= p - (fc)] p - (fc')] ... p - (fc«*-»)],
und diese Funktion hat ganze rationale Koeffizienten. Es ist
also nach (5):
[Hm(t')]p = Hm(tp~) (mod p),
also, wenn wir t = (k) setzen:
[(fc)i> _ (fc)] [(fc)s _ (fc')] ... [(k)p - (fc^-D)] = 0 (mod p).
Bedeutet also iß ein in p aufgehendes Primideal in St, so muß
wenigstens einer der Faktoren der linken Seite durch iß teilbar
sein, und daraus folgt eine Kongruenz
(12) (k)p = (k1) (mod iß),
worin (k1) irgend eine der Klasseninvarianten ist, die auch mit
(k) identisch sein kann.
5. Ist zunächst
(D, jp) = — 1,
so kann iß jedenfalls nicht vom ersten Grade sein, weil ja schon
(13) 7-^ (mod iß)
ist. Ist aber in (12) (nach § 121)
(k) = f(k, y5), k = f(k,-fö),
so folgt aus (13)
(k>y = fty», —yüö) = f(k, _ys) = k
(k)p2 = k (mod iß),
und mithin ist für alle ganze Zahlen £ des Körpers St
(u) r2 eh : (mod iß),
und iß ist vom zweiten Grade.
6. Ist zweitens
(D, jp) = -}- 1,
so gibt es, wie in § 118 bewiesen ist, zwei entgegengesetzte Klassen
l, V1 (die, wenn 1 zweiseitig ist, miteinander identisch sind), die
durch Formen mit dem ersten Koeffizienten p repräsentiert
werden können, und wenn (k) eine .beliebige Klasseninvariante
ist, so ist nach § 120 die Invariantengleichung für den Trans-
formationsgrad p:
(15) Fp(u, v) = 0
446 Achtzehnter Abschnitt. § 122.
befriedigt für
u — (fc), v = (Ik) und v — (7-1 &).
Nach dem, was am Schlüsse des § 69 bewiesen ist [Formel
(32)], folgt aber hieraus die Kongruenz
(16) . [(fe/ — (Ik)] [(lk)p — (k)] = 0 (mod p).
Wenn nun iß ein in p auf gehendes Primideal ist, so muß
einer der beiden Faktoren auf der linken Seite von (17) durch iß
teilbar sein. Welche der beiden hiernach möglichen Annahmen
wir weiter verfolgen, ist gleichgültig, da die eine in die andere
übergeht, wenn k mit l~1k und l mit IT1 vertauscht wird. Sei
also
(17) (k)p = (Ik) (mod iß).
Wenn die Kongruenz (17) für irgend einen der konjugierten
Werte (k) befriedigt ist, so gilt sie auch für jeden anderen.
Denn es ist nach § 121:.
(k') = f(k,]/D), (Ik') = f(lk,]/D),
also
(k')p = f(kp, }!D) = f(lk, \D) = (Ik') (mod iß).
Es folgt also aus (14), wenn man k durch IT^k ersetzt:
(18) (r1/^ = (7c) (mod iß),
d. h. je nachdem für l die eine oder die andere der beiden zu p
gehörigen Klassen l gesetzt wird, ist der eine oder der andere
Faktor von (16) durch iß teilbar.
Durch wiederholte Anwendung von (17) ergibt sich für jeden
beliebigen positiven Exponenten ji
(19) (k)p* = (l*k) (mod iß)
(Schluß von st auf st 1).
Wenn nun l zum Exponenten e gehört, oder e der Index von
p ist, so ist nach (19):
(20) (lef = (k) (mod iß),
und p‘ ist die niedrigste Potenz von p, die dieser Bedingung
genügt. Denn wenn noch eine niedrigere Potenz von p die Kon-
gruenz (19) erfüllt, so folgt aus (20), daß zwei verschiedene
Klasseninvarianten (k), (k') nach dem Modul iß kongruent sind.
Es wäre also ihre Differenz (k) — (k') durch iß und mithin die
Diskriminante von Hm durch p teilbar, gegen die Voraussetzung.
§ 122.
Irreducibilität.
447
Daraus ergibt sich nun wieder nach (7), daß die Kongruenz
(21) ? (mod 5ß)
für jede ganze Zahl £ in $ erfüllt ist und daraus also der Satz:
Eine Primzahl p zerfällt im Körper $ in lauter von-
einander verschiedene Primideale, deren Grad gleich
dem Index von p ist.
Wir wollen noch beweisen, daß es unter den verschiedenen
in p auf gehenden Primidealen immer eines gibt, für welches
von den beiden aus (16) folgenden Kongruenzen die Kongruenz
(17) besteht.
Dazu bemerken wir: Wenn wir die sämtlichen Zahlen des
Körpers ß in die konjugiert imaginären verwandeln, indem wir
mit —yD und jede Klasseninvariante (k) mit der entgegen-
gesetzten (k~*) vertauschen, so gehen die sämtlichen Zahlen eines
Ideals 91 in die Zahlen eines konjugiert imaginären Ideals 91' über,
das auch mit 91 identisch sein kann, und die Norm des Ideals 91
ist gleich der Norm des Ideals 91'. Ist 91 ein Primideal, so ist
auch 91' ein Primideal.
Ist nun die Kongruenz (17) nicht erfüllt, so muß nach (16)
(/ k)p = (k) (mod iß)
sein, und auch diese Kongruenz bleibt bestehen, wenn k durch
eine andere Klasse k' ersetzt wird. Setzen wir also Z~~~11 an
Stelle von k, so folgt:
(k~')p = (T'kr1) (mod iß).
Da also (k^1)1' — (T~ 1k~1) eine Zahl in iß ist, so ist (k)p— (Ik)
in dem zu iß konjugierten Ideal iß' enthalten, und es ist
(k)v = (Ik) (mod iß'),
was aus (17) durch Vertauschung von iß mit iß' hervorgeht,
7. Aus diesen Sätzen ist die Irreducibilität der Klassen-
gleichung auch nach Adjunktion von eine einfache Folge.
Sind A-, k' zwei beliebige Klassen der Diskriminante D, so
können wir k' nach § 118 in der Weise zusammensetzen: ’
k' = kll'l" ...,
daß durch die Klassen l, V, l", ... die Primzahlen p, p', p", ..,
darstellbar sind. Nach dem, was soeben bewiesen ist, können
wir also die Primteiler 5ß, 5ß', ^ß" dieser Primzahlen so wählen, daß
448
Achtzehnter Abschnitt.
§ 122.
(k)v = (kl) (mod iß),
(22) (kiy = (kW) (mod 'ß'),
(kll')p" = (kll'l") (mod iß")
Nehmen wir jetzt an, es zerfalle die Klassengleichung, es sei
also für ein variables t
Hm(t) = ^(0^(0,
so können wir, da k, k' beliebige Klassen waren, (k) unter den
Wurzeln von (t), (k') unter denen von H2(t) wählen. In der
Kette (22) gehört also das Anfangsglied (k) zu den Wurzeln (ä^)
von •Hj(t) und das Endglied (k') zu den Wurzeln (/c2) von FT2(t).
Da mindestens an einer Stelle der Kette (22) der Übergang von
den Wurzeln des einen Faktors zu denen des anderen stattfinden
muß, so gibt es ein Paar von Wurzeln (fcj), (k2), das für irgend
eine Primzahl p und ein darin aufgehendes Primideal iß der
Kongruenz
(kx)p = (k2) (mod iß)
genügt. Da nun (fcj) = 0 ist, so folgt durch den oft an-
gewandten Schluß
H^kjp = H^kp) = H^k,) == 0 (mod iß).
Da nun
H, (k2) = n[(k2) - (kJ] .
ist, so muß eine der Differenzen (k2) — (fcj) durch iß teilbar sein,
was nicht möglich ist, da p nicht in der Diskriminante von R
aufgeht.
Damit ist die Irreducibilitat der Klassenglei-
chung bewiesen; der Grad des Körpers ff ist gleich
dem Doppelten der Klassenzahl h festgestellt, und
die im vorigen Paragraphen gefundene Gruppe <5
ist als die wahre Gruppe der Klassengleichung er-
kannt.
8. Hiernach können wir alle Primzahlen p, abgesehen
von einer endlichen Anzahl von Ausnahmen (die in 2D
oder der Diskriminante von H aufgehen) in ihre Primfaktoren
im Körper ff zerlegen.
Ist (ü, jp) = —|— 1, so zerfällt p und Körper Sl in zwei kon-
jugierte Primideale ersten Grades. Ist p vom Index «, so ist
jedes in p aufgehende Primideal p vom Grade «. Ist also
P = «ßx $2
_ § 122. Irreducibilität. 449
so ist wegen 5. N(jp) = p2h, und folglich
2 h = re.
Die Anzahl der Primfaktoren, in die p im Körper ß zerfällt,
ist also gleich 2 h/e.
Ist ferner (D, p) = — 1, so sind die Primfaktoren von p
vom zweiten Grade, und ihre Anzahl ist also = h.
9. Eine interessante Folgerung ziehen wir noch aus diesen
Resultaten. Es sei (D, jp) = -f-1 und e der Index von p. Dann
ist ips durch die Form x2 — Dy2 darstellbar und
(23) p‘ = yy',
wenn zur Abkürzung
(24) y = 1 , y' =----------f-*—
gesetzt wird. Wir wissen nun, daß p in lauter verschiedene Prim-
ideale vom Grade e zerfällt. Da p ungerade ist, und x, y höchstens
den gemeinschaftlichen Teiler 2 haben, so haben y, y' keinen
gemeinsamen Primfaktor in ß. Jedem Primideal 5ß, das in y
aufgeht, entspricht ein davon verschiedenes (konjugiertes) Prim-
ideal ^ß', das aus 5ß dadurch entsteht, daß man für alle Zahlen
von 'ß die konjugiert imaginären Zahlen setzt. Es ist also y
nicht nur durch ß, sondern durch Sße teilbar.
Nach § 121 ist
(25)
v 7 \1?(®)/ \i?(®i)/ \i?(os-i)/
und nach § 72, 4 genügen die Faktoren P2 auf der linken Seite
dieses Ausdrucks einer Gleichung P2^?(P2, y3) = p, worin
<p(P2, 7ä) eine ganze algebraische Zahl ist.
Daraus folgt aber, daß P2 nicht durch eine höhere als die
erste Potenz von Iß teilbar sein kann, während doch y durch ߣ
teilbar ist. Wir schließen also aus (25), daß jede der Zahlen P2
durch die erste Potenz von ß teilbar sein muß, daß mithin alle
diese Zahlen assoziiert sind. Bezeichnet also p irgend eine
algebraische Einheit, so ist
x -I- y V— m
2------= 9 -P2S,
also ist y wirklich als «te Potenz einer im Körper ß existieren-
den Zahl dargestellt, und P2 selbst ist eine Darstellung eines
Primideals im Körper Si durch ein Hauptideal im Körper R.
TVeber, Algebra. IH. 29
450
Achtzehnter Abschnitt.
§ 123.
§ 123. Beziehungen zwischen Klasseninvarianten in den
verschiedenen Ordnungen.
Zwischen den Klasseninvarianten verschiedener Diskrimi-
nanten D = Q2A mit dem gleichen Stamm z/ bestehen alge-
braische Beziehungen, die wir jetzt aufzusuchen haben.
Es sei p eine beliebige Primzahl (auch p = 2 nicht aus-
geschlossen) und
(1) D' = p2D.
Es sei — D = m, — D' = m', also m' = p2 m, und
(2) Hm(u) = 0,
(3) = 0
seien die zu den Diskriminanten —m, —m' gehörigen Klassen-
gleichungen.
v = jfpf)
sei eine beliebige Wurzel der zweiten und
(4) A' <a'2 + B' o' -j- C = 0, B'2 — 4 A'C = B'
die primitive quadratische Gleichung, der co' genügt. A' möge,
was erlaubt ist, durch p unteilbar vorausgesetzt sein.
Wir betrachten nun die Invariantengleichung
(5) v} = 0,
deren Wurzeln sind:
(6) w==j(pc>'), c = 0, 1, 2, ...,jp —1.
Das Argument dieser Funktionen:
_____ > j co' —c
co = nco oder = ----------!—
p
genügt einer aus (4) abzuleitenden quadratischen Gleichung,
nämlich:
co — p co', A' co2 B'p co 4- Cp2 = 0,
(D co' 4“ c
P
A'p2 co2 4~ (B' — 2 A' c) p co 4~ A' c2 — B' c C = 0.
Die Diskriminanten dieser Gleichungen sind p2D' = piB,
und die erste von ihnen ist immer primitiv, die Diskriminante
§ 123. Beziehungen zwischen Klasseninvarianten. 451
der zweiten Gleichung reduziert sich nur dann auf D, wenn sie
imprimitiv ist und
B' — 2 A' c durch p,
1 ' A'2c — B' c -|- C durch p2
teilbar ist, und dann genügt die entsprechende Zahl (6) gleich-
zeitig der Gleichung (5) und der Gleichung (2). Dies trifft aber,
wie wir gleich zeigen, nur für einen Wert c zu, und folglich läßt
sich der betreffende Wert u rational durch v ausdrücken.
Denn ist zunächst p ungerade, so hat die erste Kon-
gruenz (8):
2 A' c — B' = 0 (mod p)
nur eine Wurzel, und für diese ist
(’2A'c — B')2 —p2B.= 4:A'(A'c2 — B'c -|- C') = 0 (mod p2).
Ist p = 2, so ist B' und folglich B' gerade und mithin
B' — 2 A' c immer durch 2 teilbar. Es ist dann
/ B'\2
(A'c — ^) — B = A'(A'c2 — B'c + C"),
und da B = 0 oder = 1 (mod 4) ist, so ist die linke Seite hier
durch 4 teilbar, wenn A' c----— = B (mod 2) angenommen wird.
Ai
Geht man umgekehrt von einer Gleichung
(9) A co2 —|— B co —|— C 0, B2 — 4 AG = B
der Diskriminante B aus, nimmt A relativ prim zu p an und
setzt co' = pco, so genügt co' der primitiven Gleichung
(10) J.»'2 -|- Bpco' Gp2 = 0
von der Diskriminante B' = p2 B, und wenn wir also v = j (<»')
setzen, so ist u = j (co) rational durch v ausdrückbar. Daraus
folgt also der Satz:
1. Jede Klasseninvariante für die Diskriminante B
ist rational ausdrückbar durch eine Klasseninvariante
für die Diskriminante p2B.
Um aber die Frage zu beantworten, wie viele Werte von v
zu demselben Werte von u=j(co) führen, bemerken wir, daß
die verschiedenen Werte von v, die dies leisten, Wurzeln der
Gleichung (5) und (3) sein müssen, also in einer der Formen
(ii)
29*
452
Achtzehnter Abschnitt.
§ 123.
(12)
enthalten sind. Nun haben wir aus (9):
co' = p co, A co'2 -j- Bp co' -|- Cp2 = 0,
o' — ® + C
CO = -------------------------------------,
p ..
J.jp2 co'2 -|- (B — 2 A c)p co' -]- Ac2 — B e C = 0,
deren Diskriminante B' ist. Unter den Größen (11) werden aber
nur diejenigen der Gleichung (3) genügen, für die die ent-
sprechende Gleichung (12) primitiv ist.
Die erste der Gleichungen (12) ist nach unserer Voraussetzung
stets primitiv; von den übrigen sind nur die nicht primitiv, für die
(13) Ac2 — Bc -|- (7 = 0 (mod p),
und von den Größen (11) fallen soviele aus, die nicht Lösungen
von (3) sind, als die Kongruenz (13) Lösungen hat. Bezeichnen
wir für den Augenblick die Zahl dieser Lösungen mit t, so ist
die Anzahl der Werte von v, die zu demselben Wert von w ge-
hören, (p -|- 1 — f).
Nehmen wir zunächst p = 2, so haben wir, da A ungerade
ist, folgende Fälle:
B = 0, c = C (mod 2), t = 1,
B = 1, (7=0, c = 0, 1 (mod 2), t = 2,
B = 1, (7=1 (mod 2), t = 0,
(weil c2 — c immer gerade ist). Dies läßt sich so zusammen-
fassen : ’
B = 0 (mod 4), t = 1,
B = 1 (mod 8), t — 2,
B = 5 (mod 8), t — 0.
Mit Benutzung des Zeichens (D, jp) (§ 85) können wir also
setzen:
(14) t = (B, p)1.
Ist p ungerade, so ist die Kongruenz (13) gleichbedeutend mit
(2 Ac — B)2 = B (mod jp),
und diese hat eine Lösung (2 A c — B = 0), wenn p in B auf-
geht, wenn also (D, jp) = 0 ist, zwei Lösungen, wenn B quadra-
tischer Rest von p, also (Z>, p) — -|-1 ist, und keine Lösung,
wenn B quadratischer Nichtrest, also (D, jp) = —1 ist. Also
gilt auch hier die Formel (14).
Nehmen wir daher vorläufig an, was wir gleich genauer
untersuchen werden, es seien unter den jp —|— 1 Größen
§ 123.
Beziehungen zwischen Klasseninvarianten.
453
(15)
o -(- c
p
keine zwei äquivalente, so gehören zu jedem Werte von w
(p — (D, p)] Werte v, und" wenn wir die Grade von (2) und (3)
mit h und k' bezeichnen, so ergibt sich (in Übereinstimmung mit
den Formeln § 100) folgende Beziehung:
(16) h' = [p— (D,p)]h. 2
Nach § 122 sind h und h' die Klassenzahlen der Diskrimi-
nanten D, D'.
Es handelt sich also noch um die Frage, ob unter den Größen
(15) nach Ausschluß der wegen (13) wegfallenden, noch äqui-
valente vorkommen können. Ist zunächst p a äquivalent mit
40 -, so ist:
(17* = + —i,
x 7 p a ßp co r 1
oder:
(18) ßpoA (a -|- ßcp — 8p2) cd ca — pp — 0.
Diese Gleichung muß aus (9) durch Multiplikation mit einer
ganzen Zahl g hervorgehen, und es folgt also:
ßp = g A, a -|- ßcp — 8 p2 = g B, ca — gp = gC.
Da A durch p unteilbar angenommen war, so folgt hieraus,
daß g und folglich a durch p teilbar ist. Setzen wir g = px,
a = pa', so folgt:
(19) ß = Ax, a! ßc — 8 p — Bx, ca' — y = Gx.
Setzen wir noch
(20) a' — ßc 8p = y,
so ergibt sich:
2a' = Bx 4- y,
x > 2 (/5 c — 8 p) = Bx — y,
und aus
(22) p a! 8 — ßy — 1
folgt sodann
(23) y2 — Dx2 = 4.
Der Wert x = 0 ist auszuschließen, weil sonst ß — 0 sein
müßte, was der Gleichung (22) widerspricht, und wir können
unbeschadet der Allgemeinheit x positiv annehmen. Da über-
dies B nach dem Modul 4 entweder = 0 oder = 1 ist, so
454
Achtzehnter Abschnitt.
§ 123.
bleiben zur Erfüllung von (23) nur folgende zwei Möglichkeiten
übrig:
1. D = —3, x = 1, y = + 1.
Da es für die Diskriminante — 3 nur eine Formenklasse
gibt, so können wir A = 1, B = 1, C = 1 annehmen, d. h. für
2 7t i
co die imaginäre dritte Einheitswurzel e 3 setzen, und erhalten
unter den Größen (15) drei äquivalente, indem wir y = -|- 1,
und = — 1 annehmen:
wie auch aus den Gleichungen:
co ________________ — 1 o-4-l __ — 1
p t-rP®' P Pa
erkannt wird, aus denen die Äquivalenz der drei Größen (24)
evident ist.
2. D — —4, x = 1, y = 0.
Wir können ebenso B = 0, A = C = 1, d. h. <n = i an-
nehmen und finden die zwei äquivalenten Werte:
(25) p co,
wie auch aus der Gleichung:
co
P'
—p
pco = ----—
co
folgt.
Es seien ferner zwei der Werte (3)
co 4~ c co 4- c'
p ’ p
äquivalent, so daß eine Gleichung besteht:
(26) = » + K«’ + ? =
v 1 p ap 4- ß(oo 4- c )
oder
(27) 0,2 + O3 c' + c + aP ~ SP)03 +
' ß cc' A~ KCP — d c'p — yp2 = 0,
woraus durch Vergleichung mit (9)
ß = Ax,
(28) ßc' 4- ßc 4- <&p — 8 p = Bx,
ßcc' 4- wcp — 8 c'p — yp* = Cx,
§ 124.
Klassenkörper und Ordnungskörper.
455
folgt, und wenn man wieder
(29) ' ßc' — ßc 4- ap 4- 8p = y
setzt:
zo/fi 2(/?c' + a p) = B X + y,
1 7 2(ßc — 8p) = Bx — y.
Daraus
(31) y* — Dx1 = 4 p2.
Aus (28) ergeben sich die Kongruenzen
ßcc' = Cx, ß (c 4- c') ~ B x, ß = Ax
<32) Dxi = ß*(c-cy <mod^
Soll c' von c modulo p verschieden sein, so kann hiernach
weder x noch D durch p teilbar sein und es folgt aus (32)
(33) A<e + C^^
v ' Acc = C,
und dies führt durch Elimination von c' für c auf die Kongruenz
(13), also auf den auszuschließenden Wert von c.
Fassen wir dies zusammen, so sehen wir, daß unter
den Größen (15) nur in den beiden Ausnahmefällen
D = —3, D = —4 äquivalente vorkommen, und zwar
sind im Falle D = —3 je drei, im Falle D = —4 je zwei
von ihnen äquivalent.
In diesen Fällen muß also die rechte Seite der Formel (16)
noch durch 3 oder durch 2 geteilt werden, und die Formel
bleibt also auch dann noch richtig, wenn man, wie schon früher,
für D = — 3, — 4 unter h nicht 1, sondern | und | versteht.
§ 124. Klassenkörper und Ordnungskörper.
Ist D = Q2A eine Diskriminante und A ihr Stamm, so sind
nach den Resultaten des vorigen Paragraphen die Klassen-
invariante w der Diskriminante A rational durch die Klassen-
invariante v der Diskriminante D ausdrückbar, und zu jedem w
gehören r Werte von v, wenn r nach der Formel (16), § 123 bestimmt
wird. Diese Werte von v sind die Wurzeln einer Gleichung
rten Grades, deren Koeffizienten rational von w abhängen. Die
Größen v gehören also einem Körper St(-D) über &(A) an, der
kein anderer ist als der Klassenkörper der Diskriminante D.
In bezug auf die quadratischen Körper £2 = 31 (fä) sind
beide Körper Abelsche. Wir wollen, wenn eine genauere Unter-
456 Achtzehnter Abschnitt. § 124.
Scheidung nötig ist, den Körper den Klassenkörper von <£,
$(D) den Klassenkörper für die Diskriminante D oder
den Ordnungskörper für den Führer Q nennen.
Nach den Resultaten von § 122 ist, vielleicht mit einer
endlichen Zahl von Ausnahmen,
ein Primideal p des Körpers <£ im Körper
dann und nur dann in Primideale ersten Grades
zerlegbar, wenn p in vom ersten Grade ist und
der Hauptklasse angehört, also gleich einer kom-
plexen Primzahl
x -|- w .
— -
ist.
Soll p in S(_D) in Primideale ersten Grades
zerlegt werden, so kommt noch hinzu, daß x der
durch Q bestimmten Ordnung angehöre, d. h. nach
dem Modul Q mit einer rationalen Zahl kongruent
sei (§ 96).
Neunzehnter Abschnitt.
Berechnung der Klasseninvarianten.
§ 125. Die Klasseninvariante
Wir haben schon oben bemerkt, daß außer der Funktion
j (o) noch andere Modulfunktionen zur Bildung von Klassen-
invarianten geeignet sind, und oft zu einfacheren Resultaten
Anlaß geben. Unter diesen tritt uns zunächst die Funktion (o)
entgegen, die durch (tu) definiert ist.
Wir haben im § 71 gesehen, daß zwischen den Funktionen
(1) u = Vi (m), v = y2 —L-------),
falls ad = n durch 3 nicht teilbar ist, und c durch 3 teilbar
angenommen ist, eine Transformationsgleichung
(2) (w, v) = 0
besteht. Die Funktion <bn hängt aber nur von den beiden Argu-
menten vir”, w3 ab, und in 4>„(m, u) = 0 kommt also, wenn
n = 1 (mod 3) ist, nur w3, d. h. j (co) vor; in diesem Falle kann
daher diese Gleichung kein anderes Resultat ergeben, als die
Invariantengleichung. Anders ist es aber in dem Falle
(3) n = — 1 (mod 3),
den. wir jetzt voraussetzen wollen.
Wenn einer der Werte v = u werden soll, so muß eine
Relation bestehen
e 4- 0 cj Ä „
(4) 1—j—— =------------, aö — ly=l,
v ' a ßeo a
und zugleich muß [§ 54, (15)]
(5) — a ß a ? ß ö — = 0 (mod 3)
sein. Es ist also jedenfalls co Wurzel einer quadratischen Gleichung:
(6) Beo 4- C = 0, D = B2 — 44G.
458
Neunzehnter Abschnitt.
§ 125.
Besteht umgekehrt eine solche Gleichung, so folgt durch
Vergleichung mit (4) in der früher angewandten Art, wenn x, y
ganze Zahlen sind:
8 ß = A x,
ca — ay = Cx,
' ' cß 0 a — ad = Bx,
cß — 0 a — ad — y,
woraus:
20a = Bx — y,
(8) %(cß — a8) = Bx y,
4n = y2 — Bx2.
Setzen wir A relativ prim zu 3» voraus, so muß 0=1,
a = n angenommen werden; denn nach (7) muß unter dieser
Voraussetzung x durch 0 teilbar sein, und folglich auch ca^- ay
und cß — ad, woraus folgt, daß auch a, c durch 0 teilbar sein
müßten, während doch a, c, 0 keinen gemeinsamen Teiler haben.
Also ist
2 a = B x — y, ß = Ax,
2ny = c(Bx— y) — ‘iCx, <lnd = :2cAx — Bx — y.
Die Zahlen x, y sind hier außer den in § 114, 1), 2) an-
gegebenen Beschränkungen wegen (3) noch der unterworfen,
daß y2 — Bx2 = —1 (mod 3) werde. Dadurch ist aus-
geschlossen, daß B durch 3 teilbar sei. x muß von Null
verschieden sein, und wir können es, ohne die Allgemeinheit zu
beschränken, positiv annehmen. (Eine gleichzeitige Vorzeichen-
änderung von x und y bewirkt nur eine Vorzeichenänderung von
a, ß, y, d, die ohne Belang ist.)
Ist B = — 1 (mod 3), so müssen x und y durch 3 unteilbar
sein; ist B = 1 (mod 3), so ist y durch 3 teilbar, x nicht teil-
bar. Im übrigen können die Zahlen x, y beliebig angenommen
werden. Es ist dann c bestimmt aus den beiden (miteinander
verträglichen) Kongruenzen:
. ___ J? x —I— y
cAx =--------1 3
Bx-a (m°dW)
c- o y ~ Cx
2i
und kann, da n durch 3 unteilbar ist, noch der Bedingung
c = 0 (mod 3)
unterworfen werden.
§ 125. Die Klasseninvariante y2. 459
Nun ist nach (7) ß durch 3 nicht teilbar, und daher reduziert
sich die Kongruenz (5) durch Multiplikation mit ß auf:
a -|- d = 0 (mod 3)
oder nach (7) und (3) auf
(10) B = 0 (mod 3).
Ersetzen wir in (6) to durch to + 1, so geht B über in
B + 2 J., und von den drei Zahlen J3, B 2 J., B — 2 Ä ist
eine und nur eine durch 3 teilbar. Wir nehmen also an, es sei
B selbst durch 3 teilbar, dann folgt, daß von den drei Werten
(11) ra(e’), r2(«>H-l) = e 3 y2(o), y2(o — 1) = e 3 y2(ra)
nur der erste der Gleichung
(12) •- (w, w) = 0
genügt. Die Gleichung (12) und
(13) w3 —j(co) = 0
haben daher nur eine gemeinsame Wurzel, und diese ist rational
durch j (to) ausdrückbar. Damit ist bewiesen:
1. y2(<a) ist eine Klasseninvariante, wenn to die
Wurzel einer quadratischen Form ist, deren Diskri-
minante und erster Koeffizient durch 3 nicht teil-
bar sind, während der mittlere Koeffizient durch 3
teilbar ist.
Wenden wir dies Ergebnis auf den Fall n — 2 an, so er-
halten wir zunächst aus der Gleichung (5), § 71:
(14) <P2 (w, u) = w4 — 2 u3 — 495 w2 24.33.53 = 0.
Die Gleichung
y- — l)x- = 8
ist, da D = 0 oder = 1 (mod 4) sein muß, nur für drei nega-
tive Werte von D lösbar, nämlich
D = —8, x = 1, y — 0,
(15) D = — 7, x = 1, y = ± 1,
D = —4, x = 1, y — +2.
Diesen drei Werten von D entsprechend kann man für die
Gleichung (6) die folgenden wählen:
D = — 8, o2 + 2 = 0,
D = — 7, to2 4- 3ra -|- 4 = 0,
D = — 4, ra2 4- 1 = 0
oder
460
Neunzehnter Abschnitt.
§ 125.
D = — 8,
D = -7,
D = -4,
« = V- 2, ______
3 + 1/- 7
a ——------2-----
ca = i.
Der Wert (i) ist aber (nach § 117) bekannt, nämlich = 12,
und daher muß die linke Seite von (14) durch w — 12 teilbar
sein. Da dieser Faktor bekannt ist, findet man leicht die übrigen:
«4 _ 2 u3 — 495 «2 _|_ 24.33.53 = (w — 12) (w — 20) (w + 15)2.
Da y2(o) ebenso wie j(a>) für ein rein imaginäres eo einen
positiven Wert hat, so muß der Faktor u— 20 dem Werte
D = —8 entsprechen, und wir erhalten:
(iß) z2(«) = 12,
(17) n (V^2) = 20,
(18) ?2 (~3 + j/~~7) = -15.
Es existieren außer —7 noch fünf ungerade durch 3 nicht
teilbare negative Diskriminanten:
(19) — 11, — 19, — 43, — 67, — 1631),
für die es nur eine Formenklasse gibt. Für diese ist also nach
unserem Satze:
eine ganze rationale Zahl Z.
Um diese rationalen Zahlen zu finden, wollen wir Grenzen
aufsuchen, zwischen denen sie liegen müssen, die um weniger als
eine Einheit voneinander verschieden sind.
Nach § 54, (5), (8) ist:
r, (») = f («)• - = f, (»)• +
= r.W” + +y,.
ferner nach § 34, (19):
fs ----2~ 7 ~ e 12,
') Daß nicht mehr Diskriminanten dieser Art existieren, kann bis jetzt
nur daraus geschlossen werden, daß, soweit man die Berechnung der
Klassenzahlen fortgesetzt hat, weitere Zahlen dieser Art nicht gefunden sind
[vgl. die Tafel der Klassenzahlen von Gauss (Werke, Bd. II, S. 450)].
Die Klasseninvariante y2.
461
§ 125.
also
(— 3 + ,s 256
- (--------2) = f(°J) ~ f^yi *
Setzt man also: _
(20) q = e~-’r1/“)
so erhält man [§ 24, (11)]:
z = 3 + ^)
2
= q * n (1 + -------------------
1>”° n (! g2>-l)X6
Wir machen nun Gebrauch von der für jedes echt gebrochene
positive x gültigen Grenzbestimmung:
1 -4- x <C ex. <C i—-—, e~x >1 — x,
1 1 — x
und erhalten:
9
1 < JT(1 + g2”-1) < e1-«2,
woraus
1 2 _ 1 8ä 2_----1-?.
q 3 — 256 q% <Z Z <Z q s e1-«2 — 256 t/s e *—<z2,
und indem man die obere Grenze noch vergrößert, kann man
dafür auch setzen:
2
256 qs -|-
Z <Z q s
2
8 g3
1 — 8 q — q2
6
212 gs
1 — g2’
Für m = 11 ist q ungefähr = 2-16, woraus man ersieht, daß der
Unterschied beider Grenzen:
2 6
8gS , 212 g3
1—8 ä — £2 + 1 — ä2
bereits für m = 11 und noch mehr also für die größeren Werte
von m sehr klein ist. Z ist also die zunächst über
_ 1 2.
q s — 256 q$
gelegene ganze Zahl, und dieser Wert, für die größeren m schon
q~ 3, kommen einer ganzen Zahl außerordentlich nahe. Daraus
berechnet man diese Zahlenl):
*) Man tut gut, sich bei diesen und vielen der später beschriebenen
Rechnungen ein- für allemal den Briggischen Logarithmus
log (n log e) = 0,134 934184 0
zu merken, bei dem man übrigens meist mit 7 Dezimalen ausreicht.
462
Neunzehnter Abschnitt.
§ 1261
— ya (=£+PT)=32,
-72 ,_ä + /TüFx = i)6 = 32^ \ 2i /
— Ti ( ) = 960 — 64.15, \ Ä /
— Ti' ( ) = 5280 = 32.3.5.11, X At /
— Ti । 3 +V—!63^ — 640 320 = 64.3.5.23.29.
Bei diesen Zahlen ist die Zerlegbarkeit in verhältnismäßig
kleine Primzahlen bemerkenswert.
Auch für die Diskriminante —27 existiert nur eine Klasse.
Da aber diese Diskriminante durch 3 teilbar ist, so ist nicht y8 (ca),
sondern erst j (ca) eine rationale Zahl. Man findet durch ähn-
liche Rechnung:
x O /
§ 126. Die Klasseninvarianten f(ca)il.
Die Wurzeln der kubischen Gleichung
(1) (u — 16)8 — uj(ca) = 0
sind, wie wir früher allgemein gesehen haben (§ 54),
w = f(ca)M, — f. (ca)**, — fa (ra)245
oder
/ 1 \24
(2) f(ca + 1)«, f (1 - .
Es sei nun wieder ca die Wurzel der quadratischen Gleichung:
(3) Acat-(-Bca-\-C = 0
mit der negativen Diskriminante:
(4) D = B* — 421(7,
worin A, B, C keinen gemeinschaftlichen Teiler haben, und j (ca)
sei die Klasseninvariante. Setzen wir
ca' = ca 4- 1, ca" = 1------,
1 • ca
so ist
f . Aca'2 + (B - 2 A)ca> + (A - B + C) =. 0,
k B + (7 — (B + 2 (7) ca” + Cca"2 = 0.
§ 126.
Die Klasseninvarianten f(w)24.
463
Die drei Argumente von (2) sind also die Wurzeln von äqui-
valenten quadratischen Formen.
Wir unterscheiden die drei Fälle:
1. D = 0 (mod 4). Hier ist B gerade, und A und C können
nicht beide gerade sein; von den drei Formen (3), (5) hat also
die eine zwei ungerade äußere Koeffizienten, die beiden anderen
haben einen geraden und einen ungeraden äußeren Koeffizienten.
2. Ist D = 1 (mod 8), so ist B ungerade B2 = 1 (mod 8),
A C = 0 (mod 2), also ist wenigstens einer der beiden Koeffi-
zienten gerade, und unter den drei Formen (3), (5) ist eine, aber
auch nur eine, die zwei gerade äußere Koeffizienten hat.
3. Ist D = 5 (mod 8), so ist 44C = 4 (mod 8) und die
beiden äußeren Koeffizienten A und C sind ungerade.
Wenn es nun gelingt, eine ganzzahlige Gleichung aufzustellen,
der von den drei Wurzeln (2) nur die eine genügt, so folgt
daraus, daß diese eiue Wurzel rational durch j(cj) ausdrückbar
und also eine Klasseninvariante ist.
Es besteht zwischen den Funktionen
(6) u = f(a)\ v = f 4 0 = °) (mod 2)
\ (Jj l
für einen ungeraden Transformationsgrad n (§§ 73, 74) eine Trans-
formationsgleichung :
(u, v) = 0,
und die Gleichung:
(7) ®M(w, w) = 0
ist also nach
Größen (6):
(8)
worin
(9) oder
§ 53 nur dann befriedigt, wenn für eine der
c da ______ y de?
a w —|— ß a
(J;?) C“42)
eine zur ersten oder zur zweiten Klasse (§ 36) gehörige lineare
Transformation ist.
Die Vergleichung von (8) mit (3) führt aber, wie oben, zu
den Bedingungen:
464
Neunzehnter Abschnitt.
§ 126.
ßd — Ax,
ac — y a = Cx,
ßc — 8 a ad — B x,
(10) ßc — 8 a — ad = y,
' . Bx y . Bx — y
ßc — 8a = -—ad —----------------x—S
4 « = 7/2 - Bx'1.
Nehmen wir A und n ohne gemeinsamen Teiler an, so muß
d = 1, a — n sein, denn eine in x und d aufgehende Primzahl
müßte auch in y und folglich in a c — ya und ßc — 8 a und,
wegen a8 — ßy = 1, auch in a und c aufgehen, während doch
a, c, d keinen gemeinsamen Teiler haben sollen. Aus (10) wird
w, ß, y, 8, c ebenso bestimmt, wie im vorigen Paragraphen. Es-
ergeben sich zunächst die beiden Kongruenzen
. Bx + y Bx — y „ , , .
cAx = -----c-----------Cx (mod n),
von denen die eine aus der anderen folgt, wenn x teilerfremd
zu n ist, und die Bedingung
c = 0 (mod 2)
ist damit verträglich. Weiter folgt:
Bx — y „ . Bx — y
a= -----2-, ny — — Cx + c-----------—2-,
(11)
o j c, so —|— y . j
ß = Ax^ n8 =---------------* -j- Acx.
2i
Wenn nun B und mithin B ungerade ist, so müssen, da.
wegen (9) a und Ö beide gerade oder beide ungerade sind, x und
y gerade sein; also sind ß und y gerade, und a und d müssen
ungerade sein. Folglich muß von den beiden Zahlen ±x, %y eine
gerade, eine ungerade sein. Das ist aber unabhängig davon, wie
sich A und C gegen den Modul 2 verhalten.
Wenn also von den drei Größen (2) die eine der Gleichung
(7) genügt, so tun es auch die beiden anderen, und wir können
diese drei nicht voneinander trennen.
Wir müssen daher B gerade annehmen und setzen zur
Vereinfachung:
(12) B = —4n?,
worin m eine positive ganze Zahl ist.
Wir unterscheiden:
§ 126. Die Klasseninvarianten / (w)24. 465
1. Wenn D = 4 (mod 8) ist, setzen wir
n = m, x = 1, y = 0,
« = ß = A,
y^—C, ö = (mod 2).
Die Kongruenz (9) fordert also, da nicht alle drei Koeffi-
zienten A, B, C gerade sein können, daß die beiden äußeren
Koeffizienten ungerade, der mittlere durch 4 teilbar sei, und dies
findet nur für eine der drei Formen (3), (5) statt; folglich ge-
nügt eine der drei Funktionen (2) der Gleichung (7), und ist
also Klasseninvariante.
2. D = 0 (mod 8),
n = m 1, x = 1, y = + 2,
w = ß = A,
Al
y = — C, S = ~1 (mod 2).
Al
Es müssen also auch hier die beiden äußeren Koeffizienten
ungerade B = 2 (mod 4) sein, und es verhält sich dann alles
wie oben. Damit ist bewiesen:
1. Ist co die Wurzel einer primitiven quadra-
tischen Gleichung mit negativer, durch 4 teilbarer
Diskriminante D und ungeraden äußeren Koeffi-
zienten, so ist /(oi)-4 Klasseninvariante für die Dis-
kriminante B.
Die Annahme, daß A relativ prim zu n, d. h. zu m 1
oder zu m sei, kann nachträglich als unwesentlich aufgegeben
werden.
Denn wenden wir auf w eine lineare Transformation (S) an,
so geht die Gleichung (3) bei ungeraden A, C in eine äquivalente
Gleichung über, in der die äußeren Koeffizienten dann und nur
dann beide ungerade sind, wenn (S) zur ersten oder zweiten
Klasse gehört, also wenn /’(cj)24 durch (S) ungeändert bleibt.
Man kann dann noch (S) so bestimmen, daß der erste Koeffizient
in der umgeformten Gleichung (3) zu einer beliebigen Zahl, also
auch zu n relativ prim wird.
Weber, Algebra. III. on
466
Neunzehnter Abschnitt.
§ 126.
Auf den Fall m = 1 ist dies Verfahren nicht anwendbar,
weil (M> «) für n = 1, co = i (aber auch nur für diesen Werf)
identisch verschwindet, für m — 1 haben wir aber bereits früher
gefunden (§ 83):
f(if“ = 64,
so daß also auch in diesem Falle der ausgesprochene Satz gilt.
Wenn m ungerade ist, so ist bei ungeradem A, C der mitt-
lere Koeffizient JB durch 4 teilbar; dagegen ist bei geradem m
unter der gleichen Voraussetzung B nicht durch 4 teilbar. Durch
die Substitution ct> -|- 1 für co erreichen wir aber auch im Fall
eines geraden m, daß B durch 4 teilbar wird; dann aber wird
auch C gerade. Durch die Vertauschung (co, —|— 1) geht aber
/(co)24 in —/i (co)24 über, so daß wir also unserem Satz auch den
folgenden Ausdruck geben können:
2. Ist co die Wurzel der quadratischen Gleichung:
A(o2-{-B(o~\-C— 0,
worin A ungerade, B gerade ist, so ist, je nachdem
D = 4 oder D = 0 (mod 8) ist, f (co)24 oder (co)24
Klasseninvariante.
Da A und C nicht beide gerade sein können, so sind nur
drei Fälle möglich, von denen durch die Vertauschungen
(cd, cd —|— 1),
der zweite auf den ersten und der dritte auf den zweiten zurück-
geführt wird. Wir haben also in diesen Fällen:
A = 1, C = 1 (mod 2), Klasseninvariante f (co)24,
(13) A = l, 0 = 0 „ „
A = 0, 0=1 „ „
Insbesondere ist also, wenn wir die Hauptform der Diskri-
minante — 4m, (1, 0, m), zugrunde legen, f(tf—m)24 bei unge-
radem und fx (V— m)2i bei geradem m eine Klasseninvariante.
Diese beiden Zahlen haben einen reellen positiven Wert, und
sollen in den weiter unten folgenden Rechnungen vorzugsweise
berücksichtigt werden.
Aus der Gleichung (1) schließen wir (Bd. II, § 154, 11.),
da j (cd) eine ganze algebraische Zahl ist, daß auch /(cd)24 eine
ganze algebraische Zahl sein muß, und die Form der Gleichung (1)
zeigt, daß die Norm dieser Zahl eine Potenz von 2 ist.
§ 127.
Die Potenzen von /'(«) als Klasseninvarianten.
467
§ 127. Die Potenzen von /(co) als Klasseninvarianten.
Nach der Definition von }q(<») ist:
Ist co die Wurzel einer Gleichung:
(2) A a‘- 2 B co -|- C = 0, A C — B2 = m,
deren Diskriminante —4 m durch 3 nicht teilbar ist, so können
wir, wenn nötig, durch Übergang zu einer äquivalenten Gleichung,
A, C als ungerade, A durch 3 unteilbar und B durch 3 teilbar
voraussetzen. Dann aber sind nach den beiden vorigen Para-
graphen f(ai)2i und y2(cj) Klasseninvarianten, und wir erhalten
aus (1) den Satz:
3. Ist co Wurzel einer quadratischen Form von
negativer, durch 3 nicht teilbarer Diskriminante,
deren beide äußere Koeffizienten ungerade, deren
mittlerer Koeffizient durch 6 teilbar ist, so ist
eine Klasseninvariante.
Um die Frage zu untersuchen, ob auch noch niedrigere
Potenzen von /(co) Klasseninvarianten sein können, machen wir
Gebrauch von der Formel:
(3) /(co 2>')6 =
worin r eine ganze Zahl ist; die Werte
ar = co 2r
sind die Wurzeln von äquivalenten quadratischen Gleichungen
A G)r ~p 2 Br G)r —j— (Jr 0,
worin
(4) Br = B — 2 Ar,
und hierin läßt sich r nach dem Modul 4 so bestimmen,- daß
bei ungeradem m:
(5) B,. = 0, 2, 4, 6 (mod 8)
und bei geradem m:
(6) Br = 1, 3, 5, 7 (mod 8).
Wenn es nun gelingt, eine Gleichung mit rationalen Koeffi-
zienten aufzufinden, der von den vier Werten (3) entweder nur
30*
468 Neunzehnter Abschnitt. § 127.
der eine, der dem Werte r = 0 oder zwei, die den Werten
r = 0, 2 entsprechen, genügen, so folgt, daß /(co)6 oder /(w)12
Klasseninvarianten sind.
Ist außerdem m durch 3 unteilbar, so kann man die Br alle
durch 3 teilbar voraussetzen, und es folgt dann durch Kombina-
tion mit dem Satz 1., daß auch
f(a)s = f (co)2 oder /(co)12 /(co)-8 = /(w)4
unter den Klasseninvarianten enthalten sind.
Nachdem so unser nächstes Ziel bezeichnet ist, machen wir
von dem Ergebnis des § 73 Gebrauch, daß zwischen
/. /c -|- 8 co\3 . .
--------------------------------), u = f(&y
eine Modulargleichung:
(7) (w, v) = 0
besteht, wenn
ad = n, c = 0 (mod 16)
ist. Die hieraus abgeleitete Gleichung
(8) u) = 0
ist dann und nur dann befriedigt, wenn
zq\ c + 8<u ___ y -j- ög>
a ~ a 4- ß <o'
worin f eine lineare Transformation der ersten oder zweiten
Klasse ist, die [nach § 40, (12)] der Bedingung genügt:
\^=ß)6 - - 1,
oder der damit gleichbedeutenden:
(10) ay -j- ßd 2<x2 — 2 aß — 2ad = 0 (mod 16).
Aus (9) folgt aber, wenn a der Gleichung (2) genügt, wie
wir im vorigen Paragraphen gesehen haben,
n|= y2 -|- mx2,
(11) a — Bx — y, ny ——Cx-j-c(Bx— y),
ß = Ax, nd — — Bx — y Acx.
Nehmen wir zunächst m ungerade an, so können wir n = m,
also x = 1, y = 0 setzen, und da c durch 16 teilbar ist, folgt:
a = B, ß = A, y = — mC, d = — mB (mod 8),
§ 127. Die Potenzen von f(ci) als Klasseninvarianten. 469
also ergibt (10):
(12) B (m A — (m 1) B + = 0 (mod 8).
Wenn nun m = 3 (mod 4), so ist A C = 0 (mod 4) und
der in (12) in der Klammer stehende Ausdruck ungerade, daher
ist (12) nur unter der Voraussetzung befriedigt, daß
B ~ 0 (mod 8).
Wir wollen, um Wiederholungen zu vermeiden, bei den im
folgenden auszusprechenden Theoremen ein- für allemal voraus-
setzen, daß co die Wurzel einer solchen Gleichung (3) der Diskri-
minante — 4m sei, in der A ungerade, B durch 8 teilbar sei.
Damit ist also das Theorem bewiesen:
4. Ist m = 3 (mod 4), so ist f(<o)e Klasseninvariante.
Ist ferner = 5 (mod 8), so reduziert sich die Kongruenz
(12) auf:
B 2—~ ~~ 0 (mod 8),
und diese Bedingung ist erfüllt, wenn B durch 4 teilbar ist, da-
gegen nicht erfüllt, wenn B nur durch 2, nicht durch 4 teilbar
ist. Daraus folgt:
5. Ist m = 5 (mod 8), so ist f(w)12 Klasseninvariante.
Ist m = 1 (mod 8), so läßt sich aus der Kongruenz (12)
nichts schließen. Dies stimmt mit dem Umstande überein, daß
in diesem Falle ®m(w, u) nur von m8 abhängig ist. Um auch
hier zu ähnlichen Resultaten zu gelangen, wenden wir die Trans-
formation zweiter Ordnung an. Wir nehmen in (7):
(13) n ~ 1 (mod 8)
und setzen:
uv = ±y2s,
d. h.:
= ± yj.,
oder [§ 34, (18)]:
(u) f(^y=±^y.
Die Gleichung (7) geht dadurch über in eine Gleichung:
(15) «>.(„,+£) = 0,
X U /
470
Neunzehnter Abschnitt.
§ 127.
genüge, in der
oder genauer gesagt, je nach der Wahl des Vorzeichens in zwei
Gleichungen, die außer dem Produkt
V2/-(«p
nur rationale Zahlkoeffizienten enthalten. Letzteres ersieht man
daraus, daß in der Gleichung (7) nur solche Produkte vor-
kommen, in denen 7» fc gerade ist (vgl. den Anfang von § 74).
Die Relation (14) fordert nun, daß co einer Gleichung
HR! c + + !) + ~ 1)
' a a (co -j- 1) -j- ß (<» — 1)
eine zur ersten oder zweiten Klasse ge-
0/
hörige lineare Transformation ist. Damit aber eine der beiden
Gleichungen (14) wirklich erfüllt sei, ist nach § 40, (12) noch
erforderlich:
(17) (a — ß) (k -|- ß -|- y — 8) = 0 (mod 8).
Nun folgt aber, wenn co Wurzel der quadratischen Gleichung
(2) ist, aus (16) wie oben:
d(a ß) — Ax,
d (a — ß) = B x + y, -•
(18) c(w — ß) — a(y — 8) = Cx,
c(“ + ß) — «0 + 8) = Bx — y,
2n = y2 mx2.
Ist nun, wie vorausgesetzt war,
m = 1 (mod 8),
so setzen wir:
m 4- 1 , m -I- 9
m=—— oder —j—,
je nachdem m = 1 oder ~ 9 (mod 16) ist, so daß auch n = 1
(mod 8) wird, dann ist x = 1, y = +1 oder =+3 zu setzen,
und wenn wir A relativ prim zu n voraussetzen, so wird 8 = 1,
a = n, und aus (18) folgt:
« + ß = A, M (y — 8) = — C + c(B + y),
a, — ß = B-\-y, n(y -|- 8) = — B + y + cA.
Hiernach ergibt die Bedingung (17), da B -|- y ungerade,
c = 0 (mod 16) ist:
A = C (mod 8),
§ 127. Die Potenzen von f(<u) als Klasseninvarianten. 471
was nur möglich ist, wenn B = 0 (mod 4) ist. Um aber zu
entscheiden, welche der beiden Gleichungen (15) erfüllt ist, kommt
es nach § 40, (12) darauf an, ob
(06 — ^)2 — 1 (06 _ (06 + y — d)
oder, was dasselbe ist,
(B + yy - 1 + (B + y) (JL - nC)
durch 16 oder nur durch 8 teilbar ist. Vermehrt man aber in
diesem Ausdruck B um ein ungerades Vielfache von 4, so ver-
ändert er sich um ein ungerades Vielfache von 8, woraus zu
schließen, daß, je nachdem B = 0 oder = 4 (mod 8), die eine
oder die andere der beiden Gleichungen (15) befriedigt ist.
Damit ist bewiesen:
6. Ist m = 1 (mod 8), so ist ]/2/’(<»)6 Klassen-
invariante.
In den Fällen, wo m = 3 (mod 4) ist, können wir noch
einen Schritt weiter gehen. Wir haben in § 73 neben den
Schlaeflischen Modulargleichungen auch die Gleichungen
(19) ®„(«i, «i) = 0
kennen gelernt, die zwischen
(20) - A (m)s, vx = \ — \fA —----------}
bestehen, und aus § 73, (10), (15) ergibt sich, daß, wenn n = 7
(mod 8) vorausgesetzt wird, («i, vf) rational durch
u1 Ui Mi + V1
dargestellt werden kann. Wenn wir also in (19) .
(2i) v-l = a 8 = ±A (<»)3, «i = fi (»)s
setzen, so wird
±]/23
V1 = 7-7
f<°>y
und Mj8 -|- ‘i’i3 kann rational durch /(co)24 ausgedrückt werden
[§ 34, (11)], d. h. es geht
(«i, ^i) = 0
in eine oder, nach der Wahl des Vorzeichens, zwei rationale
Gleichungen für _
i = y2 f&y
über, die wir mit
(22)
bezeichnen wollen.
F(+£) = 0
472
Neunzehnter Abschnitt.
§ 127.
Die Gleichung (22) hat aber wieder eine Gleichung der
Form (21) zur Folge, so daß in beiden die Vorzeichen überein-
stimmen, und die Gleichung (21) fordert nach § 40, (7):
(23)
c dto______y -|- d co
a a ßto'
S = 0 (mod 2),
72 — 1 -|- y (2<z — d) = 0 oder = 8 (mod 16),
und zwar gilt, je nachdem die eine oder die andere Kongruenz
stattfindet, in (21) und (22) das eine oder das andere Vorzeichen.
Nehmen wir m = n, also m = —1 (mod 8), so ergibt sich
aus (2) und (23) ganz wie oben:
ß = A, ny = — C cB,
a = B, nd — — B -\-cA,
also aus der zweiten Kongruenz (23):
C2 CB — 1 = 0 oder = 8 (mod 16),
woraus zunächst folgt, daß B jedenfalls durch 8 teilbar sein
muß; vermehren wir aber B um ein ungerades Vielfache von 8,
so geht die eine dieser Kongruenzen in die andere über, und
infolgedessen geht in (21) das eine in das andere Vorzeichen
über. Für ein bestimmtes co besteht also nur die eine der
beiden Gleichungen (22) und es folgt:
7. Ist m = 7 (mod 8), so ist y2/’(<»)s Klassen-
invariante.
Wenn wir einer durch alle bekannten Beispiele bestätigten
Induktion vertrauen dürfen, so besteht noch das folgende Theorem:
8. Ist m = 3 (mod 8), so ist f(ai)s Klasseninvariante.
Indessen fehlt hierfür noch der allgemeine Beweis.
Ist m = 2 (mod 4), so wenden wir dasselbe Verfahren an,
wie oben im Falle m = 1 (mod 8).
Wir setzen:
(24) 2 h = m y2,
und nehmen y = 0 oder = ± 2, so daß n = 1 (mod 4) wird.
Wenn wir dann in der Gleichung (19)
(25) = f2 (yj = M1 ~
setzen, so ergibt sich eine Gleichung, die nur ^^(ra)6 und
rationale Koeffizienten enthält. (19) • ist aber nur dann erfüllt
[§ 40, (7)], wenn
§ 127.
Die Potenzen von f(a>) als Klasseninvarianten.
473
(26) = ,;s„ W2)
a 2a ßca v 7
und außerdem
(27) y2 — 1 y(2a — d) = 0 (mod 16);
aus (26) und (24) folgt:
2a = B~^y, 2ny =—C , ,
a r-D \ (m0<l 16)>
ß = A, 2 no = — (B — y) v ’
und daraus schließt man wie oben:
9. Ist m = 2 (mod 4), so ist ^2 ^(jo)6 Klassen-
invariante.
Wiederum weisen sämtliche Beispiele darauf hin, daß, wenn
m = 4 (mod 8) ist, ^/(ca)12 Klasseninvariante ist. Aber
auch hierfür fehlt noch der Beweis. Wenn m durch 8 teilbar
ist, tritt eine Reduktion nicht ein.
In den Fällen 4. bis 8. ergibt sich nach 3. eine weitere
Reduktion auf die dritte Wurzel, wenn m nicht durch 3 teilbar
ist. Demnach erhalten wir folgende Fälle:
m = + 1 (mod 3),
1) m = 3 (mod 4) Klasseninvariante /(“)/
2) m = 5- (mod 8)
3) m = 1 „ VM«)2,
m = 7 „ y2/(<o),
5) m = 3 „
6) m = 2 ,, Vi/^)2,
7) m = 4 „ V2/i(«)4,
wovon freilich die Fälle 5) und 7) nur durch Induktion ge-
schlossen sind.
Die Klasseninvarianteu /(co) eignen sich ganz besonders zur
numerischen Berechnung, weil sie unter allen die einfachsten
Resultate liefern. Wir geben daher zunächst eine, größere Reihe
von Beispielen, die sich auf Grund unserer bisherigen Entwicke-
lungen leicht ableiten lassen, und die zugleich die Methoden
kennen lehren, deren man sich auch zu weiter fortgesetzten Rech-
nungen dieser Art bedienen kann.
Es wird bei diesen Berechnungen häufig die Aufgabe gestellt,
reduzible, ganze rationale Funktionen in Faktoren zu zerlegen.
Eine solche Zerlegung ist, wenn sie gefunden ist, natürlich sofort
474
Neunzehnter Abschnitt.
§ 128.
zu verifizieren; aber auch das Auf finden der Faktoren gelingt
leicht, wenigstens soweit die Rechnungen bis jetzt fortgesetzt sind,
da man häufig in den späteren Fällen früher gefundene Resul-
tate benutzen kann, und überdies die allgemeine Form der Fak-
toren kennt. Beispiele werden dies erläutern.
§ 128. Die ersten Fälle der Berechnung von — m).
Setzen wir in der kubischen Gleichung:
(1) «3 — y2 (ca) u — 16 = 0,
deren Wurzeln nach § 54
/(ca)3, — AO»)8, —AG»)8
sind, co = i, also [§ 125, (16)], y2 = 12, so folgt:
«3 — 12 w — 16 = 0,
eine Gleichung, deren einzige positive Wurzel u — 4 ist, so daß
wir in Übereinstimmung mit § 126 erhalten:
(2) _ f(i) = 1X2;
setzen wir ca = ]/—2, also y2 = 20 [§ 125, (17)], so erhalten
wir aus (1) die Gleichung:
«3 — 20 w — 16 = 0
mit der einzigen rationalen Wurzel — 4. Da aber nach den
Sätzen der beiden vorhergehenden Paragraphen A (]/—2)8 rational
sein muß, so ist:
(3) A(V=2) = 1/2.
Wir setzen ferner co = e 3 , also y2(ca) = 0 (§ 117) und
erhalten aus (1):
us — 16.
Dieser Gleichung genügt [§ 34, (19)]:
/_ i yzzäxs 16 e 3
u " \ 2 ) - f(y=^)8’
woraus der reelle positive Wert:
(4) r(V=3) = 1/2.
Um die übrigen Resultate des § 125 anwenden zu können,
setzen wir
m = 7, 11, 19, 43, 67, 163,
§ 128. Die ersten Fälle der Berechnung von /"(V-—m). 475
und benutzen die aus § 34, (19) folgende Formel:
/(<») ft ( —~ M) = e~T y 2.
Demnach ist, wenn wir
f (y— m) = x
setzen, x nach (1) die reelle positive Wurzel der Gleichung
(5) x2i -|~ Za (—3 xls — 28 =0.
Für m = 7 erhalten wir nach § 125, (18)
(6) /(y=7) = y2,
während in den anderen Fällen, nach Einsetzen der Werte für y2,
sich die Gleichung (5) erst in zwei Faktoren 12ten, diese wieder
in zwei Faktoren 6ten und schließlich diese in zwei Sten Grades
spaltet. Die so erhaltenen Gleichungen sind kubische Gleichungen
für a;8, x'4, a;2, x, von denen wir jedesmal nur die beibehalten,
die eine reelle positive Wurzel hat, der schließlich —m)
selbst genügt.
Um die erste Zerlegung zu finden, setzen wir die Gleichung
(5) in die Form:
(a;12 — ax*)2 — (bx3 c)2 — 0,
und haben die ganzen Zahlen a, b, c aus den Gleichungen:
2 a b2 — — y2, 2bc — a2, c2 = 28
zu bestimmen, also c = 4;16; die Gleichung 12ten Grades mit
positiver Wurzel lautet also:
x12 — bxs — axi — 16 = 0.
Die Zahlen a, b bestimmen sich aus den obigen Gleichungen
leicht, und so findet man schließlich die gesuchten kubischen
Gleichungen. Man erhält z. B. für m — 11 successive
x12 — 8 a;8 ~|~ 16 a;4 — 16 = 0,
x6 — ix2 — 4 = 0,
x3 — 2 x2 2 x — 2 = 0.
In den fünf Fällen des § 125 findet man folgende Gleichungen:
<7) x = f(\- 11), x3 — 2 x2 -f~ 2 x — 2 =0,
(8) x = f (V- 19), x3 — 2 x — 2 = 0,
(9) a; = f (y- 43), x3 — 2 a;2 — 2=0,
(10) * = f (y- 67), x3 — 2 a;2 — 2 a; — 2 = 0,
(11) xr = f<y—163), ,x3 — 6 a;2 -|- 4 x — 2 = 0.
476
Neunzehnter Abschnitt.
§ 129.
§ 129. Anwendung der Transformation zweiter Ordnung zur
Berechnung von Klasseninvarianten.
Die Transformation zweiter Ordnung läßt sich, wenn nötig
in mehrmaliger Wiederholung, auf alle solche Diskriminanten
— im anwenden, für die y2 mx2 eine Potenz von 2 ist, also'
z. B. auf m = 7, 15, 23, 31.
Diese Rechnungen sind aber beschwerlich, und wir werden
einfachere Wege finden, um in diesen Fällen zum Ziele zu kommen.
Bessere Dienste leistet die Transformation zweiter Ordnung, um
aus einer bekannten Klassen invariante eine neue zu finden, die zu
einer Diskriminante gehört, die das Vierfache der ersteren ist.
Dazu führen folgende Formeln:
Nach § 34 ist:
+ A(<»)s ==
AWV.C»)’ =
woraus
Das Vorzeichen der Wurzel wechselt nur für. f(ti)2i = 64r
also für w = i, und ist, solange —iw reell und größer als 1
ist, positiv zu nehmen, da die linke Seite für ein verschwindendes
g positiv unendlich wird. Es ergibt sich daraus:
oder
A(w)«f(wy [/(w)« 4- y/’(w)24 — 64J = 32,
und auf dieselbe Weise:
A(w)*A(«>)4[A(«»)12 + y/i(ra)24 + 64] = 32.
Ferner ist nach § 34, (16):
A(2w)A(w) = |/2,
woraus
(1) 2 A (2 w)8 = f (w)^ [f (w)« + Vf(w)^ - 64]
= fi (®)4 [fi (<»)12 + VA (ra)24 + 64].
Diese Formeln können dazu dienen, wenn f(w) oder A(M)
bekannt ist, f1(2ea') zu berechnen, also A (V—4 m) aus
§ 130. Berechnung von Klasseninvarianten. 477
oder A (V— m). Auf diese Weise findet man sehr leicht, wenn
man aus den Formeln des vorigen Paragraphen f(i), /i (]/—2),
/(]/—3), /(y—7) entnimmt:
(2) = 8,
(3) A(y^i6)8 = 8y2(i + y2)2,
(4) /•1(y=~8)8^ 8(1 +1/2), ___________________
(5) ÄAV- 32)8 = 32(1 +y2)2 + 8y2l/8(l + y2)4 + (l + V2).
Setzen wir:
/•^y-W = 8®,
so ist x Wurzel der biquadratischen Klassengleichung:
(6) (x2 — 24 x — 2)2 — 8(8« + l)2 = 0,
die durch Adjunktion von \2 in zwei quadratische Gleichungen
«2 — 8 (i ± yiy x — 2 (i ±1/2) = o
zerfällt. Ferner finden wir so:
<7) fi (yzri2y = 2^2 (1 + ys),
(8) Ä(1/Z:28)4 = 2 1/2 (3 + 1/7).
Auf andere Fälle werden wir diese Methode später noch
anwenden.
§ 130. Berechnung von Klasseninvarianten aus den
Schlaefli sehen Modulargleichungen.
I. Wenn wir in einer der Gleichungen zwischen u — /(m)
und v — f(na>') oder zwischen u = v — fx(nai) (§ 73),
für u einen der bekannten Werte von m) oder /i (y—m)
einsetzen, so erhalten wir eine Gleichung, welcher f(y—n2m)
oder fi (y— m2 m) genügt.
Diese Gleichung enthält unter Umständen noch fremde
Faktoren, die man aufzusuchen und zu beseitigen hat.
Ist n eine Primzahl, so erhalten wir nach § 123 vollständigen
Aufschluß über diese überflüssigen Faktoren. Geht n in m auf,
so ist in der betreffenden Gleichung ein zur Determinante — m
gehöriger Linearfaktor abzusondern, ist — m quadratischer Nicht-
rest von n, so sind überflüssige Faktoren überhaupt nicht vor-
handen, ist — m quadratischer Rest von m, so ist ein zur Diskri-
4:78
Neunzehnter Abschnitt.
§ 130.
minante —im gehöriger quadratischer Faktor abzusondern, und
•wenn m = 1 ist, so ist die nach Absonderung der fremden
Faktoren übrig bleibende Gleichung ein Quadrat.
Als Beispiele für diese Fälle nehmen -wir:
1. m = 3, n = 3, 2. m = 2, n — 5, Absonderung eines Linearfaktors, kein fremder Faktor.
3. m = 2, n = 3, Absonderung eines quadratischen Faktors.
i. m =1, n = 3, Quadrat.
5. m = 1, n == 5, Quadrat nach Absonderung eines quadratischen Faktors.
6. m = 1, n = 7, Quadrat.
Im Falle 1. hat man in der auf den Transformationsgrad
n = 3 bezüglichen Formel des § 73 zu setzen:
w3 = 2, v3 = f(j— 27)3 = 2 a;,
also
1 2
A = x'2 -I—-, B - - ix----------,
1 X- X
und folglich:
x* — i x3 2 x 1 = — 1) (x3 — 3x'2 — 3x — 1) = 0,
so daß man für m = 27 erhält:
(1) /(]/— 27)3 = 2x, x3 — 3 x‘2 — 3x — 1 = 0.
Im Falle 2. setzen wir im System II. des § 73 (n — 5):
«i = A (V=2) = ]/2, v, = A (V=75Ö) = ]/2 x,
so daß man (ohne fremden Teiler) die Gleichung 6ten Grades:
(2) - x3 + 2^ +±) = 0, A (f^5Ö) = ^2x
erhält, die sich für
1
y =-----x
x
auf den dritten Grad reduziert:
(3) ^ + 2^ + 33/ + ! = 0.
§ 130. Berechnung von Klasseninvarianten. 479
Im Falle 3. setzen wir im System II. des § 73 (n3):
M1 = 1/2, vf = A (V— 18)3 = 1/2»,
»4 — 4 »3 — 8 x — 4 = (x2 -J- 2) (»2 — 4 x — 2),
also
(4) x2 — 4» — 2 = 0, (]/—18)3 = 1/2».
Die Auflösung von (4) ergibt:
(5) x — 2 + >6.
Im Falle 4. ist:
w = f(i) = 1/2, v3 = —9)3 = 1/2^»,
A X2 I 2 T> 4
A 'n F ~91 -- 2 X —,
2 1 x2 x
xi — 4»3 —|— 8 rt? —4 = (a?2 — 2 x — 2)2 = 0,
also
(6) x2 — 2» — 2 = 0, /•(1/ZZ9)8 = l/2«,
(7) x = 1 + ys.
Im Falle 5.:
u — fff) = v- = ff$—25) = l/2»,
1 / 1 \ / 1 \ / 1 \2
»3 ; — 2[x2 ---) = (»-[---) (»---------1) =0.
1 x3 \ x2J \ xj \ x J
(8) »-1-1 = 0, /-(y=15) = 1/2 x,
tb
m * = 4^-
Endlich setzen wir für n — 7:
w = 1/2, v = /•(/— 49) =
1/ <0
und finden
0 = (»8 — 4 »7 -/ 28 xi — 32 x 16)
= (»4 — 2»3 — 2x2 — ix -|- 4)2,
woraus leicht durch Auflösung einer quadratischen Gleichung:
(10) » + 1 = 1 + y?, x =
480 Neunzehnter Abschnitt. § 130.
Auf dieselbe Weise sind die in der Tabelle am Ende auf-
geführten Klasseninvarianten für
m = 75, 36, 100, 63, 175
berechnet, und diese Rechnungen lassen sich auch noch weiter
fortsetzen.
II. Aus den Schlaeflischen Modulargleichungen läßt sich
noch auf verschiedene andere Arten für die Berechnung von
Klasseninvarianten Nutzen ziehen.
Setzen wir
w ./---
co =--------, co = V—
co '
so wird
(11) /» = f(^ =
wenn also in der Modulargleichung für den Transformations-
grad tn
u = v
gesetzt wird, so ergibt sich eine Gleichung, unter deren Wurzeln
u = f (]/— m) vorkommt. In dem System I. des § 73 ist dann
immer A = 2 zu setzen, und es ergeben sich die Formeln:
8
m — 3, B = ue-------------= 2,
ue
4
m = 5, B = m4-------------= 2,
M4
Q
m = 7, B = us -1----------= 9,
'm6
o
m = 11, B = vfi-----------Bfi — B^ — 2B — 2,
64
m = 13, B = u12------------ = 9.26,
’ m12 ’
m = 17, R = -B2 — 68B — 544 = 0,
1 w8
Q
. m =19, B = tt« — B3 — 38B2 + 252B — 648 = 0.
’ ue 1
Die Fälle m =, 3, 7, 11, 19 ergeben keine neuen Resultate,
können aber zur Verifizierung der früher gefundenen verwandt
werden; aus m = 5, 13 erhalten wir durch Auflösung einer
quadratischen Gleichung:
§ 130.
Berechnung von Klasseninvarianten.
481
(12)
(13)
f(V-5/ =1 + 1/5,
f(y—13/ = s + yi3.
Für m — 17 ist die Klassenzahl 4, also die oben angegebene
Gleichung, die in bezug auf us vom 4ten Grade ist, die Klassen-
gleichung. Löst man sie in bezug auf B auf, so erhält man:
us i 1® — 34 i io 1/17
I U8 । r ’
4 ,—
ü = 5+ +
। 2 y_ (i + W)‘
V « V — 2
Wenn man also
1/2» = f(y— 17)2
setzt, so erhält man für x die quadratische Gleichung:
(14)
i _ i + yi?
x 2
III. Wir setzen für co die Wurzel der quadratischen
Gleichung:
2co2 + 2rco + n = 0,
•worin n eine ungerade ganze Zahl bedeutet und r eine ganze
Zahl, deren Quadrat kleiner als 2m ist, also:
(15) • 2co + 2r = — —,
— v + V— w
(16) co = 4/-----------, m = 2 m — r2.
£
Es ist dann nach § 34:
r rti
(17) A (fi>) fi (2 co + 2 r) = + |/2,
und nach (15), (16):
/o\ —LI* —
(18) = e 12 y2’
(19)
r rti
/2 (®) j, / । \»
fi W + y— m)
setzen wir also, je nachdem r und folglich auch m gerade oder
ungerade ist,
(20) x — fj (y—m), x = f(y— m),
Weber, Algebra. III. gy
482 Neunzehnter Abschnitt. § 130.
so wird
rai
und diese Werte hat man für w15 in das System II., § 73 zu
substituieren, um eine Gleichung für x zu erhalten.
Indem man für r die verschiedenen zulässigen Werte setzt,
bekommt man aus (16):
n = 3, m = 6, 5, 2,
n = 5, m — 10, 9, 6, 1,
n - 7, m = 14, 13, 10, 5,
n = 11, m = 22, 21, 18, 13, 6,
n = 13, m = 26, 25, 22, 17, 10, 1,
n = 17, m = 34, 33, 30, 25, 18, 9,
n = 19, m = 38, 37, 34, 29, 22, 13, 2.
Als einfaches Beispiel wählen wir n = 7 und erhalten aus
§ 73, II.:
xs . 4 _ . ,„r- rit
T H----« — 7 + 4 V2 COS -7- •
4 1 xs ' ' 4
Daraus ergibt sich für r = 0:
(22) + § = 1 + x = A
für r = 1 das bereits bekannte
(23) /•(]/— 13)4 = 3 + ]/13,
für r = 2:
(24) A(yzziö> =12^5.
Als zweites Beispiel nehmen wir noch n = 13 und erhalten:
für r = 0, 4, also m = 26, 10 ergibt sich hieraus JB1 = 16, und
folglich nach § 73:
A7 — 6 A5 + A3 + 20A + 16 = 0,
während für r — 2, also m — 22 in dieser Gleichung in
— A zu verwandeln ist.
Man findet aber leicht die Zerlegung:
A7-6A +A + 20A + 16
v 7 =(AH-i)HA-2m8 + 2A2 + A + 4)-
§ 130. Berechnung von Klasseninvarianten. 483
Ist —ia > 1% so ist auch /^(m) > V2, denn A(ra)2 geht,
während —i» von ^2 bis ao geht, ebenfalls, und zwar stets
wachsend *), von ('2 bis oo , und folglich ist Ar negativ für
r = 0, 2, 4.
Der erste Faktor Ax -|- 1 verschwindet, wie aus dem schon
bekannten Resultat (24) hervorgeht, für r = 4; daher verschwindet
der dritte Faktor A* -|- 2 A2 -j- A1 -f- 4 für r = 0, während
At -|- 2 für r = 2 verschwindet.
Wir erhalten also nach (25):
(27) A (V^iö)2 = fiy, ?/-l = 1,
y
(28) ft (V^22)2 = V2t/, = 2,
i?
(29) (]/— 26)2 = y'2«/, _ 2«/5 — 2^ + 2y2 — ‘ly— 1 = 0.
IV. Als Beispiel für eine andere Art der Verwendung der
Schlaeflischen Modulargleichungen, die zu der sonst schwer zu-
gänglichen Klasseninvariante —41) führt, möge das Folgende
dienen.
Wir setzen:
(30) 2 h ra2 4- 2 r ra -(- )?, = 0,
. — r 4- V— m
(31) w -----------------5— -----, m = 2 n2 — r2.
Ai Yb
Es kann hierin r jede Zahl bedeuten, die m positiv macht,
die aber mit n keinen Teiler gemeinschaftlich hat [weil sonst
(30) imprimitiv ist]. Es wird dann nach § 34:
r ni
f f roz i vi e 12 V'2
(32) f‘ {») = f'P<” “ + 'M =
[2 (n g> 4" r)] — A (r V— m) = e 24 x.
4) Aus § 51, (11) folgt nämlich durch die Substitution (<o, 1—
(«)9 = - v + f. (“)’] d
o
31*
Neunzehnter Abschnitt.
§ 130.
484
also:
ACwo)
e 2i }/2
x
wenn, je nachdem r gerade oder ungerade ist,
(33) x = fi (j/— m) oder = /‘(^— m)
gesetzt wird. Nehmen wir also in der zu n gehörigen Modular-
gleichung II., § 73:
M1 = fs (»),
mi
/2\,, .
= (ü)-------Z-
\ / \f(/ /
oder
so ergeben sich zwei Gleichungen, aus denen man durch Eli-
mination von Uj eine Gleichung für x herleitet.
Um für n = 5 diese Rechnung durchzuführen, setzen wir:
triti
xf2(a) =
(34)
Ä
woraus man, entsprechend den beiden Annahmen für für ein
ungerades r die Gleichungen erhält:
f + i + 2('i’-A) = o.
(35)
____ ___ ß 24 y)
(«) - ’’
Diese Gleichungen gelten für r = 1, 3, 7, die zu den
Werten m = 49, 41, 1 gehören.
Subtrahiert man die beiden Gleichungen (35), so kann man
den Faktor | — n abwerfen, der nur für m = 1 verschwinden
kann:
Kl + & - w (i - - 2 (i + n) (i + A_) = o,
§ 131. Berechnung von Klasseninvarianten. 485
und wenn man die beiden Gleichungen (35) addiert:
Kl + v)3 — + 1/)] (1 + 1^5-)
+ 2[(l + ~ 2^] (1 - = 0.
Es ist aber nach (34):
und man erhält also eine Gleichung für a?2, wenn man (| V)
eliminiert. Diese Gleichung wird nach dem gewöhnlichen Elimi-
nationsverfahren, wenn man
x2 . V2
Z j/2
setzt, in der Form
(36) z* — 9 0* + 2O04 603 — 1902 — 170 — 6 = 0
gefunden. Hierin ist aber noch der auf die Determinante —49
bezügliche Faktor enthalten. Für diesen ist [nach Formel (10)]:
z = 2 fi.
Es muß also die linke Seite von (36) durch
02 — 40 — 3
teilbar sein, und die Ausführung der Division ergibt den für die
Determinante —41 gültigen Faktor:
04 — 5 03 -|- 302 -|- 3 0 2 = 0,
(37) z - । F .
yä 'i"/-(y-4i)
§ 131. Berechnung von Klasseninvarianten aus den irrationalen
Formen der Modulargleichungen.
In außerordentlich einfacher Weise führen vielfach die irra-
tionalen Formen der Modulargleichungen zur Aufstellung von
Klassengleichungen.
1. Im § 75 haben wir gesehen, daß, falls m = — 1 (mod 8)
ist, zwischen den beiden Funktionen:
2 J. = f(a)f(ina) + (—1) 8 [A (») (m ra) A (ra) A (m »)],
m 4- 1
jß — %_______i________________। (— I) 8___2
A(0J)A(»W0J) AC^ACw») f(co),f(ma)
486 Neunzehnter Abschnitt. § 131.
eine algebraische Gleichung besteht, und diese Gleichungen sind
dort für m = 7, 23, 31, 47, 71 aufgestellt.
Setzen wir darin:
ra = , --, mas = y—w, /’(y— m) = 1/2 x,
y— m
so wird nach § 34:
m 4-1 m 4-1
1 X X
Daraus ergibt sich z. B. für m = 23, wo A = 1 ist, die
Gleichung:
(1) /'(y— 23) = y2 x, a« — x — 1 = 0
und für m = 31:
x9 — 4 x6 4- 3 x3 — 1 = 0.
Dies ist zunächst eine kubische Gleichung für x3; man spaltet
daraus aber leicht die kubische Gleichung für x selbst ab:
(2) ' ^(y— 31) = y2 x, x3 — x^ — 1 = 0.
Ähnlich ergeben sich die Gleichungen:
(3) /•(y^47) = y2a;,
x6 — — 2x2 — 2x — 1 =0,
(4) /•(y^7i) = y2^,
x7 — 2x6 — x'=> x* x3 x2 — x — 1 — 0.
Im letzten Falle, m = 71, ist von der-unmittelbar erhaltenen
Gleichung 9ten Grades der der Aufgabe fremde Faktor (x 4- l)2
abgesondert.
2. Um zu einer weiteren Berechnungsart zu gelangen, wenden
wir die Transformation zweiter Ordnung an. Wir haben zunächst
allgemein [für ein veränderliches ra, § 34, (17)]:
f (2v)3 4- f^3 = 2
/(2»)8 - woraus: f(2 gj)8 = AH8 = = + A (CT)8 1 8 AH4 AM8’ _ /'M8 + A M8 _ 8 . AM4 AM8’
§ 131.
daraus
Berechnung von Klasseninvarianten.
487
+ a(«)8A(2®)8 = 8 + y(cj)8 + ^(cj)-8]a,
/ 2 V")
was sich nach § 34 leicht in die Form bringen läßt:
64
+ A(«)Vä(2«>P = 16 + A(«)12 +
und hieraus kann die Wurzel gezogen werden:
Q
(5) f Op f (2 + A (»)4 A (2 co)4 = f2 (rap +
Es genüge nun a der quadratischen Gleichung:
(6) 2 cP 2ra n = 0
mit ungeradem n, also:
—r 4- V—m
(7) ca = --- 4? ------» m ~ 2 w — r2-
£i
Wenn dann
(8) 1/2 x — — m)2, oder = A (V— m)2
gesetzt wird, je nachdem r ungerade oder gerade ist, so wird
r«i tTn
(9) A(»)2 = e 43
«X/
Ferner folgt aus
2» = — — — 2r
G>
nach den Formeln des § 34:
/n\
f^^ = f
(10) A(2«)=aQ^
A(2g>) = A(J)e
so daß die Gleichung (5) ergibt:
oi) ^ra)^(?y+ (-i/a^a^)4
/ mi\
_r2!i e~~\
= e 13 V8 ( x3 -—- /•
’ \ ' x3)
488
Neunzehnter Abschnitt.
§ 131.
Aus (10) folgt noch weiter:
(12) A(<»)fä(J) = y2e-^,
\w/
(13) (?) = V2
Wenn wir n = 23 und r = 0 annehmeu, so gibt die Glei-
chung § 75, (8) mit Benutzung von (12):
(14) /•(«) f (?) - A («) A (?) = 2 + V2,
woraus durch zweimaliges Quadrieren mit Benutzung von (11)
und (13) folgt:
+ -4 = 36 4- 26 1/2;
hieraus leitet man die einfachere Gleichung ab:
(15) ^+|=3-|- 1/2, ^2^ = A2(V^46)-
dz
3. Wir machen endlich noch eine Anwendung der Trans-
formationsgleichungen des § 76 für einen zusammengesetzten
Transformationsgrad auf die Determinante —39.
Setzen wir
e (tl ß (1 /— 13\ tt2 -|- ®2
« = nr=39), v = f\y~ä~)' =
so ist in der auf n = 39 bezüglichen Gleichung (22), § 76 zu
setzen:
V2 U U2 V
und die erwähnte Gleichung gibt:
#3 ^2 — 5 s — 6 = 0,
woraus nach Abwertung des Faktors 0 4“ 2 die folgende her-
vorgeht :
(16) z2 — z — 3 = 0, z = —•
Zwischen « und v besteht aber andererseits eine Trans-
formationsgleichung dritter Ordnung (§73):
w6®6 — 8 u12 -I- ®12
, , - = = z* — 6^ -4- 9^2 — 2,
M3 U6Ve 1 ’
27 I 7 i/j ß
was sich mit Hilfe von (16) auf die Form z* — 2 = ——1—
bringen läßt.
§ 132. Die Schlaeflische Modulargleichung. 489
Daraus erhält man
— 4(3 4. ^13),
4. ve — 4 (17 4- 5 j/13),
us _ = j/2 (3 4- yTs),
so daß, wenn u3 = x gesetzt wird, für x die quadratische
Gleichung folgt:
(17) x* — L±_VÜ (a; 4- !) = 0, /(V— 39)3 = x.
Wir wollen unsere Resultate jetzt noch an wenden auf zwei
Probleme, die in die allgemeine Transformationstheorie des
siebenten Abschnittes gehören.
§ 132. Die Schlaeflische Modulargleichung für den
23 sten Transformationsgrad.
Jede Klassengleichung tritt als Divisor in einer großen Zahl
von Transformationsgleiehungen auf und kann daher, wenn sie
auf andere Weise bekannt ist, zur Berechnung von Transforma-
tionsgleichungen benutzt werden. Wir nehmen als Beispiel den
23 sten Transformationsgrad.
Nach § 73 besteht, wenn
(1) « = /(«), ® = /’(23g>), c = 0 (mod 48)
gesetzt ist, eine Gleichung zwischen
B = UV -\---,
UV
und es ist schon in § 74, (14) gezeigt, daß diese Gleichung die
Form hat:
(3) A = B11 4- m, JE?10 -j----4- m10 B 4-
worin die Koeffizienten mx, ..., rationale Zahlen sind.
Statt nun diese rationalen Zahlenkoeffizienten wie dort aus den
Entwickelungen von u und v nach Potenzen von q zu berechnen,
suchen wir die Wurzeln der Gleichung (3) für u = v aus der
komplexen Multiplikation zu bestimmen.
490
Neunzehnter Abschnitt.
§ 132.
Durch Multiplikation mit w12®12 geht die Gleichung (3) in
eine Form über, welche u, v nicht im Nenner enthält, die wir
für den Augenblick mit
(4) F(u, v) = 0
bezeichnen, so daß für ein unbestimmtes x und co:
(5) F [/», x] = [x — /’(23gj)] n [- -
Wir untersuchen nun, für welche Werte von co die Funktion:
(6) F(u, u) = F[f(co), /»]
= [/•(«) - /•<23«)] n [/(«) - /(^)]
verschwindet. Es verschwindet zunächst offenbar der Faktor:
rw-O
für
Verstehen wir ferner unter r eine der Zahlen +2 oder +4,
und dementsprechend unter
m = 23 — r2
entweder 19 oder 7, so verschwinden von den Faktoren von (6)
für ra — y—m je zwei, nämlich:
j., . „/24r 4- »\
denn es ist
„/24 r + V— m\ _ ~ f(r m\
T\ 23 ) ~ 6 ' \ 23 /
= f(----------T-) =
\r — y— m/
Wir fügen noch hinzu, daß
er \ „ Gj\
/(») — ™)
für co = y— m einer endlichen Grenze zustrebt, wie man durch
Differentiation nach co erkennt (§ 54), und daraus folgt, daß
F(uy w) durch [u — teilbar ist.
§ 133. Die Kesolventen 7ten und Ilten Grades. 491
Wenn man u = v setzt, so wird
A = 2, B = u* + —,
’ ' W2 ’
und wenn u = — m), m — 7, 19, 23 gesetzt wird, so erhält
man aus § 128, (6), (8), § 131, (1) durch Elimination von u die
Gleichungen für B:
m— 7, 5 — 3 = 0,
m = 19, B^ — 6 52 10 5 — 6 = 0,
m ~ 23, 5« — 5 52 + 4 5—1 = 0.
Die beiden letzten kubischen Gleichungen sind, da sie keine
rationale Wurzel haben, irreducibel, und daraus ergibt sich ohne
Rechnung die gesuchte Modulargleichung (3):
(7) A— 2 = (5— 3)2(5S—6524-105— 6)2(5s—552-]- 45-1).
In der Abhandlung: „Ein Beitrag zur Transformationstheorie
der elliptischen Funktionen mit einer Anwendung auf Zahlen-
theorie“, Math. Annalen 43, 185, habe ich auf demselben Wege
auch noch die Transformationsgleichung für den 47sten Trans-
formationsgrad abgeleitet.
§ 133. Die Resolventen 7ten und Ilten Grades für den
7ten und Ilten Transformationsgrad.
Wir haben in § 82 gesehen, daß für den 7ten und Ilten
Transformationsgrad Resolventen der Grade 7 und 11 existieren.
Auch bei der Bildung dieser Gleichungen kann die Theorie der
komplexen Multiplikation nützliche Dienste leisten.
Wir betrachten, wenn n = 7 oder = 11 ist, die Trans-
formationsgleichung
Fn («, v) = 0,
deren Wurzeln, wenn w = /'(ca) gesetzt wird,
(1)
sind, wobei c als Index von v nach dem Modul n genommen
werden kann, während es unter dem Zeichen f durch 48 teilbar
vorausgesetzt werden muß.
Diese Gleichungen sind nach § 73:
(2) n = 7, vs — u7 v7 7 w4 v4 — 8 w v w8 = 0,
(3) n = 11, ®42— u11 ®n H u9®9— 44u7 v7 -|- 88 w8®7’
— 88u3v3 32 w® w12 = 0.
492
Neunzehnter Abschnitt.
§ 133.
Wir haben in § 73 den Einfluß der drei Vertauschungen
(c') = (ra, gj 2),
durch die u übergeht in
auf die Wurzeln der Gleichungen (2) und (3) untersucht. Dieser
Einfluß ergibt sich aus den Zusammensetzungen:
(6) c' = c -|- 2 (mod ri);
(8) cc" = — 1 (mod ri);
—— 1
(10) c'" = (mod ri),
a — ß = 1 — c'", y -|- ö = c -j- 1,
a + ß = n, n (y — ö) = (c — 1) — c'" (c 1),
und nach § 34 und § 40, (12) geht also durch die Substitutionen
(c')i (c"), (c,")i mit Rücksicht auf
2 - 2 n2 (mod 48),
die Wurzel vc über in:
und dies gilt auch für c = oo. Die Vertauschungen der Indices,
die sich so ergeben, sind:
(12) n — 7, c = oo, 0, 1, 2, 3, 4, 5, 6,
c' = oo, 2, 3, 4, 5, 6, 0, 1,
c” = 0, oo, 6, 3, 2, 5, 4, 1,
d" = 1, 6, 0, 5, 4, 2, 3, oo.
§ 133. Die Resolventen 7ten und Ilten Grades. 493
(13) n = 11, c = oo, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
c' = oo, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1,
c" = 0, oo, 10, 5, 7, 8, 2, 9, 3, 4, 6, 1,
c1" = 1, 10, 0, 4, 6, 5, 8, 7, 9, 2, 3, oo.
Als Wurzeln der Resolventen 7ten und Ilten Grades können
wir nach § 82 je eine der beiden folgenden Funktionen betrachten:
(14) n = 7,
Vf) tyr +1 ‘»v + s) (y, + 2 4 e) (vv + 4 4- ö)
'Ujv -----------------------------------------------,— 5
*y7 w4
, (v„ «v+6)(«v + 2 «r + 3)(«v + 4 «v + e)
— i y 7 u4
(15) n = 11, wv =
f») (f»+l—^44*2) (t>»4-3 — Vv+e) (w»-|-4—Vv+ s) (Pv+6~'^i’+io) ('^>'4-9 ^»4-7)
«yiiw6 ’
lV'v =
(v^—tV) (fr+1—Vv+s) ('^>'+3 ^»+7) (t>>H-4— ^»+2) (^»+5 Vv+s) (^^4-9“ ^l'4-io)
—tyiiw6 ’
worin y'7 und yil positiv genommen sein sollen.
Es tritt nun zunächst der folgende bemerkenswerte Unter-
schied zwischen beiden Fällen hervor.
Durch die beiden Vertauschungen (c'), (c'') werden im Falle
n = 7 die wv nur untereinander vertauscht, und zwar in folgen-
der Weise:
Wo, w„ W2, W-i, w4, Wf» w6,
(c') W2, W3, W4, W5, W6, Wo, Wj,
(c") Wo, w2, Wj, w6, w4, w5, ws,
während [nach (13)] im Falle n = 11 durch die Vertauschung
(c') die Größen w gleichzeitig ihr Vorzeichen ändern, so daß
folgende Vertauschungen eintreten:
Wo, Wj, w2, w3, w,t, w6, w6, w7, ws, w9, w10,
(c') -w2, -W3, -w4, -w5, -w6, -W7, -Ws, -Wj, -W10, -Wo, -Wj,
(c") Wo, w9, W6, W3, W6, W4, W2, W8, W7, W1, w10,
und ebenso verhält es sich mit w'.
Daraus folgt nun (§ 54), daß die w, Wurzeln einer Gleichung
7 ten oder 11 ten Grades :
(16) wn A1wn~1 -|- yl2w”—2 ••• An = 0
494
Neunzehnter Abschnitt.
§ 133.
sind, daß darin aber im Falle n = 7 sämtliche Ai rational von
/'(co)24 abhängen, dagegen im Falle n — 11 die Ai mit geradem
Index ebenfalls rational von /'(ß>)24 abhängen, während die mit
ungeradem Index das Produkt von f(ß>)12 mit einer rationalen
Funktion von /'(ß>)24 sind. Die Zahlkoeffizienten enthalten außer
rationalen Zahlen nur noch die Irrationalität i^7 bzw. «^11,
und demnach wollen wir diese Gleichungen bezeichnen durch
(17)
® [w,/(co)24, «^7] = 0,
O [tu, /(co)12, &yn] = 0.
Ändern wir gleichzeitig die Vorzeichen von i und w, so ergibt
sich, wie wir in §82 gesehen haben, eine Gleichung, deren
Wurzeln die Größen w' sind.
Auch bei der Anwendung der Substitution (c'") zeigt sich
für die beiden Fälle ein Unterschied.
Es ergibt sich nämlich aus (13), mit Rücksicht darauf, daß
nach (2) das Produkt sämtlicher vv den Wert ws hat, daß im
Falle n = 7 durch die Substitution (c'") die wv nur unterein-
ander vertauscht werden, und zwar in folgender Weise:
/Wo, Wj, w2, ws, w4, wä, w6\
\W6, W3, We, Wt, Wo, Wj/’
und daraus folgt, daß in diesem Falle die Koeffizienten Av
alle ungeändert bleiben, durch die Vertauschung:
Überdies kommen im Nenner dieser Koeffizienten
nur Potenzen von /(co)24 vor (§ 73), und die Potenzen von
/(co)24 steigen bis zu derselben Höhe wie die von /(co)-24.
Im Falle n = 11 gehen durch die Vertauschung (c'") die
Größen wv in die Größen w'v über, und zwar in folgender Reihen-
folge :
/Wo, Wj, w2, ws, w4, w6, w6, w7, w8, w9, w10\
\Ws, w2, w(, wö, Wo, Wo, Wo, wi, Ws, wlo, wj /
Nach (17) können wir diese Eigenschaft durch die in bezug
auf w identische Gleichung ausdrücken:
und daraus ergeben sich die folgenden Eigenschaften der Koeffi-
zienten Av'.
•§ 133. Die Resolventen 7ten und Ilten Grades. 495
Av bleibt ungeändert durch die gleichzeitige Ver-
tauschung:
(«»)' ^). Gl'n.-iVii),
und enthält bei geradem v nur die geraden, bei un-
geradem v nur die ungeraden Potenzen von /(co)12.
Auch hier treten nur Potenzen von /(co) im Nenner auf,
und die Potenzen von f(ca) steigen bis zur selben Höhe wie die
von /(co)-1.
Um über die Grade der Funktionen Av ins Klare zu kommen,
betrachten wir die Anfänge der Entwickelungen nach steigenden
Potenzen von q = eaiu>.
Es beginnt die Entwickelung von /(co) mit q 24, die von
n 1 ItiIc 1
mit q 24, von vc mit q 24H e 48 n, worin aber in der letzten
Exponentialgröße, wenn wir c auf seinen kleinsten Rest (mod n)
reduzieren, auch nach dem Modul n zu nehmen, also für
n = 7, 11:
£8 = —1 (mod 7)’
= 3 (mod 11)
zu setzen ist. Wenn wir also hiernach
2 7ti &7ti
q — e 7 oder = e 11
setzen, so erhalten wir aus (14), (15) als Anfänge der Ent-
wickelung
für n = 7 :
_ __i_
wv — q 7 qsv(q — p3)(p2 — p6)(p4 — p5) 4“ •••,
für n = 11:
6
itf\Äwv = q 22 p5r (p — p2) (p3—p6) (p4-p8) (p5—p10) (p9— p7) -/-•••
Es ist aber für n — 7:
(p — p3) (p2 — p6) (p4 — p5) = — p — p2 — p44-p3 + p54-p6,
und für n = 11:
(p — p2) (p3 — p6) (p4 — ps) (p5 — p10) (p9 — p7) =
— p — p3 — p4 — p5 — p9 -j- p2 4- p6 4~ p8 H- p7 + p10-
496
Neunzehnter Abschnitt.
§ 133.
Da 1, 2, 4 die quadratischen Reste von 7; 1, 3, 4, 5, 9 die
quadratischen Reste von 11 sind, so können diese beiden Summen
nach Bd. I, § 179 bestimmt werden, und ergeben in den beiden
Fällen: _ __
ij/7 und —i]/ll,
so daß
(18) Wv ~ 2 7 e3r H—> n = 7’
wv = —q 22 p5*1 ..., n — 11.
Hierdurch läßt sich eine obere Grenze ableiten, bis zu
der in Av die Potenzen von /“(<») höchstens ansteigen können,
wenn man noch beachtet, daß die Av als ganze rationale (und
symmetrische) Funktionen der wv darstellbar sind.
Für n — 1 ergibt sich so, da alle Exponenten von f((a)
durch 24 teilbar sein müssen, daß jij, J.2, Aa, A4, A6, A6 Kon-
stanten sind, während A7 nur die erste Potenz von /“(<»)24, und
zwar mit dem Koeffizienten — 1 [nach (18)], enthält.
Für n — 11 muß, wenn f (a>)122 die höchste in Av vor-
kommende Potenz von /'(k>) ist,
, — 5v
n
sein, und überdies muß Z mit v zugleich gerade oder ungerade
sein. Daher sind Aa, A4 konstant, A6, As enthalten die höchste
Potenz f(co)2i, A10 enthält auch /'(ca)48. Da die A mit ungeradem
Index nur ungerade Potenzen von /(ß>)12 enthalten, so ist A7 = 0,
A-i, A:> enthalten /“(<»)12, A7, A9 enthalten bis /'(k>)36, in An
steigt /“(<») bis zur 60sten Potenz an.
Für den Fall n = 7 wollen wir nun die Konstanten voll-
ständig mit Hilfe der komplexen Multiplikation bestimmen, und
zwar genügt dazu die Betrachtung der Werte der wv für o = i.
Für o = i wird
« = f(i) = ]X2,
und wenn wir diesen Wert in die Gleichung (2) einführen, und.
]/ 2 v = x
setzen, so ergibt sich:
(19) x* — 4a:’ -|- 28a:4 — 32a: + 16 = 0.
Die linke Seite dieser Gleichung ist das Quadrat des Aus-
druckes :
(20) a:4 — 2 a:3 — 2d:2 — 4x 4,
§ 133. Die Resolventen 7ten und Uten Grades. 497
so daß also die Werte von v für co — i paarweise einander
gleich werden. Aus § 119, (15), (17) folgt, wenn co = i, also
A = 1, C = 1, — 0, m = 4, p = x — 1, y = 0 gesetzt
wird, daß für cc' = — 1 (mod 7) vc = v0, wird, so daß also:
(21) + = ®o, »2 = V), «4 = f6-
Der Ausdruck (20) laßt sich in die beiden quadratischen
Faktoren:
x^ — (1 + ff) x + 2, x^ — (1 — |/ 7) x + 2
zerlegen, so daß die acht Werte von x paarweise je einer der
vier Größen _
f29) i+v? r? i - v?
( ’ 2 ± )/2’ 2. -
gleich werden, und es handelt sich noch darum, diese vier Werte
den einzelnen vv zuzuordnen. Dazu bemerken wir, daß v0
für co = i reell sind, und daß ebenso vt reell sein müssen,
weil sie gleichzeitig einander gleich und konjugiert imaginär sind.
Aus «o entsteht vv dadurch, daß man q mit einer gewissen
Einheitswurzel multipliziert; da aber die Entwickelung von v0
nach Potenzen von q nur positive Koeffizienten enthält [vgl. § 24,
(11)], so folgt, daß «o größer sein muß als v15 und mithin ist
1 +1/7 . ]/7
V2+ =V2«o = -^- + ^,
(23) r- L-
Für die beiden anderen Wurzelpaare ergibt sich:
^2 + «XX
* y2
<M) ^ = ^=+^-.'S2-
* y 2
Daß in diesen Ausdrücken das Vorzeichen von i richtig ge-
wählt ist, schließt man auf folgende Weise:
Aus (23) ist zu ersehen, daß für <o — i, also für w = ]/2",
die Wurzel w0 verschwindet, und daß also für diesen Wert A7
verschwinden muß. Nach den oben nachgewiesenen Eigenschaften
ist hierdurch Ä7 vollständig bestimmt, nämlich:
/ 64\2
(25)
Weber, Algebra. III.
32
498 Neunzehnter Abschnitt. § 133.
woraus folgt, daß für keinen anderen Wert von u24 als 64 zwei
der Werte vv einander gleich werden. Es tritt diese Gleichheit
also nur für co = i und gewisse mit i äquivalente Werte von co
ein, und daher nicht für einen anderen rein imaginären Wert
von co.
Der Anfang der Entwickelung nach steigenden Potenzen von
g ergibt nun:
, . — 2 . 48\ ./co 4- 2.48\
(26) — V; = ----?-----) — j
__ 1 4 ar
= 2iq 7-24 sin —(-•••,
so daß für einen hinlänglich großen reellen Wert von —ico die
linke Seite von (26) positiv imaginär ist. Wenn nun —ico auf
reellem Wege von oo bis 1 geht, so geht, wie wir oben gesehen
haben, t>2 — nicht durch Null. Es muß also auch für co = i
die Differenz — «6 positiv imaginär sein, wie in (24) an-
genommen ist.
Wenn man also die Werte (23), (24) in (14) einsetzt, so
ergibt sich für co = i:
w0 = 0, w6 = 0
,n„x 1 + ifi
(27) w1 = w2 — w3 = iv6 — —!- ,
M. _ *')/7(l + W
j
Danach kann für den Fall n — 7 die Resolvente vollständig
gebildet werden. Sie lautet:
/ 7-|_iy7\4/ i 1/7 (1 i i/7)2\
(28) w2(w------—2 —\w -)---------fJ
und nimmt eine einfachere Gestalt an, wenn man
i fi (1 4- iflf
w 4--5—-—/----= z*
4
setzt:
(29) a 4 _ ^<J±-^)‘) + i fjf = .
§ 133.
Die Resolventen 7ten und Ilten Grades.
499
Für den Fall n — 11 ist die entsprechende Rechnung noch
nicht durchgeführt. Verhältnismäßig einfach erhält man, wenn
man mit Benutzung der Betrachtungsweise des § 119 die Werte
von g> aufsucht, für die eine der Größen wv verschwindet:
o = i co = V—7, g> =
1—]/—7
u = ^''2, m = y2, u = 1,
und daraus
32*
Zwanzigster Abschnitt.
Die Multiplikatorgleichung in der komplexen
Multiplikation.
§ 134. Die KlasseninVariante y3(ß>).
Wir haben jetzt die Funktion
(®) = VJ(ß>) — 12=
auf deren Eigenschaft als Klasseninvariante zu prüfen.
Wir haben zunächst für ein variables <x> die Multiplikator-
gleichung Ister Stufe (§ 72, 3), wonach, wenn
(1) n = 3, c = 0 (mod 4),
die v Größe,
/ (c -j- 8 o\\6
(2) Jf = (-1)* 8^
durch die linearen Transformationen nur miteinander permutiert
werden. Setzen wir also
(3) « = 3 (®), v = 3 (—---------),
\ U> /
so besteht zwischen u, v die Invariantengleichung
(4) F(v, u) — 0,
und es ist
F(x, u) — II (x — v\
wenn das Produktzeichen sich über die v Wertsysteme von
a, b, c erstreckt. Die Summe
(5) Fu) S (*’ M)
ist für ein unbestimmtes x durch lineare Transformation un-
geändert und daher eine rationale Funktion von w. Da die Funk-
tion aber für jeden endlichen Wert von y(c) einen endlichen
§ 134. Die Klasseninvariante y3(w). 501
Wert hat, so ist sie eine ganze Funktion von J(co). Lassen
wir in (5) x in v übergehen, so ergibt sich
(6)
x ' (v)
worin il>(y,u) eine ganze rationale Funktion von w und v
ist, mit rationalen Zahlenkoeffizienten.
Lassen wir nun in (6) a in die Wurzel einer quadratischen
Gleichung der negativen Diskriminante
B = B1 2 * * * * — 4:AC
übergehen:
(7) Aco2 + Beo + G = 0,
so können einer oder mehrere der Werte v gleich u werden. Ist
dies nur für einen der v Werte v der Fall, so wird F'(y) für
v = w nicht verschwinden, und wir können nach (6) rational
durch diesen singulären Wert von u ausdrücken.
Die Gleichung u = v führt aber die Bedingung mit sich:
c —ö ß» 7 5®
a a ßco
Daraus folgt:
1 7 8 R v Bx + y ~
cp — ao =-------ca — ay = Cx,
z
(9) 4« = i/ä — Bx2,
worin x positiv angenommen werden kann.
Wir nehmen A ungerade und relativ prim zu B an. Ist
B = 1 (mod 4), so setzen wir n — — B und erhalten aus (9):
y2 + n (%2 — 4) = 0.
Der Wert x — 1 ist hiernach nur dann zulässig; wenn —B
das Dreifache einer Quadratzahl ist. Sehen wir zunächst von
diesem Fall ab, so bleibt nur
x = 2, y = 0,
und aus (8) ergibt sich:
8 = 1, ß — 2 A, a = B,
a = n, y = 2 C, 8 = B (mod 4),
a -|- ß ® = \B,
und durch die beiden letzten Gleichungen (8) ist c nach dem
Modul n bestimmt.
502
Zwanzigster Abschnitt.
§ 134.
Nach § 38 (15) ist also
g । j
(10) m = (_1)A+C+—yz>s 73(«,),
und es wird hier nur einer der Werte v = w, demnach ist Jf
und folglich auch \D % (ca) rational durch j (®) ausdrückbar.
Um auch den Ausnahmefall zu erledigen, setzen wir
n == —D —
Dann wird (9):
y2 4- 3 m2 (x2 — 4) = 0,
und diese hat die drei Lösungen:
x = 2, y — 0,
x = 1, y = + 3 m..
Die Gleichungen (8) ergeben für x = 2 wieder die Formel (10):
= (-l/+C+^iV/D373(«),
und die beiden anderen Fälle ergeben
8 = 1, a = n,
y = C, a 8 = B (mod 4),
y.D + 3 m
« + ß ® = 1—y-----
Daraus erhält man nach § 38 (15) für JZ2, die Werte
Nun sind zwar nicht die Größen JZ15 J/2, Ms einzeln, wohl
aber, wie wir gleich zeigen werden, ihre symmetrischen Funk-
tionen, z. B. ihre Summe, durch j'(co) rational ausdrückbar, und
daraus ergibt sich auch für diesen Fall, daß ]Ä)y3(a) Klassen-
invariante ist.
Von der Annahme, die wir gemacht haben, daß A relativ
prim zu 2D sei, können wir uns nachträglich befreien, da y3(ca)
durch alle linearen Transformatoren höchstens sein Zeichen
ändert. Wir haben dann den Satz:
1. Ist D = 1 (mod 4), so ist yZ)y3(ß>) Klassen-
invariante der Diskriminante JD.
§ 134. Die Klasseninvariante y3 (<«)• 503
Um den Satz vollständig zu begründen, müssen wir noch
beweisen, daß die symmetrischen Funktionen der Afj, Af2, Afs in
dem zuletzt betrachteten Ausnahmefall rationale Funktionen von
j (gj) sind. Dies erfordert, daß wir untersuchen, was aus (6) wird,
wenn für einen singulären Wert u von v der Nenner F' (v), und,
da Af endlich bleibt, auch der Zähler verschwindet. Wir lassen
zunächst wieder gj variabel und bezeichnen die Wurzeln von
(4) mit
(11) «n «2, vv.
Es mögen nun für den betrachteten besonderen Wert von gj
(12) «i, v2, ..., vi
einander gleich werden, während die übrigen t^ + i, ..., «r davon
verschieden bleiben. Wir nehmen irgend eine symmetrische Funk-
tion der Größe (12), z. B., für ein unbestimmtes t:
(13) 0 = (t — (t — u2), ..., (t — vfr,
wenn wir in 0 alle Permutationen der Größen (11) ausführen, so
bestimmen wir r Werte
(14) 0n 02, ..., 0r,
wenn __ v!
r ~ Ä! (y — Ä)!
die Anzahl der Kombinationen von v Größen zu je Ä (ohne Wieder-
holung) bedeutet. Über t können wir so verfügen, daß auch für
den singulären Wert gj nur eine der Größen (14) gleich dem
ersten 0 wird. Die 0 sind die Wurzeln einer Gleichung
<P(x, u) = 0
vom Grade r, und für den singulären Wert x = 0 bleibt (0)
von Null verschieden.
Betrachten wir nun eine symmetrische Funktion S der (12)
entsprechenden Größe
Afn ..., Afz,
so nimmt diese durch die v Kombinationen der Zahlen a, 8, c, die
zu den Werten (11) führen, gleichfalls r Werte Slt S2, ..., Sr an,
und die Summe
$(«, u) ---------- = & (x, u)
ist eine rationale ganze Funktion von x und w. Daraus folgt,
indem man x in 0 übergehen läßt:
c _ ® (0, u)
— ®'(w)
504
Zwanzigster Abschnitt.
§ 134.
Für den singulären Wert werden nun alle die Größen (12)
einander gleich und gleich u, also ß eine rationale Funktion von
w, und damit ist der gesuchte Beweis geführt.
Als bemerkenswerte Beispiele wählen wir die Fälle des § 125:
r.(-1 V~'')
r. (~ 1 +/~ 11) = 7. s
r.(~1+/=7ii?) = 8- 27 y=ri9,
7s 1 ~V~27) = 8-1L 23 V—3’
7i (~ 1 +2j/~43) = 8. 7. 81 ]/-^43,
X £j /
73 (-1 67) = 7- 8. 9. 31 y^67,
1 +2 ~~163) = 8. 27. 7. 11. 19. 127 163.
Auch hier ist die Zerlegbarkeit der rationalen Faktoren in
verhältnismäßig kleine Primzahlen auffällig. Wir geben hier
noch einige Beispiele, in denen nicht ^T), sondern Y— JD vor-
kommt.
Wir haben im § 128 gefunden:
Ä (V=2)4 = 2, /•(Y=3)s = 2, /•(Y=7)2 = 2.
Darauf wenden wir die Formeln an (§ 129):
+ ß =
und finden
Z(Y=2)8 + /-2(Y=2)8 = 4y2,
- 4(^=5)' =
v z
fi (f7?)8 - A (V'^7)8 = 6 Y7.
§ 135.
Die Klasseninvariante z2 und x.
505
Hieraus erhält man x2 und x'2 aus den Formeln [§ 54, (3)]
also ___ _
a — V—2: x2 = ()/2 — l)2,
/—ö , 2 — 1/3 (1 — V3)2
« = V-3: « = . = 2 / \
„_v=7. -8~3ri_(3-ri)’
C _ y !. V. — 16 32
§ 135. Die Klasseninvariante x2 und x.
Es ist in § 126 gezeigt, daß, wenn die Diskriminante D durch
4 teilbar ist, und die quadratische Gleichung, deren Wurzel a
ist, ungerade äußere Koeffizienten hat, f(e>)24 Klasseninvariante
für die Diskriminante D ist.
Es ist aber nach § 54 und § 34
, s , 16 „ 16
Hl v2 v'i ------- -- v2 ------- ' 2—_Z_ - ----------- .
' /’(cj)24’ /’(cj)8 f (2cj)s
Genügt nun co der Gleichung
(2) A co2 -f- B co -|- C = 0
mit der Diskriminante
D = B2 — 44C,
so genügt cj' = 2cj der Gleichung
A co'2 2 B &' -|- 4 C = 0
mit der Diskriminante 4D, und nach § 126, (13) ist daher
f, (2 co)24 Klasseninvariante für diese Diskriminante. Es ist also
x2x'2 und x6 rational ausdrückbar durch Klasseninvarianten der
Diskriminante B und 4D.
Die identische Gleichung
%2 x'2 _|_ X* x'4 -I- 2 x6
(3) z—i— -------------- = x2
- 7 1 —x0
zeigt, daß dasselbe auch für den Modul x2 gilt.
Da x2 durch jede lineare Substitution in eine rationale
(linear gebrochene) Funktion von x2 übergeht, so kann jetzt auch
die Voraussetzung, daß die Koeffizienten A, C ungerade sein sollen,
fallen gelassen werden, und wir haben den Satz:
2. Ist die Diskrimiuante B~0 (mod 4), so ist
x2(co) Klasseninvariante der Diskriminante 4D.
506
Zwanzigster Abschnitt.
§ 135.
_ Im § 134 ist ferner nachgewiesen, daß für D = 1 (mod 4)
]/Dys(co) Klasseninvariante ist. Es ist aber (§ 54)
... 8 (2 + z2 z'2) (x'2 — z2)
(4) n (<o) = -A-.-T- ---------L.
Genügt co der Gleichung (2), und setzt man:
so ergibt sich für co' die Gleichung:
(6) (A + JB + C)^ — 2(A — G)co' + (A — B + C) = 0.
Ist D = 5 (mod 8), so sind A, B, C ungerade, und ist
D = 1 (mod 8), so können wir A und C gerade annehmen, und
folglich ist in beiden Fällen (6) eine primitive Gleichung für co'
von der Diskriminante 4D. Es ist daher nach § 126, 1. f (cof)24
eine Klasseninvariante für diese Diskriminante, und da nun
nach § 34 (18)
/(«)/•(«') = yi
ist, so gilt dasselbe für f(co)24. Daraus folgt, daß z2z'2 Klassen-
invariante für 4D ist, und da man nach (4) z2 rational durch
y3 und x2 z'2 ausdrücken kann, so ergibt sich:
3. Ist die Diskriminante D = 1 (mod 4), so ist
z2 rational ausdrückbar durch eine Klasseninva-
riante der Diskriminante 4D und durch ^D.
Ist J(co) Klasseninvariaute der Diskriminaute D, so sind
j (2 co), j (| co) Klasseninvarianten für 4 D, und es ist:
7 f2 col - <2 + 16)3 - P56 + A O»)24]3
A(2co)24 - ^(co)48
_ 16 (16 z'2 -f- z4)3
z7 8 * * * x'2 ’
W r /co\24 i3 * *
• /«\ _ + 16 * *J [256 + A (co)24]3
J\‘i) ,/<o\24 A(®)48
'2\2/
_ 16(16x2 4- x'4)3
z2z'8
Hieraus ergibt sich, daß auch umgekehrt die Klasseninvarianten
der Diskriminante 4D rational durch x2 ausdrückbar sind.
§ 136.
Quadratische Transformationsgrade.
507
Um auch % (<») selbst als Klasseninvariante auffassen zu
können, wendet man die Gausssche Transformation (§ 9, § 32)
an. Danach ist:
\2/ [1 4- %(gj)]2’
woraus:
H (üj) —
*2 (?)
4-25t2(?)
Es ist also h (gj) rational ausgedrückt durch z2 (gj) und z2
gj\
V’
und gj' == genügt der Gleichung
Al
(8) 4 Am'* + 2_Bgj' + C = 0.
Ist C eine gerade Zahl, was wir annehmen können, wenn
D = 0 (mod 4) oder = 1 (mod 8) ist, so kann in (8) der
Faktor 2 weggehoben werden und die Diskriminante von (8) ist
gleich D. Ist aber C ungerade, was bei D = 5 (mod 8) not-
wendig ist, so ist die Diskriminante von (8) gleich 4D. Daraus
folgt nach 2. und 3.:
4. a) Ist D = 0 (mod 4), so ist z(gj) rational ausdrück-
bar durch die Klasseninvarianten der Diskri-
minante 4D.
b) Ist D = 1 (mod 8), so ist %(gj) ausdrückbar durch
]/Z) und durch die Klasseninvarianten der Dis-
kriminante 4Z>.
c) Ist D = 5 (mod 8), so ist z(gj) rational ausdrück-
bar durch und durch die Klasseninvarianten
der Diskriminante 16Z).
§ 136. Quadratische Transformationsgrade.
Wenn der Transformationsgrad n eine ungerade Quadrat-
zahl ist, so ist nach § 72, 5. für ein variables gj:
0)
Bedingung:
(5)
(6)
508 Zwanzigster Abschnitt. § 136.
wenn ad = n und c durch 8 teilbar ist, eine ganze algebraische
Funktion des Körpers 3t(v, u), worin
zo. • /C 4- d co\ ...
(2) g---)' u=)(co).
Es werde nun darin für a> eine Wurzel der primitiven,
quadratischen Gleichung
(3) J. gj2 -|- J5 ß> -j- C = 0,
mit negativer Diskriminante
(4) D = 52 —4XC
gesetzt, und wir nehmen ein für allemal an, daß A positiv und
relativ prim zu 2l)n sei, was keine Beschränkung ist. Soll nun
v = u werden, so ist dafür die notwendige und hinreichend»
c dco / -|- dco
a a -f- ß&'
ad — ßy — 1.
Vergleicht man (5) mit (3), so folgt (§ 114), daß es zwei
ganze positive Zahlen x, y geben muß, deren erste positiv an-
genommen werden kann und die den Bedingungen genügen:
dß = Ax, cß-{-da—ad = Bx,
. . ca — ay = Gx, —cß —|— öcc —|— = y,
' 2da = Bx y,
2 (cß — ad) = Bx — y,
und daraus wegen (6):
(8) in = y'2 — Bx2.
Ein Primteiler von d müßte, da A relativ prim zu n an-
genommen ist, in x und in y aufgehen. Dann aber auch in
ca — ay und in cß — ad,
folglich in a, d, c. Da diese drei Zahlen aber ohne gemeinschaft-
lichen Teiler sind, so muß g = 1 sein, und aus (7) ergibt sich:
« = 'Bxy, ß = Ax,
(9) H
,, a & Bx — y
ca — ny = Gx, cß — nd — ----------------—-,
Ai
daraus folgt, daß x und y keinen ungeraden gemeinschaftlichen
Teiler haben, und daß, wenn x und y gerade sind, %(Bx -|- y)
ungerade sein muß. Da wir überdies x positiv annehmen können,
§ 136. Quadratische Transformationsgrade. 509
so kommen nur eigentliche Lösungen von (8) in Betracht
(§ 114). Jede eigentliche Lösung führt aber nach (9) zu einem
Wertsystem a, ß, und durch die Kongruenzen
(10) ca~Cz, cß = —- (mod n)
zu einem bestimmten Wert von c (mod n), der auch noch durch
8 teilbar angenommen werden kann. Wenn umgekehrt <r, y
diesen Bedingungen genügen, so habe a und ß keinen gemein-
samen Teiler, wie aus
Bx — y .
a,-----—- — ßCx = — n
2t
hervorgeht. Denn danach müßte ein ungerader Teiler von a
und ß in n aufgehen, und müßte daher, da A relativ prim zu n
angenommen war, in x und folglich in y aufgehen.
Es folgt aber noch, wenn wir von den beiden Ausnahme-
fällen D = —3, JJ — —4 absehen, die uns hier überhaupt
nicht interessieren, weil für diese j(co) rational ist, daß ver-
schiedene Lösungen von (8) auch zu verschiedenen Werten c
führen. Denn nehmen wir an, daß ein und derselbe Wert von c
zu zwei verschiedenen Systemen (a, ß, /, ö) führen könnte, so
würde aus (5) eine Relation der Form
y + d a>
(0 *.-----
a -f- ßa>
folgen, und diese Substitution ist, wenn sie nicht identisch ist,
nur für die beiden erwähnten Ausnahmefälle möglich.
Demnach ist die Anzahl der «-Werte in (2), die nach
(3) gleich u werden, so groß wie die Anzahl der eigent-
lichen Lösungen der Gleichung (8).
Hat die Gleichung (8) nur eine solche Lösung, so ist der
entsprechende Wert von M rational durch u ausdrückbar. Hat
sie aber mehrere Lösungen, so sind die zugehörigen Werte von M
die Wurzeln einer rationalen Gleichung:
(11) = 0,
deren Grad in bezug auf M ebenso groß ist, wie die Anzahl
dieser Lösungeu (§ 134).
Es genügt ferner w der Klassengleichung
H_d (w) — 0.
510
Zwanzigster Abschnitt.
§ 136.
Wir können ®(Jf,u) als ganze Funktion von u darstellen
und können dann diese Funktion durch ihren größten gemein-
schaftlichen Teiler mit H_D (u) ersetzen.
Wir können a, und ß positiv annehmen. Für ß liegt dies in
den bereits gemachten Voraussetzungen. Für a können wir es
immer dadurch erreichen, daß wir B um ein Vielfaches von 2 A
vermehren, wodurch wir zu einer äquivalenten (parallelen) Form
kommen. Dadurch kann Bx -f- y positiv gemacht werden.
Bestimmen wir also den Quotienten
nach § 38, (15), so ergibt sich, da ß gerade oder ungerade ist,
je nachdem x gerade oder ungerade ist:
x = 0 (mod 2): AL = (—\ / 2 e4 a(z )« T
(12) W
x = 1 (mod 2): AL = ^0 t 2 e* + y—^(a ß
Die Quadratwurzeln
haben positiven reellen Bestandteil. Diese Werte von M genügen
also der Gleichung (11). Kommen unter ihnen gleiche vor, so
kann der Grad der Gleichung (11) durch Absonderung mehrfacher
Wurzeln auf rationalem Wege erniedrigt werden.
Da die Gleichung (11) zur Zerlegung der Klassengleichung
nach den Vorzeichen von AL angewandt werden soll, so ist es
von Wichtigkeit, zu entscheiden, ob unter den zu demselben cj
gehörigen Werten von AL in (12) solche vorkommen, die sich nur
durch das Vorzeichen unterscheiden.
Wir untersuchen, wann zwei verschiedene von den Werten
(12), etwa AL, AL', dieselbe 8te Potenz haben. Ist
(14) ALS = M's,
so muß, wenn p eine zwölfte Einheitswurzel und x, y, x', y' zwei
verschiedene Lösungen der Gleichung (8) sind:
(15) y' 4- V-D = 9 (y 4- ® V#)-
§ 136.
Quadratische Transformationsgrade.
511
Daraus folgt, daß p einer quadratischen Gleichung
genügen muß, also daß __
, . । . i + 1 + V—3
(16) 9 = oder (? = =—----------------
Al
sein muß, weil dies die einzigen nicht reellen zwölften Einheits-
wurzeln' sind, die einer quadratischen Gleichung genügen, und
q - +1 zu x = x', y = y' führen würde. Demnach muß
einem Körper angehören, der durch eine dieser Irrationalitäten 9
bestimmt ist, d. h. es muß
(17) D = — 4 m2 oder D = —-3 m2
sein. Im ersten Fall folgt aus (15)
718) y' = ±2mx’
' 2mx' = -$-y,
also nach (8):
n = m2 (x2 -f- a/2),
und da n ungerade vorausgesetzt war, muß auch m ungerade
sein; nach (18) sind y, y' und wegen (8) auch x, x' gerade, und
aus (12) folgt, da 7 und ß gerade sind:
\ Ai /
und aus (18):
y' -j- ix'my
(19) M'i = — MM
Es haben also M und M' nicht gleiche, sondern entgegen-
gesetzte 4te Potenzen.
Im zweiten der Ausnahmefälle (17) folgt in gleicher Weise
aus (15):
±2t/' = y — 3mx,
' + 2mx' = y mx.
Darauf folgt, wenn man die oberen Zeichen nimmt,
(21) m(x'y — y' x) = 2n,
und hieraus schließt man, daß m ungerade sein muß; denn wäre
m gerade, so müßte y und y' gerade sein, und nach (21) wäre
2n durch 4, also n durch 2 teilbar. Dieser Fall ist also nicht
weiter zu berücksichtigen, wenn wir ein gerades D voraussetzen.
Hiermit ist folgender Satz bewiesen:
1. Es sei D = 0 (mod 4) eine negative Diskriminante,
x, y seien zwei Zahlen ohne gemeinsamen un-
'y txm\e
. 2
M'i = (a' 4- ß' eo)6 =
512 Zwanzigster Abschnitt. § 137.
geraden Teiler und so, daß, wenn x gerade ist,
y = 2 (mod 4), ferner so, daß
n — l(«/2 — Dx2)
eine ungerade Quadratzahl ist.
Es sei ferner M durch die Formel (12) bestimmt.
Dann hat die Funktion einen Teiler
(22) 5(11,«),
der mit keiner der Funktionen
(23) ®(—Jf,u), 0(tJf,u), ®(—i,Mu)
eine gemeinsame Wurzel hat.
§ 137. Zurückführung ungerader Diskriminanten auf gerade.
Nach einem von Kronecker ausgesprochenen Satz läßt sich
die Klassengleichung unter Adjunktion von Quadratwurzeln in
so viele Faktoren zerlegen, als es für die betreffende Klassen-
gleichung Geschlechter der Formenklassen gibt, und zwar so,
daß jedem dieser Faktoren nur die Klasseninvarianten genügen,
für die die entsprechenden quadratischen Formen (X, B, C) zu
einem und demselben Geschlecht gehören. Diese Zerlegung er-
halten wir aus den im vorigen Paragraphen bewiesenen Satz 1.
Daß dieser Satz in der Form, in der wir ihn ausgesprochen
haben, sich nur auf gerade Diskriminanten D bezieht, ist für
den Beweis des Kroneckerschen Satzes keine Beschränkung.
Denn wenn D = 1 (mod 8) ist, dann ist nach § 123 der
.Klassenkörper $ (D) identisch mit dem Klassenkörper $ (4 D).
Ist aber D = 5 (mod 8), daun ist der Grad von $(4D) dreimal
so groß als der von $ (D), aber der letztere ist in dem ersteren
enthalten, und die Anzahl der Geschlechter für $ (D) und $ (4 D)
ist die gleiche (§ 104).
Ist u = j (co) eine Klasseninvariante für D = 1 (mod 8),
so sind
(1) v = j (»') = j (2 o), j 00, 3
Klasseninvarianten von 4D, und u ist eine rationale Funktion
von v:
(2) u = (p (v),
die ungeändert bleibt, welche der drei Größen (2) man auch
für v setzen mag. Alle Charaktere der Formen, deren Wurzeln
oi und co' sind, haben denselben Wert.
§ 188. Zerfällung der Klassengleidhung nach den Geschlechtern. 513
Ersetzt man in (2) v durch eine andere Klasseninvariante
derselben Diskriminante 4 D und desselben Geschlechtes, so geht
auch u in eine andere Klasseninvariante der Diskriminante D
über, bleibt aber auch in demselben Geschlecht
Läßt man also in (2) v die Klasseninvarianten eines Ge-
schlechtes der Diskriminante 4D durchlaufen, so durchläuft
u die Invarianten des entsprechenden Geschlechtes der Diskri-
minante D [indem es jeden dieser Werte dreimal, bei T) = 1
(mod 8) nur einmal annimmt], und die symmetrischen Funktionen
dieser u sind in dem gleichen Rationalitätsbereich enthalten wie
die Größen v. Ist daher die Klassenfunktion nach den
Geschlechtern in Faktoren zerlegbar, so gilt das gleiche von
-H-n(w)1)-
§ 138. Zerfällung der Klassengleichung nach den Geschlechtern.
Um den Satz 1., § 136, anzuwenden, setze man
(1) D = _B2 — iAC = — im,
und zerlege m in zwei Faktoren
(2) m = m'm",
wobei vorausgesetzt ist, daß m" ungerade und ohne
quadratischen Teiler sei.
Nun machen wir in dem Satz 1., § 136, die Annahme:
, x x = i, y - 2 (4 m' — m"),
n = (im' m")2.
a = “2B im' — m",
(4) am" = iAC — (B — m"~)2,
ß = iA.
. . a -|- ß eo = 2 i ^m' m" -(-im' — m",
= (2 ym' i
*) Die Durchführung der entsprechenden Betrachtungen für ein un-
gerades D würde zwar auch möglich sein, würde aber zahlreiche Unter-
scheidungen und Weitläufigkeiten nötig machen. Hier ist ein Punkt, wo die
Gausssche Bezeichnung und Unterscheidung von Formen erster und zweiter
Art, deren ich mich noch in der ersten Auflage bedient habe, eine gewisse
Vereinfachung des Ausdrucks mit sich bringen würde. Es hängt das mit
der Ausnahmestellung zusammen, die die Zahl 2 in der ganzen Theorie der
elliptischen Funktionen einnimmt, die in der Weierstrassschen Theorie
etwas zurücktritt, aber doch nicht ganz verschwindet. Auf der anderen
Seite ist diese Auszeichnung der Zahl 2 auch wieder die Quelle von großen
Vereinfachungen, namentlich in den numerischen Resultaten.
Weber, Algebra. III. oo
514
Zwanzigster Abschnitt.
§ 138.
1.
worin die Quadratwurzeln positiv zu nehmen sind. Sodann ist,
weil JB gerade ist
a m" = — 1
und folglich nach dem Reziprozitätsgesetz und nach (4):
also:
(6)
(7) /1 = 4,
also:
ferner:
also:
a — 1 m" + 1 । n n i * a\
—— =-------------------------------F 2 c (mod 4),
—1 „m”+ 1
i 2 = (— l)°i 2 ,
und demnach endlich nach § 136, (12), (13):
2 (2V^' + ^)3,
wofür man auch setzen kann:
7 = 4 C (mod 8), oc ~ 1 (mod 2) [§ 136, (7)],
c—i
JB 2 m' = 2 C (mod 4),
(8)
/ A \ / m" + l -
2 ^' +
m"—1 \3
i 2 ym"}
Jf =
Nach dem Satz 1. (§ 136) ist dann H—d(u) teilbar durch
eine Funktion
(.W,m),
die zu <&(—2R,«) relativ prim ist. Setzen wir
(m" -F1 — 1 \ 3 '
2f 2 ym' -\-]i 2
so ist für jede Klasseninvariante von D eine der beiden
Gleichungen
(10) <P(p,a) = 0, ®(—p,a) = 0
§ 188. Zerfällung der Klassengleichung nach den Geschlechtern. 515
befriedigt, und zwar die erste oder die zweite, je nachdem
(") (^) = +‘(^) = -1
ist.
2. Hieraus folgt, daß das Vorzeichen =+l
nicht von der besonderen Form (A, B, C), sondern nur
von der durch diese Form repräsentierten Klasse ab-
hängt, also ein Charakter der Formenklasse ist.
Nun ist die Invariante einer zweiseitigen Klasse reell, und die
Invarianten entgegengesetzter Klassen sind konjugiert imagi-
när. Für zwei entgegengesetzte Formen (A, B, C), (A,—B, C)
ist aber das Vorzeichen (11) das gleiche, und daraus folgt, daß
®(fi,u) entweder reelle oder konjugiert imaginäre Wurzeln, und
folglich reelle Koeffizienten hat, und sich daher nicht ändert,
wenn g durch den konjugiert imaginären Wert p' ersetzt wird.
Nun sind die beiden Fälle m" = 1, m" = 3 (mod 4) zu unter-
scheiden, weil es davon abhängt, welches Glied in (9) imaginär
ist. Das eine Mal kommt i nur in der Verbindung iy'm', das
andere Mal in i^m" vor, und demnach ist:
(12) <Z»(/i,w) = | [0(/i,w) + ®(/i',w)] = : m" ~ 1 , d
= vGy< m) : m''= 3 '
Die Fuuktion ’P’, und folglich auch hat reelle Koeffi-
zienten _und enthält nur die eine der beiden Quadratwurzeln
ym", y»w'. Die \m" ist nach unserer Voraussetzung immer
irrational, ]hn' ist nur dann rational, wenn m' ein Quadrat ist.
Da H(u) rationale Koeffizienten hat, so muß es, wenn m" = 1
durch n) und ’F(—und wenn m" = 3, und m'
kein Quadrat ist, durch n) und ’F (— «) teilbar sein.
Nun ändert Hf sein Vorzeichen durch die gleichzeitigen
Vorzeichenänderungen:
ritt (i, — i), (ym", — ym"):»«" = 1 .
(13) ) ' '—/ (mod 4),
(i, —i), (y>n', —y«') : m" = 3
und folglich ist, wenn nicht m" = 3, und zugleich m' ein Quadrat
ist, in beiden Fällen:
(14) H(u) = <I>(—M,u),
und diese Zerlegung ist nur dann nicht möglich, weun m" = 1
(mod 4) und zugleich m' ein Quadrat oder m' = 1 ist.
33*
516
Zwanzigster Abschnitt.
§ 138.
3. Jedes der beiden Vorzeichen (11) kommt in gleich
vielen Klassen der Diskriminante D = —4m'm" vor und
die Klassenfunktion ist durch Adjunktion von
vm", wenn m" = 1 , n
'.— (mod 4)
ym", „ m" = 3
in zwei Faktoren vom Grade \h zerlegbar, außer wenn
m" = 3 und m' ein Quadrat ist.
In diesem Ausnahmefall ist, wenn wir = 4 m' setzen,
— m" = z/ der Stamm von
D = <2äz/,
und es ist für jede durch eine Form der Diskriminante D dar-
stellbare und zu D teilerfremde Zahl A:
<2>’^ = (^) = +1
und H(u) ist mit ®(M,w) identisch.
Zerlegt man m in einer zweiten Art in zwei Faktoren
(15) m = mimi',
wo m( denselben Bedingungen genügt wie m", so erhält man in
gleicher Weise eine Zerlegung
(16) H(u) — 0(3'/,,«) <&(—_Mi,w),
und indem man den größten gemeinschaftlichen Teiler von
(Jf, u) und ® (Jfn w) aufsucht, erhält man eine Zerlegung von
H(u) in vier Faktoren:
• H(u) = 0, (w) (u) (w) (m),
vorausgesetzt, daß in ®(Jf, w) eine Quadratwurzel einer Primzahl
vorkommt, die in u) nicht enthalten ist. So fährt man
fort und zerlegt allmählich H(u) in Faktoren, deren Anzahl eine
Potenz von 2 ist.
Wir wollen die Anwendung auf die einzelnen Fälle etwas
genauer betrachten.
1) Ist m = 3 (mod 4), so sind alle Charaktere in der Form
(— \
\m"/
enthalten, und die Formel (8) reicht hin, um alle Geschlechter
voneinander zu trennen. Ist hier m" = 3, so ist m' = 1 (mod 4)
und aus (12) folgt, daß in den Teilgleichungen nur die Quadrat-
wurzeln aus solchen Zahlen vorkommen, die von der Form 4 m -|-1
§ 188. Zerfälhmg der Klassengleichung nach den Geschlechtern. 517
sind. Bezeichnen wir also mit p, p', p", ... die Primfaktoren von
m von der Form 4 m -|- 1, mit q, q', q", ... die Primfaktoren von
m von der Form' 4 m 3, so kommen in den Teilgleichungen
die folgenden Quadratwurzeln vor:
/p, yy, Vp", ..., ]lqq', 1/qq", ...;
wenn also nur ein q in m enthalten ist, so kommt rfq in den
Teilgleichungen nicht vor. Da in diesem Fall wenigstens ein q
in m aufgehen muß, so ist die Anzahl der zur Zerlegung er-
forderlichen Quadratwurzeln gleich der Anzahl der in m auf-
gehenden Primzahlen, vermindert um 1, also gleich der Anzahl
der diesem Fall entsprechenden unabhängigen Charaktere.
2) Ist
m = 1 (mod 4), m = 6, 2 (mod 8), m = 4 (mod 16),
so können nach § 105 beziehungsweise die Charaktere
\ a r vv’ \ a r \a)
durch die Charaktere von der Form
ausgedrückt werden, und es reicht also auch in diesen Fällen die
Formel (8) aus, um alle Geschlechter voneinander zu trennen.
Die Formeln (9), (12) lehren, daß in diesen Fällen zur voll-
ständigen Trennung der Geschlechter folgende Adjunktionen
nötig sind:
m = 1 (mod 4), yp, ^p", ..., tfq, ^q', tfq", ...
m = 6 (mod 8), yä, yp, ^p’, ]/p”, ..., faq', ^qq", ...
m = 2 (mod 8), j/p, yp7, \p", ..., ^2q, ^2q', ^'Zq", ...
m = 4 (mod 16), yp, ^p’, \p", ..., \'q, ^q', \q", ...
Denn im Fall m = 1 (mod 4) ist die Anzahl der q jedenfalls
gerade. Setzt man also m = qr2m", m' = qr2 und versteht
unter r2 die größte in r2m" aufgehende Quadratzahl, so ist
m" = 3 (mod 4) und die Formel (12) gibt die Adjunktion von ^q,
also ist in diesem Fall zur vollkommenen Trennung der Ge-
schlechter _____ __ _____________ ____
yp, yp', yp",..., y^, ...
zu adjungieren, und . die Anzahl der Quadratwurzeln ist gleich
der Anzahl der in m aufgehenden Primzahlen, wieder in Über-
518
Zwanzigster Abschnitt.
§ 188.
einstimmuug mit der Anzahl der unabhängigen Charaktere. Auf
ähnliche Art ergeben sich die übrigen Fälle von (16).
In den noch übrigen Fällen, nämlich m = 12 (mod 16) und
m = 0 (mod 8), ist die vorstehende Zerlegung zwar auch noch
anwendbar, in den so gewonnenen Teilgleichungen sind aber
immer noch je zwei oder je vier Geschlechter vereinigt, ent-
sprechend den Charakteren
/—1\ 72 \
\ A )' \ri/’
Wir leiten also noch eine zweite Transformationsformel wie
(8) her, indem wir die Gleichung
4 m = y2 — Dx'2
(8), § 136, folgendermaßen befriedigen:
m = m'm" = 0 (mod 4),
x = 2, y = 2 (m1 — m"'), n = (m1 im")2,
worin wieder m" ungerade und durch kein Quadrat teilbar an-
genommen ist, aber auch = 1 sein kann, und aus § 136, (9)
erhält man
a = B -|- m' — m", ß = 2 A, y = — 2 0 (mod 8),
am" = AC — (^B — m")2,
Nehmen wir der Einfachheit halber B = 0 (mod 8), was
nötigenfalls durch Übergang zu einer parallelen Form erreicht
wird, so ergibt sich m' = C (mod 8), a = C — m" (mod 8) und
folglich
.“-1 «ia/v_tn If, A+l m"—l
i 2 e4 = (—l)4 (—1) 2 i 2 ,
,a/ \m") \ni"/ \am"/ \am"J
und daraus ergibt sich nach § 136, (12), (13):
/ 9 \ / A \ / 1\ / "1"~1 »»" + 1 \3
(iS) « = -(-,)(_,)(_)(; . y„' + i .
Diese Formel ergänzt die vorige für den Fall m = 12
(mod 16), und zeigt, daß auch in diesem Falle die vollständige
Zerfällung der Klassengleichung durch Adjunktion von
, . , , Vp', •••> V«, V«", •••
geschieht.
§ 138. Zerfällung der Klassengleichung nach den Geschlechtern. 519
Ist nun m durch eine noch höhere als die zweite Potenz von
2 teilbar, so kann man, wenn der Exponent von 2 ungerade ist,
nach § 105, (7) alle Charaktere auf solche von der Form
(—\ f Z-(—\
\m"J’ \ A J \m"J
zuriickfiihren. Man setze
m = 2 r2 m",
indem man wieder unter r2 die größte in aufgehende Quadrat-
zahl versteht und wende, je nachdem m" = 1 oder = 3 (mod 4)
ist, die Formel (8) oder (18) an. Man erhält dann die vollständige
Zerfällung der Klassengleichung unter Adjunktion der Quadrat-
wurzeln aus sämtlichen in ni aufgehenden Primzahlen, aus-
schließlich ^2.
Ist aber der Exponent der höchsten in m aufgehenden Potenz
von 2 eine gerade Zahl, so genügt auch (18) noch nicht zur voll-
ständigen Zerlegung der Klassengleichung. Man kann zwar hier
wieder durch die Formeln (8), (18) durch Adjunktion sämtlicher
yp und y^ die Funktion H Zerfällen, die y'2 bekommt man aber
dadurch nicht hinein, und es bleiben also immer noch je zwei
Geschlechter in einer solchen Teilgleichung enthalten. Um auch
diese noch zu trennen, leiten wir unter der Voraussetzung, daß
m durch 8 teilbar sei, noch eine dritte Formel her.
Wir setzen
m = m'm",
x = 1, y = — im'', n = Qm' m")2.
______________ n i _________ ________
y— 7 (a ß to) = e 4 (|y>n' i /»/'),
worin wieder m" ungerade und durch kein Quadrat teilbar ist.
Hier folgt aus § 136:
(19) Jf=(-l)se4 2 + 2 y»4")’
Nachdem die Zerlegung nach den Charakteren \ durch
'die Formeln (8) und (18) erledigt ist, handelt es sich nur noch
um die Zerlegung nach den Charakteren
/—1\ Z2\
\ A )' W’
d. h. nach dem Verhalten von..J. gegen den Modul 8. Es genügt
daher, in der Formel (19) m" = 1 zu setzen, wodurch man
folgende vier Werte von M erhält:
520
Zwanzigster Abschnitt.
§ 188.
V 2
A = 1 (mod 8),
> = (— i)8 —(i — q y™)3 = ap,
y2
(20) ^-1-i
' 7 y2-
m 1 _ •
AL = (— 1) V !—=A (1 — i 1 yx>3 = A/'",
y2
A = 3 (mod 8),
= M",
A = 5 (mod 8),
A == 7 (mod 8).
Die vier Werte von AL gehen aus dem ersten hervor durch
die Vertauschungen:
(21)
-w, y2,
jr, —yi,
M", — yi,
j/'", yi,
i, j/m,
— i, — rfm,
i,
— i, — rfm.
Ist nun <P (AL, u) = 0 in demselben Sinne wie oben die
zwischen u und AL bestehende Gleichung, so sind die vier Funk-
tionen
<P(Af, w), <P(—AI, u), fb(iAL,u), <I>(—iAL, u)
ohne gemeinsamen Teiler, und wenn ®(A/, u) in H(u) enthalten
ist, so sind auch die drei anderen Funktionen <P(—AL, u),
(L>(iAL, u), a>(—iAL, w) in H(u) enthalten, da die Vorzeichen
der Irrationalitäten (20) beliebig geändert werden können. Es
ist daher
H(u) = ®(AZ,w)®(—AL, u) (i M, u) & (—iAL, u),
und es kommt also jeder der vier Fälle
A= 1, A = 3, A~ 5, A=e 7 (mod 8)
in gleich vielen Formenklassen der Diskriminante — 4 m vor.
Eine Ausnahme tritt nur dann ein, wenn m ein Quadrat
oder das Doppelte eines Quadrates ist, weil im ersten Falle
rational und daher nur die Vertauschung (Af, AI") gestattet ist,
im zweiten Falle /2 und ^m gleichzeitig ihr Zeichen ändern, also
nur die Vertauschung (AL, M') zulässig ist.
Aber es genügen auch schon diese Vertauschuugen, um die
Teilgleichung durch Adjunktion von /2 weiter zu Zerfällen.
§ 139.
Beispiele.
521
Im ersten Falle kommen nach § 105 nur die beiden Kon-
gruenzen
A — 1, A = 5 (mod 8),
im zweiten Falle nur die beiden Kongruenzen
A = 1, A = 3 (mod 8)
vor, und zwar wieder in gleich viel Formenklassen. Die voll-
ständige Zerlegung der Klassengleichung nach den Geschlechtern
erfordert, wenn m durch 8 teilbar ist, immer die Adjunktion der
Wurzeln aus sämtlichen in m aufgehenden Primzahlen, ein-
schließlich 2.
Man bemerkt, daß in diesen Betrachtungen ein neuer Beweis
der von Gauss und Dirichlet bewiesenen Sätze über die Existenz
der Geschlechter enthalten ist, freilich nur für negative Dis-
kriminanten.
§ 139. Beispiele.
Zur wirklichen Ausrechnung der Zerfällung der Klassen-
gleichung sind die Formeln des vorigen Paragraphen nur in be-
schränktem Maße anwendbar wegen des zu hohen Grades der
Transformationsgleichungen. Wir werden nachher in einem Falle
eine wenigstens nahe verwandte Methode zur Anwendung bringen.
Ist die Klassengleichung bekannt, so läßt sich meist leichter die
Zerlegung direkt finden, indem man einen Ansatz von bekannter
Form mit unbestimmten Koeffizienten macht; so findet man aus
den Formeln § 130, (2), (29), (37) die folgenden Teilgleichungen,
worin das positive Zeichen der Quadratwurzel dem Haupt-
geschlecht entspricht:
m = 50,
m = 26,
m = 41,
z2
A(V—50) =1/2^,
xz — x2 — —(x + 1),
(V^26)2 = V2 a:,
X?‘ — X2 = (x 1),
= r(y^ii)2 , _y2 _
_V2 +jf£y-4i)2’
5 + V41 , 7 4- yil
2 2 ~
522
Zwanzigster Abschnitt.
§ 189.
Um aber eine Anwendung unserer allgemeinen Methode zu
geben, nehmen wir m = 3 (mod 8) an und setzen D = —m.
Wir befriedigen die Gleichung:
4 m = y2 mx2,
m — m'm",
m' — m" , /m' 4- m"\2
» = —2—’ *“ = (—J—)•
indem wir setzen
x = 1,
wobei y und folglich n ungerade ausfällt. Es wird ferner nach
§ 136, (13)
. a /Vm'-I-«
+ 0“ = k----- 2 )
Setzen
teilbar ist,
(1)
wir unter der Voraussetzung, daß n durch 3 nicht
Ze —j— Ö
\ a )
v(°>)
so läßt sich M mit Anwendung von § 38, (15) bestimmen und
man findet, wenn m" denjenigen der beiden Faktoren m', m"
bedeutet, der modulo 4 mit 1 kongruent ist:
(a \ —w"—2 ni , , h • <! t
AA n—s— e- -— aym _
' 2
Um hiervon eine Anwendung zu machen, setzen wir n = 25, also
20 = m' -|- m",
und folglich
s m = 1, m' = 19, m = 19,
m" = 17, m' = 3, m = 51,
• m" = 13, m' — 7, m = 91,
m" — 9, m! = 11, m = 99.
Legen wir die Form
/, in' — m" X
V’ -----2--’ n)
zugrunde, so ist A = 1 zu setzen, und (2) ergibt:
no A — i^ÄÄ
m = 19, M =-----------jr-i—,
2t
„ it -^V17— «V3
m = 51, M = e 3 -l----------——,
(3) _ 2
ft1 ,, V13 — i 1/7
m = 91, Ju = 1 —I—,
’ 2 ’
q___; i/tT
m = 99, AL = e3 -—
§ 139.
Beispiele.
523
Nun genügt nach § 72, (27), (28) einer Transformations-
gleichung, die, wenn
% = j/ö 5 Jf* + 15 Jfs 25 JP 25 M
= [(jf + ^y+ 5 (m+A) + 5]
gesetzt wird, die Gestalt erhält:
(4) J(o) = r2(co)3 == + 5)..
A<
Für m — 19 erhält man hieraus den schon oben (§ 125)
gefundenen Wert
und für die drei übrigen Werte von m erhält man
j 7+y-~51) = — 2i*.27(6263 -|- 1519 ^17),
(5) n (~3+2V--—) = - 48 (227 + 63 y 13),
j 1 ~ 212 (4 591804 316 4- 799 330 532 ^33).
Hieraus kann man zu kubischen Gleichungen für
/•(yzTöi)2*, /•(yzröi)*, /•(V=^9)2*
gelangen, indem man von den Formeln Gebrauch macht (§ 34,
§ 54):
_______________________________ __ r n i
f (— r 4" V— m\ 24
h \ 2 / - fCV^)’
/_, + ££<_ / _ iS-
2 ) ’
worin r = 7, 3, 1; m = 51, 91, 99 zu setzen ist. Setzt man
also für r = 3: _____
/“(y— m) — x,
so erhält man:
(6) ;r2* y2 (co) a?16 — 162 = 0,
und für r = 7, 1: ___
/(y— = 2 a?,
für diese beiden Fälle:
(7) — [3 — 2~8 j (co)] 3^8 _ 1 = 0,
524
Zwanzigster Abschnitt.
§ 139.
wo für yä(co) und J(o) die Werte (5) einzusetzen sind. Diese
Gleichungen lassen sich noch zerlegen, und man erhält für x
seihst viel einfachere Gleichungen:
/(V— 51)3 =2«, «3 _ 4^2 _ x _ i — yi7a;2,
(8) /(V— 91) = x, x3 — 2 «2 _ x _ 2 = yi3x,
f^— 99)3 = 2x, x3 —13a:2 — 4« — 1 =i/33(2«2_]_
Die Darstellung der Klasseninvarianten j (ra) durch eine
einzige Quadratwurzel ist immer dann möglich, wenn zwei Ge-
schlechter und in jedem Geschlecht eine Klasse vorhanden ist.
Diese Werte von m finden sich in der Gaussschen Tafel der
Klassenzahlen (Werke, Bd. II, S. 450ff.) unter der Bezeichnung
II, 3, von denen die auszuwählen sind, die = 3 (mod 8) sind.
Ihre Anzahl ist aller Wahrscheinlichkeit nach endlich, wie die
erwähnte Tafel auf weist; es sind die Zahlen:
m = 35, 51, 75, 91, 99, 115, 123,
147, 187, 235, 267, 403, 427.
Wenn die Formenklassen in eine beliebige Anzahl von Ge-
schlechtern zerfallen, aber in jedem Geschlecht nur eine Klasse
enthalten ist, dann lassen sich nach dem in § 138 bewiesenen
Satze alle Klasseninvarianten durch Quadratwurzeln aus-
drücken. Von Euler und Gauss ist durch Induktion geschlossen,
daß es nur eine endliche Anzahl, nämlich 65, solcher Diskrimi-
nanten gibt ’). In der Abhandlung „Zur komplexen Multiplikation
elliptischer Funktionen“ (Mathematische Annalen, Bd. 33) habe
ich diese Zahlen alle berechnet. Sie sind auch in der Tafel der
Klasseninvarianten, die diesem Buche beigefügt ist, enthalten.
*) Euler, Nouv. Mem. de Berlin 1776, S. 338. Gauss, Disq. art. 303.
Euler ist auf diese Zahlen auf einem anderen Wege gelangt, nämlich von
der Aufgabe, große Primzahlen zu ermitteln (Vgl. die Straßburger Disser-
tation von Peter Meyer: Beweis eines von Euler entdeckten Satzes, be-
treffend die Bestimmung von Primzahlen, Straßburg 1906). Diese Zahlen
sind:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 15, 16, 18, 21, 22, 24, 25, 28, 30, 33, 37,
40, 42, 45, 48, 57, 58, 60, 70, 72, 78, 85, 88, 93, 102, 105, 112, 120, 130, 133,
165, 168, 177, 190, 210, 232, 240, 253, 273, 280, 312, 330, 345, 357, 385, 408,
462, 520, 760, 840, 1320, 1365, 1848.
Einundzwanzigster Abschnitt.
Die Normen der Klasseninvarianten f («).
§ 140. Konvergenz einer unendlichen Reihe.
Wir betrachten, eine beliebige quadratische Form
(1) y) = Ax + 2Bxy 4- Cy*
mit negativer Diskriminante
(2) — m = B* — A C,
in der vorläufig die Koeffizienten A, B, C nicht notwendig als
ganze Zahlen betrachtet werden sollen, nur sollen sie reell sein.
Nehmen wir x, y als rechtwinkelige Koordinaten in einer Ebene
an, so entsprechen den ganzzahligen Werten von x, y die Gitter-
punkte. Die Gleichung
0, y) = t
stellt für ein konstantes t eine Ellipse dar, und die Anzahl
Z(f) der Werte von tl>, für ganzzahlige x, y, die kleiner als t
sind, ist gleich der Anzahl der im Innern dieser Ellipse gelegenen
Gitterpunkte. Nach Bd. II, § 194, (5) nähert sich der Grenzwert
des Verhältnisses Z(ty.t für ein unendlich großes f, dem Flächen-
inhalt der Ellipse ij> = 1, nämlich dem Werte n : rfm. Also
haben wir
(3) Lim -AA — .
r ym
Lassen wir also in der unendlichen Reihe
i
(4) S = X , . ,
v (x, y)s
die Zahlen x, y alle ganzzahligen Werte, ausgenommen die Kom-
bination x = 0, y = 0, durchlaufen, so ist nach Bd. II, § 196, 4
S für s > 1 konvergent, und es ist
(5) Lim (s — 1) S = -£=•
v 7 s —i ym
526 Einundzwanzigster Abschnitt. § 141.
Im folgenden soll durch direkte Umformung der Summe 8
nachgewiesen werden, daß
8--------^—=
(s — 1) ym
für s = 1 einen endlichen Grenzwert hat und dieser Grenzwert
soll bestimmt werden.
§ 1«.
Wir ordnen
Die Kroneckersche GrenzformeL
die Glieder der Reihe
x,y 1
8=2? , , .
(«, y)s
Weise an, daß wir die dem verschwindenden y
zunächst in der
entsprechenden Glieder absondern und von den übrigen je zwei,
welche entgegengesetzten Werten von x und y entsprechen, zu-
sammenfassen.
So erhalten wir:
(1)
wenn zur Abkürzung
(2)
8 = M, + Ns,
(3)
y
Ms = 2 2?
1
-oo,» (Ax2 -|- 2Bxy -j- Cy^'
Ns =
den Ns für s = 1 erhält, läßt sich,
ist. Der Wert N,
Reihe für s = 1 unbedingt konvergent bleibt, direkt
bestimmen und ergibt:
(4)
gesetzt
da die
N = 1 % 1 _
Ai,„ x* —
Um das Verhalten von AIS für s = 1 zu ermitteln, zerlegen
wir die Funktion ij) — Ax2 -|- 2Bxy -|- Cy* in zwei kon-
jugiert imaginäre lineare Faktoren:
Ax2 ^Bxy Cy'2 = A(x -|- a^y) (x — K>2y),
wenn
(5)
so erklärt werden, daß j/m positiv ist.
Hierdurch wird
2 v
M = 4-2?
«1 =
co2 =
(6)
2?
1
§ 141.
Die Kronecker sehe Grenzformel.
527
Nun ist nach einem bekannten Satz aus der Theorie der
r~ Funktionen, wenn Ä eine beliebige Größe mit positiv imagi-
närem Bestandteil bedeutet:
00
1 _ (2rc)s * f
(—^y~r(s)Je §
0
worin die Potenz (•— i k)s dadurch eindeutig erklärt ist, daß, wenn
— ik — qeia gesetzt, p positiv und der Winkel ® zwischen —
und -j—w angenommen wird, (—ik'y — gseieis zu setzen ist.
Ersetzt man hierin i k durch die konjugiert imaginäre
Größe — i k', indem man zugleich einen neuen Integrationsbuch-
staben tj wählt, und multipliziert beide Gleichungen, so folgt:
i r c
<7) W =
0 0
Hierin setzen wir für k, k' die beiden konjugierten Faktoren
-f- x — von nnd führen den Integralausdruck (7)
in (6) ein.
Dadurch erhalten wir:
00 00
(8) Jfs= . [ [e2««d—5 + «>s>;)] (g^y-idgdij.
As 1 (8) 1 (S) j J
o o
Wir fassen nun das Produkt der beiden Integrale auf der
rechten Seite dieses Ausdruckes, das wir zur Abkürzung durch
(S) r=2fp>J) + v(“G + “2>i)] 1 d^dl]
0 0
bezeichnen, als Doppelintegral auf,
das sich, wenn |, ij als recht-
winkelige Koordinaten in der Ebene
gedeutet werden, über den positiven
Quadranten des Koordinatensystems
erstreckt.
Um das Doppelintegral umzu-
formen, teilen wir den Integrations-
bereich . durch eine den Winkel
halbierende Gerade in die beiden
Teile I, II (s. die Fig. 2), und sub-
stituieren im ersten Teil
Fig. 2.
528
Einundzwanzigster Abschnitt.
§ 141.
I — 1? = U, | -|- y = V,
im zweiten Teil:
i — V = —w, i + »2 = v.
Wenn man dann, wie die Figur andeutet, zuerst bei kon-
stantem u in bezug auf v integriert, so erhält man:
oo oo
C C /'ife — 'U$\s—*
W — e27rixudu + —\ dv,
0 u
00 00
f f / v% _ u^\s— 1
_j_ e~i7tixu du eni^~«("i—ft,2)+*j(ft,i + ft,2)] /--—\ dvy
0 u
oder, wenn man zur Abkürzung
00
f /<n2 »/2\S—1
(10) <p+ (w) = e*ivtv<a,i+a,d±u<-a,i-a,M (----—\ dv
u
setzt,
00 00
(11) W == j dt7lixu<p+(u)du -}- j e~27rixu<f>Ju)dit.
o o
Diese nach u genommenen Integrale zerlegen wir in lauter
solche Bestandteile, deren Grenzen die Reihe der ganzen Zahlen
sind, wir setzen also, da x eine ganze Zahl ist:
oo v v +1
(12) f e±2rTixu <p+(ii)du = S f e±27tixu <p+(u)du,
o °>” i
i
= S ( <pt (u v)du,
0
1
= j e--nixuf(u)du,
0
wenn wiederum
(13) f(u) = S <p*(u -|- v)
0,oo
gesetzt ist.
Wenn wir nun zunächst die Summation in bezug auf x aus-
führen, so können wir von der Grundformel aus der Theorie der-
Fourierschen Reihen Gebrauch machen:
(14) S 1 e^ix^f(u)du = 1 E/(0) + /“(!)]
-oo,»
= i9>±(0) + 9>±(v),
1,00
§ 141.
Die Kroneckersche Grenzformel.
529
und erhalten also, da nach (10)
00
f z^\2s —2
(15) 9>+(0) = <p_ (0) = 9>(0) = e'ris/i’(<ui + “2) f 1 dv
o
ist, aus (11), (12) und (14):
(16) i W = <p (0) + i [<p+ (,) + <p_ (r)].
— 00,00 1,00
Führen wir dies in (8) ein, so zerfällt Ms in zwei Teile:
(17) Ms = Ps + Qs,
wenn
12 srV« v
<18) ^ = ^r(s)r(g)1z>(0)’
(’2n\2s y T
<l9> ^=^T(S)l»g +
gesetzt wird.
Nach (15) ist, wenn wir für v eine neue Integrationsvariable
t durch die Gleichung
. , , x ‘InvyJm
n iv (ß>i ß>2) —----— = — t
einführen, und die Summation nach y ausführen:
v 2z42s—1
r" t2s~2dt
| ef — 1 ’
also:
(20)
(2a)2i/^
(4% ym)2s—1 r (s)2
t2s^dt
d — 1 ‘
Hieraus läßt sich der Grenzwert P leicht bestimmen,
ist nämlich das Integral
Es
(21)
£2s-2e-f
(i
1
— e-f
dl,
«/
da der in der Klammer stehende Ausdruck für t — 0 und t = oo
einen endlichen Wert behält, bis s = 1 stetig, und hat daher
den Grenzwert: 34
o
"Weber, Algebra. III.
dt = —F'(l) = 0,5772 ...
34
530
Einundzwanzigster Abschnitt.
§ 141.
Zerlegt man also das Integral (21) in seine beiden Bestand-
teile und setzt
j = F(2s - 2) =
o
so folgt:
Lim
S = 1
ht^-^dt r&s—i)
l J ef — 1 2 (s — 1)
\o
= —-T'(l),
und wenn man also die Entwickelung nach Potenzen von s — 1:
einsetzt,
(22)
F(2s — 1) = 1 + 2f'(l)(s — 1) -I-----
Lim
s = 1
p2s~2(H 1
J ef — 1 s — 1
o
= 0.
(23)
so daß
(24)
Man erhält ferner durch Entwickelung nach Potenzen von
s — 1:
(2zc)^JLs~1
(4?r (/m)25-1 F(s)2 .
nach (20):
_ (2^AS~1 / F &—*dt 1 \
s ~ (4ar ym)2^1 F(s)2 l J et — ! s — 1J
worin die noch folgenden Glieder mit s — 1 verschwinden.
Daraus folgt:
Es bleibt noch der Bestandteil Qs zu untersuchen übrig, der
für s=l einen endlichen Grenzwert Q erhält; diesen können wir
ohne weiteres durch Einsetzen des Wertes s = 1 bestimmen.
Es läßt sich nämlich in (10), solange u und y größer als
Null sind, nach Einsetzen des Wertes s = 1 die Integration
§ 141. Die Kronecker sehe Grenzformel. 531
ausführen und ergibt mit Rücksicht auf den Wert von
4
<p+(v) =-------j=^-
2 ttymy
worin a a1 oder = co2 zu setzen ist, je nachdem das obere
oder untere Zeichen in <jo+ (v) genommen wird. Durch Ausführung
der Summation nach y folgt hieraus:
» v A »
27 27 <pt(y) =---------= 27 log(l —
i,«° i,«o 2 n ym i,«>
und die Summe nach v läßt sich auf die Funktion y (co) zurück-
führen, da nach § 24, (8):
«»<» r
r](ca) = e 12 II (1 — e2 ««>'<»)
1,00
ist. Danach wird, immer für s = 1,
2 S <P±(v) = — —7= llOff --------------Tn-)-
i,oo 1,00 2 n ym \ /
Führen wir dies Resultat in (19) ein, nachdem wir dort
s=l gesetzt haben, so ergibt sich der Grenzwert von Qs:
Q ‘jr -rrS
(26)
ym
Hiernach erhalten wir aus (4), (25), (26) die folgende Grenz-
formel, deren Ableitung das Ziel dieser Betrachtung war:
x, y | jp
(27) Lim 27 =—-—;——=---------।—=—r.-------------—==
«=i (-4# + %B%y -j- Lt/2) (s — 1) y)W
2«r'(l) . sr. A ‘in 7 , . , .
=-------7/=^- + l°9 777 — IT l0g n 71 W-
| m ym 4 m ym
Aus (27) ergibt sich in Übereinstimmung mit § 140, (5):
, X’V l n
Lim (s — 1) 2? -L - l7=,
v 7 y>s y m
also nur abhängig von m, nicht von der besonderen Form
Verstehen wir also jetzt unter A, 2B, G ganze Zahlen und lassen
ein vollständiges Repräsentantensystem der zur Diskriminante
— 4 m gehörigen Formenklassen durchlaufen, so folgt
(28) Lim (5-1)27 27 =
8=1 y m
wenn h die zur Diskriminante — 4 m gehörige Klassenzahl ist.
34*
532
Einundzwanzigster Abschnitt.
§ 141.
Aus (27) leitet man eine einfachere Formel her für die
Funktion
nx 7 \ 5 ) ni '/ l n j
/•(co) = e *....\ = e2* V < 7 .
’i w ’i («>)
Ersetzt man nämlich
A durch 2 A,
B „ A + B,
C „ KA + 2B+C),
so hleiht m = AG — B* ungeändert und fflj, ca2 gehen über’ in
, »i + 1 , — 1
«h = —3—, «2 = —--------
Setzt man also
= (4 22?, C),
1 ’ tp> = [2A, 2(A-j-B), ±(A + 2B+ G)],
so ergibt sich aus (27)
(30) Lim Ci’ * _ g ‘ 1V f f W.
' ’ , = I \ *• *'7 ('m yä
Wir nehmen jetzt nicht nur A, 2 B, G, sondern auch A, B, C
als ganze Zahlen ohne gemeinschaftlichen Teiler und A ungerade
an. Dann ist tp eine primitive Form der’ Diskriminante — 4 m,
und wir betrachten zunächst die beiden Fälle
m = 1, m = 2 (mod 4).
Nehmen wir, was keine weitere Beschränkung ist, B = m + 1
(mod 2) an, d. h. B gerade oder ungerade, je nachdem m un-
gerade oder gerade ist, so ergibt sich aus
m = AG — B2:
A — G = 0 (mod 4) m ungerade,
A 0 = 0 „ m gerade,
und die Form tp' ist primitiv von’der Diskriminante — 4 m. Es
ist nach der Komposition der quadratischen Formen:
= tpatp,
wenn
/ —1_ ]\
tpo = ( 2, 2, ——) (m ungerade),
2,0,—) (m gerade),
z
§ 142. Die Nonnen- der Klasseninvarianten f (<u). 533
und folglich durchläuft gleichzeitig mit ein Repräsentanten-
system der Diskriminante — 4 m. Es durchläuft aber öj die-
selbe Wertreihe wie ra2, wenn auch in anderer Reihenfolge, und
demnach ergibt sich durch Summation der Formel (30):
(3D n = !,
wenn sich das Produkt II auf die Wurzeln mit positiv imaginärem
Teil eines vollen Formensystems mit der Diskriminante — 4 m
bezieht.
Wir werden in der Folge der Kürze wegen diese
Wertreihe der ca ein vollständiges Wurzelsystem der
Diskriminante —4m nennen.
§ 142. Die Normen der Klasseninvarianten f (ca).
Wir lassen ca ein vollständiges Wurzelsystem der Diskri-
minante — 4 m durchlaufen, und setzen voraus, daß in der Form
(A, 2B, C), deren Wurzel ca ist, A,.C ungerade, A relativ prim
zu m sei, worin keine weitere Beschränkung liegt; dann sind
nach § 126 die 24sten Potenzen von f(ca) Klasseninvarianten und
ihre Norm ist eine Potenz von 2.
In einer zweiseitigen Klasse gibt es stets einen Repräsen-
tanten von einer der beiden Formen:
(A, 0, C), (A, 2B, Jl),
worin A ungerade vorausgesetzt werden kann. Im ersten Falle
ist ca rein imaginär und folglich [§ 24, (11)]:
/“(ßj), /i(m), f2(ca)
reell und positiv; im zweiten Falle sind ca und 1: ca konjugiert
imaginär, folglich:
/» = f (_ 1)
reell und
= 6(-|), /,(«) =
konjugiert imaginär, und nach der Formel f(ca)fi (ca)f2 (ca) =)/ 2
ist auch hier f(ca) positiv.
Wir können also den Repräsentanten (A, 2B, C) immer so
gewählt annehmen, daß A und C ungerade sind und daß f(ca)
für eine zweiseitige Klasse reell und positiv wird; repräsentieren
534
Einundzwanzigster Abschnitt.
§ 142.
wir ferner zwei entgegengesetzte Klassen durch (A, + 2 B, C), so
sind die entsprechenden Werte von /"(ra) konjugiert imaginär, ihr
Produkt daher positiv, und es folgt also nach diesen Bestim-
mungen, daß das Produkt
IVO)
einen positiven reellen Wert hat, der eine Potenz von 2 ist.
Wir setzen, indem wir mit h die Klassenzahl bezeichnen, diese
Potenz = 2hTi so daß
(i)
Es wird unsere Aufgabe sein, diesen Exponenten t zu be-
stimmen. Wir schicken aber noch folgende Bemerkung voraus,
die dieser Aufgabe ein erhöhtes Interesse verleiht.
Infolge der Gleichung [§ 54, (8)]:
(2) • /‘O)24 — — 16 = 0
ist, wenn ca die Wurzel einer zur Klasse k gehörigen Form der
Diskriminante —4 m ist, f(ca) eine ganze algebraische Zahl,
und da in (2) auch durch —^((u)8, —AO)8 ersetzt
werden kann, so sind auch /’i(ßi), /aO) ganze algebraische
Zahlen. Mithin ist es auch
VO = AO) AO)-
Ist p eine ungerade Primzahl, von der — m quadratischer
Rest ist, und p durch die Formen der Klasse l (der Diskrimi-
nante — 4 m) darstellbar, so ist bei passender Bestimmung von c
nach § 118:
c -4- ca
P
die Wurzel einer zur komponierten Klasse lk gehörigen Form,
und es kann (wenn nicht gerade p = 3 ist), c durch 48 teilbar
angenommen werden. Setzen wir also:
so ist sowohl uv als 2:« eine ganze algebraische Zahl.
Wenn wir daher nach § 74
n / x , /2\ 2S
B = (u v)s 4- ( — ) 7-r-,
k 7 \P/ (uv)s
A = (-)+(-\r
\vJ 1 \uJ
§ 142. Die Normen der Klasseninvarianten f(o>). 535
setzen (wo jetzt A-, B natürlich nicht zu verwechseln sind mit
den Koeffizienten der quadratischen Form), so ist B eine ganze
algebraische Zahl, und nach § 74, (14) ist A die Wurzel einer
algebraischen Gleichung, deren Koeffizienten ganze algebraische
Zahlen sind. Es ist also A ebenfalls eine ganze algebraische
Zahl.
Da aber die beiden Quotienten ur:vr und vr:ur die Wurzeln
der quadratischen Gleichung
x2 — J.a;-|-l=0
sind, so folgt, daß
U . V
— und —
v u
ganze Zahlen, und da sie zueinander reziprok sind, Einheiten
sind.
Es sind also u und v assoziierte Zahlen.
Da man nun nach § 118 durch wiederholte Kompositionen
mit Klassen l (durch die Primzahlen darstellbar sind) von jeder
Klasse k zu jeder anderen Klasse k' derselben Diskriminante
gelangen kann, und da zwei mit einer dritten assoziierten Zahl
untereinander assoziiert sind, so haben wir den Satz:
Setzt man für co die h Wurzeln der Formen eines
Systems von Repräsentanten der Diskriminante —4>w,
so sind die h Zahlen f(<o) untereinander assoziiert; und
daraus nach (1) unmittelbar den merkwürdigen Satz, der sich
leicht an allen Beispielen bestätigen läßt:
f(a):2* ist eine ganze Zahl, und zwar eine Einheit.
1. Die Bestimmung der Exponenten t ist durch elementare
Hilfsmittel möglich, wenn m = 1 oder = 2 (mod 4) oder: m = 3
(mod 8).
Machen wir in der Gleichung mit ungeraden äußeren Koeffi-
zienten
(3) + 2J?ßj 4- C = 0
mit der Diskriminante 4(B2 — AC) = —4 m die Substitution
co' — 1 , o—l—l
co' + 1’ “ — —
so erhalten wir die Gleichung
(5) A+2 Jg+. P_ (Ä _ (})a, + A-1B+C = 0)
536 Einundzwanzigster Abschnitt. § 142.
die gleichfalls die Diskriminante —4 m hat, und worin, wenn
m = 1 oder = 2 (mod 4) ist, die beiden äußeren Koeffizienten
ungerade sind; denn es ist:
für m = 1 (mod 4), JB = 0 (mod 2), A C = 2 (mod 4),
für m = 2 (mod 4), JB = 1 (mod 2), Al ü = 0 (mod 4).
Daraus folgt, daß
und
von 24sten Einheitswurzeln abgesehen, dieselbe Wertreihe durch-
läuft. Denn ersetzt man co' durch eine äquivalente Zahl, so muß,
wenn die äußeren Koeffizienten ungerade bleiben sollen, die Sub-
stitution zur ersten oder zweiten Klasse (§ 36) gehören, und
daraus folgt aus (4), daß auch a in eine äquivalente Zahl über-
geht. Wenn aher zwei Fonnen (5) äquivalent sind, so sind
auch die entsprechenden Formen (3) äquivalent und umgekehrt.
Demnach ist
andererseits ist aher [§ 34, (18)]:
woraus sich ergibt:
(6) t = |, m = 1, 2 (mod 4),
in Übereinstimmung mit dem Resultat des vorigen Paragraphen
[§ Wl, (31)].
2. Ist sodann m = 3 (mod 8), so entsprechen einer Wurzel
co' einer Form der Diskriminante —m je drei Wurzeln von
Formen der Diskriminante —4m:
„ , co' co' 1
2(o’ 2’ 2 ’
und es sind die 24sten Potenzen der Größen:
f (^L\ —
f^co')'
Zßj' + ix yi
2 ) — f(co'y
§ 142. Die Normen der Klasseninvarianten 537
deren Produkt = 2 ist, Klasseninvariante der Diskriminante — 41).
Hiernach ist: ,
nf(a>) = 2«Ä,
also
(7) t = |, m = 3 (mod 8).
3. Für den Fall m = 7 (mod 8) können wir den Wert von r
auf diesem einfachen Wege nicht bestimmen. Es ist dazu die
im vorigen Paragraphen abgeleitete Grenzformel erforderlich.
Zunächst behandeln wir die beiden Fälle m = 3 (mod 4) gleich-
mäßig und setzen:
<jp = ax2-[-bxy-{-cy2 = (a, b, c),
(8) b2 — 4ac = —«M,
z,v 1
<p(^, yy
worin x, y alle ganzzahligen Werte, mit Ausnahme der Kombi-
nation 0, 0, durchlaufen.
Die Summe S zerlegen wir in vier Partialsummen
Son, /Soi, Si’o, Sh,
so daß x, y in SJo nur geradzahlige, in Sh nur ungeradzahlige
Werte durchläuft. In Sh durchläuft x die ungeraden, y die
geraden Zahlen und umgekehrt in Sh- Dann ist
(10) S' 2 Soo — ($oi 4" Sh) (Sl0 4" Sh) 4" (Sn 4~ Soo)-
Ersetzen wir
in Sh x, y durch
Sh Soo X, y „
„ $!o 4“ Soo X, y „
n Soo 4- $11 X1 y »
2 z, 2«/,
2 z, y,
x, 2y,
x — y, x 4- y,
so sind die neuen x, y keiner weiteren Beschränkung mehr unter-
worfen, als der, daß nicht beide zugleich verschwinden. Setzen
wir daher:
(11)
so ist
(12)
<p = (a, b, c),
9h = (4a, 2Z>, c),
tp2 — (a, 2b, 4c),
y)g = (a 4“ b 4“ (c — c:), a — b 4~
4® Soo = $',
«•.y
S’o'l 4" $00 — Elfi s,
Sio 4- $00 == ^^2 ,
^,y
Söo 4“ $n = Z'tys •
538
Einundzwanzigster Abschnitt.
§ U2.
Wir setzen a als ungerade voraus und lassen tp ein volles
Repräsentantensystem der Diskriminante —m durchlaufen. Ist
dann m = 3 (mod 8), so ist c ungerade, und qpj, <p2, <p3
durchlaufen zusammen ein Repräsentantensystem der Diskrimi-
nante — Denn unter den 3 7i Wurzeln dieser Formen
co o , 2
2’ 2ß’’ 1 ßj-4-1
kommen nach § 123 keine äquivalenten vor.
Ist dagegen m = 7 (mod 8), so ist c gerade, | | tp3 durch-
laufen je ein Repräsentantensystem der Diskriminante —m, tp2
durchläuft ein Repräsentantensystem der Diskriminante —im.
Durchläuft also tp ein Repräsentantensystem der Diskrimi-
nante — im, und setzen wir
v,v 1
03)
so ergibt sich aus (10):
(14)
m = 3
(mod 8).
m = 7
Setzen wir in den Formeln (29), (30) des vorigen Paragraphen
tp' = 2 <jp, V’ = (A 2 JE?, C),
also:
A = a,
B = b — a,
C = 4c — 2b a,
so ergibt sich:
8-> = i08 fWA'».),
2 ]'m \2
und wenn tp ein Repräsentantensystem der Diskriminante —im
durchläuft, so durchläuft tp dreimal oder nur einmal ein Re-
präsentantensystem der Diskriminante —m, je nachdem m = 3
oder = 7 (mod 8) ist Wir erhalten also, wenn s in diesen
beiden Fällen 3 oder 1 ist:
(15) Lim (ES- ^ES'\ = lilogU^p,
«=i \ 2 J ym p2
worin o die Wurzeln der. Formen tp durchläuft. Und daraus
ergibt sich nach (14):
§ 142.
Die Normen der Klasseninvarianten /'(«>).
539
Lim(4*4-2 — 3.2s)24S' =
(16) 5=1 „
Lim (4-s 4- 2 — 3.2S) 2? S =
247t. f(a) „
8 7t. f(a)
-7=log JT'-L=2 m = 7
(m ]/2
(mod 8),
(mod 8).
Es ist aber [§ 141, (28)]:
Lim (s — 1) S S =
ym
4S 4- 2 — 3.2S
Lim ----!---------
s — 1
= 2 log 2,
also:
(17)
log n = 0,
8 ^2
log 71^ = 0,
1/2
(mod 8),
(mod 8).
m = 3
m = 7
Die erste dieser Formeln gibt das bereits auf andere Weise
abgeleitete Resultat; die zweite gibt das neue:
(18) t — m = 7 (mod 8).
4. Es bleibt noch die Bestimmung von r in dem Falle übrig,
wo m durch eine höhere Potenz von 2 teilbar ist. Um auch noch
diese Bestimmung auszuführen, sei
(19)
m = 4 m',
(20) co' = —4~ / y/m, m> —
also co' die Wurzel der quadratischen Form (JL, 2B, C) der
Diskriminante —m, worin A und C als ungerade vorausgesetzt
werden können. Es sind dann
(21) ßjj = 2 m', = y
Wurzeln der Formen
(22) (A, 4B, 4 0), (4A, 4B, C),
und es sind nach § 126, (13) die 24sten Potenzen von
^(ß,]) — f2(co'X ~
Klasseninvarianten der Diskriminante —4 m..
Durchläuft co' ein vollständiges Wurzelsystem der Diskrimi-
nante — m, so durchlaufen ta, und co2 zusammen ein vollständiges
Wurzelsystem der Diskriminante —4 m (§ 123), und wir erhalten,
540
Einundzwanzigster Abschnitt.
§ 142.
wenn co ein vollständiges Wurzelsystem von Formen mit ungeraden
äußeren Koeffizienten durchläuft, mit Benutzung der Formel:
= yä,
wenn h' die zur Diskriminante —m' gehörige Klassenzahl ist:
Qh __
(23) nfw = nf^f^ = ^h'nf^
worin Ä, h' die Klassenzahlen für die Diskriminanten —4 m, —m
bedeuten. Es ist dann (§ 123):
h — 2 h'.
Sind also wie oben r, r' so bestimmt, daß
2‘ ’ 27'
Einheiten werden, so ist
nf(eo) = 2**, Df(co') = 2Ä’*',
und daraus nach (23):
(24) * = if + T-
eine Formel, die auch noch für m' = 1 gilt, wo h' = h und
die beiden Werte 2ta' und ta':2 äquivalent sind.
Durch wiederholte Anwendung dieser Formel ergibt sich,
wenn
'm = 4:lm'
ist, für ein beliebiges positives 2:
_ t' . i • 1
2'- ‘ 2 2z + i '
Fassen wir das hiermit Bewiesene zusammen, so können wir
sagen, daß folgende Größen algebraische Einheiten sind:
]/2 ’
f(s°)
y'2 ’
yi ’
m = 1, 2 (mod 4),
m = 3 (mod 8),
m = 7 (mod 8),
§ 143.
Partialnormen von f(w).
541
f(a>)
1 _ 1 ’
22 2^ + 2
1 1 ’
22 3.2>- + i
fi“)
8 143.
= ’4*m', m' = 1, 2 (mod 4),
= 4Am', mr = 4 (mod 8),
= 4Ä m', m' = 7 (mod 8).
Partialnormen von
machen von der Grenzformel (30) des § 141 noch eine
Anwendung auf die Bestimmung des Produktes
(1) nf(a>),
in dem sich das Produktzeichen II nicht über ein vollständiges
Wurzelsystem, sondern nur über die Wurzeln a der Formenklassen
eines Geschlechts erstreckt. Wir beschränken uns dabei aber
auf den Fall, daß
(2) z/ = —4 m
eine Stammdiskriminante ist, daß also m keinen quadratischen
Teiler habe und entweder = 1 oder = 2 (mod 4) ist oder, was
dasselbe ist,
(3) z/ = —4 oder = 8 (mod 16).
Es sei ö ein von z/ und 1 verschiedener Stamm teil er von
z/ und %(ö, k) der diesem Stammteiler entsprechende Charakter
der Klasse k.
Ist 8' der zu ö komplementäre Stammteiler zu 8, so ist in
diesem Falle
öd' = z/,
Z(d, fe) = z(d', fc),
und wir bekommen also alle Geschlechter, wenn wir für ö die
ungeraden Stammteiler setzen, was wir hier tun wollen. Es
sei nun wie in § 141, (29), (30):
(4) = (A,2JB, C),
# =
542 Einundzwanzigster Abschnitt. § 143.
Sind dann k, 7c0, k' die Klassen, zu denen ty' gehören,
so ist
%(ö, kf) = z(ö, ko) x(ö, k),
also
z5') k) = (S, A),
U Z(M') = (Ö, 2)(ÖM).
Ist Oj eine Wurzel der Klasse k, so ist ra2 Wurzel der ent-
gegengesetzten Klasse k~ \ in diesen beiden Klassen sind aber
die Charaktere %(ö, k~) und %(ö, li~l) dieselben. Multiplizieren
wir daher die Formel § 141, (30) mit % (ö, k~) und bilden die
Summe über alle Klassen k, so folgt:
(s) sz(ä,s)(i’A-3'±)=
\ v v / ym |/2
und wegen (5) kann man für die linke Seite schreiben:
[l_(d,2)]S*MlfJ-.
Demnach haben wir:
(ö, 2) = +1: (ö, k) log ® = 0,
,7) ym 72
' 2 a 1 ffcD k 1
(M) = “I: =
wobei rechts der Grenzwert für s = 1 zu nehmen ist.
In § 113 haben wir die Formel bewiesen:
(8) =
v / " ' 1 tys ns ns
Wenn wir mit Ä’(ö) die Klassenzahl für die Diskriminante ö
bezeichnen, so ist, wie in § 112, (8) bewiesen ist:
ö<0
(9) n V-ö
= _log£
n |/(j 7
worin die Quadratwurzeln positiv zu nehmen sind, und
_ T-y- ufö
£ ~ 2
die fundamentale positive Einheit des quadratischen Körpers mit
der Grundzahl ö ist. Für die beiden Ausnahmefälle ö = —3,.
ö = —4 gelten diese Formeln, wenn man unter K nicht die
§ 143. Partialnormen von f(<u). 543
Klassenzahl selbst, sondern den dritten Teil oder die Hälfte
davon versteht.
Nun ist ö' immer gerade und von entgegengesetztem Vor-
zeichen wie ö, und 4 m — —öd'-, danach ergehen sich aus (7)
die Formeln:
(10) 22? x (ö, k) log^S) — 0, <5=1 (mod 8),
V
= K(d)K(Ö')logE, <5 = 5 (mod 8),
worin
(11) s = <5 > 0 = 1 (mod 8),
_ T-j- <5 < 0 = 5 (mod 8)
zu setzen ist. Die erste der Formeln (10) gilt auch noch für d = 1.
Da nun für alle Klassen eines Geschlechts und für jedes d
der Charakter %(d,/c) denselben Wert hat, so sind durch (10)
und (11) die Produkte (1) bestimmt. Denn es ist nach § 113
2^%(d, &) = 0,
außer wenn k die Hauptklasse ist, und für diese ist die Summe
gleich der Anzahl g der Geschlechter. Man erhält z. B. für die
Wurzeln » des Hauptgeschlechts
(n f^\2s= n '
\ j/2 /
worin g die Anzahl der Geschlechter bedeutet, und das Produkt
links über alle Wurzeln » des Hauptgeschlechts, das Produkt
rechts über alle Stammteiler d von zf, die = 5 (mod 8) sind,
auszudehnen ist.
Um das Produkt der Klasseninvarianten für ein anderes als
das Hauptgeschlecht zu bilden, hat man die Formel (8) vor der
Summation mit z(d,fc-1) zu multiplizieren, wenn k eine Klasse
des betreffenden Geschlechts bedeutet.
Die Anwendung der Formel (10) verlangt die Kenntnis der
Klassenzahlen positiver und negativer Diskriminanten und der
Zahlen T, U. Die Klassenzahlen sind in weitem Umfange von
Gauss berechnet und aus seinem Nachlaß im zweiten Bande der
Werke, S. 450 bis 476, veröffentlicht. Für die Lösungen T, U der
Feilschen Gleichung enthält Legendres „Theorie des nombres“
oder auch der „Canon Pellianus“ von Degen eine Tabelle.
544 Einundzwanzigster Abschnitt. § 143.
Es existieren 63 negative Diskriminanten von der Eigenschaft,
daß in jedem Geschlecht nur eine Klasse enthalten ist; daß es
nicht mehr gibt, selbst daß die Zahl nur eine endliche ist, kann
freilich bis jetzt nur durch Induktion geschlossen, nicht bewiesen
werden. Die Mehrzahl dieser Diskriminanten, die bereits in
§ 139 zusammengestellt sind, ist =1, 2 (mod 4) und ohne
quadratischen Teiler oder = 8 (mod 16).
Für die ersteren lassen sich die Klasseninvarianten nach
der Formel (10) vollständig berechnen, und eine ähnliche Formel,
auf deren Bildung wir hier nicht eingehen wollen, führt auch
für die durch 8 teilbaren Diskriminanten zum Ziel.
Für die vereinzelten Diskriminanten dieser Art, die hierher
nicht passen, lassen sich die Klasseninvarianten /"(<») nach einer
der anderen Methoden berechnen *)•
Um an einem einfachen, leicht zu übersehenden Beispiele
die Rechnung durchzuführen, wählen wir m = 105 = 3. 5. 7.
Wenn wir die Werte von d, die = 1 (mod 8) sind, weglassen,
da diese in der Summe der Formeln (10) keinen Beitrag geben,
so haben wir:
d = —3, 5, 21, —35,
d' = 140, —84, —20, 12
zu setzen und erhalten, da g = 8 ist:
16 log ^~105) = K(-3) AT(U0) log T+ ^140,
|7 2 *
+ ^(5) K(- 84) log T + ^V84,
+ K(21) K(-20) log T+ ^V.20.,
+ K(- 35) ^(12) log 1/12 •
*) Vgl. des Verfassers Abhandlung: „Zur komplexen Multiplikation
elliptischer Funktionen“. Mathematische Annalen, Bd. 23. Ich mache hier
auf einen Fehler in der Gaussschen Tafel aufmerksam, den ich bei Gelegen-
heit dieser Rechnungen gefunden habe: Gauss’ Werke, Bd. II, S. 475 muß
die positive Determinante 136 die Bezeichnung IV, 2, nicht IV, 1 haben.
§ U4.
Berechnung einiger weiterer Klasseuinvarianten.
545
Es ist aber
K(— 3) = K{— 84) = 4, K(— 20) = 2, K(— 35) = 2,
#(+140) = 4, #(5) = 1, #(21) = 2, #(12) = 2 Q,
wie man aus den Gaussschen Tafeln oder hier auch leicht durch
direkte Abzählung findet.
Ferner ist nach den Legendreschen oder Degenschen
Tafeln:
log (r+iüötQ = 10g(6 + = 10g
log (T + 17) = log f1 + = pog (2 + Vö),
log T4~ J721 V = log —±V2* = 1 log (55 + 12 yil)
= log
log + j/12-~) = log (2 + Vä),
und daraus erhält man:
(^^105--)12= (2 + M (55 + 12 1/21) (6 + j/35) (2 + (G;)3,
oder was damit gleichbedeutend ist:
y2lär (y- ioö)6 - - (i +1/5)3(1/3 + V7)3 (1/5 + y?) (i + ys)3.
§ 144. Berechnung einiger weiterer Klasseninvarianten.
Nächst den Diskriminanten, bei denen in jedem Geschlecht
nur eine Formenklasse vorkommt, die wir im vorhergehenden
Paragraphen betrachtet haben, geben die einfachsten Resultate
die, welche in jedem Geschlecht zwei Formenklassen enthalten,
und unter diesen wieder die, bei denen nur zwei Geschlechter
vorkommen. Die Klasseninvarianten für diese Diskriminanten
— 4 m sind die Wurzeln quadratischer Gleichungen, deren Koeffi-
zienten nur eine Quadratwurzel enthalten. Wir setzen wieder
Stammdiskriminanten voraus, und erhalten nach der Gaussschen
Tafel die folgenden Werte von m:
r) Nach Gaussscher Bezeichnung sind die Klassenzahlen zweiter Art
zu nehmen.
Weber, Algebra. III. 35
546
Einundzwanzigster Abschnitt.
§ 144.
m = 14, 34, 46, 82, 142 = ±2 (mod 16),
m = 17, 49, 73, 97, 193 = 1 (mod 8).
Die Formenklassen des Hauptgeschlechts können in diesen
Fällen repräsentiert werden für ein gerades m durch
(I) (I, 0, m), (2,0,^),
für ein ungerades m durch
(2) (1,0, m), (2, 1,^4^)’
von denen die letztere äquivalent ist mit
. . /m + 1 w — 1 m 1\
l3) \ 2~’ 2 ’ 2 )'
Für die Formen (1) sind nach § 127, 6. die Klasseninvarianten
und für die Formen (2), (3) (§ 127, 3.)
/•(V^)2 lind 1 M _ V2
yi V2 \i - y=^J ~
und nach § 142 sind dies ganze algebraische Zahlen.
Setzen wir also, entsprechend den beiden Fällen:
(4) -- a(V— »02, f(V— w)2,
eine ganze algebraische Zahl, die nur eine Quadratwurzel enthält,
und aus § 138 erhalten wir Aufschluß, welche Quadratwurzel
darin vorkommt.
Es ist yj, wenn m = 6 (mod 8) ist, also für m = 14, 46, 142,
1 / VYl
wenn m = 2 (mod 8) ist, also für m = 34, 82, ferner
y»t im Fall eiues ungeraden m (mit Ausnahme von m = 49, wo
y7 an die Stelle tritt).
Setzen wir also
(5) x 4- -Z = a + b yP,
tZ/
so sind a, b rationale Zahlen, die höchstens den Nenner 2 haben.
Es müssen aber auch a und b positiv sein. Denn ändern wir in
(5) das Vorzeichen von tfp, so entsteht eine andere quadratische
§ 144. Berechnung einiger weiterer Klasseninvarianten. 547
Gleichung, deren Wurzeln die zum zweiten Geschlecht gehörigen
Klasseninvarianten sind, und die daher konjugiert imaginär sind,
während die Wurzeln von (5) reell sind. Daraus ergibt sich die
Größenbestimmung:
(a -|- b Vjp)2 > 4 > (a — b ;
also müssen a und b gleiches Zeichen haben. Da aber x nach
(4) positiv ist, so müssen a und b beide positiv sein.
Um a und b wirklich zu linden, braucht man nur den Aus-
druck auf der linken Seite von (5) nach (4) auf wenige Dezimalen
zu berechnen, wobei es weitaus hinreichend ist,
___
f (V— = A (V— m) = e 24
zu setzen, und die so gefundenen Dezimalen mit den Dezimalen
von ]/p zu vergleichen, um alsbald b und sodann a zu erhalten.
Die Rechnung ist überaus einfach und gibt folgende Resultate:
m — 142, x -I- — = 9 -4- 51/2”,
1 x i t >
m = 193, x -j- = 13 + yi93.
35*
Zweiundzwanzigster Abschnitt.
Cayleys Entwickelung der Modulfunktionen.
§ 145. Grenzwerte für s = 1.
In diesem Abschnitt soll eine funktionentheoretische An-
wendung der Grenzformel gegeben werden. Es bedeutet also hier
» nicht eine quadratische Irrationalzahl, sondern eine Variable
mit positiv imaginärem Bestandteil. Die Modulfunktionen ge-
hören zu den Funktionen mit natürlichen Grenzen, d. h. wenn
man sich der Grenze der Konvergenz nähert, so liegen auf dieser
Grenze, hier also auf der Achse der reellen ca, die singulären
Punkte überall dicht, so daß man diese Funktionen über diese
Grenze hinaus nicht analytisch fortsetzen kann. Cayley hat in
seinen letzten Untersuchungen Entwickelungen der Modulfunk-
tionen gegeben, die darum merkwürdig sind, weil sie das Ver-
halten der Funktionen bei der Annäherung an die Grenze augen-
fällig machen. Der Schlüssel zu diesen Entwickelungen ist die
Grenzformel § 141, (27)1 * * *).
Wenn man in dieser Formel:
(1)
i (Atfi + ‘IBxy + Oy^)s (s _ i)
2«f'(l) n A 2« . , .
—log 4m " TT log v r‘
1/m v m 1Im
(2) aq = a -|- ß i, »2 = — « -f- ß i, ß 'J> 0
*) Die erste Cayleysehe Arbeit findet sich in dem Comptes Rendus
der Pariser Akademie von 1893, Bd. 161. Weiteres in einem Briefwechsel mit
dem Verfasser dieses Buches, der im 47. Bande der mathematischen Annalen
veröffentlicht ist.
§ 14=5. . Grenzwerte für s = 1. 549
setzt, so ergibt sich
A = 1, B = a, C — a2 ß2, m = ß2,
und die Formel 1 ergibt:
x,y . , y i
________________________________________________
[(a? — ay)2 ß2y2~]s ~~ (x + g>1 y)s (x — »2 y)s
n 2 jtF(l) x , 2 ti .
~ (S— })(}-------ß------~ß log 4 ß — ~ß- loS V (ß»i) V(®2>
Das Zeichen Lim ist hier der Kürze wegen weggelassen.
Wir setzen
S — S [(# _ Ky)2 ßty2]^
worin x, y alle ganzzahligen Werte mit Ausnahme der Kombi-
nation 0,0 durchlaufen. S ist eine unbedingt konvergente Reihe,
solange s > 1 ist.
Nun teilen wir die Glieder von S in drei Arten ein, je nach-
dem die x, y gerade oder ungerade sind, und setzen
*,y j
So — ft-----------er—i—Oa x = y (mod 2),
[(x — ay)2 -|- ß2y2)s s v
x,y ।
(5) ß — —-------——j— x = 0 (mod 2),
v 1 [(x — ay)2 + ß2y2]s v '
x,y i
S» ?=0 W2)-
In ß0 sind also die Zahlen x, y entweder beide gerade oder
beide ungerade, in ß1 durchläuft x die geraden, y alle ganzen
Zahlen, in S2 ist y gerade, x beliebig. Betrachtet man die
Summe So -|- S( -j- so kommen darin alle Glieder von S vor,
und zwar die Glieder dreimal, in denen x und y beide gerade
sind. Hebt man in der Summe dieser Glieder den Faktor 4~s
heraus, so bleibt S selbst übrig, und es ergibt sich also:
(6) So + + n2 = (1 + s.
Geht man zur Grenze s = 1 über, so hat man zu setzen
1 1 «___ i
(n 1 = ^-1^1082...,
und erhält aus (3) die für s = 1 gültige Formel:
(8) So 4-^ + 5, = ^-Ilog 2.
550
Zweiundzwanzigster Abschnitt.
§ 145.
Ersetzen wir a und ß in 8 durch 2 a und 2 ß, so hat das
denselben Erfolg, als wenn wir y durch 2y ersetzen, d. h. es
geht 8 in 82 über, und demnach erhalten wir aus (3):
(9) 2 82 — (s —1)/3 ß ßXg ß
Ersetzt man a, ß durch | a, jß und multipliziert mit 4—s, so
ist der Erfolg derselbe, als ob man x durch 2 x ersetzt hätte, und
man erhält . Sj. Also nach (3) mit Rücksicht auf (7):
. Ersetzt man endlich a, ß durch |(« + 1), Iß und dann
2x — y durch so ergibt sich in gleicher Weise:
2 x , /I + <»i\- /— 1 + <»2\
und demnach mit Rücksicht auf die Formeln [§ 34, (9)]:
indem man die Formeln (9), (10), (11) von (3) subtrahiert:
8- 2 80 = ylog»i)
Q <?r
8- 2 8, = y log/-,(«!) A («2),
. 8-28, = log A (mJA (m2),
woraus sich durch Addition nach § 34, (11) die Relation (8) wieder
ergibt.
§ 146.
Ein Satz über Reihenkonvergenz.
551
In der Differenz 2 So — 8 kommen nun genau dieselben
Glieder vor wie in S, nur erhalten die, in denen x y ungerade
ist, das negative Zeichen, und wir können daher auch setzen:
__O ff ( 1 + y
— losH-,) = Lim S l(xJa!l>;+l)vr
(12) log/, (»,)/-,(«,) = Lim S [(J _
T 108 f’ = S S [(„ _ ^'+ f.,.t -
worin nun x, y alle ganzzahligen Wertpaare mit Ausnahme von
0,0 annehmen. Diese drei Formeln lassen sich nach § 34, (13), (14)
aus einer von ihnen ableiten, z. B. indem man in der zweiten
(13)
ersetzt.
ß>l, «2 durch durch + 1, — 1 »2 — 1, — 1 »2 ’
und
also
«, ß durch a + 1, ß,
und durch — a ß
a* + ß*' 4- ßs
Reihenkon vergenz.
§ 146. Ein Satz über
Wollte man in den Ausdrücken (12), § 145 die Zeichen Lim
und 2? miteinander vertauschen, also ohne weiteres unter dem
Summenzeichen s = 1 setzen, so würde man keine unbedingt
konvergente Reihen erhalten, und es muß also untersucht werden,
in welchem Sinne diese Formeln dann noch gültig bleiben.
Um diese Untersuchung durchzuführen, wollen wir zunächst
einen allgemeinen Satz aus der Reihenlehre ableiten, der eine
Verschärfung des Satzes Bd. II, § 196, 3. ist. Es sei
(i) f<i <: fG < f*s <: fG •••
eine Reihe von unendlich vielen positiven Zahlen, und Z(f)
bedeute die Anzahl diesei’ Zahlen, die nicht größer als t sind.
Dieses Z(t) soll für jedes t einen endlichen Wert haben, woraus
dann folgt, daß die mit n ins unendliche wachsen. Wir
wollen aber noch weiter voraussetzen, daß
—r1- — a -j=
t
(2)
552
Zweiundzwanzigster Abschnitt.
§ 146.
sei, worin a eine konstante (unabhängig von f), und 6 eine Funk-
tion von t, die in endlichen Grenzen eingeschlossen bleibt.
Nehmen wir zunächst an, die seien alle voneinander ver-
schieden, so ist Z(fin) = n, und aus (2) folgt:
&) — = a + ^=;
daraus folgt, daß n: fin endlich bleibt, und folglich mit veränderter
Bedeutung von 6:
n . 6
— — a -f- -=,
fn
oder, nach dem binomischen Satz, für irgend ein positives s:
. /, . 0 \
—7 ( 1 —I— —- ),
,.S \ । /'
Pn \ }nJ
worin alle die mit 6 bezeichneten Größen endliche Werte haben.
Diese Formeln gelten aber auch noch, wenn unter den
gleiche vorkommen. Denn seien etwa (wie in Bd. II, § 196, 3.)
4-15 4" 2 5 • • »5 4- l —
einander gleich und
w <C n tn -|- l,
so ist
Z(tin — 0) = m, Z(}1„) = m -|- Z,
— 0) 21 < Zfan)
P'n n P’n
1 0' , n . 0
a 4---7= 1 « T i~i
woraus (3) folgt und (4) wie oben abgeleitet werden kann.
Der Satz, den wir beweisen wollen, lautet so:
Es sei s1, s.2, ;3, ... eine unendliche Reihe positiver
oder negativer, aber endlicher Größen und
(5) El 4" E2 4" • • • + E« = ?n yn,
so beschaffen, daß dem absoluten Werte nach unter
einer endlichen Konstanten bleibt.
Dann ist
(6) 6 = h -1 h 12 । ...
ri r2 ^3
konvergent und eine stetige Funktion von s, so lange
s
2
2
ist.
§ 147. Entwickelung von f, fß ft. 553
Wegen (4) braucht dieser Satz nur bewiesen zu werden für
= n, weil die Reihe sn6/n 2 unbedingt konvergiert und
also nach bekannten elementaren Sätzen diese Eigenschaft hat.
Setzen wir also
W 6+f+-
und nach (5) en = yn\n — yn-i ]/n — 1, so wird
(8) 6 = F +
Da nun für ein unendlich großes n
~ (m + 1)0 — + >
ist, so ist die Reihe (8) unbedingt konvergent, solange s > |
ist, und daraus folgt auch für diese Reihe unsere Behauptung
nach denselben elementaren Sätzen.
§ 147. Entwickelung von f2.
Die Reihen (12), § 145 sind nun in diesem Falle. Betrachten
wir z. B. die zweite von ihnen, aus denen, wie wir gesehen
haben, die anderen hergeleitet werden können, und setzen für
Fu JGi fh» • • • die der Größe nach geordneten Werte der Funktiou
(1) (x — + ß2y2 = n.
Wir nehmen x y als rechtwinkelige Koordinaten in der Ebene
und überlagern die Ebene mit zwei Gittern, indem wir in dem
einen Gitter für die x die geraden, in dem anderen die ungeraden
ganzen Zahlen setzen.
Die Anzahl der Gitterpunkte, die im Innern der Ellipse (1)
oder auf ihrer Peripherie liegen, für die daher <i n ist, be-
zeichnen wir für die beiden Arten mit Z°(m), Z1^).
Setzen wir _ _
x = iV«, y =
so geht (1) über in
(2) (| — aij)2 + ßV = 1,
und der Flächeninhalt dieser Ellipse ist a/ß, und nach Bd. II,
§ 194, 1.:
554
Zweiundzwanzigster Abschnitt.
§ 147.
z°(0 _ jr . r0
t ~2ß+\t'
£(Q = 2L _l 21
t 2ß~^r
worin y° und y1 für t = a> endlich bleiben. Der Faktor | bei
x/2ß kommt daher, daß hier die Gittermaschen Rechtecke vom
Inhalt 2 sind. Dies ist aber in Übereinstimmung mit der
Formel § 146, (2).
Aus (3) ergibt sich
(4) z°(O-z1(f) = yV#;
worin y gleichfalls endlich bleibt.
Nun können wir die in der Formel (12), § 145 vorkommende
Summe
L(* — ««/)2 + ß2^
so schreiben:
0 =
worin die e15 f2, fs, ... nur die Werte +1 haben und
(5) -j- £a H- £s £n = Z°(n) — Z' («),
— y^n.
Damit sind die Voraussetzungen unseres Satzes § 146 erfüllt.
•Es ist also 0 für s 1> | eine stetige Funktion von s, also
insbesondere auch für s = 1, und wir erhalten aus § 145, (12):
- y 10« n»<) /(».) = S (a! j-yl'yy,.
(6) - W, (•>,) A (•>,) = 2 (J _
=S w _ 1^1 ß.^
Man kann diese Formeln auch noch anders darstellen. Wir
führen die Bezeichnung ein:
(7) S (^ - Soo : x gerade, y gerade,
= S01 : x gerade, y ungerade,
= S10 : x ungerade, y gerade,
= Sn : x ungerade, y ungerade.
§ 147. Entwickelung von f, f\, fs. 555
Dann ist
-jj- log f (»i)f f (»2) = — Sqq -|- S10 Sol — Su,
(8) -ß- log/i (»1) /i (»2) — — ^oo H- S10 — 801 + Stl,
-ß-log/a (rai)/a (raa) = —'800 — 810 -|- 801 Sn,
woraus durch Addition:
log 2 — — 3 Soo —f— S10 —|— 8n -|- Sn,
und wenn man hierdurch So„ eliminierte:
y log f (W1) f (m2) = p log 2 4- | S10 + f S01 - f S(1,
(9) . log A («0 fi (®2) = log 2 + | S10 - | S01 + 1 Sn,
P 0 P
' ^logra(«I)ra(«2) = ^log2-fS10+|S01 + |S11.
p 0 p
Diese Summen sind aber so zu verstehen, daß in allen zugleich
(x — a y)2 ß2 y2 < n
sein soll, und dann n ins Unendliche wächst. Jede einzelne
Summe 8 wird dann unendlich, aber ihre Verbindungen, wie sie
in diesen Formeln vorkommen, erhalten endliche Grenzwerte.
Wir wollen noch mit Sh* Sh, Sh die Summen bezeichnen,
die denselben Ausdruck haben wie S01, S10, ST1 nach (6), nur
mit dem Unterschied, daß x und y keinen gemeinschaft-
lichen Teiler haben sollen.
Setzen wir
S10 + 801 - 2 8n = Tn,
(x — a y)2 ß2y2 <; n,
Lim Tn = T
n — <x>
und bezeichnen mit die Summe, die aus Tn entsteht, wenn
alle Glieder ausgeschieden werden, in denen x und y beide durch
die ungerade Primzahl p teilbar sind, so ergibt sich:
T™ = Tn-LTnp-2
und durch Grenzübergang zu m = cc :
piP) __ rr (1___
\ P*)'
556
Zweiundzwanzigster Abschnitt.
§ 147.
Verfährt man so mit allen Primzahlen und setzt
Sio + Sii - 2 Sh = T',
so folgt
worin sich das Produkt II auf alle ungeraden Primzahlen p
erstreckt. Nun erhält man durch Entwickelung nach steigenden
Potenzen von p~2-.
H(\ — p~2) ~ 1 “^3* + 52 + 7^+92“! ’
_ %2
~ T’
und folglich
rn __ rpi
und indem man ebenso mit den beiden anderen Summen ver-
fährt, folgt aus (9):
log f (öl) />a) = i log 2 + (S{0 + Sh - 2 Sh),
(10) logA(rai)A(ra2) = flog 2 + (Sh - 2 Sh + «.),
logA^OAC^) = |10g2 + (-2 Sh + Sh + Sh).
Diese Formeln vereinfachen sich wesentlich, wenn man
a = 0, also
a>! = a>2 = co = i ß
setzt, also wenn man ein rein imaginäres a annimmt. Dann
wird
g, ___ 1 x ungerade, y gerade,
10 rc2 — co2 y2 xy relativ prim.
Sondert man das Glied x = +1, y — 0 ab und nimmt von
den übrigen je vier zusammen, so ergibt sich
Sio = 2 + •-_1 ,
. dy ’ vj U
worin x, y nur positive Werte durchlaufen.
Ebenso verfährt man mit den anderen Summen. Setzt man
dann
§ 148. Elementare Ableitung der Entwickelungen. 557
(u) 5 «a y-a = S1 x^y ungerade,
— U UJ — iXz
= 82 x ungerade, y gerade,
= S3 x gerade, y ungerade,
x, y positiv und relativ prim, so folgt:
ß Sio —- — 2 i co —4 i S%,
ß Soi = -|—— + 4 i S3,
♦ G)
ß Sh = 4 i Si,
und folglich ergibt sich aus (10) für ein rein imaginäres ro:
log/» = ilogyä + ^(-u> +1 - 4 Si + 2 S2 + 2 8S),
(12) log A («) = |log V2 + ^ (- m —| + 2 8X + 2 83 - 4 83),
log A («) = 1 log V 2 + g (2 ca + 1 + 2 8j - 4 S-2 + 2 83).
§ 148. Elementare Ableitung der Entwickelungen.
Man kann zu den vorstehenden Entwickelungen auch auf
dem folgenden Wege gelangen. Es ist nach einer bekannten
Formel der Analysis:
zn y; 03 )__1______i + 1
' i,«» ra2i/2 — a?2 2 cs y2 ‘ 2 y q2»— 1’
wenn q = enia ist1). Daraus durch Entwickelung nach Potenzen
von q:
(2) 27------------- =----------------- — (1 4- S ö2
v ' i,» ca2«/2 — x2 2c3y2 y \2- 1)00 u
Ersetzt man hier y durch ^y, so folgt:
(3)
und
2 03 __
i,oo C32y2 --—4 a?2
wenn man (2) von (3)
y. (—l?ta =
a)2y2 — x2
1 ni /1 . _
--------------( —k- 2? anv
03 y2 y \2 ' 1,00
abzieht:
_____i------q&n-Vv
2csy2 y 1,00 *
’) Aus der Entwickelung:
, 1 , 2^ . 2« , 2«
cotg Z I__ 2 4* z~Z _ . 2 4 2 _ 9 2
558
§ 148.
Zweiundzwanzigster Abschnitt.
Summiert man diese Formeln abermals nach y von 1 bis oo
und macht von den Formeln Gebrauch, die teils bekannt sind,
teils aus § 24, (11) folgen:
1 — 31:2 r (— 1)y _ _
y2 6 ’ y2 12’
= -logiKi-ä--!) = _iog/-1(ro)-^,
1/ Artt
n y (__1 Aw zy2 n y 7 n->
2? = -log Z7(l +92») = — log/^ro) + - llog2,
= —log 2,
y
. M-w-» = _10gD(1 = _
y
so ergibt sich:
(—I)r+»g> _ a?
i,» i,«> »2 y* — x^ ~~
- 24ra-^ + ^10^’
- t G& t • 1 J? / X
= 2^ + ^r + %*log^ra>
Die Doppelsummen auf der linken Seite dieser Formeln sind
so zu verstehen, daß zuerst die Summation in bezug auf x, dann
die Summation in bezug auf y auszuführen ist. Man kann aber
auch so summieren, daß man
(6) 0 <7 x <Z m, 0 <Z y < n, n=oo, — = oo
nimmt, und dann m und n so ins Unendliche wachsen läßt, daß
m:n unendlich wird. Daß beides dasselbe gibt, kann man auf
verschiedene Weise zeigen, z. B. durch Vergleichung der Summen
mit Integralen.
Setzt man also, wie in § 147, (10), indem man x, y an die
Bedingung (6) bindet:
CT
a>2 w2 — x'1
y x
(5) 27 2
y
a>2 y'2 — x2
(— l)v w
Gl2 -(y2 ---------
so folgt aus (5):
- Sa
= Sr
= s2
= Ss
x, y gerade,
x, y ungerade,
x ungerade, y gerade,
x gerade, y ungerade,
§ 149. Entwickelungen für die Funktion log r/ (<o). 559
So + ST - S2 - S8 = + ^log/»,
s0 - s, - s2 + s8 = - ^ + ^logAC«),
So - S, + S2 - S8 = ~ + ^logA(<4
Daraus durch Addition:
3 So — Sx — S2 — Ss = iti log ^2,
und wenn man So eliminiert:
4 S1 -1S2 - < Ss = log V2 + %ilog /•(«),
-1S, - IS2 +1S8 = log V2 + % ilog A («),
sT +1 s2 -1 s8 = 2^ + log 1/2 + ziogA («).
Man kann nun ebenso wie vorhin von den Summen S zu
den S' übergehen, in denen x, y relativ prim sind, und findet:
log /"C09) — |l°g + gj (— ~ — 4 —|— 2 Äs —|— 2 Ss),
(7) logA («) = flog V 2 + g (- « - | + 2 S1 + 2 S2 - 4 S^),
log A(ra) = |l°g + "24 (— ra — ~ S1 — 4 Sä -j- 2 Ss) •
Diese Formeln stimmen der Form nach mit § 147, (11)
überein, was insofern auffallend ist, als die Art des Grenz-
überganges beide Male eine verschiedene ist.
§ 149. Entwickelungen für die Funktion log i] (w).
Betrachten wir die Summe
(1)
' J (x co y)2s
erstreckt über alle x, y mit Ausnahme der Kombination 0, 0.
Indem man die Glieder mit y = 0 absondert, kann man
dafür setzen:
x 1 x _ 1
(2) U = 2 + 2S S (x nyy^
1,00 1, co —co.co'' 1 '
sodann ist
560
Zweiundzwanzigster Abschnitt.
§ 149-
r(2g)
[—2%i(® -j- »j/)]2s
^2TTi(& +1/w)£ £2s — 1
dl;,
Summiert man nun nach x und wendet die Fourier sehe
Reihe an: i
= i[f(o) + /•(!)],
0
so folgt: rf2 x x »
_LA__2_ X1 __________________ = X1 e27tiya)n n2s—1
(—2jrf)2s (A + k>2/)2s ’
und durch Summation nach y:
TW eX V x -1 ” „inian
1 l2s) x v 1 — V e__________r— M2»-1
(--2srf)2s -*—1 (x 4- coy)2s i 1 — ^-nian
' 1, co CO , CO ' 1, co
1 ^<71og(l-e2-“«) 2
--- -- / -------1 ’" ’
2 tc i d co
1,00
Hiernach bekommen wir durch den Grenzübergang mit Rück-
sicht auf die Definition der Funktion i?(ro) [§ 24, (8)]:
. dlogijfa») %2
2 71 t j ~~7T
do 6
Ferner ist
T’
und demnach folgt (1) und (2):
r- XT1 1 a .<71ogi;(a>)
(3) Lim >, 7---:----= —4sr«----------, v....
v 1 S=1 (x -|- eay)2s da
[zu summieren, wie zu (1) angegeben]. Wollte man hier unter dem
Summenzeichen zur Grenze übergehen, so würde man erhalten:
d^n^) = ____-1_____
d ca (x co y)2'
dann aber würde man eine nur bedingt konvergente Summe
haben, und es müßte eine genaue Art des Grenzüberganges fest-
gestellt werden. Man müßte in der xy -Ebene eine geschlossene
Kurve annehmen, innerhalb deren die Punkte x, y liegen, und
dann diese Kurve ins Unendliche hinausrücken lassen. Der Wert
der Summe wird von der Beschaffenheit dieser Kurve abhängen.
Vielleicht ergibt sich dafür die Ellipse | x a> y | = n. An sich
hat die Formel (4) keinen Sinn.
VIERTES BUCH.
KLASSENKÖRPER.
Weber, Algebra. III.
3$
Dreiundzwanzigster Abschnitt.
Der Teilungskörper.
§ 150. Die homogenen Weierstrassschen Funktionen.
Wir waren in § 114 von der Frage ausgegangen, unter welchen
Voraussetzungen eine doppelt periodische Funktion <p(u) mit den
Perioden uq, «2 eine Multiplikation <p(pu) gestattet, d. h. unter
welchen Umständen puq, pm2 sich linear und ganzzahlig durch
»!, co2 ausdrücken lassen, und waren zu dem Resultat gelangt, daß
dies bei veränderlichem »j, «2 nur möglich ist, wenn p eine
ganze rationale Zahl ist, und daß nur, wenn
(D ® ?
eine imaginäre quadratische Irrationalzahl ist, auch p eine kom-
plexe Zahl desselben Körpers wie co sein kann. Es kommt jetzt
darauf an, die aus dieser Annahme folgenden Formeln der kom-
plexen Multiplikation etwas genauer zu erforschen.
Wir wollen zunächst, als das formal einfachere, die kom-
plexe Multiplikation der Weierstrassschen elliptischen Funktion
g» (w) untersuchen, müssen dann aber auch noch die komplexe
Multiplikation der Jacobischen elliptischen Funktionen in Be-
tracht ziehen.
In den § 37, (8), § 46, (13) haben wir die Formeln für die
Homogeneität der Funktionen ö(w), ^5(11) und der Invarianten
p2, ps, 16 G — gl — 27gl abgeleitet, die wir hier noch einmal
zusammenstellen:
<5 (Zu, Z co,, Z a>2) = Z
(Z u, Z Gjj, Z gj2) =
^(Zctj, Zgj2)
g3 (1 »j, Z c2)
G (Z gjj, Z gj2)
ö (u, «2),
Z"2 p (w, Oj, ro2),
= z-4p2(»l, »2),
= A-65'3(ß’i, »2),
= Z“12 Cr(»1, <U2),
(2)
36*
564
Dreiundzwanzigster Abschnitt.
§ 150.
und die Funktionen § 46, (12), (15), (16):
----------------------= J (») — 27 • 64,
»J2 G = 28 %13 7] (g>)24
hängen von dem Verhältnis (1) ab.
In § 54, (4), (5) sind noch die eindeutigen Funktionen von o:
,,(«,) = rtw = W“-16,
„(„) = V,(„)-27.04 =
definiert.
Aus der letzten Gleichung (3) erkennt man [etwa aus der
Entwickelung von ?/(»), § 24, (8)], daß G nicht verschwinden
kann, solange » einen positiv imaginären Bestandteil hat, und
folglich können auch g3, g3 nicht beide zugleich verschwinden.
Aus den Reihenentwickelungen des § 56 ergibt sich:
(5) ö(w) = 2? am,n(^g^m gi)n । ijp
v = 2 m 3 n,
worin die rationalen Koeffizienten am,n nur Potenzen von 3 im
Nenner haben können (nach Schwarz-Weierstrass sind es
ganze Zahlen, worauf es hier aber nicht ankommt).
Ebenso ist
2^21' — 2
(6) (M) = n (| gz)m (2 ,</3)" । ijj
mit rationalen Koeffizienten Um Funktionen von zwei
Variablen zu erhalten, machen wir folgende Substitution:
Wenn von den beiden Invarianten g2, g3 keine verschwindet,
so setzen wir:
(7) w =
also /o„3\m+M /a£\m + 2ni / a„ a«
\ / \ x r '—V
und dadurch ergibt sich aus (5):
4 / (t 1
(8) r ä Ö(M) = 2Äm,njm+nu ~27'64)m+2w(2^ + i)!
Ist endlich
so setzen wir
(12)
und erhalten
(13)
§ 150. Die homogenen Weierstrassschen Funktionen. 565
worin die rationale Zahlen sind, die im Nenner nur Potenzen
von 2 und von 3 enthalten können.
In gleicher Weise ergibt sich aus der Reihenentwickelung
(6) für die ^-Funktion:
/y /y tn,n ailiV—2
(9) (w) = 2? + - 27.64)”»+^^^-^,
worin die Bm.n rationale Zahlkoeffizienten sind. Daß auch sie
nur Potenzen von 2 und 3 im Nenner haben, machen die ersten
Fälle wahrscheinlich, kommt aber für uns jetzt nicht in Betracht.
Ist g3 oder g3 gleich Null, so ist die Substitution (7) nicht
brauchbar. Ist zunächst
9s = 0,
so fallen in den Reihen für 6(w) und (w) die Glieder weg, in
denen n positiv ist. Es ist dann
M4m + 1
ö(w) — S am,o gf
— 2
W = 2? &m,0 gf m •
Wir setzen dann
_ i
(10) u — g3 4 w
und erhalten
2 m + l
g24 ö (u) = 2? Am p
(H) _1 m
2 (M) — 27i)i’
wenn JOT, Bm wieder rationale Zahlen sind.
9z = 0,
— 2
« = g3 6w,
2 w giß ^4-1
__1 n Wi6n—2
9S 3 W =
In den Entwickelungen (8), (9), (11), (13) ist
(14) A00 = l, #00 = 1, Ao = 1, Bo = 1.
566 Dreiundzwanzigster Abschnitt. § 151.
§ 151. Die komplexe Multiplikation der Funktion & (w).
Wir nehmen jetzt an, die Perioden gj2 der Funktion (u)
genügen einer quadratischen Gleichung
(1) Mgj2 + B gj2 »i Ctf = 0,
in der A, B, C ganze rationale Zahlen ohne gemeinschaftlichen
Teiler sind. Es sei A positiv, und die Diskriminante der qua-
dratischen Form (J, B, C)
(2) B2 — 4 A C = A
sei eine negative Stammdiskriminante, d. h. es enthalte A
keinen quadratischen Faktor, nach dessen Absonderung eine Dis-
kriminante übrig bleibt (§ 84).
Setzen wir
(3) gj = —,
so folgt aus (1):
(4) 2Aa> = — B + )/J,
und wenn wir \A positiv imaginär annehmen, so erhält gj einen
positiv imaginären Teil und kann als Modul einer ü- Funktion
dienen. A ist die Grundzahl eines imaginären quadratischen
Körpers, den wir mit £i bezeichnen x).
Durch die singuläre Invariante j (gj) wird der Klassenkörper
ß(z7) bestimmt, dessen Relativgrad in bezug auf $1 gleich der
Klassenzahl der Diskriminante A ist. Die ganzen Zahlen des
quadratischen Körpers 42 = sind von der Form:
(5) f* =
2
worin x und y ganze rationale Zahlen sind, die der Bedingung
x = By (mod 2)
genügen. Zu der durch (5) definierten Zahl y bestimmen wir
vier ganze rationale Zahlen a, 6, c, 8:
# -4— B y .
= - 2 , i = Ay,
a
(6)
x) Die Annahme, daß J Stammdiskriminante sei, ist hier zur Verein-
fachung gemacht. In meiner Abhandlung „Über Zahlgruppen in algebrai-
schen Körpern“ (Mathematische Annalen, Bd. L) ist diese Annahme nicht
gemacht. Man erhält dann allgemeinere Körper, die zu den Ordnungen
gehören, wie in § 124.
§ 151. Die komplexe Multiplikation der Funktion p (w). 567
woraus:
, x'1 — 4 y2 ,
(7) ad — bc — -------------- = y y' = m,
wenn
(8)
die zu y konjugierte Zahl des Körpers H ist.
Nehmen wir y von Null verschieden, so folgt aus (1) durch
Multiplikation mit y:
b w22 (a — 8) <a2 <»! — c a2 = 0,
und dafür kann man auch schreiben:
(a gjj -f- 5 <»2) g»2 = (c g»x 4~ 8 g»2) roi
oder
c 4- 8 <a
g» — — z. •
a -4 o g>
Nach (4) und (5) folgt aus (6):
/1 n\ । t. (2 A <x> 4“ R) y
(10) a 4- bco = ——iö!— p,
C 4- 8 G» = (l CO,
oder in homogener Form:
prox = «g»! 4- ög»2,
fl G»2 = C G»x 4~ 8 G»2 ,
und durch Auflösung dieser linearen Gleichungen:
y'co1 — dc^—ba^,
y' g»2 — — c w, 4- a g»2.
Daraus ergibt sich, daß ^5 (p u) eine doppelt - periodische
Funktion mit den Perioden »j, gj2 ist, und da sie außerdem eine
gerade Funktion von u ist, so läßt sie sich rational durch ^5 (u)
darstellen (§ 21). Wenn wir also mit R und P ganze rationale
Funktionen von ^5 (u) ohne gemeinschaftlichen Teiler bezeichnen,
so ist
R
(13) (jiu) = -p •
Da der Quotient (p u): (u) für u = 0, d. h. für (u) = co,
endlich bleibt, so ist der Grad von R um eine Einheit höher als
der Grad des Nenners.
568
Dreiundzwanzigster Abschnitt.
§ 152.
§ 152. Die Pole der Funktion (ft u).
Um den Grad der Funktionen R und P festzustellen, müssen
wir die Ntfllstellen von P, also die Unendlichkeitsstellen von
p(ftw), abzählen, die nicht zugleich Unendlichkeitsstellen von
p (w) sind. Es wird aber (g w): p (w) dann und nur dann
unendlich, wenn
Äi GJX —|— Ä2 GJ2
wird, wenn Äx, Ä2 ganze Zahlen sind, wenn äx gjx ä2gj2, aber
nicht (äx gjx ä2 gj2) : ft eine Periode ist. Setzen wir also
(2)
W (w)]
P«[p (u)]’
und bezeichnen mit g die Wurzeln von P„(j:), so ist
(3)
fh< GJ, -I- GJ,'
Die Zahl g ändert sich nicht, wenn 4 und Ä2 um Vielfache
von m — gg' geändert werden, weil dadurch nach (11), § 151
das Argument der ^-Funktionen um eine Periode geändert wird.
Da die Funktionen p(w) und ^j(fitt) nicht geändert werden,
wenn wir die Periode gjx, gj2 einer linearen Transformation mit
der Determinante 1 unterwerfen, so beschränken wir die Allgemein-
heit nicht, wenn wir annehmen, A sei relativ prim zu m und
wegen der Periodizität von ^j(w) können wir daher auch setzen:
/Äx gjx -I- 7», A GJ,
9 = H -------------------
Wegen der Homogenität von & (u) können wir nun gjx = 1,
gj2 = gj setzen und erhalten nach § 151, (4):
A^ = -----
und demnach ist
(4) Äx gjx ä2 A gj2 = Ä2 (—S •
Wenn wir daher
K + K —B4 = v
setzen, so ergibt sich aus (3):
(S) s = i> (4
§ 152.
Die Pole der Funktion p (an).
569
worin v ebenso wie ft eine ganze Zahl des Körpers £i ist, die
nicht durch g teilbar ist.
Ist diese Bedingung erfüllt, so ist g eine Wurzel von P^x).
Weil aber in der w-Ebene für w = 0 (modd. Oj, gj2)
unendlich in der zweiten Ordnung wird, so ist Pft(x') durch
(x — gf teilbar, es sei denn, daß
p W — 9
für u = v:g selbst in der zweiten Ordnung verschwindet; dies
tritt wegen § 46, (18) dann ein, wenn
ist, also wenn v:g eine halbe Periode ist, und also
(6) g = e15 e2, e3
wird.
1. Nach (4) ist, wenn Oj = 1, cj2 = gj gesetzt ist,
jede ganze Zahl des Körpers £1 eine Periode von (w).
Dies gilt nicht umgekehrt; da aber Aca eine ganze
Zahl in Sl ist, so muß jede Periode durch Multipli-
kation mit A in eine ganze Zahl verwandelt werden.
Daraus folgt, daß zwei Werte
s = p □’ °'=P (y)
dann und nur dann einander gleich sind, wenn
v = +v' (mod g)
ist. Denn ist g = g', so muß entweder
v 4- v' n i' — v'
—!— oder ---------
9 9
durch Multiplikation mit A in eine ganze Zahl verwandelt werden.
A ist aber relativ prim zu g, und folglich muß eine dieser beiden
Zahlen selbst ganz sein. Die Anzahl der inkongruenten Werte
von v ist aber gleich N(g) = m (Bd. II, § 165).
Lassen wir also v ein volles Restsystem nach dem Modul g
mit Ausschluß der Null durchlaufen, so bekommen wir jeden
Wert von g zweimal, außer wenn
(7) 2v = 0 (mod p),
und in diesem Falle ist einer der Werte e.
Daraus folgt:
570
Dreiundzwanzigster Abschnitt.
§. 152.
(8) = n[x — p
und PuS.x) ist vom Grade m — 1.
In dem Produkt P^ (x) kommt jeder Faktor x — g zwei-
mal vor, außer wenn g einem der e gleich ist, wenn also die
Kongruenz (7) für ein von Null verschiedenes v erfüllt werden
kann.
1) Wenn g relativ prim zu 2 ist, also wenn m ungerade
ist, so hat die Kongruenz (7) nur die Wurzel v = 0. Dann ist
P^x) ein Quadrat, und wenn S(x) eine Funktion vom Grade
j(m — 1) ist,
(9) Pu (a?) = S2, m = 1 (mod 2).
Wenn g mit 2 einen Teiler gemein hat, sind drei Fälle zu
unterscheiden.
2) Wenn p durch 2 teilbar ist, so muß v, wenn es der
Kongruenz (7) genügen soll, ein Vielfaches von |p sein, und da
es drei von Null verschiedene nach dem Modul 2 inkongruente
Zahlen in £1 gibt, so hat (7) drei Wurzeln. Es kommen also
unter den g die drei Werte e1? e2, es vor, und wir haben:
(10) P^x) — ^?'(w)2S2, m = 0 (mod 2),
worin S eine ganze Funktion vom Grade | m — 2 ist.
3) Wenn 2 im Körper Sl in zwei (gleiche oder verschiedene)
Primideale zerfällt, also wenn z7 = 0 (mod 4) oder = 1 (mod 8)
ist, so kann g durch einen dieser Primfaktoren teilbar sein, ohne
durch 2 teilbar zu sein. Dann hat die Kongruenz (7) nur eine
von Null verschiedene Wurzel und es kommt unter den Zahlen g
nur eine der drei Zahlen (6), etwa e, vor. In diesem Falle ist
(11) Pu (x) — [p (w) — e] S2,
worin S eine Funktion vom Grade | m — 1 ist.
In bezug auf die beiden besonderen Fälle g?J = 0 und g% = 0
ist noch folgendes zu bemerken.
4) Wenn g?J = 0 ist, so ist zl ~ —4, — 0, und es
ergibt sich aus der Differentialgleichung § 46, (18):
^'(w)2 = 4 p (w)3 — 5-2 p (w),
durch die mit Rücksicht auf das Anfangsglied der Entwickelung
die ^5 - Funktion eindeutig bestimmt ist.
§ 153. Die Funktion r (u). 571
Ersetzt man dann w durch iu, so folgt:
— [p'(MP = 4 — g.2 p (iw),
und daraus:
(12) p(w) = — p(w).
Die Größen g sind also einander paarweise entgegengesetzt,
eine der drei Größen gj, e2, e3 ist gleich Null, die beiden anderen
ebenfalls entgegengesetzt gleich. Daraus folgt, daß in den For-
meln (9) bis (11) die Funktion 8 in diesem Falle nur die
geraden Potenzen von & (w) enthalten kann.
5) Ist g2 = 0, so ist d — —3, j(») = 64.27, und es ist,
wenn mit p eine imaginäre dritte Einheitswurzel bezeichnet wird:
(13) («) = 9 p (e2«) — e2 (p «),
und die Wurzeln g von S ordnen sich zu dreien in der Weise:
(1<) 9, 9 9, 9*9-
Unter diesen drei Werten sind nur dann zwei einander gleich,
wenn sie alle drei verschwinden. Aus (13) aber ergibt sich, daß
dies eintritt, wenn u mit einem der Werte +1:]/—3 kongruent
wird. Denn für z7 = — 3 sind 1, p, p2 Perioden von (w), und
da nun
P — g2 _ !
V-3
ist, so ist nach (13):
( 9 \ _ . / g2 \ _ n
\p—3/ ^xyzzg/ ’
und der Wert Null kommt also unter den g dann und nur dann
vor, wenn m durch 3 teilbar ist.
Daraus folgt:
Ist z/ = —3 und m = 0 (mod 3), so ist S:^(w) eine
rationale Funktion von (w)8.
Ist z7 = —3 und m = 1 (mod 3), so ist S selbst eine
rationale Funktion von (w)s.
[Da m die Form |(a?2 3 t/2) haben muß, so kann hier m
nicht = — 1 (mod 3) sein.]
§ 153. Die Funktion t(u).
Wir führen nun nach § 150 (6), (8), (9), (10), (12), (13) eine
Funktion r = r(u) ein, die nur von zwei Argumenten w, m ab-
hängt, indem wir setzen:
572
Dreiundzwanzigster Abschnitt.
§ 153.
a)
r(u) = p (w), im allgemeinen,
(1)
b)
jp(w)2
c)
91
_ & «
wenn g3 — 0,
wenn g2 = 0.
9i
dann g wie oben eine ganze Zahl des Körpers Si
wenn
(2)
Und
ist, so können wir in allen drei Fällen setzen:
Z X
worin (5, P ganze Funktionen von r sind, die bis auf konstante
Faktoren im Falle (1) a) mit B, P des vorigen Paragraphen
übereinstimmen, in den Fällen (1) b) und (1) c) daraus durch
Erhebung ins Quadrat oder in den Kubus hervorgehen [§ 152,
4), 5)].
Wir richten den Bruch (2) so ein, daß die höchste Potenz
von t im Nenner 0 den Koeffizienten 1 hat. Die übrigen Koeffi-
zienten von 0 sind dann rational zusammengesetzt aus Größen
der Form
T
und da vg' eine Periode von r ist, so gehören diese Größen zu
den Wurzeln der Teilungsgleichung der Perioden, und sind daher,
da der Modul der entsprechenden elliptischen Funktionen eine
algebraische Zahl ist, selbst algebraische Zahlen (§ 58, § 61).
Daraus folgt:
2. Die Koeffizienten in ®(r) sind algebraische
Zahlen.
Wir erweitern den Bruch ’F: 0 durch Multiplikation von
Zähler und Nenner mit dem Produkt der konjugierten Werte
0', 0", 0'", ... unj erhalten:
(3)
~ 2V”’
worin nun Z und N ganze Funktionen von r sind, die einen
gemeinsamen Teiler enthalten können, wobei jedoch N rationale
Zahlenkoeffizienten hat.
§ 154.
Der Teilungskörper.
573
Nach § 150, (8), (10), (13) beginnt die Entwickelung von
t(m) nach steigenden Potenzen von u mit einer negativen Potenz
von u. Wir ordnen in der Gleichung
(4) t(jiu)N = Z
die Funktion Z nach fallenden Potenzen von r, entwickeln beide
Seiten nach steigenden Potenzen von u und vergleichen die
Koeffizienten gleich hoher Potenzen von u. Dann bekommen
wir für die Bestimmung der Koeffizienten von Z eine Reihe
linearer Gleichungen, deren jede folgende nur einen neuen dieser
Koeffizienten enthält, und daraus können diese Koeffizienten
successive rational berechnet werden. Beachtet man nun die
Form der Entwickelungen des § 150, so ergibt sich, daß die Koeffi-
zienten von Z rationale Funktionen von j («) und sind.
Befreit man nach dem Euklidischen Algorithmus N und Z
von gemeinschaftlichen Faktoren, so kommt man zu den Funk-
tionen 'S*’, 0 zurück, und es ergibt sich, wenn wir unter dem
Klassenkörper den Inbegriff der rationalen Funktionen von
und j(a) verstehen:
3. Die Koeffizienten der Funktionen ®(r), ’P’(r)
in (2) gehören dem Klassenkörper an.
§ 154. Der Teilungskörper.
Wenn wir (durch rationale Rechnung) die Funktion <t>(x) von
allen mehrfach darin vorkommenden Faktoren befreien, so bleibt
eine ganze Funktion T^x) von x übrig, deren Koeffizienten dem
Klassenkörper angehören, und die Wurzeln von ^(ir) sind sämt-
liche voneinander verschiedene unter den Größen
Zwei dieser Größen
/ v \ / v'\
T — , T —-
\fV \.w/
sind einander gleich,
V vf
im Falle (1) a), wenn — = + —,
v ' p — p
(1) b), wenn - = + - = ±i-,
r r p
(1) c), wenn- = ±-, ±p-,
f*'
574 . Dreiundzwanzigster Abschnitt. § 154.
worin die Kongruenz auf die Perioden bezogen wird, also (§ 152, 1.)
im Falle a), wenn v = + v',
(2) b), wenn v = + v', +iv' (mod p),
c), wenn v = + pv', +p2i''.
Es seien jetzt
(3) {i — am, p, = Ujin
zwei ganze Zahlen mit dem größten gemeinschaftlichen Ideal-
teiler m im Körper ß. Dann haben 1), und T«, einen gemein-
samen Linearteiler, wenn
und dies findet nach (2) dann und nur dann statt, wenn
(5) in', = e^v (mod ppj),
worin e eine Einheit des Körpers ß ist, also e = + 1 im all-
gemeinen, s = + 1, +?, wenn zf = —4, und e = +1, +p, +p2,
wenn zf — —3 ist. Aus (5) folgt aber, daß v durch a und vr
durch a, teilbar sein muß.
Denken wir uns v gegeben und v, gesucht, so ist die Kon-
gruenz (5) nur möglich, wenn p, v durch p teilbar ist, und da
a und a, relativ prim sind, so muß v durch a teilbar sein. Ist
a eine durch a teilbare ganze Zahl in ß, so beschaffen, daß
a: a relativ prim zu m ist, so können wir demnach
(6) v = « g (mod p)
setzen (Bd. II, § 166, 7.) und erhalten die sämtlichen voneinander
verschiedenen Werte und jeden zwei-, vier- oder sechsmal,
wenn wir £ ein volles Restsystem nach dem Modul m durchlaufen
lassen (mit Ausschluß der Null). Man erhält dann die sämtlichen
gemeinsamen Wurzeln von und TV1 in der Form
Der größte gemeinschaftliche Teiler JDm von Tu und hat
also alle die Größen (7) zu Wurzeln. Aus Din läßt sich noch
auf rationalem Wege ein Teiler Tm absondern, der nur die unter
den Größen (7) zu Wurzeln hat, in denen g relativ prim zu m
ist, wenn man JDm von allen Faktoren befreit, die es mit einem
Dm> gemein hat, wenn m' ein Teiler von ni ist. Da in dieser
§ 154. Der Teilungskörper. 575
Betrachtung in (3) m jedes beliebige Ideal in ß bedeuten kann,
so kommen wir zu folgendem Hauptsatz:
4. Ist m ein beliebiges Ideal des Körpers ß, so
existiert eine Funktion Tm in ß, deren Wurzeln
die voneinander’ verschiedenen der Zahlen sind,
wenn g ein System inkongruenter, zu m teiler-
fremder Zahlen durchläuft.
Um den Grad der Funktion Tm zu bestimmen, bemerken
wir, daß zwei Größen nur dann einander gleich sind, wenn
(8) S = «g (mod m)
ist. Es werden also so viele von den r. einander gleich, als es
modulo in inkongruente Einheiten gibt; das sind im allgemeinen
zwei, für zf == — 4 sind es vier und für z/ = — 3 sind es sechs.
Diese Zahlen verringern sich aber wiederum, wenn verschiedene
der Einheiten e nach dem Modul m kongruent sind, wenn also
1 — s durch m teilbar ist. Das kann aber nur vorkommen,
wenn m ein Teiler von 2 oder von 3 ist. Also:
5. Der Grad der Funktion Tm ist gleich der An-
zahl ^(m) (Bd. II, § 168) der nach dem Modul ni in-
kongruenten, zu tn teilerfremden Zahlen in ß,
geteilt durch die Anzahl der nach m inkongruenten
Einheiten in ß.
Die Wurzeln der Funktion Tm bestimmen einen algebraischen
Körper über dem Klassenkörper, dessen relativer Grad höch-
stens gleich dem Grade von Tm ist, und beide Grade sind gleich,
wenn Tm irreduzibel ist.
6. Diesen Körper wollen wir den Teilungs-
körper für den Modul m nennen.
Diese Teilungskörper spielen für den Körper ß eine ähnliche
Rolle, wie die Kreisteilungskörper für den Körper der rationalen
Zahlen, nur daß sich hier noch der Klassenkörper dazwischen
schiebt, zu dem es im Körper der rationalen Zahlen, ebenso wie
in jedem einklassigen Körper, kein Analogon gibt.
Nach dem Multiplikationstheorem (§ 151) kann
(9) r(gu) = Ödr(M)]
cc
rational durch r(u) ausgedrückt werden. Setzen wir u = £'—,
l1
so folgt:
(10) = =
576 Dreiundzwanzigster Abschnitt. § 155.
und folglich durch Vertauschung von g mit £':
(H) ös(rJr) = Ös,(ts),
und damit nach Bd. I, § 169:
7. Der Teilungskörper ist in bezug auf den
Klassenkörper relativ Abelsch.
Die Zahlen g, nach dem Modul m genommen, bilden bei der
Multiplikation eine Gruppe, und die Relativgruppe des Teilungs-
körpers ist mit dieser Gruppe isomorph (oder wenigstens mit
einem Teiler dieser Gruppe. Die Irreduzibilität von Tm wird
weiterhin bewiesen werden, wodurch dann die Gruppe von $m
selbst festgestellt ist).
§ 155. Multiplikation der elliptischen Funktionen für einen
ungeraden Multiplikator.
Für den Nachweis der Existenz des Teilungskörpers ist die
Benutzung der Weierstrassschen Funktion und der daraus ab-
geleiteten t-Funktion sehr zweckmäßig, und es wäre am be-
quemsten, wenn man darauf auch die weitere Untersuchung dieses
Körpers gründen könnte. Dafür aber ist die arithmetische Natur
der Multiplikationsformeln noch nicht genügend bekannt, und es
ist darum zurzeit noch notwendig, die komplexe Multiplikation
und Teilung auch der Jacobischen elliptischen Funktionen zu
betrachten.
Hierbei wollen wir den Multiplikationsformeln, die wir in § 57
abgeleitet haben, noch eine etwas andere Gestalt geben.
Wir betrachten zunächst durchweg den Multiplikator m als
ungerade Zahl. Wir setzen, wenn
den Modul der elliptischen Funktionen bedeutet, nach Kro-
necker1):
(2) Ä = + 1) = 4^4 + 54> (3)L
' \ 1 %/ /aG0) /(«/ S V /J
und entwickeln diesen Ausdruck nach steigenden Potenzen von
q = enia.
*) Zur Theorie der elliptischen Funktionen. Sitzungsbericht der Berliner
Akademie vom 29. Juli 1886.
§155. - Multiplikation der elliptischen Funktionen. 577
Man kann die Form dieser Entwickelung aus den Produkt-
formeln [§ 24, (11)]:
1 /I _|_ 02”-l\4 1 / l-LnS» \4
z = q-jn( -z—) + 16 2'2 n( XJ)
1 \ 1 4- q2v ) ~ * \1 + X /
ableiten, und findet:
(3) Z = q 2 (1 4* Z, q Z2 q2 ^3 23 4~ ' ’ •)»
worin die Konstanten Zn Z2, Zs, ... ganze rationale Zahlen sind.
Setzen wir ferner
(4) x = ]/% sn (^L z),
\y % /
so bleibt (4) nach § 45, (9) ungeändert, wenn % mit l:x vertauscht
wird. Es genügt x der Differentialgleichung
(5) (-J—) = 1 — \lx2 4- x\
v 7 \dwJ 1 1
Entwickelt man also x nach dem Taylorschen Lehrsatz in
eine Reihe nach steigenden Potenzen von w:
(6) x = w 4" ws 4" X w'a ...,
so sind die Koeffizienten JX2, ... ganze rationale
Funktionen von Z mit rationalen Zahlenkoeffizienten,
wie sich aus (5) nach der Methode der unbestimmten Koeffizien-
ten ergibt.
Benutzt man die Bezeichnung von § 42, so ist
Z-7X #31(w)
(7) x — yx sn v = ~ ; -,
v 7 #oi«
und nach § 57, IV. mit einer etwas modifizierten Bedeutung der
M, B, C, D:
xA(x')
yx sn m v — -r. , *
\.x)
/o. iL x2 B(x)
(8) cn m v = 1/ 1-------,
v f x D(x)
a Pi--------------5 CO)
dllffl'l! = VI — XX2 •
' D(x)
Hier sind A(x), B(x), C(x), JD(x) ganze rationale Funktionen
von x vom Grade |(m2 — 1), und es ist aus den Rekursions-
formeln § 57, (13), (14) zu ersehen, daß die Funktionen A, D und
das Produkt B C ganze rationale Funktionen von Ä sind, deren
Weber, Algebra. III. 37
578
Dreiundzwanzigster Abschnitt.
§ 155.
Zahlenkoeffizienten rational sind. Daß es ganze Zahlen sind, ist
wegen des Nenners 2, der zunächst auftritt, nicht zu ersehen.
Um dies näher zu untersuchen, betrachten wir die Wurzeln
der Funktion J.(ir): Sie sind, wenn gesetzt wird:
_ 2hK^-2h'iK'
(9)
h' — V sn -ßfr, h’
'Ji -|- h' co
m ’
h h' co
---!------, CO
m
worin h,h' irgend welche ganze Zahlen sein können; nur dürfen
sie nicht beide gleich Null sein. Man erhält alle Wurzeln von
A(x), wenn man h, h1 je ein volles Restsystem nach dem Modul
m durchlaufen läßt, abgesehen von der Kombination 0,0. Es ist
dann
v 71 ih z , . /2&4-1 Ä'-\2
— iS (—1)” e m 2r 1 q- 2 +
(10) Xh,W = Znivh / vy
S (— 1)” e m q^ m7
Um diesen Ausdruck nach steigenden Potenzen von q zu ent-
wickeln, muß man zunächst die niedrigste Potenz von q im Nenner
h'
auf suchen, d. h. das Glied, in dem v — so klein als möglich
wird. Dies findet statt, wenn v die zunächst an —h' /m gelegene
ganze Zahl ist. Es gibt, da m ungerade ist, nur eine solche
Zahl v, und die Formel (10) erhält die Gestalt:
(11) , । = Qi Q1Q2 Qi Qi •••>
1 ~r~ Va
worin Q1 und Q2 nach steigenden Potenzen von q geordnete Reiben
sind, deren Koeffizienten ganze algebraische Zahlen (Kreis-
teilungszahlen) sind.
Demnach läßt sich x^v nach steigenden Potenzen
von q entwickeln und die Koeffizienten dieser Entwicke-
lung sind ganze algebraische Zahlen.
Ist S eine symmetrische Funktion der xh,h’ mit rationalen
ganzzahligen Koeffizienten, so läßt auch diese sich in derselben
Weise nach Potenzen von q entwickeln. Andererseits ist S nach
dem Fundamentalsatz über symmetrische Funktionen rational durch
§ 155.
Multiplikation der elliptischen Funktionen.
579
die Koeffizienten von A (x) ausdrückbar, ist also eine ganze rationale
Funktion von Ä mit rationalen Zahlenkoeffizienten von der Form:
(12) s = s0 r + sx r-1- + sa as-2 -|---------h ss,
worin die 80, 81; 82, rationale Zahlen sind. Daß es ganze
Zahlen sind, soll eben bewiesen werden. Das ergibt sich aber
sehr einfach, wenn man in (12) für A die Entwickelung (3) ein-
setzt und dann die Koeffizienten gleich hoher Potenzen von q auf
beiden Seiten miteinander vergleicht. Man bekommt nämlich zur
Bestimmung der 80, 8n 82, ..., eine Reihe linearer Gleichungen,
deren jede folgende nur ein neues 8; und zwar mit dem Koeffi-
zienten 1 enthält, während auf der anderen Seite dieser Glei-
chungen ganze algebraische Zahlen stehen. Hiernach sind also
die So, Sx, S2, ..., ganze algebraische Zahlen, und da sie rational
sind, sind es auch ganze rationale Zahlen.
Da wir überdies nach § 57, H und (7) -4(0) und -4(oo)
kennen, so ergibt sich für A(x) der Ausdruck:
(13) A(x) = + 1 4- 3 + a2x^~6 m,
worin die ar, ..., ganze ganzzahlige Funktionen von
Z sind.
Ferner ist nach § 57, (7):
D(x) = + x”^-1 a(—\
v 7 — \x /
und folglich:
(14) + D (a:) = + 1 ai + a2 + • • +
^Das Zeichen ± in (13) und (14) ist nach § 57 bestimmt durch
m—]-]
(-i)M-
Für die Funktionen B und C gilt die Relation:
(15)
und ihre Wurzeln sind daher zueinander reziprok. Der erste und
der letzte Koeffizient sind in B und in C gleich der Einheit.
Die Wurzeln von B sind:
yh,w = sn(ßM, 4-10 =
cn
än£lh,h’
(16)
, (O
m
h 4 h co
—:, co
. m
37*
(17)
580 Dreiundzwanzigster Abschnitt. § 155.
und lassen sich in folgender Weise entwickeln:
„ + l + iry +
* m/ ß m
' (v + — )2
2J m'/ e m
lm Nenner dieses Ausdruckes kommt nur ein Glied mit
niedrigster Potenz von q vor, das man erhält, wenn man für v
die dem Bruch —h’/m zunächst gelegene ganze Zahl setzt.
Im Zähler kommt im allgemeinen auch nur ein niedrigstes
Glied vor, dessen Koeffizient eine Einheit ist. In dem besonderen
Falle, wo h’/m eine ganze Zahl ist, kommen aber im Zähler zwei
gleiche niedrigste Glieder vor, nämlich (für K = 0) v = 0, —1.
Diese geben zusammen
i „ hn
qi 2 cos —
m
und 2 cos — ist eine algebraische Einheit. [Zu schließen aus
Bd. I, § 144, (19)-]
Demnach läßt sich sowohl der Ausdruck (17), als auch sein
reziproker Wert nach steigenden Potenzen von q in der Art
entwickeln, daß der Koeffizient des ersten Gliedes den Wert 1
hat und alle übrigen Koeffizienten ganze algebraische Zahlen sind.
Daraus schließt man, ebenso wie in bezug auf A(x), daß sich
B(x)C(x) in der Weise darstellen läßt:
(18) B(x) C(x) = 4- -------|- 1, ,
worin die 6,, b2 ... ganze rationale Funktionen von Z mit ganzen
rationalen Zahlenkoeffizienten sind. Außerdem sind die Koeffi-
zienten b, die gleichweit vom Anfang und vom Ende abstehen,
einander gleich.
Betrachten wir noch die aus (8) fließende Gleichung:
(19) xA(x) — sn.mvD(x) = 0,
die in bezug auf x vom Grade m2 ist. Ihre Wurzeln sind die
Größen: _
sn v, ]/ z sn (y -|- ß^^).
Das Produkt dieser Wurzeln ist, vom Vorzeichen abgesehen,
gleich dem unabhängigen Gliede in dieser Gleichung, also gleich
+ y% sn»»:,
und daraus ergibt sich:
(20) + !—==---------- — n y% sn(v £lh,h')-
y k sn -v
'^WOFMATHEMAUOg
«-«NELL UNIVER81TY
§ 156.
Übergang zu den singulären Moduln.
581
§ 156. Übergang zu den singulären Moduln.
Wir nehmen jetzt an, daß co die Wurzel einer quadratischen
Gleichung:
(1) aco2 ba -j- c = 0
mit der negativen Stammdiskriminante
(2) z/ = b2 — kac
sei.
Ist dann j(o) die Invariante, so genügt die Größe A [§ 155,
(2)] der Gleichung 6 ten Grades:
(3) A« — 9.16 A4 — [j (co) — 27.2«] l2 -|- 64 [j (co) — 27.64] = 0,
deren Koeffizienten ganze algebraische Zahlen sind. Folglich ist
A selbst eine ganze algebraische Zahl (Bd. II, § 154, ll.)1)
und in § 135 haben wir gesehen, daß A Klasseninvariante der
Diskriminante 4 z/ oder 16 z/ ist.
Wir adjungieren also dem Klassenkörper $ (z/) die Zahl A
und erhalten einen Klassenkörper:
. 8 = ß(4z/), wenn zf = 0 (mod 4), oder = l(mod8).
8 = S(16zf), z/ = 5 (mod8).
Ist h die Klassenzahl von zf, also der Relativgrad von ß(z/)
in bezug auf den quadratischen Körper ß = Dl (|^), und h' der
Relativgrad von 8 in bezug auf ß, so ist (§ 100, § 123):
h1 — h, wenn z/ = 1 (mod 8),
(5) /d = 2Ä; „ z/ = 0 (mod 4),
h' = föh, „ zf = 5 (mod 8).
In dem ersten dieser drei Fälle ist also 8 mit St (zf) identisch.
Durch die Substitution des singulären Moduls co gehen die
Koeffizienten alf a2 ..., blf b2, ..., in § 155, (13), (18) in ganze
algebraische Zahlen über, und daraus folgt, Bd. II, § 154, 11., daß
die Wurzeln von A(%), nämlich:
(6) snßy, ganze Zahlen
und die Wurzeln von B(xy.
(7) Einheiten
v 7 ’ dnßM-’
sind.
l) Dieser Umstand ist es, der die Einführung von >. an Stelle von x
besonders empfiehlt, weil x im allgemeinen keine ganze Zahl ist, sondern
erst 4 x.
582
Dreiundzwanzigster Abschnitt.
§ 156.
Nun ist für variable % und v [§ 45, (5)]:
zox \ dn (i v, x')
(8) dn (y,%) = —). £
' v 7 cn (t v, x)
Setzen wir hierin:
„ 2hK-\--2h'iK'
v = ßÄ,w =
m
— 2h' Kr 2hiK
IV = --------'---- = ßl
1—h'yhj
m
so haben die ß' dieselbe Bedeutung für x' wie die ß für %, d. h.
sie entsprechen der Vertauschung von («,— l/o) und es ergibt
sich aus (7) und (8), daß auch
dn ßÄ
—^=.7 eine Einheit ist.
1/7
Es sind also auch
m
1 i
--= dn
(9)
m
Aus der
(10)
v \ 7)2 /
— ------=—i—j-,— algebraische Einheiten.
/h 4- h
*"(—52
§ 155, (20) folgt für i: = 0:
h,W __
•—• -D y/ x sn ßr^^* — n x^^.
ganzen Zahlen x^ sind also Teiler der
cn ß;t) h’
Formel
1. Die
Zahl m.
Wir setzen
jetzt, wenn m und n zwei ungerade Zahlen sind:
2hK 4- 2Ä'i.B7
Hh,W — -----------------
m
21K± 2l'iK'
n
und substituieren in der Formel § 155, (20):
v = Hjtv
Dadurch ergibt sich:
, . y[xsamH^v f— n
(11) ;—t=---—— — II yx sn(^Hitv 4"'ßM')>
y% snAf^,
§ 157. Komplexe Multiplikatoren. 583
worin
c2(lm hn)K -|- 2(Zm -|- b,'n)iK’
Hl>v + &h,h. = ----------------—-----------------,
und folglich sind die Faktoren des Produktes (11):
sn (Hl,v -f-
ganze Zahlen [nach (6)]. Vertauscht man in (11) wieder m und
n, so folgt:
/inx v« snn ßh)V ... „ ,.
(12) -^=---------------— ist eine ganze Zahl.
• snßM.
Dies gilt für beliebige ungerade n, also auch, wenn n relativ
prim zu m ist, für n-1 (mod m) und es ist also auch
(>t snr-'öj,^ . ,
i—t=----—— eine ganze Zahl.
|/x sn&M,
Ersetzt man hierin ä, h' durch nh, nh', so folgt, daß auch
yTx snißi A. . „ ,. . ,
'— eine ganze Zahl ist,
yx8nȧj,n'
also ist der Quotient (12) eine Einheit, oder anders ausgedrückt:
2. Durchläuft n eine Reihe ungerader, zu m teiler-
fremder Zahlen, so sind die ganzen Zahlen:
(13) snnil^h'
miteinander assoziiert.
§ 157. Komplexe Multiplikatoren.
Es genüge a> wie im vorigen Paragraphen der quadratischen
Gleichung
(1) am2 -|- beo —]— c = 0
mit negativer Stammdiskriminante
. zf = b2 — iac,
also sei:
Wir legen unseren Betrachtungen wie im vorigen Paragraphen
die Funktion
(3) ^snv = V^ = s(u)
584 Dreiundzwanzigster Abschnitt. § 157.
zugrunde, die wir als Funktion von w = u/2£ mit s(u) be-
zeichnen. Diese Funktion hat dann die durch
s(u + 1) = — s(u),
S(u -|~ gj) = s(w)
ausgedrückte doppelte Periodizität. Alle Perioden von s(u) sind
in der Form 2 m -|- nco enthalten, worin w, n ganze rationale
Zahlen sind, und gehen also durch Multiplikation mit a in ganze
Zahlen über.
Zwei Zahlen w, w', die sich nur um eine Periode unter-
scheiden, heißen kongruent nach dem Modul 2, gj:
u' = u (mod 2, gj).
Da die Funktion snr einen Wert nur zweimal im
Periodenparallelogramm annimmt, so wird nur dann
S(w) — S(u’),
wenn entweder
u = w'
(5) oder (mod 2, gj)
u = 1 — u'
ist, und s(w) verschwindet nur, wenn
w = 0, 1 (mod 2, gj)
ist.
Da jede gebrochene Zahl in SI durch Multiplikation mit einer
ganzen rationalen Zahl in eine ganze Zahl verwandelt werden kann,
so ergibt sich aus § 156, (6) der Satz:
1. Ist rj irgend eine gebrochene Zahl des Körpers
SS, so ist s(jj) eine algebraische Zahl, und wenn ins-
besondere jj so dargestellt werden kann, daß sein
Nenner relativ prim zu 2 ist, so ist s(jj) eine ganze
algebraische Zahl.
Es sei jetzt
(6) y = y -|- x ]/z7
eine ganze Zahl in &, in der x, y ganze rationale Zahlen sind ’), und
fi' = y —
die zu y konjugierte Zahl. Ferner
(7) m = y y’ — y2 — dx2
die Norm von p-, die wir als ungerade voraussetzen.
T) Im Fall eines geraden J kann hiernach ,« jede ganze Zahl aus ß
sein. Im Fall eines ungeraden J ist u eine Zahl der Ordnung [2].
§ 157. Komplexe Multiplikatoren. 585
Es ist dann nach (2)
y,-=y-\-bx-\-2aG>x,
(8) ya) = — 2cx -|- (y — ba?)cj,
m — (y bx)(y — bx) -|- 4a cx2,
woraus folgt, daß
y bx und y —-bx
ungerade sind.
Daraus ergibt sich nach (4):
S[ji(w + 1)] = —S(jiw),
s[fl(w cj)] = s(fiw).
Die Funktion s(fiw) hat also dieselben Perioden wie s(«),
und da s(ftw) eine ungerade Funktion von w ist, so kann sie
rational durch s(u) ausgedrückt werden. Wir bezeichnen mit
_4(s), D(s) ganze rationale Funktionen von s = s(u), die
übrigens nur die geraden Potenzen von s enthalten, und setzen:
(10) s(yu) = ys(u)^&-
Die Werte von S(w), für die s(fiw) Null oder unendlich
wird, sind nach 3. algebraische Zahlen, und da sich aus diesen
die Koeffizienten von A und D zusammensetzen lassen, so sind
diese auch algebraische Zahlen. Um ihre Natur näher zu be-
stimmen, denken wir uns den Bruch (10) zunächst so erweitert,
daß D rationale Koeffizienten erhält. Das geschieht dadurch,
daß wir Zähler und Nenner mit dem Produkt aller zum Nenner
konjugierten Faktoren multiplizieren. Wir können also A (s) und
D(s) in die Form setzen:
an ^(s) = ^ + A«2 + 4-,«4 + •••,
v } D(S) = A + D3s2 + As4 + ---,
worin die -A> nach unserer Voraussetzung rationale Zahlen
sind, während Au As, ..., zu bestimmen sind. Setzen wir wie in
§ 155, (4), (6):
w = 1/xv = 2^hKu,
so geht S(w) in ]/xsn(-^L) über, und die Gleichung (10) ergibt:
\]/x /
(12) —----------V / = A1 -j- As s2 + As s* 4- • • •
586 Dreiundzwanzigster Abschnitt. § 157.
Entwickelt man die linke Seite nach Potenzen von w, so sind
die Koeffizienten rational durch A und ausdriickhar, gehören
also dem Körper _
g = 9? (Ä,
an. Entwickelt man die rechte Seite in gleicher Weise und
ordnet nach den Potenzen von w, so tritt Av zuerst in dem
Koeffizienten von w’-1 auf, und zwar mit dem Faktor 1 behaftet.
Danach läßt sich Av bestimmen, wenn die früheren Koeffizienten
schon bestimmt sind, und es folgt, daß alle diese Koeffizienten
dem Körper S angehören.
Da man nachträglich wieder Zähler und Nenner des Bruches
A/D durch rationale Rechnung von gemeinschaftlichen Faktoren
befreien kann, so ergibt sich der Satz;
2. Wenn in dem Ausdruck (8) Zähler und Nenner
J.(s), D(s) von gemeinschaftlichen Faktoren befreit
sind, so gehören diese Funktionen dem Körper 8 an.
Um die Funktion A(x) darzustellen, nehmen wir den Koeffi-
zienten der höchsten Potenz von x gleich 1 an und untersuchen,
für welche Werte von w die Funktion s(p.u) verschwindet. Wir
bezeichnen einen Wert w, für den S(p.u) verschwindet, mit 2p/p.
und erhalten dann als Bedingung des Verschwindens nach (5)
eine der beiden Kongruenzen
2 p = 0, 1 (mod 2, cj).
Es ist also p eine Zahl des Körpers &, die zwar gebrochen
sein, aber keine anderen Nenuer als einen Teiler von 2 a haben
kann. Andererseits kann man p um ein Vielfaches von p. ver-
ändern, ohne daß der Wert s(2p/p.) geändert wird, und da es
nur auf den letzteren ankommt, und man der Kongruenz:
£
t» = 2^ (mod
wenn g eine ganze Zahl in £i ist, durch eine ganze Zahl p genügen
kann, so können wir p als ganze Zahl annehmen, wenn wir vor-
aussetzen, daß der erste Koeffizient a in (1) ungerade und
relativ prim zu p. sei. Diese Annahme halten wir von jetzt an fest.
Lassen wir also p ein vollständiges Restsystem nach dem
Modul mit Ausschluß der Null durchlaufen, so erhalten wir
alle Werte von S, für die A(s) verschwindet, in der Form:
§ 157.
Komplexe Multiplikatoren.
587
Es ist noch zu zeigen, daß von den Zahlen (13) keine zwei
einander gleich sind. Wäre
ohne daß p = p' (mod jx) wäre, so müßte nach (5)
ft" 1 (mod 2, gj)
sein. Es müßte also a(l tu) durch 2 teilbar sein, also auch,
wenn gj zu gj' konjugiert ist, a(l gj') durch 2 teilbar, und
mithin _
a(cj — gj') = )/zf = 0 (mod 2).
Es wäre also zf durch 4 teilbar, und {zf = ja2(ej — gj')2
wäre gleichfalls noch Diskriminante, was der Annahme wider-
spricht, daß z/ Stammdiskriminante sei1)- Hiernach sind die
Größen (13), deren Anzahl m — 1 beträgt (Bd. II, § 165), alle
voneinander verschieden, und es ergibt sich
(14) A(z) =
Die Funktion s(w) genügt nach § 44, (20) der Gleichung:
/ , gj \ 1
S « +w = —-z-v,
\ ~ 2/ s(u)’
und wegen (8) und (4):
s | p. (u + -v,
L \ 2/J s(fitt)
und demnach ergibt sich aus (10), wenn man u durch u -
* Ä
ersetzt:
n-D l-1)^ = J_______________= (-i)ca:-P(g)
J s(jzu) S(M) s(m)2(s) ’
(16) 4(s)d(l) = (-l)«D(s)D(l)-
1) Es müßte b gerade Und a b -f- c durch 4 teilbar sein, und
1 x 2
- J = (- — aj — a(a — b -f- c) wäre Diskriminante. Für eine beliebige
Diskriminante D könnte man denselben Zweck erreichen, wenn man zum
Zähler der Ausdrücke (13) eine Potenz von 2 als Faktor hinzufügte.
588 Dreiundzwanzigster Abschnitt. § 157.
Da A und D ohne gemeinschaftliche Teiler sind, so ist für
eine Variable x und eine Konstante Ä:
hxm~1A^^ = D(x),
und indem man x durch 1/x ersetzt:
JtA(x) =
und nach (16):
7i2 = (— l)ca;.
Also ist
(17) D(x) = sxn-'A^,
worin s = +1 oder = +* ist. Das hängt nach (16) davon ab,
ob cx gerade oder ungerade ist1).
Gebrauchen wir also wieder die Bezeichnung (10), jedoch jetzt
unter der Voraussetzung, daß A und D ohne gemeinschaftliche
Teiler sind, so ergibt sich:
(18) £S(fiw) — x + ^ot_2S2 -23gB_3 + ^S“-1’
und die Ax, A3, ..., sind ganze Zahlen des Körpers S,
denn sie sind die symmetrischen Grundfunktionen der ganzen
Zahlen (13).
Im besonderen ergibt sich, wenn man w = 0 setzt:
(19) Ar =
und daraus:
(20) =
/2 o\
Die S (—) sind also Teiler von u.
\P/
Aus (10) folgt:
(21) sd(s) — s(jiw)D(s) == 0,
und dies ist, wenn S(fiw) als gegeben betrachtet wird, eine
Gleichung für s(w) vom mtei1 Grade, deren Wurzeln sind:
s(M),
’) Aus § 138 ergibt sich, daß i im Körper ß enthalten ist; (17) steht
also nicht im Widerspruch mit dem Satze 2.
§ 157.
Komplexe Multiplikatoren.
589
Das Produkt dieser Wurzeln ist also, da S“ den Koeffizienten 1
hat, gleich dem negativen unabhängigen Glied, d. h. es ist:
k 7 s(w) \ r ft/’
und daraus für u = 0 wie oben:
(23) ^ = ^(7)'
Es sei jetzt jj eine gebrochene Zahl in & mit dem ungeraden
Idealnenner 0; dann folgt aus (22), daß S (ft 17)/S (17) eine ganze
Zahl ist, wenn ft eine beliebige Zahl (6) in Q ist. Nehmen wir
[i relativ prim zu 0 und setzen ft'ft = 1 (mod 0), so können wir
17 durch ersetzen und finden, daß auch eine
ganze Zahl ist, worin ft' ebenso beliebig ist wie ft. Folglich ist
auch S (17)/S (ft 17) eine ganze Zahl und mithin eine Einheit.
Wir haben also den Satz:
3. Ist 17 eine Zahl in £1 mit ungeradem Ideal-
nenner, und durchläuft (i eine Reihe relativer Prim-
zahlen zu ct, so sind die Zahlen
s(m)
miteinander assoziiert.
Noch eine weitere Folgerung ergibt sich daraus, wenn man
in (22) u = 2q1/il1 setzt:
s(2gA \ fh ftJ
\ fh /
Sind nun ft und relativ prim zu ftl5 so ist die linke Seite
nach 3. eine Einheit, und folglich müssen auch alle Faktoren der
rechten Seite
die ja ganze Zählen sind, Einheiten sein.
Auf diese Form läßt sich aber jedes s(->?) bringen, wenn
eine gebrochene Zahl in Q ist, in deren Nenner zwei verschiedene
Primideale aufgehen, falls dieser Nenner ungerade ist. Denn man
kann in diesem Falle den Nenner ft von 17 in zwei Ideale a< o2
590 Dreiundzwanzigster Abschnitt. § 158.
zerlegen, die zueinander relativ prim sind, und man kann dann
zwei ungerade ganze Zahlen oq, a2 in SI bestimmen, die zuein-
ander relativ prim sind, von denen die eine durch an die andere
durch a2 teilbar ist. Es ist dann T[ cq a2 eine ganze Zahl in SI
und man kann nach Bd. II, § 166, (4) zwei ganze Zahlen px, p2
so bestimmen, daß
vcq «2
- — Pi ~r Pa Ki
r
und daher
\ fi / \ cq a2 J
wird. Dies ist aber von der Form (25). Wir bekommen daraus
den Satz:
4. Enthält eine gebrochene Zahl jj in SI mit un-
geradem Nenner zwei oder mehr verschiedene Prim-
faktoren im Nenner, so ist s(jj) eine Einheit.
§ 158. Zerlegung der Funktion A(x).
Es seien jetzt
ji = y -j- x
/h = Vi + «i
zwei ungerade ganze Zahlen in SI von der Form § 157, (6). Es
sei m der größte gemeinschaftliche Idealteiler von y und g,,.
Setzt man also
(2) /i=ma’
fh = ma,,
so sind a und cq zwei äquivalente Ideale ohne gemeinsamen
Teiler.
Die den beiden Zahlen y, y^ entsprechenden Funktionen A(x)
bezeichnen wir mit
A(a?), A^fx),
und fragen, welche gemeinschaftliche Wurzeln diese Funktionen
haben, wann also die Gleichung:
w
erfüllt sein kann, wenn p nach dem Modul y, px nach dem Modul yr
genommen ist.
§ 158. .Zerlegung der Funktion A (x). 591
Da die Kongruenz
— _j_ 2_£i_ _ i (mo(j 2, gj)
fi pt
nicht möglich ist, was man ganz wie oben (S. 589) zeigt, so ist
für die Gleichung (3) notwendig und hinreichend:
(4) = 0 (mod 2, gj).
P-Pi
Daraus folgt:
(5) P9i = fhg (mod p^),
und dies ist nur dann möglich, wenn
(6) p = 0 (mod a), (q = 0 (mod Qj).
Sind umgekehrt die Bedingungen (5) und (6) erfüllt, so ist:
eine ganze Zahl und die Gleichung (3) ist befriedigt.
Man nehme nun eine durch o teilbare ganze Zahl in £1;
(7) « — ac,
worin c relativ prim zu p und p, ist. Wenn dann p durch a
teilbar ist, so kann man eine ganze Zahl g nach dem Modul in
aus der Kongruenz
p = «g (mod p)
bestimmen (Bd. II, § 166, 7.); dann ist
w u,
(8) «i = -y- = di c
eine durch iqc und durch kein anderes Ideal teilbare ganze Zahl,
und aus (5) ergibt sich
gi = «i £ (mod fij).
5. Wir erhalten also die gemeinschaftlichen Wur-
zeln von MU1(«) in der Form:
worin g ein vollständiges Restsystem nach dem
Modul tn durchläuft.
Hierin kann nt jedes beliebige ungerade Ideal in £1
bedeuten.
Denn man kann zu jedem solchen Ideal zwei Zahlen p, pj
von der Form (2) wählen und dann gj unter den äquivalenten
Zahlen so, daß a ungerade und relativ prim zu ppT wird.
592 Dreiundzwanzigster Abschnitt. § 159.
Sucht man den größten gemeinschaftlichen Teiler von Au und
JU1, so erhält man eine ganze Funktion J.m, deren Koeffizient
ganze Zahlen in S sind, deren Wurzeln die Größen (9) sind, nnd
wenn man endlich von Faktoren befreit, die es mit irgend
einem Am> gemein hat, in dem ni' ein echter Teiler von m ist, so
erhält man eine ganze Funktion:
(10) Tm(x) = £* — TV^1XV~1 4- — ••• ± r0,
deren Wurzeln nur die unter den Größen (8) sind, in denen §
relativ prim zu m ist.
Der Grad v dieser Funktion ist nach Bd. II, § 168 zu be-
stimmen. Wir wollen sie die Idealteilungsfunktion nennen.
Ihre Koeffizienten sind ganze Zahlen des Körpers S, und es ist
speziell
(11)
worin g ein vollständiges System inkongruenter, zu m teilerfremder
Zahlen durchläuft.
Die Wurzeln von Tm(x) sind gleich und entgegengesetzt, und
wir erhalten eine Gleichung von Graden 1/2v für die Größe
Durch Adjunktion dieser Größen zu dem Körper 2 entsteht
ein Körper $m, den wir gleichfalls Teilungskörper nennen. Er
ergibt sich aus dem Teilungskörper des § 154 durch Adjunktion
von x. Die Gruppe dieses Körpers ist in der Gruppe der Zahlen
g (mod nt) enthalten, wie leicht aus den Multiplikationsformeln
folgt.
Wir bemerken noch, daß sich der allgemeine Teilungskörper
Sm durch Anwendung des Additionstheorems auf den Fall zurück-
führen läßt, wo m eine Potenz eines Primideals in & ist.
§ 159. Primideale.
6. Ist 11 eine gebrochene Zahl des Körpers ü, die
in reduzierter Form den ungeraden Idealnenner ct
hat, und ist nt ein zu ct relativ primes Ideal, so ist
die ganze Zahl s(t?) relativ prim zu in.
Denn man nehme in £1 eine durch o teilbare^ zu 2 nt teiler-
fremde ganze Zahl p. an. Dann ist eine ganze Zahl. In
dem Produkt § 157, (23)
§ 159.
Primideale.
593
(i) o = ns(^)
kommt eine Zahl 2q vor, die mit pt} nach dem Modul p kon-
gruent ist. Folglich ist S(i?) ein Teiler von u und mithin relativ
prim zu m, wie bewiesen werden sollte.
Nehmen wir jetzt an, daß in der Formel (11), § 158
(2) r0
in ein Primideal des Körpers Si sei und setzen demgemäß
m = p, so daß £ ein volles Restsystem nach dem Modul p mit
Ausschluß der Null durchläuft.
Nehmen wir dann ft so an, daß es nur durch die erste Potenz
von p teilbar und durch ein beliebig gewähltes anderes Primideal
p' nicht teilbar ist, so kann nach dem Satz 6. nicht durch p'
teilbar sein. Nun ist Ta nur von dem Ideal p abhängig und
unabhängig davon, wie im übrigen die Zahl p genommen ist.
Folglich ist r0 nach dem Satz 6. durch kein von p verschiedenes
Primideal teilbar. Es kann aber auch p nicht in einer höheren
als der ersten Potenz in t0 auf gehen, denn die Faktoren des
Produktes (1) kommen alle unter den Faktoren des Produktes (2)
vor, und folglich ist ft durch t0 teilbar. Demnach können wir
geradezu
(3) ro = P
setzen, und da r0 eine Zahl im Körper 2 ist, so folgt:
7. Jedes ungerade Primideal des Körpers Si ist
ein Körper 2, ein Hauptideal.
Auch in der Annahme, daß p relativ prim zu a sein sollte,
liegt keine Einschränkung dieses Satzes. Denn wir können bei
gegebenem p unter den äquivalenten Formen (a, b, c), ohne A zu
ändern, eine auswählen, bei dem diese Forderung erfüllt ist.
Noch nicht bewiesen ist aber hierdurch, daß p auch im
Klassenkörper fi(zf) selbst ein Hauptideal ist. Wenigstens folgt
dies nur in dem Fall zf = 1 (mod 8), wo fi mit 2 identisch ist1).
Nach dem Satz 3., § 157 sind die Faktoren des Produktes (2)
alle miteinander assoziiert. Die Anzahl dieser Faktoren istW(p) — 1,
und demnach können wir auch setzen:
*) Vgl. hierzu § 122, wo auch der Fall der Primzahl 2 erledigt ist.
Weber, Algebra. III. 3g
594
Dreiundzwanzigster Abschnitt.
§ 160.
§ 160. Primideale ersten Grades in $m.
Es kommt nun vor allem darauf an, die Primzahlen p aufzu-
suchen, die im Körper g in Primideale ersten Grades zerlegbar
sind. Nach § 122 und § 156 sind das die Primzahlen p, die durch
die Hauptform der Diskriminante D — 4zf oder 16zf darstellbar
sind. Diese sind von der Form:
1) p = y2 — A x2, Zl = 0 (mod 4) oder = 1 (mod 8),
2) p = y2 — 4zf x2, zl = 5 (mod '8).
Ist A = 1 (mod 8), so muß der dritte Koeffizient der Form
(a, ö, c) gerade sein. Ist A ~ 0 (mod 4), so können wir c
gerade annehmen, indem wir nötigenfalls zu der Parallelform
(a, & —2 a, a —c) übergehen. Zerfällt also p in die beiden
Primfaktoren ir, tc'. so ist
1)
2) sr — y 2 x A,
und um die Multiplikationsformel § 157, (10), (17) auf u — n
anzuwenden, haben wir im letzteren Falle x durch 2 x zu ersetzen.
Wir können also in allen Fällen cx gerade und daher e = + 1
annehmen.
Die in den Darstellungen (1), 1), 2) liegenden Bedingungen
für den Modul 2 lassen sich in die eine zusammenfassen:
« = 1 (mod 2).
Setzen wir, wenn N(ri) = p ist, für den Augenblick zur
Abkürzung:
z2\ = AiX + A3x3 -|--------|- xP~2 -|- xp,
7 il>(x) = 1 Ap~.,:i2 -|- ••• + AsxP~3-i~A1xP~1,
so ist nach § 157, (18), (19)
(3) Ar = +sr,
und
(4) + s (n u) = ,
' 7 ' 7 $ (S) ’
und daraus ergibt sich durch Differentiation nach u:
zp. x . % s' (n u) <p' (s) 1p (s) — <P (s) iF (s)
( ’ ± s'(u) ~ ^(s)2
Nach § 155, (5) ist aber
S'(u)2 = 1 — |Zs2 -|- s4,
§ 160.
Primideale ersten Grades in $m.
595
und aus (5) ergibt sich durch Quadrieren mit Benutzung von (4):
4^(s)4 — WsWsP-l-Ufe)« r x , z \ ,/ x z
---— = [9>W(s) — <p'(s)^(s)]2.
Da rechts eine ganze Funktion von s steht, so muß auf der
linken Seite der Zähler durch den Nenner teilbar sein (was sich
auch aus der Betrachtung der Nullpunkte ergibt), und es folgt:
0 = jy (s) ii> (s) — <? (s) t/>' (s)]2,
wo 0 eine ganze Funktion von S ist, deren Koeffizienten ganze
Zahlen in fi sind. Es muß also das Quadrat einer ganzen
Funktion sein, deren Koeffizienten gleichfalls ganze algebraische
Zahlen sind (Bd. I, § 2; Bd. II, § 159), und es ergibt sich daraus
für ein variables x:
(6) <p' (x) tp (x) — ip' (x) <p(x) = 0 (mod st).
Hiernach läßt sich beweisen, daß die Koeffizienten A1, As,
A&, ..., Ap-2 alle durch n teilbar sind.
Von A1 wissen wir das schon. Nehmen wir also an, es sei
bewiesen für
so folgt:
A, z43, ..., Ar-l (2v + 1 <p),
<p (x) = A2l, + 1x2'' + 1 -|- •••
<p'(x) =. (2 v -j-1) Azr-j. i x2" —J— • • •
tp (x) = 1 Ap _ a x2 -|- —
(mod st)
tp' (F) = 2 Ap _ 2 x • • •
Suchen wir also in (6) den Koeffizienten von x2v, so folgt:
(2v 1) ^2» + i = 0 (mod st).
Da 2v -)- 1 <pp und p eine Primzahl ist, so ist 2v 1
relativ prim zu st, und es folgt:
(7) J.2r + i = 0 (mod st).
Setzen wir in (4) für u einen der Werte 2w|/ft, § 158, (9),
so wird S(u) eine Wurzel der Ideal-Teilungsgleichung § 158, (10),
und es folgt:
+ fi(sru) = [s(u)]*> (mod st),
und wenn wir ein Quadrat erheben:
(8) s(sru)2 = [s(m)]2?! (mod st).
Insbesondere ist also
(9)
wenn
(10)
S(u)2 = s(u)2v (mod st),
st = V1 (mod m)
38*
596 Dreiundzwanzigster Abschnitt. § 161.
ist. Die Zahl s(w)* 2 erzeugt den Körper Es ist außerdem
nach § 122 für jede Zahl p in ß:
(11) Q = Qp (mod Sß),
wenn iß ein in 5t aufgehendes Primideal in ß ist, und folglich ist
für jede ganze Zahl r in wenn iß' ein Primideal in ist:
(12) t» = t (mod iß'),
wenn die Bedingungen (10) und (1) erfüllt sind.
Daraus ergibt sich:
8. Damit eine in ü existierende Primzahl % im
Körper in Primideale ersten Grades zerfalle, ist
notwendig und hinreichend, daß
% = 1 (mod 2),
n = + 1 (mod tn).
Von einer gewissen endlichen Anzahl von Primzahlen (die in
den Diskriminanten der auftretenden Gleichungen aufgehen) ist
dabei abgesehen.
§ 161. Zahlgruppen und Idealgruppen.
Wie in § 98 und § 106 bezeichne ich mit 0 die Gesamtheit
der ganzen und gebrochenen Zahlen des quadratischen Körpers ü,
nach Ausschluß aller Zahlen, die zu einem beliebig angenommenen
S nicht teilerfremd sind. S kann eine rationale Zahl, eine Zahl
in oder auch ein Ideal sein. Ich will es den Exkludenten
nennen. In den drei Abhandlungen „über Zahlgruppen in alge-
braischen Körpern“ Q habe ich gewisse Systeme von Zahlen aus 0
unter dem Namen Zahlgruppen zusammengefaßt, die dadurch
definiert waren, daß das-Produkt und der Quotient je zweier
Zahlen einer solchen Gruppe in derselben Gruppe enthalten waren.
Eine solche Zahlgruppe kann niemals die Zahl Null enthalten,
enthält aber sicher die Zahl 12).
Im gleichen Sinne wie von Zahlgruppen können wir auch von
Idealgruppen reden, die ebenfalls ihren Exkludenten haben
können. Es kommen hierbei natürlich auch gebrochene Ideale
vor, und man bedient sich dabei nicht ohne Nutzen der Dar-
stellungsweise durch die Funktionale (Bd. II, § 169).
Q Mathematische Annalen Bd. 48, 49, 50.
2) Fueter nennt diese Gruppen „Zahlstrahlen“. Vgl. Fueter, Die
Theorie der Zahlstrahlen I, II; Crelle, Bd. 130, 132.
§ 161. Zahlgruppen und Idealgruppen. 597
Die Gesamtheit der ganzen und gebrochenen Zahlen des
Körpers der wir einen beliebigen Exkludenten S beilegen,
bildet die Zahlgruppe 0 und die Gesamtheit der Ideale 0 in dem
gleichen Sinne eine Idealgruppe.
Ebenso bildet die Gesamtheit der numerischen Einheiten
eine Zahlgruppe E und die Gesamtheit der funktionalen Ein-
heiten eine Idealgruppe E.
Die Multiplikation zweier Gruppen A und B zu dem Pro-
dukt AB geschieht dadurch, daß man jedes Element von A mit
jedem Element von B multipliziert. Ist A eine Zahlgruppe, so
ist E A eine Idealgruppe. Diese enthält aber nui‘ Hauptideale und
kann daher Hauptidealgruppe genannt werden.
Wenn die ganze Gruppe 0 in eine endliche Anzahl von
Nebengruppen nach A zerfällt:
(1) 0 = AWj —|— Accq -j— —|— Accjy
so heißt die Zahl j der Index von A und wird mit
(2) j = (0, A)
bezeichnet (wie in § 100).
Wir sprechen den ersten Satz aus:
1. Ist A eine Zahlgruppe mit endlichem Index j,
und q eine beliebige Zahl in 0, so ist in A ent-
halten.
Denn von der unbegrenzten Reihe der Potenzen 1, tj2, tj3, ...,
müssen zwei verschiedene Glieder in derselben Nebengruppe Aat
enthalten sein, und ihr Quotient, der ja auch eine Potenz von q ist,
ist in A enthalten. Der niedrigste Exponent r, für den in A
enthalten ist, erweist sich in bekannter Weise als Teiler von j.
2. Ist A eine Zahlgruppe mit endlichem Index, so
läßt sich auch die Idealgruppe 0 nach EA in eine
endliche Zahl von Nebengruppen zerlegen:
zox 0 = Ar -|- A% —H *" • —I“
= A «1 -|- A o2 -|- • • • -j- A üb,
und zwar können wir darin ax, a2, ..., als ganze Ideale in 0
wählen, da wir jedes gebrochene Ideal in 0 nach 1. durch Multi-
plikation mit einer Zahl in A in ein ganzes Ideal verwandeln
können. Wir brauchen nur für q eine Zahl zu wählen, die durch
den Nenner des Ideals teilbar ist, und mit einer genügend hohen
Potenz von q zu multiplizieren.
598
Dreiundzwanzigster Abschnitt.
§ 161.
Die Zahl _ ___
(4) h = (0, EA)
heißt die Klassenzahl des Körpers £1 nach A, und das System
Adi, Aaa,..., Aah die Idealklassen nach A. Den Satz 2. können
wir nach den allgemeinen Gruppensätzen im § 100, 12. beweisen.
Danach ist:
(Ö, EA) = (Ö, EO) (EO, EA),
(EO, EA) ~ (EO, EEA) = (0, EA),
(0, EA) (EA, A) = (0, A),
(EA, A) = (E, E'),
wenn E' die Gruppe der in A enthaltenen numerischen Einheiten
bedeutet. Folglich ist
(5) (Ö, EA) = (Ö, EO)
und (0, EO) ist die Zahl der absoluten Idealklassen in £2, also
eine endliche Zahl. Die Zahl (E, E') ist im quadratischen Körper
mit negativer Diskriminante gleich 1, wenn —1 in A vorkommt,
gleich 2, wenn —1 nicht in A vorkommt, und kann nur in den
beiden Ausnahmefällen A = — A, A =— 3 bis zu 4 oder bis
zu 6 ansteigen. _ _
Gehören an al einer Klasse A1 an, und a2, al einer Klasse Aa,
so gehören die Produkte a2 a2 und aj al in dieselbe Klasse, die
wir die Klasse A1Aa nennen. Die Klassen lassen sich also kom-
ponieren und_bilden eine endliche Abelsche Gruppe, in der die
Hauptklasse EA die Einheit ist.
Eine Zahlgruppe A soll Kongruenzgruppe heißen, wenn
sie nicht nur aus einzelnen Zahlen, sondern aus ganzen Zahl-
klassen nach einem Modul AK besteht, d. h. wenn a zu A gehört,
so sollen auch alle mit « nach dem Modul AL kongruenten Zahlen
zu A gehören; AK soll der Modul der Kongruenzgruppe heißen.
Eine Kongruenzgruppe hat immer einen endlichen Index, weil ja
schon die Anzahl der Zahlklassen nach dem Modul AL endlich ist.
Statt AK kann man auch jedes Vielfache von AL als Modul wählen.
Darum gewinnen wir auch keinen allgemeineren Begriff, wenn
wir für df ein Ideal nehmen. Wir können sogar AK als natürliche
Zahl annehmen.
Wenn ein Ideal m relativ prim zu AK ist, so kann man in
jeder durch a repräsentierten Zahlklasse eine Zahl a0 aus der
Kongruenz
162.
Die durch ein Ideal teilbaren Ideale der Hauptklasse.
599
(6) a0 = k — 0 (mod in)
bestimmen, worin tt eine ganze Zahl in £1 ist.
Daraus folgt, daß jedes im Exkludenten aufgehende Prim-
ideal e in M aufgehen muß, weil sonst a0 für m = e durch e
teilbar wäre.
Haben a und M einen gemeinschaftlichen Teiler, so haben
alle Zahlen der Form « Mi-, in der | eine beliebige Zahl ist,
denselben gemeinschaftlichen Teiler mit M. Es gibt aber in A
auch Zahlen, die relativ prim zu HA sind, z. B. die Zahl 1. Es
gilt dann der folgende Satz:
3. Ist m relativ prim zu Jf, so kann man in A
eine durch m teilbare ganze Zahl «0 — tun von der
Art bestimmen, daß n zu M und einem beliebig
gegebenen Ideal c relativ prim wird.
Hat man nämlich nach (6) eine durch m teilbare Zahl
a0 = mn
bestimmt, die zu M teilerfremd ist, so erhält man andere solche
Zahlen:
«ö = «o + M I = nt n',
wenn
I = UH
eine beliebige durch m teilbare ganze Zahl ist. Ist nun q ein in c,
aber nicht in a0 aufgehendes Primideal, so nehme man j durch
q teilbar an, dann ist n' nicht durch q teilbar. Geht aber q in c
und in «0 auf, so nehme man j durch q nicht teilbar an; dann
ist auch n' nicht durch q teilbar.
Daraus folgt:
4. Ist in ein beliebiges zu M teilerfremdes Ideal,
so gibt es in jeder Idealklasse A„ Ideale, die zu m
relativ prim sind.
Man nehme, um dies zu beweisen, ein Ideal b in der Klasse
1 und bestimme nach 3. eine Zahl
a = ab,
so daß a relativ prim zu m ist, dann gehört a in die Klasse Av
und genügt der Forderung des Satzes 4.
§ 162. Die durch ein Ideal teilbaren Ideale der Hauptklasse.
Es soll jetzt unter £1 der quadratische Körper mit
negativer Grundzahl A verstanden werden.
600 Dreiundzwanzigster Abschnitt. § 162.
In diesem Körper sei A eine Kongruenzgruppe mit dem Modul
M und dem Exkludenten S Die Gruppe A enthält, wie wir ge-
sehen haben, unendlich viele ganze Zahlen. Wir fragen nach
der Anzahl T(t) der ganzen Zahlen in die durch irgend ein
gegebenes ganzes zu AL teilerfremdes Ideal in teilbar sind, deren
Norm nicht größer als die positive Zahl t ist.
Es sei («i, w2) eine Basis von m, also nach § 91, (11):
__ ___ & -f- \~A
(1) W1 --- $22 W2 ----- $22 ---0--- ’
Hierin bedeute a22 die größte in m aufgehende ganze rationale
Zahl, a22a die kleinste durch m teilbare ganze rationale Zahl;
b ist eine Wurzel der Kongruenz:
b'2 = A (mod 4 a),
und es ist:
(2) A = b2 — Lac.
(3) N (m) = a|2 a.
Da m relativ prim zu M vorausgesetzt ist, so können wir nach
§ 161, (6) in jeder in A vorkommenden Zahlklasse nach M eine
durch m teilbare Zahl a() bestimmen. Diese Zahl hat die Form
«o = Xq y0 a2,
und wenn wir
a = a0 -L Af (xc^ + ya2)
= («o + Mx) «i + (y0 + My) a2
setzen und x, y alle positiven und negativen ganzen rationalen
Zahlen durchlaufen lassen, so durchläuft a die Gesamtheit der
durch m teilbaren und nach M mit a0 kongruenten ganzen Zahlen
der Gruppe A.
Um alle durch ni teilbaren ganzen Zahlen in A zu erhalten,
haben wir ein vollständiges Restsystem nach M in £1 zu suchen
und darunter die in A enthaltenen durch m teilbaren Zahlen «0
auszuwählen.
Soll die Norm dieser Zahl a nicht größer als t sein, so er-
gibt sich dafür, wenn wir die quadratische Form
axZ-^-bxy-lf-cy2
mit <p (x, y) bezeichnen, die Bedingung:
<P (x0 + Mx, y9 + My) [§ 91, (2), (4)].
U22 $
§ 162. Die durch ein Ideal teilbaren Ideale der Hauptklasse.
601
Nehmen wir in einer Ebene ein rechtwinkeliges Koordinaten-
system X, Y an, und bezeichnen als Gitterpunkte die Punkte
mit den Koordinaten
X = O0 Mx)
Y = Oo + My)
6^22
$22
worin x0, y0 festgehalten werden und x, y alle ganzen rationalen
Zahlen durchläuft, so wird durch dieses Gitter die Ebene in
Quadrate geteilt, deren Fläche
= 4^
V
ist, und wenn Ta die Anzahl der Gitterpunkte ist, die innerhalb
der Ellipse
V (X, K) = 1
oder auf ihrer Grenze liegen, so ist T0ö2 für ein unendliches t
it
gleich dem Flächeninhalt dieser Ellipse, also gleich
Berücksichtigt man noch die Flächenelemente ö2, die von der
Peripherie der Ellipse durchschnitten werden, aus denen man ein
Maß für den Fehler dieser Flächenbestimmung erhält, so ist
(5) To = M 2 !--)/t,
' 7 M.2 «ja a y— z/
worin _R0 eine mit unendlich wachsendem t endlich bleibende
Größe ist [Bd. II, § 194, (6)].
Einen solchen Ausdruck erhalten wir für jedes «0, und wenn
wir diese Ausdrücke alle addieren, so erhalten wir mit Rücksicht
auf (3) den Satz:
Ist A eine Kongruenzgruppe mit dem Modul M
und m ein zu M teilerfremdes Ideal in £1, ferner T
die Anzahl der in EA enthaltenen ganzen Haupt-
ideale, deren Norm nicht größer als t ist, so ist
W y=2^5) + JiV7,
worin g eine von m und t unabhängige, von Null
verschiedene Zahl und R eine mit unendlich wach-
sendem A endliche Funktion von t ist.
602
Dreiundzwanzigster Abschnitt.
§ 163.
(7)
Die Konstante g ist nach (5) näher bestimmt:
y %
9 — ----
\~A
wenn y die Anzahl der in A enthaltenen Zahlklassen nach dem
Modul M ist.
Will man unter T die Anzahl der ganzen Ideale der Haupt-
klasse EA verstehen, deren Norm nicht größer als t ist, so bleibt
(6) auch dann noch bestehen, nur hat man, wenn —1 in A vor-
kommt, die Zahl g zu halbieren, und in den beiden Ausnahme-
fällen A — — 4, A = — 3 möglicherweise noch durch 4 oder
durch 6 zu teilen.
§ 163. Die Dirichletsehen Summen.
Wir verstehen jetzt unter 0 die Idealgruppe der sämtlichen
Ideale in Si (mit Rücksicht auf den Exkludenten N); A sei eine
Kongruenzgruppe und
(1) Ä = EA,
die Gruppe der entsprechenden Hauptideale. Wir zerlegen 0 nach
§ 161, (3) in die Klassen nach A:
(2) 0 = A1 -j- A2 • • 4" Ak,
und betrachten die Summen:
(3)
Si
worin s eine positive Variable > 1 bedeutet, und a, die sämtlichen
ganzen Ideale einer Klasse A{ durchläuft.
Die Summen S, formen wir in folgender Weise um:
Da N(ai) eine der Zahlen 1, 2, 3, ... sein muß, so bezeichnen
wir mit a„ die Anzahl der Ideale der Klasse Ai, deren Norm — v
ist, und erhalten (*)
(*)
^2 । । ^4 ।
wobei, wenn eine Zahl v unter der N (a,) nicht vorkommt, a, — 0
zu setzen ist.
Bezeichnen wir mit Z (v) die Anzahl der Ideale der Klasse
Ai, deren Norm nicht größer als v ist, so erhalten wir für Z(v)
aus der Formel (6) des vorigen Paragraphen einen Grenzwert:
§ 163.
Die Dirichletschen Summen.
603
Wir nehmen nach § 161, 4. in der Klasse (Ai) 1 ein zu M teiler-
fremdes Ideal m und lassen in
(5) tn di = ä
üi die Ideale der Klasse Ai, und folglich ä die durch m teilbaren
Ideale der Hauptklasse durchlaufen; ist dann
N (üi) 4 v,
so ist
W(m)W(af) = 2V(a) 4 vW(m).
Bedeutet wie früher T die Anzahl der durch ni teilbaren Ideale
der Hauptklasse, deren Norm nicht größer als t ist, so ist, wenn
t = vN(m) gesetzt wird,
Z(v) = T,
und aus der Formel § 162, (6) ergibt sich
(6) Z(v) = gv Bvy/v,
worin g eine Zahl, die für alle Klassen Ai dieselbe ist, und B,
eine Funktion von v bedeutet, die mit unendlich wachsendem v
nicht unendlich wird.
Nach der Bedeutung von av ist
(7) av = Z(v) — Z(v — 1), Z(0) = 0
und folglich
(8) =
0,co
Setzen wir für Z(y) den Ausdruck (6), so folgt:
(9) S{ = g V— 4- SB„ (Tv (— — 7—
- } * J ^vs “ ’ \vs (p i)«7
Das zweite Glied dieser Summe:
1/T (— — -—-A
' \vs (v 4- i)v
ist unbedingt konvergent, solange s > | ist, und ist daher eine
stetige Funktion von s, die für s = 1 in
Bv
4-1)
übergeht; denn es ist
Lim4 + i^ - —2-Y) = sL.mfi,
604
Dreiundzwanzigster Abschnitt.
§ 163.
endlich. Die erste Summe in (9) ist
0«) Si = s-^r + c.,
wo Gs für s = 1 endlich bleibt, nämlich in den Wert der Euler-
schen Konstante 0,5772 ... übergeht (Bd. II, S. 723).
Berücksichtigt man dies, so ergibt sich aus (9) das Resultat:
5. Hat St die Bedeutung (3), so ist
(H) Ä = s-^ + G,
worin g eine von der besonderen Klasse Ai unab-
hängige von Null verschiedene Konstante ist, .und
G{ eine von A» abhängige Funktion von s, die für
s=l endlich bleibt.
Die Gruppe Ziten Grades der Idealklasse Äi ist eine Abelsche,
und es gibt daher h Charaktere sämtlich Zite Einheits-
wurzeln sind, darunter der Hauptcharakter Xt, der für jede
Klasse = 1 ist. Ebenso hat für die Hauptklasse jeder der
Charaktere den Wert 1. Für diese Charaktere bestehen die
Sätze:
SXx(Äi) = 0, S Xx(Äi) = 0,
(12) x = 2,3, ..., Zi, i = 2,3, ..., Ji,
^Zi(^) = -SZx(Ä) = Zi
(Bd. II, § 13). Wenn das ganze Ideal a in 0 in die Klasse Ä
gehört, so setzen wir für jedes X:
(13) Z(a) = %(Ä),
und haben so für jedes Ideal in Ö die Charaktere nach der
Gruppe A bestimmt. Für irgend zwei Ideale a und 6 aus Ö be-
steht die Relation:
(H) x (a) X (b) = x (a b).
Nun bilden wir aus Si die h Summe:
(15) Q* = £%*(Ä)Si,
wofür wir nach (3) und (13) auch setzen können:
<16> e = S(W'
§ 163.
Die Di richtet sehen Summen.
605
Darin kann % jeder der Charaktere sein, und die Summe
erstreckt sich über sämtliche Ideale a von 0. Nach (11) ist,
wenn wir
Gx =
setzen,
_ Ji G
(17) ~ s —1 11
Qx = G*., 1.
worin die Gt, G^ ..., Gh Funktionen von s sind, die für s = 1
einen endlichen Wert behalten.
Die Summen Q lassen sich in derselben Weise umformen, die
wir schon im § 197 des zweiten Bandes kennen gelernt haben.
Danach ist, wenn p irgend ein Primideal in 0 bedeutet:
-—* —-8 = i + z(p) wr + z(p)wf2s + -
i — z(t>)^(p)
_ i _i_ _i_ _i_ । . .
N(p)s N(p2)s W(p3)s ’
und da sich alle Ideale a als Produkte solcher Ideale p darstellen
lassen, so folgt:
Q = n------------------,
1 - z(p)W(p)-s’
worin sich das unendliche Produkt n auf alle Primideale p in 0
erstreckt.
Zu jedem Ideal a in 0 gehört ein gewisser Exponent tp,
d. h. es gibt einen gewissen niedrigsten positiven Exponenten <p,
für den ei'? in der Hauptklasse enthalten ist. Die Zahl tp ist
immer ein Teiler der Klassenzahl h. Wir setzen:
(19) h — e<p.
Gehört in diesem Sinne a zum Exponenten <p, so sind sämt-
liche Charaktere %s(a) <pte Einheitswurzeln, und jede <pte Einheits-
wurzel kommt darunter s mal vor (Bd. II, § 198, 1.).
Gehört also p zum Exponenten tp, so ist
[i - Z1(p)^(p)-s] [i - z2(p) ^v(p)—s] ••• [i— mp) wrs]
= [1 - N(p)-’’s]\
und es folgt aus (18):
(2°) Qi Qi • • • Qh = n ___.
606
Dreiundzwanzigster Abschnitt.
§ 163.
Es handelt sich nun um den Grenzwert, dem diese Aus-
drücke sich nähern, wenn s = 1 wird.
Was die linke Seite betrifft, so folgt aus (17), daß
j Lim (s — 1) ft = h g endlich und von Null verschieden,
(21) [Lim Q2 Qi ... Qh endlich (vielleicht Null)
ist. Zur Beurteilung der rechten Seite bemerken wir, daß die
Primideale p vom ersten oder vom zweiten Grade sind, und daß
demnach NQp) gleich einer natürlichen Primzahl oder gleich dem
Quadrat einer natürlichen Primzahl ist. Ferner stützen wir uns
auf den bekannten Satz der Analysis, nach dem ein unendliches
Produkt
(1 — Si) (1 — 32) (1 — 3s) •••
unbedingt konvergiert und einen von Null verschiedenen Grenz-
wert hat, wenn
3i + 3a + 3?. + • • •
eine unbedingt konvergente Reihe ist, und keines der & = 1 ist.
Wir teilen danach die Primideale p in zwei Arten, pn p2, und
zwar sollen die px vom ersten Grade sein und zum Exponenten
<p = 1 gehören (also e = h). Die p2 sollen entweder vom zweiten
Grade sein, oder zu einem höheren Exponenten <p gehören. Es
sind also pi die zur Hauptklasse gehörigen Primideale
ersten Grades.
Dann ist
W(p1)’’ = N(px) = P1
eine natürliche Primzahl und
mindestens die 2te (höchstens die 2Äte) Potenz einer Primzahl.
Nach dem erwähnten analytischen Satze ist dann das Produkt
77[1 - N(p.2)-^J£
für s = 1 endlich und von Null verschieden, und es folgt aus
(20), (21) der Satz:
6.
Der Grenzwert
Lim II
s = 1
g — 1
IZ[l-W(p1)-’JÄ
ist endlich, wenn p, die Primideale
der Hauptklasse Ax durchläuft.
ersten Grades
Ein besonderes Interesse nimmt die Frage in Anspruch, ob
dieser Grenzwert verschwinden kann.
§ 164.
Der Klassenkörper.
607
§ 164. Der Klassenkörper.
Zu der Zahlgruppe A in dem quadratischen Körper SS soll
ein algebraischer Körper über SS existieren, den man mit SI oder
St (A) bezeichne, von dem wir nur voraussetzen wollen:
7. Definition des Klassenkörpers.
Die Primideale px ersten Grades der Hauptklasse
JL15 und nur diese, sollen im Körper’ ®(JL) wieder in
Primideale ersten Grades zerfallen.
Es sind also nur die Primideale in SS, die wir vorhin mit p,
bezeichnet haben, die in ® in Primideale ersten Grades zerfallen.
Eine beliebige endliche Anzahl von Primzahlen können dabei
ausgenommen sein. Sie werden dann in den Exkludenten ge-
nommen.
Ist n der relative Grad des Körpers ß über SS und p eine
natürliche Primzahl, in der die Ideale pj und in SS und St
aufgehen, und bezeichnet man mit Ns, N& die absoluten Normen
im Körper SS und St, so ist
-W) = ^(Pi) = P, -^«(Pi) = P",
und folglich muß px im Körper St in n Primideale zerfallen:
(I)
Die Primideale, die in den Grundzahlen der Körper SS oder St
aufgehen, sollen immer ausgeschlossen sein. Dann sind die sß15
^ß2, ..., voneinander verschieden.
Ob ein solcher Körper Si existiert, bleibt vorläufig unentschieden.
Wir wollen untersuchen, was aus der Definition geschlossen werden
kann.
Da in jedem Ideal pj n Ideale aufgehen, so ist
(2)
worin sich das erste Produkt auf alle Ideale px des Körpers SS,
das zweite auf alle Ideale Sß ersten Grades des Körpers St er-
streckt, und nach dem für jeden beliebigen Körper gültigen
Satz I, § 197 des II. Bandes hat
(3) (s — l)ffr------------=i
für s = 1 einen von Null verschiedenen endlichen Grenzwert, der
dort auf die Klassenzahl im Körper St zurückgeführt ist. Setzen
wir zur Abkürzung
608
Dreiundzwanzigster Abschnitt.
§ 164.
p = n-.-------------
[1 - W(P1r]
so ist nach (2) und (3) für s = 1
(5) (s — 1) Pn endlich und von Null verschieden,
und nach § 163, 6.:
(6) (s — 1)FÄ endlich,
und wenn man hieraus P eliminiert, so folgt:
(s — i)»-ä endlich.
Also ist
(7) n > h.
Daraus folgt der Satz:
8. Der Relativgrad n des Klassenkörpers kann
nicht kleiner sein als die Klassenzahl h der Gruppe.
Ist n = h, so ist (s — l)^*1 für s = 1 nicht Null,
und die Summen Q2, Qs, ..., Qh sind gleichfalls von
Null verschieden.
Kann man eine Gleichung in ü vom Grade h bilden, aus
der sich ein Körper ableiten läßt, der die charakteristischen
Eigenschaften des Klassenkörpers erkennen läßt, und ist der Grad
dieses Körpers nicht größer als h, so folgt also, daß er auch
nicht kleiner sein kann, also = h sein muß. Damit ist die Ir-
reduzibilität der fraglichen Gleichung erwiesen.
Hierauf beruht der Nachweis der Irreduzibilität der Kreis-
teilungsgleichung, den wir im § 198 des II. Bandes gegeben
haben. Dort trat an Stelle von Sl der Körper der rationalen
Zahlen. Im nächsten Abschnitt werden wir noch weitere An-
wendungen hiervon machen.
Ob es Gruppen gibt, bei denen der Grad des Klassenkörpers
größer als die Klassenzahl ist, bleibt dahingestellt. Ich halte es
für unwahrscheinlich.
Wir beweisen noch, daß es höchstens einen Klassenkörper
geben kann. Jeder solche Körper wird durch Adjunktion einer
algebraischen Zahl zu ß erzeugt.
Es sei | eine den Klassenkörper = ü (|) erzeugende
ganze Zahl, die also einer in Sl irreduzibelen Gleichung
(8) /(|) = ^+air-1+a2r-2+- •• + «» = 0
genügt, in der die «j, «2, ..., a„ ganze Zahlen in £1 sind.
§ 164. Der Klassenkörper. 609
Jede ganze Zahl y des Körpers ft kann (Bd. I, § 151) in der
Form dargestellt werden:
worin <p(£) ganze Koeffizienten in Sl hat. Man kann dies in die
Form setzen:
(9) w = y0 + H------F Z«-i T“1,
worin 7, y0, ylf ..., 7„—, ganze Zahlen in Sl sind, und so, daß die
erste, 7, ein Teiler der Diskriminante von f ist. Die Prim-
faktoren von 7 schließen wir durch den Exkludenten aus.
Es sei
5ß ein Primideal ersten Grades in ft,
pj das durch teilbare Primideal ersten Grades in ü,
. p die Norm von px und von
dann ist für jede ganze Zahl r in ft:
a? = u (mod pj
und
(10) = £ (mod 5ß),
also nach (9) für jede ganze Zahl in ft:
(mod sJß).
9. Die notwendige und hinreichende Bedingung
dafür, daß ft(|) Klassenkörper sei, besteht also
darin, daß für jedes in einem p! aufgehende Prim-
ideal $ und nur für dieses die Kongruenz (10) er-
füllt sei.
Es seien nun
ft = ß(£), ft' = ß(g')
zwei Klassenkörper derselben Gruppe A. Zunächst ergibt sich
leicht, daß sie von gleichem Grade sein müssen. Denn für
beide muß die Bedingung (5) erfüllt sein. Sind also n und n'
die Grade, so muß (s — 1)«'-« für s = 1 endlich und von Null
verschieden sein, was nur möglich ist, wenn n = n' ist.
Durch Zusammensetzung von ft und ft' leiten wir einen
dritten Körper ab:
ft" = ß(^,r),
von dem wir zeigen, daß er auch ein Klassenkörper ist.
Weber, Algebra. IH. gg
610 Dreiundzwanzigster Abschnitt. § 164.
Den Körper R" können wir erzeugen durch eine Zahl:
(11) S' = «I +
in der a, a' ganze Zahlen in SI sind.
Es sei iß" ein in einem px auf gehendes Primideal in ft" und
iß, iß' die durch iß" teilbaren Primideale in ft, ft' und N (pj) — p.
Dann ist nach 9.:
(12) r = i (mod iß), gp = r (mod iß'),
und folglich ist nach (11):
(13) r* = = r (mod iß").
Ist umgekehrt die Kongruenz (13) befriedigt,- so folgen daraus
wieder die Kongruenzen (12), weil man | und £' rational [in der
Form (9)] durch ausdrücken kann.
Es ist also ft" ebenfalls Klassenkörper, und sein Grad ist
ebenso hoch wie der von ft und ft'. Es sind also | und £' pri-
mitive Zahlen von ft", und folglich sind alle diese Körper iden-
tisch (Bd. I, § 151, 3.). Ist ft ein Klassenkörper, so sind die mit
ft konjugierten Körper auch Klassenkörper und sind daher mit ft
identisch.
Damit ist der Satz bewiesen:
10. Es gibt für eine gegebene Zahlgruppe nur
einen Klassenkörper, und dies ist ein Normalkörper.
Wir wollen nun die hauptsächlichsten Eigenschaften] und
Anwendungen des Klassenkörpers in den aus der komplexen
Multiplikation stammenden Fällen näher kennen lernen.
Nehmen wir an, daß die Zahlgruppe A eine andere Gruppe
A' als Teiler von endlichem Index (A, A') enthalte, und daß
diese beiden Gruppen Klassenkörper besitzen:
ft = ft(M) = ß(i),
k 7 ft'= ft (A') = &(£'),
dann läßt sich beweisen, daß der Körper ft in ft' enthalten ist.
Sind nämlich pn pi die Primideale in SI ersten Grades der Haupt-
klassen A^Ai, dann sind die pj unter den pj enthalten. Wenn
daher p die Primzahl ist, in der p, und p] aufgeht, so ist nach 9.:
= £ (mod 5ß) für alle p, und folglich für alle pj,
£'p = (mod iß') für alle pj,
wenn iß und iß' Primideale ersten Grades in ft und ft' sind.
§ 165. Primideale in den Klassen. 611
Wir bilden jetzt den Körper:
(16) ß" = Ä(^') = ß(n,
indem wir
(17) r = «i + «'r
setzen, und bezeichnen ein Primideal ersten Grades dieses Körpers,
das in einem pj aufgeht, mit iß".
iß, iß' seien, wie oben, die durch iß" teilbaren Primideale in
ft, Dann ist nach (15) und (17)
= £" (mod iß"),
und folglich ist ft" ein Klassenkörper von A'.
Demnach ist ft" mit ft' identisch; ist eine primitive Zahl
von ft", und folglich kann jede Zahl in ft", also auch rational
durch ausgedrückt werden.
Daraus folgt:
11. Enthält eine Zahlgruppe A eine andere Zahl-
gruppe A' als Teiler von endlichem Index, und exi-
stieren die Klassenkörper ft(JL), ft(A'), so ist ft(A)
in ft(JL') enthalten.
§ 165. Primideale in den Klassen.
Wir kehren jetzt zu den Funktionen Q zurück, die wir in
§ 163, (16) durch unendliche Reihen und in § 163, <18) durch
unendliche Produkte:
(1)
ox - - n-
i-zW
dargestellt haben, worin %x einen der Charaktere der Gruppe
bedeutet und p alle Primideale in 0 durchläuft. Den Loga-
rithmus dieses Produktes entwickeln wir in folgender Weise:
los© — | 1 V Z*(E2) । 1 X1 Z* (fr3) ।
Das Vielfache von 2?ri, das in dem log() nicht näher definiert
ist, brauchen wir nicht zu kennen, da es sich mit s nur unstetig
ändern könnte, und da rechts und links stetige Funktionen von
s stehen, solange s > 1 ist, so ändert sich dieses Vielfache über-
haupt nicht mit s.
Es sei Ai eine der Klassen der Idealgruppe A und Ai die
entgegengesetzte Klasse. Dann ist nach (12), (13), (14), § 163:
1C _
2 t* (A'i) %z(a) = h oder = 0,
39*
612 Dreiundzwanzigster Abschnitt. § 166.
je nachdem das Ideal a in der Klasse At oder in einer anderen
Klasse enthalten ist. Multiplizieren wir also die Formel (2) mit
%x(Ai) und summieren in bezug auf %, so folgt:
1 x
-2?Zz(M;)log&
ll
(3) (i) j 1 (2) 1 1 (3) 1
= ZSyQjy + 2Sjv(P)2S + H >
(1) (2) (3)
worin sich die Summen 2?, 2?, 2?,... auf alle Primideale p erstrecken,
deren erste, zweite, dritte, ... Potenz in der Klasse At enthalten ist.
(2) (3)
Wir gehen in (3) zur Grenze s = 1 über; die Summen2?, 2?, ...
behalten dabei einen endlichen Wert, da ihre unbedingte Kon-
vergenz für s = 1 nicht aufhört. Dasselbe gilt von dem Teil
(!)
der Summe 2T, der sich auf Primideale von höherem als dem
ersten Grade bezieht, und es bleibt also nur noch fraglich, ob
die Summe
S n (py ’
erstreckt über alle Primideale ersten Grades der Klasse Ai, endlich
bleibt oder unendlich wird. Ersteres würde der Fall sein, wenn
es in Ai gar keine oder nur eine endliche Anzahl von Primidealen
ersten Grades gäbe.
Setzen wir aber die Existenz eines Klassenkörpers vom Grade
voraus, so folgt aus § 164, 8. und § 163, (21), daß
log Qu log Qs, •••, log Qh
endliche Grenzwerte behalten, während log unendlich wird. Die
linke Seite von (3) wird also unendlich und die rechte Seite kann
nicht endlich bleiben.
Damit ist bewiesen:
12. Wenn ein Klassenkörper existiert, dessen Grad
nicht höher ist als die Klassenzahl, so enthält jede
Klasse unendlich viele Primideale ersten Grades.
§ 166. Primideale in den Idealklassen.
Nehmen wir als Gruppe zunächst die Gesamtheit der Zahlen 0
des Körpers Sl ohne die Null, so sind die Klassen die Ideal-
klassen des Körpers ü, die, wie wir gesehen haben, den Klassen
quadratischer Formen der Diskriminante A eindeutig zugeordnet
§ 167. Primzahlen in Linearformen. 613
werden können. Nehmen wir als Gruppe die Ordnung 0' = [0]
mit dem Führer Q, die durch die Kongruenzbedingung definiert
ist, daß jede Zahl in 0' nach dem Modul Q mit einer rationalen
Zahl kongruent sein soll, so haben wir eine Kongruenzgruppe,
deren Exkludent und Modul — Q ist. Die Klassen entsprechen
den Formenklassen der Diskriminante D = Der zweite
Fall schließt den ersten in sich (für Q = 1). Der Klassenkörper
ist hier der Klassenkörper ®(D), den wir zum Unterschied von
allgemeineren als Ordnungskörper bezeichnen wollen.
Denn ist (k~) eine Klasseninvariante, so ist (§ 122)
(fc)r = (k) (mod 5ß)
nur dann befriedigt, wenn p durch die Hauptklasse der Dis-
kriminante D darstellbar ist. Dann zerfällt p in ß in zwei kon-
jugierte Primideale p, p', die durch Zahlen in 0 oder in 0'
darstellbar, also Hauptideale sind.
Der Körper Ä(z/) ist der Klassenkörper von ü im
engeren Sinne, der den Idealklassen dieses Körpers entspricht,
und auch als Haupt-Klassenkörper $(&) bezeichnet sein mag.
In jeder Idealklasse, sowohl nach 0 als nach 0', gibt es
also unendlich viele Primideale ersten Grades. Mit anderen
Worten: Ist ci ein beliebiges (zu Q teilerfremdes) Ideal, so gibt
es unendlich viele Primideale p, die mit ci nach 0' äquivalent
sind. Dann sind nach § 95 auch die den Ideialen a und p ent-
sprechenden Formen äquivalent, und p ist durch die zu ci gehörige
Form darstellbar. Damit ist der Satz bewiesen:
1. Durch jede primitive Form der Diskriminante
D sind unendlich viele Primzahlen darstellbar1).
§ 167. Primzahlen in Linearformen.
Wir definieren nun eine Zahlgruppe d in fl folgender-
maßen :
*) Dieser Satz, sowohl für negative als für positive Diskriminanten, ist
zuerst von Diriehlet bewiesen, der Beweis aber nur in einem speziellen Fall
publiziert (Bericht der Berliner Akademie 1840, Werke Bd. I, S. 497). Der
ausgeführte Beweis ist von H. Weber gegeben (Mathematische AnnalenXX,
1882). Eine gleichfalls von Diriehlet herrührende Verallgemeinerung, auf
die wir im nächsten Paragraphen zurückkommen, ist von A. Meyer be-
wiesen. (Grelles Joum., Bd. 103). Der hier im Text gegebene Beweis beruht
auf anderer Grundlage, bezieht sich aber freilich einstweilen (solange der
Klassenkörper für positive Diskriminanten nicht bekannt ist) nur auf negative
Diskriminanten.
614 Dreiundzwanzigster Abschnitt. § 167.
Es sei m ein ganzes Ideal in ü, und A bestehe aus allen
ganzen und gebrochenen Zahlen a in fl, die zu tn teilerfremd
sind und der Bedingung genügen:
(1) a = 1 (mod tn).
Nehmen wir die Primteiler von in in den Exkludenten, und
bezeichnen mit 0 die Gruppe der Zahlen in ß, so zerfällt 0
nach dem Modul tn in tp(in) Zahlklassen, worin tp(in) die Be-
deutung wie in Bd. II, § 168 hat, nämlich, wenn p die Primteiler
von tn durchläuft:
(2) ^(m) = 2V(m) ZT^i__L_y
In die Gruppe A gehören nicht bloß einzelne Zahlen, sondern
Zahlklassen nach dem Modul m. Hiernach ist:
(3) (0, A) = ^(tn).
Um die Klassenzahl für unsere Gruppe zu bestimmen, wenden
wir die Sätze des § 161 an.
Danach ist, wenn E die Gruppe der funktionalen Einheiten
und E die Gruppe der numerischen Einheiten bedeutet:
(Ö, EA) = (Ö, EO) (EO, EA),
(E0,Eä) = (EO, EEA) = (0, EA).
Weiter ist
(0, EA) (EA, A) = (0, A) = tp(tn).
(EA, A) — e ist die Zahl der nach nt inkongruenten Einheiten,
und
(Ö, EO) = H
die Klassenzahl des Körpers
(Ö, EA) = h
die Klassenzahl nach A. Daraus ergibt sich:
(4) h =
v '• e
Die Zahl e ist im allgemeinen gleich der Anzahl der Ein-
heiten in 42, also = 2, und in den beiden Ausnahmefällen
A = —4, A = —3 ist e = 4 und e = 6. Die Zahl e ist
kleiner, wenn unter den Einheiten Kongruente (modulo tn) vor-
kommen, was nur möglich ist, wenn nt ein Teiler von 2 oder
von 3 ist.
§ 167. Pi’imzahlen in Linearformen. 615
Bedeutete? die Gruppe der Einheiten oder auch eine
darin enthaltene Gruppe, so bekommen wir denselben
Wert der Klassenzahl und denselben Klassenkörper,
wenn wir EA an Stelle von A treten lassen.
Dies gilt nicht nur für diese besondere Gruppe, sondern
allgemein. Wir hätten also z. B. die Zahlen a, der Gruppe A
auch durch
es = +1 (mod m)
definieren können, denn E = —|— 1, —1 ist auch in den Aus-
nahmefällen A = —4, A = —3 eine Gruppe.
Nun läßt sich nachweisen, daß der Teilungskörper Ain der
Klassenkörper zu A ist. Schließen wir zunächst noch alle in
der Diskriminante des Teilungskörpers aufgehenden Primfaktoren
aus, und bezeichnen mit r irgend eine Zahl des Teilungskörpers,
so ist nach § 160
(5) r1’ = r (mod p)
nur dann erfüllt, wenn p ein Primideal ersten Grades in Ä
ist, das der Hauptklasse angehört. Das aber ist das Kennzeichen
des Klassenkörpers. Der Grad des Teilungskörpers ist aber nach
§154 höchstens gleich dem in (4) gegebenen Ausdruck A, folglich
ist er genau gleich h und die Teilungsgleichung irreduzibel.
Außerdem ist damit bewiesen, daß es in jeder der Idealklassen
Av nach A unendlich viele Primideale ersten Grades gibt.
Man kann diesem Satz folgenden Ausdruck geben:
Ist ß eine beliebige Zahl in 0, ci ein beliebiges Ideal in 0,
so ist durch
(6) Av = aß A
eine Klasse nach A bestimmt (§ 161), und in dieser Klasse sind
unendlich viele Primideale ersten Grades enthalten. Ein solches
Primideal ist nach (6) in der Form darstellbar:
(7) p = aßa,
worin a = 1 (mod m) ist. Setzen wir also
aß = n,
so ist
n = ß (mod in).
Daraus folgt:
2. Ist ß eine Zahl in 0, ci ein Ideal in 0, so gibt
es unendlich viele im allgemeinen gebrochene Zahlen
n in 0, die der Bedingung
Dreiundzwanzigster Abschnitt.
§ 168.
616
(8) n = ß (mod tn)
genügen, für die
(9) p = an
ein Primideal wird.
Nimmt man ci = 1, so wird n eine ganze Zahl, also eine
in ß existierende Primzahl. Der Satz lautet für diesen beson-
deren Fall:
3. Es gibt im Körper £1 unendlich viele existie-
rende Primzahlen n, deren Norm eine natürliche
Primzahl ist, die nach einem beliebigen Modul m
mit einer beliebigen zu in teilerfremden Zahl ß
kongruent sind.
Nehmen wir für den Modul nt eine ganze Zahl p in ß, so
erhalten wir folgenden Satz:
4. Ist p eine ganze Zahl in ß, so sind in der
Linearform
in der | die ganzen Zahlen von ß durchläuft und
ß relativ prim zu p ist, unendlich viele Primzahlen
enthalten.
Man hat hier eine schöne Verallgemeinerung des Satzes von
den Primzahlen in arithmetischen Progressionen (Bd. II, § 198) ').
§ 168. Reduktion der Klassengleichung in den Kreisteilungs-
körpern.
Wir definieren eine weitere Gruppe A durch folgende Be-
stimmung:
Es seien (), m zwei ganze rationale Zahlen, deren Prim-
faktoren wir in den Exkludenten 8 aufnehmen. 0 sei wie in
§ 98 die Gruppe der Zahlen in ß, und 0' die Gruppe der Zahlen
der Ordnung [0], undA bestehe aus allen ganzen und gebrochenen
Zahlen a in 0', die der Kongruenzbedingung
(1) -N(a) = 1 (mod m)
genügen. Zunächst haben wir die Klassenzahl
(2) h = (Ö, EA) = (Ö, EO') (EO', EA)
*) Für den Fall A = —4 ist dieser Beweis gegeben von H. Weber,
Grelles Journ., Bd. 129 (Dirichlet-Band), für A — —3 in einer Straßburger
Dissertation von H. Bresslau (Straßburg 1907).
§ 168. Reduktion der Klassengleiehung in den Kreisteilungskörpern. 617
zu bestimmen. Der erste Faktor ist die Klassenzahl der quadra-
tischen Formen der Ordnung 0' [§ 100, (3)], die wir mit H'
bezeichnen. Es ist also
(3) h = H (EO1, EA) = A)
(nach § 100, 13.).
Es bleibt noch (0', A) zu bestimmen.
Bedeutet p2,..., ein vollständiges Repräsentantensystem
von 0' nach A, so müssen die Zahlen
(4) W(01), JV(p2).., JV(p,)
nach dem Modul m alle verschieden sein, und jede Norm einer
Zahl in 0 ist mit einer dieser Zahlen nach m kongruent. Ist
daher Z die Gruppe der rationalen Zahlen, die Gruppe der
Zahlen z aus Z, die der Bedingung
z = 1 (mod »<)
genügen, die Gruppe der Normenreste nach w, so ist (4) ein
vollständiges Repräsentanten System von nach Jf und folglich
= (0', A) = (^ M).
Dafür kann man auch setzen (§ 100, 12.):
«y, V=
(7)
(5)
Nun ist
(6) (Z, AL) — <p(m) = mll(l —
wenn r die Primfaktoren von m durchläuft und folglich
_ FZ'y(m)
n - (Z, Hm)'
Den Klassenkörper <Q(Z) unserer Gruppe erhalten wir, wenn
wir dem Klassenkörper $(D) eine primitive mte Einheitswurzel
adjungieren:
(8) $(4) = ©
Denn die Bedingung dafür, daß ein in einer Primzahl p auf-
gehendes Primideal 5ß des Körpers $ (D, p) vom ersten Grade sei,
ist, wenn (k) eine Klasseninvariante der Diskriminante JD bedeutet:
(9) (k)p = (&)> Qp = p (mod iß),
wenn alle störenden Primzahlen, z. B. die in den Diskriminanten
der die Zahlen (k) und (p) definierenden Gleichungen, in den
Exkludenten 8 aufgenommen sind.
618 Dreiundzwanzigster Abschnitt. § 168.
Die erste der Bedingungen (9) fordert, daß p durch die
Hauptform der Diskriminante JD eigentlich darstellbar sei (§ 122),
die zweite, daß
(10) p = 1 (mod m)
sei.
Damit eiu Primideal p ersten Grades in ü, das nicht in 8
aufgeht, in DA enthalten sei, ist notwendig und hinreichend, daß
1. p ein Hauptideal, d. h..eine existierende Zahl n sei, und
daß diese Zahl n in A enthalten sei, d. h. daß
2. N(gt) — p = 1 (mod m)
sei. Diese Bedingungen stimmen genau mit den Bedingungen (9)
überein, und folglich ist $(D, p) der Klassenkörper der
Gruppe A.
Der Grad des Körpers ®(A) ist daher nicht nur höchstens,
sondern genau gleich h.
Die Zahl (Z, _Rm) ist = 1, wenn in m keine der charakte-
ristischen Primzahlen des § 108 auf geht, und dann ist der Grad
des Körpers $ (A) gleich H' <p (m). Nehmen wir umgekehrt alle
charakteristischen Primzahlen und Primzahlpotenzen in m auf,
so wird Rm = R die Gruppe der absoluten Normenreste,
und es ist
(Z, R) = 2 g,
wenn g die Anzahl der Geschlechter der Diskriminante D ist
(§ 113, 7.). Bezeichnet also Hg die Anzahl der Klassen eines
Geschlechtes, so ist H' = gHg, und die Formel (7) ergibt:
(11) h =
Nach § 138 zerfällt die Klassenfunktion H_D(u) durch Ad-
junktion von Quadratwurzeln in so viele Faktoren, als es Ge-
schlechter von Formenklassen gibt, und der Grad eines jeden
dieser Faktoren ist Hg.
Wäre nun die Klassengleichung durch Adjunktion irgend
welcher Einheitswurzeln noch weiter zerlegbar, als nach den Ge-
schlechtern, so könnte man m so annehmen, daß auch diese
Einheitswurzeln und auch tfÄ in dem Körper 8t (p) enthalten
wären.
Ist dann h" der niedrigste Grad, auf den die Klassengleichung
durch Adjunktion von Einheitswurzeln reduziert werden kann, so
ist der absolute Grad des Körpers $(D, p) höchstens gleich h" (p(m)
§ 169. Beziehung der Teilungskörper zu dem Klassenkörper. 619
und der Relativgrad in bezug auf höchstens gleich | h" <p (m),
und daraus geht nach (11) hervor, daß h" nicht kleiner als H'g
sein kann. Damit ist bewiesen:
5. Die Klassengleichung D (u) ist in dem Körper,
der alle Einheitswurzeln enthält, nicht weiter zer-
legbar als in die den Geschlechtern entsprechenden
Faktoren.
§ 169. Beziehung der Teilungskörper zu dem Klassenkörper.
Wir haben in den beiden letzten Paragraphen zwei Arten
von Gruppen betrachtet, von denen die erste zu den Teilungs-
körpern der elliptischen Funktionen, die zweite zu den Ordnungs-
körpern in Verbindung mit Einheitswurzeln führte. Zwischen
diesen besteht eine Beziehung:
Die erste Gruppe A bestand aus den Zahlen a in 0, die der
Bedingung
(1) a = +1 (mod tn)
genügten, wenn m irgend ein Ideal in £1 ist, die zweite Gruppe
A' bestand aus den Zahlen «' der Ordnung [$], die der Bedingung
(2) jV(a') = 1 (mod m)
genügten, wenn m und Q natürliche Zahlen bedeuten.
Nehmen wir an, es sei nt ein Primideal oder eine Potenz
eines Primideals, so können wir Q und m so annehmen, daß die
Gruppe A' in der Gruppe A enthalten ist.
Denn ist r eine rationale Zahl, so ist, da a' der Ordnung
[0] angehört:
(3) a' = r (mod Q), N(ar) = r2 (mod Q),
und wenn Q durch m teilbar ist:
(4) a' = r (mod m),
also nach (2) und (3)
r2 = 1 (mod m)
(5) (r — 1) (r 1) = 0 (mod m),
wir nehmen also Q durch m und m durch in teilbar an; dann
ist nach (5), wenn in, wie wir angenommen haben, ein Primideal
oder eine Potenz eines solchen ist, entweder
(6) r = 1 oder r = — 1 (mod m),
620 Dreiundzwanzigster Abschnitt. § 169.
und aus (4) folgt:
(7) a' = +1 (mod tn);
folglich ist A' in A enthalten, und nach § 164, 11. ist also $(A)
in ß(A') enthalten. Da nun nach § 158 jeder Teilungskörper sich
aus solchen zusammensetzen läßt, deren Teiler ein Primideal oder
eine Potenz eines Primideals ist, so folgt:
6. Der Teilungskörper der elliptischen Funktionen
ist zurückführbar auf Ordnungskörper und Kreis-
teilungskörper1).
*) Auf anderem Wege ist ein Teil dieses Satzes bewiesen in der Straß-
burger Dissertation von Daniel Bauer, „Über den Teilungskörper der
elliptischen Funktionen mit singulärem Modul“. Straßburg 1903.
FÜNFTES BUCH.
ALGEBRAISCHE FUNKTIONEN.
Vierundzwanzigster Abschnitt.
Algebraische Funktionen einer Variablen.
§ 170. Einleitendes.
Die Theorie der algebraischen Funktionen einer Veränder-
lichen ist der Ausgangspunkt der allgemeinen Untersuchungen
von Abel über die neuen Transzendenten, die seitdem den Namen
„Abelsche Funktionen“ erhalten haben, und die höchste Ver-
allgemeinerung der elliptischen Funktionen sind. Die Haupt-
probleme dieser Theorie sind durch die Arbeiten von Riemann,
Weierstrass, Clebsch, Brill und Noether zu einem gewissen
Abschluß gebracht. Insbesondere hat Riemann in der Vor-
stellung der mehrblätterigen (Riemannschen) Flächen ein durch
seine Anschaulichkeit außerordentlich wirksames Hilfsmittel für
die Untersuchung dieser Funktionen geschaffen.
Alle diese Untersuchungen aber, die sich einerseits auf die
Funktionentheorie, andererseits, wie beiClebsch, Brill, Noether,
auf die Methoden der rationalen Algebra (Theorie der Formen
und Invarianten oder der algebraischen Kurven) stützen, müssen
immer gewisse Einschränkungen machen, sie müssen gewisse
„Ausnahmefälle“ ausschließen und sich mit der Behandlung der
sogenannten allgemeinen Fälle begnügen. Nicht unterworfen ist
dieser Beschränkung die nach Analogie der Zahlentheorie von
Dedekind und mir ausgearbeitete Theorie der algebraischen
Funktionen, von der hier eine Übersicht gegeben werden soll1).
*) Zur Literatur über algebraische und Abelsche Funktionen sei hier
erwähnt: Abel, Mem. sui- une propriete generale d’une classe tres-etendue
de fonctions transcendentes (1826 der Pariser Akademie vorgelegt, Werke,
neue Ausgabe von Sylow und Lie, Bd. I, S. 145). Riemann, Theorie der
Abelschen Funktionen, Grelles Journ., Bd. 54, 1857, Werke 2. Aufl., Nr. 88.
Weierstrass, Vorlesungen 1875/76, Werke, Bd. IV. Clebsch, Über die
624
Vierundzwanzigster Abschnitt.
§ 171.
§ 171. Definition der algebraischen Funktionen.
Eine Variable 0 heißt eine algebraische Funktion einer un-
abhängigen Veränderlichen z, wenn die beiden Variablen durch
eine algebraische Gleichung
(1) F(ß,z) = 0
miteinander verbunden sind. F bedeutet hierin einen Ausdruck
von der Form
(2) F(ß,Z) = dg 0n —fljd”-1 —••• —ctn,
dessen Koeffizienten a0, alt ..., an ganze rationale Funktionen
von z ohne gemeinschaftlichen Teiler sind. Über die konstanten
Koeffizienten in diesen Ausdrücken machen wir weiter keine
Voraussetzung, als daß es reelle oder komplexe Zahlen sind1).
Wir setzen dabei die Funktion F(fi,z') in dem Sinne als
irreduzibel voraus, daß sie nicht in Faktoren zerfallen soll, die
selbst rationale Funktionen von 0 und z sind.
Jede ganze Funktion Cr(0,^) läßt sich nach Bd. I, § 20
nm- auf eine Weise in irreduzible Faktoren zerlegen (abgesehen
von konstanten Faktoren). Wir sagen, daß die Funktion G(ß,z)
Anwendung der Abelschen Funktionen in dei- Geometrie, Grelles Journ.,
Bd. 63, 1864. Clebsch und Gordan, Theorie der Abelschen Funktionen,
Leipzig 1866. Brill und Noether, Uber die algebraischen Funktionen und
ihre Anwendung in der Geometrie, Mathematische Annalen VII, 1874. Brill
und Noether, Die Entwickelung der Theorie der algebraischen Funktionen,
Bericht der Deutschen Mathematiker-Vereinigung 1894. Appell et Goursat,
Theorie des fonctions algebriques, Paris 1895. Über die zahlentheoretischen
Methoden: Kronecker, Über die Diskriminante algebraischer Funktionen,
Grelles Journ., Bd. 91, 1881, und: Festschrift zu Kummers Doktor-Jubiläum,
Grelles Journ., Bd. 92, 1881. Dedekind und Weber, Theorie der algebrai-
schen Funktionen einer Veränderlichen, Grelles Journ., Bd. 92, 1879. Hensel
und Landsberg, Theorie der algebraischen Funktionen einer Variablen,
Leipzig 1902. Die Form der Theorie, die im folgenden dargestellt ist, stützt
sich auf den in Bd. II, § 153 eingeführten Begriff der Funktionale, die
in dieser Form bereits in einer von Wellstein angeregten Straßburger
Dissertation von Rehfeld (1906) zur Behandlung eines speziellen Problems
der'Funktionentheorie angewandt wurden.
') Es würde nirgends eine Lücke bleiben, wenn wir uns dabei auf
algebraische Zahlen beschränken wollten. Betrachtet man 0, z als
Cartesische Koordinaten in der Ebene, so stellt die Gleichung (1) eine
algebraische Kurve dar, und man kann die Theorie dieser Kurven anwenden,
wie es Clebsch und Gordan und Brill und Noether getan haben.
Freilich haben dabei nur die reellen Werte dieser Variablen eine wirklich
anschauliche Bedeutung.
§ 171. Definition der algebraischen Funktionen. 625
dann und nur dann verschwinde, wenn unter ihren irreduziblen
Faktoren die Funktion F(ß,z) vorkommt. Dies ist die Definition
des Verschwindens, nach der, wenn man ganz korrekt sein wollte,
eine jede Gleichung Gr (0, z) = 0 als Kongruenz nach dem Modul F
aufzufassen wäre. Um nicht weitläufig zu sein, wollen wir aber
diese Ausdrucksweise hier nicht brauchen.
Wenn wir die Gleichung (1) durch a0 dividieren, so erhält
sie die Form
(3) f(fi,z) = fl« + M*"1 + M"-2 4-F Jn-rÖ + Sn,
worin die &2, ..., b„ ganze oder gebrochene rationale Funk-
tionen von z sind.
Das System aller ganzen und gebrochenen rationalen Funk-
tionen 0(0, z) von 0 und z, in denen der Nenner nicht durch F
teilbar ist, also nicht verschwindet, hat die Eigenschaft, sich
durch Addition, Subtraktion, Multiplikation und Division (außer
durch 0) zu reproduzieren, und bildet daher einen Körper
algebraischer Funktionen (Bd. I, § 146), den ich mit H
bezeichnen will.
Der Grad n der irreduziblen Gleichung (2) oder (3), also
der Gleichung niedrigsten Grades, der 0 genügt, heißt der Grad
des algebraischen Körpers in bezug auf 0 oder auch der
Grad von 0.
Ist <p(0) eine ganze Funktion von 0, deren Koeffizienten
ganze oder gebrochene rationale Funktionen von z sind, so kann
man durch Division eine Gleichung bilden:
<p(0) = /(0)2(0) + r(0),
worin ^(0) und r(0) ebensolche Funktionen wie <p sind, von
denen jedoch r(0) höchstens vom Grade n — 1 ist. Wegen
(3) ist dann
(4) <p(0) = r(0).
Ist <jp(0) nicht durch /(0) teilbar, so haben die beiden
Funktionen keinen rationalen Teiler gemein, und man kann zwei
Funktionen des Körpers /i (0), 9^ (0) so bestimmen, daß
/(ö)A (0) + 9> (0)^(0) = 1
wird (Bd. I, § 6). Da nun /(0) = 0 ist, so folgt hieraus:
Weber, Algebra. IU.
40
626 Vierundzwanzigster Abschnitt. § 171.
Man kann also jede gebrochene Funktion von 0 durch eine
ganze Funktion von 0 ersetzen und erhält so den Satz:
1. Jede Funktion t, des Körpers £1 läßt sich auf
eine einzige Weise in die Form setzen:
(6) £ = Xo -j- x-i 0 -j~ x2 02 -j- • • • -j- xn—i 0n~ \
deren Koeffizienten rationale
Funktionen von z sind.
Daß dies überhaupt möglich ist, schließt man aus (4) und
(5); daß es nur auf eine Weise möglich ist, folgt aus der Irre-
duzibilität von /(d); denn hätte man zwei verschiedene Dar-
stellungen einer und derselben Größe £ in der Form (6), so
würde ihre Differenz eine Gleichung für 0 von niedrigerem als
ntem Grade ergeben.
Wählt man n Funktionen des Körpers SZ beliebig aus:
Vi = + %?0 + ••• +
= + -------------
(?)
+ -----ix^0n-\
mit der einzigen Beschränkung, daß die Determinante
2? + x§> x^>... x^L.!
nicht identisch Null ist, so kann man durch Elimination der
Potenzen von 0 aus (6) und (7) jede Funktion g in SZ in die
Form setzen:
(8) i = yim H---------------F yny»,
deren Koeffizienten yt rationale Funktionen von z sind.
Ein solches System von Funktionen ..., yn heißt eine
Basis des Körpers SZ.
Damit ein Funktionensystem i;2, ..., eine Basis von SZ
bilde, ist notwendig und hinreichend, daß keine Gleichung von
der Form
yim + 3/2^2 H------F y«yn = 0
bestehe, in der die Koeffizienten yx, y2, ..., yn nicht sämtlich
identisch verschwinden.
So bilden die Funktionen
1, 0, 02, .... 6”-1
eine Basis von SZ.
§ 172.
Normen und Spuren.
627
Der Übergang von einer Basis t]n zu einer anderen
iji, Vz, • ••> Vn geschieht durch eine lineare Substitution:
(9) «1, 1?2, •••, i?'») = •••, i?»)
oder kürzer geschrieben
(10) (jli) =
worin L die Bedeutung bat
(11)
/(l,u ^1,2; • • •> ^1, n\
^2,1 f ^2,21 * • *1 ^2, n
\/n,l, ^m,2, •••: ^n,nj
(Bd. II, § 41).
Die Elemente li^ dieser Substitution sind rationale Funk-
tionen von z.
Das System (i/) ist dann und nur dann wieder eine
Basis, wenn die Determinante | L | dieser Substitution
nicht verschwindet.
§ 172. Normen und Spuren.
Wählt man zur Darstellung der Funktionen in Sl eine be-
liebige Basis iji, i;2, • ••> Vn, so kann man, wenn £ eine beliebige
Funktion des Körpers ist, da die Produkte gi;, im Körper ent-
halten sind, setzen:
iVi — ?/i,i Vi + 3/i,a ^2 2/i,>i
(1) t1/! = ’/u *11 T
iVn ?/n,l^l ~H ?/n,2^2 “I“ “I“ 2/w,nl/>i5
und daraus erhält man durch Elimination der 17:
3/i,i — 3/1,2, • • 5 3/1, n
(2) 3/2,1, 3/2,2 —• • 3/2, n = 0
y», 1 j 3/m,2j • •» w £
eine Gleichung, die nach Potenzen von £ geordnet, die Gestalt
erhält:
(3) tp (?) = £" -|- £n~1 H“ ' + i £ bn — 0,
in der < &2, ..., bn rationale Funktionen von z sind. Diese
Koeffizienten sind von der Wahl der Basis unabhängig. Denn
die Gleichungen (1), durch die der Übergang von der Basis
40*
628 Vierundzwanzigster Abschnitt. § 172.
zu der Basis vermittelt wird, können wir nach der Bezeich-
nung (9), (10) des vorigen Paragraphen so darstellen:
(4) W =
und demnach ergibt sich durch Übergang zu der Basis
W = LYL-1^).
Die Funktionen bt, b2, ..., b„ sind also durch die Funktion t,
vollständig bestimmt.
Die Funktion
yi,ii 3/1,2, • • yi,n
y^,i, y^, • • •, y%,n
(5) (-!)»&„ =
y^lt yn,2, •*., t/n,n
heißt die Norm der Funktion £ und wird mit N(t,) bezeichnet.
Über sie gelten folgende Sätze:
1. Wenn nicht identisch Null ist, so ist N(t,)
von Null verschieden.
Denn wenn die Determinante des Systems (1) verschwindet,
so lassen sich rationale Funktionen yt, y2, ..., y„, die nicht alle
verschwinden, so bestimmen, daß
£ («/i Vi + «/ä + —F yn yn) = o
wird, und dies fordert, da i?2, ..., yn eine Basis ist, g = 0.
2. Ist £ eine rationale Funktion von g, so ist
ihre Norm die nte Potenz dieser Funktion.
Denn ist £ rational, so reduzieren sich die Gleichungen (1)
auf die Identitäten ^tji = £ yi. Es verschwinden also in der
Determinante (5) alle Glieder mit Ausnahme der Diagonalglieder,
und diese werden alle gleich Wir drücken diesen Satz durch
die Formel aus:
N (a) = an.
3. Sind zwei Funktionen in ß, so gilt der Satz
(6) N(W) = W(£)W(£').
Denn ist nach (4):
W = (g'^) = Y’(ri,
so ist
(U'^) = YY'fä,
und daraus folgt die Formel (6), weil die Determinante einer
zusammengesetzten linearen Substitution, hier YY', gleich dem
Produkt der Determinante der Komponenten ist.
§ 172. Normen und Spuren. 629
4. Aus 2. und 3. folgt, wenn £ von Null ver-
schieden ist:
= b
und daraus für irgend zwei £':
« O =
5. Ist t eine, unbestimmte oder variable Größe,
und (p(f) die Funktion, die nach (3) für f = £ zu
Null wird, so ist
(8) q>(t) = N(t — £).
Das ergibt sich aus (1) und (2). Denn ersetzt man in (1)
£ durch £ — t, so ist dies gleichbedeutend damit, daß man yiti
durch yit i — t ersetzt und die übrigen yit & ungeändert läßt.
Zerlegen wir die Funktion <p(f), die eine rationale Funktion
von t und z ist, in ein Produkt von irreduziblen Faktoren
<p2(^> ••• so muß einer dieser Faktoren für t = £ ver-
schwinden. Sei dies (f), und
(9) (0 = ^ + H--------------F b'e-J + b'e
sei vom Grade e. Es ist dann cp1 (£) — 0 die Gleichung niedrig-
sten Grades, der £ genügt, und aus £ leitet man einen Körper
SZ-y ab, der in £1 enthalten ist und den Grad e hat. Jede Zahl y
des Körpers ßj kann, und zwar auf eine Art, in der Form dar-
gestellt werden:
(10) y = x0 + ^£ + ••• 4-
Sei ferner
(11) 6f + y1 (ff-1 -|-F yf-x + yf = 0
die Gleichung niedrigsten Grades mit Koeffizienten in der 0
genügt, also f der Relativgrad von Sl in bezug auf
Durch die ef Funktionen
kann jede Funktion des Körpers linear ausgedrückt werden, und
zwischen ihnen besteht keine lineare Gleichung mit rational von z
abhängigen Koeffizienten. Denn sonst würde 0 oder £ aus einer
Gleichung von niedrigerem Grade als f oder e entstehen. Dem-
630 Vierundzwanzigster Abschnitt. § 172.
nach bilden die Funktionen (12) eine Basis des Körpers ß, und
es folgt
(13) ef = n.
Es sind also e und f Teiler von n.
Bedeutet
(W) £x, £2, te
eine Basis des Körpers ß15 so bilden die n Größen:
(15) £20\..., fc = 0, 1, 2, 1
eine Basis von SI. Bildet man die Substitution der e Größen:
(16) (Ui)=?i&),
so ist
(17) (~w = ifj = ^(o
die Norm von £ im Körper Slt, und wenn man die Substitution
für (££i6s) im Körper SI mit der Basis (15) bildet, so ergibt sich
(£&0*) = ?!&) ^(£.0) ... W’*),
woraus
(iß) n& = \y^.
Aus der Substitutionsdeterminante | Fj | leitet man die Funktion
(jpj (f) nach der Formel (2) ab, und es folgt also nach (18):
(19) N(t-£) =
und daraus:
6. Die Funktion <jp(£) = N (t— £) ist entweder
irreduzibel oder eine Potenz einer irreduziblen
Funktion.
Ist der Exponent f dieser Potenz größer als 1, so ist der
Körper SI imprimitiv, Si, ist ein Teilkörper, und SI ist ein Körper
vom Grade f über Si, (Bd. I, § 151)..
Ist f = 1, e = n, so heißt £ eine primitive Funktion
des Körpers SI, und ßj ist mit Si identisch.
Wir kehren zii der Gleichung (2) oder (3) zurück, die, wie
wir gesehen haben, von der Wahl der Basis unabhängig ist, und
definieren den Koeffizienten
(20) —= ?/i,i 2/2,2 + ••• 4* 2/«,n = $(£)
als die Spur der Funktion £. Für die Spur ergeben sich aus
der Definition die folgenden fundamentalen Sätze, in denen £, £'
irgend zwei Funktionen in Si, und x eine rationale Funktion
bedeutet:
§ 173.
Diskriminanten.
631
S(0) — 0,
(211 S(1) S(x$) 47
s(£ + £') = s(0 + s(t,y
Alle Spuren sind rationale Funktionen von
§ 173. Diskriminanten.
Ist y2, ..., yn) = (yf) ein System von n Funktionen im
Körper Sl, so sind die n2 Spuren S(yiyk) rationale Funktionen
von z. Wir definieren als Diskriminante des Systems (1^)
die Determinante
(1) 4 (yh, ; Vn) =
$(»?!%), ..., Sfay»)
S(v'2^l), S(y2y2), ..., S(y2yn)
S^nVi), S(y„y2), .. S(y„yn)
wofür wir auch kürzer z/(^) schreiben.
Wir beweisen den Satz:
7. Die Diskriminante z/(^,) ist dann und nur
dann von Null verschieden, wenn (i^) eine Basis des
Körpers Sl ist.
Nehmen wir, um ihn zu beweisen, zunächst an, daß z/ (ijf) = 0
sei. Dann kann man nach einem elementaren Determinanten-
satz die rationalen Funktionen yu y2, ..., yn, ohne daß sie alle
Null sind, so bestimmen, daß
(2) ?/i S (>h Vk) + y2 S (y2 yk) -|-\-ynS (yn yk) ==
+ y2y2 H-------H = o
(fc = 1, 2, ..., n)
ist. Bedeutet ajj, x2, ..., xn ein beliebiges System rationaler
Funktionen, und setzt man
z3) yi’h + y2 m H--------ynyn = y,
1 J m + % H-----------F *nyn = t,
so folgt aus (2) durch Multiplikation mit xk und Summation:
(4) S(ii2) = 0.
Ist nun (yi) eine Basis, so kann | jede beliebige Funktion
in £1, also auch 1/y sein, und dann gibt die Formel (4) das
widersprechende Resultat S(l) = 0; also kann die Diskriminante
einer Basis (yi) nicht verschwinden.
632 Vierundzwanzigster Abschnitt. § 174.
Um auch das Umgekehrte zu beweisen, nehmen wir an, es
sei ('r]i) eine Basis und
(5) (iß = X(&)
eine lineare Substitution. Das System (iß ist dann und nur
dann gleichfalls eine Basis, wenn die Determinante | X | dieser
Substitution von Null verschieden ist (§ 171). Setzt man nach (5)
q’h = + ^*,2^2 + ••• +
so wird ...
2 V
SC^Vk) — iji'),
und indem man daraus die Determinante bildet:
(6) 4$, ..., iß) = ..., i?„).
Ist also von Null verschieden, so kann |X| nicht ver-
schwinden und (qi) ist eine Basis. Damit ist 7. bewiesen.
Aus (6) ergibt sich noch nach der Definition der Norm in
§172, wenn man iji = gi;,- setzt, und £ eine beliebige Funktion
in Sl ist:
(7) z/(£iß = W(£Pz/(iß.
§ 174. Die Potenzsummen.
Die Spuren der Potenzen von (i
(1) sfc = 8(0*)
sind nichts anderes als die Potenzsummen, die nach den
Newtonschen Formeln berechnet werden können. Da wir aber
hier nicht von den „Wurzeln“ der Gleichung f(ff) = 0 sprechen
dürfen, die wir noch nicht haben, so müssen diese Formeln direkt
aus der Definition der Spur abgeleitet werden.
Ist f(ff) — 0 die den Körper ß definierende Gleichung, so
setzen wir
(2) f(t) — tn a^-1 + ••• + aM-i< + an
und bilden den Quotienten:
(3) t~Q = H-
worin
l/o — 1 ®n—2 0 ~l~ • • ’ ®i0"—2 f)n~
= ®n —2 -f- —3 0 -j- • • • 0”— 2,
(4)
fln-2 = Oj 0,
i7„_i = 1.
§ 174. Die Potenzsummen. 633
Zwischen diesen Funktionen bestehen die Relationen:
0»?o == —
OtJl = Vo — «n-lVn-l,
(5) — Vi —«n-Z^n-l»
f)t]n—1 Vn— 2 ®1 ^ln — Ij
und die 17 0, ijj, ..., 17«-1 bilden eine Basis von £i, da man durch
(4) die Potenzen von 0 linear durch die 17, ausdrücken kann.
Ist also S ein© beliebige Funktion in SI, so kann man setzen:
(6) t = 2/0^0 + yiVl 4“ ••• 4~ «/n —l^n —!•
Wir leiten aus y0, y1, ..., yn-i eine Fortsetzung der Reihe
dieser rationalen Funktionen y„, yn+u «/n + 2, ••• ab, indem wir
setzen:
(7) anyr 4“ «n — 12/r+i 4“ • • • ~F ai yr+n_ 1 yr + n — 0
(r = 0, 1, 2, ...).
Dann ergibt sich aus (5) und (6):
£0 = 170 «/1 4“ *712/z + ••• 4“ ’?»-2«/»-i»
--- Vn — 1 (an?/o 4“ an — 1 ?/l 4“ 4" ®1 Vn — 1)»
= 4~ y^Vi 4“ ••• 4~ y^n-u
und allgemein für ein positives r:
(8) £ 0r = yr^O 4- yr+lVl 4- ” 4- Vr + n—l Vn —11
wie man aus (5) und (7) durch den Schluß von r auf r -|- 1
leicht bestätigt. Ordnet man diese Summe nach Potenzen von 0,
so ergibt sich ein Ausdruck von der Form
(9) £ 0r = a?o, r 4- Xl,rf) 4- ^2, r02 4“ ” 4“ Xn — l,r 6* ~ 4
worin
%0,r — yran — i 4- yr + 1an — 2 4“ ••• 4“ 2/r+n—2«1 4“ Vr + n — li
%l,r = yr«"n — 2 4“ TZr-J-l05« —3 4“ 4“ Vr + n—li
(10)
—2,r yr^i 4” y^-^-li
a-n —l,r == 2/r-
Nach der Definition der Spur [§ 172, (20)] ist aber
(11) S (£) — a?o,o 4- ^1,1 4- • • • 4- xn — 1, n — 1»
= 2/o«n-i 4- 22/i«n-2 4- 32/2a„-3 4----------F w2A»-i-
Will man diesen Ausdruck auf f = Tjr anwenden, so hat
man yr = 1, die übrigen y — 0 zu setzen und erhält
^(^14 -- (^* 4“ l)®n—r—1» $(?]n—1—r) —- (^ ^) ®r,
634
Vierundzwanzigster Abschnitt.
§ 174.
und folglich, solange r n ist, nach (4) mit der Bezeichnung (1):
(12) (n — r)ar = ars0 -]- «r-iSj -(-••• 4“ M-i -|- sr,
und wenn man die Spur von Orf(ff) = 0 nimmt:
(13) 0 = an Sr 4~ «n — 1 sr +1 —1 —Sr 4- n.
Dies sind die Newtonschen Formeln (Bd. I, § 46).
Bezeichnen wir mit
f'(t) = wt”-1 -|- (n — 1)«^”-2 ---1- 2a„_2t an_!
die abgeleitete Funktion von f(t), multiplizieren die Gleichung
(12) mit 6n~r~1 und summieren von r = 0 bis r = n — 1,
so folgt:
(14) f (ff) — Ho So 4- TJj Sj 4- • • • 4- Hn — l Sn^i,,
und wenn man für irgend ein positives k die Gleichungen (12)
mit ßn-r + ic—i multipliziert und noch so viele von den Gleichungen
(13) hinzunimmt, bis n — r 4~ k — 1 anfängt, negativ zu werden,
so ergibt sich:
(15) ff1 f (ff) = Ho Sic 4- VlSk+l 4- "4“ Vn — lSk + n — !•
Um die Norm von f'(6) zu bilden, hätte man in diesen •
Gleichungen zunächst die Basis ij», ..., rjn — i durch die Sub-
stitution (2) durch (1, 0, ff*, ..., f)n~i) auszudrücken, dann die
Gleichung (15) für k — 0, 1, ..., n — 1 zu bilden und die Deter-
minante dieses Systems zu nehmen. Statt dessen kann man die
Determinante in bezug auf die nehmen, und dann mit der
Substitutionsdeterminante:
a,
@n — 2, • • •, «i, 1
«n — 2, «n — 3 , • • •, 1, 0
n(w + l)
1, 0, ..., 0, 0
multiplizieren. Dadurch erhält man
So,
S1,
$1, ..., sn
S2, •.Sn
i n (n + 1)
(16) W'(0)] = (-1)2
Sn — i, Sn, . ... S2n — 2
Diese Determinante ist aber nach der Definition der Dis-
kriminante (§173):
z/(l, 0, 02, ..., 0«-1),
und wir haben also:
(17) Nf'(ff) = (—lfn(nV1)^1(1, 0, 0ä, ..., 0»-i).
§ 175. Ganze Funktionen von z. 635
In der Betrachtung dieses Abschnittes haben wir, dem Haupt-
ziel der Untersuchung entsprechend, die Koeffizienten av a2, •••»
als rationale Funktionen von z betrachtet. Alles bleibt aber
vollständig ungeändert, wenn wir für diese Größen irgend einen
Rationalitätsbereich festsetzen.
§ 175. Ganze Funktionen von z.
Jede Funktion <0 des Körpers £2 genügt, wie wir gesehen
haben, einer Gleichung niedrigsten Grades:
(1) coe -|- <ae~1 -f- &2 coc-2 • • • -]- be = 0,
deren Koeffizienten &15 b2, ..., be rationale Funktionen von z sind.
1. Wenn diese Koeffizienten ganze rationale
Funktionen von z sind, so heißt co eine ganze
algebraische oder kurz eine ganze Funktion von z.
Über die ganzen algebraischen Funktionen gelten die näm-
lichen Sätze, wie über die ganzen Zahlen (Bd. H, § 149).
Setzen wir
(2) Cp (t) = te 4" ^1 ie — 1 4" ^2 te~2
so ist, wie wir in § 172 gesehen haben,
(3) N(t — co) = qp (t)f (ef = n)
eine ganze Potenz von cp (t). Wenn wir daher N (t — co) nach
Potenzen von t ordnen, so werden die Koeffizienten alle wieder
ganze rationale Funktionen, also insbesondere:
2. Die Norm und die Spur einer ganzen Funk-
tion co sind ganze rationale Funktionen von z.
3. Eine rationale Funktion von z ist nur dann
eine ganze algebraische Funktion, wenn sie eine
ganze rationale Funktion ist.
Denn ist co = —b rational, so ist e = 1 und co -|- & = 0
die Gleichung niedrigsten Grades für co, also co nur dann ganz,
wenn b ganz und rational ist.
4. Jede Funktion 17 in £2 kann durch Multipli-
kation mit einer von Null verschiedenen rationalen
Funktion von z in eine ganze algebraische Funktion
verwandelt werden.
Denn jede Funktion 17 genügt einer Gleichung niedrigsten
Grades:
(4) 4- 4- ••• + i >? 4- — °>
636 Vierundzwanzigster Abschnitt. § 175.
und wenn man mit multipliziert und &0 rj = co setzt, so
erhält man eine Gleichung von der Form (1).
5. Eine Funktion co des Körpers Sl ist eine ganze
Funktion, wenn sie irgend einer Gleichung
(5) tp (co) = com -|- c,»“-1 ----p- cm_j o 4- cm = 0
genügt, in der Cj, c2, ..., cm ganze rationale Funk-
tionen sind, wenn dies auch nicht die Gleichung
niedrigsten Grades ist.
Denn ist q> (co) = 0 die Gleichung niedrigsten Grades für
co, so muß tp (t) für ein variables t durch (<) teilbar sein. Das
ist einfach der Inhalt der Gleichung (5). Es ist also
t(t) = z(0s>(0,
worin tp(t) ebenfalls eine ganze Funktion von t ist. Wenn nun,
wie vorausgesetzt, tp(t) ganze Koeffizienten hat, so müssen nach
einem Satz von Gauss auch die Koeffizienten von <p(t) und von
% (<) ganze Funktionen sein. Vgl. Bd. I, § 2, § 20, § 148 ’)•
Hieraus ergibt sich der folgende Hauptsatz:
6. Summe, Differenz, Produkt zweier ganzer Funk-
tionen in £i sind wieder ganze Funktionen.
Sind nämliph co', co" zwei ganze Funktionen in ß, die den
Gleichungen genügen:
16) co'»'4-öico'’1'-1 4------4 &4-1CO' 4- b'n, = 0,
so bezeichne man mit
die Produkte
co'1'co"’'''; v' — 0, 1, ..., n1 — 1,
v" = 0, 1, ..., n" — 1,
und mit co eine der drei Funktionen co' 4- co", co'co", dann kann
man mit Hilfe der Gleichungen (6) setzen:
COCO, = «!,! 4“ ••• 4" X^m rom’
(7) ..................................
*) Bei diesem Beweis braucht nicht die Zerlegbarkeit der ganzen
rationalen Funktionen in lineare Faktoren vorausgesetzt zu werden, sondern
nur die Zerlegbarkeit in irreduzible Faktoren. Man kann also für die
Zahlenkoeffizienten noch einen beliebigen Rationalitätsbereich festsetzen.
Wir werden aber in der Folge die Zerlegbarkeit einer ganzen rationalen
Funktion von « in lineare Faktoren, d. h. den Fundamentalsatz der Algebra,
doch voraussetzen müssen.
§ 176. Minimalbasis und Körperdiskriminante. 637
wo ffl = «' n" ist, und die ganze rationale Funktionen von z
sind. Aus (7) ergibt sich durch Elimination der co»-:
$1,1 »5 «2,U «1,2, «2,2 », • •, #1, m • •, #2, m = 0,
2, • • 5 m
und dies ist eine Gleichung für co von der Form (5).
Durch wiederholte Anwendung dieses Satzes folgt, daß jede
ganze rationale Funktion von ganzen Funktionen wieder
eine ganze Funktion ist.
7. Eine ganze Funktion co heißt durch eine ganze
Funktion co' teilbar, wenn eine dritte ganze Funk-
tion co" existiert, so daß
(8) co = co' co"
ist.
Aus dieser Definition ergibt sich ohne weiteres:
Ist co teilbar durch o/ und co' teilbar durch co", so
ist auch co durch co" teilbar.
Sind co' und co" durch co teilbar, so ist auch co' + co"
durch co teilbar.
Sind co15 co2, co3, ... durch co teilbar und coi, co2, co3, ...
beliebige ganze Funktionen, so ist auch
rol “I- »2 »2 ~j- »3 »3 “j---
durch co teilbar.
§ 176. ‘Minimalbasis und Körperdiskriminante.
Da man jede Funktion des Körpers £2 durch Multiplikation
mit einer ganzen rationalen Funktion in eine ganze algebraische
Funktion von g verwandeln kann, so gibt es auch Körperbasen,
die aus ganzen Funktionen bestehen (z. B. nach der Bezeich-
nung in § 171, (2) die Potenzen von a0Ö).
Ist nun
(1) COi, »2 5 • • »n
eine solche aus ganzen Funktionen bestehende Basis, so ist jede
in der Form
(2) co — xy coj + «2 »2 -|- • • • -|- Xn con
638
Vierundzwanzigster Abschnitt.
§ 176.
(3) co =
enthaltene Funktion, wenn die xly x2, ..., xn ganze rationale
Funktionen sind, eine ganze Funktion in £1. Es ist aber nicht
gesagt, daß auch umgekehrt in der Form (2) mit ganzen Koeffi-
zienten Xi alle ganzen Funktionen in £i enthalten sind.
Gibt es also ganze Funktionen in der Form (2), in der die
Xi nicht alle ganze rationale Funktionen sind, so können wir eine
ganze Funktion finden;
'l'l —1— *1'2 ®2 —I— " * ’ —|— •l'H
z — c ’
in der die x{ ganz und nicht alle durch ,z — c teilbar sind.
Reduzieren wir die x( auf ihre konstanten Reste (nach z — c),
so ergibt sich eine ganze Funktion co in der Form:
C, CO, —j-r <?2 CÖ2 “I- ' * * “|“ Cn
z — c ’
in der die Konstanten c,, c2, ..., cn jedenfalls nicht alle ver-
schwinden. Ist etwa c1 von Null verschieden, so können wir co,
durch co, co2, ..., con ausdrücken und erhalten eine neue ganz-
zahlige Basis von £i:
(4) co, co2, ..., con.
Für die Diskriminante ergibt sich aber nach § 173, (6) die
Beziehung:
c2
(5) z/(co, g>2, ..., co„) = Jfon “2, •••> «.)•
Beide Diskriminanten sind ganze rationale Funktionen von z,
aber die Diskriminante der Basis (4) ist von niedrigerem Grade
als die Diskriminante der Basis (1).
Wenn wir auf diese Weise fortfahren, den Grad der Dis-
kriminante zu erniedrigen, müssen wir schließlich zu einer aus
ganzen Funktionen bestehenden Basis co15 co2, ..., <o„ kommen von
der Eigenschaft, daß in der Form (2) mit ganzen rationalen X{
alle und nur die ganzen Funktionen in ausgedrückt sind.
8. Definition: Eine ganzzahlige Basis co15 co2, ..., co„
des Körpers ££ heißt eine Minimalbasis, wenn in der
F orm
(6) (0 X^ CO, “|“ X2 CÖ2 ~I— • • • ~|~ Xn G)n
mit ganzen rationalen a?15 x2, ..., x„ alle ganzen
Funktionen des Körpers £1 darstellbar sind.
Eine solche Minimalbasis existiert also immer.
§ 176. Minimalbasis und Körperdiskriminante. 639
9. Ein aus einer Minimalbasis Oj, co2, •••> «’n ab-
geleitetes System ganzer Funktionen
(7) = A.1O1 + ®»,2 «2 + • ' • + %v,n »n,
v = 1, 2, n
ist dann und nur dann eine Minimalbasis, wenn die
Determinante
(8) X = 2 + a?i,i ^2)2 ... xn,„
eine von Null verschiedene Konstante ist.
Denn hat diese Determinante, die eine rationale Funktion
von z ist, einen Linearfaktor z — c, so kann man die Konstanten
c15 c2, ..., cn so bestimmen, daß die n ganzen rationalen Funk-
tionen
Cl%l,v ~I- ^2^2,». —••• —I- CnX„^r
durch z — c teilbar werden, ohne daß alle verschwinden.
Dann ist aber
dl H- C2 G>2 H- ’ • 4~ C„ co'n
Z -- C
eine ganze Funktion, und coi, «ä, •••, «n keine Minimalbasis.
Für die Diskriminante erhält man aus (7) nach § 173, (6)
(9) z/(coi, «2, ..., co'K) = X2z/(co15 co2, ..., co„).
Daraus folgt:
10. Die Diskriminante einer Minimalbasis ist, von
einem konstanten Faktor abgesehen, von der beson-
deren Wahl der Basis unabhängig.
Die Diskriminante einer Mypmalbasis hat unter allen Diskri-
minanten aus ganzen Funktionen gebildeter Basen den niedrig-
sten Grad (daher der Name Minimalbasis). Es ist eine durch
den Körper selbst, abgesehen von einem konstanten Faktor,
eindeutig bestimmte ganze rationale Funktion von z. Sie wird
daher auch die Diskriminante des Körpers £1 genannt und
mit z/(ü) bezeichnet.
Fünfundzwanzigster Abschnitt.
Funktionale.
§ 177. Rationale Funktionale.
Wir übertragen nun den Begriff des Funktionals, der uns im
17. Abschnitt des zweiten Bandes zur Begründung der Theorie
der algebraischen Zahlen gedient hat, auf die algebraischen Funk-
tionen.
Wir adjungieren also dem Körper £i beliebige Variable und
rechnen damit nach den Regeln der Buchstabenrechnung. Es
entsteht so ein erweiterter Körper £1, dessen Elemente Funk-
tionale heißen. Der Körper £1 selbst heißt der Funktional-
körper. Die Variablen sind hier nicht im Sinne der Analysis
als Zeichen für veränderliche Zahlen, sondern als bloße Rechnungs-
symbole aufzufassen, und sind wohl zu unterscheiden von den
Variablen £, 0 des Körpers £1. Wir wollen diese Hilfsvariablen
die Funktionalvariablen nennen.
Aus dem Körper Z der rationalen Funktionen von z entsteht
durch Adjunktion der Variablen der Körper Z der rationalen
Funktionale.
Eine ganze rationale Funktion der Variablen:
® (w, v, w, ...)
mit ganzen rationalen Funktionen von z als Koeffizienten heißt
eine ganze Funktion in Z. Der größte gemeinschaftliche Teiler
der Koeffizienten von ® heißt der Teiler der Funktion, und
die Funktion heißt primitiv, wenn die Koeffizienten keinen ge-
meinschaftlichen Teiler haben. Die primitiven rationalen Funk-
tionen und ihre Quotienten werden auch Einheiten im Körper
Z genannt.
§ 177. Rationale Funktionale. 641
_Die Quotienten ganzer Funktionen in Z sind die Funktionale
in Z. Jedes Funktional A in Z kann in die Form gesetzt
werden:
(1) A = -=- = a^- = aE,
K ’ <I>2 E2 '
worin ®15 ®2, E» E2 ganze Funktionen in Z sind, darunter die Ein-
heiten Et, E2, und E ist eine Einheit in Z, die sich als gebrochene
Funktion darstellt, a ist der Quotient der Teiler von O, und O2,
also eine ganze oder gebrochene rationale Funktion von z.
Die Funktionen a und E in der Formel. (1) sind durch Ä
völlig bestimmt, abgesehen von konstanten Faktoren, die hier
die Rolle der numerischen Einheiten spielen. Wir wollen a
die „Absolute“ von A nennen. Es gilt dann der Satz:
1. Die Absolute eines Produktes ist gleich dem
Produkt der Absoluten der Faktoren,
und wir definieren:
2. Ein rationales Funktional heißt ganz, wenn
seine Absolute eine ganze Funktion von z ist.
Aus 1. folgt, daß das Produkt zweier ganzer Funktionale in
Z wieder ein ganzes Funktional ist. Dasselbe folgt auch für die
Summe und Differenz zweier ganzer Funktionale A2, A2 in Z.
Setzen wir nämlich:
— E-i — dn En
4i = «1^, 4s =
-Fi iE ^2 E,
worin a15 «2 ganze rationale Funktionen von z sind; E12 E2, E
ganze Einheiten, so ist die Absolute von A1 + A2 der Teiler der
ganzen Funktion diE2 + a2J?2, also auch eine ganze Funktion
von z. Also gilt der Satz:
3. Summe, Differenz und Produkt zweier ganzer
Funktionale in Z sind wieder ganze rationale Funk-
tionale.
Alle Einheiten und deren Reziproken sind nach der Definition
als ganz zu bezeichnen. Ist die Absolute eines ganzen rationalen
Funktionals A linear (=f z — c), so heißt A ein rationales
Primfunktional oder ein Primfunktional in Z.
Weber, Algebra, in. 4^
642
Fünfundzwanzigster Abschnitt.
§ 178.
4. Jedes ganze rationale Funktional läßt sich
in Primfaktoren zerlegen und zwar, von Einheits-
faktoren abgesehen, nur auf eine Weise.
Ist ein Produkt von ganzen Funktionalen in Z
durch ein Primfunktional teilbar, so ist wenigstens
einer der Faktoren durch dieses Primfunktional
teilbar.
§ 178. Funktionale des Körpers Sl.
Ein Funktional des Körpers Sl ist ein Ausdruck von der
Form: r . :
(1) rä = Xü -|- XT e -j-+ Xn-iÖ«-1,
wo 0 die den Körper £1 erzeugende' algebraische Funktion ist,
und xa, xt, ..., xn_t rationale Funktionale sind, cö ist nur
dann = 0, wenn alle Koeffizienten So, • • •, xn — 1 verschwinden.
Jedes Funktional, das in bezug auf 0 von höherem als dem
(n — l)ten Grad ist, kann durch den Rest der Division durch /’(0)
ersetzt, also auf den (n— l)ten Grad reduziert werden, und der
Quotient zweier Ausdrücke (1), in der der Nenner nicht = 0 ist,
kann wie in § 171, 1. auf die Form (1) gebracht werden.
Nimmt man eine beliebige Basis ;
CO1, COg,
des Körpers £1, so kann « auch in die Form
(2) rä = x1a1 a?2 g>2 xn
gesetzt werden. Wendet man dies auf die Produkte 00.; an
und setzt
(3) eacoi = x^^ -J- Xi^a^ + ••• + xiinan,
worin die xi>n rationale. Funktionale sind, so ergibt sich für i»
eine Gleichung:
(4) ^1,1 #1,2, &l,n X2,i, #2,2 CO, •••, X>2,n 11 2» • ♦ • •, n & = 0,
also:. 5. Jedes Funktional in £1 genügt einer Gleichung (5) . <p (a) = 0, worin *- (6) <p(t) = + + + X
(7) N(to) =
(8) S(ea) = xK
und die Sätze § 172, (6) n
den Normen und Spuren d<
Es ist dann, wie in § '
(9) <p(t)
und die Diskriminante e
§ 1^9. Ganze Funktionale des Körpers £1. 643
eine rationale Funktion nten Grades von/ ist, deren
Koeffizienten^, A2, ..., An Funktionale des Körpers
Z sind.
Wir definieren die Norm und die Spur des Funktionals wie
in § 172:
^1,2, •••}
^2,1, ^'2,2? •••, *^2}m
^n,l, 2, • • *5 %n,n
l “I- ^2,2 “I- ’ ' ’ “l“ xn,ni
nd (21) gelten unverändert auch von
sr Funktionale.
172, (8),
= N(t — rä),
ines Funktionalsystems ist wie in
§ 173, (1) erklärt, und wenn das Funktional <5 in einem in ß ent-
haltenen Körper eten Grades ßj enthalten ist, so genügt cä einer
Gleichung eten Grades (t) = 0. Wie in, § 172, (19) wird be-
wiesen, daß
<P(0 == E<P1 (91f (« = */)
eine Potenz von <p1 (t) ist.
§ 179. Ganze Funktionale des Körpers ££.
6. Definition. Ein Funktional ö in ß heißt ganz,
wenn es einer Gleichung:
(1) F(a) = + ••• + 4»_irä + Äm = 0
genügt, deren Koeffizienten A^, ..., Am ganze ratio-
nale Funktionale sind.
Aus dem Gaussschen Satz (Bd. I, § 2) folgt, da man nach
§177 die Primfaktoren in Z kennt, daß, wenn F(t) in Z reduzibel
ist, auch jede in F(t) aufgehende Funktion ganze Koeffizienten
hat, insbesondere also auch die Gleichung niedrigsten Grades
<p(äi) = 0, der <5 genügt.
Die notwendige und hinreichende Bedingung für ein ganzes
Funktional <a ist also die, daß
N (t — S)
bei Ordnung nach Potenzen von t ganze rationale Funktionale zu
Koeffizienten hat.
41*
644
Fünfundzwanzigster Abschnitt.
§ 180.
Wie in § 175 beweist man die Sätze:
7. Summe, Differenz, Produkt von ganzen Funk-
tionalen in £i sind wieder ganze Funktionale.
8. Ist cö ein ganzes Funktional in £i nach der Defi-
nition 6. und zugleich rational, so ist es ein ganzes
Funktional in Z (nach der Definition 2.).
9. Ist « ein ganzes Funktional in ii, so ist N(ä>)
ein ganzes Funktional in Z, und die Absolute von
N(äi) heißt die „absolute Norm von rä“.
Die absolute Norm von w ist also eine Funktion in Z.
Bezeichnen wir die absolute Norm mit Na(a), so gilt der Satz:
(2) Na(ä(ö') = Na(ä)Na(ä').
§ 180. Teilbarkeit von Funktionalen. Einheiten.
Es sind nun die Sätze von Bd. II, § 155 mit ganz geringen
Modifikationen, auf die im folgenden aufmerksam gemacht ist, zu
wiederholen. Zur Vereinfachung des Ausdruckes sollen hier mit
den kleinen griechischen Buchstaben ganze Funktionale in ß, mit
den kleinen lateinischen Buchstaben ganze Funktionale in Z be-
zeichnet sein. Dann haben wir:
1. Definition: Wenn ß von Null verschieden ist,
so heißt a durch ß teilbar, wenn a/ß = y ein ganzes
Funktional in £i ist.
2. Sind £, q, ... beliebige ganze Funktionale in Sl
und <z, ß, ... durch d teilbar, so ist auch
+ Vß +••
durch d teilbar.
3. Definition: Ein ganzes Funktional s, dessen
Reziprokes 1/s ganz- ist, d. h. ein Teiler der Zahl 1
heißt eine Einheit in £i. Eine Einheit ist Teiler
eines jeden ganzen Funktionals. Produkt und Quo-
tient zweier Einheiten sind wieder Einheiten.
4. Zwei ganze Funktionale a, ß, die gegenseitig
durcheinander teilbar sind, heißen assoziiert. Ihr
Quotient a/ß = s ist eine Einheit. Zwei Funk-
tionale <z und as sind assoziiert.
5. Ist a teilbar durch ß, so ist jedes mit a asso-
ziierte Funktional teilbar durch jedes mit ß asso-
ziierte Funktional.
§ 181. Größter gemeinschaftlicher Teiler. 645
6. Sind zwei ganze Funktionale mit einem dritten
assoziiert, so sind sie auch untereinander assoziiert.
7. Die Norm N(a) ist durch a teilbar.
Dies folgt aus der Gleichung (6), § 178: <p(a) = 0, deren
letzter Koeffizient An = + -V(<z) ist. Denn danach ist:
+ 2f(<x) = a(aM-1 -|- A-i an~2 ••• -|- An_^).
8. Ein ganzes Funktional, dessen absolute Norm
eine Konstante ist, ist eine Einheit, und umgekehrt
ist die absolute Norm einer Einheit « eine von Null
verschiedene Konstante.
Denn wenn s eine Einheit ist, so sind
N(e) und .
- ’ \e / N(e)
ganze Funktionale in Z; folglich N(e) eine Einheit in Z. Um-
gekehrt ist .N(«) durch « teilbar, also, wenn N(s) eine Einheit
in Z ist, « ein Teiler von 1, d. h. eine Einheit.
9. Es gibt ganze rationale Funktionen von z. B.
die absolute Norm von w, die durch w teilbar sind.
Ist a eine durch <z teilbare ganze rationale Funk-
tion von z von möglichst niedrigem Grade, so ist
jede andere durch a teilbare ganze rationale Funk-
tion von z durch a teilbar.
§ 181. Größter gemeinschaftlicher Teiler.
Sind a, ß, ... ganze Funktionale in £1 und x, y, ... Variable,
die in a,ß, ... nicht vorkommen, so ist
(1) d = ax ßy -----------
nach § 180, 2. ebenfalls ein ganzes Funktional, und zwar ist d
teilbar durch jeden gemeinsamen Teiler von a, ß, ... Sind
Xo, yo, ... beliebige ganze Funktionen oder Funktionale in Z, so
ist, wie jetzt bewiesen werden soll,
(2) d0 = a x0 -|- ß y0 -j- • • •
durch d teilbar. Denn bezeichnen wir die absolute Norm von d
mit D, so ist
(3) JV(d) = D E (a?, y, ...) = D E,
und E (x, y, ...) ist eine Einheit in Z, zugleich aber eine ganze
homogene Funktion der Variablen x, y, ...
646 Fünfundzwanzigster Abschnitt. § 182.
Bedeutet t eine neue Variable, so ist
N(8t — Öo) = DE(xt — x^ yt — y0, ...)r
also, wenn man nach absteigenden Potenzen von t ordnet und
den Faktor V(Ö).= DE beiderseits forthebt:
(4) N(t — = i" + Clt^ +
worin C\, C2 ... keinen anderen Nenner als E haben, und
folglich ganze Funktionale in Z sind. Demnach ist nach der
Definition § 179, 6. auch ö0: ö ein ganzes Funktional, wie be-
wiesen werden sollte.
Demnach erhalten wir folgende Definitionen:
1. Das Funktional d = ax ßy ••• und jedes
mit d assoziierte Funktional ist der größte gemein-
schaftliche Teiler von <z, ß, ...
2. Ist axßy eine Einheit, so heißen a und ß
teilerfremd oder relativ prim. Gibt es Funktionale
g, t], für die al- ßt] eine Einheit ist, so sind a, ß
relativ prim.
3. Ist a relativ prim zu ß und zu y, so ist es
auch relativ prim zu ßy.
Denn nach Voraussetzung sind
e — ax ßy, = au -j- ßv
Einheiten (x, y, u, v neue Variablen).
a(aux yv x ßuy) -|- ßyv y = s e±,
also nach ’3. a und ß y relativ prim.
4. Ist a relativ prim zu ß und ay durch ß teilbar,
so ist y durch ß teilbar.
Denn aus der Voraussetzung folgt:
ay x -|- ß yy = s y,
woraus, da e eine Einheit ist, sich der Beweis ergibt.
, § 182. Primfunktionale in Si.
1. Definition. Ein ganzes Funktional ar in Si heißt
ein Primfunktional, wenn es keine Einheit ist und
außer durch die Einheiten nur durch die mit ihm
assoziierten Funktionale teilbar ist.
§ 182. Primfunktionale in £1. 647
Daraus folgt:
2. Ist ein Produkt aß durch n teilbar, so ist
wenigstens einer der beiden Faktoren, a oder ß,
durch n teilbar.
Denn ist weder a noch ß durch n teilbar, so sind beide
relativ prim zu n und nach § 181, 3. ist n auch relativ prim
zu a ß.
3. Jedes von Null verschiedene ganze Funktional
<ö ist durch ein Primfunktional teilbar.
Denn ist a> nicht selbst ein Primfunktional, so ist es durch
ein von cj verschiedenes Funktional a teilbar. Ist
ü) — aeä',
so ist <ä' keine Einheit und
Na(jo) = Na(a)Na(jä').
Die hier vorkommenden absoluten Normen sind ganze Funk-
tionen in z und der Grad von Wa(ci') ist kleiner als der Grad
von Wa(cj). Ist iö' noch kein Primfunktional, so kann man so
fortfahren und muß schließlich auf einen Primfaktor n von ö
kommen.
In dieser Weise schließt man weiter wie in Bd. II, § 158,
wobei nur an Stelle der dort benutzten Größe der ganzen ratio-
nalen Zahlen hier die Höhe des Grades ganzer rationaler Funk-
tionen der Variablen z tritt. So erhält man auch die Sätze:
4. Jedes ganze Funktional a in ß, das keine
Einheit ist, läßt sich in eine endliche Anzahl von
Primfaktoren zerlegen, und zwar nur auf eine Weise,
wenn assoziierte Funktionale als nicht verschieden
betrachtet werden.
Im folgenden müssen wir von dem Satz Gebrauch machen,
daß eine ganze rationale Funktion von z mit numerischen Koeffi-
zienten in lineare Faktoren zerlegbar ist, mit anderen Worten,
wir müssen den Fundamentalsatz der Algebra von der Wurzel-
existenz voraussetzen. Es folgt daraus zunächst:
5. Die ganze rationale Funktion von z niedrig-
sten Grades, die durch ein Primfunktional n teilbar
ist, ist eine linearerFunktion z — c.
Nach § 180, 9. gibt es überhaupt ganz rationale Funktionen
von z, die durch a teilbar sind. Zerlegt man eine solche Funk-
648
Fünfundzwanzigster Abschnitt.
§ 182.
tion in lineare Faktoren, so muß nach 2. einer dieser Linear-
faktoren durch n teilbar sein. Es können nicht zwei verschiedene
Linearfunktionen z- — c und z — d durch dasselbe it teilbar sein,
weil sonst die von Null verschiedene Konstante c — d durch n
teilbar wäre.
6. Jede ganze Funktion ö in ß ist nach dem Mo-
dul n mit einer Konstante b kongruent, d. h. man
kann die Konstante b so wählen, das cj — b durch ar
teilbar wird.
Denn die Funktion cj genügt nach § 175 einer Gleichung:
gj" -|- «i (on~1 + • • • -f- «m-1 gj + an = 0,
worin die a1, ..., an ganze rationale Funktionen von z sind. Sind
af, ..., die Reste dieser Funktionen bei der Teilung durch
z — c, also Konstanten, so folgt:
gj" -|- afra”“1 ••• -|- aj, = 0 (mod n),
und wenn man die Funktion auf der linken Seite in Linear-
faktoren zerlegt:
(1) (gj — 6) (gj — b') (gj — &")••• = 0 (mod ar).
Es muß also wenigstens einer dieser Linearfaktoren durch ar
teilbar sein, was zu beweisen war.
Aus der nachgewiesenen einwertigen Zerlegbarkeit der Funk-
tionale in Primfaktoren ergeben sich weitgehende Folgerungen,
von denen die wichtigsten hier angeführt werden sollen.
Wenn in einem Funktional <p des Körpers ß eine gewisse
Anzahl der Hilfsvariablen, x, y, ..., nur im Zähler vorkommen,
so möge
T = y,
eine holomorphe Funktion von x, y, ... heißen. Von denen
gilt der Satz:
7. Eine holomorphe Funktion ist nur dann ein
ganzes Funktional in il, wenn die Koeffizienten der
geordneten Funktion <p ganze Funktionale sind.
Es genügt offenbar, den Satz für holomorphe Funktionen
einer Variablen
(2) (p = xm(p0 + +------1-
nachzuweisen, weil er daraus durch vollständige Induktion allge-
mein bewiesen werden kann.
Dieser Beweis ergibt sich aber aus dem Gaussschen Satz:
§ 182. Primfunktionale in 12. 649
Haben zwei holomorphe Funktionen
a — aoxh -|- ••• -|- aÄ,
ß = + 0^-1+ •.• + &
ein Produkt
7 = 7o + + 7i ^Ä + /c-1 + • • • + + k,
dessen Koeffizienten ganze Funktionale sind, so können die yOi
y15 yh+lc nur dann alle durch ein Primfunktional n teilbar
sein, wenn entweder alle a0> ßn • ••, kä> oder alle ft, ft, ..., ft
durch n teilbar sind, was ganz so bewiesen wird, wie in Bd. I, § 2.
Wenn nun (2) ein ganzes Funktional ist, ohne daß <p0, ..., <pm
ganz sind, so kann man ein ganzes Funktional ft und darin einen
Primfaktor n so bestimmen, daß
(3) % = y<p — + «i^-1 +---------1- am,
durch % teilbar ist, <z0,«j, ..., an aber nicht alle durch ar teilbar
sind.
Ist nun <p ganz, so genügt es einer Gleichung:
(4) E<pm = öj Er (pm~l + a3 E2 <pm^ 4----\-amEm
und daraus durch Multiplikation mit ft”*:
(5) E = ft (ft Et 1 + a3 E2 ft x”“2 + am Em),
worin die «j, «3, ... ganze Funktionen in Z, die E, Ex, ..., Em
Einheiten in Z sind. Die Einheiten E, Ely ..., Em können zwar
x noch enthalten, können aber holomorph angenommen werden.
Ordnen wir rechter Hand und linker Hand von (5) nach x, so
sind die Koeffizienten von E nicht alle durch n teilbar. Ebenso
sind nach dem erwähnten Satz die -Koeffizienten von %m nicht
alle durch ar teilbar, während auf der rechten Seite alle Koeffi-
zienten den Faktor ft, also auch den Faktor n haben. Das ist
unmöglich und damit unser Satz bewiesen (Bd. H, § 159).
8. Ein holomorphes ganzes Funktional <p ist der
größte gemeinschaftliche Teiler aller seiner Koeffi-
zienten.
Sind <z, ß, ... die Koeffizienten von cp, so ist <p jedenfalls
durch den größten gemeinschaftlichen Teiler von «, ß, ... teilbar.
Zerlegen wir eine Linearfunktion z — c in ihre funktionalen Prim-
faktoren, so können wir in diesen Primfunktionalen ar die Variablen
beliebig bezeichnen, und da jedes Primfunktional in einem z — c
aufgehen muß, so können wir darin die Variablen von den Vari-
ablen x, y, ... in <p verschieden annehmen. Demnach können
650 Fünfundzwanzigster Abschnitt. § 182.
wir ein von den x, y, ... freies, mit <p assoziiertes Funktional
i[> = eq> bestimmen. .Da dann <p/i[> ganz ist, so müssen nach 7.
die Koeffizienten von <p alle durch ijj, und folglich auch alle
durch <p teilbar sein. Was zu beweisen war.
Damit ist zugleich bewiesen:
9. Ein holomorphes ganzes Funktional geht in
ein assoziiertes über, wenn die Variablen anders
bezeichnet werden.
10. Jedes Funktional ä in ß geht durch Multi-
plikation mit einer Einheit in Z in ein holomorphes
Funktional über.
Denn man kann zunächst cö als Quotienten zweier ganzer
holomorpher Funktionale
to = ±
<P
darstellen. Setzt man N((f>) — cp<p', so ist, wie die Formel (4)
zeigt, in der amEm = +N(tp) ist, <f>' mit einem holomorphen
Funktional assoziiert, und es folgt:
(6) Em7b = ^.
11. Zu einem ganzen Funktional ö.kann man ein
zweites y so wählen, daß y durch beliebig gegebene
Primfunktionale jt2i... nicht teilbar wird, und daß
(7) Sft ‘ a
eine Funktion in ß wird.
Man stelle co nach 10. durch ein holomorphes Funktional <p
dar. Dessen Koeffizienten sind nach 8. alle durch to, aber nicht
alle durch StTj teilbar. Es gibt also eine Funktion wx, die durch
<o, aber nicht durch cöJtj teilbar ist.
Nun setze man:
— G) G?2 ~j CO ^*1 ^3 • • •) ^3 - ^0 ^2 ^3 • * *
und bestimme:
teilbar durch Sj, nicht teilbar durch
c n n a2i n n m2i
K3 n‘ n &31 n ii 'n ß’s 3r3-
Dann genügt
a = oCj —|— oc3 ocs —|— • • •
den Forderungen des Satzes 11.
§ 188. Basen und Basisformen der Funktionale. 651
12. Jedes ganze Funktional gj ist der größte ge-
meinschaftliche Teiler zweier Funktionen a, ß in ß.
Um dies zu beweisen, nehmen wir a — a u, teilbar durch (5,
dann ß teilbar durch cö und ß:ä> relativ prim zu fi; dann ist
ä> — ax ßy
der größte gemeinschaftliche Teiler von a und ß.
§ 183. Basen und Basisformen der Funktionale.
Es sei jetzt
(1) »1, (o2, ..., gj„
eine Minimalbasis des Körpers ß (§ 176) und
(2) otj, oc3, ..., an
eine andere Basis von ß. Die lineare Substitution, durch die
die a mit dem cj Zusammenhängen, sei:
i
(3) i fä-fa
worin die aSfi ganze Funktionen in Z sind, deren Determinante
(d) Z. — £ I i $2, 2 • • • «
nicht identisch verschwindet. Sind t\, t2, ..., tn Variable, so ist
(5) A = oCj ij a2 i3 -|- • • • un tn
der größte gemeinschaftliche Teiler von <xn <z3, •••> un-
Setzt man für tj, i3, ..., tn ganze Funktionen in Z, so ent-
stehen aus A ganze Funktionen in ß, die alle durch X teilbar sind.
1. Man nennt A eine Basisform und <z2, ..., <zn
eine Basis des Funktionals A, wenn man alle durch
A teilbaren Zahlen in ß dadurch erhält, daß man
für ti ganze Funktionen in Z setzt.
Bilden die eine solche Basis, so kann man ganze Funktionen,
g^s in Z, so bestimmen, daß
(6) are)s = Sg^sai
wird.
Daraus folgt:
(7) h C&i ti, s,
wenn
(8) ti,s = Sg®str
652 Fünfundzwanzigster Abschnitt. § 188.
gesetzt ist, und indem man für a, in (7) die Ausdrücke (3) sub-
stituiert: i
i s
(ß) ' Z G)r ---- 03} A { tg- f»
Nach der Definition der Norm (§ 172) ist also A7(Z) die
Determinante aus den Koeffizienten
s
i ts, ri
und diese kann man nach dem Multiplikationssatz der Deter-
minante in
(10) N(k) = AT
zerlegen, worin A die Bedeutung (4) hat, und T die Determinante ist:
(11) 1 = 2j +<1,! fä, 2 ... tn, n-
Hierin ist T eine homogene Funktion wten Grades der
deren Koeffizienten ganze Funktionen in Z sind. A ist selbst
eine ganze Funktion in z. Man beweist nun wie in Bd. II, § 164,
daß T eine Einheit ist. Wäre das nämlich nicht der Fall, so
hätte T irgend einen Linearfaktor z — c, und man könnte
nach einem elementaren Determinantensatz holomorphe ganze
Funktionale yi in z, die nicht alle durch z — c teilbar sind, so
bestimmen, daß
us = 3/1 G 1 + • • • ~F yn ts n
durch z — c teilbar wird (man kann den yt sogar konstanten
Koeffizienten geben, da man sie auf ihre Reste nach z — c redu
zieren kann).
Setzt man nun
® = Ml + !/ä +---------------F ym
so folgt aus (7)
Z G3 OCj —|— —F * * * —|—
und daraus folgt, weil die Ui durch Z, die Ut durch z — c teilbar
sind, daß » durch z — c teilbar ist, was der Definition der
Minimalbasis widerspricht. Demnach ergibt sich aus (10), daß A
die absolute Norin des Funktionals Z ist:
(12) WO(Z) = S ±
^11^22 •••
Für ein Primfunktional tc können wir leicht eine Basis finden.
Es können nicht alle Elemente cjj, cj3, ..., cj„ einer Minimalbasis
durch 7t teilbar sein, weil ja durch die Linearform
(13) G3 -- 3C-^ GJj —|— iZ-2 C?2 —F * * ' —F '^rl
§ 183. Basen und Basisformen der Funktionale. 653
auch die Funktion „1“ darstellbar sein muß. Nehmen wir an,
«j sei nicht durch % teilbar. Nach § 182, 6. gibt es Konstanten
cn c2, ..., cn, deren erste unbeschadet der Allgemeinheit = 1
angenommen werden kann, die den Bedingungen:
öj = 1, «2 = c2, ..., con = cn (mod %)
genügen. Wir setzen:
ai — — c)®x,
z i . x --- ^2 ^2 1
-- G)n — Cn (Oy
Daß dies eine Basis von w ist, ersieht man sofort, wenn man
die Funktion (13) so darstellt:
(15) m = a;2«2 + "• + + (-A + c2x2 + •.—cn
da a2, ..., an durch % teilbar sind, so kann m nur dann durch
% teilbar sein, wenn die ganze Funktion in Z:
-|- c2 x2 H“ ’ * * 4" cn xn
durch (g — c) teilbar und folglich co durch die Formel (5) dar-
stellbar ist. Hiernach ergeben die Formeln (10) und (14):
(16) Na(o) = g — c,
also den Satz:
2. Die absolute Norm eines Primfunktionals ist
eine lineare Funktion von g.
Dieser Satz bedeutet einen wesentlichen Unterschied zwischen
den Theorien der Zahlen und der Funktionen. In der Zahlen-
theorie gibt es Primideale verschiedener Grade, deren Norm eine
Potenz einer Primzahl ist. In der Theorie der Funktionen haben
wir nur Primfunktionale ersten Grades. Dies rührt daher, daß
wir vermöge des Fundamentalsatzes der Algebra jede ganze
Funktion einer Variablen nach dem Modul n in lineare Faktoren
zerlegen können.
Die Zahl der Primfaktoren, in die (g — c) zerfällt, ist hier-
nach n, da N (z — c) = (g — c)n ist.
Fassen wir die untereinander gleichen Primfaktoren in
Potenzen zusammen, so ist
(17) z — c =
worin
(18) n = <?2 + es 4" • "> •
wo s eine Einheit ist.
654
Fünfundzwanzigster Abschnitt.
§ 184.
§ 184. Basisform und Verzweigungsfunktional.
Unter der Basisform des Körpers £1 wollen wir die Linear-
form verstehen:
(1) T = 4" ®2^2 4" •• • 4"
in der f2, ..., tn die Funktionalvariablen sind, und deren Koeffi-
zienten öj, <u2, ..., o„ eine Minimalbasis von ß bilden. Diese
Form ist der größte gemeinschaftliche Teiler von o15 co2, ..., ra»
und folglich eine Einheit. Aus t kann man alle ganzen
Funktionen in £1 ableiten, indem man für die Variablen tlf
t2, tn ganze Funktionen in Z setzt.
Setzen wir
(2) F(f) = N(t — r) — tn 4~ Z1tH~1 4- ••• 4- Zn—it 4~ -Am
so sind die A2, ..., A„ holomorphe ganze Funktionale in
Z, und t genügt der Gleichung wten Grades:
(3) F(v) = 0.
Ist n ein Primfunktional und
Na(o) = z — c,
so kann man nach § 182, 6. die Konstanten Cj, c2, ..., cn aus
den Kongruenzen
(4) öl = cn co2 = c2, ..., <un = cn (mod zr)
bestimmen, und wenn man
(5) Tp = C] ti + c2 ^2 4“ ' 4“ tn
setzt, so ist t0 ein konstantes Funktional, und t — t0 ist
durch ji teilbar. Es ist nun zu beweisen:
3. Das Primfunktional % ist der größte gemein-
. schaftliche Teiler von t — t0 und z — c:
(6) Zt = u (t — t0) 4- v (z — c),
und wenn daher (z — c) durch eine höhere als die
erste Potenz von n teilbar ist, so ist t— t0 nur durch
die erste Potenz von a teilbar.
Zunächst ergibt sich aus der Definition § 181, daß
(7) T To = (öj Cj) 4- ti (®2 — ci) + • • • + tn (®n — Cn)
der größte gemeinschaftliche Teiler von — Cj), («2 — c2), • ••}
(a„ — cM) ist. Ist nun
(8) o = xx öj 4- x2 <u2 + • • • xn co„ = 0 (mod it),
§ 184. Basisform und Verzweigungsfunktional. 655
so ist ajj Ci -|- c2 + • • • H“ xn durch %, und weil es eine
Funktion in Z ist, durch (z — c) teilbar. Wir setzen:
X1C1 + «2C2 +-------1- XnC„ — (z — c)y
und erhalten aus (8)
(9) C3 —a;1(c31 —C1)-|-a:2(c32 —c2)-|---\-xn(an — c„) + — c)y
= (r —!-r0) + (? —
Hätte nun (r — r0) und (z — c) den gemeinschaftlichen Teiler
?rö, so könnte man nach § 182, 11. eine durch Jt teilbare, zu ö
teilerfremde Funktion ö in finden. Dem widerspricht aber die
Gleichung (9), und damit ist unser Satz bewiesen.
Es sei
(10) == Bütm ü1Zm—'x -|- ••• t -|- Bm
eine Funktion mten Grades von t, und Bo, Bu .... Bm seien ganze
holomorphe Funktionale in Z mit den Funktionalvariablen
t2, ..., tm die der Kongruenzbedingung
(11) 0(t) = 0 (mod z — c)
genügt [wie z. B. die Funktion F(t') = N(t —• v)]. Dann ist
0(vo) = 0 (mod a),
und wenn wir <%>(() durch r — r0 dividieren, so ergibt sich
(12) <P(f) = (t — ro)®i(O (mod a),
worin (f) ein holomorphes ganzes Funktional in Z ist. (weil r0
als konstantes Funktional in Z enthalten ist). Da nun in (12)
außer den Funktionalvariablen nur rationale Funktionen von z
vorkommen, so muß diese Kongruenz auch für den Modul z — c
gültig sein:
(13) <P(f) = (t — r0) Chj^) (mod z — c).
Ist %' ein zweites Primfunktional, das auch, mit % identisch
sein kann, und z — c durch nit' teilbar, und t = t'o (mod %'),
so ist (t — Tq): n relativ prim zu rf (nach 3.) und wegen (11)
ist 0x(rö) — 0 (mod %')• Daraus schließt man
®i(0 = (t - rJ)®2(0
zunächst für den Modul dann aber auch, da die Funktionale
in Z liegen, auch für den Modul (z — c). Wir haben also:
(14) <b(i) = (t — r0)(t — To) (0 (mod z — c).
Daraus schließen wir auf folgenden wichtigen Satz:
4. Es sei nach § 183, (17)
(15) z — c = ... an
656 Fünfundzwanzigster Abschnitt. § 184.
in n (gleiche oder verschiedene) Primfaktoren zer-
legt, und
(16) Tj, T2!
seien die konstanten Funktionale, denen t nach den
Modulen
(17) , ^2, *.*,
kongruent wird.
Es sei 0(f) ein ganzes holomorphesFunktional in z
vom Grade m in bezug auf f, das der Bedingung
(18) <P(r) = 0 (mod z — c)
genügt. Dann ist:
(19) <P(t) = (t — ti) (t — r2) ... (t — TnyP(t) (mod z — c),
worin ’P- ein ebensolches Funktional vom Grade
m — n ist.
Es folgt daraus:
5. Ein Funktional 0, das der Bedingung (18) ge-
nügt, kann nicht von niedrigerem als wtem Grade
sein.
Und auf die Funktion F(f) angewandt, folgt die Formel:
(20) F(t) = N(t — — rj)(f — r2) ... (t— rn) (mod z — c).
Die Kongruenz (20) können wir in folgender Weise durch
eine Gleichung ersetzen:
Wir fassen, wie in (17) des vorigen Paragraphen, in der
Zerlegung von z — c in Primfaktoren die gleichen Faktoren zu-
sammen und setzen:
(21) —c =
el e2 H“ • • • -j- em = n,
dann ist nach (20):
(22) F(f) = (t- (t - ?2> ,..(t-Tmym-\-(z - c)R(#),
worin R(f) ein ganzes Funktional zunächst in ß ist. Die Formel
(22) selbst sagt aber, daß R(f) in Z enthalten ist, und daß es
eine ganze Funktion der Funktionalvariablen t, tt, t2, ..., tn ist.
Wir können also auch die Ableitung der Gleichung (12) in
bezug auf t bilden und erhalten:
F'(f) = er (t — Ti)**-1 (t — v2y ... (t —
(23) + 62 ~ — • ••(* —
+ em(t — r2)e>(t — r.2y ... (t — (z — c) R'(t)
§ 184. Basisform und Verzweigungsfunktional. 657
und hierin liegt der Beweis des folgenden Hauptsatzes, den man
erhält, wenn man t = setzt.
6. Wenn eY = 1 ist, so ist F'(r) nicht durch «j
teilbar. Sonst ist F'(f) durch ?r|1—h aber nicht durch
teilbar. Das Gleiche gilt von den übrigen Prim-
faktoren von (z— c) und folglich ist F'(f) teiler-
fremd zu allen Primfaktoren z — c in Z, die nicht
durch das Quadrat eines Primfaktors in Si, teilbar
sind.
Es gibt also nur eine endliche Anzahl von Primfaktoren
(z — c), die durch eine höhere als die erste Potenz eines Prim-
faktors in ß teilbar sind, und F'(r) ist, in Primfaktoren zerlegt,
das Produkt aller Faktoren ji«-1, wenn die höchste in N(it)
— z — c aufgehende Potenz von ist.
Das Funktional F'(r) wird das Verzweigungsfunktional
des Körpers £1 genannt.
Für die absolute Norm des Verzweigungsfunktionals er-
halten wir:
(24) NaF'(r) = n(z — +
worin sich das Produkt TI auf alle Linearfaktoren (z — c) er-
streckt, die durch eine höhere als die erste Potenz eines Prim-
faktors teilbar sind.
Wh* können noch zeigen, daß diese absolute Norm nichts
anderes ist, als die Körperdiskriminante JD.
Um dies zu beweisen, setzen wir:
(25) F = —|— •***, 2 <^2 * * * ~H «c,n>
worin die uk<1, ..., Wj,n homogene Funktionen ftten Grades
von i2, ..., t„ sind, und die Determinante
^1,0? ^2,0? • • •? 0
(20) JJ ____ ^1,1? W2,15 ’**’ 1
^1, n — 1, ^'2, n — 1, •••? n—1
ist eine Einheit.
Denn wäre ü keine Einheit, so hätte sie wenigstens einen
Linearfaktor z — c, und man könnte die ganzen rationalen
holomorphen Funktionale y0, yL, ..., yn — i so bestimmen, daß
Mr,O«/o + Ur,iyi +---------(- = 0 (mod Z c)
wäre, ohne daß alle ys durch z — c teilbar sind.
Weber, Algebra. HL 42
658 Fünfundzwanzigster Abschnitt. § 185.
Dann würde sich aus (20) eine Kongruenz ergeben:
«/o + Jh* + 4------F S'»-!1"-1 = 0 (mod z — c),
was nach dem Satz 5. nicht möglich ist.
Nach § 174, (17) und § 176, (9) ist
NF'(r) = +^/(l, r, r2, ..., vn~J)
(27) = ± «2, ..., W„)
= ± U^-
also ist
(28) NaF'(r)=.d
die Körperdiskriminante, die hiernach durch (24) in
lineare Faktoren zerlegt ist.
Die gewonnenen Resultate benutzen wir noch zum Beweis
des folgenden Satzes:
7. Ist eine ganze Funktion in ß
(29) ö == Xx öj -|- ^2® 2 + • • • + X„On
durch jedes in z — c aufgehende Primfunktional
teilbar, so ist S(co) durch z-— c teilbar.
Die x-l, x^, ..., xn sind hier ganze Funktionen in Z. Die
Funktion co geht aus t hervor durch die Substitution
(30) ti — x^ — x%, • •., tn — xn.
Ist also co durch a teilbar, und cox = ..., co„ = c„ (mod %),
so ist
xici 4* xzcz + ••• 4" x«cn = 0 (mod %)
und folglich auch, als Funktion in Z, durch z — c teilbar. Sind
also r2, ..., vm die konstanten Funktionale, denen r nach den
Primfaktoren %2, ..., von (z — c) kongruent ist, und
gehen diese durch die Substitution (30) in r“, r“, ..., r“K über, so
sind alle diese Funktionen durch (z — c) teilbar [weil sie n. V.
durch einen Primteiler von (z — c) teilbar sind]. Nun ist nach (22)
(31) ---$(T) — elrl 4- e2r2 4“ ••• 4~
und mithin
— S(co') = Cjt» -F e2T°2 4- ••• 4- = 0 (mod z — c),
wie zu beweisen war.
§ 185. Die gebrochenen Funktionen in £1 und die
Taylorsche Entwickelung.
Eine gebrochene Funktion q im Körper ß kann auf unendlich
viele Arten durch Multiplikation mit einer ganzen Funktion v in
eine ganze Funktion p verwandelt werden. Es ist dann
§ 185.
Die gebrochenen Funktionen in £L.
659
und p heißt der Zähler, v der Nenner von ip Diese beiden
Funktionen sind durch i/ nicht vollständig bestimmt, wohl aber
sind die Funktionale bestimmt, die übrig bleiben, wenn alle
gemeinschaftlichen Funktionalfaktoren im Zähler und Nenner
herausgehoben werden. Denn ist
(2) V = =
so muß jedes Primfunktional, das in v, aber nicht in a aufgeht,
in v' aufgehen. Die so aus 7] bestimmten Funktionale « und. ß
nennen wir Zählerfunktional und Nennerfunktional von ip Um
r/ durch Funktionen darzustellen, nehme man zunächst eine Funk-
tion v, teilbar durch ß, aber sonst beliebig und setze v — ßy-,
darin kann y relativ prim zu einem beliebigen Funktional an-
genommen werden. Dann ist 7] v eine durch y teilbare ganze
Funktion, und man setze
7) v — [l = a y.
Das Funktional öc kann aber, wie wir später noch nachweisen
werden, bei gegebenem ß nicht mehr beliebig sein.
Die Funktionale ä, ß werden wir auch kurz den Zähler und
den Nenner von tj nennen.
Ist n ein Primfunktional, so gibt es Zahlen (Konstanten)
a, b, a', b', die den Kongruenzen
p = a, v = b, p' = v' = b' (mod sr)
genügen, und aus (2) folgt
,, , , a a!
ab ' = ba', T ~ = c,
1 b b .
vorausgesetzt, daß v und v' nicht durch sr teilbar sind. Es ist
dann 7} — c eine Funktion in ß, in der der Zähler, aber nicht
der Nenner durch a teilbar ist. Ist p eine ganze oder gebrochene
Funktion, in der der Zähler durch sr, aber nicht durch sz2, der
Nenner auch nicht durch n teilbar ist, so ist (17 — c): p eine
Funktion, deren Nenner nicht durch jr teilbar ist und deren Zähler
den Faktor sr einmal weniger enthält als (t; — c). Wir setzen:
V — c — qtix.
Dieselbe Betrachtung wenden wir auf an und bekommen
so eine beliebig fortzusetzende Reihe von Gleichungen:
42*
660
Fünfundzwanzigster Abschnitt.
§ 186.
*1 = c + 4>»h,
% = C1 + ^2,
Vr~1 = Cr—1 -p QVri
woraus sich ergibt:
(4) 7] = C -|- Cj p C2 p2 • • • ~F Cr—1 Qr~1 4“ 7?r 4*r-
Die Reihe der Konstanten c, c15 c2, cr_! ist durch tj voll-
ständig bestimmt und 7)t, ij2, ijr ist eine Reihe von Funk-
tionen in ß, deren Nenner nicht durch % teilbar ist.
Man könnte diesen Ausdruck die Taylorsche Entwickelung
der Funktion rj nach Potenzen von p nennen. Eine ähnliche Ent-
wickelung läßt sich auch für eine Funktion r/ geben, deren Nenner
durch 7t teilbar ist, nur daß dabei auch negative Potenzen auf-
treten: Man kann nämlich eine Potenz jy5 so bestimmen, daß
der Nenner von (fri nicht mehr durch % teilbar ist, und wenn
man auf dieses Produkt die Entwickelung (4) anwendet, so folgt:
(5) 7] = C Q~s -|- Cx p-s + 1 -|- ••• G-l 4>r—5-1 TJr Qr~S-
§ 186. Birationale Transformation.
Wir kommen jetzt zu einem Gegenstand, der das Gebiet der
algebraischen Funktionen vorzugsweise von dem der algebraischen
Zahlen unterscheidet, und der Grund dafür ist, daß die Theorie
der ganzen Funktionen und Funktionale für die Funktionen bei
weitem nicht den Charakter der Invarianz hat, wie bei den Zahlen;
das ist die birationale Transformation.
Ist irgend eine nicht konstante Funktion des Körpers ß
und N(t — die /'te Potenz einer irreduziblen Funktion eten
Grades (§ 172, 6.), so besteht zwischen z und zY eine Gleichung,
die in bezug auf zx vom eten Grade ist, deren Grad in bezug auf £,
wenn Nenner und überflüssige Faktoren weggeschafft sind, mit
e± bezeichnet werde. Diese Gleichung sei
(1) J) = 0.
Unter den verschiedenen Gleichungen dieser Form gibt es
nur eine irreduzible und diese ist sowohl in bezug auf e als in
bezug auf von möglichst niedrigem Grade (Bd. I, § 20).
Ist Ö eine primitive Funktion des Körpers ß, so ist nach
§ 172, (12)
(2)
h = 0, 1,
1 Ä; = 0, 1.
e — 1
f~ 1
§ 186. Birationale Transformation. 661
eine Basis des Körpers ß, und folglich kann jede Funktion m
in £1 in der Form dargestellt werden:
(3) = + ------
worin die g0, ..., £/_j rationale Funktionen von # und sind,
also Zahlen des durch (1) bestimmten Körpers. Setzen wir
(4) n = ef, n-L = erf,
so lassen sich die Funktionen & in jeder der beiden Formen
darstellen:
... | = xü + + x^ -|------+ x^g^,
' = y0 + yiz + y%H-----------1- y^-i ^ei~1 ,
worin die x rationale Funktionen von g, die y rationale Funktionen
von gr sind.
1. Demnach läßt sich jede Funktion m linear mit
rationalen Koeffizienten in gt darstellen durch die
Wj-Funktionen:
, . „ r = 0, 1, ..e, — 1
w s = 0,-v
die wir in irgend einer Reihenfolge mit
(7) Vl, V2,
bezeichnen, und diese Funktionen sind linear un-
abhängig, d. h. es besteht zwischen ihnen keine
lineare Relation mit rationalen Koeffizienten in gt:
tfi i/i -j- x2 -------------------------1- x„, y„t = 0,
außer wenn die alle verschwinden.
Denn f ist der niedrigste Grad einer Gleichung für 0 mit
rationalen Koeffizienten in g und gt (§ 172).
Betrachten wir nun das Funktional
(8) rx = <! 1/1 + ^2 ’la + • • • + Vm
mit den Funktionalvariablen t2, ..., tni, so ergibt sich ein System
von Gleichungen:
(9) Tj = “F 4”
worin r jede natürliche Zahl, auch 0, sein kann, und die xi>r
rationale holomorphe Funktionale in gt sind. Es ergibt sich
daraus durch Elimination der y eine Gleichung
(10) #«) = -I-1- + Am = 0
höchstens vom Grade nr mit rationalen Funktionalen in gr als
Koeffizienten.
662 Fünfundzwanzigster Abschnitt. § 186.
Es ist zu beweisen, daß dieser Grad nicht kleiner als wx
sein kann, oder was damit gleichbedeutend ist, daß die
i/2, ..., i/m rational durch rx darstellbar sind. Dies ergibt sich,
wenn man (10) nach einem der partiell differentiiert:
m'tr 'i r t»»-i _|_ ... । 8^»-i । 8 — 0
dtv -r + g^ - o.
Da nun <5z(rx) nicht verschwindet, wenn m der möglichst
niedrige Grad der Gleichung (10) ist, so erhält man daraus un-
mittelbar die gesuchte Darstellung von Also muß m =
sein. Damit ist bewiesen:
2. Das Funktional rx genügt einer irreduziblen
Gleichung »jten Grades in
Setzen wir also in (9) r = 0, 1, 2, ..., — 1, so ergibt sich
ein System linearer Gleichungen für i/x, r]2, ..., deren Deter-
minante ein nicht verschwindendes Funktional in ist, und man
kann also für die Variable .^ solche konstante Werte setzen, daß
die Determinante auch dann nicht verschwindet. Geht rx durch
diese Substitution in 0X über, so kann man aus dem System (9)
die i/x, ..., rational durch und 0X ausdrücken.
Damit ist aber bewiesen:
3. Ist eine beliebige, nicht konstante Funktion
in ß, und 0X eine zweite Funktion desselben Kör-
pers, die keiner Gleichung von niedrigerem als
wxten Grade in zr genügt, so sind alle Funktionen
des Körpers ß, also auch g und 0, rational durch
gr und 0X ausdrückbar.
Zwischen irgend zwei Funktionen a, ß des Körpers ü besteht
immer eine Gleichung mit konstanten Koeffizienten
(11) *>,(0 = 0,
und unter allen möglichen Gleichungen dieser Form ist eine von
möglichst niedrigem Grade, sowohl in bezug auf a als in bezug
auf ß.
Sechsundzwanzigster Abschnitt.
Zahlenwerte der algebraischen Funktionen.
§ 187. Der Punkt.
Es entsteht nun die Frage, wie man den algebraischen Funk-
tionen eine Bedeutung im Gebiete der Zahlen beilegen kann. Wir
setzen dabei das Gebiet der reellen und imaginären rationalen
und irrationalen Zahlen als gegeben voraus, und in diesem
Gebiete das Rechnen mit den vier Spezies. Wir erweitern dieses
Gebiet durch Hinzufügung eines Zahlzeichens „Unendlich“: oo,
und rechnen auch mit diesem Zeichen in bekannter Weise, so daß
(1) — = 0, i = 00, oo. oo = 00
' oo 0
ist, während den Symbolen
I n 0 00
00 -f- OO, 0 • 00, —1 --
— 0 00
keine Bedeutung zukommt (oder auch, in jedem einzelnen
Falle nach Bedarf, ein beliebiger Zahlwert beigelegt wird).
Der Körper £1 besteht jetzt aus allen möglichen algebraischen
Funktionen a, ß, y, ..., die nach § 186 als rationale Funktionen
von zweien unter ihnen mit Zahlenkoeffizienten dargestellt werden
können. Auf die Art dieser Darstellung kommt es zunächst
nicht an.
Wir stellen nun folgende Definition auf:
1. Wenn alle Individuen oc, ß, y, ... des Körpers 52
durch bestimmte Zahlwerte a0, ß0, y0, ... in der Weise
ersetzt werden, daß
1. a = a0, wenn a konstant,
2. (w ß)0 — «o ßo>
3. (a ß')o = Wo ß0,
4. (oc/3)o = a0ß0,
664 Sechsundzwanzigster Abschnitt. § 187.
so ordnen wir einem solchen Zusammentreffen von Werten
einen Punkt ^ß zu. Wir sagen: <x = a0, oder <x hat den Wert a0
im Punkte ^ß. Zwei Punkte 5ß und ^ß' heißen dann und nur dann
verschieden, wenn es wenigstens eine Funktion in £1 gibt, die in
und 5ß' verschiedene Werte hat.
Die Regeln 2. bis 5. versagen in den Ausnahmefällen, nämlich
2. und 3., wenn a0 und ß0 = oo sind; 4., wenn a0 = 0, /30 = oo
oder a0 = oo, ß0 — 0 wird, und 5., wenn a0 und ß0 beide = 0
oder beide = oo sind.
Trotzdem müssen die Funktionen (a + ß)0, (aß)0 und (a:/3%
auch in diesen Fällen bestimmte Werte haben, die aber nicht un-
mittelbar aus den Vorschriften 2. bis 5., sondern auf indirektem
Wege bestimmt werden.
Der Punkt ist hiernach ein zu dem Körper ü ge-
höriger invarianter Begriff, der nichts mit dem zufälligen
Umstand zu tun hat. welche der Funktionen von £1 wir als die
unabhängige Variable betrachten.
Um alle Punkte zu finden, verfahre man so: Ist ^ß ein Punkt,
so gibt es Funktionen, die in ihm einen endlichen Wert haben,
denn wenn eine Funktion a in 5ß unendlich ist, so ist 1 : a end-
lich. Eine solche Funktion nehme man als unabhängige Variable z
und bezeichne ihren Wert im Punkt mit c. Alle ganzen Funk-
tionen von z sind dann gleichfalls in 5ß endlich, denn ist co eine
ganze Funktion, die der'Gleichung
<un -|- Oi o”-1 -)-••• -]- an = 0
genügt, so muß
1 I _|_ 31 _|_ . . . _|_ *31 0
1 (z>2
in ^ß befriedigt sein, und da die a15 a2, ..., an als ganze rationale
Funktionen von z in endlich sind, so kann co nicht — oo sein.
Jede Kongruenz nach dem Modul z —• c muß daher im
Punkt ^ß in eine richtige Gleichung übergehen, auch wenn diese
Kongruenz zwischen holomorphen ganzen Funktionalen besteht.
Ist also t die Basisform von ££ in Z, so muß nach § 184, (20) die
Gleichung bestehen:
(t — tx) (t — t2) ... (t — v„) = 0.
Es muß also einer der Faktoren der linken Seite in ^ß ver-
schwinden. Ist dies t — rx, so entspricht diesem Faktor ein
Primfaktor sr von z — c. Es wird also in 5ß
(2) rax = cx, ra2 — e2, ..., con = cn,
§ 187.
Der Punkt.
665
wenn cx, c2, ..., cn die durch die Kongruenzen
(3) <ax = cx, «o2 = c2, a)n = cn (mod sr)
bestimmten Zahlwerte sind. Hierdurch sind die Werte aller ganzen
Funktionen von z im Punkt iß bestimmt. Jede ganze Funktion
a> ist nach dem Modul z — c einem Ausdruck
<*1 ®1 “I- ®2 H- '' ‘ ~I-
mit konstantem Koeffizienten a kongruent und ist dann und nur
dann durch a teilbar, wenn
Ul Cx + ^2 4~ =z o
ist. Demnach folgt:
2. Unter den ganzen Funktionen von z haben nur
die durch n teilbaren in iß den Wert 0.
Da man jede gebrochene Funktion in ß so darstellen kann,
daß Zähler und Nenner nicht zugleich durch sr teilbar sind, so
ist hierdurch der Wert einer jeden Funktion in iß bestimmt.
3. Der Primfaktor sr heißt durch den Punkt iß
erzeugt. Er kann nicht durch einen von iß ver-
schiedenen Punkt erzeugt werden.
Man kann auch umgekehrt aus jedem Primfaktor % in z
einen Punkt erzeugen.
Ist z.— c die durch sr teilbare Linearfunktion, so gebe man
der Funktion z den Wert c. Dann nehme man eine durch sr,
aber nicht durch sr2 teilbare Funktion p und setze nach § 185,
(5) für jede Funktion nj:
(4) q = a Qm Qm + 1,
worin m eine ganze rationale Zahl, eine Funktion, deren Nenner
nicht durch a teilbar ist. Der Funktion q erteile man den Wert 0
und der Funktion 17 den Wert
n]0 = 00, wenn m <Z 0,
n]0 = a, wenn m == 0,
y0 — 0, wenn m 0.
4. Die so bestimmten Werte aller Funktionen q
genügen den Bedingungen 1. bis 5. und konstituieren
also einen Punkt, der durch das Primfunktional sr
erzeugt heißt.
Man kann also aus einer einzigen Funktion z und den Prim-
faktoren der Linearformen z — c alle Punkte ableiten, in denen
666 Sechsundzwanzigster Abschnitt. § 188.
z einen endlichen Wert hat. Um auch die übrigen zu bestimmen,
muß man noch eine zweite Funktion, etwa zx — 1 :z, zu Hilfe
nehmen, die in den noch fehlenden, in endlicher Anzahl vorhan-
denen Punkten den endlichen Wert 0 hat.
Die Gesamtheit der Punkte bilden die absolute Rie-
mannsche Fläche1).
§ 188. Ordnungszahlen.
1. Ist ein Punkt, so schreiben wir jeder Funk-
tion 17, die in diesem Punkte einen endlichen und
von Null verschiedenen Wert erhält, in die Ord-
nung 0 zu.
2. Wenn co die Gesamtheit der in verschwinden-
den Funktionen durchläuft, und p eine von diesen
Funktionen ist, für die alle
co
&
endliche Werte haben, so hat p die Ordnung 1.
Man sagt auch, p wird in unendlich klein in der ersten
Ordnung.
Ist — weder Null noch Unendlich, so hat o' hiernach gleich-
em
falls die Ordnung 1. Umgekehrt ist, wenn p und q' beide die
Ordnungszahl 1 haben, q : q' und p': p weder Null noch Unendlich.
3. Ist p von der ersten Ordnung und co irgend
eine Funktion in £1, so hat co die Ordnungszahl n,
wenn Q~nco in weder Null noch unendlich wird.
Diese Bestimmung der Ordnung n ist unabhängig davon,
welche Funktion erster Ordnung wir genommen haben. Ist n
positiv, so wird co Null, ist n negativ, so wird «o unendlich, und
ist n = 0, so hat co in einen endlichen, von Null verschiedenen
Wert.
’) Nach Riemanns Theorie der algebraischen Funktionen entspricht
jeder Punkt der geschlossenen mehrblätterigen Fläche einem Punkte in unserem
Sinne. Ist z unabhängige Variable, so ist die Riemannsche Fläche «-blätterig
über die «-Ebene ausgebreitet. Als absolute Riemannsche Fläche kann
man irgend eine Fläche betrachten, auf die die Gesamtheit jener mehrblätte-
rigen Flächen eindeutig und stetig bezogen werden kann.
§ 189. Polygone. 667
Die Definition der Ordnungszahl haftet also am Punkte iß.
Sie ist für den Körper SI invariant.
Daß jede Funktion in jedem Punkte iß eine bestimmte ganze
Zahl n als Ordnungszahl erhält, ergibt sich nun aus § 185, (5).
Man nehme eine Funktion z, die in iß endlich bleibt, als
unabhängige Variable, bestimme das zu iß gehörige Prim-
funktional sr und wähle eine Funktion p, deren Zähler durch a,
aber nicht durch 3t2 teilbar ist. Diese Funktion ist von der ersten
Ordnung.
Dann kann man jede Funktion co in die Form setzen:
(1) co = a$n ihp”+1,
worin a eine von Null verschiedene Konstante ist, und n ist die
Ordnungszahl von co.
Hat q die Ordnung 1, so hat p” die Ordnung n.
Über die Ordnungszahlen gelten folgende Sätze, die alle leicht
aus (1) folgen:
4. Die Ordnung eines Produktes zweier Funk-
tionen ist gleich der Summe der Ordnungen der
Faktoren. Die Ordnung eines Quotienten ist gleich
der Differenz der Ordnungen von Zähler und Nenner.
Die Ordnung einer Summe ist gleich der niedrig-
sten unter den Ordnungen der Summanden. Kommen
unter den Summanden mehrere von gleicher niedrig-
ster Ordnungszahl vor, so kann die Ordnung der
Summe größer, aber nicht kleiner sein.
Von einer Funktion, die in iß Null in der «ten
Ordnung wird, sagt man auch, sie wird Null in der
ersten Ordnung in n zusammengefallenen Punkten.
§ 189. Polygone.
1. Definition. Komplexe von Punkten, die den-
selben Punkt auch mehrmals enthalten können,
heißen Polygone oder Vielecke (des Körpers Si).
Die Zahl der Punkte eines Polygons heißt seine Ordnung,
und ein Polygon mter Ordnung wird auch kurz ein m-Eck
genannt.
Als Bezeichnung für die Polygone sollen die Buchstaben des
großen deutschen Alphabets 91, 23, (£,... dienen.
668 Sechsundzwanzigster Abschnitt. § 189.
2. Unter dem Produkt 9123 zweier Polygone verstellt
man das Polygon, das die Punkte von 21 und 23 zu-
gleich enthält, und zwar einen Punkt 5ß, der rmal
in 91 und smal in 23 vorkommt, r -]- smal. Die Ord-
nung eines Produktes ist gleich der Summe der
Ordnungen der Faktoren.
Wenn wir also mit 5ßj, 5ß2,... verschiedene Punkte bezeichnen,
so können wir jedes Polygon 91 auf eine Weise in die Form setzen:
(1) « = $»•••
Die Punkte sind also in der Rechnung mit Polygonen die Prim-
elemente. Um auch für die Einheit einen Vertreter zu haben,
muß noch das „Nulleck“ £), das gar keinen Punkt enthält, mit-
genannt werden.
Der größte gemeinschaftliche Teiler zweier Polygone
91, 23 enthält jeden Punkt, der in 2t und 23 vorkommt, und zwar
so oft, als er in jedem von beiden vorkommt.
Das kleinste gemeinschaftliche Vielfache enthält jeden
Punkt von 21 und 23, und zwar in der höchsten der Ordnungen,
in denen er in 21 und 23 vorkommt.
3. Ist z eine Variable des Körpers 42 und n der
Grad des Körpers in bezug auf 2, so nimmt z jeden
Wert c in n Punkten an.
Denn zerlegt man z — c in seinePrimfaktoren [§ 183, (17)]:
z — c = • • •, e1 -|- e2 -|- • • • = n,
so erzeugt jeder dieser Primfaktoren einen Punkt, z. B. n1 den
Punkt Sßx, in dem die Funktion z — c Null in der e1ten Ordnung
wird. Rechnet man diesen Punkt ex fach, so erhält man ein Polygon
... von der Ordnung n, in dessen Punkten die Funktion
z — c verschwindet.
Derselbe Satz gilt aber auch für den Wert c = 00, wie man
daraus schließt, daß der Grad des Körpers 42 in bezug auf 1 : z
derselbe ist wie in bezug auf z.
4. Di e n Punkte, in denen z einen Wert c annimmt,
heißen konjugiert nach 2, und die Werte ij,, ..., ij„,
die eine Funktion q in 42 in n konjugierten Punkten
annimmt, heißen gleichfalls konjugiert nach z, und
z heißt von der Ordnung n. Die Konstanten, und
nur diese, haben die Ordnung 0.
§ 190. Verzweigungspunkte und Verzweigungszahlen. 669
§ 190. Verzweigungspunkte und Verzweigungszahlen.
Nach § 184 gibt es nur eine endliche Anzahl von Punkten,
in denen z — c Null in höherer als der ersten Ordnung wird.
Diese heißen die Verzweigungspunkte von Si in z.
Wir konstruieren ein Polygon das (e — 1) mal jeden
Punkt iß enthält, in dem z — c oder 1: z Null in der eten Ord-
nung wird. Dieses Polygon heißt das Verzweigungspolygon
von ß in bezug auf z, und seine Ordnung
(2) wz = 21 (e — 1)
heißt die Verzweigungszahl in bezug auf z1).
In § 184, (20) haben wir die Formel erhalten:
(3) N(t — t) = (t — ti) (t — t^) ... (t — t„) (mod z — c),
worin r die Basisform des Körpers ß nach z bedeutet und rx, r2,
..., rn die gleichen oder verschiedenen konstanten Funktionale,
denen t nach den Primfaktoren von z — c kongruent wird, also
die Werte, die t in den nach z konjugierten Punkten 5ßx, ^ß2,..., <ß„
annimmt. In jedem dieser Punkte muß (3) in eine richtige Glei-
chung übergehen, und daraus folgen z. B.:
(4) N(f) — ,
(5) ®(r) ==: ± H“ rn
als Werte der rationalen Funktionale N(r) und S(t) für z = c.
Setzt man für die Fünktionalvariablen rationale Funktionen von z,
so gelten entsprechende Formeln für die Funktionen in ß, vor-
ausgesetzt, daß nicht einer der Ausnahmefälle 0. 00, 00 -|- 00
ein tritt.
Ist daher ..., eine Basis von ß, und sind i;i>x, ...,
konjugierte Werte nach z von 17,-, so ist nach (5) und der
Definition der Diskriminante in § 173
(6) zZ(’?i, •••, ’l») = (£ ±»7i,i »72,2 »7m,».)2-
Stehen zwei Funktionen z und z1 in ß in einer linearen Be-
ziehung :
az b
l) Breitet man die Riemannsche Fläche über der .»-Ebene aus, so ist
n die Anzahl der übereinanderliegenden Blätter, w2 ist die Anzahl der Ver-
zweigungspunkte dieser Fläche.
670
Sechsundzwanzigster Abschnitt.
§ 191-
worin a, b, c, d Konstanten sind, deren Determinante ad —• bc
von Null verschieden ist, so sind die Verzweigungspolygone
und 3z' identisch, und daher ist auch = wy, denn wenn in
einem Punkte z — z0 oder 1 Null in der eten Ordnung wird,
so ist in demselben Punkte auch
, _ , _ (ad — bc)(z — g„)
0 (cz + 8) (c20 + 8)
oder wenn 20 unendlich, also Vo = a: c ist:
und wenn z'o = oo, also C£o -|~ d = 0 ist:
1 cz d
z' a z b
ebenfalls unendlich klein in der eten Ordnung.
Wenden wir dies auf z' = 1 : z an, so erhalten wir die Ver-
zweigungspunkte, in denen z einen endlichen Wert hat, aus der
Körperdiskriminante D nach § 184, (24), (28). Es fehlen dann
noch die Verzweigungspunkte, in denen z = oo, also z' = 0 wird,
und diese ergeben sich in gleicher Weise aus den verschwinden-
den Wurzeln der Körperdiskriminante Dy. Demnach haben wir
den Satz:
5. Die Verzweigungszahl w2 ist gleich dem Grade
der Körperdiskriminante D, vermehrt um die Anzahl
der verschwindenden Wurzeln von' Z)y .(z' = 1 : z).
§ 191. Polygonquotienten und Polygonklassen.
Eine Funktion t; in ß hat nur in einer endlichen Zahl von
Punkten eine von Null verschiedene Ordnungszahl. Die Summe
der positiven Ordnungszahlen ist ebenso groß wie die Summe der
negativen, nämlich gleich der Ordnung der Funktion n (§ 189, 4.).
Sind die Ordnungszahlen von q für jeden Punkt iß bekannt, so
ist dadurch die Funktion rj bis auf einen konstanten Faktor be-
stimmt. Denn wenn eine zweite Funktion -rj' überall dieselben
Ordnungszahlen hat, so hat -rj : i/ überall die Ordnungszahl 0 und
ist daher konstant (§ 189, 4.).
Wir bilden ein Polygon 'M, in das wir jeden Punkt, in dem
q eine positive Ordnungszahl hat, so oft aufnehmen, als diese
Ordnungszahl angibt, und ein zweites Polygon 23, in das wir in
§ 191-
Polygonquotienten und Polygonklassen.
671
entsprechender Weise die Punkte auf nehmen, in denen tj eine
negative Ordnungszahl hat. Dann sind die Polygone 91 und 93
von gleicher Ordnung, nämlich von der Ordnung der Funktion 17,
und durch diese Polygone ist die Funktion 17 his auf einen kon-
stanten Faktor bestimmt.
Wir können daher die symbolische Bezeichnung einführen:
91
(1) = &
und 91 den Zähler oder das Obereck, SB den Nenner oder das
Untereck von 7] nennen. Nach dieser Definition sind zunächst
91 und 18 relativ prim zueinander. Wir wollen aber diese Be-
zeichnung noch dadurch erweitern, daß wir, wenn SJD? ein beliebiges
Polygon ist:
TO 91 _ 91
TO93 - 18
setzen. Dann ist die Bezeichnung (1) von der Beschränkung frei,
daß 91 und SB relativ prim sein sollen. Beide Polygone sind immer
noch von gleicher Ordnung, aber diese kann größer sein als die
Ordnung von 17.
Bei dieser Darstellung der Funktionen 17 gelten dann für die
Multiplikation und Division dieselben Regeln, wie beim Rechnen
mit Zahlenbrüchen im Gebiete der natürlichen Zahlen.
In (1) können 91, 93 nicht beliebige m-Ecke sein, und die Er-
forschung der Beziehung zwischen diesen ist die große Frage, die,
in anderer Weise, durch das Abelsche Theorem beantwortet wird.
Wir stellen folgende Definition auf:
1. Können zwei w-Ecke 91, 91' Obereck und Unter-
eck einer Funktion in £1 sein, so heißen 91 und 91'
äquivalent.
In Zeichen: Gibt
zukommt, so ist
<3)
Aus der Formel
V =
.ergibt sich der Satz:
es eine Funktion t), der die Bezeichnung
91
r‘ ~ 91'
91 ~ 91'.
91 , _ 9£ y _ 9£
91'’ V ~ 91"’ 7] ~~ 91"
672
Sechsundzwanzigster Abschnitt.
§ 192.
2. Sind zwei n-Ecke mit einem dritten äquivalent,
so sind sie auch untereinander äquivalent. Man
vereinigt danach äquivalente Polygone 21, 21', ... in
einer Polygonklasse A. Jedes Polygon ist in einer,
und nur in einer Klasse enthalten.
Es existieren auch Polygone, die mit keinem anderen äqui-
valent sind, und die daher jedes für sich eine besondere Klasse
bilden. Diese heißen isolierte Polygone.
3. Ist 21 ~ 21', 23 ~ 23', so ist 2123 ~ 21'23'.
Dies folgt aus
21 23 2123
(4) ’/i — Ui — 21'23'"
Die Klasse C, der das Produkt 2123 aus den Klassen A, B
angehört, enthält daher alle Produkte aus einem Polygon der
Klasse A mit einem Polygon der Klasse B (unter Umständen
auch noch andere) und ist daher durch die Klassen A und B
vollständig bestimmt. Darauf beruht die Multiplikation (Kom-
position) der Klassen, die sich in der Formel ausdrückt:
(5) C = AB = BA.
Aus einer Gleichung zwischen drei Klassen A, B, M
MA = MB
folgt hiernach A = B. Denn ist 'Dl 21 ~ 21123, so folgt aus (2)
21 ~ 23. Ist 21 ~ 21' und
2123 = 6 und 21'23 = &',
so ist auch S ~ (£'. Wenn also 21 in <5 enthalten ist, so ist jedes
mit 21 äquivalente Polygon in einem mit (£ äquivalenten Polygon
6' enthalten.
4. Wir nennen eine Klasse C durch eine Klasse A
teilbar, wenn ein Polygon von A in einem Polygon
von C enthalten ist, und setzen
(6) AB = C.
Die Kl ässe B ist durch A und C vollständig bestimmt.
§ 192.
Wenn 21, 2IX, 9I2, ..., 21,
es s Funktionen in Si:
21,
Polygonscharen.
Polygone einer Klasse A sind, so gibt
(1)
_ ... _ 2I2 _ 21,
V1 ~ '21 ’ % ' '21 ’ “ '21
§ 192. Polygonscharen. 673
Ist 5ß irgend ein Punkt und g eine Funktion, die in diesem
Punkt die Ordnung 1 hat, so setzen wir nach § 185
V1 = ßl Qm + Qm P \
(2) ’fc = % ?m + ö2 Pm f S
Vs = cs Qm + ös Qm + \
worin e15 e2, ..., es Konstanten sind, die nicht alle verschwinden,
und 0j, 02, 0S Funktionen, die in 5ß endlich sind; m ist die
niedrigste Ordnungszahl in 3ß, die unter den Funktionen vt vor-
kommt.
Der Inbegriff der Funktionen
(3) V = C1V1 +&V2 -I------------F Cs Vs
mit Konstanten c15 c2, ..., cs heißt eine Schar. Wir bezeichnen
sie durch
(4) (71, Vs),
und nennen V2, •••> Vs eine Basis der Schar. Die Ord-
nung von v in ist nicht kleiner als m (sie ist größer, wenn
e1 ci 4“ e2 c2 4“ • • • 4“ es cs = 0 ist). Es kann aber v in keinem
Punkt unendlich werden, der nicht in 21 enthalten ist, und
auch nicht in höhere Ordnung, als der Punkt in 21 eingeht.
Wir können also setzen:
(5)
worin 21' gleichfalls zur Klasse A gehört.
Nimmt man statt 21 ein anderes Polygon 33 der Klasse A
und setzt
(6) £ =
so folgt aus 1.:
<. , «1
= ’il =
. , *2
(7) = =
und = =
21'
(8) ^v = v' — CtV) + Mi 4--F CsV's = gj--
Jedes durch den Nenner 21 und ein Konstantensystem cn
c2, ..., cs erzeugte Polygon 21' wird also auch durch jeden mit
Weber, Algebra. III.
674 Sechsundzwanzigster Abschnitt. § 192.
TI äquivalenten Nenner und dasselbe Konstantensystem erzeugt,
und dies Polygon TI' ist also nur abhängig von den Konstanten
und von den Polygonen Tb, sil2, TIS. Der Inbegriff dieser
Polygone wird eine Polygonschar mit der Basis TIX, ..., QI«
genannt und mit
(9) («!, »2, 21,)
bezeichnet.
Wenn die Polygone Tb, TI2, ..., TIS den größten gemeinschaft-
lichen Teiler TU haben, so ist dieser Teiler in allen Polygonen
der Schar enthalten und heißt der Teiler der Schar. Aber
man kann in der Schar ein Polygon TI' = TR SB so bestimmen,
daß 23 beliebig gegebene Punkte njcht enthält.
Denn ist ein Punkt Sß ftmal in TM und vmal in TI enthalten
und 9 eine Funktion, die in Sß von der ersten Ordnung ver-
schwindet, so ist in den Entwickelungen (2):
m — ii — v,
und die Entwickelung von q = TI': TI = TR23:TI lautet
q = e Qm -|- 0 Qm + *,
worin
e = e1c1 -|- e2 c2 -)-••• -f- cs.
Wählt man also die ci so, daß e nicht verschwindet, so ist
Sß nicht in SB enthalten.
Eine Schar, die einen Teiler TR hat, heißt eine uneigent-
liche Schar.
Wenn zwischen den Funktionen i?2, ..., eine Relation
von der Form besteht:
(10) ci’ii -|- c2 Vz H- ' ’' 4- Vs == 0,
in der die Konstanten c15 c2, ..., cs nicht alle = 0 sind, so be-
steht dieselbe Relation
(11) + CuVi +--------p cst]’s = 0
zwischen den Funktionen (7). Wir nennen dann diese Funktionen
linear abhängig. Dem entsprechend heißen auch die Polygone
der Schar TIX, TI2, ..., TIS linear abhängig. Man kann dann eine
der Funktionen, etwa t]s, linear durch die übrigen ausdrücken,
und die Schar (i?x, ij2, ..., ijs) ist mit (i?x, 1?2, ..., ^s_x) identisch.
Gleiches gilt von den Polygonscharen (Tb, TI2, ..., TI.,) und (2lx,
TI2, ..., Tls—i). Durch wiederholte Anwendung dieser Reduktion
kann man jede Schar durch eine linear unabhängige oder
irreduzible Basis darstellen. Zwei irreduzible Basen einer
§ 192.
Polygonscharen.
675
Schar haben gleich viel Elemente, und diese Zahl heißt die
Dimension der Schar und die Schar heißt eine s-fache.
Sind ?l15 2I2, •••> linear abhängig oder unabhängig, so gilt
dasselbe von 2)1 2(i, 2)13l2, ..., 2)i2Is.
Man kann in einer Schar der Dimension s >> 1
(12) 8 = (2G, «2, ..., 21,)
ein Polygon finden, das einen beliebigen Punkt Iß mindestens
einmal öfter enthält als der Teiler 2)1 dieser Schar.
Dieser Zweck wird erreicht, wenn man für diesen Punkt die
Entwickelung (2) ansetzt und dann eine der Konstanten cn c2,..., cs
aus der Gleichung
(13) C’i c2^2 -1- —H cs6s —- 0
bestimmt. Diese Polygone bilden dann eine Schar von der (s — 1 )ten
Dimension, deren Teiler durch 2)i$ß teilbar ist.
Dieser Satz läßt sich dahin erweitern:
5. Die Polygone einer s-fachen Schar, die durch
ein r-Eck 3t teilbar sind, bilden eine mindestens
(s — r)-fache Schar.
Ist dieser Satz schon für ein r-Eck bewiesen, so folgt er
für ein (r 1)-Eck 3t$ßfaus dem vorhergehenden. Denn durch
Hinzutreten des Punktes Iß wird entweder die Dimension nicht
verändert, wenn Iß im Teiler der durch 3t reduzierten Schar auf-
geht, oder sie wird um 1 vermindert.
Man kann das Polygon 3t so wählen, daß die Dimension von
8 genau auf (s — r) reduziert wird. Zu diesem Zweck hat man
die Punkte von 3t successive so zu wählen, daß jeder folgende
im Teiler der durch die vorangehende reduzierten Schar nicht
enthalten ist. Daraus folgt:
6. In einer s-fachen Schar gibt es mindestens
ein Polygon, das durch ein gegebenes (s — 1)-Eck
teilbar ist.
Ist die Klasse M, der alle Polygone der Schar 8 angehören,
von der mten Ordnung, so kann die Dimension s der Schar nicht
größer sein als m -|- 1. Denn sonst könnte man nach 6. in
8 ein Polygon finden, das durch ein (m -|- 1)-Eck teilbar wäre,
was widersinnig ist, da 8 nur m-Ecke enthält. Es hat daher die
Dimension s der Schar bei gegebener Klasse A ein Maximum.
Ist dieses Maximum erreicht, so sind alle Polygone der Klasse A
43*
676 Sechsundzwanzigster Abschnitt. § 193.
in S enthalten. Denn gibt es ein nicht in S enthaltenes Polygon
91s +! in A, so ist
(Sli, 2l3,2tÄ + 1)
eine Schar von der Dimension s -|- 1. Damit ist bewiesen:
7. Die Polygone einer Klasse bilden eine Schar
von einer endlichen Dimension s. Diese Zahl soll
die Dimension der Klasse heißen.
Wenn es in einer Klasse G Polygone gibt, die durch ein
Polygon 91 einer Klasse A teilbar sind, so ist G durch A teil-
bar. Ist
G = AB,
so erhält man die Dimension von B dadurch, daß man die Schar
aus C aussucht, die durch irgend ein Polygon 91 in A teilbar
ist. Diese Dimension ist also nur von den beiden Klassen A
und C abhängig und soll mit (A, G) bezeichnet werden.- Das
Zeichen für die Dimension einer Klasse A ist hiernach (0, A),
wenn O die Klasse des Nullecks ist. Wir haben dann
(14) (d, C) = (A, AB) = (0, B),
und wenn a die Ordnung der Klasse A ist, so ist nach 5.:
(15) (d, G) (0, C) - a.
Bezeichnen wir mit A die eigentliche Klasse, die man erhält,
wenn man 9)1 überall weghebt, so soll die uneigentliche Klasse
mit dem Teiler 9)1 durch 9)1 A bezeichnet sein.
8. Der Teiler einer uneigentlichen Klasse ist ein
isoliertes Polygon.
Ist nämlich 9)1 A eine uneigentliche Klasse, so läßt sich in
A ein Polygon 91 finden, das relativ prim zu 9)1 ist. Ist 9)1' mit
9)1 äquivalent, so ist 9)1'91 in 9)1 A enthalten und mithin durch
9)1 teilbar. Es ist also auch 9)1' durch 9)1 teilbar, also mit 9)1
identisch. Es gibt also in der Klasse von 9)1 nur das einzige
Polygon 9)1.
§ 193. Normalbasen.
Nach dem Vorigen können wir eine Funktion z des Körpers
Q von der nten Ordnung in der Form
§ 193. Normalbasen. 677
darstellen, worin U und U' äquivalente n-Ecke ohne gemeinschaft-
lichen Teiler sind. Eine ganze Funktion co von a ist dadurch
charakterisiert, daß sie in keinem Punkt unendlich wird, der
nicht in U enthalten ist. Folglich läßt sich eine solche Funktion
co so darstellen:
91
(2) co = —,
t ) Ur>
worin r ein positiver Exponent ist. In (2) können Zähler und
Nenner gemeinschaftliche Teiler haben. Wir können aber an-
nehmen, daß 91 nicht durch U teilbar ist. Dann hat in (2) der
Exponent r den kleinst möglichen Wert. Diese Zahl r soll
der Exponent von co in a heißen.
1. Setzen wir a' — l:a, so ist nach (1), (2):
, 11 , , 91
— U<> 03 - as'r —
und wenn 91 nicht durch U' teilbar ist, so ist r der Exponent
von co' in bezug auf a'. Die Annahme, daß 91 nicht durch U'
teilbar sei, bedeutet, daß co nicht durch a teilbar sei, und daraus
folgt, daß auch co' nicht durch / teilbar ist.
2. Der Exponent einer ganzen rationalen Funktion von a
vom mten Grade
x == (Iq —cq a —|— • • • -j— am
ist gleich m. Denn diese Funktion wird in jedem in U enthaltenen
Punkt unendlich von der mten Ordnung. Der Exponent des Pro-
duktes xcj ist gleich r m.
3. Der Exponent einer Summe
CO -— Cy GOj —Cg GOg —|— • • • —C8 G0s
ist höchstens gleich dem größten der Exponenten von coj, co2,..., cos.
4. Wir bestimmen eine Reihe ganzer Funktionen von a
^1> ^3) • • •
durch folgende recurrente Bestimmung:
1) Aj konstant (Exponent = 0),
2) A2 eine nicht rationale ganze Funktion von a mit
möglichst kleinem Exponenten r2,
3) As eine nicht in der Form
(3) Aj a?2 ^2 • • • “F xs—i 'F—i
enthaltene ganze Funktion von a mit möglichst kleinem
Exponenten rs,
678 Sechsundzwanzigster Abschnitt. § 193.
und setzen diese Reihe fort, solange man noch Funktionen As
finden kann, die nicht in der Form (3) enthalten sind.
Nach 4., 3) sind die Funktionen Ax, A2, A, in dem Sinne
linear unabhängig, daß zwischen ihnen keine lineare Gleichung
besteht mit rationalen Koeffizienten in s. Da es nicht mehr als
n linear unabhängige Funktionen gibt, so kann s nicht größer
als n sein. Andererseits gibt es, solange ist, immer noch
ganze Funktionen, die von Ax, A2, ..., As_x nicht linear abhängig
sind, und darunter auch solche von kleinstem Exponenten. Wir
erhalten also n Funktionen
(4) L = (Ax, A2,..., An),
und diese bilden eine Basis des Körpers £1 nach z. Sie bilden
eine Minimalbasis; denn wäre dies nicht der Fall, so müßte für
irgend ein s n eine Funktion xt Ax x2 A2 -|- • • • xs As durch
eine lineare Funktion z — c teilbar sein, ohne daß xs durch z — c
teilbar ist. Reduziert man auf ihre Reste nach
z — c, so ergibt sich eine Gleichung:
cx Ax -|- c2 A2 As = (z — c) ft,
worin die ..., cs konstant sind, cs von Null verschieden und
[i eine ganze Funktion ist. Es ist ft nicht in der Form (3) ent-
halten und sein Exponent ist nach 2. und 3. kleiner als der
Exponent von A„ was der Bestimmung 4. 3) widerspricht. Also:
5. Die Funktionen Ax, A2, ..., A„ bilden eine Mini-
malbasis von £1 nach z. Sie heißt eine Normalbasis.
Die Exponenten rx, r2, r3, rn dieser Funktionen genügen
der Bedingung:
(5) = 0, 1 r2 r3 ... rn.
Denn wäre rsOs_x, so hätte man nach 3. 3) As an Stelle von
As_x nehmen müssen.
Von den Funktionen A< ist keine durch z teilbar; denn wäre
As = g [i, so hätte it einen kleineren Exponenten als As und wäre
nicht in der Form (3) enthalten. Es müßte also u an Stelle
von As treten.
6. Demnach sind (nach 1.)
rx, r2, ...,
die Exponenten von
(6) Al = /nA1( A2 = ..., AJ, = z'r«ln
in bezug auf z' = l:z. und diese Funktionen sind die Elemente
einer Normalbasis von nach z'.
§ 194. Differentialquotienten. 679
Bezeichnen wir nämlich mit x'i ganze rationale Funktionen
von höchstens vom Grade m, so ist
(7) Xi — smx'i
eine ganze rationale Funktion von z. Wäre nun
i
X{ A i ,
O,s—1
so würde aus (6) und (7) folgen:
zml.s = XxiZrs~rili,
0, s-I
und dies ist unmöglich, weil die A» linear unabhängig sind; und
es kann auch keine Funktion Xs von niedrigerem Exponenten als
rs geben, weil man daraus eine Funktion As von niedrigerem
Exponenten herleiten könnte.
Die Körperdiskriminanten Dz, Dzi in bezug auf die Variable
z und st sind
D2 — z/(A,, A2, ..., An),
IK — D (Ai, A2, •.., Am) ,
und daraus folgt nach (6):
(8) Dz< = Z' 2 <»-i + »-s+ ••• + r„)
Ist also 8 der Grad von Dz, so ist
2 (fj + r2 -|------|- r„) — ö
die Anzahl der verschwindenden Wurzeln von Dz-, und es ergibt
sich nach § 190, 5.:
(9) Wz = 2 (r, r2 • • • -|- rn).
7. Die Verzweigungszahl w2 ist also immer eine
gerade Zahl.
§ 194. Differentialquotienten.
Die Differentialquotienten körinen wir, wo wir keinen Gebrauch
von der Stetigkeit machen, nicht in der gewöhnlichen Weise
einführen. Wir nehmen zwei Funktionen a, ß aus ß, zwischen
denen die irreduzible Gleichung
(1) F (a, ß) = 0
besteht, bezeichnen mit F' (a), F' (ß) die abgeleiteten Funktionen
und definieren den Differentialquotienten als Funktion des
Körpers £1 durch die Formel:
(^\ - -
W \dß) “ F'(a)‘
680 Sechsundzwanzigster Abschnitt. § 194.
Es seien a0, ßQ die endlichen Werte der Funktionen a, ß in
einem Punkt Dann ist F(a0, ß0) — 0, und wir können die
Gleichung (1) so darstellen:
(3) 0 = (a — a0) F' (a0) + (ß - ßQ) F' (ß.)
+ >[(«— «o)2 F" (a0, a0) + 2 (a — a0) (ß — ß^ F" (a0, ß0)
+ (ß-/V F"(ß0,ß0-)] + ...
Die beiden zueinander reziproken Funktionen
« — «o ß — ßo
ß — do ’ « — «0
können nicht beide in dem Punkt unendlich sein. Es sei also:
/« — «0\
\ß ~ ßo/o
der endliche Wert des ersten dieser Quotienten. Dann ergibt
sich aus (3), wenn F'(c/ß nicht Null ist:
/'n (a ~ — F'^ — (F'(ßy\ _ (da\
K ) \ß~ ßj~ F’(a0) - \F'(a)J0 ~ \dß);
Diese Gleichung besteht für alle Punkte 5ß, mit etwaiger Aus-
nahme einer endlichen Anzahl1).
1. Eine Funktion y in ß, die in allen Punkten,
mit Ausnahme einer endlichen Anzahl, der Bedin-
gung genügt:
(5)
\p — Po/o
ist mit identisch.
\dßj
Denn aus (4) und (5) folgt, daß die Funktion
/d <x\
\dß) ~ V
unendlich viele Nullpunkte hat und daher identisch verschwin-
den muß.
Die Formel (5) kann also gleichfalls als Definition des Dif-
ferentialquotienten dienen.
Daraus ergeben sich einfach die Hauptsätze über die Dif-
ferentialquotienten :
*) Unter den auszunehmendeu Punkten sind jedenfalls die enthalten, in
denen a0 oder ß„ unendlich wird. Denn für diese Punkte sind die Funk-
tionen « — «0, ß — ß0 gar nicht erklärt.
§ 194.
Differentialquotienten.
681
2. Seien a, ß, y drei Funktionen in ß; dann ist
. . /da\ zdß\ /da\
w W W7 “ W/
Denn es ist für unendlich viele Punkte
/« — «0\ /ß — ßQ\ _ /« — a0\
\ß — ßo/o V — TWo V — Wo’
und daraus folgt wie bei 1. der Satz 2.
Demnach kann man jeder Funktion a in & eine Funktion da
so zuordnen, daß für irgend zwei dieser Funktionen:
W \dß) = Fß
ein wirklicher Quotient zweier Funktionen da, d ß wird. Diese
Funktionen nennen wir die Differentiale von a,ß. Die Diffe-
rentiale der Konstanten und nur diese sind gleich Null. Die anderen
Differentiale sind alle vollständig bestimmt, wenn eines von ihnen
willkürlich (z. B. konstant) angenommen ist.
3. Sind a, ß, y, ..., beliebige Funktionen in ß,
die einer Gleichung
(8) F(a, ß, y, ...) = 0
genügen, so ist
(9) F' (a) d a F' (ß) d ß F' (y) d y • • • = 0.
Um diesen Satz zu beweisen, nehme man einen Punkt 5ß, in
dem keine der Funktionen a, ß, y ... oder da, dß, dy, ... unend-
lich oder Null wird und auch die abgeleiteten F'(a), F' (ß), F'(y)
nicht verschwinden, und ordnen wie in (3) die Funktion F nach
Potenzen und Produkten von a — aQ, ß — ß0, y — y0, ... Dann
ergibt sich, daß die Gleichung (9) für unendlich viele Punkte, und
mithin identisch erfüllt ist. Als Spezialfälle von (9) ergeben sich:
d (a ß) = d a d ß,
. d (aß) = ßda -f- adß,
' j /a\ ßda — adß
d \ß) - ß~*
Der Begriff des Differentials läßt sich ohne weiteres auf
holomorphe Funktionale übertragen, wenn die Funktional-
variablen als Konstanten betrachtet werden. Der Satz 3. und die
daraus folgenden Formeln (10) gelten dann auch noch, wenn a,
ß, y, ... holomorphe Funktionale sind und F (a, ß, y, ...) eine
ganze rationale Funktion von a, ß, y, ..., ist.
682 Sechsundzwanzigster Abschnitt. § 195.
Ist a eine ganze rationale Funktion von so ist da/dz eben-
falls eine ganze rationale Funktion, nämlich die Derivierte von
u nach z.
§ 19S. Darstellung der Differentialquotienten durch
Polygonquotienten.
Wir nehmen irgend eine Funktion z der nten Ordnung in ß
und eiue Minimalbasis coj, co2, ..., con in bezug auf z. Alle ganzen
Funktionen von z des Körpers sind dann in der Form dar-
stellbar :
(1) 03 = X. COj -|- CO2 • • • -|- Xn 03n
und gehen aus dem Basisfunktional
(2) t = #i o1
hervor, wenn für die Funktionalvariablen t2, ..., tn ganze
rationale Funktionen x., x2, ..., xn von z gesetzt werden.
Setzen wir, wie in § 184,
Ä(# — r) = F(t,z),
so genügt t der irreduzibeln rationalen Gleichung:
r(r, z) = 0,
und man erhält nach § 194, 3.:
(3) F'(r)dr + F'(z)dz = 0,
und hierin ist F (f) das Verzweigungsfunktional (§ 184).
Nach (1) und (2) ist
(4) d ß) = d r -|- co1 d x. -|- co2 d x% • • • -|- O3n d xn,
wo in dr die tt durch die Xt zu ersetzen sind, und es folgt also
aus (3) der Satz:
4. Ist 03 eine ganze Funktion von z. so ist
(5) F'(tfä- = — F (z) + co. -|---------H 4^
v 7 'dz ’ 1 x dz ' 1 dz
ein ganzes Funktional.
Andererseits ist F'(a) nach § 182, 8. durch F'(t) teilbar.
Setzen wir also:
(6) F'W^F'ft),
so ist p ein ganzes Funktional, und aus (4) ergibt sich, wenn
man die t. durch die x. ersetzt:
§ 195. Darstellung der Differentialquotienten durch Polygonquotienten. 683
(?)
* dxn\
1 d$ d $ J
dxn\
dx-
dx,
co,-,------
dz
~ 1’ydz
und daraus folgt, daß auch F' (z) (nach Ersetzung der t( durch
die Xi) durch p teilbar ist.
Wir nennen demnach, mit Rücksicht auf die geometrische
Analogie, p das Funktional der Doppelpunkte in ra, z.
Ist Sß ein Punkt, in dem z endlich und F'(r) von Null ver-
schieden ist, der also kein Verzweigungspunkt in z ist, so hat
eine ganze Funktion co von z nach 4. in iß einen endlichen
Differentialquotienten. Eine gebrochene Funktion q von z, die
in endlich ist, läßt sich als Quotient zweier ganzer Funktionen
G)':ca darstellen, deren Nenner co in Sß nicht verschwindet.
Daraus folgt:
d 'n 1 / , d a> d <o'\
-=-1 = —- g> ------co ,
dz ro2 \ dz dz J
und folglich ist dq'.dz im Punkt Sß gleichfalls endlich.
Um das Verhalten eines beliebigen Differentialquotienten
da:dß in irgend einem Punkt Sß zu erkennen, nehme man eine
Funktion z, die in Sß Null von der ersten Ordnung wird, und be-
zeichne mit r, s die Ordnungszahlen von a — a0, ß — /30 in
Punkt Sß. Für den Fall, daß a in Sß unendlich wird, setze man
«0 = 0 und erhält eine negative Ordnungszahl r. Entsprechen-
des gilt, wenn ß unendlich wird.
Dann ist nach § 185:
a — a0 — zr a',
W ß-ß0 = Z’ß',
worin a' und ß' Funktionen in £1 sind, die in Sß weder Null noch
unendlich werden.
Daraus ergibt sich nach § 194:
da , , . da'
— — rzr~1 a' zr-j—,
dz 'dz
dß ,o,i Aß'
~A~ = sz3-1 ß' -4- Z!s-~,
dz 1 dz
da'
a' dz
"cTßA
ß'dz
ß — ß0 da ______
a — a0 dß
(9)
684 Sechsundzwanzigster Abschnitt. § 195.
und wenn man in den Punkt 5ß geht:
(10) ~~ = -
' \a — a0 dß)0 s'
was ein endlicher von Null verschiedener Wert ist.
Daraus folgt:
5. Die Ordnungszahl des Differentialquotienten
da:dß in irgend einem Punkt 5ß ist gleich der
Differenz der Ordnungszahlen von a— a0 und ß — ßQ.
Ist r >• s, oder r < s, so ist
/a — a„\
= 0 “d“ =
und folglich nach (10) auch
fww') == 0 oder = oo.
W/o
Ist r = s, so folgt aus (10)
. . /da\ _/a — aQ\
J \dß)o~ \ß — ßj^
Hier ist jede Spur der Variablen z herausgefallen,
und diese Formel gilt für jeden Punkt ohne Ausnahme.
Danach lassen sich die Nullpunkte und Unendlichkeitspunkte
der Differentialquotienten genau feststellen und damit diese
Funktionen als Polygonquotienten darstellen.
Ist a die Ordnungszahl von a — a0 in einem Punkt nach
§ 188, so enthält das Verzweigungspolygon 3« den Punkt
a — Imal oder — a — lmal, je nachdem a positiv oder negativ
ist. Ist a negativ, so enthält das Nennerpolygon 'äl von a den
Punkt 5ß (—a)mal, und folglich ist in beiden Fällen der Punkt
5ß in 3«:'^2 (a — l)mal enthalten. Hat 3/s, 33, b die entspre-
chende Bedeutung für ß. so enthält also der Quotient:
3«®2
(n — b) mal den Punkt 5ß.
Die Ordnungszahl von da:d ß in 5ß ist aber nach 5. ebenso
groß, und daraus ergibt sich die Darstellung:
/12, da _ 3«SB2
' J dß' 3^’’
worin, um es zu wiederholen, 3«: 3ß die Verzweigungspolygone,
21, SB die Nenner von a, ß sind.
§ 196.
Geschlecht des Körpers £1.
685
§ 196. Geschlecht des Körpers £i.
Da in einem Polygonquotienten Zähler und Nenner von
gleicher Ordnung sind, so folgt aus der letzten Formel [§ 195, (12)]:
(1) Wa — 2 a = wß — 2 A
Bezeichnen wir also mit n die Ordnung und mit w die Ver-
zweigungszahl für eine beliebige Variable, die, wie wir im § 193
gesehen haben, eine gerade Zahl ist, so ist die ganze Zahl:
(2) p — — n + 1,
eine zu dem Körper Sb gehörige invariante ganze Zahl, die das
Geschlecht des Körpers genannt wird. Daß diese Zahl nicht
negativ sein kann, ergibt sich aus § 193, (5) und (9), wonach
(3) p = (rs — 1) + (rs — 1) -|------------1- (rMi — 1)
ist, und so aus lauter Summanden besteht, deren .keiner negativ ist.
Zwei Funktionen a, ß nennen wir ein primitives Paar des
Körpers wenn alle Funktionen in £1 rational durch a und ß
ausgedrückt werden können. Ist a von der mten, ß von der wten
Ordnung, so ist nach § 171 für ein primitives Paar notwendig
und hinreichend, daß die zwischen a und ß bestehende irreduzible
Gleichung:
n m
(4) F(a, ß) = 0
in a vom nten, in ß vom »iten Grade sei.
Es sollen die Funktionen F' (a), F' (ß) durch Polygonquotienten
dargestellt werden. Wir setzen:
worin 21, von der mten, 33, 31 von der nten Ordnung sind. 21
hat dann mit 2)1 und 23 mit 91 keinen Punkt gemein. Wir setzen:
F(a, ß~) = aoan -f- a, an-1 -f- •••-(- aM,
(6) F'(a) = + (w — l^a’1-2 -f- - a„_i,
aF' (a) = — a, an~1 — 2 a2an~2 — • • • — na„.
Aus der zweiten diesei’ Gleichungen schließt man, daß im
Nenner von F'(a) keine Punkte vorkommen, die nicht in 21 oder
in 23 enthalten sind, und aus dem dritten folgt, daß dieser
Nenner höchstens = 21”— 229m sein kann. Wir setzen also:
(?) =
686 Sechsundzwanzigster Abschnitt. § 196;
Es soll jetzt bewiesen werden, daß 2 durch das Verzweigungs-
polygon ft? teilbar ist.
Nehmen wir zunächst an, daß 31 und 33 relativ prim zu 3^
seien; dann gibt es eine ganze rationale Funktion x von ft die in
keinem Punkt von 3(J verschwindet, für die ca = xa eine ganze
Funktion von ß wird. Setzen wir
f(a>) = xnF(a, ß),
so ist:
f'(ca) — xn~iF'(oi).
Ist t die Basisform von SI in bezug auf ß, so ist nach § 182
f'(eo) durch f'(r) teilbar, und da nach Voraussetzung ß in keinem
Verzweigungspunkt unendlich wird, so ist f'(t) und folglich auch
F' (a) durch das Verzweigungspolygon 3;j teilbar, und unsere Be-
hauptung erwiesen. Wir setzen:
s = 313/»,
(») *"(«) =
Diese Formel ist hierdurch nur unter der Voraussetzung
erwiesen, daß weder a noch ß in einem der Verzweigungspunkte
unendlich wird.
Machen wir aber die lineare Substitution:
. «(«i + 1) = »Ol,
W ß(ßl + 1) = t>ßn
so ist nach § 190
und wir können die Konstanten a, b so wählen, daß ocj und ft in
keinem Punkte von 3/s unendlich werden. Wir haben nur für a
und b irgend konstante Werte zu nehmen, die a und ß in keinem
Punkte von 3;? annehmen.
Ist Fj (cq, ft) = 0 die zwischen a1, ß1 bestehende rationale
Gleichung, so ist:
Fi(“»ßi) = («i + l)”(ft + l)mF(a, ß),
oder auch nach (9):
an ßmF1 («!, ft) = an bm tß ß™ F(a, ß);
ferner da:da1 = a2: a ax2, und folglich, mit Rücksicht auf F = 0,
F1 - 0:
(10) aM—2 ßm Fi (aß) = a”-1 bm aß~2 ßß F' (a).
§ 196. Geschlecht des Körpers 11. 687
Nach (9) verschwinden a15 ft in denselben Punkten und mit
denselben Ordnungszahlen wie a, ß, und daraus ergeben sich, den
Darstellungen (2) und (4) entsprechend, die Polygondarstellungen:
(11) «i — 9^’ & — 2g/
und aus (5), (7) und (10):
2
(12) -Fi(«x) =
Damit ist die Formel (8) allgemein bewiesen.
Setzt man nach § 194, (9):
F'(a)da 4- F'(ß)dß = 0,
so folgt aus (8) und § 195, (12):
(13) =
Beide Ableitungen F'(a). F'(ß) verschwinden also in den
Punkten von 3t, und 31 heißt das Polygon der Doppelpunkte
in (a, ß).
Die Ordnung von 31M23m“2 ist ‘2n(m — 1) und daraus ergibt
sich für die Ordnung 2r von 3i eine gerade Zahl, nämlich:
2 r = 2 n (m — 1) — wa = 2m(n — 1) — Wg,
und für das Geschlecht p ergibt sich nach (2):
(14) p = (n — 1) (tn — 1) — r.
Siebenundzwanzigster Abschnitt.
Algebraische und Abelsche Differentiale.
da ___ 3H1
~ 3JU
_ 21U2 _ 2IU|
- 233’ - 233?
03 d a = 03. da,.
§ 197. Differentiale in Sl.
Sind a und zwei Variable in SS von den Ordnungen n, n1
mit den Unterecken 11, Un mit den Verzweigungsecken: 3, 3n
den Verzweigungszahlen w, wu so ist nach § 195, (12)
Setzt man
(i) 03
so wird hiernach
(2)
Ist 21U2 äquivalent mit SB3> so ist ro eine Funktion in SS,
und ist gleichfalls eine Funktion in SS. Sind a, b die Ord-
nungen von 21 und 23, so ist [§ 196, (2)]
& + ^ = «' + 2n,
' a = b 2p — 2,
wenn p das Geschlecht des Körpers SS ist.
Wir setzen jetzt in einer neuen symbolischen Bezeichnung
O) da =
und nennen diese Ausdrücke die zum Körper SS gehörigen
Differentiale.
Im Zähler und Nenner 21, 23 eines Differentials können
gemeinschaftliche Faktoren zugefügt oder weggelassen werden.
Haben 21 und 23 keinen gemeinschaftlichen Teiler, so heißt 21 das
Obereck, 23 das Untereck des Differentials dJ.
§ 197. Differentiale in £1. 689
Die Bezeichnung (5) eines Difierentiais unterscheidet sich von
der ähnlichen Bezeichnung der Funktionen in Sl dadurch, daß
der Grad des Zählers um (2^ — 2) höher ist als der des Nenners.
Die in § 194 definierte Differentiale da der Funktionen in
£i sind spezielle Fälle der allgemeinen Differentiale (5). Denn
nicht alle diese dJ sind Differentiale von Funktionen in £1.
Wir unterscheiden eigentliche Differentiale da, d. h. solche,
die Differentiale von Funktionen in £1 sind, und uneigentliche
oder Abelsche Differentiale dJ, die das nicht sind. Für die
letzteren hat J selbst keine Bedeutung und erhält eine solche
erst in der Integralrechnung, die der rein arithmetischen Methode
nicht zugänglich ist.
Ist z eine beliebige Variable in ££ und dJ ein Differential,
so ist dJ:dz eine Funktion in a, und d_J:dz ist ein Diffe-
rentialquotient. Wir unterscheiden auch hier eigentliche
und uneigentliche Differentialquotienten. Der Quotient
zweier Differentiale dJ-.dJ' ist gleichfalls immer eine Funktion
in 42 und kann ebenfalls ein Differentialquotient genannt werden.
Damit ein Polygonquotient 91: 93 das Symbol für ein Diffe-
rential sein kann, ist notwendig, daß die Differenz (a — &) der
Ordnungen von 91 und 93 gleich (2 p— 2) sei. Aber diese Be-
dingung ist nicht hinreichend; es kommt noch hinzu, daß eine
Variable » in 42 existieren muß, für die
(6) U29l ~ 3®
ist. Ist diese Forderung befriedigt, so bleibt sie erhalten, wenn
z durch irgend eine andere Variable in 42 und 91 und 93 durch
äquivalente Polygone ersetzt werden. Sind also 91', 91", ... Poly-
gone der durch 91 bestimmten Klasse A, so sind 91':93, 91":93, ...
gleichfalls Differentiale.
Ist
/ = («!, 5I2, «3, •••)
und 9l15 9I2, 9Is, ... eine Basis von A, so sind die entsprechenden
Differentialquotienten
d J, d Aq d J%
dz ’ dz ’ dz ’
die Basis einer Funktionenschar von endlicher Dimension, und wir
können
(d , d , d
die Basis einer Schar von Differentialen von derselben Dimension
nennen.
Weber, Algebra. III. 44
690 Siebenundzwanzigster Abschnitt. § 198.
Jedes Differential dj, dessen Untereck ® oder ein Teiler
von SB ist, kann dann in der Form dargestellt werden:
(7) dj Cy d -j— <?2 d ~I- d d> + •••
mit konstanten Koeffizienten.
Die einfachsten Differentiale sind die, deren Untereck das
Nulleck ist, und deren Oberecke 23 also von der Ordnung
(2p — 2) sind. Diese heißen Differentiale erster Gattung
und werden mit d W bezeichnet. Sie sind dadurch charakterisiert,
daß für jede Variable z die Polygone U223 und 3 äquivalent sein
müssen, und die 2B bilden also, ihre Existenz vorausgesetzt, eine
Polygonklasse TV, deren Dimension zu bestimmen ist.
Das Polygon 23 heißt das Grundpolygon des Differentials dW
und wird ein vollständiges Polygon erster Gattung ge-
nannt. Ist 23 = 21®, so heißen auch 21 und ® Polygone erster
Gattung und zwar Ergänzungspolygone voneinander.
Jedes Polygon, das nicht Teiler eines vollständigen Polygons
erster Gattung ist, heißt von der zweiten Gattung.
Ist 21 ein Polygon erster Gattung, so ist auch jedes mit 21
äquivalente Polygon 21' von der ersten Gattung, und wir nennen
die Klasse A von 21 eine Klasse erster Gattung. Denn ist
21® — 23, so ist AB = TU, wenn B die Klasse von ® ist, und
es ist 21'® — 23' mit 23 äquivalent, also von der ersten Gattung.
Ist also q die Anzahl der linear unabhängigen Polygone
erster Gattung, die durch ein Polygon der Klasse A teilbar sind,
so ist nach § 192, (14)
(8) ' q. = (-4, TV) = (0, B),
also gleich der Dimension der Ergänzungsklasse.
Ist A eine Klasse zweiter Gattung, so gibt es kein durch
21 teilbares Polygon erster Gattung, und es ist
(A, W) = 0.
§ 198. Die Polygonsehar erster Gattung.
Um die Dimension (0, TV) der Polygonschar erster Gattung zu
bestimmen und damit zugleich ihre Existenz nachzuweisen, nehmen
wir eine beliebige Variable z in mit dem Verzweigungseck
3 und dem Untereck 11. Ist dW ein Differential erster Gattung,
so ist
(1)
dW 23U2
W = -j— — —ö~
3
§ 198. Die Polygonschar erster Gattung. 691
eine Funktion in £1, die wir einen Differentialquotienten
erster Gattung nennen.
Ist Sß ein Punkt, in dem (# — #0) unendlich klein von der
Ordnung e wird, so kommt dieser Punkt (e — 1) mal in 3 vor,
und folglich ist [w(# — ^0)]0 = 0. Wird z in einem anderen
Punkte ^ß unendlich in der eten Ordnung, so kommt dieser
Punkt e mal in U und (e — 1) mal in 3 vor, also einmal im
Zähler von wz, und folglich ist auch in diesem Punkte (w#)0 = 0,
und diese beiden Forderungen, nämlich:
a) In jedem Punkte, in dem z einen endlichen Wert zQ hat,
ist [w(z — ^o)]o = 0;
b) In einem Punkte, in dem z unendlich wird, ist (wz)0 = 0,
sind auch ausreichend, einen Differentialquotienten erster Gattung
w zu definieren.
Um die erste Bedingung zu erfüllen, nehmen wir eine
Minimalbasis nach z:
(2) »i, «2, ..., ra,„
setzen
(3) «r, s = StcOrCOs),
so daß
(4j zi — I i 2 • • • ^n, n
die Körperdiskriminante (nach z) ist, und bestimmen eine Basis
(5) Si, • • -5 fn
aus den Gleichungen:
(6j
Ist (r, s) ein Zeichen, das = 0 ist, wenn r und s verschieden
sind, und = 1, wenn r = s ist, so kann man die rationalen
Funktionen dr> s von z so bestimmen, daß
(7) 2<ii,r di, S = (r, s)
wird, und erhält aus (6):
(8) r
und die Größen a'r,s haben keinen anderen Nenner als ^7.
Daraus ergibt sich wegen (3) und (7):
= (r, s),
44*
692 • Siebeniindzwanzigster Abschnitt. § 198.
Ist umgekehrt für ein Funktionensystem vfo, t}2, i]n die
Bedingung
(10) . S^rßfs) — (r, s)
befriedigt, so ist Tjr = a,.; denn setzt man
t
^‘itr
so folgt aus (9) und (10) xr,s = (r, s). Demnach sind die Be-
dingungen (9) und (6) vollständig gleichbedeutend.
Die Größen s{ bilden eine Basis von Sl, sind aber nicht
ganze Funktionen.. Die Basen (5) und (2) heißen zueinander
komplementär.
Die Größen
(11) . ^«2, •••>
sind ganze Funktionen, und wenn i15 t2, ...,£» Funktionalvariablen
sind, so ist
(12) s2i2 4 ••• 4 eHtn) = Zs
der größte gemeinschaftliche Teiler der Funktionen (11).
Ist
(13) r = (z — q)4 — c2)(s — c8)...
das Produkt aller voneinander verschiedenen Linearfaktoren von
4 und
(14) % == Jtj ?r2?r3 ...
das Produkt der verschieden in z/ aufgehenden Primfunktionale,
so können wir jede durch r teilbare ganze Funktion p von z
in Sl in die Form setzen:
(* = r(“L Sj x2 8% 4 • • • xn in),
worin die
5 *^2 , * * * i rationale Funktionen von z sind. Dann
erhält man nach (9)
rxt = S(QG>i),
und da durch jeden Primfaktor von r teilbar ist, so ist
S(pch) nach dem Satz § 184, 7. eine durch r teilbare ganze
Funktion in Z, und folglich Xi eine ganze rationale Funktion.
Hieraus folgt, daß
z/p = r(x1zfel x2Zs2 4 ... 4- xnZe„)
durch reZ teilbar ist, und daß sonach re ein in p aufgehendes
ganzes Funktional ist.
Wäre n ein nicht in % enthaltener Primfaktor von re, so
könnte man p so annehmen, daß es nicht durch ar teilbar ist,
§ 198. Die Polygonsehar erster Gattung. 693
und (> könnte nicht durch re teilbar sein. Ebenso schließt man,
daß jeder der Primfaktoren sr,, %2, ..., aber keiner mehr als ein-
mal in re aufgeht; also ist, von Einheitsfaktoren abgesehen,
(15) re = x.
Also genügt jede der Funktionen en e2,..; en der Bedingung ä).
Umgekehrt ist auch jede dieser Bedingung genügende Funktion w
in der Form enthalten: . ;
(16) . ' w = x^ —j- x2 e2 • • -j— xn fH,
worin die xJ,'X2, J.., xn ganze rationale Funktionen von z sind.
Denn es ist rw; eine durch % teilbare ganze Funktion, und
folglich nach (9), (16) und § 184, 7,i,
S(rwv>i) = rXi
eine durch r teilbare ganze Funktion von z, folglich
(17) Xi-— S(wa>i).\
Um also die Differentialquötienten erster Gattung zu er-
halten, hat man unter den Funktionen (16) die aüszusuchen, die
der Bedingung b) genügen. , . .
Zu dem Zweck nehmen wir für (2) die in § 193 betrachtete
Normalbasis .
und bezeichnen die dazu komplementäre Basis mit
die durch
(18) S(4fis) = (r, s)
definiert ist.
Setzen wir dann
(19) w = y^ H--------------------.+ ynyn,
so ist, wenn ri der Exponent von A,- ist, nach (1.7) . .
Nach der Definition von rt ist für< z^= - oo endlich und
wz verschwindet wegen b). Folglich muß "für z — oo
verschwinden, d. h. yi kann höchstens, vom Grade (r, — 2) sein
und enthält daher höchstens ri — 1 konstante Koeffizienten.
Da = 1, rx = 0 ist und der Grad von yY nicht negativ
sein kann, so muß yY identisch Null sein und es folgt
S(w) = 0.
694 Siebenundzwanzigster Abschnitt. § 198.
Dies ist das Abelsche Theorem für die Differential-
quotienten erster Gattung.
Um zu zeigen, daß diese Forderung über die yi für die Er-
füllung von b) auch genügt, betrachten wir die Funktionen in Si
als Funktionen von z' = 1: z. Für diese bildet
Zj = Z,r*k2, ..., k'n = z'rnXn
nach § 193, 6. eine Minimalbasis, und
= ^If^, [l’2 = zr^[l2, ..., [l'n = Zrn pn
ist nach (10) die dazu komplementäre Basis. Folglich ist z'y' = 0
für z' = 0 [nach a), auf z' angewandt], also
zn-i fq = 0,
zyi[ii = zri~1pi = 0 für z — oo,
Z
wenn der Grad von yt nicht höher als (r,- — 1) ist.
Damit ist nachgewiesen, daß alle in der Form (19) ent-
haltenen Funktionen, in denen die y{ ganze rationale Funktionen
von z, höchstens vom Grade ft — 2 sind, ’Differentialquotienten
erster Gattung sind, und daß auch umgekehrt in dieser Form
alle Differentialquotienten erster Gattung darstellbar sind, und
es folgt der Hauptsatz:
1. Die Klasse der Differentiale erster Gattung
ist von der Dimension
(0, W) == (r2 — 1) 4- (r3 — 1) -]-------1- (rn — 1) = p.
Hieraus ergibt sich noch folgendes: Ist A eine beliebige
Polygonklasse von der Ordnung a und W die Hauptklasse erster
Gattung, so ist nach § 192, (14):
(J, W) (0, TK) — a = p — a,
also, wenn a p — 1 ist:
(A W) 1.
Es gibt also, wenn a kleiner als p ist, immer Polygone erster
Gattung, die durch $ teilbar sind, und daraus folgt:.
2. Jedes Polygon von (p— 1) ter und niedrigerer
Ordnung ist von der ersten Gattung.
Nach § 192, 5. kann man, wenn m nicht größer als p ist,
ein m-Eck sDi so wählen, daß, wenn HA die durch Wi bestimmte
Klasse ist,
(fff, TF) = p — m
§ 199. Der Riemann-Rochsche Satz. 690
wird, und wenn man hier m = p setzt, so folgt, daß es Klassen
der Ordnung p von der zweiten Gattung gibt.
§ 199. Der Riemann-Rochsche Satz.
Das unter dem Namen des Riemann-Rochschen Satzes
bekannte Theorem hat den Zweck, die Dimensionen von Polygon-
klassen zu bestimmen.
Wir betrachten zunächst eine eigentliche Polygon-
klasse A von der Ordnung n, nehmen darin zwei teilerfremde
Polygone 31, 31' und setzen:
31'
S ~ 31 ’
Ist dann 31" ein anderes Polygon derselben Klasse, so
setzen wir
31" ra 31"
° ~ 31’ z ~ 31' ’
Es ist also ra eine ganze Funktion von z, und ra: z eine
ganze Funktion von l:z. Wenn also ra nicht konstant ist, so ist
der Exponent r von co gleich 1. Umgekehrt ist auch jede ganze
Funktion co von z vom Exponenten 0 oder 1 in der Form 31": 31
darstellbar.
Wir erhalten also die ganze Klasse A aus der Gesamtheit
der ganzen Funktionen von z, deren Exponent 1 ist. Diese
erhalten wir aber leicht aus der Normalbasis (Ax, Z2, ..., 2„) in z,
mit der Reihe der Exponenten rx, rs, ..., rn (§ 193). Ist die
letzte dieser Funktionen, deren Exponent gleich 1 oder 0 ist, so
ist jede ganze Funktion, deren Exponent 1 ist, in der Form
(1) = c0# ci4“ c2Z2 -j- ••• -j- c3Z3
darstellbar (c0 muß konstant sein, weil es nach der Definition
der Normalbasis eine ganze Funktion sein muß, und wenn sein
Exponent positiv wäre, so wäre der Exponent von co größer als
eins). Demnach ist
(2) (0, A) = s + 1,
und diese Zahl ist also immer 1.
Die obere Grenze n -|- 1 wird nur dann erreicht, wenn alle
r2, r8, ..., rn = 1 und folglich p = 0 ist.
Da in einer eigentlichen Klasse mindestens zwei Polygone
enthalten sind, also (0, A) 2 sein muß, so kann n = 1 nur
in dem Falle p = 0 vorkommen.
696 Siebenundzwanzigster Abschnitt. § 199.
Eine Funktion z, die nur in je einem Punkte 0 und oo wird,
also die Ordnung 1 hat, gibt es daher nur in dem Falle p = 0.
Jede Funktion in SI ist durch ein solches z rational dar-
stellbar ’).
Wenn > 2 ist, so sind jq und zpi nach § 198 Differential-
quotienten erster Gattung. Es gibt also nach (1) Polygone SB, SB'
von der ersten Gattung, die der Bedingung genügen:
spSB 212äß' SB' 21'
- 3. , W - 3
und da 21, 21' teilerfremd sind, so muß 21 in SB, 21' in SB' auf-
gehen. Es ist also A eine Klasse erster Gattung.
Ist A eine Klasse zweiter Gattung, so sind also alle Expo-
nenten rt, r2, ..., rn gleich 2 oder kleiner als 2, und es ist im
besonderen rs+1 — 2, rs+2 = 2, ..., rn = 2. Folglich ist
p = (r2 — 1) + (r3 — 1) -|-----------1- (rn — 1) = n — s,
und wir haben nach (2) den Satz:
3. Die Dimension einer eigentlichen Klasse A von
der zweiten Gattung ist
(3) (0, A) — n — p 1.
Ist ferner A eine eigentliche Klasse erster Gattung und
(4) AB = W.
die vollständige Klasse erster Gattung, so nehme man ein Polygon '-8
in B und bilde die Differentialquotienten erster Gattung:
’ 213® 2l22l'S
’ ’ w = gw = —8~’
und diese Form bleibt erhalten, wenn ® durch ein äquivalentes
Polygon ®' ersetzt wird. Die. Dimension (0, B) ist also so groß
wie die Dimension der Schar der Differentialqüotienten erster
Gattung w, die die Eigenschaft haben, daß auch 'zw noch von
der ersten Gattung ist. Damit dies der Fall sei, dürfen in dem
Ausdruck:
w — y-i. fff -|- y% Pz + • • -H Vn pn
die Grade der Funktionen y2, y2, ...,, yn nur bis zu der Höhe
— 2, r2 — 2, ..., rn.— 2, ansteigen, und daraus folgt:
l) Dieser Funktiönenkörper führt zu den von den Geometern so
genannten „Unikursalkurven“.
§ 199. Der Riemann-Rochsche Satz. 697
(0, B) == (rs+1 — 2) 4~ (r«+2 — 2) 4- ••• 4~ (r« — 2),
(5) p = (ra+1 — .1) 4- (rs + 2 — 1) -----------H (r„ — 1),
(0, B) = p — n -|- s,
und nach (2):
(0, A) - (0, B) = n-p 4- 1.
Nun ist nach § 192, (14) (0, B) = (ri, TU), und wir haben
den Riemann-Roch sehen Satz für Klassen erster Gattung:
4. Die' Dimension einer eigentlichen Klasse A
erster Gattung ist
(6) (0, 4) = n - p + 1 + (4 W).
Diese Formel schließt (3) in sich, weil für Polygone zweiter
Gattung (A, TK) = 0 ist.
Da die Dimension einer eigentlichen Klasse mindestens
gleich 2 ist, so folgt für eine Klasse zweiter Gattung:
n p 4~ 1,
und hierin ist der Beweis eines Satzes von Riemann enthalten:
5. Eine Funktion, deren Ordnung kleiner als
(p 4~ 1) ist, ist von der ersten Gattung.
Es folgt weiter daraus, daß die Klasse W der Polygone
erster Gattung eine eigentliche ist. Denn angenommen, W habe
den Teiler TR, und es sei W = 211 A, so wäre (0, TP) = (0, A)
= p. Nimmt man 31 in A relativ prim zu 211, so gibt es in W nur
ein durch 21 teilbares Polygon, nämlich 21 TU, und folglich ist
(A, TF) = 1. Demnach gibt die Formel (6):
n — 2p — 2,
also gleich der Ordnung von W. Die Ordnung von A ist also
ebenso groß wie die von W, und folglich 311 — £).
Der Satz 4. gilt unverändert auch für uneigentliche Klassen.
Um das nachzuweisen, sei zunächst A von der ersten Gattung
und vom.Teiler 311:
A = WA',
AB = W,
(7) A'B' = W, '
. B' •== TflB, (§ 192, 8.)
. (A',W) == (0, B').
Die Ordnungen von TU, A, B seien m, a, b, also a 4~ b die
Ordnung von W, d. h. .
(8) a 4~ b — 2(p — 1).
698 Siebenundzwanzigster Abschnitt. § 199-
Nach (7) und § 192 ist
(9) (0, B) (0, B') — m,
und nach (6), angewandt auf A':
(0, A) = (0, A') = a - m — p + 1 + (0, B'),
also nach (8):
(0, A) - |a < (0, B) - |5.
Da wir aber A und B vertauschen können, so ergibt sich
hieraus
(0, A) - ja = (0, B) - |5,
und wenn man
(0, B) = (A, W),
|(a — 5) = a — p 1
(0,A) = a-p+ 1 +(A W)
in genauer Übereinstimmung mit (6).
Um auch für uneigentliche Klassen zweiter Gattung den
entsprechenden Satz abzuleiten, sei
(10) A =
eine uneigentliche Klasse zweiter Gattung vom Teiler
In einer eigentlichen Klasse zweiter Gattung, C, deren
Dimension größer ist als die Ordnung a von A, gibt es nach
§ 192, 5. immer Polygone, die durch ein Polygon der Klasse A
teilbar sind, und C ist also auch durch A teilbar.
Aus § 192, (15) folgt:
(0, A) (0, C) - c + a,
und aus (3):
(0, C) = 1,
also
(11) (0, A) a — p + 1.
Nun ist A' eine eigentliche Klasse von derselben Dimension
wie A, also, wenn m die Ordnung von SR ist, nach (6):
(12) (0,4) = M = « - m - 2 -H J- (^', W),
also nach (11):
(13) (J.', W) 5 m-
Daraus folgt, daß A' von der ersten Gattung sein
muß.
Ist W = A'B', so folgt aus (13):
(14) (A',W) = (0, B') m.
§ 200. Differentiale zweiter und dritter Gattung. 699
Wäre nun (0, B') > m, so könnte man in B' ein durch 9)1
teilbares Polygon 911® finden (§ 192, 5.), und es wäre:
91'3)1® ~ 91® = 9ß
ein vollständiges Polygon erster Gattung, es wäre also 91 selbst
von der ersten Gattung; gegen die Voraussetzung. Also ist
(0, B') = (Af, W) = m und
(15) (O,A) = a-p + l.
Also gilt auch hier der Riemann-Rochsche Satz in der
Form 3.
Besteht A aus einem isolierten Polygon 911, so ist (O,A~) = 1,
also a = p, und daraus folgt:
6. Ein isoliertes Polygon zweiter Gattung muß
ein j>-Eck sein, und umgekehrt ist jedes j)-Eck
zweiter Gattung ein isoliertes Polygon.
7. Geht ein Punkt Sß im Teiler einer uneigent-
lichen Klasse zweiter Gattung A auf, und ist A = A\
so muß A' von der ersten Gattung sein.
Denn es ist nach dem Satz (6) und (15):
(0, A) = a — p 4- 1,
(O,J.') = a-p + (A',W),
(0, A) = (0, A'),
also (A', W) = 1.
§ 200. Differentiale zweiter und dritter Gattung.
Wir können jetzt die Bedingung für ein Differential:
91
(1) =
die wir in § 197, (6) mit Rücksicht auf eine Variable 2 in der
Form ausgedrückt haben:
U29l ~ 3®,
invariant darstellen, wenn wir die vollständigen Polygone erster
Gattung benutzen, wonach
U29B ~ 3
ist:
91 ~ 2ß®,
oder, indem wir die Klassen einführen:
700 Siebenundzwanzigster Abschnitt. § 200.
1. Der Polygonquotient (1) ist ein Differential,
wenn die Klassen A, B von 41 und 43 relativ prim
sind und der Bedingung genügen:
(2) A — WB.
Sind a und b die Ordnungszahlen von A und B, so ist:
(3) . a — b = 2p — 2,
und da A jedenfalls von der zweiten Gattung ist, nach § 199, (15):
(4) (O,^) = 5+p-l.
Besteht B aus einem einzelnen Punkt Sß, so ist (0, A) = p,
und die Dimension von A ist ebenso groß wie die von FF; ist daher
(2öx, sß2,..., a^)
eine Basis von W, so ist
(Sßiffi,, SßSÖ2, ..., Sßä^)
eine Basis von A. Daher ist A eine uneigentliche Klasse mit
dem Teiler Sß, und es folgt:
2. Ein einzelner Punkt Sß kann nicht üntereck
eines Differentials sein.
Hat die Klasse A einen Teiler SDt vom Grade m, so muß Söi
im Teiler von B enthalten sein; denn Dl muß in jedem der
Polygone SffiSß, und folglich, da W eine eigentliche Klasse ist, in
jedem der Sß aufgehen. Ist
Dl^' = A, WB1 = B,
so muß
(5) (O,AL) = (O,Al')
sein. Es ist aber nach (3) und (4), auf A und A' angewandt,
wenn A' von der zweiten Gattung ist:
(0, J.) = (0, Al') + m,
also (0, A) >. (0, Al'); folglich muß m — 0 sein.
Al' kann aber nur dann von der ersten Gattung sein, wenn
B ein isoliertes Polygon und B = Dl ist. Dann ist:
Al' = W, (0, A') = p,
also muß (0, Al) = p, b = 1 sein,, und wir kommen anf den
Fall des Satzes 2. Folglich: . .
3. Jedes Polygon von mehr als einem Punkt kann
üntereck eines Differentials sein.
Unter einem Differential zweiter Gattung versteht man
ein solches, dessen üntereck eine Potenz eines einzelnen Punktes iß
§ 200. Differentiale zweiter und dritter Gattung. 701
ist. Ein Differential, dessen Untereck nur aus zwei einfachen
Punkten besteht, heißt ein Differential dritter Gattung. Wir be-
weisen den Satz:
4. Jedes Differential dJ läßt sich linear und mit
konstanten Koeffizienten aus Differentialen erster,
zweiter und dritter Gattung zusammensetzen.
Dieser Satz kann nach (4) auch so ausgesprochen werden,
daß die Klasse A eine Basis
(6) 9lx, SI2, ..., 9h+x,_x
von der Art hat, daß die Quotienten
(7) dJr = ^
Differentiale von einer der drei Gattungen sind.
Um ihn durch vollständige Induktion zu beweisen, nehmen
wir an, es sei für irgend ein SB eine solche Basis gefunden, und
suchen eine ebensolche für das Untereck Sß93, wenn iß ein be-
liebiger Punkt ist. Eine solche Basis können wir in der Form
annehmen:
(8) Sß9Ix, Sß9l2, ..., W-h,-!, %b+p,
worin %j+p ein mit 9B SB Sß äquivalentes Polygon sein muß, das
den Punkt Sß nicht enthält.
Wenn der Punkt Sß in 93 auf geht, setzen wir:
93 = DJSß“,
so daß Sß nicht mehr in 91t auf geht. Das Polygon 2BSßm + 1 ge-
hört dann in eine eigentliche Klasse, in der also ein durch Sß
nicht teilbares Polygon 9t existiert.
Wir setzen dann:
9I6+jP = 9119t,
und erhalten daraus ein Differential zweiter Gattung:
/q\ j r ______ ^b+p 9t
\yl Ut,b+P 5g Sß Sß”*+1
Geht iß in 93 nicht auf, so nehme man einen in SB aufgehen-
den Punkt Sß0. Dann gehört 9B Sß0 Sß in eine eigentliche Klasse
und enthält ein durch Sß nicht teilbares Polygon 9t. Ist dann
SB = Sß0911, %>+p = 9119t,
so ist
/iM J 1 __ %Lb+p __ 9t
(10) dJb+p — — 5ßo5ß
702
Siebenundzwanzigster Abschnitt.
§ 201.
ein Differential dritter Gattung. Damit ist der Satz 4. bewiesen,
sogar mit der Verschärfung, daß die darin auftretenden Differen-
tiale dritter Gattung einen beliebigen festen Punkt 5ß0 im Untereck
enthalten.
§ 201. Die Residuen.
Ist ein Punkt, der mmal im Untereck 53 eines Differen-
tials dj aufgeht (m 5> 0), so nehme man eine Funktion 2 in Sl,
die in unendlich groß in der ersten Ordnung wird. Dann kann
man nach § 197, (1) und § 185, (5) setzen:
(1) ~ = am_2Äm-24- am_32m~a -|--------+
CV 4V
worin die a Konstanten sind, 13 eine in -5ß endliche Funktion in Sl.
Der Koeffizient —a_x von —heißt das Residuum
des Differentials dJ in bezug auf den Punkt 5ß.
Das Residuum von d J im Punkt 5ß kann nur dann von Null
verschieden sein, wenn m >0 ist, d. h. wenn der Punkt 5ß im
Untereck von dj vorkommt. Solche Punkte sollen Pole von
d J heißen.
1. Das Residuum eines eigentlichen Differentials
ist gleich Null. Denn durch Differentiation einer
Potenz von 2 kann niemals 2~1 entstehen.
Nimmt man für 2 eine Funktion die gleichfalls in
unendlich von der ersten Ordnung wird, so kann man setzen:
(2)
2 — C2X + in, = c-1^1 -|-1?2,
d2 । -2
worin die c Konstanten, 13X, 132, 133, in 5ß endlich sind.
Setzt man
— 2
m—3 »
m — 2
«m-2 ^"t~1 ,
m — 1
a0 — co,
so ergibt sich aus (1):
dJ dco . . d2 . , ,
d21 d2, d2x '
wo 13' in endlich bleibt, und darin gibt nach 1. nur der Teil
, d2
Cv 4^2
§ 201. Die Residuen. 703
einen Beitrag zu dem Gliede mit und dieser hat nach (2)
den Koeffizienten a_i. Daraus folgt:
2. Das Residuum von dJ ist von der Wahl der
Funktion g unabhängig.
Es gilt ferner noch der folgende Satz:
3. Die Summe aller Residuen eines Differentials
ist gleich Null.
Wir erweitern den Ausdruck 21/® des Difierentiais dJ\ wenn
nötig, durch Hinzufügung von Punkten im Zähler und Nenner,
so daß die voneinander verschiedenen Punkte des Unterecks
(3)
ein Polygon einer eigentlichen Klasse bilden. Die Pole von dJ
sind dann unter diesen 5ß enthalten, möglicherweise auch noch
andere Punkte, für die das Residuum von dJ gleich Null ist.
Als Nenner von d J können wir dann
(4) ® — ... Kn
nehmen, wenn wir die zuviel genommenen Punkte wieder im
Zähler zufügen.
Wir nehmen eine Funktion g in SI von der nten Ordnung,
die in jedem der Punkte und in jedem nur zur ersten Ordnung
unendlich wird, und bilden die Entwickelung für den Punkt -ß;:
(5) = a®_2-|------------H 4’ +
Wenn wir für den Koeffizienten a® den Wert 0 zulassen,
können wir in allen Punkten mit derselben Potenz an-
fangen. Die Summe der Residuen von dJ ist
-- U-___1 •
Nach § 182, 11. läßt sich ein Funktionensystem a2, •••>
so bestimmen, daß ar in dem Punkte unendlich klein in der
ersten Ordnung wird, in den übrigen Punkten endlich und
von Null verschieden bleibt.
Setzt man dann
in „
0C1 «2 • ♦ • Qi 5
so wird
= 0™ in $Jß2, ^ßs> •••> endlich und nicht = 0 in
(6) ~ ” ^ß1’ ^ß3’ ’' ^ß’!’ ” ” ” — 0 » ^ßa>
n ^ßi, ^ßai •••> 1 ,> » » == 0 iü ^ß«.
704 Siebenundzwanzigster Abschnitt. .§ 201.
Verstehen wir nun unter rationale Funktionen
von z, die nicht alle identisch = 0 sind, und setzen:
(7) = ^1 91 + «2 4»2 + • • • + 9»>
so kann nur dann für z = oo, d. h. in den Punkten
5ß2, ..., 5ß„ endlich sein, wenn die Xi für z — oo endlich bleiben,
also Brüche sind, deren Zähler nicht von höherem Grade ist als
der Nenner.
Sind nämlich die
^*2 5 * * * 5 für z = oo nicht alle end-
lich, so gibt es einen positiven Exponenten r, so daß die Pro-
dukte xrz~r, xiz~r. ..., xnz~r für z — oo endlich sind, und
mindestens eines dieser Produkte, etwa XiZ~r, von Null ver-
schieden. Dann ist
-pp2 + ••• + xnz~r9«
im Punkte 5ßx endlich und von Null verschieden, und q kann daher
in nicht endlich sein. Ebenso sieht man, daß keine Relation
von der Form
«i 9i ~|~ #2 9a ‘ 9« == 0
bestehen kann, d. h. die 9X, 92) ..., 9» bilden eine Basis nach z.
Setzen wir also
(8) 9i 91 | *^'«,2 92 | * * ’ ~|~ xitn 9» 1
so ist
(9) S(jd~z') ~ X1>1 Xn,n-
Nach (5) ist
Z^m + Qi
dz s
für z — 00 endlich und folglich gilt das gleiche von
(10) + a^Mi+2a:/!2, ..., ^t’m+2 x^n.
Es enthalten also die Funktionen zxr>s jeden der Punkte
höchstens m — 1 mal im Nenner, und
enthält jeden der Punkte 5ß2, 5ß3, ... im Zähler, ('bi im allge-
meinen nicht.)
Nun ist nach (8):
d J
91 = 91 + + •'• + ^A,»9»-
§ 201.
Die Residuen.
705
Diese Funktion muß also in s-ß2, ?ß3, ... verschwinden. In
dem Punkte Sß2 verschwindet aber zx1^1q1, zx^3q3, ..., zxi,n^n,
während p2 nicht verschwindet. Folglich muß ä'«1j2 in AFi d- b. für
z = co, verschwinden und endlich bleiben. Wir haben also:
Ist r nicht gleich s, so ist ^2irr)S für z = co endlich.
Wir definieren nun die rationale Funktion u® durch:
(11) X{>i = a^zm~2 + + ••• + a^z-1 + w(%-2,
worin die Konstante «F dieselbe sein soll wie in (5), und wir
erhalten:
T
(12) _M®],
und nach (8):
[ij® M®] 9» == 1 “1“ " “I- —1 9’—1 “I“ +1 9® + 1
-(-••• Z* Xi, n 9„.
Im Punkte ist 17® endlich und von Null verschieden,
während auf der rechten Seite alles in verschwindet. Folg-
lich muß auch w® in und, weil es rational ist, für z = oo
endlich sein, und aus (9) und (11) folgt:
(13) = H--------F Sa^z-1 + Su&z~\
Nach unserer Annahme über z enthält das Untereck 33 von
dJ keinen Punkt, in dem z einen endlichen Wert hat.
Ist ein Punkt, in dem z den endlichen Wert z0 hat, so ist
Z1JX z , 91 dJ Ü1U2 , .dJ U919I
(14) (z z0) — u, — 3$ , (z z») — gsg ,
und in 9t ist der Punkt 5ß einmal öfter enthalten als in $,
folglich ist:
(15) [(^ — = 0 (in $)•
Das ist die Forderung a) in § 198.
Ist daher Ä2, ..., ln die Normalbasis in z, und ft,, /a2, ...,
die komplementäre Basis, so ist:
(16) = 2h th + 2/ä/M--------------------F ynPn,
worin die yi ganze rationale Funktionen von z sind, woraus folgt, daß
(17) = yi [§ 198, (18)]
eine ganze rationale Funktion von z ist.
Weber, Algebra. III. 4.5
706
Siebenundzwanzigster Abschnitt.
§ 201.
Da diese Funktion hiernach keine negativen Potenzen von z
enthalten kann, so ergibt sich aus (13) der zu beweisende Satz:
= 0,
der mit der besonderen Annahme über die Variable z nichts
mehr zu tun hat.
Als spezielle Anwendung folgt hieraus, daß ein Differential
zweiter Gattung kein Residuum hat, und daß die beiden Residuen
dei’ Differentiale dritter Gattung gleich und entgegengesetzt sind.
Ein eigentliches Differential (/ö, wie wir schon gesehen
haben, hat kein Residuum, und die Residuen des „logarith-
mischen Differentials“ d<5:<3 sind ganze Zahlen, nämlich die
Ordnungszahlen in z.
Wir wollen diese Betrachtungen mit dem Beweis des folgen-
den Satzes beschließen:
4. Nennen wir Differentiale zweiter Gattung linear
abhängig, wenn eine lineare Verbindung von ihnen
und von Differentialen erster Gattung mit kon-
stanten Koeffizienten einem eigentlichen Differen-
tial gleich ist, so sind höchstens p 1 Differen-
tiale zweiter Gattung immer linear abhängig.
Um dies zu beweisen, nehmen wir ein p-Eck zweiter Gattung:
(18)
mit p verschiedenen Punkten. Ist dann 5ß ein gegebener Punkt,
so setzen wir:
(19) u = ...
und erhalten eine Klasse B, in deren Teiler jedenfalls 5ß nicht
aufgeht, weil sonst iß2 ••• nach § 199, 7. von der ersten
Gattung sein müßte. Wir können also eine Funktion in £1:
(20) 2 = j
bestimmen, in deren Untereck jedenfalls der Punkt 5ß enthalten
ist. Wir bilden nun das eigentliche Differential
(21) dz = J,
in dessen Zähler 3 (dem Verzweigungspolygon nach z) der Punkt iß
nicht auf geht, weil er in U nur einfach aufgeht, und wenn wir
dz nach § 200, 4. durch Differentiale erster, zweiter und dritter
§ 201.
Die Residuen.
707
Gattung ausdrücken, so kann die dritte Gattung nicht in diesem
Ausdruck vorkommen, weil sonst die Residuen nicht — 0 sein
könnten. Dieser Ausdruck gibt also eine lineare Abhängigkeit
zwischen den Differentialen zweiter Gattung, deren Unterecke
F, W, W, •••, sind-
Nimmt man für irgend einen positiven Exponenten m:
U = •••
und setzt
_ 91 , _ 3
— u, dz — U2,
so ist 3 durch Sß“-2, U2 durch 'ß2”1-2, folglich das Untereck von
d z durch 5ßm teilbar. Man bekommt dann eine lineare Abhängig-
keit zwischen den Differentialen mit den Unterecken
iß“, iß“-1, ..., iß2, ..., iß2,
und damit ist der Satz 4. allgemein bewiesen.
45*
TABELLEN.
Tabelle I.
Entwickelungen der sechzehn fr-Quotienten (S. 88).
(1) v durchläuft alle ganzen Zahlen von — oo bis 00 • »n»nfo + a) _ 2 i V ar ö'u (;;) ö'u («) “ v — 1
(2) + a~) = W*8'**- n ö'u (?;) ft io (a) " e2’7’*’—1
(3) »b »01 (y + g) _ o . ^-iqve!Tiv ei7tiav ar »n (v) »oi («) ? q2‘‘e'2rriv—1
(4) »ii »oo (v 4- a) _ . x-i(— l)r qv eaiv eirri,JV. » »11 (v) »00 (a) ~qiv &niv — 1
(5) »li »io fr + «) = _ o . V *"ia' . sr »io fr) »ii fr) “ " <fv e2ntv 4- 1
(6) »li »n fr + a) = n ‘ V (—SL^L. ®»lflfr)»iofr) " i g2ve2»iv 1
(7) »li »oo (v +«) _ 2 V ^aiav jr»jo (v) »oi (a) “ _|_ j
(8) »11 »01 + a) = 2 V (- 1V e2gi'avgv e”™. ®»io'(®)»oo(«) “ q2f (ä.niv i
(9) »li»oifo + a) = o;-y e(2* + i)*jfl jr »oi (v) »n (a) ~ -2-i qzv + i e2,Tiv— 1
(io) »li»oo(^+ «) = _2 y(—1)* e(21, + 1)g7a ir »oi (0 »io («) “ ’e27Ii” — 1
Ql) »n »ii + a) _ 2 ’ V g(2v + 1)gz’ag 2 ^iv « »oi (v) »oi («) “ S2”+1 eiaiv — 1
(12) 2v 4-1 »11 »10 (^ + a) _ 2 y(— e(2v + 1)aiag 2 eniv 5T»Ol(O»Oo(ö) “ “ g2v + le2.i.,_ !
. I + _ (1?) 00^(g)00^3g
g »2^(t 4-rtg)^ Xi ) (^ H“ *0 ll*G'I/*6'
i + as
I + aW? l + i?P _ (ft) L0# (<Q 00a K
(itiß 5 VIL (I 4 4 g):> (p “4” Ä) °1^1 Trß'
14-45
. _i_+_wLl±i^ rz 7 = u
’^^d+^p 4i -)^ 5 (» + «)T%1”«
. 1 + .1?g59 rr- „ _ _ (») ”& (ft) 004? *
m^d + ^P ° (n 4- ft) oo^. ttg,
•TO[pqBi
(9T)
(st)
(ti)
(ei)
ZIL
Tabelle II.
Zweite Form der Entwickelung der sechzehn
^-Quotienten (S. 91).
In den Tabellen II, III, IV, V durchläuft m die Reihe der
positiven geraden, n die Reihe der positiven ungeraden Zahlen,
also:
m = 2, 4, 6, 8, 10, ...,
n = 1, 3, 5, 7, 9, ...
Ebenso soll m' die geraden, n' die ungeraden Zahlen durch-
laufen.
(1)
(2)
011 011 + «) X IX
Q. / \ q. '7 \ = COtg 31 V + COtg 31 U
st 0n (v) 0n (a) 1
(3)
(4)
011 010 -|~ a)
31011 («) 010 («)
= cotg n v — tgst«
011 0Q1 4~a ) 1
st0ii GO 0oi («) sin st v
g2 ß— mTtia giiv
fßrtiv ______ qm
0110QO (y + g) _ 1
310n (f) 0oo («) sin st f
q 2 — m 7t i a gTt i v
ß2 7tiv ______ gm
ni ~
q2 gntnia ß—niv
ß—2 7t iv _ qm
UB - aauz—।
Aiu& Viu u —9 zt>
v .
AAU—& VAUvß S5
u
,K-.,^ -|^(1_)S:!. =
I— u
(») 00^ (ft) l0^ 3t
(» + ft) 0 Y Ilß
«5 (ituz—3
aiu —viu u& z
u
AAU& VAUU — 9
u .
(») I0e (ft)1 y x,
(n + ft) II« 4#
U^ Ai UZ—
, viuv^ u^
w® Aiuzß
o Ti -5 VI z
VAUU—v UM J Y—U
V2£ S09
l
_ (»)0I«(ft) I0«^
(n 4- «)00^ 4«
w® atuz—
»i u u9 u&
uIf AAUZ^
VAUU—«Ö
»3t nis ___ (») 1Y (a) I0^ Je
I — (» 4- ft)I0« 4«
Ai UZ
AIUZ&
Al IL—& VIUVA—gÖ
VA
4Au$ VtUVA^ Z
.^OfSOO ______________ (»)00^-(a) 0I^-2ß
in
Ai UZ —& Ul^
I
I + Wf®-)
AiU — & DiUVA—9 .5
VA
aiu& viu v0 z ®
ui _
a 2£ soo ___ (») I0^ (a) °\@ iß
I “"' (» + ft)00« '
VA5 + Al UZ ~
ViUVA^ Ulfi
VA
»«s, + »»s,- = w”<> <>);«»
Ai UZ
DAUVA& wfi
Ul 5 + AiU z^
ViUVA - VA^
q । q (») <A) 0I‘G'#
»»s,«» 4- ^st- =
•uaipqBj,
fei)
(u)
(oi)
(6)
(8)
fe)
(9)
fe)
TIA
-4- a in $
tnuu—9 g 5
u
uu “T" atuz
atu—g®
u .
u
(Z>)00^- (fi) 00^if;
(» + fi) lx#
(9l)
«5 —j“ Afciigi?
a XfZU U—9
u
uu
aiic
u
(») (<l) 00^ 2S
(» + ft) 0I« II©
(Sl)
uU ~]~~ gtjt/g—/ x
a B —5—\I J
vtuu^ U^j Jt — u
n ic soo
l
___ (») OX^ (fi) 004} 2ß
— (» + a) l0«
ub ~|~
. mir« vb
uV ~j aiuz-
Vli£U^
»it ms __________ (») lI^ (ft) 00^ ic
~—i — C° + A) 00'6' ”«
frl)
(ei)
SU
•nanaq«!
Tabelle III.
Entwickelung der ^-Quotienten in trigonometrischen
Reihen (S. 92).
zi>. '9'11'9'11 (y 4-a) , , ,
(1) —k—/ ; o. , ; = cotg st v 4- cotg sr a
J ®9'11(v) #u(a) s -r s
mm'
4~ 4 2 3 2 sin sr (m a 4- m' f)-.
zo\ 9'119'i0 (v -(- «) , ,
<2> «»„(»)»..(<) =
m ni m'
4- 4 (— 1)2 q 2 sin st (m a 4~ m' v).
frii'froiO + a) 1 । z , A
(3) —-—--------------------------k 4>,o2 sm sr(ma 4- nv).
' 7 stitn (v)#Oi (a) sinsrv 1 - 1 . 1
z^\ 9i! ttoo (y 4~ a) 1
st S'n (v) #Oo (a) sin st v
m mn
4- 4 (— 1)2 q 2 sin sr (m a 4- n v).
(5) Vertauschung von a und v in (2).
/ß\ 11 fru —I- . । ,
<6’ “ *8’"’ +*8’»
m + m' m.m.,
— 4__________(— l)-ä q^i~ sin sr (m a 4~ f)-
zy\ 91! -bpo (y 4~ Ct) _______ 1
n frio (y) 9'01 (fl) COS sr v
n — 2 fflii
4- 4 (— 1) 2 q 2 cos a (ma nv).
zgx 9n 9^01 (v 4~ <r) ________ 1
7 sr ö'jo (v) ttOo («) ~ cos sr v
m 4- n — 1 mn
4- 42(— 1) 2 q2 cos ii (ma nv).
Tabellen.
717
(9) #oi 0* J~~ fO Vertauschung von a und v in (3). ’r#o1W#n(«) V
(10) y-l Vertauschung von a und v in (7). 71 «•(,! (v) «10 (a)
(11) ^11 ^11 H“~ *-0 A X“1 ""9~ • / I f X „ Ov?/-; = 4 >, q 2 Bin®(»a + «'»). n «01 00 #oi («)
(12) #li #io (ü + «) A '( \ ' \ —\ o. / ( = 4 >, (—• 1) 2 q 2 cos st (n a 4- n v). #oi 00 #oo («)
(13) ^1^°/ Vertauschung von a und v in (4). ’t #00 («) #11 00
(14) Vertauschung von a und v in (8). n «oo (v) «10 (a)
(15) Vertauschung von a und v in (12). w «oo 00 #oi 00
(16) q, / 1 \ n + nt n n> 0 v’d.- /= - 4 V (— 1)” sin % (n a + n' v). ^#ooW#oo(«) 1 V
Tabelle IV.
Entwickelungen der elliptischen Funktionen (S. 163).
n
, 2xJV _ . xn (1 qn)q2
(1) ---- sn2Äw = 4smstv> -----!:—-
v 1 n -^1— 2 qn cos 2 n u-\~ q2n
n
. x-1 ?2
= 42jn=^smM3iM-
n
(2) cn2 Ku = 4cos3Zv2S(—-0 2 i-------—
' n 7 i — 2 qn cos 2 itu-^-q
n
= 4 2ufrp^COSW3IM-
n— 1
(3) ^dn27fM =1+4V(~1)2O gw(c°s2 3tu-r)
' ’ st 1 — 2 gn cos 2 stu g2n
m = 1 + 4^i </K cosmstw.
(4) 2K 1 = 1 1 4sin3tn V g2(1 + g”i)
n sn2 Ku sin st u 1 — gmcos2stu-(-g2”1 1 । . x-1 qn — H 4 >, sm st n u. sm 3t u 1 1 — qn
(5) 2 K cn 2 Ku m Q 2 == cotg 3t u 4- 4 sin 2nu >,, —K:—:—:—- ° 1 -4J 1 — qm cos 2 3i u qm = cotg 3t u — 4 X i~iqm n m u' m m
st sn2Xu
(6) 2 K dn 2 Ku 1 , . • (— l)2 q2 (1— qm)
st sn 2 Ku sin3TU 1 * " v" 1 g»« COS 2 3t u -|~S2” 1 . 3” = 4 >x— sm n 3t u. smstu -^-ll-(-gn
Tabellen.
719
(7)
2%'^
sr
1 1
——=- =-----------4 cos 3t ti
ch2äm cossru
m n
(_i)rgT(1 + r)
—<1 -]-2qmcos2nu-^-q2m
__. 2 nn
(8)
2 v.' K sti Ku
a cn 2 Ku
m
(— l)2 qm
= tg 3t u 4~ 4 sin 2 3t u'V’,-----;—
ö 1 1—qm cos 2 3t u 4~ q2m
_qm
= tgsru4-4^;(—l)2 ——- sin mstw.
(9)
2 K dn 2 Ku
3t cn.2 Ku
1
COS 3t U
-]-4cos3ru
g2 (1 4~ gm)
1 -f- 2 qm cos 2 3t u S2 m
1 ___ ”_____5 n«
= —-------F 4 V (— 1) 2 r-^—
COSJtU 1 v 7 1 — g’
1 1 _1V 1A-2 a" (Qn + cos 2 3t w)
3t dn2Ku 1 12gncos 2 3t u 4-g2n
m
= !+4S(—T)2 rrfr^cos,W3IM-
n — 1 n
2x%'.S?sn2-ZTw . . x—’ (—1) 2 S2 (1 — 3”)
( ) 3t dn2Ku' Sm3IM^ 14-2g«cos23tu 4-S2”
. y.
= 4 > —--------sm n it u.
<^1 — qn
(12)
2%£ cn2KM _ v (—1) 2 Q2 (l + g”)
3t dn2^u— ^l + 2g«cos23tw4-g2’‘
4 V - —g-2
^1 4- q«
cos niru.
Tabelle V.
Entwickelung der Transzendenten zweiter Gattung
(S. 164).
(1)
(2)
d log H(2 Ku) _ A£Z(2Zw) +
7tdU 7t 71
d log sn 2 Ku
Ttdu
qm
1 — 2 qm cos 2 Tt u g2m
qm
-—------sm m 7t u.
1 — qm
dlogH(2Ku-j- K) 2K7.Tr dlogcn2JTu
--- Ttdu------ = — Z(2^M) H-------,
qm
— — tg 7t u — 4 sin 2 7t u x , , „--;----------
ö -<—' l -|-2gmcos2 Ttu qm
m
(—l)Tqm .
\—-—— sm m Ttu.
1 — qm
(3)
dlog@(2Ku)
Ttdu
~ Z(2Ku),
x—i qn
i sm 2 Ttu >-----S: 5-,
"1 — 2qn cos 2 Ji u q2n
m
32 sin 7t m u
2-1 1 _ g-m ’
dlog©(2KuK)_____, dlogdn25?w
------------- -- Z1 I 2 J\. 'M/) —r- -5-
7t ' 7 Ttdu
7t du
Qn
4 sm 2Ttu >,, , -r------2.^--:——
1 -|- 2 gncos 2srM-]~ q2n
m
e
——- sm m 7t u.
— qm
Tabelle VI.
Verzeichnis von Klasseninvarianten.
(Zum neunzehnten Abschnitt.)
t = ^2, m = 1
= /2, m = 2
/(y^s) = 72, m = 3
MV^) = ^8, m = 4
= i + Vs, m = 5
=4+21/2, m = 6
f (V77?) = V2, m = 7
=8 + 81/2, m = 8
f(l'^9)3 = 1X2(1 +V'3), m = 9
2MV-10)2 = i + V5, m = 10
f (y — 11) — x, x3 — 2 a?2 + 2 # — 2 = 0, m = 11
M1/-12)4 = 2 72(1+1/3), m = 12
f (V -13)4 = 3 +1/13, m = 13
A(V-U)a =y2«, a; + l = l+y2, m = 14
/(y-iö)a = y2(i +y5), m = 15
/+y-i6)4 = 2]X8(i+y2), m = 16
/(y-17)2 = \2x, a? + | = 1 l2V7’ m = 17
A(y- 18/ =1/2(2 + V6), m = 18
f (y—19) = x, x3—2x—2 = 0, Weber, Algebra. HI. m = 19 46
722
Tabellen.
AG/-20)4 = 1/8^, a;2 = (2a; + 1), £ 2 f (V - 21)12 = (1/3 +1/7)3 (3 +1/7)2, /i(|/ —22)2 = V2(l +1/2), /(]/ — 23) -- ]/2a;, x* — x — 1 = 0, A (y - 24)24 = 29 (i + y2)2 (2+ys)3 (yä + yä)3, •jy8f(y_25) = i+1/5, . _ A (y - 26)2 = y2 X, x3 - X* = 3 + ^- (x + 1), f (y —27)3 = 2a;, x3 — 3a;2 — 3a; — 1 = 0, A(y-28)4 = 21/2 (3 +1/7), /•(y — 29)4 = 2a;, 2 x3 — 9 a;2 — 8 x — 5 = y29 (a; + l)2, fi (y - 30)6 = 2 y2 (3 + yiö) (2 + ys), /(y — 31) = y2a;, a>3 — a:2 — 1 = 0, /•/y-32)8 = 8a>, m = 20 m = 21 m = 22 m = 23 m — 24 m — 25 m = 26 m = 27 m = 28 m = 29 m = 30 m — 31 m = 32
a;2 — 8 (1 +1/2)2a; — 2 (1 + yiä) = 0, y2f(y-33)6 = (3+yu) (i+1/3)3, _ /.(V-34)1 = V2«, + =++ f(y —35) = x, a;3 — 2 = (1 +1/5) (a;2 — a;), A(y-36)3=^8a;, a;2 — 4a; — 2 = 2 yi(x + 1), /• (y — 37)4 = 2(6+y37), //y —38)2 = y2a;, xa — 2a;2 — (2a: + 1) (1 + ^2) = 0, f (y—39/ = ys x, x^ = i), a (y—4o)8 = 2 (1 + yö)a (1+y2)2 (3+yiö), f(y-41) ^y2a;, m = 33 m = 34 m = 35 m — 36 m = 37 m — 38 m = 39 m — 40 m — 41
, + lY_^1(;e + l) + Lil® = o,
Tabellen.
723
V8A (V — 42)° =(2V2-]- V7) (3 + yj)’, - - m = 42 f (Y —43) = x, x3 — 2 a:2 — 2 = 0, m = 43 /j(y —44)4 = föx, m = 44 (a:8 — 6o:2+8a: — 3) — yil(2a:2—2'a: + 1) = 0, /(y-45)12= 2(2 + V5)s(y3+y5)\ m — 45 A(V — 46)2 = ißx, x + - = 3 +1/2, m = 46 X f (y — 47) = y2a:, m = 47 x6 — x3 — 2x2 — 2x — 1 = 0, //y — 48)8 = m = 48 81^2 (1+ys) (y2+y3)2 (1+y2)2,. f (y-49)2 = y2a?, a: + - = 2 + 1/7, m = 49 X /j(y — 50) = ]//2a:, x3— x2 = (a: + 1), m = 50 f (y—51)8 = 2 a:, x3 —4 a:2—x—l=yi7a?2, m = 51 A(y —52)4 = y8a:, m = 52 x2 _ 2 (4 + yi3)a: — 3+01/13 = °> Ai
f (y — 55) = y2 x, x2 — x = m = 55 y2/(y — 57)6 = (1 + ys)8 (13 + 3 yi9), m = 57 y^jf/y —58)2 = 5 + y29, m = 58 /i(y— 60)12= m = 60 y25 (1+1/5)2 (2+ys)8 (y3 + yK)8, • f (y — 63)8 = 1/8 O’, m = 63 y7 (x2 — x + 1) =yä(x2 + 3 a: — 1), f (y — 67) = x, x3 — 2x2 — 2x — 2 = 0, m = 67 V8/i(y-70)2 =(l+yö)2 (l+M m = 70 /•(yz^71) = \2x, m = 71 x2 — 2 a:6 — a:5 + a;4 + a:3 + a:2 — x — 1 =0, 46*
724
Tabellen.
fi (j/ _ 72)24 = 2« (2 V6)4 (1 -y ]/2)9 (2 4 ]/3)6, m — 72
f (y^73)2 = V2XV, x + 1 = 5+ V^, m = 73
X M
—75) = x, xa — 2 a:2 — 2x — 4 = 2^5 x, m = 75
VöA(V —78)6 = (3 +V13)3 (5 +y26), m = 78
/i(y^82)2 = fix, x + ± = 15 ^41 m = 82
16 f (y^85)4 = (1 + V5)4 (9 -|- ysö), m = 85
/i(y=88)s = 4(i+y2)2(3+yTi)2(7y2+syii), m = 88
f (y — 91) = x, xa — 2 x‘2 — x — 2 = y 13 x, m — 91
2 f (y.—93)12 = (3 yi 4- V31)3 (39 4 7 VäT)2, m = 93
f (<=97)2 = 1/2^, x 4- 1 = m = 97
f (y—99)8 = 2 a?, m = 99
x* — 13 a?2 — 4 a: — 1 = fis^x* 4- x),
^24 (y—100) = x, m = 100
o:2 — x — 1 = yK(4 H- l)i
(y— io2)6 = y23 (i 4- y2)s (syi+y i7)a, m = 102
yä^fcy—105)6 =
(14- yö)3 (1+yä)3 (1/3+y?)3 +y?), m = 105
/i(y—112)8 = m = 112
y27 (14- y2)4 (2 yi 4- y?)2 (3 4- yv),
8 fr (y^l2Ö)24 =(14 y3)6 (1 + W (V2 + ys)6 rn = 120
(y 3 + yö)6 (y 5 + y 6)3 (3+y 10)2,
y^7/1! (y—iso)2 = (14- yö)3 (3 4- y 13), m = iso
2f (y—133)4 = (3 -4 y'7)2 (ö y4 4- 3 yiö), m = 133
A(y-142)2 = y2 x, x 4 - == 9 4- ö y2, m - 142
Tabellen.
725
f (j/— 163) — x, x* — 6a:2 _|_ ±x _ 2 = 0, m — 163
29 f (]/—16ö)12 = (1 + Vö)6 (^3 4- j/ö)6 m = 165
(35/5-1-2 yn)2 (yn -4 vik)8 .
26A(V—168)24= (1 + 5/3)12 (1 4- (2)4 m = 168
(3 + VO“ (V3 + ((6 4- (7)8 ((7 + (8)2,
/((—175) =5/2^, m = 175
2 a;8 — 4 a;2 4- a; — 3 — l/ö(2a;2 — x 4- 1),
((—177)6 = (23 4- 3 (59) (1 4-j/Ö)9,. m = 177
y^y/y-190)2 = (i 4- yö)s (3 4- yiö), m = 190
f (y—193)2 = yä'ir, x 4- i = 13 -|- yi93, m = 193
y^fXy—210)6 = m - 210
(i + V5 )S(V2 4- ys)3(ys 4- V7)s(5 yK 4- yi4),
fXy-232)8 = m = 232
2 (1 4- yü)6 (5 4- y29)2 (99 4- 13 Vö8),
/^y—24o)“=5/217 (i4-yö)2(2+y3)s(yi+y5)8 m — 240
(1+yä)6 (3 4- yiö)6 (yi 4- ys y (ys. 4- yöy,
2 f (y— 253)4 = (54- y23)2 (13 yn 4- 9 5/23), m = 253
yi18/1 (y—273)6 = m = 273
(3 4~yis)s (i +ys)8 (y3 4-V7)s (nyis4- iöVt),
8 /i (y—28o)8 = (14- ys)4 (14- yn2 (3 4- y?)2 m = 280
(ys + W (y7 + ys)a (5 ys + 3 yn),
26A(y— 312)24= (1 4-yä)18 (3 4-Vis)6 (5/2 4-ys)6 m = 312
(21/34- yij)6 (35/34- y26)8 (5 4- 5/20)2,
y215/i(y—330)6 = (1 4-1/5)6 m = 330
(y&+M (yn+yiö)8 (yiö+yn),
1/219f (y— 345)6 = (1 4- Vö)6 m = 345
(14-ys)8 (3 yö 4-yny (15 ys 4-7 yn),
216^- (y_ 357)8 — m — 357
(5/3 4- yT)12 (3 4- y?)6 (5/17 4- yöi)8 (114- yiiö)2,
1/27 (y- 385)2 = m = 385
(1+yö )2 (3+yn) (ys+yy) (y?+yn),
726
Tabellen;
/i(y^4Ö8)24=(l-+y3)12(l/2+l/3)lä(l+y2)8 m = 408
(7 -4- yäl)8 (31/2-4- V17)* (51/2-4- l/äl)3,
l/29/i(l/—462)8 = (yä-4-1/7)8 m = 462
(1/6 -4-1/7 )s (1/7 4- yn)8 (22yn+39 y?),
25/’1(l/—52°)8 = (1-|-1/5)8(1-1-1/2/(3-I-1/13)2 m = 520
(3 -|- 1/1Ö)2 (5 -|-1/26) (57 -|- 5 yiBÖ),
2fi(l/—^60)8 = (l + Vö)6 (3 4-1/1Ö)2(13-|-31/19)2 ™ — 760
(31/2-1-1/19)2 (21/5-4-1/19)2 (511/1Ö 37 1/19),
212/1 (V—840)24= (1/3 + l/ö)12 (1 4-1/2)8 m = 840
(1 +1/3)8 (1 4-1/5/ (3 +1/7)8 (3 + 1/TÖ)8
(i^+^^-^/^+v?)8 _
(1/14 -|- 1/15)8 (31/3-4-2 1/7)2 (51/5-1-31/14)2,
224fi(V— W)24= (14-l/3)18(l4-1/5)12(1 4-1/2)6 m = 1320
(3 41/10)43 + 1/1T)8 (V3+V5)6 45 +1/6 )8
(1/11 +1/15)8 (3 y5 4- 2 y 11)6 (4 y2 4- yss)6
(31/6 4- y55)s (yiö 4- yii)2,
231/-(y_ 1365)12= (y3+y7)12(l +yö)8(3 +y7)6 m = 1365
(3 4- y 13)6 (1/3 4- yK)8 (21/34- y 13)6
(y 35 4-1/39)8 (3 y? 4- y65)2,
221/i (y— 1848)24 =(14- yä)12 (1/2 4-1/3)12 m = 1848
(3 4- y? )12 (3+yn)8 (ys 4- y? )e (ye 4- y?)8
(y? 4- yn)8 (21/24- y? y (7 yi + 3 yny
(51/34- yn)8 (yn 4- yn)8 (22 yn 4- 39 y? y-
ALPHABETISCHES REGISTER.
(Die Zahlen geben die Seiten an. Die Definitionen verkommender Konstanten und Funk-
tionen sind unter den Stichwörtern Konstante, Funktion, Modulfunktien nachgewiesen,)
Abbildung, eindeutige 6.
Abelsche Differentiale 689.
— Relationen 205 ff.
Abelsches Theorem 44, 671, 694,
Abgeleitete Ideale 353.
Absolute eines rationalen Funktionals
641.
Absolute Normenreste 394.
— Norm eines Funktionals 644.
— Primfunktionals 653.
Additionstheorem der elliptischen Inte-
grale 43 ff.
— von cn, dn, sn 50, 142 ff.
— der p-Funktion 162.
— der ft-Funktionen 76 ff.
— von 0(v), H(v) 142.
Algebraische Darstellung von 135 ff.
---der Thetanullwerte 135 ff.
— Funktionen 624.
Allgemeine Teilungsgleichung 216.
Amplitude 49.
Anzahl der Geschlechter 409.
Äquivalenz, allgemeine, verschärfte 366.
— in Ordnungen 361 ff.
— von Formen 331.
— — — im quadratischen Körper
347 ff.
Argument von 3- 68.
Arithmetische Natur der Klassenfunk-
tion 426 ff.
Assoziierte Funktionale 641.
Basis eines Funktionals 651.
— eines Funktionenkörpers 626.
— einer Ordnung 353.
Bäsisform 356, 651.
— eines Primfunktionals 653.
Birationale Transformation 660.
Cauchy 54.
Oayleys Entwickelung der Modulfunk-
tionen 548.
Charakter der T-Funktion 64.
— einer ganzen Funktion 53.
— einer quadratischen Form 381.
Charakteristik der T-Funktion 64.
Concordante Formen 428.
Darstellung von Zahlen durch quadra-
tische Formen 376 ff.
Dekomposition von Substitutionen 99ff.
Derivierten von .9 81 ff.
Differentiale 631, 688.
— , Abelsche 689.
— , eigentliche 689.
— , elliptische 4.
— erster Gattung 690.
— zweiter und dritter Gattung 690, 699.
Differentialgleichung für K 168.
Differentialquotienten 679.
— erster Gattung 691.
— , Darstellung durch Polygonquo-
tienten 683.
Dimensionen einer Polygonschar 675.
Dirichletsche Grenzformel 404.
— Summen 602.
Diskriminante 321 ff.
— der Invariantengleichung 431 ff.
— des quadratischen Körpers 339.
— einer Ordnung 351.
728
Alphabetisches Register.
Diskriminante im algebraischen Funk-
tionenkörper 631.
Diskriminantenform, Zahlen von 321.
Doppelpunkte 687.
Doppelt periodische Funktionen 57.
--------der zweiten Art 59.
Doppelverhältnis 6.
Eigentliche Darstellbarkeit 366.
— Teilungsgleichung 216.
— Transformation 103.
Einheiten im Teilungskörper 589.
— , funktionale 644.
Einheitsfunktionen 55.
Einhellige Formen 428.
Einige Formen 428.
Elliptische Differentiale 4.
— Differentialgleichungen 139, 166.
— Funktionen Jacobis 137 ff.
— Integrale 3.
— Kurven 19, 23.
Entgegengesetzte Formen 372.
Entwickelung von log y (<u) 559.
Euler 17.
Exponent einer ganzen Funktion 677.
Formen zu einer Idealbasis 332.
Formenklassen 333.
Fremde Zahlen 358.
Fundamentale Einheiten 398 ff.
Fundamentalsatz für Ö-Funktionen 69.
Funktionale 363.
— im Körper 42 642.
— , rationale 639.
Funktion cn, dn, sn 49.
— E(v) 154 ff.
— H(u) 141.
— p(w) 150.
— 0 (u, v) 157.
— a(u) 116.
— T 61.
— ö (u) 141.
— Z(v) 154 ff.
— Z(u) 161.
Gal oissche Gruppe der Teilungs-
gleichung 208.
— — — Transformationsgleichung
284 ff., 305 ff.
Ganze Funktionale in Sl 643.
— Funktionen 55, 635.
— rationale Funktionale 641.
Gattung der Integrale 39.
— von Punkten 39.
Gausssche Summen 328.
— Transformation 105 ff., 146.
Gebrochene Funktionen 658.
Gehörig, zu einer Gruppe 178.
Genera von Formenklassen 382.
Geschlecht des Körpers 685.
Geschlechter von Formenklassen 382.
------r Idealklassen 388, 395 ff.
Gitterpunkte 402.
Grad eines algebraischen Funktionen-
körpers 625.
Grundzahl 339.
Gruppe der Idealklassen 598.
— von Kollineationen 98.
— der Teilungsgleichung 208 ff.
— des Teilungskörpers 576.
— der Transformationsgleichungen
284 ff., 305 ff.
Gudermannsche Bezeichnung der
elliptischen Funktionen 49.
Hauptcharakteristiken 72.
Hauptordnung 351.
Haupt-S-Funktionen 72.
Haupttransformationen 100.
— 2. Ordnung 105.
— ungerader Ordnung 110 ff.
Hermite 16.
Hermitesche Transformation 17.
Holomorphe Funktionen 648.
Homogene Variabein 4.
— W eierstrasssche Funktionen 564.
Idealgruppen 596.
Idealklassen 333.
— nach den Ordnungen 362 ff.
Idealteilungsfunktion 592.
Index 430.
— eines Gruppenteilers 597.
Integrale der ersten, zweiten, dritten
Gattung 39, 43, 154, 690, 699.
— , elliptische 3.
Invarianten, der elliptischen Funk-
tionen 13, 15.
— der ft(x) 15, 152.
Invariantengleichung 237 ff.
Irreduzibilität der Klassengleichung
442, 619.
— des Klassenkörpers 608.
Isolierbedingungen 401.
Isolierte Polygone 672.
Alphabetisches Register.
729
Jacobi sehe Bezeichnung der ellipti-
schen Funktionen 49.
— Funktionen ö (v), H (v) 141.
— Modulargleichungen 273 ff.
, — ^-Formeln 80.
— Transformation 30.
— Transzendenten 153, 157.
Klassenfunktion 421.
Klassengleichung 421.
Klasseninvarianten 420, Tabelle VI.
— , Berechnung 457 ff.
— derselben Diskriminante 435.
Klassenkörper 422, 607, 620.
— und Ordnungskörper 455.
Klassenzahl 405 ff.
Klassenzahlrelationen 423.
Kollineationen 97.
Komplement des Moduls 9.
Komplementärer Modul 9.
Komplementäre Stammteiler 382.
Komplexe Multiplikation 414 ff.
— — der Jaeobischen elliptischen
Funktionen 583.
----von p(«) 566.
Komposition der Formen 335.
—-------in den Ordnungen 369 ff.
----Klassen 370.
------- Ordnungen 373 ff.
----quadratischen Formen 428 ff.
Kongruenz (nach w„ <u.2) 57.
Kongruenzgruppe 178, 598.
Kongruenzmoduln 178.
Konstante eu es, es 151.
— r)lt >]<, 118, 161.
— x 9, 137.
— K, K' 139 ff., 168 ff.
— q_ 83.
Körper algebraischer Funktionen 625.
Körperdiskriminante 637.
Kovarianten der f4(x) 16.
Kroneckersche Gr'enzformel 526f.
— Klassenzahlrelation 423.
Kurven, elliptische 19.
— , rationale 19.
L andensche Transformation 105 ff.,
146.
Legendre 9.
Legendre sehe Relation 156 (161,118).
L eg end resches Symbol 322, 385 ff.
--------, erweitertes 323.
Lineare Abhängigkeit 70.
Lineare Abhängigkeit der Funktionen
/(“)> /,(«>), AW 114.
— — der >9-Funktionen 103.
— Fundamentaltransformationen 101.
— Substitution 6, 8.
— Transformation 5, 8, 98.
— — von cn, dn, sn 147 ff.
— — — r/ (w) 124.
— — der Funktionen f (<u), f\ (w),
AW 114, 132.
----von a 118.
----der .'/-Funktionen 103 ff., 130.
Linearformen, Primzahlen in den 613.
Minimalbasis im Funktionenkörper
637.
Modulargleichung 36, 226.
— in irrationaler Form 269 ff.
—, Jacobische 273 ff.
Modularkorrespondenzen 280 ff.
Modul der elliptischen Integrale 9.
— — — — durch Thetanullwerte
dargestellt 137.
----Kongruenzgruppe 598.
----^-Funktion 68.
Modulfunktionen 177.
—, >)(<«) 85, 112 ff.
—, /(“), Ä("), AW 85f., 112ff.
—, tM, 71(1») 179.
—, JW 153, 174 ff.
Monodromiegruppe der Teilungsglei-
chung 212 ff.
Multiplikation der elliptischen Funk-
tionen 190 ff., 576.
— des elliptischen Differentials mit 2:
18.
— von p (w) 196 ff.
— bei Transformationen 97.
Multiplikator einer Transformation 31.
Multiplikatorgleichung 37, 226.
— erster Stufe 249 ff.
Jformalbasen 676.
Normalform des elliptischen Differen-
tials 9.
— , Lege.ndresche 13.
— , Weierstrasssche 13.
Normalintegrale der drei Gattungen 43.
Normen im algebraischen Funktionen-
körper 627.
Normenreste 389.
— der Primzahlpotenzen 390 ff.
Normenrestgruppen 389 ff.
730
Alphabetisches Register.
Ordnung der doppelt periodischen
Funktionen 58.
-----Nullpunkte 54.
— •— T-Funktion 61, 67.
-----Unstetigkeitspunkte 54.
Ordnungen im quadratischen Körper
351.
Ordnungsgruppe 358.
Ordnungskörper 455.
Ordnungszahlen 666.
Parallele Formen 361, 377.
Partielle Differentialgleichung für 9 71.
Periodenparallelogramm 56.
Periodenteilung 204.
Periodizität, allgemeine 56.
— von cn, dn, sn 51.
Periodizitätsfaktor 61.
Pole von p (u, u) 568.
Polygone in algebraischen Körpern 667.
Polygonklasse 671.
Polygonquotienten 671.
Polygonschar erster Gattung 672.
Polygonscharen 672.
Positive Idealbasen 331.
Potenzsummen 632.
Primäre Ideale 353,
Primdiskriminanten 322.
Primfunktionale 646.
Primideale ersten Grades im Teilungs-
körper 594.
— in den Klassen 611.
Produktdarstellung der .9-Funktionen
83 ff.
Punkt im algebraischen Körper 661.
Punkte der 1., 2., 3. Gattung 39.
Quadratische Klassengleichungen 546.
— Körper 338 ff.
— Substitutionen 13.
Rationale Integrale 4.
Raumkurve vierter Ordnung 23.
Reihendarstellung der .9 - Funktionen
86 ff.
Reihenentwickelung der elliptischen
Funktionen, Tabelle IV, 162 ff.
— — Transzendenten 2. Gattung,
Tabelle V.
-----p-Funktion 185 ff.
-----«/-Funktionen 182 ff., 186.
-----^-Quotienten, Tabelle I, II, HI.
Reihenkonvergenz 553.
Residuen 54, 702 ff.
Residuensumme 703.
Resolventen für den 5. Tranäformations-
grad 309 ff.
Reziproke Substitution 98.
Reziprozitätsgesetz der quadratischen
Reste 345.
Riemann-Rochscher Satz 695.
Riemannsche Fläche 666.
Satz von Cauchy 54.
Schläfli sehe Modulargleichungen
256 ff.
----für Primzahlgrad 265 ff.
— — für zusammengesetzten Grad
274 ff.
Sigma-Funktionen 116.
----durch & dargestellt 122 ff.
Sigmanullwerte 119 ff.
Singuläre Moduln 419.
— Perioden 413 ff.
— Werte der Modulfunktionen 419.
----von j (<u) 418.
Spuren im algebraischen Funktionen-
körper 627.
Stammdiskriminante 321.
Stamm einer Diskriminante 321.
Stammteiler einer Diskriminante 380.
Substitutionen, ganze 6.
— , Hermitesche 17.
— , lineare 6, 8.
—, quadratische 13.
Symbol von Legendre 322.
--------, erweitertes 323.
Symbolische Multiplikation von Stamm-
teilern 380 ff.
Taylor sehe Entwickelung 660.
Teilbarkeit der Funktionale 644.
Teiler einer uneigentlichen Polygon-
klasse 674.
— eines Ideals 353.
—, größter gemeinschaftlicher von
Funktionalen 645.
Teilung der elliptischen Funktionen 200.
— — — — mit singulärem Modul
588.
— — Perioden 204.
Teilungsgleichung 202.
— , allgemeine, eigentliche 216.
— , auf Transformationsgleichungen
zurückgeführt 217 ff.
— , ihre Gruppe 208 ff.
Alphabetisches Register.
731
Teilungskörper 573, 592, 620.
— und Klassenkörper 620.
Thetafunktion 68 ff.
Thetanullwerte 85.
Thetaquotienten 88 ff.
Transformation von Differentialen 5.
— , Gausssche 33.
— , Hermitesche 17.
— , Jacobische 32.
— , Landensche 34.
— 2. Grades 32.
— 3. Grades 35.
— der T-Funktionen 94.
Transformationsgleichung 221.
— , Bildung der 225 ff.
— erster Stufe 246.
— für und y8 247 ff.
Transformationsgrad 94, 234.
Transformationszahl 94, 234.
Uneigentliche Äquivalenz 331.
— Diskriminanten 321.
— Polygonklassen 674.
Unstetigkeitspunkte 53.
V ertauschung von Argument und Para-
meter 157.
Verwandte T-Funktionen 65.
— 0-Funktionen 70.
Verzweigungspolygon 669.
Verzweigungspunkt 669.
Verzweigungszahl 669.
Weierstrass 13.
Weierstrasssche Primfaktoren 56.
— p-Funktion 150.
— a-Funktionen 116.
— Transzendenten 2. und 3. Gattung
160 ff.
Wurzeln der Transformationsgleichung
231.
Wurzelsystem, vollständiges 533.
Zahlgruppen 358, 596.
Zahlringe 351.
Zerfällung der Klassengleichung 616.
Zusammensetzung der Transforma-
tionen 95 ff.
Zweiteilung der elliptischen Funktionen
200.
Berichtigungen zum ersten Bande.
(Kleinere Versehen, die der Leser leicht selbst verbessert, sind hier nicht aufgeführt.)
Seite 185, Zeile 4 v. o. lies (m — s)(n — s) + s statt (m — s)(n — s) nach
einigen leicht ersichtlichen Änderungen in den letzten Zeilen von
Seite 184.
„ 186, Formel (4) lies n/t -\-mr statt nr 4- m,u.
„ 195, Zeile 7 v. o. lies zwei statt drei.
„ 198, „ 13 v. o. „ U2 statt U\.
„ 215, „ 7 v. u. „ A:r! statt Xrs.
„ 221, Formel (13) und (14) lies r~1 statt r.
„ 246, Zeile 6 v. u. ist 0, zu streichen.
„ 320, Formel 7 das zweite *(«)0(ä)1 durch (x) 0 (x)2 zu ersetzen.
„ 339, Zeile 4 v. u. lies reellem statt imaginärem.
n y> 445, 487, n n 19 v. o. 13 v. o. n n unlösbar statt lösbar. (mod p) statt (mod m).
n 541, 9 v. o. 5? u statt w.
n 552, 11 V. 0. n gf/-n statt tyln.
657, „ 7 v. u. ist hinter „Normalgleichung“ einzuschalten: mit reellen Wurzeln.
Berichtigungen zum zweiten Bande.
Seite 231, 232. Bei der Anwendung, die hier von dem Satze 4 gemacht ist,
wurde übersehen, daß die Invarianten selbst zum Rationalitäts-
bereich gehören, daß also die Darstellung von J als rationale
Funktion von 0 eine reine Identität (J — J~) ist. Demnach ist
der Absatz Seite 231 unten von „Aus diesem Satze“ bis 232 oben
„unentschieden bleiben“ zu streichen.
„ 640, Zeile 14 v. o. lies jF'(r) statt F'(t').
„ 697, „ 13 v. u.: Die hier folgende Schlußweise muß folgendermaßen
abgeändert werden:
Aus (13) ergibt sich durch Multiplikation mit gs und Sum-
mation :
— nxSäsgs 4- au < 2gsXs < 2<5'sgs -f- au.
Berichtigungen zum dritten Bande.
733
Setzt man
n*z#,\g,\ = g,
so ist um so mehr, da die Summe der absoluten Werte nicht
kleiner ist, als der absolute Wert der Summe:
(14) —«/ + ««< 2gs7.s < g + au.
Man setze nun
— g 4- au = a, g + au -- a'
ad = — a = 2 g
und erhält:
(15) a < 2gsls < a'.
Ersetzt man u durch u' = u + d, so geht a in a' über (das
wäre bei der Formulierung des Textes nicht der Fall), und wenn
man a" = «' + ad = g + au' setzt, und wenn ebenso von
u' abhängt wie von «, so ergibt sieh
«' < Sgs'-'s < a".
Durch Fortsetzung dieses Verfahrens wird eine Reihe von ganzen
Zahlen
’A V, • •
den folgenden Bedingungen gemäß bestimmt.
Von hier kann wie im Text Seite 698 oben fortgefahren
werden. Der Text auf S. 697 wird richtig durch folgende vier
Korrekturen:
Seite 697, Zeile 13 v. u. lies nh S<)'s\ gs\. statt 'kSäsys.
„ 11 v. u. „ —g statt —ng.
„ 3 v. u. „ — g „ — ng.
„ 1 v. u. „ 2g „ (« + 1)0.
Berichtigungen zum dritten Bande.
Seite 28, Formel (23) lies K2 statt K...
„ 124, Formelsystem (8) lies u statt
„ 180, Zeile 9 v. u. lies a‘ß<)' „ a*ßy.
„ 185, letzte Zeile und Seite 186, Formel (6), (7) lies g,2 statt g2.
„ 333, Zeile 8 v. o. lies äquivalent, wenn statt äquivalent. Wenn.
„ 340, Zeile 4 v. u. lies a!2 statt «12.
„ 394, „ 18 v. o. b) ist — 5 zu streichen.
„ 525, Formel (1) lies A x'1 statt A x.
Verlag von Friedr. Vieweg & Sohn in Braunschweig.
Das graphische Einmaleins
oder die Rechentafel, ein Ersatz für den Rechenschieber, entworfen
von Gustav Herrmann,
Geh. Reg. - Rath und Professor an der König!. technischen Hochschule zu Aachen.
8. geh. Preis 1,20 Jb
Lehrbuch der Variationsrechnung
von Adolf Kneser,
Professor der angewandten Mathematik an der Universität in Dorpat.
Mit 24 in den Text eingedruckten Abbildungen, gr. 8. geh. Preis 8 Jb
Lehrbuch der politischen Arithmetik
für höhere Handelsschulen (Handelsakademien) und zum
Selbstunterricht bearbeitet von
F. S. Holzinger,
Professor an der öffentlichen Handelsakademie in Linz.
Zweite unveränderte Auflage, gr. 8. Preis geh. 3 Jb, geb. 3,40 Jb
Hauptsätze der
Differential- und Integral-Bechnnng,
als Leitfaden zum Gebrauch bei Vorlesungen zusammengestellt
von Dr. Robert Fricke,
Professor an der technischen Hochschule zu Braunschweig.
Vierte Auflage. Mit 74 in den Text gedruckten Figuren, gr. 8.
Preis geh. 5 Jb, geb. 5,80 Jb
Vier- und fünfstellige Logarithmentafeln
nebst einigen
physikalischen Konstanten.
Royal-8. Preis kart. 0,80 Jb
G. Lejeune-Dirichlets
Vorlesungen über die Lehre von den einfachen
und mehrfachen bestimmten Integralen.
Herausgegeben von G. Arendt.
Mit eingedruckten Abbildungen, gr. 8. Preis geh. 12 Jb, geb. 13 Jb
Ausführliches Verlagsverzeichnis kostenlos.
Verlag von Friedr. View eg & Sohn in Braunschweig.
Siebenstellige gemeine Logarithmen
der Zahlen von 1 bis 108000 und der Sinus, Cosinus, Tangenten und
Cotangenten aller Winkel des Quadranten von 10 zu 10 Secunden nebst
einer Interpolationstafel zur Berechnung der Proportionaltheile
von Dr. Ludwig Schrön,
Director der Sternwarte und Professor zu Jena, Mitgliede der Kaiserlich Leopold. Carolin,
deutschen Akademie der Naturforscher und der gelehrten Gesellschaften zu Breslau,
Frankfurt a. M., Halle und Jena.
Vierundzwanzigste revidirte Stereotyp-Ausgabe. Imp.-8. geh.
Tafel I und II. (Logarithmen der Zahlen und der trigonometrischen Functionen.)
Preis 4,20
Tafel III. Interpolationstafel (Supplement zu allen Logarithmentafeln). Preis 1,80 Jb
Tafel I. Die Logarithmen der Zahlen. (Für Solche, welche Tafeln für trigonome-
trische Rechnungen nicht nöthig haben.) Preis 2,40
Fünfstellige
logarithmische und trigonometrische Tafeln.
Herausgegeben von
Dr. O. Schlömilch,
weil. K. S. Geheimrat a. D.,
Mitglied der Königl. Sächsischen Gesellschaft der Wissenschaften zu Leipzig, der Königl.
Schwedischen Akademie zu Stockholm, der Kaiserl. Leopoldinischen Akademie usw.
Galvanoplastische Stereotypie. Wohlfeile Schulausgabe.
Zwanzigste Auflage. 8. Preis geh. 1 Jb, geb. 1,30 Jb
Abgekürzte Multiplikations-Rechentafeln
für sammtliche Zahlen von 2 bis 1000.
Nebst einem Anhang: Enthaltend die Quadratzahlen von 1 bis 1000.
Entworfen und herausgegeben von
J. Ernst,
Kaiserlicher Cassen-Controleur a. D., Gassen- und Rechnungs-Revisor
des Kreises Kreuznach.
kl. 4. Preis geb. 4 geb. in Lnwd. 5
Partielle Differentialgleichungen
und deren Anwendung auf physikalische Fragen. Vorlesungen von
Bernhard Riemann.
Für den Druck bearbeitet und herausgegeben von
Karl Hattendorff.
Dritte Auflage. Mit Holzstichen, gr. 8. geh. Preis 8 Jb
Ausführliches Verlagsverzeichnis kostenlos.