ПРИКЛАДНАЯ МАТЕМАТИКА
Восьмое издание
Том 2
Математический анализ


APPLIED MATHEMATICS for business, economics, life sciences, and social sciences
Eight Edition
Raymond A. Barnett
Merritte College
Michael R. Ziegler
Marquette University
Karl E. Byleen
Marquette University
Prentice
Hall
Prentice Hall
Pearson Education, Inc.
Upper Saddle River, NJ 07458


ПРИКЛАДНАЯ МАТЕМАТИКА
Восьмое издание
Том 2
Математический анализ
Реймонд А. Барнетт
Колледж Мерритта
Майкл К. Циглер
Колледж Маркетта
КарлЭ. Байлин
Колледж Маркетта
АЦАЛЕКШиКА
Москва • Санкт-Петербург
2021


ББК 22.143 Б25
УДК 510.2
ООО “Диалектика”
Зав. редакцией С. Н. Тригуб
Перевод с английского докт. физ.-мат. наук Д. А. Клюшина, В. В. Марченко, А, В. Романенко, О. М. Ядренко
Под редакцией докт. физ.-мат. наук Д. А. Клюшина
По общим вопросам обращайтесь в издательство “Диалектика” по адресу: infо.dialektika@gmail.com, http://www.dialektika.com
Барнетт, Реймонд А., Циглер, Майкл Р,. Байлин, Карл Э.
Б25 Прикладная математика, 8-е изд. Том 2. Математический анализ. : Пер. с англ. — СПб.: ООО “Диалектика”, 2021 — 1100 с.: ил. — Парал. тит. англ.
ISBN 978-5-907114-37-1 (рус., том 2)
ISBN 978-5-907114-35-7 (рус., многотом.)
ББК 22.143
Все названия программных продуктов являются зарегистрированными торговыми марками соответствующих фирм.
Никакая часть настоящего издания ни в каких целях не может быть воспроизведена в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая фотокопирование и запись на магнитный носитель, если на это нет письменного разрешения издательства Prentice Hall, Inc.
Copyright © 2021 by Dialektika Computer Publishing.
Authorized translation from the English language edition published by Prentice Hall, Copyright © 2003, 2000, 1997, 1994, 1991, 1988, 1985, 1983 by Pearson Education, Inc., Upper Saddle River, New Jersey 07458.
All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording or by any information storage retrieval system, without permission from the Publisher.
Научно-популярное издание
Реймонд А. Барнетт, Майкл Р. Циглер, Карл Э. Байлин Прикладная математика, 8-е издание. Том 2 Математический анализ
ООО ’’Диалектика", 195027, Санкт-Петербург, Магнитогорская ул., д. 30, лит. А, пом. 848
ISBN 978-5-907114-37-1 (рус, том 2)
ISBN 978-5-907114^35-7 (рус, многотом 1)
ISBN 0-13-065580-5 (англ.)
©ООО “Диалектика”, 2021
© 2003 by Pearson Education, Inc.


Оглавление
Часть III. Математический анализ 10
Глава 8. Производная И
Глава 9. Построение графиков и оптимизация 163
Глава 10. Дифференцирование 271
Глава 11. Интегрирование 345
Глава 12. Практические задачи интегрального исчисления 471
Глава 13. Исчисление многих переменных 540
Глава 14. Дифференциальные уравнения 640
Глава 15. Теория вероятностей и математический анализ 702
Часть IV. Приложения 780
Приложение А. Основные алгебраические понятия и законы 781
Приложение Б. Специальные темы 870
Приложение В. Основные справочные сведения 952
Приложение Г. Графики элементарных функций 961
Ответы к упражнениям 964
Предметный указатель 1086


Содержание
Часть III. Математический анализ 10
Глава 8. Производная 11
8.1 Основы теории пределов 12
8.2 Пределы и непрерывность 37
8.3 Производная 61
8.4 Производные постоянных, степенных функций и сумм 85
8.5 Производные произведений и частных 104
8.6 Цепное правило: дифференцирование сложных функций 116
8.7 Маржинальный анализ в бизнесе и экономике 129
Глава 9. Построение графиков и оптимизация 163
9.1 Первая производная и построение графиков 164
9.2 Вторая производная и построение графиков 190
9.3 Методы построения графиков: универсальный и углубленный 213
9.4 Оптимизация. Глобальный максимум и минимум 237
Глава 10. Дифференцирование 271
10.1 Константа е и непрерывно начисляемые сложные проценты 272
10.2 Производные логарифмических и экспоненциальных функций 283
10.3 Цепное правило: общая форма 300


Содержание
7
10.4 Неявное дифференцирование 317
10.5 Связанные скорости 326
Глава 11. Интегрирование 345
11.1 Первообразные и неопределенные интегралы 346
11.2 Интегрирование методом замены переменной 367
11.3 Дифференциальные уравнения: рост и затухание 383
11.4 Геометрическая и численная интерпретации определенных
интегралов 401
11.5 Определенный интеграл как предел суммы. Основная теорема
интегрального исчисления 425
Глава 12. Практические задачи интегрального исчисления 471
12.1 Площадь фигуры, ограниченной кривыми 471
12.2 Интегрирование в экономических задачах 490
12.3 Интегрирование по частям 510
12.4 Таблицы интегралов 521
Глава 13. Исчисление многих переменных 540
13.1 Функции нескольких переменных 540
13.2 Частные производные 555
13.3 Максимум и минимум функции 569
13.4 Поиск максимумов и минимумов методом множителей Лагранжа 582
13.5 Метод наименьших квадратов 597
13.6 Двойные интегралы по прямоугольным областям 615
Глава 14. Дифференциальные уравнения 640
14.1 Основные понятия 641
14.2 Разделение переменных 657
14.3 Линейные дифференциальные уравнения первого порядка 674
Глава 15. Теория вероятностей и математический анализ 702
15.1 Несобственные интегралы 703
15.2 Непрерывные случайные величины 715
15.3 Математическое ожидание, стандартное отклонение и медиана 736
15.4 Специальные распределения вероятностей 753
Часть IV. Приложения 780
Приложение А. Основные алгебраические понятия и законы 781
А.1 Множества 785


8
Содержание
А.2 Алгебра и действительные числа 794
А.З Операции с полиномами 802
А.4 Факторизация полиномов 811
А.5 Операции с рациональными выражениями 819
А.6 Целочисленные степени и экспоненциальная форма записи числа 827
А.7 Дробные степени и корни 835
А. 8 Линейные уравнения и неравенства одной переменной 844
А.9 Квадратные уравнения 858
Приложение Б. Специальные темы 870
Б.1 Последовательности, ряды и суммы рядов 870
Б.2 Арифметические и геометрические последовательности 879
Б.З Бином Ньютона 889
Б.4 Приращения и дифференциалы 893
Б.5 Правило Лопиталя 904
Б.6 Двойные интегралы по сложным областям 916
Б.7 Интерполяционные полиномы и разделенные разности 931
Приложение В. Основные справочные сведения 952
Приложение Г. Графики элементарных функций 961
Ответы к упражнениям 964
Предметный указатель 1086


Часть III
Математический анализ


8
Производная
■ 8.1. Основы теории пределов
■ 8.2. Пределы и непрерывность
■ 8.3. Производная
■ 8.4. Производные постоянных, степенных функций и сумм
■ 8.5. Производные произведений и частных
■ 8.6. Цепное правило: дифференцирование сложных функций
■ 8.7. Маржинальный анализ в бизнесе и экономике
■ Ключевые слова, основные обозначения и формулы
■ Общие правила дифференцирования
■ Решение практических задач
■ Домашнее задание 8.1. Минимальные средние затраты
■ Домашнее задание 8.2. Численное дифференцирование с помощью графической утилиты
Введение
Чем отличаются алгебра и математический анализ? Вероятно, наиболее точно различие между этими двумя дисциплинами выражают слова статический и динамический. В алгебре решаются уравнения относительно определенного значе¬


12
Часть III. Математический анализ
ния или переменной — в ней оперируют статическими понятиями. В математическом анализе исследуют, как изменение одной переменной влияет на другую переменную, — здесь рассматриваются динамические понятия.
На рисунке, показанном ниже, проиллюстрированы три основные задачи математического анализа. Возможно, читатель удивится, узнав, что все три задачи — казалось бы, такие разные — связаны между собой математическими зависимостями. Решение этих задач и отслеживание взаимосвязи между ними привело к образованию нового раздела математики математики. Исаак Ньютон (Isaac Newton) (1642-1727) в Англии и Готтфрид Вильгельм фон Лейбниц (Gottfried Wilhelm von Leibniz) (1646-1716) в Германии одновременно и независимо разработали его и назвали математическим анализом. Час новых идей пробил!
а) найти уравнение касательной в точке (хр для заданной функции у =Дх)
орость этой очке
б) определить мгновенную скорость падающего тела
в) найти площадь фигуры, ограниченной графиками функций у =д(х), х = а, х = b и осью х
Кроме задач, изображенных на рисунке, математический анализ позволяет решить множество других важных проблем. До последнего времени математический анализ использовался преимущественно в физических науках, но сейчас он находит применение во многих других областях знаний.
8.1. 	Основы теории пределов
■ Функции и графики: краткий обзор
■ Пределы
■ Вычисление пределов
■ Пределы разностных отношений
Основой математического анализа является понятие предела. Эта концепция помогает точно описать поведение величины /(х), когда переменная х близка по значению, но не равна определенной величине с. В этом разделе применен комбинированный — численный, графический и алгебраический — подход к вычислению


Глава 8. Производная
13
пределов. Основное внимание будет уделено именно построению и объяснению концепции, а не формальным математическим подробностям.
Функции и графики: краткий обзор
График функции у = f(x) = х+ 2 представляет собой набор всех упорядоченных пар (х,/(х)). Например, если х = 2, то /(2) = 4, а (2,/(2)) = (2,4) — это точка на графике f. На рис. 8.1 показаны точки (—1, /(—1)), (1, /(1)) и (2, /(2)), лежащие на графике функции /. Следует отметить, что значения —1, 1 и 2, принадлежащие области определения, относятся к оси т, а значения /(—1) = 1, /(1) = 3 и /(2) = 4, лежащие в области значений, относятся к оси у.
Рис. 8.1. График функции /(х) = х + 2
Иногда, если дано значение х, значение f (х) удобно находить непосредственно с помощью графика функции /. Эта процедура вкратце рассмотрена в примере 8.1.
Пример 8.1 (Поиск значения функции по ее графику). Заполните следующую таблицу, используя заданный график функции д.
х д(х) ^2
1
3
4
Решение. Чтобы найти значение д(х), необходимо проследовать по вертикали от значения х, лежащего на оси х, до графика функции д, а затем по горизонтали переместиться до соответствующего значения д(х), отложенного на оси у (проследите за пунктирной линией).


14
Часть III. Математический анализ
X
-2
4,0
1
2,5
3
1,5
4
1,0
Упражнение 8.1.
Заполните следующую таблицу, используя заданный график функции h.
х h(x) ^2
-1 О
1
2
3
4
Пределы
В двух следующих примерах будут даны основные представления о пределе.
Пример 8.2 (Анализ предела). Пусть /(ж) = х + 2. Рассмотрим численно, графически и алгебраически поведение функции /(х), если значения х приближаются к числу 2.
Решение. Чтобы численно исследовать поведение функции /(ж) для величин х в окрестности числа 2, следует построить таблицу ее значений (табл. 8.1).
Таблица 8.1. Таблица значений функции /(х)
X
1,5
1,8
1,9
1,99
1,999 -<■ 2 <- 2,001
2,01
2,1
2,2
2,5
Л®)
3,5
3,8
3,9
3,99
3,999 -» 4 <- 4,001
4,01
4,1
4,2
4,5
Численные значения, приведенные в таблице, указывают на то, что если величина х близка к числу 2, то соответствующее значение /(х) близко к числу 4.
Чтобы графически изучить поведение функции /(х), нужно построить ее график для значений ж, лежащих в окрестности числа 2 (рис. 8.2, а). Тонкие вертикальные линии на рис. 8.2, а соответствуют значениям х, которые стремятся к числу 2 с обеих сторон. Соответствующие горизонтальные линии определяют значения функции /(х), стремящиеся к числу 4, по мере того, как переменная х


Глава 8. Производная
15
стремится к числу 2 с обеих сторон. На рис. 8.2, б показан график функции /, а также таблица значений х и /(х) на экране калькулятора Texas Instruments TI-83. Если провести по графику курсором, его координаты в таблице подсвечиваются. Это отчетливо демонстрирует важность взаимосвязи между графиком функции и ее значениями.
Рис. 8.2. График функции /(ж) = х + 2
Наконец, чтобы изучить поведение алгебраически, нужно просто отметить, что если величина х стремится к числу 2, то значения т + 2 должны стремиться к числу 2 + 2 = 4. Собрав вместе все эти факты, можно сделать вывод, что
lim (х + 2) = 4 или z + 2 —► 4, если х —> 2.
х—>2
Следует также отметить, что /(2) = 4. Таким образом, значение функции в точке 2 и предел функции в точке 2 совпадают. Иначе говоря,
lim (ж + 2) = / (2) .
X—>2
Это означает, что на графике функции f в точке х = 2 нет разрывов или дыр. ■
Упражнение 8.2.
Пусть /(ж) = х + 1.
1. 	Заполните следующую таблицу.
X
0,9
0,99
0,999 — 1 «-
1,001
1,01
1,1
/(я)
?
?
? —► ? <—
?
?
?
2. Постройте график функции f(x) = х + 1.
3. Используя таблицу, график и алгебраическое выражение х + 1, найдите значение
lim (х + 1).
х—>1


16
Часть III. Математический анализ
4. 	Воспользуйтесь аналогичным подходом для вычисления пределов
lim(x + l) и lim (х 4-1).
х—>0 х—>3 ■
Результаты, полученные в примере 8.2 и упражнении 8.2, вполне прогнозируемые. Следующий пример уже менее очевиден.
Пример 8.3 (Анализ предела). Пусть
д-2 — Л
Даже если функция не определена в точке х = 2 (в которой числитель и знаменатель равны 0), можно все же спросить, как ведет себя функция д(х), если число х находится в окрестности двойки? Числитель, стремящийся к нулю, — это сила, толкающая дробь в направлении нуля. Знаменатель, стремящийся к нулю, — это другая сила, толкающая дробь в сторону больших чисел. Как же эти две силы уравновешиваются?
Решение. Проделывая все то же, что и ранее, необходимо построить таблицу значений функции д(х) (табл. 8.2).
Таблица 8.2. Значения функции д(х)
X
1,5
1,8
1,9
1,99
1,999 -> 2
<- 2,001
2,01
2,1
2,2
2,5
9(®)
3,5
3,8
3,9
3,99
3,999 -» 4
— 4,001
4,01
4,1
4,2
4,5
Следует отметить, что эти значения совпадают со значениями /(х) = х + 2 в табл. 8.1. Это означает, что между функциями f и д существует алгебраическая зависимость.
9 =
х2 — 4 (х — 2) (х + 2)
х — 2 х — 2
= х + 2,
х 2.
Таким образом, д(х) = f(x) для всех значений х, за исключением точки х = 2. Это означает, что график функции д совпадает с графиком функции / (рис. 8.2), за исключением того, что из графика д “выколота” точка с координатами (2,4), как показано на рис. 8.3.
Поскольку поведение функции (х2—4)/(х —2) в точках из окрестности числа 2, но не равных 2, совпадает с поведением функции х + 2 в той же окрестности, выполняется следующее соотношение.
х2 — 4
lim = lim (х + 2) = 4.
ж—>2 х - 2 ж—>2
Итак, предел функции д существует, даже несмотря на то, что функция в этой точке не определена. ■


Глава 8. Производная
17
Рис. 8.3. График функции д(х) с “выколотой” точкой
Упражнение 8.3.
Повторите решение примера 8.3 и найдите предел ■
Примечание
Исследование графика функции д(х) = (т2 — 4)/(х — 2) (из примера 8.3) с помощью графической утилиты может не выявить дыру в точке х = 2 (рис. 8.4). Это происходит из-за того, что существует разница между координатами точек на плоскости (бесконечное множество) и координатами пикселей на экране (конечное множество). Во многих графических утилитах самый простой способ сделать эту дыру видимой — выбрать параметры окна вывода так, чтобы точка х = 2 была средней точкой интервала, на котором задана функция (рис. 8.5). Следует отметить, что графическая утилита не отображает координату у, соответствующую х = 2, поскольку значение #(2) не определено. В задачах 75 и 76 практикума 8.1 показан другой способ масштабирования окна, позволяющий сделать дыры видимыми на графике.
Рис. 8.4. График функции
9 (х) = ^2 Для -3 z 5
5
—71
Х=2
¥=
1
Рис. 8.5. График функции
9 (х) = Для -1 х 5


18
Часть III. Математический анализ
Дадим неформальное определение предела. Строгое определение нам пока не требуется, но оно дано в сноске1.
Предел
Говорят, что
lim f (х) = L или f(x) —► L, когда х —> с,
х—>с
если значение функции /(ж) стремится к единственному действительному числу L, когда переменная х стремится к числу с, но не равно с (с любой стороны от с).
(Примечание. Существование предела в точке с никак не влияет на значение функции в точке с. Фактически число с может даже не находиться в области определения f (см. пример 8.3). Однако функция должна быть определена по обеим сторонам от точки с.)
В следующем примере рассматривается функция модуля.
f (®) = \х
—х, если х < О,
<
х, если х 0.
/(-2) = |-2|i= Н^2)':=2
/(3) = |3| = 3
График функции f показан на рис. 8.6.
Рис. 8.6. График функции /(ж) = |х|
Пример 8.4 (Анализ предела). Пусть h(x) = |т| /х. Исследуйте поведение функции h(x) для значений х в окрестности нуля, не равных нулю, используя таблицу и график. Найдите предел lim^o h(x), если он существует.
1 Чтобы неформальное определение стало точным, нужно более строго отнестись к применению слова стремится. Это означает следующее: говорят, что /(я) = L, если для каждого числа
е > 0 существует такое число d > 0, что |/(х) — L\ < е, когда 0 < |х — с| < d. Это определение, как правило, используется для вычисления отдельных пределов и доказательства их разнообразных свойств, помогающих находить конкретные пределы. (Несмотря на то что интуитивное представление о пределе существует довольно давно, строгое определение было дано только в девятнадцатом столетии немецким математиком Карлом Веерштрассом (Karl Weierstrass) (1815-1897).)


Глава 8. Производная
19
Решение. Функция h определена для всех действительных чисел, за исключением нуля. Например,
Не определена
Вообще, функция h(x) равна числу —1 для всех отрицательных х и единице для всех положительных х, В табл. 8.3 и на рис. 8.7 показано поведение функции h(x) в окрестности нуля.
Таблица 8.3. Значения функции h(x)
X -2 -1 0,1 -0,01
-0,001 -ч.
0 <- 0,001 0,01 0,1 1 2
/i(a:) -1 -1 -1 -1
-1 ->
-1/1 <- 1 1 111
Рис. 8.7. Поведение функции h(x) в окрестности нуля
Находится ли функция h(x) вблизи какого-то определенного значения, когда аргумент х находится вблизи нуля (с любой стороны от него)? Нет, поскольку функция h(x) равна числу —1 для х < 0 и единице для х > 0. Следовательно, можно сказать, что
lim — не существует.
х—>0 X
Таким образом, в точке х = 0 не существует ни сама функция Д(т), ни ее предел. Однако в нуле существует предел справа и предел слева, хотя они не равны между собой. (Этот момент будет дополнительно обсуждаться ниже.) ■


20
Часть III. Математический анализ
Упражнение 8.4.
Постройте график функции
и найдите предел limx_>2 h(x), если он существует. ■
В примере 8.2 было удобно исследовать значения функции /(т), когда переменная х стремится к числу 2 слева, а затем, когда х стремится к числу 2 справа. Как показывает пример 8.4, значения функции h(x) стремятся к двум разным числам в зависимости от направления, и вполне естественно назвать эти значения “предел слева” и “предел справа”. Такие результаты наводят на мысль, что при обсуждении пределов будут весьма полезными понятия односторонних пределов.
Говорят, что
lim f (х) = К, Выражение х —► с~ читается как "х стремится к числу с слева" х—>с~ и означает, что х —► с и х < с.
где число К называется пределом слева (или левосторонним пределом), если функция /(т) стремится к значению К, когда переменная х стремится к числу с слева на действительной числовой оси. Говорят, что
lim / (х) = L, Выражение х —► с+ читается как "аг стремится к числу с справа" х—>с+ и означает, что х —► с и х > с.
где число К называется пределом справа (или правосторонним пределом), если функция /(ж) стремится к значению L, когда переменная х стремится к числу с справа на действительной числовой оси.
Существование предела
Для существования предела необходимо, чтобы существовали и были равны пределы слева и справа.
В примере 8.4
ж кг
lim — = —1 и lim — = 1.
х z^0+ х
Поскольку левосторонний и правосторонний пределы не равны, то
lim — не существует.
ж->0 х
Пример 8.5 (Графический анализ предела). Проанализируйте поведение функции f(x), график которой изображен на рис. 8.8, вблизи следующих точек.
1. -1. 2. 1. 3. 2.


Глава 8. Производная
21
Рис. 8.8. График функции /(ж)
Решение.
1. 	Поскольку в нашем распоряжении есть только график, чтобы связать значение х с соответствующим значением /(ж), следует воспользоваться вертикальными и горизонтальными прямыми. Легко видеть, что для любых значений х в окрестности числа —1 соответствующие значения f(x), определяемые горизонтальными линиями, близки к единице.
lim f(x) = l, х—» — 1“
lim f (x) = 1,
x—► — 1 +
lim f (x) = 1,
x—► — 1
/(-1) = 1.
2. 	Для любых значений x, близких к единице, но не равных ей, вертикальные и горизонтальные прямые указывают на то, что соответствующие значения f(x) близки к числу 3. Однако “выколотая” точка (1,3) свидетельствует о том, что /(1) ф 3.


22
Часть III. Математический анализ
lim f (х) = 3, >1_
lim+ f (x) = 3,
lim f (x) = 3, X—>1
/(1) = 5.
3. Разрыв на графике в точке х = 2 указывает на то, что поведение вблизи этой точки сложнее, чем в двух предыдущих случаях. Если переменная х приближается к числу 2 слева, соответствующие горизонтальные прямые пересекают ось у вблизи точки 2. Если переменная х приближается к числу 2 справа, соответствующие горизонтальные прямые пересекают ось у вблизи точки 5. Таким образом, односторонние пределы в данном случае отличаются.
lim f (х) = 2,
х—>2_
lim / (х) = 5,
lim/(x)
х—>2
не существует,
/(2) = 2.
Упражнение 8.5.
Проанализируйте поведение функции /(х), график которой изображен на рис. 8.9 вблизи следующих точек.
1. В окрестности нуля.
2. В окрестности единицы.
3. В окрестности числа 3. ■


Глава 8. Производная
23
Рис. 8.9. График функции f(x)
Вычисление пределов
Таблицы и графики очень полезны для исследования пределов, в особенности если в рассматриваемой точке происходит что-то необычное. Однако большое количество пределов, вычисляемых в математическом анализе, не представляют собой ничего необычного, и их можно быстро вычислить, используя незначительные алгебраические упрощения, немного интуиции и основные свойства пределов. Основы этого подхода образует следующий перечень свойств пределов.
Теорема 8.1 (Свойства пределов). Пусть f и д — две функции. Предположим, что
lim f (х) = L lim д (х) — М,
х—>с х—>с
где L и М — действительные числа (оба предела существуют). Тогда
1. lim [f (х) + д (ж)] = lim f (х) + lim д(х) = L + М;
х—*с х—>с х—>с
2. lim [f (ж) — д (ж)] = lim f (ж) — lim д(х) = L — М;
х—>с х—>с х—>с
3. lim kf (ж) = к lim f (х) = kL для любой постоянной к;
х—*с х—>с
если М / 0;
5. lim
х—>с
/(х) 'Sj/W L
д (ж) lim д (х) М’
х—*с
6. lim х/f (ж) — г/lim f (ж) — y/L для четных п L > 0. х->с у у х_>с
Задание 8.1.
Свойства, перечисленные в теореме 8.1, можно переформулировать с помощью коротких устных утверждений. Например, в свойстве 1 просто утверждается, что предел суммы равен сумме пределов. Запишите устную формулировку остальных свойств теоремы 8.1. ■


24
Часть III. Математический анализ
Пример 8.6 (Использование свойств пределов). Вычислите предел Итж_>з(я;2 - — 4х).
Решение. Прежде всего следует отметить существование следующего очевидного предела.
lim х — 3.
х—>3
(Здесь утверждается только, что если переменная х стремится к числу 3, то значения тождественной функции /(ж) = х также стремятся к числу 3.) Теперь можно воспользоваться этим пределом и свойствами пределов.
lim (х2 — 4rr): = lim х2 — lim 4х : = Свойство 2
х—>3 ' х—>3 х—>3 ;
! — ( lim х ) • ( lim х ) — lim 4х ! — Свойства 3 и 4
! \х—>3 / \х—>3 / х—>3 !
= 3-3-43 =-3.
После определенной практики вы научитесь пропускать этапы в выделенном пунктиром блоке и будете записывать такие выражения следующим образом.
lim (х2 — 4х) = 3 • 3 — 4 • 3 = —3.
Упражнение 8.6.
Вычислите предел lim^ (х2 + 5х). ■
Что будет, если попытаться оценить такой же предел, как в примере 8.6, но в случае, когда переменная х стремится к неопределенному числу, например, числу с? Повторяя проделанное в примере 8.6, получим
lim (х2 — 4х) = с • с — 4 • с = с2 — 4с.
х—*с ' '
Если положить /(ж) = х2 — 4х, получим следующий результат.
lim f (ж) = lim (х2 — 4х) = с2 — 4с = f (с).
х—>с х—>с 4 '
Итак, этот предел можно найти, просто вычислив значение функции f в точке с. Очевидно, что вычисление предела стало бы значительно проще, если бы можно было найти такую функцию, для которой
lim f (х) = f (с).
х—>с
(8.1)


Глава 8. Производная
25
Оказывается, существует множество функций, удовлетворяющих условию (8.1). Подробное обсуждение этих функций будет продолжено в следующем разделе. Теперь же следует отметить, что если
/(х) = апхп + an_ixn_1 Ч h а0
является полиномиальной функцией, то свойства в теореме 8.1 подразумевают,
что
lim f (х) = lim (апхп + an_ixn_1 + F ao) =
x—>c x—>c ' '
= anxn + an_ixn_1 4 h a0 = f (c).
Для рациональной функции
гМ-п®
W d(x)’
где n(x) и d(x) — полиномиальные функции и d(c) ф 0, используя свойство 5 и тот факт, что полиномы п(х) и d(x) удовлетворяют условию (8.1), получаем
ч „(х) „(х)
1,т г (х) = Ьш
= г (с).
Эти результаты подытожены в теореме 8.2.
Теорема 8.2 (Пределы полиномиальных и рациональных функций).
1. lim f (ж) = f (с), f — произвольная полиномиальная функция; ж—>с
2. lim г (х) — г (с), г — произвольная рациональная функция с ненулевым
х—-с
знаменателем в точке х = с. ■
Пример 8.7 (Поиск пределов). Вычислите следующие пределы.
1. lim (х3 — 5х — 1). 2. lim х/2а?2 + 3.
ж->2 v 7 х->-1
з. lim ,2+.
X—>4 Зх + 1
Решение.
1. lim (т3 - 5х - 1) = 23 - 5 • 2 - 1 - -3.
ж->2 V 7
2. lim У2х2 + 3 = / lim (2х2 + 3) -
X ► 1 X 1
= ^2- (-1)2 + 3 = Уб.
2х _ 2-4 8
’ х™ Зх + 1 _ 3-4 + 1 “ 13‘
Теорема 8.2
Свойство 6
Теорема 8.2
Теорема 8.2


26
Часть III. Математический анализ
Упражнение 8.7.
Вычислите следующие пределы.
1. lim (х4 — 2х + 3). 2. lim л/Зх2 — 6.
х—>—1 х 7 х—>2
Важно отметить, что на некоторые свойства пределов налагаются ограничения. В частности, если
lim f (а?) = 0 и lim д (х) = О,
то поиск предела
может вызвать некоторые затруднения, поскольку свойство 5 (предел отношения) не выполняется, когда Итх_>с <7(2:) = 0. Часто для вычисления результата приходится прибегать к математическим преобразованиям или другим методам. Согласно примерам 8.3 и 8.4
и
lim — не существует.
х->2 х
Эти два примера демонстрируют, что для поиска предела (8.2) недостаточно просто знать, что Итж_>с /(х) — 0 и limx^c д(х) = 0. В зависимости от выбранных функций f и д предел (8.2) может существовать или не существовать. Следовательно, если задан предел (8.2), а пределы limx_>c /(х) = 0 и Птж_>с g(z) = 0, то говорят, что предел (8.2) не определен или, точнее, является неопределенным выражением 0/0.
Предупреждение. Выражение 0/0 не является действительным значением и его нельзя использовать в качестве значения предела. Если предел имеет неопределенность 0/0, то, чтобы определить, существует ли предел, и вычислить его значение, если он существует, необходимо провести дополнительный анализ.
Задание 8.2.
Воспользуйтесь алгебраическими, численными и/или графическими методами для анализа каждого из следующих неопределенных выражений.
3. lim ~
2^1 (X - I)2


Глава 8. Производная
27
Пределы разностных отношений
Пусть функция f задана на открытом интервале, содержащем число а. Одним из наиболее важных пределов в математическом анализе является предел разностного отношения.
lim /_(» + ;>)-/(»)
h->0 h
Если
lim [/ (а + h) - f (а)] = О,
h—>U
как это часто бывает, то предел (8.3) является неопределенным выражением. В следующем примере показано несколько полезных методов вычисления пределов разностных отношений.
Пример 8.8 (Предел разностного отношения). Найдите предел
lim
/ (3 + h) — / (3) h
для функции /(ж) = 4х — 5.
Решение.
Поскольку предел имеет неопределенность 0/0 и свойство 5 теоремы 8.1 неприменимо, были сделаны алгебраические упрощения. |
Упражнение 8.8.
Вычислите предел
lim /(4^)-/(4)
h—о h
для функции /(х) = 7 — 2х.
Задание 8.3.
Ниже приведено неправильное решение примера 8.8, основанное на ложных утверждениях, обозначенных Объясните, в чем заключаются ошибки.
lim h->0
/(3
/(3)
/ lim h—О
4(3 + h) - 5 - 4 • 3 - 5 h
—10 + 4Л.
= lim ;
л—о h
.. Ю + 4 lim
h->0
= -6.


28
Часть III. Математический анализ
Пример 8.9 (Предел разностного отношения). Вычислите предел
Ит/(-5 + Ц-/(-5)
h—>0 h
для функции /(х) = |х + 5|.
Решение.
lim/(-5 + >»)-/(-5)
h—>0 h
- lim К-5+ Ю + 51-1-5 + 51 h—>0 h
lim h->o
\h\
— не существует. h
Поскольку предел имеет неопределенность 0/0 и свойство 5 теоремы 8.1 неприменимо, были сделаны алгебраические упрощения. Смотрите пример 8.4.
Упражнение 8.9.
Вычислите предел
lim+!+•++!>
h->0 h
для функции f(x) = \x — l
Пример 8.10 (Предел разностного отношения). Найдите предел
Вт/(2 + л)_/(2)
h—>0
h
для функции f (#) = у/х.
Решение.
у/2 4" 7i — л/2
Um/(2 + Д)-/(2) = hm
h->0 h h—>Q
— lim h—>Q
= lim h—>0
h
VzTh-Vi h
2 + h —2
\/2 + ~h 4“
\/2 + h 4~ \/2
Неопределенность 0/0.
Разложим числи¬
тель на множители.
h + ~h 4~
1
(А-В)(А4В) = = А2 — В2.
h


Глава 8. Производная
29
Упражнение 8.10.
Вычислите предел
h—>0 h
для функции f (ж) = у/х.
Ответы к упражнениям
8.1.
х -2-101234 h(x) 1,0 1,5 2,0 2,5 3,0 3,5 4,0
X
0,9
0,99
0,999 — 1
<- 1,001
1,01
1,1
л®)
1,9
1,99
1,999 -> 2
<- 2,001
2,01
2,1
3) lim (z + 1) = 2.
х—>1
4) lim (x + 1) — 1, x—>0
lim (x + 1) — 4.
8.3. 2.
8.4.
lim
x->2
x-2
|z-2|
не существует.


30
Часть III. Математический анализ
8.5. 1) lim f (х) = 0;
х—
lim / (х) - 0;
X—>0+
lim f (х) = 0;
х—>0
f (0) = 0.
2) lim f (x) = 1;
x—>1_
lim f (x) = 2;
x—>1 +
lim f (x) не существует;
x—>1
f(1) не определено.
3) lim f (x) = 3;
x—>3
lim f (x) = 3;
X—>3+
lim f (x) = 3;
X
/(3) = 2.
8.6. -6.
8.7. 1) 6. 2) Уб. 3)
8.8. —2.
8.9. He существует.
Практикум 8.1
А В задачах 1-10 требуется вычислить пределы, если они существуют.
1. 	lim 4х.
х—>3
3. 	lim (х + 5). х—► —4
5. 	lim х (х — 4). а?—>2 v 7
2. 	lim 3z.
x—>—2
4. 	lim (x — 3). x—>5
6. 	lim x(x + 3).
x—►—1
7.
lim
х->-3 х +
5
8. lim .
ж->4 x
9. 	lim \/5x + 4.
10. 	lim ^/16 — 7x.
x->0
Вычислите пределы, указанные в задачах 11-20, при условии, что Ппъ^з /(х) = 5 и limx^3 g(x) = 9.
И. lim [f (х) - g (х)]. 12. lim [f (x) + g (x)].
x—>3 x—>3


Глава 8. Производная
31
14. lim —2/ (х).
х—>3
16. limi •$(*)]•
х
18. lim у/g (x).
20. lim
X—>3 Зд (ж)
13. Iim4p(x).
х 3
15. lim
х-з д (х)
17. lini у/ f (х).
19. 	lim
я—з 2/ (х)
В задачах 21-24 требуется нарисовать график функции, удовлетворяющей данным условиям.
*21. f (0) = 1; lim f (х) = 3; lim f (x) = 1. z->0“ x-»o+
* 22. f (1) = —2; lim f (x) = 2; lim f (x) = —2. x—>1“ x—>1 +
*23. /(—2) = 2; lim f (x) = 1; lim f (x) = 1.
x->-2~ x—>-2+
*24. f (0) = -1; lim f (x) = 2; lim f (x) = 2.
x—>0~ x—>0+
В задачах 25-28, воспользовавшись графиком функции f, приведенным ниже, вычислите указанные пределы и значения функции.
25. а)
в)
26. а)
в)
27. а)
в)
*д)
lim /(х). б)
х—>0~
limf(x). г)
х—>0
lim /(х). б)
х—>1~
lim f (®). г)
х—>1
lim f (х). б)
Х-.2-
lim/(x). г)
х—>2
Можно ли переопределить значение /(
Аргументируйте свой ответ.
lim /(х).
х^о+ v 7
/(0).
lim / (х).
х—>1 +
/(!)•
lim /(х).
z->2+
/(2).
!) так, чтобы limx_>2 f (х) = f (2)?
28. a) lim f (x). 6) lim /(x).
B) lim/(x). г) Д4).
x—>4
*д) Можно ли переопределить значение /(4) так, чтобы lima;_>4 f (х) = f (4)? Аргументируйте свой ответ.


32
Часть III. Математический анализ
В задачах 29-32, воспользовавшись графиком функции д, приведенным ниже, вычислите указанные пределы и значения функции.
29. a) lim g(x). б) lim g(x).
х—>1“ х—>1+
в) limg(x). г) р(1).
х—>1
*д) Можно ли переопределить значение р(1) так, чтобы limx_>ip(x) = р(1)? Аргументируйте свой ответ.
30. a) lim g(x).
х—>2~
в) limp (ж).
х—>2
б)
г)
lim о (аг).
х—>2+
5(2).
31. a) lim р(х). б) lim р(х).
х—>3“ х—»з+
в) lim о (я). г) р(3).
х—>3
*д) Можно ли переопределить значение д(У) так, чтобы Нт1_з д(х) = д (3)? Аргументируйте свой ответ.
32. a) lima._4- д (х). в) Птг^4д(х).
б) limI_>4+ д (я).
г) Р(4).
Б В задачах 33-52, используя свойства пределов, алгебраические упрощения, таблицы значений и/или графики, вычислите пределы, если они существуют.
х2 — 9
, x2 - 25
33.
Ит
34.
lim r .
х—►—3 х + 3
x—» —5 x + 5
|х - 11
x — 3
35.
lim 1 1.
36.
lim :
z->l+ X — 1
x->3- |x — 3
lx- 11
x — 3
37.
lim J -1.
38.
lim 1 or
T->1- X — 1
x->3+ \x - 3|
lx — 11
, x — 3
39.
lim 1 1.
40.
lim | ,r
x—>1 X — 1
ж->з |x — 3|
x —2
x 3
41.
lim o
42.
lim ——.
x—>1 x2 — 2x
x->l x2 + 3x
x — 2
. x + 3
43.
lim o
44.
lim — — .
x—>2 x2 — 2x
x->-3 x2 + 3x
, x2 — x — 6
, x2 + x — 6
45.
lim n .
46.
lim
x—>2 x + 2
x—>3 X -f~ 3


Глава 8. Производная
33
47.
lim
х->-2
X2 - X - 6
z + 2
48.
lim
x—»—3
x2 + x — 6
x + 3
49. lim
z—3
x
x + 3
x-3 \ x2 - 9 /
50. lim +
i-2\j + 2 x2-4J
52. 	lim ( 7- + Vx2 4- 3
\ x — 1
Для каждой функции в задачах 53-60 вычислите предел
h->o h
53. 	/(х) = 3z + 1.
55. /(rr) = x2 + 1.
57. 	f (z) = yfi - 2.
59. 	/(ж) = |rr — 2| -3.
54. 	/(x) = 5x - 1.
56. /(#) = x2 — 2.
58. 	f (x) = 1 + y/x.
60. 	/(x) = 2-F|x-2|.
* 61. Используя таблицу значений, опишите поведение следующих пределов.
a) lim
х-»0~ х
б) lim -.
z->0+ х
* 62. Используя таблицу значений, опишите поведение следующих пределов.
a) lim —z.
х->0" х2
б)
lim -т.
х->0+ х2
В
63. 	Пусть f имеет вид
/(х) =
1 -F тх,
4 — тх.
если х < 1, если х > 1,
где т — константа.
а) Постройте график функции / при т = 1 и вычислите пределы lim^i- f (х) и lim^^i-b /(я).
б) Постройте график функции f при т = 2 и вычислите пределы lim^^x- f (я) и Нтя-^ f (ж).
в) Найдите такое значение т, для которого lim^}- f (х) — lim^^i-h / (ж), и постройте соответствующий график функции /.
*г) Кратко опишите каждый график. Чем график из п. в отличается от графиков пп. а и б?
64. 	Пусть f имеет вид
, , ч | —Зт + 0,5я; если х < 2;
f (*) = С о
13т — х; если х > 2,
где т — константа.
а) Постройте график функции f при т = 0 и вычислите пределы lim^^- f (#) и limx_>2+ / (я)-
б) Постройте график функции f при т = 1 и вычислите пределы Итж_>2- f и Итх_2+ /(*)•


34
Часть III. Математический анализ
в) Найдите такое значение т, для которого f (х) — limI_2+ /(я),
и постройте соответствующий график функции /.
г) Кратко опишите каждый график. Чем график из п. в отличается от графиков пп. а и б?
В задачах 65-68 требуется вычислить следующие пределы (здесь а — действительная
постоянная величина).
65. lim
Zi—>0
(а + Д)2 — а2 h
66 Um [3 (а +/1) — 2] — (Зп - 2) h—>0 h
67. lim
Ai->0
\4 + А - \/a
—k—■ 0> °-
1 1
68. lim a / 0.
h—о h
В задачах 69-74, используя таблицу значений, оцените каждый предел с точностью
до трех десятичных знаков.
а:10 — 1
69. lim , .
х—>1 X — 1
х15 - 1
70. lim
х—>1 X — 1
71. 	lim .
х—>0 X
73. 	lim (Ц-х)1/х.
х—>0
V — 1
72. 	lim .
х->0 X
74. 	lim (1 + 2х)1/х.
х—>0
Для решения задач 75-80 необходимо воспользоваться графической утилитой. При изучении пределов с помощью утилиты удобно выбрать значения Хт[п и Хтах так, чтобы координаты, отображаемые на экране, имели конечное количество десятичных знаков. В задачах 75 и 76 описан простой способ, которым это можно сделать.
75. 	Пусть Xmin = 0. Используя метод проб и ошибок, найдите такое целое число п, для которого координата х точки, отображаемой на экране, равна целому числу, когда Хтах = п.
*76. Задано произвольное значение Хтт- Пусть
X
max
— -^Gnin h ' Tl^
где п — целое число, полученное в задаче 75. Проанализируйте свойство координаты х точки, отображаемой на экране, если h — 0,5 и если h = 0,1.
В задачах 77-80 постройте график каждой функции и, воспользовавшись опциями изменения масштаба и отслеживания, изучите левосторонний и правосторонний пределы для указанного значения (значений) величины с. Для выбора значений Xmin u А'шах воспользуйтесь идеями, изложенными в задачах 75 и 76.
77. /(х) =
х4 - Юж2 + 24
4 — х2
с = —2, с = 2.
78. /(*) =
ж4 - 12х2 + 27
х2 — 9
с = —3, с = 3.
79. f(x) =
х3 — 9х
|х2 — 9| ’ С
80. f (х) = |^2 _ ; с = -2, с = 2.


Глава 8. Производная
35
Применение математики
Экономика и бизнес
81. Тарифы на телефонную связь. Тариф на междугородные телефонные звонки из штата в штат длительностью до 20 минут составляет 0,99 долл, и 0,07 долл, за каждую последующую минуту или ее часть.
а) Дайте определение кусочно-заданной функции стоимости F(x) междугороднего звонка из штата в штат длительностью х минут.
б) Постройте график функции F(x) для 0 < х 40.
в) Вычислите пределы Итх_2о- F(x), lima._>2o+ F и Нтж_>20 F (х), если они существуют.
82. WWW Тарифы на телефонную связь. Тариф на междугородные телефонные звонки из штата в штат длительностью до 10 минут равен 0,09 долл, и 0,18 долл, за последующую минуту или ее часть.
а) Дайте определение кусочно-заданной функции стоимости G(x) междугороднего звонка из штата в штат длительностью х минут.
б) Постройте график функции G(x) для 0 < х < 40.
в) Вычислите пределы Ит^ю- G (ж), lima._,10+ G (т) и limx_>io G (х), если они существуют.
*83. Тарифы на телефонную связь. Вернемся к задачам 81 и 82. Сравните стоимость услуг телефонной связи в обоих случаях для звонков длительностью менее 20 минут.
* 84. Тарифы на телефонную связь. Вернемся к задачам 81 и 82. Сравните стоимость услуг телефонной связи в обоих случаях для звонков длительностью больше 20 минут.
WWW Компания реализует одежду, украшенную вышивкой, и товары народных промыслов. В следующей таблице указаны скидки, предлагаемые компанией при разных объемах оптовых закупок х, выраженных в долларах. Приведенные в ней значения являются исходными данными задач 85 и 86.
Скидка при оптовой продаже (за вычетом налога)
Объем заказа х, долл.
Скидка, %
300 х < 1000
3
1000 < х < 3000
5
3000 X < 5000
7
5000 х
10
85. 	Скидка при оптовой продаже. Предположим, что величина скидки определяется по общему объему заказа. Иначе говоря, если величина х удовлетворяет неравенству 300 < х < 1000, то стоимость всего заказанного товара уменыпа-


36
Часть III. Математический анализ
ется на 3%. Если величина х удовлетворяет неравенству 1000 х < 3000, то стоимость заказанных товаров удешевляется на 5%, и т.д.
а) Пусть х — объем заказа до вычитания скидки. Запишите определение кусочно-заданной функции цены с учетом скидки D(x).
б) Используя односторонние пределы, исследуйте предел D(x), когда переменная х стремится к 1000 или к 3000.
86. Скидка при оптовой продаже. Предположим, что величина скидки определяется для каждого объема заказа отдельно. Иначе говоря, цена с учетом скидки для покупки на 4000 долл, вычисляется следующим образом.
300 + 0,97 • 700 + 0,95 • 2000 + 0,93 • 1000 = 3809.
а) Пусть х — объем заказа до вычитания из него скидки скидка. Запишите определение кусочно-заданной функции цены с учетом скидки Р(х).
б) Используя односторонние пределы, исследуйте предел Р(х), когда переменная х стремится к 1000 или 3000.
*в) Сравните этот метод начисления скидок с методом, описанным в задаче 85. Всегда ли в одном из них цена будет ниже, чем в другом?
Биологические науки
87. WWW Борьба с загрязнением.. Штрафы промышленным предприятиям, загрязняющим среду, составляют 20 долл, за каждую тонну выбрасываемых в атмосферу вредных веществ, если их объем не превышает 4000 т. На выбросы свыше 4000 тонн штрафы не предусмотрены. Запишите определение кусочно-заданной функции F(x\ описывающего общую сумму штрафа, начисляемого за выбросы на х тонн загрязняющих веществ в год. Чему равен предел функции F(z), когда переменная х стремится к значению 4000 или 8000?
88. Борьба с загрязнением. Рассмотрите условие задачи 87. Штраф промышленного предприятия за выброс в атмосферу тонны загрязняющих веществ рассчитывается по формуле А(х) = F(x)/x. Запишите определение кусочно-заданной функции А(х). Чему равен предел функции А(х), когда переменная х стремится к значению 4000 или 8000?
Социальные науки
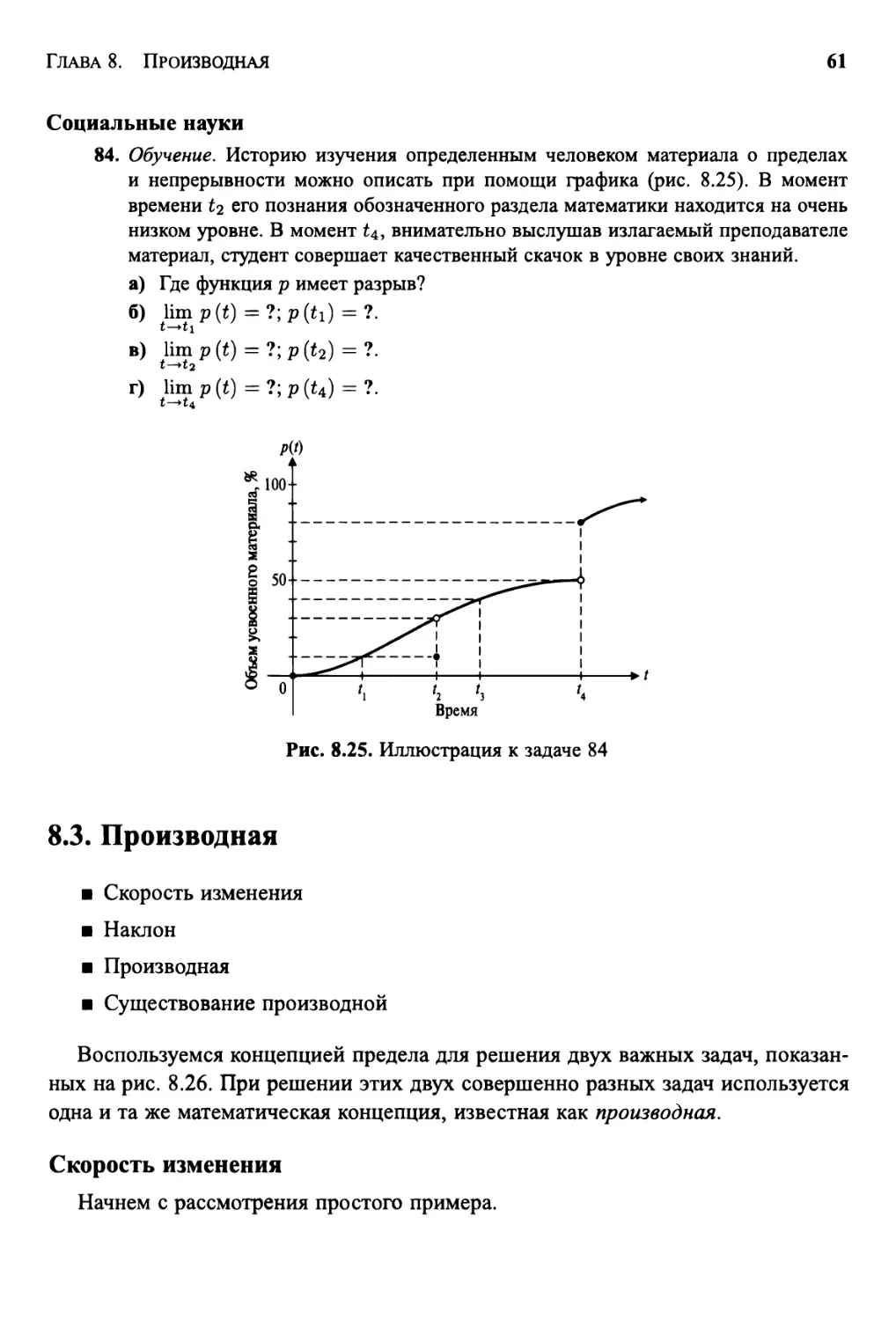
89. 	Активность избирателей. Кусочно-определенные функции часто применяются для предсказания результатов выборов. Для каждой из функций / и <?, показанных ниже, найдите пределы, когда переменная х стремится к числу 5 или 10.
f № = <
0,8 — 0,08х;
если х 5;
если 5 < х < 10;
0; если 10 < х.
д(х) =
0;
0,8 - 0,04а:2
1;
-3;
если х 5;
если 5 < х < 10;
если 10 < х.


Глава 8. Производная
37
8.2. 	Пределы и непрерывность
■ Непрерывность
■ Свойства непрерывности
■ Бесконечные пределы
■ Решение неравенств с использованием свойств непрерывности
В теореме 8.2 из раздела 8.1 утверждается, что если f — полиномиальная функция или рациональная функция с ненулевым знаменателем в точке х = с, то
lim f (х) = f (с). (8.4)
х—>с
Говорят, что функция, удовлетворяющая условию (8.4), непрерывна в точке х = с. Твердое понимание непрерывности функций важно для построения и анализа графиков. Как станет видно позже, свойства непрерывности являются также основой простого и эффективного метода решения неравенств — инструмента, который будет широко использоваться в последующих разделах.
Непрерывность
Сравним графики, показанные на рис. 8.10, которые обсуждались в примерах 8.2 и 8.4 из раздела 8.1. Следует отметить, что два из них имеют разрывы, т.е. их нельзя нарисовать, не оторвав карандаш от бумаги. Если говорить нестрого, функция непрерывна на интервале, если ее график можно нарисовать, не отрывая карандаш от бумаги. Функция, график которой имеет разрыв в точке х = с, называется разрывной в этой точке. Функция f (рис. 8.10, а) непрерывна для всех значений х. Функция д (рис. 8.10, б) является разрывной в точке х = 2, но непрерывной на любом интервале, не содержащем двойки. Функция h (рис. 8.10, в) имеет разрыв в точке х = 0, но является непрерывной на любом интервале, не содержащем нуля.
Большинство графиков функций, описывающих природные явления, непрерывны, тогда как многие графики, используемые в экономических и финансовых расчетах, имеют разрывы. В частности, на рис. 8.11, а показан график изменения температуры воздуха в течение суток, — явление непрерывного характера. А график на рис. 8.11, б изображает количество товара, хранящегося на складе, в каждый из дней рабочей недели — абсолютно дискретную величину.
Задание 8.4.
1. 	Кратко опишите изменение температуры, показанное на рис. 8.11, а. Укажите самую высокую и самую низкую температуру в течение обозначенного периода, а также моменты времени, в которые эти значения были зафиксированы.


38
Часть III. Математический анализ
a)Um/(x) = 4, б)Нт#(х) = 4, в) предел lim h(х) не существует,
Д2) = 4 значение g(2) не определено. значение Л(0) не определено.
Рис. 8.10. Примеры непрерывных и разрывных функций
Время с начала суток Дни недели
а) температура в течение суток б) объем товара, хранящегося на
складе в течение недели
Рис. 8.11. Примеры непрерывных и дискретных графиков
2. 	Кратко опишите изменения в количестве товара, хранящегося на складе, показанные на рис. 8.11, б. Оцените величины изменений и укажите моменты времени, в которые эти изменения произошли. ■
Итак, мы приходим к следующему формальному определению непрерывности. Непрерывность
Функция f непрерывна в точке х = с, если выполняются следующие условия.
1. Существует предел Нтж_>с f (х).
2. Существует значение /(с).
3. \imx^cf (х) = f (с).
Функция непрерывна на открытом интервале2 (а, Ь), если она непрерывна в каждой точке этого интервала.
Если одно или несколько из этих трех условий не выполняются, то функция разрывается в точке х = с.
2Способы обозначения интервалов описаны в приложении А.8.


Глава 8. Производная
39
Задание 8.5.
Постройте график функции, которая разрывается в точке, поскольку для нее не выполняется условие 1 определения непрерывности. Сделайте то же для условий 2 и 3. ■
Пример 8.11 (Непрерывность функции, заданной графиком). Воспользовавшись определением непрерывности, проанализируйте непрерывность функции, график которой показан на рис. 8.12.
Рис. 8.12. График разрывной функции
Решение. Начнем с определения точек разрыва. При изучении графика на нем можно обнаружить разрывы в точках х — —4, —2, 1 и 3. Теперь нужно определить, какие условия в определении непрерывности не выполняются в каждой из этих точек. Везде нужно найти значение функции, а также ее предел в рассматриваемой точке.
Разрыв в точке х = —4.
lim f (т) = 2; Поскольку односторонние пределы отличаются, предел не
существует (раздел 8.1)
lim / (ж) = 3;
lim f (ж) не существует;
/(-4) = 3.
Таким образом, функция f не является непрерывной в точке х = —4, поскольку не выполняется условие 1.
Разрыв в точке х = —2.
lim f (х) = 5;
х—>-2~
lim f (ж) = 5;
Кружок в точке (—2,5) указывает на то, что число 5 не является значением функции f в точке —2. Поскольку нигде на вертикальной прямой х = 2 нет жирной точки, значение /(—2) не определено
lim /(ж) = 5;
х—>—2
f (—2) не существует.


40
Часть III. Математический анализ
Таким образом, функция f не является непрерывной в точке х = —2, поскольку не выполняется условие 2.
Разрыв в точке х = 1.
lim f (z) = 4;
lim /(z) = 1;
x—>1 +
lim f (x) не существует;
x—>1
f (1) не существует.
Таким образом, функция f не является непрерывной в точке х = 1, поскольку не выполняется ни условие 1, ни условие 2.
Разрыв в точке х = 3.
lim f (х) = 3; Жирная точка с координатами (3; 1) указывает на то, что
ж—3- /(3) = 1.
lim f (х) = 3;
х—>3+
lim f (z) = 3;
/(3) = 1.
Условия 1 и 2 выполняются, но функция f не является непрерывной в точке х — 3, поскольку не выполняется условие 3.
Найдя все точки разрыва и проанализировав их характер, можно сделать вывод, что функция f непрерывна везде, за исключением точек х = —4, —2, 1 и 3. ■
Упражнение 8.11.
Воспользовавшись определением непрерывности, исследуйте функцию, график которой показан на рис. 8.13. ■
Рис. 8.13. График разрывной функции
Важно уметь локализовать точки разрывов в функциях, заданных уравнениями.


Глава 8. Производная
41
Пример 8.12 (Непрерывность функций, заданных уравнениями). Воспользовавшись определением непрерывности, исследуйте каждую функцию в указанной точке (точках).
1. 	/(ж) = х + 2 в точке х — 2. 2. д (ж) — в точке х = 2.
3. 	h (ж) = в точках х — 0 и х — 1.
Решение.
1. Функция / непрерывна в точке х = 2, поскольку
lim f (я;) = 4 = f (2) См. рис. 8.10, а
х—>2
2. Функция д не является непрерывной в точке х — 2, поскольку д(2) = 0/0, т.е. ее значение в точке 2 не определено (см. рис. 8.10, б).
3. Функция h не является непрерывной в точке х — 0, поскольку /г(0) = |0| /0, т.е. ее значение в точке 0 не определено. Кроме того, предел limx_,o h(x) не существует.
Функция h непрерывна в точке х = 1, поскольку
lim — — 1 — h (1). См. рис. 8.10, в
х—>1 X ■
Упражнение 8.12.
Воспользовавшись определением непрерывности, исследуйте каждую функцию в указанной точке (точках).
1. 	/(х) = х + 1 в точке х = 1.
2.
9(х) =
х2 — 1
х — 1
в точке х = 1.
h (ж) =
3.
— в точках х = 2 и х = 0. кг - 2
Аналогично односторонним пределам можно рассматривать одностороннюю непрерывность. Например, говорят, что функция непрерывна справа в точке х = с, если f (ж) = f (с), и непрерывна слева в точке х = с, если
lim^c- f (ж) = f (с). Функция непрерывна на замкнутом интервале [а, Ь], если она непрерывна на открытом интервале (а, Ь), а также справа в точке а и слева в точке Ь,
На рис. 8.14, а показана функция, которая непрерывна на замкнутом интервале [—1,1]. На рис. 8.14, б показана функция, которая непрерывна на полуоткрытом интервале [0, оо).


42
Часть III. Математический анализ
а) функция f непрерывна на отрезке [—1,1]
Рис. 8.14. Непрерывность на замкнутом и полуоткрытом интервалах
б) функция д непрерывна на луче [0, оо)
Свойства непрерывности
www Функции имеют также важное свойство общей непрерывности.
Если две функции непрерывны на одном и том же интервале, то их сумма, разность, произведение и отношение непрерывны на том же интервале, за исключением значений х, при которых знаменатель равен нулю.
Эти свойства вместе с теоремой 8.3, сформулированной ниже, позволяют определить интервалы непрерывности для некоторых важных видов функций, не строя их графиков и не пользуясь тремя свойствами из определения.
Теорема 8.3 (Свойства непрерывности некоторых конкретных функций).
1. Постоянная функция /(ж) = к, где к — константа, непрерывна при всех х.
Функция f(x) = 7 непрерывна при всех х.
2. 	Для положительного целого п функция f(x) = хп непрерывна для при х.
Функция /(аз) = аз6 непрерывна при всех аз.
3. 	Полиномиальная функция непрерывна при всех х.
Функция 2аз3 — Заз2 + аз — 5 непрерывна при всех аз.
4. 	Рациональная функция непрерывна для всех х, за исключением тех значений, при которых знаменатель равен нулю.
Функция
аз2 + 1
аз — 1
непрерывна при всех аз, за исключением точки а? = 1, значения, при котором знаменатель обращается в нуль.


Глава 8. Производная
43
5. 	Для положительных нечетных целых чисел п функция у/ f (я) непрерывна везде, где непрерывна функция f(x).
Функция V®2 непрерывна при всех х.
6. 	Для положительных четных целых чисел п функция у/ f (х) непрерывна везде, где функция /(х) непрерывна и неотрицательна.
Функция \/х непрерывна на интервале [0, оо).
Пункты 3 и 4 соответствуют аналогичным пунктам теоремы 8.2 в разделе 8.1. Они здесь повторяются для того, чтобы подчеркнуть их важность.
Пример 8.13 (Использование свойств непрерывности). Воспользовавшись теоремой 8.3 и общими свойствами непрерывности, найдите области непрерывности следующих функций.
х
1. f(x) = х2 — 2х + 1.
(ж + 2) (ж — 3) ’
4. f (ж) = у/х - 2,
Решение.
1. Поскольку f — полиномиальная функция, она непрерывна при всех х.
2. Поскольку f — рациональная функция, она непрерывна при всех ж, за исключением точек —2 и 3 (значений, при которых знаменатель обращается в нуль).
3. Полиномиальная функция х2 — 4 непрерывна при всех х. Поскольку число п = 3 — нечетное, функция f непрерывна при всех х.
4. Полиномиальная функция х — 2 непрерывна при всех х и неотрицательна
при всех х 2. Поскольку число п = 2 — четное, функция f непрерывна при х 2 или на интервале [2, оо). ■
Упражнение 8.13.
Воспользовавшись теоремой 8.3 и общими свойствами непрерывности, найдите области непрерывности следующих функций.
1. f(x) = х4 + 2х2 + 1.
3. f (х) = у/х — 4.
4. 	f (ж) = + 1.


44
Часть III. Математический анализ
Бесконечные пределы
Функция является разрывной в любой точке с, в которой Нтж_>с/(х) не существует. Например, если односторонние пределы в точке х = с не совпадают, то предел не существует и функция разрывается в точке х — с (см. рис. 8.12). Еще одна ситуация, в которой предел может не существовать, касается функций, значение которых становится очень большим, когда аргумент х стремится к числу с. Для описания такого характера поведения часто используется знак сю. Чтобы проиллюстрировать подобный случай, рассмотрим функции
= и 9^) = ^.
График функции f на рис. 8.15, а указывает на то, что если аргумент х находится вблизи нуля слева от него, то значение f(x) равно очень большому отрицательному числу, а если аргумент х находится вблизи нуля справа от него, то оно равно очень большому положительному числу. В обоих случаях предел не существует. Однако для описания поведения графика в точке х — 0 удобно воспользоваться символом сю. Таким образом, можно записать
lim f (х) = —сю и lim f (х) = сю.
х—>0“ х—>0+
Поскольку эти два утверждения описывают разные типы поведения, невозможно записать одно выражение для предела, чтобы описать характер графика в точке х = 0.
НпД = эс lim 4 = оо
х-о X ^о’х2
lim А = оо
х-0 X2
Рис. 8.15. Функции, стремящиеся к бесконечности


Глава 8. Производная
45
Из графика функции д на рис. 8.15, б видно, что, когда аргумент х находится вблизи нуля с любой из сторон, значение д(х) равно очень большому положительному числу. В этом случае предел функции д(х), когда аргумент х стремится к нулю, также не существует. Однако поведение графика д вблизи нуля можно описать с помощью выражения
lim д (х) — оо.
х—>0
Для обеих функций /ид прямая х = 0 (вертикальная ось) является вертикальной асимптотой. Все эти рассуждения подытожены в нижеприведенной врезке.
www Вертикальные асимптоты
Если предел функции / не существует, когда аргумент х стремится к числу с слева, поскольку функция /(х) становится равна очень большим положительным числам (или очень большим отрицательным числам), говорят, что3
lim / (х) = оо (или —оо).
х—>с~
Если это происходит, когда аргумент х стремится к числу с справа, говорят, что
lim / (ж) = оо (или —оо).
Если оба односторонних предела ведут себя одинаково, то говорят, что
lim / (х) — оо (или —оо).
Если справедливо любое из вышеперечисленных утверждений, то прямая х = с является вертикальной асимптотой для графика у = f(x).
Пример 8.14 (Пределы в точках разрыва). Рассмотрим функцию
Используя при необходимости знаки оо и — оо, опишите поведение этой функции во всех точках разрывов и найдите все вертикальные асимптоты.
3Строгое определение такого выражения для предела имеет следующий вид: Итд._с- f (а?) — = оо, если для любого N > 0 существует такое d > 0, при котором f(x) > N, когда с — d < х < с. Можно сделать аналогичные утверждения для предела справа, неограниченных пределов и пределов для очень больших отрицательных чисел.


46
Часть III. Математический анализ
Решение. Сначала разложим на множители знаменатель и найдем точки разрывов.
ж4 — х2 = х2(х2 — 1) = х2(х — 1)(ж + 1).
Таким образом, функция f имеет разрывы в точках х = — 1, 0 и 1. Воспользуемся вычислительным подходом для оценки поведения функции f(x) вблизи каждой точки разрыва.
Поведение функции в точке х = — 1 показано в следующей таблице (значения функции /(ж) округлены до ближайшего целого числа).
Таблица 8.4. Поведение функции /(ж) вблизи числа — 1
X
-1,01
-1,001
-1,0001 -> -1
<- -0,9999
-0,999
-0,99
98
998
9998 —> оо
-оо -10002
-1002
-102
Проанализировав характер значений /(х) вблизи точки х = — 1 (табл. 8.4), можно видеть, что для значений х, лежащих вблизи числа —1 слева, значения /(т) равны большим положительным числам, а для значений х, лежащих вблизи числа —1 справа, значения /(ж) равны большим отрицательным числам. Таким образом, для описания поведения в точке х = — 1 нужно использовать односторонние пределы.
1 — х 1 — X
lim —j х = оо и lim —А = —оо.
х4 — xz я->-1+ ж4 — хл
Это указывает на то, что для графика у = f(x) линия х = —1 является вертикальной асимптотой.
Поведение функции /(х) в точке х = 0 показано в следующей таблице (значения /(х) округлены до ближайшего целого числа).
Таблица 8.5. Поведение функции f(x) вблизи числа О
X
-0,01
-0,001 -►
0 <- 0,001
0,01
/(а=)
-10101
-1001001 ->
-оо <- -999001
-9901
Поскольку значения f(x) для точек х вблизи нуля с любой стороны от него равны очень большим отрицательным числам (табл. 8.5), то для описания поведения в точке х = 0 можно воспользоваться следующим выражением.
Таким образом, вертикальной асимптотой для графика у = /(ж) является прямая х = 0 (ось у).
Поведение функции /(ж) в точке х = 1 показано в следующей таблице (значения /(х) округлены до трех десятичных знаков).


Глава 8. Производная
47
Таблица 8.6. Поведение функции /(ж) вблизи числа 1
х 0,9
0,99
0,999 -+ 1 <-
1,001
1,01
1,1
/(ж) -0,650
-0,513
-0,501 -» -0,5 <-
-0,499
-0,488
-0,394
Значения в табл. 8.6 указывают на то, что значение limx_i /(ж) существует. Подтвердим это, воспользовавшись алгебраическими упрощениями (следует отметить, что предел является неопределенным выражением).
Неопределенное выражение 5
1 — ж
05 — 1
= -1, 05 / 1
Поскольку этот предел существует, в точке х = 1 нет вертикальной асимптоты.
На графике у = f(x) (рис. 8.16) показано поведение, определяемое следующими выражениями для пределов.
lim f (ж) = оо; х—»—1“
lim / (ж) = —оо;
х—►—1+
lim f (ж) = —оо; х—>о
lim f (ж) = —0,5.
х—>1
Рис. 8.16. Вертикальные асимптоты графика функции /(ж) =
О построении и анализе графиков, имеющих асимптоты, более подробно будет рассказано в разделе 9.3. ■


48
Часть III. Математический анализ
Упражнение 8.14.
Рассмотрим функцию
_ х-З
(Х) х2-4ж + 3’
Используя по необходимости знаки оо и — оо, опишите поведение этой функции во всех точках разрывов и найдите все вертикальные асимптоты. ■
Предупреждение.
На рис. 8.17, а показан график функции f из примера 8.14, построенный с помощью графической утилиты. Может показаться, что графическая утилита нарисовала вертикальную асимптоту, проходящую через точку х = -1, но в действительности это не так. Как показано в примере 8.14, точки, находящиеся вблизи числа —1 слева, имеют большие положительные координаты у, в то время как точки, находящиеся вблизи числа —1 справа, имеют большие отрицательные координаты у. Для данной шкалы х в этой графической утилите на экране нет точек, имеющих координату —1. Утилита просто соединила последнюю точку слева от числа —1с первой точкой справа от него. Поскольку эти точки на экране не видны, создается впечатление, что эта линия является вертикальной асимптотой. На рис. 8.17, б показана та же функция в значительно меньшем масштабе у. Теперь обе точки четко видны, и график кажется непрерывным в точке х = — 1, что, как известно, неправда. При построении графиков функций с вертикальными асимптотами при помощи графических утилит сначала необходимо выполнить операции, описанные в примере 8.14, и найти асимптоты. Не стоит полностью полагаться на встроенные алгоритмы визуализации графической утилиты.
5
Рис. 8.17. Особенности работы графической утилиты
50
Решение неравенств с использованием свойств непрерывности
В математическом анализе одним из основных инструментов изучения графиков является специальный линейчатый график, называемый знаковой диаграммой. Эта диаграмма будет широко использоваться в последующих разделах. В настоящем обсуждении процедура построения знаковых диаграмм будет основана на анализе свойств непрерывности.


Глава 8. Производная
49
Предположим, что функция / непрерывна на интервале (1,8) и /(х) 0 при
любых значениях х на этом интервале. Предположим также, что /(2) = 5 — положительное число. Может ли функция /(ж) быть отрицательной при каком-либо значении х на интервале (1,8)? Нет. Если бы, к примеру, значение /(7) было равно —3, как это показано на рис. 8.18, то мы не смогли бы соединить точки (2,5) и (7, —3) непрерывной линией, не пресекая ось х между точками 1 и 8 хотя бы один раз. (Пересечение оси х нарушило бы предположение о том, что /(х) О при любых значениях х на интервале (1,8).) Таким образом, можно сделать вывод, что функция f(x) должна быть положительной при всех значениях х на интервале (1,8). Если бы значение /(2) было отрицательным, то, используя аналогичные рассуждения, можно было бы показать, что функция /(х) должна быть отрицательной на всем интервале (1,8).
Лх)
5-- *(2,5)
ч—I—I—I—I—
5
Л
(7,-3)
-5
Рис. 8.18. Перемена знака
В общем случае, если f — непрерывная функция и f(x) 0 на интервале (а, Ь), то /(х) не может изменять знак на интервале (а, Ь). Это квинтэссенция теоремы 8.4.
Теорема 8.4 (Знаковые свойства на интервале (а, Ь)). Если f — непрерывная функция на интервале (а, Ь) и /(х) / О при любых значениях х на (а, Ь), то либо /(х) > О при всех значениях х на (а, Ь), либо /(х) <0 при всех значениях х на (а,Ь). ■
Теорема 8.4 является основой эффективного метода для решения разнообразных неравенств. Он проиллюстрирован в примере 8.15.
Пример 8.15 (Решение неравенства). Решите неравенство
х + 1
х-2
> 0.
Решение. Начнем с того, что перепишем левую часть неравенства в виде функ¬
ции /:
/(*) =
х -I-1
х — 2’


50
Часть III. Математический анализ
Рациональная функция f является разрывной в точке х = 2 и /(т) = 0 при х = — 1 (дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю). Нарисуем на действительной числовой оси точки ж = 2 и ж = -1, которые назовем точками разбиения (рис. 8.19). (Следует отметить, что точка 2 “выколота”, поскольку функция не определена при х = 2.) Точки разбиения 2 и —1 определяют три открытых интервала (—оо, —1), (—1,2) и (2,оо). На каждом из этих интервалов функция f является непрерывной и не равна нулю. Из теоремы 8.4 известно, что функция f(x) не меняет знак ни на одном из этих интервалов. Таким образом, знак /(ж) на каждом из этих интервалов можно найти, выбирая пробное число на каждом из них и вычисляя значение f(x) для этого числа. Поскольку в качестве пробного можно взять любое число из каждого подинтервала, выберем такие числа, для которых легко проводить расчеты: —2, 0 и 3. Результаты показаны в табл. 8.7.
—I ♦ 1 1 0 1—► %
-2-10123
Рис. 8.19. Результаты проверки
Таблица 8.7. Проверочные числа
X
/(®)
-2
1
4
(+)
0
1
2
(-)
3
4
(+)
Знак функции f(x) для каждого пробного числа будет таким же, как и ее знак на всем интервале, содержащем это пробное значение. Используя данную информацию, можно построить знаковую диаграмму для функции f(x).
Теперь, пользуясь знаковой диаграммой, можно легко записать решение для данного неравенства.
f (х) > 0 для
представление в виде неравенств представление в виде интервалов
Большинство неравенств, с которыми нам придется сталкиваться, будут строгими (> или <). Если необходимо решить неравенства вида или то нужно


Глава 8. Производная
51
просто включить конечную точку х любого интервала, если функция f определена в этой точке и удовлетворяет данному неравенству. Например, если вернуться к знаковой диаграмме в примере 8.15, то решение неравенства будет иметь следующий вид.
/ (х) > О для
х — 1 или х > 2
(—сю, —1] U (2, оо)
представление в виде неравенств представление в виде интервалов
Вообще, для заданной функции f все значения х, в которых она имеет разрыв или обращается в нуль, называются точками разбиения. Эти точки определяют открытые интервалы, на которых функция /(х) не меняет знак. Используя проверочные числа на каждом интервале, можно построить знаковую диаграмму для функции /(х) на действительной числовой оси. Затем можно очень легко определить, где /(х) < 0 или /(ж) > 0, т.е. решить неравенство /(ж) < 0 или /(ж) > 0.
Процедура построения знаковых диаграмм подытожена в нижеприведенной врезке.
Построение знаковых диаграмм
Дана функция /.
Этап 1. Найти числа (точки) разбиения.
а) Найти все точки, в которых функция f имеет разрыв. (Рациональные функции разрываются во всех значениях х, в которых знаменатель обращается в нуль.)
б) Найти все точки, в которых /(ж) = 0. (Для рациональных функций это происходит в точках, где числитель равен нулю, а знаменатель — нет.)
Этап 2. Отобразить числа, найденные на первом этапе на действительной числовой оси, разбив числовую ось на интервалы.
Этап 3. Выбрать пробные числа из каждого открытого интервала, полученного на втором этапе, и найти значения /(х) для каждого пробного числа, чтобы определить, будет ли функция /(х) положительной (+) или отрицательной (—) на каждом из этих интервалов.
Этап 4. Построить знаковую диаграмму, используя разбиение действительной числовой оси, полученное на втором этапе. На ней будут показаны знаки функции /(х) на каждом из открытых интервалов.
(Примечание. По знаковой диаграмме легко найти решение неравенств /(х) < 0 или /(х) > 0.)
Упражнение 8.15. х2 _
Решите неравенство — <0. ■
х — 3


52
Часть III. Математический анализ
Задание 8.6.
Пусть yi = (х + 1)/(х — 2), а у2 = У1/ \yi\- На рис. 8.20 показан график функции у2, построенный с помощью графической утилиты. Проанализируйте связь между этим графиком и знаковой диаграммой, построенной при решении примера 8.15. ■
2
Ответы к упражнениям
8.11. Функция f не является непрерывной в точках х = —3, —1, 2 и 4.
х — —3: limx_>_3 f (х) = 3, но значение /(—3) не существует;
х = —1: /(—1) = 1, но предел 1ппж_>_1 f (х) не существует;
х — 2: Нша;_>2 f (я) — 5, но значение /(2) = 3;
х = 4: предел limx_>4 f (х) не существует и значение /(4) не существует.
8.12. 1) Функция f непрерывна в точке х - 1, поскольку f (х) = 2 =
= /(!)•
2) Функция д не является непрерывной в точке х = 1, поскольку значение д(1) не определено.
3) Функция h не является непрерывной в точке х = 2 по двум причинам: значение h(2) не существует и предел limx_>2 h (х) не существует.
4) Функция h непрерывна в точке х - 0, поскольку limx_>o h (х) = — 1 = = ^(0).
8.13. 1) Поскольку f — полиномиальная функция, f непрерывна для всех х.
2) Поскольку f — рациональная функция, она непрерывна при всех значениях х, за исключением точек —1 и 4, в которых знаменатель обращается в нуль.
3) Полиномиальная функция х — 4 непрерывна при всех значениях х и неотрицательна при х 4. Поскольку число п = 2 — четное, функция f непрерывна при всех х 4, т.е. на интервале [4, оо).


Глава 8. Производная
53
4) 	Полиномиальная функция ж3 + 1 непрерывна при всех значениях х. Поскольку число п = 3 — нечетное, функция f непрерывна при всех значениях х.
8.14. Функция f имеет вертикальную асимптоту в точке х = 1, поскольку
f (х) = —оо и lima._>1+ f (ж) = оо. Кроме того, функция f имеет разрыв в точке х = 3, поскольку значение /(3) не определено, однако в точке х = 3 нет вертикальной асимптоты, поскольку Ишх_>з f (ж) = 0,5.
8.15. -оо < х < -1 или 1 < х < 3; (—оо, -1) U (1,3).
Практикум 8.2
А В задачах 1-6 требуется построить вероятный график функции, которая удовлетворяет заданным условиям в точке х = 1, и проверить, является ли функция f непрерывной в этой точке.
1. f (1) = 2 и lim f (я) = 2. 2. f (1) = -2 и lim f (х) = 2.
X —>1 х—>1
3. f (1) = 2 и lim f (x) = —2. 4. f (1) = — 2 и lim f (x) = —2.
x—>1 x—>1
5. 	/ (1) = —2, lim f (x) = 2 и lim f (x) = —2.
6. f (1) = 2, lim f (x) = 2 и lim f (x) = —2.
x—*1“ x—>1+
В задачах 7-10 требуется построить вероятный график функции, которая непрерывна при всех значениях х, за исключением точки х = 1, и удовлетворяет заданным условиям в точке х = 1.
7. lim f (х) = —оо. 8. lim f (х) = оо.
х—>1 х—»1
9. lim / (х) = —оо и lim f (х) = оо. 10. lim f (х) = оо и lim f (х) = —оо.
X—>1“ х—>1+ х—>1~ х—>1 +
Используя теорему 8.3, найдите области, в которых функции в задачах 11-16 явля¬
ются непрерывными.
11. 	/(х) = Зх — 4.
13. g (х) =
Зх
х -1-2’
12. 	h{x) = 4 — 2х.
14. 	Ж-_.
х — 4
15. т (х) =
х -F 1
(х - 1) (х + 4)’
16. п (х) =
х — 2
(х - 3) (х + 1) ’
Б В задачах 17-20 рассматривается функция f, показанная на графике. Используя гра фик, вычислите пределы, указанные ниже.


54
Часть III. Математический анализ
Выполните следующие задания при произвольных значениях с.
1) Найдите lim f (х), lim f (х), lim f (x) и /(с).
x—>c— x—>c+ x—*c
* 2) Непрерывна ли функция f в точке с? Объясните свой ответ.
17. с = 1. 18. с = 2.
19. с = —2. 20. с = —1.
21. 	Дана следующая функция f:
если х целое, если х не целое.
а) Постройте график f.
б) lim f (ж) = ?.
В) Л2) = ?.
г) Непрерывна ли функция f в точке х = 2?
д) Где функция f имеет разрыв?
22. 	Дана следующая функция д:
если х четное целое;
если х не является четным целым.
а) Постройте график д.
б) lim д (я) = ?.
В) 5(1) = ?■
г) Непрерывна ли д в точке х = 1?
д) Где функция д имеет разрыв?
В задачах 23-32, воспользовавшись при необходимости знаками — оо или оо, опишите поведение функции в окрестности каждой точки разрыва и найдите все вертикальные асимптоты.
*23. f(x) = —Ц-.
J ' х + 3
х^ 4- 4
* 25. h (ж) = —-
х2 - 4
* 24. g (ж) = -
*26. k(x} =
х2 — 9 х2 4-9*
*27. F (х) =
х2 — 4 х2 + 4’
* 28. G (я) =
х2 + 9
9 — х2
*29. Н (х) =
х2 — 2х — 3 х2 — 4х + 3 ’
*30. К (х) =
х2 + 2х — 3
х2 — 4х + 3
*31. Т (ж) =
&Е-16
ж4 — &г3 + 16ж2 ’
*32. =
6х + 9 х4 + 6ж3 -I- 9ж2
В задачах 33-38 требуется решить неравенства, пользуясь знаковой диаграммой. Представьте ответ в виде неравенства и в виде интервала.
33. 	х2 — х — 12 < 0.
34. 	х2 — 2х — 8 < 0.


Глава 8. Производная
55
35. 	х2 + 21 > 10х.
36. 	х2 -I- 7х > —10.
37.
х2 -I- 5х
х — 3
>0.
38.
х — 4 х2 4- 2х
<0.
В задачах 39-44, используя графическую утилиту, приблизительно вычислите координаты точек разбиения для каждой функции f(x) с точностью до двух десятичных знаков. Затем решите следующие неравенства.
1) /(*) > 0, 2) /(х) < 0.
Запишите ответ в виде интервала.
39. /(х) = х3 — Зя2 — 2х 4- 5.
40. /(х) = х3 4- Зх2 — 4х — 8.
41. /(х) = х4 — 6х2 4- Зх + 5.
42. /(х) = х4 — 4х2 — 2х 4- 2.
43. f (х) =
3 + 6х — х3
х — 1
44. f (х) =
х3 — 5х 4-1
х 4- 1
Используя теорему 8.3, найдите области, в которых функции в задачах 45-52 непрерывны. Представьте ответы в виде интервалов.
45. v^6.
47. УЬ^х.
49. v/x2^?9.
51. у/х2 4-1.
46. у/7^х.
48. \/^8.
50. з/4-х2.
52. ^+2.
В задачах 53-58 постройте график функции f, найдите все точки разрывов и проанализируйте поведение функции f в этих точках.
*53. /(х) = j
1 4" х,
если х < 1;
,5-«:
если х 1.
*55./(х) = j
1 4- х,
если х 2;
1 5 — х,
если х > 2.
если х < 0;
*57. /(х) = <
1,
если х = 0;
если х > 0.
♦54. /(х) = J
х2,
если х 1;
2х,
если х > 1.
1
*56./(*) = j
Гх2,
если х 2;
[2х,
если х > 2.
'1,
если х < 0;
*58. /(х) = <
0,
если х = 0;
1-F х, если х > 0.
В задачах 59-62 найдите все точки разрывов функции f и проанализируйте ее поведение в этих точках, используя графическую утилиту. (Подсказка. Выберите значения Xmjn и Xmax лшк, чтобы предполагаемые точки разрыва оказались в центре интервала (Хт[п, Хтах).)
* 59. f (х) = х 4-
|2х — 4|
х — 2
* 60. f (х) = х 4-
|3х + 9|
х 4~ 3
*61. /(х) =
х2 — 1 |х| — 1 ’
♦62. /(х) =
х3 -8
|х| — 2
В
63. 	Пользуясь графиком функции g (рис. 8.21), ответьте на следующие вопросы
а) 	Непрерывна ли функция g на открытом интервале (—1,2)?


56
Часть III. Математический анализ
б) Непрерывна ли функция д справа от точки х = — 1? Выполняется ли равенство д(х) = д (-1)?
в) Непрерывна ли функция q слева от точки х = 2? Выполняется ли равенство НтЛ-5(.)Д(2)?
г) Непрерывна ли функция д на замкнутом интервале [—1,2]?
д(х) = -х2 + 2х + 2
Рис. 8.21. Иллюстрация
к задаче 63
64. 	Пользуясь графиком функции f (рис. 8.22), ответьте на следующие вопросы.
а) Непрерывна ли функция f на открытом интервале (0,3)?
б) Непрерывна ли функция f справа от точки х = 0? Иначе говоря, действительно ли lim^o-h f (х) = f (0)?
в) Непрерывна ли функция f слева от точки х = 3? Иначе говоря, действитель- но ли Пт^^з- f(x) = f (3)?
г) Непрерывна ли функция f на замкнутом интервале [0,3]?
Дх)=?-2х + 2
Рис. 8.22. Иллюстрация к задаче 64
В задачах 65-66 рассматривается функция целой части числа, которая обознача ется И и определяется следующим образом:
[ж] = наибольшее целое < х.


Глава 8. Производная
57
Например,
[—3,6] = наибольшее целое —3,6 - —4, [2] = наибольшее целое ^2 = 2,
[2,5] = наибольшее целое < 2,5 = 2.
График f(x) = [я] представлен ниже. На нем показано, что
М = -2
для
—2 х < -1,
Ы = -1
для
—1 х < 0,
Ы = о
для
0 < х < 1,
[®1 = 1
для
1 < х < 2,
И = 2
для
2 х < 3.
и т.д.
Рис. 8.23. Иллюстрация к задачам 65 и 66
65. а) Непрерывна ли функция f справа от точки х = О?
б) Непрерывна ли функция f слева от точки х = О?
в) Непрерывна ли функция f на открытом интервале (0,1)?
г) Непрерывна ли функция f на замкнутом интервале [0,1]?
д) Непрерывна ли функция f на полуоткрытом интервале [0,1)?
66. а) Непрерывна ли функция f справа от точки х = 2?
б) Непрерывна ли функция f слева от точки х = 2?
в) Непрерывна ли функция f на открытом интервале (1,2)?
г) Непрерывна ли функция f на замкнутом интервале [1,2]?
д) Непрерывна ли функция f на полуоткрытом интервале [1,2)?
В задачах 67-70 постройте вероятный график функции f, которая непрерывна для всех действительных чисел и удовлетворяет указанным условиям. Найдите точки пересечения графика f с осью х.
67. f(x) < 0 на интервалах (—сю, —5) и (2, оо); /(х) > 0 на интервале (—5,2).
68. /(ж) > 0 на интервалах (—оо, —4) и (3, оо); f(x) < 0 на интервале (—4,3).


58
Часть III. Математический анализ
69. f(x) < 0 на интервалах (—оо, —6) и (—1,4); /(х) > 0 на интервалах (—6, -1) и (4, оо).
70. /(х) > 0 на интервалах (—оо, —3) и (2,7); /(х) < 0 на интервалах (-3,2) и (7, оо).
*71. Функция /(х) = 2/(1 — х) удовлетворяет условиям /(0) = 2 и /(2) = —2. Становится ли функция f равной нулю в какой-либо точке на интервале (—1,3)? Противоречит ли это теореме 8.4? Объясните свой ответ.
*72. Функция /(х) = 6/(х - 4) удовлетворяет условиям /(2) = -3 и /(7) = 2. Становится ли функция f равной нулю в какой-либо точке на интервале (0,9)? Противоречит ли это теореме 8.4? Объясните свой ответ.
* 73. Функция f непрерывна и не равна нулю на интервале (0,4), а также непрерывна и не равна нулю на интервале (4,8). Кроме того, /(2) = 3 и /(6) = -3. Проанализируйте справедливость следующего утверждения и проиллюстрируйте сделанные выводы с помощью графиков: либо /(4) = 0, либо функция f имеет разрыв в точке х = 4.
*74. Функция f непрерывна и не равна нулю на интервале (—3,1), а также непрерывна и не равна нулю на интервале (1,4). Кроме того, /(—2) = -3 и /(3) = 4. Проанализируйте справедливость следующего утверждения и проиллюстрируйте сделанные выводы с помощью графиков: либо /(1) = 0, либо функция f имеет разрыв в точке х = 1.
Применение математики
Экономика и бизнес
75. 	Почтовый тариф. Доставка заказного письма в 2001 году стоила 0,34 долл, за первую унцию (или любую ее часть) и 0,21 долл, за каждую последующую унцию (или ее часть).
а) Запишите определение кусочно-заданной функции стоимости почтовой доставки заказного письма Р(х), весом х унций.
б) Постройте график функции Р(х) на интервале 0 < х 5.
*в) Является ли функция Р(х) непрерывной в точках х = 4,5 и х = 4? Объясните свой ответ.


Глава 8. Производная
59
76. 	Тариф на телефонную связь. Тариф на междугородные телефонные звонки составляет 0,15 долл, за первую минуту (или любую ее часть) и 0,10 долл, за каждую последующую минуту (или ее часть).
а) Запишите определение кусочно-заданной функции стоимости R(x) междугородного звонка длительностью х минут.
б) Постройте график функции R(x) на интервале 0 < х < 6.
*в) Является ли функция R(x) непрерывной в точке х = 3,5? В точке х = 3? Объясните свой ответ.
*77. Почтовый тариф. Проанализируйте разницу между функцией Q(x) = 0,34 + -I- 0,21 [я] и функцией Р(х), заданной в задаче 75.
* 78. Тариф на телефонную связь. Проанализируйте разницу между функцией S(x} = = 0,15 + 0,1 И и функцией R(x), заданной в задаче 76.
79. 	Тарифы на природный газ. В табл. 8.8 показаны тарифы на природный газ, установленные региональным коммунальным предприятием Middle Tennessee Natural Gas Utility на летний период. Потребители вносят фиксированную месячную оплату независимо от объема потребленного газа.
а) Запишите определение кусочно-заданной функции месячной платы S(я) для потребителя, расходующего х термов тепла за летний месяц.
б) Постройте график функции S(x).
в) Является ли функция S(x) непрерывной в точке х = 50? Объясните свой ответ.
Таблица 8.8. Летние тарифы (май-сентябрь)
Базовый тариф
5,00 долл.
Менее 50 термов4
Свыше 50 термов
0,63 долл, за терм
0,45 долл, за терм
80. Тарифы на природный газ. В табл. 8.9 приведены тарифы на природный газ, установленные региональным коммунальным предприятием Middle Tennessee Natural Gas Utility District на зимний период. Потребители вносят фиксированную месячную оплату независимо от объема потребленного газа.
а) Запишите определение кусочно-заданной функции месячной платы S(x) для потребителя, расходующего х термов тепла за зимний месяц.
б) Постройте график функции S(x).
в) Является ли функция S(x) непрерывной в точках х = 5 и х = 50? Объясните свой ответ.
81. Заработок. Продавец персональных компьютеров получает месячный оклад в размере 1000 долл, и 5% комиссионных от месячного объема продаж, превышающего 10 000 долл. Если месячный объем продаж превышает 20 000 долл.,
британская тепловая единица (Бте) — это количество теплоты, необходимое для повышения температуры одного фунта воды на один градус по Фаренгейту, а терм — это 100000 Бте.


60
Часть III. Математический анализ
Таблица 8.9. Зимние тарифы (октябрь-апрель)
Базовый тариф
5,00 долл.
Менее 5 термов Следующие 45 термов Свыше 50 термов
0,69 долл, за терм
0,65 долл, за терм
0,63 долл, за терм
то продавец получает премию в размере 500 долл. Пусть функция E(s) описывает заработок продавца в зависимости от месячного объема продаж s.
а) Задайте функцию E(s) на интервале 0 s 30000.
б) Найдите значения lims_>i0 ооо Е (s) и 22(10 000).
в) Найдите значения lims_>2oooo Е (s) и 22(20000).
г) Является ли функция Е непрерывной в точке s = 10 000? В точке s = 20 000?
82. Аренда оборудования. Компания сдает в аренду офисную технику на следующих условиях: принтеры за 10 долл, в день или за 50 долл, на 7 дней. Пусть С(х) — стоимость аренды принтера на х дней.
а) Постройте функцию С(х) для 0 х 10.
б) Найдите lims_>4)5 С (х) и (7(4,5).
в) Найдите lims_>s С (х) и (7(8).
г) Является ли функция С непрерывной в точках х = 4,5 и х = 8?
Биологические науки
83. Рост численности животных. В медицинской лаборатории разводят кроликов. Их численность ДГ(2) в произвольный момент времени t, зависит от количества родившихся и умерших кроликов. В момент рождения или смерти очередного кролика, функция 7V, как правило, имеет разрыв (рис. 8.24).
а) Где функция N имеет разрыв?
б) Um АГ (t) = ?; W (t5) = ?.
в) lim N (f) = (t3) = ?•
Рис. 8.24. Иллюстрация к задаче 83


Глава 8. Производная
61
Социальные науки
84. 	Обучение. Историю изучения определенным человеком материала о пределах и непрерывности можно описать при помощи графика (рис. 8.25). В момент времени t2 его познания обозначенного раздела математики находится на очень низком уровне. В момент внимательно выслушав излагаемый преподавателе материал, студент совершает качественный скачок в уровне своих знаний.
а) Где функция р имеет разрыв?
б) lim p(t) = = 2.
t—
в) limp(t) = ?; p(i2) = ?•
t—
r) lim p (t) = ?; p (t4) = ?.
8.3. 	Производная
■ Скорость изменения
■ Наклон
■ Производная
■ Существование производной
Воспользуемся концепцией предела для решения двух важных задач, показанных на рис. 8.26. При решении этих двух совершенно разных задач используется одна и та же математическая концепция, известная как производная.
Скорость изменения
Начнем с рассмотрения простого примера.


62
Часть III. Математический анализ
а) найти уравнение касательной в точке (хр У]) для заданной функции у =Дх)
сорость )ЭТОЙ точке
б) определить мгновенную скорость падающего тела
Рис. 8.26. Две основные задачи математического анализа
Пример 8.16 (Анализ дохода). Доход от продажи х пластиковых цветочных горшков (в долларах) описывается функцией
7?(т) = 20т — 0,02т2, 0 т 1000
график которой показан на рис. 8.27.
1. Как изменится доход, если вместо 100 реализовать 400 горшков?
2. Как в среднем изменится доход при таком изменении объема производства?
Рис. 8.27. График функции
R(x) — 20т — 0,02т2


Глава 8. Производная
63
Решение.
1. 	Изменение дохода описывается формулой
71(400) - Я(100) = 20 • 400 - 0,02 • 4002 - (20 • 100 - 0,02 • 1002)
= 4800 - 1800 = 3000 долл.
Таким образом, с увеличением производства со 100 горшков до 400, доход возрастет на 3000 долл.
2. 	Чтобы найти среднее изменение дохода, следует разделить величину изменения дохода на величину изменения производства.
Я (400) - Я (100) _ 3000
400- 100 “ 300
= 10 долл.
Таким образом, если производство возрастает со 100 горшков до 400, среднее изменение дохода составляет 10 долл, на горшок. ■
Упражнение 8.16.
Вернемся к функции дохода, описанной в примере 8.16.
1. Как изменится доход, если вместо 600 реализовать 800 горшков?
2. Как в среднем изменится доход при таком изменении объема производства? ■
Вообще, если дана функция у = f(x) и аргумент х меняет свое значение с величины а на а + h, то функция у меняет свое значение с величины /(а) на /(a-F/i). Средняя скорость изменения равна отношению изменения величины у к изменению переменной х.
Средняя скорость изменения функции Средняя скорость изменения функции у = f(x) на промежутке от х = а до х = а + h равна
f (а + Л.) - f (a) f(a + h)-f(a)
{a + h)-« ~ h ' <8-5)
Как отмечалось в разделе 8.1, математическое выражение (8.5) называется разностным отношением. Предыдущие рассуждения указывают на то, что разностное отношение можно интерпретировать как среднюю скорость изменения функции. В следующем примере проиллюстрирован еще один способ интерпретации этого отношения: скорость движения объекта.
Пример 8.17 (Скорость). Маленький стальной шарик, сброшенный с башни, пролетает у футов за х секунд, что приблизительно описывается формулой
у - /(х) - 16х2.


64
Часть III. Математический анализ
На рис. 8.28 показано положение шарика на оси координат (положительное направление — вниз) в конце 0, 1, 2 и 3 секунды.
64
144
◄— Положение тела на старте (х = 0 с)
ч Положение тела через х = 1 с
(у = 1612 = 16 футов)
4 Положение тела через х = 2 с
(у = 16*22 = 64 футов)
Положение тела через х = 3 с (у = 16 32= 144 футов) Уровень земли
У
Рис. 8.28. Положение падающего шарика (примечание: ось у направлена вниз)
1. Найдите среднюю скорость на промежутке от х = 2 с до х = 3 с.
2. Найдите и упростите выражение для средней скорости на промежутке от х = 2сдот = 2 + /гс, h 0.
3. Найдите предел выражения, полученного при решении п. 2 при h —> 0, если он существует.
4. Проанализируйте возможные способы интерпретации предела, полученного при решении п. 3.
Решение.
1. 	Напомним формулу d = rt, которую можно переписать в виде
d Пройденное расстояние _
г — - — = Средняя скорость.
t Затраченное время
Например, если человек добирается из Сан-Франциско в Лос-Анджелес (расстояние примерно 420 миль) за семь часов, то средняя скорость его движения будет равна
d 420 «п
г = - = = 60 миль в час.
t 7
Иногда человек будет перемещаться быстрее, иногда медленнее, но средняя скорость движения будет равна 60 миль в час. В нашей задаче средняя


Глава 8. Производная
65
скорость падения стального шарика в промежутке времени с х = 2 с по х = 3 с определяется следующим образом.
_ Пройденное расстояние
Средняя скорость = — =
Затраченное время
_ / (3) — / (2) _
3-2
16 • З2 - 16 • 22 _ х
= = 80 футов в секунду.
Таким образом, если у = f(x) — положение падающего мячика, то средняя скорость просто равна средней скорости изменения функции f(x) за время х. Таким образом, существует еще одна интерпретация разностного отношения (8.5).
2. 	Выполняя аналогичные вычисления, получим следующий результат.
Пройденное расстояние
Средняя скорость = — =
Затраченное время /(2 + /i)-/(2) = h
_ 16• (2 + /г)2 - 16 • 22 _
_ h ~
_ 64 + 64/i + 16/t2 - 64 _
= М64 + 1Щ = 64 + 16Л1
Отношение приращения
Упрощаем неопределенное выражение 0/0
h^O.
Следует отметить, что если h = 1, то средняя скорость равна 80 футам в секунду и совпадает с результатом, полученным в п. 1.
3. 	Предел выражения для средней скорости, полученного при решении п. 2 при h —► 0, равен
/ (2 + fe) — / (2)
lim h->0
= lim (64 + 16/i) =
h
= 64 фута в секунду.
4. 	Средняя скорость на постоянно уменьшающемся интервале стремится к 64 футам в секунду. Этот предел можно интерпретировать как скорость мячика в момент, когда мячик пролетел ровно 2 с. По этой причине величина 64 фута в секунду представляет собой мгновенную скорость в момент времени х = 2 с. Следовательно, мы решили одну из основных задач математического анализа (см. рис. 8.26, б). ■


66
Часть III. Математический анализ
Упражнение 8.17.
Для падающего стального мячика из примера 8.17 найдите следующие параметры.
1. Среднюю скорость на временном промежутке с х — 1 с по х = 2 с.
2. Среднюю скорость (в упрощенной форме) на временном промежутке cx = lcnox = l + hc, h^O.
3. Мгновенную скорость в момент х = 1 с. ■
Задание 8.7.
Напомним функцию дохода из примера 8.16: R(x) = 20х — 0,02z2. Вычислите предел
v R (100 + /г) — R (100) lim — т
h—>о h
Проанализируйте возможные способы интерпретации этого предела. ■
Идеи, которые были развиты в примере 8.17, не ограничиваются только средней скоростью движения. Их можно применять и к средней скорости изменения любой функции.
Мгновенная скорость изменения функции
Мгновенная скорость изменения функции у = f(x) в точке х = а равна
lim/(-+'■)-/(<■), (86)
h—>о h
если этот предел существует.
Прилагательное мгновенная часто опускают, подразумевая, что фраза скорость изменения всегда означает мгновенную скорость изменения, а не среднюю скорость. Аналогично скорость движения всегда означает мгновенную скорость изменения пройденного расстояния со временем.
Наклон
До сих пор интерпретации разностного отношения были, по сути, численными. Теперь рассмотрим геометрическую интерпретацию этой величины. Линия, проходящая через две точки на графике, называется секущей. Если (а, / (а)) и (а + Д, /(а + Ji)) — две точки на графике у = f(x), то, воспользовавшись формулой для расчета наклона из раздела 8.3, можно найти наклон секущей, проходящей через эти две точки (рис. 8.29).
Наклон секущей = +
(а + h) — а
= f(a + h)-f (а)
h
Разностное отношение


Глава 8. Производная
67
Таким образом, разностное отношение можно интерпретировать и как среднюю скорость изменения, и как наклон секущей.
Пример 8.18 (Наклон секущей). Дана функция f(x) = х2.
1. Найдите наклон секущей, если а = 1и h = 2и1 соответственно. Постройте график у = f(x) и две секущие.
2. Найдите и упростите уравнение наклона секущей для а — 1 и произвольного числа h, не равного нулю.
3. Найдите предел выражения, полученного при решении п. 2.
4. Проанализируйте возможные интерпретации предела, вычисленного при решении п. 3.
Решение.
1. 	Если а — 1 и h — 2, секущая проходит через точку (1;/(1)) = (1; 1) и (3; /(3)) — (3; 9) с наклоном
/ (1 + 2) — / (1) _ З2 — I2
2 2
Если а = 1 и h = 1, секущая проходит через точку (1; /(1)) — (1; 1) и (2; /(2)) = (2; 4) с наклоном
/(1 + 1) -/(1) _ 22 — I2 _ о
1 - " 3-
График у = f(x) и две секущие показаны на рис. 8.30.


68
Часть III. Математический анализ
2. 	Для а — 1 и произвольного числа h, не равного нулю, секущая проходит через точку (1; /(1)) = (1; 1) и (1+Д; /(l + /i)) = (l+/i; (l+/i)2) с наклоном
/(1 + Д)-/(Д) (1 +/i)2 — I2 =
h h
_ 1 + 2/t + /г2 - 1 _
h
_ h (2 + Д) _
“ h ~
= 2 + h, h^O.
3. Предел выражения для наклона секущей, полученного при решении п. 2,
равен
lim + f = Rm (2 + h) = 2.
h—>0 h h—>0
4. 	Как можно было видеть в ходе решения п. 3, предел выражения для наклона секущей, проходящей через точку (1; /(1)), равен 2. Если построить график прямой, проходящей через точку (1; /(1)), с наклоном, равным 2 (рис. 8.31), то эта линия будет предельной для секущих. Наклон, полученный из предела выражения для секущих, называется наклоном графика в точке х — 1, а линия, проходящая через точку (1;/(1)) с таким наклоном, называется касательной. Таким образом, мы решили еще одну из основных задач математического анализа (см. рис. 8.26, а). ■
Упражнение 8.18.
Задана функция /(х) = х2.
1. Вычислите наклон секущей, если а — 2 и h = 2 и 1 соответственно.
2. Выведите и упростите уравнение наклона секущей для а = 2 и произвольного числа h, не равного нулю.


Глава 8. Производная
69
Дх)=л21
ftx)
10
Секущая: наклон равен 4
Секущая: наклон равен 3
Касательная: наклон равен 2
5
—5—4—3—2—1
1 2 3 4 5
Рис. 8.31. Касательная
3. Вычислите предел выражения, полученного при решении п. 2.
4. Вычислите наклон графика и наклон касательной в точке а = 2.
Идеи, изложенные в предыдущем примере, подытожены в следующем определении.
Наклон графика
Если дано уравнение у = f(x), то наклон графика в точке (а; /(а)) равен (8.7)
при условии, что предел существует. Наклон графика также равен наклону касательной в точке (а; /(а)).
Как известно из планиметрии, касательная к окружности — это прямая, которая проходит через одну и только одну точку окружности (рис. 8.32, а). Хотя это определение нельзя обобщить на все графики функций, связь между графиками функций и их касательными аналогична (рис. 8.32, б). Предел (8.7) является одновременно и математическим определением касательной, и методом аппроксимации ее наклона.
Производная
Как показано выше, предел разностного отношения можно интерпретировать как скорость изменения функции, как скорость движения или как наклон касательной. Кроме того, этот предел позволяет решить две основные задачи, поставленные в начале главы. Теперь можно ввести новые понятия, в определении которых упоминается предел разностного отношения. Следуя традициям, будем использовать букву х вместо буквы а и рассматривать разностное отношение
/ (ж + Д) - / (ж)
h


70
Часть III. Математический анализ
Рис. 8.32. Касательные
как функцию, зависящую от аргумента h при фиксированном значении х, когда приращение h стремится к нулю.
Производная
Производной функции f(x) в точке х называется величина
Г' ( \ Г f{x + ti) - /(х)
/ (х) = lim — f > если этот предел существует.
h—>0 h
Если величина f(x) существует для всех значений х на открытом интервале (а, Ь), то функцию f называют дифференцируемой на (а, Ь).
(В определении дифференцируемости слева или справа вместо /г —► 0 в определении, данном выше, используют выражения h 0“ или h —> 0+ соответственно.) Процесс определения производной от функции называется дифференцированием, т.е. производную от функции получают путем ее дифференцирования.
Интерпретация производной
Производная функции f — это новая функция Областью определения функции /' является подмножество области определения функции /. Производная имеет множество применений и интерпретаций. Ниже перечислены некоторые из них.
1. 	Наклон касательной. Для любого аргумента х из области определения функции /' величина ff(x) представляет собой наклон касательной к графику f в точке


Глава 8. Производная
71
2. Мгновенная скорость изменения. Для любого аргумента х из области определения функции /' значение f(x) является мгновенной скоростью изменения функции у = f(x), зависящей от переменной х.
3. Скорость движения. Если функция /(я) задает положение движущегося объекта в момент времени х, то v = ff(x) — скорость объекта в этот момент времени.
В примере 8.19 проиллюстрирован двухэтапный процесс определения производных, который будет использоваться в разделе повсеместно. В последующем мы сформулируем правила определения производных, не требующие вычисления пределов. Однако, чтобы полностью разобраться в понятии производной и способах ее применения, сначала необходимо освоить процедуру ее непосредственного вычисления.
Пример 8.19 (Вычисление производной). Вычислите производную функции f(x) = 4х — х2.
Решение.
Этап 1. Построим разностное отношение.
f (х + h) - f (ж) _ [4 (x + ti) — (х + П)2] - (4х - X2) _
h ~ h
4х + 4/г — х2 — 2xh — h2 — 4х + х2 ~ h =
4h — 2xh -h2
~ h ~
Ji (4 — 2х — h)
= h =
— 4 — 2x — h, h / 0.
Этап 2. Найдем предел разностного отношения.
/' (®) = Ии
п,—>U
/ (х + h) - / (х) h
= lim (4 — 2х — h) = 4 — 2х.
Таким образом, если /(ж) = 4х — х2, то /'(ж) = 4 — 2х. Производная /' — это новая функция, полученная из функции /. ■
Упражнение 8.19.
Вычислите производную функции /(ж) = 8х — 2х2.


72
Часть III. Математический анализ
Пример 8.20 (Вычисление наклона касательной), www В примере 8.19 рассматривалась функция /(т) = 4х — х2. Производная этой функции равна /'(*) = = 4 — 2х. Таким образом, наклон касательной к графику f в любой точке (*;/(*)) равен
т — f'(x) — 4 — 2х.
1. Найдите наклон графика f в точках х = 0, х - 2 и х - 3.
2. Постройте график у = f(x) = 4х — х2 и, используя значения наклона, вычисленные при решении п. 1, начертите касательные к графику в точках х = 0, х = 2 и х = 3.
Решение.
1. 	Пользуясь выражением = 4 — 2х, находим
/'(0) = 4 - 2 • 0 = 4,
/'(2) = 4-22 = 0,
/'(3) = 4 - 2 • 3 = -2.
Наклон в точке а? = О
Наклон в точке х = 2
Наклон в точке х = 3
Упражнение 8.20.
В упражнении 8.19 рассматривалась функция /(х) = 8х — 2х2. Используя производную, выполните следующие задания.
1. Найдите наклон графика f в точках х = 1, х = 2 и х = 4.
2. Постройте график функции у = f(x) = 8х — 2х2 и, используя значения
наклона, найденные при решении п. 1, начертите касательные к графику в точках х = 1, х = 2их = 4. ■
Задание 8.8.
В примере 8.19 было показано, что производная от функции f(x) = 4х - х2 равна /'(х) = 4 — 2х, а в примере 8.20 был построен график функции f(x) и несколько касательных.


Глава 8. Производная
73
1. Постройте графики f и /' в одной и той же системе координат.
2. График функции /' — прямая линия. Является ли он касательной к графику /? Объясните свой ответ.
3. Найдите точки, в которых график /' пересекается с осью х. Чему равен
наклон касательной к графику f для этих значений х? Опишите связь между наклоном касательной функции и точками пересечения производной с осью х. ■
Примечание: вычисление производных в графических утилитах
Вернемся к значениям f(x), вычисленным в примере 8.20, а. В некоторых графических утилитах, например, в большинстве графических калькуляторов, есть встроенная процедура численного дифференцирования, вычисляющая приближенные значения /'(*) для любого заданного значения х. На рис. 8.33, а показано численное дифференцирование с помощью графического калькулятора TI-83. В других утилитах, чтобы найти алгебраические формулы для производных и впоследствии вычислить значения этих формул для указанных значений х, используется символьное дифференцирование. На рис 8.33, б продемонстрировано символьное дифференцирование с помощью пакета программ Maple V.
nDeriuCVi>Х>0)
4 nDeriv(Yi
0 nDeriu<Yi
-2
• f:=4*x-xA2;d:=diff(f,x);
2 f := 4х - х d := 4x - 2
• x:=0;d;x:=2;d;x:=3;d;
x := 0
4
x := 2
0
x := 3
-2
а) численное дифференцирование: yl=4x-xA2
б) символьное дифференцирование: f:=4*х-хЛ2
Рис. 8.33. Численное и символьное дифференцирование
Дифференцирование — это основа математического анализа, поэтому очень важно научиться самостоятельно выполнять эту операцию, не используя технические средства. Однако для проверки проделанной работы можно воспользоваться численным дифференцированием с помощью графической утилиты.
Пример 8.21 (Вычисление производной). Вычислите производную функции f (х) = у/х + 2.
Решение. Используя двухэтапный процесс, найдем следующий предел.
|im/(x + /.)-/W
h—о h


74
Часть III. Математический анализ
Этап 1. Построим разностное отношение.
f(x + h)-f(x) _ (Vx + h + 2) “ (\А + 2) _ h ~ h ~
_ у/х + h - у/х
~ h *
Поскольку это отношение представляет собой неопределенность вида 0/0, его нужно преобразовать, приведя числитель к рациональному виду.
у/х + h — yfx h
у/х + h + у/х х + h — х
\/х + h + у/х fa ^у/х + h + у/х^
h
х h +
1
у/х -И h + у/х"
h 0.
h
Этап 2. Найдем предел разностного отношения.
Таким образом, производная от функции f (ж) = у/х + 2 равна /' (х) = = 1/(2у/х). Область определения функции f представляет собой луч [0, оо). Поскольку значение /'(О) не определено, областью определения функции /' является луч (0, оо) — подмножество области определения функции /. ■
Упражнение 8.21.
Вычислите производную функции f (ж) — у/х + 4. ■
Пример 8.22 (Анализ продаж). Суммарный объем продаж компании (млн. долл.) через t месяцев определяется выражением S (t) = y/t + 2. Найдите значения 5(25) и S'(25) и дайте их интерпретацию. Используя этот результат, найдите суммарный объем продаж через 26 и 27 месяцев.


Глава 8. Производная
75
Сравните результат со значениями 5(25) и S'(25), вычисленными с помощью графической утилиты.
Решение. Функция суммарного объема продаж S имеет такой же вид, как и функция f в примере 8.21, — изменены только буквы, обозначающие функцию и независимую переменную. Следовательно, производные 5" и /' также имеют одинаковый вид.
S (t) — \/t + 2;
f (£) — у/х + 2;
Вычислив функции S и S' в точке t = 25, получим следующие значения.
5(25) = ^25 + 2 = 7;
S'(25) = 2^=0-L
На рис. 8.34 показаны результаты проверки полученных результатов со значениями, вычисленными с помощью графической утилиты. Таким образом, через 25 месяцев суммарный объем продаж составит 7 млн. долл, и будет расти со скоростью 0,1 млн. долл. (100000 долл.) в месяц. Если бы эта мгновенная скорость изменения продаж оставалась постоянной, продажи возросли бы на 7,1 млн. долл, через 26 месяцев, на 7,2 млн. долл, через 27 месяцев и т.д. Хотя функция 5' не является постоянной, эти значения позволяют достаточно точно определить будущие суммарные объемы суммарных продаж. ■
25^
25
7 nDeriv(Yi,X,25> .1000000001
Рис. 8.34. Функция
yi = >/х + 2
Упражнение 8.22.
Объем суммарных продаж компании (млн. долл.) через t месяцев определяется выражением S (f) — \/t + 4. Найдите значения 5(12) и 5'( 12) и дайте их интерпретацию. Используя полученный результат, найдите суммарный объем продаж через 13 и 14 месяцев. (Воспользуйтесь производной, найденной в упражнении 8.21.)


76
Часть III. Математический анализ
Сравните результат со значениями 5(12) и S'(12), вычисленными с помощью графической утилиты. ■
Вернемся к примеру 8.22. Было бы полезно сравнить оценки суммарного объема продаж, полученные с использованием производной, с соответствующими точными значениями функции 5(t).
Точные значения Вычисленные значения
5(26) = ^26 + 2 = 7,099...» 7,1;
5(27) = + 2 = 7,196...» 7,2
Для этой функции вычисленные значения очень неплохо согласуются с точными значениями функции S(t). Для других функций результат числовых вычислений может оказаться не настолько точным.
Использование значения скорости изменения функции в точке для оценки значения функции в окрестности точки — это простой, но важный способ применения производной.
Существование производной
Существование производной в
в точке х = а.
'(а) =
Если предел в точке х = а не существует, говорят, что функция f является недифференцируемой в точке х = а, или значение /,(ж) не существует.
Задание 8.9.
Пусть /(х) = |х — 1|.
1. Постройте график функции /.
2. Заполните следующую таблицу.
точке х = а зависит от существования предела f (a + h) - f (а)
lim 7 k . (8.8)
h
-0,1 -0,01
-0,001 ->0<- 0,001 0,01
0,1
/(l + h)-/(l) h
? ?
? —►? <— ? ?
?
3. Вычислите предел 1ш1^_>о если он существует.
4. Используя результаты, полученные при решении пп. 1-3, определите, существует ли значение /'(1).
Повторите решение пп. 1-4 для функции д (х) = tyx — 1. ■


Глава 8. Производная
77
Как найти на графике функции f точки, в которых значения f'(a) не существуют? В принципе, невозможно описать все случаи, в которых предел в формуле (8.7) не существует. Однако можно перечислить несколько наиболее общих ситуаций, в которых производная f(a) не существует (рис. 8.35).
а) разрыв в точке х = а
Лх)
Л*)
в) вертикальная касательная в точке х = а
/W
г) вертикальная касательная в точке х = а
Рис. 8.35. Недифференцируемая в точке х = а функция f
1. Если на графике точка х = а представляет собой “выколотую” точку или разрыв, то значение /'(а) не существует (рис. 8.35, а).
2. Если на графике функции f точка х = а является точкой излома, то значение f'(a) не существует, и у графика нет касательной в точке х = а (рис. 8.35, б). (На рис. 8.35, б левосторонняя и правосторонняя производные существуют, но они не равны между собой.)
3. Если график f в точке х = а имеет вертикальную касательную, то значение f'(а) не существует (рис. 8.35, в и г).
Ответы к упражнениям
8.16. 1) -1600 долл.
2) 	-8 долл, на горшок.
8.17. 1) 48 футов в секунду.
2) 32 + 16Л.
3) 32 фута в секунду.
8.18. 1) 6,5.
2) 4 + h.
3) 4.
4) Оба равны 4.
8.19. /'(т) = 8 - 4х.
8.20. 1) /'(1) = 4; f (2) = 0; /'(4) = -8.


78
Часть III. Математический анализ
8.21. f'(x) = l/(2v<rT4).
8.22. S(12) = 4; S"(12) = 0,125; через 12 месяцев суммарный объем продаж составит 4 млн. долл, и будет расти со скоростью 0,125 млн. долл. (125 000 долл.) в месяц. Суммарный объем продаж составит приблизительно 4,125 млн. долл, через 13 месяцев и 4,25 млн. долл, через 14 месяцев.
Практикум 8.3
А В задачах 1 и 2 требуется вычислить указанные величины для функции у = /(х) = = 5 — х2 и дать им интерпретацию, используя график, показанный ниже.
а) 	/(2) -/(1)
.> JmMa.
h^Q h
/(—!) — /(—2) } -1 - (-2) ’ в) lim/(-2 + frW(-2).
h->0 h
h
/ (—2 + fe) — / (—2)
3. 	Вычислите указанные величины для функции /(х) = Зх2.
а) 	Средняя скорость изменения функции /(х), если значение х изменяется с 1 на 4.


Глава 8. Производная
79
б)
в)
г) Д) е)
Наклон секущей, проходящей через точки (1;/(1)) и (4;/(4)) на графике у = А*)-
Наклон секущей, проходящей через точки (1; /(1)) и (1Ч- /(1 + fo)), h ф 0. Упростите полученный ответ.
Наклон графика в точке (1; / (1)).
Мгновенная скорость изменения функции /(ж) в точке х = 1.
Наклон касательной в точке (1; /(1)).
ж) Уравнение касательной в точке (1; /(1)).
4. Вычислите указанные величины для функции f(x) = Зж2.
а)
б)
в)
г) Д) е)
Средняя скорость изменения функции /(я), если значение х изменяется с 2 на 5.
Наклон секущей, проходящей через точки (2;/(2)) и (5;/(5)) на графике У = Д®).
Наклон секущей, проходящей через точки (2; /(2)) и (2 -I- Ai; /(2 -I- /i)), h 0. Упростите полученный ответ.
Наклон графика в точке (2; /(2)).
Мгновенная скорость изменения функции /(х) в точке х = 2.
Наклон касательной в точке (2; /(2)).
ж) Уравнение касательной в точке (2; /(2)).
В задачах 5-12, используя двухэтапный процесс, вычислите функцию f'(x) и значения /'(1), Г(2)и/'(3).
5. Дт) = 4.
7. Дт) = 2т — 3.
9. /(х) = 2 — х2.
11. f (i) = 3 +
X
Б Задачи 13 и 14 касаются графика функции у = f(x) = х2 +х, показанного на рисунке.
6.
8.
10.
12.
/(*) = -з. f(x) = 4х + 3.
/(ж) = 2х2 + 5.
/(*) = |.


80
Часть III. Математический анализ
13. а) Вычислите наклон секущей, соединяющей точки (1; /(1)) и (3; /(3)).
б) Вычислите наклон секущей, соединяющей точки (1; f (1)) и (1 + h\ f (1 + h)).
в) Вычислите наклон касательной в точке (1; / (1)).
г) Вычислите уравнение касательной в точке (1; / (1)).
14. а) Вычислите наклон секущей, соединяющей точки (2; /(2)) и (4; /(4)).
б) Вычислите наклон секущей, соединяющей точки (2; /(2)) и (2 + Л; /(2 + h)).
в) Вычислите наклон касательной в точке (2; /(2)).
г) Вычислите уравнение касательной в точке (2; /(2)).
В задачах 15 и 16 предполагается, что объект движется вдоль оси у таким образом, что его положение в момент времени х определяется выражением у — f(x) = х2 +х (значения у измеряются в метрах, а х — в секундах). Вычислите следующие величины.
15. а) Средняя скорость движения (средняя скорость изменения величины т/, зави¬
сящей от аргумента ж), когда переменная х меняет свое значение с 1 на 3.
б) Средняя скорость движения, когда аргумент х меняет свое значение с 1 на
1 “F h.
в) Мгновенная скорость в точке х = 1.
16. а) Средняя скорость движения (средняя скорость изменения величины у, зави¬
сящей от аргумента х), когда х меняет свое значение с 2 на 4.
б) Средняя скорость движения, когда аргумент х меняет свое значение с 2 на
2 -h h.
в) Мгновенная скорость в точке х = 2.
В задачах 17-22 вычислите функцию f'(x), используя двухэтапный процесс, требующий вычисления пределов. Определите значения /'(1), /'(2) w /'(3).
17. /(ж) = Ьх - 2х2. 18. /(х) = Зх - 4х2.
19. f (z) = 4 - 2y/i. 20. f (z) = 6^ - 7.
21- f = ttv 22- f =
x + 3 z — x
В задачах 23-30рассматривается функция F, показанная ниже на графике. Используя график, определите, существует ли функция Ff(x) в каждой из указанных точек х.
23. х = а.
25. х = с.
24. х = Ь.
26. х = d.


Глава 8. Производная
81
27. х = е.
29. х = д.
28. х = f.
30. х = h.
31. Дана функция /(х) = х2 — 4х.
а) Вычислите функцию /'(*)•
б) Вычислите наклон касательных к графику функции f в точках х = 0, 2 и 4.
в) Постройте график f и начертите касательные в точках х = 0, 2 и 4.
32. Дана функция f(x) = х2 + 2х.
а) Вычислите /'(х).
б) Вычислите наклон касательных к графику функции f в точках х — — 2, — 1
и 1.
в) 	Постройте график f и начертите касательные в точках х = — 2, — 1 и 1.
33. Предположим, что объект движется вдоль прямой так, что в момент времени х он находится в точке у = f(x) = 4х2 — 2х. Вычислите функцию мгновенной скорости v = /'(х), а также скорость движения в моменты времени х = 1, 3 и 5 с (величина у измеряется в футах).
34. Повторите решение задачи 33, если /(х) = 8х2 — 4х.
В задачах 35-38, воспользовавшись опциями изменения масштаба и отслеживания в графической утилите, вычислите координаты точек на графике у = f(x) вблизи (0, /(0)). Затем, используя наклон секущей, вычислите приближенное значение /'(0) с точностью до двух десятичных знаков. (Если в используемой графической утилите предусмотрена процедура численного дифференцирования, сравните полученные результаты.)
35. 	/(х) = 2х.
37. 	f (я) = л/2 + 2х - х2.
36. 	f(x) = 3*.
38. 	f (х) = у/3 — 2х — х2.
39. Пусть f(x) = х2, g(x) = х2 - 3 и /г(х) = х2 + 1.
*а) Как связаны между собой графики этих функций? Как предположительно будут связаны между собой производные от этих функций?
б) Используя двухэтапный процесс, вычислите производную от функции т(х) = = х2 + С, где С — произвольная действительная постоянная.
40. Пусть /(х) = 2х, g(x) = 2х — 1 и Zi(x) = 2х + 2.
*а) Как связаны между собой графики этих функций? Как предположительно будут связаны между собой производные этих функций?
б) Используя двухэтапный процесс, вычислите производную отт(х) = 2x4-С, где С — произвольная действительная постоянная.
41. *а) Дайте геометрическое толкование следующему утверждению: если /(х) =
= С — постоянная функция, то /'(х) = 0.
б) Используя двухэтапный процесс, проверьте утверждение п. 1.
42. *а) Дайте геометрическое толкование следующему утверждению: если /(х) =
= тх + b — линейная функция, то /'(х) = т.
б) Проверьте утверждение п. 1, используя двухэтапный процесс.


82
Часть III. Математический анализ
В
В задачах 43-46 постройте график функции f и определите точки, в которых она
является недифференцируемой.
43. /(х) =
если х < 1, если х 1.
{Г1'
если х < О, если х О.
44. f (х) =
46. /(х) =
|2х,
(6-я, р-Х2
I2’
если х <2, если х 2.
если х < О, если х > О.
В задачах 47-52, рассматривая предел, требуется определить, является ли функция f дифференцируемой в точке х = О.
lim h—о
/(Q + fc)-/(Q) h
47. f(x) = |х|. 48. f(x) = 1 - |ж|.
49. /(ж) = ж1/3. 50. /(ж) = х2/3.
51. f (х) = \/1 — х2. 52. f (ж) = \/1 + х2.
53. 	Мяч, брошенный с воздушного шара, пролетает у = 16ж2 футов за х секунд. Когда мяч ударится об землю, если в момент, когда он был брошен, воздушный шар находился на высоте 576 футов? Какова будет скорость мяча в момент удара об землю?
54. 	Повторите решение задачи 53, если в момент броска воздушный шар находился на высоте 1024 фута.
Применение математики
Экономика и бизнес
55. Доход. Доход от продажи х автомобильных кресел для младенцев (долл.) определяется формулой
R(x) = 60z — 0,025z2;
0 х 2400.
а) Вычислите среднее изменение дохода, если размеры производства изменятся с 1000 автомобильных кресел до 1050.
б) Вычислите функцию R!(ж), используя двухэтапный процесс.
*в) Вычислите величину дохода и мгновенную скорость изменения дохода при производстве 1000 автомобильных кресел и дайте интерпретацию этих результатов.
56. Прибыль. Прибыль от продажи х автомобильных кресел для младенцев (долл.) определяется формулой
Р(х) = 45х - 0,025л?2 - 5000;
0 < х < 2400.


Глава 8. Производная
83
а) Вычислите среднее изменение величины прибыли, если размеры производства изменятся с 800 автомобильных кресел до 850.
б) Вычислите функцию Р'(х), используя двухэтапный процесс.
*в) Вычислите величину прибыли и мгновенную скорость изменения прибыли при уровне производства 800 автомобильных кресел и дайте интерпретацию этих результатов.
57. Анализ продаж. Суммарный объем продаж компании (млн. долл.) через t месяцев задан формулой
S (t) = 2^ГР10.
а) Вычислите функцию 5'(t), используя двухэтапный процесс.
*б) Вычислите значения 5(15) и S'(15). Дайте интерпретацию этих результатов. *в) Используя результаты, полученные при решении п. б, вычислите общий объем продаж через 16 и 17 месяцев.
58. Анализ продаж. Суммарный объем продаж компании (млн. долл.) через t месяцев задан формулой
5 (t) = 2>/t 4- 6.
а) Вычислите функцию 5'(t), используя двухэтапный процесс.
*б) Вычислите значения 5(10) и 5'(10). Дайте интерпретацию этих результатов. *в) Используя результаты, полученные при решении п. б, вычислите общий объем продаж через 11 и 12 месяцев.
59. WWW Добыча полезных ископаемых. Объем производства цинка в США (тыс. тонн) описывается формулой
p(t) = 14Z2 - 6,6t + 602,4;
где t — время в годах и t = 0 соответствует 1995 году.
а) Вычислите функцию p'(t), используя двухэтапный процесс.
*б) Вычислите объем производства в 2010 году, мгновенную скорость изменения объема производства в 2010 году и дайте интерпретацию этих результатов.
60. WWW Потребление полезных ископаемых. Потребление меди в США (тыс. тонн) описывается формулой
p(t) = 27t2 - 75t + 6015,
где t — время в годах и t = 0 соответствует 1990 году.
а) Вычислите функцию р'(£), используя двухэтапный процесс.
*б) Вычислите размер годового потребления меди в 2010 году, мгновенную скорость потребления меди в 2010 году и дайте интерпретацию этих результатов.
61. Потребление электроэнергии. В таблице 8.10 приведены объемы потребления электроэнергии (млрд. кВт) коммунальным и коммерческим секторами Соединенных Штатов Америки за 1990 год.
а) Пусть переменная х описывает время (в годах), где х = 0 соответствует 1990 году, а функция у описывает соответствующие продажи в жилом секторе. Постройте уравнение квадратичной регрессии, введя эти данные в графическую утилиту.


84
Часть III. Математический анализ
WWW Таблица 8.10. Объемы потребления электроэнергии (млрд. кВт)
Год
Коммунальный сектор
Коммерческий сектор
1990
924
751
1991
955
766
1992
936
761
1993
995
795
1994
1008
820
1995
1043
863
1996
1082
887
1997
1075
928
1998
1128
969
1999
1146
983
*б) Вычислите значения Р(20) и 7?'(20), а затем дайте интерпретацию этих результатов, если у = R(x) — регрессионное уравнение, построенное при решении п. а. Округлите результат до десятой доли миллиарда.
62. WWW Потребление электроэнергии. Воспользуйтесь данными из табл. 8.10.
а) Пусть переменная х описывает время (в годах), где х = 0 соответствует 1990 году, а функция у — объем потребления электроэнергии коммерческим сектором. Постройте уравнение квадратичной регрессии, введя эти данные в графическую утилиту.
*б) Вычислите значения С(20) и С'(20), а затем интерпретируйте полученные результаты, если у = С(х) — регрессионное уравнение, найденное при решении п. а. Округлите результат до десятой доли миллиарда.
Биологические науки
63. Загрязнение воздуха. Концентрация озона (частей на млрд.) в воздухе метрополитена в летний период определяется уравнением
P(t) = 80+12t —i2,
где t — время в часах, a t = 0 соответствует 9 часам утра.
а) Вычислите функцию используя двухэтапный процесс.
*б) Вычислите значения Р(3) и Р'(3). Дайте интерпретацию полученных результатов.
64. Медицина. Температура тела пациента (в градусах по Фаренгейту) через t часов после принятия жаропонижающего препарата равна
F(()=98+f±i.
а) Вычислите функцию F'(t), используя двухэтапный процесс.
*б) Вычислите значения Р(3) и F' (3). Интерпретируйте полученные результаты.


Глава 8. Производная
85
Социальные науки
65. Детская смертность. Количество детских смертей на 100000 рожденных мальчиков в Соединенных Штатах Америки составляет приблизительно
/(t) = 0,011t2 -i + 29,8,
где t — время в годах и t = 0 соответствует 1960 году.
а) Вычислите функцию /'(£), используя двухэтапный процесс.
*б) Вычислите количество умерших мальчиков в 2000 году, мгновенную скорость изменения количества умерших мальчиков в 2000 году и интерпретируйте полученные результаты.
66. Детская смертность. Количество детских смертей на 100 000 рожденных девочек в Соединенных Штатах Америки составляет приблизительно
/(t) = 0,008t2 - 0,74t + 23,
где t — время в годах и t = 0 соответствует 1960 году.
а) Вычислите функцию /'(£), используя двухэтапный процесс.
*б) Вычислите количество умерших девочек в 2000 году, мгновенную скорость изменения количества умерших девочек в 2000 году и интерпретируйте полученные результаты.
8.4. 	Производные постоянных, степенных функций и сумм
■ Производная постоянной функции
■ Правило дифференцирования степенных функций
■ Производная функции, умноженной на константу
■ Производная суммы и разности
■ Решение практических задач
В предыдущем разделе было показано, что производная функции /, зависящей от переменной х, равна f (х) = lim
h—>о
f(x + h)-f (ж)
h
если предел существует. Для вычисления производных использовались это определение и двухэтапный процесс. В этом и следующих разделах будут обозначены правила, позволяющие находить производные от многих функций, не прибегая к вычислению предела.
Введем несколько важных обозначений.


86
Часть III. Математический анализ
Обозначение производной
Производная функции у = /(х) может обозначаться следующим образом:
Каждая из обозначенных выше форм записи лучше всего подходит для обозначения производной только в отдельных ситуациях. Набравшись немного опыта, вы научитесь с легкостью их различать.
Производная постоянной функции
Предположим, что
f (ж) = С, Постоянная функция
где С — константа.
Геометрически график функции /(т) = С — это горизонтальная прямая с углом наклона, равным 0 (рис. 8.36). Следовательно, можно ожидать, что f'(x) — 0. Покажем, что это действительно так, используя определение производной и двухэтапный процесс, описанный ранее.
Определение /'(®)
Наклон = О
Лх) = С
С
0
х
Этап 2. lim 0 = 0.
Рис. 8.36. График постоянной функции
Таким образом,
f'W = 0.
Можно сделать следующий вывод.


Глава 8. Производная
87
Правило дифференцирования постоянной функции
Если у — f(x) = С, то /'(ж) = 0.
Кроме того у’ = 0 и dy/dx = 0.
(Примечание. Запись С' = 0 или -^-С = 0 означает, что у1 — = 0, где у = С.)
dx dx
Пример 8.23 (Дифференцирование постоянной функции).
1. Если f(x) = 3, то /'(а?) = 0.
2.
Если у = —1,4, то у' = 0.
dy
3. Если у — 7г, то — = 0.
dx
4.
d „„ —23 = 0. ах
■
Упражнение 8.23.
Вычислите следующие производные.
1. /'(х) для /(х) = —24;
2.
у' для у = 12;
- dy /=
3. — для у = -V7;
4.
d ( \
■
Правило дифференцирования степенных функций
Функция вида f(x) = xk, где к — действительное число, называется степенной. Ниже перечислены наиболее распространенные степенные функции.
/(х) = х; h(x) = х2; m(x) = х3;
п (х) — \/х, р (х) — \/х.
Задание 8.10.
1. Ясно, что функции /, h и т в формулах (8.9) — это степенные функции. Объясните, почему функции пир также являются степенными функциями.
2. Область определения степенной функции зависит от показателя степени. Найдите область определения каждой из следующих функций.
г(а?) = х4; s(x) = ж-4; t(x) = я1/4;
и(х) = х"1/4; v(x) = х^\ w(x) = х~^\ н
Для вычисления производных от многих степенных функций можно использовать определение производной и двухэтапный процесс, описанный в предыдущем разделе.
Если
/(х)= х2,
то
/'(*) =
= 2х.
Если
/(х)= х3,
то
/'(я) =
= Зх2
Если
/(х)= X4,
то
/'О) =
= 4х3
Если
/(х)= х5,
то
/'(*) =
= 5х4


88
Часть III. Математический анализ
Отметим закономерность, присущую этим вычислениям. В каждом случае показатель степени функции f становится коэффициентом функции а показатель степени /' уменьшается на единицу. Вообще, для любого положительного целого п справедливо следующее правило.
Если f(x) = хп, то /Х(х) —пхп~х. (8.10)
Чтобы доказать формулу (8.10) для любого действительного числа п, можно воспользоваться более строгими методами.
Правило дифференцирования степенных функций
Если у — f(x) = хп, где п — действительное число, то
/'(х) = nxn_1.
Кроме того, у' = пхп~х и dy/dx = пхп~\
Задание 8.11.
1. Опишите устно правило дифференцирования степенной функции.
2. Если f(x) = х9 чему равно /'(х)? Покажите, как эту производную можно
получить из правила дифференцирования степенной функции. В
Пример 8.24 (Дифференцирование степенных функций).
1. Если /(х) = х5, то /'(х) = 5х5-1 = 5х4.
2. Если у = х25, то у' = 25х25-1 = 25х24.
3. Если у — х_3, то = —Зх-3-1 = —Зх-4 = — Д,.
4. _lz5/3 = Ёх(5/3)-1 = Ёх2/3.
dx 3 3
Упражнение 8.24.
Вычислите следующие производные.
1. 	/'(ж) для /(ж) = X6.
- dy -2
3. 	— для у = х L.
dx
В некоторых случаях, прежде чем применять правило степеней, необходимо использовать свойства показателей, чтобы переписать выражение.
2. yf для у = х30.
4. -jU/2.
dx


Глава 8. Производная
89
Пример 8.25 (Дифференцирование степенных функций).
1. Выражение /(х) = 1/х4 можно переписать в виде /(х) = ж-4. Следовательно,
f (х) = — 4ж-4-1 = — 4z-5, или —
X
2. Выражение у = у/х можно переписать в виде у = ж1/2. Следовательно,
= 1 -1/2
2 2 ’
или
1
2у/х'
или
-1
3^'
Упражнение 8.25.
Вычислите следующие производные.
1. 	/'(ж) для / (т) = -. 2. у' для у -
X
dx у/х
Производная функции, умноженной на константу
Пусть /(т) = ки(х), где к — константа, а и — функция, дифференцируемая в точке х. Тогда, используя двухэтапный процесс, получаем следующее.
! f (x + h) - f (ж) _ ки (х + Д) - ки (ж)
и(х + h) — и (ж)
- к
h
h
h
Этап 2.
Нт / (х + /1) - / (ж)
и{х + h) —и(х) _
= к lim h->0
= ки’ (ж).
h
'и(х + ti) — и (ж)
lim kg (я?) = к lim g (ас)
X —*с х—+с
Определение и' (аз)
h
= lim к h—>0
h
Таким образом, справедливо следующее правило.
Производная дифференцируемой функции, умноженной на константу, равна производной этой функции, умноженной на константу.
Правило дифференцирования константы, умноженной на функцию Если у = f(x) = ku(x), то
/'(ж) = fcu'(x).
, dy _ du
Кроме того, у — ки и — = к—.
ах ах


90
Часть III. Математический анализ
Пример 8.26 (Дифференцирование функции, умноженной на константу).
1. Если /(ж) — Зх2, то f (х); = 3 • 2х2-1 i = 6х.
л „ х3 1 о dy\ 1 „ о, : 1 9
2. Если у = — — —Xй, то —; = - • 3xd 1 ; = -х.
*66 ' 2
4. Л
0,4
d
0,4
= —0,4x_3/2i = 0,4
(—3/2)—1
dx
Vx^
dx
T3/2
dx ;
2
= —0,6х 5/2, или
Упражнение 8.26.
Вычислите следующие производные.
1. /'(x) для /(x) = 4x5.
dy t4
i ' 1
3' У ДЛЯу= 3^3’
d 0,9 dx yfx
Производная суммы и разности
Пусть /(х) = и(х) + г>(х), если и'(х) и г/(х) существуют. Тогда, используя двухэтапный процесс, получим следующие результаты.
Этап J f(x + h)-f (х) _ [u (х + ft) + v (х + ft)] - [it (х) + v (х)] _
ft ft
и (х + ft) + V (х + ft) — и (х) — V (х)
Этап 2.
h->0 ft
= lim
h—>0
lim [<j (x) + ft (x)] = lim g (x) + lim ft (x)
x—>C x—>C x—>C
u(x + h)—u(x} v(x + h) — v(x)
lim — 7 — + lim — —
-►0 ft h->0
— u'lx) + v'(x).
Таким образом, справедливо следующее правило.
Производная суммы двух дифференцируемых функций равна сумме их производных.
Аналогично можно показать следующий факт.


Глава 8. Производная
91
Производная разности двух дифференцируемых функций равна разности их производных.
Объединив эти утверждения, получим правило дифференцирования суммы и разности.
Правило дифференцирования суммы и разности
Если у — f(x) = и{х) ± v(z), то
/'(ж) = и'(ж) ± v'(x).
Кроме того,
у' = и' ± V1-,
(Примечание. Это правило обобщается на сумму и разность произвольного количества функций.)
Используя правила, установленные ранее, можно вычислить производные от всех полиномиальных и множества других функций.
Пример 8.27 (Дифференцирование сумм и разностей).
1.
Если /(ж) = Зх2 -I- 2х, то
2.
Если у = 4 + 2ж3 — Зх \ то
3.
4.
dy _ d dx dx
5-^Зх
= Аж-2/3_3 =
dx
3
d 5
d 2 d х3 : dxx4 dx 9 ;
dx Зх2
^--3.
Зх2/3
Упражнение 8.27.
Вычислите следующие производные.


92
Часть III. Математический анализ
1. /'(х) для /(х) = Зх4 — 2х3 + х2 — 5х + 7.
2. у' для у = 3 — 7х-2.
3. для у = 5х3 — yfx.
dx
d (_3_ £ _ хЛ
dx \ 4х х3 8 ) И
Решение практических задач
Пример 8.28 (Мгновенная скорость движения). Объект движется вдоль оси у (шкала в футах) таким образом, что его положение в момент времени х (шкала в секундах) задается формулой
/(х) = х3 — 6х2 + 9х.
1. Вычислите функцию мгновенной скорости движения v.
2. Вычислите скорость в моменты времени х = 2сих = 5с.
3. Найдите момент(ы) времени, в который(ые) скорость движения равна 0 футов в секунду.
Решение.
1. v — f (х); — (х3)' — (6x2)z + (9x)z; — Зх2 — 12х + 9.
2. /'(2) = 3 • 22 — 12 • 2 + 9 = —3 фута в секунду, /'(5) = 3 • 52 — 12 • 5 + 9 — 24 фута в секунду.
3. v = /'(х) = Зх2 — 12х + 9 = 0,
3(х2 - 4х + 3) = 0,
3(х — 1)(х — 3) = 0,
х = 1; 3.
Таким образом, v = 0 футов/с в моменты х = 1 с и х = 3 с. ■
Упражнение 8.28.
Повторите решение примера 8.28 для функции /(х) = х3 — 15х2 + 72х. ■
Пример 8.29 (Уравнение касательной). Пусть /(х) = х4 — 6х2 + 10.
1. Вычислите /'(х).
2. Решите уравнение касательной в точке х — 1.
3. Найдите такое значение х, при котором касательная будет горизонтальной.


Глава 8. Производная
93
Решение.
1. 	f (х); - (х4)' - (бх2)' 4- (10)';
= 4х3 - 12®.
2. У~У1 = m(x-xi),
У - 5 = —8(х - 1), у = —8х + 13.
Ух = f (Я!1) = f (1) = I4 - 6 • I2 + 10 = 5 т — f' (хх) = f (1) = 4 • I3 - 12 • 1 = -8 Касательная в точке х = 1
3. 	Поскольку наклон горизонтальной линии равен 0, необходимо решить урав¬
нение /'(х) = 0 для х.
f (х) = 4х3 — 12х = 0;
4х (х2 - 3) = 0;
4х (х + у/З^ (х — \/з) = 0;
х = 0; —у/З] у/З. м
Упражнение 8.29.
Повторите решение примера 8.29 для функции /(х) = х4 — 8х3 + 7. ■
Замечание.
В примере 8.29 для решения уравнения /Х(х) = 0 использовались специальные алгебраические методики. Для приблизительного решения уравнений подобного вида можно использовать графическую утилиту. На рис. 8.37 показано решение уравнения из примера 8.29.3. Следует отметить, что графическая утилита выдает приблизительные значения для — у/З и у/З в десятичном представлении.
10
-10
10
Рис. 8.37. Решение уравнения = 4х3 - 12х
10
В бизнесе и экономике скорость изменения определенной величины часто дает возможность понять суть исследуемого явления или процесса. Производителей, например, может интересовать не только уровень общих затрат С(х), но также скорость их изменения при различных объемах производства.


94
Часть III. Математический анализ
www В экономике термином предельный обозначают скорость изменения (т.е. производную) исследуемых величин. Таким образом, если
С(х) = общие затраты на производство х единиц продукции,
то
С'(х) = предельные затраты =
= мгновенная скорость изменения величины общих затрат С (я), на производство единицы продукции при общем объеме производства, равном х.
Пример 8.30 (Предельные затраты). Предположим, что общие затраты С(х) (тыс. долл.) на производство х парусных яхт в год описываются следующей функцией, график которой показан на рис. 8.38.
С(х) = 575 + 25® - 0,25®2; 0 < х 50.
Рис. 8.38. Предельные затраты
1. Вычислите величину предельных затрат при производстве х яхт в год.
2. Вычислите величину предельных затрат при производстве 40 яхт в год и дайте интерпретацию этого результата.
Решение.
1. 	Величина предельных затрат при производстве х яхт в год равна
С (®)i = (575)' + (25®)' - (0,25х2)' j = 25 — 0,5®.


Глава 8. Производная
95
2. 	Величина предельных затрат при производстве 40 яхт в год равна
С,(40) = 25 — 0,5 • 40 = 5; или 5000 долл, на яхту.
При уровне производства 40 яхт в год общие затраты растут со скоростью 5000 долл, за шлюпку. ■
Упражнение 8.30.
Предположим, что величина общих затрат С(х) (тыс. долл.) на производство х парусных яхт в год описывается функцией
С(х) = 500 4- 24а; — 0,2а;2; 0 < х С 50.
1. Вычислите величину предельных затрат при производстве х яхт в год.
2. Вычислите величину предельных затрат при производстве 35 яхт в год и дайте интерпретацию полученным результатам. ■
В описании предельных затрат, приведенных в примере 8.30.2, производная указывает характер изменения исходной величины. Однако существует еще один способ интерпретации значения производной, который широко используется в экономике. Вернемся к результатам, полученным в примере 8.30.2. Если скорость роста общих затрат в расчете на яхту равна 5000 долл, при производстве 40 яхт в год, то при увеличении объема производства до 41 яхты в год общие затраты вырастут на 5000 долл. Таким образом производная показывает, насколько вырастут затраты при включении в годичный производственный план еще одной яхты. Исходя из этого, предельные затраты можно определить следующим образом.
Функция предельных затрат
Если С(х) — это общие затраты на производство х единиц продукции, то функция предельных затрат С'(т) указывает приближенную величину затрат на производство дополнительной единицы продукции сверх обозначенного объема производства.
Пример 8.31 (Предельные затраты). Вернемся к функции общих затрат, заданной в примере 8.30.
С(х) = 575 + 25х — 0,25а?2; 0 х 50.
1. Используя функцию предельных затрат, оцените величину затрат на производство 31-й яхты.
2. Используя функцию общих затрат, вычислите точную величину затрат на производство 31-й яхты.


96
Часть III. Математический анализ
Решение.
1. Из примера 8.30 известно, что С'(х) = 25 - 0,5z. Следовательно,
С'(40) = 25 — 0,5 • 30 = 10; или 10000 долл, на яхту.
Величина затрат на производство 31-й яхты приблизительно равна 10 000 дол
2. Точная величина затрат на производство 31-й яхты составляет
(Общие затраты \ / Общие затраты \
на производство 1 — I на производство 1 =
31-й яхты / \ 30-й яхты /
= С(31) - С (30) =
= 1109,75 - 1100 = 9,750 долл.
Следует отметить, что приближенная величина предельных затрат, равная 10 000 долл., очень близка к точному значению. ■
Упражнение 8.31.
Вернемся к функции общих затрат, заданной в примере 8.30.
С(ж) = 500 + 24т - 0,2s2; 0 < х 50.
1. Используя функцию предельных затрат, вычислите приближенную величину затрат на производство 41-й яхты.
2. 	Используя функцию общих затрат, вычислите точную величину затрат на производство 41-й яхты. ■
Замечание. Производную всегда можно считать мгновенной скоростью изменения функции, как это показано в примере 8.30. Интерпретация функции предельных затрат как приблизительной величины затрат на выпуск дополнительной единицы продукции — это частный случай, который применим к функции общих затрат. Такая интерпретация справедлива также для к функции общей прибыли, но не применима к большинству других экономических функций, которые будут рассматриваться далее.
Ответы к упражнениям
8.23. 	Все равны 0.
8.24. 	1) 6ж5.
2) 	ЗОж29.
3) 	—2ж_3 = —2/ж3.


Глава 8. Производная
97
4) 8.25. 1) —х 2, или—1/х2.
2) |x-V3, или 2/(3\/х).
3) -|х-3/2, или —l/^x/x3).
8.26. 1) 20х4.
2) х3/3.
3) —х-4, или — 1/х4.
4) — 0,Зх-4/3, или —0,3/ v'x4.
8.27. 1) 12х3 — 6х2 + 2х — 5.
2) 14х_3, или 14/х3.
3) 15х2 — |х-3/4, или 15х2 — 1/ (4х3/4).
4) 3/(4х2) — (12/х4) — (х3/2).
8.28. 1) v = Зх2 - ЗОх + 72.
2) /'(2) = 24 фута/с, /'(5) = —3 фута/с.
3) х = 4сих = 6с.
8.29. 1) /'(х) = 4х3 - 24х2.
2) у = —20х + 20.
3) х - 0 и х = 6.
8.30. 1) С"(х) = 24 - 0,4х.
2) С" (35) = 10, или 10 000 долл, на яхту при объеме производства 35 яхт величина общих затрат растет со скоростью 10 000 долл, за яхту.
8.31. 1) С'(40) — 8, или 8000 долл.; величина затрат на производство 41-й шлюп¬
ки приблизительно равна 8000 долл.
2) С(41) — С(40) = 7,8, или 7800 долл.
Практикум 8.4
А Вычислите производные, указанные в задачах 1-18.
1. /'(х) для /(х) = 7. 2. з~3.
dx
4. у' для у = xG.
, dy g
3. — для у = х.
dx
dx


98
Часть III. Математический анализ
7. у' для у = х 4.
8. -j- для у = х 8. ах
10. f'(x) для /(а:) = а:9/2.
13. f'(x) для f(x) = 5а:2.
15. у' для у = 0,4а:7.
12. у’ для у =
»■ i
16. /'(х) для /(х) = 0,8х4.
Задачи 19-24 связаны с функциями fug, которые удовлетворяют условиям f(2) = 3 и д'(2) = —1. В каждой задаче для указанной функции h найдите значение h'(2).
19. h(x) = 4/(х).
21. h(x) = /(x) +p(x).
23. h(x) = 2f(x) — 3g(x) + 7.
20. 	h(x) = 5g(x).
22. h(x) = f(x) - g(x).
24. h(x) = —4/(x) + 5g(x) — 9.
Б Вычислите производные, указанные в задачах 25-48.
25. f (2а:-5).
dx v 7
27. /'(а:) для / (а:) =
хч
d -!
29. .
dx 2х2
31. f(x) для f(x) = —За:1/3.
33. 4- (2,4а;2 -3,5а:+ 4).
dx v 7
35. для у = Зх5 — 2х3 + 5.
dx
37. (Зх"4 +
dx v
39. для у =
dx
41. 4- (3*2/3 -
dx v
43. — (^- -
dx \х3/5
d 1
dx у/х'
47. — для 1/ =
В задачах 49-52 вычислите следующие функции и величины.
1) ГИ;
45.
— 3,2х 2 + х. у/Х
26. yf для у = —4x x.
du —3
28. / длят/= —. dx xb
30. yf для у =
32. для у = — 8xx/4. dx
34. у' для у = Зге2 + 4х — 7.
36. f'(x) для /(ж) = 2,6x3 — 6,7x + 5,2.
38. у' для у = 2x 3 — 4x x.


Глава 8. Производная
99
2) наклон графика f в точках х = 2 и х = 4;
3) уравнение касательной в точках х = 2 и х = 4;
4) значение (значения) х, при которых касательная будет горизонтальной.
49. f(x) = 6х — х2. 50. f(x) = 2х2 4- 8х.
51. f(x) = Зх4 - бх2 - 7. 52. /(х) = х4 - 32х2 + 10.
Если объект движется вдоль оси у (шкала в футах) так, что его положение в момент времени х (шкала в секундах) задается функциями, указанными в задачах 53-56, найдите следующие зависимости и величины:
1) функцию мгновенной скорости движения v =
2) скорость движения в моменты времени х = 0 секунд и х — 3 секунды;
3) моменты времени, в которые v = 0.
53. /(ж) = 176х - 16х2. 54. f(x) = 80х - 10х2.
55. f(x) = x3 — 9x2 + 15#. 56. f(x) = x3 - 9x2 + 24x.
В задачах 57-64 необходимо использовать графическую утилиту. В каждой задаче найдите f(x) и приблизительное значение(ия) х (с точностью до двух десятичных знаков), в котором(ых) график f имеет горизонтальную касательную.
57. f (х) = х2 — Зх — 4у/х. 58. f (ж) = х2 + х — 10^.
59. f (х) = З^х4 — 1,5х2 — Зх. 60. f (х) = З^х4 — 2х2 + 4х.
61. /(ж) = 0,05х4 -h 0,1х3 - 1,5х2 - 1,6х 4- 3.
62. /(х) = 0,02х4 - 0,Оба;3 - 0,78х2 + 0,94х + 2,2.
63. f(x) = 0,2х4 - 3,12а;3 + 16,25а:2 - 28,25а; + 7,5.
64. f(x) = 0,25а;4 - 2,6а;3 + 8,1а;2 - 10х + 9.
65. Пусть /(х) = ах2 + Ьх + с, а 0. Напомним, что график функции у = f(x) — это парабола. Используя производную /'(х), получите формулу для координаты х вершины этой параболы.
* 66. Теперь, научившись находить производные, объясните, почему больше нет необ¬
ходимости помнить формулу для координаты х вершины параболы.
67. Приведите пример функции кубической параболы, имеющей следующие свойства.
а) У нее нет горизонтальной касательной.
б) У нее есть одна горизонтальная касательная.
в) У нее есть две горизонтальные касательные.
* 68. Может ли у кубической полиномиальной функции быть больше двух горизон¬
тальных касательных? Объясните.
В Вычислите все производные в задачах 69-72.
\ г/ \ 10x4-20
69. /'(х) для /(х) =
X
d х4- Зх3 + 5
х2
71.
dx
dy х2 + 25
70. / для у =
dx хЛ
. 2х5 - 4х3 + 2х
72. у для у = -3


100
Часть III. Математический анализ
В задачах 73 и 74 требуется проверить каждое утверждение, используя определение производной и двухэтапный процесс.
73. -^-х3 = Зх2. 74. -^-х4 = 4х3.
ах ах
*75. Область определения степенной функции /(ж) = я1/3 — это множество всех действительных чисел. Найдите область определения производной f'(x). Проанализируйте характер графика у = f(x) для всех значений х, не входящих в область определения /'(х).
*76. Область определения степенной функции f(x) = х2/3 — это множество всех действительных чисел. Найдите область определения производной f(x). Проанализируйте характер графика у = f(x) для всех значений х, не входящих в область определения /'(х).
Применение математики
Экономика и бизнес
77. Предельные затраты. Величина общих затрат (в долларах) на производство х теннисных ракеток в день равна
С(х) = 800 + 60x-0,25z2;
0 х 120.
а) Вычислите величину предельных затрат при производстве х ракеток.
*б) Вычислите величину предельных затрат при производстве 60 ракеток и объясните полученный результат.
в) Вычислите точную величину затрат на производство 61-й ракетки и сравните ее с результатом, найденным при решении п. б.
*г) Вычислите значение С"(80) и объясните полученный результат.
78. Предельные затраты. Величина общих затрат (в долларах) на производство х портативных радиоприемников в день равна
С(х) = 1000 + ЮОх - 0,5х2;
0 х 100.
а) Вычислите величину предельных затрат при производстве х радиоприемников.
*б) Вычислите величину предельных затрат при производстве 80 радиоприемников и проинтерпретируйте результат.
в) Вычислите точную величину затрат на производство 81-го радиоприемника и сравните ее с результатом, найденным при решении п. б.
*г) Вычислите значение С'(50) и объясните полученный результат.


Глава 8. Производная
101
79. 	Производство автомобилей. Годовое производство лимузинов в Соединенных Штатах Америки за разные годы характеризуется данными, приведенными в табл. 8.11.
WWW Таблица 8.11. Объем производства лимузинов
Год
Количество лимузинов, шт
1980
2500
1985
6500
1990
4400
1995
3400
2000
5700
а) Пусть переменная х — это время, прошедшее с 1980 года, а функция у описывает соответствующий объем производства лимузинов в США. Введите в графическую утилиту данные, приведенные в табл. 8.11, и найдите кубическое уравнение регрессии.
*б) Если у = L(x) обозначает уравнение регрессии, найденное при решении п. а, вычислите значения £(12) и £'(12) с точностью до ближайших сотых и объясните полученные результаты.
*в) Повторите решение п. б для значений £(18) и L'(18).
80. 	Регистрация автотранспорта. Общее количество зарегистрированных лимузинов в Соединенных Штатах Америки за определенный год приведено в табл. 8.12.
WWW Таблица 8.12. Количество лимузинов в США
Год
Количество зарегистрированных лимузинов
1985
4000
1990
7000
1995
8900
2000
11000
а) Пусть переменная х — это время, прошедшее с 1980 года, а функция у описывает соответствующее количество владельцев лимузинов в США. Введите в графическую утилиту данные, приведенные в табл. 8.12, и найдите кубическое уравнение регрессии.
*б) Если у = L(x) обозначает уравнение регрессии, найденное при решении п. а, вычислите значения £(18) и £'(18) с точностью до сотни долларов и объяните полученные результаты.
* 81. Предельные затраты. На рис. 8.39 приведен график общих затрат (в долларах) еженедельного производства микроволновых печей. Оцените, что больше: приблизительная величина затрат на производство 101-й печи или приблизительная величина затрат на производство 401-й печи? Увеличивается или снижается доходность производства, проиллюстрированного графиком рис. 8.39, с ростом его объема. Объясните.


102
Часть III. Математический анализ
Количество печей, шт.
Рис. 8.39. Иллюстрация к задаче 81
* 82. Предельные затраты. На рис. 8.40 приведен график общих затрат (в долларах) еженедельного производства микроволновых печей. Оцените, что больше: приблизительная величина затрат на производство 101-й печи или приблизительная величина затрат на производство 401-й печи? Увеличивается или снижается доходность производства, проиллюстрированного графиком рис. 8.40, с ростом его объема. Объясните.
Количество печей, шт.
Рис. 8.40. Иллюстрация к задаче 82
83. Реклама. Анализ данных, собранных за предыдущие периоды, показал (рис. 8.41), что объем продаж моторных катеров N(z) зависит от затрат на рекламу х (в тысячах долл.) следующим образом.
N (х) = 1000 - 5 < х 30.
X
а) Найдите функцию N(x).
б) Вычислите значения N'(10) и N'(20). Объясните полученные результаты.
* 84. Зависимость спроса от цены. Предположим, что люди готовы покупать х фунтов шоколадных конфет в день по цене р долл, за четверть фунта. Эта зависимость описывается таким уравнением.
180
х — 10 -I ; 2 < р 10.
Р


Глава 8. Производная
103
График этой функции показан на рис. 8.42. Вычислите спрос и мгновенную скорость изменения спроса как функции цены, если цена составляет 5 долл. Дайте краткое объяснение полученным результатам.
Рис. 8.42. Иллюстрация к задаче 84
Биологические науки
85. Медицина. У человека ростом х дюймов сердце бьется с частотой у ударов в минуту, что описывается таким эмпирическим уравнением
у = 590х“1/2; 30 < х 75.
Вычислите мгновенную частоту пульса при разном росте.
а) 36 дюймов. б) 64 дюйма.
86. Экология. Угольная электростанция выбрасывает в окружающий воздух сернистый газ. Его концентрация С(х) в миллионных долях определяется уравнением
где х — расстояние от электростанции в милях. Вычислите мгновенную концентрацию сернистого газа на следующих расстояниях от электростанции.
а) х = 1 миля; б) х = 2 мили.


104
Часть III. Математический анализ
Социальные науки
87. Обучение. Предположим, что человек осваивает у новых понятий за х часов, что описывается уравнением
у = 50VS; 0 < х < 9,
график которого изображен рис. 8.43. Вычислите скорость обучения в конце указанных временных отрезков.
а) К концу первого часа. б) К концу девятого часа.
88. Обучение. Предположим, человек осваивает у новых понятий за х часов, что описывается уравнением
у = 21^2; 0 < х 8.
Вычислите скорость обучения в конце следующих временных отрезков.
а) К концу первого часа. б) К концу восьмого часа.
8.5. 	Производные произведений и частных
■ Производные произведений
■ Производные частных
Правила вычисления производных, рассмотренные в предыдущих разделах, существенно расширяют возможности по их применению во многих практических задачах. В этом и следующем разделах мы рассмотрим еще несколько полезных правил.
Производные произведений
В разделе 8.4 мы выяснили, что производная суммы равна сумме производных. Будет ли производная произведения произведением производных?


Глава 8. Производная
105
Задание 8.12.
Пусть F(t) — х2\ S(x) = х3 и /(х) = F(x)S(x) — х\ Какое из следующих
выражений равно /'(х)?
1. F'(x)S'(x).
3. F'(x)S(x).
2. F(x)S"(x).
4. F(x)5'(x) + F'(x)S(x). a
Сравнивая различные выражения, перечисленные в задании 8.12, легко понять, что производная произведения не равна произведению производных, а имеет несколько более сложную зависимость.
Используя определения производной и двухэтапный процесс, можно доказать следующее правило.
Производная произведения двух функций равна сумме первой функции, умноженной на производную второй функции, и второй функции, умноженной на производную первой функции.
www Правило дифференцирования произведений
Если
У = = F(x)S(x)
и производные F'(x) и S'(x) существуют, то
Кроме того,
f(x) = F(x)S'(x) + S(x)F'(x).
y' — FS' + SF1, T- = FT- + S^T-
dx dx dx
Пример 8.32 (Дифференцирование произведения). Используя два разных мето¬
да, вычислите производную /'(ж) для функции
f(x) = 2т2 (Зя4 — 2).
Решение.
Метод 1. Используем правило дифференцирования произведения
fix) = 2х2(3х4 - 2)' + (Зх4 - 2)(2х2)7 = = 2х2 • 12х3 + (Зх4 - 2) • 4х = = 24х5 + 12х5 - 8х = Первую функцию умножаем на производную второй и добавляем вторую функцию, умноженную на производную первой
= Збя5 — 8х.


106
Часть III. Математический анализ
Метод 2. Сначала выполним умножение, а затем возьмем производную.
/(х) = 2х2(3х4 — 2) = бх6 — 4х2, f'(x) — Збх5 — 8х.
Упражнение 8.32.
Используя два разных метода, вычислите /'(х) для /(х) = Зх3(2х2 — Зх + 1). ■
До сих пор все произведения, с которыми мы сталкивались, можно было дифференцировать любым из методов, продемонстрированных в примере 8.32. В последующих разделах мы покажем, что есть ситуации, в которых просто необходимо использовать правило дифференцирования произведения. Если не оговорено противное, для дифференцирования всех произведений в этом разделе необходимо использовать именно это правило.
Пример 8.33 (Касательная). Пусть /(х) = (2х — 9)(х2 + 6).
1. Вычислите уравнение касательной к графику /(х) в точке х = 3.
2. Вычислите значение(я) х, при котором(ых) касательная является горизонтальной.
Решение.
1. 	Сначала найдем /'(х).
f'(x) = (2х — 9)(х2 + б)7 + (х2 + 6)(2х — 9)7 = — (2х — 9) • 2х + (х2 + 6) • 2.
Теперь найдем уравнение касательной в точке х = 3:
У~У1 =m(x-xi), у - (-45) = 12(х - 3), у = 12х - 81.
У1 = /(®1) = /(3) = -45
т = /'(Ж1) = /'(3) = 12
Касательная в точке х = 3
2. 	Касательная является горизонтальной при любом значении х9 при котором У'(х) = 0, так что
/'(х) = (2х - 9) • 2х + (х2 + 6) • 2 = 0,
бх2 - 18х + 12 = 0,
х2 — Зх + 2 = 0,
(х — 1)(х — 2) — 0,
х = 1; 2.
Касательная является горизонтальной в точках х = 1 и х = 2.


Глава 8. Производная
107
Упражнение 833.
Повторите решение примера 8.33 для функции /(х) = (2х + 9)(z2 — 12). ■
Как показано в примере 8.33, способ, которым записывается производная /'(х), зависит от того, что с ней приходится делать. Если нас интересует только значение /'(х) при определенном значении х, подойдет правило, использованное при решении п. 1. Однако, если нужно решить уравнение f'(x) = 0, необходимо произвести умножение, как это было сделано при решении п. 2.
Производные частных
Как и в случае с произведением, производная частного двух функций не равна частному производных этих функций.
Задание 8.13.
Пусть Т(х) = х5, В(ж) = х2 и
Какое из следующих выражений равно /'(х)?
Выражения в задании 8.13 предполагают, что производная частного двух функций приводит к более сложному выражению, чем можно было бы ожидать.
Вообще, если Т(х) и В (я) — две произвольные дифференцируемые функции и можно показать, что
В (ж) Г (х) - Т (х) В' (х) [В (т)]2
Таким образом, справедливо следующее правило.
Производная частного двух функций равна разности знаменателя, умноженного на производную числителя, и числителя, умноженного на производную знаменателя, деленной на квадрат знаменателя.


108
Часть III. Математический анализ
WWW Правило дифференцирования частного
Если
У = f (®) =
в (ж)
и производные Т'(х') и В'(х) существуют, то
В (х) Т' (х) - Т (х) В' (х)
[ВЫ]2
Кроме того,
dT dB
= ВТ'— ТВ' dy = В^-Т^с
У В2 ’ dx В2
Пример 8.34 (Дифференцирование частных).
1. Вычислите производную f(x) функции f (х) = •
2. Вычислите производную у' функции у — ,
3. Вычислите производную используя правило дифференцирования,
а также разбивая дробь на две дроби.
Решение.
, _ (2х — 1) (х2)'-х2 (2х — 1)' _
‘ 7 * (2т - I)2
(2х — 1) ♦ 2х — х2 • 2 (2х - I)2
4т2 — 2х — 2х2
(2х-1)2
2х2 — 2х
~ (2х —I)2'
, (х3 + 1) (х2 — x)z — (х2 — х) (х3 + 1)Z
2‘ У = (х3 + I)2
(х3 + 1) (2х — 1) — (х2 — х) • Зх2
= (х3 +1)2 =
2х4 — х3 + 2х — 1 — Зх4 + Зх3
= (х3 +1)2 =
—х4 + 2х3 + 2х — 1
(х3 + I)2
Знаменатель умножаем на производную числителя, вычитаем числитель, умноженный на производную знаменателя, и делим результат на квадрат знаменателя


Глава 8. Производная
109
3. 	Метод 1. Воспользуемся правилом дифференцирования частных.
ri^-3 dx х2 (я2)2
х2 • 2х — (ж2 — 3) • 2х ж4 2х3 — 2х3 + бх бх 6
X4 X4 X3 ’
Метод 2. Разобьем исходную дробь на две дроби.
*2-3 _ А _ А _ i _ 3ж-2.
О О О )
XZ XZ XZ
4- (1 - Зх-2) =0-3 (-2) х~3 = dx 4 ' хл
Сравнивая методы 1 и 2, легко понять, что часто, прежде чем слепо использовать формулу дифференцирования, стоит выполнить алгебраические преобразования. ■
Упражнение 8.34.
1. 	Вычислите производную /'(ж) функции / (ж) =
2ж
ж2 + 3
2.
Зд?
Вычислите производную yf функции у = —z Т
d 2 + х3
3. 	Вычислите производную =—
ах х6
двумя способами.
Задание 8.14.
Объясните, почему в выражении, указанном ниже, используется знак 7^, а затем вычислите правильное значение производной.
dx3 Зх2
dx х2 + Зх + 4 2х + 3 ■
Пример 8.35 (Анализ продаж). Объем продаж видеоигр S (в тысячах штук) через t месяцев после выпуска рассчитывается по формуле
125t2
t2 + 100’


110
Часть III. Математический анализ
1. Вычислите функцию S'(t).
2. Вычислите значения 5(10) и S" (10). Дайте интерпретацию этих результатов.
Сравните ответ с результатами, полученными с помощью графической утилиты.
3. Используя результаты, полученные при решении п. 2, оцените суммарный объем продаж через 11 месяцев.
Решение.
1. S' (t) =
(t2 + 100) (125t2)' - 125t2 (t2 + 100)'
(t2 + 100)2
(t2 + 100) (250t) - 125i2 (2t) _
(t2 +100)2
250t3 + 25 OOOf — 250t3 _
(t2 +100)2
25 000t
2 ’
(t2 + 100)
125 • 1П2
2'5(10) = й^ю = 62’5и5'(10> =
25000-10
—z о = 6,25.
(102 + 100)2
Суммарный объем продаж через десять месяцев составит 62 500 игр, причем эта величина растет со скоростью 6250 игр в месяц. На рис. 8.44 показан результат проверки ответа с помощью графической утилиты.
3. Суммарный объем продаж в следующем месяце возрастет приблизительно на 6250 игр. Таким образом, приблизительный суммарный объем продаж через 11 месяцев составит 62 500 + 6250 = 68 750 игр. ■
Упражнение 8.35.
Вернемся к примеру 8.35. Предположим, что объем продаж S (в тысячах штук) через t месяцев после выхода игры рассчитывается по формуле
S(4) =
150t
t + з


Глава 8. Производная
111
62.5 nDeriu<Vi> Х>10)
6.25
Рис. 8.44. Функция
У1 ~ х2 + 100
1. Вычислите функцию S'(t).
2. Вычислите значения S(12) и S"(12). Дайте интерпретацию этих результатов.
Сравните ответ с результатами, полученными с помощью графической утилиты.
3. Используя результаты, полученные при решении п. 2, оцените объем продаж
через 13 месяцев. ■
Ответы к упражнениям
8.32. ЗОя4 - Збж3 + 9ж2
8.33. 1) у = 84а? - 297.
2) х = —4, х = 1.
8.34. 1)
8.35. 1) S'(t) = ъ
' (t + 3)2
2) S(12) — 120; S"(12) = 2. Через 12 месяцев суммарный объем продаж составит 120 000 игр, и эта величина будет расти со скоростью 2000 игр в месяц.
3) 122 000 игр.


112
Часть III. Математический анализ
Практикум 8.5
В задачах этого практикума потребуется находить как обычную, так и упрощенную формы производной. При проверке полученных результатов сначала убедитесь в корректности выбора правил дифференцирования и только затем переходите к анализу алгебраических преобразований. Если не оговорено противное, при вычислении производных произведений следует применять правило дифференцирования без предварительного умножения алгебраических выражений.
А В задачах 1-18 вычислите функцию f(x) и упростите результат.
2. 	/(х) = 5х2(х3 + 2).
4. 	/(ж) = (Зх + 2)(4х — 5).
10. f(x) = (Зх + 5)(х2 - 3).
12. /(х) = (0,5х - 4)(0,2х + 1).
16. /(х) = (а:2 - 4) (а:2 + 5).
х2 — 4
1. /(х) = 2а:3(а:2 — 2).
3. /(ж) = (х- 3)(2х - 1).
( . 2х + 3
7-/« = ТТ2-
9. /(а:) = (а:2 + 1)(2а: — 3).
11. У(х) = (0,4а: + 2)(0,5х - 5).
J v J 2х - 3
15. /(х) = (х2 + 2)(х2 — 3).
В задачах 19-24 рассматриваются функции fug, которые удовлетворяют условиям /(1) = 3, /'(1) = 2, #(1) = 5 и </(1) = —3. В каждой задаче вычислите значение h'(l) для указанной функции h.
19. h{x) = f(x)g(x).
20- =
9Щ
21 h fa:) = &
f(x)'
22. h(x) = f(x)f(x).
24./г(х) = J-r.
Б В задачах 25-32 вычислите указанные производные и упростите результат.
25. f'(x) для /(а:) = (2а: + 1)(а:2 - За:). 26. у1 для у = (а:3 + 2х2)(3х - 1).
[(3 - 0,4а:3) (0,5а:2 - 2а:)].
/'(х) для/(а:) = 2^Т1-
dy х4 — х3
ТхДляу = 1^Т-
27.
29.
31.
30.
32.
для у = (2,5х - х2)(4х + 1,4). 28.
. 5х — 3
для?/= .
х2 + 2х
d х2 — Зх + 1
dx х2 — 1
В задачах 33-36 вычислите производную f'(x) и постройте уравнение касательной к графику f в точке х = 2.
33. /(х) = (1 + Зх)(5 — 2х).
34. /(х) = (7 — Зх)(1 + 2х).


Глава 8. Производная
113
В задачах 37-40 вычислите f'(x) и значение (значения) х, при котором (которых) f\x) = 0.
37. f(x) = (2s - 15)(s2 + 18). 38. f(x) = (2z - 3)(s2 - 6).
В задачах 41-44 вычислите функцию f(x) двумя способами: используя правила дифференцирования произведений и частных, а также после предварительного упрощения выражений.
41. /(ж) = £3(я:4 — 1). 42. /(ж) = rr4(rr3 — 1).
>4-1 г/ \ х3 + 9 ла t < \ я4 + 4
43‘ f х = —~з~ • 44« f (*) = —
X X
В В задачах 45-56 вычислите все производные и упростите результат.
45. f'(x) для /(ж) = (2ж4 — Зх3 + х)(х2 — х + 5).
для у = (х2 — Зх + 1)(я3 + 2х2 — х).
ах
d Зх2 - 2х + 3 . х3 - Зх + 4
. 48. и для и = —- . dx 4х2 + 5х — 1 2х2 + 3х — 2
для у = 9х1//3(а;3 + 5). 50. [(4ггх/2 - 1) (Зх1/3 + 2)].
51. f'(x) для f (s) = 52. у’ для у = j^+~r
d х3 — 2х2 dy х2 — Зх -1-1
46.
47.
49.
53- dx^^- dx""y~ ■
(2х2 — 1) (х2 + 3)
55. f(x) для / (я) = А + ).
2х — 1
56. »- для , = (д3 + 2) (г2 _ 3).
В задачах 57-60 рассматривается функция вида f(x) = [u(x)]n, где и(х) — дифференцируемая функция.
57. Используя правило дифференцирования произведений, покажите, что если п = — 2, то /'(х) = 2и(х)и,(х),
58. Используя правило дифференцирования произведений и результаты задачи 57, покажите, что /'(я) = 3[и(ж)]2и'(ж), если п = 3.
59. Исходя из результатов задач 57 и 58, запишите формулу для f'(x) при произвольном п.
60. 	Используя правило дифференцирования отношений, вычислите функцию f'(x), если п = — 1. Согласуется ли этот результат с формулой, полученной в задаче 59?


114
Часть III. Математический анализ
В задачах 61-64 требуется вычислить приближенное значение(ия) х (с точностью до двух десятичных знаков), в котором(ых) график функции f имеет горизонтальную
касательную.
61. f(x) — (х2 + 4)(х2 — 2х).
x, + i ■
62. /(х) = (х2 + 3)(х2 + 4х).
ГГ \ х3 + 15х - 1 64-/м= ^+1 •
Применение математики
Экономика и бизнес
65. Анализ продаж. Суммарный объем продаж компакт-дисков S (тыс. шт.) описывается формулой
on/2
s<‘> = ^n»'
где t — количество месяцев, прошедших с момента поступления компакт-дисков в продажу.
а)
*б)
в)
Вычислите функцию Sf(t).
Вычислите значения 5(10) и S"(10). Дайте интерпретацию этих результатов. Используя результаты, полученные при решении п. б, оцените суммарный объем продаж через 11 месяцев.
66. Анализ продаж. Телекоммуникационная компания предлагает услуги оператора кабельного телевидения. Общее количество абонентов N (тыс. чел.) через t месяцев после запуска службы определяется по формуле
N(1) = ^
V 7 t + 5
а) Вычислите функцию
*б) Вычислите значения 7V(15) и Л7 (15). Дайте интерпретацию этих результатов, в) Используя результаты, полученные при решении п. б, оцените суммарный объем продаж через 16 месяцев.
67. Зависимость спроса от цены. Согласно классической экономической теории, объем спроса х на свободном рынке сокращается с ростом цены р (см. рис. 8.45). Предположим, что количество компакт-дисков х, еженедельно приобретаемых в розничной сети по цене р долл., рассчитывается по формуле
4000
0,1р + 15
10 р 70.
а) Вычислите функцию dx/dp.
*б) Определите спрос и мгновенную скорость изменения спроса как функцию цены, если цена составляет 40 долл. Дайте интерпретацию этих результатов.
в) Используя результаты, полученные при решении п. б, оцените спрос, если цена возрастет до 41 долл.


Глава 8. Производная
115
68. Зависимость предложения от цены.. Также, согласно классической экономической теории, объем предложения х на свободном рынке увеличивается с ростом цены р (см. рисунок). Предположим, что количество компакт-дисков х, еженедельно поставляемых в розничную сеть по цене р долл., рассчитывается по
формуле
ЮОр
10 0^70.
0,1р + 1
а) Вычислите функцию dx/dp.
*б) Найдите предложение и мгновенную скорость изменения предложения в зависимости от цены, которая составляет 40 долл. Дайте интерпретацию этих результатов.
в) Используя результаты, полученные при решении п. б, оцените предложение, если цена возрастет до 41 долл.
Биологические науки
69. Медицина. Препарат вводится пациенту в вену на ее правой руке. Концентрация препарата в крови, регистрируемая в левой руке (мг/куб. см.) через t часов после
инъекции, задается формулой
а) Вычислите функцию С (х).
*б) Вычислите значение С'(0,5) и С"(3). Дайте интерпретацию результатов.
70. 	Чувствительность к препарату. Через час после приема препарата в количестве х мг температура тела пациента Т(х), выражаемая в градусах Фаренгейта, рассчитывается по формуле
Г(дт) = я;2 (1 - ^) ; 0
Скорость Г'(ж), с которой изменяется температура Т в зависимости от величины дозы препарата х, называется чувствительностью тела к дозировке.


116
Часть III. Математический анализ
N (х)
а) Вычислите функцию Т'(х), используя правило дифференцирования произведений.
б) Вычислите значения Г'(1), Т'(3) и Г'(6).
Социальные науки
71. 	WWW Обучение. На заре создания количественной теории обучения (приблизительно 1917 год) Л. Л. Терстоун (L. L. Thurstone) выяснил, что количество успешно выполненных человеком действий 7V(x) в зависимости от количества тренировочных упражнений х, описывается формулой
ЮОх + 200
х + 23
а) Вычислите мгновенную скорость изменения величины обучения N'(x) как функцию, зависящую от количества тренировочных упражнений х.
б) Вычислите значения N'(4) и А7 (68).
8.6. 	Цепное правило: дифференцирование
сложных функций
■ Дифференцирование степенных функций
■ Комбинирование правил дифференцирования
В этом разделе будет разработано правило дифференцирования степенных функций — особый вариант очень важного цепного правила, рассмотренного в главе 10. Кроме того, мы впервые столкнемся с некоторыми видами произведений, которые нельзя упростить с помощью умножения и которые необходимо дифференцировать, используя правило дифференцирования степенных функций.
Дифференцирование степенных функций
Мы уже широко использовали правило дифференцирования степенных функций
-^-хп = пхп~\ (8.11)
ах
Теперь хотелось бы обобщить это правило так, чтобы можно было дифференцировать функции типа [u(x)]n, где и(х) — дифференцируемая функция. Останется ли правило (8.11) справедливым, если х заменить на и(т)?
Задание 8.15.
Пусть и(х) = 2т2 и /(ж) = [и(ж)]3 = 8ж6. Какое из следующих выражений равно
1. 3[ц(х)]2.
2. 3 [и'(ж)]2.
3. 3 [-и(х)]2 и'(х).


Глава 8. Производная
117
Вычисления в задании 8.15 показывают, что нельзя обобщить правило степеней, просто заменив в уравнении (8.11) переменную х на функцию и(х).
Как же можно найти формулу для производной от [и(я)]п, где и(х) — произвольная дифференцируемая функция? Рассмотрим производные функций [и (ж)]2 и [и(х)]3 и попробуем выявить общую структуру искомого правила. Поскольку [и(х)]2 — и(х)и(х), то, используя правило дифференцирования произведений, запишем
= и (ж) и' (х) + и (х) и' (ж) = (8-12)
= 2и (х) и' (х).
Поскольку [u(x)]3 = [u(x)]2u(x), используя правило дифференцирования произведений и уравнение (8.12), запишем
= 1хи + =
= [и (х)]2 и' (х) + и (х) [2и (х) и' (х)] = = 3 [и (х)]2 и1 (х).
Подставляем уравнение (8.12)
d dx
[U(x)]2.
Продолжая тем же образом, можно доказать следующее правило.
А dx
[и (ж)]п = п [и (х)]п 1 и' (х),
где п — положительное целое.
(8.13)
Прибегая к более формальным доказательствам, можно показать, что формула (8.13) справедлива для всех действительных чисел п. Как бы там ни было, мы получили общее правило дифференцирования степенных функций.
www Общее правило дифференцирования степенных функций
Если и(х) — дифференцируемая функция, п — любое действительное число и
у = /(х) = [u(x)]n ,
то
/'(х) = п [u(x)]n_1 и'(х).
Это правило часто записывают более компактно в виде
/ , d ~~ „п 1 du , v
= пи и , или —и = пи —, где и = и (х).
dx dx


118
Часть III. Математический анализ
Общее правило дифференцирования степенных функций представляет собой особый вариант очень важного и полезного правила дифференцирования, называемого цепным правилом (в русскоязычной литературе это правило называется правилом дифференцирования сложных функций. — Прим. ред.). По существу, цепное правило позволит дифференцировать составное выражение f [<7(2)], если известно, как дифференцировать f(x) и д(х). Отложим детальное обсуждение цепного правила до главы 10.
Пример 8.36 (Дифференцирование степенных функций). Вычислите функ- цию
1. f{x) = (Зх + I)4. 2. /(х) = (х3 + 4)7.
3.
/(®) =
1
(х2 + х + 4)3
4. f (х) — у/З — х.
Решение.
1. / (х) = (Зх + I)4 ;
f (x)i = 4 (Зх + I)3 (Зх + 1)' i =
= 4(3х + 1)33 =
= 12 (Зх + I)3 .
Пусть и = Зж + 1, п = 4.
du
— = 3 dx
du dx
2. f (x) = (x3 + 4)7 ■
f1 (x); = 7 (x3 + 4)6 (x3 + 4)Z; =
= 7 (x3 + 4)6 3x2 =
= 21x2 (x3 + 4)6.
Пусть u = ж3 + 4, n — 7.
du dx
du ~
— = Зж2 dx
3.
1
(x2 + x + 4)3
/ (z) =
(x2 + x + 4) 3 ;
Пусть и = ж2 -|- x 4, n = —3.
f' (x) = —3 (x2 + x + 4) 4 (x2 + x + 4)'; =
„ i du nu71-1 — dx
= —3 (x2 + x + 4) 4 (2x + 1) =
-3(2x + l)
du
— = 2x + 1 dx
(x2 + x + 4)4


Глава 8. Производная
119
— л/З — х = (3 — х)1/2 ;
Пусть и =;
i= i (3 - х:)-1/2(3 - □.)< =
„ 1 du пи"-1 — dx
= |(3-гГ1/2(-1) =
du dx
Упражнение 8.36.
Вычислите функцию
1. /(х) = (5х + 2)3.
3.
/(®) =
1
(ж2 + 4)2
2. /(ж) = (х4 - 5)5.
4. f (ж) = \/4 - х.
Следует отметить, что дифференцирование каждой функции в примере 8.36 проводилось в два этапа. Сначала применялось общее правило дифференцирования степенных выражений, а затем вычислялось значение du/dx. Немного попрактиковавшись в вычислении производных, вы научитесь дифференцировать сложные функции в один этап. Поступая так, не забывайте включать в результат множитель du/dx. Например,
^(х6 + 1)4 = 4(х5 + 1)35х4;
А(15 + 1)4/4(хЬ + 1)3.
Правильно
Отсутствует du/dx = 5sc4
Если положить и(х) = х, то du/dx = 1, и общее правило дифференцирования степенных выражений переходит в обычное правило дифференцирования степенных функций, рассмотренное в разделе 8.4. Сравните следующие выражения.
~—хип / пи"-1.
dx
Правило дифференцирования степенных выражений.
Общее правило дифференцирования степенных функций.
За исключением и (х) = X + к, когда du/dx = 1.
Комбинирование правил дифференцирования
В следующих примерах общее правило дифференцирования степенных функций применяется совместно с другими правилами дифференцирования.
Пример 8.37 (Касательные). Постройте уравнение прямой, касательной к графику f в точке х = 2 для функции f (ж) = х2\/2х + 12.


120
Часть III. Математический анализ
Сравните ответ с результатами, полученными с помощью графической утилиты.
Решение.
/ (ж) = т2\/2х + 12 =
= ж2 (2х + 12)1/2;
f (ж) = х2-^- (2х 4-12)1/2 + (2х + 12)1/2 -j—x2 = ах ах
= х2 | (2х + 12)_1/2 • 2 + (2х + 12)1/2 • 2
Воспользуемся правилом дифференцирования произведений
Для дифференцирования (2а? + 12)1/2 следует воспользоваться общим правилом дифференцирования степенных функций, а для дифференцирования ж2 — обычным.
Точка
Наклон
У — У1 = т(х — ®1)
Касательная
На рис. 8.46, а показаны значения /(2) и /'(2), а на рис. 8.46, б — график функции у = f(x) и касательная в точке х = 2. Следует отметить, что для проверки проделанной работы был построен график уравнения у — 17ж — 18. Здесь не использовалась встроенная процедура построения графика касательной. Такая процедура дала бы подобный график, но по нему нельзя было узнать, правильное ли уравнение найдено для касательной. В
Yi nDerivCYi
2
16
17.00000022
а)
Рис. 8.46. Графики функций из примера 8.37


Глава 8. Производная
121
Упражнение 8.37.
Вычислите функцию f'(x) и уравнение прямой, касательной к графику функции f в точке х — 3 для f (ж) - ж\/15 — 2х.
Сравните ответ с результатами, полученными с помощью графической утилиты. ■
Пример 8.38 (Касательная). Вычислите значение(я) х, в котором(ых) касательная к графику функции
х3
~ (2 — Зж)5
проходит горизонтально.
Решение. Воспользуемся правилом дифференцирования частных:
, м _ (2 - Зх)5 £х3 - х3£ (2 - Зх)5 _ Г <12 ”
[(2-Зж)5]
_ (2 - Зж)5 Зх2 - ж35 (2 - Зж)4 (-3) (2 - Зж)10
_ (2 - Зж)4 Зж2 [(2 - Зж) + 5ж] _
(2 - Зж)10
_ Зж2 (2 + 2ж) _ 6ж2 (ж + 1)
~ (2 - Зж)6 ” (2 — Зж)6 '
Для дифференцирования а?3 следует воспользоваться обычным правилом дифференцирования степенных выражений, а для дифференцирования (2 — За?)6 — общим.
Поскольку дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю, очевидно, что /'(я) = 0 в точках х = — 1 и ж = 0. Таким образом, график функции f имеет горизонтальные касательные в точках х — — 1 и х = О.в
Упражнение 8.38.
Вычислите значение(я) х, в котором(ых) касательная к графику функции
/(*) =
(2 - Зж)2
проходит горизонтально. ■
Пример 8.39 (Комбинирование правил дифференцирования). Запишите функцию / из примера 8.38 в виде произведения, а затем продифференцируйте.


122
Часть III. Математический анализ
Решение.
т3
f (х) = е = х3 (2 — Зх)-5 ;
J к ’ (2 - Зх)5 V 1 f' (х) — х3-^- (2 — Зх) 5 + (2 — Зх) 5 -j-x3 —
ах ах
= х3 (-5) (2 - Зх)-6 (-3) + (2 - Зх)-5 Зх2 =
- 15х3(2 - Зх)-6 + Зх2(2 - Зх)-5.
Мы получили выражение для /'(х) без проведения упрощений. Этого вполне достаточно для получения ответов только на некоторые, но далеко не все вопросы. Например, если нужно решить уравнение /'(х) = О? то выражение придется упростить алгебраическими методами.
(2 - Зх)6 + (2 - Зх)5 (2 - Зх)6 + (2 - Зх)6
15х3 + Зх2 (2 — Зх) Зх2 (5х + 2 — Зх)
(2 — Зх)6 (2 — Зх)6 ’
Упражнение 8.39.
Запишите функцию f из упражнения 8.38 в виде произведения, а затем продифференцируйте.
Как показано в примере 8.39, любое частное можно преобразовать в произведение и продифференцировать, используя правило дифференцирования произведений. Однако, если производную необходимо упростить, чаще всего, проще воспользоваться правилом дифференцирования частных. (Сравните алгебраические упрощения в примере 8.39 с преобразованиями в примере 8.38.) Есть один особенный случай, в котором предпочтительнее использовать метод отрицательных степеней, — когда функция представляет собой дробь с постоянным знаменателем.
Пример 8.40 (Альтернативные методы дифференцирования). Вычислите функцию /'(х) двумя способами, если


Глава 8. Производная
123
Решение.
Метод 1. Воспользуемся правилом дифференцирования частных.
(_ ^2 + 9)3i4-4j(^ + 9)3 _ J ~ Г п <1 2 “
[(г2 + 9)3]
(х2 + 9)3 • 0 — 4 [3 (ж2 + 9)2 • 2х]
= (х2 + 9)6 =
—24х (х2 + 9)2 —24х
(х2 + 9)6 _ (х2 + 9)4'
Метод 2. Перепишем функцию в виде произведения и воспользуемся общим правилом дифференцирования степенных функций.
/(1) = ^гЬ>? = 4(12 + 9)~3;
f (х) = 4(-3) (х2 + 9)-1.2х =
Какой метод предпочтительнее? ■
Упражнение 8.40. 5
Вычислите функцию /'(х) двумя способами, если f (х) = ■
(х3 + 1)
Ответы к упражнениям
8.36. 1) 15(5х + 2)2.
2) 20х3(х4 - 5)4.
3) —4х/(х2 + 4)3.
4) -1/(2х/4=х).
8.37. f (х) - х/15 - 2х - . Х ; у = 2х + 3.
4 ’ д/15 - 2х У
8.38. х = 0, х = 2.
8.39. —6х3 (Зх - 2)_3 + Зх2 (Зх - 2)-2 = 3x2 ~
(Зх 2)
—ЗОх2
(х3 + 1)3’
8.40.


124
Часть III. Математический анализ
Практикум 8.6
В задачах этого практикума потребуется находить как исходную, так и упрощенную формы производной. При проверке полученных результатов сначала убедитесь в корректности выбора правил дифференцирования и только затем переходите к анализу алгебраических преобразований.
А В задачах 1-6 замените знак ? выражением, которое сделает указанное уравнение справедливым.
1. (Зх + 4)4 = 4 (Зх + 4)3 ?
ах
2. (5 - 2х)6 = 6 (5 - 2х)5 ?
dx
Х = 3(4 —2т2)2 JL
4-,|(3*2+7)5 = 5(зх2+7)4^
5. 4- (1 + 2х + Зх2)7 = 7 (1 + 2х + ах 4 7 v
Зх2)6 ?
6. 4“ (4 — 3z — 2х2)8 = 8 (4 - Зх — dx v v
2х2)7 ?
В задачах 7-20, используя общее правило дифференцирования степенных выражений, найдите функцию f'(x) и упростите результат.
1. /(х) = (2х + 5)3.
8. /(х) = (Зх - 7)5.
9. /(х) = (5 - 2х)4.
10. /(х) = (9 — 5х)2.
11. /(х) = (4 + 0,2х)5.
12. /(х) = (6 - 0,5х)4.
13. /(х) = (Зх2 + 5)5.
14. /(х) = (5х2 — З)6.
15. /(х) = (х3 - 2х2 + 2)8.
16. /(х) = (2х2 + х + I)7.
17. f(x) = (2х - 5)1/2.
18. /(х) = (4Х + 3)1/2.
19. /(х) = (х4 + I)-2.
20. /(х) = (х5+2)-3.
В задачах 21-24 найдите функцию fix')
и уравнение прямой, касательной к графику f
в указанных точках х. Вычислите значение(я) х, в котором(ых) касательная будет
горизонтальной.
21. /(х) = (2х - I)3; х = 1.
22. /(х) = (Зх — I)4; х = 1.
23. /(х) = (4х - З)1/2; х = 3.
24. f(x) = (2х + 8)1/2; х = 4.
В задачах 25-44, используя общее правило дифференцирования степенных выражений, вычислите функцию dy/dx и упростите результат.
25. у = 3(х2 - 2)4.
26. у = 2(х3 + 6)5.
27. у = 2(х2+Зх)~3.
28. у = З(х3 + х2)-2.
29. у = у/х2 + 8.
30. у = (/Зх - 7.
31. у = (/Зх + 4.
32. у = у/2х — 5.
33. у — tfOfix + 3,6.
34. у = (/1,6х - 4,5.
35. у = (х2 — 4х + 2)1/2.
36. у= (2х2 + 2х — З)1/2.
37. у =
У 2х + 4
38. у = „ 1
у Зх — 7


Глава 8. Производная
125
39. у =
1
(ж3 + 4)5
40. у =
1
(ж2 — З)6
41. v — —п .
4ж2 - 4ж + 1
42. у =
1
2х2 — Зх + 1
43. у =
4
у/х2 — Зж
44. у =
3
\Jx — х2
В задачах 45-50 найдите функцию ff(x) и уравнение прямой, касательной к графику f
в указанных точках х.
45. /(х) = х(4 — х)3; х = 2.
47. /(х) =
х
(2ж - 5)3
49. 	f (х) = х\/2х + 2; х = 1
46. f(x) = х2(1 — ж)4; х = 2.
гг4
48. f (х) = 7); х = 4
к ’ (Зж — 8)2
50. 	/ (ж) = x\Jx — 6; х = 7
х = 3
В задачах 51-56 найдите функцию f(x) и значение(я) х, в котором(ых) касательная проходит горизонтально.
51. 	/(х) = х2(х — 5)3.
53. f (х) =
х
(2ж + 5)2
55. 	f (ж) = у/х2 — 8ж + 20.
52. 	/(ж) = ж3(ж —7)4.
54-/м=^4-
56. 	f (ж) = у/х2 + 4ж + 5.
В задачах 57-62 вычислите приближенное значение(я) х (с точностью до двух деся тичных знаков), в котором(ых) график функции f имеет горизонтальную касатель ную.
57. 	/(х) = х(х — 1)(х2 — 5).
59. /(х) = (х3 — 2х2)(х2 + 1).
61. 	f (х) = \/х4 — 6х2 + х + 12.
58. 	/(х) = х(х — 2)(х + 3)(х — 4).
60. /(х) = (х3 -I- Зх2)(х2 + 4).
62. 	f (х) = \/х± — 4х3 + 4х 4- 20.
В
В задачах 63-74 вычислите каждую производную и упростите результат.
63. 	^[з^ + 1)3].
65.
d (ж3 - 7)4
dx 2х3
67. А[(21-3)!(2^ + 1)3].
69. (4х2\/х2 — 1).
dx v 7
71.
dx у/х - 3
73. 4у(2ж-1)3 (ж2 + З)4.
м-^И*3-з4
d Зх2
бб. 	— Q.
dx (ж2 5)3
б8.^-1)3(^-2)3]. 70. 4 (Зжл/2ж2 + 3).
d ж2
72. 	_
dx у/х2 +1
d / 4ж + 1
Тх\ 2ж2 + Г


126
Часть III. Математический анализ
Применение математики
Экономика и бизнес
75. 	Предельные затраты. Величина общих затрат (сотен долл.) на производство х калькуляторов в день рассчитывается по формуле
С (а?) = 10 Ч- \/2х + 16; 0 < х < 50,
график которой показан на рис. 8.47.
Объем производства, шт.
Рис. 8.47. Иллюстрация к задаче 75
а) Вычислите величину предельных затрат при производстве х калькуляторов в день.
*б) Вычислите значения С'(24) и С" (42) и объясните полученные результаты.
76. Предельные затраты. Величина общих затрат (сотен долл.) на производство х видеокамер в день равна
С (х) = 6 + \/4я + 4; 0 х 30.
а) Вычислите величину предельных затрат при производстве х видеокамер в день.
*б) Вычислите значения С" (15) и С'(24) и объясните полученные результаты.
77. Зависимость предложения от цены. Количество стереосистем х, еженедельно поставляемых в сеть розничных магазинов по цене р долл., задается формулой
х = 80 у/р + 25 - 400; 20 О Ю0,
график которой показан на рис. 8.48.
а) Вычислите функцию dx/dp.
*б) Вычислите предложение и мгновенную скорость изменения предложения как функцию цены, если цена составляет 75 долл. Дайте интерпретацию полученных результатов.


Глава 8. Производная
127
Цена, долл.
Рис. 8.48. Иллюстрация к задачам 77 и 78
78. Зависимость спроса от цены. Количество стереосистем х, еженедельно приобретаемых в сети розничных магазинов по цене р долл., задается формулой
х = 1000 — 60\/р + 25; 20 р 100,
график которой показан на рис. 8.48.
а) Вычислите функцию dx/dp.
*б) Вычислите спрос и мгновенную скорость изменения спроса как функцию цены, если цена составляет 75 долл. Дайте интерпретацию полученных результатов.
79. Сложные проценты. Допустим, на банковский депозит внесена сумма 1000 долл, при годовой процентной ставке г, а сложные проценты начисляются ежемесячно. Сумма на счету в конце четвертого года составит
А = 1000 (1 + ^г)48 долл.
Вычислите скорость изменения суммы А как функции, зависящей от процентной ставки г.
80. Сложные проценты. Допустим, что на депозит внесена сумма 1000 долл, при годовой процентной ставке г, а сложные проценты начисляются каждые полгода. Сумма на счету в конце пятого года составит
А = 100 (1 + |г)10 долл.
Вычислите скорость изменения суммы А как функции, зависящей от процентной ставки г.
Биологические науки
81. 	Рост бактерий. Численность бактерий у в некой среде через х дней описывается формулой
У = (3 • Ю6)
У(х2 - I)2
Вычислите функцию dy/dx.


128
Часть III. Математический анализ
82. 	Загрязнение. В результате сильной утечки из септического резервуара в небольшое озеро курортной зоны попало большое количество болезнетворных бактерий. Департамент здравоохранения рассчитал, что через t дней после внесения в озеро антибактерицидного средства численность бактерий в кубическом сантиметре воды составит
С (t) = 500 (8 - f)2 ; 0 sj t «s 7.
а) Вычислите функцию C'(t), используя общее правило дифференцирования степенных выражений.
*б) Вычислите значения С (1) и С (6) и объяните полученные результаты.
Социальные науки
83. 	WWW Обучение. В 1930 году Л. Л. Терстоун нашел следующую формулу, описывающую зависимость времени обучения Т от количества изучаемых понятий п.
Т = f (п) — уп\/п — а.
к
Здесь а, с и к — эмпирические константы. Предположим, что для отдельного человека время Т (в минутах), затрачиваемое на изучение п понятий, равно
Т — f (п) = 2п\/п — 2.
а) Вычислите функцию dT/dn.
*б) Вычислите значения /'(11) и /'(27) и проинтерпретируйте результаты.


Глава 8. Производная
129
8.7. 	Маржинальный анализ в бизнесе и экономике
■ Предельные затраты, доход и прибыль
■ Решение практических задач
■ Предельные средние затраты, доход и прибыль
Предельные затраты, доход и прибыль
www Одним из важных применений математического анализа в бизнесе и экономике является маржинальный анализ. Ранее мы уже ввели понятие предельных затрат. Экономисты говорят также о предельном доходе и предельной прибыли. Напомним, что слово предельный обозначает мгновенную скорость изменения, т.е. производную.
Предельные затраты, доход и прибыль
Пусть х — объем (количество) продукции, выпускаемой за определенный интервал времени.
Общие затраты = С(х).
Предельные затраты = С'Сг).
Общий доход = R(x).
Предельный доход = 7?'(х).
Общая прибыль = Р(х) = R(x) — С(х).
Предельная прибыль = Р'(х) = R'^x} — С'(х) =
— (предельный доход) — (предельные затраты)
Предельные затраты (доход или прибыль) — это мгновенная скорость изменения затрат (дохода или прибыли) при заданном объеме производства.
Важно помнить: когда рассматривается функция затрат С(х), подразумевается, что она описывает общие затраты на производство х изделий. Чтобы найти точную величину затрат на производство отдельного изделия, нужно вычислить разницу двух последовательных значений С(х).
Общие затраты на производство (х + 1) изделий = С(х + 1).
Общие затраты на производство х изделий = С(х).
Точная величина затрат на производство (х + 1)-го изделия = С(х -I-1) — С(х).
Как отмечалось в разделе 8.4, функцию предельных затрат можно использовать для вычисления приблизительной величины затрат. Чтобы убедиться в этом,


130
Часть III. Математический анализ
необходимо вернуться к определению производной.
С' (х) — lim
/1—>0
С (х + h) — С (х) h
С' (х) » С (ж + К) - С (ж),
Предельные затраты
h ф 0;
Д = 1.
Таким образом, величина предельных затрат приблизительно равна С(х + 1) — — С(х), т.е. точной величине затрат на производство (х 4- 1)-го изделия. Эти наблюдения подытожены ниже и проиллюстрированы на рис. 8.49.
Предельные затраты и точная величина затрат
Если С(х) — величина затрат на производство х изделий, то функция предельных затрат показывает приблизительные затраты на производство (т + 1)-го изделия.
Предельные затраты Точная величина затрат С'(х) « С(х + 1) - ОД
Дайте аналогичную интерпретацию для функции общего дохода и функции общей прибыли.
Пример 8.41 (Анализ затрат).
Компания производит топливные баки для автомобилей. Величина общих затрат на производство х баков в неделю (в долларах) равна
С(ж) = 10000 + 90х - 0,05х2.
1. Вычислите функцию предельных затрат.
2. Вычислите значение С'(500) и опишите словесно получаемый результат.


Глава 8. Производная
131
3. 	Вычислите точную величину затрат на производство 501-го бака и проанализируйте связь между этим результатом и предельными затратами, найденными при решении п. 2.
Проверьте все расчеты с помощью графической утилиты.
Решение.
1. С"(я) = 90 - 0,1гг.
2. С'(500) = 90 - 0,1 • 500 = 40 долл.
К функции предельных затрат, без сомнения, можно применить стандартную интерпретацию производной. Следовательно, при уровне производства 500 баков в неделю величина общих затрат растет со скоростью 40 долл, в неделю. Можно воспользоваться также специфической интерпретацией предельных затрат, т.е. 40 долл. — это приблизительная величина затрат на производство 501-го бака.
3. С(501) = 10000 + 90 • 501 - 0,05 • 5012 =
= 42 539,95 ДОЛЛ. Общие затраты на производство 501 бака в неделю.
С(500) = 10000 + 90 • 500 - 0,05 • 5002 =
= 42 500,00 ДОЛЛ. Общие затраты на производство 500 баков в неделю. 0(501) - 0(500) = 42 539,95 - 42 500,00 =
= 39,95 ДОЛЛ. Точная величина затрат на производство 501-го бака.
Сравнивая эти результаты с предельными затратами, вычисленными при решении п. 2, легко видеть, что величина предельных затрат действительно неплохо аппроксимирует точную величину затрат на производство 501-го бака.
Проверка этих вычислений продемонстрирована на рис. 8.50. ■
nDeriv<Vi,X,500>
40
500- >X:Yi
42500
501- »X:Yi
42539.95
Рис. 8.50. Значения функции
У1 = 10 000 + 90а: — 0,05а:2


132
Часть III. Математический анализ
Упражнение 8.41.
Компания производит автоматические коробки передач для автомобилей. Общие затраты на производство х коробок передач в неделю (в долларах) равна
С(х) = 50000 4- 600т - 0,75т2.
1. Вычислите функцию предельных затрат.
2. Вычислите значение С" (200) и опишите словесно получаемый результат.
3. Вычислите точную величину затрат на производство 201-й коробки передач и проанализируйте связь между этим результатом и предельными затратами, найденными при решении п. 2.
Проверьте все расчеты с помощью графической утилиты. ■
Для сравнения полезно вычислять как приблизительную величину затрат С'(х), так и точную величину затрат С(х + 1) — С(х). Однако на практике предельные затраты анализируются значительно чаще, чем точные, поскольку функцию предельных затрат намного легче представлять графически. На рис. 8.51 показан график функции затрат, рассмотренной в примере 8.41, и касательные в точках х = 200 и х = 500. На графике явно видно, что с ростом производства наклон касательной уменьшается. Следовательно, затраты на производство следующего бака также снижаются, что указывает на правильно организованный производственный процесс. О графическом анализе подробно рассказано в главе 9.
Рис. 8.51. Функция С(х) = 10 000 -I- 90# — 0,05ж2
Решение практических задач
Теперь обсудим, каким образом цена, спрос, доход, затраты и прибыль оказываются связанными между собой в типичных прикладных задачах. Хотя в уравнении зависимости спроса от цены независимая переменная может представлять


Глава 8. Производная
133
как цену, так и спрос, чаще всего в функциях, описывающих взаимосвязь между предельными доходами, затратами и прибылью, в качестве такой переменной выбирают именно спрос.
Задание 8.16.
Чтобы определить спрос на новые радиоприемники, отдел маркетинга провел исследование рынка, результаты которого представлены в табл. 8.13.
Таблица 8.13. Зависимость спроса от цены
Спрос X, шт.
Цена р, долл.
3000
7
6000
4
1. Предполагая, что связь между ценой р и спросом х линейна, постройте уравнение зависимости спроса от цены и запишите результат в виде х = f(p). Постройте график уравнения и найдите область определения /. Проанализируйте эффект роста цены при снижении спроса.
2. Решите уравнение, найденное в п. 1, относительно р, получив уравнение вида р = д(х). Постройте график уравнения и найдите область определения функции д. Проанализируйте эффект роста цены при снижении спроса. ■
Пример 8.42 (Производственная стратегия).
Отдел маркетинга настаивает на выпуске новых радиоприемников. Проведя исследование рынка, сотрудниками отдела было получено следующее уравнение зависимости спроса от цены.
X = 10000 — 1000р. х- спрос при ценер. (8.14)
Решая уравнение (8.14) относительно переменной р, получаем следующую зависимость.
р = 10 — 0,001ж, (8.15)
где х — это количество радиоприемников, которые, вероятнее всего поступят в розничную сеть по цене р долл.
Финансовый отдел определил следующую функцию затрат.
С(х) = 7000 + 2х, (8.16)
где 7000 долл. — это приблизительные постоянные затраты (стоимость оборудования и накладные расходы), а 2 долл. — приблизительные переменные издержки на производство одного радиоприемника (включают оплату труда, стоимость материалов, затраты на маркетинговые исследования, рекламу, хранение, доставку и т.п.).


134
Часть III. Математический анализ
1. Найдите область определения функции, описывающей зависимость спроса от цены (8.15).
2. Вычислите функцию предельных затрат С' (ж) и дайте ее интерпретацию.
3. Найдите функцию дохода, как функцию переменной х, и ее область определения.
4. Вычислите предельный доход для значений х = 2000, 5000 и 7000. Объясните полученные результаты.
5. Постройте график функции затрат и функции дохода в одной системе координат, найдите точку пересечения этих графиков и проинтерпретируйте результаты.
6. Вычислите функцию прибыли и ее область определения, постройте график этой функции.
7. Вычислите предельную прибыль для значений х = 1000, 4000 и 6000. Объясните полученные результаты.
Решение.
1. Поскольку цена р и спрос х должны быть неотрицательными, О 0 и
р = 10 - 0,001х > 0;
10 0,001х;
10000 х.
Таким образом, допустимыми значениями х будут 0 х 10 000.
2. Величина предельных затрат С'(ж) = 2. Поскольку эта величина постоянна при любом объеме производства, затраты на производство одного дополнительного радиоприемника составят 2 долл.
3. Доход — это сумма /?, получаемая компанией при производстве и реализации х радиоприемников по цене р долл. Его величина определяется следующим выражением.
R = (Объем продаж) • (Цена радиоприемника) = хр.


Глава 8. Производная
135
Доход R можно выразить как функцию переменной р, используя уравнение (8.14), или как функцию переменной х, используя уравнение (8.15). Как отмечалось ранее, в предельных функциях независимая переменная обычно представляет количество изделий х. Исходя из этого, функция дохода имеет следующий вид.
R(x) = хр = ж(Ю — 0,001ж) = На основе уравнения (8.15) (8.17)
— Юж — 0,001ж2.
Поскольку уравнение (8.15) определено только для 0 х < 10000, область определения функции дохода тоже задается отрезком 0 х 10 000.
4. Предельный доход описывается следующим выражением.
R'(ж) = 10 - 0,002ж.
Для объемов производства ж = 2000, 5000 и 7000 получим такие результаты.
Я'(2000) = 6, Л'(5000) = 0, Я'(7000) = -4.
Следовательно при производстве 2000,5000 и 7000 радиоприемников в неделю доход с единицы продукции будет изменяться приблизительно на 6, 0 и —4 долл. Иначе говоря, при увеличении еженедельного объема производства до 2000 радиоприемников доход будет расти. При дальнейшем увеличении еженедельного объема производства до 5000 радиоприемников доход не изменится, а при выходе на объем 7000 радиоприемников в неделю доход будет падать.
5. Графики функций 7?(ж) и С(ж) в общей системе координат, показаны на рис. 8.52. Точки пересечения кривых дохода и затрат называются точками безубыточности (используются также синонимы “критическая точка”, “порог рентабельности”, ’’точка самоокупаемости” и “точка нулевой прибыли”. — Примеч. ред.\ поскольку при таких уровнях производствах доход равен затратам — компания не зарабатывает, но и не терпит убытков. Точки безубыточности можно вычислить следующим образом.
С (ж) = R (х);
7000 + 2ж = Юж — 0,001ж2;
0,001ж2 - 8ж + 7000 = 0;


136
Часть III. Математический анализ
Ж2 — 8000х + 7 000 000 = 0; Решение квадратного уравнения
(см. приложение А.9).
8000 ± х/80002 — 4 • 7 000 000
х = г
_ 8000 ± V36000000
2
_ 8000 ± 6000
_ 2 = 1000; 7000.
77(1000) = 10 • 1000 - 0,001 ■ 10002 = 9000;
С(ЮОО) = 7000 + 2 • 1000 = 9000;
77(7000) = 10 • 7000 - 0,001 • 70002 = 2 1 000;
(7(1000) = 7000 + 2 • 7000 = 21000.
Таким образом, точками безубыточности будут точки (1000; 9000) и (7000; 21 000), как показано на рис. 8.52. Внимательно их изучив, можно заметить, что затраты превышают доходы при объемах производства от 0 до 1000, а также от 7000 до 10 000. Следовательно, при производстве такого количества продукции компания терпит убытки. С другой стороны, при объеме производства от 1000 до 7000 доход больше затрат, и компания получает прибыль.
Еженедельный объем производства, шт.
Рис. 8.52. Графики функций затрат и дохода


Глава 8. Производная
137
6. Функция прибыли вычисляется как
Р(аг) = Я(ж) - С(х) =
= (Юж - 0,001а;2) - (7000 + 2х) =
= -0,001а;2 + 8а; - 7000.
Область определения функции затрат представляет собой луч х 0, а область определения функции дохода — отрезок 0 < х 10 000. Таким образом, область определения функции прибыли — это множество значений х, в которых определены обе функции, т.е. 0 х 10 000. График функции прибыли показан на рис. 8.53. Следует отметить, что координаты х точек безубыточности на рис. 8.52 — это точки пересечения функции прибыли с осью х. Кроме того, на интервалах, где затраты превышают или меньше дохода, прибыль отрицательна и положительна соответственно.
Р(х), долл.
юооо ■
-10 000 ■
/ 5000 \ 10 000
Г Объем производства, шт.
\
-20 000 -
\
-30000 -
Рис. 8.53. График функции прибыли
7. Предельная прибыль рассчитывается по формуле
Р'(я) = —0,002х + 8.
Для объемов производства 1000, 4000 и 6000 шт. в неделю получаем следующие значения предельной прибыли.
р'(Ю00) = 6, Р'(4000) = 0, Р'(бООО) = —4.
Это означает, что при объемах производства 1000, 4000 и 6000 радиоприемников в неделю прибыль с единицы продукции будет изменяться приблизительно на 6, 0 и —4 долл. Иначе говоря, при увеличении еженедельного объема производства до 1000 радиоприемников прибыль будет расти, при росте объема производства до 4000 шт. в неделю прибыль не меняется,


138
Часть III. Математический анализ
а при увеличении его до 6000 шт. в неделю прибыль падает. Очевидно, что объем производства, обеспечивающий получение максимальной прибыли, составляет 4000 шт. в неделю. ■
Точки безубыточности можно также найти, используя графическую утилиту. Точки безубыточности для примера 8.42 показаны на рис. 8.54.
www Исследование, проведенное в примере 8.42, необычайно важно, поскольку описывает взаимосвязь между основополагающими понятиями экономического и математического анализа. В следующей главе вы познакомитесь с отдельной методикой вычисления объема производства и отпускной цены, при которых достигается максимальная прибыль.
Упражнение 8.42.
Выполните следующие задания, используя функции дохода и прибыли из примера 8.42.
1. Вычислите значения В!(3000) и Я'(6000) и объясните полученные результаты.
2. Вычислите значения Р'(2000) и Р'(7000) и объясните полученные результаты. ■
Задание 8.17.
Пусть
С(т) = 12000 + 5х и R(x) = 9х - 0,002т2.
Объясните, почему ниже используется знак Затем найдите верное выражение для функции прибыли.
Р(т) = Р(т) - С(т) / Эх - 0,002т2 - 12 000 + 5т. и


Глава 8. Производная
139
Предельные средние затраты, доход и прибыль
Иногда полезно провести маржинальный анализ средних затрат (затраты на единицу продукции), среднего дохода (доход на единицу продукции) и средней прибыли (прибыль на единицу продукции).
Предельные средние затраты, доход и прибыль
Если х — объем продукции, производимой за определенный промежуток времени, то
Доход на единицу продукции:
Затраты на единицу продукции: средние затраты = С (х) = ——;
х
предельные средние затраты = С' (х) = —С (ж). ах
nr \ R(x>)
средний доход = R(x) = —
X
предельные средний доход = R! (ж) = —R (х). ах
Р (х)
Прибыль на единицу продукции: средняя прибыль = Р (ж) = —— ;
X
предельные средняя прибыль = Р' (х) = —Р (#). ах
Пример 8.43 (Анализ затрат).
Небольшой машиностроительный завод производит буры для нефтедобывающей промышленности. Аналитический отдел завода установил, что величина общих затрат на производство х буров в день (в долларах) вычисляется по формуле
С(ж) = 1000 + 25а; - 0,hr2.
1. Вычислите функции С (аг) и С1 (я).
2. Вычислите значения С (10) и С' (10) и объясните полученный результат.
3. Используя результаты решения п. 2, вычислите приблизительную величину средних затрат на производство одного бура при выпуске 11 буров в день.
Решение.
„ ч С(х) 1000 + 25а: - 0,1а:2
1. 	С (х) — —— =
X X
ЮОО or о .
= 1- 25 — 0,1а:;
х
. d . 1000 п ,
С " dx^ ~ х^ _0,1'
Функция средних затрат
Функция предельных средних затрат


140
Часть III. Математический анализ
2‘ с(10) = + 25“°Л10) =124 д°лл-;
С' (10) = - ОД = -10,10 долл.
При объеме производства 10 буров в день средние затраты на производство одного бура составляют 124 долл., и они растут со скоростью 10,10 долл, на один бур.
3. 	Если объем производства увеличится на один бур, то средние затраты на производство бура снизятся приблизительно на 10,10 долл. Таким образом, величина средних затрат на производство одного бура при выпуске 11 буров в день равна приблизительно 124 — 10,10 = 113,90 долл. ■
Упражнение 8.43.
Рассмотрим функцию затрат на производство радиоприемников из примера 8.42.
С(х) = 7000 + 2гг.
1. Вычислите функции С (х) и С' (х).
2. Вычислите значения С (100) и С' (100) и объясните полученный результат.
3. Используя результаты решения п. 2, вычислите приблизительную величину
средних затрат на производство радиоприемника при объеме производства, равном 101 шт. в день. ■
Задание 8.18.
Студент получил следующее решение упражнения 8.43.
С (х) — 7000 + 2х, Затраты
С' (х) = 2; Предельные затраты
С' (х) 2
= —. "Средние" предельные затраты
X X
Объясните, почему последняя функция — это не то же, что функция предельных средних затрат. I
Предупреждение.
1. 	Чтобы вычислить функцию предельных средних затрат, необходимо сначала определить функцию средних затрат, а затем вычислить ее производную. Как показано в задании 8.18, если выполнять эти два этапа в обратном порядке, то получится другая функция, которая не имеет значимых экономических интерпретаций.


Глава 8. Производная
141
2. 	Следует напомнить, что функция предельных затрат имеет две интерпретации: обычной производной, описывающей мгновенную скорость изменения, и экономической характеристики, определяющей приблизительные затраты на производство (х + 1)-го предмета. Последняя интерпретация никак не соотносится с функцией предельных средних затрат. Возвращаясь к примеру 8.43, при интерпретации С' (х) = —10,10 долл, будет некорректно утверждать что величина средних затраты на производство следующего бура приблизительно равна 10,10 долл. Фактически фраза “величина средних затрат на производство следующего бура” не имеет смысла. Концепция усреднения применяется к совокупности элементов, а не к одному элементу. Приведенные выше примечания справедливы также для функций дохода и прибыли.
Ответы к упражнениям
8.41. 1) С"(я) = 600 - 1,5гг.
2) С'(200) = 300. При производстве 200 коробок передач величина общих затрат растет со скоростью 300 долл, на коробку передач. Кроме того, приблизительная величина затрат на производство 201-й коробки передач равна 300 долл.
3) С(201) — С(200) = 299,95 долл. Величина предельных затрат из п. 2 неплохо аппроксимирует точное значение.
8.42. 1) R' (3000) = 4. При производстве 3000 радиоприемников увеличение объ¬
ема производства на единицу продукции приводит к росту дохода приблизительно на 4 долл.
R' (6000) = —2. При производстве 6000 радиоприемников увеличение объема производства на единицу продукции приводит к снижению дохода приблизительно на 2 долл.
2) Р'(2000) = 4. При производстве 2000 радиоприемников увеличение объема производства на единицу продукции приводит к росту прибыли приблизительно на 4 долл.
Р'(7000) = —6. При производстве 7000 радиоприемников увеличение объема производства на единицу продукции приводит к снижению прибыли приблизительно на 6 долл.
2) С (100) = 72 долл.; С" (100) = —0,70 долл. При производстве 100 ра¬
диоприемников величина средних затрат на производство одного радиоприемника равна 72 долл, и растет со скоростью 0,70 долл.
3) Приблизительно 71,30 долл.


142
Часть III. Математический анализ
Практикум 8.7
Применение математики
Экономика и бизнес
1. Анализ затрат. Величина общих затрат на производство х кухонных комбайнов (в долларах) равна
С(х) = 2000 + 50а: - 0,5а:2.
а) Вычислите точную величину затрат на производство 21-го кухонного комбайна.
б) Используя функцию предельных затрат, вычислите приблизительную величину затрат на производство 21 -го кухонного комбайна.
2. Анализ затрат. Величина общих затрат на производство х электрогитар (в долларах) равна
С(а:) = 1000 + 100а: - 0,25а:2.
а) Вычислите точную величину затрат на производство 51-й электрогитары.
б) Используя функцию предельных затрат, вычислите приблизительную величину затрат на производство 51-й электрогитары.
3. Анализ затрат. Величина общих затрат на производство х автомобильных кузовов (в долларах) равна
С(ж) = 60000 + 300х.
а) 	Вычислите средние затраты на производство одного кузова, если производится всего 500 кузовов.
*б) Вычислите предельные средние затраты при производстве 500 кузовов и объясните полученные результаты.
в) Используя результаты решения пп. а и б, вычислите приблизительную величину средних затрат на производство одного кузова при общем объеме производства 501 шт.
4. Анализ затрат. Величина общих затрат на издание х словарей (в долларах) равна
С(х) = 20 000 + 102.


Глава 8. Производная
143
а) 	Вычислите средние затраты на выпуск словаря, если издается 1000 словарей.
*б) Вычислите предельные средние затраты при производстве 1000 словарей и объясните полученные результаты.
в) 	Используя результаты решения пп. аиб9 вычислите приблизительное значение средних затрат на выпуск словаря при объеме производства 1001 шт.
5. Анализ прибыли. Общая прибыль от продажи х скейтбордов (в долларах) равна
Р(х) = 30# — 0,3л?2 — 250; 0 х 100.
а) Вычислите точную прибыль от продажи 26-го скейтборда.
б) Используя функцию предельной прибыли, вычислите приблизительную величину прибыли от продажи 26-го скейтборда.
6. Анализ прибыли. Общая прибыль от продажи х портативных стереосистем (в долларах) равна
Р(ж) = 22х — 0,2х2 — 400; 0 х 100.
а) Вычислите точную прибыль от продажи 41-й стереосистемы.
б) Используя функцию предельной прибыли, вычислите приблизительную величину прибыли от продажи 41-й стереосистемы.
* 7. Анализ прибыли. Общая прибыль от продажи х видеокассет (в долларах) равна
Р(х) = 5х — 0,005х2 — 450; 0 х 1000.
Оцените предельную прибыль для заданных значений х и объясните полученные результаты.
а) 	х = 450. б) х = 750.
* 8. Анализ прибыли. Общая прибыль от продажи х фотоаппаратов (в долларах) равна
Р(х) = 12а: - 0,02а:2 - 1000; 0 х 600.
Оцените предельную прибыль для заданных значений х и объясните полученные результаты.
а) 	х = 200. 6) х = 350.
9. 	Анализ прибыли. Общая прибыль от продажи х газонокосилок (в долларах) равна
Р(х) = 30а: - 0,03а:2 - 750; 0 < х 1000.
а) 	Вычислите среднюю прибыль на газонокосилку, если производится 50 газонокосилок.


144
Часть III. Математический анализ
*б) Вычислите предельную среднюю прибыль при производстве 50 газонокосилок и объясните полученный результат.
в) 	Используя результаты решения пп. а и б, вычислите среднюю прибыль на газонокосилку, если производится 51 газонокосилка.
10. Анализ прибыли. Общая прибыль от продажи х грилей на углях (в долларах) равна
Р(х) = 20ж — 0,02ж2 — 320; 0 < х 1000.
а) 	Вычислите среднюю прибыль на гриль, если производится 40 грилей.
*б) Вычислите предельную среднюю прибыль при производстве 40 грилей и объясните полученный результат.
в) 	Используя результаты решения пп. а и б, вычислите среднюю прибыль на гриль, если производится 41 гриль.
11. Анализ доходов. Ценар (в долларах) и спрос х для некой модели радиоприемника с таймером связаны уравнением
х = 4000 — 40р.
а) Выразите цену р через спрос х и найдите область определения этой функции.
б) Вычислите доход R(x) от продажи х радиоприемников с таймером и объясните полученный результат. Какова область определения R1
*в) Вычислите предельный доход при производстве 1600 радиоприемников и объясните полученный результат.
*г) Вычислите предельный доход при производстве 2500 радиоприемников и объясните полученный результат.
12. Анализ доходов. Цена р (в долларах) и спрос х для некой модели парового утюга связаны уравнением
х = 1000 — 20р.
а) Выразите цену р через спрос х и найдите область определения этой функции.
б) Вычислите доход R(x) от продажи х паровых утюгов и объясните полученный результат. Какова область определения R?
*в) Вычислите предельный доход при производстве 1600 паровых утюгов и объясните полученный результат.
*г) Вычислите предельный доход при производстве 2500 паровых утюгов и объясните полученный результат.
13. Доход, затраты и прибыль. Уравнение зависимости спроса от цены и функция затрат на производство циркулярных станков имеют вид.
х = 600 — ЗОр и С(х) — 7200 + 60х,
где х — количество станков, продаваемых по цене р долл., а С(х) — общие затраты на производство х станков (в долларах).
а) 	Выразите цену р как функцию спроса х и найдите область определения этой функции.


Глава 8. Производная
145
б) Вычислите величину предельных затрат.
в) Выразите функцию дохода и установите область ее определения.
г) Вычислите предельный доход.
*д) Вычислите значения 7?'(1500) и Я'(4500) и объясните полученные результаты.
е) Постройте в одной и той же системе координат графики функций затрат и дохода для 0 < х < 6000. Найдите точки безубыточности и укажите области убытков и прибыли.
ж) Выразите прибыль как функцию переменной х.
з) Вычислите предельную прибыль.
*и) Вычислите значения Р'(1500) и Р'(ЗООО) и объясните полученные результаты.
14. Доход, расход и прибыль. Уравнение зависимости спроса от цены и функция затрат на производство телевизоров имеют следующий вид:
х = 9000 - ЗОр и С(х) = 15 000 + ЗОж,
где х — количество телевизоров, продаваемых по цене р, долл., а С(х) — общие затраты на производство х телевизоров (в долларах).
а) Выразите цену р как функцию спроса х и найдите область определения этой функции.
б) Вычислите предельные затраты.
в) Выразите функцию дохода и установите область ее определения.
г) Вычислите предельный доход.
*д) Вычислите значения Я'(3000) и /?'(6000) и объясните получаемые результаты.
е) Постройте в одной и той же системе координат графики функций затрат и дохода для 0 < х < 9000. Найдите точки безубыточности и укажите области убытков и прибыли.
ж) Выпазите прибыль как функцию переменной х.
з) Вычислите предельную прибыль.
*и) Вычислите значения Р'(1500) и Р'(4500) и объясните получаемые результаты.
15. Доход, затраты и прибыль. Компания планирует производить и продавать новую модель электрического тостера на два ломтика. После проведения всестороннего исследования рынка, отдел маркетинга сделал следующие оценки: недельный спрос равен 200 тостерам при цене 16 долл, за штуку и 300 тостерам при цене 14 долл, за штуку. Финансовый отдел выяснил, что постоянные еженедельные затраты составят 1400 долл., а переменные издержки (в расчете на единицу продукции) будут равны 4 долл.


146
Часть III. Математический анализ
а) Предположим, что связь между ценой р и спросом х линейна. Используя оценки отдела маркетинга, выразите величину р как функцию, зависящую от переменной х9 и найдите область определения этой функции.
б) Выразите доход как функцию, зависящую от переменной х, и установите область определения этой функции.
в) Предположим, что функция затрат линейна. Используя оценки финансового отдела, выразите зависимость затрат от переменной х.
г) Постройте в одной и той же системе координат графики функции затрат и функции дохода для 0 х 1000. Найдите точки безубыточности и укажите области убытков и прибыли.
д) Выразите прибыль как функцию переменной х.
*е) Вычислите приближенное значение предельной прибыли при х = 250 и х = 475 и объясните полученные результаты.
16. Доход, затраты и прибыль. Компания, упомянутая в задаче 15, также планирует производить и продавать модель тостера на четыре ломтика. Для этого тостера оценки отдела маркетинга таковы: недельный спрос равен 300 тостерам при цене 25 дол. за штуку и 400 тостерам при цене 20 долл, за штуку. По оценкам финансового отдела постоянные еженедельные затраты составлят 5000 долл., а переменные издержки будут равны 5 долл.
а) Предположим, что связь между ценой р и спросом х линейна. Используя оценки отдела маркетинга, выразите величину р как функцию, зависящей от переменной х, и найдите область определения этой функции.
б) Вычислите доход как функцию, зависящую от переменной х, и установите область определения этой функции.
в) Предположим, что функция затрат является линейной. Используя оценки финансового отдела, выразите зависимость затрат от переменной х.
г) Постройте в одной и той же системе координат графики функций затрат и дохода для 0 х 800. Найдите точки безубыточности и укажите области убытков и прибыли.
д) Выразите прибыль как функцию переменной х.
♦е) Вычислите приближенное значение предельной прибыли при х = 325 и х = 425 и объясните полученные результаты.
17. Доход, затраты и прибыль. Общие затраты и общий доход от производства и продажи х горнолыжных костюмов (в долларах) составляют соответственно
С(х) = 24х + 21900 и R(x) = 200яг - 0,2а?2; 0 < х < 1000.


Глава 8. Производная
147
а) Вычислите значение х, при котором график R(ж) имеет горизонтальную касательную.
б) Вычислите функцию прибыли Р(х).
в) Вычислите значение х, при котором график Р(х) имеет горизонтальную касательную.
г) Постройте в одной и той же системе координат графики С(х), R(x) и Р(х) для 0 х < 1000. Найдите точки безубыточности и точки пересечения графика Р(х) с осью х.
18. Доход, затраты и прибыль. Общие затраты и общий доход от производства и продажи х фенов (в долларах) составляют соответственно
С(ж) = 5х + 2340 и R(x) = 40а: — 0,1х2; 0 х 400.
а) Вычислите значение х, при котором график R(x) имеет горизонтальную касательную.
б) Вычислите функцию прибыли Р(х).
в) Найдите значение х, при котором график Р(х) имеет горизонтальную касательную.
г) Постройте в одной и той же системе координат графики С(х), R(x) и Р(я) для 0 х 400. Найдите точки безубыточности и точки пересечения графика Р(х) с осью х.
19. Анализ безубыточности. Уравнения зависимости спроса от цены и функция затрат для производства садовых шлангов имеют следующий вид.
р = 20 — \/х и С(х) — 500 + 2х.
Здесь х — количество садовых шлангов, которые можно продать по цене р долл., аОД - общие затраты на производство х садовых шлангов (в долларах).
а) Выразите доход как функцию х.
б) Постройте в одном окне графики функций затрат и дохода для 0 х 400. Используя методы аппроксимации, найдите точки безубыточности с точностью до ближайшего целого.
20. Анализ безубыточности. Уравнения зависимости спроса от цены и функция затрат на производство шелковых шарфов ручной работы имеют следующий вид.
р = 60 — 2\/х и С'(я) = 3000 4- 5х.
Здесь х — количество шарфов, которые можно продать по цене р долл., а С(х) — общие затраты на производство х шарфов (в долларах).
а) Выразите доход как функцию переменной х.
б) Постройте в одном окне графики функций затрат и дохода для 0 х 900. Используя методы аппроксимации, найдите точки безубыточности с точностью до ближайшего целого.


148
Часть III. Математический анализ
21. 	Анализ безубыточности. В табл. 8.14 содержатся данные о цене, спросе и полных затратах на производство диаскопических проекторов, где р — оптовая цена проектора (в долларах) при спросе х проекторов, а С — общие затраты (в долларах) на производство х проекторов.
Таблица 8.14. Цена, спрос и затраты на производство диаскопических проекторов
ж, шт.
р, долл.
С,долл.
3190
581
1 130 000
4570
405
1241000
5740
181
1410000
7330
85
1620000
а) Постройте уравнение квадратичной регрессии, описывающее взаимосвязь спроса и цены, используя х в качестве независимой переменной.
б) Постройте уравнение линейной регрессии, описывающие общие производственные затраты, используя х в качестве независимой переменной. Вычислите приблизительные постоянные затраты и переменные издержки в расчете на проектор. Округлите ответ до ближайшего доллара.
в) Найдите точки безубыточности. Округлите ответ до ближайшего целого.
г) Укажите диапазон цен, в котором компания будет получать прибыль. Округлите ответ до ближайшего доллара.
22. 	Анализ безубыточности. В табл. 8.15 содержатся данные о цене, спросе и общих затратах на производство спортивных тренажеров, где р — оптовая цена тренажера (в долларах) при спросе х тренажеров, а С — общие затраты (в долларах) на производство х тренажеров.
Таблица 8.15. Цена, спрос и общие затраты на производство тренажеров
X, шт.
р, долл.
С,долл.
2910
1435
3 650000
3415
1280
3 870 000
4645
1125
4190 000
5330
910
4380 000
а) Постройте уравнение линейной регрессии описывающее зависимость спроса от цены, используя х в качестве независимой переменной.
б) Составьте уравнение линейной регрессии, описывающее общие производственные затраты, используя в качестве независимой переменной величину х. Вычислите приблизительные постоянные затраты и переменные издержки в расчете на тренажер. Округлите ответ до ближайшего доллара.
в) Найдите точки безубыточности. Округлите ответ до ближайшего целого.
г) Определите диапазон цен, при которых компания будет получать прибыль. Округлите ответ до ближайшего доллара.


Глава 8. Производная
149
Ключевые слова, основные обозначения и формулы
8.1. Пределы. Предел; функция абсолютного значения; предел слева; левосторонний предел; предел справа; правосторонний предел; свойства пределов; пределы полиномиальных и рациональных функций; неопределенное выражение 0/0; разностное отношение;
lim /(х); lim /(х); lim /(х);
X—>С х—>с~ х—>с+
/(a + h) — f(a) Ит /(а+/г)-/(а) h 1 h—»о h
8.2. Пределы и непрерывность. Непрерывность в точке; непрерывность на открытом интервале; разрыв в точке; непрерывность справа; непрерывность слева; непрерывность на закрытом интервале; общие свойства непрерывности; свойства непрерывности отдельных функций; вертикальная асимптота; решение неравенств с использованием свойств непрерывности; знаковая диаграмма; проверочное количество; количество разбиения
lim f(x) = f(c), если функция f в точке х = с непрерывна; х—>с
lim f(x) = оо; lim f(x) = —оо.
х—х—►с
8.3. Производная. Средняя скорость изменения; отношение приращения; средняя скорость движения; мгновенная скорость движения; мгновенная скорость изменения; секущая; наклон графика; наклон касательной; производная; дифференцирование; дифференцируемость; интерпретации производной; недифферен-
цируемость;
f'(T\ /(^ + Л) -
8.4. 	Производные от констант, степенных выражений и сумм. Обозначение производной; правило дифференцирования постоянных функций; правило дифференцирования степенных выражений; правило дифференцирования константы, умноженной на функцию; правило дифференцирования сумм и разностей; функ¬
ция предельных затрат;
m У;
dx
8.5. Производные от произведений и отношений. Правило дифференцирования произведений; правило дифференцирования отношений.
8.6. Цепное правило: дифференцирование сложных функций. Общее правило дифференцирования степенных выражений; цепное правило; комбинирование правил дифференцирования.
8.7. Маржинальный анализ в бизнесе и экономике. Предельные затраты; предельный доход; предельная прибыль; точные затраты; уравнение зависимости спроса от цены; функция затрат; функция дохода; предельный доход; точки безубыточности; функция прибыли; предельная прибыль; средние затраты; предельные


150
Часть III. Математический анализ
средние затраты; средний доход; предельный средний доход; средняя прибыль; предельная средняя прибыль;
С"(ж); С (я); С' (х); Я'(я); Я(ж); Я'(х); Р'(х); Р(ж); Р’(х).
Общие правила дифференцирования
-j- [u(ar) ± v(z)] = u'(x) + v'(x)-, dx
[F(x)S(a;)] = F(x)S'(x) + S(x)F'(x); d T(x) _ B(x)T'(x) — T(x)B'(x) dx B(x) [B(x)]2
[-и(ж)]п = n [u(x)]n_1 u'(x).
Упражнения для повторения  * 1
Выполните все упражнения этого обзорного раздела и сравните результаты с ответами, помещенными в конце книги. Ответы ко многим упражнениям на повторение приводятся вместе с номером соответствующего раздела (курсивом). Если у вас возникают затруднения при решении какой-либо задачи, повторите материал соответствующего раздела.
Во многих задачах этого практикума требуется найти производную. Большинство ответов нужно представить, как в упрощенной, так и исходной форме производной. При проверке полученных результатов сначала убедитесь в корректности выбора правил дифференцирования и только затем переходите к анализу алгебраических преобразований.
А
1. 	Вычислите указанные величины для функции у = f(x) = 2х2 + 5.
а) Изменение величины у, если переменная х меняется с 1 до 3.
б) Среднюю скорость изменения величины у как функции, зависящей от переменной х, если значение х меняется с 1 до 3.
в) Наклон секущей, проходящей через точки (1;/(1)) и (3;/(3)) на графике У = /(я)-
г) Мгновенную скорость изменения величины у как функции, зависящей от переменной х, в точке х = 1.


Глава 8. Производная
151
д) Наклон касательной к графику у = f(x) в точке х — 1.
е) /'(!)•
2. 	Используя двухэтапный процесс вычисления производной, рассчитайте производную /'(х) функции /(х) = —Зх + 2.
3. 	Пусть Unis-,! /(х) = 2 и limx_>i р(х) = 4, вычислите следующие значения,
а) 	Нт (5/(х) + Зд(х)). б) lim (/(х)р(х)).
х—>1 х—>1
.)
д(х)
В задачах 4-6, используя график f, показанный ниже, вычислите указанные пределы и значения функций.
4. a) lim /(х).
х—*1~
В) lim/(я)- X—>1
5. a) lim /(х).
х—*2~
В) lim/(x).
х—>2
6. a) lim /(х).
х—>3 —
В) lim/(ж).
х—>3
б) lim /(х).
х—>1+
г) /(1).
6) lim /(х).
х->2+
Г) /(2).
б) lim /(х).
х->3+
Г) /(3).
В задачах 7-9, используя график функции f, показанный на рисунке ниже, ответьте
на каждый вопрос.
7. 	a) lim f (х) = ?.
х—►!
в) 	Непрерывна ли функция f в точке х = 1?


152
Часть III. Математический анализ
8. a) lim / (х) = ?. б) /(2) = ?.
х ) 2
в) 	Непрерывна ли функция / в точке х = 2?
9. а) lim/(x) = ?. б) /(3) = ?.
х—>3
в) 	Непрерывна ли функция f в точке х = 3?
10. 	Используя двухэтапный процесс, вычислите производную /'(а;) функции / (ж) = = 5 а;2.
11. Пусть /(5) = 4, /'(5) = —1, (/(5) = 2, д'(5) = —3. Вычислите значение Л'(5)
для каждой из следующих функций.
a) h(x) = 2f(x) + 3<?(х).
в) м*)=
б) h(x) = /(х)р(х). г) h(x) = [/(х)]2.
12. Замените знак ? в уравнении выражением, которое сделает равенство справед¬
ливым.
(За;2 + 4х + 1)5 = 5 (За;2 + 4а; + 1)4 ? .
В задачах 13-24 вычислите функцию f'(x) и упростите результат.
13. f(x) = Зх4 - 2х2 + 1.
14. f(x) = 2а;1/2 — За;.
15. f(x) = 5.
17. / (х) = ^ + 0,25х4.
19. f(x) = (х2 — 1)(х3 — 3).
21-^)=Л2-
23. /(х) = (2х - З)3.
1 а;2
|6-^> = ^+г
18. /(х) = (2х — 1)(Зх + 2).
20. /(х) = (0,2х - 1,5)(0,5х + 0,4).
22. /(х) = 1 .
24. /(х) = (х2 + 2)"2.
Б В задачах 25 и 26 рассматривается функция f, показанная на следующем графике.
25. a) lim f (а;) = ?. б) lim f (а;) = ?.


Глава 8. Производная
153
в)
Д)
26. а)
в)
Д)
lim/(x) = ?. г) /(2) = ?.
х—>2
Непрерывна ли функция f в точке х = 2?
lim f (х) = ?. б) lim f (х) = ?.
lim/(x) = ?. г) Л5) = ?.
х—>5 Непрерывна ли функция / в точке х = 5?
В задачах 27-29 решите каждое неравенство. Запишите ответ в виде интервала. Используя графическую утилиту для построения графиков в задаче 29, вычислите приблизительные координаты точек разбиения с точностью до двух десятичных знаков.
27. х2 - х < 12.
х — 5
28. —г- > 0.
х2 + Зх
29. х3 + х2 — 4я — 2 > 0.
30. Пусть У(х) = 0,5х2 — 5.
а)
б)
Вычислите наклон секущей, проходящей через точки (2; /(2)) и (4; /(4)).
Вычислите наклон секущей, проходящей через точки (2; /(2)) и (2 +/г; /(2 + + /г)), h / 0.
Вычислите наклон касательной в точке х = 2.
в)
В задачах 31-39 вычислите указанную производную и упростите результат.
31. для у = Зх4 — 2ж~3 + 5. ах
32. У для у = (2х2 — Зх + 2)(я2 + 2х — 1).
33. /'(х) для / (х) — 2а: 3 4
(х-1)
0 9
35. д'(х) для д(х) = 1,8^х +
2 ’
39.
37. \/х3 - 5. 38. для у = + 4
ах ах xz
d (х2 + 2)4
dx 2х — 3
40. Для у = f(x) = х2 -И 4 выполните следующие задания.
а) Вычислите наклон графика в точке х = 1.
б) Постройте уравнение касательной в точке х = 1 в виде у = тх + Ь.
41. Повторите проделанное в задаче 40 для /(х) = х3(х -И I)2.
В задачах 42-45 вычислите значение(я) х, при котором(ых) касательная проходит горизонтально.
42. /(ж) = 10# — х2.
43. /(ж) = (х + 3)(я2 — 45).
45. f(x) = х2(2х — 15)3.


154
Часть III. Математический анализ
В задачах 46-48 вычислите приблизительное значение(я) х (с точностью до двух десятичных знаков), в котором(ых) график f имеет горизонтальную касательную.
46. /(х) = х4 — 2х3 — 5х2 + 7х. 47. f(x) = - .
48. /(х) =
5х4 — 40х2
(х2 + 1)2 ■
49. 	Объект движется вдоль оси у (шкала в футах) так, что в момент времени х (шкала в секундах) он находится в точке у = /(х) = 16х2 — 4х. Вычислите следующие функции и величины.
а) Функцию мгновенной скорости движения.
б) Скорость движения в момент времени х = 3 секунды.
50. 	Объект движется вдоль оси у (шкала в футах) так, что в момент времени х (шкала в секундах) он находится в точке у = f(x) = 96х — 16х2. Вычислите следующие функции и величины.
а) Функцию мгновенной скорости движения.
б) Момент (моменты) времени, в которых скорость равна нулю.
*51. Пусть /(х) = х3, д(х) = (х — 4)3 и h(x) = (х + З)3.
а) Как связаны между собой графики f, д и h? Проиллюстрируйте сделанные выводы, построив графики /, д и h в одних и тех же координатных осях.
б) Как, предположительно, будут связаны между собой производные от этих функций? Проиллюстрируйте сделанные выводы, построив графики д' и h' в одних и тех же координатных осях.
*52. Пусть /(ж) — дифференцируемая функция, а к — ненулевая постоянная. Для каждой функции д кратко опишите связи между графиками функций f и д. Сделайте то же самое для графиков f' и д'.
а) д(х) = f(x + k). б) g(x) = f(x) + k.
В задачах 53-57 найдите области, в которых f будет непрерывной. Выразите ответ в интервальном представлении.
53. /(ж) = х2 - 4. 54. /(х) =
55. f(x) = . 56. /(х) = у/Ь-х2.
х£ + Зх — 4
57. f(x) = V^x2.
В задачах 58-61 вычислите значения указанных пределов. При необходимости вос-
пользуйтесь знаками оо и — оо.
58. lim *.
х—>з_ 3 — X
60. lim 1.
х—»з 3 - X
59. lim * + 1.
z->3+ 3 — X
61. lim l + 12. (3 - x)2
В задачах 62-71 найдите предел, если он существует.
62. lim21-’
я?->3 X + 5
63. lim (2x2 — x + 1).


Глава 8. Производная
155
х - 4 ’
66. lim
х—>4~
68. lim
х—>4
к-4|
х — 4 *
70. lim + /(2) f{x} = х2 + 4
я—о h
71. lim
/1—0
f (x + h) — f (ж)
h
для / (x) =
1
ж + 2
72. Пусть
_, ч х3 — 4х2 — 4х + 16 /W= la:2 — 4 ■
Постройте график f и, воспользовавшись опциями изменения масштаба и отслеживания, изучите левосторонний и правосторонний пределы для указанных значений с.
а) с = —2.
б) с = 0.
в) с = 2.
В задачах 73 и 74, используя определение производной и двухэтапный процесс, вычислите функцию f'(x).
73. 	f(x) = х2 — х. 74. f (х) = у/х — 3.
В В задачах 75-78 рассматривается функция f, показанная на следующем рисунке. Определите, дифференцируема ли функция f при указанных значениях х.
75. х = 0. 76. х = 1.
77. х — 2. 78. х = 3.
В задачах 79-82 найдите f'(x) и упростите результат.
х3
X +1)4
81. f (х) = 82. f (х) = ~^=.
х у/х2 + 4
* 83. Область определения степенной функции /(ж) = я1/5 — это множество всех действительных чисел. Найдите область определения производной f'(x). Проанализируйте характер графика у = f(x) для всех х, не входящих в область определения /'(я).


156
Часть III. Математический анализ
84. 	Пусть f имеет вид
если х
если х
где т — константа, а)
Постройте график функции f для т — lim f (х) и х—>1~
и вычислите значения
Пт / (ж).
х—► !+
б)
Постройте график функции / для т =
lim f (х) и
х—>1“
2 и вычислите значения
lim / (х) •
х—>1+
О
в)
*г)
Найдите такое значение т, при котором выполняется равенство lim / (х) = lim f (х),
х—>1“ х—>1 +
и постройте график функции f для этого значения т.
Дайте краткое описание каждого графика. Чем график из п. в отличается от графиков, построенных при решении пп. а и б?
85. 	Пусть /(х) = 1 — |х — 1|, 0 х 2 (см. рис. 8.55).
Рис. 8.55. Иллюстрация к задаче 85
а)
в)
б)
lim h—>0+
г) Существует ли/'(I)?
/(1 + /1)-/(1)
h
= ?
Применение математики
Экономика и бизнес
86. 	WWW Тарифы на природный газ. В следующей таблице приведены тарифы на природный газ, установленные региональным коммунальным предприятием Middle Tennessee Natural Gas Utility на зимний период. Потребители платят фиксированную месячную плату независимо от объема потребленного газа.
а) Запишите определение кусочно-заданной функции месячной платы S(x) для потребителя, расходующего х термов за зимний месяц.


Глава 8. Производная
157
Тарифы на природный газ
Ежемесячная плата за подключение к газопроводу 7,47 долл.
Первые 90 термов 0,4 долл, за терм
Свыше 90 термов 0,2076 долл, за терм
б) Постройте график S(x).
в) Непрерывна ли S(x) в точке х = 90?
87. Анализ затрат. Величина общих затрат на производство х телевизоров (в долларах) равна
ОД) = 10000 + 200х - 0,1х2.
а) Вычислите точную величину затрат на производство 101-го телевизора.
б) Используя функцию предельных затрат, вычислите приблизительные затраты на производство 101-го телевизора.
88. Анализ затрат. Величина общих затрат на производство х велосипедов (в долларах) равна
С(х) = 5000 + 40х + 0,05ж2.
а) Вычислите общие и предельные затраты на производство 100 телевизоров и объясните полученный результат.
б) Вычислите средние и предельные средние затраты на производство 100 телевизоров и объясните полученный результат.
89. Анализ затрат. Величина общих затрат на производство х лазерных принтеров в неделю (в долларах) показана на рис. 8.56. Что больше, приблизительные затраты на производство 201-го или 601-го принтера? Более или менее эффективным становится производственный процесс, описываемый этим графиком, при росте объема производства? Объясните свой ответ.
Объем производства, шт.
Рис. 8.56. Иллюстрация к задаче 89
90. 	Анализ затрат. Пусть
р = 25 — 0,01а: и С(х) = 2х + 9000, 0 х 2500.


158
Часть III. Математический анализ
Используя обозначенную выше зависимость предложения от цены и функцию затрат на производство рассчитайте следующие показатели.
а) Вычислите функции предельных затрат, средних затрат и предельных средних затрат.
б) Выразите доход через х и вычислите функции предельного дохода, среднего дохода и предельного среднего дохода.
в) Вычислите функции прибыли, предельной прибыли, средней прибыли и предельной средней прибыли.
г) Найдите точку (точки) безубыточности.
*д) Определите размер предельной прибыли при х = 1000, 1150 и 1400 и объясните полученные результаты.
е) 	Постройте график R = R(ж) и С = С(х) в одной и той же системе координат и найдите области доходов и убытков.
91. 	Обучение сотрудников. В компании по производству компьютерных комплектующих было установлено, что, в среднем, новый служащий через t дней обучения по месту работы может собрать компонентов, что составляет
AT(t) =
40t
t -|- 2
а) Вычислите среднюю скорость изменения функции N(t) за период с 3-го по 6-й день.
б) Вычислите мгновенную скорость изменения функции N(t) на 3-й день.
* 92. Анализ продаж. Данные об объемах продаж за предыдущие учетные периоды, предоставленные производителем бассейнов, позволяют сделать вывод, что суммарное количество бассейнов N (в тысячах штук), реализованных за год, описывается уравнением
N (t) —
где t — количество месяцев с начала года. Вычислите значения 7V(5) и А'(5) и объясните полученные результаты.
93. 	Потребление природного газа. В табл. 8.16 содержатся данные о потреблении природного газа в США в миллиардах кубических футов.
WWW Таблица 8.16. Потребление газа в США
Год Объем потребленного газа, млрд. куб. футов
I960
12,0
1970
21,1
1980
19,9
1990
18,7
2000
21,9
а) Пусть переменная х описывает время (в годах), где х = 0 соответствует 1960 году, а переменная у представляет объем потребления природного газа


Глава 8. Производная
159
в США. Введите эти данные в графическую утилиту и постройте уравнение кубической регрессии.
*б) Допустим, что у = 7V(x) — это уравнение регрессии, найденное при решении п. а. Вычислите значения ДГ(50) и 7V'(50) и дайте интерпретацию полученных результатов.
94. 	Анализ безубыточности. В табл. 8.17 содержатся данные о цене, спроса и затратах на производство кренделей, где р — цена кренделя при дневном спросе х кренделей (в долларах), а С — общие затраты на производство х кренделей (в долларах).
Таблица 8.17. Цена и спрос на крендели
X
р, долл.
С, долл.
125
9
740
140
8
785
170
7
850
200
6
900
а) Постройте уравнение линейной регрессии, описывающее связь между спросом и ценой, используя в качестве независимой переменной величину х.
б) Составьте уравнение линейной регрессии для функции затрат, считая х независимой переменной. Используя это уравнение, найдите приблизительные величины постоянных затрат и переменных издержек в расчете на крендель.
в) Найдите точки безубыточности.
г) Укажите диапазон цен, придерживаясь которых булочная будет получать прибыль.
Во всех ответах округлите цену в долларах до ближайшего цента.
Биологические науки
95. 	Загрязнение. Установка для очистки сточных вод подключена к ливневой канализации, которая отводит стоки к центру большого озера. Концентрация отходов С(х), частиц на миллион, на расстоянии х метров от конца трубопровода равна приблизительно
С(х) = 500(я + I)-2.
Какова мгновенная скорость изменения концентрации на расстоянии 9 метров от места стока? На расстоянии 99 метров?
* 96. Медицина. Температура тела пациента (в градусах Фаренгейта) через t часов после принятия жаропонижающего лекарства равна
F (t) = 98 +
4
y/t 4* 1
Вычислите значения F(3) и F'(3). Дайте интерпретацию этих результатов.


160
Часть III. Математический анализ
Социальные науки
97. Обучение. Процесс изучения N понятий за t часов описывается уравнением N (t) = 2Vt.
Вычислите скорость обучения через указанное время.
а) 1 час. б) 4 часа.
Домашнее задание 8.1. Минимальные средние затраты
www Если С(х) — общие затраты на производство х изделий, то функция предельных затрат С'(х) позволяет вычислить приблизительную величину затрат на производство следующего изделия, в то время как функция средних затрат С (т) позволяет вычислить среднюю величину затрат в расчете на уже произведенное изделие. Таким образом, функция Cf(x) указывает затраты на выпуск следующего изделия, в то время как функция С (х) указывает затраты на выпуск всех изделий, которые были произведены на данный момент. С учетом этой разницы может показаться странным, что между двумя данными функциями есть тесная связь. Как будет показано, информация, полученная путем сравнения значений С" (я) и С (т), может помочь найти уровень производства с минимальной величиной средних затрат.
1. 	Величина общих затрат на производство х единиц продукции (в долларах) составляет
С(ж) = 0,01гг2 + 40а: + 3600.
Вычислите функции С"(х) и С (а:) и заполните табл. 8.18.
Таблица 8.18. Общие и средние затраты
х С'(х) С(х)
100
200
300
400
500
600
700
800
900 1000
2. 	Повторите вычисления для функции
С(ж) = 0,00016ж3 - 0,12а:2 + 30а; + 10000.


Глава 8. Производная
161
3. Изучите значения в таблице, заполненной при решении пп. 1 и 2, и опишите поведение каждой функции. Есть ли у каждой из этих функций минимальное значение? Чему оно равно и какой точке соответствует? Какая связь существует между минимальной величиной средних затрат и предельными затратами при уровне производства, соответствующем минимальным средним затратам?
4. Если в вашем распоряжении есть графическая утилита, подтвердите наблюдения, сделанные при решении п. 3 и постройте графики функций С" (я) иё(4
5. Следующие утверждения могут помочь доказать наличие связи, обнаруженной в результате наблюдений в ходе решения п. 3. В каждом пункте нужно заполнить пустое место словом “увеличит” или “снизит” и обосновать сделанный выбор.
1) Если С'(х) < С (х) (т.е. затраты на выпуск следующего изделия меньше
средних затрат на выпуск уже произведенных изделий), то увеличение производства на одно изделие средние затраты.
2) Если С'(х) > С (х) (т.е. затраты на выпуск следующего изделия больше
средних затрат на выпуск уже произведенных изделий), то увеличение производства на одно изделие средние затраты.
6. Проанализируйте справедливость следующего утверждения для произвольной функции затрат С(х): если минимальное значение функции С (х) соответствует уровню производства х, то при таком уровне производства С"(х) = С(я)?
7. В пп. 1 и 2 для иллюстрации связи между функциями Cf (х) и С (х) использовались квадратичная и кубическая функции. Однако наиболее важным типом функций затрат является линейная функция. Чтобы увидеть, почему в задаче не используется линейная функция затрат, попытайтесь провести параллель с заключениями, сделанными выше, для функции затрат
С(х) = ЗОж + 12000.
Противоречат ли какие-нибудь из сделанных заключений утверждениям, полученным в результате решения пп. 5 и 6?


162
Часть III. Математический анализ
Домашнее задание 8.2. Численное дифференцирование с помощью графической утилиты
В большинстве утилит для построения графиков есть встроенная процедура, позволяющая найти приблизительное значение производной от функции, которая часто обозначается nDeriv (обратитесь к руководству по работе с графической утилитой). Например, при вызове nDeriv(ж3, а?, а) будет найдено приблизительное значение производной от у — х3 в точке а.
1. Вычислите с помощью графической утилиты значение nDeriv(x3, х, а) для о = 1, 2, 3, 4 и 5 и сравните результат с соответствующими значениями функции
-j-x3 = Зх2.
ах
2. Введите в редактор формул графической утилиты функции = х3, у2 — Зх2
и ?/з = nDeriv(yi, х, х). Постройте график функций у2 и у$ на отрезках —2 ^х 2, —2 2 и проанализируйте взаимосвязь между этими гра¬
фиками. Чтобы подкрепить сделанные выводы, воспользуйтесь функцией отслеживания или таблицами значений.
В большинстве графических утилит для вычисления приблизительного значения производной используется следующее среднее значение разностных отношений при фиксированном значении h (центральная разность. — Прим, ред.}
1 / / (ж + /г) - / (ж) /(x-fe) ~/(ж)\ = f(x + h)-f(x-h)
2\h -h J 2h
Таким образом, для данного значения а и фиксированного значения h nDeriv(/(x), х, а) = —ty. (8. j 8)
3. Используя уравнение (8.18), найдите и упростите выражение nDeriv(/(x), х,а) для функции /(х) = х3. Сравните значения упрощенного выражения со значениями функции nDeriv, полученными при решении п. 1, и проверьте, можно ли найти фиксированное значение h для данной графической утилиты. Обратитесь к руководству по работе с графической утилитой и проверьте, можно ли изменить это значение.
4. Пусть /(х) = |х|. Чему равна функция nDeriv(/(x), х, 0)? Дифференцируема ли функция /(х) в точке х = 0?
5. Повторите решение п. 4 для функции /(х) = 1/х2.
6. Почему при использовании функции nDeriv для вычисления приблизительного значения производной функции /(х) необходимо знать точки, в которых /7(х) не существует?


Построение графиков и оптимизация
■ 9.1. Первая производная и построение графиков
■ 9.2. Вторая производная и построение графиков
■ 9.3. Методы исследования графиков: универсальный и углубленный
■ 9.4. Оптимизация. Глобальный максимум и минимум.
■ Ключевые слова, основные обозначения и формулы
■ Домашнее задание 9.1. Максимизация прибыли
■ Домашнее задание 9.2. Минимизация расходов
Введение
С исторической точки зрения одной из основных причин возникновения математического анализа была потребность в эффективных инструментах построения графиков функций. Еще совсем недавно студенты рисовали графики вручную. Теперь все изменилось. В настоящее время графики функций, заданные уравнения, можно построить с помощью специального высокопроизводительного программного обеспечения. Означает ли это, что старый математический аппарат больше не нужен? Совсем наоборот — для эффективного применения современных компьютерных технологий требуются специалисты, прекрасно разбирающиеся не только в вычислительной технике, но и методах построения и анализа графиков.
В первых трех разделах главы рассматриваются принципы построения графиков и математические инструменты их анализа. Исследуемые функции могут


164
Часть III. Математический анализ
задаваться как уравнениями или табличными данными, так и словесным описанием или вспомогательными графиками. В последнем разделе методы исследования графиков будут применены для решения задач оптимизации, относящихся к наиболее важным практическим проблемам, решаемым методами математического анализа.
Посильную помощь в изучении последующего материала будут сведения, изложенные в разделе 2.1. В частности, в дальнейших суждениях мы будет опираться на следующий факт.
График полинома положительной степени п имеет по крайней мере п — 1 точек экстремума и не более п действительных нулей, т.е. точек пересечения с осью х.
9.1. 	Первая производная и построение графиков
■ Возрастающие и убывающие функции
■ Локальный экстремум
■ Условия существования экстремума
■ Анализ графиков
Поскольку по производной можно судить о наклоне графика функции в заданной точке, возникает предположение, что с ее помощью можно исследовать и другие его свойства. Как будет показано ниже, производная позволяет получить большое количество информации о форме графика. Кроме того, с ее помощью можно найти максимум и минимум функции без построения ее графика. Аналитические отделы производственных предприятий часто используют этот метод для определения условий получения максимальной прибыли или минимальных затрат. Помимо этого, анализ функции по ее производной находит применение в фармакологии, позволяя определить дозировки препаратов, обеспечивающие максимальный лечебный эффект. Область практического применения метода чрезвычайно широка.
Возрастающие и убывающие функции
Задание 9.1.
На рис. 9.1 показан график функций у = /(х) и знаковая диаграмма ее производной f(x). Здесь
f(x) — х3 — Зх
и
f'(x) = Зх2 — 3 — 3(х + 1)(х — 1).
Опишите поведение графика функции f на интервалах, где знак ее производной /'(а?) является постоянным и в точках его изменения. ■


Глава 9. Построение графиков и оптимизация
165
-1 1
Рис. 9.1. Графики функций у = f(x) и знаковая диаграмма ее производной
Если проследить за графиком функции слева направо, то на разных интервалах он может то возрастать, то убывать. Например, с одной стороны, график функции f(x) = х3 — Зх, изображенный на рис. 9.1, на интервале (—ос, —1) идет вверх. Это означает, что на этом интервале функция /(ж) является возрастающей1, а наклон ее графика положителен (f'(x) > 0). С другой стороны, на интервале (—1,1) график функции f(x) идет вниз. Следовательно, на этом интервале функция f(x) является убывающей, а наклон ее графика отрицателен (/'(х) < 0). И наконец, на интервале (1, оо) график функции /(х) снова идет вверх, т.е. она снова становится возрастающей и /'(х) > 0. В точках х = — 1 и х = 1 наклон графика равен нулю (/'(х) = 0), т.е. касательные в этих точках направлены горизонтально.
Итак, если на интервале (а, Ь) выполняется условие /'(х) > 0 (наклон графика положителен) (рис. 9.2), то функция /(х) возрастает (У), а ее график идет вверх (слева направо). Если же на интервале (а, Ь) выполняется условие /'(х) < 0 (наклон графика отрицателен), то функция /(х) убывает (\), а ее график идет вниз (слева направо).
Задание 9.2.
На рис. 9.3 показаны графики функций /(х) = х2 и д(х) = |х|. Обе функции убывают слева от точки х = 0 и возрастают справа от нее. Как связаны между собой график каждой из этих функций в точке х = 0 и значения их производных в этой точке? ■
Строго говоря, функция f(x) называется возрастающей на интервале (а, Ь), если из условия а < Xi < Х2 < Ъ следует, что /(хг) > /(xi). Функция f(x) называется убывающей на интервале (а, Ь), если из условия а < xi < Х2 < b следует, что /(хг) < /(xi).


166
Часть III. Математический анализ
Рис. 9.2. Наклон графика функций у = f(x)
www Возрастающие и убывающие функции
Дх) fix)
Направление графика функции f
Примеры
+ Возрастает /
— Убывает
Вверх /
Вниз
Рис. 9.3. Графики функций у — f(x) ^у — д(х)
Пример 9.1 (Определение интервалов возрастания и убывания функции). Рассмотрим функцию f(x) — 8х — х2.
1. В каких точках х касательная к графику этой функции проходит горизонтально?
2. При каких значениях х функция /(ж) возрастает? При каких значениях х она убывает?
3. Нарисуйте график функции /(х). Изобразите касательную к ее графику в какой-нибудь точке.


Глава 9. Построение графиков и оптимизация
167
Решение.
1. /'(ж) = 8 - 2® = О,
х = 4.
Таким образом, касательная к графику функции проходит горизонтально только в точке х = 4.
2. Чтобы определить интервалы, на которых выполняются условия f'(x) > О или /'(х) < 0, построим знаковую диаграмму для функции f'(x). Напомним, что точками разбиения интервала в этой диаграмме являются значения переменной х, в которых функция равна нулю или имеет разрыв. Таким образом, знаковая диаграмма для функции /'(ж) должна содержать точки, в которых производная равна нулю или имеет разрыв. Из решения п. 1 нам известно, что f(x) = 8 — 2х = 0 в точке х = 4. Поскольку функция f'(x) = 8 — 2х является полиномом, она непрерывна во всех точках х. Построим знаковую диаграмму функции /'(т) на интервалах (—оо, 4) и (4, оо), используя в качестве точек разбиения числа 3 и 5.
/'W
Л*)
-►X
Итак, на интервале (—оо, 4) функция /(ж) возрастает, а на интервале (4, оо) — убывает.
Упражнение 9.1.
Выполните пример 9.1 для функции f(x) = х2 — 6х + 10.


168
Часть III. Математический анализ
Как показано в примере 9.1, структура знаковой диаграммы оказывает существенное влияние на способ оценки производной при анализе графика функции f. Главную роль в этой диаграмме играют точки разбиения интервала. Как известно, если /'(с) = 0, то график функции у = f(x) имеет горизонтальную касательную в точке х = с. Однако среди точек разбиения есть и такие, в которых значение /'(с) не определено вообще2. Есть два типа таких точек: значение /(с) в которых либо вообще не определено, либо оно задано, но наклон касательной в точке х = с не определен.
Критические значения функции f
Точки х из области определения функции /, в которых выполняется условие У'(х) = 0 или производная f'(x) не существует, называются критическими значениями функции /. Они всегда являются точками разбиения интервала в знаковой диаграмме для функции /'(х), однако помимо них в нее входят и другие точки.
Важно понимать, что, хотя значение функции ff(x) в критической точке х = с может не существовать, точка с всегда входит в область определения функции f.
Критические значения всегда входят в область определения функции f.
Рассмотрим пример, иллюстрирующий взаимосвязь между критическими значениями и точками разбиения.
Пример 9.2 (Критические значения и точки разбиения). Найдите точки разбиения для функции критические значения функции f и определите интервалы, на которых функция f возрастает и убывает соответственно.
1. /(ж) = 1 + х3. 2. /(ж) = (1 - х)1/3. 3. /(ж) = —
х — 2
Решение.
1. 	/(х) = 1 + х3; f'(x) — Зх2 = 0;
х = 0.
Единственной точкой разбиения интервала для функции f является точка х = 0. Поскольку она принадлежит области определения функции /, точка нуль одновременно является критическим значением функции f.
Знаковая диаграмма для функции /'(х) = Зх2 (точка разбиения: х = 0) выглядит следующим образом.
2Предполагается, что значение f'(c) не определено ни в одной точке разрыва функции f(x).
Существуют функции, производные которых являются разрывными в точке х = с, несмотря на то, что значение f'(c) определено. Однако в нашей книги такие примеры не рассматриваются.


Глава 9. Построение графиков и оптимизация
169
Пробные значения
/W
X
/'(®)
-►X
-1
3(+)
1
3(+)
Л*)
Анализ знаковой диаграммы показывает, что функция / (ж) возрастает на интервалах (—оо, 0) и (0, оо). Поскольку функция f(x) в точке х = 0 является непрерывной, отсюда следует, что функция /(х) является возрастающей при всех значениях х.
Рис. 9.4. График функции у = f(x)
2. /(ж) = (1 - ху/3 /'(х) = - j(l - z)-2/3 = 3(1_^)2/3-
Чтобы найти точки разбиения для функции отметим, что производная является непрерывной при всех значениях х, за исключением точек, в которых знаменатель равен нулю. Иначе говоря, значения /'(1) не существует, а функция /' разрывается в точке х = 1. Поскольку числитель является константой и равен —1, при всех значениях х выполняется условие /'(т) 0.
Следовательно, точка х = 1 является единственной точкой разбиения интервала для функции Поскольку эта точка принадлежит области определения функции у, значение х = 1 одновременно является критическим. В знаковой диаграмме символ ND обозначает факт, что функция f'(x) в точке х = 1 не определена.
Знаковая диаграмма для функции f{x) = —1(1 — ж)-2/3 = 3(Х Д^2/з выглядит следующим образом (единственная точка разбиения: х = 1).


170
Часть III. Математический анализ
Пробные значения
ш
X
—►X
0
Ч(-)
ftx)
2
-И-)
Анализ знаковой диаграммы показывает, что функция /(т) убывает на интервалах (—оо, 1) и (1, оо). Поскольку функция /(ж) в точке х = 1 является непрерывной, отсюда следует, что функция f(x) является убывающей при всех значениях х. Итак, непрерывная функция может убывать (или возрастать) на интервале, содержащем значения х, при которых функция У'(х) не определена. График функции /(ж) показан на рис. 9.5. Обратите внимание на то, что, поскольку производная в точке х = 1 не определена, касательная в этой точке является вертикальной. Сформулируем это правило в более общем виде: касательная в точке х = с проходит вертикально, если функция f непрерывна в этой точке и по мере приближения к ней величина |/'(ж) | возрастает до бесконечности.
3.
= Й2 Ш
Чтобы найти точки разбиения для функции отметим, что производная является непрерывной при всех значениях х, за исключением точки х — 2. Следовательно, точка х = 2 является единственной точкой разбиения интервала для функции Однако эта точка не принадлежит области определения функции /. Таким образом, значение х = 2 не является критическим и у функции вообще нет критических значений.
Знаковая диаграмма для функции f(x) = / 2^ выглядит следующим образом (единственная точка разбиения: х = 2).


Глава 9. Построение графиков и оптимизация
171
/W
Я*)
Пробные значения
X
/'(*)
1
-1 (-)
3
-1(-)
Анализ знаковой диаграммы показывает, что функция /(х) убывает на интервалах (—ос, 2) и (2, оо). График функции /(ж) показан на рис. 9.6. ■
Рис. 9.6. График функции /(х)
Упражнение 9.2.
Найдите точки разбиения для функции критические значения функции f и определите интервалы, на которых функция f возрастает и убывает соответственно.
1. 	/(ж) = 1 - х3. 2. /(ж) = (1 + я)1/3. 3. /(ж) =-. ■
X
Задание 9.3.
Некий студент проанализировал знаковую диаграмму, построенную при решении примера 9.2.3, и пришел к выводу, что функция /(х) = 1/(х — 2) убывает при всех значениях х, за исключением точки х = 2. Однако /(х) = — 1 < /(3) - = 1. Это наводит на подозрения, что данная функция является возрастающей. Чем объясняются расхождения между ответом, полученным нами, и выводом, к которому пришел студент? В чем заключается ошибка студента? ■
Замечание.
1. 	Не следует считать, что все точки разбиения интервала для функции /' являются критическими значениями функции /. Это условие выполняется


172
Часть III. Математический анализ
только в том случае, если точка разбиения принадлежит области определения функции /.
2. 	Открытые интервалы, на которых функция возрастает или убывает, всегда принадлежат области определения функции.
Локальный экстремум
Если график функции сначала идет вверх, а затем — вниз, точка, в которой он изменяет направление, называется локальным максимумом. Если график функции сначала идет вниз, а затем — вверх, точка, в которой он изменяет направление, называется локальным минимумом. На рис. 9.7 функция достигает локального максимума в точках сз и eg, а локального минимума — в точках С2 и С4. Говорят, что значение /(с) является локальным максимумом, если существует интервал (т, п), содержащий точку с и удовлетворяющий следующему условию:
/(ж) /(с) при всех х е (т, п).
Максимум называется локальным, поскольку это условие должно выполняться только в окрестности точки с.
Число /(с) называется локальным минимумом, если существует интервал (т, п), содержащий точку с и удовлетворяющий следующему условию:
/(х) /(с) при всех х € (т, п).
Локальный максимум или минимум называется локальным экстремумом. Точка на графике, в который достигается локальный экстремум, называется точкой экстремума. Итак, на рис. 9.7 локальный максимум достигается в точках сз и Сб, а локальный минимум — в точках С2 и С4. Все эти точки являются точками экстремума. Обратите внимание на то, что значение /(сз) не является наибольшим на графике, изображенном на рис. 9.7. Позднее мы покажем, как найти наибольшее и наименьшее значения функции, а пока сосредоточимся на поиске точек локального экстремума.


Глава 9. Построение графиков и оптимизация
173
Как найти эти точки по уравнению функции, не рисуя ее график? Для этого необходимо проверить критические значения функции. Локальные экстремумы функции f на рис. 9.7 достигаются в тех точках, в которых производная равна нулю (точки С2 и сз) или в тех точках, где производная не существует (точки и cq). Иначе говоря, точками локального экстремума являются только критические значения функции /.
Теорема 9.1 (Существование локального экстремума). Если функция f непрерывна на интервале (а, Ь), число с принадлежит этому интервалу и значение /(с) является локальным экстремумом, то либо /'(с) = 0, либо значение /'(с) не существует (не определено). ■
Теорема 9.1 гласит, что локальный экстремум достигается только в критических точках, однако отсюда не следует, что каждая критическая точка является точкой локального экстремума. На рис. 9.7 точки ci и являются критическими (наклон функции в этих точках равен нулю), но функция не достигает локального максимума или минимума в этих точках.
Итак, стратегия поиска экстремальных точек проста. Сначала необходимо найти все критические точки функции /, а затем проверить, достигает ли функция локального максимума или минимума в этих точках.
Условия существования экстремума
Если функция f(x) существует по обе стороны от критического значения с, чтобы выяснить, является ли точка (с, /(c)) точкой локального максимума, минимума или ни тем, ни другим, необходимо проанализировать знак функции Все возможные варианты перечислены во врезке “Необходимое условие локального экстремума”.
/'(с) = 0: горизонтальная касательная
а) Де) — локальный минимум
б) Де) — локальный максимум
в) Де) — ни локальный минимум, ни локальный максимум
Рис. 9.8. Локальные экстремумы
г) Дс)— ни локальный минимум, ни локальный максимум


174
Часть III. Математический анализ
www Необходимое условие локального экстремума
Предположим, что число с является критическим значением функции /, т.е. значение /(с) определено и либо f(c) = 0, либо значение /'(с) не существует. Построим знаковую диаграмму для функции /'(с) на интервале, содержащем точку с.
Знаковая диаграмма
/(с)
Лх)
/(с) — локальный минимум. Если знак функции /'(х) в точке с изменяется с отрицательного на положительный, значение /(с) является локальным минимумом.
Дх)
Дх)
/(с) — локальный максимум. Если знак функции /'(х) в точке с изменяется с положительного на отрицательный, значение /(с) является локальным максимумом.
Лх)
Лх)
/(с) не является локальным экстремумом. Если знак функции /'(х) в точке с не изменяется с отрицательного на положительный, значение /(с) не является ни
Лх)
локальным максимумом, ни локальным минимумом.
f\x)
/(с) не является локальным экстремумом. Если знак функции /'(х) в точке с не изменяется с положительного на отрицательный, значение /(с) не является ни
Лх)
локальным максимумом, ни локальным минимумом.
Пример 9.3 (Поиск локальных экстремумов). Рассмотрим функцию /(х) = = х3 — 6т2 + 9# + 1.
1. Вычислите критические значения функции /.
2. Найдите локальные максимумы и минимумы.
3. Постройте график функции /.
Решение.
1. 	Найдем в области определения функции /(ж) точки, в которых выполняется условие /'(х) = 0 либо производная не существует.
/(ж) = Зж2 - 12х + 9 = О,
3(х2 — 4х + 3) = О,
3(ж — 1)(х — 3) = О,
X = 1 или X = 3.


Глава 9. Построение графиков и оптимизация
175
Функция /'(х) определена при всех значениях х. Критическими значениями являются числа х = 1 и х = 3.
2. 	Чтобы проверить выполнение условия существования экстремума, проще всего построить знаковую диаграмму для функции f'(x) при всех значениях х. Точками разбиения интервала для функции f'(x) являются значения х = 1 и х = 3 (они являются критическими и для функции /(х)).
Знаковая диаграмма для функции /'(ж) = 3(ж — l)(z — 3) выглядит следующим образом.
Пробные значения
Дх)
X
/'(*)
—►X
0
9(+)
2
-З(-)
Лх)
4
9(+)
Локальный Локальный
максимум минимум
Анализ знаковой диаграммы показывает, что функция f возрастает на интервале (—оо, 1), имеет локальный максимум в точке х = 1, убывает на интервале (1, 3), достигает локального минимума в точке х = 3 и возрастает на интервале (3, оо). Эти факты перечислены в следующей таблице.
X
/'(®)
/(®)
График функции f
(-00,1)
+
Возрастает
Направлен вверх
X = 1
0
Локальный максимум
Горизонтальная касательная
(1,3)
-
Убывает
Направлен вниз
х = 3
0
Локальный минимум
Горизонтальная касательная
(3,оо)
-и
Возрастает
Направлен вверх
Значение /'(с) не определено, но число Де) существует
а) Лс) — локальный
минимум
б) Дс) — локальный
максимум
в) Дс) — ни локальный минимум, ни локальный
г) 	Лс) — ни локальный минимум, ни локальный
максимум
максимум
3. 	Используя информацию, полученную при решении п. 2, можно построить график функции /.


176
Часть III. Математический анализ
X
/'(*)
0
1
1
5
2
3
3
1
4
5
Упражнение 9.3.
Рассмотрим функцию f(x) = x3 — 9ж2 + 24ж — 10.
1. Найдите критические значения функции /.
2. Найдите локальные максимумы и минимумы.
3. Постройте график функции f.
Замечание.
Локальные экстремумы легко найти с помощью графической утилиты. На рис. 9.9, а показан график функции, изученной в примере 9.3. Локальный максимум и минимум легко распознаются на графике, но как вычислить их координаты? Для этого можно применить два метода, перечисленных ниже. Подробности этих методов излагаются в руководствах, которые сопровождают соответствующие программы. Проверьте, можно ли с помощью вашей графической утилиты построить график производной. Если это возможно, то вам не придется вычислять производную и вводить в программу ее значения.
1. Постройте график производной и найдите ее критические значения с помощью встроенной процедуры. Проанализируйте график, изображенный на рис. 9.9, б, и убедитесь, что точка х = 1 является критическим значением, в котором функция достигает локального максимума (см. рис. 9.9, а). Критическое значение, в котором функция достигает локального минимума, вычисляется точно так же.
2. Постройте график функции и вычислите координаты ее локальных максимума и минимума с помощью встроенной утилиты. На рис. 9.9, в показано, что локальный минимум достигается в точке х = 3 (вычисления являются приближенными). Локальный максимум вычисляется точно так же.
Как убедиться в том, что вы нашли все локальные экстремумы функции? В целом, это довольно сложная задача. Однако, если функция является полиномом,


Глава 9. Построение графиков и оптимизация
177
а) у = х3 — бх2 + 9х + 1
Рис. 9.9. Приближенное вычисление локальных экстремумов с помощью графической утилиты
верхний предел для количества локальных экстремумов определить довольно просто. Поскольку точки локальных экстремумов представляют собой точки пересечения графика производной с осью х, количество локальных экстремумов не может превышать количество таких точек. Этот факт подтверждается следующей теоремой.
Теорема 9.2 (Точки пересечения с осью х и локальные экстремумы полиномиальных функций). Если f = апхп + an_ixn_1 + ... + а\х + ао, ап О является полиномом n-й степени, то функция f имеет не более п точек пересечения с осью х и не более п — 1 экстремумов. ■
Теорема 9.2 не гарантирует, что каждый полином n-й степени имеет ровно п — 1 локальных экстремумов. Она утверждает только, что их количество не превышает числа п — 1. Например, кубический полином в примере 9.3 имеет два локальных экстремума, а кубический полином в примере 9.2.1 не имеет ни одного.
Анализ графиков
www Производная позволяет не только создавать, но и анализировать графики, выясняя связи между функцией и скоростью ее роста. Рассмотрим этот процесс на следующих примерах.
Пример 9.4 (Экспорт и импорт сельскохозяйственной продукции). Несколько последних десятилетий экспорт сельскохозяйственной продукции в США превышал импорт, обеспечивая положительный платежный баланс. Однако этот баланс на протяжении всего периода подвергался значительным колебаниям. График, изображенный на рис. 9.10, иллюстрирует скорость изменения баланса внешней торговли на протяжении 15-летнего периода. Здесь B(t) — баланс внешней торговли, млрд, долл., a t — время, лет.
* 1. Опишите график функции у = B(t) и укажите ее локальные экстремумы.
2. 	Нарисуйте эскиз графика функции у = B(t),


178
Часть III. Математический анализ
Рис. 9.10. Скорость изменения баланса внешней торговли
Решение.
1. График производной у = B'(t) содержит ту же самую информацию, что и знаковая диаграмма. Иначе говоря, по графику легко определить, что функция B'(t) является положительной на интервале (0, 4), обращается в нуль в точке t = 4, является отрицательной на интервале (4, 12), снова обращается в нуль в точке t = 12 и вновь становится положительной на интервале (12, 15). Следовательно, первые четыре года баланс внешней торговли возрастал, затем достиг локального максимума, потом восемь лет убывал, достиг локального минимума, а в последние три года вновь возрастает.
2. Точный график невозможно построить, не зная фактических значений функ¬
ции у = B(t). Однако мы в состоянии набросать его эскиз, продемонстрированный на рис. 9.11. Обратите внимание на то, что ось у на этом графике не размечена, поскольку нам не известны значения функции у = B(t). ■
Рис. 9.11. Характер изменения баланса внешней торговли


Глава 9. Построение графиков и оптимизация
179
Упражнение 9.4.
График, изображенный на рис. 9.12, аппроксимирует скорость изменения доли США на мировом рынке автомобильных двигателей на протяжении 20 лет. Здесь S(t) — доля США в производстве автомобильных двигателей, выраженная в процентах, at — количество лет.
Рис. 9.12. Скорость изменения доли США мировом на рынке автомобильных двигателей
* 1. Опишите график функции у = S(t) и укажите ее локальные экстремумы.
2. 	Нарисуйте эскиз графика функции у = S(t). ■
Пример 9.5 (Анализ дохода). График, изображенный на рис. 9.13, иллюстрирует общий доход Г?(х) от продажи х книжных полок, выраженный в долларах.
1. Опишите график предельного дохода у = Rf(t) и укажите точки ее пересечения с осью х,
2. Нарисуйте эскиз графика функции у = R'(t).


180
Часть III. Математический анализ
Решение.
1. Как следует из графика (см. рис. 9.13), функция 7?(х) возрастает на интервале (0, 550), достигает локального максимума в точке х = 550, а затем убывает на интервале (550, 1000). Следовательно, функция предельного дохода R'(x) положительна на интервале (0, 550), обращается в нуль в точке х = 550 и является отрицательной на интервале (550, 1000).
2. Эскиз графика функции у = R'(t) продемонстрирован на рис. 9.14. ■
ка предельного дохода
Упражнение 9.5.
График, изображенный на рис. 9.15, иллюстрирует общий доход R(x) от продажи х письменных столов, выраженный в долларах.
Рис. 9.15. График общей прибыли
1. Опишите график предельного дохода у = R'(t) и укажите точки его пересечения с осью х.
2. Нарисуйте эскиз графика функции у = Rf(t). ■


Глава 9. Построение графиков и оптимизация
181
Сравнивая примеры 9.4 и 9.5, можно заметить, что график производной (см. пример 9.4) предоставляет больше информации о функции, чем график самой функции (см. пример 9.5). В следующем разделе мы покажем, как можно извлечь дополнительную информацию о производной из графика самой функции.
Ответы к упражнениям
9.1. 	1) Горизонтальная касательная в точке х — 3.
2) Убывает на интервале (—оо, 3), возрастает на интервале (3, оо).
9.2. 1) Точка разбиения: х = 0; критическое значение: х = 0. Убывает при всех
значениях х.
2) Точка разбиения: х = —1; критическое значение: х = —1. Возрастает при всех значениях х.
3) Точка разбиения: х = 0; критических значений нет. Убывает на интервалах (-оо, 0) и (0, ос).
9.3. 1) Критические значения: х = 2, х = 4.
2) Локальный максимум в точке х = 2, локальный минимум в точке х = 4.
9.4. 	1) Доля США на мировом рынке шесть лет убывала, достигла локального минимума, затем 10 лет возрастала, достигла локального максимума, а затем последние четыре года постоянно убывала.


182
Часть III. Математический анализ
9.5. 	1) Предельная прибыль положительна на интервале (0, 450), равна нулю в точке х = 450 и отрицательна на интервале (450, 1000).
Практикум 9.1
А В задачах 1-8 исследуется следующий график функции.
1. Укажите интервалы, на которых функция /(х) возрастает.
2. Укажите интервалы, на которых функция /(ж) убывает.
3. Укажите интервалы, на которых f'(x) < 0.
4. Укажите интервалы, на которых /'(х) > 0.
5. Укажите точки, в которых /'(х) = 0.
6. Укажите точки, в которых функция /'(х) не существует.
7. Укажите точки, в которых функция /(х) достигает локального максимума.
8. Укажите точки, в которых функция /(х) достигает локального минимума.
В задачах 9 и 10 функция f(x) непрерывна на интервале (—оо, оо), имеет критические значения в точках х = а, Ь, с и d. Используя знаковую диаграмму для функции определите, имеет ли функция f(x) локальные максимумы или минимумы.
9.


Глава 9. Построение графиков и оптимизация
183
10.
Б В задачах 11-24 необходимо указать интервалы, на которых функция f(x) возрастает, убывает, а также определить точки локальных экстремумов.
11. /(х) = х2 — 8х + 8.
13. /(х) = —2х2 - 16х - 25.
15. f(x) = х3 + 4х — 5.
17. /(х) = -х3 + 9х2 - 15.
19. /(х) = 2х3 - Зх2 - 36х.
21. /(х) = х4 — 18х2.
23. /(х) = -х4 + 32х.
12. /(ж) = х2 + 4х — 2.
14. /(ж) = —Зх2 + 12# — 5.
16. f(x) — —х3 — 4х + 8.
18. f(x) = х3 — 12х2 + 36х.
20. /(х) = —2х3 + Зх2 -1- 120гг.
22. f(x) = —х4 + 50х2.
24. /(х) = х4 + 4х.
В задачах 25-30, используя графическую утилиту, необходимо приближенно вычислить критические значения функции f(x) с точностью до двух десятичных знаков, указать интервалы, на которых функция f(x) возрастает, убывает, а также опре-
делить точки локальных экстремумов.
25. f(x) = х4 + х2 + х.
27. f(x) = х4 — 4х3 + 9х.
29. f(x) = х4 — 2х3 — 5х2 4- 4х.
26. /(х) = х4 4- х2 — 9х.
28. /(ж) = х4 + 5х3 - 15х.
30. /(ж) = х4 4- 2х3 — 4х2 — 6х.
В задачах 31-36 необходимо указать интервалы, на которых функция f(x) возрастает или убывает, а также нарисовать ее график. Изобразите на нем горизонталь-
ные касательные.
31. /(х) = 4 4- 8х — х2.
33. /(х) = х3 — Зх 4-1.
35. /(х) = 10 - 12х + 6х2 - х3.
32. /(х) = 2х2 — 8х + 9.
34. /(х) = х3 — 12х 4- 2.
36. /(х) = х3 4- Зх2 4- Зх.
В задачах 37-44 функция f(x) непрерывна на интервале (—оо, оо). Нарисуйте возможный график функции, используя знаковую диаграмму.
37.
х -2-1012
f(x) -1 1231
38.
X
-2-101 2
/(®)
1 3 2 1-1


184
Часть III. Математический анализ
39.
X
—2
-1
0
2
4
/(я)
2
1
2
1
0
40.
X
—2
-1
0
2
3
Л®)
-3
0
2
-1
0
41. /(-2) = 4, /(0) = 0, /(2) = -4.
/'(-2) = 0, /'(0) = 0, /'(2) = 0.
/'(ж) > 0 на интервалах (—оо, —2) и (2, оо).
/'(#) < 0 на интервалах (—2,0) и (0,2).
42. /(-2) = -1, /(0) = 0, /(2) = 1. /'(-2) = 0, /'(2) = 0.
> 0 на интервалах (—оо, —2), (—2, 2) и (2, оо).
43. /(-1) = 2, /(0) = 0, /(1) = —2.
/'(—1) = 0, /'(1) = 0, значение /'(0) не определено.
/'(х) > 0 на интервалах (—оо, —1) и (1, оо).
/'(х) < 0 на интервалах (—1,0) и (0,1).
44. /(-1) = 2, /(0) = 0, /(1) = 2.
/'(—1) = 0, /'(1) = 0, значение /'(0) не определено.
/'(х) > 0 на интервалах (—оо, —1) и (0,1).
/'(х) < 0 на интервалах (—1,0) и (1, оо).
Задачи 45-50 связаны с функциями j\ — /в и их производными д\ — д^. Используя графики, приведенные на рис. 9.16 и 9.17, найдите для каждой функции fi соответствующую производную gi.
45. А.
47. 	/3.
49. 	/5.
46. /2.
48. /4.
50. /6.


Глава 9. Построение графиков и оптимизация
185
Рис. 9.16. Графики функций fa — fa
Рис. 9.17. Графики функций д± — да


186
Часть III. Математический анализ
В задачах 51-56, используя график функции у = /'(ж), необходимо указать интервалы, на которых функция f(x) возрастает, убывает, а также определить точки локальных экстремумов.
51. 52.
53. 54.
55. 56.
В задачах 57-60, используя график функции у = найдите интервалы, для ко¬
торых ff(x) > 0, интервалы, для которых f'(x) < О, и значение х, для которого f'(x) — 0. Изобразите возможный график функции у = f(x).
57. 58.


Глава 9. Построение графиков и оптимизация
187
59.
60.
В В задачах 61-72 необходимо указать интервалы, на которых функция f(x) возрастает, убывает, а также определить точки локальных экстремумов, не строя ее график.
4
61. 	f(x) = х Н—.
х
63. 	/(ж) = 1 Ч h —.
X X2
65‘
67. 	/(х) = х4(х - 6)2.
69. 	/(х) = 3(х - 2)2/3 + 4.
71. 	f(x) = 2у/х - х, х > 0.
62. 	/(х) = - + х.
х
64. 	/(ж) = 3 - - -
X X2
“■ = JTT
68. 	f(x) = х3(х — 5)2.
70. 	/(х) = 6(4 — х)2/3 + 4.
72. 	/(х) = х — 4^х, х > 0.
* 73. Пусть /(х) = х3 + кх, где к — константа. Сколько локальных экстремумов имеет эта функция? Нарисуйте эскиз ее графика.
а) к > 0.
б) fc<0.
в) к = 0.
*74. Пусть /(х) = х4 + кх2, где к — константа. Сколько локальных экстремумов имеет эта функция? Нарисуйте эскиз ее графика.
а) к > 0. б) к < 0. в) к = 0.
Применение математики
Экономика и бизнес
75. Анализ прибыли. На рис. 9.18 приведен график функции прибыли Р(х), выражаемой в долларах, от продажи х электрических дрелей.
*а) Опишите график предельной прибыли у = Р'(х) и укажите точки его пересечения с осью х.
б) Нарисуйте возможный график функции у = Р'(х).
76. Анализ доходов. На рис. 9.19 приведен график общего дохода Р(х), выражаемого в долларах, от продажи х электрических дрелей.
*а) Опишите график предельного дохода у = Rf(x) и укажите точки его пересечения с осью х.
б) Нарисуйте эскиз графика функции у = R'(x).


188
Часть III. Математический анализ
77. WWW Анализ цены. На рис. 9.20 приведен график, отражающий скорость изменения цены ветчины на протяжении 70 месяцев. Здесь B(t) — цена фунта нарезанной ветчины (в долларах), at — время, (в месяцах).
*а) Опишите график функции у — B(t) и укажите точки его локальных экстремумов.
б) Нарисуйте возможный график функции у = B(t).
78. WWW Анализ цены. На рис. 9.21 приведен график, отражающий скорость изменения цены яиц на протяжении 70 месяцев. Здесь E(t) — цена дюжины яиц (в долларах), at — время (в месяцах).
Б'(0
Рис. 9.20. Иллюстрация
к задаче 77
Рис. 9.21. Иллюстра¬
ция к задаче 78
*а) Опишите график функции у — E(t) и укажите точки его локальных экстремумов.
б) Нарисуйте возможный график функции у = E(t).
79. 	Средние затраты. Компания, выпускающая в день не более 150 тостеров, несет следующие производственные расходы: постоянные затраты — 350 долл., издержки на производство одного тостера — 20 долл., амортизационные издержки — 0,05х2 долл. Общие производственные расходы при выпуске х тостеров в день описываются формулой
С(х) = 0,05х2 4- 20z 4- 320; 0 < х < 150.


Глава 9. Построение графиков и оптимизация
189
а) Чему равны средние производственные затраты С (х) при выпуске х тостеров в день?
б) Найдите критические значения функции С (ж), интервалы, на которых она возрастает или убывает, а также точки локальных экстремумов, не рисуя график.
80. Средние затраты. Компания, выпускающая в день х (0 < х < 200) миксеров, несет следующие производственные расходы: постоянные затраты — 450 долл., издержки на производство одного миксера — 30 долл., амортизационные издержки — 0,0&г2 долл.
а) Чему равны средние производственные затраты С (ж) при выпуске х миксеров в день?
б) Найдите критические значения функции С (х), интервалы, на которых она возрастает или убывает, а также точки локальных экстремумов, не рисуя график.
81. Маржинальный анализ. Покажите, что прибыль растет на интервале (а, 6), если во всех точках этого интервала предельный доход превышает предельные затраты. (Подсказка. Р(х) = R(x) — С(х).)
82. Маржинальный анализ. Покажите, что прибыль на интервале (а, Ь) убывает, если во всех точках этого интервала предельный доход не превышает предельные затраты.
Биологические науки
83. Медицина. Лекарство вводится в кровь пациента путем инъекции в правую руку. Концентрация лекарства в левой руке через t часов после инъекции аппроксимируется формулой
= 0 < t < 24.
Найдите критические значения функции C(f), интервалы, на которых концентрация лекарства возрастает или убывает, а также точки локальных экстремумов, не рисуя график.
84. Медицина. Концентрация лекарства C(t) в крови через t часов после приема аппроксимируется формулой
C(t) =
0,16t
i2 + 4t + 4’
0 < t < 12.
Найдите критические значения функции C(t), интервалы, на которых концентрация лекарства возрастает или убывает, а также точки локальных экстремумов, не рисуя график.


190
Часть III. Математический анализ
Социальные науки
85. 	Политика. Популярность политика через t месяцев после начала предвыборной компании описывается следующей формулой.
8 4t
P(f) = ^t49+°’1; 0<*<24-
Здесь P(t) — доля людей, которым известна фамилия кандидата. Найдите критические значения функции P(t), интервалы, на которых популярность возрастает или убывает, а также точки локальных экстремумов, не рисуя график.
9.2. 	Вторая производная и построение графиков
■ Выпуклость
■ Точки перегиба
■ Исследование функции с помощью второй производной
■ Анализ графиков
В разделе 9.1 показано, что первая производная позволяет выяснить интервалы, на которых функция возрастает или убывает. В этом разделе мы покажем, что с помощью второй производной можно получить дополнительную информацию о форме графика.
Выпуклость
Рассмотрим функции
/(х) = х2 и д(х) = у/х
на интервале (0, сю). Поскольку
f'(x) = 2х > 0 при 0 < х < оо
и
>0
при
0 < х < оо,
обе функции /(х) и д(х) являются возрастающими на интервале (0, оо).
Задание 9.4.
1. Опишите разницу между графиками функций (рис. 9.22).
2. Заполните следующую таблицу и укажите, чем отличаются друг от друга значения производных функций f и д, а также их графики.


Глава 9. Построение графиков и оптимизация
191
Рис. 9.22. Графики функций /(ж) = х2 и д{х) = у/х
Будем говорить, что график функции является выпуклым вверх, если охватывает некую область снизу. Аналогично график функции называется выпуклым вниз, если он охватывает некую область сверху. Итак, график, изображенный на рис. 9.22, а, является выпуклым вверх, а на рис. 9.22, б — выпуклым вниз. Математическая формулировка понятия выпуклости позволит нам в дальнейшем более подробно анализировать графики функций.
Рассмотрим наклоны графиков функций f и д в разных точках (рис. 9.23). Анализ этих графиков приводит нас к двум выводам. Во-первых, на рис. 9.23, а мы видим, что функция /'(х) (наклон касательной) является возрастающей и график функции /(т) расположен над касательной. Во-вторых, на рис. 9.23, б мы видим, что функция д'(х) является убывающей и график функции д(х) расположен под касательной.
а) Дх)=х2
б) 5(х)=Л
Рис. 9.23. Наклоны графиков функций f(x) = х2 тл д(х) = у/х


192
Часть III. Математический анализ
Исходя из этих наблюдений, мы можем сформулировать следующее утверждение.
График функции f называется выпуклым вверх на интервале (а, Ь), если функция f'(x) на этом интервале возрастает, и выпуклым вниз, если функция f'(x) на этом интервале убывает.
С геометрической точки зрения график функции является выпуклым вверх на интервале (а, Ь), если в каждой точке этого интервала он лежит выше касательной, и выпуклым вниз, если в каждой точке интервала он лежит ниже касательной.
Как определить, является ли функция возрастающей или убывающей? В разделе 9.1 мы использовали для этого первую производную. Следовательно, чтобы выяснить, является ли функция f{x) возрастающей или убывающей, необходимо вычислить ее производную, т.е. функцию f"(x). Эта производная называется второй производной функции f. Кроме того, вторая производная имеет и другие обозначения.
Вторая производная
Пусть у = /(х). Тогда вторая производная функции f вычисляется по формуле
Кроме того, для обозначения второй производной используются следующие символы.
www Вернемся к исследованию функций, упомянутых в начале главы.
/(а?) = х2,
f'{x) = 2х,
ГЫ =
При х > 0 выполняется условие f"(x) > 0. Следовательно, функция f(x) возрастает, и график функции f является выпуклым вверх (рис. 9.23, а). При х > 0 выполняется условие дн(х) < 0. Следовательно, функция № убывает, и график функции д является выпуклым вниз (рис. 9.23, б).


Глава 9. Построение графиков и оптимизация
193
Выпуклость
Рассмотрим интервал (а, Ь).
Не следует путать выпуклость с направлением графика вверх или вниз. Как показано на рис. 9.24, график функции может быть выпуклым вверх и при этом возрастать, убывать и даже менять направление.
/”(х) > 0 на интервале (а, Ь) Выпуклость вверх
а) функция f \х) является отрицательной и возрастает. График функции Дх) убывает
а b
б) функция f '(х) возрастает от отрицательных значений до положительных. График функцииДх) сначала убывает, а затем возрастает
/”(х) < 0 на интервале (а, Ь) Выпуклость вниз
в) функция/'(х) является положительной и возрастает. График функции Дх) возрастает
г) функция/' '(х) является положительной и убывает. График функции Дх) возрастает
а b
д) функция/ '(х) убывает от положительных значений до отрицательных. График функции Дх) сначала возрастает, а затем убывает
е) функция/'(х) является отрицательной и убывает. График функцииДх) убывает
Рис. 9.24. Примеры выпуклых графиков
Пример 9.6 (Определение выпуклости графика). Рассмотрим функцию /(х) = = х\ Укажите интервалы, на которых функция f выпукла вверх, и интервалы, на которых она выпукла вниз. Нарисуйте график этой функции.


194
Часть III. Математический анализ
Решение. Чтобы выяснить выпуклость графика, необходимо определить знак функции f"(x).
/(ж) = X3-
f'(x) = Зх2;
f"(x) = 6х.
Знаковая диаграмма функции = 6х выглядит следующим образом.
Пробные значения
/"(X)
X
/"(*)
-1
-б(-)
х 1
6(+)
График функции/
Итак, график функции f является выпуклым вниз на интервале (—оо, 0) и выпуклым вверх на интервале (0, оо). Форма графика показана на рис. 9.25. ■
Рис. 9.25. График функции
f(x)=x*
Упражнение 9.6.
Выполните пример 9.6 для функции f(x) = l — x3, ■
График функции, рассмотренной в примере 9.6, в точке (0,0) изменяет направление выпуклости. Эта точка называется точкой перегиба (inflection point).
Точки перегиба
Задание 9.5.
Как связаны между собой изменение направления выпуклости в точке х = 0 и значения второй производной следующих функций в окрестности этой точки?
1. 	/(ж) = х3. 2. д(х) — я4/3. 3. h(x) = х4. ■
Точкой перегиба называется точка, в которой график функции изменяет направление выпуклости (например, выпуклость вверх изменяется на выпуклость


Глава 9. Построение графиков и оптимизация
195
вниз, и наоборот). Поскольку направление выпуклости изменяется, функция fff(x) также должна менять свой знак. Определить, в какой точке функция изменяет свой знак, можно с помощью точек разбиения3 (см. раздел 8.2). Итак, рассмотрим следующую теорему.
Теорема 9.3 (Точки перегиба). Если функция у = f(x) непрерывна на интервале (а, Ь) и имеет точку перегиба х = с, то либо = 0, либо значение f"(c) не существует. В
Обратите внимание на то, что точкой перегиба может быть только одна из точек разбиения функции /"(ж), однако не любая точка разбиения функции f'(x) является точкой перегиба.
Точка разбиения с функции f"(x) является точкой перегиба графика функции f, только если выполняются следующие два условия.
1. Функция f"(x) изменяет знак в точке а
2. Точка с принадлежит области определения функции f.
На рис. 9.26 продемонстрировано несколько типичных случаев.
с
Л*)
в)/'(с) = 0
Рис. 9.26. Точки перегиба
Л*)
г) значение /’(с) не определено
Если значение /'(с) существует и функция в точке х = с изменяет знак, то касательная в точке (с, /(c)) всегда лежит ниже графика, выпуклого вверх, и выше графика, выпуклого вниз (см. рис. 9.26, а-в).
Пример 9.7 (Поиск точек перегиба). Найдите точки перегиба функции /(т) = = х3 — бх2 + 9х + 1.
3Как и для первой производной, будем предполагать, что, если функция /" разрывается в точке с, то значение f"(c) не существует.


196
Часть III. Математический анализ
Решение. Поскольку точками перегиба могут быть только точки, в которых функция /"(х) изменяет знак, построим знаковую диаграмму для этой функции.
/(ж) = х3 — 6х2 + 9х + 1, f'(x) = Зх2 — 12х + 9, /"(х) = 6х - 12 = 6(х - 2).
Знаковая диаграмма для функции /"(х) = 6(х — 2) выглядит следующим образом (точка разбиения: х = 2).
График функции f
Пробные значения
/"W
X
/"(®)
X
1
-б(-)
3
6(+)
Точка перегиба
Анализ знаковой диаграммы показывает, что график функции f имеет точку перегиба в значении х = 2. График функции f продемонстрирован на рис. 9.27. (См. также пример 9.3 из раздела 9.1.) ■
Упражнение 9.7.
Найдите точки перегиба функции f(x) = х3 — 9х2 + 24т —10. (Сравните с ответом, полученным при решении упражнения 9.3 из раздела 9.1.) ■


Глава 9. Построение графиков и оптимизация
197
Замечание.
Точки перегиба трудно определить с помощью графической утилиты, однако их довольно просто найти, используя встроенные процедуры для решения уравнений. Исследование графика функции /(ж) из примера 9.7 (рис. 9.28, а) показывает, что точка перегиба должна быть расположена где-то между локальным максимумом в точке х = 1 и локальным минимумом х = 3. График второй производной и процедура решения уравнений (рис. 9.28, б) приводят нас к выводу, что точка перегиба имеет координату х = 2.
5
, J
к
-5
а) = х3 - бх2 + 9х + 1
5
(tool Х=2
Z.
-5
б) у2 = бх — 12
Рис. 9.28. Точки перегиба
Следует помнить, что точки разбиения функции /"(ж) являются лишь кандидатами на точки перегиба. Для того чтобы точка разбиения была точкой перегиба, функция f должна быть определена в точке х = с, а вторая производная должна изменять знак в этой точке. Рассмотрим следующий пример.
У(х) = ж4, д(х) =
X
/'(х}=4х3, д'(х) = —
х£
f"{x) = 12ж2, д"(х) =
х°
В каждом из этих вариантов точка х = 0 является точкой разбиения для второй производной, но не является точкой перегиба ни для одного из перечисленных графиков. Функция f не имеет перегиба в точке х = 0, поскольку функция /"(я) не изменяет знак в этой точке (см. рис. 9.29, а). Функция д не имеет перегиба в точке х = 0, поскольку значение ^(0) не определено (рис. 9.29, б).
Исследование функции с помощью второй производной
С помощью второй производной можно найти локальные экстремумы функции. Предположим, что функция f удовлетворяет условиям /'(с) = 0 и f'(c) > 0.


198
Часть III. Математический анализ
Рис. 9.29. Графики функций /(ж) = х4 и д(х) = ±
Во-первых, поскольку > 0, то4 > 0 во всех точках х некоторого
интервала (m,n), содержащего точку с. Итак, график функции f на интервале (тп, п) должен быть выпуклым вверх. Отсюда следует, что функция f'(x) на этом интервале возрастает. Поскольку /'(с) = 0, функция f(x) в точке х = с должна изменять знак. Следовательно, значение /(с) представляет собой локальный минимум (см. рис. 9.30). Подобным образом, при /'(с) = 0 и < 0 значение /(с) будет представлять локальный максимум. В случае, когда = 0 и f"(c) = 0, вторая производная не предоставит нам полезных сведений о поведении функции f в окрестности точки х = с; значение /(с) может представлять локальный минимум, максимум или не быть ни одним из них.
Ч 1 F
men
а) если /'(с) = 0 и f"(c) > 0, то Дс) — локальный минимум
а) если /’(с) = 0 и/"(с) < 0, то Дс) — локальный максимум
Рис. 9.30. Определение локальных экстремумов с помощью второй производной
4Фактически мы предполагаем, что функция f"(x) является непрерывной на некоем интервале, содержащем точку с. Функция, для которой значение f"(c) существует, но при этом вторая производная f" (х) не является непрерывной на некоем интервале, содержащем точку с, представляет собой скорее исключение, чем правило.


Глава 9. Построение графиков и оптимизация
199
Анализируя знак второй производной, можно легко найти локальные максимумы и минимумы. Этот тест особенно удобен, если вам не хочется рисовать графики функций. В противном случае для поиска точек экстремума можно использовать анализ знаков первой производной.
Поиск локальных максимумов и минимумов с помощью второй производной Пусть точка с представляет собой критическое значение функции f(x).
Если условие f'(c) = 0 не выполняется или значение f"(c) не существует, необходимо исследовать первую производную.
Г(С)
/"(С)
График функции f:
f(c)
Пример
0
+
Выпуклый вверх
Локальный минимум
0
-
Выпуклый вниз
Локальный максимум
0
0
?
Критерий не работает
Пример 9.8 (Поиск локальных экстремумов). Найдите локальные максимумы и минимумы указанных функций, используя вторую производную, если это возможно.
1. f(x) = х3 — бх2 + Эх + 1.
2. /(ж) = — 4х5 + 25ж4.
6
Решение.
1. Сначала найдем первую и вторую производные и вычислим критические значения.
/(ж) = х3 — бх2 + Эх + 1;
f'(x) = Зх2 - 12х + 9 = 3(я - 1)(я - 3);
/,z(z) = бх — 12 = 6(ж — 2).
Критическими значениями являются числа х = 1 и х = 3.
/Z,(l) = — 6 < 0 Локальный максимум в точке а? = 1
/ZZ(3) = б > 0 Локальный минимум в точке х = 3
2. f(x) = - 4z5 + 25гг4;
о
f\x) = х5 — 20х4 + 100а:3 = х3(х — 10)2;
/"(х) = 5я4 - 80х3 + ЗООх2.
Критическими значениями являются числа х = 0 и х = 10.
fn(0) = 0 При обоих критических значениях вторая производная равна нулю, f" (10) = 0 следовательно, необходимо проанализировать первую производную.


200
Часть III. Математический анализ
Знаковая диаграмма для функции /(х) = х3(х — 10)2 (точки разбиения: 0 и 10).
Пробные значения
/'W
X
/'(®)
Лх)
X
-1
1 И
-121 (-)
81 (+)
1331 (+)
Анализ диаграммы показывает, что функция /(х) имеет локальный минимум в точке х = 0 и не имеет локальных экстремумов в точке х = 10. ■
Упражнение 9.8.
Найдите локальные максимумы и минимумы указанных функций, используя вторую производную, если это возможно.
1. /(х) = х3 — 9х2 + 24х — 10.
2. /(х) = 10х6 - 24х5 + 15х4. ■
Многие студенты ошибочно полагают, что из условия f"(c) = 0 следует, что значение /(с) не является локальным экстремумом. Пример 9.8.2, демонстрирует, что это не так. Как видим, если f”(c) = 0, то в точке с локальный экстремум может как существовать, так и не существовать. Если /"(с) = О или значение f "(с) не определено, необходимо анализировать первую производную.
Анализ графиков
Анализ графика позволяет выявить интервалы, на которых функция возрастает или убывает, а также определить выпуклость графика на разных отрезках числовой прямой.
Пример 9.9 (Анализ графиков). На рис. 9.31 показан график производной функции /. Опишите график функции /, используя имеющуюся информацию, и нарисуйте его эскиз.
Решение. Анализируя знак первой производной, можно узнать, на каких интервалах функция f возрастает или убывает. В то же время, знак второй производной подсказывает нам, на каких интервалах функция f является выпуклой вверх или вниз. Информация, полученная на основе графика функции приведена в табл. 9.1, а эскиз графика функции f продемонстрирован на рис. 9.32. ■
Упражнение 9.9.
На рис. 9.33 показан график производной функции /. Опишите график функции /, используя имеющуюся информацию, и нарисуйте его эскиз. ■


Глава 9. Построение графиков и оптимизация
201
Таблица 9.1. Свойства функции f
X
f'(x) (рис. 9.27)
f(x) (рис. 9.28)
—оо < х < — 2
Является отрицательной
Является убывающей
и возрастает
и выпуклой вверх
х = —2
Локальный максимум
Точка перегиба
—2 < х < 0
Является отрицательной
Является убывающей
и убывает
и выпуклой вниз
х = 0
Локальный минимум
Точка перегиба
0 < х < 1
Является отрицательной
Является убывающей
и возрастает
и выпуклой вверх
х — 1
Пересекает ось х
Локальный минимум
1 < х < оо
Является положительной
Является возрастающей
и возрастает
и выпуклой вверх
Пример 9.10 (Максимальная скорость изменения).
В результате маркетинговых исследований было установлено, что затраты на рекламу в размере х тыс. долл, обеспечивают объем продаж N(x), описываемый следующей формулой.
ДГ(х) = 2000 - 2т3 + 60х2 - 450т, 5 х < 15.
При каких значениях х скорость изменения объема продаж в зависимости от расходов на рекламу возрастает или убывает? Вычислите максимум этой функции. Нарисуйте график функций 7V и 7V' в одной и той же системе координат и прокомментируйте их.
Решение. Скорость изменения объема продаж в зависимости от расходов на рекламу вычисляется по следующей формуле.
N'(x) = —6х2 + 120х - 450 = -6(х - 5) (х - 15).


202
Часть III. Математический анализ
Рис. 9.33. График функции /'(т)
Чтобы определить интервалы, на которых эта функция возрастает или убывает, необходимо вычислить функцию N"(x), т.е. вторую производную.
N"(x) = -12т + 120 = 12(10 - т).
Информация, полученная в результате анализа знаковых диаграмм функций АГ'(т) и ^"(т), представлена в табл. 9.2.
Таблица 9.2. Свойства функций ТУ'(т) и ^"(т)
X
N"(x)
N'(x)
N'(x)
N(x)
5 < т < 10
+
+
Возрастает
Возрастающая, выпуклая вверх
х = 10
0
+
Локальный максимум
Точка перегиба
10 < т < 15
+
Убывает
Возрастающая, выпуклая вниз
www Итак, функция N'(x), т.е. скорость изменения объема продаж в зависимости от расходов на рекламу, возрастает на интервале (5, 10) и убывает на интервале (10, 15). Графики обеих функций показаны на рис. 9.34. Анализ графика функции Nf(x) показывает, что максимумом функции АГ(т) является значение 7V'(10) = 150. Обратите внимание на то, что в точке х = 10 функция АГ'(т) имеет локальный максимум, а функция АГ(т) — перегиб. Эта величина называется точкой сокращающихся доходов, поскольку после нее скорость изменения объема продаж снижается. В
Упражнение 9.10.
Повторите решение примера 9.10 для функции N(x) = 5000 - т3 + 60т2 - 900т, 10 т 30. I


Глава 9. Построение графиков и оптимизация
203
Точка сокращающихся доходов
Рис. 9.34. Графики функций 2V(x) и N'(x)
Ответы к упражнениям
9.6. Выпуклая вверх на интервале (—оо, 0). Выпуклая вниз на интервале (0, оо).
9.7. Точка перегиба в точке х = 3.
9.8. 1) /(2) — локальный максимум, /(4) — локальный минимум.
2) /(0) — локальный минимум, в точке х = 1 нет ни одного локального экстремума.
9.9.
Л*)


204
Часть III. Математический анализ
X
Л®)
/(я)
—оо < х < — 1
Является положительной
Является возрастающей
и убывающей
и выпуклой вниз
х = —1
Локальный минимум
Точка перегиба
-1 < X < 1
Является положительной
Является возрастающей
и возрастающей
и выпуклой вверх
X = 1
Локальный максимум
Точка перегиба
1 < х < 2
Является положительной
Является возрастающей
и убывающей
и выпуклой вниз
х = 2
Пересекает ось х
Локальный максимум
2 < х < оо
Является отрицательной
Является убывающей и выпуклой
и убывающей
вниз
9.10. Функция N'(x) возрастает на отрезке (10, 20), убывает на отрезке (20, 30). Максимальная скорость изменения объема продаж равна 7V'(20) = 300, х = 20 — точка сокращающихся доходов.
Практикум 9.2
А В задачах 1-8 исследуется следующий график функции.
1. Укажите интервалы, на которых функция /(ж) является выпуклой вверх.
2. Укажите интервалы, на которых функция /(ж) является выпуклой вниз.
3. Укажите интервалы, на которых выполняется условие f”(x) < 0.


Глава 9. Построение графиков и оптимизация
205
4. Укажите интервалы, на которых выполняется условие /"(о:) > 0.
5. Укажите интервалы, на которых функция /'(о:) возрастает.
6. Укажите интервалы, на которых функция /'(я) убывает.
7. 	Укажите точки перегиба.
8. Укажите локальные экстремумы функции /'(*)•
В задачах 9-12 необходимо сопоставить каждому графику соответствующие
9. 	/'(х) > 0 и /"(а:) > 0 на (а, Ь).
11. 	/'(а:) < 0 и f'(x) > 0 на (а, 6).
10. 	f'(x) > 0 и /"(а:) < 0 на (а, 6).
12. 	/'(а:) < 0 и /"(а:) < 0 на (а, 6).
В задачах 13-20 необходимо найти указанные производные.
13. f"(x) для /(а;) = 2а:3 — 4а:2 + 5х — 6.
14. д"(х) для д(х) = —х3 + 2х2 — Зх + 9.
15. h'f(x) для h(x) = 2а:-1 - За:-2. 16. к”(х) для к(х) = —6а:-2 + 12а:-3.
17. d2y/dx2 для у = х2 — 18а:1/2. 18. d2y/dx2 для у = х3 — 24а:1/3.
19. у" для у = (х2 + 9)4. 20. у" для у = (а?2 — 16)5.
Б В задачах 21-32 найдите все локальные максимумы и минимумы, используя вторые производные, если это возможно (график строить не требуется). Если вторую производную применить нельзя, проанализируйте первую производную.
21. 	/(а:) = 2х2 — 8х + 6.
23. 	/(а:) = 2х3 - Зх2 - 12а? - 5.
25. 	/(а:) = 3-х3 + 3х2 - Зх.
27. 	/(а:) = а:4 - 8а:2 + 10.
29. 	/(а:) = а?6 + За:4 + 2.
31. 	/(а:) = х + —.
22. 	f(x) = 6х — х2 + 4.
24. 	/(а:) = 2х3 + Зх2 — 12х — 1.
26. 	/(а:) = х3 + 6а:2 + 12х + 2.
28. 	f(x) = х4- 18а:2 + 50.
30. 	f(x) = 4 — а?6 — 6а:4.
32. 	f(x) = х -I- —.
В задачах 33-38 найдите интервалы, на которых график функции f является выпуклым вверх или вниз, а также все точки перегиба.
33. 	/(а:) = а:4 + 6а:2.
35. 	/(а:) = х3 — 4а:2 + 5а: — 2.
37. 	/(а:) = —а:4 + 12а:3 - 12х + 24.
34. 	f(x) = х4 + 6х.
36. 	f(x) = —х3 — 5а:2 + 4а: — 3.
38. 	/(а:) = х4 - 2х3 - 36а: + 12.
В задачах 39-44 найдите локальные максимумы или минимумы, если они есть. Предполагается, что функция f(x) является непрерывной на всей числовой оси.
39. 	(2, f (2)), если /'(2) = 0 и /"(2) > 0.


206
Часть III. Математический анализ
40. (4,/(4)), если /'(4) = 1 и /"(4) < 0.
41. (-3, /(-3)), если /'(_3) = 0 и /"(-3) = 0.
42. (-1, /(-1)), если /'(-1) = 0 и /"(-1) < 0.
43. (6, /(6)), если /'(6) = 1 и /"(6) не существует.
44. (5, /(5)), если /'(5) = 0 и /"(5) не существует.
В задачах 45-52 предполагается, что функция f является непрерывной на всей числовой оси. Используя приведенную информацию, нарисуйте ее возможный график.
X
-4-2-1 0 2 4
/(®)
0 3
1,5 0 -1 -3
Дх)
Г(х)
X
-4-2-1024
/(®)
0-2-1013
/'(X)
/"(X)
X
-3 0 1 2 4 5
/(я)
-4 0 2 1 -1 0
/'(х)
X


Глава 9. Построение графиков и оптимизация
207
X
-4 -2 0 2 4 6
/(®)
0 3 0 -2 0 3
/"W
49. /(0) = 2, /(1) = 0, /(2) = —2;
/'(0) = 0, /'(2) = 0;
/'(ж) > 0 на (—оо, 0) и (2, оо);
f ix) < 0 на (0,2);
Г(1)=0;
f'(x) > 0 на (1,оо);
f'lx) < 0 на (—оо, 1).
50. /(-2) = —2, /(0) = 1, /(2) = 4;
/'(-2)=0, /'(2) = 0;
f(x) > Она (-2,2);
/'(ж) < 0 на (—оо, —2) и (2, оо);
Г(0) = 0;
f'(x) > О на (-00,0);
f'lx) < 0 на (0, оо).
51. /(-1) = 0, /(0) = —2, /(1) = 0;
/'(0) = 0, /'(—l) и /'(1) не определены;
f ix) > 0 на (0,1) и (1,оо);
f ix) < 0 на (-оо, -1) и (—1,0);
//7(-1) = 0 и /"(1) не определено;
f'lx) > 0 на (-1,1);
f"(x) < 0 на (—оо, —1) и (1, оо).
52. /(0) = —2, /(1) = 0, /(2) = 4;
/'(0) = 0, /'(2) = 0 и /'(1) не определено;
/'(ж) > 0 на (0,1) и (1,2);
f(x) < 0 на (—оо, 0) и (2, оо);
/"(1) не определено;
f'lx) > 0 на (-оо, 1);
f'lx) < 0 на (1, оо).
В задачах 53-60 необходимо найти локальные максимумы и минимумы, а также точки перегиба. Нарисуйте эскизы графиков каждой из указанных функций, изобразив касательные в точках локальных экстремумов и в точках перегиба.
53. /(ж) = х3 — 6ж2 + 16. 54. f(x) = х3 — 9ж2 4- 15ж + 10.
55. /(ж) = х3 + х + 2. 56. f(x) = 1 — Зж — х3.


208
Часть III. Математический анализ
57. Дт) = (2 - т)3 НН 1.
59. 	f(x) = х3 — 12т.
58. 	f(x) = (1 + т)3 — 1.
60. 	f(x) = 27x — x3.
В задачах 61-64, используя графики функции у = f'(x) необходимо построить график функции у = f(x).
61.
63.
62.
64.
Для решения задач 65-70 необходимо применить графическую утилиту и вычислить точки перегиба с точностью до двух десятичных знаков. Укажите интервалы, на которых графики функций являются выпуклыми вверх и вниз соответственно.
65. f(x) = 0,25т4 - 2т3 + 1,5т2 + 21т + 15.
66. Дт) = 0,25т4 - З,5т3 + 12т2 + 21т.
67. Дт) = т5 + 2т4 + 4т2 - 5.
68. Дт) = х5 — Зт4 + т3 — т2 + 10.
69. /(т) = т5 — Зт4 — т3 + 7т2 — 2.
70. Дт) = т5 — 2т4 — Зт3 -И 4т2 + 4т + 5.
В задачах 71-74 предполагается, что функции f, f и f" являются непрерывными на всей числовой оси.
71. Как определить точки перегиба графика функции у = Дт), исследуя график функции у — f'(x)l
72. Как узнать, возрастает или убывает функция у = f'(x), исследуя график функции у = f(x)2
73. Как найти локальные максимумы и минимумы функции у = ff(x), исследуя график функции у = /(х\?


Глава 9. Построение графиков и оптимизация
209
74. 	Как найти локальные максимумы и минимумы функции у = f(x), исследуя график функции у = f(x)?
В В задачах 75-78 требуется найти точки перегиба, не строя график.
75. /(х) =
1 z2 + 12‘
77. /(х) =
х
z2 + 12’
76. /(х) =
78. f (х) =
х2 + 12
х2 + 12’
Применение математики
Экономика и бизнес
79. WWW Инфляция. Одним из наиболее распространенных характеристик инфляции является скорость изменения индекса потребительских цен (Consumer Price Index — CPI). Газетные заголовки пугают тем, что она постоянно возрастает. Что можно сказать о графике индекса потребительских цен?
80. WWW Инфляция. Еще один показатель инфляции — это индекс розничных цен (Producers Price Index — PPI). В правительственных отчетах говорится, что скорость изменения индекса розничных цен снижается. Что можно сказать о графике индекса розничных цен?
81. Анализ затрат. Некая компания производит осветительные приборы на нескольких заводах. На рис. 9.35 показан график общих затрат С(я) (в долларах) на производство х настольных ламп в неделю на заводе А. Обсудите форму графика функции предельных затрат С (ж) и оцените эффективность производства.
Объем производства, шт.
Рис. 9.35. График функции затрат на заводе А
82. 	Анализ затрат. Компания, упомянутая в задаче 81, производит осветительные приборы на заводе Б. На рис. 9.36 показан график общих затрат С(х) (в долларах) на производство х настольных ламп в неделю на заводе Б. Обсудите форму графика функции предельных затрат С" (ж) и оцените эффективность произвол-


210
Часть III. Математический анализ
Объем производства, шт.
Рис. 9.36. График функции
затрат на заводе Б
83. Доход. Отдел маркетинговых исследований компьютерной компании провел в крупном городе пробные продажи новой продукции. Выяснилось, что зависимость цены р (в долларах) от недельного спроса х приближенно описывается формулой
р = 1296 — 0,12л;2; 0 < х < 80.
Итак, еженедельный доход можно вычислить по следующей формуле.
R(x) = хр = 1296ж2 - 0,12а;3; 0 < х < 80.
а) Найдите локальные экстремумы функции доходов.
б) На каких интервалах график функции доходов является выпуклым вверх, а на каких — вниз?
84. Прибыль. Предположим, что функция затрат для предприятия, упомянутого в задаче 83, приближенно описывается формулой
С(ж) = 830 + 396ж.
а) Найдите локальные экстремумы функции затрат.
б) На каких интервалах график функции затрат является выпуклым вверх, а на каких — вниз?
85. Реклама. Некая компания выяснила, что, затратив на рекламу х тыс. долл., она сможет продать N(x) единиц своей продукции. Зависимость объема продаж от затрат на рекламу описывается следующей формулой.
7V(x) = -Зж3 + 225х2 - ЗбООж + 17000, 10 х 40.
а) При каких затратах на рекламу скорость изменения объема продаж ЛГ'(Ж) возрастает, а при каких - убывает?
б) Найдите точки перегиба графика функции ЛГ(ж).
в) Постройте графики функций 2\Г(х) и ДГ'(:г) в одной и той же системе координат.
г) Найдите максимум скорости изменения объема продаж.


Глава 9. Построение графиков и оптимизация
211
86. Реклама. Некая компания выяснила, что, затратив на рекламу х тыс. долл., она сможет продать 7V(x) единиц своей продукции. Зависимость объема продаж от затрат на рекламу описывается следующей формулой.
АГ (я) = —2х3 + 90х2 - 750х + 2000, 5 х < 25.
а) При каких затратах на рекламу скорость изменения объема продаж N'(x) возрастает, а при каких — убывает?
б) Найдите точки перегиба графика функции N(x).
в) Постройте графики функций N(x) и N'(x) в одной и той же системе координат.
г) Найдите максимум скорости изменения объема продаж.
87. Реклама. Автомобильный салон рекламирует свою продукцию по телевидению. Данные об эффективности рекламной кампании приведены в следующей таблице. Здесь х — месячное количество рекламных объявлений, а у — месячный объем продаж автомобилей.
Количество рекламных объявлений, х
Объем продаж автомобилей, у
10
325
12
339
20
417
30
546
35
615
40
682
50
795
а) Постройте уравнение кубической регрессии, связывающее объем продаж с количеством поданных рекламных объявлений, используя эти данные и графическую утилиту.
б) Сколько рекламных объявлений должен подать автомобильный салон, чтобы достичь максимального объема продаж? Округлите ответ до целых чисел.
88. 	Реклама. Музыкальный магазин рекламирует свою продукцию по радио. Данные об эффективности рекламной кампании приведены в следующей таблице. Здесь х — месячное количество рекламных объявлений, а у — месячный объем продаж компакт-дисков.
Количество рекламных объявлений, х
Объем продаж компакт-дисков, у
10
345
14
488
20
746
30
1228
40
1671
50
1955


212
Часть III. Математический анализ
а) Постройте уравнение кубической регрессии, связывающее объем продаж с количеством рекламных объявлений, используя эти данные и графическую утилиту.
б) Сколько рекламных объявлений должен подать магазин, чтобы достичь максимального объема продаж? Округлите ответ до целых чисел.
Биологические науки
89. Рост численности бактерий. В колонию бактерий ввели определенное количество химического вещества, стимулирующего их рост. Через t минут число бактерий приближенно описывается следующей формулой.
AT(t) = 1000 + 30i2 - t3, 0 < t < 20.
а) На каких интервалах функция N' (t) возрастает, а на каких — убывает?
б) Найдите точки перегиба графика функции N(t).
в) Постройте графики функций и N'(t) в одной и той же системе координат.
г) Найдите максимум скорости роста.
90. Чувствительность к лекарственным препаратам. Через час после приема х мг лекарственного препарата изменение температуры тела Т(ж), определяемой по шкале Фаренгейта, приближенно описывается следующей формулой.
Т(х) = х2 (1 - ; 0 < х < 6.
Производная функции Т(х) называется чувствительностью тела к препарату.
а) На каких интервалах функция Tf(x) возрастает, а на каких — убывает?
б) Найдите точки перегиба графика функции Т(ж).
в) Постройте графики функций Т(х) и Г(х) в одной и той же системе координат.
г) Найдите максимум функции Tf(x).
Социальные науки
91. Обучение. Время Т (мин.), которое необходимо человеку для усвоения п понятий, приближенно описывается следующей формулой.
Т(п) = 0,08п3 — 1,2п2 + 6п; п 0.
а) На каких интервалах функция Т(п) возрастает, а на каких — убывает?
б) Найдите точки перегиба графика функции Т(п). Постройте графики функций Т(п) и Г'(и) в одной и той же системе координат.
в) Найдите минимум функции Г(п).


Глава 9. Построение графиков и оптимизация
213
9.3. 	Методы построения графиков: универсальный и углубленный
■ Бесконечные пределы
■ Вертикальные асимптоты
■ Общие принципы построения графиков
■ Построение графиков функций согласно общим принципам
■ Решение пратических задач
В разделе рассматриваются методы построения графиков с помощью понятий, введенных ранее. Однако прежде, чем приступить к построению графиков, необходимо исследовать поведение функций при стремлении переменной х к бесконечному пределу.
Бесконечные пределы
Важным элементом анализа графиков является исследование поведения функции при стремлении переменной к бесконечному пределу. Напомним, что бесконечность обозначается символом оо. Мы будем писать, что х оо, если переменная х неограниченно возрастает, и х —► — оо, если она неограниченно убывает.
Начнем с исследования степенных функций хр и 1/хр, где р — положительное действительное число.
Задание 9.6.
1. 	Заполните следующую таблицу.
X
100 1000 10000 100000 1000000
X2
Х/х2,
2. Опишите поведение функции х2 при неограниченном увеличении переменной х, используя введенные выше обозначения.
3. Повторите решение задачи для функции \)х2, ■
Если р — положительное действительное число, то при увеличении переменной х функция хр возрастает. Этот факт записывается следующим образом.
хр оо при х —> оо или lim хр = оо.
х—>оо
Поскольку величины, обратные к очень большим числам, являются очень маленькими, при увеличении переменной х функция 1 /хр стремится к нулю. Этот факт


214
Часть III. Математический анализ
записывается так.
1/хр —> 0 при х оо или lim — = 0. х—>оо Хр
Графики функций /(х) = х2 и д(х) = 1/х2 представлены на рис. 9.37.
При неограниченном уменьшении переменной х степенные функции ведут себя почти так же, за исключением двух особенностей. Во-первых, если число х является отрицательным, то степень хр не является действительным числом ни при одном четном показателе р. Во-вторых, если степень хр является действительным числом при всех показателях р, она может стремиться как к оо, так и к — оо в зависимости от величины р. Например,
lim х2 = оо, но lim х3 = —оо.
х—>—оо х—►—оо
Линия у — 0 (ось х) на рис. 9.37 называется горизонтальной асимптотой функции р(х). Линия у = b называется горизонтальной асимптотой графика У = f(x)9 если функция f(x) стремится к числу b при неограниченном убывании или возрастании переменной х. Этот факт записывается следующим образом.
lim f(x) = b или lim /(х) = b.
х—>—оо х—>оо
В первом случае при больших отрицательных значениях переменной х график приближается к горизонтальной линии у = b (рис. 9.38). Во втором случае график функции приближается к горизонтальной линии у = Ь при больших положительных значениях переменной х.
Теорема 9.4 (Пределы степенных функций при х —> ±оо). Если р — положительное действительное число, а к — произвольная действительная константа, то


Глава 9. Построение графиков и оптимизация
215
1. 	lim — — 0, 2. lim — — О,
х—►—оо Хр х—>оо Хр
3. 	lim кхр — ±оо, 4. lim кхр = ±оо,
х—►—оо х—>оо
при условии, что число хр является действительным при отрицательных значениях х. Пределы в пунктах 3 и 4 могут быть равными как —оо, так и оо, в зависимости от значений к пр. ■
Следует помнить, что символ оо не является числом, к которому стремится переменная х. Он используется только для того, чтобы подчеркнуть, что переменная х неограниченно возрастает. Как указывалось в разделе 8.2, если предел равен оо, это означает, что его не существует. Кроме того, необходимо отметить, что свойства пределов 1-6 в теореме 8.1 из раздела 8.1 сохраняются, если заменить выражение х —► с при х —► оо или х —► —оо.
Перейдем к исследованию поведения полиномов и рациональных функций, когда х стремится к бесконечности.
Пример 9.11 (Предел полинома на бесконечности). Рассмотрим полином
р(х) = 2ж3 — х2 — 7х + 3.
Чему равен предел полинома р(ж) при х —> оо или х —► —оо?
Решение. Поскольку предел степенных функций вида \/хр стремится к нулю при х —> оо или х —> — оо, удобно перейти к обратным величинам. Вынесем за скобки член полинома р(гс) с наибольшей степенью.
pW = 213 (1__L__L + _L).
Используя теорему 9.4 и свойства пределов, получим следующий результат.


216
Часть III. Математический анализ
Итак, при больших значениях х
1 7_ 3
2х 2х2 2х3
Поскольку 2а?3 —> ос при х ос,
lim (2а;3 — х2 — 7х + 3) = lim 2х3 \ 1 — —Д 4- -Д? | = оо.
х—юо 4 7 х—>оо у 2х 2xz 2х6 J
Аналогично, поскольку 2о?3 —> — оо при х —> — оо,
(1 7 3 \
1 — ) = —оо.
2х 2хл 2х6 J
Итак, поведение полинома р(х) при больших значениях переменной х определяется поведением его старшего члена 2х3. ■
График функции р(х), построенный с помощью графической утилиты, представлен на рис. 9.39.
Рис. 9.39. График функции р(о?) = 2о?3 — х2 — 7х + 3
Упражнение 9.11.
Рассмотрим полином р(х) = —4а:4 + 2а:3 + За:. Чему равны пределы полинома р(о?) при х —> ос и х —> —оо? ■
Выводы, сделанные при решении примера 9.11, можно распространить на произвольные полиномы.
Теорема 9.5 (Пределы полиномов при х —► ±ос). Если
р(о?) = апхп + an_io?n_1 Н h а^х + ао, ап 0, п 1,


Глава 9. Построение графиков и оптимизация
217
то
lim р (ж) = lim апхп = ±ос
х—>оо х—>оо
и
lim р(х) = lim апхп = ±ос.
х—►—оо х—>—оо
Эти пределы равны —оо или оо в зависимости от чисел ап и п. ■
Полином нулевой степени р(х) = ао является константой, а его предел при х —► ±оо равен ао- Теорема 9.5 утверждает, что при х —> ±оо полином, степень которого выше единицы, не может быть определенным числом. Следовательно, такие полиномы не могут иметь горизонтальных асимптот.
Задание 9.7.
Опишите зависимость поведения полинома от поведения его старшего члена. ■
www Поскольку рациональная функция представляет собой частное двух полиномов, для исследования ее поведения на бесконечности можно воспользоваться величинами, обратными к степеням переменной х. Например, рассмотрим рациональную функцию
,, ч 2х1  2 - 5х + 9
/W=3^ + 4x-8'
Вынесем за скобки старшие члены полиномов в числителе и знаменателе.
/(х) =
Зх2
1 - — —
2 2х 2х2
3 ' “ 4 8 '
Зх Зх2
Используя теорему 9.4, получаем следующий результат.
2
3
lim f (х) = lim
х—>оо х—>оо
lim f (х) = lim
х—►—оо х—►—оо
1 2х + 2х2 j Г'2 1-0 + 0 !
4 	_ 8 !“3’1 + 0-0 I
Зх Зх2 /
2
3
и
/
2
3
1 2х + 2х2 ] Г 2 Г-0 + 6 ;
4 8 3 ‘1 + 0-0 !
+ Зх Зх2 /
2
3’
Итак, поведение рациональной функции при х —> ±ос определяется отношением старших членов числителя и знаменателя. Обобщим полученный результат в виде следующей теоремы.


218
Часть III. Математический анализ
Теорема 9.6 (Пределы рациональных функций при х —*■ ±оо и горизонтальные асимптоты). Если
_ атхт + + • • • + а^х + ао _j_ п L _j_ n
то
lim f (x) - lim и lim f (x) = lim
х—юо x—>oo bnXn X—►—oc x—>—ос ЬпХп
Существуют три варианта таких пределов.
1. Если т < п, то Пшя-юо f (х) = lim^-oo f (х) = 0 и линия у = 0 (ось х) является горизонтальной асимптотой функции /(х).
2. Если т = п, то f (х) = lim^-oo f (x) = и линия у =
является горизонтальной асимптотой функции f(x).
3. Если т > п, то limT_f (х) = limx_f (х) = ±оо в зависимости от чисел т, п, ат и Ьп, а функция /(ж) не имеет горизонтальных асимптот. ■
Обратите внимание на то, что в первых двух вариантах пределы функции f(x) при х —> ±ос одинаковы. Следовательно, рациональная функция не может иметь более одной горизонтальной асимптоты.
Задание 9.8.
Первое утверждение теоремы 9.6 можно сформулировать так.
Если степень числителя меньше степени знаменателя, то ось х является горизонтальной асимптотой.
Сформулируйте аналогичным образом второе и третье утверждения этой теоремы. ■
Пример 9.12 (Горизонтальные асимптоты рациональных функций). Найдите горизонтальные асимптоты следующих функций.
1- f (я) =
5х3 - 2х2 + 1
4х3 + 2х — 7 ’
2.
/(*) =
Зх4 — х2 + 1
8х6 - 10
,, , 2ж5 — х3 — 1
6ж3 + 2х2 —7’
Решение.
1 атхт 5х3 5
Ьпхп 4х3 4*
(Здесь и далее используются обозначения, введенные в теореме 9.6. — При- меч. ред.)
Горизонтальной асимптотой функции /(ж) (теорема 9.6.2) является линия
У = I


Глава 9. Построение графиков и оптимизация
219
атхт __ Зх4 _ 3
Ьпхп 8х6 8х2 ’
Горизонтальной асимптотой функции /(х) (теорема 9.6.1) является линия У = о.
3 атхт _ 2х5 _ х2
Ьпхп бх3 3
Функция /(х) не имеет горизонтальных асимптот (теорема 9.6.3). ■
Упражнение 9.12.
Найдите горизонтальные асимптоты следующих функций.
1- / (®) =
4х3 — 5х + 8
2х4 — 7
2.
/ (*) =
5х6 + Зх
2х5 — х — 5
, f ( ' _ 2х3 — х + 7
4х3 + Зх2 —100’
Вертикальные асимптоты
www Кроме горизонтальных функция может иметь вертикальные асимптоты. Способ их определения задает следующая теорема.
Теорема 9.7 (Определение вертикальных асимптот). Пусть /(х) = n(x)/d(x), где функции п(х) и d(x) являются непрерывными в точке х = с. Если в этой точке знаменатель равен нулю, а числитель — нет, то линия х = с является вертикальной асимптотой графика функции /. ■
(Замечание. Поскольку рациональная функция представляет собой частное двух полиномов, непрерывных на всей числовой оси, данная теорема распространяется и на них.)
Если f(x) = n(x)/d(x), причем п(с) = 0 и d(c) = 0, то предел функции /(х) представляет собой неопределенность, и теорему 9.7 к этой функции применять нельзя.
к /•/ \ v п(х) О
lim j (х) = lim , Неопределенность -
х >с х >с а \Х) ®
В этих ситуациях необходимо провести алгебраические преобразования.
Пример 9.13 (Определение вертикальных асимптот). Найдите все вертикальные асимптоты функции
х2 + х — 2
х2 — 1
Решение. Пусть п(х) = х2 + х - 2 и d(x) = х2 — 1. Разложим знаменатель на множители.
d(x) = х2 — 1 — (х — 1)(х + 1).


220
Часть III. Математический анализ
Поскольку d(—1) = 0 и n(—1) = —2^0, из теоремы 9.7 следует, что прямая х = — 1 является вертикальной асимптотой. С другой стороны, d(l) = 0, но п(1) = 0, поэтому на точку х = 1 теорема 9.7 не распространяется. Следовательно, необходимо провести алгебраические упрощения.
Пт/(х) = Нтж2 + Х / = = lim (X- 1)(х + 2) = ж->1 (х — 1) (х + 1)
х + 2 = lim —
х—>1 X + 1 _ 3 “ 2*
Поскольку предел Нтж_4 f (х) существует, функция f не имеет вертикальной асимптоты в точке х = 1 (рис. 9.40). ■
Упражнение 9.13.
Найдите все вертикальные асимптоты функции f (х) =
Общие принципы построения графиков
www Итак, мы овладели весьма эффективными методиками анализа графиков и можем без труда создавать их эскизы. Эти методики можно реализовать с помощью графических утилит или других компьютерных программ.


Глава 9. Построение графиков и оптимизация
221
Принципы построения графика функции у = f(x)
Этап 1. Проанализируйте функцию /(х).
1) Найдите область определения функции /(х). Областью определения функции /(х) является множество всех действительных чисел, при которых /(х) является действительным числом.
2) Найдите точки пересечения графика с осями х и у. Точкой пересечения графика с осью у является значение /(0). Точками пересечения графика с осью х являются корни уравнения /(ж) = 0.
3) Найдите асимптоты. Для поиска асимптот следует применять теоремы 9.6 и 9.7. Если эти теоремы применить нельзя, необходимо вычислить пределы функции в точках разрыва, а также при х —► ±оо.
Этап 2. Проанализируйте функцию f'(x). Найдите все критические значения функции /(х) и точки разбиения функции /'(х). (Помните, что любое критическое значение функции /(х) является точкой разбиения функции /'(ж), однако некоторые точки разбиения функции f'(x) могут не быть критическими значениями.) Постройте знаковую диаграмму функции f'(x), определите интервалы, на которых функция f(x) возрастает или убывает, и найдите локальные максимумы и минимумы.
Этап 3. Проанализируйте функцию Постройте знаковую диаграмму
функции /"(я), определите интервалы, на которых график функции /(ж) является выпуклым вверх или вниз, и найдите точки перегиба.
Этап 4. Нарисуйте эскиз графика функции f. Нарисуйте асимптоты, определите точки пересечения графика с осями, точки локальных максимумов и минимумов, а также точки перегиба. Используйте всю информацию, полученную на этапах 1-3. В области неопределенного поведения функции график необходимо строить по точкам.
Построение графиков функций согласно общим принципам
Проиллюстрируем общие принципы построения графиков на примерах.
Пример 9.14 (Построение графика согласно общим принципам). Проанализируйте функцию
/(х) = ж4 - 2х3,
следуя общим принципам построения графиков. Нарисуйте эскиз графика этой функции.
Решение.
Этап 1. Проанализируйте функцию f(x) = х4 — 2х3.


Ill
Часть III. Математический анализ
1. Область определения: вся числовая ось.
2. Точка пересечения с осью у: /(0) = 0.
Точки пересечения с осью х: /(0) = 0,
х4 - 2х3 = 0, х3(х — 2) = 0,
х = 0; 2.
3. Асимптоты. Поскольку функция f является полиномом, у нее нет ни горизонтальных, ни вертикальных асимптот.
Этап 2. Проанализируйте функцию f'(x) = 4х3 — 6х2 — 4х2 (х — |).
Критические значения функции /(х): 0 и
Точки разбиения функции /'(х): 0 и |.
Знаковая диаграмма для функции f(x) выглядит следующим образом.
Пробные значения
/'(х)
X
/"(®)
-1
-ю (-)
X
1
-2(_)
Лх)
2
-8 (+)
Локальный минимум
Итак, функция /(х) на интервале (—оо, |) убывает, а на интервале (|, оо) возрастает. Точка локального минимума: х = |.
Этап 3. Проанализируйте функцию f" (х) = 12х2 — 12х = 12х(х — 1).
Точки разбиения функции /"(х): 0 и 1.
Знаковая диаграмма для функции /"(х) выглядит следующим образом.
Пробные значения
/"(X)
X
/"(*)
-1
24 (+)
X
1
2
—з (—)
График функции f
2
24 (+)
Точка Точка
перегиба перегиба
Итак, на интервалах (—оо, 0) и (1, оо) график функции /(х) является выпуклым вверх, а на интервале (0,1) — выпуклым вниз. Точки перегиба: х = 0 и х = 1.


Глава 9. Построение графиков и оптимизация
223
Этап 4. Нарисуйте эскиз графика функции f(x).
Пробные значения
X
/"(*)
0
0
1
-1
3
27
2
16
2
0
Упражнение 9.14.
Проанализируйте функцию /(а;) = х4+4ж3, следуя общим принципам построения графиков. Нарисуйте эскиз графика этой функции. ■
Пример 9.15 (Построение графика согласно общим принципам). Проанализируйте функцию f(x) = (х — 1)/(х — 2), следуя общим принципам построения графиков. Нарисуйте эскиз графика этой функции.
Решение,
Этап 1. Проанализируйте функцию f (х) =
1. Область определения: вся числовая ось, за исключением точки х = 2.
2. Точка пересечения с осью у: f (0) = =
Точки пересечения с осью х. Поскольку дробь равна нулю, когда числитель равен нулю, а знаменатель — нет, точкой пересечения графика с осью х является значение х = 1.
3. Горизонтальная асимптота: а^.п = j = 1.
Итак, горизонтальной асимптотой является линия у = 1.
Вертикальная асимптота. Знаменатель равен нулю, когда х — 2, а числитель в этой точке не равен нулю. Следовательно, вертикальной асимптотой является линия х = 2.
Этап 2. Проанализируйте функцию ff (х) — 4 — -1
\х~ 2) \х~
Критические значения функции f(x)\ отсутствуют.
Точка разбиения функции ff(x): х — 2.
Знаковая диаграмма для функции f'(x) выглядит следующим образом.


224
Часть III. Математический анализ
/'(X)
Лх)
Пробные значения
X
Л®)
1
-1 (-)
3
-1 (-)
Итак, функция f(x) убывает на интервалах (—оо, 2) и (2, оо). Точек локального экстремума нет.
Этап 3. Проанализируйте функцию f" (ж) = . 2 ,2 •
(х—2)
Точка разбиения функции fff(x): х = 2.
Знаковая диаграмма для функции /"(х) выглядит следующим образом.
/"(*)
Пробные значения
X
/"(*)
1
-2 (-)
3
2(+)
График функции f
Итак, на интервале (—оо, 2) график функции f(x) является выпуклым вниз, а на интервале и (2, оо) — выпуклым вверх. Поскольку в точке х = 2 функция не определена, значение х = 2 не является точкой перегиба, несмотря на то, что в этой точке функция f"(x) меняет знак.
Этап 4. Нарисуйте эскиз графика функции f(x).
Лх)
Пробные значения
X
/"(®)
-2
3
4
0
1
2
1
0
3
2
-1
5
2
3
3
2
4
3
2


Глава 9. Построение графиков и оптимизация
225
Упражнение 9.15.
Проанализируйте функцию /(ж) = 2ж/(1 — х), следуя общим принципам построения графиков. Нарисуйте эскиз графика этой функции. ■
Решение практических задач
Пример 9.16 (Средние затраты). Рассмотрим функцию затрат С(х) =
= 5000 +0,5ж2, где х — объем производства. Проанализируйте график функции средних затрат, придерживаясь основных принципов исследования графиков и нарисуйте его эскиз. Найдите функцию предельных затрат и постройте ее график в той же системе координат.
Решение. Функция средних затрат имеет следующий вид.
= . . 5000 + 0,5ж2 5000 пг
С (ж) - - = + 0,5ж.
X X
Этап 1. Проанализируем функцию С (х).
1. Область определения. Поскольку отрицательные значения переменной х не имеют смысла, а значение С (0) не определено, областью определения функции является множество всех положительных действительных чисел.
2. Точки пересечения с осью х\ нет.
3. Горизонтальная асимптота: а^п = = 0,5гг.
Следовательно, горизонтальных асимптот нет.
Вертикальная асимптота: линия х = 0, поскольку знаменатель в этой точке равен нулю, а числитель — нет.
Наклонные асимптоты. Некоторые графики имеют асимптоты, которые не являются ни горизонтальными, ни вертикальными. Такие асимптоты называются наклонными. Если х — большое положительное число, то величина 5000/х очень мала. Следовательно,
ч 5000 г С (х) = И 0,5х « 0,5гг.
х
Иначе говоря,
lim ГС (ж) — 0,5x1 = lim = 0.
х—>оо L J х—>ОО X
Отсюда следует, что график функции у = С(х) при х —> оо стремится к прямой у = 0,5х. Эта линия является наклонной асимптотой функции у = С(х).


226
Часть III. Математический анализ
Этап 2. Проанализируем функцию С' (ж).
Критическое значение функции С (х)\ 100.
Точки разбиения функции С' (х): 0 и 100.
Знаковая диаграмма для функции выглядит следующим образом.
С’(х)
ОД
Пробные значения
X
<?'(*)
50
-1,5 (-)
125
0,18 (+)
Локальный
минимум
Итак, функция С (т) на интервале (0,100) убывает, на интервале (100, оо) — возрастает, а в точке х = 100 имеет локальный минимум.
Этап 3. Проанализируем функцию С" (ж) = 10Д0°-
Функция С" (х) положительна при всех положительных действительных значениях переменной х. Следовательно, график функции у — С (х) на интервале (0, сю) является выпуклым вверх.
Этап 4. Нарисуем эскиз графика функции у = С (х). Этот график продемонстрирован на рис. 9.41.
Функция предельных затрат равна С'(ж) = х. Ее график также представлен на рис. 9.41. ■
Рис. 9.41. График функции У = С(х)


Глава 9. Построение графиков и оптимизация
227
Данный рисунок иллюстрирует важный экономический принцип.
Минимум средних затрат достигается, когда уровень средних затрат равен величине предельных затрат.
Упражнение 9.16.
Рассмотрите функцию затрат С(х) = 1600 + 0,25х2, где х — объем производства.
1. Проанализируйте график функции средних затрат, придерживаясь основных принципов исследования графиков, и нарисуйте его эскиз. Найдите функцию предельных затрат и постройте ее график в той же системе координат. Найдите все наклонные асимптоты.
2. Вычислите величину минимальных средних затрат. ■
Ответы к упражнениям
9.11. р (х) = —4х4 (1 — — 4^3) « — 4х4 при больших значениях х (по абсолют¬
ной величине).
lim р(х) — —оо, lim р(х) = —оо.
х—»—оо х—>оо
9.12. 1) у = 0.
2) Ни одной горизонтальной асимптоты.
9.13. х = 1.
9.14. 	Область определения: (—оо,оо).
Точка пересечения с осью у\ /(0) = 0.
Точки пересечения с осью х: —4; 0.
Асимптоты: нет.
Убывает на интервале (—оо, —3), возрастает на интервале (—3, оо), локальный минимум достигается в точке х = —3.
Выпуклая вверх на интервалах (—оо, —2) и (0, оо), выпуклая вниз на интервале (—2,0).
Точки перегиба: х = — 2, х = 0.
X
X
/(®)
—4
0
-3
—27
—2
-16
0
0


228
Часть III. Математический анализ
9.15. 	Область определения: вся числовая ось, за исключением точки х = 1. Точка пересечения с осью у: /(0) = 0.
Точка пересечения с осью х: 0.
Горизонтальная асимптота: у = —2.
Вертикальная асимптота: х = 1.
Возрастает на интервалах (оо, 1) и (1, оо).
Выпуклая вверх на интервале (—оо, 1), выпуклая вниз на интервале и (1, оо).
X
/(®)
-1
-1
0
0
1
2
2
3
2
-6
2
—4
5
5
2
9.16. 	1) Область определения: (0, оо).
Точки пересечения: нет.
Вертикальная асимптота: х = 0.
Наклонная асимптота: у = 0,25т.
Возрастает на интервале (0, 80), убывает на интервале (80, оо). Локальный минимум достигается в точке х = 80.
Выпуклая вверх на интервале (0, оо).
2) Величина минимальных средних затрат равна 40 и достигается в точке х — 80.


Глава 9. Построение графиков и оптимизация
229
Практикум 9.3
А В задачах 1—14 исследуется следующий график функции.
1. Укажите интервалы, на которых выполняется условие f(x) < 0.
2. Определите интервалы, на которых выполняется условие f'(x) > 0.
3. Укажите интервалы, на которых функция f(x) возрастает.
4. Определите интервалы, на которых функция f(x) убывает.
5. Найдите точки локальных максимумов функции f(x).
6. Укажите точки локальных минимумов функции f(x).
7. Определите интервалы, на которых выполняется условие f"(x) < 0.
8. Укажите интервалы, на которых выполняется условие /"(а;) > 0.
9. Определите интервалы, на которых график функции f(x) является выпуклым вверх.
10. Укажите интервалы, на которых график функции /(а;) является выпуклым вниз.
11. Найдите точки перегиба функции /(а;).
12. Укажите горизонтальные асимптоты функции f(x).
13. Определите вертикальные асимптоты функции f(x).
14. Найдите точки пересечения графика функции /(ж) с осями х и у.
В задачах 15-24 необходимо вычислить указанный предел.
15. 	lim (-5а;3 + 7х — 9).
х—>оо
17. 	lim (5а?4 + 2х3 + 7).
х—>оо
16. 	lim (4а;3 + 5а?2 + 3). х—>оо
18. 	lim (За;6 - 2а:5 + 7 а;). х—►—оо
21.
lim
я—>оо
Зх3 + Ьх
9х2 — 4
20.
lim
х—>оо
2х2 + 5
5а;2-2’
23.
lim
х—> — оо
2х2 — 5х
За;3 + 7 ’
22.
24.
lim
х—>оо
2х - 7 5а;2+ 2’
lim
х—► — оо
Зх3 -5
2а;2+9’


230
Часть III. Математический анализ
В задачах 25-36 необходимо найти все горизонтальные и вертикальные асимптоты.
25. /(х) =
27. /(*) =
29. f (а;) =
31. /(а?) =
33. f (х) =
Зх — 4
х х2 - 4 х2 + 4’
х
х2 — 1 ’
X3 х2 — 16’ 2х2 + х — 3 х2 — 2х + 1 ’ Зх2 2х + 5 2х2 + Зх — 20
26. /(*) =
28. /(х) =
30. / (х) =
32. f (х) =
34. f(х) =
36. f (х) =
Зх х — 4’ х2 -I- 9 х2 - 9’
х3 х2 + 1 ’
Зх х2 + 3’ 5х2 — 2х -I-1
2х2 -5х-3‘
2х2 + х — 6
х2 + 4х + 4
38. /(х) = Зх2 — х3.
40. /(х) = (2 — х)(х + I)2.
42. /(х) = х4 — 4х3.
z ч 2х — 4
44-/w = 772'
46. /И = *-±£.
35. f (х) =
Б В задачах 37-46 требуется исследовать функцию f и нарисовать ее возможный график.
37. /(х) = х3 — бх2.
39. /(х) = (х + 4)(х — 2)2.
41. /(х) = 8х3 — 2х4.
43./и = —.
43./И = ^.
В задачах 47-54 требуется построить график функции f, используя предоставленную информацию. Предполагается, что функция f непрерывна в области определения, а в таблице перечислены все точки пересечения ее графика с осями координат.
47. Область определения: вся числовая ось. f (х) = 2.
X
-4 -2 0 2 4
0-20-20
X
Ш
X
48. Область определения: вся числовая ось. lim^-oo f (х) = —3; lim^oo f (х) = = 3.
X
-2-10 12
/(я)
0 2 0 -2 0


Глава 9. Построение графиков и оптимизация
231
X
/И
Г(х)
X
49. 	Область определения: вся числовая ось, за исключением точки х = —2. limx__2- f (х) = оо; lima.^_2+ f (х) = -оо; lim^^ f (х) = 1.
X
—4
0
4
6
/(*)
0
0
3
2
/'(х)
X
/"(X)
X
50. 	Область определения: вся числовая ось, за исключением точки х = 1. f (х) = оо; lim^^ f (х) = оо; f (х) = -2.
X
-4-2 0 2
0-200
Лх)
х
ш
X
51. Область определения: вся числовая ось, за исключением точки х = — 1. /(-3) = 2, /(-2) = 3, /(0) = -1, /(1) = 0.
/'(х) > 0 на интервалах (—оо, —1) и (—1, оо).
/"(х) > 0 на интервалах (-оо, -1) и f"(x) < 0 на интервале (-1, оо). Вертикальная асимптота: х = — 1.
Горизонтальная асимптота: у = 1.
52. Область определения: вся числовая ось, за исключением точки х = 1. /(0) = —2, /(2) = 0.
f'(x) < 0 на интервалах (—оо, 1) и (1, оо).
/"(х) < 0 на интервале (—оо, 1).
/"(х) > 0 на интервале (1, оо).
Вертикальная асимптота: х = 1.
Горизонтальная асимптота: у = — 1.


232
Часть III. Математический анализ
53. Область определения: вся числовая ось, за исключением точек х = — 2 и х = 2. /(-3) = -1, /(0) = 0, /(3) = 1,
f'(x) < 0 на интервалах (—сю, —2) и (2, сю).
/'(х) > 0 на интервале (—2,2).
f"(x) < 0 на интервале (—оо, —2) и (-2,0).
/"(х) > 0 на интервале (0,2) и (2, оо).
Вертикальная асимптота: х = —2 и х = 2.
Горизонтальная асимптота: у = 0.
54. Область определения: вся числовая ось, за исключением точек х = —1 и х = 1. /(—2) = 1, /(0) = 0, /(2) = 1,
/'(х) > 0 на интервалах (-оо, —1) и (0,1).
f(x) < 0 на интервале (—1,0) и (1, оо).
/"(х) > 0 на интервалах (—оо, —1); (-1,1) и (1, оо).
Вертикальная асимптота: х = —1 и х = 1.
Горизонтальная асимптота: у = 0.
* 55. Теорема 9.5 гласит, что
lim (апхп + an_ixn_1 Н h «о) = ±оо.
х—юо v 7
Каким условиям должны удовлетворять числа п и аП9 чтобы предел был равен оо? Каким условиям должны удовлетворять числа п и аП9 чтобы предел был равен —оо?
* 56. Теорема 9.5 также гласит, что
lim (апхп + ап-±хп~1 + • —И ао) = ±сю.
Каким условиям должны удовлетворять числа п и аП9 чтобы предел был равен оо? Каким условиям должны удовлетворять числа п и аП9 чтобы предел был равен —оо?
* 57. Пусть р(х) = х3 — 2х2.
а) Вычислите пределы lim^^oo р' (х) и lim^^^ р" (х). Опишите поведение графика функции р(х) при больших положительных значениях переменной х.
б) Вычислите пределы limz^_ocp/ (х) и lim^-oop" (х). Опишите поведение графика функции р(х) при больших (по абсолютной величине) отрицательных значениях переменной х.
* 58. Решите задачу 57 для функции р(х) = х4 — 2х3.
В В задачах 59-60 покажите, что линия у = х является наклонной асимптотой для графика функции у = /(ж) и нарисуйте его эскиз.
59. 	f (х) = х + -. 60. f (х) = х — -.
х х
В задачах 61-72 требуется исследовать функцию у = f(x) и нарисовать ее возможный график.
61. /(ж) = х3 — х. 62. /(х) = х3 + х.
63. /(х) = (х2 + 3)(9 — х2). 64. /(х) = (х2 + 3)(х2 — 1).


Глава 9. Построение графиков и оптимизация
233
65. f(x) = (х2 — 4)2. 66. /(х) = (х2 — 1)(х2 — 5).
67. /(х) = 2х6 - Зх5. 68. /(х) = Зх5 - 5х4.
В задачах 73-80 необходимо применить общие принципы построения графиков и, пользуясь графической утилитой, вычислить с точностью до двух десятичных знаков точки пересечения графика с осью х, критические значения, а также точки перегиба.
73. /(ж) = ж4 - 5х3 + Зх2 + 8х - 5.
74. f(x) = я4 + 2гг3 — 5х2 — 4я + 4.
75. /(т) = х4 - 21х3 + 100х2 + 20z + 100.
76. /(ж) = х4 - 12z3 + 2&г2 + 76z - 50.
77. f(x) = -х4 - х3 + 2х2 - 2х + 3.
78. f(x) = —х4 + х3 + х2 + 6.
79. /(ж) = 0,1х5 + 0,Зя4 - 4ж3 - 5х2 + 40х + 30.
80. f(x) = х5 + 4х4 - 7х3 - 20х2 + 20х - 20.
Применение математики
Экономика и бизнес
81. Доход. Отдел маркетинговых исследований компьютерной компании провел в крупном городе пробные продажи новой продукции. Выяснилось, что зависимость между ценой р (в долларах) и недельным спросом х приближенно описывается следующей формулой.
р(х) = 1296 - 0,12ж2; 0 х 80.
Итак, недельный доход можно вычислить по такой формуле.
R(x) = хр = 1296ж — 0,12ж3; 0 х 80.
Нарисуйте график функции R(x).
82. Прибыль. Предположим, что функция затрат С(х) (в долларах) для производства, упомянутого в задаче 81, имеет следующий вид.
С(х) = 830 + 396ж.
а) Запишите формулу прибыли Р(х).
б) Постройте график функции Р(ж).


234
Часть III. Математический анализ
83. 	Загрязнение. Оказалось, что компьютерные компании, расположенные в Силиконовой долине (Калифорния), загрязняют подземные воды, закапывая в землю контейнеры с токсическими химическим веществами. Агентство по контролю за качеством воды требует от компаний принять срочные меры по предотвращению загрязнения подземных вод, накладывая на них штраф, который должен покрыть затраты на исследование и очистку загрязненных территорий. Предположим, что сумма штрафа (млн. долл.) вычисляется по следующей формуле.
2х
р = \; о х < 1.
1 — X
Здесь х — доля ликвидированного загрязнения.
а) На каких интервалах функция Р(х) возрастает, а на каких — убывает?
б) На каких интервалах график функции Р(х) является выпуклым вверх, а на каких — вниз?
в) Найдите горизонтальные и вертикальные асимптоты.
г) Найдите точки пересечения графика с осями хну.
д) Нарисуйте эскиз графика функции Р(х).
84. 	Обучение сотрудников. В компании по производству компьютерных комплектующих было установлено, что в среднем после t дней обучения сотрудник способен собрать N(t) компонентов в день.
loot t + 9’
t 0.
а) На каких интервалах функция N(t) возрастает, а на каких — убывает?
б) На каких интервалах график функции AT(t) является выпуклым вверх, а на каких — вниз?
в) Найдите горизонтальные и вертикальные асимптоты.
г) Найдите точки пересечения графика с осями х и у.
д) Нарисуйте эскиз графика функции 7V(t).
85. 	Сервисное обслуживание. Первоначальная стоимость офисного копировального аппарата равна 3200 долл. Стоимость его обслуживания составляет 300 долл, за первый год, а затем каждый год увеличивается на 100 долл. Общая стоимость копировального аппарата через п лет выражается следующей формулой.
С(п) = 3200 -И 250п 4- 50n2, п 1.


Глава 9. Построение графиков и оптимизация
235
а) Выведите формулу для вычисления средней стоимости аппарата за год С (п) через п лет.
б) Постройте график функции С (п).
в) Когда функция С (п) достигнет минимума? (Этот показатель часто называют моментом замены оборудования.)
86. 	Затраты на строительство. Руководство завода желает построить огороженный прямоугольный склад площадью 20000 кв. футов, используя в качестве одной из сторон ограждения стену завода (рис. 9.42). Пусть х — расстояние (в футах) от здания до противоположной ограды. Докажите, что длину забора, необходимого для огораживания склада, можно вычислить по формуле
Рис. 9.42. Складской двор
а) Постройте график функции L.
б) Какие размеры прямоугольника позволяют минимизировать длину ограды?
87. 	Средние и предельные затраты. Общие ежедневные затраты на производство х парковых скамеек (в долларах), задаются следующей формулой.
С(х) = 1000 + 5я + 0,1х2.
а) Постройте графики функций средних и предельных затрат в одной и той же системе координат. Изобразите наклонные асимптоты.
б) Найдите минимум средних затрат.
88. 	Средние и предельные затраты. Общие ежедневные затраты на производство х столов для пикника (в долларах) задаются следующей формулой.
ОД) = 500 + 2х + 0,2а:2.
а) Постройте графики функций средних и предельных затрат в одной и той же системе координат. Изобразите наклонные асимптоты.
б) Найдите минимум средних затрат.
89. 	Минимизация средних затрат. Данные, приведенные в следующей таблице, описывают общие ежедневные затраты у (в долларах) на производство х порций пиццы.
а) Постройте уравнение квадратичной регрессии для вычисления общих затрат, используя графическую утилиту.


236
Часть III. Математический анализ
Количество порций х
Общие затраты у
50
395
100
475
150
640
200
910
250
1140
300
1450
б) Найдите минимальное значение общих затрат (с точностью до цента) и соответствующий объем производства (с точностью до единицы).
90. 	Минимизация средних затрат. Данные, приведенные в следующей таблице, описывают общие ежедневные затраты у (долл.) на производство х порций пиццы.
а) Постройте уравнение квадратичной регрессии для объема общих затрат, используя графическую утилиту.
б) Найдите минимум общих затрат (с точностью до цента) и соответствующий объем производства (с точностью до единицы).
Количество порций х
Общие затраты у
50
595
100
755
150
1110
200
1380
250
1875
300
2410
Биологические науки
91. 	Медицина. Лекарственный препарат вводится пациенту в вену на правой руке. Концентрация препарата в левой руке через t часов описывается следующей формулой.
CW"t2 + r
Постройте график функции С.
92. 	Физиология. Изучая скорость сокращения мышц у лягушек при разных нагрузках, исследователи У. Фемс (W. О. Fems) и Дж. Марш (J. Marsh) выяснили, что этот показатель уменьшается при увеличении нагрузки. В частности, зависимость скорости сокращения мышц S (см/с) от нагрузки w (г), выражалась следующей формулой.
5(w) =
26 + 0,06w
w
w 5.
Постройте график функции S.


Глава 9. Построение графиков и оптимизация
237
Социальные науки
93. 	Память. Среди студентов, изучающих психологию, провели эксперимент, выясняющий их способность к запоминанию новой информации. Каждый студент в течение дня должен был запомнить 30 специальных знаков. В течение каждого из последующих 30 дней студентам нужно было вспомнить как можно больше этих знаков. Оказалось, что среднее количество воспроизводимых студентами знаков прекрасно описывается следующей формулой.
5t + 20
t 1.
Постройте график функции 7V(t).
9.4. 	Оптимизация. Глобальный максимум и минимум
■ Глобальный максимум и минимум
■ Решение практических задач
Рассмотрим одно из наиболее важных применений производной — поиск глобальных максимума или минимума функции. Как указывалось ранее, специалистов по экономике часто интересует объем производства, приносящий максимальную прибыль, медицинских работников — время, за которое концентрация лекарства в крови достигнет максимума, а архитекторы стремятся вынести промышленные предприятия за границы города, минимизируя загрязнение воздуха. Любые задачи такого типа являются задачами оптимизации, для решения которых необходимо вычислить глобальный максимум или минимум определенной функции.
Глобальные максимум и минимум
Во-первых, необходимо выяснить, что представляет собой глобальный максимум или минимум! Говорят, что значение / (с) является глобальным максимумом функции У, если
/(с) > /(я)
при всех значениях переменной х в области определения. Аналогично значение /(с) является глобальным минимумом функции У, если
/(с) /(ж)
при всех значениях переменной х в области определения. На рис. 9.43 продемонстрировано несколько типичных примеров.
Задание 9.9.
Рассмотрим функции f,gnh, графики которых показаны на рис. 9.44.


238
Часть III. Математический анализ
а) глобальных максимума и минимума нет. Локальный максимум: х = -2. Локальный минимум: х = 2
б) глобальный максимум: х = 0. Глобального минимума нет
в) глобальный минимум: х = 0. Глобального максимума нет
Рис. 9.43. Глобальные экстремумы функций
а) Дх) = 1 — |х|
Рис. 9.44. Графики функций f,gnh
1. Какие из этих функций являются непрерывными на отрезке [—1,1]?
2. Найдите глобальные максимум и минимум каждой из функций на отрезке [—1,1], если они существуют, и укажите, в каких точках они достигаются.
3. Предположим, что функция р непрерывна на отрезке [—1,1] и удовлетворяет
условиям р(—1) = 0 и р(1) = 0. Нарисуйте эскиз ее графика. Имеет ли эта функция глобальный максимум или минимум? Как изменить график функции р, чтобы она не имела глобальных максимума и минимума на отрезке [—1,1]? ■
Во многих практических приложениях область определения функции ограничена физическими законами. Если область определения представляет собой отрезок, можно применить следующую теорему.


Глава 9. Построение графиков и оптимизация
239
Теорема 9.8 (Экстремальное значение5). Функция /, непрерывная на отрезке [а, Ь] (см. раздел 9.1), достигает на нем глобального максимума и минимума. ■
Необходимо помнить, что значения глобального максимума и минимума зависят как от функции /, так и от отрезка [а, Ь]. Проиллюстрируем четыре разных ситуации (рис. 9.45).
Дх)
Лх)
б) [а, />] = [4,10]
Глобальный максимум Л5) = Ю5
Глобальный максимум , Я5) = 105=Д11) I
Г) [«,*] = [3,11]
в) [М] = [4,8]
/ Д8) = 78
I Глобальный / минимум
5
■ > 1 ■
Рис. 9.45. Глобальные экстремумы функции /(х) = х3 — 21ж2 + 135ж — 170 на разных отрезках
! ЯЗ) = 73=Л9) Глобальный минимум
Во всех вариантах глобальный максимум достигается либо в критической точке, либо на конце отрезка. Функция может иметь на отрезке только один глобальный максимум и минимум, хотя каждый из них может достигаться в нескольких точках (см. рис. 9.45, г).
Глобальный экстремум (если он существует), всегда достигается либо в критических точках, либо на концах отрезка.
Итак, чтобы найти глобальный максимум и минимум непрерывной функции, определенной на отрезке, необходимо просто найти все ее критические значения, вычислить значения функции в критических точках и на концах отрезка, а затем выбрать наибольшее и наименьшее значения среди этих величин.
www Поиск глобального максимума и минимума непрерывной функции на отрезке [а, Ь]
Этап 1. Убедитесь, что функция f является непрерывной на отрезке [а, Ь].
Этап 2. Найдите критические значения функции f на отрезке [а, Ь].
Этап 3. Вычислите функцию f на концах отрезка [а, Ь] ив критических точках.
5Вторая теорема Вейерштрасса. — Примеч. ред.


240
Часть III. Математический анализ
Этап 4. Глобальный максимум функции f на отрезке [а, 6] является наибольшей величиной среди чисел, найденных на этапе 3.
Этап 5. Глобальный минимум функции f на отрезке [а, Ь] является наименьшей величиной среди чисел, найденных на этапе 3.
Пример 9.17 (Поиск глобальных экстремумов). Найдите глобальные максимум и минимум функции
/(х) = а?3 + За;2 — 9х — 7
на указанных интервалах.
1. 	[-6,4]. 2. [-4,2]. 3. [-2,2].
Решение.
1. Функция f непрерывна на всем отрезке.
/(ж) = Зх2 + бх — 9 = 3(ж — l)(z + 3).
Итак, точки х — — 3 и х = 1 являются критическими точками функции f на отрезке [—6,4]. Вычислим ее значения в точках —6, —3, 1 и 4, а затем выберем среди них максимальное и минимальное.
/(—6) = —61, Глобальный минимум
/(-з) = 20,
/(1) = -12,
/(4) = 69. Глобальный максимум
2. Отрезок: [—4,2].
X
/(ж)
-4
13
-3
20
Глобальный максимум
1
-12
Глобальный минимум
2
-5
3. 	Отрезок: [—2,2].
х /(ж)
-1
15
Глобальный максимум
1
-12
Глобальный минимум
2
-5
Критическая точка х = — 3 в таблицу не включена, поскольку она не принадлежит интервалу [-2,2]. ■


Глава 9. Построение графиков и оптимизация
241
Упражнение 9.17.
Найдите глобальные максимум и минимум функции
/(х) = т3 — 12ж
на указанных интервалах.
1. [-5,5]. 2. [-3,3]. 3. [-3,1]. ■
Предположим, что мы хотим найти глобальные максимум и минимум непрерывной функции на открытом интервале. Поскольку теорему 9.8 в этой ситуации применить нельзя, теперь нельзя утверждать, что функция обязательно имеет глобальный экстремум на исследуемом интервале. Примеры функций, не имеющих глобальных экстремумов, продемонстрированы на рис. 9.46.
а) на интервале (—оо, оо) нет абсолютных экстремумов, —1 <Дх) < 1 при всехх (Дх) * 1 или — 1 ни при одном х)
б) на интервале (1,2) нет абсолютных максимумов, 3 < fix) < 5 при всех х е (1,2) (fix) * 3 или 5 ни при одном х€(1,2))
в) на интервале (-1,1) нет абсолютных экстремумов. График имеет вертикальные асимптоты х = —1 и х = 1
Рис. 9.46. Функции, не имеющие глобальных экстремумов
Чтобы определить глобальный экстремум на открытом интервале или убедиться. что его не существует, лучше всего проанализировать график функции. Однако в одной ситуации, которая достаточно часто встречается в практических приложениях, эту задачу можно решить без построения графика. Часто бывает, что функция f непрерывна на интервале I и имеет только одну критическую точку с (интервал I может быть любым — открытым, полуоткрытым или замкнутым). Если существует значение для поиска глобального экстремума можно прибегнуть к анализу второй производной.


242
Часть III. Математический анализ
Применение второй производной для поиска глобальных максимума и минимума на интервале I, на котором функция f имеет только одну критическую точку с
Г(с)
Г(с)
/(с)
Пример
0
+
Глобальный минимум
< / >»*
0
-
Глобальный максимум
0
0
Критерий не работает
Пример 9.18 (Поиск глобальных экстремумов на открытом интервале). Найдите глобальный минимум функции
f(x) = х + -
X
на интервале (0, оо).
Решение.
4 _ х2 — 4 (х — 2) (х + 2) х2 х2 х2 '
На интервале (0, оо) существует только одна критическая точка функции /: х = 2. Поскольку /"(2) = 1 > 0, глобальным минимумом функции f на интервале (0, оо) является значение /(2) = 4. ■
Упражнение 9.18.
Найдите глобальный максимум и минимум функции
/(т) = 12 - X - -
X
на интервале (0, оо). В
Решение практических задач
www Рассмотрим несколько практических задач, связанных с поиском глобальных экстремумов. Для начала перечислим этапы решения подобных задач. Первый шаг является наиболее сложным. Лучше всего проиллюстрировать решение оптимизационных задач несколькими примерами.


Глава 9. Построение графиков и оптимизация
243
Этапы решения прикладных задач оптимизации
Этап 1. Определите переменные, функцию /, интервал Z, а затем сформулируйте задачу в следующем виде.
Максимизировать (или минимизировать) f(x) на интервале I.
Этап 2. Найдите глобальный максимум (или минимум) функции f на интервале I и значения переменной х, при которых он достигается.
Этап 3. Используйте решение задачи для ответа на поставленные вопросы.
Пример 9.19 (Максимизация дохода и прибыли). Некая компания производит и реализует х радиоприемников в неделю. Ниже приведены функция еженедельных затрат и уравнение зависимости цены от спроса.
С(х) = 5000 + 2ж;
р = 10 - 0,001ж; 0 X 10 000.
Найдите следующие величины.
1. Максимальный доход.
2. Максимальную прибыль, объем производства, при котором достигается максимум прибыли, и цену, по которой компания должна продавать радиоприемники, чтобы достичь максимальной прибыли.
Решение.
1. Доход, получаемый от продажи х радиоприемников по цене р долл., вычисляется следующим образом.
Я(ж) — хр — ж(Ю — 0,001а?) = Юж — 0,001а?2.
Следовательно математически задача записывается так.
Максимизировать /?(ж) = Юж — 0,001ж2; 0 ж 10 000.
Я'(ж) = 10 - 0,002ж;
10 - 0,002ж = 0;
ж = 5000. Единственное критическое значение
Для поиска глобального экстремума воспользуемся второй производной.
R"(x) = —0,002 < 0 при всех ж.
Итак, максимальный доход равен следующей величине.
Мах Я(ж) = Д(5000) — 25 000 долл.


244
Часть III. Математический анализ
2. Прибыль = доход — затраты.
Р(ж) = Я(х) - С(х) - Юж - 0,001я2 - 5000 - 2х = 8х - 0,001ж2 - 5000.
Математически задача записывается следующим образом.
Максимизировать Р(ж) = 8х — 0,001 х2 — 5000 при 0 < х < 10 000, Р'(ж) = 8 - 0,002ж;
8 - 0,002х = 0;
х = 4000; Р"(х) = —0,002 < 0 при всех х.
Поскольку х — 4000 — единственное критическое значение и Р"(ж) < 0, получаем следующий результат.
МахР(х) = Р(4000) = 11000 долл.
Вычисляя уравнение цены в точке х = 4000, определим оптимальную цену радиоприемника.
р = 10 - 0,001 • 4000 = 6 долл.
Итак, максимальная недельная прибыль, равная 11000 долл., достигается при выпуске 4000 радиоприемников и продаже их по цене 6 долл. Обратите внимание на то, что этот объем продукции не совпадает с объемом, гарантирующим максимальный доход. ■
Результаты решения примера 9.19 приведены на рис. 9.47. Легко видеть, что прибыль достигает максимума, когда
Р'(т) = Д'(ж) _ С'(т) = 0,
т.е. когда предельная прибыль равна предельным затратам (скорость увеличения прибыли равна скорости увеличения затрат при выпуске 4000 радиоприемников в неделю). Обратите внимание на то, что наклоны обеих кривых в этой точке равны.
Упражнение 9.19.
Решите пример 9.19 для функции
С(т) = 90000 +30т,
р — 300 — при 0 < х 9000. ■


Глава 9. Построение графиков и оптимизация
245
Рис. 9.47. Прибыль и доход
Пример 9.20 (Максимизация прибыли). Правительство решило обложить компании, выпускающие радиоприемники, специальным налогом: по два доллара с каждого радиоприемника. Сколько радиоприемников в неделю должна выпускать компания теперь, чтобы достичь максимальной прибыли. Чему равна максимальная еженедельная прибыль? Какую цену должна установить компания на свою продукцию, чтобы гарантировать максимальную еженедельную прибыль? Решение. Налог, равный двум долларам, изменил формулу затрат.
С(ж) = исходные затраты + налог = = 5000 + 2х + 2х = 5000 + 4х.
Новая функция прибыли выглядит следующим образом.
Р(х) = 7?(х) — С(х) = 6х — 0,001а;2 — 5000 при 0 х 10000.
Итак, мы должны решить следующую задачу.
Максимизировать Р(аг) = бх — 0,001а;2 — 5000 при 0 х 10 000;
Р'(х) = 6 - 0,002а:;
6 — 0,002а? - 0;
х = 3000;


246
Часть III. Математический анализ
Р"{х) = —0,002 < 0 при всех х. Мах Р(х) = Р(3000) = 4000 долл.
Вычисляя уравнение цены в точке х = 3000, определим оптимальную цену радиоприемника.
р = 10 — 0,001 • 3000 = 7 долл.
Итак, максимальная прибыль за неделю, равная 4000 долл, за неделю, достигается при выпуске 3000 радиоприемников в неделю и продаже их по цене 7 долл, за штуку. Несмотря на то что налог увеличил себестоимость продукции на два доллара, оптимальная цена радиоприемника увеличилась только на один доллар. Оставшийся доллар с каждого радиоприемника снижает максимальную прибыль компании до 7000 долл. ■
Упражнение 9.20.
Решите пример 9.20 для функции
С(х) = 90 000 + ЗОх,
р = 300 — при 0 ж < 9000,
если правительство решило взимать 20 долл, налога с каждой единицы выпущенной продукции. Сравните результаты с ответом, полученным при анализе упражнения 9.19, п. 2. I
Пример 9.21 (Максимальная урожайность). Фермер, выращивающий грецкие орехи, выяснил, что если на одном акре земли растут 20 ореховых деревьев, то каждое дерево приносит в среднем 60 фунтов орехов в год. Предположим, что каждое новое посаженное дерево (вплоть до пятнадцатого) снижает среднюю урожайность всех ореховых деревьев на два фунта в год. Сколько ореховых деревьев необходимо посадить на одном акре земли, чтобы получить максимальный урожай?


Глава 9. Построение графиков и оптимизация
247
Решение. Обозначим через х количество дополнительных деревьев, посаженных на одном акре земли. Тогда выполняются следующие соотношения.
20 + х = общее количество деревьев на одном акре земли,
60 — 2х = урожайность каждого дерева,
урожайность одного акра земли = общее количество деревьев на акрех
х урожайность дерева,
Y(х) = (20 + х)(60 — 2х) = 1200 + 20ж — 2х2 при 0 х 15.
Итак, мы должны решить следующую задачу.
Максимизировать Y(z) = 1200 + 20ж — 2х2 при 0 х 15,
У'(я) = 20 - 4х,
20 — 4х = 0,
х = 5.
Y"(x) = — 4 < 0 при всех х.
Следовательно,
Мах У (я) = У (5) = 1250 футов на акр.
Итак, чтобы достичь максимальной урожайности, равной 1250 фунтов грецких орехов на один акр земли, на одном акре необходимо посадить 25 деревьев. ■
Упражнение 9.21.
Повторите решение примера 9.20, если на одном акре земли изначально росли 30 ореховых деревьев, а добавление каждого нового дерева снижает урожайность дерева на один фунт. ■
Задание 9.10.
В примере 9.21 введение обозначения х для количества дополнительно высаженных деревьев на одном акре земли позволило легко решить поставленную задачу. Однако такая возможность существует не всегда. Предположим, что х — общее количество ореховых деревьев, высаженных на одном акре земли, а у — урожайность одного дерева. Тогда урожайность одного акра равна ху,
1. Найдите величины у при х = 20иж = 21. Постройте уравнение прямой, проходящей через эти точки.
2. Используя уравнение, построенное в п. 1, выразите урожайность одного акра через величины х или у, а затем примените эту переменную для решения примера 9.21.
3. Сравните этот метод решения задачи со способом, описанным в примере 9.21. Какой из них понятнее и проще для вычислений? В


248
Часть III. Математический анализ
Пример 9.22 (Максимальная площадь). Фермер желает пристроить прямоугольный загон к стене конюшни так, чтобы эта стена стала одной из сторон загона. Длина стены — 60 футов. При каких размерах загона его площадь является максимальной, если в распоряжении фермера есть следующее количество материалов.
1. 160 футов жердей.
2. 250 футов жердей.
Решение.
1. Для начала разметим стороны прямоугольника, как показано на рисунке.
Площадь загона равна
А — (х + 60)у.
Для того чтобы максимизировать площадь, необходимо определить зависимость между переменными х и у, а затем выразить величину А как функцию одной из этих величин. В данном случае зависимость между переменными х и у можно определить с помощью общей длины имеющихся жердей.
х + у + 60 + х + у = 160,
2х + 2у — 100,
у - 50 — х.
Итак,
А(х) — (х + 60) (50 — х).
Теперь необходимо выяснить допустимые значения переменной х, т.е. область определения функции А. Поскольку фермер желает использовать все имеющиеся жерди, число х не может быть отрицательным. Поскольку символ у обозначает другую сторону загона, число у также не может быть отрицательным. Итак,
у = 50 - х 0,
50 х.


Глава 9. Построение графиков и оптимизация
249
Областью определения функции А является отрезок [0,50]. Следовательно, необходимо решить следующую задачу.
Максимизировать А(х) = (х + 60) (50 — т) при 0 х 50.
А(т) = 3000 — Ют — х2,
А'(т) = -10 - 2т,
-10 - 2т = 0,
х = —5.
Поскольку число х = — 5 не принадлежит отрезку [0,50], оно не является критическим значением. Функция А(х) непрерывна на отрезке [0,50], поэтому ее глобальный максимум достигается на одном из концов отрезка.
А(0) = 3000, Максимальная площадь
.4(50) = 0.
Если х — 0, то у = 50. Следовательно, загон имеет максимальную площадь, если длины его сторон равны 60 и 50 футов соответственно.
2. 	Если фермер имеет в своем распоряжении 250 футов жердей, то вычисления выглядят следующим образом.
х + у + 60 + х + у — 250,
2х + 2у = 190, у = 95 — х.
Следовательно, необходимо решить следующую задачу.
Максимизировать А(т) = (х + 60) (95 — т) при 0 х 95.
А(х) = 5700 + 35т — х2 у
А'(х) = 35 - 2т,
35 — 2т = 0,
35
х = — = 17,5. Единственная критическая точка


250
Часть III. Математический анализ
= —2 < 0 при всех ж, МахА(ж) = Л(17,5) = 6006,25, у = 95 - 17,5 = 77,5.
Итак, загон имеет максимальную площадь, если длины его сторон равны 77,5 фута каждая. ■
Упражнение 9.22.
Повторите решение примера 9.22, если длина стены амбара равна 80 футам. ■
Замечание.
Для вычисления критических значений удобно использовать графические утилиты. Графики, представленные на рис. 9.48, подтверждают результаты решения примеров 9.22.1 и 9.22.2.
а) А(х) = (х + 60) (50 - х) б) Л(х) = (х + 60) (95 - х)
Рис. 9.48. Графики, построенные с помощью графической утилиты
Пример 9.23 (Управление запасами), www Звукозаписывающая студия
предполагает, что спрос на ее новый компакт-диск на протяжении следующего года достигнет 20 000 заказов. Хранение одного компакт-диска на складе на протяжении одного года стоит 0,5 долл. Если же компании придется выпустить дополнительное количество компакт-дисков, на наладку оборудования придется затрать 200 долл. Сколько компакт-дисков компания должна выпустить за один производственный цикл, чтобы минимизировать затраты на хранение продукции и наладку оборудования?


Глава 9. Построение графиков и оптимизация
251
Решение. Такие задачи называются задачами управления запасами. Одним из основных предположений в этой задаче является равномерность спроса. Например, если производственный год состоит из 250 рабочих дней, ежедневный спрос должен быть равным 20000/250 = 80 компакт-дисков. Компания может выпустить все 20 000 компакт-дисков в начале года. Это позволит минимизировать затраты на наладку производства, но значительно увеличит затраты на хранение продукции. С другой стороны, компания могла бы выпускать по 80 компакт-дисков в день. Это минимизирует затраты на хранение продукции, но поднимет расходы на наладку производства. Оптимальное решение лежит где-то посередине. Введем следующие обозначения.
х — количество компакт-дисков, выпущенных за производственный цикл,
у — количество производственных циклов.
Очевидно, что общие затраты, связанные с наладкой производства, составляют 200?/. А чему равна величина затрат на хранение продукции? Если спрос является равномерным, количество компакт-дисков, хранящихся на складе, колеблется от нуля до х, причем среднее количество единиц хранения равно х/2. Этот результат проиллюстрирован на рис. 9.49.
Количество товара на складе
Среднее
количество
Первый Второй Третий Четвертый
Производственные циклы
Рис. 9.49. Управление запасами
Поскольку величина затрат на хранение одного компакт-диска на протяжении года равна 0,5 долл., общие затраты на хранение равны 0,5ж/2 = 0,25z, а общие затраты выражаются следующей формулой.
Общие затраты = затраты на наладку + затраты на хранение
С = 200?/ + 0,25х.
Для того чтобы представить общие затраты С как функцию одной переменной, мы должны выяснить зависимость между величинами х и у. Если компания выпускает х компакт-дисков в течение каждого из у производственных циклов, значит,


252
Часть III. Математический анализ
общее количество произведенных компакт-дисков равно ху. Итак,
ху = 20 000,
20000
Очевидно, что величина х больше или равна единице, но меньше или равна 20 000. Следовательно, мы должны решить такую задачу.
Максимизировать
С (х) = 200 • + 0,25х;
X
4000000 _
h 0,25х;
X
4000000  5 + 0,25.
хг
0 < х 20000,
С (ж) =
С" (г) =
Вычисления выглядят следующим образом.
4000000 п
+ 0,25 = 0;
X
2 4000000
х2 = :
0,25 ’
х2 = 16000000,
х = 4000
( х 8 000000
с^ = x3 >
Значение —4000не является критическим, поскольку 1 X 20 000.
при х 6 (1, 20 000).
0
Следовательно,
MinC(x) = С(4000) = 2000.
20 000 „ у = = 5.
у 4000
Итак, чтобы минимизировать затраты, компания должна выпускать по 4000 ком¬
пакт-дисков пять раз в год. ■
Упражнение 9.23.
Повторите решение примера 9.23, если затраты, связанные с наладкой про¬
изводства, составляют 250 долл., а величина затрат на хранение одного компакт- диска на протяжении одного года равна 0,40 долл.


Глава 9. Построение графиков и оптимизация
253
Ответы к упражнениям
9.17. 1) Глобальный максимум: /(5) — 65; глобальный минимум: /(—5) = —65.
2) Глобальный максимум: /(—2) = 16; глобальный минимум: /(2) = —16.
3) Глобальный максимум: /(—2) = 16; глобальный минимум: /(1) = —11.
9.18. /(3) = 6.
9.19. 1) МахЯ(ж) = Я(4500) = 675 000 долл.
2) МахЯ(ж) = 21(4050) = 456750 долл., р = 165 долл.
9.20. Мах/?(ж) = /?(3750) — 378 750 долл., р = 175 долл., цена увеличивается на 10 долл., прибыль уменьшается на 78 000 долл.
9.21. Мах У (ж) = У (15) = 2025 фунтов/акр.
9.22. 1) 80 на 40 футов.
2) 82,5 на 82,5 фута.
9.23. Необходимо выпускать по 5000 компакт-дисков четыре раза в год.
Практикум 9.4
А В задачах 1-10 исследуется следующий график функции. Найдите глобальный максимум и глобальный минимум этой функции на указанных отрезках.
1. 	[0; 10].
5. 	[1; 10].
9. 	[2; 5].
2. 	[2; 8].
6. 	[0;9].
10. [5; 8].
3. 	[0;8].
7. 	[1;9].
4. 	[2; 10].
8. 	[0;2].
В задачах 11-16 необходимо найти глобальный максимум и глобальный минимум указанной функции, если они существуют.
11. 	/(ж) = х1  2 — 2х + 3.
12. 	/(ж) = х2 4- 4х — 3.


254
Часть III. Математический анализ
13. 	/(х) = — х2 — бх + 9. 14. /(х) = —х2 + 2х + 4.
15. /(х) = х3 + х. 16. /(х) = —х3 — 2х.
Б В задачах 17-22 необходимо найти глобальный экстремум указанной функции, если он существует.
17. Глобальный максимум функции
12 /(х) = 20 — Зх ; х > 0.
х
18. Глобальный минимум функции
9 /(х) = 4 + х + —; X > 0.
х
19. Глобальный минимум функции
64 /(х) = 10 + 2х + х > 0.
xz
20. Глобальный максимум функции
/(х) = 20 - 4х — ; х > 0.
х2
21. Глобальный максимум функции
/(а;) = 20 + 15а; - 2а:2 -х > 0.
X
22. Глобальный минимум функции (с точностью до двух десятичных знаков)
/(х) = 20 — 7х + 4х2 +
х
х > 0.
В задачах 23-26 необходимо найти глобальный максимум и глобальный минимум функ¬
ции, если они существуют на указанном интервале.
23. /(х) = х3 — бх2 + 9х — 6
а) [-1;5]. б)
24. /(х) = 2х3 - Зх2 - 12х + 24
а) [-3;4]. б)
25. /(х) = (х — 1)(х — 5)3 + 1
а) [0;3]. б)
26. /(х) = х4 — 8х2 + 16
а) [—1;3]. б)
В Ответьте на следующие вопросы.
[-1;3].
в) [2; 5].
[-2;3].
в) [-2;1].
[1;7].
в) [3,6].
[0;2].
в) [-3;4].
27. 	Как разделить 10-дюймовую линию на два отрезка так, чтобы произведение двух длин было максимальным?
28. 	Какие числа необходимо добавить к пяти и вычесть из пяти, чтобы их произведение было максимальным?


Глава 9. Построение графиков и оптимизация
255
29. Найдите два числа, разность которых равна 30, а произведение — максимально.
30. Найдите два положительных числа, сумма которых равна 60, а произведение — максимально.
31. При каких длинах сторон прямоугольника, периметр которого равен 100 см, его площадь максимальна?
32. При каких длинах сторон прямоугольника, площадь которого равна 225 см2, его периметр минимален? Чему равен этот периметр?
В задачах 33-36 рассматривается прямоугольная площадь, ограниченная забором, стоимость которого равна В долл, за фут. Существует ли решение поставленных задач? Какие экономические выводы можно сделать, решив указанные задачи оптимизации?
* 33. Минимизируйте стоимость забора при заданной площади.
* 34. Максимизируйте стоимость забора при заданной площади.
* 35. Максимизируйте площадь при фиксированной стоимости забора.
* 36. Минимизируйте площадь при фиксированной стоимости забора.
Применение математики
Экономика и бизнес
37. WWW Максимальная прибыль и доход. Некая компания выпускает и продает х телевизоров в месяц. Функция затрат и уравнение зависимости цены от спроса имеют следующий вид.
С(х) = 72 000 + 60а;,
р — 200—0 х SS 6000.
ои
а) Вычислите максимальный доход.
б) Найдите максимальную прибыль, объем производства, при котором достигается максимальная прибыль, и цену, которую следует установить на телевизоры.
в) Предположим, что правительство решило взимать с каждого телевизора дополнительный налог в размере 5 долл. Сколько телевизоров должна выпускать компания, чтобы гарантировать максимальную прибыль? Чему равна максимальная прибыль? Какую цену теперь необходимо установить?
38. Максимальная прибыль и доход. Повторите решение задачи 37 для следующих функции затрат и уравнения зависимости цены от спроса.
ОД = 60000 + 60я,
р = 200-^-, 0^x^ 10000.


256
Часть III. Математический анализ
39. 	Максимальная прибыль. В таблице приведены данные о цене и спросе, а также затраты на производство циркулярных пил, где р — оптовая цена пилы, долл., х — годовой спрос и С — общие затраты на производство х пил.
X
р
с
950
240
130000
1200
210
150000
1800
160
180000
2050
120
190000
а) Постройте модель квадратичной регрессии для зависимости цены от спроса, где независимой переменной является величина х.
б) Постройте уравнение линейной регрессии для зависимости затрат от объема производства, где независимой переменной является величина х.
в) Чему равна максимальная прибыль? Какую оптовую цену должна установить компания, чтобы получить максимальную прибыль?
40. 	Максимальная прибыль. В таблице приведены данные о цене и спросе, а также затратах на производство аэрографов, где р — оптовая цена, долл., х — объем годового спроса и С — общие затраты на производство х штук аэрографов.
а) 	Постройте модель квадратичной регрессии для зависимости цены от спроса, где независимой переменной является величина х.
X
р
С
2300
98
145000
3300
84
170000
4500
67
190000
5200
51
210000
б) Постройте модель линейной регрессии для зависимости затрат от объема производства, где независимой переменной является величина х.
в) Чему равна максимальная прибыль? Какую оптовую цену должна установить компания, чтобы получить максимальную прибыль?
41. Прокат автомобилей. Агентство по прокату автомобилей предоставляет в аренду своим клиентам 200 машин по цене 30 долл, в день. Увеличение стоимости проката на один доллар приводит к падению спроса на пять автомобилей в день. При какой цене агентство получит максимальный доход? Чему он равен?
42. Доход от аренды. Трехсоткомнатный отель в Лос-Анджелесе полностью заполняется при стоимости комнаты, равной 80 долл, за ночь. Увеличение стоимости аренды на один доллар приводит к уменьшению заполняемости на три номера. Предположим, что стоимость обслуживания одного снимаемого номера равна 10 долл, в день. Какую цену за аренду должно установить руководство отеля, чтобы получить максимальную валовую прибыль? Чему равна эта прибыль?
43. Сельское хозяйство. Владелец вишневого сада выяснил, что при высадке 30 деревьев на одном акре каждое дерево приносит 50 фунтов вишни за сезон. При


Глава 9. Построение графиков и оптимизация
257
высадке дополнительного дерева (вплоть до 20) средняя урожайность деревьев снижается на один фунт. Сколько деревьев следует высадить на одном акре сада, чтобы получить максимальный урожай? Чему он равен?
44. Сельское хозяйство. Владелец грушевого сада выбирает оптимальный момент для сбора и продажи фруктов. Если весь урожай собрать в один день, он получит 30 центов за фунт. Каждое дерево приносит в среднем 60 фунтов груш, пригодных для продажи. В течение следующих четырех недель урожайность каждого дерева в среднем вырастет на 6 фунтов, однако за это время цена будет падать на 2 цента в неделю. Когда следует собрать и продать урожай, чтобы получить максимальный доход? Чему он равен?
45. Производство. Коробки для конфет изготавливаются из прямоугольных картонных заготовок, размером 8 на 12 дюймов. Затем в каждом углу прямоугольника вырезаются одинаковые квадраты, а полученная фигура образует коробку. Какой должна быть сторона вырезаемого квадрата, чтобы объем коробки был максимальным?
46. Упаковка. Почтовая служба принимает лишь пакеты, сумма длины и обхвата которых не превышает 108 дюймов.
Рис. 9.50. Почтовая бандероль
а) Определите размеры прямоугольной коробки, удовлетворяющей требованиям почтовой компании, и имеющей максимальный объем. Чему он равен?
б) Найдите размеры (радиус и высоту) цилиндрического контейнера, удовлетворяющего требованиям почтовой компании и имеющего максимальный объем. Чему он равен?
47. Затраты на строительство. Необходимо построить забор, огораживающий прямоугольную площадь, равную 800 кв. футам. Три стороны забора изготавливаются из материала, который стоит 6 долл, за фут. Материал для четвертой стороны стоит 18 долл, за фут. Определите длины сторон прямоугольника, минимизирующие затраты на изготовление забора.
48. Затраты на строительство. Владелец склада решил возвести забор, чтобы огородить участок, примыкающий к его владениям. Одной из сторон забора


258
Часть III. Математический анализ
Рис. 9.51. Склад и забор
должна стать стена склада (рис. 9.51). Найдите размеры забора, при которых достигается максимальная площадь огораживаемой территории при следующих условиях.
а) В распоряжении строителей есть 240 футов жердей.
б) В распоряжении строителей есть 400 футов жердей.
49. Управление запасами. Издательство продает 50 000 экземпляров книги в год. Хранение одного экземпляра книги в течение года стоит один доллар. Настройка производства для выпуска дополнительных экземпляров книги стоит 1000 долл. Сколько книг должна выпускать компания за один производственный цикл, чтобы минимизировать затраты на наладку производства и хранение напечатанных экземпляров?
50. Эксплуатационные затраты. Стоимость топлива, потребляемого тепловозом за час, равна v2/4 долл., где v — скорость поезда, миль/ч. (Обратите внимание на то, что стоимость топлива пропорциональна квадрату скорости.) Другие эксплуатационные затраты, включая оплату труда машинистов, равны 300 долл./ч. С какой скорость поезд должен проехать 360 миль, чтобы минимизировать эксплуатационные затраты?
51. Затраты на строительство. Небольшой курорт, расположенный на острове, решил провести водопровод, начало которого находится на расстоянии 5 миль от берега (рис. 9.52). Обозначим через х длину участка водопровода, проложенного по берегу.
Рис. 9.52. Водопровод


Глава 9. Построение графиков и оптимизация
259
а) Предположим, что затраты на прокладку водопровода по дну водоема в 1,4 раза больше, чем затраты на его прокладку по земле. Чему должна быть равна величина х, чтобы минимизировать затраты?
б) Предположим, что затраты на прокладку водопровода по дну озера в 1,1 раза больше, чем затраты на его прокладку по земле. Чему должна быть равна величина х, чтобы минимизировать затраты? (Сравните решение с ответом к задаче 56.)
52. Производственные расходы. Компания решила производить консервы в банках емкостью 12 унций (приблизительно 22 куб. дюймов) в виде правильных цилиндров. Найдите размеры (радиус и высоту) банки, для изготовления которой затрачивается минимальное количество жести. Предположим, что крышки банок вырезаются из квадратных заготовок, а их стенки изготавливаются из прямоугольника.
Биологические науки
53. Дезинфекция водоемов. Вода в озере, в котором часто купаются отдыхающие, время от времени подвергается дезинфекции. Предположим, что через t дней после дезинфекции концентрация бактерий в кубическом сантиметре воды описывается следующей формулой.
C(t) = 30i2 - 240f + 500, 0 t 8.
Через сколько дней после дезинфекции концентрация бактерий станет минимальной? Чему равна эта концентрация?
54. 	Концентрация препарата. Концентрация C(f) некого лекарственного препарата в крови пациента через t часов после приема описывается следующей формулой.
С(1) =
0,16t
t2 + 4t + 4‘
Через сколько часов после приема концентрация лекарства в крови пациента станет максимальной? Чему равна эта концентрация?
55. Затраты на содержание лаборатории. Каждый год в лабораторных экспериментах используются 500 белых мышей. Стоимость питания каждой мыши равна 4 долл, в год. Заказ каждой мыши стоит 10 долл. Сколько мышей следует заказать за один раз, чтобы минимизировать затраты на их питание и обслуживание заказа?
56. Затраты на полет. Некоторые птицы избегают летать на крупными озерами в дневное время. (Предполагается, что затраты энергии на полет над водой больше, чем на полет над землей, поскольку днем воздух над землей, как правило, поднимается вверх, а над водой — опускается вниз.) Предположим, что из гнездовья, расположенного на берегу озера, взята взрослая птица. Ее отвозят на остров, расположенный в пяти милях от берега (рис. 9.53), а затем отпускают.
а) 	Предположим, что лететь над озером в 1,4 раза труднее, чем над землей. Сколько миль птица должна пролететь над берегом, чтобы попасть в свое гнездо, затратив минимум энергии?


260
Часть III. Математический анализ
Рис. 9.53. Траектория полета птицы
б) 	Предположим, что лететь над озером в 1,1 раза труднее, чем над землей. Сколько миль птица должна пролететь над берегом, чтобы попасть в свое гнездо, затратив минимум энергии? (Сравните ответ с решением задачи 51.)
57. Ботаника. Предположим, что высота (в футах) определенного растения через t месяцев определяется по следующей формуле.
H(t) = 4i1/2 - 2t; 0 < t < 2.
Сколько времени потребуется растению, чтобы достичь максимальной высоты? Чему она равна?
58. Загрязнение. Два промышленных завода расположены друг от друга на расстоянии 10 миль (рис. 9.54). Предположим, что концентрация вредных пылевидных веществ (частиц на миллион) обратно пропорциональна квадрату расстояния от источника. Завод Ai выбрасывает в атмосферу в восемь раз больше вредных веществ, чем завод А2. Концентрация пылевидных веществ в произвольной точке расстояния между заводами задается следующей формулой.
С'(х) = ^ + —-jj 0,5 < х < 9,5; к > 0.
х1 (10 - х)
Насколько далеко от завода Ai концентрация загрязнения достигнет минимума?
Рис. 9.54. Заводы
Социальные науки
59. 	Политика. Оценки социологов показывают, что численность населения, имеющего право голоса в некоем городе (тыс. чел.), будет расти по следующей формуле.
2V(t) = 30 + 12t2 - t3.


Глава 9. Построение графиков и оптимизация
261
Здесь t — время, измеряемое годами. В какой момент скорость роста числа избирателей станет максимальным?
60. 	Обучение. Согласно данным отдела кадров крупной сети продовольственных магазинов в среднем учетчик запоминает Р% информации из прейскуранта через х часов после начала работы. Функция Р(х) имеет следующий вид.
Р(х) = 9бж — 24ж2, 0 х < 3.
Через какое время учетчик запомнит максимальное количество информации? Чему равен этот максимум?
Ключевые слова, основные обозначения и формулы
9.1. 	Первая производная и графики. Возрастающие и убывающие функции; графики, направленные вверх и вниз; критические значения; локальный экстремум; локальный максимум; локальный минимум; экстремум; определение локального экстремума с помощью первой производной.
9.2. 	Вторая производная и графики. Выпуклость вверх; выпуклость вниз; вторая производная; выпуклость и вторая производная; точка перегиба; определение локальных максимумов и минимумов с помощью второй производной; точка
сокращающихся доходов.
/"(*);
у
//
9.3. 	Методы построения графиков. Горизонтальная асимптота, поведение на бесконечности степенных, полиномиальных и рациональных функций; определение вертикальных асимптот; этапы построения графиков (нахождение области определения функции, точек пересечения графика с осями координат, горизонтальных и вертикальных асимптот; анализ первой производной для поиска интервалов возрастания и убывания функций, локальных экстремумов; анализ второй производной для поиска интервалов, на которых график функции является выпуклым вверх или вниз, а также определение точек перегиба); наклонные асимптоты.
9.4. 	Оптимизация: глобальный максимум и минимум. Глобальный максимум; глобальный минимум; глобальный экстремум функции на отрезке; анализ второй производной для поиска глобального максимума и минимума; задачи оптимизации; задача управления запасами.
Упражнения для повторения
Выполните все упражнения этого обзорного раздела и сравните результаты с ответами, помещенными в конце книги. Ответы ко многим упражнениям на повторение приводятся вместе с номером соответствующего раздела (курсивом). Если у вас возникают затруднения при решении какой-либо задачи, повторите материал соответствующего раздела.


262
Часть III. Математический анализ
А В задачах 1-8 исследуется следующий график функции. Найдите на оси х точки или интервалы, соответствующие указанному поведению функции f.
1. Функция f(x) возрастает.
2. f'(x) < 0.
3. График функции /(ж) является выпуклым вниз.
4. Локальный минимум.
5. Глобальный максимум.
6. Значение /'(*) близко к нулю.
7. Значение /'(х) не существует.
8. Точки перегиба.
В задачах 9 и 10 требуется построить график функции f, используя приведенную информацию. Предполагается, что функция f является непрерывной в области определения, а в условии перечислены все точки пересечения ее графика с осями координат.
9. Область определения: вся числовая ось.
X
-3-2-10 2 3
/(®)
0 3 2 0 -3 0
Л*)
X
10. 	Область определения: вся числовая ось.
/(-2) = 1,/(0) = 0,/(2) = 1;
/'(0) = 0, /'(ж) < 0 на (-00,0); f(x) > 0 на (0, оо);
/"(—2) < 0 на (—оо, —2) и (2, оо); f"(x) > 0 на (-2,-2);
lim / (х) = 2, lim / (х) = 2.
х—^ — оо х—юо


Глава 9. Построение графиков и оптимизация
263
11. Найдите /"(я) для функции f(x) = х* + 5я3.
4
12. Найдите уп для функции у = Зх Н—.
х
Б В задачах 13-16 исследуется функция
f(x) = х3 — 18х2 + 81ж.
13. Используя функцию /, выполните следующие задания.
а) Найдите область определения функции /.
б) Найдите все точки пересечения графика /.
в) Найдите все горизонтальные и вертикальные асимптоты графика f.
14. Используя функцию выполните следующие задания.
а) Найдите все критические значения функции /.
б) Найдите точки разбиения для функции
в) Найдите все интервалы, на которых функция f возрастает или убывает.
г) Найдите все локальные максимумы и минимумы.
15. Используя функцию выполните следующие задания.
а) Найдите все интервалы, на которых график функции f является выпуклым вверх или вниз.
б) Найдите все точки перегиба.
16. Постройте график функции /.
В задачах 17-20 исследуется функция
У = /(*) =
Зх
х + 2’
17. Используя функцию /, выполните следующие задания.
а) Найдите область определения функции /.
б) Найдите все точки пересечения графика /.
в) Найдите все горизонтальные и вертикальные асимптоты графика /.
18. Используя функцию выполните следующие задания.
а) Найдите все критические значения функции /.
б) Найдите точки разбиения для функции
в) Найдите все интервалы, на которых функция f возрастает или убывает.
г) Найдите все локальные максимумы и минимумы.
19. Используя функцию выполните следующие задания.
а) Найдите все интервалы, на которых график функции f является выпуклым вверх или вниз.
б) Найдите все точки перегиба.
20. Постройте график функции /.
21. Используя график функции у = f'(x), приведенный на рис. 9.55, опишите график функции у = f(x). Изложите ваши выводы в виде таблицы (см. пример 9.9 из раздела 9.2).


264
Часть III. Математический анализ
Рис. 9.55. График функ¬
ции у = f(x)
22. 	Проанализируйте график, представленный на рис. 9.55. Какой из следующих графиков относится к функции у = /"(х)?
а) б)
в)
23. Используя вторую производную, найдите все локальные экстремумы функции
f(x) = х3 — бх2 — 15# — 12.
24. Найдите глобальный максимум и минимум функции (если они существуют).
/(х) = х3 — 12х + 12, — 3 < х 5.
25. Найдите глобальный минимум функции (если он существует).
у =/(х) = х2 + х > 0.
х£


Глава 9. Построение графиков и оптимизация
265
В задачах 26-31 необходимо вычислить указанные пределы.
26. lim (—2ж3). 27. lim (х3 — 2х2).
В задачах 32 и 33 необходимо найти горизонтальные и вертикальные асимптоты, если они существуют.
* 34. Пусть у = f(x)— полиномиальная функция с локальными минимумами в точках х = а и х = Ь, а < Ь. Должна ли функция f(x) иметь хотя бы один локальный максимум между точками а и Ь? Обоснуйте свой ответ.
*35. Производной функции f(x) — х~г является функция /'(ж) = —х~2. Поскольку /'(г) < 0 при х ф 0, можно ли утверждать, что функция /(я?) убывает при всех х, за исключением точки х = 0? Обоснуйте свой ответ.
*36. В чем заключается разница между точкой разбиения для функции /'(я) и критическим значением функции /(ж). Приведите примеры.
В
37. 	Найдите глобальный максимум функции /'(я), если
f(x) = 6z2 — х3 + 8.
Постройте графики функций / и /' в одной и той же системе координат на отрезке 0 х 4.
38. Найдите два положительных числа, произведение которых равно 400, а сумма — минимальна. Чему равна минимальная сумма?
39. Пусть /(х) = (х — 1)3(х + 3). Примените общие принципы построения графика и нарисуйте его эскиз.
Решая задачи 40 и 41, примените общие принципы построения графика и опишите его поведение. Все вычисления выполняйте с точностью до двух десятичных знаков.
40. /(ж) = х4 + х3 — 4я2 - Зх + 4.
41. /(ж) = 0,25х4 - 5я3 + 31х2 - 70гг.
Применение математики
Экономика и бизнес
42. 	WWW Анализ цен. График, приведенный на рис. 9.56, аппроксимирует скорость изменения цены помидоров на протяжении 60 месяцев. Здесь р(1) — цена фунта помидоров, at — время (в месяцах).


266
Часть III. Математический анализ
а) Опишите график функции у = p(t) и укажите все его локальные экстремумы и точки перегиба.
б) Постройте график функции у = p(t).
43. Максимальные доход и прибыль. Некая компания производит и продает х электрических печей в месяц. Формула затрат и уравнение зависимости цены от спроса имеют следующий вид.
ОД = 350# + 50 ООО;
р = 500 - 0,025а?; 0 х 20 000.
а) Найдите максимальный доход.
б) Сколько печей должна выпускать компания, чтобы достичь максимальной прибыли? Чему она равна? Какую цену следует установить на электрические печи?
в) Предположим, что правительство решило взимать с каждой электрической печи дополнительный налог в размере 20 долл. Сколько печей должна выпускать компания, чтобы гарантировать максимальную прибыль? Чему равна максимальная прибыль? Какую цену теперь необходимо установить?
44. Затраты на строительство. Необходимо построить забор, огораживающий прямоугольную площадь. Три стороны забора изготавливаются из материала, который стоит 5 долл, за фут. Материал для четвертой стороны стоит 15 долл, за фут. Определите длины сторон прямоугольника, обеспечивающего минимальные затраты на изготовление забора.
а) Предположим, что площадь участка равна 5000 тыс. кв. футов. Определите длины сторон забора, гарантирующие минимум затрат.
б) Предположим, что площадь участка равна 3000 тыс. кв. футов. Определите длины сторон забора, гарантирующие максимальную площадь охвата.
45. Доход от аренды. Двухсоткомнатный отель во Фресно полностью заполняется при стоимости комнаты, равной 40 долл, за ночь. Увеличение стоимости аренды на один доллар приводит к уменьшению заполняемости на четыре номера. Предположим, что стоимость обслуживания одного снимаемого номера равна


Глава 9. Построение графиков и оптимизация
267
8 долл, в день. Какую цену за аренду должно установить руководство отеля, чтобы получить максимальную валовую прибыль? Чему равна эта прибыль?
46. 	Управление запасами. Компьютерный магазин продает 7200 дискет в год. Хранение одной дискеты в течение года стоит 0,20 долл. Заказывая дополнительное количество дискет, магазин должен заплатить 5 долл, за обработку одного заказа. Сколько заказов должен сделать магазин, чтобы минимизировать затраты на хранение дискет и обработку дополнительных заказов?
47. Средние затраты. Общие затраты на производство х мусорных баков описываются следующей формулой.
С(х) = 4000 + Юж + 0,1а;2.
Найдите минимальную величину средних затрат. Постройте графики функции средних и предельных затрат в одной и той же системе координат. Найдите наклонные асимптоты.
48. Средние затраты. Данные, приведенные в следующей таблице, описывают общие ежедневные затраты у (в долларах) на производство х дюжин шоколадных пирожных.
Количество дюжин X
Общие затраты у
50
119
100
187
150
248
200
382
250
505
300
695
а) Постройте уравнение квадратичной регрессии общих затрат, используя графическую утилиту.
б) Найдите минимальное значение общих затрат (с точностью до цента) и соответствующий объем производства (с точностью до единицы).
49. 	Реклама. Магазины, торгующие бытовой техникой, заказывают рекламу на телевидении. В следующей таблице приведены величины: х — количество рекламных роликов, показанных в течение месяца и у — объем продаж холодильников.


268
Часть III. Математический анализ
Количество роликов, X
Объем продаж холодильников, у
10
271
20
427
25
526
30
629
45
887
48
917
а) Постройте уравнение кубической регрессии, описывающее зависимость объема ежемесячных продаж холодильников от количества телевизионных рекламных роликов.
б) Сколько рекламных роликов необходимо показать за месяц, чтобы достичь максимальной скорости изменения объемов продаж по отношению к объему рекламы, и сколько холодильников будет продано при этом? Округлите ответ до ближайшего целого числа.
Биологические науки
50. Дезинфекция водоемов. Озеро, в котором купаются отдыхающие, подвергается периодической дезинфекции. Предположим, что через t дней после дезинфекции концентрация бактерий в кубическом сантиметре воды описывается следующей формулой.
C(t) = 20t2 - 120* + 800, 0 < t < 9.
Через сколько дней после дезинфекции концентрация бактерий станет минимальной?
Социальные науки
51. Политика. Оценки социологов показывают, что численность населения, имеющего право голоса в некоем городе (тыс. чел.) будет расти по следующей формуле.
IV(f) = 10 + 6t2 - t3, 0 < t 5.
Здесь t — время, измеряемое годами. В какой момент скорость роста числа избирателей станет максимальной?
Домашнее задание 9.1. Максимизация прибыли
www Максимальная прибыль и доход. Некая компания выпускает и продает х кондиционеров в месяц. Формула затрат и уравнение зависимости цены от спроса имеют следующий вид.
С(ж) = 180^ + 20000,
р = 200 - 0,001, 0 х < 100 000.


Глава 9. Построение графиков и оптимизация
269
1. Найдите максимальную прибыль.
2. Сколько кондиционеров должна выпускать компания, чтобы достичь максимальной прибыли? Чему она равна? Какую цену следует установить на кондиционеры?
3. Предположим, что правительство решило взимать с каждого кондиционера дополнительный налог в размере 18 долл. Какую прибыль получит государство от этой меры?
4. Предположим, что правительство решило взимать с каждого кондиционера дополнительный налог в размере 23 долл. Какую прибыль получит государство от этой меры?
5. Предположим, что правительство решило взимать с каждого кондиционера дополнительный налог в размере t долл. При каком значении переменной t прибыль государтсва достигнет максимума? Чему равна максимальная прибыль?
Домашнее задание 9.2. Минимизация затрат
Два курорта, расположенных на разных островах, решили проложить кабель от каждого острова к источнику электрического тока, находящегося на берегу (рис. 9.57). Величина затрат на прокладку силовой линии по дну озера прямо пропорциональна его длине, поэтому руководство курортов решило минимизировать его длину.
Рис. 9.57. Схема прокладки силовых линий
1. 	Предположим, что береговая линия является прямой. Обозначим через f общую длину силовой линии, а через х — координату источника электрического тока, расположенного на берегу (рис. 9.58). Найдите функцию постройте графики функций f(x) и f(x) (используя процедуру численного дифференцирования) и вычислите величину х, обеспечивающую минимальную общую длину кабеля.


270
Часть III. Математический анализ
Рис. 9.58. Система координат (прямая линия берега)
2. 	Повторите решение п. 1, предполагая, что береговая линия имеет форму параболы, описываемой уравнением у = 0,02х2 — 2 (рис. 9.59).
Рис. 9.59. Система координат (параболическая береговая линия)


10
Дифференцирование
■ 10.1. Константа е и непрерывно начисляемые сложные проценты
■ 10.2. Производные логарифмических и экспоненциальных функций
■ 10.3. Цепное правило: общая форма
■ 10.4. Неявное дифференцирование
■ 10.5. Связанные скорости
■ Ключевые слова, основные обозначения и формулы
■ Дополнительные правила дифференцирования
■ Упражнения для повторения
■ Домашнее задание 10.1. Эластичность спроса
■ Домашнее задание 10.2. Точка сокращения доходов
Введение
Эта глава завершает обсуждение тем, связанных с производными. Сначала мы рассмотрим дифференцирование выражений, содержащих экспоненциальные и логарифмические функции, а затем будут изучены прикладные задачи. Прежде чем продолжить, возможно, будет полезно повторить некоторые наиболее важные свойства экспоненциальных и логарифмических функций, описанные главе 2.


in
Часть III. Математический анализ
10.1. 	Константа е и непрерывно начисляемые сложные проценты
■ Константа е
■ Непрерывно начисляемые сложные проценты
В главе 2 с помощью неформальных рассуждений была введена показательная функция с основанием е и описаны непрерывно начисляемые сложные проценты. Теперь, когда мы освоили понятие предела, можно дать точное определение константы е и непрерывно начисляемых сложных процентов.
Константа е
Иррациональное число е является удобным основанием как для показательных, так и для логарифмических функций. Причина, по которой именно это число выбирается в качестве основания, станет понятной после того, как мы выведем формулу дифференцирования экспоненциальной функции ех и натурального логарифма lnj?.
В главе 2 число е неформально определялось как иррациональное число, приблизительное значение которого можно найти с помощью выражения [1 + (1/п)]п, взяв достаточно большое значение п. Теперь после введения понятия предела можно дать формальное определение числа е как одного из следующих пределов.
www Число е
е — lim (1 + —либо е — lim (1 + s)1/5 : n—>оо у п J з->0 7
е = 2,718281828459...
Мы будем использовать обе формы пределов. (Примечание, Если s = 1/п, то s —> 0, если п ос.)
Доказательство того, что такие пределы существуют и равны числу, находящемуся между 2 и 4, довольно сложно и не рассматривается в нашей книге. Многие люди неверно полагают, что предел этих выражений равен единице, поскольку “1 + s стремится к единице, когда s —> 0, а единица в любой степени равна единице”. Немного поэкспериментировав с калькулятором, можно убедиться в обратном. Рассмотрим следующую таблицу значений s и f(s) = (1 + s)1/5 и график, показанный на рис. 10.1, для значений s, близких к нулю.
в стремится к 0 слева —> 0 <— з стремится к 0 справа
з —0,5
-0,2
-0,1
-0,01 -> 0 «- 0,01 0,1 0,2 0,5
(1 4- s)1^ 4,0000
3,0518
2,8680
2,7320 -> е «- 2,7048 2,5937 2,4883 2,2500


Глава 10. Дифференцирование
273
Рис. 10.1. Значения функции /($) = (1-F s)1/3
Вычислите самостоятельно несколько табличных значений с помощью калькулятора, а также найдите несколько значений, при которых переменная s еще ближе к нулю. Следует отметить, что функция в точке s = 0 имеет разрыв.
Кто в действительности открыл число е, до сих пор остается спорным вопросом. Оно получило свое название после того, как великий математик Леонард Эйлер (1707-1783) вычислил значение е с точностью до 23 десятичных знаков, используя выражение [1 + (1/п)]п.
Непрерывно начисляемые сложные проценты
Теперь рассмотрим, как число е совершенно естественно появляется в такой важной прикладной задаче, как начисление сложных процентов. Давайте сначала рассмотрим простые проценты, затем сложные проценты и только после этого перейдем к непрерывно начисляемым процентам.
Если капитал Р взят взаймы под годовой процент г,1 то через t лет начисления простых процентов заемщик будет должен кредитору сумму А, равную
А = Р + Prt = Р(1 4~ rt). Простые проценты (10.1)
С другой стороны, если проценты начисляются п раз в год, заемщик будет должен кредитору сумму А, равную
/ r\nt
А = Р ^1 4 J , Сложные проценты (10.2)
Здесь г/п — процентная ставка за период начисления процентов, a nt — количество таких периодов. Предположим, что значения Р, г и t в уравнении (10.2) остаются неизменными, а число п возрастает. Будет ли сумма А расти бесконечно, или же она будет стремиться к какому-нибудь предельному значению?
^сли г — процентная ставка, записанная 100т% — это ставка в виде процентов. Например, если г = 0,12, имеем 100г% = 100-0,12% = 12%. Следовательно, выражения 0,12 и 12% эквивалентны. Если не указано противное, во всех формулах этой книги число г рассматривается в десятичной форме.


274
Часть III. Математический анализ
Прежде чем приступать к решению общей задачи о пределах, проведем вычислительный эксперимент. Если Р = 100 долл., г = 0,06, at = 2 года, то
А = 100
Несколько значений А, вычисленных для некоторых значений п, показаны в табл. 10.1. Самая большая прибыль наблюдается на первом этапе. Затем с ростом п прибыль снижается. Оказывается, когда п становится все больше и больше, А стремится к 112,75 долл.
Таблица 10.1. Результаты вычислительного эксперимента
Частота начисления
п
л ( 0,06\2п
А = 100 (14 1 , долл.
Ежегодно
1
112,3600
Раз в полгода
2
112,5509
Ежеквартально
4
112,6493
Ежемесячно
12
112,7160
Еженедельно
52
112,7419
Ежедневно
365
112,7486
Ежечасно
8760
112,7496
Задание 10.1.
1. Предположим, что на сберегательный счет положено 1000 долл., которые дают 6 простых процентов прибыли. Сколько будет на счету через 2 года?
2. Предположим, что на сберегательный счет положено 1000 долл., которые дают 6 сложных процентов в год. Сколько будет на счету через 2 года, если проценты начисляются ежегодно? Каждые полгода? Ежеквартально? Еженедельно?
3. Как часто нужно начислять проценты при ставке 6%, чтобы на счету через
два года было 1150 долл.? ■
Теперь вернемся к общей задаче. Зафиксировав в уравнении (10.2) числа Р, г и t и вычисляя следующий предел, можно получить интересный и полезный результат.
пЛ r\nt тэт Д r\^/r)rt
lim Р I 1 4 1 — Р lim 114 ) — Умножим показатель степени
п—>сю \ п/ п—юо \ п/ на r/т и обозначим з = г/п.
Следует отметить: п —► оо подразумевает, что з —► О.


Глава 10. Дифференцирование
275
= Р1нп[(1 + 5Г]Г1 = =p[linj(l+s)‘/-]rt = = Pert.
Воспользуемся свойством пределов, указанным в сноске2 lim (1 + з)1/в = е
«—►о
Результирующая формула называется формулой непрерывно начисляемых сложных процентов (continuous compound interest formula). Эта формула очень важна и широко используется в бизнесе и экономике.
Непрерывно начисляемые сложные проценты
А = Pert,
где Р — капитал; г — годовая номинальная процентная ставка с непрерывным начислением сложных процентов; t — время, лет; А — сумма на момент времени t.
Пример 10.1 (Вычисление непрерывно начисляемых сложных процентов). Какая сумма будет на счету через два года, если 100 долл, вложены под 6%, начисляемых непрерывно?3 Сколько будет накоплено процентов?
Решение.
А = Pert =
— 100е®’®®’2« 6% эквивалентно г = 0,06
« 112,7497 долл.
(Сравните этот результат со значениями, полученными в табл. 10.1.) Накопленная сумма будет равна 112,7497 — 100 = 12,7497 долл. ■
Упражнение 10.1.
Какая сумма (с точностью до цента) будет на счету через пять лет при исходном зачислении на него 100 долл, при годовой номинальной процентной ставке, равной 8%, начисляемых ежегодной? Начисляемых раз в полгода? Начисляемых непрерывно? ■
Пример 10.2 (www График роста объема инвестиций). Банк Union Savings предлагает 5-летние депозитные сертификаты с годовой ставкой 5,75%, начисляемых непрерывно. Постройте график накопленной суммы, как функции 2Используем следующее новое свойство пределов: если f(x) существует, то
liniz^c [/(х)]р = [lim^-^c f(x)]p, при условии, что последнее выражение относится к действительным числам.
3 Следуя общепринятым традициям, выражение “под 6 сложных процентов, начисляемых непрерывно” означает “при годовой номинальной процентной ставке 6%, начисляемых непрерывно”.


276
Часть III. Математический анализ
времени для пятилетнего периода при инвестировании в депозитные сертификаты на 1000 долл.
Решение. Постройте график функции
А = 1000e°’°575t, ООО.
Построим таблицу значений, используя калькулятор, затем обозначит в координатном пространстве соответствующие точки и соединим их плавной кривой.
t, лет
А,долл.
0
1000
1
1059
2
1122
3
1188
4
1259
5
1333
Упражнение 10.2.
Постройте график накопленной суммы, как функции времени для четырехлетнего периода, если в депозитные сертификаты с годовой ставкой 5,51%, начисляемых непрерывно, инвестировано 5000 долл. ■
Пример 10.3 (Вычисление времени роста). Сколько времени понадобится, чтобы инвестиции объемом 5000 долларов выросли до 8000 долларов при ставке 5%, начисляемых непрерывно?
Решение. Необходимо решить уравнение А = Pert относительно t.
А = Pert;
8000 = 5000е°’°5<; eo,O5t = 1б.
lne°’05t = In 1,6;
0,05t = In 1,6;
, In 1,6
0,05 ’
t» 9,4 года.
Разделим обе части уравнения на 5000 и поменяем их местами.
Возьмем натуральный логарифм от обеих частей (напомним, что logb Ьх = ж).
На рис. 10.2 показан альтернативный метод решения примера 10.3 с помощью графической утилиты.


Глава 10. Дифференцирование
277
Рис. 10.2. Функции t/1 = бОООе0,05*; у2 = 8000
Упражнение 10.3.
Сколько времени понадобится, инвестиции объемом 10000 долларов выросли до 15 000 долларов при ставке 9%, начисляемых непрерывно. ■
Пример 10.4 (Время удвоения капитала). Сколько понадобится времени, чтобы капитал удвоился, если он вложен под 6,5%, начисляемых непрерывно?
Решение. Необходимо решить уравнение А = Pert относительно t для заданных А = 2Р и г = 0,065.
Разделим обе части уравнения на Р и поменяем их местами.
Вычислим натуральный логарифм выражений по обе стороны уравнения.
2Р = Pe°’065f; e0,065t _ 2- lne°’065t - In 2;
0,065i = In 2;
ln2
* _ 0,065’
t a 10,66 года.
На рис. 10.3 показан альтернативный метод решения уравнения e0,065t = 2 из примера 10.4 с помощью графической утилиты.
Упражнение 10.4.
Сколько понадобится времени, чтобы капитал утроился, если он вложен под 5,5%, начисляемых непрерывно? ■


278
Часть III. Математический анализ
Задание 10.2.
Рассматриваются три варианта вложения 10000 долл.: под 7%, начисляемых ежегодно, под 6%, начисляемых ежемесячно, и под 5%, начисляемых непрерывно.
1. Какой вариант будет наилучшим для вложения 10 000 долл, на 8 лет?
2. На какой срок нужно вложить деньги, чтобы самым прибыльным оказался
третий вариант? ■
Ответы к упражнениям
10.1. 146,93 долл.; 148,02 долл.; 149,18 долл.
10.2. А = 5000е°’О561(.
t, лет
А, долл.
0
5000
1
5289
2
5594
3
5916
4
6258
О
н—► /
4
10.3. 4,51 года.
10.4. 19,97 года.
Практикум ЮЛ
А В задачах 1 и 2, используя калькулятор, вычислите приближенное значение А с точностью до двух десятичных знаков.
1. А = ЮООе0’*  1* для t = 2, 5 и 8.
2. А = 5000e°’°8t для t = 1, 4 и 10.
3. Постройте график суммы на счету как функции времени для периода 8 при начальной инвестиции 6000 долл, под 10%, начисляемых непрерывно.
4. Постройте график суммы, лежащей на счету, как функции времени для периода 6 при начальной инвестиции 4000 долл, под 8%, начисляемых непрерывно.
Б В задачах 5-10 требуется решить уравнения относительно t или г с точностью до двух десятичных знаков.
5. 2 = e°’06t. 6. 2 = е0’03*. 7. 3 = е°’н.
8. 3 = е°’25г. 9. 2 = е5г. 10. 3 = е10г.


Глава 10. Дифференцирование
279
В В задачах 11 и 12 требуется заполнить каждую таблицу с точностью до пяти десятичных знаков, используя для вычислений калькулятор.
п
[1 + (1/п)]п
10
2,59374
100
1000
10000
100000
1000000
10000000
1
00
е = 2,718281828459...
S
(1 + s)1/»
0,01
2,70481
-0,01
0,001
-0,001
0,0001
-0,0001
0,00001
-0,00001
0
е = 2,718281828459...
* 13. Используя калькулятор и таблицу значений, исследуйте предел
lim (1 -I- .
п—>оо
Существует ли этот предел? Если да, то чему он равен?
* 14. Используя калькулятор и таблицу значений, исследуйте предел
Существует ли этот предел? Если да, то чему он равен?
15. 	Можно показать, что число е удовлетворяет неравенству Проиллюстрируйте этот факт, построив графики функций
У1 = (1 + 1/гг)п,
у2 = 2,718281828 » е,
Уз = (1 + l/n)n+1
в одном окне графической утилиты на отрезке 1 < п 20.


280
Часть III. Математический анализ
16. 	Покажите, что
е3 = lim (1 + -)"
п—>оо \ п/
для любого действительного числа s. Проиллюстрируйте этот факт для $ = 2, построив графики функций
У1 = (1 + 2/п)п,
У2 = 7,389056099 « е2,
в одном окне графической утилиты на отрезке 1 п 50.
Применение математики
Экономика и бизнес
17. WWW Непрерывное начисление процентов. Банк Provident Bank продает десятилетние депозитные сертификаты, которые приносят прибыль в размере 5,51%, начисляемых непрерывно.
а) Сколько будет стоить такой сертификат через 10 лет, если в него было вложено 10000 долл.?
б) Сколько времени должно пройти, чтобы стоимость сертификата составила 15 000?
18. WWW Непрерывное начисление процентов. Банк Provident Bank также продает трехлетние депозитные сертификаты, которые приносят прибыль в размере 5,28%, начисляемых непрерывно.
а) Сколько будет стоить такой сертификат через три года, если в него было вложено 10000 долл.?
б) Сколько времени должно пройти, чтобы стоимость сертификата составила 11 000 долл.?
19. Текущая стоимость. Кредитный билет по завершении 10-летнего срока будет стоить 20 000 долл. Во сколько нужно оценить билет сейчас, если он приносит прибыль в размере 5,2%, начисляемых непрерывно?
20. Текущая стоимость. Кредитный билет по завершении пятилетнего срока будет стоить 50 000 долл. Во сколько нужно оценить билет сейчас, если он приносит прибыль в размере 6,4%, начисляемых непрерывно?
21. Непрерывное начисление процентов. Инвестор купил ценные бумаги на сумму 20 000 долл. Пять лет спустя эти ценные бумаги были проданы за 30 000 долл. Каков должен быть размер годовой номинальной процентной ставки, чтобы получить равноценный доход от вложения 20000 долл., если проценты начислялись непрерывно?
22. Непрерывное начисление процентов. Семья заплатила за дом 40000 долл, наличными. Пятнадцать лет спустя они продали этот дом за 100000 долл. Каков должен быть размер годовой номинальной процентной ставки, чтобы получить равноценный доход от вложения 40 000 долл., если проценты начислялись непрерывно?


Глава 10. Дифференцирование
281
23. Текущая стоимость. Решая уравнение А = Pert относительно Р, получим значение
Р = Ae~rt,
описывающей текущую стоимость капитала А, накопленного через t лет при размещении его под годовой номинальной процентной ставкой г, которая начисляется непрерывно.
а) Постройте график Р = ЮОООе-0’08*; 0 О 50.
б) Нт*_юо ЮОООе-0,08* = ?. (Сделайте приблизительную оценку, используя результат решения п. а.)
(Вывод. Чем больше времени пройдет до накопления суммы А, тем меньше текущая стоимость, как и следовало ожидать.)
24. Текущая стоимость. Возвращаясь к задаче 23, через сколько лет будет накоплена сумма 10000, текущая стоимость которой равна 5000 долл.?
25. Время удвоения капитала. Сколько должно пройти времени, чтобы капитал удвоился, если он вложен под 7%, начисляемых непрерывно?
26. Время удвоения капитала. Сколько должно пройти времени, чтобы капитал удвоился, если он вложен под 5%, начисляемых непрерывно?
27. Время удвоения капитала. Под какую номинальную процентную ставку нужно вложить капитал, чтобы он удвоился через 8 лет?
28. Время удвоения капитала. Под какую номинальную процентную ставку нужно вложить капитал, чтобы он удвоился через 10 лет?
29. Время роста капитала. Клиент банка, собирающийся инвестировать 20 000 долл., решил разделить капитал на части, положив 10 000 долл, под 7,2%, начисляемых непрерывно, и 10000 долл. — под 8,4%, начисляемых ежегодно. Используя метод графической аппроксимации, определите, сколько времени пройдет, прежде чем общий капитал на обоих счетах вырастет до 35 000 долл.
30. Время роста капитала. Инвестор внес 5000 долл, на счет со ставкой 8,8%, начисляемых непрерывно, и 7000 долл, на счет со ставкой 9,6%, начисляемых ежегодно. Используя метод графической аппроксимации, определите, сколько времени пройдет, прежде чем общий капитал на обоих счетах вырастет до 20 000 долл.
*31. Время удвоения капитала.
а) Покажите, что время удвоения капитала t (в годах) при годовой процентной ставке г, начисляемой непрерывно, равно
t - —
г


282
Часть III. Математический анализ
б) Постройте график уравнения времени удвоения капитала из п. а на отрезке 0,02 г 0,30. Обоснованы ли такие ограничения на величину г? Объясните.
в) Вычислите время удвоения капитала (в годах, с точностью до двух десятичных знаков) для г = 5, 10, 15, 20, 25, 30%.
* 32. Процентная ставка удвоения капитала.
а) Покажите, что процентная ставка г, при которой капитал с непрерывно начисляемыми процентами удвоится через t лет, равна
In 2 г ~ ~Т'
б) Постройте график уравнения процентной ставки удвоения капитала из п. а на отрезке 1 < t < 20. Обоснованы ли такие ограничения на величину t? Объясните свой ответ.
в) Вычислите процентные ставки удвоения капитала для t = 2, 4, 6, 8, 10 и 12 лет.
Биологические науки
33. Радиоактивный распад. Уравнение, описывающее процесс распада радиоактивных веществ, имеет следующий вид.
Q = Qoert.
Здесь
Qo — количество вещества в момент времени t = 0,
г — скорость распада,
t — время в годах,
Q — количество вещества в момент времени t.
Сколько понадобится времени, чтобы распалась половина имеющегося количества радия, если считать его скорость распада равной г = —0,0004332? (Этот временной промежуток называется периодом полураспада вещества.)
34. Радиоактивный распад. Скорость распада изотопа углерода-14 равна г = —0,0001238. Сколько понадобится времени, чтобы распалась половина имеющегося количества углерода-14? (Воспользуйтесь уравнением радиоактивного распада из задачи 33.)
35. Радиоактивный распад. Период полураспада изотопа цезия — 30 лет. Какова скорость распада этого изотопа? (Воспользуйтесь уравнением радиоактивного распада из задачи 33.)
36. Радиоактивный распад. Период полураспада изотопа стронция составляет 90 лет. Какова скорость распада этого изотопа? (Воспользуйтесь уравнением радиоактивного распада из задачи 33.)


Глава 10. Дифференцирование
283
Социальные науки
37. Численность населения. Уравнение, описывающее рост численности населения Земли на коротких временных интервалах, имеет вид:
P = Poert,
где
Ро — численность населения в момент времени t = 0,
г — скорость роста численность населения,
t — время, лет,
Р — численность населения в момент времени t
Сколько понадобится времени, чтобы численность населения Земли удвоилась, если она продолжит расти с текущей скоростью 1,3% в год?
38. WWW Численность населения. Сколько понадобится времени, чтобы численность населения США удвоилась, если она продолжит расти со скоростью 0,85% в год?
39. WWW Численность населения. В некоторых странах численность населения удваивается каждые 50 лет. С какой скоростью растет численность население? (Воспользуйтесь уравнением из задачи 37.)
40. WWW Численность населения. В некоторых странах численность населения удваивается за 200 лет. С какой скоростью увеличивается численность населения? (Воспользуйтесь уравнением из задачи 37.)
10.2. 	Производные логарифмических
и экспоненциальных функций
■ Формулы вычисления производных 1п х и ех
■ Методы построения графиков
■ Решение практических задач
В этом разделе обсуждаются формулы для производных функций 1пж и ех. Оказывается, самые простые формулы для производных получаются, если из всех возможных вариантов основания для логарифмической и показательной функций log6 х и Ьх выбрать Ь, равное числу е.
Задание 10.3.
1. Используя график функции f(x) = 2х, показанный на рис. 10.4, начертите касательные для нескольких значений х, вычислите приблизительную величину их наклона и постройте график /'(ж). Где находится график производной: выше или ниже графика /(ж) = 2х?
2. Используя график функции д(х) = 3х, показанный на рис. 10.5, начертите касательные для нескольких значений х, вычислите приблизительную


284
Часть III. Математический анализ
Рис. 10.4. График функции /(х) = 2х Рис. 10.5. График функции д(х) = 3х величину их наклона и постройте график д'Ю- Где находится график про¬
изводной: выше или ниже графика д(х) = Зж?
Легко видеть, что в задании 10.3, в котором /(ж) = 2х, графики функций f(x) И /'(*) выглядят почти одинаково, а график f'(x) всегда находится ниже графика /(х). Аналогично для д(х) = 3х графики функций д(х) и д'(х) выглядят почти одинаково, а график д' (ж) всегда находится выше графика д(х). Следовательно, должна существовать показательная функция, равная своей производной, основание которой лежит между числами 2 и 3. Далее вы увидите, что показательная функция с основанием е = 2,718... обладает именно таким свойством, т.е.
Мы выведем также формулу для производной функции натурального логарифма
dx х
Формулы вычисления производных 1п х и е®
Выведем формулу для вычисления производной функции
/(ж) = Ina? = logez, х > 0
используя определение производной
и двухэтапный процесс, рассмотренный в разделе 8.3.


Глава 10. Дифференцирование
285
Этап 1. Сначала упростим разностное отношение.
f (х + /г) — f (ж) _ In (х + h) — In х _
h = h =
— - [In (х + ti) — In ж] = h
Воспользуемся тем, что
In А — In В = In —.
Чтобы преобразовать выражение, домножим его на 1 = х/х.
Воспользуемся тем, что р In А = In Ар.
Этап 2. Вычислим предел. Пусть s = h/x. При фиксированном значении х из условия h —► 0, следует, что s —► 0.
— In х = lim dx h—>0
/ (ж + Ь) - / (ж) h
Пусть 8 = h/x. Следует отметить, что h —► О подразумевает, что а —► О
= hij[ln(1+s)1/,] =
= — In l"lim (1 + s)1/*8] —
x Ls->ov 7 J
= — In e =
x
1
Воспользуемся определением числа е
In е = loge е = 1.
X
Таким образом,
В следующем разделе будет показано, что в общем случае
Это несколько более сложный результат, чем тот, что получен выше, за исключением ситуации, когда Ь = е.


286
Часть III. Математический анализ
В процессе поиска производной от ех воспользуемся (без доказательства) тем фактом, что
А-»о h
Задание 10.4.
Вычислите
eh - 1
h
для следующих значений h\ —0,1; —0,01; —0,001; —0,0001; 0,0001; 0,001; 0,01;
0,1. Дают ли основания эти вычисления сделать вывод, что
eh - 1 lim —— = 1? h
Проанализируйте результат.
Применим теперь к экспоненциальной функции /(т) = ех двухэтапный процесс.
Этап 1. Сначала упростим разностное отношение.
f (х + /г) - f (х) ea:+h — ех
= = Воспользуемся тем, что еа+° = еае°. h h
exeh — ех
— = Вынесем за скобки е®.
h
Этап 2. Вычислим предел для результата, полученного на этапе 1.
d г* = lim f (I + 1 W
dx h—>0
„ /
h
'eh- 1\
= lim e
l —
7 1 —
h—>0 \
„ I
4 /
'eh-l\
= e lim
i —
. i —
h—>o \
< h J
= exl =
ex.
Воспользуемся предположительным значением предела, указанным выше.
Таким образом,
dx


Глава 10. Дифференцирование
287
В следующем разделе будет показано, что
-bx = bx\nb.
х
Это также является несколько более сложным результатом, чем тот, что получен выше, за исключением ситуации, когда b — е.
Два только что полученных результата объясняют, почему функция ех настолько широко используется, что она получила даже специальное название — экспоненциальная функция.
Производные от функции натурального логарифма и экспоненциальной функции
dx х' dx
www Эти формулы производной можно совместно использовать с правилами дифференцирования, рассмотренными в главе 8 для дифференцирования разнообразных функций.
Пример 10.5 (Вычисление производных). Вычислите производную f'{x) для следующих функций:
1. /(х) = 2е® + 3 In х.
3. 	/(х) = (1пх)4.
4. /(х) = 1пх4.
Решение.
= 2ех + 3 • - = 2ех + -
; х j е ~ е^—х0 ;
;. f (х) =: dx . ..2 dx : = Правило ! I I •
(х3)
Правило дифференцирования частных.
х3ех — ех3х2 _ х2ех (х — 3) ех (х — 3)
х3ех — ех3х2 _ х2ех (х
3. (In ж)4 = 4 * (In ж)3 4“ 1пя = ах ах
Правило дифференцирования степенных выражений для функций
4.
(In ж)3
X
ilnx4 = ^(41na;) =
Свойство логарифмов
X X
X X


288
Часть III. Математический анализ
Упражнение 10.5.
Вычислите производную f'(x) для следующих функций.
1. /(х) = 41пх — 5ех.
2. /(х) = х2ех.
3. /(х) = 1пх3.
4. /(х) = (1пх)3.
Предупреждение.
—ех хе ах
dx
Правило дифференцирования степеней нельзя использовать для дифференцирования показательной функции. Правило дифференцирования степенных выражений применяется к показательным выражениям вида хп, где показатель степени — константа, а основание — переменная. В показательном выражении вида ех основание — это константа, а показатель степени — переменная.
Методы построения графиков
Воспользовавшись методами, описанными в главе 9, можно с помощью первой и второй производных получить полезную информацию о графиках функций у = 1пхну = ех.С помощью формул вычисления производной, полученных выше, можно построить табл. 10.2.
Таблица 10.2. Поведение функций у = 1пх и у = ех
In я?
е®
у = In х х > 0
у' = \/х > 0 ж > 0
у" = —1/х2 <0 х > 0
у = ех —оо < х < оо
у' =■ ех > 0 —оо < ж < оо
у" = ех > 0 —оо < х < оо
Из таблицы следует, что обе функции возрастают, и график у = In а; всегда является выпуклым вверх, а график у = ех всегда является выпуклым вниз. Можно показать, что limx_>0+ In ж = —оо, a Ипг^-оо ех = 0. Таким образом, ось у — это вертикальная асимптота для графика у = In х9 а ось х — это горизонтальная асимптота для графика ех. Графики обеих функций показаны на рис. 10.6.
Следует отметить, что если перегнуть страницу по пунктирной линии у — х, то два графика точно совпадут (см. раздел 2.3). Также обратите внимание на то, что оба графика не ограничены при х оо. Сравнивая эти графики с графиком функции у = х (пунктирная линия), можно сделать вывод, что ех растет быстрее, чем переменная х, а 1пх растет медленнее, чем переменная х.
Рост экспоненциальных и логарифмических функций
%р In X
lim — =0, р > 0 и lim = 0, р > 0.
х—>ОО еХ ж—>ОО Хр


Глава 10. Дифференцирование
289
Рис. 10.6. Функция ех непрерывна на интервале (—сю, сю), а функция In ж — на интервале (0, оо)
Пределы, записанные во врезке, означают, что функция ех растет быстрее, чем любая положительная степень переменной х, а функция In х растет медленнее, чем любая положительная степень переменной х.
Теперь применим методы построения графиков к несколько более сложной функции.
Пример 10.6 (Методика построения графиков). Проанализируйте функцию /(т) = хех, следуя методике построения графиков, рассмотренной в разделе 9.3. Соберите всю необходимую информацию и постройте график /.
Решение.
Этап 1. Проанализируем f(x): f(x) = хех.
1) Область определения: все действительные числа.
2) Пересечение с осью у: /(0) = 0.
3) Пересечение с осью х: хех = 0 только при х = 0, поскольку ех > 0 для любых х (см. рис. 10.6).
4) Вертикальные асимптоты: нет.
Горизонтальные асимптоты. У нас нет пока средств для вычисления пределов, позволяющих охарактеризовать поведение функции f(x) при х —► — оо и ж ->оо. Однако следующие таблицы значений дают возможность составить представление о характере графика f при х —► —оо и х —> оо.


290
Часть Ш. Математический анализ
X
1
5
10 —> оо
2,72
742,07
220 264,66 ^оо
X
-1
-5
— 10 —> —оо
-0,37
-0,03
-0,00045 -> 0
Этап 2. Проанализируем функцию
f (х) = х^ех + ех
d_ dx
= хех + ех = ех (х + 1);
Критическая точка функции /(ж): —1. Точка разбиения для функции f'(x): — 1. Знаковая диаграмма для функции f(x).
Лх)
Ах)
X
Пробные значения
X
/'(я=)
-2
-в’2 (-)
0
1(+)
Таким образом, /(ж) убывает на интервале (—ос, —1), имеет локальный минимум в точке х = 1 и возрастает на интервале (—1, оо). (Поскольку ех > 0 для всех х, нет необходимости находить значение е~2, чтобы, используя пробное число —2, сделать вывод, что —е 2 < 0.)
Этап 3. Проанализируем функцию
rw=e^(I+1)+(I+1)^e.=
= ех + (ж + 1) ех = ех (х + 2).
Знаковая диаграмма для функции /"(х) (точка разбиения равна —2).
Лх)
X
График функции f
Пробные значения
X
/"(®)
-3
-е-3 (-)
-1
с’1 (+)
Точка перегиба


Глава 10. Дифференцирование
291
Таким образом, график f является выпуклым вверх на интервале (—оо, —2), имеет точку перегиба в точке х = — 2 и является выпуклым вниз на интервале (—2,оо).
Этап 4. www Построим график f, используя информацию, полученную на этапах 1-3.
Пробные значения
X
/(®)
-2
-0,27
-1
-0,37
0
0
Упражнение 10.6.
Проанализируйте функцию /(х) = xlnx. Соберите всю необходимую информацию и постройте график /. ■
Решение практических задач
Пример 10.7 (Максимизация прибыли).
Отдел маркетинговых исследований сети зоомагазинов провел пробные продажи аквариумных насосов (и других товаров) в нескольких торговых точках города. Выяснилось, что недельный спрос на аквариумные насосы описывается следующей зависимостью.
р = 12 — 2 In х, 0 < х < 90.
Здесь х — недельный объем продаж, ар долл. — цена одного насоса. Предположим, затраты на производство насоса равны 3 долл., сколько он должен стоить, чтобы недельная прибыль была максимальной?


292
Часть III. Математический анализ
Решение. Требуется вычислить цену, при которой недельная прибыль будет максимальной. Однако проще сначала вычислить количество насосов, обеспечивающее максимальную недельную прибыль. Уравнение дохода имеет следующий вид.
R(x) — хр — 12х — 2х1пх.
Уравнение затрат записывается так:
С(х) - Зх,
а уравнение прибыли имеет вид
Р(х) = R(x) - С(х) =
— 12х — 2х In х — Зх —
— 9х — 2т1пх.
Таким образом, необходимо решить следующую задачу.
Максимизировать Р(х) = 2х — 2ж1пх, 0 < х < 90.
Pf (ж) = 9 — 2х • - — 2 In х —
х
= 7 — 21nz = 0;
2 In я = 7;
Ina; = 3,5;
х = е3’5;
Р"(х) = -2 - - =
X X
Поскольку х = е3,5 — единственное критическое значение и Р"(е3,5) < 0, то недельная прибыль достигает максимума, когда х — е3,5 « 33 и р — 12 — 2 In е3,5 = = 5 долл. ■
На рис. 10.7 показан альтернативный метод поиска максимального значения Р(х) из примера 10.7, в котором используется графическая утилита.
Рис. 10.7. Функция yi = 9х — 2а: In а;


Глава 10. Дифференцирование
293
Упражнение 10.7.
Решите задачу примера 10.7, если насос обходится сети зоомагазинов в 3,5 долл. ■
Ответы к упражнениям
10.5. 	1) 4/х - 5ех.
2) хех(х + 2).
3) 3/х.
4) 3 • (1пх)2/х.
10.6. 	Область определения: (0,оо).
Пересечение с осью у: нет ( значение /(0) не определено).
Пересечение с осью х: х = 1.
Функция возрастает от луче на (е-1, сю) и убывает на луче (0, е-1).
Локальный минимум достигается в точке х = е-1 « 0,368.
Функция является выпуклая вниз на луче (0, сю).
X
5
10
100 —> оо
f(x)
8,05
23,03
460,52 —► оо
X
0,1
0,01
0,001
0,0001 -> 0
/(я)
-0,23
-0,046
-0,0069
-0,00092 -> 0
10.7. 	Прибыль достигает максимума при х = е3,25 « 26 и р — 5,50 долл.
Практикум 10.2
Ответы на большинство задач из этого практикума содержат как обычную, так и упрощенную форму производной. При проверке полученных результатов сначала убедитесь в корректности применения правил дифференцирования и только после этого переходите к анализу алгебраических преобразований.
А В задачах 1-8 вычислите указанные производные и упростите результат.
1. 	/'(ж) для /(ж) = 2ех + 31пх.
3. 	для у = 4ех - Зхе. ах
5. 	у' для у = 1пж3.
2. 	д'(х) для д(х) = 5ех — 61пж.
4. 	для у = — 7ех 4- 9хе. ах
6. 	у' для у = (1пх)3.
8. 4 In Я6.


294
Часть III. Математический анализ
Б В задачах 9-32 вычислите f (х) и упростите результат.
9. f(x) = ж4 In х.
11. /(х) = х3ех.
13'^> = ?Т9'
15.
X4
17. /(х) = (х + 2)3 In х.
19. /(х) = (х + 1)3ех.
23. f(x) — x(lnх)3.
25. f(x) = (4 —5еж)3.
27. f (х) = \/1 + lnx.
29. /(х) = хех — ех.
31. /(х) = 2х2 In х — х2.
10. /(аг) = х3lnx.
12. /(х) = х4ех.
14^w=^-
'г'Г
18. /(х) = (х — I)2 Inх.
20. /(х) = (х - 2)3еж.
22./(х) = ^.
24. /(х) = х(1пх)2.
26. 	/(х) = (5 —lnx)4.
28. / (х) =
30. /(х) = xlnx — х.
32. f (х) = х2 ех — 2хех + 2ех.
В задачах 33-36 постройте уравнение касательной к графику у = /(х) для указанного
значения х.
33. /(х) = ех; х = 1. 34. /(х) = ех; х = 2.
35. /(х) = 1пх; х = е. 36. /(х) = lnx; х = 1.
* 37. Студент утверждает, что касательная к графику /(х) = ех в х = 3 проходит через точку (2,0) (рис. 10.8). Верно ли это? Будет ли касательная в х = 4 проходить через точку (3,0)? Аргументируйте свой ответ.
Рис. 10.8. Иллюстрация
к задаче 37
*38. Студент утверждает, что касательная к графику /(х) = lnx в х = 3 проходит через начало координат (см. рис. 10.9). Верно ли это? Проходит ли касательная в точке х = 4 через начало координат? Аргументируйте свой ответ.


Глава 10. Дифференцирование
295
Рис. 10.9. Иллюстрация к задаче 38
В задачах 39 и 40 нужно воспользоваться следующими свойствами показательных и логарифмических функций (см. разделы 2.2 и 2.3).
(аь)с = аЬс, 1па6 = Ina + In b.
*39. Вычислите производные функции у = е2х, у = е3х и у = е4х. Какова производная функции у = екх для произвольной константы fc? Обоснуйте ответ.
* 40. Вычислите производные от функций у = 1п(2я), у = 1п(3я) и у = 1п(4х). Какова производная функции у = ln(fca;) для произвольной константы к! Обоснуйте ответ.
В В задачах 41-46 вычислите указанный экстремум каждой функции для х > 0.
41. Абсолютный максимум функции
f(x) = 5х — 2х1пх.
42. Абсолютный максимум функции
/(ж) = 4х1пх — 7х.
43. Абсолютный максимум функции
44. 	Абсолютный максимум функции
45. Абсолютный максимум функции
f(x) = ж2(3 - In х).
46. Абсолютный максимум функции
f(x) = я3 (In я — 2).
В задачах 47-54 примените стратегию построения графиков, рассмотренную в разделе 9.3, к функции f, соберите необходимую информацию и постройте график.
47. /(х) = 1 — ех. 48. f(x) = 1 — In х.


296
Часть III. Математический анализ
49. /(ж) = х — In я. 50. f(x) = ех — х.
51. fix') = (3 - х)ех. 52. f(x) = (х - 2)ех.
53. f(x) = x2hix. 54. f (х) =
х
В задачах 55-58 необходимо воспользоваться графической утилитой. Вычислите критическое значение функции f(x) с точностью до двух десятичных знаков, найдите интервалы, на которых функция f(x) возрастает и убывает, и вычислите локальный экстремум.
55. 	f(x) = ех — 2х2. 56. f(x) = ех + х2.
57. f(x) = 20 In ж — ех. 58. /(ж) = я2 — Зя In я.
В задачах 59-62, используя метод графической аппроксимации, вычислите точки пересечения функций f(x) и д(х) (с точностью до двух десятичных знаков).
59. /(х) = е®; д(х) = я4.
(Следует отметить, что существуют три точки пересечения, причем при больших значениях х функция ех превышает функцию я4.)
60. /(ж) = е®; д(х) = х5.
(Следует отметить, что существует две точки пересечения, причем при больших значениях х функция ех превышает функцию я5.)
61. /(я) = 1пя; #(я) = я1//5.
(Следует отметить, что при больших значениях я функция In я не превышает функцию я1/5.)
62. /(я) = In я; д(х) = я1/4.
(Следует отметить, что при больших значениях я функция In я меньше, чем функция я1//4.)
Применение математики
Экономика и бизнес
63. 	Максимальная прибыль. Национальная продовольственная служба предложила организаторам спортивных соревнований по всей стране концессионный договор на поставку продуктов питания. Ее отдел маркетинга провел исследование спроса на хот-доги увеличенного размера, реализуемые в течение среднестатистического футбольного матча. Было обнаружено, что спрос на новые хот-доги описывается следующей формулой.
р = 5 — In я, 5 < я 50.
Здесь я — количество хот-догов (тыс. шт.), продаваемых на протяжении одной игры по цене р долл. Сколько должен стоить хот-дог, чтобы прибыль от одной игры была максимальной, если концессионер платит 1 долл, за хот-дог?


Глава 10. Дифференцирование
297
64. Максимальная прибыль. Во время концертного тура спрос на футболки с символикой рок-группы описывается следующей формулой.
р — 15 — 4 In ж, 1 х < 40.
Здесь х — количество футболок (тыс. шт.), продаваемые в ходе одного концерта по цене р долл. Сколько они должны стоить, чтобы прибыль от одного концерта была максимальной, если каждая футболка обходится группе в 5 долл.?
65. Максимальная прибыль. Региональная сеть универмагов собрала данные об объемах недельных продаж определенной марки джинсов (см. таблицу). Одни и те же джинсы предлагались по различным ценам — от обычной цены 35,99 долл, до самой низкой отпускной цены 23,99 долл. Каждая пара джинс этой марки обходится сети универмагов в 20,00 долл. Используя уравнение логарифмической регрессии (р = а + b 1п х), найдите цену (с точностью до ближайшего цента), при которой прибыль будет максимальной.
Объем продаж, х
Цена за пару (долл.), р
21543
23,99
14029
25,99
12130
27,99
9169
29,99
6964
31,99
5506
33,99
4187
35,99
66. Максимальная прибыль. Компания посылочной торговли специализируется на продаже спортивной обуви. Отдел маркетинговых исследований установил недельный спрос на определенную модель обуви для разных ценовых уровней (табл. 10.3). Компания может купить эту модель обуви у производителя по цене 62 долл, за пару. Используя уравнение логарифмической регрессии (р = а + Ь 1п х), вычислите цену (с точностью до ближайшего цента), при которой прибыль достигает максимума.
67. Минимальные средние затраты. Затраты на производство х единиц продукции описываются формулой
С(х) = 600 -I- ЮОж - 100 In х, х 1.


298
Часть III. Математический анализ
Таблица 10.3. Таблица к задаче 66
Спрос, х
Цена за пару (долл.), р
4312
74
3064
79
2499
84
2047
89
1823
94
1781
99
Вычислите минимальные средние затраты.
68. Минимальные средние затраты. Затраты на производство х единиц продукции описываются формулой
С(х) = 1000 + 200х - 200lnx, х 1.
Вычислите минимальные средние затраты.
69. Максимальный доход. Косметическая компания планирует разметить рекламу новой линейки губных помад. Отдел маркетинговых исследований провел пробные продажи новой линейки помад в тщательно отобранном крупном городе и обнаружил, что спрос описывается формулой
р=10е“х, 0 х 2,
где х — недельный объем продаж (тыс. шт.), по цене р долл, за штуку.
а) При какой цене недельный доход Я(х) = хр достигает максимума? Каков максимальный недельный доход в рассматриваемом городе?
б) Постройте график R для 0 х 2.
70. Максимальный доход. Повторите решение задачи 69, используя уравнение спроса р — 12е-1, 0 < х < 2.
Биологические науки
71. Артериальное давление. Чтобы найти связь между весом и систолическим кровяным давлением у здорового ребенка, был проведен эксперимент. Используя клинические записи о состоянии здоровья 5000 детей, медики обнаружили, что систолическое кровяное давление описывается формулой
Р(х) = 17,5(1 + lnx); 10 х 100,


Глава 10. Дифференцирование
299
где Р(х) измеряется в миллиметрах ртутного столба, а х — в фунтах. Какова скорость изменения кровяного давления как функции веса при весе 40 фунтов? При весе 90 фунтов?
72. Артериальное давление. Постройте график уравнения артериального давления из задачи 71.
73. Концентрация препарата. Концентрация препарата в крови через t часов после введения описывается формулой
C(t) = 4,35e_t; 0 t 5,
где C(t) — концентрация в миллиграммах на миллилитр.
а) Какова скорость изменения концентрации через 1 час? Через 4 часа?
б) Постройте график С.
74. Загрязнение воды. Использование кристаллов йода — это популярный способ, которым небольшое количество загрязненной воды можно сделать пригодной для питья. Кристаллы, помещенные в одноунциевую бутылку воды, будут растворяться до тех пор, пока раствор не станет насыщенным. После насыщения половина этого раствора заливается в контейнер с загрязненной водой, объем которого равен кварте (1,14 л), и приблизительно через час вода становится пригодной для питья. Полупустая одноунциевая бутылка затем снова наполняется и повторно используется аналогичным образом. Предположим, что концентрацию йода в одноунциевой бутылке через t минут после того, как в нее были добавлены кристаллы, приблизительно можно описать уравнением
C(t) = 250(1 - e_f), t > 0,
где C(t) — концентрация йода в микрограммах на миллилитр.
а) Какова скорость изменения концентрации через 1 минуту? Через 4 минуты?
б) Постройте график С для 0 < К 5.
Социальные науки
75. WWW Физиология: стимул/реакция. В физиологии закон стимула-реакции Вебера- Фечнера (Weber-Fechner) имеет вид
R = A;In
*->0
где R — ответ, S — текущий уровень стимуляции, a So — минимально регистрируемый уровень стимуляции. Вычислите функцию dR/dS.
76. Психология: обучение. Уравнение, описывающее средний уровень овладения навыками машинописи имеет вид
N(t) = 10 Н- 6 In t > 1,
где 7V(t) — количество слов в минуту, которые печатаются через t часов обучения и практических занятий (два часа в день, пять дней в неделю). Каким будет уровень овладения навыками машинописи через 10 часов обучения и практических занятий? Через 100 часов?


300
Часть III. Математический анализ
10.3. 	Цепное правило: общая форма
■ Суперпозиция функций
■ Цепное правило
■ Обобщенные правила дифференцирования
■ Другие логарифмические и показательные функции
Задание 10.5.
1. Как было показано ранее, функция /(ж) = ех равна своей производной. Используя график функции д (х) = ех2, изображенный на рис. 10.10, объясните, почему функция д(х) не равна собственной производной.
2. Используя график функции h (х) = 2хех2 на рис. 10.11, объясните, почему
функция h(x) может быть производной от функции д(х). (В этом разделе будет показано, что функция h(x) действительно является производной функции д(х).') ■
Рис. 10.10. График функции
9^=ех2
Рис. 10.11. График функции h (х) = 2хех2
В разделе 8.6 была описывалось цепное правило дифференцирования степенных функций.
4- [и ип = П [и (х)Г-1 и1 (ж). ах
Например, (х2 — 3)
dx
5
= 5 (х2 - З)4 — (х2 - 3) = = Юж (ж2 - З)4


Глава 10. Дифференцирование
301
Это общее правило дифференцирования степенных выражений представляет собой отдельный вариант одного из наиболее важных правил дифференцирования — цепного правила, которое позволяет выражать производные довольно сложных функций через производные более простых функций.
Предположим, требуется вычислить производную функции
тп (х) = In (2х + 1) или п(х) = е3х2~1.
Нам известны формулы для вычисления производных функций lnx и ех, а также полиномиальных функций. Однако они неприменимы к указанным комбинациям. Для вычисления производных функций, являющихся функциями более простых функций, производные которых известны, используется цепное правило. По этой причине раздел начинается с краткого обзора суперпозиции функций.
Суперпозиция функций
Рассмотрим функцию тп детально:
m(x) = 1п(2ж + 1).
Функция тп представляет комбинацию функции натурального логарифма и линейной функции. Чтобы удостовериться в этом, пусть
у — f(u) — In и и и — д(х) — 2х + 1.
Тогда у можно выразить через функцию, зависящую от переменной х.
у - /(u) = /[^(х)] = 1п(2х + 1) = т(х).
В таком случае говорят, что функция тп является суперпозицией двух более простых функций f и д. (Проще говоря, функцию тп можно считать функцией функции.)
www Суперпозиция функций
Функция тп является суперпозицией функций f и д, если
т(х) = /[р(х>].
Областью определения функции тп является множество всех чисел х, лежащих в области определения функции д, а значения функции д(х) образуют область определения функции /.
Пример 10.8 (Суперпозиция функций). Пусть /(и) — еи, д(х) = Зх2 + 1 и тп(у) = г>3/2. Вычислите следующие функции.
1. /[я(х)|; 2. 3. m[p(x)].


302
Часть III. Математический анализ
Решение.
1- f[g№] = еэ(1) - е3х2+1.
2. g[f(u)] = 3[/« + 1 = 3(eu)2 + 1 = 3e2u + 1.
3. m[y(ar)] = [у(ж)]3/2 = (Зж2 + I)3/2. ■
Упражнение 10.8.
Пусть /(u) — In и, у(ж) = 2ж3 + 4 и m(v) = v~5. Вычислите следующие функции.
1- ЖХ)Ь 2. g[f(u)]; 3. m[y(x)]. ■
Пример 10.9 (Суперпозиция функций). Запишите каждую функцию в виде суперпозиции натурального логарифма или экспоненциальной функции и полинома.
1. 	у = 1п(х3 — 2х2 + 1). 2. у — ех2+4.
Решение.
1. Пусть
У = /(«) = lnu,
и = д(х) = ж3 — 2х2 + 1.
Проверка, у — /[у(ж)] = 1п[у(ж)] = 1п(х3 — 2х2 + 1).
2. Пусть
У = f(u) = еи,
и — д(х) — х2 + 4.
Проверка, у = /[у(ж)] = ед(-х> = ех2+4. ■
Упражнение 10.9.
Повторите проделанное в примере 10.9 для функций
1. у = e2x3+7. 2. у = 1п(х4 + 10). ■
Цепное правило
Слово цепное отражает тот факт, что функция образуется с помощью суперпозиции (как, например, функции в примере 10.8). Цепное правило позволяет выражать производные сложных функций через производные функций, образующих суперпозицию.
Предположим, что функция


Глава 10. Дифференцирование
303
является суперпозицией функций /ид, где
y = f(u) И I4 = ^(x).
Требуется выразить производную dy/dx через производные функций / и д. Из определения производной (см. раздел 8.3) имеем
dy т (х + h) — т (х\
- lim — - —
dx h—>о h
Подставим m(x + h) =
= f[g(x +h)] urn (a?) = f[g (®)].
= lim -
Цд{х + П)\-/[д(х)\ h
Домножим на 1 = g (® 4- h) — g (x)
g(x + h) -
- 9 (®)'
= lim
'/[g(x + h)] — / [p (□?)]
g(x + h) -g(x)'
h->0
g(x + h) — g(x)
= lim
7 [p + Ml - f b С*)]
g(x + li) -g(x)'
h->0
g(x + h) — g (x)
h
(10.3)
Во втором множителе формулы (10.3) можно распознать разностное отношение функции з(х). Чтобы первый множитель можно было интерпретировать как разностное отношение функции /(и), нужно положить к = д(х + Д) — д(х). Поскольку и = д(х)9 запишите
и + к; = д (ж) + д (х + h) - д (х) • = д (х + К).
Подставляя этот результат в уравнение (10.3), имеем
dy _ .. Г/ (u + fc) - / (u) д(х + h) — д (х) dx h-^o к h
(Ю.4)
Если предположить, что к = [<?(х + /г) — д(х)] —> 0, когда h —» 0, можно вычислить предел каждого разностного отношения в уравнении (10.4).
dy = L / (n + fc) - / (u) dx к
=/'{u) д'{x)—
lim g(x + fe) -g(x)
h->0 h
dy du du dx
Этот результат корректен при довольно общих условиях и называется цепным правилом, однако он остается поверхностным, поскольку в нем игнорируется множество скрытых проблем. Формальное доказательство цепного правила выходит за рамки этой книги, поэтому ограничимся его формулировкой.


304
Часть III. Математический анализ
www Цепное правило
Если функции у — f(u) и и = д(х) образуют суперпозицию функций
У = т(х) = /[^(ж)],
ТО
dy dy du dy du
при условии, что — и —- существуют.
dx du dx du dx
Или, что то же самое,
т'(х) = /'[д(хУ]д'(х), при условии, что и </(#) существуют.
Пример 10.10 (Цепное правило). Вычислите функцию dy/dx при следующих условиях.
1. 	у = 1п(х2 — 4х + 2). 2. у = е2ж3+5. 3. у — (Зх2 + I)3/2.
Решение.
1. Пусть у = In и и и = х2 — 4х + 2. Тогда4
dy; dy du ;
dx \ du dx •
U - (2x - 4) =i
\___u__
= —2 (2x — 4) = Поскольку и = x2 — 4я? + 2.
x 4x 4" 2
_ 2s-4
x2 — 4x + 2
2. Пусть у = еи и и = 2х3 + 5. Тогда
dy \ dy du ;
dx \ du dx •
:= eu (бх2) =:
= 6т2е2а;3+5. Поскольку и = 2ж3 + 5.
4Приобретя некоторый опыт использования цепного правила, действия, указанные в пунктир¬
ных рамках, как правило, можно будет производить в уме.


Глава 10. Дифференцирование
305
3. 	Есть два метода.
Метод 1. Цепное правило: общая форма. Пусть у = и3/2 и и = Зх2 + 1.
Тогда
dy i dy du ;
dx \ du dx ;
;= • 6x =:
:...2 :
= (Зх2 + l)1/2 • 6x =
= 9x (Зх2 + l)1/2 , или
Поскольку и = Зя?2 + 1.
9хз/3х2 + 1.
Метод 2. Цепное правило: степенное выражение (общее правило дифференцирования степенных выражений).
^(з^ + 1)3/2 = з(з^ + 1)1/2А(312 + 1) =
М®)]п = n[u(a:)]n_1 ^u(®).
= | (Зх2 + 1)1/2 • бх =
— 9х (Зх2 + 1)1/2 , или 9х\/3х2 + 1. ■
Обобщенное правило дифференцирования степенных выражений, изложенное в разделе 8.6, можно вывести, используя цепное правило следующим образом. Дано у — [u(x)]n, пусть у — vn и = и(х). Тогда
dy dy dv
dx dv dx
— nvn~i-j—u (x) =
dx
= n[u (x)]n_1 ^u (x).
Поскольку V = и (ж).
Упражнение 10.10.
Вычислите функцию dy/dx при следующих условиях.
1. у = е3ж4+6. 2. у = 1п(х2 + 9х + 4).
3. 	у = (2х3 + 4)“5 (используйте оба метода).
Цепное правило можно расширить на случай суперпозиции трех и более функций. Например, если у = w — g(u) и и = /г(х), то
dy dy dw du dx dw du dx


306
Часть III. Математический анализ
Пример 10.11 (Цепное правило). Вычислите функцию dy/dx для функции у = = Л(а;) = е1+(Ьх)2
Решение. Следует отметить, что функция h имеет форму у = ew, где w = 1 + и2, а и = Ina;. Таким образом,
dy! dy dw du _ !
dx: dw du dx :
\=ew-2u--= i
: x :
!= • 2u * — = ! Поскольку w = 1 + u2
: x ;
;= gl+O1137) • 2 In X • — =; Поскольку и = In x.
• x__>
= - • lnx • е1+(1пж) .
X
Упражнение 10.11.
Вычислите производную dy/dx функции у — /i(x) = [ln(l + еж)]3. ■
Обобщенные правила дифференцирования
На практике при использовании цепного правила нет необходимости вводить дополнительные переменные, как это делалось в примерах 10.10 и 10.11. Вместо этого, воспользовавшись цепным правилом, можно расширить правила дифференцирования отдельных функций до обобщенных правил дифференцирования суперпозиций так же, как это было сделано выше. Аналогичные методы можно применить к функциям вида у = и у = 1п[/(х)] (см. задачи 71 и 72 в практикуме 10.3). Все эти результаты собраны в нижеприведенной врезке.
Обобщенные правила дифференцирования
И (<■ = "[/ИГ1/'И-
(10.5)
(10.6)
Ае/(х) = (х) .
dx
(Ю.7)
При использовании натуральных логарифмов, степенных или экспоненциальных выражений можно либо применять цепное правило, рассмотренное ранее, либо специальные формулы дифференцирования, которые основаны на цепном правиле. Применяйте то правило, которое вам кажется проще. В примере 10.12 будут использованы обобщенные правила дифференцирования.


Глава 10. Дифференцирование
307
Пример 10.12 (Обобщенные правила дифференцирования).
1.
= е2х 2х =
ах ах
Используем формулу (10.7)
2х
2 = 2е2х.
2.
3.
1 d / 2 л\
—q ~~г~ + 9) = Используем формулу (10.6)
X2 + 9 dx х 7
1 ~ 2х
о
X2
+ 9
х2 + 9’
\2 d { _2\
= 3-
(1+е,
) &(1+е)
= Используем формулу (10.5)
= 3-
|2О
Используем формулу (10.7)
= 3-
12 2 ех -2х =
= 6жех2 (1 + е*2)2.
= е
Упражнение 10.12.
Вычислите следующие производные.
1. ^-1п(х3 + 2х). 2. АеЗх2+2
dx v ' dx
Другие логарифмические и показательные функции
В большинстве практических задач, в которых встречаются логарифмические или показательные функции, предпочтительным основанием является число е. Производные от функций у = log^x и у = Ьх можно получить, выразив эти функции через натуральный логарифм и экспоненциальную функцию.
Сначала найдем связь между logb х и In х для произвольного основания Ь, b > 0 и b 1. Некоторые из приведенных далее выкладок могут быть вам знакомы.
у = logbx
by = х
In bv = In х у In Ь — In х y=^i'nx-
Преобразуем в показательное выражение.
Возьмем натуральный логарифм от обеих частей.
Напомним, что In bv = у In b.
Решим относительно у.


308
Часть III. Математический анализ
Таким образом,
log^ X — -—-lnx. Формула замены основания5 (10.8)
In о
Дифференцируя обе части уравнения (10.8), получим
1 d In Ь dx
lnx =
1
lnb
Задание 10.6.
1. На рис. 10.12 изображены графики функций /(х) = log2x и д(х) = log4x. Какой график какой функции принадлежит?
Рис. 10.12. Графики функций /(х) =
= /(х) = log2 X и #(х) = log4 X
2. Постройте графики функций /'(х) и </(*)•
3. Функция /(х) связана с функцией д(х) так же, как производная /'(х) связана
с производной Что это за связь? ■
Пример 10.13 (Дифференцирование логарифмических функций). Вычислите функцию f'(x) при следующих условиях.
1. /(х) = log2 X. 2. /(х) = lg(l + X3).
Решение.
Используем формулу (10.8).
1
х
5Уравнение (10.8) — это особый случай обобщенной формулы замены основания для логарифмов (которую можно вывести аналогичным образом): logb х = (loga x)/(loga b).


Глава 10. Дифференцирование
309
Напомним, что lgr = log10 г.
Используем формулу (10.8).
1 / Зх2 \
In 10 \1 4- х3)
Упражнение 10.13.
Вычислите функцию f'(x) при следующих условиях.
1. Дх) = lgx. 2. /(х) = log3(x + х2).
Теперь следует найти связь между Ьх и ех для произвольного основания Ь, Ь > 0 и 6 ± 1.
у = Ьх] Возьмем натуральный логарифм от обеих частей.
In у = In Ьх =
— X In Ь — Если In А = В, то А = ев.
у = ехЫх.
Таким образом,
bx = ex\nb (Ю.9)
Дифференцируя обе части уравнения (10.9), получим
—bx = bI,n6lnb = bxlnb.
dx
Пример 10.14 (Дифференцирование показательных функций). Вычислите производную /'(х) при следующих условиях.
1. Дх) = 2х. 2. f (х) = 10®5+®.
Решение.
1. /(т) = 2х = ех1п2; Используем формулу (10.9).
/'(х) =exln2ln2 = 2xln2.
2. Дх) = 10х +х = е(х Используем формулу (10.9).
/'(х) = е(х5+х)1п10 (5х4 + 1) In 10 =
= 10х5+х (5х4 + 1) In 10. а
Упражнение 10.14.
Вычислите функцию f(x) при следующих условиях.
1. Дх) = 5х. 2. f (х) = 4х2+3х. ■


310
Часть III. Математический анализ
Ответы к упражнениям
10.8. 1) 1п(2х3 + 4).
2) 2- (In и)3 + 4.
3) (2х3 + 4)-5.
10.9. 1) у = f(u) = еи; и = д(х) = 2ж3 + 7.
2) у = /(u) = In и; и = д(х) = ж4 + 10. 10.10. 1) 12х3е3х4+6  7 *.
2) 2ж + 9
х2 + 9х + 4
3) -30ж2(2ж3 + 4)-6.
10.11.
10.12.
Зех [In (1 + ех)]2
1 + ех
1)
х3 + 2х
2) 6же3х2+2.
3)
10.13. 1)
2)
—8хе_х2 (2 + е~х2)3.
1 1
In 10 х
1 /1 + 2х\
In 3 \ х + х2 )
10.14. 1) 5х In 5.
2) 4х2+3х (2х + 3) In 4.
Практикум 10.3
А В задачах 1-6 вычислите функцию f[g(х)].
1. f(u) = и3; д(х) = Зх2 + 2. 2. /(и) = и4; д(х) = 1 — 4х3.
3. f(u) = In и; д(х) = 2х2 + 5. 4. /(и) = In и; д(х) = Зх4 + 10.
5. f(u) = еи; д(х) = -х2. 6. f(u) = еи; д(х) = Зх3.
Запишите все сложные функции в задачах 7-12 в виде у = f(u); и = р(х).
7. у = (Зх2 — х + 5)4. 8. у = (2х3 + х + З)5.
9. у = 1п(3х2 — 2х + 9). 10. у = 1п(х4 + х2 + 12).
11. у = е1+ж+а;2. 12. у = e*4+2*2+5.
В задачах 13-18 выразите величину у через переменную х. Используя цепное правило, найдите dy/dx, а затем выразите функцию dy/dx через переменную х.
13. у - и2; и = 2 + ех. 14. у = и3; и - 3 — lnx.


Глава 10. Дифференцирование
311
15. у = еи; и = 2 — а;4.
17. 	у = In и; и = 4а;5 — 7.
16. у = еи; и = х6 + 5а?2.
18. 	у = lniz; и = 2 + За;4.
В задачах 19-52 вычислите производную и упростите результат. (Для некоторых из этих задач ответы в конце книги содержат как общую, так и упрощенную форму производной. При проверке полученных результатов сначала убедитесь в корректности применения правил дифференцирования и только после этого переходите к анализу алгебраических преобразований.)
19. 	1п (ж - 3). ах
21. -^-ln(3-2t). dt
23. -у-Зе2®. ах
25 — 2e_4t
25‘ dt е ■
27. 	-^-ЮОе-0’03®. ах
29. In (х + I)4. ах
20. In (w + 100).
dw
22. In (4-5т/).
dy
24. -^2еЧ dy
26. ^-6e"3r. dr
28. 	41000e°’06t. dt
30. -7- In (x 4-1)-3. dx
31. 	4- (2e2x -3ex +5). dx ' 7
33. —e3x2~2x. dx
35. In (t2 + 3t).
37.A1„(^ + 1),/2.
41. 4- (e21 - I)4.
dx v 7
J p2x
43. 	— — .
dx x2 + 1
47. (e~x Ina;). dx
d 1
dx In (1 + x2) ’
51. s/ln (1 — a;2).
“■s'1- '~e
34. —ex3~ 3a:2+i. dx
36. In (a;3 — 3a;2). dx v 7
38.А1п(11 + 5Г.
d e®+1
44. 	3 7
dx x + 1
46. (1 — x) e2x.
dx
48. 4--^-
dx ex + 1
d 1
dx In (1 — a;3) *
S2.
*53. Опишите соотношение между графиками функций у = lnz и у = logb х для Ь> 1.


312
Часть III. Математический анализ
*54. Опишите соотношение между графиками функций у = 1пх и у = logfex для О < b < 1.
В В задачах 55-60, используя методику построения графиков, описанную в разделе 9.3, к функции f, соберите все необходимую информацию и постройте график.
55. /(ж) = 1 - е~х. 56. /(ж) = 2 - Зе~2х.
57. /(ж) = 1п(1 - х). 58. f(x) = 1п(2т + 4).
59. f (х) = е-0,5*2. 60. f(x) = 1п(ж2 + 4).
В задачах 61 и 62 выразите величину у через переменную х. Используя цепное правило, вычислите функцию dy/dx и выразите ее через переменную х.
61. 	у = 1 + w2; w = In и; и = 2 + ех. 62. у = In w; w = 1 + еи; и = х2.
В задачах 63-70 вычислите каждую производную.
63- 10§2 (З*2 - 1).
65. -^10®2+:г. dx
67. log3 (4ж3 + 5я + 7). dx 7
ф) _^_2ж3—
dx
ы.
66. -^-81_2х2. dx
70. 4-10lni.
71. Используя цепное правило, выведите формулу.
1 /(я)
/'(*)•
72. Используя цепное правило, выведите формулу.
=e/(*)f (д;).
*73. а) Используя графики функций f(x) = 1п(я2+1) пд(х) = 1/(х2+1) (рис. 10.13), объясните, почему д(х) не является производной f(x).
Рис. 10.13. Иллюстрация к задаче 73
б) Вычислите производную f'(x) и постройте ее график.


Глава 10. Дифференцирование
313
* 74. а) Сколько раз нужно применить цепное правило, чтобы вычислить производную от функции f (х) =
б) Постройте такую функцию р(х), чтобы для вычисления ее производной понадобилось три раза применить цепное правило.
75.* Предположим, студент утверждает, что функции /(х) = ln[5(x2 + З)4] и д{х) = = 41п(х2+3) имеют одинаковые производные, поскольку он ввел в графическую утилиту функции /(х), р(х), /'(х) и р'(х), но на экране появилось только три графика (рис. 10.14). Верны ли его рассуждения? Совпадают ли функции /'(х) и д'(х)? Аргументируйте свой ответ.
ylBln (5*<хл2+3)л4> у2В41п (хл2+3) y3Bn0er(ybx>x) у4Вп0ег(у2>х>х)
б)
а)
Рис. 10.14. Иллюстрация к задаче 75
76.* Предположим, студент утверждает, что функции /(х) = (х -И 1) ln(x + 1) — х и д(х) = (х + I)1/3 должны иметь одинаковые производные, поскольку он ввел данные экране /(х), р(х), f'(x) f'(x) и д'(х) в графическую утилиту, а на экран (рис. 10.15) было выведено только три графика. Верны ли его рассуждения? Совпадают ли функции /'(х) и р'(х)? Аргументируйте свой ответ.
у1В(х+1>*1п (х+1)-х у2В(х+1)л(1/3) уЗВп0ег(уЬх,х) у4Вп0ег(у2>х>х)
б)
а)
Рис. 10.15. Иллюстрация к задаче 76


314
Часть III. Математический анализ
Применение математики
Экономика и бизнес
77. Максимальный доход. Предположим, что уравнение зависимости цены от спроса на х единиц товара, полученное на основе эмпирических данных, имеет вид
р = 100е_0,05х,
где х — дневной объем продаж при цене р долл, за единицу. Вычислите объем производства и цену, при которых доход достигает максимума. Каким будет максимальный доход?
78. Максимальный доход. Повторите действия задачи 77, используя следующую зависимость цены от спроса
1Ое-°’04*.
79. Максимальная прибыль. Вернемся к задаче 77. Используя методы аппроксимации, вычислите объем производства и цену, при которых прибыль достигает максимума, если ежедневные постоянные затраты составляют 400 долл., а переменные издержки в расчете на единицу продукции равны 6 долл. Какова максимальная прибыль? (Подсказка. Постройте графики у — Р(х) и у = Pf(x) в одном и том же окне.)
80. Максимальная прибыль. Вернемся к задаче 78. Используя методы аппроксимации, вычислите объем производства и цену, при которых прибыль достигает максимума, если ежедневные постоянные затраты составляют 30 долл., а переменные издержки в расчете на единицу продукции равны 0,70 долл. Какова максимальная прибыль? (Подсказка. Постройте графики у = Р(х) и у = Р'(х) в одном и том же окне.)
81. Максимальная прибыль. Компания посылочной торговли компьютерным оборудованием собирает данные о недельном спросе на модемы Data-Link при различных уровнях цены р (см. таблицу). Компания покупает модемы у производителя по 100 долл, за штуку. Используя уравнение экспоненциальной регрессии (р = abx), вычислите цену (с точностью до ближайшего цента), при которой недельная прибыль достигает максимума.
Спрос, х Цена модема р, долл.
412
169,95
488
149,95
575
139,95
722
129,95
786
119,95
82. 	Максимальная прибыль. Компания посылочной торговли компьютерным оборудованием продает 100-мегабайтные диски. Данные в следующей таблице описывают недельный спрос на эти диски при различных уровнях цены р. Компания


Глава 10. Дифференцирование
315
покупает диски у производителя по 6 долл, за штуку. Используя уравнение экспоненциальной регрессии (р = abx), найдите цену (с точностью до ближайшего цента), при которой недельная прибыль достигает максимума.
Спрос, х Цена диска р, долл.
578
16,95
942
14,95
1218
13,95
1758
11,95
2198
10,95
83. 	Ликвидационная стоимость. Ликвидационная стоимость самолета S (в долларах) через t лет составляет приблизительно
S(t) = 300000e_0,lt.
Какой будет скорость обесценивания (долларов в год) через один год? Через 5 лет? Через 10 лет?
84. Стоимость перепродажи. Цена перепродажи автомобиля R (в долларах) через t лет составляет приблизительно
S(t) = 2OOOOe_o,15t.
Какой будет скорость обесценивания (долларов в год) через один год? Через 2 года? Через 3 года?
85. Реклама и максимальная прибыль. Компания звукозаписи выпустила новый компакт-диск с записями очень популярной музыкальной группы. Прежде чем начать общенациональную рекламную компанию, отдел маркетинговых исследований провел пробные продажи дисков в крупном городе. Целью исследований было определение длительности рекламной компании, обеспечивающей максимальную прибыль. Оказалось, что доля людей из целевой группы из 50 000 покупателей компакт-дисков, которые приобрели диски через t дней после начала телевизионной рекламы, равна 1 — е~0,03г. Если от продажи каждого компакт- диска будет получено 4 долл., общий доход через t дней после начала рекламной акции составит приблизительно
R(t) = 4- 50000- (1 - e_0,03t), t > 0.
Затраты на телевизионную рекламу составляют
0(f) = 4000 4- 3000t, t > 0.


316
Часть III. Математический анализ
а) Сколько дней должна идти телевизионная реклама, чтобы общая прибыль была максимальной? Какова максимальная общая прибыль? Какую долю целевого рынка образуют покупатели компакт-дисков, когда будет достигнута максимальная прибыль?
б) Постройте график функции прибыли.
86. Продвижение на рынок и максимальная прибыль. Повторите действия задачи 85, используя уравнение дохода
R(t) = 3-60000- (1 — e_0,04t).
Биологические науки
87. Артериальное давление и возраст. Исследовательская группа, используя клинические записи, разработала следующую приблизительную математическую модель, описывающую связь между систолическим кровяным давлением и возрастом:
Р(х) = 40 + 251п(х + 1), 0 < х 65,
где Р(ж) — давление, измеряемое в миллиметрах ртутного столба, а х — возраст в годах. Какова скорость изменения давления по достижении 10-летнего возраста? 30 лет? 60 лет?
88. Биология. Дрожжевая культура, содержащаяся при комнатной температуре (68 градусов по Фаренгейту), помещена в холодильник, поддерживающий постоянную температуру 38 градусов по Фаренгейту. Через t часов температура культуры Т составит приблизительно
Т = 30e_0,58t + 38, t > 0.
Какова скорость изменения температуры культуры в конце первого часа? В конце четвертого часа?
89. Рост численности бактерий. Одна бактерия холеры делится каждые 0,5 часа, образуя две таких же бактерии холеры. Если изначально в колонии было 5000 бактерий, то через t часов в ней будет
A(t) = 5000 • 22‘
бактерий. Вычислите функцию A'(t), а также значения А'(1) и А'(5) и проин- терпретируйте результаты.
90. Бактериальный рост. Повторите решение задачи 89 для начальной колонии из 1000 бактерий, в которой одна бактерия делится каждые 0,25 часа.
Социальные науки
91. Социология. Дэниэл Ловенталь (Daniel Lowenthal), социолог из Колумбийского университета, провел пятилетнее исследование продаж популярных мелодий в зависимости от их позиции в чартах. Он обнаружил, что средний объем продаж ЛГ(п) мелодии, находящейся на п-й позиции, составляет приблизительно,
N(n) = A'le’0’09’"'11; 1 < п 20,
где Ni — объем продаж мелодии, занимающей первую позицию. Постройте график N для 7Vi = 1000 000 мелодий.


Глава 10. Дифференцирование
317
92. 	Политология. Томас У. Касстивенс (Thomas W. Casstevens), политолог из Оклендского университета, изучал сменяемость кадрового состава в законодательных органах. Он и его команда обнаружили, что количество членов выборного законодательного органа, постоянно находящихся на службе, через t лет после выборов приблизительно описывается функцией
N(t) = Noe~ct.
В частности, при выборах в Палату представителей США в 1965 году эта формула принимает вид
JV(t) = 434e_0,0866t.
Какой будет скорость смены кадрового состава через 2 года? Через 10 лет?
10.4. 	Неявное дифференцирование
■ Специальное обозначение функции
■ Дифференцирование неявных функций
Специальное обозначение функции
Уравнение
у = 2 - Зж2 (10.10)
определяет функцию /, где у — зависимая, а х — независимая переменная. Используя обозначение функции, можно записать
у = /(х) или /(х) = 2 - Зх2.
Чтобы сократить до минимума количество используемых символов, уравнение (10.10) часто записывают в виде
у = 2 - За;2 = у(х)
где у одновременно является и зависимой переменной, и обозначением функции. Это обозначение весьма удобно и двойная роль символа у не создает никаких противоречий. Другими примерами такой записи могут служить следующие функции.
х = 2t2 — St + 1 = х (£), z = \/^2 ~ = z (и),
r=(7^ = r(s)'
Этот тип обозначения позволяет упростить математические выкладки и сократить объем формул, записываемых в дальнейших вычислениях.


318
Часть III. Математический анализ
До сих пор мы рассматривали функции, у которых была только одна независимая переменная. Эту концепцию можно обобщить и на другие переменные (глава 13). Например, выражение
F(x, у) = х2 - 2ху 4- Зу2 - 5
определяет функцию F, имеющую две независимые переменные.
Дифференцирование неявных функций
Рассмотрим уравнение
Зх2 + у — 2 = 0 (10.11)
и решим его относительно переменной у,
у = 2 — 3х2. (10.12)
Оба уравнения определяют одну и ту же функцию, в которой х используется в качестве независимой переменной, а у — в качестве зависимой. Уравнения (10.12) можно записать в виде
У = f(x),
где
/(х) = 2 — Зх2, (10.13)
получив явный (четко сформулированный) закон, позволяющий находить значения у для любых значений х. С другой стороны, величина у в уравнении (10.11) — это та же величина у, что и в уравнении (10.12), только в уравнении (10.11) она задается неявным образом, а не выражается явно, как функция х. Таким образом, можно сказать, что уравнения (10.12) и (10.13) задают функцию f явно, а уравнение (10.11) задает ее неявно.
Процесс, в ходе которого уравнение, определяющее функцию неявно, используется для вычисления производной зависимой переменной по независимой переменной, называется неявным дифференцированием (implicit differentiation). Продифференцируем уравнение (10.11) неявно, а уравнение (10.12) — явно и сравним результаты.
Прежде всего, в уравнении
Зх2 у — 2 = 0
будем рассматривать величину у как функцию, зависящую от переменной т, — т.е. у = у(х) — и запишем
Зх2 + у(х) — 2 = 0.


Глава 10. Дифференцирование
319
Затем продифференцируем обе части уравнения по х.
6а; + у' - 0 = 0.
Поскольку величина у является функцией х, но не выражена явно, для обозначения производной можно просто записать
Теперь решим уравнение относительно у'.
у7 = —6т.
Следует отметить, что такой же результат получается, если использовать уравнение (10.12), дифференцируя его непосредственно.
У - 2 - За:2; у7 — —6т.
Зачем нужно неявное дифференцирование? Почему бы не решить уравнение относительно величины у, выразив ее через переменную х, и не продифференцировать ее непосредственно? Ответ на этот вопрос состоит в том, что существует множество уравнений вида
Г(ж,у) - 0,
(10.14)
которые либо сложно, либо невозможно решить относительно переменной у, явно выразив эту величину через переменную х (в частности, попробуйте сделать это для уравнений х2у5 — Зху + 5 = 0 или еу — у = Зх). Однако можно показать, что при довольно общих условиях, налагаемых на функцию F, уравнению (10.14) может удовлетворять одна или несколько функций, в которых у — зависимая переменная, ах — независимая. Чтобы вычислить производную у' при таких условиях, уравнение (10.14) следует продифференцировать неявно.
Задание 10.7.
1. Сколько можно провести касательных к графику на рис. 10.16, если х = 0, 1, 2, 4 или 6?
2. Нарисуйте касательные, рассмотренные при решении п. 1, и вычислите приближенное значение их наклона.
3. Объясните, почему график на рис. 10.16 не является графиком функции. ■
Пример 10.15 (Неявное дифференцирование). По заданной функции
F(x, у)-х2 + у2- 25
(10.15)
вычислите производную у7 и наклон графика в точке х = 3.


320
Часть III. Математический анализ
у
х2+у2 = 25
Рис. 10.17. Окружность
Рис. 10.16. Кардиоида
Решение. Рассмотрим график функции х2 + у2 — 25 = 0 (окружности, см. рис. 10.17) и проинтерпретируем полученные результаты с геометрической точки зрения. Из графика становится ясно, что уравнение (10.15) не описывает функцию. Однако, если на переменные наложить определенные ограничения, то уравнение (10.15) может описывать несколько функций. Например, и верхняя, и нижняя половины окружности описываются функцией. Точки на каждой половине окружности, соответствующие точке х = 3, можно вычислить, подставив значение х = 3 в уравнение (10.15), и решив его относительно у.
z2 + у2 - 25 = 0,
З2 + у2 = 25,
Таким образом, точка (3,4) находится на верхней половине окружности, а точка (3, —4) — на нижней. Эти результаты будут использованы немного позже. Пока продифференцируем уравнение (10.15) неявно, рассматривая величину у как функцию, зависящую от переменной х, т.е. у = f(x).
х2 + у2 - 25 = 0,
Применим цепное правило.


Глава 10. Дифференцирование
321
Решим уравнение относительно у', выразив эту величину через а? и у.
Выразим ответ через х и у.
www Таким образом, для вычисления производной у' нам не пришлось решать уравнение х2 + у2 — 25 = 0 относительно величины у, выражая ее через переменную х. Выразив производную у' через переменные х и у, можно, воспользовавшись уравнением у' = —xfy, вычислить величину у' для любой точки на графике z2 + у2 — 25 = 0 (за исключением точки у = 0). В частности, для точки х — 3 оказалось, что точки (3,4) и (3, —4) лежат на графике. Следовательно, наклон графика в точке (3,4) равен следующей величине.
3
= —Наклон графика в точке (3,4).
(3,4) 4
Наклон графика в точке (3, —4) равен такому значению.
3 3
(3,-4)
-4 4’
Наклон графика в точке (3, —4).
Символ
(а,Ь)
означает, что производная у' вычисляется в точке х = а и у = Ь. Графическая интерпретация результатов проведена на исходном графике и показана на рис. 10.18. ■
То, что в примере 10.15 величина у' выражается через переменные х и у, не такой уж большой недостаток. Следует только помнить, что если требуется вычислить величину у' для определенных значений х и у9 скажем, (а?о, уо), то эта упорядоченная пара должна удовлетворять исходному уравнению.


322
Часть III. Математический анализ
Упражнение 10.15.
Постройте график функции х2 + у2 — 169 = 0, используя неявное дифференцирование, вычислите производную у' и наклон графика в точке х — 5. ■
Пример 10.16 (Неявное дифференцирование). Вычислите уравнение(я) каса- тельной(ых) к графику
у — ху2 + х2 + 1 — 0 (10.16)
в точках, в которых х = 1.
Решение. Сначала найдем величину у для х — 1:
у — ху2 + х2 + 1 - 0,
у - l2y2 + I2 + 1 - 0,
У - у2 + 2 - 0,
У2 - У - 2 = 0,
(у-2)(у + 1) = 0,
у = -1; 2.
Таким образом, при х = 1 на графике есть две точки: (1,—1)и(1,2). Дальше найдем наклон графика в этих двух точках, дифференцируя неявно уравнение (10.16).
Воспользуемся правилом дифференцирования произведений и цепным правилом d о для — ху .
dx
Решим уравнение относительно у', собрав все слагаемые, содержащие у', с одной стороны.
(1 - 2ху) у' = у2 - 2т;
, _ у2 - 2х
У ~ 1 — 2ху
Теперь вычислим наклон в каждой точке.
,1 = (—I)2 —2-1 = 1-2 = -1 = _1
У 1(1-1) 1 —2-1-(—1) 1 + 2 3 3’
.1 22 - 2 • 1 4 — 2 2 2


Глава 10. Дифференцирование
323
Уравнение касательной в точке (1,-1):
У - У1 = ТП (х - ;
у + 1 = -| (х - 1);
у +1 = —
v - -±х- ?
У 3х 3’
Уравнение касательной в точке (1,2)
У - У1 = тп (х - a?i);
2/ — 2 = —|(ж — 1);
у — 2 = — + |;
у=_?Х+|.
Упражнение 10.16.
Повторите действия примера 10.16 для уравнения х2 + у2 — ху — 7 = 0 в точке х = 1. ■
Задание 10.8.
Наклон касательной к графику у2 + Зху + 4х = 9вх = 0 можно вычислить одним из следующих способов: неявно дифференцируя уравнение или решая явно уравнение относительно величины у, выражая ее через переменную х (используя формулу для вычисления корней квадратного уравнения), а затем вычисляя производную. Какой из этих двух методов эффективнее? Объясните свой ответ, и
Пример 10.17 (Неявное дифференцирование). Вычислите производную х' для функции х = x(t), заданной неявно уравнением
tlnx = хе1 — 1,
и найдите значение х' в точке (t, х) = (0,1).
Решение. Важно помнить, что х — это зависимая переменная, at — независимая. Следовательно, нужно продифференцировать обе части уравнения по t (используя по необходимости правило дифференцирования произведений и цепное правило), а затем решить его относительно х'.
Неявно дифференцируем no t.
t lnx = хе* — 1.
t F lnx = хе + x e ,
x
: x' _ f :
; x • t F x • lnx = x • xe 4- x • e x
; X ;
tx' + xlnx = x2et + xe*x',
Избавимся от дроби.
txf — хе*х' = x2e* — xlnx,
х О.
Решим относительно х'.
Вынесем за скобки х'.
(t — xe*) xz = x2e* — x In x, . x2e* — xlnx x =
t — хе1


324
Часть III. Математический анализ
Теперь, как и требовалось, вычислим значение х' в точке (t,x) = (0,1).
,| _ (1)*  1 2е° —llnl _
Х 1(0,1) 0 — 1е°
Упражнение 10.17.
Вычислите производную х' для функции х — x(t), заданной неявно уравнением
1 + х Inf = tex,
и найдите значение х' в точке (t, х) = (1,0). ■
Ответы к упражнениям
10.15.
10.16.
у' = —х/у; если х = 5, у = ±12, следовательно, у'\ 12^
_ _5_
12-
, у - 2х 4 14 1 14
у = ; у = —х , у = —х 4 .
У 2у — х У 5 5 У 5 5
ПИ У' 1(5,-12) =
10.17.
z tex — х , |
Х tint —t2ex’ W)
Практикум 10.4
А В задачах 1-4 вычислите производную у двумя способами:
1. неявно дифференцируя данное уравнение, а затем решая его относительно у1,
2. решая уравнение относительно величины у, а затем непосредственно дифференцируя.
1. 	Зх + 51/ + 9 = 0. 2. — 2х + 61/ — 4 = 0.
3. 	Зх2 - 41/ - 18 = 0. 4. 2х3 + 51/ - 2 = 0.
В задачах 5-22, используя неявное дифференцирование, вычислите производную у'
и значение у' в указанной точке.
5. 	у- 5х2 +3 = 0; (1,2).
7. 	х2 - у3 - 3 = 0; (2,1).
9. 	у2 + 2у + Зх = 0; (-1,1).
11. 	ху-6 = 0; (2,3).
13. 	2ху + у + 2 = 0; (-1,2).
15. 	х2у - Зх2 - 4 = 0; (2,4).
6. 	5а3 -у- 1 = 0; (1,4).
8. 	2/2+х3 + 4 = 0; (-2,2).
10. 	у2 — у — 4z = 0; (0,1).
12. 	Зху - 2х - 2 = 0; (2,1).
14. 	2у + ху - 1 = 0; (-1,1).
16. 	2х3у - х3 + 5 = 0; (-1,3).


Глава 10. Дифференцирование
325
17. 	еу = х2+у2\ (1,0).
19. 	х3 - у = lnj/; (1,1).
21. 	х In у -F 2т/ = 2ж3; (1,1).
18. 	х2 — у = (2,0).
20. 	1п?/ = 2?/2— х; (2,1).
22. 	хеу — у = х2 — 2; (2,0)
В задачах 23 и 24 вычислите производную х' для функции х = x(t), заданной неявно данным уравнением. Найдите значение производной х' в указанной точке.
23. 	х2 - t2x 4-t3 + 11 = 0; (-2,1). 24. х3 - tx2 - 4 = 0; (-3, -2).
В задачах 25 и 26 рассматривается уравнение и график, показанные на рисунке.
(х-1)2 + (у-1)2=1
25. Используя метод неявного дифференцирования, вычислите наклон касательной в точках на графике, в которых х = 1,6. Проверьте полученный ответ, визуально оценив наклон графика на рисунке.
26. Используя метод неявного дифференцирования, вычислите наклон касательной в точках на графике, в которых х = 0,2. Проверьте полученный ответ, визуально оценив наклон графика на рисунке.
В задачах 27-30 постройте уравнение(я) касательной(ых) к графику указанного уравнения в точке(ах) с указанными значениями х.
27. 	ху — х — 4 = 0; х = 2.
29. 	у2 - ху - 6 = 0; х = 1.
28. 	Зх -h ху + 1 = 0; х = —1.
30. 	ху2 — у — 2 = 0; ж = 1.
*31. Вычислите у' двумя способами: сначала неявно продифференцировав уравнения, затем решив уравнение явно относительно величины у, которая выражается через переменную х, если хеу = 1. Какой из методов предпочтительнее? Аргументируйте свой ответ.
* 32. Объясните, почему сложно решить уравнение х3 + у + хеу = 1, где у — явная функция х. Вычислите наклон касательной к графику уравнения в точке (0,1).
В В задачах 33-40 вычислите у' и наклон касательной к графику каждого уравнения в указанной точке.
33. 	(1 + у)3 + у = х + 7; (2,1).
35. 	(х - 2у)3 = 2у2 - 3; (1,1).
37. 	У7 + j/2 - х3 + 4 = 0; (2,3).
39. 	ln(zi/) = у2 - 1; (1,1).
34. 	(у - З)4 - х = у, (-3,4).
36. 	(2х - j/)4 - у3 = 8; (-1, -2).
38. 	6-Уг/3 + 1 - 2х3/2 -2 = 0; (4,2)
40. 	ехУ-2х = у + 1; (0,0).


326
Часть III. Математический анализ
41. Составьте уравнение(я) касательной(ых) в указанной точке на графике уравнения
у3 - ху - х3 = 2,
где х — 1. Округлите все приближенные значения до двух знаков после запятой.
42. Вернемся к задаче 41. Составьте уравнение (уравнения) касательной (касательных) в точке (точках) на графике, где у = — 1. Округлите все приблизительные значения до двух знаков после запятой.
Применение математики
Экономика и бизнес
В задачах 43-46, используя уравнение зависимости спроса от цены, вычислите скорость изменения величины р в зависимости от переменной х методом неявного дифференцирования (х — объем продаж при цене р долл.).
43. 	х = р2 — 2р + 1000. 44. х = р3 — Зр2 + 200.
45. 	х = У10 000-р2. 46. х = У1500-р3.
Биологические науки
47. Биофизика. В биофизике уравнение
(L + m)(V + n) = fc
называется фундаментальным уравнением мышечных сокращений (fundamental equation of muscle contraction), где m9nnk — постоянные, a V — скорость сокращения мышечных волокон для мышцы, подверженной нагрузке L. Вычислите функцию dL/dV методом неявного дифференцирования.
48. Биофизика. В задаче 47, используя метод неявного дифференцирования вычислите функцию dV/dL.
10.5. 	Связанные скорости
Руководство профсоюза обеспокоено тем, что скорость роста заработной платы отстает от скорости роста прибыли компании. Директор автосалона желает знать, насколько сильно снизятся объемы продаж в результате прогнозируемого роста процентных ставок. Инвесторы пристально изучают связь между скоростями роста индекса Доу-Джонса и валового внутреннего продукта за последние 50 лет.
В каждой из описанных ситуаций рассматриваются две величины — в первом случае, например, заработная плата и прибыль, изменяющиеся со временем. Попытаемся выявить точную связь между скоростями роста (или снижения) двух величин. Начнем обсуждение таких связанных скоростей с рассмотрения простейших ситуаций, в которых связанными величинами являются расстояние и скорость движения.


Глава 10. Дифференцирование
327
Пример 10.18 (www Связанные скорости и движение). У стены стоит 26-футовая лестница (рис. 10.19). С какой скоростью низ лестницы будет удаляться от стены в момент, когда он находится от нее на расстоянии 10 футов, если верх лестницы сползает вдоль стены со скоростью 2 фута в секунду?
Рис. 10.19. Сползающая
вдоль стены лестница
Решение. Многие полагают, что, поскольку лестница имеет постоянную длину, низ лестницы будет удаляться от стены с той же скоростью, с какой верх лестницы смещается вниз вдоль стены. Сейчас вы убедитесь, что это не так.
Пусть в произвольный момент времени х — расстояние, на которое отстоит от стены нижний край лестницы, а у — высота, которой достигает верхний край края лестницы (см. рис. 10.19). Переменные х и у изменяются со временем, т.е. х = x(t) иу = y(t). Кроме того, переменные хну связаны между собой теоремой Пифагора
x2 + i/2 = 262. (10.17)
Неявно дифференцируя уравнение (10.17) по времени t и используя по необходимости цепное правило, получим
Скорости dx/dtii dy/dt связаны между собой уравнением (10.18), поэтому подобные задачи называются задачами о связанных скоростях (related rates problem).
Дальнейшее решение заключается в вычислении величины dx/dt, если х = 10 футов, зная, что dy/dt = —2 (величина у убывает с постоянной скоростью, равной двум футам в секунду). Теперь в нашем распоряжении есть все величины, которые необходимы для решения уравнения (10.18) относительно dx/dt, за исключением величины у. Для х — 10 величину у можно вычислить, используя


328
Часть III. Математический анализ
уравнение (10.17).
102 + у2 = 262;
у = \/262 — 102 = 24 фута.
Подставим dy/dt = —2, х = 10 и у = 24 в уравнение (10.18), а затем решим его относительно dx/dt.
2 • io| + 2 • 24 • (-2) = 0;
dx -2 • 24 • (-2) л „ х
— = = 4’8 ФУ™ в секУНДУ-
Таким образом, низ лестницы удаляется от стены со скоростью 4,8 фута в секунду. ■
Упражнение 10.18.
Допустим, у стены стоит 26-футовая лестница (см. рис. 10.19). С какой скоростью верх лестницы будет двигаться вниз в момент, когда он опирается на стену на высоте 24 фута, если низ лестницы удаляется от стены со скоростью 3 фута в секунду? в
Задание 10.9.
1. При каких значениях переменных х и у из примера 10.18 производная dx/dt равна двум (т.е. равна скорости, с которой лестница сползает вниз вдоль стены)?
2. При таких условиях производная dx/dt будет больше 2? Меньше 2? в
Советы по решению задачи о связанных скоростях
Этап 1. Нарисовать схему, если это целесообразно.
Этап 2. Определить все необходимые переменные, включая те, скорость изменения которых дана, и те, скорость изменения которых нужно вычислить.
Этап 3. Записать все заданные скорости изменения и скорости изменения, которые нужно найти, в виде производных.
Этап 4. Составить уравнение, связывающее переменные, полученные на этапе 2.
Этап 5. Неявно продифференцировать уравнение, найденное на этапе 4, используя по необходимости цепное правило, и подставить в него все заданные значения.
Этап 6. Решить уравнение относительно производной, обозначающей неизвестную скорость.


Глава 10. Дифференцирование
329
Пример 10.19 (www Связанные скорости и движение). Предположим, что две моторные лодки выехали из одной точки в один и тот же момент времени. Как быстро будет меняться расстояние между ними через два часа, если первая движется на север со скоростью 15 миль в час, а вторая — на восток со скоростью 20 миль в час?
Решение. Прежде всего, начертим схему, показанную на рис. 10.20.
Рис. 10.20. Схема движения лодок
Переменные х, у и z изменяются со временем. Следовательно, их можно рассматривать как функции времени: х — x(t\ у = y(t) и z = z(t), заданные неявно. Теперь имеет смысл взять от каждой переменной производную по времени. Согласно теореме Пифагора
г2 = т2 + 2/2. (10.19)
Известно также, что
dx dy
— = 20 миль в час и — = 15 миль в час. dt dt
Вычислите производную dz/dt в конце второго часа, т.е. когда х = 40 миль, а у = 30 миль. Чтобы сделать это, следует продифференцировать обе части уравнения (10.19) по t и решить его относительно dz/dt.
Теперь у нас есть все, что необходимо, за исключением переменной z. Из уравнения (10.19) можно узнать, что при х = 40 и у = 30 переменная z равна 50. Подставляя известные величины в уравнение (10.20), получим
= 2 • 40 • 20 + 2 • 30 • 15,
= 25 миль в час. dt
Таким образом, лодки будут расходиться со скоростью 25 миль в час.


330
Часть III. Математический анализ
Упражнение 10.19.
Повторите решение примера 10.19 на конец третьего часа движения лодок. ■
Пример 10.20 (Связанные скорости и движение). Предположим, что точка движется вдоль кривой х2 + у2 = 5 (рис. 10.21). В точке (—3,4) ее координата х растет со скоростью 0,4 единицы в секунду. Как быстро в этот момент изменяется координата у?
Рис. 10.21. Окружность
Решение. Поскольку переменные ж и у изменяются со временем, обе эти величины можно рассматривать как функции времени.
x = x(t) и у = у(£),
Однако они ограничены, так что
х2 + у2 = 25.
Теперь требуется вычислить производную dy/dt, зная, что х = —3, у = 4 и dx/dt = 0,4. Неявно дифференцируя обе части уравнения (10.21) по переменной t, получаем
х2 + у2 = 25;
dy dt
Разделим обе части уравнения на 2.
Подставим х = —3, у = 4 и dac/dt = 0,4 и решим уравнение относительно dy/dt.
= 0,3 единицы в секунду.


Глава 10. Дифференцирование
331
Упражнение 10.20.
Предположим, что точка движется вдоль кривой у3 = т2. В точке (—8,4) ее координата у растет со скоростью две единицы в секунду. Как быстро в этот момент изменяется координата т? ■
Пример 10.21 (Связанные скорости и бизнес). Предположим, что при производстве радиоприемников, уравнения затрат, дохода и прибыли имеют следующий вид.
С = 5000 + 2т,
R = Ют — 0,001т2
Р = R — С,
Уравнение затрат.
Уравнение дохода.
Уравнение прибыли.
Объем производства составляет т радиоприемноков в неделю. Вычислите скорость роста следующих величин.
1. Затраты.
2. Доход.
3. Прибыль.
Предполагается, что исходный объем производства равен 2000 радиоприемникам, причем он растет со скоростью 500 приемников в неделю.
Решение.
1. С — 5000 + 2т; Подразумевается С = C(t) и х = a?(t).
Подразумевается С = C(t) и а? = a?(t).
dC „ dx dx
— = 0 + 2— = 2—.
dt dt dt
Поскольку x = 2000, dx/dt = 500,
— - 2 • 500 = 1000 долл, в неделю.
Затраты увеличиваются со скоростью 1000 долл, в неделю.
2. 	R = Юж — 0,001ж2;
Поскольку, если х — 2000, dx/dt = 500,
— — [10 — 0,002 ■ 2000] • 500 = 3000 долл, в неделю.
Доход растет со скоростью 3000 долл, в неделю.


332
Часть III. Математический анализ
3. 	Р = R - С;
dP _ dR _ dC _
dt dt dt
= 3000 — 1000 = Результаты решения пп. 1 и 2
= 2000 долл, в неделю.
Прибыль растет со скорость 2000 долл, в неделю. ■
Упражнение 10.21.
Повторите вычисления примера 10.21 для объема производства 6000 радиоприемников в неделю. I
Задание 10.10.
1. Предположим, что в примере 10.21 x(t) — 500£ + 500. Вычислите время и объем производства, при которых прибыль достигает максимума.
2. Предположим, что x(t) = t*  1 2 + 492t + 16. Вычислите время и объем производства, при которых прибыль достигает максимума.
3. Объясните, почему не обязательно знать формулу для x(t), чтобы вычислить
объем производства, при котором прибыль достигает максимума. ■
Ответы к упражнениям
10.18. dy/dt = —1,25 фута/с.
10.19. dz/dt = 25 миль/час.
10.20. dx/dt = 6 единиц/с.
10.21. 1) dC/dt = 1000 долл, в неделю.
2) dR/dt = —1000 долл, в неделю.
3) dP/dt = —2000 долл, в неделю.
Практикум 10.5
А В задачах 1-6 предполагается, что х = x(t), а у = у/t}. Вычислите указанную скорость, имея остальную информацию.
1. у — х2 + 2; dx/dt — 3, когда х = 5; вычислите dy/dt.
2. у = х3  4 5 6 — 3; dx/dt = —2, когда х = 2; вычислите dy/dt.
3. х2 + у2 = 1; dy/dt = —4, когда х = —0,6, а у = 0,8; вычислите dx/dt.
4. х2 + у2 = 4; dy/dt = 5, когда х = 1,2, а у = —1,6; вычислите dx/dt.
5. х2 + Ъху + у2 = 11; dx/dt = 2, когда х = 1, а у = 2; вычислите dy/dt.
6. х2 — 2ху — у2 = 7; dy/dt = —1, когда х = 2, а у = —1; вычислите dx/dt.


Глава 10. Дифференцирование
333
Б
7. Точка движется вдоль кривой ху = 36. Когда точка находится в положении (4,9), ее координата х растет со скоростью 4 единицы в секунду. Как быстро в этот момент изменяется координата у?
8. Точка движется вдоль кривой 4а:2 -F 9г/2 = 36. Когда точка находится в положении (3,0), ее координата у убывает со скоростью 2 единицы в секунду. Как быстро в этот момент изменяется координата х!
9. Лодка подтягивается к причалу, как показано на рисунке. Как быстро будет уменьшаться расстояние между лодкой и причалом, когда до причала останется 30 футов, если тянуть веревку со скоростью 3 фута в секунду.
Рис. 10.22. Иллюстрация к задачам 9 и 10
10. Вернемся к задаче 9. Предположим, что расстояние между лодкой и причалом убывает со скоростью 3,05 фута в секунду. Как быстро будет подтягиваться веревка в момент, когда лодка находится на расстоянии 10 футов от причала?
11. Камень, брошенный в спокойное озеро, вызывает расходящуюся по кругу рябь. Как быстро будет меняться площадь ряби в момент, когда ее радиус равен 10 футам, если он растет со скоростью 2 фута в секунду? (Воспользуйтесь формулами S = TrR2, тг « 3,14.)
12. Вернемся к задаче И. Как быстро будет меняться длина окружности расходящейся по кругу ряби в момент, когда ее радиус равен 10 футам? (Воспользуйтесь формулами L = 2ttR, it « 3,14.)
13. Радиус сферического надувного шара растет со скоростью 3 см в минуту. Как быстро будет меняться его объем в момент, когда радиус равен 10 см? (Воспользуйтесь уравнением V = ^itR3, 7г « 3,14.)
14. Вернемся к задаче 13. Как быстро будет расти площадь поверхности сферы, если радиус равен 10 см? (Воспользуйтесь уравнением S = 4irR2, тт « 3,14.)
15. Закон Бойля-Мариотга для газа в замкнутом сосуде утверждает, что если объем остается постоянным, то давление Р и температура Т связаны уравнением
где к — константа. Какова скорость изменения давления при температуре 250 К и давлении 500 фунтов на квадратный дюйм, если температура растет со скоростью 3 К в час?


334
Часть III. Математический анализ
16. Закон Бойля-Мариотта для газа в замкнутом сосуде утверждает, что если температура остается постоянной, то давление Р и объем V связаны уравнением
VP = k,
где к — константа. Какова скорость изменения давления при объеме 1000 кубических дюймов и давлении 40 фунтов на квадратный дюйм, если объем убывает со скоростью 5 кубических дюймов в секунду?
17. У вертикальной стены стоит 10-футовая лестница. Предположим, что низ лестницы отодвигается от стены с постоянной скоростью 3 фута в секунду. С какой скоростью верх лестницы будет сползать вниз (отрицательная скорость) в момент, когда низ лестницы находится на расстоянии 6 футов от стены? (Подсказка. Воспользуйтесь теоремой Пифагора а2 + Ь2 = с2, где с — длина гипотенузы прямоугольного треугольника, а а и b — длины двух катетов.)
18. Метеозонд подымается вертикально со скоростью 5 метров в секунду. Наблюдатель стоит на земле на расстоянии 300 метров от точки, с которой был выпущен зонд. С какой скоростью будет меняться расстояние между наблюдателем и зондом, если зонд находится на высоте 400 метров?
В
19. Уличный фонарь находится наверху 20-футового столба. Человек, ростом 5 футов, удаляется от столба со скоростью 5 футов в секунду. С какой скоростью верхушка тени человека будет удаляться от столба, если человек находится на расстоянии 20 футов от него?
20. Вернемся к задаче 19. С какой скоростью будет удлиняться тень человека, если он находится на расстоянии 20 футов от столба?
* 21. В сферический надувной шар накачивают гелий со скоростью 4 кубических фута
в секунду. Как быстро будет расти радиус шара через 1 минуту? Через 2 минуты? Может ли радиус шара в какой-то момент времени расти со скоростью 100 футов в секунду? Объясните свой ответ.
* 22. Точка движется вдоль оси х с постоянной скоростью 5 единиц в секунду. В какой
точке ее расстояние от точки (0,1) будет расти со скоростью 2 единицы в секунду? Со скоростью 4 единицы в секунду? Со скоростью 5 единиц в секунду? Со скоростью 10 единиц в секунду? Объясните свой ответ.
23. Точка движется вдоль кривой у = ех + х + 1 таким образом, что ее координата х постоянно растет со скоростью 3 единицы в секунду. Как быстро будет меняться координата у, когда точка пересечет ось х!
24. Точка движется вдоль кривой х3 + у2 = 1 таким образом, что ее координата у постоянно растет со скоростью 2 единицы в секунду. В какой точке (точках) координата х будет расти со скоростью 1 единица в секунду?


Глава 10. Дифференцирование
335
Применение математики
Экономика и бизнес
25. Скорость изменения затрат, дохода и прибыли. Предположим, что при производстве калькуляторов уравнения затрат, дохода и прибыли имеют вид
С = 90000 + ЗОя,
3
Я = 300х- —,
30’
Р = R - С,
где х — это недельный объем производства. Вычислите скорость изменения следующих величин.
а) Затраты. б) Доход. в) Прибыль.
Предполагается, что при выпуске 6000 калькуляторов объем производства растет со скоростью 500 калькуляторов в неделю.
26. Скорость изменения затрат, дохода и прибыли. Повторите вычисления задачи 25 для уравнений
С = 72 000 + 60z,
х2
R — 200# — —,
30’
P = R-C,
если при выпуске 1500 калькуляторов объем производства растет со скоростью 500 калькуляторов в неделю.
27. Реклама. В розничном магазине обнаружили, что размеры недельных продаж s и недельные затраты на рекламу х (обе величины выражены в долларах) связаны уравнением
S = 60000 - 40000е_0,ООО5а:.
Текущие недельные затраты на рекламу составляют 2000 долл., и растут со скоростью 300 долл, в неделю. Вычислите текущую скорость изменения объема продаж.
28. Реклама. Повторите вычисления задачи 27 для уравнения
s = 50 000 - 20 ОООе-0’0004*.
29. Цена-спрос. Цена товара р (долл.) и спрос на него х связаны уравнением
2х2 -I- Ьхр -I- 50р2 = 80 000.
а) Вычислите скорость изменения спроса, если цена равна 30 долл, и растет со скоростью 2 долл, в месяц.
б) Вычислите скорость изменения цены, если спрос равен 150 единиц и падает со скоростью 6 единиц в месяц.


336
Часть III. Математический анализ
30. Цена-спрос. Повторите вычисления задачи 29 для уравнения
х2 + 2хр + 25р2 = 74 500.
Биологические науки
31. Загрязнение. Из нефтяного танкера, севшего на мель, вытекает нефть, образующая круглое нефтяное пятно, толщиной около 0,1 фута (см. рис. 10.23). Чтобы вычислить скорость dV/dt (в кубических футах в минуту), с которой нефть вытекает из танкера, было установлено, что при радиусе пятна R = 500 футов, оно увеличивается со скоростью 0,32 фута в минуту (dR/dt — 0,32). Вычислите функцию dV/dt, используя значение 7Г « 3,14.
Рис. 10.23. Иллюстрация к задаче 31
Социальные науки
32. 	Обучение. Начинающий работник сборочного конвейера после выполнения х операций производит одну операцию за Т минут. Этот процесс описывается урав¬
нением
Т = 6
Вычислите производную dT/dt после того, как было выполнено 36 операций, если dx/dt = 6 операций в час, где t — время в часах.
Ключевые слова, основные обозначения и формулы
10.1. Константа е и непрерывно начисляемые сложные проценты. Определение константы е; непрерывно начисляемые сложные проценты
А = Pert.
10.2. Производные логарифмических и экспоненциальных функций. Формулы производных натурального логарифма и экспоненциальной функции; свойства графиков у — lnx и у = ех.
10.3. Цепное правило: обобщенная форма. Сложная функция; цепное правило; обобщенные формулы для производных; формулы производных функций у = logb х и у = Ьх.


Глава 10. Дифференцирование
337
10.4. Неявное дифференцирование. Специальная форма записи функций; функции, заданные явно; функции, заданные неявно; неявное дифференцирование
y = у = у(х); F(x,y) = 0; 2/'|(аЬ)-
10.5. Связанные скорости. Связанные скорости
X - z(t); у = y(t).
Специальные правила дифференцирования
1
х
1пх = ах
1
/(я)
/'(я),
Ae/w = е/ыу (х)
ах
J-Ai
In6dx ПХ lnb ’
^ьх = ^_ех'пЬ = exinb\nb = &*lnb, dx dx
dy dy du dy dy dw du dx du dx*  1  2 dx dw dx dx
и так далее.
Упражнения для повторения
Выполните все упражнения этого обзорного раздела и сравните результаты с ответами, помещенными в конце книги. Ответы ко многим упражнениям на повторение приводятся вместе с номером соответствующего раздела (курсивом). Если у вас возникают затруднения при решении какой-либо задачи, повторите материал соответствующего раздела.
А
1. Используя калькулятор, вычислите с точностью до ближайшего цента значение А = 2000е°-°9‘ для t = 5, 10 и 20.
В задачах 2-4 вычислите указанные производные.
2. 4- (гЬх + Зе1). 3. -^е2х~3  4.
dx dx
4. 	у' для у = 1п(2ж -|- 7).


338
Часть III. Математический анализ
5. Пусть у = In и, а и = 3 + ех.
а) Выразите у через х.
б) Используя цепное правило, найдите dy/dx, а затем выразите dy/dx через переменную х.
6. Вычислите производную у' функции у = у(х), заданной неявно уравнением 2у2 — Зх3 — 5 = 0, и найдите ее значение в точке (х, ?/) = (1,2).
7. Вычислите функции dy/dt и dx/dt для уравнения у = Зх2 — 5, где х = x(t) и у = y(t\ когда х = 12.
Б
8. Постройте график функции у = ЮОе-0,1*.
* 9. Используя калькулятор и таблицы значений, исследуйте предел
Существует ли этот предел? Если да, то чему он предположительно равен?
В задачах 10—15 вычислите указанные производные.
ю. i[(w+in4 н.
d ех
12. - 13. у' для у = 1п(2х3 — Зх).
dx хь
14. /'(х) для f (х) = е^3"^2. 15. dy/dx для у = е~2х 1п5х.
16. Вычислите уравнение касательной к графику у = f(x) = 1 + е~х в точке х = 0. В точке х = —1.
17. Вычислите производную у' функции у = у(х), заданной неявно уравнением х2 — Зхт/ + 4т/2 = 23, и наклон графика в точке (—1,2).
18. Вычислите производную х' функции х = x(t), заданной неявно уравнением х3 — 2t2x + 8 = 0, и ее значение в точке (t, х) = (-2,2).
19. Вычислите производную у' функции у = у(х), заданной неявно уравнением х — у2 = еу,и ее значение в точке (1,0).
20. Найдите производную у' функции у = т/(х), заданной неявно уравнением 1пт/ = = х2 — у2, и вычислите ее значение в точке (1,1).
21. Точка движется вдоль кривой у2 — 4х2 = 12 таким образом, что, когда (х, у) = = (1,4), ее координата х убывает со скоростью 2 единицы в секунду. Найдите скорость изменения координаты у.
22. У стены стоит 17-футовая лестница. Как быстро верх лестницы будет подыматься вверх, если ее основание, находящееся на расстоянии 8 футов от стены, толкают к стене со скоростью 0,5 фута в секунду?
23. Вода из водонагревателя протекает на пол. Образуется круглая лужа, площадь которой растет со скоростью 24 квадратных дюйма в минуту. Как быстро будет увеличиваться радиус лужи R в момент, когда он составляет 12 дюймов? (S = = tvR2)


Глава 10. Дифференцирование
339
В В задачах 24-27 требуется найти величину абсолютного максимума f(x) для х > 0.
24. 	/(ж) = 11х — 2х 1пх. 25. /(ж) = 10хе_2х.
26. /(ж) = Зх — х2 4- е~х. 27. f (х) =
В задачах 28 и 30 необходимо проанализировать функцию f, применяя методику построения графиков, рассмотренную в разделе 9.4, и построить график.
28. /(х) = 5 — Ъе~х. 29. /(х) = х3 lnx.
30. Пусть у — w3, w = lniz, а и = 4 — ех.
а) Выразите величину у через переменную х.
б) Используя цепное правило, вычислите производную dy/dx, а затем выразите dy/dx через переменную х.
В задачах 31-36 вычислите указанные производные.
31. у' для у = 5х2"1. 32. log5 (х2 - х).
33. -p-v/ln (х2 + х).
dx
34. Найдите производную у' для функции у = у(х), заданной неявно уравнением еху = х2 + у 4-1, и вычислите ее значение в точке (0,0).
* 35. Камень, брошенный в спокойное озеро, вызывает расходящуюся по кругу рябь.
Предположим, что ее радиус растет с постоянной скоростью 3 фута в секунду. Покажите, что площадь не будет расти с постоянной скоростью. В каком случае скорость роста площади будет наименьшей? Наибольшей? Объясните.
* 36. Точка движется вдоль кривой у = х3 таким образом, что ее координата у растет
с постоянной скоростью 5 единиц в секунду. Всегда ли скорость роста координаты х больше, чем скорость роста координаты у! Объясните свой ответ.
Применение математики
Экономика и бизнес
37. Время удвоения капитала. Сколько понадобится времени, чтобы капитал удвоился, если он вложен под 5 сложных процентов, начисляемых при следующих условиях?
а) Ежегодно. б) Непрерывно.
38. Непрерывное начисление процентов. Если 100 долл, вложены под 10 сложных процентов, начисляемых непрерывно, через t лет сумма (в долларах) составит
А = 100е°’“.
Вычислите функцию а также величины А'(1) и А'(10).


340
Часть III. Математический анализ
39. Маржинальный анализ. Уравнение зависимости спроса на холодильники объемом 14 кубических футов от отпускной цены имеет вид
р(х) = ЮООе-0’021,
где х — месячный спрос, ар — цена в долларах. Составьте уравнение предельного дохода.
40. Максимальный доход. Для зависимости спроса от цены из задачи 39 вычислите объем производства и цену за штуку, при которых доход будет максимальным. Каким будет максимальный доход?
41. Максимальный доход. Постройте график функции дохода из задач 39 и 40 для 0 х 100.
42. Максимальная прибыль. Вернемся к задаче 39. Вычислите цену (с точностью до ближайшего цента), при которой прибыль будет максимальной, если каждый холодильник обходится магазину в 220 долл. Какой будет максимальная прибыль (с точностью до ближайшего доллара)?
43. Максимальная прибыль. В следующей таблице показаны данные о дневном спросе х на пирожные со взбитыми сливками, реализуемые на выездных ярмарках, при различных уровнях цен р. Используя уравнение логарифмической регрессии (р = а + b In х), вычислите цену (с точностью до ближайшего цента), при которой прибыль будет максимальной, если затраты на производство пирожного со взбитыми сливками составляют один доллар.
Спрос, х Цена пирожного (долл.), р
3125
1,99
3879
1,89
5263
1,79
5792
1,69
6748
1,59
8120
1,49
44. Минимальные средние затраты. Затраты на производство х единиц продукции составляют
С(я) = 200 + 50х — 50 In х, х 1.
Вычислите минимальные средние затраты.
45. Уравнение спроса. Дано уравнение спроса
х = х/5000-2р3,
вычислите скорость изменения р, зависящей от переменной х, неявно дифференцируя уравнение (х — объем продукции, которую можно продать по цене р долл.).


Глава 10. Дифференцирование
341
46. Скорость изменения дохода. Компания выпускает новую видеоигру и может продать сразу весь тираж. Доход (в долларах) составляет
х2 R = 36# — —,
20’
где дневной тираж составляет х игр. Вычислите скорость роста дохода, если при производстве 250 игр в день он растет со скоростью 10 игр в день.
Биологические науки
47. Концентрация препарата. Концентрация препарата в крови через t часов после инъекции составляет приблизительно
C(t) = 5e_0,3t,
где C(t) — концентрация в миллиграммах на миллилитр. Какова скорость изме- нения через 1 час? Через 5 часов?
48. Заживление ран. Круглая рана на руке затягивается со скоростью 45 квадратных миллиметров в день (скорость сокращения площади раны). Как быстро будет уменьшаться радиус R в момент, когда R = 15 миллиметров? (А = ttR2.)
Социальные науки
49. Обучение сотрудников. В сборочном цеху новый рабочий через t дней обучения по месту работы в среднем может собрать
АГ(<) = 10(1 - e_0,4t)
единиц продукции.
а) Какова скорость обучения через один день? Через пять дней?
б) Постройте график функции N для 0 < t < 10.
50. Обучение сотрудников. Новый рабочий на производственной линии после выполнения х операций осуществляет операцию за Т минут. Этот процесс описывается уравнением
Т’2(1 + М
Вычислите скорость сокращения времени выполнения каждой операции dT/dt, если после девятикратного повторения операции скорость сокращения составляет dT/dt = 3 операции в час.
Домашнее задание 10.1. Эластичность спроса
www В общем случае считается, что при снижении цены на товар спрос на него растет, а при увеличении цены спрос на товар падает. Чтобы измерить чувствительность спроса к изменению цены, пользуются понятием эластичность


342
Часть III. Математический анализ
спроса, которое обозначается Е(р) и является пределом относительного изменения спроса х, деленного на относительное изменение цены р. Следовательно, если х = f(p) — уравнение зависимости цены от спроса, то
Поскольку рост цены обычно приводит к снижению спроса, можно ожидать, что величина Е(р) будет отрицательной. Если Е(р) = — 1, то 10 процентный рост цены приводит к 10 процентному снижению спроса, и при этом говорят, что спрос имеет единичную эластичность. Если Е(р) = —4, то 10 процентный рост цены приводит к 40 процентному снижению спроса. Выражая такую чувствительность спроса к цене, говорят, что спрос эластичен, когда Е(р) < -1. Если Е(р) = —0,25, то 10 процентный рост цены приводит всего лишь к 2,5 процентному снижению спроса; выражая такого рода чувствительность спроса к цене, говорят, что спрос неэластичен, когда Е(р) > —1.
1. 	Рассмотрите уравнение цены-спроса
х = /(р) = 10 000 - 500р, 0 О 20.
Вычислите эластичность спроса при р = 4, 7, 10, 13 и 16 и для каждого случая скажите, будет ли спрос эластичным, неэластичным или же у него единичная эластичность.
2. Постройте график эластичности спроса Е(р) и график дохода J?(p) как функции цены, а также график прямой у = — 1. Используя графики, объясните связь между эластичностью и возрастающим/убывающим характером поведения функции дохода.
3. Повторите решение п. 2 для уравнения зависимости цены от спроса
х = / (р) = \/144 - 2р, 0 С р < 72.
4. 	Предположим, что х = д(р) — произвольное уравнение цены-спроса, в котором функция д(р) является дифференцируемой. Пусть соответствующая функция дохода имеет вид 7?(р) = хр = д(р\р> Покажите, что Rf(p) = = д(р)[Е(р) + 1]. Объясните, почему доход растет с ростом цены тогда и только тогда, когда спрос неэластичен.


Глава 10. Дифференцирование
343
Домашнее задание 10.2. Точка сокращения доходов6
В табл. 10.4 приведены данные об объеме продаж процессоров электронных таблиц для ПК через х месяцев после выпуска продукта. Точка сокращения доходов соответствует значению переменной х, при котором скорость изменения объема продаж достигает своего максимального значения. В разделе 9.2 было показано, что для описания такой ситуации можно использовать полиномиальное регрессионное уравнение третьей степени.
Таблица 10.4. Объем продаж
Срок реализации (месяцев), х
Объем продаж, тыс. копий
4
71
8
182
12
305
16
405
20
450
1. Получите уравнение кубической регрессии Р(х) для данных, приведенных в табл. 10.4, и найдите точку сокращения доходов (с точностью до двух десятичных знаков).
www Кубическая полиномиальная модель хорошо описывает данные для 4 < х 20, но плохо для х > 20. В улучшенной модели, которую можно использовать для предсказания поведения при х > 20, применяется функция роста по логистической кривой, имеющая вид
£(х)= с -Ьх- (10.22)
1 + ае °х
2. Постройте модель логистической регрессии £(х) для данных, приведенных в табл. 10.4, и вычислите по этой модели точку сокращения доходов (с точностью до двух десятичных знаков).
3. Постройте графики функций Р(х) и L(x') для Xmin = 4, Xmax = 20, Ymin = 0 И Ymax = 500. Есть ли какие-нибудь существенные отличия в описаниях данных, которые обеспечивают эти две функции?
4. Повторите решение п. 3, увеличив значение Хтах до 30.
5. Вычислите предел lim^oo L (х) (с точностью до ближайшего целого). Значение этого предела называется пропускной способностью модели. Сравните пропускную способность со значением функции L(x) в точке сокращения доходов, найденным при решении п. 2.
6Выполняя это задание, необходимо использовать графическую утилиту, поддерживающую функции логистической регрессии.


344
Часть III. Математический анализ
6. 	В табл. 10.5 приведены сведения об объеме продаж нового текстового процессора. Постройте уравнение логистической регрессии для этих данных, найдите точку сокращения доходов (с точностью до двух десятичных знаков) и пропускную способность (с точностью до ближайшего целого).
Таблица 10.5. Объем продаж текстового процессора
Срок реализации (месяцев), х
Объем продаж, тыс. копий
4
151
8
204
12
327
16
480
20
530
Покажите, что для произвольной функции в уравнении (10.22) пропускная способность равна с, точка сокращения доходов равна 1па/6, а значение функции в точке сокращения доходов составляет с/2.


11
Интегрирование
■ 11.1. Первообразные и неопределенные интегралы
■ 11.2. Интегрирование методом замены переменной
■ 11.3. Дифференциальные уравнения: рост и затухание
■ 11.4. Геометрическая и численная интерпретации определенных интегралов
■ 11.5. Определенный интеграл как предел суммы. Основная теорема интегрального исчисления
■ Ключевые слова, основные обозначения и формулы
■ Основные свойства и формулы вычисления интегралов
■ Упражнения для повторения
■ Домашнее задание 11.1. Формула Симпсона
■ Домашнее задание 11.2. Нормальное распределение
Введение
В предыдущих трех главах мы изучали дифференциальное исчисление. Теперь рассмотрим вторую важную часть математического анализа — интегральное исчисление. В главе исследованы следующие типы интегралов: неопределенный и определенный. Несмотря на внешние различия между ними, основная теорема интегрального исчисления утверждает, что обе формы интегралов тесно связаны между собой и представляют операцию, обратную дифференцированию.


346
Часть III. Математический анализ
11.1. 	Первообразные и неопределенные интегралы
■ Первообразные
■ Геометрическая и вычислительная интерпретация первообразных
■ Первообразные и неопределенные интегралы: алгебраические выражения
■ Первообразные и неопределенные интегралы: экспоненциальные и логарифмические выражения
■ Решение практических задач
У большинства операций в математике есть обратные операции — сложение и вычитание, умножение и деление, возведение в степень и извлечение корня. Вы уже знаете, как находить производные разнообразных функций. В этом и следующих разделах рассматривается операция вычисления первообразной (восстановление функции по ее производной). Эта операция является обратной по отношению к дифференцированию. Функция F называется первообразной функции /, если F'(x) = /(ж). Мы исследуем эту операцию с геометрической, вычислительной и алгебраической точек зрения. Кроме того, в разделе выводятся специальные формулы для вычисления первообразных с помощью алгебраического подхода, напоминающего способ выведения формул для вычисления производных.
Первообразные
Задание 11.1.
1. Вычислите первообразную функции 2х.
2. Сколько существует первообразных функции 2х и как они между собой связаны?
3. Какое обозначение следует использовать для представления первообразной
функции 2х? ■
Что представляет собой первообразная функции х2?
х3 п
— является первообразной функции х ,
поскольку
d f х3\ о dx = Х
Следует отметить, что
dx
d ( х3 \
dx\~^~1T)
dx


Глава 11. Интегрирование
347
Следовательно, функции
также являются первообразными функции ж2, так как производная от них равна х2. Оказывается, что первообразной функции х2 является функция
х3
— + С для произвольного действительного числа С,
поскольку
Таким образом, первообразная функции — это не одна уникальная функция, а целое семейство.
Описывает ли выражение
х3
— + С, где С — произвольное действительное число
О
все первообразные функции х2? Как следует из теоремы 11.1, приведенной без доказательства, ответ на этот вопрос является утвердительным.
Теорема 11.1 (Первообразные). Если производные от двух функций равны между собой на открытом интервале (а, 6), то эти функции могут отличаться только на постоянную величину. Иначе говоря, если F и G — дифференцируемые функции на интервале (a, i>) и F'(x) — G'(x) для всех х на интервале (а, 6), то F(x) = = G(x) + к, где к — произвольная постоянная. ■
Геометрическая и вычислительная интерпретация первообразных
Задание 11.2.
Пусть f'(x) = 1.
1. Что можно сказать о графике произвольной дифференцируемой функции /, исходя из того, что /'(ж) = 1?
2. Постройте в одной и той же системе координат график трех первообразных функций у = f(x), удовлетворяющих условиям /(0) = —2, /(0) = 0 и /(0) = 2. Опишите геометрическую связь между этими графиками. ■
Некоторые характеристики первообразной можно представить визуально, используя понятие наклона. Если дан график производной от функции у = можно построить предположительный график первообразной функции /, показывающий ее характерную форму. Напомним некоторые свойства, перечисленные в табл. 11.1.


348
Часть III. Математический анализ
Таблица 11.1. Свойства графика функции у = /(х), полученные из графика у = f'(x)
Л®)
График у = f(x)
Положительная Отрицательная Возрастающая Убывающая
Возрастающая Убывающая Выпуклая вниз Выпуклая вверх
Пример 11.1 (Анализ графика у = f(x) по заданному графику у = f'(x)). Дан график у — f'(x), показанный на рис. 11.1. Постройте вероятный график трех первообразных функции /, для которых /(0) = -1, /(0) = 0 и /(0) = 2, используя для них общую систему координат.
Рис. 11.1. Парабола
Решение. В табл. 11.2 собрана информация, полученная из графика у — f'(x).
Таблица 11.2. Свойства функций /(ж) и /'(х)
X
Л®)
График у = f(x)
0 < х < 1
Положительная и убывающая
Возрастающая и выпуклая вверх
х = 1
Пересечение с осью х
Локальный максимум
1 < х < 3
Отрицательная и убывающая
Убывающая и выпуклая вверх
х = 3
Локальный минимум
Точка перегиба
3 < х < 5
Отрицательная и возрастающая
Убывающая и выпуклая вниз
х = 5
Пересечение с осью х
Локальный минимум
3 < х < 6
Положительная и возрастающая
Возрастающая и выпуклая вниз
Функция /(х) — одна из первообразных функции поскольку все первообразные имеют уравнение у = f(x) + C. Следовательно, график любой первообразной функции можно получить из графика любой другой первообразной функции путем параллельного переноса вдоль оси у. Нам известно начало каждого из графиков у = f(x)9 а также их общая форма на интервале (0,6). На рис. 11.2 показаны возможные графики трех первообразных, имеющих требуемые характеристики. ■


Глава 11. Интегрирование
349
Рис. 11.2. Графики пер¬
вообразных
Упражнение 11.1.
По графику функции у = показанному на рис. 11.3, постройте вероятный график
трех первообразных /, удовлетворяющих условию /(0) = —1, /(0) = 0 и /(0) = 1, используя одну и ту же систему координат. ■
Рис. 11.3. График произ¬
водной из упражнения 11.3
Первообразные и неопределенные интегралы: алгебраические выражения
Теорема 11.1 гласит, что если производные от двух функций равны, то эти функции могут отличаться только на константу. Для представления семейства первообразных функции /(х) используется неопределенный интеграл
j f (ж) dx.
Тогда первообразную функции f(x) можно записать следующим образом.
f f (ж) dx = F (х) + С, если F' (х) = f (х).


350
Часть III. Математический анализ
Символ J называется знаком интеграла, а функция f(x) называется подынтегральной функцией. Символ dx означает, что первообразная вычисляется по переменной х. Произвольная константа С называется постоянной интегрирования. Возвращаясь к предыдущим рассуждениям, можно записать
2 > я3 d (х3 2
х dx = —- + С, поскольку —- I — + С 1 = х .
3 dx \ 3 )
Конечно, в неопределенном интеграле можно использовать не только переменную х. Например,
f 2j t3 „ d ft3 \ 2
t dt = — + С, поскольку — — + С I = t ,
J 3 dt \ 3 J
или
f 2 > f U3 Л 2
it du = — + С, поскольку — I — + C-I = и .
Тот факт, что неопределенное интегрирование является обратной операцией к дифференцированию, за исключением добавления константы, можно выразить в символической форме следующим образом
Производная от неопределенного интеграла от функции f(x) равна функции /(®).
Неопределенный интеграл от производной от функции F(a?) равен функции F(a?) + С.
Как и для производной, можно вывести формулы и описать особые свойства, позволяющие вычислять неопределенные интегралы многих часто встречающихся функций. Для начала перечислим несколько формул, которые можно установить, дифференцируя первообразную и неопределенный интеграл, а также свойства производной, рассмотренные в главе 8.
Формулы и свойства неопределенных интегралов
ч
J к dx = кх + С.
хп+1
2.
xndx = + С, п —1.
-
п + 1
3.
kf (х) dx = к | f (ж) dx.
4.
[f (х) ± g (а:)] dx = [ f (х) dx ±
g (х) dx.
Докажем формулу 2 и свойство 3 (истинность остальных утверждений можно показать аналогичным образом). Чтобы доказать формулу 2, просто продифференцируем правую часть. Таким образом,
(п + 1)хп
п + 1
+ 0 = zn,
п —1.


Глава 11. Интегрирование
351
(Следует отметить, что формулу 2 нельзя использовать в случае, когда п = — 1, т.е., когда подынтегральная функция равна х~\ или 1/х. Неопределенный интеграл от функции х~х = \/х будет рассмотрен далее.)
Чтобы доказать свойство 3, предположим, что F — такая функция, что F\x) = /(ж). Тогда
k р (х) dx = к(х) dx = k(F (х) + CJ = kF (х) + кСъ
и, поскольку [fcF(x)]' = kFf(x)dx = kf(x),
j kf (x) dx = kF' (x) dx = kF (x) + C2.
Выражения kF(x) 4- kCi и kF(x) + kC2 описывают один и тот же набор функций, поскольку Ci и С2 — произвольные действительные числа. Таким образом, свойство 3 доказано.
Предупреждение. Свойство 3 утверждает, что постоянный множитель можно выносить за знак интеграла. Переменный множитель нельзя выносить за знак интеграла.
Постоянный множитель Переменный множитель
= 5j xxl2dx, j xxx!2dx Ф x j x^2dx.
Воспользуемся теперь этими формулами и свойствами.
Пример 11.2 (Вычисление неопределенных интегралов).
1. §dx — 5х + С.
Свойство 4 можно распространить на суммы и разности прозвольного количества функций.
_ f 3dx Г _ _2, Зх 2+1 _ о л _
5. —5- = Зх 2dx = —-—- + С = —Зх 1 + С.
J х2 J —2 +1
f Г ?.(2/3)+1
6. I 5\fu?du = 5 I u2/3du = 5 2 —Ь С =
?у5/з
= 5— + С = Зи5/3 + С.


352
Часть III. Математический анализ
Для проверки любого из результатов, полученных в примере 11.2, достаточно продифференцировать конечный результат, чтобы получить подынтегральную функцию в исходом неопределенном интеграле. При вычислении неопределенного интеграла не следует забывать о произвольной константе С.
Упражнение 11.2.
Вычислите следующие неопределенные интегралы.
1. 	dx. 2.
3. (2х5 - Зх2 + 1) dx.
4. 14v^w^dw.
5' j (2l2/3 - Ji) dx-
Пример 11.3 (Вычисление неопределенных интегралов).
i- =j (S - ?) ^= = j (х — Зх-2) dx = := xdx — з I x~2dx = :
2.
— бд/S^ dx = (bx ^3 — бх1/2) dx =
';= 2 x_1/3dx — 6 j xl/2dx = ;
: x(_i/3)+i ж(1/2)+1 :
i= 2 ; — 6 —i И- C —;
; -|+i i+i i

= 2—-6—+ C =
= Зх2/3 - 4a:3/2 + C.
Упражнение 11.3.
Вычислите следующие неопределенные интегралы.
1. j xi~Jx3dx. 2. j (s^ - dx.
Первообразные и неопределенные интегралы: экспоненциальные и логарифмические выражения
Выведем формулы интегрирования для функций ех и \/х. (Как указано в приведенной выше врезке, к выражению а:-1 = 1/х формула 2 не применяется.)


Глава 11. Интегрирование
353
Формулы вычисления неопределенных интегралов
5. f exdx = ех + С.
fl ( ,
6. — dx = In р| + С, х 0.
Формула 5 непосредственно следует из формулы вычисления производной экспоненциальной функции, рассмотренной в главе 10. Из-за абсолютного значения | ж| формула 6 не является прямым следствием формулы вычисления производной натурального логарифма. Покажем, что
d , | | 1
— In kr = -, х Ф 0. dx х
Рассмотрим два варианта: х > 0 и х < 0.
Вариант 1. х > 0:
d - | | d _
—— In |rr| = — In x = Поскольку I®I = Ж ДЛЯ X > 0.
dx dx
1
x
Вариант 2. x < 0:
J__d
—x dx
(-*)
-1 1
Поскольку IXI = —X ДЛЯ X < 0.
—X X
Таким образом,
— lnlxl = - , x Ф 0
dx х
и, следовательно,
| -dx = In |х| + С, х ф 0.
Что можно сказать о неопределенном интеграле функции In xl Отложим ответ на этот вопрос до изучения раздела 12.3, где этот интеграл будет вычислен методом интегрирования по частям.
Пример 11.4 (Интегрирование экспоненциальных и логарифмических выражений).
| ^2ех + dx\ = 21 exdx + 3 j-dx =•
= 2ex + 31n |дг| + C.
Упражнение 11.4.
Вычислите интеграл j* (| — 4еж) dx. ■
(Примечание. Общие принципы интегрирования показательных и логарифмических функций рассматриваются в разделе 11.2.)


354
Часть III. Математический анализ
Решение практических задач
Рассмотрим теперь несколько примеров практического применения неопределенного интеграла, чтобы понять, зачем нужны первообразные.
Пример 11.5 (Построение кривых). Составьте уравнение кривой, которая проходит через точку (2,5), если ее наклон в точке х задан уравнением dy/dx — 2х.
Решение. Необходимо вычислить такую функцию у = f(x), чтобы выполнялось условие
Если dy/dx = 2х, то
(И-1)
(П.2)
(И.З)
и
Поскольку у = 5 при х = 2, можно вычислить такое значение С, при котором
5 = 22 + С.
Таким образом, С = 1, а
у = х2 + 1
является частной первообразной, единственной из всех первообразных, заданных в уравнении (11.3), которая удовлетворяет одновременно и уравнению (11.1), и уравнению (11.2) (рис. 11.4). I
Рис. 11.4. График функции у = х2 + С
Посмотрим, чем отличаются примеры 11.5и11.1,в которых вероятный график функции восстанавливался с помощью графика ее производной. В примере 11.5 было составлено уравнение первообразной, график которой проходит через точку (2,5). Следовательно, можно построить точный график первообразной.


Глава 11. Интегрирование
355
Задание 11.3.
Постройте график производной у = f'(x) = 2х из примера 11.5 и, пользуясь информацией, полученной с помощью этого графика, подтвердите, что форма графиков первообразных совпадает с формой, показанной на рис. 11.4. ■
Упражнение 11.5.
Составьте уравнение кривой, которая проходит через точку (2,6), если ее наклон в точке х задан уравнением dy/dx = Зх2. В
В некоторых ситуациях проще вычислить скорость изменения величины, чем само изменение за данный промежуток времени (например, скорость роста популяции, скорость роста предприятия, скорость затягивания раны, скорость обучения или потери знаний). Если дана функция скорости (производная) и известно значение зависимой переменной при данном значении независимой переменной, то (если функция скорости не слишком сложна), как правило, исходную функцию можно найти путем интегрирования.
Пример 11.6 (Функция затрат). Вычислите функцию затрат С(х) и величину затрат на производство 20 единиц продукции, если предельные затраты на производство х единиц продукции заданы формулой
С'(х) = 0,3а2 + 2х,
а постоянные затраты равны 2000 долл.
Решение. Напомним, что предельные затраты — это производная от функции затрат, и что постоянные затраты — это расходы при нулевом уровне производства. Таким образом, задача сводится к вычислению функции С (а?) при следующих условиях.
С'(х) = 0,3а2 + 2а; С(0) = 2000.
Вычислим неопределенный интеграл функции 0,3а2 4- 2а и определим значение произвольной постоянной, используя условие С(0) = 2000,
= 0,1а3 + х2 + К.
Поскольку С описывает затраты, для обозначения постоянной интегрирования используется буква К.
Примем во внимание условие
С(0) = 0,1 • О3 + О2 + Д' = 2000.
Следовательно, К = 2000 и частная функция затрат имеет вид
С'(я) = 0,1а?3 + х2 + 2000.
Теперь найдем значение С(20) — затраты на производство 20 единиц продукции. С(20) = 0,1 • 203 + 202 + 2000 =
= 3200 долл.
График функции затрат показан на рис. 11.5.


356
Часть III. Математический анализ
Объем производства, шт.
Рис. 11.5. Функция затрат
Упражнение 11.6.
Вычислите функцию дохода 7?(х), если предельный доход составляет
R\x) = 400 — 0,4rr,
а при нулевом объеме производства дохода нет. Каким будет доход при производстве 1000 изделий? ■
Пример 11.7 (Реклама). Чтобы увеличить аудиторию слушателей, FM-радиостан- ция проводит активную рекламную кампанию. На данный момент у станции 27 000 постоянных слушателей, но ожидается, что количество постоянных слушателей S(t) будет расти со скоростью
S'(t) = 60t1/2
слушателей в день, где t — количество дней, истекших с начала кампании. Сколько должна длиться рекламная кампания, чтобы количество постоянных слушателей возросло до 41 000?
Решение, Необходимо решить уравнение S(t) = 41 000 относительно t при условиях
5(f) = 60t1/2 и 5(0) = 27000.
Прежде всего, выполним интегрирование и вычислим функцию S(t):
S (t) = —
ts/2
= 60—2— 4“ C —
2 = 40f3/2 + C.
Поскольку
5(0) = 40 • 03/2 + C = 27000,
C = 27000 и
5(f) = 40f3/2 + 27000.


Глава 11. Интегрирование
357
Теперь необходимо решить уравнение S(t) = 41 000 относительно t:
40t3/2 + 27 000 = 41 000;
40£3/2 = 14000;
«3/2 = 350;
t = 3502/3; Воспользуемся калькулятором. = 49,664419...
Таким образом, рекламная кампания должна длиться приблизительно 50 дней. ■
В графических утилитах для решения уравнения S(t) = 41000 из примера 11.7 предлагается альтернативный подход (рис. 11.6).
Рис. 11.6. Графики функций т/1 = 40х1,5 + 27000, т/2 = 41000
Упражнение 11.7.
Месячный тираж журнала Computing News составляет 640 000 экземпляров. В связи с выходом на рынок нового журнала такой же тематической направленности ожидается, что месячный тираж Computing News, описываемый функцией C(t), будет снижаться со скоростью
C\t) = -6000£1/3
экземпляров в месяц, где t — количество месяцев, прошедших с момента появления на рынке нового журнала. Сколько понадобится времени, чтобы тираж журнала Computing News снизился до 460 000 экземпляров в месяц? ■
Предупреждение.
Г
1. exdx # + С.
J х + 1
Правило интегрирования степенных выражений применимо только к функциям вида хп, где показатель степени п —действительная константа, не равная —1, а основание х — переменная. Функция ех имеет переменный показатель степени х и постоянное основание е. Правильное выражение для вычисления первообразной функции ех имеет вид
Г exdx = ех + С.


358
Часть III. Математический анализ
2. Р Интеграл от произведения не равен произведению интегралов. Правильное выражение имеет вид
f х4
х (х2 4-2) dx = (х3 4- 2х) dx = — 4- х2 4- С.
3. Не все элементарные функции имеют элементарные первообразные. Однако, вычисляя первообразные, если они существуют, можно существенно упростить решение некоторых задач.
Ответы к упражнениям
11.1.
11.2. 1) х + С.
2) ft5 + C.
О
3) (х6/3) - х3 + х + С.
4) |w8/5 + C.
5) pi5/3 + х~3 + С.
5
11.3. 1) |х3-4х2 + С.
2) 6т4/3 - 12а:1/2 + С.
11.4. 51п|х| -4еж +С.
11.5. у = х3 - 2.
11.6. Я(х) = 400а - 0,2а:2; Я(1000) = 200 000 долл.
11.7. t — 403/4 « 16 месяцев.
Практикум 11.1
А В задачах 1—18 нужно вычислить неопределенный интеграл. (Проверяется дифференцированием.)


Глава 11. Интегрирование
359
5. j t 4dt.
6. j t7dt.
7. j 2irdt.
8. j e dt.
9. j 3u6du.
10. 12?z5du.
11. j (1 + 3u2) du.
12. j (8 - u3) du.
13. j 5e‘dt.
14. j 7,67e‘dt.
15. [-dz.
16. [
J z
J
17. x (1 + x) dx.
18. f x2 (1 — x2) dx.
В задачах 19-22 каждый график является графиком производной у = Для каждого из них в одной и той же системе координат постройте вероятные графики трех первообразных функций f, удовлетворяющих условиям /(0) = —2, /(0) = 0 и /(0) = 2, соответственно.
19.
21.
20.
22.
В задачах 23-32 вычислите все первообразные для каждой производной.
23. = 200а:4.
ах
25. = 24 - 6а:.
ах
27. =2и5- Зи2 - 1.
du
dx с
24. —- = 42t5. dt
26. = За;2 - 4а;3.
dx
28. = 3 - 12t3 - 9t5.
dt


360
Часть III. Математический анализ
29.
dx
= ех + 3.
32.
— х — ех.
du dv
Б В задачах 33 и 34 проанализируйте справедливость каждого утверждения. Если утверждение всегда истинно, объясните почему. Если нет, приведите контрпример.
* 33. а) Если п — целое число, то хп+1/(п -hl) — это первообразная функции хп.
б) 	Функция f(x) = 7г — первообразная функции д(х) = 0.
* 34. a) f (ж4 + х2) dx = х4 + х2 + С.
Могут ли три графика, перечисленные в задачах 35-38, быть первообразными одной и той же функции? Объясните свой ответ.
35.
36.
37.
38.
В задачах 39-60 нужно вычислить неопределенный интеграл. (Проверяется диффе¬
ренцированием.)
j 20т1/3. 41. j 9t_4dt. «■В
39.
40.
42.
44.
f §dm
J m2
45.
f dx
J 4т3
46.
10u3/2d?z.
j 8f 5dt.


Глава 11. Интегрирование
361
ч
4 + Udu.
и
ч
ЧЧ)
dx.
51.
(Ч‘ ■ i
- 2^ dx.
53.
dx.
ч
| dx.
ч
f ех - Зх л
1 4 dx~
59.
12 + 5z - 3z3 , л dz.
И
ЧЧг*
5«-1 Ч’ + Js)'''
52-Ж~з+1>
54-1 й dx-
58.1
60. |<1±^
В задачах 61-64 каждый график является графиком производной у = Для
каждого из них в одной системе координат постройте вероятные графики трех первообразных функций f, удовлетворяющих условиям /(0) = —2, /(0) = Ou /(0) = 2 соответственно.
61.
63.
62.
64.
В задачах 65-74 требуется вычислить частную первообразную каждой производной, удовлетворяющую заданным условиям.
65. = 2х - 3; у (0) = 5. 66. = 5 - 4х; у (0) = 20.
ах ах
67. С"(х) = бх2 - 4х; С(0) = 3000. 68. Я'(х) = 600 - 0,6х; Я(0) = 0.


362
Часть III. Математический анализ
„ dx 20 „л dJt 100
6’-S = 7i’’(1> = 40' ™- = = m
71. =■ 2х~2 + Зх-1 — 1; у (1) = 0. 72. = Зх-1 + х-2; у (1) = 1.
dx dx
73. = 4е* - 2; х (0) = 1. 74. = 5ег - 4; у (0) = -1.
UjL Ul/
75. Составьте уравнение кривой, которая проходит через точку (2,3), если ее наклон задан формулой
dy Л 1
-—= 4х — 3 ах
для всех х.
76. Составьте уравнение кривой, которая проходит через точку (1,3), если ее наклон задан формулой
= 12а:2 - 12а: ах
для всех х.
В В задачах 77-82 требуется вычислить неопределенные интегралы.
__ f Х~1 _ 1
78.] Л.
„„ Г 1 - За:4 ,
«»■ ]
81- | A’^2Xdx- 82. j
Для каждой производной в задачах 83-88 найдите первообразную, удовлетворяющую заданным условиям.
83-^^;М<4)=5-
dy 5а:+ 2
КГ1Г’(1>=0
87. р' (аг) = р(1) = 20.
В задачах 89-92 вычислите, как указано, производную или неопределенный интеграл.
77.
79.
2х4 — х .
z—dx. хл
х5 — 2х ,
-л—dx. х4
х2ех — 2х
84.^
ах
S6. dt
1 — х^ _;/?(!)= 4.
88. р' (а:) = р(1) = 15.
89.
-а (IV*)


Глава И. Интегрирование
363
Применение математики
Экономика и бизнес
93. Функция затрат. Предельные средние затраты на производство х спортивных часов составляют
C'(;r) = -^, С (100) = 25,
где С (х) — средние затраты в долларах. Вычислите функцию средних затрат и функцию затрат. Какими будут постоянные затраты?
94. WWW Возобновляемый источник энергии, В 1998 году объем потребления электроэнергии из возобновляемых источников в США составило 6,98 квадриллионов британских тепловых единиц (т.е. 6,98 • 1015 Бте). С 1960 года потребление росло со скоростью
/'(*) = 0,004/; + 0,062,
где t — количество лет, прошедших с 1960 года. Вычислите функцию f(t) и оцените объем потребления электроэнергии из возобновляемых источников в США в 2020 году.
* 95. Производственные затраты. На рис. 11.7 показан график функции предельных затрат на производство х тысяч наручных часов в месяц, где затраты С (ж) измеряются в тысячах долларов в месяц.
Объем производства, тыс. шт.
Рис. 11.7. Иллюстрация
к задаче 95
а) Используя показанный выше график, опишите форму графика функции затрат С (ж), когда х растет от 0 до 8000 наручных часов в месяц.
б) Дано уравнение функции предельных затрат
С"(х) = Зх2 - 24гг + 53.
Вычислите функцию затрат, если ежемесячные постоянные затраты при нулевом объеме производства составляют 30 000 долл. Какими будут затраты на производство 4000 наручных часов в месяц? На производство 8000 наручных часов в месяц?


364
Часть III. Математический анализ
в) Постройте график функции затрат для 0 х 8. (Сравните форму графика с результатами анализа, полученными при решении п. а.)
г) Почему график функции затрат на обоих концах круче, чем посередине?
* 96. Доход. На рис. 11.8 показан график функции предельного дохода от продажи х тысяч наручных часов в месяц.
Рис. 11.8. Иллюстрация
к задаче 96
а) Используя показанный выше график, опишите словами форму графика функции дохода Я(х), когда х растет от 0 до 1000.
б) Составьте уравнение функции предельного дохода (линейная функция, показанная на рис. 11.8).
в) Постройте график функции дохода на интервале [0, 1000]. (Сравните форму графика с результатами анализа, полученными при решении п. а.)
г) Составьте уравнение зависимости цены от спроса и определите цену, при которой спрос составит 700 единиц.
97. Анализ продаж. Предполагается, что месячные продажи некой модели персонального компьютера будут снижаться со скоростью
5'(t) = —25«2/3
компьютеров в месяц, где t — время в месяцах, a S(t) — ежемесячный объем продаж. Компания планирует прекратить выпуск данной модели компьютера, когда объем ежемесячных продаж упадет до значения 800 компьютеров. Вычислите функцию S(t), если в исходный момент (t = 0) месячный объем продаж равен 2000 компьютеров. Сколько еще времени компания будет производить обозначенную модель компьютера?
98. Анализ продаж. Скорость изменения объема ежемесячных продаж картриджей с новой видеоигрой описывается формулой
5'(t) = 500f1/4, 5(0) = 0,
где t — количество месяцев, прошедших с момента выпуска видеоигры, a S(t) — месячный объем продаж картриджей. Вычислите функцию S(t). Когда месячные продажи составят 20 000 картриджей?


Глава 11. Интегрирование
365
99. 	Анализ продаж. Повторите решение задачи 97, если S"(t) = — 25t2/3 — 70, а все остальные данные остаются неизменными. Используя графическую утилиту, найдите приближенное решение уравнения S(t) = 800 с точностью до двух десятичных знаков.
100. Анализ продаж. Повторите решение задачи 98, если S'(t) = 500/1/4 4- 300, а все остальные данные остаются неизменными. Используя графическую утилиту, найдите приближенное решение уравнения S(t) = 20000 с точностью до двух десятичных знаков.
101. WWW Затраты на рабочую силу и обучение сотрудников. Военный подрядчик начал производство новой системы управления реактивным снарядом. На основе данных, собранных во время сборки первых 16 систем управления, руководитель производством вывел следующую функцию, описывающую эффективность использования рабочей силы:
р(х) = 2400х_1/2,
где р(х) — это количество человеко-часов, затрачиваемых на сборку х-й единицы системы управления. Например, после сборки 16 систем управления скорость сборки составляет 600 человеко-часов на единицу, а после сборки 25 систем управления, скорость сборки составляет 480 человеко-часов на единицу. Эффективность производственного процесса возрастает с повышением квалификации сотрудников, которая в свою очередь растет с увеличением объема производства. Сколько человеко-часов L(x) понадобится для сборки первых х единиц, если для сборки первых 16 единиц затрачено 19200 человеко-часов? Сколько часов понадобится для сборки первых 25 систем управления?
102. Затраты на рабочую силу и обучение сотрудников. Сколько человеко-часов L(x) понадобится для сборки первых х систем управления, если эффективность использования рабочей силы в задаче 101 рассчитывается по формуле
5(х) = 2000х_1/3?
Сколько понадобится для сборки первых 27 систем управления?
Биологические науки
103. 	Рост и вес. У среднестатистического человека скорость изменения веса W (в фунтах) как функция роста h (в дюймах) приблизительно рассчитывается по формуле
= 0,0015/г2.
ап
Вычислите функцию W(h), если 1У(60) = 108 фунтов. Найдите также вес человека ростом 5 футов и 10 дюймов.


366
Часть III. Математический анализ
104. Заживание раны. Какой будет площадь раны А через 10 дней, если она изменяется со скоростью, равной приблизительно
= —4£-3, 1 t 10,
at
где t — время в днях, и А(1) = 2 см2?
Социальные науки
105. Урбанизация. Скорость роста численности населения N(t) в населенном пункте через t лет после получения статуса города приблизительно составляет
= 400 + 600VI, 0 t с 9.
at
Сколько человек будет проживать в городе через 9 лет, если на момент получения этого статуса его численность населения была равна 5000?
106. Обучение. В масштабных исследованиях эффективности обучения принимает участие начальный класс средней школы с языковым уклоном. В одном из экспериментов детям предлагали запомнить список из 50 слов. Целью исследования было определить скорость запоминания списка за различные периоды времени на протяжении 5-часового учебного занятия. Было обнаружено, что средняя скорость обучения всего класса обратно пропорциональна времени, потраченному на изучение, и приблизительно составляет
v'(t) = y, 1 < t 5.
Каким будет среднее количество слов, усвоенных учениками через t часов для 1 t 5, если в среднем через один час изучения они запоминают 15 слов? Каким это значение будет через четыре часа изучения? (Округлите ответ до ближайшего целого числа.)


Глава 11. Интегрирование
367
11.2. 	Интегрирование методом замены переменной
■ Применение цепного правила в обратном порядке
■ Интегрирование методом замены переменной
■ Другие методы подстановки
■ Решение практических задач
Многие формулы для вычисления неопределенных интегралов, введенные в предыдущем разделе, основываются на соответствующих формулах вычисления производных. Теперь рассмотрим процедуры и формулы вычисления неопределенных интегралов, основанные на цепном правиле дифференцирования.
Применение цепного правила в обратном порядке
Напомним цепное правило.
^f[9&)]=f'[g(x)]g' (х).
Выражение в правой части формулы образуется путем вычисления производной от внешней функции f и умножения на производную от внутренней функции д. Если подынтегральное выражение представлено в виде ff[g(x)]g'(x), то можно без труда найти первообразную и неопределенный интеграл.
Использование цепного правила в обратном порядке
j f Iff (я)] У (z) dx = f [5 (*)] + C. (11.4)
Задание 11.4.
1. Какое из следующих выражений имеет первообразную ех -1?
д?2ех3_1, Зя:2ех3_1, Зже^3-1.
2. Какое из следующих выражений имело бы первообразную е*3-1, если бы оно было умножено на постоянный множитель? На переменный множитель?
Зяе*3-1, £2e®3_1. в
Вычислим неопределенный интеграл
(11.5)
Подынтегральная функция имеет вид, соответствующий выражению из цепного правила е9^д\х\ которое равно производной от е9^. Поскольку


368
Часть III. Математический анализ
то
Зх2ех rdx = ех 1 + С.
Чем следующий неопределенный интеграл отличается от интеграла (11.4)?
| х2ех xdx.
(И.6)
В нем отсутствует постоянный множитель, равный числу 3. Иначе говоря, функция х2ех _1 с точностью до постоянного множителя является производной функции ех _1. Однако, поскольку постоянный множитель можно выносить за знак интеграла, то при вычислении неопределенного интеграла от функции ех _1 не возникает никаких проблем. Следует умножить и разделить интеграл на число 3 и вынести множитель | за знак интеграла. Эта процедура эквивалентна умножению интеграла (11.6) на единицу.
(И.7)
Производная от правой части уравнения (11.7) равна подынтегральному выражению интеграла (11.6). Это можно проверить самостоятельно.
Чем следующий неопределенный интеграл отличается от интеграла (11.5)?
(И.8)
Степень переменного множителя х в формуле (11.8) на единицу меньше, чем в формуле (11.5). Это серьезное отличие. Как бы заманчиво это ни было, нельзя преобразовать интеграл (11.8), умножая его на переменный множитель х и вынося из-под знака интеграла множитель 1/ж, как это было сделано с числом 3 в уравнении (11.7). Если бы можно было вынести за знак интеграла множитель 1/х, то почему бы сразу не вынести из-под знака интеграла всю подынтегральную функцию? Тогда взятие неопределенного интеграла сводилось бы к тривиальной задаче и не давало желаемого результата — вычисления первообразной от подынтегральной функции.
Формулы интегрирования
Зх2ех ~xdx = ех —1 Н- С7; Подынтегральное выражение соответствует
J цепному правилу.
Подынтегральное выражение можно свести к выражению, соответствующему цепному правилу.
Зхеж rdx = ? Подынтегральное выражение нельзя свести
J к выражению, соответствующему цепному
правилу.
Предупреждение. Постоянный множитель можно выносить за знак интеграла, а переменный — нет.


Глава 11. Интегрирование
369
Иногда результат интегрирования можно просто угадать. В этом нет ничего плохого. Следует только проверить результат методом обратного дифференцирования. Если результат правильный, то можно продолжать дальше, если же нет, нужно испытать другой подход.
Как показано в разделе 10.3, цепное правило позволяет обобщить формулы вычисления производных функций хп, ех и 1пх на функции [/(^)]п, е^х^ и 1п[/(х)]. Цепное правило также можно использовать для обобщения формул вычисления неопределенных интегралов, рассмотренных в разделе 11.1.
Общие формулы вычисления неопределенных интегралов
!• [ (/ (*)]" /' (z) dx = + С, п/ -1.
2. 	\ef^f'(x)dx = ef^ + С.
L
(®)
Каждую формулу можно проверить, воспользовавшись цепным правилом и показав, что производная от функции справа равна подынтегральному выражению слева. Например, выражение
А [еЛ*)+с] = ef^f(x)
доказывает формулу 2.
f (x)dx = ln\f(x)\+C.
j (Зх + 4)10 • 3dx =
1.
2.
Пример 11.8 (Применение цепного правила в обратном порядке).
(Зх + 4)11
— \-С. Формула 1, где f (ж) = Зх + 4, а f(x) = 3.
Проверка: ± (Зх + 4) i = (Зх + 4)10 (3).
| ех -2xdx = ex +С. Формула 2, где / (х) = а:2, а/'(х) = 2аз.
d „2, d о \ 2
Проверка: — е ; = е — х2 ; = е • 2х.
dx • dx •
- 3x2dx = In 11 + я3| + С. Формула 3, где f (ж) = 1 + ж3, а f' (ж) = Зж2.
J 1 + х6
А Ц + (1 + х3) _ _L_ . 3jA
3.
Упражнение 11.8.
Вычислите следующие неопределенные интегралы.
1. (2х3 - З)20 • 6x2dx. 2. j е5х • 5dx.
3. 	| , * „ • 2xdx.
J 4 + x2


370
Часть III. Математический анализ
Интегрирование методом замены переменных
При использовании формул 1, 2 и 3 главное — распознать вид подынтегральной функции. Иногда в таких формулах сложно выделить функции /(ж) и ff(x). В этих ситуациях можно выполнять замену переменной, чтобы упростить подынтегральную функцию. Метод замены переменной, который сейчас рассматривается, будет очень полезен при дальнейшем обучении интегрированию.
Прежде всего, введем понятие дифференциала. Как известно, производная представляет собой выражение dy/dx, причем это обозначение считается единым целым. Теперь мы определим dy и dx как две отдельные величины, частное от деления которых равно /'(*)•
Дифференциалы
Пусть у = f(x) — дифференцируемая функция.
1. Дифференциал dx независимой переменной х — это произвольное действительное число.
2. Дифференциал dy зависимой переменной у — это произведение f'(x) и dx, т.е.
dy = f'(x)dx.
С понятием дифференциала связаны определенные математические тонкости, которые подробно обсуждаются в курсах высшей математики. В рамках нашей книги дифференциал рассматривается как вспомогательный инструмент, позволяющий вычислять неопределенные интегралы. Результат же всегда можно проверить путем дифференцирования.
Пример 11.9 (Дифференциалы).
1.
Если у = f(x) = гг2, то
dv. = f (я) dx ;
= 2х dx.
2.
Если и = д(х) — е3х, то
du\ = д' (х) dx ; =
= 3e3xdx.
3.
Если w = h(t) = 1п(4 + 5*),
то
к
dw< = hf (*) dt! = — dt.
• 4 + 5*
Упражнение 11.9.
1. Вычислите дифференциал dy для у = f(x) = х3.
2. Вычислите дифференциал du для и = h(x) — 1п(2 + я2).
3. Вычислите дифференциал dv для v = g(t) = e~5t. ■
Рассмотрим метод замены переменной на нескольких примерах.
Пример 11.10 (Замена переменной). Вычислите неопределенный интеграл
j (х2 + 2х + 5)5 (2х + 2) dx.


Глава 11. Интегрирование
371
Решение. Если
и = х2 + 2х + 5,
то дифференциал от и равен
du = (2х + 2)dx.
Следует отметить, что du — это один из множителей в подынтегральном выражении. Поставим и вместо х2 + 2х + 5, a du вместо (2х + 2)dx и получим
Поскольку и = х2 + 2х + 5.
(х2 + 2х + 5)5 (2х + 2) dx = |и5du =
и6
= _ + с =
= (х2 + 2х + 5)6 + С.
о
Проверка: (х2 + 2х + 5)6 = • 6 • (х2 + 2х + 5)5 (х2 + 2х + 5) =
dx 6 7 6 ’ dx 4 7
= (х2 + 2х + 5)5 (2х + 2).
Упражнение 11.10.
Вычислите неопределенный интеграл J (х2 — Зх + 7) (2х — 3) dx методом замены переменной. ■
Метод замены переменной носит такое название, поскольку переменная х заменяется на переменную и. Подставляя и = /(х) и du = f(x)dx в формулы 1, 2 и 3, получим обобщенные формулы неопределенных интегралов, показанные в следующей врезке.
Общие формулы вычисления неопределенных интегралов
f ип+г
4. undu = + С, —1.
J п + 1
5. j eudu = еи + С.
6. I — du = In |u| -h С.
J и
Эти формулы справедливы, если и — это независимая переменная или функция другой переменной, a du — дифференциал этой переменной.
Пошаговое описание метода замены переменной вычисления неопределенного интеграла приведено в следующей врезке.


372
Часть III. Математический анализ
Вычисление интеграла методом замены переменной
Этап 1. Подобрать переменную, упрощающую подынтегральное выражение. В частности, следует попытаться выбрать такое и, чтобы дифференциал du был множителем подынтегрального выражения.
Этап 2. Выразить подынтегральное выражение через величины и и du, полностью исключив исходную переменную и ее дифференциал.
Этап 3. Вычислить значение нового интеграла, если это возможно.
Этап 4. Выразить первообразную, вычисленную на этапе 3, через исходную переменную.
Пример 11.11 (Замена переменной). Применяя замену переменной, вычислите следую¬
щие неопределенные интегралы.
1. j (Зх + 4)6 ■ 3dx.
Решение.
1. Если положить и = Зж + 4, то du = Sdx и
d (Зх + 4)7 _ 7(3x + 4)6 d
Воспользуемся формулой 4.
Поскольку и = Зя? + 4.
Проверка.
dx 7
7 dx
(Зж + 4) = (Зж + 4)6
3.
2. 	Если положить и = t2, то du = 2tdt и
ef2 • 2tdt = еи du =
Воспользуемся формулой 5.
= еи + С = = ее + С.
Поскольку и = t2.
d .2 .2 d п /2
Проверка, —е = е —t = е • 2t. dt dt
e5w • 5dw.
Упражнение 11.11.
Применяя метод замены переменной, вычислите следующие неопределенные интегралы.
1. (2ж3 — З)4 • 6x2dx. 2.
Предупреждение. Интегрирование методом замены переменной — это эффективный, но, к сожалению, не универсальный способ вычисления неопределенных интегралов. Например, при вычислении интегралов J ех dx или J (In ж) dx он не работает.


Глава 11. Интегрирование
373
Другие способы подстановки
Для того чтобы воспользоваться методом замены переменной (подстановки), подынтегральное выражение должно допускать представление его через величины и и du. В некоторых случаях, перед тем как делать замену переменных, приходится сначала преобразовывать подынтегральное выражение и только затем применять одну из формул интегрирования. Одна из таких задач рассматривается в примере 11.12.
Пример 11.12 (Метод подстановки). Вычислите следующие неопределенные интегралы.
1. л * dx. 2. I te~l dt.
J 4x + 7 J
3. 	j 4z2 \Лг3 + 5 dx.
Решение.
1. 	Если и = 4д? + 7, то du = ^dx. Чтобы подынтегральное выражение в точности преобразовать к виду формулы 6, не достает множителя, равного числу 4. Помня, что постоянный множитель можно выносить за знак интеграла, сделаем следующее.
[ -7^-^dx = f -^—-dx =
J 4х + 7 J 4х + 74
= 1 [ -—^—-4dx =
4 J и
1, | ,
= - In u + C =
4
= j In |4x + 7| + C.
Подставим и = 4а? 4- 7 и du = 4dx.
Воспользуемся формулой 6.
Проверка.
Поскольку и = 4а? + 7.
1 1 d
4 4х 4- 7 dx
1
4я 4- 7’
2. Если и = —t2, то du = —2tdt. Заменяя переменную, получим следующее выражение.
Подставим и = —t2 и du = —2tdt.
Воспользуемся формулой 5.
Поскольку и = —t2.


374
Часть III. Математический анализ
d ( 1 j.2'X 1 j.2 d / n\
- (__e- 'j = --e- - (-/ )
3. 	j 4х2а/х3 + 5dx = 4 j v6e3 + 5 • x2dx =
-^e e (—20 = te ‘2
Вынесем 4 за знак интеграла и выполним такие же операции, что и раньше.
Подставим и = х3 + 5 и du = 3x2dx.
Воспользуемся формулой 4.
Поскольку и = х3 + 5.
Проверка.
4
3
4
3
(^ + S)1/2^(«3 + 5) =
(x3 4- 5)1/2 • Зх2 = 4я2\Лг3 + 5.
Упражнение 11.12.
Вычислите следующие интегралы.
!. р-3^.
2.
-^dx- xz — 9
3.
5t2 (t3 + 4) 2 dt.
Даже если невозможно найти замену переменной, которая в точности сведет подынтегральное выражение к одной из интегральных формул, подстановка поможет упростить подынтегральную функцию, к которой можно будет применить другой метод.
Пример 11.13 (Метод подстановки). Вычислите интеграл Х dx.
J ух + 2
Решение. Повторяя предыдущие рассуждения, положим и = х -И 2, тогда du = dx и
I
X
д/я + 2
dx =
-^du. у/и
Следует отметить, что эта подстановка не полна, поскольку не все подынтегральное выражение выражено через и и du. Как отмечалось ранее, за знак интеграла можно


Глава 11. Интегрирование
375
выносить только постоянный множитель, поэтому из-под него нельзя вынести переменную х. Вместо этого, следует вернуться к изначальной замене, выразить переменную х через величину и и, воспользовавшись полученным в результате уравнением, завершить подстановку.
и = х 4- 2;
и — 2 = х.
Выразим х через и.
Подставим это выражение для х.
Таким образом,
х
и — 2 ,
du =
, dx —
J Ух + 2
,ь.
= | (и1/2 — 2и-1/2) du = • = | и1/2du — 21 u~^2du •
иЭ/2 1/2
— з 2 1 4- С —
2 2
= |(z + 2)3/2-4(s + 2)1/2 + C'.
Упростим подынтегральное выражение
Поскольку и = х 4- 2.
j Г о
Проверка. — - (я + 2)3//2 - 4 (я + 2)1/2 dx 3
= (я + 2)1/2 — 2 (я 4-2)”1/2 =
х + 2 2 х
(х + 2)1/2 (х + 2)1/2 (х + 2)1/2‘
Упражнение 11.13.
Вычислите интеграл J* х\/х 4-1 dx. В
Решение практических задач
Пример 11.14 (Зависимость цены от спроса). Отдел маркетинговых исследований крупной сети супермаркетов установил, что в одном из магазинов предельная цена р'(х) зубной пасты определенной торговой марки при спросе х тюбиков в неделю описывается формулой
р'(х) = —О,О15е_о’°1ж.
Определите уравнение зависимости цены от спроса, если при цене тюбика пасты 2,35 долларов недельный спрос составляет 50 тюбиков. Вычислите недельный спрос соответствующий цене 1,89 долларов.


376
Часть III. Математический анализ
Решение.
=
—0,015е_о’О11<£г =
= -
-0,015
e-°'01xdx =
-0,015 j
Ге-о,о1х-0’01с/х =
1 -0,01
= -
-0,015
-0,01
| е-0’01® (—0,01) da: =
— 1,5 eudu =
Подставим и = —0,01® и du = —0,01d®.
= l,5eu + С =
= 1,5е_0’01ж + С. Поскольку и = —0,01®.
Вычислим константу С, учитывая, что
р(50) = 1,5е~0,01’50 + С = 2,35 долл.
С = 2,35 — 1,5е-0’5 = Воспользуемся калькулятором
= 2,35-0,91 =
= 1,44 долл.
Таким образом,
р(х) = 1,5е_0,01х + 1,44.
Чтобы вычислить спрос при цене 1,89 долл., решим уравнение р(х) — 1,89 относительно х.
l,5e“°’01x + 1,44 = 1,89;
1,5е_0,01х = 0,45;
e-o,oi® = Од
—0,01т = 1п 0,3;
х = —100 In 0,3 « 120 тюбиков. ■
В графической утилите предусмотрен альтернативный подход к решению уравнения р(т) = 0,89 из примера 11.14 (рис. 11.9).
Упражнение 11.14.
Предельная цена р'(т) зубной пасты определенной торговой марки при объеме предложения х тюбиков в неделю описывается формулой
р'(х) = 0,001е°’01ж.
Определите уравнение зависимости цены от предложения, если поставщик готов поставить 100 тюбиков в неделю по цене 1,65 долл. Сколько тюбиков должен предложить поставщик по цене 1,98 долл.? ■


Глава 11. Интегрирование
377
Рис. 11.9. Функция 1/1 = 1,5е 0’01ж + 1,44,
У2 = 1,89
Задание 11.5.
В каждом из следующих примеров объясните, почему был использован знак После этого решите задачу, используя либо метод замены переменных, либо любой другой способ.
1. (х2 4- З)2 dx = Г (ж2 + З)2 —dx =4
j (*2 +3)2 •2xdx-
^l-_dx = ^dxt u=l°x + 3.
/ In |u| + C.
Предупреждение.
1. Переменную нельзя выносить за знак интеграла!
2. Перед применением формул интегрирования 11.4-11.6 подынтегральное выражение нужно выразить исключительно через величины и и du.
Ответы к упражнениям
11.8. 1) ^-(2х3-3)21+С.
2) е5х + С.
3) 1п|4 + х21 + С или 1п(4 + х2) + С, поскольку 4 + х2 > 0.
11.9. 1) dy = 3x2dx.
2х
2) du = -da?.
2 + х2
3) dv - —3e~5tdt.
11.10. | (x2 - Зх + 7)5 + С.
5
11.11. 1) 1 (2z3 -З)5 +C.
5
2) e5w + C.
11.12. 1) -|e-3l + C.
tJ


378
Часть III. Математический анализ
2) In |rr2 - 9| + С.
3) + +
11.13. I (x + 1)5/2 - I (x + 1)3/2 + C.
o 3
11.14. p(x) = O,leo,olx + 1,38; 179 тюбиков.
Практикум 11.2
А В задачах 1-40 требуется вычислить неопределенные интегралы и проверить результат путем дифференцирования.
(4х — З)2 • 4dx.
4
(7x 4-1)3 • 7dx.
3.
(х2 + 1)4 • Zxdx.
4-J
(z5 — 2)2 • 5z4dx.
5-
е2х ■ 2dx.
‘■J
ex • 3x2dx.
7. I
[ -—• 4x3dx.
8.
r 1
exdx.
J
1 1 + X4
1 + ex
[* (х + З)10 dx.
10.
(x — 3)-4 dx.
ч
I* (6£-7)“2dt
!2.J
1" (5t + l)3 dt.
13.
(t2 4-1)5 tdt.
14.
(t3 +4)-2 t2dt.
ч
xex dx.
4
[ e~0,01xdx.
17.
———-dx.
18.
f X 9dx.
5x + 4
j
1 1+x2
19.
[ e^dt.
20.
[ 3 dt.
1
] 2-t
Г t
Г t2
21.
.dt.
22.
.dt.
1 (3t2 + l)4
1 (t3 - 2)5
Г x2
f x
23.
9dx.
24.
-dx.
1 (4 — x3)
1 (5-2a;2)5
25.
xy/x + 4dx.
26.
ху/х — 9dx.
27.
f Л dx.
28.
f * dx.


Глава 11. Интегрирование
379
29. | х (х — 4)9 dx.
31. 	р11 (1 +е2')3<Ь.
33. 	[л \+I ,<1*.
35. j (2х + 1) ex2+x+1dx.
37. j (ех - 2х)3 (ех - 2) dx.
39. [ Х3+Х 4dx.
J (х4 + 2х2 + I)4
В задачах 41-46 предполагается, что указанное решение было сдано на проверку студентом.
1) Как проверить решение?
2) Правильное это решение или нет? Если решение неправильное, объясните, в чем ошибка и как ее можно исправить.
3) Для каждого неправильного решения найдите правильное и проверьте результат путем дифференцирования.
*41. Г — dx = In |2х — 3| + С. *42. [ Х dx = In |х2 + 5| + С.
J 2х - 3 J х2 + 5 1 1
x\x*dx = exi + С. * 44. f e4l_5da: = е4*’5 + С.
*43.
*45. [2 (х2 - 2)2dx = „ 2) + С.
J Зх
*46. | —10х • (х2 — З) -4 dx = (х2-3)_5 + С.
В В задачах 47-58 требуется вычислить неопределенный интеграл и проверить результат с помощью дифференцирования.
47. j х \/За:2 + 7 dx. 48. j х2 л/2 х3 + 1 dx.
49. 	jx(x3 + 2)2dx. 50. j® (х2 + 2)2 dx.
51. 	j x2 (x3 + 2)2 dx. 52. j (x2 + 2)2 dx.
53. f . Х[ dx. 54. [ . dx.
55. [ ^dx. 56. [ -?—dx.
J x J 1 + ex
57. [ ^e~1/xdx. 58. | —}—dx.
J x2 J xlnx


380
Часть III. Математический анализ
В задачах 59-64 требуется вычислить первообразную каждой производной.
59. = 7t2 (Z3 + 5)6.
at
61 dy = 3t
‘ dt
dp ех + е~х
dx (е* - е~х)
60. = 10п (п2 - 8)7.
dn ' '
dy _ 5х2
о2» — а «
dx (хз _ 7)4
dm In (£ — 5)
64. 	—— = —.
dt t — Ь
Используя метод замены переменной, выведите формулы интегрирования в задачах 65 и 66. Затем проверьте результат обратным дифференцированием.
65. j eaudu =^еаи +С, а / 0.
f 1 1
66. -du = - In \аи + b\ + С, а 0.
J аи + о а
Применение математики
Экономика и бизнес
67. 	Зависимость цены от спроса. Предельная цена детского шампуня при спросе х бутылок в неделю описывается формулой
-6000
(За; + 50)2 ’
Составьте уравнение цены-спроса, если недельный спрос при цене 4 долл, за бутылку равен 150 шт. Каким будет недельный спрос при цене 2,50 долл.?
68. 	Зависимость цены от спроса. Предельная цена при уровне предложения х бутылок детского шампуня в неделю описывается формулой
р' {х) =
300
(За; + 25)2'
Составьте уравнение зависимости цены от спроса, если поставщик шампуня предлагает к поставке 75 бутылок в неделю по цене 1,60 долл, за бутылку. Какой объем поставок может предложить поставщик при цене 1,75 долл, за бутылку?
69. 	Функция затрат. Недельные затраты на производство х пар теннисных туфель описываются формулой
С'^ = 12 + ГИ’
где С(х) — общие затраты в долларах. Вычислите функцию затрат, если постоянные затраты составляют 2000 долл, в неделю. Какими будут средние затраты в расчете на пару туфель, если каждую неделю производится 1000 пар?


Глава 11. Интегрирование
381
70. Функция дохода. Недельный предельный доход от продажи х пар теннисных туфель описывается формулой
R' (х) = 40 - 0,02а; + -55L; R (0) = 0,
х 4-1
где R(x) — доход в долларах. Вычислите функцию дохода. Найдите доход от продажи 1000 пар туфель.
71. Маркетинг. Автомобильная компания готова выпустить новую серию автомобилей, сопровождая выпуск общенациональной рекламной кампанией. После проведения пробных продаж в специально выбранном городе отдел маркетинговых исследований пришел к выводу, что через t месяцев после начала кампании в масштабах страны ежемесячный объем продаж (в миллионах долларов) будет расти со скоростью
S'(t) = 10 - 10е“°’н; 0 24.
а) Каким будет суммарный объем продаж S(t) через t месяцев после начала кампании в масштабах страны, если предположить, что вначале кампании объем продаж был равен нулю?
б) Каким будет суммарный объем продаж через 12 месяцев после начала кампании?
в) Когда предполагаемый общий объем продаж достигнет 100 миллионов долларов? Используя графическую утилиту, вычислите приближенный ответ с точностью до двух десятичных знаков.
72. Маркетинг. Повторите решение задачи 71, если скорость роста ежемесячных продаж описывается формулой
S'(t) = 20 - 20e~°*ost; 0 t 24.
73. WWW Нефтедобыча. Используя данные за первые три года добычи, а также геологические исследования, руководство нефтедобывающей компании оценило, что нефть будет выкачиваться из месторождения со скоростью
R (*) = -152. + 5, 0 t 20,
t 1
где R(t) — скорость добычи (в тысячах баррелей в год) через t лет после начала разработки месторождения. Сколько баррелей нефти Q(t) будет давать месторождение первые t лет, если Q(0) = 0? Сколько баррелей будет добыто за первые 9 лет?
74. Добыча нефти. Предположим, что скорость добычи нефти в задаче 73 оказалась равной
а) Когда скорость добычи будет максимальной?
б) Сколько баррелей нефти, Q(t), будет давать месторождение первые t лет, если Q(0) = 0? Сколько баррелей будет добыто за первые 5 лет?


382
Часть III. Математический анализ
в) 	Сколько времени понадобится (с точностью до ближайшей десятой доли года), чтобы добыть четверть миллиона баррелей нефти?
Биологические науки
75. Биология. Дрожжевая культура растет со скоростью W'(x) = O,2eo,lt г в час. Каким будет ее вес через t часов, если вначале культура весила 2 г? Каким он будет через 8 часов?
76. Медицина. Скорость заживления раны на кожном покрове (см2/день) приблизительно равна A'(t) = —0,9е_о,и. Какова площадь раны A(t) будет через t дней, если сначала ее площадь была равна 9 см2? Какого размера она достигнет через 5 дней?
77. Загрязнение. Зараженное озеро очищается с помощью бактерицидного средства. Скорость роста вредоносных бактерий через t дней после очистки составляет
dTV dt
2000t
iTt2’
0 t 10,
где N(t) — число бактерий на миллилитр воды (поскольку производная dN/dt — отрицательная, число вредоносных бактерий уменьшается).
а) Вычислите минимальное значение dN/dt.
б) Вычислите функцию N(f), а затем число бактерий через 10 дней, если изначально их число составляло 5000 бактерий на миллилитр.
в) В какой момент времени (с точностью до двух десятичных знаков) число бактерий достигнет 1000 бактерий на миллилитр?
78. 	WWW Загрязнение. Из нефтяного танкера, выброшенного на риф, вытекает нефть. В результате образуется нефтяное пятно, которое расходится в стороны со скоростью, приблизительно описываемой уравнением dR dt
где R — радиус круглого пятна (в футах) через t минут. Вычислите радиус пятна через 16 минут, если в момент t = 0 он был равен 0.
Социальные науки
79. Обучение. В отдельно рассматриваемом экономическом колледже было установлено, что через t недель после записи на 15-недельный курс машинописи средний студент печатает со скоростью N'(t) = 6e_0,lf слов в минуту. Сколько слов в минуту N(t) предположительно будет печатать студент после t недель обучения машинописи, если в начале курса студент мог печатать 40 слов в минуту? Сколько он сможет печатать после окончания курса?
80. Обучение. В том же колледже было установлено, что через t недель после записи на 15-недельный курс стенографии средний студент записывает текст на слух со скоростью N'(t) — 12e_0,06t слов в минуту. Сколько слов в минуту N(t) предположительно сможет застенографировать студент после t недель обучения, если в начале курса он не мог набрать под диктовку ни одного слова? Сколько он сможет застенографировать после окончания курса?


Глава 11. Интегрирование
383
81. 	Поступление в колледж. Запланированная скорость набора студентов, поступающих в новый колледж оценивается уравнением
= 5000 (t 4-1)_3/2 , О 0, at
где E(t) — планируемое число принятых в колледж за t лет. Вычислите планируемое количество студентов, набранных в колледж за 15 лет, если в самый первый год (t = 0) поступило 2000 человек.
11.3. 	Дифференциальные уравнения: рост и затухание
■ Дифференциальные уравнения и поля направлений
■ Повторное рассмотрение задачи непрерывного начисления сложных процентов
■ Закон экспоненциального роста
■ Численность населения, радиоактивный распад и скорость обучения
■ Сравнительный анализ процессов экспоненциального роста
В предыдущем разделе рассматривались уравнения вида
3^ = 6я2 — 4ж, р' (х) — —400е“о,О4:Е.
ах
Такие уравнения называются дифференциальными. Вообще говоря, уравнение является дифференциальным, если в него входит неизвестная функция и одна или несколько производных. Рассмотрим еще несколько примеров дифференциальных уравнений.
= ку, у" - ху' + х2 = 5, = 2ху.
Первое и третье уравнение называются уравнениями первого порядка, поскольку в каждое из них входит первая производная и нет производных более высокого порядка. Второе уравнение называется уравнением второго порядка, поскольку в него входит вторая производная и нет производных более высокого порядка. Поиск решений различных типов дифференциальных уравнений (функций, удовлетворяющих этим уравнениям) является предметом целых книг и курсов на эту тему. Ниже рассмотрены только самые значительные и наиболее часто применяемые уравнения первого порядка, имеющие непосредственное практическое значение.
Сначала мы рассмотрим несколько уравнений первого порядка с точки зрения полей направления. Затем используем их для описания непрерывно начисляемых сложных процентов и, в заключение, обобщим изученную методику на разнообразные явления роста.
Дифференциальные уравнения и поля направлений
Продемонстрируем концепцию поля направления на нескольких примерах. Рассмотрим дифференциальное уравнение первого порядка
(Н.9)


384
Часть III. Математический анализ
Функция f является решением уравнения (11.9), если величина у удовлетворяет этому уравнению для всех значений х из области определения функции /. С геометрической точки зрения уравнение (11.9) описывает наклон фазовых траекторий, проходящих через точку (х,у). Например, если у = f(x) — решение уравнения (11.9), проходящее через точку (0,2), то наклон графика f в точке (0,2) равен
= 0,2 • 2 = 0,4.
ах
Это можно указать, нарисовав короткий отрезок касательной в точке (0,2), как показано на рис. 11.10, а. На этом рисунке показаны также аналогичные отрезки для точек (—3,1) и (2,3). Предполагая, что график f проходит через все эти три точки, можно построить приблизительный график этой функции, показанный на рис. 11.10, б.
Рис. 11.10. Наклон графика
Если продолжать рисовать отрезки касательных в каждой точке координатной сетки на рис. 11.10 — для такой задачи проще воспользоваться компьютером, чем делать все вручную, — то получится поле направлений. Поле направлений для дифференциального уравнения (11.9), построенное с помощью компьютера, показано на рис. 11.11. В общем случае, поле направлений для уравнения первого порядка можно получить, рисуя отрезки касательных, найденных из уравнения, в каждой точке координатной сетки. При более глубоком рассмотрении этой темы, изучая поля направлений, можно узнать довольно много о характере и поведении фазовых траекторий дифференциальных уравнений первого порядка. Наша тема намного проще.
Задание 11.6.
1. Проведите на рис. 11.10, а отрезки касательных к фазовым траекториям дифференциального уравнения (11.9), проходящим через точки (—3, -1), (0,2) и (2, -3).
2. Постройте на рис. 11.10, б приблизительный график фазовой траектории, проходящей через эти три точки. (Предварительно повторно нарисуйте отрезки касательных.)


Глава 11. Интегрирование
385
Рис. 11.11. Поле направлений
3. 	Сделайте предположение относительно того, какой тип функции из всех элементарных функций, рассмотренных в первых двух главах, может быть решением дифференциального уравнения (11.9). ■
Если вы предположили, что решение уравнения (11.9) — это экспоненциальная функция, то примите поздравления. Покажем теперь, что функция
у = Се°'2х
(11.10)
является решением уравнения (11.9) для любого действительного числа С. (Ниже будет показано, как получить уравнение (11.10) непосредственно из уравнения (11.9).) Для этого подставим функцию у = Се0,2х в уравнение (11.9), чтобы убедится в том, что левая часть равна правой части для всех действительных х.
левая часть :
= 4- (Се0-2*) = О,2Се0’2*; ах ах '
правая часть :
0,2у = 0,2Се°’2х.
Следовательно, уравнение (11.10) является решением уравнения (11.9) для любого действительного числа С. При каких значениях С получатся фазовые траектории, проходящие через точки (0,2) и (0, —2) соответственно? Подставляя координаты каждой точки в уравнение (11.10) и решая его относительно С (задача для самостоятельного решения), получим
у = 2е°'2х и у = -2е°'2х, (П-11)
в чем можно без труда убедиться. Графики уравнений (11.11) показаны на рис. 11.12 и подтверждают результаты, показанные на рис. 11.11,6.
Задание 11.7.
1. 	Постройте на рис. 11.10 приблизительную фазовую траекторию, проходящую через точку (0,3), и фазовую траекторию, проходящую через точку (0, —3).


386
Часть III. Математический анализ
Рис. 11.12. Графики уравнений
у = 2е0,2х и у = —2е0,2х
2. 	Используя графическую утилиту, постройте в одном и том же окне графики функции у = Се0,2х для С = —4, —3, —2, 2, 3, 4. Обратите внимание на то, как эти фазовые траектории согласуются с отрезками касательных в поле направления, показанном на рис. 11.12. в
Как отмечалось выше, построение поля направления вручную — слишком сложная задача для человека. В координатной сетке 20 на 20 понадобится нарисовать 400 отрезков касательных! Для рутинной работы такого типа предназначены компьютеры. В нескольких задачах из практикума 11.3 дана иная интерпретация полей направления.
Повторное рассмотрение задачи непрерывного начисления процентов
Пусть Р — исходная стоимость капитала, а А — стоимость капитала в момент времени t. Вместо того, чтобы рассчитывать текущий капитал через исходный капитал, на который начисляются проценты по заданной ставке, давайте считать, что темп (скорость) прироста капитала в произвольный момент времени t пропорционален его текущей стоимости. Поскольку dA/dt — темп прироста А со временем t, получаем уравнение
dA
-^=гА, А(0) = Р, А, Р > 0, (11.12)
где г — некая константа. Требуется найти функцию А = A(t), которая удовлетворяет этим условиям. Умножая обе части уравнения (11.12) на величину 1/Л, получим
1 dA
A dt ~Г'
Теперь проинтегрируем обе части по t.


Глава 11. Интегрирование
387
In |А| = rt + С; |А| = А, поскольку А > О.
In А = rt 4- С.
Преобразуем последнее уравнение в эквивалентную экспоненциальную форму
А = ert+C = Определение логарифмической функции: у = In аз
тогда и только тогда, когда х = ev.
= ecert. Свойство показательной функции: bmbn = brn+n.
Поскольку А(0) = Р, вычислим значение A(t) = ecert при t = 0 и приравняем его значению Р:
А(0) = eceQ = ес = Р.
Отсюда следует, что ес = Р, и можно переписать функцию А = ecert в виде
А = Pert.
Эта формула для вычисления непрерывно начисляемых сложных процентов совпадает с формулой, полученной в разделе 10.1, и описывает ситуацию, в которой капитал Р инвестируется на t лет при номинальной годовой ставке г с непрерывно начисляемыми сложными процентами.
Закон экспоненциального роста
Вообще говоря, если скорость изменения величины Q со временем пропорциональна самой величине в данный момент и Q(0) = Qq, то, повторив предыдущие рассуждения, придем к следующему выводу.
Закон экспоненциального роста
Если = rQ и Q (0) = Qo, то Q = Qoert, at
где Qo — величина в момент t = 0, г — скорость роста (выраженная через десятичное число), t — время, Q — величина в момент времени t.
Константа г в законе постоянного роста иногда называется постоянной роста или скоростью роста. Последний термин может вводить в заблуждение, поскольку скорость роста величины Q со временем равна dQ/dt, а не г. Следует отметить, что если г < 0, то и dQ/dt < 0 и Q убывает. Этот тип роста называется экспоненциальным спадом.
Если известно, что скорость роста некой величины пропорциональна ей самой, то эта величина показывает экспоненциальный рост. В таких ситуациях вычисления можно выполнять с помощью формулы, приведенной во врезке, не прибегая к решению дифференциального уравнения. Закон экспоненциального роста применим не только к финансовым задачам, требующим вычисления непрерывно начисляемых сложных процентов, но и к задачам, описывающим многие другие процессы и явления, — рост численности населения, радиоактивный распад, истощение природных ресурсов и так далее.


388
Часть III. Математический анализ
Численность населения, радиоактивный распад и скорость обучения
Как показано на рис. 11.13, население планеты достигло одного миллиарда в 1804 году, двух миллиардов — в 1927 году, трех миллиардов — в 1960 году, четырех миллиардов — в 1974 году, пяти миллиардов — в 1987 и шести миллиардов — в 1999 году. Рост численности населения за определенный промежуток времени часто можно приблизительно описать уравнением экспоненциального роста.
Рис. 11.13. Рост населения
планеты
Пример 11.15 (Рост численности населения). Население Индии в 2000 году
(t = 0) составило приблизительно миллиард человек. Пусть величина Р описывает численность населения Индии (в миллиардах) через t лет после 2000 года, которая непрерывно растет на 1,3% в год.
1. Составьте уравнение, описывающее рост численности населения Индии после 2000 года, предполагая, что скорость роста 1,3% остается неизменной.
2. Каким будет предполагаемое население Индии в 2030 году (с точностью до десятой доли миллиарда)?
3. Постройте график уравнения, найденного при решении п. 1 за период с 2000 по 2030 год.
Решение.
1. Применив закон экспоненциального роста, получим
dP
— =0,013Р; Р(0) = 1,0.
Таким образом,
Р = 1,Ое°’013‘. (11.13)
2. Используя уравнение (11.13), можно оценить население Индии в 2030 году (t = 30).
Р = 1,Ое0’013'30 = 1,5 миллиарда человек.
3. 	График показан на рис. 11.14.


Глава 11. Интегрирование
389
Рис. 11.14. Население Индии
Упражнение 11.15.
Каким будет население Индии в 2015 году (с точностью до десятой доли миллиарда), если предположить, что скорость роста останется прежней? ■
Пример 11.16 (Рост численности населения). При какой скорости роста численность населения Канады удвоится через через 100 лет?
Решение. Задача заключается в вычислении константы г при заданных Р = 2Pq и t = = 100:
Р = PQert
2Р0 = Рое1ООг,
2 = е100г,
Возьмем натуральный логарифм от обеих частей и поменяем их местами.
100т = In 2,
In 2
Г~ 100’
w0,0069, или 0,69%.
Упражнение 11.16.
Численность населения Нигерии увеличивается по экспоненциальному закону. Вычислите время удвоения численности населения (с точностью до ближайшего года), если его прирост составляет 2,1% в год. ■
Теперь давайте перейдем к описанию еще одного явления, подчиняющегося закону экспоненциального роста — радиоактивному распаду. В 1946 году Уиллард Либби (Willard Libby) (позже получит Нобелевскую премию в области химии) обнаружил, что концентрация радиоактивного изотопа углерод-14 в тканях животных и растений поддерживается на одном и том же уровне в течение всей жизни организма, и начинает снижаться после его смерти за счет явления радиоактивного распада. При этом скорость уменьшения концентрации изотопа углерод-14 пропорционально ее величине. Следовательно,


390
Часть III. Математический анализ
что указывает на полную применимость закона экспоненциального роста. Было установлено, что скорость распада изотопа углерод-14 равна 0,0001238; таким образом, г = —0,0001238, поскольку распад предполагает отрицательную скорость роста.
Пример 11.17 (Археология). При проведении археологических раскопок была найдена часть человеческой кости. Определите предположительный возраст кости (с точностью до ближайших 100 лет), если концентрация изотопа углерод-14 в кости составляет 10% от исходной величины.
Решение. Используя закон экспоненциального роста
= -0,000123 8Q, Q(0) = Qo,
at
приходим к выводу, что
Q = Q0e-°’0001238t,
и задача сводится к вычислению такого значения t, при котором Q = 0,lQo (поскольку текущая концентрация изотопа углерод-14 составляет 10% от величины Qo, регистрируемой в момент смерти человека). Таким образом,
O,lQo
0,1
1п0,1
t
На рис. 11.15 показано решение примера 11.17 в окне графической утилиты.
= Q0e-°’0001238t;
_ 0,0001238*.
= lne-°’0001238t; 1п0,1
«18 600 лет.
-0,0001238
Рис. 11.15. Функция т/i =
= g—0,0001238s. У2 = Од


Глава 11. Интегрирование
391
Упражнение 11.17.
Оцените возраст кости в примере 11.17 (с точностью до 100 лет), если концентрация изотопов углерод-14 в ней равна 50% от исходного значения. ■
Процесс приобретения определенных навыков, например набора текста или плавания, часто можно описать с помощью математической модели, предполагающей наличие максимально достижимого уровня, скажем М, и существование линейной зависимости между скоростью обучения и разницей между достигнутым у и максимально возможным М уровнями. Формально она записывается как
= к (М - у), у (0) = 0.
Этот тип задач также сводится к закону экспоненциального роста. Прежде всего, умножая обе части первого уравнения на l/(Af — у), получим
1 dy = к М-у dt
а затем проинтегрируем каждую часть по переменной t.
— In |u| = kt + С,
— ]n(M — y) = kt + C,
In (M — y) = —kt — C.
Заменим переменную: и = M — у и du = —dy = = -^dt.
dt
Подставим M — у = и.
Знак абсолютного значения необязателен.
(Почему?)
Приведем последнее уравнение к экспоненциальному виду.
М — у = e~kt-c- М - у = e~ce~kt;
у = М — e~ce~kt.
Теперь положим у(0) = 0. Отсюда следует, что у(0) = М — е~се° = 0.
Решая это уравнение относительно е~с, получим
е~с = М,
и окончательное решение принимает вид
у = М - Me~kt - М(1 - e~kt).


392
Часть III. Математический анализ
Пример 11.18 (Обучение). Оказалось, что расстояние у (в футах), которое может проплыть обучающийся плаванию человек за минуту спустя t часов тренировки, составляет приблизительно
у = 50(1 — e_0,04t).
Какова скорость повышения навыка плавания (с точностью до двух десятичных знаков) будет достигнута через 10 часов тренировок?
Решение.
у = 50- 50e_o,O4t;
y'(t) = 2e_0,04t;
2/(10) = 2е-0,0410 « 1,34 фута за час. ■
Упражнение 11.18.
Чему в примере 11.18 будет равна скорость повышения уровня (с точностью до двух десятичных знаков) через 50 часов тренировки? ■
Сравнительный анализ процессов экспоненциального роста
Графики и уравнения табл. 11.3 представляют наиболее часто применяемые модели экспоненциального роста. Их можно условно разделить на две категории — описывающие процессы ограниченного и неограниченного роста. Для каждой модели указан короткий (далеко неполный) список областей ее практического применения. В них перечислены только наиболее очевидные задачи.
Ответы к упражнениям
11.15. 1,2 миллиарда человек.
11.16. 33 года.
11.17. 5600 лет.
11.18. 0,27 фута/час.
Практикум 11.3
А В задачах 1-8 для каждого дифференциального уравнения вычислите общее или част¬
ное решение.
1.
3.
= 4,16т.
_ ^0,5х
dy „-2
dx
2.
2
X
dx dy dx
— х2 — т; у (0) = 0.
dx
—2хе~х2;у(0) = 3.
6. = ^’У = °'
8. = е*-3; т/(3) = —5.


О с
& 3 И Д
О ю
о
&
&
о
S а
о
8
S о
о я xg 1 о 2
о я ео
S о
£
S
£
О
•
•
•
•
Таблица 11.3. Модели экспоненциального роста
к о
1 w
s 6 § s as
о § И Р
& § &
О О и


394
Часть III. Математический анализ
Б В задачах 9-14 рассматриваются следующие поля направлений.
У У
а) б)
* 9. Какое поле направлений соответствует дифференциальному уравнению dy/dx = = х — 1? Вкратце обоснуйте свой ответ.
*10. Какое поле направлений соответствует дифференциальному уравнению dy/dx — = —xl Вкратце обоснуйте свой ответ.
11. Решите дифференциальное уравнение dy/dx = х — 1 и вычислите частное решение, проходящее через точку (0, —2).
12. Решите дифференциальное уравнение dy/dx = —х и вычислите частное решение, проходящее через точку (0,3).
13. Постройте график частного решения, вычисленного в задаче 11 на соответствующем рисунке, показанном выше.
14. Постройте график частного решения, вычисленного в задаче 12, на соответствующем рисунке, показанном выше.
В задачах 15-20 для каждого дифференциального уравнения вычислите общее или частное решение.
dy о 1С dy с
15- Л =гу- ,б- Л = ~89'
П.^ = -0,5у,у (0) = 100. 18. - 0,1»; у (0) = -2,5.
dx dx
19. — = —8х. 20. — = -St.
dt dt
В задачах 21-28 рассматриваются следующие поля направлений.
4
У
ЧЧ1ЧЧЧЧЧ ЧЧЧЧЧЧЧЧ % Ч Ч Ч % Ч % % чччччччч
чччччччч чччччччч
ч ч
* * * * * *
**********

;*
/ / /
/ »
/ /
* *5
• •
III
•t1
• >
• •
• t
•»
9 9
9 9 9
9 9 9
• •
1 1
t 1
1 1
9 9
• • •
9 9 9
1 I
1 1
1 1
• •
' •
1 1
а)
5
)
1111111111
9999999999
9999999999
9999999999
9999999999
чччччччччч чччччччччч 1ЧЧЧЧЧЧЧЧЧ Ч 11 % % % t % 11
чччччччччч чччччччччч чччччччччч чччччччччч
» » » 1 » » 1 » t »
t t I t t 1 1 > 1 1
б)


Глава 11. Интегрирование
395
* 21. Какое поле направлений соответствует дифференциальному уравнению dy/dx =
= 1 -yl Вкратце обоснуйте свой ответ.
* 22. Какое поле направлений соответствует дифференциальному уравнению dy/dx =
= ?/ + 1? Вкратце обоснуйте свой ответ.
23. Покажите, что у = 1 — Се~х — решение дифференциального уравнения dy/dx = = 1 — у для любого действительного числа С. Вычислите частное решение, проходящее через точку (0,0).
24. Покажите, что у = Сех — 1 — решение дифференциального уравнения dy/dx = = у + 1 для любого действительного числа С. Вычислите частное решение, проходящее через точку (0,0).
25. Постройте график частного решения, найденного в задаче 23, на соответствующем рисунке, показанном выше.
26. Постройте график частного решения, найденного в задаче 24, на соответствующем рисунке, показанном выше.
27. Используя графическую утилиту, постройте графики у = 1 — Се~х для С =
= -2, -1, 1 и 2 для — 5 х < 5, — 5 у < 5. Обратите внимание на то,
как фазовые траектории согласуются с направлениями отрезков касательных в соответствующем поле направления, показанном выше.
28. Используя графическую утилиту, постройте графики у = Се~х — 1 для С =
= —2, —1, 1 и 2 для — 5 х 5, — 5 у < 5. Обратите внимание на то,
как фазовые траектории согласуются с направлениями отрезков касательных в соответствующем поле направления, показанном выше.
В задачах 29-36, используя графическую утилиту, постройте графики для указанных примеров различных типов экспоненциального роста из табл. 11.3.
29. 	Неограниченный рост.
у = 1000e°’°8t,
0 < £ 15,
0 О 3500.
31. Экспоненциальное затухание. р = lOOe-0'05*,
0 < х < 30,
0 < р 100.
33. Ограниченный рост.
N = 100(1 - e_0,05t),
0 t 100,
О < N 100.
30. 	Неограниченный рост.
у = 5250e°’12t,
0 10,
0 О 20000.
32. 	Экспоненциальное затухание. р = 1000е_о,О8х,
0 х 40,
0 О юоо.
34. 	Ограниченный рост.
N = 1000(1 - е_0’07‘),
0 t < 70,
0 1000.


396
Часть III. Математический анализ
35. Логистический рост.
1000
36. Логистический рост.
400
N = 1 + 999e-°-4t ’ _ 1 + 99e-°’4t ’
0 < t < 40; 0 s? t < 30;
0 < N 1000. 0 < N 400.
*37. Покажите, что максимальное значение скорости логистического роста, dy/dt — = ку(М — у), соответствует значению у = М/2.
* 38. Вычислите значение t, при котором значение логистической функции
М
У ~ 1 + ce~kMt
равно 7И/2.
*39. WWW Пусть Q(t) обозначает численность населения планеты в момент времени t. В 1967 году население планеты насчитывало 3,5 миллиарда человек и росло оно со скоростью 2,0% в год, а в 1999 году оно насчитывало 6 миллиардов человек и росло со скоростью 1,3% в год. В каком году, 1967 или 1999, значение dQ/dt (скорость роста Q со временем t) было больше? Аргументируйте свой ответ.
* 40. Вернемся к задаче 39. Объясните, почему функция численности населения планеты Q(t) не удовлетворяет закону экспоненциального роста.
Применение математики
сумму А, лежащую
Экономика и бизнес
41. Непрерывно начисляемые сложные проценты. Вычислите на счете через t лет, если
dA
— = 0,08А и А (0) = 1000.
dt
42. Непрерывно начисляемые сложные проценты. Вычислите на счете через t лет, если
dA
— = 0,12А и А (0) = 5250.
dt
43. Непрерывно начисляемые сложные проценты. Вычислите на счете через t лет, если
dA
— = г А А (0) = 8000 А (2) = 9020.
44. Непрерывно начисляемые сложные проценты. Вычислите сумму А, лежащую на счете через t лет, если
dA
~—=тА А (0) = 5000 А (2) = 7460.
dt
сумму А, лежащую
сумму А, лежащую


Глава 11. Интегрирование
397
45. Зависимость цены от спроса. Предельная цена dp/dx при спросе х единиц продукции в неделю пропорциональна цене р. При цене 100 долл, недельный спрос отсутствует (р(0) = 100), а при цене 77,88 долл, недельный спрос составляет пять единиц продукции (р(5) = 77,88).
а) Составьте уравнение зависимости цены от спроса.
б) Какой будет цена при спросе 10 единиц продукции в неделю?
в) Постройте график уравнения зависимости цены от спроса на отрезке 0 х 25.
46. Зависимость цены от предложения. Предельная цена dp/dx при предложении х единиц продукции в неделю пропорциональна цене р. При цене 10 долл, недельное предложение отсутствует (р(0) = 10), а при цене 12,84 долл, недельное предложение составляет 50 единиц продукции (р(50) = 12,84).
а) Составьте уравнение зависимости цены от предложения.
б) Какой будет цена при предложении 10 единиц продукции в неделю?
в) Постройте график уравнения зависимости цены от предложения на отрезке 0 х 250.
47. Реклама. С помощью телевизионной рекламы производитель пытается представить новый товар как можно большему числу покупателей. Предположим, что скорость ознакомления покупателей с новым товаром пропорциональна количеству людей, которые ранее ничего не знали о рекламируемом товаре из L просмотревших ее. В начале рекламной кампании товар был неизвестен ни одному покупателю, а через 10 дней о нем знало 40% из L просмотревших телевизионную рекламу. Математически условия задачи выражаются следующей формулой.
dN
— = fc (L - N), N (0) = 0, N (10) = 0,4L. dt
а) Решите дифференциальное уравнение.
б) Какой процент из L телезрителей будет оповещен о новом товаре через пять дней после начала кампании?
в) Сколько понадобится дней, чтобы ознакомить с новым товаром 80% из L телезрителей?
г) Постройте график решения п. а ддя 0 < t < 90.
48. Реклама. Предположим, что дифференциальное уравнение из задачи 47 имеет вид
dN
— = k(L-N), N (0) = 0, N (10) = 0,lL. dt
*а) Дайте словесную интерпретацию выражению Af(10) = 0,lL.
б) Решите дифференциальное уравнение.
в) Сколько понадобится дней, чтобы оповестить 50% из L телезрителей?
г) Постройте график решения п. а для 0 < t С 300.


398
Часть III. Математический анализ
Биологические науки
49. Биология. В относительно чистом объеме воды интенсивность света снижается согласно закону
^ = ~W, 7(0) =/о,
где I — интенсивность света на расстоянии х футов от поверхности. В Саргассовом море, в районе островов Вест-Индии к = 0,00942. Выразите функцию I в зависимости от переменной х и глубины, на которой интенсивность света вполовину меньше, чем на поверхности.
50. Артериальное давление. При определенных условиях давление крови Р в самой большой артерии человеческого тела (аорте) между двумя ударами пульса меняется со временем t согласно закону
dP
-£ = -аР, PW=Po,
где а — постоянная. Вычислите функцию Р = P(t), удовлетворяющую обоим условиям.
51. 	Концентрация препарата. Пациенту была сделана инъекция лекарственного препарата. Скорость снижения его концентрации в организме Q пропорциональная самой концентрации. Пусть скорость уменьшения концентрации лекарственного препарата составляет 4% в час. Таким образом,
dQ dt
= —0,04Q;
где t — время в часах.
а) Объем введенного препарата равен 3 мл (Q(0) = 3). Вычислите функцию Q = Q(t), удовлетворяющую обоим условиям.
б) Сколько миллилитров препарата (с точностью до двух десятичных знаков) будет находиться в организме через 10 часов?
в) Сколько понадобится часов (с точностью до двух десятичных знаков), чтобы в организме остался только 1 мл препарата?
г) Постройте график решения п. а.
52. 	Простая эпидемия. Рассмотрим обособленную общину из 1000 человек. Один из ее членов по возвращению домой из другой общины заболел гриппом. Предположим, что в родном сообществе никто не был заражен гриппом и все люди в нем восприимчивы к этому заболеванию. В одной из математических моделей эпидемии гриппа предполагается, что болезнь распространяется со скоростью, прямо пропорциональной количеству зараженных N и количеству тех, кто еще не заразился — в данном случае, 1000 — N. Эта модель представлена следующей математической формулой.
— = fc7V(1000 - N), N (0) = 1. dt


Глава 11. Интегрирование
399
Здесь N — количество людей, зараженных гриппом, через t дней. Для к = 0,0004 можно показать, что N(t) равно
= 1000
W 1 + 999е-°’4*’
а) Сколько людей будет заражено гриппом через 10 дней? Через 20 дней?
б) Сколько понадобится дней, чтобы гриппом заразилась половина общины?
в) Вычислите предел limt-^oo 7V(t).
г) Постройте график функции N = N(t) для 0 < t < 30.
53. WWW Авария на АЭС. Одним из опаснейших изотопов, выброшенных в окружающую среду в результате аварии на Чернобыльской АЭС в 1986 году, был цезий-137. Найдите скоростью распада этого изотопа, если три года спустя в экосистеме осталось 93,3% цезия-137, выброшенного при аварии.
54. WWW Инсектициды. Во многих странах использование инсектицида ДДТ запрещено из-за его длительного неблагоприятного воздействия. Через пять лет после того, как в определенной стране прекратилось использование ДДТ, его количество в экосистеме снизилось до 75% от присутствовавшего в момент введения запрета. Вычислите скорость снижения количества ДДТ.
Социальные науки
55. Археология. В древней могиле обнаружен череп. Установлено, что в нем содержится 5% от исходного количества изотопа углерода-14. Оцените возраст черепа. (См. пример 11.17.)
56. Обучение. Установлено, что количество слов в минуту 7V, которое обучающийся машинописи человек может набрать в минуту через t часов практических занятий, приблизительно описывается следующей формулой.
N = 100(1 - e_0,02t).
Характерный график такой функции можно найти в табл. 11.3 (ограниченный рост). Какой будет скорость повышения уровня квалификации через 10 часов практических занятий? Через 49 часов практических занятий?
57. Поведение небольших социальных групп. При изучении поведения людей в небольших группах социологи Стефан (Stephan) и Мишлер (Mischler) обнаружили, что, если разместить членов дискуссионной группы из 10 человек согласно количеству их выступлений, то, функция N(k), описывающая порядок выступления к-ro человека, приблизительно задается следующей формулой.
AT(fc) = Ю^Ю.
Здесь Ni — количество выступлений первого участника. Оцените, сколько раз шестой участник принимал участие в дискуссии, если в определенной дискуссионной группе из 10 человек N± = 180. Сколько раз выступал десятый участник?


400
Часть III. Математический анализ
58. Восприятие. Один из старейших законов математической психологии — это закон Вебера-Фечнера (Weber-Fechner), открытый в середине девятнадцатого столетия. Он описывает чувственное восприятие человеком раздражителей различной интенсивности, включая нагрузку, звук, свет, шок, вкус и т.д. В одной из формулировок закона утверждается, что скорость изменения воспринимаемого раздражения S обратно пропорциональна интенсивности раздражителя R. Следовательно,
dS__ к dR ~ R'
где к — постоянная. Если считать, что Rq является пороговым уровнем, при котором все еще можно ощущать раздражение (минимально определяемое значение громкости звука, интенсивности света, силового воздействия и т.д.), то можно записать
ЭД) = 0.
Вычислите функцию S в зависимости от R, удовлетворяющую приведенным выше условиям.
59. Распространение слухов. Группа из 400 родителей, родственников и друзей с волнением ожидает в аэропорту Кеннеди чартерный рейс, которым прилетают студенты, проживавшие в Европе в течение всего учебного года. Самолет опаздывает из-за плохих погодных условий. Одному из родителей показалось, будто он услышал, что система радиосвязи самолета вышла из строя, и он поделился этой новостью с несколькими друзьями, которые в свою очередь передали ее своим друзьям и т. д. Социологи пристально изучили этот процесс и обнаружили, что слухи распространяются со скоростью, прямо пропорциональной количеству тех, кто о них слышал, х, и количеству тех, кто о них не слышал, Р — х, где Р — общее количество людей. Рассматриваемая ситуация описывается следующей математической моделью (в данном случае Р = 400).
= 0,001а; (400 - х); х(0) = 1.
dt
Здесь t — время (в минутах). Можно показать, что
1 + 399е-°’4‘'
Характерный график такой функции можно найти в табл. 11.3 (логистический рост).
а) Сколько человек услышат слух через 5 минут? Через 20 минут?
б) Вычислите предел lim^oo a;(t).
в) Постройте график функции x(t) для 0 t 30.
60. Распространение слухов. Сколько в задаче 59 понадобится времени (с точностью до ближайшей минуты), чтобы пущенный кем-то слух дошел до половины группы, состоящей из 400 человек?


Глава 11. Интегрирование
401
11.4. 	Геометрическая и численная интерпретации определенных интегралов
■ Площадь под графиком функции
■ Площадь под графиком, скорость и расстояние
■ Площадь под графиком и полное изменение функции
Первые три раздела этой главы были посвящены неопределенному интегралу — множеству всех первообразных данной функции. В этом и следующем разделах будет введена связанная с этим понятием концепция определенного интеграла. В этом разделе будет использоваться интуитивный, неформальный подход. В следующем разделе данная концепция будет рассмотрена более строго.
Чтобы ввести понятие определенного интеграла, рассмотрим площадь, ограниченную графиком функции /, осью х и вертикальными прямыми х = а и х = Ь, как показано на рис. 11.16. Если график функции /(х) нарисован в области положительных значений, то он задает верхнюю границу фигуры, расположенной под ним и ограниченной линиями х = а и х = Ь.
Рис. 11.16. Площадь фигуры под кривой у = f(x)
Операция вычисления площади окрашенной серым цветом области на рис. 11.16 обо значается символом определенного интеграла.
ъ
площадь под кривой\
а
J
Точное определение этого символа будет дано в разделе 11.5, в котором будет также показано, как определенный интеграл функции на интервале [а, 6] связан с неопределенным интегралом (первообразной) функции. Для простоты вначале функция f(x) будет ограничена только положительными значениями — вскоре это ограничение будет снято. Предполагается также, что все рассматриваемые функции непрерывны на любом рассматриваемом интервале.
Удивительно, но помимо расчета площади, с помощью определенных интегралов можно вычислять полное изменение функции на интервале, исследуя ее производную. Например, по заданной функции скорости (производной) или таблице ее значений можно


402
Часть III. Математический анализ
вычислить расстояние, которое пролетел стальной шарик, брошенный с моста, в течение определенного интервала времени, или же дополнительные затраты, связанные с увеличением объема производства.
Площадь под графиком функции
Как же все-таки вычислить площадь окрашенной серым цветом области на рис. 11.16? Иначе говоря, как вычислить площадь фигуры, ограниченной графиком функции /(х) = = 0,25х2 + 1, осью х и вертикальными прямыми х = 1 и х = 5? (Это громоздкое выражение, как правило, сокращается до: “площадь фигуры, расположенной под графиком функции /(х) = 0,25х2 4-1отх = 1дож = 5”.) В этой ситуации нельзя применять стандартные геометрические формулы вычисления площади, однако можно косвенно воспользоваться формулой определения площади прямоугольника. Чтобы увидеть, как это делается, рассмотрим метод приближенного вычисления площади фигуры, расположенной под кривой, разбивая ее на прямоугольники. Этот метод позволяет достичь любого уровня точности, но полученная величина все равно будет приближенной. Для начала разделим интервал [1,5] на оси х на четыре равные части.
(Обычно длину подынтервалов обозначают Дх. Это выражение читается как “дельта икс”. Знак Д обозначает греческую прописную букву “дельта”.) Затем на каждом подынтервале построим прямоугольники, высота которых равна значению функции в крайней слева точке подынтервала (рис. 11.18).
Рис. 11.17. Чему равна площадь окрашенной серым цветом области?
Рис. 11.18. Левосторонние прямоугольники
Суммируя площади прямоугольников на рис. 11.18, получим левостороннюю сумму (left sum) четырех прямоугольников, которая обозначается £4 и равна
L4 = /(1) ■ 1 + /(2) ■ 1 + /(3) • 1 + /(4) • 1 =
= 1,25 + 2,00 + 3,25 + 5 = 11,5.


Глава 11. Интегрирование
403
Из рис. 11.18 ясно, что, поскольку /(ж) — возрастающая функция, в левосторонней сумме Z/4 площадь недооценивается. Таким образом,
5
11,5 = Z/4 < j (0,25я2 + 1) dx = площадь фигуры.
1
Задание 11.8.
Переоценивалась или недооценивалась бы реальная площадь фигуры, расположенной под кривой, в левосторонней сумме £4, если бы функция /(ж) убывала на интервале [1,5]? Объясните свой ответ. ■
Предположим теперь, что для вычисления высоты прямоугольников, построенных на подынтервалах, выбиралась крайняя справа точка каждого подынтервала. Накладывая этот результат поверх рис. 11.18, получим рис. 11.19.
Рис. 11.19. Левосторонние и правосторонние прямоугольники
Суммируя площади правосторонних прямоугольников на рис. 11.19, получим правостороннюю сумму (right sum) четырех прямоугольников, обозначаемую Я4, которая равна
Я4 = /(2) • 1 + /(3) • 1 + /(4) • 1 + /(5) • 1 =
= 2,00 + 3,25 + 5,00 + 7,25 = 17,5.
(Сравните величины Я4 и L4 и обратите внимание на то, что значение R4 можно получить из числа £4, удалив площадь одного прямоугольника и добавив площадь другого.) Из рис. 11.19 ясно, что, поскольку функция /(х) — убывающая, в правосторонней сумме R4 площадь переоценивается, откуда можно сделать вывод, что реальная площадь находится между 11,5 и 17,5. Иначе говоря,
5
11,5 = L4 < j (0,25а;2 + 1) dx < R4 = 17,5.
1
(11.14)


404
Часть III. Математический анализ
Поскольку реальная площадь лежит между оценочными значениями справа и слева, можно ожидать, что их среднее значение ближе к действительной величине.
Задание 11.9.
Переоценивалась бы или недооценивалась реальная площадь под кривой в правосторонней сумме Т?4, если бы функция /(ж) убывала на интервале [1,5]? Объясните свой ответ.и
Первое приближение к значению площади фигуры, расположенной под кривой, вычисленной по формуле (11.14), является довольно грубым, однако описанный здесь метод можно развить, увеличивая точность получаемого результата путем деления интервала [1,5] на все большее количество подынтервалов. Конечно, такая задача слишком громоздка для ручных расчетов, но с ней прекрасно справляются компьютеры.1 На рис. 11.20 показана аппроксимация фигуры левосторонними и правосторонними прямоугольниками, разбивающих ее на 16 равных частей.
Рис. 11.20. Аппроксимация фигуры прямоугольниками
В этом случае
Дх = = 0,25;
L16 = f (1) • Дж + f (1,25) • Дж + • • • + / (4,75) • Дж = 13,59; 7?i6 = f (1,25) • Дж + f (1,50) • Дж + ••• + / (5) • Дж = 15,09.
Таким образом, теперь известно, что площадь фигуры, расположенной под кривой, находится между 13,59 и 15,09.
5
(И.15)
1
Графические утилиты позволяют выполнять подобные вычисления (см. предисловие).


Глава 11. Интегрирование
405
При разбиении на 100 равных частей компьютерные расчеты дают следующие результаты.
5
14,214 = Lioo < j (0,25х2 + 1) dx < R100 = 15,454,
1
(11.16)
среднее =
£ioo + Яюо
14,214 + 14,454
= 14,334.
2
2
Чтобы оценить пригодность выбранного метода аппроксимации для практического использования нужно рассчитать его погрешность. Погрешностью аппроксимации будем называть абсолютное значение разности между аппроксимированным и точным значениями.
Задание 11.10.
Если а и b — координаты двух точек на действительной числовой оси, расстояние между этими двумя точками равно \Ь — а|. При оценке погрешности аппроксимации будут использованы следующие неравенства, определяющие соотношения расстояний на числовой оси.
1. Если х лежит между а и b на числовой оси, то
|ж — а| \Ь — а| и |ж — Ь\ < \Ь — а|.
2. Если А = то
I® - Л| с | |Ь - а|.
Дайте словесную и геометрическую интерпретацию каждого из этих неравенств. ■
Функция является монотонной на интервале [а, 6], если она либо возрастает на [а, Ь], либо убывает на [а, Ь]. Следующее примечание, касающееся монотонных функций, является основой для оценки погрешности вычисления площади с помощью левосторонней или правосторонней суммы.
Если f — монотонная функция, то площадь фигуры под графиком f(x) всегда меньше правосторонней суммы Ln и левосторонней суммы Rn для любого целого числа п.
Рассмотрим положительную монотонную функцию?/ = /(ж), показанную на рис. 11.21. Если jk f (я) dx — реальное значение площади под графиком функции у = f(x) от х = а до х = Ь, то эта площадь лежит между значениями Ьпн Rn. Таким образом, при аппроксимации этой площади с помощью величин Ln или Rn возникает погрешность, которая меньше абсолютного значения разности между левосторонней и правосторонней суммами \Rn — Ln\. Эта разность в точности равна сумме площадей белых прямоугольников, показанных на рис. 11.21.
Таким образом,
погрешность < |Лп - Ьп| = I/ (6) - f («)| &х = \f (5) - f (а)| -— п
Если для аппроксимации используется среднее значение левосторонней и правосторонней суммы, предел погрешности уменьшается вдвое.


406
Часть III. Математический анализ
Рис. 11.21. Разность площадей \Rn - Ln\ = \f(b) — f(a) \ Ьх
Пределы погрешностей для левосторонней, правосторонней суммы и их среднего значения (для монотонных функций)
Если функция f(x) монотонна на интервале [а, Ь] и
ь
I = / (я) dx,
а
Ln — левосторонняя сумма,
Rn — правосторонняя сумма,
д Ln
Ап~ 2 ’
то справедливы следующие пределы погрешностей:
п
\1-Ап\<\ЦЬ)-Ца)\Ь-^.
Эти формулы не только позволяют оценивать погрешности определенных аппроксимаций, Ln, Rn или Ап, но, что еще важнее, с их помощью можно узнать, насколько большим должно быть значение п, чтобы погрешность была меньше определенной величины.
Пример 11.19 (Приближенное вычисление площади). Задана функция /(х) = 9 — — 0,25х2. Вычислите приближенную площадь фигуры, расположенной под кривой у = = /(х) от х = 2 до х = 5.
1. Построим график функции на интервале [0,6], затем нарисуем левосторонние и правосторонние прямоугольники на интервале [2,5] для п = 6.
2. Вычислим величины Lg, Rq и Aq9 а затем определим погрешности для каждой из этих величин.


Глава 11. Интегрирование
407
3. 	Насколько большим нужно выбрать п для вычисления сумм Ln, Rn и АП9 чтобы приближенное значение (9 — 0,25ж2) dx находилось в пределах 0,05 от истинного значения?
Решение.
1. 	Дж = 0,5.
2. 	L6 = f (2) • Дж + f (2,5) • Дж + / (3) • Дж + / (3,5) • Дж + / (4) • Дж + + f (4,5) • Дж = 18,53;
RQ = f (2,5) • Дж + f (3) • Дж + f (3,5) • Дж + f (4) • Дж +
+ f (4,5) • Дж + f (5) • Дж = 15,91;
= U + R. = пл2
Оценки погрешностей для сумм Lq и Rq выглядят следующим образом.
погрешность \f (5) - / (2)| = |2,75 - 8| • 0,5 = 2,625.
6
Оценка погрешности для величины имеет следующий вид.
погрешность <
2,625
2
= 1,3125.
3. 	Для сумм Ln и Rn найдем такое п, чтобы погрешность 0,05.
^0,05;
|2,75 - 8| - 0,05;
п
15,75 0,05п;
п
15,75
0,05
= 315.
Найдем такое число п, чтобы погрешность суммы Ап не превышала 0,05.
1/(6)-/И ^0,05;
|2,75 - 8| 0,05;
2п


408
Часть III. Математический анализ
7,875 0,05п;
п
7,875
0,05
= 157,5;
п 158. Округляем до ближайшего целого.
Упражнение 11.19.
Задана функция f(x) = 8 — 0,5ж2. Вычислите приближенную площадь фигуры, расположенной под кривой у = f(x) от х = 1 до х = 3.
1. Постройте график функции на интервале [0,4]. Затем нарисуйте левосторонние и правосторонние прямоугольники на интервале [1,3] для п = 4.
2. Вычислите суммы Lq, Rq и Aq, а затем оцените погрешности для каждой из этих величин.
3. Насколько большим нужно выбрать п для вычисления сумм Ln9 Rn и Ап, чтобы
приблизительное значение (8 — 0,5ж2) dx находилось в пределах 0,5 от истинного значения? I
Если функция f не монотонна, площадь может и не лежать между левосторонней и правосторонней суммами, и тогда оценки погрешности, рассмотренные выше, нельзя применять на всем интервале. Однако, конечно же, интервал [а, Ь] можно разделить на подынтервалы, на каждом из которых функция f будет монотонной, а затем выполнить описанные выше действия на каждом из них (рис. 11.22).
До сих пор в рассуждениях предполагалось, что график у = /(х) находится над осью х, т.е. функция f(x) положительна на интервале [а, Ь]. Если часть (или весь) график находится под осью х, то для некоторых (или для всех) значений х, функция f(x) будет отрицательной, а величина /(ж) Ах будет отрицательной площадью прямоугольника, лежащего под осью х (рис. 11.23). В этом случае левосторонняя и правосторонняя суммы, Ln и Rn, будут суммами площадей прямоугольников, расположенных над осью х и площадей прямоугольников, расположенных под осью х, взятых со знаком минус. Как правило, такие площади называются площадями со знаком, поскольку положительные величины соответствуют площадям, а отрицательные величины соответствуют площадям со знаком минус.
Рис. 11.22. Немонотонная функция
Рис. 11.23. Площади со знаком


Глава 11. Интегрирование
409
Все эти наблюдения приводят к следующей расширенной интерпретации знака определенного интеграла.
Знак определенного интеграла для функций с отрицательными значениями
Если функция /(ж) положительна для некоторых значений х на [а, Ь] и отрицательна для остальных значений, то знак определенного интеграла
ь
f (х) dx
а
обозначает совокупную сумму площадей фигур, расположенных между графиком у = — f(x) и осью х, взятых со знаком, где площади над осью х считаются положительными, а площади под осью х считаются отрицательными (рис. 11.24, где А и В — действительные площади указанных областей).
Рис. 11.24. Интеграл J** f (х) dx =
= -А + В
Если функция f(x) монотонна и принимает как отрицательные, так и положительные значения на интервале [а, Ь], как показано на рис. 11.23 и 11.24, процесс аппроксимации интеграла J** / (я) dx с помощью сумм Ln, Rn и Ап, включая применение соответствующих формул вычисления погрешности, остается таким же, как и в случае, когда f(x) ограничивается только положительными значениями.
Площадь под графиком, скорость и расстояние
Обратим теперь внимание на, казалось бы, не связанные между собой задачи, в которых рассчитываются расстояние, скорость и время. В главе 8 сначала было введено понятие средней скорости:
Пройденное расстояние
Средняя скорость = — , (I l.17)
Затраченное время


410
Часть III. Математический анализ
а затем была определена концепция мгновенной скорости как предела отношения приращений.
ds s(t + h) — s (t)
—- = lim =
dt h,—>o h
s(t + At) - s(t)
= lim , В отношении приращении вместо величины h
At часто используется обозначение At.
Здесь s — положение движущегося объекта в момент времени t. Теперь проанализируем процесс в обратном порядке, т.е. сначала рассмотрим функцию скорости либо в виде уравнения, либо в виде табличных значений, а затем вычислим расстояние. За основу возьмем уравнение (11.17), переписанное в следующем виде.
Расстояние = Скорость • Время. (11.18)
Чтобы сделать дальнейшее описание понятнее, рассмотрим конкретные примеры.
Если пренебречь сопротивлением воздуха, то мгновенная скорость стального шарика, брошенного с моста (рис. 11.25), описывается уравнением
r(t) = 32t,
где r(t) — скорость в футах в секунду спустя t секунд. (Следует отметить, что из-за гравитации скорость, с которой падает шарик, растет со временем.) Какое расстояние пролетит шарик между первой и четвертой секундами? Чтобы ответить на этот вопрос, рассмотрим площадь под кривой r(t) = 32t от t = 1 до t = 4. Как получить расстояние из площади? Чтобы связать эти величины, разделим интервал [1,4] на три равные части и оценим площадь фигуры, расположенной под кривой, используя суммы L$ и 7?з, как показано на рис. 11.26.
Площадь первого левостороннего прямоугольника = r(l)At.
С одной стороны,
r(l)At = Скорость в конце первой секунды • 1 с =
= Расстояние, пройденное с момента t = 1 до момента t = 2
при постоянной скорости г(1).
Поскольку функция r(t) на интервале [1,2] растет, то значение г(1) — это минимальная скорость на этом интервале. Следовательно, величина r(l)At недооценивает реальное расстояние, пройденное стальным шариком с момента t = 1 до момента t = 2.
Площадь первого правостороннего прямоугольника = г(2) At.
С другой стороны
г(2) At = Скорость в конце второй секунды • 1 с =
= Расстояние, пройденное с момента t = 1 до момента t = 2
при постоянной скорости г(2).


Глава 11. Интегрирование
411
Рис. 11.25. Стальной шарик, падающий с моста
w| 1 L J Ч Э
Рис. 11.26. Разбиение отрезка с шагом Дж = 1
Поскольку функция r(t) на интервале [1,2] растет, то величина г(1) — это максимальная скорость на этом интервале. Следовательно, величина г(2)Д£ переоценивает реальное расстояние, пройденное стальным шариком с момента t = 1 до момента t = 2.
Аналогичный анализ применим и ко второму, и к третьему прямоугольнику, поэтому можно сделать вывод, что
Расстояние, пройденное
с момента t = 1 до момента t = 4 Повторяя проделанное для произвольного числа п, можно записать
Расстояние, пройденное
с момента t = 1 до момента t = 4
Это выражение означает, что реальная площадь фигуры, расположенной под кривой функции скорости r(t) = 32t от t = 1 до t = 4, является точным расстоянием, которое стальной шарик пролетает с момента t = 1 до момента t = 4, т.е.
4
г (t) dt =
1
Расстояние, пройденное с момента t = 1 до момента t =


412
Часть III. Математический анализ
Площадь под графиком, скорость и расстояние
Если г = r(t) — положительная функция скорости объекта, движущегося по кривой, то
ь
Результирующее расстояние, пройденное с момента t = а до момента t = b
а
Полное изменение положения
с момента t = а до момента t = b
Пример 11.20 (Площадь под графиком, скорость и расстояние).
1. Используя функцию скорости r(t) = 32t, рассмотренную выше, оцените расстояние, которое стальной шарик пролетит с момента t = 1 до момента t = 4, используя Aq. Вычислите оценку погрешности для этой суммы.
2. Каким должно быть число п, чтобы погрешность суммы Ап не превышала 0,5 фута?
Решение.
1. At =
4-1
6
= 0,5;
L6 = г (1) At + г (1,5) At + г (2) At + г (2,5) At + г (3) At + г (3,5) At = 216;
R6 = г (1,5) At + г (2) At + г (2,5) At + г (3) At + г (3,5) At + г (4) At = 264;
216 + 264
2
= 240 футов.
Приблизительное расстояние, пройденное с момента t = 1 до момента t = 4.
Погрешность < \г (4) — г (1)| = 24 фута.
2 • 6 Таким образом,
Расстояние, пройденное с момента t = 1 до момента t =
г (t) dt = 240 ± 24 фута.
(Примечание. Выражение J* г (t) dt = 240 ± 24 фута — общепринятый и удобный способ представления выражения 240 — 40 f (t) dt 240 + 24, и мы будем придерживаться его в дальнейшем.)
2. Решим неравенство для оценки погрешности.
г (4)-4(1)|
144
п
^0,5;
^0,5;
п 288.
Упражнение 11.20.
1. Используя функцию скорости r(t) = 32t, оцените расстояние, которое стальной шарик пролетит с момента t = 2 до момента t = 5, используя сумму Л6. Вычислите оценку погрешности для этой суммы.
^6 =
b — а
п


Глава 11. Интегрирование
413
2. Каким должно быть число п, чтобы погрешность при использовании Ап не превышала один фут? ■
Площадь под графиком и полное изменение функции
Напомним (см. главу 8), что предельные затраты (доход или прибыль) — это мгновенная скорость изменения затрат (дохода или прибыли) в расчете на единицу продукции при заданном объеме производства. Рассмотрим на наглядных примерах, как связаны между собой предельные затраты, изменение общих затрат и площадь фигуры под кривой соответствующей функции.
Предположим, некая компания во Флориде строит скоростные моторные катеры. Предельные затраты при различных объемах производства даны в табл. 11.4, где х — количество катеров, построенных за месяц, а предельные затраты С'(х) выражены в тысячах долларов.
Таблица 11.4. Предельные затраты на постройку катеров
X, шт
5
10
15
20
25
С"(х), тыс. долл.
24
20
17
15
14
Интересно было бы оценить дополнительные затраты (изменение общих затрат) при переходе с объема производства, равного пяти катерам к объему, равному 25 катерам в месяц. Для этого построим график на основе значений в табл. 11.4, а также изобразим на нем правосторонние и левосторонние прямоугольники, как показано на рис. 11.27.
Рис. 11.27. Разбиение отрезка с шагом Дж = 5
Предположим, что, как указано на рисунке, непрерывно убывающая кривая, описывающая соответствующую функцию предельных затрат, проходит через каждую точку в табл. 11.4, но уравнение этой кривой неизвестно. (Такая ситуация в реальных практических задачах встречается довольно часто.) Тем не менее все-таки можно оценить полное


414
Часть III. Математический анализ
изменение затрат, повторяя действия, равнозначные выполняемым выше при вычислении расстояния по заданной скорости.
Площадь первого левостороннего прямоугольника = C,(5)Arc.
С одной стороны,
(Приблизительные затраты на строительство\ следующего катера при объеме производства I • 5 =
5 катеров /
= Приблизительные дополнительные затраты на увеличение объема производства с 5 до 10 катеров в месяц.
Поскольку функция С'(х) убывает на интервале [5,10], значение С"(5) — это максимальная скорость на этом интервале. Следовательно, величина С" (5) Ах переоценивает дополнительные затраты на увеличение производства с 5 до 10 катеров в месяц.
Площадь первого правостороннего прямоугольника = С"(10)Ая.
С другой стороны,
(Приблизительные затраты на строительство\ следующего катера при объеме производства • 5 = 10 катеров у
= Приблизительные дополнительные затраты на увеличение объема производства с 5 до 10 катеров в месяц.
Поскольку функция С'(т) убывает на интервале [5,10], значение С"(5)— это минимальная скорость на этом интервале. Следовательно, величина С" (10) Дж недооценивает дополнительные затраты на увеличение производства с 5 до 10 катеров в месяц.
Аналогичный анализ применим и ко второму, третьему и четвертому прямоугольнику, поэтому можно сделать вывод, что
< /Дополнительные затраты на увеличение объема\ <
4 \ производства с 5 до 25 катеров в месяц J 4‘
Это выражение показывает, что реальная площадь фигуры, расположенной под графиком функции предельных затрат у = С'(х) соответствует дополнительным затратам на увеличение объема производства с 5 до 25 катеров в месяц. Следовательно,
25
С' (х) dx — (Д°полнительные затРаты на увеличение объема\ ' у производства с 5 до 25 катеров в месяц у
5


Глава 11. Интегрирование
415
Площадь под графиком и полное изменение функции
Если у = F'(x) — функция скорости (производная), то совокупная сумма площадей фигуры, расположенной между графиком у = F'(x) и осью х от х = а до х = Ь, взятых со знаком, соответствует полному результирующему изменению F(x) от х = а до х = Ь. В строгом математическом виде это утверждение записывается следующим образом.
ь
j F1 (х) dx =
Полное изменение функции
F (х) от х = а до х = b
а
Неформально, определенный интеграл дает возможность вычислить полное изменение функции по скорости ее изменения. Приведенные выше рассуждения подводят к ключевому пункту математики — основной теореме интегрального исчисления, которая будет рассмотрена в разделе 11.5.
Пример 11.21 (Изменение затрат и площадь фигуры под графиком функции).
Вернитесь к табл. 11.4 и рис. 11.25 и, используя сумму Л4, оцените дополнительные затраты (общее изменение затрат) при переходе с объема производства, равного 5 катерам, к объему, равному 25 катерам в месяц. Вычислите погрешность вычислений.
Решение.
^х = 5,
Z/4 = С' (5) Дх + С1 (10) Дх + С" (15) Дх + С' (20) Дх = 380 тыс. долл. Переоценка = С" (10) Дх + С' (15) Дх + С' (20) Дх + С' (25) Дх = 330 тыс. долл. Недооценка л 380 + 330 осс
А4 = = 355 тыс. долл.
Оценка погрешности суммы А4 выглядит следующим образом.
25 — 5
Погрешность < \(У (5) — С' (25)| = 25 тыс. долл.
Таким образом, дополнительные затраты (общее изменение затрат) при переходе с объема производства 5 катеров к объему производства 25 катеров в месяц составляют
25
j С (х) dx = 355 000 ± 25 000 долл.
5 ■
Упражнение 11.21.
Вернитесь к табл. 11.4 и рис. 11.25 и, используя сумму Л2, оцените дополнительные затраты (общее изменение затрат) при переходе с объема производства 10 катеров к объему производства 20 катеров в месяц. Определите погрешность вычислений. ■


416
Часть III. Математический анализ
Ответы к упражнениям
11.19. 1) Дх = 0,5.
2) = 12,625; R4 = 10,625; А4 = 11,625; погрешность для L4 и R4 равна 2, предел погрешности для А4 равен 1.
3) п > 16 для Ln и Rn, п> 8 для Ап.
Расстояние, пройденное
с момента t = 2 до момента t = 5
2) п 144.
Дополнительные затраты на увеличение
производства с 10 до 20 катеров в месяц
j = 172 500 ± 12 500 долл.
Практикум 11.4
А Задачи 1-10 связаны с оценкой площади фигуры, расположенной под кривыми, на рис. 11.28, а-г от х — 1 до х — 4. В каждом случае разделите интервал на три равных подынтервала.
1. Постройте левосторонние и правосторонние прямоугольники на рис. а и б.
2. Постройте левосторонние и правосторонние прямоугольники на рис. виг.
3. Используя результаты задачи 1, вычислите суммы L3, R$ и А3 для рис. а и 6.
4. Используя результаты задачи 2, вычислите суммы ±3, Я3 и А3 для рис. виг.
*5. Замените соответствующие знаки вопроса в оценках сумм £3 и Я3. Объясните сделанный выбор.
4 4
1 1
*6. Замените соответствующие знаки вопроса в оценках сумм L3 и Я3. Объясните сделанный выбор.
4
1
4
? < v (х) dx ?
1
7. 	Рассчитайте пределы погрешности для сумм L3, R3 и А3, найденных в задаче 3 для обоих графиков.


Глава 11. Интегрирование
417
Рис. 11.28. Иллюстрация к задачам 1-10
8. 	Рассчитайте пределы погрешности для сумм £3, Я3 и А3, найденных в задаче 4 для обоих графиков.
* 9. Используя результаты предыдущих задач, дайте геометрическую интерпретацию следующего выражения.
4
j f (х) dx = 16,5 ± 3,5.
1
*10. Используя результаты предыдущих задач, дайте геометрическую интерпретацию следующего выражения.
4
j и (х) dx = 10,5 ± 3,5.
1
11. 	Стрела выпущена вертикально вверх с начальной скоростью 128 футов в секунду. Если пренебречь сопротивлением воздуха, скорость ее подъема (в футах в секунду) спустя t секунд определяется зависимостью, график которой показан на рис. 11.29.
а) Оцените высоту, которую достигнет стрела, вычисляя левостороннюю и правостороннюю суммы, а также их среднее, разбив исследуемый интервал на


418
Часть III. Математический анализ
Рис. 11.29. Иллюстрация к задаче 11
четыре равных подынтервала. (Значения можно взять непосредственно из графика.) Вычислите пределы погрешности полученных результатов.
*б) Объясните, как площади прямоугольников в аппроксимации правосторонней и левосторонней суммами в п. а связаны с расстоянием.
в) На сколько равных частей необходимо разбить интервал [0,4], чтобы величина Ап аппроксимировала высоту, достигнутую стрелой, с точностью до 1 фута?
12. 	Вернувшись к задаче 11 и вычисляя левостороннюю и правостороннюю суммы, а также их среднее, а также разбив рабочий интервал на два равных подынтервала, оцените расстояние, которое пролетит стрела за первые две секунды полета. Оцените пределы погрешности полученных результатов.
Б В задачах 13 и 14 требуется проанализировать справедливость каждого утверждения. Если утверждение всегда истинно, объясните почему. Если нет, приведите контрпример.
* 13. а) Функция /(ж) = х2 — 2х монотонная на интервале [0,2].
б) Функция /(ж) = х2 — 2х монотонная на интервале [1,3].
* 14. а) Если f — функция, монотонная на интервале [а, 6], то площадь фигуры под
графиком f(x) больше, чем левосторонняя сумма Ln, и меньше, чем правосторонняя сумма Rn, для любых положительных целых п.
б) Если площадь фигуры под графиком /(ж) на интервале [а, Ь] одновременно равна и левосторонней сумме Ln и правосторонней сумме Rn для любых положительных целых n, f — постоянная функция.
В задачах 15 и 16 рассматривается приведенный ниже рисунок, на котором показано два участка земли, расположенных вдоль реки.


Глава 11. Интегрирование
419
15. 	Один человек, заинтересованный в покупке обоих участков земли, показанных на рисунке, хочет быстро оценить их общую площадь. Для береговой линии реки уравнения нет, поэтому он должен использовать среднее значение правосторонней и левосторонней сумм прямоугольников, покрывающих площадь. Береговая линия длиной в 1000 футов разделена на 10 равных частей. В конце каждого подынтервала было измерено расстояние от базовой линии до реки. Результаты измерений записаны в таблице. Пусть х — расстояние, измеренное от левого конца базовой линии, a h(x) — расстояние от базовой линии до реки в точке х. Оцените общую площадь обоих участков, используя сумму Аю, и вычислите предел погрешности этой величины. На сколько подынтервалов следует разбить базовую линию, чтобы погрешность суммы Ап не превышала 2500 кв. футов?
X
0 100 200 300 400 500 600 700 800 900 1000
h(x)
0 183 235 245 260 286 322 388 453 489 500
16. Оцените по отдельности площадь каждого участка в задаче 15, вычислив сумму А5, и определеите предел погрешности обоих результатов. Длина береговой линии каждого участка равна 500 футов.
17. Автомобиль движется со скоростью 75 миль в час (110 футов в секунду). Водитель резко нажимает на педаль тормоза. В течение 7 секунд, понадобившихся для остановки, скорость автомобиля в конце каждой секунды регистрируется специальным датчиком и записывается в таблицу.
t
0
1
2
3
4
5
6
7
r(t)
110
85
63
45
29
16
5
0
Здесь — это скорость (в футах в секунду) спустя t секунд, 0 < t < 7.
а) Оцените расстояние, пройденной до полной остановки, вычислив среднее значение левосторонней и правосторонней сумм для семи равных подынтервалов. Вычислите предел погрешности полученного результата.
б) На сколько равных подынтервалов нужно разбить интервал [0,7], чтобы величина Ап аппроксимировала длину тормозного пути с точностью до 5 футов?
18. Оцените в задаче 17 расстояние, пройденное за первые 3 секунды после нажатия на педаль тормоза, рассчитав среднее значение левосторонней и правосторонней сумм для трех равных подынтервалов. Вычислите предел погрешности полученного результата. На сколько равных подынтервалов нужно разбить интервал [0,3], чтобы величина Ап аппроксимировала расстояние с точностью до 10 футов?
19. На рисунке показан график функции, не монотонной на интервале [0,5]. Вычислите площадь под кривой на этом интервале.
а) Найдите точку Р на оси х, которая разделяет интервал [0,5] на такие две части, что функция /(х) является монотонной на каждой из них.
б) Разделите интервал [0,5] на пять подынтервалов и постройте на нем прямоугольники правосторонних и левосторонних сумм.


420
Часть III. Математический анализ
Рис. 11.30. Иллюстрация
к задаче 19
*в) Опишите поведение левосторонних и правосторонних прямоугольников слева и справа от точки Р в контексте переоценки и недооценки реальной площади.
г) Используя подходящее сочетание правосторонней и левосторонней сумм, найдите такие числа N\ hN2, при которых
5
М f (х) dx TV2’
о
20. 	Используя подходящее сочетание правосторонней и левосторонней сумм, найдите такие числа N± и N2 из задачи 19, при которых
4
Ni j f (ж) dx 7V2*
о
В Задачи 21 и 22 касаются рисунка, показанного ниже.
*21. Аппроксимируйте интеграл J2 (0,25х2 — 4) dx, используя суммы Rq и Вычислите для каждой из них предел погрешности. (Все значения округлите до двух десятичных знаков.) Объясните, что представляет собой этот определенный интеграл на интервале [2,5] в геометрическом смысле.


Глава 11. Интегрирование
421
22. Аппроксимируйте интеграл (0,25а;2 — 4) dx, используя суммы £5, Я5 и А5. Вычислите для каждой из них предел погрешности. (Все значения округлите до двух десятичных знаков.) Объясните, что представляет собой этот определенный интеграл на интервале [1,6] в геометрическом смысле.
В задачах 23-26, используя графическую утилиту, найдите интервалы, на которых каждая функция является монотонной.
23. /(х) = е-2. 24./(ж) = _|—.
25. Да;) = х4 - 2х2 + 3. 26. f (х) = ех2.
В задачах 27-32 для аппроксимации определенного интеграла с заданной точностью используется левосторонняя сумма Ln, правосторонняя сумма Rn или их среднее Ап. Какое число п необходимо выбрать в каждом случае? (Каждая функция монотонна
на указанном интервале.)
3
10 р
27. lnrrdx = Rn ± 0,1.
28. ln (х2 + 1) dx = Ln ± 0,5.
1
J 0
3 р
4 p
29. \xxdx = Ln ± 0,5.
30. Xхdx = Rn± 0,5. J
J
1
1
3
3 p
31. e~x2dx = An±0,5.
32. Iex2dx = An ± 0,5.
0
J
0
* 33. Объясните, почему справедливо выражение
ь
f (я) dx = lim Ln, п—юс
если функция f монотонна на интервале [а, Ь].
* 34. Объясните, почему справедливо выражение
ъ
f (х) dx = lim Rn,
п—юо
a
если функция f монотонна на интервале [а, Ь].
Применение математики
Экономика и бизнес
35. 	Затраты. Компания производит горные велосипеды. Исследовательский отдел построил график (рис. 11.31), на котором величина С'(х) измеряется в долларах, а х — месячный объем производства велосипедов. Оцените рост затрат при


422
Часть III. Математический анализ
Рис. 11.31. Иллюстрация
к задачам 35 и 36
переходе с объема производства 300 на 900 велосипедов в месяц. Используйте среднее значение левосторонней и правосторонней суммы для двух равных подынтервалов и вычислите пределы их погрешностей.
36. 	Затраты. Вернувшись к задаче 35, оцените рост затрат при переходе с нулевого объема производства к производству 600 велосипедов в месяц, используя левостороннюю и правостороннюю суммы для двух равных подынтервалов. Замените соответствующие знаки вопроса значениями £2 и R2:
600
о
37. Непрерывно начисляемые проценты. Десять тысяч долларов положено на счет, скорость изменения суммы на котором через t лет после начального вложения составляет
A'(t) = 800eo,O8t.
Как изменится сумма на счету с конца второго года до конца шестого? Оцените сумму на счету, используя левостороннюю и правостороннюю суммы для четырех равных подынтервалов. (Все величины вычислите с точностью до ближайшего доллара.) Замените соответствующие знаки вопроса значениями £4 или R4:
6
? < j 800e°'08Mt < ?.
2
38. Непрерывно начисляемые проценты. Одна тысяча долларов положена на счет, скорость изменения суммы на котором через t лет после начального вложения составляет
A'(t) = 50e°'O5t.
Как изменится сумма, лежащая на счету с конца второго года до конца шестого? Оцените сумму на счету, используя среднее значение левосторонней и правосторонней суммы для четырех равных подынтервалов. Вычислите пределы погрешности полученных результатов. (Все величины вычислите с точностью до ближайшего доллара.)


Глава 11. Интегрирование
423
39. 	Обучение сотрудников. Компания, производящая компьютерные комплектующие, установила, что в среднем новый работник после t дней обучения в процессе выполнения своих обязанностей может собирать N(t) комплектующих в час, как показано в таблице (производительность труда нового работника непрерывно растет с рабочим временем).
t
0
20
40
60
80
100
120
N(t)
10
51
68
76
81
84
86
Используя среднее значение левосторонней и правосторонней сумм, оцените количество комплектующих, произведенных новым работником за первые 60 и за последующие 60 дней. Для каждого случая используйте три равных подынтервала. Вычислите пределы погрешности для каждой величины.
40. 	Обучение сотрудников. Для нового работника из задачи 39, используя левостороннюю и правостороннюю суммы, оцените количество комплектующих, произведенных на временном интервале [20,100]. Замените соответствующие знаки вопроса значениями L± или R±.
100
20
41. Доход. Исследовательский отдел сети супермаркетов составил следующее уравнение зависимости цены от спроса на пиво категории “премиум”, продаваемого блоками из шести банок.
р = 8 — —- 0 х С 300 Цена-спрос
50
Здесь х — количество блоков, продаваемых в день по цене р долларов за каждый. Из этого уравнения были получены уравнения дохода и предельного дохода, а также их графики, показанные на рис. 11.32.
*а) Дайте геометрическую интерпретацию выражения R' (х) dx и опишите изменение дохода.
б) Аппроксимируйте R' (х) dx, вычислив среднее значение левосторонней и правосторонней сумм для четырех равных подынтервалов. Определите пределы погрешностей этих сумм.
в) Оцените значение J?(200) - /1(100). Как эта величина связана с решением п. а?
42. Доход. Вернитесь к задаче 41.
*а) Дайте геометрическую интерпретацию выражения J*^ R' (ж) dx и опишите изменение дохода.
б) Аппроксимируйте R' (х) dx, вычислив среднее значение левосторонней и правосторонней сумм для четырех равных подынтервалов. Определите пределы погрешности этих сумм.
в) Оцените значение 7?(300) — 12(100). Как эта величина связана с решением п. а?


424
Часть III. Математический анализ
Биологические науки
43. 	WWW Медицина. Приблизительные значения скорости заживления ссадины на коже A'(t) (в кв. см. в день) даны в нижеприведенной таблице.
t
0123456789 10
A'{t)
0,90 0,81 0,74 0,67 0,60 0,55 0,49 0,45 0,40 0,36 0,33
A(t) — это площадь раны после t дней заживления.
а) Аппроксимируйте площадь ссадины, которая заживет за первые пять дней, вычисляя левостороннюю и правостороннюю суммы для пяти равных подынтервалов.
б) Замените соответствующие знаки вопросов величинами L$ и Я5.
5
? < j A' (t) dt < ?.
О
44. Медицина. Вернемся к задаче 43. Аппроксимируйте площадь ссадины, которая заживет за вторые пять дней. Вычислите среднее значение левосторонней и правосторонней сумм для пяти равных подынтервалов. Определите пределы погрешности для этих сумм.
Социальные науки
45. WWW Обучение. В ходе исследований эффективности обучения психолог обнаружил, что в среднем скорость запоминания списка специальных символов после


Глава 11. Интегрирование
425
х дней практических занятий, А7 (я), приблизительно описывается нижеприведенной таблицей значений.
X
0
2
4
6
8
10
12
N'(x)
29
26
23
21
19
17
15
Здесь N(x) — количество специальных символов, запомненных после х дней практических занятий. Аппроксимируйте количество специальных символов, которые были запомнены с 6 по 12 день, используя среднее значение левосторонней и правосторонней сумм для трех равных подынтервалов. Вычислите погрешность этой величины.
46. 	Обучение. Используя данные из задачи 45, аппроксимируйте количество специальных символов, запомненных с 1 по 6 день, используя левостороннюю и правостороннюю суммы для трех равных подынтервалов. Замените соответствующие знаки вопроса значениями £з и 7?з.
6
о
11.5. 	Определенный интеграл как предел суммы. Основная теорема интегрального исчисления
■ Определенный интеграл как предел суммы
■ Основная теорема интегрального исчисления
■ Смысл определенного интеграла: среднее значение
В предыдущем разделе было представлено интуитивное и неформальное описание понятия определенного интеграла и основной теоремы интегрального исчисления. Символ определенного интеграла J* f (х) dx использовался для обозначения совокупной суммы площадей фигуры, ограниченной графиком у = f(x) и осью х от х = а до х = Ь. (На рис. 11.33 числа А, В и С — действительные площади соответствующих областей.)
Было также установлено, что если /(ж) описывает скорость, то выражение J** f (ж) dx можно интерпретировать как общее результирующее изменение первообразной /(ж) на отрезке от х = а до х = Ь. В частности, если /(ж) = С (ж) — предельные затраты на производство х изделий, то число С* (ж) dx определяет общее изменение затрат при переходе от объема производства а к объему производства Ь.
Определенный интеграл как предел суммы
Уточним теперь некоторые концепции из предыдущего раздела. Сначала дадим строгое определение формулы суммирования площади левосторонних и правосторонних прямоугольников, Ln и Rn соответственно. Если интервал [а, Ь] разбит точками а = хо, Ж1,..., хп = Ь на п равных подынтервалов, длина которых равна Дж = (Ь — а)/п, то, используя


426
Часть III. Математический анализ
Рис. 11.33. Интеграл f (z) dx = А — В + С
операцию суммирования (см. приложение Б.1), можно записать:
/ (zfc-i) Az = f (z0) Az 4- / (zi) Az + • • • 4- f (zn-i) Az;
k=i
Rn = ^f (Zfc) Az = f (zi) Az + f (z2) Az 4 h f (zn) Az.
k=i
Для аппроксимации интеграла J* f (z) dx можно также использовать другие суммы площадей прямоугольников, например, формулу средних точек1. В формуле средних точек высота каждого прямоугольника равна значению функции /(z) в центре каждого подынтервала, а не значению в одной из его крайних точек. Формула средних точек имеет следующий вид.
Az 4-/
Zi 4- z2
2
Az 4 h f
&x.
На рис. 11.34 продемонстрировано использование формулы средних точек при аппроксимации интеграла (0,25z2 — 4) dx для п = 5, 10 и 20 (естественно, все вычисления выполнены на компьютере).
Задание 11.11.
Обозначим символом А (рис. 11.34) точную площадь фигуры, ограниченной графиком и осью z на интервале от точки х = 1 до точки х — 4, а символом В — точную площадь фигуры, ограниченной графиком и осью z на интервале от точки х = 4 до точки х = 6. Сформулируйте обоснованное предположение о значении следующего предела, выразив его через площади А и В, и обоснуйте свое утверждение.
lim Мп = 2
п—>оо ■
2Такие суммы называются квадратурными. — Прим. ред.


Глава 11. Интегрирование
427
Рис. 11.34. Вычисление площади фигуры под графиком функции /(х) = = 0,25х2 - 4 с помощью формулы средних точек
Перейдем к понятию определенного интеграла в форме, которая не только охватывает как частные случаи все предыдущие рассуждения, но и раскрывает возможности для множества других интерпретаций и практических применений.
Определенный интеграл
Пусть f — непрерывная функция, заданная на закрытом интервале [а, Ь] и
1. а = хо < xi < • • • < xn-i < хп = Ь,
2. Ахк = хк- Хк-1 для к = 1, 2, ..., п,
3. Axfc —► 0, когда п —► оо,
4. Xk-i ск хк для fc = 1, 2,..., п.
Тогда величина
г
/(x)dx = lim 52/(cfc) Axfc = lim [/(ci) Дх1 + / (c2) Дх2 + Ь/(сп)Дхп]
I n—>oo * * n—►ОС
a ^=1
называется определенным интегралом функции f от а до 6, где /(ж) — подынтегральная функция, а — нижний предел, а b — верхний предел.
При вычислении определенного интеграла отрезок [а, Ь] делится на п подынтервалов произвольной длины таким образом, чтобы длина каждого подынтервала Дх^ = хк — — Xk-i стремилась к нулю при бесконечном росте п. Затем на каждом из п подынтервалов выбирается точка ск и формируется сумма
52 f (Cfc) &Хк = f (ci) +f (c2)Дх2 +•••+/ (c«) д^п,
fc=l
которая называется суммой Римана (названной в честь знаменитого немецкого математика Георга Римана (Georg Riemann) (1826-1866)).


428
Часть III. Математический анализ
Можно показать, что при условиях, указанных в определении, сумма Римана всегда существует и равна действительному числу. Если выполняется условие 3, предел не зависит от характера разбиения [а, Ь] на подынтервалы, если же выполняется условие 4, то он не зависит и от выбора точек с*А Важно помнить, что независимо от исходной интерпретации в конкретной задаче определенный интеграл всегда можно интерпретировать геометрически как площадь со знаком, так же, как производную всегда можно интерпретировать геометрически через наклон.
Формулы суммирования площадей левосторонних и правосторонних прямоугольников, а также формула средних точек, рассмотренные выше, — это относительно простые суммы Римана, в которых все подынтервалы имеют одинаковую длину, а точки сь выбираются закономерным образом, являясь крайними или центральными точками подынтервалов. Для аппроксимации определенного интеграла можно использовать любую из этих сумм. Чтобы этими аппроксимациями можно было пользоваться, нужно найти формулы вычисления пределов погрешности для немонотонных функций.
Пределы погрешностей для сумм Ln, Rn и Мп Пусть
ь
I = j f (z) dx,
а
Ln — сумма площадей левосторонних прямоугольников, Rn — сумма площадей правосторонних прямоугольников, Мп — сумма значений в средних точках.
Пределы погрешности формулы суммирования площадей левосторонних и правосторонних прямоугольников
Если |/'(х)| < By для любых х на [а, Ь], то
I — Ln |
В1 (Ъ - а)2
2п
Вг (Ь - а)2
2п
I-Rn\>
Пределы погрешности формулы средних точек
Если |/"(х)| < В2 для любых х на [а, Ь], то
\1~Мп\
В2 (6 - а)3
24п2
Пример 11.22 (Пределы погрешности). Пусть
з
I = j (4х — х3) dx. -1
3В этой книге рассматриваются только пределы сумм Римана, для которых подынтервалы [а, Ь] имеют одинаковую длину. В этом случае условие 3 выполняется автоматически.


Глава 11. Интегрирование
429
На рис. 11.35 приведены графики у = f'(x) и у = f'(x) для подынтегральной функции /(х) = 4х — х3, которыми можно будет воспользоваться при необходимости.
Рис. 11.35. Графики функций у = ff(x) и у = /"(х)
1. Каким следует выбрать значение п, чтобы величины Ln или Rn аппроксимировали интеграл I с погрешностью не более 0,5?
2. Каким следует выбрать значение п, чтобы величина Мп аппроксимировала интеграл I с погрешностью не более 0,5?
Решение.
1. 	Выберем такое число п, чтобы
Вх (Ь - а)2
2п
^0,5;
где Bi — произвольный верхний предел величины |/'(х)| на интервале [-1,3]. (Предупреждение. Используется верхний предел величины |/'(х) |, а не функции /'(х).) Из графика у = f(x) на рис. 11.35, а, видно, что в качестве величины Bi можно выбрать любое число, равное 23 или больше. Выберем Bi = 23. (Графики у = f'(x) часто используются для вычисления верхнего предела |/'(х)| на интервале [а, Ь], если его сложно получить алгебраическим путем.) Таким образом,
368.
2. 	Выберем такое число п, чтобы выполнялось неравенство
В2 (Ь - а)3
24п2


430
Часть III. Математический анализ
где В2 — произвольный верхний предел величины |/"(х)| на интервале [—1,3]. Из графика у = на рис. 11.35, б, видно, что в качестве оценки В2 можно выбрать любое число, равное 18 или больше. Выберем В2 = 18. Таким образом,
18 [3 - (-1)]3
24п2
18-64
24 • 0,5
^0,5;
18-64
24 • 0,5
п
Поскольку п— положительное число.
= 9,8; или
10.
(Примечание. Для формулы средних точек необходимо всего 10 подынтервалов, чтобы получить такую же точность, как при использовании формул суммирования левосторонних и правосторонних прямоугольников на основе 368 подынтервалов. В обоих случаях точность может быть значительно выше, чем указано, но эти формулы для пределов погрешностей дают гарантированный результат для указанного значения п. Еще одна квадратурная сумма — формула Симпсона, — которая, как правило, дает более точный результат при определенном значении п, будет рассмотрена в домашнем задании.) ■
Упражнение 11.22.
Рассмотрим интеграл / = (х2 — 4z) dx.
1. Каким следует выбрать значение п, чтобы величина Ln или Rn аппроксимировала интеграл I с погрешностью не более 0,1?
2. Каким следует выбрать значение п, чтобы величина Мп аппроксимировала интеграл I с погрешностью не более 0,1? ■
Задание 11.12.
Объясните разницу между определенным интегралом f (х) dx и неопределенным интегралом J f (х) dx, указав, что описывает каждый из них. ■
В следующей врезке сформулировано несколько важных свойств определенного интеграла. Следует отметить, что свойства 3 и 4 соответствуют свойствам 3 и 4 неопределенных интегралов, описанным ранее в разделе 11.1.
Свойства определенных интегралов
где к — константа.


Глава 11. Интегрирование
431
Большинство из этих свойств непосредственно следуют из определения интеграла. Их применение продемонстрировано в примере 11.23.
Пример 11.23 (Свойства определенного интеграла). Если
2
xdx = 2,
о
2
jx2dx=
О
Упражнение 11.23.
Используя те же значения интегралов, что даны в примере 11.23, вычислите следующие
величины.
з
2
О
3. 3xdx.
2
2
2. j (9ж2 — 4х) dx. о
-2
4. j 3xdx.
-2
о


432
Часть III. Математический анализ
Основная теорема интегрального исчисления
Перейдем к одному из наиболее важных постулатов математики — основной теореме интегрального исчисления. Для начала рассмотрим еще раз интерпретацию неопределенного интеграла предельных затрат, рассмотренную выше.
Если С"(х) описывает предельные затраты на производство х единиц продукции, то jk (j' (ж) dx определяет общее изменение затрат при изменении объема производства с х = а на х = b (рис. 11.36). Общее изменение затрат можно найти, пользуясь формулой C(b) — С (а), где С(х) — функция затрат, представляющая собой первообразную функцию предельных затрат С\х). Таким образом, можно записать
ъ j С (i) dx = С (b) - С (а). а
Рис. 11.36. С' (х) dx — общее изменение затрат
В общем случае, поскольку F'(x) — мгновенная скорость изменения в точке х,
ь
F* (х) dx описывает общее изменение F(cc) от ® = а до а? = Ь.
а
Однако оно также равно F(b) — F(a). Следовательно,
ъ
F' (ж) dx = F (b) — F (а).
а
Этот примечательный результат оказывается справедливым при довольно общих условиях.


Глава 11. Интегрирование
433
Основная теорема интегрального исчисления4
Если f — непрерывная функция, определенная на закрытом интервале [а, 6], a F — произвольная первообразная функции /, то
ь
j f (х) dx = F (ж) а
b
= F(b)-F(a),
F'(x) = f(x).
а
С помощью первообразной функции f(x) можно точно и быстро найти значение определенного интеграла J** f (х) dx, т.е. предела суммы Римана на интервале [а, Ь]. Для этого следует найти значения первообразной в крайних точках а и b и вычислить их разность. Конечно, если функция /(ж) дана в виде таблицы значений или графика, либо первообразную функции /(ж) найти непросто, либо она не существует (распространенная ситуация в действительных задачах), то необходимо прибегнуть к аппроксимации, т.е. квадратурным формулам. Запись F (ж) | обозначает полное изменение функции F(x) от точки х = а до точки х = Ь и представляет промежуточный этап вычисления определенного интеграла в основной теореме.
Теперь становится ясно, почему методы вычисления неопределенных интегралов были рассмотрены до этого раздела — вы получили в свое распоряжение эффективные методики вычисления первообразных широкого класса элементарных функций, которыми можете воспользоваться, применяя основную теорему интегрального исчисления. Важно помнить следующее.
В основной теореме можно использовать любую первообразную функции f(x). Чаще всего, выбирают самую простую первообразную, полагая С = 0, поскольку любое другое значение С сократится при вычислении разности F(a) — F(b).
В следующем примере с помощью основной теоремы будут найдены значения разнообразных определенных интегралов.
Пример 11.24 (Вычисление определенных интегралов). Вычислите интеграл
2
j ^2х + Зех — dx.
1
Решение.
2
1
2
2
+ 3ех
— 41п |ж|
1
1
= (22 - I2) + (Зе2 - Зе1) - (41п2-41п1) = = 3 + Зе2 — Зе — 41п 2 « 14,24.
4 В русскоязычной литературе это правило называется формулой Ньютона-Лейбница. — При- меч. ред.


434
Часть III. Математический анализ
Упражнение 11.24.
Вычислите интеграл Д (4х — 2ех + |) dx. ■
Вычисление определенного интеграла — это двухэтапный процесс. Сначала вычисляется первообразная, а затем — разность между ее значениями. Если для вычисления первообразной приходится применять метод замены переменной, можно использовать два способа, описанных в следующем примере.
Пример 11.25 (Определенный интеграл и метод замены переменной). Вычислите интеграл
5
О
Решение» Решим эту задачу методом замены переменной двумя разными способами.
Метод 1. Выполняя подстановку в неопределенном интеграле, найдем первообразную как функцию переменной х, а затем вычислим значение определенного интеграла.
Подставим и = sc2 + 10 и du = 2xdx.
= | [ -du =
2 J и
= - ln |u| + С =
= i ln (x2 + 10) + C.
Поскольку и = x2 + 10 > 0.
Выберем С = 0 и, используя первообразную | In (ж2 + 10), вычислим значение определенного интеграла.
5
j --|Г = Iln <l! +
0
1 1
= - In 35- -In 10 «0,626.
о 2 2
Метод 2. Сделаем подстановку непосредственно в определенном интеграле, меняя как переменную, так и пределы интегрирования. В определенном интеграле
I^Tioda:’
о
верхний предел равен х = 5, а нижний — х = 0. Чтобы сделать подстановку и = х2 + 10 в этом определенном интеграле, необходимо заменить пределы интегрирования соответствующими значениями переменной и.
х = 5, значит и = 52 + 10 = 35. Новый верхний предел.
х = 0, значит и = О2 + 10 = 10. Новый нижний предел.


Глава 11. Интегрирование
435
Таким образом,
Ы
0
= f -du =
2 J и
Упражнение 11.25.
Используя оба метода, описанных в примере 11.25, вычислите интеграл
[ —^—dx.
J 2х + 4
О
Пример 11.26 (Определенные интегралы и замена переменной). Используя метод 2, описанный в примере 11.25, вычислите интеграл
1
| \/5 — tdt,
-4
Решение. Если и = 5 — t, то du = —dt и
* = 1, t=-4,
значит и = 5 — 1 = 4. значит и = 5 — (—4) = 9.
Новый верхний предел.
Новый нижний предел.
Следует отметить, что для переменной и нижний предел больше, чем верхний. Следует быть внимательным и не перепутать местами эти два значения при подстановке в определенный интеграл.
1
| Vх 5 — tdt = — -4
1
х/5 — £ (—dt) =
-4
4
= — j y/udu =
9
4 = — j и1/2 du =
9


436
Часть III. Математический анализ
'16 _ 54'
3 3
Упражнение 11.26.
Используя метод 2, описанный в примере 11.25, вычислите интеграл
5
Задание 11.13.
Объясните, почему в каждом из выражений используется знак и запишите правильный
результат.
2.
1.
#е2.
5 5
-dx - -du,
J 2х + 3 2 J и
2 2
и = 2х + 3,
du = 2dx.
Пример 11.27 (Изменение прибыли). Компания производит х телевизоров в месяц. Месячная предельная прибыль (в долларах) описывается следующей формулой.
Р'(х) = 165 - 0,1х; 0 х 4000.
На данный момент компания производит 1500 телевизоров в месяц, но она планирует расширить производство. Вычислите общее изменение месячной прибыли, если месячный объем производства вырастет до 1600 телевизоров.
Решение.
Р (1600) -Р (1500) =
1600
(165 — 0,1х) dx —
1500
1600
= (165i - 0,05я?2)
1500
= [165 • 1600 - 0,05 • 16002] - [165 • 1500 - 0,05 • 15002] = = 136 000 — 135 000 =
= 1000.
Таким образом, при увеличении месячного объема производства с 1500 до 1600 единиц месячная прибыль возрастет на 1000 долл. ■


Глава 11. Интегрирование
437
Упражнение 11.27.
Повторите расчеты примера 11.27, если
Р'(х) = 300 - 0,2х; 0 х 3000,
и месячный объем производства возрастает с 1400 до 1500 телевизоров. ■
Пример 11.28 (Номинальный период эксплуатации). Компания, предоставляющая услуги в сфере развлечений, сохраняет данные о прибыли, приносимой каждой видеоигрой, установленной в павильоне игровых автоматов. Предположим, что функции C(f) и R(t) описывают соответственно общие совокупные затраты и доход (в тысячах долларов) через t лет после установки видеоигры, и что
C'(t) = 2, R'(t) = 9e~°’5t.
Значение t, при котором C’(t) = R'(t), называется периодом номинальной эксплуатации игры.
1. Определите номинальный период эксплуатации игры с точностью до ближайшего года.
2. Вычислите общую прибыль, полученную за номинальный период эксплуатации игры.
Решение.
1. R' (t) = С" (*);
9e-°,5t = 2;
2 e-o,5t _ . Преобразуем уравнение к логарифмическому виду.
У
-0,5* =
2
t = — 2 In - « 3 года.
Таким образом, номинальный период эксплуатации игры равен трем годам. Этот результат проиллюстрирован на рис. 11.37.
2. Общая прибыль, накопившаяся за номинальный период эксплуатации, равна
з
Р (3) - Р (0) = j Р' (t) dt =
о
3
= j [я' (t) - с (t)] dt = о
3
(ge-o,5t _ 2) dt =
о
Напомним: j eaxdx = -eax + C.


438
Часть III. Математический анализ
= (- 18e_0’5t - 2t) 3
о
= (—18е-1,5 - 6) - (-18е° - 0) =
= 12 — 18е 1,5 « 7,984; или 7,984 долл.
Рис. 11.37. Номинальный период эксплуатации
Упражнение 11.28.
Повторите решение примера 11.28, если C"(t) = 1, a R'(t) = ■
Пример 11.29 (Численное интегрирование с помощью графической утилиты).
Вычислите интеграл
2
j е~х2 dx
-1
с точностью до трех десятичных знаков.
Решение. Первообразная подынтегральной функции е~х2 не является элементарной функцией, поэтому для вычисления значения определенного интеграла нельзя воспользоваться основной теоремой. Вместо этого воспользуемся процедурой численного интегрирования, предусмотренной в графической утилите. Эта процедура является более мощным инструментом аппроксимации, чем формулы суммирования левосторонних и правосторонних прямоугольников, рассмотренные в разделе 11.4. Из рис. 11.38 видно, что
2 j = 1,629.
-1 ■


Глава 11. Интегрирование
439
fnInt<eA<-X*>,X, -1,2)
1.628905524
Рис. 11.38. Интегрирование с помощью графической утилиты
Упражнение 11.29.
Вычислите интеграл
4 я
1,5
с точностью до трех десятичных знаков.
Смысл определенного интеграла: среднее значение
Напомним, что производная функции f в разделе 8.3 определена как
/' (х) = lim
v h->0
/ (х -Н h) - / (x) h
Вычислить значение этого выражения непосредственно довольно сложно, но его легко найти в некоторых практических задачах (наклон, мгновенная скорость движения, скорость изменения и т. д.). Как только становится ясно, что речь идет о производной, можно попытаться вычислить ее, используя формулы и правила дифференцирования.
Аналогично вычислить определенный интеграл, используя определение
ь
f (х) dx = lim [f (ci) ДХ1 + f (c2) Дх2 + ■■■ + f(cn) Дхп], I n—>oo
a
(1119)
как правило, непросто. Однако выражение, указанное в его правой части, естественным образом возникает во многих частных задачах. В подобных случаях для вычисления определенного интеграла можно воспользоваться основной теоремой, если есть возможность вычислить первообразную. В противном случае интеграл можно аппроксимировать с помощью формулы суммирования площадей прямоугольников. Проиллюстрируем вышесказанное, найдя среднее значение непрерывной функции.
Предположим, что температура F (в градусах по Фаренгейту) в центре мелководного озера с 8 утра (t = 0) до 6 вечера (t = 10) в мае меняется приблизительно так, как показано на рис. 11.39.
Как вычислить среднюю температуру воды с 8 утра до 6 вечера? Известно, что среднее значение конечного числа величин ai, аг, • • •, вычисляется по следующей формуле.
ai + аг + • • • + ап
Среднее = .
п


440
Часть III. Математический анализ
Количество часов после 8 утра
Рис. 11.39. Изменение температуры
А что делать с непрерывной функцией, имеющей бесконечное количество значений? Кажется логичным разбить временной интервал [0,10] на п равных подынтервалов, вычислить температуру в точке на каждом подынтервале, а затем использовать среднее этих значений для аппроксимации среднего значения непрерывной функции F = F(t) на интервале [0,10]. Можно ожидать, что точность аппроксимации будет повышаться с ростом п. Фактически это приводит к следующему определению: предел среднего значения п величин при п —> оо называется средним значением функции F на интервале [0, 10], если этот предел существует.
Средняя температура для п значений
= 1 [Г(<х) + F(t2) + ••• + F(tn)],
(11.20)
где tk — точка на k-м подынтервале. Будем называть предел уравнения (11.20) при п —► оо средней температурой на интервале [0,10].
Уравнение (11.20) отчасти похоже на выражение (11.19), за исключением только Д^. Это можно исправить, умножая уравнение (11.20) на величину (5 — а)/(6 — а), которая изменит его вид, но не значение.
т—- • - [F (*1) + F (t2) + о — a nL
+ * • • F (tn) ]


Глава 11. Интегрирование
441
Таким образом,
Теперь предел внутри скобок имеет такой же вид, как выражение (11.19) — т.е. является определенным интегралом. Таким образом,
ь
/Средняя температура на\ _ у интервале [а, Ь] = [0,10] у —
а
10
10_0 j (_f2 +10i + 50)dt =
'^(“i + 5t2 + 5O0
Вычислим определенный интеграл, используя основную теорему.
о
ю
о
Вообще говоря, если повторить описанные выше операции для произвольной непрерывной функции f на интервале [а, Ь], то получится следующая общая формула.
Среднее значение непрерывной функции f на интервале [а, Ь]
ь
j f (х) dx.
а
Задание 11.14.
На рис. 11.40 прямоугольник имеет такую же площадь, что и площадь фигуры, расположенной под графиком у = f(x) от точки х = а до точки х = Ь. Объясните, как среднее значение /(х) на [а, Ь] связано с высотой прямоугольника. ■
Пример 11.30 (Среднее значение функции). Вычислите среднее значение функции f(x) = х — Зх2 на интервале [—1,2].
Решение.
2
5
Упражнение 11.30.
Вычислите среднее значение функции g(f) = 6t2 — 2t на интервале [—2,3].


442
Часть III. Математический анализ
Рис. 11.40. График функции у = f(x)
Пример 11.31 (Средняя цена). Дано уравнение зависимости цены от спроса: р = D(x) = 1ООе~0’051.
Вычислите среднюю цену (в долларах) в диапазоне спроса [40,60].
Решение.
Средняя цена =
60
ЮОе
1
60-40
0,051 dx =
40
100 f
_ 20 J 6
0,05xdx =
Воспользуемся формулой
eaxdx = — еах, а / О.
а
40
° —0,05х
0,05
60
40
f
= 100 (е 2 — е 3) « 8,55 долл.
Упражнение 11.31.
Дано уравнение зависимости цены от предложения:
р = S(x) = Юе°’05х.
Вычислите среднюю цену (в долларах) на интервале предложения [20,30].


Глава 11. Интегрирование
443
Ответы к упражнениям
11.22. 1) п > 270.
2) п 5.
11.23. 1) 38.
2) 16.
3) -6.
4) 0.
5) 108.
11.24. 16 + 2е — 2е3 + 51пЗ и —13,241.
11.25. | (In 6 — In 4) « 0,203.
11.26. 2.
11.27. 1000 долл.
11.28. 1) -2 In « 4 года.
15
2) 11 - 15е-2 « 8,970; или 8970 долл.
11.29. 8,017.
11.30. 13.
11.31. 35,27 долл.
Практикум 11.5
А Задачи 1-6 касаются следующего рисунка с указанными площадями.
Площадь А = 2,33
Площадь В = 10,67
Площадь С = 5,63
о
1. f (х) dx = ?.
/ (х) dx = ?.
а
f (х) dx = ?.
а
f (ж) dx = ?.
0
о
6. 10/ (ж) dx = ?.
о


444
Часть III. Математический анализ
В задачах 7-20 вычислите интеграл.
3
7. 12xdx.
2
4
9. j 5dx.
3
3
j (2ж — 3) dx.
1
4
j (4 — я2) dx.
-3
1 24xndx.
о
1
| e2xdx.
о
3,5
2x~rdx.
1
11.
13.
15.
17.
19.
8.
10.
12.
14.
2
3x2dx.
1
20
12
3
j (6x + 5) dx.
1
2
(x2 — 4z) dx.
16.
18.
-1
2 j 30x5cLe. о
1 | e5xdx.
-1
2 f dx
20-1
1
Б В задачах 21-24 используется рисунок из задач 1-6.
ь
22. j f (х) dx = 1.
О
а
24. 	f (х) dx = ?.
ь
о
21. j f (x) dx = 2.
b
0
23. j f (x) dx = 2.
c
25. В примере 11.20 из раздела 11.4 для оценки расстояния, которое стальной шарик, брошенный с моста, пролетит в течение временного интервала [1,4], использовалась функция скорости r(t) = 32t, а также формулы суммирования левосторонних и правосторонних прямоугольников. Вычислите это расстояние, используя определенный интеграл и основную теорему интегрального исчисления.
26. Повторите действия задачи 25 для временного интервала [2,5].
В задачах 27-44 вычислите интеграл.
2
27. j (2х~2 - 3) dx.
1
2
28. j (5 - 16х“3) dx.
1


Глава 11. Интегрирование
445
4
29. j %\/xdx.
1
з
31. 12 (z2 — 4)5 xdx.
2
9
33. -dx.
J x - 1 з
10
35. 	j e_0,05i:da:.
-5
хе х dx.
43.
25
30. —=dx.
J Vx
4
1
32. 32 (a;2 + 1)7 xdx.
0
8
34. -dx.
J x + 1 2
25
36. 	j e~°'01xdx.
-10
38.
e
4
40. | z\/4 — xdx.
о
1
42. j xex2dx.
о
«• j
-2
37. j '^dt.
1
2
39. jx\/4 — x2dx.
о
1
41.
о
X2 + 1 ,
dx.
x
-2
В задачах 45-52 выполните следующие задания.
1) Вычислите среднее значение каждой функции на указанном интервале.
2) Используя графическую утилиту, постройте график функции и вычислите ее среднее значение.
45. /(z) = 500 - 50z; [0,10]. 46. д(х} = 2х + 7; [0,5].
47. 	f(t) = 3t2 - 2t; [-1,2]. 48. g(t) = 4t - 3t2; [-2,2].
49. f (z) = [1,8]. 50. g (z) = л/zTT; [3,8].
51. /(z) = 4e-°’2a:; [0,10]. 52. /(z) = 64e°’08a;; [0,10].


446
Часть III. Математический анализ
В задачах 53-58 используется рисунок, показанный ниже.
53. Используя сумму значений в средних точках М±, аппроксимируйте интеграл
8
I = j (0,25ж2 - 4) dx.
О
Вычислите пределы погрешности этой суммы.
54. Используя сумму значений в средних точках Мз, аппроксимируйте интеграл
6
I = j (0,25х2 — 4) dx.
о
Вычислите пределы погрешности этой суммы.
* 55. Вычислите интеграл I = (0,25х2 — 4) dx, используя основную теорему. Рас¬
считав сумму значений в средних точках М4, вычислите точное значение погрешности \1 — М±\. Лежит ли эта погрешность в допустимых пределах, вычисленных в задаче 53? Объясните свой ответ.
* 56. Вычислите интеграл I = (0,25х2 — 4) dx, используя основную теорему. Рас¬
считав сумму значений в средних точках М$, вычислите точное значение погрешности \1 — 7Из|. Лежит ли эта погрешности в допустимых пределах, вычисленных в задаче 54? Объясните свой ответ.
57. При каком числе п сумма значений в средних точках Мп аппроксимирует интеграл
8
I = j (0,25х2 - 4) dx
О
с погрешностью, не превышающей 0,05?
58. При каком числе п сумма значений в средних точках Мп аппроксимирует интеграл
6
I = j (0,25х2 - 4) dx
о
с погрешностью, не превышающей 0,05?


Глава 11. Интегрирование
447
В В задачах 59-62 требуется переписать указанные выражения в виде J** f (ж) dx и вычислить их значения, используя основную теорему интегрального исчисления.
59. lim [(1 - с?) До: 4- (1 - с2) Ах 4 |- (1 — с£) Да;], где Да: = и ск = 2 +
4" = 1, 2, ..., п.
60. lim [(с? - 3) Да: 4- (с2 - 3) Да; 4 1- (с2 - 3) Да;], где Да: = и Cfc =
Го°°4-^,А: = 1, 2, ..., п.
61. lim [ (Зс? - 2ci 4- 3) Да: -4 (Зс? — 2сг 4- 3) Да: 4 И (Зс^ — 2сп + 3) Да?], где
Да: = и ск = 2 4- к™, к = 1, 2, ..., п.
62. lim [ (4с? 4- Зс? — 5) Да: 4- (4с? 4- Зс? — 5) Да: 4- h (4с^ 4- Зс£ — 5) Да:], где
Дя = и cfc = 1 4- к±, к = 1, 2, ..., п.
В задачах 63-68 вычислите интегралы.
з
63. 	j х\/2х2 - 3dx.
2
65. [ „ *—-dx.
J х2 - 2х + 3 о
67. [ 6 X~eX2dx.
J (е ® + е®)2
64. j ху/Зх2 + 2dx.
о
66. [ dx.
J 2х2 4- 4а; 4- 4 i
68. f
J t - 5
6
В задачах 69-72 используется тот факт, что функция натурального логарифма выражается через определенной интеграл.
69. 	Все расчеты округлите до четырех десятичных знаков,
а) 	Аппроксимируйте выражение
2
1п2 = j
1
используя сумму значений в средних точках для п = 5. Вычислите пределы погрешности.
б) 	Вычислите значение 1п 2 непосредственно с помощью калькулятора.


448
Часть III. Математический анализ
в) 	Вычислите реальную погрешность для суммы значений в средних точках. (Воспользуйтесь результатами решения пп. а и б и выражением расчета погрешности |1п2 — М5|.) Находится ли это значение в допустимых пределах, вычисленных при решении п. а?
70. 	Все расчеты округлите до четырех десятичных знаков.
а) 	Аппроксимируйте выражение
з
1
используя сумму значений в средних точках для п = 10. Вычислите предел погрешности.
б) Вычислите значение In 3 непосредственно с помощью калькулятора.
в) Вычислите реальную погрешность для суммы значений в средних точках. (Воспользуйтесь результатами решения пп. а и б и выражением погрешности |1п 3 — M5I.) Находится ли это значение в допустимых пределах, вычисленных при решении п. al
71. 	Какое значение п нужно выбрать, чтобы погрешность аппроксимации In 2 методом суммирования значений в средних точках из задачи 69 не превышала 0,0005?
72. 	Какое значение п нужно выбрать, чтобы погрешность аппроксимации 1пЗ методом суммирования значений в средних точках из задачи 70 не превышала 0,0005?
В задачах 73-76, используя метод численного интегрирования, вычислите значение каждого определенного интеграла (с точностью до трех десятичных знаков).
3,5
73. 	xlnzckr.
1,7
2 75' j Thdx- -2
1
74. ех dx.
-1
Применение математики
Экономика и бизнес
77. 	Затраты. Компания производит горные велосипеды. Исследовательский отдел получил следующую функцию предельных затрат.
С (я) = 500 - 0^1^ 900.
Здесь С'(х) измеряется в долларах, а х — месячный объем производства. Вычислите увеличение затрат при росте месячного объема производства с 300 до 900 велосипедов. Запишите определенный интеграл и вычислите его значение.


Глава 11. Интегрирование
449
78. Затраты. Возвращаясь к задаче 77, вычислите увеличение затрат при росте месячного объема производства с нулевого уровня до 600 велосипедов. Запишите определенный интеграл и вычислите его значение.
79. Ликвидационная стоимость. Новое промышленное оборудование сначала быстро обесценивалось, а по прошествии некоторого времени падение цены замедлилось. Предположим, что скорость (долл./год), с которой меняется остаточная стоимость фрезерного станка, приблизительно описывается следующей формулой.
V'(t) = f(t) = 500(t - 12), 0 10.
Здесь V (t) — стоимость станка через t лет. Какова стоимость станка станка за первые 5 лет? За вторые 5 лет? Запишите соответствующие интегралы и вычислите их.
80. Эксплуатационные затраты. Эксплуатационные затраты на содержание многоквартирного дома, как правило, увеличиваются с его возрастом. По сделанным за прошлые периоды записям руководство ЖЭК установило, что скорость роста эксплуатационных затрат (долл./год) на содержание определенного многоквартирного комплекса приблизительно равна
М'(х) = f(x) = 90х2 + 5000,
где х — возраст квартирного комплекса в годах, а М (ж) — общие (совокупные) затраты на эксплуатацию в течение х лет. Запишите определенный интеграл, который будет определяет общие эксплуатационные затраты за период с конца второго года по конец седьмого года, начиная с момента введение дома в эксплуатацию, и найдите его значение.
81. Обучение сотрудников. В компании, производящей компьютерные комплектующие, было установлено, что в среднем новый работник после t дней обучения может собрать на рабочем месте Д/(£) компонентов, как показано в следующей таблице (производительность труда нового работника обычно растет с рабочим временем, пока не достигнет определенного уровня).
t
0
20
40
60
80
100
120
N(t)
10
51
68
76
81
84
85
а) Составьте уравнение квадратичной регрессии и отобразите в одном окне калькулятора график этого уравнения и набор данных.
б) Используя уравнение регрессии и процедуру численного интегрирования, вычислите с помощью графической утилиты приблизительное количество комплектующих, собранных новым работником за первые 100 дней работы.
82. 	Обучение сотрудников. Вернемся к задаче 81.
а) Составьте уравнение кубической регрессии и отобразите в одном окне калькулятора график этого уравнения и набор данных.
б) Используя уравнение регрессии и процедуру численного интегрирования, вычислите с помощью графической утилиты приблизительное количество компонентов, собранных новым работником за вторые 60 дней работы.


450
Часть III. Математический анализ
83. Номинальный период эксплуатации. Общие совокупные затраты C(t) и доход R(t) (тыс. долл.) от эксплуатации фотокопировального аппарата удовлетворяют соответственно уравнениям
C'(t) = ^t и fl'(t) = 5te-‘2,
где t — время в годах. Определите номинальный период эксплуатации аппарата с точностью до ближайшего года. Каков размер общей прибыли, полученной за номинальный период эксплуатации аппарата?
84. Номинальный период эксплуатации. Общие совокупные затраты C(t) и доход R(t) (тыс. долл.) от эксплуатации угольной шахты удовлетворяют соответственно уравнениям
C'(t) = 3 и R'(t) = 15е_0,1<,
где t — период функционирования шахты в годах. Определите номинальный период эксплуатации шахты с точностью до ближайшего года. Каков размер общей прибыли, полученной за номинальный период эксплуатации шахты?
85. Средние затраты. Общие затраты на производство х автомобильных кузовов (в долларах) составляют С(х) = 60000 + ЗООх.
а) Вычислите средние затраты (в расчете на единицу) при производстве 500 кузовов. (Подсказка. Средние затраты на единицу продукции описываются функцией С (х).)
б) Вычислите среднее значение функции затрат на отрезке [0,500].
*в) Проанализируйте разницу между решениями пп. а и б.
86. Средние затраты. Общие затраты на издание х словарей (в долларах) составляют С(х) = 20000 + Юх.
а) Вычислите средние затраты (в расчете на единицу) при издании 1000 словарей.
б) Вычислите среднее значение функции затрат на отрезке [0,1000].
*в) Проанализируйте разницу между решениями пп. а и б.
87. Затраты. Предельные затраты при различных месячных объемах производства наручных часов приведены в следующей таблице. Объем производства х указан в тысячах штук, а предельные затраты С(х) — в тысячах долларов.
X
0 1 2345 6 78
с"(®)
58 30 18 9 5 7 17 33 51
а) Составьте уравнение квадратичной регрессии и в одном окне калькулятора отобразите график этого уравнения и набор данных.
б) Используя уравнение регрессии и процедуру численного интегрирования, аппроксимируйте с помощью графической утилиты (с точностью до доллара) рост затрат при увеличении месячного объема производства с 2000 до 8000 часов.
88. 	Затраты. Вернемся к задаче 87.
а) Составьте уравнение кубической регрессии и в одном окне калькулятора отобразите график этого уравнения и набор данных.


Глава 11. Интегрирование
451
б) Используя уравнение регрессии и процедуру численного интегрирования, аппроксимируйте с помощью графической утилиты (с точностью до ближайшего доллара) рост затрат при увеличении месячного объема производства с 1000 до 7000 часов.
89. 	Предложение. Функция предложения описывается следующей формулой.
р = 5(ж) = 10(е0,02:Е - 1).
Вычислите среднюю цену (в долларах) на отрезке [20,30].
90. 	Спрос. Функция зависимости цены от спроса описывается следующей формулой.
ПГ А 1000 р = D (х) = .
х
Вычислите среднюю цену (в долларах) на отрезке [400,600].
91. 	Затраты на оплату труда и обучение. Подрядчик министерства обороны приступил к производству ракетных систем управления. На основе данных, собранных при выпуске первых 16 систем, руководитель производства получил следующую функцию производительности рабочей силы.
д(х) = 2400х х/2.
Здесь д(х) — это число человеко-часов, затрачиваемых на сборку х-й системы управления. Сколько приблизительно человеко-часов понадобится для сборки с 17-й по 25-ю систему управления? (Подсказка. Положите а = 16 и b = 25.)
92. 	Затраты на оплату труда и обучение. Сколько приблизительно человеко-часов понадобится для сборки с 9-й по 27-ю систему управления, если производительность рабочей силы в задаче 91 составляет
р(х) = 2000х_1/3.
(Подсказка. Положите а = 8 и b = 27.)
93. Инвентаризация. Магазин заказывает 600 единиц товара каждые три месяца. Если товар монотонно распродается (убывает) до 0 к концу каждого третьего месяца, то количество такого товара на складе магазина I в произвольный момент времени в течение года описывается графиком, показанным на рис. 11.41.
а) Запишите функцию объема товара, хранимого на складе магазина, в течение первых трех месяцев (предполагая, что она непрерывна). (Ее график — это прямая линия, соединяющая точки (0,600) и (3,0).)
б) Какое среднее количество товара будет находиться на складе магазина в трехмесячный период?
94. Повторите решение задачи 93 при заказе 1200 единиц товара каждые четыре месяца.
95. Добыча нефти. Используя данные первых трех лет добычи, а также результаты геологических исследований, руководство нефтедобывающей компании определило, что нефть из месторождения будет выкачиваться со скоростью
Д(<) = ГИ + 5,


452
Часть III. Математический анализ
Время, мес.
Рис. 11.41. Иллюстрация к задаче 93
где R(t) — скорость или темп отбора нефти (в тысячах баррелей в год) спустя t лет после начала разработки месторождения. Сколько приблизительно баррелей нефти будет добыто из месторождения в течение первых 10 лет? С конца 10-го до конца 20-го года добычи?
96. WWW Добыча нефти. Сколько приблизительно баррелей нефти будет добыто из месторождения в течение первых пяти лет, если установлено, что темп ее отбора в задаче 95 равен
Я(<) = ^^-+3, 0 < t 20,
Сколько будет добыто в течение вторых пяти лет?
97. Прибыль. Пусть R(t) и C(t) описывают соответственно общую совокупную прибыль и затраты (в долларах) на добычу нефти из некой скважины, где t — время в годах. Графики производных функций R и С за пятилетний период показаны на рис. 11.42. Используя сумму значений в центральных точках при п — 5, аппроксимируйте общую совокупную прибыль от скважины за этот пятилетний период. Необходимые значения функции найдите по графику.
Рис. 11.42. Иллюстрация к задачам 97 и 98
98. Доход. Используя рис. 11.42 и формулу суммирования значений в средних точках при п = 5, аппроксимируйте средний годовой доход от нефтяной скважины.
99. Недвижимость. Землемер составил показанную ниже таблицу, в которой указано вертикальное расстояние (в футах) от дороги до противоположного края


Глава 11. Интегрирование
453
земельного участка (ширина участка) через каждые 600 футов его ширины, начиная с отметки 300 футов (рис. 11.43). Используя приведенные значения и формулу суммирования значений в средних точках, вычислите площадь участка неправильной формы.
X
300
900
1500
2100
л®)
900
1700
1700
900
Рис. 11.43. Иллюстрация к задаче 99
100. 	Повторите решение задачи 99 для следующих измерений, собранных в таблице.
X
200
600
1000
1400
1800
2200
/(®)
600
1400
1800
1800
1400
600
Биологические науки
101. Биология. Ожидается, что вынутая из морозильной камеры дрожжевая культура весом 2 г при более высокой температуре будет расти со скоростью W'(t) = = O,2eo,lt г в час. На сколько вырастет вес дрожжевой культуры в течение первых 8 часов? На сколько увеличится ее вес с конца 8-го по конец 16-го часа?
102. Медицина. Скорость заживления раны на коже (в квадратных сантиметрах в день) приблизительно равна A'(i) = — О,9е~о,1<. Вначале рана имела площадь 9 см2. На сколько изменится площадь за первые пять дней? За вторые пять дней?
103. Температура. Какой будет средняя температура (в градусах Фаренгейта) в аквариуме в течение двухчасового периода, если она изменяется согласно следующему закону?
C(t) = t3 - 2t + 10, 0 t «С 2.
104. Медицина. Препарат вводится в кровь пациенту через правую руку. Концентрация препарата в тканях левой руки через t часов после инъекции составляет
C(i) =
0,14t
t2 + l’
Какой будет средняя концентрация препарата в тканях левой руки в течение первого часа после инъекции? В течение первых двух часов после инъекции?


454
Часть III. Математический анализ
105. 	WWW Медицина: дыхание. Физиологи, чтобы получить график объемной скорости потока вдыхаемого и выдыхаемого воздуха используют аппарат под названием пневмотахограф. На рис. 11.44 показана часть такого графика для фазы вдоха у пациента, не подверженного физическим нагрузкам. Площадь фигуры, расположенной под этим графиком, соответствует общему объему воздуха, вдыхаемого в течение фазы вдоха. Используя формулу суммирования значений в средних точках при п = 3, аппроксимируйте площадь фигуры под графиком. Необходимые значения функции найдите по графику.
Рис. 11.44. Иллюстрация
к задачам 105 и 106
106. Медицина: дыхание. Используя результаты, полученные при решении задачи 105, найдите приблизительный средний объем воздуха, находящихся в легких в течение фазы вдоха.
Социальные науки
107. Политика. В течение избирательной кампании уровень осведомленности общественности о кандидате на место в Конгресс составила приблизительно
Р(<) = ^П9+0>1; °^24’
где t — время в месяцах с начала кампании, a P(t) — доля избирателей в неком округе, которые помнят имя кандидата. Какова средняя доля избирателей, которые будут помнить имя кандидата в течение первых семи месяцев с начала кампании? В течение первых двух лет с начала кампании?
108. Состав населения. Было обнаружено, что в силу различных факторов численность детей в большом городе сначала увеличивается, а затем резко падает. Сколько в среднем детей насчитывалось в городе в течение шестилетнего периода, если известно, что их численность за этот период рассчитывается по формуле
7V(t) = _lt2+t + 4, 0 < t < 6?
Предполагается, что функция N = N(t) непрерывна, как показано на рис. 11.45.


Глава 11. Интегрирование
455
Рис. 11.45. Иллюстрация
к задаче 108
Ключевые слова, основные обозначения и формулы
11.1. Первообразные и неопределенные интегралы. Первообразная; неопределенный интеграл; знак интеграла; подынтегральное выражение; постоянная интегрирования.
11.2. Интегрирование методом замены переменной. Применение цепного правила в обратном порядке; обобщенные формулы вычисления неопределенных интегралов; дифференциалы; метод замены переменной; замена переменной.
11.3. Дифференциальные уравнения: рост и затухание. Дифференциальное уравнение; уравнение первого порядка; уравнение второго порядка; поле направлений; непрерывно вычисляемые сложные проценты; закон экспоненциального роста; константа роста; скорость роста; экспоненциальное затухание; рост численности населения; радиоактивный распад; неограниченный рост; ограниченный рост; логистический рост.
= rQ; Q = Qoert.
11.4. Геометрическая и численная интерпретация определенных интегралов. Площадь под кривой; знак определенного интеграла; формула левых прямоугольников; формула правых прямоугольников; монотонная функция; пределы погрешности суммы левосторонних и правосторонних прямоугольников, а также формулы суммирования значений в средних точках; площади со знаком; скорость, площадь и расстояние; скорость, площадь и общее изменение функции.
ь
j* f (^0 Rn] Ап.
а
11.5. Определенный интеграл как предел суммы; основная теорема интегрального исчисления. Формулы суммирования левосторонних и правосторонних прямоугольников, а также значений в средних точках; пределы погрешности суммы левосторонних и правосторонних прямоугольников, а также значений в средних точках; определенный интеграл как предел суммы Римана; подынтегральная функция; нижний предел; верхний предел; свойства определенных интегралов;


456
Часть III. Математический анализ
основная теорема интегрального исчисления; номинальный период эксплуатации; смысл определенных интегралов; среднее значение непрерывной функции.
ь
f(x)dx-
ь
- F(b) - F(a);
а
а
п
к=1
1
b — а
ь
j f(x)dx.
а
Основные свойства и формулы вычисления интегралов
kdx = кх + С,
j kf(x)dx = к f(x)dx,
j (/(х) ± д(х\) dx = f(x)dx + j g(x)d;
j undu =
j eudu = e“ + C,
| eau du = ^eau + C,
[ —du — ln |u| + C,
J и
a
f(x)dx = 0,
a
b a
j f(x)dx = —
a b
b b
kf(x)dx = к f(x)dx, к — константа, a a
b b b
j (/(x) ± g(x)) dx = f(x)dx ± jg(x)d'.
a a
b c b
j f(x)dx = j f(x)dx + f(x)d;
a a c
ип+1
, 1 + С,
П + 1
п ± -1,
а 7^ О,
и / О,
f(x)dx,
и
1х,
кг,
а
lx.


Глава 11. Интегрирование
457
Упражнения для повторения
Выполните все упражнения этого обзорного раздела и сравните результаты с ответами, помещенными в конце книги. Ответы ко многим упражнениям на повторение приводятся вместе с номером соответствующего раздела (курсивом). Если у вас возникают затруднения при решении какой-либо задачи, повторите материал соответствующего раздела.
А Вычислите следующие интегралы.
р
20 p
1. (бх + 3) dx.
2. 5dx.
10
9
3. j (4 - f2) dt.
0
4. j (1 — t2)3 tdt.
5. [1 + u4rfu. J и
1
6. j xe~2x dx.
0
В задачах 7 и 8 вычислите следующие производные и неопределенные интегралы.
7’ dx (Iе X dx\
8. j (\/4 + 5x) dx.
9. Найдите функцию у = /(ж), удовлетворяющую следующим условиям.
^=Зх2-2, /(0) = 4.
*10. Опишите график первообразной функции /, график производной которой изображена на рис. 11.46.
Рис. 11.46. Иллюстрация к задачам 10 и 11
11. 	Опишите графики трех возможных первообразных функции /, производная которой изображена на рис. 11.46, при условиях /(0) = —2, /(0) = 0 и /(0) = 2.


458
Часть III. Математический анализ
12. Вычислите первообразные.
а) = 8х3 — 4а? — 1. б) = е( — 4t_1.
dx dt
13. Вычислите интеграл Jx (х2 4-1) dx с помощью формулы суммирования значений в средних точках при п = 2. Оцените погрешность этого приближения.
14. Вычислите интеграл ]*х (ж2 + 1) dx с помощью основной теоремы интегрального исчисления и оцените фактическую погрешность \1 — ЛГ2|-
15. Вычислите интеграл j^7 f(x)dx, используя формулу суммирования значений в средних точках при п = 4 и следующие табличные значения.
X
3
7
11
15
/(я)
1,2
3,4
2,6
0,5
16. Вычислите среднее значение функции /(х) = бгг2 + 2х на отрезке [—1,2].
17. Какой прямоугольник имеет ту же площадь, что и фигура, ограниченная графиком функции f{x) = бх2 4- 2х на отрезке [—1,2] (см. задачу 16)?
Б Вычислите интегралы, используя график и величины площадей, приведенные на следующем рисунке.
Площадь А = 1
Площадь В = 2
Площадь С = 2
Площадь D = 0,6
Ь
18. j 5f(x)dx.
а
d
20. | f(x)dx.
b
d
22. f(x)dx.
о
ь
24. f(x)dx.
c
c
b
c
a
a
b
0
25. f(x)dx.
d
* 26. Опишите график первообразной функции, производная которой изображена на рис. 11.47. Чем один график первообразной функции f(x) отличается от другого?
27. 	Опишите графики трех возможных первообразных функции /, производная которой изображена на рис. 11.47, при условиях /(0) = —1, /(0) = 0 и /(0) = 1.


Глава 11. Интегрирование
459
Рис. 11.47. Иллюстрация к задачам 26 и 27
В задачах 28-33 используется поле направлений, изображенное на рис. 11.48.
5
Ч Ч Ч Ч Ч I t I I I ЧЧЧЧЧЧЧЧ11 ЧЧЧЧЧЧЧЧ11 ЧЧЧЧЧЧЧЧ11 Ч Ч Ч Ч Ч Ч Ч I I I ЧЧЧЧЧЧЧЧ11 ЧЧЧЧЧЧЧЧЧ1 ЧЧЧЧЧЧЧЧЧ1 ***ччхччч Ч ***>***•<•444
—5* »«>*^^//// «*«*ХХ///// I ZZZZZ////I /////////I /✓//////fl //////// I I ////// I I I I ////// f f I I / / / / / f I I I I /////fillip
I I I I I I I I t »
I I f f f / / / / /
Iff/////// Iff/////// Iff/////// If//////// f / // // // // ////////// /////////*• ////****--
ччч**-*-*«.-.Э ЧЧЧЧЧЧ*.*** 1ЧЧЧЧЧЧЧЧЧ 1ЧЧЧЧЧЧЧЧЧ 1ЧЧЧЧЧЧЧЧЧ 11ЧЧЧЧЧЧЧЧ I 1 ч ч ч ч ч ч ч ч 11ЧЧЧЧЧЧЧЧ 11ЧЧЧЧЧЧЧЧ I I I I I ч ч ч ч ч
Рис. 11.48. Иллюстрация к задачам 28-33
28. 	Ответьте на следующие вопросы.
а) Чему равен наклон решения уравнение в точках (2,1) и (—2, —1)?
б) Чему равен наклон решения уравнения = у в точках (2,1) и (—2, —1)?
*29. Решению какого уравнения, или соответствует поле направ¬
лений, изображенное на рисунке? Обоснуйте свои ответ.
30. 	Докажите, что функция у = Сх2 является решением уравнения для
любого действительного числа С.
31. 	Найдите частное решение уравнения проходящее через точки (2,1)
или (—2, —1).
32. Постройте графики двух частных решений задачи 31.
33. Используя графическую утилиту, постройте графики функций у = Сх2 для значений С = —2, —1, 1 и 2 на отрезках — 5 х 5 и — 5 у < 5.


460
Часть III. Математический анализ
В задачах 34-44 вычислите следующие интегралы.
1
0
34.
д/1 + xdx.
35.
х2 (х3 + 2)
J -1
J -1
be~ldt.
Г 1 4- t2
36.
37.
dt.
J t
1
1
38.
хе3х dx.
39.
[ * dx.
J V2~x
-3
3
3
40.
Г 2dx.
41.
[ 2dx.
1 1 + х2
J (1 + x2)2
0
0
%
х3 (2х4 4- 5)5 dx.
43.
[ e X -dx.
Jr«+3
Г ех
44.
.dx.
J
1 (еж + 2)2
45. Вычислите функцию у = f(x), удовлетворяющую следующим условиям.
= Зх-1 - /(1) = 5.
46. Составьте уравнение кривой, проходящей через точку (2,10), если ее наклон при каждом значении х описывается уравнением
dy dx
= 6x4-1.
В задачах 47-50 описывается следующая ситуация. Модель ракеты взлетает в воздух с начальной скоростью, равной 160 футов в секунду. Пренебрегая сопротивлением воздуха, скорость ее полета r(t) можно описать следующим графиком.
47. 	Вычислите высоту подъема ракеты, используя формулу суммирования левосторонних и правосторонних прямоугольников, а также значений в средних точках для пяти подынтервалов разбиения. (Значения функции легко определить по графику.) Вычислите пределы погрешности этих сумм.


Глава 11. Интегрирование
461
* 48. Как площади прямоугольников, используемых в квадратурных суммах, связаны с расстоянием?
49. На сколько интервалов необходимо разбить интервал [0,5], чтобы сумма Ап аппроксимировала высоту подъема ракеты с точностью до одного фута?
50. Запишите определенный интеграл, выражающий высоту подъема ракеты и вычислите его. (Подсказка. Сначала составьте уравнение скорости полета.)
51. Выполните следующие задания.
а) Вычислите среднее значение функции f (х) = Зу/х на отрезке [1,9].
б) Изобразите график функции f (х) = Зу/х и ее среднее значение на отрезке [1,9] в одной и той же системе координат.
В В задачах 52-56 вычислите следующие интегралы.
52.
53. р(х3 - l)2cfc.
[ х dx. I у/б - X
7 Г
54.
55. д?х/16 — xdx.
0
1 р
56.
х (х 4-1)4 dx.
-1
57. Вычислите функцию у = f(x), удовлетворяющую следующим условиям.
^=9х2е< ДО) = 2.
58. Решите следующее дифференциальное уравнение.
dN
— = 0,067V, 7V(0) = 800, N > 0.
dt
Задачи 59-63 связаны с вычислением определенного интеграла
1
о
(У этой подынтегральной функции нет первообразной, представленной элементарной функцией.)
59. Постройте график функции f (х) = е~х* на отрезке [0,1].
60. Вычислите интеграл I с помощью формулы суммирования значений в средних точках при п = 5.
61. Вычислите функцию f"(x) и покажите, используя графическую утилиту, что величина |/"(х) | не превосходит числа 2 на интервале [0,1].
62. Используя результаты решения задачи 61, вычислите пределы погрешности величины М5, указанной в задаче 60.


462
Часть III. Математический анализ
63. Используя результаты решения задачи 62, определите, сколько интервалов разбиения п необходимо выбрать, чтобы величина Мп аппроксимировала интеграл I с погрешностью, не превосходящей 0,0005.
В задачах 64-67 постройте графики следующих функций и укажите характер их изменения: неограниченный рост, экспоненциальный спад, ограниченный рост или логистический рост.
64. N = 50 (1 — e-°>07t); 0 t 80, 0 < N 60.
65. р = 500е-°'°3‘; 0 < х 100, 0 < р 500.
66. А = 2ООе0,08; 0 < t С 20; 0 < А < 1000.
61-N= 1 + 90е-о,з«> 00^25, 0^100.
В задачах 68-70 вычислите интегралы, используя графическую утилиту.
0,6
68. I . dx.
-0,5
3
69. x2exdx.
-2
70.
2,5 lnx .
~^~dx
J
0,5
Применение математики
Экономика и бизнес
71. Затраты. Компания выпускает горные лыжи. Отдел маркетинговых исследований выяснил, что функция предельных затрат С (ж) выглядит так, как показано на рис. 11.49. Здесь С\х} — предельные затраты (в долларах), ах — недельный объем производства (пар лыж). Оцените изменение функции предельных затрат при изменении недельного объема производства с 200 до 600 пар лыж. Примените формулы суммирования левосторонних и правосторонних прямоугольников для вычисления интегралов при разбиении интервала интегрирования на два равных подынтервала. Замените знаки вопроса в неравенстве значениями и Л2.
600
200
* 72. Затраты. Объясните, каким образом изменение производственных затрат связано с суммами левосторонних и правосторонних прямоугольников использованными при решении задачи 71.
73. 	Затраты. Предположим, что функция предельных затрат, упомянутая в задаче 71, линейна. Составьте ее уравнение и запишите определенный интеграл, выражающий рост затрат при изменении недельного объема производства с 200 до 600 пар лыж. Вычислите этот определенный интеграл.


Глава 11. Интегрирование
463
Рис. 11.49. Иллюстрация
к задаче 71
74. Прибыль и объем производства. Недельная предельная прибыль при выпуске х единиц продукции приближенно описывается формулой
Р'(х) = 150- 0 0^40.
Чему равно общее изменение прибыли при изменении недельного объема производства с 10 до 40 единиц? Запишите определенный интеграл и вычислите его.
75. Функция прибыли. Предположим, что предельная прибыль от производства х единиц продукции в день описывается формулой
Р\х) = 100 - 0,02ж, Р(0) = О,
где Р(х) — прибыль (в долларах). Вычислите функцию прибыли Р, а также прибыль, полученную при дневном производстве 10 единиц продукции.
76. Истощение месторождения. Вначале из нефтяной скважины удавалось добывать 60 000 баррелей в неделю, но со временем объем добычи нефти стал сокращаться со скоростью 4000 баррелей в год. Итак, если функция P(t) представляет собой общий объем добычи (тыс. баррелей), то
P'(t) = f(t) = 60 - 4f, 0 t 15.
Запишите определенный интеграл, позволяющий найти общий объем добычи через 15 лет работы, и вычислите его.
77. Инвентаризация. Предположим, что объем товара, хранящегося на складе, с течением времени t сокращается по следующему закону.
I(t) = 10 4-36t —3t2, 0sUs?12.
Чему равен средний объем хранящегося на складе товара во втором квартале?
78. Зависимость цены от спроса. Предположим, что зависимость цены от спроса описывается функцией
р = $(х) = 8(е0’05® - 1).
Вычислите среднюю цену (в долларах), если спрос изменяется в интервале [40,50].


464
Часть III. Математический анализ
79. 	Обучение сотрудников. Компания, выпускающая звукозаписывающую аппаратуру, выяснила, что в среднем новый сотрудник может собрать деталей за рабочую смену после t дней обучения. Эта зависимость описывается следующей таблицей значений.
t
0
10
20
30
40
50
N(t)
5
10
14
17
19
20
а) Вычислите среднее значение левосторонней и правосторонней сумм А5 при равномерном разбиении интервала на пять подынтервалов и оцените общее количество деталей, собранных сотрудником после 50 дней обучения. Оцените погрешность этой величины.
б) Постройте уравнение квадратичной регрессии и ее график.
в) Вычислите общее количество деталей, собранных сотрудником после 50 дней обучения, используя уравнение квадратичной регрессии и графическую утилиту.
80. Номинальный период эксплуатации. Общие затраты C(t) и общий доход R(t) (тыс. долл.) угольной шахты описываются формулами
C"(t) = 3 и R'(t) = 20е_о’“.
Здесь t — возраст шахты. Вычислите номинальный период эксплуатации шахты, начиная с ближайшего года. Какую общую прибыль принесет шахта за время своего существования?
81. Маркетинг. Отдел маркетинговых исследований автомобильной компании выяснил, что месячный объем продаж (млн. долл.) новой модели автомобиля изменяется по следующему закону.
s'(t) = 4e’°’08t, 0 < t < 24.
Здесь t — количество месяцев, прошедших с момента выпуска модели в серию. Чему равен общий объем продаж модели S(t) через t месяцев после выпуска, если в момент выхода на рынок эта величина была равна нулю? Чему равна эта величина через 12 месяцев после выпуска? За какое время общий объем продаж достигнет 40 млн. долл.?
Биологические науки
82. WWW Загрязнение. На рисунке изображен график концентрации загрязняющих веществ C(t) в промышленной зоне на протяжении 12 часов. Вычислите среднее значение концентрации таких веществ за этот период, используя метод суммирования значений по средним точкам и разбив отрезок на шесть подынтервалов. Значения функции определите по графику.


Глава 11. Интегрирование
465
t
Время, ч
83. Заживление раны. Площадь небольшой раны изменяется по следующему закону
dA ~ г,
— = —5t-2, 1 С 5.
at
Здесь t — количество дней, а А(1) = 5 см2. Какова будет площадь раны через пять дней?
84. Загрязнение. Агентство по охране окружающей среды выяснило, что скорость просачивания токсических химических веществ отходов со свалки в грунт (галлонов в год) описывается формулой
1000
(l+t)2’
где t — время существования свалки, измеряемое в годах. Вычислите общее количество токсических веществ, просочившихся в грунт за четыре года.
85. Численность населения. Численность населения Мексики в 2000 году равнялась 100 млн. чел. и росла со скоростью 1,5 % в год.
а) Сколько людей будет жить в Мексике в 2025 году, если скорость роста численности населения останется неизменной?
б) Через какое время численность населения Мексики удвоится при неизменной скорости роста?
Социальные науки
86. Археология. Скорость распада изотопа углерод-14 равна г = —0,0001238. Части кости животного, найденной при археологических раскопках, содержит 4% исходного количества этого изотопа. Оцените возраст находки.
87. Обучение. Средний студент школы бизнеса, обучающийся набору текста, через t недель занятий улучшает навык со скоростью N'^t) = 7е_0,1< слов в минуту. Предположим, что в начале курса студент мог набирать текст со скоростью 25 слов в минуту. Сколько слов в минуту он будет вводить через t недель обучения? Предположим, что курс обучения длится 15 недель. Какой скорости набора текста достигнет студент по окончании курса обучения?


466
Часть III. Математический анализ
Домашнее задание 11.1. Формула Симпсона
Описание формулы Симпсона
Сумма площадей левосторонних прямоугольников Ln, сумма площадей правосторонних прямоугольников Rn> средняя сумма площадей левосторонних и правосторонних прямоугольников Ап и сумма значений в средних точках Мп представляют собой квадратурные формулы, предназначенные для вычисления интегралов. Если функция / возрастает, формула суммы площадей правосторонних прямоугольников переоценивает определенный интеграл, а формула суммы площадей левосторонних прямоугольников — недооценивает (рис. 11.50).
Ь
Ln f (x)dx Rn.
а
Рис. 11.50. Квадратурные формулы левосторонних и правосторонних прямоугольников
Формула средней суммы площадей Ап аппроксимирует интеграл монотонной функции лучше, чем формулы суммирования левосторонних и правосторонних прямоугольников. Эта сумма часто называется формулой трапеций и обозначается как Тп, поскольку средняя площадь соответствующих левостороннего и правостороннего прямоугольника равна площади трапеции (см. рис. 11.51). Складывая величины Ln и Rn и разделяя их пополам, получим Тп = Ап. Это и есть формула трапеций. Сумма значений в средних точках Мп, как и величина Тп, лучше аппроксимирует определенный интеграл монотонной функции, чем формулы суммирования площадей левосторонних и правосторонних прямоугольников.
Ln — (J (^о) "И f (#1) + • ’ • + f fan-l)) А#- Формула суммирования
площадей левосторонних прямоугольников
Rn = (J (#i) 4- f (#2) + ••• + / (жп)) Аж. Формула суммирования
площадей правосторонних прямоугольников
Тп — (J (^о) + 2/ (Ж1) -I F 2/ (жп_1) + f (жп))
Формула трапеций
+ /
Дж.
Формула суммирования значений в средних точках
Прямоугольник в формуле суммирования значений в средних точках имеет такую же площадь, что и трапеция, косая сторона которой образована касательной (см. рис. 11.51). В целом, если функция является выпуклой или вогнутой, погрешность формулы трапеций вдвое выше, чем погрешность формулы суммирования значений в средних точках.


Глава 11. Интегрирование
467
Ь
Tn f(x)dx Мп.
Рис. 11.51. Формула трапеций
Это означает, что взвешенное среднее двух оценок, в котором сумма значений в средних точках учитывается дважды, лучше аппроксимирует значение интеграла, чем каждая из квадратурных формул по отдельности. Это правило называется формулой Симпсона и записывается следующим образом.
$2п =
2Мп + Тп
3
Формула Симпсона
(И.21)
Формула трапеций содержит значения подынтегральной функции в (n + 1) точках (включая точки а и Ь), а формула суммы значений в среднх точках — в п точках. В то же время формула Симпсона содержит значения подынтегральной функции в (2n +1) точках (включая точки а и Ь). Чтобы применить формулу Симпсона, следует разделить отрезок [а, Ь] на 2п равных подынтервалов, вычислить подынтегральную функцию в каждой точке разбиения, а затем применить формулы суммирования в средних точках и трапеций для п интервалов. Итак, формула Симпсона требует разбиения интервала интегрирования на четное количество одинаковых подынтервалов.
1. 	Для Дх = (Ь - а)/4 формула Симпсона
S4 =
2ЛГ2 4- Т2
3
принимает вид
Si = (f (х0) +4/(xi) + 2/ (х2) + 4/(х3) + /(х4)) —.
Сравнение погрешностей
Чтобы оценить эффективность методов интегрирования, следует сравнить их погрешности при одинаковом количестве точек разбиения п. Выполните эту процедуру для пяти квадратурных формул, Ln, Rn, Мп, Тп и S2n, рассмотренных выше, вычислив определенный интеграл, значение которого известно заранее, а затем сравните полученные погрешности.
2. 	Рассмотрим интеграл
12
4
Три десятичных знака


468
Часть III. Математический анализ
Таблица 11.5. Значения подынтегральной функции
X
4
5
6
7
8
9
10
11
12
1/х
0,250
0,200
0,167
0,143
0,125
0,111
0,100
0,091
0,083
Таблица 11.6. Погрешности квадратурных формул
~ Z Rn — I — I Тп — I S2n — I
п — 2 0,401 0,002
п = 4 —0,009
Заполните табл. 11.6, используя значения подынтегральной функции, приведенные в табл. 11.5.
Из результатов, приведенных в табл. 11.6, следует, что точность квадратурной формулы зависит от количества точек разбиения п.
Таблица 11.7. Зависимость погрешности квадратурных формул от количества точек разбиения п
Rn
Гп
&2п
1
1
1
2п -
2
4
16
1
Точность увеличивает¬
1
Точность увеличивает¬
1
Точность увеличивает¬
10nio
ся на один десятичный
102
ся на два десятичных
104
ся на четыре десятич¬
знак
знака
ных знака
Мы уже отмечали, что формулы Ln и Rn для постоянной функции дают точный результат. Аналогично формулы Мп и Тп дают точный результат для постоянной и линейной функций. А для каких функций дает точный ответ формула Симеона? Оказывается, эта формула является точной для всех подынтегральных функций, представляющих собой полиномы, степень которых не превышает трех. Однако формула Симпсона практически не применяется в компьютерных программах, поскольку существуют более производительные алгоритмы аппроксимации. Например, в большинстве графических утилит используется алгоритм интегрирования Гаусса-Кронрода (Gauss-Kronrod), погрешность которого равна нулю для всех подынтегральных функций, представляющих собой полиномы, степень которых не превышает пяти.
3. 	Примените формулу Симеона для приближенного вычисления интеграла
10
2
при 2п = 4 и 2п = 8. Вычислите величину S^n с тремя десятичными знаками.
4. 	Применение более производительного алгоритма показало, что I = 27,159. Вычислите погрешность \I — Sin | с двумя десятичными знаками.


Глава 11. Интегрирование
469
Применение
Применим формулу Симпсона для вычисления затрат. (Заметим, что для этого не обязательно строить уравнение регрессии, как это предусмотрено в графической утилите.)
Некая компания выпускает и продает популярные солнечные очки. Ее финансовый отдел собрал данные (табл. 11.8) о предельных затрат (в долларах) на производство х пар солнечных очков в час.
Таблица 11.8. Предельные затраты
X
50 100 150 200 250 300 350 400 450
С'(х)
21,80 16,95 15,31 14,50 14,00 13,66 13,42 13,25 13,11
5. Предположим, что компания выпускает 50 пар очков в час и планирует повысить объем производства до 450 пар очков в час. Оцените общее изменение затрат, используя формулы Ln и Rn и подходящее значение п. Насколько близки приближенные значения общего изменения затрат к реальным величинам?
6. Примените формулу Симпсона для решения задачи 5.
Домашнее задание 11.2. Нормальное распределение
Одна из наиболее важных функций в теории вероятностей и математической статистике описывает плотность нормального распределения. Ее колоколообразный график часто называют кривой нормального распределения (рис. 11.52).
Рис. 11.52. Плотность нормального распределения
Можно показать, что площадь фигуры, расположенной под кривой нормального распределения от —оо до оо, для любого действительного числа р и любого положительного действительного числа а всегда равна единице. Таким образом, площадь фигуры, ограниченной кривой нормального распределения на отрезке [а, Ь], является частью общей площади фигуры, расположенной под этой кривой от — оо до оо. Рассмотрим плотность нормального распределения на следующем примере.
Отдел качества завода по производству 100-ваттных лампочек проверил крупную выборку товара и выяснил, что средняя продолжительность работы лампочек равна пяти часам (р = 5) при стандартном отклонении, равном одному часу (а = 1). (Стандартное отклонение измеряет разброс плотности нормального распределения вокруг среднего зна¬


470
Часть III. Математический анализ
чения, или математического ожидания. Малое стандартное отклонение характерно для высоких и узких нормальных кривых, а большое — для плоских и широких.) Кривая нормального распределения для значений ц = 5 и а = 1 показана на рис. 11.53. Площадь фигуры, расположенной под этой кривой между 500 и 600 часами, представляет собой долю лампочек, продолжительность работы которых больше пяти часов и меньше шести. Иначе говоря, эта площадь равна вероятности того, что лампочка, случайным образом извлеченная из генеральной совокупности лампочек, проработает больше 500 часов, но не больше 600.
Рис. 11.53. Плотность нормального рас¬
пределения для значений /1 = 5 и а = 1
1. Запишите определенный интеграл, выражающий вероятность того, что лампочка, случайным образом извлеченная из генеральной совокупности лампочек, проработает больше 500 часов, но не больше 600.
2. Вычислите определенный интеграл из п. 1 с помощью формулы суммирования значений в средних точках при разбиении интервала интегрирования на пять равных частей. Объясните смысл полученного результата.
3. Вычислите функцию Постройте график функции у = f"(x) на отрезке [5,6]
и покажите, что функция |/"(х)| на этом отрезке не превышает 0,4.
4. Вычислите пределы погрешности величины Мп в п. 2, используя результат решения п. 3.
5. Используя результаты решения п. 3, определите, насколько большим должно быть число п, чтобы погрешность формулы суммирования в средних точках не превышала 0,00005.
6. Предположим, что площадь фигуры, расположенной под кривой нормального распределения от точки 5 до оо, равна 0,5. Чему равна вероятность случайно выбрать лампочку, срок службы которой больше 600 часов? Объясните ход своих рассуждений.
7. Чему равна вероятность случайно выбрать лампочку, срок службы которой меньше 500 часов? Объясните ход своих рассуждений.
8. Используя графическую утилиту, определите вероятность случайно выбрать лампочку, срок службы которой больше 450 часов, но меньше 550 часов. Решите эту задачу для лампочки, срок службы которой больше 350 часов, но меньше 650 часов.
9. Постройте графики кривой нормального распределения для д = 8иа = 1,2иЗ. Как параметр а влияет на форму нормальной кривой?


12
Практические задачи интегрального исчисления
■ 12.1. Площадь фигуры, ограниченной кривыми
■ 12.2. Интегрирование в экономических задачах
■ 12.3. Интегрирование по частям
■ 12.4. Таблицы интегралов
■ Ключевые слова, основные обозначения и формулы
■ Упражнения для повторения
■ Домашнее задание 12.1. Анализ концентрации дохода по исходным данным
■ Домашнее задание 12.2. Рынок зерна
Введение
В этой главе рассматриваются дополнительные темы, связанные с интегрированием. Поскольку все они совершенно не зависят друг от друга, их можно рассматривать в любом порядке, а определенные разделы при необходимости можно даже пропустить.
12.1. 	Площадь фигуры, ограниченной кривыми
■ Площадь фигуры между кривой и осью х
■ Площадь фигуры между двумя кривыми
■ Практическая задача: распределение доходов


472
Часть III. Математический анализ
В главе 11 мы выяснили, что определенный интеграл f (х) представляет собой сумму площадей фигур, лежащих между графиком функции у = /(х) и осью х от точки х = а до точки х = Ь, причем площадь над осью х учитывается со знаком “плюс”, а площадь под осью х — со знаком “минус” (рис. 12.1). В этом разделе рассматривается применение определенного интеграла для вычисления площади фигур, лежащих между кривой и осью х, а также между двумя кривыми. Эти площади всегда являются неотрицательными величинами, поскольку площадь может представляться только положительным значением.
Рис. 12.1. Графическое представление
интеграла f (х) dx = — А 4- В
Площадь фигуры между кривой и осью х
На рис. 12.1 величина А соответствует площади фигуры, лежащей между кривой у = = f(x) и осью х от точки х = а до точки х = с, а величина В — площади фигуры, расположенной между кривой у = f(x) и осью х от точки х = с до точки х — Ь. Обе эти величины являются положительными. Поскольку на отрезке [с, Ь\ выполняется условие /(х) 0, то
ь
| f (х) dx — В.
с
Кроме того, поскольку на отрезке [а, с] выполняется условие /(х) 0, то
f (х) dx = —А,
а
ИЛИ
с с
А = - f (х) dx = j [-/ (х)] dx.
а а
Таким образом, площадь фигуры, лежащей между графиком отрицательной функции и осью х, равна определенному интегралу функции, взятой со знаком минус.


Глава 12. Практические задачи интегрального исчисления
473
Задание 12.1.
Постройте график такой функции /, чтобы на отрезке [1,5] выполнялось условие f{x) 0. (Записывать уравнение не нужно.) Постройте график функции у = —f(x) на том же интервале в той же системе координат. Объясните, как эти рисунки связаны с рассуждениями, приведенными выше. ■
Все предыдущие интерпретации основывались на трактовке определенного интеграла как предела суммы Римана.
ь ри а
п
dx = lim V f (с*:) Дх*;.
n—>oo '
k=l
На рис. 12.2 показан частный случай суммы Римана, демонстрирующий применение формулы суммы значений в средних точках для вычисления величины М$ на интервале [а, Ь]. Произведение отрицательно для всех прямоугольников на отрезке [а, с]
и положительно для всех прямоугольников на отрезке [с, Ь\. Таким образом, величины /(cfc)Axjt представляют собой площади прямоугольников, взятые со знаком минус на отрезке [а, с], а величины —/(с^)Дх^ являются реальными площадями прямоугольников на этом отрезке. Следовательно, для отрезка [а, с], на котором выполняется условие f(x) < 0, справедливо следующее утверждение.
п
Площадь = lim У [-/ (с*)] =
п—>ое ' к=1
с
j [-/ (*)] dx.
а
Рис. 12.2. Площадь и суммы Римана
Однако на отрезке утверждение.
[с, Ь\, где выполняется условие /(х) 0, справедливо следующее
п л
Площадь = lim /(cfc)Axfc= \f(x)dx.
п—»ОО '
fc=l J


474
Часть III. Математический анализ
Площадь фигуры между кривой и осью х
Для функции /, непрерывной на отрезке [а, Ь], площадь фигуры, лежащей между кривой у = и осью х от точки х — а до точки х = Ъ, можно найти по следующим формулам.
Если /(х) > 0 на отрезке [а, Ь], то площадь = j f (х) dx.
а
Ъ
Если /(ж) 0 на отрезке [а, Ь], то площадь = [-/ (х)] dx.
Если на некотором отрезке функция f(x) меняет знак (как показано на рис. 12.1), площадь между графиком f и осью х можно получить, разделив интервал на подынтервалы, на которых функция f имеет постоянный знак, найдя площади на каждом из этих подынтервалов и просуммировав эти площади.
Пример 12.1 (Площадь между кривой и осью х). Вычислите площадь фигуры, ограниченной графиками /(х) = бх — х2 и у = 0 для 1 х 4.
Решение. Прежде всего построим график функции /(х) (рис. 12.3). (Решение любой задачи, связанной с вычислением площади, должно начинаться с построения графика.) Поскольку на отрезке [1,4] выполняется условие /(х) 0, то
= 24.
Упражнение 12.1.
Вычислите площадь фигуры, ограниченной графиками /(х) = х2 + 1 и у = 0 на отрезке 1 х С 3. |
Пример 12.2 (Площадь фигуры между кривой и осью «). Вычислите площади фигур, лежащих между графиком /(х) = х2 — 2х и осью х, на указанных отрезках
1. [1,2]. 2. [-1,1].
Решение. Прежде всего построим график функции /, показанный на рис. 12.4.


Глава 12. Практические задачи интегрального исчисления
475
Рис. 12.3. График функции Рис. 12.4. График функции
/(х) = 6х — х2 f(x) = х2 — 2х
1. Из графика следует, что для чисел 1 < х < 2 выполняется условие /(ж) < О, следовательно, нужно интегрировать
2
Л1 = J [-/ («)] dx =
1
|« 0,667.
2. Поскольку из графика видно, что f(x) 0 на отрезке [—1,0] и /(ж) 0 на отрезке
[0,1], для вычисления этой площади потребуется два интеграла.
А = + Аз =
о 1
/ (ж) dx + j [-/ (ж)] dx = -1 о
0 1
(х2 - 2х) dx -h j (2х — х2) dx = -1 о


476
Часть III. Математический анализ
Упражнение 12.2.
Вычислите площадь фигуры, лежащей между графиком функции /(т) = х2 — 9 и осью х на указанных отрезках.
1. [0,2]. 2. [2,4]. в
Площадь фигуры между двумя кривыми
Теперь рассмотрим площадь, ограниченную функциями у = f(x) и у = д(х), где /(т) д(х) 0 для а х Ь, как показано на рис. 12.5.
/Площадь А между \ _ /ПлощальА
\ f (ж) И д (х) ) ~ ^под f (х)/
ь
Площалъ под д(х)
Площади вычисляются от х — а до х = Ъ над осью х.
f (х) dx -
д (х) dx
а а
Ъ
[/ (*) - 9 (*)] dx.
а
Воспользуемся свойством определенного ингерала 4 (раздел 11.5).
Рис. 12.5. Графики функций у — = /(я) и у = р(х)
В этой формуле не требуется, чтобы функции f(x) или д(х) оставались положительными на интервале [а, Ь]. Более общий результат представлен в следующей врезке.


Глава 12. Практические задачи интегрального исчисления
477
Площадь фигуры между двумя кривыми
Если функции fug непрерывны и /(я) д(х) на отрезке [а, Ь], то площадь фигуры, ограниченной кривыми у = /(ж) и у = д(х) на отрезке а х Ь, вычисляется по следующей формуле.
ъ
А = [f(x)~ 9 (ж)] dx-
Задание 12.2.
Сумма Римана для интеграла, описывающего площадь фигуры, расположенной между графиками у = f(x) и у = д(х), имеет вид
п
52 [/ (ct) - 9 (cfc)]
fc=l
Если f(x) д(х), каждое слагаемое в этой сумме представляет собой площадь прямоугольника с высотой f(ck) — g(ck) и шириной Ах*;. Проанализируйте взаимосвязь между этими прямоугольниками и площадью фигуры, лежащей между графиками функций У = /(*) и У = 9(х)- ■
Пример 12.3 (Площадь фигуры между двумя кривыми). Вычислите площадь фигуры, ограниченную графиками f (ж) = + 3, д(х) = —х2 + 1, х = — 2, и х = 1.
Решение. Прежде всего нарисуем эту фигуру (рис. 12.6), а затем запишем определенный интеграл и найдем его значение. Из графика следует, что /(#) д(х) для — 2 х 1, так что
Упражнение 12.3.
Вычислите площадь фигуры, ограниченной графиками /(х) = х2 — 1, д (х) — — ^х — 3, х — — 1 и х = 2. ■


478
Часть III. Математический анализ
Рис. 12.6. Графики f (х) = |х+3,
д(х) — —х2 + 1, х = —2, и х = 1
Пример 12.4 (Площадь между двумя кривыми). Вычислите площадь фигуры, ограниченной графиками /(х) = 5 — х2 и р(х) = 2 — 2х.
Решение, Прежде всего построим графики f и д9 как показано на рис. 12.7. Поскольку в формулировке задачи нет никаких предельных значений х, соответствующие значения необходимо определить по графику. Как показано на рисунке, график f — это парабола, а график д — это прямая. Площадь, ограниченная этими двумя графиками, находится между точкой пересечения графиков слева и точкой пересечения графиков справа. Чтобы найти эти точки пересечения, решим уравнение /(х) = д(х) относительно х.
/(х) = д(х),
5 — х2 = 2 — 2х,
х2 — 2х — 3 = О,
х = —1; 3.
Рис. 12.7. Графики /(х) = 5 - х2 и д(х) = = 2 — 2х


Глава 12. Практические задачи интегрального исчисления
479
Всегда можно проверить эти значения, подставив их в исходные уравнения. (Следует отметить, что фигура, лежащая между графиками для х < —1, слева не ограничена, а фигура между графиками для х > 3 не ограничена справа.) На рис. 12.7 показано, что /(х) д(х) на интервале [—1,3], так что
А= j [/(х)
-1
= Ь
-1
+ 2х — х2) dx
— (2 — 2x)j dx =
Г З31
= з-з + з2- —
о
3
-1
- 3 • (-1) + (-1)2 -
Упражнение 12.4.
Вычислите площадь фигуры, ограниченной графиками f(x) = 6-х2 ид(х) = х. ■
Пример 12.5 (Площадь между двумя кривыми). Вычислите площадь фигуры, ограниченной графиками /(ж) = х2 — х и д(х) = 2х для — 2 х < 3.
Решение. Графики f и д показаны на рис. 12.8. Изучив график, можно увидеть, что /(х) д(х) на интервале [—2,0], но д(х) f(x) на интервале [0,3]. Таким образом, для вычисления площади понадобится найти два интеграла.
о
Al = j [f (х) - д (х)] dx = f(x) >9 О) на [-2, о]
-2
0
= | [х2 — х — 2х] dx =
-2
о
= | (ж2 — Зж) dx =
-2
3
= j [д (х) - f (ж)] dx = д(х) f (®) на [о, з] о


480
Часть III. Математический анализ
з
j [2х — (ж2 — ж)] dx = о
з
j (Зя — х2) dx =
о
Рис. 12.8. Графики функций
f(x) = х2 — х и д(х) = 2х
Общая площадь между двумя графиками равна
26 9 79
Л = Л1+Л2 = ^ + ^ = ^«13,167.
о 2 о ■
Упражнение 12.5.
Вычислите площадь фигуры, ограниченной графиками f(x) — 2х2 и д(х) = 4 - 2х для —2 X С 2. g
Пример 12.6 (Вычисление площади методом численного интегрирования). Вычислите площадь фигуры (с точностью до трех десятичных знаков), ограниченной графиками f (х) = е~х и д(х) = х2 — 1.
Решение. Прежде всего воспользуемся графической утилитой, построим графики функций f и д и найдем точки пересечения графиков (рис. 12.9, а). Легко видеть, что график f имеет колоколообразную форму, а график д представляет собой параболу. Отметим также, что /(ж) д(х) на интервале [—1,131; 1,131]. Вычислим теперь площадь Л, используя


Глава 12. Практические задачи интегрального исчисления
481
метод численного интегрирования (рис. 12.9, б).
1,131
А = f [е-1* - (х2 - 1)] dx = 2,876.
-1,131
2
а)
Гп1пЪ(ел( -Хл2)-<
ХЛ2-1),Х>-1.131» 1.131) 2.875501719
Рис. 12.9. Результаты вычислений
Упражнение 12.6.
Вычислите площадь фигуры (с точностью до трех десятичных знаков), ограниченной графиками f(x) = х21п х и д(х) = Зх — 3. ■
Практическая задача: распределение доходов
Бюро переписи населения США собрало и проанализировало множество данных, касающихся распределения доходов среди семей в Соединенных Штатах Америки. Бюро сообщило, что за 1997 год 20% беднейших семей получили 4% всех семейных доходов, а 20% богатейших семей получили 47% таких доходов. В табл. 12.1 и на рис. 12.10 дана подробная картина распределения семейных доходов в 1997.
Таблица 12.1. Распределение семейных доходов в Соединенных Штатах Америки в 1997 году
Уровень доходов, долл.
X
У
Ниже 21 000
0,20
0,04
Ниже 36 000
0,40
0,14
Ниже 54 000
0,60
0,30
Ниже 80 000
0,80
0,53
График у = f(x) на рис. 12.10 называется кривой Лоренца, которая, как правило, вычисляется с помощью регрессионного анализа, т.е. путем аппроксимации набора данных на заданном интервале определенной элементарной функцией. Переменная х описывает суммарную долю семей, уровень доходов которых не превышает заданный, а переменная у описывает суммарную долю всех семейных доходов. Например, точка (0,40; 0,14) в табл. 12.1 указывает на то, что 40% семей (доход которых ниже 36 000 долл.) получают 14% общего дохода всех семей; точка (0,60; 0,30) указывает на то, что 60% семей получают 30% общего дохода всех семей и т.д.


482
Часть III. Математический анализ
Рис. 12.10. Кривая Лоренца
Абсолютное равенство доходов наступило бы тогда, когда площадь между кривой Лоренца и кривой у — х стала бы равна 0. В этом случае кривая Лоренца имела бы вид у = х, и все семьи получали бы равные доли общего дохода. Иначе говоря, 5% семей получало бы 5% дохода, 20% семей получало бы 20% дохода, 65% семей получало бы 65% дохода и т. д. Максимально возможная площадь между кривой Лоренца и кривой у = х равна j, т.е. площади треугольника, лежащего под графиком у = х. В этом случае возникло бы абсолютное неравенство — весь доход был бы сосредоточен в руках одной семьи, а остальные семьи не имели бы дохода. В действительности кривая Лоренца лежит между этими двумя крайностями. Однако по мере роста окрашенной серым цветом области начинает расти неравенство в распределении доходов.
Отношение площади, ограниченной графиком у — х и кривой Лоренца у = /(т), к площади треугольника, лежащего под прямой у = х от точки х — 0 до точки х = 1, называется показателем концентрации дохода. Площадь, ограниченная графиками у = х и у = f(x) равна интегралу $q[x — f (х)] dx, а площадь треугольника под прямой у = х равна
Показатель концентрации доходов
Если у = f(x) — уравнение кривой Лоренца, то
1
показатель концентрации доходов = 2 j [х — f (ж)] dx.
о
Показатель концентрации доходов всегда больше нуля и меньше единицы.
Нуль соответствует абсолютному равенству — доходы равномерно распределяются между всеми людьми, а единица соответствует абсолютному неравенству — один человек получает весь доход, а остальные не получают ничего.


Глава 12. Практические задачи интегрального исчисления
483
Чем ближе показатель концентрации доходов к нулю, тем ближе распределение доходов к равномерному. Чем ближе этот показатель к единице, тем ближе положение к ситуации, когда весь доход сосредоточен в одних руках. Показатель концентрации доходов используется для сравнения распределения доходов в разные моменты времени, между различными группами людей, до и после выплаты налогов, между различными странами и т. п.
Пример 12.7 (Распределение доходов). Кривая Лоренца для распределения доходов в определенной стране в 1990 году описывается функцией f(x) = х2,6. Экономисты предсказали, что кривая Лоренца в этой стране в 2010 году будет иметь вид д(х) = х1,8. Вычислите показатель концентрации дохода для каждой кривой и объясните полученные результаты.
Решение. Кривые Лоренца показаны на рис. 12.11.
а) кривая Лоренца в 1990 году б) прогнозируемая кривая
Лоренца в 2010 году
Рис. 12.11. Кривые Лоренца
Показатель концентрации доходов 1990 году (см. рис. 12.11, а) равен
Прогнозируемый показатель концентрации доходов в 2010 году (см. рис 12.11, б) равен
1
2
о
1
[х - д (х)] dx = 2 j [х — х1’8]
о
dx = 2
Если предположение корректно, то показатель концентрации доходов будет падать, а доход в 2010 году будет более равномерно распределен по сравнению с 1990 годом. ■
Упражнение 12.7.
Повторите решение примера 12.7, если предполагаемая кривая Лоренца в 2010 году будет иметь вид р(х) = х3,8. ■


484
Часть III. Математический анализ
Ответы к упражнениям
А = | (х*  1 2 + 1) dx = ~
-1
1) А = j (9 — х2) dx =
о
f f4  * * 7
(9 — х2) dx + (х2 — 9) dx = 6.
2 3
А= j [(х2 _ i) _ (_| _ з)] dx = = 9)75.
-1
2
г 125
А - [(б — х2) — х] dx = ~ 20,833.
-з
1 2 [(4 - 2х) - 2х2] dx + j [2х2 - (4 - 2а:)] dx = у « 12,667.
-2
12.6. 0,443.
12.7. Показатель концентрации доходов приблизительно равен 0,538. В 2010 году доходы будут распределены менее равномерно.
12.1.
12.2.
12.3.
12.4.
13,333.
2) А =
12.5. Л =
1
Практикум 12.1
А Задачи 1-6 связаны с рис. 12.12 а-г. В задачах 1-4 запишите определенные интегралы, описывающие площади областей, залитых серым цветом.
1. Окрашенная серым цветом область на рис. 12.12, б.
2. Окрашенная серым цветом область на рис. 12.12, а.
3. Окрашенная серым цветом область на рис. 12.12, в.
4. Окрашенная серым цветом область на рис. 12.12, г.
* 5. Объясните, почему интеграл J** h (х) dx не описывает площадь фигуры, лежащей между графиком у = /г(х) и осью х от точки х = а до точки х = b на рис. 12.12, в.
*6. Объясните, почему интеграл [—h (х)] dx описывает площадь фигуры, лежащей между графиком у = Ji(x) и осью х от точки х = а до точки х = b на рис. 12.12, в.
В задачах 7-16 требуется вычислить площадь фигуры, ограниченной графиками с указанными уравнениями на заданных интервалах. Вычислите ответ с точностью до трех десятичных знаков.
7. у = —2х — 1; у = 0, 0 < х < 4.
8. у — 2х — 4; у = 0, — 2 < х < 1.


Глава 12. Практические задачи интегрального исчисления
485
в)
г)
Рис. 12.12. Иллюстрации к задачам 1-6
9. у = х2 + 2; у = 0, -1 х 0.
11. 	у = х2 — 4; у = 0, — 1 х < 2.
13. 	у = ех; у = 0, — 1 х 2.
15. у = -1/t; у = 0, 0,5 t 1.
10. 	у = Зх2 + 1; у = 0, — 2 х 0.
12. 	у = Зх2 - 12; у = 0, -2 х 1.
14. у = е~х; у = 0, -2 х 1.
16. у = — 1/t; у = 0, 0,1 t 1.
Б Задачи 17-26 касаются рисунков а и б. В задачах 17-24 запишите определенные интегралы, описывающие указанные заштрихованные площади на заданных отрезках.
б)
Рис. 12.13. Иллюстрации к задачам 17-26
17. На отрезке [а, Ь] на рис. 12.13, а. 18. На отрезке [с, d] на рис. 12.13, а.
19. На отрезке [6, d\ на рис. 12.13, а. 20. На отрезке [а, с] на рис. 12.13, а.


486
Часть III. Математический анализ
21. На отрезке [с, d] на рис. 12.13, б. 22. На отрезке [а, Ь] на рис. 12.13, б.
23. На отрезке [а, с] на рис. 12.13, б. 24. На отрезке [6, d] на рис. 12.13, б.
*25. Обращаясь к рис. 12.13, б, объясните, как, используя определенные интегралы и функции fag, можно вычислить площадь фигуры, ограниченной двумя функциями от точки х = а до точки х = d.
*26. Обращаясь к рис. 12.13, а, объясните, как, используя определенные интегралы, можно вычислить площадь фигуры, ограниченной графиком у = f(x) и осью х от точки х = а до точки х = d.
В задачах 27-42 требуется вычислить площадь фигуры, ограниченной графиками заданных функций на заданных отрезках (если они указанны). Вычислите ответ с точностью до трех десятичных знаков.
27. 	у = —х; у = 0; — 2 < х < 1.
29. 	у = х2 - 4; у = 0; 0 х 3.
31. 	у = 4 - х2; у = 0; -3 х 4.
33. 	у = —2х + 8; у = 12; -1 х 2.
35. у = Зх2; у = 12.
37. 	у — 4 — х2; у = —5.
39. 	у = х2 + 1; у = 2х — 2; — 1 х < 2.
41. 	у = е°’5х; у = 1 х < 2.
X
28. 	у — —х -h 1; у = 0; — 1 < х < 2.
30. 	у = 4 — х2; у = 0; 0 < х < 4.
32. 	у = х2 — 4; у = 0; —4 < х < 3.
34. 	у = 2х + 6; у = 3; — 1 < х < 2.
36. у - х2\ у = 9.
38. 	у = х2 - 1; у = 3.
40. 	у = х2 — 1; у = х — 2; — 2 < х < 1.
42. 	у = у = —ех; 0,5 < х 1.
х
В задачах 43-46 постройте графики уравнений и найдите наиболее важные точки пересечения, используя графическую утилиту. Затем вычислите площадь фигуры, ограниченной кривыми. Запишите ответы с точностью до трех десятичных знаков.
43. 	у = 3 — 5х — 2х2; у = 2х2 4- х — 2; 44. у = 3 — 2х2; у — 2х2 — 4х;
45. у — — 0,5х 4- 2,25; у = —. 46. у = х — 4,25; у = —
х х
В В задачах 47-54 вычислите площадь, ограниченную графиками указанных функций на заданных отрезках (если они заданы). Вычислите ответ с точностью до трех десятичных знаков.
47. у — 10 — 2х; у = 4 4- 2х; 0 < х < 4.
49. у — х3; у = 4х.
51. у = х3 — Зх2 - 9х 4- 12; у = х 4- 12.
53. у = х4 — 4х2 4-1; у = х2 — 3.
48. у = Зх; т/ = х + 5;0Сх<5
50. у = х3 4-1; у = х 4-1.
52. у = х3 — бх2 4- 9х; у = х.
54. у = х4 — бх2; у = 4х2 — 9.
В задачах 55-60 постройте графики уравнений и найдите наиболее важные точки пересечения, используя графическую утилиту. Затем вычислите площадь фигуры, ограниченной кривыми. Запишите ответы с точностью до трех десятичных знаков.
55. у = х3 — х2 4- 2; у — —х3 4- 8х — 2.
56. у = 2х3 4- 2х2 — х; у = —2х3 — 2х2 4- 2.


Глава 12. Практические задачи интегрального исчисления
487
57. 	у = е х; у = 3 — 2х. 58. у = 2 — (х + I)2; у = еж+1.
59. у = ех\ у = 5х — х3. 60. у = 2 — ех; у = х3 4- Зх2.
В задачах 61-64 вычислите площадь фигуры, ограниченной графиками указанных функций на заданных отрезках (если они указаны), используя процедуру численного интегрирования, предусмотренную в графической утилите. Запишите ответы с точностью до трех десятичных знаков.
61. у = е~х\ у = \/1пх; 2 х С 5.
62. у = х2 -I- Зх + 1; у = ееХ; — 3 х < 0.
63. у = ех ; у = х + 2. 64. у = 1п(1пх); у = 0,01х.
Применение математики
В следующих задачах, чтобы яснее представлять себе каждое задание и правильно проинтерпретировать результаты, полезно построить графики.
Экономика и бизнес
* 65. Добыча нефти. Пользуясь данными, собранными в первые три года добычи,
а также результатами геологических исследований, руководство нефтедобывающей компании выяснило, что через t лет после начала разработки нефть из месторождения будет выкачиваться со скоростью, равной
д(*  *) = ГИо + 10,
где R(t) — скорость или темп добычи (в тысячах баррелей в год). Вычислите площадь между графиком R и осью t на отрезке [5,10] и объясните полученный результат.
*66. Добыча нефти. Вернитесь к задаче 65. Вычислите площадь фигуры, лежащей между графиком R и осью t на отрезке [5,15], и объясните полученный результат, если установлено, что скорость добычи равна
Я ~ t2 + 25 25,
* 67. Номинальный период эксплуатации. Компания, предоставляющая услуги в сфе¬
ре развлечений, сохраняет данные о прибыли, приносимой каждой видеоигрой, которая установлена в павильоне игровых автоматов. Предположим, что функции C(t) и R(t) описывают соответственно общие затраты и доходы (в тысячах долларов) через t лет после установки игры. Вычислите площадь между графиками С' и R' на отрезке оси t от 0 до конца номинального периода эксплуатации, если
Cf(t) = 2 и 7?' = 9e-°’3t.
* 68. Номинальный период эксплуатации. Повторите решение задачи 67, если
Cf(t) = 2t и R' = 5te"0’lr


488
Часть III. Математический анализ
* 69. Распределение доходов. В рамках исследования влияния Второй мировой войны на экономику Соединенных Штатов Америки специалисты, используя данные Бюро переписи населения США, получили следующие кривые Лоренца для распределения доходов в Соединенных Штатах в 1935 и 1947 годах.
f(x) = я2’4, Кривая Лоренца для 1935 года
д(х) = ж1,6. Кривая Лоренца для 1947 года
Вычислите показатель концентрации доходов для каждой кривой Лоренца и объясните полученный результат результат.
* 70. Используя данные Бюро переписи населения США, специалисты получили следующие кривые Лоренца для распределения доходов в Соединенных Штатах в 1962 и 1972 годах.
Кривая Лоренца для 1962 года
Кривая Лоренца для 1972 года
Вычислите показатель концентрации доходов для каждой кривой Лоренца и объясните полученный результат.
*71. WWW Распределение национального богатства. Кривые Лоренца можно также использовать в качестве относительной меры распределения совокупного богатства страны. Используя данные отчета Объединенного комитета по вопросам экономики конгресса США, специалисты получили следующие кривые Лоренца для распределения национального богатства Соединенных Штатов Америки в 1963 и 1983 годах:
f(x) = x1Q, Кривая Лоренца для 1963 года
д(х) = х12. Кривая Лоренца для 1983 года
Вычислите показатель концентрации доходов для каждой кривой Лоренца и объясните полученный результат.
* 72. Распределение доходов. Правительство небольшого государства планирует радикально изменить систему налогообложения для того, чтобы добиться более равномерного распределения доходов. Кривые Лоренца для текущего распределения доходов и для предполагаемого распределения доходов после принятия закона об изменении порядка налогообложения даны ниже. Вычислите показатель концентрации доходов для каждой кривой Лоренца. Обеспечит ли предложенное изменение более равномерное распределение доходов? Объясните свой ответ.
/(ж) = х2’3, Текущая кривая Лоренца
д(х) = 0,4х + 0,6ж2. Предполагаемая кривая Лоренца после внесения изменений в налоговое законодательство


Глава 12. Практические задачи интегрального исчисления
489
73. 	Распределение национального богатства. Данные в таблице описывают распределение богатства в стране.
X
0 0,20 0,40 0,60 0,80 1
У
0 0,12 0,31 0,54 0,78 1
а) Используя метод квадратичной регрессии, составьте уравнение кривой Лоренца для этих данных.
б) Используя уравнение регрессии и процедуру численного интегрирования, вычислите приблизительное значение показателя концентрации доходов.
74. 	Распределение национального богатства. Вернемся к задаче 73.
а) Используя метод кубической регрессии, составьте уравнение кривой Лоренца для этих данных.
б) Используя уравнение кубической регрессии и процедуру численного интегрирования, вычислите приблизительное значение показателя концентрации доходов.
Биологические науки
* 75. Биология. Дрожжевая культура растет со скоростью W'(t) = O,3eo,lt г/ч. Вычис¬
лите площадь фигуры, лежащей между графиком W' и осью t на отрезке [0,10] и объясните результаты.
* 76. WWW Истощение природных ресурсов. В Соединенных Штатах Америки мгно¬
венная скорость изменения спроса на лесоматериалы в миллиардах кубических футов в год начиная с 1970 года (t = 0) изменялась приблизительно следующим образом
Q'(t) = 12 + 0,006£2, 0 t 50.
Вычислите площадь фигуры, лежащей между графиком Q' и осью t на отрезке [15,20], и объясните полученный результат.
Социальные науки
* 77. Обучение. Исследование эффективности обучения проводится в классах с язы¬
ковым уклоном общеобразовательной школы. В эксперименте использовался список из 50 слов. Целью исследовангия было измерение скорости запоминания слов из списка в различные моменты времени в течение непрерывного пятичасового учебного занятия. Было установлено, что средняя скорость запоминания всего списка слов обратно пропорциональна времени, потраченному на изучение, и приблизительно равна
Вычислите площадь фигуры, лежащей между графиком V и осью t на отрезке [2,4], и объясните полученные результаты.
*78. Обучение. Повторите решение задачи 77, если положить V'(t) = 13/t1/2, а интервал заменить на [1,4].


490
Часть III. Математический анализ
12.2. 	Интегрирование в экономических задачах
■ Плотность вероятностей
■ Непрерывный источник доходов
■ Будущая стоимость дохода от непрерывного источника
■ Баланс спроса и предложения
В этом разделе описано множество важных примеров применения интегралов при решении самых разных экономических задач. В нем рассмотрены три независимые темы: плотности вероятностей, непрерывные потоки доходов, а также баланс спроса и предложения. Их можно рассматривать в любом порядке.
Плотность вероятностей
Рассмотрим возможность применения определенного интеграла для вычисления вероятностей с интуитивной точки зрения. Для более строгой трактовки данного предмета необходимо использовать специальное интегральное выражение J^° f (ж) dx, которое нами еще не рассматривалось.
Предположим, что возможным исходом эксперимента является произвольное действительное число на отрезке [с, d]. Например, переменная х может описывать коэффициент IQ, рост человека в дюймах или срок службы электрической лампочки в часах. Будем считать, что х — непрерывная случайная величина.
В определенных ситуациях можно вычислить функцию /, зависящую от независимой переменной х, которую можно использовать для вычисления вероятности того, что исход эксперимента х будет лежать в отрезке [с, d]. Такая функция, называемая плотностью вероятностей, должна удовлетворять следующим трем условиям (рис. 12.14).
а) б)
Рис. 12.14. Плотность вероятностей
1. f(x) 0 для действительных х.
2. Площадь фигуры, лежащей под графиком функции /(х) на интервале (—сю, сю) равна единице.
3. Если [с, d] — отрезок на интервале (—сю, сю), то
d
Р (с х < d) =
f (ж) dx.


Глава 12. Практические задачи интегрального исчисления
491
Задание 12.3.
^е_гс/4, если х О,
О в противном случае.
1. Объясните, почему /(х) 0 на интервале (—оо, оо).
2. Вычислите интегралы J*j° f (х) dx, Jq° f (x) dx и Jq° f (x) dx.
3. Исходя из решения п. 2, определите, чему предположительно равна площадь фигуры, лежащей под графиком /(х) на интервале (—оо, оо)? ■
Пример 12.8 (Продолжительность телефонных разговоров). Предположим, что длительность телефонных разговоров (в минутах) по общественному телефону- автомату — это непрерывная случайная величина с функцией плотности вероятностей, показанной на рис. 12.15.
/(t) = J ie_t/4> если 1 > °>
1 0 в противном случае.
Рис. 12.15. Плотность вероятностей
1. Вычислите вероятность того, что случайно выбранный разговор будет длиться от 2 до 3 минут.
2. Найдите такое число b (с точностью до двух десятичных знаков), чтобы вероятность того, что случайно выбранный разговор продлится от 2 до b минут, была равна 0,5.
Решение.
з
1. 	P(2^t^3) =
= -е“3/4 + е*1/2«0,13.


492
Часть III. Математический анализ
2. 	Необходимо найти такое число Ь, при котором Р(2 < t < 6) = 0,5.
ь
j |е t>/4dt = 0,5.
2
-е“ь/4 + е“1/2 = 0,5. е-ь/4 = е-о>5-О,5.
— = In (е-0,5 — 0,5) .
Решим относительно Ь.
b = 8,96 мин.
Таким образом, вероятность того, что случайно выбранный разговор продлится от 2 до 8,96 мин., равна 0,5. ■
Упражнение 12.8.
1. Вычислите вероятность того, что в примере 12.8 случайно выбранный разговор продлится 4 минуты или меньше.
2. Найдите такое число b (с точностью до двух десятичных знаков), чтобы вероятность
того, что случайно выбранный разговор продлится b минут или меньше, была равна 0,9. ■
В домашнем задании 11.2 была рассмотрена одна из наиболее важных плотностей вероятности — плотность нормального распределения вероятностей, график которого показан на рис. 12.16.
1 e_(z-/x)2/2<т2 — математическое ожидание
Рис. 12.16. Нормальная кривая
Можно показать (хотя эти и не просто), что площадь фигуры, лежащей под кривой нормального распределения на рис. 12.16 на интервале (—оо,оо), точно равна единице. Поскольку интеграл J е~х dx не выражается через элементарные функции (т.е. первообразную нельзя выразить в виде конечной комбинации элементарных функций), то вероятность


Глава 12. Практические задачи интегрального исчисления
493
как правило, вычисляется путем соответствующих замен переменных с последующим использованием статистических таблиц, содержащих значения площадей фигур фигур, лежащих под кривой нормального распределения (т.е. нормальной кривой с параметрами // = 0 и а = 1). Эти таблицы приводятся в большинстве учебников по математике. Такие таблицы можно построить, используя квадратурные формулы, описанные в разделе 11.5. Однако, как правило, для этих целей используются компьютеры, в которых применяются более совершенные вычислительные алгоритмы. В некоторых калькуляторах также предусмотрена функция вычисления площади фигуры, лежащей под кривой нормального распределения.
Непрерывный источник доходов
Для начала рассмотрим простой пример, имеющий очевидное решение, а затем обобщим полученные результаты на более сложные ситуации.
Предположим, некая женщина учредила доверительный фонд, который будет приносить ее племяннику 2000 долл, в год в течение десяти лет. Сколько денег получит племянник благодаря доверительному фонду в конце десятого года? Поскольку за весь период начислений было всего десять платежей по 2000 долл., он получит
10 • 2000 = 20 000 долл.
Рассмотрим теперь эту же задачу с другой точки зрения, которая может оказаться полезной при решении более сложных задач. Предположим, что поток доходов непрерывен и скорость его равна 2000 долл, в год. На рис. 12.17 площадь фигуры, лежащей под графиком /(£) = 2000 между точками 0 и t, представляет собой доход, накопленный через t лет, считая от момента учреждения доверительного фонда. Например, для t = | года доход будет равен | • 2000 = 500 долл., для t = j года доход будет равен j • 2000 = 1000 долл., для t = 1 год доход будет равен 1 • 2000 = 2000 долл., для t = 5,3 года доход будет равен 5,3 • 2000 = 10 600 долл., а для t = 10 лет доход будет равен 10 • 2000 = 20 000 долл. Общий доход за десятилетний период, т.е. площадь фигуры, лежащей под графиком функции f(t) = 2000 между точками 0 и 10, представляет собой определенный интеграл
10 ю
2000Л = 2000t = 2000 • 10 - 2000 • 0 = 20 000 долл.
о 0
Обобщим теперь идею непрерывного источника доходов на менее очевидную задачу.
Рис. 12.17. Непрерывный доход


494
Часть III. Математический анализ
Пример 12.9 (Непрерывный источник доходов). Скорость изменения доходов, получаемых от торгового автомата, размещенного в аэропорту, равна
f(t) = 5000e°’O4t,
где t — время в годах с момента установки автомата. Вычислите общий доход, полученный от автомата за первые пять лет эксплуатации.
Решение. Площадь фигуры, лежащей под графиком функции скорости изменения дохода между точками 0 и 5, описывает общее изменение дохода за первые пять лет (рис. 12.18) и, следовательно, равна определенному интегралу.
5
Валовый доход = j 5000e°,04fdt =
о
= 125 000eo,O4t 5
О
= 125 ОООе0,04’5 - 125 ОООе0’040 =
= 152 675- 125 000 =
= 27 675 долл.
Результат округлен до ближайшего доллара
Таким образом, за первые пять лет эксплуатации торговый автомат принес доход в размере 27 675 долл. а
Время, лет
Рис. 12.18. Непрерывный источник доходов
Упражнение 12.9.
Возвращаясь к примеру 12.9, вычислите общий доход (с точностью до ближайшего доллара), полученный в течение вторых пяти лет эксплуатации автомата. ■
В действительности доход от торгового автомата, как правило, не получают в виде единичного платежа в конце года, несмотря на то, что скорость высчитывается на годовой основе. Доход обычно собирается ежедневно или еженедельно. В задачах подобного типа важным предположением является то, что доход в действительности поступает


Глава 12. Практические задачи интегрального исчисления
495
непрерывным потоком, т.е. доход является непрерывной функцией времени, а скорость изменения — мгновенной. Скорость изменения называется скоростью непрерывного потока доходов.
Общий доход при непрерывном потоке доходов
Если f(t) — скорость изменения непрерывного потока доходов, общий доход, полученный в течение периода, прошедшего с момента t = а до момента t = b, равен
ь
j f W dt.
а
Будущая стоимость дохода от непрерывного источника
В разделе 10.1 рассматривалась формула вычисления непрерывно начисляемых сложных процентов
А = Pert,
где Р — сумма инвестиции (или текущая стоимость), А — накопленный капитал (или будущая стоимость), г — скорость непрерывного начисления сложных процентов, рассчитываемых по годовой ставке (выражается десятичным числом), at — время в годах. Например, если инвестиции суммой 10000 долларов за год увеличивается на 12 непрерывно начисляемых сложных процентов, то через пять лет их стоимость (с точностью до доллара) будет равна
А = ЮОООе0’12 5 = 18221 долл.
Обобщим концепцию расчета будущей стоимости на доход, получаемый от непрерывного источника. Предположим, что /(t) — скорость изменения непрерывного потока доходов, а полученный доход сразу же инвестируется под непрерывно начисляемые проценты с годовой ставкой г. Нам уже известно, как вычислить доход от непрерывного источника, полученный через Т лет, но как определить будущую стоимость такого дохода и величину начисляемых на него процентов? Поскольку доход поступает непрерывным потоком, то нельзя использовать формулу А = Pert. Она справедлива только для одноразового вклада Р, но не для непрерывного потока инвестиций. Вместо нее следует воспользоваться суммой Римана, которая позволит применить формулу А = Pert повторно. Вначале разделим временной отрезок [0, Т] на п равных сегментов длиной At и на каждом из них выберем произвольную точку с^, как показано на рис. 12.19.
Общий доход, полученный за период времени от t = t^-i до t = tk, равен площади фигуры, расположенной под графиком /(t) на этом подынтервале, и приблизительно равен /(cfc)At, т.е. площади закрашенного серым цветом прямоугольника на рис. 12.19. Доход, полученный за этот период времени, будет представляться процентами, начисляемыми в течение приблизительно Т — Ск лет. Таким образом, если воспользоваться формулой будущей стоимости А = Pert ддя Р = f(ck) At и t = Т — с^, то будущая стоимость дохода, получаемого за период времени от t = tk-i до t = будет приблизительно равна
f (с/J Ate(T_Cfc)r.


496
Часть III. Математический анализ
Рис. 12.19. Разбиение интервала интегрирования
Сумма приблизительных значений, подсчитанная на п подынтервалах разбиения, равна
f (ci) Ate(T-C1> + / (с2) Ate<T-C2> + ■■■ + / (ск) = ^f (ск)
к=1
Эта сумма имеет вид суммы Римана, и предел этой суммы равен определенному интегралу (см. раздел 11.5). Таким образом, будущая стоимость дохода от непрерывного источника равна
т
FV = f (t) er(T-t}dt.
О
Поскольку г нТ — константы, можно записать следующую формулу.
FV =
т т
j f (t) erTe~rtdt = erT j f (t) e~rtdt. о о
(12.1)
Последнее выражение использовать намного удобнее, поскольку найти значение такого интеграла проще, чем в исходном выражении.
Будущая стоимость дохода от непрерывного источника
Если f(t) — скорость изменения непрерывного потока доходов, 0 Н Т и доход инвестируется под непрерывно начисляемой процентной ставкой г, то будущая стоимость FV инвестиций по истечении Т лет будет равна
т т
FV = j f (t) er(T-‘)dt = erT j f (t) e~rtdt.
0 0
Будущая стоимость дохода от непрерывного источника равна накопленному капиталу, полученному от непрерывного источника (доход и проценты) за Т лет.
Вернемся теперь к доверительному фонду, учрежденному любящей тетушкой для своего племянника. Предположим, что получаемые из доверительного фонда 2000 долл, он вкладывал по мере их поступления под восемь непрерывно начисляемых сложных процентов. Рассмотрим непрерывный поток доходов со скоростью 2000 долл, в год. Какой


Глава 12. Практические задачи интегрального исчисления
497
будет стоимость капитала (с точностью до доллара) в конце десятого года? Используя определенный интеграл для вычисления будущей стоимости, получим
т
о
10
FV = е0’08 10 2 0 00е_о’О8*бЙ = г = 0,08, т = ю, / (t) = 2000.
о
10
= 2ОООе0,8 e_0’08t<ft =
О
= 2000е°’8
‘e-0,08f
_ -0,08
10 о
= -25 ОООе0’8 [е-°’°810 - е-°’08 0] = 30639 долл.
Таким образом, спустя десять лет племянник получит 30639 долл., включая проценты. Сколько составят проценты? Поскольку он получил 20 000 долл, из доверительного фонда, проценты равны разнице между будущей стоимостью и доходом. Таким образом, величина
30 639 - 20 000 = 10 639 долл.
представляет собой проценты, начисленные на доход, полученный из доверительного фонда за десятилетний период.
Задание 12.4.
Предположим, что доверительный фонд учрежден таким образом, что племянник будет получать 2000 долл, в год в течение 20 лет от непрерывного источника доходов, вкладываемые под восемь непрерывно начисляемых сложных процентов. Когда стоимость капитала достигнет 50 000 долл.? ■
Применим теперь аналогичный способ анализа к примеру 12.9, в котором рассматривается задача об игровых автоматах.
Пример 12.10 (Будущая стоимость от непрерывного источника доходов). Используя для вычисления скорости изменения доходов, который приносят торговый автомат в примере 12.9, формулу
/(«) = 5000е°’О4‘,
вычислите будущую стоимость капитала при непрерывно начисляемой ставке, равной 12%, в течение пяти лет, и общую сумму начисленных процентов. Запишите ответ с точностью до доллара.
Решение. Воспользовавшись формулой
т
FV = erT [ f (t) e~rtdt
о


498
Часть III. Математический анализ
для г = 0,12, Т = 5 и /(<) - 5ОООе0,044, получим
5
FV = е0’12'5 j 500Oe°’o4<e_o,12trfZ =
о
5
= 5ОООе0,6
e-°’08Mt =
О
= 5ОООе0,6
5
О
= 5000е°’6 (-12,5е-0’4 + 12,5) =
= 37 545 долл.
Округлено до ближайшего доллара
Таким образом, будущая стоимость капитала при 12 непрерывно начисляемых сложных процентах в течение пяти лет будет равна 37 545 долл.
В примере 12.9 было показано, что общий доход, получаемый от торгового автомата за пятилетний период, равен 27 675 долл. Разница между будущей стоимостью и доходом равна начисленным процентам. Таким образом, величина
37545 - 27675 = 9870 долл.
представляет собой проценты, начисленные на доход, получаемый от торгового автомата в течение пятилетнего периода. ■
Упражнение 12.10.
Повторите решение примера 12.10 при ставке, равной девяти непрерывно начисляемым сложным процентам. ■
Баланс спроса и предложения
Пусть р = D{x) — уравнение зависимости цены от спроса на товар, где х — объем товара, приобретаемого по цене р, долл, за единицу. Предположим, что р — это текущая цена, а х — это объем товара, продаваемого по такой цене. Кривая зависимости цены от спроса, приведенная на рис. 12.20, указывает на то, что если цена выше р, то спрос х меньше, чем х, хотя часть покупателей все же приобретает товар по более высокой цене. Покупатели которые согласны платить больше, чем р, но получают возможность приобрести его по цене р, сэкономят. Давайте попробуем вычислить общую сумму, сэкономленную всеми покупателями, которые согласны заплатить за этот товар цену, превышающую р.
Чтобы решить задачу, рассмотрим интервал [q, Ck + Дж], где сь + Дж < ж. Если бы на этом интервале цена оставалась постоянной, экономия на каждой единице равнялась бы разнице между D(сь), ценой, которую готов заплатить покупатель, и р, ценой, которую он платит в действительности. Поскольку Дж описывает объем товара, приобретенного на заданном интервале, то общая сэкономленная всеми покупателями сумма будет приблизительно равна величине
[D (с/J - р] Дж, (Экономия на единице товара) • (Объем товара)


Глава 12. Практические задачи интегрального исчисления
499
Рис. 12.20. График зависимости цены
от спроса
которая представлена площадью окрашенного серым цветом прямоугольника, показанного на рис. 12.20. Если разделить отрезок [0, х] на п равных сегментов, общая сэкономленная всеми покупателями сумма будет приблизительно равна величине
п
[Г> (ci) - р] Дх + [£) (с2) - р] Дх + • • • + [£> (с„) - р] Дх = [D (ск) - р] Дх,
к—1
которую можно рассматривать как сумму Римана для следующего интеграла.
X j [D (ж) — р] dx. о
Таким образом, потребительская выгода равна этому интегралу.
Потребительская выгода
Если (х, р) — точка на графике зависимости цены от спроса р = D(x) для определенного товара, то потребительская выгода CS при цене р равна величине
X CS = j [D (я) — р] dx, о
представленной площадью фигуры, лежащей между графиками р = р и р = D(x) от точки х = 0 до точки х = х, как показано на следующем рисунке.


500
Часть III. Математический анализ
Потребительская выгода соответствует общей сумме, сэкономленной потребителями, которые согласны заплатить за товар больше, чем р = р9 но все же имеют возможность приобрести его по цене р = р.
Пример 12.11 (Потребительская выгода). Вычислите потребительскую выгоду при цене 8 долл., если зависимость цены от спроса представлена уравнением
р = D(x) = 20 — 0,05т.
Решение.
Этап 1. Вычислим величину т, т.е. спрос при цене р = 8. р = 20 - 0,05т.
8 = 20 - 0,05т.
0,05т = 12.
т = 240.
Этап 2. Построим график, как показано на рис. 12.21.
Рис. 12.21. График зависимости цены от спроса


Глава 12. Практические задачи интегрального исчисления
501
Этап 3. Вычислим потребительскую выгоду (площадь окрашенной серым цветом области на графике).
CS = j [D(x)-p\dx =
о
240
= (20 — 0,05х — 8)dx =
о
240
0
(12 — 0,05rr) dx
= (12х - 0,025х2) U40 = 2880 - 1440 = 1440 долл.
Таким образом, общая сумма, сэкономленная покупателями, которые согласны заплатить за товар более высокую цену, равна 1440 долл. ■
Упражнение 12.11.
Повторите решение примера 12.11 для цены 4 долл. ■
Если р = S(x) — уравнение зависимости цены от предложения товара, р — текущая цена, а х — текущее предложение, то некоторые производители все же будут согласны предложить некоторый объем товара по цене, ниже чем р. Дополнительный доход, который они получат при более высокой цене, называются выгодой производителей. Его величину также можно вычислить с помощью определенного интеграла (аналогично тому, как рассчитывалась потребительская выгода).
Выгода производителей
Если (х,р) — точка на графике зависимости цены от предложения р = S(x), то выгода производителей PS при цене р равна величине
X PS = j [р — S (х)] dx, о
представленной площадью фигуры, ограниченной графиками р = р и р = S(x) от точки х = 0 до точки х = х, как показано на рисунке.
Выгода производителей соответствует общему дополнительному доходу производителей, которые согласны предложить товар по цене, ниже чем р = р, хотя все еще могут продать его по цене р = р.


502
Часть III. Математический анализ
Пример 12.12 (Выгода производителей). Вычислите выгоду производителей при цене 20 долл, при следующей зависимости цены от предложения.
р = П(х) = 2 + 0,0002а:2.
Решение.
Этап 1. Вычислим х, т.е. предложение при цене р = 20:
р = 2 + 0,0002х2;
20 = 2 + 0,000252;
0,0002а:2 = 18;
х2 = 90000;
х = 300. Это единственное решение, поскольку ж 0.
Этап 2. Построим график, как показано на рис. 12.22.
Рис. 12.22. График зависимости цены от предложения
Этап 3. Вычислим выгоду производителей (представленную площадью окрашенной серым цветом области на графике).
х 300
PS = [р - S (a:)] dx = [20 - (2 + 0,0002а:2)] dx =
о о
о
300
= 5400 — 1800 = 3600 долл.
300
о
о
Таким образом, общая выгода производителей, которые согласны предложить товар по более низкой цене, равна 1440 долл. ■


Глава 12. Практические задачи интегрального исчисления
503
Упражнение 12.12.
Повторите решение примера 12.12 для цены 4 долл. ■
На рынке конкурентных рынках цена товара определяется балансом между предложением и спросом. Если р = D(x) и р = S(х) — это соответственно уравнения зависимостей цены от спроса и предложения товара, а (я, р) — точка пересечения графиков этих уравнений, то число р называется равновесной ценой, а число х — равновесным количеством. Равновесная цена определяет выгоду, как потребителей, так и производителей товара.
Пример 12.13 (Равновесная цена и выгода). Вычислите равновесную цену, а затем — выгоду потребителей и производителей при равновесном уровне цен, если
р = D(x) = 20 — 0,05х и р = S(x) = 2 + 0,0002х2.
Решение, Этап 1. Найдем точку равновесия. Приравняем D(x) к S(x) и решим полу¬
ченное уравнение.
D(x) = S(x);
20 - 0,05а; = 2 + 0,0002ж2; 0,0002х2 + 0,05х - 18 = 0;
х2 + 250ж — 90 000 = 0;
х = 200; -450.
Поскольку х не может быть отрицательным, то существует единственное решение х = 200. Равновесную цену можно найти, используя уравнение для D(x) или S(x). Чтобы проверить результат, воспользуемся обоими уравнениями.
р = D (200) =
= 20 - 0,05 • 200 = 10.
= S (200) =
= 2 + 0,0002 • 2002 = 10.
Таким образом, равновесная цена составляет р = 10, а равновесное количество — х = 200.
Этап 2. Построим кривые, как показано на рис. 12.23.
Этап 3. Вычислим потребительскую выгоду.
х
CS = j [D (a:) -p]dx =
о
200
j (20 - 0,05а; - 10) dx =
о
200
(10 — 0,05а;) dx =
о
= (10а: - 0,025а:2)
= 2000 - 1000 = 1000 долл.


504
Часть III. Математический анализ
Рис. 12.23. Кривые зависимости цены от спроса и предложения
Этап 4. Вычислим выигрыш производителя.
х
PS = j [р - S (a:)] dx =
о
200
= j (10 - (2 + 0,0002а:2)) dx = о
200
= j (8 - 0,0002а:2) dx = о
= ^8а? - 0,0002у)
200
0
1600
= 1600 — ~ 1067 долл.
В графической утилите предусмотрен альтернативный подход к вычислению равновесной точки из примера 12.13 (рис. 12.24, а). Чтобы вычислить выгоду потребителей и производителей, можно прибегнуть к методу численного интегрирования (рис. 12.22, б).
Упражнение 12.13.
Повторите решение примера 12.13 для
р = D(x) = 25 — 0,001х2 и р = S(x) = 5 + 0,1ж.


Глава 12. Практические задачи интегрального исчисления
505
а)
fnInt<20-.05*X-l 0,Х,0,200)
1000 fnlnt<10-<2+.000 2*Хл2),Х,0,200) 1066.666667
Рис. 12.24. Вычисление выгоды в графической утилите
Ответы к упражнениям
12.8. 0,63.
12.9. 9,21 мин.
12.10. 33 803 долл.
12.11. FV = 34691 долл.; проценты = 7016 долл.
12.12. 2560 долл.
12.13. 133 долл.
12.14. р = 15; CS = 667 долл.; PS = 500 долл.
Практикум 12.2
А В задачах 1-4 требуется вычислить значение каждого определенного интеграла с точностью до двух десятичных знаков.
5
0
5
2. j e°’08(5_t)dt. о
30
f ео,об<ео,12(зо-4)^
4. j 1000e°>O3te°-15(2O-f)<ft. о
Б В задачах 5 и 6, прежде чем вычислять значение выражений, определите, какие из них равны между собой. Затем вычислите значение каждого выражения с точностью до двух десятичных знаков.
8
5. 	a) j е°-07(8-‘)(Й.
о
8
в) е0,56 j e-°’07tdt.
о
8
0


506
Часть III. Математический анализ
ю
6. 	a) j 2000eo’O5‘e°’12(lo_t)<ft. о
10
в) 2ОООе0,05 f e°’12(10_t)rft.
10
б) 2000е1,2 j e~Ofindt.
О
о
Применение математики
Экономика и бизнес
Если не указано противное, вычислите все задачи с точностью до доллара.
7. 	Ожидаемый срок службы (в годах) определенной модели радиоприемников — это непрерывная случайная величина с плотностью вероятностей
№)={2/(’+2)2'
если х 0,
в противном случае.
а) Вычислите вероятность того, что случайно выбранный радиоприемник прослужит максимум 6 лет.
б) Вычислите вероятность того, что случайно выбранный радиоприемник прослужит от 6 до 12 лет.
в) Постройте график у = f(x) для [0,12] и закрасьте область, площадь которой определяет ответ на задачу п. а.
8. 	Срок хранения (в годах) определенной марки батареек для ручных фонариков — это непрерывная случайная величина с плотностью вероятностей
/(*) =
|1/(х + I)2,
если х 0,
в противном случае.
а) Вычислите вероятность того, что случайно выбранная батарейка имеет срок хранения, не превышающий трех лет.
б) Вычислите вероятность того, что случайно выбранная батарейка сохранит рабочие характеристики от 3 до 9 лет.
в) Постройте график у = f(x) на отрезке [0,10] и закрасьте область, площадь которой определяет ответ на задачу п. а.
9. 	Решая задачу 7, найдите такое число d, при котором вероятность того, что случайно выбранный радиоприемник прослужит не больше d лет, равна 0,8.
10. 	Решая задачу 8, найдите такое число d, при котором вероятность того, что случайно выбранная батарейка имеет срок хранения не более d лет, равна 0,5.


Глава 12. Практические задачи интегрального исчисления
507
11. 	Производитель дает гарантию на изделие сроком в один год. Время, за которое
изделие выходит из строя после его продажи, описывается плотностью вероят¬
ностей
/(*) =
Г О,О1е-°’01*,
1°
если t 0,
в противном случае,
где t — время, мес. Какова вероятность того, что у случайно выбранного покупателя изделие выйдет из строя в течение следующих отрезков времени?
а) В течение гарантийного периода.
б) В течение второго года после покупки.
12. 	В определенном городе дневное потребление воды (в тысячах галлонов) в расчете на один дом является непрерывной случайной величиной с плотностью вероятностей
/0,15е-°№,
/Ы = |о
если х 0,
в противном случае.
Вычислите вероятность того, что в случайно выбранном доме будет потребляться следующий объем воды.
а) Не более 400 галлонов воды в день.
б) От 300 до 600 галлонов воды в день.
13. Какова вероятность того, что изделие в задаче 11 прослужит по крайней мере один год? (Подсказка. Напомним, что общая площадь фигуры, расположенной под кривой плотности вероятностей, равна единице.)
14. Какова вероятность того, что жилой дом в задаче 12 будет потреблять более 400 галлонов воды в день? (См. подсказку к задаче 13.)
15. Вычислите общий доход, полученный благодаря непрерывному источнику доходов за первые пять лет, если скорость изменения дохода равна f(t) = 2500 долл, в год.
16. Вычислите общий доход, полученный благодаря непрерывному источнику доходов за первые десять лет, если скорость изменения дохода равна f(t) = = 3000 долл, в год.
*17. Объясните результат, полученный в задаче 15, построив график и дав его словесное описание.
* 18. Объясните результат, полученный в задаче 16, построив график и дав его словесное описание.
19. Вычислите общий доход, полученный благодаря непрерывному изменения дохода доходов за первые два года, если скорость изменения дохода равна f(t) = = 400eo,O5t долл, в год.
20. Вычислите общий доход, полученный благодаря непрерывному источнику доходов за первые три года, если скорость изменения дохода равна f(t) = 600e°,06t долл, в год.


508
Часть III. Математический анализ
*21. Объясните результат, полученный в задаче 19, построив график и дав его словесное описание.
* 22. Объясните результат, полученный в задаче 20, построив график и дав его словесное описание.
23. WWW Начиная со своего двадцатипятилетия, человек ежегодно вносит на пенсионный счет сумму, равную 2000 долл. Будем считать ежегодные вклады непрерывным источником доходов. Какая сумма будет накоплена на счете через 40 лет, когда человек выйдет на пенсию в возрасте 65 лет, если деньги на счету вложены под пять непрерывно начисляемых сложных процента? Сколько будут составлять проценты от конечной суммы?
24. Предположим, что в задаче 23 человек начал регулярно вносить вклады на пенсионный счет в возрасте 30 лет, а сумма на счету размещена под шесть непрерывно начисляемых сложных процентов. Будем считать ежегодные вклады непрерывным источником доходов. Сколько денег будет находиться на счете через 35 лет, когда человек выйдет на пенсию в возрасте 65 лет? Сколько будут составлять проценты от конечной суммы?
25. Вычислите будущую стоимость капитала, представленного доходом от непрерывного источника, размещенного под 6,25 непрерывно начисляемых процента. Скорость изменения дохода от непрерывного источника составляет /(f) = = 1650e~°’02t долл, в год.
26. Вычислите будущую стоимость капитала, представленного доходом от непрерывного источника, размещенного под 5,75 непрерывно начисляемых процента. Скорость изменения дохода от непрерывного источника составляет /(£) = = 2000eo,O6t долл, в год.
27. Вычислите проценты, оговоренные в задаче 25.
28. Вычислите проценты, оговоренные в задаче 26.
29. Инвестору предоставлен выбор между двумя вариантами вложения капитала: в известный магазин одежды и в новый компьютерный магазин. Каждый вариант требует одинаковых начальных вложений и каждый из них будет представлять непрерывный источник доходов в виде десяти непрерывно начисляемых сложных процентов. Скорость изменения доходов от магазина одежды равна f(t) = 12 000 долл, в год, а скорость изменения доходов от компьютерного магазина предположительно будет равна g(t) = 10 000eo,O5t долл, в год. Сравнивая будущие стоимости инвестиций, определите, какая из них представляет лучший выбор для последующих пяти лет.
30. Повторите решение задачи 29. Какая из инвестиций представляет лучший выбор для последующих 10 лет?
31. У инвестора есть 10000 долл., которые можно вложить либо в облигации, которые подлежат оплате через пять лет, либо в бизнес-проект, представляющий непрерывный источник доходов в течение следующих пяти лет со скоростью изменения f(t) = 2000 долл, в год. Какой вариант лучше, если и облигации, и непрерывный источник доходов приносят восемь непрерывно начисляемых сложных процента в год?


Глава 12. Практические задачи интегрального исчисления
509
32. Повторите решение задачи 31. Как лучше инвестировать имеющийся капитал, если скорость изменения доходов для бизнес-проекта равна f(t) = 3000 долл, в год?
33. Предприятие планирует купить оборудование, которое будет приносить непрерывный поток доходов в течение восьми лет со скоростью равной f(t) = = 9000 долл, в год. Если непрерывный поток доходов размещен под 6,95 непрерывно начисляемых сложных процентов, каким должен равнозначный вклад, размещенный под такой же процентной ставкой, чтобы обеспечить такую же будущую стоимость, как и непрерывный поток доходов? (Такой вклад называется текущей стоимостью непрерывного потока доходов.)
34. Вернитесь к задаче 33. Вычислите текущую стоимость непрерывного потока доходов при ставке, равной 7,65 непрерывно начисляемых сложных процентов, в течение 12 лет, если скорость изменения доходов равна f(t) = ЮООе0,03* долл, в год.
35. Вычислите будущую стоимость при ставке, равной г непрерывно начисляемых сложных процентов, в течение Т лет при скорости изменения непрерывного потока доходов f(t) = к, где к — постоянная.
36. Вычислите будущую стоимость при ставке, равной г непрерывно начисляемых сложных процентов, в течение Т лет при скорости изменения непрерывного потока доходов f(t) = kect, где с и к — постоянные, с^г,
37. Вычислите потребительскую выгоду при при цене товара р = 150 долл, и следующей зависимости цены от спроса.
р = D(x) = 400 — 0,05а;.
38. Вычислите выигрыш потребителя при цене товара р = 120 долл, и следующей зависимости цены от спроса.
р = D(x) = 200 — 0,02а;.
* 39. Объясните результаты задачи 37, построив график и кратко описав его.
*40. Объясните результаты задачи 38, построив график и кратко описав его.
41. Вычислите выгоду производителя при цене р = 67 долл, и следующей зависимости цены от предложения.
р = S(x) = 10 4- 0,lx -I- 0,0003а;2.
42. Вычислите выигрыш производителя при цене р = 55 долл, и следующей зависимости цены от предложения.
р = S(x) = 15 + 0,1а; + 0,003а;2.
* 43. Объясните результаты задачи 40, построив график и кратко описав его.
* 44. Объясните результаты задачи 41, построив график и кратко описав его.


510
Часть III. Математический анализ
В задачах 45-52 требуется вычислить выгоду потребителей и производителей при равновесной цене для заданных зависимостей цены от спроса и предложения. Постройте график, на котором можно отобразить получаемые результаты. Округлите все значения до ближайшего целого числа.
45. р - D(x) = 50 — 0,lx; р = S(x) - 11 + 0,05х.
46. р = D(x) = 25 - 0,004х2; р = S(x) = 5 + 0,004х2.
47. р = D(x) = 80е“о’оо1х; р = S(x) = ЗОе0’0011.
48. р = D(x) = 185е-0’0051; р = 5(х) = 25е°’005а:.
49. р = D(x) = 80 - 0,04х; р = S(x) = ЗОе0’0011.
50. р = D(x) — 190 — 0,2х; р = S(x) = 25е0,005х.
51. р = D(x) = 80е-°’ОО1а;; р = 5(х) = 15 -F 0,0001х2.
52. р = £)(х) = 185е_0,005:г; р = S(x) = 20 + 0,002х2.
53. WWW В следующих таблицах приведены данные о зависимостях цены от спроса и предложения сои на зерновом рынке, где х — объем товара (в тысячах бушелей), ар — цена бушеля (в долларах).
Цена и спрос Цена и предложение
X
р = D(x)
X
р = S(x)
0
6,70
0
6,43
10
6,59
10
6,45
20
6,52
20
6,48
30
6,47
30
6,53
40
6,45
40
6,62
Используя уравнение квадратичной регрессии, смоделируйте зависимость цены от спроса. Используя уравнение линейной регрессии, смоделируйте зависимость цены от предложения.
а) Вычислите равновесное количество (с точностью до трех десятичных знаков) и равновесную цену (с точностью до ближайшего цента).
б) Методом численного интегрирования найдите выгоду потребителей и производителей при равновесной цене.
54. 	Повторите решение задачи 53, используя при моделировании обеих зависимостей уравнения квадратичной регрессии.
12.3. 	Интегрирование по частям
В разделе 11.1 мы обещали рассмотреть точный способ вычисления неопределенного интеграла
К"1’
поскольку ни один из описанных на тот момент методов интегрирования не позволял найти первообразную от 1пх. В этом разделе будет рассмотрен очень полезный прием,


Глава 12. Практические задачи интегрального исчисления
511
интегрирование по частям, который позволяет найти не только указанный выше интеграл, но и многие другие интегралы вида
Метод интегрирования по частям применяется также для получения многих других формул интегрирования, описанных приводятся в учебниках по математике. Многие из этих формул рассмотрены в следующем разделе.
Метод интегрирования по частям основывается на формуле дифференцирования произведений. Если f и д — дифференцируемые функции, то справедливо выражение
4; [/ (*) 9 (*)] = f (*) 9' (*) + 9 (*) f (*),
которое можно переписать в эквивалентной форме
f (*) д' (х) = 4 (х) в (*)] - 9 № Г (*) •
Интегрируя обе части, получим
Первый интеграл справа от знака равенства составляет f(x)g(x) + С. (Почему?) На данный момент опустим постоянную С, приняв ее в расчет после вычисления остальных интегралов, и получим следующую формулу.
f (х) д' (ж) dx = f (х) д(х) — I g (®) f' (х) dx.
Это выражение можно привести к более подходящей форме, полагая и = f(x) и v = = д(х). Тогда du = f(x)dx ndv = gf(x)dx. Сделав такую подстановку, получим формулу интегрирования по частям.
Интегрирование по частям
udv = uv — I vdu.
Эта формула оказывается полезной, если интеграл слева сложно или невозможно проинтегрировать, используя стандартные формулы. Если и и dv выбраны удачно — это наиболее важная часть метода, — то может оказаться, что вычислить интеграл справа проще, чем интеграл слева. Эта формула является чрезвычайно важным инструментом интегрирования, который применяется во многих, хотя и не всех, случаях. Результат применения метода очень просто проверить, продифференцировав его, чтобы получить исходное подынтегральное выражение (обязательно выработайте такую привычку). Важность рассмотренной формулы будет продемонстрирована на нескольких примерах.
Пример 12.14 (Интегрирование по частям). Вычислите интеграл J xexdx, используя формулу интегрирования по частям, и проверьте результат.


512
Часть III. Математический анализ
Решение. Прежде всего запишем формулу интегрирования по частям.
| udv = uv — j vdu. (12.2)
Теперь попытаемся найти такие и и dv в интеграле J* xexdx9 при которых интеграл J vdu в правой части формулы (12.2) проще вычислить, чем интеграл J* udv = J* xexdx в ее левой части. По большому счету, существует только два подходящих варианта выбора и п dv в интеграле J xexdx.
I
Вариант 1 и dv
Вариант 2 и dv
ех xdx.
Мы рассмотрим только первый вариант, а второй вам предстоит разобрать самостоятельно (задание 12.5).
В первом варианте и = х, a dv = exdx. Исходя из формулы (12.2), чтобы записать пра¬
вую часть, следует вычислить функции du следующей схеме. Пусть
и = х,
Тогда
du = dx,
v. Дальше необходимо действовать согласно
dv = exdx.
К функции v можно добавить произвольную константу, однако для простоты она будет всегда полагаться равной нулю. Общая произвольная константа интегрирования будет добавлена в конце метода. Подставляя полученный выше результат в формулу (12.2), получим.
vdu
xexdx = хех
= хех — ех + С
Интеграл в правой части очень просто вычислить.
Теперь добавим произвольную постоянную С.
Проверка.
(хех - ех + С) = хех + ех — ех = хех. dx
Задание 12.5.
Рассмотрите второй вариант в примере 12.14, используя формулу интегрирования по частям, и объясните, почему такой выбор является неудачным. ■
Упражнение 12.14.
Вычислите интеграл J xe2xdx. ■


Глава 12. Практические задачи интегрального исчисления
513
Пример 12.15 (Интегрирование по частям). Вычислите интеграл J xlnxdx.
Решение, Как и в предыдущем примере, существуют два варианта выбора и и dv.
Вариант 1 и dv
Вариант 2 и dv
Ina: xdx.
Вариант 1 неудачен, поскольку неизвестно, как вычислить первообразную функции lnx.
Поэтому перейдем к варианту 2 и положим и = In а: и dv = х dx. Далее нужно выполнить те же операции, что и в примере 12.14. Пусть
и = lnx,
dv = х dx.
Тогда
du — dx, х
j dv = j x dx, x2
V =
Подставим полученные результаты в формулу интегрирования по частям:
I 	и dv = uv — v du
x hi xdx = lnx —— -——dx =
2 	J 2 x
X2 f X
= — lnx — — dx = Вычислить этот интеграл не составляет труда.
2 J 2
х2 1 я2
= — \пх - — + С.
d (х2 х2 \ х2 1 х
Проверка, — — lnx + С 1 = xlnx + — = xlnx.
dx у 2 4 j 2x2
Упражнение 12.15.
Вычислите интеграл J х In 2х dx. ■
Самые внимательные из вас, выполняя задание 12.5, могли заметить заметить, что некоторые варианты выбора функций и и dv приводят к появлению интегралов, еще более сложных, чем исходные. Это не означает, что в вычислениях или формуле интегрирования по частям есть какая-то ошибка. Это просто означает, что определенные варианты выбора функций и и dv не упрощают задачу. В некоторых задачах может вообще не оказаться ни одного подходящего варианта. Эти и некоторые другие наблюдения по выбору функций и и dv собраны в следующей врезке.


514
Часть III. Математический анализ
Интегрирование по частям: выбор функций и и dv
Для J и dv = uv — J* vdu справедливо следующее.
1. Произведение и dv должно быть равно исходному подынтегральному выражению.
2. Должна существовать возможность проинтегрировать функцию dv (предпочтительно, используя стандартные формулы или простые подстановки).
3. Новый интеграл J* v du не должен быть сложнее, чем исходный интеграл J* и dv.
4. Для интегралов, содержащих функцию хреах, следует попробовать подстановку
и = хр и dv = еах dx.
5. Для интегралов, содержащих функцию xp(ln x)q, следует попробовать подстановку
и = (1пх)9 и dv = хр dx.
В некоторых случаях можно вычислить значение исходного интеграла, применив формулу интегрирования по частям несколько раз. В следующем примере проиллюстрирован именно такой случай.
Пример 12.16 (Многократное интегрирование по частям). Вычислите интеграл J x2e~xdx.
Решение, Следуя рекомендациям из приведенной выше врезки, выберем следующие подстановки.
и = х2, dv = e~xdx.
Тогда
du = 2х dx, v — —е~х,
x2e~xdx = х2 (—е_ж) — j (—е_х) 2xdx = — х2е~х + 12xe~xdx. (12.3)
Используя стандартные формулы, значение нового интеграла найти не удается, но все же он проще, чем исходный интеграл. Если к нему снова применить формулу интегрирования по частям, то получится еще более простой интеграл. Для интеграла J xe~xdx выберем следующие подстановки.
и = х, dv = e~xdx.
Тогда
du = dx, v = —е~х,
Константу выберем равной нулю.
(12.4)


Глава 12. Практические задачи интегрального исчисления
515
Подставляя уравнение (12.4) в уравнение (12.3), получим
x2e~xdx = — х2е~х + 2 (—хе~х — е_х) + С = Добавим произвольную константу
= —х2е~х - 2хе~х - 2е~х + С (12.5)
Проверка. (-х2е~х - 2хе~х - 2е~х + С) = х2е~х - 2хе~х + 2хе~х - 2е~х + 2е~х = = х2е~х. ■
Упражнение 12.16.
Вычислите интеграл J x2e2xdx. ■
Пример 12.17 (Интегрирование по частям). Вычислите значение интеграла J^lnxdx и дайте геометрическую интерпретацию полученному результату.
Решение. Прежде всего вычислим интеграл Jlnxdx, а затем вернемся к вычислению определенного интеграла. Следуя совету 5, приведенному во врезке (для р = 0), выберем следующие подстановки.
и = Ina;, dv = dx.
Тогда
Следовательно,
Следует отметить, что это очень важный результат, о котором упоминалось в начале раздела. Вычислим определенный интеграл:
е
е
1п х dx = (a; In х — а;)
1
= (elne — е) — (1 In 1 — 1) = (е — ё) — (0 — 1) = 1.
1
Этот интеграл описывает площадь фигуры, расположенной под кривой у = In я от точки х = 1 до точки х = е, как показано на рис. 12.25. ■
Рис. 12.25. График функции у = Ina;


516
Часть III. Математический анализ
Упражнение 12.17.
Вычислите интеграл Д In Зх dx. ■
Задание 12.6.
Попытайтесь применить формулу интегрирования по частям к интегралу J ех dx и объяснить, почему она не позволяет добиться конечного результата. ■
Ответы к упражнениям
12.14. 	^е21 -^е2х + С.
2 4
12.15. 1п2х — —- + (7.
2 4
12.16. ^-е2х - хе2* + ±е2х + С.
2 2 4
12.17. 	2 In 6 - 1пЗ - 1« 1,4349.
Практикум 12.3
А В задачах 1-4 требуется вычислить интегралы, используя метод интегрирования по частям. Предполагается, что, если в подынтегральное выражение входит функция натурального логарифма, выполняется условие х > 0.
х2 In х dx.
2. xe^xdx.
х3 ln x dx.
Б
* 5. Предположим, что следующий интеграл вычисляется методом интегрирования
по частям: J (х + I)5 (х + 2) dx. Какой из вариантов подстановки для функции и лучше выбрать: и = (х + I)5 или и = х + 2? Объясните сделанный выбор, а затем вычислите интеграл.
* 6. Предположим, что следующий интеграл вычисляется методом интегрирования
по частям: J (5х — 7) (х — I)4 dx. Какой из вариантов подстановки для функции и лучше выбрать: и = 5х — 7 или и = (х — I)4? Объясните сделанный выбор, а затем вычислите интеграл.
Задачи 7-20 смешанные — в некоторых из них необходимо применить интегрирование по частям, а для решения других можно воспользоваться методами, которые были рассмотрены в предыдущих главах. Вычислите интегралы, предполагая, что, если в интеграл входит функция натурального логарифма, выполняется условие х > 0.
8. (х — 1) е Xdx.
7. xe~xdx.
10. хе х dx.


Глава 12. Практические задачи интегрального исчисления
517
1
1
11.
(х — 3) exdx.
12.
(ж + 1) exdx. J
J с
0
в
2
г
13.
In 2х dx.
14.
]
1
15.
J
16.
[ f dx.
J x3 + 5
17.
J
18.
[ &X dx.
J e' + l
19.
\/х In х dx.
20.
J v*
В задачах 21-24 необходимо проиллюстрировать каждый интеграл рисунком и объяснить его геометрический смысл.
* 21. Задача 11. * 22. Задача 12.
*23. Задача 13. *24. Задача 14.
В Задачи 25-42 смешанные — в некоторых из них необходимо применить интегрирование по частям вместе с методами, которые были рассмотрены ранее, в других может потребоваться использовать формулы интегрирования по частям повторно. Когда в подынтегральное выражение входит функция 1п#(х), предполагается, что
> 0.
25.]
x2exdx.
26.
j x3exdx.
27. I
| xeaxdx, a 0.
28.
j ln (ax) dx, a > i
e
2
2,.
I>-
30.
j x3ex dx.
1
1
2 p
2 p
31.
In (z + 4) dx.
32.
In (4 — z) dx.
0
J 0
33.]
J xex 2dx.
34.
j xex+rdx.
35.
zln (1 + x2) dx.
36.
jz ln (1 + z) dx.
37. j
ex ln (1 + ex) dx.
38.
J v*
f (lnz)2 dx.
40.
j x (lnz)2 dx.
41.
I (lnz)3 dx.
42.
x (lnz)3 dx.


518
Часть III. Математический анализ
В задачах 43-46 требуется построить график каждого уравнения на указанном интервале, используя графическую утилиту, и вычислить с ее помощью площадь фигуры, лежащей между данной кривой и осью х. Найдите ответ с точностью до двух десятичных знаков.
43. у = х — 2 — lnx; 1 х 4. 44. у = 6 — х2 — lnx; 1 х 4.
45. у = 5 — хех; 0 х 3. 46. у = хех + х — 6;0^х^З.
Применение математики
Экономика и бизнес
47. Прибыль. Предельная прибыль (в миллионах долларов в год) составляет
Вычислите общую прибыль, полученную за первые пять лет производства (с точностью до ближайшего миллиона долларов), используя соответствующий определенный интеграл.
48. Добыча. Предполагается, что через t месяцев скорость добычи нефти из месторождения (тыс. баррелей в месяц) будет равна
Я(0 = 10te_o,lt.
Вычислите общий объем добычи за первый год разработки месторождения (с точностью до ближайшей тысячи баррелей), используя соответствующий определенный интеграл.
* 49. Прибыль. Объясните результаты решения задачи 47, построив график и описав
его словами.
* 50. Добыча. Объясните результаты решения задачи 48, построив график и описав
его словами.
51. Непрерывный источник доходов. Вычислите будущую стоимость капитала при ставке, равной восьми непрерывно начисляемым сложным процентам, в течение пяти лет поступления дохода от непрерывного источника со скоростью
/(0 = 1000 - 200/.
52. Непрерывный источник доходов. Вычислите будущую стоимость капитала при ставке, равной десяти непрерывно начисляемым сложным процентам, в течение четырех лет поступления дохода от непрерывного источника со скоростью
/(/) = 1000 - 250/.
53. Распределение доходов. Вычислите показатель концентрации доходов для кривой Лоренца
у = хех~1.


Глава 12. Практические задачи интегрального исчисления
519
54. 	Распределение доходов. Вычислите показатель концентрации доходов для кривой Лоренца
у = х2е1-1.
* 55. Распределение доходов. Объясните результаты решения задачи 53, построив гра¬
фик и описав его словами.
* 56. Распределение доходов. Объясните результаты решения задачи 54, построив гра¬
фик и описав его словами.
57. Анализ продаж. Предполагается, что объем продаж некой модели персонального компьютера будет снижаться со скоростью
S'(f) =
компьютеров в месяц, где t — время в месяцах, a S(t) — месячный объем продаж компьютеров. Компания планирует прекратить производство указанной модели компьютеров, когда объем ежемесячных продаж достигнет 800 компьютеров. Вычислите функцию S(t), если объем ежемесячных продаж в исходный момент (t = 0) равен 2000 компьютерам. Как долго, с точностью до ближайшего месяца, компания будет продолжать производить эти компьютеры?
58. Анализ продаж. Скорость изменения объема ежемесячных продаж картриджей с новой видеоигрой составляет
S'(t) = 3501n(f + l), 5(0) = 0,
где t — количество месяцев, истекших с момента выпуска видеоигры, a S(t) — ежемесячный объем продаж картриджей. Найдите функцию S(t). Когда, с точностью до ближайшего месяца, объем ежемесячных продаж достигнет уровня 15 000 картриджей?
59. Потребительская выгода. Вычислите потребительскую выгоду (с точностью до ближайшего доллара) при цене р = 2089 долл, для зависимости цены от спроса
р = D(x) = 9 — 1п(х + 4).
Воспользуйтесь значением х, вычисленным с точностью до ближайшей единицы (с избытком).
60. Выгода производителей. Вычислите выгоду производителей (с точностью до ближайшего доллара) при цене р = 26 долл, для зависимости цены от предложения
р = S(x) = 51n(x + 1).
Воспользуйтесь значением х, вычисленным с точностью до ближайшей единицы (с избытком).
* 61. Выгода потребителей. Объясните результаты решения задачи 59, построив гра¬
фик и описав его словами.
* 62. Выгода потребителей. Объясните результаты решения задачи 60, построив гра¬
фик и описав его словами.


520
Часть III. Математический анализ
Биологические науки
63. WWW Загрязнение. Концентрация загрязняющего вещества через t часов после прекращения работы фабрики на один день равна
201n(t + l)
С (ч = о— частиц на миллион.
(t + l)2
Вычислите среднюю концентрацию за период времени от момента t = 0 до момента t = 5.
64. WWW Медицина. После приема таблетки содержащийся в нем лекарственный препарат начинает поступать в кровь пациента. Скорость роста концентрации препарата в крови через t минут после приема таблетки равна
R(t) = te~Q'2t.
Вычислите общее количество препарата, которое попадет в кровь в течение 10 минут после приема таблетки.
Социальные науки
65. Обучение. В неком бизнес-колледже было установлено, что средний студент, записавшийся на курс машинописи, через t недель занятий улучшает обозначенный навык со скоростью
N'(t) = (t + 6)e_0,25t слов/мин.
за неделю. Сколько слов в минуту N(t) предположительно слов будет набирать студент после t недель занятий, если в начале курса он печатает со скоростью 40 слов в минуту? Сколько времени (с точностью до ближайшей недели) понадобится студенту, чтобы достичь скорости набора 70 слов в минуту? Сколько слов в минуту студент должен набирать в конце курса?
66. Обучение. В этом же бизнес-колледже было установлено, что средний студент, записавшийся на начальный курс стенографии, через t недель занятий улучшает навык набора текста на слух со скоростью
N'(t) = (t + 10)e_0,lt слов/мин.
в неделю. Сколько слов в минуту N(t) предположительно стенографирует студент после t недель занятий, если в начале курса он имел нулевой навык стенографии (т.е. не мог набрать под диктовку ни одного слова)? Сколько времени (с точностью до ближайшей недели) понадобится студенту, чтобы достичь скорости стенографирования 90 слов в минуту? Сколько слов в минуту студент должен уметь стенографировать в конце курса?
67. Политика. Количество избирателей (тыс. чел.) в определенном городе равно
ДГ(0 = 20 + 4Z -
где t — время, лет. Вычислите среднее количество избирателей за период времени с момента t = 0 до момента t = 5.


Глава 12. Практические задачи интегрального исчисления
521
12.4. 	Таблицы интегралов
■ Использование таблиц интегралов
■ Подстановка и таблицы интегралов
■ Формулы приведения
■ Решение практических задач
Таблица интегралов — это список формул интегрирования, используемый для вычисления интегралов. Люди, которым часто приходится вычислять сложные интегралы, используют таблицы, содержащие сотни формул. Такие таблицы приведены во многих учебниках математики. В табл. В.2 приложения В содержится короткий список формул интегрирования. Некоторые из этих формул можно получить, используя методы интегрирования, описанные ранее, в то время как для вычисления других требуются методы, которые здесь не рассматривались. Однако каждую из формул можно проверить путем дифференцирования правой части.
Использование таблиц интегралов
Формулы, приведенные в табл. В.2 (и в более подробных таблицах интегралов), упорядочены по категориям, таким как “Интегралы, содержащие выражения а + Ьи\ “Интегралы, содержащие выражения %/и2 — а2” и т. п. Здесь и — переменная интегрирования. Все остальные символы обозначают константы. Чтобы воспользоваться таблицей для вычисления интеграла, прежде всего необходимо найти категорию, которая наиболее близка к виду подынтегрального выражения, а затем определить формулу в этой категории, к которой можно точно привести подынтегральное выражение, присваивая константам конкретные значения. Этот процесс проиллюстрирован в следующем примере.
Пример 12.18 (Интегрирование с помощью таблиц). Используя табл. В.2, вычислите интеграл | (5+2lf(4-3j)
Решение, Поскольку подынтегральное выражение
= (5 + 2х) (4 - Зх)
является рациональной функцией, в которую входят выражения а+Ьи и c+du, рассмотрим формулы с 15 по 20 в табл. В.2 и попробуем определить, нельзя ли привести функцию / (я?) к одной из них. Сравнивая подынтегральное выражение в формуле 16 с функцией /(ж), легко увидеть, что оно совпадет с /(ж), если положить а = 5, b = 2, с = 4 и d = —3. Полагая и = х и подставляя значения а, Ъ, с и d в формулу 16, получим
Г и 1 / а с \
7—, г W—m~ldu=~L — I-ln|a + btt| --ln|c + du| I Формулой
J (а + bu) (с + du) ab — be \b d )
j (5+ 2^4-3.)^ = 5(-3)-2-4 (i 15 + 2ll - ln I4 - 4 + c =
а Ъ c d a- d — b- c = 5 ■ (—3) -2-4 = -23
= 11115 + 2xl “ ln I4 “ 3xl + C-


522
Часть III. Математический анализ
Следует отметить, что постоянная интегрирования С не включена ни в одну из формул, приведенных в табл. В.2. Однако константу С обязательно следует включать в первообразную. ■
Упражнение 12.18.
Используя табл. В.2, вычислите интеграл J (ь+ъх)\1+х)йх' ■
Пример 12.19 (Интегрирование с помощью таблиц). Вычислите значение интеграла f4 J dx
J3 т^25-т2
Решение, Прежде всего воспользуемся табл. В.2 и вычислим интеграл
ху/25-х2<1Х'
Поскольку в подынтегральную функцию входит выражение \/25 — х2, рассмотрим формулы с 29-й по 31-ю и выберем формулу 29 со значениями а2 = 25 и а = 5.
1
иу/а2 — и2
а + — и2
и
I
Формула 29
[ 1 tto = -|ln
J a;\/25 — х2 5
5 -h V25 - х2
х
+ С.
Таким образом.
4
3
5 + л/25 — х2
х
5 + 3
4
5 + 4
3
4
3
= —11п2 + 11пЗ - 11п1,5 ~ 0,0811.
5 5 5
Упражнение 12.19.
Вычислите значение интеграла: J** dx-
Подстановка и таблицы интегралов
Как показано в примерах 12.18 и 12.19, если интеграл, значение которого требуется вычислить, можно привести точно к одному из табличных, вычисление неопределенного интеграла сводится к простой подстановке правильных констант в подходящую формулу. Как поступить, если интеграл нельзя свести к одной из формул в таблице? Во многих случаях в этой ситуации следует применять подстановку, позволяющую преобразовать данный интеграл к одной из табличных формул. Рассмотрим несколько примеров.
Пример 12.20 (Подстановка и таблицы интегралов). Вычислите интеграл J y16^2_25 (^х-


Глава 12. Практические задачи интегрального исчисления
523
Решение. Чтобы связать этот интеграл с одной из формул, содержащих выражение у/и2 - а2 (формулы 40 и 45), отметим, что, если и = 4х, то
и2 = 16х2 и л/16гс2 - 25 = у/и2 - 25.
Воспользуемся подстановкой и — 4х и преобразуем этот интеграл к стандартному виду.
г х2 If — и2
. ^=dx = - . 16 =du = Подстановка: и = 4а?, du = 4 do?, а? =
J V16x2 - 25 4 J y/u2 _ 25 4
If u2
= 777 z -dU.
64 J y/u2 - 25
Значение последнего интеграла можно вычислить, используя формулу 44 со значением а = 5.
и2
. у/и2 — а2
[ г х1
J ч/16ж2 - 25
du = - (иу/и2 — а2 + a2 In |u + у/и2 — а2|)
_ 1 Г Ц2 _ Воспользуемся формулой 44
> 64 J \/и2 — 25 со значением а = 5.
= (ид/и2 — 25 + 25In |и + \/и2 — 25^ + С = Подставим и = 4а?.
“ 128
Формула 44
Упражнение 12.20.
Вычислите интеграл J \/9х2 — 16 dx. ■
Пример 12.21 (Подстановка и таблицы интегралов). Вычислите интеграл J
Решение. Ни в одну из формул в таблице не входит четвертая степень. Однако, если положить и = х2, то
д/#4 4-1 = \/и2 + 1,
а это выражение встречается в формулах с 32 по 39. Следовательно, подставляя функцию и = х2, получим следующее выражение.
1 1 f 1
. X dx = - \ . du. Подстановка: и = а?2, du = 2а? do?.
J 2J x/^+i
В последнем интеграле можно распознать формулу 36 со значением а = 1:
[ -du = In \и + у/и2 + а21
J V и2 + а2 I 1
[ Х -dx = х [ 1 du =
J \/х4 + 1 2 J у/и2 -h 1
= ln |u + д/^2 + 1] + C =
Z I I
= i ln lx2 4- 4-11 4- C.
Zi I I
Формула 36
Воспользуемся формулой 36 co значением a = 1.
Подставим и = а?2.


524
Часть III. Математический анализ
Упражнение 12.21.
Вычислите интеграл J* х\/х4 + ldx.
Формулы приведения
Пример 12.22 (Использование формул приведения). Используя табл. В.2, вычислите интеграл J x2e3xdx.
Решение. Поскольку в подынтегральное выражение входит функция е3х, рассмотрев формулы 46-48, делаем вывод, что для этой задачи можно воспользоваться формулой 47. Полагая в формуле 47 и = х, п = 2 и а = 3, получим
Формула 47
Следует отметить, что выражение в правой части уравнения по-прежнему содержит интеграл, но показатель степени х понижен до единицы. Формулы такого типа называются формулами приведения и предназначены для многократного применения до тех пор, пока не будет получен интеграл, значение которого можно вычислить. Применяя формулу 47 к интегралу J xe3xdx при п = 1, имеем
х2е3ж
3
2 (хе3х
3
х2е3х
3
2хе3х
9
j e3xdx.
Последнее выражение содержит интеграл, значение которого вычислить просто.
Сделав последнюю подстановку и добавляя постоянную интегрирования, получаем следующий результат.
х2е3ж
3
2хе3х
9
+ С.
Упражнение 12.22.
Используя табл. В.2, вычислите интеграл J* (lnx)2 dx. ■
Решение практических задач
Пример 12.23 (Выгода производителей). Вычислите выгоду производителей при цене 20 долл, и следующей зависимости цены от предложения.


Глава 12. Практические задачи интегрального исчисления
525
Решение.
Этап 1. Вычислим величину х, предложение при цене р = 20:
5х
500 —ж’
20 =
5х
500-я’
10000 - 20х = 5х;
10000 = 25я;
х = 400.
Этап 2. Построим график, как показано на рис. 12.26.
Рис. 12.26. График функции р —
— S{x) —
Этап 3. Вычислим выгоду производителей (площадь фигуры, окрашенную серым цветом на графике).
400
ч
о
10000 —25я
dx.
500 - х


526
Часть III. Математический анализ
Используем формулу 20 со значениями а = 10000, b = —25, с = 500 и d = — 1.
' a + bu bu ad — be
du — 1 - ln |c + du\ Формула 20 J c + du d d*  1 2  3
400
PS = (25rr + 25001П |500 — rr|)
о
= 10 000 + 2500 ln 1100| -2500ln |500| = « 5976 долл.
р = D (х)
Упражнение 12.23.
Вычислите потребительскую выгоду при цене 10 долл, для зависимости цены от спроса
20х - 8000
х - 500 ■
Задание 12.7.
Применяя к подынтегральному выражению из примера 12.23 алгебраические преобразования, включая деление столбиком, покажите, что
5х _ — 5х _ 2500
500 — х х — 500 х — 500
Используя этот результат, вычислите неопределенный интеграл в примере 12.23, не прибегая к табличным формулам. I
Ответы к упражнениям
1 + X
5 + Зх
12.18. + I In
2 \ 5 + Зх ) 4
-1— « 0,0058.
1200
12.20. (Зха/9х2 — 16 — 16In |3х + х/9х2 — 1б|) + С.
12.21. (х2\/х4 + 1 + In |х2 + \/х4 +1|) + С.
12.22. x(lnx)2 — 2х1пх + 2х + С.
12.23. 3000 4- 2000 In 200 - 2000 In 500 « 1167 долл.
12.19.
+ С.
Практикум 12.4
А В задачах 1-14, используя табл. В.2, вычислите неопределенные интегралы. fl fl
1. -dx. 2. -dx.
% х (1 + х) J X2 (1 -|- х)
3. 	I 5 dx. 4. [ dx.
J (3 + х)2(5 + 2х) J (5 + 2х)2(2 + х)


Глава 12. Практические задачи интегрального исчисления
527
6. [ 1 da
J :гх/16 + х
>».]
Г 1
х2\/х2 — 16
12.
х3 \nxdx.
14.
5 + 2е3г dX'
В задачах 15-20 вычислите значение определенных интегралов. Для вычисления первообразной воспользуйтесь табл. В.2.
I
15.
3 4- х
dx.
16.
[ -—^dx.
J (6 + х)2
2
7
17. — 77- zdx.
J (3 + х) (14-х)
о
4
19. [ . J dx.
J х/х2 4- 9 о
18- f V7-. \dx.
J (3 4- x) (1 4- x) о
5
20. [ \J x2 — 16dx.
Б В задачах 21-32, используя методы подстановок и табл. В.2, вычислите неопределен¬
ные интегралы.
44^
22. j x2\/9x2 — ldx.
23. [ Д dx.
J у/х4 - 16
24. j xy/x4 — 16dx.
25. |х2\/я6 4- 4dx.
26. f dx.
J x/z6 4- 4
. Г 1
f x/#4 4- 4 ,
27. t dx.
28. dx.
J х3\/4 — х4
J x
Г ех
Г ex
29‘ J (2 + ех) (3 + 4ex)dX
30. 9 dx.
J (4 4-ex)2 (2 4-e1)
Г In X
f 1
31. —. dx.
32. dx.
J хх/4 4- lnx
J xlnxx/4 4- lnx
задачах 33-38, используя табл. В.2,
вычислите неопределенные интегралы.
33. j x2eZxdx.
34. j x2e~*xdx.
35. j x3e~xdx.
36. | x3e2xdx.
37. f(lnx)3dx.
38. f(lnx)4dx.


528
Часть III. Математический анализ
Задачи 39-46 — смешанные. Некоторые из них требуют использования табл. В. 2, а другие можно решить, применяя методы, которые были рассмотрены ранее.
5
3
4
41-1
2
45. [ . Х dx.
J ^2^1
40. j — §dx.
3
4
42. —~dx.
J (x2 - l)2
2
44. 	|
46. f . x2 dx.
J
В задачах 47-50 требуется вычислить площадь фигуры, ограниченной графиками у = f(x) и у = д(х) с точностью до двух десятичных знаков. Примените графическую утилиту и найдите точки пересечения графиков с точностью до двух десятичных знаков.
47. / (х) = 10 ; д(х) = х2 + Зх. 48. f (х) = д/1 + х2\ д(х) — Зх — х2.
\/х2 4-1
49. / (ж) = х\/4 + х\ д(х) — 1 + х. 50. / (х) = Х ; д(х) = х — 2.
уж + 4
Применение математики
Используя табл. В.2, вычислите значения всех интегралов, входящих в решения задач 51-74.
Экономика и бизнес
51. Потребительская выгода. Вычислите потребительскую выгоду при цене р — = 15 долл, для зависимости цены от спроса
р = D (х) =
7500 - ЗОх
300 — х
52. 	Выгода производителей. Вычислите выигрыш производителей при цене р = = 20 долл, для зависимости цены от предложения
р = s (х) =
Юж
300 — х
53. Потребительская выгода. Постройте график зависимости цены от спроса и уравнения цены р = 15 из задачи 51. Площадь какой фигуры выражает потребительскую выгоду?
54. Выгода производителей. Постройте график зависимости цены от предложения и уравнения цены р = 20 долл, из задачи 52. Площадь какой фигуры выражает выгоду производителей?


Глава 12. Практические задачи интегрального исчисления
529
55. Затраты. Компания производит горные лыжи. Ее постоянные затраты составляют 25 000 долл., а величина предельных затрат равна
. 250 +Юж
с w = TTW
где С(х) — общие затраты на производство х пар лыж. Вычислите функцию затрат С(х) и установите объем производства (с точностью до единицы), при котором затраты составляют 150000 долл. Чему равны затраты (с точностью до доллара) при производстве 850 пар лыж?
56. Затраты. Компания производит портативные CD-плейеры. Ее постоянные затраты составляют 25 000 долл, в неделю, а предельные затраты равны
65 + 20Х
1 7 1 + 0,4^
где С(х) — общие затраты на производство х плейеров в неделю. Найдите функцию затрат С(х) и установите объем производства (с точностью до единицы), при котором затраты составляют 52 000 долл, в неделю. Чему равны затраты (с точностью до доллара) при производстве 700 плееров в неделю?
57. Непрерывный источник доходов. Вычислите будущую стоимость капитала при ставке, равной десяти непрерывно начисляемых сложных процента, через 10 лет для непрерывного источника доходов, поступающих со скоростью f(t) = 50t2.
58. Непрерывный источник доходов. Вычислите будущую стоимость капитала при ставке, равной восьми непрерывно начисляемых сложных процента, через 5 лет для непрерывного источника доходов, поступающих со скоростью f(t) = 200Л
59. Распределение доходов. Вычислите показатель концентрации доходов для кривой Лоренца
у — ±х\/1 + Зх.
60. Распределение доходов. Вычислите показатель концентрации доходов для кривой Лоренца
у = |з:2\/1 + Зх.
* 61. Распределение доходов. Постройте график прямой у = х и кривую Лоренца
из задачи 59 на интервале [0,1]. Проанализируйте влияние уменьшения площади фигуры, ограниченной прямой у = х и кривой Лоренца, на справедливое распределение доходов.
* 62. Распределение доходов. Постройте график прямой у = х и кривую Лоренца
на интервале [0,1] из задачи 60. Проанализируйте влияние увеличения площади фигуры, ограниченной прямой у = х и кривой Лоренца, на справедливое распределение доходов.
63. 	Маркетинг. После пробных продаж богатой клетчаткой сорта крупы отдел маркетинга крупного производителя пищевых продуктов установил, что месячный объем продаж (в миллионах долларов) через t месяцев после выпуска данного сорта крупы на рынок будет расти со скоростью
I2
(W


530
Часть III. Математический анализ
Найдите общий объем продаж S(t) через t месяцев после начала продаж, если исходный объем продаж равен нулю. Найдите общий объем продаж в течение первых двух лет после появления нового сорта крупы на рынке.
64. 	Средняя цена. В магазине уцененных товаров уравнение цены-спроса для моторного масла высшего сорта описывается следующим уравнением
р — D (х) = =,
v 7 ^100 +бх
где х — количество канистр масла, которое можно продать по цене р долл. Вычислите среднюю цену на отрезке спроса [50,250].
* 65. Маркетинг. Продемонстрируйте на графике объем продаж нового сорта крупы
из задачи 63 и объясните его геометрический смысл.
* 66. Зависимость цены от спроса. Изобразите в одной и той же системе координат
график зависимости цены от спроса и график средней цены на отрезке [50,250]. Опишите, как связаны между собой площади фигур, лежащих под этими двумя кривыми на отрезке [50,250].
67. Прибыль. Предельная прибыль небольшого автосалона, продающего х автомобилей в неделю, равна
Р' (х) = хд/2 + Зх,
где Р(х) — прибыль, долл. Прибыль автосалона от продажи одного автомобиля в неделю равна 2000 долл. Вычислите функцию прибыли и количество автомобилей, которое следует продавать (с точностью до единицы), чтобы получить недельную прибыль 13 000 долл. Какую еженедельную прибыль (с точностью до доллара) будет иметь автосалон при продаже 80 автомобилей?
68. Доход. Предельная прибыль компании, производящей и реализующей х калькуляторов на солнечных батареях в неделю, равна
Й'М = 7ГТЕ' л(0) = 0’
где Я(х) — доход, долл. Вычислите функцию дохода и недельный объем продаж (с точностью до единицы) для получения дохода 10000 долларов. Какой доход (с точностью до доллара) имеет компания, если она продает 1000 калькуляторов в неделю?


Глава 12. Практические задачи интегрального исчисления
531
Биологические науки
69. 	WWW Загрязнение. Из нефтяного танкера, выброшенного на риф, вытекает нефть. Скорость радиального растекания нефтяного пятна описывается формулой
dR _ 100
~dt ~
t >0,
где R — радиус круглого пятна (в футах) через t минут. Вычислите радиус пятна через четыре минуты, если в момент t = 0, радиус был равен нулю.
70. 	WWW Загрязнение. Концентрация загрязняющего вещества (частиц на миллион) в течение 24-часового периода приблизительно равна
С (t) = tV24 - t, 0 < t sj 24,
где t — время в часах. Вычислите среднюю концентрацию загрязнения за период времени с момента t = 0 до момента t = 24.
Социальные науки
71. Обучение. Человек запоминает N слов со скоростью, которая приблизительно
равна
N' (0 - , t^0,
Vt2 + 25
где t — количество часов непрерывного обучения. Вычислите общее количество слов, выученных за первые 12 часов непрерывного обучения.
72. Политика. Количество избирателей (тысяч человек) в неком округе приблизи-
тельно равно
500
/М=2 + Зе-’
где t — время в годах. Вычислите среднее количество избирателей за период с момента t = 0 до момента t = 10.
*73. Обучение. Объясните решение задачи 71 с геометрической точки зрения.
*74. Политика. Постройте в одной системе координат график функции у = f(t) и прямую, описывающую среднее количество избирателей на интервале [0,10] из задачи 72. Опишите, как связаны между собой площади фигур, лежащих под этими двумя кривыми на отрезке [0,10].


532
Часть III. Математический анализ
Ключевые слова, основные обозначения и формулы
12.1. Площадь фигуры, ограниченной кривыми. Площадь фигуры, лежащей между кривой и осью х; площадь фигуры, лежащей между двумя кривыми; распределение доходов; кривая Лоренца; абсолютное равенство; абсолютное неравенство; показатель концентрации доходов.
12.2. Интегрирование в экономических задачах. Плотность вероятностей; нормальная плотность вероятностей; непрерывный источник доходов; прибыль от источника доходов; общий доход; будущая стоимость непрерывного источника доходов; потребительская выгода; выгода производителей; равновесная цена; равновесное количество.
12.3. Таблицы интегралов. Интегрирование по частям; выбор и и dv;
udv = uv — vdu.
12.4. 	Интегрирование с помощью таблиц. Таблица интегралов; подстановка и таблицы интегралов; формулы приведения.
Упражнения для повторения
Выполните все упражнения этого обзорного раздела и сравните результаты с ответами, помещенными в конце книги. Ответы ко многим упражнениям на повторение приводятся вместе с номером соответствующего раздела (курсивом). Если у вас возникают затруднения при решении какой-либо задачи, повторите материал соответствующего раздела.
Все численные ответы следует находить с точностью до трех десятичных знаков, если не оговорено другое.
А В задачах 1-3 требуется записать определенные интегралы, представляющие собой площади фигур, закрашенных серым цветом на следующем рисунке, на указанных интервалах.
1. Интервал [а, Ь]. 2. Интервал [Ь, с]. 3. Интервал [а, с].
4. Изобразите фигуру, лежащую между графиками функций т/ = 1пхи1/ = 0на интервале [0,5; е], и вычислите ее площадь.
В задачах 5-10 требуется вычислить значение каждого интеграла.
5.


Глава 12. Практические задачи интегрального исчисления
533
7.
9. [ „dx.
J х (1 4- X)
’■ 1 rhdx-
1 x2\/l 4- x
Б
В задачах 11-14 требуется записать определенные интегралы, представляющие собой площади фигур, закрашенных серым цветом на следующем рисунке, на указанных
интервалах.
11. Интервал [а, Ь]. 12. Интервал [6, с].
13. Интервал [b,d\. 14. Интервал [a, d].
15. Изобразите фигуру, ограниченную графиками функций у = х2 — бх 4- 9 и ?/ = = 9 — х, и вычислите площадь этой фигуры.
В задачах 16-21 требуется вычислить значение каждого интеграла.
1
16.
xexdx.
17.
0
г
18.
\/9х2 - 49 dx.
19.
20.
х2 lnx dx.
21.
[ , f dx.
J у/х2 4-16
о
j te~°’5tdt.
[ \ dx.
J 1 + 2ex
22. Изобразите фигуру, ограниченную указанными графиками, и найдите ее площадь. При решении п. б найдите точки пересечения и площадь фигуры с точно-
стью до двух десятичных знаков.
а) у = х3 — бх2 4- 9х; у = х.
б) у = х3 — бх2 4- 9х; у = х 4“ 1.
В В задачах 23-30 требуется вычислить значение каждого интеграла.
23.
24.
x (lnx)2 dx.
J
1 X
25.
* dx.
26.
[ * dx.
x/x2 — 36
J л/х4 - 36
i p
p
27.
xln (10 — x) dx.
28.
(Ina;)2 dx.
о


534
Часть III. Математический анализ
29.
хе 2х dx.
31. 	Используя функцию численного интегрирования, предусмотренную в графической утилите, вычислите площадь фигуры, лежащей в первом квадранте под графиком
6
У~ 2 + 5е~х
и над графиком у = 0,2я + 1,6 (с точностью до трех десятичных знаков).
Применение математики
Экономика и бизнес
32. 	Гарантийный срок службы. Производитель выдает на свои изделия годичную, а на запасные части — двухлетнюю гарантию. Время, прошедшее до поломки изделия с момента покупки, выражается плотностью вероятностей
/(«) =
Г 0,21е—0,214,
если t О,
в противном случае.
Какова вероятность того, что у выбранного случайным образом покупателя изделие сломается в течение указанного срока?
а) В течение первого года гарантии.
б) В течение второго года гарантии.
* 33. Гарантийный срок службы. Постройте график плотности вероятностей для задачи 32 на интервале [0,3] и дайте геометрическую интерпретацию решения задачи 32, б.
34. Функция дохода. Недельный предельный доход от продажи х фенов для волос составляет
R'(x) = 65 - 61n(x + 1), Я(0) = О,
где R(x) — доход в долларах. Вычислите функцию дохода и объем производства (с точностью до ближайшей единицы) при недельном доходе 20 000 долл. Каким будет недельный доход (с точностью до доллара) при производстве 1000 фенов для волос?
35. Непрерывный источник доходов. Скорость непрерывного потока доходов (долл./год) для пятилетнего периода составляет
/(t) = 2500е°'О5‘, 0 < t 5.
а) Постройте график у = f(t) на интервале [0,5] и заштрихуйте фигуру, площадь которой равна общему доходу, полученному с конца первого года по конец четвертого.
б) Вычислите общий доход, полученный с конца первого года до конца четвертого.


Глава 12. Практические задачи интегрального исчисления
535
36. 	Будущая стоимость доходов от непрерывного источника. Непрерывный поток доходов в задаче 35 вкладывается по мере своего поступления под 15 непрерывно начисляемых сложных процентов.
а) Вычислите будущую стоимость (с точностью до доллара) в конце пятилетнего периода.
б) Вычислите проценты (с точностью до доллара), полученные в течение этого пятилетнего периода.
* 37. Распределение доходов. Экономический отдел получил следующие кривые Лоренца для текущего и прогнозируемого через 10 лет распределения доходов в определенной стране.
f(x) = 0,lx + 0,9х2. Текущая кривая Лоренца
д(х) = х1’5. Прогнозируемая кривая Лоренца
а) Постройте график функции у = х и текущую кривую Лоренца в одной системе координат на интервале [0,1], а в другой системе координат постройте график функции у = х и прогнозируемую кривую Лоренца на том же интервале.
б) Что можно сказать, изучая площади фигур, ограниченных кривыми Лоренца и графиком у = х: более или менее равномерно будет распределен доход через десять лет?
в) Вычислите показатель концентрации доходов для текущей и прогнозируемой кривой (с точностью до одного десятичного знака). Что теперь можно сказать о распределении доходов через 10 лет? Он будет более или менее равномерным?
38. Выгода потребителей и производителей. Вычислите выгоду потребителей и производителей при равновесной цене для каждой пары зависимостей цены от спроса и предложения. Постройте графики выгоды потребителей и производителей. Округлите все значения до ближайшего целого.
а) р = D(x) = 70 — 0,2х; p=S(x) = 13 + 0,0012а:2.
б) р = D(x) = 70 — 0,2а:;
р = S(x) = 13е0,006х.
39. Выгода производителей. В следующей таблице содержатся данные о цене и предложении свиней на животноводческом рынке, где х — вес (тыс. фунтов), а р — цена за фунт (центы)
а) Постройте уравнение квадратичной регрессии и определите спрос при цене 52,50 цента за фунт.
б) Используя процедуру численного интегрирования, вычислите выгоду производителей (с точностью до доллара) при цене 52,50 цента за фунт.


536
Часть III. Математический анализ
Зависимость цены от предложения
X
р = S(x)
0
43,50
10
46,74
20
50,05
30
54,72
40
59,18
Биологические науки
40. 	WWW Усвоение препарата. Скорость, с которой организм выводит препарат (в миллилитрах в час) равна
R(t) = ,
(t -hl) (t + 2)
где t — количество часов, которое прошло с момента принятия препарата. Сколько препарата будет выведено из организма в течение первого часа после приема? В течение четвертого часа?
41.* Опишите геометрический смысл решения задачи 40, используя графическую утилиту.
42. 	Медицина. Время, затраченное врачом на прием пациента (в часах), описывается функцией плотности вероятности
4 Л
о
если 0 t 3, в противном случае.
а)
б)
Какова вероятность того, что врач проведет со случайно выбранным пациентом менее одного часа?
Какова вероятность того, что врач проведет со случайно выбранным пациентом более одного часа?
* 43. Медицина. Опишите геометрический смысл решения задачи 42, 6.
Социальные науки
44. Политика. Скорость роста числа избирателей в городе со временем t (в годах) предположительно равна
МИ = ^°°Ц,
(1 + 12)
где ?V(t) измеряется в тысячах человек. Насколько вырастет число избирателей за следующие три года, если 7V(0) — текущее количество населения, принимающего участие в выборах?


Глава 12. Практические задачи интегрального исчисления
537
45. 	Психология. Лабораторных крыс обучали поиску выхода из лабиринта, поощряя ее пищевыми шариками. После седьмого успешного эксперимента было установлено, что плотность вероятности успешного нахождения выхода из лабиринта за определенное время (в минутах) в течение восьмой попытки равна
если £ > О,
в противном случае.
Какова вероятность того, что случайным образом выбранная лабораторная крыса после семи успешных попыток закончит восьмой эксперимент менее чем за 2 мин.? (Напомним, что площадь фигуры, лежащей под кривой плотности вероятности на числовой прямой, равна единице.)
Домашнее задание 12.1. Анализ концентрации доходов на основе необработанных данных
Это домашнее задание можно выполнить, не пользуясь графической утилитой, хотя программа позволит ускорить необходимые расчеты.
Вначале рассмотрим необработанные данные о распределении доходов, которые Бюро переписи населения США представило в табличной форме (табл. 12.2). Исходя из этих данных, сравним распределение доходов среди белого и афроамериканского населения в Соединенных Штатах Америки в 1997 году. Воспользуемся численным, геометрическим и символьным подходами. Прежде всего запишем в таблицу координаты точек, лежащих на кривой Лоренца. Затем для каждого набора точек составим уравнение кривой Лоренца в виде /(ж) = хр. Проинтерпретируем распределение доходов с геометрической точки зрения, построив график кривой Лоренца и график у = х для обоих наборов
www Таблица 12.2. Распределение доходов населения
Семьи, 1997 г Раса
Верхний предел для каждой пятой части, долл.1
Самая низкая Вторая
Третья
Четвертая Верхние 5%2
Всего
20586
36000
53616
80000
137080
Белые
22 576
38000
55783
82442
142400
Афроамериканцы
11396
21875
36 052
57000
95684
Распределение общего дохода для каждой пятой
части, %
Семьи, 1997 г
изкая
ВС св
ысокая
Раса
и
ВС
ВС
И Ои
09
ф
№
£
св а
£
о sa
ВС св
И
И
св
2
S
S
в
&
и
г*
м
£
и
ф
М
Всего
4,2
9,9
15,7
23,0
47,2
20,7
Белые
4,6
10,2
15,7
22,8
46,8
20,7
Афроамериканцы
3,4
9,1
15,6
25,1
46,6
17,6
Источник'. Бюро переписи населения США, Министерство торговли США


538
Часть III. Математический анализ
данных. Наконец, вычислим показатель концентрации доходов белого и афроамериканского населения и проанализируем полученный результат. (См. анализ кривых Лоренца в разделе 12.1.)
Этап 1. Численный анализ. Заполните табл. 12.3 и табл. 12.4, используя данные из табл. 12.2. Округлите уровни доходов до ближайшей тысячи долларов и представьте проценты в десятичном виде с точностью до двух десятичных знаков. Следует помнить, что х описывает совокупный процент семей в данной категории, а у описывает соответствующий совокупный процент доходов, полученных этими семьями. Опишите словами смысл последних двух строк в табл. 12.3 и табл. 12.4 после их заполнения.
Таблица 12.3. Распределение доходов между афроамериканскими семьями, 1997 г
Уровень доходов
X
У
Ниже 11 000 долл.
0,20
0,03
Ниже
0,13
Ниже
Ниже 57 000 долл.
0,80
Таблица 12.4. Распределение доходов между белыми семьями, 1997 г
Уровень доходов
X
У
Ниже 23 000 долл.
0,20
0,05
Ниже
0,15
Ниже
Ниже 82 000 долл.
0,80
Этап 2. Геометрический анализ
1) Для каждой таблицы постройте отдельные графики, отмечая точки из столбцов х и у в табл. 12.3 и табл. 12.4. Кроме того, на каждом графике постройте прямую у = х на интервале [0,1].
2) Найдите такое число р (с точностью до одного десятичного знака), при котором график функции /(х) = хр проходит через точку (0,20; 0,03) в табл. 12.3. Постройте эту кривую на отрезке 0 х 1. Кроме того, найдите такое число q (с точностью до одного десятичного знака), для которого функция д(х) — xq проходит через точку (0,20; 0,05) в табл. 12.4. Постройте эту кривую на отрезке 0 х 1. Повторите эту процедуру для всех остальных точек в каждой таблице. Сравните все графики, построенные на основе табл. 12.3, и выберите значение р, при котором достигается наилучшая аппроксимация данных. Сделайте то же самое для всех графиков, построенных на основе табл. 12.4.
3) Можно ли, исходя из графиков, построенных при решении п. 2, сделать заключение о том, что распределение доходов белых и афроамериканских семей стало более справедливым?
Этап 3. Символьный анализ. Пользуясь значениями р и д, полученными на этапе 2.2, вычислите показатель концентрации доходов для белых и афроамериканских семей и проанализируйте результат.
Последняя пятая часть не имеет верхнего предела. 2Нижний предел для верхних 5%.


Глава 12. Практические задачи интегрального исчисления
539
Домашнее задание 12.2. Рынок зерна
В таблицах, приведенных ниже, содержатся данные о зависимостях цены от спроса и предложения на пшеницу на зерновом рынке, где х — количество бушелей пшеницы (в тысячах), ар — цена за бушель (в центах).
Зависимость цены от спроса Зависимость цены от предложения
X
р = D(x)
X
р = S(x)
20
345
20
311
25
336
25
312
30
323
30
321
35
320
35
323
40
318
40
326
45
307
45
338
1. Для каждого набора данных постройте модели квадратичной, логарифмической и экспоненциальной регрессии.
2. Сравните модели из пункта 1, используя сумму квадратов остаточных погрешностей (см. задачу 2.2 в разделе 2).
3. Используя модели, которые наилучшим образом описывают данные, аппроксимируйте предложение и вычислите спрос, при котором удерживается цена, равная 3,50 долл, за бушель, 3,25 долл, за бушель и 3,00 долл, за бушель.
4. Используя модели, которые наилучшим образом аппроксимируют данные, вычислите равновесное количество и равновесную цену.
5. Используя процедуру численного интегрирования, вычислите выгоду потребителей и производителей при равновесной цене.


13
Исчисление многих переменных
■ 13.1. Функции нескольких переменных
■ 13.2. Частные производные
■ 13.3. Максимум и минимум функции
■ 13.4. Поиск максимумов и минимумов методом множителей Лагранжа
■ 13.5. Метод наименьших квадратов
■ 13.6. Двойные интегралы по прямоугольным областям
■ Ключевые слова, основные обозначения и формулы
■ Упражнения для повторения
■ Домашнее задание 13.1. Планирование города
■ Домашнее задание 13.2. Численное интегрирование и функции многих переменных
13.1. 	Функции нескольких переменных
■ Функции нескольких независимых переменных
■ Примеры функций нескольких переменных
■ Трехмерная система координат
Функции нескольких независимых переменных
В разделе 1.1 мы рассматривали понятие функции одной независимой переменной. Теперь мы расширим это понятие на большее количество переменных. Начнем с простого примера.


Глава 13. Исчисление многих переменных
541
Единственным товаром небольшой компании являются стандартные доски для серфинга. Еженедельные постоянные затраты на производство одной доски составляют 500 долл., а переменные издержки — 70 долл. Функция общих недельных затрат имеет следующий вид.
ОД = 500 + 70ж. (13.1)
Здесь х — недельный объем производства досок для серфинга. Функция затрат зависит только от одной независимой переменной х. Каждому значению переменной х из области определения функции С соответствует одно и только одно число С(х) в области значений функции С.
Допустим теперь, что компания принимает решение производить доски для профессионального спорта. Пусть еженедельные постоянные затраты на одну спортивную доску составляют 200 долларов, а переменные издержки — 100 долларов. Тогда функцию затрат (12.1) нужно переписать так.
ОД у) = 700 + 70а; 4-100?/. (13.2)
Здесь С(х,у) — еженедельные затраты на производство х стандартных досок и у досок для профессионального спорта. Уравнение (13.2) является примером функции двух независимых переменных, хну. Разумеется, если в будущем компания будет расширять производственную линию, то в функции затрат будут появляться новые переменные, по одной на каждый новый тип досок.
Вообще, уравнение вида z = f(x, у)
определяет функцию двух независимых переменных, если для каждой допустимой упорядоченной пары (ж, у) существует одно и только одно значение z9 определяемое f(x,y). Переменные хну называются независимыми переменными, а переменная z — зависимой переменной. Множество всех допустимых упорядоченных пар составляет область определения функции, а множество всех соответствующих им значений /(х, у) — область значений функции. Если не указано обратное, будем считать, что областью определения функции, заданной уравнением z = f(x,y), является множество всех упорядоченных пар, состоящих из действительных чисел (ж, у) таких, что f(x,y) также является действительным числом. Отметим однако, что в некоторых практических задачах имеются ограничения, которые могут сужать область определения.
Аналогично можно определить и функцию трех независимых переменных w = = /(т, у, г), и функцию четырех независимых переменных u = f(w, х, у, z) и т.д. В этом разделе мы в основном сосредоточимся на функциях двух независимых переменных.
Пример 13.1 (Вычисление функции двух независимых переменных). Для определенной выше функции расходов С(х, у) = 700 + 70ж + 100?/ вычислите значение С(10,5).
Решение.
С(10,5) = 700 + 70 • 10 + 100 • 5 = 1900 долл. в
Упражнение 13.1.
Вычислите значение С(20,10) для функции затрат из примера 13.1. ■


542
Часть III. Математический анализ
Пример 13.2 (Вычисление функции трех независимых переменных). Вычислите значение /(3,0, —1) для функции f(x, т/, z) = 2х2 — Зху + 3z + 1.
Решение.
/(3,О, -1) = 2 • З2 - 3 • 3 • О + 3 • (-1) + 1 = 18 - О - 3 + 1 = 16. в
Упражнение 13.2.
Вычислите значение /(—2,2,3) для функции из примера 13.2. ■
Пример 13.3 (Функции прибыли, затрат и доходов). Исследовательский отдел компании, выпускающей доски для серфинга, вывел следующие функции зависимости цены от спроса для каждой модели.
р = 210 — 4я + т/, q = 300 + 100х — 12т/.
Здесь р — цена стандартной доски, q — цена спортивной доски, х — недельный спрос на стандартные доски, у — на спортивные.
1. Вычислите функцию недельных доходов R(x, у) и значение Я(20,10).
2. Пусть функция еженедельных затрат имеет вид
С(х, у) = 700 + 70х + 100т/.
Вычислите функцию недельной прибыли Р(ж, у) и значение Р(20,10).
Решение.
(Спрос на \ / Цена \ / Спрос на \ / Цена \
стандартные I • I стандартной I 4- I спортивные I • I спортивной I доски у \ доски у у доски У у доски У
R(x, у) =xp + yq =
= х(210 — 4х + т/) + 7/(300 + х — 12т/) =
= 210ж 4- 300т/ — 4ж2 + 2ху — 12т/2;
Р(20,10) = 210 • 20 + 300 • 10 - 4 • 202 + 2 • 20 • 10 - 2 • 102 =
= 4800 долл.


Глава 13. Исчисление многих переменных
543
2. Прибыль = доходы — затраты.
Р(х, у) = R(x, у) - С(х, у) =
= 210х + 3001/ - 4х2 + 2ху - 12у2 — 700 — 70х — 100у =
= 140х 4 200у — 4а;2 + 2ху — 12у2 — 700;
Р(20,10) = 140 • 20 + 200 • 10 - 4 • 202 + 2 • 20 • 10 - 12 • 102 - 700 =
= 1700 долл. ■
Упражнение 13.3.
Повторите решение примера 13.3 для следующих функций затрат и зависимости цены от спроса.
р = 220 — 6х + у;
q = 300 + Зх — Ют/;
С(ж, у) = 40х -I- 80т/ -I- 1000. ■
Примеры функций нескольких переменных
Многие из рассмотренных ранее понятий можно представить в виде функций двух или более переменных. Ниже приведены примеры нескольких из них:
Площадь прямоугольника А(х,у) = ху
Объем параллелепипеда
V(x,y,z) = xyz
Объем прямого кругового цилиндра
Простые проценты
Сложные проценты
V(r, h) = irr2h
A(P,r,t) = P(1 + rt)
(p \ nt
1+n)
A — текущая стоимость,
P — капитал,
г — годовая ставка, t — время в годах
А — текущая стоимость,
Р — капитал,
г — годовая ставка, t — время в годах, п — количество периодов начисления


544
Часть III. Математический анализ
IQ
Q(Af, С) = — • 100
Сопротивление течению крови в сосуде (закон Пуазейля)
Г*
Q = IQ — коэффициент интеллектуального развития, М — МА — умственный возраст,
С = С А — календарный (фактический) возраст
R — сопротивление,
L — длина сосуда, г — радиус сосуда, к — константа
Пример 13.4 (Дизайн упаковок). Товар, выходящий с производственной линии, упаковывается в открытые сверху коробки квадратного сечения, показанные на следующей рисунке. Пусть длина (и ширина) основы коробки (в дюймах) равна х, а высота (в дюймах) — у. Вычислите количество материала М(х, у), необходимое для производства одной такой коробки, и значение М(5,10).
Решение.
Площадь основания = х2
Площадь боковой грани = ху
Поверхность = (Площадь основания) + 4 • (Площадь боковой грани) М(х) = х2 + 4ж?/,
М(х) = 52 + 4 • 5 • 10 = 225 кв. дюймов. ■
Упражнение 13.4.
Для условий примера 13.4 вычислите объем коробки V(x,y) и значение У(5,10).и
В следующем примере рассматривается производственная функция Кобба-Дугласа (Cobb-Douglas)
/(х,у) = кхтуп,
где к, т, п — положительные константы ит + п = 1. В экономике эта функция используется для описания объема производства f(x,y) от затрачиваемого труда х и у единиц капитала (расходов на производственные помещения, оборудование, инструменты и т.п.). Функция Кобба-Дугласа также используется для определения производительности труда в отдельной отрасли промышленности или группе отраслей, принимающих участие в выпуске одного и того же типа продукции, или даже для вычисления ее общенационального объема производства.


Глава 13. Исчисление многих переменных
545
Пример 13.5 (Производительность). Производительность сталелитейного производства можно приближенно представить функцией
f(x,y) = 10x°V’8;
где х — объем затрачиваемого труда, а у - затрачиваемый капитал. Предположим, что на производство единицы стали затрачивается использует 3000 единиц труда и 1000 единиц капитала. Сколько единиц стали при этом производится?
Решение. Объем производства стали описывается выражением
/(3000,1000) = 10 • ЗООО0’2 • 1ООО0'8»
«12 457 ед. Используем калькулятор ■
Упражнение 13.5.
Вернемся к примеру 13.5. Вычислите объем производства стали, если на ее выплавку затрачивается 3000 единиц труда и 1000 единиц капитала. ■
Трехмерная система координат
Далее мы вкратце рассмотрим графики некоторых функций двух независимых переменных. Поскольку функция вида z = включает две независимые переменные х
и у и одну зависимую переменную z, то для построения ее графика требуется трехмерная система координат. Трехмерную систему координат можно построить с помощью трех взаимно перпендикулярных числовых осей, пересекающихся в их началах (рис. 13.1). В такой системе координат каждой точке однозначно сопоставляется тройка чисел z), и наоборот, каждой тройке чисел однозначно соответствует точка
в пространстве.
Рис. 13.1. Прямоугольная система координат.
Пример 13.6 (Прямоугольные координаты). Определите положение точки (—3,5,2) в прямоугольной системе координат.


546
Часть III. Математический анализ
Решение.
Упражнение 13.6.
Определите координаты вершин прямоугольного параллелепипеда, изображенного на рисунке.
Задание 13.1.
Представьте, что находитесь перед комнатой с прямоугольными стенами, которые пересекаются под прямыми углами. Пусть началом трехмерной системы координат служит точка пересечения пола, противоположной стены и стены, расположенной слева. При этом каждая пространственная точка внутри комнаты имеет неотрицательные координаты. Тогда координатная плоскость z = 0 (или, что то же самое, плоскость ху) будет “полом”, а плоскость z — 2f параллельная к ней, но расположенная на 2 единицы выше, — “потолком” комнаты. Дайте словесное описание таким плоскостям.
1. 	х = 0. 2. х = 3. 3. у = 0.
4. у = 4. 5. х — —1. ■
Как выглядит график функции z — х2 + у21 Если положить i = 0 и построить график z — О2 + у2 в плоскости yz, то получится парабола. Если же положить у = 0 и построить график z = х2 4- О2 в плоскости xz, то получится также парабола, но расположенная в пространстве по-другому. Можно показать, что график функции z = х2 + у2 получается


Глава 13. Исчисление многих переменных
547
вращением любой из парабол вокруг оси z (рис. 13.2). Этот чашеобразный рисунок является поверхностью, которая называется параболоидом.
В общем случае графиком функции вида z = будет некая поверхность. Гра¬
фиком функции такого типа является набор всех упорядоченных троек чисел, которые удовлетворяют ее уравнению. Часто построение графика функции трех независимых переменных представляется довольно сложным процессом, и мы не будет останавливаться на его детальном рассмотрении в этой книге. Далее вы познакомитесь всего с несколькими наглядными примерами изображения графиков функции в трехмерном пространстве, которые впоследствии будет применяться при поиске их экстремумов (максимумов и минимумов). Заметим, что функция z = f(x, у) = х2+у2 имеет локальный минимум в точке (х,у) = (0,0) (см. рис. 13.2). На рис 13.3 показана функция с локальным максимумом в точке (ж, у) = (0,0).
Рис. 13.2. Параболоид
Рис. 13.3. Локальный максимум:
/(0,0) = 4
Для поверхности, изображенной на рис. 13.4, точка (ж, у) = (0,0) называется седловой точкой, которая не является ни максимумом, ни минимумом. Отметим, что для х = 0 седловая точка является локальным максимумом, а для у = 0 — локальным минимумом. Более подробно локальные максимумы и минимумы будут рассмотрены в разделе 13.3.
Задание 13.2.
1. Пусть f(x,y) = х2 + у2. Сечением этой поверхности плоскостью х = 2 является парабола z = f(2,y) = 4 + у2 (рис. 13.5). Объясните, почему сечением поверхности f(x,y) = х2 + у2 плоскостью, параллельной плоскости yz, всегда является парабола, ветви которой направлены вверх (рис. 13.5). Объясните, почему сечением поверхности /(ж, у) = х2 + у2 плоскостью, параллельной плоскости xz, всегда является парабола, ветви которой направлены вверх.
2. Пусть д(х, у) = у2 —х2. Объясните, почему сечением поверхности р(х, у] — у2 —х2
плоскостью, параллельной плоскости yz, всегда является парабола, ветви которой направлены вверх (рис. 13.4). Объясните, почему сечением поверхности f(x,y) = = х2 — у2 плоскостью, параллельной плоскости xz, всегда является парабола, ветви которой направлены вниз. ■


548
Часть III. Математический анализ
Рис. 13.4. Седловая точка (0,0,0) Рис. 13.5. Парабола
В некоторых графических утилитах предусмотрена процедура, позволяющая отображать поверхности (подобных изображенным на рис. 13.3-13.5), соответствующие функциям нескольких переменных. Другие же, например, графический калькулятор, используемый для построения графиков в этой книге, приспособлены для построения графиков функций только одной независимой переменной. Используя последние модели калькулятора можно строить графики сечений поверхности плоскостями, параллельными yz или xz. Используя описанные возможности, можно получить четкое представление о поведении графика функции двух независимых переменных.
Пример 13.7 (Построение сечений).
1. Опишите сечения графика /(х, у) = 2х2 + у2 плоскостями у = 0, у = 1, у = 2, у = 3 и у = 4.
2. Опишите сечения графика f(x,y) = 2х2 + у2 плоскостями х — 0, х — 1, х = 2, х = 3 и х = 4.
Решение,
1. Сечением графика /(х, у) = 2х2 + у2 плоскостью у = 0 является график /(х, 0) =
= 2х2 в этой же плоскости. Форму сечения можно определить, построив график функции yi = 2х2 с помощью графической утилиты (рис. 13.6). Аналогично графики функций у2 = /(х, 1) = 2х2-Н 1,2/з = /(х,2) = 2х2+4, у4 = /(х,3) = 2х2+9 и 2/5 = 4) = 2х2 + 16 являются остальными четырьмя сечениями поверхности
(рис. 13.6). Каждое из них представляет собой параболу, ветви которой направлены вверх. Сопоставьте графики на рис. 13.6 и действительные сечения поверхности /(х, 2/) = 2х2 4- у2, показанные на рис. 13.7.
2. Пять сечений параболоида представляются графиками функций 2/1 = х2, 2/2 = 2 +
+ z2, 2/з = 8 + х2, 2/4 = 18 -Ь х2 и 2/5 = 32 + х2, изображенных на рис. 13.8. (Заметим, что замена буквы независимой переменной с х на у никак не влияет на вид графика.) Все пять сечений представляют собой параболы, ветви которой направлены вверх. а


Глава 13. Исчисление многих переменных
549
Рис. 13.6. Графики функций Рис. 13.7. Параболоид 2/1 = 2х2,
2/2 = 2х2 + 1,
2/з = 2х2 + 4,
2/4 = 2х2 + 9,
у5 = 2х2 + 16
Рис. 13.8. Графики функций
2/1 = х2,
2/2 = 2 + х2,
1/з = 8 + х2,
7/4 = 18 + X2, 2/5 = 32 + х2
Упражнение 13.7.
1. Опишите сечения графика д(х, у) =у2 — х2 плоскостями 2/ = 0,2/ = 1, У = 2,2/ = 3 и у = 4.
2. Опишите сечения графика д(х, у) = у2 — х2 плоскостями х = 0, х = 1, х = 2,
I = 3 и I = 4. ■
Ответы к упражнениям
13.1. 3100 долл.
13.2. 30.
13.3. 1) R(x, 2/) = 220х + 3002/ - 6х2 + 4^2/ ~ Юу2; Я(20,10) = 4800 долл.
2) Р(х, у) = 180х + 2202/ - 6х2 + 4x2/ - Юг/2 - Ю00; Р(20,10) = 2200 долл.


550
Часть III. Математический анализ
13.4. V(x,y) = х2у; V(5,10) = 250 дюйм3.
13.5. 17411 единиц.
13.6. А(0,0,0); С(2,4,0); G(2,4,3); 17(0,4,0).
13.7. 1) Сечением является парабола, ветви которой направлены вверх.
2) Сечением является парабола, ветви которой направлены вниз.
Практикум 13.1
А В задачах 1-10 требуется вычислить указанные значения функций f(x,y) = 7ху — 8
ug(x,y) = 4х — у2 + 12.
1. /(0,0).
3. /(-3,1).
5. ff(0,0).
7. 5(2,-1).
2. /(2,1).
4. /(2,-7).
6. 5(0,-1).
8. 5(-1,2).
9. #(3,4) - 6/(3,4). 10. /(-2,5) + 9<?(-2,5).
Б Вычислите указанные значения приведенных ниже функций.
11. А(2,3) для А(х,у) = ху.
М
13. Q(12,8) для Q(M, G) = — • 100.
15. V(2,4) для V(г, h) = ттг2Н.
17. Я(1,2) для R(x, у) = —5т2 + бху - 4у2 + 200т + 300?/.
18. Р(2,2) для Р(т, у) = —х2 -I- 2ху - 2у2 — 4т + 12?/ + 5.
19. Я(6,0,5) для R(L,r) = 0,002^.
г4
20. £(2000,50) для L(w,v) = (1,25 • 10-5)wv2.
21. А(100; 0,06; 3) для А(Р; г; t) = Р + Prt.
22. А(10; 0,04; 3; 2) для А(Р; г; i; п) = Р (1 +
т
23. Р(0,05; 12) для P(r; Т) = j 4000 e_rf dt.
О т
24. Г(0,07; 10) для F(r; Т) = 4000 er(T“t) dt.
о
25. Пусть Р(т,?/) = х2 + еху — у2. Вычислите все значения переменной т, для которых выполняется условие Р(т, 2) = 0.
26. Пусть G(a, 5, с) = а3 4- Ь3 + с3 — (ab + ас + Ьс) — 6. Вычислите все значения переменной т, для которых выполняется условие G(2,6,1) = 0.


Глава 13. Исчисление многих переменных
551
В
27. Для функции /(х, у) = х2 + 2у2 вычислите выражение
/(х 4-/г, у) -/(х, у)
h
28. Для функции f(x,y) = х2 + 2у2 вычислите выражение
/(x,y4-fc) ~/(х,у)
к
29. Для функции f(x, у) = 2ху2 вычислите выражение
/(д 4-/г, у) ~ Ж у) h
30. Для функции f(x, у) = 2ху2 вычислите выражение
Ж У 4-А:)-Дж, у)
к
31. Определите координаты точек Е и F на рисунке к упражнению 13.6 (см. выше).
32. Определите координаты точек В и Н на рисунке к упражнению 13.6 (см. выше).
В задачах 33-38 примените графическую утилиту для объяснения свойств графиков указанных сечений.
*33. Пусть f(x,y) = ж2.
а) Объясните, почему сечения поверхности z = f(x, у) плоскостями, параллельными у = 0, являются параболами.
б) Опишите сечения этой поверхности плоскостями ж = 0, ж = 1 и ж = 2.
в) Опишите вид поверхности z = f(x, у).
*34. Пусть f(x,y) = у/4 - у2.
а) Объясните, почему сечения поверхности z = f(x,y) плоскостями, параллельными х = 0, являются полуокружностями радиуса 2.
б) Опишите сечения этой поверхности плоскостями у = 0, у = 2 и у = 3.
в) Опишите вид поверхности z = f(x, у).
*35. Пусть f(x,y) = у/Зб — ж2 — у2.
а) Опишите сечения этой поверхности плоскостями у = 1, у = 2, у = 3, у — 4 и у = 5.
б) Опишите сечения этой поверхности плоскостями ж = 0, ж = 1, ж = 2, х = 3, х = 4 и х = 5.
в) Опишите вид поверхности z = f(x, у).
* 36. Пусть /(ж, у) = 100 + Юж + 251/ — х2 — 51/2.
а) Опишите сечения этой поверхности плоскостями у = 0, у = 1, у = 2, пу = 3.
б) Опишите сечения этой поверхности плоскостями ж = 0, ж = 1, ж = 2, и ж = 3.
в) Опишите вид поверхности z = /(ж, у).


552
Часть III. Математический анализ
*37. Пусть /(я, т/) = е (*2+А
а) Объясните, почему /(а, 6) = f(c,cT), если (а,Ь) и (с, d) — точки, которые лежат на одной окружности с центром в начале координат плоскости ху.
б) Опишите сечения этой поверхности z — f(x,y) плоскостями х — 0, у = О и х = у.
в) Опишите вид поверхности z = f(x, у).
*38. Пусть f(x,y) = 4 — у/х2 + у2.
а) Объясните, почему /(а, 6) = f(c, d), если (а, 6) и (с, d) — точки, которые лежат на одной окружности с центром в начале координат плоскости ху.
б) Опишите сечения этой поверхности z = f(x,y) плоскостями х = 0, у = О и х = у.
в) Опишите вид поверхности z = f(x, у).
Применение математики
Экономика и бизнес
39. Функция затрат. Небольшая компания производит доски для серфинга — стандартную и спортивную модели. Предположим переменные издержки на производство стандартной модели равны 70 долл., а спортивной модели — 100 долл. Ежемесячные постоянные затраты составляют 2000 долл., а функция ежемесячных затрат задается выражением
С(х, у) = 2000 + 70z + 100?/.
Здесь хну — месячный объем производства соответственно стандартных и спортивных моделей. Вычислите значения <7(20,10), <7(50, 5) и (7(30,30).
40. Реклама и объем продаж. Предположим, компания еженедельно расходует х тыс. долл, на рекламные объявления в печатных изданиях и у тыс. долл, на телевизионную рекламу. Еженедельные продажи задаются выражением
S(x,y) = 5х2у3.
Вычислите значения 5(3,2) и 5(2,3).
41. Функция доходов. В супермаркете продается два сорта кофе: сорт А по цене р долл, за фунт и сорт В по цене q долл, за фунт. Функции ежедневного спроса на сорты А и В соответственно задаются уравнениями
х = 200 — Ьр + 4д,
у — 300 + 2р — 4q
(обе величины в фунтах). Определите функцию дневного дохода R(p,q). Вычислите значения Я(2,3) и Я(3,2).


Глава 13. Исчисление многих переменных
553
42. 	Функции затрат, доходов и прибыли. Компания производит трех- и десятискоростные велосипеды. Функции недельного спроса и затрат задаются уравнениями
р = 230 — 9ж 4- у, q = 130 + х — 4г/,
С(х, 1/) = 200 + 80х + 301/,
где р — цена десятискоростного велосипеда (в долларах), q — цена трехскоростного велосипеда, х — недельный спрос на десятискоростные велосипеды, у — на трехскоростные, С(х,у) — функция затрат. Определите функции недельных доходов Я(х, у) и прибыли Р(х, у). Вычислите значения Я(10,15) и Р(10,15).
43. 	Производительность. Производственная функция Кобба-Дугласа для нефтеперерабатывающего производства имеет вид
f(x,y) = 20а;0’V’6;
где х — объем затраченного труда, у — стоимость затраченного капитала. Пусть в производство вложено 1200 единиц труда и 1700 единиц капитала. Какой объем бензина при этом будет произведен?
44. Производительность. Нефтеперерабатывающий завод из примера 43 выкоплен другой компанией, руководство которой приняло решение повысить объем производства за счет удвоения затрат труда и капитала. Воспользуйтесь функцией Кобба-Дугласа, заданной в примере 43, для вычисления объема производства бензина при увеличении указанных затрат. Как повлияет на производство повышение затрат труда и капитала?
45. Будущая стоимость. На пенсионный счет ежегодно вносится сумма 2000 долларов под 9% годовых.
а) Сколько денег будет находиться на пенсионном счету через 30 лет? Воспользуйтесь формулой
i
где Р — периодичность начислений, i — процентная ставка, установленная на период начисления, п — количество начислений (периодов), F = FV = = будущая стоимость.
б) Воспользуйтесь графической утилитой и вычислите процентную ставку, обеспечивающую доход 500000 долл, за 30 лет.
46. 	Дизайн упаковки. Отделу доставки компании нужно разработать дизайн прямоугольной упаковки, открытой сверху и разделенной посередине (рис. 13.9). Пусть размеры упаковки (в дюймах) составляют х9 у и z.


554
Часть III. Математический анализ
Рис. 13.9. Иллюстрация к задаче 46
а) Определите количество материала М (х, у, z), необходимое для производства такой упаковки, и вычислите М(10,12,6).
б) Допустим, что коробка имеет квадратное основание и объем 720 куб. дюймов. Используя графическую утилиту, вычислите размеры коробки, для производства которой требуется минимум материала.
Биологические науки
47. 	Биология морей. Время погружения с аквалангом приближенно определяется уравнением
где Т — время погружения (в минутах), V — объем воздуха (закачанного в баллон при атмосферном давлении), х — глубина погружения в футах. Найдите значения Т(70,47) и Т(60,27).
48. 	WWW Течение крови. Согласно закону Пуазейля сопротивление R течению крови прямо пропорционально длине сосуда L, и обратно пропорционально четвертой степени его радиуса г. Эта зависимость выражается уравнением
Вычислите значения Я(8,1) и Я(4; 0,2).
49. 	WWW Физическая антропология. При изучении классификации человеческих черепов антропологи часто используют понятие черепной индекс. Этот индекс С прямо пропорционален ширине головы W и обратно пропорционален длине головы L (обе величины определяются при рассмотрении черепа сверху), т.е. описывается уравнением
C(W,L) = 100—,
Б
где W — ширина (в дюймах), L — длина (в дюймах). Вычислите значения С(б, 8) и <7(8,1; 9).


Глава 13. Исчисление многих переменных
555
Социальные науки
50. Исследование безопасности. Длина тормозного пути автомобиля описывается формулой
L(w, v) = kwv2,
где к — константа, w — вес автомобиля в фунтах, v — скорость автомобиля в милях в час. Вычислите значения £(2000,40) и L(3000,60) при к — 0,0000133.
51. Психология. Коэффициент умственного развития (IQ) определяется как умноженное на 100 отношение умственного возраста (МА) к фактическому (календарному) возрасту (СА), т.е. имеет место уравнение
Q(M,C) = ^-100,
где Q = IQ, М = МА и С = СА. Вычислите значения Q(12,10) и <2(10,12).
13.2. 	Частные производные
■ Частные производные
■ Частные производные второго порядка
Частные производные
На данный момент нам уже хорошо известно, как дифференцировать многие функции одной переменной и как описывать получаемые результаты. А как поступать с функциями нескольких переменных? Вернемся к примеру производства досок для серфинга, приведенному в начале этого раздела.
Для производства стандартных досок для серфинга, функция затрат имеет вид
С(х) = 500 + 70я.
Дифференцируя эту функцию по переменной х9 получим функцию предельных затрат
С'(ж) = 70.
Поскольку предельные затраты постоянны, то сумма, равная 70 долл., — это изменение расходов при увеличении объема выпускаемой продукции на одну единицу.
Если предприятие производит две модели досок, стандартную и спортивную, то функция затрат имеет вид
С (я, у) = 700 + 70ж -I-1001/.


556
Часть III. Математический анализ
Теперь будем считать, что при дифференцировании функции по переменной х значение переменной у остается неизменным. Обозначим такую производную как Сх(х, у). Аналогично при дифференцировании функции по переменной у значение переменной х также считается фиксированным. Такая производная обозначается Су(х, у). Производные такого типа имеют следующий вид.
Сх(х,у) = 70,
Су(х,у) = 100.
Обе такие производные называются частными производными. В данном примере они описывают функцию предельных затрат. Первая производная описывает изменение затрат при увеличении объема производства стандартной модели на одну единицу (при неизменном объеме выпуска спортивной модели), а вторая — изменение расходов при увеличении объема производства спортивной модели на одну единицу (при неизменном объеме выпуска стандартной модели).
В общем случае, если z — f(x,y), то частная производная функции f по переменной х, обозначаемая как dzjdx, fx или /ж(х, у), определяется как
при условии, что такой предел существует. Легко видеть, что это — обычная производная по переменной х, если переменная у считается постоянной. Поэтому все свойства производных, рассмотренных в главах 8 и 10, остаются справедливыми и для частных производных.
Аналогично частная производная функции f по переменной у, обозначаемая как dz/dy, fy или fy(x, у), определяется как
Если переменная х фиксирована, то эта функция совпадает с обычной производной по переменной у.
Аналогичные определения можно сформулировать для функций трех и более независимых переменных.
Пример 13.8 (Частные производные). Вычислите следующие выражения для функции z = f(x, у) = 2х2 - Зх21/ + бу + 1.
1. dzjdx.
2. 	Д(2,3).
Решение.
1. 	z = 2х2 — Зж21/ + 5?/ + 1. Дифференцируя эту функцию по переменной х и считая переменную у постоянной, получим следующий результат.
—— = 4х — бху. дх
2. 	z — f(x, у) = 2х2—Зх2у+бу+1. Сначала вычислим производную по переменной х. Из решения п. 1 известно, что
fx(x,y) = 4х- бху.


Глава 13. Исчисление многих переменных
557
Далее вычисляем значение производной в точке (2,3).
/ж(2,3) = 4 • 2 — 6 • 2 • 3 = —28.
Альтернативный подход к решению примера 13.8.2 состоит в подстановке значения у = 3 в функцию f(x,y) и построении графика функции /(я,3) = — 7х2 + 16, которая является сечением поверхности z = /(х, у} плоскостью у = 3. Далее следует определить наклон касательной к графику при х = 2. Итак, мы получаем Д(2,3) = —28 (рис. 13.10).
Рис. 13.10. График функции j/х = —7х2 + 16
Упражнение 13.8.
Вычислите следующие выражения для функции f из примера 13.8.
1. dz/dy. 2. Д(2,3).
Пример 13.9 (Вычисление частных производных с помощью цепного правила). Вычислите следующие выражения для функции z = f(x, у) = ех +у .
1. dz/dx. 2. Л(2,1).
Решение.
1. 	Используя цепное правило (z = еи, и = и(х\ у — константа), получим следующий результат.
dz = + = 2хех'+У2.
dx дх
2.
д(х2 + у2) ду
/у(2,1) = 2 • 1 • е241’ = 2е5.
Упражнение 13.9.
Вычислите следующие выражения для функции z = f(x, у) = (х2 + 2ху)5.
1. dz/dy. 2. A(i,o).


558
Часть III. Математический анализ
Пример 13.10 (Прибыль). Функция прибыли при производстве досок для серфинга, из примера 13.3 имела вид
Р(ж, у) = 140х + 2001/ — 4х2 + 2ху — 12у2 — 700.
Вычислите значения Рх(15,10), Рх(30, 10) и дайте интерпретацию результатов.
Решение.
Рх(х, у) = 140 - &г + 2у,
Я(15,10) = 140 - 8 • 15 + 2 • 10 = 40,
РДЗО,10) = 140 — 8 • 30 + 2 • 10 = -80.
Это значит, что при недельном объеме производства 15 стандартных и 10 спортивных досок увеличение выпуска стандартных досок на единицу (при неизменном объеме изготовления спортивных досок — 10 единиц в неделю) приведет к увеличению прибыли приблизительно на 40 долларов. При недельном объеме производства 30 стандартных и 10 спортивных досок увеличение производства стандартных досок на единицу (при неизменном объема выпуска спортивных досок — 10 единиц в неделю) приведет к уменьшению прибыли приблизительно на 80 долларов. а
Упражнение 13.10.
Для функции прибыли из примера 13.10 вычислите значения 7^(25,10), Ру(25,15) и опишите полученные результаты. а
Задание 13.3.
Пусть Р(х,у) — функция прибыли из примера 13.10 и упражнения 13.10.
1. Допустим, что объем производства спортивных досок остается постоянным — 10 шт. в неделю. При каком объеме производства стандартных досок прибыль будет максимальной? Вычислите максимальную прибыль.
2. Допустим, что объем производства стандартных досок остается постоянным —
25 шт. в неделю. При каком объеме производства спортивных досок прибыль будет максимальной? Вычислите максимальную прибыль. в
Пример 13.11 (Производительность). Производительность крупного предприятия по производству компьютерного оборудования приближенно описывается функцией Кобба-Дугласа
f(x, у) = 15х°’4у°'6
при затратах х единиц труда и у единиц капитала. Частная производная fx(x,y) описывает скорость изменения производительности по отношению к затратам труда и называется предельной производительностью труда. Частная производная fy(x,y) представляет собой скорость изменения производительности по отношению к затратам капитала и называется предельной производительностью капитала. Пусть компания затрачивает 4000 единиц труда и 2500 единиц капитала. Вычислите предельную производительность труда и капитала. Что можно сделать для увеличения доходов компании: увеличить затраты труда или капитала?


Глава 13. Исчисление многих переменных
559
Решение.
fx(x,y) = 6x °'6у°’6
fx (4000,2500) = 6 • 4000“°’62500°’6«
«4,53
fy(x,y) = 9х°’4у~0,4
(4000,2500) = 9 • 4000°'42500“°’4«
«10,86
Предельная производительность труда
Предельная производительность капитала
При текущем уровне затрат 4000 единиц труда и 2500 единиц капитала увеличение затрат труда на одну единицу (при неизменных затратах капитала в 2500 единиц) приводит к росту объема производства приблизительно на 4,53 единицы. Увеличение расхода капитала на одну единицу (при неизменных затратах труда в 4000 единиц) приводит к росту объема производства приблизительно на 10,86 единицы. Стало быть, руководству компании целесообразно сконцентрироваться на увеличении затрат капитала. ■
Упражнение 13.11.
Производительность предприятия по изготовлению самолетов приближенно описывается функцией Кобба-Дугласа
f(x, у) = 40х°’3у0’7
при затратах х единиц труда и у единиц капитала.
1. Вычислите производные у) и fy(x, у).
2. Пусть текущие затраты компании составляют 1500 единиц труда и 4500 единиц капитала. Вычислите предельную производительность труда и предельную производительность капитала.
3. Что можно сделать для увеличения доходов компании: увеличить затраты труда
или затраты капитала? ■
Частные производные имеют простую геометрическую интерпретацию, как показано на рис. 13.11. Пусть значение переменной х фиксировано, скажем, х = а. Тогда значение fy(a, у) задает наклон кривой, получаемой пересечением плоскости х = ас поверхностью z — f(x, у). Аналогичную интерпретацию можно дать производной Д(гг, Ь).
Задание 13.4.
Пусть /(х, у) = х2у — 2ху2 4- 3. Рассмотрим поверхность z = f(x, у).
1. Сечением поверхности плоскостью х = 2 является кривая /(2,1/) = 41/ — 4i/2 + + 3, которая представлена параболой. Вычислив производную, определите наклон касательной к этой параболе в у — |.
2. Проверьте ответ с помощью частных производных.
3. Объясните, почему сечение поверхности плоскостью у = 1 также является параболой. Вычислив производную, определите наклон касательной к этой параболе в х = 3.
4. Проверьте ответ с помощью частных производных. ■


560
Часть III. Математический анализ
Рис. 13.11. Геометрическая интерпретация
Частные производные второго порядка
Функция
X = f(x,y) = ^у7
имеет две производные первого порядка
= fx = fx(x, у) = fa?y7 ИЛИ = fy = fy(x, у) = 7х4у6
С другой стороны, у каждой из этих частных производных тоже существуют частные производные, которые называются частными производными второго порядка функции z = f(x,y). Обобщая различные обозначения для частных производных первого порядка, запишем четыре производные второго порядка для функции z = f(x, у) = х4у7 в следующем виде.
Эквивалентные обозначения
- г ( \ д f dz\ /Д 3 7\ ш 2 7
/„ = ~ (W) = 28Х»/.
Л. = /..(*.«) = = Л (W) - 28xss«.
f„ = /„(*,») = (g) = (W) = 42*У.
Для вычисления смешанной частной производной d2z/dxdy = fxy(x,y) функция z — f(x,y) сначала дифференцируется по переменной х, а переменная у считается постоянной. Далее результат вычисления дифференцируется по переменной у, а переменная х считается постоянной. При вычислении другой смешанной частной производной


Глава 13. Исчисление многих переменных
561
d2z/dydx = /ух(Х)У) порядок вычислений изменяется на противоположный, однако результат будет тот же, т.е. fxy = fyx. Существуют функции, у которых fxy ф fyx, однако они имеют узкую область практического применения. Для всех функций, с которыми нам придется иметь дело в этой книге, выполняется условие fxy = fyx.
Примем следующее определение.
Частные производные второго порядка
Пусть z = /(ж, у), тогда
Jxx Jxx\ ,У) дх2 дх удх J , f _ , / ч _ 92Z _ д (dz\
fxy - fxy(x,y) - дудх - ду J ,
fyx - fyx(x,y) ~ дхду~ дх J >
fyy ~ fyy&v) - ду2 - ду \^дуJ •
Пример 13.12 (Частные производные второго порядка). Пусть z — f(x,y) = Зя2 — — 2ху3 + 1. Вычислите следующие функции.
d2z и d2z дх ду ду дх *
2.
дх2
3» fyx(2> !)♦
Решение.
1. Сначала будем дифференцировать функцию по переменной х, а затем — по переменной у. Получим следующий результат.
dz ду
d2z _ д (dz\ _ д , 2ч дхду дх \ду) дх' ХУ '
-бу2.
2. 	Сначала будем дифференцировать функцию по переменной х, а затем по перемен ной у. Получим следующий результат.
dz „ _о
— = 6х - 2у3, ОХ
d2z д (dz\ д , Зч 2
a,sx = д Дэх) = а„ 2’>= '
3. Дифференцируя дважды по переменной х, найдем следующие выражения.
dz дх
= бх - 2y3,
d2z _ а /дх\ _
дх2 дх \дх)
4. 	Сначала найдем функцию fyx(ж, ?/), а затем вычислим значение этой функции в точке (2,1). Напомним еще раз, что для поиска функции fyx нужно сначала дифференцировать функцию f по переменной у, а затем по х.
fy(x,y) = ~бху2, fyx(x,y) = -бу2, И
fyx(2,1) = -6 • I2 = -6.


562
Часть III. Математический анализ
Упражнение 13.12.
Пусть z = Дх, у) = х3у — 2у4 + 3. Вычислите следующие выражения.
1. d2z. ду дх
з. ДД2,з).
d2z
ду2'
4. /у1(2,3). ■
Ответы к упражнениям
13.13. 1) = -Зх2 + 5.
ду
2) Д(2,3) = -7.
13.14. 1) 10я(я2 + 2xi/)4.
2) 10.
13.15. (25,10) = 10 — объем производства при х = 25 и у = 10. Увеличение переменной у на единицу при постоянном значении переменной х приводит к увеличению доходов приблизительно на 10 долларов; Ру (25,15) = —110: увеличение переменной у на единицу при постоянном значении переменной х приводит к уменьшению доходов приблизительно на 110 долларов.
13.16. 1) fx(x,y) = 12х~°'7у°’7; fy(x,y) = 28х°’3у~°’3.
2) Предельная производительность труда «25,89. Предельная производительность капитала «20,14.
3) Увеличить затраты труда.
13.17. 1) Зя2.
2) -24у2.
3) 12.
4) 12.
Практикум 13.2
А В задачах 1-4 считается, что z = f(x,y) = 7 — 2х + 5у. Вычислите указанные
функции или значения.
1. dzjdx.
3. /у(1,2).
2. дг/ду.
4. Д(1,2).
В задачах 5-10 считается, что z = f(x,y) = 6х2у + Зу3. Вычислите указанные
функции или значения.
5. dzjdy. д2 z
' ду2'
9. А (2,3).
6. dzjdx.
8‘ дх2'
10. А(2,3).


Глава 13. Исчисление многих переменных
563
В задачах 11-18 считается, что С(х,у) = 5х2 —6ху + 3у2—4х+10у —15. Вычислите
указанную функцию или значения.
11. Сх(х,у).
13. С,(2,2).
15. СХу(х,у).
, Схх(х, у).
12. Су(х,у).
14. Су(2,2).
16. Сух(х,у).
18. Суу(х,у).
Б В задачах 19-24 считается, что S(x,y) = 4х3у+у In х. Вычислите указанные функции или значения.
19. Sx(x,y). 20. Sy(x,y).
21. 5У(2,1). 22. 5,(2,1).
23.
Sxy (х^у). 24. SyX(x, у).
В задачах 25-32 считается, что z = f(x,y) = е4х2+3у. Вычислите указанные функции
или значения.
25.
dz дх'
дхду
29. /^(1,0).
31. А40,1).
26.
28.
dz
ду
д2 z дудх'
30. лдо,1).
32. /^(1,0).
В задачах 33-42 требуется найти выражения fx(x, у) и fy(x, у) для указанных функций.
33. 	f(x,y) = (х2 - у3)3.
35. 	/(х,7/) = (Зх22/-1)4.
37. 	f(x,y) = 1п(я2 + у2).
39. f(x,y) = y2exy2.
34. 	f(x,y) = у/2х-у2.
36. 	f(x,y) = (3 + 2ху2)3.
38. 	f(x,y) = 1п(2х - Зу).
40. f(x,y) = х3ех2у.
42. /(ж, у) =
2х2у
х2 + у2'
* 43. а) Пусть f(x, у) = у3 + 4у2 — 5у + 3. Покажите, что df/dx = 0.
б) Объясните, почему существует бесконечное количество функций д(х,у), удовлетворяющих условию дд/дх = 0
*44. а) Приведите пример функции, для которой д f /дх = 3 и д f /ду = 2. б) Сколько таких функций существует? Объясните ответ.
В задачах 45-50 вычислите производные fXx(x,y)> /ху(х,У)> fyx&y) и fyy(x,y) для каждой из указанных функций f.
45. f(x, у) = х2у2 +х3 + у.
47. f(x,y) = 7.-^-
У х
49. 	f(x,y) = хеху.
46. 	f(x,у) = х3у3 +х + у2.
х2 и2
48. f(x,y) = .
У х
50. 	f(x,y) = xln(xy).


564
Часть III. Математический анализ
В
51. Для функции
Р(х, у) = -х2 -I- 2ху — 2у2 — 4х + 12у — 5
вычислите все значения переменных х и у, для которых одновременно выполняются равенства
Рх(х,у) = 0 и Ру(х,у) = 0
52. Для функции
С(х, у) = 2х2 -I- 2ху 4- Зу2 — 16х — 18т/ + 54
вычислите все значения переменных хиу, для которых одновременно выполняются равенства
Сх(х,у)=0 и Су(х,у) = 0.
53. Для функции
F(x, у) - х3 — 2х2у2 — 2х — 4у + 10
вычислите все значения переменных хиу, для которых одновременно выполняются равенства
Fx(x,y)=0 и Fy(x,y)=0.
54. Для функции
G(x, у) = х2 In у — Зх — 2у + 1
вычислите все значения переменных хиу, для которых одновременно выполняются равенства
Gx(x,y) = 0 и Gy(x,y)=0.
★ 55. Пусть f(x, у) = Зх2 4- у2 — 4х — Оу + 2
а) Вычислите минимальное значение функции /(х, у) при у = 1.
б) Объясните, почему этот результат не является минимальным значением функции f(x,y).
* 56. Пусть /(х, у) = 5 — 2х + 4у — Зх2 — у2.
а) Вычислите минимальное значение функции /(х, у) при х = 1.
б) Объясните, почему этот результат не является максимальным значением функции f(x,y).
57. Пусть /(х, у) = 4- х4у + Зх?/2 4- у5.
а) Используя графическую утилиту, вычислите такое число с (с точностью до трех десятичных знаков), при котором значение /(с, 2) является максимумом функции f(x,y) при у = 2.
б) Вычислите выражения /х(с, 2) и fy(c, 2).
58. Пусть f(x,y) = ex + 2еу 4- Зх?/2 4-1.
а) Используя графическую утилиту, вычислите такое число d (с точностью до трех десятичных знаков), при котором значение /(1, d) является максимумом функции f(x,y) при х = 1.
б) Вычислите значения fx (1, d) и fy (1, d).


Глава 13. Исчисление многих переменных
565
В задачах 59 и 60 покажите, что указанные функции удовлетворяют уравнению fxx(x,y) + fyy(x, у) = 0.
59. 	f(x, у) = 1п(т2 + у2). 60. f(x, у)=х2 - Зху2.
61. Для функции f(x, у) = х2 + 2у2 вычислите следующие выражения.
lim fr+Лф/М б) 11ю №.» + *)-№,■<
h—>o h fc->o k
62. Для функции f(x, у) = 2xy2 вычислите следующее значение.
а) iim /(Ж + М)-/(*,!/) б) lim f(x,y + k)~ f(x,y)
h—0 h * k—>Q k
Применение математики
Экономика и бизнес
63. Функция прибыли. Предприятие производит два типа калькуляторов: х единиц типа Ану единиц типа В. Недельная прибыль и затраты описываются функциями
Я(х, у) = 80х + 901/ + 0,04x1/ — 0,05х2 — 0,05т/2,
С(х, У) = 8х + 61/ + 20 000.
Вычислите значения Рж(1200,1800) и Ру( 1200,1800) и дайте интерпретацию полученного результата.
64. Реклама и сбыт. Компания тратит х долларов на рекламу в печатных изданиях и у долларов на телевизионную рекламу. Недельный объем продаж компании описывается функцией
S(x,y) = 10x°’4y°’8.
Вычислите значения Sx (3000,2000) и 5^(3000,2000) и объясните полученные результаты.
65. Уравнения спроса. В супермаркете продается два сорта кофе: сорт А по цене р долларов за фунт и сорт В по цене q долларов за фунт. Функции ежедневного спроса для сортов АнВ представлены уравнениями
х = 200 — 5р + 4д,
у = 300 + 2р — 4q.
Вычислите выражения дх/др и ду/др и объясните полученные результаты.
66. Функции дохода и прибыли. Компания производит десяти- и трехскоростные велосипеды. Еженедельный спрос и затраты описываются функциями
р — 230 — 9х +1/,
q = 130 -h х — 41/,
С(х, у) = 200 -I- 80х + 301/,


566
Часть III. Математический анализ
где р — цена десятискоростного велосипеда (в долларах), ад — цена трехскоростного велосипеда, х — ежедневный спрос на десятискоростные велосипеды, у — ежедневный спрос на трехскоростные велосипеды, и С (ж, у) — функция затрат. Вычислите функции Rx (10, Ру (10, 5) и объясните полученные результаты.
67» Производительность. Средняя производительность промышленной отрасти некой страны третьего мира задается функцией
f(x,y) = 10z°’7V’25
при затратах х единиц труда и у единиц капитала.
а) Вычислите функции fx(х, у) и fy(x, у).
б) Пусть в рассматриваемый момент времени промышленная отрасль затрачивает 600 единиц труда и 100 единиц капитала. Вычислите предельную производительность труда и капитала.
в) Какой из показателей нужно поощрять к повышению для достижения большей предельной производительности — затраты труда или капитала?
68. 	Производительность. Производительность предприятия по выпуску автомобилей приближенно описывается функцией:
f (я, у) = 50^/^ = 5Ож0,5?/0’5
при затратах х единиц труда и у единиц капитала.
а) Вычислите функции fx(x, у) и fy(x, у).
б) Пусть в рассматриваемый момент времени предприятиезатрачивает 250 единиц труда и 125 единиц капитала. Вычислите предельную производительность труда и капитала.
в) Какой из показателей следует повысить для достижения большей предельной производительности — затрат труда или капитала?
В задачах 69-72 речь идет о следующем. Если увеличение спроса на один из товаров вызывает понижение спроса на другой, то такие товары называются конкурирующими, или замещающими. (Примером таких продуктов являются лицензионные и “пиратские” диски.) Если же увеличение спроса на один из товаров повышает спрос на другой, то такие товары называются дополняющими. (Примером таких товаров могут служить рыбацкие лодки и моторы к ним.) Чтобы проверить, являются товары конкурирующими или дополняющими, можно использовать частные производные. Рассмотрим функции зависимости спроса от цены для двух товаров.
X = ftp, g)
У = 9<Р, ч)
Функция спроса на товар А
Функция спроса на товар В
Переменные хиу представляют собой объем продажи товаров А и В соответственно при цене р и q. Обычно, если цена товара А растет при неизменной цене товара В, то спрос на товар А падает. Это значит, что fp(p,q) < 0. Далее, если А и В — конкурирующие товары, то спрос на товар В вырастет, т.е. gp(p, q) > 0. Аналогично, если цена товара В растет при неизменной цене товара А, то спрос


Глава 13. Исчисление многих переменных
567
на товар В падает. Это значит, что gq(p,q) < 0. Наконец, если А и В — конкурирующие товары, то спрос на товар А вырастет, т.е. fq(p,q) > 0. Таким образом, мы приходим к следующему критерию, принимая во внимание подобный анализ для дополняющих товаров.
Дополняющие и конкурирующие товары
Частные производные
Товары А и В
Я(РЛ) > 0ирр(р,д) > 0
Я(р, (?) < 0 и gp(p, q) < 0 >Qngp(p,q) ^0 fq(p,Q) ^0идр(р,д) > 0
Конкурирующие Дополняющие Нет определения Нет определения
Используйте обозначенные критерии в задачах 69-72 для определения отношения между указанными товарами (конкурирующие, дополняющие или ни то, ни другое)
69. Спрос на товар. Функции, описывающие недельный спрос на масло и маргарин в супермаркете, имеют следующий вид.
х = f(p> <?) = 8000 — 0,09р2 + 0,08q2 Масло
У = 9(Pi Q) = 15 000 -I- 0,04p2 — 0,3g2 Маргарин
70. Спрос на товар. Функции, описывающие недельный спрос на кофе сортов А и В в супермаркете, имеют следующий вид.
z = /(р, д) = 200 — 5р + 4g Koqpe, сорта А
У = g(p,q) = 300 + 2р — 4g Кофе сорта В
71. Спрос на товар. Функции, описывающие месячный спрос на лыжи и лыжные ботинки в спортивном магазине, имеют следующий вид.
х = /(р5 Q) = 800 — 0,004р2 — 0,003д2 Лыжи
У = &(Р> q) = ООО — 0,003р2 — 0,002#2 Лыжные ботинки
Теннисные ракетки
Теннисные мячи
72. 	Спрос на товар. Функции, описывающие месячный спрос на теннисные ракетки и теннисные мячи в спортивном магазине, имеют следующий вид.
х = Яр, ?) = 500 - 0,5р - q2
У = р(р, <?) = Ю 000 - 8р - 100<?2


568
Часть III. Математический анализ
Биологические науки
73. WWW Медицина, Следующая эмпирическая формула выражает площадь А поверхности тела среднего человека (в квадратных дюймах) через его вес w (в фунтах) и рост h (в дюймах).
А = f(w,h) = 15,64w°’425/i0’725.
Знание площади тела человека может быть полезно при изучении, например, гипотермии (потеря тепла организмом вследствие изменения физических характеристик среды).
а) Вычислите функции fw(w, h) и fh(w,h).
б) Пусть вес ребенка — 65 фунтов, а рост — 57 дюймов. Вычислите значения /w(65,57) и fh(65,57) и объясните полученные результаты.
74. Течение крови. Согласно закону Пуазейля сопротивление R течению крови в сосуде прямо пропорционально от длине сосуда L и обратно пропорционально четвертой степени радиуса сосуда г.
R(L, г) = к\ к — константа
Вычислите значения #ь(4; 0,2) и Rr (4; 0,2) и опишите полученные результаты.
Социальные науки
75. Физическая антропология. При изучении рас и человеческих групп антропологи часто используют черепной индекс С, который прямо пропорционален ширине головы W и обратно пропорционален ее длине L (при изучении сверху). Черепной индекс определяется следующим уравнением.
W C(W,L) = 100—.
т
W — ширина в дюймах
L — длина в дюймах
Вычислите величины Сцл(6, 8) и 6^(6, 8).
Рис. 13.12. Иллюстрация к задаче 75


Глава 13. Исчисление многих переменных
569
76. 	Исследование безопасности. При идеальных условиях длина тормозного пути автомобиля (в футах) описывается формулой:
L(w, v) = kwv2,
где к — константа, w — вес автомобиля в фунтах, v — скорость автомобиля. Вычислите значения Lw (2500,60) и Lv(2500,60) при к = 0,0000133 и опишите полученные результаты.
13.3. 	Максимум и минимум функции
Теперь мы можем перейти к поиску локальных максимумов и минимумов функций вида z = обобщив метод, основанный на использовании производной второго
порядка, для функции одной переменной. Для начала допустим, что производные второго порядка функции f существуют в некоторой круговой области в плоскости ху. Это значит, что поверхность z = f{x}y) не имеет заострений, разрывов и изломов. Иначе говоря, мы будем иметь дело с поверхностями без изломов (рис. 13.13), разрывов (наподобие земных разломов) или точек заострения (наподобие дна ямки для гольфа).
Рис. 13.13. Примеры поверхностей
Кроме того, мы не будем рассматривать предельные точки и описывать теорию абсолютного максимума или минимума. Несмотря на это ограничение, методы, к рассмотрению которых мы сейчас перейдем, могут использоваться при решении широкого спектра задач.
Говорят, что значение /(а, 6) является локальным максимумом, если существует круг в области определения функции / с центром в точке (а, 6), для точек (ж, у), внутри которого выполняется условие:
/(а,Ь) f(x,y)
Аналогично значение /(а, Ь) является локальным минимумом, если существует круг в области определения функции f с центром в точке (а, &), для точек (х,у), внутри которого выполняется условие.
f(x,y)


570
Часть III. Математический анализ
На рис. 13.14, а изображен локальный максимум, на рис. 13.14, б — локальный минимум, а на рис. 13.14, в — седловая точка, которая не является ни локальным максимумом, ни локальным минимумом.
а)
б)
в)
Рис. 13.14. Локальные экстремумы и седловая точка
Чему равны значения /ж(а, 6) и fy(a, 6), если значение /(а, Ь) соответствует локальному максимуму или минимуму при условии, что частные производные существуют в круге с центром в точке (а,Ь) в области определения? Из рис. 13.14 следует, что /х(а,Ь) = 0 и fy(a, Ь) = 0, поскольку касательные прямые к данным кривым являются горизонтальными. Теорема 13.1 гласит, что этот интуитивный вывод — правильный.
Теорема 13.1 (Локальные экстремумы и частные производные). Пусть значение /(а, Ь) является локальным экстремумом (локальным максимумом или локальным минимумом) функции f. Если обе производные fx и fy существуют в точке (а, 6), то
(13.3)
Обратное утверждение неверно. Если /х(а,6) = 0 и Д(а,6) = 0, то значение f(a, b) не обязательно является локальным экстремумом. Например, точка (a,b, f(a,b)) может быть седловой точкой (см. рис. 13.14, в).
Теорема 13.1 дает необходимое (но не достаточное) условие того, что значение функции /(а, Ь) является локальным экстремумом. Поэтому следует сначала найти все точки (а, Ь), которые удовлетворяют уравнениям /х(а, Ь) = 0 и fy(a, b) = 0, а затем проверить, является ли значение /(а, Ь) локальным экстремумом или седловой точкой. Точки (а, 6), для которых выполняются условия (13.3), называются критическими.
Задание 13.5.
1. Пусть f(x,y) = у2 4- 1. Объясните, почему функция f(x,y) имеет локальный минимум в каждой точке на оси х. Убедитесь в том, что каждая точка оси х является критической точкой. Почему график этой функции можно назвать “желобом”?
2. Пусть д(х, у) — х3. Покажите, что каждая точка оси у является критической точкой.
Объясните, почему функция д(х,у) не имеет локальных экстремумов на оси у. Почему график этой функции можно назвать “спускным желобом”? ■


Глава 13. Исчисление многих переменных
571
Достаточные условия того, что данная точка является локальным экстремумом или седловой точкой, определены в приведенной ниже теореме 13.2. Для проверки используются частные производные второго порядка. (Как и теорема 13.1, теорема 13.2 приводится без доказательства.)
Теорема 13.2 (Определение типа экстремума с помощью частных производных). Дано.
1. Функция z = /(х, у).
2. Ь) = 0 и fy(а, 0=0 (точка (а, Ь) является критической).
3. Существуют частные производные второго порядка функции f в некоторой круговой окрестности с центром в точке (а, 0.
4. А = /хх(о, 0, В = fxyfai 0» С = fyy(ci, 0.
Вариант 1. Если АС — В2 > 0 и А < 0, то значение /(а, 0 является локальным максимумом.
Вариант 2. Если АС — В2 > 0 и А > 0, то значение /(а, 0 является локальным минимумом.
Вариант 3. Если АС — В2 < 0, то значение /(а, 0 является седловой точкой.
Вариант 4. Если АС — В2 = 0, то значение /(а, 0 нельзя классифицировать с помощью этого критерия. ■
Для иллюстрации применения теоремы 13.2 найдем локальный экстремум для очень простой функции, для которой решение почти очевидно: z = f(x,y) = х2 4- у2 + 2. Из формы графика этой функции (рис. 13.15) видно, что она имеет локальный минимум в точке (0, 0). Применим теорему 13.2.
Рис. 13.15. Параболоид
Этап 1. Поиск критических точек. Найдем точку (х,1/), для которой одновременно выполняются условия fx(x, у) = 0 и fy(x, у) — 0.
А (я, у) = 2х = о,
х = 0,
fv(x,y) = 2у = 0,
У = 0.


572
Часть III. Математический анализ
Единственной критической точкой является (а, Ь) = (0,0).
Этап 2. Вычислим значения А = /Х1(0,0), В = fxy(0,0) и С ~ fyy^'> 0)*
fxx^i у) — 2, fxy (#) у) 0, /уу(х,У) = 2,
поэтому А = /жх(0,0) = 2.
поэтому В = fxy(0,0) = 0.
поэтому С = fyyffi, 0) = 2.
Этап 3. Вычислим значения АС — В2 и попытаемся классифицировать точку (0,0) согласно теореме 13.2.
АС-В2 = 2-2-О2 = 4>0 и А = 2 > 0.
Итак, выполняется второй вариант, указанный в теореме 13.2. Следовательно, значение /(0,0) = 2 является локальным минимумом.
Теперь рассмотрим, как с помощью теоремы 13.2 можно найти экстремумы функций, не рисуя их графики.
Пример 13.13 (Поиск локальных экстремумов). Воспользуйтесь теоремой 13.2 и найдите локальные экстремумы функции
/(х, у) = -х2 - у2 + 6я + 8г/ - 21.
Решение.
Этап 1. Поиск критических точек. Найдем точку (гг, ?/), для которой одновременно выполняются условия fx(x, у) = 0 и fy(x, у) = 0.
fx(x, у) = —2х + 6 = 0, fy(x, у) = —2у + 8 = 0,
х = 3, у = 4.
Единственной критической точкой является (а, Ь) = (3,4).
Этап 2. Вычислим значения А = fxx(3,4), В = /Ж2/(3,4) и С = fyy & 4).
fxx (х> у) — —2, fxy(x, у) = 0, fyy(x> у) — —2,
поэтому А — /хх(3,4) = —2. поэтому В = /Х2/(3,4) = 0.
поэтому С — fyy(3,4) = -2.
Этап 3. Вычислим значение АС — В2 и попытаемся классифицировать точку (3,4) согласно теореме 13.2.
АС -В2 = -2 • (-2) — О2 = 4 > 0 и А = —2 < 0.
Итак, выполняется первый вариант, указанный в теореме 13.2. Следовательно, значение /(3,4) =4 является локальным максимумом. ■
Упражнение 13.13.
Воспользуйтесь теоремой 13.2 и найдите локальные экстремумы функции
/(х, у) = X2 + у2 - 10х - 2у + 36.


Глава 13. Исчисление многих переменных
573
Пример 13.14 (Функция, имеющая несколько критических точек). Воспользуйтесь теоремой 13.2 и найдите локальные экстремумы функции
f(x,y) = х3 + у3 - бху.
Решение.
Этап 1. Найдем критические точки функции /(ж, у) = х3 + у3 — бху.
fx(z,y) = Зх2 - бу = О, бу = Зх2,
1 2
у = -X ,
* 2
!у(х,у) = Зу2 - 6х = О, Зту2 = 6х,
3 G*2)= ба:’
~х4 = 6х,
4
Зх4 - 24х = О,
Зх(х3 — 8) = О,
х = 0 или х = 2,
У = 0 или у=^-22 = 2.
Решаем уравнение относительно переменной у
(13.4)
Используем уравнение (13.4) для исключения переменной у
Решаем уравнение относительно переменной х
Критическими являются точки (0,0) и (2,2).
Поскольку у функции есть две критические точки, то вычисления этапа 2 и 3 придется выполнять дважды.
Точка (О, 0)
Этап 2. Вычисляем значения А = fxx(Q, 0), В = fxy(fi, 0) и С = fyy(fi, 0).
fxx У} — 6х,
поэтому
А = /то(0,0) = 0.
fxy(x> У) — —6,
поэтому
в = fxy (0,0) = -1
fyyfay) = 61/,
поэтому
С =/„„(0,0) = 0.
Этап 3. Вычисляем значения АС — В2 и пытаемся классифицировать точку (0,0) согласно теореме 13.2.
АС - В2 = 0 • 0 - (-6)2 = -36 < 0.
Иначе говоря, выполняется третий вариант, указанный в теореме 13.2. Это значит, что точка (0,0) является седловой точкой функции f.
Теперь рассмотрим вторую критическую точку (2,2).


574
Часть III. Математический анализ
Точка (2, 2)
Этап 2. Вычислим значения А = fxx(2,2), В = fxy(2,2) и С = fyy(2,2).
fxx(x,y)
= бх,
поэтому
А =
/^(2,2) = 12.
fxy(x, у)
= -6,
поэтому
В =
/1у(2,2) = —6.
fyy(x, У)
= бу,
поэтому
С =
/уу(2,2) = 12.
Этап 3. Вычислим значение АС — В2 и попытаемся классифицировать точку (0,0) согласно теореме 13.2.
АС-В2 = 12- 12- (-6)2 = 108 > 0 и А = 12 > 0
Иначе говоря, выполняется второй вариант, указанный в теореме 13.2. Таким образом, значение /(2,2) = —8 является локальным минимумом. ■
Выводы, полученные в примере 13.14, можно проверить графически, построив сечения поверхности функции /. Сечения плоскостями у = 0, х = 0, у = х и у = — х (все плоскости проходят через начало координат (0,0)) являются графиками функций /(х,0) = ж3, /(0,?/) = ?/3, f(x,x) = 2х3 — бх2 и /(х, — х) = бх2 соответственно, как показано на рис. 13.16, а (заметим, что первые две функции имеют одинаковые графики). Сечения плоскостями у = 2, х = 2, у = хиу = 4 — х (все плоскости проходят через точку (2, 2)) являются графиками функций /(х, 2) = х3 — 12х + 8, /(2, у} = у3 — 12у + 8, /(х, х) = 2х3 — бх2 и /(х, 4 — х) = х3 + (4 — х)3 + бх2 — 24х соответственно, как показано на рис. 13.16, б (первые две функции имеют одинаковые графики). Последний рисунок иллюстрирует тот факт, что если функция f имеет локальный минимум в точке (2,2), то каждое ее сечение плоскостью, проходящей через точку (2,2), также будет иметь локальный минимум со значением —8 в точке (2,2). С другой стороны, на рис. 13.16, а одна часть сечений имеет локальный максимум в точке (0,0), другая — локальный минимум, а некоторые сечения не имеют ни того, ни другого.
Рис. 13.16. Применение графической утилиты
10
fl 1
Х=2
V=-b
10
б) — 12х+ 8
у2 = 2х3-6х2
у3 = х2 + (4 —х)3 4- бх2 —24х
Упражнение 13.14.
Воспользуйтесь теоремой 13.2 и найдите локальные экстремумы функции f(x,y) = х3 + у2 - бху.


Глава 13. Исчисление многих переменных
575
Задание 13.6.
Пусть /(х, у) = х4 + у2 + 3, д(х, у) = 10 - х2 - у4 и h(x, у) = х3 + у2.
1. Покажите, что единственной критической точкой каждой из функций является точка (0,0).
2. Объясните, почему функция /(х, у) имеет локальный минимум в точке (0,0), функция р(х,т/) имеет локальный максимум в точке (0,0), а функция h(x,y) не имеет ни того, ни другого в этой точке.
3. Согласуются ли результаты с теоремой 13.2? Аргументируйте ответ. ■
Пример 13.15 (Прибыль). Пусть функция годовой прибыли компании, изготавливающей доски для серфинга, имеет вид
Р(х, у) = -22х2 + 22ху - II?/2 + 110х - 44?/ - 23,
где х — годовой объем производства обычных досок (тыс. шт.), у — годовой объем производства спортивных досок (тыс. шт.), а Р — прибыль (тыс. долл.). Сколько нужно производить досок каждого вида, чтобы получить максимальную прибыль? Чему будет равна эта прибыль?
Решение.
Этап 1. Найдем критические точки.
Рх(х, у) = —44х + 22у + 110 = 0,
Р3/(х, у) = 22х — 22у — 44 = 0.
Решив эту систему, выясним, что единственной критической точкой является точка (3,1).
Этап 2. Вычислим значения А = РЖ1(3,1), В = Рху(Ъ, 1) и С = Руу& 1).
Ргх(^?2/) = —44,
РтУ(х, У) = 22,
Руу(х>У) = —22,
поэтому поэтому поэтому
А = Рхх(3,1) = —44.
В = Рху(3,1) = 22.
С = Pw(3,l) = -22.
Этап 3. Вычислим значение АС — В2 и попытаемся классифицировать точку (3,1) согласно теореме 13.2.
АС - В2 = -44 • (-22) - 222 = 484 > 0 и А= -44 < 0.
Иначе говоря, выполняется первый вариант, указанный в теореме 13.2. Следовательно, значение Р(3,1) = 120 является локальным минимумом. Максимальная прибыль, равная 120 000 долл., получается при ежегодном производстве 3000 стандартных досок и 1000 спортивных. ■
Упражнение 13.15.
Повторите решение примера 13.15 для функции
Р(х, у) = —66х2 + 132х?/ — 99?/2 -И 132х — 66?/ — 19.


576
Часть III. Математический анализ
Пример 13.16 (Дизайн упаковки). Отделу доставки компании требуется разработать прямоугольную упаковку без верха, разделенную посередине. Объем коробки должен составлять 48 кубических дюймов. Вычислите размеры коробки, на изготовление которой расходуется минимальное количество материала.
Рис. 13.17. Коробка
Решение. Рассмотрим рис. 13.17. Количество материала, необходимое для производства коробки, задается следующей формулой.
Передняя и Основание задняя стенки
М = ху + 2xz
Боковые стенки и перегородка
+ 3yz
(13.5)
Объем коробки равен следующей величине.
V — xyz — 48.
(13.6)
Поскольку теорема 13.2 выполняется только для функций двух независимых переменных, следует использовать уравнение (13.5) для исключения одной из переменных в уравнении (13.6).
М = ху + 2xz + 3yz —
Подстановка z = 48/ху
96 144
= ху -\ 1 .
у X
Таким образом, задача сводится к поиску минимального значения функции
х > 0 и у > 0.


Глава 13. Исчисление многих переменных
577
Этап 1. Найдем критические точки.
144
Мх(х,у) = у г =0,
144
У = xz
96 Му(х,у) =х- = 0,
У
96 X = -о,
У2
96
х ’
96
х ’
96
X
20736 —— = 216, 96
х = 6,
144 ,
у = = 4.
У 36
У2 =
20 736 _ х4
х3 =
(13.7)
Решим уравнение относительно у2
Используем уравнение (13.7) для исключения переменной у и решения относительно переменной х
Умножаем обе части равенства на а?4/96 (напомним, что ж > О)
Для поиска переменной у используем формулу (13.7).
Итак, единственной критической точкой является (6,4).
Этап 2. Вычислим значения А — МХХ(Ъ, 4), В = Мху(б, 4) С = Муу(6,4).
Мхх(х,у) = — ,
Мху^Х, у) = 1,
\ 192
Муу(х,у) = —,
поэтому
поэтому
поэтому
OQQ
А = Мех(6,4) = ^|
4
3‘
В = Мху(6,4) = 1-
С - Мга(6,4) = ~ = 3.
Этап 3. Вычислим значение АС — В2 и попытаемся классифицировать точку (6,4) согласно теореме 13.2.
АС - В2 = ^ • 3 - I2 = 3 > 0 и а = — > 0. о и
Иначе говоря, выполняется второй вариант, указанный в теореме 13.2. Это значит, что у функции М(ж, у) есть локальный минимум в точке (6,4). Если х = 6, а у = 4, то
~ _ 48 _ 48 _ 2
ху 6-4
Таким образом, затраты материала будут минимальны, если размеры коробки составляют 6x4x2 дюймов. в
Упражнение 13.16.
Вычислите размеры коробки из примера 13.16, при которых расход материала будут минимальными, а объем равен 384 куб. дюйма. ■


578
Часть III. Математический анализ
Ответы к упражнениям
13.13. Значение /(5,1) = 10 является локальным минимумом.
13.14. Функция f имеет седловую точку (0,0). Значение /(8,18) = —108 является локальным минимумом.
13.15. Локальный минимум достигается при значениях х = 2 и у = 1; Р(2,1) = 80. Максимальная прибыль в 80 000 долларов получается при производстве 2000 стандартных досок и 1000 спортивных.
13.16. 12 х 8 х 4 дюймов.
Практикум 13.3
А В задачах 1-4 вычислите производные fx(x, у) и fy(x, у) и объясните, руководствуясь теоремой 13.1, почему функция f(x,y) не имеет локальных экстремумов.
* 1. f(x, у) = 4х + 5у — 6.
* 2. f(x, у) = 10 — 2х — Зу + х2.
* 3. f(x, у) = 3,7 - 1,2х + 6,8?/ + 0,2г/3 + х4.
* 4. f(x, у) = х3 - у2 + 7х + Зу + 1.
В задачах 5-24 найдите локальные экстремумы функций с помощью теоремы 13.2.
5. f(x, у) = б-х2 - 4х- у2. 6. f(x, у) = 3 - х2 - у2 + бу.
7. f(x, у) = х2 + у2 +2х - бу + 14. 8. f(x, у) = х2 + у2 - 4х + бу + 23.
Б
9. 	f(x, У) = ху + 2х — Зу — 2.
10. f(x, у) = х2 — у2 + 2х + бу — 4.
11. f(x, у) = —Зх2 + 2ху — 2у2 + 14т + 2у + 10.
12. f(yc, у) = —х2 + ху - 2у2 + х + Юу - 5.
13. f(x, у) = 2х2 — 2ху + Зу2 — 4х — 8у + 20.
14. f(x, у) = 2х2 - ху + у2 - х - бу + 8.
15. f(x,y)=exy.
17. f(x, у) = х3 + у3 - Зху.
19. f(x, у) = 2х4 + у2 - 12ху.
21. f(x,y) = х3 - Зху2 + бу2.
23. f(x, у) =у3 + 2х2у2 - Зх - 2у + 8.
24. /(я, у) = х In у + х2 — 4х — бу + 3.
* 25. Объясните, почему функция f(x, у) ных экстремумов.
16. f(x,y) = х2у - ху2.
18. /(х, у) = 2у3 - бху - х2.
20. f(x,y) = Збху - х4  * * 7 * 9 10 11 12 13 14 15 - 2у2.
22. f(x, у) = 2х2 — 2х2у + 6?/3.
х2 имеет бесконечное количество локаль-


Глава 13. Исчисление многих переменных
579
* 26. а) Найдите локальные экстремумы функций /(х, у) = х + у, д(х, у) = х2 + у2 и h(x,y) = ж3 + у3.
б) Какие локальные экстремумы имеет функция /(х, у) = хп + уп, где п — положительное целое число?
27. а) Покажите, что точка (0,0) является критической точкой для функции
/(х, у) = и4е2/Ч-х2?/4-Ы, однако исследовать ее характер с помощью частных производных второго порядка нельзя.
б) Применяя сечения (как в примере 13.14), определите характер критической точки (0,0) функции f (локальный максимум, минимум или седловая точка)?
28. а) Покажите, что точка (0,0) является критической для функции д(х,у) =
= еху 4- х2у3 -I- 2, однако исследовать ее характер с помощью частных производных второго порядка нельзя.
б) Применяя сечения (как в примере 13.14), определите характер критической точки (0,0) функции д (локальный максимум, минимум или седловая точка)?
Применение математики
Экономика и бизнес
29. Максимальная прибыль для ассортимента товаров. Предприятие ежегодно производит два типа калькуляторов: х тыс. шт. модели А и у тыс. шт. модели В. Функции годовых доходов и затрат (млн. долл.) имеют следующий вид.
R(x,y) = 2х 4- Зр,
С(ж, у) = х2 — 2ху 4- 2у2 4- 6# — 9у 4- 5.
Определите, сколько калькуляторов каждой модели нужно производить для получения максимальной прибыли. Чему равна максимальная прибыль?
30. Уменьшение расходов за счет автоматизации. Ежегодные затраты на оплату труда и обслуживание автоматических производственных линий описываются следующей функцией.
С(х, у) = 2х2 4- 2ху 4- Зр2 — 16# — 181/ 4- 54.
Здесь переменная х соответствует ежегодным затратам на оплату труда, а переменная у — затратам на обслуживания автоматических линий (обе величины измеряются миллионами долларов). Определите, сколько следует расходовать на каждый пункт сметы для минимизации общих затрат. Каким будет минимальный уровень таких затрат?
31. Увеличение прибыли. В магазине продаются две модели недорогих калькуляторов. Магазин платит 6 долл, за модель А и 8 долл, за модель В. В отделе маркетинга были определены следующие функции еженедельного спроса для двух конкурирующих товаров.
х = 116 — ЗОр + 20д, Уравнение спроса для модели А
у = 144 4- 16р — 24q, Уравнение спроса для модели В


580
Часть III. Математический анализ
где р — отпускная цена модели A, q — модели В.
а) Определите спрос на каждую из моделей, если р = 10 долл., a q = 12 долл. Выполните то же задание для р = 11 долл, и q = 11 долл.
б) Какова должна быть отпускная цена калькулятора каждой модели для достижения максимальной еженедельной прибыли? Чему равна максимальная еженедельная прибыль? (Подсказка'. С = бх + Sy, R = рх + qy, Р = R - С.)
32. Увеличение прибыли. В магазине продаются два типа фотопленки. Магазин платит 2 долл, за пленку типа А и 3 долл, за пленку типа В. В отделе маркетинга были определены следующие дневные функции спроса для двух конкурирующих товаров.
х = 75 — 40р + 25д, Уравнение спроса для пленки типа А у = 80 + 20р — 30q, Уравнение спроса для пленки типа В
где р — отпускная цена пленки типа A, q — пленки типа В.
а) Найдите спрос на каждую из пленок, если р = 4 долл., a q — 5 долл. Выполните то же задание для р = 4 долл, и q = 4 долл.
б) Какова должна быть цена пленки каждого типа для достижения максимальной ежедневной прибыли? Чему равна максимальная ежедневная прибыль? (Подсказка'. С = 2х + Зу, R = рх + qy, Р = R — С.)
33. WWW Минимизация расходов. Станция приема сигнала спутникового телевидения расположена в точке Р(х,у) так, что сумма расстояний от нее до городов А, В и С — минимальна (рис. 13.18). Найдите координаты точки Р, при которых расходы на обустройство сети кабельного телевидения в трех городах будут минимальны.
34. Минимизация расходов. Повторите решение задачи 33, заменив координаты точки В на В(6,9) и точки С на С(9,0).
35. Минимальные затраты материала. Прямоугольная коробка без верха с двумя параллельными отделениями (рис. 13.19) должна иметь объем, равный 64 кубическим дюймам. Определите размеры коробки, при которых на ее изготовление уходит минимальное количество материала.


Глава 13. Исчисление многих переменных
581
Рис. 13.19. Иллюстрация к задаче 35
36. 	Минимальные затраты материала. Прямоугольная коробка без верха с двумя пересекающимися перегородками (рис. 13.20) должна иметь объем, равный 72 кубическим дюймам. Определите размеры коробки, при которых на ее изготовление уходит минимальное количество материала.
Рис. 13.20. Иллюстрация к задаче 36
37. 	Максимальный объем. Службой доставки выдвинуто требование, что суммарная длина и обхват прямоугольной упаковки не должны превышать 120 дюймов (рис. 13.21). При каких соответствующих ограничениям размерах пакета объем коробки будет максимальным?
Рис. 13.21. Иллюстрация к задаче 37
38. 	Максимальный объем. При перевозке коробку с грузом укрепляют в трех направлениях, как показано на рис. 13.22. На это выделяется 150 дюймов металлизиро-


582
Часть III. Математический анализ
Рис. 13.22. Иллюстрация к задаче 38
ванной ленты с возможным превышением на 6 дюймов из-за наложения ленты при креплении по 2 дюйма в каждом направлении. Определите максимальный объем коробки, которую можно укрепить указанным способом.
13.4. 	Поиск максимумов и минимумов
методом множителей Лагранжа
■ Функции двух независимых переменных
■ Функции трех независимых переменных
Функции двух независимых переменных
Рассмотрим чрезвычайно эффективный метод решения отдельного класса задач поиска максимумов и минимумов. Этот метод был разработан Жозефом Луисом Лагранжем (Joseph Louis Lagrange) (1736-1813), выдающимся французским математиком восемнадцатого века. В честь автора метод назван методом множителей Лагранжа. Сначала мы рассмотрим суть этого метода на простом примере, а затем изложим общую суть метода в форме теоремы.
Фермер намерен построить два загона для скота одинаковой площади вдоль уже существующего забора (рис. 13.23), располагая 720 футами материала для строительства забора. Какими должны быть длины х и у для заграждения максимально возможной площади? Чему при этом будет равна максимальная площадь?
Рис. 13.23. Загон для скота


Глава 13. Исчисление многих переменных
583
Общая площадь задается следующим уравнением.
f(x,y) = ху.
Если значения х и у ни чем не ограничены, эта величина может принимать сколь угодно большое значение. Однако в данном случае количество материалов для строительства забора ограничено 720 футами. Поэтому значения хиу нужно выбрать согласно уравнению
Зх + у = 720.
Это ограничение приводит к следующей задаче поиска максимума и минимума.
Найти максимум функции f(x,y)=xy (13.8)
при условии Зх + у = 720 или Зх + у — 720 = 0. (13.9)
Это частный случай общей формулировки класса задач следующего вида.
Найти максимум (или минимум) функции z = f(x, у) (13.10)
при условии д(хчУ) = 0. (13.11)
Конечно, можно попробовать выразить с помощью уравнения (13.11) переменную у через переменную х (или наоборот, х через у) и подставить в уравнение (13.10). Тогда задача будет сведена к поиску экстремума функции одной переменной и может быть решена методами, описанными в разделе 9.4. Однако, если уравнение (13.11) окажется сложнее уравнения (13.9) и его решение относительно одной из переменных очень сложно или невозможно вообще, этот подход не работает. Метод множителей Лагранжа применяется к функции д(х,у) непосредственно, не требуя решения уравнения (13.11) относительно одной из переменных. Более того, этот метод легко использовать для произвольного количества переменных, которые могут удовлетворять более, чем одному ограничению.
Итак, опишем общий метод. С помощью функций /иди уравнений (13.10) и (13.11) составим новую функцию F.
F(x,y,X) = f(x,y) + Хд(х,у). (13.12)
Здесь А (маленькая греческая буква “лямбда”) называется множителем Лагранжа. Суть метода изложена в теореме 13.3.
Теорема 13.3 (Метод множителей Лагранжа для функции двух переменных). Каждый локальный максимум или минимум функции z = /(ж, у), удовлетворяющий условию д(х, у) = 0, является точкой (хо, ув), для которой тройка чисел (хо, уо, А) будет решением системы уравнений
Fx^x, Уч А) 0,
Уч =
Fx(x,y, А) = 0,
где F(x,y, А) = f(x,y) + Хд(х,у) — функция, для которой существуют частные производные первого порядка. ■


584
Часть III. Математический анализ
Решим задачу, связанную с проектированием загона для скота, методом множителей Лагранжа.
Этап 1. Сформулируем задачу в виде уравнений (13.10) и (13.11).
Найти максимум функции /(х, у) = ху
при условии д(х, у) = Зх + у — 720 = 0.
Этап 2. Построим функцию F, вводя множитель Лагранжа А:
F(x, у, А) = f(x, у) + Хд(х, у) = ху + А(3х + у - 720).
Этап 3. Найдем решение системы Fx = 0, Fy = 0, F\ = 0. (Решения называются критическими точками функции F.)
Fx — У И- ЗА — 0,
Fv — х А — 0, F\ = Зх + у — 720 = 0.
По первым двум уравнениям
У - -ЗА,
х = —А.
Подстановка найденных выражений для у и х в третье уравнение и вычисление значения А дает следующий результат.
-ЗА - ЗА = 720,
-6А = 720,
А = —120.
Таким образом,
у = -3 • (-120) = 360 футов,
х = —(—120) = 120 футов.
Следовательно, единственной критической точкой функции F является точка (^о,2/о,Ао) = (120,360,-120).
Этап 4. Согласно теореме 13.3, если функция f(x,y) имеет локальный максимум или минимум, удовлетворяющий дополнительному условию д(х, у) = 0, он расположен в точке х = 120 ну = 360. Вид экстремума можно исследовать с помощью процедуры, приведенной в теореме 13.2 из раздела 13.3, однако мы этого делать не будем. (Заметим, что теорему 13.2 нельзя применить непосредственно к функции /(ж, у) в точке (120,360), поскольку эта точка не является критической для функции f(x,y) без учета ограничений.) В данном случае мы просто констатируем, что максимум функции f(x,y) достигается в точке с координатами х — 120 и у = 360. Следовательно,
шах/(я,?/) = /(120,360) = 120 • 360 = 43 200 кв. футов.


Глава 13. Исчисление многих переменных
585
Ниже перечислены ключевые вычислительные этапы метода множителей Лагранжа.
Метод множителей Лагранжа
Этап 1. Формулируем задачу в следующем виде.
Найти максимум (или минимум) функции z — f(x, у)
с учетом ограничения д(х, у) = О
Этап 2. Строим функцию F.
F(x, у, А) = f(x, у) + Хд(х, у).
Этап 3. Вычисляем критические точки функции F, т.е. решаем систему уравнений
Fx(x,y, Л) = О, -^/(•^5 У) ^) О, F\(x,y, А) = 0.
Этап 4. Если единственной критической точкой функции F является точка (я0, Уо, Ао), будем считать, что точка (а?о, т/о) соответствует решению рассматриваемой задачи. Если у функции F имеется несколько критических точек, следует вычислить значение функции z = f(x,y) для (а?о, З/о) в каждой критической точке (^о? З/о, Ао) функции F. В рассматриваемом нами классе задач наибольшее из этих значений является максимумом функции f(x,y) с учетом ограничения д(х,у), а наименьшее — минимумом функции f(x,y) с учетом ограничения 9&,у).
Пример 13.17 (Минимум функции с учетом ограничений). Найдите минимум функции /(ж, у) = х2 + у2 при ограничении х + у = 10.
Решение.
Этап 1. Найти максимум функции f(x,y) = х2 + у2
при условии <7 (я, у) = х 4- у — 10 = 0.
Этап 2. F(z, 2/, А) = х2 + у2 4- Х(х + у - 10).
Этап 3. Fx = 2х 4- А = 0,
Fy = 2у 4- А = 0,
Fx = х 4- у - Ю = 0.
Из первых двух уравнений следует, что х = —А/2иу = —А/2. Подставляя эти результаты в третье уравнение, получаем
_1д _ = Ю,
2 2
-А = 10,
А = -10.


586
Часть III. Математический анализ
Таким образом, единственной критической точкой является точка (хо, уо, Ао) = = (5,5,-10).
Этап 4. Поскольку (5,5, —10) является единственной критической точкой функции F, то (этап 4 в нашей процедуре)
min/(a:, у) =/(5,5) = 52 + 52 = 50. и
Поскольку функция д(х,у) из примера 13.17 довольно проста, метод поиска условного экстремума, альтернативный методу множителей Лагранжа, заключается в решении уравнения д(х,у) = 0 относительно переменной у. После подстановки его в функцию f(x,y) получим функцию h(x) = f(x, 10 — х) = х2 + (10 — х)2, которая зависит только от одной переменной х. Далее ищем минимум функции h(x). Получаем min/(x,t/) = f(5,5) = 50. Успех этого подхода зависит от возможности найти решение уравнения относительно одной из переменных, поэтому он не всегда бывает успешным.
Рис. 13.24. График функ¬
ции h(x) = х2 + (10 — х)2
Упражнение 13.17.
Найдите максимум функции /(х, у) = 25 — х2 — у2 при ограничении х + у = 4. ■
На рис. 13.25 и 13.26 показаны результаты, полученные при решении примера 13.17 и упражнения 13.17 соответственно.
Задание 13.7.
Рассмотрите задачу о поиске минимума функции /(х,?/) = Зх2 + 5у2 при ограничении д(х,у) = 2х + Зг/-6 = 0.
1. Вычислите значения функции f(x,y) для целых значений переменных х и у в интервалах О^ж^ЗиО^^З. Отметьте результаты вычислений на рис. 13.27 для указанных точек (х,у).
2. Постройте график функции связи д(х, у) — 0.
3. Определите приблизительно положение минимума функции f на основе вычислений, выполненных в п. 1.
4. Найдите условный минимум функции f методом множителей Лагранжа. ■


Глава 13. Исчисление многих переменных
587
Рис. 13.25. Поверхность f(x,y) = х2 + у2 и плоскость д(х, у) = х + у — 10 = 0
Рис. 13.26. Поверхность /(ж, у) = 25 - х2 - у2 и плоскость д(х, у) = х + у — 4 = 0
у
2и О О дз
О О да
ppg.
0 1 2 3
Рис. 13.27. Результаты вычислений
Пример 13.18 (Производительность). Производственная функция Кобба-Дугласа для нового вида продукции задается формулой
N(x,y) = 16х°'25у°'75,


588
Часть III. Математический анализ
где х — объем труда, у — объем капитала, затраченных на выпуск 7V(z, ?/) единиц продукции. Затраты на единицу труда равны 50 долл., а на единицу капитала — 100 долл. Допустим, что производственный бюджет равен 500 000 долл. При каких объемах капитала и труда будет достигнут максимальный объем производства? Каков максимальный объем производства?
Решение. Затраты на х единиц труда и у единиц капитала равны 50ж+100?/. Ограничение производственного бюджета суммой в 500 000 долл, соответствует уравнению
50ж + 100?/ = 500 000.
Этап 1. Найти максимум функции N(x,y) = 16z0,25?/0’75
при условии д(х, у) = 50х + 100?/ - 500 000 = 0.
Этап 2. F(x, у, А) = 16ж0’25?/0’75 + А(50х + 100?/ - 500 000).
Этап 3. Fx = 4z“°’7V’75 + 50А = 0,
Fy = 12z°’2V0’25 + 100А = 0,
Fa = 50х + 100?/ - 500000 = 0.
Из первых двух уравнений получим следующий результат.
Л = _ 2^0,75 °,75 и Л=3 0,25 -0,25
25 25 у
Следовательно,
Лж-0,75 0,75 = _ 1^0,25 -0,25
25 У 25 У
2 3
25 V 25
3 у = -х
У 2
Умножим обе части равенства на ®°’7V’26
(Будем считать, что х # О И у # о)
Подставляя найденное выражение для переменной у в третье уравнение и решая относительно х, получаем следующее.
50я + 100 • |х- 500000 = 0,
200а; = 500000, х = 2500.
Поэтому
у = | • 2500 = 3750
и
А = -F 25OO-0,75 • 375O0,75 « -0,1084.
25
Единственной -0,1084).
критической точкой функции F является точка (2500,3750.


Глава 13. Исчисление многих переменных
589
Этап 4. Поскольку функция F имеет только одну критическую точку, максимум производительности достигается при затратах 2500 единиц труда и 3750 единиц капитала (см. этап 4 в методе множителей Лагранжа). Итак,
тах^х.у) = 2V(2500,3750) = 16 • 2500°’253750°’75 « 54 216. в
На этапе 3 было найдено отрицательное значение множителя Лагранжа. Этот эффект называется предельной производительностью денег и приблизительно соответствует увеличению объема производства для каждого дополнительно затраченного доллара. В примере 13.18 увеличение бюджета с 500000 до 600000 долл, приведет к увеличению объема производства приблизительно на
0,1084 • 100000 = 10840 единиц.
Заметим, что если перед построением функции F(x, у. А) привести ограничение
50# + 1001/ — 500 000 = 0
к виду
х + 2у — 10 000 = 0,
то корректно интерпретировать значение - А уже нельзя. Поэтому в задачах о предельной производительности упрощать уравнение связи не стоит.
Упражнение 13.18.
Производственная функция Кобба-Дугласа для нового вида продукции задается формулой
N(x,y) = 2Ох°’5у0’5,
где х — объем труда, у — объем капитала, затраченных на выпуск N(x,y) единиц продукции. Затраты на единицу труда составляют 40 долл., а на единицу капитала — 120 долл.
1. Пусть производственный бюджет равен 300 000 долл. При каких объемах капитала и труда будет произведено максимальное количество продукции? Каким будет максимальный объем производства?
2. Найдите предельную производительность денег в этом случае и приблизитель¬
но оцените повышение объема производства при увеличении бюджета до 40 000 долл. ■
Задание 13.8.
Рассмотрите задачу о минимуме функции f(x,y) = 4 - х2 — у2, учитывая ограничения д(х,у) = у~х2 + 1 = 0.
1. Вычислите значения функции f(x,y) = 3, если точка (х, у) лежит на окружности единичного радиуса с центром в начале координат. Какое значение будет принимать функция f(x, у), если точка (х, у) лежит на окружности, радиус которой равен 2, с центром в начале координат? Ответьте на тот же вопрос, если радиус равен трем (рис. 13.28).
2. Объясните, почему некоторые точки параболы у — х2 4-1 = 0 лежат внутри окружности х2 4- у2 = 1.


590
Часть III. Математический анализ
3. Можно ли утверждать, руководствуясь выводом, сделанным в п. 2, что условный максимум функции f(x,y) больше трех? Аргументируйте ответ.
4. Найдите условный максимум функции /(ж, у) методом множителей Лагранжа. ■
Функции трех независимых переменных
Выше отмечалось, что метод множителей Лагранжа также применим и для функций, которые зависят от произвольного количества переменных с любым количеством ограничений. Ниже приводится теорема о способе применения метода множителей Лагранжа для функции трех переменных с одним ограничением. Далее рассматривается пример, демонстрирующий преимущество этого метода по сравнению с методом, использованным в разделе 13.3.
Теорема 13.4 (Метод множителей Лагранжа для функции трех переменных). Каждый локальный максимум или минимум функции w = f(x, ?/, z), удовлетворяющий ограничению д(х, у, z) = 0, является точкой (жо, уо, го), для которой четверка (а?о, Уо, го, А) служит решением системы
Fx(x,y,z, А) = 0,
Fy(x,y,z, А) = 0, Fz(x,y,z, А) = 0, Fx(x,y,z, А) = 0,
где для функции F(x, у, z, А) = /(х, у, z) + А#(х, т/, z) существуют все необходимые частные производные. ■
Пример 13.19 (Дизайн упаковок). Прямоугольная коробка без верха с двумя отделениями должна быть собрана с использованием 162 квадратных футов картона (рис. 13.22). При каких размерах коробки ее объем будем максимально возможным?
Решение. Задача сводится к поиску максимума функции
V(x,y,z) = xyz


Глава 13. Исчисление многих переменных
591
Рис. 13.29. Упаковочная коробка
при условии, что общее количество материала, необходимое для изготовления коробки, равно 162 кв. дюйма. Следовательно, переменные х, у, и z должны удовлетворять уравнению
ху -F 2xz 4- ^yz = 162.
Этап 1. Найти максимум функции V(x, у, z) = xyz
при условии <7(т, у, z) = ху + 2xz + 3yz — 162 = 0.
Этап 2. F(x, 1/, г, Л) = xyz + Х(ху + 2xz + 3yz — 162).
ЭтапЗ. Fx = yz 4- Х(у + 2z) = 0,
Fy = xz 4- Л(х -h 3z) = 0,
Fz = xy 4- A(2x 4- 3?/) = 0,
F\ = xy 4- 2xz + 3yz — 162 = 0.
Из первых двух уравнений получаем следующие результаты.
у 4- 2z х + 3z
Исключая переменную Л, приходим к следующему выводу.
—yz —xz
у + 2z х 4- Зг ’
—xyz — 3yz2 — —xyz — 2xz2]
3yz2 = 2xz2; Будем считать, что z / О
Зх — 2х;
3
X — -v.
2У
Из второго и третьего уравнений получаем следующие результаты.
л ~xz х ~xz
х 4- 3z ’ 2х 4- Зу


592
Часть III. Математический анализ
Исключая переменную Л, приходим к следующим уравнениям.
—XZ —ху
у + 3z 2х 4- 3z ’
—2x2z — 3xyz = —х2у — 3xyz\
2x2z = x2y; Будем считать, что х О
2z = у;
1
Z=2y-
Подставляя х = и z = в четвертое уравнение, получим следующий результат.
|г/ • У + 2 • |у • ~у + Зу • - 162 = 0;
3 , 3 2 3 2
2У + 2У + 2У = 162;
У2 = 36;
Будем считать, что у > 0
У = 6;
а: = | - 6 = 9;
Используем х = ^у
z = - • 6 = 3.
2
Используем z = ^у
Итак,
— 6 • 3 3 —yz
Л = ~“ = — -• Используем А =
6 + 2-3 2 7 l/ + 2z
Поэтому единственной критической точкой, для которой значения переменных х, у и z являются положительными числами, оказывается четверка (9, 6, 3, —
Этап 4. Коробка с максимальным объемом имеет размеры 9x6x3 дюймов. ■
Упражнение 13.19.
Коробка, описанная в примере 13.19, должна быть собрана из 288 кв. дюймов картона. Найдите размеры коробки, при которых ее объем будет максимальным. ■
Допустим, нам нужно решить пример 13.19 методом, изложенным в разделе 13.3. Для начала нужно выразить из уравнения ограничений одну переменную, скажем, перемен-
ную 2, через другие.
162 — ху
2х + Зу
Переменную z можно исключить из функции объема и свести задачу к поиску максимума
функции
тл/ \ 162 _ ХУ
Vfc») = xs2i + 3s.
Метод множителей Лагранжа позволяет избежать вычисления громоздких производных функции V.


Глава 13. Исчисление многих переменных
593
Ответы к упражнениям
13.17. Max f(x, у) = /(2,2) = 17 (рис. 13.26).
13.18. 1) 3750 единиц труда и 1250 единиц капитала; max7V(x,?/) = 7V(3750,1250) «
« 43 301 единиц.
2) Предельная производительность денег « 0,1443; увеличение объема производства « 5774 единиц.
13.19. 12 х 8 х 4 дюймов.
Практикум 13.4
/(х, у) = 2ху
х + у = 6.
/(х, у) = бху
у — X — 6.
/(х, у) = х*  1 2  3 4 * * 7 8 9 10 11 12 + у2
Зх + 4у = 25.
f(x,y) = 25 -X2 - у2
2гг 4- у = 10.
А Используйте метод множителей Лагранжа для решения задач 1-4.
1. Найти максимум функции
при ограничении
2. Найти минимум функции
при ограничении
3. Найти минимум функции
при ограничении
4. Найти максимум функции
при ограничении
Б В задачах 5 и 6 примените теорему 13.1 и объясните, почему у приведенной функции не существует максимума или минимума.
* 5. Найти минимум функции
при ограничении
* 6. Найти максимум функции
при ограничении
Решите задачи 7-16 методом множителей Лагранжа.
7. Найдите максимум и минимум функции
при ограничении
8. Найдите максимум и минимум функции
при ограничении
9. Найдите максимальное произведение двух чисел, сумма которых равна 10.
10. 	Найдите максимальное произведение двух чисел, разность которых равна 10.
/(х,у) = 4х - Зу 2х + Ьу = 10.
f(x,yj = Ъх + Ьу + 24
Зх -I- 2у = 4.
/(х, у) = 2ху х2 + у2 = 18.
/(х, у) = х2 - у2 х2 + у2 = 25.
В Решите следующие задачи
11. Найдите максимум функции
при ограничении
12. Найдите максимум функции
при ограничении
/(x,y,z) = х2 + у2 + z2 2х — Зу + 3z = —28.
/(x,y,z) = xyz
2x + y + 2z= 120.


594
Часть III. Математический анализ
13. Найдите максимум и минимум функции
при ограничении
14. Найдите максимум и минимум функции
при ограничении
15. Найдите максимум и минимум функции
при ограничении
16. 	Найдите максимум и минимум функции при ограничении
f(x,y,z) = х + у + z х2 + у2 + z2 = 12.
f(x,y,z) = 2x + 4y + 4z х2 + у2 +z2 = 9.
/(z, у) = У + ху2
х + у2 = 1.
f(x,y) = х + еу х2 + у2 = 1.
В задачах 17 и 18, используя теорему 13.1, объясните, почему у приведенной функции
не существует максимума или минимума.
*17. Найти минимум функции
при ограничении
*18. Найти минимум функции
при ограничении
х — 2у — 6. f(x,y) = х3 + 2у3
6х — 2у = 1.
*19. Рассмотрите задачу поиска максимума функции f(x>y) при ограничении д(х, у) = 0, где д(х, у) = у — 5. Объясните, почему эту задачу можно решить без использования метода множителей Лагранжа.
*20. Рассмотрите задачу поиска максимума функции при ограничении
д(х,у) = 0, где д(х,у) = 4х — у + 3. Объясните, почему эту задачу можно решить без использования метода множителей Лагранжа.
21. 	Рассмотрите задачу поиска максимума функции /(ж, у) = е~(х2+у2^ при ограничении д(х, у) = х2 4- у — 1 = 0.
а) Выразите переменную у из уравнения связи и, подставив этот результат в функцию f(x,y), найдите функцию h(x), зависящую от одной переменной. Постройте график функции h(х) и решите исходную задачу максимизации путем поиска максимума функции h(x). Ответ округлите до трех десятичных знаков.
б) Проверьте полученный ответ с помощью метода множителей Лагранжа.
22. 	Рассмотрите задачу поиска максимума функции
f(.x,y) =х2 + 2у2
при ограничении д(х,у) = уех2 — 1 = 0.
а) Выразите переменную у из уравнения связи и, подставив этот результат в функцию /(ж, у), найдите функцию h(x), зависящую от одной переменной. Постройте график функции h(ж) и решите исходную задачу максимизации путем поиска максимума функции h(x). Ответ округлите до трех десятичных знаков.
б) Проверьте полученный ответ с помощью метода множителей Лагранжа.


Глава 13. Исчисление многих переменных
595
Применение математики
Экономика и бизнес
23. Бюджет минимальных затрат. Компания производит две модели телевизоров: х единиц модели А и у единиц модели В в неделю. Общие затраты (в долларах) описываются функцией
С(х,у) = бх2 + 12т/2.
Отделом логистики выдвигается дополнительное условие:
х + у = 90.
Сколько телевизоров каждой модели нужно производить еженедельно, чтобы минимизировать затраты? Чему равны минимальные затраты?
24. Бюджет максимального объема производства. Месячный бюджет фирмы на материалы и оплату труда составляет 60 тыс. долл. Если на оплату труда расходуется х тыс. долл., а на материалы — у тыс. долл., то объем производства описывается функцией
N(x, у) = 4ху — 8х.
Как распределить затраты на материалы и оплату труда, чтобы получить максимальное значение функции 7V? Чему равно максимальное значение функции N?
25. Производительность. Консалтинговой компанией получена следующая функция Кобба-Дугласа для производства определенного вида продукции.
N(x,y) = 50х°’8у°’2,
где х — объем труда, а у — объем капитала, затрачиваемых на производство N(x,y) единиц продукции. Затраты труда составляют 40 долл., а затраты капитала — 80 долл.
а) Пусть производственный бюджет составляет 400 тыс. долл. Как распределить эту сумму для достижения максимального объема производства? Чему равен максимальный объем производства?
б) Вычислите предельную производительность денег в рассматриваемом случае и приблизительно оцените увеличение объема производства при расширении бюджета на 50 тыс. долл.
26. Производительность. Маркетинговым отделом предприятия получена следующая функция Кобба-Дугласа для определенного вида продукции.
N(x,y) = 10х°’6у°’4,
где х — объем труда, а у — объем капитала, затрачиваемых на производство 7V(x, у) единиц продукции. Затраты труда составляют 30 долл., а затраты капитала — 60 долл.
а) Пусть производственный бюджет составляет 300 000 долл. Как распределить эту сумму для достижения максимального объема производства? Чему равен максимальный объем производства?


596
Часть III. Математический анализ
б) Вычислите предельную производительность денег в рассматриваемом случае и приблизительно оцените увеличение объема производства при расширении бюджета на 80 000 долл.
27. 	Максимальный объем. Прямоугольная коробка без верха разделена посередине двумя пересекающимися перегородками. На ее изготовление уходит 192 кв. дюймов картона (рис. 13.30). При каких размерах коробки ее объем будет максимальным?
Рис. 13.30. Иллюстрация к задаче 27
28. 	WWW Максимальный объем. Согласно правилам почтовой службы сумма длины и обхвата упаковки не должна превышать 120 дюймов (рис. 13.31) При каких размерах листа почтового картона можно упаковать коробку максимального объема, удовлетворяющего этим требованиям?
Рис. 13.31. Иллюстрация к задаче 28
Биологические науки
29. Сельское хозяйство. Вдоль уже существующего забора (рис. 13.32) необходимо построить три загона для скота одинаковой площади. На строительство забора выделено 400 футов материала. Какими должны быть длины хну для ограждения максимально возможной площади? Чему при этом будет равна максимальная площадь?
30. Минимизация затрат на питание. Рацион питания семейства морских свинок должен еженедельно обеспечивать из 25 600 калориями. При включении в него двух видов пищевой смеси получается 200хт/ калорий для х килограммов смеси М и у килограммов смеси N. Килограмм смеси М стоит один доллар,


Глава 13. Исчисление многих переменных
597
Рис. 13.32. Иллюстрация к задаче 29
а килограмм смеси N — два доллара. Какое количество смесей каждого типа нужно использовать, чтобы минимизировать недельные затраты на питание? Чему равны такие минимальные затраты? Замечание: х 0 и у 0.
13.5. 	Метод наименьших квадратов
■ Аппроксимация методом наименьших квадратов
■ Решение практических задач
Аппроксимация методом наименьших квадратов
Регрессионный анализ — это процесс подбора элементарной функции, лучше других аппроксимирующей набор заданных точек методом наименьших квадратов. Общие принципы регрессионного анализа рассмотрены в главе 2. Теперь с помощью рассмотренных в разделе 13.3 методов оптимизации мы сможем изучить принципы, лежащие в основе метода наименьших квадратов. Начнем с линейной регрессии, поиска уравнения прямой, которая “наилучшим образом” аппроксимирует заданный набор точек.
Предположим, руководству предприятия необходимо приближенно найти функцию затрат на производство некоторой продукции. Величины затрат известны лишь для некоторых объемов производства, перечисленных в табл. 13.1. Несмотря на то что точки не лежат на одной прямой (рис. 13.33), похоже, что функция затрат имеет линейный характер. По этой причине аналитический отдел предприятия предложил аппроксимировать функцию затрат линейной функцией, т.е. подобрать значения а и b так, чтобы прямая
у = ах + Ъ
в некотором смысле была “наилучшим приближением” функции затрат.
Таблица 13.1. Исходные значения затрат
Объем производства, Затраты, х (тыс. шт.) у (тыс. долл.)
2 4
5 6
6 7
9 8
8


598
Часть III. Математический анализ
х
Объем производства, сотен шт.
Рис. 13.33. Значения функции затрат
Как понимать выражение “наилучшее приближение”? Поскольку прямая у = ах + b не может проходить через все четыре точки, целесообразно рассмотреть разности ординат точек, построенных по данным таблицы, и соответствующих ординат точек, лежащих на прямой. Каждая из этих разностей называется остатком (рис. 13.34). Например, для абсциссы х = 2 соответствующая точка из табл. 13.1 имеет координаты (2, 4), а точка на прямой задается координатами (2, 2а + Ь), поэтому разность будет равна
4 	- (2а + Ь) = 4 - 2а - Ъ.
Все остатки исходного набора данных приведены в табл. 13.2.
Таблица 13.2. Остатки
X
У
ах + Ь
Остаток
2
4
2,0 -|- b
4 - 2а - b
5
6
5а + 6
6 — 5а — b
6
7
6а -|- b
7 — 6а — b
9
8
9а+ Ь
8 — 9а — b
Критерий “наилучшего приближения” формулируется так: требуется найти такие значения коэффициентов а и Ь, чтобы сумма квадратов остатков была минимальной. Получающаяся в результате прямая называется прямой наименьших квадратов или регрессионной прямой. Для ее поиска необходимо минимизировать функцию
F(a, b) = (4 - 2а - Ь)2 4- (6 - 5а - Ь)2 + (7 - 6а - Ъ)2 + (8 - 9а - Ь)2.
Этап 1. Найдем критические точки.
Fa(a, 6) = 2(4 - 2а - 6)(-2) + 2(6 - 5а - 6)(-5) +
+ 2(7 - 6а - Ь)(-6) + 2(8 - 9а - Ь)(-9) =
= -304 + 292а + 446 = 0;


Глава 13. Исчисление многих переменных
599
Объем производства, сотен шт.
Рис. 13.34. Остатки
Гь(а, 6) = 2(4 - 2а - 6)(-1) + 2(6 - 5а - 6)(-1) +
+ 2(7 - 6а - 5)(-1) + 2(8 - 9а - 6)(-1) =
= -50 + 44а + 86 = 0.
После деления каждого уравнения на число 2 получим систему
146а + 226 = 152,
22а 46 = 25.
Решение этой системы (0,58; 3,06) является единственной критической точкой.
Этап 2. Найдем значения А = Faa(a, 6); В = Fab(a, 6); С = Fbb(a, 6).
Faa(a, Ь) = 292, поэтому А = Faa(0,58; 3,06) = 292.
Fab(a, 6) = 44, поэтому В = Fab(0,58; 3,06) = 44.
Fbb(a, 6) = 8, поэтому С = Fbb(0,58; 3,06) = 8.
Этап 3. Вычислим значение АС — В2 и найдем тип критической точки (а, 6) согласно теореме 13.2 раздела 13.3.
АС - В2 = 292 • 8 — 442 = 400 > 0 и А = 292 > 0
Следовательно, выполняется вариант 2, указанный в теореме 13.2, и функция F(a, 6) имеет локальный минимум в критической точке (0,58; 3,06).
Таким образом, прямая наименьших квадратов для приведенных данных выглядит следующим образом.
у = 0,58z + 3,06 Прямая наименьших квадратов
При таком выборе коэффициентов а и 6 сумма квадратов остатков минимальна (рис. 13.35).


600
Часть III. Математический анализ
Объем производства, сотен шт.
Рис. 13.35. Регрессионная прямая
Эта линейная функция теперь может быть использована для определения показателей, обычно связанных с функцией затрат, — например, общие затраты, предельные затраты, средние затраты и т. п. Например, общие затраты на производство 2000 единиц продукции приближенно равны
у = 0,58 • 20 + 3,06 = 14,66, или 14 660 долл.
Функция предельных затрат равна
= 0,58.
ах
Функция средних затрат равна
0,58х + 3,06
У = •
х
Рассмотрим общий случай. Задан набор п точек (a?i, з/i), (^2,2/2), . • •, (хп, Уп)- Задача состоит в определении уравнения прямой у = ах+ Ь9 для которой сумма квадратов остатков является минимальной. Сумму квадратов остатков можно представить в следующем виде.
F(a>= 52 ^ук ~ахк ~ь)2-
к=1
Заметим, что в этом выражении переменными величинами являются числа а и 6, а значения Xk и уь считаются известными. Для минимизации функции F(a, 6) вычислим частные производные по переменным а и b и приравняем их к нулю.
п
Fa(a, b) = ^2(ук- ахк - Ь) (-хк) = 0, к=1
Fb(a, b) = 52 2 (.Ук - ахк - 6) (-1) = 0.
к=1


Глава 13. Исчисление многих переменных
601
После деления каждого уравнения на число 2 и упрощения выражений оказывается, что каждый из коэффициентов уравнения прямой наименьших квадратов у = ах + b удовлетворяет системе нормальных уравнений (normal equations).
п \ / п \ п
) а + (52^ ) Ь = ^2ХкУк,
к=1 / \fc=l / fc=l
п \ n
^2хк\а + пЬ = ^2ук.
к=1 / к=1
Приближение методом наименьших квадратов
Для заданного набор п точек , j/i), (^2,2/2), • • •, Уп) коэффициенты прямой наименьших квадратов у = ах + b удовлетворяют уравнениям
п \ / П \ п
^2хк I а+ I ]Ь = ^хкУк, Л=1 / \fc=l / к=1
п \ п
У^хк\ a + nb = У^ ук. ,к=1 / fc=l
(13.13)
Решение этой системы имеет вид
п п п
п 52 хкУк - 52 хк 12 Ук
к=1 *:=! к=1
п п
52,Ук-а52хк
к=1 к=1
п
(13.14)
(13.15)
Теперь вернемся к табл. 13.1 и вычислим суммы, которые нужны для записи решений нормальных уравнений. Результаты приведены в табл. 13.3.
Таблица 13.3. Промежуточные результаты
хк
Ук
ХкУк
*2к
2
4
8
4
5
6
30
25
6
7
42
36
9
8
72
81
Сумма 22
25
152
146
Нормальная система уравнений (13.13) имеет вид
14ба 4- 226 = 152, 22а 4~ 46 — 25.


602
Часть III. Математический анализ
Решения этой системы выражаются формулами (13.14) и (13.15)
4 • 152 — 22 • 25
4•146 — 222
25 - 0,58 • 22 _
= 0,58;
3,06.
Сравним результаты с результатами п. 1. Заметим, что табл. 13.3 обеспечивает удобный формат представления данных для дальнейших вычислений.
В большинстве утилит есть встроенные процедуры аппроксимации данных методами линейной регрессии, позволяющие находить решения системы нормальных уравнений, которые получаются приравниванием к нулю производных суммы квадратов. Поэтому при решении действительной практической задачи достаточно ввести точки данных и воспользоваться процедурой линейной регрессии для поиска прямой у = ах + Ь, которая наилучшим образом описывает целевые данные (рис. 13.36). Вам не придется отдельно вычислять ни частные производные, ни суммы квадратов.
Т1—
Ti—
Тз
б
9
ч б ? в
1<1)=2
а)
»inReg y=ax+b а=. 58 Ь=3.06 г=.9803789355
Рис. 13.36. Результаты аппроксимации в графической утилите
Задание 13.9.
1. Изобразите четыре точки (0,0), (0,1), (10,0), (10,1). Какая прямая будет “наилучшим” описанием этих данных? Воспользуйтесь формулами (13.14) и (13.15) для проверки сделанного вывода.
2. Изобразите в координатном пространстве четыре точки (0,0), (0,10), (1,0), (1,10). Какая прямая будет “наилучшим” описанием этих данных? Воспользуйтесь формулами (13.14) и (13.15) для проверки сделанного вывода.
3. Если в обоих случаях предположение было неверным, найдите причину ошибки.и
Метод наименьших квадратов можно также использовать для поиска квадратичной функции у = ах2 + Ьх -И с, которая наилучшим образом описывает исходный набор данных. В этом случае сумма квадратов остатков является функцией трех переменных.
п
F(a, b,c) = ^2 (ук - ахк - Ьхк - с) .
к=1


Глава 13. Исчисление многих переменных
603
Вычислим частные производные и приравняем их к нулю.
п
Fa(a, Ь, с) = 52 2 (ук - ахк - Ьхк - с) (-х^) = 0, fc=i
п
Fb(a, b, с) = 52 2 (.Ук ~ ахк - Ъхк - с) (~хх) = 0, к=1
Гс(а, Ь, с) = 52 2 (Ук ~ axl - Ьхк - с) (-1) = 0. fc=i
Получаемая в результате система трех линейных уравнений называется системой нормальных уравнений квадратичной регрессии.
В графическом калькуляторе имеется встроенная процедура решения задач квадратичной регрессии. Для этого достаточно ввести координаты заданных точек. На рис. 13.37 приведены вычисления для данных табл. 13.1.
XI
тз
б
9
ч
6
7
В
1<1>=2
а)
3uadRe9 y=ax2+bx+c а=-. 0416666667 b=1.038333333 с=2.06
в) Ух = -0,0417x2 + 1,0383а: + 2,06
Рис. 13.37. Получение уравнения квадратичной регрессии
Задание 13.10.
1. Используя рис. 13.36 и 13.37, определите, какой из методов — линейной или квадратичной регрессии — обеспечивает минимальную сумму квадратов остатков для данных табл. 13.1. Аргументируйте ответ.
2. Проверьте свое предположение вычислением суммы квадратов для каждого
случая. а
Метод наименьших квадратов оказывается действенным в других типах регрессии — например, кубической, квадратичной, логарифмической, экспоненциальной или другой степенной регрессионной модели. Подробно некоторые из них рассмотрены в отдельных упражнениях, размещенных в конце этого раздела.
Решение практических задач
Пример 13.20 (Проверка знаний). В табл. 13.4 приведены результаты экзаменов по математическому анализу, проведенных в середине и в конце семестра, группы из 10 студентов.


604
Часть III. Математический анализ
Таблица 13.4. Результаты экзаменов
Середина семестра
Конец семестра
Середина семестра
Конец семестра
49
61
78
77
53
47
83
81
67
72
85
79
71
76
91
93
74
68
99
99
1. Используя формулы (13.13), (13.14) и (13.15), составьте нормальные уравнения для прямой наименьших квадратов, аппроксимирующей данные из табл. 13.4.
2. Используя метод линейной регрессии, предусмотренный в графической утилите, постройте прямую наименьших квадратов.
3. Используя прямую наименьших квадратов, предскажите оценку, которую может получить в конце семестра студент, набравший 95 баллов в середине семестра.
Решение.
1. 	В табл. 13.5 указан удобный способ вычисления сумм, необходимых для поиска коэффициентов а и Ь.
Таблица 13.5. Промежуточные результаты
Xfc
Ук
ХкУк
Х1
49
61
2989
2401
53
47
2491
2809
67
72
4824
4489
71
76
5396
5041
74
68
5032
5476
78
77
6006
6084
83
81
6723
6889
85
79
6715
7225
91
93
8463
8821
99
99
9801
9801
Сумма 750
753
58440
58496
Последняя строка в табл. 13.5 содержит следующие результаты.
10 10 10
5? хк = 750 5? У* = 753 52 ХкУк = 58 440
fc=l к=1 к=1
Нормальные уравнения имеют следующий вид.
10
^хк = 58496
fc=i
58496а+ 7505 = 58440,
750а + 105 = 753.


Глава 13. Исчисление многих переменных
605
Используя формулы (13.14) и (13.15), получаем такие результаты.
10 • 58 440 - 750 ■ 753 19 650 _
а~ 10 -58496- 7502 _ 22460 ~ ’
t 753 - 0,875 • 750 „ _
Ь = = 9,675.
Прямая с наименьшей суммой квадратов приближенно описывается уравнением
у = 0,875я + 9,675.
2. 	Введем данные во встроенную процедуру линейной регрессии. Результаты приведены на рис. 13.38. (Расхождения между ними и значениями а и Ь, полученными выше, вызваны округлением.)
пп
ТП
ТП
61
53
47
67
72
71
76
74
6В
7В
77
ВЗ
В1
1 <1
=49
inReg y=ax+b а=.874888691 Ь=9.683348175 г=.9285049257
в)
Рис. 13.38. Результаты аппроксимации в графической утилите
3. 	Если я = 95, то у = 0,875-95 +9,675 « 92,8 — предполагаемая оценка (рис. 13.38, в). Если считать экзаменационную оценку целым числом, то результатом предсказания будет округленное значение 93. ■
Упражнение 13.20.
Повторите решение примера 13.20 для данных, приведенных в табл. 13.6. ■
Таблица 13.6. Результаты экзаменов
Середина семестра
Конец семестра
Середина семестра
Конец семестра
54
50
84
80
60
66
88
95
75
80
89
85
76
68
97
94
78
71
99
86


606
Часть III. Математический анализ
Пример 13.21 (Расход топлива). Объем жидкого топлива, используемого для обогрева домов в Соединенных Штатах, равномерно снижается на протяжении нескольких десятилетий. В табл. 13.7 приведены данные о доле домохозяйств, использовавших жидкое топливо для обогрева с 1960 по 1991 гг. Воспользуйтесь данными, приведенными в таблице, и определите процент домов в Соединенных Штатах, которые будут предположительно использовать жидкое топливо для обогрева помещений в 2010 году.
Таблица 13.7. Доля домохозяйств, использующих жидкое топливо для обогрева
Год
Доля, %
Год
Доля, %
1960
32,4
1985
14,1
1970
26,0
1989
13,3
1975
22,5
1993
12,9
1980
18,1
1997
10,9
Решение. Введем данные, считая, что значение х = 0 представляет 1960 год, х = 10 — 1970 год и так далее, и применим процедуру линейной регрессии, как показано на рис. 13.39.
L1
L3 2
0
10
15
20
25
29
33
32.4
26
22.5
10.1
14.1
13.3
12.9
lz =<з:
2.4» 26? 22....
а)
LinReg y=ax+b а=“. 599026764 Ь=31.42944039 гг=.9665472977 г=-. 9831313736
40
О в)
Рис. 13.39. Процедура линейной регрессии
Из рис. 13.39 следует, что формула прямой, построенной с помощью метода наименьших квадратов, выглядит так: у = —0,60х 4- 31,43. Ожидаемая доля домов, обогреваемых жидким топливом, в 2010 году (соответствует х = 50) равен —0,60 ♦ 50 + 31,43 = 1,43%.■
Упражнение 13.21.
В 1950 году основным источником тепловой энергии был уголь, тогда как процент домов, отапливаемых жидким топливом, составлял всего 22,1 %. Дополните данные из примера 13.21 информацией за 1950 год, вычислите соответствующую линию наименьших квадратов и дайте новую оценку доли потребления жидкого топлива в 2010 году. Объясните причину расхождений между двумя прогнозами. в
Задание 13.11.
В табл. 13.8 приведены данные о количестве А (мг) радиоактивного изотопа галлий-97, используемого при диагностике злокачественных опухолей, и время его распада t (ч).


Глава 13. Исчисление многих переменных
607
Таблица 13.8. Распад ра¬
диоактивного изотопа
t, ч
А, мг
0
50,0
5
46,4
10
43,1
15
39,9
20
37,1
1. Поскольку данные описывают процесс радиоактивного распада, то можно ожидать экспоненциальной зависимости величины А от времени t, т.е. А = aebt ддя некоторых постоянных а и Ь. Покажите, что если А = aebt9 то отношение между величинами 1п А от t является линейным.
2. Вычислите In А для каждой точки данных и постройте прямую, которая наилучшим образом описывает данные (In A, t).
3. Найдите величины а и Ь, которые соответствуют “наилучшему” приближению.
4. Проверьте результат вычисления на калькуляторе с помощью процедуры экспоненциальной регрессии. в
Ответы к упражнениям
13.20. 1) у = 0,85ж + 9,47.
ТЗ
50
60
66
75
ВО
76
6В
7В
71
ВЧ
ВО
вв
95
=54
inReg y=ax+b
а=.8504140787
Ь=9.466873706
г=.8959772625
3) 90,3.
13.21. у = -0,38х + 25,87; 6,87%.
Практикум 13.5
А В задачах 1-6 требуется найти прямую наименьших квадратов и изобразить ее вместе с исходными данными.
1 1
2 3
3 4
4 3
X
У
х X
У
1
-2
1
8
2
-1
2
5
3
3
3
4
4
5
4
0


608
Часть III. Математический анализ
X
У
э- X
У
о.
X
У
1
20
1
3
1
2
2
14
2
4
2
3
3
11
3
5
3
3
4
3
4
6
4
2
Б В задачах 7-14 требуется найти прямую наименьших квадратов и использовать результат для вычисления значения у при указанном значении х.
X
У
8.
X
У
1
3
1
0
2
1
3
1
2
2
3
6
3
0
3
4
Вычислите значение у для х
= 2,5.
Вычислите значение у для х =
3.
10.
X
У
X
У
0
10
-5
60
5
22
0
50
10
31
5
30
15
46
15
20
20
51
15
15
Вычислите значение у для х
= 25.
Вычислите значение у для х =
20.
12.
X
У
X
У
-1
14
2
-4
1
12
6
0
3
8
10
8
5
6
14
12
7
5
18
14
Вычислите значение у для х
= 2.
14.
Вычислите значение у для х —
15.
X
У
ж у
X
У
ж у
0,5
25
9,5 12
0
-15
12 11
2
22
11 11
2
-9
14 13
3,5
21
12,5 8
4
—7
16 19
5
21
14 5
6
-7
18 25
6,5
18
15,5 1
8
-1
20 33
Вычислите значение у для х = 8. Вычислите значение у для х = 10.
15. 	Для поиска коэффициентов параболы
у — ах2 + Ьх + с,


Глава 13. Исчисление многих переменных
609
которая является наилучшим приближением для точек (1,2), (2,1), (3,1) и (4,3), необходимо минимизировать сумму квадратов остатков
F(a, 6, с) = (а 4- b + с — 2)2 + (4а + 2Ь + с - I)2 +
4~ (9а 4~ 3d 4- с — I)2 4~ (16а 4~ 45 4~ с — З)2,
решив систему нормальных уравнений
Fa(a,b, с) = 0, Fb(a, b, с) = 0, Fc(a,b,c) = 0
для переменных а, b и с. Постройте эту параболу и изобразите точки данных.
16. 	Повторите решение задачи 15 для точек (—1, —2), (0,1), (1,2) и (2,0).
В задачах 17 и 18 речь идет о системе нормальных уравнений и формулах для переменных а и Ь, приведенных в тексте.
*17. Проверьте формулы (13.14) и (13.15), решив нормальную систему уравнений (13.13) относительно величин а и Ь.
* 18. Пусть числа
являются средними значениями координат хну соответственно. Покажите, что точка (ж, у) удовлетворяет уравнению наименьших квадратов у = ах + Ь.
* 19. а) Допустим, что п = 5 и абсциссы точек (#i, i/i), (#2, Уъ), • • •, (жп,Уп) равны —2, —1, 0, 1, 2. Покажите, что из системы (13.13) следует, что
а =
ТхкУк
ТА
и параметр Ъ равен среднему значению набора чисел у^
б) Покажите, что вывод, полученный при решении п. а, остается верным даже тогда, когда среднее значение координат х равно нулю.
* 20. а) Приведите набор из шести точек, одна половина которого лежит выше ре¬
грессионной прямой, а вторая — под ней.
б) Приведите набор из шести точек, у которого только одна точка лежит выше регрессионной прямой, а остальные — выше.
*21. а) Найдите линейную и квадратичную функции, которые наилучшим образом приближают данные (0; 1,3), (1; 0,6), (2; 1,5), (3;3,6) и (4; 7,4). (Результаты округлите до двух десятичных знаков.)
б) Какая из двух функций наилучшим образом описывает данные? Объясните ответ.
* 22. а) Найдите линейную и квадратичную функции, которые наилучшим образом
приближают данные (Г, 3,2), (2; 4,2), (3; 4,7), (4; 5,0) и (5; 5,3). (Результаты округлите до двух десятичных знаков.)
б) Какая из двух функций наилучшим образом описывает данные? Объясните ответ.


610
Часть III. Математический анализ
*23. Опишите нормальные уравнения для кубической регрессии. Сколько нужно уравнений и переменных? Какой метод можно использовать для решения этой задачи?
*24. Опишите нормальные уравнения для регрессии четвертого порядка. Сколько нужно уравнений и переменных? Какой метод можно использовать для решения?
Применение математики
Экономика и бизнес
25. 	Производство автомобилей. В таблице приведены данные по производству автомобилей в Канаде за период с 1990 по 1999 годы.
Объем производства автомобилей в Канаде
Год
Количество, тыс. шт.
Год
Количество, тыс. шт.
1990
1928
1995
2408
1991
1888
1996
2397
1992
1961
1997
2571
1993
2246
1998
2568
1994
2321
1999
3026
а) Постройте регрессионную прямую, считая что в 1990 г. выполнялось условие х = 0.
б) Примените прямую наименьших квадратов для оценки годового объема производства автомобилей в Канаде в 2010 г.
26. 	Производство говядины. В таблице приведены данные по производству говядины в Соединенных Штатах за период с 1990 по 1999 гг.
Объем производства говядины в Соединенных Штатах
Год
Вес, млн. фунтов
Год
Вес, млн. фунтов
1990
22 743
1995
25222
1991
22917
1996
25 525
1992
23 086
1997
25 490
1993
23 049
1998
25 760
1994
24 386
1999
26493
а) Постройте регрессионную прямую, считая что в 1990 г. выполнялось условие х = 0.
б) Примените прямую наименьших квадратов для оценки годового объема производства говядины в Соединенных Штатах в 2012 году.
27. 	Максимизация прибыли. Маркетинговый отдел крупной сети аптек провел в двух курортных регионах пробные продажи нового солнцезащитного крема в пластиковой бутылке емкостью четыре унции. Варьируя цены на протяжении лета и выяснив объем ежемесячного спроса, отдел получил данные, приведенные


Глава 13. Исчисление многих переменных
611
в следующей таблице, где у — месячный объем продаж (тыс. шт.), ах- цена бутылки (в долларах).
X, долл.
у, тыс. шт.
5,0
2,0
5,5
1,8
6,0
1,4
6,5
1,2
7,0
1,1
а) Составьте уравнение спроса, используя метод наименьших квадратов.
б) Пусть затраты на продажу бутылки солнцезащитного крема в сети аптек равны четырем долларам. Какую цену следует установить, чтобы получить максимальную месячную прибыль? (Подсказка. Используйте результаты решения п. а для С = 4т/, R = ху и Р = R — С.)
28. 	Максимизация прибыли. Маркетинговый отдел сети супермаркетов провел в крупном городе пробные продажи новой смеси орешков, продаваемых в упаковках емкостью по восемь унций. Варьируя цены в течение года и выяснив объем ежемесячного спроса, отдел получил данные, приведенные в таблице, где у — месячный объем продаж (в тыс. пгг.), ах- цена упаковки (в долларах).
X, долл. у, тыс. шт.
4,0
4,2
4,5
3,5
5,0
2,7
5,5
1,5
6,0
0,7
а) Найдите уравнение спроса, используя метод наименьших квадратов.
б) Пусть затраты на продажу упаковки смеси орешков в сети супермаркетов равны трем долларам. Какую цену следует установить, чтобы получить максимальную месячную прибыль?
Биологические науки
29. 	Медицина. При погружении человека под воду циркуляция крови в коже и в мышцах снижается, что приводит к понижению пульса. В медицинском центре были проведены исследования группы десяти двухлетних детей. По условиям эксперимента лицо ребенка кратковременно погружали в воду и затем измеряли пульс. В следующей таблице приведены значения частоты пульса для различных температур воды.
а) Пусть Т — температура воды (в градусах Фаренгейта), а Р — частота сердечного пульса (количество ударов в минуту). Используя метод наименьших квадратов, найдите линейную зависимость между величинами Т и Р.
б) Используя результаты решения п. а, определите значения Р при Т — 57.


612
Часть III. Математический анализ
Температура воды, °F Частота пульса
50
15
55
13
60
10
65
6
70
2
30. 	Биология. В биологии существует эмпирическое биоклиматическое правило для умеренного климата, известное несколько сотен лет. Согласно этому правилу период цветения растений, появления насекомых и созревания фруктов обычно наступает с задержкой на 4 дня по мере повышения высоты над уровнем моря на каждые 500 футов. Это правило выражается формулой
d = 8h, 0 < h 4,
где d — время задержки, a h — высота (в тысячах футов). Для проверки этого закона были проведены эксперименты, в ходе которых записывались разности между моментами начала цветения одних и тех же яблочных деревьев одного сорта на различных высотах. Результаты приведены в следующей таблице.
h
<1
0
0
1
7
2
18
3
28
4
33
а) Используя метод наименьших квадратов, определите зависимость величины h от переменной d. Выполняется ли стандартное биоклиматическое правило d — Sh хотя бы приблизительно?
б) Сколько времени пройдет до начала цветения яблочных деревьев исследуемого сорта на высоте 3,5 тысячи футов над уровнем моря? (Для ответа используйте линейное уравнение, полученное при решении п. а.)
31. 	Глобальное потепление. В следующей таблице приведены значения средней температуры поверхности Земли за период с 1885 по 1995 годы.
WWW Средняя температура поверхности Земли
Год
°F
Год
°F
1885
56,65
1945
57,13
1895
56,64
1955
57,06
1905
56,52
1965
57,05
1915
56,57
1975
57,04
1925
56,74
1985
57,36
1935
57,00
1995
57,64
а) Постройте регрессионную прямую, используя значение х = 0 для 1885 года.


Глава 13. Исчисление многих переменных
613
б) Оцените среднюю температуру поверхности Земли в 2085 году с помощью прямой наименьших квадратов.
32. 	Загрязнение воздуха, В следующей таблице приведены данные об объемах загрязняющих веществ, выбрасываемых в воздух в Соединенных Штатах.
WWW Объем загрязняющий веществ, выбрасываемых в воздух в США
Год
Объем загрязнений, млн. т
Год
Объем загрязнений, млн. т
1989
179,6
1994
174,6
1990
170,5
1995
161,4
1991
172,5
1996
160,9
1992
169,0
1997
160,6
1993
169,6
1998
154,3
а) Вычислите регрессионную прямую, используя значение х = 0 для 1989 года.
б) Используя прямую наименьших квадратов, оцените объем загрязнения воздуха в Соединенных Штатах в 2015 году.
Социальные науки
33. 	Политология. Принадлежность к экономическому классу и партийная принадлежность не были изобретением “Нового курса” Франклина Рузвельта. Они относятся ко времени Эндрю Джексона (Andrew Jackson) (1767-1845). Поль Ла- зарсфельд (Paul Lazarsfeld) из Колумбийского университета в ноябре 1950 года опубликовал в журнале Scientific American статью, в которой привел результаты статистических исследований о зависимости между экономической и партийной принадлежностью. Данные, взятые из статьи, приведены в следующей таблице.
Политическая принадлежность, 1836 г
Количество адми- Оценочная величина нало- Доля голосов, отданных нистративных рай- га на недвижимость на че- за демократическую паронов ловека, сотни долл. тию, %
12
1,7
51
3
2,1
49
1
2,3
53
5
2,4
36
2
3,6
65
11
3,7
35
10
4,7
29
4
6,2
40
6
7,1
34
9
7,4
29
8
8,7
20
7
11,9
23
а) Допустим, что величина А задает среднюю величину налога на недвижимость в заданном административном районе в 1836 г., а величина D — процент голосов, отданных за демократическую партию в 1836 г. Используя


614
Часть III. Математический анализ
метод наименьших квадратов, найдите линейную зависимость между величинами D и А.
б) Предположим, что в среднем налог на недвижимость равен 300 долл. Как изменится в таком случае процент голосов, отданных за демократическую партию?
34. 	Образование. В приведенной ниже таблице приведен рейтинг GPA группы из 10 учеников, рассчитанный на основании их оценок, получаемых на протяжении семестра в средней школе и колледже.
Рейтинг GPA
Средняя школа
Колледж
Средняя школа
Колледж
2,0
1,5
3,0
2,3
2,2
1,5
3,1
2,5
2,4
1,6
3,3
2,9
2,7
1,8
3,4
3,2
2,9
2,1
3,7
3,5
а) Постройте линию наименьших квадратов для этих данных.
б) Вычислите средний балл GPA студента колледжа, общий средний балл в котором равен 3,5.
в) Вычислите средний балл GPA студента средней школы, общий средний балл в которой равен 2,7.
35. 	Олимпийские игры. В следующей таблице приведены значения рекордов в соревнованиях прыжков с шестом с 1896 по 2000 гг.
WWW Рекорды в прыжках с шестом
Год
Высота, футы
Год
Высота, футы
1896
10,81
1956
14,96
1900
10,82
1960
15,43
1904
11,50
1964
16,73
1906
11,60
1968
17,71
1908
12,17
1972
18,04
1912
12,96
1976
18,04
1920
13,46
1980
18,96
1924
12,96
1984
18,85
1928
13,78
1988
19,35
1932
14,16
1992
19,02
1936
14,27
1996
19,42
1948
14,10
2000
19,35
1952
14,93
а) Используя графическую утилиту, постройте регрессионную прямую, полагая х = 0 для 1896 года.
б) Оцените рекордное значение высоты для прыжков с шестом в 2016 году.


Глава 13. Исчисление многих переменных
615
13.6. 	Двойные интегралы по прямоугольным областям
■ Введение
■ Определение двойного интеграла
■ Среднее значение функции в прямоугольной области
■ Двойные интегралы и объем
Введение
В одном из предыдущих разделов мы обобщили понятие производной на функции нескольких переменных. Как построить аналогичное обобщение для интеграла и как интерпретировать результат? Для начала посмотрим на интегрирование как на операцию, обратную к дифференцированию. Для функции нескольких переменных можно построить первообразную функцию по одной из переменных, считая все остальные переменные постоянными. Иначе говоря, операция вычисления частной первообразной представляет собой операцию, обратную частному дифференцированию. Будем обозначать вычисление первообразной по переменной х при фиксированной переменной у как J* f(x, у) dx. Аналогично вычисление первообразной по переменной у при фиксированной переменной х обозначается как J* /(х, у) dy.
Пример 13.22 (Вычисление частной первообразной). Вычислите следующие первообразные.
2. (бх?/2 + Зх2) dx.
Решение,
1. 	Считая переменную х постоянной величиной и используя свойства первообразной функции из раздела 11.1, получим следующий результат.
= бх y2dy + Зх2 dy =
= бх • + Зх2?/ + С(х).
о
— 2ху3 + Зх2у + С(х)
Символ dy указывает на то, что вычисление первообразной функции 6а?|/2 + Зге2 проводится только по переменной у, а переменная гс считается постоянной
Заметим, что постоянная интегрирования является произвольной функцией, зависящей только от переменной х, поскольку для каждой такой функции
Проверка, Проверим правильность полученного ответа частным дифференцированием.
Q
— Г2хг/3 + Зх2?/ 4- С(х)1 = бх2у + Зх2 + 0 = бху2 + Зх2. оу


616
Часть III. Математический анализ
2. 	Теперь постоянной величиной будем считать переменную у.
x2dx =
В этом случае постоянная интегрирования является произвольной функцией Е(у), зависящей только от переменной у.
Проверка.
[Зх2?/2 + х3 + = вху2 + Зх2 + 0 = бху2 + Зх2.
Упражнение 13.22.
Вычислите следующие интегралы.
1. (4х?/ + 12х22/3) dy.
2.
+ 12х2?/3) dx.
Обобщив понятие первообразной на функции двух переменных, можно приступать к вычислению определенных интегралов
ъ
f(x,y)dx или
d
а
С
Пример 13.23 (Вычисление частной первообразной). Вычислите следующие интегралы, подставляя пределы интегрирования для переменной у в интеграле по dy и пределы для переменной х в интеграле по dx.
2
1. j (бх?/2 + Зх2) dy. о
1
2. (бх?/2 -I- Зх2) dx.
о
Решение.
1. Из примера 13.22.1 известно, что
(бх?/2 + Зх2) dy = 2х?/3 + Зх2?/ + С(х).
Согласно свойствам интеграла для функции одной переменной для вычисления определенного интеграла можно использовать любую первообразную. Поэтому, вы-


Глава 13. Исчисление многих переменных
617
бирая С(х) = 0, получим следующий результат.
у=2
у=о
= [2х • 23 + Зх2 • 2] - [2х ■ О3 + За;2 • 0] = = 16а: + 6а:2.
2. Из примера 13.22.2 известно, что
(ба?!/2 + 3a;2) dx = Зх2у2 + х3 -И Е(у).
Поэтому, полагая Е(у) = 0, получим следующий результат.
1
(бху2 4- За;2) dx = (Зх2у2 + а;3)
Х — 1 я=О
о
= [Зу2 • I2 + I3] - [Зу2 • О2 + О3] = = Зу2 + 1.
Упражнение 13.23.
Вычислите следующие интегралы.
1 з
1. j (4ху 4- 12л;2j/3) dy. 2. j (4ху 4- 12а;2т/3) dx.
о о
Заметим, что в результате вычисления определенного интеграла функции двух переменных f(x,y) по переменной у получается функция, зависящая только от одной переменной х, или константа. Аналогично, вычисляя определенный интеграл от функции f(x,y) по переменной х, получим функцию, зависящую только от одной переменной у, или константу. Каждую из этих функций далее можно интегрировать по оставшейся переменной.
Пример 13.24 (Вычисление повторных интегралов). Вычислите следующие повторные интегралы.
1 Г2
1.
о Lo
j (бху2 4- За:2) dy dx.
Г1
2
2. j j (бху2 4- За:2) dx dy. о
_о


618
Часть III. Математический анализ
Решение.
1. Из примера 13.23.1 известно, что
2
| (бжт/2 + Зж2) dy = 16ж + 6ж2.
о
По этой причине
1 Г2 1 1
| j (бжт/2 + Зж2) dy dx = j (16ж + 6ж2) dx =
о
о |_0
х—1
х=0
= (8ж2 + 2ж3)
= (8 • I2 + 2 • I3) - (8 • О2 + 2 • О3) = 10.
2. Из примера 13.23.2 известно, что
j (бжт/2 о
+ Зж2) dx = Зу2 + 1.
По этой причине
2 dy = j (Зу2 + 1) dy =
О
= (у3 + у)
у=2
3/=о
= (23 + 2) - (О3 + 0) = 10.
Для вычисления последних двух интегралов в примерах 13.23.1 и 13.23.2 в качестве альтернативы основной теореме интегрального исчисления можно использовать процедуру численного интегрирования, поскольку подынтегральное выражение в каждом из интегралов (16ж + 6ж2) dx и (З?/2 + 1) dy является функцией только одной переменной (рис. 13.40).
Упражнение 13.24.
Вычислите следующие интегралы.


Глава 13. Исчисление многих переменных
619
Гп1пШ6*Х+ё*ХА2| ,Х,0,1)
10 fnInt<3*YA2+l,Y, Э,2)
10
Рис. 13.40. Численное интегрирование
Определение двойного интеграла
Заметим, что ответы в примерах 13.24.1 и 13.24.2 совпадают. Это свойство позволяет дать следующее определение двойного интеграла.
Двойной интеграл
Двойным интегралом функции f(x, у) в прямоугольной области
-R = {(я, у) I а < х b, c^y^d}
называется интеграл
1
b f(x,y)dA = j
1
d dx = j
~b
| f(x,y)dx
dy.
R
а
_с
с
_d
В двойном интеграле f(x, у) dA, функция f(x, у) называется подынтегральным выражением, a R — областью интегрирования (region of integration). Обозначение dA указывает на то, что интегрирование проводится по двумерной области. Интегралы
II
f(x,y)dy
dx
называются повторными. Порядок записи дифференциалов dx и dy соответствует последовательности вычисления интегралов. Приведенное выше определение двойного интеграла по прямоугольной области не является самым общим. Однако в рассматриваемых нами случаях оно эквивалентно общему определению.
Пример 13.25 (Вычисление двойного интеграла). Вычислите интеграл
в области
R = {(х, у) | 1 х 3, -1 у 2}


620
Часть III. Математический анализ
Решение. Область интегрирования изображена на рис. 13.41.
Рис. 13.41. Область интегрирования
Рассмотрим различные способы выбора порядка интегрирования.
3 2
| (z + у) dА = j (х + у) dy dx = R 1 -1
з
у=2
i/=-i
2 3
J (x + у) dA = j(z + y) dx dy =
R -1 1
2
х=3
dx =
dx =
х—'З
х—1
-1
2
-1
х=1
dy =


Глава 13. Исчисление многих переменных
621
= (4 + 2у) dy = (4у + у2)
-1
= (8 + 4) — (—4+1) =
= 12- (-3) = 15.
Упражнение 13.25.
Вычислите интеграл двумя способами.
Пример 13.26 (Двойной интеграл показательной функции). Вычислите следующий интеграл.
2хех*+у dA в области R = {(х, у) | 0 < х < 1, — 1 < у < 1}
R
Решение. Область интегрирования показана на рис. 13.42.
J 2xex2+v dA
R
1 1
2хех +ydx dy =
-1 о
f Г 2
37 = 1"
= в* +У
-U
Х=0
dy =
Упражнение 13.26.
Вычислите интеграл
J ~2еХ^У в области R = {(ж,у) | 0 х 1, 1 у 2} . R


622
Часть III. Математический анализ
Рис. 13.42. Область
интегрирования
Среднее значение функции в прямоугольной области
В разделе 11.5 определение среднего значения функции f(x) в интервале [а, Ъ] выглядело так.
ь
[ /(х) dx.
о — a J
а
Это определение легко распространить на функции двух переменных в прямоугольной области. Заметим, что выражение (b — a)(d — c) в знаменателе приведенной ниже формулы представляет собой площадь прямоугольника R.
Среднее значение в прямоугольной области
Средним значением (average value) функции /(х, у) в прямоугольнике
R = {(х, у) | а х 6, с у d}
является интеграл
R
Пример 13.27 (Среднее значение функции). Вычислите среднее значение функции /(х, у) = 4 — — ±у в прямоугольной области R = {(ж, у) | 0 < х 2, 0 < у 2}.


Глава 13. Исчисление многих переменных
623
Решение. Область интегрирования R изображена на рис. 13.43.
(l-id-c) I/(1'9)" - (2-0X2-0) f (4 Ч1 4») dA =
R R
2 2
4- -гг- -у) dxdy =
о о
Рис. 13.43. Область интегрирования
На рис. 13.44 изображена поверхность z = f(x,y). Согласно нашим вычислениям среднее значение z лежит над областью R. ■
Упражнение 13.27.
Вычислите среднее значение функции f(x,y) = х + 2у в прямоугольной области R = = {(х,у) I 0 < х 2, 0 у 1}. ■
Задание 13.12.
1. Какая из двух функций, f(x,y) = к —х2 — у2 или д(х,у) = 4 — х — у, имеет большее среднее значение в прямоугольной области R = {(я, у) | 0 < х 1, 0^i/^l}?
2. Проверьте вывод, вычислив двойные интегралы. ■


624
Часть III. Математический анализ
Рис. 13.44. Поверхность z = /(х, у)
Двойные интегралы и объем
Определенные интегралы функций одной переменной позволяют вычислять площади фигур, поэтому нет ничего удивительного в том, что интегралы функций можно использовать для вычисления объемов.
Вычисление объема тела, ограниченного поверхностью
Если в прямоугольной области R = {(х.у) | а х Ь, с у d} выполняется условие f(x,y) 0, то объем тела, расположенного между поверхностью f(x,y) и прямоугольником Я, вычисляется по формуле
V = J/(z12/)dA.
R
Доказательство этого утверждения можно найти в более специализированном учебнике.
Пример 13.28 (Объем). Вычислите объем тела, ограниченного поверхностью f(x,y) = = 1 + х2 + у2 и прямоугольником R = {(х, у) | 0 х 1, 0 < у < 1}.
Решение, Область R показана на рис. 13.45, а тело — на рис 13.46.


Глава 13. Исчисление многих переменных
625
Х=1
х=0
dy =
Рис. 13.45. Область R
Рис. 13.46. Тело
Упражнение 13.28.
Вычислите объем тела, ограниченного поверхностью f(x,y) = 1 + х + у и прямоугольником R = {(ж, у) | 0 х 1, 0 у С 2}. ■
Задание 13.13.
Рассмотрите тело, расположенное под графиком функции f(x,y) = 4 — у2 над прямоугольником R = {(х, у) | 0 х < 3, 0 у < 2}.
1. Объясните, почему сечения этого тела любой плоскостью, параллельной координатной плоскости yz, имеют одинаковые площади, и вычислите их.
2. Вычислите площади сечений тела плоскостями у = 09у=±ку = 1.
3. Вычислите объем тела двумя способами. ■
Ответы к упражнениям
13.22. 1) 2ху2 + Зх2у* + С(х).
2) 2х2у 4- 4х3т/3 + Е(х).
13.23. 1) 2z + 3x2.
2) 181/+ Ю83/3.


626
Часть III. Математический анализ
13.24. 1) 36.
2) 36.
13.25. 12.
13.26. е-2е1/2 + 1.
13.27. 2.
13.28. 5 кубических единиц.
Практикум 13.6
А В задачах 1-8 требуется найти первообразную и с ее помощью вычислить определенный интеграл.
1. а)
12x2y3dy.
2. а)
12x2y3dx.
3..) ]
(4ж + бу 4- 5) dx.
4-а> ]
(4ж + бу + 5) dy.
5.а>]
[ * dx.
1 у/у + X2
\vi^dy-
' In ж ,
7. .)
dy.
ху
8..) _
1 ху
б) j 12x2y3dy.
О
2
б) j 12х2т/3(/х.
-1
3
б) j (4х + бу + 5) dx. -2
4
б) 	j (4х + 61/ + 5) dy.
1
б) [ dx.
1
1
Б В задачах 9-16 требуется вычислить указанные интегралы.
2 1
9.
12т2!/3 dy dx (см. задачу 1).
-1 о
1 2
10.
12x2y3dxdy (см. задачу 2).
о -1


Глава 13. Исчисление многих переменных
627
4 3
11. j | (4х + 61/ + 5) dx dy (см. задачу 3).
1 -2
3 4
j j (4х + 61/ + 5) dy dx (см. задачу 4). -2 1
5 2
[к
е е2
Г 1П X , , .
dydx (см. задачу 7).
J J ху
1 1
12.
13.
15.
X
dxdy (см. задачу 5).
+ х2
14.
16.
X
dydx (см. задачу 6).
0 1 у/у + Х^
е2 е
Г
dxdy (см. задачу 8).
. J ху
1 1
В задачах 17-20 необходимо вычислить двойной интеграл двумя способами.
R
R
R
R
2 5
В задачах 21-24 требуется найти среднее значение каждой функции в указанной прямоугольной области.
21. /(гс,у) = (х + у)2, R = {(х,у) | 1 х 5, -1 у 1}.
22. f(x,у) = х2 + у2, R = {(х,у) | -1 х 2, 1 s$ у 4}.
23. f(x,y) = х/у, R = {(х,у) | 1 х 4, 2 у < 7}.
24. f(x,y) = х2у3, R = {(ге, а/) | -1 < х < 1, 0 < у 2}.
В задачах 25-28 требуется вычислить объем тела, ограниченного указанной поверхностью и заданным прямоугольником.
25. /(х, у) = 2 - х2 - у2, R = {(х, у) | 0 < х < 1, О у 1}-
26. /(х, у) = 5 - х, R = {(х, у) | О < х 5, О < у < 5}.
27. /(х, у) = 4 - у2, R = {(х, у) | О < х < 2, О < у < 2}.
28. /(х,у) = e~x~v, R= {(х, у) | О х 1, О у 1}.
В В задачах 29-32 требуется вычислить двойной интеграл. Внимательно отнеситесь к выбору порядка интегрирования. В каждой из задач процесс вычисления одним способом проще, чем другим.
29. 	J хеху dA, R = {(ж, у) | О х 1, 1 у 2}.
R


628
Часть III. Математический анализ
*33. Докажите, что Jg (1 — у) dx dy = 0. Может ли такой интеграл представлять объем тела? Аргументируйте ответ.
*34. а) Вычислите средние значения функций f(x,y) = х + у, д(х,у) = х2 + у2 и h(x, у) = х3 + т/3 в прямоугольной области
R = {(я, 2/) | о х 1, 0 у 1}.
б) Увеличивается или уменьшается среднее значение функции /с(х, у) = хп+уп в прямоугольной области
= {(х, у) | 0 х 1, 0 у 1}
при увеличении числа п? Аргументируйте ответ.
в) Увеличивается или уменьшается среднее значение функции к(х,у) = хп+уп в прямоугольной области
R2 = {{x,y) |0^х^2, О^т/^2}
при увеличении числа п? Аргументируйте ответ.
35. Пусть /(х, у) = х3 + у2 — е~х — 1.
а) Вычислите среднее значение функции /(х, у) в прямоугольной области R =
= {(х,у) | —2 ^х^ 2,-2 2}.
б) Изобразите в области R все точки (х, у), ддя которых f(x,y) = 0.
в) Для каких точек (х,у) в области R функция f(x,y) больше нуля? Меньше нуля? Аргументируйте ответ.
36. Вычислите размеры квадрата S с центром в начале координат, среднее значение функции /(х, у) = х2еу в котором будет больше 100.
Применение математики
Экономика и бизнес
37. 	Принцип мультипликатора. Предположим, Конгресс США установил единовременное десятипроцентное возмещение налоговых платежей при инвестировании в экономику у млрд, долл., где 5 у 7. Если каждое физическое лицо или корпорация от каждого доллара полученной прибыли тратит долю х,


Глава 13. Исчисление многих переменных
629
где 0,6 х 0,8, то согласно принципу мультипликатора в экономике общее количество истраченных денег S (млрд, долл.) выражается формулой
Чему равен средний расход при указанных пределах переменных хну? Запишите соответствующий двойной интеграл и вычислите его.
38. Принцип мультипликатора. Повторите решение задачи 36 для 6 у 10 и 0,7 х 0,9.
39. Производственная функция Кобба-Дугласа. Предположим, некая отрасль промышленности затрачивает х тысяч единиц труда, где 10 х < 20, и у миллионов единиц капитала, где 1 у < 2, на производство N единиц некой продукции. Функция производительности выражается формулой
N(x,y) = х°'75у0’25.
Чему равен средний объем производства при указанных пределах изменения переменных х и у? Постройте соответствующий двойной интеграл и вычислите его.
40. Производственная функция Кобба-Дугласа. Повторите решение задачи 39 для
^,2/)=x°V’5
при 10 х 30 и 1 < у 3.
Биологические науки
41. WWW Заселение территорий. Для изучения распространения популяций некоторых видов насекомых биологи сконструировали искусственную среду обитания размерами 16 футов в длину и 12 — в ширину. Единственная доступная пища в этой среде сосредоточена в центре. Биологи измеряют концентрацию насекомых на квадратный фут в точке, расположенной на расстоянии d от места нахождения кормушки (рис. 13.47). Функция концентрации насекомых приближенно задается формулой
С = 10-Id2.
Какова средняя концентрация насекомых в этой среде? Выразите величину С в виде функции, зависящей от переменных хну. Запишите и вычислите соответствующий двойной интеграл.
Рис. 13.47. Иллюстрация к задаче 41


630
Часть III. Математический анализ
42. 	Заселение территорий. Повторите решение задачи 41 для квадратной искусственной среды обитания со стороной 12 футов и функцией концентрации вида
Рис. 13.48. Иллюстрация к задаче 42
43. WWW Загрязнение. Завод тяжелой промышленности, расположенный в центре небольшого городка, выбрасывает в атмосферу мелкодисперсные загрязняющие вещества (рис. 13.48). Допустим, что концентрация загрязнения (частиц на миллион) в точке, расположенной на расстоянии d от завода, выражается формулой
С = 100 - 15d2.
Чему равна средняя концентрация загрязняющих веществ в воздухе города, если он занимает прямоугольную область размером 4x2 мили. Выразите величину С как функцию переменных х и у, Запишите и вычислите соответствующий двойной интеграл.
44. Загрязнение. Повторите решение задачи 43 для города, границы которого образуют прямоугольник, имеющий 8 миль в длину и 4 — в ширину. Функция концентрации загрязнения выражается формулой
С = 100 - 3d2.
Социальные науки
45. Исследование безопасности. В идеальных условиях длина тормозного пути автомобиля выражается формулой
L = 0,0000133rry2,
где х — вес автомобиля (в фунтах), а у — скорость автомобиля (миль/ч). Чему равна средняя длина тормозного пути для автомобилей, вес которых изменяется в интервале 2000-3000 фунтов, а скорость — от 50-60 миль/ч? Запишите и вычислите соответствующий двойной интеграл.
46. Исследование безопасности. Повторите решение задачи 45 для автомобилей, вес которых находится в интервале 2000-2500 фунтов, а скорость — 40-50 миль/ч.
47. Психология. Коэффициент умственного развития Q человека с ментальным возрастом х и фактическим возрастом у определяется с помощью формулы
Q(x,y) = 100—.
У


Глава 13. Исчисление многих переменных
631
В группе шестиклассников ментальный возраст колеблется между 8 и 16 годами, а фактический — между 10 и 12. Чему равно среднее значение коэффициента умственного развития в выбранной группе? Запишите и вычислите соответствующий двойной интеграл.
48. 	Психология. Повторите решение задачи 47 для группы школьников с ментальным возрастом между 6 и 14 годами и фактическим возрастом — между 8 и 10 годами.
Ключевые слова, основные обозначения и формулы
1. Функции нескольких переменных. Функции двух независимых переменных; функ¬
ции двух независимых переменных; производственная функция Кобба-Дугласа; трехмерная система координат; тройка чисел параболоид; поверхность;
седловая точка.
z = /(*,y); w = f(x,y,z)
2. Частные производные. Частная производная функции f по переменной ж; частная производная функции f по переменной у; предельная производительность труда; предельная производительность капитала; производные второго порядка.
dz
dz ду'
fx(x,y); fv(x,y);
d1  2  3 4 5 6z
dx2
— fxx У) 5
d2z dydx
— fxy(X) УУ
d2Z dxdy
d2z
dy2
— fyxfa y)]
= fyy(x, УУ
3. Максимум и минимум функции. Локальный максимум; локальный минимум; седловая точка; критическая точка; анализ по второй производной.
4. Поиск максимумов и минимумов методом множителей Лагранжа. Связь; множитель Лагранжа; критическая точка; метод множителей Лагранжа для функции двух переменных; предельная производительность денег; метод множителей Лагранжа для функции трех переменных.
5. Метод наименьших квадратов. Приближение наименьшими квадратами; регрессионный анализ; метод наименьших квадратов; линейная регрессия; прямая наименьших квадратов; регрессионная прямая; нормальные уравнения.
6. Двойные интегралы по прямоугольным областям. Двойные интегралы по прямоугольным областям; двойные интеграл; подынтегральная функция; область интегрирования; повторный интеграл; среднее значение в прямоугольной области; объем под поверхностью.


632
Часть III. Математический анализ
R
V = j/(x,i/)dA.
R
Упражнения для повторения
Выполните все упражнения этого обзорного раздела и сравните результаты с ответами, помещенными в конце книги. Ответы ко многим упражнениям на повторение приводятся вместе с номером соответствующего раздела (курсивом). Если у вас возникают затруднения при решении какой-либо задачи, повторите материал соответствующего раздела.
А
1. Вычислите производные /(5,10), fx(x,y) и /у(х,у) для функции f(x,y) = = 2000 + 40х + 70г/.
2. Вычислите производные d2zfdx2 и d2z/dxdy для функции z = х3у2.
3. Вычислите интеграл J (бод2 + 4t/) dy.
4. Вычислите интеграл J (бод2 4- 4?/) dx.
5. Вычислите интеграл J*j 4ху dy dx.
* 6. Вычислите производные /х(ж, у), fy(x, у) для функции /(ж, у) = 6 + 5х — 2у + +Зт2+я3 и объясните, почему функция /(ж, у) не имеет локального экстремума.
Б
7. Вычислите значения /(2,3), fy(x,y) и Д(2,3) для функции f(x,y) = Зя2 - - 2ху 4- у2 - 2х + Зт/ - 7.
8. Вычислите выражение [fxx(2,3)][/2/2/(2,3)] - [fxy(2,3)]2 для функции f(x,y) = = —4х2 4- 4ху — Зу2 4- 4z + Ют/ 4- 81.
9. Пусть f(x,y) = х 4- Зу и д(х, у) = х2 + у2 — 10. Найдите критические точки функции F(x, у, А) = /(х, у) 4- Хд(х, у).
10. 	С помощью прямой наименьших квадратов для данных, приведенных в таблице, оцените значение у при х = 10.
X
У
2
12
4
10
6
7
8
3
11. 	Для области R= {(х, у) | — 1^д:^1,1^т/^2} вычислите двойной интеграл JJ (4х -F 6т/) dA двумя способами.
R


Глава 13. Исчисление многих переменных
633
в
12. Вычислите производные fx, fy, и fxy для функции f(x, у) = ех +2у.
13. Вычислите производные fx, и fxy для функции f(x,y) = (х2 + у2)5.
14. Найдите критические точки и проверьте существование экстремумов функции
/(ж, у) = х3 - 12х + у2 - бу.
15. С помощью метода множителей Лагранжа найдите максимум функции f(x,y) = = ху при условии 2х + Зу = 24.
16. С помощью метода множителей Лагранжа найдите максимум функции f (я, у ,z) = = х2 +у2 + z2 при условии 2х + у + 2z = 9.
17. Постройте прямую наименьших квадратов для данных, приведенных в таблице.
X
У
X
У
10
50
60
80
20
45
70
85
30
50
80
90
40
55
90
90
50
65
100
110
18. Вычислите среднее значение функции /(я, у) = х2/3у^3 в прямоугольной области
R = {(ж, у) | -8 х 8, 0 у 27}.
19. Вычислите объем тела, ограниченного поверхностью z = Зх2 + З?/2 и прямоугольником
R = {(х,у) | 0 х 1, -1 у 1}.
* 20. Предскажите среднее значение функции /(х, у) = х+у в прямоугольной области R = {(#, 1/) | — Ю < х 10, —10 у 10} не производя никаких вычислений. Проверьте результат, вычислив соответствующий двойной интеграл.
*21. а) Вычислите такие размеры квадрата S которых среднее значение функции
с центром в начале координат, при
f(x,y) =
У + 10
в области S равно 5.
б) Может ли существовать такой квадрат с центром в начале координат, для которого среднее значение функции
ех
У+ 10
в этой области равно 0,05? Аргументируйте ответ.
* 22. Объясните, почему функция /(ж, у) = 4х3 — 5у3 не имеет максимума или минимума при условии Зх 4- 2у = 7.


634
Часть III. Математический анализ
Применение математики
Экономика и бизнес
23. Максимальная прибыль. Предположим, некое предприятие производит х единиц продукции Ану единиц продукции В (сотен штук в месяц). Функция месячной прибыли (в сотнях долларов) описывается формулой
Р(х, у) = — 4х2 + 4хт/ — Зу2 + 4х + Ют/ -I- 81.
*а) Вычислите значение Рх(1,3) и проанализируйте полученный результат.
б) Какой объем продукции каждого вида должна производить компания для получения максимальной прибыли? Чему равна максимальная прибыль?
24. Минимальные расходы материала. Прямоугольная коробка без верха, разделенная на шесть отделений (рис. 13.49), должна иметь объем, равный 96 куб. дюймам. Найдите размеры коробки, при которых расход материала на ее изготовление будет минимальным.
Рис. 13.49. Иллюстрация к задаче 24
25. 	Прибыль. В таблице приведены объемы годовой прибыли некой компании за пятилетний период (млрд. долл.). Вычислите прибыль этой компании в шестом году с помощью уравнения линейной регрессии.
Год
Прибыль
1
2
2
2,5
3
3,1
4
4,2
5
4,3
26. 	Производительность. Производственная функция Кобба-Дугласа для некой продукции имеет вид
N(x,y) = 10х0,8у0,2;
где х — объем труда, ат/ — объем капитала, затрачиваемых на производство N единиц продукции.
а) 	Вычислите предельную производительность труда и капитала при х = 40 и у — 50. Какой из показателей нужно увеличить для повышения производительности — затраты труда или капитала?


Глава 13. Исчисление многих переменных
635
б) Пусть затраты единицы труда составляют 100 долл., а единицы капитала — 50 долл., бюджет на производство продукции — 10000 долл. С помощью метода множителей Лагранжа определите объемы труда и капитала, при которых достигается максимальный объем производства. Вычислите предельную производительность денег и приблизительно оцените повышение объема производства при увеличении бюджета на 2000 долл.
в) Пусть 50 х < 100, 20 < у 40. Вычислите средний объем производства. Запишите соответствующий определенный интеграл и вычислите его.
Биологические науки
27. 	Биология моря. Функция, определяющая максимальное время погружения аквалангиста, имеет вид
где Т — время погружения в минутах, V — объем закачанного в балон воздуха (куб. футов, измеренного при атмосферном давлении), х — глубина погружения в футах. Вычислите значения Тж(70,17) и проанализируйте результат.
28. 	Загрязнение. Завод тяжелой промышленности, расположенный в центре маленького города, выбрасывает в атмосферу мелкодисперсные загрязняющие вещества. Допустим, что концентрация загрязнения (частиц на миллион) на расстоянии d от завода описывается формулой
С = 100 - 24</2.
Допустим, что размеры города составляют 4 мили в длину и 4 мили в ширину. Какова будет средняя концентрация частиц в городе? Выразите величину С через переменные х и у, запишите соответствующий двойной интеграл и вычислите его.
Социальные науки
29. Социология. Социолог Йозеф Кавана (Joseph Cavahaugh) изучал зависимость количествам телефонных звонков п за некоторый период между двумя удаленными городами с населением Pi и Р2 соответственно, от расстояния между ними d. Формула, выражающая эту зависимость для недельного периода, имеет вид
Р1Р9
n(P!,P2,d) = 0,001-^.
Вычислите значение п(100 000,50 000,100).
30. Образование. В начале семестра студенты сдают квалификационный экзамен по иностранному языку для проверки их уровня подготовки. Такой же экзамен они сдают и в конце семестра. С помощью прямой наименьших квадратов вычислите оценку, которую получит студент на втором экзамене, если на первом он получил 40 баллов.


636
Часть III. Математический анализ
Первый экзамен
Второй экзамен
30
60
50
75
60
80
70
95
90
90
31. 	WWW Плотность населения. В следующей таблице приведены данные о плотности населения на квадратную милю в Соединенных Штатах за 1900-2000 годы.
Плотность населения в Соединенных Штатах
Год
Плотность населения, чел./кв. милю
Год
Плотность населения, чел./кв. милю
1900
25,6
1960
50,6
1910
31,0
1970
57,4
1920
35,6
1980
64,0
1930
41,2
1990
70,4
1940
44,2
2000
77,8
1950
50,7
а) Постройте прямую наименьших квадратов, полагая х — 0 для 1900 года.
б) Используя линейную регрессию, оцените плотность населения в Соединенных Штатах в 2010 году.
в) Повторите оценку методами квадратичной и экспоненциальной регрессии.
32. 	Продолжительность жизни. В таблице приведены данные о ожидаемой средней продолжительности жизни мужчин и женщин в некоторых странах Центральной и Южной Америки.
Средняя продолжительность жизни в странах Центральной и Южной Америки
Мужчины
Женщины
Мужчины
Женщины
62,30
67,50
70,15
74,10
68,05
75,05
62,93
66,58
72,40
77,04
68,43
74,88
63,39
67,59
66,68
72,80
55,11
59,43
а) Постройте прямую наименьших квадратов для этих данных.
б) Используя линейную регрессию, оцените среднюю продолжительность жизни женщин в центрально- или южноамериканской стране, если продолжительность жизни мужчин в ней составляет 60 лет.
в) Повторите оценку методами квадратичной и логарифмической регрессии.
33. 	WWW Доля женщин в трудовых ресурсах. Из приведенной ниже таблицы можно заключить, что среди японских женщин много таких, кто намерен оставить на


Глава 13. Исчисление многих переменных
637
время работу, чтобы выйти замуж и воспитывать детей, однако вернуться к ней после взросления детей.
Доля женщин в трудовых ресурсах Японии, 1997 г.
Возраст, лет
Доля работающих женщин, %
Возраст, лет
Доля работающих женщин, %
22
73
47
72
27
65
52
68
32
56
57
59
37
63
62
42
42
71
а) Объясните, почему от модели кубической регрессии можно ожидать лучшего описания этих данных, чем от линейной и квадратичной.
б) Проверьте предположение, изобразив точки данных в одной системе координат с кривыми линейной, квадратичной и кубической регрессии.
Домашнее задание 13.1. Планирование города
Комитет по планированию города должен принять решение о местах расположения нового зоопарка и новой больницы. Поступления в бюджет города напрямую зависят от двух заводов, расположенных вблизи его центра. Оба загрязняют атмосферу мелкодисперсными веществами и это обстоятельство должно быть принято во внимание комиссией при выработке окончательного решения. Было решено, что новый зоопарк будет построен в наименее загрязненном районе на окраине города, а новый госпиталь — в наименее загрязненном районе в двух милях от центра.
Город занимает прямоугольную территорию с размерами 10 миль в направлении с востока на запад и 6 миль с севера на юг. Если выбрать систему координат с началом в центре прямоугольника (т.е, в центре города), то первый завод имеет координаты (—1,1), а второй — (1,0). В точке с координатами (ж, у) уровень загрязнения первого завода описывается функцией Ci = 200 — (di)2, где di — расстояние от точки до первого завода. Аналогично уровень загрязнения второго завода описывается функцией С2 = 200 — (с^)2, где d2 — расстояние от точки (ж, у) до второго завода.
1. Найдите точку в пределах города, в которой концентрация загрязняющих веществ максимальна.
2. Найдите точки на границах города, в которых концентрация загрязняющих веществ максимальна и минимальна.
3. Вычислите среднюю концентрацию загрязняющих веществ в городе.


638
Часть III. Математический анализ
4. На окружности с центром в центре города и радиусом в две мили найдите точки, в которых концентрация загрязняющих веществ максимальна и минимальна.
5. Определите оптимальное расположение новой больницы и зоопарка.
Домашнее задание 13.2. Численное интегрирование функций многих переменных
Определенный интеграл /(х, у) dx является пределом сумм Римана (см. раздел 11.5) вида
п
k=\
Аналогично двойной интеграл /(х, г/) dxdy в прямоугольной области R — {(х,у) | является пределом сумм вида
7П П
j=i k=i
где а х0 < хг < х2 < ■. ■ < хт = Ь, с = у0 < у! < у2 < ■ ■ ■ < уп = d, ^_i < cj С xj для j = 1,2,..., т и yk-i < dk < ук для к = 1,2,... ,п.
Оказывается, что такие методы численного интегрирования, как формула Симпсона (см. домашнее задание 11.1), применимы также и для приближенных вычислений двойных интегралов. Рассмотрим пример такого вычисления.
Пример 13.29 (Использование формулы Симпсона для вычисления двойных интегралов). С помощью формулы Симпсона приближенно вычислите интеграл
4 6 j (х2у + 2у2 + Зх + 1) dy dx, о о
разделяя интервал [0,4] на четыре равные части, а [0,6] — на шесть равных частей.
Решение. Вычислим значения функции /(х, у) = х2у + 2у2 + Зх + 1 в 35 узлах сетки, образованной указанным разбиением интервалов (табл. 13.9).
Таблица 13.9. Значения функции в узлах сетки
у = о
1
2
3
4
5
6
х = 0
1
3
9
19
33
51
73
150
1
4
7
14
25
40
59
82
186
2
7
13
23
37
55
77
103
258
3
10
21
36
55
78
105
136
366
4
13
31
53
79
109
143
181
510


Глава 13. Исчисление многих переменных
639
Далее воспользуемся формулой Симпсона для каждого из шести равных подынтервалов, соответствующего строке таблицы, и обозначим результаты вычисления как Rj, записывая в последний столбец. Например, полагая д(у) = f(xo, у), получим
А?/
Яо = [р(1/о) + 4g(j/i) + 2с?(з/2) + 4р(у3) + 25(54) + 45(1/5) + 5(55)] -у = = [1 + 4- 3 + 2- 9 + 419 + 3-33 + 4-51 + 1-73]| = 150.
О
Наконец, используем формулу Симпсона для четырех равных подынтервалов оставшегося интервала для значений 7?0, -Ri, R2, R3 и R±.
5 	= [Яо + 47?! + 2Я2 + 42?з + Я4] =
и
= [150 + 4 • 186 + 2 • 258 + 4 • 366 + 510] | = 1128.
О
Таким образом, двойной интеграл J* (х2у + 2у2 + Зх + 1) dydx приблизительно равен 1128. ■
В примере 13.29 двойной интеграл можно вычислить как повторный. Точное значение двойного интеграла также равно 1128. Нет ничего удивительного в том, что применение формулы Симпсона для полиномов третьего и более низких порядков дает точный результат. Метод, описанный выше, может быть использован и в случаях, когда невозможно найти первообразную для функции f(x,y) или тогда, когда для функции f(x,y) нет явной формулы, а есть только таблица некоторых значений.
1. Вычислите двойной интеграл в примере 13.29 как повторный.
2. Покажите, что формулу Симпсона для интеграла в примере 13.29 можно использовать и в обратном порядке: сначала для столбцов табл. 13.9 вычисляются значения Со, Ci, Сг, Сз, С4, С5, Сб, а затем применяется формула Симпсона.
3. С помощью формулы Симпсона вычислите приближенно интеграл
з з
116~^Х о о
разделяя каждый из интервалов на шесть равных подынтервалов и вычисляя значения функции f(x,y) = е~(х +г/ > с точностью до четырех десятичных знаков в каждом из 49 узлов построенной решетки.
4. Повторите решение п. 3, используя для вычисления значений Rj вместо формулы Симпсона подпрограмму численного интегрирования, предусмотренную в графической утилите.
5. Известно, что объем тела, ограниченного поверхностью функции f (х, у) = = е~^х +у ) и первым квадрантом, равен тг/4. Сравните результаты решения пп. 3 и 4 с этим значением и объясните причину различия.


14
Дифференциальные уравнения
■ 14.1. Основные понятия
■ 14.2. Разделение переменных
■ 14.3. Линейные дифференциальные уравнения первого порядка
■ Ключевые слова, основные обозначения и формулы
■ Упражнения для повторения
■ Домашнее задание 14.1. Закон Торричелли
■ Домашнее задание 14.2. Метод Эйлера
Введение
Математические модели многих процессов в природе и обществе лучше всего строить на основе представления о скорости их проистечения. Например, скорость роста численности популяции может быть пропорциональна размеру популяции или разности между ним и некоторым фиксированным пределом. В подобных случаях скорость процесса или явления можно кратко выразить с помощью дифференциальных уравнений, например
= ky, ^=k(M-y), ^=ky(M-y).
Такие дифференциальные уравнения моделируют несколько типов экспоненциального роста — неограниченный, ограниченный и логистический (см. табл. 11.3). К сожалению, не существует единого метода решения всех возможных дифференциальных уравнений. В этой главе после введения основных понятий будут рассмотрены методы решения всего нескольких типов дифференциальных уравнений, которые имеют очень важное практическое применение.


Глава 14. Дифференциальные уравнения
641
14.1. 	Основные понятия
■ Решение дифференциального уравнения
■ Неявное решение
■ Решение практических задач
В этом разделе рассматриваются основные понятия, описанные в разделе 11.3, и вводится понятие решения дифференциального уравнения, включая явное и неявное представление. Конкретные методы решения дифференциальных уравнений будут рассмотрены в следующих двух разделах.
Решение дифференциального уравнения
Дифференциальное уравнение — это уравнение, содержащее неизвестную функцию, как правило обозначаемую у, и одну или несколько ее производных. Например, выражение
у' = 0,2ху (14.1)
является дифференциальным уравнением. Поскольку в этом уравнении содержится только первая производная неизвестной функции, оно называется дифференциальным уравнением первого порядка. В общем случае, порядок дифференциального уравнения — это наивысший порядок производной неизвестной функции, встречающийся в уравнении.
Следует отметить, что в уравнении (14.1) для обозначения производной функции у по переменной х вместо выражения dy/dx используется символ у'. Это распространенная практика при записи дифференциальных уравнений. Если не оговорено противное, далее будет предполагаться, что у — это функция независимой переменной х, а у' обозначает производную у по переменной х.
Задание 14.1. Рассмотрим дифференциальное уравнение
у' = 2х (14.2)
1. Какие из следующих функций удовлетворяют этому уравнению?
у = х2, у = 2х2, у = х2 + 2.
2. Существуют ли другие функции, удовлетворяющие уравнению (14.2)? Какой вид должны иметь все эти функции?
3. Рассмотрите возможные методы решения произвольного дифференциального уравнения вида
у' = f(x). в
На рис. 14.1, а показано поле направлений уравнения (14.1). Напомним (см. раздел 11.3), что поле направлений дифференциального уравнения получается путем построения отрезков касательных, найденных из уравнения, в каждой точке координатной сетки. Оно позволяет дать геометрическую интерпретацию общих принципов решения уравнения. Из-за огромного количества отрезков прямых, поля направлений, как правило,


642
Часть III. Математический анализ
WWW
1 \ X X X X X \ X X \ -
[х/ / J И ■-■/// > <« -XX///
'и"?
/ / / / /- , / / / м
: --ччЧ
’'ХХ X X X -\ХХ XX Sx х 1 \
б)
Рис. 14.1. Поле направлений для уравнения у' = 0,2x1/
строятся с помощью графической утилиты. На рис. 14.1, б показано поле направлений для уравнения yf = 0,2ху, построенное с помощью графического калькулятора TI-83 Plus.
Рассмотрим теперь функцию
т/ = 2е°’1аЛ
производная которой равна
У1 = 2е°’1ж2 • 0,2х = О,4хе0’112.
Подстановка функций у и у' в уравнение (14.1) приводит к соотношениям
у' = 0,2ху
0,4хе°’1х2 = 0,2ж • 2е°’1х2,
0,4хе°’1х2 =0,4хе°’1х2,
которые являются справедливыми для любых значений х. Это указывает на то, что функция у = 2е0,1х является решением уравнения (14.1). Однако эта функция — не единственное решение. Фактически, если С — произвольная постоянная, то, подставляя функции


Глава 14. Дифференциальные уравнения
643
у = Се0,1х2 и у' = О,2хСео,1х2 в уравнение (14.1), получим тождество
у' = 0,2жу
0,2хСе°'1х2 = 0,2хСео'1х\
Оказывается, все решения уравнения у' = 0,2ху можно получить из выражения у = = Се°'1х , присваивая константе С соответствующие значения. По этой причине функция у = Се011 называется общим решением уравнения (14.1). Совокупность функций вида у = Се0,1® называется семейством решений уравнения (14.1). Функция у = 2e0,hE , которую можно получить, полагая в общем решении С = 2, называется частным решением уравнения (14.1). Другими частными решениями являются функции
2, = _2е°’1ж2,
С =—2,
У = -е°’1х2,
С = -1,
у = о,
С = 0,
У-е^х2,
С = 1.
Эти частные решения (вместе с полем направлений уравнения (14.1)) изображены на рис. 14.2. Обратите внимание на то, как частные решения согласуются с направлениями, указанными полем направлений.
Рис. 14.2. Частные решения уравнения у' = 0,2а;?/
Замечание: нахождение общих решений.
Большинство, но не все, дифференциальные уравнения первого порядка имеют общее решение, в которое входит произвольная постоянная. Если найдена функция, такая как у = = Се°'1х , удовлетворяющая данному дифференциальному уравнению для произвольного значения постоянной С, то эта функция является общим решением.


644
Часть III. Математический анализ
Пример 14.1 (Проверка решения дифференциального уравнения). Покажите, что функция
у = Сх2 + 1
является общим решением дифференциального уравнения
ху' = 2у — 2.
В одних и тех же координатных осях постройте графики частных решений, для которых С = -2, -1, 0, 1 и 2.
Решение, Подставляя функции у = Сх2 + 1 и у' = 2Сх в дифференциальное уравнение, получим
ху' = 2у — 2
х • 2Сх = 2(Сх2 + 1) — 2,
2Сх2 = 2Сх2 + 2-2,
2Сх2 = 2Сх2.
Это значит, что функция у = Сх2 + 1 является общим решением. Графики частных решений, соответствующих константам С — —2, —1, 0, 1 и 2, показаны на рис. 14.3. ■
Рис. 14.3. Частные решения уравнения ху' = 2у —2
Упражнение 14.1.
Покажите, что функция
у = Сх + 1
является общим решением дифференциального уравнения
ху' = у - 1.
В одних и тех же координатных осях постройте графики частных решений, для которых
С = —2, -1, 0, 1 и 2. ■


Глава 14. Дифференциальные уравнения
645
Во многих практических задачах нужно будет находить частные решения у(х), удовлетворяющие начальным условиям вида у(хо) = у о. В таком случае значение константы С в общем решении следует выбирать таким образом, чтобы оно удовлетворяло начальным условиям, т.е. чтобы фазовая траектория (из семейства фазовых траекторий) проходила через точку (z0, уъ).
Пример 14.2 (Поиск частного решения). Используя общее решение в примере 14.1, найдите частное решение дифференциального уравнения ху' = 2у — 2, удовлетворяющее указанным условиям, если такое решение существует.
1. 	2/(1) = 3. 2. 2/(0) = 3. 3. 7/(0) = 1.
Решение,
1. Начальное условие 2/(1) — 3. Из примера 14.1 следует, что общее решение дифференциального уравнения имеет вид
2/ = Сх2 + 1.
Подстановка значений х = 1и2/ = 3в это общее решение приводит к следующему результату.
3 = С-12 + 1 = С + 1,
С = 2.
Таким образом, частным решением, удовлетворяющим начальному условию 2/(1) = = 3, является функция
у = 2х2 + 1.
Смотрите график на рис. 14.3 с пометкой С = 2.
2. Начальное условие y(Q) = 3. Подстановка значений х = Ои2/ = Зв общее решение приводит к следующему соотношению.
3 = С02 + 1.
Независимо от того, какое значение С будет выбрано, С ■ О2 = 0 и это уравнение сводится к соотношению
3 = 1,
которое всегда неверно. Таким образом, не существует частного решения данного дифференциального уравнения, которое удовлетворяло бы начальному условию 2/(0) = 3.
3. Начальное условие 2/(0) = 1. Подстановка значений ж = 0и2/ = 1в общее решение приводит к следующим соотношениям.
1 = С • О2 + 1,
1 = 1.
Это равенство справедливо для всех значений С. Следовательно, все решения этого дифференциального уравнения удовлетворяют начальному условию 2/(0) = 1 (см. рис. 14.3). ■


646
Часть III. Математический анализ
Замечание: характер частных решений.
Ситуация, проиллюстрированная в примере 14.2, весьма распространена. Большинство дифференциальных уравнений первого порядка, с которыми нам придется встречаться, имеют единственное частное решение, удовлетворяющее данным начальным условиям. Однако необходимо осознавать: существует возможность того, что дифференциальное уравнение может не иметь ни одного частного решения, удовлетворяющего данным начальным условиям, или того, что оно может иметь много частных решений, удовлетворяющих данному начальному условию.
Упражнение 14.2.
Используя общее решение, определенное в упражнении 14.1, найдите частное решение дифференциального уравнения ху' = у—1, которое удовлетворяет указанному начальному условию, если такое решение существует.
1. 	3/(1) = 2. 2. 7/(0) = 2. 3. 7/(0) = 1. .
Неявные решения
Применение метода, рассмотренного в этом разделе, всегда приводит к неявному решению дифференциального уравнения. В большинстве дифференциальных уравнений, которые здесь рассматриваются, явный вид решения можно найти позже, решая неявное уравнение относительно зависимой переменной.
Задание 14.2.
Пусть у — функция, заданная неявно уравнением
ху = С, где С — константа. (14.3)
1. Продифференцировав неявно уравнение (14.3), найдите дифференциальное уравнение, в которое входят у и у'.
2. Решите уравнение (14.3) относительно величины у и убедитесь, что результат удовлетворяет дифференциальному уравнению, выведенному при решении п. 1. ■
Пример 14.3 (Проверка неявного решения). Пусть функция у задана неявным уравнением
у3 + еу — х4 = С. (14.4)
Покажите, что функция у удовлетворяет дифференциальному уравнению
(Зу2 + ey\yf = 4ж3.
Решение. Воспользуемся неявным дифференцированием и покажем, что функция у удовлетворяет данному дифференциальному уравнению.
Следует помнить, что —хп = пхп 1 dx
и — ех = е®, но — уп = пуп~1у' dx dx
d .
и —ev = еуу , поскольку у является dx
функцией х.


Глава 14. Дифференциальные уравнения
647
Итак, выполненные вычисления показывают, что любая функция у9 заданная неявным уравнением (14.4), является решением этого дифференциального уравнения. Явную формулу для функции у в данном случае найти нельзя, поскольку она не выражается через конечное количество комбинаций элементарных функций. ■
Упражнение 14.3.
Пусть функция у задана неявным уравнением
у + еу2 - х2 = С. (14.5)
Покажите, что функция у удовлетворяет дифференциальному уравнению
(l + 2yey2^y'= 2х. и
Пример 14.4 (Поиск явного решения). Покажите, что функция у удовлетворяет дифференциальному уравнению
УУ1 - х,
если она задана неявно уравнением
у2-х2 = С.
Найдите явное выражение для частного решения, удовлетворяющего начальному условию 2/(0) = 2.
Решение. Используя неявное дифференцирование, получим
у2 -х2 = С,
2уу' - 2х = 0, 2уу' = 2х, уу' = х.
Следовательно, функция у удовлетворяет данному дифференциальному уравнению. Подставляя в уравнение у2 — х2 = С значения х = 0 и у = 2, получим следующий результат.
у2 -X2 = С,
22 - О2 = С,
4 = С.
Следовательно, частное решение, удовлетворяющее условию 2/(0) = 2, является реше¬
нием уравнения
= 4,
или
у2 = 4 + х2.


648
Часть III. Математический анализ
Решая последнее уравнение относительно у, получим два явных решения:
У1 (х) = -\/4 + гг2 и у2 (х) = - \/4 + х2.
Первое из этих двух решений удовлетворяет условию
У1 (0) = V4 + 02 = V4 = 2,
в то время как второе решение удовлетворяет условию
У1 (0) = - \/4 + 02 = -V4 = —2.
Следовательно, частным решением дифференциального уравнения уу' — х, удовлетворяющим начальному условию р(0) = 2, является функция
у (х) = \/4 + z2.
Проверка,
у'(х) = | (4 + X2) 1/2 2х =
X
\/4 + х2
уу' = X
\\/4 + х2/
X = X
■
Упражнение 14.4.
Покажите, что функция у удовлетворяет дифференциальному уравнению
W = 1,
если она задана неявно уравнением
У2 - х = С.
Найдите явное выражение для частного решения, удовлетворяющего начальному условию 2/(0) = 3. .
Решение практических задач
WWW В экономике часто изучают цену на товар за определенный период, поэтому вполне естественно рассматривать цену как функцию времени. Пусть функция p(t) — цена определенного товара в момент времени t. Если функция p(t) стремится к предельному значению р, когда t стремится к бесконечности, то говорят, что цена на этот товар динамически стабильна, а р называют равновесной ценой. (Позднее это определение равновесной цены будет связано с определением, которое было дано в разделе 12.2.) Чтобы изучить поведение цены как функции времени, экономисты часто предполагают, что цена удовлетворяет дифференциальному уравнению. Этот подход проиллюстрирован следующими примерами.


Глава 14. Дифференциальные уравнения
649
Пример 14.5 (Динамически стабильная цена). Предположим, что цена p(t) удовлетворяет дифференциальному уравнению
= 10 - 0,5р; t > 0.
1. Покажите, что функция
p(t) = 20 - Ce_0,5t
является общим решением данного дифференциального уравнения, и найдите значение
р = lim р (t).
t—>оо
2. В одной и той же системе координат постройте графики трех частных решений, удовлетворяющих начальным условиям р(0) = 40, р(0) = 10 и р(0) = 20.
3. Проанализируйте долговременное поведение цены этого товара.
Решение.
1. р(£) =20-C'e~°’5t;
p'(t) = 0,5Ce~°’5t.
Подставляя эти зависимости в дифференциальное уравнение, получим следующий результат.
g = W-0,5р.
0,5Ce°’5t = 10 - 0,5 (20 - Се-0’5*) = = 10 - 10 + O,5Ce_o,5t = = O,5Ce_o,5t.
Следовательно, функция p(t) = 20 — Ce~0,5t является общим решении диффе- ренциального уравнения. Чтобы найти равновесную цену, необходимо вычислить значение предела lim^^ р (£).
Р = Дт ₽(*) =
= lim (20 - Ce~0,5t) =
t—>оо v 7
= 20 - C lim e_0,5t = lim e-°-6t = о
t—>OO t—>oo
= 20-CO.
= 20.
2. Для того чтобы построить графики трех частных решений, необходимо найти значение постоянной С для каждого из указанных начальных условий. В каждом случае


650
Часть III. Математический анализ
будет использоваться уравнение
р(0) =
= 20 - Се° = 20 -
-с-
р(0) =
= 40;
р(0) = Ю;
р(0) = 20:
20 - С =
= 40;
20 - С = 10;
20 - С = 20:
С =
= -20;
С = 10;
С = 0;
p(t) =
= 20 + 20е~°’5‘.
p(t) = 20 - 10e“°’5t.
p(t) = 20
Графики решений показаны на рис. 14.4.
Рис. 14.4. Частные решения уравнения = Ю - 0,5р
3. 	Равновесная цена р не зависит от постоянной С и, следовательно, от начального значения функции цены р(0) (см. рис. 14.4). Если р(0) > р, то цена убывает по мере приближения к р как к предельному значению. Если р (0) < р, то цена растет по мере приближения к р как к предельному значению. Если р (0) = р, то цена остается постоянной для всех значений t. ■
Упражнение 14.5.
1. Покажите, что функция
p(t) = 25 - Ce“°’2t
является общим решением дифференциального уравнения
ф
— = о dt
t > 0.
0,2р;
Вычислите равновесную цену р.
2. В одной и той же системе координат постройте графики трех частных решений, удовлетворяющих начальным условиям р(0) = 40, р(0) = 5 и р(0) = 25.
3. Проанализируйте долговременное поведение цены этого товара. ■


Глава 14. Дифференциальные уравнения
651
Ответы к упражнениям
14.1.
14.2. 	1) у = х+1.
14.3.
2) Частное решение не существует.
3) у = Сх 4-1 для любого С.
d d -.2 d о d
dxУ dx dx dx
yf + ey22yy' - 2x = 0;
(1 4- 2yey2^ y' = 2x.
14.4. у (т) = \/9 4- x.
14.5. 1) p = 25.
3) Если p (0) > p, то цена убывает по мере приближения к р как к предельному значению. Если р (0) < р, то цена растет по мере приближения к р как к предельному значению. Если р (0) = р, то цена остается постоянной для всех значений t.


652
Часть III. Математический анализ
Практикум 14.1
А В задачах 1-6 покажите, что данная функция является общим решением указанного
дифференциального уравнения.
1. у = Сх2; ху' = 2у.
1 С >
Ъ.у=—; ху' = -у.
х
5. 	у - 4 + Се1; у' = у - 4.
2. 	у = С(х - I)2; (х - 1)у' = 2у. (J
4. 	у= ——(х +1)1/' = -у.
х +1
6. 	у = 1,5 + Ce~2t; у' = 3 - 2у.
В задачах 7-10 требуется определить, какое из следующих полей направлений а-г соответствует указанному дифференциальному уравнению. Кратко обоснуйте свой ответ.
7. 	ху' = 2у (из задачи 1). 8. (х — Y)y' = 2у (из задачи 2).
9. ху' = —у (из задачи 3). 10. (х + 1)у' = —у (из задачи 4).
В задачах 11-14, используя подходящее поле направлений из задач 7-10 (а, б, в или г), необходимо построить графики частных решений, для которых С = —2, —1, 0, 1 и 2.
11. у = Сх2 (из задачи 1). 12. у = С(х — I)2 (из задачи 2).
задачи 3). 14. у = —
х
Б В задачах 15-20 покажите, что данная функция у является общим решением указанного дифференциального уравнения. Найдите частное решение, удовлетворяющее данному начальному условию.
15. у = 3 + Зх + Сех; у' — у - Зх; 1/(0) = 4.
16. у = — 4 — 4х + Сех; у' - у + 4х; i/(0) = 1.
(из задачи 4).


Глава 14. Дифференциальные уравнения
653
17. у = хе х + Се х; у' = —у + е х; у(0) = 0.
18. у = хе2х + Се2®; у' = 2у + е2х; у(0) = 0.
С
19. у = 2х + —; ху' = 4х -у; у(1) = 1.
X
(J
20. у = -Зх Ч ; ху' + у = -6х; г/(1) = 2.
х
В задачах 21-24, пользуясь процедурой неявного дифференцирования, покажите, что если функция у задана неявным уравнением, то она удовлетворяет указанному дифференциальному уравнению.
21. у3 + ху - х3 = С; (З?/2 + х)у’ = Зх2 - у.
22. у + х3у3 — 2х = С; (1 + x3y2)yf = 2 — Зя2?/3.
23. ху + еу2 — х2 = С; (х + 2.уеу2^ у' = 2х — у.
24. у+ еху - х = С; (1 + хеху\у' = 1 - уеху.
В задачах 25-28, пользуясь процедурой неявного дифференцирования, покажите, что если функция у задана неявным уравнением, то она удовлетворяет указанному дифференциальному уравнению. Найдите явное выражение для частного решения, удовлетворяющего данному начальному условию.
25. у2 + х2 = С; уу' = -х; у(0) - 3.
26. у2 + 2х2 = С; уу1 = -2х; у(0) = -4.
27. 1п(2 - у) = х + С; у' = у - 2; у(0) = 1.
28. 1п(5 - у) = 2х + С; у' = 2(у - 5); у(0) = 2.
В задачах 29-32, используя общее решение дифференциального уравнения у, найдите частное решение, удовлетворяющее начальному условию. Постройте графики частных решений для х 0.
29.
у = 2 + Се х\у' = 2-у. а) 2/(0) = 1.
б)
2/(0) = 2.
В)
2/(0) = 3.
30.
У = 4 + Се~х; у' =4 -у. а) 2/(0) = 2.
6)
2/(0) = 4.
в)
2/(0) = 5.
31.
у = 2 + Сех; у' = у - 2. а) 2/(0) = 1.
б)
2/(0) = 2.
В)
2/(0) = 3.
32.
У = 4 + Се1; у' = у - 4. а) 2/(0) = 2.
б)
2/(0) = 4.
в)
2/(0) = 5.
В задачах 33-36 запишите дифференциальное уравнение, соответствующее данному описанию скорости. Объясните, что означает каждый символ в этом уравнении.
* 33. Количество работников корпорации растет со скоростью 650 чел. в год.
* 34. Кровяное давление в аорте между ударами сердца растет со скоростью, пропор¬
циональной кровяному давлению.
* 35. Вынутая из печи пицца остывает со скоростью, пропорциональной разнице меж¬
ду температурой пиццы и комнатной температурой 72°Е


654
Часть III. Математический анализ
* 36. Вынутое из холодильника молоко нагревается со скоростью, пропорциональной разнице между комнатной температурой и температурой молока.
В В задачах 37 и 38, используя общее решение дифференциального уравнения у, найдите частное решение, удовлетворяющее указанному начальному условию. Постройте графики частных решений для х 0.
37-У=1+Х-х;^ = 0’^(10-^
а) 2/(0) = 1. б) у(0) = 10. в) 2/(0) = 20.
(Подсказка. Частное решение п. а в точке х = 1п 9 соответствует точке перегиба.)
38‘ У = l + Ce-1’ У> = °’2j/(5 _
а) 2/(0) = 1. б) 2/(0) = 5. в) 2/(0) = 10.
(Подсказка. Частное решение п. а в точке х — 1п 4 соответствует точке перегиба.)
В задачах 39 и 40, используя общее решение дифференциального уравнения у, найдите частное решение, удовлетворяющее указанному начальному условию.
39. у = Сх3 + 2; ху' = 3?/ — 6.
а) 7/(0) = 2. б) 2/(0) = 0. в) 7/(1) = 1.
40. у — Сх4 -И 1; ху' = 42/ — 4.
а) 2/(0) = 1. б) 2/(0) = 0. в) 2/(1) = 2.
В задачах 41 и 42 используйте следующие размеры окна/области отображения графической утилиты. -Xmin ~ ~ 5, l^nin ~ 1/тах ~
41. Известно, что функция 2/ = z + Ce_x — это общее решение дифференциального уравнения у' + у = 1 + х.
а) В одном и том же окне постройте графики частных решений, для которых С = 0, 1, 2 и 3.
*б) Что общего между графиками решений для С > 0?
в) В одном и том же окне постройте графики частных решений, для которых С = 0, -1, —2 и -3.
*г) Что общего между графиками решений для С < 0?
42. Повторите решение задачи 41, если известно, что функция у = х + С/х является частным решением дифференциального уравнения ху' = 2х — у.
Применение математики
Экономика и бизнес
43. 	Стабильность цены. Предположим, что цена на товар p(t) удовлетворяет дифференциальному уравнению
а) Покажите, что функция
dp dt
= 0,5 - 0,1р.
р(1) = 5 - Се-0,1*


Глава 14. Дифференциальные уравнения
655
является решением этого дифференциального уравнения, и вычислите значение предела
р = lim р (t).
t—>оо
б) Постройте графики частных решений, удовлетворяющих начальным условиям р(0) = 1 и р(0) = 10.
*в) Проанализируйте долговременный характер поведения цены на этот товар.
44. 	Стабильность цены. Предположим, что цена на товар p(f) удовлетворяет дифференциальному уравнению
а) Покажите, что функция
является решением этого дифференциального уравнения, и вычислите значение предела
р = lim р (t).
t—>oo
б) Постройте графики частных решений, удовлетворяющих начальным условиям р(0) = 2 и р(0) = 8.
*в) Проанализируйте долговременный характер поведения цены на этот товар.
45. Непрерывно начисляемые сложные проценты. Предположим, что на счет с непрерывной скоростью поступает доход равный 200 долл, в год, приносящий восемь непрерывно начисляемых сложных процентов. Сумма на счету А через t лет удовлетворяет дифференциальному уравнению
= 0,08А + 200.
dt
а) Покажите, что функция
А = Се0’08* - 2500
является решением этого дифференциального уравнения.
б) Постройте графики частных решений, удовлетворяющих начальным условиям А(0) = 0 и А(0) = 1000.
*в) Сравните долговременный характер поведения двух частных решений п. б. Проанализируйте влияние значения А(0) на стоимость капитала.
46. Непрерывно начисляемые сложные проценты. Предположим, что со счета с непрерывной скоростью снимается сумма 500 долл, в год, приносящая десять непрерывно начисляемых сложных процентов. Тогда сумма, на счету А через t лет удовлетворяет дифференциальному уравнению
= ОДА-500.
dt
а) Покажите, что функция
А = 5000 + Се0’14
является решением этого дифференциального уравнения.


656
Часть III. Математический анализ
б) Постройте графики частных решений, удовлетворяющих начальным условиям 4(0) = 4000 и 4(0) = 6000.
*в) Сравните долговременный характер поведения двух частных решений п. б. Проанализируйте влияние значения 4(0) на сумму на счету.
Биологические науки
47. WWW Численность популяции — закон роста Верхалста. Предположим, что количество бактерий в культуре N(t) в момент времен t удовлетворяет закону Верхалста
dN
— = 100 - 0,57V.
dt
а) Покажите, что функция
2V(t) = 200 - Ce~°’5t
является решением этого дифференциального уравнения, и вычислите значение предела
N = lim N (t),
t—юо
где N — равновесная численность популяции.
б) Постройте графики частных решений, удовлетворяющих начальным условиям 7V(0) = 50 и р(0) = 300.
*в) Проанализируйте долговременный характер изменения численности бактерий.
48. Численность популяции — логистический рост. Предположим, что популяция определенного вида животных N(t) в контролируемой среде обитания в момент времени t удовлетворяет закону логистического роста
./V (1000 — 7V).
dt 500 v ’
а) Покажите, что функция
является решением этого дифференциального уравнения, и вычислите значение предела N = lim^oo N (£).
б) Постройте графики частных решений, удовлетворяющих начальным условиям 7V(0) = 200 и р(0) = 2000.
*в) Проанализируйте долговременный характер изменения численности популяции.


Глава 14. Дифференциальные уравнения
657
Социальные науки
49. 	WWW Распространение слухов — закон роста Гомпертца. Предположим, что скорость распространения слухов удовлетворяет уравнению роста Гомпертца
dt
где N(t) — количество людей, до которых уже дошел слух в момент времени t. а) Покажите, что функция N (t) = Се~2е °’5* является решением этого диффе-
Покажите, что функция N (t) = Се 2е °’5* является решением этого дифференциального уравнения, и вычислите значение предела N = lim^^ N (t).
б) Постройте графики частных решений, удовлетворяющих начальным условиям N(0) = 100 и р(0) = 200.
*в) Проанализируйте влияние значения 7V(0) на долговременный характер распространения слухов.
14.2. 	Разделение переменных
■ Разделение переменных
■ Экспоненциальный рост
■ Ограниченный рост
■ Логистический рост
Разделение переменных
Ниже описывается метод разделения переменных, позволяющий решать дифференциальные уравнения вида
ЛуУ = 9&).
(14.6)
Неформально этот метод уже использовался в разделе 11.3 при выводе нескольких важных законов экспоненциального роста. Далее мы приведем более строгое его описание.
Задание 14.3.
Используя алгебраические преобразования, запишите следующие уравнения в форме f(y)y' = 9(х) или объясните, почему это невозможно.
1. у' = х2у. 2. У = х2 + ху. 3. у' = х2у + ху. ■
Решение дифференциальных уравнений методом разделения переменных основывается на формуле замены переменной в неопределенных интегралах. Если у = у(х) — дифференцируемая функция от х, то
(Н.7)
Если функция у(х) является решением уравнения (14.7), то у'(х) также должна удовлетворять это уравнение. Иначе говоря,


658
Часть III. Математический анализ
Подставляя д(х) вместо /[y(x)]i/(х) в уравнение (14.7), получим
f (У) dy = j д (х) dx.
Таким образом, решение у(х) уравнения (14.6) задается неявным образом. Если вычислить значения обоих неопределенных интегралов и решить результирующее уравнение относительно величины у, то получится явное решение дифференциального уравнения (14.6).
Эти рассуждения подытожены в теореме 14.1.
Теорема 14.1 (Разделение переменных). Решение дифференциального уравнения
f(y)y' =
выражается неявно уравнением
j f (у) dy = j
д (ж) dx.
Использование этого метода будет продемонстрировано на нескольких примерах.
Пример 14.6 (Метод разделения переменных). Решите уравнение у' = 2ху2.
Решение.
Домножим на 1/з/2, чтобы разделить переменные.
Преобразуем к уравнению, содержащему неопределенные интегралы.
Найдем значение каждого неопределенного интеграла.
Объединим две постоянные интегрирования в одну произвольную постоянную.
Решим относительно у.
Общее решение
Проверка.
dx \ х2 + С) у' = 2ху2.
2х 2 о ( 1 V
(х2+С)2 к ~^+С)
2х j 2х
(х2 + С)2 ~ (х2 + С)2 ’
(х2 + С)2'
Подставим у' — 2ж/(®2 + С)2 и у1 = -1/(ш2 + С)2.
Следовательно, решение — правильное. (Необходимо выработать привычку проверять решения каждого дифференциального уравнения. С этого момента в большинстве примеров, рассмотренных в тексте, вам придется выполнять такую проверку самостоятельно.) ■


Глава 14. Дифференциальные уравнения
659
Упражнение 14.6.
Решите уравнение у' = 4х3у2.
В некоторых случаях общее решение, полученное методом разделения переменных, не включает в себя все решения дифференциального уравнения. Например, постоянная функция у = 0 также удовлетворяет уравнению в примере 14.6. (Убедитесь в этом.) Однако решение у = 0 нельзя получить из выражения
1
ни при каком значении постоянной С. Решения такого типа называются сингулярными и, как правило, рассматриваются в более углубленных курсах. Здесь не будут делаться попытки найти сингулярные решения каких-либо из рассматриваемых дифференциальных уравнений.
Пример 14.7 (Метод разделения переменных). Найдите общее решение уравнения
(1 + х2)у' = 2х(у - 1).
Затем найдите частное решение, удовлетворяющее начальному условию т/(0) = 3.
Решение. Прежде всего, найдем общее решение: (1 + х2} у' = 2х(у-1).
У1 = 2х у — 1 1 4- х2
f dy _ f 2xdx J У - 1 J 1 + x2 * ln \y - 1| = ln (1 4- x2) 4- C,
Домножим на 1/(14-ж2) и 1/(у—1) чтобы разделить переменные. Преобразуем к уравнению, содержащему интегралы.
Вычислим значение каждого неопределенного интеграла.
где С — произвольная постоянная. Следует отметить, что две постоянные интегрирования всегда можно объединить в одну произвольную постоянную. Кроме того, следует отметить, что вместо выражения |1 4- х2|, можно использовать выражение (14-х2), поскольку выражение 1 + х2 всегда положительное. Чтобы решить последнее уравнение относительно величины у, приведем его к экспоненциальному виду:
|у - 1| = eln(1+:r2)+c =
= е<'е1п(1+а: ) = Воспользуемся свойством е1п г = г.
= ес (1+х2).
Можно показать, что замена выражения ес произвольной постоянной К позволяет опустить знак модуля в левой части последнего уравнения1. Результирующее уравнение можно затем использовать для нахождения общего решения исходного дифференциального
!В любой задаче, в которой используется разделение переменных, можно предположить, что уравнения
е1п1/(2/)1 = есд(х') и №) = Кд(х)
эквивалентны (обе величины С и К — произвольные постоянные). Доказательство этого предположения связано со свойствами модуля и показательных функций.


660
Часть III. Математический анализ
уравнения. Таким образом,
у — 1 = К(1 + х2)-,
у = 1 + К(1 + х2). Общее решение
Чтобы найти частное решение, удовлетворяющее условию = 3, подставим х = 0 и у = 3 в общее решение и решим уравнение относительно К.
3 	= 1 + #(1 + 0);
К = 2;
у — 1 + 2(1 -I- х2) = 3 + 2х2. Частное решение ■
Упражнение 14.7.
Найдите общее решение уравнения
(2 + ж4)у' = 4х3(у —3).
Затем найдите частное решение, которое удовлетворяет начальному условию 2/(0) = 5. ■
Задание 14.4.
Пусть у — положительная величина, изменяющаяся со временем t, например, цена товара, количество препарата в крови или численность населения страны. Если функция у удовлетворяет дифференциальному уравнению
dy , ,
— = ky, к — константа, at
то говорят, что скорость изменения у со временем t пропорциональна у. Если к > 0, величина у увеличивается (растет); если к = 0, у — постоянная; если к < 0, величина у уменьшается (убывает, или затухает). Для каждого из следующих дифференциальных уравнений дайте краткое словесное описание скорости изменения величины у и проанализируйте возможность ее роста/убывания.
1. 	^ = к. 2. =к(100-у). 3. =ку (100-у). .
Экспоненциальный рост
WWW Вернемся теперь к изучению закона экспоненциального роста, который впервые был рассмотрен в разделе 11.3. На этот раз основной акцент будет сделан на поиске соответствующих законов роста в конкретных практических задачах и на использовании метода разделения переменных для решения соответствующих дифференциальных уравнений. Начнем с обычного закона экспоненциального роста.
Закон экспоненциального роста
Если скорость изменения величины у со временем t пропорциональна самой этой величине, то функция у удовлетворяет дифференциальному уравнению
К экспоненциальному росту относится и ситуация, когда функция у возрастает, и ситуация, когда она убывает (затухает).


Глава 14. Дифференциальные уравнения
661
Пример 14.8 (Анализ физического процесса). Нафталиновый шарик определенного состава испаряется со скоростью, пропорциональной его объему, теряя половину своего объема каждые четыре недели. Как долго будет эффективен нафталиновый шарик, если исходно его объем равен 15 см3, и шарик становится неэффективным, если его объем уменьшается до 1 см3?
Решение. Нафталиновый шарик испаряется со скоростью, пропорциональной его объему. Следовательно, если V — объем нафталинового шарика через t недель, то
Поскольку начальный объем составляет 15 см3, известно, что V(0) = 15. Через четыре недели объем шарика будет составлять половину от исходного объема, т.е. У (4) = 7,5. Итак, получаем следующую модель экспоненциального затухания.
У(0) = 15; У (4) = 7,5.
В этой задаче необходимо вычислить значение t, которое удовлетворяет уравнению V(t) = 1. Прежде всего воспользуемся методом разделения переменных, чтобы найти общее решение дифференциального уравнения.
ЛУ dt
= kV
^dV V~dt
= к.
In У = kt + C,
Здесь можно записать In V вместо In | V|, поскольку V > О.
У — — ecekt = Aekt. Общее решение
Здесь А = ес — положительная постоянная. Теперь воспользуемся начальным условием, чтобы найти константу А.
У(0) = Ае° = А = 15.
V(f) = 15efct.
Далее воспользуемся условием У (4) = 7,5 и найдем константу к.
V (4) = 15е4/с = 7,5;
4fc = In 0,5;
У (t) = 15е^/4)1п0,5. Частное решение


662
Часть III. Математический анализ
График V(t) показан на рис. 14.5. Чтобы установить, как долго будет эффективен нафталиновый шарик, вычислим такое t, при котором V = 1.
V(t) = l;
15е<‘/4)1п0’5 = 1;
(t/4) In 0,5 _ 1 .
_ 15’
t 1
- ln0,5 = In—;
4 15
41n Л
t = 1 « 15,6 недели. ■
ln0,5
Рис. 14.5. Экспоненциальное затухание
Упражнение 14.8.
Повторите решение примера 14.8, если нафталиновый шарик теряет половину своего объема каждые пять недель. ■
Вернемся к решению примера 14.8. Для вычисления константы к (рис. 14.6) и решения уравнения V(t) = 1 (рис. 14.7) можно воспользоваться процедурой поиска точек пересечения при помощи графической утилиты.
20
./
Intersection х=-.17згввв
7=7.5
-10
Рис. 14.6. У1 = 15е41; у2 = 7,5 к к -0,1733
к « 15,6 недели


Глава 14. Дифференциальные уравнения
663
Ограниченный рост
В некоторых ситуациях существует верхний (или нижний) предел значений, которые может принимать переменная. Наличие такого предельного значения приводит к закону ограниченного роста.
Закон ограниченного роста
Если скорость изменения величины у со временем t пропорциональна разнице между у и предельным значением М, то функция у удовлетворяет дифференциальному уравнению
Когда речь идет об ограниченном росте, к нему относится как ситуация, когда функция у возрастает и стремится к числу М снизу, так и ситуация, когда она убывает и стре¬
мится к числу М сверху.
Пример 14.9 (Рост продаж). Ожидается, что годовые продажи новой компании будут расти со скоростью, пропорциональной разности между годовым объемом продаж и верхним пределом, равным 20 млн. долл. Вначале объем продаж был равен нулю, а на втором году деятельности — вырос до 4 млн. долл.
1. На какой объем продаж может рассчитывать компания в течение 10-го года?
2. В каком предположительно году объем продаж достигнет 15 млн. долл.?
Решение. Если S — объем продаж (млн. долл.) в течение t лет, то математическая модель этой задачи будет иметь следующий вид.
(И.8)
5(0) = 0; 5(2) = 4.
Это модель ограниченного роста. В п. 1 требуется вычислить значение 5(10), а в п. 2 — решить уравнение 5(t) = 15 относительно величины t. Прежде всего, разделив переменные в (14.8) и проинтегрировав обе части, получим следующий результат.
— ln(20 - 5) = kt + С;
In (20 - 5) = -kt - С;
20 - S = e~kt~c = е~се = Ae~kt;
Здесь можно записать — ln(20 — S) вместо — In |20 — S|, поскольку О < S < 20.
А=е-С
Общее решение
Теперь воспользуемся условиями 5(0) = 0 и 5(2) = 4, чтобы найти постоянные Аи к.
S 	(0) = 20 - Ае° =
= 20 - А = 0;
А = 20;


664
Часть III. Математический анализ
S(t) = 20 — 20e_fct;
S (2) = 20 - 20e_2fc = 4; 20e_2fc = 16;
-2k = = о 8-
20 ’ ’ —2k = In 0,8;
*=-^0,1116;
S (t) = 20 — 20е^/1  2  * * * * *)ln0,8. Частное решение
График S(t) показан на рис. 14.8. Следует отметить, что верхний предел является горизонтальной асимптотой.
1. 5(10) = 20 - 2Ое51п0,8 « 13,45 млн. долл.
2. 5 (t) = 20 - 20e(t/2) ln °’8 = 15;
20e(t/2)lnO’8 = 5;
Jt/2)ln0,8 _ A —0 25-
6 	" 20 " ’ ’
t
- ln0,8 = ln0,25;
t =
21n0,25
ln0,8
» 12,43 года.
Годовые продажи превысят 15 млн. долл, на 13-м году.
Упражнение 14.9.
Повторите решение примера 14.9, если объем продаж в течение второго года равен
3 млн. долл. ■


Глава 14. Дифференциальные уравнения
665
Логистический рост
WWW Если величина сначала начинает расти экспоненциально, а затем приближается к предельному значению, то говорят, что она имеет логистический рост.
Закон логистического роста
Если скорость изменения величины у со временем t пропорциональна самой величине и разности между у и предельным значением М, то функция у удовлетворяет дифференциальному уравнению
= ky (М - у).
Теоретически функции, удовлетворяющие закону логистического роста, могут быть возрастающими или убывающими, однако на практике убывающие логистические функции встречаются редко.
Пример 14.10 (Рост численности популяции). При изучении реснитчатых простейших было показано, что скорость роста численности парамеций Paramecium caudatum в среде с ограниченным объемом пропорциональна произведению самой численности и разности между верхним пределом, равным 374, и численностью. Предположим, что изначально в лабораторной среде содержится 25 парамеций. Через один час в ней будет 125 парамеций. Сколько парамеций будет в лабораторной среде через два часа?
Решение, Если Р — количество особей парамеций в среде в момент времени t, то для этой задачи подходит следующая модель логистического роста.
J=fcP(375-P);
Р(0) = 25; Р(1) = 125.
Требуется вычислить значение Р(2). Прежде всего, разделим переменные и преобразуем выражение к равнению, содержащему неопределенные интегралы.
1 dP _ Р(375-Р) dt ~ ’ .[рртЬр)"’’ Н (14”
Значение интеграла в левой части уравнения (14.9) можно найти либо с помощью тождественных преобразований2, либо воспользовавшись формулой 9 из приложения В.2.
2Если нет желания пользоваться приложением В.2, то для вычисления значения этого интеграла и решения всех остальных задач на логистический рост в практикуме 14.2 можно воспользоваться алгебраическим тождеством


666
Часть III. Математический анализ
Воспользуемся формулой 9 со значениями и = Р, а = 375 и b = -1.
I
1
и (а + Ьи)
du =
1
— In а
и
а + Ъи
1р(375-р/Р 375 1П
Р
375-Р
Формула 9
Поскольку 0 < Р < 375, то знак модуля можно опустить.
Возвращаясь к уравнению (14.9), получим следующий результат.
= j к dt = kt + D;
= 375fct + 375D;
= e375fct+375D _ eBteC.
D — константа.
В = 375fc, C = 375D.
P = 375eBtec - PeBtec-,
P (eBtec + 1) = 375estec;
375estec p - eetec + 1;
_ 375
1 + Ae~Bt
Домножим числитель и знаменатель на e~Bte~c и положим А = е~с.
Общее решение
Теперь воспользуемся условиями Р(0) = 25 и Р(1) = 125, чтобы найти константы А и В.
P(Z) =
375
1 + 14e_Bt
F(l) =
375
1+14е~в
= 125;
375 = 125 + 1750e
-в.
_в _ 250 _ 1
E _ 1750 _ 7’ —В = lnl = — 1п7;
7
В = 1п7;
P(t) =
375
1 + 14e_tln7’
Частное решение
Чтобы установить численность популяции через два часа, необходимо вычислить значение Р(2).
375
Р (2) = 1 + 14е-21п7 « 292 парамеции.


Глава 14. Дифференциальные уравнения
667
График P(t) показан на рис. 14.9. Такая S-образная кривая типична для функций логистического роста. Следует отметить, что верхний предел является горизонтальной асимптотой. ■
Рис. 14.9. Логистический рост
На рис. 14.10-14.12 показан альтернативный, графический подход к поиску постоянных Л и В, а также значения Р(2) в примере 14.10.
Рис. 14.10. Ш = гН; „,=25,4 = 14
Рис. 14.11. В1 = 1ТЩ
у2 = 125, В «1,9459
Р(2) « 292; Логистический рост


668
Часть III. Математический анализ
Упражнение 14.10.
Повторите решение примера 14.10, если изначально парамеций было 15, а через один час их стало 150. I
Ответы к упражнениям
14.6. у = -l/(z4 + С).
14.7. Общее решение: у = 3 + К(2 + х4); частное решение у = 5 + х4.
14.8. 19,5 недели.
14.9. 1) 11,13 млн. долл.
2) На 17-м году (t « 17,06 лет).
14.10. 343 парамеции.
Практикум 14.2
А В задачах 1-4 запишите дифференциальное уравнение, описывающее скорость изменения указанной величины.
* 1. Годовой объем продаж компании у растет со скоростью 100 тыс. долл, в год.
* 2. Годовой объем продаж компании у растет со скоростью, пропорциональной са¬
мому годовому объему продаж.
* 3. Численность рыбы в озере у растет со скоростью, пропорциональной разности
между численностью популяции и верхним пределом 10 000 рыб.
*4. В сообществе, состоящем из 100 000 человек, количество человек, заболевших инфекционным заболеванием, растет со скоростью, пропорциональной произведению количества зараженных и здоровых людей.
В задачах 5-8 опишите словесно скорость изменения величины, удовлетворяющей указанным дифференциальным уравнениям и проанализируйте характер возрастания/ убывания этой величины.
*5. Годовой объем продаж компании у (в млн. долл.) удовлетворяет уравнениям dy/dt = 0,lj/ и ?/(0) = 2.
*6. Годовой объем продаж компании у (в млн. долл.) удовлетворяет уравнениям dy/dt = 0,1(8 - у) и у(0) = 2.
*7. Количество людей, уже знакомых со слухом, описывается уравнением dy/dt = = 0,2у(5000 - у) и 7/(0) = 1.
*8. Концентрация препарата в крови пациента у (в мл.) описывается уравнением dy/dt = —0,2у и у(0) = 5.
В задачах 9-12 требуется показать, что к каждому из уравнений можно применить метод разделения переменных, записав его в виде f(y)y' = g(x).
9. ху' = у2. 10. у' + ху = 2х.
х 2
11. ху' + ху = Зу. 12. у' Ч— = -.
У У


Глава 14. Дифференциальные уравнения
669
В задачах 13-22 требуется найти общее решение каждого дифференциального уравнения. Затем найдите частное решение, удовлетворяющее начальному условию.
13. у' = Зх2; 2/(0) = -1.
15. у' = |; 2/(1) = 2.
17. у' = у; 2/(0) = 10.
14. у1 = 2е2®; 2/(0) = 5.
■6. »(1) = 2.
18. у' = у- 10; 2/(0) = 15.
19. у' = 25 - у, 2/(0) = 5.
21. 2/=-; 2/(1) = 5; х > 0.
X
20. у' = Зх2у; у (0) =
22. у' = 2/(-1) = 2е.
Б В задачах 23-32 требуется найти общее решение каждого дифференциального уравнения. Затем найдите частное решение, удовлетворяющее начальным условиям.
23. у' = 2/(1) = 3.
24. у> > У(°) = 2-
25. у' = уех\ 2/(0) = Зе.
27. у' = 2/(0) = In2.
29. у' = ху + х; 2/(0) = 2.
26. у' = —у2ех; 2/(0) =
28. У1 = 2/2(2х + 1); 2/(0) =
30. у' = (2х 4- 4) (2/ - 3); 2/(0) = 2.
31. у1 = (2 - у)2ех; 2/(0) = 1.
д.1/2
32. у' = 3/(1) = 7.
(У-5)
В задачах 33-38 требуется найти общее решение каждого дифференциального уравнения. Не нужно пытаться найти явное выражение для решения.
1 + X2
33-’ = 1+,’-
35. хуу' = (14- х2)(1 4- у2).
_ . , 6х — 9х2
34. у' = — —.
22/4-4
36. (ху2 — х)у' = х2у — X2.
37. х2еуу' = х3 4- х3еу.
, хех
38. у' = -—.
In у
В В задачах 39-44 требуется найти явное выражение для частного решения каждого
дифференциального уравнения.
2
39. хуу' = lnx; 3/(1) = 1.
40. у' = у(о) = 2.
У
41. ху' = Ху/у 4- 2у/у; 2/(1) = 4.
43. уу' = хе~у3; 2/(0) = 1.
42. у' = х(х - 1)1/2(2/ - 1)1/2; 2/(1) = 1-
44. уу' = х(1 4- 2/2); 3/(0) = 1.
В задачах 45-48 проанализируйте, почему метод разделения переменных не дает возможности найти явное решение дифференциального уравнения у = h(x).
* 45. у' + ху = 2.
* 47. 3yyf = ех2 + у.
* 46. у' — 5х2у = ех.
> 9*2 + 2
*48. у' = —- .
5t/4 — 6


670
Часть III. Математический анализ
49. 	Во многих прикладных задачах, описывающих процессы ограниченного роста, предельное значение М не известно заранее, и его нужно найти, исходя из имеющихся данных. Предположим, что скорость изменения величины у со временем пропорциональна разности между у и неизвестным верхним пределом М, и что у = 0, когда t = 0. Из закона ограниченного роста следует, что
у = М(1 - e~kt), М>0,к>0.
а) Используя данные, приведенные в таблице, составьте два уравнения, которым должны удовлетворять М и к, и решите каждое из них относительно М.
t
1
1,5
У
3
4
б) Используя графическую утилиту и уравнения, выведенные при решении п. а, аппроксимируйте значение М с точностью до одного десятичного знака.
50. 	Вернемся к задаче 49. Предположим, что скорость изменения величины у со временем пропорциональна разности между у и неизвестным верхним пределом М9 и что у = 10, когда t = 0. Из закона ограниченного роста следует, что
у = М + (10 — M)e~kt, М>0,к>0.
а) Используя данные, приведенные в таблице, составьте два уравнения, которым должны удовлетворять М и к, и решите каждое из них относительно М.
t
1
5
У
9
7
б) Используя графическую утилиту и уравнения, выведенные при решении п. а, аппроксимируйте значение М с точностью до одного десятичного знака.
Применение математики
Экономика и бизнес
51. WWW Непрерывно начисляемые сложные проценты. Сберегательный банк предлагает депозитный сертификат, приносящий 5,5 непрерывно начисляемых сложных процентов. Какова будет стоимость инвестиций через 5 лет?
52. WWW Непрерывно начисляемые сложные проценты. Банк Equitable Federal предлагает депозитный сертификат, приносящий 4,9 непрерывно начисляемых сложных процентов. Какова будет стоимость капитала размером 10 тыс. долл, четыре года спустя?


Глава 14. Дифференциальные уравнения
671
53. Реклама. Компания заказывает рекламу своего товара на радиостанции, постоянная аудитория которой насчитывает 100000 человек. Предположим, что скорость, с которой люди узнают о новом товаре, пропорциональна числу тех, кто о нем уже слышал.
а) Сколько понадобится времени на то, чтобы о товаре узнали 50 000 человек, если в начале рекламной кампании о товаре не знал никто, а через 7 дней о нем узнали 20 000 человек?
*б) Предположим, что компания недовольна результатами рекламмной кампании и хочет сократить время извещения 50000 человек об их товаре до 14 дней. Сколько людей должны узнать о товаре в течение первых 7 дней, чтобы это произошло?
54. Реклама. Перед началом рекламной кампании только 10% потенциальных покупателей товаров определенной торговой марки знали о ее существовании. Спустя одну неделю после начала кампании о торговой марке узнали 20% покупателей. Предположим, что доля проинформированных покупателей растет со скоростью, пропорциональной произведению доли проинформированных и доли непроинформированных покупателей.
а) Какой процент покупателей будет помнить о торговой марке через пять недель после начала рекламной кампании?
*б) Предположим, что заказчик недоволен результатами рекламной кампании и хочет добиться того, чтобы после первой недели рекламной кампании название торговой марки знали 25% покупателей. Как это повлияет на долю покупателей, которые будут помнить название торговой марки спустя 5 недель после начала рекламной кампании?
55. Анализ физического процесса. Производитель исследует свойства нового дезодоранта. Активный компонент испаряется со скоростью, пропорциональной количеству этого компонента. Половина этого компонента испаряется в течение первых 30 дней с момента нанесения дезодоранта. Как долго один из таких дезодорантов будет оставаться эффективным, если он становится неэффективным после того, как испарится 90% активного компонента?
56. WWW Корпоративные прибыли. Согласно данным Комитета экономического анализа США, общие корпоративные прибыли в промышленном секторе экономики США в 1995 году составляли 576,8 млрд, долл., а в 2000 году — 946,2 млрд. долл. Какими будут общие корпоративные прибыли в 2010 году, если они растут со скоростью, пропорциональной общим корпоративным прибылям?
57. Рост объема продаж. Предполагается, что годовой объем продаж новой компании будет расти со скоростью, пропорциональной разности между объемом продаж и верхним пределом, равным пяти миллионам долларов. Когда объем продаж достигнет четырех миллионов долларов, если вначале он был равен нулю, а за первые четыре года деятельности составил один миллион долларов?
58. Анализ продаж. Годовой объем продажи компании упал с восьми миллионов долларов два года тому до шести миллионов долларов на сегодняшний день. Вычислите годовой объем продаж через три года, если он будет продолжать падать


672
Часть III. Математический анализ
со скоростью, пропорциональной разности между объемом продаж и нижним пределом, равным трем миллионам долларов.
59. Анализ продаж. Новая компания изначально имела нулевой объем продаж, в течение первого года он составил два миллиона долларов, а в течение третьего года — пять миллионов долларов. Если предположить, что годовые продажи S растут о скоростью, пропорциональной разности между объемом продаж и неизвестным верхним пределом М, то согласно закону ограниченного роста
S(t) = М (1 - e~kt), М>0,к>0,
где t — время (лет), a S(t) — объем продаж (млн. долл.). Используя методы аппроксимации, найдите константу к с точностью до одного десятичного знака и значение М с точностью до ближайшего миллиона. (См. задачу 49.)
60. Анализ продаж. Вернемся к задаче 59. Вычислите приближенное значение к с точностью до одного десятичного знака и М с точностью до миллиона, если объем продаж в течение третьего года составлял четыре миллиона долларов, а все остальные показатели остались неизменными.
WWW Закон поглощения тепла Ньютона гласит, что скорость изменения температуры объекта пропорциональна разности между температурой объекта и температурой окружающей среды. Используя этот закон, сформулируйте модели для задач 61-64, а затем решите их, используя методы, рассмотренные в этом разделе.
61. Производство. В ходе одного из этапов производственного процесса металлический прут нагревается в печи до тех пор, пока его температура не достигнет 500° F. В печи поддерживается постоянная температура 800° F. Перед помещением в печь температура прута равна 80° F. Через две минуты после помещения в печь температура увеличивается до 200° F. Через сколько времени нужно вынуть прут из печи?
62. Производство. На следующем этапе производственного процесса, рассмотренного в задаче 61, нагретый прут необходимо охладить в чане с водой, пока его температура не достигнет 100° F. Температура воды в чане поддерживается на уровне 50° F. Через сколько времени можно будет вынуть прут из воды, если температура прута в момент погружения в воду равна 500° F, а после пяти минут нахождения в воде он остывает до 400° F?
Биологические науки
63. Приготовление пищи. Пирог вынули из печи, температура которой равна 325° F, и поместили в морозилку с постоянной температурой 25° F. После того как пирог продержали в морозилке один час, его температура стала равна 225° F. Какой будет температура пирога, если его продержать в морозилке четыре часа?
64. Приготовление пищи. Мясо для жарки вынули из холодильника, температура которого равна 20° F, и поместили в духовку с постоянной температурой 350° F. После того как мясо продержали в духовке один час, его температура стала равна 185° F. Какой будет температура мяса, если его продержать в духовке три часа?


Глава 14. Дифференциальные уравнения
673
65. Численность популяции. Бактериальная культура растет со скоростью, пропорциональной их численности. Изначально культура содержала 100 бактерий. Через один час в ней насчитывалось 140 бактерий.
а) Сколько бактерий будет в культуре через пять часов?
б) Когда в культуре будет насчитываться 1 000 бактерий?
66. Численность популяции. Бактериальная культура растет в среде, которая может обеспечить жизнедеятельность максимум 1100 бактерий. Скорость роста численности бактерий пропорциональна произведению количества бактерий и разности между 1100 и количеством бактерий. Изначально культура содержала 100 бактерий. Через час в ней было 140 бактерий.
а) Сколько бактерий будет в культуре через пять часов?
б) Когда в культуре будет насчитываться 1000 бактерий?
67. Простая эпидемия. Эпидемия гриппа распространяется в группе, состоящей из 50000 человек, со скоростью, пропорциональной произведению количества инфицированных и здоровых людей. Изначально было инфицировано 100 человек, а 10 дней спустя — 500.
а) Сколько людей будет инфицировано через 20 дней?
б) Когда будет инфицирована половина группы?
68. Экология. Популяция рыб в большом озере уменьшается со скоростью, пропорциональной разности между численностью популяции и нижним пределом, равным 5000 рыб.
а) Определите численность популяции через шесть лет, если она уменьшилась с 15 000 рыб три года тому назад до 10 000 рыб на сегодняшний день.
*б) Допустим, численность популяции рыбы через шесть лет составит 8000, указывая на то, что озеро может прокормить больше чем исходный нижний предел, равный 5000 рыбам. Предполагая, что скорость роста численности популяции по-прежнему пропорциональна разности между численностью популяции и неизвестным нижним пределом М, вычислите приближенное значение М с точностью до тысячи.
Социальные науки
69. Чувственное восприятие. Человек подвергается физическому воздействию, которое является измеримой величиной, однако измерить интенсивность результирующего ощущения сложно. Если s — величина воздействия, a Z(s) — интенсивность ощущения, то экспериментальные данные говорят о том, что
где к — некоторая константа. Выразите величину I как функцию, зависящую от переменной s.
70. 	Обучение. Количество слов в минуту ДГ, которое может напечатать человек, возрастает по мере приобретения навыка. Предположим, что скорость набора текста N пропорциональная разности между N и верхним пределом, равным 140 символам. Разумно будет предположить, что вначале человек совсем не умел наби¬


674
Часть III. Математический анализ
рать тексты. Следовательно, N = 0, когда t = 0. После 10 часов практических занятий человек может набирать текст со скоростью 35 слов в минуту.
а) Сколько слов в минуту сможет напечатать человек после 20 часов практических занятий?
б) Сколько часов придется заниматься человеку, чтобы научиться набирать текст со скоростью 105 слов в минуту?
71. 	Распространение слухов. Слухи распространяются в общине, насчитывающей 1000 человек, со скоростью, пропорциональной произведению количества тех, кто их слышал, и количества тех, кто их не слышал. Инициаторами слухов выступали пять человек, а через день о них знали 10 человек.
а) Сколько человек будет знать слухи через семь дней?
б) Сколько понадобится времени, чтобы слухи распространились среди 850 человек?
14.3. 	Линейные дифференциальные уравнения первого порядка
■ Повторение правила дифференцирования произведений
■ Основной метод решения линейных дифференциальных уравнений первого по рядка
■ Решение практических задач
Повторение правила дифференцирования произведений
Метод решения дифференциальных уравнений, рассматриваемый в этом разделе, частично основан на правиле дифференцирования произведений функций. Напомним, что, если F и S — две дифференцируемые функции, то
(F5)' = FS' + F'S.
В главе 8 было описано правило дифференцирования произведений, в которых функции F и S известны заранее. Теперь наша цель — научиться распознавать суммы двух слагаемых, представляющие собой производную произведения функции.
Задание 14.5.
Поставьте в соответствие каждой сумме слева производную произведения функций справа (здесь у — неизвестная дифференцируемая функция).
1. x2yf 4- 2ху\
2. e~2xyf - 2е~2ху;
1 	1 / 2
3- -,у -
4. ех у' + 2хех у.
1- ;
3. (е-2^)';
4. (х2у)'.
Как должны быть связаны между собой функции т(х) и п(я), если т(х)у' + п(х)у — производная произведения этих функций? ■


Глава 14. Дифференциальные уравнения
675
Основной метод решения дифференциальных уравнений первого порядка
Дифференциальное уравнение, которое можно представить в виде
у' + f(x)y = д(х)
называется линейным дифференциальным уравнением первого порядка. Например, уравнение
х
(14.10)
является линейным дифференциальным уравнением первого порядка, в котором f(x) = = 2/х и д(х) = х. Это уравнение нельзя решить методом разделения переменных. (Попытайтесь разделить переменные, чтобы убедиться в справедливости сказанного.) Вместо этого изменим вид уравнения, умножая обе его части на х2.
х2у' + 2ху = х3.
(Н.П)
Почему мы выбрали именно функцию х2? Ответ на этот вопрос дадим позднее. Прежде всего, посмотрим, как такой выбор помогает решить задачу.
Поскольку (х2)' = 2х, левая часть уравнения (14.11) является производной произведения функций.
х2у' + 2ху = (х2у)'.
Следовательно, уравнение (14.11) можно переписать в виде
(х2у)' = х3.
Теперь обе части уравнения можно проинтегрировать следующим образом.
т4 х2у = — + С.
Решая уравнение относительно величины у, получим общее решение
Функция х2 , которая использовалась для преобразования исходного уравнения к уравнению, которое можно решить, называется интегрирующим множителем. Оказывается, существует отдельная формула, позволяющая вычислить интегрирующий множитель для произвольного линейного дифференциального уравнения первого порядка. Более того, этот интегрирующий множитель можно затем использовать для вычисления решения дифференциального уравнения, как это было сделано выше. Формула для интегрирующего множителя и процесс решения дифференциального уравнения первого порядка описаны во врезке.


676
Часть III. Математический анализ
WWW Решение линейного дифференциального уравнения первого порядка
Этап 1. Записываем уравнение в стандартном виде.
У1 + f(x)y = g(x).
Этап 2. Вычисляем интегрирующий множитель.
/(х) = e^(l)dl.
(При вычислении интеграла J f (х) dx константу интегрирования следует по- дожить равной нулю.)
Этап 3. Умножаем обе части уравнения, представленного в стандартном виде, на интегрирующий множитель /(ж). Теперь левая часть уравнения должна иметь вид [Дя)у]'-
[Д*)3/]' = I(x)g(x).
Этап 4. Интегрируем обе части уравнения.
Цх)у = I / (ж) g (х) dx.
(При вычислении интеграла JI (х) g (т) dx следует учесть произвольную постоянную интегрирования.)
Этап 5. Решая уравнение относительно переменной у, получаем общее решение.
Пример 14.11 (Использование интегрирующего множителя). Решите уравнение 2ху' + -И?/ = Ют2.
Решение.
Этап 1. Умножая обе стороны на 1/(2т), получим уравнение, записанное в стандартном виде.
у1 -И — у = 5т. f (х) = и g (х) = 5х.
2т 2ас
Этап 2. Найдем интегрирующий множитель.
I (х) = e-ff(x)dx =
= eJ [l/(2x)]dx _
= e(l/2)lnz =
= eln*1/2 =
= xV2.
Будем предполагать, что х > О, и в качестве постоянной интегрирования выберем нуль.
г In t = ln tr,
elnr = r, r > 0.
Интегрирующий множитель.


Глава 14. Дифференциальные уравнения
677
Этап 3. Умножим обе части уравнения, записанного в стандартном виде, на интегрирующий множитель.
х1!2^ -I- -х х!2у = 5z3/2
Левая сторона должна иметь вид
[I (а?) у]'.
(х^у)' = 5я3/2.
Этап 4. Интегрируем обе части уравнения.
5x3/2cfo; Учтем произвольную постоянную
интегрирования в правой части.
х1/2у = 2ж5/2 + С.
Этап 5. Решим уравнение относительно величины у.
2 С
= 2х Ч . Общее решение. ■
Упражнение 14.11.
Решите уравнение xyf + Зу = 4х. ■
Следует отметить, что в примере 14.11, чтобы избежать применения модуля в интегрирующем множителе, предполагается, что х > 0. Во многих задачах этого раздела требуется вычислять выражения вида lh'(x)/h(x>)]dx. Чтобы избежать сложностей, связанных с использованием модуля, будем предполагать, что h(x) > 0. Это упростит процесс решения. Выпишем несколько удобных формул (в первой формуле, согласно п. 2, постоянная интегрирования равна нулю).
Основные формулы интегрирования, содержащие функцию натурального логарифма Если h(x) > 0, то
dx = In h (х) и eln h(^ = h (я). h yXj
Если линейное дифференциальное уравнение записано в стандартном виде, то умножение обеих частей уравнения на интегрирующий множитель всегда преобразует его левую часть в производную функции 1(х)у. Следовательно, можно пропустить п. 3 и 4 и перейти непосредственно к п. 5. Этот подход будет проиллюстрирован на следующем примере. Вам решать, что проще — выполнять процедуру поэтапно или воспользоваться формулой из п. 5.
Пример 14.12 (Использование интегрирующего множителя). Найдите частное решение уравнения
у' + 2ху = 4х,
удовлетворяющее начальному условию 2/(0) = 5.


678
Часть III. Математический анализ
Решение. Поскольку уравнение уже записано в стандартном виде, найдем интегрирующий множитель
Цх) = ej2xdx = ех\ f(x) = 2x
Переходя сразу к п. 5, имеем
У = дд p(x)p(or)d® = = [ ех • 4xdx =
ех J
= е~х2 j 4теж2(/х =
= е-х\2ех2 + С).
= 2 + Се~х\
д (ж) = 4®
Пусть и = х2, du = 2х dx.
Общее решение.
Подставляя а: = 0и^ = 5в общее решение, получим следующий результат.
5 = 2 + С;
С = 3;
_ г
у = 2 + Зе . Частное решение.
Упражнение 14.12.
Найдите частное решение уравнения у' + Зх2?/ = 9х2, удовлетворяющее начальному условию ?/(0) = 7. I
Предупреждение.
1. 	При интегрировании обеих частей таких уравнений, как
(ж1/2 г/)' = 5я3/2,
следует помнить, что
х^2у — 5x3/2dx 2х5/2.
В первообразной нет слагаемого "+С".
Запомните: при вычислении интеграла
I (ж) g (х) dx
необходимо учитывать постоянную интегрирования. Если эта постоянная пропущена, то необходимо найти общее решение дифференциального уравнения. Корректную процедуру поиска значения такого интеграла можно найти на этапе 4 примера 14.11.
1. -^2 j 4хех dx j кхе??dx = j 4х dx.
Аналогично тому, что переменный множитель нельзя выносить за знак интеграла, переменный множитель за знаком интеграла нельзя сокращать с множителем под знаком интеграла. Корректную процедуру вычисления такого интеграла можно найти в примере 14.11.


Глава 14. Дифференциальные уравнения
679
Решение практических задач
Если Р — исходная сумма, вложенная под 100г непрерывно начисляемых сложных процентов, а А — сумма на счету через t лет, то, как можно было видеть в разделе 11.3, функция А удовлетворяет уравнению экспоненциального роста
НА
^^гА, Л(0) = Р.
Теперь предположим, что с этого счета деньги снимаются непрерывно со скоростью т долл, в год. Тогда сумма на счету А в момент времени t должна определяться уравнением Скорость изменения суммы А
dA dt
( Скорость роста суммы А благодаря непрерывному начислению сложных \ процентов /
гА
Скорость, с которой деньги снимаются
т,
или
dA
— гА = —т. (14.12)
dt
Задание 14.6.
Как изменится уравнение (14.12), если деньги не снимаются, а непрерывно вкладываются
со скоростью т долл, в год? ■
Пример 14.13 (Непрерывно начисляемые сложные проценты). Изначально на счет, приносящий восемь непрерывно начисляемых сложных процентов, была внесена сумма 10000 долл. Затем деньги непрерывно снимались со скоростью 1000 долл, в год до тех пор, пока деньги на счету не были исчерпаны. Вычислите сумму, находящуюся на счету, в произвольный момент времени t. Когда эта сумма станет равной нулю? Сколько всего денег может быть снято с такого счета?
Решение. Сумма А, находящаяся на счету в произвольный момент времени t, описывается (см. формулу (14.12)) уравнением
dA
— - 0,08А = -1000; А (0) = 10 000.
dt
Интегрирующий множитель для этого уравнения равен
I (t) = ~^dt = e_0,08t. f (t) = -0,08.
Умножая обе части дифференциального уравнения на функцию I(t) и следуя процедуре, описанной выше, получим такой результат.
e-0.08t^4 _ 0;08е-о,озел = _1000e_o,O8t;
dt
(е-°>08‘Л)' = — 1000e_o,o8t;


680
Часть III. Математический анализ
е_0’08‘Л = j — 1000e_o’08tdi =
= 12 500e_0,08t + С;
А — 12 500 + Ce0,08t. Общее решение.
Применяя начальное условие 4(0) = 10 000, получаем следующий результат.
4(0) = 12 500+ С = 10000.
С = -2500.
A (t) = 12 500 — 25ООе0,084. Сумма, лежащая на счету в произвольный момент времени t.
Чтобы установить, когда сумма, лежащая на счету, станет равной нулю, необходимо решить уравнение 4(4) = 0 относительно величины t.
4(4) = 0;
12 500 - 2500e°-O8t = 0;
12 500 = 2500eOO8t;
5 = e0,08t;
In 5
t = ——- ~ 20,118 года.
0,08
Таким образом, сумма на счету будет исчерпана через 20,118 года (на рис. 14.13 проиллюстрирован альтернативный подход к решению этой задачи с помощью графической утилиты). Поскольку деньги снимаются со счета со скоростью 1000 долл, в год, всего со счета будет снято
1000-20,118 = 20118 долл. а
Рис. 14.13. т/i = 12 500 - 2500е°’°8х
Упражнение 14.13.
Повторите решение примера 14.13, если сумма на счету размещена под пять непрерывно начисляемых сложных процентов. ■
Пример 14.14 (Равновесная цена). В экономике предложение S и спрос D на товар часто можно рассматривать как функцию цены p(t) и скорости изменения цены p'(t). (Следовательно, величины S и D в конечном счете являются функциями


Глава 14. Дифференциальные уравнения
681
времени t.) Равновесная цена в момент времени t является решением уравнения S = D.
Если функция p(t) — решение этого уравнения, то долгосрочная равновесная цена равна
р = lim р (t).
t—>OO
Например, если
D = 50 — 2p(t) -I- 2p'(t), S = 20 + 4p(t) + 5p'(t)
и p(0) = 15, то равновесная цена в момент времени t является решением уравнения
50 - 2p(t) + 2p'(t) = 20 + 4p(t) + 5p'(t).
После упрощений уравнение принимает следующий вид.
p'(t) + 2p(t) = 10, f (t) = 2 и g(t) = 10.
Таким образом, после преобразований исходное уравнение стало линейным дифференциальным уравнением первого порядка с интегрирующим множителем
I (t) = 2dt — e2t.
Переходя непосредственно к п. 5, получаем следующий результат.
р(*) = ^ |10e2tdf =
= e~2t (5e2t + C);
p(t) = 5 + Ce~2t.
p(0) = 5 + C = 15;
C= 10;
p (t) = 5 + 10e~2f;
p = lim (5 -I- 10e~2*) = 5.
t->oo v 7
Общее решение.
Равновесная цена в момент времени t
(рис. 14.14).
Долгосрочная равновесная цена. ■
Рис. 14.14. Равновесная цена


682
Часть III. Математический анализ
Упражнение 14.14.
Вычислите равновесную цену в момент времени t и долгосрочную равновесную цену, если D = 70 + 2p(t) + 2p'(t), S = 30 + 6p(t) 4- 3p'(t) и p(0) = 25. ■
Пример 14.15 (Борьба с загрязнением). На производстве установлен сборный резервуар емкостью 1000 галлонов, используемый для контроля выбросов загрязняющих веществ в канализационную систему. Изначально резервуар содержит 500 галлонов воды. Каждый галлон воды содержит два фунта загрязняющих веществ. Кроме того загрязненная вода, содержащая пять фунтов загрязняющих веществ на галлон, закачивается в резервуар со скоростью 100 галлонов в час и полностью перемешивается с имеющейся в резервуаре водой. Одновременно с этим однородно перемешанная вода из резервуара выливается в канализацию со скоростью 50 галлонов воды в час. Этот процесс продолжается пять часов. Вычислите следующие величины в конце пятичасового периода.
1. Общее количество загрязняющих вещество в резервуаре.
2. Скорость (в фунтах на галлон), с которой загрязняющее вещество выливается в канализацию.
Рис. 14.15. Система очистки сточных вод
Решение. Пусть p(t) — общее количество загрязняющих веществ в резервуаре (в фунтах) через t часов после начала исследования процесса. Поскольку резервуар изначально содержит 500 галлонов воды и каждый галлон воды содержит два фунта загрязняющих веществ, то
р(0) = 2 • 500 = 1000. Исходное количество загрязняющего вещества в резервуаре
Так как загрязненная вода вливается в резервуар и выливается из него с разной скоростью и с разной концентрацией загрязняющих веществ, то скорость изменения количества загрязняющего вещества в резервуаре будет зависеть от скорости, с которой загрязняющее вещество поступает в резервуар, и скорости, с которой оно убывает из резервуара.
(Скорость изменения X / Скорость поступлениях / Скорость убыванияХ
количества загрязняющего I = I загрязняющего I — I загрязняющего вещества J у вещества J у вещества у


Глава 14. Дифференциальные уравнения
683
Если найти выражение для двух скоростей в правой части уравнения, то получится дифференциальное уравнение, содержащее функцию p'(t).
Поскольку вода, содержащая пять фунтов загрязняющего вещества на галлон, попадает в резервуар с постоянной скоростью 100 галлонов в час, загрязняющее вещество попадает в резервуар со скоростью
(5 фунтов X /100 галлонов\ ,
• = 500 фунтов в час.
на галлон у у в час у
Как быстро загрязняющее вещество покидает резервуар? Поскольку общее количество загрязняющего вещества в резервуаре растет, скорость, с которой загрязняющее вещество покидает резервуар, зависит от количества загрязняющего вещества в резервуаре в момент времени t и количества воды в резервуаре в момент времени t. Поскольку каждый час в резервуар попадает 100 галлонов и только 50 галлонов его покидает, количество воды в резервуаре растет во скоростью 50 галлонов в час. Следовательно, количество воды в резервуаре в момент времени t равно
(
Исходное количество воды
Скорость поступления (галлонов в час)
500 +
50t
Продолжительность процесса
Концентрация загрязняющих веществ в произвольный момент t равна
/ Общее количество X
р (t) у загрязняющего веществау _ Концентрация (количество в галлоне)
500 + 50t ’ (Общее количество воды) загрязняющих веществ.
Поскольку вода покидает резервуар со скоростью 50 галлонов в час, скорость, с которой его покидает загрязняющее вещество, равна
50р (t) = p(t)
500 50Z 10 И-1
Таким образом, скорость изменения p(t) должна удовлетворять уравнение
(Скорость изменения X / Скорость поступлениях / Скорость убыванияХ
количества загрязняющего I = I загрязняющего I — I загрязняющего I
вещества у \ вещества у \ вещества у
p(t)
10 + t'
p'W
500
Получаем следующую модель.
р' (t) = 500 -
Р(*)
10 +1
р(0) = 1000,


684
Часть III. Математический анализ
или
p' (t) + ^7? (0 = 5°;
J ф _ eJ dt/(10+t) _ eln(10+t) _ = 10 +1;
p(f) = ioTfPoo(lo + z)rfz =
1 [250 (10 +t)2 + c];
C
10 + t’
Линейное дифференциальное уравнение первого порядка, в котором f (t) = 1/ (10 + t) и д (t) = 500.
Интегрирующий множитель
Переходим непосредственно к п. 5.
10 + t
р (t) = 250 (10 + f) +
(j
1000 = 250 -10 + —; 10
й=-1500;
С = -15 000;
р (t) = 250 (10 +1) -
15 000
10 + t’
Общее решение
Начальное условие: р (0) = 1000.
Частное решение (рис. 14.16)
Рис. 14.16. Количество загрязняющих вещество в резервуаре
. Чтобы определить общее количество загрязняющего вещества через пять часов, необходимо вычислить значение р(5).
р (5) = 250(15) —
15 000
15
= 2750 фунтов.


Глава 14. Дифференциальные уравнения
685
2. 	Через пять часов резервуар будет содержать 750 галлонов воды. Скорость, с которой загрязняющее вещество выбрасывается в канализационную систему, равна
2750
750
« 3,67 фунта на галлон.
Упражнение 14.15.
Повторите решение примера 14.15, если вода выливается из резервуара со скоростью 75 галлонов в час. ■
Ответы к упражнениям
14.11. 1(х) = х3; у = х + С!х3.
14.12. I (х) = ех3 \ у = 3 4- 4е_х3.
14.13. A(t) = 20000 - 10000e°’°5t; А = 0, когда t = (In 2)/0,05 « 13,863 лет; всего со счета будет снято 13 863 долл.
14.14. 	p(t) = 10 + 15e_4t; р = 10.
14.15. 	р (t) = 125 (20 +t) -
1) 2375 фунтов;
12 000000
(20 +1)3 ’
2) Приблизительно 3,77 фунта/галлон.
Практикум 14.3
Во всех задачах, в которых встречается выражение 1пД(я), предполагается, что h(x) > 0.
А В задачах 1-4 необходимо ответить на вопрос: является ли дифференциальное уравнение линейным уравнением первого порядка? Если это так, найдите такие функции f(x) и д(х), при которых уравнение можно переписать в виде у' + f(x)y = g(x).
1. yf = ky. 2. у' = k(M - у).
3. 	у' = ку(М — у). 4. у' = кх2(М — у).
В задачах 5-12 необходимо заменить каждый знак ? такой функцией, зависящей от переменной х, которая превратит подынтегральную функцию в производную произведения, а затем вычислить первообразную. В качестве постоянной интегрирования
необходимо взять нуль.
ч
1 (x3yf + Чу) dx.
6. j (e2xyf + ?i/) dx.
7.
f {е~3ху' + ly) dx.
8. j (a№V + ?y^ dx.
9-
f (2y' + 4x3i/) dx.
10. j (?y' + 0,2e°’2^) dy.
И.
[ (?y' - 0,5e~°’5xy) dx.
u- j (v -


686
Часть III. Математический анализ
В задачах 13-24 необходимо найти интегрирующий множитель, общее решение и частное решение, удовлетворяющее данному начальному условию.
13. 	у' + 2у = 4; 7/(0) = 1.
15. 	у1 + у = е~2х; у(0) = 3.
17. 	у' -у = 2ех; 1/(0) = —4.
19. 	у' + у = 9х2е~х; у(0) = 2.
14. 	у' ~3у = 3; 2/(0) = -1.
16. 	у' - 2у = е3®; 1/(0) = 2.
18. 	у' + 4т/ = Зе-4^; 1/(0) = 5.
20. 	у' - Зу = 6д/хе3х; у(0) = -2
21. 	ху' + у = 2х; у(1) = 1.
23. 	ху' +2у = 10х3; 1/(2) = 8.
22. 	ху' -Зу = 4х; у(1) = 1.
24. 	ху' -у= Л;у(2) = 3. х£
Б В задачах 25-34 необходимо для каждого уравнения найти интегрирующий множитель, а затем общее решение.
25. yf + ху = 5х.
27. 	у' — 2у = 4х.
29. 	ху' + у = хех.
26. у' — 2ху = бх.
28. 	у' + у = х2.
30. 	ху' + 2у = хе3х
31. 	ху' + у = х\пх.
33. 	2ху' + Зт/ = 20ж.
32. 	ху' — у — х\пх.
34. 	2ху' — у = бх2.
В задачах 35-38, предполагается, что указанное “решение ” было сдано на проверку студентом, изучающим этот курс.
1) Как правильно проверить каждое из этих решений?
2) Правильное или неправильное решение получил студент? Если решение неправильное, объясните, в чем заключается ошибка и как ее можно исправить.
3) Запишите правильное решение для каждого неправильного решения и проверьте результат.
*35. Уравнение:
у1 + -у = (х + I)2 •
X
Решение:
1 Г 2
у = - 1 т (ж + 1) dx =
х J
= з +1)3 + с.
, 2
*36. Уравнение:
у + —у = х — 1. X
Решение:
У = j X2 (х - 1) dx =
= | (х - I)2 + С.
*37. Уравнение:
у' + 3у = е~х.
Решение:
у = Л е21(й? =
1 -X 2е '


Глава 14. Дифференциальные уравнения
687
*38. Уравнение: уг — 2у = ех.
Решение: у — е2х e~xdx =
= -ех.
В В задачах 39-44 необходимо найти общее решение двумя способами. Используйте сначала интегрирующий множитель, а затем — метод разделения переменных.
39. у' = 40. у' =
X X + 1
, 2х + 2ху , 4х + 2ху
4L 9 - "•9 =
43. 	у' = 2я(1/ + 1). 44. У = Зх2(у + 2).
*45. Используя интегрирующий множитель, найдите общее решение для модели неограниченного роста
^-=kv dt У'
(Подсказка. Следует помнить, что первообразная нуля равна произвольной постоянной.)
*46. Используя интегрирующий множитель, найдите общее решение для модели
ограниченного роста
* 47. Проанализируйте, как упростится процесс решения уравнения
У' + Л*)у =
если функции f(x) и д(х) являются соответственно константами а ф 0 и Ь, и найдите его общее решение.
* 48. Проанализируйте, как упростится процесс решения уравнения
у' + f(x)y = д(х),
если д(х) = 0 для всех х, и найдите его общее решение.
Применение математики
Экономика и бизнес
49. Непрерывно начисляемые сложные проценты. Начальная сумма, равная 20000 долл., размещена под 4,8 непрерывно начисляемых сложных процента. Со счета ежегодно с постоянной скоростью снимается 3000 долл, до его полного обнуления. Вычислите сумму на счету в произвольный момент времени t. Когда сумма станет равной нулю? Сколько всего денег будет снято со счета?


688
Часть III. Математический анализ
50. Непрерывно начисляемые сложные проценты. Начальная сумма, равная 50000 долл., размещена под 4,5 непрерывно начисляемых сложных процента. Со счета ежегодно с постоянной скоростью снимается 5400 долл, до его полного обнуления. Вычислите сумму на счету в произвольный момент времени t. Когда сумма станет равной нулю? Сколько всего денег будет снято со счета?
51. Непрерывно начисляемые сложные проценты. Начальная сумма Р долл, размещена под 4,75 непрерывно начисляемых сложных процента. Со счета ежегодно с постоянной скоростью снимается 1900 долл, до его полного обнуления. Через 10 лет, в течение которых деньги непрерывно снимались со счета, сумма на счету, стала равна нулю. Вычислите величину начального вклада Р.
52. Непрерывно начисляемые сложные проценты. Начальная сумма, равная Р долл., размещена под 4,25 непрерывно начисляемых сложных процента. Со счета ежегодно с постоянной скоростью снимается 3400 долл, до его полного обнуления. Через пять лет, в течение которых деньги непрерывно снимались со счета, сумма на счету, стала равна нулю. Вычислите величину начального вклада Р.
53. Непрерывно начисляемые сложные проценты. Начальная сумма, равная 5000 долл., размещена под семь непрерывно начисляемых сложных процента. Со счета ежегодно с постоянной скоростью снимается 2100 долл. Вычислите сумму на счету в произвольный момент времени t. Сколько денег будет находиться на этом счету через пять лет?
54. Непрерывно начисляемые сложные проценты. Начальная сумма, равная 10 000 долл., размещена под 6,25 непрерывно начисляемых сложных процента. Со счета ежегодно с постоянной скоростью снимается 5000 долл. Вычислите сумму на счету в произвольный момент времени t. Сколько денег будет на этом счету через 10 лет?
55. Непрерывно начисляемые сложные проценты. Начальная сумма, равная 10 000 долл., вложена во взаимный фонд. Дополнительные инвестиции совершаются со скоростью 1000 долл, в год. Через 10 лет фонд оценивается в 30 000 долл. Какой была ставка непрерывно начисляемых сложных процентов для этого фонда в течение 10-летнего периода? Выразите ответ в процентах с точностью до двух десятичных знаков.
56. Непрерывно начисляемые сложные проценты. На счет некого учреждения в доверительном фонде поступила сумма 100 000 долл. Дополнительные инвестиции совершаются со скоростью 1000 долл, в год. Деньги снимаются со счета со скоростью 20 000 долл. Через пять лет в доверительном фонде осталось 15 000 долл. Какой была ставка непрерывно начисляемых сложных процентов для указанного счета в течение пятилетнего периода? Выразите ответ в процентах с точностью до двух десятичных знаков.
57. Зависимости спроса и предложения. Предложение S и спрос D на определенный товар удовлетворяют уравнениям
S = 35-2p(t) + 3p'(f), £> = 95-5p(t) + 2p'(f).


Глава 14. Дифференциальные уравнения
689
Вычислите равновесную цену в момент времени t и долгосрочную равновесную цену, если р(0) = 30.
58. Зависимости спроса и предложения. Предложение S и спрос D на определенный товар удовлетворяют уравнениям
S = 70 - 3p(t) 4- 2p'(f),
Z? = 100-5p(t)+p'(t).
Вычислите равновесную цену в момент времени t и долгосрочную равновесную цену, если р(0) = 5.
Биологические науки
59. Загрязнение. Сборный резервуар емкостью 1000 галлонов заполнен 200 галлонами воды. Изначально каждый галлон воды в резервуаре содержит два фунта загрязняющих веществ. Вода, содержащая три фунта загрязняющего вещества на галлон, поступает в резервуар со скоростью 75 галлонов в час, а равномерно перемешанная вода вытекает из резервуара со скоростью 50 галлонов в час. Сколько фунтов загрязняющего вещества будет находиться в резервуаре через два часа? С какой скоростью (в фунтах на галлон) загрязняющее вещество будет вытекать из резервуара через два часа?
60. Загрязнение. Повторите решение задачи 59, если вода поступает в резервуар со скоростью 100 галлонов в час.
61. Загрязнение. Повторите решение задачи 59, если вода поступает в резервуар со скоростью 50 галлонов в час.
62. Загрязнение. Повторите решение задачи 59, если вода поступает в резервуар со скоростью 150 галлонов в час.
63. Загрязнение. Вернемся к задаче 59. В какой момент времени в резервуаре будет находиться 1000 фунтов загрязняющих веществ? Округлите ответ до одного десятичного знака.
64. Загрязнение. Вернемся к задаче 62. В какой момент времени в резервуаре будет находиться 1500 фунтов загрязняющих веществ? Округлите ответ до одного десятичного знака.


690
Часть III. Математический анализ
В статье, опубликованной в журнале College Mathematics Journal (Jan. 1987, 18:1), Артур Сигал (Arthur Segal) предложил следующую модель описания процесса набора
и потери человеком веса.
С.
3500
Здесь w(t) — вес человека (в фунтах) после t дней потребления С калорий в день. Воспользуйтесь предложенным уравнением для решения задач 65-68.
65. Потеря веса. Человек, весящий 160 фунтов, перешел на диету, потребляя 2100 калорий в день. Сколько будет весить этот человек через 30 дней соблюдения такой диеты? Сколько человеку понадобится времени, чтобы потерять 10 фунтов? Вычислите предел Нгщ-юо w (t) и проанализируйте результат.
66. Потеря веса. Человек, весящий 200 фунтов, перешел на диету, потребляя 2800 калорий в день. Сколько будет весить этот человек через 30 дней соблюдения этой диеты? Сколько человеку понадобится времени, чтобы потерять 25 фунтов? Вычислите предел Нгщ-юо w (t) и проанализируйте результат.
67. Потеря веса. Человек, весящий 130 фунтов, хочет похудеть на пять фунтов в течение 30-дневного периода. Сколько калорий в день должен потреблять такой человек, чтобы достичь своей цели?
68. 	Потеря веса. Человек, весящий 175 фунтов, хочет похудеть на 10 фунтов в течение 45-дневного периода. Сколько калорий в день должен потреблять такой человек, чтобы достичь своей цели?
Социальные науки
WWW В 1960 году Уильям К. Истес (William К. Estes) предложил следующую модель оценки успеваемости учеников одного класса.
Здесь k(t) — знания ученика через t недель (выражаемые в процентах и оцениваемые по выполненным экзаменационным заданиям), 1 — коэффициент обучаемости, характеризующий способность ученика к обучению (выражается в процентах и определяется по коэффициенту интеллектуального развития или другим аналогичным показателям), а А — константа, представляющая собой долю полезного времени, которое ученик провел за изучением предмета (чтение книг, посещение лекций и т. п.). Используя эту модель, решите задачи 69 и 70.
69. 	Теория обучения. Студенту, записавшемуся на курс испанского языка, в первый день занятий дали предварительный тест, чтобы определить уровень его начальных знаний по предмету. Результаты предварительного теста, коэффициенты обучаемости и доли полезного времени двух студентов приведены в таблице. Используя модель Истеса, предскажите уровень знаний каждого студента после 6 недель занятий.


Глава 14. Дифференциальные уравнения
691
Предварительная оценка
Коэффициент обучаемости, %
Доля полезного времени, %
Студент А
0,1(10%)
0,8
0,9
Студент Б
0,4(40%)
0,8
0,7
70. 	Теория обучения. Вернемся к задаче 69. Когда у обоих студентов будет одинаковый уровень знаний? Округлите ответ до одного десятичного знака.
Ключевые слова, основные обозначения и формулы
14.1. Основные понятия. Дифференциальное уравнение; дифференциальное уравнение первого порядка; порядок; поле направлений; решение; общее решение; семейство решений; частное решение; начальное условие; неявное решение; динамически стабильная цена; равновесная цена.
14.2. Разделение переменных. Разделение переменных; сингулярное решение; закон экспоненциального роста; закон ограниченного роста; закон логистического роста;
j f (у) dy = j
g (r) dx-,
dy dt
14.3. 	Линейные дифференциальные уравнения первого порядка. Линейное дифференциальное уравнение первого порядка; интегрирующий множитель; общее решение; равновесная цена в момент времени t; долгосрочная равновесная цена.
у'+ = g(x\, I(x) = Kx'>dx-
Упражнения для повторения
Выполните все упражнения этого обзорного раздела и сравните результаты с ответами, помещенными в конце книги. Ответы ко многим упражнениям на повторение приводятся вместе с номером соответствующего раздела (курсивом). Если у вас возникают затруднения при решении какой-либо задачи, повторите материал соответствующего раздела.
А В задачах 1 и 2 требуется показать, что данная функция является общим решением указанного дифференциального уравнения.
\.у = Су/х; 2ху' = у.
2. у = 1 + Се х/3; Зу' + у = 1.


692
Часть III. Математический анализ
В задачах 3 и 4 требуется найти соответствие между полями направлений и дифференциальными уравнениями. Кратко обоснуйте свой ответ.
у
У
3
з / / z z X
/ ХХХХхххххх- -■ /ХХХХхххх««» ХХХХхх»-----
-3
X -- Z
X -- X
✓ -- X
X X Z X X ✓
х Z Z Z Z ✓
X Z Z
Z /
✓
Z Z Z /
X X
Z X Z
X
а)
✓ Z ✓ ✓ /
Z Z Z /
Z
Z
Z
Z
Z
✓
X
X Z Z Z
✓
X Z
Z Z ✓ /
X X
Z
Z
/
X
б)
X
\ X * - \ х х х \ \ s х
6
X
3. 	2ху' — у (из задачи 1),
4. 	Зу' + у = 1 (из задачи 2).
В задачах 5 и б, используя соответствующее поле направлений для задач 3 и 4, необходимо построить графики частных решений, полученных при С = — 2, — 1, О, 1 и 2.
5. 	у = Су/х; (из задачи 1). 6. у = 1 + Се ®/3; (из задачи 2).
В задачах 7 и 8 необходимо записать дифференциальное уравнение, которое описывает скорость изменения указанной величины.
* 7. Цена товара у убывает со скоростью, пропорциональной разности между ценой и нижним пределом, равным 5 долл.
* 8. Цена товара у растет со скоростью, пропорциональной цене.
В задачах 9 и 10 необходимо кратко описать словами скорость изменения данной величины, удовлетворяющей указанному дифференциальному уравнению, и проанализировать характер роста/убывания этой величины.
* 9. Количество людей у, заразившихся инфекционным заболеванием, удовлетворяет
уравнениям dy/dt = 0,2?/(50 ООО — у) и ?/(0) = 1.
* 10. Количество радиоактивного вещества у (в граммах), выброшенного в атмосферу в результате аварии ядерного реактора, удовлетворяет уравнениям dy/dt = = -0,001?/ и 2/(0) = 100.
В задачах 11—14 необходимо определить, можно ли данное дифференциальное уравнение записать в форме, допускающей решение методом разделения переменных, f(y)y' = в форме линейного дифференциального уравнения у' + f(x)y = g(x), в обеих формах, или его нельзя записать ни в одной из этих форм.
11. у' + Зх2?/ + 9 = еж(1 — х + у). 12. у' + 10?/ + 25 = Зху2.
13. у' + Зу = ху 4- 2х — 6. 14. у2у' — ^хех~у.
В задачах 15-20 необходимо найти общее решение.
17. у' = Зх2у2.
19. у' = -у + х6.
х


Глава 14. Дифференциальные уравнения
693
Б В задачах 21-28 необходимо найти частное решение, удовлетворяющее данному условию.
21. 	у' = 10 - у; у(0) = 0.
23. у' = 2уе~х- у(0) = 1.
25- у> = ^Т5;г/(0) = 0-
х (1 +
27-^= 1 + ж2 ;У(0) = 1’
22. 	у' + у = х; з/(0) = 0.
24^ = 7TT^ = L
26. у' + -у = In я; 2/(1) = 2.
X
28. 	?/' + 2ху = 2е_а;2; ?/(0) = 1.
29. 	Решите следующее дифференциальное уравнение двумя способами. Используйте сначала интегрирующий множитель, а затем — метод разделения переменных.
ху' - 4у = 8.
*30. Приведите пример уравнения, которое можно решить, используя интегрирующий множитель, но нельзя решить методом разделения переменных. Решите это уравнение.
*31. Приведите пример уравнения, которое можно решить методом разделения переменных, но нельзя решить, используя интегрирующий множитель.
32. 	Найдите общее решение следующего дифференциального уравнения, а затем найдите частное решение, удовлетворяющее указанным начальным условиям.
ху' -5у = -10;
а) 	2/(0) = 2. б) 2/(0) = 0. в) 2/(1) = 1.
33. Найдите явное выражение для частного решения дифференциального уравнения УУ' = я, удовлетворяющего начальному условию 3/(0) = 4.
34. Известно, что у = х3 + Сх — это общее решение дифференциального уравнения ху' — у = 2х3.
а) Постройте графики решений, полученных при С = 0, 1, 2 и 3.
*б) Что общего у графиков решений для С > 0?
в) Постройте графики решений, полученных при С = 0, —1, -2 и —3.
*г) Что общего у графиков решений для С < 0?
35. Скорость изменения величины у со временем t пропорциональна разности между у и неизвестным верхним пределом М и у = 0, когда t = 0. Из закона ограниченного роста следует, что
у = М(1 - М > 0, к > 0.
а) Используя данные, приведенные в таблице, найдите два уравнения, которым должны удовлетворять величины М и к, и решите каждое из них относительно М.
t
2
5
У
4
7


694
Часть III. Математический анализ
б) 	Используя графическую утилиту и уравнение из п. а, найдите приблизительное значение М с точностью до одного десятичного знака.
Применение математики
Экономика и бизнес
36. WWW Обесценивание. Новый холодильник стоит 500 долл. Стоимость 20-летнего холодильника равна 25 долл. Найдите стоимость холодильника через пять лет после покупки, если скорость изменения стоимости пропорциональна самой стоимости.
37. Рост объема продаж. Скорость роста годового объема продаж компании пропорциональна разности между ним самим S и верхним пределом, равным 200 000 долл. Предполагается, что 5(0) = 0.
а) Сколько понадобится времени, чтобы годовой объем продаж достиг 150000 долл., если за первый год объем продаж составил 50 000 долл.?
*б) Предположим, компания недовольна результатами и хочет, чтобы объем продаж достиг 150 000 долл, за три года. Какими должны быть продажи за первый год, чтобы это смогло произойти? Округлите ответ до ближайшей тысячи долларов.
38. Стабильность цены. Предложение S и спрос D на определенный товар удовлетворяют уравнениям
S — 100 + р +р' и 79 = 200 - р — р'.
а) Вычислите равновесную цену р в момент времени t.
б) Вычислите долгосрочную равновесную цену р.
в) Постройте графики частных решений, удовлетворяющих начальным условиям р(0) = 75 и р(0) = 25.
*г) Проанализируйте долгосрочное поведение цены на этот товар.
39. Непрерывно начисляемые проценты. Исходная сумма, равная 60 000 долл, размещена под пять непрерывно начисляемых сложных процента. Ежегодно со счета снимается 5000 долл, до его полного обнуления. Вычислите сумму на счету в произвольный момент времени t. Когда сумма, находящаяся на счету, станет равной нулю? Сколько всего денег будет снято со счета?
40. Непрерывно начисляемые проценты. Во взаимный фонд изначально вложено 15 000 долл. Дополнительные инвестиции осуществляются со скоростью 2000 долл, в год. Через 10 лет фонд оценивается в 50000 долл. Какой была ставка непрерывно начисляемых сложных процентов для этого фонда в течение 10 летнего периода? Выразите ответ в процентах с точностью до двух десятичных знаков.
Биологические науки
41. Урожайность. Урожайность зерна y(f) (в бушелях на акр) удовлетворяет урав-
нению
= 100 + е * - у. dt


Глава 14. Дифференциальные уравнения
695
Вычислите величину у в произвольный момент времени, если ?/(0) = 0.
42. Загрязнение. Сборный резервуар емкостью 1000 галлонов исходно вмещает 100 галлонов незагрязненной воды. Вода, содержащая два фунта загрязняющего вещества на галлон, поступает в резервуар со скоростью 75 галлонов в час, а равномерно перемешанная вода вытекает из резервуара со скоростью 50 галлонов в час.
а) Вычислите общее количество загрязняющего вещества в резервуаре через два часа. Округлите ответ до одного десятичного знака.
б) Когда резервуар будет содержать 700 фунтов загрязняющего вещества? Округлите ответ до одного десятичного знака.
43. Экология. Популяция птиц на острове уменьшается со скоростью, пропорциональной разности, между численностью популяции и нижним пределом 200 птиц.
а) Вычислите численность популяции через четыре года, если он уменьшился с 1000 птиц пять лет тому назад до 500 птиц на сегодняшний день.
б) Предположим, что четыре года спустя популяция насчитывает 400 птиц что указывает на большую вместимость острова, чем предполагалось. Считая, что скорость изменения численности популяции остается пропорциональной разности между ее размером и неизвестным нижним пределом М, найдите приблизительное значение М с точностью до ближайшего целого.
Социальные науки
44. Распространение слухов. Некто распространяет слухи в группе из 200 человек. Скорость распространения слухов пропорциональная числу людей, которые их еще не слышали. Через два дня слухи дошли до 10 человек.
а) Сколько человек узнает о слухах через пять дней?
б) Сколько понадобится времени, чтобы о слухах узнали 100 человек?
Домашнее задание 14.1. Закон Торричелли
WWW Представим себе, что вода вытекает через отверстие в стенке резервуара (рис. 14.17). Обозначим через h высоту столба воды над отверстием. При больших значениях h вода убывает очень быстро, поскольку ее скорость вытекания очень велика. При малых значениях h вода убывает медленнее, поскольку ее скорость вытекания небольшая. Можно предположить, что производная dh/dt пропорциональна величине h, т.е. функция h удовлетворяет дифференциальному уравнению
(14.13)
где к — константа. Однако дифференциальные уравнения
= kh2 dt
и
(14.14)
(14.15)


696
Часть III. Математический анализ
также означают, что по мере уменьшения величины h вода течет все медленнее. Какое из уравнений лучше моделирует процесс вытекания воды из резервуара? На этот вопрос можно ответить, проведя следующий простой эксперимент.
Рис. 14.17. Вытекание воды из отверстия
Просверлите небольшое отверстие диаметром приблизительно 4 мм в нижней части прозрачного пластикового контейнера. (Не обязательно, чтобы весь контейнер был цилиндрическим — подойдет 2-литровая бутылка из-под газированного напитка или контейнер из-под стеклоомывателя.) Проградуируйте отрезок ленты и наклейте ее его на цилиндрическую часть бутылки, так чтобы высоту h можно было измерить с точностью до миллиметра (см. рис. 14.17). Наполните бутылку водой, закрыв отверстие пальцем, а затем откройте его, позволив воде свободно вытекать (не забудьте подставить под струю емкость для сбора вода). Запустите секундомер в момент, когда высота столба воды достигнет некой начальной отметки (например, 11,0 см). Запишите с интервалом 10 или 15 секунд высоту столба воды по мере ее убывания (выберите такой интервал времени, чтобы сделать приблизительно десять измерений, прежде чем струя воды не станет очень тонкой).
1. Постройте табл. 14.1 и запишите полученные данные в первые два столбца. В случае необходимости (в зависимости от рабочих характеристик установки) можно изменить 15-секундный временной интервал и количество строк таблицы.
2. Найдите частные решения Нъ и h$ соответственно дифференциальных уравнений (14.13)—(14.15), которые удовлетворяли бы одновременно первой и последней точкам записанных в таблицу данных (табл. 14.1).
3. Рассчитав значения hi, /12 и /13, заполните последние три столбца таблицы.
4. Постройте графики функций /и, /12 и /13 и нанесите точки данных в общей системе координат.
5. Пользуясь результатами решения пп. 3 и 4, определите, какая из функций hx, h,2 и /13 лучше моделирует процесс вытекания воды из резервуара.
Закон Торричелли утверждает, что скорость dh/dt пропорциональна квадратному корню из h (для емкости с постоянной площадью сечения). Закон назван в честь Евангелиста Торричелли (1608-1647), изобретателя ртутного барометра.


Глава 14. Дифференциальные уравнения
697
Таблица 14.1. Пример записи экспериментальных данных
Время, с
Высота столба воды, см hi h2
0
15
30
45
60
75
90
105
120
135
150
165
180
11,0 11,0 11,0 11,0
9.8
8.9
7.9
7.1
6.2
5.4
4,6
4,0
3.4
2,8
2.4
1.9 1,9 1,9 1,9
6. 	Проанализируйте, в какой мере полученный результат подтверждает закон Торричелли.
Домашнее задание 14.2. Метод Эйлера
В этом разделе описаны методы решения только определенных классов дифференциальных уравнений. Однако многие дифференциальные уравнения не имеют решений, которые можно выразить в виде конечной комбинации элементарных функций. В этом случае решение необходимо аппроксимировать. Рассмотрим метод аппроксимации произвольной задачи с начальным условием вида
у' = у), у(а) = С, а^х ^Ь. (14.16)
Чтобы не путать точное решение задачи с начальным условием и результатами аппроксимации, будем называть функцию у = у(х) точным решением задачи (14.16), если
у' = у(х)) для а х b и у(а) = С.
Следует отметить, что точное решение всегда является частным. В общие решения входит произвольная постоянная, которую нельзя аппроксимировать численно.
Рассматриваемый здесь метод аппроксимации решений задач с начальным условием называется методом Эйлера. Этот метод основывается на следующих наблюдениях относительно наклона прямой: если тп — наклон отрезка прямой, проходящего через точки (хо,?/о) и (xi,т/i), а Дх = xi—xo — изменениевеличиных,то yi = ув+птАх (рис. 14.18).
Чтобы объяснить суть метода Эйлера, рассмотрим следующую задачу с начальным условием.
у' = У, 1/(0) = 1. (14.17)
Конечно, это очень простое уравнение, решение которого имеет вид у = ех. Изучение этого простого уравнения даст возможность сравнить приближенное решение с точным. Аппроксимируем решение задачи (14.17) на интервале 0 х 1. Чтобы сделать это,


698
Часть III. Математический анализ
Рис. 14.18. Иллюстрация к описанию метода Эйлера
разобьем интервал [0,1] на пять подынтервалов длиной Дх = 0,2 и найдем приблизительные значения решения в конечных точках каждого из этих интервалов. Напомним из предыдущих рассуждений о полях направлений, что в данной точке на плоскости уравнение у' = у указывает наклон касательной к решению, проходящему через эту точку (рис. 14.19).
Наклон в данной начальной точке (0, т/(0)) = (0,1) равен yf = 1. Построим отрезок прямой с наклоном, равным единице, выходящий из точки (0,1) и заканчивающийся в точке (0,2, т/i) (рис. 14.20). Исходя из предыдущих наблюдений относительно наклона, можно сделать вывод, что
t/i = i + o,2.i = i,2«t/-o,2.
Рис. 14.19. Поле наклона для у' = у
Рис. 14.20. Аппроксимация г/(0,2)
1. 	Вычислите наклон в точке (0,2,1,2), постройте отрезок прямой с таким наклоном, выходящий из точки (0,2,1,2) и заканчивающийся в точке (0,4,7/2), а затем, используя величину 7/2, вычислите приблизительное значение т/(0,4).


Глава 14. Дифференциальные уравнения
699
2. Повторите решение п. 1 и вычислите приблизительные значения ?/(0,6), т/(0,8) и ?/(1). На рис. 14.21 показаны отрезки прямой, соединяющие приближенные значения у(х), а на рис. 14.22 этот график накладывается на график точного решения.
3. Формула (14.18) в методе Эйлера является рекурсивной, т.е. каждое приблизительное значение выражается через предыдущее значение. Убедитесь, что эта формула дает те же приблизительные значения, что и формулы, найденные при решении пп. 1 и 2.
4. Проанализируйте связь между формулой (14.18) и наклоном отрезка прямой, показанной на рис. 14.18.
Рис. 14.21. Ломаная, приближающая точное решение
Рис. 14.22. Графики точного и приближенного решения
Метод Эйлера
Если у (ж) — точное решение задачи с начальным условием
у'= у(хо)=Уо,
хо, я?1, ..., хп — последовательность значений, для которых
хк = xk-i + Дх, к = 1, 2, ..., п,
и ?/1, у2, ..., уп — последовательность значений, для которых
Ук = Ук-i + f(xk-i,yk_i)&x, к = 1,2,..., п, (14.18)
то
3/(xfc)«2/fc, А: = 1,2, ...,n.
5. 	Расстояние между последовательными значениями х9 Ах называется длинной шага. В данном случае использовалась шаги равной длины. Будет ли процедура корректной, если шаги будут разной длины?


700
Часть III. Математический анализ
6. Рассмотрим следующую задачу с начальным условием:
?/ = 2/ + 7ж - 3, 3/(0) = 1. (14.19)
7. Найдите точное решение задачи (14.19).
8. Аппроксимируйте решение на отрезке 0 < х 1, используя метод Эйлера с длинной шага Дж = 0,2. Постройте таблицу для сравнения приблизительных значений с точными.
9. Повторите решение п. 7 для длины шага Дж = 0,1.
10. Чтобы сравнить точное решение п. 7 с приблизительным решением п. 8, полученным с помощью графической утилиты, введите значения хь и приблизительные значения уь в программу. Затем введите точное решение в редактор функций и постройте графики в одном и том же окне. Повторите эту процедуру для приблизительного решения п. 8. Вычисление приблизительных значений и построение их графика легко автоматизировать, написав короткую программу. В табл. 14.2 перечислены программы для нескольких графических калькуляторов, а на рис. 14.23 проиллюстрировано использование одной из этих программ для обработки данных задачи п. 8. Обратите внимание на то, что название функции f(x, у) нужно вводить прописными буквами в кавычках (рис. 14.23, а). В программе для калькулятора TI-85/TI-86 также требуются вводить кавычки, но название функции указывается строчным буквами.
11. Расстояние между точным и приблизительным решением описывает погрешность аппроксимации. Исходя из построенных таблиц и графиков, объясните, как изменится погрешность при вычислении следующего значения? Какой будет погрешность при увеличении шага?
До сих пор мы рассматривали только уравнения, точные решения которых известны. Рассмотрим теперь уравнение, точное решение которого нельзя найти ни одним из описанных ранее методов:
?/ = - + -• 2/(1) = 1
х у
12. Используя метод Эйлера с длиной шага 0,2, вычислите приблизительное значение 2/(2).
13. Повторите решение п. 12, сокращая шаг, пока приблизительное значение у (2) не будет найдено с точностью до одного десятичного знака.


Глава 14. Дифференциальные уравнения
701
Таблица 14.2. Программы графических калькуляторов аппроксимации методом Эйлера
TI-82/TI-83 TI-85/TI-86*
(0}-> L1
{0}-» xStat
(0}-> L2
{0}-> yStat
Input "ХО? ",Х
Input "X0: ”,x
Input "YO? ”,Y
Input "YO: ",y
Input ’’DELTA X? ”,D
Input "DELTA x: ",D
Input "NBR OF STEPS? ”,N
Input "NUMBER OF STEPS: ",N
Input ”F(X,Y)? ”,Yo
Input ”f(x,y): ",Y
FnOff 0
ST> Eq(Y, y9)
0-» I
FnOff 9
Lbl A
0-* I
X-> Li (1+1)
Lbl A
Y—> L2 (1+1)
x-»x Stat(I+l)
X+Yo*D—» Y
y->yStat (1+1)
X+D-> X
y+y9*D—» у
1+1-» I
X+D—» x
If I>N
1+1-» I
Stop
If I>N
Goto A
Stop Goto A
* В калькуляторе TI-86 предусмотрена встроенная процедура Euler, поэтому собственную программу следует назвать иначе, например, Eulr.
prSnEULER «0? 0 ?0? 1
DELTA X? .2
1BR OF STEPS? 5
"Y+7X-3 Done
Xi
Ti
Тз
0
1
.2
.6
.4
.4
.6
.44
76B
1.4416
1 (?) =
б) вывод
в) график точного и приближенного решений
а) ввод
Рис. 14.23. Выполнение программы аппроксимации методом Эйлера в графическом калькуляторе TI-82/TI-83


15
Теория вероятностей и математический анализ
■ 15.1. Несобственные интегралы
■ 15.2. Непрерывные случайные величины
■ 15.3. Математическое ожидание, стандартное отклонение и медиана
■ 15.4. Специальные распределения вероятностей
■ Ключевые слова, основные обозначения и термины
■ Упражнения для повторения
■ Домашнее задание 15.1. Бета-распределение
■ Домашнее задание 15.2. Распределение хи-квадрат
Введение
В разделе 12.2 кратко описаны инструменты математического анализа применяемые при решении задач теории вероятностей. В настоящей главе эта тема будет рассмотрена более подробно. В начале главы вводится концепция несобственного интеграла и другие базовые понятия. Затем в ней обсуждаются наиболее известные распределения вероятностей, а в завершение — подробно описывается нормальное распределение.


Глава 15. Теория вероятностей и математический анализ
703
15.1. 	Несобственные интегралы
■ Несобственные интегралы
■ Практическая задача: стоимость капитала
Несобственные интегралы
Рассмотрим интегральные выражения, имеющие широкое применение не только в теории вероятности, но и в других разделах математики. Ранее было введено понятие определенного интеграла
ь
j/(x)cLr. (15.1)
а
Оно подразумевало, что функция f непрерывна на отрезке [а, Ь]. Расширим теперь смысл выражения (15.1) на бесконечную прямую.
Задание 15.1.
Для каждой из следующих функций найдите площадь фигуры, ограниченной графиком от х = 1 до х = b, b > 1 (рис. 15.1). Проанализируйте характер изменения этой площади по мере увеличения числа Ь.
= = х~5/4- 2- = = х-4/5. а
Рис. 15.1. Графики функций f (х) = = х (х) = = я-4/5
Исследуем конкретный пример, который будет служить основной нескольких общих определений. Как понимать следующее выражение?
Построив график /(я) = 1/ж2, х 1 (рис. 15.2), можно отметить, что для произвольного фиксированного значения b > 1 величина f (х) dx — это площадь фигуры, расположенной между графиком у = 1/х2, над осью х и между точками х = 1 и х = Ь.


704
Часть III. Математический анализ
Рис. 15.2. График функции
f(x) = 1/х2
Посмотрим, что произойдет, если устремить b —► оо, т.е. вычислим следующий предел.
Можно ли было ожидать такой результат? Независимо от того, насколько большим будет число Ь, площадь фигуры, лежащей под графиком от точки х = 1 до точки х = Ь, никогда не превысит единицы, а в пределе она будет равна ей (рис. 15.3). Следовательно,
оо Ъ
1 1
Рис. 15.3. График функции f(x) = 1/z2
Этот интеграл представляет собой пример несобственного интеграла. В общем случае
выражения вида
ъ
f (ж) dx,
— оо / (х) dx,
— ОО


Глава 15. Теория вероятностей и математический анализ
705
где f — непрерывная функция на указанном интервале, называются несобственными интегралами. (Эти интегралы “несобственные” потому, что их интервал интегрирования неограничен, на что указывает использование символа оо. Существуют и другие типы несобственных интегралов, в которых интервалы интегрирования содержат точки разрыва функции, но здесь они рассматриваться не будут.) Строгое определение каждого типа интегралов, приведенных выше, дано в следующей врезке.
Несобственные интегралы
Если f — непрерывная на указанном интервале функция, и указанный предел существует,
то
1.
2.
3.
оо b
j f (х) dx = Jim | f (x) dx, a a
b b
f (x) dx = lim f (x) dx,
J a—ooj
— oo a
oo c oo
f (x)dx = j f (x) dx + j f (ж) dx.
— oo
— оо с
Здесь с — произвольная точка на интервале (—ос. ос), выбранная таким образом, чтобы оба несобственных интеграла справа существовали.
Пример 15.1 (Вычисление несобственного интеграла). Вычислите следующий интеграл, если он сходится.
оо
2
Решение,
оо
1
2
Поскольку In 6 —> оо, когда 6 —► ственный интеграл расходится.
ь
dx f dx
— = lim — =
X b—>oo J X
2
Г ib"
= lim (lnrr) =
= lim (ln b — ln 2).
b—»oo
oo, то предела не существует. Следовательно, несоб-
Ъ—>оо
Упражнение 15.1.
Вычислите значение следующего интеграла, если он сходится.
dx
3


706
Часть III. Математический анализ
Пример 15.2 (Вычисление несобственного интеграла). Вычислите значение следую¬
щего интеграла, если он сходится
2
exdx.
— оо
Решение.
Интеграл сходится.
Упражнение 15.2.
Вычислите следующий интеграл, если он сходится.
-1 j x~2dx.
-оо ■
Пример 15.3 (Вычисление несобственного интеграла). Вычислите следующий интеграл, если он сходится.
ОО
Т
J (1+I2)2
— оо
Решение.
оо
0 оо
——zdx = Г (1 + х2) 2 2х dx + (1 + ж2)
(1 + х2) J J
— оо —оо О
О Ь
= lim j (1 + я2) 2 2х dx + Jim j (1 + ж2) 22xdx =
а
'(l + Q-1
_2
2х dx =
lim
а—► — оо
-1
О'
+ lim
Ь—>оо
•оо
О
(1 + а;2)
-1
-1 ЬЗ
а
0
lim
а—► — оо
+ lim
Ъ—>оо
+1
= —1 + 1 = 0. Интеграл сходится.


Глава 15. Теория вероятностей и математический анализ
707
Упражнение 15.3.
Вычислите следующий интеграл, если он сходится.
Задание 15.2.
Пусть
если 0 < х < 1; в противном случае.
1. Постройте график функции /(х) и объясните, почему она не является непрерывной в точках х = 0 и х = 1.
2. Вычислите интеграл J** f (ж) dx,
3. Проанализируйте поведение несобственного интеграла J^° f (я) dx. ■
В теории вероятности часто встречаются функции, которые равны нулю на одном или нескольких интервалах действительной оси. Несобственные интегралы таких функций можно упростить, удалив интервалы, на которых функция равна нулю. Этот процесс проиллюстрирован в следующем примере.
Пример 15.4 (Вычисление несобственного интеграла). Найдите значение интеграла /Хо f (Х) dx’ еСЛИ
если X > 0;
0 в противном случае.
Решение. Функция / имеет разрыв в точке х = 0 (рис. 15.4). Однако, поскольку /(ж) = 0 для х < 0, можно поступить следующим образом.
оо оо
f(x)dx = f(x)dx = f(x) = о для х < 0.
-оо 0
= [_!_^ =
J (х + 2)2
о 4 7
ь
= lim ~dx —
b^ooj (ж + 2)2 о
= lim |-4(х + 2)"1
Ь-+оо 0
= lim + 2^ =
Ъ—>оо у Ь -4- 2 J
= 2
Интеграл сходится.


708
Часть III. Математический анализ
Рис. 15.4. График функции /(х) из примера 15.4
Упражнение 15.4.
Вычислите интеграл f (х) dx, если
4х — х2, "о
если 0 х 4; в противном случае.
Пример 15.5 (Добыча нефти). Предполагается, что через t лет нефть из нефтяной скважины будет отбираться со скоростью R(t) миллионов баррелей в год, которая равна
R(t) = 8е-°’05* — 8e_0,lt.
Вычислите общее количество нефти, которая будет добыта из этой скважины.
Решение. Общий объем нефти, добытой за Т лет эксплуатации скважины, равно R(t)dt (рис. 15.5). В какой-то момент в будущем скорость годовой добычи станет настолько низкой, что работа скважины станет экономически невыгодной. Однако, поскольку неизвестно, когда это произойдет, уместно предположить, что скважина будет функционировать бесконечно, а для вычислений можно воспользоваться несобственным интегралом. Следовательно, общее количество добытой нефти приблизительно равно
т
R (t) dt =
о
т
т j(8e_0’05t — 8e_0,lt)cli =
О
lim
(-160e~°’O5t +80е_о’н)
т'
Т—юо
0 _
= lim (- 160е“°’05Т + 8Ое_о,1Т + 80)
Т->оо V 7
= 80, или 80 000 000 баррелей.
Общий объем добытой нефти за любой конечный промежуток времени [0, Т] меньше, чем 80 000 000 баррелей, и, чем больше величина Т, тем ближе это число к 80 000 000 баррелям. На рис. 15.6 показан общий объем добытой нефти на интервале [0, Т] для значений Т(= X) от 50 до 110 лет. ■


Глава 15. Теория вероятностей и математический анализ
709
X
Ml
so
67.405
60
72.252
70
75.241
B0
77.096
90
7B.232
100
7B.926
110
79.347
ViB-160eA(
-.05X...
Рис. 15.5. График функции R(t) =
= ge-o,O5t _ 8e-o,it
Рис. 15.6. Общее количество добытой нефти на интервале [0, X]
Упражнение 15.5.
Скорость годовой добычи из нефтяной скважины (в миллионах баррелей) равна
R(t) = 4e_0,lt - e~°’2t.
Предполагая, что скважина будет эксплуатироваться бесконечно, найдите общий объем добытой нефти. в
Практическая задача: стоимость капитала
Напомним, что если капитал вложен под г непрерывно начисляемых сложных процентов на Т лет, то текущая стоимость PV и будущая стоимость FV связаны между собой формулой вычисления непрерывно начисляемых сложных процентов (см. раздел 10.1)
FV = PVerT,
которую можно также переписать в виде
FV = erTPV.
Эта зависимость справедлива как для одиночных вкладов, так и для доходов от непрерывных источников. Следовательно, если /(£) — непрерывный источник доходов, то будущая стоимость будет равна (см. раздел 12.2)
т
FV = егТ | f (t) e~rtdt. Будущая стоимость.
о
Используя формулу непрерывно начисляемых сложных процентов, можно определить, что текущая стоимость равна
т
PV = e~rTFV = e~rTerT j / (t) e~Ttdt.
0


710
Часть III. Математический анализ
Поскольку е тТегТ = 1, получаем следующий результат
т
PV = j f (t) e~rtdt. Текущая стоимость.
О
Если в формуле для текущей стоимости величину Т устремить к оо, то получится несобственный интеграл, который представляет собой стоимость основного капитала непрерывного источника доходов.
Стоимость основного капитала бесконечного источника доходов
Непрерывный источник доходов называется бесконечным, если доход от него поступает всегда. Стоимость основного капитала CV бесконечного источника доходов f(t) при ставке г непрерывно начисляемых сложных процентов — это текущая стоимость на временном интервале [0, оо), т.е.
оо
CV = f (t) e~rtdt.
о
Понятие стоимости основного капитала позволяет определить ценность вложения (в денежном исчислении при текущей стоимости денег), которое будет приносить доход в течение неограниченного периода времени.
Пример 15.6 (Стоимость основного капитала). Семья сдала в наем нефтедобывающей компании права на разработку месторождения в обмен на пожизненные годовые выплаты, равные 1200 долл. Вычислите стоимость основного капитала такой аренды при ставке, равной пяти непрерывно начисляемым процентам.
Решение. Годовые выплаты нефтяной компании можно рассматривать, как непрерывный источник доходов, поступающих со скоростью f(t) — 1200. (Трактовка последовательности периодических платежей как непрерывного потока доходов, поступающих с постоянной скоростью, даже если доход начисляется только в конце каждого периода, является весьма распространенной практикой.) Таким образом, стоимость основного капитала будет равна
оо
CV = f(t)e~rtdt;
О оо
CV = j 1200е-° 05tdt =
О
Т
= lim
Т—юо о
1200е
0054t =
= lim
Т—>оо
—24ОООе_0,05*
т~
о
= lim (—24ОООе_о,О5Т + 24000) = 24 000 долл. Т—юо Х '


Глава 15. Теория вероятностей и математический анализ
711
Упражнение 15.6.
Повторите решение примера 15.6, если ставка равна шести непрерывно начисляемым сложным процентам. ■
Ответы к упражнениям
15.2. 1.
15.3. Расходится.
32
15.4. -.
15.5. 35 000 000 баррелей.
15.6. 20 000 долл.
Практикум 15.1
А В задачах 1-16 требуется вычислить значение каждого сходящегося несобственного Б
интеграла.
оо
' dx х4 *
1
оо
j10~6xcte.
о
оо
j e~x/1  2dx.
о
1.
3.
5.
7.
9.
И.
dx
13.
1
оо
6. j e~xdx. о
оо
1
10.
оо
dx
(я+1)3’
оо
0
14.
ОО dx
ж1’01 *
1
оо
16. 0,01 j e~°’lxdx.
О


712
Часть III. Математический анализ
В задачах 17-22 необходимо построить график функции у = /(х) и вычислить значение интеграла / (х) dx, если он сходится.
17. /(х) =
18. f (х) =
19. /(х) =
fl + х2,
1°
(2 + х,
1°
Ге-ОДх,
1°
если 0 х < 2;
в противном случае.
если 0 х < 3;
в противном случае.
если х 0;
в противном случае.
20. / (х) =
21. f (х) =
22. /(х) =
(2 - е-0,2®,
1°
fW + 2),
1°
U/(x+ l)2,
1°
если х 0;
в противном случае.
если х 2;
в противном случае.
если х 1;
в противном случае.
В задачах 23-26 необходимо проанализировать справедливость каждого утверждения. Если утверждение всегда истинно, объясните почему. Если нет, приведите контрпример.
*23. Если f — непрерывная возрастающая функция на интервале [0,оо), такая, что /(х) > 0 для всех х, то интеграл J^° f (х) dx расходится.
*24. Если f — непрерывная убывающая функция на интервале [0,оо), такая, что /(х) > 0 для всех х, то интеграл J^° f (х) dx сходится.
*25. Если f — непрерывная функция на интервале [1,оо), такая, что /(х) > 0 для всех х, и /(х) > 10 для 1 х 1000, то интеграл f (х) dx расходится.
* 26. Если f — непрерывная функция на интервале [1, оо), такая, что 0 < /(х) 0,001
для всех х, то интеграл f (х) dx сходится.
В задачах 27-36 требуется вычислить значение F(b), затем, используя графическую утилиту, оценить предел Нгпь—ос F(b).
ь
ь
27. F (Ь) =
X4'
1»-FW = \T3.
1
1
1
ь
29. F (Ь) =
[10_6xdx.
Г 108
30. F (b) = _^dx.
0
i
1
ь
b
31. F (Ь) =
e~x/2dx.
32. F (6) = j e~xdx.
о
о


Глава 15. Теория вероятностей и математический анализ
713
33. F (Ь) =
з4-г<ь>=Ш-
1
35. F (Ь) = j
О
dx
(я+1)2’
ь
36. F (b) = j
О
dx
(х + 1)3
* 37. Сходится ли интеграл f (х) dx, если функция f непрерывна на луче [0, оо)
и интеграл f (ж) dx сходится? Объясните свой ответ.
* 38. Расходится ли интеграл J^° f (ж) dx, если функция f непрерывна на луче [0, оо)
и интеграл f (х) dx расходится? Объясните свой ответ.
В В задачах 39-48 необходимо вычислить значение каждого сходящегося интеграла.
оо
39. 	| ^e~x/kdx, к >0.
О
оо
41-1 ib"1-
— оо
оо
40. —dx, р > 1.
J хр
1
оо
42. j xe~x*dx.
— оо
оо
44. j (е~х + 2еж) dx.
о
оо
Г е~х
48. - dx
J 1 + е-*
Применение математики Экономика и бизнес
49. Стоимость основного капитала. Пожизненная годовая рента за земельную собственность составляет 6000 долл. Вычислите стоимость основного капитала при ставке, равной пяти непрерывно начисляемым сложным процентам.
50. Стоимость основного капитала. Пожизненная годовая рента за земельную собственность равна 10000 долл. Вычислите стоимость основного капитала при ставке, равной четырем непрерывно начисляемым сложным процентам.
51. Стоимость основного капитала. Доверительный фонд приносит бесконечный поток доходов со скоростью
/(£) = 1500е°,04< долл, в год.


714
Часть III. Математический анализ
Вычислите стоимость основного капитала при ставке, равной семи непрерывно начисляемым сложным процентам.
52. 	Стоимость основного капитала. Доверительный фонд приносит бесконечный поток доходов со скоростью
/(t) = 1000eo,O2t долл, в год.
Вычислите стоимость основного капитала при ставке, равной шести непрерывно начисляемым сложным процентам.
* 53. Стоимость основного капитала. Вернемся к задаче 49. Проанализируйте вли¬
яние на стоимость основного капитала увеличения ставки до 6% и уменьшения ее до 4%. Объясните результат.
* 54. Стоимость основного капитала. Вернемся к задаче 50. Проанализируйте вли¬
яние на стоимость основного капитала увеличения ставки до 5% и уменьшения ее до 2%. Объясните результат.
55. 	Добыча. Скорость (норма) отбора природного газа из месторождения (млрд. куб. футов в год) задается уравнением (см. следующий рисунок)
R(t) = 3e"°’2t - 3e“°’4t.
а) Вычислите общую добычу, предполагая, что скважина будет функционировать бесконечно.
б) Когда объем добычи достигнет 50% от общего объема добытого газа? Округлите ответ до двух десятичных знаков.
56. 	Добыча. Скорость (норма) отбора из нефтяной скважины (млрд. куб. футов в год)
задается уравнением
lOOOt
(50 + i2)2 ’
а) Вычислите общий объем добычи, предполагая, что скважина будет функционировать бесконечно.
б) Когда объем добычи достигнет 50% от общего объема добытого газа? Округлите ответ до двух десятичных знаков.


Глава 15. Теория вероятностей и математический анализ
715
Биологические науки
57. 	WWW Загрязнение. По оценкам исследователей, скорость утечки токсичных веществ со свалки через t лет будет равна R(t) галлонов в год, где
Я(*) =
500
(W
Вычислите общее количество токсических веществ, которые вытекут со свалки, предполагая, что утечка длится бесконечно.
58. 	Усвоение препарата. При приеме лекарственного препарата организм усваивает не все его количество. Один из способов определения количества усвоенного препарата заключается в измерении скорости вывода его из организма. Какое количество препарата будет выведено из организма при скорости
R(f) = Зе 0,lt — Зе 0,3t мл/мин.,
где t — время в минутах с момента принятия препарата?
Социальные науки
59. 	WWW Иммиграция. Чтобы контролировать рост численности населения, государство планирует ввести в действие новые иммиграционные законы. Аналитики оценили, что скорость иммиграции в страну через t лет после изменения законодательства будет равна
„, ч 400
R (tj = — — млн. иммигрантов в год.
Вычислите общее количество иммигрантов, которые прибудут в страну за время действия новых законов, предполагая, что они введены навечно.
15.2. 	Непрерывные случайные величины
■ Непрерывные случайные величины
■ Плотность вероятности
■ Интегральная функция распределения
Непрерывные случайные величины
Теория вероятностей связана с вычислением предельной частоты исходов эксперимента, если исход каждого испытания случаен. Например, при подбрасывании правильной монеты невозможно предсказать, что выпадет: орел или решка. Однако теория вероятности позволяет предсказать, что монета упадет орлом приблизительно в 50% испытаний.
Значения, присвоенные каждому исходу эксперимента, определяют функцию, называемую случайной величиной. Рассмотрим эксперимент, в котором подбрасывается три монеты, и функцию X, значениями которой является количество выпавших орлов. Возможные исходы эксперимента и соответствующие значения функции X приведены в табл. 15.1.


716
Часть III. Математический анализ
Таблица 15.1. Количество орлов, выпавших при подбрасывании трех монет
Пространство выборок S
Количество выпавших орлов X(ej)
ei: PPP
0
е2: РРО
1
е3: POP
1
е4: ОРР
1
е5: РОО
2
е§'. ОРО
2
е7: OOP
2
е8: ООО
3
Поскольку совокупность возможных исходов этого эксперимента является ограниченным множеством, функция X называется дискретной случайной величиной.
Ситуация усложняется, если эксперимент имеет бесконечное количество исходов. Представим себе следующую ситуацию: включим электрическую лампочку и оставим ее светиться до тех пор, пока она не перегорит. Какая-то лампочка может оказаться бракованной и не загореться вообще. Другая может отработать 50 или 100 лет. Пусть X — функция, значениями которой являются ожидаемые сроки службы лампочек (в часах). Теоретически нет никаких оснований исключать какие-либо значения ожидаемого срока службы лампочки из интервала [0,ос). Следовательно, можно предположить, что функция X принимает любые значения из интервала [0, оо), и тогда она называется непрерывной случайной величиной.
Непрерывная случайная величина
Непрерывная случайная величина X — это функция, принимающая числовые значения, описывающие каждый исход эксперимента. Совокупность возможных значений X является интервалом действительных чисел. Этот интервал может быть открытым или закрытым, а также ограниченным или неограниченным.
Термин непрерывный здесь применяется в ином смысле, чем в разделе 8.2. В данном случае он отражает тот факт, что значения случайной величины принадлежат непрерывному множеству действительных чисел, такому как [0, сю), а не дискретному множеству, такому как {0,1,2,3} или {2,4,8,...}.
Задание 15.3.
Для каждого из следующих экспериментов определите, является ли указанная случайная величина дискретной или непрерывной.
1. Подбрасываются два кубика. Значение X является суммой очков на верхних поверхностях кубиков.
2. Дротик бросается в круглую мишень для игры в дартс. Значение X является расстоянием от дротика до центра мишени.
3. Отделение банка открыто 10 часов в сутки. Значение X является количеством клиентов, обслуживаемых за день.
4. Отделение банка открыто 10 часов в сутки. Значение X является временем (в минутах), которое каждый клиент проводит в очереди. ■


Глава 15. Теория вероятностей и математический анализ
717
Плотность вероятности
Если X — дискретная случайная величина, то вероятность того, что ее значение попадет в данный интервал, можно вычислить путем суммирования. Рассмотрим эксперимент, в котором подбрасываются три монеты. Пусть значение X соответствует количеству выпавших орлов. Распределение вероятностей для величины X показано в табл. 15.2 и проиллюстрировано гистограммой (рис. 15.7). Обозначим вероятность того, что значение X окажется между числами 0 и 2 включительно, через Р(0 < X < 2), и вычислим ее путем суммирования.
Р(0 < X 2) = Р (X = 0) + Р (X - 1) + Р (X = 2) = | | | ?
Таблица 15.2. Распределение вероятностей
Количество выпавших орлов, X
0
1
2
3
Вероятность, р(х)
1
8
3
8
3
8
1
8
Рис. 15.7. Гистограмма распреде¬
ления вероятностей
Если X — непрерывная случайная величина, то такой подход неприменим. Поскольку теперь функция X может принимать любые действительные значения на отрезке [0,2], невозможно записать вероятность Р(0 < X < 2) в виде конечной и даже бесконечной суммы. (Каким было бы второе слагаемое в такой сумме, т.е. какое “следующее” действительное число после нуля? Подумайте над этим.) Вместо этого необходимо ввести функцию нового типа, называемую плотностью распределения вероятностей, и воспользоваться интегралами, входящими в эту функцию, для вычисления вероятности того, что непрерывная случайная величина лежит на заданном интервале. К примеру, плотность распределения вероятностей можно использовать для вычисления вероятности того, что фактическое количество некоего вещества может быть больше 11,9 и меньше 12,1 унции, или что скорость автомобиля, участвовавшего в дорожно-транспортном происшествии, была больше 60 и меньше 65 миль в час.


718
Часть III. Математический анализ
Для простоты в формулировках определений и формулах мы будем предполагать, что значение непрерывной случайной величины может быть любым действительным числом, т.е. что оно принадлежит прямой (—сю, оо).
Плотность распределения вероятностей
Функция /(х) является плотностью распределения вероятностей (или плотностью вероятности. — Примеч. ред.) непрерывной случайной величины X, если
1. /(х) > 0 для всех х е (—сю, оо),
оо
2. j f (х) dx = 1.
— оо
3. Вероятность того, что X лежит на отрезке [с, d] равна
d
Р (с < X d) — j f (х) dx.
с
j f(x)dx = Вероятность (c<X<d)
Область значений величины X = (—оо, оо) — область определения функции /.
Пример 15.7 (Использование плотности распределения вероятностей). Пусть
/12х2 - 12х3, /м = |0
если 0 х 1; в противном случае.
Постройте график функции f и убедитесь, что она удовлетворяет первым двум условиям в определении плотности распределения вероятностей. Затем вычислите каждую из следующих вероятностей и проиллюстрируйте результат графически.
1. 	Р(0,4 X 0,7). 2. Р(Х 0,5).
3. Р(Х > 0,6). 4. Р(Х = 0,3).
Решение. График функции f (рис. 15.8) указывает на то, что /(х) 0 для всех х. Кроме
того,
оо 1
| f (х) dx = j (12х2 — 12х3) dx — (4х3 — Зх4) | = 1.
— оо О


Глава 15. Теория вероятностей и математический анализ
719
Рис. 15.8. Плотность распределения вероятностей
0,7
1. Р (0,4 X 0,7) = j f (х) dx =
0,4
0,7
(12а:2 - 12х3) dx = (4х3 - Зх4) I ’ = 0,4725. к / \ / |0,4
0,4
Следует отметить, что f (я?) = О для х < О.
= 0,3125.


720
Часть III. Математический анализ
1
3. Р (X 0,5) = j f (х) dx = Следует отметить, что f (х) = 0 для х > 1.
0,6
1
= (12z2 - 12х3) dx = (4х3 - Зх4) | = 0,5248.
0,6
0,3
4. 	Р (X = 0,3) = j f (т) dx = 0. Свойство определенных интегралов (раздел 11.5).
0,3
X


Глава 15. Теория вероятностей и математический анализ
721
Упражнение 15.7.
Пусть
„, х I бх — бх2, если 0 < х < 1;
f (*) = ) п
10 в противном случае.
Постройте график f и убедитесь, что эта функция удовлетворяет первым двум условиям в определении плотности распределения вероятностей. Затем вычислите каждую из следующих вероятностей и проиллюстрируйте результат графически.
1. Р(0,3 < X 0,8).
3. Р(Х > 0,4).
2. Р(Х < 0,7).
4. Р(Х = 0,5). в
Вероятность в примере 15.7.4 демонстрирует фундаментальное различие между дискретной и непрерывной случайными величинами. В дискретном случае известно распределение вероятности Р(х), которое задает вероятность каждого возможного значения случайной величины. Следовательно, если с — одно из значений случайной величины, то Р(Х = с) = Р(с). В непрерывном случае вероятностью того, что значение случайной величины принадлежит определенному интервалу, задается интегралом плотности распределения вероятностей. Если с — произвольное действительное число, то вероятность того, что исход в точности равен с, равна
с
Р (X = с) = Р (с X с) = f (х) dx = 0.
с
Следовательно, Р(Х = с) = 0 для любого числа с.
Тот факт, что Р(Х = с) = 0, также подразумевает, что исключение любой из конечных точек не изменит вероятности того, что случайная величина лежит на данном интервале, т.е.
ь
Р(а<Х <b)=P(a<X ^b) = P(a^X <b)=P(a^X ^b)=^f(x)dx.
а
Пример 15.8 (Использование функцию плотности распределения вероятностей). Используя функцию плотности распределения вероятностей из примера 15.7, вычислите вероятности Р(0,1 < X 0,2) и Р(Х > 0,9).
Решение.
0,2
Р (0,1 < X «С 0,2) = j f (х) dx =
0,1
0,2
= j (12х2 — 12х3) dx =
o,i
. 10,2
= (4х3 - Зх4)
' 7 lo,i
= 0,0272 - 0,0037 = 0,0235.


722
Часть III. Математический анализ
ОО
Р (X > 0,9) = f (т) dx =
0,9
1
j (12х2 — 12х3) dx =
0,9
= (4z3 - Зх4)
,9
= 1 - 0,9477 = 0,0523.
Упражнение 15.8.
Используя функцию плотности распределения вероятностей из упражнения 15.7, вычислите вероятности Р(0,2 X < 0,4) и Р(Х < 0,8). ■
Пример 15.9 (Срок хранения). Срок хранения (в месяцах) определенного препарата — это непрерывная случайная величина с плотностью вероятности (рис. 15.9)
0 в противном случае.
Рис. 15.9. Плотность распределения вероятностей срока хранения препарата
Вычислите вероятность того, что срок хранения препарата лежит в указанных интервалах.
1. Между 10 и 20 днями.
2. Не более 30 дней.
3. Более 25 месяцев.


Глава 15. Теория вероятностей и математический анализ
723
20
Решение.
10
30
30
2. Р (X 30) = j f (х) dx = j
50 2dx = Ге + 50)2
о ' 7
-50
х 4- 50
30
о
3. Р (X > 25) = j f (х) dx = j
OO
50 2dx.
_ (x + 50)2
25 25
Значение этого несобственного интеграла можно вычислить непосредственно, используя методы, описанные в разделе 15.1. Однако есть и другой метод, в котором не нужно прибегать к вычислению несобственных интегралов. Поскольку f описывает плотность распределения вероятностей, можно записать
oo
1 = j f {x} dx =
— OO
oo
J (x + 50)2 о
25 oo
Г 50 J
= ~dx +
J (x + 50)2 о
Ь с Ь
j f (ж) dx = j f (ж) dx + j f (x) dx a a c
50 2dx.
J (x + 50)
25
Решая последнее уравнение относительно [50/(х + 50)2] dx, имеем
оо
Следовательно, Р (X > 25) = |.
Упражнение 15.9.
Вычислите вероятность того, что срок хранения препарата в примере 15.9 лежит в указанных интервалах.
1. Между 50 и 100 днями.
2. Не более 20 дней.
3. Более 10 месяцев. ■


НА
Часть III. Математический анализ
Интегральная функция распределения
Задание 15.4.
Пусть
/(х) =
если 0 < х 2;
в противном случае
и
если х < 0; если 0 х 2;
если х > 2.
1. Постройте график каждой функции.
2. Является ли функция f плотностью распределения вероятностей? А функция F?
3. Есть ли какая-нибудь связь между функциями f и F?
4. Вычислите значение J*f (х) dx.
5. Можно ли воспользоваться функцией F, чтобы вычислить значение интеграла
в п. 4? ■
Всякий раз при вычислении вероятности для непрерывной случайной величины необходимо находить первообразную плотности распределения вероятностей. Эта первообразная используется так часто, что удобно дать ей отдельное название.
Интегральная функция распределения
Если f — плотность распределения вероятностей, то соответствующая интегральная функция распределения F имеет следующий вид
х
F(x) = P(X^x)= f(t)dt.
— ОО
Более того,
Р (с X d) = F (d) - F (с).
На рис. 15.10 показана геометрическая интерпретация этой концепции.
а) интегральная функция б) плотность распределения в)
распределения
Рис. 15.10. Интегральная функция распределения
Следует отметить, что F (ж) = J*® f (f) dt — это функция, зависящая от верхнего предела интегрирования х, а не от переменной интегрирования t. Сформулируем несколько


Глава 15. Теория вероятностей и математический анализ
725
важных свойств интегральной функции распределения. Эти свойства следуют непосредственно из того факта, что с геометрической точки зрения функцию F(x) можно интерпретировать как площадь фигуры, лежащей под графиком функции у = f(t) от —сю до х (см. рис. 15.10).
Свойства интегральных функций распределения
Если f — функция распределения, a F (х) = J* f (t) dt — соответствующая интегральная функция распределения, то
1. F'(x) = f(x) везде, где функция f непрерывна.
2. 0 F(x) < 1, —ос < х < ос.
3. F(x) не убывает на интервале (—оо, —оо)1.
Пример 15.10 (Использование интегральной функции распределения). Найдите интегральную функцию распределения для плотности вероятности в примере 15.7 и, воспользовавшись ею, вычислите вероятность Р(0,1 < х < 0,9).
Решение. Если х < 0, то
X
F(x)= j f(t)dt =
— ОО
если 0 я? 1, в противном случае.
/(I1 =
Если 0 х 1, то
х Ох
F(x)= j f(t)dt= j /(t) + j/(t)dt =
— oo —oo 0
X
= 0 +
о
= 4x3 - Зя4.
’функция F(x) является неубывающей на интервале (а, Ь), если F(xi) F(xi) ддя а < xi <
< Х2 <Ь.


726
Часть III. Математический анализ
Следовательно,
если х < О, если 0 х 1, если х > 1.
Таким образом (рис. 15.11),
Р(0,1 X <: 0,9) = Г(0,9) - Г(0,1) = 0,9477 - 0,0037 = 0,944.
а)
Рис. 15.11. Плотность вероятности и интегральная функция распределения
Упражнение 15.10.
Найдите интегральную функцию распределения для плотности вероятности в упражнении 15.7 и, воспользовавшись ею, вычислите вероятность Р(0,3 х 0,7). ■
Пример 15.11 (Срок хранения). Возвращаясь к определению срока хранения препарата в примере 15.9, предположим, что фармацевт при продаже хочет быть на 95% уверенным в том, что препарат еще годен к употреблению. Сколько нужно хранить препарат, чтобы он не потерял лекарственные свойства?
Решение. Пусть х — количество месяцев, в течение которых препарат хранился до момента продажи. Обозначим вероятность того, что срок хранения препарата меньше, чем количество месяцев, в течение которых он пролежал на полке, через Р(0 X х). Фармацевт хочет, чтобы эта вероятность была равной 0,05. Следовательно, необходимо решить уравнение Р(0 X < х) = 0,05 относительно величины х. Прежде всего найдем интегральную функцию распределения F. Легко видеть, что для х < 0 выполняется условие Р(х) = 0. А какое условие выполняется при х 0?
х
X
F(x) =
о
50
(50 +1)2
dt =
50 1
-50
50 + x
50
50 + x
x
50 + x'
Следовательно,
F(x) =
f°,
[x/ (50 + x),
если x < 0, если x 0.
-(-1) = 1-


Глава 15. Теория вероятностей и математический анализ
727
Теперь, чтобы уравнение Р(0 X х) было равно 0,05, сведем его к следующему.
Fix)- F (0) = 0,05; F(0) = о
х = 2,5 + 0,05#;
0,95а: = 2,5;
х « 2,6.
Если препарат продан в течение первых 2,6 месяцев хранения, то вероятность того, что он еще годен к употреблению, равна 0,95. ■
На рис. 15.12 показан альтернативный метод решения примера 15.11 с помощью графической утилиты.
Hrtl М-Д2 Hott
4ViBfnInt<50/(50 +Х>/Ч2,Х?0,Х) чУгВ.05
\7з =
\7м = \Ys = \7б =
Рис. 15.12. Решение примера 15.11 с помощью графической утилиты
Упражнение 15.11.
Повторите решение примера 15.11, если фармацевт хочет, чтобы вероятность годности препарата к употреблению, была равна 0,99. ■
Ответы к упражнениям
15.1.


728
Часть III. Математический анализ
1) 0,68
2) 0,784
3) 0,648
4) 0
15.2. 0,248; 0,896.


Глава 15. Теория вероятностей и математический анализ
729
15.3. 1) 1.
О, если х < О,
Зх*  2 — 2х3  * * * 7 8 9, если 0 < х < 1; Р (0,3 < X < 0,7) = 0,568.
1, если х > 1.
15.5. Приблизительно | месяца, или 15 дней.
Практикум 15.2
А В задачах 1 и 2 постройте график и покажите, что функция f удовлетворяет первым двум условиям в определении плотности распределения вероятностей.
если 0 < х 4,
0 в противном случае.
< |ж2, если 0 х 3, 0 в противном случае.
В задачах 3-6 определите, является ли функция f плотностью распределения вероятностей? Объясните свой ответ.
если — 4 х 0,
в противном случае.
, если 0 < х < 4,
в противном случае.
если х = 1,
в противном случае.
если х 1,
в противном случае.
7. Используя функцию из задачи 1, вычислите указанные вероятности. Проиллюстрируйте каждую из них графически.
а) 	Р(1 X 3). б) Р(Х 2). в) Р(Х > 3).
8. Используя функцию из задачи 2, вычислите указанные вероятности. Проиллюстрируйте каждую из них графически.
а) 	Р(1 X 2). б) Р(Х > 1). в) Р(Х < 2).
9. Используя функцию из задачи 1, вычислите указанные вероятности.
а) 	Р(Х = 1). б) Р(Х > 5). в) Р(Х < 5).
*3. /(z) = | 8 ’
*4./(х) = |^2
*6. /(х) = Н’


730
Часть III. Математический анализ
10. Используя функцию из задачи 2, вычислите указанные вероятности.
а) 	Р(Х = 2). б) Р(Х>4). в) Р(Х<4).
11. Найдите интегральную функцию распределения, соответствующую функции в задаче 1, и постройте ее график.
12. Найдите интегральную функцию распределения, соответствующую функции в задаче 2, и постройте ее график.
13. Используя интегральную функцию распределения из задачи 11, вычислите указанные вероятности.
а) 	Р(2 X 4). б) Р(0<Х<2).
14. Используя интегральную функцию распределения из задачи 12, вычислите указанные вероятности.
а) 	Р(0 X 1). б) Р(2 < X < 3).
15. Используя интегральную функцию распределения из задачи И, вычислите значения х, удовлетворяющие следующим уравнениям.
a) 	P(0^X^x) = J. б) Р(0<Х^х) = ^.
16. Используя интегральную функцию распределения из задачи 12, вычислите значения х, удовлетворяющие следующим уравнениям.
a) P(0^X^z) = J. б) Р(О^Х^х) = 1
о 04
Б В задачах 17 и 18 постройте график и покажите, что функция f удовлетворяет первым двум условиям в определении функции плотности распределения вероятностей. 2/ (1 + я)3 , если х 0,
0 в противном случае.
2/ (2 4- х)2 , если х 0,
0 в противном случае.
19. Используя функцию из задачи 17, вычислите указанные вероятности.
а) Р(1^Х^4). б) Р(Х>3). в) Р(Х^2).
20. Используя функцию из задачи 18, вычислите указанные вероятности,
а) Р(2 X 8). б) Р(Х 3). в) Р(Х < 1).
21. Найдите интегральную функцию распределения, соответствующую функции в задаче 17, и постройте ее график.
22. Найдите интегральную функцию распределения, соответствующую функции в задаче 18, и постройте ее график.
23. Используя интегральную функцию распределения из задачи 21, вычислите значения х, удовлетворяющие следующим уравнениям.
а) Р(0<Х«$х) = р б)Р(Х>х) = 4
4 10
24. Используя интегральную функцию распределения из задачи 22, вычислите зна¬
чения х, удовлетворяющие следующим уравнениям, а) Р(0^Х^х) = ^. б)Р(Х>х) = |.
17. /(х) =
18. /(х) =


Глава 15. Теория вероятностей и математический анализ
731
В задачах 25-28 найдите соответствующую интегральную функцию распределения. Постройте графики обеих функций (в отдельных координатных системах).
— |х2, если 0 х < 2,
О в противном случае.
| - |х2, если -1 х 1,
О в противном случае.
| -I- |х3, если -1 х 1,
О в противном случае.
| \/х, если 0 х 4,
О в противном случае.
В задачах 29-32, используя графическую утилиту, найдите приблизительное значение х (с точностью до двух десятичных знаков), которое удовлетворяет уравнению относительно указанной интегральной функции распределения F(x).
29. Р(0 < X х) = 0,2 для Г(х) из задачи 25.
30. P(-l X х) — 0,4 для Р(х) из задачи 26.
31. Р(—1 X х) = 0,6 для Р(х) из задачи 27.
32. Р(0 < X < х) = 0,7 для Р(х) из задачи 28.
Для каждой функции f в задачах 33-36 найдите такую постоянную к, при которой функция kf является плотностью распределения вероятностей, или объясните, почему такой константы не существует.
\/х, если х 1,
0 в противном случае.
1/х4, если х 1,
0 в противном случае.
1/я3, если х 1,
0 в противном случае.
l/v^, если х 1,
0 в противном случае.
* 37. Может ли функция
F(x) =
f2-2z,
1°
если 0 < х < 1,
в противном случае
быть интегральной функцией распределения? Объясните свой ответ.


732
Часть III. Математический анализ
* 38. Может ли функция
„ . х I 0,5 — 0,5х3, если — 1 х < 1,
F (х) = <
10 в противном случае
быть интегральной функцией распределения? Объясните свой ответ.
В
В задачах 39 и 40, используя графическую утилиту, постройте график функции f и вычислите интеграл f (х) dx для N = 1, 2 и 3. Проанализируйте доказательства того, что f является плотностью распределения вероятностей.
*39. /(ж) = /—е~0,5а;2. *40. f (х) — ^_е~2(ж~1)5)2.
V27T V27t
В задачах 41-44 функция F(x) является интегральной функцией распределения непрерывной случайной величины X. Найдите плотности распределения вероятностей f(x), соответствующие каждой функции F(x).
0,
если х < 0,
41. F(x) = <
я2,
если 0 х 1,
л
если х > 1.
1
°,
если х < 1,
42. F (х) =
1 Iх
— если 1 х 3,
1
1л
если х > 3.
'о,
если х < 0,
43. F(x) = <
6х2
— &г3 + Зх4, если 0 х 1,
Л
если х > 1.
44. f(x) = J
(1/я3) , если х 1,
I 0 в противном случае.
В задачах 45 и 46 найдите соответствующие интегральные функции распределения.
X,
если 0 х 1,
2-
я, если 1 < х 2,
0
в противном случае.
1 4’
если 0 х 1,
1
2 ’
если 1 < х 2,
1 4’
если 2 < х 3,
0
в противном случае.


Глава 15. Теория вероятностей и математический анализ
733
Применение математики
Экономика и бизнес
47. 	Потребление электроэнергии. Дневной спрос на электроэнергию (в миллионах киловатт-часов) в большом городе является непрерывной случайной величиной с плотностью распределения вероятностей
J 0,2 —0,02а:,
если 0 С х < 10, в противном случае.
*а) Вычислите значение интеграла f (х) dx и проанализируйте результат.
б) Какова вероятность того, что дневной спрос на электроэнергию будет меньше восьми миллионов киловатт-часов?
в) Какова вероятность того, что пяти миллионов киловатт-часов будет недостаточно, чтобы удовлетворить дневной спрос?
48. 	WWW Потребление бензина. Дневной спрос на бензин (в миллионах галлонов) в большом городе является непрерывной случайной величиной с плотностью распределения вероятностей
Го,4- 0,0&г,
/w=v>
если 0 < х < 5,
в противном случае.
*а) Вычислите значение интеграла J* f (х) dx и проанализируйте результат.
б) Какова вероятность того, что дневной спрос на бензин будет меньше двух миллионов галлонов?
в) Какова вероятность того, что трех миллионов галлонов будет недостаточно, чтобы удовлетворить дневной спрос?
49. 	Режим разделения времени. В компьютерной сети, работающей в режиме разделения времени, время ответа на запрос пользователя (в секундах), является непрерывной случайной величиной с плотностью распределения вероятностей
/(х) =
если х 0,
в противном случае.
*а) Вычислите значение интеграла J*0 f (ж) dx и проанализируйте результат.
б) Какова вероятность того, что ответ на пользовательский запрос будет получен в течение одной секунды?
в) Какова вероятность того, что пользователю придется ожидать ответа более четырех секунд?
50. 	Время ожидания. Время, которое тратит клиент, ожидая обслуживания в банке (в секундах), является непрерывной случайной величиной с плотностью распределения вероятностей
если х 0,
в противном случае.


734
Часть III. Математический анализ
*а) Вычислите значение интеграла f (ж) dx и проанализируйте результат.
б) Какова вероятность того, что клиент будет ожидать менее трех минут?
в) Какова вероятность того, что клиенту придется ожидать обслуживания более пяти минут?
51. 	Спрос. Недельный спрос на рубленые бифштексы (в тысячах фунтов) в сети супермаркетов является непрерывной случайной величиной с плотностью распределения вероятностей
/(*) = <
0,03ял/100 — ж2,
О
если 0 х 10, в противном случае.
а) Какова вероятность того, что будет раскуплено более 4000 фунтов рубленных бифштексов?
б) Менеджер мясного отдела заказал 8000 фунтов рубленых бифштексов. Какова вероятность того, что спрос не превысит это количество?
в) Менеджер хочет, чтобы вероятность того, что спрос не превысит заказанное количество, была равна 0,9. Сколько для этого нужно заказать рубленых бифштексов?
52. 	Спрос. Недельный спрос на журнал о спорте (тыс. экз.) в определенном городе является непрерывной случайной величиной с плотностью распределения вероятностей
/(ж)=<(125^25 Х2
если 0 х 5,
в противном случае.
а) Поставщик журнала в этот город заказал 3000 экземпляров журналов. Какова вероятность того, что спрос не превысит это количество?
б) Какова вероятность того, что спрос не превысит 4000 экземпляров?
в) Поставщик хочет быть на 95% уверенным, что спрос не превысит заказанное количество. Сколько экземпляров нужно для этого заказать?
Биологические науки
53. 	Продолжительность жизни. Продолжительность жизни определенного микроорганизма (в минутах) является непрерывной случайной величиной с плотностью распределения вероятностей
/(*) =
{ 5000 (iCte3 ж4) >
если 0 < х < 10,
в противном случае.
а) Какова вероятность того, что микроорганизм проживет по меньшей мере семь минут?
б) Какова вероятность того, что микроорганизм проживет не более пяти минут?


Глава 15. Теория вероятностей и математический анализ
735
54. 	Продолжительность жизни. Продолжительность жизни растения определенного вида (в месяцах) является непрерывной случайной величиной с плотностью распределения вероятностей
если 0 х < 6, в противном случае.
а) Какова вероятность того, что одно из этих растений проживет по меньшей мере четыре месяца?
б) Какова вероятность того, что одно из этих растений проживет максимум пять месяцев?
55. 	Срок хранения. Срок хранения скоропортящегося препарата (в днях) является непрерывной случайной величиной с плотностью распределения вероятностей
/(ж) = |800х/(400 + х2)2,
если х О,
в противном случае.
а) Какова вероятность того, что препарат будет иметь срок хранения не более 20 дней?
б) Какова вероятность того, что срок хранения препарата превысит 15 дней?
в) Когда должен истечь срок, в течение которого нужно использовать препарат, если клиент требует, чтобы вероятность годности препарата к использованию составляла 0,8?
56. Срок хранения. Повторите решение задачи 55, если
200ж/ (100 + ж2)2 , если х 0,
0 в противном случае.
Социальные науки
57. Обучение. Количество слов в минуту, которое начинающая машинистка может напечатать после одной недели практических занятий, является непрерывной случайной величиной с плотностью распределения вероятностей
{J_„-х/20
20е ’
0
/(ж) =
если х 0,
в противном случае.
а) Какова вероятность того, что начинающая машинистка сможет печатать по меньшей мере 30 слов в минуту после одной недели практических занятий?
б) Какова вероятность того, что она сможет печатать по меньшей мере 30 слов в минуту после одной недели практических занятий?
58. 	WWW Обучение. Количество часов, необходимое для того, чтобы шимпанзе выполнила новое задание, является непрерывной случайной величиной с плотностью распределения вероятностей
/(*) =
если 0 < х 3, в противном случае.


736
Часть III. Математический анализ
а) Какова вероятность того, что шимпанзе выполнит задание за первый час?
б) Какова вероятность того, что шимпанзе не выполнит задание за первые
два часа?
15.3. 	Математическое ожидание, стандартное отклонение и медиана
■ Математическое ожидание и стандартное отклонение
■ Альтернативная формула вычисления дисперсии
■ Медиана
Математическое ожидание и стандартное отклонение
Для описания наборов статистических данных используют математическое ожидание, характеризующее центр распределения, и стандартное отклонение, представляющее меру разброса значений. Эти термины используются для описания и дискретных, и непрерывных случайных величин. Например, если X — дискретная случайная величина, описывающая количество выпавших орлов при подбрасывании трех монет (табл. 15.3), то математическое ожидание и стандартное отклонение вычисляются следующим образом.
Стандартное отклонение = у Дисперсия
,8660.
Следует отметить, что эти величины были вычислены с использованием конечных сумм и вероятностей из табл. 15.3.
Расширение этих идей на непрерывные случайные переменные предполагает применение интегралов и плотностей распределения вероятностей.


Глава 15. Теория вероятностей и математический анализ
737
Таблица 15.3
X
0 12 3
р(х)
13 3 1
8 8 8 8
Математическое ожидание и стандартное отклонение непрерывной случайной величины
Пусть /(ж) — плотность распределения вероятностей непрерывной случайной переменной X. Тогда математическим ожиданием является число
оо р = Е (X) = | xf (ж) dx,
— оо
дисперсией —
оо V(X)= j (х-р)2 f(x)dx,
— ОО
а стандартным отклонением —
а= УУ(х).
Математическое ожидание непрерывной случайной величины характеризует центр распределения ее значений, а стандартное отклонение — разброс ее значений относительно математического ожидания. Эта ситуация проиллюстрирована на рис. 15.13. Большая часть площади под кривой находится вблизи математического ожидания. На рис. 15.13, б стандартное отклонение в четыре раза больше, и фигура, лежащая под графиком, значительно более размыта.
Пример 15.12 (Вычисление математического ожидания, дисперсии и стандартного отклонения). Вычислите математическое ожидание, дисперсию и стандартное отклонение функции если 0 < х 1, в противном случае.
Решение,
оо
= £?(%)= j xf(x)dx
— оо
оо
V (х) = j (х - р)2 f (х) dx =
— ОО
1
= j х (12rr2
о
— 12а;3) dx =
j(12х3
О
— 12а?4) dx =
Математическое ожидание (среднее значение)
Н-
х2 — 12a;3) dx =


738
Часть III. Математический анализ
1
о
f /108 2 468 з 132 4 5\ ,
= j Ы* +VX -12’ )* = О
г = £
о 25
Дисперсия
Стандартное отклонение
б) а = 4
Рис. 15.13. Влияние математического ожидания на форму графика плотности распределения вероятностей
Упражнение 15.12.
Вычислите математическое ожидание, дисперсию и стандартное отклонение функции
если 0 < х 1, в противном случае.
Задание 15.5.
Рассмотрим функцию плотности распределения вероятностей
если 0 х 2, в противном случае.


Глава 15. Теория вероятностей и математический анализ
739
1. Вычислите математическое ожидание /х.
2. Вертикальная прямая х = /х делит фигуру, лежащую под графиком функции
У = на две части. Равны ли площади этих областей? Если нет, найдите такое число тп, при котором вертикальная прямая х = т делит эту фигуру на две области с равными площадями. ■
График плотности распределения вероятностей, рассмотренной в примере 15.12, показан на рис. 15.14, а, на котором также отмечены площади фигур, лежащих слева и справа от указанного математического ожидания (вычисления пропущены). Выполняя задание 15.5, легко обнаружить, что прямая, проходящая через математическое ожидание, не делит фигуру, лежащую под графиком функции /, на две области с равными площадями. Значение х, соответствующее такому разбиению, называется медианой, и будет рассмотрено ниже. Если заштрихованную область на рис. 15.14, а нарисовать на куске древесины постоянной толщины и обрезать древесину по внешнему контуру области, то полученный в результате объект, находясь на клине, окажется в положении равновесия в точке, соответствующей математическому ожиданию /х = 0,6 (рис. 15.14, б). По этой причине математическое ожидание /г часто называют параметром положения центра распределения.
а) б)
Рис. 15.14. Плотность распределения вероятностей


740
Часть III. Математический анализ
Пример 15.13 (Срок службы). Срок службы электрической лампочки определенной марки (в часах) является непрерывной случайной величиной с плотностью распределения вероятностей
f (х) = *
loo 2оооо*£’ если 0 х 200,
0 в противном случае.
1. Каков средний срок службы одной из рассматриваемых электрических лампочек?
2. Какова вероятность того, что лампочка прослужит дольше среднего?
Решение.
1. 	Поскольку значение этой случайной величины представляет собой количество часов, которое прослужит лампочка, то ее математическое ожидание является средним сроком службы. Следовательно,
оо 200
Е(Х)= j г/Ий = j * ~ =
— оо 0
200
0
м/1 * ’ (гбб1’
—
60000 )
200
0
200
3
» 66,67 часа.
2. 	Вероятность того, что лампочка прослужит больше часов равна
оо 200
Р(Х>^)= j f(x)dx = j
200/3 200/3
х I dx =
20 000 )
—
40000 J
200
200/3
Упражнение 15.13.
Повторите решение примера 15.13, если функция плотности распределения вероятностей равна
/(х) =
1 1
200 90 000
я,
если 0 х 300,
в противном случае.
0
Альтернативная формула вычисления дисперсии
Множитель (х—/д)2 в формуле для вычисления V(X) вносит определенную сложность в нахождение значения интеграла. Чтобы упростить эту формулу, можно воспользоваться


Глава 15. Теория вероятностей и математический анализ
741
свойствами определенного интеграла.
оо
(х — д)2 f (я;) dx =
— оо
оо
= j (я;2 - 2я?/1 + /12) / (х) dx =
— оо
оо
= j [x2f (х) - 2xfj. f (x) + Д2/ (x)] dx
— OO
oo oo
= j x2 f (x) dx — j 2/zx/ (x) dx +
— oo —oo
oo
+ j p2/ (z) dx =
— OO
oo oo
= j x2f (я?) dx - 2/z j xf (x) dx +
— oo —oo
oo
+ M2 j f (®) dx =
— OO
Алгебраические преобразования
Алгебраические преобразования
Свойство определенного интеграла
Свойство определенного интеграла
оо
j xf(x)dx = fJL,
— оо
оо
j f (ж) dx = 1.
— оо
х
Как правило, вычислить интеграл JX (х - м)2 f (я) dx.
Теорема 15.1 (Альтернативная формула вычисления дисперсии).
■2f(x)dx проще,
чем интеграл
oo
V (x) = j x2f (я:) dx — (i2.
— oo
Пример 15.14 (Вычисление дисперсии). Используя теорему 15.1, вычислите дисперсию в примере 15.12.


742
Часть III. Математический анализ
Решение. Из примера 15.12 имеем: /z = xf (х) dx = |. Следовательно,
оо
х2 f (ж) dx —
— ОО
1 2
= - = 0,4.
о 0
если 0 ж 1; в противном случае.
Упражнение 15.14.
Используя теорему 15.1, вычислите дисперсию в упражнении 15.12.
Пример 15.15 (Вычисление математического ожидания, дисперсии и стандартного отклонения). Вычислите математическое ожидание, дисперсию и стандартное отклоне¬
ние функции
если х 1,
в противном случае.
Решение.
mi
R г
= lim
2
1 R—>oo


Глава 15. Теория вероятностей и математический анализ
743
Упражнение 15.15.
Вычислите математическое ожидание, дисперсию и стандартное отклонение функции
если х 2,
в противном случае.
Медиана
Еще одним параметром, характеризующим свойства случайных величин, является медиана — значение, которое делит фигуру, лежащую под графиком плотности распределения вероятностей, на две равные части (рис. 15.15). Если число т — медиана, оно должно удовлетворять уравнению
Р(Х^т) = |.
В общем случае для решения этого уравнения предварительно необходимо найти интегральную функцию распределения.
Рис. 15.15. Медиана
Пример 15.16 (Вычисление медианы). Вычислите медиану непрерывной случайной величины с плотностью распределения вероятностей
если х 1,
в противном случае.
Решение.
Этап 1. Найдем интегральную функцию распределения. Для х < 1 выполняется условие F(x) = 0. Если х > 1, то
X
1
Г(г)


744
Часть III. Математический анализ
Этап 2. Решим уравнение Р (X т) — | относительно величины т.
F(m) = P(X m);
1 _ 1
2 m3 ’ m3 = 2;
т = \^2.
Следовательно, медиана равна \/2 « 1,26. ■
На рис. 15.16 показан альтернативный метод решения примера 15.16 с помощью графической утилиты.
НфН Plots
\YiBfnInt<3XZs "4? X, ЬХ) чУгВ.5
\Уч = чУ5 = \Yfi =
1
-1
Рис. 15.16. Решение примера 15.16 с помощью графической утилиты
Упражнение 15.16.
Вычислите медиану непрерывной случайной величины с плотностью распределения вероятностей
(24/х4,
1°
/(*) =
если х 2,
в противном случае.
Задание 15.6.
Рассмотрим плотность распределения вероятностей /, заданную графиком, изображенным на рис. 15.17. Существует ли у нее медиана? Сколько медиан имеет эта функция? Объясните свой ответ. ■
Пример 15.17 (Срок службы). Вычислите медиану для срока службы электрической лампочки в примере 15.13.


Глава 15. Теория вероятностей и математический анализ
745
Рис. 15.17. Функция плотности распределения вероятностей
Решение.
Этап 1. Найдем интегральную функцию распределения. Если х < 0, то F(x) = 0. Если 0 х 200, то
X
F(x)= j f(t)dt =
— ОО
если О х 200, в противном случае.
40000 J
100 х 40000Х ‘
Если х > 200, то
х
— оо
200 х
j f(t)dt+ j /(t) 0 200
dt — 0 1 0 — 1.
Следовательно,
— оо
F(x) =
40 000Х ’
если х < 0, если 0 < х 200, если х > 200.
0
Этап 2. Решим уравнение Р (X т) = | относительно величины т.
F(m) = P(X <m) = i
1 lol
—т т =
100 40 000 2
т2 - 400m -I- 20 000 = 0.
Решение должно находиться в пределах О т 200.


746
Часть III. Математический анализ
Это квадратичное уравнение имеет два решения: 200 + 100\/2 и 200 — 100\/2. Поскольку значение т должно лежать на отрезке [0,200], то правильным ответом является второе решение.
Таким образом, срок службы, соответствующий медиане, равен 200 - 100д/2 « 58,58 часа. ■
Упражнение 15.17.
Вычислите медиану для срока службы электрической лампочки в упражне нии 15.13. ■
На рис. 15.18 показаны математические ожидания и медианы двух плотностей распределения вероятностей, рассмотренных в этом разделе (см. примеры 15.13, 15.15, 15.16 и 15.17). Как отмечалось ранее, математическое ожидание и медиана, как правило, не равны между собой.
Рис. 15.18. Графики плотностей распределения вероятностей
Ответы к упражнениям
15.12. /z=|;V(X) = l; а «0,2236.
15.13. 1) 125 часов;
15.14.
2)
133
288'
1
20’
15.15. м = 3; V(X) = 3; а = « 1,732.
15.16. т = ^16 = 2\/2 « 2,52.
15.17. т = 450 - 150\/5 « 114,59 часа.


Глава 15. Теория вероятностей и математический анализ
747
Практикум 15.3
А В задачах 1-6 требуется вычислить математическое ожидание, дисперсию и стандартное отклонение.
1- / (*)
2- f (х)
3. f (х)
4. f (х)
(Зх2
1°
если 0 х < 2, в противном случае.
если 0 < х < 1,
в противном случае.
если 2 < х 5,
в противном случае.
если 1 < х < 3,
в противном случае.
4 - 2х, *0
/(*) =
если 1 < х < 2, в противном случае.
если 2 х 4,
в противном случае.
В задачах 7—12 вычислите медиану.
7- f(x)={
если 0 х 1, в противном случае.
если 0 х 4, в противном случае.
если 2 < х < 4, в противном случае.
если 1 х < 3, в противном случае.
11- f (х) =
2х,
П./(х) = {
2-
0
если 0 х < 4, в противном случае.
если 0 С х < 1,
в противном случае.


748
Часть III. Математический анализ
А (*) =
/2 (х) =
Б В задачах 13 и 14 рассматриваются случайные величины Ху и с плотностями распределения вероятностей Д и Д соответственно, где
0,5, если 0 х 2,
О в противном случае,
0,25, если — 2 < х 2,
О в противном случае.
* 13. Объясните, как по графикам Д и /2 предсказать, какая из переменных Ху и Х2 имеет большее математическое ожидание. Проверьте ответ, вычислив математическое ожидание каждой величины.
* 14. Объясните, как по графикам Д и Д предсказать, какая из переменных Ху и Х2 имеет большую дисперсию. Проверьте ответ, вычислив дисперсию каждой величины.
В задачах 15 и 16 рассматриваются случайные величины Ху и Х2 с плотностями распределения вероятностей ду и д2 соответственно, где
0,5,
если 0 < х < 1,
0,25,
если 1 х 3,
0
в противном случае,
0,5,
если 0 < х < 1,
0,125,
если 1 х 5,
0
в противном случае.
* 15. Объясните, как по графикам ду и д2 предсказать, какая из переменных Ху и Х2
имеет большую медиану. Проверьте ответ, вычислив медиану каждой величины.
* 16. Объясните, как по графикам ду и д2 предсказать, какая из переменных Ху и
имеет большее математическое ожидание. Проверьте ответ, вычислив математическое ожидание для каждой величины.
В задачах 17-20 требуется вычислить математическое ожидание, дисперсию и стандартное отклонение случайных величин со следующими плотностями распределения вероятностей.
4/х\ если х 1,
0 в противном случае.
5/х6, если х 1,
0 в противном случае.
64/х5, если х 2,
0 в противном случае.
81/т4, если х 3,
0 в противном случае.


Глава 15. Теория вероятностей и математический анализ
749
В задачах 21 и 22, используя графическую утилиту, вычислите приближенно математическое ожидание, дисперсию и стандартное отклонение случайных величин с указанными плотностями распределения вероятностей, заменяя интеграл по интервалу (—оо, ос) интегралом по отрезку [—10,10].
21. /(х) = -^=e-4x~V2.
V 27Г
22. /(х) = —е-(х+2,1)2/3,92.
к ’ 1,4^
В задачах 23-30 вычислите медиану случайной величины с указанной плотностью распределения вероятностей.
1/х, если 1 х е,
О в противном случае.
1/(2я), если 1 х е2,
О в противном случае.
23. /(х) =
24. f (х) =
25. /(х) =
26. /(х) =
(4/(2 + х)2,
1°
|2/(1 + х)2,
27. / (х) = /
1/(1+ х)2,
О
если 0 х < 2, в противном случае.
если 0 х < 1,
в противном случае.
если х О,
в противном случае.
29. /(х) =
Г3/(3 + х)2,
1°
если х О,
в противном случае.
(2е-21,
1°
если х О,
в противном случае.
30. /(х) =
если х О,
в противном случае.
В задачах 31 и 32, используя график интегральной функции распределения F, вычислите медиану. (Предполагается, что каждый участок графика F является отрезком прямой.) Является ли медиана единственной? Объясните свой ответ.
*32.


750
Часть III. Математический анализ
В задачах 33 и 34, используя график плотности распределения вероятностей f, найдите интегральную функцию распределения F. (Предполагается, что каждый участок графика f является отрезком прямой.) Вычислите медиану. Является ли медиана единственной? Объясните свой ответ.
*33. *34.
В В задачах 35 и 36 необходимо определить, является ли функция f{x) непрерывной плотностью распределения вероятностей случайной величины с математическим ожиданием р и стандартным отклонением а, где а и b — константы. Вычислите интегралы, выразив результаты через величины а, Ь, р и а.
оо
*35.
(ах + b) f (х) dx.
— оо
оо
* 36. j (х — a)2 f (х) dx.
— оо
37. / (х) =
38. f (х) =
Квартилями плотности распределения вероятностей называются точки х\, х% и х%, которые делят фигуру, лежащую под графиком этой функции, на четыре равные части. Вычислите квартили плотностей распределения вероятностей, указанных в задачах 37-40.
jx, если 0 х 2,
0 в противном случае.
Зх2, если 0 < х < 1,
0 в противном случае.
39. /(х) =
40. f (х) =
/з/(3 + х)2,
1°
/1/(1+*)2,
1°
если х > 0,
в противном случае.
если х 0,
в противном случае.
В задачах 41-44, используя графическую утилиту, приближенно вычислите медианы указанных плотностей распределения вероятностей f (с точностью до двух десятичных знаков).
/. / ч |4х —4х3, если 0 х 1,
41. f (х) =
0 в противном случае.
Зх — Зх5, если 0 х 1,
0 в противном случае.
43. f (х) =
если х 1,
в противном случае.


Глава 15. Теория вероятностей и математический анализ
751
если х 1,
в противном случае.
Применение математики
Экономика и бизнес
45. 	Оплата труда. Затраты строительного подрядчика (тыс. долл.) в расчете на каждого сотрудника представлены непрерывной случайной величиной с плотностью распределения вероятностей
/м = |0,08(20-х),
если 15 х 20,
в противном случае.
а) Вычислите затраты на оплату труда.
б) Вычислите медиану затрат на оплату труда.
46. 	WWW Потребление электроэнергии. Суточное потребление электроэнергии в большом городе (в миллионах киловатт-часов) является непрерывной случайной величиной с плотностью распределения вероятностей
/о,2-О,О2х,
если 0 < х < 10, в противном случае.
а) Вычислите ожидаемое суточное потребление электроэнергии.
б) Вычислите медиану суточного потребления электроэнергии.
47. 	Время ожидания. Время (в минутах), которое клиент банка проводит в ожидании обслуживания является непрерывной случайной величиной с плотностью распределения вероятностей
/м=
если х 0,
в противном случае.
Вычислите медиану продолжительности ожидания.


752
Часть III. Математический анализ
48. 	Долговечность изделия. Срок службы автомобильного аккумулятора (в годах) является непрерывной случайной величиной с плотностью распределения вероятностей
|е_х/2, если х О,
О в противном случае.
Вычислите медиану срока службы аккумулятора.
49. 	Потребление воды. Суточное потребление воды в небольшом городе (в миллионах галлонов) является непрерывной случайной величиной с плотностью распределения вероятностей
1/(1 + я2)3/2, если х О,
О в противном случае.
Вычислите ожидаемое суточное потребление воды.
50. 	Потребление бензина. Суточное потребление бензина в большом городе (в миллионах галлонов) является непрерывной случайной величиной с плотностью распределения вероятностей
4/(4 + я2)3/2, если х 0,
0 в противном случае.
Вычислите ожидаемое суточное потребление бензина.
Биологические науки
51. 	Продолжительность жизни. Продолжительность жизни определенного микроорганизма (в минутах) является непрерывной случайной величиной с плотностью распределения вероятностей
/(х) =
если 0 х 10, в противном случае.
Вычислите среднюю продолжительность жизни одного из таких микроорганизмов.
52. 	Продолжительность жизни. Продолжительность жизни растения определенного вида (в месяцах) является непрерывной случайной величиной с плотностью распределения вероятностей
^(6х — х2), если 0 х 6,
0 в противном случае.
Вычислите среднюю продолжительность жизни одного из таких растений.
53. WWW Срок хранения. Срок хранения скоропортящегося препарата (дней) явля¬
ется непрерывной случайной величиной с плотностью распределения вероятно¬
стей
( 800х/(400 + х2)2,
1°
если х 0,
в противном случае.
/(*) =
Вычислите медиану срока хранения.


Глава 15. Теория вероятностей и математический анализ
753
54. 	Срок хранения. Повторите решение задачи 53, если
/(*) =
Г200х/(100 + х2)2,
1°
если х О,
в противном случае.
Социальные науки
55. 	Обучение. Количество часов, которое шимпанзе тратит на выполнение новой задачи, является непрерывной случайной величиной с плотностью распределения вероятностей
/(х) =
если 0 С х < 3, в противном случае.
Сколько предположительно часов потратит шимпанзе на выполнение очередного задания?
56. 	Явка на выборах. Количество зарегистрированных избирателей (тыс. чел.), которые проголосовали на местных выборах в маленьком городе, является непрерывной случайной величиной с плотностью распределения вероятностей
если 4 х 8, в противном случае.
а) Вычислите ожидаемое количество проголосовавших избирателей.
б) Вычислите медиану количества проголосовавших избирателей.
15.4. 	Специальные распределения вероятностей
■ Равномерное распределение
■ Экспоненциальное распределение
■ Нормальное распределение
Теперь, изучив общие свойства плотностей вероятности, можно рассмотреть несколько конкретных функций, которые широко используются на практике.
Равномерное распределение
Задание 15.7.
Рассмотрим случайную величину X с плотностью распределения вероятностей
/(я)
если 0 < х 10, в противном случае.
Постройте график функции f(x) и вычислите указанные вероятности.
1. 	Р(0 X 1) и Р(2 X 3), Р(6 < X 7), Р(9 X 10).


754
Часть III. Математический анализ
2. Р(а < X < а + п), если а О, п О и а + п 10.
3. Какова вероятность того, что случайная величина X лежит на интервале I длиной
п, принадлежащем отрезку [0,10]? Зависит ли эта вероятность от расположения интервала /? Объясните свой ответ. ■
Плотность распределения вероятностей, рассмотренная в задании 15.7, может оказаться весьма полезной. В следующем примере мы сделаем некоторые общие выводы о функциях подобного вида.
Пример 15.18 (Время ожидания).
На некую остановку автобус приходит каждые 30 минут. Если человек пришел на автобусную остановку в произвольный момент времени (т.е., не зная расписания автобуса), то случайная величина X, описывающая время, которое человек проведет на остановке, ожидая следующего автобуса, будет равномерно распределена на отрезке [0,30]. Следовательно, вероятность того, что величина X лежит на небольшом интервале фиксированной длины не зависит от расположения этого интервала на отрезке [0,30]. Таким образом, вероятность того, что время ожидания пассажира будет находиться между 0 и 5 минутами равна вероятности того, что время ожидания будет находиться между 5 и 10 минутами, а также вероятности того, что эта величина будет находиться между 18 и 23 минутами. Можно показать, что плотность распределения вероятностей этой равномерно распределенной случайной переменной имеет следующий вид.
/(*) =
если 0 < х < 30,
в противном случае.
Следовательно,
5 _ £ _ 1
30 ” 30 ” 6’
1
6’
1
6’
Каждую из таких вероятностей можно представить в виде площади фигуры, лежащей под графиком функции f на рис. 15.19. ■


Глава 15. Теория вероятностей и математический анализ
755
Рис. 15.19. Плотность равномерного распределения вероятностей
Упражнение 15.18.
Используя плотность распределения вероятностей из примера 15.18, вычислите вероятность того, что время ожидания пассажира будет лежать в следующих интервалах.
1. От 0 до 10 мин.
2. От 10 до 20 мин.
3. От 17 до 27 мин. а
В общем случае, если исход эксперимента лежит на отрезке [а, Ь], и, если вероятность исхода, лежащего на небольшом интервале фиксированной длины, не зависит от расположения этого небольшого интервала на отрезке [а, Ь], то говорят, что непрерывная случайная величина в этом эксперименте является равномерно распределенной на отрезке [а,Ь]. Плотность вероятности равномерно распределенной случайной величины имеет следующий вид (рис. 15.20).
/(*)
если а < х 6, в противном случае.
Поскольку /(&) > Ои
оо Ъ
ь а
ь
Ь — а
а
Ъ — а
= 1,
функция f удовлетворяет необходимым условиям плотности распределения вероятностей.
Рис. 15.20. Плотность равномерного распределения вероятностей


756
Часть III. Математический анализ
Если F — это соответствующая интегральная функция распределения, то для х < а выполняется условие F(z) = 0. Для а х b имеем
х а
b — а b — а
х — а b — а
Если х > Ь, то F(x) — 1.
Используя методы, рассмотренные в предыдущем разделе, можно показать, что (см. задачи 49-52 в практикуме 15.4)
Эти свойства подытожены в следующей врезке.
Плотность равномерного распределения вероятностей
/(*) =
если а х < Ь, в противном случае;
Математическое ожидание
Стандартное отклонение
М = | (а + Ь); а = (Ь — а).
VY2
Пример 15.19 (Электрический ток). Электрический ток в домашней сети протекает под действие равномерно распределенного напряжения от 110 до 120 В. Какова вероятность того, что напряжение в сети больше 113 В, но меньше 118 В?
Решение. Поскольку напряжение равномерно распределено на отрезке [110,120], оно имеет следующую плотность вероятности
если 110 < х 120, в противном случае.
Тогда
118
113
118
113
118 113
То- _ IF
1
2
Упражнение 15.19.
Какова вероятность того, что напряжение в примере 15.19 равно по меньшей мере 116 В? ■


Глава 15. Теория вероятностей и математический анализ
757
Экспоненциальное распределение
Задание 15.8.
Установите связь между положительными постоянными а и Ь, которые определяют следующую функцию плотностью вероятности.
если х О,
в противном случае.
Непрерывная случайная величина имеет экспоненциальное распределение и называется экспоненциально распределенной случайной величиной, если ее плотность вероятности определяется экспоненциальной функцией, т.е.
/(*) =
f(l/A)e-/\
1°
если х О,
в противном случае, где А — положительная константа. Экспоненциальные случайные величины используются во многих практических задачах, включая изучение продолжительности телефонных разговоров, время, которое клиент ожидает обслуживания в банке, и срок службы частей и компонентов механизмов.
Поскольку /(х) 0 и
j f (х) dx = j X!xdx =
— оо О
R
= lim f ^-e~x/xdx = н—ooj А о
Iя
= lim =
Я—оо \ / |0
= lim (~e~R/x + 1") = 1, Я—оо \ /
функция f обладает свойствами плотности вероятности. Если F — это интегральная функция распределения, то F(x) = 0 для х < 0. Для х 0 имеем
X X
— оо О
0


758
Часть III. Математический анализ
Чтобы вычислить медиану, решим уравнение
F(m)=P(X^m) = |,
1 _ =
1
2’
_ — р-т/Х
2
т
Г
т = —AIn - = Ain2.
2
Примечание: In = — In 2.
Чтобы показать, что = А и а = А, можно воспользоваться методом интегрирования по частям. Здесь он подробно рассматриваться не будет. Достаточно познакомиться с основными свойствами экспоненциального распределения, приведенными в следующей врезке.
Пример 15.20 (Частота звонков). Промежуток времени между телефонными звонками, поступающими на коммутатор крупной юридической фирмы, является экспоненциальной случайной величиной. Средний промежуток между звонками равен 20 секундам. Какова вероятность того, что в течение следующих 30 секунд звонки поступать не будут, если только что был принят предыдущий телефонный звонок?


Глава 15. Теория вероятностей и математический анализ
759
Решение. Пусть X — случайная величина, представляющая собой промежуток времени между телефонными звонками, измеренный в секундах. Поскольку среднее значение промежутка равна 20 с, выполняется условие /1 = А = 20. Следовательно, плотность вероятности случайной величины X описывается следующей функцией.
х/20, если х 0,
0 в противном случае.
Кроме того,
— e~x^20dx = j f(x)dx 4- j f(x)dx = 1
о 30
30
= 1 - f 1e-x'20dx =
J 20
0
130
= 1 - (-e-l/20) = e-1,5 « 0,223.
' 'Io
F(X>30) = j
30
Упражнение 15.20.
Какова вероятность того, что в течение следующих 10 секунд телефонные звонки в примере 15.20 поступать не будут, если только что был принят очередной звонок? ■
Нормальное распределение
Рассмотрим теперь самую важную из всех плотностей вероятности — плотность нормального распределения вероятностей. Эта функция является ядром огромного количества статистических теорий, а также сама по себе служит полезным инструментом при решении различных задач.
Непрерывная случайная величина X имеет нормальное распределение и называется нормально распределенной случайной величиной, если ее плотность вероятности имеет следующий вид.
СГ\/27Г
где р — произвольная постоянная, а а — положительная постоянная. Можно показать, хотя это непросто, что
и
оо
j f (х) dx = 1
— оо
оо
Е(Х) =
xf (х) dx = /1,
— оо
оо
V (ж) = j (х — р)2 f (х) dx = а2.
— оо
Таким образом, р — это математическое ожидание нормально распределенной случайной величины, а а — ее стандартное отклонение. График функции /(ж) всегда является


760
Часть III. Математический анализ
Рис. 15.21. Нормальное распределение вероятности
колоколообразной кривой, которая называется нормальной. На рис. 15.21 показаны три нормальные кривые для различных значений р и а.
Стандартное отклонение является мерой разброса нормально распределенной случайной величины относительного математического ожидания. Небольшое стандартное отклонение указывает на сосредоточение значений случайной величины в небольшом интервале вокруг математического ожидания и, следовательно, на более высокую и узкую кривую. Большое стандартное отклонение указывает на существенный разброс вокруг математического ожидания и, следовательно, на широкую и плоскую кривую. Следует отметить, что каждая нормальная кривая на рис. 15.21 симметрична относительно вертикальной прямой, проходящей через математическое ожидание. Это справедливо для любой нормальной кривой. Следовательно, прямая х = р делит область, лежащую под нормальной кривой, на две части с равными площадями. Поскольку общая площадь фигуры, ограниченной нормальной кривой, всегда равна единице, площадь каждой из этих областей равна 0,5. Это означает, что медиана нормально распределенной случайной величины всегда равна математическому ожиданию (рис. 15.22).
Рис. 15.22. Математическое ожидание и медиана нормальной случайной величиной


Глава 15. Теория вероятностей и математический анализ
761
Плотность нормального распределения вероятностей
f (х) = <т > 0.
Математическое ожидание д/ Медиана
Стандартное отклонение а
х
График f(x) симметричен относительно прямой х = ц.
Интегральная функция нормального распределения имеет вид
х
F(x) = ^= [ e-(‘-M)2/(2<T)2dt.
J
— ОО
Функцию F(a?) невозможно представить в виде конечной комбинации элементарных функций. Более того, вероятность
d
P(c^X^d) = —^= f
<тл/2тг J
С
невозможно вычислить с помощью первообразной.
Однако для вычисления приблизительных вероятностей такого типа можно воспользоваться процедурой численного интегрирования, предусмотренной в графической утилите, как показано на рис. 15.23. Здесь продемонстрировано вычисление вероятности Р(0 X < 1,5), где X — нормально распределенная случайная величина с параметрами // = 0 и а = 1.
-Х2/2),Х,0,1.5 )
.4331927987
Рис. 15.23. Численное интегрирование с помощью графической утилиты
Для вычисления вероятностей, имеющих нормальное распределение, можно также использовать таблицы. Примечательно, что площадь фигуры, лежащей под нормальной кривой между математическим ожиданием /1 и заданным количеством стандартных отклонений вправо (или влево) от д, остается неизменной независимо от формы нормальной кривой. Например, площадь фигуры, лежащей под нормальной кривой с параметрами = 3 и а = 5 от точки ц = 3 до точки /1 + 1,5а = 10,5, равна площади фигуры, лежащей под нормальной кривой с параметрами ц = 15 и а = 2 от точки /1 = 15 до точки /л = = 15 + 1,5а = 18. Обратите внимание на то, что залитые черным цветом области области


762
Часть III. Математический анализ
на рис. 15.24 имеют одинаковые площади. Следовательно, такие площади можно легко найти с помощью стандартной нормальной кривой, т.е. нормальной кривой с нулевым математическим ожиданием и единичным стандартным отклонением. Фактически, если величина z представляет собой количество стандартных отклонений, отмеряемых по оси х от математического ожидания д, то площадь фигуры, лежащей под нормальной кривой от // до // + za, равна площади фигуры, лежащей под стандартной нормальной кривой от 0 до z (рис. 15.25). В табл. III приложения В указаны соответствующие значения для стандартной нормальной кривой.
0.2
0
Рис. 15.24. Фигуры, ограниченные нормальными ограниченные нормальными кривыми
0 z z
Рис. 15.25. Площади фигур и значения z
В последующих рассуждениях основное внимание будет уделено использованию табл. III из приложения В для вычисления площадей фигур, лежащих под нормальной кривой. При желании эти вычисления можно выполнить с помощью графической утилиты.
Пример 15.21 (Вероятность нормального распределения). На заводе выпускаются электрические лампочки со сроком службы, имеющим нормальное распределение с математическим ожиданием, равным 500 ч, и стандартным отклонением, равным 100 ч. Какой процент электрических лампочек прослужит от 500 до 670 ч?
Решение. Чтобы ответить на этот вопрос, прежде всего установим, на расстоянии скольких стандартных отклонений находится число 670 от математического ожидания, равно-


Глава 15. Теория вероятностей и математический анализ
763
го 500. Это легко установить, разделив расстояние между числами 500 и 670 на стандартное отклонение, равное 100. Таким образом,
670 - 500
100
170 , _
100 = 1'70'
Иначе говоря, число 670 находится на расстоянии 1,7 стандартного отклонения от математического ожидания, равного 500. Обратившись к табл. III из приложения В, видим, что значению z — 1,7 соответствует число 0,4554. Поскольку общая площадь под нормальной кривой равна 1, можно сделать вывод, что 45,54% всех произведенных электрических лампочек прослужит от 500 до 670 часов (рис. 15.26). ■
Рис. 15.26. Срок службы электрической лампочки — положительное значение z
Упражнение 15.21.
Какой предположительно процент электрических лампочек в примере 15.21 прослужит от 500 до 750 часов? ■
Пример 15.22 (Вероятность нормального распределения). Какова вероятность того, что лампочка, выбранная случайно из всей партии выпущенной продукции (см. пример 15.21), прослужит от 380 до 500 часов?
Решение. Чтобы ответить на этот вопрос, прежде всего вычислим величину z.
х — 380 — 500 . _ _
z = ™— = —1,20.
а 100
Как правило, удобнее всего нарисовать приблизительный график кривой нормального распределения и обозначить на нем имеющиеся данные (рис. 15.27).
В табл. III из приложения В не включены отрицательные значения z, но, поскольку нормальная кривая симметрична относительно вертикальной прямой, проходящей через математическое ожидание, можно просто воспользоваться абсолютным значением (положительным значением) z из таблицы. Таким образом, площадь, соответствующая величине z = —1,20, равна площади, соответствующей значению z = 1,20, т.е. числу 0,3849. Поскольку площадь фигуры, лежащей под всей нормальной кривой, равна единице, вероятность того, что выбранная случайным образом электрическая лампочка прослужит от 380 до 500 часов, равна 0,3849. ■


764
Часть III. Математический анализ
Рис. 15.27. Срок службы электрической лампочки — отрицательное значение z
Упражнение 15.22.
Какова вероятность того, что выбранная случайным образом электрическая лампочка в примере 15.22 прослужит от 400 до 500 часов? ■
Ответы к упражнениям
15.18. 	1)
15.19. j.
15.20. е”0’5» 0,607.
15.21. 49,38%.
15.22. 0,3413.
Практикум 15.4
А В задачах 1-4 найдите плотность вероятности f и соответствующую интегральную функцию распределения F для непрерывной случайной величины X в следующих случаях.
1. X равномерно распределена на интервале [0,2].
2. X равномерно распределена на интервале [3,6].
3. X — экспоненциальная случайная величина с параметром А =
4. X — экспоненциальная случайная величина с параметром А = |.


Глава 15. Теория вероятностей и математический анализ
765
В задачах 5-8 вычислите математическое ожидание, медиану и стандартное отклонение непрерывной случайной величины X в следующих случаях,
5. X равномерно распределена на интервале [1,5].
6. X равномерно распределена на интервале [2,8].
7. X — экспоненциальная случайная величина с параметром Л = 5.
8. X — экспоненциальная случайная величина с параметром Л = 3.
В задачах 9-16, используя табл. III приложения В, вычислите площадь фигуры, лежащей под стандартной нормальной кривой от 0 до указанного значения z.
9. 1. 10. 2. И. -3. 12. -1.
13. 0,9. 14. -1,7. 15. 2,47. 16. -1,96.
Дано нормальное распределение с математическим ожиданием 50 и стандартным отклонением 10. Используя табл. III приложения В, вычислите площадь фигуры, лежащей под этой нормальной кривой между математическим ожиданием и значением, указанным в задачах 17-24.
17. 65. 18. 75. 19. 83. 20. 79.
21. 45. 22. 38. 23. 42. 24. 26.
Б В задачах 25 и 26 рассматриваются случайные переменные Х± и Х2 с плотностями распределения вероятностей Д и Д соответственно, где
. . . f 0,4, если -1,25 < х < 1,25, /2 (х) = <
10 в противном случае.
* 25. Объясните, как по графикам функций Д и Д предсказать, какая из величин Х±
или Х2 имеет большее стандартное отклонение. Проверьте сделанное предсказание, вычислив стандартное отклонение каждой величины.
* 26. Объясните, как по графикам функций Д и Д предсказать, какая из величин
или Х2 имеет большую медиану. Проверьте сделанное предсказание, вычислив медиану каждой величины.
В задачах 27 и 28 рассматриваются случайные переменные Х\ и Х2 с плотностями распределения вероятностей д\ и д2 соответственно, где
1 -(»-1)2/2
✓
е_х, если х 0,
0 в противном случае.
* 27. Объясните, как по графикам pi и д2 предсказать, какая из величин Xi или Х2
имеет большую медиану. Проверьте сделанное предсказание, вычислив медиану каждой величины.
91 (я) =
92 (х) =


Часть III. Математический анализ
766
*28. Объясните, как по графикам д± и д? предсказать, какая из величин Xi или X? имеет большее математическое ожидание. Проверьте сделанное предсказание, вычислив математическое ожидание каждой величины.
В задачах 29-32 непрерывная случайная величина X характеризуется математическим ожиданием р. Вычислите величину р, а затем — вероятность Р(Х р) для следующих вариантов.
29. X равномерно распределена на интервале [0,4].
30. X равномерно распределена на интервале [0,10].
31. X — экспоненциальная случайная величина с параметром А = 1.
32. X — экспоненциальная случайная величина с параметром А = 2.
В задачах 33-36 непрерывная случайная величина X характеризуется математическим ожиданием р и стандартным отклонением а. Вычислите величины р и а, а затем — вероятность Р(р — а < X р + сг) для следующих случаев.
33. X равномерно распределена на интервале [-5,5].
34. X равномерно распределена на интервале [-2,2].
35. X — экспоненциальная случайная величина с медианой т = 6 In 2.
36. X — экспоненциальная случайная величина с параметром т = 4 In 2.
Дана нормальная случайная величина X с математическим ожиданием, равным 70, и стандартным отклонением, равным 8. Вычислите вероятности, указанные в задачах 37-44.
37. F(60 < X 80).
38. F(50 < X 90).
39. Р(62 < X < 74).
40. Р(66 < X 78).
41. Р(Х > 88).
42. Р(Х > 90).
43. Р{Х 60).
44. Р(Х 56).
В задачах 45-48 рассматривается нормальная случайная величина X с математическим ожиданием р и стандартным отклонением а. Используя графическую утилиту со встроенной процедурой численного интегрирования, вычислите указанные вероятности.
*45. Вычислите вероятность Р(р — а X р + ст) с точностью до четырех десятичных знаков, подставив р = 0 и следующие значения.
а) а = 0,5. б) а = 1. в) а - 2.
Объясните результаты.
*46. Вычислите вероятность Р(р - 2а X р + 2а) с точностью до четырех десятичных знаков, подставив р — 0 и следующие значения.
а) а = 0,5. б) а = 1. в) а = 2.
Объясните результаты.
* 47. Вычислите вероятность Р(р — Зег X р + Зег) с точностью до четырех
десятичных знаков, подставив р = 0 и следующие значения.
а) ст = 0,5. б) а = 1. в) а — 2.
Объясните результаты.
* 48. Изменятся ли вероятности в задачах 45-47, если р = 5?


Глава 15. Теория вероятностей и математический анализ
767
В В задачах 49-52 рассматривается равномерно распределенная случайная величина X с плотностью вероятностей
если а х Ь, в противном случае.
49. Покажите, что р = (а + Ь)/2.
50. Покажите, что т = (а + Ь)/2.
51. Покажите, что x2f (х) dx = (62 + ab + а2)/3.
52. Покажите, что V(X) = (b — а)2/12.
* 53. Используя процедуру численного интегрирования, предусмотренную в графической утилите, вычислите приближенное математическое ожидание, медиану и стандартное отклонение случайной величины с плотностью вероятностей
если х > 0,
в противном случае.
Объясните, почему интеграл по интервалу (—оо, оо) можно заменить интегралом по отрезку [0,10]. Убедитесь, что полученный результат согласуется с результатами, которых можно ожидать для экспоненциальной функции распределения.
* 54. Используя процедуру численного интегрирования, предусмотренную в графической утилите, вычислите приближенное математическое ожидание, медиану и стандартное отклонение случайной величины с плотностью вероятностей
7(х) =
(0,36е-°’36;Е,
1°
если х 0,
в противном случае.
Объясните, почему интеграл по интервалу (—оо, оо) можно заменить интегралом по отрезку [0,100]. Убедитесь, что полученный результат согласуется с результатами, которых можно ожидать для экспоненциальной функции распределения.
В задачах 55-58 рассматривается случайная величина X с плотностью вероятности
/(*)
(р/хр+1,
1°
если х 1,
в противном случае,
где р — положительная постоянная. Эта случайная величина часто называется случайной величиной Парето2.
55. Убедитесь, что функция f обладает свойствами плотности вероятности и вычислите математическое ожидание. Какие ограничения нужно наложить на число р, чтобы гарантировать, что математическое ожидание существует?
2Эта случайная величина названа в честь Вильфредо Парето (1843-1923), итальянского социолога и экономиста. Будучи известным благодаря своим теориям политических процессов, Парето также разработал новые области применения математики в экономике.


768
Часть III. Математический анализ
56. Вычислите стандартное отклонение. Какие ограничения нужно наложить на число р, чтобы можно было гарантировать, что стандартное отклонение существует?
57. Вычислите медиану.
58. Математическое ожидание и медиана для равномерно распределенной случайной величины равны между собой так же, как математическое ожидание и стандартное отклонение экспоненциально распределенной случайной переменной. Используя график, проиллюстрируйте связь между математическим ожиданием, медианой и стандартным отклонением случайной величины Парето. Вычислите приблизительные значения абсцисс точек пересечения с точностью до двух десятичных знаков.
Применение математики
Экономика и бизнес
59. Время ожидания. Время, в течение которого соискатель ожидает экзамена на получение водительских прав (в минутах), равномерно распределено на отрезке [0,40]. Какова вероятность того, что соискатель будет ожидать более 25 минут?
60. Время ожидания. Время ожидания посадки на самолет в крупном аэропорту (в минутах), равномерно распределено на отрезке [0,60]. Какова вероятность того, что пассажир будет ожидать посадки менее 20 минут?
61. Связь. Продолжительность телефонных разговоров (в минутах) распределена экспоненциально. Средняя продолжительность разговора (математическое ожидание) равна трем минутам. Какова вероятность того, что разговор продлится менее двух минут?
62. Время ожидания. Время, в течение которого водитель ожидает обслуживания непосредственно в автомобиле является экспоненциальной случайной величиной. Среднее время ожидания (математическое ожидание) равно четырем минутам. Какова вероятность того, что водитель будет ожидать более пяти минут?
63. Техническое обслуживание. Период времени между поломками копировального аппарата является экспоненциальной случайной величиной. Половина копировальных аппаратов требует ремонта в течение первых двух лет эксплуатации. Какова вероятность того, что копировальный аппарат потребует ремонта в течение первого года эксплуатации?
64. Поломка комплектующих. Срок службы компьютерных комплектующих является экспоненциальной случайной величиной. Половина комплектующих выходит из строя в течение первых трех лет. Комплектующие продаются с годовой гарантией. Какова вероятность того, что компьютерная комплектующая выйдет из строя в течение гарантийного срока?
65. Продажи. Годовой объем продаж отдельного менеджера компании, торгующей кассовыми аппаратами, имеет нормальное распределение. Средний годовой объем продаж (математическое ожидание) равен 200 000 долл, со стандартным отклонением, равным 20 000 долл. Какая предположительно доля менеджеров по продажам показывает годовой объем продаж более 240 000 долл.?


Глава 15. Теория вероятностей и математический анализ 769
66. Гарантии. Срок службы автомобильного аккумулятора имеет нормальное распределение. Средний срок службы (математическое ожидание) равен 170 неделям со стандартным отклонением, равным 10 неделям. Какая предположительно доля проданных аккумуляторов будет возвращена до конца гарантийного периода, если гарантия длится три года?
67. WWW Контроль качества. Завод производит прецизионную деталь, длина которой описывается нормально распределенной случайной величиной с математическим ожиданием, равным 100 мм, и стандартным отклонением, равным 2 мм. Все детали, имеющие отклонение от среднего более 5 мм, должны быть отбракованы. Какая средняя доля деталей должна быть отбракована?
68. Контроль качества. Завод производит деталь, ширина которой является нормально распределенной случайной величиной с математическим ожиданием, равным 7,55 см и стандартным отклонением, равным 0,02 см. Все детали, имеющие отклонение от математического ожидания более 0,05 см, должны быть отбракованы. Какая в среднем доля выпущенной партии будет забракована?
Биологические науки
69. WWW Продолжительность жизни. Время смерти с момента заболевания пациента определенной болезнью распределено экспоненциально. Вероятность того, что пациент умрет через год, равна 0,3.
а) Каково ожидаемое время смерти?
б) Какова вероятность того, что пациент проживет дольше, чем ожидаемое время смерти?
70. Продолжительность жизни. Повторите решение задачи 69, если вероятность того, что пациент умрет через год, равна 0,5.
71. Медицина. Время заживления пореза определенного типа имеет нормальное распределение со средним временем заживления, равным 240 ч, и стандартным отклонением, равным 20 ч. Какая доля людей, имеющих такой порез, выздоровеет спустя 8 дней после травмы или раньше?
72. Сельское хозяйство. Высота стебля кормового растения — это нормально распределенная величина со средним значением 38 дюймов и стандартным отклонением, равным 1,5 дюйма. Какая доля кормовых растений с высотой более 40 дюймов?
Социальные науки
73. Обучение. Время, необходимое взрослому человеку для запоминания последовательности случайных цифр (в минутах), является экспоненциальной случайной величиной. Среднее время равно двум минутам. Какова вероятность того, что взрослому человеку для запоминания цифр понадобится более пяти минут?
74. Поведение животных. Время, необходимое кролику для нахождения пути в лабиринте (в минутах), распределено экспоненциально. Среднее время равно 30 секундам. Какова вероятность того, что кролик найдет путь в лабиринте менее, чем за минуту?


770
Часть III. Математический анализ
75. Градуировка кривой. Экзаменатор проградуировал кривую, предполагая, что оценка теста имеет нормальное распределение. Средняя оценка соответствует 70 баллам, а стандартное отклонение равно 8 баллам. Вычислите количество баллов для каждого интервала шкалы, если экзаменатор хочет распределить оценки следующим образом: 10% — А, 20% — В, 40% — С, 20% - D и 10% — F. Округлите ответ до одного десятичного знака.
76. Психология. Тест, предназначенный для выявления агрессивно и пассивно настроенных личностей, был стандартизирован на большой группе людей. Оценочные баллы имеют нормальное распределение со средним значением, равным 50, и стандартным отклонением, равным 10. Верхние десять процентов шкалы соответствуют высокому показателю агрессивности, следующие 20% шкалы — умеренной агрессивности, средние 40% — средней агрессивности, следующие 20% баллов — умеренной пассивности, а 10% баллов в нижней части шкалы — высокой пассивности. Чему равен разброс баллов? Округлите ответ до одного десятичного знака.
Ключевые слова, основные обозначения и формулы
15.1. 	Несобственные интегралы. Несобственный интеграл; сходящийся интеграл; расходящийся интеграл; бесконечный поток доходов; стоимость основного капитала;
оо
j У (х) dx =
а
Ъ
f (х) dx =
Ь
а
— ОО
оо
с
j у (х) dx +
— ОО
CV =
f(t)e rtdt.
о
15.2. 	Непрерывные случайные переменные. Дискретная случайная переменна; непрерывная случайная переменная; плотность распределения вероятностей; интегральная функция распределения;


Глава 15. Теория вероятностей и математический анализ
771
15.3. 	Математическое ожидание, стандартное отклонение и медиана. Математическое ожидание; среднее значение; дисперсия; стандартное отклонение; альтернативная формула вычисления дисперсии; медиана.
оо
Математическое ожидание: р = Е (X) = j xf (я) dx;
— оо
оо
Дисперсия: V (х) = j (ж - р)2 f (х) dx
—оо
оо
= j х2 f (х) dx — р2;
—оо
Стандартное отклонение: а = y/V (X);
Медиана: решение уравнения Р (X < т) = относительно величины т.
Zi
15.4. 	Специальные распределения вероятности. Равномерно распределенная случайная величина; плотность равномерного распределения; экспоненциальное распределение; экспоненциальная случайная величина; плотность экспоненциального распределения; нормальное распределение; нормально распределенная случайная величина; плотность нормального распределения; кривая нормального распределения; стандартная нормальная кривая.
Плотность равномерного распределения вероятностей:
если а < х < Ь;
в противном случае
Плотность экспоненциального распределения вероятностей:
если х 0;
в противном случае;
Плотность нормального распределения вероятностей: /(х)= 1 а>0.
CTV27r
Упражнения для повторения
Выполните все упражнения этого обзорного раздела и сравните результаты с ответами, помещенными в конце книги. Ответы ко многим упражнениям на повторение приводятся вместе с номером соответствующего раздела (курсивом). Если у вас возникают затруднения при решении какой-либо задачи, повторите материал соответствующего раздела.


772
Часть III. Математический анализ
А В задачах 1-3 вычислите значение каждого несобственного интеграла, если он сходится.
ОО
О
2.
оо
[ —Ц- dx.
J X + 1
о
В задачах 4-7 рассматривается непрерывная случайная величина X с плотностью распределения вероятностей
если 0 х 2, в противном случае.
4. Вычислите вероятность Р(0 X 1) и проиллюстрируйте ответ на графике.
5. Вычислите математическое ожидание, дисперсию и стандартное отклонение.
6. Вычислите соответствующую интегральную функцию распределения и постройте ее график.
7. Вычислите медиану.
8. Вычислите вероятность Р(100 X 118), если X — нормальная случайная величина с математическим ожиданием, равным 100, и стандартным отклонением, равным 10.
В задачах 9 и 10 найдите плотности распределения вероятностей f и соответствующую интегральную функцию распределения F для непрерывной случайной величины в следующих вариантах.
9. Величина X равномерно распределена на интервале [5,15].
10. Величина X является экспоненциальной случайной величиной с параметром
В задачах 11 и 12 ответьте, является ли f плотностью распределения вероятностей. Объясните свой ответ.
*11. /(я) = е-<
0,75 (х2 — 4ж + 3) , если 0 х < 4,
0 в противном случае.
Б В задачах 13-16 рассматривается непрерывная случайная величина X с плотностью распределения вероятностей
если х 1,
в противном случае.
13. Вычислите вероятность Р(1 X 4) и проиллюстрируйте ответ на графике.
14. Вычислите математическое ожидание, дисперсию и стандартное отклонение.
15. Вычислите соответствующую интегральную функцию распределения и постройте ее график.
16. Вычислите медиану.


Глава 15. Теория вероятностей и математический анализ
773
В задачах 17-20 рассматривается экспоненциально распределенная случайная величина X.
17. Вычислите плотность распределения вероятностей, если Р(4 X) = е~2.
18. Вычислите вероятность Р(0 X ^2).
19. Вычислите соответствующую интегральную функцию распределения.
20. Вычислите математическое ожидание, стандартное отклонение и медиану.
21. Дано нормальное распределение с математическим ожиданием, равным 50, и стандартным отклонением, равным 6. Вычислите площадь фигуры, лежащей под нормальной кривой на указанных отрезках.
а) 	От 41 до 62. б) От 59 до бесконечности.
22. Дана нормальная случайная величина X с математическим ожиданием, равным 82, и стандартным отклонением, равным 8. Вычислите следующие вероятности.
а) 	Р(84 X 94). б) Р(Х > 60).
В задачах 23 и 24 вычислите значение каждого несобственного интеграла, если он сходится.
О оо
23. I exdx. 24. [ ^-^dx.
J J (x + 3)2
-oo 0
* 25. Сходится ли интеграл J^° f (x) dx, если функция f непрерывна на интервале
[—1, сю) и интеграл J^°x f (х) dx сходится? Объясните свой ответ.
В задачах 26 и 27 найдите такую постоянную к, при которой kf является плотностью распределения вероятностей, или объясните, почему такой постоянной к не существует.
е_10х, если х 0,
0 в противном случае.
е101, если х 0,
0 в противном случае.
28. Вычислите вероятность Р(Х < р), если X — экспоненциально распределенная случайная величина с медианой т = 3 In 2 и математическим ожиданием р.
В
29. Вычислите математическое ожидание и медиану непрерывной случайной величиной с плотностью распределения вероятностей
*26. Цх) =
*27. /(*) =
/и = {“/(1+5)3’
если х 0,
в противном случае.
30. 	Используя графическую утилиту, вычислите приблизительное значение медианы (с точностью до двух десятичных знаков) непрерывной случайной величины


114
Часть III. Математический анализ
с плотностью распределения вероятностей
/(х) + если^1,
1 0 в противном случае.
31. Вычислите значение интеграла J*^ ^^^dx, если он сходится.
32. Вычислите интеграл, если f — непрерывная плотность вероятности с математическим ожиданием /г и стандартным отклонением ст, а параметры а, b и с — константы. Выразите результат через параметры //, сг, а, Ъ и с.
оо
j (ат2 + Ьх + с) f (т) dx.
— оо
В задачах 33-36 рассматриваются случайные переменные и с плотностями распределения вероятностей Д и Д соответственно, где
0,25те_ж/2; если х О,
О в противном случае,
0,0625т3е“х/2; если т О,
О в противном случае.
*33. Объясните, как по графикам Д и Д предсказать, какая из величин Х\ или Х2 имеет большее математическое ожидание.
* 34. Объясните, как по графикам Д и Д предсказать, какая из величин Х^ или Х2 имеет большую дисперсию.
35. Проверьте прогноз, сделанный в задаче 33, вычислив приближенно математические ожидания величин Xi иХ2, используя метод численного интегрирования.
36. Проверьте прогноз, сделанный в задаче 34, вычислив приближенно дисперсии случайных величин Х^ и Х2, используя метод численного интегрирования.
Применение математики
Л (*) =
/2 (ж) =
Экономика и бизнес
37. 	Добыча. Скорость добычи из нефтяной скважины (в миллионах баррелей в год) равна (см. следующий рисунок)
R(t) = 12e_0,3t - 12e_0,6t


Глава 15. Теория вероятностей и математический анализ
775
а) Предполагая, что скважина будет эксплуатироваться бесконечно, вычислите общий объем добытой нефти.
б) Когда добыча из скважины достигнет 50% от общего объема добычи? Округлите ответ до двух десятичных знаков.
38. 	Спрос. Менеджер кинотеатра установил, что недельный спрос на попкорн (в фунтах) описывается непрерывной случайной величиной с плотностью распределения вероятностей
0,02 (1 - 0,01а;); если 0 х 100,
0 в противном случае.
*а) Вычислите интеграл J^0 f (x)dx и проанализируйте результат.
б) Какова вероятность того, что имеющегося попкорна хватит, чтобы удовлетворить недельный спрос, если в начале недели запасы составляют 50 фунтов?
в) Сколько попкорна потребуется в начале недели, если вероятность того, что предложение превысит недельный спрос, была равна 0,96?
39. Стоимость основного капитала. Пожизненная годовая рента недвижимого имущества составляет 2400 долл. Вычислите стоимость основного капитала при ставке, равной шести непрерывно начисляемым сложным процентам.
40. Заявка на предоставление кредита. Доля заявок на государственные кредитные карточки (выраженная в десятичном представлении от 0 до 1), которые были обработаны в день их получения, является непрерывной случайной величиной с плотностью распределения вероятностей
если 0 < х 1, в противном случае.
а) Какова вероятность того, что по меньшей мере 20% полученных заявок будет обработано в день их поступления?


776
Часть III. Математический анализ
б) Сколько предположительно заявок будет обработано в день их получения?
в) Чему равна медиана доли заявок, обработанных в день их поступления?
41. Поломка компьютера. Производитель установил, что промежуток времени между поломками выпускаемых компьютеров описывается экспоненциально распределенной случайной переменой со средним периодом между поломками, равным 4000 часам. Предположим, что определенный компьютер был только что отремонтирован.
а) Какова вероятность того, что компьютер проработает следующие 4000 часов без поломок?
б) Какова вероятность того, что компьютер сломается в течение следующих 1000 часов?
42. Срок службы автомобильной шины. Срок службы шины с радиальным расположением корда определенной марки (в милях) описывается нормальной случайной величиной с математическим ожиданием, равным 35 000 милям, и стандартным отклонением, равным 5000 миль. Какова вероятность того, что шина выйдет из строя на протяжении первых 25 000 миль пробега?
43. Отбор персонала. Количество баллов, набранных в отборочном тесте соискателями на должность технического специалиста, имеет нормальное распределение с математическим ожиданием, равным 100, и стандартным отклонением, равным 10. Вычислите приблизительную долю соискателей, принимавших участие в тестировании, которые набрали количество указанное количество баллов.
а) От 92 до 108. б) 115 или больше.
Биологические науки
44. 	Медицина. Срок хранения определенного препарата (в месяцах) является непрерывной случайной величиной с плотностью распределения вероятностей
№) = {10/(1 + 1оЛ
если х 0,
в противном случае.
*а) Вычислите интеграл / (х) dx и проинтерпретируйте результат.
б) Какова вероятность того, что препарат будет пригоден к употреблению через пять месяцев?
*в) Чему равна медиана срока хранения?
45. Продолжительность жизни. Продолжительность жизни с момента заболевания собаки определенной болезнью (в месяцах) описывается экспоненциально распределенной случайной величиной. Вероятность того, что собака проживет более одного месяца равна е~2.
а) Какова вероятность того, что после заражения болезнью собака проживет более двух месяцев?
б) Какова средняя продолжительность жизни после заражения?
46. Усвоение препарата. Скорость, с которой препарат выводится из организма (в миллилитрах в час), равна
R(t) = 15e“°’2t - 15e_0,3t


Глава 15. Теория вероятностей и математический анализ
777
где t — количество часов, прошедших с момента приема препарата.
а) Сколько всего препарата будет выведено из организма?
б) Сколько понадобится времени, чтобы из организма было выведено 50% об щего количества препарата? Округлите ответ до двух десятичных знаков.
Социальные науки
47. WWW Тестирование. Оценки в тесте на умственное развитие шестилетних детей имеют нормальное распределение с математическим ожиданием, равным 108, и стандартным отклонением, равным 12. Какой предположительно процент детей наберет 135 или более баллов?
48. Политика. Скорость изменения со временем количества избирателей в городе (в годах) приблизительно равна
100t
(1 + *2)2’
где N(f) измеряется в тысячах человек. Насколько вырастет количество избирателей в течение следующих трех лет, если ДГ(О) — текущее количество избирателей? Насколько возрастет количество избирателей, если оно будет непрерывно расти с этой скоростью?
Домашнее задание 15.1. Бета-распределение
WWW Теорема Байеса, названная в честь пресвитерианского священника Томаса Байеса (1702-1763), в последние годы имеет широкое прикладное значение. Она показывает высокую эффективность исследования случайных величин, значения которых можно выразить в виде долей или процентов. В частности, одной из таких переменных, которая широко используется в статистике, является случайная бета-величина. Как правило, случайная бета-величина применяется для описания процента ресторанов быстрого питания, которые начали получать прибыль в течение первого года деятельности, процента времени в году, в течение которого завод-изготовитель простаивал, потребления природного газа как доли общего объема, и доли анкет соискателей на рабочую должность, резюме которых содержат ошибки.
Непрерывная случайная величина имеет бета-распределение3 и называется случайной бета-величиной, если ее плотность вероятности является бета-функцией
у (х) = {(0 + О3 + 2)хР (! - х) >
если 0 < х < 1, в противном случае,
где (3 — постоянная, /3^0. Значение /3, как правило, определяют, исходя из результатов конкретных экспериментов. Значение случайной бета-величины можно выразить в виде доли или процента. Однако перед выполнением вычислений, связанных со случайной бета-величиной, проценты необходимо переводить в дольные части.
3Существует более полное определение бета-распределения, но оно здесь рассматриваться не будет.


778
Часть III. Математический анализ
1. Покажите, что функция f обладает свойствами плотности распределения вероятностей.
2. Постройте графики функции f для (3 = 0,1, 2 и 3. Опишите графики функции f при произвольных /3 > 1, включая расположение всех локальных экстремумов и точек перегиба на интервале (0,1).
3. Вычислите математическое ожидание и стандартное отклонение.
4. Вычислите интегральную функцию распределения.
5. Вычислите медиану для (3 = 0 и (3 = 1.
6. Вычислите приближенное значение медианы (с точностью до двух десятичных знаков) для (3 = 2 и (3 ~ 3.
Домашнее задание 15.2. Распределение хи-квадрат
Непрерывная случайная величина имеет распределение хи-квадрат с 2т степенями свободы (где т — положительное целое), если ее плотность вероятности равна
(т-1)!2" хт~1е~х^2, если 0 < X < оо,
О в противном случае.
При т — 1 (и только в этом случае) функция f(x) является плотностью экспоненциального распределения вероятностей.
Распределение хи-квадрат естественным образом связанно с нормальным распределением. Оно также имеет множество применений в статистическом анализе. Например, распределение хи-квадрат используется для исследования расхождений между мнениями мужчин и женщин, также при оценке рейтинга поддержки президента.
1. Используя графическую утилиту, покажите, что функция f обладает свойствами плотности распределения вероятностей при т — 1, 2, 3, 4 и 5. Проанализируйте, почему интеграл по интервалу (—оо,оо) можно заменить интегралом по отрезку [О, 50].
2. Постройте графики функции f для т = 1, 2, 3 и 4. Как изменяются графики при возрастании т?
3. Используя численное интегрирование, найдите приближенное математическое ожидание распределения хи-квадрат при тп = 1,2,3,4и5. Используя полученные ответы, запишите предположительную формулу для математического ожидания распределения хи-квадрат с 2т степенями свободы.
4. Используя численное интегрирование, найдите приближенную дисперсию распределения хи-квадрат при т = 1, 2, 3, 4 и 5. Используя полученные ответы, запишите предположительную формулу для дисперсии распределения хи-квадрат с 2т степенями свободы.
5. Используя численное интегрирование, найдите приближенную медиану распределения хи-квадрат при т = 1, 2, 3, 4 и 5. Как медиана изменяется с ростом величины т?


Часть IV
Приложения


A
Основные алгебраические понятия и законы
А.1. Множества
А.2. Алгебра и действительные числа
А.З. Операции с полиномами
А.4. Факторизация полиномов
А. 5. Операции с рациональными выражениями
А.6. Целочисленные степени и экспоненциальная форма записи числа
А. 7. Дробные степени и корни
А. 8. Линейные уравнения и неравенства одной переменной
А.9. Квадратные уравнения
Введение
В приложении А рассматриваются основные алгебраические принципы, которые обычно изучаются в более ранних курсах. Приведенный здесь материал можно изучать до знакомства с основной частью книги или использовать как справочник. Пробелы в знаниях алгебры можно выявить решая задачи, приведенные в начале раздела А. 1. В ответах, помещенных в конце книги, указаны разделы приложения А, с которыми нужно ознакомиться, чтобы устранить их.


782
Часть IV. Приложения
Проверка знаний алгебры
Выполните все упражнения этого раздела и сравните результаты с ответами, помещенными в конце книги. Ответы ко всем упражнениям приводятся вместе с номером раздела приложения А, в котором они обсуждались.
1. Определите истинность (И) или ложность (Л) каждого из приведенных утверждений.
а) 	7 {4,6,8}. б) 8 С {4,6,8}.
в) 0^{4,6,8}. г) 0 с {4,6,8}.
2. Замените знаки вопроса в приведенных ниже утверждениях, которые описывают использование соответствующего свойства действительных чисел.
а) Коммутативность умножения (•): x(y + z) = 2.
б) Ассоциативность сложения (+): 2 + (х + у) = ?.
в) Дистрибутивность: (2 + 3)ж = ?.
В задачах 3-7речь идет о следующих полиномах:
а) Зх — 4, б) х + 2,
в) Зх2 + х — 8, г) х3 + 8.
3. Просуммируйте все четыре полинома.
4. Вычтите из суммы полиномов б и г сумму полиномов а и в.
5. Вычислите произведение полиномов виг.
6. Какую степень имеет полином г?
7. Чему равен коэффициент во втором слагаемом полинома в?
В задачах 8-13 выполните указанные вычисления и упростите результат.
8. 5д:2 — Зх[4 — 3(х — 2)]. 9. (2х + у)(3х — 4?/).
10. (2а — 36)2. 11. (2х — у)(2х + у) — (2х — у)2.
12. (т2 -I- 2тп — n2)(m2 — 2тп — п2). 13. (х — 2т/)3.
14. Запишите в экспоненциальной форме следующие числа.
а) 4065 000 000 000. б) 0,0073.
15. Запишите в стандартной десятичной форме следующие числа.
а) 2,55 108. б) 4,06 • 10“4.
16. Пусть U = {2,4,5,6,8}, М = {2,4,5} и N = {5,6}. Найдите следующие множества.
a) MUN. б) МП N.
в) (MUN)'. г) MC\Nf.
17. Проанализируйте диаграмму Венна, приведенную на следующем рисунке. Сколько элементов содержится в каждом из приведенных ниже множеств?


Приложение А. Основные алгебраические понятия и законы
783
a) A U В. в) (A U В)'.
18. 	Определите истинность (И) или ложность (Л) каждого из приведенных утверждений.
а) Натуральное число является рациональным.
б) Периодическая десятичная дробь является иррациональным числом.
9tz8v6
21. —-—
23. 6(x_3t/2)-2.
25. (ЭоЧ"2)1/2.
27. (x1/2 + 7/1/2)2.
19. Приведите пример целого числа, которое не является натуральным.
В задачах 20-28 необходимо представить ответы в форме, включающей только целочисленные степени. Все переменные, фигурирующие в задачах, являются положительными действительными числами.
20. 6(хт/3)5.
22. (2 • 105)(3 • 10_3).
24. т?/3и2/3.
5° 3-2
26- 32 + 2-2 •
28. (Зх1/2 - у1/2)(2х1/2 + Зу1/2).
В задачах 29-34 требуется разложить полиномы на множители с целыми коэффициентами. Если это нельзя сделать, объясните, почему.
29. 12х2 + 5х — 3. 30. 8х2 — 18хт/ 4- 9т/2.
31. t2 — 4t — 6. 32. 6n3 — 9n2 — 15n.
33. 	(4x — t/)2 — 9x2.
34. 	2x2 + 4x7/ — 5t/2.
В задачах 35-40 требуется упростить приведенные выражения. Все неправильные
дроби преобразуйте в правильные.
35.
5Ь За3 6а2 Ь2
37 х - х + 4 х2 — 16 х2 — 4х’
39. 1+h~ 7.
h
36.
38.
40.
Зх 1
Зх2 — 12х бх
у — 2 У2 + 2т/
7/2 - 4т/ + 4 ’ у2 + 4т/ + 4 *
а? 1 +т/ 1 х-2 — у~2
41. Каждое из приведенных ниже утверждений иллюстрирует одно из перечисленных свойств действительных чисел или одно из определений, относящееся к действительным числам. Определите, какое из свойств относится к каждому из утверждений.


784
Часть IV. Приложения
Коммутативность (+, •) Ассоциативность (+, •)
Единичный элемент (+, •) Обратный элемент (+, •) Деление Изменение знака
Дистрибутивность Вычитание Добавление нуля
а) (-7) - (-5) = (-7) + Н-5)]. б) 5u + (3^ + 2) = (3v + 2) + 5u.
в) (5m — 2)(2m + 3) = (5m — 2)2m + (5m — 2)3.
г) 9 • (4y) = (9 • 4)y. д) U =
— (v — w) v — w
e) 	(x-y) + 0 = (x-y).
42. Из 100 студентов первого курса 70 изучают математику, 45 — английский язык , а 25 — одновременно и математику, и английский язык.
а) Сколько студентов выбрали математику или английский язык?
б) Сколько студентов выбрали английский язык, но не математику?
43. Представьте выражение б^Ух2 — 7^/(х — I)3 в виде дробных степеней.
44. Представьте выражение 2а;1/2 — Зт2/3 в виде радикалов.
45. Представьте выражение в виде ахр + bxqy а и b — целые числа, а р и q
рациональные числа.
В задачах 46 и 47 преобразуйте знаменатель в рациональный вид.
Зх х - 5
46. -j=. 47. — F.
v3x у/х — у5
В задачах 48 и 49 преобразуйте числитель в рациональный вид.
48.
у/х — 5
х — 5
49.
у/и + h — у/й h
В задачах 50-54 решите уравнения относительно переменной х.
5°. И-^- = 2- 51. х2 = 5х.
52. Зх2 - 21 = 0. 53. х2 - х - 20 = 0.
54. 2х = 3 + -.
X
В задачах 55-57решите неравенства относительно переменной х и укажите решения на числовой оси.
55. 2(х + 4) > 5х - 4. 56.1-^^^.
О Z
57. —2 < | - 3 < 3.
В задачах 58 и 59 выразите переменную у через переменную х.
58. 2х — Зу = 6. 59. ху — у = 3.
* 60. Всегда ли верно утверждение Ас В, если АГ\В = А? Аргументируйте ответ.


Приложение А. Основные алгебраические понятия и законы
785
Применение математики
61. Экономика. Уровень валового производства в Соединенных Штатах в 1998 году составлял 8 511 000000000 долл, при населении 270 300000 человек. Запишите долю валового производства на человека в экспоненциальной (научной) и стандартной десятичной форме, округляя ответ с точностью до доллара.
62. Инвестиции. Инвестор располагает суммой, равной 60000 долл. Пусть одна часть суммы инвестируется под 8%, а вторая — под 14%. Какие суммы нужно инвестировать для каждой процентной ставки, чтобы общий доход составлял 12% от всей суммы?
63. Анализ безубыточности. Продюсер образовательного видео выяснил, что съемки нового фильма будут стоить приблизительно 72 000 долл., а затраты на выпуск видеокассеты равна 12 долл, за единицу. Сколько видеокассет следует выпустить, чтобы не понести убытки, если оптовая цена одной видеокассеты 30 долл.?
А.1. Множества
■ Обозначения и свойства множеств
■ Операции с множествами
■ Решение практических задач
В этом разделе рассматриваются основные понятия теории множеств. Идеи и обозначения теории множеств позволяют не только формулировать математические утверждения ясно и точно, но и являются необходимыми для понимания основ теории вероятностей.
Обозначения и свойства множеств
Множеством называется любая совокупность объектов, определенная так, что всегда можно сказать, принадлежит данный объект указанной совокупности или нет. Для обозначения конкретных множеств часто используются прописные буквы, например, А, В и С. Каждый объект, принадлежащий множеству, называется элементом множества. Обозначение
а е А значит “элемент а принадлежит множеству А”,
а £ А значит “элемент а не принадлежит множеству А”.
Множество без элементов называется пустым. Например, множество людей ростом более 20 футов является пустым.
0 значит “пустое множество”.
Множество обычно определяется или перечислением всех элементов в фигурных скобках {}, или указанием правила, которое определяет элементы множества. Например, если Р(х) — некоторое утверждение относительно х, то
S = {х | Р(х)} значит “S является множеством таких величин х, ддя которых выражение Р(х) является истинным”.


786
Часть IV. Приложения
Напомним, что вертикальная черта в фигурных скобках означает “такой, что”. В приведенном ниже примере иллюстрируются оба способа определения множества — перечисление и правило.
Пример А.1 (Описание множеств).
Правило Перечисление
{х | х — выходной день недели} = {Суббота, воскресенье}
{я | я2 = 4} = {-2,2}
{х | х — положительное нечетное число} = {1,3,5,...} а
Многоточие (...) в третьем множестве примера А. 1 указывает на то, что последовательность чисел по закономерности, которая понятна из приведенных первых трех чисел, продолжается бесконечно. Первые два множества в примере А.1 являются конечными (интуитивно понятно, что все элементы множества можно пересчитать, используя конечный набор чисел), а последнее множество является бесконечным (интуитивно понятно, что процесс пересчета элементов множества бесконечен). Если множество задается перечислением элементов, то каждый элемент нумеруется только один раз. Порядок, в котором нумеруются элементы множества, не имеет значения.
Упражнение А.1.
Пусть G — множество всех чисел, для которых выполняется равенство х2 = 9.
1. Задайте множество G с помощью правила.
2. Задайте множество G перечислением элементов.
3. Определите истинность или ложность следующих утверждений: 3 G G,
9 0 G. ■
Если каждый элемент множества А является элементом множества В, то множество А называется подмножеством множества В. Например, множество всех студенток является подмножеством всех студентов группы. Если множества А и В состоят из одних и тех же элементов, то говорят, что эти множества равны.
Л сВ А = В
А(£В
А/В
значит “множество А является подмножеством множества В” значит “множества Л и В имеют одни и те же элементы” значит “множество Л не является подмножеством множества В” значит “множества Л и В не состоят из одинаковых элементов”
Легко доказать, что
множество 0 является подмножеством любого множества.
Пример А.2 (Обозначения множеств). Пусть Л = {-3,-1,1,3}, В = {3,-3,1,-1} и С = {—3, —2, —1,0,1,2,3}. Каждое из перечисленных ниже утверждений — истинно?
Л = В
С/Л
0 с л
Лес
С£Л
0 С С
Лев
Вс л
0 л


Приложение А. Основные алгебраические понятия и законы
787
Упражнение А.2.
Пусть А = {0,2,4,6}, В = {0,1,2,3,4,5,6} и С = {2,6,0,4}. Проверьте истинность или ложность каждого из приведенных ниже утверждений.
1. 	А С В. 2. А с С. 3. А = С.
4. 	С С В. 5. В ^А. 6. 0 С В. ■
Пример А.З (Подмножества). Перечислите все подмножества множества {а, Ь, с}.
Решение.
{а,Ъ,с}, {а, 6}, {а, с}, {Ь, с}, {а}, {&}, {с}, 0. в
Упражнение А.З.
Перечислите все подмножества множества {1,2}. ■
Задание А.1.
Какое из приведенных ниже утверждений является истинным?
1. 	0 С 0. 2. 0 е 0. 3. 0 = {0}. 4. 0 С {0}. ■
Операции с множествами
Объединением множеств А и В называется множество A U В, содержащее все элементы множеств А и В.
Объединение
AU В = {х | х е А или х е В}.
Здесь слово “или” используется так, как обычно в математических высказываниях. Это значит, что х может быть элементом любого из множеств А или В.
Для наглядного представления отношений между множествами применяются диаграммы Венна. На рис. А.1 показано объединение множеств. Заметим, что
АсАиВ и В с A UB.
Рис. А.1. Закрашенная область изображает множество A U В
Пересечением двух множеств А и В называется множество А П В, состоящее из всех элементов, которые принадлежат множествам А и В одновременно.


788
Часть IV. Приложения
Пересечение
Аг\в = {х | # е А и х ев}.
Отношение между множествами показано на диаграмме Венна на рис. А.2. Заметим, что
АГ\ВсА и АП В с В.
Рис. А.2. Закрашенная область изображает множество АПВ
Если АП В = 0, то множества А и В называются непересекающимися. Иллюстрация приведена на рис. А.З.
Рис. А.З. А П В = 0; множества А и В являются непересекающимися
Множество U, состоящее из всех возможных элементов, называется универсальным. Все остальные множества являются подмножествами U.
Определим еще одну операцию над множествами, которая называется дополнением. Дополнением множества А (по отношению к универсуму U) называется множество А' элементов U, которые не принадлежат А (рис. А.4).
Дополнение
Ar = {х EU \ х £ А}
Пример А.4 (Объединение, пересечение и дополнение). Пусть А = {3,6,9}, В = = {3,4,5,6,7}, С = {4,5,7} и U = {1,2,3,4, 5, 7,8,9}. Тогда
AUB= {3,4,5,6,7,9}
АП В = {3,6}
А П С = 0 Множества А и С не пересекаются
В' = {1,2,8,9} .


Приложение А. Основные алгебраические понятия и законы
789
U
Рис. А.4. Дополнением множества А является множество А'
Упражнение А.4.
Пусть R = {1,2,3,4}, S = {1,3,5,7}, Т = {2,4} и U = {1,2,3,4,5,7,8,9}. Найдите следующие множества.
1. 	RUS. 2. Rr\S. 3.SDT. 4. S'. ■
Решение практических задач
Пример А.5 (Исследование рынка). Случайно выбранные 100 студентов заполнили анкету, содержащую следующие вопросы.
1. Есть ли у вас телевизор?
2. Есть ли у вас автомобиль?
3. Есть ли у вас телевизор и автомобиль?
На вопрос 1 получено 75 утвердительных ответов, на вопрос 2 — 45 и на вопрос 3 —
35.
1. У скольких студентов есть телевизор или автомобиль?
2. У скольких студентов нет ни телевизора, ни автомобиля?
Решение. Для решения этой задачи применим диаграммы Венна. Будем считать, что U — множество всех студентов (100),
Т — множество всех студентов, у которых есть телевизор (75),
С — множество всех студентов, у которых есть автомобиль (45),
Т А С — множество всех студентов, у которых есть телевизор и автомобиль (35).
Количество элементов пересечения вычисляются так:
40 = 75 - 35
10 = 45 - 35
15 = 100 - (40 4-35-1- 10)
1. Количество студентов, у которых есть телевизор или автомобиль, равно количеству элементов множества Т U U. Возникает иллюзия, что это количество студентов равно сумме количества элементов множества Т плюс количество элементов множества С, т.е. 75 4- 45 = 120, но это число больше общего количества студентов!


790
Часть IV. Приложения
В чем же ошибка? Количество элементов в пересечении множеств (35) вычислено дважды. Правильным ответом, как следует из диаграммы Венна, будет следующее число.
40 + 35 + 10 = 85.
2. 	Количество студентов, у которых нет ни телевизора, ни автомобиля, является количеством элементов множества (Т U 17)', т.е. 15. ■
Упражнение А.5.
Вернитесь к примеру А.5.
1. У скольких студентов есть автомобиль, но нет телевизора?
2. У скольких студентов нет ни автомобиля, ни телевизора? ■
Заметим, что в примере А.5 слово “и” ассоциировалось с пересечением множеств, а слово “или” — с объединением.
Задание А.2.
Найдите количество студентов, которое содержится в множестве (Т П С) А С в примере А. 5. Опишите это множество с помощью диаграммы Венна. ■
Ответы к упражнениям
А.1. 1) {х | х1  2 = 9}.
2) {-3,3}.
3) Верно: верно.
А.2. Все верны.
А.З. {1,2}, {1}, {2}, 0.
А.4. 1) {1,2,3,4,5,7}.
2) {1,3}.
3) 0.
4) {2,4,6,8,9}.
А.5. 1) 10 элементов множества Т' П С.
2) 65 элементов множества (Т Г) С)'.
Практикум А.1
А Определите истинность (И) или ложность (Л) утверждений в задачах 1-8.
1. 4 е {2, 3,4}.
3. 	{2,3} 6 {2,3,4}.
5. 	{3,2,4} С {2,3,4}.
7. 	0£{2,3,4}.
2. 	6 £ {2,3,4}.
4. 	{3,2,4} = {2,3,4}.
6. 	{3,2,4} €{2,3,4}.
8. 	0 = {0}.


Приложение А. Основные алгебраические понятия и законы
791
В задачах 9-20 определите результирующее множество, используя метод перечисле¬
ния элементов.
9. 	{1,3,5} U {2,3,4}-
11. 	{1,3,4} П {2,3,4}.
13. 	{1,5,9} А {3,4,6,8}.
10. 	{3,4,6,7} U {3,4,5}.
12. 	{3,4,6,7} А {3,4,5}.
14. 	{6,8,9,11} П {3,4,5,7}.
15. 	{х | х - 2 = 0}.
17. 	{х | х2 = 49}.
16. 	{х |х + 7 = 0}.
18. 	{а: | х2 = 100}.
19. {х | х — нечетное число между 1 и 9, включительно}.
20. {х | х — месяц, начинающийся с буквы М}.
21. Для U = {1,2,3,4,5} и А = {2,3,4} найдите множество А'.
22. Для U — {7,8,9,10,11} и А = {7,11} найдите множество А'.
В задачах 23-34 речь идет о приведенной ниже диаграмме Венна. Сколько элементов содержится в каждом из приведенных множеств?
23. А.
26. В'.
29. А' А В.
32. (A U В)'.
24. V.
27. A U В.
30. А А В'.
33. А' А В'.
25. А'.
28. А А В.
31. (А А В)'
34. U'.
35. Пусть R = {1,2,3,4}, Т = {2,4,6}. Найдите следующие множества, а) {х | х € R или х е Т}. б) RUT.
36. Пусть R = {1,3,4}, Т = {2,4,6}. Найдите следующие множества.
а) {х | х € R и х 6 Г}. б) Я А Т.
37. Пусть Р = {1,2,3,4}, Q = {2,4,6} и R = {3,4,5,6}. Найдите множество ВU (СПЯ).
38. 	Пусть Р, Q и Я — множества, определенные в задаче 37. Найдите множество ЯП (Q U Я).
В задачах 39-48 обсудите истинность каждого утверждения. Для помощи используйте диаграммы Венна. Если утверждение верно, объясните, почему, если нет, приведите контрпример.
* 39. Если А С В, то А А В = А.
* 41. Если A U В = А, то А С В.
* 43. Если А А В = 0, то А = 0.
* 40. Если А С В, то A U В = А.
* 42. Если А А В = А, то А с В.
* 44. Если А = 0, то А А В = 0.


792
Часть IV. Приложения
* 45. Если А с В, то Л' с В'. * 46. Если А с В, то В' с А'.
* 47. Пустое множество является элементом любого множества.
* 48. Пустое множество является подмножеством любого множества.
49. Сколько подмножеств у каждого из приведенных ниже множеств?
а) {а}. б) {а,Ь}.
в) {а, Ь, с}. г) {a, b, с, d}.
50. Пусть множество А содержит п элементов. Выразите количество элементов множества А через число п.
* 51. Совпадают ли множества 0 и {0}? Аргументируйте ответ.
*52. Совпадают ли множества {0} и {0, {0}}? Аргументируйте ответ.
Применение математики
Экономика и бизнес
Исследование рынка. В задачах 53-64 речь идет об опросе 1000 пассажиров общественного транспорта. Оказалось, что 600 пассажиров читают новости, 500 — слушают музыку, а 300 — делают и то, и другое. Используются следующие обозначения.
N — множество пассажиров, читающих новости,
М — множество пассажиров, слушающих музыку.
Следуя методу, описанному в примере А.5, найдите количество пассажиров в каждом из приведенных множеств.
53. N U М. 54. N А М. 55. (W U МУ.
56. (7V А МУ. 57. N' А М. 58. N А М'.
59. Множество пассажиров, читающих новости или слушающих музыку.
60. Множество пассажиров, читающих новости и слушающих музыку.
61. Множество пассажиров, не читающих новости или не слушающих музыку.
62. Множество пассажиров, не читающих новости и не слушающих музыку.
63. Множество пассажиров, слушающих музыку, но не читающих новости.
64. Множество пассажиров, читающих новости, но не слушающих музыку.
65. Выборы руководства. Управление компанией, состоящее из президента и трех вице-президентов, которые обозначаются с помощью множества {Р, Vi, V3}, намеревается сформировать комитет из двух человек из своего окружения. Сколькими способами можно избрать комитет? Иначе говоря, сколько существует способов выбрать двух человек из множества четырех человек?
66. Подсчет голосов. Управление компанией из задачи 65 провело выборы следующим образом: у президента имеется два голоса, и у каждого из вице-президентов — по одному голосу. Для выбора в комитет кандидату нужно получить три голоса. Найдите все минимальные побеждающие комбинации, т.е. перечислите


Приложение А. Основные алгебраические понятия и законы
793
все подмножества множества {Р, Vi, V2, V3}, в которых представлено ровно три голоса “за”.
Биологические науки
Группы крови. При переливании крови у пациента должны быть те же антигены, что и у донора. У человека может быть три или более антигена А, В или Rh, либо ни одного из них. Возможны восемь типов крови, как показано на диаграмме Венна, где U — множество всех рассматриваемых людей.
U
Здесь множество А— обозначает людей, у которых есть антиген А, но нет В и Rh, О-\ у которых есть антиген Rh, но нет ни А, ни В; АВ обозначает людей,
у которых нет антигена Rh, и т. п.
С помощью диаграмм Венна определите типы крови, указанные в множествах, приведенных в задачах 67-74.
67. А П Rh.
70. 	AUB.
73. А! П В.
68. А П В.
71. 	(A U В)'.
74. Rh' П А.
69. A U Rh.
72. (AU В U ВЛ)'.
Социальные науки
Социальные группы. Р. Д. Льюс (R. D. Luse) иА.Д. Пэрри (A. D. Perry) при исследовании социальных групповых структур структур (Psychometrica, 1949, 14:95-116) использовали теорию множеств для определения людей, относящихся к близкому кругу друзей. Пусть G — множество всех людей в исследуемой группе и С С G. Множество С будет близким кругом друзей, если выполняются следующие условия.
1) В множестве С содержится по крайней мере три элемента.
2) Для любых a, be С справедливы утверждения aRb и bRa.
3) Для любого элемента а С существует по крайней мере один элемент be С, для которого выполняется условие aRb, bRa или оба одновременно.
(Замечание. Выражение aRb обозначает, что “а относится к b”, “а предпочитает Ь”, “а такое же, как Ь” и т.п. Разумеется, выражение aRb значит, что “а не относится к Ь” и т.п.)
* 75. Сформулируйте утверждение 2 словами.
* 76. Сформулируйте утверждение 3 словами.


794
Часть IV. Приложения
А.2. Алгебра и действительные числа
■ Множество действительных чисел
■ Действительная числовая ось
■ Основные свойства действительных чисел
■ Другие свойства действительных чисел
■ Свойства дробей
Правила операций над символами в алгебре сильно зависят от свойств действительных чисел. В данном разделе мы рассмотрим основные свойства этой числовой системы. Для ясности и простоты будем только формулировать основные понятия и обозначения. Основные свойства множеств изложены в разделе А. 1.
Множество действительных чисел
Какая числовая система используется чаще всего? Это система действительных чисел. Говоря неформально, действительное число — это число, которое можно записать в десятичном виде. В табл. А. 1 описано множество действительных чисел и некоторые наиболее важные его подмножества, а на рис. А.5 продемонстрированы связи между ними.
Таблица А.1. Множество действительных чисел
Обозначение
Название
Описание
Примеры
N
Натуральные
Последовательно перечисляемые
1,2,3,...
числа
числа (также называются положительными целыми числами)
Z
Целые числа
Числа вида ±п, где п — натураль¬
...-2,-1,0,
ные числа, и нуль
1,2,...
Q
Рациональные
Числа, которые можно предста¬
-4; 0; 1;
числа
вить в виде а/b, где а и b — целые
5’3’
числа, и b 0; числа, представи¬
3,67; -0,333;
мые в десятичном виде в конечном виде или с бесконечным периодом
5,2727271
I
Иррациональные
Числа, представимые в десятич¬
V2; тг, &7;
числа
ном виде в бесконечном виде (без
1,414213...;
периода)
2,71828182...
R
Действительные
Рациональные и иррациональ¬
числа
ные числа
Множество
натуральных чисел
содержит числа вида ±п, где п —
натуральное чис-
ло, и нуль. Множество всех рациональных чисел содержит все целые числа, а также дроби, числитель и знаменатель которых являются целыми числами, а частное не относится к целым числам. И, наконец, множество всех действительных чисел содержит все рациональные и иррациональные числа.
1 Черта сверху обозначает, что этот символ (или группа символов) повторяется бесконечно.


Приложение А. Основные алгебраические понятия и законы
795
Рис. А.5. Множество действительных чисел и его наиболее важные подмножества
Действительная числовая ось
Существует взаимно-однозначное соответствие между точками действительной прямой и элементами множества действительных чисел. Так, каждому числу соответствует только одна точка прямой и, наоборот, каждой точке прямой можно поставить в соответствие только одно действительное число. Прямая, ассоциированная с множеством действительных чисел (рис. А.6), называется действительной числовой осью, или более просто — числовой осью. Каждое число, ассоциированное с точкой на действительной числовой оси, называется координатой.
Рис. А.6. Действительная числовая ось
Точка с координатой 0 называется началом координат. Стрелка на правом конце отрезка указывает положительное направление оси. Координаты всех точек по правую сторону от нуля называются положительными действительными числами, а по левую — отрицательными действительными числами. Число 0 не является ни положительным, ни отрицательным.
Основные свойства действительных чисел
Теперь рассмотрим некоторые основные свойства действительной числовой системы, руководствуясь которыми можно выполнять тождественные преобразования.
Основные свойства действительных чисел
Пусть а, b и с — произвольные элементы множества действительных чисел R.


796
Часть IV. Приложения
Свойства сложения
Ассоциативность.
а + (5 + с) = (а + Ь) + с.
Коммутативность.
а + b = b + d.
Тождественность.
Число 0 является единственным нейтральным элементом отно-
сительно операции сложения, т.е. 0 + а = а + 0 = а для любого элемента а множества R.
Обратный элемент. Для каждого элемента а множества R элемент —а является единственным обратным элементом относительно операции сложения, т.е. (—а) + а = = а + (—ft) — 0.
Свойства умножения
Ассоциативность.
(аб)с = а(6с).
Коммутативность. Тождественность.
ab = Ьа.
Число 1 является единственным нейтральным элементом отно-
сительно операции умножения, т.е. 1 • а = а • 1 = а для любого элемента а множества R,
Обратный элемент. Для любого ненулевого элемента а множества R элемент 1 /а является единственным обратным элементом относительно операции умножения, т.е. а • 1/а = 1/а • а = 1.
Свойства дистрибутивности
а(Ь + с) = ab 4- ас (а 4- Ъ)с = ас + Ьс
Не стоит пугаться названий этих свойств. Идеи, которые они представляют, довольно просты. В самом деле, эти свойства используются при выполнении арифметических вычислений повсеместно.
Свойства коммутативности относительно операций сложения и умножения достаточно привычны. Они означают, что порядок сложения или умножения двух действительных чисел не влияет на результат. Например,
7 	4-2 = 24-7 и 3-5 = 5-3.
Являются ли операции вычитания и деления коммутативными? Иначе говоря, верно ли, что а — b = b — а или а 4- b = b 4- а, где а и b — действительные числа (исключая деление на 0)? Оказывается, нет.
8-6^6-8 и 10 4-5^54-10
Почему, при вычислении суммы и произведения
3 + 24-6 и 3-2-6
нам не нужны скобки, чтобы указать, какие числа складываются или умножаются первыми? Ответ содержится в свойствах ассоциативности этих операций. Согласно этим свойствам можно записать следующие выражения.
(3 + 2) + 6 = 3 + (2 + 6) или (3 • 2) • 6 = 3 • (2 • 6)


Приложение А. Основные алгебраические понятия и законы
797
Таким образом, группировать слагаемые или множители можно как угодно. Будут ли операции вычитания и деления ассоциативными? Оказывается, нет.
(12 — 6) — 2 7^ 12 — (6 — 2) или (12 -F 6) Ч- 2 12 Ч- (6 2)
Чтобы убедиться в этом, достаточно вычислить обе части этих выражений.
В операции сложения свойства коммутативности и ассоциативности позволяют менять порядок действий, а также добавлять или исключать скобки, если это необходимо. Это утверждение верно для операции умножения, но неверно для вычитания и деления.
Какое число можно прибавить к заданному числу и получить опять заданное число? Какое число можно умножить на заданное число и получить опять заданное число? Ответы на эти вопросы: числа 0 и 1 соответственно, поэтому числа 0 и 1 называются единичными элементами. Это значит, что для произвольных действительных чисел а и Ь выполняются следующие условия.
0 + 5 = 5 и (ci + 6) + 0 = (о + 6),
1-4 = 4 и (а + Ь)-1 = (а + Ь).
Теперь рассмотрим обратные элементы. Для каждого действительного числа а существует единственное число —а такое, что а + (—а) = 0. Число —а называется аддитивной инверсией числа а. Иногда числа а и —а называют противоположными. Например, аддитивной инверсией числа 7 является число —7, поскольку 7 + (—7) = 0.
Число —а не обязательно является отрицательным. Если число а отрицательно, то число —а положительно, а если число а положительно, то число —а отрицательно.
Для каждого ненулевого действительного числа а существует единственное действительное число 1/а такое, что а • 1/а = 1. Число 1/а называется мультипликативной инверсией числа а или обратным к числу а. Например, обратным к числу 4 является число поскольку 4 • | = 1 (заметим, что число 4, в свою очередь, является обратным к числу |). У числа 0 нет обратного числа.
Перейдем к свойствам дистрибутивности, в которых фигурируют обе операции — сложение и умножение. Рассмотрим следующие два выражения.
5 - (3 + 4) = 5 • 7 = 35, 5 • 3 + 5 • 4 = 15 + 20 = 35.
Итак,
5 • (3 + 4) = 5 • 3 + 5 • 4.
Таким образом, умножение на число 5 сводится к умножению на него слагаемых суммы 3 + 4. В общем случае в системе действительных чисел умножение является дистрибутивным относительно сложения. Приведем еще два примера.
9(m + n) = 9т + 9п, (7 + 2)u = 7а + 2и.
Пример А.6 (Свойства действительных чисел). Определите, какое из свойств действительных чисел иллюстрируется указанным утверждением.


798
Часть IV. Приложения
Утверждение
Свойство
1. ar(j/ + z) = (у + z)x
2. 5(2?/) = (5 • 2)у
3. 2 + (7 + т/) = 2 + (т/ + 7)
4. 4z + 6z = (4 + 6)z
Коммутативность (•) Ассоциативность (•) Коммутативность (+) Дистрибутивно сть
5. 	Если т + п — 0, то п = —т Свойство обратного элемента (+) ■
Упражнение А.6.
Определите, какое из свойств действительных чисел иллюстрируется указанным утверждением.
1. 8 + (3 + у) = (8 + 3) + у.
2. (х + у) + z = х + (у + z).
3. (а + Ь)(я + у) = а(х + у) + Ь(х + у).
4. 5ху + 0 = 5ху.
5. Если ху = 1, х ф 0, то у = 1/ж. I
Другие свойства действительных чисел
Операции вычитания и деления можно определить с помощью операций сложения и умножения соответственно.
Вычитание и деление
Для произвольных действительных чисел а и b справедливы следующие утверждения.
Вычитание а - b = а + (-6) 7 - (—5) = 7 + [-(-5)] = 7 + 5 = 12.
1 19
Деление а 4-6 = а--, Ь 0, 94-4 = 9-- = -.
Ъ 4 4
Это значит, что при вычитании числа b из числа а к числу а необходимо прибавить число —Ь (аддитивную инверсию числа 6). При делении чисел а и b необходимо умножить число а на мультипликативную инверсию числа 6. Заметим, мультипликативной инверсии числа 0 не существует.
Делить на 0 нельзя!
Приведенные ниже свойства обратных элементов следуют из свойств и определений, указанных ранее.
Свойства обратных элементов
Для произвольных действительных чисел а и b справедливы следующие утверждения.
1. — (—а) = а.
2. (—a)b = — (ab) = a(—b) = —ab.
3. (—а)(—Ъ) = ab.
4. (—1)а = —а.


Приложение А. Основные алгебраические понятия и законы
799
Отметим также следующие важные свойства нулевого элемента.
Свойства нуля
Для произвольных действительных чисел анЬ справедливы такие утверждения.
1. а • 0 = 0 0-0 = 0, -35 -0 = 0
2. а • b = 0 тогда и только тогда, когда а = 0 или Ь = 0.
Если (3® + 2)(® — 7) = О, то 3® + 2 = О или ® — 7 = О.
Задание А.З.
Множество чисел называется замкнутым относительно некоторой операции, если действие этой операции над элементами множества дает элемент того же множества. Например, множество действительных чисел R замкнуто относительно операций сложения, умножения, вычитания и деления (исключая деление на ноль). Замените каждый знак вопроса в приведенной ниже таблице на буквы И (истинно) или Л (ложно) и проиллюстрируйте каждое утверждение примером (определения множеств N, Z9 Q, I и R приведены в таблице А.1).
о
О
©
©
X
X
я -
X
х
й X
4 X
й
2 5 з
2 5 В
2 5 Я
2
g- Ё И
Я Q й а © я
S я 8
I “ S © S я s
П Ё
1 = Е
ЬЁ я
1 8 S
Ж я ч
х н ч еп © 3
м © £
Я Г «л СО © X
« н а м е ч
9
9
9
9
Z
9
9
9
9
Q
9
9
9
9
I
9
9
9
9
R
И
И
И
И
Свойства дробей
Напомним, что частное а+ Ь (при b ф 0), записанное в виде а/b, называется дробью. Число а называется числителем, а число b — знаменателем.
Свойства дробей
Для любых действительных чисел a, b, с, du к (деление на 0 исключается) выполняется:
1. 	у = тогда и только тогда, когда ad = be
b d
4 6
— = —, поскольку 4 • 9 = 6 • 6.
6 9
2 	Исключая деление на 0.


800
Часть IV. Приложения
Ответы к упражнениям
А.6. 1) Ассоциативность (+).
2) Коммутативность (+).
3) Дистрибутивность.
4) Единичный элемент (+).
5) Обратный элемент (•).
Практикум А.2
Все переменные считаются действительными числами.
А В задачах 1-6 замените каждый из знаков вопроса выражением, которое иллюстрирует указанное свойство действительных чисел.
1. Свойство коммутативности (•): uv = ?.
2. Свойство коммутативности (+): х + 7 = ?.
3. Свойство ассоциативности (+):3 + (7 + 1/) = ?.
4. Свойство ассоциативности (•): x(yz) = ?.
5. Единичный элемент (•): l(u + v) = ?.
6. Единичный элемент (4-): 0 + 9m = 1.
В задачах 7-26 определите истинность (И) и ложность (Л) каждого из утверждений.
7. 	5(8т) = (5 • 8)т. 8. а + cb = а + Ьс.
9. 	5х -F 7х = (5 -F 7)х.
11. 	7-11 = 7+ (-11).
13. (х + 3) + 2х = 2х + (х + 3).
14. (4х + 3) + (х + 2) = 4х + [3 + С
15 2х _ 2х
-(х + 3) (х + 3)’
1’. (-3) • = 1.
19. — х2у2 = (—1)х2у2.
10. 	uv(w + х) — UVW + UVX.
12. 8 4-(—5) = 8 • (+Y
\ —О/
+ 2)].
., 2х 2х
16. =
— (х —3) х —3
18. -0,5 4- 0,5 = 0.
20. [—(х 4- 2)](—Зх) = (х 4- 2)х.


Приложение А. Основные алгебраические понятия и законы
801
а с _ а + с fc 1
b d b -J- d к 4- b 1 4- b
23. (х + 8)(х 4- 6) = (х + 8)х + (х + 8) • 6.
24. и(и — 2v) + v(u — 2v) = (u 4- v)(u — 2v).
25. Если (x - 2)(2x + 3) = 0, то или x - 2 = 0, или 2x + 3 = 0.
26. Если x - 2 = 0 или 2x 4- 3 = 0, то (x — 2)(2x + 3) = 0.
Б
* 27. Пусть uv = 1. Обязательно ли какое-либо из чисел и и v должно быть равным 1?
Объясните ответ.
* 28. Пусть uv = 0. Обязательно ли какое-либо из чисел и и v должно быть равным 0?
Объясните ответ.
* 29. Определите истинность (И) и ложность (Л) каждого из утверждений.
а) Все целые числа являются натуральными.
б) Все рациональные числа являются действительными.
в) Все натуральные числа являются действительными.
* 30. Определите истинность (И) и ложность (Л) каждого из утверждений.
а) Все натуральные числа являются целыми.
б) Все действительные числа являются иррациональными.
в) Все рациональные числа являются действительными.
31. Приведите пример действительного числа, которое не является рациональным.
32. Приведите пример рационального числа, которое не является целым.
33. Укажите, какому множеству (или множествам) N (натуральных чисел), Z (целых чисел), Q (рациональных чисел) или R (действительных чисел) принадлежат приведенные ниже элементы.
а) 8. б) у/2. в) -1,414. г)
34. Укажите, какому множеству (или множествам) АГ, Z, Q, R (см. задачу 33) принадлежат приведенные ниже элементы.
а) -3. б) 3,14. в) тг. г) |.
* 35. Определите истинность (И) и ложность (Л) каждого из приведенных ниже утвер¬
ждений. Для ошибочных утверждений приведите контрпример, заменяя а, b и с действительными числами. Для всех действительных чисел а, b и с: а) (а 4- Ь) + с = а + (6 + с). б) (а — Ь) — с = а — (Ь — с),
в) (аЬ)с = а(Ьс). г) (а 4- Ь) 4- с = а 4- (Ь 4- с).
* 36. Определите истинность (И) и ложность (Л) каждого из приведенных ниже утвер¬
ждений. Для ошибочных утверждений приведите контрпример, заменяя а и Ь действительными числами. Для всех действительных чисел а и Ь:
а) а + b = b 4- а. б) а — b = b — а.
в) ab = Ьа. г) а 4- b = b 4- а.


802
Часть IV. Приложения
В
37. Пусть с = 0,151515..тогда 100с = 15,1515 ... и
100с - с = 15,1515... - 0,151515...
99с = 15;
_ 15 _ 5 С_ 99 ~ 33'
Преобразуйте число 0,090909... в десятичную дробь этим же методом (все периодические дроби являются рациональными числами и, наоборот, каждое рациональное число является периодической дробью).
38. Повторите решение задачи 37 для числа 0,181818...
В задачах 39 и 40 с помощью калькулятора представьте каждое число в десятичном виде с той точностью, на которую он рассчитан. Обратите внимание на периодичность дроби для рационального числа и непериодичность для иррационального.
”4 “4 «-Ш-
«4 «4 45-^- *4
А.З. Операции с полиномами
■ Натуральные степени
■ Полиномы
■ Приведение подобных членов
■ Сложение и вычитание
■ Умножение
■ Комбинированные операции
В этом разделе рассматриваются основные операции с полиномами. Этот математический объект часто возникает в разных задачах. Наш обзор начинается с короткого анализа натуральных степеней. Целые и рациональные степени подробно обсуждаются в следующих разделах. (Натуральные, целые и рациональные числа являются важными частями действительной числовой системы, см. табл. А.1 и рис. А.5 в разделе А.1.)
Натуральные степени
Определение натуральной степени выглядит следующим образом.
Натуральная степень
Пусть п — натуральное число, Ь — произвольное действительное число,
Ьп = Ь *Ь ... - Ъ п множителей Ь
З5 = 3 • 3 • 3 • 3 • 3 5 множителей 3
В этом случае число п называется показателем, а число b — основой.
С помощью этого определения легко получить первое свойство степеней.


Приложение А. Основные алгебраические понятия и законы
803
Теорема А.1 (Первое свойство степеней). Для производных натуральных чисел тип и произвольного числа b справедливо следующее утверждение.
ЬтЬп = bm+n (2t4)(5t3)'= 2-5t3+^\ = lot7. В
Полиномы
Алгебраические выражения получаются с помощью констант и переменных, а также алгебраических операций сложения, вычитания, умножения, деления, вычисления степеней и извлечения корней. Полиномами называются определенные типы алгебраических выражений. Полином относительно одной переменной х получается сложением и вычитанием констант и слагаемых вида ахп9 где п — натуральное число, а а — произвольное действительное число. Полином относительно двух переменных х получается сложением и вычитанием констант и слагаемых вида ахтуп9 где тип — натуральные числа, а а — произвольное действительное число. Полиномы для трех или более переменных
определяются аналогичным образом.
Полиномы
Не полиномы
1
х — у
8
0
Зх3 — бх + 7
бх + 3
X
X2 + у2
2х2 — 7ху — 8у2
9j/3 + 4у2 - у + 4
Vx3 — 2х
2х-2 — Зх-1
2х — Зу + 2
и5 — 3u3v2 + 2uv4 — v4
Полиномы довольно часто встречаются в математике. Для удобства их классифицируют по порядку. Если каждое слагаемое в выражении полинома включает только одну переменную, возведенную в степень, то порядком слагаемого называется его степень. Если слагаемое состоит из произведения степеней различных переменных, то порядком слагаемого называется сумма степеней множителей. Порядком полинома называется порядок наибольшего ненулевого слагаемого. Любая ненулевая константа представляет собой полином нулевого порядка. Число 0 также является полиномом, но неопределенного порядка.
Пример А.7 (Порядок полинома).
1. Порядок первого слагаемого в выражении 5ж3 + \/?>х — | равен трем, порядок второго слагаемого равен единице и третьего — нулю. Итак, порядок полинома равен трем, т.е. совпадает с максимальным порядком среди всех слагаемых.
2. Порядок первого слагаемого в выражении 5u3v2 — \/7uv2 равен пяти, а порядок второго слагаемого равен трем, поэтому порядок всего полинома равен пяти. ■
Упражнение А.7.
1. Задан полином 6я5 + 7х3 — 2. Чему равен порядок первого слагаемого? Второго слагаемого? Третьего слагаемого? Всего полинома?
2. Задан полином 2u4v2 — 5tw3. Чему равен порядок первого слагаемого? Второго
слагаемого? Всего полинома? ■


804
Часть IV. Приложения
В заключение отметим еще несколько терминов из классификации полиномов. Полином, который состоит из одного слагаемого, называется одночленом, из двух слагаемых — двучленом, из трех — трехчленом.
Приведение подобных членов
Понятие коэффициента является наиболее важным в процедуре приведения подобных слагаемых. Коэффициентом слагаемого полинома называется константа, стоящая перед соответствующей степенью переменной. Если константа пропущена или указан только знак то коэффициент считается равным единице. Если указан только знак то коэффициент считается равным —1. Поэтому для полинома
5х4 — х3 — Зх2 + х — 7\ = 5х4 + (—1)х3 -I- (—3)х2 + 1х + (—7);
коэффициент при первом слагаемом равен 5, при втором слагаемом 1, при третьем —
—3, при четвертом — 1 и при пятом 7.
Ниже приведены свойства дистрибутивности, которые являются наиболее важными в процедуре приведения подобных членов.
Свойства дистрибутивности действительных чисел
1. а(Ь + с) = (b + с)а = аЬ + ас
2. а(Ь — с) = (6 — с) а = ab — ас
3. а(Ь -|- с -|-... 4“ /) — ab + ас + ... 4~ af
Два члена полинома называются подобными, если они являются одинаковыми степенями одной и той же переменной. Коэффициенты полинома могут совпадать, но это не обязательно. Поскольку постоянные члены содержат переменную в нулевой степени, все константы являются подобными членами. Если в полиноме имеется несколько подобных членов, то их можно сгруппировать в одно слагаемое, используя свойства дистрибутивности. Процедура приведения подобных членов иллюстрируется следующим примером.
Зх2?/ — 5ху2 + х2у — 2х2у =!3х2?/ + х2у — 2х2у — 5ху2 = !
=: (Зх2т/ + х2у - 2х2у) — 5ху2 =! =; (3 -|- 1 — 2)х2у - 5ху2 = ;
= 2х2у — Ъху2.
Использование свойств действительных чисел описано в приложении А.2. Весь процесс вычисления можно формализовать следующим образом.
Подобные члены полинома приводятся путем сложения их коэффициентов.
Как упростить выражение вида 4(х — 2у) — 3(2х — 7у)? Преобразуем выражение со скобками с помощью свойств дистрибутивности, а затем приведем подобные члены.
4(х — 2у) — 3(2х — 7у) = 4х — Sy — бх + 21?/ = —2х + 13?/.
Пример А.8 (Исключение скобок). Исключите скобки и упростите выражение:
Используется свойство дистрибутивности


Приложение А. Основные алгебраические понятия и законы
805
1. 	2(3х2 - 2х + 5) + (х2 + Зх - 7)! = 2(3х2 - 2х + 5) + 1(х2 + Зх - 7)! = = 6х2 — 4х + 10 + х2 + Зх — 7 =
= 7х2 — х + 3.
2. 	(х3 - 2х - 6) - (2х3 - х2 + 2х - 3) =
; = 1(х3 - 2х - 6) + (-1)(2х3 - х2 + 2х — 3) ■ = = х3 — 2х — 6 — 2х3 + х2 — 2х + 3 =
= —х3 + х2 — 4х — 3.
В этом месте будьте внимательны со знаком!
3. 	[Зх2 — (2х -|-1)] — (х2 — 1) = [Зх2 — 2х — 1] — (х2 — 1) =
= Зх2 — 2х — 1 — х2 + 1 =
= 2х2 — 2х.
В первую очередь устраняем внутренние скобки
Упражнение А.8.
Исключите скобки и упростите выражение.
1. 3(u2 — 2и2) + (и2 + 5г>2).
2. (m3 — 3m2 + т — 1) — (2т3 — т + 3).
3. (х3 — 2) — [2х3 — (Зх + 4)].
Сложение и вычитание
Сложение и вычитание полиномов можно свести к процедуре раскрытия скобок и приведения подобных членов, как показано в примере А.9.
Пример А.9 (Сложение полиномов). Сложите полиномы “по горизонтали” и “столбиком”.
х4 — Зх3 + х2, —х3 — 2х2 + Зх и Зх2 — 4х — 5.
Решение. Сложение “по горизонтали”.
(х4 — Зх3 + х2) + (—х3 — 2х2 + Зх) + (Зх2 — 4х — 5) = = х4 - Зх3 + х2 — х3 - 2х2 + Зх + Зх2 - 4х - 5 = = х4 — 4х3 + 2х2 — х — 5.
Сложение “столбиком” сводится к приведению подобных членов и суммированию их коэффициентов.
х4 — Зх3 + х2
— х3 — 2х2 + Зх
Зх2 — 4х — 5
х4 — 4х3 + 2х2 — х — 5 в
Упражнение А.9.
Сложите указанные полиномы “по горизонтали” и “столбиком”.
Зх4 — 2х3 + 4х2, х3 — 2х2 — 5х и х2 + 7х — 2. в


806
Часть IV. Приложения
Пример А.10 (Вычитание полиномов). Вычтите полином 4а:2 — За: + 5 из полинома х2 - 8 двумя способами: “по горизонтали” и “столбиком”.
(х2 — 8) - (4х2 - Зх + 5) = или х2 - 8
— х2 — 8 — 4х2 + Зх — 5 = ~ + Зх — 5 <— Здесь нужно изме-
о о . _ — Зх + Зх —13 нить знак и сложить
= -Зх2 + Зх - 13.
выражения ■
Упражнение А.10.
Вычтите полином 2х2 — 5х + 4 из полинома 5х2 — 6 двумя способами: “по горизонтали” и “столбиком”. I
Умножение
При вычислении произведения алгебраических выражений наиболее существенно используются как свойства дистрибутивности, так и остальные свойства операций с действительными числами.
Пример А.11 (Произведение полиномов).
(2а: - 3)(3а:2 - 2х + 3)1 = 2а?(3а:2 - 2х + 3) - 3(3а:2 - 2х + 3) i =
= 6а:3 — 4а:2 + 6а: — 9а:2 + 6а: — 9 =
= 6а:3 - 13а:2 + 12а: - 9.
Решение. Используя умножение “столбиком”, получаем следующий результат.
Зх2 — 2х + 3
2х — 3
бх3 — 4х2 -|- бх
— 9х2 + бх — 9
бх3 — 13х3 + 12х — 9 . н
Упражнение А.11.
Вычислите произведение полиномов
(2а: — 3)(2а?2 + За: — 2).
Чтобы вычислить произведение двух полиномов, необходимо поочередно умножить каждое слагаемое одного полинома на слагаемые другого полинома, а затем привести подобные члены.
Довольно часто встречаются произведения биномов, поэтому целесообразно придумать процедуру, с помощью которой можно записать произведение сразу, исходя из простого наблюдения. Для поиска произведения (2х — 1)(3х + 2) поступим следующим образом:
Внешнее и внутренние произведения являются подобными слагаемыми, поэтому их можно объединить в одно слагаемое
Для ускорения вычислений действия, отмеченные рамкой, производятся в уме.


Приложение А. Основные алгебраические понятия и законы
807
Некоторые произведения биномов встречаются достаточно часто, поэтому полезно знать сокращенные формулы для их вычисления. Приведенные ниже формулы легко доказать, раскрывая скобки в левых частях.
Некоторые произведения биномов
1. (а — b)(a -I- Ь) = а2 — Ь2.
2. (а + 6)2 = a2 + 2ab + b2.
3. (а — Ь)2 = а2 — 2аЬ + Ь2.
Задание А.4.
1. Опишите связь между формулой 1 и площадями прямоугольников, изображенных на рисунке.
(а — Ь)(а + Ь) = а1 — Ь2
а
а + Ь
а — Ь а
b
а b
b
2. Создайте аналогичные рисунки для геометрической интерпретации формул 2 и З.и
Пример А.12 (Некоторые произведения биномов). Вычислите произведения, выполняя расчеты в уме.
1. 	(2т-Зт/)(5т + 21/). 2. (За — 26) (За + 26).
3. (5т-З)2. 4. (m + 2n)3.
Решение.
1. (2т — + 2у)\ = Юж2 -I- 4ху — 15ху — бу2 ; =
= 10х2 — 11ху — бу2.
2. (3а-26)(3а + 26)! = (3а)2-(26)2! =
= 9а2 - 462.
3. (5т - З)2: = (5т)2 - 2 • 5т • 3 + З2 : =
= 25т2 — 30т + 9.


808
Часть IV. Приложения
4. (т + 2п)3 = (т + 2п)2(т + 2п) =
= (m2 + 4mn 4- 4n2)(m + 2n) =
= т2(т 4- 2n) 4- 4тп(т -I- 2n) 4- 4n2(m 4- 2n) =
= m3 4- 2m2n 4- 4m2n 4- 8mn2 4- 4mn2 4- 8n3 =
= m3 4- 6m2n 4- VZmn2 4- 8n3. ■
Упражнение A.12.
Вычислите произведения, выполняя расчеты в уме.
1. (4u — 3v)(2u 4-v). 2. (2ху 4- 3)(2ху - 3).
3. 	(т 4-4n)(m — 4п). 4. (2и — 3v)2.
5. (2ж - у)3. ■
Комбинированные операции
В завершение этого раздела изучим несколько примеров, в которых иллюстрируется использование всех операций, рассмотренных выше. Заметим, что при преобразовании выражений в первую очередь обычно упрощается внутренняя группа символов. Это значит, что сначала устраняются круглые скобки ( ), затем квадратные [ ], и после этого фигурные { }, если они имеются.
Умножение и деление по приоритету предшествует сложению и вычитанию, а вычисление степеней — умножению и делению.
Пример А.13 (Комбинированные операции). Проведите указанные вычисления и упростите результат:
1. Зж — {5 — 3[ж — ж(3 — ж)]} = Зж — {5 — 3[ж — Зж 4- ж2]} =
= Зж — {5 — Зж + 9ж — Зж2} =
= Зж — 5 + Зж — 9ж 4- Зж2 =
= Зж2 — Зж — 5.
2. (ж - 2у)(2ж 4- Зу) - (2ж 4- у)2 = 2ж2 - ху - бу2 - (4ж2 4- 4жт/ 4- у2) =
= 2х2 — ху — бу2 — 4х2 — 4ху — у2 =
= —2ж2 — Ьху — 7у2. в
Упражнение А.13.
Проведите указанные вычисления и упростите результат.
1. 2t - {7 - 2[t - t(4 4-1)]}. 2. (u - 3u)2 - (2u - v)(2u 4- v). B
Ответы к упражнениям
A.7. 1) 5, 3, 0, 5.
2) 	6, 4, 6.
А.8. 1) 4u2 - v2.


Приложение А. Основные алгебраические понятия и законы
809
2) —тп3 — Зт2 + 2т — 4.
3) -х3 + Зх + 2.
А.9. Зх4 - Зх3 - Зх2 + 2х - 2.
А.10. Зх2 4- 5х - 10.
А.11. 4х3 - 13x4-6.
А.12. 1) 8u2 - 2w - 3v2.
2) 4х2т/2 — 9.
3) m2 - 16n2.
4) 4?z2 — 12ш? + 9v2.
5) 8x3 — 12x2i/ 4- бхт/2 — y3.
A.13. 1) -2t2 - 4t - 7.
2) — 3u2 — 3uv 4- 10г>2.
Практикум A.3
А В задачах 1-8 речь идет о следующих полиномах:
а) 2х — 3;
б) 2х2 — х + 2;
в) х3 4- 2х2 —х + 3.
1. 	Чему равна степень полинома в?
3. 	Вычислите сумму полиномов бив.
5. Вычтите полином б из полинома в.
7. 	Умножьте полином б на полином в.
2. 	Чему равна степень полинома а?
4. 	Вычислите сумму полиномов а и б.
6. 	Вычтите полином а из полинома б.
8. 	Умножьте полином а на полином в.
В задачах 9-30 проведите указанные вычисления и упростите результат.
9. 	2(и - 1) - (Зи + 2) - 2{2и + 3).
11. 4а-2а[5-3(а + 2)].
13. (а 4- Ъ)(а — Ь).
15. 	(Зх-5)(2х + 1).
17. 	(2х — Зу)(х + 2у).
19. 	(Зт/4-2)(3у — 2).
21. 	(Зт 4- 7п)(2тп — 5п).
23. 	(4m + 3n)(4m — Зп).
25. 	(Зи 4- 4и)2.
27. 	(и — Ь)(а2 + ab И- &2).
29. 	(4а: + Зт/)2.
10. 	2(х - 1) 4- 3(2х - 3) - (4а: - 5)
12. 	2у - Зу[4 - 2(т/ - 1)].
14. (т — п)(т 4- п).
16. 	(4f-3)(t-2).
18. 	(Зх 4- 2у)(х - Зу).
20. 	(2т - 7) (2т 4-7).
22. 	(бх — 4?/)(5а: 4- Зу).
24. 	(Зх — 2у)(3х + 2у).
26. 	(4х — у)2.
28. 	(a + b)(a2 — ab + b2).
30. 	(Зх 4- 2)2.
Б В задачах 31-44 проведите указанные вычисления и упростите результат.
31. 	т — {т — [т — (т — 1)]}.
33. 	(х2 — 2ху 4- у2)(х2 4- 2ху 4- у2).
35. 	(За - Ь)(3а 4- Ь) - (2а - ЗЬ)2.
32. 	2х - 3{х 4- 2[х - (х 4- 5)] + 1}
34. 	(2х2 4- х — 2)(х2 — Зх 4- 5).
36. 	(2х - I)2 - (Зх 4- 2)(3х - 2).


810
Часть IV. Приложения
37. 	(тп — 2)2 — (т — 2)(т + 2). 38. (х — 3)(х + 3) — (х — З)2.
39. (ж - 2у)(2х + у) - (х + 2у)(2х - у).
40. (Зт + п)(т — Зп) — (m + 3n)(3m — п).
41. (u + v)3. 42. (х — у)3.
43. (х — 2у)3. 44. (2т — п)3.
45. Вычтите сумму последних двух полиномов из суммы первых двух: 2х2 — 4ху + + у2, Зху - у2, х2 - 2ху - у2, -X2 + Зху - 2у2.
46. Вычтите сумму первых двух полиномов из суммы последних двух: Зт2 — 2т+5, 4т2 — т, Зт2 — Зт — 2, т3 + т2 + 2.
В В задачах 47-50 проведите указанные вычисления и упростите результат.
47. (2х - I)3 - 2(2х - I)2 + 3(2х - 1) + 7.
48. 2(х - 2)3 - (х - 2)2 - 3(х - 2) - 4.
49. 2{(х - 3)(z2 - 2х + 1) - х[3 - х(х - 2)]}.
50. — 3x{z[a; — х(2 — ж)] — (х + 2)(х2 — 3)}.
*51. Пусть заданы два полинома с порядками тип, причем т больше п. Какой порядок будет у произведения этих полиномов?
* 52. Какой порядок будет у суммы полиномов из задачи 51?
* 53. Как изменится ответ задачи 51, если полиномы будут одного порядка?
* 54. Как изменится ответ задачи 52, если полиномы будут одного порядка?
* 55. Покажите на конкретном примере, что в общем случае (а + 6)2 а2 + Ь2. При
каких условиях, налагаемых на переменные а и 6, имеет место равенство?
* 56. Покажите на конкретном примере, что в общем случае (а — Ь)2 а2 — Ь2. При
каких условиях, налагаемых на переменные а и Ь, будет иметь место равенство?
Применение математики
Экономика и бизнес
57. Инвестиции. Представьте себе, что у вас есть 10000 долл., которые необходимо инвестировать частично под процентную ставку, равную 9%, и частично — под процентную ставку, равную 12%. Пусть х — сумма, которая инвестируется под ставку, равную 9%. Составьте алгебраическое выражение, которое описывает годовую прибыль от обеих инвестиций, и упростите результат.
58. Инвестиции. Представьте себе, что у вас есть 100 000 долл, для инвестиций. Пусть х долл. — сумма, которая составляет краткосрочные инвестиции с прибылью, равной 7%. Такая же сумма инвестируется под ставку, равную 9%. Оставшиеся средства вкладываются в облигации с высоким рейтингом, приносящие прибыль 11%. Составьте алгебраическое выражение, которое описывает годовую прибыль от этих трех инвестиций, и упростите результат.


Приложение А. Основные алгебраические понятия и законы
811
59. Общая выручка. На музыкальное шоу нужно продать четыре тысячи билетов. Пусть х билетов продаются по цене 10 долл, за каждый, втрое большее количество билетов — по цене 30 долл., а оставшиеся билеты — по цене 50 долл. Составьте алгебраическое выражение, которое описывает выручку от продажи всех билетов (считая, что все они проданы), и упростите результат.
60. Общая выручка. На концерт нужно продать шесть тысяч билетов, одну часть по цене 9 долл., а остальные — по цене 15 долл. Пусть х — количество билетов стоимостью в 9 долл. Составьте алгебраическое выражение, которое описывает валовой доход от продажи всех билетов (считая, что все они проданы), и упростите результат.
Биологические науки
61. Питание. В пищевой смеси А содержится 2% жиров, а в смеси В — 6% жиров. Необходимо приготовить 10 кг комбинированной смеси, состоящей из компонентов А и В. Пусть в нее входит х кг смеси А. Составьте алгебраическое выражение, которое описывает общее количество жиров в получаемой пищевой смеси, и упростите результат.
62. Питание. В одной унции пищевого продукта М содержится восемь единиц кальция, а в одной унции пищевого продукта N — пять единиц кальция. Из этих пищевых продуктов производится 160 унций комбинированной смеси. Пусть для этого использовано х унций продукта М. Составьте алгебраическое выражение, которое описывает общее количество кальция в такой смеси, и упростите результат.
А.4. Факторизация полиномов
■ Общие множители
■ Факторизация методом группировки
■ Факторизация полиномов второго порядка
■ Некоторые специальные формулы факторизации
■ Комбинирование методов факторизации
Говорят, что полином представлен в факторизованной форме, если он записан в виде произведения двух или более полиномов. Следующие полиномы представлены в факторизованной форме.
4ж2?/ — бху2 = 2ху(2х — Зу) х2 - х — 6 = (ж — 3)(я + 2)
2ж3 — 8х = 2х(х — 2)(х + 2)
5т2 + 20 = 5(т2 4- 4)
Если не указано обратное, наше изложение будет ограничено разложением полиномов на полиномы с целыми коэффициентами.
Полином с целыми коэффициентами называется полностью факторизованным, если каждый из множителей нельзя представить в виде произведения двух полиномов с целыми коэффициентами (за исключением произведения самого множителя и числа 1). Все полиномы, которые приведены выше, как мы убедимся позже, факторизованы полностью.


812
Часть IV. Приложения
Запись полинома в факторизованной форме является довольно сложной задачей. Однако ее успешное решение позволяет упростить многие алгебраические выражения, и, кроме того, упрощает решение некоторых видов уравнений и неравенств. В процессе разложения полиномов на множители (факторизации) ключевую роль играют свойства дистрибутивности действительных чисел.
Общие множители
В общем случае первым шагом любой процедуры факторизации является вынесение за скобки множителей, которые являются общими для всех слагаемых.
Пример А. 14 (Общие множители). Вынесите за скобки множители, общие для всех слагаемых.
1. 	Зх3?/ — бх2?/2 — Зх?/3.
2. 	3?/(2?/ + 5) + 2(2?/ + 5).
Решение.
1. Зх3?/ — бх2?/2 — Зх?/3; = (Зху)х2 — (Зху)2ху — (Зху)у2 ; =
= 3rry(rc2 - 2ху - у2).
2. Зу(2у + 5) + 2(2у + 5)Г= М2у + 5) + 2(2у + 5) i =
= (Зу + 2)(2у + 5).
Упражнение А.14.
Вынесите за скобки множители, общие для всех слагаемых.
Факторизация методом группировки
В некоторых случаях полиномы удается факторизовать, группируя слагаемые, как показано в примере А.14, 2. Далее факторизация производится аналогично. Эффективность этой процедуры демонстрируется в следующем подразделе, где рассматривается разложение полиномов второго порядка на полиномы первого порядка (если такие полиномы существуют).
Пример А.15 (Факторизация группировкой). Факторизуйте следующие полиномы методом группирования членов.
1. Зх2 — Зх — х + 1. 2. 4х2 — 2ху — вху + Зу2.
3. 	у2 + xz + ху + yz.
Решение.
1. 	Зх2 — Зх — х + 1 = (Зх2 — Зх) — (х — 1) = Сгруппируем первые два и по¬
следние два слагаемых вместе
= Зх(ж — 1) — (х — 1) = Вынесем общие множители из
= (ж - 1)(3х — 1)
каждой группы за скобки. Тогда общий множитель (а? — 1) выносится за скобки


Приложение А. Основные алгебраические понятия и законы
813
2. 4х2 — 2ху — бху + Зу2 = (4х2 — 2ху) — (Gxy — Зу2) =
= 2х(2я: — у) - Зу(2х — у) = = (2х — у)(2х — у).
3. Если сгруппировать первые два и последние два слагаемых в выражении у2 + xz + + ху + yz, то окажется, что в каждой группе нет общего множителя. Однако, если поменять местами средние два слагаемых, то процедуру можно повторить.
у2 + XZ + ху + yz = у2 + ху + XZ + yz =
= (у2 + ху) + (xz + yz) =
= у(у + х) + z(x + у) =
= у(х + у) + z(x + у) =
= (x + y)(y + z). в
Упражнение А.15.
Факторизуйте следующие полиномы методом группирования членов.
1. 	бгг2 + 2ж + Эх + 3. 2. 2и2 + 6uv — 3uv — 9v2.
3. 	ас + bd + be 4- ad. ■
Факторизация полиномов второго порядка
Теперь перейдем к задаче разложения полиномов второго порядка вида
2х2 — ох — 3 или 2х2 + Зху — 2у2
на полиномы первого порядка с целыми коэффициентами. Поскольку большое количество полиномов второго порядка таким способом факторизовать невозможно, полезно знать способ проверки существования искомых множителей с целыми коэффициентами. В описанном здесь методе факторизации для этой цели используется ас-тест. Если множители существуют, то с помощью этого теста их легко найти.
ас-тест проверки факторизуемости
Если в полиномах вида
ах2 + Ьх + с или ах2 + Ьху + су2 (А. 1)
произведение ас можно разложить на множители р и q таким образом, что сумма р и q равна коэффициенту b в среднем слагаемом, или, иначе говоря, существуют такие целые числа р и q, что
pq = ас и р + q = Ь, (А.2)
то полином можно разложить на полиномы первого порядка с целыми коэффициентами. Если не существует целых чисел р и q, удовлетворяющих уравнению (А.2), то полиномы вида (А.1) нельзя факторизовать на полиномы первого порядка с целыми коэффициентами.


814
Часть IV. Приложения
Если существуют целые числа р и q, удовлетворяющие уравнению (А.2), то процедура факторизации продолжается следующим образом. Разложим среднее слагаемое в (А.1) с помощью тождества b = р + qf тогда
ах2 + Ьт + с = ах2 + рх + qx + с, ах2 + Ьху + су2 = ах2 + рху + qxy + су2.
Далее необходимо поочередно сгруппировать первые два и последние слагаемые, как в примере А. 15. Эта процедура всегда приводит к результату, независимо от того, в каком порядке записаны средние два слагаемых.
Ниже для прояснения процедуры приведено несколько примеров. После небольшой тренировки большинство вычислений можно будет проводить мысленно, а сам процесс вычисления будет быстрым и эффективным.
Пример А.16 (Факторизация полиномов второго порядка). Разложите, если возможно, приведенные ниже полиномы второго порядка на полиномы первого порядка с целыми коэффициентами.
1. 	4т2 — 4х — 3. 2. 2х2 — Зх — 4. 3. 6т2 — 25ху + 4?/2.
Решение.
1. 4т2 — 4т — 3.
Этап 1. Проверим возможность факторизации с помощью ас-теста. Сравнивая выражение 4т2 — 4т — 3 с общей формой ат2 + Ьх + с, получаем, что а = 4, Ъ = — 4 и с — —3. Умножая коэффициенты а и с, получаем:
ас = 4 • (—3) = -12.
Ниже приведен список всех пар целых чисел, произведение которых равно —12. Они называются фактор-парами числа —12. Попробуем подобрать фактор-пару, сумма элементов которой равна b = — 4, среднему коэффициенту в выражении 4т2 — 4т — 3 (на практике этап 1 обычно делается в уме и занимает меньше времени). Заметим, что для фактор-пары 2 и —6 сумма равна —4. Поэтому согласно ас-тесту полином 4т2 — 4т — 3 можно представить в виде произведения полиномов первого порядка с целыми коэффициентами (т.е. факторизовать).
PQ
1 - (-12)
-1 • 12
2 • (—6) Все фактор-пары числа —12 = ас
-2-6
3-(-4)
—3-4
Этап 2. Разбиваем среднее слагаемое с помощью равенства b = p+q и заканчиваем факторизацию. Для этого с помощью равенства —4 = 2 + (—6) разложим


Приложение А. Основные алгебраические понятия и законы
815
средний член полинома 4х2 — 4а? — 3 и проведем группирование членов.
4х2 — 4х — 3 = 4а?2 + 2х — 6х — 3 =
= (4х2 -I- 2х) — (6х + 3) =
= 2х(2х + 1) - 3(2® + 1) =
= (2х + 1)(2х —3).
Результат легко проверяется вычислением произведения. Коэффициенты должны совпасть с коэффициентами исходного полинома.
2. 2х2 - Зх - 4
Этап 1. Проверим возможность факторизации с помощью ас-теста.
ас = 2 • (-4) = -8.
Может ли число —8 иметь фактор-пару, сумма которой равна —3? Ни для одной их перечисленных ниже фактор-пар сумма не равна —3 = 6, среднему коэффициенту в выражении 2х2 — Зх — 4. Поэтому согласно ас-тесту полином 2х2 — Зх — 4 нельзя разложить на полиномы первого порядка с целыми коэффициентами. Такой полином называется нефакторизуемым.
рд
-1-8
1 • (—8) Все фактор-пары числа —8 = ас
-2-4
2 •(-<)
3. 6х2 - 25х£/ + ^у2
Этап 1. Проверим возможность факторизации с помощью ас-теста.
ас = 6 • 4 = 24.
Перечисляя в уме все фактор-пары числа 24 и имея в виду, что их суммы должны быть равны — 25 = 6, получим, что если р = — 1 и q = — 24, то
pq = — 1 • (—24) = 24 = ас
и
р + q = -1 -к (-24) = -25 = b
Поэтому полином является факторизуемым.
Этап 2. Разбиваем среднее слагаемое с помощью равенства b = р + q и заканчиваем факторизацию, группируя члены. Иначе говоря, применим равенство —25 = — 1 + (—24) и завершим факторизацию полинома 6х2 — 25хр + 4р2


816
Часть IV. Приложения
следующим образом.
бх2 — 25xi/ + 41/2 = бх2 — ху — 24xi/ + 41/2 =
= (бх2 — ху) — (24ху — 4у2) = = х(бх — у) — 4у (бх — у) =
= (бх - у)(х - 4у),
Проверку результата проведите самостоятельно.
Упражнение АЛ6.
Разложите, если возможно, приведенные ниже полиномы второго порядка на множители с целыми коэффициентами.
1. 2x2 4- llx — 6.
2. 4x2 4-llx — 6. 3. 6x2 4- 5xi/ — 4y2. ■
Некоторые специальные формулы факторизации
Приведенные ниже формулы позволяют факторизовать некоторые часто встречающиеся полиномы. Формулы легко получить, вычисляя произведения, стоящие в правых частях.
Некоторые специальные формулы факторизации
Полный квадрат Полный квадрат Разность квадратов Разность кубов Сумма кубов
и2 4- 2uv 4- v2 = (iz 4- v)2. и2 — 2uv + v2 = (iz — v)2.
и2 — v2 = (iz — v)(u 4- v).
u3 — v3 = (u — v)(u2 + uv + v2). u3 4- v3 = (u 4- v)(u2 — uv 4- v2).
Предупреждение. Заметим, что полинома и2 + v2 нет в этом списке формул факторизации. Причина в том, что
и2 -I- v2 ф (аи + bv)(cu + dv)
ни для каких действительных коэффициентов а,Ь, си d.
Пример АЛ7 (Факторизация). Факторизуйте полностью следующие полиномы.
1. 4m2 — 12mn 4- 9п2. 2. х2 — 161/2.
3. 	z3 - 1. 4. m3 4- n3.
5. a2 -4(6 + 2)2.
Решение.
1. 4m2 — 12mn 4- 9n2 = (2m — 3n)2.
2. x2 — 16i/2; = x2 — (4t/)2 • = (x — 4y) (x 4- 4y).
3. z3 - 1 = (z - l)(z2 + z + 1).
4. m3 4- n3 = (m 4- n)(m2 — mn 4- n2).
5. a2 — 4(6 4-2)2 = [a — 2(6 4-2)] [a 4-2(6 4-2)]. ■


Приложение А. Основные алгебраические понятия и законы
817
Упражнение А. 17.
Факторизуйте полностью следующие полиномы.
5. 9(т-3)2 — 4п2.
Задание А.5.
1. Проверьте приведенные ниже формулы факторизации полинома и4 — и4.
и4 — v4 = (и — v)(u 4- v)(u2 4- v2) —
= (и — -и)(и3 + u2v -F uv2 + v3)
2. Какая закономерность прослеживается в следующих формулах.
и2 — v2 — (и — v)(u 4- v).
и3 — v3 = (и — v)(u2 + uv 4- v2).
и4 - v4 = (и — v)(u3 4- u2v 4- uv2 4- г>3).
3. 	С помощью закономерности, полученной в п. 2, запишите аналогичные выражения для и5 — -и5 и и6 — V6. ■
Комбинирование методов факторизации
В заключение этого раздела рассмотрим несколько задач факторизации полиномов, в которых необходимо использовать несколько приемов, рассмотренных выше. В общем случае при факторизации полинома сначала необходимо вынести за скобки все множители, общие для всех слагаемых (если таковые имеются). Далее используются остальные описанные выше приемы, пока полином не будет представлен в факторизованной форме.
Пример А.18 (Комбинирование методов факторизации). Факторизуйте полностью следующие полиномы.
1. Зх3 - 48х.
3. 3m4 — 24mn3.
2. 3u4 — 3u3v — 9u2v2.
4. 	Зж4 - 5z2 + 2.
Решение.
1. Зх3 - 48х = 3rr(x2 — 16) = Зж(х — 4)(ж 4- 4).
2. 3114 — 3t?v — 9u2v2 = Зи2 (и2 — uv — Зг>2).
3. 3m4 — 24mn3 = 3m(m3 — 8n3) = 3m(m — 2n)(m2 + 2mn 4- 4n2).
4. 3x4 - 5z2 + 2 = (3x2 - 2)(x2 - 1) = (3x2 - 2)(z - l)(z + 1).
Упражнение A. 18.
Факторизуйте полностью следующие полиномы.
1. 18ж3 — Зх. 2. 4m3n — 2т2п2 + 2тп3.
3. 2t4 - 16t 4. 2т/4 - 5т/2 - 12.


818
Часть IV. Приложения
Ответы к упражнениям
А.14. 1) 2ху(х2 — кху — Зу2).
2) 	(2я-7)(Зя-2).
А.15. 1) (3z + l)(2x + 3).
2) (и -I- 3v)(2u — 3v).
3) (а + b)(c + d).
А.16. 1) (2х-1)(ж4-6).
2) Факторизация невозможна.
3) (Зх + 4у)(2х-у).
А.17. 1) (х + Зу)2.
2) (Зх — 2у)(3х + 2у).
3) (2т — 1)(4т2 + 2т + 1).
4) (х + yz)(x2 - xyz + y2z2).
5) [3(m — 3) — 2n][3(m — 3) 4-2п].
A.18. 1) 2x(3x-2)(3x + 2).
2) 2mn(2m2 — mn + n2).
3) 2t(t — 2)(t2 + 2t + 4).
4) (2y2 + 3)(y — 2)(y + 2).
Практикум A.4
А В задачах 1-8 вынесите за скобки все множители, которые являются общими для всех слагаемых.
1. 	6т4 - 9т3 - Зт2.
3. 8?z3v — 6iz2v2 + 4ui’3,
5. 	7т(2т — 3) + 5(2т — 3).
7. 	а(3с + d) — 4b(3c + d).
2. 	6z4 - &r3 - 2х2.
4. 	Юге3?/ + 20з722/2 — 15xi/3
6. 	5х(х -hl) — 3(х 4-1).
8. 	2w(y — 2z) — х(у — 2z).
В задачах 9-18 факторизуйте полиномы с помощью группировки членов
9. 	2х2 - х 4- 4х — 2.
11. Зу2 -Зу + 2у-2.
13. 	2х2 + 8я — х — 4.
15. wy — wz + ху — xz.
17. ат — Ьп — Ьт 4- ап.
10. х2 — Зх 4- 2х — 6.
12. 2х2 — х 4- 6х — 3.
14. 6х2 4- 9ж — 2х — 3.
16. ас 4- ad 4- be 4- bd.
18. ab 4~ 6 4“ 2д 4- 3b.
20. 2х2 4- Зх — 3.
22. х2 — 4ху — 12у2.
Б В задачах 19-56 полностью факторизуйте полиномы. Если полином нельзя факторизовать, объясните, почему.
19. Зу2 - у - 2.
21. и2 — 2uv — 15v2.


Приложение А. Основные алгебраические понятия и законы
819
В
23. 	т2 — 6т — 3.
25. 	w2x2 — у2.
27. 9m2 — 6mn + п2.
29. у2 +16.
31. 	4z2 - 28z + 48.
33. 	2а:4 - 24а:3 + 40а:2.
35. 4а:?/2 — 12ху + 9х.
37. 	6т2 — тп — 12п2.
39. 4u3v — uv3,
41. 	2а:3 — 2а:2 + 8х.
43. г3 -t3.
45. а3 + 1.
24. 	х2 + х — 4.
26. 	25т2 — 16п2.
28. х2 4- Юху + 25?/2.
30. и2 + 81.
32. 	бх2 + 48а: 4- 72.
34. 	2у3 - 22у2 + 48^/.
36. 16а:2з/ — 8ху 4- у.
38. 	6s2 + 7st - 3t2.
40. х3у — 9ху3.
42. 	Зт3 — 6т2 4- 15т.
44. т3 4- п3.
46. с3 - 1.
47. (а: 4-2)2 -9у2.
49. 5?z2 4- 4ш? — 2v2.
51. 	6(а: — у)2 4- 23(а: — у) — 4.
53. ?/4 - Зу2 - 4.
55. 	27а2 + а5Ь3.
48. (а-Ь)2 — 4(с —d)2.
50. За:2 — 2ху — 4у2.
52. 	4(А + В)2-5(А + В)-6.
54. т4 — п4.
56. 	s4t4 — 8st.
В задачах 57-60 обсудите истинность каждого из утверждений. Если утверждение верно, объясните, почему. Если ложно, приведите контрпример.
*57. Если п — положительное целое число, превышающее 1, то полином ип — vn является факторизуемым.
* 58. Если тип — положительные целые числа, и m п, то полином ит — vn
невозможно факторизовать.
* 59. Если п — положительное целое число, превышающее 1, то полином ип 4- vn
является факторизуемым,
* 60. Если к — положительное целое число, то полином u2fc+1 4- является фак¬
торизуемым.
А.5. Операции с рациональными выражениями
■ Приведение к младшим членам
■ Умножение и деление
■ Сложение и вычитание
■ Составные дроби
Теперь мы переходим к рассмотрению дробных выражений. Дробным выражением называется частное двух алгебраических выражений (деление на нуль исключается). Если


820
Часть IV. Приложения
числитель и знаменатель являются полиномами, то в этом случае выражение называется рациональным. Приведем некоторые примеры рациональных выражений.
1 5 х + 7 х2 — 2х + 4
х3 + 2х ’ х ’ Зх3 — 5х + 1 ’ 1
В этом разделе рассматриваются основные свойства рациональных выражений, в частности умножение, деление, сложение и вычитание.
Поскольку все переменные являются действительными числами, то в большинстве рассматриваемых свойств рациональных выражений ключевую роль играют свойства действительных чисел, которые обсуждались в приложении А.2.
Если не оговаривается обратное, всегда считается, что переменные принимают такие значения, при которых деление на нуль исключено.
В качестве примера рассмотрим рациональное выражение
2х + 5
х(х + 2) (а? - 3) *
Здесь считается, что переменная х не может быть равной нулю, —2 и 3, поскольку при таких значениях знаменатель равен нулю.
Приведение к младшим членам
Основную роль в процессе приведения к младшим членам играют фундаментальные свойства дробей, которые можно для удобства представить в следующем виде.
Фундаментальные свойства дробей
Если а, b и к — действительные числа, и Ь, к / 0, то:
ка _ а 5 • 2 _ 2 х(х + 4) _ ж
kb~b' 5^7 ~ 7’ 2(« + 4) “ 2’ ж 4>
С помощью этого свойства (если читать формулу слева направо) можно сократить все общие для числителя и знаменателя множители данной дроби. Эта процедура называется приведением дроби к младшим членам. В этом случае числитель и знаменатель делится на ненулевой общий множитель.
Это свойство можно сформулировать иначе, если читать формулу справа налево — умножение числителя и знаменателя на ненулевой множитель. Эта процедура называется приведением дроби к старшим членам. Ниже мы будем использовать это свойство в обоих направлениях.
Пример А.19 (Приведение к младшим членам). Приведите к младшим членам каждое из рациональных выражений.
6ж2 + х — 1 _ (2х + 1)(3х — 1)
2х2 — х — 1 (2ж + 1)(х —1)
Зж - 1
Факторизуем одновременно числитель и знаменатель
Делим числитель и знаменатель на общий множитель (2ж + 1)
х — 1


Приложение А. Основные алгебраические понятия и законы
821
ж4 — 8я _ х(х — 2) (ж2 4- 2х + 4) _ Зя3 — 2х2 — Зх х(х — 2) (Зя + 4)
_ я2 + 2х + 4
“ Зя+ 4 ■
Упражнение А. 19.
Приведите к младшим членам каждое из рациональных выражений.
я2 — 6я + 9 я3 — 1
я2 — 9 ’ я2 — 1 ’ И
Умножение и деление
Поскольку значения переменных ограничены действительными числами, то умножение и деление рациональных выражений подчиняется тем же правилам, что и умножение и деление дробей действительных чисел, описанных в разделе А.2.
Умножение и деление
Пусть а, Ь, с и d — действительные числа. Тогда:
, а с ас . . . л 3 х Зх
1. 7 • - = —, b, d/0; = —
bdbd 5 ж+ 5 5(ж + 5)
а с ad , , п х 3 ж + 5
' b ' d~ b с’ ,С’ ’ 5 ’ ж + 5 5 ж
Задание А.6.
Опишите процесс вычисления произведения и частного двух рациональных выражений.■
Пример А.20 (Умножение и деление). Выполните указанные операции и приведите выражения к младшим членам.
1.
10я3т/ я2 — 9 _
Зя?/ + 9у 4я2 — 12я
10я3у
_ 5я2
4 v 4 я — 2
Факторизуем числители и знаменатели. Затем сокращаем числитель и знаменатель на общий множитель
2 	— я —
2 (я - 2) = 2^^2)
1
2
Ъ — а = — (а — Ь)
Часто выражение удобнее записать в ином виде
Упражнение А.20.
Выполните указанные операции и приведите выражения к младшим членам.
1.
12я2?/3 j/2 + 6т/ + 9
2ху2 -I- бху Зу3 + 9?/2
5


822
Часть IV. Приложения
Сложение и вычитание
Поскольку переменные принимают только действительные значения, применим правила сложения и вычитания действительных дробей.
Сложение и вычитание
Пусть а, b и с — действительные числа. Тогда:
1 “ + = Ь/0; - + 8 +
Ь Ъ 6 ж + 5 ж + 5 ж + 5
а с _ а — с х х + 7 _ х — (ж + 7)
b b b ’ ’ Зх2!/2 Зх2у2 Зх2у2
Таким образом, при сложении или вычитании рациональных выражений с одинаковыми знаменателями необходимо сложить или вычесть числители и записать получившийся результат в числитель результирующего выражения с тем же знаменателем. Если знаменатели не совпадают, то выражения приводятся к общему знаменателю, а затем процедура проводится, как указано выше.
Из всех возможных общих знаменателей наиболее удобен наименьший общий знаменатель (НОЗ). Обычно наименьший общий знаменатель очевиден, в других случаях его можно найти с помощью процедуры, описанной ниже.
Наименьший общий знаменатель
Наименьший общий знаменатель двух или более рациональных выражений вычисляется следующим образом.
1. Полностью факторизуем знаменатель каждого выражения (на множители с действительными коэффициентами).
2. Определяем, какие множители в знаменателе данного выражения отсутствуют в знаменателях других выражений.
3. Перемножаем общие множители с максимальными степенями.
Пример А.21 (Сложение и вычитание). Запишите выражение в виде дроби и приведите к младшим членам.
3 5 _ 11 4 5ж 3 1 1 2
10 6 45 9х 61/2 ' х — 1 х х2 — 1
Решение.
1. Для поиска наименьшего общего знаменателя разложим на множители каждый знаменатель.
10 = 2-5 1
6 	= 23 I
45 = З2 5 J
НОЗ = 2 . З2 • 5 = 90


Приложение А. Основные алгебраические понятия и законы
823
Далее, используя фундаментальные свойства дробей, сделаем каждый из знаменателей равным 90.
3 5 11 9-3 15-5 2 11
10 + 6 “ 45 “ 9 ■ 10 + 15-6 _ 2-45 '
Г”27'"75'”'22':_
■_7. 90 + 90 .. 90J ~
_ 27 + 75 - 22 _ 80 _ 8
90 _ 90 _ 9’
2. I НОЗ = 2 . З2®!/2 = 18XV2.
Gy2 = 2- Зу2 j
4 	5х „ 2у2 •4
И 1 = —
9х бу2 2у2-9х
Зх • 5х
Зх • бу2
18а?2/2
+ W
Sy2 - 15ж2 4- 18од2
1&Е7/2
3 1 1 2 _ 1 1 _ 2 _ НОЗ = х(х -1) х
* х — 1 X х2 -1 х — 1 х (я-1) (я 4-1) х(® + 1)
_ х(х + 1) — (я — 1)(я + 1) — 2х _
х(х — 1)(ж 4-1)
х2 4- х — х2 4-1 — 2х
х(х - 1)(х 4-1)
1 — X _
х(х — 1)(х 4-1)
_ —1
4-1) х(х 4-1) ’
Упражнение А.21.
Запишите выражение в виде дроби и приведите к младшим членам.
5 	_ £ £
L 28 10 + 35
3 2 1 1
* х2 — 4х 4- 4 х х — 2 *
1 _ 2х-Ы 3 4х2 Зж2 + 12ж
Задание А.7.
Ан
Чему равно выражение -*-?
Каков результат вычисления выражения 16 4- 4 4- 2 на калькуляторе?
Чем отличаются выражения 16 4- (4 4- 2) и (16 4- 4) 4- 2?
16
Как использовать черту дроби для разграничения этих двух вариантов в записи -|-?и


824
Часть IV. Приложения
Составные дроби
Дробные выражения, у которых числитель или знаменатель, или оба одновременно, являются дробями, называются составными. Часто составную дробь требуется записать в виде простой дроби, у которой и числитель и знаменатель являются полиномами. В этом процессе нет ничего принципиально нового — требуется только правильно применить понятия и методы, изложенные выше.
Пример А.22 (Упрощение составных дробей). Преобразуйте выражение в простую дробь и приведите к младшим членам.
11 _L _ JL
1 5 + h 5 х2 у2
h ' У’
X у
Решение. Выражения будем упрощать различными методами — каждый из них удобен для определенного класса задач.
1. 	Это выражение будем упрощать, преобразовывая отдельно числитель и знаменатель в простую дробь и затем вычисляя частное дробей.
5-5-h 1_
5(5 + Д) ’ h ~
-h _ -1
5(5 + h)/i “ 5(5-h/i)’
2. 	В методе, который применяется для упрощения этого выражения, используется фундаментальное свойство дробей
а
Ь
ка kb'
Ъ,к ф 0.
Умножим числитель и знаменатель на НОЗ каждой дроби, в данном случае это
+ XI/ + X2)
xy^-^xJ(j/ + х)
у2 + ху + X2
ху(у + х)
или
х2 + ху + у2
ху(х + у)


Приложение А. Основные алгебраические понятия и законы
825
Упражнение А.22.
Преобразуйте выражение в простую дробь и приведите к младшим членам.
1 1
1. 2 + fa 2
Ответы к упражнениям
Практикум А.5
А В задачах 1—18 проведите указанные операции и приведите результат к младшим
членам.
d5 _о_\
За ’ \6а2 4d3/
_ х2 х 1
3. 1 .
12 18 30
4m — 3 3 2m — 1
18m3 4m 6m2
j;2 — Q
7‘ x2-3x + (x2~x~ 12)‘
9.- — —^—.
x x — 3
3 2
x2 - 1 x2 — 2x + 1’
4 _ -1 _ JL
‘ 18 28 42’
3x + 8 2x — 1 5
4x2 x3 8x' 8.
2x2 + lx + 3
4x2 - 1
4- (x + 3).
10.
12.
2 _ 2
m m + 4
1 1
a2 - 62 + a2 + 2ab + b2 ’


826
Часть IV. Приложения
13.
х — 1
X + 1
-1.
14. тп - 3 -
тп — 1 тп — 2’
15.
3
а — 1
2
1 — а
5
х — 3
2
3 — х
2х _ х —4 х2 — 16 х2 4- 4х’
тп + 2 тп
тп2 — 2тп т2 — 4 ’
Б В задачах 19-30 проведите указанные операции и приведите результат к младшим членам. Каждую из составных дробей запишите в виде простой дроби и приведите результат к младшим членам.
, л х2 х — 1 1
19. 1 .
х2 + 2х -I-1 Зх + 3 6
20. У-
’ У2 - У - 2 у2 + 5у - 14
2 — х х2 + 4х + 4
21. • .
2х 4- х2 х2 — 4 с 4-2 с-2 с
23. 1 .
5с — 5 Зс — 3 1 — с
1+3-
25. —J.
х
X
1 _ J_
27 2(х + Д) 2х
2
у2 + 8у + 7'
22.
24.
26.
28.
30.
у X
9 — т2
тп2 + 5т + 6
тп + 2 тп — 3’
х + 7 + у + 9 ах — Ьх Ьу — ау'
х
1 1
х + h х h
15
Представим, что “решения ” задач 31-38 даны студентом
1) Являются ли решения верными? Если решение неверно, объясните, по какой причине, и укажите, как получить правильное решение.
2) Приведите правильное решение для каждого неверного решения.
х2 + 4х + 3 х2 + 4х Л х2 — Зх — 4 х2 — Зх
= х + 4. * 32. =
х х — 4
*31.
*33.
*34.
*35.
*36.
х + 3 (х + h)2 — х2 h (х + /г)3 — х3 h х2 — Зх х2 — 2х — 3
2
х — 1 х2 — 1
*32.
х
— х — 3.
= (х + I)2 — х2 = 2х + 1.
- = (х + I)3 — х3 = Зх2 + Зх + 1.
о х2 — Зх + х — 3 + X - 3 = — — = 1.
х2 — 2х — 3
х + 3 2х + 2 — х — 3 1
х2 — 1 х 4-1


Приложение А. Основные алгебраические понятия и законы
827
*37.
2х2  3
х2 — 4
х
х-2
*38. я +
х-2 х2 -Зх +2
2х2 — х2 — 2х _ х х2 — 4 х + 2 ’
х + х — 2 2
х2 — Зх + 2 х — 2 ’
В
Преобразуйте каждую из составных дробей в простую дробь и приведите результат к младшим членам.
А.6. Целочисленные степени и экспоненциальная форма записи числа
■ Целочисленные степени
■ Экспоненциальная форма записи числа
Рассмотрим основные операции над целочисленными степенями, особенности экспоненциального представления чисел и их использования.
Целочисленные степени
Сформулируем определение целочисленной степени.
Определение ап
Для целого числа п и действительного числа а справедливы следующие утверждения.
1. 	Если п — положительное целое число, то
ап = а • а
а, п множителей а.
54 = 5 • 5 • 5 ♦ 5
2. Если п = О,
а° = 1, а / 0. 12° = 1
0° не определено.
3. Если п — отрицательное целое число, то
ап — , а 0.
а~п
1
а-(-з)
1
а
з
(Если п — отрицательное целое число, то — п — положительное.) Замечание. Можно показать, что для всех действительных чисел


828
Часть IV. Приложения
Приведенные ниже свойства полезны при вычислениях с целочисленными степенями.
Теорема А.2 (Свойства степеней). Для произвольных целых чисел тп, п и действительных чисел а, Ь выполняются следующие свойства.
1. атап = ат+п;
asa~3 = а8+<-3)
= аъ
2. (ат)п = атп;
(а’2)3
= а3(-2)
= а~в
3. (ab)m = атЬт;
(аЬ)"2
= а~2Ь~2
/ а \т ат
/а\б
_ а5
4. - ) = —,
Ь ф 0;
\ Ь / Ьт
\ь)
“ ЬБ
ат
1
а-3 _
1
1
5. — = ат~п =
, а 0.
ап
fln-m ’ '
аг
а7-(—3)
= а10
Задание А.8.
Свойство 1 из теоремы А.2 можно сформулировать так.
Для вычисления произведений двух степеней с одинаковыми основами следует сложить показатели и записать результат с той же основой.
Сформулируйте остальные свойства, приведенные в теореме А.2. Что легче запомнить — формулу или ее словесную формулировку? I
Пример А.23 (Преобразование степенных форм). Преобразуйте выражения и запишите ответ в степенной форме с положительным показателем.
Упражнение А.23.
Преобразуйте выражения и запишите ответ в степенной форме с положительным показателем.
1. 	З^-Зт/3.
2. тп2тп 6.
3. (u3v 2) 2.


Приложение А. Основные алгебраические понятия и законы
829
&Е 2у 4
бх-5?/2
Пример А.24 (Преобразование в простую дробь). Запишите выражение a.Li^1 в виде простой дроби с положительными показателями.
Решение, Сначала заметим, что
1 — х ж(1 — х) я-1-! 1
Распространенная ошибка
Исходное выражение является сложной дробью и упрощается следующим образом.
1 — X
х~т — 1
1 — X
Умножаем числитель и знаменатель на х для устранения внутренних дробей
X
я(1 — х)
ж(1 - х)
— = X.
1 - X
Упражнение А.24.
Запишите выражение * в виде простой дроби с положительными показателями. ■
Экспоненциальная форма записи числа
В практических задачах часто приходится иметь дело с очень большими числами. Вот несколько примеров таких ситуаций.
“С точностью до миллиарда долларов, государственный долг в Соединенных Штатах в 1998 году был равен
5 526000000 000 долл."
“По прогнозам в 2025 году на Земле будут жить
7 896 000 000 человек. "
Часто встречаются и очень маленькие числа. Вот несколько примеров их использования.
“Интенсивность звука человеческого голоса равна
0,000000000316 ватт/кв. см."
Вообще говоря, с обычной формой записи таких чисел работать довольно неудобно. Числа из первого и последнего примера нельзя ввести в большинство калькуляторов в том виде, в котором они записаны. Однако, используя показательную функцию, определенную


830
Часть IV. Приложения
для всех целых чисел, любое конечное десятичное число можно представить в виде произведения числа от 1 до 10 и целой степени числа 10.
а -10", 1 < а < 10 а — десятичное число,
’ п — целое число.
Запись числа в такой форме называется экспоненциальным представлением. Ниже приведены некоторые примеры записи чисел в стандартном десятичном и экспоненциальном форматах.
Десятичный и экспоненциальный формат представления чисел
7 = 7 • 10°
0,5 = 5 • 10"1
67 = 6,7 • 101
0,45 = 4,5 -10-1
580 = 5,8 • 102
0,0032 = 3,2 • 10~3
43 000 = 4,3 104
0,000045 = 4,5 • 10“5
0,000000391 = 3,91 • 10-7
73400 000 = 7,34-107
Заметим, что степень числа 10 соответствует числу позиций, на которые нужно переместить десятичную запятую, чтобы получить число от 1 до 10. Степень положительна, если запятая перемещается в левую сторону, и отрицательна — если в правую. Положительные показатели соответствуют числам, превышающим или равным 10, отрицательные — положительным числам, которые меньше 1, нулевой показатель соответствует числам, которые превышают или равны 1, но меньше 10.
Пример А.25 (Экспоненциальный формат числа).
1. Каждое из чисел представьте в экспоненциальном виде.
7320 000 и 0,00000054
2. 	Каждое из чисел представьте в стандартном десятичном виде.
4,32 • 106 и 4,32 ■ 10“5
Решение.
1. 7320 000;= 7.320000 -106
! Сдвиг на шесть позиций влево •
• Положительная степень >
0,00000054:= 0,00000054 • 10’7'
• Сдвиг на семь позиций вправо •
7,32 • 106
:= 5,4 • 10“7
Отрицательная степень
2. 4,32 • 10® = 4320000
I f
Сдвиг на шесть позиций вправо
Положительная степень, равная 6
4 32
4,32 • IO"® = = = 0^0000432 Сдвиг на пять позиций влево
Отрицательная степень, равная —5


Приложение А. Основные алгебраические понятия и законы
831
Упражнение A.2S.
1. Представьте следующие числа в экспоненциальной форме.
47100; 2443000000; 1,45.
2. Представьте следующие числа в стандартной десятичной форме.
3,07 108 ; 5,98 • 10"6.
Задание А.9.
В научных и графических калькуляторах вычисления можно проводить как в экспоненциальной, так и в десятичной форме. Если результат вычислений слишком велик или слишком мал для отображения на экране, то большинство калькуляторов автоматически выводят результат в экспоненциальном виде. Прочтите инструкцию к своему калькулятору и поэкспериментируйте с некоторыми операциями над очень большими или очень маленькими числами в обоих режимах — экспоненциальном и десятичном. Например, докажите следующий результат.
216700000000 24
0,0000000000000788 ’ ■
Ответы к упражнениям
А.23.
1)
бу7.
1
2)
Л •
т4
3)
V4
U6
4)
У*-
5)
4а;3
Зу6
А.24.
X
х -
-1
А.25.
1) 4,7 •
104, 2,443 • 109, 1,45 • 10°.
2) 307000000; 0,00000598.
Практикум А.6
А В задачах 1-14 требуется упростить каждое из выражений и представить ответ в виде положительных степеней. Значения переменных таковы, что деление на нуль
исключено.
1. 2а;-9.
2. Зу“5.
з. 3
4. А.
2w-7
4я-9
5. 2аГ8а:5.
6. Зс-9с4.
w~s
7. —
т-11
8. —г
т~5


832
Часть IV. Приложения
9. 5v8v~8. 10. 7d~4d4. И. (а~3)2. 12. (64)“3.
13. 	(х62/_3)~2. 14. (а-364)-3.
В задачах 15-20 требуется представить каждое число в экспоненциальном виде.
15. 	82 300 000 000. 16. 5 380 000. 17. 0,783.
18. 	0,019. 19. 0,000034. 20. 0,000000007832.
В задачах 21-28 требуется представить каждое число в стандартной десятичной форме.
21. 	4 • 104. 22. 9 • 106. 23. 7 • 10_3. 24. 2 • 10"5.
25. 	6,171 • 107. 26. 3,044 • 103. 27. 8,08 • 10"4. 28. 1,13 • 10"2.
Б В задачах 29-38 требуется упростить каждое из выражений и представить ответ в виде положительных степеней.
10_3•104 10-17•10-5
29. (22 + 31)0. 30. (W)o. 31. io_u 1о_2. 32. 1Q_3 1Q_14-
33. 	(5х2т/-3)-2. 34. (2m-3n2)-3. 35. ^4- 36* 7ГЧ7ГТ-
v у v ’ 2•10-5 6•10“4 frr-3!/-1 9m~4n3
6а:2?/-4 ’ 12m-1n-1’
В задачах 39-42 требуется записать каждое из выражений в форме ахр + bxq или ахр + bxq + схг, где а, b и с — действительные константы, р, q и г — целые числа. Например,
2а:4 — За:2 + 1! 2а:4 Зх2 1 ! 3 1
~ ! = —« Ч ~ \ = х х Ч—х
2х3 ; 2а:3 2а:3 2а:3 ; 2 2
39.
7 а:5 — х2
4а:5
Зя4 — 4а?2 — 1
4а?3
40.
42.
5а:3 — 2
За:2
2а:3 — За:2 Ч- х
2Ж2
В задачах 43-46 требуется записать каждое выражение только через положительные показатели и как простые дроби, приведенные к младшим членам.
За?2(а: — I)2 — 2а:3(а: — 1)
• (^ТГ)4 •
45. 	2а:_2(а? — 1) — 2а:_3(а: — I)2.
5а:4(а? Ч- З)2 — 2а:5(а: + 3)
(^ЙЗ)4 ’
46. 2х(х Ч- З)-1 — х2(х Ч- 3)“2.
В задачах 47-50 представьте каждое выражение в экспоненциальном виде и упростите результат. Ответ запишите двумя способами: в экспоненциальном виде и в стандартной десятичной форме.
9 	600 000000
1600 000-0,00000025
_ 1250 000-0,00038
49 I
0,0152
60 000 - 0,000003
8* 0,0004-1500000
0,00000082-230000 ‘ 625 000-0,0082
* 51. Каким будет результат вычисления 2з2 на калькуляторе?


Приложение А. Основные алгебраические понятия и законы
833
* 52. Вернемся к задаче 51. В чем заключается разница между числами 2(3 ) и (23)2? *53. Если п = 0, свойство 1 в теореме А.2 принимает вид amaQ = am+° = ат. Как можно использовать это равенство для определения а0?
*54. Если т = —п, свойство 1 в теореме А.2 принимает вид а~пап = aQ = 1. Как можно использовать это равенство для определения а_п?
В В задачах 55-58 представьте выражения в виде простых дробей, приведенных к млад¬
шим членам.
55.
58 ху 2 -ух 2
—х~х
и + V U~r -h f_1 ’
Применение математики
Экономика и бизнес
В задачах 59 и 60 речь идет о данных, приведенных в табл. А.2.
Таблица А.2. Активы пяти крупнейших банков США
Банк
Активы, долл.
Citigroup, Нью-Йорк BankAmerica, Сан-Франциско Chase Manhattan, Нью-Йорк Bank One, Чикаго
J.P. Morgan, Нью-Йорк
667400000000
617679000000
365 875000000
261496000000
261067000000
Финансовое состояние.
а) Запишите активы банка Citigroup в экспоненциальном виде.
б) После преобразования в экспоненциальный вид найдите отношение активов банка Citigroup к активам банка Chase Manhattan. Ответ представьте как в экспоненциальном, так и в стандартном десятичном виде.
в) Повторите решение п. б, поменяв в отношении банки местами.
60. Финансовое состояние.
а) Запишите активы банка BankAmerica в экспоненциальной форме записи.
б) После преобразования в экспоненциальный вид найдите отношение активов банка BankAmerica к активам банка J.P Morgan. Ответ представьте как в экспоненциальном, так и в стандартном десятичном виде.
в) Повторите решение п. б, поменяв в отношении банки местами.
В задачах 61 и 62 речь идет о данных, приведенных в табл. А.З.
61. Государственный долг. Проведите указанные вычисления в экспоненциальном виде и представьте окончательный ответ в стандартной десятичной форме.
а) 	Чему был равен государственный долг на душу населения в 1998 году (с точностью до доллара)?


834
Часть IV. Приложения
Таблица А.З. Государственный долг США, проценты по долгу и численность населения
Год
Государственный долг, долл.
Проценты по долгу, долл.
Численность населения, чел.
1990
1998
3 233 300000000
5 526200000000
264 800000000
363 800000000
248765170
270299000
б) Чему были равны проценты по долгу на душу населения в 1998 году (с точностью до доллара)?
в) Сколько составляли проценты по долгу в 1998 году (с точностью до двух десятичных знаков)?
62. Государственный долг. Проведите указанные вычисления в экспоненциальном виде и представьте окончательный ответ в стандартной десятичной форме.
а) Чему был равен государственный долг на душу населения в 1990 году (с точностью до доллара)?
б) Чему были равны проценты по долгу на душу населения в 1990 году (с точностью до доллара)?
в) Сколько составляли проценты по долгу в 1990 году (с точностью до двух десятичных знаков)?
Биологические науки
Загрязнение воздуха. Стандарт качества воздуха определяется максимальной концентрацией загрязняющих веществ в нем. Концентрация загрязняющих веществ обычно измеряется в миллионных долях (ррт). Стандарт в 30 ррт определяется так.
30 = ’..Г =3 ■10-5=О'00003 =<,’003%-
В задачах 63 и 64 выразите данный стандарт
1) в экспоненциальном виде,
2) в стандартном десятичном формате,
3) в процентах.
63. Допустимая концентрация угарного газа в воздухе (усредненная за период 8 часов) равна 9 ррт.
64. Допустимая концентрация оксида серы в воздухе (усредненная за год) равна 0,03 ррт.
Социальные науки
65. Борьба с преступностью. В 1998 году в Соединенных Штатах доля насильственных преступлений составляла 566,4 на 100000 человек при общей численности населения 270,3 млн. чел. Сколько всего было насильственных преступлений в этом году? Представьте ответ в экспоненциальном виде, а затем преобразуйте его в стандартный десятичный вид (с точностью до тысячи).


Приложение А. Основные алгебраические понятия и законы
835
66. 	Плотность населения. Численность населения Соединенных Штатов в 1998 году составляла 270,3 млн. чел. при общей площади территории, равной 3 539 000 кв. миль. Чему равна плотность населения? Представьте ответ в экспоненциальном виде, а затем преобразуйте его в стандартный десятичный вид (с точностью до одного десятичного знака).
А.7. Дробные степени и корни
■ Корень п-й степени действительного числа
■ Рациональные степени и корни
■ Свойства корня
В этом разделе рассматривается общее понятие корня п-й степени, а также степенной функции с рациональными показателями.
Корень n-й степени действительного числа
Рассмотрим квадрат со стороной г общей площадью 36 кв. дюймов. Итак,
г2 = 36.
Следовательно, квадрат числа г равен 36. Говорят, что число г является квадратным корнем из величины Ь, если г2 = Ь. Аналогично число г является кубическим корнем из величины Ь, если г3 = Ь.
Корень п-й степени
Для произвольного натурального числа п величина г является корнем п-й степени из числа Ь, если тп = Ь.
Так, число 4 является квадратным корнем из числа 16, поскольку 42 = 16, а число -2 — кубическим корнем из числа —8, поскольку (—2)3 = —8. Однако (—4)2 = 16, поэтому —4 также можно считать квадратным корнем из числа 16. Можно показать, что у каждого положительного числа есть два квадратных корня, два корня четвертого порядка и, вообще, два корня п-й степени, если п — четное число. У отрицательных чисел нет квадратных корней, корней четвертого порядка и, вообще, корней п-й степени, если п — четное число. Причина в том, что не существует такого действительного числа, четная степень которого отрицательна. Для нечетных степеней ситуация проще. Каждое действительное число имеет только один кубический корень, один корень пятого порядка и, вообще, один корень п-й степени, если п — нечетное число.
В системе комплексных чисел корни имеют более общие свойства. Однако в данной книге мы ограничимся действительными корнями из действительных чисел. Итак, под “корнем” всегда подразумевается “действительный корень”.
Рациональные степени и корни
Рассмотрим символы, которые используются для описания корней п-й степени. Если п — натуральное число, превышающее единицу, то для обозначения корня п-й степени из действительного числа b используются следующие символы.
Ь1/п, или Vb.


836
Часть IV. Приложения
Степенная форма записи удобна тем, что (Ь1/71)71 = Ь, если считать, что свойства степенной функции распространяются и на рациональные степени. Вторая форма называется корнем n-й степени. Ниже символ у/~ называется знаком корня, число п — степенью корня, а число а — подкоренным выражением.
Степень
|—Знак корня
Подкоренное выражение
Если степень корня равна двум, она, как правило, не указывается. Поэтому квадратные корни обозначаются как y/b, а не как \/b. Для корней n-й степени используются обозначения Ъ1/п и у/b. Если существует два действительных значения корня из заданного числа, то положительное значение корня называется арифметическим значением корня п-й степени.
Пример А.26 (Вычисление корней). Вычислите каждое из значений.
1. 	41/2 и х/4.
3. 	(-4)1/2 и у<=4.
5. 	(—8)1/3 и ^8.
2. 	— 41/2 и —\/4.
4. 	81//3 и \/8.
6. 	—81/3 и -^8.
Решение.
1. 41/2 = уД = 2(^4 7 ±2).
2. —41/2 = -74 = —2.
3. (—4)1/2 и 7=4 не являются действительными числами.
4. 81/3 = 78 = 2.
5. (-8)1/3 = 7=8 - -2.
6. —81/3 - -78 = -2.
Упражнение А.26.
Вычислите каждое из значений.
1. 161/2.
2. -716.
4. (-9)1/2. 5. (781)3. ■
Распространенная ошибка
Символ л/4 представляет собой одно число 2, а не ±2. Не путайте число У4 с решениями уравнения х2 = 4, которые обычно записываются как х = ±74 = ±2.
Теперь перейдем к определению Ьг, если г = т/п — рациональное число.


Приложение А. Основные алгебраические понятия и законы
837
Рациональные степени
Пусть тип — целые числа, не имеющие общих множителей, b — действительное число, причем для четного значения п число b — положительное. Тогда справедливы следующие утверждения.
ьт/
п
82/Э = (81/3)2 = (^8)2 = 22 = 4; g2/3 = (82)1/3 = ^2 = ^4 _ 4>
b-m/n= 1 b^Q 8-2/3 = J_ = l
Ьт/п §2/3 4
Заметим, что при указанных ограничениях на числа т, п и b оба определения степени 6m/n — эквивалентны между собой.
Все свойства целых степеней, перечисленные в теореме А.2 раздела А.6, выполняются и для рациональных степеней при условии, что для четного значения п число b — положительное. Далее в тексте, если не указано обратное, переменные считаются положительными действительными числами.
Пример А.27 (Переход от рациональной степени к знаку корня и наоборот). Перейдите от степенной формы записи к знаку корня.
1. X1/7 = ^/х.
2. (3u2v3)3 или (\/3u2v3)3. первая запись предпочтительнее
Перейдите от знака корня к степенной форме записи.
4. Уб = б1/5
5. — vCr2 = —х2/3.
6. \/а:2 -Н З/2 = (х2 + t/2)1/2. Заметим, что (х2 + у2)1/2 х + у. Почему?
Упражнение А.27.
Перейдите от степенной формы записи к знаку корня.
1. 	г?/5. 2. (6я2з/5)2/9. 3. (3xt/)-3/5.
Перейдите от знака корня к степенной форме записи.
4. 	У&и. 5. -</(2^7. 6. ^/х3 + т/3. а
Пример А.28 (Вычисления с рациональными степенями). Упростите каждое из выражений и запишите результат с помощью положительных степеней. Если в ответе есть рациональные степени, выразите их с помощью знака корня.
1. Зх1/3.2тХ/2 = 6xV3+l/2 = бх5/6 = 6^5
2. (-8)5/3 = [(-8)1/3]5 = (—2)5 = -32.


838
Часть IV. Приложения
3. (2х^3у-2/3? = 8ху~2 =
У2
/4х^3\1/2 _ ^2х3/6 _ 2 2 _ 2
4‘ ~ xV4 _ д.1/4-1/6 - х1/12 - ■
Упражнение А.28.
Упростите каждое из выражений и запишите результат с помощью положительных степеней. Если в ответе есть рациональные степени, запишите их с помощью знака корня.
1. 	93/2. 2. (-27)4/3. 3. 5у1/4 ■ 2а/1/3.
/8х1/2\ Х/3
4. 5. .
Задание А.10.
Вычислите оба корня.
163/2 = /[б3 = (\/16)3.
272/3 = V272 = (>/27)2.
Какая из форм более удобна для вычисления вручную? ■
Пример А.29 (Вычисления с рациональными степенями). Вычислите произведения и запишите результат с помощью положительных степеней.
1. 	3i/2//3(2t/1/3 — у2). 2. (2iz1//2 + и1/2)^1/2 — Зг?/2).
Решение.
1. 32/2/3(2т/1/з _ ^^"’^/з+Г/з"" з^/з;?; = Qy _ Зу8/з
2. (2U1/2 + v1/2)(w1/2 — Зг;1/2) = 2и — би1/2?;1/2 — 3v. ■
Упражнение А.29.
Вычислите произведения и запишите результат с помощью положительных степеней.
1. 	2с1/4(5с3 — с3/4). 2. (7а;1/2 — ?/1/2)(2ж1/2-h З?/1/2). ■
Пример А.30 (Вычисления с рациональными степенями). Представьте выражения в виде ахР + где аиЬ — действительные, а р и q — рациональные числа.
Решение.
2у/х — Зу/т2
_ 2а;1/2 - За:2/3 _
Переход к степенной форме
Разбиение одной дроби на две
2^х
2а;1/3
2а;1/2 За;2/3
2а;1/3 2а;1/3
= а;1/6 - 1,5а:1/3.
Упражнение А.30.
Представьте выражение 5 в виде ахр + byq, где а и b — действительные, а р и q —
рациональные числа. ■


Приложение А. Основные алгебраические понятия и законы
839
Свойства корня
Рассмотрим несколько свойств корня, позволяющие упрощать выражения.
Пример А.31 (Свойства корня). Упростите выражения, используя свойства корня.
1. </(3zV)4-
Решение.
2. #8^2.
1. ^(Зя4?/3)4 = Зя4?/3
2. = ^16 = = 2
Свойство 1
Свойства 1 и 2
Свойство 3 и 1
Упражнение А.31.
Упростите выражения, используя свойства корня.
1. \/(я3 + ?/3)7. 2. {/8?/3
Задание А.11.
Вычислите произведение
Как использовать этот результат для упрощения выражений с корнями?
Возникает вопрос: в какой форме лучше всего представить выражение, содержащее корни. Этот вопрос имеет много ответов. Все зависит от того, что мы собираемся делать с полученным выражением. При выведении некоторых формул иногда удобно избавиться от корней. Этот процесс называется приведением числителя или знаменателя к рациональному виду. Данная процедура иллюстрируется примерами А.32 и А.ЗЗ.
Пример А.32 (Приведение знаменателя к рациональному виду). В каждом из выражений приведите знаменатель к рациональному виду.
6я ~ 6 х — 4
1- 2. 3. —-.
>/2ж \/7--У5 х/5 + 2
Решение.
* 6я 6я а/2я 6я\/2я п г—
1. —= = г • = —т— = 3^2я.
\Г1х у2я у2я 2я
6 _ 6 V7+ у/5 _ 6 (\/7 + л/5)
У7- \/5 “ /7-V5 ’ У7 + ^ “ 2
2.
3(х/7 + л/5).


840
Часть IV. Приложения
3 х — 4 _ х — 4 у/х + 2 у/х + 2
V^-2 (х - 4) (^/ж - 2)
_/= ~ \ = Vх ~ 2
у/х — 2 х — 4
Упражнение А.32.
В каждом из выражений приведите знаменатель к рациональному виду. 12аЬ2 9 „ х2 — у2
у/ЗаЬ \/б + х/3' у/х-у/у'
1.
2.
Пример А.ЗЗ (Приведение числителя к рациональному виду). В каждом из выражений приведите числитель к рациональному виду.
\/2 3 + у/т у/*2 4- h — \/2
2^' 9-т ’ Х h ’
Решение.
t л/2 _ у^2 _ 2 _ !
2^/3 _ 2\/3 ’ >/2 ~ 2\/б ”
З-F у/т _ 3 -I- у/т 3 — у/т _ 9 — т _ 1
9 — т 9 — m 3 — у/т (9 — тп) (3 — у/т) 3 — у/т ’
у/2 4- h — д/2 \/2 4~ h — у/2 у/2 4- h 4- \/2
h h у/24~ h 4- \/2
_ h - 1 h (\/2 + Ъ 4~ д/2) у/2 4- h 4- \/2 В
Упражнение А.ЗЗ.
В каждом из выражений приведите числитель к рациональному виду.
. \/3 2 — у/п \/3 4~ h — у/З
1. —2. — . 3. . ■
3\/2 4 - п h
Ответы к упражнениям
А.26. 1) 4.
2) —4.
3) -3.
4) Не является действительным числом.
5) 27.
А.27. 1)
2) у/(бх2?/5)2 ИЛИ (у/бх2у5)2.
3) l/{/(3xj/)3.
4) (9м)1/4.
5) — (2а:)4/7.
6) (а:3 + т/3)1/3 (не х + у).


Приложение А. Основные алгебраические понятия и законы
841
А.28. 1) 27.
2) 81.
3) 10у7/12 = 10
4) 16у/х3.
5) 2/х1/13 = 2/ tyx.
А.29. 1) 10с13/4 — 2с.
2) 	14х + 19гг1/2у1/2 - Зу.
А.30. 2,5х"7/6 - 2х-1.
А.31. 1) х3 + у3.
2) 2у.
3) 2х.
А.32. 1) 4Ъу/ЗаЬ.
2) 3(\/б- у/3).
3) (х + у) (у/х + ^/у).
А.ЗЗ. 1) -L.
2) 2 + ^-
3) 1—г-
\/3 -И h -|- \/3
Практикум А.7
А В задачах 1-6 представьте каждое из выражений в виде радикала, не упрощая ответ.
1. 	бх3/5. 2. 7J/2/5. 3. (4ху3)2/5.
4. 	(7х2у)5/7. 5. (х2 +1/2)1/2. 6. х1/2 + 3,1/2.
В задачах 7-12 представьте каждое из выражений в виде рациональной степени, не упрощая ответ.
7. 5'Ух3.
10. У(3т4п)2. 11. &х+#У- 12. ^/х2 + у3.
В задачах 13-24 вычислите значение каждого из выражений, если оно существует.
9. У(2х2у)3.
8. 7mVri7.
13. 251/2.
14. 641/3.
15. 163/2.
16. 163/4.
17. -361/2.
18. -323/5.
19. (-36)1/2.
20. (-32)3/5.
/ 4\3/2
2'- (й)
п. Г4Г
23. 9“3/2.
24. 8'2/3.


842
Часть IV. Приложения
В задачах 25-34 упростите каждое выражение и запишите результат с помощью положительных степеней, считая, что все переменные — положительные действи¬
тельные числа.
25. z4/5z-2/5.
26. у 3/7у^.
29. (8т3?/-6)1/3.
„ ™2/3
27.
т-1/3’
30. (4-а-2?;4)1/2
8т-1/3
33. —
12т1/4
В задачах 35-40упростите каждое из выражений, используя свойства корня и считая, что все переменные — положительные действительные числа.
35. {/(2 т+ 3)5. 36. </(7 + 2т/)3. 37. /18rW.
38. \/2аЗ\/32а5. 39.
40
V^y
Б В задачах 41-48 упростите каждое выражение и запишите результат с помощью положительных степеней.
41. Зх3/4 (4а;1/4 — 2т8). 42. 2т1/3 (Зт2/3 — т6).
43. (Зи1/2 - v1/2) (г?/2 _ 4^1/2). 44. (а1/2 + 2d1/2) (а1/2 - 3d1/2).
45. (5т1/2 + п1/2) (5т1/2 - п1/2). 46. (2т1/2 - Зт/1/2) (2т1/2 + Зт/1/2).
47. (Зх1^ - yi/2)2. 48. (j.i/2 + 2г/1/2)2.
Представьте выражения, приведенные в задачах 49-54, в виде ахр + byq, где a ub — действительные, р и q — рациональные числа.
Ух* + 2
2^ ’
З^/т2 + у/х
5т
12у^-3
4^/т
2\/тЗ + {/т
Зт
Т2 — 4у/х
2^с *
В задачах 55-60 приведите знаменатели к рациональному виду.
55.
58.
12mn2
3
\/т + 4
5б.
\/7т
59 Пх-у)2 ’ Ух~Уу'
57.
2
Ух — 2
За — 3d
I. F.
\/а + у d
В задачах 61-66 приведите числители к рациональному виду.
64.
д/2(а -j- 7i) — л/2а
Vi ~ Ух
h
t — X
Ух -I- h — у/х h
Ух- Уу
Ух + уу'


Приложение А. Основные алгебраические понятия и законы
843
В задачах 67-70 перечислены некоторые распространенные ошибки при вычислениях с рациональными степенями. В каждом из случаев приведите числовой пример, который показывает, что левая часть выражения не всегда равна правой.
67. 	(х -I- з/)1/2 ж1/2 + т/1/2. 68. (ж3 4- т/3)1/3 х 4- у.
В В задачах 71-78 обсудите истинность каждого из утверждений. Если утверждение верно, объясните, почему. Если же утверждение ложно, приведите контрпример.
* 71. Если г < 0, то у числа г нет кубических корней.
* 72. Если г < 0, то у числа г нет квадратных корней.
* 73. Если г > 0, то у числа г есть два квадратных корня.
* 74. Если г > 0, то у числа г есть три кубических корня.
* 75. Корни четвертого порядка числа 100 равны -/16 и —/16.
* 76. Квадратными корнями числа 2/6 — 5 являются числа Уз - л/2 и У2 - Уз.
* 77. \/355 - 60У35 = 5/7 - б/5.
*78. /7 - 5/2 = 1 - /2.
Упростите выражения, приведенные в задачах 79-84, записывая их как простые или отдельные дроби с положительными степенями, приведенные к младшим членам.
79. -|(х - 2)(х + З)-3/2 + (х + 3)_1/2.
80. 2(х-2)-1/2 - i(2x + 3)(x-2)"3/2.
gl /-1)1/2-Д-|'(д~1)~1/2
о, (2х - 1)V2 - (х + 2) • | • (2х - 1)-V2.2
81 2x^-1 •
(х + 2)2/3 — х • |.(х + 2)-1/з
(х + 2)4/3
2(3х - I)1/3 - (2х + 1) • | • (3® - 1)_2/3 • 3
84‘ (Зх - I)2/3 '
Вычислите значения выражений в задачах 85-90 с помощью калькулятора.
85. 223/2. 86. 155/4. 87. 827-3/8.
88. 	ЮЗ-3/4. 89. 37,097/3. 90. 2,8768/5.
Вычислите значения выражений, приведенных в задачах 91 и 92, на калькуляторе и определите, какие пары выражений имеют одинаковые значения. Проверьте эти результаты алгебраически.
91. а) /3 + /5.
в) 1 + /3.
д) /8 + /60.
б) /2 + /3 + /2 - /3.
г) /10 + б/З.
е) /б.


844
Часть IV. Приложения
92. а) 2\/2 + \/5. б) ч/8.
в) \/3 + \/7. г) \/3 + \/8 + \/з - ^8.
д) х/10 + л/84. е) 1 + х/5-
А.8. Линейные уравнения и неравенства одной переменной
■ Линейные уравнения
■ Линейные неравенства
■ Решение практических задач
В уравнение
3 	- 2(х + 3) = - 5
и неравенство
| + 2(3я - 1) > 5
неизвестная величина входит только в первой степени. В общем случае уравнением первого порядка, или линейным уравнением относительно одной переменной, называется любое уравнение, представленное в следующем виде.
Стандартная форма ах + b = 0, а / О (А.З)
Если символ равенства = в формуле (А.З) заменить на символы <, >, ^ или то получившееся в результате выражение называется неравенством первого порядка, или линейным неравенством.
Решением уравнения (или неравенства) относительно одной переменной называется число, при подстановке которого вместо переменной уравнение (или неравенство) становится верным. Множество, состоящее из всех решений, называется множеством решений. Когда говорят о процессе решения уравнения (или неравенства) подразумевают процедуру поиска множества решений.
Начнем с повторения понятия эквивалентных равенств и эквивалентных неравенств. Если уравнение (или неравенство) с помощью некоторой процедуры преобразуется в другое уравнение (или неравенство) с таким же множеством решений, то такие уравнения (или неравенства) называются эквивалентными. Основная идея решения уравнений (или неравенств) состоит в преобразовании исходного уравнения (или неравенства) в более простые эквивалентные формы. Этот процесс продолжается до тех пор, пока не получится уравнение (или неравенство) с очевидным решением.
Линейные уравнения
Процедура решения линейных уравнений опирается на следующие свойства равенства.


Приложение А. Основные алгебраические понятия и законы
845
Свойства равенства
Эквивалентное уравнение получается в результате следующих операций.
1. Если к каждой стороне исходного уравнения добавляется (или вычитается) одна и та же величина.
2. Если каждая часть исходного уравнения умножается (или делится) на одну и ту же ненулевую величину.
Рассмотрим несколько примеров, чтобы напомнить процедуру решения линейных уравнений.
Пример А.34 (Решение линейных уравнений.). Найдите решение уравнения и проверьте ответ.
8х - 3(т - 4) = 3(я - 4) + 6.
Решение.
8х — 3(х — 4) = 3(я — 4) + 6,
&г — Зх + 12 = Зх — 12 + 6,
5т + 12 = Зя — 6,
2я = -18,
х = —9.
Проверка.
8я — 3(я — 4) = 3(я — 4) -И 6,
8 	• (-9) - 3[(—9) - 4] X 3[(-9) - 4] + 6,
-72-3- (-13) = 3- (-13) + 6,
-33 = -33. ■
Упражнение А.34.
Найдите решение уравнения и проверьте ответ.
Зх - 2(2я - 5) = 2(я + 3) - 8.
Задание А.12.
Согласно свойству равенства 2 умножение обеих частей уравнения на одну и ту же ненулевую величину приводит к эквивалентному уравнению. На какое наименьшее положительное число следует умножить обе части приведенного ниже уравнения, чтобы получить уравнение, не содержащее дробей?
х +1 х 1
~3 4 = 2 ■


846
Часть IV. Приложения
Пример А.35 (Решение линейных уравнений). Найдите решение уравнения и проверьте ответ.
х + 2 х
2 	з 5
Решение. Какие действия следует выполнить над уравнением
х + 2 х
~‘з = 5’
чтобы избавиться от знаменателей? От знаменателей можно избавиться, умножив обе части равенства на одно и то же число, кратное обоим знаменателям. Для всех дробей НОЗ (наименьший общий знаменатель) равен 6. Это как раз то число, которое нам нужно! Разумеется, для умножения подойдет любой общий знаменатель, однако с помощью НОЗ получается наиболее простое уравнение. Таким образом, умножая обе части уравнения на число 6, получим следующий результат.
3(i + 2) — 2х == 30^
Зх + б — 2х = 30,
х = 24.
Проверка.
х + 2 х
2 3 “ ’
24 + 2 24 2 с
Т “5’
13-8 = 5,
Упражнение А.35.
Найдите решение уравнения и проверьте ответ.
х +1 х 1
4 	= 2 ■
Во многих практических задачах формулы или уравнения требуется преобразовывать в эквивалентные формы. В этом отношении следующие примеры довольно типичны.
Пример А.36 (Преобразование формулы с одной переменной). Используя формулу вычисления суммы простых процентов А = Р + Prt, выразите следующие величины.


Приложение А. Основные алгебраические понятия и законы
847
1. Переменную г через остальные переменные.
2. Переменную Р через остальные переменные.
Решение.
1.
P(l + rt) = А,
Поменяем части уравнения местами
Выносим переменную г в правую часть Разделим обе части уравнения на Pt
Поменяем части уравнения местами
Вынесем за скобки переменную Р (используя свойство дистрибутивности)
Разделим обе части уравнения на (1 + rt)
Р =
А
1 + rt*
Упражнение А.36.
Используя формулу М = Nt + Nr, выразите следующие величины.
1. Переменная t.
2. Переменная N.
Линейные неравенства
Прежде чем перейти к решению линейных неравенств, напомним, какое значение имеют символы < (меньше) и > (больше). Если а и b — действительные числа и существует положительное число р такое, что а + р = Ь, то
а < b Число а меньше числа Ь
Естественно, если к действительному числу добавить положительную величину, то сумма будет больше исходного числа. Это как раз то, что утверждается в определении. Если а < Ь, то можно также записать
b > а Число Ь больше числа а
Пример А.37 (Неравенства).
1. 3 < 5,
Поскольку 3-|-2 = 5.
2. -6 < —2,
Поскольку —6 + 4 = —2.
3. О > -10,
Поскольку —10 < 0.
Упражнение А.37.
Замените знаки вопроса на символы < или >.
1. 	2 ? 8. 2. -20 ? 0. 3. -3 ? - 30. а
Символы неравенства имеют однозначную геометрическую интерпретацию на действительной числовой оси. Если а < Ь, то число а расположено на оси левее числа Ь. Если с > d, то число с расположено на числовой оси правее значения d (рис. А.7). Проверьте эту геометрическую интерпретацию для случая неравенств из примера А.37.


848
Часть IV. Приложения
Рис. А.7. а < b и с > d
Задание А.13.
Замените знаки вопроса на символы < или >.
1. -1 ? Зи 2 - (-1) ? 2 - 3.
2. -1 ? 3 и —2 • (-1) ? - 2-3.
3. 12 ? -8иу? у.
4.12?.8ик4
На основе этих примеров опишите, как изменится неравенство, если обе его части умножить на число. ■
Перейдем к решению линейных неравенств с одной переменной. Напомним, что под решением неравенства понимается такое число, подстановка которого в качестве значения переменной дает верное неравенство. Множество всех таких решений называется множеством решений. Говоря о процессе решения неравенства, мы подразумеваем поиск его множества решений. Процедура решения линейных неравенств с одной переменной во многом напоминает процедуру решения линейных уравнений с одной переменной, но существует одно важное различие, указанное ниже.
Свойства неравенств
Следующие операции приводят к эквивалентному неравенству.
1. Добавление к обеим частям или вычитание из обеих частей одного и того же числа.
2. Умножение или деление обеих частей исходного неравенства на положительное число.
Следующая операция приводит к неравенству, противоположному по отношению к исходному.
3. Умножение или деление обеих частей исходного неравенства на отрицательное число.
Замечание. Умножение и деление на нуль запрещены.
Таким образом, с неравенствами можно проводить те же операции, что и с уравнениями. Однако при этом необходимо учитывать, что смысл неравенства меняется, если обе его части умножаются на отрицательное число. В противном случае смысл неравенства не меняется. Например, рассмотрим истинное утверждение
-3 > -7.
Умножая обе части на число 2, получим следующее неравенство.
—2 > -14.


Приложение А. Основные алгебраические понятия и законы
849
Смысл неравенства остался прежним. Если умножить обе части неравенства — 3 > — 7 на число —2, то левая часть станет равной числу 6, а правая будет равна числу 14. Следовательно, чтобы неравенство осталось истинным, его знак необходимо поменять на противоположный.
6 	< 14
Если а < Ь, то двойное неравенство а < х < b означает, что х > а и х < Ь, т.е. значение х находится между значениями а и Ь. Остальные варианты и удобные обозначения с помощью интервалов приведены в табл. А.4. Отметим, что конечная точка области обозначается квадратной скобкой, если она входит в неравенство, и круглой скобкой, если не входит.
В связи с данными, приведенными в табл. А.4, полезна следующая терминология: если а < Ь, то интервал [а, Ь], который включает обе точки, называется замкнутым интервалом, интервал (а, Ь), который не включает ни одну из точек, называется открытым интервалом, а интервалы вида (а, Ь] и [а, Ь) называются полуоткрытым и полузакрытым интервалами соответственно.
Таблица А.4. Форматы представления неравенств
Интервал
Неравенство
Изображение на числовой прямой
[а, 6]
а х < b
[а, 6)
а С х < b
(а, 6]
а < х <6
(а,Ь)
а < х < b
(—оо, а]
х а
(—оо, а)
х < а
[6, оо)3
х b
(*>, оо)
х > b
3Символ оо (читается “бесконечность”) не является числом. Запись [Ь, оо) используется, чтобы охарактеризовать интервал, который начинается в точке Ъ и продолжается бесконечно в правую сторону. Запись [Ь, оо] не имеет смысла, поэтому ее никогда не употребляют.


850
Часть IV. Приложения
Пример А.38 (Запись и графическое представления интервалов в неравенствах).
1. Запишите [—2,3) как двойное неравенство и представьте на графике.
2. Запишите х > — 5 как интервал и представьте на графике.
Решение,
1. Запись [—2,3) эквивалентна — 2 < х < 3.
2. 	Запись х —5 эквивалентна [—5, сю).
Упражнение А.38.
1. Запишите (—7,4] как двойное неравенство и представьте на графике.
2. Запишите х < 3 как интервал и представьте на графике. ■
Задание А.14.
В решении примера А.37 показан график неравенства х — 5. Какой вид имеет график неравенства х < —5? Как выглядит соответствующий интервал? Опишите отношение между этими множествами. в
Пример А.39 (Решение линейного неравенства). Решите линейное неравенство и изобразите область его решений.
2(2х + 3) < 6(х — 2) + 10.
Решение,
2(2х + 3) < 6(х - 2) + 10,
4х + 6 < бх — 12 + 10,
4х + 6 < бх — 12 + 10,
4х + б < бх — 2,
—2х + 6 < —2,
—2х < —8,
х > 4, или (4, оо).
Заметим, что смысл неравенства изменился
после умножения обеих частей на —2
Обратите внимание на то, что при изображении множества решений неравенства х > 4 мы использовали круглую скобку в точке 4, поскольку точка 4 не входит в интервал. ■


Приложение А. Основные алгебраические понятия и законы
851
Упражнение А.39.
Решите линейное неравенство и изобразите область его решений.
3(ж — 1) 5(ж + 2) - 5. а
Пример А.40 (Решение двойного неравенства). Решите неравенство и изобразите область его решений.
-3 < 2х + 3 9.
Решение. Речь идет о таких значениях переменной х, для которых число 2ж+3 находится между —3 и 9. Поступаем так же, как и выше, только теперь переменную х оставим посередине.
-3 < 2х + 3 9,
; - 3 - 3 < 2ж + 3 - 3 9 - 3, ;
—6 < 2х < 6,
—3 < х 3, или (—3,3].
Упражнение А.40.
Решите неравенство и изобразите область его решений.
—8 Зж — 5 7. а
Заметим, что обычно линейное уравнение имеет только одно решение, тогда как линейное неравенство — бесконечно много решений.
Решение практических задач
Для полной реализации алгебраического потенциала необходимо уметь переводить практические задачи на математический язык. Иными словами, нужно уметь представлять словесные задачи в математической форме.
Первый пример относится к важной концепции анализа безубыточности. Любое производственное предприятие несет затраты С и получает доходы R. Компания является убыточной, если R < С, безубыточной, если R = С, и прибыльной, если R> С. Затраты включают постоянные затраты, например, накладные расходы, расходы на проектирование и сборку, и переменные издержки, которые определяются объемом произведенной продукции и ценой.
Пример А.41 (Анализ безубыточности). Студия звукозаписи производит компакт-диски. Постоянные затраты для определенного типа дисков составляют


852
Часть IV. Приложения
24000 долл., включая затраты на запись мастер-копии, дизайн и организацию производства. Переменные издержки составляют 6,20 долл, на диск и включают затраты на изготовление, распространение и авторский гонорар с каждого диска, произведенного и проданного через розничную торговую сеть. Предполагается, что розничная цена диска равна 8,70 долл. Сколько дисков нужно произвести и продать, чтобы достичь уровня безубыточности?
Решение. Пусть
х — количество произведенных и проданных дисков,
С — затраты на производство х дисков,
R — доход от продажи х дисков.
Компания будет безубыточной, если R = С, причем
С = постоянные затраты + переменные издержки =
= 24000 долл. + 6,202 долл.
R = 8,702 долл.
Вычислим такое значение переменной х, для которого R — С, т.е.
8,72 = 24000 + 6,22
2,52 = 24 000
х = 9600 компакт-дисков
Для х = 9600 получаем следующий результат.
£ = 24000 + 6,22= R
= 24000 + 6,2-9600 = = 83 520 долл.
R = 8,702 =
= 8,70 • 9600 = = 83 520 долл.
Упражнение А.41.
Найдите точку безубыточности в примере А.41, если постоянные затраты составляют 18 000 долл., переменные издержки — 5,20 долл, за диск, а цена продажи диска в розничной торговой сети — 7,60 долл. ■
Область применения алгебры настолько широка и разнообразна, что невозможно выработать единый, универсальный метод решения любых задач. Однако на начальном этапе решения задачи полезно следовать таким рекомендациям.
Советы по решению задач, выраженных в словесной форме
1. Внимательно прочитайте условие задачи.
2. Запишите наиболее важные факты и отношения.
3. Определите неизвестные величины и обозначьте их разными символами.
4. Запишите уравнение (или неравенство) относительно неизвестных величин и данных задачи.
5. Решите уравнение (или неравенство).
6. Запишите все решения, которые требуются в исходной задаче.
7. Проверьте решения исходной задачи.


Приложение А. Основные алгебраические понятия и законы
853
Пример А.42 (Индекс потребительских цен). Индекс потребительских цен (Consumer Price Index — CPI) является мерой среднего изменения цен за указанный период по отношению к базовому периоду, индекс CPI которого принимается равным 100. Индекс учитывает цены на основные товары потребления и услуги и регулярно публикуется Бюро статистики труда. В табл. А.5 приведены значения индекса CPI за некоторые годы в период с 1960 по 1998 годы. Каким должен быть чистый годовой доход в 1998 году, чтобы обеспечить такую же покупательскую способность, как годовой доход 13 000 долл, в 1960 году? Ответ укажите с точностью до доллара.
Таблица А.5. Индекс CPI
(1982 - 1984 = 100)
Год
CPI
1960
29,6
1970
38,8
1980
82,4
1990
130,7
1998
163,0
Решение. Чтобы заработная плата в 1998 году обеспечивала такую же покупательную способность, как и в 1960 году, отношение годовых сумм должно быть равным отношению соответствующих индексов CPI. Пусть х обозначает годовой доход в 1998 году, тогда нужно решить уравнение
х 163,0
13 000 = 29,6 ’
163,0
х = 13 000 • = 71588 долл, в год. ■
29,6
Упражнение А.42.
Чему должен быть равен чистый годовой доход в 1970 году, чтобы обеспечить такую же покупательную способность, как годовой доход, равный 75 000 долл, в 1998 году? Ответ укажите с точностью до доллара. ■
Ответы к упражнениям
А.34. х — 4.
А.35. х — 2.
А.36. 1)
2)
А.37. 1)
2)
3)
t = -
N
N =
М
t + r
<.
<.
>.


854
Часть IV. Приложения
А.38. 1) - 7 < х sj 4.
2) (-оо,3).
А.39. х — 4 или [—4, оо).
АЛО. -1 х < 4, или [-1,4).
А.41. 7500 дисков.
А.42. 17853 долл.
Практикум А.8
А Решите задачи 1-6.
2. Зт/ — 4 = бу — 19.
4. х - 3 > —2.
1. 	2m + 9 = 5m — 6.
3. 	x + 5 < —4.
5. 	—Зж > -12. 6. —4ж 8.
Решите задачи 7-10 и изобразите область их решений.
8. 	—2ж -|-8 < 4.
10. — 3 < у — 5 < 8.
7. -4ж - 7 > 5.
9. 2 ж + 3 5.
Решите задачи 11-26. т/ 1
!1' 7 _ * 1 = 7
13. | > —2. 15.?=4-|.
3 6
Б
17. 10ж + 25(ж — 3) = 275.
19. 3 - у 4(т/ - 3).
X X 6
21. ~ ~ — ~.
5 6 5
т 3
23. —— 3 < - — т.
5 5
25. 0,1(ж-7) + 0,05ж = 0,8.
18. -3(4 - х) = 5 - (х + 1). 20. х-2 2(ж — 5).
_ 1
“ 2
т/
3 '
У
3
24-“-5>i+2-
26. 0,4(u + 5) - 0,3u = IT.
22 У-
4


Приложение А. Основные алгебраические понятия и законы
855
Решите задачи 27-30 и постройте графики.
27. 2 Зх - 7 < 14. 28. -4 < Ьх + 6 < 21.
29.-4^?С + 32^ 68. 30.-1 ^ + 5 И.
5 3
В Решите задачи 31-38 относительно указанной переменной. 2
31. Зх — 4у = 12 относительно у. 32. у = —~х + 8 относительно х.
и
33. Ах + By = С относительно у (считая, что В 0).
9
35. F = -С + 32 относительно С.
5
34. у — тх + Ь относительно т.
5
36. С = - (F — 32) относительно F.
38. U = ЗС — 2CD относительно С.
Решите задачи 39 и 40 и постройте графики.
39. -3 4 - 7х < 18. 40. -1 < 9 - 2и 5.
* 41. Что можно сказать о знаках величин а и Ь в каждом случае? б) ab < 0.
а
г> ь<0-
* 42. Что можно сказать о знаках величин а, b и с в каждом случае?
a) abc > 0. б)
37. А — Вт — Вп относительно В.
a) ab > 0.
в) ?>0.
ab
— < 0.
с
а2
Vc<0-
Если с — d = — 1, то с ? d.
в) > 0. г)
*43. Замените знаки вопроса знаком < или >.
а) 	Если а — b = 2, то а ? Ь. б)
* 44. Для каких величин end выполняется неравенство c + d < с — dl
*45. Пусть а и Ь — положительные числа и b/а больше единицы. Тогда разность а — b — положительна или отрицательна?
*46. Пусть а и b — отрицательные числа и b/а больше единицы. Тогда разность а - Ь — положительна или отрицательна?
В задачах 47-52 обсудите истинность каждого из утверждений. Если утверждение верно, объясните, почему. Если нет, то приведите контрпример.
*47. Если пересечение двух открытых интервалов — не пусто, то это пересечение является открытым интервалом.
* 48. Если пересечение двух замкнутых интервалов — не пусто, то это пересечение
является замкнутым интервалом.
* 49. Объединение любых двух открытых интервалов — открытый интервал.
* 50. Объединение любых двух замкнутых интервалов — замкнутый интервал.
*51. Если пересечение двух открытых интервалов — не пусто, то их объединение является открытым интервалом.


856
Часть IV. Приложения
* 52. Если пересечение двух замкнутых интервалов — не пусто, то их объединение является замкнутым интервалом.
Применение математики
Экономика и бизнес
53. Загадка. Выручка от продажи 8000 билетов на джазовый концерт составила 165 000 долл. Пусть билеты продавались по ценам 15 долл, и 25 долл. Сколько билетов каждого типа было продано?
54. Загадка. Паркомат рассчитан на монеты в 10 и 25 центов. Пусть в нем имеется 100 монет на общую сумму 14,50 долл. Сколько монет каждого типа находится в паркомате?
55. Инвестирование. Инвестиции составляют 12 000 долл., причем часть суммы инвестируется под 10%, а вторая часть — 15%. Сколько нужно вложить под каждую процентную ставку для получения 12% прибыли со всей суммы?
56. Инвестирование. Сумма инвестиций составляет 20 000 долл., причем часть суммы инвестируется под 8%, а вторая часть — 12%. Сколько нужно вложить под каждую процентную ставку для получения 11% прибыли со всей суммы?
57. Инфляция. Пусть цена автомобиля изменяется одновременно с индексом CPI (табл. А.5 из примера А.42). Какова будет цена автомобиля в 1998 году (с точностью до доллара), если в 1970 году аналогичная модель стоила 5000 долл.?
58. Инфляция. Пусть изменение цен на дом происходит наряду с изменением индекса CPI (табл. А.5 из примера А.42). Какова была цена на дом в 1960 году (с точностью до доллара), если в 1998 году он стоил 200000 долл.?
59. Анализ безубыточности. Постоянные затраты (накладные расходы, авансовые выплаты, редактирование, допечатная подготовка и т.п.) на издание нового популярного романа составляют 55 000 долл., а переменные издержки (затраты на бумагу, печать, логистику и т.п.) — 1,60 долл, за экземпляр. Пусть книга отпускается дистрибьюторам по цене 11 долл. Найдите точку безубыточности для издательства.
60. Анализ безубыточности. Издательство выпускает новую книгу, постоянные затраты на которую составляют 92 000 долл., а переменные издержки — 2,10 долл, за экземпляр. Пусть книга отпускается дистрибьюторам по цене 15 долл. Какой тираж нужно продать, чтобы издание было безубыточным?
61. Анализ безубыточности. Издателю из задачи 59 стало известно, что из-за повышения цен на бумагу переменные издержки на издание романа выросли до 2,10 долл, за экземпляр.
*а) Продумайте возможные стратегии для компании, чтобы справиться с возросшими затратами.
б) 	Предположим, что издательство продолжает продавать книги по цене 11 долл. Какой в этом случае тираж нужно продать, чтобы издание было прибыльным?


Приложение А. Основные алгебраические понятия и законы
857
в) 	Предположим, издательство не намерено увеличивать тираж романа. По какой цене нужно отпускать издание при новых условиях, чтобы оно оставалось прибыльным?
62. Анализ безубыточности. Издателю из задачи 60 стало известно, что из-за повышения цен на бумагу переменные издержки на издание романа выросли до 2,70 долл, за книгу.
*а) Придумайте возможные стратегии для компании, чтобы справиться с возросшими расходами.
б) Пусть компания продолжает продавать книги по цене 15 долл. Какой в этом случае тираж нужно продать, чтобы издание было прибыльным?
в) Предположим, издательство не намерено увеличивать тираж романа. По какой цене нужно отпускать издание при новых условиях, чтобы оно оставалось прибыльным?
Биологические науки
63. Исследование дикой природы. Сотрудник общества рыболовов и охотников оценил общее количество особей радужной форели в типичном озере по общепринятому методу ловли и маркирования рыбы. Он выловил сетью, маркировал, а затем отпустил 200 особей радужной форели. Спустя неделю (этого времени достаточно, чтобы маркированные рыбы смешались с остальными) он опять выловил 200 рыб, среди которых оказалось восемь уже маркированных. Оцените общее количество рыб в озере, допуская, что отношение количества маркированных рыб в озере к общему числу рыб такое же, как и во втором улове.
64. Экология. За сутки температура на антарктической станции меняется в интервале от —49°F до 14°F (то есть —49 < F < 14). Каким будет интервал температур в градусах Цельсия? (Примечание: F = |С + 32.)
Социальные науки
65. Психология. Коэффициент умственного развития IQ определяется как результат деления ментального возраста МА, вычисляемого в ходе тестирования, и календарного (фактического) возраста СА, умноженного на 100. Например, если у ребенка ментальный возраст равен 12 лет, а фактический — 8 лет, то коэффициент IQ, вычисленный таким образом, равен 150. Пусть у 9-летней девочки IQ равен 140. Вычислите ее ментальный возраст.
66. Антропология. При изучении генетических групп в антропологии используется показатель, называемый черепным индексом. Он указывает отношение ширины головы к ее длине (при измерении сверху), выраженное в процентах. Он рассчитывается следующим образом.
„ _ ЮОТУ
Здесь С — черепной индекс, W — ширина головы, L — длина головы. У племени индейцев в Баха, Нижняя Калифорния в среднем черепной индекс равен 66, а ширина головы в среднем — 6,6 дюйма. Чему равна в этом случае средняя длина головы индейцев?


858
Часть IV. Приложения
Рис. А.8. Иллюстрация к задаче 66
А.9. Квадратные уравнения
■ Решение методом вычисления квадратного корня
■ Решение методом факторизации
■ Формула корней квадратного уравнения
■ Формула корней квадратного уравнения и метод факторизации
■ Практическая задача: предложение и спрос
Квадратным уравнением одной переменной называется уравнение вида
ах2 + Ьх + с = 0, а О,
где х — переменная, а, b и с — константы. Эту форму записи уравнения будем называть стандартной формой. Оба уравнения
5х2 - За; + 7 = 0 и 18 = 32t2 - 12t
являются квадратными уравнениями, поскольку они записаны в стандартной форме или могут быть к ней преобразованы.
В данном разделе мы ограничимся поиском действительных решений квадратных уравнений.
Решение методом вычисления квадратного корня
Простейший тип квадратного уравнения не содержит линейного слагаемого.
ах2 + с = 0, а 0 0.
Метод решения такого уравнения специального вида основан на прямом использовании свойств квадратного корня.
Свойство квадратного корня
Если а2 = Ь, то а = \/b.
Задание А.15.
Укажите, являются ли перечисленные пары уравнений эквивалентными.


Приложение А. Основные алгебраические понятия и законы
859
1. 	х2 = 4 и х = 2.
2. 	х2 = 4 и х = —2.
3. 	х = л/4 и х = 2.
4. 	х = y/i и х = —2.
5. 	х — —\/4 и х = 2.
Пример А.43 (Метод квадратного корня). Воспользуйтесь свойствами квадратного корня для решения приведенных уравнений.
1. 	х2 - 7 = 0. 2. 2х2 — 10 = 0.
3. Зя2 -И 27 = 0.
4. 	(ж - 8)2 = 9.
Решение.
1. х2 - 7 = 0,
х2 = 7, Квадрат какого действительного числа равен 7?
х = ±\/7. Сокращенное обозначение для л/7 и — у/т
2. 2х2 - 10 = 0,
2х2 = 10,
х2 = 5, Квадрат какого действительного числа равен 5?
х = ±у/5.
3. Зх2 + 27 = 0,
Зх2 = -27,
х2 = —9. Квадрат какого действительного числа равен —9?
У этого уравнения нет действительных решений, поскольку квадрат действительного числа не может быть отрицательным.
4. (х - 8)2 = 9,
х — 8 = ±\/9,
х — 8 = ±3,
х = 8 ± 3 = 5 или 11. ■
Упражнение А.43.
Воспользуйтесь свойствами квадратного корня для решения приведенных уравнений.
1. х2 - 6 = 0. 2. Зх2 -12 = 0.
3. 	х2 + 4 = 0. 4. (х + 5)2 = 1. ■
Решение методом факторизации
Если левую часть квадратного уравнения, записанного в стандартной форме, можно факторизовать, то уравнение решается довольно быстро. Метод решения методом факторизации основан на следующем важном свойстве действительных чисел (см. приложение А.2).
Если а и b — действительные числа, то аЬ = 0 тогда и только тогда, когда а = 0 или Ь = 0 (или оба числа равны нулю одновременно).


860
Часть IV. Приложения
Пример А.44 (Метод факторизации). Решите уравнение методом факторизации, используя целые коэффициенты, если это возможно.
1. За;2 - 6а: - 24 = 0. 2. Зг/2 = 2у. 3. х2 - 2а: - 1 = 0.
Решение.
1. За;2 - 6а: - 24 = 0, х2 — 2а; — 8 — 0,
Разделим обе части на число 3, поскольку оно является общим множителем всех слагаемых
Факторизуем левую часть, если это возможно
(х - 4)(х + 2) = 0,
х + 4 = 0
или х + 2 = 0,
х = —4 или
х = —2.
2. Зу2 = 2у,
Зу2 - 2у = 0.
У&у - 2) = 0,
Решение у = О будет потеряно, если обе части разделить на у. (Выражения 3j/2 = 2у и Зу = 2 не эквивалентны).
у = 0 или
Зт/ - 2 = 0,
у = 0 или
Зу = 2,
у = 0 или
3. х2 — 2х — 1 = 0
Это уравнение не может быть факторизовано с целыми коэффициентами. Его решение мы найдем позже другим методом. ■
Упражнение А.44.
Решите уравнения методом факторизации, используя целые коэффициенты, если это возможно.
1. 2х2 + 4х — 30 = 0. 2. 2х2 = Зт. 3. 2х2 — 8т + 3 = 0. ■
Заметим, что уравнение вида т2 = 25 может быть решено как методом вычисления квадратного корня, так и методом факторизации, причем результаты будут одинаковыми (как и должно быть). Решите это уравнение обоими методами и сравните результаты.
Отметим также тот факт, что метод факторизации применим и для полиномиальных уравнений с более высокими степенями. Рассмотрим следующее уравнение.
х3 — х = 0,
х (х2 — 1) = 0, х(х — 1)(х + 1) = 0,
X = 0 ИЛИ X = 1 или х - —1.
Решение: ж = 0,1,— 1.
Убедитесь, что эти значения являются решениями исходного уравнения.


Приложение А. Основные алгебраические понятия и законы
861
Методы вычисления квадратного корня и факторизации просты и эффективны. Однако существуют квадратные уравнения, которые имеют простую форму, но не могут быть решены ни одним из этих методов. Например, как упоминалось в примере А.44.3, полином в уравнении
х2 - 2х - 1 = О
невозможно разложить на множители с целыми коэффициентами. Необходимость решать подобные уравнения приводит к хорошо известной и широко применяемой формуле корней квадратного уравнения.
Формула корней квадратного уравнения
Существует метод выделения полного квадрата, с помощью которого можно решить любое квадратное уравнение. После краткого обзора этого метода мы выведем с его помощью известную формулу корней квадратного уравнения. Эта формула позволяет механически находить решение любого квадратного уравнения.
Задание А.16.
Замените знаки ? такими числами, чтобы в результате получалось правильное равенство.
1. (ж + I)2 = х2 + 2х 4- ?. 2. (х 4- 2)2 = х2 4- 4х 4- ?.
3. (х 4- З)2 = х2 4- бх 4- ?. 4. (х 4- 4)2 = х2 4- 8х 4- ?.
Замените знаки ? такими числами, чтобы получаемый в результате трехчлен был полным квадратом.
5. х2 4- Юх 4- ?. 6. х2 4- 12х 4- ?. 7. х2 4- Ьх 4- ?. ■
Метод выделения полного квадрата основан на преобразовании квадратного уравнения в стандартной форме
ах2 4- Ьх 4- с = О
к виду
(х + А)2 - В,
где А и В — некоторые константы. Решения последнего уравнения легко найти рассмотренным выше методом вычисления квадратного корня (если существуют действительные решения).
Рассмотрим уравнение из примера А.44.3.
х2 — 2х — 1 = 0. (А.4)
Поскольку левую часть нельзя разложить на множители с действительными коэффициентами, прибавим единицу к обеим частям уравнения.
х2 — 2х = 1. (А.5)
Теперь попробуем найти число, которое нужно прибавить к обеим частям уравнения, чтобы выделить в левой части полный квадрат полинома первого порядка. Квадрат двучлена имеет следующий вид.
(х 4- т)2 = х2 4- 2тх 4- т2.


862
Часть IV. Приложения
Легко видеть, что третье слагаемое в правой части равно квадрату половинного коэффициента при х во втором слагаемом правой части. Поэтому для получения полного квадрата в левой части уравнения (А.5) следует прибавить к обеим частям половину коэффициента при х, т.е. число (-|)2 = 1. (Это правило выполняется только тогда, когда коэффициент при х2 равен единице, т.е. а = 1.) Тогда
х2 - 2х + 1 = 1 + 1.
Левая часть является полным квадратом двучлена х — 1, поэтому
(х - I)2 = 2.
Квадрат какого числа равен 2?
х — 1 = ±\/2
х = 1± у/2
Уравнение (А.5) решено!
Попробуем применить этот же метод для решения общего квадратного уравнения
ах2 + for + с = О, а ± О (А.6)
и решить его для всех х раз и навсегда, в терминах коэффициентов а, b и с. Для начала умножим обе части уравнения (А.6) на 1/а, откуда получаем следующий результат.
b с „ х2 + -х — — 0.
а
а
Прибавим к обеим частям число —с)а.
2 Ъ
х —х = — а
с
а
Теперь выделим полный квадрат в левой части уравнения, добавляя к обеим частям половину коэффициента при х, т.е. (6/2а)2 = 62/4а2.
2 b Ь2 Ь2 с
! + -Я Н = .
а 4а2 4а2 а
Записывая левую часть как полный квадрат и собирая слагаемые в левой части в одну дробь, получаем следующий результат.
( b \2 Ь2 — 4ас
Г+ 2а) = 4а2 ’
Теперь решаем это уравнение методом вычисления квадратного корня.
b lb2 — 4ас
2а=±\1 4а2
b lb2 — 4ас Х = ~2а±\ 4а2
Поскольку ±\/4а2 = ±2а для произвольного действительного числа а


Приложение А. Основные алгебраические понятия и законы
863
Это выражение называется формулой корней квадратного уравнения и записывается в виде дроби.
Формула корней квадратного уравнения
Если ах2 + Ьх + с = 0, а 0, то
—Ь ± \/Ь2 — 4ас
Эта формула обычно используется для решения квадратных уравнений, когда методы вычисления квадратного корня и факторизации не подходят. Величина Ь2 — 4ас под знаком корня называется дискриминантом. Значение дискриминанта дает полезную информацию о решениях уравнения, все возможные случаи перечислены в табл. А.6.
Таблица А.6. Значения дискриминанта
Ь2 — 4ас
ах2 + Ьх + с = 0
Положительно
Равно нулю Отрицательно
Два действительных решения Одно действительное решение Нет действительных решений
Пример А.45 (Формула корней квадратного уравнения). Решите уравнение х2 — 2х — — 1 = 0 с помощью формулы корней квадратного уравнения.
Решение, х2 — 2х — 1 = О
—b zb \/b2 — 4ас
х = = а=1Ь=-2с=—1
2а
^-(-2)±У(-2)2-4-1.(-1)_
2-1
2 zb у/8 2zb2\/2 г-
= —-— = = 1 zb \/2 « -0,414 или 2,414
Проверка, х2 — 2х — 1 = 0
Когда х = 1 + х/2, то
(1 + >/2) 2 — 2 (1 -I- л/г) — 1 = l-ь 2/2 + 2 - 2 - 2/2 -1 = 0.
Когда х = 1 — х/2, то
(1 - х/г) 2 — 2 (1 — х/^) — 1 = 1 — 2/2 + 2 - 2 + 2/2 -1 = 0. и
Упражнение А.45.
Решите уравнение 2х2 — 4х — 3 = 0 с помощью квадратичной формулы.


864
Часть IV. Приложения
Если попробовать решить уравнение х2 — бх + 11 = 0 с помощью рассмотренной
выше формулы, то получим
6±У^8
Х~ 2
Эти значения не являются действительными числами. (Почему?)
Формула корней квадратичного уравнения и метод факторизации
В разделе А.4 задача факторизации была ограничена разложением полинома на множители с целыми коэффициентами. Если данный полином нельзя представить в виде произведения полиномов с целыми коэффициентами, то говорят, что полином не факторизуется в целых числах.
Допустим, что нужно факторизовать полином
х2 - 19а? - 372
(А.7)
Чем больше значения коэффициентов полинома, тем сложнее применять ас-тест, рассмотренный в разделе А.4. Однако применение формулы корней квадратного уравнения позволяет очень просто факторизовать любой полином с целыми коэффициентами, если это возможно. Рассмотрим этот метод на примере полинома (А.7), а затем обобщим результат.
Начнем с решения соответствующего квадратного уравнения с помощью общей формулы.
х2 - 19а? - 372 = 0.
-(-19) ± У(-19)2 - 4 ■ 1 ■ (-372)
2
19 ±43
2
= -12
ИЛИ
31.
Поэтому
х2 - 19х - 372 = [х - (-12)][х - 31] = (х + 12)(х - 31).
Если найти произведение множителей правой части, то получится полином в левой части.
Что стоит за этой процедурой? В приведенных ниже теоремах мотивируется и обобщается этот процесс.
Теорема А.З (Теорема о факторизуемости). Полином второго порядка ах2 + Ьх + с может быть представлен в виде произведения полиномов первого порядка с целыми коэффициентами тогда и только тогда, когда число у/Ь2 — 4ас — целое. ■
Теорема А.4 (Теорема о факторизации). Если числа г\ и Г2 являются решениями уравнения ах2 + Ьх + с = 0, то
ах2 + Ьх + с = (х — п) (х — Г2).


Приложение А. Основные алгебраические понятия и законы
865
Пример А.46 (Факторизация методом вычисления дискриминанта). Факторизуйте, если возможно, следующий полином с целыми коэффициентами.
1. 4х2 - 65х + 264. 2. 2х2 - ЗЗх - 306.
Решение.
1. 4х2 - 65я + 264.
Этап 1. Проверка факторизуемости.
Vb2 - 4ас = >/(—65)2 -4-4-264 = 1.
Поскольку результат является целым числом, то полином может быть разложен на множители первого порядка с целыми коэффициентами.
Этап 2. Разложим на множители, используя теорему о факторизации. Вычислим решения соответствующего квадратного уравнения с помощью общей формулы.
4д: 65а: + 264 — 0, ^Получено на этапе 1
-(-65) ± 1^ 33
х — — = — или 8.
2-4 4
Поэтому
2. 2х2 - ЗЗх - 306.
Этап 1. Проверка факторизуемости.
у/b2 - 4ас = у^-ЗЗ)2 - 4 • 2 • (-306) = \/3537.
Поскольку х/3537 не является целым числом, то полином не раскладывается на множители с целыми коэффициентами. ■
Упражнение А.46.
Разложите полином на множители с целыми коэффициентами, если это возможно.
1. Зх2 - 28х - 464. 2. 9х2 + 320х - 144.
Практическая задача: предложение и спрос
Изучение предложения и спроса является одной из наиболее важных задач экономики. В общем случае производители склонны выпускать больше продукции при росте цены и уменьшать объем производства при ее падении. Аналогично потребители склонны покупать меньшее количество товара при росте цены и большее — при ее падении. В результате ситуация динамически изменяется при колебаниях цен, предложения и спроса до тех пор, пока цена не примет такое значение, при котором предложение уравновешивается спросом. В экономической теории такая точка называется точкой равновесия. Если цена увеличивается относительно равновесного значения, то предложение растет, а спрос — падает и наоборот, при падении цены ниже равновесного значения предложение падает, а спрос — растет.


866
Часть IV. Приложения
Пример А.47 (Предложение и спрос). Уравнения, описывающие недельные предложение и спрос на шезлонги в летний период на крупном курорте, имеют следующий вид.
х 3
140 + 4
5670
Уравнение предложения
Уравнение спроса
Уравнение предложения показывает, что поставщик намеревается продать х единиц товара по цене р дрлл. Уравнение спроса значит, что потребитель собирается приобрести х единиц товара по цене р долл. При каком объеме товара предложение равно спросу? Чему равна цена товара в этом случае?
Решение. Положим правую часть уравнения предложения равной правой части уравнения спроса и решим получившееся уравнение относительно переменной х.
х 3 _ 5670
140 + 4 _
х2 + 105х = 793800
х2 + 105а? — 793 800 = 0
Умножим обе части на 140®, это наименьший общий знаменатель
Запишем уравнение в стандартной форме
Используем формулу корней квадратного уравнения
_ -105 ± ^/Юб2 -4 -1 ■ (-793800)
Х~ 2
х = 840 единиц
Отрицательный квадратный корень следует отбросить, поскольку отрицательное количество единиц товара не имеет смысла: его нельзя ни произвести, ни продать. Подставляя значение х = 840 в уравнение предложения или в уравнение спроса, получим величину равновесной цены (здесь используется уравнение спроса).
5670 5670 п „
” - — = 840 = 6J5
Таким образом, при цене 6,75 долл, поставщик сможет продать, а потребители купят
840 шезлонгов в неделю. ■
Упражнение А.47.
Повторите решение примера А.47, если в конце летнего сезона уравнения предложения и спроса имеют следующий вид.
х 1
Р= 80 “ 20
1264
Р =
Уравнение предложения
Уравнение спроса
х


Приложение А. Основные алгебраические понятия и законы
867
Ответы к упражнениям
А.43. 1) ±л/б.
2) ±2.
3) Не имеет действительных решений.
4) -6, -4.
А.44. 1) -5,3.
2) 0, j.
3) Невозможно разложить на множители с целыми коэффициентами. А.45. (2 ±710)/2.
А.46. 1) Невозможно разложить на множители с целыми коэффициентами.
2) (Эх - 4)(х 4- 36).
А.47. 320 шезлонгов по цене 3,95 долл.
Практикум А.9
В приведенных ниже задачах необходимо найти только действительные решения. Если действительных решений нет, объясните, почему.
А В задачах 1-4 решите уравнения методом вычисления квадратного корня.
1. 2х2 - 22 = 0.
3. (ж - I)2 = 4.
2. Зт2 —21 = 0.
4. (х + 2)2 = 9.
В задачах 5-9 решите уравнения методом факторизации.
5. 2и2 — 8и — 24 = 0.
7. х2 = 2х.
6. 3z2 — l&r + 15 = 0.
8. п2 — Зп.
В задачах 9-12 решите уравнения с помощью формулы корней квадратного уравнения.
9. х2 — 6х — 3 = 0.
11. 3u2 + 12u + 6 = 0.
10. т2 ± 8т ±3 = 0.
12. 2х2 - 20х - 6 = 0.
Б В задачах 13-30 решите уравнения любым из методов.
13. 2х2 = 4х.
15. 4и2 — 9и = 0.
17. 8гг2 + 20х = 12.
19. х2 = 1 — х.
21. 2х2 = 6х - 3.
23. у2 - 4у = -8.
25. (х + 4)2 = 11.
27. - = р.
Р
2 3
29. 2- - =
т2 т
14. 2х2 = -Зх.
16. 9у2 - 25 = 0.
18. 9х2 — 6 = 15х.
20. т2 = 1 — Зт.
22. 2х2 = 4х - 1.
24. х2 — 2х = —3.
26. (у - 5)2 = 7.
28. х - - = 0.
и и*


868
Часть IV. Приложения
32. х2 - 28х - 128.
34. х2 + 52х -|- 208.
36. Зх2 - 32х - 140.
38. бх2 - 427х - 360.
В задачах 31-38 представьте полиномы в виде произведения полиномов первого порядка с целыми коэффициентами. Используйте формулу корней квадратного уравнения и теорему факторизации.
31. х2 + 40х - 84.
33. х2 - 32х + 144.
35. 2х2 + 15х - 108.
37. 4х2 + 241х - 434.
В
39. В соотношении А = Р(1 + г)2 выразите переменную г через переменные А и Р, т.е. локализуйте переменную г в левой части уравнения (с коэффициентом, равным единице). В правой части должно быть алгебраическое выражение, включающее величины А и Р (но не число г). Ответ запишите, используя только положительные квадратные корни.
40. Решите уравнение х2 + тх + п = 0 относительно х в терминах тип.
*41. Рассмотрим квадратное уравнение
х2 + 4х 4- с = 0,
где с — действительное число. Укажите связь между значениями величины с и тремя типами решений, перечисленных в табл. А.6.
* 42. Рассмотрим квадратное уравнение
х2 — 2х + с — 0,
где с — действительное число. Укажите связь между значениями величины с и тремя типами решений, перечисленных в табл. А.6.
Применение математики
Экономика и бизнес
43. 	Предложение и спрос. Компания продает оптом некую марку шампуня. В отделе маркетинга компании были получены следующие уравнения недельного предложения и спроса.
X 1
р =
450 + 2
Уравнение предложения
6300
р =
X
Уравнение спроса
При каком объеме товара предложение равно спросу? Чему равна цена товара в этом случае?


Приложение А. Основные алгебраические понятия и законы
869
Уравнение предложения
Уравнение спроса
44. Предложение и спрос. Импортер поставляет некую модель автоматического фотоаппарата в сеть магазинов метрополитена. В летний период уравнения недельного предложения и спроса имели следующий вид.
х ₽=6+9 24840
Р =
х
При каком объеме товара предложение равно спросу? Чему равна стоимость единицы товара в этом случае?
45. Процентная ставка. Пусть Р долл, инвестируются под 100г процентов ежегодно. По истечении двух лет сумма вырастет до А = Р(1 + г)2. Под какую процентную ставку была инвестирована сумма, равная 100 долл., если через два года она выросла до 144 долл.? (Замечание. Если А = 144 и Р = 100, то нужно найти г.)
46. Процентная ставка. Используя формулу из задачи 45, вычислите процентную ставку для инвестиций объемом 1000 долл., если через два года вклад вырос до 1210 долл.
Биологические науки
47. Экология. Важным фактором эрозии почв является скорость течения грунтовых вод. Для измерения скорости потока воды v (в футах за секунду) в поток помещают L-образную полую трубку так, что конец которой погружен в воду против течения, а второй — направлен вверх. Вода в трубке поднимется на некоторую высоту h (в футах) над уровнем потока. Из школьного курса физики известно, что v2 = 64h. Какова скорость воды, если h = 1 фут или 0,5 фута?
Социальные науки
48. Исследование безопасности. Важно знать, какое наименьшее количество футов d проедет автомобиль от момента начала торможения до полной остановки (учитывая время реакции водителя) при различных скоростях его движения v (в милях в час). В отделе исследования безопасности была получена формула d = 0,044v2 + l,lv. Допустим, что длина тормозного пути равна 550 футов. Оцените скорость автомобиля в момент начала торможения.


Б
Специальные темы
БД. Последовательности, ряды и суммы рядов
Б.2. Арифметические и геометрические последовательности
Б.З. Бином Ньютона
Б.4. Приращения и дифференциалы
Б.5. Правило Лопиталя
Б.6. Двойные интегралы по сложным областям
Б.7. Интерполяционные полиномы и разделенные разности
Б.1. Последовательности, ряды и суммы рядов
■ Последовательности
■ Ряды и суммы рядов
Перечисляя квадраты чисел, вы, возможно, запишете такую строку.
1,4,9,16,25,36...
Однако назвать все квадраты чисел невозможно, поскольку их бесконечно много. И все же существуют способы, с помощью которых можно представить всю совокупность подобных чисел сразу. Например, можно написать так.
1,4,9,..., и2, п е N.
Здесь символ N обозначает множество натуральных чисел. Список таких чисел называется последовательностью (sequence). Именно последовательности являются предметом исследования в этом разделе.


Приложение Б. Специальные темы
871
Последовательности
Рассмотрим следующую функцию.
У(п) = 2п+1, (Б.1)
область определения которой представляет собой множество всех натуральных чисел N. Отметим, что
/(1) = 3, /(2) = 5, /(3) = 7,...
Функция f является примером последовательности. Вообще говоря, последовательность — это функция, областью определения которой является множество возрастающих целых чисел. Как правило, для обозначения последовательностей используются специальные обозначения.
Область значений функции /(п) более компактно можно обозначить символом ап. Тогда вместо формулы (Б.1) получим следующую запись.
dfi — 2ть 1
Областью определения этой функции считается множество всех натуральных чисел, если не указано обратное. Элементы области значений называются членами последовательности. Число ai называется первым элементом последовательности, а число ап — п-м членом.
<21 = 2 • 1 1 = 3,
0-2 = 2 • 2 4- 1 = 5,
ап = 2п + 1.
Упорядоченный список элементов
3,5,7,..., 2n + 1,...,
полученный путем перечисления всех элементов области значений описанной выше функции, часто неформально также называют последовательностью. Кроме того, последовательности часто обозначают с помощью фигурных скобок, например, {ап}. В частности, последовательность нечетных чисел 3,5,7,..., 2п + 1 можно представить в следующем виде: {2n +1}.
Если областью определения последовательности является конечное множество возрастающих целых чисел, то последовательность называется конечной. Если же областью определения последовательности является бесконечное множество возрастающих целых чисел, то последовательность называется бесконечной. Например, последовательность {2п + 1} является бесконечной.
Пример Б.1 (Запись последовательности). Запишите первые четыре члена следующих последовательностей.
1. 	ап = Зп — 2.


872
Часть IV. Приложения
Решение.
1. 	1,4,7,Ю
Упражнение Б.1.
Запишите первые четыре члена следующих последовательностей.
1. 	ап = -п + 3. 2.
Задание Б.1.
1. 	Укажите следующий элемент последовательности.
2,4,8,
Варианты ответов:
1) 16,
2) 14,
2. 	Сравните первые четыре члена следующих последовательностей.
1) ап = 22,
2) Ьп = п2 - п + 2,
6
3) сп = 5п-\ 9.
п
Какая из этих последовательностей совпадает с последовательностью, описанной в п. 1? ■
Итак, мы научились определять первые члены последовательностей по заданным формулам. Теперь рассмотрим обратную задачу. Иначе говоря, можно ли определить последовательность, указав первые три-четыре ее члена? И как вывести формулу для вычисления n-го члена последовательности с помощью предыдущих элементов? Как правило, если у нас нет дополнительной информации, мы вынуждены отрицательно ответить на первый вопрос. Как показывает задание Б.1, первые несколько членов разных последовательностей могут совпадать. Простым перечислением первых трех членов невозможно однозначно задать всю последовательность. Можно даже показать, что, перечислив первые т членов последовательности, мы не сможем задать ее полностью, поскольку она содержит бесконечное количество элементов.
Отвечая на второй вопрос, мы должны определить общую формулу для вычисления n-го члена некоей последовательности, первые члены которой совпадают с заданными. Это вполне можно сделать. Зная некий шаблон, мы способны определить общий вид элементов, который он описывает. Рассмотрим эту ситуацию на следующем примере.
Пример Б.2 (Определение общего члена последовательности). Определите общий член последовательности по указанным четырем элементам.
1. 	3,4,5,6,... 2. 5,-25,125,-625,...


Приложение Б. Специальные темы
873
Решение,
1. Поскольку члены последовательности представляют собой целые числа, следующие друг за другом, формулу для вычисления ее членов можно записать так: ап — п, п 3. Если областью определения последовательности должно быть множество всех натуральных чисел, ее общий член должен иметь следующую формулу: bn = п + 2.
2. Каждый из членов последовательности можно задать в виде произведения степени числа 5 и степени числа —1.
5 = (—1)°51 = ai,
-25 = (-l)^2 =а2,
125 - (—1)253 = а3,
625 = (—1)354 = а4.
Если областью определения последовательности должно быть множество всех натуральных чисел, ее общий член должен иметь следующую формулу.
ап = и
Упражнение Б.2.
Определите общий член последовательности по указанным четырем элементам.
1.3,6,9,12,... 2. 1,-2,4,-8,... ■
Как правило, существует несколько способов задания n-го члена последовательности (см. решение примера Б.2.1). Однако, если не указано иное, мы будем предполагать, что областью определения последовательности является множество всех натуральных чисел.
Ряды и суммы рядов
Если ai, а,2, ..., ап, • • - — это последовательность, то выражение
ai + 02 + + • • • + яп + ...
называется рядом. Если последовательность является конечной, то соответствующий ряд также называется конечным. В данном разделе мы рассмотрим только один конечный ряд.
1,3,5,7,9;
1 + 34-5 + 7 + 9.
Обратите внимание на то, что ряд очень легко подсчитать.
1 + 3 + 5 + 7 + 9 = 25.


874
Часть IV. Приложения
Ряды часто представляют в очень компактном виде с помощью знака суммы. Рассмотрим следующий пример.
6
£ fc2 = З2 + 42 + 52 + 62 = 9 + 16 + 25 + 36 = 86.
к=3
2
(4А: + 1) = (4 • 0 + 1) + (4 • 1 + 1) + (4 • 2 + 1) = 1 + 5 + 9 = 15.
к=0
В каждом из этих примеров ряд, стоящий в правой части равенства, вычислялся путем подстановки в левую часть последовательных значений индекса суммирования к, начиная с номера, указанного ниже суммы знака S, и заканчивая номером, стоящим выше этого символа. В роли индекса суммирования может выступать любая буква, а не только буква к, причем суммирование может начинаться с любого целого числа и завершаться также любым целым числом, которое больше начального значения индекса суммирования или равно ему. Рассмотрим следующую последовательность.
111 _1_
2’ 4’ 8’ ’’2™’
Ряд, соответствующий этой последовательности, имеет такой вид.
ill _L _ V —
2 + 4 + 8 4 Н2"_2^2>-
J —1
Пример Б.З (Знак суммирования). Запишите ряд не используя знак суммы
и не вычисляя ее.
Решение.
\ к 1 2 3 4 5
к2 + 1 _ I2 + 1 + 22 + 1 + З2 + 1 + 42 + 1 + 52 + 1 =
к=1
_ 1 2 2 А 5
“ 2 + 5 + 10 + 17 + 26’ ■
Упражнение Б.З.
Запишите ряд не используя знак суммы и не вычисляя ее. ■
Задание Б.2.
1. Найдите наименьшее значение п, при котором ряд ^2aLi £2+1 больше 3.
2. Найдите наименьшее значение п, при котором ряд г? больше 0,99 или 0,999.и
Если члены ряда поочередно являются то положительными, то отрицательными, такой ряд называется знакопеременным.
Пример Б.4 (Знак суммирования). Запишите знакопеременный ряд
1 _ 1 1 _ 1 _ 1
2 _ 4 + 6 _ 8 + 10 “ 12 ’
используя знак суммы, при следующих условиях.


Приложение Б. Специальные темы
875
1. Начальное значение индекса суммирования к равно 1.
2. Начальное значение индекса суммирования j равно 0.
Решение.
1. Перемену знака можно описать с помощью числа (- l)fc+1, которое равно то +1, то —1 в зависимости от индекса к. Остальную часть членов ряда можно представить в виде дроби . Следовательно, ряд можно записать так.
liii 1 1  * * _ A (-i)fc+1
2_4 + 6_8 + 10 12 ~ 2к ’
к—1
2. 	Перемену знака можно описать с помощью числа (—1)\ которое равно то +1, то —1 в зависимости от индекса j. Остальную часть членов ряда можно представить в виде дроби 2(ДХ) • Следовательно, ряд можно записать так.
1
2
ill 1 1 А (-1/
4 + 6 8 + 10 12 _ 2 О' + 1) ’
Упражнение Б.4.
Запишите знакопеременный ряд
1 1 _ £ £
3 	+ 9 27 + 81’
используя знак суммы, при следующих условиях.
1. Начальное значение индекса суммирования к равно 1.
2. Начальное значение индекса суммирования j равно 0. ■
Знак суммирования позволяет компактно представить любой список чисел, даже если эти числа не порождаются формулой. Например, предположим, что студенты в группе, состоящей из 10 человек, получили на экзамене следующие оценки.
87,77,95,83,86,73,95,68, 75,86.
Обозначим оценки студентов буквами ai, а2, аз,..., аю. Тогда среднюю оценку студентов можно вычислить по следующей формуле.
1 ю 1
— V ак = — (87 + 77 + 95 + 83 4- 86 + 73 + 95 + 68 + 75 + 86) =
10 	10 4  * * 7 fc=l
= Т • 825 = 82,5.
В статистике используется следующая формула для вычисления арифметического среднего а списка, состоящего из п чисел ai, а2, аз, ..., an.


876
Часть IV. Приложения
Пример Б.5 (Арифметическое среднее). Вычислите арифметическое среднее чисел 3, 5, 4, 7, 4, 2, 3 и 6.
Решение.
я — — ' ак — — (3 + 5 + 4 + 7 + 4 + 2 + 3 + 6) — — • 34 — 4,25.
о 7” о о
Упражнение Б.5.
Вычислите арифметическое среднее чисел 9, 3, 8, 4, 3 и 6.
Ответы к упражнениям
Б.1.
1)
2)
Б.2.
1)
2)
2, 1, 0, -1.
11 11 ~2’ 4’ _8’ 16’ я^ — Зт?..
яп = (—2)n_1.
„ 3 4 5 6
2 + 2 + 3 + 4 + 5‘
Б.4. 1)
к=1
2)
j=0
Б.5. 5,5.
Б.З.
3fc-i •
Практикум Б.1
А В задачах 1-6 необходимо вычислить первые четыре элемента последовательности.
1. ап = 2п + 3.
2. ап = 4п — 3.
3. On
Ti 2 п + 1 ’
2п 4- 1
2п
5. 	яп = (-3)n+1.
7. 	Запишите 10-й член последовательности из задачи 1.
8. 	Запишите 15-й член последовательности из задачи 2.
9. 	Запишите 99-й член последовательности из задачи 3.
10. 	Запишите 200-й член последовательности из задачи 4.


Приложение Б. Специальные темы
877
В задачах 11-16 необходимо записать ряд, не используя знак суммы, и вычислить его.
6
и. 52 fc.
k=i
и. £ (-2)fc.
к=0
12. £ к2.
к=1
15-ДУ
7
13. 52 (2к-з).
к=4
4 1 'W-
В задачах 17-20 необходимо вычислить арифметическое среднее чисел, указанных в списке.
17. 5, 4, 2, 1 и 6. 18. 7, 9, 9, 2 и 4.
19. 96, 65, 82, 74, 91, 88, 87, 91, 77 и 74. 20. 100, 62, 95, 91, 82, 87, 70, 75, 87 и 82.
Б В задачах 21-26 необходимо вычислить первые пять членов последовательности, а - И-"'1 “п “ 2"
21.
22.
23.
24.
an = (—l)n (n — I)2. _1-(-1)п
О-п —
25.
26.
В задачах 27-42 необходимо вывести общую формулу для вычисления п-го члена последовательности по ее первым четырем членам.
27. -2,-1, 0,1,...
29. 4, 8, 12, 16, ...
31 1 3 5 7
2’ 4’ 6’ 8””
1, —2, 3, —4,...
1, -3, 5, -7, ...
2 4 8
1( 5’ 25’ 125’ “
9 4 4
ГУ* fY***
«А/ *А/ «А/ j • • 9
33.
35.
37.
39.
41.
гр
*А/ } *4/ } «А/ } «А/ } • •
28. 4, 5, 6, 7,...
30. -3, -6, -9, -12, ...
32 1 ? * 4 2’ 3’ 4’ 5’ ’ ’'
34. —2, 4, -8, 16, ...
36. 3, -6, 9, -12, ...
4 16 64 256
8‘ 3’ 9 ’ 27’ 81 ”
40. 1, 2х, Зх2, 4х3,... х2 х3 х4
42‘х’ Т’ У’ Т’ ■■
В задачах 43-50 необходимо записать ряд в развернутом виде, не вычисляя его.
43. £ (-l)fe+1 (2fc - l)2.
fc=l
2A: + 3
5
47. £ xk~l.
fc=i
4 	('-l')fex2fc+1
49 У2 ИУ
fc=o 2fc +1
2к
(—2)fc+1
2fc + l ’
(-!)*
к2-к'
4
44. 12
к=1
46. £
к=3
3 1
48. £ irrfc+1. к=1 к
4 (—l)fca:2fc
50. у * .
к=о U + 2


878
Часть IV. Приложения
В задачах 51-54 необходимо записать ряд, используя знак суммы, при следующих условиях.
1) Начальное значение индекса суммирования равно нулю.
2) Начальное значение индекса суммирования равно единице.
51. 2+ 3 + 4 +5+ 6.
1
4’
В задачах 55-58 необходимо записать ряд, используя знак суммы, при условии, что начальное значение индекса суммирования равно единице.
3 4
55,2+2 + 3 + '” +
п + 1
п
58. 1-4 + 9 + (-1)п+1п2.
В В задачах 59-62 необходимо оценить корректность приведенных утверждений. Если утверждение истинно, объясните почему, если нет — приведите контрпример.
* 59. Для каждого целого положительного числа п сумма ряда 1 + | + | + ”’ + ^ меньше четырех.
* 60. Для каждого целого положительного числа п сумма ряда | + | + | + +
меньше единицы.
* 61. Для каждого целого положительного числа п сумма ряда | — | +1 Н —
больше или равна |.
* 62. Для каждого целого положительного числа п сумма ряда 1 — | + | — | Н h
+ больше или равна |.
Некоторые последовательности задаются рекуррентными формулами, т.е. п-й член выражается через один или несколько предыдущих членов. Например, если последовательность ап задана формулой
ai = l и ап = 2an_i + 1 при 2,
тогда
(2 2 = 2di + 1 = 21 + 1 = 3,
(2з = 2а2 + 1 = 23 + 1 = 7,
(Z4 = 2(1з + 1 = 2’7 + 1 = 15
и т.д. В задачах 63-65 требуется вычислить первые пять членов указанных последовательностей.
63. 	ai = 2 и ап = 3an_i + 2 при п 2. 64. = 3 и ап = 2an_i - 2 при 2.
65. ai = 1 и an = 2an_i при п > 2. 66. ai = 1 и ап = -|an_i при п 2.
Если А — положительное действительное число, то последовательность, заданную рекуррентными формулами при п 2,


Приложение Б. Специальные темы
879
можно использовать для аппроксимации числа с любой требуемой точностью. В задачах 67 и 68 необходимо вычислить первые четыре члена этой последовательности для указанного числа А и сравнить четвертый член последовательности со значением \/А, вычисленным с помощью калькулятора.
67. А = 2. 68. А = 6.
69. Последовательность, заданная рекуррентными формулами = 1, ап = an_i + 4- ап_2 при п 3, называется последовательностью Фибоначчи. Вычислите первые десять членов последовательности Фибоначчи.
70. Последовательность, заданная формулой Ьп = > тесно связана с по¬
следовательностью Фибоначчи. Вычислите первые десять членов этой последовательности (с точностью до трех десятичных знаков) и опишите зависимость членов этой последовательности от членов последовательности Фибоначчи.
Б.2. Арифметические и геометрические
последовательности
■ Арифметическая и геометрическая прогрессии
■ Формулы вычисления n-го члена прогрессии
■ Формулы суммирования конечного арифметического ряда
■ Формулы суммирования конечного геометрического ряда
■ Формулы суммирования бесконечного геометрического ряда
■ Решение практических задач
В большинстве случаев вычислить сумму произвольного количества членов последовательности, не прибегая к их суммированию, довольно сложно. Однако некоторые специальные последовательности — арифметическая и геометрическая — обладают свойствами, позволяющими вывести формулу для вычисления их суммы.
Арифметическая и геометрическая прогрессии
С одной стороны, последовательность 5, 7, 9, 11, 13, ..., 5 + 2(п — 1), ..., в которых каждый последующий член больше предыдущего на 2, представляет собой типичный пример арифметической прогрессии. С другой стороны, последовательность 5, 10, 20, 40, 80, ..., 5 • 2n_1, ..., в которой каждый последующий член образуется путем умножения предыдущего на число 2, является геометрической прогрессией.
Арифметическая прогрессия
Последовательность ai, а2,..., ап,... называется арифметической прогрессией, если существует константа d, называемая разностью, такая что
an, ап,—i — d.
Иначе говоря,
ап = an_i + d при всех п > 1.


880
Часть IV. Приложения
Геометрическая прогрессия
Последовательность ai, аг,..., ап, • • • называется геометрической прогрессией, если существует ненулевая константа d, называемая знаменателем, такая что
= Г.
1
Иначе говоря,
ап = ran i при всех п> 1.
Задание Б.З.
1. Опишите все арифметические прогрессии с разностью, равной двум.
2. Опишите все арифметические прогрессии со знаменателем, равным двум. ■
Пример Б.6 (Запись последовательности). Укажите, какие из первых четырех членов последовательности образуют арифметическую или геометрическую прогрессию.
1. 	1,2,3, 5,... 2. -1,3,-9,27, ...
3. 3, 3, 3, 3, ... 4. 10; 8,5; 7; 5,5; ...
Решение.
1. Поскольку 2—1 5—3, разность между соседними элементами последовательности
не постоянна, следовательно, она не является арифметической прогрессией.
2. Указанная последовательность является геометрической прогрессией со знаменателем, равным —3.
3. Последовательность является арифметической прогрессией, разность которой равна нулю. Одновременно она представляет собой геометрическую последовательность, знаменатель которой равен единице.
4. Последовательность является арифметической прогрессией с разностью, равной
— 1,5. Она не является геометрической прогрессией. ■
Упражнение Б.6.
Укажите, какие из первых четырех членов последовательности образуют арифметическую или геометрическую прогрессию.
1. 	8; 2; 0,5; 0,125; ... 2. -7, -2, 3, 8, ... 3. 1, 5, 25, 100, ... а
Формулы вычисления n-го члена прогрессии
Если {ап} — арифметическая прогрессия с разностью d, то
а2 = Ql + d,
аз = а2 — ^1 Н" 2d,
CI4. = (2$ d = CL} + 3d.


Приложение Б. Специальные темы
881
Формула вычисления п-го члена арифметической прогрессии
an = ai -F (п — l)d при всех п > 1.
(Б.2)
Аналогично, если {ап} — геометрическая прогрессия со знаменателем г, то
02 = ОХГ,
2
О3 — О2Г — 017* ,
04 = О3Г = 01Г3.
Формула вычисления п-го члена геометрической прогрессии
ап = ахгп 1 при всех п > 1.
(Б.З)
Пример Б.7 (Вычисление n-го члена арифметической и геометрической прогрес¬
сий).
1. Предположим, что первый и десятый члены арифметической прогрессии равны 3 и 30 соответственно. Вычислите 40-й член прогрессии.
2. Предположим, что первый и десятый члены геометрической прогрессии равны 3 и 30 соответственно. Вычислите 40-й член прогрессии.
Решение,
1. Применим формулу (Б.2), где а\ = 3 и аю = 30 и вычислим разность d.
ап = ai + (п- l)d, (210 = ОХ + (10 — l)d,
30 = 3 + 9d, d = 3.
Следовательно,
040 — 3 4~ 39 • 3 — 120.
2. Применим формулу (Б.З), где ai = 3 и аю = 30 и вычислим знаменатель г.
ап - air" х,
30 = Зг9, г9 = 10,
г = 101/9.
Следовательно,
/ \ 39
а40 = 3 • (101/9) = 3 • 1039/9 = 64633,041.


882
Часть IV. Приложения
Упражнение Б.7.
1. Предположим, что первый и 15-й члены арифметической прогрессии равны -5 и 23 соответственно. Вычислите 73-й член прогрессии.
2. Вычислите восьмой член геометрической прогрессии
1 _J_ 1
64’~32’ 16’ ■
Формулы суммирования конечного арифметического ряда
Если ai, а2> • • •, ап — конечная арифметическая прогрессия, то соответствующий ряд ai + 02 + • • + оп называется конечным арифметическим рядом. Мы выведем две простые и очень полезные формулы вычисления сумм конечных арифметических рядов. Обозначим через d разность арифметической прогрессии oi, 02, ..., оп, а через Sn — сумму ряда oi + о2 4 И ап. Тогда
Sn = oi + (oi + d) + • • • 4- [01 + (n — 2)d] -|- [01 (п — l)d].
Изменим порядок суммирования на противоположный.
Sn = [01 4- (n — l)d] 4" [01 Н- (п — 2)d] 4- • • • 4- (01 4- d) 4~ 01.
Сложим эти два равенства почленно.
2Sn = [2oi 4- (n — l)d] 4~ [2ai 4~ (м — 2)d] 4~ • • • 4~
4~ (2oi 4~ (п — l)cQ 4~ (2oi 4~ (п — 1)с/) •
Все п слагаемых в правой части равенства одинаковы, поэтому справедлива следующая формула.
2Sn = п [2oi 4- (n — l)d].
Это приводит нас к следующему выводу.
Сумма конечного арифметического ряда: первая формула
Sn = " [2ai + (n - l)d]. (Б.4)
Заменяя величину
2oi 4- (n — l)d
в выражении
- [oi + О! + (п - l)d]
значением ап из формулы (Б.2), получим вторую полезную формулу вычисления суммы конечного арифметического ряда.
Сумма конечного арифметического ряда: вторая формула
а П г т
*Ьп — ~ [^1 4~ anj.
(Б.5)


Приложение Б. Специальные темы
883
Пример Б.8 (Вычисление суммы конечного арифметического ряда). Вычислите сумму первых 30 членов арифметической последовательности
3, 	8, 13, 18, ...
Решение. Применим формулу (Б.4) с параметрами п = 30, ai = 3 и d = 5.
30
S30 = — [2 • 3 + (30 - 1) • 5] = 2265.
2 И
Упражнение Б.8.
Вычислите сумму первых 40 членов арифметической последовательности
15, 13, 11, 9, ... а
Пример Б.9 (Вычисление суммы конечного арифметического ряда). Вычислите сумму четных чисел, которые больше 31 и меньше 87.
Решение. Сначала вычислим индекс п, используя формулу (Б.2).
= «1 -h (п - l)d,
86 = 32 + (п - 1)2,
п = 28.
Теперь, используя формулу (Б.5), найдем величину S28-
„ П г !
[Qi + ап\,
•S28 = у [32 + 86] = 1652. в
Упражнение Б.9.
Вычислите сумму нечетных чисел, которые больше 24 и меньше 208. ■
Формулы суммирования конечного геометрического ряда
Если ai, а.2, ..., ап — конечная геометрическая прогрессия, то соответствующий ряд ai + аг + • • ’ + an называется конечным геометрическим рядом. Мы выведем две простые и очень полезные формулы для вычисления сумм конечных геометрических рядов. Обозначим через г знаменатель геометрической прогрессии ai, a2,..., an, а через Sn — сумму ряда ai + a2 Н 1- ап. Тогда
Sn = ai + air + air2 H h airn_1.
Умножим обе части равенства на число г.
rSn = а±г + air2 + air3 + h airn_1 + airn.


884
Часть IV. Приложения
Вычтем первое равенство из второго.
rSn — Sn = a^r + air2 + air3 + • • • +
+ airn_1 + airn - (ai + a±r + air2 4 h airn_1)
(r - l)5n = airn - ab
Решая последнее уравнение относительно Sn, приходим к следующему выводу.
Сумма конечного геометрического ряда: первая формула
Sn =
ai (rn - 1)
г — 1
г 1.
(Б.6)
Поскольку ап = а\гп \ т.е. ran = airn, формулу (Б.6) можно переписать в ином виде.
Сумма конечного геометрического ряда: вторая формула
Sn =
г a^j ai
г — 1
(Б.7)
г ± 1.
Пример Б. 10 (Вычисление суммы конечного геометрического ряда). Найдите сумму первых десяти членов геометрической прогрессии.
1; 1,05; 1,052; ...
Решение. Применим формулу (Б.6) с параметрами ai = 1, г = 1,05 и п = 10.
Sn
Sn
«1 (rn -1) ,.
r-1 ’
1 (l,O510 - 1) _ 0,6289
1,05-1 ~ 0,05
Упражнение Б.10.
Вычислите сумму первых восьми членов геометрической прогрессии.
100; 100-1,08; 100-1,082; ...
Формула суммирования бесконечного геометрического ряда
Задание Б.4.
1. Сумма конечного геометрического ряда для любого числа п при а± = 5 и г = | вычисляется по формуле (Б.6).
Как ведет себя величина Sn при увеличении числа п?
2. Повторите решение п. 1 при ai = 5 и г = 2. ■


Приложение Б. Специальные темы
885
Как ведет себя величина Sn при неограниченном увеличении числа п? Чтобы найти ответ на этот вопрос, перепишем формулу (Б.6) в следующем виде.
_ аггп ai
1 - •
Г — 1 Г — 1
Легко видеть, что при — 1 < г < 1 величина гп стремится к нулю, когда число п неограниченно возрастает. Итак, первый член формулы, приведенной выше, при больших значениях п будет пренебрежимо малым, а величина Sn будет очень близка к значению второго члена, т.е. —а\/(г — 1) (это выражение можно переписать в виде ai/(l — г). Итак, если —1 < г < 1, сумма бесконечного геометрического ряда определяется по следующей формуле.
Формула суммирования бесконечного геометрического ряда
Sx = -1 < г < 1. (Б.8)
1 — г
Если г — 1 или г 1, бесконечный геометрический ряд не имеет суммы.
Решение практических задач
Пример Б.11 (Выплата займа). Один человек взял взаймы 3600 долл, на три года и обязался погасить заем за счет ежемесячных платежей. При этом он согласился каждый месяц выплачивать по 100 долл, и 1% оставшейся суммы. Какую сумму он выплатит за три года?
Решение. Рассмотрим процедуру выплаты долга во времени.
+
Итак, общая стоимость долга равна
1 + 2 + • •• + 34 + 35 + 36.
Эти числа образуют конечную арифметическую прогрессию с параметрами п = 36, ai = 1 и азб = 36. Следовательно, можно применить формулу Б.5.
п
Sn = — [о-i -|- ап\ ;
536 = у [1 + 36] = 666.
Следовательно, общая стоимость трехлетнего долга составит 666 долл.


886
Часть IV. Приложения
Упражнение Б.11.
Повторите решение примера Б.11, если сумма долга равна 6000, а срок его погашения равен пяти годам. ■
Пример Б.12 (Моделирование экономической ситуации). Правительство решило стимулировать экономический рост, приняв программу возврата переплаченных налогов. Предположим, что вам возвращено 600 долл, и вы потратили на дополнительные товары и услуги 80% этой суммы, и каждый человек, которому вы заплатили, также потратил 80% своих денег и так далее. В соответствии с принципом мультипликатора в экономике снижение налога на 600 долларов вызывает лавинообразный эффект. Какая общая сумма при этом будет потрачена, если рассматриваемый процесс длится бесконечно?
Решение. Необходимо вычислить сумму бесконечного геометрического ряда, в котором первый член равен ai = 0,8 • 600 = 480 долл., а г = 0,8. Используя формулу (Б.8), получим следующий результат.
Итак, предполагая, что процесс будет протекать так, как мы его описали, можно ожидать, что возврат налогов суммой 600 долл, приведет к увеличению расходов на 2400 долл. ■
Упражнение Б.12.
Повторите решение примера Б.12, если налоги возвращаются в размере 1000 долл.
Ответы к упражнениям
Б.6. 1) Геометрическая прогрессия со знаменателем г = Прогрессия не является арифметической.
2) Арифметическая прогрессия с разностью d = 5. Прогрессия не является геометрической.
3) Последовательность не является ни арифметической, ни геометрической прогрессией.
Б.7. 1) 139.
2) —2.
Б.8. -960.
Б.9. 10 672.
Б.10. 1063,66.
Б.11. 1830.
Б.12. 4000.


Приложение Б. Специальные темы
887
Практикум Б.2
А В задачах 1 и 2 необходимо по первым трем элементам последовательности распознать вид прогрессии, вычислить разность или знаменатель, а также следующие два члена.
1. Определите, является ли данная последовательность арифметической или геометрической прогрессией.
а) -11,-16,-21,... б) 2,-4,8, ...
в) 1,4, 9, ... г)
7 7 2 16 18
2. Определите, является ли данная последовательность арифметической или геометрической прогрессией.
а) 5, 20, 100, ... б) -5, -5, -5, ...
в) 7; 6,5; 6; ... г) 512, 256, 128, ...
Б В задачах 3-8 необходимо распознать вид прогрессии и вычислить ее сумму.
Е (-i)fe+1. fc=l
200
4. S3.
/с=1
6. 3 - 9 + 27 З20.
7. 5 + 4,9 + 4,8 + • • ■ + 0,1.
1 -
1
10Q2’
Пусть ai, аг, аз,ап,... — арифметическая прогрессия. В задачах 9-14 необходимо
вычислить указанные величины.
9. 	а\ = 7\ d = 4, аг = аз —
11. 	ai = 2, d = 4, й21 = ?, S31 = 2.
13. ai = 18, П20 = 75, S20 = 7.
10. 	ах = —2, d = -3, а2 = 7,а3 = 7.
12. 	ai = 8, d = —10, ai5 = ?, S23 = ?
14. 	ai = 203, азо — 261, S30 = ?.
Пусть а±, а2, а3, ..., ап, ... — геометрическая прогрессия. В задачах 15-24 необходимо вычислить указанные величины.
15. ai = 3, г = —2, а2 = ?, а3 = ?, а4 =
16. ai = 32, г = — -, а2 = 7, аз = ?, а4
17. ai = 1, 07 = 729, г = —3, S7 = ?.
19. 	ai = 100; г = 1,08; а10 = ?.
21. ai = 100, ад = 200, г = 7.
23. 	ai = 500; г = 0,6; Slo = ?; = ?.
25. S4i = £ (3k + 3) = ?.
k—1
18. 	ai = 3, a7 = 2187, r = 3, S7 = ?.
20. 	ax = 240; r = 1,06; ai2 = ?.
22. 	ai = 100, аю = 300, r = ?.
24. 	ai = 8000; r = 0,4; Si0 = ?; = 7.
50
26. 	S5o = E (2k - 3) = 7.
k=l
27. Ss = £ (—2)*-1 = ?. 28. S8 = £ 2k = ?.
fc=l fc=l
29. Вычислите сумму всех нечетных чисел, которые больше 12 и меньше 68.
30. Вычислите сумму всех четных чисел, которые больше 23 и меньше 97.


888
Часть IV. Приложения
31. 	Вычислите сумму бесконечного геометрического ряда (если она существует).
а) 2,4,8,...
32. 	Вычислите сумму бесконечного геометрического ряда (если она существует).
а) 16,4,1,...
б) 1,-3,9,...
В
33. Вычислите сумму /(1) + /(2) 4- /(3) + • —И /(50), если /(ж) = 2х — 3.
34. Вычислите сумму р(1) + р(2) + <?(3) + • • • + д( 100), если g(t) = 18 — 3t.
35. Вычислите сумму /(1) + /(2) + /(3) 4 h /(10), если /(я) = (1)*.
36. Вычислите сумму р(1) 4- #(2) 4- #(3) 4- • • • 4- <?(10), если д(х) = 2х.
37. Докажите, что сумма первых п нечетных положительных целых чисел равна п2.
38. Докажите, что сумма первых п четных положительных целых чисел равна п4-п2.
*39. Если г = 1, то ни первая, ни вторая формулы для суммирования конечных геометрических рядов не корректны. Выведите формулу для вычисления суммы конечного геометрического ряда, если г — 1.
* 40. Можно ли утверждать, что если все члены бесконечного геометрического ряда
меньше единицы, то его сумма меньше 1000? Аргументируйте свой ответ.
* 41. Существует ли конечный геометрический ряд с параметрами ai = 1 и ап = 1,1,
сумма которого равна 100? Аргументируйте свой ответ.
* 42. Существует ли конечный геометрический ряд с параметрами ai = 1 и ап — 1,1,
сумма которого равна 105? Аргументируйте свой ответ.
* 43. Существует ли бесконечный геометрический ряд с параметром = 10, сумма
которого равна 6? Аргументируйте свой ответ.
*44. Существует ли бесконечный геометрический ряд с параметром — 10, сумма которого равна 5? Аргументируйте свой ответ.
Применение математики
Экономика и бизнес
45. Погашение займа. Один человек взял в долг 4800 долл, и обязался погасить заем за два года, выполняя ежемесячные платежи. При этом он согласился каждый месяц выплачивать по 200 долл, и 1% оставшейся суммы. Сколько всего денег он выплатит за два года?
46. Погашение займа. Один человек взял в долг 5400 долл, и обязался погасить заем за 18 месяцев, выполняя ежемесячные платежи. При этом он согласился каждый месяц выплачивать по 300 долл, и 1,5% оставшейся суммы. Сколько всего денег он выплатит за 18 месяцев?
47. Субсидирование экономики. Правительство приняло программу субсидий, в рамках которой населению выплачены 5 000 000 долл. Предположим, что каждый гражданин или министерство, получившие деньги, потратили 70% этой суммы,


Приложение Б. Специальные темы
889
а каждый получатель денег, также потратил 70% от нее и так далее. Насколько увеличатся расходы (ai = 3 500 000)?
48. Субсидирование экономики. Правительство снизило налоги, в результате чего каждому гражданину были возвращены налоги в сумме 1200 долл. Предположим, что они в среднем тратят 65% этой суммы, а все получатели этой суммы также тратят 65% от нее и так далее. Насколько увеличатся расходы людей?
49. Сложный процент. Предположим, инвестор положил в банк 1000 долл, под 5% годовых. Обозначим через А сумму денег, лежащих на счету через п лет. Стоимость капитала, рассчитанная за каждый год, образует геометрическую прогрессию со знаменателем 1 -I- 0,05 = 1,05. Вычислите суммы, которые будет лежать на счету через 10 и 20 лет. (Подсказка. Нарисуйте временную диаграмму начислений.)
50. Сложный процент. Предположим, инвестор положил в банк Р долл, под 100г% годовых. Обозначим через А сумму денег, лежащих на счету через п лет. Стоимость капитала, рассчитанная за каждый год, образует геометрическую прогрессию со знаменателем 1 + г. Запишите формулу для вычисления суммы, которая будет лежать на счету через п лет. (Подсказка. Нарисуйте временную диаграмму начислений.)
Б.З. Бином Ньютона
■ Факториал
■ Доказательство теоремы о биноме Ньютона
Бином Ньютона, имеющий вид (а+5)п, встречается намного чаще, чем можно было бы предположить. Коэффициенты разложения бинома Ньютона играют важную роль в теории вероятностей. Биномиальная формула позволяет разложить бином Ньютона при любом натуральном числе п. Поскольку в эту формулу входят факториалы, сначала необходимо дать определение этого понятия.
Факториал
Факториалом натурального числа п, обозначаемым как п!, называется произведение первых п натуральных чисел. Факториал нуля по определению равен единице.


890
Часть IV. Приложения
Пример Б.13 (Факториалы). Вычислите следующие величины. 8! 8-7!
1. 	5! = 5 • 4 • 3 ■ 2 • 1 = 120. 2. - = —- = 8.
7! 7!
,10! 10-9-8-7! _
’■ 7' 7- ™
Упражнение Б.13.
Вычислите следующие величины.
1. 4!
Во многих приложениях математики и статистики используется следующая важная формула.
Если 0 г п, то
Пример Б.14 (Вычисление Сп>г). Вычислите следующие величины.
1 С 9! 9!_9-87!_
L Сэ’2 2! (9-2)! 2!7! 2-7! 36'
2 С 5! - 5! - 5! - 1
’ 5,5 5! (5-5)! 5!10! 5!
Упражнение Б.14.
Вычислите следующие величины.
1. С5,2- 2. Сб,0-
Доказательство теоремы о биноме Ньютона
Для начала разложим бином Ньютона при некоторых небольших числах п.
(а 4* 6)1 = d 4- 6,
(a -J- 6)2 = а2 2а6 4~ 62,
(а Я- 6)3 — а3 4~ За2 6 4“ Заб2 4- 63,
(а 4- 6)4 = а4 4- 4а36 4- 6а262 4- 4а63 4- 64,
(а 4- 6)5 = а5 + 5а46 4- 10а362 4- 10а263 4- баб4 4- б5.
Выводы
1. Разложение бинома (а 4- б)п состоит из n + 1 членов.
2. Степени числа а слева направо уменьшаются на единицу.
3. Степени числа 6 слева направо увеличиваются на единицу.
4. Сумма степеней чисел а и 6 в каждом слагаемом равна п.


Приложение Б. Специальные темы
891
5. 	Коэффициент при каждом слагаемом получается из коэффициента предыдущего слагаемого путем его умножения на предыдущий показатель степени числа а и деления на номер этого члена в биномиальном разложении. Например, в разложении бинома (а + Ь)4 коэффициент при третьем слагаемом получается из коэффициента при втором слагаемом путем умножения числа 4 (коэффициента второго слагаемого) на число 3 (показатель степени числа а во втором слагаемом) и деления на число 2 (номер предыдущего члена). (Иначе говоря, коэффициент в третьем слагаемом равен (4 • 3)/2 = 6.)
Сформулируем эти свойства в более общем виде.
Итак, мы получили формулу для вычисления коэффициентов разложения бинома Ньютона. (Формальное доказательство этой формулы, основанное на принципе математической индукции, выходит за рамки нашей книги.)
Бином Ньютона
(а + b}n = Cnfian + СпЛап-Ч + Сп,2ап~2Ь2 + ■■■ + Сп,пЬп.
Пример Б.15 (Разложение бинома Ньютона). Разложите в ряд бином (u + г?)6.
Решение.
(и + г»)6 = Сб,о^6 + C6,iu5v + C6)2^4v2 +
4" Сб,зи2и4 + С6,4Л4 + Cq^uv^ 4- C6,6V6 = = и6 + 6u5v 4- 15ti4v2 4- 2O'u3,u3 4- 15iz2v4 4- 6?w5 4- v6.
Упражнение Б.15.
Разложите в ряд бином (х 4- 2)5. В
Пример Б. 16 (Разложение бинома Ньютона). Вычислите шестой член разложения бинома (х — I)18.
Решение.
Шестой член = Cis,5^13(-1)5
5! (18 — 5)!Ж
• (-1) = -8568а?13.


892
Часть IV. Приложения
Упражнение Б.16.
Вычислите четвертый член разложения бинома (х - 2)20. .
Задание Б.5.
1. Используя формулу для вычисления величины Cn>r, найдите следующую сумму.
Сб,о + C6,i + Сб,2 4“ С*б,з И- Сб,4 4- С*6,5 4- Сб,б-
2. Запишите разложение бинома Ньютона при следующих параметрах: п = 6, а = 1 и b = 1. Сравните результат с ответом, полученным при решении п. 1.
3. Вычислите следующую сумму для произвольного натурального числа п.
^*п,0 4“ Сп,1 4“ £п,2 4“ ’ * ’ 4~ Сп,п- в
Ответы к упражнениям
Б.13.
1)
24.
2)
7.
3)
336.
Б.14.
1)
10.
2)
1.
Б.15.
X5
+ Юж4 + 40а;3 + 80а;2 + 80ж + 32.
Б.16.
-9
420а;*  17.
Практикум Б.З
А В задачах 1 и 2 необходимо по первым трем элементам последовательности распознать вид прогрессии, вычислить разность или знаменатель, а также следующие два члена.
Б
1.
5.
9.
6!.
2. 7!.
3
9! ’
, 20!
4' 19!’
12!
6 10!
7. —.
2!3!
8 2L 8‘ 3!4!’
“эТ
6--бГ
6!
7!
”• 4!(7 —4)!'
И.
3!17!
12.^
50!2!
5!(6 — 5)! ’
^5,3-
14. С7>3.
15. С6,5.
16. С7,4.
18. Сб>5.
19. С18Д5-
20. С18,з
13.
17.
Разложите в ряд каждый из биномов, указанных в задачах 21-26.
21. (а4-&)4. 22. (m + n)5. 23. (х — I)6.
24. (и - 2)5. 25. (2а - Ь)5. 26. (х - 2у)5.
Вычислите указанный член разложения биномов, указанных в задачах 27-32.
27. 	(ж — I)18; 5-й член. 28. (х — З)20; 3-й член.


Приложение Б. Специальные темы
893
29. (р + д)15; 7-й член. 30. (р + д)15; 13-й член.
31. (2х + у)12; 11-й член. 32. (2ж + р)12; 3-й член.
В
33. Докажите, что Сп,0 = Сп,п при п 0.
34. Докажите, что СП)Г = СПуП-г при п г 0.
35. Приведенная ниже диаграмма называется треугольником Паскаля. Напишите следующую строку этой диаграммы. Как эти числа связаны с коэффициентами биномиального разложения?
* 36. Почему сумма элементов в каждой строке треугольника Паскаля представляет
собой некую степень числа 2? (Подсказка. Положите а = b = 1 и примените разложение бинома.)
* 37. Почему знакопеременная сумма элементов в каждой строке треугольника Пас¬
каля (например, 1-4 + 6 — 4 + 1) равна нулю?
*38. Докажите, что Cn,r = n~^C>n,r-i при п > г > 1.
*39. Докажите, что Cn>r_i + Cn>r = Cn+i>r при n > г > 1.
Б.4. Приращения и дифференциалы
■ Приращения
■ Дифференциалы
■ Приближенные вычисления с помощью дифференциалов
Понятие дифференциалов использовалось в главах И и 12 при изучении методов вычисления неопределенных интегралов. Настало время поглубже разобраться в понятии дифференциала, используя свойства приращений.
Приращения
Иногда необходимо определить, как изменяются значения функции у — f(x) при небольших изменениях переменной х. Например, если у — это прибыль, а х — цена товара, необходимо выяснить, как изменится прибыль при небольших колебаниях цены.
Пусть у = f(x) = х3 и переменная х изменяется от 2 до 2,1. Тогда величина у изменяется от у = /(2) = 23 = 8 до у = /(2,1) = 2,13 = 9,261. Изменения величин х и у называются приращениями и обозначаются как Дж и Др соответственно (читается


894
Часть IV. Приложения
как “дельта-икс” и “дельта-игрек”). Итак, мы можем записать следующие вычисления.
Дх = 2,1 — 2 = 0,1. Изменение переменной х
Лу = /(2,1) - /(2) = 2,13 - 23 =
= 9,261 — 8 = 1,261. Изменение переменной у
Следует помнить, что приращения Дж и Дт/ не являются произведениями — здесь оба символа (и дельта, и буква) образуют единое обозначение.
Приращения
Дх = х2 — xi Ду = У2 - У1 =
х2 = Xi + Дх = /(х2) - /(xj = f(xi + Дх) - f(xi)
Приращение Д?/ представляет собой изменение величины у, когда переменная х изменяется на Дж. Приращение Дж может быть как положительным, так и отрицательным.
(Примечание. Приращение Дт/ зависит от функции /, переменной ж и приращения Дж.)
Пример Б.17 (Приращения). Рассмотрим функцию у = /(ж) =
1. Вычислите величины Дж, Д1/ и Дт//Дж для чисел Ж1 = 1 и ж2 = 2.
2. Вычислите величину для чисел Ж1 = 1 и Дж = 2.
Решение.
1. 	Дж = ж2 — Ж1 = 2 — 1 = 1.
Ду = f Ы - f Ы = /(2) - /(1) = | | = |.
Ду = / (х2) - f (да) = 1 = 3
Дж ж2 — Ж1 1 2
/ (хх + Дх) — / (хх) = /(1 + 2) —/(1) =
Дж 2
/(3)-/(1) ы 4 п
2 2 2' 1
2.


Приложение Б. Специальные темы
895
Упражнение Б. 17.
Рассмотрим функцию у = /(х) = х2 + 1.
1. Вычислите величины Дх, Ау и Д?//Дх для чисел х\ = 2 и Х2 = 3.
2. Вычислите величину для чисел xi = 1 и Дх = 2. в
В примере Б. 17 мы столкнулись с новым обозначением уже известной нам величины
f(x + h) — /(х)
(Б.9)
h
Как правило, буква h обозначает приращение Дх. Итак, выражение (Б.9) принимает следующий вид.
Следовательно, производную можно определить как предел отношения приращений (если этот предел существует), т.е.
ИЛИ
/(х +Дх) -/(х)
Дх
/' (х) = lim
Дт—»оо
(Б. 10)
Задание Б.6.
Предположим, что у = f(x) — функция, областью определения которой является вся числовая ось. Опишите область значений функции /, если приращение Дт/ всегда равно нулю.
Дифференциалы
Предположим, что предел отношения (Б. 10) существует. Тогда при малых приращениях Дх отношение приращений Д?//Дх является хорошей аппроксимацией производной /'(х). С другой стороны, производная /'(х) является хорошей аппроксимацией отношения приращений Ду/Дх. Запишем этот факт следующим образом.
(Б.11)
Умножая обе части соотношения (Б.11) на Дх, получим следующий результат.
(Б.12)
Из уравнения Б.12 следует, что величина /'(х)Дх является хорошей аппроксимацией приращения Д1/, когда приращение Дх мало.
Принимая во внимание большое практическое и теоретическое значение величины /'(х)Дх, исследователи присвоили ему особое название — дифференциал — и стали обозначать отдельным символом — dy, или df.
dy = f'(x)Ax, или df = f'(x)Ax.


896
Часть IV. Приложения
Например,
d (2х3) = (2х3)' Дх = 6х2  1Дх, d(x) = (х)'Дх = 1Дх = Дх.
Во втором примере скобки после символа d можно опустить.
dx = Ах.
Дифференциалы
Если у = f(x) — дифференцируемая функция, то дифференциалом dy, или df, называется произведение производной /'(х) и приращения dx, где dx = Ах.
dy = f(x)dx или df = ff(x)dx,
где
dx = Ах.
Примечание. Дифференциал dy (или df) фактически является функцией, зависящей от двух независимых переменных — х и dx. Изменение хотя бы одной из них или обеих приводит к изменению значения dy (или df).
Пример Б.18 (Дифференциалы). Вычислите дифференциал функции /(х) = х2 + Зх при следующих параметрах.
1. х = 2, dx = 0,1. 2. х = 3, dx = 0,1. 3. х = 1, dx = 0,02.
Решение.
dy — f'(x)dx = (2х + 3)dx
1. 	При х = 2 и dx = 0,1 dy = (2 • 2 + 3) • 0,1 = 0,7.
2. 	При х = 1 и dx = 0,1
^ = (2-3 + 3)-0,1 = 0,9.
3. 	При х = 1 и dx = 0,02
dy = (2-1 + 3)-0,02 = 0,1.
Упражнение Б.18.
Вычислите дифференциал функции /(х) = у/х + 3 при следующих параметрах.
1. х = 4, dx = 0,1.
2. 	х = 9, dx = 0,12.
3. 	х = 1, dx = 0,01.
Итак, у нас есть две интерпретации символа dy/dx. Скажем, в примере Б. 18 отношение dy/dx для функции /(х) = х3 + Зх при х = 2 и dx = 0,1 можно вычислять по-разному:
или
Производная
dy = 0,7
dx 0,1
Отношение дифференциалов


Приложение Б. Специальные темы
897
Приближенные вычисления с помощью дифференциалов
Выше было показано, что при малых приращениях Да? справедливо приближенное равенство
(я), или &y^f\x)kx.
Кроме того, поскольку
dy = f'(x)dxy
имеет место приближенное равенство
Д|/ « dy.
Иначе говоря, величину Дт/ можно считать приближением дифференциала dy.
Чтобы дать геометрическую интерпретацию этого факта, необходимо вспомнить основные свойства наклона. Как показано на рис. Б.1, вертикальное изменение положения линии равно произведению наклона на горизонтальное изменение.
Рис. Б.1. Геометрическая интерпретация дифференциала
Рассмотрим касательную к графику функции у = f(x) (рис. Б.2). Поскольку значение производной /'(х) представляет собой наклон касательной в точке х, а дифференциал dx — горизонтальное смещение касательной, то вертикальное смещение касательной равно dy = f'(x).
Пример Б.19 (Графики и таблицы приращений и дифференциалов).
1. Постройте графики функций Дт/ и dy (относительно независимой переменной Дх = dx) для функции /(х) = бх — х2 при х = 2.
2. Вычислите значения функций Д1/ и dy (относительно независимой переменной Дх = dx) для функции /(х) = бх — х2 при х = 2 и Дх = dx = 0,1; 0,2 и 0,3.
Решение.
1. Ьу = /(2 + Дх) - /(2) = 6(2 + Дх) - (2 + Дх)2 - 8.
Поскольку /'(х) = 6 — 2х, то dy = (6 — 2 • 2)dx = 2dx. Для построения графиков этих функций можно воспользоваться графической утилитой (рис. Б.З). (Обратите внимание на то, что в графической утилите независимая переменная Дх обозначается буквой X.) Из рис. Б.З следует, что дифференциал представляет собой линейное приближение приращения, причем при уменьшении значений Дх = dx оно становится все более точным.


898
Часть IV. Приложения
Рис. Б.2. Геометрическая интерпретация дифференциала
Рис. Б.З. Геометрическая интерпретация дифференциала
2. Требуемые величины можно вычислить с помощью графика (рис. Б.З) (Дт/ = 0,19 при Дх = 0,1) и записать в виде таблицы (рис. Б.4). Для Дх = dx = 0,1; 0,2 и 0,3 соответствующие значения приращения Дт/ равны 0,19; 0,36 и 0,51, а дифференциал dy равен 0,2; 0,4 и 0,6. ■
Vi
Vz
.1
.2
.2
.4
.3
.51
.6
Vi=.l*
Рис. Б.4. Таблица приращений
Упражнение Б.19.
Повторите решение примера Б.19 при х = 4, Дх — dx — —0,1; —0,2 и —0,3.


Приложение Б. Специальные темы
899
Задание Б.7.
Предположим, что у = /(х) — дифференцируемая функция. Объясните, почему график функции dy (зависящей от независимой переменной Дх) представляет собой прямую линию, проходящую через начало координат, при фиксированном значении х. ■
Пример Б.20 (Затраты и доход). Некая компания производит и продает х транзисторных радиоприемников в неделю. Затраты и доход описываются следующими формулами.
С(х) = 5000 -F 2х,
R(x) = 10х - , 0 х 8000.
Найдите приближенные изменения дохода и прибыли, если производство возрастет с 2000 до 2010 единиц в неделю.
Решение. Аппроксимируем приращения ДТ? и ДР дифференциалами dR и dP соответственно, используя величины х = 2000 и dx = 2010 — 2000 = 10.
х^
Р(х) = 10х — ———,
v 7 1000’
dR = R'(x)dx = (10 - dx = (10 - ) • 10 = 60 долл, в неделю,
\ 500/ \ 500 /
Р(х) = Я(х) - С(х) = 10х - - 5000 - 2х = 8х - - 5000,
dP = P'(x)dx = ^8 — dx = ^8 — • 10 = 40 долл, в неделю.
Упражнение Б.20.
Повторите решение примера Б.20, если объем производства возрастает с 6000 до 6010. ■
Сравнивая результаты решения примера Б.20 и упражнения Б.20, легко увидеть, что увеличение объема производства с 2000 до 2010 единиц в неделю приводит к увеличению дохода и прибыли, однако увеличение объема производства с 6000 до 6010 единиц, наоборот, приводит к уменьшению этих показателей.
Завершая обсуждение, необходимо отметить, что, несмотря на то, что дифференциалы можно использовать для аппроксимации определенных величин, погрешность такого приближения в некоторых ситуациях может оказаться существенной. В принципе, чем меньше приращение Дх, тем точнее аппроксимация Дт/ « dy.
Ответы к упражнениям
Б.17. 1) Дх = 1, Дт/ = 5, Дт//Дх = 5.
2) 4.
Б.18. dy = -^-=dx.
2у/Х


900
Часть IV. Приложения
1) 0,025.
2) 0,02.
3) 0,005.
X
Vi
Vz
1 1 1
.6 .4 .2
Vi=.19
Б.20. dR = —20 долл./неделю, dP = —40 долл./неделю.
Практикум Б.4
А В задачах 1-6 необходимо вычислить указанные величины для функции у — f(x) = Зт2.
1. Дт, Д?/, Д^/Дт при Ti = 1 и т2 = 4.
2. 	Дт, Дт/, Дту/Дт при Ti = 2 и т2 = 5.
3.
4.
f (д?1 + Дт) - /(ti) Дт
/(Т1 + Дт) - f (тх) Дх
при тх = 1 и т2 = 2.
При XI = 2 И Т2 = 1.
5. 	Дт//Дт при тх = 1 и т2 = 3.
6. 	Дт//Дт при тх = 2 и т2 — 3.
В задачах 7—12 необходимо вычислить дифференциал dy указанных функций. т*  1 2
8. у = 200т .
У 30
10. у = т3(60 — т).
7.
9.
у — 30 + 12т2 — т3.
12. у = 52лД.
11.
590
3/ /— '
\/Х
Б В задачах 13 и 14 необходимо вычислить указанные величины для функции у = /(т) = = Зт2.
f (2 + Дт) - f (2)
13. а) Вычислите величину —
Дт
f f (2)
б) К чему стремится величина — при Дт —> 0?
Дх


Приложение Б. Специальные темы
901
f (3 + Дж) - f (3)
14. а) Вычислите величину
/\т
/(3 4- Аж) - f (3)
б) К чему стремится величина при Дж —► 0?
Дж
В задачах 15 и 18 необходимо вычислить величину dy для функции у = fix) = Зж2.
15. у = (2ж 4- I)3. 16. ?/ = (Зж 4- 5)5.
ж ж2
У *2+ 9 У (х + 1)2
В задачах 19-22 необходимо вычислить величины dy и Дт/ для указанных функций.
19.
20.
у = f(x) = ж2 — Зж 4- 2, ж = 5, dx = Нх = 0,2.
У = = 30 4- 12ж2 — ж3, ж = 2, dx = Их = 0,1.
у = f(x) = 75 ^1 — , ж = 5, dx = Дж = —0,5.
у = /(ж) = 100 ^ж —ж = 2, dx = Нх = —0,1.
Куб, длина сторон которого равна 10 дюймам, покрывается слоем пластмассы толщиной 0,2 дюйма. Оцените объем оболочки, используя дифференциалы.
21.
22.
23.
24. 	Сфера, радиус которой равен 5 см, покрывается слоем льда, толщиной 0,1 сантиметра. Оцените объем ледяной сферы, используя дифференциалы. (Напомним, что V = |7ГГ3.)
В
В задачах 25-28 необходимо выполнить следующие задания.
1) Постройте график функций Ну и dy относительно независимой переменной Их = dx по заданной функции f(x) в указанной точке х.
2) Вычислите величины Ну и dy для функции f(x) при указанных значениях х и Нх = = dx.
25. /(ж) = ж2 4- 2ж 4- 3; ж = —0,5; Дж = dx = 0,1; 0,2 и 0,3.
26. /(ж) = ж2 4- 2ж 4- 3; ж = —2; Дж — dx = —0,1; —0,2 и —0,3.
27. /(ж) = ж3 — 2ж2; ж = 1; Дж = dx = 0,05; 0,10 и 0,15.
28. /(ж) = ж3 — 2ж2; ж = 2; Дж = dx = —0,05; —0,01 и —0,15.
В задачах 29-32 необходимо выяснить корректность приведенных утверждений, аргументировав свой ответ.
* 29. Если график функции у = f(x) представляет собой прямую линию, то функции Ну и dy относительно независимой переменной Дж = dx для функции /(ж) в точке ж = 3 совпадают.
*30. Если график функции у = f(x) представляет собой параболу, то функции Ну и dy относительно независимой переменной Дж = dx для функции /(ж) в точке ж = 0 совпадают.
*31. Предположим, что функция у = f(x) является дифференцируемой, а ее областью определения является вся числовая ось. Если все дифференциалы dy в точке ж = 2 равны нулю, то функция /(ж) является постоянной.


902
Часть IV. Приложения
*32. Предположим, областью определения функции у = f(x) является вся числовая ось. Если все приращения Дт/ в точке х = 2 равны нулю, то функция f(x) является постоянной.
33. Вычислите дифференциал dy, если у = \/Зх2 — 2х + 1.
34. Вычислите дифференциал dy, если у — (2х2 — 4) у/х + 2.
35. Вычислите дифференциал dy и приращение Дт/, если у = 52у/х, х — 4 и Аж = = dx = 0,3.
36. Вычислите дифференциал dy и приращение Дт/, если у = ^=, х = 64 и Дх = = dx = 1.
Применение математики
Решите следующие задачи, используя дифференциалы.
Экономика и бизнес
37. 	Реклама. Руководство компании выяснило, что объем продаж N зависит от расходов на рекламу х тыс. долл.
7V(x) = 60ж — ж2, 5 < х 30.
Насколько увеличится объем продаж при увеличении расходов на рекламу с 10 до 11 тыс. долл, или с 20 до 21 тыс. долл.?
38. Зависимость цены от спроса. Предположим, что спрос (в фунтах) на шоколадные конфеты в сети бакалейных магазинов при цене х долл, за фунт описывается формулой
D = 1000-40а;2, 0 х < 5
Насколько увеличится спрос, если цена вырастет с 3,00 долл, до 3,20 долл.?
39. Средние затраты. Средние затраты на производство теннисных ракеток С описываются следующей формулой.
С =
х 1.
Здесь х — объем производства в час. Насколько изменятся средние затраты на производство ракеток, если объем производства увеличится с 20 до 25 ракеток в час или с 40 до 45 ракеток в час?
40. 	Доход и прибыль. Предприятие ежемесячно производит и продает х телевизоров. Формулы, описывающие затраты и доход, имеют следующий вид.
С(ж) = 72 000 + бОя,
х2
R(x) = 200ж — —-, 0 < ж < 6000.
oU
Насколько увеличится доход и прибыль, если объем производства увеличится с 1500 до 1510 телевизоров в месяц или с 4500 до 4510 телевизоров в месяц?


Приложение Б. Специальные темы
903
Биологические науки
41. Частота пульса. Средняя частота пульса у (ударов в минуту) у здорового человека ростом х дюймов описывается следующей формулой.
590 у = 30 х 75.
у/х
Насколько изменится частота пульса при изменении роста с 36 до 37 дюймов или с 64 до 65 дюймов?
42. Измерения. Птичье яйцо отдаленно напоминает сферу. Предположим, что внутренний радиус яйца равен 5 мм, а внешний — 5,3 мм. Чему равен объем скорлупы. (Напомним, что V = |тгт3.)
43. Медицина. Пациент принимает лекарство для расширения сосудов. Предположим, что радиус артерии увеличивается с 2 до 2,1 мм. Насколько увеличится площадь ее поперечного сечения? (Площадь поперечного кругового сечения артерии равна А = 7гг2.)
44. Чувствительность к лекарству. Через час после приема х мг лекарства, температура тела человека Т (по шкале Фаренгейта) описывается следующей формулой.
Т = X2 (1 - , 0 X 6.
Аппроксимируйте температуру тела при следующих условиях.
а) Доза лекарства увеличивается с 2 до 2,1 мг.
б) Доза лекарства увеличивается с 3 до 3,1 мг.
в) Доза лекарства увеличивается с 4 до 4,1 мг.
Социальные науки
45. Обучение. Количество слов в минуту, которое может напечатать человек после t недель обучения, описывается следующей формулой.
N = 75 (1 - |) , 3 х 20.
Насколько изменится эта величина, если продолжительность обучения увеличится с 5 до 5,5 недель?
46. Обучение. Количество слов в минуту, которые может запомнить человек за х часов, описывается следующей формулой.
у = 52\/я, 0 х С 9.
Насколько изменится эта величина, если продолжительность обучения увеличится с 1 до 1,1 часа или с 4 до 4,1 часа?
47. Политика. Количество избирателей в определенном городе с течением времени изменяется по следующей формуле.
N(i) = 30 + 12t2 -t3, 0 t 8.


904
Часть IV. Приложения
Здесь t — количество лет. Как изменится количество избирателей в данном городе при следующих условиях?
а) Величина t изменяется с 1 до 1,1 года.
б) Величина t изменяется с 4 до 4,1 года.
в) Величина t изменяется с 7 до 7,1 года.
Б.5. Правило Лопиталя
■ Введение
■ Правило Лопиталя и неопределенные выражения вида 0/0
■ Односторонние пределы и пределы на оо
■ Правило Лопиталя и неопределенные выражения вида оо/оо
Введение
Умение вычислять разнообразные пределы — один из навыков, необходимых для успешного применения методов математического анализа. Пределы играют главную роль при построении теории производной, а также являются важным инструментом для построения графиков. Основные задачи, касающиеся пределов, были рассмотрены в главах 12 и 15. Чтобы эффективно решать подобные задачи, необходимо познакомиться с некоторыми дополнительными методами вычисления пределов.
В этом разделе будет рассмотрен важный и часто применяемый метод вычисления пределов дробных выражений под названием правило Лопиталя. Это правило названо в честь французского математика маркиза де Лопиталя (Marquis de L’Hopital) (1661-1704), которого считают автором первого учебника по математическому анализу. Чтобы пользоваться правилом Лопиталя, необходимо очень хорошо разбираться в свойствах пределов отдельных элементарных функций. На рис. Б.5 представлен обзор пределов некоторых функций, содержащих различные степени переменной х.
lim х = —оо
-3 ы=°° lim Д =оо х-»0“ х lim Д =ос
б)У=*
3
11тД =0
X->00
lim 5? =0
х—*—ос
а),У=х
Рис. Б.5. Пределы, содержащие различные степени х


Приложение Б. Специальные темы
905
Пределы на рис. Б.5 легко обобщить на функции вида /(ж) = (х — с)п и д(х) = = 1/(х — с)п. В общем случае, если п — нечетное целое число, пределы, содержащие выражения вида (х — с)п или 1/(х — с)п, в которых число х стремится к числу с (или ±оо) ведут себя так же, как пределы, содержащие величины х и 1/х9 в которых число х стремится к нулю (или ±оо). Если п — четное целое число, то пределы, содержащие эти выражения, ведут себя так же, как пределы, содержащие величины х2 и 1/ж2, в которых переменная х стремится к нулю (или ±оо).
Пример Б.21 (Пределы, содержащие степени х — с).
1.
lim
х—2
5
(х-2)4
= 00.
Сравните с lim — на рис. Б.5 х—>0 я>
2. 	lim « = — оо.
(ж -I- I)3
Сравните с lim — на рис. Б.5 ас—►О- ®
3.
lim
х—>оо
4
(х - 9)6
= 0.
Сравните с lim — на рис. Б.5 х —>оо Xя
4. 	lim Зт3 = — оо.
х—» — оо
Сравните с lim х на рис. Б.5
X—► — оо
Упражнение Б.21.
Вычислите следующие пределы.
7
6
1. lim ,.
Z-3+ (х - З)5
2. lim тг.
х—-4 (х + 4)6
3. lim —~ .
(х + 2)
4. lim 5т4.
х—>оо
На рис. Б.6 повторно рассмотрены некоторые пределы, содержащие экспоненциальные или логарифмические функции.
а) у = ех
lim е~х = оо
х—00
6)у = е х
в) у = lnx
Рис. Б.6. Пределы, содержащие экспоненциальные и логарифмические функции
Пределы на рис. Б.6 также можно обобщить на случай других простых экспоненциальных и логарифмических выражений.


906
Часть IV. Приложения
Пример Б.22 (Пределы, содержащие экспоненциальные и логарифмические выражения).
1. lim 2е3х = оо.
Сравните с lim ех на рис. Б.6
2. lim 4е_5х = 0.
Сравните с lim е“® на рис. Б.6
3. lim In (х + 4) = оо.
Сравните с lim In х на рис. Б.6
4. lim In (х — 2) = —оо. х—>2+
Сравните с lim In х на рис. Б.6
®—>о+
Упражнение Б.22.
Вычислите следующие пределы.
1. lim 2е_6х.
2. lim Зе2х.
3. 	lim In (х + 4).
4. 	lim ln (х — 10).
Теперь, повторив свойства пределов некоторых основных функций, можно перейти к рассмотрению основной темы этого раздела, правила Лопиталя — мощного инструмента вычисления пределов определенных типов.
Задание Б.8.
Из рис. Б.6 следует, что
lim е х = 0 и lim In (1 + Зе х) = 0.
Существует ли предел
lim 1п(1+Зе-)?
х—»оо е х
Если да, то чему он равен? Обоснуйте ответ, используя графический метод.
Правило Лопиталя и неопределенные выражения вида 0/0
Напомним, что предел
является неопределенным выражением 0/0 (раздел 8.1), если
lim f (х) — 0 и lim д (х) = 0.
Свойство отношений пределов из раздела 8.1 в данном случае неприменимо, поскольку limx_+c д (х) = 0.
Предел неопределенных выражений 0/0 может как существовать, так и не существовать. Без дополнительного изучения нельзя сказать, какое из этих утверждений истинно.
Каждый из следующих пределов содержит неопределенное выражение 0/0.


Приложение Б. Специальные темы
907
Значение первого предела можно вычислить, выполнив некоторые алгебраические упро-
щения.
.. я;2-4 (я-2) (ж+ 2) .. z .
lim — = lim = lim (х + 2) = 4.
®->2 х-2 х->2 X - 2 х-> 2
Однако второй предел подобным образом найти нельзя. Вместо этого следует обратиться к чрезвычайно эффективному правилу Лопиталя, которое приводится без доказательства. Это правило можно применять к пределам, содержащим неопределенные выражения 0/0.
Теорема Б.1 (Правило Лопиталя для неопределенных выражений 0/0: вариант 1). Для действительного числа с, если f (х) = 0 и 1ш1ж_>с д (я) = 0, то
lim
х—»с
/(*)
9(х)
lim
х—>с
9' (®) ’
при условии, что второй предел существует или равен +оо или — оо.
Пример Б.23 (Правило Лопиталя). Вычислите предел lim^-^i
Решение. Этап 1. Убедимся, что правило Лопиталя применимо.
lim (ех — е) = е1 — е = 0 и lim (ж — 1) = 1 — 1 = 0. х—»1 х—>1
Итак, правило Лопиталя действительно применимо.
Этап 2. Применим правило Лопиталя.
lim
х—>1
выражение. .
р/° : А (е» _ е) ■
• = lim '
х — 1 : ®-»1 а . . !
= lim =
х—>1 1
Правило Лопиталя
Свойство пределов ■
е
1
Упражнение Б.23.
Вычислите предел lima;_>4 е*^4 • ■
Замечание. В правиле Лопиталя запись f{x)/gf(x) означает, что производная от f(x) делится на производную от р(х).
В правиле Лопиталя для раскрытия неопределенного выражения 0/0 производная числителя делится на производную знаменателя.


908
Часть IV. Приложения
Функции
g g*E
У1 = . И у2 =
х — 1 1
из примера Б.23 — это две разные функции (рис. Б.7), но обе функции имеют одно из тоже значение предела, число е, когда переменная х стремится к единице. Хотя функция у\ в точке х = 1 не определена, график функции у± позволяет проверить ответ, полученный при решении примера Б.23.
5
0
Yi
Yz
.9
2.5В6В
2.4596
.99
2.7047
2.В912
.999
1
2.7169 ERROR
2.715В
NWvH
1.001
2.719В
2.721
1.01
2.7319
2.7456
1.1
2.В5ВВ
3.0042
72=2.71828182846
Рис. Б.7. Вычисление предела с помощью графической утилиты
Пример Б.24 (Правило Лопиталя). Вычислите предел limx_>o ^4
Решение.
Этап 1. Убедимся, что правило Лопиталя применимо.
lim In (1 -I- х2\ = ln 1 = 0 и lim х4 = 0. я—О v 7 х—О
Итак, правило Лопиталя действительно применимо.
Этап 2. Применим правило Лопиталя.
выражение, о/о ; 1п(1 + а;2); lim — -
х—>0
d и dxX
х4
lim
х—>0
In (1 -I- Ж2)
Ж4
= lim
х—>0
4x3
Правило Лопиталя
= lim z—>0
1
2x2 (1 4- x2)
Алгебраическое преобразование
= oo.
Вертикальная асимптота в точке х = 0
Последнее выражение является следствием того, что прямая х = 0 служит вертикальной асимптотой для функции
= 2х2 (1 + z2)’
и по мере приближения величины х к нулю слева или справа значения f(x) становятся очень большими (рис. Б.8). ■


Приложение Б. Специальные темы
909
100
о
Рис. Б.8. График функции
f (Х) = 2x2(l+z2)
Упражнение Б.24.
Вычислите предел lim^i ^21)3 • ■
Пример Б.25 (Правило Лопиталя неприменимо). Вычислите предел lim^i
Решение.
Этап 1. Убедимся, что правило Лопиталя применимо.
lim In х = ln 1 = 0, но lim х — 1 0.
х—>1 х—*1
Увы, правило Лопиталя не применимо.
Этап 2. Вычислим предел, используя другой метод. В данном случае можно применить свойства отношений для пределов из раздела 8.1, откуда следует, что
lnx lim lnx lim — =
х->1 х lim х
In 1
~Г
= 0.
0
1
Следует отметить, что применение правила Лопиталя привело бы к неверному
результату.
d ,
lnx dx^nX г Vх
lim / lim = lim Ц- = 1.
x->l X ®-»l d x->l 1
diX ■
Упражнение Б.25.
Вычислите предел lim^o
Замечание. Как показано в примере Б.25, не все отношения, входящие в пределы, являются неопределенными выражениями 0/0.
Прежде чем использовать правило Лопиталя, необходимо обязательно убедиться, что оно применимо.
Пример Б.26 (Повторное применение правила Лопиталя). Вычислите предел
х2


910
Часть IV. Приложения
Решение,
Этап 1. Убедимся, что правило Лопиталя применимо.
lim х2 = 0 и lim (ех - 1 — х) = 0. х—>о х—>о
Итак, правило Лопиталя действительно применимо.
Этап 2. Применим правило Лопиталя.
выражение, ,
0/0 : d ~ \
х2 : : 2х
lim -л ; = lim , dx ; = lim
z—>о ех — 1 — х> х—>о d z ч : х—»о ех — 1
; —- \ех — 1 — х) ;
• dx •
Поскольку limx_>o 2ж = 0 и lim^o (ех — 1) = 0, новый предел также является неопределенным выражением 0/0 и к нему можно снова применить правило Лопиталя.
Этап 3. Применим правило Лопиталя повторно.
lim
х—>0
выражение, ,
°/о i —2х '
2х : Ад ;
— = lim ех -1 I »—.о а ;
: -1’;
lim — =
х->о ех
Таким образом,
.. я2 v 2т 1. 2
lim = lim = lim — = 2.
х—>0 ех — 1 — х I—>о ех — 1 х—>о ех
Подтверждение того, что предел при х —> 0 равен числу 2, приведено на рис. Б.9. На рисунке показан график функции
х2
ш= —i—
ех — 1 — х
и таблица отдельных значений у у.
Упражнение Б.26.
Вычислите предел limx_>o ~—~2~2ж• ■
Односторонние пределы и пределы на оо
Кроме пределов, в которых переменная х стремится к числу с, в главах 8 и 9 были рассмотрены односторонние пределы и пределы выражений, когда переменная х стремится к бесконечности. Правило Лопиталя справедливо также и в этих случаях.
Теорема Б.2 (Правило Лопиталя для неопределенных выражений 0/0: вариант 2 (для односторонних пределов и пределов на бесконечности)). Первый вариант правила Лопиталя (теорема Б.1) остается справедливым, если запись х —► с заменить везде, где она встречается, одной из следующих записей:
х —> с+, х —> с~, х —> оо, х —> —оо. а


Приложение Б. Специальные темы
911
X
Vi
‘.1 -.01 -.001 0 .001 .01 .1
2.0672
2.0067
Ж
1.9993
1.9933
1.9339
Vi=ERROR
Рис. Б.9. График и значения функции тц =
Например, если lima:_oo У (х) = 0 и lim^oo д (т) = 0, то
lim = Um
д' (ж) ’
при условии, что второй предел существует или равен +оо или — оо. Аналогичные правила можно записать для х —► с+, х —> с~ и х —> —оо.
Пример Б.27 (Правило Лопиталя для односторонних пределов). Вычислите предел lim^1+
Решение.
Этап 1. Убедимся, что правило Лопиталя применимо.
lim In х = 0 и lim (х — I)2 = 0.
х—*1+ X—>1+
Итак, правило Лопиталя действительно применимо.
Этап 2. Применим правило Лопиталя.
выражение,
о/о : lim ■"* j_)
X—►!+ (x — I)2 ■ X-
lim
х—►!+
lim
х—>1+
= 00.
Правило Лопиталя
Алгебраическое преобразование
Свойство пределов
Последний результат является следствием того, что
lim — = оо.
®->1+ х — 1
Упражнение Б.27.
Вычислите предел


912
Часть IV. Приложения
Пример Б.28 (Правило Лопиталя для односторонних пределов). Вычислите предел
Решение.
Этап 1. Убедимся, что правило Лопиталя применимо.
lim In (1 + е х) = In (1 + 0) = In 1 = 0 и х—юс v 7
lim е~х = 0.
х—>оо
Итак, правило Лопиталя действительно применимо.
Этап 2. Применим правило Лопиталя.
lim
х—юо
выражение , _
0/0 ; d п (л , -хм ;
ln(1 + e~*); lim ^[ ( )]j
I — 11И+г—»ос ;
I х |
: dx :
е~х
lim
я;—юо
= lim
х—>оо 1 е'
-e~*/(l + e-x) =
—е~х
1
—х
Правило Лопиталя
Алгебраическое преобразование
Свойство пределов
Упражнение Б.28.
Вычислите предел Ит^-оо
111(1+26*)
ех
I
Правило Лопиталя и неопределенные выражения вида оо/оо
В разделе 9.3 рассматривались методы вычисления пределов таких рациональных функций, как
2х2 4х3 Зх3
lim ——lim -—-. lim ———-.
х—>оо X3 + 3 X—>ос 2х2 + 5 х—>оо 5х3 + 6
Каждый из этих пределов является неопределенным выражением вида оо/оо. В общем случае, если lim /(х) = ±оо и lim g(x) = ±оо, то выражение
х—»с х—»с
х—>с g (Ж
называется неопределенным выражением оо/оо. Более того, во всех трех рассмотренных выше пределах выражение х с можно заменить выражениями х с+, х —> с“, х —> ос или х —> — оо. Можно показать, что правило Лопиталя также применимо и к этим неопределенным выражениям вида оо/оо.
Теорема Б.З (Правило Лопиталя для неопределенных выражений оо/оо: вариант 3). Первый и второй варианты правила Лопиталя для неопределенных выражений 0/0 справедливы также и в случае, если пределы функций f и g являются бесконечными, т.е. оба предела могут быть равны либо +оо, либо -оо. ■


Приложение Б. Специальные темы
913
Например, если lima._c+ / (ж) = оо и limI_c+ д (х) = —оо, то к выражению lim [f (х)/д (х)]
X—кут
можно применить правило Лопиталя.
Пример Б.29 (Правило Лопиталя для неопределенных выражений оо/оо). Вычисли- те предел .
Решение.
Этап 1. Убедимся, что правило Лопиталя применимо,
lim lnx = оо и lim х2 = оо.
х—>оо х—>ос
Итак, правило Лопиталя действительно применимо.
Этап 2. Применим правило Лопиталя.
lim
х—»ос
выражение,
оо/оо ! lnx ;
5—! = 11т Xz I х—>оо
— lnx дх
dx
= 0.
Правило Лопиталя
Алгебраическое преобразование
Свойство пределов
Упражнение Б.29.
Вычислите предел Пт^-оо g
Пример Б.ЗО (Правило Лопиталя для неопределенных выражений оо/оо). Вычислите предел lim^oo
Решение.
Этап 1. Убедимся, что правило Лопиталя применимо.
lim ех = оо и lim х2 = оо.
х—>ос ж—юо
Итак, правило Лопиталя действительно применимо.
Этап 2. Применим правило Лопиталя.
выражение, ,
оо/оо ; d !
г еХ • г dxe г еХ :
lim • = lim — = lim —. •
х—>оо I х—>оо Д о х—»оо 2х !
1 Т2 I
Поскольку lim^oo ех — оо и lim^oo 2х = оо, этот предел представляет собой неопределенное выражение оо/оо, и правило Лопиталя можно применить снова.


914
Часть IV. Приложения
Этап 3. Применим правило Лопиталя.
lim
х—>оо
выражение, оо/оо ! ех •
2х :
Итак,
ех ех
lim — = lim — = lim —- = оо.
я—►оо х—юс 2х х—>оо 2
Упражнение Б.30.
Вычислите предел lim^^oo ■
Задание Б.9.
Пусть п — положительное число. Как с помощью правила Лопиталя доказать, что
г еХ lim — = оо.
т—юс Хп
Следует ли отсюда, что функция ех растет быстрее, чем любая степень числа х?
Ответы к упражнениям
Б.21. 1) оо.
2) оо.
3) 0.
4) оо.
Б.22. 1) оо.
2) 0.
3) —оо.
4) оо.
Б.23. е4.
Б.24. оо.
Б.25. 0.
Б.26. 2.
Б.27. -оо.
Б.28. 2.
Б.29. 0.
Б.30. оо.


Приложение Б. Специальные темы
915
Практикум Б.5
А В задачах 1-14 вычислите пределы с помощью правила Лопиталя.
х4 - 16
1. lim
х—>2 X3 — 8
. v z2+x-6
3* пт —z— —
х->2 X2 + 6ж — 16
5. lim
х—»0 X
7. lim ln(1 + fa).
х—>0 х
.. 2z2 + 7
lim ——
x~>oo + 9
p3x lim —.
x—>oo x
X2 lim -—. x^oe lnx
В задачах 15-18 правило Лопиталя не применимо. Объясните причину. Если предел существует, вычислите его с помощью другого метода.
v £2 + 5я + 4 1- е~Х
*15. lim —-—. *16. lim -—.
х—>1 х6 + 1 X—>оо In а;
*17. lim Ж + 24. *18. lim —-5.
(х - 2)4 з (х + З)5
Б В задачах 19-42 в одних вариантах правило Лопиталя применимо не всегда, а в других его следует применить несколько раз.
9.
11.
13.
2. lim
X—>1 х3 — 1
... х2 — 8х + 16 4. lim —z
х—>4 х1 — ох + 4 1п X
х — 1 е2ж — 1
о х
Зх4 + 6 lim —
х—юо + 5
lim
х—юо е4ж In я
lim ——.
X—ЮО Д?4
6. lim
х—►!
8. lim
X
10.
12.
14.
Проверьте ответы, построив график функции.
20.
22.
24.
Зя + 1-е3х lim 5
X—>0 X2,
lim
х—-1
In (ж + 2)
х + 2
In (1 + 2х)
lim
х—>0“
26.
lim
х—>0+
In (1 + х)
\Jx


916
Часть IV. Приложения
34.
lim
х—»оо
4х2 + 9х
5х2 + 8 ’
36. lim —.
х—too X6
38.
40.
42.
.. 1+е-*
nm
rr—► —оо 1 }
1п(1 + 2е ®) lim -—у- г.
х—too In (1 + е х)
е2х — 1 — 2х — 2х2
lim „
х->0 х6
43. limx_0+ (ж In х).
(Подсказка: перепишите выражение в виде х In х = •)
44. 1шъг_>0+ (-/Jinx).
(Подсказка: перепишите выражение в виде у/х In х = ^//2.)
В задачах 45-48 число п является положительным. Вычислите следующие пределы.
45.
In х lim .
х—»оо Хп
С
47. lim —.
х—too Хп
Хп
46. lim -—.
х—too ma?
48. lim —.
x—too ex
Покажите, что в задачах 49-52 повторное применение правила Лопиталя не приводит к решению.
Оцените пределы, построив график функции.
49.
л/1 + я2
lim
x—too X
50.
lim .
х->-оо 5/4 + Х2
51.
v'x3 + 1
lim
х—t — oo X
52. lim . x2 ™ +1)2
Б.6. Двойные интегралы по сложным областям
■ Регулярные области
■ Двойные интегралы по регулярным областям
■ Изменение порядка интегрирования
■ Вычисление объема с помощью двойных интегралов
В данном разделе рассматривается концепция двойных интегралов, которая уже обсуждалась в разделе 13.6. Для начала проанализируем пример и введем несколько новых терминов.


Приложение Б. Специальные темы
917
Регулярные области
Пусть R — область, изображенная на рис. Б. 10. Опишем ее с помощью следующих неравенств.
R = {(х,у) \ х у 6х — х2, 0 х < 5}
Рис. Б.10. Регулярная ж-область
Область R можно представить в виде объединения сегментов, ограниченных вертикальными линиями от точки (х,д(хУ) до точки (я, /(ж)), где 0 х < 5. Любая область, которую можно разбить подобным образом, называется х-регулярной.
Рассмотрим область S, изображенную на рис. Б.11. Опишем ее с помощью следующих неравенств.
S 	= {(х,у) I у2 О 0 + 2, -1 О О}
Рис. Б.11. Регулярная ^-область
Область S можно представить в виде объединения сегментов, ограниченных горизонтальными линиями, проходящими от графика функции h(y) = у2 до графика функции k(y) — У+2 на отрезке [—1,2]. Любая область, которую можно разбить на горизонтальные сегменты подобным образом, называется ^/-регулярной.


918
Часть IV. Приложения
Регулярные области
Область R в плоскости ху называется х-регулярной, если существуют функции /(ж) и д{х), а также числа а и Ь, удовлетворяющие следующим условиям.
R = {(я, У) I 9(х) /(ж), а х Ь} .
Область S в плоскости ху называется ^/-регулярной, если существуют функции h(y) и к {у), а также числа с и d, удовлетворяющие следующим условиям.
s = {(я,у) I Ку) х < Ку), с^х d}.
Геометрическая интерпретация этих определений приведена на рис. Б. 12.
Рис. Б. 12. Примеры регулярных областей
Замечание. Область не является ^/-регулярной, если существует горизонтальная линия, которая не лежит целиком внутри области. Аналогично область не является х-регуляр-


Приложение Б. Специальные темы
919
ной, если существует вертикальная линия, которая не лежит целиком внутри области (рис. Б. 12).
Пример Б.31 (Х-регулярная область). Область R ограничена графиками функций у = = 4 — х2 ну = х — 2, О 0 и осью у. Опишите эту область с помощью неравенств.
Рис. Б.13. Иллюстрация к примеру Б.31.
Решение. Область R можно разбить на сегменты, проведя вертикальные линии от графика функции у = х — 2 до графика функции у = 4 — х2. Итак, область R является х- регулярной. С помощью неравенств эта область описывается следующим образом.
R = {(х,у) | х - 2 у 4 - х2, 0 х 2} . а
Замечание. Область R в примере Б.З 1 одновременно является и ^-регулярной, поскольку
■R = {(я, J/) I 0 < ® < fc(y), -2 С У 4} ,
где
fc(y) =
2 + У,
у/4~У,
если — 2 у < О, если 0 < у < 4.
Следует отметить, что функция к(у) является кусочно-заданной, поэтому последнее описание области R выглядит немного сложнее.


920
Часть IV. Приложения
Упражнение Б.31.
Область R ограничена графиками функций х = 6 —уих — у2,у^Ои осью х. Опишите эту область с помощью неравенств.
Пример Б.32 (Описание регулярных областей). Область R ограничена графиками функций х + у2 = 9 и х + Зу = 9. Нарисуйте и опишите эту область с помощью неравенств, рассматривая ее и как х-регулярную, и как ^-регулярную.
Решение.
Проверка ^-регулярности
Область R можно разбить на сегменты, проведя вертикальные линии от графика функции х + 31/ = 9 до графика функции х -I- у2 = 9. Итак, область R является х-регулярной. Чтобы описать х-регулярную область R с помощью неравенств, необходимо решить уравнения относительно переменной у.
z + 3?/ = 9, Зу = 9 — х, а = з-^.
х + у2 = 9,
у2 = 9 - х,
у = \/9 — х.
Поскольку график функции расположен в первом квадранте, выбираем положительный квадратный корень.
Итак,
R — {(х,у) | 3 — < у д/9 — х, 0 < х 9} .
Проверка ^-регулярности
Область R можно разбить на сегменты, проведя горизонтальные линии от графика функции х + Зу = 9 до графика функции х + у2 = 9. Итак, область R является ^/-регулярной. Чтобы описать ^-регулярную область R с помощью неравенств, необходимо решить уравнения относительно переменной х.
х + Зу = 9,
х = 9 — Зу.
х + у2 = 9,
х = 9 — у2.


Приложение Б. Специальные темы
921
Итак,
R = {(х,у) |9-Зт/^д;^9-х2,0^7/^3}. а
Упражнение Б.32.
Повторите решение примера Б.32 для области Я, ограниченной графиками функций 2у — х = 4 и у2 — х = 4.
Задание Б.10.
А
Е
I
О U
Гласные буквы А, Е, I, О и U, изображенные на рисунке, можно считать областями на плоскости. Одна из этих областей является х-регулярной, но не ^/-регулярной, другая — ^/-регулярной, но не х-регулярной, третья — и ж-, и ^/-регулярной, а две остальные — ни тем, ни другим. Укажите эти буквы. ■
Двойные интегралы по регулярным областям
Распространим двойное интегрирование на х-, и ^-регулярные области. Обратите внимание на то, что порядок интегрирования теперь зависит от природы области R. Если область R является ж-регулярной, первое интегрирование выполняется по переменной у, а если область R является ^-регулярной, первое интегрирование выполняется по переменной х.
Пределы внешнего интеграла всегда являются постоянными, а пределы внутреннего — переменными.


922
Часть IV. Приложения
Двойное интегрирование по регулярным областям X-регулярная область
Если R = {(х, у) | д(х) у /(х), а х Ь}9 то
J F (х, у) dA =
R
а
dx.
Y-регулярная область
Если R = {(ж, у) | h(y) ^х к(у), с^у d}, то
J F (ж, у) dA =
R
d fc(y)
I i
c \h(y)
F(x, y)dx
dy.
Пример Б.ЗЗ (Вычисление двойных интегралов). Вычислите интеграл 2ху dA, где
R — область, ограниченная графиками функций у = —х и у = х2, х 0, а также линией х = 1.


Приложение Б. Специальные темы
923
Решение. Анализ рисунка показывает, что область R является х-регулярной.
R = {(я,у) I -х у х2, 0 х 1} .
Итак,
1 [>
J 2ху dA = j j 2ху dy dx =
R
о
—x
1
[x5 — x3] dx =
0
Упражнение Б.ЗЗ.
Вычислите интеграл 3xt/2cL4, где R — область из примера Б.ЗЗ. ■
Пример Б.34 (Вычисление двойных интегралов). Вычислите интеграл
(2х + у) dA,
R
где R — область, ограниченная графиками функций у = у/х, х -I- у = 2 и линией у = 0.


924
Часть IV. Приложения
Решение. Анализ рисунка показывает, что область R является ^/-регулярной.
R = {(х,у) \у1  2 ^х ^2- у, 0 т/ 1} .
Итак,
1 J (2х + у) dA = r о
2-2/
j (2х + у) dx
У2
dy =
1
о
(х2 + ух)
1
= j { [(2 - У? + У (2 - у)\ - [(у2)2 + У (у2)] }dy = о
1
(4 - 2у - у3 - у4) dy =
О
= ^4у -у2- iy4 - Jy5)
2/=1
У=0
1
4 5/ 20
Упражнение Б.34.
Вычислите интеграл {у — 4х) dA, где R — область из примера Б.34. ■
Пример Б.35 (Вычисление двойных интегралов). Область R ограничена графиками функций у = у/х и у — jx. Вычислите интеграл 4z?/3dA двумя способами.


Приложение Б. Специальные темы
925
Решение. Анализ рисунка показывает, что область R является как х-, так ^-регулярной.
R = {(х, у) | у у/х, 0 < х 4 R = {(х, у) | у2 х 2у, 0 у < 2} .
Х-регулярная область
V-регулярная область
Интегрирование по х-регулярной области приводит к следующему результату.
4
ч
у/х
ч
ixy3dy
dx =
0
х/2
4 Г
У=\/х~
ху4
dx =
J
0
у=х/2_
Ч Ч - й1') *=
о
Интегрирование по ^/-регулярной области приводит к следующему результату.
dy =
2zV
х=2у
х=у2
dy -
[2 (2?/)2 г/3 — 2 (у2)2 j/3] dy =
ч


926
Часть IV. Приложения
2
= j (8?/5 - 2у7) dy =
О
Упражнение Б.35.
Область R ограничена графиками функций у = хиу = ±х2. Вычислите интеграл 4х3?/ dA двумя способами. ■
Изменение порядка интегрирования
В примере Б.35 показано, что
4
у/х
4xy3dy
J
2
dx =
J
~2у kxy^dx
0
х/2
0
J
У2
dy.
В целом, если R является как х-, так и ^/-регулярной, то оба повторных интеграла равны. В прямоугольных областях изменение порядка интегрирования не вызывает особых трудностей. Как следует из примера Б.35, в более сложных областях эта задача не так проста. Рассмотрим следующий пример. Поскольку нас интересует только процесс интегрирования, а не его результат, подынтегральное выражение уточнять не будем.
Пример Б.36 (Изменение порядка интегрирования). Измените порядок интегрирования в интеграле J1 [Jo 1 f у)dy\ dx-
Решение, Указанный порядок интегрирования свидетельствует о том, что область является х-регулярной.
R = {(я,2/)|0Су^я-1,
Чтобы убедиться в том, что область R одновременно является и ^-регулярной, построим следующий график (рис. Б. 14). Теперь область можно описать с помощью неравенств.
Итак,
R = {(х, у) | у 4-1 х 3, 0 у 2} .
3
~х — 1 с
2
■ 3
1
f(x,y)dy
_ о
dx =
0
-З/Ч
f (х, у) dx
-1
Упражнение Б.36.
Измените порядок интегрирования в интеграле
[Jo Х f у') dy\ dx-
Задание Б.11.
Опишите трудности, связанные с вычислением интеграла Jo Jx2 хеу dy dx, и способы их преодоления с помощью изменения порядка интегрирования. ■


Приложение Б. Специальные темы
927
Рис. Б.14. Область R
Вычисление объема с помощью двойных интегралов
В разделе 13.6 показано, как с помощью двойного интеграла вычисляется объем твердого тела с прямоугольным основанием. Если границу тела можно задать функцией областью определения которой является регулярная область R (не обязательно прямоугольная), то двойной интеграл этой функции также представляет собой объем соответствующего твердого тела.
Пример Б.37 (Вычисление объема тела). Область R ограничена графиками функции х + у = 1, у = 0 и х = 0. Вычислите объем твердого тела, ограниченного графиком z = 1 - х — у и областью R.
Решение.
Из рисунков следует, что область R является как х-, так и ^/-регулярной. Попробуем вычислить интеграл, считая область R ж-регулярной.
R = {(*,у)\0^у^1-х, 0 ж 1} .
Итак, объем твердого тела вычисляется следующим образом.
х — у) dA —
1 Г1-х
1 1 ” х ~ у>) dy о L о
dx =


928
Часть IV. Приложения
1
о
1
у=1—х~
dx =
у=0
(1 — х) — х (1 — х) — | (1 — х)2 dx =
о
1
1=1
Упражнение Б.37.
Область R ограничена графиками функции у + 2х = 2, у = 0 и х = 0. Вычислите объем твердого тела, ограниченного графиком z = 2 — 2х — у и областью R. ■
Ответы к упражнениям
Б.31. R = {(х,у) | у2 < х 6 - у, 0 у < 2}.
Б.32. Область R является как х-, так и ^/-регулярной.
Б.ЗЗ.
40
77
Б.34.
20
Б.35. ™
2 4-у
j f (х, у) dx dy. о 2
Б.37. |.
3
Б.36.
Практикум Б.6
А В задачах 1-6 необходимо описать с помощью неравенств область, ограниченную
графиками указанных функций. Описывая х- и у-регулярную область R в задачах 1
и 2, воспользуйтесь операциями над множествами и неравенствами. Решая задачи 3-6
можете воспользоваться наиболее удобными обозначениями.
1. у = 4 - х2, у = 0, 0 < х 2. 2. у = х2, у = 9, 0 < х 3.


Приложение Б. Специальные темы
929
3. 	у — х3, у = 12 — 2х, х = 0.
5. 	у2 = 2х, у = х — 4.
4. 	у = 5 - х, у = 1 + х, у = 0.
6. 	у = 4 + Зх — х\ х + у = 4,
8.
В задачах 7—10 необходимо вычислить интеграл.
2 У j ху dx dy. о о
4?
10. 	j (х2 + 2т/) dy dx.
1 X
1 X
7. j j (х + у) dy dx.
о о
1 у/У
9. j j (2х + у) dx dy.
О 7/3
Б В задачах 11-14 требуется описать область R и определить характер ее регулярности.
*11. R = {(х,у) | |х| 2, |y| 3}. *12. R = {(x,y) | 1 x2 + y2 4}.
* 13. R = {(x, y) | x2 + y2 1, |x| 2, 0 у 2}.
*14. Я = {(х,1/)Пх| + ЫС1}.
15.
В задачах 15-20 необходимо вычислить указанные интегралы.
j (х2 + у2) dA9
R
R = {(#> У) I О С У С 2х9 0 х < 2).
16. J 2x2ydA9
R
R = {(х, у) | 0 у 9 — х2, -3 х < 3}.
17. |(х + у-2)3<М,
я
R = {(я, у) I о х у + 2, 0 у 1}.
18. J (2х 4- Зу) dA,
я
R = {(я,у) | у2 —4 у < 4 — 2у, 0 у 2}.
19. j ex+vdA,
я
R= {(^> у) I -X У X, О S? х ^2}.
20. f dA,
V л/х2 + у2
R = {(я,у) | о < X с ^/4У ~ У2, 0 у 2}.
В задачах 21-26 область R ограничена графиками указанных функций. Опишите ее с помощью неравенств и вычислите интегралы.
21. у = х -h 1, у = 0, х = 0, х = 1, J \/1 + х + ydA.
R


930
Часть IV. Приложения
22. у = х2,у = у/х, J 12^2/ dA.
R
23. у = 4х - х2, у = 0, J у/у + x2dA.
R
24. у = 1 + Зу, х = 1 - у, у = 1, рж + у + I)3 dA.
R
25. у = 1 - у/х, у = 1 + у/х, х — 4, | х (у - I)2 dA.
R
В задачах 27-32 необходимо вычислить указанный интеграл, нарисовать область интегрирования, изменить порядок интегрирования и снова вычислить интеграл в соответствии с новым порядком интегрирования.
2 У
27.
(х + 2у) dy dx.
28. (з/ — х)4 dx dy.
31.
3 З—х
29.
о о
о о
2 4х
О х/4
30. (1 + 2у) dydx.
о х3
4 2\/У
30.
х dy dx.
32. (1 + 2ху) dxdy.
В задачах 33-36 требуется вычислить объем твердого тела, ограниченного поверхностью f(x,y) и областью R.
33. f(x, у) = 4 — х — у, область R ограничена графиками х + у = 4, у = 0, х = 0.
34. f(x, у) = (х — у)2, область R ограничена графиками у = х, у = 2, х = 0.
35. у) = 4, область R ограничена графиками у = 1 — х2, у = 0,
36. /(х, у) = кху, область R ограничена графиками у = Vl — х2, ?/ = 0,
В В задачах 37-40 необходимо изменить порядок интегрирования и вычислить интеграл.
2 4
1 1
37. [ [ 1 2 dx-
J J 1 + У2
1 1
38. L/Г — x2dx dy.
О у
4 2
0 yfi


Приложение Б. Специальные темы
931
В задачах 41-46 требуется изобразить область интегрирования с помощью графической утилиты, найти точки пересечения ее границ с осями координат, описать область R с помощью неравенств и вычислить интеграл. Все вычисления необходимо проводить с точностью до двух десятичных знаков.
41.
У =
= 14- у/х, у = х2, х = 0, ж dA. 42. JU
у = 1 + у = X, X = 0,
x dA.
R
R
43.
У =
- \/х, У = 1 — у = 0, 24xi/ dA. 44.
у = x3, у = 1 — x, у = 0,
JU
48xy dA.
JU R
R
45.
У =
- е~х, у = 3 — х, tydA. 46.
у = ex,y = 2 + x, II 8y dA. JU
JU
R
R
В задачах 47-50 необходимо вычислить интеграл с точностью до трех десятичных знаков, используя графическую утилиту.
47.
2 9-х2
| j yex2dydx. о о
49.
10 lny
11
1 1+1/
у/х
1 + ?/2
dxdy.
Б.7. Интерполяционные полиномы и разделенные разности
■ Введение
■ Интерполяционный полином
■ Таблицы разделенных разностей
■ Решение практических задач
Уравнение пучка прямых с центром в одной точке, позволяет построить полином, проходящий через две заданные точки на плоскости, координаты х которых отличаются друг от друга. В связи с этим возникает вопрос: можно ли построить полином, проходящий через три, четыре или большее количество заданных точек на плоскости? Изучив это раздел, вам станет понятно, что на этот вопрос существует утвердительный ответ. Кроме того, существуют несколько методов построения таких интерполяционных полиномов. Как правило, интерполяционные полиномы используются для вычисления ординат точек, не входящих в заданное множество. Например, компания, занимающаяся розничными продажами, может хранить информацию о ценах и объемах спроса на разные товары. Цену на товар, объем спроса на который не указан в таблице, можно вычислить с помощью интерполяционного полинома. Помимо этого, интерполяционные полиномы широко используются в компьютерной графике для построения гладких кривых, проходящих через заданные точки.


932
Часть IV. Приложения
Введение
Как правило, полиномы записываются в стандартном виде, т.е. показатели степени переменной х или возрастают, или убывают. Например, оба полинома, показанных ниже, записаны в стандартном виде.
р(х) = 14- х2 — 2ж3, q(x) = —Зж5 + 2х4 — 5х.
В данном разделе мы будем записывать полиномы по-разному, в зависимости от ситуации.
Задание Б.12.
Рассмотрим точки, приведенные в табл. Б. 1.
Таблица Б.1. Координаты
точек на плоскости
X
1
2
3
4
У
4
7
4
1
1. Пусть pi (ж) = а0 + «1 (х — 1). Определите коэффициенты а0 и а\ так, чтобы график функции у = pi (ж) проходил через первые две точки, указанные в табл. Б. 1.
2. Пусть Р2^х) = ад + ai(x — 1) + а^х — 1)(х — 2). Определите коэффициенты а0, ai и аъ так, чтобы график функции у = Р2(х) проходил через первые три точки, указанные в табл. Б. 1.
3. ПустьР2(х) = ao + ai(# — 1) + а2(я — 1)(х —2) + аз(я — 1)(я —2)(х —3). Определите
коэффициенты ао, ai, аг и аз так, чтобы график функции у = рз(х) проходил через все четыре точки, указанные в табл. Б.1. ■
Проиллюстрируем основные понятия на следующих примерах.
Пример Б.38 (Приближенное вычисление дохода). Компания собрала данные о доходах (тыс. долл.), полученных от продажи определенного товара при указанных объемах производства (тыс. единиц). Оцените уровень предполагаемого дохода, если компания производит 3000 или 7000 единиц продукции.
Решение. Для решения этой задачи достаточно построить кусочно-линейную аппроксимацию искомой функции, используя уравнение прямой, проходящей через две заданные точки (рис. Б. 15).
Несмотря на то что этот вид аппроксимации весьма полезен в некоторых приложениях, у него есть несколько серьезных недостатков. Во-первых, как правило, кусочно-линейная аппроксимация в каждой точке имеет излом и не является дифференцируемой. Во-вторых, кусочно-линейная аппроксимация требует применения разных формул для разных последовательных пар, указанных в таблице (рис. Б. 15).
Для преодоления перечисленных недостатков мы предложим метод построения полинома, принимающего в точках из табл. Б.2 значения, совпадающие со значениями функции R(x). Полученная функция является дифференцируемой, задается единой формулой и позволяет аппроксимировать значения функции R(x) в любой точке отрезка от 1 до 8.


Приложение Б. Специальные темы
933
Рис. Б.15. Кусочно-линейная аппроксимация функции R(x)
Таблица Б.2. Доход R при заданных объемах производства
X
1
4
6
8
R(x)
65
80
40
16
Предположим, что функция р(х) является полиномом, значения которого совпадают со значениями функции R(x) в точках из табл. Б.2. Вместо записи функции р(ж) в виде суммы степеней переменной х представим ее в следующем виде, используя первые три значения из табл. Б.2.
р(х) = а0 + ai(x - 1) + а2(х - 1)(ж — 4) 4- а3(я - 1)(ж - 4)(я - 6).
Как мы убедимся в дальнейшем, это значительно упростит нашу задачу.
Поскольку р(х) в заданных точках принимает значения, перечисленные в табл. Б.2, можно записать следующие уравнения.
65 = Я(1) = р(1) = а0; (Б.13)
80 = 7?(4) = р(4) = а0 + 3ai; (Б. 14)
40 = Я(6) = р(4) = ао + 5ai + Юаг; (Б.15)
16 = R(8) = р(8) = ао 4" 7ai 4- 28а2 4~ 56а3. (Б.16)
Из уравнения (Б.13) следует, что ао = 65. Решая уравнение (Б. 14) относительно коэффициента ai, получаем следующий результат.
ai = ^(80 — а0) = ^(80 — 65) = 5.
Аналогично, решая уравнения (Б.15) и (Б. 16), приходим к следующим выводам.
“2 = Б) (40 ~а°~ 5ai) = Б)(40 “ 65" 25) = _5’
а3 = (16 - a0 - 7ai - 28а2) = ^(16 - 65 - 35 + 140) = 1.
56 56


934
Часть IV. Приложения
Итак,
р(х) = 65 4- 5(х — 1) — 5(ж — 1)(я — 4) + (я — 1)(т — 4)(а? — 6).
Значения полинома р(х) в точках, приведенных в табл. Б.2, совпадают со значениями функции R(x). Кроме того, с помощью полинома р(х) можно приближенно вычислить значение функции R(x) в любой точке отрезка [1,8].
Рис. Б.16. Полином р(х) = 65+5(я—1) —
— 5(я — 1)(х — 4) + (х — 1)(я — 4)(х — 6)
При объеме производства, равном 3000 шт., доход R(3) аппроксимируется следующей формулой.
Я(3) « р(3) = 65 4-5-2 — 5-2- (-1) 4- 2 • (—1) • (-3) = 91 тыс. долл.
При уровне производства, равном 7000 шт., доход R(7) аппроксимируется следующей формулой.
Я(7) « р(7) = 65 + 5- 6- 5- 6- 3 + 6- 3-1 = 23 тыс. долл. н
Упражнение Б.38.
Оцените уровень предполагаемого дохода, если компания из примера Б.38, производит 2000 или 5000 единиц продукции. ■
Поскольку доход компании в примере Б.38 был задан с помощью таблицы, у нас нет никакой информации о значениях функции Д(ж) в точках, не совпадающих с точками из табл. Б.2. Следовательно, мы ничего не можем сказать о точности аппроксимации дохода с помощью полинома р(х). Как указывалось ранее, в некоторых случаях кусочнолинейная аппроксимация может оказаться наилучшим выбором. Основное преимущество полинома р(х) — его дифференцируемость, возможность задания с помощью одной формулы и совпадение с заданными значениями в указанных точках.
Интерполяционный полином
Процедуру, описанную выше, можно использовать для аппроксимации любой функции, заданной с помощью таблицы. Полиномы, построенные таким образом, называются интерполяционными.


Приложение Б. Специальные темы
935
Интерполяционные полиномы
Пусть функция /(ж) задана с помощью таблицы, содержащей (n + 1) точек.
X
Xq
Хг . .
• хп
/(®)
Уо
У1 ..
• Уп
Интерполяционным полиномом, аппроксимирующим функцию /(х), называется полином р(ж), степень которого не превосходит числа п, удовлетворяющий следующим условиям.
р(*о) = Уо = f(x0), p(*i) = У1 =
Р(х„) = Уп = f(xn).
Интерполяционный полином Ньютона имеет следующий вид.
р(х) = а0 + ai (я - яо) + а2 (х - ж0) (х - х\) Ч F
Ч- @>п (х я0) (*£ *£].) • • • (•£ Хп—1) .
Обратите внимание на то, что функция f(x) и ее интерполяционный полином проходят через одни и те же заданные точки (рис. Б.16). Существует ли интерполяционный полином, аппроксимирующий функцию f(x), но не совпадающий с полиномом р(х). Справедливо следующее утверждение.
Существует только один интерполяционный полином, степень которого не превосходит числа п, проходящий через точки, заданные в таблице.
Степень любого другого полинома, проходящего через заданные точки, должна быть больше числа п. Процедура построения интерполяционного полинома описана в следующей врезке.
Процедура построения интерполяционного полинома
Этап 1. Запишите интерполяционный полином Ньютона р(ж) с неопределенными коэффициентами.
Этап 2. Используя условия p(xi) = yi, i = 0,1,..., п, сформируйте систему, состоящую из (п Ч-1) линейных уравнений относительно неопределенных коэффициентов. Не изменяйте порядок следования уравнений в этой системе. Такие системы уравнений называются системами с нижнетреугольными матрицами.
Этап 3. Решите каждое из уравнений системы, начиная с первого, и последовательно вычислите все неопределенные коэффициенты интерполяционного полинома Ньютона, выражая коэффициент с наибольшим индексом через предыдущие коэффициенты. Такой метод вычисления коэффициентов называется прямой подстановкой.


936
Часть IV. Приложения
Пример Б.39 (Построение интерполяционных полиномов). Постройте интерполяционный полином, аппроксимирующий функцию, заданную следующей таблицей.
X
0 12 3
/(я)
54-3-4
Решение.
Этап 1. Интерполяционный полином Ньютона р(х) выглядит следующим образом.
р(х) = ад + ai# + &2х(х — 1) + азх(х — 1)(х — 2).
Этап 2. Нижнетреугольная система уравнений относительно коэффициентов интерполяционного полинома Ньютона приведена ниже.
ао = 5, ао + ai = 4.
ао + 2ai + аг = —3, ао + 3ai + баг + баз = —4.
р(0) = /(О) = 5 р(1) = f (1) = 4 р(2) = /(2) = -3
р(3) = /(3) = -4
Этап 3. Решая систему методом прямой подстановки, приходим к следующим результатам.
ао — 5,
ai = 4 — ао = 4 — 5 = —1,
аг = - (—3 — ао — 2ai) = 3 — 5 + 2) = —3,
аз = — (—4 — ао — 3ai — баг) = — 4 — 5 + 3-1- 18) = 2.
о о
Итак, интерполяционный полином Ньютона имеет следующий вид.
р(х) = 5 — х — Зя(я — 1) + 2х(х — 1)(д: — 2).
Эта форма записи интерполяционного полинома очень удобна для вычисления его значений. Однако для выполнения других операций, например, дифференцирования, интегрирования, а также для построения графика, следует привести подобные члены и записать полином в стандартном виде.
р(х) = 2ж3 — 9я2 + 6ж + 5.
График этого полинома представлен на рис. Б. 17. ■
Упражнение Б.39.
Постройте интерполяционный полином, аппроксимирующий функцию, заданную следующей таблицей.
X
-1
0
1
2
/(®)
5
3
3
11


Приложение Б. Специальные темы
937
Рис. Б.17. Полином
р(х) = 2х3 — 9х2 + бх + 5
Задание Б.13.
Рассмотрим точки, приведенные в таблице, и соответствующий интерполяционный полином.
X
1
3
6
У
3
7
13
р(х) = х3 — 10х2 + 29х — 17
1. Докажите, что полином р(х) проходит через все заданные точки в таблице.
2. Является ли полином р(х) интерполяционным относительно данных таблицы? Если нет, постройте соответствующий интерполяционный полином.
3. Как связаны между собой количество точек в таблице и степень интерполяционного
полинома? ■
Таблицы разделенных разностей
Рассмотрим простую процедуру вычисления коэффициентов интерполяционного полинома Ньютона ао, ai, ..., ап. Для этого еще раз вернемся к табл. Б.2.
Коэффициентами интерполяционного полинома Ньютона, построенного по этой таблице, являются числа ао = 65, ai = 5, а2 = —5 и аз = 1. Чтобы минимизировать количество вычислений, связанных с полиномом Ньютона, запишем таблицу разделенных разностей. Для начала запишем в первых двух столбцах значения координат хну. Затем вычислим отношение разности двух последовательных значений переменной у к разности двух последовательных значений переменной х (табл. Б.З). Эти дроби называются разделенными разностями первого порядка.
Чтобы заполнить второй столбец, повторим процесс, используя для определения числителя разделенные разности первого порядка, а для вычисления знаменателя — разность между двумя последовательными значениями х, разделенными одной точкой (табл. Б.4).
Чтобы заполнить третий столбец, повторим процесс, используя для определения числителя разделенные разности второго порядка, а для вычисления знаменателя — разность между двумя последовательными значениями х, разделенными двумя точками (табл. Б.5).


938
Часть IV. Приложения
Таблица Б.З. Разделенные разности первого порядка
•Efc
Ук
Разделенные разности первого порядка
1
65
80 - 65 _
7-
4-1
4
80
40 - 80 _
-40
= -20
6-4
2
6
40
16-40
-24
= -12
8-6
2
8
16
Таблица Б.4. Разделенные разности второго порядка
Ук
Разделенные разности первого порядка
Разделенные разности второго порядка
1
65
5
4
80
-20
6
40
-12
8
16
-20 - 5 _ —25 _
6-1 ” “
-12 - (-20) _ 8
8-4 ~ 4
Таблица Б.5. Разделенные разности третьего порядка
ait
Ук
Разделенные разности первого порядка
Разделенные разности второго порядка
Разделенные разности третьего порядка
1
65
5
4
80
-5
-20
2 - (-5) _ 7 _
8-1 7
6
40
2
-12
8
16
Мы разделили этот процесс на несколько таблиц, чтобы упросить изложение. На практике все эти операции выполняются над одной и той же таблицей. Немного потренировавшись, вы научитесь быстро заполнять таблицы разделенных разностей (табл. Б.6).
Как использовать эту таблицу? Запишем в строку числа, расположенные по диагонали, начиная со второго столбца.
65 5
-5 1


Приложение Б. Специальные темы
939
Таблица Б.6. Разделенные разности — окончательная форма
Ук
Разделенные разности первого порядка
Разделенные разности второго порядка
Разделенные разности третьего порядка
1
65
; 80 - 65
4-1
4
80
Н20-5 J 5
: 6-1 :
;4°-80_; 20
i2 - <-5) - i.
: 6-4 :
; 8- 1 ;
6
40
: —12 - (-20)
: 8-4 1
: 8-6 :
8
16
Как видим, эти числа являются искомыми коэффициентами интерполяционного полинома Ньютона (см. пример Б.З8). Итак, табл. Б.6 содержит всю информацию, необходимую для построения интерполяционного полинома
р(х) = 65 + 5(ж - 1) - 5 (я - 1)(я — 4) + (ж — 1)(я — 4)(ж — 6).
Таблица разделенных разностей проста в использовании и поэтому часто применяется при компьютерных вычислениях.
Таблица разделенных разностей и интерполяционные полиномы
Пусть функция /(ж) задана с помощью таблицы, содержащей (n + 1) точек, где х$ < < х^ < • • • < хп.
X
Xq
. .
хп
/(®)
Уо
У1 ..
Уп
Таблица разделенных разностей вычисляется следующим образом.
Столбец 1. Координаты х из исходной таблицы.
Столбец 2. Координаты у из исходной таблицы.
Столбец 3. Разделенные разности первого порядка, вычисленные по первому и второму столбцу.
Столбец 4. Разделенные разности второго порядка, вычисленные по первому и третьему столбцу.
Столбец п + 2. Разделенные разности n-го порядка, вычисленные по первому и (п+1) столбцу.


940
Часть IV. Приложения
Коэффициенты интерполяционного полинома Ньютона
р(х) = а0 + (х - х0) + а2(х - х0) (х - xi) Н F
+ ап(х- х0) (х - xi)... (х - xn_i)
записаны в первых ячейках каждого столбца таблицы разделенных разностей, начиная со второго столбца.
Замечания.
1. Перед началом вычислений точки в исходной таблице должны быть упорядочены по возрастанию координаты х. Если этого не сделать, коэффициенты полинома будут вычислены неправильно.
2. Поскольку каждый столбец таблицы разделенных разностей зависит от всех чисел, записанных в предыдущем столбце, необходимо полностью выполнять вычисления, несмотря на то, что нас интересуют только первые элементы столбцов.
3. Существуют альтернативные методы построения интерполяционных полиномов. Например, можно записать искомый полином в стандартной форме
р(х) = Ь$х3 4- b2x1  2 + bix + 60
и сформировать систему уравнений относительно неопределенных коэффициентов.
р(1) = 63 4- Ь2 + bi + bo = 65,
р(4) = 64Ьз + 16&2 4~ 461 4* Ьо = 80, р(6) = 2166з + З662 4" 661 4~ 6о — 40, р(8) = 51263 + 6462 4- 861 +Ь0 = 16.
Вычисления, которые необходимо выполнить, чтобы решить эту систему, намного сложнее, чем вычисления, связанные с таблицей разделенных разностей.
Пример Б.40 (Построение интерполяционных полиномов). Построим интерполяционный полином, аппроксимирующий функцию, заданную следующей таблицей.
Таблица Б.7. Узлы интерполяции
X
0 12 3 4
/(®)
35 25 19 —7 -29
1. Вычислите таблицу разделенных разностей.
2. Постройте интерполяционный полином.
Решение.
1. 	Таблица разделенных разностей выглядит следующим образом.


Приложение Б. Специальные темы
941
Ук
Й О. £ « 5 е л S CU ВТ
О 35
25 - 35
1
25
: -6 - (-10)
; 2-о ;
'19-25 ■
: 2-1 =; 6
:-10-2 ; л
: з-о =; 4
2
19
;-26-(-6)=:
: 3-1 ’ : 4-0 :
7 19 26
2-<-Ю) -4
: з — 2 :
■4-1 ;
3
—7
: -22 - (-26) ■„
1 4 — 2 ■
:-29-(-7)_: : 4 — 3 ;
4
-29
2. 	Интерполяционный полином Ньютона имеет следующий вид.
р(ж) = ао + ai# + а2ж(ж — 1) + а^х(х — 1)(я — 2) + а±х(х — 1)(я — 2)(я — 3).
Подставляя значения из таблицы разделенных разностей, получим следующий результат.
р(х) = 35 — 10я + 2х(х — 1) — ^х[х — 1)(ж — 2) + 2я(я — 1)(я — 2)(я — 3) =
= 35 — 32ж 4- Збж2 — 16ж3 + 2д;4 Стандартная форма
Детали перехода к стандартной форме здесь не указаны. Наши вычисления подтверждаются расчетами, выполненными с помощью графической утилиты (рис. Б. 18).и
Упражнение Б.40.
Постройте интерполяционный полином, аппроксимирующий функцию, заданную следующей таблицей.
1. Вычислите таблицу разделенных разностей.
2. Постройте интерполяционный полином. ■


942
Часть IV. Приложения
1ЙИ
0
35
1
25
г
19
3
-7
ч
•29
ViB35-
-32Х+;
ЗбХг-...
Рис. Б.18. Результаты расчетов
Таблица Б.8. Узлы интерполяции
X
0
1
2
3
4
5
1
-1
—7
1
Задание Б.14.
Для вычисления таблицы разделенных разностей можно использовать графическую утилиту. В частности, на рис. Б. 19, показана таблица разделенных разностей, вычисленная с помощью калькулятора TI-83, а также входные данные и результаты расчетов.
IPROGRAMs INTERP
•Lz+Lj
•din<Ls)+М !For(I,2,M,1> sFor<J>M>I>“1>
: CLs < J)-l_3 < J-l)) /<Li<J)-Li<J-I+l ) )-»Lz C J)
: End
:Endг Pause L?
<0,1,2,3,4>-»Ь
{0 1 2 3 4} <35,25,19,-?,-29 }->Lz
<35 25 19 -7 -2... prgnINTERP
<35 -10 2 -4 2} I
а) программа
б) входные данные и результаты
Рис. Б. 19. Результаты расчетов
Введите эти данные и операции в калькулятор TI-83 (или его аналоги — Примеч. ред.) и выполните расчеты. ■
Решение практических задач
Пример Б.41 (Запасы). В неком магазине хранится 8000 единиц нового товара. Объем запасов I через t недель записан в табл. Б.9.
Таблица Б.9. Запасы
t
0
2
4
6
8
8000
5952
3744
1568
0
Вычислите объем запасов через пять недель и средний объем запасов на протяжении пяти недель после получения заказа, используя интерполяционный полином.


Приложение Б. Специальные темы
943
Решение. Таблица разделенных разностей выглядит следующим образом.
tfc Ik
ta « S о S st
Q О
0
8000
-1024
2
5952
-20
-1104
4
4
3744
4
-1088
12
6
1568
76
-784
8
0
Интерполяционный полином задается следующей формулой.
p(t) = 8000 - 1024t - 20t(t - 2) + 4t(t - 2)(t - 4) + t(t - 2)(t - 4)(t - 6).
После упрощений приходим к следующему выводу.
p(t) = f4 - 8t3 - 10004 + 8000.
Объем запасов через пять недель равен следующей величине.
р(5) = 54 - 8 • 53 - 1000 • 5 + 8000 = 2625 шт.
Средний объем запасов на протяжении первых пяти недель выражается следующей формулой.
5 5
Нр(‘)Л=Н(‘4 о о
- 8£3 - 1000t + 8000) dt =
= | Q<5 - 2t4 - 500t2 + 8000^ =
= (625- 1250 - 12 500 + 40000) - | 0 =
5 5
= 5375 шт.
Упражнение Б.41.
Вернитесь к примеру Б.41 и вычислите приближенный объем запасов через семь недель и средний объем запасов на протяжении первых семи недель. ■


944
Часть IV. Приложения
Ответы к упражнениям
Б.38. р(2) = 88 000 долл., р(5) = 61 000 долл.
Б.39. р(х) = 5 — 2(х + 1) + (х + 1)х + (х + 1)х(х — 1).
Б.40. 1)
•Efe Ук
0
5
—4
1
1
1
—2
-1
2
-1
—2
1
-6
3
3
—7
7
8
4
1
2) р(х) = 5 — 4х + х(х + 1) — х(х — 1)(х — 2) + х(х — 1)(х — 2)(х — 3) = = 5 - 13х + 15х2 - 7х3 + х4.
Б.41. 657 шт., 4294,2 шт.
Практикум Б.7
А В задачах 1-4 необходимо выполнить следующие задания.
1) Построить интерполяционный полином Ньютона по заданной таблице.
2) Записать соответствующую нижнетреугольную систему уравнений.
3) Применить для вычисления коэффициентов интерполяционного полинома метод прямой подстановки.
X
1 3 4
Z.
X
-1
1
2
/(®)
2 6 11
/(я)
1
3
7
X
-10 2
4
4.
X
-1
0
2 3
/(®)
6 5 15
-39
/(®)
5
1
5 1


Приложение Б. Специальные темы
945
В задачах 5-10 необходимо построить таблицу разделенных разностей и записать
интерполяционный полином.
3.
X
ч л л О*
12 3 х
1 2 3
/(®)
4 8 14 /(ж)
1 3 7
/.
X
-10 12 х
-10 12
/(®)
-3139 f(x)
5 6 3 2
X
—2
1
2
4
1U.
X
-1
0
3
5
/(я)
25
10
17
13
f(x)
17
10
25
5
Б Ответьте на следующие вопросы.
* 11. Можно ли интерполировать таблицу, содержащую координаты трех точек, ли¬
нейным, квадратичным или кубическим полиномом? Аргументируйте свой ответ.
* 12. Можно ли интерполировать таблицу, содержащую координаты четырех точек,
линейным, квадратичным или кубическим полиномом? Аргументируйте свой ответ.
В задачах 13-20, используя интерполяционный полином, необходимо вычислить значение функции, заданной с помощью таблицы.
X
-4
0
4
8
f(x)
-64
32
0
224
а) /(2)
~ ?.
б)
/(6)« г
X
-5
0
5
10
f(x)
250
50
10
Ю -350
а) /(-3)«?.
б)
/(8)«?.
X
-1
0 1
4
f(x)
0
0 0
15
а) /(2)
« ?.
б)
/(3)«?.
X
-2
0 2
6
f(x)
0
0 0
-96
а) /(1)
~ ?.
б)
X
—4
—2
0
2
4
f(x)
24
2
0
-6
8
а) /(-3)«?.
б) /(!)«?.


946
Часть IV. Приложения
X
-6 —2
0
2
6
19 3
10
3
19
а) /(1)
б) /(5)«?.
X
-3 —2
-1
1
2
3
-24 -6
0
0
6
24
а) /(-0,5) «?.
б) /(2,5) «?
X
-3 —2
-1
0
1
2 3
40 0
0
4
0
0 40
а) 	/(-2,5)«?. б) /(1,5) «?.
В задачах 21-30 необходимо построить интерполяционный полином. Нарисуйте график полинома и укажите точки, координаты которых перечислены в таблице.
21.
X
-2
0
2
2
0
2
23. '
X
0
1
2
—4
—2
0
25. 1
X
-1
0
2
3
0
2
0
—4
27. ■
X
—2
-1
0
1 2
1
5
3
1 5
29.
X
—2
-1
0
1 2
f(x)
-3
0
5
0 -3
22. ■
X
-2
0
2
f(x)
2
0
—2
24. ■
X
0
1
2
—4
-3
0
26.
X
-3
-1
0
1
f(x)
0
4
3
0
28.
X
—2
-1
0
1
2
f(x)
-8
0
2
4
12
30.
X
-1
0
1
2
3
f(x)
6
2
0
-6
2
Постройте уравнение регрессии четвертого порядка с помощью графической утилиты и сравните результаты с интерполяционными полиномами четвертого порядка, полученными при решении соответствующих задач.
31. Задача 27. 32. Задача 28.
33. Задача 29. 34. Задача 30.
В
35. 	В таблице приведены значения функции /(х) = у/х.


Приложение Б. Специальные темы
947
Постройте по этой таблице интерполяционный полином. Сравните результаты интерполяции со значениями функции f(x) = у/х и заполните следующую таблицу.
X
1
2 3 4 5
6 7 8 9
р(х)
1
2
3
у/х
1
2
3
36. 	В таблице приведены значения функции f(x) = 6/у/х.
X
1 4 9
6 3 2
Постройте по этой таблице интерполяционный полином. Сравните результаты интерполяции со значениями функции f(x) — Q/y/х и заполните следующую таблицу.
X
123456789
р(х)
6 3 2
Ь/т/х
6 3 2
37. 	В таблице приведены значения функции f(x) = 10х/ (1 4- ж2).
X
-2-1012
/(®)
-4 -5 0 5 4
Постройте по этой таблице интерполяционный полином. Сравните результаты интерполяции со значениями функции f(x) = Юж/ (1 + ж2) и постройте их графики в одной и той же системе координат.
38. 	В таблице приведены значения функции /(ж) = (9 — ж2) / (1 + ж2).
X
-2-1012
/(®)
1 4 9 4 1
Постройте по этой таблице интерполяционный полином. Сравните результаты интерполяции со значениями функции /(ж) = (9 — ж2) / (1 + ж2) и постройте их графики в одной и той же системе координат.
39. Составьте уравнение параболы, график которой проходит через точки (—Ж1, 2/1), (О, у2) и (ж1, 2/1), где Ж! > 0 и t/х у2.
40. Составьте уравнение параболы, график которой проходит через точки (0, 0), (Ж1, 2/1) и (2Ж1, 0), где хг > 0 и уг / 0.


948
Часть IV. Приложения
Применение математики
Экономика и бизнес
41. 	Наличный резерв. В таблице указан запас денежных средств (тыс. долл.) небольшой компании. Здесь t — количество месяцев, отсчитываемых с начала года.
t
0 4 8 12
C(t)
2 32 38 20
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома приблизительное количество наличных денежных средств (тыс. долл.) через шесть месяцев.
в) Вычислите с помощью интерполяционного полинома приблизительный средний объем денежных средств в первом квартале.
42. 	Складские запасы. В магазине промышленных товаров хранятся 147 газонокосилок. В таблице приведен объем запасов через t месяцев после получения заказа.
t
0 12 3
I(t)
147 66 19 0
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома приблизительное среднее количество газонокосилок, хранящихся в магазине на протяжении трех месяцев.
43. 	Распределение доходов. Распределение доходов среди населения США в 1999 г. описывалось кривой Лоренца у = f(x).
X
0 0,2 0,8 1
/(ж)
0 0,04 0,52 1
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома приблизительное значение показателя концентрации дохода (с точностью до четырех десятичных знаков).
44. 	Распределение доходов. Вернемся к задаче 43. Применив налоговые меры, направленные на более справедливое распределение доходов, правительство США добилось, чтобы распределение доходов среди населения США описывалось кривой Лоренца у = д(х), значение которой приведено в следующей таблице.
X
0 0,2 0,8 1
g(x)
0 0,06 0,54 1


Приложение Б. Специальные темы
949
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома приблизительное значение показателя концентрации дохода (с точностью до четырех десятичных знаков).
45. 	Максимальный доход. В следующей таблице приведены данные о доходах R (тыс. долл.) от продажи х тыс. ламп.
X
2 4 6
R(x)
24,4 36 34,8
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома приблизительный доход от продажи 5000 ламп.
в) Определите с помощью интерполяционного полинома объем производства, гарантирующий максимальный доход.
46. 	Минимальные средние затраты. В таблице приведены затраты С (тыс. долл.) на производство х тыс. микроволновых печей.
X
1 3 5
С(ж)
215 535 1055
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома приблизительный доход от продажи 4000 микроволновых печей.
в) Определите с помощью интерполяционного полинома объем производства, гарантирующий минимальную величину средних затрат.
Биологические науки
47. 	Температура. В таблице приведена температура С, в градусах Цельсия, поддерживаемая в виварии в течение t часов.
t
0 12 3 4
C(t)
14 13 16 17 10
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома приблизительную среднюю температуру на протяжении четырех часов.
48. 	Концентрация препарата. В таблице приведена концентрация С, мг/куб. см, лекарственного препарата в крови пациента через t часов после приема.
t
0 1 2 3 4
C(t)
0 0,032 0,036 0,024 0,008


950
Часть IV. Приложения
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома количество времени, которое понадобится для того, чтобы концентрация лекарства достигла максимального значения.
49. 	Дезинфекция. Озеро, расположенное в зоне отдыха, время от времени подвергается антибактериальной обработке. В таблице указана концентрация бактерий С (единиц/куб. см.) через t дней после дезинфекции.
t
0 2 4 6
C(t)
450 190 90 150
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома количество времени, которое понадобится для того, чтобы концентрация бактерий достигла минимального значения.
50. 	Дыхание. Для определения объемной скорости потока R вдыхаемого и выдыхаемого воздуха используется пневмотахограф. На рисунке показан график скорости потока вдыхаемого воздуха, полученный при обследовании некого пациента.
Время, с
а) Постройте интерполяционный полином, используя точки t = 0, 1, 2, 3, отмеченные на графике.
б) Используя интерполяционный полином, вычислите средний объем вдыхаемого воздуха.
Социологические науки
51. 	Регистрация избирателей. В таблице указано количество избирателей в административном округе за 30 лет.
t
0
10
20
30
N(t)
10000
13500
20000
23 500


Приложение Б. Специальные темы
951
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома среднее количество избирателей в течение первого двадцатилетнего периода.
52. 	Регистрация избирателей. В таблице указано количество избирателей в административном округе за 10 лет.
t
0
4
6
10
N(t)
15 000
18800
22 200
26000
а) Постройте интерполяционный полином.
б) Вычислите с помощью интерполяционного полинома год, в котором количество избирателей росло с максимальной скоростью.


в
Основные справочные сведения
Таблица ВЛ. Основные геометрические формулы
1. 	Подобные треугольники
1) Два треугольника называются подобными, если два угла одного треугольника равны двум углам другого треугольника.
2) Если два треугольника подобны, то их соответствующие стороны пропорциональны.
а b с
a' bf d
с
с
2. 	Теорема Пифагора


Приложение В. Основные справочные сведения
953
Продолжение табл. В. 1
3. Прямоугольник
А = ab Площадь
Р — 2а + 2Ь Периметр
4. Параллелограмм
h — высота
А — ah = ab sin в Площадь
Р — 2а + 2Ь Периметр
5. 	Треугольник
h — высота
А = ±hc
Р = а + b + с
s = (а + b + с)
А = y/s(s — a)(s — b)(s — с)
6.
а
Площадь
Периметр
Полупериметр
Трапеция
Основание а параллельно основанию Ь.
h — высота
A = ±(a + b)h Площадь
Площадь: формула Герона
7. Круг
R— радиус
D — диаметр
D = 2R
А = тгТ?2 = j7rZ)2
Площадь
С = 2ttR - TtD
Длина окружности
% = *
тг» 3,14159
Для любого круга


954
Часть IV. Приложения
Окончание табл. В. 1
8. Параллелепипед
V = аЬс Объем
Р = 2аЬ -|- 2ас + 2Ьс Площадь поверхности
9. Прямой круглый цилиндр
R— радиус h — высота
V = nR2h
Объем
S = 2тгЯН
Т = 2tvR(R + h)
Площадь боковой поверхности
Площадь поверхности
10. Прямой круглый конус
R— радиус h — высота
$ — длина образующей
V = yrR2h
S = 7Г Rs = nRy/R2 + h2
Объем
Площадь боковой поверхности
Т = kR(R + $) = 7гТ? (r + \/ R2 + h2} Общая площадь
' ' поверхности
11. Сфера
R— радиус
D — диаметр
D = 2R
V = = |тгГ>3 Объем
S = 47гЯ2 = 7г£>2
Площадь поверхности


Приложение В. Основные справочные сведения
955
Таблица В.2. Формулы интегрирования
(Примечание. Во всех интегралах постоянная интегрирования опущена. Переменная и — это переменная интегрирования; все остальные символы являются константами.)
1.
Интегралы, содержащие ип
г un+1
undu = -,п —1.
J П4-1
2. j u"rdu = j -du = ln\u\.
Интегралы, содержащие выражение a 4- bu, a/0nb/0
3.
4.
5.
6.
7.
8.
9.
10.
11.
[ 1 -du = - ln
J и (a 4- bu) a
f 1 1
J u2 (a 4- bu) au
I 1
I
а 4- Ьи
- Ъ ,
аи= 1- —z In
а2
а+ Ьи и
~^du = , " . + Ду1п
и (а 4- Ьи) а (а 4- Ьи) а
1 , а 4- 2Ьи
а+ Ьи 2Ь,
-du = —-— — 4- In
u2(a + bu) а2и(а + Ьи) а3
Интегралы, содержащие выражение а2 — и2, а > О f 1 1
13. ~2 2du = 1П
J и2 - а2 2а
14. [ 2 1 2du ~ ^Г1П
J а2 - и2 2а
12.
а + Ьи
и
и — а и + а и + а и — а
1
и
Интегралы, содержащие выражения (a + bu) и (c + du), b 0, d 0 и ad — be / 0
c + du
a + bu


956
Часть IV. Приложения
и
Продолжение табл. В.2
'*■ j (fl + ^c + du)du = (sln 1“ + ta| - 21,1 |c + M ■
u2 1 1 / a2 | | с2 \
= 1 l_^ 1 T
1 1 d
— — +
17.
J (a 4- bu) (c + du)
[ 1 du = —7~~; 4 1 o In
J (a 4- bu) {c 4- du) ad — bca + bu (ad — be)
[ u d _ a 1 c j
J (a 4- bu)2 (c 4- du) b {ad — be) a 4- bu {ad — be)2
Г a 4- bu 1 bu ad —be . . . .
J 2722^ = 22 + -2Г-ln|c + <i“'■
Интегралы, содержащие выражение y/a + bu, a/ОиЬ/О
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
с + du
a + bu
c + du
a + bu
— 2 У (a + bu)3
yj a + budu= ——— .
3b
u\/a + budu = 2 ~ \/ (a + bu)3.
9 , — 2 (15b2u2 — 12abu + 8a2) Г "T
u2 yja + bu du = — 105^3 ~ V (a + •
1
J у/a+ bu
u
du =
105b3
2y/a + bu
b ’
2 (bu — 2a) / —
2 (3b2 u2 — 4abu + 8a2) ,
-—
у/a+ bu — y/a
J. y/a+ bu + y/a y/a + bu b
■ — — t= In
au 2ayja у/д 4~ bu 4~ y/a
Интегралы, содержащие выражение y/a2 — u2, a > О
, a > 0.
у/a + bu — y/a
, a > 0.
29.
— du = — - ln
a + y/a2 — u2
•
Uy/a2 — u2 a
u
a + y/a2 — u2
u
_л f 1 . y/a2 - u2
J u2 у/a2 — u2 a2u
31. f U-du = y/a2 — u2 — aln
J u
Интегралы, содержащие выражение y/u2 + a2, a > 0
32.
u
y/u2 + a2du = | (uy/u2 + a2 + a2 ln\u + ^/u2 4- a2|) .


Приложение В. Основные справочные сведения
957
Продолжение табл. В.2
33.
34.
35.
36.
37.
j u2y/u2 + a2du = [u (2u2 + a2) \/u2 -F a2 — a4 ln |iz + y/u2 + a2|] . I IT
Г y/u2 + d
J
[ ' -
J y/u2 + a2
[ 1 -
J uy/u2 + a2
[ . U -du = 1 (uy/u2 -F a2 —
J y/rfT^2 2 V v
f 1
a + ^/u2 -F a2
u
u I I
du = In u + y/u2 + a2\.
du = - In a
и
a + yV + a2
a2 ln\u + д/u2 -F a2 j) .
y/u2 + a2
, du = — —— .
J u2y/u2 + a2
Интегралы, содержащие выражение ^/u2 — a2, a > 0
38.
39.
y/u2 — a2du = (uy/u2 — a2 — a2 ln |ti + y/u2 — a2|) .
j u2y/u2 — a2du = [u (2u2 — a2) y/u2 — a2 — a4 ln \u + y/u2 — a2|] ’ y/u2 -a2 | -|
du = — — F In \u + y/uz — az\.
u I I
.— du = ln \ u + y/u2 — a21.
y/u2 - a2 I V I
j ^du = (uy/и2 — a2 + a2 ln |n + \/u2 — a2|) .
[ * ■Л„_У/ц2-а2.
J u2y/u2 - a2 a2u
Интегралы, содержащие выражение ewa, a 0
40.
41.
42.
43.
44.
45.
' y/u2 — a2
U2
1
46.
eaudu = .
J a
47.
j uneaudu = U'
48.
[ 1 du =
J c + deau
- - [u^e^du.
a a J
= - - — ln|c + de“ul, c/0. c ac
Интегралы, содержащие выражение ln u
49. In u du = u ln u — u.


958
Часть IV. Приложения
Окончание табл. В. 2
50.
51.
52.
flnu 1 2
du = - (lnu) .
Ju 2V '
f un+1
un\nudu = lniz o, n Ф —1.
J n+1 (n + 1)2
| (lnu)n du = u (lnu)n — n j (lnu)n_1 du.
Интегралы, содержащие тригонометрические функции, зависящие от аргумента au, a О 53.
54.
55.
56.
57.
58.
59.
60.
61.
П - 1 Г п_2
Ч (sin сш)
п J
- ——- [ (cosau)”-2 du, п 0.
п J
du, п/0.
62.


Приложение В. Основные справочные сведения
959
Таблица В.З. Площадь под кривой нормального распределения
Площадь под кривой нормального распределения от 0 до z, z О
Z
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,0
0,0000
0,0040
0,0080
0,0120
0,0160
0,0199
0,0239
0,0279
0,0319
0,0359
0,1
0,0398
0,0438
0,0478
0,0517
0,0557
0,0596
0,0636
0,0675
0,0714
0,0753
0,2
0,0793
0,0832
0,0871
0,0910
0,0948
0,0987
0,1026
0,1064
0,1103
0,1141
0,3
0,1179
0,1217
0,1255
0,1293
0,1331
0,1368
0,1406
0,1443
0,1480
0,1517
0,4
0,1554
0,1591
0,1628
0,1664
0,1700
0,1736
0,1772
0,1808
0,1844
0,1879
0,5
0,1915
0,1950
0,1985
0,2019
0,2054
0,2088
0,2123
0,2157
0,2190
0,2224
0,6
0,2257
0,2291
0,2324
0,2357
0,2389
0,2422
0,2454
0,2486
0,2517
0,2549
0,7
0,2580
0,2611
0,2642
0,2673
0,2704
0,2734
0,2764
0,2794
0,2823
0,2852
0,8
0,2881
0,2910
0,2939
0,2967
0,2995
0,3023
0,3051
0,3078
0,3106
0,3133
0,9
0,3159
0,3186
0,3212
0,3238
0,3264
0,3289
0,3315
0,3340
0,3365
0,3389
1,0
0,3413
0,3438
0,3461
0,3485
0,3508
0,3531
0,3554
0,3577
0,3599
0,3621
1,1
0,3643
0,3665
0,3686
0,3708
0,3729
0,3749
0,3770
0,3790
0,3810
0,3830
1,2
0,3849
0,3869
0,3888
0,3907
0,3925
0,3944
0,3962
0,3980
0,3997
0,4015
1,3
0,4032
0,4049
0,4066
0,4082
0,4099
0,4115
0,4131
0,4147
0,4162
0,4177
1,4
0,4192
0,4207
0,4222
0,4236
0,4251
0,4265
0,4279
0,4292
0,4306
0,4319
1,5
0,4332
0,4345
0,4357
0,4370
0,4382
0,4394
0,4406
0,4418
0,4429
0,4441
1,6
0,4452
0,4463
0,4474
0,4484
0,4495
0,4505
0,4515
0,4525
0,4535
0,4545
1,7
0,4554
0,4564
0,4573
0,4582
0,4591
0,4599
0,4608
0,4616
0,4625
0,4633
1,8
0,4641
0,4649
0,4656
0,4664
0,4671
0,4678
0,4686
0,4693
0,4699
0,4706
1,9
0,4713
0,4719
0,4726
0,4732
0,4738
0,4744
0,4750
0,4756
0,4761
0,4767
2,0
0,4772
0,4778
0,4783
0,4788
0,4793
0,4798
0,4803
0,4808
0,4812
0,4817
2,1
0,4821
0,4826
0,4830
0,4834
0,4838
0,4842
0,4846
0,4850
0,4854
0,4857
2,2
0,4861
0,4864
0,4868
0,4871
0,4875
0,4878
0,4881
0,4884
0,4887
0,4890
2,3
0,4893
0,4896
0,4898
0,4901
0,4904
0,4906
0,4909
0,4911
0,4913
0,4916
2,4
0,4918
0,4920
0,4922
0,4925
0,4927
0,4929
0,4931
0,4932
0,4934
0,4936
2,5
0,4938
0,4940
0,4941
0,4943
0,4945
0,4946
0,4948
0,4949
0,4951
0,4952
2,6
0,4953
0,4955
0,4956
0,4957
0,4959
0,4960
0,4961
0,4962
0,4963
0,4964


960
Часть IV. Приложения
Окончание табл. В.З
Z
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
2,7
0,4965
0,4966
0,4967
0,4968
0,4969
0,4970
0,4971
0,4972
0,4973
0,4974
2,8
0,4974
0,4975
0,4976
0,4977
0,4977
0,4978
0,4979
0,4979
0,4980
0,4981
2,9
0,4981
0,4982
0,4982
0,4983
0,4984
0,4984
0,4985
0,4985
0,4986
0,4986
3,0
0,4987
0,4987
0,4987
0,4988
0,4988
0,4989
0,4989
0,4989
0,4990
0,4990
3,1
0,4990
0,4991
0,4991
0,4991
0,4992
0,4992
0,4992
0,4992
0,4993
0,4993
3,2
0,4993
0,4993
0,4994
0,4994
0,4994
0,4994
0,4994
0,4995
0,4995
0,4995
3,3
0,4995
0,4995
0,4995
0,4996
0,4996
0,4996
0,4996
0,4996
0,4996
0,4997
3,4
0,4997
0,4997
0,4997
0,4997
0,4997
0,4997
0,4997
0,4997
0,4997
0,4998
3,5
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
3,6
0,4998
0,4998
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
3,7
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
3,8
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
3,9
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000


г
Графики элементарных функций
Основные функции
Тождественная функция /»=х
-5--
Абсолютная величина sW = 1*1
Квадратичная функция А(х) = х2
Кубическая функция т(х) = х3
Квадратный корень л(х)=\/х
Кубический корень р(х) = №


962
Часть IV. Приложения
Полиномы первого порядка
т > О Возрастающая
Линейная функция
Дх) = тх + Ь
Дх) = тх + b
Дх)
ь
т = 0
Горизонтальная
Постоянная функция Дх) = Ь
Полиномы второго порядка
f(x) = ах2 + Ьх + с = а(х - й)2 + к
Показательные и логарифмические функции
Показательная функция f(x) = b*
Показательная функция Дх) = Ь*
Логарифмическая функция Дх)= logtx


Приложение Г. Графики элементарных функций
963
Типичные полиномы, степень которых больше двух
Полином третьей степени /(х)= х3—х2—14х+11
Полином четвертой степени
/(х) = ?-Зх’-9х2 + 23х + 8
Типичные рациональные функции
Преобразования графиков
Горизонтальный перенос 9(х)=/(х+3) й(х) = /(х —2)
Растяжение, сжатие и
Вертикальный перенос j(x) =f(x) + 2 й(х)=/(х)-3
зеркальное отражение S(x) = 2/(x) й(х)= —0,5/(х)


Ответы к упражнениям
Глава 8
Практикум 8.1
1. 12. 3. 1. 5. —4.
9. 3. 11. —4. 13. 36.
17. у/5. 19. 1,4.
21. 23.
7. -1,5.
15.
I СЛ
25. а) 2.
б) 2.
в) 2.
г) 2.
27. а) 1.
б) 2.
в) Не существует.
г) 2.
д) Нет.


Ответы к упражнениям
965
29. а) 1.
б) 2.
в) Не существует.
г) Не существует.
д) Нет.
31. а) 1.
б) 1.
в) 1.
г) 3.
д) Да. Доопределите <?(3) = 1.
33.
-6.
35. 1.
37. -1.
39. He существует.
41.
1.
43. 0,5.
45. -1.
47. -5.
49.
2
3*
51. 0.
53. 3.
55. 4.
57.
1
2\/2‘
59. He существует.
61. а) Предела нет. Значения функции при стремлении величины х к нулю слева становятся большими отрицательными числами.
б) 	Предела нет. Значения функции | при стремлении величины х к нулю справа становятся большими положительными числами.
63. a) lim /(ж) = 2,
х—*1“
lim f(x) = 3.
х—>1 +
б) lim f{x) = 3,
X—>1“
lim f(x) = 2.
x—► ! +
в) 	m = 1,5.


966
Ответы к упражнениям
г) 	График, построенный при решении задачи 1, делает скачок из точки (1, 2) в точку (1, 3). График, построенный при решении задачи 2, делает скачок из точки (1,3) в точку (1, 2). График, построенный при решении задачи 3, непрерывен. У него нет
ни разрывов, ни скачков.
65. 2а. 67. Д=.
27а
73. 2,718.
69. 10. 71. 0,693.
75. Типичные значения п в разных калькуляторах таковы: в TI-81 — 95, в TI-82 и TI-83 — 94, в TI-85 - 126.
77. 	lim f(x) = lim f(x) = 2, x—► —2 x—>—2+
lim f(x) — lim /(#) — 2. z—>2 x—>2+
79. lim /(x) = —3,
x—> — 3~
lim f(x) = 3.
x—► —3+
в) Все три предела равны 0,99.
85. a) P(X) = <
0,97x;
0,95a?;
0,93a?;
0,9z;
если 0 < x < 300, если 300 x < 1000, если 1000 x < 3000,
если 3000 x < 5000,
если x 5000.


Ответы к упражнениям
967
б) 	Предел Нтх_>юоо не существует, поскольку limx_>1000- D(x) = 970,
a limx_>1000+ D(x) = 950. Предел limx_>3ooo D(x) не существует, поскольку Нпт^зооо- D(x) = 2850, а lima._>3Ooo+ D(x) = 2790.
20а;, если 0 < х < 4000,
80 000, если х 4000.
б) 	Птж_4ооо F(x) = 80000, limx^8Ooo F(x) = 80 000.
89. 	Предел limx_^5 f(x) не существует. limx_>i0 /(ar) = 0; limx^5 д(х) = 0; limx^i0^(x) = 1.
Практикум 8.2
1. Функция f непрерывна в точке х = 1, поскольку lima;_>i f(x) — /(1).
3. Функция f является разрывной в точке х = 1, поскольку limx_>i /(х) /(1).
5. 	Функция f является разрывной в точке х = 1, поскольку предел limx_>i f(x) не существует.


968
7.
11.
13.
15.
17.
19.
21.
23.
25.
27.
29.
31.
33.
35.
Ответы к упражнениям
/W
▲
Все значения х.
Все значения х, за исключением точки х = — 2.
Все значения х, за исключением точек х = — 4 и х ~ 1.
а) f(x) = 2; Птх^1+ /(ж) = 1; предел limx^i f(x) не существует; Д1) = 1.
б) Нет, поскольку предел Итж_>1 f(x) не существует.
а) limx__2- Дх) = 1; limx^_2+ /(х) = 1; limx^_2 Дх) = 1; /(-2) =
б) Нет, поскольку lim^-2 /(х) 7^ f (-2).
а) 	Лх)
5-
• • • <
1 1 1 1 1
► • • •
ним
—5'
1.
2.
Нет.
д) 	Все целые числа.
Функция f является разрывной в точке х = —3; Иш^-з- f(x) — — оо;
limx_>_3+ /(ж) = оо; линия х = — 3 является вертикальной асимптотой.
Функция h является разрывной в точке х = —2; limx__2- h(x) = оо;
limx^_2+ h(x) = —оо; линия х = —2 является вертикальной асимптотой. Функция h является разрывной в точке х = 2; limx_>2- h(x) = —оо; lima._>2+ h(x) = оо; линия х = 2 является вертикальной асимптотой.
Функция f непрерывна на всей числовой оси и не имеет вертикальных асимптот.
Функция Н является разрывной в точке х = 1; Н(х) = —оо;
Н(х) = оо; линия х = 1 является вертикальной асимптотой. Функция Н является разрывной в точке х = 3, поскольку 1ппж_>з Н(х) — 3, но значение Я(3) не существует. Линия х = 3 не является вертикальной асимптотой.
Функция Т является разрывной в точке х = 0; Нгпж^0- Т(х) = — оо;
limx_0+ Т(т) = —оо; линия х = 0 (ось у) является вертикальной асимптотой. Функция Т является разрывной в точке х = 4; limx_>4- Т(х) = оо; lima._>4+ Т(я) = оо; линия х = 4 является вертикальной асимптотой.
-3 < х < 4; (—3;4).
х < 3 или х > 7; (—оо; 3) U (7; оо).


Ответы к упражнениям
969
37. -5 < х < 0 или х > 3; (—5; 0) U (3; сю).
39. а) (-1,33; 1,20) U (3,13; оо).
б) (-оо; —1,33) U (1,20; 3,13).
41. а) (-оо; -2,53) U (-0,72; оо).
б) (-2,53; -0,72).
43. а) (-2,15; -0,52) U (1; 2,67).
б) (-оо; -2,15) U (-0,52; 1) U (2,76; оо).
45. [6, оо).
47. (—оо; оо).
49. (—оо; —3] U [3, оо).
51. 	(—оо; оо).
53. 	Поскольку /(х) = 2 и /(ж) = 4, предел lim^i /(х) не существует
и функция f имеет разрыв в точке х = 1.
55. Функция f непрерывна во всех точках х.
57. 	Поскольку Итх_>о/(я) = 0 и /(0) = 1, Итх_>о/(я) Ф /(0) и функция / имеет разрыв в точке х = 0.
59. Поскольку limx_>2- /(#) = 0 и lima._>2+ /(^) = 4, предел Птж_>2 /(#) не существует.
Более того, значение /(2) не определено. Следовательно, функция f в точке х = 2 имеет разрыв.
61. Поскольку значения /(—1) и /(1) не определены, функция f в точках i = 1 их = -1 имеет разрывы, даже несмотря на то, что /(ж) = /(х) = 2.


970
Ответы к упражнениям
63. а) Да.
б) Да.
в) Да.
г) Да.
65. а) Да.
б) Нет.
в) Да.
г) Нет.
Д) Да.
67. 	Точки пересечения графика с осью х: х = 5; 2.
69. Точки пересечения графика с осью х: х = —6; —1; 4.
71. 	Нет, но это не противоречит теореме 8.4, поскольку функция f является разрывной в точке х = 1.
73. На графиках продемонстрированы возможные ситуации. Из теоремы 8.4 следует, что должно выполняться хотя бы одно из условий.
если 1 < х 2,
если 2 < х 3,
если 3 < х 4,
если 4 < х 5,


Ответы к упражнениям
971
б) Р(х),долл.
1,20
1,00
0,80
0,60
0,40
0,20-
-—I—I—I—I—к
0 1 2 3 4 5
х
в) Да; нет.
81. а) E(s), долл.
1 1 I » S
0 10 000 20 000 30 000
б) Итт^юооо ^(5) = Ю00; Е(ЮООО) = 1000 долл.
в) Предел limx_2oooo E(s) = 20 000; Е(20000) = 20 000 долл. 83. а) ^2, £з, ^4> ^б> ^7-
б) lim^t6Ar(t) = 7;7V(t5) = 7.
в) Предел Пт*_>*3 N (t) не существует; N (t3) = 4.
Практикум 8.3
1. а) —3; наклон секущей линии, проходящей через точки (1, /(1)) и (2, /(2)).
б) —2; —h\ наклон секущей линии, проходящей через точки (1, /(1)) и (1 + /г, /(1 + + h\).
в) —2; наклон касательной линии в точке (1, /(1)).
3. 	а) 15.
б) 15.
в) 6 ЗЛ.
г) 6.


972
Ответы к упражнениям
д) 6.
е) у = бх — 3.
5. f'(x) = 0; /'(1) = 0; Г(2) = 0; /'(3) = 0.
7. 	/'(х) = 2; /'(1) = 2; /'(2) = 2; /'(3) = 2.
9. /'(х) = —2х; /'(1) = -2; /'(2) = -4; /'(3) = -6.
11. 	Г (х) = -^; /'(1) = -2; /' (2) = f (3) = -2~.
13. а) 5.
б) 3 + h.
в) 3.
г) у = Зх — 1.
15. а) 5 м/с.
б) 3 + h м/с.
в) 3 м/с.
17. /'(х) = 5 - 4х; /'(1) = 1; /'(2) = -3; /'(3) = -7.
19. 	f (х) = /'(1) = -1; /'(2) = /'(3) =
21. /'(х) = -1/(х + З)2; /'(1) = -1/16; /'(2) = -1/25; /'(3) = -1/36.
23. Да. 25. Нет.
27. Нет. 29. Да.
31. а) /'(х) = 2х - 4.
33. v = f'(x) — 8х - 2; 6 футов/с; 22 футов/с; 38 футов/с.
35. 0,69. 37. 0,71.
39. а) Графики функций д и h получаются из графика f с помощью вертикальных переносов.
б) 2х.
41. а) Наклон графика функции равен нулю во всех точках.


Ответы к упражнениям
973
43. Функция f не является дифференцируемой в точке х = 1.
45. Функция / является дифференцируемой во всех точках числовой оси.
47. Нет.
49. Нет.
51. /'(0) = 0. 53. 6 с; 192 футов/с.
55. а) 8 ,75 долл.;
б) R'(x) = 60 — 0,05х.
в) Р(1000) = 35000; Я'(1000) = 10. При выпуске 1000 автомобильных кресел прибыль достигает 35 000 долл, и будет возрастать со скоростью 10 долл, за каждое
дополнительное кресло.
57. a) S'(t) = , 1 .
х/Г+10
б) S(15) = 10; *S"(15) = 0,2. Через 15 месяцев общий объем продаж достигнет 10 млн. долл., возрастая со скоростью 0,2 млн. долл., т.е. 200000 долл, в месяц.
в) Прогнозируемый общий объем продаж через 16 месяцев достигнет 10,2 млн. долл., а через 17 месяцев — 10,4 млн. долл.
59. a) p'(t) = 28t - 6,6.
б) 	р(15) — 3653; р'(15) = 413,4. В 2010 г. объем производства достигнет 3653,4 тыс. тонн цинка. Это количество будет расти со скоростью 413,4 тыс. тонн в год.
61. a) QuadReg
y=ax2+bx+c а=". 0583731517 Ь=-1.509819783 с=50.23597577
б) 	В 2010 г. объем потребления достигнет 1546,8 млрд. кВт ч и будет расти со скоростью 41,9 млрд. кВт ч в год.
63. a) P'(t) = 12 - 2t.
б) Р(3) = 104; Р'(3) = 6. Через три часа концентрация озона достигнет 103 частей на млрд., возрастая со скоростью 6 частей на млрд, в час.


974
Ответы к упражнениям
65. a) f'(t) = 0,022t - 1.
б) /(40) = 7,4; /'(40) = —0,12. В 2000 г. количество умерших девочек на 100 000 новорожденных сократится до 7,4, убывая со скоростью —0,12 смертей на 100000 новорожденных в год.
Практикум 8.4
1. 0. 3. 9а?8.
5.
За?2. 7. -4а:-5.
9. р/3. 11.
13.
10а;. 15. 2,8а:6.
2
17. 19. 12.
о
21.
2. 23. 9.
25. —10х_6 = — 10/х6.
27.
-16а;-5 = —16/а?5.
29. х~3 = 1/х3.
31.
-а:"2/3 = -1Д2/3.
33. 4,&г — 3,5.
35.
15а?4 - 6а:2.
37. -12а;-5 - 4х~3 = -Д2 - 4/х3.
хь
39.
-р2 + 2аГ4 = --Д+ Д
2 2х2 а?4
41. 2а?-1/3 - ^“2/3 = ДД -
3 х1'6
5
43.
5 а? ' +ЗХ ! ~ 5а:8/5
За?2/3
лс 1 -4/3 _ 1
5‘ 3 _ Зх4/3'
0,6 хЗ/2
47. —0,6а?-3/2 + 6,4а?-3 + 1 = ■
6,4 1
Н о" + 1.
X6
49. а) /'(а:) = 6 - 2х.
б) /'(2) = 2; f (4) = —2.
в) у = 2а? + 4; у = -2а? + 16.
г) а? = 3.
51. а) /'(а?) = 12а;3 - 12а?.
б) /'(2) = 72; f (4) = 720.
в) у = 12х - 127; у = 720а: - 2215.
г) х = -1; 0; 1.
53. 	a) v = /'(и) = 176-32а:;
б) /'(0) = 176 футов/с. /'(3) = 80 футов/с.
в) 5,5 с.
55. a) v = /'(и) = За?2 - 18а: + 15;
б) /'(0) = 15 футов/с. /'(3) = —12 футов/с.
в) х = 1 с, х = 5 с.
57. f(x) = 2а? - 3 - 2а:”1/2 = 2а: - 3 -
J 1 ’ а:1/2
59. /'(а?) = 4^5 - За: - 3; х = -2,90.
61. /'(а?) = 0,2а;3 + 0,3а;2 - Зх - 1,6; х = -4,46; -0,52; 3,48.
63. /'(а;) = 0,8а;3 - 9,36а;2 + 32,5а; - 28,25; х = 1,30.
65. х = —Ь/(2а).


Ответы к упражнениям
975
67. а) х3 + х.
б) х3.
в) ж3 — X,
69. -20х"2 = —20/ж2.
71. 	2х - 3 - Юж"3 = 2х - 3 - 10/х3.
75. Областью определения функции /'(х) является вся числовая ось, за исключением точки х = 0. В этой точке график функции у = f(x) является гладким, однако касательная в ней является вертикальной линией.
77. 	а) С(х) = 60 - х/2.
б) С" (60) = 30 долл, за ракетку. При объеме производства, равном 60 ракеткам, скорость изменения общих затрат равна 30 долл, за ракетку. Итак, затраты на производство дополнительной ракетки приближенно равна 30 долл.
в) 29,75 долл.; предельные затраты близки к 30 долл, за ракетку.
г) С'(80) = 20 долл, за ракетку. При объеме производства, равном 80 ракеткам, скорость изменения полных затрат равна 20 долл, за ракетку. Итак, величина затрат на производство дополнительной ракетки приближенно равна 20 долл.
79. a) QuadRe9
y=ax2+bx+c а=". 0583731517 Ь=-1.509819783 0=50.23597577
б) В 1992 г. компания выпустила 3900 лимузинов, а уровень производства уменьшился на 400 штук в год.
в) В 1998 г. компания выпустила 3900 лимузинов, а уровень производства увеличился на 600 штук в год.
81. Приближенная величина затрат на производство 101-й микроволновой печи больше, чем затраты на производство 401-й микроволновой печи. Поскольку предельные затраты уменьшаются, производственный процесс становится более эффективным.
83. a) N\x) = 3780/х2.
б) 	7V'(10) = 37,8. Если на рекламу затрачивается 10000 долл., объем продаж увеличивается со скоростью 37,8 катера на каждую тысячу долл. ЛГ(20) = 9,45. Если на рекламу затрачивается 20 000 долл., объем продаж увеличивается со скоростью 9,45 катера на каждую тысячу долл.
85. а) -1,37 ударов/мин.
б) -0,58 ударов/мин.
87. а) 25 понятий/ч.
б) 8,33 понятий/ч.
Практикум 8.5
1. 2х3 • 2х + (х2 — 2) • 6ж2 = 10х4 — 12я2.
3. (ж - 3) • 2 + (2х - 1) • 1 = 4х - 7.


976
5.
7.
9.
11.
13.
15.
17.
19.
25.
27.
29.
31.
33.
35.
37.
39.
41.
43.
45.
47.
49.
51.
53.
Ответы к упражнениям
(х — 3) • 1 — х • 1 3
(х - З)2 (х — З)2
(х - 2) ■ 2 - (2х + 3) • 1 _ 7
(х — 2)2 (х — 2)2
(х2 + 1) • 2 + (2х - 3) • 2х = 6х2 - 6х + 2.
2 ’
и- 4
1.
(0,4х + 2) • 0,5 + (0,5х - 5) • 0,4 = 0,4х - 1.
(2х - 3) • 2х - (х2 + 1) • 2 _ 2х2 - 6х - 2 (2х - З)2 _ (2х - З)2
(х2 + 2) • 2х + (х2 — 3) • 2х = 4х3 — 2х.
(х2 - 2) ■ 2х - (х2 + 2) 2х _ 10х
(х2 - З)2 _ “ (х2 - 3)
(2х + 1)(2х - 3) + (х2 - Зх)•2 = 6х2 - 10х - 3.
(2,5х - х2) • 4 + (4х + 1,4)(2,5 - 2х) = -12х2 + 17,2х + 3,5.
(х2 + 2х) ■ 5 — (5х — 3) (2х + 2) _ —5х2 + 6х + 6
(х2 + 2х)2 (х2 + 2х)2
(х2 — 1) ■ (2х — 3) — (х2 — Зх + 1) • 2х Зх2 — 4х + 3
(х2 -1)2 = (х2-1)2 '
/'(х) = (1 + Зх)(-2) + (5 - 2х) • 3; у = -Их + 29.
г. . . (Зх - 4) • 1 - (х - 8) • 3
f М 1 (Зх-4 s =5х-13
f'(x) = (2х — 15) • 2х + (х2 + 18) • 2 = 6(х — 2)(х - 3); х = 2; х = 3. .. . . (х2 + 1) • 1 - х • 2х 1-х2
f _ (х2 + I)2 “ (х2 + 1)2’ * Х ~ _1; Х = L
7х6 - Зх2.
(2х4 - Зх3 + х) (2х - 1) = (х2 - х + 5) (8х3 - 9х2 + 1) = 12х5 - 25х4 + 52х3 - — 42т2 — 2т + 5.
(4т2 + 5т - 1) (6т - 2) - (Зт2 — 2т + 3) (8т + 5) 23т2 - 30т - 13
(4т2 + 5т — I)2 (4т2 + 5т — I)2
9т1/3 • Зт2 + (т3 + 5) • (Зт-2/3) = 15.
(т2 — 3) • 2т-2/3 — 6т1/3 • 2т —Ют2 — 6
(т2 — З)2 (т2 — З)2 т2/3
X-2/3 (Зх2 - 4х) + (х3 - 2х2) 4/3 + -X4/3.
\ о / 3 о


Ответы к упражнениям
977
(х2 + 1) [(2а:2 — 1) • 2х + (а:2 + 3) • 4а:] — (2а:2 — 1) (а:2 + 3) • 2а: ' (а:2 + I)2
4а:5 + 8а:3 + 16а:
(а:2 + I)2
59. /'(х) — п[и(т)]п_1'и'(я:).
61. х = 1,21.
63. х = —3,72; х = —1; х = 1,36; х — 3,36.
ч о/ / х (*2 + 50) ’ 180t “ 90*2 ’ 2t 9000*
65. 	a) (^) — о о •
(t2 + 50)2 (t2 + 50)2
б) 	S(10) = 60; S'(10) = 4. Через 10 месяцев общий объем продаж достигнет 60000 компакт-дисков, причем продажи будут расти со скоростью 4000 компакт-дисков
в месяц.
в) 	Приблизительно 64 000 компакт-дисков.
2 ’
67 а) -- (ОДР-Ы) ‘0-4000-0,1 _ 400
■а)ф_ (0,1р + 1)2 “ (0,1р + 1)
dx
б) х = 800; — = —16. При цене, равной 40 долл., объем спроса упадет до 800 плей-
dp
еров в неделю, уменьшаясь со скоростью 16 компакт-дисков.
в) Приблизительно 784 плейера.
69. a) С'(<) = ^ + 1)-°’14-2°’14-2< = °’14-°’У.
V ' (t2 + l)2 (t2 + l)2
6) 	C"(0,5) = 0,0672. Через 0,5 ч концентрация будет расти со скоростью 0,0672 мг/см3 в час. С"(3) — —0,0112. Через 3 ч концентрация будет расти со скоростью 0,0112 мг/см3
3000
(а; + 32)2
Практикум 8.6
1. 3.
3. —4х.
5. 2 -И бх.
9. -8(5 - 2а:)3.
13. 30а; (За:2 + 5)4.
17. (2а: - 5)_1/2
1
(2х —5)1/2'
7. 6(2а: + 5)2.
11. 5(4 + 0,2а:)4 • 0,2 = (4 + 0,2а:)4.
15. 8 (а:3 - 2х2 + 2)7 (За:2 - 4а:).
19. —8а:3 (х4 + 1)~3= ~&Х\.
' 1 (а:4 +1)3
21. /'(а:) = 6(2а: - I)2; у = 6г - 5; а: = |.
2 2
23. 	/'(а?) = 2(4а: - 3)_1/2 = _ ^1/2; у = -а: + 1; ни одной точки.
25. 24а:(а:2 - 2)3.
2
3


978
27.
29.
33.
35.
37.
41.
43.
45.
47.
49.
51.
53.
55.
57.
61.
63.
65.
67.
69.
71.
73.
Ответы к упражнениям
4 •
1
-6(^ + 3»)-(21 + 3) - 6(2* + 3)
\хл + Зх)
х (а:2 + 8) 1,/2 = -—ттй * 31. (За; + 4)_2/3 =
V ’ (а;2+8)1/2 (За; + 4)2/3
(0,8а; + 3,6)—3/4 • 0,8 = ——
4 (0,8а; + З,6)3/4
(а:2 - 4х + 2)~1/2 (а; - 2) = * ~ 2
V 7 (а:2 — 4а; + 2)1/2
-2 (2а; + 4)’2 = 39. -15а;2 (а;3 + 4)-6 =
(-8а: + 4) (4а;2 - 4а; + 1) ~2 = - * 3.
—2(2а; - 3) (х2 - Зх)~3/2 -= ~2(2х~3)
(х2 — Зх)3/2
/'(х) = (4 — х)3 — Зх(4 — х)2 = 4(4 — х)2(1 — х); у = —16х + 48.
£,( ч (2х - 5)3 - 6х(2х - 5)2 —4х — 5
> (1> =1!,=-171+54-
f'(x) = (2а: + 2)1/2 + а?(2а; + 2)_1/2; у = |а; -
/'(а;) = 2х(х — 5)3 + Зх2(х — 5)2 = 5а;(а; — 5)2(а; — 2); х = 0; 2; 5.
... . (2а; + 5)2 - 4х (2а: + 5) 5 - 2а: 5
7 w * (2?W = (2?W;' = i
гы = ы - + 20)-_ 4) = (i2 J;+420)1/2;
59. х = 0; 1,55.
; х — 4.
х = -1,49; 0,48; 1,77.
х = -1,77; 0,88; 1,69. 18х2 (х2 + 1)2 + 3 (х2 + 1)3 = 3 (х2 + 1)2 (7х2 + 1).
24х5 (х3 — 7)3 — (х3 — 7)4 бх2 3 (х3 — 7)3 (Зх3 + 7)
4х6 2х4
(2а:- З)2 ■ 12а; (2а;2 + 1)2 + (2я:2 + 1)3 • 4(2а: - 3) = 4 (2а;2 + 1)2 (2а; - 3) (8а;2 - 9а; +1). 4а;3 (а;2 - 1)“1/2 + 8х (а;2 - 1)1/2 = — 3 _ 8*
(а;2
(а: — З)1/2 • 2 — а; (а: — 3)~1/2 _ а; - 6
(а; - З)3/2 ’
(2а; - I)3 (а;3 + З)4] [8а;(2а; — I)3 (а:2 + 3) + 6 (а;2 + 3) (2а: - I)2] = (2а?— 1)1?/
х (11х2 - 4х + 9).
_ 1)V2-
х — 3


Ответы к упражнениям
979
75. а) С (я) = (2х + 16)“1/2 = —
(2х + 16)1у/
б) 	С'(24) = 1/8, т.е. 12,50 долл. При объеме производства, равном 24 калькуляторам, общие затраты будут расти со скоростью 12,50 долл, за калькулятор. Кроме того, затраты на производство 25-го калькулятора приближенно равны 12,50 долл. С'(42) = = 1/10. При объеме производства, равном 42 калькуляторам, величина общих затрат будет расти со скоростью 10,00 долл, за калькулятор. Кроме того, величина затрат на производство 43-го калькулятора приближенно равна 10,00 долл.
77. а) = 40 (р + 25)"1/2 =
Ф (р + 25)1'2
б) 	х = 400 и dx/dp = 4. При цене 75 долл, спрос равен 400 стереосистемам, увеличиваясь со скоростью 4 шт./долл.
79. 4000 (1 + .
(4 ■ 106)х
‘ (х2 - 1)5/3 •
83. a) /'(n) = п(п - 2)-V2 + 2(n - 2)1/2.
б) 	/'(11) = у = 9,67. Если список содержит И пунктов, время обучения возрастает со скоростью 9,67 мин. на пункт. /'(27) = у = 15,4. Если список содержит 27 пунктов, время обучения возрастает со скоростью 15,4 мин. на пункт.
Практикум 8.7
1. а) 29,50 долл.
б) 	30 долл.
3. а) 420 долл.
б) С' (500) = —0,24. При объеме производства, равном 500 кузовов, величина средних затрат снижается со скоростью 24 цента за кузов.
в) Приблизительно 419,76 долл.
5. а) 14,70 долл.
б) 	15 долл.
7. 	а) Р'(450) = 0,5. При производстве 450 видеокассет прибыль растет со скоростью 50 центов за кассету.
б) Р'(750) = —2,5. При объеме производства, равном 750 видеокассет, прибыль падает со скоростью 2,50 долл, за кассету.
9. а) 13,50 долл.
б) Р' (50) = 0,27 долл. При производстве 50 газонокосилок средняя прибыль от продажи одной газонокосилка возрастает со скоростью 0,27 долл, за единицу.
в) Приблизительно 13,77 долл.
11. 	а) р = 100 — 0,025а;; область определения: 0 С х < 4000.
б) Р(х) = ЮОгг — 0,025я2, область определения: 0 < х < 4000.
в) Я'(1600) = 20. При объеме производства, равном 1600 радиоприемников, прибыль растет со скоростью 20 долл, за единицу.


980
Ответы к упражнениям
г) 	R!(2500) = —25. При объеме производства, равном 2500 радиоприемников, прибыль растет со скоростью 25 долл, за единицу.
13. 	а) р = 200 — ±х; область определения: 0 х 6000.
б) С"(х) = 60.
в) 7?(х) = 200х - я2/30; область определения: 0 х 6000.
г) R'(x) = 200 —х/15.
д) Л' (1500) = 100. При объеме производства, равном 1500 станков, прибыль растет со скоростью 100 долл, за единицу. В'(4500) = —100. При объеме производства, равном 4500 станков, прибыль падает со скоростью 100 долл, за единицу.
е) Точки безубыточности: (600; 108 000) и (3600; 288 000).
ж) Р(х) = —х2/30 4- 140х - 72 000.
з) Р(х) = —х/15 + 140.
и) Я'(1500) = —100. При объеме производства, равном 4500 станков, прибыль растет со скоростью 40 долл, за единицу. 71'(3000) = —60. При объеме производства, равном 3000 станков, прибыль падает со скоростью 60 долл, за единицу.
15. а) р = 20 — 0,02х; область определения: 0 х 1000.
б) Р(х) = 20х — 0,02х2; область определения: 0 < х 1000.
в) С(х) = 4х + 1400.
г) Точки безубыточности: (100; 1800) и (700; 4200).
д) Р(х) = 16х - 0,02х2 - 1400.
е) Р'(250) = 6. При объеме производства, равном 250 тостеров, прибыль растет со скоростью 6 долл, за единицу. Р'(475) — —3. При объеме производства, равном 475 тостеров, прибыль падает со скоростью 3 долл, за единицу.
17. а) х = 500.
б) Р(х) = 176х - 0,2х2 - 21900.
в) х = 440.


Ответы к упражнениям
981
г) 	Точки безубыточности: (150; 25 500) и (730; 39 420). Точки пересечения графика Р(х) с осью х: х = 150 и х = 730.
19. a) R(x) = 20# — ж3/2.
б) Точки безубыточности: (44; 588) и (258; 1016).
21. a) JQuadReg
y=ax2+bx+c а=1.4101002Е’5 b=“.2732556676 0=1320.924694
б) Постоянные расходы « 721680 долл. Переменные издержки = 121 долл.
в) (713; 807703), (5423;1 376227).
г) 254 О 1133.
Упражнения для повторения
1. а) 16.
б) 8.
в) 8.
г) 4.
Д) 4.
е) 4. (8.3)
2. f'(x) = -3. (8.3)
3. а) 22.


982
4.
5.
6.
7.
8.
9.
10.
И.
12.
14.
16.
18.
19.
20.
21.
22.
23.
Ответы к упражнениям
б) 8.
в) 2. (8.1)
а) 1.
б) 1.
в) 1.
г) 1. (8.1)
а) 2.
б) 3.
в) Не существует.
г) 3. (8.1)
а) 4.
б) 4.
в) 4.
г) Не существует. (8.1)
а) Не существует.
б) 3.
в) Нет. (8.2)
а) 2.
б) Не определена.
в) Нет. (8.2)
а) 1.
б) 1.
В) Да. (8.2) f(x) = 10х. (8.3)
а) -11.
б) -14.
в) 5/2.
г) -8. (8.4, 8.5, 8.6)
бх + 4. (8.4)
х-'«-з=^-з.(8.0
-х_3 + х = - Д + х. (8.4)
13. 12а?3 - 4х. (8.4)
15. 0. (8.4)
17. —2х-5 + х3 = -Д- + х3. (8.4)
х°
(2х - 1) • 3 = (Зх + 2) • 2 = 12х + 1. (8.5)
(х2 — 1) • Зх2 + (х3 — 3) • 2х = 5х4 — Зх2 — 6х. (8.5) (0,2х - 1,5) • 0,5 + (0,5х 4- 0,4) • 0,2 = 0,2х - 0,67. (8.5)
(х2 + 2)-2-2х-2х _ 4 — 2х2 (х2 + 2)2 _ (х2 + 2)2
(-1H3I+2,”-3-^?-<86)
3(2х - З)2 ■ 2 = 6(2х - З)2. (8.6)


Ответы к упражнениям
983
24.
25.
26.
27.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
44.
46.
з •
—2 (х2 + 2) • 2х = (8.6)
к 7 (х2 + 2)3
3.
3.
3.
3.
28. (—3;0) U (5;оо). (8.2)
а) 4.
б) 6.
в) Не существует.
г) 6.
д) Нет. (8.2)
а)
б)
в)
г)
Д) Да. (8.2)
(-3;4).(5.2)
(-2,34; -0,47) U (1,81; оо). (8.2)
а) 3.
б) 2 + 0,5/г.
в) 2. (5J)
12х3 + бх-4 = 12х3 + 4. (8.4)
X*
(2х2 - Зх + 2) (2х + 2) + (х2 + 2х - 1) (4х - 3) = 8х3 + Зх2 - 12х + 7. (8.5)
(х - I)2 ■ 2 - (2х - 3) • 2 • (х - 1) _ 4 — 2х
(х — I)4 (х-1)3'^
(х2 - 1) [2(2х + 1) • 2] + (2х + I)2 • 2х = 2(2х + 1) (4х2 + х - 2). (8.5, 8.6) 1 ^-5)^(3^).
(2х - 3) • 4 • (х2 + 2)3 ■ 2х - (х2 + 2)4 ■ 2 _ 2 (х2 + 2) (7х2 - 12х - 2)
(2х - З)2
а) т = /'(1) = 2.
б) у = 2х + 3. (8.3, 8.4)
а) т = /'(1) = 16.
б) у = 16х - 12. (8.3, 8.5)
х = 5. (8.4)
(2х - З)3
. (8.5, 8.6)
х — —2; х = 2. (8.5)
х = -1,34; 0,58; 2,26. (8.4)
43. х = —5; х = 3. (8.5)
45. х = 0; х = 3; х = у. (8.5)
47. х = -0,41; 1,80. (8.5)


984
Ответы к упражнениям
48. х = -0,89; 0,89. (8.5, 8.6)
49. a) v = f'(x) = 32х - 4.
б) /'(3) = 92 футов/с. (8.4)
50. a) v = f(x) = 96т — 32.
б) х = 3 с. (8.4)
51. а) График функции д получается из графика функции f путем сдвига на четыре единицы вправо, а график функции h — путем сдвига на три единицы влево.
б) График функции д' получается из графика функции f путем сдвига на четыре единицы вправо, а график функции h' — путем сдвига на три единицы влево. (8.3,8.6)
52. 	а) График функции д получается путем горизонтального переноса графика функции f, а график функции д' — путем горизонтального переноса графика функции б) График функции д получается путем вертикального переноса графика функции /, а график функции д' — путем вертикального переноса графика функции (8.3)
53. (—оо; оо). (8.2)
54. 	(-оо; 2) U (2; оо). (8.2)
55. 	(-оо; -4) U (-4; 1) U (1; оо). (8.2)
56. (—оо; оо). (8.2)
57. [-2; 2]. (8.2)
59. -оо. (8.2)
61. оо. (8.2)
63. 16. (8.1)
65. 1/6. (8.1)
67. 1. (8.1)
58. 	оо. (8.2)
60. Не существует. (8.2)
62. 3/8. (8.1)
64. -1. (8.1)
66.-1. (8.1)
68. 	Не существует. (8.1)
70. 4. (8.1)
72. 	a) limI__2- f(x) = -6; lima,__2+ f(x) = 6; предел lima:__2 f(x) не существует.
б) limx_o f(x) = 4.
в) limx__2- f(x) = 2; Итж__2+ f(x) = -2; предел Итж_,_2 f(x) не существует. (8.1)


Ответы к упражнениям
985
73. 2х - 1. (8.3)
75. Нет. (8.3)
74.
76. Нет. (8.3)
77. Нет. (8.3)
78. 	Да. (8.3)
79. 	(х - 4)4 • 3 • (х + З)2 + (х + З)3 • 4 • (х - 4)3 = 7х(х - 4)3(х + З)2. (8.5, 8.6) (2г + 1) 5х4 — z5 ■ 4 ■ (2х + I)3 • 2 х>(2х + 5) ,
8°- (2ГЛ? = (2г + I!' '(S'5' 8 5)
83. Областью определения функции /'(ж) является вся числовая ось, кроме точки х = 0. В этой точке график функции у = f(x) является гладким, но имеет вертикальную касательную. (8.3)
84. a) f(x) = 1; f(x) = -1.
6) f(x) = -1; limx_>1+ f(x) = 1.
в) m = 1.
г) 	Графики в пп. а и б имеют разрывы в точке х = 1, а график в п. в — нет. (8.2)


986
Ответы к упражнениям
85. а) 1.
б) -1.
в) Не существует.
г) Нет. (8.3)
7,47 -I- 0,4х; если 0 < х 90,
24,786 + 0,2076я; если 90 < х.
87. а) 179,90 долл.
б) 180 долл. (8.7)
88. а) С*(100) = 9500; С"(100) = 50. При объеме производства, равном 100 велосипедам, общие затраты составляют 9500 долл., возрастая со скоростью 50 долл, на велосипед, б) С(100) = 95; С'(100) = —0,45. При объеме производства, равном 100 велосипедам, средние затраты равны 95 долл., убывая со скоростью 0,45 долл, на велосипед. (8.7)
89. Приблизительные затраты на производство 201-го принтера выше, чем приблизительные затраты на производство 601-го принтера. Поскольку предельные затраты убывают, эффективность производственного процесса повышается. (8.7)
90. а) С'(х) = 2; С (х) = 2 + 2222; С'(х) = -2222.
б) R(x) =хр = 25х — 0,01х, R’(x) = 25-0,02х; R (х) = 25-0,01х; R' (х) = -0,01.
в) Р{х) = R(x) - С(х) = 23х - 0,01х2 - 9000; Р'(х) = 23 - 0,02х; Р(х) = 23 - - 0,01х - Р' (х) = -0,01 + §222.
г) (500; 10 000) и (1800; 12 600).
д) Р'(ЮОО) = 3. Прибыль возрастает со скоростью, равной 3 долларам за зонтик. Р'(1150) = 0. Прибыль не растет. Р'(1400) = 0. Прибыль убывает со скоростью, равной 5 долларам за зонтик.
е)
91. 	а) 2 компонента в день.
б) 3,2 компонента в день. (8.5)


Ответы к упражнениям
987
92. 	Л^(5) = 15; N'(5) = 3,833. Через пять месяцев общий объем продаж равен 15 000 бассейнов, возрастая со скоростью 3833 бассейнов в месяц. (8.6)
y=ax3+bx2+cx+d а=.001225
0819285714 564642857
d=12.08428571
б) N(50) = 38,6; N'(50) = 2,6. В 2010 г. потребление природного газа достигнет
38,6 трлн. куб. футов, возрастая со скоростью 2,6 трлн. куб. футов в год. (8.3)
94. a) Linfeeg
у=ах+Ь
_ -.0384180791
Ь=13.59887006
-.9897782666
а=
г=
б) Постоянные затраты: 484,21 долл., переменные издержки на производство и продажу одного кренделя: 2,11 долл.
LinReg
y=ax+b а=2.107344633
Ь=484.2090395 г=.9939318704
в) (51; 591,15), (248; 1007,62).
г) 4,07 < р < 11,64 долл. (8.7)
95. С"(9) = -1 частиц на миллион/м. (8.6)
96. F(3) = 100; F'(3) = —0,25. Через три часа температура тела достигнет 100°F, уменьшаясь со скоростью 0,25°F/4. (8.6)
97. 	а) 10 понятий в час.
б) 5 понятий в час. (8.4)
Глава 9
Практикум 9.1
1. (a, b); (d;f); (g,h). 3. (b, с); (c,d); (f;g).
5. c, d, f. 7. b, f.
9. Локальный максимум в точке х = а; локальный минимум в точке х = с; в точках х — b и х = d локальных экстремумов нет.
11. Убывает на интервале (—ос; 4); возрастает на интервале (4; оо); локальный минимум в точке х = 4.
13. Возрастает на интервале (—оо; —4); убывает на интервале (—4; оо); локальный максимум в точке х — —4.
15. Возрастает на всей числовой оси; локальных экстремумов нет.
17. Убывает на интервалах (—оо; 0) и (6; оо); возрастает на интервале (0; 6); локальный минимум в точке х = 0; локальный максимум в точке х = 6.


988
Ответы к упражнениям
19. Возрастает на интервалах (—оо; —2) и (3; оо); убывает на интервале (—2; 3); локальный максимум в точке х = —2; локальный минимум в точке х = 3.
21. Убывает на интервалах (—оо; —3) и (0; 3); возрастает на интервалах (—3; 0) и (3; оо); локальные минимумы в точках х = — 3 и з? = 3; локальный максимум в точке х — 0.
23. Возрастает на интервале (—оо; 2); убывает на интервале (2; оо); локальный максимум в точке х — 2.
25. Убывает на интервале (—оо; —0,39); возрастает на интервале (—0,39; оо); локальный минимум в точке х = — 0,39.
27. Убывает на интервалах (—оо; —0,77) и (1,08; 2,69); возрастает на интервалах (—0,77; 1,08) и (2,69; оо); локальные минимумы в точках х = —0,77 и х = 2,69; локальный максимум в точке х — 1,08.
29. 	Убывает на интервалах (—оо; —1,22) и (0,35; 2,38); возрастает на интервалах (—1,22; 0,35) и (2,38; оо); локальные минимумы в точках х = —1,22 и х = 2,38; локальный максимум в точке х = 0,35.
31. Возрастает на интервале (—оо; 4). Убывает на интервале (4; оо). Горизонтальная касательная в точке х — 4.
33. Возрастает на интервалах (—оо; — 1), (1; оо). Убывает на интервале (—1; 1). Горизонтальная касательная в точке х — —1; 1.
35. Убывает на всей числовой оси. Горизонтальная касательная в точке х = 2.
х


Ответы к упражнениям
989
45. д4. 41. д6.
51. Возрастает на интервале (—1; 2); убывает на интервалах (—оо; -1) и (2; оо), локальный минимум в точке х = — 1; локальный максимум в точке х = 2.
53. 	Возрастает на интервалах (—1; 2) и (2; оо); локальный минимум в точках х = — 1
55. Возрастает на интервалах (—2; 0) и (3; оо); убывает на интервалах (—оо; -2) и (0; 3); локальные минимумы в точках х = — 2 и х = 3; локальный максимум в точке х — 0.


990
Ответы к упражнениям
57. /'(х) > 0 на интервалах (—оо; -1) и (3; оо); /'(ж) < 0 на интервале (-1; 3); /'(ж) = = 0 в точках х = — 1 и гс = 3.
59. 	/'(х) > 0 на интервалах (—2; 1) и (3; оо); ff(x) < 0 на интервалах (—оо; —2) и (1; 3); /'(х) = 0 в точках х = —2, х = 1 и х = 3.
61. Критические значения: х = —2; х = 2; возрастает на интервалах (—оо; —2) и (2; оо); убывает на интервалах (—2; 0) и (0; 2); локальный максимум в точке х = —2; локальный минимум в точке х = 2.
63. Критическое значение: х = —2; возрастает на интервале (—2; 0); убывает на интервалах (—оо; —2) и (0; оо); локальный максимум в точке х = —2.
65. Критические значения: х = 0; х = 4; возрастает на интервалах (—оо;0) и (4;оо); убывает на интервалах (0; 2) и (2; 4); локальный максимум в точке х — 0; локальный минимум в точке х = 4.
67. 	Критические значения: х = 0; х — 4; х = 6; возрастает на интервалах (0; 4) и (6; оо); убывает на интервалах (—оо; 0) и (4; 6); локальный максимум в точке х = 4; локальные минимумы в точках х = 0 и х = 6.
69. 	Критическое значение: х = 2; возрастает на интервале (2; оо); убывает на интервале (—оо; 2); локальный минимум в точке х = 2.
71. Критическое значение: х = 1; возрастает на интервале (0; 1); убывает на интервале (1; оо); локальный максимум в точке х — 1.
73. 	а) Нет ни критических значений, ни локальных экстремумов. Функция возрастает на всей числовой оси.
б) Есть два критических значения: х = ±у/—к/3. Функция возрастает на интервале
(—оо; — у/—к/3), достигает в точке х = —у/—к/3 локальный максимум, убывает на интервале /с/З; ^—к/З), достигает в точке у/—к/3 локальный минимум
и снова возрастает на интервале (у/—к/3\ оо).
в) Существует единственное критическое значение: х = 0. Локальных экстремумов нет. Функция возрастает на всей числовой оси.


Ответы к упражнениям
991
75. а) Предельная прибыль больше нуля на интервале (0;600), равна нулю в точке х = 600 и меньше нуля на интервале (600; 1000).
77. а) На протяжении первых 15 месяцев цена убывает, достигает локального минимума, на протяжении следующих 40 месяцев возрастает, достигает локального максимума, а затем 15 месяцев убывает.
б) B(t)
I I
I I
I I
I I
I I
I I
- I I I I I I I I I I I I I I ■» /
10 30 50 70
320
79. а) С (ж) = 0,05а: + 20 + .
х
б) Критическое значение: х = 80; убывает на интервале 0 < х < 80; возрастает на интервале 80 < х < 150; локальный минимум в точке х = 80.
81. Функция Р(х) возрастает на интервале (а; Ь), если Р'(х) = R!(x) — С'(х) > 0 на интервале (а; 6), иначе говоря, если R'(ж) > С'(х) на интервале (а; Ь).
83. Критическое значение: t = 1; возрастает на интервале 0 < t < 1; убывает на интервале 1 < t < 24; локальный максимум в точке t = 1.
85. Критическое значение: t = 7; возрастает на интервале 0 < t < 7; убывает на интервале 7 < t < 24; локальный максимум в точке t = 7.
Практикум 9.2
1. (а, с); (с; d); (е, д). 3. (d, е); (д, h). 5. (а, с); (с; d); (е, д).
1. d, е, д. 9. 3. 11. 4.
13. 12х - 8. 15. 4х_3 - 18х-4. 17. 2 + |^_3/2.
19. 8 (х2 + 9)3 + 48х2 (х2 + 9)2 = 8 (х2 + 9)2 (7х2 + 9).
21. /(2) = —2 — локальный минимум.
23. /(-1) = 2 — локальный максимум; /(2) = —25 — локальный минимум.
25. Локальных экстремумов нет.
27. /(—2) = —6 — локальный минимум. /(0) = 10 — локальный максимум. /(2) = — 6 — локальный минимум.
29. /(0) = 2 — локальный минимум.


992
31.
33.
35.
37.
39.
41.
43.
45.
49.
53.
55.
Ответы к упражнениям
/(—4) = — 8 — локальный максимум; /(4) = 8 — локальный минимум.
Выпуклая вверх на всей числовой оси; точек перегиба нет.
Выпуклая вниз на интервале (—ос; |); выпуклая вверх на интервале (|; оо); точка перегиба: х —
Выпуклая вниз на интервалах (—оо; 0) и (6; оо); выпуклая вверх на интервале (0; 6); точки перегиба: х = 0 и х = 6.
Локальный минимум.
Определить невозможно.
Ни одного.
51.
Локальный максимум в точке х = 0, локальный минимум в точке х = 4, точка перегиба: х = 2.
Точка перегиба: х = 0.


Ответы к упражнениям
993
57. Точка перегиба: х = 2.
59. Локальный максимум в точке х = — 2, локальный минимум в точке х = 2, точка перегиба: х = 0.
—оо < х < — 1
х = —1
— 1 < х < 0
X
0<
= 0 х < 2
х
2 < х < оо
Является положительной
и убывающей
Точка пересечения с осью х Является отрицательной и убывающей
Локальный минимум
Является отрицательной и возрастающей
Локальный максимум
Является отрицательной и убывающей
Является возрастающей и выпуклой вниз
Локальный максимум
Является убывающей и выпуклой вниз
Точка перегиба
Является убывающей и выпуклой вверх
Точка перегиба
Является убывающей и выпуклой вниз
= 2


994
Ответы к упражнениям
X
ГЮ
—оо < х < — 2
Является отрицательной и
воз-
Является убывающей и выпук¬
растающей
лой вниз
х = —2
Локальный максимум
Точка перегиба
—2 < х < 0
Является отрицательной и
убы-
Является убывающей и выпук¬
вающей
лой вниз
х = 0
Локальный минимум
Точка перегиба
0 < х < 2
Является отрицательной и
воз-
Является убывающей и выпук¬
растающей
лой вверх
х = 2
Локальный максимум
Точка перегиба
2 < х < оо
Является отрицательной и
убы-
Является убывающей и выпук¬
вающей
лой вниз
65. Точки перегиба: х = 0,27 и х = 3,23; выпуклая вверх на интервалах (—оо;0,27) и (3,73; оо); выпуклая вниз на интервале (0,27; 3,73).
67. 	Точка перегиба: х = —1,40; выпуклая вверх на интервале (—1,40; оо); выпуклая вниз на интервале (—оо; —1,40).
69. Точки перегиба: х = —0,61, х = 0,66 и х = 1,74; выпуклая вверх на интервалах (-0,61; 0,66) и (1,74; оо); выпуклая вниз на интервалах (—оо; —0,61) и (0,66; 1,74).
71. Если функция /'(х) достигает в точке х = с локальный экстремум, то она должна изменять свое поведение: с возрастания на убывание или наоборот. Следовательно, график функции у = f(x) в точке х — с изменяет направление выпуклости, т.е. точка х = с является точкой перегиба.
73. Если точка х = с является точкой перегиба графика функции у = /(х), то функция /(х) в этой точке должна изменять направление выпуклости. Функция /'(х) должна изменять свое поведение: с возрастания на убывание или наоборот, а точка х = с является точкой локального экстремума функции f(x).
75. Точки перегиба: х = — 2 и х = 2.
77. Точки перегиба: х = —6, х = 0 и х = 6.
79. График CPI является выпуклым вверх.
81. График функции у = С'(х) является положительным и убывающим. Поскольку предельные затраты убывают, производственный процесс при возрастании объемов производства становится более эффективным.
83. а) Локальный максимум в точке х = 60.
б) Выпуклая вниз на всем интервале (0; 80).


Ответы к упражнениям
995
85. а) Возрастает на интервале (10; 25); убывает на интервале (25; 40). б) Точка перегиба: х = 20.
г) МахЛГ'(я) = N'(25) = 2025.
87. a) CubicReg y=ax5+bx2+cx+d а=-.005 b=.485 с=-1.85 d=300
б) Чтобы продавать 574 автомобиля в месяц, необходимо сделать 32 рекламных объявления.
89. а) Возрастает на интервале (0; 10); убывает на интервале (10; 20).
б) Точка перегиба: t = 10.
г) N'(10) = 300.
91. а) Возрастает на интервале (5; оо); убывает на интервале (0; 5). б) Точка перегиба: п = 5.
Практикум 9.3
1. (—оо; Ь), (0; е), (е;д).
5. х = 0.
3. (b;d), (d;0), (р; оо).
7. 	(—оо;а), (d;e), (Л;оо).


996
9.
13.
17.
21.
25.
27.
29.
31.
33.
35.
37.
39.
41.
Ответы к упражнениям
(а; 6), (e;h). х = d, х = е. оо.
00.
11. х = а, х = h,
15. —оо.
19. -3/2.
23. 0.
Горизонтальная асимптота: у = 3, вертикальная асимптота: х = 0.
Горизонтальная асимптота: у = 1, вертикальных асимптот нет.
Горизонтальная асимптота: у = 0, вертикальные асимптоты: х = — 1, х = 1.
Горизонтальных асимптот нет, вертикальные асимптоты: х = —4, х = 4.
Горизонтальная асимптота: у = 2, вертикальная асимптота: х = 1.
Горизонтальная асимптота: у = 3/2, вертикальные асимптоты: х = —4, х = 5/2.
Область определения: вся числовая ось. Точка пересечения графика с осью у: 0; точки пересечения графика с осью х: 0; 6. Возрастает на интервалах (—оо; 0) и (4; оо). Убывает на интервале (0;4). Локальный максимум в точке х = 0. Локальный минимум в точке х = 4. Выпуклая вверх на интервале (2; оо). Выпуклая вниз на интервале (—оо; 2). Точка перегиба: х = 2.
Область определения: вся числовая ось. Точка пересечения графика с осью у. 16; точки пересечения графика с осью х: —4; 2. Возрастает на интервалах (—оо; —2) и (2;оо). Убывает на интервале (—2; 2). Локальный максимум в точке х = —2. Локальный минимум в точке х = 2. Выпуклая вверх на интервале (0;оо). Выпуклая вниз на интервале (—оо; 0). Точка перегиба: х = 0.
Область определения: вся числовая ось. Точка пересечения графика с осью у: 0; точки пересечения графика с осью х: 0; 4. Возрастает на интервале (—оо;3). Убывает на интервале (3; оо). Локальный максимум в точке х = 3. Выпуклая вверх на интервале (0; 2). Выпуклая вниз на интервалах (—оо; 0) и (2; оо). Точки перегиба: х = 0 и х = 2.


Ответы к упражнениям
997
43. Область определения: вся числовая ось, за исключением точки х = 3. Точка пересечения графика с осью у: —1; точка пересечения графика с осью х: —3. Горизонтальная асимптота: у = 1. Вертикальная асимптота: х = 3. Возрастает на интервалах (-оо;3) и (3; оо). Выпуклая вверх на интервале (3; оо). Выпуклая вниз на интервале (—оо;3).
45. Область определения: вся числовая ось, за исключением точки х = 2. Точка пересечения графика с осью у: 0; точка пересечения графика с осью х: 0. Горизонтальная асимптота: у = 1. Вертикальная асимптота: х = 2. Возрастает на интервалах (—оо; 2) и (2; оо). Выпуклая вверх на интервале (2; оо). Выпуклая вниз на интервале (—оо; 2).


998
Ответы к упражнениям
55. При любых значениях п 1. Если а > 0, предел равен оо, а если а < 0, предел равен —оо.
57. а) Нш^-^оо р' (х) = оо; lim^^ р" (х) = оо. График функции у - f(x) возрастает и является выпуклым вверх при больших положительных числах х.
б) 	limx_,_oop' (х) = оо; lim^-oop" (ж) = —оо. График функции у = f(x) возрастает и является выпуклым вниз при больших отрицательных числах х.
59. Область определения: вся числовая ось, за исключением точки х = 0. Вертикальная асимптота: х = 0. Возрастает на интервалах (—оо; —1) и (1; оо). Убывает на интервалах (—1;0) и (0;1). Локальный максимум в точке х = — 1. Локальный минимум в точке х = 1. Выпуклая вверх на интервале (0;оо). Выпуклая вниз на интервале (—оо;0).
X
61. Область определения: вся числовая ось. Точка пересечения графика с осью у: 0; точки пересечения графика с осью х: —1; 0; 1. Возрастает на интервалах (—оо; -^/3) и (х/3/3;оо). Убывает на интервале (—х/З/3; х/З/З). Локальный максимум в точке х — —х/З/З. Локальный минимум в точке х = х/З/З. Выпуклая вверх на интервале (0; оо). Выпуклая вниз на интервале (—оо; 0). Точка перегиба: х = 0.
X
63. Область определения: вся числовая ось. Точка пересечения графика с осью у: 27; точки пересечения графика с осью х: —3; 3. Возрастает на интервалах (—оо; -х/3) и (0; х/З). Убывает на интервалах (—х/З; 0) и (\/3; оо). Локальный максимум в точках х — — х/З их = х/З. Локальный минимум в точке х = 0. Выпуклая вверх на интервале (—1; 1). Выпуклая вниз на интервалах (—ос; —1) и (1; оо). Точки перегиба: х = — 1 и х = 1.


Ответы к упражнениям
999
65. Область определения: вся числовая ось. Точка пересечения графика с осью у: 16; точки пересечения графика с осью х: —2; 2. Убывает на интервалах (—оо; —2) и (0; 2). Возрастает на интервалах (—2; 0) и (2;оо). Локальный минимум в точках х = — 2 и х = 2. Локальный максимум в точке х = 0. Выпуклая вверх на интервалах (—оо;—2v/3/3) и (2\/3/3; оо). Выпуклая вниз на интервале (—2\/3/3; 2\/3/3). Точки перегиба: х = —2\/3/3 и х = 2\/3/3.
67. Область определения: вся числовая ось. Точка пересечения графика с осью у: 0; точки пересечения графика с осью х: 0; 1,5. Убывает на интервалах (—оо;0) и (0; 1,25). Возрастает на интервале (1,25; оо). Локальный минимум в точках х = 1,25. Выпуклая вверх на интервалах (—оо;0) и (1;оо). Выпуклая вниз на интервале (0; 1). Точки перегиба: х = 0 и х = 1.
69. Область определения: вся числовая ось, кроме точек ±2. Точка пересечения графика с осью у: 0; точка пересечения графика с осью х: 0. Горизонтальная асимптота: у = 0. Вертикальные асимптоты: х = —2; х = 2. Убывает на интервалах (—оо; —2), (2; 2) и (2;оо). Выпуклая вверх на интервалах (—2;0) и (2;оо). Выпуклая вниз на интервале (—оо; —2) и (0; 2). Точка перегиба: х = 0.


1000
Ответы к упражнениям
71. Область определения: вся числовая ось. Точка пересечения графика с осью у: 1. Горизонтальная асимптота: у = 0. Возрастает на интервале (—оо; 0).Убывает на интервале (0; оо). Локальный максимум в точке х = 0. Выпуклая вверх на интервалах (—оо; — \/3/3) и (\/3/3; оо). Выпуклая вниз на интервале (—^3/3; д/З/З). Точки перегиба: х = —д/З/З и х = х/З/З.
73. Область определения: вся числовая ось. Точки пересечения графика с осью х: —1,18; 0,61; 1,87; 3,71. Точка пересечения графика с осью у: —5. Возрастает на интервале (—0,53; 1,24) и (3,04; оо). Убывает на интервале (—оо; —0,53) и (1,24; 3,04). Локальные минимумы в точках х = —0,53 и х = 3,04. Локальный максимум в точке х = 1,24. Выпуклая вверх на интервалах (—оо; 0,22) и (2,28; оо). Выпуклая вниз на интервале (0,22; 2,28). Точки перегиба: х = 0,22 и х = 2,28.
75. Область определения: вся числовая ось. Точки пересечения графика с осью х: 8,01; 13,36. Точка пересечения графика с осью у: 100. Возрастает на интервале (—0,10; 4,57) и (11,28; оо). Убывает на интервале (—оо; —0,10) и (4,57; 11,58). Локальный максимум в точке х = 4,57. Локальные минимумы в точках х = —0,10 и х = 11,28. Выпуклая вверх на интервалах (—оо; 1,95) и (8,55; оо). Выпуклая вниз на интервале (1,95; 8,55). Точки перегиба: х = 1,95 и х = 8,55.
77. Область определения: вся числовая ось. Точки пересечения графика с осью х\ —2,40; 1,16. Точка пересечения графика с осью у\ 3. Убывает на интервале (-1,58; оо). Возрастает на интервале (—оо;—1,58). Локальные минимумы в точках х = —2,27 и х = 3,82. Локальные максимумы в точках х = —5,59 и х = 1,65. Выпуклая вниз на интервалах (—оо; —0,88) и (0,38; оо). Выпуклая вверх на интервале (—0,88; 0,38). Точки перегиба: х = —0,88 и х = 0,38.
79. Область определения: вся числовая ось. Точки пересечения графика с осью х: —6,68; —0,72. Точка пересечения графика с осью у: 30. Убывает на интервалах (—5,59; —2,27) и (1,65; 3,82). Возрастает на интервалах (-оо; -5,59), (-2,27; 1,65) и (3,85; оо). Локальные минимумы в точках х = —2,27 и х = 3,82. Локальные максимумы в точках х = —5,59 и х = 1,65. Выпуклая вверх на интервалах (—4,31; —0,40) и (2,91; оо). Выпуклая вниз на интервалах (—оо; —4,31) и (—0,40; 2,91). Точки перегиба: х = —4,31, х = -0,40, х = 2,91.


Ответы к упражнениям
1001
83. а) Возрастает на интервале (0; 1).
б) Выпуклая вверх на интервале (0; 1).
в) Линия х = 1 является вертикальной асимптотой.
г) График пересекает оси х и у в начале координат.
85. а)
б)
б) 25 в точке х = 100.
89. а)
3uadRe9 y=ax2+bx+c
а=. Ь=.
с=316
0100714286
7835714286


1002
Ответы к упражнениям
б) 	Минимальная величина средних затрат, равная 4,35 долл., достигается при выпуске 177 порций пиццы в день.
Практикум 9.4
1. Min/(ж) = /(0) = 0; Мах/(я) = /(10) = 14.
3. Min/(я) = /(0) = 0; Мах/(ж) = /(3) = 9.
5. Min/(ж) = /(1) = /(7) = 5; Мах/(я) = /(3) = /(9) = 14.
7. Min/(ж) = /(1) = /(7) = 0; Мах/(я) = /(3) = /(9) = 9.
9. Min/(ж) = /(5) = 7; Мах/(ж) = /(3) = 9.
11. Min/(ж) = /(1) = 2; максимума нет.
13. Мах/(ж) = /(—3) = 18; минимума нет.
15. Абсолютного экстремума нет. 17. Мах/(х) = /(2) = 8.
19. Min/(x) = /(4) = 22. 21. Мах/(ж) = /(3,87) = 46,29.
23. а) Мах/(я) - /(5) = 14. Min/(ж) = /(—1) = —22.
б) Max f [x) = /(1) = —2. Min/(x) = /(—1) = —22.
в) Max f ix) = /(5) = 14. Min/(ж) = /(3) = -6.
25. а) Мах/(х) = /(0) = 126. Min f(x) = /(2) = -26.
б) Max fix) = f(7) = 49. Min/(x) = /(2) = —26.
в) Max f (x) = /(6) = 6. Min/(я) = /(3) = —15.
27. Точно пополам. 29. 15 и —15.
31. 	Квадрат длины стороны, равной 25 см. Максимальная площадь = 625 см2.
33. Пусть х и у — длины сторон прямоугольника и А — его фиксированная площадь. Требуется минимизировать функцию С = 2Вх 4- 2АВ/х, х > 0. Эта математическая задача всегда имеет решение, что соответствует интуитивным предположениям.
35. Пусть х и у — длины сторон прямоугольника, а С — фиксированная стоимость забора. Требуется минимизировать функцию С = х(С — 2Вх)/(2В), 0 х С/(2В). Эта математическая задача всегда имеет решение, что соответствует интуитивным предположениям.
37. а) МахВ(х) = Я(3000) = 300 000.
б) Максимальная прибыль равна 75 000 долл. Она достигается при выпуске 2100 телевизоров по цене 130 долл.
в) Максимальная прибыль равна 64 687,50 долл. Она достигается при выпуске 2025 те левизоров по цене 132,5 долл.


Ответы к упражнениям
1003
39. а)
QuadReg у=ах2+Ьх+с а=*2.352941е "5 Ь=‘.0325964781 0=288.9535407
б)
LinReg y=ax+b а=53.50318471
Ь=82245.22293
в) Максимальная прибыль равна 118 996 долл. Она достигается при цене 195 долл, за пилу.
41. 35 долл.; 6125 долл. 43. 40 деревьев; 1600 фунтов.
45. (10 — 2у/7)/3 = 1,57 кв. дюйма. 47. 20 футов на 40 футов.
49. 	10 000 книг за пять циклов.
51. а) х = 5,1 мили.
б) х ~ 10 миль.
53. 4 дня; 20 бактерий/см2. 55. 50 мышей в одном заказе.
57. Один месяц; два фута.
59. Четыре года, отсчитывая от текущего момента.
Упражнение для повторения
1. (a;ci), (с3;с6) (9.1, 9.2)
3. (а;с2), (с4;с5), (с7; £>). (9.1, 9.2)
5. ci, с6. (9.1)
7. с4) с6. (9.1)
11. f"(x) = 12х2 + 30т. (9.2)
2. (с1;с3), (с6;Ь) (9.1, 9.2)
4. с3. (9.1).
6. С1, с3, с$. (9.1)
13. а) Вся действительная ось.
б) Точка пересечения графика с осью у: 0; точки пересечения графика с осью х: 0; 9.
в) Вертикальных и горизонтальных асимптот нет. (9.3)
14. а) 3; 9.
б) 3; 9.
в) Возрастает на интервале (—оо; 3) и (9; оо); убывает на интервале (3; 9)
г) Локальный максимум в точке х = 3; локальный минимум в точке х = 9. (9.3)
15. а) Выпуклая вверх на интервале (—оо; 6); выпуклая вниз на интервале (6; оо). б) Точка перегиба: х = 6. (9.3)


1004
Ответы к упражнениям
16. (9.3) f(x)
17. а) Вся числовая ось, кроме точки —2.
б) Точка пересечения графика с осью у: 0; точка пересечения графика с осью х: 0.
в) Горизонтальная асимптота: у — 3. Вертикальная асимптота: х = —2. (9.3)
18. а) Нет.
б) —2.
в) Возрастает на интервале (—сю; —2) и (—2; сю).
г) Ни одного. (9.3)
19. а) Выпуклая вверх на интервале (—оо; —2); выпуклая вниз на интервале (—2; оо).
X
Г(х)
/(®)
—оо < х < — 2
Является отрицательной и воз¬
Является убывающей и выпук¬
растающей
лой вниз
х = -2
Точка пересечения с осью х
Локальный минимум
—2 < х < 0
Является положительной и воз¬
Является возрастающей и вы¬
растающей
пуклой вверх
х = — 1
Локальный максимум
Точка перегиба
-1 < х < 1
Является положительной и воз¬
Является возрастающей и вы¬
растающей
пуклой вниз
х =1
Локальный минимум
Точка перегиба
1 < X < 00
Является положительной и воз¬
Является возрастающей и вы¬
растающей
пуклой вверх


Ответы к упражнениям
1005
(9-2)
22. 3. (9.2)
23. Локальный максимум в точке х = — 1. Локальный минимум в точке х = 5. (9.2)
24. Min f(x) = f(2) = —4. Мах/(я) = /(5) = 77. (9.4)
25. Min f(x) = f(2) = 8. (9.4) 26. -oo. (9.3)
27. -oo. (9.3) 28. oo. (9.3)
29. 2. (9.3) 30. oo. (9.3)
31. 0. (9.3)
32. Горизонтальная асимптота: у = 0; вертикальных асимптот нет. (9.3)
33. Горизонтальных асимптот нет; вертикальные асимптоты: х = — 2, х = 2. (9.3)
34. Да. Поскольку функция f(x) непрерывна на отрезке [а,Ь], у нее существует абсолютный максимум на отрезке [а, Ь]. Однако концы интервала являются локальными минимумами, следовательно, абсолютный максимум должен достигаться во внутренней точке. (9.4)
35. Нет. Функция может возрастать или убывать только в своей области определения. Правильно говорить, что функция убывает на интервалах (—сю; 0) и (0, оо). (9.7)
36. Критическим значением функции f(x) является точка разбиения для функции Г(х), принадлежащая области определения функции /. Например, если f(x) = х~г, то число 0 является точкой разбиения для функции f'(x) = —х~2, однако эта точка не является критической по отношению к функции /, поскольку число 0 не принадлежит ее области определения. (9.1)
37. Max f'(x) = f'(2) = 12. (9.4)
38. Оба числа равны 20. Минимальная сумма равна 40. (9.4)
39. Область определения: вся числовая ось. Точки пересечения графика с осью х: -3; 1. Точка пересечения графика с осью у: —3. Горизонтальных и вертикальных асимптот нет. Возрастает на интервале (—2; оо). Убывает на интервале (—оо; —2). Локальный


1006
Ответы к упражнениям
минимум в точке х = -2. Выпуклая вверх на интервалах (—сю; —1) и (1; оо). Выпук лая вниз на интервале (—1; 1). Точки перегиба: х = — 1 и х = 1. (9.3)
40. Область определения: вся числовая ось. Точки пересечения графика с осью х: 0,79; 1,64. Точка пересечения графика с осью у: 4. Возрастает на интервалах (—1,68; —0,35) и (1,28; оо). Убывает на интервалах (—оо; —1,68) и (—0,35; 1,28). Локальные минимумы в точках х = —1,68 и х = 1,28. Локальный максимум в точке х = —0,35. Выпуклая вверх на интервалах (-оо; —1,10) и (0,60; оо). Выпуклая вниз на интервале (-1,10; 0,60). Точки перегиба: х = —1,10 и х = 0,60. (9.3)
41. Область определения: вся числовая ось. Точки пересечения графика с осью х\ 0; 11,10. Точка пересечения графика с осью у: 0. Возрастает на интервалах (1,87; 4,19) и (8,94; оо). Убывает на интервалах (—оо; 1,87) и (4,19; 8,94). Локальные минимумы в точках х = 1,87 и х = 8,94. Локальный максимум в точке х = 4,19. Выпуклая вверх на интервалах (—оо; 2,92) и (7,08; оо). Выпуклая вниз на интервале (2,92; 7,08). Точки перегиба: х = 2,92 и х = 7,08. (9.3)
42. а) В течение первых 15 месяцев график цены возрастает и является выпуклым вверх, достигая локального максимума в точке t = 15. На протяжении следующих 15 месяцев график цены убывает и является выпуклым вниз, достигая точки перегиба t = 30. В течение следующих 15 месяцев график цены убывает и является выпуклым вверх, достигая локального минимума в точке t = 45. Оставшиеся 15 месяцев график цены возрастает и является выпуклым вверх.
43. а) Мах^(х) = Л(ЮООО) = 2 500000 долл.
б) Максимальная прибыль равна 175 000 долл. Она достигается при выпуске 3000 электрических печей по цене 425 долл.
в) Максимальная прибыль равна 119 000 долл. Она достигается при выпуске 2600 электрических печей по цене 435 долл.
44. а) Длина стороны забора, изготавливаемой из дорогого материала, 50 футов, а остальных — 100 футов.
б) Длина стороны забора, изготавливаемой из дорогого материала, 75 футов, а остальных — 150 футов. (9.4)


Ответы к упражнениям
1007
45. 	49 долл.
47. Min С (х) = С (200) = 50. (9.5)
46. 12 заказов в год. (9.4)
у
48. а)
QuadReg y=ax2+bx+c
а=.0061285714
Ь=.1224285714 с=102.2
б) MinC(x) = С(129) = 1,71 долл. (9.5)
49. a) CubicReg
y=ax3+bx2+cx+d а=-.01 b=.83 c= -2.3 d=221
б) Чтобы продавать по 588 холодильников в месяц, необходимо дать 28 рекламных объявлений. (9.5)
50. Три дня. (9.7)
51. Два года, отсчитывая с текущего момента. (9.7)
Глава 10
Практикум 10.1
1. 1221,40 долл.; 1648,72 долл.; 2225,54 долл.
5. 11,55.
7. 10,99.


1008
Ответы к упражнениям
9. 0,14.
n
[1 + (1/n)]"
10
2,59374
100
2,70481
1000
2,71692
10 000
2,71815
100 000
2,71827
1000000
2,71828
10 000000
2,71828
oo
e = 2,718281828459...
17. а) 17349,87 долл.
б) 	7,36 лет.
19. 11 890,41 долл. 21. 8,11%.
б) 	lim 10 OOOe_0,08t = 0. t—>оо
25. 9,90 года. 27. 8,66%.
29. 7,3 года.
31. а) А = Pert; 2Р = Pert; 2 = ert; rt = ln 2; t = —.


Ответы к упражнениям
1009
Хотя параметр г может быть любым положительным числом, резонно ограничить область его изменения, поскольку в большинстве случаев доходность инвестиций колеблется от 2% до 30%.
в) 	Время удвоения капитала (лет): 13,86; 6,93; 4,62; 3,47; 2,77 и 2,31 соответственно.
33. t = - In 0,5/0,00043332 « 1600 лет.
37. 53,3 лет.
Практикум 10.2
1. /'(х) = 2ех + -.
X
35. г = In 0,5/30 «-0,0231.
39. 1,39%.
3. = 4е* - Зегг6-1.
ах
6 (Inя)5
7. —
х
11. х3ех + Зх2еж = х2ех(х + 3)
X
9. т3 + 4х3 In я = ж3(1 4- 41пх).
(я2 + 9) ех — 2хех ех (х2 — 2х -И 9)
13, (х2 + 9)2 = (х2 + 9)2
с х3 — 4х3 In х 1 — 4 In х
15’ = х$ ■
17. 3(х 4- 2)2 lnx 4- = (х 4- 2)2(31пх 4-
х
19. (х 4- 1)3ех 4- 3(ж 4- 1)2еж = (х 4- 1)2еж(х 4- 4).
х + 2
х
21. 	2»е- - + 1) с- _ (lni), + 3(lni)2 _ (hll)2(llla; + 3).
(еж) ех
25. 3(4 - 5е®)2(—5ех) = -15еа:(4 - бе1)2. 27. J (1 + lnx)_1/2 1 =
2 х 2ж(14-1пх) '
29. хех 4- ех — ех = хех. 31. 2х2- + 4х\пх — 2х = 4ж1пх.
х
33. у = ех. 35. у = —х.
е
37. Да, он прав. При любом действительном числе с уравнение касательной к графику функции у = ех в точке (с; ес) имеет вид у — ес = ес(х — с). Следовательно, касательная проходит через точку (с — 1; 0).
39. ~^екх = кекх при любой константе к. 41. Мах/(я) = /(е1,5) = 2е1,5 « 8,963. ах
43. Мах/(ж) = /(2) = е2/4« 1,847. 45. Мах/(ж) = Де2’5) = е5/2 « 74,207.
47. Область определения: вся числовая ось. Точка пересечения графика с осью у: 0; точка пересечения графика с осью х: 0. Горизонтальная асимптота: у = 1. Убывает на интервале (—оо; оо). Выпуклая вниз на интервале (—оо; оо).


1010
Ответы к упражнениям
49. Область определения: (0; оо). Вертикальная асимптота: х = 0. Возрастает на интервале (1; оо). Убывает на интервале (0; 1). Локальный минимум в точке х = 1. Выпуклая вниз на интервале (0; оо).
51. Область определения: вся числовая ось. Точка пересечения графика с осью у: 3; точка пересечения графика с осью х: 3. Горизонтальная асимптота: у = 0. Возрастает на интервале (—оо; 2). Убывает на интервале (2; оо). Локальный максимум в точке х = 2. Выпуклая вверх на интервале (—оо; 1). Выпуклая вниз на интервале (1; оо). Точка перегиба: х = 1.
53. Область определения: (0; оо). Точка пересечения графика с осью х: 1. Возрастает на интервале (е-1/2; оо). Убывает на интервале (0; е-1/2). Локальный минимум в точке х = е-1/2. Выпуклая вверх на интервале (е-3/2; оо). Выпуклая вниз на интервале (0; е-3/2). Точка перегиба: х — е-3/2.
55. Критические значения: х = 0,36; х = 2,15. Возрастает на интервале (—оо; 0,36) и (2,15; оо). Убывает на интервале (0,36; 2,15). Локальный максимум в точке х = 0,36. Локальный минимум в точке х = 2,15.


Ответы к упражнениям
1011
57. Критическое значение: х = 2,21. Возрастает на интервале (0; 2,21). Убывает на интервале (2,21; оо). Локальный максимум в точке х = 2,21.
59. (-0,82; 0,44), (1,43;4,18), (8,61; 5503,66).
61. (3,65; 1,30), (332 105,11; 12,71). 63. р = 2 долл.
65. р = 27,57 долл. 67. Min С (х) = С (е7) « 99,91 долл.
69. а) Максимальный недельный доход равен 3680 долл, при цене 3,68 долл, за штуку.
71. При весе, равном 40 фунтам, артериальное давление будет возрастать со скоростью 0,44 мм рт. ст. на каждый дополнительный фунт. При весе, равном 90 фунтам, артериальное давление будет возрастать со скоростью 0,19 мм рт. ст. на каждый дополнительный фунт.
73. а) Через один час концентрация будет уменьшаться со скоростью 1,60 мг/мл в час. Через четыре часа концентрация будет уменьшаться со скоростью 0,08 мг/мл в час.
75. dR/dS = k/S.
Практикум 10.3
1. (Зх2 + 2)3.
5. е~х\
9. у = In-и; и = Зх2 — 2х + 9.
13. у = (2 4- ех)2; dy/dx = 2ех (2 + ех).
3. ln (2х2 + 5).
7. у = и\ и = Зх2 — х + 5.
11. у = еи; и = 1 + х + х2.
15. у = е2"*4; = -4z3e2-<
17. у = In (4z5 - 7)
dy _ 20ж4
dx 4х5 — 7
19.
2
3 — 2t
25. -8е~Ч
23. бе2®.
1
х — 3


1012
Ответы к упражнениям
29.
33.
37.
41.
43.
45.
47.
51.
53.
55.
57.
59.
. 31. 4е2ж - Зеж.
х + 1
(6х-2)е^^. 35.^1
х , 4[ln(f2 + l)]3-2t = 8i[ln(t2 + l)]3
х2 + 1‘ t2 + l t2 + l
4 (е2х - l)3 • 2е2х = 8е2х (е2х - 1)3.
(х2 + 1) • 2е2х — е2х ■ 2х 2е2х (а;2 — х + 1)
(х2 +1)2 = (а?2 +1)2
(х2 + 1) (—е~х) + е~х ■ 2х = е~х (2х -х2-1).
С~Х с-х1пх~е~Х(1~х1Пх) 49 2Х
х х ' ' (1 +а;2) [ln(i + Z2)]2’
2х
_ 3(1 —х2) [In (1 — я;2)]2/3
График функции у = logdx получается из графика функции у = lnx с помощью вертикального растяжения, если 1 < b < е, и вертикального сжатия, если b > е.
Область определения: (—оо; оо). Точка пересечения графика с осью у: 0; точка пересечения графика с осью х: 0. Горизонтальная асимптота: у = 1. Возрастает на интервале (—оо; оо). Выпуклая вниз на интервале (—оо; оо).
Область определения: (—оо; 1). Точка пересечения графика с осью у: 0; точка пересечения графика с осью х: 0. Вертикальная асимптота: х = 1. Убывает на интервале (—оо; 1). Выпуклая вниз на интервале (—оо; 1).
Область определения: (—оо; оо). Точка пересечения графика с осью у: 1. Горизонтальная асимптота: у = 0. Возрастает на интервале (—оо; 0). Убывает на интервале (0; оо). Локальный максимум в точке х — 0. Выпуклая вверх на интервалах (—оо; —1) и (1; оо). Точки перегиба: х = — 1 и х = 1.


Ответы к упражнениям
1013
у = 1 + [In (2 +
61.
63.
67.
73.
75.
77.
79.
81.
83.
85.
87.
89.
,x}]2.dy = 2еж In (2 + е1) ' Л ’ dx 2 + ех
12а;2 + 5
(4х3 + 5х + 7)1пЗ’
65. (2х + 1) ■ IO®2*1 • In 10.
69. г*3-12*4®4-1 (Зх2 - 2х + 4) In 2.
а) Когда функция f(x) убывает, функция д(х) является неотрицательной.
2х х2 + Г
б) г (я) =
Максимальный доход, равный 735,80 долл., достигается при выпуске 20 единиц товара в день по цене 36,79 долл, за штуку.
Максимальный доход, равный 224,61 долл., достигается при выпуске 17 единиц товара в день по цене 42,74 долл, за штуку.
159 68 долл.
—27145 долл./год; —18196 долл./год; —11036 долл./год.
а) 	23 дня; 26 685; около 50%.
2,27 мм рт. ст./год; 0,81 мм рт. ст./год; 0,41 мм рт. ст./год.
A'(t) = 2 • 1п2 • 5000е2Нп2 = 10000 • 1п2 • 22*; А'(1) = 27726 бактерий/ч (скорость изменения численности в конце первого часа). А1 (5) = 7 097 827 бактерий/ч (скорость изменения численности в конце пятого часа).


1014
Ответы к упражнениям
91. N(n)
1 000 000-
800 000
600 000
400 000
200 000
0
5 10 15 20 *
Практикум 10.4
—4
5. у' = 10х; 10.
9. У' = —;
У 2у + 2
2у .
2я -|- 1
2±- ;2.
еУ — 2у ’ 6д2у — у In у 2
х + 2у __3 ,| 3
6; 1,8) 4’ 1(1,6; 0,2) 4
2 12 3 12
5 5 ’У 5 5
1 1
3 (1 + у)2 + 1 ’ 13’
13. yf =
17. У' =
21. у' =
33. у' =
4.
15. у' =
23. х' =
41. у = 0,63я + 1,04.
4
3’
6-2?/
х
Зя2?/
Г+i’
-1.
2tx - 3Z2
2х — t2
27. у = —х + 5.
3 (ж - 2у)2 3
6 (х — 2у)2 + 4у ’ Ю
39. у' =
43. р' =
У
2ху2 — х
1
2р — 2
3
4
У
, 00 000-р2
45. р = — -
Р
dL = — (L + m) dV V + n
Практикум 10.5
1. 30.
5. -16/7.
9. Приблизительно —3,03 футов/с.
13. 3768 куб. см./мин.
17. -9/4 футов/с.
3. -16/3.
7. Убывает со скоростью 9 единиц/с.
11. dA/dt « 126 кв. футов/с.
15. 6 фунтов/кв. дюймов/ч.
19. 20/3 футов/с.


Ответы к упражнениям
1015
21. 0,0214 футов/с; 0,0135 футов/с; да, в момент t = 0,00019 с.
23. 3,835 единиц/с.
25. a) dC/dt = 15 000 долл.в неделю.
б) dR/dt = —50000 долл, в неделю.
в) dP/dt = 1,53 долл, в месяц.
31. Приблизительно 100 куб. футов/мин.
Упражнение для повторения
1. 3136,62 долл.; 4919,21 долл.; 12 099,29 долл. (10.1)
3. 2е2х_3. (10.2)
7. dy/dt = 216. (10.4)
8. 	Область определения: (—оо; оо). Точка пересечения графика с осью у: 100. Горизонтальная асимптота: у = 0. Убывает на интервале (—оо; оо). Выпуклая вверх на интервале (—оо; оо).
7 	(lnz)6 + l
10. — < (10.3)
11. х5(1 + 6lnx). (70.2)
13.
6х2 — 3 2х3 - Зх
. (10.3)
14. (Зх2 - 2х) е®3-®2. (10.3)
16. у = -х + 2; у = —ex + 1. (10.2)
18‘х' = з^; "4-(704)
15.
1 — 2х In Ъх хе2х
17. у' =
19. У' =
. (10.3)
Зу — 2х 8
8у — Зх’ 19
(10.4)
1
е» + 2/
1. (10.4)


1016
Ответы к упражнениям
20.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
33.
35.
36.
37.
, _ 2ху 2 у ~ 1 + 2у2’ 3' 0,27 футов/с. {10.5) 21. dy/dt = —2 единицы/с. (10.5)
dR/dt = 1/л ~ 0,318 дюймов/мин. (10.5)
Max f(x) = /(4,5) = 2е4’5 « 180,03. (10.2)
Мах/(я) = /(0,5) = 5е-1 « 1,84. (10.3)
Мах/(я) = /(1,373) = 2,487. (10.2)
Мах/(х) = /(1,763) = 0,097. (10.2)
Область определения: (—оо; оо). Точка пересечения графика с осью у: 0. Точка пересечения графика с осью х: 0. Горизонтальная асимптота: у = 5. Возрастает на интервале (—оо; оо). Выпуклая вниз на интервале (—оо; оо).
Область определения: (0; оо). Точка пересечения графика с осью х: 1. Возрастает на интервале (е_1//3; оо). Убывает на интервале (0; е-1/3). Локальный минимум в точке х = е-1/3. Выпуклая вверх на интервале (е 5/6; оо). Выпуклая вниз на интервале (0; е-5/6). Точка перегиба в точке х — е-5/6.
а) 	у = [In (4 - е*)]3.
dy _ -Зе* [In (4-е*)]2 dx 4 — еж
. (10.3)
2х5*2-1 In 5. (10.3)
2х — 1 X2 — X
34. у' =
. (10.3)
2х + 1
2 (х2 + х) ^/1п (х2 + х)
. (10.3)
2х - ехуу
хеху — 1
0. (10.4)
Скорость увеличения площади прямо пропорциональна радиусу R. Следовательно, она минимальна, когда R = 0, и не имеет максимального значения. (10.5)
Да, при < х < (10.5)
а) 15 лет.
б) 13,9 года. (70.7)


Ответы к упражнениям
1017
38. A'(t) = 10е°’“; А'(1) = 11,05 долл./год; А'(10) = 27,18 долл./год. (70.7)
39. R'(x) = (1000 - 20х)е~°’О2х. (10.3)
40. Максимальная доход, равный 18 394 долл., достигается при выпуске 50 единиц товара в месяц по цене 367,88 долл, за штуку. (10.3)
42. 549,15 долл.; 9864 долл. (10.3) 43. 1,52 долл. (10.2)
44. MinC(x) = С(е5) « 49,66 долл. (10.2)
, - (5000-2р3)1/2
45. р' = —i F 7—. (10.4) 46. dR/dt = 110 долл./день. (70.5)
3pz
47. —1,111 мг/мл в час; —0,335 мг/мл в час. (10.3)
48. dR/dt = —3/(27г), приблизительно 0,477 мм/сут. (10.5)
49. а) К концу первого дня скорость обучения составляет 2,68 единицы в день, а концу пятого дня — 0,54 единицы в день.
б) 	(10.3) N(t)
50. 	dt/dt = —\/Tl« —0,037 мин. на операцию в час. (10.5)
Глава 11
Практикум 11.1
1. 2,7а: + С.
5. -Г3/3 + С.
9. 	Зи2/7 + С.
13. 5е* + С.
17. х2/2 + гс3/3 + С.
3. а:9/9 + С.
7. 2-7г£ + С.
11. и + и3 + С.
15. 3|lnz| + С.


1018
Ответы к упражнениям
19.
23.
27.
31.
33.
35.
37.
39.
43.
47.
51.
55.
59.
61.
65.
69.
73.
77.
81.
85.
21.
у = 40а:5 + С.
у = — и3 — и + С.
х = 5 In 111 t Н- С.
а) Ложь.
б) Истина.
25. Р = 24т - Зх2 + С.
29. у = ех + Зх + С.
Нет, поскольку один график нельзя получить из другого с помощью вертикального переноса.
Да, поскольку один график можно получить из другого с помощью вертикального
переноса.
15а:4/3 + С.
2у/й + С.
4 In |u| + и + С.
2а:5 + 2а:-4 -2х + С.
3 5 _2
-х3 + 2х 2 + С.
5
—4z-3 - |z-2 — 31n|z| +С.
41. -ЗГ3 + С.
45. —х~2/8 + С.
49. а:3 + 2а:-1 + С.
53. 2а:3/2 + 4а:1/2 + С.
57. ех/4 - За:2/8 + С.
63.
у = х2 — За: + 5.
х = 40д/<.
х = 4е* — 2t — 3.
х2 + х 1 + С.
ех — 21п |ж| + С.
у = За:5/3 + За:2/3 - 6.
67. С(х) = 2х3 - 2х2 + 3000.
71. у = —2а:-1 + 31п |ат| — х + 3.
75. у = 2х2 — За: + 1.
79. ^а;2 + а:-2 + С.
83. М = Z + t-1 + ?.
4
87. р(х) = Юж-1 + 10.


Ответы к упражнениям
1019
89. х3. 91. х* + Зх2 + С.
93. 	С (х) = 15 + —; С(х) = 15а; + 1000; С(0) = 1000 долл.
X
95. а) Функция затрат возрастает на интервале от 0 до 8, является выпуклой вниз на интервале от 0 до 4 и выпуклой вверх — на интервале от 4 до 8. Точка перегиба: х = 4. б) С(х) = х3- 12х2 + 53а; + 30; С(4) = 114000 долл.; С(8) = 198000 долл.
г) 	При низких и высоких объемах производства заводы часто оказываются неэффек- тивными.
97. S(t) = 2000 - 15ts/3; 8О3/5 « 14 месяцев.
99. S(t) = 2000 - 15£5/3 — 70t; t« 8,92 месяцев.
101. L(x) = 4800а;1/2; L(25) = 24000 человеко-часов.
103. W(h) = 0,0005/i3; W(70) = 171,5 фунтов.
105. 19400.
Практикум 11.2
1. |(4x-3)3+C.
5. е2х + С.
9. 1(х + 3)п+С.
13. 1(*2 + 1)в + С.
17. | In |5х + 4| + С.
5
21. -^(3t2 + l)"3 + C.
25. | (х + 4)5/2 - | (х + 4)3/2 + С. О о
29. ±-(х - 4)11 + ^(х - 4)10 + С.
11 о
33. - In [4 + 2х + х21 -F С.
37. 7 (еж - 2т)4 + С.
4
3- 5 С*2 + т)4 + С-
7. In (1 + а:4) + С.
11. -i(6t - 7)"1 + С.
6
15. ^ех2 + С.
19. —е1_< + С.
23. | (4-х3)’1 + С.
27. |(х - З)3/2 + 6(х - З)1'2 + С.
31. | (1 + е2*)4 + С. О
35. + С.
39. --1 (х4 + 2х2 + 1)_3 + С.


1020
Ответы к упражнениям
41.
43.
45.
47.
51.
55.
59.
63.
69.
71.
73.
75.
а) Необходимо продифференцировать правую часть и сравнить ее с подынтегральным выражением, стоящим в левой части.
б) Нет, так как [In |2х — 3| + С] = Если и = 2х — 3, то du = 2dx.
в) „
1 2х - 3 2 1
2x-3dX= 21п12ж 31+ С-
Проверьте-. £ [| In |2х - 3| + С] =
а) Необходимо продифференцировать правую часть и сравнить ее с подынтегральным выражением, стоящим в левой части.
б) Нет, т.к. [е*4 + с] = 4я3ех4 х3ех\ Если и = х4, то du = 4x3dx. В подынтегральном выражении нет множителя 4.
в) j x3ex*dx — j 4x3ex*dx = + С.
Проверьте: [|еж4 + = х3ех4.
а) Необходимо продифференцировать правую часть и сравнить ее с подынтегральным выражением, стоящим в левой части.
б) Нет, так как + с] = 3x4 3^22 ~4 2(х2 — 2)2. Если и = х2 — 2, то du =
= 2xdu. Оказывается, студент вынес из-под знака интеграла переменную величину (см. ниже пример неправильного вычисления).
в) j 2(ж2 — 2)2dx = j (2х4 — 8х2 + Проверьте: [|х5 — |х3 + 8z + С
1(Зх2 + 7)3/2 + С.
|(х3 + 2)3 + С.
|(1пх)4 + С.
х = — (t3 + 5) + С.
р = - (ех - е~хГ1 + С.
С(х) = 12х + 5001n(x + 1) + 2000;
2 , 8 о
I dx = -хь — -х3 + 8х + С.
5 3
= 2х4 - 8х2 + 8 = 2 (х2 - 2)2 .
49. -I- -I- 2х2 4- С.
53. | (2х4 + 3)1/2 + С.
57. е~^х + С.
61. т/ = 3(<2-4)1/2 + С'.
67. р(х) = 2000/(Зх -I- 50); 250 бутылок. (1000) = 17,45 долл.
а) S(t) = 10t + 100e_0,lt - 100; 0 t 24.
б) S(12) « 50 млн. долл.
в) 18,41 месяцев.
Q(t) = 100 ln(t 4-1) + 5t; 0 t < 29; Q(9) « 275 тыс. баррелей. Иф) = 2е°’и; И/(8)^4,45г.


Ответы к упражнениям
1021
77. а) —1000 бактерий/мл в день.
79. N(t) = 100 — 60e_0,lt; 0 t < 15; N(15) ~ 87 слов/мин.
81. E(t) = 12 000 - 10 000(t + 1)_1/2; Е(15) = 9500 студентов.
Практикум 11.3
1. у = 2,08х2 4- С. 3. у = 2е°’5а; + С.
X3 X2 2
= У У’ 7. у = е + 2.
Рисунок б. При х = 1 наклон dy/dx = 1 — 1 = 0 для любого значения у. При х = 0 наклон dy/dx = 0 — 1 = —1 для любого значения у. Оба эти условия согласуются с полем направлений, изображенным на рисунок б.
т2 2
у=--х + С-9у=--х
5.
9.
И.
15.
19.
у = Ce2t.
х = Ce~st.
21. Рисунок а. При у = 1 наклон dy/dx = 1 — 1=0 для любого значения х. При у = 2 наклон dy/dx = 1 — 2 = —1 для любого значения х. Оба эти условия согласуются с полем направлений, изображенным на рисунке а.
27.
О
О


1022
Ответы к упражнениям
37. Проанализируйте вторую производную функции /(у) = ку(М — у).
39. 1999. 41. А = 1000e°’O8t.
43. А = 8000e°’O6t.
45. а) р(х) = 100е_о,О5ж.
б) 60,65 долл, за штуку.
47. а) N = L(1 - e-°’051t). б) 22,5%.
49. I = /ое"0’009421; х « 74 фута.
51. a) Q = Зе"0’044.
б) Q(10) = 2,01 мл.
в) 27,47 ч.
53. 0,023117.
55. Приблизительно 24 200 лет.


Ответы к упражнениям
1023
57. 104 раза; 67 раз.
59. а) 7 человек; 353 человека, б) 400.
Практикум 11.4
1.
3. 	Рисунок а\ L3 = 13; R3 = 20; А3 = 16,5. Рисунок 6: L3 = 14; R3 = 7; Л3 = 10,5.
5. L3 J**/(x)dx Я3; R3 < J* (j(x)da: < L3; поскольку функция /(ж) возрастает, величина L3 недооценивает площадь, а 7?3 — переоценивает. Поскольку функция д(х) убывает, верно обратное утверждение.
7. Оба рисунка. Предел погрешности вычисления величин L3 и Я3 равен 7. Предел погрешности вычисления величины Аз равен 3,5.
9. Точная площадь фигуры, лежащей под графиком функции у = f(x), отличается от среднего арифметического левой и правой суммы не более чем на 3,5 единицы. Аз = 16,5.
11. a) L3 = 320, R4 = 192, Л4 = 256. Предел погрешности вычисления величин £3 и R3 равен 128. Предел погрешности вычисления величины А± равен 64.
б) Высота каждого прямоугольника представляет собой мгновенную скорость, а основание — время. Расстояние равно произведению скорости на время.
в) п > 256.
13. а) Ложь.
б) Истина.
15. Аю = 311100 кв. футов. Предел погрешности равен 25 000 кв. футов; п 100.
17. а) А7 = 298 футам. Предел погрешности равен 55 футов.
б) п > 77.
19. а) Р = 2.


1024
Ответы к упражнениям
б)
в) Слева от точки Р = 2 формула левых прямоугольников недооценивает истинную площадь, а формула правых прямоугольников — переоценивает. Справа от точки Р = 2 формула левых прямоугольников переоценивает истинную площадь, а формула правых прямоугольников — недооценивает.
5
г) 26 С j f(x)dx < 39.
о
21. Lq = —3,53; R6 = —0,91; Aq = —2,22. Предел погрешности вычисления величин Lq и Rq равен 2,63. Предел погрешности вычисления величины А6 равен 1,31. С геометрической точки зрения определенный интеграл на отрезке [2; 5] представляет собой сумму площадей фигур, ограниченных кривой и осью х между точками х = 2 и х = 5. Площади фигур, расположенных над осью х9 учитываются с положительным знаком, а площади фигур, расположенных под осью х,— с отрицательным.
23. (-оо; 0], [0; оо). 25. (-оо; -1], [-1; 0], [0; 1], [1; оо).
27. п 22. 29. п > 104.
31. п 30.
33. Обозначим определенный интеграл в левой части через I. Тогда
Выражение справедливо, поскольку при п —► оо предел правой части равен нулю.
35. А2 = 180000 долл., погрешность = 30 000 долл.
37. Lt = 4251 долл.; Я4 = 4605 долл.; 4251 J® 800e°>084t < 4605.
39. Первые 60 дней: А$ = 3240 штук, погрешность = 660 штук; вторые 60 дней: Аз = 4920 штук, погрешность = 100 штук.
41. а) Интеграл R' (х) dx представляет собой площадь фигуры, лежащей под кривой предельных затрат между точками х = 100 и х = 200. Он также равен общему изменению дохода за счет увеличения объема продаж со 100 до 200 блоков в день.
б) Л4 = 200 долл.; погрешность равна 50 долл.
в) 200 долл.; величины Я(200) - Я(100) и R' (ж) dx равны общему изменению дохода за счет увеличения объема продаж со 100 до 200 блоков в день. Следовательно,
R! (х) dx = Я(200) - Я(100).
43. a) L3 = 3,72 см2; У?2 = 3,37 см2.


Ответы к упражнениям
1025
5
б) 3,37 A' (t) dt 3,72.
о
45. А3 = 108 символов, погрешность равна шести символам.
Практикум 11.5
1. -2,33.
5. 1,067.
9. 5.
13. | « —2,333.
17. | (е2 - 1) « 3,195.
21. -10,67.
25. 240 футов.
29. 14.
3. 8,34.
7. 5.
11. 2.
15. 2.
19. 2 In 3,5 «2,506.
23. -5,04.
27. —2.
31. 56 = 15625.
33. In 4 « 1,386.
37. 1/2.
41. J (1 -е”1) «0,316.
4
35. 20 (е0,25 - е-°-5) « 13,550.
39. 8/3 « 2,667.
43. -| -1п2«-2,193.
45. а) Среднее значение функции /(х) равно 250.
47. а) Среднее значение функции /(х) равно б)
(Среднее значение /(г) =
49. а) Среднее значение функции /(ж) равно Ц « 1,61.


1026
Ответы к упражнениям
51.
53.
57.
61.
65.
69.
71.
75.
79.
81.
а) Среднее значение функции /(х) равно 2 (1 - е 2) « 1,73.
5
59. j (1 - х2) dx = -36.
2
— 2х + 3) dx = 1610.
2,214.
5
j 500 (t — 12) dt = -23 750 долл.; о
а)
QuadReg y=ax*+bx+c а=_.0082142857 b=1.528571429 с=16
,566.
— 11250 долл.
| ^500 - dx = 180 000 долл.
130
б) 6505.


Ответы к упражнениям
1027
83. Номинальный период = \/1п55 « 2 года; общая прибыль = || — |е 4 ~ 2,272, или 2272 долл.
85. а) 420 долл.
б) 135 000 долл.
QuadReg y=ax2+bx+c a=3.074675325 b= -24.98073593 c=55.56363636
б) 100 505 долл.
89. 5Ое0,6 — 5Ое0,4 — 10 » 6,51 долл. 91. 4800 человеко-часов.
93. а) I = —200t + 600.
з
б) j (—200t + 600) dt = 300.
о
95. 100 In И 4- 50 « 290 тыс. баррелей; 100 In 21 — 100 In 11 + 50 « 115 тыс. баррелей.
97. 10000 долл. 99. 3120 000 кв. футов.
101. 2е0,8 - 2 « 2,45 г; 2ех’6 - 2е°>8 = 5,45 г.
103. 10°С. 105. 1,1 л.
107. 0,6 In 2 + 0,1 « 0,516; (4,2 In 625 + 2,4 - 4,2 ln 49)/24 « 0,546.
Упражнения для повторения
1. 3x2 + 3z + C. (11.1)
3. -207. (77.5)
5. ln|u| + Ju4 + C. (11.1)
7. e~x2. (11.1)
9. у = f(x) = x3 — 2x + 4. (11.3)
10. 	Возрастает на отрезке [0; 2], убывает локальный максимум в точке х = вертикального переноса. (77.7)
2. 50. (77.5)
4. 	-I(l_f2)4 + C. (11.2)
6. 	0,216. (11.5)
8. 	>/4 + 5х + С. (11.1)
отрезке [2; 4]; выпуклая вниз на отрезке [0; 4]; Графики первообразных рисуются методом
И. (77.7)


1028
Ответы к упражнениям
12.
13.
15.
17.
18.
20.
22.
24.
26.
27.
28.
29.
31.
32.
34.
36.
38.
а) 2гг4 — 2х2 — х + С.
б) е‘ — 41n|i| + С. (11.1)
5 j (х2 + 1) dx = 44 ± 1,333. (11.5) 14. 45,444; \1 - М2\ = 1,333. (11.5)
1
30,8. 	(11.5). 16. 7. (11.5)
Ширина = 2 — (—1) = 3; высота = среднее значение функции f(x) = 7. (11.5)
-10. (11.4,11.5) 19. 0,4. (11.4, 11.5)
1,4. (11.4, 11.5) 21. 0. (11.4, 11.5)
0,4. (11.4, 11.5) 23. 2. (11.4, 11.5)
-2. (11.4, 11.5) 25. -0,4. (11.4, 11.5)
Возрастает на отрезках [0; 1] и [3; 4], убывает на отрезке [1; 3]; выпуклая вниз на отрезке [0; 2]; выпуклая вверх на отрезке [2; 4]; локальный максимум в точке х = 1; локальный минимум в точке х = 2. Графики первообразных рисуются методом вертикального переноса. (11.1)
(11.1)
а) 1; 1.
б) 4; 4. (11.3)
dy/dx = 2у/х. Наклоны графика, вычисленные в задаче 28.1, согласуются с приведенным полем направлений. (11.3)
| ■ 23/2 « 1,886. (11.5)
-5е-‘ + С. (11.1)
^е3х2 + С. (11.2)
6
35. | «0,167. (77.5)
6
37. (1 + е2).(77.7)
39. 2 (л/5 - 1) « 2,472. (77.5)


Ответы к упражнениям
1029
40.
42.
44.
45.
46.
47.
48.
49.
50.
51.
52.
54.
55.
57.
59.
60.
I In 10 « 1,151. (11.5) 41. 0,45. (11.5)
(2а;4 + 5)6 + С. (11.2) 43. - In (е~х + 3) + С. (11.2)
— (е* + 2)-1 + С. (11.2)
у = f(x) = 3 In |х| + а;-1 + 4. (11.2, 11.3)
у = За;2 + х - 4. (11.3)
L$ = 480 футов; Я5 = 320 футов; А5 = 400 футов; погрешности величин и R$ равны 160; погрешность величины равна 80. {11.4)
Высота каждого прямоугольника представляет собой мгновенную скорость, а основание — время. Расстояние равно произведению скорости на время. {11.4) п > 400. {11.4)
Высота = J® (160 - 32t) dt = 400 футов. (11.4)
а) Среднее значение функции f(x) равно 6,5.
б) /(*)
I I I 1 I I t Ы I
0'510
х
53. *а;8 - |а;5 + ^х2 + С. (11.2)
8 5 2
56. « 4,267. (11.5)
15
58. N = 800e°’O6t. (11.3)


1030
Ответы к упражнениям
1
62. I = j e~x2dx = М5 ± 0,00334 = 0,74805 ± 0,00334. (11.5)
о
63. п > 13. (11.5)
64. Ограниченный рост.
65. 	Экспоненциальный распад.
66. 	Неограниченный рост.
67. Логистический рост.
68. 1,167. (77.5)
69. 99,074. (77.5)


Ответы к упражнениям
1031
70.
71.
72.
73.
74.
75.
76.
77.
79.
80.
81.
82.
84.
85.
86.
87.
-0,153. (/7.5)
600
L2 = 180000 долл.; R2 = 140000 долл.; 140000 | C'(x)dx 180000. (11.4)
200
Высота прямоугольника, равная С"(ж), представляет собой величину предельных затрат на производство х единиц продукции, т.е. приближенную себестоимость единицы продукции при заданном объеме производства. Ширина прямоугольника представляет собой объем производства, превышающий значение х = 200. Следовательно, произведение себестоимости и количества произведенной продукции равно числу, на которое увеличиваются производственные затраты. Чем больше объем производства, тем точнее формула. {11.4)
600
f (бОО - dx = 160 000 долл. (77.5)
200
40
(iso ~ Io)dx = 4425 долл' (77’5)
10
Р(х) = ЮОгг - 0,01а:2; Р(10) = 999 долл. (11.3)
15
j (60 — 4t) dt = 450 тыс. баррелей. {11.5)
о
109 штук. {11.5) 78. 16е2,5 — 16е2 — 8 « 68,70 долл. {11.5)
а) As = 725; погрешность = 75.
QuadReg ч=ах2+Ьх+с а= 005 Ь=.55 с=5
в) 729. {11.4, И-5)
Номинальный период = 10 In ™ « 19 лет; общая прибыль = 143 — 200е-1,9 « « 113 086 долл. {11.5)
S{t) = 50 - 5Ое~°’08* « 31 млн. долл.; — (In 0,2)/0,08 « 20 месяцев. {11.3)
6,5 частиц на миллион. 83. 1 см2. {11.3)
800 галлонов. {11.5)
а) 145 млн.
б) Около 46 лет. {11.3)
-In 0,04
0,0001238
«26 000 лет. {11.3)
7V(£) = 95 — 70е 0,lt; 7V(15) « 79 слов/мин. {11.3)


1032
Ответы к упражнениям
Глава 12
Практикум 12.1
ь
а
Ъ
3. j [—Л(ж)] dx.
а
5. Поскольку заштрихованная фигура на рисунке в расположена ниже оси х, h(x) С 0. Следовательно, величина h(x)dx является отрицательной.
7. 	20. 9. 7/3 « 2,333.
11. 	9.
15. 0,693.
13. 7,021.
ь
а
19.
ь f
j f(x)dx + j [—/(ж)]
dx.
d
21. j [f(x) - g(x)] dx.
c
a
c
d c
23. [/(x) - p(x)] dx + j [p(x) - /(x)] dx.
С b
25. Чтобы определить точки пересечения b и с, решим уравнение /(ж) = д(х) на интервале [a, d\. Затем обратим внимание на то, что на отрезке [а, Ь] выполняется неравенство
/(х) > д(х), а на отрезке [Ь, с] — д(х
довательно, площадь = $ba[f(x) — д('
27.
2,5.
29. 7,667.
35.
32.
37. 36.
43.
18.
45. 1,858.
51.
101,75.
53. 8.
59.
8,290.
61. 3,166.
f(x), а на отрезке [с, d] — f(x) д(х). Сле- )] dx + Л ^(Х) _ dx + fc [/(Х) “ dx-
31. 23,667.
33. 15.
39. 9.
41. 2,832.
47. 17.
49. 8.
55. 17,979.
57. 5,113.
63. 1,385.
65. Общий объем производства за период с конца пятого года по конец десятого года равен 50 + 100 In 20 - 100 In 15 « 79 тыс. баррелей.
67. 	Общая прибыль на протяжении пяти лет эксплуатации равна 20—30е_1,5«13,306 тыс.
долл.
69. 1935: 0,412; 1947: 0,231; наиболее равномерно доход был распределен в 1947 г.
71. 1963: 0,818; 1983: 0,846; наименее равномерно совокупный доход был распределен в 1983 г.
73. а) /(х) = 0,3125х2 + 0,7175х - 0,015.
б) 0,104.
75. Общий вес дрожжей на протяжении 10 часов равен Зе - 3 ~ 5,15 г.
77. Среднее количество слов, заученных на протяжении двух часов, равно 15 In 4 — - 151п2«10.


Ответы к упражнениям
1033
Практикум 12.2
1. 4.12.
5. а) 10,72.
б) 3,28.
в) 10,72.
7. а) 0,75.
б) 0,11.
в)
3. 509,14.
9. 	8 лет.
11. а) 0,11.
б) 0,10.
13. P(t > 12) = 1 - Р(0 t 12) = 0,89.
15. 12 500 долл.
17.
Если f(t) — скорость непрерывного потока доходов, то общий доход за пять лет равен площади фигуры, лежащей под графиком функции у = f(t) между точками t = 0 и t = 5.
19. 8000 (е0,15 - 1) « 1295 долл.
21.
Если /(£) — скорость непрерывного потока доходов, то общий доход за три года равен площади фигуры, лежащей под графиком функции у = f(t) между точками t = 0 и t — 3.


1034
Ответы к упражнениям
23. 255 562 долл.; 175 562 долл. 25. 20 000 (е0’25 - е'0’08) « 7218 долл.
27. 875 долл.
29. Магазин одежды: FV = 120000 (е0,5 — 1) « 77847 долл.; компьютерный магазин: FV = 200 000 (е0,5 — е0,25) « 72 939. Лучше вложить средства в магазин одежды.
31. Облигация: FV = ЮОООе0,4 « 14918 долл.; бизнес: FV = 25 000 (е0,4 - 1) « « 12 296 долл. Лучше вложить средства в облигации.
к
33. 55 230 долл. 35. - (егТ - 1). 37. 625 000 долл.
39.
Площадь залитой цветом области представляет собой величину потребительской выгоды, т.е. общую сумму, сэкономленную покупателями, которые согласны заплатить более 150 долл, за единицу товара, имея возможность приобрести его по более низкой цене.
41. 9900 долл.
43.
Площадь заштрихованной области представляет собой величину выгоды производителей, т.е. общую прибыль, которую получат производители, согласные поставлять товар по цене меньше 67 долл., имея возможность поставлять его по цене 67 долл.
45. CS = 3380 долл.; PS = 1690 долл.


Ответы к упражнениям
1035
47. CS = 6980 долл.; PS = 5041 долл.
49. CS = 7810 долл.; PS = 8336 долл.
51. CS = 8544 долл.; PS = 11507 долл.
53. а) х = 21,457; р = 6,51 долл.
б) CS = 1,774 долл.; PS = 1,087 долл.
Практикум 12.3
S. « = х + 2; 11 + 2)^+1)‘ - <5^ + С.
7. -Ze"1  *-е’1 + С. 9. Ь'"+С.
|1
11. (хех — 4ех) = —Зе + 4 « —4,1548.
1о
I3
13. (х1п2т-ж) = (31п6 —3) - (In2 — 1) «2,6821.
15. In (х2 + 1) + С. 17. (1пж)2/2 + С.


1036
Ответы к упражнениям
19.
21.
23.
25.
29.
31.
35.
37.
39.
41.
43.
47.
49.
2 з/21пх_4 3/2 с
3 9
Интеграл равен площади фигуры, ограниченной графиком функции у = (х — 3)ех и отрезком оси х от точки х = 0 до точки х = 1.
Интеграл равен площади фигуры, ограниченной графиком функции у = In 2х и отрезком оси х от точки х = 1 до точки х = 3.
(х2 - 2х + 2) ех + С. 27.
Г_^_1Г = _? + 1й0,2М2.
\ х х) х е
61п6 — 41п4 — 2 « 3,205. \
(1+ х2) In (1 + х2) - | (1 + х2) + С.
(1 + е1) In (1 + е®) - (1 + еж) + С.
х(1п х)2 — 2х\пх + 2х + С.
х(1пх)3 — Зх(1пх)2 + бх 1п х — бх + С.
~^ + с. а2
33. хех~2
- ех~2 + С.
1,56. 45. 34,98.
5
(2t — te~^ dt = 24 млн. долл.
о


Ответы к упражнениям
1037
Общая прибыль за первые пять лет (млн. долл.) равна площади, ограниченной кривой предельной прибыли Pf(t) = 2t — te^ и отрезком оси t от точки t = 0 до точки t = 5.
51. 3278 долл. 53. 0,264.
55.
Концентрация дохода равна площади фигуры, ограниченной прямой у = х и кривой Лоренца у = xex~1f поделенной на площадь фигуры, ограниченной прямой у = х и отрезком оси х от точки х = 0 до точки х — 1.
57. 	S(t) = 1600 + 4OOeo,lt — 40te0,lt; 15 месяцев.
59. 977 долл.
61.
Потребительская выгода равна площади, ограниченной кривой зависимости цены от спроса р = 9 — 1п(ж -I- 4), кривой цены у = р = 2,089 и отрезком оси х от точки х = 0 до точки х = х = 1000. Эта величина представляет собой количество потребителей, желающих сэкономить более 2089 долл.
63. 2,1388 частиц на миллион.
65. AT(f) = —4fe_0,25t — 40e“°’25t 4- 80; 8 недель; 78 слов/мин.
67. 20 980.
Практикум 12.4
1. In
X
1 + X
2(х - 32)
3
5.
+ С.
х
+ С.
3.
1
3 + я
7. -In
4~ 2 In
5 + 2х
3 И- х
1 + У1 - я2
X
+ С.
+ С.
11. ^-х31пх — ^х3 + С. о У
15. 9 In | —2 «1,6492.
13. x-lnjl + e1! + С.


1038
Ответы к упражнениям
17.
21.
23.
25.
27.
31.
35.
37.
39.
43.
49.
53.
55.
57.
61.
63.
|Ш у «0,4377.
19. In За 1,0986.
_ У4х2 + 1 + 21п |2а. + у4а,2 + J + с
X I I
In |х2 + \/х4 — 1б| + С.
(х3у/х6 + 4 + 41п |х3 + \/х6 + 4h + С.
\/4 - х2
8х2
+ С.
2
-(1пх — 8)\/4 + Ina: + С.
29. | In
5
3 + 4ег
2 + ех
—х3е х — За:2е х — бхе х — бе х + С.
х(1пх)3 — За:(1па:)2 + бх In х — ба: + С.
64
Т’
] . г
X
5,48.
41. | In ? а 0,2939.
47. 31,38.
51. 3000 + 1500 In | а 1352 долл.
О
С(х) = 200а; + 10001п(1 + 0,05а:) + 25 000; 608; 198 773 долл.
100 ОООе - 250 ООО « 21828 долл. 59. 0,1407.
По мере уменьшения площади фигуры, ограниченной двумя кривыми, кривая Лоренца стремится к прямой у = х, а распределение доходов становится все более равномерным.
S(t) = 1 +1 — —1 — 2 In 11 + t|; 24,96 — 2 In 25 « 18,5 млн. долл.
1 с


Ответы к упражнениям
1039
Месяцы
Общий объем продаж (млн. долл.) за первые два года (24 месяца) равен площади фигуры, ограниченной графиком функции у = S'(t) и отрезком оси t от точки t = 0 до точки t = 24.
67. Р (х) = (2 + За:)3/2 - 2000,83; 54; 37932 долл.
135
69. 1001пЗ « 110 футов. 71. 60 In 5 « 97 слов.
73.
Время обучения, ч
Площадь фигуры, ограниченной графиком функции у = N'(t) и отрезком оси t от точки t = 0 до точки t = 12, равна общему количеству слов, заученных за указанное время.
Упражнения для повторения
ь
1. f(x)dx. (12.1)
а
b с
3. j f(x)dx + j[—/(a:)]da:. (12.1)
a b
4. Площадь = 1,153.
2- j[-/(z)]<£r. (12.1). b
5. 	-xe4x - -le41 + C. (12.3, 12.4)
4 16
6. lnx — ^x2 + C. (12.3, 12.4)


1040
Ответы к упражнениям
7.
9.
10.
11.
13.
14.
15.
16.
18.
19.
20.
22.
+ С. (12.4)
\Л + я — 1
\/l -h яг H- 1
8.
+ С. (12.4)
12.
С
[p(z) - f(x)]dx. (12.1)
ь
x
1 + x
+ с. (12.4) 1^ + 1°
\/1 + Я 1  ~ 1п
х 2
ь j lf(x)-g(x)]dx. (12.1) а
с d
j [д(х) - f(x)] dx + j [/(x) - g(x)] dx. (12.1) b c
bed
j [f(x) - g(x)]dx + j [</(x) - f(x)]dx + j [/(x) - g(x)]dx. (12.1)
Площадь = 20,833.
С
Зх + \/9x2 - 49 ) + C. (12.4)
1. (12.3, 12.4) 17. — -81n8 + 81n4« 1,955.
^3rr\/9a;2 — 49 — 49 ln
_2te-°’5t - 4e_0,5t + C. (12.3, 12.4)
In# — -|- C. (12.3, 12.4) 21. x — ln |1 + 2ex| + C. (12.4)
о 9
а) 	Площадь = 8.


Ответы к упражнениям
1041
б) 	Площадь = 8,38.
23. ^(1пх)3 + С. (12.2)
и
24. ^а:2(1пх)2 — ^ж21пх + ^х2 + С. (12.3,12.4)
25. у/х2 - 36 + С. (12.2) 26. | In |х2 + у/х4 - 361 + С. (12.4)
27. 50 In 10 - 42 In 6 - 24 « 15,875. (12.3, 12.4)
28. x(lnx)2 -2xlnx + 2x + C. (12.3,12.4)
29. ~е-х2 + С. (12.2)
30. — ^х2е~2х - ^е~2х - ~е~2х + С. (12.3, 12.4)
31. 1,703. (12.1)
32. а) 0,189.
6) 0,154. (12.2)
33.
Вероятность того, что изделие выйдет из строя на протяжении двухлетнего гарантийного срока, равна площади фигуры, ограниченной графиком плотности вероятности у = f(t) и отрезком оси t от точки t = 3 до точки t = 2.
34. R(x) = 65я — 6[(х -I-1) 1п(я + 1) — я]; 618 фенов в неделю; 29 506 долл. (12.3)
35. а)
б) 8507 долл.


1042
Ответы к упражнениям
36. а) 20 824 долл.
б) 6623 долл. (72.2)
37. а)
б) Распределение является более равномерным, поскольку площадь фигуры, ограниченной двумя кривыми, уменьшается.
в) Текущая стоимость = 0,3; будущая стоимость = 0,2; через 10 лет доход будет распределен более равномерно. {12.1)
36. 	a) CS = 2250 долл.; PS = 2700 долл.
б) CS = 2890 долл.; PS = 2278 долл. (72.2)
39. а) 25 403 фунтов.
б) PS = 121,6 долл. (72.2)
40. 4,522 мл.; 1,899 мл. (77.5, 12.4)
41. (77.5, 72.7)


Ответы к упражнениям
1043
42. 0,667; 0,333. (72.2)
43. (72.2)
Вероятность того, что доктор затратит на случайно выбранного пациента больше одного часа, равна площади фигуры, ограниченной графиком плотности вероятности у = f(t) и отрезком оси t от точки t = 1 до точки t = 3. (12.2)
44. 45000. (11.5, 12.1)
45. 0,368. (12.2)
Глава 13
Практикум 13.1
1. -8.
3. -29.
5. 12.
7.
19.
9. -448.
11. 6.
13. 150.
15.
16тг.
17. 791.
19. 0,192.
21. 118.
23.
36095,07.
25. -1,926; 0,599.
27. 2х + h.
29. 2у2.
31. £7(0; 0; 3); F(2\ 0; 3).
33. a) z = х2 в плоскости у = с, где с — произвольная константа.
б) Ось у; горизонтальная прямая, параллельная оси у и проходящая через точку (1; 0; 1); горизонтальная прямая, параллельная оси у и проходящая через точку (2;0;4).
в) Параболическая “впадина”, лежащая над осью у.
35. 	а) Верхние полукруги, центры которых лежат на оси у.
б) Верхние полукруги, центры которых лежат на оси х.
в) Верхняя полусфера, радиус которого равен 6, а центр лежит в начале координат.
37. 	а) Числа а2 + Ь2 и с2 + d2 равны квадрату радиуса круга.
б) Колоколообразные кривые, достигающие в начале координат максимума, равною единице.
в) Колокол, максимум которого равен единице и достигается в начале координат, а ветви раходятся во все стороны до бесконечности.
39. 4400 долл.; 6000 долл.; 7100 долл.
41. R(p,q) = -5p2 + 6pg-4g2 + 200p + 300<7; 71(2,3) = 1280 долл.; 7?(3,2) = 1175 долл.
43. 30 065 единиц.
45. а) 272 615,08 долл.
б) 12,2%.
47. Т(70,47) « 29 мин.; Т(60,27) = 33 мин.


1044
Ответы к упражнениям
49. С(6; 8) = 75; 0(8,1; 8) = 90.
51. 0(12,10) « 120, 0(10,12) и 83.
Практикум 13.2
1. -2.
3. 5.
5. 6х2 + 92/2.
7. 18г/.
9. 72.
11. 10х — бу — 4.
13. 4.
15. -6.
17. 10.
19. 12х2у+-.
X
21. 32 +In 2.
23. 12х2 + -
X
25. 8хе4ж2+5^.
27. 40хе4т2+5^.
29. 40е4.
31. 8е5.
33. /Х(х,у) = 6х (х2
-2/3)2; /у(*,У) =
-9j/2 (х2 - у3)2.
35. /Х(х,у) = 24x2/ (Зя?2?/ - 1)3; fy{x,y) = 12х2 (Зх22/ - 1)3.
37. Л(х,2/) = 2х/ (х2 +«/2); fy(х, у) = Ъу/ (х2 + у2).
39. fx(x,y) = у4еху2\ fy(x,y) = 2ху3еху2 + 2уеху2.
41. fx(x,y) = 4xi/2/ (х2 + у2)2; fy(x,y) = -4х2у/ (х2 + у2)2.
45. fxx(x, у) = 2у2 + 6х; fxy(x, у) = 4ху = fyx(x, у); fyy(x, у) = 2х2.
47. fxx(x,y) = —2у/х3; fxy(x,y) = -\/у2 + 1/х2 = fyx(x,y}-, fyy(x,y) = 2х/у3.
49. fxy(х, у) = (2у + Х2/2) еху; fxy(x, у) = (2у + х2у) еху = fyx(x, у); fyy(x, у) = х3еху.
51. х — 2 и у = 4. 53. х — 1,200 и у = —0,695.
55.»>43.
б) Значения функции /(0,2/), например, меньше чем -у.
57. а) с = 1,145.
б) /х(с, 2) = 0;/у(с, 2) = 92,021.
59. fxx(x, у) + fyy(x, у) = (2у2 - 2х2) / (х2 + у2}2 + (2х2 - 2у2') / (х2 + у2)2 = 0.
61. а) 2х.
б) 42/.
63. Рх (1200,1800) = 24; при производственном плане (1200,1800) прибыль увеличится приблизительно на 24 доллара на каждый дополнительный калькулятор типа А; Р1/(1200,1800) = -48; при производственном плане (1200,1800) прибыль уменьшится приблизительно на 48 долларов на каждый дополнительный калькулятор типа Б.
65. дх/dp = — 5: увеличение цены кофе сорта А на один доллар уменьшит уровень спроса на кофе сорта Л на 5 фунтов при любом уровне цен (р, q); ду/dp = 2: увеличение цены кофе сорта А на один доллар увеличит уровень спроса на кофе сорта В на 2 фунта при любом уровне цен (р, д).
67. а) Д(х,2/) = 7,5х_0,252/0’25; /У(х,у) = 2,5х°’75у~°’75.
б) Предельная производительность труда = Д(600,100) « 4,79. Предельная производительность капитала = /у (600,100) « 9,58.
в) Капитал.
69. Конкурирующие.
71. Дополняющие.


Ответы к упражнениям
1045
73. a) fw(w,h) = fh^h) = ll,34w0’425/i_0,275.
6) 	/w(65,57) = 11,31: площадь тела человека, имеющего вес, равный 65 фунтам, и рост, равный 57 дюймам, увеличивается со скоростью 11,31 кв. дюймов на каждый дополнительный фунт веса (при фиксированном росте); Д(65,57) = 21,88: площадь тела человека, имеющего вес, равный 65 фунтам, и рост, равный 57 дюймам, увеличивается со скоростью 21,99 кв. дюймов на каждый дополнительный дюйм роста (при фиксированном весе).
75. С\у(6,8) = 12,5: если W = 6 и L = 8, то при увеличении ширины головы на один дюйм (при фиксированной высоте) черепной индекс возрастает приблизительно на 12,5 единицы; СТ, (6,8) = —9,38: если W = 6 и L = 8, то при увеличении высоты головы на один дюйм (при фиксированной ширине) черепной индекс уменьшается приблизительно на 9,38 единицы.
Практикум 13.3
1. /Ж(ж, у) = 4; fy(x, у) = 5; функции fx(x, у) и fy(x, у) никогда не равны нулю.
3. fx(x,y) = -1,2 4- 4х3; fy(x,y) = 6,8 + 0,6т/2; функция fy(x,y) никогда не равна нулю.
5. /(—2,0) = 10 — локальный максимум.
7. /(—1,3) = 4 — локальный минимум.
9. Функция f имеет седловую точку (3; —2).
11. /(3,2) = 33 — локальный максимум.
13. /(2,2) = 8 — локальный минимум.
15. Функция f имеет седловую точку (0; 0).
17. 	Функция f имеет седловую точку (0; 0); /(1,1) = — 1 — локальный минимум.
19. Функция f имеет седловую точку (0; 0); /(3,18) = —162 и /(-3,-18) = —162 — локальные минимумы.
21. В точке (0; 0) критерий не выполняется; функция / имеет седловые точки (2; 2) и (2;-2).
23. Функция / имеет седловую точку (0,614; —1,105).
25. Функция /(ж, у) является неотрицательной и равна нулю, если х = 0. Следовательно, функция / имеет локальные минимумы в каждой точке оси у.
27. б) Локальный минимум.
29. 2000 калькуляторов модели А и 4000 калькуляторов модели В, МахР = Р(2,4) = = 15 млн. долл.
31. а) При р = 10 долл, и q = 12 долл, х = 56 и у = 16; при р = 11 долл, и q = 11 долл. х = 6 и у = 56.
б) Максимальная еженедельная прибыль, равная 288 долл., достигается при р = = 10 долл, и q = 12 долл.
33. Р(х,у) = Р(4,2).


1046
Ответы к упражнениям
35. 8 дюймов на 4 дюйма на 2 дюйма.
37. 20 дюймов на 20 дюймов на 40 дюймов.
Практикум 13.4
1. Мах/(х,у) = /(3,3) = 18.
3. Min/(х, у) =/(3,4) = 25.
5. Система уравнений Fx = — 3 + 2Л = 0 и Fy = 4 + 5Л = 0 не имеет решения.
7. Мах /(х, у) = /(3,3) = /(-3, -3) = 18; Min /(х, у) = /(3, -3) = /(-3,3) = -18.
9. Максимальное произведение равно 25, когда каждый сомножитель равен 5.
11. Min /(х, у, z) = /(-4,2, -6) = 56.
13. Мах/(х,у,г) = /(2,2,2) = 6; Min/(x,y,z) = /(-2,-2,-2) = -6.
15. Мах/(х,у) = /(0,217; 0,885) = 1,055.
17. Система уравнений Fx = ех + А = 0 и Fy = Зеу — 2А = 0 не имеет решения.
19. Максимизировать функцию /(ж, 5), зависящую только от одной переменной.
21. a) Max f(x,y) = /(0,707; 0,5) = /(-0,707; 0,5) = 0,47.
23. 60 единиц модели А и 30 единиц модели В гарантируют минимальные затраты, равные 32 400 долл, в неделю.
25. а) 8000 единиц труда и 1000 единиц капитала; Max7V(x, у) = TV(8000,1000) « « 263 902 единиц.
б) Предельная производительность денег « 0,6598; увеличение объема производства « 32 990 единиц.
27. 8 х 8 х 8/3 дюймов.
29. х = 50 футов и у = 200 футов; максимальная площадь равна 10000 кв. футов.
Практикум 13.5
7. у = -1,5х + 4,5; у = 0,75 при х = 2,5.
9. у = 2,12ж + 10,8; у = 63,8 при х — 25.
11. у = —1,2а? -I-12,6; у = 10,2 при х = 2.
13. у = —1,53# + 26,67; у - 14,4 при х = 8.


Ответы к упражнениям
1047
21. а) у = 1,52а: — 0,16; у = 0,73а;2 — 1,39а: + 1,30.
б) Квадратичная функция.
23. Нормальные уравнения образуют систему, состоящую из четырех линейных уравнений относительно четырех переменных а, Ь, с и d, которую можно решить методом Гаусса.
25. а) у = 110,5а: + 1834;
б) 4044000.
27. а) у = —0,48а: + 4,38;
б) 6,56 долл, за бутылку.
29. а) Р = -0,66Т + 48,8;
б) 11,18 ударов в минуту.
31. а) у = 0,0086а? + 56,48; б) 58,19 °F.
33. a) D = -3,1Л + 54,6;
б) 45%.
35. а) у = 0,0871а: + 10,80; б) 21,25 фута.
Практикум 13.6
1. а) За:2?/4 4- С(х).
б)
3. а)
б)
5. а)
б)
7. а)
б)
Зя2.
2х2 + вху + 5я + Е(у). 35 -|- 301/.
у/у + х2 + Е(уУ, Vy + ^~ у/у- !i^ + cW.
X
21пт
X
9. 9.
15. 1.
11. 330.
17. 16.
1
(а: + y)2dydx =
-1
32
3 ’
13. (56 - 20\/5)/3.
19. 49.
4 7
23. у- f —dydx = In ~ 0,6264.
15 J J ?/ 2 2


1048
Ответы к упражнениям
25. 4/3 куб. ед.
1 2
в) В точках, лежащих в правой полуплоскости, функция больше нуля, а в точках, лежащих в левой полуплоскости, — меньше.
0,8 7
37. — I I —-—dy dx = 30 ln 2 « 20,8 млрд. долл.
0,4 J J 1 - х
0,6 5
20 2
39. j jх0’75 у0’25 dydx = (21’25 - 1) (201’75 - 101-75) «8,375.
10 1
8 6
41- ife J J [10-
1
1 Z 2 2\1 j j 20
— [х + у ) dydx= — насекомых на кв. фут.
10
-8 -6
2 1
j [100 — 15 (х2 + у2)] dy dx — 75 частиц на миллион.
4J
-2 -1
3000 60
j 0,0000133ху2dy dx « 100,86 футов.
2000 50
16 12
47. j j 100|di/ dx = 600 ln 1,2 «109,4.
8 10
45.—^—
10000
Упражнения для повторения
1. /(5,10) = 2900; fx{x,y) = 40; /У{х,у) = 70. {13.1, 13.2)
2. d2z/dx2 = вху2; д2г/дхду = 6ж2у. {13.2)
3. 2ж?/3 + 2у2 + С(ж). {13.6) 4. Зж2?/2 + 4ху + Е{у). {13.6)
5. 1. {13.6)
6. У) = 5 + 6 + Зж2; fy{x, у) = -2; функция /у(ж, у) никогда не равна нулю. {13.3)
7. /(2,3) = 7; fy(ж, у) = -2ж + 2у + 3; fy{2,3) = 5. {13.1, 13.2)


Ответы к упражнениям
1049
8.
10.
11.
12.
13.
14.
15.
16.
17.
19.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
-8 • (-6) - 42 = 32. (73.2)
у = — 1,5а: + 15,5; у = 0,5 при х = 10. (13.5)
18. 	(13.6)
fx(x,y) = 2хех2+2у", fy(x,y) = 2ех2+2у; fxy(x,y) = 4хех2+2у. (13.2) fx(x,y) = 10а: (a:2 + i/2)4; fxy(x,y) = 80ху (х2 +у2)3. (13.2)
f(2,3) = —25 — локальный минимум; седловая точка: (—2; 3). (13.3)
18. —. (13.6)
5
20. 0. {13.6)
а) 12,56.
б) Нет. {13.6)
Система уравнений Fx = 12ж2 + ЗА = 0, Fy = —15у2 + 2А = 0 и РЛ = Зх + 2у — 7 = 0 не имеет решения. {13.4)
а) Рх(1,3) = 8. Прибыль будет возрастать на 8000 долл, на каждые 100 дополнительных единиц продукции вида Л, если объем производства продукции вида Б фиксирован на уровне (1; 3).
б) При выпуске 200 единиц продукции вида А и 300 единиц продукции вида Б\ Р(2,3) = 100 тыс. долл. — локальный максимум. {13.2, 13.3)
8 	дюймов на 6 дюймов на 2 дюйма.
у = 0,63ж + 1,33; прибыль на шестом году равна 5,11 млн. долл. {13.4)
а) Предельная производительность труда « 8,37. Предельная производительность капитала «1,67. Менеджеру следует стимулировать рост производительности труда.
б) 80 единиц труда и 40 единиц капитала; MaxN(x,?/) = N(80,40) « 696 единиц. Предельная производительность капитала « 0,0696. Увеличение объема производства « 139 шт.
1 ТТ о я 0 2 (401,2 — 201,2) (1001,8 — 501,8)
в) удод J j 10x°’8y°’2dy dx = ± Уё = 621 единиц. (73.4)
50 20
Тж(70,17) = -0,924 мин/фут при V = 70 куб. футов и х = 17 футов. {13.2)
216
2 2
[100 — 24 (х2 + т/2)] dy dx = 36 частиц на миллион. {13.6)
-2-2
50 000. {13.1)
у - -х 4- 48; у = 68 при х = 40. {13.5)
а) у = 0,4933х + 25,20.
б) 84,40 чел. на кв. милю.
в) 89,30 чел. на кв. милю; 97,70 чел. на кв. милю.


1050
Ответы к упражнениям
32. 	а) у = 1,069а: + 0,522.
б) 64,68 года.
в) 64,78 года; 64,80 года. {13.5)
Глава 14
Практикум 14.1
7. в.
11. у ,С=1
/ г=\
19. у = 2х —
х
17. у = хе х.
25. у = у/9 - х2.
27. у = 2- ех.
29. а) т/ = 2 - е~х.
б) У = 2.
в) у = 2 + е х.
31. а) у = 2 - ех.
б) у = 2.
в) у = 2 + ех.


Ответы к упражнениям
1051
33. 	dN/dt = 650; t — время (лет), N = N(t) — количество сотрудников в момент t, dN/dt = N' — скорость изменения количества сотрудников.
35. dT/dt = —к(Т — 72); t — время, Т = T(t) — температура пиццы в момент t, к — положительный коэффициент пропорциональности, dT/dt = Т' — скорость изменения температуры пиццы (отрицательная, поскольку пицца остывает).
37. а) у =
10
1+9е-ж’
б) у = Ю.
в) У~ Г“
10
0,5е-*‘
39. а) у = Сх3 И- 2 для любого числа С.
б) Решения не существует.
в) у = 2 - х3.
б) Каждый график уменьшается до локального минимума, а затем возрастает, стре-
г) 	Каждый график возрастает на всей числовой оси, стремясь к прямой у = х при неограниченном увеличении переменной х.


1052
Ответы к упражнениям
43. а) р = 5.
б) p(t) = 5 — 4e_0,lt; p(t) = 5-1- 5е_0,1<.
Р
1 1 1 1—н-
0 5 10 15 20 25
45. б) A(f) = 25ООе0,08* - 25 00; A(t) = 3500e°’O8t - 2500.
Практикум 14.2
1. dy/dt = 100000. 3. dy/dt = fc( 10000 - у).
5. В настоящее время годовой объем продаж равен 2 млн. долл. Объем продаж растет прямо пропорционально ему самому.


Ответы к упражнениям
1053
7.
9.
13.
15.
17.
19.
21.
23.
25.
27.
29.
31.
33.
35.
37.
41.
45.
47.
49.
51.
53.
55.
59.
63.
65.
В общине, состоящей из 5000 человек, слухи распространяются со скоростью, прямо пропорциональной количеству человек, уже слышавших их, и количеству человек, которые о них еще не знают.
1,1 1t 1 , 3-х
~ъУ = -• 11. -у = .
yz х ух
Общее решение: у = х3 + С; частное решение: у = х3 — 1.
Общее решение: у = 2 In я + С; частное решение: у = 2 Ina; -И 2.
Общее решение: у = Сех; частное решение: у = 10ех.
Общее решение: у = 25 — Се~х; частное решение: у = 25 — 20е~®.
Общее решение: у = Сх\ частное решение: у = 5х.
Общее решение: у = (Зх 4- С)1/3; частное решение: у = (Зх 4- 24)1/3.
Общее решение: у = Се&х; частное решение: у = 3ee*.
Общее решение: у = In (е® 4- С); частное решение: у = In (ех + 1).
Общее решение: у = Сех2/2 — 1; частное решение: у = Зе®2/2 — 1.
Общее решение: у = 2 — 1/ (е® + С); частное решение: у = 2 — е х.
1 з 1 з
У + -у3 = х + -х3 + С.
i In 11 + у21 = ln |х| + (x2/2) 4- С или ln (1 + 7/2) = ln (x2) + x2 + C. z
ln (1 + ev) = ^x2 + C. 39. у = ^/1 + (lnx)2.
у = | [x + ln (x2) + 3]2 . 43. у = ^/ln(x2 + e).
Это дифференциальное уравнение невозможно записать в виде f(y)y' = р(х). Подынтегральное выражение е*2 не имеет элементарной первообразной.
а) М = 3/(1 - e"fc); М = 4/(1 - е~1’5к).
б) 7,3.
5000е°’275 « 6582,65.
ч 71п0,5 „„
а) мГ22дня'
б) 100000 (1 - е°'51п0’5) « 29300 человек.
30 In 0,1
« 100 дней.
In 0,5
57.
41n0,2
1п0,8
« 29 лет.
к = 0,2; М = 11 млн. долл.
61.
21n(5/12)
ln(5/6)
~ 9,6 мин.
25 + 300e4ln<2/3> «84,26°F.
a) 100e51nl
б)
ln 10  « lnl,4
,4 « 538 бактерий.
6,8 ч.


1054
Ответы к упражнениям
67. а)
б)
50000
1 + 499e21n<"/4")
ss 2422 человека.
10 In (1/499)
1п(99/499)
38,4 дня.
69. I = Ask.
71. а)
1000
| _|_ 199е71п(99/199)
« 400 человек.
б)
1п(3/3383)
1п(99/199)
« 10 дней.
Практикум 14.3
1. Да; /(я) = —к, д(х) = 0.
3. Нет; уравнение содержит член у2, т.е. является нелинейным.
5. f (х3у' 4- Зя2?/) dx = х3у. 7. f (e~3xyf — Зе_3ж?/) dx = е~3ху.
9.
(я4?/ + 4я3?/) dx = я4?/.
0,5е“°’5х?/) dx = е~0,3ху.
13. I = е2х; у = 2 + Се~2х; у = 2- е~2х.
15. 	/(я) = ех; у = е~2х + Се~х; у = —е~2х + 4е~х.
17. 	1(я) = е~х; у = 2хех 4- Сех; у = 2хех — 4еж.
19. 1(я) = ех; у = Зх3е~х 4- 2е~х. 21. /(я) = я; у = я 4- (С/х); у = х.
23. 	/(я) = я2; у = 2я3 4- (С/я2); у = 2я3 — (32/я2).
25. 1(я) = ех2'2; у = 5 4- Се"*2/2. 27. /(я) = е~2х; у = -2я - 1 4- Се2х.
29. 1(х) = х; у — ех - ех/х 4- (С/х). 31. 1(х) = х; у = |я1пя - |я 4- (С/х).
33. 1(х) = я3/2; у = 4я 4- Ся-3/2.
35. б) Решение не верно. Множитель 1/я, стоящий перед знаком интеграла, и множитель я в подынтегральном выражении не компенсируют друг друга.
В) У = ^Х3 4- -Я2 4- -Я 4- (С/х).
37. б) Решение не верно. Пропущена константа интегрирования.
в) 	у — + Се~3х.
39. у = 1 4- (С/х). 41. у = С(1 4- я2) - 1.
43. у = Сех2 - 1. 45. у = Cekt.
47. у= (b/а) + Се~ах.
49. A(t) = 62 500 - 42 500e°’°48t; 24105 долл.
51. 15 124,60 долл.
53. A(t) = 35000e°-O7t - 30000; 19667,36 долл.
55. 5,23%. 57. p(t) = 20 + 10e~3t; р = 20.
59. 622 фунта; Щ и 2,5 фунта на галлон.


Ответы к упражнениям
1055
61. 600 — 2ООе_0,5 « 479 фунта; 3 — е“0,5 ~ 2,4 фунта на галлон.
63. 6,2 часа.
65. 120 + 4Ое-0,15 « 154 фунта; — (1п |)/0,005 « 58 дней. Если долго соблюдать диету, вес будет стремиться к 120 фунтам.
67. 17’5 (^^е-вдб015) Л 1647 кал0Рий-
69. Студент А: 0,9 - 0,8е"4’8 « 0,8934, т.е. 89,34%. Студент Б: 0,7 - 0,Зе~4’8 « 0,6975, т.е. 69,75%.
Упражнения для повторения
3. б. (14.1)
5. (14.1) у
4. а. (14.1)
7. dy/dt = —к(у — 5), к > 0. (14.2) 8. dy/dt = ку, к > 0. (14.2)
9. Скорость распространения болезни прямо пропорциональна произведению количе¬
ства заболевших и здоровых людей. (14.2)
10. Количество радиоактивного вещества в данный момент равно 100 г. Оно будет убывать прямо пропорционально первоначальному количеству. (14.2)
11. Линейное уравнение первого порядка: у' + (Зх2 - ех) у — (1 — х)ех — 9. (14.2, 14.3)
12. Ни одна из форм. (14.2, 14.3)
13. 	Форма с разделенными переменными: (у + 2) 1у' = х — 3; линейное уравнение
первого порядка: у' + (3 — х)у — 2х — 6. (14.2, 14.3)
14. Форма с разделенными переменными: у2еуу' = 4хех. (14.2, 14.3)
15. у = С/х4. (14.2)
17. у = -1/ (х3 + С). (14.2)
19. у = |х7 + Сх5. (14.3)
21. у = 10 - 10е_х. (14.2, 14.3)
23. у = е2е~2е~х. (14.2)
25. у = у/х2 + 16 - 4. (14.2)
16. 	у = |х2 + (С/х4). (14.3)
18. 	у = ех + Се2ж.
20. 	у = С(2 + х) - 3. (14.2)
22. 	у = х - 1 + е~х. (14.3)
24. 	у = (х2 + 4) / (х + 4). (14.3)
1 1 19
26. 	у = -xlnx - -х + у (1/х2). (14.3)


1056
Ответы к упражнениям
27.
29.
32.
33.
34.
35.
36.
38.
39.
40.
42.
43.
у = у/1+2х2. (14.2) 28. у = (2х + 1)е~х . (14.3)
у = —2 + Сх4. (14.2, 14.3)
у = —2 + Сх5.
а) у = 2 + Сх5, где С — произвольная константа. {14.2, 14.3)
б) Частного решения не существует.
в) у — 2 -хъ. (14.2, 14.3)
у = у/х2 + 16. (14.2)
б) График возрастает и пересекает ось х только в точке х = 0.
в) 5
-5
г) 	Каждый график имеет локальный максимум и локальный минимум, пересекая ось х трижды. (14.1)
а) М = 7/ (1 - e_5fc), М = 4/ (1 - е~2к).
б) 9,2. (14.2)
500е-°’251п2° « 236,44 долл. (14.2)
а) р = 50 + Ае 1
б) р = 50.
в) (14.1, 14.2) i
1
75^
< р = 50 + 25е-'
50-
25:
^ZP = 5O - 25е-'
о!
1 2 Г
A(t) = 100000 - 40000e°’°5t; (1п2,5)/0,05 « 18,326 лет; 91630 долл. (14.3)
4,82%. (14.3) 41. у = 100 + te~4. (14.3)
а) 211,1 фунта.
б) 10,3 ч.
а) 337 птиц.
б) 357 птиц. (14.2)


Ответы к упражнениям
1057
44. а) 200 — 199е(5/2) 1п("/199) « 23 человека.
б)
21п(100/199)
1п(190/199)
30 дней. {14.2)
3. Расходится.
7. Расходится.
11. Расходится.
15. 1.
19. 10.
Глава 15
Практикум 15.1
1. 1/3.
5. 2.
9. 1.
13. Расходится.
17. 14/3.
23. Истина.
25. Ложь.
О
эт-- 5 - = 5'
0.4
0


1058
Ответы к упражнениям
33. F(b) = 2y/b — 2; lim F(b) = оо.
39. 1.
37. Да.
41. Расходится.
43. 1/2.
45. Расходится.
47. Расходится.
49. 120 000 долл.
51. 50000 долл.
53. Повышение процентной ставки на 6% приводит к снижению стоимости капитала на 100000 долл., а уменьшение процентной ставки на 4% приводит к повышению стоимости капитала на 150 000 долл. В целом, повышение процентной ставки приводит к уменьшению объема капитала, необходимого для образования потока доходов.
55. а) 7,5 млрд. куб. футов.
б) 6,14 лет.
57. 500 галлонов.
59. Приблизительно 8 000 000 иммигрантов.
Практикум 15.2
4
1. Из графика следует, что /(я) 0. j f(x)dx = 1.
о
3
5. Нет.
1


Ответы к упражнениям
1059
2
0
4
3
1
9. а)
f(x)dx -
0.
-1
оо
б)
f(x)dx =
0.
5
5
в)
f(x)dx -
= 1.
— оо
'0,
если х < 0,
11. F(x) = <
, если 0 < х < 4.
I1-
если х > 4.
13. а) Г(4) - Г(2) = 3/4. б) Г(4) - Г(0) = 1/4.
15. 	а) 2.
б) 4/3.


1060
Ответы к упражнениям
17. Из графика следует, что
оо
dx = 1.
19. а) | = 0,21.
J (1 + х)3
ОО
f 2 1
б) ~dx =
J (1 + х)3 16
3
.) [-^=1
о
1
(1+х)2 ’
если х < 0,
если х 0.
б) 3.
0, если х < 0,
если 0 х 2, если х > 2.


Ответы к упражнениям
1061
27.
29.
33.
35.
39.
41.
43.
45.
47.
49.
Г(х) =
0,
< | + iz2 + |z4,
1,
если х < —1, если — 1 х 1, если х > 1.
ад
31. х « 0,44.
Такой константы не существует, поскольку интеграл
2.
оо
f(x)dx расходится.
1
37. Нет.
0,683; 0,954; 0,997.
1
0
если 0 < х С 1,
в противном случае.
.. , (12х - 24х2 + 12а;3,
- |о
если 0 < х < 1,
в противном случае.
F(x) =
'о,
^х2
2х ’
2х - |х2 - 1,
Л
если х < 0,
если 0 х < 1, если 1 х < 2, если х > 2.
а) Вероятность того, что ежедневный спрос будет колебаться от 2 до 6 млн. кВт ч, равна 0,48.
8
б) (0,2 - 0,02х) dx = 0,96.
о
10
в) (0,2 - 0,02х) dx = 0,25.
5
а) 	Вероятность того, что продолжительность обработки запроса будет колебаться от 5 до 10 с, равна 0,239.


1062
Ответы к упражнениям
1
б) j ^e~x/wdx = 1 - е-1/10 » 0,0952.
О
1
— e~x/wdx = 1 - е"2/5 « 0,6703.
J Ю
о
' / 843/2
51. а) 0,003ху 100 - x2dx = « 0,7699.
о
8
б) j О,ООЗД7л/юо - x2dx = 0,784.
о
в) ^100 — 1002/3 « 8858 фунтов.
ю
-Д- (10а;3 - х4) dx = 0,47178.
J 5000 v 7
7
5
6) j^(ltteS"’‘')'b = s=IW875-
о
20
[ 800ж - 0 5
J (400 + x2ydX ~ °Д
о
оо
в)
53. а)
55. а)
б)
в)
57. а)
б)
800а;
ox^dx = 0,64.
J (400 + х2)2
15
10 дней.
оо
f J_e-^/20dx = е-1,5 0 223.
J 20
30
оо
[ ^-e~x/20dx = е~4 а 0,018.
J
80
Практикум 15.3
1. 4/3; 2/9; 0,471. 3. 3,5; 0,75; 0,866.
5. 4/3; 1/18; 0,236. 7. 1/л/2 « 0,707.
9. л/10 « 3,162. И. 4-2х/2 и 1,172.
13. Математическое ожидание случайной величины равно единице, а Х2 — нулю.
15. Медиана случайных величин Ху и Х2 равна единице.
17. 4/3; 2/9; 0,471. 19. 8/3; 8/9; 0,943.
21. 	1,00; 0,25; 0,50. 23. е5 « 1,649.
25. 2/3. 27. 1.


Ответы к упражнениям
1063
29. (In 2)/2 » 0,347.
31. F(x) = 1/2 при любом значении х, удовлетворяющем условию 0 х < 2,5. Медиана не является единственной.
33. F(x) = <
х - ±х2,
1
1х2-2х^1,
если х < 0, если 0 х < 1,
если 1 < х < 2,
если 2 < х < 3,
1, если я >3.
F(x) = 1/2 при любом значении х, удовлетворяющем условию 1 С х 2. Медиана не является единственной.
35. a/i + Ь.
37. хх = 1; х2 = \/2 « 1,414; х3 = \/3 « 1,732.
39. xi = 1; х2 = 3; х3 = 9.
43. 1,47.
45. а) 50/3 «16 667 долл.
б) 	20 - 5\/2/2 « 16 464 долл.
47. 31п 2 « 2079 мин.
51. 20/3 « 6,7 мин.
55. 1,8 ч.
41. 0,54.
49. 1 млн. галлонов.
53. 20 дней.
Практикум 15.4
(о,
в
если 0 < х < 2, противном случае.
если х < 0, если 0 х 2, если х > 2.
3. /(х) = <
если х 0,
в противном случае.
2®, если х 0,
в противном случае.
5. р, = 3; т = 3; а = 2/х/З ~ 1,155. 7. /1 = 5; т = 5 In2 « 3,466; а = 5.
9. 0,3413. 11. 0,4987.
13. 0,3159. 15. 0,4932.
17. 0,4332. 19. 0,4995.
21. 0,1915. 23. 0,2881.
25. Стандартное отклонение случайной величины Х± равно единице, а Х2 — 0,722.
27. 	Медиана случайной величины Х± равна единице, а Х2 — 0,693.


1064
Ответы к упражнениям
29. ц = 2; 1/2. 31. ц = 1; 1 - е'1 « 0,632.
33. ц = 0; <т = 5/\/3 « 2,887; 1/у/З « 0,577.
35. ц = 6; а = 6; 1 - е"2 « 0,865. 37. 0,7888.
39. 0,5328. 41. 0,0122.
43. 0,1056.
45. а) 0,6827.
б) 0,6827.
в) 0,6827. Вероятность того, что нормально распределенная случайная величина лежит в окрестности математического ожидания на расстоянии, не превышающем одного стандартного отклонения, равно 0,6827.
47. а) 0,9973.
б) 0,9973.
в) 0,9973. Вероятность того, что нормально распределенная случайная величина лежит в окрестности математического ожидания на расстоянии, не превышающем трех стандартных отклонений, всегда равна 0,9973.
53. 0,2; 0,139; 0,2.
55. р = р/(р— 1) прир > 1. Если 0 р 1
57. т = ^2.
61. 1 - е"2/3  * « 0,487.
65. 2,28%.
69. а) —1/(1п0,7)« 2,8 года.
б) 	в-1 « 0,368.
71. 0,82%.
то математического ожидания не существует.
59. | = 0,375.
63. 1 - (1/л/2) «0,293.
67. 1,247%.
73. е"2-5 « 0,082.
75. Для А: 80,2 и выше; для В: 74,2 — 80,2; для С: 65,8 — 74,2; для D: 59,8 — 65,8; для F: 59,8 и ниже.
Упражнения для повторения
1. 1/2. (15.1)
3. 8. (15.1)
2. Расходится. (15.1)
4. 0,75. (15.2)
2 2 \/2
5. д = - « 0,6667; V(x) = - « 0,2222; а = « 0,4714. (15.3)
О У о
если х < 0,
если 0 < х 2, {15.2)
если х > 2.


Ответы к упражнениям
1065
1.
8.
9.
10.
И.
12.
13.
14.
15.
16.
2 - х/2 « 0,5858. (15.3)
0,4641. (75.4)
/(х) =
J 10’
0
(
F(x) =
/(*) =
F(x) =
если 5 х < 15, в противном случае.
если х < 5,
— 5), если 5 х 15,
1 если х > 15.
5е 5х, если х 0,
0 в противном случае.
1-е 5х, если х 0,
0 в противном случае.
U5.4)
Нет. Площадь фигуры, лежащей под графиком функции /, не равна единице. {15.2)
Нет. При некоторых значениях переменной х функция f становится отрицательной. {15.2)
« 0,9688.
/to
г п
ц = - и 1,6667; V(x) = — « 2,2222; а = -у/5 « 1,4907. (15.3) о У о
если х 1,
в противном случае.


1066
Ответы к упражнениям
17.
18.
19.
20.
21.
22.
23.
25.
27.
28.
29.
30.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
ре-ж/2,
1 - е-1 « 0,6321. (15.2)
если х 0,
в противном случае.
если ж > 0,
в противном случае.
(15.4)
(/5.4)
р = 2; а = 2; т = 2 In 2 « 1,3863. (75.4)
а) 0,9104.
б) 0,0668.
а) 0,3345.
б) 0,9970. (15.4)
1. (15.1) 24. (15.1)
Да. (75.7) 26. к = 10. (75.2)
Такой константы не существует, поскольку интеграл J^° f(x)dx расходится. (75.2)
Р(Х 3) = 1 - е-1 « 0,6321. (15.4)
р = = 2,0711. (15.3)
1,68. (15.3) 31. 1. (15.1)
аа2 + ар? + Ьр + с. (15.3)
График функции /2 сдвинут вправо относительно графика функции Д, поэтому математическое ожидание случайной величины Х2 больше, чем математическое ожидание случайной величины Х±. (15.3)
По сравнению с графиком функции Д, график функции f2 имеет больший разброс, поэтому дисперсия случайной величины Х2 больше, чем дисперсия случайной величины Xi.
Математическое ожидание случайной величины Х2 равно 6, а Х± — 4. (15.3) Дисперсия случайной величины Х2 равна 12, а Х± — 8. (15.3)
а) 20 000 000 баррелей.
б) 4,09 лет. (75.7)
а) Вероятность того, что еженедельный спрос будет колебаться от 40 до 100 фунтов, равна 0,36.
б) 5 = 0,75.
в) 80 фунтов. (15.2)
40000 долл. (75.7)
а) 0,896.
б) 50%.
в) 50%. (75.2, 15.3)
а) е-1 « 0,3679.
б) 1 - е-°’25 и 0,2212. (75.4)
0,0228. (75.4)


Ответы к упражнениям
1067
43. а) 60,46%.
б) 7,35%. (15.4)
44. а) Вероятность того, что срок годности лекарства будет колебаться от 2 до 8 месяцев, равна и 0,2778.
б) j « 0,6667.
в) 10 месяцев. (15.2, 15.3)
45. а) е-4 « 0,0183.
б) 1/2 месяцев. (15.2, 15.3)
46. а) 25 мл.
б) 6,93 года.
47. 1,22%. (15.4) 48. 45 000; 50 000. (15.1)
Приложение А
Проверка знаний алгебры
1. а) Истина.
б) Истина.
в) Ложь.
г) Истина. (АЛ)
2. а) (у + z)x.
б) (2 + х) + у.
в) 2х + Зх. (А.2)
3. х3 + Зх2 + Зх - 2. (А.З) 4. х3 - Зх2 -Зх + 22. (А.З)
5. За?5 4- х4 - 8а:3 + 24а;2 + 8т - 64. (А.З)
6. 3. (А.З)
8. 	14т2 - 30т. (А.З)
10. 	4а2 - 12а£> + 962. (А.З)
12. 	т4 — 6т2п2 + п4. (А.З)
14. а) 4,065 х 1012.
б) 7,3 х IO"3. (А.6)
15. а) 250000000.
б) 0,000406. (А.6)
16. а) {2,4,5,6}.
б) {5}.
в) {8}.
г) {2,4}. (А. 1)
17. а) 28.
б) 5.
в) 4.
г) 10. (А.1)
1. 1. (А.З)
9. 6т2 — 5ху — 4j/2. (А.З)
11. 4ху - 2у2. (А.З)
13. х3 — 6х2у + 12я?т/2 — 8у3. (А.З)


1068
Ответы к упражнениям
18.
19.
20.
22.
24.
26.
28.
30.
31.
32.
34.
35.
37.
39.
41.
42.
43.
45.
47.
49.
51.
53.
55.
а) Истина.
б) Ложь. (А.2)
Например, 0 и —3. Можно привести бесконечное количество примеров. (А.2)
6х5у15. (А.6) 21. 3u4/u2. (А.6)
6 	• 102. (А.6)
и1/3. (А.7)
(А.6)
бх -I- 7Х1/2!/1/2 — 31/. (Л. 7)
23. 	х6/у4. (А.6)
25. За2/Ь. (А.7)
27. х + 2Х1/2?/1/2 + у. (А.7)
29. (Зх - 1)(4х + 3). (А.4)
(4х - 31/) (2х - 31/). (А.4)
Полином не раскладывается на множители с целыми коэффициентами. (А. 4)
Зп(2п — 5)(п + 1). (А.4) 33. (х — у)(7х — у). (А.4)
Полином не раскладывается на множители с целыми коэффициентами. (А.4)
12а3Ь - 40Ь2 - 5а
30а3Ь2
36.
7х — 4
6х(х — 4) ’
(J.5)
—8(х + 2)
х(х — 4)(х + 4)
(А.5)
38.
У + 2 у(у - 2) ’
(Л.5)
-1
7(7+ h)'
(А.5)
40.
ху
у-х
(А.7)
а) Вычитание.
б) Коммутативность (+).
в) Дистрибутивность.
г) Ассоциативность (•).
д) Изменение знака.
е) Добавление нуля (+).
а) 90.
б) 45. (А.1)
6х2/5 - 7(х - I)3/4. (А. 7)
2-^х~1/2.(А.Т) у/^+у/5. (А.7)
. 1 -. (А.7)
\J и -|- h -|- у/и
X = 0,5. (А.9)
х = —4; 5. (А.9)
х < 4, или (—оо; 4). (А.8)
44. 2^1-3^. (А.7)
46. x/Зж- (А.7)
48.
1
у/х — 5
(Л.5)
50. х = 2. (А.8)


Ответы к упражнениям
1069
57. 2 х < 12, или [2; 12]. (А.8)
58. у = |ж - 2. (А.8)
59. у = 3/(х - 1). (А.8) 60. Да. (Л.7)
61. 3,1487 ♦ 104 = 31487 долл, на человека. (А.6)
62. 20000 долл, при ставке 8%; 40000 долл, при ставке 14%. (А.8)
63. 4000 видеокассет. (А.8)
Практикум А.1
1. Истина.
3. Истина.
5. Истина.
7. Истина.
9. {1,2,3,4,5}.
И. {3,4}.
13. 0.
15. {2}.
17. {-7,7}.
19. {1,3,5,7,9}.
21. А' = {1,5}.
23. 40.
25. 60.
27. 60.
29. 20.
31. 95.
33. 40.
35. а) {1,2,3,4,6}. б) {1,2,3,4,6}.
37. {1,2,3,4,6}.
39. Истина.
41. Ложь.
43. Ложь.
45. Ложь.
47. Ложь.
49. а) 2.
б) 4.
в) 8.
г) 16.
51. Нет.
53. 800.
55. 200.
57. 200.
59. 800.
61. 200.
63. 200.
65. 6.
67. А+, АВ+.
69. А-, А+, В+, АВ-, АВ+, О+.
71. О+, О-.
73. В-, В+.
75. Каждый член клики связан с другими членами клики.
Практикум А.2
1. UV.
7. Истина.
13. Истина.
19. Истина.
25. Истина.
3. (3 + 7) 4- у.
9. 	Истина.
15. Истина.
21. Ложь.
27. Нет.
5. и -h v.
11. Истина.
17. Истина.
23. Истина.


1070
Ответы к упражнениям
Ложь. Истина. Истина.
29. а)
б)
в)
31. Например, \/2 или 7г. Таких чисел бесконечно много.
33. а) W, Z, Q, R.
б) R.
в) Q, R.
35. а) Истина.
б) Ложь, поскольку, например, (8 — 4) — 2 (8 — 4) - 2.
в) Истина.
г) Ложь, поскольку, например, (8/4)/2 / 8/(4/2).
37. 1/11.
39. а) 2,166666666...
б) 4,85257569...
в) 0,437500000...
г) 0,261261261...
9.
13.
17.
Практикум А.З
1. 3. 3. х3 -|- 4х2 — 2я -Н
5. х3 + 1. 7. х5 + Зх4 - 2т3 +
—5и + 2. 11. 6а2 + 6а.
а2 — Ь2. 15. 6ж2 — 7х — 5.
2х2 + ху — б?/2. 19. 9?/2 — 4.
21. 6т2 — тп — 35п2. 23. 16т2 — 9п2.
25. 9u2 + 24iw + 16v2. 27. а3 - Ь3.
29. 16я2 + 24ги/ + 91/2. 31. 1.
33. х4 - 2х2у2 + у4. 35. 5а2 + 12аЬ - 105:
37. —4т + 8. 39. —бху.
41. и3 + За2г> + Зш;2 + v3. 43. х3 — бх2у + 12од
45. 	2х2 — 2ху -|- Зу2. 47. 8ж3 — 20ж2 + 20х
49. 4х3 — 14х2 + 8х — 6. 51. т + п.
53. Не изменится.
55. (1 + I)2 I2 + I2; либо а, либо b должны быть равны нулю.
57. 0,09х + 0,12(10000 - х) = 1200 - 0,03z.
59. Юд: + 30 • Зх + 50 • (4000 - х - Зх) = 200 000 - 100z.
61. 0,02ж + 0,06(10 — х) = 0,6 — 0,04ж.
Практикум А.4
1. Зт2 (2т2 — Зт — 1).
5. (7т + 5)(2т — 3).
3. 2uv (2и2 — 3uv + 2v2).
7. (a-4b)(3c + d).


Ответы к упражнениям
1071
9. (2х- 1)(я + 2).
13. (z + 4)(2z- 1).
17. (а — 6)(т 4- п).
21. (и - 5v)(u 4- 3v).
25. (wx — y)(wx + у).
29. He раскладывается.
33. 2x2(x — 2)(x — 10).
37. (2n — 3m) (3m 4- 4n).
41. 2x (x2 — x + 4).
45. (a -F 1) (a2 — a -h 1).
49. He раскладывается.
53. (j/-2)(y + 2) (y2 + l).
57. Истина.
Практикум A.5
1. 8d6.
5.
9.
13.
17.
15m2 + 14m - 6
36m3
x — 6
x(x — 3)
2
x — 1
x2 4- — 16
x (x — 4) (z 4* 4) ’
11. (1/-1)(31/ + 2).
15. (w + x)(y - z).
19. ^y + 2^y-l).
23. He раскладывается.
27. (3m — n)2.
31. 4(z — 3)(z — 4).
35. x(2y - 3)2.
39. uv(2u — v)(2u -I- v).
43. (r - t) (r2 +rt +12).
47. [(z + 2) - 3y] [(x + 2) + Зт/].
51. (6x — 61/ — 1)(ж - у -I- 4).
55. a2(3 -I- ab) (9 — Sab 4- a262).
59. Ложь.
_ 15x2 4-10# — 6
3. .
180
x(x — 4) ’
x — 5
1L (x-l)2(z + l)’
25. —.
x — 3
x — v
29. y-.
x + y
31. а) Неверно.
6) x 4-1.
33. а) Неверно.
6) 2x 4- h.
7x2 - 2x - 3
19' 6(x + l)2 '
„ -17c+ 16
15(c - 1) ’
2rr(x 4- h) ’
35. а) Неверно.
x2 — x — 3 x + l
37. а) Правильно.
6)


1072
Ответы к упражнениям
3(х + h)2x2
Практикум А.6
1. 2/х9.
5. 2/х3.
9. 5.
13. у6/х12.
17. 7,83 • 10"1.
21. 40000.
25. 61710 000.
29. 1.
33. уб/25х\
37. 4у3/Зх5.
41. ^-х — 1х-1 — -уя-3.
4 4
хл
49. 3,125 • 104; 31250.
55. uv.
59. а) 6,674 - 1011.
б) 1,8241.
в) 0,5482.
61. а) 20 445 долл.
б) 1346 долл.
в) 6,58%.
63. а) 9 • 10~6.
б) 0,000009.
в) 0,0009%.
65. 1531 000.
41. х.
3. 3w7/2.
7. 1/w5.
11. 1/а6.
15. 8,23 • Ю10.
19. 3,4-10-5.
23. 0,007.
27. 0,000808.
31. 1014.
35. 4 • 102.
”• I - г-
4 4
х2(х — 3)
(ж — I)3
43.
47. 2,4- 1О10; 24000 000 000.
51. 64.
Ьс(с + Ь) с2 + Ьс + Ь2
Практикум А.7
1. б^Ух3.
5. у/х2 + у2, а не х + у.
9. (2а:2у)3/5.
13. 5.
17. -6.
3. ^/(4ху3)2.
7. 5а:3/4.
И. а:1/3 + у1/3.
15. 64.
19. Не рациональное число (и даже не действительное).


Ответы к упражнениям
1073
21. 8/125.
25. т2/5.
29. 2х/у2.
33. 2/Зх7/12.
37. бх3.
41. 12х - бх35/4.
45. 25т — п.
49. i»‘'3+a.-l/3
23.
27.
31.
35.
39.
43.
47.
51.
55.
59.
63.
67.
71.
75.
79.
83.
87.
91.
3.
7.
11.
15.
19.
23.
1/27.
т.
ху2/2.
2х + 3.
2.
Зи — 13U1/2!;1/2 + 41/.
9х — бх1/2?/1/2 + у.
57.2VEH2
х-2
хуу/Ьху
69. Один из вариантов: х = у = 1.
73. Истина.
77. Ложь.
81. ~ 2
2(х — I)3/2
85. 103,2.
89. 4588.
Практикум А.8
1. т = 5.
5. х 4.
7(Х~У) (у/х + у/у).
1
у/х -\-h + у/~х
Один из вариантов: х = у = 1.
Ложь.
Истина.
х + 8
2(х + З)3/2 ‘
х + 6
3(х +2)5/3 ’
0,0805.
а и Э; б и е; в и г.
х < -9.
х < —3, или (—оо; —3).
9. -1 х 2, или [-1; 2].
у = 8.
13. х > —6
17. х = 10.
21. х = 36.
У = 8. у>3. т < 3


1074
Ответы к упражнениям
25. х = 10.
27. 3 < х < 7, или [3; 7).
29. -20 < С < 20, или [-20; 20].
31. у = ^х — 3.
33. у = ~{А/В)х + (С/В) = (-Ах 4- С)/В.
35. С = (F - 32). 37. В = А/(т - п).
39. -2 < х 1, или (-2; 1].
41. а и в: а > 0 и b > 0 или а < 0 и b < 0. биг:а>0иЬ<® или а < 0 и b > 0.
43. а) >;
б) <.
45. Отрицательная.
49. Ложь.
47. Истина.
51. Истина.
53. 3500 билетов по цене 15 долл.; 4500 билетов по цене 25 долл.
55. 7200 долл, при ставке 10%; 4800 долл, при ставке 15%.
57. 21 005 долл.
59. 5851 книга.
61. б) 6180 книг.
в) Не меньше 11,50 долл.
63. 5000. 65. 12,6 года.
Практикум А.9
1. ±>/п.
5. —2; 6.
9. 3 ± 2а/3.
13. 0; 2.
17. 1/2; -3.
21. (3 ± у/З) /2.
25. —4 ± у/П.
29. -1/2; 2.
3. -1; 3.
7. 0; 2.
11. —2 ± у/2.
15. ±3/2.
19. (-1 ± ^5) /2.
23. Действительного решения нет.
27. ±v/3.
31. (х — 1)(х±42).
33. Полином не раскладывается на множители с целыми коэффициентами.
35. (2х - 9)(х + 12). 37. (4х - 7)(х + 62).
39. r = y/AjP-1.


Ответы к упражнениям
1075
41. Если с < 4, существуют два разных действительных корня; если с = 4, существует один кратный действительный корень; если с > 4, уравнение не имеет действительных корней.
43. 1575 бутылок по 4 долл, каждая. 45. 0,2, т.е. 20%.
47. 8 футов/с; 4\/2, т.е. 5,66 футов/с.
Приложение Б
Практикум Б.1
1. 5, 7, 9, 11.
5. 9, —27, 81, -243.
9.^.
100
13. 5 + 7 + 9 + 11 = 32.
1 1 4’ 8’
16’ 32’
3 9 _27 81
2’ 4’ 8 ’ 16'
29. ап = 4п.
33. ап = (-1)п+1п.
41. ап = (-l)"4-1^2"-1.
, 3 4 5 6
Х 2’ 3’ 4’ 5‘
7. 23.
11. 1 + 2 + 3 + 4 + 5 + 6 = 21.
15 1 — — 1 _ 1111
’ + 10 + 100 + 1000 ~ 1000'
19. 82,5.
23. 0, 4, 0, 8, 0.
27. ап = п — 3.
31. ап = (2п — 1)/2п.
35. ап = (- 1)п+1(2п - 1).
39. ап = хп.
43. 1 - 9 + 25 - 49 + 81.
47. 1 + х + х2 + х3 + а;4.
4 8 16 32
7 + 9 + И + 13’
1 1
51. a) J2(fc + 1).
к—1
б) ЕЬ + 2).
а=1
4
53. а) Е
к=1 3
J=1
(-l)fc+1 к
(~l)j j + 1 ’


1076
Ответы к упражнениям
61. Истина.
65. 1, 2, 4, 8, 16.
55-
/с=1
59. Ложь.
63. 2, 8, 26, 80, 242.
67-1-1й'5й;“4 = йй’“1>414216;'/2“!1’414214^
69. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.
Практикум Б.2
1. а) Арифметическая; d = —5; —26; —31.
б) Геометрическая; г = 2; —16; 32.
в) Ни то, ни другое.
г) Геометрическая; г = -; —; —.
3 54 162
3. Геометрическая; 1.
7. Арифметическая; 127,5.
11. a2i = 82, 531 = 1922.
15.
19.
23.
27.
31.
33.
а2 = —6, аз = 12, а4 — —24. аю = 199,90.
Sio = 1242, 5оо = 1250.
-85.
а) Не существует.
б) Soo = | = 1,6.
2400.
37. Положим а1 = 1ис? = 2в формуле Sn
39. Sn = nay,
43. Да.
47. Около 11670 000 долл.
5. Ни то, ни другое.
9. а2 = 11, аз = 15.
13. 	S20 = 930.
17. S7 = 547.
21. г = 1,09.
25. 2706.
29. 1120.
35. 0,999.
= (n/2) [2ai + (n — l)d].
41. Нет.
45. 48 + 46 Ч I- 4 + 2 = 600 долл.
1628,89 долл.; 2653,30 долл.
49.
Практикум Б.З
1. 720.
5. 1320.
9. 6.
13.
17.
10.
10. 1140.
6.
19. 816.
3.
7.
11.
15.
10.
1.
21. C4fia4 + С4>4а3Ь3 + C4>2a2b2 4- C4t3ab3 + С4,4Ь4 = а4 + 4а3Ь + 6а252 4- 4аЬ3 + Ь4.
23. х6 - бх5 4- 15х4 - 20х3 4- 15х2 - бх 4-1.
25. 32а5 - 80а45 - 40а362 - 40а2 63 + ЮаЬ4 - Ь5.
27. ЗОбОх14. 29. 5005pV-


Ответы к упражнениям
1077
31. 264х2т/10.
35. 1 5 10 10 5; 1 6 15 20 15 6 1.
33. Сп,о =
п! п!0!
Практикум Б.4
1. Ах = 3; А?/ = 45; Дт//Ах = 15.
5. 12.
13. а) 12 + Ах.
б) 12.
15. dy = 6(2х + l)2dx.
19. dy = 1,4; Аз/ = 1,44.
3. 12.
7. dy = (24х — Зх2) dx.
11 	я 295 J
1L АУ = ~^dx-
9 	— х2
17. du = — dx.
У (х2 + 9)2 21. dy = -3; Ду = -з|.
23. 120 кв. дюймов.
29. Истина.
33. dy =
6х — 2
3 (Зх2 - 2х + 1)2/3
31. Ложь.
35. dy = 3,9; Ay = 3,83.
37. Увеличится на 40 единиц; увеличится на 20 единиц.


1078
Ответы к упражнениям
39. —2,50 долл.; 1,25 долл.
43. 1,26 кв. мм.
47. а) Увеличится на 2100 человек.
б) Увеличится на 4800 человек.
в) Увеличится на 2100 человек.
41. —1,37 долл./мин.; —0,58 долл./мин.
45. 3 слова в минуту.
Практикум Б.5
1. 8/3.
3. 1/2.
9. 0.
11. 00.
17. оо.
19. 8.
25. оо.
27. 1/3.
33. 0.
35. 0.
41. 1/3.
43. 0.
\/1 + X2
49. lim
= 1.
z—>ое X
2
¥1=Ш+Х2)/Х
0
10
Х=10 Y=
1.00Ч9В76
-1
5. 1.
7. 4.
13. оо.
15. 5.
21. 0.
23. оо.
29. —2.
31. —оо.
37. 0.
39. 1/4.
45. 0.
47. оо.
х/х3 + 1
51. lim
= 1.
х—>оо
X
2
Практикум Б.6
1. R = |О, у) : 0 < у < 4 - аг2; 0 х < 2}. R = {&,у) л/4 — у; 0 < у С 4}.
3. Область R является регулярной по переменной х.
R = {(ж, у) : х3 у < 12 - 2х- 0 х 2}.


Ответы к упражнениям
1079
5.
Область R является регулярной по переменной у.
7. 1/2. 9. 39/70.
11. 	Область R представляет собой прямоугольник с вершинами (±2; ±3) и является регулярной по обеим переменным.
13. Область R представляет собой сегмент круга с центром в начале координат и единичным радиусом, а также с вершинами в точках (±2; 0) и (±2; 2). Вершины в область не включаются. Область является регулярной по переменной х.
15. 56/3. 17. -3/4.
21. R = {(ж, у) : 0 у х + 1; 0 х 1}.
1 х4“1
j у/1 + x + ydydx = (б8 - 24/15.
о о


1080
Ответы к упражнениям
25. R = {(х, у) : 1 - у/х у 1 + у/х; 0 < х < 4}.
4 H-\/i
j j х(у - l)2 dydx=^.
0 1-^i
3 3 — y
' f 27
27. (x+ 2y)dxdy =—.
о о
2
15
0 4y2
31.


Ответы к упражнениям
1081
4 4—х
33.
о
(4 — х — у) dx dy = о
32
3 ’
35.
j j 4dxdy=8-.
о о
4 у/У
37. f [ л о dxdy = In 17. J J i + r
о 0
39.
1 x/x
j 4yex dy dx = e — 1. о о
41. R = {(x,y) : x2 у 1 + < x 1,49}.
1,49 1+у/х
xdydx «0,96.
43. R = {(x,y) : y3 x 1 - y;0 у < 0,68}.
0,68 1-y
| 24x1/ dx dy « 0,83.


1082
Ответы к упражнениям
45. R = {(ж, у) : е х < у < 3 — х; —1,51 < х 2,95}.
Регулярная область по переменной х.
R = {(ж, у) : -In?/ х 3 - у; 0,05 у 4,51}.
Регулярная область по переменной у.
2,95 З-ж 4,51 3-у
I 4ydxdy= I 4ydx dy «40,67.
-1,51 е-х2 0,05 - ln у
47. 323 402. 49. -3,354.
Практикум Б.7
1. а) р(х) = ао + ai(^ - 1) + а2(х - 1)(я - 3).
б) ао — 2, а^ = 2, а2 = 1.
в) р(ж) = 2 + 2(х - 1) 4- (х - 1)(х — 3).
3. а) р(х) = а0 + ai(x + 1) + а2(х + 1)ж 4- а3(х + l)z(x - 2).
б) ао = 6, ai = -1, а2 = 2, а3 = -2.
в) р(х) = 6 - (х 4-1) 4- 2(х + 1)х - 2(х 4- 1)х(х - 2).
Хк
Ук
Первая разделенная разность
Вторая разделенная разность
1
4
4
2
8
1
6
3
14
Ук
Первая разделенная разность
Вторая разделенная разность
Третья разделенная разность
-1
-3
4
0
1
-1
2
1
1
3
2
6
2
9


Ответы к упражнениям
1083
хк
Ук
Первая разделенная разность
Вторая разделенная разность
Третья разделенная разность
-2
25
-5
1
10
3
7
-1
2
17
-3
—2
4
13
11. р(х) = 25 — 5(х + 2) + 3(х + 2)(х — 1) — (х + 2)(х — 1)(х — 2).
13. р(х) = —64 + 24(х + 4) — 4(х + 4)х + (х + 4)х(х — 4);
а) 8.
б) 56.
15. р(х) = ^(х + 1)х(х — 1).
а) 1,5.
б) 6.
17. р(х) = 24- 11(х + 4) + ^(х + 4)(х + 2) — ^(х + 4)(х + 2)х+ ^(х + 4)(х + 2)х(х — 2).
2 2 8
а) у = 7,125.
б) -у = -2,875.
19. р(х) = —24 — 18(гг + 3) — 6(х + 3)(х + 2) + (я + 3)(я + 2)(яг + 1).
а) 3/8 = 0,375.
б) 105/8 = 13,125.
21. р(х) = 2 — (я + 2) + + 2)х — |х2.
х


1084
Ответы к упражнениям
25. р{х) — 2(ж + 1) — (х + 1)ж = 2 + х — х2.
27. р(х) — 1 + 4(ж -I- 2) — 3(х + 2)(я + 1) + (я + 2)(х + 1)я = х3 — Зх -I- 3.
29. р(х) = —3 + 3(я + 2) + (х + 2)(х + 1) - 2(х 4- 2)(а? + 1)ж + (х + 2)(х 4- 1)ж(ж - 1) =
31. р(х) = х3 — Зх 4- 3. Два полинома идентичны.
33. р(х) = х* — 6х2 4- 5. Два полинома идентичны.
35. р(х) = 1 + - 1) - 4j(iz: - 1)(х - 4).
X
123456789
p(x)
1 1,4 1,7 2 2,3 2,5 2,7 2,9 3
y/x
1 1,4 1,7 2 2,2 2,4 2,6 2,8 3
37. р(х) — — 4 4- (х + 2) + 3(я: + 2)(х + 1) — (х + 2)(х + 1)ж — (х + 2)(х + 1)а: = 6х — х3.
39. у = У2 + (у1- уг) х21х}.
41. a) p(t) = 2 + 7,5t - 0,75t(t - 4) = 2 + 10,5* - 0,75i2.


Ответы к упражнениям
1085
б) С(6) « 38, т.е. 38 000 долл.
в) Приблизительно 15 500 долл.
43. а) р(х) = 0,2 + 0,75а:(х — 0,2) + 1,25ж(а: — 0,2) (ж — 0,8) = 0,25х — 0,5х2 + 1,25а:3. б) 0,1146.
45. а) р(х) = 24,4 + 5,8(х - 2) — 1,6а:(х — 2)(а: — 4) = 15,4ж — 1,6х2.
б) Я(5) « 37, т.е. 37 000 долл.
в) Приблизительно 4813 лампы.
47. a) р(/) = 14 - t + 2t(t - 1) - t(t - l)(t - 2) = 14 - 5t + 5t2 - t3.
б) Приблизительно 14,7°C.
49. a) p(t) = 450 - 130/ + 20/(/ - 2) = 450 - 170/ + 20/2.
б) Приблизительно 4,25 дней.
51. a) p(f) = 10000 + 350/ 4- 15/(/ - 10) - t(t - 10)(/ - 20) = 10 000 - 45/2 - /3.
б) Приблизительно 14 000 зарегистрированных избирателей.


Предметный указатель
А
Абсолютное неравенство, 482 равенство, 482
Анализ предложения и спроса, 865 регрессионный, 597
Аппроксимация кусочно-линейная, 932
Асимптота вертикальная, 45 горизонтальная, 218
Ассоциативность, 796
Б
Бином Ньютона, 891
В
Величина равновесная, 503
Выгода потребителей, 499 производителей, 501
Выражение алгебраическое, 803 дробное, 819
подкоренное, 836 рациональное, 820
Г
График выпуклый вверх, 192 выпуклый вниз, 192
д
Двучлен, 804
Диаграмма
Венна, 787 знаковая, 51
Дискриминант, 863 Дисперсия, 737 Дистрибутивность, 797 Дифференциал, 370; 895
Дифференцирование неявное, 318 произведения, 105 разности функций, 91 сложных функций, 118 степенной функции, 88; 117 суммы функций, 91 частного, 108
Дополнение, 788


Предметный указатель
1087
Доход, 134
на единицу продукции, 139 общий, 495 предельный, 135 средний, 139
Дробь, 799 простая, 824 составная, 824
3
Задача
о предельной производительности, 589
о связанных скоростях, 327 управления запасами, 251
Закон логистического роста, 665 ограниченного роста, 663 Торичелли, 696 экспоненциального роста, 660
Затраты предельные, 94; 129 средние, 139 средние, 139 точные, 130
Знаменатель, 799 геометрической прогрессии, 880 Значение
критическое, 168 среднее, 622
И
Инверсия аддитивная, 797 мультипликативная, 797
Индекс
CPI, 853 суммирования, 874
Интеграл неопределенный, 349 несобственный, 705 определенный, 409; 427
Интегрирование
по частям, 511
К
Квартиль, 750
Коммутативность, 796 Координата, 795 Корень
n-й степени, 835 квадратный, 835 кубический, 835 Коэффициент полинома, 804 Кривая Лоренца, 481
м
Максимум
глобальный, 237 локальный, 172; 569 Математическое ожидание, 737 Медиана, 743
Метод
замены переменной, 371 линейной регрессии, 597 наименьших квадратов, 597 неопределенных множителей Лагранжа, 582
разделения переменных, 657 Эйлера, 697
Минимум
глобальный, 237
локальный, 172; 569 Множество, 785
бесконечное, 786 конечное, 786 пустое, 785
Множитель
интегрирующий, 675
Н
Наклон, 69
Начало координат, 795 Неравенство
линейное, 844
первого порядка, 844
О
Область
^-регулярная, 917
^/-регулярная, 917 интегрирования, 619 Объединение, 787 Ограничение, 583


1088
Предметный указатель
Одночлен, 804
Остаток, 598
Ось
числовая, 795
п
Параболоид, 547
Первообразная, 346
Пересечение, 787
Плотность
вероятностей, 490
распределения вероятностей, 718
Площадь под графиком функции, 402 Площадь фигуры
со знаком, 408
Поверхность, 547
Погрешность аппроксимации, 405 Подмножество, 786
Поле направлений, 383; 641 Полином
интерполяционный, 931
Ньютона, 935
нефакторизуемый, 815
нулевого порядка, 803
относительно двух переменных, 803 относительно одной переменной, 803
полностью факторизованный, 811 Полный квадрат, 816
Порядок
полинома, 803
слагаемого, 803
Последовательность, 871 Постоянная
интегрирования, 350; 678
Правило
дифференцирования обобщенное, 306
Лопиталя, 907
цепное, 304; 367
Предел, 18
односторонний, 20
слева, 20
справа, 20
Представление числа
десятичное, 830
экспоненциальное, 830
Прибыль
на единицу продукции, 139 предельная, 129; 137 Приведение дроби
к младшим членам, 820 к старшим членам, 820 Принцип мультипликатора, 629 Приращение, 894
Прогрессия арифметическая, 879 геометрическая, 880
Производительность
капитала предельная, 558 предельная денег, 589 труда предельная, 558
Производная, 70
вторая, 192 частная, 556 второго порядка, 560 первого порядка, 556
Проценты
сложные n-кратное начисление, 273 непрерывно начисляемые, 275; 386
Прямая наименьших квадратов, 598 регрессионная, 598
Р
Разность арифметической прогрессии, 879 квадратов, 816 кубов, 816 разделенная
второго порядка, 938 первого порядка, 937 Распределение бета, 777 нормальное, 759 равномерное, 753


Предметный указатель
1089
хи-квадрат, 778 экспоненциальное, 757 Решение, 642
общее, 643 сингулярное, 659 точное, 697 частное, 643
Ряд, 873 арифметический, 882 геометрический, 883 знакопеременный, 874
С
Семейство решений, 643
Система координат трехмерная, 545
Скорость изменение мгновенная, 66 средняя, 63
Случайная величина дискретная, 716 непрерывная, 716
Стандартное отклонение, 737 Степень
натуральная, 802 рациональная, 837 целочисленная, 827 Стоимость
основного капитала, 710 предельная, 94
Сумма кубов, 816 левосторонняя, 402 правосторонняя, 403 Римана, 427
Суперпозиция функций, 301
Т
Таблица интегралов, 521
Теорема Пифагора, 952
Точка безубыточности, 135 критическая, 570; 584 перегиба, 194 равновесия, 865 разбиения, 51
седловая, 570
экстремума, 172
Треугольник Паскаля, 893 Трехчлен, 804
У
Уравнение
дифференциальное, 383; 641
второго порядка, 383
линейное, 675
первого порядка, 383; 641 зависимости цены от спроса, 133 квадратное, 858 линейное, 844
первого порядка, 844 Условие
начальное, 645
Ф
Фактор-пара, 814
Факториал, 889
Факторизация полинома, 811 Формула
Терона, 953 квадратичная, 863 приведения, 524 Симпсона, 466; 467 средних точек, 426 суммирования значений в средних точках, 466
суммирования площадей левосторонних прямоугольников, 466
суммирования площадей правосторонних прямоугольников, 466 трапеций, 466
Функция
бета, 777
возрастающая, 166 дохода, 135 затрат, 133
Кобба-Дугласа, 544 монотонная, 405 непрерывная, 38
слева, 41


1090
Предметный указатель
справа, 41 подынтегральная, 350 предельных затрат, 95 прибыли, 137 распределения, 724 степенная, 87 убывающая, 166
ц
Цена
динамически стабильная, 648 равновесная, 503; 648; 681 долгосрочная, 681
Ч
Числитель, 799
Число
действительное, 794
иррациональное, 794 натуральное, 794 рациональное, 794 целое, 794
Член
последовательности, 871
э
Экстремум
локальный, 172 Эластичность
единичная, 342 спроса, 342
Элемент
нейтральный, 797 обратный, 797


ПРИКЛАДНАЯ МАТЕМАТИКА
ВОСЬМОЕ ИЗДАНИЕ
Т0М1
ОСНОВЫ И ЛИНЕЙНАЯ АЛГЕБРА
Реймонд А. Барнетт Майкл Р. Циглер Карл Э. Байлин
www.willlamspublishing.com
Восьмое издание книги Прикладная математика Том 1 Основы и линейная алгебра представляет собой изложение курса дискретной математики и математического анализа, предназначенного для студентов соответствующих специальностей. Подбор тем и их относительная независимость друг от друга позволяют легко адаптировать книгу для любых высших учебных заведений. Авторы сделали акцент на активной работе в аудитории и сильной обратной связи между преподавателем и студентами. Текст написан на доступном для студентов уровне, одновременно авторы сохранили математическую строгость и точность изложения. Основное внимание уделяется методам решения задач, а не математической теории. Доказательства теорем приводятся, только если это необходимо для объяснения математической идеи. Книга изобилует примерами и упражнениями, описывающими разнообразные ситуации, возникающие в процессе деятельности бизнесменов, экономистов, биологов, медиков и социологов.
ISBN 978-5-907114-36-4
в продаже


КОНКРЕТНАЯ МАТЕМАТИКА
2-е издание
Рональд Л. Грэхем, Дональд Э. Кнут, Орен Паташник
КОНКРЕТНАЯ МАТЕМАТИКА МАТЕМАТИЧЬХЖИ)'. ОСНОВЫ
ИНФОРМАТИКИ
нгого; ШДАННС . . \ \г. ; - •
www.williamspublishing.com
В основу данной книги положен одноименный курс лекций Станфордского университета. Название “конкретная математика” происходит от слов “КОНтинуальная” и “дисКРЕТНАЯ” математика. Назначение данной книги — обеспечить читателя техникой оперирования с дискретными объектами, что совершенно необходимо для математиков, работающих в области информатики. Книга ориентирована в первую очередь на практиков (хотя и теоретики найдут в ней много полезного), и изобилует массой конкретных примеров и упражнений. Конкретность изложения абстрактного материала — еще одно пояснение названия книги. Широта охвата столь различных тем в одной книге могла бы вызвать подозрения в некоторой легковесности, если бы не имена ее авторов — известных американских математиков. Тем не менее слово “легкий” к книге вполне применимо, так как стиль изложения достаточно далек от сухого академизма. Как признаются сами авторы, они считают математику развлечением, и они сделали все, чтобы читатели книги получили от ее прочтения не только знания, но и удовольствие.
в продаже
ISBN 978-5-8459-1923-6


Дискретная математика и комбинаторика
Джеймс Андерсон
Дискретная
МАТЕМАТИКА
И КОМБИНАТОРИКА
ДЖЕЙМС АНДЕРСОН
www.dialektika.com
Данная книга содержит доступное для начинающего читателя и достаточно полное изложение основных разделов дискретной математики. Особое внимание в ней уделено математической логике. Автор считает это важным как для развития техники доказательств, так и в более широком аспекте развития логического мышления. Кроме оснований математической логики, в книге изложены основы теории множеств, теории графов, теории алгоритмов, комбинаторики, элементы теории вероятностей. Она содержит обширные сведения по алгебре и теории чисел.
Книга планировалась автором как основа односеместрового или двусеместрового курса по дискретной математике. Первые восемь глав закладывают основы знаний по предмету и образуют относительно самостоятельную часть, поэтому преподаватель имеет определенную свободу в выборе материала остальных глав. Чтение книги требует некоторой математической культуры, хотя для изучения основных глав достаточно будет знаний по математике в объеме средней школы.
ISBN 978-5-907144-07-1
в продаже


ГЛУБОКОЕ ОБУЧЕНИЕ И TENSORFLOW ДЛЯ ПРОФЕССИОНАЛОВ
Сантану Паттанаяк
Глубокое обучение и TensorFlow
для профессионалов
Математический подход к построению систем искусственного интеллекта на Python
www.williamspublishing.com
Данная книга представляет собой углубленное практическое руководство, которое позволит читателям освоить методы глубокого обучения на уровне, достаточном для развертывания готовых решений. Прочитав книгу, вы сможете быстро приступить к работе с библиотекой TensorFlow и заняться оптимизацией архитектур глубокого обучения. Весь программный код доступен в виде блокнотов iPytnon и сценариев, позволяющих с легкостью воспроизводить примеры и экспериментировать с ними. Благодаря этой книге вы:
• овладеете полным стеком технологий глубокого обучения с использованием TensorFlow и получите необходимую для этого математическую подготовку;
• научитесь развертывать сложные приложения глубокого обучения в производственной среде с помощью TensorFlow;
• сможете проводить исследования в области глубокого обучения и выполнять самостоятельные эксперименты в TensorFlow.
ISBN: 978-5-907144-25-5 в продаже


ИСКУССТВО ПРОГРАММИРОВАНИЯ
ТОМ 1. ОСНОВНЫЕ АЛГОРИТМЫ
З-е издание
Дональд Э. Кнут
КЛАССИЧЕСКИЙ ГРУД
ИСПРАВЛЕН? ЮГ, И ДОПОЛНЕННОЕ ИЗДАНИЕ
Искусство программирования
ТОМ 1
Основные алгоритмы
Третье издание
ДОНАЛЬД э. кнут
www.williamspublishing.com В первом томе представлено полное введение в теорию получисленных алгоритмов, причем случайным числам и арифметике посвящены отдельные главы. В книге даны основы теории получисленных алгоритмов, а также их основные примеры. Тем самым установлено прочное связующее звено между компьютерным программированием и численным анализом. Особого упоминания заслуживает предложенная Кнутом в этом третьем издании новая трактовка генераторов случайных чисел, а также рассмотрение способов вычислений с помощью формальных степенных рядов.
ISBN 978-5-907144-23-1 в продаже


ИСКУССТВО
ПРОГРАММИРОВАНИЯ
ТОМ 2. ПОЛУЧИСЛЕННЫЕ АЛГОРИТМЫ З-е издание
Дональд Э. Кнут
КЛАССИЧЕСКИЙ ТРУД
ИСПРАВЛЕН! ЮЕ И ДОПОЛНЕННОЕ И ЗДАНИЕ
Искусство программирования
ТОМ 2
Подучисленные алгоритмы Третье издание
ДОНАЛЬД э. кнут
www.williamspublishing.com
Во втором томе представлено полное введение в теорию получисленных алгоритмов, причем случайным числам и арифметике посвящены отдельные главы. В книге даны основы теории получисленных алгоритмов, а также их основные примеры. Тем самым установлено прочное связующее звено между компьютерным программированием и численным анализом. Особого упоминания заслуживает предложенная Кнутом в этом третьем издании новая трактовка генераторов случайных чисел, а также рассмотрение способов вычислений с помощью формальных степенных рядов.
SBN 978-5-907144-15-6
в продаже


ИСКУССТВО ПРОГРАММИРОВАНИЯ том з. сортировка и поиск 2-е издание
Дональд Э. Кнут
КЛЛ< ГИЧЕСКИЙ ТРУД
И(Т 1РЛ&ЛИ i ЛОЕ И ДО! JOAHEHI ЮН ИЗДАНИЕ
Искусство программирования
IOM3
Сортироши и поиск
Второе издание
ДОНАЛЬД э. кнут
www.williamspublishing.com
Во втором издании третьего тома содержится полный обзор классических алгоритмов сортировки и поиска. Представленная в нем информация дополняет приведенное в первом томе обсуждение структур данных. Автор рассматривает принципы построения больших и малых баз данных, а также внутренней и внешней памяти. В книге приведена подборка тщательно проверенных компьютерных алгоритмов и представлен анализ их эффективности. Кроме того, специальный раздел посвящен методам оптимальной сортировки и описанию новой теории перестановок и универсального хеширования.
ISBN 978-5-907144-41-5
в продаже


ИСКУССТВО ПРОГРАММИРОВАНИЯ
ТОМ 4, А. КОМБИНАТОРНЫЕ АЛГОРИТМЫ
Часть 1
Дональд Э. Кнут
KA.'V' И’ИСКИН <руд но «юг РВДАПШ
Искусство программирования
f ОМ 4. А
Комбина горные йлгорцтмы Часть 1
ДОНАЛЬД э. кнут
www.dialektika.com
В этом томе рассматриваются методы, позволяющие компьютерам эффективно работать с задачами гигантского размера. Рассматриваемый материал начинается с булевых функций и технологий и трюков работы с битами, затем всесторонне рассматривается генерация всех кортежей и перестановок, всех сочетаний и разбиений, и всех деревьев. Комбинаторный поиск — богатая и важная тема, и Кнут приводит слишком много нового, интересного и полезного материала, чтобы его можно было разместить в одном или двух (а может быть, даже в трех) томах. Одна эта книга включает около 1500 упражнений с ответами для самостоятельной работы, а также сотни полезных фактов, которые вы не найдете ни в каких других публикациях. Том 4А определенно должен занять свое место на полке рядом с первыми тремя томами этой классической работы в библиотеке каждого серьезного программиста.
ISBN 978-5-907144-06-4
в продаже


МАТЕМАТИКА ДЛЯ ЧАЙНИКОВ 2-Е ИЗДАНИЕ
Марк Зегарелли
ВЕДЬ ЭГО ГАК ПРОСТО!
Математика
Марк Зегарелли
чайников
Освойте обыкновенные дроби, десятичные дроби и проценты
Научитесь решать  ■
www.dialektika.com
Многие школьники на этапе перехода от арифметики к алгебре почему-то начинают испытывать страх перед математикой. Эта книга поможет вам разобраться с любыми математическими трудностями. Здесь вы найдете все необходимое для освоения школьного курса математики и перехода к изучению алгебры и геометрии. Начав со знакомства с числами, дробями и процентами, вы затем освоите более сложные темы, такие как единицы измерения, множества и алгебраические уравнения. Основные темы книги:
• множители, делители
и кратные;
• обыкновенные дроби, десятичные дроби и проценты;
• основные геометрические фигуры и тела;
• диаграммы и графики;
• экспоненциальная запись числа, единицы измерения, статистика и множества;
• введение в алгебру.
ISBN:978-5-907144-62-0 в продаже


МАТЕМАТИКА СБОРНИК ЗАДАЧ ДЛЯ ЧАЙНИКОВ З-Е ИЗДАНИЕ
Марк Зегарелли
www.dialektika.com
Этот сборник задач окажет помощь в усвоении основных математических понятий, проработке примеров практических задач и поэтапном анализе их решений. Пользуясь этим пособием, читатель может на практике освоить простые и десятичные дроби, научиться выполнять основные арифметические операции над числами, решать алгебраические уравнения, вычислять площади и объемы геометрических форм и тел, строить графики в двумерной координатной плоскости и ознакомиться с различными системами счисления.
Книга адресована всем желающим изучить математику и поможет им преодолеть невольный страх перед этой дисциплиной.
ISBN 978-5-907144-11-8
в продаже