Ф. П. Васильев
Лекции
по методам
решения
экстремальных
задач
Издательство
Московского университета
1974

ОГЛАВЛЕНИЕ
Предисловие ........ 5
Глава 1. Минимизация функций одной переменной 7
§ 1. Постановка задачи .'.... 7
§ 2. Задачи А и Б. Строго квазивыпуклые функции .... 8
§ 3. Оптимальный пассивный поиск в задачах А и Б . * . . 11
§ 4. Последовательный поиск 16
§ 5. Метод деления отрезка пополам 18
16. Оптимальный последовательный поиск для задачи А . . . 20
§ 7. Оптимальный последовательный поиск для задачи Б . 27
§ 8. Метод золотого сечения 32
§ 9. Метод ломаных : 35
§ 10. Выпуклые функции. Метод касательных 38
§ И. Метод парабол 44
§ 12. О* некоторых других методах минимизации ..... 47
Глава 2. Минимизация функций многих переменных 51
§ 1. Постановка задачи. Обозначения. Вспомогательные сведения 51
§ 2. Градиентный метод 65
§ 3. Метод проекции градиента 72
§ 4. Метод возможных направлений . 77
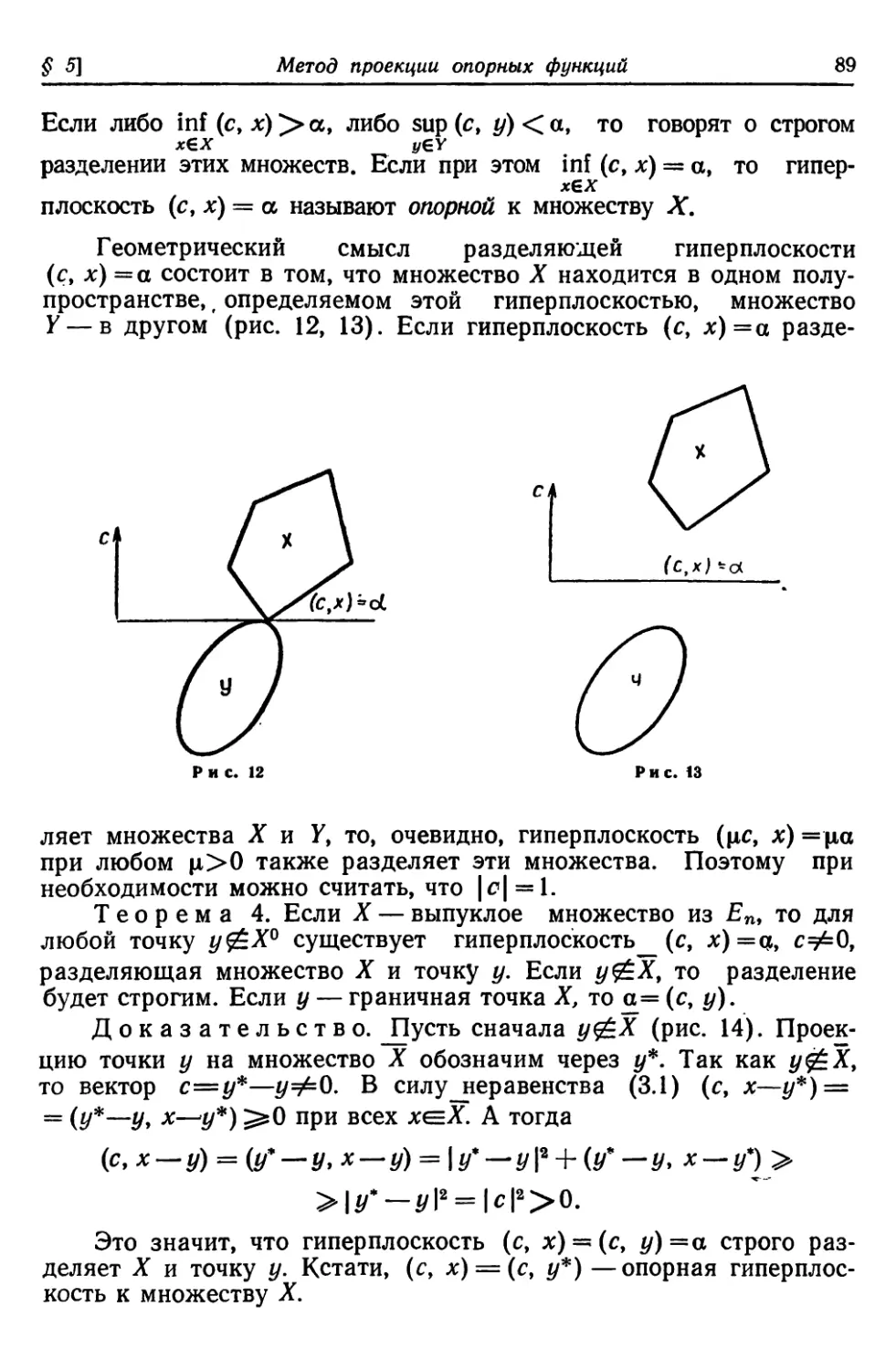
§ 5. Метод проекции опорных функций -. 84
§ 6. Метод условного градиента , 96
§ 7. Метод сопряженных градиентов 101
§ 8. Метод Ньютона * 107
§ 9. Метод штрафных функций 117
§ 10. Теорема Куна — Таккера 121
§ 11. Элементы линейного программирования ....... 131
§ 12. О методе случайного поиска и некоторых других методах . 148
Глава 3. Принцип максимума Л. С. Понтрягина 155
§ 1. Постановка задачи оптимального управления . . w » . . 155
§ 2. Формулировка принципа максимума Л. С. Понтрягина . . 159
§ 3. Приближенное решение краевой задачи принципа максимума 168
§ 4. Связь между принципом максимума и классическим вариаци-
онным исчислением 177
Глава 4. Динамическое программирование. Проблема синтеза ... 181
§ 1. Схема Р. Беллмана. Проблема синтеза для дискретных систем 481
§ 2. Схема Н. Н. Моисеева 191
§ 3. Дифференциальное уравнение Р. Беллмана . 198
§ 4. Проблема синтеза для систем с непрерывным временем. Оцен-
ка погрешности 203
Глава 5. Достаточные условия оптимальности 213
§ 1. Достаточные условия оптимальности для задач с закрепленным
временем 213
§ 2. Достаточные условия оптимальности для задач с незакреплен-
ным временем 222
§ 3. Достаточные условия оптимальности для дискретных управляе-
мых систем. Оценка погрешности 227
Глава 6. Методы минимизации в функциональных пространствах 232
§ 1. Вспомогательные сведения 233
§ 2. Некоторые методы минимизации функционалов . ... 247
§ 3. Задача оптимального управления со свободным правым концом 257

§ 4. Градиент функционала, связанного с дискретной управляемой
системой. Условия оптимальности . .' 27>
§ 5. Минимизация квадратичного функционала. Примеры . . . 284
§ 6. Оптимальное управление процессом нагрева стержня . . 294
§ 7. Оптимальное управление процессом колебания струны . . ЗОО
Глава 7. Методы решения задач быстродействия 308
§ 1. Постановка задачи 308-
§ 2. Вспомогательный аппарат. Критерии управляемости и опти-
мальности 314
§ 3. р-метод 321
§ 4. Приложения 327"
Глава 8. Регуляризация некорректно поставленных экстремальных задач 337
§ 1. О некорректно поставленных задачах минимизации . 337
§ 2. Метод регуляризации А. Н. Тихонова 339»
§ 3. Регуляризация при вычислении с погрешностями .... 349-
§ 4. Регуляризация с помощью аппроксимации множества 351
§ 5. Усиленная регуляризация * 353»
Глава 9. Разностные аппроксимации задач оптимального управления 35S
§ 1. Разностная аппроксимация для одной задачи минимизации
квадратичного функционала 355=
§ 2. Разностная аппроксимация задачи об оптимальном нагреве
стержня 361'
Литература . . 364

Предисловие
В последние десятилетия весьма актуальными стали вопросы наилучшего
(в том или ином смысле) управления различными процессами физики,
техники, экономики и др. Сюда относится, например, задача огранизации
производства с целью получения максимальной прибыли при заданных
затратах ресурсов; задача управления системой гидростанций и водо-
хранилищ с целью получения максимального количества электроэнергии;
задача о космическом перелете из одной точки пространства в другую
наибыстрейшим образом или с наименьшей затратой энергии; задача о
быстрейшем нагреве печи до заданного температурного режима и многие
другие задачи. К таким проблемам приводят также многие задачи вычис-
лительной математики, как, например, задача наилучшего приближения
функций, задача минимизации невязки уравнения и др.
В математической постановке задачи сводятся к отысканию экстре-
мума (максимума или минимума) некоторой функции или функционала
J (и), выражающего собой качество (цену) управления и из заданного
множества V некоторого пространства. Требование принадлежности
управления и некоторому множеству V выражает собой- ограничения,
обычно вытекающие из ограниченности наличных ресурсов, возможностей
технической реализации управления, нежелательности каких-либо запре-
щенных (аварийных) состояний и т. п. Задачи отыскания экстремума
функционала J (и) на множестве U принято называть экстремальными за-
дачами. Заметим, что задача максимизации функционала J (и) на множе-
стве U эквивалентна задаче минимизации функционала —Пи) на том же
множестве U, поэтому можно ограничиться рассмотрением задач мини-
мизации.
С 50-х годов теория экстремальных задач обогатилась фундамен-
тальными результатами, потребности практики способствовали бурному
развитию методов приближенного решения экстремальных задач.
В основу настоящей книги положен курс лекций по численным мето-
дам решения экстремальных задач, который автор в течение ряда лет чи-
тает студентам 3—4-го курса факультета вычислительной математики и
кибернетики Московского университета. В книге изложены основы наи-
более часто используемых на практике методов приближенного решения
экстремальных задач, теоретическое обоснование и краткая характеристи-
ка этих методов. Содержание книги можно разделить на две части.
К первой относятся две первые главы, где рассматриваются методы мини-
мизации функций конечного числа переменных, во второй части — методы
минимизации функционалов, заданных на множествах из функциональных
(в основном гильбертовых) пространств и связанных с процессами, опи-
сываемыми системами обыкновенных дифференциальных уравнений или
уравнениями с частными производными.
Заманчиво было изложить методы минимизации в общем виде на
языке функционального анализа в первой же части лекций, охватив при
этом как частный случай многие методы минимизации функций конечного
числа переменных и различных других классов функционалов. Однако

такой способ изложения, несмотря на свою привлекательность и удобства
для читателя-знатока, видимо, все же труден для первого знакомства с
предметом, не говоря уже о том, что он не может отразить всю специфику
конечномерных задач.
Таким образом, принятое в книге расположение материала объяс-
няется стремлением автора, с одной стороны, сделать книгу, доступной
читателям, владеющим математикой в объеме программ технических вузов
и желающим впервые ознакомиться с теорией и методами решения экстре-
мальных задач, с другой стороны, сохранить математическую строгость
изложения. По этой причине материал, требующий для своего полного
усвоения знаний элементов функционального анализа, излагается в более
поздних главах книги. Заметим, впрочем, что отсутствие знаний по функ-
циональному анализу не будет мешать пониманию и усвоению излагае-
мых в этих главах основ методов и иллюстрирующих их конкретных .при-
меров экстремальных задач, если только читатель будет готов некоторые
утверждения принять не в их максимально общей форме.
Многие параграфы завершаются упражнениями, помогающими усво-
ить содержание основного текста и дополняющими его. Объем книги
заставил автора ограничиться лишь / небольшим количеством примеров
экстремальных задач, иллюстрирующих описываемые в книге методы.
Список.литературы, приводимый в конце книги,-никак не может претен-
довать на библиографическую полноту и не имеет целью отразить исто-
рические аспекты и чей-либо приоритет в рассматриваемых вопросах, а
содержит лишь те работы, которые были непосредственно использованы
в книге или близко примыкают к ней, дополняя ее содержание.
Нумерация формул, теорем, лемм, определений, упражнений в каж-
дом параграфе самостоятельная; ссылки на материалы, расположенные в
пределах данного параграфа, имеют вид (А), вне данного параграфа, но
в пределах данной главы — (В. А) вне данной главы — (С. В. А), где
С — номер главы, В — номер параграфа, в котором находится упоми-
наемая формула, теорема или другой материал с номером А. Так, напри-
мер, теорема 3 из §*1 главы 2 в пределах данного § 1 именуется просто
теоремой 3, в других параграфах 2-й главы — теоремой 1.3, в других
главах — теоремой 2.1.3. Аналогично, при ссылках на § В главы С в
пределах главы С .этот параграф будет именоваться просто § В, вне гла-
вы С — § С. А. Значок А в тексте означает окончание доказательства
теорем, лемм.
Автор выражает глубокую благодарность академику А. Н. Тихонову
за внимание и поддержку при написании книги, В. Г. Карманову,
М. С. Никольскому, Н. X. Розову, прочитавшим книгу в рукописи и сде-
лавшим ряд ценных замечаний, И. С. Березину, взявшему на себя труд
по научному редактированию книги и своими советами способствовавшему
улучшению содержания книги, устранившему многочисленные погрешности
изложения. Автор весьма признателен В. Г. Курилову, В. И. Селиверсто-
вой, А. С. Стрекаловскому за большую помощь в подготовке рукописи
к изданию.
Автор будет благодарен читателям за все замечания по содержа-
нию книги.

Глава 1
Минимизация функций одной переменной
§ 1. ПОСТАНОВКА ЗАДАЧИ
•
Пусть на множестве U={u: a^u^.b} числовой оси, где а и
Ь — заданные числа, —оо^а<6^|+оо, определена функция
J (и). Под задачей минимизации функции J (и) на множестве U
будем понимать следующее: 1) найти «/*= inf J (и); 2) если на U.
нижняя грань достигается, то найти точку ы*е£/, в которой
J(u*)=J*\ 3) если нижняя грань не достигается на £/, то указать
последовательность ы0, ии ...; и*, ...; Uh^U (&=0, il, ...) такую, что
Пт,/(иЛ) = /\ Точку u*^U со свойством /(«*)=/* называют тон-
fe-»oo
кой минимума J (и) на £/, а последовательность {Uk}^U со свой-
ством: limJ(uk)= J* называют минимизирующей последователь-
Л-юо
ностью для функции J (и) на U.
Что нам известно из классического математического анализа о
методах решения этой задачи? Допустим, что J (и) кусочно-непре-
рывная и кусочно-гладкая функция на U. Тогда, как известно [126],
минимум J (и) на U может достигаться лишь в тех точках wet/, в
которых или //(а)=0, или У'(и) не существует, или J (и) терпит
разрыв, или же, в точках, являющихся граничными для множества
V. Такие точки принято называть точками, подозрительными на
минимум. Если точки, подозрительные на минимум, найдены, то
среди них нужно выбрать те, в которых, в самом деле достигается
минимум. Для этого обычно исследуется знак производной J'(u)
в окрестности подозрительной точки или знак второй производной
J"(u) в этой точке, если J"(u) существует. В результате такого
отбора определяются точки, в которых достигается, вообще говоря,
лишь локальный минимум J (и) на U. Чтобы найти абсолютный
минимум J (и) на £/, остается перебрать все точки локального ми-
нимума и из них выбрать точку с наименьшим значением функции,
если таковая существует.
Описанным способом поиска минимума можно воспользовать-
ся во всех тех случаях, когда функции и ее производные имеют
достаточно простой вид, и без особых трудностей удается реали-
7

8 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [Гл. I
зовать указанную выше схему отбора точки абсолютного миниму-
ма. К сожалению, этот подход лишь в редких случаях позволяет
решить задачу минимизации функции J (и) на С/. Дело р том, что
вычисление производной J (и) в практических задачах зачастую
представляет большие трудности и нередко даже неизвестно, су-
ществует ли производная в интересующей нас точке. Возможно,
например, функция J (и) задана лишь таблично или лишь извест-
но, что в любой точке ие U значение J (и) может быть вычислено
с нужной точностью, а сама- функция задана неявно. В тех слу-
чаях, когда производная все же явно вычислена, решение уравне-
ния J'(u) =0 может встретить серьезные трудности.
Поэтому важно иметь методы минимизации, не требующие вы-
числения производной и основанные лишь на вычислении значений
функции в каких-либо специально подбираемых точках. В прак-
тических задачах вычисление значений функции также может ока-
заться весьма трудоемким делом, и здесь большую ценность приоб-
ретают методы, позволяющие решить задачу минимизации с тре-
буемой точностью на основе вычислений значений функции в воз-
можно меньшем количестве точек.
§ 2. ЗАДАЧИ А И Б. СТРОГО КВАЗИВЫПУКЛЫЕ ФУНКЦИИ
Прежде чем переходить к изложению методов минимизации
функций одной переменной уточним постановку задачи.
Пусть функция J (и) определена на отрезке [a, b]={u:a^Z
^u^b} и достигает на [а, Ь] своей нижней грани, и пусть тре-
буется минимизировать ее на [а, Ь]. В зависимости от того, инте-
ресует ли нас только точка минимума и*, или же наряду с и* мы
интересуемся еще и значением /(w*), следует различат*» две по-
становки задачи минимизации [56]:
Задана А: Найти точку и*е[а, Ь] и значение
/(<0= inf J{u) = J\
Задача Б: Найти точку #*е[а,&], в которой /(«*)=/* (не
интересуясь самим значением /(а*)).
Для приближенного решения этих задач обычно поступают
следующим образом: 1) вычисляют значения функции в каких-либо
специальным образом подбираемых п точках щ, щ, ..., ип из от-
резка [а, 6]; 2) перебором значений J(Ui) среди точек {щ} (i=
= 1, ..., п) выделяют точку йПу в которой J (ип) = min J (щ);
3) из точек а, 6, и\у ..., ип определяют точку ап, ближайшую к
ип слева, и точку ЬПу ближайшую к ип справа; 4) в качестве и*
принимают какую-либо точку ип из отрезка [аПу Ьп]. При реше-
нии задачи А часто полагают un = ип (с вычисленным'значением

§ 2] Задачи А и Б. Строго квазивыпуклые функции 9
J(un))', в задаче Б можно, например, взять #*=—(ап+Ьп) (зна-
чение J(u„) здесь нас не интересует).
Понятно, что такой порядок действий имеет смысл лишь в тех
случаях, когда у нас есть основание считать, что и*е(ап, Ьп]. Од-
нако нетрудно подобрать функцию (даже непрерывную), для ко-
торой и*£[ап> Ьп]. Укажем один важный класс функций, для ко-
торых всегда и*^[ап> Ьп\
Определение 1. Функция J (и), определенная на множестве
U={u : а^:и^Ь}9 называется строго квазивыпуклой на Г/, если
существуют числа а, Р, а^а^р^&, такие, что: 1) J(u) строго
монотонно убывает при а^и<.а (если а<а^'р^6); 2) J (и)
строго монотонно возрастает при р<и^& 1(если a^a^ip<6);
3) J(u)=J* = \nU(u) при а<и<Ср (если а^а<р^6); 4) в точ-
иеи
ках и=а и и=р выполняются условия:/(а)^/*приа=а^р^^;
У (а — 0) = lim J(u)>J(a)>r при а<а<р<6; /(&)>/* при
и-мх—О
a^a^^=b; J ф + 0)= Vim J(u)> J ф)>Г при а<а<р<6; и
наконец, в случае а<а=Р<& :/*^/(a)^max{/(a—0), 7(a+0}
(эквивалентное и более изящное определение см. ниже в упраж-
нении 3) [135].
Множество всех строго квазивыпуклых функций на отрезке
а^и^Ь обозначим через Q[a9 b]. Вот примеры таких функций:
Ji(u)=u2^Q[a> b] при любых a, b; J2(u) = \и\ +a+sign(и)^Q[a,b]
при любых a, b\ Jz(u)= V '' ^ I принадлежит Q[a, Ь] при
" J— 1, w = 0J
любых a, ft. Функция
/*(«) = )'"'' uut°o}eQ[0'1]> но ^l"1* П.
Очевидно, строго квазивыпуклая функция на U локальных ми-
нимумов не имеет, или, точнее говоря, любая точка локального
минимума такой функции одновременно является точкой ее ((абсо-
лютного) минимума на U. Если а<р, то нижняя грань J (и) на U
всегда достигается; если <х=р, то нижняя грань может и не до-
стигаться'. Множество всех тех функций из Q[at 6], которые до-
стигают своей нижней грани на [а, 6], хотя бы в одной точке а*,
обозначим через Q*[a, 6].
Задачи А и Б мы будем рассматривать на классе функций
Q*[at &], 0<&—а<оо. Для функций этого класса, очевидиц спра-
ведливо утверждение: если J(un) ^min{/(an), J(bn)}t an<.un<bn>
то на отрезке [ant' bn] существует хотя бы одна точка минимума
J (и) на [at Ь]. Поэтому намеченная выше схема поиска минимума
оправдана.

10 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ \Гл. J
Определение 2. Пусть J(u).^Q*[at b] и пусть вычислены
значения 1{щ) в некоторых точках {wje[a, ft], (i=l, ..., п). Ска-
жем, что тройка точек an, &n, ип, локализует точку минимума J (и)
на {а, &] по точкам {щ} (i=l9 ..., п)_у если: 1) ап, &п, ип содержат-
ся среди точек а, 6, иь ..., ип; 2) J(Un) =minJ(щ)\ 3) an<un<.bn\
__ i<t</i
4) кроме wn,'интервалу an<w<6n не принадлежит ни одна из то-
чек ии_ ип (т. е. на интервале ап<и<Ьп имеется лишь одна
точка ип, в которой вычислено значение функции).
На практике часто бывает, что мы заранее ограничены числом
точек {wi, ..., an}e[a, &], в которых можно вычислить значение
функции J (и). Такое ограничение естественно во всех тех случа-
ях, когда каждое вычисление J (и) трудоемко. Например, значения
J {и) могут определяться в результате дорогостоящего эксперимен-
та или сложных вычислений на ЭВМ. Возникает вопрос, как нуж-
но выбирать точки и\, ..., ип и как вести поиск минимума, или, ко-
роче, какой должна быть стратегия поиска минимума, чтобы по
наблюдениям значений функции в этих точках определить точку
минимума и* с наименьшей возможной погрешностью? Кроме то-
го, одна и та же стратегия поиска, примененная к различным
функциям из некоторого класса, по-видимому, будет давать раз-
личные погрешности в определении и*: для некоторых «удачных»
функций эта погрешность может оказаться равной нулю, для дру-
гих «неудачных» функций погрешность может быть значительной.
Как же выбирать стратегию поиска, чтобы она давала по возмож-
ности меньшую погрешность даже для самых «неудачных» функ-
ций из данного класса, например класса Q*[a, &]?
Оказывается, при ответе на эти вопросы следует различать за-
дачи А и Б. Поясним это на примере п=2. Пусть /(m)gQ*[0, 1],
пусть минимум J (и) на (0, 1] достигается в точке м*е[0, 1]. Возь-
мем точки их=—(1 — б), и2 =— (1+б),0<6<0, 1 и вычислим зна-
чения /(Hi), J(u2). Может оказаться, что J(u\) ^]J(u2). Тогда
ы*е[0, и2]. В задаче А в этом случае в качестве приближения к и*
естественно принять точку и*2 = их с уже вычисленным значением
J{u{) «/(и*). При этом гарантированная точность есть \и* — ы*2\ <
<—=—, поскольку в худшем случае для некоторых функций из
Q*[0, 1] может быть и*=0. В задаче Б в качестве приближения к
и* можем принять и£ = —(1 + 6) —середину отрезка [0, и2], ибо
значение J(ul) здесь нам не требуется, и получим лучшую гаран-
тированную точность \и*—и*|< —(1+6), чем в задаче А. Слу-

§ 3}
Оптимальный пассивный поиск в задачах А и Б
11
чай J{ti\)>J(ti2) рассматривается аналогично и приводит к тем
же оценкам |и* —и*| для задач А и Б. Заметим, что для зада-
1 2
чи А возможен более лучший выбор точек иг = —и иг = —,
о о
дающий гарантированную на классе Q*[0, 1] точность, равную —,
о
в то время как для задачи В такой выбор точек гарантирует по
сравнению с предыдущим меньшую точность.
Наконец, еще одна тонкость: при решении задачи А или Б,
оказывается, следует различать два принципиально различных
способа выбора точек ии ..., иП9 в которых вычисляются значения
функции: 1) все точки ии .., ип задаются заранее, до начала вы-
числений (до начала экспериментов) — это пассивный поиск;
2) эти точкет выбираются последовательно в процессе поиска с
учетом результатов предыдущих вычислений (экспериментов) —
это последовательный поиск. Об этом речь пойдет в следующих
параграфах.
Упражнения. 1. Как нужно доопределить функцию J(u) =
= Uul , , в точке и=0, чтобы 7(и)е=0[0,1]?Q[-1, 1]? Q[-l, 0]?
2. Как нужно доопределить функцию / (и) = { ' ^ \
I— и-к А, и<0\
в точке и = 0, чтобы J(u)£Q[0,1]? Q[— 1,0]? Q[—1,1]? Q[a,6]
при любых a, 6? Рассмотреть случаи А = 0; +1; — 1.
3. Доказать, что функция J (и) строго квазивыпукла на проме-
жутке £/={и: a^zu^:b} тогда и только тогда, когда J(au+
+ (1—a)v)^.max{J(u)\ J(v)} при всех w, ие£/ и всех а,0<а<1,
причем равенство может достигаться лишь при J(u)=J(v).
4. Если /i(w), /2(w)eQ[a, 6], то будут ли принадлежать Q[at b]
следующие функции: J\{u)+J2(u)t J\(u)—J2(u), J\(u)-J2(u),
/i(")//2(")?
5. Как следует выбирать две точки ии w2e[0, 1], чтобы точку
минимума J(u)^Q*[Qy 1] найти с наилучшей точностью, гарантиро-
ванной для всех функций из Q*[0, 1] в случае задач А и Б?
§ 3. ОПТИМАЛЬНЫЙ ПАССИВНЫЙ ПОИСК В ЗАДАЧАХ А И Б
Определение 1. Пусть 7(tt)EQ*[a, b]. Скажем, что на от-
резке (a, Ь] задана пассивная стратегия Рп> если: 1) на [a, Ь] за-
ранее задаются все п точек {щ} (i=l, ..., п)у Uo=a^U\<.u2<....
... <wn^«n+i=6 и вычисляются значения 1(щ) (t=l, ..., п)\
2) путем сравнения величин 1(щ) (t=l, ..., п) определяются точ-
ка uk, в которой / (uk) = min J(ut)9 и отрезок [uk-u uk+i]t содер-
жащий точку м* минимума J (и) на [a, Ь] (таким образом, точки

12 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [Гл. 1
Uk-i, uk, tih+i локализуют точку минимума); 3) имеется правило, по
которому одна из точек w*6[«bb«Hi] принимается в качестве
приближенного значения для w*. Поиск минимума, осуществляе-
мый с помощью пассивной стратегии, будем называть пассивным
поиском [230].
Возьмем две пассивные стратегии Pn={ui} uPn = {ui} на
[а, Ь]. Какая из этих стратегий лучше? Как их сравнивать? При от-
вете на эти вопросы будем различать задачи А и Б.
1. Начнем с задачи А. Пусть для некоторой функции /(и)е
^Q*[a, b] с помощью пассивной стратегии Pn={u>i} (*=1, .., п)
среди точек {иг}е[а, Ь] выбрана точка uk9 J(uk) = min J(ut) и от-
i<t<fi
резок [uk-u Uk+iii содержащий точку и* минимума J (и) на [а, Ь].
В задаче А в качестве приближения к н* принимаем точку и*п = uk,
допуская при этом погрешность
\и*~ип\<тах{"Н-1 — uk> »k — ил-i}.
Очевидно любой другой выбор и* с вычисленным J(u^) для
некоторых функций из Q*[a, b] приведет к большей погрешности.
Для любой фиксированной стратегии Рп={щ} нетрудно указать
функцию /(tt)eQ*[a, 6], для которой отрезок [uh-U uk+i]> содержа-
щий точку щ*у будет совпадать с любым из наперед йзятых от-
резков [Ui-x, U{+{\ (/=1, 2, ..., п) и погрешность \и* — и*п\ будет как
угодно близкой к max{^+i—uif щ—щ-\) (например, если
Шах {щ+\—Uu Ui—Ui-i}=Ui+\—щ, то можно взять
' — и -\- ui+i—е при и^.щ+1—е,
— (ut+i— Ui-i)(u — ut+i + е) при и>и{+1—е,
где е достаточно малое положительное число). И поскольку
заранее неизвестно, какой из отрезков, [#t-i, Щ+\] содержит и*, мы
вынуждены рассчитывать на самую «неудачную» функцию J(u)^
^Q*[#, b] и в качестве гарантированной на Q*[af &] точности в оп-
ределении и* с помощью стратегии Рп должны взять максималь-
ную из возможных погрешностей;
max max {w*+i — и{> ut — щ-\} = max {wl+i — u{) = L* (Pn, b — a).
Величина L% (Pny b — a) от J(u)^Q*[ayb] не зависит и ха-
рактеризует стратегию Рп на классе функций Q*[atb].
Теперь естественно считать, что пассивная стратегия Рп луч-
ше другой пассивной стратегии Рп$ если
/*(Ря,6-а) <LUP'n,b-a).
JB(u) = \

$ 3) Оптимальный пассивный поиск в задачах А и Б 13
Обозначим
I*(b — a) = izAl£(Pn9 b-a)t
Рп
где нижняя грань берется по всем пассивным стратегиям.
Определение 2. Пассивную стратегию Рп назовем опти-
мальной для задачи А, если Ln(b — а) = Ln (Р*, 6 — а).
Теорема 1. Для задачи А при всех п^\ оптимальная пас-
сивная стратегия существует, единственна и имеет вид
Доказательство. Прежде всего, очевидно Ln(P*n> Ь — а) =
= —.Для любой другой пассивной стратегии Рп={щ) : Д==
п+ 1
i=a0^tti<w2< — <wn^«n+i==& всегда найдется отрезок [uh,
Uk+i] длины t/ft+i—uk > — ибо в противном случае сумма
п -f-1
длин всех отрезков [ui9 ui+i] (f=0, 1, ..., п) будет меньше длины
отрезка [а, Ь]. Следовательно,
Ln (Рп> Ь - а) = max {и,+1 - щ) > -^L
<Xf <п п + 1
для любой пассивной стратегии Рп, причем равенство здесь дости-
гается только при Рп = Рп. А
2. Теперь перейдем к задаче Б. Пуеп> с помощью пассивной
стратегии Pn={Ui} для некоторой функции 7(«)eQ*[a, b] найден
отрезок [Wft-i, Wfc+i], содержащий точку а* минимума J (и) на [а, 6].
В задаче Б значение J(и*) нас не интересует, поэтому в качестве
приближения к w* можем взять и*=—(tfe-i + и*н)» допуская
при этом погрешность |н* — ы*|<— (wa+i—w^-i) (любой другой
выбор и*п может привести к увеличению погрешности при соот-
ветствующем выборе 7(«)sQ*[a, &]). Эта погрешность зависит от
выбора стратегии Рп и функции /(w)eQ*[a, 6]/Для любой фик-
сированной пассивной стратегии Рп={и{} нетрудно указать функ-
цию /(w)eQ*[a, &], для которой отрезок [uh-\rU>h+\\ содержащий
точку и*, будет совпадать с любым из наперед взятых отрезков
[Ui-u "я-i] (*=1, ..., п), и погрешностьIи* — и*п\ будет как угодно
близкой к —(щ+х —a*_i) (см., например, функцию Je(u) из п. 1).
И поскольку заранее неизвестно, какой из отрезков [ai-ь #г-м] со-
держит и*, мы вынуждены рассчитывать на самую «неудачную»

14 МИНИМИЗАЦИЯ ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ* [Гл. 1
функцию J (и) из Q*[a> b] и в качестве гарантированной на Q*[a>b]
точности в определении w* с помощью стратегии Рп взять макси-
мальную из возможных погрешностей:
max — (щ+х — щ-\) = Ln (Ря, Ь —а).
1<;<п 2.
Величина Ln(Pn, Ь — а) от /(w)eQ*[a, b] не зависит и характери-
зует стратегию Рп на классе функции Q*[at b].
Определение 3. Пассивную стратегию Р*п назовем оптималь-
ной для задачи Б, если L* (Рп, 6 — а) = L* (& — а) = inf L* (Ря, b—'a)*
где „вжняя граАь бередя „о всем пассивным срат^м. upa«,™
Р*п назовем е-6птимальной, если Z,J?(Р®, Ь—а)<L*[Ь — а) + е, е>0.
Теорема 2. Для задачи Б при всех нечетных n=2m+l
(m^O) существует бесконечно много оптимальных пассивных стра-
тегий, причем La (Ь — а) = """а
2 (т +1)
Доказательство. Возьмем пассивную стратегию Рд = {^} из
точек v2i = о-+1—=^- (i =1,2 m), а точки t^+i (г ±= 0, 1, ...
т+ 1
..., т) расположим на отрезке [а, 6] как угодно, лишь бы
l>2f-l < 02* <ЧМ+1» Чм+1 ?2*-1 < 7^ •
/71+ I
Очевидно, Ln (Рп, Ь — а) = ~~а , С другой стороны, /для любой
2 (т +1)
пассивной стратегии Ря = {щ} Имеем
£* (Л*> Ь— а) = — max (а^ — и<_0 >
2 i<f<»
> —max {6 — u2mt и2т — ^2m-2, • • • > и4—и2> '#2 — а} >
Ь — а
2(/п+1)
-1|?(Р;,6-а).
Следовательно, стратегии Ря оптимальны и Ln(b—a) =
> — а
2(«+1)
Теорема 3. Для задачи Б при всех четных л = 2/тг(т>1)
оптимальной пассивной стратегии не существует;
' 2 (« + !)'

§ 3] Оптимальный пассивный поиск в задачах А и Б 15
В качестве е-оптимальной стратегии можно взять
m-J- 1 m-f- 1
где 0<8<;
t = l,2, ... ,m,
b—a
*2(m+l)
Доказательство. Прежде, всего
ИЛ Ь-а) = i™ fa+, -■>,-,) = i-fc-a) = j^ + f.
Покажем, что Ln(Pn> b — a)>—""~a для любой пассивной страте-
гу +1)
гии Рп = {wj, a0 = а < йх <w2< ... <ип < Ь = wn+i. Имеются две
возможности: либо и2 ]> и = аН—^^Ц либо и2 < и. Если и2 > а, то
пг-\-1 ♦
£* (Л,, 6 — а) = 4" max (и<+1 — w£_i) >-^-(иг — а)>
2 1<*<п 2
. 1 /— ч Ъ — а
> — (и — а) =
2 v 2(m+l) "
Если же w2<w, то max (w^-i—Wi_i)>H2— а. В самом деле,
1<£<п
если бы max (tii+i— w*-i) <и2— а, то u2i+\—W2*-i < u2 — a, t =
1<е<л
= 1,2, ...,m, и, кроме того, wx— a<w2— a. Сложив последние
неравенства, будем иметь6 — a<(m + 1) (w2 — a)<(/n+ l)(w —a) =
= 6 — a; получили противоречие/ Таким образом,
L%(Pn,b— a) = 4- max (ин-i —^-i) = l5-i(Pi-b 6—«i).
2 2<f<ft
где P„_i—пассивная стратегия на [и1У 6], составленная из точек
и2> #з> • • • >ип стратегии Рп. Но п— 1 = 2/я— 1 —нечетное число, и
в силу теоремы 2 L%-\{P'n-u b — Uj) > ~~% - Следовательно,
2/п
Ц(Рп.Ь-а)>-—>
2пг 2пг 2 (т +1)
Таким образом. 1« (Р„, Ь — а)>—"~"fl> для любой пассивной стра-
r f v п 2(m + i)
тегии Рл, причем Ll(Pi b — а)< 2^{) +е Для любого б, 0<
< е < 77-^7- Следовательно, L% (Ь - а) = .*~g А
2 (т + 1) 2 (т + 1)

16 МИНИМИЗАЦИЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ [Гл. t
Из теорем 2—3 непосредственно вытекает
Следствие 1. Для любой пассивной стратегии Рп={ш} на
отрезке [а, Ь] существует функция 7(w)eQ*[a, b\ такая, что для
тройки точек аПу bnt ип> локализующей точку минимума J (и) на
[a, Ь] по точкам и\9 ..., ип, справедливо неравенство
bn-an>-^- = 2L*(b-a),
т-\-1
где т = — для четных п, т= п~~ для нечетных я(п > 1),
2 * 2
Как видим, при решении задачи Б с помощью пассивных стра-
тегий предпочтительнее брать четное число п=2т, поскольку
^2m+i (b — a) = Lom (b — a) =
и увеличение числа точек на единицу существенно не улучшает
точность.
§ 4. ПОСЛЕДОВАТЕЛЬНЫЙ ПОИСК
Пассивный поиск -используется, как правило; лишь в тех слу-
чаях, когда можно одновременно провести п независилСых экспери-
ментов, но нет возможностей (например, не хватает времени), для
того, чтобы ставить эти эксперименты последовательно, друг за
другом; с учетом результатов предыдущих экспериментов. Между
тем интуитивно ясно, что при выборе наилучших действий следует
использовать информацию о результатах действий, которые мы
уже произвели, и во всех тех случаях, когда это возможно, гораз-
до эффективнее использовать последовательный поиск [230].
Определение 1. Пусть 7(a)eQ*[a, b]. Скажем, что на от-
резке [а, Ь] задана последовательная стратегия Рп, если: 1) задано-
правило выбора первых нескольких точек иь и^у ..., и8^[а, Ь\.
(l^s^n), из которых определяются три точки а8, bs, ^локали-
зующие точку минимума J (и) на [а, Ь] (см. определение 2.2);.
2) если l^s<fi, то по известному правилу на отрезке [as, bs] вы-
бирается несколько точек и8+ь •••> «л (\^s<.k^.n) и среди точек
us, us+u ..., Uk определяется тройка а&, Ь&, й&, локализующая точку
минимума; если &<п, то на [а&, fc/J по некоторому правилу выби-
раются последующие несколько точек Ид+ь—»Um (l^s<.k<.m^.n)
и среди йь, Ufc+i, ...С Um определяется Очередная локализующая
тройка От* Ьт, йт и т. д. Этот процесс продолжается до тех пор„
пока не будет выбрана последняя м-я точка и определена соответ-
ствующая тройка an, bn, йп, локализующая точку и* минимума
J (и) на [a, Ь]\ 3) имеется правило, по которому одна из точек
и*п 6 [ап, Ьп] принимается в качестве приближения для и*.

§4]
Последовательный поиск
17
Очевидно: [a, b] => [aS9 bs] => [ak, bk] =э ... => [ал, 6Л], J(un) =
= min /(и,) an<Cun<bn9 ал<и*<&„ и на интервале ал<и<6/1Г.
кроме йп> нет точек с вычисленным значением функции. Отсюда
ясно, что*можно ограничиться рассмотрением только таких после-
довательных стратегий Рп, согласно которым в задаче А прини-
мается Un = ип, а в задаче Б — и\ = — [ап + 6л], ибо любой:
другой выбор приближения и*п для и* из (ап, 6П] может привести
для некоторых функций 7(«)GQ*[a, 6] к увеличению погрешности
Поиск минимума, осуществляемый с помощью последователь*
ной стратегии, будем называть последовательным поиском.
Указанный выше, способ выбора и* в задаче А приводит к
погрешности \ип — и*\ < max {Ьп — и*п, ип — ап}, причем для любой
фиксированной последовательной стратегии Рп нетрудно указать
функцию 7(w)sQ*[a, 6], для которой эта погрешность будет как
угодно близкой к тах{&д — и*п> ип — ап}. Для выбранной страте-
гии Рп в качестве точности, гарантированной на классе Q*[a, b]„
естественно теперь взять число
&% (Рп>Ь—а)= sup max {bn — иЛ> < — ап).
J€Q4aM
Определение 2. Последовательную стратегию Рп назовем
оптимальной для задачи А, если
ti(Plb — a) = inltflPn9b — a) = ti(b-a),
где нижняя грань берется по всем последовательным стратегиям.
Стратегию Р\ назовем е-оптимальной, если б£(Рл, b—a)<i
<fi» (b — я)+е, e>0. Для задачи Б аналогично определяются
погрешности
\»m-»n\<-lr(bn-an), ЬБп(РП9Ь-а) =
= sup -±-{Ья-ая)9 &пъ(Ь-а) = т\Ьпъ{Рп9Ь-а)9
JeQ'la.b] 2 Рп
понятия оптимальной и е-оптимальной стратегий.
Допустим, что мы построила какую-либо последовательную»
оптимальную (или е-оптимальную) стратегию гп для минимиза-
ции функций из класса Q*[a, b]. Пусть теперь на каком-то другом
отрезке [с9 d] нам нужно минимизировать функцию из Q*[c, d\.
Возникает вопрос: нельзя ли стратегию Рп.Для отрезка {а, Ь] ис-

18 МИНИМИЗАЦИЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ [Гл. 1
пользовать для построения оптимальной (или е-оптимальной) стра-
тегий поиска минимума на отрезке [с, dp Для ответа на этот воп-
рос возьмем линейное преобразование v = —^- (и — а) + с, пере-
b — а
водящее отрезок [а, Ь] в [с, d]9 и каждой функции G(ti)eQ*[c,d]
поставим в соответствие функцию
J(u)^G{±^(u-a) + c^eQ*[a,b].
Очевидно, 'при этом между классами функций Q*[a, b] и Q*[c, d]
будет установлено взаимно-однозначное соответствие. Теперь ес-
тественно принять следующее
Определение 3. Применением стратегии Рп к отрезку [с, d]
для минимизации функции G(u)eQ*[c, d] будем называть после-
довательный выбор точек
Vt = 4—- (^ —а) +^€ [^э d], (i = 1, 2,... ,п)
о — а
по тем же правилам и в той же последовательности, по которым
выбираются точки щ^[а, b] (t=l, 2, ..., п) с соответствующими
номерами при применении стратегии Рп для минимизации функ-
ции J(u)==G (——^- (и — а) + с j на отрезке [а, 6].
После принятия такого определения имеет смысл говорить о
стратегиях Рп безотносительно к отрезку,- на котором ищется ми-
нимум строго квазивыпуклой функции. Нетрудно видеть, что для
любой стратегии Рп и любого числа а>0 имеют место равенства
б£(Рл,а(Ь-а)) = аб£(Рл, 6-а), б£(а(6-а)) =аб£(6-а).
Аналогичным свойством однородности по переменной b—а обла-
дают также величины Ъп(Рп>Ь — а)% &п(Ь — а) для задачи Б: чем
меньше длина отрезка, тем лучше гарантированная точность в оп-
ределении точки минимума с помощью одной и той же страте-
гии Рп.
Естественно распространить определение 3 и на пассивные
стратегии. Тогда величины
Lt(Pn> b-a)t L%(b-a), Lbn(Pn, b-a), L*(b-a)
будут обладать упомянутым выше свойством однородности по
переменной Ъ—а.
§ 5. МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
Простейшим примером последовательной стратегии является
метод деления отрезка пополам [230]. Суть этого метода проста.

§5]
Метод деления отрезка пополам
\9
Пусть 7(t/)eQ*(a, b], а и* — точка минимума J (и) на [a, Ь]. Возь-
мем точки
Ч = -J (а + Ь — б), и 2 = JL (а + 6 + б) = а + Ь ■ — ulf
где 6=const, 0<б<6—а. Величина б может характеризовать по-
грешность измерений величины и и ограничена снизу возможно-
стями измерительного прибора. Точки ti\9 и% расположены симмет-
рично на отрезке [a, Ь]9 при ма-
лых б делят [a, Ь] почти попо-
лам — отсюда название метода.
Далее, вычисляем и сравниваем
значения /(wi), J{u2). Если
J(ui)^Hu2)> т0 полагаем
а\=а, b\ = ii2\ если же J(u{)>
>/(«2)>то a\=uub\ = b (рис.1).
В результате получим отрезок
[du Ь{\> содержащий точку а*
минимума функции J (и) на U,
причем
, Ь~а+Ь
Рис. 1
Если отрезок [яа-j, bk-i], содержащий точку и*, уже изве-
стен и
то дальше на этом отрезке поступаем аналогичным образом. А имен-
но, берем точки
— flft-i + bk~i — б __ gj?.i + bk-\ + б .
И2*-1 = 2 * 2Л 2—'— —
расположенные симметрично на отрезке [ak-u 6fe-i]> и вычислим зна-
чения J(ii2k-\)> «Г (****)• Если J(u2k-\)KJ(u2k)y то полагаем afe = afe-u
&* = "2*> если У (tf2*-i) > / (u2k), то- аЛ = н2*-ь h = fr*_i. Отрезок
\ak> h] содержит точку и* минимума; его длина
Ьь — ak =
Ь — а
=^+(l__L)e>e.
Допустим, что требуемое число вычислений n=2k значений
функций мы провели и остановились на отрезке [ан, Ьъ\. Тогда в

20 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [Гл. t
качестве приближения для точки минимума а* в задаче Б примем
ип = — (ak + bk), допустив при этом погрешность
В задаче А примем
Un=U2k-l При J(U2k-\)<J(u2k)t Un = U2k ПрИ J (U2k-\)> J (u2k)
с уже известным значением J(un); допускаемая при этом погреш-
ность
\u*-tin\<bk-ak < JjZ£- + 6.
Зная величину погрешности в определении и* при Л-кратном де-
лении отрезка пополам, легко подсчитать число n=2k вычислений
значений функции для получения и* с нужной точностью е,
е>6>0.
Заметим, если для функции J(u)^Q[ayb] нижняя грань J (и)
на U не достигается, то при 6^-0, £->оо описанный метод позволя-
ет строить минимизирующую последовательность — для этого до-
статочно, например, взять упомянутые выше величины #Л, л =
=2£(£=1,2, ...)♦ Метод деления отрезка пополам может быть ис-
пользован для поиска минимума произвольной непрерывной функ-
ции на отрезке [а, Ь], однако в результате придем, вообще говоря,
к точке локального минимума.
Сравнивая полученные выше оценки погрешности \и*— ип\
для функций из класса Q*[a, b] с оценками из теорем 3.1 и 3.3, не-
трудно убедиться в преимуществе метода деления отрезка пополам
по сравнению с пассивным поиском уже при небольших n=2k.
Однако существуют последовательные стратегии, которые лучше
метода деления отрезка пополам.
§ 6. ОПТИМАЛЬНЫЙ ПОСЛЕДОВАТЕЛЬНЫЙ ПОИСК
ДЛЯ ЗАДАЧЛ А
Оказывается, оптимальная последовательная стратегия для за-
дачи А связана со знаменитыми числами Фибоначчи, и поэтому
эту стратегию будем называть стратегией, или планом, Фибо-
наччи.

§6]
Оптимальный последовательный поиск для задачи А
21
Как известно [56], числа Фибоначчи определяются так: /7п+2=
=Fn+\+Fn, (-я=1, 2, ...); Fi=F2=l. Нетрудно показать, что
Перейдем к описанию* плана Фибоначчи Фп (п^1). Пусть
J(M)eQ*[a, b]. При /1=1 план Ф\ прост: берем ux = —^— и вы.
числяем значение J(u\). Полагая U\ = uv определим точку мини-
мума н* с погрешностью
|л* *i ^ Ь — а Ь — а
\u-m\K-j- —.
Пусть теперь я>2. Тогда план Фп начинается с выбора двух
точек
ux = a + ~i-ib-a)9 aa = a + -|5±L-(6-a) = a + 6—иъ
расположенных на отрезке [а, Ь] симметрично, и вычисления значе-
ний J(ux)f J(u2). Если y(ttx)</(a2), то полагаем а2 = а, Ь2 = и29
Щ = ui> если же ' (ui) > J (и%)> то a2 = Щ.% Ь% = 6, и2 = и2, В резуль-
тате получаем отрезок [а2, Ь2] длины
_ Ь2 — а2 = Ь — их = и2~а= *+|. (6 —а)>
содержащий точку и* и точку и2, а2<и2<62, в которой
/ (и2) = min {J (и±), J (uj).
Заметим, что точка и2 совпадает с одной из точек
^ = я2 + -^—(Ь2-а2) = а2 + -р^-(Ъ-а) (при J(ud<J(ujy
ИЛИ
= а2 + Ь2— и2 (при J (их) >/ (и2))ч
Далее на отрезке [а2, Ь2] выбираем следующую точку и3~а2 + Ь2 —
— и2, вычисляем J(u9) и сравнением величин J(u2)9 J (и9) находим
ловый отрезок [а8, Ьв] и т. д. (рис. 2). В общем случае, пусть точ-

22 МИНИМИЗАЦИЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ [Гл. /
^ЛЧ^Ч6
(п-4,ига*$(6 а), иу-а. 1(6-а))
Р и с._2
ки и1э ... , wft(2<£<tt) уже выбраны, пусть найден отрезок
[<*k> h] длины #
содержащий тощсу и* и точку uk, ak<uk<C.bk> с вычисленным зна-
чением J(uk) = min J(ui)f причем точка uk совпадает с одной из
KKk
точек
а;-аЛ + ^ьЛ^(ЬА—aft) = aA + -%=&^(ft —а)
ИЛИ
^ = ^ + 4*^ <**-**) = **+^^
^n-Л+з **я+а
Если &<>, то на отрезке [ak, bk] выбираем следующую точку:
Uk+\ = ak+ bk—ukt симметричную с uk на этом отрезке и совпада-
ющую с одной из точек u'k, ukt отличной от ик. Вычислим значение
J(Wfe_j-i) и сравним с J{uk). Пусть для определенности ^ = ^<w^=
= Uk+i (случай uk+\ = «л < uk = и* рассматривается аналогично). Тог-
да при J(uk)<J {Uk+\) полагаем о*+1 = akf bk+l == Mfe+b tfft+i = ал.
Если же J(uk) > У (iik+\), то a*+1 = ил, bk+\ = &*, tfft+i = uk+i- в Ре-
зультате получаем отрезок [ak+u &ft+i] длины
содержащий точки и* и uk+u ak+\ < Wfe+i < *Н-ь с известным значе-
нием J(afe+i)= min J(a£), причем точка Мн-i совпадает с одной из
точек

# 6] Оптимальный последовательный поиск для задачи А 23
иш = ak+l + "-" {bk+l - аш) = аш + n~k (b — a)
ИЛИ
uk+l = ak+x + Fn~k+1 {bk+x — ak+1) =
fn-k+2
= ац-i + f*"*+1 Ф — a) = аж + 6fc+i — u'k+x,
и Т. Д.
Если & = я, то процесс заканчиваем и полагаем ип= ип с вы-
численным значением J(u)=s min/(W;). Заметим, что при k = n
г ^ т *****
длина отрезка [ап, Ьп\ равна
ьп—ап= ' (Ь — а) = ——'-,
И ТОЧКИ
u'n = an+ Fl ф—а) =ап
^Я+2 ^Я+2
F2 /t _ч _ , 6 —a
(6 — д) = ал +
гЛ+2 *П+2
совйадают_и делят отрезок [ад, Ьп] пополам. Таким образом, прини-
мая ип = ип = ия = иЛ> мы допускаем погрешность
независимо от выбора функции J (u)£Q*[af Ь]. Нетрудно видеть, что
для функции / (и) = и 6 Q* [а, 6] план Ф„ дает погрешность в опре-
делении и* = а, в точности равную —=^-. Следовательно,
6*(ФД, 6-а) = -^Ц/г>1).
План Фибоначчи Фп полностью описан [56], [230].
Отметим одно замечательное свойство плана Фп: применение
плана Ф«— k+i к отрезку [а&, &ь], полученному в результате пер-
вых k шагов плана Фибоначчи ФЛ, равносильно дальнейшему про-
должению плана Фп на этом отрезке [а&, bu], (l^k^Zn). Этот факт
вытекает из того, что первые две точки плана Фп*-к±\ совпадают
с точками u'k, Uk, или, что то же самое, с точками uk, Uk+\ пла-
на Фп.
План Фибоначчи Фп прост и удобен для использования на
ЭВМ.

24 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [Гл. /
Теорема 1. Для задачи А план Фп является оптимальным;
6*(ФД, 6-a) = inf6£(P„, b-a) = tf(b-a)=-^-.
Других оптимальных последовательных стратегий нет.
Доказательство будем проводить индукцией по п. При п=1у
очевидно, все утверждения теоремы верны. Пусть оптимальность
плана Ф* и единственность оптимальной последовательной страте-
гии доказаны при всех k=l9 2, ..., п—11 (л^2). Покажем, что тог-
да план Фп оптимален и других оптимальных стратегий нет. Возь-
мем произвольную последовательную стратегию Рп (п^2). Со-
гласно определению 4.1 стратегии Рп вначале выбираются точки
ии ..., u8^[at b] (I^s^m), и сравнением величин J(u\)y ..., J(us)
находится отрезок [as, b8], содержащий точку минимума и* и точку
й8 с вычисленным значением / (us) = min J{ut). Не умаляя общ-
l<i<s
яости, можем считать, что 2^5^п. В самом деле, задание одной
точки щ (5=1) ничего не добавляет к известной информации о
том, что а^.и*^:Ь, и поэтому остается переходить сразу ко второ-
му шагу стратегии Рп, заключающемуся в задании следующих не-
скольких точек и2, .., us (5^2), что, конечно, равносильно заданию
точек щ9 иг, ..., и3 (s^2) с самого начала, на первом же шаге
стратегии Рп. Итак, 2^5^л. ~
Отдельно рассмотрим случай s=2^n, когда стратегия Рп на-
чинается с выбора двух точек щ, и^ a^tti<CM2^6. Начальные
точки плана Фп обозначим через
и\ = а + -^— (Ь — a), u2=a + J^-(b — ay.
Fn+2 Fn+ъ
Начнем со случая иг<^и\. Если /(«i)>/(«2), то точка а* мини-
мума будет находиться на отрезке [щ9 Ь] длины Ъ — иг>Ь — и\у
причем для поиска и* на этом отрезке мы можем вычислить зна-
чение функции J (и) еще в п—1 точках, включая точку гё2=и2.
Если даже точка й2 на отрезке {ци Ь] расположена так удачно а
допускает применения оптимального (в силу индукции) плана Фп-\
на [u\9 b] с участием точки м2, то и в этом случае/гарантированная
погрешность в определении и* будет больше, чем при применении
плана Фп на [a, Ь]:
б* {Ра,Ь-а)> Ы.1 (Ф-ь Ь - и,) = ±=2±- > -р- =
= ±^- = ЬА(Фп,Ь-а).

§ 6] Оптимальный последовательный поиск для задачи А 25
Таким образом, стратегии Рп, начинающиеся с выбора двух
точек ии и2у a^U\<.U2^bt где «i<Wi, заведомо неоптимальны.
Аналогичные рассуждения показывают, что стратегии Рп с выбо-
ром точки u2>U2 также не могут быть оптимальными.
Пусть теперь и{^>и\. В худшем случае точка и* может на-
ходиться на отрезке [а, и\] длиной
* F
ux — a^>ui—а = —-—(Ь — а),
Fn+2
и на поиск и* на этом отрезке в нашем распоряжении остается
еще п—2 вычисления значений функции. Но если даже стратегия
Рп такова, что дальнейший поиск и* на [а, щ] совпадает с опти-
мальным планом Фп-2, то и в этом случае гарантированная по-
грешность в определении и* будет больше, чем при применении
плана Фп на [а, Ь\.
ti(Pn. Ь-а)>Ь*-2(Фп-2, u1.-a)=^^>^ff- =
= Л=Л- = Ь£(Фп,Ь-а).
ГП+2
Таким образом, стратегии РП9 начинающиеся с двух точек
ни u2t a^Ui<.U2^b> где ^.>«*, заведомо неоптимальны. Ана-
логично доказывается неоптимальность стратегии Рп вг случае
и2<и2.
Остается рассмотреть случай и± = и\> и2 = и2, когда первые две
точки стратегии Рп и плана Фп совпадают, и сравнение величин
J_(u\)} JJ112) приведет к отрезку [a2i bl], содержащему точки и* и
и2 с J (и2) = min {J (и*), Jiul)}. На поиск и* на этом отрезке в на-
шем распоряжении остается вычисление значений функции еще в
п — 1 (п > 2) точках, включая точку и2. Продолжением плана Фп на
отрезке [а2, 6J является план Фп-\ на этом отрезке, являющийся
единственной оптимальной последовательной стратегией по предполо-
жению индукции. Поэтому любое отклонение стратегии Рп на \а2,
Ь2] от Фп приведет лишь к увеличению гарантированной погрешно-
сти:
б^(Ря,6-а)>б^1(Фя«ь bl-al) =Ь${Фп,Ь-а)
при РпфФп. Таким образом, среди стратегий РЛ, начинающихся с
выбора двух точек их, и2 6 [а, Ь] (5=2), наилучшей является план
Фибоначчи Фп. В частности, при п = 2 наилучшим будет план Ф2.

26 МИНИМИЗАЦИЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ [Гл. t
Наконец, перейдем к рассмотрению пбследовательных стратегий
Рп% начинающихся с выбора s точек и19 и2, ... , ws6 [a, 6J, 2<s <
</г. В этом случае, сравнивая значения J(«i), ... , J{us), мы най-
дем отрезок [aSi 6S], содержащий точки и* и us, as<us<bs с вы-
численным значением J(a^) = min J(u{). Согласно следствию 3.1 при
любых, даже самых наилучших действиях на классе Q* [а, Ь] будем
иметь bs — as > —=^-, где т = -^- при четном st т = ——— при
нечетном s(m> 1). В то же самое время, оказывается, первые s ша-
гов плана Фп приводят к отрезку [al, b*s] меньшей длины
Ь\ - as = -Z^±± (b-a) <±^<bs-as.
Fn+2 m + 1
Это вытекает из следующих неравенств:
2Fn+2>(s+l)/wH* при s=2m+l, 3<s<n, (1)
2Fn+2>(s + 2)F/I_s+3 при s=2m, 4<s<n. (2)
Справедливость неравенства (1^ при s=3 и (2) при s=4 легко
установить с помощью индукции по п. При всех 5^4, оказывает-
ся, верно более сильное неравенство (2), вытекающее из монотон-
ного убывания (5+2) Fn_s+3 при возрастании 5 от 5=4 до s=n:
(s + 2) Frt_s+3 = (s + 2) Fn-s+2 +(s + 2) Fn-s+l >
>(s + 2)Fn-$+2 + F„_s+2 = (s + 3) Fn-s +2.
При поиске точки и* на отрезке [а$, bs] можно вычислить зна-
чения функции еще в п—s+1 точках этого отрезка, включая точку
ws. Если даже точка us Ha[as, bs] расположена очень удачно и до-
пускает применение оптимального (в силу индукции) плана Фп-s+i
на отрезке [aSi bs] с участием точки uSi мы сможем получить лишь
б£(/>„,&-а) >б£_5+1(Ф„_Ж( bs-as)= -^£->-^fi_ =
= _Ёр£_ = б*(Ф„, 6-а).
^Л+2
Таким образом, случай 2<s</2 также рассмотрен. ^
Теперь нетрудно ответить на следующий практически важйый
вопрос: сколько следует произвести наблюдений значений J (и),
чтобы с заданной точностью е>0 определить точку w* минимума
7(tt)eQ*[a, &]? Количество необходимых для этого наблюдений

§ 7] Оптимальный последовательный поиск для задачи Б 27
в задаче А равно наименьшему из чисел п, удовлетворяющих не-
равенствам
<е<— или Fn+\< <^Л+2.
Fn+2 гП+1
Очевидно также, длина отрезка [а, &], на котором можно найти
точку и* минимума функции /(w)eQ*[a, b] с заданной точностью
е>0, произведя п наблюдений значений J {и), не превышает
fFn+2-
§ 7. ОПТИМАЛЬНЫЙ ПОСЛЕДОВАТЕЛЬНЫЙ ПОИСК
ДЛЯ ЗАДАЧИ Б
Теорема 1. Для задачи Б наименьшая возможная гаранта-,
рованная на классе Q*[a, b] погрешность равна 6„ (Ь— а) = ——^-,
однако оптимальной последовательной стратегии Рп при п>\ не
существует.
Доказательство. Прим=1 независимо от выбора точки
#i £ [я> Ь] (и даже не вычисляя значения J (иг)) можем положить
* а 4-b i * * i ^ Ь—а Ь — а ^
щ = —-— с погрешностью \и —и\ | < = . Очевидно,
2 2 2/*2
любой другой выбор и* может привести лишь к большей погреш-
ности. Теперь покажем, что для любого е, 0 <е<—^-, и лю-
бого я> 1 можно построить последовательный план Ф„, для кото-
рого
- „_ <Ььп(Фьп,Ь-а)<-^- + г.
План Ф„ будем строить следующим образом. На отрезке [а, Ь\ сна-
чала реализуем описанный при решении задачи А фибоначчиев план
Фя-1= ф£_1 и получим отрезок [ап_ь Ьп-\\ длины
Оп-\ —ап-\ = ,
содержащий точку минимума и* и точку
с вычисленным значением
/ (йд_,) = min / (w,) (п > 2, а2 = а, 6Х = Ь)

28 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ. [Гл. Т
После этого положим ип = ип-\ + е, вычислим значение J (ип) и оп«
ределим "точку ип следующим образом:
ип =
— (ац-i + ип)9 если J (ип^) < /(ип)9
-i- (art-i + б/i-i), если J(un-i)>J(un).
Принимая (/я в качестве приближения для и*, допустим погрешность
*г—м
"ад " '
Я+1
Таким образом, план Ф„, гарантирующий погрешность, как угодно
близкую к
6 —А
2Fn+1
, построен при всех п >2 (рис. 3).
"А "*
(n*4,uf* а+$ (6а), и2* а > $ (6-а))
Рн с. 3
Далее докажем, что
8* (6 — а) = inf 6* (Ря, 6 —а) = J^£L при всех п = 1, 2,
а также убедимся в том, что &п(Р„, * — а)>~^ для любой пос-
ледовательной стратегии Рп при всех" п > 2. Как было показано
выше, при я= 1 имеем 6? (6 — а) = ■ *""*■. При л = 2, очевидно,
Ai 2
ДБ/о t ч^ & —а ^ — fl
ЫР>, *-«)>—7-=—57"
для любой стратегии Р2. С другой стороны, для "любого е>0 мож-
но указать стратегию Фз, для которой

§ 7] Оптимальный последовательный поиск для задачи Б 29
Следовательно,
bB2(b-a)=inib*2(P2tb-a) = ,
причем нижняя грань здесь не достигается. Сделаем индуктивное
предположение: пусть
для любой последовательной стратегии Pk при всех & = 2, 3, .•..
п — 1, (п > 3), и докажем, что тогда
bUb-a)=J^-<bBn(Pnt Ь-а)
для всех последовательных стратегий Рп.
Возьмем произвольную последовательную стратегию Рп
(я^З). Согласно определению 4.1 стратегии Рп вначале выбира-
ются точки in, и2, ..., wse[a, 6], (I^s^az). Как и в задаче А, не
умаляя общности, можем считать, что 2^'s^n (см. доказатель-
ство теоремы €. 1).
Сначала рассмотрим случай s = 2 < л, когда стратегия Рл начи-
нается с выбора двух точек а^их<и2КЬ. Начальные точки пла^
на ф£-1 на [a, Ь] обозначим через
*Wi Fn+i
Возможно u% < w* или uL > иь Пусть сначала иг < и1. Тогда в худ-
шем случае u*£[uit b], причем для поиска и* на [и19 Ь] можно»
вычислить значение функции еще в п — 1 точках этого отрезка,,
включая тбчку Ъ2 с известным значением J (и2). В [силу предполо-
жения индукции при любом выборе точек и3, , йп и любом рас-
положении точки и2 на [uv b] точку и* можно получить с гаранти-
рованной погрешностью, большей
Следовательно,
Ь—их ^ Ъ — их _ ь — а
2Fn * 2Fn "" 2Fn+1
Ь*п(РП9Ь-а)>.Ь-а
2F>
n+i
Для любых стратегий Рм начинающихся с выбора двух точек и1г
иг> a<£/1<w2<*, где иг<ии Аналогичные рассуждения показы-
вают, что для стратегий Рп с выбором точки и2 >u2(s = 2) также

30 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [Гл. 1
ЬБп(Рп>Ь-а)>Ь а
2Fn+1
Пусть теперь и^и]. В'худшем случае точка и* может на-
ходиться на отрезке [а, и\] длиной
и1^-а>щ—а = п~х (Ь — а),
Fn+i
и для установления этого обстоятельства мы должны сделать по
крайней мере три вычисления значений функции, причем хотя бы
одно из них во внутренней точке отрезка [а, и{\. Следовательно, для
поиска и* на [а, и{\ в своем распоряжении мы имеем самое боль-
шее п—2 вычисления значений функции на этом отрезке. Однако
по предположению индукции
сБ / ч Hi— а ^ их—а Ь — а
6/i-2(Wi —а) = —h >"
2F/I-1 %Fn-i 2F/1+1
так что
ЬБп(Рп, Ь — а) > Ь~а и при %>м1.
Аналогично доказывается это неравенство для случая u2<Cul. Та-
ким образом, для всех стратегий Рп% начинающихся с выбора двух
точек и19 щ 6 [a, b] (s = 2), имеем
ЬБп(Рп> Ь-а)>-±р-(п>3).
Перейдем к рассмотрению последовательных стратегий Рп, начи-
нающихся с выбора s точек и19 и2У , us 6 [a9b]9 2<s<n. В этом
случае, сравнивая значения /(их),_... , J(us), найдем отрезок [as, bs],
содержащий точки и* и uS9 as<.us<dbs) с вычисленным значением
J(us)= min J{ut)4 Согласно следствию 3,1 при любых даже самых
наилучших действиях на классе Q*[at b] будем иметь
6>^ Ь — CL S ^ Л
s — as> —--, гдет=—>2
т + \ 2
при четном .5, т = > 1 при нечетном 5 > 3.
Далее нам понадобятся неравенства:
2Fn+i>(s + 1) Fn-s+2 при всех s = 2т + 1, 3 <5<п
и
2Fn+\>(s + 2)Fn-S +2 при всех s = 2/п, 4<s<п, (1)

§ 7] Оптимальный последовательный поиск для задачи Б 31
справедливость которых при s < п — 1 вытекает из неравенств
(6.1—2), а при s = n (1) просто доказать с помощью индукции
по п.
Если в стратегии Рп оказалось s = п, то
ПУ п% ' ^ 2(m+l) 2F„+1
в силу следствия 3.1 и неравенств (1) при s — n. Поэтому пусть
3<s<n—1. Однако в этом случае первые s шагов плана Фп-\
приводят к отрезку [aSt bl] меньшей длины:
&;-*; = -^_(fr_a)<-^-<6s-aS(
^Л+1 « + 1
что вытекает из неравенств (1). Дли получения отрезка [as, bs] нам
понадобилось s значений функции, поэтому для поиска и* на [aS9 bs]
мы имеем в распоряжении _еще п — s + 1 значение функции на этом
отрезке, включая точку us с известным J(us). Однако по предпо-
ложению индукции
6rt_s+1 (6 — а) =
поэтому
6ьп(Рп,Ь-а)> °°-а° >
^S As
2Frt-s+2
bs — fls ^_a
Таким образом, доказано, что бд(РЛ, 6 — a)>—~^- для любой
2Fn+i
последовательной стратегии P„(ai>2), и, кроме того, для любого е,
0<б<—=—, существует стратегия Ф„, для которой
2^Л+1
Следовательно,
Ьвп(Ь-а)= inffi£(P„, &-с)= Ь~а
Заметим, что величина s на практике не может быть сколь
угодно малой в силу ограниченных возможностей измерительных
приборов, ЭВМ и т. п. Пусть е>0 — тот наименьший сдвиг между
числами, который можно измерить, и пусть 0<е<-гтР—• Учи-
тывая конечность числа е, вместо описанного выше плана Фъп
можно использовать следующий более точный и полностью сим-

32 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [Гл. J
метричный план [230]. Этот план начинается с двух симметричных
на [а, Ь] точек
u1 = a + -J^-(b-a)+ <~1>лр* е.и^а+Ь-и^
Если после k вычислений функции найден отрезок [аЛ, bk\ (А>1;
^ = 0, Ьг = Ь)9 содержащий точки и* и uk с вычисленным значени-
ем J(uk)= min J(ut)> то следующая точка берется так: Uk+\ =
^ufc + fyfe—wa и т- Д. После п вычислений получим отрезок [ап, Ьп],
и можем положить ип = "^ п . С ^помощью индукции нетрудно
доказать, что
Теперь можно ответить на вопрос: сколько следует произвести
.наблюдений значений J (и), чтобы с заданной точностью 6>0 оп-
ределить точку и* минимума /(M)eQ*[a, b\> Количество необхо-
димых для этого наблюдений равно наименьшему из чисел п, удов-
летворяющих неравенству
2Fn+1 Fn+i 2
Очевидно также, что гарантированная наименьшая возможная
-длина отрезка [аП9 Ьп], содержащего точку и* минимума J(u)^
^Q*[a, &], который может быть получен по наблюдениям значений
этой функции в п точках (п^2), задаваемых последовательно,
всегда больше 2бд (Ь — а) = —^—. Наконец, длина отрезка [а, Ь],
Fn+i
на котором с заданной точностью б>0 можно найти точку и* <ми-
нимума /(w)sQ*[a, b] по п наблюдениям значений J (и), меньше
§ 8. МЕТОД ЗОЛОТОГО СЕЧЕНИЯ
Описанные выше планы Фибоначчи являются эффективным
методом отыскания точки и* минимума функции 7(w)eQ*[a, b].
Однако, к сожалению, нельзя воспользоваться планами Фибонач-
чи, не зная заранее числа п предполагаемых наблюдений значений
■(функции, ибо выбор первых точек щ, и>2 в этих планах требует
.знания числа п. Между тем на практике встречаются ситуации,
когда число п по каким-либо причинам не может быть заранее
определено. Иногда желательно не ограничивать себя каким-то
наперед заданным числом л наблюдений значений J (и) и прово-

§ s]
Метод золотого сечения
33
дить наблюдения до тех пор, пока, не удовлетворится какой-либо
интересующий нас критерий, попутно стараясь, однако, чтобы ис-
пользуемый метод поиска по возможности скорее привел к точке
минимума. В этом случае можно пользоваться методом деления
отрезка пополам, не требующим знания числа п наблюдений зна-
чений J (и). Однако существует еще один метод, который также
не зависит от намечаемого числа п значений J (и) и который при
достаточно больших п почти столь же эффективен, как и метод
Фибоначчи. Это — метод золотого сечения [230].
Как известно, золотым сечением отрезка называется деление
отрезка на две неравные части так, чтобы отношение всего отрезка
к большей части равнялось отношению большей части к меньшей.
Нетрудно проверить, что золотое сечение отрезка [а, Ь] произво-
дится двумя симметрично расположенными точками
и1 = <Н -—(6—а) и и2=а+Ь — и± =
= а+ ~1 {Ь — а)> иг<и29
причем
±=± = ±=jL в ь~а = "*-" = 1±У£~ 1,618033989.
Ь — иг их — а иг — а Ь — и2 2
Замечательно здесь то, что точка и\ в свою очередь производит
золотое сечение отрч\зка [я, и2]: здесь
и2 — их<их — а = Ь — и2, — = —1 .
их — а и2 — U\
Аналогично точка а2 производит золотое сечение отрезка [ии Ь].
Опираясь на это свойство золотого сечения, можно предложить
следующий метод поиска точки и* минимума функции J(u)£ Q*[a, b].
А именно сначала на отрезке [а, Ь] берем точки иг и и2, задающие
золотое сечение отрезка [а, Ь] = [а19 Ьг]. Сравнивая J(ux) с J(u2)t
находим новый отрезок [aj, b2], а2<#*<62, причем
b2 — a2 = u2 — a = b — u1 = *Ъ~~ (Ь — а),
и на отрезке [а2, Ь2У находится точка и29 совпадающая с одной из
точек их или и2, в которой J (и2) = min J(щ) и производящая золо-
тое сечение отрезка [а2, Ь2]. Далее берем симметричную с и2 точку
из = а2 + Ь2 — и2, также производящую золотЬе сечение отрезка
[^2» Ь2]> вычисляя значение J(u3) и сравнивая его с J(u2), находим

34 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [Гл. I
новый отрезок [а3, Ьь], я3<а*<&3, и т' Д- Пусть уже известен от-
резок
-*—^—J (6 — а) и известна
точка ил, ah<un<bn, производящая золотое сечение отрезка {ап> Ьп]
и ^совпадающая с одной из точек ul9 ut, ... , ип, в которой
J(un) — m\nJ-{Ui). Тогда в— качестве ип+\ возьмем точку
un+i = an + bn — иЛ, также производящую золотое сечение отрезка
[ал, Ьп]9 вычисляем значение J(Un+\) и, сравнивая с J(un), находим
новый отрезок
№п+1> Ьп+\], CLn+l < #* < Ьп+\,
и т.. д. Процесс продолжаем до тех пор, пока не получим и* с до-
статочной точностью или пока не выполнится другой интересующий
нас критерий.
Пусть мы остановились на /г-м шаге (п > 2) и нашли отрезок
[ап% Ья], ал<и*<6я, а также точку ил> ап<ип<Ьп, с вычислен,
ным значением /(wn) = min/(кЛ, производящую золотое сечение от-
резка [ал, &„]. Заметим, что для этого нам понадобилось п вычис-
лений^ значений функции. Если мы решаем задачу А, то полагаем
Un = ип с погрешностью
\и* — ип\<тах{Ьп — ип, ип — ап}= ( ~l )(fri — <**) =
Ь — а .
Если решаем задачу Б, то полагаем ип = * п с погрешно-
стью

§9]
Метод ломаных
35
Для сравнения с методами Фибоначчи для решения задач А и Б
заметим, что при больших п число
"V 2 ) ST'
/Г
Поэтому при достаточно больших п погрешность, получаемая при
применении метода золотого сечения к решению задач А и Б, боль-
ше соответствующей погрешности метода Фибоначчи всего в
/н^у_1_ 1708
V 2 J vt
раз. Отношение погрешности метода золотого сечения к погрешности
метода деления отрезка пополам при решении задачи А равно
/ 2/2" у
К2»(0,87...)«^2.
Отсюда видно, что уже при не очень больших п преимущество ме-
тода золотого сечения становится ощутимым.
На практике иногда сочетают метод золотого сечения с мето-
дом Фибоначчи: на первой стадии поиска минимума применяют ме-
тод золотого сечения, затем, задавшись некоторым натуральным
числом л, переходят к плану Фибоначчи Фп и на этом заканчива-
ют поиск.
Упражнение. Пусть заданы m чисел: а\, аг, ..., dm — и пусть
известно, что минимум minak=ap достигается при каком-то един-
ственном р, l^ip^m, причем а\^а2^ ... >аР, ap<ap+i<; ...^Om.
Как организовать п выборок из чисел а\9 аг, ..., а™, чтобы ар=
= mmak найти как можно точнее? Существует ли наилучшая стра-
тегия определения р?
§ 9. МЕТОД ЛОМАНЫХ
В этом параграфе рассмотрим один простой метод минимиза-
ции функций J (и), удовлетворяющих условию Липшица на отрез-
ке [а, &], позволяющий найти минимум с любой наперед заданной
точностью [85, 182]. Напомним
Определение 1. Говорят, что функция J (и) удовлетворяет
условию Липшица на отрезке Га, Ь\ если существует такая по-
стоянная L>0, что \J(u)—J(v) \^:L\u—'v\ при любых и, ue[fl, &].
Пользуясь -формулой конечных приращений Лагранжа, не-
трудно показать, что непрерывная на отрезке функция J (и) с ку-
сочно-непрерывной производной удовлетворяет условию Липшица
с константой L=sup|/'(w) |.

36 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [Гл. 1
Зафиксируем произвольную точку v отрезка [а, Ь] и определим
функцию K(ut v)=J(v)— L\u—v\ переменной и, a^.u^.b. Нетруд-
но видеть, что функция К(и9 v) кусочно-линейна, K(vt v)=J(v)f
К(и, v)^J(u) при всех и, а^и^Ь.
Опишем метод ломаных. В качестве начального при*
ближения может быть взята любая точка u0£[at Ь]. Далее состав-
ляем функцию /С(и, и0) = J(и0) — L\и — и0\ и следующую точку иг
определяем из условия min/С (и, u0) = K(uv и0) (очевидно, их = а
или «! = &). Зная иь определяем К (и, и±)> составляем новую функ-
цию Рх(и) = max К (и, ut) и находим и2 из условия Рг(и2) = min Рг{и)
i=0,l а^и^Ь
(рис. 4). Пусть точки u0t и19 ... , ид(л>1) уже известны. Тогда
составим функцию
Рп(и) = max/С (я, щ) = max {/([(и, ип), Рп-\{и))
(примем Р0(и) = К(и% и0)) и следующую точку ип+\ найдем из усло-
вия Рп (un+i) = min Рп (и) и т. д. Если min Рп (и) достигается в
нескольких точках, то в каче-
стве ип+х берем любую из
них.
Для доказательства сходи-
мости этого метода нам пона-
добятся следующие свойства
Рп(и)9п=0, 1,2,...: 1) Рп(и) —
непрерывная кусочно-линейная
функция и график ее представ-
ляет собой ломаную линию,
состоящую из отрезков пря-
мых с угловым наклоном L
или — L\ 2) Рп(и)^Рп+\(и)у
Pn(u)^J(u) при любых
и, а^и^Ь и любых я=0, 1,
2,...; 3) Pn(Ui)=J(Ui) при
всех * = 0, 1,..,п, ибо J(Ui) =
=K(uiy Ui)^Pn(Ui) < J{Ui);
4) Pn(u) удовлетворяет усло-
вию Липшица на отрезке
[а, Ь] с константой L.
А
4
1 а /
К
в
г%
у
и
В
)4f
• •>
U2U!
А
\°'и,
\
с
ХЪС - график функции K(u,uJ,
А В, - график К (и ,uf), А ВС.в^график
Р,(и), А2ВгСг-график К (и,иг)МЪ?Ь?£2^-
график Р2(и)
Рис. 4
Теорема 1. Построенная выше последовательность {ип} та-
кова, что: 1) lim Pn(Wn+i)=/*==inf/(H) =/(*/*); 2) любая пре-

* 91
Метод ломаных
37
дельная точка и последовагельностгг {ип} является точкой мини-
мума функции J (и); 3) если J (и) достигает своего минимума на
отрезке [а, Ь] в единственной точке а*, то вся последовательность
{ип} сходится к а*.
Доказательство. Прежде всего заметим, что последователь-
ность Pn(tin+\) монотонно возрастает и ограничена сверху;
Рп-х (йп) = min/V-! (и)]< Pn-i (un+i) < Рп (ил-н),
Рп (и^,) = min Рп (и) < />„ (и') < J (и*).
Следовательно, существует UmPnr{un+i) = P\<J*. Покажем, что
Р* = J\ Пусть и — произвольная предельная точка последовательно-
сти {и„}. Тогда существует подпоследовательность^^}, сходящая^к
и, причем можем считать, что Л<л2< • •• <[я*Он-1<3 Так
как
О < J (щ) — Рп (un+i) «= Рл (и,) — Рп («„+!) < I | и, — «д+il
при. любом п и любых t, 0< *<[/*, то полагая здесь 1 = л*_ь
n=nk — 1, получим 0<J(urtfr-1)—Pn^^XLI^^—>nft|. От-
сюда при k ->- оо имеем
У < / (в) = lim/ (i^) - lim Pftj._, (ипЛ = P* < Л
*->oo fc-»oo " ■
т. e. hmPn(un+i) = J* = J(u).
Л-*оо
Первое и второе утверждения теоремы доказаны. Третье утверждение
теоремы теперь является простым следствием первых двух. А
Описанный метод ломаных имеет ряд достоинств. Он позволя-
ет получить приближенное значение точки абсолютного минимума
функции J (и) на [а, 6] и сходится при любом выборе начальной
точки щ, лишь бы функция J (и) удовлетворяла условию Липшица.
Метод ломаных не требует существования производной J'(u) во
всех точках отрезка, наличия строгой квазивыпуклости /(w), кро-
ме того, функция J (и) может иметь сколько угодно локальных и
абсолютных минимумов на отрезке [а, Ь]. Если константа Липшица
L функции J (и) известна, то метод ломаных прост и удобен для
использования на ЭВМ. На каждом шаге этого метода требуется
решить простую задачу минимизации кусочно-линейной функции
Рп(и), сводящейся к перебору известных вершин ломаной Рп(и),
причем перебор здесь существенно упрощается, ибо ломаная Рп (и)
отличается от Pn_i(a) не более чем двумя новыми вершинами.

38 МИНИМИЗАЦИЯ ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ [Гл. 1
Нетрудно модифицировать-описанный метод ломаных так, чтобы
последовательность Pn(un+i) строго монотонно возрастала.
В работе [83] показано, что метод ломаных близок к опти-
мальным методам поиска минимума на классе функций, удовлет-
воряющих условию Липшица. Оптимальная стратегия поиска ми-
нимума строго квазивыпуклых функций, удовлетворяющих усло-
вию Липшица, рассмотрена в работе [241].
§ 10. ВЫПУКЛЫЕ ФУНКЦИИ. МЕТОД КАСАТЕЛЬНЫХ
Для минимизации некоторых классов функций можно исполь-
зовать более эффективные варианты метода ломаных. Опишем
одну модификацию метода .ломаных, пригодную для поиска мини-
мума выпуклых функций, когда в качестве звеньев ломаных бе-
рутся отрезки касательных к графику функции.
Определение 1. Функция J (и), определенная на. отрезке
а^и^Ь, называется выпуклой, если
J(au + [l — a]v)<aJ(u) + (\—a)J{v) (1)
при всех и, v£[a> b] и всех а, 0<а<1.
Когда а пробегает отрезок [0, 1], точки (aw+(l—a) v, aJ(u) +
+ (1— a)J(v)) на плоскости переменных (u9J) пробегают хордуЛВ,
соединяющую точки А=,(и, J(u)) и В= (и, J(v)) на графике
функции. Поэтому неравенство (1) имеет простой геометрический
смысл: график выпуклой функции на любом отрезке '[и, t>]s[a,.ft]
находится ниже хорды, соединяющей точки графика функции на
концах отрезка [и, v]. Примерами функций, выпуклых на любом
отрезке из области своего определения, могут служить следующие
элементарные функции: и2, и, —иу |к|, eu, erw, —1шг. Функция
sinw выпукла на отрезке — яг^и^О и невыпукла при О^и^л.
Более подробное изучение выпуклых функций отложим до сле-
дующей главы, а здесь отметим лишь некоторые свойства выпук-
лых функций, необходимые для описания метода касательных
(см. также упражнения в конце настоящего параграфа).
Теорема 1. Пусть функция J (и) выпукла и непрерывно диф-
ференцируема на отрезке [а, Ь]. Тогда: 1) справедливо неравенство
J(u)>J(v) + J'(v)(u-v) (2)
при всех w, ye[a, b] (иначе говоря, график гладкой выпуклой
функции лежит выше графика любой ее касательной); 2) произ-
водная Г (и) не убывает на [а, &]; 3) J (и) удовлетворяет на [a, Ь]
условию Липшица с константой L=max{|/'(a+0) |, |/'(6—0) |}.

§ т
Выпуклые функции. Метод касательных
39
Доказательство. Перепишем неравенство (1) в виде
J(v-\-a(u—v))—J(v)^a[J(u)—J(v)]. К левой части этого неравен-
ства применим формулу Лагранжа о конечных приращениях. По-
лучим
•/'(о + бсф — v))a(u— v)<£a[J(u) — J (v)], 0<6<1,
или
J'(v + fa(u — v))(u — v)<J(u) — Jm(v)
при всех 0 < а < 1. Отсюда при а -► + 0 сразу придем к неравен-
ству (2).
Переменные и и v в (2) .равноправны. Меняя их ролями, по-
лучим j(v)^J(u)+J'(u)(v—и) при всех и, иё[а, Ъ\ Сложим по-
следнее неравенство с (2) почленно. Будем иметь [J'(u)—/'(у)]
(и—v)^0 при всех и, v^[ay Ь\ что равносильно неубыванию про-
изводной J'(u) на отрезке [а, Ь]. Следовательно, /'(а+0Х/'(и)<
J'(b—0) при всех и, а^и^Ь. С помощью формулы Лагранжа о
конечных приращениях отсюда имеем
\J(u)-J(v)\=\J'(t)(u-v)\<L\u-v\
при всех и, v£[a, b], где a<£<6, L = тахШ' (а + 0)|,
№ (6-0)|}. А
Обозначим через U* множество точек глобального минимума
функции J (и) на отрезке [а, Ь\ т. е. U*={u: a^zu^b, J(u) =
=/* = inf/(H)}. Возможны следующие три случая: 1) U* — пус-
тое множество (примером такой функции может служить J(u)=u
при 0<к^1, /(0) = 1 на отрезке [0, 1]); 2) О* состоит из одной
точки и* (примером служит функция J(u)=u2 на отрезке [—1,1]);
3) U* состоит более чем из одной точки (примером служит J(u) =
= \и\ + \и—1| на отрезке fc-4, 2]). В последнем случае существу-
ет отрезок (р, у]^[а, 6], все внутренние точки которого принадле-
жат £/*, а концы этого отрезка могут и не принадлежать U* (при-
мер: /(w)s=0 при 0<а^1, /,(0) = 1). В самом деле, если и* и и*е
el/*, u*^v*9 то
/*</(aa*+(ll— a)u*X<x/(tt*) + (l— a)J(v*)=J*
Следовательно, /(aa*+(l—a)u*)=/* при всех ae[0, 1], т. е. весь
отрезок [a*, i>*]c:C/*. Теперь остается взять p=inf£/*, y=suP^*- А
Теорема 2. Всякая выпуклая на отрезке [а, &] функция J (и),
достигающая своей нижней грани на этом отрезке, принадлежит
подмножеству Q*[a, b] строго квазивыпуклых функций на [а, Ь].
Доказательство. По условию U* непусто. Обозначим
P=inf£/*, Y=sup[/*. Как было замечено выше, либо U* состоит
из одной точки и.* и тогда р=у=и*, либо P<y и тогда все точ-
ки интервала p<w<v принадлежат U*9 т. е. /(и)=/* при Р<м<

40 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [Гл. t
<у. Далее, если а<р, то 1(ц) строго монотонно убывает при а<
<w<p и Нт/(ы)=/(р)=/*, ибо в противном случае, как нетруд-
«-►Э—о
но видеть, функция J (и) не может быть выпуклой на [а, Ь]. Анало-
гично, если у<.Ь, то J (и) строго монотонно возрастает при у<.и<.
[<Ь и UmJ(u)=J(y)=J*. Таким образом, 7(«)eQ*[a, &]. А
Пусть функция J (и) выпукла и непрерывно дифференцируема
на отрезке (а, Ь\ Согласно теореме* 2/(и) принадлежит Q*[af b\.
Опишем метод касательных для ее минимизации. Через L(u, v)
будем обозначать линейную функцию L(ut v)==J(v)-\-J'(v)(u—v)
переменной и, a^.u^:b при каждом фиксированном v^[a9 b]. В си-
лу теоремы 1 J(u)^L(uy v) при всех ме[а, 6]. В качестве началь-
ного приближения может быть взята любая точка Wo^fa, b\ Далее
составляем функцию L(u, щ) и следующую точку щ определяем
из условияminL (utUo)=L(u\tUo) (очевидно и\=а или U\=b).
Пусть Г(ио)ФО, ибо если /,(^о)=0, то, как следует из нЪравей-
ства (2) при у=Оо, точка tio будет точкой минимума, и процесс на
этом прекращается. Зная ии определяем L(u9u\)9 составляем но-
вую функцию Pi (и) =maxL (а, щ) и находим щ, из условия Р\ (и2) =
=minPi(u) (рис. 5). Пусть точки щу ии ..., Un (n^l) уже извест-
J
0
АВ-график функции Ни ип)
CD -график Ltu.u,),AED -график
P,(u).PQ -график L(u,u9) AMND-
график Р2(и)
Рие. 5
ны и Г(ип)Ф0 1(если J'(un)=0, то из (2) при v=un следует, что
tin — искомая точка минимума). Тогда составляем функцию
Рп(и) = max L (w, ul) = max{L(u9 ип), P,*-i(tt)}
(естественно принять P0(u) = L(u, и0))> и следующую точку ип+\
находим из условия Рп (ип+\) = min Рп (и) и т. д.

§ т
Выпуклые функции. Метод касательных 41
Нетрудно видеть, что Рп(и) —непрерывная кусочно-линейная
функция, и график ее представляет собой ломаную-, состоящую из
отрезков касательных к графику функции J (и). Поэтому описан-
ный метод естественно назвать методом касательных.
Теорема 3. Пусть функция J (и) выпукла и непрерывно диф-
ференцируема на отрезке [а, 6], и пусть построенная выше после-
довательность {ип} такова, что 1'(ип)ф0, п=0, 1, Тогда:
1) НтРя(М = ^= inf П")\
2) последовательность {tin} имеет не более двух предельных
точек, совпадающих с и*=тШ*, w**=sup£/*, где U* — множест-
во точек минимума J (и) на [а, Ь]. Если U* состоит из одной точки
и*, то limun=:w*.
П->оо
Доказательство. Заметим, что при выполнении условий
теоремы функция J (и) удовлетворяет условию Липшица с кон-
стантой L=max{|/'(a) |, \У(Ь)\) (см. теорему 1). Кроме того,
согласно неравенству (2) L(uf un)^J(u) при всех и^[а, Ь] и всех
п=0, 1, Тогда ломаная Рп(и), построенная из отрезков каса-
тельных указанным выше способом, обладает свойствами 1)—4),
сформулированными перед теоремой 9.1. Поэтому буквальным пов-
торением доказательства теоремы 9.1 можно убедиться, что любая
предельная точка, последовательности {ип} принадлежит множест-
ву U*. Однако J (и) непрерывна и строго квазивыпукла на [а, 6],
поэтому О* либо представляет собой отрезок а*^м^|ц**, либо
состоит из единственной точки а*. По условию 1'(ип)ф0 и, сле-
довательно, Un$EU*. Тогда предельными для последовательности
{ип} могут быть лишь точки и* или ы**, а в случае и*=и** имеет
место равенство limun=u*. А
П-»оо
При описании метода касательных выше предполагалось суще-
ствование производной J'(u) во всех точках we[a, b]. Однако этот
метод может быть приспособлен для поиска минимума любой вы-
пуклой функции на отрезке [а, &], лишь бы она достигала своей
нижней грани на этом отрезке. Дело в том, что выпуклая на [a, Ь]
функция во всех внутренних точках этого отрезка непрерывна,
имеет конечные левые и правые производные
J'(u + 0)=Um '<» + *>-■'<"> f
J'(u-0)= lim Hu)-J(u-h) f
, Л-Ч-0 h
причем У (и—0)^:J'(u+0) (см. ниже упражнение 2). Поэтому в
описанном выше методе касательных можно принять L(u, ип) =
=J(ttn)+J'n* (и—tin) у где Jn — произвольная постоянная, удовлет-

42 МИНИМИЗАЦИЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ [Гл. I
воряющая неравенствам У(ип—0) <;/п^/'("п+0); неравенство
J(u)^L(u; ип)> а^и^Ь, при этом сохранится (см. упражнениеЗ).
На практике удобнее брать Уп из условия |/д| =min{|//(wn—0) |,
\J'(Un+0) |}. Если при некотором п окажется, что J'(un—0)^0^
^'/ (йп+0), то Wn — точка минимума (см. упражнение 4), и в
этом случае процесс прекращается. Чтобы избежать возможных
равенств //(а+0)=—оо или J'(b—0)=+оо, удобно начинать про-
цесс поиска с точек Uo=a+ho и щ = Ь—к\ с тем, чтобы следующее
приближение м2 взять из условия минимума Р2(и) = max{L(w, и0);
L(u, Ui)}. Здесь Ао, h\— положительные величины, выбираемые
из условия, чтобы /'(a+fto+О) и J'(b—h\—0) помещались в раз-
рядной сетке ЭВМ. Если окажется, что J'(a+h0+Q) и J'(b—h0—0)
положительны [отрицательны], то точку минимума следует искать
на отрезке a^u^.a+h0 [b—hi^.u^.b) с помощью ' методов, не
требующих вычисления производной функции.
При такой модификации метод касательных пригоден для по-
иска минимума любой выпуклой функции на любом конечном от-
резке; утверждения теоремы 3 остаются при этом справедливыми.
Поскольку ломаная из отрезков касательных аппроксимирует
функцию J (и) лучше, чем ломаная из § 9, то следует ожидать,
что метод касательных для выпуклых функций, вообще говоря,
сходится быстрее метода ломаных, из § 9. Оптимальная стратегия
поиска минимума выпуклых функций описана в работе [242].
Упражнения. 1. Если J (и) выпуклая функция на отрезке [а, 6],
то
J(u)-J(v) ^ /(ш)-/(о) ^ J(»)-/(g) (3)
М — V W—V w—и
при всех и, v, w, a^.v<u<w*£:b. Доказать. Выяснить геометри-
ческий смысл этих неравенств.
/Указание. Использовать выпуклость функции и представ-
ление u=<tv+(l—a)w, где и<Са<го,<х= ———, 0<а< 1.
w—V
2. Доказать, что выпуклая на отрезке [а, Ь] функция J (и) во
всех внутренних тачках отрезка непрерывна и имеет конечные ле-
вые и правые производные У(и±0)у причем У(и — 0)^:У(и+0),
we (а, 6). Доказать, что У(и+0) — неубывающая непрерывная
справа функция, У (и—0) — неубывающая непрерывная слева
функция.
Указание. Пользуясь неравенствами (3), доказать, что
' /(q)-J(n-T) ^ 7(и)-/(и-*) ^ J(u + h)-J(u)
х h f h
^ J(» + X)—J(u) ^y
X
при всех т, ht лишь бы 0<Л<т; и% и±т, и±Ле[а, b].

§ т
Выпуклые функции. Метод касательных
43
3. Если J (и) выпукла на отрезке [а, Ь\ то
J(u)>J(v)+J'n-(u-v) (5)
при всех и, vy а<а<6, а<у<6, где j'n — произвольное число,
такое, что J'(v — 0)<Jn<J'(о + 0).
Указание. Воспользоваться доказательством неравенства
(2), рассмотрев случаи u>v и u<.vt и неравенством /'(о—0)^
</'(*+0).
4. Точка w.*e[a, b] является точкой минимума выпуклой функ-
ции J (и) на отрезке [а, Ь] тогда и только тогда, если /'(и*+0)^0,
/'(и*—0)^0. В частности, если Г (и*) существует и а<и*<Ь, то
//(и*)=0. Доказать.
Указание. Принять в (5) Jn=0.
5. Доказать, что выпуклая на отрезке [а, 6] функция J (и) диф-
ференцируема почти всюду на этом отрезке.
Указание. Воспользоваться монотонностью функций
Г (и—0), /'(и+0) и показать, что Г (и—0)=Г(и+0) во всех точ-
ках непрерывности J'(u-\-0) (или Г (и—0)).
6. Доказать, что выпуклая на отрезке [а, Ь] функция J (и)
удовлетворяет условию Липшица на каждом отрезке a^M^fi,- ле-
жащем строго внутри [а, 6]. На примере функции /(«)=— J/l—и2
М ^1 убедиться, что в общем случае здесь нельзя полагать
a=a, р=6.
Указание. Пользуясь неравенствами (3), (4), показать, что
/'(<* +0)< JW-JW <j'(p-0)
и — V
при всех a<w, a<p.
7. Доказать, что выпуклая на отрезке {а, 6] функция J (и) аб-
солютно непрерывна на каждом отрезке а^и^р, лежащем стро-
го внутри [а, Ь\
8. Для того чтобы дифференцируемая функция J (и) на отрез-
ке [a, Ь] была выпуклой, необходимо и достаточно, чтобы произ-
водная J'(u) не убывала на [а, 6]. Необходимость доказана в тео-
реме 1; докажите достаточность.
9. Для того чтобы дважды дифференцируемая функция J (и)
на отрезке [a, Ь] была выпуклой, необходимо и достаточно, чтобы
/"(а)^О при a^u^ib. Доказать.
10. Для выпуклости функции J (и) на интервале а<и<Ь не-
обходимо и достаточно существования такой функции l(v)9 a<

44 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ {Гл. /
<и<&, чтобы J(u)^J(v)+l(v)(u—v) при всех а, а<.и<.Ь. До-
казать. Покажите, что l(v)=J'(v) почти всюду.
11. Если J (и) выпукла и монотонно возрастает на отрезке
[а, &], а функция u=z(x) выпукла на отрезке c^.x^d9 и z(x)^
е[а, &] при ^&[c,d], то J(z(x)) выпукла на [c9d\. Доказать.
§ 11. ЛЕТОД ПАРАБОЛ
В двух предыдущих параграфах минимизируемая функция
J (и) аппроксимировалась кусочно-линейными функциями Рп(и), и
исходная задача заменялась последовательностью задач миними-
зации функций Рп{ц). Однако вместо кусочно-линейных функций
в качестве аппроксимирующих функций Рп(ц) могут быть выбра-
ны и другие классы функций. Если Рл(и), л=0, 1, ..., достаточно
хорошо аппроксимируют исходную функцию J (и) равномерно на
всем рассматриваемом отрезке и, кроме того, задача минимиза-
ции Рп(и) при каждом п решается просто, то упомянутый подход
к поиску минимума может оказаться весьма эффективным. В этом
параграфе остановимся на методе парабол, приспособленном для
поиска минимума строго квазивыпуклых функций, хорошо аппрок-
симирующихся параболами.
Итак, пусть /(«)eQ*[a, b] и пусть требуется определить точ-
ку и* минимума J (и) на [a, Ь] с заданной точностью е>0.
Определение 1.Тройку точек {и—т, и, v+h} (ft, т>0) на-
зовем удачной, если каждая из этих точек принадлежит отрезку
[а, Ь] и, кроме того, A-=J(v)— J(v— т)^0, A+=J(v)— J(v+h) sg:0,
Д-+Д+<0.
Теорема 1. Если тройка точек {v—т, t\ v+h} удачная, то
через точки (v—т, J(v—т)), (v, J(v))t (v+h, J(v+h)) на плоско-
сти (a, /) можно провести параболу L(u)=pu2+qu+c с коэффи-
циентом р>0, причем точка w=- — . — минимума L(u) при
2 р
—оо<а<+оо удовлетворяет неравенству
\v — a;| < — тах{т, А}.
Доказательство. Искомая парабола является обычным
интерполяционным многочленом и имеет вид [19]
£(«)-(---—£У <U-M- — » JL(u-v)+J(v).
\ % п J х-\~ п п
(1)

§ 11}
Метод парабол
45
Так как тройка точек {и — т, vt v + h) удачная, то
^ \ х h J % + hZ
и минимум L(u) на числовой оси —ос<и< + оо достигается^в
точке
2 ТД+ + ЛД- '
Отсюда следует, что
k 2 т|Д+|+А|Д-| ^2 Д '- '
Последнее неравенство доказывается элементарно, простым рассмот-
рением случаев Л2| А~| — т2| Д+| >0 и А2| Д-| —т2| Д+|<0. А
Опишем метод парабол в сочетании с методом золотого се-
чения. Пусть сделано k шагов (&^3) метода золотого сечения и
найден отрезок [аку bk], содержащий точку минимума и* функции
J (и) на [а, Ь]. Примем гипотезу о том, что функция J (и) на от-
резке [ah, bh] хорошо аппроксимируется параболой. Если строго
квазивыпуклая функция J (и) достаточно гладкая на отрезке [ак, bk]
и сам отрезок [a*, bk] имеет достаточно малую длину, cKiak^u*^.
bk<.b, то такая гипотеза вполне правдоподобна, поскольку в окре-
стности внутренней точки минимума гладкая (функция, вообще го-
воря, близка к параболе. Далее возьмем одну из точек tik, произ-
водящих золотое сечение отрезка [а*, Ьк], и вычислим значение
J(uh) (если только оно еще не было вычислено на последнем шаге
метода золотого сечения). Если bk—Ял^е, то точку uk принимаем
за точку минимума и*, и процесс на этом заканчивается. Пусть
bk—Q>k>v- Тогда проверяем, является ли тройка {а&, Uk, bh) удач-
ной или нет. "Если эта тройка неудачная, то делаем следующий шаг
метода золотого сечения, находим отрезок [cik+u bk+\] и с ним по-
ступаем так же, как с отрезком [а*, Ьъ\.
Пусть тройка {ak, uki bk) удачная, и пусть Wk — точка мини-
мума параболы (1) с v=Uk, r=rh=tik—aky h=hk=bh-—
—uk. Согласно теореме 1
\ч — щ\<\т**{Къ)*
Положим аА=тах{|ыЛ — wk\\ е/4}.
Нетрудно проверить, что ик — ak, uk + ak€[ak, bk]. Вычислим
Д7 = J(uk)—J(uk — ak), A? = J(uk) — J(uk + ak).

46 МИНИМИЗАЦИЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ \Гл. 1
В зависимости от знаков А* , AJJ" возможны 4 случая. 1. Afe <0,
&t < О, А7 + Ал" < 0. Это значит, что тройка {uk — иЛ, иЛ, и* + <**} —
удачная. Полагаем а^\ = uk — ak, bk+\ = tik+<ik и с отрезком
[afe+ь bk+\] поступаем так же, как с предыдущим отрезком [ak> bk].
2. А^<0, Д/|">0. Тогда полагаем ak+\ = и*, bk+\ = 6Л и с отрезком
[а/г+ь 6л+1] поступаем так же, как с [ak, bk]. 3. ДГ>0, Д^<0.
Тогда принимаем aft+i = ak, 6fe+i -%ис отрезком [а*+ь frft+i] пос-
тупаем так же, как с'[а£, 6ft]; 4. Д£">0, А^">0. Тогда на[аЛ, 6Л[де*
лаем следующий шаг метода золотого сечения, находим отрезок
[ak+\, bk+\] и с ним поступаем так же, как с предыдущим отрезком
[ak, bk]. Впрочем, если заранее известно, что функция J (и) строго
квазивыпукла на [ak, bk]9 то последний случай возможен лишь при
А^=А^ = 0, т. е.
j(u) = J*= inf J (и)
при uk — akKu<£uk+ak. Здесь остается принять в качестве точки
минимума любую точку из отрезка [uk — ak, uk + ak]f и процесс
поиска на этом заканчивается.
Повторяя описанный процесс многократно, получим последо-
вательность вложенных стягивающихся отрезков [аь, bk]:
[ан+и bk+\] с [akt bk]9 bk+i — ak+\ < ~ (bk — ak).
Отсюда видно, что на классе функций Q*[a, b] метод парабол по
скорости сходимости не уступает методу золотого сечения и ненам-
ного уступает ему по числу вычислений значений функции J (и).
Если, же функция 7(«)eQ*[fl, b], хорошо аппроксимируется пара-
болой хотя бы в некоторой окрестности точки минимума, то метод
парабол может оказаться гораздо лучше плана Фибоначчи и по
скорости сходимости, и по числу вычислений значений функции.
Разумеется, это не противоречит оптимальности плана Фибоначчи,
ибо этот план был выработан из расчета на «наихудшую» функцию
из класса Q*[a, b], что не исключает возможности построения бо-
лее эффективных методов поиска минимума на «хороших» под-
классах из Q*[a, b]. Для функций, не являющихся строго квазивы-
пуклыми, описанный метод парабол приводит, вообще говоря,
лишь к точке локального минимума.
Нетрудно модифицировать метод парабол так, чтобы можно
былс пользоваться параболами (1) при выполнении лишь условия
1 -<0> не требуя неположительности величин А+, А-. Од-
т h
нако при этом следует иметь в виду, что точка минимума такой

§ щ
О некоторых других методах минимизации
47
параболы на отрезке, [v—т, v+h] может не совпадать с точкой ми-
нимума параболы на всей числовой оси.
Другой вариант метода парабол описан в (201].
§ 12. О НЕКОТОРЫХ ДРУГИХ МЕТОДАХ МИНИМИЗАЦИИ
1. Описанные выше методы позволяют с заданной точностью
решить задачу минимизации строго квазивыпуклых функций, а на
других классах функций эти методы (кроме метода ломаных) мо-
гут привести к точке локального минимума. Задача определения
глобального минимума функций, не являющихся строго квазивы-
пуклыми, в общем случае весьма трудна, и методы решения таких
задач в настоящее время разработаны еще недостаточно.
Здесь мы остановимся на одном методе поиска глобального
минимума функций, основанном на информационно-статистическом
подходе [212], [213]. Для некоторых достаточно широких классов
функций (подробное статистическое описание этих классов см. в
работе [212]) удается построить оценки апостериорной вероятности
расположения глобального минимума на основе уже проведенных
испытаний, заключающихся в вычислении значений минимизируе-
мой функции в определенных точках щ, щ9 ..., uk из отрезка [а, Ь].
На основе этих оценок затем можно получить оценку максимума
информации о расположении точки минимума и указать простое
правило выбора следующей точки wa+ь Отсылая читателя за под-
робностями к работам [212],д [213], здесь ограничимся лишь опи-
санием самого метода.
Пусть требуется минимизировать функцию J (и) на отрезке
[а, Ь]. Процесс поиска минимума начинается с двух точек Ио=а,
щ=Ь9 и вычисления величины
Л __1/(ц,)-/(ц0)|
«1 — "о
После чего полагается
^f/Лпри А2>0,
I 1 при А1 = 0,
где г=const>/1 представляет собой параметр алгоритма, выбирае-
мый вычислителем. В качестве следующей точки #2 берется точка
Предположим, что точки щ, ии ..., Uk (k^2) уже известны.
Произведя при необходимости перенумерацию этих точек, можно
считать, что a=«o<tti<... <Uh-i<.tik=b. Далее определяются
величины

48 МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ \Гл. J
l<S<fc "s — US-1
и
mfe =
rAfe при Ал>0,
1 при Ал = 0.
Затем составляется функция
^(g) = ^(n,-g-i) + |y(^-/(tt^)|2 -2[J(as) + J(^i)]
"s — MS-1
целочисленного аргумента s, 1 <s<£, и простым перебором значе-
ний Rk(s) определяется тот номер s=*skt для которого Rk(sk) =
= max Rk(s). Если us.—ws._i<e, где e>0 — заданная точность,
l<s<fe Л *
то процесс поиска прекращается и точка us принимается в качестве
искомой точки минимума. Если же us.—Us.^i >е, то полагаем
Uk+\ = — (Usk + Usk-i) —
J (uSk) - J (Ug^)
2mk
Из определения tnk, очевидно, следует ttSfe-iO*+i<«sfe. Теперь ос-
тается перенумеровать точки w0, uv ... ,uk, uk+\ в порядке возраста-
ния и перейти к определению следующей точки Uk+2 аналогичным
образом. Метод поиска минимума описан.
В качестве иллюстрации приведем результаты применения опи-
санного метода для отыскания минимума функции
J (и) = sin и + sin -^-> + In и— 0,84а + 3
о
на отрезке 2,7^w<7,5 [213]. График функции J (и) приведен на
рис. 6, там же вертикальными
штрихами на оси Ои отмечено рас-
положение точек щ при г=2,
е=0,01; группа из 14 точек, распо-
ложенных вблизи точки глобально-
го минимума, изображена черным
прямоугольником. Как видим, из
28 точек, в которых вычислялись
значения функции в ходе поиска
минимума, большая часть (21 точ-
ка) расположена вблизи точки гло-
бального минимума.
С целью проверки описанного метода были проведены чис-
ленные эксперименты на большом количестве задач минимизации
при различных г>1, е>0 [212]. В частности, была проведена ми-
Рис. 6

§ т
О некоторых других методах минимизации
49
нимизация 20 функций, представляющих собой выборку из функций
вида
где |а*|^1, |&г|^1> 4^JV^14, коэффициенты aiy Ь^ и целое чис-
ло N представляют собой значения независимых равномерно рас-
пределенных случайных величин. При г=2, е=0,002 среднее число
вычислений значений функции оказалось равным 29. При этом
лишь для одной из 20 функций был найден локальный минимум
вместо глобального. Поиск минимума при г=3, е=0,002 для тех
же функций потребовал в среднем 40 вычислений значений функ-
ции, причем во всех случаях был найден глобальный минимум.
Другие эксперименты также показали, что с ростом г повышается
надежность поиска, но одновременно увеличивается и среднее чис-
ло вычислений значений функции. При фиксированном г надеж-
ность возрастает с уменьшением е.
2. Кратко остановимся на методах минимизации, когда на зна-
чения функции J (и) в каждой точке и накладываются случайные
ошибки или, как говорят, помехи. Такая ситуация, в частности,
имеет место в том случае, когда значения функции J (и) получают-
ся в результате измерений какой-либо физической величины. При
наличии помех многие рассмотренные выше методы непригодны
для поиска минимума функции, и здесь целесообразно пользовать-
ся методом стохастической аппроксимации [45], [230].
Опишем один из вариантов этого метода. Наблюдаемые в экс-
перименте значения J (и) в точке и обозначим через z(u). Будем
предполагать, что наблюдения J (и) возможны в любой фиксиро-
ванной точке и, —оо<и<+оо, и не содержат систематических
ошибок. Тогда для поиска минимума функции J (и) при —оо<а<
<+оо может быть использована следующая процедура Кифера—
Вбльфовица [45], [230]:
ип+1 = ип-апг{и» + с>*-г(и»-с»\ 11^1,2, (1)
Сп
где последовательности {ап}9 {сп} заданы и удовлетворяют условиям
ОО 00
ап>0> сп>°> lima„=limc„ = 0, Yап = + оо, V (-22-Y<oo.
(2)
Например, можно взять ап = —, сп = -п-, п = 1, 2, .... При доста-
п п '4
точно широких предположениях относительно функции J (и) и вероят-

МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ \Гл. 1
ностных характеристик случайной величины z (и) можно доказать схо-
димость по вероятности последовательности {ип}9 определяемой фор-
мулами (1), к точке глобального минимума J (и) [45].
Практическое применение метода (1) показало, что его схо-
димость, вообще говоря, сильно замедляется в тех случаях, когда
слева от точки минимума и* график функции имеет крутой спуск,
справа от и* — крутой подъем, а на остальных участках функции
J (и) изменяется медленно. Тогда на пологих участках шаги поис-
ка \ип+\—tin\ могут стать очень малыми, а на крутых участках,
наоборот, достаточно большими, и в результате большая часть вре-
мени на поиск может быть затрачена на чрезмерно медленные
спуски на пологих участках и последующие большие скачки че-
рез точку минимума с попаданием на другой пологий участок.
В таких ситуациях может оказаться полезной следующая так на-
зываемая нормализованная процедура Кифера — Вольфовица
[230}:
un+i = un— assign(z(un + cn) — z(un — сп))9 м= 1, 2,... , (3)
где последовательности {an}, {сп} удовлетворяют условиям (2) и,
как обычно, sign*=l при х>0, sign#=—1 при *<0, sign#=0
при х=0. Сходимость процесса (3) можно ускорить, если длину
шага {ап} менять лишь при изменении знака z(un+cn) —
—z(un—сп), сохраняя ап постоянным в остальных случаях [230].
Различные варианты метода стохастической аппроксимации,
строгое обоснование этого метода и различные приложения можно
найти в работе [45]. Другой метод поиска минимума при наличии
помех описан в работе [213].

Глава 2
Минимизация функций многих переменных
§ 1. ПОСТАНОВКА ЗАДАЧИ. ОБОЗНАЧЕНИЯ. ВСПОМОГАТЕЛЬНЫЕ
СВЕДЕНИЯ
1. Пусть на некотором множестве U m-мерного евклидова
пространства Ет задана функция J (и) переменных (а1,..., ит) = и.
Будем рассматривать задачу минимизации функции J (и) на
множестве £/, понимая под этим следующие вопросы: 1) найти
/*=inf/(tt); 2) если на U нижняя грань достигается, то найти
и€С/
точку и*е£/, в которой /(и*) =/*; 3) если нижняя грань не дости-
гается на Ut то указать последовательность {an}"c:t/, для которой
lim J(un) =J** Точку u*^U со свойством /(и*)=/* называют
-►оо
точкой минимума J (и) на £/, а последовательность {un}czU со
свойством lim/(wn)=7* называют минимизирующей последова-
тельностью для функции J(u) на U.
Умение эффективно решать задачи минимизации функций
конечного числа переменных на заданных множествах определяет
успех в решении многих задач прикладного характера. Современ-
ная теория экстремальных задач позволяет свести многие экстре-
мальные задачи в бесконечномерных пространствах к задачам
минимизации функций конечного числа переменных, и в связи с
этим значение эффективных вычислительных алгоритмов поиска
экстремума^ функций конечного числа переменных в последнее
время еще более возросло.
Что известно из классического анализа о методах решения
поставленной задачи? Если и* — точка минимума гладкой функ-
ции J (и) на всем пространстве Ету то [126]
^1 = 0, (1 = 1,2,...,/я). (1)
Точка и*, являющаяся решением системы уравнений (1), назы-
вается стационарной -ъчкой функции J (и). Если стационарные
точки найдены, то среди них нужно выбрать те точки, в которых
в самом деле достигается минимум. Для этбго нужно провести,
дополнительное исследование поведения функции в окрестности
стационарной точки. Если функция J (и) дважды непрерывно

52 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
дифференцируема, то наряду с системой (1) рассматривается
квадратичная форма
Ет &J(u*) £/£/
которая в точке минимума должна быть неотрицательно опреде-
ленной. Если эта квадратичная форма положительно определена,
то w* есть точка, вообще говоря, локального минимума функ-
ции J (и). Чтобы найти абсолютный минимум, остается перебрать
все точки локального минимума и из них выбрать точку с наи-
меньшим значением функции, если таковая существует.
Создается впечатление, что изложенный классический подход
в основном решает задачу минимизации достаточно гладких функ-
ций на всем пространстве. В действительности же на этом пути
обычно встречаются такие вычислительные трудности, которые
делают необходимым поиск других "методов решения. Например,
отыскание стационарных точек из системы (1) сама по себе весьма
серьезная задача, по трудности сравнимая, быть может, с исход-
ной задачей минимизации. Далее, если множество 1]фЕт, то
минимум функции может достигаться на границе множества U,
и в этой точке условие (1), вообще говоря, не будет выполняться.
Разумеется, на этом основании классический подход не может
быть исключен из арсенала методов минимизации. В некоторых
простых (но, к сожалению, редких) ситуациях классический под-
ход просто незаменим и дает полное решение задачи минимиза-
ции в аналитическом виде через различные параметры задачи.
К настоящему времени разработано и исследовано на сходи-
мость довольно много методов минимизации функций многих пере-
менных. В наших лекциях будут рассмотрены некоторые наиболее
часто используемые на практике итерационные методы, позволяю-
щие при определенных условиях строить последовательности {ип}>
которые являются минимизирующими или сходятся к точке мини-
мума. Часть из этих методов пригодна для поиска минимума
функции на всем пространстве £т, часть — на ограниченных мно-
жествах U, а некоторые методы нетрудно приспособить к поиску
минимума как при £/=£т, так и при 11фЕт, причем может быть
U ограничено или не ограничено. Мы остановимся также на од-
ном общем приеме, позволяющем свести задачу минимизации
функции-на ОфЕт к последовательности задач минимизации на
всем пространстве Ет, — здесь речь идет о так называемом методе
штрафных функций. Будет изложена вычислительная схема каж-
дого из этих методов, при некоторых предположениях на функции и
множество U будет доказана их сходимость, а в ряде случаев по-
лучим оценку скорости сходимости и дадим краткую характе-
ристику методов. При этом рассмотрим лишь основные ва-

§ 1] Постановка задачи. Обозначения. Вспомогательные сведения 53
рианты излагаемых методов, чтобы ознакомить читателя с основа-
ми этих методов, полагая, что знание основ методов облегчит
читателю изучение литературы по данному вопросу, позволит ему
без особого труда самостоятельно разобрать тот или иной алго-
ритм и выбрать подходящую модификацию метода или самому
придумать новую его модификацию, исходя из особенностей кон-
кретной задачи.
Чем руководствоваться при выборе метода, каковы критерии,
по которым можно сравнивать различные методы? Довольно рас-
пространенный критерий оценки метода — скорость сходимости, и
при этом считают, что чем выше скорость сходимости, тем лучше
метод. Конечно, чем быстрее сходится метод, тем меньшее число
итераций необходимо для получения решения с заданной точ-
ностью. Однако при оценке метода важное значение имеет не
столько скорость сходимости метода, сколько общий объем вычис-
лений, требуемый для получения решения с заданной точностью.
А общий объем вычислений зависит не только от числа итераций,
но и от трудоемкости вычислений на каждой итерации. Нередко
бывает, что при решении конкретной задачи выгоднее применять
метод, который хотя и сходится медленнее и, следовательно, тре-
бует большого числа итераций, но расчет каждого шага итерации
этого метода осуществляется просто и требует небольшого числа
машинных операций, и суммарный объем вычислений для решения
задачи с нужной точностью оказывается меньше, чем при приме-
нении другого, более быстро сходящегося метода, если каждый
шаг итерации последнего связан с трудоемкими вычислениями.
В том случае, когда свойства минимизируемой функции из-
вестны мало, то, видимо, сначала полезно применять грубые и
простые методы минимизации (быть может, даже метод простого
перебора значений функции на сетке с небольшим числом узлов),
а затем на основе накопленной при этом информации о функции
перейти к более точным методам. Например, при минимизации
достаточно гладких функций сначала можно применить какой
либо вариант градиентного метода, который вблизи точки мини-
мума обычно начинает сходиться очень медленно, а затем на
основе полученного приближения точки минимума перейти к ме-
тоду Ньютона, каждый шаг которого хотя и более трудоемок, но
общий объем вычислений может оказаться небольшим из-за
быстрой сходимости метода Ньютона вблизи точки минимума.
При выборе метода минимизации наряду с общим объемом
вычислений следует принимать во внимание также и устойчивость
метода по отношению к погрешностям, область сходимости мето-
да, степень гладкости и другие свойства минимизируемой функ-
ции, сложность вычислений значений функции и ее производных,
используемых в методе, требуемый объем памяти, удобство реа-
лизации на ЭВМ и т. д.

54 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
2. .Для описания и изучения методов минимизации нам понадо-
бятся отдельные формулы и факты из классического анализа. При-
мем следующие обозначения: Ет — евклиддво пространство размер-
(и1\
ности т; и = I : I — вектор-столбец или точка пространства Ет с
\ит)
координатами и*9 i = 1, 2, , т\ иТ = (и\ , ит)— вектор-строка;
Л = {aif} — матрица порядка п х т с элементами аи (i = 1, 2, ... , л;
/=1,2, ,т); матрицу, полученную транспонированием Л, будем
/л
обозначать через АТ или А*; аг6 = (а,Ь)Егп = V а'У— скалярное про-
изведение двух векторов а и Ь из Ет ; | а \Е = К(я> я)ят~~ евклидова
норма вектора а € £m; Au = v — произведение матрицы А на вектор-
столбец и у представляющее собой вектор-столбец v£En с координа-
т т
тами ^Vfl^'; [(Л£, £) = V a^fc'V — квадратичная форма с сим-
метрической матрицей Л порядка /яхт; \\А Ц^ = sup \Au\e — норма
матрицы А порядка пхт. Там, где не могут возникнуть недоразуме-
ния, индексы пространств в обозначениях скалярных произведений,
норм векторов и матриц, знак транспонирования в обозначении век-
/ Jtti {и)
тор-строки мы будем опускать. Пусть далее /'
диент функции J (и) в точке и,
(J* (и) \
\Jum (U) )
\JUmu*% • • • yJumum/
матрица вторых производных функции J (и) в точке и\ здесь
1 . ^ dj(u) . дЧ(и) .
Cp(U) — множество всех функций, обладающих на U непрерывными
частными производными до порядка р включительно; о (а) — величи-
на, бесконечно малая относительно a-при а->0, т. е. limo (а)-а"*1 = 0.
а-»0
Как известно, для любых а, 66 Ет имеет место неравенство Ко-
ши — Буняковского: |(а, 6)|<\а\ • \Ъ|, причем знак равенства при
а, ЬФО возможен тогда и только тогда, когда a = ab, a = const.
Далее, |Ли|Ел'<||Л||п,т |и|ят Для любых матриц Л порядка./г х т и
любых и 6 Ет.

§ 1] Постановка задачи. Обозначения. Вспомогательные сведения 55
Если J(ti)£&>(U)t u + aheU при 0<а<1, то
J(u + h)—J(u) = (J'(u),h)+o(\h\) при р=1, (2)
J(u + h)-J(u) = (J'(u),h)+±(J"(u)h,h) + o(\h\*) при р = 2. (3)
Рассмотрим функцию g (а) — J {и + aft) одной переменной а, 0 <
<а<1, при фиксированных и9 А, предполагая, что u + ah£U при
всех а, 0<а< 1. Если /(и)6 0(1/)> то g(a)6CP[0, lj, причем
g' (а) = (/' (и + aft), А), (р > 1), g" (а) = (/" (а + aft) ft, ft) (р > 2). (4)
В самом деле, если, например, /(^бС2^, то, заменив в формуле
(3) и на и + aft, ft на Дай, получим
g(a + Да)—g(a) = Да(/'(и + aft),ft) +
+ Y Да2(У" (а + aft) ft, ft) + о (| Да|2).
Отсюда следует, что g(a)6C2[0, 1] и верны формулы (4).
Выпишем следующие формулы классического анализа для функ-
ции g(a):
a
g(«)-g(0) = g'(e,a)a = jV (')<# = £'(0)a+ -±-£*(e2a)a»,
о
g' («) — Г (0) = ag" (в3а), 0 < 6, < 1.
Полагая в этих формулах a= 1 и пользуясь равенствами (4),
получим
/ (и + А) - J (и) = g (1) -g (0) = (/' (a + exft), ft) =
= jV(" + tf»),A)<#, (5)
о
J (u + h) - / (и) = (У (и), A) + -J- С (" + &Л) Л. Л). (6)
(/'(u + ft)-/' (u)th) = £' (l)-g' (0) = (J* (к + в8А)А,А). (7)
3. В настоящее время наиболее полно исследованы задачи
минимизации выпуклых функций на выпуклых -множествах. Раз-
дел экстремальных задач, рассматривающий такие задачи, часто
называют выпуклым программированием. Приведем определения
выпуклых множеств и функций, докажем некоторые их свойства.
По поводу выпуклых множеств и функций см. работы [39, 46, 73,
88, 97, 114, 116, 127, 128, 133, 134, 199, 229, 260, 269] и др.

56 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
Определение 1. Множество U называется выпуклым,
если <xu+(l—a)v^U при любых u, v^U и любых а, О^а^-1,
т. е. отрезок v+a(v—и)у где 0^а^1, соединяющий любые две
точки и, v множества, также принадлежит множеству.
Таким образом, формулы (2—7) справедливы при всех
и, u+h^Uy если {/ — выпуклое множество, а функция J (и) доста-
точно гладкая.
Определение 2. Функция J(u)9 определенная на выпук-
лом множестве U, называется выпуклой, если
J(au + (1 — a) v)<£aJ(u) + (1 —a) J (v) (8)
при всех и, tie(/ и всех a, O^a^l. Если в (8) равенство воз-
можно только при а=0 и а=1, то J (и) называется строго выпук-
лой функцией.
Теорема 1. Если J (и) выпуклая функция на выпуклом
множестве Ut то всякая точка локального минимума J (и) одно-
временно является точкой ее абсолютного минимума на U. Мно-
жество U* всех точек минимума J (и) на U выпукло (если оно не
пусто). Если J (и) строго выпуклая функция на U, то она может
достигать своего минимума на U не более, чем в одной точке.
Доказательство. Пусть и* — точка локального мини-
мума J (и), т. е. существует такая окрестность О точки w*, что
/(w*)^/(a) при всех и^О и u^U. Пусть вопреки утверждению
существует такая точка v^U, что /(a*)>/(i>). Так как
u=u* + a(v—u*)&0()U при всех достаточно малых а, 0<а<1, то
с учетом выпуклости функции J (и) будем иметь.
J(u*)<J(u* + a(v — *0)<а/(и) + (1— a) J (и*) < J (и*).
Противоречие. Следовательно, и* — точка абсолютного минимума
J (и) на U.
Далее, если выпуклая функция достигает своего минимума в
двух различных точках и*, и*е£/, то она достигает минимума во
всех точка отрезка, соединяющего эти две точки. Это следует из
соотношений
J (и*) = / (if )< / (aw* + (1 — a) v*) < a/ (и*) + (\—a)J (vm) = J(u*)t
превращающихся в равенства при всех a, O^a^l. Однако в слу-
чае строго выпуклой функции такое равенство невозможно при
0<а<1. А
Теорема 2. Если выпуклая функция J(u)^Gl(U) на вы-
пуклом множестве £/, то
(J'(v)f u — v)<cJ(u) — J(v)><(J'(u)> u — v) при всех и, v£U.
(9)
Доказательство. Перепишем неравенство (8) в виде
J(v+a(u—v))— J(v)^.a[J(u)— J(v)]. К левой части этого нера-

§ 1] Постановка задачи. Обозначения. Вспомогательные сведения 57
венства применим формулу (5): J(v+a(u—v))— J(v)=a(J'(v+
+6а(и—v)), u—v), 0sg6<l, и получим (J'(v+tia(u-+ v)), u—v)^.
^.J(u)—J(v) при всех а, 0<а^1. Отсюда при а->~+0 вытекает
левое неравенство (9). Поменяв в полученном неравенстве роля-
ми и и v, получим правое неравенств (9). £
Теорема 3. Для того чтобы выпуклая функция J (и) еС1 (U)
достигла своего минимума на выпуклом множестве U в точке
м*е£/, необходимо и достаточно, чтобы
(/' (и*), и — и") > 0 при всех и 6 U. (10)
Если и*— внутренняя точка множества /У, то условие (10) экви-
валентно равенству /'(и*)=0.
Доказательство. Необходимость. Пусть u*^U — точка
минимума J (и) на U. Тогда при любом u^U, и а, 0<а<1, с по-
мощью формулы (2) имеем
0</(и* + сф — и*)) — J(u*) = a(J'(u), и — и*) + о(а),
или
0 <</'(«0. a-iO+-£&L.
а
Отсюда при а-Я) сразу получим условие (10). Заметим, что
условием выпуклости J (и) мы здесь не воспользовались, так что
условие минимума (10) необходимо для всех J(u)^Cl(U), если
U — выпуклое множество.
Если и* — внутренняя ?очка множества U и h — произволь-
ный вектор из ЕШу то u=u^ + ah^U при всех достаточно малых
а, |а|^.ао. Полагая в (10) и=и*+ай, получим а(/'(и*), h)^0
при всех а, |а|^ао, что возможно только при (/'(и*), А)=0.
В силу произвола h отсюда имеем Г (и*) =0.
Достаточность. Пусть J (и) — выпуклая функция, пусть
для некоторой точки и* выполнено условие (10). Тогда из левого
неравенства (9) при o=w* получим 0sg:(/'(tt*), и—и*)^
^J(u)—J(u*) при всех u^U, т. е. и*—точка минимума.А
Заметим, что условие минимума (10) является обобщением
условия (1) на случай, когда ИфЕт и точка минимума и* может
лежать на границе множества.
Так как при и=и* (10) превращается в равенство, то условие
(10) может быть переписано в эквивалентном виде
min (/'(и*), и—w*)=0.
Определение 3. Функция J (и), определенная на выпук-
лом множестве £/, называется сильно выпуклой, если существует
такая постоянная х>0, что
/(<ш+(1— a)v)<aJ(u) + (l— a)J(v) — а(1— а)к\и — v\2 (U)
при всех u,v£U и всех а, 0 <а < 1.

58 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл.
Очевидно, сильно выпуклая функция J (и) выпукла и даже
строго выпукла. Примером сильно выпуклой функции является
/(и) = (и, и)=и*, (х=1).
Теорема 4. Для того чтобы J(u)^Cl(U) на выпуклом
множестве U была сильно выпуклой функцией, необходимо и
достаточно, чтобы существовала такая константа |i>0, что
(J'(v) — J'(u), v — u)>\l\v — и\2 при всех и9 v£U. (12)
Доказательство. Необходимость. Пусть J(u) —
сильно выпуклая функция из Cl(U). В неравенстве (11) при
а = — имеем
i|._.P<i[,W_,(£±l)] + .L[,W_,(i±!)]
при всех и, у 6 U. (13)
К каждой квадратной скобке применим правое неравенство (9).
Получим
*\u-v\*<2(j'(u),^) + 2(j'(vb ^) =
= (J'(v) — J'(u), v — u)
при всех и, v^U. Остается в неравенстве (12) принять |х=х.
Достаточность. Пусть J(u)^Cl(U) и удовлетворяет
неравенству (12). Покажем, что тогда J (и) — сильно выпукла, при-
чем в неравенстве (11) тогда можно принять к =—\i. С помощью
формулы (5) будем иметь
aJ(u) + (l—a)J(v) — J(au + (l — a)v) =
= a[J (u) — J (v)]—[J(v + a(u — v)) — J (v)] =
l l
= a^(J,(v + t(u — v))t u — v)dt—a С (J' {v + ta(u — v))> u—v)dt =
о о
l
= af(/,(y+ t(u — v)) — J' (v + ta(u— v)),
о
(v+(u-v)t)-(v + ta(u-v)))—^—>
l
>^J 7(1—«Г |И~Р|2^= -|ца(1-а)|и-*|*
0
при всех ut v£U и 0<a<l. A

§ 1] Постановка задачи. Обозначения. Вспомогательные сведения 59
Теорема 5. Для того чтобы функция /(и)еС2(£7) на вы-
пуклом множестве U, имеющем внутренние точки, была сильно
выпуклой, необходимо и достаточно, чтобы существовала такая
константа |х>0, что
УШ, Е)>|*|Е|1 при всех иеи и l£Em. (14)
Доказательство. Необходимость. Пусть J (и) —
сильно выпукла и /(«)eC2(t/). Пусть сначала и — внутренняя
точка множества /У, а £ — произвольная точка из Ет. Тогда
v = u+el^,U при всех достаточно малых е, |е|^ео. Из форму-
лы (7) с учетом неравенства (.12) имеем
e(J'(ii + e6)--J'(ii)f 1) = гЦГ(и + вг1)1Л)>е^\1\\ 0<8<1.
Следовательно, (/"(и) 6, |) =lim (/"(w+6eg) g, g)>|x|£|2 при всех
8-» О
£e£m. Если и — граничная точка U, то существует такая после-
довательность йнутренних точек {ип}е1/, что мп-*-а(/1г->-оо)# Для
внутренних точек по доказанному выполняется (/"(Ип)£,£)^М<|£|2
при всех £e£w. Пользуясь непрерывностью /"(и), отсюда прр
п-+оо получим неравенство (14) и для граничных точек U.
Заметим, что если выпуклое множество U не имеет внутрен-
них точек в Ет> то оно лежит в некоторой гиперплоскости прост-
ранства Ет (см. ниже упражнение 5.5). В этом случае множество U
можно поместить в пространство меньшей размерности и все рас-
суждения проводить в этом пространстве. Нетрудно придумать
функцию в Ет, которая в пространстве Ег(г<,т) сильно выпукла,
а в Ет не выпукла (например, /(и1, и2) = (и1)2—(и2)2 при и2=0).
Достаточность. Пусть /(и)еС2([/) и удовлетворяет
условию (14). Отсюда с помощью формулы (7) при h = v—и
имеем
(J'(v) — J'(u)t v — u) = (J"(u + Q(v — u))(v — u)9 v — u)>
>\i\u — v\2
при всех и, uet/. Тогда согласно теореме 4 J (и) сильно выпукла,
и в неравенстве (11) можно принять х = -К-. Заметим, что при
доказательстве достаточности существование внутренних точек
U не использовалось. А
Замечание. Полезно уяснить связь между константами
х и |i из неравенств (11), (12) и (14). Как видно из доказа-

60 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
тельства теорем 4 и 5, при выполнении (12) и (14) с некоторой
константой |л в неравенстве (11), по крайней мере, можно принять
х = -£-. Если же достаточно гладкая функция сильно выпукла
с константой х в (И), то в (12), (14), по крайней мере, можно
взять |i=x. Можно ставить вопрос о более точном определении
этих констант:
х = х = inf **(ц) + (1~~а)J(t>)~"J(<ш + (1 ~"q)v) в (11)
1 u,v£U a(l-a)fa-u|2 V h
0<a<l
ц = ц1= inf (J'(u)l, l) в (14);
1*1=1
и аналогично в (12). Из изложенного ясно, что |л1>х для [любого
х из (11) и хх>-^ для любого (1 из (12), (14), в частности,
Ниже в ряде случаев от градиента J'(u) сильно выпуклой
функции будем требовать выполнения условия Липшица:
\J'(u)— J'(v) | <L|u—и| при всех u, v^U, L=const>0. Как увяза-
на константа L с x и ji? Применяя к левой части (12) неравенство
Коши — Буняковского и используя условие Липшица для /'(ы),
сразу получим L^ji^b частности Ь^щ. А тогда L^fii^xi^x
при любом х>0 из (if).
Теорема 6. Если ы* — точка минимума сильно выпуклой
функции J (и) на выпуклом множестве t/, то
\и — и*|2< — [J(u) — J(u*)] при всех «61/, (15)
X
где х>0 — константа из (11). Если, кроме того, J(u)£Cl(U), то
\i\u-аЧ1 <(/'("). и—и*), \i\u — u'\<\J'(u)\,
0<£j(u)-J (w*) < —fa' (it) Р (16)
при всех иеС/, где jx>0 — константа из (12) или (14) (в силу
замечания к теореме 5 в оценке (15) можно взять х = -t\
Доказательство. Если в неравенстве (13) примем
v=u* и учтем, что /(«*)<J ( U U \ то сразу придем к (15).

§ 1] Постановка задачи. Обозначения. Вспомогательные сведения 61
Так как согласно теореме 3 в точке минимума (/'(и*), и—и*)^0,
ме(/, то из (12) при v=u* получим
|||и-*Т <(/'(«). и — иГ)<№(и)\.\и — и*\.
Первые два неравенства (16) доказаны. Наконец, если восполь-
зуемся правым неравенством (9) при и = м*, то
J(u)-J(u*)<(J'(u), u-tf)<\J'(u)\-\u—um\
и отсюда с учетом уже доказанной оценки \i\u—м*| ^ |/'(и) |
получим третье неравенство (16).^
Теорема 7. Если /(и) — сильно выпуклая непрерывная
функция на замкнутом выпуклом множестве U (в частности, воз-
можно, U=Em)9 то: 1) 1(и) ограничена снизу на U,т.е.inf J(u) =
=/*>'—оо; 2) существует и притом единственная точка u*^U,
такая, что /(н*)=/*; 3) множество M(v) = {u:u&U, J(u)^J(v)}
ограничено при любом v^U.
Доказательство. Если U — ограниченное замкнутое
множество, то утверждения теоремы следуют из классического
анализа [126]. Пусть U — неограниченное множество. Возьмем
произвольную точку ие[/. В силу непрерывности J (и) для любого
е>0, в частности при е=и>0, найдется такое б>0, что
\J(u)— J(v) |^х при всех wet/, \и—v\^.8. Следовательно,
J(u)^J(v)— к при всех u^U, \и—v\^.&. Пусть теперь \и—а|;»6.
Тогда величина а0 = < 1, и при а = ао из (11) получим
|н — v[
(hJ(u)>J(v+a0(u — v)) — (l—a0)J(v) + Ka0(l — a0)\u — v\2.
Так как а01и — v\ = б, то J (v + а0 (и — v)) — J (v) > — к в силу оп-
ределения б, и
<x>0J(u)> — k + a>0J(v) + *а0(1 —a0)\u — v\2,
или
J(u)>J(v) + *(l-aQ)\u-v\* *- = /(*)_<
— x\u-v\(6'+-j) + k\u-v\*
при всех и6Uу \и—t>|>6. Далее воспользуемся неравенством
вытекающим из очевидного неравенства 2|а&|<а2 + &2. Будем иметь
J(u)>J(v) + f\u-v\*^f(8 + ±-y (17)

62 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
при всех и^и, \u — у|>6. На самом деле это неравенство верно
при всех и 6 £/, ибо
для точек u£U, \u —1>|<8 также имеем /(w)>J(v) — k>J(v) +
Из оценки (17) тогда следует, что
J(u)>J(v)-f(6+±y
при всех u£Ut т. е. J (и) ограничена снизу на U. Далее из (17)
имеем J (и) -> + оо при | и | -юо, и 61/. Тогда для любого числа
Л > 0, в частности при А = | J (v) |, найдется такое В > 0, что
J(u)>\J(v)\ при всех w££/, \и — v\>B. Отсюда ясно, что
/•=infj(a)= inf /(«)</(d).
Так как пересечение множества U и шара |и—и|^В есть
замкнутое ограниченное (и даже выпуклое) множество, то непре-
рывная функция J (и) на этом пересечении достигает своей ниж-
ней грани в некоторой точке а*, причем /(#*)=/*. Единствен-
ность такой точки !г* следует из строгой выпуклости J (и) и тео-
ремы 1.
Ограниченность множества M(v) = {u: u^U, J(u)^.J(v)} при
любом v^U вытекает из неравенства (17): \и —1>|<8+ —- при
о
всех u^M(v). J^
По поводу других свойств выпуклы* функций и выпуклых
множеств см. также § 3, 4. Здесь мы докажем еще две леммы,
полезные в дальнейшем.
Лемма 1. Пусть С/ —выпуклое множество в Emy J(u)&
&Cl(U) и Г (и) удовлетворяет условию Липшица: \У(и)— /'(tr) | ^С
^L|w—v\ при всех и, v^Ut L=const>0. Тогда
J(v) — J(u)>(J'(v)t v—u) \v — u\2 при всех и, v£U.
(18)
Доказательство. Положим в* формуле (5) h = v— и. По-
лучим
-1
J(v) — J(u)= f (J'{u + a(v — u))t v — u)da = (J'(v)f v—u) +
о

§ Т\ Постановка задачи. Обозначения. Вспомогательные сведения 63
+ С (J'(u + a(v — и)) — J' (v), v — u)da.
о
Поскольку
(J' (и + a (v — и)) — J' (v), v — и) > — | J' {и + a (v — и)) —
— J'(v)\-\o — и\> — L(l— a)\v- и\\ 0<<х<1,
то
1
J(v) — J(u)>(J'(v)9 v — и) — L\v — w|2f(l— <x)da =
о
= (/», *_„)—Li|i,_a|«. A
Лемма 2. Пусть имеется последовательность {an}t
я = 0, 1, 2, такая, что а„>0, ал— ап+\> Аа2п при всех
n>no>0 (/l=const>0). Тогда" а„< °"1" при всех п>я0.
Ля
Доказательство. С учетом условия леммы имеем
1 __ Qfe-^+i ^ Л ak
ak+\ аЬ Wk+\ a*+i
при всех Л > п0. Просуммируем это неравенство по k от п0 до я — 1
и получим > Л (л — м0), откуда > Л (п — п0), или
ал< — при всех я>/г0. Однако < п при
л (л — п0) п — п0 п
п>п0, следовательно, a„< п°+ , n>rtQ. А
Лл
Упражнения. 1. Доказать, что пересечение любого числа вы-
пуклых множеств выпукло. Верно ли это утверждение для объеди-
нения множеств? Доказать, что замыкание выпуклого множества
выпукло.
2. Пусть функции /*(#)(*= 1, 2,..., р) выпуклы на множест-
ве1 U. Доказать, что функция J(u)= V a^(w) выпукла на U
р
При ЛЮбЫХ 0*^0.
3. Привести пример двух выпуклых функций, произведение
которых невыпукло. При каких условиях произведение двух выпук-
1 Во всех упражнениях этого параграфа предполагается, что V — выпук-
лое множество в Em.

64 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
лых функций выпукло? Достаточно ли для этого положительности
сомножителей?
4. Пусть функции Jа (и) выпуклы на U при всех аеЛ, где
А — некоторое заданное множество индексов. Доказать, что
функция" J (и) = sup /а (и) выпукла на U.
а€А
5. Функция J (и) выпукла на U тогда и только тогда, если
функция g(t)=J(u+t(v—и)) одной переменной ty 0^/^1, яв-
ляется выпуклой при любых и, v^U. Если J (и) сильно выпукла,
то g(t) сильно выпукла. Доказать.
6. Если J (и) выпукла на С/, то
при любых
п
<х,>0, £а,= 1, uteU,
где п — произвольное натуральное число. Доказать.
7. Доказать, что J (и) выпукла на U тогда и только тогда,
когда множество А = {а=(и\ ..., ит, Q = (u, <|) : ueC/, l^J(u)}
выпукло в пространстве Ет+\.
8. Для выпуклости функции J(u)^Cl(U) на U необходимо и
достаточно, чтобы J{u)—J(v)^(J'(v), и—v) при всех и, v^U.
Доказать (см. теорему 2).
9. Для выпуклости J(u)^C2(U) на U достаточно, чтобы
(/"(w)ig, 1)^0 при всех u^U и всех £е£т. Доказать (ср. теоре-
му 5).
10. Доказать, что если функции /f(w)(t=l, 2,...,•/*) выпуклы
на U, то множество Ui={u:u^U, Ji(u)^.aif /=1, 2, .., п] выпук-
ло (й{ — заданные числа).
11. Если J (и) выпукла на С/, то'множество M(v) = {u:u^U,
J(u)^J(v)} выпукло при любом v^U. Доказать. Верно ли обрат-
ное утверждение?
12. Функция J (и) у заданная на выпуклом множестве £/, назы-
вается квазивыпуклой, если J(av+(\—a)w)^max {/(и), J(v)}
при всех и, v^U и а, 0^а^1. Всякая ли выпуклая функция
квазивыпукла и наоборот? Доказать, что J (и) квазивыпукла на U
тогда и только тогда, когдча множество M(v) = {и: u^U, J(u)^.
^J(v)} выпукло при всех v&U.
13. Функция J (и), заданная на выпуклом множестве U, назы-
вается равномерно выпуклой, если существует непрерывная строго
возрастающая функция y(t), 0^t< + oot Y(0)=0, такая, что
J(au+(l — a)v)<aJ(u) + (l—a)J(v) — a(l—a)y(\u — v\)

§2]
Градиентный метод
65
при всех и, v^U, O^a^l. Доказать, что если J (и) равномерно
выпукла на замкнутом выпуклом множестве U, то все утвержде-
ния теоремы 7 сохраняют силу.
14. Доказать, что J (и) =аи2+Ьи+с, и^Е{ — сильно выпукла
при любом ц>0.
15. Пусть J(u) = — (Аи, и) — (Ь, и), где А — заданная сим-
метрическая матрица порядка mXm, Ь — заданный вектор из Ет.
Доказать, что: а) если (Л|, |)^0 при всех ge£m, то J (и) выпукла
на Ет\ б) если А —положительно определена, то J (и) сильно вы-
пукла на Ету причем в качестве константы х из неравенства (11)
можно взять и = -^-, где К\ — наименьшее собственное число
матрицы А. Вывести формулы Г (и) =Аи—Ь и J"(u) =А.
16. Пусть J (и) = \Аи—Ь\2У где А —заданная матрица порядка
пХт, Ъ — заданный вектор из Еп. Доказать, что J (и) выпукла
на Ет. Если А*А—невырождена, то J (и) сильно выпукла на Ет
(здесь А* — транспонированная матрица). Найти /'(и), J"(u).
§ 2. ГРАДИЕНТНЫЙ МЕТОД
Пусть дана функция J(u)^Cl(Em)t Как известно [126], в точ-
ке и, в которой 1'(и)Ф0, направление наибыстрейшего возраста-
ния функции совпадает с направлением градиента J'(u) в этой
точке, а направление наибыстрейшего убывания — с направле-
нием антиградиента —J'(u). Это следует из формулы (1.2) и не-
равенства Коши — Буняковского: —|/'(и) | |ft| ^ (/'(и), А)^
^|/'(и)||Л|» если учесть, что правое неравенство превращается
в равенство только при h = <xJ'(u), левое—только при h= —aJ'(u),
a=const^0. Это свойство градиента может быть положено в
основу итерационного метода минимизации функции, известного
под названием градиентного метода [3, '19, 27, 35, 46, 76, 79, 82,
109, 135, 149, 165, 161, 164, 170, 177, 188, 193, 229, 230, 235, 239,
251—253, 260] и др.
Этот метод предполагает выбор некоторой начальной точки ио.
Общих правил выбора и0 нет; в тех случаях, когда имеется априор-
ная информация об области расположения искомой точки мини-
мума, точку и0 стараются выбрать в этой области. Им-ея u0f далее
строят последовательность {ип} по правилу
Un+i = ип — anJ' (un)t ап = const > 0 (п = 0, 1, 2, ...).
(1)
Если 1'(ип)Ф0> то можно подобрать такое аЛ>0, чтобы /(wn+i)<
<J(un). В самом деле, из формулы (1.2) следует

Ьб МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
при всех достаточно малых ап>(>. Если L'(un)=09 то ип — стацио-
нарная точка, и в этом случае процесс (1) прекращается, и при
необходимости проводится дополнительное исследование поведения
функции в окрестности точки ип для выяснения того, достигается
ли в точке и минимум J (и) или нет.
1. Существуют различные способы выбора величины ап в фор-
муле (1). В зависимости от способа выбора ап можно получить
различные варианты градиентного метода. Здесь мы остановимся
на варианте, называемом методом скорейшего спуска и предпола-
гающим выбор ап из условия
gn Ы = mfngn (a), gn (а) = J (ип — а/' (ип)). (2)
Отсюда сразу имее'М /(«o)^/(wi)^/(m2)^ ...
Возникают вопросы. Возможен ли выбор ап из условия (2) >
Будет ли \\rnJ (ип) = J* = inf J (и)? Для получения положитель-
ного ответа на эти вопросы на функцию J(u)^Cl(Em) приходится
накладывать дополнительные, довольно жесткие ограничения.
Теорема 1. Пусть функция
J (и) € С1 (£m), inf J (и) = J* > — оо,
u£Em
и градиент/7(и) удовлетворяет условию Липшица: \J'(u)— J'(v) |<^
^:L\u—v\, L=const>0. Пусть щ — произвольная фиксированная
начальная точка, и последовательность {ип} получена из условий
(1), (2). Тогда lim/,(wn)=0.
Если, кроме того, J (и) выпукла и множество М(и0) = {и:
J(u)^.J(u0)) ограничено, то последовательность {ип} является
минимизирующей и любая ее предельная точка будет точкой ми-
нимума J (и) на Emt причем в случае единственности точвд мини-
мума к ней сходится вся последовательность {цп}. Справедлива
оценка
0<J(un)-J*<2D*L-±- (я=1, 2,...), (3>
п
где Z)= sup \и — v\ — диаметр множества М(и0).
utv€M(u0)
Если J (и), кроме того, сильно выпукла на Emt то
0<J(un)-J*<[J(u0)-J*]cr,
\un-u*\*<-±-[J(un)-J*]q" (n = 0t 1,...), (4)
где q= 1 £-, 0<<7<1> и = const > О из теоремы 1.4.

S 2]
Градиентный метод
67
Доказательство. Если при некотором п^О окажется
//(«п)=0, то из условий (1), (2) формально получаем ип=ип+х =
= ... , и утверждение теоремы lim//(wn)=0 становится тривиаль-
ным. Поэтому будем считать 1'(ип)Ф0 (п=0, 1, ...). Так как
/(ttn+i)=gn(an)^£n(a)=/(tfn—о.Г{ип)) при всех а^О, то из
неравенства (1.18) при v=un, u=un—raJ'(un) имеем
J (ип) - Цип+х) > J (ип) -J(un- *J> (ип)) > si (1 - -^-) I /' (un) |2
при всех a>0 и всех n = 0, 1, 2,... . Следовательно:
«'('O — /(fti+i) > maxa А — 4" сЛ|/' (un) \2 =
= -^|/'("i.)lf>0 (n = 0, 1,...). (5)
Таким образом, последовательность {J(un)} строго убывает. Но
/ (ип) > JT > — оо, поэтому существует 1 im J (и„), и V (ип) —
— /(wn+i)->0 при п->оо. Из оценки (5) тбгда имеем UmJ' (ип) = 0.
Пусть теперь J (и) выпукла, и множество- М(ио) ограничено.
Поскольку М(#о)> кроме того, замкнуто в силу непрерывности
J (и) (и даже выпукло), то J (и) достигает, своей нижней грани на
М(щ)> а стало быть, и на Ету хотя бы в одной точке м*е
М(и0) : J(u*)=J*. Тогда с помощью неравенства (1.9) имеем
0<J(uJ~J(tf)<(J'(un)9 un-u*)<D\J'(un)\ (л = 0, 1,...).
(б)
Так как </'(ыл)->-0, то отсюда следует lim J (ип) = J(u*) = J*t т. е.
П-*оо
последовательность {ип} является минимизирующей. Так как {ип}£
£М(и0), то последовательность {ип} имеет хотя бы одну предельную
точку v* = lim ип.. Но /(a) непрерывна, поэтому J* = lim / (wnJ =
= /(у*). Если J (и) достигает своего минимума в единственной точке
и\ то lim ип = и*.
Для доказательства оценки (3) обозначим an = J(un)—/*. Из
неравенств (5), (6) следует ап — ап+х>-±j-\J'iun)\\ an<D\J'{ип)Ъ
а тогда
ал — ал¥Х>-^а* (« = 0,1,2,...).
Так как ап>0 (если an = 0, то ип — точка минимума), то с по-
мощью леммы 1.2 отсюда получаем оценку (3).

68 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
Наконец, пусть J (и) сильно выпукла, и по-прежнему /(и) 6
6 С1 (£„,), «/' (и) удовлетворяет условию Липшица. Согласно теоре-
ме 1.7 тогда сохраняют силу все предыдущие рассуждения. Докажем
оценки (4). Из теоремы 1.6 имеем 0<а„<— \J'(un)\2. Отсюда и
из оценки (5) вытекает ап — ап+\ > — ял, или
an+i<(l— ~j-)an = qan(n = 0> 1. ••■)•
Следовательно, an<a0^(n = 0, 1, --.) — первая из оценок (4) полу-
чена. Вторая оценка (4) непосредственно следует из первой и нера-
венства (1.15). Остается заметить, что О < q = 1 — < 1, ибо
H<L,(cm. замечание к теореме 1.5). А
Для функций J(u)^Cl(Em) описанный метод скорейшего
спуска при т = 2 имеет простой геометрический смысл: оказывает-
ся, точка ип+и определяемая условиями (1), (2), лежит на луче
и(<х) =ип—aJ'(un) (a^O) в точке его касания линии уровня
Гп-и = {и : J (и) =/(wn+i)}. Это вытекает из следующих, двух факто-
ров: 1) градиент функции в фиксированной точке v всегда перпен-
дикулярен линии уровня T(v) = {и: J(u)=J(v)} в точке и. В самом
деле, если u=u(t) некоторое параметрическое уравнение линии
уровня Г(у), то J(u(t)) = J(v)= const Поэтому
^r(J(u(t))) = (J'(u(t)), d(t)) = 0,
т. е. градиент в каждой точке Г (v) перпендикулярен касательному
направлению к Г (а) в этой точке; 2) направление J'(un) является
касательным к линии уровня Гп+ь что в силу предыдущего равно-
сильно равенству (Jf(un), J'(un+i)) =0. Последнее следует из усло-
вия (2) и формулы (1.4)
8'п К) = — W М> J' ("«+0) = 0 при ап > 0.
Из рис. 7, 8 видно, 4to чем ближе линия уровня J(u)= const
к окружности, тем быстрее сходится метод скорейшего спуска.

§2]
Градиентный метод
69
В тех случаях, когда поверхности уровня сильно вытянуты, то
этот метод может сходиться очень медленно. Приемы ускорения
сходимости в таких случаях будут обсуждены ниже, в п. 4.
2. Известны и другие способы выбора величины ап в формуле
(1). Простейшим из них является выбор an = a = const. При этом
на каждом шаге проверяется условие монотонности: /(wn+i)<
</(wn). Если оно нарушается, то а дробится до тех пор, пока не
восстановится монотонность; время от времени полезно пробовать
увеличить а с сохранением монотонности.
В тех случаях, когда заранее известна величина Г = inf J (и),
то в равенстве (1) можно взять an—[J(un) —J*]\J'(un) |"2—это
абсцисса точки пересечения прямой /=/* и касательной к кривой
J=gn(a) в точке (gn(Q), 0) плоскости (/, а). Еще два способа
выбора ап можно получить из методов, описанных в § 3, 5 при
U = Em.
3. Если способ определения ап выбран, то итерации (1) про-
должают до выполнения тех или иных критериев окончания счета.
На практике часто используются критерии |wn+i—wn|^e, или
\J(un+i)— J(un) | ^е, или |//(wn)|<'8 и другие; возможны сочета-
ния различных критериев. Разумеется, к этим критериям надо от-
носиться критически, ибо они могут выполняться и вдали от иско-
мого минимума.
Следует заметить также, что вблизи точки минимума градиент
J'(un) близок к нулю, и метод (1) становится слишком чувстви-
тельным к выбору ап, отыскание более точных приближений точки
минимума w* затрудняется, так как расстояние \ип—и*\ пере-
стает уменьшаться. Поэтому вблизи точки и* целесообразно
использование других, более тонких методов, опирающихся на
квадратичную аппроксимацию функции в окрестности каждого
приближения (см. § 7, 8).
4. Как уже отмечалось, метод скорейшего спуска и другие
варианты градиентного метода медленно сходятся в тех случаях,
когда поверхности уровня функции J (и) сильно вытянуты и функ-
ция имеет так называемый «овражный» характер. Это означает,
что небольшое изменение некоторых переменных приводит к рез-
кому изменению значений функции — эта группа переменных
характеризует «склон оврага», а по остальным переменным, за-
дающим направление «дна оврага», функция меняется незначи-
тельно (да рис. 9 изображены линия уровня «овражной» функции
двух переменных). Если точка лежит на «склоне оврага», то на-
правление спуска из этой точки будет почти перпендикулярным к
направлению «дна оврага», и в результате приближения {ип}9
получаемые градиентным методом, будут поочередно находиться
то на одном, то на другом «склоне оврага». Если «склоны оврага»

70 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
достаточно круты, то такие скачки «со склона на склон» точек ип
могут сильно замедлить сходимость градиентного метода.
Для ускорения сходимости этого метода при поиске миниму-
ма «овражной» функции можно предложить4 следующий эвристи-
ческий прием, называемый овражным методом [67]. Сначала опи-
шем простейший вариант этого метода.
В начале поиска задаются две точки й<ь йь из которых произ-
водят спуск с помощью какого-либо варианта градиентного мето-
да и получают две точки u0t щ на «дне оврага». Пусть, например,
J(щ) <j(u0). Тогда полагают
I"i— "о I
где h — положительная постоянная, называемая овражным шагом.
Из точки й2, которая, вообще говоря, находится на «склоне овра-
га», производят спуск с помощью градиентного метода и опреде-
ляют следующую точку и2 на «дне оврага». Если уже известны
точки Uo, Uu ..., un (п^2) и J(un)<.J(un-\), то из точки
Un+l = Un-r Л
I "л— Ия-il
совершают спуск с помощью градиентного метода и находят
следующую точку an+i на «дне оврага» (см. jpnc. 9; спуск из точки
йп в точку ип, состоящий, быть может, из нескольких итерацион-
ных шагов градиентного метода, на рис. 9 условно изображен от-
резком прямой, соединяющей точки йпу ипу м=0, 1, ...).
Величина овражного шага h подбирается эмпирически с уче-
том информации о минимизируемой функции, получаемой в ходе
поиска минимума [67]. От правильного выбора h существенно за-

§2]
Градиентный метод
П
висит скорость сходимости метода. Если шаг h велик, то на кру-
тых повоторах «оврага» точки йп могут слишком удаляться от
«дна оврага» и спуск из точки йп в точку ип может потребовать
большого объема вычислений. Кроме того, при больших h на кру-
тых поворотах может произойти выброс точки йп из «оврага» и
правильное направление поиска точки минимума будет потеряно.
Если шаг слишком мал, то поиск может очень замедлиться и
эффект от применения овражного метода может стать незначи-
тельным.
Эффективность овражного метода может существенно возрас-*
ти, если величину овражного шага выбирать переменной, реаги-
рующей на повороты «оврага» с тем, чтобы: 1) по возможности
быстрее проходить прямолинейные участки на «дне оврага» за
счет увеличения овражного шага; 2) на крутых поворотах «оврага»
избежать выброса из «оврага» за счет уменьшения овражного
шага; 3) добиться по возможности меньшего отклонения точек йп
от «дна оврага» и тем самым сократить объем вычислений, тре-
буемый на градиентный спуск из точки йп в точку иП9 га=0, 1, 2,....
Интуитивно ясно, что для правильной реакции на поворот «оврага»
надо учитывать «кривизну дна оврага», причем информацию о
«кривизне» желательно получить, опираясь на результаты преды-
дущих итераций овражного метода.
В работе [211] предлагается следующий способ выбора
овражного шага:
hn+l - К • c"sa«-cosa*-i, п = 2, 3, (7)
где ап — угол между векторами ип — ип-и ип—«л-ь т. е.
_„ _ fin — Чп-и Un — U>n-i)
\"п~ И/1-1 II «я— «Л-ll
постоянная с>1 является параметром алгоритма. Точка ид+1 тогда
определяется так:
u„+i = un+ Un^Un'1 .hn+x (при /(wn)</(wn_i)).
I "/I — ИЛ.! |
Разность cos ап—cosan_i в равенстве (7) связана с «кривизной
дна оврага», и, кроме:того, обладает важным свойством указывать
направление изменения «кривизны». А именно при переходе с участ-
ков «дна оврага» с малой «кривизной» на участки с большей «кривиз-
ной» будем иметь cos an—cos an-i<0 (см. рис. 10). Тогда в силу соот-
ношения (7) An+i<An,T. е. овражный шаг уменьшается, приспосабли-
ваясь к повороту «дна оврага», что, в свою очередь, приводит к
уменьшению выбросов точки йп+\ на «склоны оврага». При пере-
ходе с участков «дна оврага» с большей «кривизной» на участки

72 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
°г
°7~~
и
П+г
Рис.
Ч
~f
и
10
О >
/к?
U
п~?
о А
JLT*
Г
Гл^у
0
п
-^0
=* п-2
<
±ц
h.j
с меньшей «кривизной», наоборот, cos ал — cosan-i>0, поэтому
овражный шаг увеличится и появится возможность сравнительно
быстро пройти участки с малой «кривизной», в частности, прямо-
линейные участки на «дне оврага». Если «кривизна дна оврага»
. на некоторых участках остает-
ul _j *Ь ся постоянной, то разность
cosan—cosan-i будет близка к
нулю, и поиск минимума на
таких участках будет прово-
диться с почти постоянным
шагом, сформированным с
учетом величины «кривизны»
при выходе на рассматривае-
мый участок.
Параметр с в равенстве
(7) регулирует чувствитель-
ность метода к изменению «кривизны дна оврага», и правильный
выбор этого параметра во многом определяет скорость движения
по «оврагу». Некоторые эвристические соображения по поводу вы-
бора с и другие аспекты применения овражного метода обсужде-
ны в работе [211].
Выражение (7) для овражного шага удобнее преобразовать
так:
hn+i = hnccosa"-cosa"-i = hn„{ccosan-™«n-2 = = ft2ccosan-COS0\
откуда окончательно
Ад+1 = Kccos\ К = V~c°sai = const > 0, п = 2, 3, ...
Другой способ ускорения сходимости градиентного метода за-
ключается в выборе подходящей замены переменных u=g(Q
с тем, чтобы поверхности уровня функции /(#(£)) в пространстве
переменных £ были близки к сферам [251—253].
Упражнение. Опишите метод скорейшего спуска для функций
J(u) из упражнений 1.15 и 1.16. Укажите явное выражение для ап
из условия (2). Пользуясь теоремой 1, оцените скорость сходи-
мости.
§ 3. МЕТОД ПРОЕКЦИИ ГРАДИЕНТА
Рассмотрим задачу минимизации функции J(u)^Cl(U) для
случая, когда \]фЕт. Непосредственное применение градиентного
метода из § 2 здесь невозможно, ибо при каком-либо п точка ип
из (2.1) может не принадлежать U. Однако нетрудно избежать эту
неприятность, если, каждый вновь полученный член последователь-

§3)
Метод проекции градиента
73
ности (2.1) проектировать на множество U. В результате мы при-
дем к так называемому -методу проекции градиента.
1. Для точного описания этого метода нам понадобятся вспо-
могательные сведения.
Определение 1. Проекцией точки и^Еш на множество
UczEm называется точка Pu(u)^Uy удовлетворяющая условию
\u — Pu(u)\ = inl\u — v\ = p(utU)t
где р(и, И) —расстояние от точки и до множества U.
Если u^U, го очевидно, что Ри(и)=и. Нетрудно указать
множества U, когда проекция точки на это множество не сущест-
вует или определяется неединственным образом.
Теорема 1. Если множество UczEm замкнуто и выпукло, то
для всякой точки и^Ет существует и притом единственная проек-
ция Ри{и) на это множество. Справедливы неравенства
(Ри{и)—иу v — Pu(u))>0 при всех v£U, (1)
\Pu(u)—Pv(v)\<C\u — v\ при всех u,v£Em. (2)
Доказательство. Рассмотрим непрерывную функцию
g(v) = \v—«|2 переменного v^Em при произвольном фиксирован-
ном UGEilw
Нетрудно проверить тождество g(av+(l—a)w) =
= ag(v) + (l—a)g(w)—a(l—a)\v—w\2y справедливое при всех
v, w^Em и O^a^l. Следовательно, g(v) сильно выпукла на
всем пространстве и согласно теореме 1.7 достигает своего мини-
мума на замкнутом выпуклом множестве U в единственной точке
v9 w^Em и O^a^l. Следовательно, g(v) сильно выпукла на
при всех yet/, причем'равенство достигается только при v = v*.
Остается принять Pu(u)=v*.
Докажем неравенство (1). Согласно теореме 1.3 для достиже-
ния функцией g(v) минимума на U в точке а* необходимо и доста-
точно, чтобы (g' (v*)t v—v*)^zQ при всех v<=U. Поскольку
g'(v) =2(v—и) и v* = Pu(u), то отсюда сразу получаем нера-
венство (1). Далее из (1) имеем
(Ри (и) - иу Ри (v) - Ри (и)) > 0, (Ри (v) -v, Ри (и) —-Рц (v)) > 0.
Сложив эти два неравенства, получим
0<(Pu(v)—Pu(u)9 Pu(u) — u — Pu(v) + v),
или
\Ри(и) — Pu(v)\*<(Pv(v) — Ри{и), v — u)<\Pu(u) — Pu(v)\\v — u\*
Разделив это неравенство на \Ри(и)— Pu(v) \¥=09 придем к нера-
венству .(2). Если же \Ри(и)— /V(t>)|=0, то (2), очевидно, также
верно. ^

74 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
2. Опишем метод проекции .градиента. Пусть начальное при-
ближение u0^ U "известно. Строим последовательность {ип} по
правилу
un+i = Pu(un — anJ'(un))9 п= 0,1,2,... (3)
где an=const>0. Существуют различные способы выбора вели-
чины ап в равенстве (3), и в зависимости от этого можно получить
различные варианты метода проекции градиента. В частности, ап
можно выбирать из условий
J (tin) — J (И/ж) > e I un — ия+112, an > 0, (4)
где un+i имеет вид (3), e>0 —некоторое фиксированное число.
Ниже будет показано, что при некоторых ограничениях на функ-
цию такой выбор ап возможен. Если же в (4) может быть лишь
ап=0, то процесс прекращается и при необходимости проводится
дополнительное исследование точки ип на минимум.
Если Us=sEmt то (3) переходит в (2.1) и метод (3), (4) пре-
вращается в обычный градиентный метод § 2, а условие (4) для
выбора ап перепишется в виде [82]
J(un)-J(un+l)>eal\J'(un)\\
Теорема 2. Пусть U — замкнутое выпуклое множество,
функция J(u)^Cl(U) и ограничена снизу на С/, градиент J'(u)
удовлетворяет условию Липшица: \J'(u)— J'(v) \ ^L\u—v\ при
всех u, v^Uy L=const>0. Пусть щ — произвольная начальная
точка из U и величины ап в (3) выбираются из условий [156]
0<в1<а.< 2 \ (5)
L + 2е
2
где ei, е — заданные числа, 0<ег<С » е>0. Тогда по-
следоватёльность {ип} из (3) удовлетворяет условию (4) и
\un—un+i\-+0 (м->оо).
Если, кроме того, J (и) выпукла, и множество М(и0) = {и:
С.и^и, J(u)^.J(u0)} ограничено, то последовательность {ип} яв-
ляется минимизирующей и любая ее предельная точка и* будет
точкой" минимум a J (и) на С/, причем в случае единственности точки
минимума вся последовательность {ип}-+и* (п-^оо). Справедлива
оценка
0<art = /(^)-/*<-^-.-i-, я =1,2, (6)
е п
где
Г = inf J (и), С = sup | /' (и) | + — D,
U М(и0) Bi

§s\
Метод проекции градиента
75
D — диаметр множества1 М(и0).
Если, кроме того, J (и) сильно выпукла на (7, то
K-wT< L> л=1,2, ... (7)
х • е п
Доказательство. Прежде всего, если в (1) принять и = ип —
— anJ'(ип) и учесть (3), то получим
(ип+\ — ип + anJ' (ип), и — un+i) > О,
или
(/' (ип), и — ип+х) > (ип — ип+и и — ип+\) при всех и 6 U,
л= 1,2, ... (8)
Заметим, что если при каком-либо п оказалось, что un = un+i,
то из (8) следует (J'(un), и—ип)^0 при всех иеС/, т. е. ип —
стационарная точка J (и) на U, которая в случае выпуклости функ-
ции будет точкой ее минимума на U,
Воспользуемся формулой (1.18) при v=uny и=ип+\. Получим
J(un) — J(un+i) >(J'(un)y ип — ип+х) — -^Цип — ип+1\*.
Отсюда с учетом условий (5) и неравенства (8) при и = ип получим
J (ип) — / (ип+1) > (-±- — ^) К — Un+i |2 >
>e\un — un+l\*>0, n = 0, 1,2, (9)
Как видим, выбор an из (5) здесь гарантирует выполнение нера-
венства (4). Далее, из (9) (или (4)) следует, что последователь-
ность {J(un)}y убывает. Так как /(ип)^/*>'—оо, то существует
lim/(wn), и, следовательно, J(un)— /(нп+1)-И)(п-мх>). А тогда из
Л-»оо
(9) имеем \ип—un+i\-+-6(n-+oo).
Пусть теперь J (и) дополнительно удовлетворяет еще условию
выпуклости и множество М(и0) ограничено. Ясно, что {цп}^М(и0)
и /* = inf/(w). Поскольку J (и) непрерывна, то она на ограничен-
ны
1 Ограниченность \J'(u)\ на М(и0) следует из ограниченности множества
-М(ио), условия Липшица для J'(u) и неравенств
I/'(и) К !/'(«)-''(«•)!+ \J'(u0)\<L\u-u6\ + \J'(u0)\<LD + \J'(u0)\.

76 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. Ь
ном замкнутом множестве М(и0) достигает своей нижней грани в
некоторой точке w*ef/, причем /(и*)=7*. Согласно теореме 1.2
0<£ап = /(ал)-/(!Г) <(/' (ua)9 un-u*) =
= W foi). Ия — Mft+l).— (/' (ия), U* — Un+i).
Отсюда с учетом (5) и неравенства (8) при u = u* получим
О < ал < (J' (ип), ип — ип+\) (un — ия+ь и* — ип+х) <
<(sup |/'(и)| + —)|ал-^+1|-С|^-^+1|. (10)
Так как \un—un+\\->0(nr+oo)9 то an=J(un)— /*->0, т. е. последо-
вательность {ип} минимизирующая. А тогда любая предельная
точка последовательности {ип} является точкой минимума и в
случае единственности точки минимума и* вся последовательность
{un}-*u* (и-+оо). Из неравенств (9), (10) имеем
ап — ап+1>^а2пУ (п = 0, 1, 2, ...).
Так как ап>0 (если ап=0, то ип — точка минимума), то отсюда
с помощью леммы 1.2 получим оценку (6). Наконец, из (6) и тео-
ремы 1.6 следует оценка (7). А
В тех случаях, когда константа Липшица L для J'(u) неиз-
вестна, при выборе ап вместо условия (5) следует использовать
условие (4). В этом случае часто полагают <xn = a=const>0 и на
каждом шаге проверяют выполнение условия монотонности:
J(un+i) </(un). Если оно нарушается, то а дробится до тех пор,
пока не восстановится монотонность; время от времени следует
пробовать увеличить а с сохранением монотонности. Величина е>0
в (4) является параметром алгоритма и в каждой задаче подби-
рается эмпирически. Следует иметь в виду, что если величина е
слишком мала, то метод (3), (4) может сходиться медленно, если
она слишком велика, то может затрудниться выбор ап из (4). Еще
один способ выбора an в (3) будет рассмотрен в § 5. Другие ва-
рианты метода проекции градиента, обсуждение различных вычис-
лительных аспектов этого метода см. в работах [9, 10, 31, 35, 97,
114, 116, 149, 155, 170, 189, 193, 235, 239, 267] и др.
Следует заметить, что задача отыскания проекции точки и
на заданное множество U сама, в свою очередь, является задачей
минимизации функции g(v) = \v—и\2 на этом множестве, и уме-
ние решать эту задачу во многом обеспечивает эффективность ис-
пользования метода проекции градиента при минимизации функ-
ций. Для некоторых множеств £/, когда, например, U есть шар в
Еш или параллелепипед с гранями, параллельными осям коорди-

§4]
Метод возможных направлений
77
нат, или гиперплоскость, или полупространство, задача проекти-
рования точки решается просто в явном виде, и реализация мето-
да проекции градиента в этом случае не вызывает особых затруд-
нений. Если же задача проектирования для своего решения тре-
бует применения тех или иных итерационных методов, то эффек-
тивность метода проекции градиента, вообще говоря, снижается.
Упражнения. 1. Доказать, что, для того чтобы точка w из вы-
пуклого замкнутого множества UczEm была проекцией какой-либо
точки и пространства £т, необходимо и достаточно, чтобы
(w — и, V — ш)>0 при всех v£U (11)
(см. теорему 1). Выяснить геометрический смысл неравенства (11)
на плоскости.
2. Найти проекции заданной точки и££т на следующие мно-
жества:
a) £/ = {a:oi<a'<p|f t= 1,2, ...,m}; 6)U={u:\u — u1\<£\R};
в) U = {u:(clt w — ut)=0}; г) (/ = {й:(с1,^м1)<0};
д) U = {u:(clru — иг) = 0, {сьи — и2)<0},
где точки ии и2> векторы С\Ф0, с2ф0> числа /?, а*, рг, t=l, 2,..., m
считаются известными.
3. Пусть Си Сг, .-., Ср — линейно-независимая система т-мерных
векторов, щ9 u2f..., Up — заданные точки евклидова пространства
Ет. Пусть U=\v : v<=Emy (ciy v—Ui)=0, i=l, 2, ..., /^ — пересече-
ние p гиперплоскостей в Em. Показать, что проекцию любой точки
и^Ет на множество U можно представить в виде
р
w=и+j] V/»
где Ль Яг, ..., Яр определяются из следующей линейной алгебраиче-
ской системы уравнений:
р
2 h (cr ct) = fa» Щ — и),1=1929 , р.
/=i
Указание. Воспользоваться неравенством (11).
, 4. Описать метод проекции градиента для минимизации функ-
ций из упражнений 1.15—16 на множествах U из упражнений 2,3.
§ 4. МЕТОД ВОЗМОЖНЫХ НАПРАВЛЕНИЙ
1. В этом параграфе рассмотрим один метод минимизации
функции J (и) на множестве 11фЕту близкий по своей идее к ме-
тоду проекции градиента. Будем предполагать, что множество U

78 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл: 2
задается так: t/={K:ft(«)<0(i=l,...,s)}, где gi(u) —известные
функции, определенные на всем пространстве Ет. Метод возмож-
ных направлений опишем (следуя [116]) для линейной функции
/(w) = (c, и), где сфО — заданный вектор из Ет. Это обстоя-
тельство не умаляет общности рассуждений, ибо если в исходной
задаче ввести новую переменную g и дополнительное ограничение
go(g, u)=J(u)—1^0, то в пространстве Ет+\ переменных (£, и) =
= (£, и1,..., ит) получим эквивалентную задачу: минимизировать
линейную функцию /i(g, w)=£ на множестве
tfi = {(£. и):ft(6. w)<0(t = 0, ..., s)},
где g0(l, u)=J(u)—%, gid> u)^gi(u) (/=1, ..., 5). Заметим, что
этот прием сведения задачи минимизации нелинейной функции к
задаче минимизации линейной функции за счет увеличения коли-
чества переменных может быть полезен и при испрльзовании дру-
гих методов, если, конечно, добавление ограничения ft(i, и) =
=J(u)—1^0 не затруднит реализацию выбранного метода из-за
возможной сложности работы с множеством U\. Непосредственное
описание метода возможных направлений для исходной задачи
см. в работе [114].
Итак, пусть требуется минимизировать функцию /(и) = (с, и),
сФОпа множестве U={u : ft(«)<0(f=l„.., s)}.
Определение. Направление рфО в точке u^U назы-
вается возможным, если достаточно малое перемещение из точку и
в направлении р не выводит за пределы множества [/, т. е. сущест-
вует такое а0>0, что u+ap^U или g«(u+ap)^0(i=l,...,s) при
всех а, О^а^ао. Возможное направление р называется подходя-
щим, если (/'(и), р) = (с, р)<0> т. е. функция J (и) в окрестности
точки и убывает при движении по направлению р.
Прежде чем переходить к описанию метода возможных на-
правлений, выведем критерий оптимальности для рассматриваемой
задачи.
Теорема 1. Пусть U={u : ft(w)<0(i=l, ...,$)}> тле gi(u) —
выпуклые функции из С1(Ет), и пусть множество U имеет внут-
реннюю точку и0. Тогда, для того чтобы точка u*^U была точкой
минимума /(и) = (с, и) на £/, необходимо и достаточно, чтобы ми-
нимальное значение функции v(a)s=£ переменной a=(g, р) =
= d> Р1, -, Рт) на множество A = {a=d> Р) (с> Р)^%>
(ft (M*),pX6npm'e/*, |р<|<1 (*=1, ..., т)} равнялось нулю:
minv (a)=0; здесь множество индексов /* = {i: 1 ^i^s,gi(u*)=0}
А
всегда непусто, так как и* — граничная точка U.
Доказательство. Необходимость. Пусть и* — точ-
ка минимума J (и) на U. Тогда и* — граничная точка множества и
и множество индексов /* непусто. Пусть minv(a)=£* достигается

#4]
Метод возможных направлений
79
в точке а*=(|*, р*). Так как а=0еЛ, то £*^v(0)=0. Покажем,
что g*=0. Если g*<0, то р*Ф0 и направление р* будет подходя-
щим. В самом деле, из условий gi(u)^Cl(Em) и gi(u*)=*0 при
ie/* следует
£<("* +«Р*) =ft(^ + ар*)-&(*0 = ato'(a* + бар*), p*) <a-^<0
при /s/*, а при i£I* gi(u* + ap*)<0 для всех достаточно
малых a>0. Кроме того, (с, p*)^g*<0. Существование подходя-
щего направления р* в точке и* противоречит тому, что и* — точ-
ка минимума. Следовательно, £* = 0.
Достаточность. Пусть при некотором и*6 V выяснилось,
что /* Ф 0 и min v (a) = £* = 0. Покажем, что и* — точка минимума
А
J (и) на_£/. Пусть это не так. Тогда существует такая точка u(:U,
что J (u)<^J(u*). Можем считать, что и — внутренняя точка "множе-
ства (/, так как по условию существует внутренняя точка и0 и, сле-
довательно, точки- v = и + а(и0 — и), 0<а<1, являются внутрен-
ними (см. упражнение -5.1) и неравенство J (и*) > / (и) = J (и) +
+ а(с1 и0 —и) сохранится при всех достаточно малых а>_0. Однако
■если и — внутренняя точка U н J(u)<J(u*)9 [то точка а = (£, р),
где р = w— и*, принадлежит множеству А при некоторых £<'0.
В^самом деле,
(С, р) =/(«)- /(!!•)< 0, fe' (к*), p)=(g'l(u*), й-й*) <
при 1*6/*,_и остается взять £ = тах{(с, р); (gt-(«*)> р) (*6/*)}<0.
Тогда v (а) = | < 0 = §* = mf v (а). Противорелие. Следовательно,
л
и* — точка минимума J (и) на U. А
2. Опишем метод возможных направлений, предполагая, что
множество U удовлетворяет условиям георемы 1. На каждом шаге
итераций находятся точка Uk^U и число 6а>0. В качестве началь-
ного приближения выбираются произвольная точка u0^U и произ-
вольное число 6о>0, например 6о=1 (о выборе и0 см. ниже). Пусть
для некоторого k^O точка uh^U и число 6л>0 уже найдены.
Тогда следующее приближение ищем так.
1. Сначала определяем множество индексов /ft={j: l^isg:
^s> —8h<Cgi(Uh)^:0}. Из определения Ih следует, что gi(uh)^
^—бА при i<£Ik.
2. Затем решаем задачу минимизации функции v(a)=?| пере-
менных a— (g, р) = (£, р1, ..., рт) на множестве Ак={а=(1, р)

80 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
(су /7^|, (g'i(uk), р)<£ при it=Iky |p*'|<l(i=l,...,/n)}. Так как
Ah — замкнутое ограниченное множество, a v(a)=£ непрерывна на
Ак, то существует такая точка ak = (Ёь pi) б Ak, что min v (a) =
= v (afe) = gj. При этом а=0еЛл, поэтому Й < v (0) — 0. Если
окажется, что £* <0, то р*ф0 и /7* является направлением, веду-
щим строго внутрь множества Иу причем вдоль р* функция J (и)
убывает. Таким образом, решая задачу минимизации v(a) на
множестве Л^, находим подходящее направление р*, в некотором
смысле наилучшее. Заметим, что задача минимизации v(a) на Ah
является хорошо известной "задачей линейного программирования
и может быть эффективно решена методами, дающими решение
за конечное число шагов (см. ниже § 11). Пусть эта задача реше-
на и найдено (*£, р\) = ak.
3. Далее вычисляем новое значение параметра £:
( 6к9 если &< — ЬкУ
[ 0,58Л, если — вЛ<6л<0.
Может оказаться, что £*=0. В этом случае нужно проверить, не
является ли точка ик точкой минимума J (и) на U. Для этого
решаем новую задачу линейного программирования: найти мини-
мум функции v(a) =£ на множестве
Al = {а = (6, р): (с, р) < Б, to' (иЛ), р)< g
при ig/ь |p'|<l(f = 1, ... , т))у
где /fe={i:Kt<s,grt(^)=0}.
Пусть minv(a) достигается на а — (Й, р&). Если окажется, что
л*
Ife = 0, то в силу теоремы 1 точка ик _будет искомой точкой, и про-
цесс на этом заканчивается. Если же Й<0, то полагаем 8fe+i=0,56^
и переходим к п. 4.
4. Наконец, полагаем uk+x = uk + akpk, где pk = pk при £*<0, а
если ^ = 0 и Efe<0> то рк = рь а число аЛ = тта^, где аЛ/ есть
наименьший положительный корень уравнения gt (uk 4- apk) = 0 (/ =
= 1, ... , s) (если при некоторых i окажется, что gt(uk + apkX0
при всех aj>0, то условно принимаем аы = + оо). Очевидно»
J (Uk+x) = / (Wj + CCk (Cy pk) < J (Uk) И Uk+lEEU.
Метод возможных направлений описан. Кратко остановимся
на отыскании начального приближения u0^Uy т. е. отыскании
какого-либо решения системы неравенств (вообще говоря, нели-

§4]
Метод возможных направлений
81
нейной) gi(u)^0(i=l,...9s). Оказывается, для определения и0
может быть использован только что описанный метод возможных
направлений. А именно этим методом нужно решить задачу мини-
мизации функции v(a)=g на множестве Л'={а=(|, и) :gi(u)^:l,
£=1, 2,_..., sy. Так как по условию U содержит внутреннюю точку
щ9 то a0= (£о, «о), где f0 = max g( (и0) < 0, будет принадлежать
Л', и, следовательно, minv(a)<0. Поэтому для того, чтобы полу-
А'
чить искомое начальное приближение Ыо,.нет необходимости точно
решать эту вспомогательную задачу. Здесь достаточно, начиная
с произвольной точки ио£ £m, проделать некоторое конечное
число шагов описанного метода возможных направлений, пока не
придем к точке ao=(!o, и'0)^А', для которой |о^О. Как видим,
метод возможных направлений может быть использован для ре-
шения нелинейных систем неравенств.
Теорема 2.Пусть U={u:gi(u)^0 (t=l,...,s)},n*e gi(u) —
выпуклые функции из С1 (Em), пусть U ограничено и имеет внут-
ренние точки. Тогда последовательность {и&}, полученная описан-
ным выше методом возможных направлений, такова, что:
1) /(цк) = (с, uk)-W* = inf J{u)\
2) любая ее предельная точка и* будет точкой минимума J(u)
на U9 а в случае единственности точки минимума вся последова-
тельность {Uh}~+U*.
Доказательство. Так как {J(uk)} монотонно убывает и
/ (uk) > У* >—оо, то существует lim J (uk) и / (uk)—J(uk+\) ->*0(£->oo).
Покажем, что Sk->0(k-*oo). Последовательность {bk} положительна
и монотонно убывает, следовательно, существует lim6^=6-0.
Предположим, что 6>0. Пусть kn — номер итерации, когда проис-
ходит дробление параметра бл, т. е. —bkn<lln<0 и 8^+i = 0,56fc #
Если lim6^ = 6>0, то процесс деления пополам заведомо конечен
и, более того, "найдется такой номер jV0, что 8k = 6 и ^ < — б при
всех &>JV0. Пусть и* — предельная точка {uk}. Ясно, что u*€U.
Выбирая при необходимости подпоследовательности, можем считать,
что uk-+u* (k->оо). Пусть /* = {i: 1 / < s, — б < gc (и*) <0}. В
силу непрерывности gt (и) имеем — б < g( (uk) < 0 при всех &>Л^ >N0
и i 6 /*. Следовательно, /* с: Ik при всех k Nx. Тогда
(с9 pk) = (c, р*)<Й<— 6, (gl(uk)9 pk)<lk< — б
при всех i£ Г и всех &>Л^. Так как последовательность {pk} огра-
ничена, то она имеет предельную точку р* При необходимости вы-

£2 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
<5ирая подпоследовательность, можем считать, что pk-+p*. Тогда при
k-*»оо из предыдущих неравенств имеем (с, р*)< — б<О,
(ft («О» Р*)< —S<0 при всех *£/*. Кроме того, gt («*)< — б при
*^/* по определению /*.
s Таким образом, р*фО и направление р* является подходящим
для точки и*. Пусть а* = min а*, где щ — наименьший ПОЛОЖИТеЛЬ-
ный корень уравнения gt {и* + ар*) = 0 (i = 1, ... , s) (если при не-
которых i окажется, что gt (и* + ар*) < 0 при всех а>0, то условно
полагаем а* = + оо). Тогда &(м* + аР*)<0 ПРИ всех а, 0<а<а*,
и * = 1,... , s. В силу непрерывности #*(ы) имеем &(и* + арл)<0
при всех k>N2>Nl9 0<а<а* и t== 1, ... , s. Это означает, что
ak > а* > 0 при всех Л > N2. Тогда 0<а*б <—ak (с, pk)=J(uk) —J(iik+\)
при всех £>#2, что противоречит соотношению J(uk) — J(uk+\)-+-
-> 0 (k -* оо). Следовательно, bk ->- О (Л -► оо) и последовательность
{£„}, когда bkn+i = 0t5bkn и — бЛл<^л<0, не обрывается ни при
каком п (конечно, здесь предполагаем, что метод возможных направ-
лений не приводит к искомой точке минимума за конечное число
шагов — в этом случае теорема очевидна). Отсюда вытекает, что
|£я-*0 при п->оо.
Теперь покажем, что J(uk)-*J*> Пусть и* —' предельная точка
{Ukn}. Можем считать, что ukn-+u*. Обозначим /* = {t:l<t<s,
gi(u*) = 0}t так что gt(u*X0 при i£I\ Покажем, что hn^r
при всех я>#8. Для этого обозначим тах&(и*) = —6*<0. Тогда
&(«0< —8* ПРИ все* i <£ **• Так как бл-*0 и g, (tf*J-*-ft(w*)('= 1,... ,s),
то найдется такой номер N^ что при всех л > #3 будет gt(Uk)< —
-0.56*<-6fe/j для 1£Г и -0.5б*<^.(^п)<0=^(^)
для /6/*. Это и означает, что Г—Li\п при всех я>#8. Пусть и*
не является точкой минимума J (и) на £/. В силу теоремы 1 тогда
существует число £<0, и вектор рфО> такие, что, (с, р)<Е,
(ft (и*)» р) <1 (* б /*), |р'|< 1 (*" = 1, т). Из непрерывности
gl (и) следует, что (# (и*л), р)< I" при всех n>NA>Nani€ Ikfi с:/*.
Па определению g^ тогда имеем g£ <1 < 0 при я > Af4, что проти-
воречит соотношению Й -►•О^-^оо). Следовательно, и* — точка ми-
нимума J (и) на [/ и J(ukn) -+J (и*) = J*. Поскольку J(uk) монотон-
но убывает, то и вся последовательность J(uk)-+<J*. Тогда любая
предельная точка последовательности {uk} является точкой минимума
J (и) на Uу а в случае единственности точки минимума вся последо-
вательность {иЛ}-ка\ ▲

§4)
Метод возможных направлений
83
3. Остановимся на вопросе об оценке погрешности метода воз-
можных направлений, а именно укажем простой способ оценки
сверху разности J(uh)— 7*^0 при фиксированном k. В силу вы-
пуклости gi(u) и теоремы 1.2 имеем
0 > ft (а) > ft (иА) + (gl (uk)9 и — uk)
при всех и 6 U и t = 1, ... , s. Это означает, что
UaUk = {u:{gi{uk)y и — uk)+gt(uk)<0 (i= 1, ... , s)}.
Тогда пип«/(и)<гшп/(и) = J* и приходим к следующей оценке по-
uk и
грешности:
0<J(uk) — J*<£j(uk) — minJ(u) (k = 0, 1, 2,...). (1)
uk
Эта оценка достаточно удобна на практике, поскольку задача
минимизации J (и) на Uh является стандартной задачей линейного
программирования. Следует заметить, что если минимальные зна-
чения J (и) на U и Uk не близки, то оценка (1) может оказаться
слишком грубой.
Такой прием получения оценки погрешности не зависит от
способа получения-величины uk и может быть использован при
работе с другими методами минимизации во всех тех случаях,
когда удается найти множество !/*, содержащее I/, для которого
задача минимизации J (и) на" Uk может быть решена достаточно
просто.
Всюду выше от подходящего направления рл(£=0, 1,...) мы
требовали |pl|< 1 ({ = 1, ... , m). Это делалось для того, чтобы
множество Ak было ограниченным и, следовательно, задача мини-
мизации линейной функции v(a)s==| на множестве Ak имела,
смысл. Возможны и другие способы нормировки вектора рн, на-
пример
m
IpJ3 = £Ip*I*<i.
В зависимости от способа нормировки вектора ри можно получить
различные модификации метода возможных направлений. По воп-
росам практического применения и сходимости различных вариант
тов метода возможных направлений подробнее см. в работах
[79, 109, 114, 116, 135, 149, 177, 193, 196, 239, 260].
Упражнения. 1. Доказать эквивалентность двух задач миними-
зации функций: J (и) на множестве U={u : gi(u) ^Г0(£=1,..., s)} vt
/j(g, u)=l на множестве £/i = {(g, и) : /(wX£, ft(^X0(t =
= l,...,s)}.

84 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
2. Доказать, что линейная функция J(u) = (cy u)y сФО может
достигать своего минимума (и максимума) лишь в граничной
точке U.
3. Для того чтобы точка и0 была внутренней точкой [гранич-
ной точкой], множества V={u : gi(u)^.0(i=lt...,s)}, gi(u)^
eC(£w), необходимо и достаточно, чтобы gi(u0)<0 при всех
i=l,...,s [gi(u0)=0, хотя бы при одном значении i, l^t^s].
Доказать.
§ 5. МЕТОД ПРОЕКЦИИ ОПОРНЫХ ФУНКЦИИ
1. В описанных выше методах минимизации функций многих
переменных мы предполагали существование градиента функций
в каждой точке множества U, В этом параграфе рассмотрим один
метод минимизации при более слабых ограничениях на функцию.
Пусть задана функция J (и) на некотором множестве U.
т
Определение 1. Линейная функция (/, и) = V ltu^ пе-
ременной ие£/, определяемая вектором /= (/ь /2,..., 1Ш), назы-
вается опорной к функции J (и) в точке v^U, если
J(u)>J (v) + (/, и — v) при всех и 6 V. (1)
Вектор / назовем опорным вектором для функции J (и) в точке
tiel/.
Неравенство (1) геометрически означает, что гиперповерх-
ность, определяемая функцией g=/(w), лежит не ниже гиперпо-
верхности, определяемой линейной функцией £=(/, и—b)+J(v),
причем при u = v эти две гипер-
поверхности имеют общую точку
(рис. 11). Если J (и) — выпукла
и eC^t/), где U — выпуклое
множество, то согласно теоре-
ме 1.2 J(u)—J(v)^(J'(v)t u—v)
при всех u^U, т. е. функция
g=(/'(u), и), является опорной к
f(u) в точке v, а градиент
J'(v) — опорный вектор в этой
" точке. Однако функция может
риси иметь опорный вектор и в тех
случаях, когда J'(u) не сущест-
вует. Например J(u) = \u\ в точке и=0 не имеет производных,
однако имеет бесконечно много опорных векторов /, |/|^1., в этой
точке, та*к как если |/|^1, то (/, и)^\и\ при всех и^Ет. Заме-
тим, что \и\ — выпуклая функция. Оказывается, это не случайно.
Ниже будет выяснена глубокая связь между выпуклыми функция-

§ 5}
Метод проекции опорных функций
85
ми и функциями, которые в каждой точке обладают опорной
функцией.
Понятие опорного вектора обобщает понятие градиента и
играет большую роль при исследовании экстремальных задач в
общей постановке [73], [97], [99], [199], [269]. Различные свойст-
ва опорных векторов, техника их вычисления в конечномерных и
бесконечномерных пространствах изучались в работах [73, 99, 199]
и др. Здесь мы приведем без доказательства два свойства опор-
ных векторов, которые могут оказаться полезными при вычислении
таких векторов.
Пусть функции Ji(u) в точке v имеют опорные векторы
lt (i = 1, 2, ... , р). Тогда: 1) функция
р
* (U) = У, aiJi (U)> а* = C0Ilst > °
Р
в этой точке имеет опорный вектор / = V а,/,; 2) функция
t=i
J (и) = max J{ (и) в точке v имеет опорный вектор
ККр
' = £ уА.
где Yi — произвольные числа, такие, что Y*>0> У. Y* = 1» а мн°-
жество индексов / (v) = {i: 1 < i < р, / (v) = /4 {v)}9 в частности,
можно взять l = lit i£I(v).
С помощью опорных функций можно просто сформулировать
критерий минимума.
Теорема 1. Для того чтобы функция J (и) достигала абсо-
лютного минимума на некотором множестве U в точке и*е£/,
необходимо и достаточно, чтобы нулевой вектор /=0 был опорным
к J (и) в точке и*.
Доказательство. Необходимость. Если и* — точка миниму-
ма, то J {и) ^>J(u*) + (0, и — u*) = J(u*) при всех u£U, т. е. нуле-
вой вектор является опорным в точке и*.
Достаточность. Если нулевой.вектор оказался опорным
к J (и) в точке и*, то J(u)^J(u*) + (0, u—u*)=J(u*) при всех
u^U. Следовательно, и* —точка минимума J (и) на U. ^
Перейдем, к описанию метода проекции опорных функций для
решения задачи минимизации функции J (и) на выпуклом множест-
ве U. Предположим, что J (и) в каждой точке иеУ имеет опорный

86 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
вектор l(u). Тогда .метод проекции опорных функций заключает-
ся в построении последовательности {ип} по правилу [187]
un+i = Pu(un-an j^ у ал>0,/2 = 0, 1, (2)
В зависимости от*способов выбора ап в (2) можно получить
различные варианты этого метода. Если J (и) выпукла и ^Cl(U)
на выпуклом множестве U, то l(un)=J'(un), и метод (2) превра-
щается в метод проекции градиента. Если U=Em, то Pu(u)=ut и
метод (2) в этом случае является непосредственным обобщением
градиентного метода на случай негладких функций. Будем пред-
полагать, что в (2) 1(ип)=£0(п=0, 1, 2,...), ибо при 1(ип)=0 в
силу теоремы 1 в точке ип функция J (и) достигает своего мини-
мума на U. Рассмотрим один вариант метода проекции опорных
функций. Именно в (2) в качестве и0 зафиксируем любую точку
из f/, а {ап} выберем произвольно, лишь бы удовлетворялись
условия [187]
00
а„>0, а„->0(/г-*оо), £а„=+оо (3)
(например, ап = п = 0, 1, J.
Теорема 2. Пусть U выпуклое замкнутое множество в Ет9
имеющее хотя бы одну внутреннюю точку (в частности, возможно
U = Em). Пусть функция J (и) непрерывна на £/, inf/(«) = /*>—оо
и во всех точках v 6 V функция J (и) имеет опорную функцию £ =
= (/ (v), и?}. Тогда для последовательности {ип}> построенной соглас-
но (2— 3), при любом начальном и06£/ справедливо равенство1
lim J(un) = «Г, или, иначе говоря, существует подпоследователь-
Л-»оо т
ность {ип}, такая, что J(uns) -W(s->oo). (В формулировке теоремы
требования на функцию J (и) можно уточнить и ослабить; см. ниже
теоремы 6, 7, 8.)
Доказательство. Прежде всего заметим, что при выполне-
нии условий теоремы последовательность {ип} из (2 — 3) определя-
ется однозначно (разумеется, если 1(ип) = 0, то ип — точка,минимума,
1 Напомним, что число а = lim ап — нижний предел последовательности
Я-»оо
{ап}, если все предельные точки {ап} не меньше а и существуеттакая подпос-
ледовательность {ап.}, что ап. -+а (£-•» ос). Верхний предал \\тап—Ь мож-
но определить так: Ь = — lim (— ап).
П-»оо

§ 5]
Метод проекции опорных функций
S7
и итерации прекращаются). Пусть вопреки утверждению теоремы
lim J (ип) = J* + 2е, е > 0. Рассмотрим множество
Л-»оо
Me = {u:ueU, J{u)<J* + z}.
Покажем, что это множество имеет внутреннюю точку. Пусть н0 —
внутренняя точка U, существование которой вытекает из условия
теорему. По определению' J* существует такая точка v£U, что
J(v)</* + 8/2. Так как точки u = v + a(u0 — v) при всех а, 0<
<<а<1, являются внутренними для множества U (см. ниже упраж-
нение 1) и функция, J (и) непрерывна, то. можно указать точку ие =
= v + а„(8) (ио — v)» которая вместе с шаром f/б = {и: | и — ие | < 6}
принадлежит U и / (и) < J* + е при всех и 6 Ue. Следовательно,
иг — внутренняя точка Ме и Ut с: Ме. Так как / (ип) > J* + е при
всех л>Л^!>0, то J(un)>J* + e>J(u) при всех и6£/в> или 0>
-p*J(u) — J (ип) > (/ (ип), и — ип) при всех и 6 £/а и п > ЛГ1# В част-
ности,
и = ые + б/ (ип) \1{ип) I-16 f/6,
поэтому
0>(/(И«), "в —«« + «/(«„) |/(Ия) |-») = ('(Wn). «B-tt«) + e|/(M«)|.
или (/(ия), ис —иЛ)< —6|/(иЛ)| при всех n>Nv Тогда, учитывая
сжимающее свойство операции проектирования (см. неравенство 3.2),
имеем
| ие- ип+112 = | Ри (иг) - Ра (ип - anl (ип) \ I (ип) f-1) I2 <
<\ue-un + an!(un)\l(un)\-i\*=\ue-uh\* + a2n +
+ 2an{l(un)t ue—lun)\l(un)\-*<\ue — un\* + a2n — 2an8 =
= \ue — un\* — 8an + an(an—8).
Так как ая->-0, то an — б<0 при всех n>N%9 и, следовательно,
\ие — un+i\2<\ue — ип\2 — а„8,
#ли
ъп8 < | ие — ип |2 — | ие — un+i |2 при всех n>N3 = max {Nu N2}.
просуммируем это неравенство по п от некоторого N > N3 до N + р.
Получим
N+P
& £ а«<1"в — Un\2 — \иг — ^+p+il2<|we — uN\2 при всех р>0.
00
Однако это противоречит условию V ап = + оо. А
п=*1

88 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
Если проекцию точки ,на множество U и опорные функции
l(un) найти несложно, то метод (2—3) очень прост. Однако этот
метод, вообще говоря, немонотонный: необязательно J(un+\)^
^J(un)t поэтому близость J(un) к /* трудно проверяема. Различ-
ные варианты метода опорных функций, а также другие методы
минимизации негладких функций описаны, например, в работах
'[35, 96, 109, 154, 187—189, 193, 251—253].
2. Выясним вопрос, какие функции обладают опорными функ-
циями во всех точках выпуклого множества U^Em?
Теорема 3. Для того чтобы функции /(«), определенная на
выпуклом множестве £/, имела опорную функцию во всех точках
множества £/, необходимо, чтобы J (и) была выпуклой на U.
Доказательство. Возьмем произвольные точки и, v6 U и
число а, 0 < а < 1. По условию / (и) во всех точках множества U
имеет опорные функции. В частности, для точки ua=oui + (l—a) v
существует вектор /а, что
J(W)—J (Ua) > (lay W — Ua) При BCeX W 6 U.
Примем здесь последовательно w •■== и и v. Получим
J {it) —J (Ua) > (/а, и — иа)9 J(v) — J (ua) > (/а, V — Ua).
Умножим первое из этих неравенств на а, второе — на 1 — а и сло-
жим. Будем иметь
aJ(u) + (l—a)J(y) — J(au + (1 — а)и)>(/а, иа — иа) = 0.
Отсюда и из произвольности и, v£U, 0<а<1 следует выпук-
лость J (и). А
Однако существуют выпуклые функции, не имеющие опорных
функций в некоторых точках области определения. Например, вы-
пуклая функция J(u) = —1/1—и? в точках и=±1 не имеет
опорных. Заметим, что точки и=±1 являются граничными для об-
ласти определения этой функции. Оказывается, это неслучайно.
Ниже будет показано, что всякая выпуклая на U функция во
внутренних точках U имеет -опорную функцию. Для доказательст-
ва этого факта нам понадобятся некоторые вспомогательные све-
дения.
3. Пусть X — некоторое множество в евклидовом пространст-
ве Еп. Замыкание множества X в Еп обозначим через X, множест-
во всех внутренних точек X — через Х°.
Определение 2. Пусть X и Y — два множества из Ет.
Гиперплоскость (с, *)=a=const с направляющим вектором сфО
называется разделяющей множества X и У, если (с, *)^а^(с, у)
при всех х^Х и f/еУ, или, иначе говоря,
inf (с, х) > a > sup (с, у).

§ 5]
Метод проекции опорных функций
89
Если либо inf (с, х) > а, либо sup (с, у) < а, то говорят о строгом
разделении этих множеств. Если при этом inf (с, *) = а, то гипер-
х€Х
плоскость (с, х) = а называют опорной к множеству X.
Геометрический смысл разделяющей гиперплоскости
(с, х)=а состоит в том, что множество X находится в одном полу-
пространстве, f определяемом этой гиперплоскостью, множество
Y — в другом (рис. 12, 13). Если гиперплоскость (с, х)=а разде-
СА
(С,х) *о(
*)-d
Рис. 12
Рис. 13
ляет множества X и Y, то, очевидно, гиперплоскость (цс, я) ={ш
при любом |i>0 также разделяет эти множества. Поэтому при
необходимости можно считать, что |я| = 1.
Теорема 4. Если X — выпуклое множество из Еп, то для
любой точку у£Х° существует гиперплоскость^ (с, х)=а,у с=£0,
разделяющая множество X и точку у. Если y&zX, то разделение
будет строгим. Если у — граничная точка X, то а= (с, у).
Доказательство. _Пусть сначала у£Х (рис. 14). Проек-
цию точки у на множество X обозначим через */*. Так как уф=Х,
то вектор с=у*—уфО. В силу_неравенства (3.1) (с, х—#*) =
= (у*—у у х—у*) ^0 при всех х^Х. А тогда
(с, х — у) = (у* — у, х — у) = \у*~у\* + (у*— Уу * — #*)>
>\УШ-У\* = \с\*>0.
Это значит, что гиперплоскость (с, х)=*(с, у)=а строго раз-
деляет X и точку у. Кстати, (с, х) = (с, у*) —опорная гиперплос-
кость к множеству X.

90
МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
[Гл. 2
Теперь пусть у— граничная точка X (рис. 15). Тогда сущест-
вует последовательность-{yk}£Xy Уь~*У (&->оо). В силу доказан-
ного существуют гиперплоскости (ck% х) = (cki yk), \ck\= 1, разделя-
ющие множество X и точкц yk'-(ck> х) >(с*> Ук) ПРИ в^х х£Х.
Последовательность {ck} имеет хотя бы одну предельную точку сл
Это значит, что некоторая подпоследовательность ckn-*c (п ->-оо),
причем \с\= 1. Так как (Ckn, х) > (сЛ , ykn) при х£Х9 то при п-нэо
отсюда получим (с, х) > (с; */) при всех х 6 X. Следовательно, гипер-
плоскость (с, л:) = (с, у) = а разделяет X и yt более того, она явля-
ется опорной к X в точке f/ € ^. А
fc,x-y*) = 0
Рис. 14
(с,х-у) = 0
Теорема 5. Пусть А и В — два заданных выпуклых множест-
ва в Ent не имеющие общих точек. Тогда существует гипер-
плоскость (с, х) =<х, разделяющая эти множества. При этом если
А и В имеют общую граничную точку у, то а= (с, у).
Доказательство. Возьмем множество Х=А—В. По
определению х^Х тогда и только тогда, когда существуют такие
а^А и 6е£, что *=а—Ь. Нетрудно видеть, что X — выпуклое
множество. В самом деле, пусть Xi=ai—bi&X, а^А, &геВ(*=1,2)«
Так как А и В выпуклы, то
а = аа±+ (1 — а)а26 Л, b=abx + (1 — а)Ь2£В
при всех а, 0^а^1. А тогда д;=ал:1+(1—а)х2=а—Ь^Х при
всех a, O^a^l. Покажем, что х=0 не является внутренней точ-
кой X. Для этого прежде всего заметим, что О^Х тогда и только
тогда, когда А и В имеют общую точку uq. Если бы 0eZ°, то
существовал бы шар |^|^б, целиком принадлежащий X, что воз-
можно, если только шар |a^-a0|^6 принадлежит множествам, А
и В. Однако Л и В не имеют общих внутренних точек. Следова-
тельно, 0 не может быть внутренней точкой X.

§ 5]
Метод проекции опорных функций
91
Тогда в силу теоремы 4 существует гиперплоскость (с, х)=0,
сФОу разделяющая множество X и точку */=0. Это значит, что
(с, х)^0 при всех д;еХ, или (с, а—6)^0, или (с9 a)^(ct b) при
всех аеЛ, 6еВ. Гиперплоскость (с, х)=а, где а — произвольное
число, удовлетворяющее неравенству inf (с, а) > а > sup (с, 6),
аел бея
разделяет множества Л и В. Если ^ — общая граничная точка А
и В, то inf (с, а) = sup (с, 6) = (с, (/) = а. А
Л В
4. Вернемся к вопросу о существовании опорных функций.
Теорема 6. Пусть U — выпуклое множество из ЕШу имею-
щее внутренние точки (в частности, возможно U=Em). Для того
чтобы функция J (и) у определенная на Ut имела опорную функ-
цию во всех внутренних точках £/, необходимо и достаточно, чтобы
J (и) была выпуклой на U.
Доказательство. Необходимость следует из теоремы 3.
Докажем достаточность. Пусть J (и) выпукла на U, и пусть v —
произвольная внутренняя точка множества U. В т+1-мерном про-
странстве Em+\=EiXEm переменных а=(£, и1,..., um) = (lt и)
определим множество
A={a=(l,u):ueU, 6 >/(«)}•
Покажем, что А выпукло. В самом деле, пусть ai = (£b Wi)&4,
#2= (62. и>2)^А. Из выпуклости U имеем aui + (1—a)ti2^U при всех
O^as^l. Из выпуклости J (и) следует:
J(au±+ (1 — a)w2)<a J(ux) + (1 — a) J(u2) <
<a|1 + (l — a)6«. 0<a<l.
Следовательно, aai+ (1—a)a2^A при всех a, O^a^l. Выпук-
лость А доказана. Точка a=. (/(a), v)y очевидно, граничная для 'А.
Тогда в силу теоремы 4 существует гиперплоскость (с, a)=a=
= (с, a), c=(vo, /о)¥=0, опорная к множеству А в точке а. Это
значит, что
(с, а — а) = v0 [| — J (v)] + (/0, и — v) > 0 при всех a = (£, и) 6 А,
(4)
т. е. при всех we(/, £^/(w). В частности, при u = v имеем
voU—HV)]^Q ПРИ всех l^Hv)> что возможно только при Vo^O.
Покажем, что vo>0. Если бы v0=0, то из (4) имели бы (/0, и—v)^0
при всех u^U. Но v — внутренняя точка множества Uy и послед-
нее неравенство возможно только при /о=0. Тогда с= (vo, k) =0, что
противоречит условию сфО. Следовательно, vo>0. Разделим нера-
венство (4) на vo>0. Получим
£ —/(и)>( ^, и — сЛ при всех u£U

92 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
и всех £>J(tt). В частности, при \ = J{u) отсюда вытекает
J(u)—,J(v) > ( -£-, и— v\ при всех u£U.
Следовательно, вектор / = — [является опорным к J (и) в точ-
ке v. ±
На примере функции J (и) = — У\ — и2 мы уже убедились,
что для существования опорной функции в граничных точках мно-
жества U выпуклости J (и) на U недостаточно. Здесь справедлива
Теорема 7. Пусть U — выпуклое множество из £т, имеющее
внутренние точки, ИфЕт. Для того чтобы функции /(и), опреде-
ленная на £/, имела опорную функцию во всех точках из U, необ-
ходимо и достаточно, чтобы J (и) была выпуклой на U и для
всякой граничной точки ug{/ существовала постоянная L = L (v) ^0,
такая,,что J(u)^J(v)—L(v)\u—v\ при всех u^U.
Доказательство. Необходимость. Пусть J (и) во
всех точка v^U имеет опорный вектор l(v). Тогда J (и)—J(v)^
^(l(v)y и—v)^—U(y)||w—v\ при всех u^U (в частности, в
граничных точках U) и остается принять L(v) = \l(v)\. Выпук-
лость J (и) следует из теоремы 3.
Докажем достаточность. Пусть J (и) выпукла на U и для каж-
дой граничной точки v множества U существует постоянная
L=L(v), такая, что. J(u)^J(v)—L\u—v\ при всех u^U. Сущест-
вование опорных функций во внутренних точках U следует из тео-
ремы 6. Пусть v — граничная точка U. В пространстве Ет+\
переменных а=(£, и1,..., ип) = (£, и) рассмотрим два множества:
А = {а = (%, u):ueu, g<J(y)-L \u-v\}
и
B = {6=(6,i0:n€l/f l>J{u)).
Покажем, что А выпукло. Пусть
пусть 0<а<1. В силу выпуклости U тогда аи±+ (1 — a) u2(zU, a
из lt < J (v) — L | щ — v | (t = 1, 2) имеем
oii+(l—oL)lt<J(v)—L{alu1 — v\ +(l-a)K-o|)<
<У(с;) —L |а«! + (1 — а)н2 — v\.v
Следовательно, aax + (1 — a) a2 6 Л при всех a, 0 < a < 1. Анало-
гично доказывается выпуклость В.
Далее, множества А и В не имеют общих внутренних точек,
ибо если (£, м)еЛ, то координата £^/(t>)— L|m—v\^J(u) при

§5]
Метод проекции опорных функций
93
всех ii^U по условию; если (|, w)eB, то g^/(w)> а точки
(/(«), м) являются граничными для В. Точка а=(/(и), v)—об-
щая граничная точка множеств А и В. Тогда в силу теоремы 5
существует гиперплоскость (с, а) = (с> а)=а, с= (vo, /о) ¥=0, разде-
ляющая множества Л и В. Это значит, что (с, а)^(с, а)^(с, Ь)
при всех а^Л и 6еВ, или же vol+(lotu)'^VoJ(v) + (loiv)^vor\+
+.(/о, и) при всех (£, м)еЛ и (т!,«)еВ. Отсюда имеем неравен-
ства
v0 [Ч — / (v)] < (/0, ^ - и)< v0 [I - J (v)] (5)
для всех wet/, &</(ti)—1|и—и|, r\^J(u). В частности, если
w=i>, то из (5) следует, что v0[r\—J(v)]^0 при всех т]^/(у), это
возможно только при vo^O. Покажем, что v0<0. Если бы v0=0,
то из (5) имели бы (/о, v—и) =0 при всех u^U. Это равенство
возможно только при /о=0, ибо U по условию имеет внутренние
точки. Тогда £=(v0, /о)=0, что противоречит условию сФО. Сле-
довательно, vo<0. Разделим неравенства (5) на vo<0. Будем
иметь л — J(v) > ( -,и— о\ при всех u^U и r\^J(u).
В частности, при г)=/(ы) отсюда вытекает
Это значит, что вектор / = ^ является опорным к J (v) в точ-
ке v. ±
5. В заключение этого параграфа остановимся на связи между
понятиями непрерывности и выпуклости функций. Существуют
выпуклые функции (например, J(u)=u2 при и<0, 7(0) = 1 на
£/={«: и<;0}), терпящие разрыв в граничных точках множества.
Однако можно показать (см. [39, 269]), что если U — выпуклое
множество из Ет с внутренними точками, то выпуклая на U функ-
ция J (и) непрерывна во всех внутренних точках множества U и,
более того, она обладает градиентом J'(u) почти всюду на U.
Здесь ограничимся доказательством менее тонких результатов,
справедливых, однако, как увидим ниже, и в бесконечномерных
пространствах.
Определение 3. Функция / (и), заданная на некотором мно-
жестве С/, называется полунепрерывной снизу [сверху] в точке
fcs£/f если для любой последовательности {ы/Jef/, uh-+u(k-+oo)
имеет место соотношение
lim J (uk) > J (и) [limJ (uk) < / (и)].

94 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
Как известно из классического анализа, для непрерывности
J (и) в точке u^U необходимо и достаточно, чтобы
lim J (uk) = lim J (uk) = / (и)
для любой последовательности K}g[/, иъ-+и (k-+oo).
Теорема 8. Пусть J (и) выпуклая функция на выпуклом
множестве U. Если в точке v^U функция J (и) имеет опорную
функцию, то она полунепрерывна сдазу в этой точке. Если, кроме
того, J (и) ограничена сверху в некоторой окрестности точки v9 то
она непрерывна в точке v.
Доказательство. Пусть {ик} — произвольная последо-
вательность, такая, что uk^U (k=0$ 1,...) и uk-+v (ft-^oo). Так
KaKJ(uk)^J(v)+\(l, uh—v), то^ lim J(uk) >J(v). Далее, no yc-
ловию существует постоянная S>0, что J(u)^C для всех wet/,
\u—v |<;8. Поэтому с учетом выпуклости J (и) имеем
J(uk)=J((l—a)v + afv L(t> —w*))<
<Z(l—a)J(v)+aj(v -(t> — w*))<0 — a)J(v)+aC
для всех a, 0<a<l, и всех номеров k, лишь бы —\v~w&|<6.
a
Отсюда lim /(wfe)<(l — a)J(v) + aC при всех a, 0<a<l. Сле-
довательно, здесь можно положить a-* + 0, тогда получим
lim /(w*)<J(v). Из полунепрерывности функции сверху и снизу
вытекает ее непрерывность. Д
Упражнения. 1. Если и0 — внутренняя точка выпуклого мно-
жества U и v — произвольная точка из замыкания Ut то точки
Ua = v + a(uo—v) при всех а, 0<а<;1, будут внутренними точками
U. Доказать.
Указание. Если шар \и—и0|^6 принадлежит £/, то шар
\и—wa|<<;a6 также ef/.
2. Доказать, что если А и В — два выпуклых замкнутых мно-
жества, не имеющие общих точек, и хотя бы одно из них ограни-
чено, то существует гиперплоскость (/, х) =>а, строго разделяю-
щая их, т. е. (/, &)^Tz<<x+e<;(/, а) при всех а^А, ЬеВ и неко-
тором 8>0. Верно ли это утверждение, если оба множества не-
ограничены?

§ 5]
Метод . проекции опорных функций
95
3. Пусть точки Ui(i = Ot 1,..., гп) таковы, что векторы
Ui—uo(i=l, 2,... m) линейно независимы. Образуем множество
m m_
S = iu: и = V сад при всев9зможных а4- >0, V а^ = ll
t=0 i=0
называемое выпуклой оболочкой множества точек и0,..., ит, или
симплексом, натянутым на эти точки. Доказать, что S — выпук-
лое множество, и точка u0^S является внутренней точкой S в
пространстве Ет тогда и только тогда, если
т т
U0 "= J] а1и1 ПРИ ai > °> J] ai = ! •
*=0 i=0
Доказать, что если точки м0,..., ит принадлежат некоторому вы-
пуклому множеству U, то симплекс SczU.
4. Точка Wo является внутренней точкой выпуклого множества
UczEm тогда и только тогда, если равенство (/, и—и0) =0 при всех
u^U может выполняться только при /=0, т. е. выпуклое множе-
ство с внутренними точками не может лежать ни в одной гипер-
плоскости в Ет. Доказать.
Указание. Доказать существование точек Щ,..., um^U9
для которых векторы М\—и0,..., Um—Wo линейно независимы, и
воспользоваться упражнением 3.
5. Выпуклое множество UaEm не имеет внутренних точек тог-
да и только тогда, если существует вектор 1Ф0 такой, что
(1У и—и0)=0 при всех u^U9 т. е. множество U лежит в некоторой
гиперплоскости (точку щ можем считать принадлежащей U).
6. Пусть J (и) — выпуклая функция на выпуклом множестве
[/, пусть u+el^U при всех е, 0^е<ео. Доказать, что J (и) имеет
производную по направлению./: х
dJ(u) = Ит /(к + еО-.Л(ц)
41 е-н-0 е
где |/|= 1. Доказать [199], что
dJ (и) , |ч
—±L= sup (c,l)9
dl сем(и)
где М(и)—множество всех опорных к J (и) векторов в точке и.
7. Найти все опорные векторы для функций: a) J (и) = \и— 11 +
+ |и+1|, U£EX\ б) J(U\U*) = |W1_W2|_K + „2|; в) J(w) =
= max {и2; и + 2}, и 6 Ег.
8. Найти все опорные векторы для J(u1tu?)= sup \иг + иЧ\.
0<<<1

96 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [ГЛч 2
9. Описать метод проекции опорных функций для задачи ми-
нимизации функции
J (и1, и2) = тах\Р + иЧ+и2\ при 0 <*/<"< 1 (t = 1,2).
10. Как нужно доопределить функцию J(u) = щ- в точке
и = 0, чтобы она стала полунепрерывной снизу?
11. Пусть J (и) определена, конечна и полунепрерывна снизу
в каждой точке замкнутого ограниченного множества UczEm.
Доказать, что тогда J (и) ограничена снизу на U и достигает на О
своей точной нижней грани.
§ 6. МЕТОД УСЛОВНОГО ГРАДИЕНТА
Рассмотрим один метод, пригодный для минимизации функ-
ции на ограниченном множестве. А именно пусть U — ограничен-
ное выпуклое замкнутое множество в Ет, и пусть задана функция
J(u)^Cl(U). В качестве начального приближения возьмем неко-
торую точку и0^и. Если известно n-е приближение иПу то прира-
щение функции J (и) в точке ип_ пред ставимо в виде
J(u)—J(un) = (J'(un), и—ип) + о(\и — ип\).
Возьмем главную линейную часть этого приращения Jn (и) =
в (/' (ип), и — ип) и определим вспомогательное приближение ип из
условия
Jn(un) = minJn(u) = m\n(J' (ия"), и — ип). (1)
Так как множество U замкнуто и ограничено, а линейная функ-
ция Jn(u) непрерывна, то такая точка un^U существует. Сразу же
заметим, что
min Jn (и) = Jn (ип) < Jn (ип) = 0.
и
Если окажется, что /п(мп)=0, то с учетом (1) имеем
(/'(ип), и—ип)^0 при всех u^U. Согласно теореме 1.3 это озна-
чает, что tin удовлетворяет необходимому условию минимума.
В этом случае итерации прекращаются, и для выяснения того,
будет ли ип точкой минимума J (и) на U, нужно дополнительно
исследовать поведение функции в окрестности этой точки. В част-
ности, если J (и) выпукла на U и /n(wn)=0, то ип в самом деле
будет точкой минимума. В дальнейшем будем предполагать, что

§6]
Метод условного градиента
97
/п(^п)<0. Тогда заведомо ипфип, и в качестве следующего приб-
лижения ип+\ принимаем
un+i=un + an{un — un), 0<аЛ<1. (2)
В силу выпуклости множества U точка Un+\&U. В зависимости
от способов выбора величины ап в (2) можно получить различные
варианты описанного метода, именуемого в литературе методом
условного градиента [35, 82, 97, 155, 229] и др. Рассмотрим неко-
торые из них.
1. Пусть ап в (2) (выбирается «из условия [97, 229]
gn (ап) =min gn (a), gn (а) = J (ип + а (ип — ип)). (3)
<Ха<1
Для определения ап могут быть использованы методы гл. 1. При
таком выборе ап последовательность {/(#п)} не возрастает, так
как
J (Цп) = gn (0) > gn К) = J ("*+i) •
Теорема 1. Пусть U — замкнутое выпуклое ограниченное
множество из Ет, пусть J(u)^Cl(U) и градиент J'(u) удовлетво-
ряет условию Липшица: \J'(u)— J'(v) \^,L\u—v\ при всех
и, v^U, L=const>0. Пусть uq — произвольная начальная точка
из U и последовательность {ип} определена согласно условиям
(1)-(3). Тогда
Jn(Un)=(J'(Un)> ип — ип)->0 (/г->оо).
Если, кроме того, J (и) выпукла на U, то последовательность
{ип} является минимизирующей и любая ее предельная точка
будет точкой минимума J (и) на U, причем в случае единственно-
сти точки минимума к ней сходится вся последовательность {ип}.
Справедлива оценка
0^an = J(un)-J(u*)<—, п=1,2, (4)
п
где и* — точка минимума J (и) на U, а С — постоянная, незави-
симая от nt С>0.
Если, кроме того, J (и) сильно выпукла на f/, то
\ип-и*?<—, л=1,2,
гДе х = const >0 из (1.11). t л ж„^
Доказательство. Обозначим D = sup \u-v\-диаметр мно-
utv£U

98 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
жества U. По условию множество U ограничено, поэтому D<oo.
Так как J(un+l) = gn(an) <gn (a) = / (un + a (un — un)) при всех a,
0< a < 1, то, пользуясь неравенством (1.18) при v = uny u = un +
+ <x(un — un)y получим.
J(Un)— J(Un+l}> — «(/'(Wj, Ur— Un) — YL\Un — Un\2>
Отсюда
>o.\Jn{un)\-±-LD\ 0<a<l, n = 0, 1, (5)
0<\Jn(un)\<^LD*+JiUn)~JiUn+l)
при всех a, 0<a<;l и я=0, 1,... Так как J(un) не возрастает и
J(un)^J*>—оо, то {J(un)} сходится и J(un)— /(wn+1)->0 при
tir+oo. Поэтому, переходя в предыдущем неравенстве к пределу
прип-^оо, будем иметь
0<\im\Jn(Un)\<lto\Jn(un)\<±LD*
Я^£ я-*00 z
при всех а, 0<а<1. Отсюда при а-^ + 0 получим, что предел
\imJn(un) существует и равен нулю.
Л-ЮО
Пусть теперь J (и) выпукла на U и и* — точка минимума J (и)
на U. Тогда с помощью неравенства (1.9) и условия (1) получаем
0<an = J(un)-J(u*)<(J'(un)t ип-и*) =
= -Jn («О < -Л («*), п = О, 1, ... (6)
Это неравенство может служить хорошей апостериорной оценкой
при практическом использовании метода (1) — (3).
Так как /п(Ып)-*0 при Яг-^оо, то из (6) имеем (J(un)-+-
J(u*)=J*9 т. е. {ип} — минимизирующая последовательность.
Из непрерывности J (и) следует, что любая" предельная точка по-
следовательности {ип} является точкой минимума J (и) на U.
В случае единственности точки минимума и* вся последователь-
ность {ип}-+и*.
Докажем оценку (4). Так как Jn{un)"^^ при_я-*оо, то най-
дется число п0 > 1,- такое, что величина a = ' п[Цп" будет удов-
летворять^неравенству 0<.а<1 при всех я>л0. Тогда максималь-
ное значение функции a | Jn (ип) | — LD2 переменной а при

§ 6] Метод условного градиента 99
-г--оо<а< + оо, которое достигается при а=а, будет совпадать с
максимальным значением этой функции на отрезке 0 < а < 1 при всех
л>я0. Поэтому, полагая в оценке (5) а = а, получим
ап — an+i = J(ип) — /(ип+ 0 > -^-\Jn(un)\2, п>п0.
Отсюда и из неравенств (6) следует
аЛ — a"+i>-fijpal> п>по- (7)
Так как аЛ>0 (если аЛ = 0, то ип — точка минимума), то с помощью
2LD2
леммы 1.2 из (7) имеем аЛ< (п0+ 1) при всех п>1ц. Для по-
п
лучения оценки (4) теперь остается принять С = max {2ID2;a0}x
X (n0+l).
2С
Оценка \ип — и* I2 < , п = 1, 2, ... для сильно выпуклых
ОСП
функций является следствием неравенства (1.15) и оценки (4). А
2. Рассмотрим еще один вариант метода условного -градиента,
когда ап ъ (2) выбирается из условия [82]
ЛЮ— J(tin + an(an — un))>Baa\Jn(un)\, 0<аЛ<1, (8)
где е — параметр алгоритма, 0<е<;1. Ниже будет показано, что
при некоторых ограничениях на функцию такой выбор ап возмо-
жен. На практике сначала берут ап=\ и проверяют условие (8).
Если оно выполнено, то оставляют ап = 1. Если же (8)
при ап=1 не выполнено, то производят дробление ап до тех пор,
пока не выполнится (8), стараясь при этом остановиться на зна-
чении <хп, по возможности близком к единице.
Теорема 2. Пусть U — замкнутое ограниченное выпуклое
множество з Em, J(u)s=Cl(U) и |/'М— J'ip) |<L|w—v\,
и, v^U, L = const>0. Тогда можно построить последовательность
{ип}9 удовлетворяющую условиям (1), (2), (8), для которой
Если, кроме того, J (и) выпукла на U, то последовательность {ип}
является минимизирующей и любая ее предельная точка будет
точкой минимума J (и) на U, причем в случае единственности точ-
ки минумума к ней сходится вся последовательность {ип}. Спра-
ведлива оценка
О < ап = / (ип) — Г < -?- (п = 1, 2,...), (9)
п

100 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [ГЛ. 2
где /*= inf J (u)9 а £>0 — некоторая константа, не зависящая от л.
Доказательство. Сначала покажем, что при выполнении
условий теоремы величину ап из (8) можно искать в виде [82, 155]
an=Ynpn, где
p„ = min(l; 'jf^1 ), 0<81<Yn<^f^ (n = 0.1,--.). (Ю)
a e,^ — заданные параметры алгоритма, 0 <вг < ~~8*, 0<е<1.
Возможно, или
\йп-ипР & К-%Р
где D—диаметр множества У. В обоих случаях имеем
0<Р„ '""""_"' ' <1; min{l;-b^ai<p;,<l (я = 0,1,...).
(")
Заметим, что если ип = ип или /п("п)=0, то ип — стационарная
точка. В этом случае, как уже говорилось выше, итерации прекра-
щаются и при необходимости проводится дополнительное изуче-
ние поведения функции в_ окрестности точки ип. В дальнейшем
будем предполагать, что ипФип, /п(«п)=7^0.
Из формулы (1.18) при 0 = м„, u = Un+i имеем
Lai -
J(un)-J(Un+l)>an\Jn(un)\ f-\ua — ua\* =
V 2 Un(tln)\ J
Отсюда с учетом (10—11) получим
^(uJ-/(Wл+1)>aJ/Л^)l(l-^)>aлвЦЛ^)l>
>818min{l;-b^^||J/l(^)l (n = 0,l,...). (12)
Повторяя рассуждения, аналогичные проведенным в доказатель-
стве предыдущей теоремы, из (12) имеем /п(йп)-*0 (п-мх>), а
также убеждаемся в том, что в случае выпуклости J (и) последо-
вательность {ип} будет минимизирующей.

§7]
Метод сопряженных градиентов
101
Так как Jn (ип)-*0, то
min{l;^|J^^)l} = ^I^W!
притчвсех*п>л0, и неравенство (12) перепишется ь виде
Согласно оценке (6) |«7Л(«Л)|>ял, поэтому
я„ — Ял+i >-^-f-я„» п>п0.
С помощью леммы 1.2 отсюда имеем
<*„<-£-•-2!±1, п>п0;
88! П
в оценке (9) остается принять В = тах{ ; а0\ (я0 + 1)-А
Упражнение. Описать различные варианты метода условного
градиента для функций J(u) упражнений 1.15—16, когда
U={u: \и—Wi|<#}, или £/=={ы:аг-^а*<р*, *=1,...,т},
Hie£w, /?, а», р< заданы.
Написать оценки (4), (9) с указанием явных выражений для
констант С, В через данные рассматриваемой задачи.
§ 7. МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ
1. Пусть функция J(u)^Cl(Em). Для минимизации этой функ-
ции на всем пространстве Ет можно использовать метод сопря-
женных градиентов, суть которого заключается в построении сле-
дующего итерационного процесса. Пусть начальное приближение
«о известно. Далее строим последовательность {ип} по правилам
Un+i = un — anpn (n = 0, 1, ...). (1)
Ро = J' ("о)> Рп = /' К) - $прп-Х (п = 1, 2,...), (2)
где величины ал, Р„ выбираются из условий
gn(ccn) = mingn(a)f gn(a)^J(un — apn) (3)
H
( (J'(un)t J'bLn^-J'jUn)) ne/
рл= I/'("*-!) I2 ' 19 (4)

102 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
а множества индексов Л, h таковы, что /iU^2={0, 1, 2,...}, 0е/2.
В зависимости от выбора множеств Л, h можно получить различ-
ные варианты метода сопряженных градиентов. В частности, если
/i=0, ^2={0, 1, 2,...}, то Рп=0 при всех л, и метод превратится
в уже известный нам метод скорейшего спуска. Если 4={0},
/i = {l, 2,...}, то получим обычный, классический вариант метода
сопряженных градиентов. Если /2={0, s, 25, 3s,...}, то придем к
так называемому s-шаговому методу скорейшего спуска (на прак-
тике часто принимают s, равным размерности м). Те значения я,
для которых рп=0, называют моментами обновления метода. Оче-
видно, что J(u0)^J(Ui)^. . .^J(Un)^....
Оказывается, метод сопряженных градиентов сходится, вооб-
ще говоря, быстрее градиентного метода и в то же время нена-
много сложнее метода скорейшего спуска. Более того, для задачи
минимизации квадратичной функции метод сопряженных градиен-
тов в отличие от градиентных методов сходится за конечное число
шагов (см. ниже теорему 1). Отсюда следует, что эффективность
метода сопряженных градиентов возрастает на завершающем эта-
пе поиска минимума, когда последовательные приближения близки
к точке минимума, ибо в'окрестности минимума достаточно глад-
кая функция, вообще говоря, близка к квадратичной выпуклой
функции. Это обстоятельство подтверждается также й практиче-
ским опытом решения конкретных задач минимизации.
Принятая здесь схема (1) — (4) метода сопряженных градиен-
тов предложена и исследована в работе [190]'; обзор других схем
и модификаций, обсуждение практического опыта применения
этого метода см. в работах [27, 35, 84, 149, 166, 170, 190, 235, 266].
Перейдем к исследованию сходимости метода сопряженных
градиентов (1) — (4). Для этого сначала докажем некоторые свой-
ства последовательностей, получаемых по формулам (1) — (4).
Лемма 1. Пусть J(u)^Cl(Em). Тогда при любом выборе
множества индексбв Л, /2, лишь бы /iU/2={0, 1, 2,...}, 0е/2, по-
следовательности {ип}, {рп} удовлетворяют соотношениям
(/'("*+i),P*) = 0, (J'(un)iPn)^\J'(u^ (п=0, 1,...) (5)
и
\Pn\2=\J'(un)\2 + ti\Pn-i\*>\J'(»n)\2 (/1=1,2,...). (6)
Доказательство. Соотношения (6) являются простым
следствием равенств (2), (5), поэтому достаточно доказать (5).
Воспользуемся методом полной математической индукции. Так
как ро=//("о), то второе из равенств (5) при п=0 очевидно, а
1 Следует заметить, что в [190] выражение для рп дано с точностью до зна-
ка. Это проще всего обнаружить проверкой условия (Арп, pn-i)=0, имеющего
место для квадратичных функций (см. ниже лемму 2); эта же ошибка по-
вторена в работе (35].

§7]
Метод сопряженных градиентов
103
равенство (J'{u{), ро) = («f'(wi), /'(«о)) =0 следует из того, что
£о(ао)=° при ао>0 и go(ao)>° ПРИ «о^О и формулы (1.4).
Пусть равенства (5) имеют место при некотором м^О. Пока-
жем, что тогда (5) верно и для /г+1. В самом деле, если an>0,
то согласно (3)
ё'п К) = — iJ' ("я — <*пРп) >Рп) = — (*' (*и-0 > Рп) = 0.
Если же ап = 0, то ип+\ = ип и
0 <£ (0) = - (/' (ип), рп) = - (/' (ип), V (ип)- РпРп-г) =
= -\J'(un)\2 = -\J'(un+i)\2<o,
следовательно, //(ttn+i) = 0 и (J'(un+i),pn) = 0. Наконец,
(Г (ип+1), рп+1) = (/' (ип+х)у J' (Un+l) - Pn+lPn) = I J9 (<M-i) I2. A
2. Сначала остановимся на случае квадратичной функции
J(u) = ±(Au9u)-ib9u)9 (7)
где А — известная симметричная положительно определенная
матрица порядка mYjny Ь — заданный вектор. К задаче миними-
зации такой функции сводится решение системы линейных алге-
браических уравнений Аи=Ь. В самом деле, здесь
J'(u) = Au—b. (8)
Так как J (и) — выпуклая (и даже сильно выпуклая) функция, то
согласно теореме 1.3 min/{a) будет достигаться в точке и* тогда
и только тогда, когда /'(«*) =Аи*—Ь=0.
Для минимизации функции (7) применим метод сопряженных
градиентов. Так как
gn (a) = J'(un — арп) = -±- а? (Арп, рп) — а (Г (ип)9 рп) + J (ип),
то min gn (а) достигается при
k(APn,Pn) (Арп,\Рп)
Преобразуем выражение для рл. Для этого прежде всего заметим, что
/' (ип) — J' (un+i) = anApnt п = 0, 1, (10)
Это равенство непосредственно следует из (1), (8). Пользуясь
исходными формулами (1) —(4) и равенствами (5), (10), полу-
чаем

104 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
(Г (и»), Г (ifc-i) - *' К)) = ал_! (/' (un), Арп-{), | J' (ц-i) |2 =
= (У (ил_0, p^O = (/' (a*-i) — /' (и*), Рд-i) =
= ад-i (Лрд-ь P*-i) (л = 1, 2, ...).
Следовательно,
(Лрл-i, Pn-i)
Как видим, для функции (7) метод (1) —(4) при /2={0},
iTj=){l, 2, ...} совпадает с методом сопряженных градиентов,
описанным, например, в работе [9].
Лемма 2. Если /2={0}, Л={1, 2, ...}, то для последова-
тельностей {ttn}, {рп}> получаемых по формулам (1), (2), (9),
(11), справедливы соотношения
V'{ud.Pi) = 0 (*>/), (/'("*W ("/)) = <> (1ф])9
(р„Лр/) = 0 (1фП, i,/ = 0, 1,2,... (12)
Доказательство проведем по индукции. Имеем (J'(Hi), р0) =
= C(*i). /'(Ц>)) = 0всилу (5);
(Mt Ро) = (Pi> АРо) =У («i) — PiPo» АРе) = 0
в силу (11). Предположим, что равенства (12) доказаны для всех
i, /<я при некотором п>1 и покажем, что (12) тогда будут верны
при всех i, /<я+ 1. Для этого достаточно доказать, что
(}' (a„+i), pt) = (J\(un+i), J' (ui}) = (ря+1, Лр,)]= 0, I = 0, 1,... , п.
Сначала убедимся в том, что (J'(wn+i), pt) = 0. При i = n это сле-
дует из (5), а при t</i с учетом (10) и предположения индукции
будем иметь
(/' (ид+1), Pl) = (У (ия) — Мрл, Рд = 0.
Тогда
tf' (Ии-i). /' (а,)) = (/' (Ии-i). Pi + fcpi-i) = 0?
при i = 1, 2,... ,rt и при i = 0
(/' (цн.0, J' (i/0)) = (/' (ия+1), р0) = 0.
Наконец, с учетом (2), (10) и предположения индукции при "всех i,
в<*<п имеем
(Apn+U Pi) = (Р/И-Ь Лрг) = (/' (Ид+i) -* рЛ+1рЛ, Лр<) =
= (/' (кя+1), Лр,) = — (Г (ия+1), /' (и,) - J' (к,+1)) = 0,

§7]
Метод сопряженных градиентов
105
а в случае i = n (рп+и Арп) = (Г (un+i) — fin+lpn> Арп) = 0 в [силу
формулы (11). А
Теорема 1. Если h={0}t Л={1, 2,...}, то метод сопря-
женных градиентов для квадратичной функции (7) сходится к
точке минимума не более, чем за m шагов (ш — размерность и).
Доказательство. Как следует из леммы 2, последова-
тельность {J'(un)}9 получаемая методом сопряженных, градиентов,
ортогональна: (/'(н*), 1'{щ))=Ъ (i¥=j> *, /=0, 1, 2,...). Однако в
/n-мерном пространстве не может быть более чем m ненулевых
взацмно ортогональных векторов. Следовательно, найдется наи-
меньший номер я, ft^Ai^m, такой, что //("п)=0. Так как J (и) —
выпуклая функция, то ип—точка минимума функции (7) в Em. А
3. Рассмотрим метод сопряженных градиентов для сильно вы-
пуклых функций.
Теорема 2. Пусть J (и) — сильно выпукла на Ет,
J(u)^Cl(Em)> и \J'(u)— J'(v)\ y^L\a—v\ при всех и, v^Emt
L=const. Тогда при любом выборе множества индексов h, 0е/2
и любом начальном приближении ио для последовательности {ип}
из (1) — (4) справедливы оценки
0<an=J(un) — Jm<a0q«, !ип — и*|2<— а^, л=0, 1, ...,(13)
И>
где
l8
/*=inf J(u) = J(u*)-Q=l- / ,0<q<\,
и€Ет [2L ([l2 + La)
\
Ц —константа из (1.12).
Доказательство. Из теоремы 1.7 следует, что нижняя
грань J (и) на Ет конечна и достигается в единственной точке и*:
/(«*)=/*. Функция gn(a)=J(un—арп) при рпФ0 также сильно
выпукла при ct^O, поэтому ап из условия (3) определяется одно-
значно. Можно считать, что рп¥=0, <хп>0, 1'(ип)Ф0 при всех
п=0, 1,... , ибо в противном случае У(ип)=0, и ип=и* — точка
минимума. В силу выбора ап: J(un+i)^J(un—арп) при всех
а^О. Поэтому с помощью формулы (Ы8) при v=un, и=ип—арп
будем иметь
/ (ип) — J (un+i) > J (ип) —J(un — арп) >
>a(J'(un),pn)—^\рп\\ а>0.
Используя второе равенство (5), отсюда получаем"
J(un)-J(ul^l)>a\J'(un)\i--^\pn\\ а>0, п = 0,1,... (14)

106 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
Далее докажем оценку
Y^IPnl2<U/(«n)l2,Y = L(1H!LV.Z). « = 0, 1, (15)
По теореме 1.4 (J'(un) — J'(un-{), u„—m»_i) >ц|ыя —u„_i [2, а
так как «„ — «n_i =—a„_ip„_i, то с учетом соотношений (5), (6)
имеем цс£_, | p„_i |2 < a„_i (/' (un-i), pn-i) = a„_i | /' («n_i) |2, или
!*«„_! I p^-! I2 -< | ^' («»_i) I2- Тогда из (4)
JB ,<:\J'M\L\un-un.1\ U'^Uon-ilPn-il _ L I J'Ы I
4Ря| |/'(«n-i)|s ^ |Mfcw.|fl»-il» Ц |P„-il *
ИЛИ
|(Ulp«-.l<—l^(«„)l.
Подставим это неравенство в (6)- и получим
IPn|2=U4^|2 + P«IPa-l|2<(l+-^)|J'(^)|2,
что равносильно (15).
Теперь нетрудно доказать оценки (13). С учетом неравенства
(15) и (14) имеем ап— ап+х > a(l ^-) I «^ ("*) I2 при любых а>0.
Следовательно,
ап-ап+х >тах a (l-J±-)\J> (un)\* =-У- \J'(un)\* (л = 0, 1, ...).
Ho | J' (wrt) |2 > цал (см. теорему 1.6), поэтому ап — ап+\ > -—^ ап,
или ал+1< (1 — -^l ]art = qant (л = 0, 1, ...). Отсюда имеем ал<
-СОД* (п-=0, 1, ...). Вторая из оценок (13) немедленно следует из
первой оценки и неравенства (1.15) при u = un. Остается заметить,
что 0<<7<1, ибо ii КL (см. замечание к теореме 1.5). А
4. В заключение заметим, что для минимизации гладкой
функции J (и) на замкнутом выпуклом множестве ИфЕт можно
использовать метод проекции сопряженных градиентов по схеме:
un+i=Pu(Un—anPn) (я=0, 1.,...)» где pn определяется согласно
(2), (4), величина an>0 выбирается из условия монотонности
^(«n)^/(ttn+i). Этот метод позволяет за конечное число шагов
найти точку минимума квадратичной функции (7) на параллелепи-
педе [190]; в общем случае сходимость метода проекции сопряжен-
ных градиентов, по-видимому, не исследована.

§ S]
Метод Ньютона
107
Упражнения. 1. Показать, что точка ип> полученная методом
сопряженных градиентов для функции (7) при /2={0}, есть точка
минимума J (и) на гиперплоскости, проходящей через точку щ и
натянутой на векторы {J'(uk)} (k=0t 1,..., п— 1). Опираясь на
лемму 2, выяснить геометрический смысл метода сопряженных
градиентов [19].
2. Описать метод сопряженных градиентов для функции
J(u) = \Au—b\2 из упражнения 1.16.
§ 8. МЕТОД НЬЮТОНА
1. Пусть функция J(u)^C2(U), где U — заданное множество
в Ет, в частности, может быть U=Em. Для решения задачи ми-
нимизации J (и) на U можно использовать метод Ньютона, заклю-
чающийся в следующем [155]. Пусть взято некоторое начальное
приближение u0^U. Если уже известно /г-е приближение Ип, то
приращение функции /(а)еС2(U) в точке ип можно представить
в виде
J{u)*-J(un)={J'(un), и^ип) + —-{Г{ип){и — ип), и — ип) +
+[о\\и-ип\)\
Возьмем квадратичную часть этого приращения:
•ММ = (J' ("п)> и — ип) + —{У (ип)(и — ип), и — ип).
Следующее приближение ип+\ определяем из условия минимума
Jn(u) на U:
Jn(un+l) = min Jn(u). (1)
В случае, когда U = Em, в точке минимума \Jn(u) на U произ-
водная /п(и) = У(ип) + У(ип)(и — ип) обращается в нуль, т. е.
J'n ("n+i) = J' (ип) + J" ("«) (un+i — ип) = 0. Если матрица Г (ип) не-
вырождена, то отсюда будем иметь un+i = ип— [J*(un)]-lJ' {ип)>
/г = 0, 1,.... Как видим, в случае [/ = £т описанный итера-
ционный процесс превращается в хорошо известный метод Нью-
тона [19] для решения уравнения /'(w)=0, определяющего стацио-
нарные точки функции J {и). Отсюда происходит название метода
и в общем случае.
Будем предполагать, что имеется некоторый эффективный
алгоритм для решения задачи (1) при каждом я=0, 1, 2,...
В случае U=Em таким алгоритмом может служить метод сопря-
женных градиентов, описанный в предыдущем параграфе, а так-

Ю8 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
же различные другие методы (см., например, [19] > решения систем
линейных алгебраических уравнений J'(un) +J"(un) (Un+i—un) =0.
В случае 1)фЕт при решении задачи (1) можно воспользоваться
одним из методов, описанных в предыдущих параграфах.
Нужно заметить, что задача (1) в общем случае может ока-
заться весьма трудоемкой. Но несмотря на это, применение метода
Ньютона во многих случаях оправдано, ибо он сходится значи-
тельно быстрее, например, градиентных методов, если только на-
чальное приближение выбрано достаточно близко к искомой точке
минимума функции. Обычно метод Ньютона и его модификации
применяют на завершающем этапе поиска минимума, когда с по-
мощью каких-либо более грубых, но менее трудоемких методов
уже найдена некоторая точка, достаточно близкая к точке мини-
мума.
Теорема 1. Пусть 7(и)еС2(£/) на выпуклом замкнутом
множестве U^Em, пусть |i|6|2.<(/"(tt)£, £) при всех £<=£т и
wsl/, и \\J"(u)— J"(v)\\^L\u—v\ при всех u9 V(=U, где \xf L —
некоторые положительные константы. Тогда задача (1) разреши-
ма при всех /г=0, 1, Кроме того, если начальное приближение
щ выбрано так, что ^=— \и{—м0|<1, то имеет место следующая
оценка скорости сходимости метода Ньютона:
00
К-и-К^^Ч-^-ТЗ^г- (" = 0,1,...). (2)
где и* — точка минимума J (и) на U.
Д оказ ательство. По условию (/"(а)|, £)^ц,|£|2 при всех
и^О и l^Em, n = const>0. Отсюда и из теоремы 1.5 вытекает,
что функция J (и) сильно выпукла на И> и, следовательно, соглас-
но теореме 1.7 ограничена снизу на U и достигает своей нижней
грани в единственной точке н*е[/. Далее, поскольку
Jn(u)=J"(un)9 то функция /п(и) также сильно выпукла на U и
достигает своей нижней грани в единственной точке ип+1е£Л
Таким образом, задача (1) всегда имеет и притом единственное
решение. Применив теорему 1.3 к функции Jn(u)f получим
(Jn(Un+\)> и — un+i)>0, u£U9 л = 0, 1,... (3)
Так как Jn (и) = /' (ип) + Г (ип) (и — ип), [то (3) перепишется в виде
(J'(un)+J"(un)(un+i — un)9 u — un+i)>0, ueu, /i = 0, 1,
(4)
Может случиться, что ип+1=ип. Тогда и*=ип+{ = ип. В самом
деле, в этом случае из (4) имеем (J'(un), u—un)^Q9 u&U. Со-

§ 8}
Метод Ньютона
109
гласно теореме 1.3 это означает, что в точке и*=ип функция J (и)
достигает своего минимума на I/, и, следовательно, задача решена.
Поэтому ниже всюду будем считать ип+1Фип(п=0, 1,...).
В (4) положим и=ип. Получим (J'(un) +J"(un) (wn+i—^n),
un—Un+_\)^0. С учетом этого неравенства и условия теоремы
имеем
|А|«п+1— Ия|1<(^(ия)(Ия+1 — Un), ИЛ+1—Ил)<(/'(«л). Un — Un+x),
л = 0, 1,..» (5)
Оценим (/' (ип)9 ип — ип+\) сверху. Для) этого в (3) заменим п на
п — 1. Получим (Jn-i(un)*r^u — ип) *> 0,1/: и б U (п > 1). В частности,
при u = un+i отсюда находим (J'n-\(un)> un — un+i)<0. С учетом
этого неравенства, формулы (1.7) и условия Липшица для J"(u) бу-
дем иметь
(/' (Un), Un — Un+x) < (Jf (Un) — j'tTi (Un), Un — Un+X) =
= (/' (ип) — У {ип-\) — J" (un-i) (ип — wrt_i), ип — un+i) =
= ([/" (Ut-i + Q(un— И/i-l)) — ^ (Wn-l)] «— Un-l),Un — Wii+l) <
<L\un — un-i\2\un — un+l\, n=l, 2,%..
Подставив полученную)(оценку Bj (5), получим
\un+i-unI <^un-Un-xW n\= 1, 2, .. .Ц (6)
Так как по условию q= — 1^ —WeKl1» то из (6) 'ПРИ п= 1 вы"
г1»
текает |Оа —"il< —<72- «Сделаем индуктивное предположение:
\un-un^\<j.g^l(n>^
Тогда из (б) имеем, что
l«n+1-^i<^(f)V*-')*=i^
Следовательно,

ПО МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
Отсюда находим.
/п—1 т—1 оо
i4.-*.i<_£i*«-%i<S-t«'<S^^<f-rf?- *
-*0 (7)
при т>п-^оо. Таким образом, последовательность {ип} фундамен-
тальна и поэтому сходится к некоторой точке и*. В силу замкну-
тости множества V точка «*et/. Переходя, к пределу в (7) при
/п-^оо, получим
00
|и'-ил|<-£У]<72* (л-0, 1,...).
Теперь остается убедиться в том, что и* — точка минимума /(и)
на U. Так как /(и1еС*(£/), то /'("nW("*)> /"(un)+/'>*) при
Пг^оо. Поэтому переходя к пределу в (4) при л-^оо, будем иметь
(/'(w*), и—и*)^0 при всех wet/. В силу теоремы 1.3 и выпук-
лости /(ы) это означает, что ы* есть точка минимума J (и) на f/.J^
Как видно из оценки и как подтверждает практика, метод
Ньютона сводится очень быстро, если начальное приближение щ
выбрано достаточно близким к точке минимума и*. Однако если
хорошего начального приближения щ нет, то метод Ньютона за-
частую расходится. В этом можно убедиться, на простом примере.
Возьмем фунвдию
•'<«>'=-15Г"* + т(1 + т)"'
при | и |< б,
J(u)=±u* + 2\u\-±b
при \и\ > 8, u£Elt
где б — произвольное малое положительное число, 0<б<1. Не-
трудно убедиться в том, что /(m)eC2(£i) и J"(u)^zl, так что
J (и) сильно .выпуклая функция. Эта функция достигает своего
минимума на Е\ в точке ы*=0. В качестве начального приближе-
ния возьмем ыо=б. Применяя метод Ньютона, получим последо-
вательность
«„ = ««-. IT""'? =(-!)"2 («=1, 2,...).,
которая расходится, хотя начальное приближение отличается от
и*=0 на малое число б.

* S]
Метод Ньютона
111
2. Возникает вопрос, нельзя ли изложенный выше метод
Ньютона видоизменить так, -чтобы модифицированный метод не
был столь чувствителен к выбору начального приближения? Такие
модификации метода Ньютона существуют, см., например, [81], [82].
Опишем одну из этих модификаций. Пусть U — выпуклое
замкнутое множество, /(w)eC2([/). Пусть выбрано произвольное
начальное приближение u0^U. Если un^U уже известно, то сле-
дующее приближение un+if^U находим так. Возьмем главную
квадратичную часть
Jn (и) = (/' (ип)9 и — ип) + -у (Г (ип) (и — ип), и —ип)
приращения J(u)—J(un)=Jn(u)+o(\u^-un\2) и определим вспо-
могательное приближение йп из условия:
Jn(un) = min Jn(u). (8)
Сразу заметим, что Jn(wrt)<Jn(ип) = 0. Далее полагаем
un+i = ип + ап (ип — ип), (9)
где ап выбирается из условий
ЛЦп) — J(un + a>n(Un — un))>ean\Jn(un)\t '0<<х„<1, (10)
г — некоторое фиксированное число, 0<е<1. Если ип не являет-
ся точкой минимума J (и) на U, то при некоторых ограничениях
на функцию J (и) можно доказать возможность выбора <гёЛ, ап,
ип+1 из условий (8—10) (см. ниже теорему 2), причем для ускоре-
ния поиска минимума желательно выбирать ап как можно* ближе
к 1. Метод (8—10) — естественное обобщение одного из вариан-
тов метода условного градиента (см. (6.1—2), (6.8)). В методе
условного градиента учитывалась лишь линейная часть прираще-
ния J (и)—J(un), а здесь учитывается квадратичная часть этого
приращения. Выбор <хп из (10) практически можно осуществлять
так же, как и в методе условного градиента. Именно сначала бе-
рец <хЛ=1 и проверяем условие (10). Если оно выполнено, то
оставляем <хп=1; если же (10) при ап = 1 нарушается, то
производим дробление ап до тех пор пока неравенство (10) не
выполнится, стараясь остановиться на значении ап, как можно
близком к 1. При некоторых ограничениях на функцию J (и) ука-
занный выбор ап может быть произведен за конечное число дроб-
лений. Замечательно также и то, что независимо от выбора на-
чального приближения описанный метод будет сходиться, причем
начиная с некоторой итерации, он превратится в метод Ньютона,
обретая, свойственную этому методу высокую скорость сходи-
мости.

112 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Лл. 2
Таким образом, метод (8—10) ненамного сложнее метода
Ньютона, по скорости сходимости не уступает ему и в то же вре-
мя не столь чувствителен к выбору начального приближения, как
метод Ньютона. При наличии эффективных методов минимизации
квадратичной функции Jn(u) на и метод (8—10) можно с успехом
применять для минимизации достаточно гладких функций.
Теорема 2. Пусть U — замкнутое выпуклое множество,
/(a)e=C2(t/), ^^(/"МЬ £><Л1Ш2 при всех 1<=Еп и всех
u^U, и пусть \\J"{u)—J"(v\\\^L\u^-v\ при всех и, vt=U, где р,
М9 L — положительные константы. Пусть ei — некоторое число,
0<е!<— -Ь (1-е).
Тогда на отрезке ei^ct^l при каждом п существуют числа <хп,
удовлетворяющие условиям (10) и среди них найдется максималь-
ное. Подставляя это максимальное <tn в (9) для любого началь-
ного приближения uo&Ut получим последовательность {tin}, для
которой: 1) {/(иЛ)} монотонно убывает и стремится к
/*=inf/(a) (л-^оо); 2) существует такой номер Ло=Яо(е), что
<7 =— 1*4+1 — 4rJ<lt и a«=lt Un+\ = un
I*
при всех п^Поу т. е. метод (8—10) с номера п=п0 превращается
в метод Ньютона, и, следовательно, будет верна оценка (2) при
всех п^По.
Доказательство. По условию (/"(и)£, £)^ц,|||2 при всех
«е(/ и l^Em, |x=const>0. Следовательно, J (и) — сильно выпук-
лая функция и в силу теоремы 1.7 ограничена снизу на U и до-
стигает своей нижней грани в единственной точке u*et/. Посколь-
ку /rt(u)=,T(wn), то функция Jn(u) также сильно выпукла_на U
и достигает своей нижней грани в единственной точке un^U.
Может случиться, что ип=ип. Тогда и* = ип = ип. В самом деле,
применив теорему 1.3 к функции ^п(и), имеем
(J'n(un), и — йп)>0,
или
(/' (ип) + J"(ип) (ип — ип), и — ип) > 0, иеи.
Если ип=ип, то отсюда следует, что (J'(un), u—un)^Q,_u^U.
В силу теоремы 1.3 и выпуклости J (и) заключаем, что и* = ип = ип,
и задача решена. Поэтому ниже будем считать, что ипФип, и,
следовательно, Jn(un)<Jn(Un)=0 при всех п=0, 1, 2,... Пока-
жем, что на отрезке ei^a^l существуют числа an, удовлетво-
ряющие условиям (10).

§ *1
Метод Ньютона
113
Обозначим иа=ип+^(ип—ип), 0<;«^1. Из выпуклости функ-
ции Jn (и) следует, что ш
К (Ua)<aJn(un) + (1 —a) Jn(un) = aJn(un)<0.
Тогда из формулы
/(^а)-/(^ = /Л^) + -^((^(^+ва(^-«Л))-
— J"(un))(un — un), un — un)t 0<а<1 (11)
будем иметь
J{un) — J(ua)> — Jn(ua)—^{M — \i)\un — un |2>а|7а(ип)| —
-I-yMl^-aJ2, 0<о<1. (12)
Так как Jn(u) сильно выпуклая функция и достигает своего мини-
мума на U в точке Un> то согласно теореме 1.6
|ия —ц,|*< — [Jn(un)-Jn(un)]^ — \Jn("n)\> л = 0, 19...
(Л р,
(13)
Подставим эту оценку в (12). Получим
J{Un) — J(tia)>a(A aj|Jn(wrt)|>oe|Jrt(in)|
при всех а, е1"<а<— <1. Таким образом,
множество тех а=аПэ Для которых выполнено условие (10), непу-
сто. Из непрерывности J (и) следует, что множество таких а зам-
кнуто и, следовательно, это множество содержит свою верхнюю
грань ап=^1. В соответствии с (9) полагаем ип+\ =,^аЛ.
Покажем, что для получаемой таким образом последователь-
ности {ип} при любом выборе начального приближения Uo^U
верны все утверждения теоремы.
Прежде всего с учетом <xn^ei из (10) имеем
lU(Un)— J(Un+\)>[Mn\Jn(un)\>eex\Jn(un)\>Ot п = 0, 1,...
(14)
Следовательно, {J{ur)} монотонно убывает и, кроме toix>, /(ил)>
>J*=iniJ(u)>—oo. Тогда существует UmJ(un) и Xim'lJ (tin+i)—
U Л-*оо ' Д-*оо

П4 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
— J (uJ] = 0. Из (14) теперь имеем | Jn (ип) \ -* 0, а из (13)—
\ип — ип\-+0(п-+оо). Следовательно, существует такой номер
от
ло = /го(8)» чт<> \Мп~"яК1""8 ПРИ всех п>по- Из (11) с
учетом условия Липшица для J"(u) и оценки (13)^|для всех а,
&i < а < 1, тогда имеем
J(un)—J(ua)>a\Jniun)\ —К — "nl8>
>Un("„)|a(l-^|u„-«„|) >о»|/я(в«)1
при всех я>п0. Это означает, что (10) выполнено при всех а„,
в1<а„<1 и, следовательно, максимальное среди таких а„ есть
ая = 1 при всех п > п0. А тогда согласно (9)
«»+i = й'п» *п (Ил+0 = К ("«) = mjnК (и),
т. е. начиная с номера п = /г0, рассматриваемый метод превращается
в метод Ньютона с начальным приближением иПш, таким, что
<7= —|ип0-и—Ищ|<1- Поэтому оценка (2) будет верна при всех
И*
п>п0. А
. Существуют и другие способы выбора an в (9), например, в
работах [81], [82] ап предлагается искать из условия минимума
функции J(un+u(un—ип)) переменной а при ti^a^l. О методе
Ньютона см. также в работах {4, 19, 27, 35, 46, 75, 81, 82, 97, 130,
152, 155, 170, 193, 235] и др.
3. На каждом шаге метода Ньютона и его модификации при-
ходится решать достаточно трудоемкую задачу минимизации квад-
ратичной части Jn(u) приращения J (и)—J(ип) на множестве U.
В частности, метод Ньютона для минимизации сильно выпуклой
функции J {и) на всем пространстве приводит к итерационному
процессу
ип+\ = ип — (J" (ип))-1 J' (ип), п = 0, 1, ... ,
на каждом шаге которого требуется обращать матрицу J"(un).
Возникает вопрос, нельзя ли построить методы минимизации,
обладающие высокой скоростью сходимости, как метод Ньютона,
и в то же время требующие меньшего объема вычислений на каж-
дой итерации?
В настоящее время такие методы известны. Они приспособле-

§8]
Метод Ньютона
115
ны для поиска минимума функции на всем пространстве и в общих
чертах сводятся к итерационному процессу:
ип+\ =и„ — anAnlJ'(un), л = 0, 1 (15)
где апфО скалярный множитель, Ап — квадратная матрица
т-ного порядка, такая, что \\Лп—/"(ап)||->0 (п-^оо).
Следуя [86], опишем один из способов выбора матрицы Ап и
величины ап в процессе (15). Зафиксируем какую-либо последо-
вательность векторов /о, г и..., Гп, .. *, обладающую свойствами:
1) kn|-^0 при /г-^оо; 2) существует число Y>0> такое, что опре-
делители Ап матриц, столбцами которых являются нормирован-
ные векторы
гп гп—\ ггь-т+1
\ra\ ' ^n-ll ' I'/i-m+ll'
удовлетворяют неравенству An^Y при всех м=т—1, т,...
В -остальном последовательность {гп} произвольна. Например,
можно взять
^0 = ^0^1» • • • > гт—\ — ^т—1 ^т> гт = **nfil* • • • » ^2т—1 =
= ^2m—1 £т> г2т == ^2т^1» • • • » Гя = Лп £ц-ь . . . #
где е/= (0, ..., О, 1, 0, ..., 0) —единичный вектор по оси Ом,
i — остаток от деления целого числа п на целое число
т, O^i^.m—1, последовательность Л,п-*0 при я-^оо, Яп>0 при
всех п=0, 1,...
Пусть последовательность {гп} с указанными свойствами уже
выбрана. Тогда матрица Ап в соотношении (15) при каждом фик-
сированном п^т—1 определяется из системы линейных алгебраи-
ческих уравнений
4Л-7 = /' (Un-j + rn-j) — ^ (И/*-/)» / = 0,1,..., т — 1.
(16)
Если полученная [при этом матрица Ап невырождена, то нахо-
дят Ап1 и при выполнении условия (AnlJ'(un), J'(un))>0 присту-
пают к выбору величины ап в (15). Для этого вначале полагают
<*п = <*Л> где
\_
i-mlni-l; R Г «'^' Ч»-»»*]2\.йп-ип = -А71 J>(un),
X L l"n-«nl» J /
R = const > 0, и проверяют справедливость неравенства
J(И/и-О — J(««)<еа„(J'(u„), «»<-"„)> 0<е<— (17)

116 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
(постоянные R, е являются параметрами алгоритма). Если нера-
венство (17) выполняется, то останавливаются на выборе ап=ап,
находят ип+\ по формуле (15) и переходят к следующей итера-
ции. Если же неравенство (17) не выполняется при ап = ап, то
производят дробление ап (например, последовательным делением
пополам) до тех пор, пока (17) не окажется справедливым, и
полученную в результате дробления величину принимают в каче-
стве ап в (15).
Если при каком-либо п^т—1 матрица Ап, определенная из
системы (16), окажется вырожденной или же (Ai^ J' (ип)9
J'(un))^0, то либо изменяют вектор гЛ и заново строят
матрицу Ап> либо полагают Ап=Е (Е — единичная матрица) и
ап в (15) выбирают, пользуясь каким-либо вариантом градиент-
ного метода; я-й шаг метода при всех п^т—1 описан. Если
О^/г^т—2, то в (15) можно принять Ап=Е и <хп при
я=0,1,..., т—2 выбирать, как в градиентном методе.
Пусть Rn— матрица, столбцами которой являются векторы т„,
Гд_1,..., [гп-m+i, a Qn — матрица, составленная из столбцов
У К + Гп)\— J' («й), . . . , /' (Un-m+i + Гп-n+i) — J' (Un-m+i).
Тогда^система (16) для определения Ап. может быть записана в виде
следующего матричного уравнения: AnRn = Qn. Отсюда видно, что
если Rn, Qn невырождены, то матрица Ап определяется однозначно,
Ап1 существует и A£l = RnQnl. Заметим, что матрицы /?д, <2„*отли-
чаются от Rn+\ и соответственно Qn+i лишь/одним столбцом! Это
обстоятельство позволяет получить^ достаточно простые и удобные
рекуррентные соотношения, связывающие матрицы А^+\ и ДГ1 [86].
Благодаря этим рекуррентным соотношениям существенно уменьша-
ется трудоемкость обращения матрицы Ап, и метод (15) — (17) ока-
зывается более экономичным по сравнению с описанными выше ме-
тодом Ньютона и его модификацией.
Отдельно остановимся на случае, когда векторы гп в (16) вы-
бираются по закону: rn = A,ne*+i, где i — остаток от деления п на
т, 0^/^т—1, числа %п>0 и Яп-^0 при /i->-oo, ^=(0,..., 0, 1,
0, ..., 0) — единичный вектор по оси Ou\ t=l, 2, ..., т.
Тогда система (16) решается в явном виде и, как нетрудно видеть,
матрица Ап будет состоять из столбцов
/>„..,+ У.< ei)-/'("„__<) У ("n-i+i + V-w g2) - У K-i+i)
i * а »• • • >

§9]
Метод штрафных функций
117
У K-t-g + K-i-l ет) - «Г (я^-!)
V-i—1
Для сравнения вспомним, что матрица Г(и) состоит из столбцов
дГ (и)
dui
dJ' (и)
ди™
W (и)
ди*дит
&J(u)
дитдит
Отсюда видно, что столбцы матрицы Ап представляют собой
разностную аппроксимацию соответствующих столбцов матрицы
У"(и) в специально выбираемых точках, и метод (15) — (17) пре-
вращается в разностный вариант метода Ньютона. Поэтому мож-
но ожидать, что метод (15) —(17) будет обладать высокой ско-
ростью сходимости. Строгое Доказательство этого факта для силь-
но выпуклых функций J(u)^C2(Em) проведено в работе [86]. Та-
ким образом, метод (15) — (17) имеет скорость сходимости, близ-
кую к скорости сходимости метода Ньютона и в то же время
является более экономичным по сравнению с методом Ньютона с
точки зрения количества вычислений производных минимизируе-
мой функции и трудоемкости обращения матрицы Ап на каждом
шаге. Для квадратичной функции, определяемой равенством
(7.7), метод (15) — (17) сходится за конечное число шагов [86].
Различные варианты метода (15) — (17), обзор близких методов и
библиографию см. в [84], [86], [258].
Отправляясь от соотношений (15) —(17), в работе [87] постро-
ен быстросходящийся метод минимизации, не требующий вычисле-
ния производных минимизируемой функции. В этом методе выра-
жения градиента, встречающиеся в соотношениях (15) —(17), за-
меняются разностными отношениями функции в подходящим обра-
зом выбранных точках. Другие методы минимизации функций, не
требующие вычисления производных минимизируемой функции,
описаны в работах [235], [262], [265]; библиографию и обзор см. в
[87], [265]. Эти методы удобно применять в тех случаях, когда вы-
числение производных минимизируемой функции связано со зна-
чительными трудностями.
§ 9. МЕТОД ШТРАФНЫХ ФУНКЦИИ
Пусть функция J (и) определена на всем пространстве Ет и
требуется минимизировать J (и) на множестве ифЕт. Идея мето-
да штрафных функций заключается в замене исходной задачи

118 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
задачей минимизации однопараметрического семейства функций
Jk(u)=J(u)+Pk(u) на всем пространстве, где Ph(u) — функция,
выражающая собой «штраф» за нарушение ограничений wet/,
a k — параметр, регулирующий величину «штрафа».
Для примера возьмем задачу на условный экстремум из клас-
сического анализа: найти минимум функции J (и) на множестве
U = {u:gi(u) = Qy i=l,2,...,s}, (1)
где J(u)t gi(u) — заданные функции, определенные на всем про-
странстве -£т« Рассмотрим функцию Jk(u)=J(u)+kg(u), где
s
lg(u) = У] g* (и)> k — достаточно большое положительное число.
Слагаемое kg(u)^Ph(u) служит «штрафом» за нарушение усло-
вия u^U: если u^U, то Pft(a)=0, а если u&J, то Ph(u)>0 и
при небольшом нарушении ограничения g(u)=0 величину «штра-
фа» можно сделать как угодно большой" за счет выбора больших
k>0. Далее будем решать задачу минимизации Jk(u) на Ету
используя те или иные известные методы минимизации. Пусть
h{ti) достигает своего минимума на Ет в точке Uk. Можно наде-
яться, что с ростом k функция /а (и) будет достигать минимума в
таких точках ик> которые все точнее и точнее удовлетворяют огра-
ничению g(и) = 0, и, кроме того, Л (uk)-*J* = inf J (и).
Определение 1. Функцию Ръ.(и) называют штрафной
функцией множества U, если Ph(u)^0 при всех ие£т и k>0, и
( 0, если и 6 U,
lim Pk(u) = \ , , 77
а-ч-оо I + оо, если и g U.
Приведем примеры штрафных функций для множеств, зада-
ваемых с помощью одного неравенства
U={u:ueEm,g(u)<0}, (2)
где g(u) — известная функция, определенная на всем простран-
стве.
Заметим, что в таком виде представимы широкие классы мно-
жеств. Например, множества, задаваемые системой неравенств
ftM<0(i=l s), нетрудно записать в виде (2): для этого
в (2) достаточно взять
где принято обозначение [g(w)]+=max{0; g(u)}. Множества вида
S
(1) также записываются в виде (2) при g(u)=J\gf(u).
*«=i

§9]
Метод штрафных функций
119
В качестве штрафной функции множества (2) могут служить,
например, следующие функции:
Pk(и) = k[g(и)]+. Pk(«о =k(to(")l+)2>
Pk (и) = -1 **<">, Р* (и) = (1 + to(«)]+)*- 1
и др. В зависимости от метода, применяемого для минимизации
функции Jh(u)=J(u)+Pk(u) на Ет% при выборе штрафной функ-
ции надо учитывать ее гладкость, удобство вычисления значений
функции и ее производных и т. п.
Важно заметить, что нет необходимости точно решать задачу
минимизации /&(«) на Ет при фиксированном £>0, а нужно лишь
позаботиться о том, чтобы с ростом k эта задача решалась все
точнее и точнее. А именно обычно берут какую-либо функцию
€=e(Aj)>0 при &>0, е(&)->-0 при й-^оо и с помощью того или
иного метода минимизации определяют точку Uk> такую, чтобы
Л= inf Jk(u)<Jk(uk)<£Jl + B(k), k>0. (3)
и*Ет
Теорема 1. Пусть функции /(«), g(u) определены и непре-
рывны на £m, inf У(и)> — оо, пусть и= {и :g(u)^.Q}. Пусть
Ет
штрафная функция множества U имеет вид Pk(u)=Qh(g(u))
(см. выше примеры), причем; 1) для каждого k функция Qk(g)
определена, непрерывна и неотрицательна при эсех g;
2) Qh(g)>0, монотонно -возрастает по g и limQk(g) = +°о при
Л-*оо
g>0; 3) если g^O, то Qh(g)-*0 (&-*+оо) равномерно относи-
тельно g^O. Пусть {tik} определены из условий (3) при некоторых
е(£)>0, е(А)-^0при*-^+с».
Тогда: 1) lim J(uk)^J* = inf/(и), lim g(wA)<0; 2) если мно-
гое «ее/ л-»+оо
жество {uk} при Л->- + оо будет иметь хотя бы одну предельную
точку и*, то и* — точка минимума J (и) на U; 3) если множество
Ub = {u:g (и) < 6} ограничено хотя бы. при одном б = б0 > 0, то
lim J(uk) = J*, p (uk, U) = inf\uk — u\-V0 (k->-oo) и любая предель-
*-*» ueu
ная точка {uk} при k -* + оо будет точкой минимума У (и) на U, а в
случае единственности точки минимума \uk — ы*|'-*0 (&->-оо).
Доказательство. Пусть {t/m} — какая-либо минимизирующая
последовательность J (и) на (/, т. е. am6t/ и J{vrn)-+*J*(m-+oo).
Возьмем произвольное е>0. Тогда найдутся такие числа т0>0,
*о>0, что /(t;m)</* + e, е(£)<е, Pk(vm) = Qk(g(vm))<e при всех
(n>m0 и £>£0. Следовательно, с учетом (3) получаем

120 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
J(uk)<Jk(uk)<Jl + s(k)<Jk(vm)+e =
= J (vm) + Pk(vm) +e<J* + 36.
Отсюда в силу произвольности е>0 имеем lim J(uk)^J*. Далее»
Qk (ё (и*)) = h (uk) — J (uk) <J* + 3b — inf / (u) < oo при всех ft > ft0.
Em
Это возможноЦтолько при limg(aл)<0,, ибо [ъ противном случае
А-*оо
существовала бы последовательность Ukn> для которой limg(u*) =
= а>0 и
0<^(т)<^(гК))^ + °° (л-*оо).
Наконец, пусть и*— предельная точка множества {uk} при ft-*с»,
*. е. существует последовательность Ukn -* а* (л-*оо).}; Тогда
lim g (мь) = g (и*) <-; о, т. е. и* 6 £/. Следовательно,
J* < / (и*) = lim / (uk) < lim J (и*) < У,
[•П-*оо Л-*оо
т. е. J (и*) = /\ Последнее утверждение теоремы теперь очевидно.^
Если множество U задается несколькими ограничениями типа
неравенств или равенств, то на практике часто бывает целесооб-
разно штрафовать не все из этих ограничений, а только некоторые
из них. А именно пусть f/={w:weC/1 и gi(u)^.0, *=1, 2,..., 5}, где
U\ — множество достаточно простого вида и реализация тех или
иных методов минимизации функций на множестве U{ не встречает
больших затруднений. Тогда на ограничения £<(к)^0(/=1, 2,...,s)
можно наложить штраф с помощью какой-либо штрафной функ-
ции Рн(и) и перейти к задаче минимизации функции
h(u)=J(u)+Pk(u) на множестве 0{. Теорема 1 и ее доказатель-
ство и в этом случае полностью сохраняют силу, причем все рас-
смотрения достаточно провести на множестве U\\ в частности,
здесь нет необходимости задавать функции J (и), gi(u), Pk(u) на
всем пространстве Ет.
Метод штрафных функций дает простую и универсальную схе-
му решения задач минимизации на множествах 1}фЕт и часто
применяется на практике. Однако, как показывает численный
опыт, при больших значениях ft нахождение точек Uh, удовлетво-
ряющих условиям (3), с ростом ft становится все более трудным.
Это связано с тем, что с ростом ft методы минимизации, исполь-
зуемые для определения tih, сходятся все более „медленно, и, кро-
ме того, оперирование с большими числами ft также вносит допол-

§ щ
Теорема Куна — Таккера
121
нительные погрешности в вычисления. Поэтому на практике целе-
сообразно поступать Следующим образом. Сначала нужно задать
достаточно быстро возрастающую последовательность k=kn
(например, &п = 10п, п=19 2,...) и использовать метод штрафных
функций до таких возможно больших я, пока удается получить
достаточно быстрое убывание функции J (и) q небольшой затратой
машинного времени. При этом для малых п слишком точное ре-
шение задачи минимизации Jk(u) нецелесообразно, и успех в при-
менении метода штрафных функций часто зависит от согласован-
ного выбора величин кп и e(ftn)=en. Если на этом пути не уда-
лось получить решение с требуемой точностью и процесс движения
к минимуму при некоторых п сильно замедлился, то далее прибе-
гают к услугам других более тонких и, вообще говоря, более тру-
доемких методов минимизации, позволяющих получить решение
задачи с требуемой точностью. Решение, полученное с помощью
метода штрафных функций на одном этапе, полезно использовать
в качестве начального приближения на следующем этапе.
Различные аспекты метода штрафных функций рассматрива-
лись, например, в работах [27, 35, 75, 109, 155, 170, 171, 192, 229,
235, 260]. Подробное изложение различных вариантов метода
штрафных функций, обсуждение вычислительных аспектов этого
метода, большое число примеров можно найти в книге [235].
В работах [55, 229] исследован другой способ учета ограничений
типа (2), заключающийся в специальном выборе нелинейного
преобразования координат, позволяющем перейти от задачи на
условный экстремум к задаче.поиска экстремума функции на всем
пространстве.
§ 10. ТЕОРЕМА КУНА — ТАККЕРА
В этом параграфе рассмотрим теорему Куна — Таккера, за-
нимающую важное место в теории выпуклого программирования.
Эта теорема представляет собой обобщение классического метода
множителей Лагранжа [126] для определения экстремума при на-
личии ограничивающих условий на случай, когда последние содер-
жат не только равенства, но и неравенства.
Будем рассматривать задачу минимизации J (и) переменных
и= (и\ и2,..., ит) на множестве
U{u:ueULi gt(u)<0 (t=l,2,...,s), ft(a) = 0 (i = 1, 2, ... ,p)},
где Ui — заданное множество в ЕШу функции J (и), gi(u), gi(u)
определены на U{. В частности, возможно, f/is£m, или
(Л={«:ы*>0(/=1,2,...,т)}.
В дальнейшем для каких-либо двух векторов х= (х\, ..., хп),
*/= (у\..., уп) будем писать х^у, понимая под этой записью
выполнение следующих неравенств: xi'^yi(i=l9 2,.., п). Если же
х*>у* (f=l, 2,.., n)t то будем писать х>у. Тогда сформулирован-

122 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
ную задачу- минимизации можно кратко записать в следующем
виде:
min/(a), U={u:uZUl9g(u)<Q9g(u) = 0}9 (1)
«ее/
где g= (gu ..., gs)9 g= (gu ..., gp). Условия g(u) =0 называют огра-
ничениями типа равенств, условия g(u)^0 — ограничениями типа
неравенств. Разумеется, условие u^Uu возможно, представимо
посредством ограничений указанных типов, однако нам будет
удобнее сохранить это условие именно в таком виде.
Введем переменные к ^ (ji, ji), Ji = (ji^. • • , £s)> И = (^i» > Ир)
и составим функцию: L (u9 X) = J(u) + (ц, g (u)) + (ц, g (u))9 называе-
мую функцией Лаеранжа задачи (1).
Определение 1. Точку (и\ Я*), u*eUl9 ЪГ = (£*, и*), |?>0
называют седловой точкой функции Лагранжа L (а, Я) в области
игхА19 где Л!=-{Я=:((Г, |A):]ie£s, £>0, fi€£p}, если
L(и*, Я)<L(u\ V) <L(u9 V) при всех a € tfi, X6Лх. (2)
Теорема 1. Для того чтобы точка u*^U\ была точкой ми-
нимума функции /(и) на £/, достаточно существования точки
A,*eAi, такой, чтобы пара (и*, X*) была седловой точкой L(u, %)
в области I/iXAi.
Доказательство. По условию точка («*, Я*) eL^XAi —
седловая точка L(u, А,), т. е.
/ («О + (й, г («О) + (и, в («О) < J (*) + <Р, g (Ю) +
+ (И*, £ («О) < J (и) * (Р, i (")) + (|i#, £ (и)) (3)
при всех'и 6 L^ и К£Аг. Покажем, что тогда u*£U. Из левого не-
равенства (3) при |Г"= |х* имеем (ц* — ц, g(u")) >0 при любых ц€£р,
что возможно только при g(u*) =0. Далее, при ц = |а* левое нера-'
венство (3) дает (ц* — И,#(и*))>0 при всех ц>0, что_возможно
только при g\ff) < 0. В самом деле, если" здесь ^зять fi = (|it,...
... ,j2_b №,№+ь ,Й?), то будем иметь (£ — №)£<("') >0 при
всех ji; > 0, откуда gf (a*) <0 (i = 1, 2, , s). _Таким образом,
*? 6 £/. Заметим, что если gt (и*) < 0, то обязательно ц/" = 0, и поэтому
ff- Й№(Ю = 0, t = 1,2, ,s. (4)
Отсюда и из g (и*) ±= 0 следует
ОЛ £("*)) = 0, Г,£(*О) = 0. (5)

§ щ
Теорема Куна — Таккера
123
Так как (i*>0, то с учетом равенств (5) из правого неравенства (3)
при любом и 6 U будем иметь J {и*) < J (и) + (ц\ g (и)) + (ц*, g (и)) <
<J(u), т. е. /(a*) = inf /(и). А
Теорема 1 доказана без каких-либо ограничений на функцию
J (и) и множества £Л, U. Обратное утверждение, к сожалению,
неверно и при довольно жестких ограничениях на данные задачи
(1), как, например, выпуклость функций J (и), g{u)> g(u) и вы-
пуклость множества U\. Чтобы убедиться в этом, достаточйо взять
J(u)=—u9 Ui = {u:u^0}, g(u)=u2. Здесь множество U состоит
из одной точки н=0 и min/(w)=/(0)=0, w* = 0, но функция
L(u, Х) =—и+Хи2 при w^O, Х^О вообще не имеет седловых точек
типа (2). Однако теорему 1 можно обратить, если функция J (и)
и множество U\ выпуклы и, кроме того, множество U удовлетво-
ряет некоторым дополнительным условиям регулярности.
Определение 2. Множество U={u:u^Uu g(u)^O), где
U\ — выпуклое множество в ЕШу gi(u) — выпуклые функции на
1/1(1=1, 2 ,..., s), назовем регулярным, если^ля любого Я=ц,^0,
ХфО существует точка uet/ь такая, что (Я, g(v))<0.
Для регулярности множества U достаточно существования
точки v^U\9 для которой g(v)<0 (условие Слейтера). Множество
U будет регулярным и _тогда, когда существуют точки
Ui^U (.1 = 1, .., s), такие, что gi(tk)<.Ot i=l, ..,5. В этом случае
точка
s
v = — V «j б Ux и удовлетворяет неравенству g (v) < 0.
Теорема'2 (теорема Куна — Таккера). Пусть множество
И—{и:и^ии g(u)^.0}y где U{ выпукло, gi(u) — выпуклые функ-
ции на Z7i(/=1, 2,Г., 5), удовлетворяет условию регулярности, и
J (и) является выпуклой на U\. Тогда, для того чтобы в точке
u*^U\ достигался минимум функции J (и) на множестве U, необ-
ходимо и достаточно существования точки А,*^0, такой, 4Tojnapa
(и*Д*) образует седловуюточку функцииL(u,X)=J(u)-{'(X9g(u))
в области f/iXAi, где Ai = {X: Ae£s, Я>0}.
Доказательство. Достаточность доказана в теореме 1.
Докажем необходимость. Пусть w* — точка минимума J (и) на U.
Покажем, что тогда функция L(u9 X) в области t/iXAi имеет сед-
ловую точку (и*, X*). Для этого в 5 + 1-мерном пространстве пере-
менных а=(£о, 6) = (So, ib.., h) введем два множества А и В
следующим образом:
А = (J Ли,

124 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
где
Ат = {а = &, 0 : g >*(а), Ь > / (*)>,
Множества Л и В не имеют общих внутренних точек. В самом деле,
если 6=(5о, 6)€Д°э то К0, £о <'("*)• В то время как для точек
я = (£о> 5)6 Л имеем l0>J(u)^>J(u*)y в случае и6 U, а если же
u£Ul9 но u£Uy то найдется такой номер i, l<t<s, что £^>
>&(и)>0. Таким образом, Л° П 5°= 0. Далее, Л и В — выпук-
лые множества в £s+i. В самом деле, если aL = (£о, £0 6 Л ({=1,2),
то существует ^ 6 U\ такое, что «а* 6 ЛИ/. Покажем, что тогда
оа = аа1 + (1-а)а2=(а^ + (1-а)^, с# + (1-а)£2)€ Л„а
при любом а, 0 < а < 1; здесь иа = анх + (1 — а) и2 6 Ux в силу вы-
пуклости Ux. Из выпуклости J(a), #(и) имеем
g(ua) <oig(uJ + (1 -e:)g(wa)< ag1 + (1 -а)£2,
/(«а) <aJ(uj'+ (I-a) J(u2) <agj + (1 —о)&
Следовательно, aa 6 ЛИа cz Л при любом а, 0 < а < 1. Аналогично
доказывается выпуклость В.
Согласно теореме 5.5 тогда существует гиперплоскость
(с, a)=a=const с направляющим вектором c=(v0, АО^О, кото-
рая разделяет множества Л и В. Это значит, что
(c9b)<a<(cfa), a£A, Ь£В. (6)
Левое неравенство (6) возможно лишь *при с^О, ибо во множе-
стве В' содержатся точки &=(£о, £) со сколь угодно большими по
модулю отрицательными координатами. Покажем, что vo>0. Если
допустить vo=0, то из c=(v0, /о)¥=0 следует 10Ф0. В силу регу-
лярности множества U тогда найдется такая точка veU\9 что
('о, g(v))<0. Положим в (6) a=(J(v)f g(v)l(=AvczA9
6=(/(w*), 0)еЯ. При vo=0 получим неравенство (4>, g(v))^0,
противоречащее определению v. Следовательно, vo>0, /о^О.
Примем теперь в (6) а = (J (u), g(u)) 6 Аи с Л, 6 = (/ (и*), 0) 6 В.
Будем иметь v07 (н*)< v0/(и) + (/0, g(w)), или если разделить на
v0>0 и принять X* = -£-, то
v0
У (и*) <£ J (и) + (Г, g(u)) при любом a 6 Ux. (7)

* щ
Теорема Куна — Таккера
125
В частности, при и = и* отсюда следует, что 0 < (k*9 g(u*)). Но
^*>0, g («*)<0, поэтому возможно лишь равенство (A,*, g(u*)) = 0.
Так как (Я, g(u*)) <0 при лю_бом V>0, то из (7) окончательно имеем
L(u9 Xе) = J(u) + (Г, в(«)) >'(«0 = '(«•) + (**. *(«0) =
= L (и*, Г) > / (а*) + (Л, g (и*)) = L (и\ X)
при всех u£UX9 Я>0.А
На примере простой задачи min (—u)t U={u:u^0f ы2.^0}
мы убедились выше, что теорема 2 неверна для выпуклых мно-
жеств без дополнительного требования регулярности. Однако если
множество U определяется линейными уравнениями и неравен-
ствами, то теорема Куна — Таккера, оказывается, верна без до-
полнительных условий регулярности. Важную роль при установ-
лении этого факта и в некоторых других вопросах играет следую-
щая теорема.
Теорема 3 (теорема Фаркаша)-. Пусть даны векторы
Ci = (cil9 ci2y... ,cim) (i = 1, 2, ... ,р)
и
Ъ = {cilt ci29 ,ctj (i = 1, 2, ... ,n).
Пусть Q — множество всех тех векторов /=(/ь..., lm)^Emy ко-
торые удовлетворяют условиям
(^/) = 2><А=° (^=1,2, ...,р),
/-1
6,/) = £^/,<0 (*=1,2,...,/*).
У-1
Тогда для того, чтобы некоторый вектор у= (Уи..., Ут) удовле-
творял неравенству
т
(У, I) = £ М < 0 пРи всех / 6 Q, (8)
необходимо и достаточно, чтобы у можно было представить в виде
линейной комбинации векторов й, с\
р *
У = %№+%№> (9)

126 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
где \it > 0, i = 1, 2, ... ,л, аць { = 1, 2, ... , р, могут быть произ-
вольными ([114], [116], [134] и др.).
Доказательство. Достаточность. Пусть вектор у пред-
ставим в виде (9). Тогда при любом /£Q имеем
(у, I) = ffihici, 0 + £ fc й. 1) = У ЙЙ. /)<о,
*=i (=i t=i
т. е. неравенство (8) справедливо при любом /6Q.
Необходимость. Пусть вектор у удовлетворяет условию
(8). Покажем, что тогда имеет место представление (9). В про-
странстве Ет введем множество
Z={z=(z\ ,гт):г=£^, + £йсь jl, >0,
i = 1, 2, ... ,п, ць t = 1, 2, ... ,p —произвольны!.
Нетрудно видеть, что множество Z — выпукло и замкнуто (дока-
жите!). Для доказательства теоремы достаточно установить, что
y^Z. Предположим, что y&zZ. Тогда согласно теореме 5.4 сущест-
вует гиперплоскость (/, z—у)=0 с направляющим вектором
1= {К • •, 1т) ¥=0, строго разделяющая множество Z и точку у, т. е.
(/, z—у)<0 при всех z^Z. Заметим, что поскольку OeZ, то
(/, у) >0. Покажем, что teQ. В самом деле,
(/, z) = £ щ (с,, /) +£ й {ch I) < (/, у) = const
i=\ 1=2
при всех. Цг^О и произвольных |Шг» что возможно только при
(ct, 0 =0, *= 1, 2,.., р, (а, I) ^0, i= 1, 2,. t, п9 т. е. /efi. По усло-
вию (8) тогда (у, I) ^0, в то время как по построению (/, у) >0.
Пришли к противоречию, которое и доказывает теорему. А
Рассмотрим следующую задачу: найти
min/(*/), £/ = L=( : W>0> /6/, Ли = 6, Ли<&1, (Ю)
где / — некоторое заданное подмножество индексов / среде 1</<^
(в частности, возможно, / = 0, или / = {/:!</< т})\

§10] w Теорема Куна — Танкера 127
заданные матрицы и векторы. Если р=0 или s=0, тогда убудем
считать, что в (10) ограничения Аи=Ь или соответственно Аи^Ь
отсутствуют. _
Пусть _Л*, Л* — матрицы, полученные транспонированием
матриц Л, А соответственно; (Au)it (Au)i — t-тые координаты_век-
торов-столбцов Аи, Аиу полученных умножением матриц Л, А со-
(иХ\
ответственно на вектор-столбец и=\ • J; ит=(и],... ит) —
\ит)
вектор-строка (впрочем, если это не может привести к недоразу-
мениям, знак Т в обозначении вектор-строки будем часто опус-
m
кать); (и, а) = £ и1 а1— скалярное произведение векторов-столб-
цов ы, а^Ет\ е,= (0,..., 0, 1, 0,... 0) — /-тый единичный коор-
динатный вектор;
\a>pi) W/ VW VW
t-тые столбцы матриц Л, Л, Л*, Л* соответственно. В этих обозна-
чениях имеем
mm т
= (Л?, и), (Ли)4 = (Л-, w), и' = (ери),
и задача (10) может быть записана в виде (1): найти minJ(u),
«ее/
и = {и:иеиг, гЛ«) = оО)-*1 = о (*=i,...,P),
&(и)^(А1и)-Ь(<0 (t=l,...,s)},
где ^ = {^^6^, w'>0, i6/}.
Теорема 4. Пусть /(ы) — гладкая выпуклая функция на
множестве U\. Тогда, для того чтобы точка и*е£/ была решением
задачи (10), необходимо и достаточно существования точки
Г = (^,ЮеЛ1 = {Х = (^|1) :peESf ц>0, ц££р},
такой, чтобы пара (и*, Я*) образовала седловую точку вида (2)
для функции L(u, Я)=/(ы) + (|л, Аи—b) + (\it Au—b) на множе-
стве UxXAi.

128 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ • [Гл. 2
Доказательство. Достаточность доказана в теореме 1.
Докажем необходимость. Пусть и* — точка минимума функции
J (и) на U. Покажем, что функция L(u, X) на множестве ^iXAi
имеет седловую точку (и*, %*). Направление /=(А,••, 1т) ФО на-
зовем возможным в точке и*, если существует число а0>0, такое,
что tt=u*+.atet/, т. е.
ui=ui* + ali>0 (iei)> A(u* + at) = b, Л(и* + <х/)<&
при всех а, 0<а<Оо. Введем множества индексов
ft = {l:l<i<s9 (АО, = &<>, Il = {i:tei. и<* = 0}.
Нетрудно видеть, что направление 1^0 будет возможным в точке
и*тогдаитолько тогда, если Л/=0, (Л/)^ <0 (* 6 /J), /, >0 (i 6 /2), или
(Ль /)=0 (I = 1, ... 9р)*($91) <0 (*€ 1\),
(-^0^=^Г<0 (fgTk (11)
Заметим также, что в силу выпуклости множества V направление /
будет возможным тогда и только тогда, когда существуют точка
ttgi/, ифи* и число е>0, такие, что 1 = е(и — и*). Поэтому в си-
лу теоремы 1.3 будем иметь (J'(u*)f и~ и*)>0 при всех u(-U или
(У (а*), /) >0 для любого /, удовлетворяющего условиям (11). Поло-
жим в_теореме 3 у = —У' (а*), с^ = Л*, а в качестве ^ возьмем век-
торы Л/ при i£l\ и — ^ при i 6 /2- Как вытекает из (11) и неравен-
ства (—/'(аф),/)<0, все условия теоремы 3 выполнены, и, следо-
вательно, существуют числа й>0 (i'6/i), Й>0 (f 6 /2) и Pi(i =
= 1,2,..., р), такие что [
-/'(«•)*£>'*' + ££Л+ £ц1(-е£). (12)
Положим Г = ф*, (х*),; где ц* = (ц^,. ^, ц^), j? = (jit,... ,$.*), Hi и
ц\ взяты из (12), недостающие числа n*(t'^/t) положены равными
нулю. Тогда (12) можно переписать в виде?
J' (и*) + Ау + Л V = £ $et, ? > 0, ИХЙР€ #• (13)
Покажем, что (и\ V) — седловая точка функции L(«, A,).= /(u) +
+ (ji, i4u—ft) -f (ц, Ли —6) на множестве l/x х Лх. В самом деле,
L (и, Г) - L {и\ Г) = J(u) — J (и*) + (F, А (и - и')) + ((Л А (и — и'))

§10}
Теорема Куна — Таккера
129
Для гладкой выпуклой функции всегда J (и) —J (и*) >'(/' (и*)у и—и*),
поэтому с учетом (13) для любого и £UX получим
L (и, Г) — L (и\ Г) > (/' (и*) + АУ + ЛV\ и — и*) =
= £ Wi(e»u-u*)= £.^(w'-wO = J] И>>0.
*€/J t€/2 «6/g
Наконец, при всех К 6 Лх будем иметь
1(«Л r)-L(w*, Я) = (|T-|i, А*' —6) + ((1*-ц, АГ-6) =
так как ц<>0, (Ли* —&);<0 при i^/i-A
Теоремы 2 и 4 являются частным случаем следующей более
общей теоремы, которую также принято называть теоремой Ку-
на — Таккера. _
Теорема 5. Пусть U={u:u^Uu g(u)^:0± g(u)=0\, где
Ui—заданное выпуклое множество из Emy g(u) = (g\(u)t ..., gs(u))>
g(u) = (g\(u)> ^ gp("))> причем функции gi(u), i—l9 2, ..., s, и
часть функций g%(u) при t = l, 2^..., r.^s являются линейными,
т. е. существуют векторы аг-, а*_ и числа 6*, &*, такие, что
gi(u) = (ai9 и)—Ьи * = 1, 2,..., р, gi(u) = (au и)—Ъи *=1, 2,..., г,
а остальные функции gi(u), /=г+1,..., s, выпуклы на £Л и не
являются линейными (возможно, что s=0 или г=0, или г=5, или
р=0, т. е. некоторые из ограничений g(u).<C.O или g(w)=0 могут
отсутствовать в представлении множества U). Пусть существует
точка v<=Uu такая, что gi(v)<0 при /=г+1,..., 5 (если r=s, то
это условие отсутствует), и пусть J (и) выпуклая функция на U\.
Тогда, для того .чтобы в точке u*^U\ достигался минимум функ-
ции J (и) на множестве £/, необходимо недостаточно существова-
ния точки Я*=(|г*, fi*)eAi = {X=(jbi, \х) \i^Es, \х^0у \i^Ep}, та-
кой, чтобы ^ара (и*, Я*) образовала седловую точку вида (2) для
функции Лагранжа L(u, X)=J(u) + (\x9 g(u)) + (\x g(u)) на мно-
жестве U\XA\.
Доказательство этой теоремы см., например, в работе [269],
§28.
Теорема Куна — Таккера имеет многочисленные приложения
в теории экстремальных задач. В частности, с помощью этой тео-
ремы в следующем параграфе будет доказан ряд важнейших
теорехм линейного программирования. Теорема Куна — Таккера

130 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
является также основой многих итерационных методов минимиза-
ции, сводящихся к поиску седловой точки функции Лагранжа.
Различные варианты теоремы Куна —'Таккера и ее обобщения, а
также применения этой теоремы к изучению экстремальных задач
см, в работах [25—27, 73, 79, 89, 109, 111, 114, 116, 119, 133, 134,
149, 170, 191, 196, 199, 235, 239, 256, 260, 269] и др.
Не вдаваясь в подробности, укажем на следующий итерацион-
ный процесс:
un+i = PUt (un — anL'u (uni Xn)), K+i = Pa, (К + ая£я ("«> K))>
/i = 0, 1,... ,
где параметр an^0 можно выбирать из тех же соображений, как
это делалось в градиентных методах. Конечно, здесь нужно пред-
полагать, что проектирование на множество U\ осуществляется
просто. Иногда часть ограничений, задающих множество U, сле-
дует отнести к ограничениям, определяющим U\, или к ограни-
чениям g(u)^:0, #(н)=0, руководствуясь удобством вычисления
проекции Put(u). Заметим, что проектирование на Ai осуществ-
ляется совсем просто:
РлЛЬ) =
У
. и J
где A,=(i4i)f л' =
\i\ если \i* > 0
0, если и'<0.
Также просто вычисляется проекция PUt(u)t если U\ = {u : ы^0}-
Существуют и другие способы построения итерационных про-
цессов, в которых итерации по переменной и делаются с использо-
ванием одного метода (например, метода Ньютона), а по перемен-
ной Я — с помощью другого метода (например, градиентного ме-
тода). В тех случаях, когда задача минимизации функции
L(u, X) на U\ при фиксированном XeAi решается легко, можно
предложить следующий итерационный процесс:
L(un+\, Xn) = minL(uf Хп), К+\ = P\t (К + <*rtU (иЛ, К))>
u£Ut
/i = 0f 1,...
Упражнение_1. Пусть множество U={u:u^Uu g(u)^0}9 где
Ux — выпукло, gi(u)t *=1, 2,..., s — гладкие выпуклые функции
на U\9 является регулярным и J (и) — гладкая выпуклая ^функция
на Uи Тогда, для того чтобы в точке w* достигался минимум J (и)
на U, необходимо и достаточно существования, - точки А,*, такой,,
что

•§ щ
Элементы линейного программирования
131
umeu19 (L'u(u\ г), и—n*)>of иеи19 (Н)
Г>0, ^(*ЛГ)<0, X^(if, Г)=0, t=l, 2,..., s (15)
{если £Л = {и: w^O}, то условия (14) можно записать в виде, сим-
метричном условиям (15):
и* > 0, L'u (и\ V) > 0, uf L'ui (и\ V) = О,
i=l, 2 тп). Доказать. (Этот результат носит название теоре-
мы Куна — Таккера в дифференциальной форме [116, 134, 149,
256] и др.)
§ П. ЭЛЕМЕНТЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
1. Под линейным программированием понимается часть тео-
рии экстремальных задач, 'изучающая задачи минимизации (или
максимизации) линейных функций на множествах, задаваемых
системами линейных равенств и неравенств. Общая задача линей-
лого программирования следующая: найти
min (с, и)\ U = {u:u'>Q(i£ /), Аи = Ь, Аи <&}, (1)
где с^Ещ, Ь^ЕР> b^Es — заданные векторы, А — заданная мат^
рица порядка рХ^, А — заданная матрица порядка $Х>я, / —
заданное подмножество индексов / среди l^i^m (подробнее
обозначения см. в задаче (10.10)).
К задаче (1) сводятся многие задачи технико-экономического
содержания ([54, 74, 114, 118, 132—134, 257] и др.). Кроме того,
реализация ряда методов минимизации нелинейных функций так-
же может привести к задаче (1) как вспомогательной (см., напри-
мер, §4, 6).
Поскольку задача (1) является частным случаем рассмотрен-
ной выше задачи (10.10), тр к (1) также применима теорема 10.4,
нз которой вытека^т^следующая так называемая основная теоре-
ма линейного программирования.
Теорема 1. Для того чтобы точка а* была решением за-
дачи _(1), необходимо и достаточно существования точки
Я,*=(р*, |i*), такой, что
^*>0(*6/), Аи* = 6, Аи*<Ь, р\{Аи* — 6)t-=0(* = 1,... , s),
(2)
ц*>0, (с+ЛУ+Л*|О,>0(*€7),
(с + Лу+Л*^=О(10/), I (3)
и'*(с + АУ + ЛУ); = 0 (i=l,2,..., /и),

132 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
здесь сохранены обозначения из задачи (10.10). Из (2), (3) сле-
дуют равенства
ОЛ Аи* — Ь) = 0, (j?f Ай* — Ь) = 0, (и\ с + АУ + Л V) = 0.
(4)
Доказательство. Составим функцию Лагранжа задачи
(1):
Ни, Ц = (с, ы) + (ц, Аи — 6) +(ft, Аи — Ь) =
= (с + Л> + Л>, и) — (Ь, \х)-(Ь, й).
Согласно теореме 10.4 точка и* будет решением задачи (1) тогда
и только тогда, когда функция L(u, Х)_ на множестве
t/iXAi, C/i = {m:m*5s0(;ge/)}, Ai={A,= (h, ц) : ц^.0} имеет седло-
вую точку (и*, %*), т. е.
{с, и*) + (и, АиГ -Ь) + (ц, А** - Ь) <{(с, и*) + (ц', Аи'-Ь) +
+ (j?, Ли' - Ь) = (с + лу + лу, «о - (*. (О - (*. й*) <
< (с + АУ + Л*й*. и) - (Ь, ц*) -(Ь, и*). « € Ut, X € Ах
или в равносильном виде: для некоторого V = (ц*, ц*) £ Аи
(ц — ц", Ли* — 6) + (Й — Й*» Аи*—Ь)«£0 при всех Я= (й, ц) € Лх,
(5)
а для некоторого и* 6 £/
(с + Л*ц* + Л V, а — и*) > 0 при всех и 6 1/1в (6)
Нетрудно видеть, что соотношения (5), (6) эквивалентны соотно-
шениям (2), (3). В самом деле, если верны соотношения (2), (3), то
из них, очевидно, [вытекают (5), (6). Покажем обратное. Пусть име-
ют место соотношения (5), (6). Тогда из (5)- при \i = \i* получим
(|i — \i*, Аи* — 6)<0 для любого \i£Ep, что возможно только при
Аи* ==_&. Далее, при pi = \i* из (5) следует (|i —|Г, Аи* — 6)<0 при
всех (4 > 0, что возможно тольно при Ли* < &. В самом деле, если
здесь _взять й = (jij,... , ц-_ь ~jfit,_ j^+i , ... , £), _то получим
(Ц; — И?) (Ли* — b)i < 0 при всех \it >_0, откуда (Ли* — b)t < 0,
£= 1, 2 [&. В частности, если (Аи* — 6)^<0, то обязательна
|Л{ = 0, поэтому [1е (Ли* — b)t = 0 при всех t = 1,2,... , s. Соотноше-
ния (2) получены.

§ щ
Элементы линейного программирования
133
Аналогично условие (6)
(с + Л V + & F, и - и*) = £ (с + АУ + Л V), (и* - иГ) +
+ £ (с + ЛV + JIV), (к'-«/) > О,
'£'
выполняющееся при всех н*^0 (is/) и произвольных и{(1£1),
приводит к соотношениям (3). Таким образом, существование сед-
ловой точки функции L(uf X) на tAXAi эквивалентно соотноше-
ниям (2), (3). Отсюда и из теоремы 10.4 следует справедливость
теоремы 1. А
Оказывается, задача (1) тесно связана со следующей задачей:
найти
min [(bt и) + (&, й]> Л = {X = (jl, р): ц > 0,
(S, Ц)6Л
(С + л>+ Л>)£ > 0(i 6 /), (с + -41* + Л*й, = 0 (i<£ /)},
(7)
называемой двойственной задачей по отношению к (1). Эту связь
выражает следующая теорема, называемая первой теоремой двой-
ственности.
Теорема 2. Задачи (1) и (7) либо обе не имеют решения,
либо обе имеют решения, причем в последнем случае
(с «♦) = -(&, io-(6f й), (8)
где и* — решение задачи (1), X* = (\im9 (Г) — решение задачи (7).
Доказательство. Составим функцию Лагранжа для двой-
ственной задачи
Lx (К и) = (6, |i) + (67 й - J "'(* + Л> + Л* ц)« -
- £ a'(c + 4V + #i0i = (ft. И) + (£ Й-
— (и, с + Л^ + Л>)==-1(и, Я),
которая отличается, от функции Лагранжа L(u, X) исходной зада-
чи лишь знаком. Согласно теореме 10.4 двойственная задача (7)
имеет решение ^*=(|л*, |ы*)еЛ тогда и только тогда, когда функ-
ция Li(Xt и) на A\XU\ имеет седловую точку (A,*, u*)^AiXU{:
Ll(X,it9u)^Ll(X*9 u*)^Li(X, и*) при всех Хе=Аи u<=UY. Так как

134 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
L(u, к)=—L\(Xt и), то из последних неравенств следует, что если
(Я*, и*) — седловая точка функции Li(X, и) на A\XUU то (w*,
X*) — седловая точка L(ut X) на U\XA\ и наоборот. Таким обра-
зом, функции L(u, X) и Li (К и) одновременно имеют седловую
точку или ее не имеют. Согласно теореме 10.4 это означает* что
задачи .(1) и (7) либо обе не имеют решения, либо обе имеют ре-
шения. Из сказанного также следует, что точки и* и %*= (\х*, \х*)
будут решениями задач (1) и (7) соответственно тогда и только
тогда, если выполняются соотношения (2), (3). Для получения
равенства (8) теперь достаточно воспользоваться равенствами
(4). А
Теорема 3. Для того чтобы точки u*^U и Х*=(\х*, |1*)еЛ
были решениями задач (1) и (7) соответственно, необходимо и
достаточно, чтобы
(с, tf)=-(ft, |0-(6, JO. (8)
Доказательство. Необходимость доказана в теореме 2.
Остается доказать достаточность. Пусть для некоторых u*^U и
Я*=(|л*, [г*)^Л имеет место равенство (8). Тогда из условий, оп-
ределяющих t/иЛ, имеем
(с, и) > — (Л> + Л*ц, и) = — (Аи, ц) — (Ли, fi) >
> — (6, и) — (6, \i) при всех и 6 (/, Л = (ц, (i) 6 Л. (9)
В частности, при X = X* = (ц*, ц*) с учетом условия (8) отсюда бу-
дем иметь (с, и) > — (6, [О — (£> И*) = (с> и*) ПРИ всех и € £Л т- е.
(с, w*) = min(c, и). Аналогично при и = и* из (9) и (8) следует
(6, и) + (6, ц) > - (с, и*) = (bt ji*) + (b9 ]0 при всех. Я = (ц, ц) 6 Л,
т. е. (Ь, и*) + (Ь у?) = min[(6, ц) + (&, у)\. А
2. Ниже будем рассматривать так называемую каноническую
задачу линейного программирования: найти
min (с, и), £/ = {и > 0, Ли = 6}, (10)
ы€С/
получающуюся из общей задачи (1) при / = {t:l<t<m}, А = 0,
6 = 0, s = 0. Заметим, что общая задача (1) введением дополнитель-
ных переменных может быть сведена к канонической задаче. В са-
мом деле^ положим v = Ъ—Аи, ul=xs/ — а/, где i&I9 a>' = max {0;
и?) > 0, wl = max {0; — и*} > 0, ив пространстве переменных
v9 и'(*€/), т1% т1{гф,1) рассмотрим задачу: найти

§ щ
Элементы линейного программирования
135
min CVер* + Т ft (wi — W')) |
при условиях
v>09 u*>0 (it I), ш<>0, w<>0 (*£/), | (n)
(см. обозначения к задаче (10.10)). Как видим, в задаче (11) все
переменные неотрицательны, остальные ограничения имеют толь-
ко вид равенств, и после переобозначений задачу (11) ~нетрудно
записать в виде (10). Остается заметить, что точка v*9 и*(i£I)9
w*, w* (£ §£/) будет решением задачи (11) тогда-и только тогда,
когда точка и* с координатами и**(1£1) и и* = w* — wl* (i £1)
будет решением задачи (1), так что задачи (1) и (11) эквивалент-
ны.
Изложенный метод сведения общей задачи (1) к канониче-
скому виду на практике, однако, применяется редко, поскольку это
приводит к чрезмерному увеличению размерности переменных.
В то же время разработку и исследование различных методов ре-
шения задач линейного программирования удобно проводить для
задач, з~аписанных в каноническом виде или в виде так называе-
мой основной задачи линейного программирования: найти
min (с, и); U = {и: и > 0, Ли <Ъ}. (12)
Исходная задача (1) легко сводится к виду (12), если ограниче-
ния типа равенств Аи=Ь заменить на два ограничения типа нера-
венств Аи^-b и (—А)и^.—Ь, а переменные u\(i^I) заменить,
как выше, разностью w%—W{. Разумеется, в зависимости от спе-
цифики задачи можно указать и другие более удобные способы
перехода от задачи (1) к задачам вида (10) или (12), позволяю-
щие избежать чрезмерного увеличения размерности задачи или,
быть может, иногда даже приводящие к сокращению числа пере-
менных и ограничений. Методы, разработанные для решения за-
дачи (10) или (12), затем часто удается модифицировать так, что-
бы их можно было применять к задачам линейного программиро-
вания в более общей форме.
В настоящих лекциях ограничимся изложением симплекс-ме-
тода, приспособленного для решения канонической задачи (10),
полагая, что знание основ метода в таком виде позволит читате-

136 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
лю без особых усилий самостоятельно .ознакомиться по имеющей-
ся литературе с симплекс-методом и другими методами, приме-
няемых к решению задач линейного программирования в различ-
ных формах. Более подробное изложение теории, методов и раз-
личных приложений линейного программирования можно найти,
например, в {Работах [54, 74, 89, 114, 116, 118, 132—134, 149, 219,
220, 226, 232, 235, 256, 257]. При изложении симплекс-метода для
задачи (10) будем следовать схеме, принятой в работе [134].
3. Выпишем двойственную к (10) задачу: найти
min(6, Я), А = {Х-ЛеЕр, с + А*%>0} (13)
и переформулируем теоремы 1—3 применительно к задачам (10),
(13).
Теорема 4. Для того чтобы точка w*e£w была решением
задачи (10), необходимо и достаточно существования точки
Х*е£р, такой, что
н*>0, Аи* = Ь, <? + Л*Г>0, и'> + Л*Г), = 0, t = l,...,m.
Задачи (10) и (13) либо обе не имеют решения, либо обе имеют
решения, причем для того, чтобы точки u*^U и Я*еЛ были ре-
шениями соответственно задач (10) и (13), необходимо и доста-
точно, чтобы (с, и*)=—(6, X*).
В задачах линейного программирования важное значение
'имеет понятие угловой (или крайней) точки множества.
Определение 1. Точка а множества AczEn называется
угловой (или крайней) точкой этого множества, если представле-
ние a=aai+(l—а)а2 при аь а2еЛ и 0<а<1 возможно лишь при
a=ai = a2. Иначе говоря, в А не существуют точек а\, а2, а\фа2,
при которых представление а=аах+(\—а)а2 возможно для како-
го-либо а, 0<а<1. Геометрически это означает, что угловая точка
не может быть внутренней точкой любого отрезка, принадлежаще-
го множеству.
Теорема 5. Всякое выпуклое замкнутое ограниченное мно-
жество АсиЕп имеет хотя бы одну угловую точку, и любая точка
ЙеЛ может быть представлена в виде выпуклой линейной комби-
нации конечного числа угловых точек а\, #2, ...,я& множества Л,
т. е.
__ k к
a = £aA, a;>0, i = 1, 2, ... , k, £<X;=1. (14)
Доказательство проводится с помощью индукции по
размерности пространства ЕПу в котором задано множество А.
Если л=1, то А есть-отрезок и справедливость теоремы очевидна.

§ т
Элементы линейного программирования
137
Пусть теорема верна для всех выпуклых замкнутых ограниченных
множеств в пространстве Еп-Х(п~^2). Пусть Л — выпуклое
замкнутое ограниченное множество в Еп. Возьмем какую-либо
граничную точку а_множества Л и построим в этой точке гипер-
плоскость (с, а—я)=0, сфО, опорную к множеству Л, т. е.
(с, а)^(су 3)=а при всех а^А. Общие точки множества А и
этой гиперплоскости обозначим через Л0. Очевидно, А0 — выпук-
лое замкнутое ограниченное множество, и, кроме того, Л0 может
быть помещено в некоторое евклидово пространство £n-i- По
предположению индукции существуют угловые точки а\9 -.. ,ял
k k
множества А0 и числа а^>0, V щ = 1, такие, что а — V <ад.
t=i *=i
Остается лишь показать, что точки а\9 а2,... ,ад являются угловы-
ми и для множества Л. Пусть а* = аа'+(1— а)а", а7, а/7еЛ,
0<а<1. Покажем, что такое представление возможно только при
а'=а"=а{. Так как (с, а'».(£\ а), (с, а")^(с9 а), (с, а,) = (с, а),
то
(с, af) = а (с, а') + (1 — а) (с, а") > (с, а) = (с, а,),
что возможно только при (с, а7) = (с, а") = (с, а), т. е. а7, а"еЛо.
Но аг- — угловая точка Л0, поэтому представление a* = aa7+
+ (1—а)а77, а7, а"^А0, 0<а<1 возможно только при cii = a'=a".
Тем самым доказано существование угловых точек множества Л
и, кроме того, получено представление (14) для любой граничной
точки множества Л.
Пусть теперь а — внутренняя точка множества Л. Через точ-
ку а проведем какую-либо прямую L. Пересечение L(]A есть отре-
зок с концами &i, b2t принадлежащими границе множества Л,
причем для некоторого а, 0<а<1 имеем: a=a&i+(l—a)b2. В
силу доказанного для граничных точек имеет место представле-
ние (14). Поэтому найдутся угловые точки ац9 ai2,..., Оцц мно-
жества А и положительные числа atl,... , aiki, Va£/= 1, такие,
/=i
ki
что bt = J] aiya£/, t = 1, 2. Тогда
У«=1
_ kt ft,
a = £ aa,,^,. + J] (1 — a) a^,.
/=i /=i
Приведя подобные члены и выбрасывая нулевые слагаемые, при-
дем к представлению (14). Д

138 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
Теорема 6. Если задача (10) имеет решение, то найдется
угловая точка множества U, также являющаяся решением этой
задачи.
Доказательство. Пусть и* — решение задачи (10).
Возьмем множества
т т
A = hi:u>0, 2]ы'<Л!} и B={w:w>0, Va' = AlL
*=i e=i
т
где М = 1 + V #'*>0. Очевидно, множества АъВ непусты, ограни-
чены, выпуклы, замкнуты, причем и* £А9 и* £ В. Тогда пересечение
Uf\A является ограниченным выпуклым замкнутым множеством и
k
и* 6 U[)A. По теореме 5 тогда существует представление и*= V ща1$
t=i
где at—угловые точки множества U(]A9 at>0(t'=l, 2,..., k)>
k
У\ щ = 1. Так как at 6 £/, то
*=i
(с, а<) > (с, и*) = inf (с, w) (t = 1, 2, .., , А).
с/
Умножим эти неравенства на o&i>0 и сложим. Будем иметь
к к
{с, и*) < £ щ (с, а<) = (с, £ сад) = (с, а*),
i=i i=i
что возможно только при (с, и*) = (с, at) (i = lf 2, ... , А). Таким
образом, точки alf a2, ... , ak также являются решением задачи (10).
.Остается показать, что среди этих точек а19 ... , ak хотя бы одна
является угловой точкой множества U.
Заметим, что среди точек а\ аь найдется точка щ ф.Ву ибо
к
в противном случае и* = V озд 6 В. Докажем, что такая точка
i=\
й{ — угловая точка U. В самом деле, пусть a*=awi+(l—a)u2t
щ9 u2^Uf 0<а<1. Покажем, что такое представление возможно
лишь при U\ = u2=ai. Для этого возьмем точки w;=a;+Y(wj—<к) =
=УЩ+(1—Y)ai(/=1»2), принадлежащие U при всех y, O^y^I-
Так как аг$ЕВ, то можем выбрать y, 0<y<I1 столь малым, чтобы
т
Vt0/<M. Таким образом, wu w2^V(]A. Кроме того, так как
t=i
ai = at/i+(l—a)«2, 0<a<l, то простые выкладки показывают, что
аг-=аШ1+ (1—а)иу2, 0<а<1. Однако щ— угловая точка множества

§ It]
Элементы линейного программирования
139
U[)A, Wi, w2^U(]Ar поэтому последнее представление для а* воз-
можно лишь при ai=wi = w2. А тогда ai — ui = u2. Таким образом,
ах — угловая точка U и (с, af) = inf (с, и). ±
Как видим, угловые точки в задаче (10) играют важную роль.
В связи с этим полезно иметь простой алгебраический критерий
для угловой точки множества U задачи (10).
Теорема 7. Для того чтобы точка иФО, u^U была угловой
точкой множества U, необходимо и достаточно, чтобы: 1) сущест-
вовали невырожденная квадратная матрица
Б =
e*i/i
e<i/
''А
aiJi
aikik
справедливо равенство
и вектор Ь =
о/.
и =
и'*
Ви = Ь, \В\ф09
Ьь
L К
, такие, что для
(15)
где aij — элементы матрицы Л, bi — координаты вектора Ь\
2) координаты вектора и, не входящие в й, заведомо равны нулю
(заметим, что если u=0^U, то и = 0 — всегда угловая точка U).
Столбцы матрицы Л, входящие в матрицу В, называются базисом
угловой точки и.
Доказательство. Необходимость. Пусть иФО —
угловая точка множества U. Пусть (Au)i = bi(i= 1,... ,р),
ш>0 (/=1,...,к), Ш=0 (/=/с+1,.. .,т) (этого всегда можно
добиться, перенумеровав при необходимости координаты векторов
и и Аи). Обозначим
П1>
<*ИГ
А =
л =
011
><tpi
\<хр1,... , арк)
- п
(* = 1, 2,..., k), ы = 1 • |>0.
V «*

140 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
Покажем, что векторы Alt Л2, ... , Ak линейно независимы.
21
zk
Пусть вопреки утверждению существует вектор z = | • | Ф 0, та-
кой, что V zfi4i= Az = 0. Возьмем ux = [ "^
£х \ о
(U—82 \
о )
6 Ет. Так как и > 0, то при достаточно малых
8>0 будем иметь wi^O, м2^0, кроме того, Л«1 = &, Аи2=Ь, т. е.
wb u2^Uy щфи2. Однако и=—(^i + ^2), что противоречит оп-
ределению угловой точки и множества U. Следовательно, векторы
Аи ... ,Ak линейно независимы, и_ранг матрицы А равен./с. Тогда
р^к, и, вычеркнув из матрицы А р—к строк, линейно выражаю-
щиеся через остальные строки Л, получим искомую квадратную
невырожденную матрицу порядка кХк и соответствующий век-
тор 6, для которых Ви = Ь. Попутно мы доказали, что матрицу В
можно выбрать так, что ее порядок будет совпадать с числом не-
нулевых координат угловой точки.
Достаточность. Пусть точка и6 U и удовлетворяет усло-
вию (15). Пусть и = аи1 + (1 г— а) и2 при некоторых их, w2 € £/ и
0<а<1. Покажем, что такое представление и возможно только
при и = их = и2. В самом деле, если \ф\п г= 1, 2, ... , k, то из
О < а< 1, и{ > 0, и2 > 0 имеем 0 = V = аи{[ + (1 — а) и!2 > 0, что
возможно только при и{ = и2 = 0 \\ф\ГУ г= 1, 2,... , Л). Тогда
из Ащ—Ь следует, что Bty =6, где щ = \ ! |(i= 1, 2). Однако
| £ j г£ 0, поэтому и1 = и2 = и, а тогда и1 = и2 = и. Следовательно,
г/ — угловая точка £/. А
Таким образом, для решения задачи (10) достаточно пере-
брать угловые точки множества U. В силу теоремы 7 число угло-
вых точек U конечно, так как число невырожденных миноров
матрицы А конечно. Однако даже в задачах не очень большой
размерности число угловых точек может быть столь большим, что
простой перебор угловых точек U может оказаться невозможным
за разумный промежуток времени даже при использовании самых

§11] \ Элементы линейного программирования 141
быстродействующих ЭВМ. Идея многих методов решения задач
линейного программирования заключается в построении такого
упорядоченного перебора угловых точек, при котором значение
функции (с, и) убывает при переходе от одной угловой точки к
другой. На этой идее основан и симплекс-метод, к изложению ко-
торого мы сейчас переходим.
4. Напоминаем, что в задаче (10) матрица А имеет порядок
рХпг, поэтому ранг матрицы А удовлетворяет неравенству:
rangi4^min (р\ пг). Если бы rang А = пг, то это означало бы, что
множество U состоит не более чем из одной точки, и задача ми-
нимизации (с, и) в этом случае становится тривиальной. Поэтому
будем считать, что и=ф9 rang A=p<m—этого всегда можно
добиться, исключив из равенств (Au)i = bu /=1,2,...,/?, линейно-
зависимые. Кроме того, симплекс-метод будем излагать в предпо-
ложении невырожденности задачи (10).
Определение 2. Угловая точка иФО множества V назы-
вается невырожденной, если соответствующая матрица В из тео-
ремы 7 имеет порядок p=rang/4<m. и число положительных
координат точки и в точности равно /?. Задача (10) называется
невырожденной, если невырождена каждая угловая точка множе-
ства U.
Пусть известна некоторая угловая точка и множества U. В
силу невырожденности задачи и теоремы 7 можем считать, что
/ аи,... , а1р
и =
и =
>0, В = \
иР
Д/71>
/71» • ' ' » "РР
\В\Ф0, Ви = Ь. Пусть с = \
Рассмотрим вектор
и— аВ~х Ak
0
*Чь=
0
а
0
<*ik
А = | : I, Л = р+ 1, ... , m, а>0,
1рк>

142 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
где а — ft-тая компонента вектора ua,k (ft>p). Так как и>0, то
найдется а0 > 0, такое, что иа,к > О при всех а, 0 < а < с^. Кроме
того,
р _ _ _
Aua,k.= V Д (а — аВ-1 Лл); + Aka = B(u — aB~l Ak) + Aka = Bu = b
при всех а, поэтому iia.k 6 U при 0 < а < а0. Далее,
(с, На,*) = (с, и — аВ-1 А) + ас* = (с, й) — а [(с, В"1 Ak) — ck].
Обозначим Дй = (с, В-1 ЛЛ) — ск\ тогда (с, ыа,ь) = (с, и) — аДЛ (ft =
= р + 1,... , т). Величины ДЛ имеют смысл и при ft = 1, 2,_... , р»
при этом согласно определению^ обратной матрицы В-1 Ak = ek> и по-
этому ДА = (с, В"1 ЛЛ) — ск = (с, еЛ) — сЛ = 0 (ft = 1, 2,..., р)л В за-
висимости от знаков величин Дъ (В-1ЛЛ)£ возникают три возможно-
сти.
I. Все величины Аь<:0 (к=1,2,... ,т). В этом случае, ока-
зывается, и* = и является решением задачи (10). В самом деле,,
возьмем Л,*=—(В_1)*с. Тогда
0>ДЛ = (с, В-М,)-сЛ = ((В-Тс"; ЛЛ)-с, = -(Г, ЛЛ)-
— ck(k= 1,... , m),
что равносильно неравенству c-f i4*V>0. Далее,
(С, Ua%k) |а=о = (*, ~") = (С, В"1 6) = ((В~ТF, 6) = - (6, V).
Таким образом, Я*—решение двойственной задачи (13), и в силу тео-
ремы 4 тогда и* = и — решение задачи (10).
II. Найдется такой номер ft>p, что Aft>0, В-1Лл<0 (напо-
минаем, что Ал = 0 при ft = 1,..., р). Тогда задача (10) не имеет решения.,
В самом деле, в этом случае uajk >_0, Аиа%к = Ь> т. е. иа,к 6 U при:
всех а>0. А тогда (с, аа^)=(с, и) — aAfe-» — оо при а-»+оо, №
inf (с, и) = —оо.
и€С/
IIL Найдутся такие ft>p и i^p, что Д&>0, (B-MfeJ^O-.
В этом случае делается итерационный шаг — переходят к следую-
щей угловой точке wao, &, где
a = a0 = min (дг~'ь)' , 4 = {t:l<t<p, (В-* 4)i>0}^ 0..
^U (Br1 Aiit
Так как В-16 = и>0, то <х0>0. Покажем, что иао,*€£/. Посколь-
ку Аиал к = Ь при всех а, то достаточно установить, что иа^ь > О*

# 11] Элементы линейного программирования 143
или (и — а0В-{ Ak)t >0, i =^ 1,... , р. Это очевидно для тех t, для
которых (В-Мл);<0. Пусть (В-1 Д^ > 0, т. е. i£Ik. Тогда
0<а0<-^^-= f , илиа<-ао(В-Мл)<>0
при всех i б /л. Таким образом, uaotk 6 £/•
Покажем, что wao,fe — угловая точка (/..Пусть минимум [в опре-
делении а0 достигается при некотором i = s 6 /*:
a0= min-i^^ £l»k>o. (16)
Тогда <, fe = u* — a0 (Б"1 Ak)s = (B~i 6) s — a0 (fi-14)s = 0. В матри-
це В = (Alt Л2,... , Ap) выбросим столбец As и дополним столбцом
Ак\ новую матрицу обозначим через С = (Al9... , Л_ь Л+ь • • • » ^pf
Лл), кроме того, вектор-столбец с координатами ul^,... , w^1>
-"at1» • • Л ««о» w«a = ao обозначим через u^k. Будем иметь
р р
+ а0Лл = Ви = Ь.
Далее, убедимся в том, что |С|=т^0# Пусть
Cz= £ г,Л* + 2*Л=0.
Так как
Д = В(5-МЛ)= J] Л (В-1 Л)£,
то
С*^ J 2Л+г*2Л(5-Мй),= £ [гН-(В-1Л)^*]Л +
i=l,i?bs t=l («1, i*s
Из линейной независимости Al9 Л2,... , Лр тогда следует, что
^ + (В"14),гЛ = 0 0=1, 2,..., р, /=^s), z,(5-M,)s = 0.
Но (5-МЛ)5>0 по определению s€^, поэтому zk = 0t а тогда все
я, = 0 (i=l,..., р, i=^=s), т. е. 1? = 0. Следовательно, |С|^=0,
C5ae,ft = Ь. В силу теоремы 7 точка tia^k является угловой для U.

144 МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
При этом (с, ua<hk) = (с, и) — а0Дл<(с, и) = (с, и), i. е. значение
функции (с, и) строго уменьшилось. Тем самым описан один итера-
ционный шаг симплекс-метода.
По условию задача (10) невырожденная, поэтому число поло-
жительных компонент у вектора uaotk равно р. Поскольку т — р ну-
левых координат у вектора ua<ttk известны: и«0 = и^1 = ... = и%^1 =■
= и%£1 = ... = Ua0 = 0, то все остальные координаты Ua0 = (и —
— a0B~l Ak)'i {i = 1,... , р, i ф s), w£0 = a0 будут положительными.
Это, кстати, означает, что в невырожденных задачах номер s, на ко-
тором достигается минимум в (16), определяется однозначно.
В вырожденной задаче такой номер s, вообще говоря, опреде-
ляется неединственным образом, и, более того, величина ао из.
(16) в этом случае может оказаться равной нулю, поскольку мот
жет быть равной нулю координата (В~1Ь)$=и8. Таким образом, в.
вырожденных задачах возможно зацикливание, когда значение
функции (с, и) при переходе от одной угловой точки к другой
не убывает и через некоторое число итераций происходит возвра-
щение к прежней угловой точке (см. упражнение 7). Для преодо-
ления явления зацикливания симплекс-метод следует несколько-
модифицировать; за подробностями отсылаем читателя к работам
[114, 116, 133, 134, 257] и др.
При использовании симплекс-метода производится перебор
только тех угловых точек, в которых значение функции (с> и) не
возрастает, поэтому симплекс-метод дает значительный выигрыш,
по сравнению с простым перебором и позволяет решать задачи
линейного программирования довольно больших размеров. Разу-
меется, при больших размерах задачи и при неудачном выборе
начальной угловой точки объем работы может оказаться значи-
тельным и при использовании симплекс-метода или его модифика-
ций.
5. Приведем формулы, связывающие последовательные итера-
ции симплекс-метода в случае невырожденной угловой точки и~
Обозначим
Л = Ь, uik = (В-1 Ak)h i = 1, 2, ... , р, k = 0, 1 т\.
Ио/ = А/=(*. В-М/) —с,= £сЛ/ — cJt /=1, 2,..., т\
Иоо = (с> и).
Параметры щ$ назовем параметрами итерации для угловой точ-
ки и; через v^ обозначим параметры итерации для новой угловой
точки v = ua<i,k> получаемой описанным выше симплекс-мето-
дом.

§ 11] Элементы линейного программирования 145-
Заметим, что параметры и^у t = 1,2,... ,р, /=0,1,...,/п, одно-
значно определяются из соотношений
*=1
Аналогично параметры vy могут быть определены соотношениями
р
i=i
где £' = £, a Al9... , Л-i, Л+ь ... , А» л* — столбцы
i=i i=i
матрицы С. С учетом этого замечания нетрудно получить простые
связи между параметрами u(i и ъц
Ъц = иц — Щк — > 1 = 0, 1,..., Р, 1Ф*\ Чк/=—.
/=0,1 т. (17)
В самом деле, по условию u?k = (В"1 ЛЛ)5>0 (см. п. 4). Из равен-
ства
ЛЛ = В(Я-МЛ) = £ ЛЛ„
*=i
тогда имеем
f=l
Так как l<s<p и
A8 = fiAiuts = B(B^As)=BeSf
i=\
где е$ — s-тый столбец единичной матрицы порядка р х р, то u£s = О
при i^s и wss= 1. Поэтому равенство (18) можно переписать в виде
A. = f-Ak + y(uls-ulk^\At.
Usk Ad \ Usk
f=l

146 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
^
Далее, при / = 0, 1, ... , mt /^fcs с учетом (18) полупим*
р р f
А, = В (В-* Aj) = £ M/ = 2j4«i/ + ^./ =
i=l
Сравнивая полученные представления Ah j = 0, 1,... , m с соотно-
шениями
определяющими tr//f получим формулы ^ (17) при всех ЬФЪ. Остается
рассмотреть случай i = 0. Так как
р
voj = 2'СЛ/ + Wki — Ch i =* 1> 2> • • • > m'
i =1
по определению, то с учетом уже доказанных формул (17) при t#0
имеем
Р
"sj
(]![]СЛ*— **) = </ — "о* ^. / = Ь 2,... , т.
i=l
Наконец, из (16) и равенства (с, v) = (с, Ha0ffe) = (ct «) — а0Дъ до-
казанного в п. 4, следует/ что
^оо = %ю — aowoA = woo ~~ U0k*
usk
•Формулы (17) полностью доказаны.
Полученные формулы (17), связывающие параметры угловых
точек на одном шаге симплекс-метода, весьма просты и могут
быть использованы для численного решения на ЭВМ невырожден-
ных задач линейного программирования симплекс-методом.
6. Как выбрать начальную угловую точку? Оказывается,
отыскание угловой точки множества U={u:u^hy Au=b} в свою
очередь весьма трудоемкая задача, сравнимая с исходной зада-
чей (10). Мы здесь опишем один из наиболее распространенных
приемов отыскания угловых точек, использующий тот же сим-
ллекс-метод.

§ 11] Элементы линейного программирования 147
Рассмотрим такую вспомогательную задачу линейного про-
граммирования: найти
(19>
Без ограничения общности можем считать, что &^.0, ибо в про-
тивном случае соответствующую строчку ограничений (Au)i=bi
мы бы умножили на (—1). Для задачи (19) можно сразу указать
угловую точку. Это будет точка ( j (см. теорему 7) и, следова-
тельно, для решения задачи (19) можно применять симплекс-ме-
тод (или его модификации в случае вырожденной задачи) и найти,
ее решение.
Теорема 8. Пусть ( )—решение задачи (19), пусть
(')
Тогда если <р* = 0, то и* — угловая точка множества U\ если ф*>0„
то U = 0 и задача (10) становится тривиальной.
Доказательство. Прежде всего ясно, что задача (19) имеет
р
решение, так как W ф 0 и линейная функция V vl > 0 на W. Да-
лее, поскольку эта задача решается симплекс-методом, та
•угловая точка множества W. В частности, если <р* = 0, то
у* = 0и ( ] —угловая точка W. Очевидно, тогда и* —угловая
точка U. Если- же ср* > 0, то [U — пустое множество. В самом деле,
если бы существовала точка u£,U, то [ ] 6 W. Но тогда I ]—
решение задачи (19) и <р* = 0 — противоречие. Д
Упражнения. 1. Выяснить геометрический смысл задач линей-
ного программирования, взяв в задачах (10) и (12) т=2, т=3.
2. "На велосипедном заводе выпускают гоночные и дорожные
велосипеды. Производство устроено так, что вместо двух дорож-
ных велосипедов завод может выпустить один гоночный, причем
гоночный велосипед приносит в 1,5 раза больше прибыли. Завод
может произвести 700 дорожных велосипедов в день, однако склад
может принять не более 500 велосипедов в день. Сколько нужна

148 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
выпускать в день, гоночных и сколько дорожных велосипедов для
того, чтобы завод получал максимальную прибыль? («Квант»,
1971, № 3). Для решения этой задачи применить симплекс-метод.
3. В пунктах А и В расположены кирпичные заводы, а в
пунктах С и Д — карьеры, снабжающие их песком. Ежесуточно
заводу А нужно 40 т песка, заводу В — 50 г, а карьер С ежесуточ-
но добывает 70 т песка, карьер Д — 30 т. Стоимость перевозки
тонны песка с карьера С на завод А равна 2 руб., на завод. В —
<3 руб., с карьера Д на завод А — 5 руб., на завод В — 5 руб.
Нужно организовать ежесуточное снабжение заводов песком так,
чтобы полная стоимость перевозок была наименьшей («Квант»,
1971, № 3): Для решения этой задачи применить симплекс-метод.
4. По аналогии с теоремой 4 для задачи (12) сформулиро-
вать условия разрешимости и оптимальности, пользуясь теорема-
ми 1—3.
5. Для того чтобы задача (1) (и, следовательно, двойствен-
ная задача (7)) имела решение, необходимо и достаточно,* чтобы
Иф0 и (с, и) ограничена снизу на U. Доказать.
6. Для того чтобы задача (1) (и, следовательно, задача (7))
имела решение, необходимо и достаточно, чтобы ИФфу АФф.
Доказать.
7. Решить задачу min {cf и) = и?—иА+и5—и6 при условиях
.a'-ftt3—2w4—3w5+4w6=0, и2+4иъ—ЗиА—2и5+и6=0, uz+u* + u*+
+ u6+u7=l, w^O, /=1,2...,7. Показать, что в этой задаче мож-
но получить зацикливание, если с помощью симплекс-метода ор-
ганизовать перебор угловых точек, соответствующий перебору
«базисных столбцов в следующем порядке:
(Л3, Л2, Л7) —>* (Л3, Л4, Л7)—>*(Л6, Л4, Л7) —*(Лб, Лв, Л7) —у-
-*(Al9 Лв, Л7)—►•(Л1, Л2, Л7) (Л3, Л2, Л7).
Любопытно отметить, что длина циклов в задачах линейного про-
граммирования меньше шести не бывает ([257], стр. 389).
§ 12. О МЕТОДЕ СЛУЧАЙНОГО ПОИСКА И НЕКОТОРЫХ
ДРУГИХ МЕТОДАХ
Наряду с описанными выше методами минимизации функ-
ций m переменных существует большая группа методов поиска
минимума, объединенных под названием метода случайного поис-
ка [79], [204]. Метод случайного поиска в отличие от ранее рас-
смотренных методов характеризуется намеренным введением эле-
мента случайности в алгоритм поиска. Многие варианты метода
случайного поиска сводятся к построению последовательности
{ип} по правилу

$ 12] О методе случайного поиска и некоторых других методах 149
Ищ.1 = Ия + <*ЛБ, Л = 0, 1,..., (1)
где ап — некоторая положительная величина, g = (g1,... ,gm) —
какая-либо реализация m-мерной случайной величины g с извест-
ным законом распределения. Например, компоненты |* случайного
вектора | могут представлять независимые случайные величины,
распределенные равномерно на отрезке [—1,1]. Как видим, орга-
низация случайного поиска минимума функции m переменных свя-
зана с наличием датчика (или генератора) случайных чисел, об-
ращаясь к которому в любой момент можно получить какую-либо
реализацию m-мерного случайного вектора g с заданным законом
распределения. Такие датчики могут быть получены на основе
стандартных программ, обычно имеющимися в библиотеках под-
лрограмм на ЭВМ.
1. Приведем несколько вариантов метода случайного поиска
минимума функции J (и) на множестве U^Em, предполагая, что
л-е приближение un^U(п^О) уже известно.
а) Алгоритм с возвратом при неудачном шаге [204]. Смысл
этого алгоритма заключается в следующем. С помощью датчика
случайного вектора получают некоторую его реализацию g и в
пространстве Ет определяют точку vn = tin + a£„ a=const>0. Если
vn^U и J(Vn)<J(un), то сделанный шаг считается удачным, и в
этом случае полагается un+i = vn. Если vn^Uy но J(vn)^J(un)t
или же vn£ U, то сделанный шаг считается неудачным и пола-
гается ип+\=ип. Если окажется, что un = un+\ = ... = un+N для
достаточно больших N, то точка ип может быть принята в каче-
стве приближения искомой точки минимума.
б) Алгоритм наилучшей пробы [204]. Берутся какие-либо s
реализаций g*1),..., g<s) случайного вектора g и вычисляются значения
функции J (и) в тех точках w=wn + ag(0,i=l,2,..., s, которые при-
надлежат множеству U. Затем полагается wn+i=«n + ag(*°\nie ин-
декс to определяется условием
/(ия + «БМ)= min /(ия + аБ<'>).
Величины s>l и a^=const>0 являются параметрами алгоритма.
в) Алгоритм статистического градиента [204]. Берутся какие-
либо 5 реализаций |(1),... >1{S) случайного вектора g и вычисляются
разности
~bJ{? = J{un + 4lV)r-J(unl
для всех ип+уЦ1^и. Затем полагают рп =—VgWAJ^*, где
У .
сумма берется по всем тем /, l^t'^s, для которых un±yl<l)^U.

150 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
Если un + apn^U, то принимается un+\ = un+upn. Если же
Un + apn $=U, то повторяют описанный процесс с новым набором
из 5 реализаций случайного вектора £. Величины s>l, а>0, у>0
являются параметрами алгоритма. Вектор рп называют статисти-
ческим градиентом. Если, U=Em, s=m и векторы £(i) являются не-
случайными и совпадают с соответствующими единичными вектора-
ми ei= (0,.., 0, 1, 0,.., 0), 1=1, 2,.., т, то описанный алгоритм,
как нетрудно видеть, превращается в разностный аналог градиент-
ного метода.
2. В описанных вариантах а), б), в) метода случайного поис-
ка предполагается, что закон распределения случайного вектора £
не зависит от номера итераций. Такой поиск называют случайным
поиском без обучения. Алгоритмы случайного поиска без обучения
не обладают «способностью» анализировать результаты предыду-
щих итераций и выделять направления, более перспективные в
смысле убывания минимизируемой функции, и сходятся, вообще го-
воря, медленно.
Между тем ясно, что от метода случайного поиска можно ожи-
дать большей эффективности, если на каждой итерации учитывать
накопленный опыт поиска минимума на предыдущих итерациях и
перестраивать вероятностные свойства поиска так, чтобы направле-
ния ■£, более перспективные в смысле убывания функции, станови-
лись более вероятными. Иначе говоря, желательно иметь алгорит-
мы случайного поиска, которые обладают способностью к самообу-
чению и самоусовершенствованию в процессе поиска минимума в
зависимости от конкретных особенностей минимизируемой функ-
ции. Такой поиск называют случайным поиском с обучением [204].
Обучение алгоритма осуществляют посредством целенаправленного
изменения закона распределения случайного вектора | в зависимо-
сти от номера итерации и результатов предыдущих итераций таким
образом, чтобы «хорошие» направления, по которым функция убы-
вает, стали более вероятными, а другие направления — менее ве-
роятными. Таким образом, на различных этапах методу случайного
поиска с обучением приходится иметь дело с реализациями случай-
ных векторов £ с различными законами распределения. Имея в ви-
ду это обстоятельство, итерационный процесс (1) удобнее записать
в виде
ип+\ = ип + an%ny п = 0, Г,... , (2)
подчеркнув зависимость случайного вектора £ от л.
В начале поиска закон распределения случайного вектора
£=£о выбирают с учетом имеющейся априорной информации о
минимизируемой функции. Если такая информация отсутствует, то
поиск обычно начинают от случайного вектора £о = (Ёо> • • • , £о*)>
компоненты £о,* = 1, 2,..., т, которого представляют собой незави-
симые случайные величины, распределенные.равномерно на отрез-

£ 12] Ь методе случайного поиска и некоторые других методах 151
ке [—1, 1]. Для обучения алгоритма в процессе поиска часто берут
семейство случайных векторов l=l(w)t зависящих от параметров
ш= (w\ ..., wm)t и при переходе от л-го шага итерации к /г+1-му
шагу имеющиеся значения параметров wn заменяют новыми зна-
чениями wn+i с учетом результатов предыдущего поиска.
Приведем два варианта метода случайного поиска с обучением
для минимизации функции J (и) на всем пространстве Ет.
а) Алгоритм покоординатного обучения [204]. Пусть имеется
семейство случайных векторов % = l(w) = (g1,..., £m), каждая коор-
дината %{ которых принимает два значения: |г'=1 с вероятностью
рг и gi =—1 с вероятностью 1—р\ где вероятности р{ зависят от
параметра wl следующим образом:
0 при w£ < — 1,
-1-(1 + ш0 при |ш'|<1, (3)
1 при до<> 1,
р'=
i= 1, 2, ... , т.
Пусть начальное приближение и0 уже выбрано. Тогда для опреде-
ления следующего приближения _щ в формуле (2) при л=0 берет-
ся какая-либо реализация случайного вектора ,|0=|(0), соответ-
ствующего значению параметров w = wo=*(0t 0, ..., 0). Приближе-
ние и2 определяется по формуле (2) при я=1 с помощью случай-
ного вектора £i=£(0). Пусть известны приближения Uq9 щ% ...» ttn
и значения параметров wnLi=(wln-u wmn-\) при некотором
л^1. Тогда полагаем
Wn = pQyLl — б Sign [{J (Un-x) — J (Un-2)) (Un-\ — Un-2)\,
i=*l, 2,... , m\ и = 2, 3, ... , (4)
где величина P^O называется параметром забывания, 6^0 —
параметром интенсивности обучения, р + 6>0. При определении
следующего приближения wn+i в формуле (2) берем какую-либо
реализацию случайного вектора l=l(wn)9 wn — (wn, ... , а#).
Из формул (3), (4) видно, что если переход от точки #п_2 к
точке ип-\ привел к уменьшению значения функции, то вероятность
выбора направления ип-\—ип-2 на следующем шаге увеличивается.
И наоборот, если при переходе от ип-2 к ип-\ значение функции
увеличится, то вероятность выбора направления r/n-i—ип-2 на сле-
дующем шаге уменьшается. Таким образом, формулы (4) осуще-
ствляют обучение алгоритма. Величина 6^0 в (4) регулирует ско-
рость обучения: чем больше 6>0, тем быстрее обучается алгоритм;
при 6 = 0, как видно, обучения нет. Величина р^0 в формулах (4)
регулирует влияние предыдущих значений параметров на обуче-
ние алгоритма; при р=0 алгоритм «забывает» предыдущие значе-

152 МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. т
ния wn-i. Для устранения возможного чрезмерного детерминиро-
вания алгоритма и сохранения способности алгоритма к достаточна
быстрому обучению на параметры iafn накладываются ограничения
1^л|<^, и при нарушении этих ограничений wln заменяют-
ся ближайшим из чисел С{ или—cit /=1,2,..., m. Величины р, 6,.
Ci являются параметрами алгоритма.
Вместо формул (4), посредством которых производится обу-
чение алгоритма, часто пользуются другими формулами [204]:
wi = pO>Ll — 6 (/ (ип-х) — (J (Un-2)) (4-1 — 4-2),
1=1, 2, ..., m; я = 2, 3, ... (5)
Описанный алгоритм покоординатного обучения имеет тот не-
достаток, что поиск и обучение происходят лишь по одному из 2"*
направлений £= (g1,..., gw), где либо |г= 1, либо |* =—1. Отсутст-
вие «промежуточных» направлений делает покоординатное обуче-
ние немобильным в областях с медленно изменяющимися направ-
лениями спуска. От этого недостатка свободен следующий алго-
ритм.
б) Алгоритм непрерывного самообучения [204]. Пусть имеет-
ся семейство случайных векторов ё = fe (ее;) = —=—! , где
\f] + W\
Wic=(w\ ..., wm) — параметры обучения, r\= (V, • •., Лт) — СЛУ"
чайный вектор, координаты if которого представляют собой неза-
висимые случайные величины, распределенные равномерно на
отрезке [—1, 1]. Поиск начинается с рассмотрения случайных
векторов £о=£(0), gi=£(0), реализации которых используются при
определении приближений w0, их по формулам (2). Обучение
алгоритма при п^2 призводится так же, как в алгоритме поко-
ординатного обучения, с помощью формул (4) или (5). При боль-
ших значениях \wn\ влияние случайной величины г\ уменьшается:
и направление ln=?i(Wn) становится более детерминированным и
близким к направлению wn. Во избежание излишней детермини-
рованности метода на параметры wn = (wn, ... , ш/£) накладыва-
ются ограничения |t^n|<^= const, и при нарушении этих Огра-
ди
ничении wn заменяется на -—- с.
\wn\
Более подробные рассмотрения различных вариантов метода-
случайного поиска, их сравнительные характеристики, вычисли-
тельные аспекты метода случайного поиска см. в работах [79],.
(204].
3. Приведенные алгоритмы случайного поиска с обучением
показывают, что процесс обучения в ходе поиска сопровождается
уменьшением фактора случайности и "увеличением степени детер-
минированности алгоритма поиска минимума, направляя поиск

# 12] О методе случайного поиска и некоторые других методах 153
преимущественно^ по направлениям убывания функции. В то же
время наличие случайного фактора в выборе направления дает
возможность алгоритму «переучиваться», если свойства функции
в -районе поиска изменились или предыдущее обучение было не-
точным. Случайный поиск с обучением в некотором смысле зани-
мает промежуточное положение между случайным поиском без
обучения и детерминированными методами поиска минимума из
предыдущих параграфов. Разумеется, и в методах предыдущих
параграфов можно обнаружить в том или ином виде элементы
самообучения алгоритма, однако наличие случайного фактора в
алгоритме делает метод случайного поиска более гибким и поэто-
му более приспособленным к поиску минимума многоэкстремаль-
ных функций, т. е. функций со многими глобальными и локальны-
ми минимумами в рассматриваемой области.
Следует сказать, что задача отыскания глобального миниму-
ма многоэкстремальных функций существенно более трудна, и ме-
тоды решения таких задач в настоящее время разработаны недо-
статочно. Для изучения поведения многоэкстремальных функций и
поиска их глобального минимума наряду с методом случайного
поиска [204] может быть использован также овражный метод
[67], [211]. Для функций, удовлетворяющих условию Липшица,
здесь можно предложить метод, обобщающий метод ломаных из
главы 1, однако его реализация с возрастанием размерности про-
странства весьма усложняется [85]. Другие методы минимизации
многоэкстремальных функций изложены в работах [103, 174, 214}.
4. Весьма усложняет решение задачи минимизации функций
многих переменных наличие помех, когда на значения функции
J (и) в каждой точке и накладываются случайные ошибки. В этих
случаях можно использовать метод стохастической аппроксимации
([45, 79, 230] и др.). Одним из вариантов этого метода является
процедура Кифера — Вольфовица, краткое описание которой бы-
ло дано в § 1.12 применительно к задачам минимизации функций
одной переменной. Для функций m переменных эта процедура
приводит к построению последовательности {ип} по закону
„I _ „t п * ("я + спед — z(un — cnet)
i= 1, 2, ... , m; n = 0, 1, ... ,
где ei= (0,— ,0, 1, 0,..., 0), z(u) — наблюдаемые в эксперимен-
те значения функции J (и) в точке иу последовательности {ап},
{сп} удовлетворяют условиям (1.12.2). Различные варианты мето-
да стохастической аппроксимации, строгое обоснование этого ме-
тода и различные приложения можно найти в работе [45]. Для
минимизации функции при наличии помех могут быть использо-
ваны также метод случайного поиска [204] и некоторые другие
методы [ПО, 214].

МИНИМИЗАЦИЯ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ [Гл. 2
5_. В заключение настоящей главы следует сказать, что в дан-
ной главе мало или даже совсем не затронуты важные, но пока,,
к сожалению, малоизученные вопросы устойчивости изложенных,
методов по отношению к,различным погрешностям вычисления и
округления, вопросы накопления, анализа и использования инфор-
мации в процессе счета, критерии точности и окончания счета и
другие вопросы, требующие немалого искусства вычислителя при
решении задачи минимизации конкретной функции с помощью
того или иного метода.
В стороне остались также вопросы, связанные с выбором оп-
тимальных стратегий поиска минимума на. определенных классах
функций. Следует сказать, что оптимальные стратегии поиска ми-
нимума функций многих переменных зачастую имеют довольно
сложное описание, что затрудняет их практическое использование.
Заметим, что задача поиска экстремума функций многих перемен-
ных хорошо укладывается в общую схему исследования операций,
разработанную в работе [69]. Это обстоятельство используется
в работах [215, 216] для построения оптимальных стратегий поис-
ка экстремума на классе функций, удовлетворяющих обобщенному
условию Липшица. Обзор оптимальных методов минимизации на
различных классах функций см. в работе [120]. Общий обзор
методов минимизации функций конечного числа переменных и биб-
лиографию см. в работах [34, 70, 75, 79, 81, 82, 84, 86, 87, 96, 97,
109, ПО, 114, 116, 118, 133, 135, 138, 149, 155, 164, 170, 188, 193,
229, 230, 235, 239, 265] и др.

Глава 3
Принцип максимума Л. С. Понтрягина
В этой главе рассмотрим задачи оптимального управления
процессами, описываемыми системами обыкновенных дифференци-
альных уравнений. К таким задачам приводят многие прикладные
задачи, в частности, задачи механики космического полета ([75,.
130, 142, 152, 246] и др.). Выдающуюся роль в развитии теории
оптимального управления сыграл академик Л. С. Понтрягин, ко-
торый сформулировал необходимые условия оптимальности, изве-
стные под названием принципа максимума [195]. Этот фундамен-
тальный результат составил математическую основу теории опти-
мального управления, послужил мощным толчком как в развитии
современной теории экстремальных задач, так и в создании чис-
ленных методов решения таких задач.
§ 1. ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Сначала остановимся на некоторых конкретных задачах. Как
известно ([75], стр. 129), при определенных условиях движение
центра масс космического аппарата и расход массы описываются
следующей системой дифференциальных уравнений:
r = t>, v = g-?r+F, G=^-gq, 0<*<7\ (1)
о
где t — время, r=r(t) = (ru r2, г3) — радиус-Ъектор центра масс
аппарата, v=v(t) = (vu v2, vz) — скорость центра масс, G=G(t) —
текущий вес аппарата, g — коэффициент пропорциональности
между массой и весом, P=P(t) — (p\t p2i ръ) — вектор тяги дви-
гателя, q=q(t) — массовый расход рабочего вещества,
F=F(rt t) = (Fi, F2i Fz) — вектор ускорения от гравитационных
сил. Предположим, что фазрвые координаты r(t), v(t), G(t) ап-
парата в начальный момент /=0 известны:
r(0) = r0, v(0)=vOt G(0) = Go. (2)
Величины q=q(t), P=P(t) являются управлением, и, задавая их
по-разному, можно получить различные фазовые траектории (ре-
шения) задачи (1), (2). Конструктивные возможности аппарата,
ограниченность ресурсов рабочего вещества накладывают на уп-
равления ограничения, например, следующего вида:
?min<9(0<<7max> Л*1п < I Р (0 К Кы ° < < < Т. (3)
155

156
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
[Гл. ?
Кроме того, на фазовые траектории также могут быть наложены
некоторые ограничения, вытекающие, например, из условий того,
чтобы вес аппарата был не меньше определенной величины, или:
траектория полета проходила вне определенных областей космиче-
ского пространства (областей повышенной радиации) и др. Здесь
возникают задачи выбора управлений q(t), P(t) из условий (3)
так, чтобы траектории системы (1), (2) удовлетворяли наложен-
ным ограничениям и, кроме того, некоторый целевой функционал
принимал свое минимальное или максимальное значение. Напри-
мер, возможны задачи [75]: 1) попасть в заданную точку или об-
ласть космического пространства за минимальное время; 2) в за-
данный момент попасть в заданную область пространства с задан-
ной скоростью и с максимальным весом аппарата или с минималь-
ной затратой энергии; 3) достичь определенной скорости за мини-
мальное время и т. п.
Эти задачи являются частным случаем более общей задачи
оптимального управления, к формулировке которой мы перехо-
дим.
Пусть некоторый управляемый процесс описывается системой
обыкновенных дифференциальных уравнений
*' = №, *\ ..., *\ и\ и\ ... , иг, 0, t0<t<T9
i= 1, 2, ... , л,
или в векторной форме:
* = /(*, и, 0, t0<t<T, (4>
где х= (х1,..., хп) — величины, характеризующие процесс в каж-
дый момент t и называемые фазовыми координатами управляемо-
го объекта, и= (и1,..., иг) — параметры управления («положе-
ние рулей» системы), определяющие ход процесса; функции
/*(х, и, t) (i=l, 2, ..., п), описывающие внутреннее устройства
объекта и учитывающие различные внешние факторы, предполага-
ются известными.
Для того чтобы ход управляемого процесса (4) был опреде-
лен на некотором отрезке to^Zt-^T, прежде всего необходимо за-
дать параметры управления и=(и\ и2,..., иг), например, как
функции времени u=u(t) = (ul(t)y..., ur(t))\ to^t^T. Будем
предполагать, что параметры управления и в каждый момент t
принадлежат некоторой области управлений V(t), которая может
быть любым множеством некоторого r-мерного евклидова прост-
ранства Ег (в частности, может быть V(t)=Er). Управление
u = u(t) назовем допустимым, если его координаты иЩ)
(/=1,2,..., г) явлются кусочно-непрерывными [или ограниченны-
ми измеримыми] функциями и u(t)^V(t) при t0^t^T [почти

§ I] Постановка задачи оптимального управления 157
всюду]. Множество всех допустимых управлений обозначим че-
рез U.
Возьмем некоторое управление u(t)^Uy t^t^T, и в (4)
положим u = u(t):
* = /(*, u{t)y t)y t0<t<T. (5>
Под решением этого уравнения будем понимать непрерывное ре-
шение интегрального уравнения
x(t) = \f(x(т), и (т), т) dx + х (g. (6>
и
Будем предполагать, что функции f{(x, и, t) определены и
непрерывны вместе со своими частными производными fxf (х, и, t}
(i, /= 1, ... , п), где х^Еп, u(t)^V(t)t to^t^T. При этих ус-
ловиях может быть доказано существование и единственность ре-
шения уравнения (5) с заданными начальными условиями x(t0)r
определенное на некотором отрезке t(y^t^.Tu t0<Ti^.T [194,
254]. В дальнейшем будем рассматривать только те допустимые
управления u(t)y для которых решение уравнения (5) существует
на всем отрезке *о^/<: Г.
Построенное в определенном выше смысле решение уравне-
ния (5) с начальным условием x(t0) будем называть решением»
или траекторией, уравнения (5), соответствующим допустимому
управлению u=u(t)^U и начальному условию x(t<>) и будем
обозначать через x(t)=x(t,u) t^t^T. Точку л:(/0) будем назы-
вать левым концом траектории, точку х(Т) —правым концом тра-
ектории x(t, и).
Теперь перейдем к непосредственной формулировке задачи оп-
тимального управления. Пусть в пространстве Еп заданы многооб-
разия S0(0» Si (О и некоторое множество G(t)y t&^t^T, и пусть
задан функционал
J(u)=[r(xyuJ)dt + 0(x(T))i
где функция f°(xyuyt) определена и непрерывна вместе с частными
производными /°/ (/=1,2, , п) при (*, uyt)£G (t) х V (t) X [/0, Г],
Ф (х) — определена и непрерывна при х 6 G (Т) f| 5/ (Г).
Задача оптимального управления заключается в том, чтобы
найти такое допустимое управление u=u*(t)^U, чтобы соответ-
ствующая ему траектории x=x*(t)=x(ty и*) удовлетворяла усло-
виям **(/<>)<=ЗДо), x*(T)ezSi(T)9 x*(t)<=G(t)y t0^t^Ty и функ-
ционал J (и) достигал своей точной нижней грани: J (и*) =inf J (и) =

Ш
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
[Гл. 3
= /*; здесь нижняя грань берется по всем u{t)^Uy для которых соот-
ветствующая траектория x(tyu) определена при t^t^T и удов-
летворяет условиям x(to,u)^So(t0)t x(Ttu)<=Si(T)/x(tyu)^G(t)t
'о</<7.
Такое управление u*(t) будем называть оптимальным управлени-
ем, x*{t)=x{tyu*)y to^t^T — оптимальной траекторией, а пару
(и*(t),х*(t)), *о^t^T — оптимальным решением рассматриваемой
-задачи. Заметим, что задача отыскания максимума J {и) легко сво-
дится к сформулированной задаче, если заметить, что sup/(w) =
= — inf (—J (и)).
Мы часто будем пользоваться следующей более краткой фор-
мулировкой задачи оптимального управления: найти минимум
функционала
J(u) = $P(xyuyt)dt + Q)(x(T)) (7)
to
лрй условиях
i = f(x9u9t)9 t0<t<T, (8)
x (t0) € S0 (g, x(T) 6 S/ (Г), x (t) 6 G (0, U < t < T, (9)
u = u(t)eU = {u(t):u(t)eV(t)t t0<t<£T) (10)
(подразумевая, конечно, что u(t) берется из класса кусочно-не-
прерывных или ограниченных измеримых функций).
Множество G(t) называют ограничением на фазовые коорди-
наты х= (х\...ухп) или просто фазовым ограничением.Может слу-
читься, что G(t)==En при всех t^[t0y 7], тогда задача (7) —(10)
называется задачей оптимального управления без ограничений на
фазовые координаты и вэтом случае условиеx(/)eG(/),f0^<7,
в (9) не пишется. Если же G{t)^sEny то задачу (7) — (10) называ-
ют задачей оптимального управления с ограничениями на фазовые
координаты.
Далее, многообразие S0(t) [или Si(t)] может не зависеть от
-Времени и состоять из одной точки, тогда говорят, что в задаче
(7)—(10) левый [или соответственно, правый] конец закреплен;
■если же S0(t) [или Si(01 t0^t^.Ty совпадает со всем простран-
ством Епу то говорят, что левый [или соответственно правый] ко-
нец .свободный и в этом случае условие x(t0)^So(t0)[x(T)^Si(T)]
в (9) не пишут; наконец, если S0(0[Si(01 *о<^<^7, представляют
собой некоторую гиперповерхность или кривую в ЕПу то левый
^правый] конец называется подвижным.
В задаче (7) — (10) моменты времени t0 и Т в общем случае
могут быть неизвестны, тогда они зависят от управления и подле-
жат определению, В частности, если /°=1, Ф(л;)=е0, то J(u) =

§ 2] Формулировка принципа максимума Л. С. Понтрягина 159'
= Г—to, и задачу (7) — (10) в этом случае называют задачей бы-
стродействия. Если же в задаче (7) — (10) моменты t0, Т извест-
ны, то задачу (7) — (10) называют задачей оптимального управ-
ления с закрепленным временем.
Если p(xtu,t)=f)(x,u) (/=0, 1, ..., п) и множества S0(t),.
Si(t), G(t) не зависят от t, то задачу (7) — (10) называют авто-
номной.
Наряду со сформулированной выше задачей в теории опти-
мального управления рассматриваются задачи с запаздыванием, с*
параметрами, с изопериметрическими условиями, с дискретным
временем и т. д. ([5; 8, 21, 24, 26, 27, 34, 48, 59—61, 75, 80, 100, 101,
115, 123, 139—142, 157, 160, 161, 171, 195, 205, 206, 228, 232, 234,
236, 238, 259] и др.; обзор работ см. в [60]? [1401).
Упражнения. 1. Если u=u(t) —кусочно-непрерывно, то непре-
рывное решение уравнения (6) кусочно-дифференцируемо и в точ-
ках непрерывности x(t) удовлетворяет уравнению (5). Доказать.
2. Доказать, что в случае ограниченного измеримого управле-
ния непрерывное решение уравнения (6) абсолютно непрерывно и
почти всюду удовлетворяет уравнению (5).
§ 2. ФОРМУЛИРОВКА ПРИНЦИПА МАКСИМУМА
Л. С. ПОНТРЯГИНА
Рассмотрим задачу оптимального управления (1.7—10) прет
1/(^ = 1/, G(/)=£n, to^t^T. Будем предполагать, что либо
Si(t)=En, либо Si(t)ss{(x9t) :hi(x,t)=0, i=l, 2, ..., п^п}, где
функции hi(x,t) непрерывно дифференцируемы по (x,t)^EnX
X[ta Т] и система векторов
W • -j*' ' l^T' —| U - 1, A • • • ,/г2)
линейно независима при всех (х, t)£Si(t)y причем в случае закрепг
ленного правого конца ht (х, t) = х1 — х\ (r=l,2, fnx = n).
Аналогично, пусть либо S0(t) = En, либо
S0(*)={(*, t) :gt {х91) = 0,. i = 1, 2, ... ,n0 <n),
где функцииgi (x, f) непрерывно-дифференцируемы no (*, t)£EnX[t0t T\
и система векторов <(-~Ц , ——, —i (i = 1, 2, ^n0) линей-
t ox1 dxn dt J
но независима при всех (x, t)€S0(t), причем в случае закрепленного
левого конца gL (х, f) =s х* — *', i = 1, 2, , п0 = п.
Сначала рассмотрим случай, когда моменты t0, Т закреплены.
Для формулировки принципа максимума наряду с системой
(1.8) рассмотрим следующую систему линейных дифференциаль-
ных уравнений относительно вспомогательных (дополнительно
вводимых) переменных t|)(0 = OMOt •••> ^п(0):

160
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
[Гл. 3
п
/-о
тде фо(*)гФо— некоторая постоянная. Если взять какое-либо до-
пустимое управление u=u(t) и соответствующую ему траекторию
jc=x(t,u) и подставить их в (1), то получим линейную систему, из
которой однозначно определяется вектор ty(t)9 to^t^T, при лю-
бых начальных условиях и любой заданной фо. Вектор 1|э(/) часто
называют импульсом, а самое систему (1)—сопряженной систе-
мой.
п
Составим функцию Н(ху i|>, %, u,t) = \\ №*(х> и> 0» называе-
мо
мую функцией Гамильтона — Понтрягина. Тогда, как легко прове-
рить, системы (1.8) и (1) можно записать в следующем симмет-
ричном виде:
х
I —
дН ;, дН
w¥=-i*-{i=l'2'---'n)-
При фиксированных х, \|э, ф0, t функция Н (х91|?, t|)o, и, t) стано-
вится функцией лишь параметра u^V и тогда имеет смысл гово-
рить о sup Н(х, i|), г|)0, и, t) *=М(х, t|), г|)0, t). Если точная верхняя
грань значений непрерывной функции Н достигается в некоторой
точке mgV, то М (х, if, t|?o, t) есть максимум значений функции Н
лри фиксированных (х, ф, фо» f) • Поэтому нижеследующую теорему,
дающую необходимое условие оптимальности, называют принципом
.максимума [195].
Теорема 1. Пусть x*(t), u*(t)t t0</<Т — оптимальное реше-
ние задачи (1.7—10) при V(t) = V, G(t)=Eny t0<£t<£T; пусть мо-
менты /0, Т заданы. Тогда необходимо существуют непрерывная век-
тор-функция ф*(/) и постоянная t|)J, такие, что
1) ♦;«>, 1ф;|2+$;[^(о]2^о,^0<^<г; (2)
2) ф*(Л удовлетворяет системе (1) [при x = x*(t), U = u*(t)t
% = %\
3) при любом t£[t0,T] функция \Н (x*(t), ф*(0, %, и, t) пере-
менного и 6 V достигает в точке и = и* (t) максимума
н (*♦ (о, г (о> *;, и* (о, о = sup я (х* (о, ф* (о, *;,«, о; (з)
«6V

§ 2] Формулировка принципа максимума Л. С. Понтрягина 161
4) выполнены условия трансверсальности на левом и правом
концах, т. е. вектор ф*(Г) ортогонален к многообразию Sj(T) в
точке л:*(Г), вектор t|?*(.*o) ортогонален к многообразию So(t0) в
точке **(/о)> или короче: t|)*(/0)-LSo('o), ty*(Т)JSi(T).
Подробнее расшифруем условие трансверсальности для случая
различных режимов на правом конце траектории:
а) если правый конец свободен,То. условие ty*(T)J_Si(T)=En
озна[чает ty*(T)=0;
i б) если правый конец подвижен, то это условие гарантирует
существование таких постоянных аь а2,..., ani, что
^Л-Да, *^Л, *-1.....«; (4)
в) если правый конец закреплен, то условие -ф*(Г) _L ^(Г) ЕЕ-*!
тривиально — оно всегда выполнено.
Аналогично условие трансверсальности на левом конце траек-
тории означает, что:
а) если x(t0) свободен, то \|>*(*о)=0;
б) если *(А)) подвижен, то существуют такие постоянные
Ъи Ь2у ..., &по, что
4W°|>i ад(^Ц (*=1,2,...,п); (5)
в) если л:(/о) закреплен, то условие трансверсальности всегда
выполнено.
Теорему 1 мы сформулировали для случая, когда допустимое
управление u(t) является кусочно-непрерывным. В случае же ог-
раниченных измеримых управлений ее формулировка полностью со-
храняется, только соотношение (3) следует понимать в смысле
почти всюду на fo^£<7\
Доказательство теоремы 1 можно найти в работе, [195]. Один
случай этой теоремы будет доказан ниже в § 6.3.
Обсудим вопрос о возможностях применения теоремы 1 к ре-
шению задачи оптимального управления (1.7—10) при V(t) = Vr
G(t)=En с заданными t0, Т. Как следует из теоремы 1, оптималь-
ным может быть лишь то управление u(t)^U и соответствующая
ему траектория x(t)=x(t,и)у которые удовлетворяют следующим
условиям:
*' = /*(*. М), t0<t<T, 1=1,2, ...,п, (6)
/=о

162
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
[Гл. 3
t0<t<T, ;= 1,2, ... ,п,
x(tjes,(tj,x(T)estm, (s)
Ч> (t0) J_ S0 (t0) в точке x (У, у (Т) ±5Х (Г) в точке х (Г),. (9)
i|>e = const<0, Шг + £ |%(0I2=^0, *0<*<7\ (10)
Я(*,г|),о|>0, M(0,0 = suptf(*,%i|>o,M), *<,<*< Г. (11)
Здесь фо,.*ф(*) также являются неизвестными и подлежат опреде-
лению. Таким образом, из условий (6) — (11) нужно определить
2п+г функций **(*), фг(0 (i=l, 2, .., n), ul{t) (i=l, 2, .., г) и пЬ-
стоянную фа^О. Сразу возникает вопрос: достаточно ли информа-
ции, содержащейся в (6) — (11), чтобы определить указанные ве-
личины?
Рассмотрим прежде всего соотношение (11), из которого, во-
обще говоря, можно найти функцию
и = и(*,г|>,г|>0,0. (12)
Задача отыскания функции (12) нам уже знакома (см. гл. 2): здесь
надо максимизировать функцию Н(х, г|),фо, w, t) конечного числа
переменных (ц\ ..., иг)еУ при фиксированных (дс, ф, фо, 0- Во
многих практических задачах удается получить явное аналитиче-
ское выражение для функции (12).
Предположим, что функция (12) уже известна, и подставим ее
в;(6)-(7):
* = /(*, afr, 4>,ft,Q,<). i^-^^^^u^^09t)ft) (13)
В результате получили систему 2п дифференциальных уравнений
первого порядка с 2л неизвестными функциями x(t)y y(t). Как
известно, общее решение этой системы зависит от 2/г произволь-
ных числовых параметров (таковыми, например, могут быть на-
чальные условия x(t0), \|э(*о)). Напоминаем, что постоянная г|)0 в
(13) пока тоже неизвестна. Можно ли выбрать эти 2п параметров
и величину фо так, чтобы можно было удовлетворить условиям
(8) —(10)?
Заметим, что функция Н(х9 ф, ф0, и, t) является линейной од-
нородной функцией переменных i|)0, t|)i, ..., i|?n, поэтому
u(x, аф, а\|?о, t)=u(xtty,tyo, t) для любой функции а=а(0>0,
fo^/<:7\ Следовательно, система (13), а также и условия транс-
версальности (9) сохранят свой вид, если все величины фо/фь»., фп
умножить на один и тот же произвольный множитель а>0. Иначе
говоря, условия (6) — (11) определяют величины фо, фь •••» Фп лишь

§ 2] Формулировка принципа максимума Л. С. Понтрягина 163
с точностью до множителя а>0, и этим множителем мы можем
распорядиться по нашему усмотрению. На практике чаще всего
полагают
где 7—некоторый подходящим образом выбранный момент вре-
мени. Если заранее ясно, что i|?o<0, то можно принять tyo=—1.
В наших рассуждениях для определенности будем считать
Ыа + У1%('о)12=1.'*о<0. (14)
Теперь нетрудно убедиться, что имеющимися 2п параметрами
системы (13) и величиной г|з0 можно, вообще говоря, распорядиться
так, чтобы удовлетворить условиям (8), (9), (14). В самом деле,
если левый и правый концы траектории x(t) закреплены: *(*0)=*<ь
x(T)=xit то получаем 2п условий (условия трансверсальности (9)
в этом случае выполняются автоматически), которые вместе с* (14)
можно, вообще говоря, удовлетворить за счет выбора упомянутых
2п параметров и величины фо. Если левый конец закреплен, а пра-
вый— свободный, то x(t0)=x0, ф(Г)=0, и опять имеем 2л усло-
вий. Если левый конец закреплен, а правый — подвижный, то
*('а) = *о. Ч>(Г)= J|e' *М*^,Л. М*(Т).Т) = 0 (/=1,2, ...,*,),
т. е. всего 2п-\гП\ условий, которые вместе с условием (14) можно, во-
обще говоря, удовлетворить соответствующим выбором 2п пара-
метров системы (13) и величин ^о, Дь а2, ...,аП1. Аналогично мджно
проверить, что число параметров совпадает с числом условий для
выбора этих параметров во всех остальных возможных случаях
граничных режимов (8)', (9).
Таким образом, принцип максимума дает «достаточную» ин-
формацию для решения поставленной задачи оптимального управ-
ления, и можно ожидать, что имеются лишь отдельные, изолиро-
ванные траектории системы (13), удовлетворяющие условиям
(6) — (11). Лишь эти отдельные изолированные траектории и могут
оказаться оптимальными, причем их оптимальность, конечно,
нужно отдельно проверить ибо теорема 1 дает, вообще говоря, не-
обходимое условие оптимальности.
Как видим, принцип максимума дает изящно и просто выпи-
сываемые необходимые условия оптимальности и приводит к спе-
циального вида краевой задаче (13), (8) —(10), которую естест-

164^ ПРИНЦИП. МАКСИМУМА Л. С. ПОНТРЯГИНА [Гл. 3
венно назвать краевой задачей принципа максимума. Если из ка-
ких-либо соображений заранее известно, что поставленная задача
оптимального управления имеет решение, и соответствующая крае-
вая задача принципа максимума также выделяет единственное ре-
шение, то последнее как раз и будет оптимальным решением. На
этом пути решены многие практически важные задачи оптималь-
ного управления, ранее казавшиеся неприступными. Следует, ко-
нечно, заметить, что практическое решение краевой задачи прин-
ципа максимума часто связано с большими трудностями и тре-
бует разработки специальных алгоритмов.
Кратко остановимся еще на случае, когда моменты t0 или Т
заранее неизвестны и подлежат определению. Здесь мы ограничим-
ся следующей теоремой [195].
Теорема 2. Пусть x*(t), u*(t), t^t^T — оптимальное ре-
шение задачи (1.7—10) при V(t) = Vy G(i)=Eny *<></< Г; пусть
начальный момент времени t0 известен, а конечный момент Т за-
ранее неизвестен. Тогда остаются справедливыми все утверждения
теоремы 1 и, кроме того, имеет место равенство
#(**(0, *Ч0. *и *(0.0 =
^гшум.гю9ъ.*ы.4 ^ tto<t<Tt (1Б0
т
если правый конец закреплен или свободен, а в случае подвижного
правого конца это равенство заменяется на такое:
я(*чо,*чо,*о.«• (о.о = ~Sfl' dhj(x*n)tT) +
+ fW(T),**(T),*o,**(T),T) drto<t<Tt m
- J dt
т
где постоянные au a^ ..., ani те же самые, что ив (4).
Таким образом, принцип максимума и в этом случае приво-
дит к краевой задаче (13), (8)—(10), а наличие неизвестной ве-
личины Т здесь «компенсируется» появлением -дополнительного
условия, получаемого из (15) при t=T.
В сформулированных выше теоремах 1, 2 задача (1.7—10) рас-
смотрена в предположении.V(t)zz=Vy G(t)=En, t^t^T. О прин-
ципе максимума для задачи (1.7—10), когда имеются фазовые ог-
раничения, см.. в работах [5, 27, 55, 10U 141, 195] и др. Следует
сказать, что краевая задача принципа максимума в этом случае
имеет более сложный вид.

§ 2] Формулировка принципа максимума Л. С. Понтрягина 165
Для иллюстрации теорем 1—2 рассмотрим примеры.
Пример I. Минимизировать интеграл J (и) = — ( (х2 + и2) dt
о
при условиях х=—ах+и, х(0)=х0. Здесь x0f а, Т — заданные по-
стоянные; на управление и не наложены никакие дополнительные
ограничения.
Согласно теореме 1 составим функцию
Н = %\{х2 + и2)+ЪЛ-ах + и)
и выпишем сопряженную систему
%= —^аЪ — Ъо*-
Так как правый конец х(Т) свободен, то из условия трансверсаль-
ности имеем ^1(Г)=0. Отсюда следует, что фо<0 (если бы
^о=0, то ^(^ssO, и нарушено условие (2) теоремы 1). Поэто-
му можем принять \|эо=—1. Тогда функция
Н = - (л:2 + и2) + ^и — а^х
достигает своего максимума по и при u=tyu и краевая задача
принципа максимума запишется в виде
х=— ах + уг, % = аг|)1 + д:, x(0)=*0, г|)(71) = 0.
Эта линейная краевая задача легко решается. В частности, отсюда
следует, что подозрительным на оптимальность является управ-
ление
(Я — а) + (Х + а)е2%т
Оказывается, оно в самом деле оптимально (см. пример 6.3.1).
Пример2. Пусть материальная точка движется по оси Ох
по закону х=и9 где и — скалярный управляющий параметр,
|и|^1. Требуется найти такое кусочно-непрерывное управление
u(t), \u(t)\^l, &<;£<: Г, чтобы точка, выйдя из начального по-
ложения х(0) = 1 с нулевой скоростью, пришла в начало коорди-
нат с нулевой скоростькГза минимальное время.
В фазовых координатах х1=х9 х2=х эта задача сводится к
задаче наибыстрейшего перехода от точки (1,0) в точку (0,0),
когда движение происходит по закону: х1=х2, х2=и, |и|<^1.

166
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
[Гл. 3
Согласно теореме 2 составим функцию Н = % + $хх2 + \{уг и
выпишем сопряженную систему
Отсюда tfo (t) = clt ip2 (t) =c2 — cxt9 clf c2 — постоянные. Из условия
max Я имеем u (t) = sign (c2 — cj). Следовательно, оптимальное уп-
равление (если оно существует) является кусочно-постоянной
функцией, принимающей значение ±1 и имеющей не более одной
точки переключения tu при переходе через которую u(t) меняет
знак.
Нетрудно убедиться* что фазовая траектория, выходящая из
(1,0) и соответствующая управлениям u(t) = + l при t^O или
u(t)=— 1 при t^JO, или
u(t) = l+1> .°<'«i.
1-1, *!<*,
никогда не будет проходить через точку (0,0). Остается рассмо-
треть управление
1+1, *1<*.
Этому управлению соответствует траектория {xl(t), x2(t)}:
•2tlt t>tx.
l0.5*2-2^ + *?+l, txKt9 \t-
Из условия xl(T)=x2(T)=0 находим /i = l, Г=2. В качестве ве-
личин фо, фь №, требуемых в принципе максимума, можно принять
фо=0, ф1 =—1; ^2=*— 1. Можно доказать, что найденные управ-
ление и траектория будут оптимальными (см. пример 5.2.2).
Упражнения. 1. С помощью принципа максимума решить за-
дачу быстродействия для системы xl*=x?t х2=и при условиях
x(to)(=S0t x(T)<=Su [w|^l, где S0={xl=0, л;2=0} или
S0={\xl\2+\x2\2—1=0},или 5о={^—1=0, *2=0},а S{ = {xl=0}
или5;={|^|2+к212-4=0}.
2. Сформулировать принцип максимума для задачи (1.7—10)
при условиях, когда f(x, u, t)*z=A(t)x+B(t)u+F(t)t Л —матрица
порядка пХп\ В — матрица пХг, F — «-мерный вектор, и, кроме
того, V='{u:\u*\^l, i=l, 2, ..., г}, G(t)==Ent t0^t^T.
3. Показать, что в задаче: найти минимум J (и) = Г(х2 — и2)
dt

§ 2] Формулировка принципа максимума Л. С. Понтрягина 167
при условиях х=и, лг(0) = 1, *(3) = 1, |и|^1, оптимальное управ-
ление не существует, а минимизирующая последовательность un(t)
имеет вид
М') =
1, 0</<1,
2л ^ "^ " 2л
(-1)* при 1 + ^<;<1+ *±1, Л = 0, 1, ... ,2/г—1,
+[1, 2<*<3
(на отрезке 1^£<2 имеем дело с так называемым скользящим
режимом [63, 142J). Что дает здесь применение принципа макси-
мума?
1
4. Найти минимум функционала J(u)= ^sinudt при условиях
о
x=cosu, х(0)=0, *(1) = 1, |и|^—. Показать, что u*(t)=0 —
оптимальное управление, и убедиться в том, что в принципе мак-
симума здесь надо принять фо=0.
5. Применить принцип максимума к задаче: минимизировать
J(u)= t\x(t)\*dt при условиях х=и, *(0) = 1, х(Т) = 1, \и\^19
о
Т>0 задано. Показать, что при Т>2 оптимальное управление не
может быть однозначно определено из принципа максимума.
6. Применить принцип максимума к задаче: минимизировать
функционал J (и) = (*л;2*#при условиях х=и, л;(0)=0, |«|^1. По-
казать, что краевая задача принципа максимума имеет бесконечно
много решений, соответствующих управлениям
un(t)= ± sign ["cos(2/1+1)яЛ (л = 0, 1 ...).
Убедиться в том, что a*(/)sO — оптимальное управление. Пока-
зать, что последовательность {un(t)} является минимизирующей.
7. Показать, что задача минимизации функционала
J(u) = jV(a—I)2
dt
при условиях х=щ *(0)=0, х(Г) = 1, Т задано,
ft^w^l, при Г=1 имеет единственное оптимальное решение, а
при Г>1 имеет бесконечно много решений. Изменится ли этот
вывод, если снять ограничения на и?

168
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
[Гл. 3
§ 3. ПРИБЛИЖЕННОЕ РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
ПРИНЦИПА МАКСИМУМА
Если ввести вектор-функцию y(t) = (xl(t), ..., xn(t), t|)i(f), ...,
t|)n(0)> то краевая задача принципа максимума (2.13), (2.8—10)
может быть записана в виде
У = Г(У,Ъ, t0<t<£T, (1)
Pi(y(t0))=0, '=l,2,...,/n, (2)
Qi(l/^)) = 0, ' = 1.2, ,s, (3)
где m-\-s=2n. При этом в случае неизвестного Т согласно теореме
2.2 сюда нужно присоединить соответствующее дополнительное ус-
ловие (2.15), взятое при^=7\
Полученная краевая задача не является классической задачей
Коши, так как часть краевых условий задана при t=tQy а часть —
при t=T, и приближенное решение таких задач сопряжено с не-
малыми трудностями. —
Здесь ограничимся описанием двух наиболее известных мето-
дов, которые могут быть использованы для приближенного реше-
ния краевой задачи (1)—(3): метода прогонки в сочетании с ите-
рациями и метода стрельб, а также остановимся на некоторых
трудностях численной реализации этих методов. Для простоты
будем предполагать, что моменты t0) Т в (1) —(3) известны.
1. Метод прогонки с итерациями. Опишем этот ме-
тод сначала для линейной задачи, когда итерации не требуются.
Именно пусть задача (1) — (3) имеет вид
y = D(t)y + d(t)y t0<t<Ty (4)
(я/, И'о)) = а*> '=1.2, ,ю, (5)
[№,*(T))I=Pi. '=1^2, ,s, (6)
где D(t) — известная матрица порядка 2/2 х 2я, d(i)—заданная век-
тор-функция размерности^ [2пу аь = (а\, , af) (' =1,2, , m),
Ь{ = (b\y •.. yb?) (' = 1, ,s)—две заданные линейно независимые
системы m + s = 2n векторов, постоянные ah fy также заданы.
Метод прогонки для решения задачи (4) — (6) заключается в
следующем. Сначала находят вектор-функции Z\(t)\ ..., zm(t), ре-
шая линейные задачи Коши:
Z;(0 = -D'(0*b МУ=аь '=1,2, ,«; (7)
здесь £>*—матрица, полученная транспонированием матрицы D.
Далее, из линейной алгебраической системы 2п уравнений с 2п
неизвестными

§ 3] Приближенное решение краевой задачи принципа максимума 169
| (г1(Т),у1)=а1+ Ud(i)9zt(t))dt (i = 1,2,... 9m) (8)
I (»ьй) = Р|, t=l,°2, ,s. (9)
определяют yi = (*/}, >у\п)- И, наконец, решая еще одну линей-
ную задачу Коши:
У = DXf)y + d(f),t.<t<Т\ у(Т) = уи (Ю)
получают искомое решение y(t) задачи (4) —(6).
В самом деле, полученная из (10) функция y(t) является ре-
шением системы (4) и в силу (9) удовлетворяет граничным усло-
виям (6). Покажем, что y{t) удовлетворяет также и граничным
условиям (5). Действительно, согласно (7), (8), (10) имеем
т
fa, у Л)) = fe (g, у (t0)) = - J-jL (*, (о, У(/)) # + (z, (г), у (Г)) =
и
т
= - f [&, У) + <*i, Й]Л + fe (Т), yi) =
и
т
= - J [(- D* г/, z<) + ft, jty) + fef d)] A + to (T),») =
г
= - j (г, (0, d (*)) Л + ft (Г), yi) = щ (i = 1, 2, , т).
Здесь мы воспользовались равенством (D*2,*/) = (2,Ity). Таким об-
разом, найденная из (10) функция y{t) есть решение задачи
(4)-(6).
HefpyAHO дать описание метода прогонки и в разностной фор-
ме. Для этого дифференциальные уравнения (7), (10) следует за-
менить разностными с помощью какой-либо известной разностной
схемы (например, по схеме Эйлера, Адамса, Рунге — Кутта и др.
[20]) и решать получающиеся разностные задачи Коши. При вы-
числении интеграла в правой части (8) можно пользоваться из-
вестными квадратурными формулами [19].
В нелинейном случае для. решения задачи (1) — (3) можно
применить метод прогонки в сочетании с итерациями. Для этого
задачу (1) — (3) линеаризуют каким-либо образом и решение ис-
ходной задачи ищут как предел последовательности решений со-
ответствующих линейных задач. Для отыскания решений линейных
задач на каждом шаге итераций используют тот или иной вариант

170
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
[Гл. 3
метода прогонки. Например, отправляясь от некоторого начального
приближения yo(t), приближения y\(t)9 ..., t/h(t), можно искать
как решения линейных краевых задач
Ук+х = F(yk,t) + Ak(t) (ук+{-ук), t0<t<T,
PiM*)) + ( №у«» , yk+i(t0)-yk(to)) =0> t=l,...,/n,(H)
* = !,...,s, fc = 0, 1,2,...,
где Д*и)—некоторая известная матрица, —-и —-=*- —гради-
ду ду
енты функций Р{(у) и Qi(f/) соответственно. К сожалению, ника-
ких общих правил выбора матриц Ak(t) не существует. В тех слу-
чаях, когда F(yft) гладкая функция, полезно принять Ak(t) =
_—{Укк)> Однако следует сказать, что F(y, t) лишь в ред-
ду
ких задачах является гладкой функцией. Дело в том, что управле-
ние u=u(xt t|), i|>o, t), определяемое из условия max Я (я, ф, %, uy /),
часто бывает негладким или даже разрывным, и в этом случае от
правых частей (2.13) и, следовательно, от F(y,t) какой-либо глад-
кости ожидать не приходится. Матрицы Ah(t) следует выбирать
исходя из соображений удобства численного решения краевой за-
дачи (11) на каждом шаге итераций и условий сходимости итера-
ций к решению исходной задачи (1) —(3). Выбор Ah(t) в каждой
конкретной ситуации является искусством.
2. Метод стрельб заключается в следующем. Из условий
(2), вообще говоря, можно выразить m координат вектора y(t0)
через остальные s=2n—m координат. Пусть для определенности
первые m координат у1 (to), ..., ym(to) однозначно выражаются че-
рез остальные координаты yi(to)=a)i(ymrhl(to)t ...» y2n{U))>
t=l,2,...,m. Зададим каким-либо образом ym+i(!t0)=ii (t=l,...,s),
тогда однозначно определяются у*(<о)=(0|(Л1> ..., К8) (1=1, ..., m).
Тем самым каждому набору параметров %= (А,1, ..., is) соответству-
ет вектор y(to)=yo(X). Решая задачу Коши для системы (1) с
начальным условием y(to)=yo(h)> получим вектор-функцию
у(*Д), to^.t^T, которая при любом выборе X удовлетворяет
граничным условиям (2). Подставим у (Г, X) в граничные усло-
вия (3) и получим функции Qi(y(TtX))^(pi(X)t i=l 5, пара-
метров К=(%\ ..., Xs). Для удовлетворения граничным условиям
(3) параметры X следует выбрать так, чтобы К удовлетворяли сле-
дующей, вообще говоря, трансцендентной системе уравнений:
<р£ (%) = ф, (Х\ ... , V) = 0 (i = 1, 2, ... , s). (12)

§ 3] Приближенное решение краевой задачи принципа'максимума 171
Тем самым краевая задача принципа максимума оказалась
сведенной к задаче отыскания корней системы (12). Для решения
системы (12) могут быть применены известные методы [19]. В ча-
стности, эта система может быть сведена к эквивалентной задаче
s
минимизации функции <р (К) = \\ ф* (К), для решения которой
можно использовать рассмотренные в гл. 2 методы минимизации
функций конечного числа переменных.
Следует подчеркнуть, что вычисление значений функций фг(Х)
в некоторой точке Х9 вообще говоря, достаточно трудоемко, так как
для этого надо решить задачу Коши для системы (1) 2п уравнений
с начальным условием y(to)=yo(X). Поэтому при отыскании кор-
ней системы (12) (или минимизации введенной выше .функции
ф(Х)) важно использовать быстро сходящиеся методы, требующие
сравнительно небольшого количества вычислений функции
<р(А,). Здесь часто используют метод Ньютона, применение которо-
го, как показывает опыт, требует от вычислителя немалого искус-
ства, в частности, умения удачно выбрать начальное приближение.
Частные производные функций q>i(X), необходимые при вычисле-
нии градиента, при этом обычно заменяют соответствующими раз-
ностными отношениями.
В том случае, когда задача (1) — (3) линейна и имеет вид
(4) — (6), применение метода стрельб существенно упрощается. Для
этого систему векторов а\, .••> я™ из условия (5) произвольным об-
разом дополняют до базиса пространства Е2п векторами
йщ+и ..-, Я2п. После чего определяют вектор-функцию го (О из за-
дачи Коши:
'z0 = D(t)z0 + d(t)t t0<t<Ty
(ai,z0(t0)) = ai(i= 1, ... ,/n); (am+u z0(t0)) = 0, t=l, ,s,
а вектор-функции Z\(t), ..., zs(t) из следующих задач Коши:
г, = D (*)*,, t0<t<Ty
fo. M'o)) = 0 (*= 1,2, ... ,m), (dm+i, z3(g) = fii/,
t= 1, ,s, / = 1, ,s,
где 6ij —символ Кронекера (6ij=l при i=<j и 8tj=0 пдо t#=/).
Тогда функция
^ = #(*Д) = г0(0+£ЯЧ(0
будет решением системы (4), удовлетворяющим при любых
Х=(А,1, Xs) условиям (5). Для определения решения задачи

172 ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [ГА. 3
(4) — (6) теперь остается подставить найденную функцию y(t, X)
в (6) и определить Я1, ..., Xs из получающейся при этом линейной
алгебраической системы
£ V {bt, zy (Г)) = р< - (bh z0 (Т)) (i = 1, 2, , s).
Как видим, применение метода стрельб к решению линейной
краевой задачи (4) — (6) требует решения s+1 задачи Коши (для
определения z0(t), ..., zs(t)) и 5+2 систем линейных алгебраиче-
ских систем (для определения Zo(t0), ..., г8{{0) и параметров К).
В нелинейном случае для решения задачи (1) — (3) можно при-
менить описанный метод стрельб в сочетании с итерациями, когда
на каждом ujare итераций решается линеаризованная задача (см.,
например, задачу (11)).
3. Эффект «неустойчивости» и пути его преодо-
ления. Следует заметить, что практическое применение методов
стрельб и прогонки часто наталкивается на серьезную трудность,
связанную с быстрым ростов некоторых координат вектор-функции
y(t) и переполнением разрядной сетки ЭВМ даже в тех случаях*
когда отрезок интегрирования t^t^T невелик. Например, если
исходная система (1.4) имеет вид x=Ax+B(uyt), где А— посто-
янная матрица порядка пХл» и, кроме того, f°(x,uyt)=f°(u,t), то
система (2.1) для ty(t) может быть записана так: ^=—Л*ф, где
Л*— матрица, полученная транспонированием Л. Отсюда видно,
что корни характеристического уравнения матрицы (—А*) отли-
чаются от корней характеристического уравнения матрицы А толь-
ко знаком и, следовательно, исходной устойчивой системе для х в
этом случае будет соответствовать неустойчивая сопряженная си-
стема уравнений для яр.
Один прием для преодоления эффекта «неустойчивости» был
предложен в работе [2J. Впоследствии этот прием был описан и
развит в работах [1, 243] с учетом специфики краевой задачи
принципа максимума. Для изложения этого приема нам будет
удобнее работать с расширенным вектором <ф=(ф0, я|)(/)) =
— СФо, ^i(0» ^n(0)=^(0» удовлетворяющим системе урав-
нений
ii = -t^Ji^tr±'i = 0'1' •"• (13)
полученной добавлением к системе (2.1) еще одного уравнения при
t=0. Такое расширение системы (2.1) не меняет существа дела
и не «портит» краевую задачу принципа максимума' (2.13),

§ 3] Приближенное решение краевой задачи принципа максимума 173
\
\
(2.8—10), так как функция Н (и вообще вся задача) не зависит
от переменной 1 х°, поэтому % = — = 0, т. е. \|)o=const. (Эта
прежний параметр из теоремы 2.1. Далее, как было замечено
выше, умножение вектора ty(t) = (ty0f ty(t)) на положительную
скалярную функцию |х(0>0 (в силу однородности функции
л __
Н(х> 'Ф, и, t)= V tyfl (xtutt) по переменной г|?) не меняет вида
управления u=u(xt ф, 0»определяемого из условия max Н (х9 ф, и, /),
а также не влияет на условия трансверсальности. Поэтому вместо
вектор-функции ф(/)"» являющейся решением «неустойчивой» си-
стемы (13), можно попытаться искать другую вектор-функцию
р(') = (ро(0> р(0)в1*('Ж0> и(0>°> которая будет опреде-
ляться из некоторой «устойчивой» системы уравнений
ft = ft(*.«.M) (' = 0,1, ,/г). (14)
В результате краевая задача (2.13), (2.8—10) будет заменена на
задачу
*'=/'(*, М), t0<t<Ty i= 1,2, ,л;
ft = ft(^.".P. ?). t0<t<T, i = 0, 1, ... ,л,
^(g6 50(g, ^(7)6^(7), (15)
P Co) = (Pi ft>)> > Р/г (*«)) J_ S0 (f0) в точке x (g,
P (Л = (P! (Г), ... , 9n (T)) J_ Sx(T) в точке x(Г),
Po(0<0, |р(0|2 = £р?(0=£0,
где и=и(*,г£t)=u(x,pyt) определяется из (2.11). В силу построе-
ния системы (14) имеет p(t)=ix(t)ty(t)t \i(t)>0. Поэтому из
краевой задачи (15) можно определить те же самые подозритель-
ные на оптимальность управления и траектории, что и из задачи
(2.13), (2.8—10), с той, однако, разницей, что при удачном выборе
системы (14) эффект «неустойчивости» будет отсутствовать или
значительно снизится.
1 Впрочем, систему (1.8) иногда полезно расширить введением переменной
х° посредством условий i°=f0(*, и, t), х°(*0)=0. [195].

174 ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [Га. 3
Таким образом, требуется построить систему вида (14), кото-
рая обладала бы следующими двумя свойствами: 1) любые два
решения i|)(t) и р(/) соответственно систем (13), (J.4) (при од-
них и тех же x=x(t), u=u(t)), для_ которых _р(*о)=а+(*о),
a=const>0, связаны соотношением p(0=n(*) + (0> [i{t)>09
n
t^t^T; 2) |p(*)| = (Vp^/))7, — невозр^астающая функция вре-
fc-0 ,
мени. '
Следуя работе [243], укажем некоторые приемы построения
системы (14) с требуемыми свойствами. Сначала остановимся на
линейном случае, когда система (13) для * имеет вид
* = C(o+f t0<t<T. (16)
Наряду с этой системой рассмотрим еще систему
P=C(*)p+e(M)pf t0<t<Ty (17)
где е(р, t) некоторая скалярная функция. Оказывается, при подхо-
дящем выборе функции е(р, t) система (17) будет обладать нуж-
ными; свойствами. Это вытекает из следующих лемм.
Лемма 1. Если +(0—решение системы (16) с начальным
условием + (*о), а p(t) —решение системы (17) с начальным усло-
вием р(*о), если p(ifo)=a^(4)=7^0, a=const>0, то существует
такая непрерывная функция ia(*)>0, что p(t)=[i(t)ty(t)y to^ts^T.
Доказательство. Обозначим tMQ = - > Ро(0 = - t
Ш)\ _ 1р(01
где |z\ = V(z,z). Так как Ф0 = -^ [ -Дг-, -4=- —^-, то, под-
V ; т? 1*1 \ 1 + 1 1 + 1/ 1 + 1
ставляя_сюда выражение для ty(t) из (16), получим г|>0 = С (/) t|>0—
—(С(ОФ0» ФсО+о- Аналогично для р0(£) имеем
Ipl Vlpl IpI/ Ipl
— (Cpo, Po)Po —^(P» 0(Po> Po)Po = C(0p0 — (Cp0, Po) p0
независимо от выбора функции е(р, t). Таким образом, +0(*) и pQ(t)
являются решением одной и той же системы дифференциальных
уравнений z = Cz — (Cz, z) z при одном и том же начальном условии
z(t0)=%(to)=~P0(to)= -^-.
I t (<о) I

§ 3] Приближенное решение краевой задачи принципа максимума -175
В силу единственности решения задачи Коши имеем
й(0-Р.(<), или -М-шш-В®-, t0<t<T.
Ж01 1р(')1
Остается положить {д. (/) = JililL, ^
\V(t)\ _ _
Лемма 2. Если е (р, t) > ( ?'р , то для любого непрерывно-
Р2
го решения p(t) системы (17) величина \p(t)\ = (V р^(0)1/вбудетне-
убывающей функцией, а если е(р, *) <—IIJMJL^ то |р(*)| будет не-
Р2
возрастающей функцией»
Доказательство. Так как
Y1T(р2) = (р' р) = (С(')р' р) + *(р>0(р, Р) =
= ?[-^- + .(р,о].
то в первом случае будем иметь (р2) > 0, во втором случае—
dt
rd —
-—(Р2)<0» откуда и следует справедливость леммы.А
dt
На основе леммы 2 можно предложить различные функции е(р, t)9
для которых норма \p(t)\ решения системы (17) не будет возра-
стать. Например, можно взять е(р,0——\\C(t)\\,rrne ||С||—норма
матрицы, соответствующая евклидовой норме вектора. Так как
|(Ср,р")|<||С|||р|2, то ^(p,0=-||C(0IK-i%ElL, и в силу
Р2
леммы 2 |р(0 | не будет возрастать. Однако практическое вычис-
ление IIС (£) || часто бывает затруднительным, поэтому, имея в виду
оценку
«С(/)|2< £|С17(012,
можно положить
*(р.о=-( j; \Сц{тг)4'

176 ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [Гл. 3
или даже е(р, *)=—Стах, где постоянная
Cmax>max( £|C^0I2)V*,
t\/=0
Сц (t) —элементы матрицы C{t). Заметим, что приведенные функции
е(р, t) от р не зависят, и система (17) остается линейной относи-
тельно р.
В некоторых случаях выбор е(р, 0<— Р может при-
вести к столь быстрому убыванию |р(0|> что |р(0| может обра-
титься в машинный нуль. Во избежании этого можно принять
е(р,<)=е(р2), где е(г) —непрерывная функция одной переменной,
удовлетворяющая условиям e(r)^Cmax при г<гь е(г)^—Стах
при г^г2у \е(г)\^Стлх при r^r^lr^ где Т\ и г2 — подходящим
образом выбранные положительные числа, t\<ir2. Например, мож-
но положить
еО^-гс^-^^ + с,
Г\ — '1
max'
Из леммы 2 в этом случае следует, что если ri^p2(/0)^/2, то-
ri<^P2(0-*Cr2 во все моменты t^[t0T\; если' p2(*o)<ri или
Р2(*о)>г2, то величина p2{t) будет стремиться с течением времени
попасть в полосу r^p2(t)^r2 и остаться в этой полосе в после-
дующие моменты времени. О других-способах выбора е(р, t) см.
в работах [1, 243].
Если система (13) нелинейна и неустойчива, то может ока-
заться полезным рассмотрение системы
п
Pi = 2 ca9j + *(Р> 0Pt С = 0, 1, , л),
/«-о
где Ctj = '-j и функция е (р, t) выбирается одним из вышеуказан-
ных способов [243].
Об использовании принципа максимума для решения конкрет-
ных прикладных задач, о методах решения возникающих при этом
краевых задач см. в работах [1, 2, 27, 34, 44, 75, 130, 141, 144, 146,
147, 152, 171, 243, 246] и др.

§ 4] СвЬзь с классическим вариационным исчислением 177
§ 4. СВЯЗЬ МЕЖДУ ПРИНЦИПОМ МАКСИМУМА И КЛАССИЧЕСКИМ
ВАРИАЦИОННЫМ ИСЧИСЛЕНИЕМ
Основной задаче! классического вариационного исчисления,
как известно [68, 254], является следующая задача: среди всех
непрерывных кривых x*=x(t)9 to^t^f, имеющих кусочно-непре-
рывные производные x(t) и удовлетворяющих условиям *(f0)&So,
x(T)eSi, найти такую, которая доставляет функционалу
J = ]f*{x{t)9k{t)9t)dt
минимальное значение. Здесь x(t) = (xl(t)9 ..., xn(t))9 S0 и Si—за-
данные множества в Еп. Буд^м предполагать, что функция
f°(x9u9t) непрерывна и имеет непрерывные производные /$,/£,/?,
fuu f°uxt fuu при (*, uJ)<=EnXEnX[tot+oo]. Далее в этом парагра-
фе для простоты ограничимся случаем закрепленного левого конца
{x(to)=Xo9 t0 задано), а правый конец х(Т) либо закреплен
(х(Т)=хи Т задано), либо свободный (Sis£n, Т задано), либо
является подвижным и лежит на заданной гладкой кривой
Si={(xtt) :х—<p(f)=0}, Т не задано.
Обозначим х=и и запишем рассматриваемую задачу в экви-
валентном виде как задачу оптимального управления: минимизи-
т
ровать функционал J(u)= Г f°(x9 u9i)dt при условиях х=*и9
*о<*<Г; x(t0)=x0, x(T)€=Siy*u(t)^V=En.
Для исследования этой задачи воспользуемся принципом мак-
симума Понтрягина. Согласно теоремам 2.1—2 нужно выписать
функцию Гамильтона — Понтрягина:
Я = %Р(х, и, t) + (г|>, и) = Н (х9 ф, и9 t)9 (1)
и сопряженную систему
* = — 1Г = — *J°x(x,u9f)9 i|)0 = const<0. (2)
ox
Для оптимального решения u(t)9 x(t)=x(t9u) должно выполнять-
ся необходимое условие
H(x(t)91>(0, u(t)91) = maxH(x(t)9i|>(0, v, t)9 t0 <t<T9 (3)
где ty(t) решение системы (2) при u=u(t)9 x=x(t9u). Так как в
данном случае множество значений управления V совпадает со
всем пространством Еп, то условие (3) может соблюдаться лишь
в стационарной точке, т. е.
H^ifA <*W, u(t)9t) + *(/) = 0. (4)

178 ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [Гл. 3
Отсюда ясно, что tpo^O, так как в противном случае \|>(/)=0 (см.
условие (2.2) теоремы 2.1). Следовательно, можно считать, что
Uo=—/. Тогда соотношения (1)—(4) перепишутся в виде
#(*, *, и, t) - - /• (*, u, t) + (*, а). (5)
*«#(*.".<). t0<t<T, (6)
Я (* (0, * (0. и (0, t) = max Я (* (*), <p.(t),v,t), t0<t< Т, (7)
* (0 = Л (* (0. и (0. fl. t0<t<T. (8)
Из уравнения (6) имеем ty(t) = f /^(а: (f), w (/), *)Л + $('•)» поэтому
с учетом (8) получим
f°u (х(*), tf (f), 0 = J/2](*С), и(0,0 Л + «(t0). (9)
Уравнение (9) называется уравнением Эйлера в интегральной
форме; здесь и(*)=*(0- Если (9) продифференцировать по t, то
получим уравнение Эйлера классического вариационного исчисле-
ния в дифференциальной форме
-£- (fu(x(t), u(t), t))-f°x (x(t), и (*).<) =0, u{t) = x(t). (90
Далее, необходимым условием достижения функцией
H(x(t)t ty(t), и, t) максимума при u=u(t) является неположи-
тельность квадратичной формы
2 Hutj (х (0, ty(t),u (/), t) U/ < 0 при любых £ = (Ъ19 Ъ ... , у,
«./-1
или если учесть выражение (5) для Я, то
2 /«V (*(0, и (0,0 М/ > 0, £6 £я, t0 < t < Т (10)
Условие (10) называется необходимым условием Лежандра.
В частности, при п=1 отсюда имеем
f°uu(x(t),u(t)tt)>0, t.<t<T.

§ 4] Связь ^ с классическим вариационным исчислением 179
Теперь выведем необходимое условие Вейерштрасса. Для это-
го перепишем условие (7) с учетом (5), (8) в следующем виде:
0< Я (*(*), i|?(/), u(t),t)-H(x(t)9 ЧКО, v% t) = /•(*(/), v, t)-
-f°(x(t),u(t)ft)-(v-u(t)tf°u(x(t),u(t),t)). (11)'
Это неравенство справедливо при любых t/eFs£n и t0^t^T9
если u(t)9 x(t)—оптимальное решение исходной задачи. Введем
в рассмотрение функцию
E(t9 х9 uf v)mej*(x9 v, t)-P(xt и9 t)-(v-u9 fu{x9 и9 *)), (12)
называемую функцией Вейерштрасса. Известное в классическом
вариационном исчислении необходимое условие Вейерштрасса
тогда немедленно следует из (11):
E(t9x(t)9u(t)9v)>09 fe<*<7\ v£En.
Далее, из принципа максимума следует непрерывность
вектор-функции t|>(/) и функции H(x(t)9ty(t)9u(t)9t) =
=maxH(x(t)9 ii>(t), v9 t) по переменной t9 t0<,t^T (см. пред-
v€En
ставления (2.15) в теореме 2.2). Поэтому с учетом соотношений
(5), (8) имеем
[f°u(x(t)9u(t)9t)]t = Q9 (13)
[(и (t),f°u(x(t)9u(t)9 t))-fo(x(t)9 u(t)9 t)]t = 0, tb<t<T9
здесь принято обозначение [z(t)]t=z(t-\-Q)—z(t — 0). Поскольку
равенства (13) выполнены при всех t9 to^.t^T9 то они сохраняют
силу и в те моменты t9 когда функция x(t) может иметь излом,
т. е. производная x(t) терпит разрыв. Таким образом, если учесть
связь u(t)=x(t)9 условия (13) превращаются в известные из клас-
сического вариационного исчиления условия Эрдмана — Вейер-
штрасса в точках излома кривой x(t).
Перейдем к рассмотрению условий на правом конце оптималь-
ной кривой x(t). Если конец х(Т) свободен, то в силу теоремы 2.1
<ф(Г)=0 и с учетом выражения (8) имеем
fu(x(T)9u(T)9T) = 0. (14)
Если правый конец х(Т) подрижен, точнее, лежит на заданной кри-
вой Sie= {(х91): hj {х9 f) = xf — фу (t) = 0, /=1,2,..., п}9 то соглас-
но теоремам 2.1 — 2 существуют такие постоянные al9 а29... 9аП9 что
^(Т) = ^а/^у^^, Н(х(Т)МТ), и(Т),Т) =
/=1

ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [Гл. 3
= _£а/ ам^т) = £ а^{т) = ^/(Т)ф/(Г) = (1|)(Г)) ф(г)).
Так как Я(х, i|>, w, 0 = (Ф» u) — f°(x> u> О и Ф(0 выражается форму-
лой (8), то последнее равенство можно переписать так:
f°(x(T)9u(T),T)+(fu(x(T),u(T)tT), ф(Г)-и(7)) = 0. (15)
Условия (14), (15) при учете связи x(t)=u(t) выражают собой
известные в классическом вариационном исчислении условия
трансверсальности для свободного и соответственно подвижного
правого конца. N
Таким образом, в случае V=En из принципа максимума сле-
дуют все основные необходимые условия, известные в классическом
вариационном исчислении [68, 254]. Однако если V — замкнутое
множество и УфЕп, то соотношение (4),вообще говоря,не выпол-
няется. Более того, имеются примеры, когда и условие Вейер-
штрасса в этом случае не имеет места ([195], стр. 284). Принцип
максимума, являясь естественным обобщением условия Вейер-
штрасса из классического вариационного исчисления, имеет то су-
щественное преимущество перед условием Вейерштрасса, что он
применим для любого (в частности, и замкнутого) множества
V^Er и для более общих задач. Заметам, что именно случай
замкнутого множества Ve£r наиболее интересен в прикладных
вопросах, поскольку значения оптимальных управлений чаще всего
лежат на границе V.

Глава 4
Динамическое программирование.
Проблема синтеза
В этой главе остановимся на методе динамического програм-
мирования, часто используемом при численном решении задач оп-
тимального управления при наличии фазовых ограничений. Заме-
тим, что принцип максимума может быть сформулирован и для
задач с фазовыми ограничениями, однако получающаяся при этом
краевая задача будет иметь еще более сложный вид ([5, 27, 55, 101
141, 195] и др.), и трудности при ее численном решении значитель-
но возрастают. Поэтому для численного решения таких задач ча-
сто бывает выгоднее использовать метод динамического програм-
мирования. Изложение этого метода начнем с простейшей схемы
Р. Беллмана [6, 14—18, 27, 34, 54, 206, 234, 259], затем опишем бо-
лее совершенную и удобную для практики схему Н. Н. Моисеева
[167—169, 171].
§ 1. СХЕМА Р. БЕЛЛМАНА. ПРОБЛЕМА СИНТЕЗА
ДЛЯ ДИСКРЕТНЫХ СИСТЕМ
1. Рассмотрим следующую задачу оптимального управления:
минимизировать функционал
- /(«) = f/Ч*. «, t)dt-hO(x(T))9 (1)
при условиях х'= f(x, и, t), t0<£t^Tt (2)
*(*)€G(f), t0<t<T, (3)
u=u(t)eV(t)t to^t^T, u(t) —кусочно-непрерывна (4)
(подробное описание обозначений см. в § 3.1; множества S0(t0)
и Si(T) из (3.1.7—10) нам здесь удобнее включить в фазовые от-
раничения G(t)9 to^t^T); моменты t0t Т будем считать извест-
ными.
Для приближенного решения этой задачи разобьем отрезок
*о^^<, Т на N частей точками *о<*г<«.<'л-1<*л=7' и, приняв
эти точки в качестве узловых, интеграл в (1) заменим квадратур-
ной формулой прямоугольников, а уравнения (2)—разностными
уравнениями с помощью простейшей явной схемы Эйлера [20].
В результате мы придем к следующей дискретной задаче опти-
мального управления: минимизировать функционал

182 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
/о (х, Мо) = 5] ^(*" Ul) + ф {Xn)>
t=0 (5)
f°t(Xi, «i)= /°(*Ь «j, ^)ft+i—/|)
при условиях
^+i = -F« (*i. «»)e**+ft+i — h)f{xu щ, tt), (6)
t = 0, 1 N—l,x0 = xeG0,
xteGtw-G{td, i=0, 1 AT, (7)
No=("o. «i. ••• . "tf-i), »j€V{™V(^), * = 0,1,2 N— 1.
(8)
Заметим, что задача (5) — (8) имеет также и самостоятельный
интерес и возникает при описании управляемых импульсных систем.
Если задать какие-либо дискретное управление [щ]0=(и0, ии
..., uN-\) и начальное условие xo=x^G0y то система (6) однознач-
но определяет соответствующую дискретную траекторию '[jt*]0=
= (х0=х, хи ..., xN). Зафиксируем некоторое xgG0 и через До(*)
обозначим множество управлений [иг-]0, таких, что: 1) выполнены
условия (8); 2) дискретная траектория [дсг]о, соответствующая уп-
равлению [щ]о и выбранному начальному условию х0=х, удов-
летворяет фазовым ограничениям (7). Управление [иДо^Ао(х) и
соответствующую траекторию [хД0 будем называть допустимыми
для выбранного начального состояния х. Множество До(*) может
быть пустым или непустым. Если Ao(*)=0 ПРИ всех *sGo, то
условия (6)—(8) несовместны и функционал (5) определен на
пустом множестве. Поэтому, чтобы задача (5) — (8) имела смысл,
естественно требовать существования хотя бы одной точки x^G0,
для которой Ао(х)Ф0. Обозначим X0=){x:x^Go9 Ао(х)Ф0}.
Тогда задача (5) —(8) может быть сформулирована совсем крат-
ко: минимизировать функционал /<>(*, [Иг]о) при [щ]о^А0(х) и
х^Х0. В результате мы пришли к уже известной нам задаче мини-
мизации функции n+Nr переменных х, Ио, Щ, ...» Un-u и для ее
рещения можно использовать методы из гл. 2. Однако в практиче-
ских задачах число n-\-Nr обычно бывает столь большим, что не-
посредственное использование методов гл. 2, вообще говоря, силь-
но осложняется. Вызывает трудности также и то обстоятельство,
что множества До(#) и Х0, на которых минимизируется 10 (х, [щ]о),
заданы неявно. Для преодоления этих трудностей используют ме-
тод динамического программирования, позволяющий свести задачу
(5) — (8) к последовательному решению более простых задач ми-
нимизации функций меньшего числа переменных.
2. Для изложения метода динамического программирования
нам понадобятся следующие вспомогательные задачи: минимизи-
ровать функционал

§ 1] Схема )> Беллмана. Проблема синтеза для дискретных систем 183
h (*. [Щ\к) = £ F°i (xi9 щ) + Ф (xN) (9)
при условиях
Xi^ = Ft{xiy щ)9 i=k9 k+l9...9 N—l9 xk = x£Gk9 (10)
xteGi9 i = kt k+l9...9 N, (11)
[Щ]к = ("л, Иц-i. • •. Илг-i), a, € Viy i = A, k + 1,... , W — 1,
(12)
где точка x и целое число k фиксированы, x^Gh9 O^k^N—l.
Через Да(^) обозначим множество всех управлений [щ]к, таких,
что: 1) выполнены условия (12); 2) соответствующая траектория
[xi\k= (Xk=xt хк+и ..., xN) из (10) удовлетворяет фазовым ограни-
чениям (11). Нетрудно видеть, что если ХоФ09 то Ак(х)Ф0 хотя
бы при одном x^Gk. Введем функцию inf Ik (х9 [щ]к) = Bk(x)9
fe=0, 1, ..., N— 1 называемую функцией Беллмана задачи (5) — (8).
. Покажем, что функция Беллмана удовлетворяет следующим
рекуррентным соотношениям, называемым уравнением Беллмансь:
Bk(x)= inf [F°k(x, u)+Bk+l(Fk(x9 и))], k = 09 1.....ЛГ-1,
u£Dk(x)
BN(x) = 0(x)9 (13)
где Dk(x) —множество всех, тех ие^, для которых существует
хотя бы одно управление [wt]ft= (uh, uk+\, ..., uN-i)^Ak(x) с ком-
понентой Uk=u. Очевидно, что множество Dk(x) и Ah(x) оба пусты
или непусты одновременно, и поскольку xk+\=Fh(x9и), то для не-
пустоты этих множеств необходимо и достаточно, чтобы
Справедливость соотношения (13) при k = N—1 очевидным об-
разом вытекает из условия BN(x) = <b(x) и представления
/jv_i (х9 [wjtf-i) = F^_i (х9 и) + ф (FN-\ (х9 и))9 верного для любого
и 6 DN-i (х) = Длг-1 (х)={и: и £ VN-U *n = -Fat—i (*» ") 6 Gtf, * 6 GN-X).
Докажем (13) при k9 0<£<N—1. Для этого сначала убедимся в
том, что
Bk(х) < Inf [F°k(x9 и) + Bk+i (Fk (x9 и))]. (И)
Возьмем произвольное u£Dk(x) (разумеется, предполагаем, что
1>к(х)Ф@). Тогда xk+i=Fk(x, и) и Ак+х(хк+\)Ф 0. По определе-
нию Bk+i(xk+i)= inf h+\(xk+u [иАк+\)9 для любого е>0 найдет-
ся управление [w?]fe+i 6 Aft+1(^/f+1)> такое, что Bk+i(xk+{) <h+\(xk+l9

184 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
[u1]k+\)<Bk+i (xk+l) + е. Поскольку [щ]к = (а, н£ц, • • • ,«5r-i) € ДЛ(*),
то Bk(x)<Ik(x, № = /^(*, u)+Ik+l(xk+u [uei]k+i)<F°k(xt и) +
+ Bk+i(xk+i) + e==Fl(x, u) + Bk+l{Fk{x, и)) + е. В силу произволь-
ности u£Dk(x) и величины е>0 отсюда следует неравенство (14).
Теперь покажем, что в (14) на самом деле знак неравенства мож-
но заменить знаком равенства. По определению inf Ik (ху [щ]к) = Bk(x),
для каждого е>0 найдется такое управление [v*]к6 А* (*), что,
Я*М<Л (*. WW <Bk (х)]+ е.
Но
поэтому
F°*(*, vt)+Bk+l(Fk(xt vl))<F°k(x, vl) + Ik+l(Fh(xt vl), Ын-O =
= '*(*> №h):<Bk(x)+e.
Так как и^бД^х), то отсюда имеем
inf [Fl(xt u)+Bk+l'(Fk(x9 u)))<Bk(x)+e9
u£Dk(x)
или в силу произвольности 6>0
inf [Fl(x, u)+Bk+i(Fk(xt u))]<Bk(x). (15)
Из (14) — (15) немедленно следует соотношение (13).
'Пользуясь уравнением Беллмана (13), можно последовательно
определить функции Bk(x) и их области определения Xki
k=N, №— 1, ..., 1, 0. А именно В^(х)==ф(л;), Xne= Gn — известны.
Если известны Bh+i{x) и Xk+\ (k^N—l)9 то для определения
Вл(х) нужно решить задачу минимизации функции <р (ху и) =
= Fk(x,u)+Bk+\ (Fk(x,u)) переменных и=(и\ ..., иг) на известном
множестве Dk (х) = {и : и^ V*, Fh (х, и) ^Хк+\}. Для этого могут
быть использованы методы глав 1, 2. Очевидно, функция Вк{х)
определена в точке х тогда и только тогда, когда Би{х)Ф0.
Таким образом, при определении значений Bh(x) одновременно
находится и область ее определения
Xk = {x:xeGk, Ок(х)ф0}^{х:.хеОк, Ьк(х)Ф0}.
Так как Ак(х)ф0 хотя бы при одном x^Gh, то ХкФ0, k=N,
tf-1, ..., 1, 0.
Заметим, что для широкого класса задач оптимального управ-
ления знак inf в правой части (13) можно заменить на min. Об
этом говорит

§ 1] Схема Р. Беллмана. Проблема синтеза для дискретных систем 185
Теорема 1. Пусть множества Gk, &=0, 1, ..., Nt замкнуты,
множества Vh, 6=0, 1, ..., N— 1, замкнуты и ограничены, и функции
F°k (ху и)у Fh(xyu) непрерывны по совокупности аргументов (*, и)
при x^Gh, weKft, ft=0, 1, ..., N—l, Ф(х) —полунепрерывна снизу
на множестве GN. Тогда: 1) множества Xhy &=0, 1, ..., Ny замкнуты,
множества Dk(x), k=Q, 1, ..., N—l, замкнуты и ограничены равно-
мерно по x^Xh; 2) нижняя грань в правой части (13) достигается
хотя бы при одном u=Uk(x)^Dk(x); 3) функция Въ(х) полунепре-
рывна снизу на Xh, k=0f 1, ..., N (см. определение 2.5.3).
Доказательство. По условию Gn=Xn замкнуто, Ф(л;) =
= BN(x) полунепрерывна снизу на XN. Сделаем индуктивное
предположение: пусть Xk+\ замкнуто, Bk+\(x) полунепрерывна
снизу на Xh+i при некотором ky 0-^.k^N—l. Докажем, что тогда
Xk замкнуто и на Xh справедливы все утверждения теоремы.
Так как Dk(x) = {u: u^Vh, Fk(x,u)^Xk+i}^Vk, a Vk ограни-
чено, то Dh(x) ограничено равномерно по x^Xk.
Докажем замкнутость Dk (х) при любом фиксированном х 6 Xk
Пусть vm£Dk(x) (m=l, 2,...), vm-+v(m->-oo). Эю значит» что.
Vm€Vk, Fk(xy vm)eXk+i(m=lt 2,...). Из^замкнутости Vk, Xk+l и
непрерывности Fk (х; v) сразу имеем
veVk, UmFk(xy vm) = Fk(xt v)6Xk+\,
т. e. v£Dk(x). Замкнутость Dk(x) доказана.
Покажем замкнутость Xk = {*: x 6 Gk, Dk (x) Ф 0}. Пусть
ym£Xk{m=\y 2, ...), ym->-y(m->oo). Из замкнутости Gk следует,
что y£Gk. Если мы еще покажем, что Dk(y)^0y то это будет
означать, что y£Xk9 и замкнутость Xk будет доказана. Так как
Dkbjm)^®* то существует такое ~vme Vky что Fk(ymy vm)eXk+i
(m=l, 2,...)- В силу компактности Vk из последовательности
{vm} можно выбрать подпоследовательность {vm }->-а€ Vk(n-*oo). По-
скольку Xk+i замкнуто, Fk (ху и) непрерывна, то lim Fk (ym , vm ) =
П-»оо
= Fk(y> v)£Xk+b т. e. v£Dk(y). Таким образом, Dk(y)=£0t
Далее, функция <р(ху и) == F\ (ху и) + Bk+\ (Fk (ху и)) при каждом
фиксированном x£Xk полунепрерывна снизу по u£Dk(x). Это сле-
дует из непрерывности F°k(xy и)у Fk(xy и) и полунепрерывности сни-
зу Bfe+i (л:). Поскольку Dk(x)—замкнутое ограниченное множество,
то ф(*, и) при каждом фиксированном x£Xk достигает своей ниж-
ней грани на Dk (х) хотя бы в одной точке и = uk (х) 6 Dk (х) (см. уп-
ражнение 2.5.11, теорему 6.1.1). Таким образом, Bk {х) = inf ф (ху и) =
u€Dk(x)
= ф(*, uk(x)) в силу уравнения Беллмана (13).-
Остается еще доказать полунепрерывность снизу Bk (х) на Xk.
Пусть UmBk(z)= limBk(ym)t z, ху ут6Хкут-+х(т-*оо)у Bk(ym) =

186 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
= ф(Уш. ик(Ут)). Так как uk(ym)eDk(ym)eVkf то в силу компакт-
ности Vk последовательность {uk(ym)}(fn = 1, 2, ...) имеет хотя бы
одну предельную точку v£Vk. Можем считать, что сама последова-
тельность * {ик(ут)}-+.v(m-*oo). Поскольку Fk(х, и) непрерывна,
Xk+\ замкнуто и, кроме того, Fk(ym, uk(ym))£Xk+u то lim Fk(ymt
т-*оо
"ftW) = ^(^^^+i- Это значит, что v£Dh{x). Тогда
limВк (х) = lim Bk (ym) = lim q> (ym, uk (ym)) > <p (x9 v) >
> inf ф(л;, u)-=[Bk(x)t Полунепрерывность £Л(лг) на Л^ доказана. А
u£Dk(x)'
Приведенное доказательство сохраняет силу, если от Fk(x, и)
потребовать лишь ее полунепрерывность снизу по (#,и).
3. Предположим, что нам удалось найти функции Bk(x) из
условий (13) и, кроме того, пусть также известны функции
uk(x)^Dk(x)9 x^Xk, &=0, l,...,Af—1, на которых достигается
нижняя грань в-правой части (J3). Тогда, оказывается, решение
задач (5)^(8) и (9) —(12) выписываются совсем просто. А имен-
но оптимальное управление [щ]0 и соответствующая траектория
[4]0 Для задачи (5) —(8) определяются следующим-образом:
сначала из условия
iniB0(x) = B0(x*0) (16)
х€Хй
находят х16 Х0, затем последовательно полагают
ио = и0(4), х\ = F0(4, и0), и\ = и%{х\)у х*2 = Fx (Хи Щ), ...
, x*n = Fn-i(xn-u илм). (17)
Оптимальное управление [щ\к и траектория [х\]к для задачи (9) —
(12) определяются аналогично
4 = *, ик = uk (4), 4+i = Fk (4, 4),... , xN = FN-i (4г-ь uN-i).
(18)
Для доказательства этих утверждений введем вспомогательные
функции
Rt (х, u) = Bt+l (Ft (х, u)) — Bt (x) + Fat(x, и), i = О, 1,... , N— 1.
(19)
Очевидно, уравнение Беллмана (13) тогда можно переписать в экви-
валентном виде

§ 1] Схема Р. Беллмана. Проблема синтеза для дискретных систем 187
inf Rk(xy и) = 0, £ = 0, 1,..., N—U Вм(х) = Ф(х).
u€Dk(x)
(20)
Кроме того, с помощью функций Rt (xt и) значение функционала (9)
на любом управлении [щ]к 6 А* (х) и х 6 Xk выражается так:
h (х, № = £ Ri (*,, а,) + 5, (х) (21)
*=*
при всех & = 0, 1,..., #—1. В самом деле, учитывая равенство
BN(x) = Q>(x)t из (10), (19) имеем
tf-l JV-1
что равносильно (21).
Теорема 2. Пусть выполнены условия теоремы 1 и множе-
ство Go ограничено. Пусть найдены функции Bh(x) из (13) и их
области определения Хку а также функции u=uk(x), x^Xk,
&=0, l,...,Af— 1, на которых достигается нижняя грань в уравне-
нии (13) (или (20)). Тогда оптимальное управление [и*]0 и тра-
ектория [х*]о для задачи (5) — (8) определяются соотношениями
(16), (17).
Доказательство. Прежде всего заметим, что существова-
ние х*0 6 Х0, удовлетворяющего условию (16), следует из полуне-
прерывности снизу Bq{x) на ограниченном замкнутом множестве
Xq^Gq. Далее, из определения щ{х), [и*]0, [х*]0 и эквивалентно-
сти записей уравнения Беллмана (13) и (20) имеем
*i(*\ ^)=0, * = 0, 1,..., N-L (22)
розьмем произвольные х^Х0) управление [иЦо^Ао(х) с соответ-
ствующей траекторией (*<]0 из (6). Так как Ui^Di(Xi)> то из урав-
нения (20) и определения щ{х) следует
inf Rt (xh и) = Ri (xi9 щ (xt)) = 0 < Rt (xi9 щ)% (23)
f = 0, 1,... , N-U
С помощью формулы (21) при А = 0сучетом соотношений (16), (22),
(23) получаем

188 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
М*> 1"Ло)— А>(*о, [tk]0)= J] [Ri(*i> щ)—ЯЛ*и "!)] +
+ В0(х) — В0(4)>0
для Л1рбых х6ЛГ0 и ИобА0(х). А
Теорема 3. Пусть известны Bh(x)f x^Xh из (13), а также
функции Uk(x)t на которых достигается нижняя грань в уравне-
нии (13) (или (20)). Тогда оптималные управления [щ\к и тра-
ектория [xi\k для задачи (9) — (12) определяются формула-
ми (IS).
Доказательство. Возьмем произвольное управление
fe]fteAft(x) и соответствующую траекторию [Xi]k из (10). Очевид-
но, соотношения (22), (23) остаются справедливыми и здесь при
всех i=k, £+1, ..., Af— 1. Поэтому оптимальность [t£]k устанав-
ливается с помощью формулы (21) так же, как в теореме 2. Д
Заметим, что inf Ik(xt [щ]к) =Ik(x, [u]k) = Bk(x). Это сле-
дует из формулы (21) с учетом равенств (22). Тем самым пока-
зано, "что функции Bk(x)t определяемые из (13), в самом деле
являются функциями Беллмана для задачи (5)—(8).
4. В теории оптимального управления и ее приложениях важ-
ное место занимает так называемая проблема синтеза, заключаю-
щаяся в построении функции u=u(xtt)t представляющей собой
оптимальное управление при условии, что в момент t объект нахо-
дится в точке х фазового пространства. Такая функция и(х, t) на-
зывается синтезирующей.
Теорема 3 показывает, что решение уравнения Беллмана (13)
равносильно решению проблемы синтеза для задачи (5) — (8).
В самом деле, функция Uk(x), на которой достигается нижняя
грань в (13), является синтезирующей, так как если в момент k
объект находится в точке х^Хк, то дальнейшее оптимальное дви-
жение объекта определяется условиями *г+1=Л(*г, M*i))> i=kt
k+l, ..., N— 1, xk=x, (если x ф Xh, то Ak(x)=0t т. е. движение
с соблюдением условий (10) — (12) невозможно). Достаточные ус-
ловия существования синтезирующей функции для задачи (5) — (8)
приведены в теореме 1.
5. В практических задачах получить явное выражение для
функций Uk(x)t на которых достигается нижняя грань в уравне-
нии (13) или (20), часто бывает затруднительно, да к тому же 6
некоторых задачах указанная нижняя грань может вообще не до-
стигаться. Поэтому на практике часто приходится иметь дело с
функциями Uk(x), которые реализуют нижнюю грань в (13) или
(20) лишь приближенно. Оказывается, при некоторых условиях
такие функции ик(х) могут быть взяты в качестве приближенной
синтезирующей функции для задачи (5) — (8).

§ 1] Схема Р. Беллмана. Проблема синтеза для дискретных систем 189
Теорема 4. Пусть функции Bk(л:), х6^, k = 0, 1, ... , N,
удовлетворяют уравнению Беллмана (13), и функции ukm(x)£Dk(x)9
/и= 1, 2, таковы, что UmRi(x, uim(x)) = 0. Пусть, кроме того,
найдены точки х0гп£Х0, для которых limB0(xm) = inf В0(х). Постро-
т-»оо х£Хо
им управление [щт]0 и соответствующую траекторию [*1т]0^следую-
щим*образом:
и0т*~ Щт \хот)у х1т == F0(X0mi иот)> и1т ==Щт \х1т)> • • • >
xNm = Fn—1 (*W— 1,т. #W—1,т).
Тогда последовательность [wtml0 является минимизирующей для зада-
чи (5) —(8), т. е. Нт70(д:0т, [uim]0) = inf inf/0(*, k]0) =/J.
m-»oo x£X0 &o(x)
Доказательство. Возьмем произвольную точку х6 Х0 и
произвольное управление [Ui]0£A0(x) с соответствующей траекторией
[x;]0 из (6). С помощью формулы (21) при & = 0 тогда имеем
N-\
t=0
+ B0\(x)-B(;(x0m)t m=l,~2,...
В этом равенстве можно перейти к пределу при т-^оо, так как
правая часть по условию имеет предел. В результате получим
n-\
Io(x> [щ]оУ—^т10(хш> [uim]0)= YRi(xit щ) +
л*"*50 "
+'В0'(х)-\п1В0(х)>0,
хех0
так как Ri(xh щ)> inf Rt(xiy и) = 0 в силу (13) или (20). Из
произвольности х£Х0 и [wt]o^oW следует /J > lim/0(*0m, [и1т]0).
m-*oo
С другой стороны, /0(*0m, [«im]0)>/o, m=l, 2 Поэтому
Uml0(xm, [uim]0) = l'o. A
m-»oo
Теорема 5. Пусть функции 5;(*), Wtm(*)> i=&, £+1, ...,
N—1, m=l, 2, ..., удовлетворяют условиям теоремы 4. Построим
управления [uim]k и соответствующие траектории [Xim]k следующим
образом:
xkm ^ Х> Ukm = ukm (xkm)> xk+l, т = Fk (xkm> Ukm)>
uk+lf m = #*+!. m (Xk+lf m), • • • , *tf/n = Fn—\ (*7V-1, m, ^^-1, m).

190 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
Тогда последовательность [ulm]k (m= 1, 2, ...) является минимизи-
рующей для задачи (9) — (12), т. е.
limIk (*, [uim]k) = I*k= inf 4 (x, [Щ]к) = Bk (x).
Доказательство. Возьмем произвольное [(*.<]&€ Ад(x) с со-
ответствующей траекторией [х^ из (10). С помощью формулы (21)
тогда имеем
N-1
m=l, 2,...
Теперь равенство limlk(xt [ultn]k) = Ik доказывается так же, как и в
теореме 4. Соотношение l\ = Bk {х) следует из формул (21) при
Щ = иш> xi = хш> когДа >я-*оо. ^
Как видим, функции uim(x) из теоремы 4 дают приближенное
решение проблемы синтеза для задачи (5)—(8), ибо если в мо-
мент k объект находится в точке x&Xk, то движение объекта по
закону
*+1.т = Л(*«т. Uim(xiJh i = *. k+lt...9 N—lt
Чт = х> w= 1, 2, ...
при больших т доставляет функционалу /*(*, [щ]к) значения, как
угодно близкие к оптимальному /£.
6. Резюмируя содержание настоящего параграфа, заметим,
что метод динамического программирования позволяет свести за-
дачу (5) — (8) к последовательности, вообще говоря, более про-
стых задач минимизации функций меньшего числа переменных для
определения Bk(x), Uk(x), определить абсолютный минимум функ-
ционала (5) при условиях (6) — (8), а также решить проблему син-
теза для этой задачи. Этот метод дает значительный выигрыш в
объеме вычислений по сравнению с простым перебором всевозмож-
ных допустимых управлений и траекторий, поскольку при вычис-
лении Bk(x), ик(х) достаточно рассмотреть лишь такие управления,
которые переводят точку х в точку Xh+i=Fb(xt и)} и дальнейшее
движение из точки хи+\ осуществить по оптимальной траек-
тории, отбрасывая все неоптимальные. Указанные достоинства ме-
тода динамического программирования, простота схемы и приме-
нимость к широкому классу задач с фазовыми ограничениями
делают этот метод весьма привлекательным, и его широко исполь-
зуют при решении задач типа (5) — (8).

§2]
Схема Н. Н. Моисеева
191
Можно показать, что при некоторых ограничениях решение
дискретной задачи (5)—(8) при измельчений шага сетки (точнее,
при max | /f+1 — ^ | ->. О (JV ->•оо)) будет близко в некотором
смысле к решению непрерывной задачи (1) — (4); (см. гл. 9).
Следует, однако, сказать, что аналитическое выражение для
Bh(x), Uh(x) при всех x^Xk в общем случае найти не удается,
и на практике приходится ограничиваться приближенным вычисле-
нием Bk(x), Uk(x) в некоторых заранее выбранных узловых точках,
используя какие-либо методы минимизации функций (например,
методы из гл. 1, 2). Согласно (13) при вычислении Bk(x) нужно
знать значения Bk+{ (Fk (х, и)) при некоторых и, и здесь возможны
случаи, когда точка xh+\ = Fh(xtи) не принадлежит заранее выб-
ранному множеству узловых точек, а следовательно, значение
Bh+i(Xk+\) заранее не вычислено. Разумеется, можно дополнитель-
но вычислить недостающее значение Bk+i(x), но это может при-
вести к чрезмерному расширению множества узловых точек, ибо
для его вычисления нужны значения ранее вычисленных функций
Bh+2(x), ..., BN(x) в новых дополнительных точках. На практике
в таких случаях недостающее значение Вц+\(х) получают с по-
мощью интерполяции по значениям Bh+\ (х) в близлежащих узло-
вых точках, что, естественно, снижает точность метода.
Следует также заметить, что принятый выше способ аппрок-
симации задачи (1) — (4) с помощью разностной задачи (5) — (8)
довольно груб, поскольку опирается на простейший метод ломаных
Эйлера для интегрирования дифференциальных уравнений и квад-
ратурную формулу прямоугольника. Ниже опишем схему Н. Н. Мо-
исеева, которая не требует интерполяции и оставляет достаточную
свободу при выборе способа аппроксимации задачи (1) — (4).
§ 2. СХЕМА Я. Н. МОИСЕЕВА
1. По-прежнему будем рассматривать задачу (1.1—4). Для
приближенного решения этой задачи, как и раньше, разобъем от-
резок t^t^T на N частей точками to<Zt\<z...<Cttf—i<ztN:=:T.
На множестве Gi=G(U) возьмем некоторую дискретную сетку
точек Xij^Gi\ следуя [171], множество всех точек выбранной сетки
будем называть шкалой состояний и обозначать через #*, i=0,
1, ..., N. Шкалы состояний Я* и Яг+1 будем называть соседними.
На двух соседних шкалах Яг- и #г+1 возьмем точки *е#* и
уеЯ1+1 и рассмотрим вспомогательную задачу: минимизировать
функционал
Ji (х9 У,и)= Г /° (х (t), u (t)t t) dt (x, у — фиксированы) (1)
h

192 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
при [условиях
x(t) = f(x(t),u(t)yt)t UKtKU+u *(ti)=x9 x(tw) = y9 (2)
x(t)eG(t), *,<*<*,+!, (3)
и (t) кусочно-непрерывна и и (t) 6 V (t) при tt < t <^+i, (4)
i=0, 1, ..., N—\. Следуя [171], задачу (1)—(4) будем называть
элементарной операцией, соединяющей точки х и у. Через Ы\х9у)
обозначим множество всех управлений u(t) из (4), для которых
соответствующая траектория x(t) удовлетворяет всем условиям
(2) —(3). Положим Mt(x9 у)= inf Ji(x,y,u)\ если Ai(x9y)=0t
и£А.(х,у)
то будем считать Л1г(*,*/) =+оо по определению.
Пусть все точки всех соседних шкал попарно соединены эле-
ментарными операциями. Если inf Jt (xt г/, и) достигается на
некотором управлении щ(t) еДг-(дс, у) и соответствующей траекто-
рии Xi(t), то величина
N— 1
£ Mt (*4f *H-I./,+1)'"+ Ф (XN.IN), *0,/о = Х
выражает собой значение исходного функционала (1.1) на управ-
лении u(t)=Ui(t) и соответствующей траектории x(t,u)=Xi(t),
ti^t.^ti+u i=0, 1, ..., JV— 1, x(t0)=x? при соблюдении всех огра-
ничений f 1.2—4). Поэтому исходную задачу (1.1—4) естественно
аппроксимировать задачей отыскания минимума суммы
N-1
£ Mi (*«./,. *Ж.//+1) + Ф С^АГ./лг)
t=0
по всевозможным наборам точек
(*о./0 = ху xujl, ... , xN,iN), хи. 6 Я, (/ = 0, 1, , N)
при всех x^Hq. Такая аппроксимация задачи (1.1—4) имеет
смысл, конечно, и в том случае, когда inf Ji(xtytu) не дости-
гается при каких-либо х, у, i. Очевидно, приведенная аппроксима-
ция задачи (1.1—"4) более гибкая и лучше приспособлена для
приближенного решения этой задачи, чем схема Беллмана, ибо
здесь предоставляется свобода в выборе способа реализации эле-
ментарной операции (1) — (4), и, кроме, того, рассмотрение лишь
таких траекторий, концы которых лежат в известных точках со-
седних шкал, избавляет нас.от необходимости интерполирования.
На способах реализации элементарной операции остановимся
ниже.

§2]
Схема Н. Н. Моисеева
193
Описанная аппроксимация задачи (1.1—4) имеет простой
геометрический смысл. А именно траекторию Xi(t) из (2), на кото-
рой достигается inf Jt (xt уу и), назовем дугой, соединяющей
точки х, у, а число Mi(x, у) —длиной этой дуги (i=0, 1, ..., N—l).
Дуги, последовательно соединяющие пары точек xtj., *i+U;+1 со-
седних шкал #г-, #i+i, '=0, 1, .., N—1, назовем путем, соединяю-
щим шкалы Н0 и HNy проходящим через точки а:0/о, хцх% >xNjNt
и в качестве его длины примем число
N—1
Тогда наша задача сведется к отысканию кратчайшего пути, сое-
диняющего шкалы Н0 и HN.
2. Обозначим
Ck (х) = inf { J] Mi (xijr *f+i,/|+1) + Ф(*м/„)),
где нижняя грань берется по всем наборам точек
(xkjk = х9 xk+uk+ii... txN}N)t xif{ 6 Hh i = k, k + 1, N.
Иначе говоря, Ck(x) выражает собой кратчайшее расстояние между
фиксированной" точкой *6 Hk и шкалой HN.
Докажем, что функции Ch(x) удовлетворяют следующим ре-
куррентным соотношениям:
Ck (х) = inf {Mk (х, у) + Ck+l (у)}, k = 0, 1, , N- 1;
y£Hk+1 (5)
С„(х) = Ф(х),
аналогичным уравнению (1.13). Справедливость (5) при k=N— 1
следует из определения CN-\{x)y CN(x). Покажем (5) при других
k, 0^.k<.N— 1. Для этого сначала убедимся в том, что
Ck(x)< inf {Mk(xiy)+Ck+l(y)}y xeHk. (6)
Возьмем произвольное !/еЯЛ+ь По определению Ck+\(y) для лю-
бого е>0 найдется путь, соединяющий точку у со шкалой HNi
длина которого не превышает Cfc+i(y)+e- Если этот путь «удли-
нить», добавив к нему дугу, соединяющую точки х и у, то получим
путь, соединяющий точку x^Hk со шкалой HNt длина которого не
превышает Mh(x, y)+Ch+i(y)+e. Поэтому заведомо Ck(x)^.

194 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
^Mk(xfy)+Ck+\(y)+e. В силу произвольности точки y^Hk+\ и
величины е>0, отсюда имеем неравенство (6).
Теперь покажем, что в (6) на самом деле знак неравенства
можно заменить знаком равенства. По определению Ck(x) для
любого е>0 найдется путь, соединяющий точку x^Hk со шкалой
HN, длина которого не превосходит Сд (х) +г. Пусть этот путь про-
ходит через точку ye^Hk+\. Ясно, что отрезок этого пути
от уе до HN не меньше Ck+\(y*), и поэтому весь путь от х до
HN не меньше Mh(xtye)+Ch+i(ye). Следовательно, Mh(x9ye) +
+Ck+i(ye)<^Ck(x)-\-e. Так как г/ееЯЛ+ь то отсюда имеем
inf; {Мк(х9у) + Сц.г(у)}<Сь(х) + е
или в силу произвольности е>0 —
inf {Mk (х,у) + СЛ+1 (у)} < Ck (х).
Сравнивая это неравенство с (6), немедленно получаем требуемые
соотношения (5).
3. Соотношения (5) могут быть использованы так же, как и
уравнение Беллмана (1.13). Опишем порядок работы с этими со-
отношениями в предположении, что каждая из шкал состоянии
Hiy i=l9 2, ..., N, содержит конечное число pi точек. Заметим, что в
этом случае в (5) вместо inf можно писать min. Функция CN(x) =
==ф(#), x^HN нам известна. Для вычисления Cn-i(x) с помощью
элементарных операций соединим попар'но все точки шкал HN-\ и
HN. Сравнивая Pn-i-Pn величин MN-\(x9у)+Ф(у) при всевозмож-
ных *e#jv_i, y^HNt найдем
min [MN-{ (х, у) + Ф (у)] = CN-i (х),
y£HN
а также точку y=yN-\(x)^HNt на которой этот минимум дости-
гается. Если Ck+i(x) и y=yk+i(x) при ^еЯА+1 уже известны, то
лпя вычисления Ch(x), x^Hk соединим элементарными операция-
ми всевозможные пары точек из шкал Hk и Hk+i- Перебором
Ph-ph+\ величин Mh(x9y)+Ch+\(y) при всех хеЯа, y^Hk+i найдем
min [Mk (х, у) + Ck+l (у)] = Ck(x)t
а также точку у = yk (х) 6 #/н-ь х 6 Hk9 на которой этот минимум
достигается, и т. д» для всех k = N, N— 1, ... , 1, 0. На вычисле*
ние всех Ck (х) и у = yk (х) при x£Hkt k = 0, 1, .., 9N— 1, понадо:
N— 1
бится перебор V рь • pt+i величин. Наконец, находим х*£Н0 из
условия Св (л:*) = inf С0 (х). Для этого нужно перебрать еще р0 величин.
хен.

§ 2] Схема Н. Н. Моисеева 195
Затем, определяем последовательно точки х\ = у0(х*0), х*2 = Ух(х\)>...
•••> xn = ^-! (xjv-i)' ПУТЬ> проходящий через найденные точки
*о> *I» »*#> будет кратчайшим среди всех путей, соединяющих
крайние шкалы Я0, HN.
В самом деле, по определению yk(x)9 &=0,1,...,W—1, и х\$.Нк,
& = О, 1, , N, имеем
СЛК)=^К,^+1) + СЛ+1(4+1), А = 0, 1, ,#-1. (7)
Возьмем произвольный путь, соединяющий шкалы Я0 и HNi про-
ходящий через точки х0у хи ..., *jv, х^Н{ (i=0, 1, .., Af). Так как
хк+\^Нк+и то согласно (5) будем иметь
Ск (хк) < Af* (xkt гк+х) + Сш fak+i).
Отсюда и из (7) тогда следует
Mk К *ш) + Ck+i (х^х) -Ск (*р = 0< Мк (хк> а+0 +
+ СЛ+1(хА+1) —СЛ(**), £ = 0,1,...,#-1.
Просуммируем это неравенство по k от нуля до N— 1. Получим
//—1
£ Ai4 (xh x*k+ll+ Cn (Sn) - C0 (xl) <
Л=0
< £ МЛ (*Л, *ж) + CN {xN) — C0 (x0).
*=0
Ho
поэтому
C0(x^infC0(x)<C0(x0),
J]1 л* (*;, 4+1) + ф og < £ м$хк, xk+l) + ф m
для любых путей, соединяющих шкалы Н0 и //#. Таким образом,
путь, проходящий через точки л^, x*v yx*N, в самом деле, крат-
чайший.
Если u*(t) и x*(t)y ^<<</i+>i, представляют собой управление
и соответствующую траекторию, на которых приближенно реали-
зуется элементарная операция (1) — (4) при х = х*(, y = x*+v то
в качестве приближенного решения исходной задачи (1.1—4) мож-
но взять управление и* (t) = и* (t) и траекторию х* (t) = х* (t)f
*<^*<A+i 0=0, 1, ..., ЛГ-1).

1<)6 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
Аналогично доказывается, что путь, проходящий через точки
*; = *€//*, *;+1 = ук (К) € Нь+и ... ,^ = ^-1(^_1)€ЯЛГ>
является кратчайшим между точкой x^Hk и шкалой ffN. Это
означает, что функция ук{х) дает нам приближенное решение
проблемы синтеза для задачи (1.1—4).
Заметим, что определение кратчайшего пути между шкалами
N—1
Hq и HN по описанной схеме потребовало перебора Vp/-Pn-i+
t=0
+ р0 величин, в то время как полный перебор всех путей, как
нетрудно видеть, потребовал бы сравнения po-p\-...-pN величин.
Таким образом, уже при не слишком больших pi перебор с по-
мощью соотношений (5) по сравнению с полным перебором дает
существенную экономию памяти ЭВМ и машинного времени. Такая
экономия достигается в результате того, что при вычислении
Ck(x) из (5) рассматриваются лишь пути, проходящие через все-
возможные точки x^Hk и y^Hk+i и соединяющие точки j/e//ft+i
со шкалой HN кратчайшим образом, и тем самым все некратчай-
шие пути, соединяющие у^Нк+\ со шкалой HN, из рассмотрения
полностью исключаются.
4. Для получения более точного решения задачи (1.1—4) необ-
ходимо взять более густую сетку точек на шкалах и увеличить
число шкал. Однако при этом число перебираемых величин, даже
при использовании описанной выше схемы перебора, катастрофи-
чески быстро растет, и уже при небольших размерностях векто-
ров х и и становится невозможным решить задачу о кратчайшем
пути за разумное время с помощью самых лучших современных
ЭВМ. В этом случае часто используют прием, известный под на-
званием метода блуждающих трубок [171]. Суть этого приема за-
ключается в следующем.
Сначала берут небольшое число шкал с небольшим количе-
ством точек на них и по описанной выше схеме поиска находят
кратчайший путь 1\9 соединяющий крайние шкалы Н0 и HN. Затем
уменьшают шаг сетки на каждой шкале, путь U окружают некото-
рой «трубкой» из путей, проходящих вблизи U по точкам новой
сетки. Для построения трубки вокруг U на каждой шкале
обычно берут небольшие окрестности точки, через которую прохо-
дит /i, и рассматривают пути, проходящие через выбранные точки.
С помощью описанной выше схемы перебора находят кратчайший
путь в полученной трубке; все пути вне этой трубки в переборе
пока не участвуют. Таким образом получают новый улучшенный
путь /2, длина которого не превышает длины 1\. Далее, сохраняя
прежние шкалы и точки на них, окружают путь h новой трубкой
и находят следующее приближение /3 и т. д., продолжая процесс

§2]
Схема Н. Н. Моисеева
197
до тех пор, пока трубка не перестанет «блуждать» и впервые по-
лучится равенство /s=/s+i. После этого измельчают сетку на каж-
дой шкале, окружают путь ls новой трубкой и продолжают поиск
кратчайшего пути описанным приемом блуждающих трубок. Про-
цесс измельчения сетки на шкалах и поиска кратчайшего пути
указанным способом повторяют, пока два кратчайших пути, полу-
ченные после двух последовательных измельчений сетки, не совпа-
дут с удовлетворительной точностью. Затем увеличивают число
шкал, т. е. сгущают сетку по времени, и повторяют процесс поиска
методом блуждающих трубок с постепенным измельчением сетки
на шкалах состояний до удовлетворительного совпадения двух по-
следовательных приближений. Попеременно измельчая сетку на
шкалах состояния и сетку по времени, поиск с помощью блуждаю-
щих трубок продолжают до получения приближенного решения
исходной задачи с достаточной точностью. Изменение шагов сеток
на шкалах состояния и по времени должно быть согласованным;
например, в случае равномерных сеток эти шаги должны удовлет-
ворять соотношению \Ax\=o(At) [169].
Оказывается, метод блуждающих трубок во многих случаях
существенно сокращает число переборов, и с его помощью удалось
решить многие практически важные задачи, ранее казавшиеся не-
приступными. В то же время следует заметить, что метод блужда-
ющих трубок.позволяет определить, вообще говоря, лишь локаль-
но-кратчайший путь между крайними шкалами при фиксирован-
ной сетке, поскольку на каждом шаге в переборе участвуют лишь
пути, попавшие в трубку. Другой прием поиска кратчайшего пути
между шкалами описан в работах [143, 145, 240].
5. Успех в применении описанных в этом параграфе методов
приближенного решения задачи (1.1—4) во многом зависит от
умения строить элементарные операции (1) — (4). По существу,
элементарная операция представляет собой экстремальную задачу
той же трудности, что и исходная задача. Однако малость отрезка
'*^*</«+i позволяет здесь сделать ряд упрощающих предположе-
ний. Прежде всего, если шаг сетки по времени достаточно мал, то
элементарную операцию строят исходя из условий (1), (2), (4),
полагая, что дуги траекторий, соединяющих точки соседних шкал,
или не нарушают фазовых ограничений (3), или этим нарушением
можно пренебречь. Далее, вместо минимизации функционала (1)
при условиях (2), (4) часто ограничиваются построением какого-
либо допустимого управления и соответствующей траектории,
удовлетворяющих условиям (2), (4), и в качестве длины дуги
Mi(xyy) берут значение функционала (1) на полученных управле-
нии и траектории.
Во многих задачах полезно задаться каким-либо семейством
управлений u(t) =u(t, си ..., cm)t зависящих от параметров
си с2, ..., сш (т^п)\ например, это могут быть алгебраические или

198 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
тригонометрические многочлены с коэффициентами си ..., сШ9 или
кусочно-постоянные функции со значениями с\9 ..., ст и т. п. Зна-
чения этих параметров затем можно определить из системы п
уравнений с т неизвестными
f *(*)# = J f(x(t)9u(t9cl9c%9...,cj9t)dt=y — x9 (8)
h h
u(t.cl9...,cjev(tt)9
используя для этого различные методы [19]. Если т>п9 то пара-
метры си ..., ст отсюда будут определяться, вообще говоря, неод-
нозначно, и свободные параметры можно использовать для мини-
мизации функционала (1). Для упрощения системы (8) дифферен-
циальное уравнение (2) часто заменяют более простыми уравне-
ниями
*(<) = /(*, ii(Of t)9 или *(/) = / (-£±£ u(t)9ty
или другими более точными разностными уравнениями [171]; здесь
возможно использование линеаризованной системы
*(0 = f(x,u(t)91) + (fx(*>»(t)> 0, x{t)-x).
При решении задачи (1), (2), (4) часто применяется также прин-
цип максимума в сочетании с различными упрощающими приема-
ми, описанными выше. Другие способы построения элементарных
операций и примеры решенных конкретных задач см. в работах
[169, 171].
§ 3. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ Р. БЕЛЛМАНА
В этом параграфе будет введена функция Беллмана для ис-
ходной задачи оптимального управления и получено дифференци-.
альное уравнение Беллмана, являющееся предельным для уравне-
ния (1.13) при неограниченном измельчении сетки по времени.
Ограничимся рассмотрением частного случая задачи (1.1—4): ми-
нимизировать функционал
J(u) = §f»(x9u9t)dt+Q>(x(T)) (1)
при условиях
х = f{x, и91)9t0<t<T9 х(t0) = х09 (2)
и(t) кусочно-непрерывна, и(t) 6 V, *0 < * < 7\ (3)

§ 3]
Дифференциальное уравнение Р. Беллмана
199
где моменты t0 ,Г и точка х0 предполагаются известными; множе-
ство V замкнуто и от t не зависит. Будем также предполагать, что
функции f°(xtutt), f(jc,u,t)9 Ф(х) непрерывны по совокупности
своих аргументов. Наряду с этой задачей нам понадобиться следую-
щая вспомогательная задача: минимизировать функционал
/'(*, и) = j7°(*(r), и(т), x)dx + 0(x(T)) (4)
при условиях
*(т) = /(*(т),1|(т),т), /<т<7\ *(*) = *, (5)
и(х) кусочно-непрерывна, m(t)eV, t^jx^T, (6)
где точка х и момент tt t^t^T, фиксированы. Через A(x?t)
обозначим множество всех управлений и=и(х), t^x^T, таких,
что: 1) выполнены условия (6); 2) соответствующие траектории
*(т, и) системы (5) определены на всем отрезке £<т^7\
Введем функцию inf J* (х, и) = В (х, t)9 называемую функ-
ff€A(*,f)
цией Беллмана задачи (1) —(3). Покажем, что при некоторых
предположениях функция B(x9t) удовлетворяет дифференциально-
му уравнению с частными производными специального вида.
А именно будем предполагать, что: 1) функция B(xtt) непрерывно
дифференцируема по совокупности {x9t)\ 2) для всякого аеУ и
всех х9 t9 t&^t<.T, найдется ЛОО, t+M^T, и кусочно-непрерыв-
ное управление d(t)gV, t+At^.x<^T, такие, что управление
и(х)
(и, t<£x<£t+At9
\v(x), t + M<x<T,
принадлежит A(x9t); 3) для всех х9 t, t(y^t<.T, нижняя грань
функционала (4) при условии (5) — (6) достигается хотя бы при
одном управлении м*(т)еД(х,<) и соответствующей траектории
х(%9 и*).
Следует сразу же заметить, что сделанные предположения
1)—3) сильно сужают класс рассматриваемых задач оптимального
управления. В частности, функция Беллмана В(х9 t) может не быть
непрерывно дифференцируемой даже в простейших задачах опти-
мального управления (см. ниже упражнение 7).
Пусть B(x(t + АО, *0, t + АО = J'+Д*(х(t + At9 и)9 иГ)9
и** = и** (т) € А (х (t + At, и*); t + At)9 Д*>0.
Так как управление
ц(т)=КМ, t-<T<t + M9
1«Г(т), t+At<x<T.

200 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
принадлежит Д(*, t), то
B(x,t)<J*(x,u(x)) = J P{x{T9U*)9lt(%)9%)dX +
t
t+At
+ B(x(t + At9tt),t + At) = j P(x(x9tt)9u*(x)9x)dx +
t
t+At
+ /<+*< (x(t + At, и-), О < j H* (*. и*), "* W> *) dx +
t
+ ./*+* (x(t + At, u*)9 it) = J* (x, и*) = В(x, t).
Следовательно,
l(x,t) = J*(x,u*)= j f°(x{x9u*)9u*(x),x)dx +
+ B(x(t + At,u*)tt + At). (8)
Далее, возьмем произвольное «eV и составим управление
u(x)^A(x,t) согласно предположению (7). Пусть этому управле-
нию соответствует траектория х(х9 и) из (5). При сделанных пред-
положениях существует управление v* (х) еД(x(t'+At, и), t+At)
такое, что
/<+д< (x(t + А*, и), v*(т)) = B(x(t + At, и), t + At).
Тогда управление
В\
-(T)=U, *<т</ + Д*,
W(t), t + At<x<T,
принадлежит Д(*, t)9 поэтому
__ t+At
B{x9t)<J*(x,u(x))= J f°(x(x,u)fuix)dx + B(x(t + At,u),t + At).
t
Отсюда и из (8) следует
t+At
j f°(x(x, и*), u*(x),x)dx + B(x(t + At, u*),t + At)-
t
t+At
— B(x,t) = 0< j f°(x(xy u),u, x)dx +
+ B(x(t + At,u), t + At) — B(x,t).

§ 3]
Дифференциальное уравнение Р. Беллмана
201
Разделим это неравенство на Д/>0 и перейдем к пределу при
&t-++0. Получим
/i(jg>if(f + 0)>Q+<IB(JCtf + 0,<l')>0-0<
dt
<r>(x,u,t)+ dB(x(t + 0,u),nf uev> to<t<T. (9)
at
Полная производная —(*( + >u )» ) c учетом уравнения (5) пред*
ставляется в виде
^(t + 0,u*),t) ={BAxJ)J(xu.{t + 0ht))+Bt{xt)
Аналогично
dB(*('+°'"M) = (в, (*, О, /(*, и, 0) + в, (,, t).
at
Из (9) тогда имеем
/• (*, а*(* + 0), 0 + (5,(*, t), f (х, и* (t + 0), t) + Bt (x91) =0 <
</° (x, u91) + (Bx(x, t), /(*, uy t)) + Bt (xt t)
при всех и 6 V. Так как V замкнуто и и* (£+.0)6 V, то последнее
неравенство может быть переписано в виде
min [Bt (xt t) + (Bx (x9 t), f (x9 u, t)) + f» (xt u, t)] = 0, t0 < t < T. (10)
Полученное соотношение называется уравнением Беллмана.
К этому уравнению добавим начальное условие
В(х,Т) = Ф(х). (11)
Таким образом, для определения функции Беллмана имеем
задачу (10), (11), которую естественно назвать задачей Коши—
Беллмана [14—18, 24, 27, 34, 195, 206, 233] и др.). Заметим, что
присутствие знака min в левой части (10) весьма осложняет изу-
чение таких уравнений, и на сегодняшний день задача Коши —
Беллмана исследована недостаточно. В тех случаях, когда удается
найти решение задачи (10), (11), то нетрудно получить оптималь-
ные решения задачи (1) — (3) и (4) — (6), а также указать синте-
зирующую функцию для задачи (1) — (3). Об этом речь пойдет в
следующем параграфе.
Упражнения. 1. Показать, что к задаче минимизации функции
tf-l
J (и0, ul9 .. ♦ , uN) = £ Jt (ui9 щ+г) + JN (uN)

202 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
векторных переменных ы0, ul9 , им при щ 6 Vi (t = 0, 1, ... ,N)
можно применить метод динамического программирования.
Указание. Ввести функцию
JV-1
Вк (и) = min [ £ Jt (щ, ut+i) + JN (uN)],
где минимум берется по всем наборам \{uk = и, uk+\9... , uN)9 щ 6 Vi
(i = k9 k + 1, ... , jV), и показать, что
Я* (и) = min [Jk(и, v) + Bk+l (*)], (k - 0, 1,... 9N- 1),
2. Написать и исследовать уравнения (1.13), (2.5), (3.10) для
г
задачи: минимизировать функционал J (и) = fx2(t)dt при усло-
6
виях x=A(t)x+K(t)u(t)+f(t), 0^t^T9x(0)=xoi где х=(х\
...., хп)9 A(t)9 K(t), f(t)— матрицы с известными непрерывными
элементами, Хо, Т заданы; управление u(t) = (ul(t)9 ..., ur(t)) ку-
сочно-непрерывно и удовлетворяет ограничениям |иг'(/) [<^1,
/=1,2, ..., г, или £1^(0 12<1.
3. Решить предыдущую задачу, заменив функционал на
J(u) = (c9x(T))9 где с=(с\9 сп)—заданный вектор, или на
J(u)=x*(T).
4. Пусть в задаче (1.1—4) 1(и)=Ф(х(Т))9 (/°(х9и91) =0).
Показать, что схема Беллмана позволяет решить проблему синтеза
для этой задачи. Провести аналогичные исследования для схемы
Моисеева.
5. Найти функцию Беллмана В(х, t) для задачи: минимизиро-
вать функционал
т
J(u) = §u2(t)dt + x2(T)
о
при условиях x(t)=u9 Jt(0)=Jt0, (я=г=1).
6. Вывести дифференциальное уравнение Беллмана для зада-
чи быстродействия: минимизировать J(u)=T—10 (to задано) при
условиях x=f(x9u,t)9 t0^t^J\x(to)=x09 x(T)=xl9 u(t)^V9 t^t0.
7. Показать," что функцияБеллмана В (х91) для задачи из при-
мера 3.2.2. не является непрерывно дифференцируемой.

§ 4)
Проблема синтеза. Оценка погрешности
203
§ 4. ПРОБЛЕМА СИНТЕЗА ДЛЯ СИСТЕМ С НЕПРЕРЫВНЫМ
ВРЕМЕНЕМ. ОЦЕНКА ПОГРЕШНОСТИ
Проблема синтеза для задачи (1.1—4) с непрерывным време-
нем заключается в построении функции u=u(x,t), представляю-
щей собой значение оптимального управления при условии, что в
момент t объект (1.2) находится в точке х фазового пространства.
Как отмечалось в § 1, такая функция и (xj) называется синтези-
рующей, и с ее помощью дальнейшее оптимальное движение объ-
екта определяется условиями x(x)=f(x(x)9н.(л;,т),т), £^т<Г;
x(t)=x.
Решение проблемы синтеза для задачи (1.1—4) экви-
валентно решению следующих задач: определить управление
и(х) =#*(*, *,т), доставляющее функционалу
Л (*, и {%)) = Г /о (х (т), и (т), т) dx + Ф (х_(Т)) (1)
минимальное значение при условиях
x(x) = f(x(x),u(x),x), *<т<Г; *(*) = *, (2)
*(T)€G(T)f *<т<7\ (3)
и = и (х) 6 V (т), t < х < Г; управление и (т) кусочно-непрерывно, (4)
для каждого фиксированного x^G(t) и для каждого фиксирован-
ного момента времени t, to^.t<T. Зная функцию и*(дс,/,т), синте-
зирующую функцию можно получить сразу: и(х, t)=u*(x,ty t) для
всех x^G(t) и всех t^[t0,7], для которых задача (1)—(4) имеет
решение.
При решении проблемы синтеза для дискретных систем важ-
ную роль сыграло уравнение Беллмана (1.13). По аналогии попро-
буем использовать дифференциальное уравнение Беллмана для ре-
шения проблемы синтеза для задачи (1.1—4) с непрерывным вре-
менем. Для этого отвлечемся от тех ограничительных условий, при
которых выводилось уравнение Беллмана (3.10), и рассмотрим
следующую задачу Коши — Беллмана:
inf [(Вх (х, 0, /(*, и. 0) + Bt (*, t) + /° (*, w, t)] = 0, (5)
ueva)
*€G(0. t0<t<T,
В(х,Т) = Ф(х), xeG(T) (6)
для определения функции В(х, t). Если ввести функцию
R(*, и, t) - (Вх(х, 0, /(х, и, 0) + Bt (х, t)+P(x,u,t)9 (7)

204 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
то задача (5), (6) перепишется в виде
inf Д(*,М) = 0, *€G(f), t.<t<T; В(х9Т) = Ф(х)9 x£G(T). (8)
«€V(0
Оказывается, решение задачи Коши — Беллмана (5), (6), (или
(8)) равносильно решению проблемы синтеза для задачи (1.1—4).
Точнее, справедлива
Теорема 1. Пусть функция В (xtt) кусочно-непрерывна,
кусочно-гладка и удовлетворяет условиям (5), (6), (или (8)) при
x^G(t)9 t^i^T. Пусть для каждой пары (х(х),и(х))9 удовлет-
воряющей условиям (2) — (4), функция В(л;(т),т) переменной т
непрерывна и кусочно-гладка на отрезке t^x^T при всех x^G(t)
и t9 to^t<T. Пусть u=u(x9t) кусочно-непрерывная функция, на
которой реализуется нижняя грань в (5) или (8). Тогда функция
u=u(x9t) представляет собой решение проблемы синтеза для за-
дачи (1.1—4).
Доказательство. Возьмем некоторый момент t9 t^t<.T,
точку x^G(t) и через D£t, Т\ обозначим множество всех пар
(х(х)9и(х)), t^x^T, удовлетворяющих условиям (2) —(4). Рас-
смотрим задачу Коши:
х (т) = /(*(т), и (х (т), т), т), t <т < 7; * (*) = х. (9)
Пусть эта задача имеет решение **(т), определенное на от-
резке £<т<;7\ и пусть jc*(t)eG(t), t^x^T. Положим
а*(т)=и(**(т),т), *<^т<7\ Очевидно, (**(т), u*(x))eDJt9T\.
Покажем, что пара (** (т), и* (т)) является оптимальным решени-
ем задачи (1) — (4). Для этого прежде всего выведем формулу
J4x9u(x)) = J Д(*(т), и(х)9 x)dx + В(х9Ч)9 (10)
справедливую при всех (x(x),u(x))^DJ[t9 Т] и при всех фиксиро-
ванных x&G(t)9 t<y^t<:T'9 здесь R(x9u9t) взята из (7).
Всюду на отрезке i^z^T, за исключением, быть может, ко-
нечного числа точек, имеем
dB(*(T)'T) = Я(*(т), и(т), т)-/°(*(т), «(т), т).
ах
Так как по условию B(x(x)tx) непрерывна на [t9T]9 то, интегрируя
последнее тождество с учетом условия (6), получим
т т
ф(х(Т))-В(х91) = f R(x(x)9 и(х)9 x)dx- f/Ч*(т), u(x)9 x) dx9
i ' t

§4]
Проблема синтеза. Оценка погрешности
205
что равносильно (10). Далее, из условия (8) имеем
#(*, и, т)> inf R(x, и, x) = R(xf и(х, т),т)==0,
u£V(x)
где меУ(т), jceG(t), ^5^^- Отсюда следует, что для любой
пары (х(т), и (т)) eDJt9 7] справедливо неравенство
R(x(x)9u(x)ix)>0 = R(x*(x)itf(x),x)9 /<т<7\ (11)
А тогда с помощью формулы (10) и условия x*(t)=x(t)=x
сразу получим
J4x9u(x))-Jt(x,u*(x)) = $[R(x(x)yu(x),x)-
-R(x'(x)tu*(x)yx)]dx>0
при всех x(x)tu(x))^D3lt,T\. ±
Кстати, из (10), (11) следует, что
J* (х, и* (т)) = inf /< (*, и (т)) == 5 (х, t).
DXU,T]
Как видим^в рассматриваемом случае В(х, t) есть функция Бел-
лмана задачи (1.1—4). Теперь нетрудно получить решение задачи
(1.1-4).
Теорема 2. Пусть функции В(х, t), u(xtt) при *€G(0,
t0<t<CT, удовлетворяют всем условиям теоремы 1, и точка x*Q on*
ределена из условий
fi(*;,g=infB(*,g, *;е*#,
где X0 = {x:xeG(t0), Dx[t0t Т]Ф 0}. Тогда траектория **(t)€G(t),
UКх <Т, определяемая из (9) при t —10, х = х*- и управление
и* (т) = и (х* (т), т), t0 < х < Г, представляют собой оптимальное ре-
шение задачи (1.1 — 4).
Доказательство. Возьмем произ вольные х^Х0 и
(*(т), м(т))еД^[/о>Т]. Неравенство (И) при t=t0, очевидно, так-
же справедливо. Поэтому с учетом определения хо из формулы
(10) имеем
J(u)-J(u*)^J*>(x, u{x))-JU (*;, и* (т)) = j [R(x(x), u(x)t x)-r-
u
- R (x* (t), u* (x), t)] dx + B (x, g - В (xl g > 0
при всех допустимых u(x) из (1.2—4). ^

206 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
2. Заметим, что теоремы 1—2 не работают в тех случаях,
когда нижняя грань в (5) не достигается и приходится иметь дело
с функциями, приближенно реализующими эту нижнюю грань.
Аналогично при решении задачи с подвижным левым концом
irrf В (х, t^ также может не достигаться. В таких случаях могут
х£Х9
оказаться полезными следующие две теоремы.
Теорема 3. Пусть функция В(х,t) удовлетворяет всем ус-
ловиям теоремы 1, и пусть имеется последовательность функций
uk(x,x) (k=l9 2, ...), таких, что:
1) Uk(x,x) определена, кусочно-непрерывна и ^(^т)еУ(т)
при всех x^G(x)9 to^n^T;
2) решение xh(x) задачи Коши:
x(x)=f(x(x)9uk(x(x)9x)9x)9 *<т<Г; *(*) = * (12)
существует и xk(x)£G(x) при t<т<Г;
т
3)' lim Г R(xk(т), uk (т), т) dx = 0,
Л-юо J
где uk(x)=u(xh(x)9x)9 £<т<;Г, (ft=l, 2, ...,).Тогда последователь-
ность (л*(т), Uk(x)) (k=l9 2, ...) является минимизирующей для
задачи (1)—(4) и, таким образом, функция uk(x, t); &=1, 2,
осуществляет приближенный синтез.
Доказательство. Возьмем произвольную пару
(x(x)9ti(x))eDolttT] при некоторых фиксированных t9 to^t^T,
x^G(t). Согласно формуле (10) и условиям xk(t)=x(t)=x тогда
имеем
т
JHx9u(x))-J*(x9uk(x)) = ^[R(x(x)tu(x)9x)-R(xk(x)9ruk(x)9x)]dx.
t
По условию теоремы правая часть этого равенства имеет предел
при Л->оо, поэтому и левая часть имеет предел. Поскольку в
силу (8)
R(x(x),u(x),x)> inf R(x(x)tu9x) = 09 *<т<7\
u£V(T)
ТО
т
J* (*, и (т))- lim J* (х9 uk (т)) = f R(х (т), и (т), т) dx > 0
при любых (х(х)9 u(x))eDx[t9 Т]. Следовательно,
Г* = inf J* (х, и (т)) > lim Л (xt ик (т)).

§ 4] t Проблема синтеза. Оценка погрешности
207
С другой стороны,
Ji(x9uk(x))>J^9 k = 1,2,
поэтому lim У (х, uk (т)) = J**. J±
Теорема 4. Пусть функция В (л:, t) [ довлетяоряет всем ус-
ловиям-теоремы 1, и пусть последовательность {хь) такова, что
xk 6 Х0 и lim В (xki t0) = inf В (лг, *0).
Кроме того, пусть имеется последовательность функций
Uk=Uk (x,t)> обладающая свойствами 1)—3) из теоремы 3 при
t=t0, x=xh. Тогда последовательность пар (**(т), uk(x))t
to^x^T, где uh(x)=uk(xk(x)fx)9 a Xh(x) —решение задачи Коши
(12) при t=to, x=Xh, является минимизирующей для задачи
(1.1-4).
Доказательство этой теоремы опирается на формулу (10) при
t=t0 и полностью аналогично доказательству теоремы 3.
3. Умение решать проблему синтеза крайне важно в различ-
ных прикладных задачах оптимального управления. В самом деле,
пусть управляемый процесс описывается условиями (1.1—4), и
пусть известна синтезирующая функция u(xtt). Тогда техническое
осуществление оптимального хода процесса обычно производится
по схеме: с измерительного прибора, замеряющего в каждый мо-
мент t фазовое состояние x(t)> на ЭВМ или какое-либо другое вы-
числительное средство подается величина x(t)y вычисляется зна-
чение управления u(t)=u(x(t)^t)f после чего оптимальное в дан-
ном положении управление u(t) передается на исполнительный
механизм, непосредственно регулирующий требуемое течение уп-
равляемого процесса.
Как вытекает из вышеизложенных теорем 1—4, для решения
проблемы синтеза для задачи (1.1—4) достаточно решить задачу
Коши — Беллмана (5), (6). Однако явное аналитическое выраже-
ние решения В(х, t) этой задачи и функции и(х, t), на которой
может достигаться нижняя грань в (5), удается лишь в редких
случаях, поэтому задачу (5), (6) приходится решать приближенно.
Наиболее удобными и эффективными при решении задачи (5), (6),
по-видимому, являются методы, изложенные выше в § 1, 2, ибо
рекуррентные соотношения Беллмана (1.13) и Моисеева (2.6) по
существу представляют собой некоторую дискретную аппроксима-
цию задачи (5), (6)" (В(х, tk) &Bk(x) &Съ,(х)). Однако здесь воз-
можны и иные подходы. В тех случаях, когда удается получить
явное выражение для и=и(х, t, Bx)^V(t), на котором достигается
нижняя грань в левой части (5), то, подставив такое и в (5), при-
дем к обычной задаче Коши для квазилинейного уравнения с част-

208 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ, ПРОБЛЕМА СИНТЕЗА \Гл. 4
ными производными первого порядка, и здесь тогда можно вос-
пользоваться известным арсеналом численных методов (разност-
ные методы, метод характеристик, метод прямых и т. п.) [20].
В. Ф. Кротов ![142] предлагает искать решение В(х91) задачи
(5) — (6) в виде многочлена по переменным х\ х29 ..., хп с неоп-
ределёнными коэффициентами, зависящими от времени:
тх mt тп
tt«=0 t,=o irt=o
Если подставить это выражение для В(х, t) в (5)—(6), то для оп-
ределения t^pilit...in(t) получится система дифференциальных урав-
нений следующего вида:
Bt (х, t) = V £ ^,.,л (t) (*)'' ... (#)'» =
tt=0 in=o
= inf F(^0 о(0, ^mx...mn{f)9x9u9t)9 (13)
с начальным условием
mt тп
S £ *1лР)(^-М^фм, хео(Т). (И)
Если Ф(дс), inf F являются многочленами относительно х19 ..., хп9
то, приравняв коэффициенты при одинаковых степенях в (13)— (14),
получим задачу Коши для системы дифференциальных уравнений
относительно iit..j (t), записанной в нормальной форме Коши
(см. ниже пример 1). Для- ее решения можно использовать различ-
ные численные методы решения задачи Коши (методы Адамса,
Рунге —Кутта и т. д.) [20].
Если же Ф (х) или inf У7 не являются многочленами относи-
u£V(t)
тельно хх хп9 то условия (13), (14) не могут быть, вообще гово-
ря, удовлетворены во всей области G(t)9 t0<^t^T9 ни при каком
выборе N=(m\+l) (m2+l) — (^n+l) коэффициентов %!...*„ (*)•
В этом случае в [142] предлагает задать в области G(t) N. кривых
Si(0t •••> 1^(0 и рекомендуется определять ^...^(0 из условия
удовлетворения (13), (14) не всюду в G(t)9 а лишь на этих кри-
вых. Этот подход перекликается с известными методами коллока-
ции и интегральных соотношений и приводит к задаче Коши для

§4]
Проблема синтеза. Оценка погрешности
209
системы обыкновенных дифференциальных уравнений, не разре-
шенных относительно производной tytt...in(t) (эти производные в
уравнения будут входить линейно). Кривые h(t), ..., £^(*)» во-пер-
вых, должны образовать достаточно густую сетку в области
G(t), fa^t^T, и, во-вторых, иметь достаточно простое аналити-
ческое выражение (например, семейство прямых, параллельных
осям координат, семейство парабол и т. п.).
Пример 1. Пусть требуется минимизировать функционал
т
/(ы) = ^u*(t)dt + №(T)
6
при условиях х = и, х (0) = х0\ и —и (t) — кусочно-непрерывная ска-
лярная функция; числа Г, х0 заданы, A, = const>0.
Задача (5), (6) здесь имеет вид
inf [Bx{xf t)u + Bt(x, t) + и*] = -±&х(х, t)+Bt(xtt) = 0, х£Е1%
0</<Г; В(х, Т) = %х\ хеЕг.
Функцию В (х, t) будем искать в виде многочлена В (дс, t) = ip0 (t) +
+ ^i (0 х + % (0 **• Подставим в предыдущие уравнения
г(Ъ + ^)* + % + Ъ* + № = 0, *£Е19 0<t<T;
4
to СП + *i (П х + Уг (Т) *» = Хх\ х 6 Ev
Приравнивая коэффициенты при одинаковых степенях х, придем к
следующей задаче Коши:
to-4"1fi==0, ti-tita=0, Ъ — Ц-=0> 0<t<T-,
фо(Г) = 0, %(Г) = 0, %(Т)=К
Отсюда находим
^(0-^(0-0, !,(»)■ _яД) + 1 •
Таким образом, функция Беллмана здесь имеет вид
я(М)= Кх2
_Л.(^ —Г)+ 1
синтезирующей является функция
u(xJ) = — — Bx = -
7 2 х Я (^ — Г) — 1

210 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
4. Предположим, что, пользуясь тем или иным методом, уда-
лось получить некоторое приближенное решение B(xf t) задачи
(5), (6). Если эта функция получена разностным методом (напри-
мер, методами § 1, 2) на какой-то дискретной сетке точек, то до-
определим ее (например, интерполяцией) во всех точках области
x^G(t), t&^t^T, до некоторой непрерывной, кусочно-гладкой
функции В(х, t). Тогда функции u=u(x9t), на которой точно или
приближенно реализуется inf R(x, и, t) можем принять в каче-
u£V(t)
стве приближенного решения проблемы синтеза для задачи
(1.1—4). Это значит, что приближенное решение (х(х)9 и(х)) зада-
чи (1) — (4) будем определять из условий
*(т) = /(*(т),и(*(т),т),-г), /<т<Г; x(t)=xt
- (15)
*(t)6G(t), и(х) = и(х[(х)9х), г<т<7\
Приближенное решение исходной задачи (1.1—4) находится
аналогично: сначала определим точку х0^Х0у на которой точно или
приближенно реализуется inf B(xt /0), затем, решая задачу Коши
же*» _
(15) при_ t=t0, х=Хо, найдем траекторию _х(х) и управление
и(х)=и(х,(х)9х), /<><т^7\ Найденную пару (х(х)9 и(х)) примем
в качестве приближенного решения задачи (1.1—4). Спрашивает-
ся, какая при этом будет допущена погрешность?
Теорема 5. Пусть функция B(x,t) кусочно-непрерывна, ку-
сочно-гладка при xezG(t), *o<*<7\ и В(х9Т)=Ф(х) xeeG(T)
(подчеркнем, что В(х91) не обязана быть решением уравнения
(5)). Пусть для каждой пары (#(т), u(x))^Dx(t9 Т) функция
В(х(х)9х) переменной т непрерывна и кусочно-гладка на отрезке
^т^Г при всех лееG(t), to^.t<.T. Тогда для любой.фиксирован-
ной пары (х (т), и (т)) еDJY, Т\ справедлива оценка
0<J4*,^(0W*'<M^), (16)
где
Г*= inf J'(x9 и(х))
Dxlt.T]
- т _ _
*t (и) = J [R (х(т), и (т), т) - Rmin (т)]dx9
#min(*) = inf inf R(x9 u9 r);
функция R(x9 и, x) определена равенством (7). Кроме того, для
любой пары (х(х)9 u(x))^DXo[t0, Т] справедлива оценка
0 < /'• (*0, и (т)) - Г < е0 (х09 и), (17)

<М]
Проблема синтеза. Оценка погрешности
211
где
Т
Г = inf inf J*o (х9 и (*)), е0 (х0, Ъ) = f [R (х (т), й (т), т) —
х£Хй Dx[t0lT] £
— Rmm W] dr + 5 (*0, О - inf 5 (*, t0)9
Доказательство. При выполнении условий настоящей
теоремы формула (10), очевидно, остается справедливой. Возьмем
произвольную пару (*(т),u(x))^D3lt9 7]. Пользуясь формулой (10),
имеем
7
J* (х9 и (0) - /< (л:, а (т)) = \ [R (х (т), и (т), т) -
— R(x(x)9 u(x)9x)]dx<et(u).
Так как е*(й) не зависит от (x(x)9u(x))^DJtf9T\9 то отсюда сразу
получаем оценку (16).
Аналогично, взяв произвольную допустимую пару
(x(x),u(x))^DXU,Т\ при некотором дсеХо, с помощью формулы
(10) получаем
т
= §[R(x(x),~u(x)f х)~R(x(х), u(x)9x)]dx + B(x09t0) —
to
— В(х9 *0)<е0(л;0,и),
откуда немедленно следует оценка (17). А
В тех случаях, когда конструктивное описание множества Х0
затруднительно, в выражении для ео(х9 й) вместо Xq часто берут
G(t0). Очевидно, при такой замене величина ео(х0,й) может лишь
увеличиться.
Из полученных^ оценок (16), (17) видно, что чем ближе
R (х(х), и(х), т) к #min (т), В (x0i t0) — к inf В (х910), тем меньше
хехй
погрешность. Отсюда ясно, что при практических вычислениях же-
лательно выбирать функцию В(х9 t), которая удовлетворяет урав-
нению (5) по возможности точнее, -а функция u(x9t) должна по-
точнее реализовать inf R(x9 и91). Тогда на парах (х(х)9и(х))9 оп-
u£V(t)
ределяемых из (15 )при различных x^G(t) и t^[t0y Т] (в частно-
сти, x=Xot t=to)t погрешность в определении минимального зна-
чения функционала будет небольшой.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ПРОБЛЕМА СИНТЕЗА [Гл. 4
Если полученная точность неудовлетворительная, то надо ис-
кать новые функции В(х, t), u(x,t), используя, например, упомя-
нутые выше методы решения задачи Коши — Беллмана с дальней-
шим дроблением разностной сетки или увеличением степени мно-
гочлена и числа кривых {li(t)}^G(t) и т. п. Постепенно уточняя
функции В (х, t), и (дс, t), вообще говоря, можно построить последо-
вательности Вт(х, t), Um(x,t)t для которых погрешность монотонно
убывает. Если окажется, что при т-^оо погрешность стремится к
нулю, то функцию Um(x, t) при достаточно больших т можно при-
нять в качестве приближенной синтезирующей функции.
Различные аспекты проблемы синтеза рассмотрены в работах
[13, 14—18, 24, 27, 160, 171, 195, 229] и др.
Упражнения. 1. Решить проблему синтеза для задачи миними-
зации функционала
т
J(u) = — Ux2+u2)dt
о
при условиях X = — X + и, X (0) = х0.
2. Найти решение задачи Коши — Беллмана для задачи ми-
нимизации функционала
т
J (и) = т II(a {t)' х {t)) + b{u {t)> t)] dt+(c> x [T])
0
при условиях x=A(t)x+C(u(t)tt)9 <ХКГ; x(0)=x0,u(t)eEV(t);
u(t) кусочно-непрерывно, где известными предполагаются мо-
мент Г, матрица A(t) порядка пХп, n-мерные вектор-функции
C(u,t), a(t), скалярная функция b(u,i), /г-мерные векторы дсо, с и
множества V(/)s£r, O^tf^T*
Указание. Функцию В(х,t) искать в виде многочлена
первой степени переменных х=(х\ ..., jc71) : В(х, t) = (ty(t)fx).

Глава 5
Достаточные условия оптимальности
При решении задач оптимального управления часто возникает
следующий вопрос: будут ли на самом деле оптимальными те уп-
равления и соответствующие им траектории, которые мы нашли,
используя какие-либо точные или приближенные методы решения
таких задач? Такой вопрос, например, естественно возникает,
когда управление и траектория найдены из краевой задачи прин-
ципа максимума, поскольку принцип максимума выражает собой
необходимое условие оптимальности, не являясь в общем случае
достаточным для оптимальности. Известные к настоящему времени
достаточные условия оптимальности либо опираются на свойство
выпуклости данных задачи, либо тесно связаны с динамическим
программированием [23, 24, 59, 141, 142, 161, 206]. Здесь ограни-
чимся изложением подхода В. Ф. Кротова [142].
§ 1. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ ДЛЯ ЗАДАЧ
С ЗАКРЕПЛЕННЫМ ВРЕМЕНЕМ
1. Рассмотрим следующую задачу оптимального управления:
минимизировать функционал
J(u)=J(x(t)t u(t)) =
= f /•(*(*), и (0, t) dt + Ф, (x (T)) + Ф0 (x (t0)) (1)
при условиях
x(t) = f(x(t),u(t), t), t0<t<T, (2)
x(t)eG(t), t0<t<T9 (3)
и = и(t) 6 V(t)> t0<Ct<Tt и (t) кусочно-непрерывна, (4)
где моменты /<ь Т будем считать известными, Фо(*) и Ф\(х) —за-
данные функции. Подробное описание остальных обозначений см.
в § 3.1; граничные условия при t=\to и t=T включены в ограниче-
ния 0(0-
Пару (x(t), u(t)) назовем допустимой на отрезке t0^t^:Tt
если управление u(t)^V(t)t а функция x(t) непрерывна, кусочно-
гладка на tb^t^T, удовлетворяет условиям (2), (3). Множество
всех допустимых пар (x(t), u(t))t t^t^T, обозначим через
D[to9T\. В пространстве £ПХ£Г введем множество Dt точек (х,и)

214.
ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ
[Гл. 5
следующим образом: (x9u)^Du если существует допустимая пара
(х(т),и(т))е/)[*о> Л» такая, что x(t)—x9 u(t)=u (в точках разры-
ва управления для определенности будем считать, что u(t) =
=u(t—0)). Проекцию множества Dt на пространство Еп обозна-
чим через Хи проекцию Dt на Ег — через Vt. Иначе говоря, если
х^Хи то существует пара (х(х)9u(x))^D[to9 7]), такая, что x(t) =х
(конечно, тогда u(t)&Vt). Очевидно, XtsG(t)9 VtsV(t),
Dt^XtXVu to^t^T. Возьмем функцию К(х9t)9 определенную и
кусочно-непрерывную при х^Хи tv^t^T, обладающую кусочно-
непрерывными ЧаСТНЫМИ ПрОИЗВОДНЫМИ Хх=(КхЧ ...» Kxn)t Ки и
составим функции
R(x9 и. t) = (КЛ*. 0. /(*. «. 0) + Kt(x91) + /•(*, и9 t),
(5)
г.(х) = К(х9 g + Ф0(х), гх(х) = -К(х,Т) + Фг (х).
Лемма 1. Если пара (x(t)9 u(t))^D[to9 Т\ и функция
K(x(t)9,t) переменной t непрерывна и кусочно-гладка на [to,T]t то
функционал (1) при u=u(t) может быть представлен в виде
/(а)«/(*(0.и(О) =
= \R(x(t)9u(t)9t)dt + rx(x(T)) + r0{x(t0)). (6)
Г.
Доказательство, Заметим, что
-^MbJL.^iKx(x(t),t),f(x(t),u(t),t))+Kt(x(t),t) =
at
= RJx (t)9 u(t)91) -f»(x (0, u(t)91) (7)
всюду на отрезке [t09 T\9 за исключением, быть может, конечного
числа точек. Так как K(x(t)9t) непрерывна по t9 то, интегрируя
тождество (7) на [t09T\9 получим
Т Т Т
§~R(x (о, «(/), t)'dt- \f°{x(0. «(0, t)dt = $^£2k±dt =
и и и
= K(x(T),T)-K(x(t0),t0) =
= -г1(х(Г)) + Ф1(х(Г))-г0(л;(д) + Ф0(д;(д),
что равносильно равенству (6). А
Нетрудно видеть, что формула (6) сохраняет силу, если
K(x(t)9t) абсолютно-непрервна на [to9T] и почти всюду на ро» Л

§ п
Задачи с закрепленным временем
215
выполняется тождество (7). Формула (6) является обобщением
аналогичной формулы (4.4.10).
2. Во всем дальнейшем изложении в этой главе большую роль
играют функции (5) и формула (6). Воспользуемся ими сначала
для получения оценки погрешности. Допустим, что, решая задачу
(1) — (4) с помощью какого-либо метода, мы нашли допустимую
пару (x(t)9u(t))^D[to, Т\ и хотим узнать, как велика погрешность
J (и)— inf J (и).
D[t0,T]
Лемма 2. Пусть функция К(х, t) такова, что формула (6)
верна для любой допустимой пары (x(Qtu(t))^D[t0t 7j. Тогда для
любой фиксированной пары (x(t),u(t))^D[to, Т\ справедлива
оценка ч
0<J(u)— inf J(u)<£e(u),
где
в(а)н|1«ИО.й(о,о-1?п1п(01л+га*(П)-
и
— rlm|n 4" fo\x (*0/) Г0лЦгГ>
#min(0= inf R(x,ji9t)9 rlmIn= inf rt(x)9 romIn = inf r0(x). (8)
(x,u)£Dt xeXT *G**e
Доказательство. Возьмем произвольную допустимую пару
(х (/), u(f))^D [/0, Т]. Согласно формуле (6) будем иметь
т
J(ly-J(u)= §[R(x(t),u(t), t)-R(x(t),u(t),t)]dt +
и
+ rt(x[T])-r1(x(T)) + r0(x(t0))- r0(x(t0)) <в(и).
Так как е(й) не зависитот (x(t)9 u(t))e-D[to9Tl то отсюда имеем
0</(и) — inf J(u)<s(u). А
Полученная оценка погрешности является естественным обоб-
щением оценок из теоремы 4.4.5.
Замечание. Лемма 2, очевидно, остается справедливой,
если множества Du Xto, Хт в соотношениях (8) заменить на более
широкие множества. Это обстоятельство полезно иметь в виду при
практическом использовании оценки из леммы 2. Дело в том, что
часто бывает затруднительно дать удобное для работы конструк-
тивное описание множеств Du Xt0, Хт и тогда в соотношениях (8)
вместо этих множеств можем взять более широкие множества,

216 ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ [Гл. 5
имеющие простое конструктивное описание. Например, вместо (8)
можно принять
tfmm (*) = inf inf R (х, и, 0, rlmin =
x€G(t) u£V(t)
= inf r^x), romIn= inf r0(x), (9)
x£G(T) xeG(t0)
иногда можно даже^считать #mJn(0 = inf inf R(x, u, t), или
x£En ueV(()
Rmin = inf inf R(x, и J).
lx£En ueEr
3. Перейдем к рассмотрению достаточных условий оптималь-
ности для задачи (1) — (4). Напомним, что по определению пара
(x*(t),u*(t))^D[to, Т\ называется оптимальной, или оптимальным
решением задачи (1) — (4), если
inf / (х (0, и (0) = J (х* (0, и* (0) = / (и*) = Г.
Dlt0tT]
Теорема 1. Для оптимальности пары (#*(0>u*(t))^D[t0, Т\
достаточно существования функции К(х, t), такой, что формула (6)
верна для любой допустимой пары (x(t),u(t))^D[tot Т\ и, кроме
того,
R{x*(t), и* (0, t) = Rmin (0, t0 <t<T, гг (*' (Г)) = rlm|n, (10)
Г0 (X Wo)) = r0mln»
где Rm\n(t)y /lmim ^omin определяются согласно (8) или (9).
Доказательство. Возьмем произвольную пару
(x(t),u(t))^D[tot Т\. Согласно формуле (6) будем иметь
/ (х (t), и (/)) - / (** (0, и* (0) = J(u)-J(и*) = J [R (х (t), и (0, 0 -
и
-R (** (0, и* (0, 0] dt + гг(х (Т)) - гг (*• (Г)) + г0 (х (t0))-
т
-r0(x*(t0)) = j[#(* (0, a(f), 0 -Rmm(t)]dt+ гг(х (Т)) -
— 'tain + г0 (* (t0)) — romn > 0
Отсюда следует
/(",)=D[i;V(*(0,"(0)-A

§ л
Задачи с закрепленным временем
217
Проиллюстрируем теорему 1 на примере.
Пример 1. Пусть требуется минимизировать функционал
J (и) = $(x2 — u)dt при условиях x(t)=u(t), \u(t) |^1, х(0) =
=*(1)=0.
Здесь G(0) = G(1) = {0}, G(t)=Eu 0<t<l. Очевидно, пара
(#*(/) =0, #*(,*) =0) является допустимой. Покажем, что она оп-
тимальна. Для этого возьмем функцию K(x,t)=x. Тогда
R = KxU + Kt + (x2-u) = x\ г0(х)^х, гг(х) = -х.
Очевидно, что формула (6) здесь верна для любой допустимой
пары. Далее, первое из условий (10) достаточно проверить на мно-
жестве Е\ХЕ\ : inf Rz=0=R(x*(t), u*(t)). Наконец, множества
Xq, Х\ СОСТОЯТ ИЗ ОДНОЙ ТОЧКИ ДС = 0, ПОЭТОМУ Г1т1П=0 = Г1(л;*(1)),
/*отгп=0=А'о(^*(0)).Согласно теореме1 пара (я*(0—0>и*(<0=0)
оптимальна.
4. При практическом решении задачи (1) — (4) с использова-
нием тех или иных приближенных методов минимизации мы обыч-
но получаем некоторую последовательность пар (Xk(t)ttih(t))&
^D[to> Т\, на которых значения функционала J (и) убывают.
И здесь возникает вопрос, является ли построенная последова-
тельность {Xk, Uk} минимизирующей, т. е. будет ли limJ(xk9uk) =
fe-*oo
= inf J(x, w)=J*? Задача построения минимизирующей последо-
diux\
вательности особенно актуальна в том случае, когда нижняя грань
функционала Ц) не достигается на множестве Д*о, Л- Для про-
верки того, будет ли та или иная последовательность минимизи-
рующей, может быть использована следующая теорема, обобщаю-
щая теорему 1.
Теорема 2. Для того чтобы некоторая последовательность
пар {Xk(t),Uk(t)}^D[to> Т\ была минимизирующей, достаточно су-
ществования такой функции К(ху t), что: 1) формула (6) верна
для любой пары (x(t),u(t))\
2) lim Г R(xk(t), uk(t)tt)dt=\Rmn(t)dt; (11)
*o *o
3) lim rx (xk (7)) = rlmln, lim r0 (xk (t0)) = r0mln> (12)
rAe ^min (*). rimm, romin определяются согласно (8) или (9).
Доказательство. Возьмем произвольную допустимую пару
(х (0> u(t))- Согласно формуле (6) будем иметь

218 ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ [Гл. S
J (и)-J (ик) = §[R(x (0, и (О, t)-R (хк (О, ик (О, 01 dt +
и
+ гг (х (Т)) - г, (хк (Т))]+ г0 (х (t0)) - г0 (хк (О).
Так как правая часть этого равенства по условию теоремы имеет
предел при А-»оо, то и левая часть имеет предел. Поэтому
J (и)- UmJ(uk)= \[-Rmn(t) + R(x(t).u(t), t)]dt +
fe-ЮО У
+ 'i (х (Т)) — rlmln — romIn + r0 (x (t0)) > 0,
откуда J (и) > lim J (uk) при любых (x[(t), и (t)) 6 D [t0, T\. Следова-
ft-юв
тельно, J* = inf J (и) > lim J (uk). Однако / (uk) > J* при всех k =
ОД.Г] ft-*»
= 1,2, поэтому lim/(aA) >«Г. Таким образом,
fe->oo
lim J (ик) = Г. A
ft-»oo
Рассмотрим пример, иллюстрирующий теорему 2.
Пример 2. Пусть требуется минимизировать функционал
J(u)= f (*2 — и2) Л при условиях х = и, | и| < 1, х (0) = 0.
Возьмем функции
М0 =
+ 1,
— 1.
**(') =
при < t < ,
* ft ^ ft 2ft #
при—+ — </< — + —
ft 2ft ft ft
m
,__ прИ _<,<_ + _
ft ' F ft2ftftft'
где m=0, 1, ..., k—1, ft=l, 2, Нетрудно проверить, что пара
(jCfe(0,^ft(0) является допустимой для рассматриваемой задачи.
Покажем, что последовательность этих пар является минимизи-
рующей. Возьмем К0М) = 1. Тогда
R = x2 — и2, Rmln (t) = min min (x2 — и2) = — 1,
x£Et 1и|<1
r0(x) = l, г,г(х) = —\.

§ п
Задачи с закрепленным временем
219
Так как
u2k(t) = l, 0<Xk(t)<-±,
то
^R{xk{t),uk{t)J)dt-+\Rm{n{t)dt = -\.
о о
Кроме того, гх (хк (1)) = гшш = — 1, r0(xk (0)) = r0mln = 1. Согласно
теореме 2 последовательность (xk (/), uk(t)) является минимизирую-
щей.
Заметим, что в этом примере inf J(u) = — 1 не достигается ни
D
на какой допустимой паре. В самом деле, если x2(t)E=Q, то в силу
уравнения x=u(t)=0 и /(0)=0>—1; если же х2(ЦФ0у то
«/(и)>— {u2(t)dt^—1 (здесь имеем дело с так называемым
о
скользящим режимом [63, 142]).
5. Использование приведенных выше достаточных условий оп-
тимальности требует знания функции K(xt t), с помощью которой
строятся функции J?, г0, Г\ в соответствии с формулами (5). Как
найти такую функцию K(xt t)t каким условиям она удовлетворяет?
Определение 1. Функцией Кротова задачи (1) — (4), соот-
ветствующей паре (x*(t)fu*(t))^D[t0t 7], назовем всякую функцию
К(Ху t), которая удовлетворяет всем условиям теоремы 1. Анало-
гично функцией Кротова, соответствующей последовательности пар
(xh(t), uk(t))^D[t0f 7], назовем всякую функцию K(xtt)t которая
удовлетворяет всем условиям теоремы 2.
Заметим, что если существует хотя бы одна функция Кротова
K(x,t)t то функцией Кротова является также К(х, t)=K(x, 0 +
+a(t), где a(t)—произвольная непрерывная, кусочно-гладкая на
t0<C.t^T функция (или абсолютно непрерывная на [t0t Т\). В част-
ности, если взять
а(0 = — f#nnn WdT + rlmln,
т
то функции, R(x, и, t), гх(х)9 г0(х), соответствующие K=K+at та-
ковы, что R(x, и, t) =#(*, и, t) —Rm\b{t)y поэтому inf R(xf и, t) =0,
(x,u)GDt
аналогично
'г W = ri (x) — r-шп и inf Tx (x) = 0,
xSXT

220
ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ
[Гл. 5
и, наконец,
r0(x)=r0(x) + a(t0) и inf r0(*) = romln + cc(g
xtXto
отличается от r0min на постоянную а(*о). Поэтому в теоремах 1, 2
без ограничения общности можем принять #min(0—0, rimm=0.
С учетом этого замечания из теорем 1, 2 имеем следующие ус-
ловия для определения функции Кротова:
R (*, и, t) ^(Кх (х, 0, /(*, и, 0) + Kt (х, t) + r (х, и, t) > 0, (13)
(x,u)eDtt t0<t<T,
г1(х)^-К(хуТ) + Ф1(х)>0, xtXr, (14)
г0(х)=К(х^0) + Ф0(х)>г0ЩП9 хеХи, (15)
причем здесь неравенства превращаются в равенства при x=x*(t),
u=u*(t) в случае теоремы 1 (разумеется, в (14) и (15) равенства
должны получиться при х=х*(Т) и *=**(£<)) соответственно), а в
случае теоремы 2 равенства в (13) — (15) достигаются в пределе
при &->+°° в следующем смысле:
JR(xk(t), МО, t)dt-+0, r1(xk(T))^0t
и
r0(xk (t0)) -+romln (ft -* + °o).
Задачу (13)—(15) назовем задачей Коши— Кротова. Эта за-
дача необычна тем, что, во-первых, здесь имеем дело не с диффе-
ренциальными уравнениями, а с дифференциальными неравен-
ствами с частными производными, во-вторых, эта задача тесно
связана с конкретной допустимой парой (x*(t)y u*(t)) или после-
довательностью допустимых пар (*ь(0»*М0)> ft==l> 2, ..., которые
подозреваются на оптимальность и на которых неравенства
(13) — (15) должны превратиться в равенства в указанном выше
смысле. Такие задачи на сегодняшний день почти не исследованы.
Заметим также, что удобное для работы конструктивное опи-
сание множеств Du XUy Хт часто отсутствует, что затрудняет прак-
тическое использование задачи Коши — Кротова в столь общем
виде (13) — (15). Поэтому полезно рассматривать задачу Коши —
Кротова при некоторых упрощающих предположениях. В частно-
сти, в соответствии с соотношениями (9) в задаче (13) — (15) мно-
жества Du Xto, Хт можно заменить на множества G(t)XV(t) (или
даже £nXV(0)> G(t0)y G(T) соответственно. В ряде случаев функ-
ция К (х, t) может быть найдена из условий
inf [(Кх(х, <), /(*, и9 t)) + Kt (х, t) + /•(*, uy t)] = 0, (16)

S l)
Задачи с закрепленным временем
221
x6Xi9 t0<t<T,
К(хуТ) = Фг(х), х£Хт, (17)
К (х, t0) + Ф0 (х) > r0min, х 6 XUt (18)
где Vt — проекция множества Dt на пространство Ег\ иногда мно-
жество Xt здесь можно заменить на G(t) (или даже на £п), мно-
жество Vt — на V(t). Следует, однако, помнить, что подобные уп-
рощения задачи (13) — (15) могут не привести к цели, ибо упро-
щенная задача может не иметь решения, в то время как задача
(13) — (15) может оказаться разрешимой.
Знание функции K(x,t) из (16), (17) и функции и(хуt)^Vtf
на которой достигается нижняя грань в (16), позволяет найти оп-
тимальную траекторию задачи (1) — (4): для этого сначала надо
найти точку x0£Xt9 из условия r0(x0)= inf г0(х), затем решить
задачу Коши x=f(x,u(xft),t), t^t^T, x(t0)=x0. Оптимальность
получающейся траектории x(ty и управления u(t)=u(x(t)t t) вы-
текает из теоремы 1. Если же нижняя грань в (16) или inf г0(х)
не достигаются, то, зная функцию K(xtt) из (16), (17) и пользу-
ясь теоремой 2, можно построить минимизирующую последова-
тельность для-задачи (1) — (4).
Нетрудно видеть, что изложенный выше подход к задачам оп-
тимального управления тесно связан с динамическим программи-
рованием и является его естественным обобщением. А именно
уравнения (16), (17) при замене Vt на V{t), Хт на GT превраща-
ются в уравнения (4.4.5—6), и в этом случае функция Кротова
K(x9t) тождественно совпадает с функцией Беллмана В(х, t). По-
вторив рассуждения §4 гл. 4 легко убедиться, что для функции
К(х,t) из (16), (17) справедливы утверждения теорем 4.4.1—4
для задачи (4.4.1—4).
Однако следует сказать, что функция Кротова K(x,t) опреде-
ляется из более широких условий (13) — (15), и она может суще-
ствовать даже тогда, когда функция Беллмана не существует.
Далее, подход Кротова позволяет установить оптимальность допу-
стимых пар или последовательностей, не решая задачу синтеза, так
как при этом подходе проводится более тонкое, чем в динамиче-
ском программировании, индивидуальное исследование каждой до-
пустимой пары или последовательности, подозрительной на опти-
мальность. В' то же самое время, когда нужно решать проблему
синтеза, связанную с задачей (4.1.1—4), метод Кротова превра-
щается в метод динамического программирования. Такая гибкость
метода Кротова делает его весьма привлекательным.
т
Упражнение. Минимизировать функционал J(u)= {(и2— х2) dt

222 ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ [Гл. $
при условиях x=u(t)f х(0) =х(Т)=0. Показать, что пара
х* (0=0, u*(t)ss'0 является оптимальной при 0<Г<я.
Указание. Функцию Кротова искать в виде К(х9 t)=ty(t)x2.
§ 2. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ ДЛЯ ЗАДАЧ
С НЕЗАКРЕПЛЕННЫМ ВРЕМЕНЕМ
Рассмотрим задачу: минимизировать функционал
Пц> to, Т) = Г/•(* (*), u(t)9 t)dt + O0(x (to), t0)+Ox{x (Г), T) (1)
при условиях
*x(t)=f(x(t), u(t)9t), t0<t<T9 (2)
*(0€G(0. t0<t<T9 (3)
м=м(/)бУ(<), u(t) кусочно-непрерывна при t0^.t^T9 (4)
где моменты t°9 Т в отличие от задачи (1.1—4) неизвестны и под-
лежат определению из условий
'о€т0, Геть *0<7\ (5)
то, Ti — заданные множества на числовой оси —оо<^<+оо. В ча-
стности, если /°«1, Oo^Oi^O, то придем к задаче быстродей-
ствия.
Как и в § 1, пару (x(t), u(t))9 удовлетворяющую условиям
(2) — (4), назовем допустимой на отрезке to^t^iT, и множество
всех допустимых пар на этом отрезке обозначим через D[t0, Т\.
Объединение множеств D[t0, Т] по всем U9 Т9 удовлетворяющим ус-
ловиям (5), обозначим через D. В пространстве ЕпхЕг введем
множество Dt точек \(х9 и) следующим образом: (х, u)^Du если
существует допустимая пара (х(т)9 м(т))е/), такая, что x(t)=x,
u(t)=u (в точках разрыва управления для определенности примем
u(t)=u(t—0)). Проекцию множества Dt на пространстве Еп обоз-
начим через Хи проекцию Dt на Ег— через Vt. Очевидно, Xt^G(t)9
VtsV(t)9 DtsXtXVt.
Величины йбт0, Т*£хг и пару (x*(t), u*(t))£D[t*09 Т*] назовем
оптимальными, если
J(u'(t)9tl r) = inU(u,t09T)=J*9
где нижняя грань берется по всем (х (/), u(t))£D[t0, Т] при все-
возможных *06т0, Т^хг.
Скажем, что последовательности
totk6 т0, Tk 6 ть (xk(0, uk (t)) eD[t0tki Tk] (k = 1, 2, ...)

§2]
Задачи с незакрепленным временем
223
минимизируют функционал J(u,'t0t Т)% если
J(UkJ*> Тк)-+Г (Л-»оо).
Для формулировки достаточных условий оптимальности, как
и в § 1, введем функции:
R(x, и, t) = (Кх(х. 0. /(*, "> t)) + Kt(x91) + Р(х9 и, 0,
г0 (*, *.)> К (х, g + ф;Цх, у, гД*. Г) = -* (х, Т) + <J>t (х9 Г),
где К (х, t) — кусочно-непрерывная и кусочно-гладкая функция при
х 6 Xtt tomin < t < Гтах, *0mln = inf t0f 7max = sup T
(предполагаем, что tomln<Tmax).
Если (*(*)» tf(0)eD[f0, Л и функция K(x(t), t) переменной t
непрерывна и кусочно-гладка при t0^\t^Tt то, как и в лемме 1.1,
нетрудно убедиться в справедливости представления
т
J(u(t), t0f Т) = §R(x (t),u(t)t t)dt + rx(x(T), T) + r0 (x(t0), t0). (6)
Теорема 1. Для того чтобы последовательности t0tk^x0,
Ть^Ти (Xh(t), uk(t))^D[t0tkt ТУ), A=l, 2, ..., минимизировали
функционал J (и, /0, Т), достаточно существования та£ой функции
К(х, t), что:
1) формула (6) верна для любой допустимой пары (x(t),
u(t))^D[to, Т\ при всех /о^то, Т&\\
Ч
2) lim f R(xk(t)tuk(t),t)dt = Ot Rmln(t)= inf R(x,u,t) = 0;
'ok r
3) lim rx (xk (Tk), Tk) = rlmIn = inf inf rx (x, 7),
fe-*oo T£xt xexT
lim r0 fo (tok), tok) = romln = inf inf r0 (*, *0).
(Для получения формулировки достаточных условий оптимальности
для фиксированных ^о€т0, Т*£хъ (x*(t), u*(t))eD[t*0t Т*] в этойтео-.
реме надо принять tok = f0, Tk = Т*9 xk (t) ==x* (Q, uk (t) = u* (t), и
все предельные переходы заменить простыми равенствами.)
Доказательство. Возьмем произвольные *0€то> Т£%1 и
(x(t), u(t))£D[t0fT]. Согласно формуле (6) будем иметь
J(u(t), t09T)-J(uk (t), tok, Tk) = J*(*(/), u(t), t) dt-

224
ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ
[Гл. 5
'ok
+ r0 {x (t0), t0) — r0(xk (tok), tok).
Так как правая часть этого равенства по условию теоремы имеет
предел при £->*оо, то и левая часть имеет предел. Поэтому
J (и (t), t0, Т) - lim J (uk (t), tok, Tk) = \\R(x(t), и (t), t) -Rmla (Щ dt+
•0
+ гг(x(Г), Т)-гШп + r0(х(g, t0)-rmia >0,
откуда
J (u(t),t0,T)> lim J (uk(t), tok, Tk)
при любых t0 6 т0, Г 6 т1э {x (t)f и (t)) 6 D [t0, T]. Следовательно,
Г = inf J(u, *e, T) > lim J (uk (t), toki Tk).
А-юо
Однако J (uk (t), t0k, Tk) > Г при всех k = 1, 2, ... , поэтому
lim J(uk(t),tok9Tk) = J\ A
В теореме 1 множество Dt часто заменяют на G(t)XV(t)9
Xto — na G(t0), Хт — на G(T) (см. замечание к лемме 1.2). Дей-
ствуя по аналогии с § 4 гл. 4 и § 1 настоящей главы, предлагаем
читателю самостоятельно выписать задачу Коши—Кротова, а так-
же рассмотреть вопросы приближенного решения проблемы синте-
за для задачи i(l)—(5).
Пример 1. Требуется наибыстрейшим образом перевести
точку х=(х\ х2) из начала координат (0, 0) в точку (1, 0) при
условии, когда движение точки подчиняется условиям [236]
& = -(х*)* + и\ х* = иу |а(0|<1, 0<*<7\
Здесь G (0) = {(0, 0)}, G (Т) = {(1,0)}, G (t) _ Е2 при 0«Г
V(t) = {u:ueElt\u\<l}t t0 = #0 = 0}, т1 = {Г:Г>0};
J (и, Т) = Т.
Построим последовательности: 1) {Tk}y где Tk — корень уравне-
ния (Т — I)3 = 12 (Т — 1) — , расположенный в | пределах
1<Г<1+*-2/3(*=1> 2,...); 2) {uk(t)}t 0</<Г*, где
uk(t) = +l при -^<*<il + -L, m = 0, !,..•, ft-1,

§2]
Задачи с незакрепленным временем
225
и при К*<у(Гй+1); "*(') = — 1 при
Y + -^-<*<-7 + T' « = o.i *-L ипри
-±-(Гл + 1 )<t<Г»; 3) {**(0} = {(4(0. 4(0> — траектории, соот-
ветствующие управлению uk(t), 0^t<CTk; xlk(Q) = xl{0)=0,
4(7*) =1,
4(ГА) = 0, (l-Л 3)f<4(0«. 0<4(0<"A 3.
0<*<ГЙ, *=1, 2,...
Покажем, что Г4-+»1=7'\ где Т* — оптимальное время. Для
этого возьмем функцию К(х, *)s=— х1. Тогда /?(х, и, *)=з(л:2)* —
г* г*
inf inf R(x, u,t)=0, (' Я (**(*), uk(t),t)dt= Г 14(0 Is Л-
-/(|M')I2-1)# = f\x*K®№ + 0(k + oo); rQ(xf 0)^0
при *€G(0); гх(л:, 7) = 1 при *€О(Г),^Г>0.
Кроме того, очевидно, формула (6) справедлива для всех до-
пустимых (#(/), и(/))еЦ0, Т\, 7^0. В силу теоремы 1 тогда J(uh,
Th)z=Tk-+l = T* (Г* — оптимальное время). Минимизирующие по-
следовательности ГА, xk(t), uh(t), k=l, 2, ..., для рассматривае-
мой задачи построены. Остается заметить, что эта задача опти-
мального решения не имеет, т. е. inU(u, Т) не достигается, и мы
имеем дело с так называемым скользящим режимом [63, 142].
Приведем еще одно достаточное условие оптимальности, ка-
сающееся задачи быстродействия.
Теорема 2. Пусть в задаче (1) —(5): /°=1, Ф0=Ф1=0,
Т1={Г: Г^/о}, начальный момент U закреплен. Пусть имеются
последовательности Th<=xx, (xh(t), uh(t))eD[to9 Tk) (k=l9 2, ...),
где Th-+T*>tQ. Для того чтобы Г* было оптимальным временем,
достаточно существования функции К (х> t), такой, что:
1) формула (6) верна для любой допустимой пары (x(t),
u(t))(=D[t0t Т\ при всех 7>*0;

226
ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ
[Гл. 5
2) lim f R(xk(t), uk(t), t)dt= f Rmin(t)dt, Rmtn(t)= inf R(x,u9f);
to *o *
T*
3) f Wmi„(0-ll*<0 при любых T,t0<T<r;
т
4) limrj(xk(Tk)t Tk) = rlmin = inf inf rx(xt 7),
Л-»оо <#<Г<Г* x£XT
\imr0(xk(t0), *0)=romin = inf r0(*, t0).
(Для получения формулировки достаточного условия оптимально-
сти для фиксированных T*>tQ, (x*(t), ~u*(t))^D[t0t Т*] в этой
теореме надо принять 7\=Г*, xh(t)-=x*(t)9 uk(t)=u*(t) и все
предельные переходы заменить простыми равенствами.)
Доказательство. Пусть выполнены все условия теоремы,
и пусть тем не менее Г* не является оптимальным временем. Тогда
существуют момент Т и пара (x(t), u(t))^D[t0t T]t такие, что
Г<Г*. Согласно формуле (6) будем иметь
J (и, T)-J(uk(t)t Tk) = T-Tk = ]R(x(t)$ ц(0, t)dt-
л>
-j Я (МО. МО. t)dt + rx{x{T), T)-rx(xk(TJ9 Tk) +
+ r0(x(t0)> 'о)—MM'o). g.
T*
Отсюда при k -* + oo получим T — T* = — Г /?mln (*) Л +
+ \R(x(t),u(t), 0*+М*(Л, T)-rlmn + r0(x(t0)tt0)-romln>
и
>-] Rmn(t)dt>T-T\
т
Полученное противоречие доказывает теорему. А
Пример 2. Пусть требуется наибыстрейшим образом переве-
сти точку х= (х\ х2) из положения (1,0) в начало координат (0,0)
при условии, когда движение точки подчиняется условиям х{=-х\
х*=и, |а(*)|<1, 0<«Г.
Возьмем Г* = 2; u*(t)= — 1 при 0</<И и.а*(0= + 1 при*
1<^2; соответствующую траекторию x{*(t) = l—0.5*2 при O^t^t
<4 uxl*(t)=0.5(t—2)2 при 1^^2; x2*{t)=—t при 0^<1 И

§ 3] Дискретные управляемые системы. Оценка погрешности 227
x2*(t)=t—2 при 1^г^:2. Указанные управления и траектория
легко находятся из принципа максимума (см. пример 3.2.2.).
Покажем, что они являются оптимальными. Возьмем функцию
К(х, t)=xl—(t—l)x2. Тогда R(x, и, t)=Kx^x2+Kx^u+Kt+\ =
= _(*_1)И+1, r0(x9 0)^1 при Jte=G(0) = {(l, 0)}, п(х9 Т)^0
при x^G(T) = {(0, 0)}. Очевидно,
inf lnlR(x9 и, t)=—\t-V\+l = Rmln(t)=R(x*(t), u'{t), t),
jKminW—1J*=—J|<-1|*<0
г T
при всех Г<2, и формула (6) верна для всех допустимых пар.
В силу теоремы 2 момент Г*=2 и пара i(x*(t), а*(*))еД0, 2] оп-
тимальны.
Заметим, что функция Беллмана в этой задаче имеет разрывы
первой производной как раз на оптимальной траектории [24, 195], в
то время как функция Кротова К (х, t) является просто много-
членом.
Упражнения. 1. Решить проблему синтеза для задачи быстрей-
шего перевода точки х= (х\ х2) из заданного состояния (х\, х\) =
=х0ФО в начало координат при условиях
а)* = *\ > = и(*). U(0I<1, 0</<Г;
б)^=ха, *=-*-+*(*), |а(0|<1, 0<*<Г;
в) х1 = х2.+ и\ *=*—& + и*, |а'(/)|<1 (/=1, 2), 0<*<Г.
2. Перевести точку х = (х1, х2, х3) из начала координат# в точку
Х\ = (а, 0, 0) быстрейшим образом, если х1 = х2, х2 = х3\ х3 = u(t)f.
|ы(/)|<1, 0</<Г; а = const. Показать, что оптимальное время
Г* = ^32Й.
Указание. В задачах 1—2 функцию Кротова искать в виде
многочлена первой степени по л: с коэффициентами, зависящими
от времени.
§ 3. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ ДЛЯ ДИСКРЕТНЫХ
УПРАВЛЯЕМЫХ СИСТЕМ. ОЦЕНКА ПОГРЕШНОСТИ
1. Рассмотрим задачу: минимизировать функционал
' (М) = £; p°t fo. щ)+Ф0 (х.)+Фх ш (1)
1=0

228 ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ \Гл. 5
при условиях
хш = Ft (xi9 щ)9 i = 0, 1, 2,... , N— 1, (2)
XttQi, uievt9 t = 0, 1, 2,..., N9 (3)
где
*< = (*{, 4, ..., хЧ)9 F{ = (F\9..., F?)f a, = (ai,..., и£); мно-
жества GiG£m, V£C£r, * = 0, 1, ... , N, заданы; функции F{ (x9 u)
определены при (x, u)&GiXVi9 t=0, 1, ..., N9 /=0, 1, ..., n\ функ-
ции Фо(х) и Ф\\(х) определены при *eG0 и x^GN соответственно;
/ — дискретное время, 1=0, 1, ..., N, момент N будем считать из-
вестным.
Как мы убедились в § 4.1, к таким задачам приводит разност-
ная аппроксимация задачи оптимального управления с непрерыв-
ным временем. Задача (1) — (3) имеет также и самостоятельный
интерес и возникает при описании управляемых систем с дискрет-
ным временем ([6, 26, 59, 119, 196, 231, 234] и др.).
Если задать управление [и*]= (wo, ии ..., иь) и начальное усло-
вие х0=а, то из уравнений (2) однозначно определяется дискрет-
ная траектория [xi]=(x0t хи ..., л:^). Пару ([х{]9 [и*]) назовем до-
пустимой, если она удовлетворяет условиям ((2), (3). Множество
всех допустимых пар обозначим через D. Допустимую пару
([*<], [u*i]) назовем оптимальной, если /([w<J) = inU ([иЛ) = Г. По-
D
следовательность допустимых пар ([**,&], [uitk])> й=1, 2, .... назо-
вем оптимальной, если она минимизирует функционал (1), т. е.
Нт/(КЛ) = Г
2. В пространстве ЕпхЕг введем множество D* точек (xf и)
следующим образом: ,(*, u)^Di9 если существует допустимая пара
([хш], [Ит])^А такая, что Х{=х9 щ=>и. Далее, через Х{ обозначим
множество всех тех JceGi, для которых существует хотя бы одно
u^Vi такое, что (х9 а)еО<.
Возьмем функцию Ki(x)9 определенную при x^Xiy t=0, 1,
..., N и положим
Rt (х, и) = Kt+i (F( (xt и)) -Ki (х) + F°t (х9 и)9 i = 0, 1, N-l9
г#(*)==*о (*) + *•(*). гг(х, u) = -Kn(x) + ФЛх) + F°N(x, и).
(4)
С помощью этих функций значение функционала (1) на любой до-
пустимой паре' можно представить в виде
1 (Ы) = £ Ъ (*i> ид + ri (**. *n) + ro(*»)• (б)
<=0

# 3] Дискретные управляемые системы. Оценка погрешности 229
В самом деле,
£ я, <*„ «,) = £ iicJ+1 (*+,)-*, (*,я + £ ^ to, «<) =
1=0 f=0 t=0
АЛ—I
= *лг(xN) —Ко(х0) + £ F?(*,, а,) = /([аЛ) — rx(xNi uN) — г0(хв),
что равносильно (5).
Теорема 1. Для оптимальности последовательности допусти-
мых пар ([*{,*], [tktb\), fc=l, 2, ..., достаточно существования функ-
ции /С<(*)» t=0, 1, ..., N, такой, что:
-1;
1) lime,to*v ^) = /?<min= Jnf #,(*, а), £«0, 1...... AT
*-»*• («.«ДО*
2) limrx(*w, ам)»'ДП|П= inf rt(x, а);
Hnir0(%) = rlraIn= inf r0(*).
(Для получения формулировки достаточного условия оптимально-
сти для фиксированной пары ([х]], [u\])^D здесь надо принять
*!* = *«. Щк = и*1> '=0, 1, ...,#,
и все предельные переходы заменить равенствами.)
Доказательство. Возьмем произвольную допустимую па-
ру ([Xi], [щ]). С помощью формулы i(5) имеем
лг—1
— rx(xNkf uNk)+r0(x0) — r0(x0tk), k= 1, 2, ...
В этом равенстве можно переходить к пределу при Л-^оо, так как
правая часть по условию имеет предел. Получим
/(1^])-Нт/([а,Л)= УШъ, Щ)-Ътп] +
+ ^i (Xn, U>n) — ^lmln + г0(*o) — rO mln > °-
Следовательно,
/•=inf/([al])>lim 7([M)-
Однако / ([ии]) > Г, Л = 1, 2, ... , поэтому lim/ ([a^J) = /\ A

230 ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ [Гл. $
3. Определение 1. Функцией Кротова задачи (1)—<3), со-
ответствующей допустимой паре ([xi]9 [Ui])£D или последова-
тельности пар ([Xik],[tiik]) е/),Л=1,2,..., назовем всякую функцик>
Ки(х), t=0, 1, ..., N, удовлетворяющую условиям теоремы 1.
Заметим, что если существует хотя бы одна функция Кротова
Ki(x), f=Q,, 1, ..., N9 то функция Ki(x)+a,i при любых <хи i =
=0,1, ..., N9 также является функцией Кротова. Поэтому без ог-
раничения общности в теореме 1 можем принять /?гтш=0, i=
=0, 1, ..., N— 1, rimln=0, ибо в противном случае функцию /(*(*>
заменим новой функцией /С< (*)+«*> ГДе
TV—1
Щ = J] Rjmln + ^lmln» ^ = 0, 1,...„, N—l9 а^=+Г1ш,п.
Таким образом, функция Кротова для допустимой пары ([**], [щ]}
или последовательности ([х^], [*йл]), Л==1;- 2, ...г согласно теореме L
удовлетворяет условиям
Я, (х, и) = tf«+1 (F, (х, и)) - Кс (х) + F°t (х9 и) > О, (х9 и) £ Dl9
i = 0, 1,..., N—l, (6>
M*. a)= —tf^ + O^+FJ^*, «)>0, (*, «)6^
^oW = ^oW + Фо (*) > >omin,
причем неравенства здесь должны обратиться в равенства, при
дс = д^, и = щ9 или при jc=JCift, u=uih в пределе, когда &->-оо, t=
=0, 1, ..., N.
Возможно определение функции Кротова из условий
inf [Ki+x{Ft{x9 a)) + F?(*. и)] — Кй{х)шш0, x£Xi%
* = 0, 1,..., ЛГ—1, (7>
inf FSr (*, a) -/C*(*) + Ф%(х) = 0, д:6 **,
где Di(x)—множество всех тех aeV*, для которых (х9 u)^Dit i—
=0, 1, .... N-\.
Сравнение условий (6), (7) с уравнением Беллмана (4.1.13)'
показывает, что функция Кротова Ki(x) является более широким
понятием, чем функция Беллмана Bi(x).
Определение функции К$(х)9 удовлетворяющей условиям (7),.
и управления и=щ(х)9 на которой реализуется нижняя грань в*
левой части уравнений (7), равносильно решению задачи (1) — (3)
и соответствующей ей проблемы синтеза (при ф0^0). Это утверж-
дение доказывается так же, как аналогичные теоремы 4.1.2—5. За-

£ 3] Дискретные управляемые системы. Оценка погрешности 231
метим, что при некоторых ограничениях на данные задачи (1) — (3)
-существование функции Кротова Ki(x)9 удовлетворяющей условиям
(7), является необходимым условием оптимальности [142] i(cm., на-
лример, теорему 4.1.1).
4. Допустим, что мы взяли некоторую функцию Ki(x) и уп-
равление и=щ(х), x^Xit удовлетворяющее условию
inf Ъ(х, u) = Ri(xt щ(х)), inf гг(х, u) = rl(x, uN(x)),
u£D.(x) uSVN
где функции Ru r\ взяты из (4). Пусть траектория {*i]=i(*o, ..., xN)
удовлетворяет условиям (2), (3) при щ=щ{хг) и некотором хо=
= х0^Х0.. Примем пару ([Х{], [щ=щ(Х{)]) в качестве приближен-
ного решения задачи (1) — (3) и оценим получающуюся при этом
погрешность 1([щ])—/*. С помощью формулы (5) для любых ([**],
{щ]) eZ) имеем
ЛГ—I _ _ _ _
/(Ы)—/(N) = 2 lRt(*i, 4) — Ri(Xi, ul)]+ri(xNt uN) —
— rx (xNy uN) + r0 (*0) — r0 (*0) < £ [— R( mln + Rt (x£, щ)\ +
t=0
.+ rx (xn, un) — rx min — r0 mIn + r0 Ц) = e ([u$1
откуда
/(M)-inf/(M<e([51]). (8)
D
Как видим, эта оценка будет тем лучше, чем точнее удовлетворя-
ются условия (6) (или условия /(7) и r0(x0)= inf г0(х)). Оценка
х€Хо
(8) может быть полезна при решении задач оптимального управ-
ления с использованием тех или иных вариантов динамического
программирования, описанных выше.
Упражнение. Вывести условия оптимальности для задачи ми-
нимизации функционала
ПЫ) = £ [<а„ xt) + b£(u{)] +Кс xN)
при условиях xi+\ = AtXi + Bt (и{), uteVlt i = 0, 1, ... , N — 1;
л:0 = а, где At — матрица порядка п х п; Bit аь с, а — /г-мерные
векторы, bi(u) — скалярная функция переменной иеУг^£г, i=
= 0, 1, ..., N-L
Указание. Функцию Ki(x) искать в виде многочлена первой
степени по х: Ki(x) = (фг, х), пользуясь условиями (7).

Глава 6
Методы минимизации
в функциональных пространствах
Выше мы занимались экстремальными задачайи: минимиза-
цией функций конечного числа переменных (гл. '1, 2) и задачами
оптимального управления, связанными с системами обыкновенных:
дифференциальных уравнений (гл. 3—5). Наряду с этими
задачами большой интерес для практики представляют задачи:
оптимального управления процессами, описываемыми уравнения-
ми с частными производными, задачи наилучшего приближения
функций и др. Оказывается, что все эти задачи можно трактовать
как экстремальные задачи в подходящим образом выбранных
функциональных пространствах и для их исследования использо-
вать аппарат и методы функционального анализа. Такая трактовка
позволяет выявить общие закономерности, присущие широким
классам экстремальных задач, создавать и исследовать общие ме-
тоды решения таких задач. В последние годы теория экстремаль-
ных задач в функциональных пространствах, методы их решения:
разрабатывались весьма интенсивно, и количество работ в этой
области продолжает расти (см., например, [3, 4, 7, 10, 30, 35, 46, 53„
64, 65, 73, 81, 82, 97, 99—101, 108, 121, 122, 128, 129, 135, 139, 142,.
148, 153—156, 161, 162, 175, 187, 195, 199, 218, 221, 229, 250, 2561
и др.).
В настоящей главе рассмотрим ряд методов, которые часто ис-
пользуются для минимизации функционалов на множествах иа.
гильбертовых или банаховых пространств и являются естествен-
ным обобщением методов гл. 2; остановимся на применениях этих:
методов к некоторым классам задач, часто встречающимся в.
приложениях.
Для понимания содержания настоящей главы вполне достаточ-
но знаний основных сведений о банаховых и гильбертовых прост-
ранствах и о функциях действительного переменного в объеме
обычных университетских курсов; необходимые сведения можно-
почерпнуть, например, в книгах [88, 127, 131, 137, 165, 210, 245].
Некоторые определения и теоремы, используемые при описании
методов минимизации и их исследовании, приведены в § 1. Изло-
жение методов минимизации применительно к конкретным задачам
оптимального управления в § 3—7 ведется в терминах, связанных
с этими задачами, и для своего понимания не требует знанийс
функционального анализа.

§ п
Вспомогательные сведения
233
§ 1. ВСПОМОГАТЕЛЬНЫЕ СВЕДЕНИЯ
Говоря о банаховых и гильбертовых пространствах, всюду ни-
же будем иметь в виду вещественные сепарабельные пространст-
ва, не оговаривая этого в дальнейшем. Для краткости банаховы
пространства будем называть ^пространствами, гильбертовы —
//-пространствами. Если не оговорено противное, термины «зам-
кнутость», «непрерывность», «ограниченность», «сходимость» будут
дониматься в сильном смысле, т. е. в смысле нормы соответствую-
щих пространств. Норму элемента (или, как будем иногда гово-
рить, точки, вектора) в пространстве В будем обозначать через
Л иIIв или просто ||а||, если ясно, о каком пространстве идет речь;
-аналогично скалярное произведение двух элементов ut v ъ Я-про-
странстве будем обозначать (ы, v)H или просто \(и, v). Под В* бу-
дем понимать пространство, сопряженное к банаховому простран-
ству В; напоминаем, что В* состоит из линейных ограниченных
функционалов, определенных на В. Примем также обозначения;
U — замыкание множества, £/, IP — множество внутренних то-
чек U.
1. При исследовании экстремальных задач в бесконечномер-
ных пространствах большую роль играют такие понятия, как гра-
диент функционала, выпуклость множеств и функционалов и др.
Эти понятия естественным образом обобщают соответствующие
понятия, которыми мы пользовались в гл. 2 при изучении задачи
минимизации функций конечного числа переменных.
Определение 1. Функционал J (и), заданный на множест-
ве U некоторого банахова пространства В, называется дифферен-
цируемым в точке u&U в смысле Фреше, если при всех Ле5, для
которых w-f-ftet/, приращение функционала можно представить
в виде
j(u + h)-J(u) = (J'(u), h) + o(\hl), (1)
где J'(и) —некоторый линейный ограниченный функционал на В
(т. е. /'(a)efi*), (J'(и), К) — результат применения функционала
J'(u) к элементу А, ," —►•О при ||А||-й). Главная линейная
IIЛ ||
часть приращения функционала, равная (У(и), Л), называется диф-
ференциалом Фреше функционала J (и) в точке u^U, а сам функ-
ционал J'(u) называется первой производной или градиентом
функционала J (и) в точке u^U.
Если В — гильбертово пространство, то сопряженное к нему
лространство В* согласно теореме Рисса—Фреше может быть
отождествлено с В, и поэтому дифференциал (/'(w), h) можно рас-
сматривать как скалярное произведение некоторого элемента
J'(u)^B на элемент Л<=В.

234 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. &
Заметим, что из представления (1) следует
lim IS2±2*kzlM ша (j>(U),h).
Напомним, что сопряженное пространство В* само является ба-
наховым с нормой || с ||д* = sup (с, и) для каждого с 6 В*. Отсюда
1М1В<1
имеем |(/'(и), Л)|<||/'(и)1ИА||в.
Определение 2. Функционал J (и) называется непрерывно»
дифференцируемым на множестве U в смысле Фреше, если J'(u)
существует при всех u^U и ||/'(и+А)— J'{u)\\B*-*-0 при ||А||-*0;
и, u-\-h^U. Множество всех функционалов, непрерывно дифферен-
цируемых на U в смысле Фреше, будем обозначать через Cl(U)„
Очевидно, всякий функционал J(u)eCl(U) непрерывен на LL
Определение 3. Говорят, что градиент J'(u) функционала
J(u)^Cl(U) удовлетворяет условию Липшица на множестве U,
если \J'(u) — J'{v)\b*<^L\u — v\\B при всех и, v*=U; L=const>0
-называют константой Липшица.
Определение 4, Билинейным функционалом называется ве-
щественная функция Q{u, v) двух аргументов (и9 y)efl, являю-
щаяся линейным функционалом по каждому аргументу при фикси-
рованном другом. Билинейный функционал называется ограни-
ченным, если существует число С, такое, что \Q(u9 v)\^C\\u\\*\\v\\
при всех и, v^B; число
||Q||= sup|Q(tt, о)|
тогда называется нормой билинейного функционала. Билинейный
функционал называется симметричным, если Q(v, u)=Q(u, v) при
всех и, v^B. Симметричный ограниченный билинейный функцио-
нал Q(u, v) при u=v порождает квадратичный функционал
Q(u, и) с нормой IIQI = sup | Q(u,u)\.
N1=1
Понятие квадратичного функционала является естественным
обобщением понятия квадратичной формы
г
(Au, а)= J аци'и?
в евклидовом пространстве. Чтобы подчеркнуть это сходство, квад-
ратичный функционал Q(tf, и) будем обозначать через {Quy и).
Примером простейшего квадратичного функционала в гильбертовом
пространстве является квадрат нормы элемента: (и, и)=и2=
={(Еи, и) f где Е — тождественный оператор.
Определение 5. Функционал J (и), заданный на множестве
U банахова пространства В, называется дважды дифференцируе-

i ц
Вспомогательные сведения
235
мым в точке u^U в смысле Фреше, если при всех h^B, для ко-
торых м+Ле£/, приращение функционала можно представить в
виде
J(u + h)-J(u) = (J'(u), h) + ±V(u)h9 А) + о(|ЛР), (2)
где J'(u) —градиент функционала, a \(J"(u)hy h) —квадратичный
функционал, называемый вторым дифференциалом J (и) в точке
u^U;— J —» 0 при || h || -► 0. Функционал J (и) называется
II л ||2
дважды непрерывно дифференцируемым на множестве U в смысле
Фреше, если J (и) дважды дифференцируем по Фреше в каждой
точке
иеи и sap\(J'(u + v)h, h) — (JT(u)h9 h)\ =
HftlNl
= \\r(u + v)-r(u)\\^0
при ||v Ц-^0, и-f *>(=[/.
Множество всех функционалов, дважды непрерывно диффе-
ренцируемых ца Uв смысле Фреше, будем обозначать через С2(С/).
Пример 1. Пусть А — симметричный линейный ограниченный
оператор, определенный на всем гильбертовом пространстве Я и
действующий из Я в Я; Ь — заданный элемент из Я. Тогда функ-
ционал J(u) = — (Аи, и) — (6, и) принадлежит С2(Н), причем,
как нетрудно убедиться, разложение (2) в данном случае будет
иметь вид
J(u + h) — J(u) = {Au — 6, h) + \{Ah, h).
Следовательно, J'(u)=Au—6, J"(u)=A.
Пусть /(tf)eO(f/) (p= 1 или 2), пусть щ h — некоторые фик-
сированные элементы рассматриваемого В-пространства, u+<xh^U
при всех а, О^а^Ч. Нетрудно видеть, что тогда формулы (2.1.4—
7) и их вывод остаются без изменений и для функционалов 7(и)е
<=Cp{U).
2. При исследовании экстремальных задач в В-пространст-
вах, как и в конечномерном случае, большую роль играют выпук-
лые множества и функционалы.
Определение 6. Множество U из некоторого В-простран-
ства называется выпуклым, если аи+(1—a)v^U при всех и, v^U
и всех а, 0^а^1, т. е. отрезок u-{-a(v—и), 0^'a^l, соединяю-
щий любые две точки w, v множества, также принадлежат мно-
жеству.

236 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. б
Определение?. Функционал J (и), определенный на выпук-
лом множестве С/, называется выпуклым, если
j(au + (1 — a)v) <aJ(u) + (l — a)J(v) (3)
при всех uf ueJ/ и всех а, О^а^'1. Если в (3) равенство возмож-
но только при а=0 и а=1, то функционал J (и) называют строго*
выпуклым.
Сравнивая эти определения с определениями 2.1.1—2, видим,
что выпуклость у функций и функционалов определяется совершен-
но одинаково, поэтому неудивительно, что многие свойства выпук-
лых функций остаются верными и для функционалов. В частности,
теоремы 2.1.1—3 и их доказательства остаются справедливыми и в
В-пространствах, нужно лишь в формулировках этих теорем и до-
казательствах слово «функция» заменить на «функционал». Впро-
чем, скоро убедимся, что в бесконечномерных пространствах такая
аналогия может быть продолжена далеко не всегда.
Определение 8. Говорят, что функционал J (и) достигает
в точке u*^U своего абсолютного минимума (или просто миниму-
ма) на множестве U, если /(и*)^/(и) при всех u^U. Функцио-
нал J (и) достигает в точке u*^U своего локального минимума на
множестве [/, если существует окрестность 0={и: неС/, 6>0,
\\и—и*||<6} точки и*, такая, что J(u*)^J(u) при всех ыеО.
Ясно, что всякий абсолютный минимум является и локальным,
но обратное, вообще говоря, неверно.
3. Вопрос о достижении функционалом своей нижней грани на
множестве из некоторого В-пространства более тонкий, чем в ко-
нечномерном случае. А именно теорема Вейерштрасса из класси-
ческого анализа о том^ что функция, непрерывная на замкнутом ог-
раниченном множестве конечномерного пространства, достигает
своей нижней грани на этом множестве, в В-пространствах оказы-
вается неверна. Проиллюстрируем это обстоятельство на приме-
рах.
1
Пример 2. Функционал J (и) = f (х2 — и2) dt на множестве
U = {u = u(t):u(t)eL2[0, 1], И0|<1, х = и9 *(0) = 0>,
как мы видели в примере 5.1.2, не достигает своей нижней граню
inf/(a)=—1. Заметим, что здесь множество U ограничено и зам-
кнуто в L^O, 1] (оно даже выпукло), а функционал J (и) непреры-
вен в норме LJ[0, 1] (однако J (и) невыпуклый).
Пример Зу Функционал
о 1
J(u)= [u(t)dt— [u(t)dt

§ 1] Вспомогательные сведения 237
на шаре
U = {u = u(t):u(t)eC[-lM |а(0|<1>
пространства С[—11, 1] также не достигает своей нижней грани
inf/(w)=—2, хотя J (и) непрерывен в норме С[— 1, 1], выпуклый
(он даже линейный), а множество U ограничено, замкнуто в
С[—1, 1}, выпукло. Заметим, что пространство С[—1, 1] нерефлек-
сивно.
Напомним некоторые определения, которые нам понадобятся
ниже для формулировки обобщенной теоремы Вейёрштрасса, при-
годной в В-пространствах.
Определение 9. Говорят, что последовательность ип из не-
которого ^В-пространства слабо сходится к элементу и^В, если
lim (с, lij = (с, и) для любого функционала с из сопряженного
пространства В*.
Если В — гильбертово пространство, то согласно теореме Рис-
са—Фреше (см., например, [127], стр. 132, [137], стр. 177) В=В*,
поэтому слабая сходимость ип к и в этом случае означает, что
lim(c, ип) = (с, и) для любого се5.
Л-*оо
Определение 10. Множество U из 5-пространства назы-
вается компактным [слабо компактным] (или секвенциально ком-
пактным [слабо компактным]), если из любой последовательности
{Ufc}e£/ можно выбрать хотя бы одну подпоследовательность {ukn}9
которая сходится [слабо сходится] к некоторому u^U.
Определение 11. Функционал J (и), заданный на некото-
ром множестве U 5-пространства, называется полунепрерывным
снизу [слабо полунепрерывным снизу] в точке ые£/, если для лю-
бой последовательности {aft}et/, которая сходится [слабо сходится]
к и при п-^оо, имеет место соотношение lim J (ип) ^J(u). Функ-
П-*от
ционал J (и) полунепрерывен снизу [слабо полунепрерывен снизу]
на множестве U't если он полунепрерывен снизу [слабо полунепре-
рывен снизу] в каждой точке u^U.
Функционал J (и) называют полунепрерывным сверху [слабо
полунепрерывным сверху] на множестве (/, если функционал —J\(u)
полунепрерывен снизу [слабо полунепрерывен снизу] на U.
Нетрудно видеть, что для непрерывности [слабой непрерывно-
сти] функционала необходимо и достаточно, -чтобы он был полу-
непрерывен [слабо полунепрерывен] как сверху, так и.снизу.
Примером слабо полунепрерывного снизу функционала яв-
ляется норма элемента в Б-пространстве: J(u) = \\u\\ i(cm., напри-
мер, [127], стр. 173, теорему 1 или [165], стр. 217).
Очевидно, из слабой непрерывности [слабой полунепрерывно-
сти сверху или снизу] следует непрерывность [полунепрерывность

238 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. в
сверху или снизу соответственно]; обратное неверно. Например,
функционал J(u) = \\u\\ непрерывен, но не является слабо непре-
рывным.
Следующая теорема обобщает теорему Вейерштрасса из клас-
сического анализа.
Теорема 1. Всякий полунепрерывный снизу [слабо полуне-
прерывный снизу] функционал J (и) на компактном [слабо компакт-
ном] множестве U 5-пространства ограничен снизу и достигает на
U своей нижней грани.
Доказательство. Сначала покажем, что inf/(#) = /*>
>—оо. В противном случае найдется последовательность {w^'Jet/,
такая, что /(иь)-*-—оо (&-*оо). Так как U компактно [слабо ком-
пактно], то существует подпоследовательность {и^}, сходящаяся
[слабо сходящаяся] к некоторому элементу а*е!Л Из полунепре-
рывности снизу [слабой полунепрерывности снизу] J (и) следует
lim J (ukn) >./(а*) > — оо. Противоречие. Таким образом, /*>
Я-*оо
>—оо. Далее, пусть {е&} — произвольная числовая последователь-
ность, такая, что ел>0, е*-Я) (&-мх>).
По определению нижней грани inf J(u) = J* для каждого k
существует элемент Uk^U, для которого J*^J(tik) ^/*+«а- Так
как U компактно [слабо компактно], то существует подпоследова-
тельность йкп, сходящаяся [слабо сходящаяся] к некоторому
элементу u*^U. Из полунепрерывностй снизу [слабой полунепре-
рывности снизу] J (и) и неравенств
J* < J (ukfl) < J* + %п при п -* оо имеем
J* < J (и*) <Jim J (ukn) <J\ т. е. / (и*) = Г. А
/1-»00
Для того чтобы было удобно пользоваться теоремой »1, жела-
тельно иметь достаточно простые критерии компактности [слабой
компактности] множеств и полунепрерывности снизу [слабой полу-
непрерывной снизу] функционалов в В-пространствах. Приведем
один широко известный критерий слабой компактности, часто при-
меняемый в прикладных задачах.
Теорема 2. Замкнутое ограниченное выпуклое множество в
рефлексивном 5-пространстве (в частности, в гильбертовом про-
странстве) слабо компактно.
Доказательство этой теоремы можно найти, например, в рабо-
те [127]: она является следствием теоремы 2 на стр. 173 [127] и
теоремы 1 на стр. 180 [127] (см. также [88], стр. 461). Подчеркнем,
что в этой теореме замкнутость и ограниченность множества пони-
маются в смысле нормы 5-пространства. Это обстоятельство часто

§ 1]
Вспомогательные сведения
239
облегчает проверку условий теоремы в практических задачах. При-
меры важнейших рефлексивных В-пространств с указанием их ос-
новных свойств приведены в работе [88], гл. IV (см. таблицу на
стр. 408—413).
Далее, остановимся на одном критерии слабой полунепрерыв-
ности снизу функционалов, связанном со свойством выпуклости.
Теорема 3. Выпуклый функционал J (и) слабо полунепре-
рывен снизу на выпуклом множестве U В-пространства тогда и
только тогда, когда J (и) полунепрерывен снизу на U.
Доказательство. Необходимость очевидна. Докажем до-
статочность. Пусть J (и) полунепрерывен снизу на U (в* частности,
может быть J (и) просто Непрерывен). Это значит, что если после-
довательность {uh}^U сходится к u^U по норме, то limJ(uk)>J(u).
Л-*оо
Пусть теперь последовательность {uk}^U слабо сходится к
ug(/. Выбирая при необходимости подпоследовательность, можем
считать, что сама последовательность {J(Uk)} обладает свойством:
lim J(uk) = lim J(uk). Из известной теоремы Мазура (см! [127],
стр. 173, теорема 2; см. также ниже упражнение 20) следует, что
для каждого номера k=l9 2, найдутся такое целое m^k и та-
кие действительные числа
m
Vkmi>Q> i=*k, k+ 1, ... , Ш, Y^akml= 1»
m
что последовательность vk = V akmiUi будет сходиться к и по норме
В-пространства, т. е. \\vk — и\\~>0 (Л-*оо). Тогда lim J(vk) > J (и).
С учетом выпуклости J (и) имеем
m m
J iPk) = ^ (E актьЩ) < V <*kmiJ (Щ) < SUP J (Щ).
Однако lim sup J (uj) = lim J(uk), поэтому переходя к пределу при
&-*оо в предыдущем неравенстве, получим
J (и) < Ит J (vk) < lim sup J (щ) = lim J (uk). ±
Из теорем 1—3 сразу следует
Теорема 4. Выпуклый полунепрерывный снизу (в частности,
непрерывный) функционал на замкнутом ограниченном выпуклом
множестве рефлексивного ^-пространства (в частности, гильберто-
ва пространства) достигает на этом множестве своей нижней
грани.

240 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
Теоремы 1,4 служат основой многих теорем существования
решений экстремальных задач; примеры таких задач см. ниже в
§ 3—7. Ряд теорем, содержащих различные достаточные условия,
гарантирующие достижение функционалом своей нижней гцани на
заданном множестве ^-пространства можно найти в работах [46]
<гл. III), [186].
4. В дополнение к теореме 3 остановимся еще на других усло-
виях слабой полунепрерывности снизу функционалов — эти усло-
вия связаны с понятием опорного (функционала.
Определение 12. Пусть J (и) — функционал, определен-
ный на множестве U банахова пространства В. Линейный непре-
рывный (функционал /, определенный на В, называется опорным к
функционалу J (и) в точке v^U, если J(u) ^/ (v) -+-(/, u—v) при
всех иеС/.
Если J (и) выпуклый и принадлежит C{(U)9 где U — выпуклое
множество, то согласно теореме 2.1.2 J(u)—J(v)^(J'(v)9 u—v)
при всех wef/, т. е. l=J'(v) —опорный функционал к J (и) в точ-
ке v. Таким образом, понятие опорного функционала обобщает
понятие градиента на случай негладких функционалов. Различные
свойства опорных функционалов, технику вычисления и их исполь-
зования при исследовании экстремальных задач в функциональных
пространствах можно найти, например, в работах [73, 99, 199] и др.
Нетрудно видеть, что теоремы 2.5.1, 2.5.3, 2.5.8 и их доказа-
тельства остаются справедливыми и в ^-пространствах, нужно
лишь в формулировках и доказательствах этих теорем слово
«функция» заменить на «функционал», Еш на В.
Для получения условий существования опорных функционалов,
аналогичных теоремам 2.5.6—7, нам потребуются теоремы разде-
лимости выпуклых множеств в В-пространствах.
Определение 13. Пусть X и Y — два множества из не-
которого банахова пространства В. Линейный непрерывный функ-
ционал сФО, определенный на В, называется разделяющим мно-
жества X и Y, если существует действительное число а, такое, что
(с, х)^а^(с, у) при всех дсеХ и уеУ, или, иначе говоря
inf (с, х)> <x>sup (с, у).
х£Х y£Y
Если либо inf (с, х)>а, либо sup(c,#)<<x, то говорят о
х£Х y€Y
строгом разделении этих множеств. Если inf (с, х) — а, то функ-
хех
ционал с часто называют опорным ко множеству X.
Справедливы следующие две теоремы, имеющие широкое при-
менение при исследовании экстремальных задач в функциональных
пространствах.
Теорема 5. Пусть X — выпуклое множество банахова прост-
ранства Ву содержащее хотя бы одну внутреннюю точку (Х°Ф0),
и пусть Y — непустое выпуклое множество в В, причем X°()Y=0.

§ п
Вспомогательные сведения
241
Тогда существует функционал с, разделяющий эти два множества.
Если X и У имеют общую граничную точку х0у то
inf (с, х) = sup (с, у) = (с, х0) = а.
х€Х x£Y
Заметим, что в отличие от конечномерного случая ,(см. теоре-
мы 2.5.4—5), требование существования внутренней точки хотя бы
одного из множеств в теореме 5 не может быть опущено (см. уп-
ражнение 5).
Теорема 6. Пусть X, У— непустые и непересекающиеся вы-
пуклые множества в ^-пространстве, такие, что X замкнуто, а У
компактно ((в частности, У может состоять из одной точки). Тогда
существует функционал /, строго разделяющий X и У.
Доказательство этих двух теорем можно найти в работе [245},
гл. II, § 9 (см. также (88], стр. 452).
Теорема 7. Пусть множество U банахова пространства В
выпукло и имеет хотя бы одну внутреннюю точку (в частности,
возможно U==B). Тогда, для того чтобы функционал J {и) во всех
точках v^U имел опорный функционал, необходимо и достаточно,
чтобы J (и) был выпуклым на U и для всякой точки v^U суще-
ствовала постоянная L=L(v)^Q, такая, что I(u)^I(v)—L(v)X
•X\\u—v\\ при всех ие£/.
Доказательство. Необходимость доказывается так же,
как в теореме 2.5.7.
Достаточность. Пусть /(и) выпуклый на U и для каждого
v&U существует постоянная L=L(y)^0, такая, что I(u)^J(v) —
—L\\u—1>|| при всех u^U. По аналогии с доказательством теоремы
2.5.7 введем банахово пространство В\=Е\ХВ элементовх= (g,и),
? — действительное число, и^В\ в качестве нормы х возьмем
11*11*,= |51 +1И|в. Зафиксируем точку v^U и в Вг рассмотрим два
множества:
X = {x=(t,u):u6U, l<J(vy-L\\u-v\\}
и
Y = {y = &u):ueu, l>J{u)}.
Очевидно, множества X и У выпуклы в В\ и не имеют общих
внутренних точек — это проверяется так же, как в теореме 2.5.7.
Покажем, что множество X имеет внутреннюю точку. По условию
множество U имеет внутреннюю точку v0. Это значит, что сущест-
вует шар |]и—0О||^6 (6>0), целиком принадлежащий U. Пока-
жем, что точка лг0= (go, fo), где lo=J(v)—L\\v—v0\\—6(l+L)t яв-
ляется внутренней для X. Для этого достаточно показать, что шар
К={х : \\х—ЯоНв^б} принадлежит X. Возьмем произвольную точ-
ку *=(6, и)(=К, т. е. \\x—Xo\\Bl = \£—b>\+\\u—Vo\\^6. Отсюда
|и-«Ь11<в. £о-б<£<1о + 6.

242 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. &
Поэтому и 6 [/ и
Klo + b = J(v)—Llv — vJ-6(l+L) + b =
= J(v)—L\\v—u + u — v0\\ — 8L<J(v) —
— L\\u — V\\ + L\\u — v0\\ — L8</(i;) — L\\u — v\\.
Таким образом, если x = (|, u) 6 /С, то u£U и £</(и) — L||a — u|[„
т. е. х£Х. Следовательно, /С с X и л:0 — внутренняя точка X.
Точка x=(J(v), v) является общей граничной точкой мно-
жеств X и У. В силу теоремы 5 существует разделяющий эти мно-
жества функционал сФО: (с, х)^(с, х)=а^(с, у) при всех
х^Х, y^Y. Заметим, что всякий функционал с из сопряженного
пространства В\ представим в виде c=(vo, 'о), где vo — действи-
тельное число, /о'е£*, и результат применения с к элементу х=
= (£, и) можно записать в виде (с, x)=V(yg-h(/o, и). Поэтому усло-
вие разделимости множеств X и Y перепишется в виде vo|+i(/o, ti) ^
^v0/(tO + (/0, u)^v0ri+('o, и) при всех (g, и)еХ и (т), к)еК, ил»
vdfe—/(^)}^(/о, у—wj^vdri—J(v)] при всех wef/, т|^/(и) и 1^
^/(у)— £||м—i>||. Эти неравенства совпадают с (2.5.5), и. даль-
нейшее доказательство проводится так же, как в теореме 2.5.7. А
Во внутренних точках множества U существование опорного
функционала может быть доказано при условиях, отличных от ус-
ловий предыдущей теоремы.
Теорема 8. Пусть U — выпуклое множество банахова про-
странства Б, имеющее внутренние точки (возможно U=B), н
пусть выпуклый на U функционал J (и) ограничен сверху в окрест-
ности некоторой точки v0, являющейся внутренней точкой U. Тогда
J (и) имеет опорный функционал во всех внутренних точках мно-
жества U.
Доказательство. Как и в предыдущей теореме, введем
банахово пространство В\=Е\ХВ элементов *=(£, и) с нормой
||jc||b, = |£|+И#Ив. В этом пространстве рассмотрим множество
X={x=\(if и) : u^U, l^J(u)}. Очевидно, X — выпуклое множест-
во в В\. Покажем, что X имеет внутреннюю точку. По условию
J(и) ограничен в окрестности некоторой внутренней точки v0t по-
этому существуют такие постоянные А и 6>0, что J(u)^A для
всех ые£/, \\и—tioll^e. Так как v0 внутренняя точка множества [/,,
то можем считать, что шар- \\и—t>oll^!6 целиком принадлежит U»
Покажем, что тогда'точка #о=(£о, 0О), гДе 1о=А+6, является
внутренней для X. Для этого достаточно показать, что шар
K = {x:\\x-xJBi<b)
принадлежит X. Пусть х= (£, а)е/С, т. е.

i П
Вспомогательные сведения
243
Отсюда \\и—iy<«6, go—&^?<1о+б. Поэтому g^lo—6=4^7 (u)
для всех и из \\и—Police. Таким образом, если *=(£, и)е/С, то
u^U, a £^/(и), т. е. х^Х. Следовательно, КаХ и *о— внутрен-
няя точка X.
Возьмем произвольную внутреннюю т^чку v^U. Точка х=
.= (/(у), и) является граничной для X. В силу теоремы 5 суще-
ствует_функционал_с= (vo, 1о)ФО, разделяющий множество X и
точку х: (сух)^(с,х) или (с,х—*)=v0(£—J(v)) + {lo, и—а)^0при
всех u^Ut %^J(u). Полученное неравенство совпадает с неравен-
ством (2.5.4) и дальнейшее доказательство такое же, как в теореме
2.5.6. А
Заметим, что принятое в теореме 8 требование ограниченности
сверху J (и) в окрестности некоторой внутренней точки v0 равно-
сильно непрерывности J (и) в этой точке — это следует из теоремы
2.5.8.
Ряд других теорем, содержащих различные условия слабой
полунепрерывности снизу функционалов, существования опорных
функционалов, а также выражающих связи этих понятий с выпук-
лостью, гладкостью, ограниченностью функционалов см., например,
в работах [46, 73].
5. Как и в конечномерном случае, в теории выпуклого програм-
мирования в бесконечномерных пространствах важное место зани-
мает теорема Куна—Таккёра. Здесь ограничимся следующим ва-
риантом этой теоремы. _
Теорема 9. Пусть U={u:u^Uu gi(u)^Q, t=l, 2, ..., s},
где U\ — заданное выпуклое множество из банахова пространства
В, функционалы gi(u)9 i=l, 2, ..., s, определены и выпуклы на U\.
Пусть множество U\ удовлетворяет следующему условию регуляр-
ности: для любого вектора l(=EStJ=£0 существует элемент ае£/ь
такой, что (/, g(v))<zOt где g=(gu ..., gs). Тогда, для того чтобы
выпуклый на U\ функционал J {и) достигал в точке а*е£А своего
минимума на U, необходимо и достаточно существования точки
Я* = (Х*и , %]) 6 Es, Я* > 0, такой, что пара (и*, >,*) образует сед-
ловую точку функционала L(uy X)=J(u) + (X, g(u)) в области
U\XAU Ai = {l:X^ESt k^zO} в следующем смысле: L(tf*, Л)^
^L(tt*, X*)^\L(uy А*) при всех u<=Uu ШЛь
Доказательство этой теоремы проводится дословно также, как
и теоремы 2.10.2. Теорему Куна — Таккера в более общей форму-
лировке и различные ее приложения см., например, в работах [73,
119, 135, 141, 199, 256] и др.
6. Наконец, остановимся на классе сильно выпуклых функцио-
налов в гильбертовых пространствах.
Определение 14. Функционал J (и), определенный на вы-

244 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
пуклом множестве V гильбертова пространства, называется сильно
выпуклым, если существует такая постоянная х>0, что
J(au + (l— a)v)<£aJ(u)+(l— a)J(v) — ха(1 — а)|и — оЦ1
при всех и, v&U и всех а, 0^а^1.
Очевидно, сильно выпуклый функционал J (и) будет рыпуклым
и даже строго выпуклым. Примером сильно выпуклого функцио-
нала является /(и) = ||и||2 с х=1.
Нетрудно убедиться, что теоремы 2.1.4—6 и их доказательства
остаются справедливыми и в Я-пространствах, нужно лишь в фор-
мулировках и доказательствах этих теорем слово «функция» заме-
нить на «функционал», Ет на Н.
Теорема 10. Пусть U — замкнутое выпуклое множество
гильбертова пространства И (в частности, возможно U=H)9 а
J (и)—сильно выпуклый непрерывный функционал на (/. Тогда:
1) J (и) ограничен снизу на U: inf «/(и) = «/*>— оо; 2) существу-
uuU
ет и притом единственная точка и*е£/, в которой достигается ниж-
няя грань J (и) на U: /(а*)=/*; 3) множество M(v) = {u : u^Uy
J(u)^.J(v)} выпукло, замкнуто и ограничено при любом v^U*
Эта теорема доказывается точно так же, как и теорема 2.1.7,
однако вместо классической теоремы Вейерштрасса здесь следует
использовать теорему 4. Заметим, что в теореме 10 в отличие от
теорем 1,4 ограниченность множества U не требуется.
При изложении методов минимизации, как и в конечномерном
случае, нам понадобится понятие проекции элемента на мно-
жество.
Определение 15. Проекцией точки и на множество U в
5-пространстве называется точка Pi/(u)e£/, удовлетворяющая ус-
ловию \\и—Ри(и)\\=р(и, U), где р(и, (/)= inf \и— v\\—расстояние
от точки и до множества I).
Очевидно, если wet/, то Рц)(и)=и. Теорема 2.3Л и ее дока-
зательство без изменений сохраняют силу в гильбертовых простран-
ствах.
Упражнения. 1. Сохраняют ли силу утверждения, высказанные
в упражнениях 2.1.1—13, 2.5.1—6, в Я-пространствах? В-простран-
ствах?
2. Доказать, что множество U={u=u(t)^L£09 1], |u(/)|^U
O^i^l} не имеет внутренних точек в L^O, 1]. Будет ли U компакт-
ным в 1г[0, 1}? Слабо компактным?
3. Пусть а(/), р(/) —некоторые функции из L^O, 1], а(*)<
<Р(0, 0<1/<1. Доказать, что U={u=u(t)<=LA0y 1], a(t)^u(t)<£
^p(f)., 0^*<1} слабо компактно в LJL0, 1}. Будет ли U компакт-
ным в L$pt 1]? Имеет ли U внутренние точки в L2 (0, 1]? В С[0, 1]?

§ п
Вспомогательные сведения
24S
1
4. Пусть J (и) = f f(u(i)) dty где /(и)—непрерывная функция на
о
£ь а) Доказать, что J (и) непрерывен в С[0, Ц но может быть раз-
рывным в Ь£0, 1]; б) Доказать, что если \f(u+h)— f(u) | <
<C(\u\\h\ + \h\2) при всех и, h*=Ex -(C=const>0), то J(u) не-
прерывен в Z,2[0, И]. в) Если f(u) полунепрерывна снизу, то будет
ли J (и) полунепрерывным снизу в С[0, 1]? L^O, 1]? г) Доказать,
что если f(u)^Cl(Ex) и f'(u) удовлетворяет условию Липшица на
Еи то J (и) у дифференцируемый функционал в L2[0, 1]. д) Дока-
зать, что если f(u) выпукла [сильно выпукла] в Е\\ то J (и) выпук-
лый [сильно выпуклый] в lutO, 1]. Следует ли из выпуклости
[сильной выпуклости] J (и) выпуклость [сильная выпуклость] f(u)>
е) Доказать, что если f(u) выпукла и удовлетворяет условию п. б),,
то J (и) достигает своей нижней грани на множестве U из упраж-
нения 3.
5. В пространстве h последовательностей и= (и1, и2, ..., ип, ...)
с нормой ||«(|=| *У\и*\2 W»<oo рассмотреть множество U={u : «е/2„
|wn| <— ,п=1, 2, ...} («гильбертов кирпич» [88], стр. 490). До-
п
казать, что 1) U выпукло, замкнуто, ограничено и компактно в /2;
2) U не имеет внутренних точек в /2; 3) не существует функциона-
ла, разделяющего U и точку и=(и\ ..., ип, ...), |wn|<—»я=1,2,...
6. Доказать, что в точке 4w=(«1, ..., ипу ...), для которой
|ип| =— хотя бы при одном n^sl, можно провести опорный функ-
п
ционал ко множеству U из упражнения 5.
7. Пусть Р — линейное нормированное пространство всех мно-
гочленов на отрезке [0, 1] с нормой
п п
и(t)|| == max \u(t)\. Положим /(и) => V |а,-1 для и(t) = V af 6 P.
Показать, что J (и)—выпуклый функционал, однако не является
непрерывным на Я. (Указание. Рассмотреть последовательность
ип (t)=tn—/n+1.) Будет ли J (и) полунепрерывным снизу на Р?
8. Доказать, что функционал /(и) = ||ц|| дифференцируем в
£j>[0, 1] <(1</?< + оо) всюду, кроме и=0, и найти J'(u). Будет ли
J (и) дифференцируем в Li{0, 1]? С[0, 1]?
9. Доказать, что функционал J(u) = \\u\\ в //-пространстве
дифференцируем во всех точках иФО. Найти У (и).
10. Пусть А — оператор из примера 1. Доказать, что если А —
положительный оператор (т. е. (Ащ и)^0 при всех меЯ), то

246 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
функционал J (и) = — (Аи, и) — (Ь, и) из примера-1 выпуклый, и
задачи минимизации J (и) на Я и решения уравнения Аи=Ь экви-
валентны.
11. Пусть А — оператор из примера 1. Доказать, что если А —
сильно положительный оператор (т. е. (Аи, и)^у\\и\\2 при всех
и^Н, Y=const>0), то функционал J (и) = —(Аи, и) — (6, и) из
примера 1 сильно выпуклый и в Я достигает своей нижней грани
на единственном элементе и*, являющемся единственным решением
уравнения Аи=Ь (это обстоятельство лежит в основе метода Рит-
да решения уравнений Аи=Ь).
12. Доказать, что в рефлексивном В-пространстве ||с|| =
= тах (с, и) при всех сеВ*.
ц«11<1
13. Пусть J (и) —выпуклый функционал на выпуклом откры-
том множестве V В-пространства. Доказать, что следующие четыре
утверждения эквивалентны: 1) J (и) полунепрерывен сверху в точ-
ке v\ 2) J (и) непрерывен в точке v\ 3) J (и) ограничен в окрест-
ности точки v\ 4) J (и)' ограничен сверху в окрестности точки v
(см. [73]).
14. Для того чтобы функционал /(«), заданный в В-простран-
стве был полунепрерывен снизу [слабо полунепрерывен снизу], не-
обходимо и достаточно, чтобы множество Uc={u: J(u)^.C) было
замкнутым [слабо замкнутым] при любом вещественном С. Дока-
зать ([46], стр. 97—99).,
15. Если на открытом выпуклом множестве U ^-пространства
задан конечный выпуклый функционал J {и), то в каждой точке
v^U он имеет опорный функционал и, следовательно, слабо полу-
непрерывен снизу. Доказать ([46], стр. 104—107).
16. Слабо полунепрерывный снизу функционал /(м),- удовлет-
воряющий условию lim J (и) = + оо, в рефлексивном В-прост-
ранстве достигает своей нижней грани ([46], стр. 119). Доказать.
17. Доказать, что J(u) — \\u—и0\\ на любом выпуклом замкну-
том множестве U рефлексивного ^-пространства достигает своей
нижней грани (теорема существования проекции ио на U или эле-
мента наилучшего приближения к заданному элементу ио&В).
18. Пусть U — множество из В-пространства с непустой внут-
ренностью, и пуёть для некоторого функционала с^В* известно,
что i(c, и)=0 при всех u^U. Доказать, что тогда с=0.
19. Прямым произведением двух линейных пространств В\ и
Вг называется линейное пространство B=BiXB2 упорядоченных
пар х= (хи х2), У=(Уи У2) ...,* где хи У^В{ (/=1, 2) с правилами
сложения х+у= (хх+уи Х2+У2) и умножения на число ах= (ахи

§ 2] Некоторые методы минимизации функционалов 247
ахг). Доказать, что если В\ и В2 — банаховы пространства, то
B=B\XB2 также банахово с нормой IWMIUil^+И*Нв,, и сопря-
женное к В пространство В* представимо в виде В* = J}\ х В^.
20. Теорема Мазура гласит ({127], стр. 173): если последова-
тельность ии ti2, ..., иПу в линейном нормированном (в частности,
в банаховом) пространстве В слабо сходится к элементу и, то для
всякого б>0 найдется такая выпуклая комбинация
п п п
Х\ щщ (aL > 0, V а; = 1) элементов {щ}, что IIи—V а^иЛ <е.
Вывести отсюда утверждение, использованное при доказательстве
теоремы 3.
Указание. Применить теорему Мазура к последовательности
Uky Uk+u «., Un, при е=—, Л=1, 2,
к
§ 2. НЕКОТОРЫЕ МЕТОДЫ МИНИМИЗАЦИИ ФУНКЦИОНАЛОВ
Пусть J (и) — некоторый функционал, определенный на мно-
жестве U Я-пространства. Будем рассматривать задачу минимиза-
ции J (и) на С/, понимая под этим следующие вопросы: 1) найти
J* =■ inf J (и)\ 2) указать последовательность {ип}е£/, для которой
lim J(ип) = У*, или же, если это возможно, найти точку и*е£/,
такую, что /(#*)=/*.
Описание наиболее известных и часто применяемых методов
минимизации функционалов в Я-пространствах внешне ничем не
отличается от описаний аналогичных методов в конечномерных
пространствах.
1. Градиентный метод (случай £/=Я). Предполагается, что
Jlu)^Cl(H). Строится последовательность {ип} по правилу ([3, 27,
35, 46, 47, 57, 59, 75, 82, 102, 111, 135, 147, 148, 155, 161, 164, 171,
193,229,244,255]):
un+\ = un—(XnJ'(Un), числа ап>0, я=0, 1, (1)
Если 1'(ип)ф0, то можно подобрать ап>0, что J(un+\)<J(un).
Это следует из (1.1). Если при каком-либо п^О Г(ип)=0, то
нужно провести дополнительное исследование поведения J (и) в ок-
рестности ип для выяснения того, будет ли ип точкой минимума
J (и) на Я. В частности, если J (и) выпуклый функционал, то необ-
ходимость в таком исследовании отпадает, так как согласно теоре-
ме 2.1.3 в точке ип, где J/(un)=0i достигается минимум J (и) на Я.
Здесь и во всех излагаемых ниже методах начальная точка
Uo^U предполагается известной. На практике начальное прибли-

248 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
жение выбирают исходя из конкретных особенностей задачи; об-
щих правил выбора tio, к сожалению, не существует.
В зависимости от способа выбора ап в (1) можно получить
различные варианты градиентного метода. Перечислим некоторые
из них:
а) ап определяется из условия tningn(a)^gn(an)f где gn(a)s
06^0
^5=/(an—aJ'(un)) — этот вариант градиентного метода принято
называть методом скорейшего спуска;
б) если ||У' (u) — J'(0)| <L||tf—v\ при всех u,v€Ht L = const >0,
то a„ может быть выбрано из условий е1<аЛ< , где elf
2
« —параметры алгоритма, выбираемые вычислителем, 0 <ех < ,
Li ""j- Л&
*>0. В частности, возможно е = —, гг = ап = —;
в) art выбирается из условия
/(ип) -J(un-anJ' (ип)) >ea*1|/' (ип)||2, а„ >0,
где е — параметр алгоритма, е>0;
г) <х„ = РЛ(/' (^Л) iF"1» где фп) — произвольная последовательность
со свойствами
99
Рп>0, РЛ-*0 (я-*оо), £ Р„=+оо (например, р„ = -^rj-)'.
д) если заранее известна величина «/* = inf J (и), то можно взять
I/'ЫР '
е) в некоторых случаях отправляются от некоторого началь-
ного an=a и, произведя необходимые дробления а, ограничивают-
ся таким выбором an, чтобы J(ип+\) <J(ип).
Приведем теорему сходимости метода скорейшего спуска.
Теорема 1. Пусть функционал J (и) определен на гильбер-
товом пространстве Н\ J (и) 6 С1 (#), inf / (и) = Г > — оо, и гради-
•ент J'{u) удовлетворяет условию Липшица ||/'(и)— J'(v)\\^L\\u—
—v\\, L=const>0, и, уеЯ. Пусть {ип}—последовательность, по-
лученная методом скорейшего спуска при некотором начальном
щ^Н (см. выше, п. а)). Тогда UmJ'(un) = 0. Если, кроме того,
Д-»00
J (и) выпуклый функционал и множество М<(и0) = {и : J (и) ^/(и0)}
ограничено, то последовательность {ип} является минимизирующей

§ 2] Некоторые методы минимизации функционалов 249
и любая ее слабая предельная точка будет точкой минимума J (и)
на Я, причем в случае единственности точки минимума к ней слабо-
сходится вся последовательность {ип}; справедлива оценка скоро*
сти сходимости
О</(*„)-/•<—, л=Ь2,
п
где D = sup || а — v J — диаметр множества М (и0).
u,v£M(u9)
Если J (и), кроме того, сильно" выпуклый функционал на Я, то
{tin} сходится к единственной точке минимума и* по норме прост-
ранства Я, причем
0<J(un)-J*<[J(u0)~J*)q", fa-iff <
<— И"о)-Л<Л /1 = 0,1,...,
И-
где<7=1 —, 0<?<1, а ц>0 константа из теоремы 2.1.4-
Доказательство этой теоремы полностью аналогично доказа-
тельству теоремы 2.2.1. В частности, вывод (2.2.5—6) остается та-
ким же, только лишь для обоснования существования точки и* из-
оценки (2.2.6) здесь нужно использовать выпуклость, замкнутость,
и ограниченность множества М(ио) и сослаться на теорему 1.4.
Существование хотя бы одной слабой предельной точки v* после-
довательности {ип} следует из слабой компактности М(и0) (см.-
теорему 1.2). Пусть tink-+v* слабо в Я. Тогда равенство J(v*)=J*
вытекает из слабой полунепрерывности J (и) (см. теорему 1.3) и:
соотношений У* = lim / (ип) = lim / (щ,) > / (v*) > J*. Все осталь-
/1-*» &-ЮО
ные рассуждения из доказательства теоремы 2.2.1 полностью со-
храняют силу и здесь.
Сходимость градиентного метода, когда параметр ап из (1)
выбирается согласно п. б), следует из теоремы 2 при £/=Я (см.
ниже).
2. Метод проекции градиента (случай 11фН). Предполагает-
ся, что J(u)^Cl(U). Строится последовательность {ип} по прави-
лу ([9, 10, 31, 35, 75, 97, 124, 135, 155, 158, 159, 171, 179, 189, 193,,
244, 255, 267])
un+i = Ри (ип — anJ' (ип)), числа ап > 0, л = 0, 1, ..., (2>
в предположении возможности указанной здесь операции проек-
тирования точки ип—апГ{ип) на множество U.
Перечислим некоторые способы выбора параметра ап в (2):
а) если \\J'(u)— J'(v) \\^L\\u—v\\ при всех и, ие£/, I=const>
>0, то ап может быть выбрано так же, как в пункте 1 б);

250 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
б) ап определяется из условия J(un)— J(un+i)^e\\un—wn+ill2,
где un+i имеет вид (2), е — параметр алгоритма, е>0;
в) ап можно выбирать, как это указано в п. 1е).
Теорема 2. Пусть функционал J (и) определен .на выпуклом
замкнутом множестве U гильбертова пространства Я, J'(u)^C1(U)f
inf J {и) — J* > — oo, и градиент J' (и) удовлетворяет условию Лип-
шица ||/' (и) — J' (v)||<I||и — v||, L = const > 0, utv £ U. Пусть
u0 — произвольная начальная точка из U . и последовательность {ип}
определена по формуле (2) с выбором параметра ап из условий
2
0О1<ап< , elf е — заданные положительные числа,
L + 2е
0<ех< 2 . Тогда
J(un)—J(un+l)>e\\un — un+lf, п = 0, 1, ... ,Hm|K — "»+il = 0
{если U=Ht то равенство Hm||wn—«fo+i||= 0 равносильно lim/' (ил)=0).
Д-ЮО /1-+00
Если, кроме того, J (и) —выпуклый функционал, и множество
М(и0) = {и: Met/, /(и)г^/(ыо)} ограничено, то последователь-
ность {ип} является минимизирующей, и любая ее слабая предель-
ная точка будет точкой минимума J (и) на £/, причем в случае един-
ственности точки минимума к ней слабо сходится вся последова-
/■*
тельность {ип}; справедлива оценка 0 < J (ип) — J* < ——, С\ =
и
= const>0, /1=1, 2, ...
Если J (и), кроме того, сильно выпуклый функционал на С/,'то
{ип} сходится к единственной точке минимума и* по норме про-
странства Я, причем \\ип — u*f < ——, /i=l, 2, ..., C2=const>0.
Доказательство этой теоремы полностью аналогично доказа-
тельству теоремы 2.3.2 с той лишь разницей, что вместо классиче-
ской теоремы Вейерштрасса здесь нужно использовать теорему
1.4 так же, как это мы делали только что при доказательстве тео-
ремы 1.
Если множество U имеет вид U={u: g%(u) ^0, i=l, 2, ..., s},
где gi(u) —заданные функционалы из СЦН), то для минимизации
функционала J(u)^Cl(H) на U можно применить метод возмож-
ных направлений [59, 117, 135, 193, 196]; один из вариантов этогс
метода в Я-пространствах может быть описан также, как в § 2.4.
3. Метод проекции опорного функционала. Пусть выпуклый
функционал J (и) в каждой точке и замкнутого выпуклого множе-
ства U имеет опорный функционал 1(и).

§ 2] Некоторые методы минимизации функционалов 251
Метод проекции опорных функционалов заключается в пост-
роении последовательности {ип} по правилу
u*+i = Pu(un-an J™ \ п = 0 ,
\ ||/(«я)Ц /
где ап — произвольная последовательность со свойствами ап>0>.
ап -*0 (/г->-оо), V аь = оо ( например, ап = 1
Теорема 2.5.2 о сходимости описанного метода и ее доказательство
полностью сохраняют силу и в Я-просгранствах. О методах мини-
мизации негладких функционалов см., например, в работах [35, 154,
155, 187, 189, 193].
4. Метод условного градиента. Пусть U — выпуклое замкну-
тое ограниченное множество в Я-пространстве, пусть функционал
J(u)^Cl(U). Метод условного градиента заключается в следую-
щем: если ип (п^О) уже известно, то берем главную линейную
часть Jn(u) = (J'(un)y и—ип) приращения J(u)—J(un) = (J'(un)9
и—ип) +о(\\и—ип||)" и определяем вспомогательное* приближение
йп^0 из условия
Jn (йп) = min Jn (и) или (/' (иа)9 ип) = min (У (ип), и). (3>
Затем полагаем [35, 36, 82, 93, 94, 97, 124, 154, 155, 179, 229]
ип+\ = ип + ап(ип — ип), 0<<хл<1, (4>
где ап может быть выбрано, например, одним из следующих спосо-
бов—а), б), в):
а) gn Ю = min gn (a), gn (а) = J(ип + а (ип — ип)), (5>
(Ха<1
б) J (ип) — J {un+i) >еап | Jn (йп) |, 0 < ап < 1, где е — параметр
алгоритма, 0 < е < 1;
в) если ||/' (и) — J' (о)||<L||и — v|| при всех u,v£U, L =
= const > 0, то ап можно определить так: ал = УлРя> гДе Рл =
= min|l; '_л(ц^'—I гг<уп< , вг и е — параметры алго-
I lUn-Unf I L
ритма, 0<е1 <— — , 0<е<1. Заметим, что приведенное здесь
описание метода условного градиента сохраняется без изменений
и в 5-пространствах.
Теорема 3. Пусть U — выпуклое замкнутое ограниченное
множество в Я-пространстве (или рефлексивном ^-пространстве),.

252 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 9
лусть функционал J(u)^C4U), inf /(u) = 7*> — оо и градиент
J'(u) удовлетворяет условию Липшица \\J'(u)—J'(v)\\^L\\u—v\\
лри всех щ v^U, L=const>0. Тогда последовательность {ип},
удовлетворяющая условиям (3) —(5), существует и Jn(un) =
= (/'(ип), йп—ип)->0 (п-+оо) при любом выборе u0^U.
Если, кроме того, J (и) выпуклый функционал на £/, то после-
довательность {ип} является минимизирующей и любая ее слабая
лредельная точка будет точкой минимума J (и) на (/, причем в слу-
чае единственности точки минимума к*ней слабо сходится вся по-
следовательность {tin}* Справедлива оценка
О <ал = /(ия)-/♦<-£-, 11=1,2, (6)
п
тде С — положительная константа, независимая от п.
Доказательство. Пусть начальное приближение u0^U
выбрано произвольно. Пусть уже известно ип (п^О). Так как
Jn(u) = (J'(un), и—ип) линейный (и тем более выпуклый) непре-
рывный функционал, то существование элемента un^Ut удовлетво-
ряющего условию (3), следует из теоремы 1.4.
Доказательство утверждения Jn(un)-+0 (п-+~оо) проводится
дословно так же, как в теореме 2.6. h Если /(и) выпуклый функ-
ционал, то существование а*е£/, /(w*)=/*! следует из теоремы
1.4, а тот факт, что {ип}—минимизирующая последовательность,
является следствием неравенств (2.6.6).
В силу теоремы 1.2 множество U слабо компактно, поэтому
последовательность {ип} имеет хотя бы одну слабую предельную
точку t>*e£/, являющуюся слабым пределом некоторой подпосле-
довательности {unk}. Но J (и) слабо полунепрерывен снизу, поэ-
тому
Г = lim J (ип) = lim / (tink) > J (v*) > J\
т. e. J(v*)=J*. Если J (и) достигает своего минимума в единствен-
лой точке и*у то вся последовательность {ип} слабо сходится к и*.
Оценка ((6) выводится совершенно так же, как и подобная
оценка (2.6.4) в теореме 2.6.1. А
Формулировку и доказательство теоремы сходимости метода
условного градиента, когда величина а^ в (4) выбирается соглас-
но пп. б), в), предоставляем читателю, заметив лишь, что это де-
лается совершенно так же, как в теореме 2.6.2.

§ 2] Некоторые методы минимизации функционалов 253
5. Метод сопряженных градиентов. Пусть функционал J (и) 6
6 С1 (Я). Построим последовательность !ыл} по правилам [35, 124,
166, 179, 190]
И/Ч-1 = ип — апрПУ п= 0, 1, 2,
Ро = *' К). P/i = ^' Ю —РиР»-1. "*- 1, 2,...,
где величины ап, рл выбираются из условий
£„(<*/i) = min £*(<*)» gn{p) = l{*n — *Pn>*
а>0
Р* =
(/'Ы,/'(«*1-|)"-/'Ы) „г.
и/'("*-!) IF
10, л€/2,
а множества индексов /i, /2 таковы, что /il)/2={0. 1, 2, ...}• Ое/2.
На практике часто принимают /2={0, щ9 п2, ...}, где 0</ii<
:<;л2< ... — заданная последовательность, например пл=Л$, s —
некоторое натуральное число, &=0, 1, 2, ..., . Если /2={0}, 1\=
= {1, 2, ...}, то этот метод превратится в метод скорейшего спуска.
Сходимость метода сопряженных градиентов для сильно выпуклых
функционалов в Я-пространствах доказывается совершенно так же,
как в теореме 2.7.2.
Приведенное здесь описание метода сопряженных градиентов
предполагает, что U=H. Если же ИфИ, то можно использовать
проекцию описанного метода un+i=Pu(un—<xnPn)> выбирая ап>0,
например, из условия J(un+i)<.J(un).
6. Метод Ньютона [4, 27, 35, 46, 75, 81, 82, 130, 152, 155, 193].
Пусть U — выпуклое замкнутое множество в //-пространстве (или
в 5-пространстве), функционал J(u)^C2(U). Пусть tin (л>0) уже
известно. Тогда берем главную квадратичную часть
Jn(u)^(Jf (un)t u~un) + ^(J"(un)(u^un)f u-un)
приращения J(u)—J(un)=Jn(u)+o(\\u—un\\2) и определяем вспо-
могательное приближение ип из условия
Jn(un) = minJn(u).
Затем полагаем
Un+i = un + an(u — un)9 0<аЛ<1,
где ап может быть выбрано, например, одним из следующих спо-
собов:

254 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
а) ап=1, л=0, 1, 2, {здесь имеем дело с методом Ньютона
в его классическом виде);
б) gn К) = min gn (a), gn (а) s*J(un + a (ип — ип))\
0<а<1
в) J(Un)— J(un+i)^Ean\Jn(un) \, где е —параметр алгорит-
ма, 0<е<|1, а величина ац выбирается как можно ближе к 1„
0<ап^1. Сходимость вариантов а), в) метода Ньютона доказы-
вается совершенно так же, как в теоремах 2.8Л—2, сходимость
варианта б) см. в работе [82].
7. Метод штрафных функционалов (27, 35, 75, 155, 162, 176,
192, 229, 244]. Пусть g(u) —некоторый функционал, определенный
на заданном множестве V\ банахова пространства В (возможно»
Ui=B). Пусть
U = {u:utUl9 g(u)<0}. (7>
Заметим, что множества вида (7) охватывают такие множест-,
ва как Ui={u: u^Uu А(")=0}, поскольку U0={u:u^Uu g(u) =
=Н2(и)^0}. Если же Uq={u:ueeUu gi(u)^0 (*=1, 2, ♦.., s)}, та
это множество также представимо в виде (7). Для этого достаточ-
но взять
s
g (и) = V [gt (и)]+, где \gt (w)]+ = max {gt (и); 0}.
Определение 1. Функционалы Pk(u) (k=l, 2, ...) называ-
ются штрафом или штрафными функционалами для ограничения:
g(u)^0 на множестве U\9 если: 1) Pk(u)^0 при всех u^U\ к
k=l, 2, ...; 2) limPk(u)=0 при u^U, \\mPk(u) = + oo при и^иЛг
но u£ U.
Примеры штрафных функционалов: Pk (и) = Ak [g {u)]+t Pk (и) =
= Ak([g(u)]+)z, pk(u)= еАьт и т. п., где Ak — некоторая пос-
ледовательность, Ak^>0 (k = 1, 2, ...), Ak->+оо при &->оо (ср„
с §2.9).
Пусть на множестве U\ задан функционал, J (и), и пусть тре~
буется минимизировать J (и) на множестве U вида (7). Заменим
эту задачу последовательностью задач минимизации функционалов»
Jh(u)=J(u)+Pk(u)f k=l, 2, ..., на множестве Uu где Pk(u) —
штраф для ограничения g(u)^0 на U\. При каждом k задача ми-
нимизации Jk(u) на 1)\ может быть решена приближенно каким*
либо методом (например, одним из вышеописанных методов).
В прикладных задачах нужно стараться представить множе-
ство U в виде (7) так, чтобы множество Uu входящее в (7), имело

§2]
Некоторые методы минимизации функционалов
255
достаточно простой вид, а реализация тех или иных методов ми-
нимизации Jk(u) на U\ не встречала чрезмерных затруднений
(например, 1)\ может быть шаром в пространстве В; возможно
также £/i==B).
Предположим, что с помощью каких-либо методов минимиза-
ции получена последовательность {иъ}, удовлетворяющая усло-
виям
Jl= inlJk(u) <£Jk(uk) <Jl+ ek, ukeU±] ft =1,2, ..., (8)
где ел>0, еь-*0 при Л-^оо.
Теорема 4. Пусть функционалы J (и), g(u) определены и
непрерывны на множестве U\ из банахова пространства В, пусть
inf J{u)> — оо. Пусть штрафной функционал для ограничения
4l£Ut
g(u)^0 на f/i имеет вид Ph(u)=Qh(g(u))> причем: 1) для каж-
дого k функция Qk(g) одной переменной непрерывна и неотрица-
тельна при всех g\ 2) Qk(g)>0 при £>0, монотонно возрастает
но g и lim Qk (g) = + оо при g>0; 3) если же gs£0, то Qh(g)-+0
Л-*оо
нри &-*оо равномерно по g^O.
Тогда для последовательности {uk}t полученной из условий
<8), имеет место lim g(tik) <0,
lim J (uk) < J* = inf / (и).
Если, кроме того, В рефлексивно, U\ — выпуклое замкнутое
множество, g(u), J (и) — выпуклые функционалы на U\ и множе-
ство Ub={u:u^U\t g(u)^8} ограничено при некотором б=бо>0,
то lim J (uk) = J* и любая слабая предельная точка и* последо-
fc-ЮО
вательности {uh} будет принадлежать U и /(#*)=/*, а«в случае
•единственности точки минимума {ии}-*и* при &->о6 слабо в В.
Доказательство. Пусть {i>m}—какая-либо последовательность,
минимизирующая J (и) на U, т. е. vm£U и J (vm)-*-J*(m-><oo). Возь-
мем произвольное е>-0. Тогда существуют числа т0, Л0>0, такие,
что 7 (vm) < J* + е, efc < е, Qfe (g (Vm)) < e при всех^ m > m0, £ > £0.
Из неравенств (8) тогда следует / (uk) < /^ (^) < J*k + efe < Jk (vm) +
+ e = / (ym) + Qk (g (vm)) + e < /* + Зе. Отсюда в силу произвольно-
сти е>0 имеем limJ(uk)^J\ Далее, Qk(g(uk)) = Jk{uk) — J(uk)<£
-< J* + 3e — inf /(#)< + оо при всех & > £0. Это возможно только
при lim g(uk) К 0, ибо в противном случае существовала бы подпо-
fc-*-foo
следовательность {#*„}, Для которой limg1^) = а>0 и 0<

256 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. б
<Q^(y)< ®kn ^ ^Uk^"*"+ °° прИ n""*°°' ПеРвое {утверждение
теоремы доказано.
Пусть теперь множество Ut9 = {и: и 6 Ult g (и) < б0} ограничено,
кроме того, l/ee выпукло и замкнуто. Следовательно, согласно тео-
реме 1.2 U^ слабо компактно. Так как limg(^)<0, то uk^U^
при всех k>k0, и из {ик} можно выбрать хотя бы одну подпосле-
довательность {ukt)(kn-*-oo), слабо сходящуюся к некоторой точке
«*6l/ed. Но g(u) слабо полунепрерывен снизу (см. теорему 1.3), по-
этому g(u*)<\img(ukn)<\img(uk)<0. Следовательно, iC£[/. А
тогда, пользуясь слабой полунепрерывностью J (и), имеем /*</(а*)]<
<Нт/(ыЛл) <Нт7(иЛ) <«/*, т. е. J(u*)=:j*. В силу произвольно-
сти слабой предельной точки и* последовательности {uk} отсюда име-
ем UmJ(uk) = J\ Если ит — единственная точка минимума J (и) на
ft-* со
V, то {uk}-+u* при &-*оо слабо в В. ±
Условия, при которых -из limg(u*)<0, uk€Ut следует
р (uk, U) = inf||uk — и||->0 (k->• оо), рассматривались в работах [46,
153, 1551.
8. Метод множителей Лагранжа. Теорема Куна—Таккера мо-
жет быть положена в основу различных итерационных методов
минимизации функционала J (и) на множествах вида U={u:u^U\r
i<(ttX0, t = l, 2, ..., s; gi(u)=09 i = l, 2, .,., /?}, где U{ — заданное
выпуклое множество гильбертова пространства Я, функционалы
J (и), gi(u) определены, выпуклы на U\ и принадлежат С4(£Л)»
£<(и) — линейные функционалы на Я. Эти методы сводятся к по-
иску седловой точки функции Лагранжа L(u, K)=J(u) + (\it
£(и)) + (|*э ё(и)) на множестве
игхАг, A1={X=(ji, ji):]ie£s, Ц>0, и6^р}.
Здесь возможен следующий итерационный процесс:
un+i = PUt(un — anL'u(un, К)), K+\ = PAt(K + anL'b(un, К))у
л = 0, 1,...,
или
L(цп+и К) = minL(а, Хп), К+х = Рл% (К + <*пU(ип, К))*
ueut
п = 0, 1,...,
и другие [111, 119, 135, 256].

§ 3] Задача оптимального управления со свободным правым концом 257
§ 3. ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ СО СВОБОДНЫМ
ПРАВЫМ КОНЦОМ
1. Обозначим через £гг)[<0, T] = l£} пространство вектор-функ-
ций и = u(t) = (игЦ), ... , иг (/)), t0< t <7\ с конечной нормой
т
IMlL(r)= (f \u(t)%rdtyi*. Очевидно, эта норма порождается скаляр-
ов
ным произведением
(и, v)L<r) = ](и(t)9v(t))B,dt:\\иЦг) =V(u, u)Lp>
и пространство L{2r)[t0, Т] — гильбертово. Здесь, как и в гл. 2, под
Ет понимаем евклидово пространство векторов г = (гг, ... , гт) со
т
скалярным произведением (у, z)Efn = V ylzl с нормой | г \Ет = V(z, z)Efn;
норму матрицы А = faiy} (t = 1,... п\ j = 1, ... , т) будем обозна-
чать ||A(|ntm = sup|i4z|£/i, где верхняя грань берется по шару |г\втК 1.
Там, где не могут возникнуть недоразумения, индексы пространств
в обозначениях норм и скалярных произведений будем опускать.
Рассмотрим следующую задачу оптимального управления: мини-
мизировать функционал
/(a) ={/•(*, utt)dt + 0(x(T)) (1)
при условиях
x=f(xtut't), t0<t<T9 *(*о) = *о; (2)
tt = a(<)€l/ClPpif т\, (3)
где х =(**,..., хп), u=(u\...t иг), функции /=(/4,..., /п), /°, Ф пред-
полагаются известными, U — заданное множество из l^r)[t0i Г],
моменты t0, Т и начальная точка х0 заданы. Будем предполагать,
не оговаривая этого в дальнейшем, что для каждого u(t)^U соот-
ветствующее решение х (t9 и) задачи (2) определено на всем отрезке
[t0y Т], и функционал (1) принимает конечное значение.
Ниже будут сформулированы достаточные условия дифферен-
цируемое™ и выпуклости функционала (1) при условиях (2), (3),
доказана справедливость принципа максимума для задачи (1) —
(3), кратко обсуждены возможности использования методов § 2
для приближенного решения этой задачи. Примем обозначения

258 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
Л | дх* дх" \ jf_
дх I ;,: ■ " • Г ди
др = / df° df° \ dp ^ г ер ор\
дх \ дх* * ''' ' дх" )' аи \ ди* * " *' * диг )'
( дФ дФ \
U дхп Г
дФ
дх
Теорема 1. Пусть функции /°, /, Ф непрерывны по совокуп-
ности своих аргументов вместе со своими частными производными
по переменным х, и при л:е£п, u^Er, t0^.t^:fy и пусть выполне-
ны следующие условия Липшица:
|/(* + Д*. и +А, *)-/(*, ut t)]Bn<LQHx\BH+\h[a^ (4)
I дФ(х + Ьх) *дФ(х) 1 ^ПАН ,~
|а/(* + А*/и + а. *) а/(лг, а, о
I а* а*
дР(х + Ьх, u + h, t) дР(х, и, t)
|^<1(|Д*|£л+|А|£г), (6)
\ г<Ь(\&х\вя + \А\Вг), (8)
•\pr<L(\&x\Bn+\hlBr) (9)
* |£n<i(l^k + l*k), (7)
а/(* + А*, ii + ft, *) а/(л:, а, /)
aw ди
I а/°(* + А*, а +Л, Q дР(х9 и, t)
I du ди
(константы Липшица для всех функций здесь обозначим одной
буквой L, так как величины этих констант для нас не будут суще-
ственными). Тогда функционал (1) при условиях (2), (3) непре-
рывен и дифференцируем по u=u(t) в норме L**[t09 Г J, причем
его градиент
/'(«) = (4 (*),..•!. J'r(t))6Ur)[t0,n
в точке u=u(t)^U представим в виде
Jt{u) = _M(*(t).W).»(t).t) ^ to<t<T> (10)
ди #
где
Щх9 », и, t)=-P(xt и, /) + (+, /(*, a, 0)v^" =

§ 3] Задача оптимального управления со свободным правым концом 259
x(t) = x(t, и) — решение задачи (2) при u = u(t)t а вектор4>ункция
ty(t)=syp(tt w) = (t|>1(/), ... , tyn(t)) определяется из условий
*-- »*ио. ♦.«(«), о t ,о<,<г> (12)
Ъ(Г)-~ дф^ , ,= 1,2 п. (13)
Доказательство. Пусть u=u(t), u+h=u(t)+h{t)^Uy
пусть x(t)=x(t,*), x{ty u+h)=x(tf u)+Ax(t), t0^t^T, соответ-
ствующие этим управлениям решения задачи (2) ,/(и) и J(u+h) =
= J(u)+AJ(u) — соответствующие значения функционала (1). Из
(2) следует, что приращение Ax(t) удовлетворяет условиям
А* = /(*(*) +A*, u(t) + h(t), t)-f(x(t), u(t), t), (14)
t0<t<T; A*(*e) = 0.
Так как
Ф(* + А*)-Ф(*)=( ^(* + ед*> , д^, 0<6<1,
то из (1) получаем
А/(и) = J [/•(*+A*, tf+Л, *)-/•(*. "> <)1<«+
и
+ (-2^2L, Д*(л) + *х, (15)
где
/<?Ф(*(Г) + ед*(Г)) аФ(х(Г)) AwtV\
^"Ч * Тх * х{1))'
IR^LlbxiT)?. (16)
С учетом соотношений (12) — (14) имеем
г
*о *• '•
Г

260 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
Подставляя полученное выражение в (15) и используя функцию
Н(ху у, и, t)=—f°(x; и, t) + (ty, f(x, и, t)), получим следующее
представление для приращения функционала:
т
Д/(и) = - [[Н(х + Ьх9 Ч>, u + h, t)-H{xy % и, t)\dt +
и
+ [( »<''♦• »'*> ,bxy+Rx. (17)
Из формулы конечных приращений следует
Н(х+Ах, % u + h, t) = H{x, ф, и, t) +
+ /ЭЯ(* + 8А*. ф, Ц + 6А. Q д \ /дН(х+%Ьх, у, и + 6/t, о ^ h\
0<е<1.
Подставим это равенство в (17); будем иметь
А/(«) —J( »"СМР. *ОТ. «И. 0 ,fc(Q)tf + J?t (18)
где /?=/?! + #2 + #8
д _ (удярс+еддс,, fr, и+е/», <> ад (ж, ч>, ц, <) д,\Л
<.
(19)
д = _ г/<?#(*+вд*. Ф, g + e/t, о _ эя<*, ч>, и, о ^ А\ d/> (2(^
Оценим остаточный член в формуле (18). Так как
дх дх дх
то с учетом условий Липшица (6), (7) имеем
\b\<Q+\*h)Lf№\% + \&*[h\)*9
где [ф||с= SUP 1ЧК'» и)К°° в СИЛУ Непрерывности $(t, и) на
u<t<r

§' 3] Задача оптимального управления со свободным правым концом 261
[Уо, Т] (напоминаем, что в наших рассуждениях u=u(t) —
фиксированное управление nat/CZZi [*0> Т].- Аналогично, с уче-
том условий (8), (9) из (20) будем иметь
\**\<V+\WL$(\bx\\h\ + \hftdt.
и
Следовательно,
|/?|<1|Дл;(Г)|а+(1+1ф|к;)1|(|Ал:(01 + |А(0|)2Л. (21)
и
Для дальнейшей оценки остаточного члена R формулы (18)
нам понадобится одна лемма, которая часто приводится в курсах
лекций по обыкновенным дифференциальным уравнениям и из-
вестна как лемма Гронуолла.
Лемма 1. Если функция y(t)^L\[t0, Т] и удовлетворяет
неравенствам
0<<p(t)<a + bt<p(r)dr9 /0</<Г, a, 6 = const>0, (22)
то верна оценка
0<(f(t)<aebi^o)9 t0<t<T; (23)
если же
г
0<ф(0<в + *|ф(*)<*т, t0<t<T а, Ъ-const>0, (24)
t
то верна оценка
0<q>(0<ae*<r-'), t0<t<T. (26)
t
Доказательство. Обозначим R(t) = b fq>(T)dt. С учетом
(22) имеем R = b<f>(t)^b(a+R(t)), или R—bR^ab. Умножая обе
части этого неравенства на е-*«-'«>, получим
Интегрирование этого неравенства от /о до t с учетом /?(*о)=0
приводит к оценке
0 < R (t) е-*«-'о> < а — ш?-*«-Ч или 0 < R {t) < aeb<*-*J — а.

262 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 5
Отсюда и из (22) сразу получаем (23). Оценка (25) выводится
из (24) аналогично с помощью функции
т
t
Продолжим доказательство теоремы 1. Из соотношений (14) для
А* (О с учетом условия (4) имеем
t T
<L§\bx(t)\dt + L$\h(t)\(tt.
Приняв в2(22), (23)
Ф(0=ЧЛ*(01. a = Lf\h(t)\dt9 b = L,
и
придем к^оценке
\bx{t)\<Cx\\K((t)\dt, С^&Г-и, t0]<tl<T. (26)
to
Воспользуемся неравенством Kouiit—Буняковского и перепишем
оценку (26) в виде
||Дх(')1с« max |Д*(/)| <Cx/f=^ *-(%«• (27)
Подставим полученную оценку в (21) и окончательно получим
\R\ <С2|| h(t)fL(r). Таким образом, в формуле (18) для прира-
щения функционала первое слагаемое — линейный относительно
h(t) ограниченный функционал на L2r)[tQy Т]9 а второе слагаемое
имеет порядок || A (Of ж ДО. Согласно определению 1.1 это означа-
ет, что функционал (1) при условиях (2), (3) дифференцируем и
его градиент имеет вид (10). Д
Итак, для вычисления градиента функционала (1) при. усло-
виях (2) в точке u=u(t)^U нужно последовательно решить две
задачи Коши: (2) и (12), (13), и найденные при этом x(t) =
=х (t, и), я|>(;)жф(/, и) подставить в (10). При решении упомя-
нутых задач Коши можно использовать различные приближенные
методы [20].
Формулы градиентов функционалов в задачах оптимального
управления, связанных с системами обыкновенных дифференци-

# 3] Задача оптимального управления со свободным правым концом 263
альных уравнений, содержащих параметры и запаздывающие ар-
гументы, можно найти в работе [35].
2. Зная формулу градиента, нетрудно расписать методы
пп. 1—5 из § 2 применительно к задаче (1) — (3).
Например, метод проекции градиента здесь будет иметь вид
«*..<*> = Pu{un(t) + «„ dH{x{t' Un)' +£ "">' Un(t)'f) ),
/г=0, 1, ..., где ап>0 выбирается, как в п. 2 § 2. Пусть здесь
U = {u = u(t)e W [t0i Т]: щ (0 <ц'(0 < р, (*), t, < t <7\
*=1. 2,..., г}, (28)
где ai(t)9 Pt(0 — заданные кусочно-непрерывные функции, cti(tf)^
<фг(0> ^о^^1^, * = 1, 2,..., г. Нетрудно видеть, что множество U
выпукло, замкнуто и ограничено в Lvr)[t0y Т] и, следовательно, в
силу теоремы 1.2 слабо компактно в Lp[t0t Т]. Проектирование
на множество V осуществляется очень просто: если функция
2(9 = (2*(*)...., аГ(*))€1И'#. Г],
то ее проекция PuZ={pi(t), ..., рг(0) на множество V имеет вид
Л(')И
2' (/), если о, (*) <*(*)< МО.
О|(0, если *'(/)< М0> (29)
МО. если **(*)> МО. t^<t<T9 *=1,2,...,г.
Так же нетрудно выписать для множества (28) явное выражение
для ^„(0= {*4(0> ••• » Mrt(0) в методе условного градиента
juw-W'b если ^'(o>;oi (30)
1М9. если У{'(0<0 J
/,(/),_gg(«<^.*g.4j.M0.<)t w<r, f= 1, 2 г.
Для решения задачи (1) — (3) при каких-либо дополнительных
условиях на фазовые координаты можно использовать метод
штрафных функционалов. Например, если правый конец траекто-
рии закреплен, т. е. х(Т)=Хъ то в качестве штрафа для такого
ограничения часто берут Pk(ti) =k\x(T, и)—Xi|% если же имеются

264 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Л*. 6
фазовые ограничения А^х*^, u)^Bit Аи Bit t=l, 2, ..., m^.nt —
известные константы, то штрафом может служить функционал
Т m
Pk(u) = -L^exp{k(x'(t, u)-B<) (*'(', «)-4)}<#;
to f=l
Если функции f, f°, Ф удовлетворяют условиям теоремы 1 и Pk(u)
дифференцируем при условиях (2), (3), то функционал Jk(u) =
=J(u)+Pk(u) также дифференцируем при условиях (2), (3), и
для получения выражения-для градиента J'k(u) можно восполь-
зоваться рецептами теоремы 1.
Следует сказать, что дифференцируемость функционала (1)
при условиях (2), (3) в теореме 1 доказана при довольно жест-
ких ограничениях на данные задачи. Очевидно, теорема 1 остает-
ся справедливой, если в правых частях неравенств (5) —(9)
вместо |Д*| взять о(1), вместо |Ди| взять |Am|v, 0<y=const^1.
В этом случае для остаточного члена R формулы (18) нетрудно
получить оценку R = o(\\h\\Lir)). В практических задачах такую
оценку для R зачастую удается получить и при меньших ограни-
чениях на исходные данные.
3, Приведем достаточные условия для того, чтобы градиент
функционала (1) при условиях (2), (3) удовлетворял условию
Липшица, которое фигурирует во многих теоремах различных ме-
тодов минимизации.
Теорема 2. Пусть выполнены все условия теоремы 1, и
пусть, кроме того,
|/(*, и9 t)\<A± + A2\xl А1У Аг = const>0, (31)
а множество U (3) имеет вид
U = {u = u(t)eL(2r)[t0J T]:u(t)eV(t)
почти всюду при
t0<t<T}9 (32)
где V(t) — заданное множество из Ег, такое, что V0 = U V(t)
tt<t<T
замкнуто и ограничено в Ег. Тогда градиент функционала (1) при
ограничениях (2) удовлетворяет условию Липшица на множест-
ве (32).
Доказательство. Распишем формулу (10) для градиента
с учетом определения (11) функции Я(х, -ф, и, t):
J>(U)= <У°(*(*, и). u(t)f t) ц df(x(tt и), u(Q, t)
ди ' ди
t0<t<T, u = u(t)eu.

§ 3] Задача оптимального управления со свободным правым концом 265
|ф(/, » + *)-¥<*, «)|,
Пользуясь условиями (8), (9), отсюда имеем
\J>(u + h)-J'(u)\<L(l+H(t, u)jc){\bx(t)\ + \h(t)\) +
II df (x(t, u + h), u(t) + h(t), t)
I du
u(t), u(t) + h(t)tU.
Так как (a + b)2 < 2 (a2 + б2), то
г
\\J'(u + h)-J'(u)\\Lp<{4L41 + m, «>|с)»^(|Ах(/)|« +
+ ift(or)^+2j|a/(Jt(<,"+;),M+/t><)[ не. «+/0-W. «)1^},/>
(33)
Из этого неравенства видно, что для доказательства теоремы
достаточно получить оценки
|*(*. «)|о<С„ |*(<, «)|с<С„
Ж', *» + *)- + (*. u)h<Ct[\h(t)\dtt
I1
(34)
(35)
где С2, Сз, С4 — положительные константы, независящие от выбо-
ра и9 u+h^U. В самом деле, тогда множество G={(x9 и9 t) а
1*1 ^С2, u^Vq9 to^t^T} ограничено и замкнуто в ЕпХЕгхЕи
Поэтому
sup
G
дПх'и'()\<М< + оо,
да
и подставляя оценки (27), (34), (35) в неравенство (33), получим
условие Липшица'для градиента.
Приступим к доказательству оценок (34), (35). Из условий
(2), (31) имеем
t
\x(t, ")1 = |*о+ J/(*(*, и), и(%)9 г)4т|<|*0| +
и
t
+ A1(T — tJ + A%$\x(xt ii)|Л.
Полагая в (22), (23) <p(t)mm\x(t9 и)\9 a=.\x0\+Ai(T—t0)9 b=A2f

266 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
сразу придем к первой из оценок (34) с С2= (\х0\ +А\(Т—*о))ехр
(А2(Т—10)) независимо от выбора u = u(t)^U.
Далее, из (12), (13) имеем
,..,, Л| I дФ(х (Г, и)) , С Г Д/°(*(т. и), и(х). х)
1*(М01-| jx +J[ Тх
_%(Ti и) */(*(*. 4, *(т),т) ]<frj.
ограниче-
Так как непрерывные функции I—-, гт— . "л
ны в G некоторой константой М>0, то из предыдущего равенства
следует
Ж*, и)|<ЛГ(1 + Г-д+Лфф(*, «)|*.
t
Полагая в (24), (25) <p(*) = |t|?(f, u)\t a=M(l+T—t0), b=M, полу-
чим вторую оценку (34). Наконец, полагая Д\|)(*)—ip(*, u+h) —
—t|>(rt, а) из (12), (13) с учетом неравенств (5)—(7) и ограни-
ченности | -j- < М на G, будем иметь
\W)\<L\&*(T) | + L(1 +|| 4Jfttt)|c)J(|A*(0l + |A(0l)« +
+ АГ ||А*(т)|Л.
Подставляя сюда оценки (26), (34), придем к неравенству
|А*(01<С,Г|Л(0|Л + А«||А*(т)|А.
Для получения оценки (35) остается принять в (24), (25)
4. Воспользуемся некоторыми формулами, полученными при
доказательстве теоремы 1, и дадим простое доказательство прин-
ципа максимума Понтрягина для задачи (1) — (3), (32).

§ 3] Задача оптимального управления со свободным правым концом 267
Теорема 3. Пусть функции /°, /, Ф непрерывны по совокуп-
ности своих аргументов вместе со своими частными производными
по переменной х и удовлетворяют условиям (4) — (7), и пусть
множество V(t) из (32) не зависит от t: V(t) = V, to^t^T. Пусть
управление u(t)^U и соответствующая траектория #(*)=#(/, и),
U^t^T, образуют оптимальное решение задачи (1)—(3), (32).
Тогда
H(x(t), г|>(0, u(t), *)=тахЯ(*(0, *(*),«,*), (36)
где Н(х9 -ф, и, t)=—f°(xt и, t) + (tyt f(xt и, t))t a <b(t) является ре-
шением задачи (12) —(13).
Доказательство. Подставим в формулу (17) разложение
Н(х+Ьх, г|>, u + h, t) = H(x, i|), u + ht t) +
+ ^mx + B&x£.u + h.f> ^ 0<6<K
Получим
Д/(и) = - [[H(x(t)t Ч?(0, u(t) + h(t), 0-
-H(x (t), * (0, и (О, t)] dt + R, (37)
где /?=/?i+#2, R\ взято из (16), #2 определяется формулой вида
(19). Справедлива оценка
to
получаемая так же, как и оценка (21). Используя оценку (26),
имеем
\R\<Ce(j\h(t)\dty, Ce = LC?+(l+||o|)|b)[C?(r-g + CJL.
(38)
Доказательство равенства (36) проведем в предположении, что
u(t) — кусочно-непрерывна на [t0i Т] (для определенности можно
считать
u(t0) = u(to + 0)> u(t)=u(t-0), *0</<Г).
Пусть равенство (36) не имеет места при некотором те [to, Т].
Тогда существуют такие v^V и а=const>0, что
ьН{х(х)у <ф(т), vy т)-2а>#(*(т), <ф(т), и(%), т).

268 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
Так как u(t) кусочно-непрерывна, a x(t)f i|)(0> #(*» Ф» и» 0 не"
прерывные функции своих аргументов, то
g(f)mH(x{t), *(*), v, t)-H(x(t), *(<), и©, *)>а
на некотором отрезке *i^^2> содержащем т. Возьмем прира-
щение h(t) специального «игольчатого» вида h(t)s3v—u(t) при
U^d^t2 и h(t)ss0 вне [t%9 tb]. Тогда из оценки (38) с помощью
неравенства Коши—Буняковского будем иметь
|/?1<Св(||А(0|Л)2<^-УСв^|А(012^.
При этом можно считать U—^>0 столь малым, что
и
Из (37) тогда получим
x[-a + Cej|ft(0l2^]<0,
что, однако, противоречит оптимальности управления u=u(t).
Аналогично доказывается равенство (36), если
но u(t) необязательно
кусочно-непрерывно. В этом случае условие u(t)^V и равенство
(36) следует понимать в смысле почти всюду на [/0, Т]. ±
5. Остановимся на следующей задаче оптимального управле-
ния, связанной с линейными системами: минимизировать функ-
ционал
J(u) = jf°(xt u,t)dt + <b(x(T)) (39)
и
при условиях
x = A(t)x + B(t)u+'f(t), t.<t<T9 x(t0) = x0y (40)
u = u(t)6U<^W[t0t 7], (41)
где x = (jc1, ... , xn), и = (a1, ... , ur), U — заданное множество из
A(t)y B(t) — заданные матрицы порядка пХп и пХг соответст-

§ S] Задача оптимальнее управления со свободным правым концом 269
венно, f(t) — известная вектор-функция; моменты t0, Т и началь-
ная точка Хо заданы.
Теорема 4. Пусть f°(x9 и9 t)9 Ф(х) определены при х^ЕП9
и&ЕГ9 t^[t0j Т]9 непрерывны по-совокупности своих аргументов
вместе с частными производными по переменным х и и, и выпол-
нены условия Липшица (5), (7), (9); пусть компоненты матриц
A(t)9 B(t) и вектор-функции f(t) кусочно-непрерывны на [t0> Т].
Тогда функционал (39) при условиях (40) непрерывно дифферен-
цируем в /4г)[*о> Т]9 и еготрадиент Г (и) Вт точке
вычисляется по формуле
/'(Ц)Д а/М*(*)» «(<),*) ^^m{th t.<t<T, (42)
ои
где x(t) = x(t, и) решение задачи (40) при u]=u(t)9 ty(t) = ty(t, и)—
решение задачи
^М®.*(*>.* _A.m, u<t<Tt *(ту—2*£«3L.
OX ox
(43)
матрицы A*(t)9 B*(t) получены транспонированием матриц
A(t), B(t). Кроме того, градиент J'(и) удовлетворяет условию
Липшица на Lp[t09 Т].
Доказательство. Справедливость формулы (42) устанав-
ливается дословным повторением доказательства теоремы 1.
Далее, из формулы (42) по аналогии с (33) здесь получим
||/Ча + А)_/Чм)цг)<(4^|(|А^(012+|А(012)^ +
и
+ 2 sup \\&(t)l*\\AW)\*dtY!\
Отсюда видно, что для доказательства выполнимости условия
Липшица для градиента J'(u) достаточно получить оценки (26),
(35). Оценка (26) для |Дх(0|, очевидно, справедлива и здесь,
причем в качестве константы С и как нетрудно проверить, можно
взять Ci=5maxexp(i4max (T—t0))9 где
An« = sup ||Л(0«, £тах= sup \\B(t)\\.
t><t<T u<t<T
Далее, для Аф(0ввФ(^ u+h)—Hp(t9 и) из (43) с учетом условия
(7) будем иметь

270 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ. ПРОСТРАНСТВАХ [Гл. 6
I А-ф(01 ^ ЛтахJ | Л^(х) 1 rfx + Ьf Лл:(Г)1 + Z. J (| Ал:(01 + IЛ(01) ^.
Используя оценку (26) и лемму 1, приходим к оценке (35). А
При необходимости нетрудно выписать явное выражение кон-
станты Липшица для градиента через величины Лщахэ #max, L,
Т—/0; предоставляем сделать это читателю. Напоминаем, что зна-
ние константы Липшица для J'(u) может оказаться полезным при
использовании некоторых методов минимизации.
Укажем достаточные условия выпуклости и сильной выпуклос-
ти функционала (39) при условиях (40).
Теорема 5. Пусть выполнены все условия теоремы 4. Пусть
функция Ф(*) выпукла по х на ЕПу а f°(x, и, t) выпукла по сово-
купности переменных (х, и), т. е.
f*(ax + (l-a)y, au + (l-a)v, t) <af°(x, u, t) + (1 -a)/°G/, v, t)
(44)
при любых a, O^a^l, xf y^En, uf v^Er и t^[t0, T]. Тогда функ-
ционал (39) при условиях (40) является выпуклым и достигает
своей нижней грани на всяком выпуклом замкнутом ограниченном
множестве U из Zir)^0» Т\, причем для оптимальности и=и*(£)е
е[/ в задаче (39) — (41) необходимо и достаточно выполнения
неравенства
J(yfrg.O.*(0.*_y(Wt и% u(t)-uUt))Erdt>0,
u(t)eu. (45)
Если u*(t) — внутренняя точка множества (/, то условие (45) равно-
сильно условию
J>(u')^ f>P(x(t,u*),u*(t),t) fl.(0f(,plO_0, t0<t<T.
ди
(46)
Если же вместо (44) имеет место неравенство
7°(ax+(l -а)*/, аи + (1— a)v, t)<af°(x, и, t) +
+ (1—a)/°(t/, v, t)— >(1— a)x|w — v\\ x = const>0 (47)
при всех a, O^a^l, л, #<=£г, и, уе£г, *<=[*0, Т]9 то функционал
(39) является сильно выпуклым на L{2r) [£0> Т], и задача (39) —
(41) имеет и притом единственное решение на любом замкнутом,
выпуклом множестве Ud^[t0f Г].

§ 3] Задача оптимального управления со свободным правым концом 271
Доказательство. Нетрудно проверить, что решения зада-
чи (40) обладают свойством:
x(t, au + (l—a)v) = ax(t, u) + (l—a)x(t, v)
при любом а и любыхu=u(t),v=v(t) 6I2[t0,T].Тогда выпуклость
[сильная выпуклость] J (и) на 1$г) [re, Т] является простым след-
ствием выпуклости Ф(х) и условия (44) [условия (47)]. Сущест-
вование оптимального управления u=u*(t) в задаче (39) — (41)
на всяком выпуклом замкнутом ограниченном множестве U из
Lir) [*о» Л тогда следует из теоремы 1.4; условия (45), (46) выте-
кают из теоремы 2.1.3 и формулы (42). Последнее утверждение
вытекает из теоремы 2.1.7. ^
Пример 1. Пусть требуется минимизировать функционал
т
J(u) = ±-Ux* + u*)dt
при условиях х = — ах + иу 0 < t < Т9 х (0) = x0f и = и (t) 6 La[0, Г]>
где а, х0, Г>0 — заданные числа.
Здесь Ф=е0 и /° = — (лг2 + и2) удовлетворяет условию (47),
поэтому J (и) сильно выпуклый и на L2[0, Т] достигает своего
минимума в единственной точке u=u*(t). Поскольку
H = --L(x* + u*) + %(-ax+u)
и задача (43) имеет вид ф=аг|> -f х9 $(Т) =0, то
Условие (46) тогда приводит к оптимальному управлению и* (t) еэ
ssipCO» O^t^T. Этот же результат был получен в примере 3.2.1
с помощью принципа максимума.
Две интересные задачи вида (39) — (41) рассмотрим в следую-
щем параграфе.
Упражнения. 1. Пусть
1
/ (и) = j* (и2 — ах2) dx, где х = и (t) б L2 [0, 1], х (0)=0, а = const,
о
При каких значениях параметра а функционал J (и) будет выпук-
лым? Сильно выпуклым в £г[0, 1]? Будет ли J (и) непрерывным
в £г[0, 1]? Дифференцируем ли он в МО, 1]?

272 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫ^ ПРОСТРАНСТВАХ [Гл. 6
2. Пусть: а) функции f°(x, и, /), /(*, и9 t)9 Ф(х) непрерывны
по (х, и9 t)^EnxErX[t0, Т]\ б) f(x, щ t) удовлетворяет условию
Липшица (4); в) \fb(x9 u+h, *)—И*. и9 t) \^C(\h\2+\u\\h\)9
С=const. Доказать, что тогда функционал (1) при условиях
(2) непрерывен в /,2Г)[*о> Л-
3. Пусть: a) f°(x9 и, t)9 Ф(х) непрерывны по совокупности сво-
их аргументов при (*, и, t)GEnXEtx[to9 Т]; б) /°(л;, и9 t) выпук-
ла по и. Доказать, что тогда функционал (39) при условиях (40),
(41) достигает своего минимума на любом выпуклом замкнутом
ограниченном множестве U из Zir)I*0> Т].
Указание. Показать, что /(и) слабо полунепрерывен
снизу в l£}[t09 Т].
4. Пусть выполнены все условия теоремы 5 (кроме, быть мо-
жет, условия (47)), U — выпуклое замкнутое ограниченное, мно-
жество из LP[t0, Г], g(x9 t) — непрерывна по (х9 t)^EnX[to> Т]
и выпукла по х. Если существует хотя бы одна траектория x(t9 и),
удовлетворяющая условиям (40), (41), и такая, что g(x (t9u)9t)^.09
to^t^fT, то задача (39)—(41) при дополнительном условии
g(x(t)9 /)^0, t0^t^\T имеет решение. Доказать.
5. Пусть
/'(*, и9 <)«/!(*, 0 + £/*/(*, 0и'(* = О, 1,...,/г),
где /i, f2i непрерывны по (х9 t)eEnx[t0, Т]9 \f}(x9 t)\<Al\x\ +
+АгЛ!г]{х\ 0|<^8 (А = const >0). Доказать, что тогда функцио-
нал (1) при условиях (2) достигает своей нижней грани на любом
выпуклом замкнутом ограниченном множестве U из Lir)[t09 Г].
Указание. Доказать слабую непрерывность J (и) в1^г) [t0t Т].
6. Пусть выполнены все условия теоремы 5 (кроме, быть мо-
жет, условия (47)), и пусть
U={u = u(t)eL^[t09 T]:u(t)eV
почти всюду при t0^.t^T}9 где V — выпуклое множество из Ег.
Доказать, что тогда принцип максимума (36) является необходи-
мым и достаточным условием оптимальности в задаче (39) — (41).
Указание. Доказать выпуклость функции —Н {х9 -ф, и91) по и
и воспользоваться неравенством (45).
7. Пусть заданы */(/)€ 12Л)[*о» Т] и точка у£Еп. Доказать, что
функционал
J{a) = a \\u(t)\*dt + $ \\x(t, u)-y(t)\*dt + y\x(T9 u) — y\*

§ 4\ Градиент функционала дискретной системы. Условия оптимальности 273
(<*> Р, Y = const) при условиях (40) дважды дифференцируем в
^2Г)1^о» Л- Доказать, что если а, р, Y>°» то J (и) при условиях
(40) выпуклый, а если же а>0, (J, у>^> то сильно выпуклый в
Lp[t0, Т].
8. Пусть требуется минимизировать функционал
/(a) = j[(a(t), x) + b(t, u)]dt + (cf х(Т))
и
при условиях
x = A(t)x + B(t, и), t0<:t<CT; x(t0) = x0,
u(t)eu={u = u(t)eLjf)[t0, T]:u(t)ev
почти всюду при to^t^Z\T}, где V — заданное множество из Ег,
A{t) — матрица порядка пХп с кусочно-непрерывными элемен-
тами, a(t) и B(ty и) — кусочно-непрерывные n-мерные вектор-
функции, b(t, и) — кусочно-непрерывная функция, дго, с — задан-
ные векторы из Еп\ моменты Uy Т заданы. Доказать, что для
оптимальности пары (u(t), x(t)) необходимо и достаточно выпол-
нения условия
(г|>(0, BV, ti(t)))-b(tf а(0) = тах[(г|)(/), B(tt u))-b(tt и)],
где
y = -A*(t)ty + a(t)f у(Т) = -с.
Указание. Заметить, что при этих условиях в формуле (18)
Я = 0.
§ 4. ГРАДИЕНТ ФУНКЦИОНАЛА, СВЯЗАННОГО С ДИСКРЕТНОЙ
УПРАВЛЯЕМОЙ системой, условия ОПТИМАЛЬНОСТИ
1. Рассмотрим следующую задачу оптимального управления с
дискретным временем: минимизировать функционал
П[Щ])= Nf£F°t(xi9 Щ) + Ф(х„) (1)
при условиях
xt+x = Fi(xh щ), i = 0, 1, ... , N — 1; х0 = а, (2)
[Щ] = (и0,... , ия-д-.щЕУь t=0, 1,... , #— 1, (3)
где хь = (xl, ... , *?), щ = (ul ... , и[), функции Ft = (F\9... , F?),
J7?, Ф предполагаются известными, Vi— заданное множество из Ег,
натуральное число Л^1 и начальная точка а заданы.

274 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. ь
Задача (1)—(3) уже изучалась нами выше. В § 4.1 с помощью
динамического программирования исследовалась проблема синтеза
для этой задачи, в § 5.3 рассматривались достаточные условия
оптимальности. В настоящем параграфе сформулируем достаточ-
ные условия дифференцируемости, выпуклости функционала (1)
при условиях (2), (3), а также выведем необходимые условия
оптимальности. Будем пользоваться следующими обозначениями:
dFi
L —
дх
дх*
dF\
дх"
dF?
дх*
dF?
~дх*
dFnt
дх"
dFj_
ди
ди*
диг
dF1}
ди*
дх ~~ \ дх* ' "# * дх" ) '
дФ /ЗФ
дх \ дх*
i \ ди* '
п J
~duF
ди!
дФ
д#
Через U£ [О, N] обозначим гильбертово пространство вектор-
функций дискретной переменной [щ] = (ио, щ, ..., uN-i) со скаляр-
ным произведением
//—1
([ui]> fa])L<D= J] («I. ViK
i=0
и с нормой
ЛГ—1
ад=(2>и,)*\
i=0
Пусть U — множество всех дискретных управлений [щ] = (и0, ...
...,a#_i), удовлетворяющих условию (3); очевидно U CZ Ljr) [0. N].
Заметим, что функционал (1) представляет собой функцию Nr
переменных и0, и\у ..., Ия_ь Если функции Fi(x, и) непрерывны, а
Fu Ф полунепрерывны снизу по совокупности переменных
(ху u)^EnxVi, множества V*, t=0, 1, ..., N—1, замкнуты и огра-
ничены в Ег, то функция I([Ui\) полунепрерывна снизу, и сущест-
вование оптимального управления [щ]9 на котором функционал
(1) достигает своей нижней грани при условиях (2), (3), следует
из теоремы 1.1.
Для приближенного решения задачи (1) — (3) могут быть
использованы методы гл. 2, однако непосредственное применение
этих методов может встретить затруднения из-за большого числа

§ 4] Градиент функционала дискретной системы. Условия оптимальности 275
переменных. При рассмотрении задачи (1)—(3) в пространстве
Lp [0, N] будем иметь дело с N векторными переменными, и ме-
тоды § 2 здесь могут оказаться более удобными.
Выведем формулу градиента функционала (1) при условиях
(2), (3) в пространстве W [О, N].
Теорема 1. Пусть функции i7?, Fit Ф непрерывны по со-
вокупности своих аргументов вместе со своими частными производ-
ными по переменным х, и при *e£n, weVi, t=0, 1, ..., N—1.
Кроме того, пусть
|^(* + Д*, u + fy-FUx, u)\En<L(\bx\En + \h\Er) (4)
при всех xf х+Ах и всех и, u+h^Viy i=^Q, 1, ..., N—1. Тогда функ-
ционал (1) при условиях (2), (3) непрерывен и дифференцируем
в норме Li [О, N], причем его градиент /'([tti]) в точке [щ]^11
представим в виде
ПЫ)"{-Щ<Л^,ид. i = 0, l....,JV-l}€ir»[0,JV],
(5)
где
Hi(x, *, a) = -F?(*, «) + <*. Ft(x, и)), ^L-(^Lf ... , «A),
(6)
[Xi] — (x0f xu ..., xN) — дискретная траектория задачи (2), соот-
ветствующая выбранному управлению [щ]^и, а вектор-функция
[tyi] — СФ-ь Фо, .... ^n-i) определяется из условий
dHl(xi ъ,щ) |е,0, 1,...,Л7-1; (7)
дх
дФ(х„)
W-1 = —
дх
Доказательство. Пусть [а*], [и*] + [А*]е£/, пусть [хг] и
[Х{] + [А**] — соответствующие этим управлениям дискретные
траектории задачи (2), а / ([щ]) и / ([Ui}+[hj])=I([iii])+AI —
соответствующие значения функционала (1). Из (2) следует, что
приращение [Ах{] удовлетворяет условиям
Axi+i^Fl(xt + ^xh tib+h^ — F^ щ) (i = 0, 1, ... , N—l);
Д*о = 0. (8)
Так как
ф{х + Ьх)-ф(х)=(^*(*±^!<}-уАху 0<6<1,

276 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 5
то из (1) получаем
//—1
(9)
где
дх дх
С учетом соотношений (7), (8) [имеем
ЛГ—1
ЛГ—1
i=0
АГ—1
Подставляя полученное выражение в (9) и используя функцию
H{(xf -ф, и)у получим следующее представление для приращения
функционала:
А/= ~2 [fftiXi + bxt, ft, щ + Ю—Н^ ft, и,)—
Из формулы конечных приращений следует
Я, (ж< + Д*„ ifc, ^ + А,) = Я, (*„ %, щ) +
+ / аяг(^+егАдсь фь u< + 9f/tf) ^ д \
+ /аяг(*, + егдд^,, ц + щ ^ 0<в|<1>
t = 0, 1,..., Я—1.
Подставим это равенство в предыдущее представление для А/; будем
иметь

§ 4] Градиент функционала дискретной системы. Условия оптимальности 277
ЛГ-1
д/ = -£( dHl(Xt,J"Ui) .fr) + *. *-*i + fr + Jfc (11>
1=0
N—1
^--2j 1 jt Тх—• д*<>
(12>
лг—1
R'--L { Та to * \1*
Для оценки остаточного члена R формулы (11) нам понадобится
одна лемма, представляющая собой дискретный аналог леммы
Гронуолла.
Лемма 1. Если некоторые величины <рг-, /=0, 1, ..., N, удов-
летворяют неравенствам
0<Ф0<а, 0<<рж<а+&£ фт, 1 = 0, 1,..., N— 1,
т=0
(14>
то справедлива оценка
0<Ф,<а(1 + 6)<( i = Q,\,..-,N; (15)*
если же
0<ф{_, <a + b J] фт, t = 0, 1,.». , N— 1; 0<флг_1<а,
(16>
то верна оценка
0<Ф,<а(1+6)^~i, i = 0, 1,..., ЛГ-1. (17>
Доказательство можно провести по индукции. При fe=0 по
условию О^фо^в. Если неравенство 0^фт^а(1+6)т верно при,
всех /л=0, 1, ..., U то из (14) следует
i
0 <ФН-1 <а + Ь £ а(1 + 6)™ = а(Г+ 6)4-1.
Аналогично можно убедиться, что из. (16) вытекает оценка (17). J^

278 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 9
Продолжим доказательство теоремы 1. Из соотношений (8)
для [AXi] с учетом условия (4) имеем
m=0 m=0
I A*+l| = I £(Д*т+1- Axj| < £ I AU +
N—1
+ L-J]aAxw| + |Aw|)<(l.+ L) £|A*J+I £ |Am|.
Полагая в (14)f (15)
« = L£|AJ, 6=1 + L, Vl = |AX||f
получим оценку
lAJiKCxJIAil, Сх = 1(2 + £)", t = 0, 1, 9N. (18)
Из условий теоремы следует непрерывность функций
дФ dHt дЩ т
, —-, —- по совокупности своих аргументов. Тогда с уче-
\дх дх ди
том оценки (18) из выражений (10), (12), (13)^ заключаем, что
остаточный член R в формуле (11) имеет порядок о (II [А*] II). Та-
ким образом, в формуле (11) для приращения функционала пер-
вое слагаемое является линейным ограниченным функционалом
относительно [Ы] на LP[0y N], а второе слагаемое имеет порядок
о (II [ft*] II). Это значит, что функционал (1) при условиях (2), (3)
дифференцируем и его градиент имеет вид (5). А
2. Зная формулу градиента, нетрудно расписать методы
пп. 1—5 § 2 применительно к задаче (1) — (3). Например, метод
проекции градиента здесь приводит к построению последователь-
ности [Ui]n=(u0ny ..., tftf-i.n) по формулам
Щ,п+\ = гуЛЩ,п + ап т у t = U, 1, ... , /V— 1,
л = 0, 1,
где ап>0 выбирается как в п. 2 § 2, [xi]п = (х0п, ,.v xn,n), [i|>i]n =
= (^-i,n, ..., iN_ifn) — решения задач (2) и (7) соответственно
при [и{] =\щ] п.
Приведем достаточные условия для того, чтобы градиент функ-
ционала (1) при ограничениях (2), (3) удовлетворял условию
Липшица.

§ 4] Градиент функционала дискретной системы. Условия оптимальности 279
Теорема 2. Пусть выполнены все условия теоремы 1 и
пусть функции
дФ dFj dF? dF{ a/f
дх дх дх ди ди
удовлетворяют условию Липшица по совокупности (xt u)^EnxVir
i=0, 1, ..., N—1, с константой L>0 (эти условия полностью анало-
гичны условиям (3.5—9), и поэтому подробно выписывать их здесь
не будем). Пусть, кроме того,
1^/(*, и)К4+ЛИ> AvA2 = const>0 (19)
при всех х^Еп, u^Vu и множества V{, i—09 1, ..., N—1, из (3>
замкнуты и ограничены в Ег. Тогда градиент функционала (1)
при ограничениях (2), (3) удовлетворяет условию Липшица.
Доказательство этой теоремы полностью аналогично доказа-
тельству теоремы 3.2; предлагаем читателю провести его само-
стоятельно.
3. Перейдем к выводу необходимых условий оптимальности
для задачи (1) — (3).
Теорема 3. Пусть выполнены все условия теоремы 1. Пусть
[щ]—оптимальное управление, [xi] — соответствующая ему тра-
ектория системы (2), т. е. / (["*])= inf / ([#/]), где нижняя грань
берется по всем [и{\ из условий (2), (3). Пусть [ty*] — решение
задачи (7), соответствующее управлению [щ]. Тогда необходимо
выполняются неравенства
( m {Х\*' "д . «,-«;)«>. 1=0. 1 N-1 (20)
при всех tii^Vu для которых 'и] + а (щ — щ) 6 Vt при любых а,
0^<а^1, причем если ut — внутренняя точка множества Vu то
6Щ(Л"Ъ ,;о. (21)
ди
функции Ht (х, % и) определяются равенствами (6).
Доказательство. Положим в формуле (11) х{ = х], ifo = i|>*,
ui = иi\ получим
Д/ = - 2 Г'*4'*' ° • *•) + °<*Ш. (22)

280 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
Пусть щ — произвольная точка из Viy для которойщ + а(щ — щ) 6
€К, при всех а, 0^|а^1. Возьмем в (22)
[Am] = (0, , 0, ht = а (щ—и})у 0, , 0).
Очевидно, при таком выборе [hm] управление [ui] + [А*]е£/, и
тогда в силу оптимальности [щ] из (22) получим
0<A/ = -(,9ff<(^' "'> , «(«,-«;>) +о(«Ц[М|Ь, 0<.<.1.
Поделив обе части этого неравенства на а>0 и перейдя к пределу
при а-*+0, сразу придем к неравенству (20). Если Ui— внут-
ренняя точка V{, то в (20) можно положить
щ = щ+г ^
ди
:eVt- при некотором е>0, что сразу приведет к равенству (21). Д
Если V* — выпуклое множество, то условие (20), очевидно,
выполнено для любого ^еУ,«. Если V* выпуклы при всех /=0, 1, ...
..., N—1, то неравенства (20) в силу формулы (5) равносильны
-одному неравенству
(/'(К1), 1«Л-К]|)лг>>о
ори всех [иг]е£/, что совпадает с условием оптимальности (2.1.10)
теоремы 2.1.3.
Таким образом, согласно' теореме 3 оптимальным может быть
лишь управление [щ\ 6 U, удовлетворяющее условиям (20). Од-
нако условия (20) не дают ответа на вопрос, как связано управле-
ние [и*] с экстремальными точками функции Ht(xu ^i, #) на
множестве К*. В частности, нельзя ли по аналогии с системами
с непрерывным временем утверждать, что оптимальное управление
{iii\ удовлетворяет принципу максимума
Ht (*;, %> "д = max Ht \xu itf, u)9 i = 0, 1, ... , N- 1? (23)
Ведь необходимое условие оптимальности тем ценнее, чем меньше
управлений, подозрительных на оптимальность, оно выделяет.
В этом смысле условие (23) явно имело бы преимущество перед
условиями (20), так как неравенства (20) могут выполняться не
только в тех точках, где имеет место (23), но и в других точках,
в которых, например, = 0. К сожалению, оказы-

§ 4\ Градиент функционала дискретной системы. Условия оптимальности 281
вается, что в управляемых системах с дискретным временем прин-
цип максимума, вообще говоря, не имеет места: на оптимальном
управлении функция Ht(x*iy ур\, и) может и не достигать своего
абсолютного максимума по иеУг-.
Пример 1. ([231], стр. 170). Пусть фазовое состояние си-
стемы описывается уравнением
*+i = *< + 2ult #+i = — х\ + yt + и] (i = 0, 1); х0 = 3; у0 = 0.
Требуется минимизировать функционал /(а0, "0 =—#2—Ф(*2, fte)
при условии
Ы = (Ц>. "i) е U = {(tt0, их): | щ | < 5 (I = 0; 1)}.
Нетрудно вычислить явное выражение
1(и0,и1) = 3(и0 + 2)*-и\ + 6.
Откуда следует, что оптимальное управление (tto, и\) имеет вид
и0= — 2, щ =з 5 (возможность Щ = — 5 предоставляем читателю
рассмотреть самостоятельно), а оптимальная траектория
*о = 3, х\ = — 1, х*2 = 9; #S = 0; у] = — 5; ^ = — 19;
минимальное значение функционала равно /*=—19.
Составим функцию
Hi(xtt yi9 Ъц:Ъи)™%(*< + 2^) + Ч>2*(— *2i+ yi+ ti2i) (i = 0,1).
Система (7) имеет вид i|>M_i =% —2^*,, t|>2,i-i = tyaf (' = 1;0);
дф л u дФ ,
Подставив сюда оптимальные (**, #*•), получим %J>ti = 0, Ф*о = 2;
*|>2i= 1; ^20= 1. Тогда
Н0 (*о, J/J, я|)10, я|>20, и) = (и + 2)2 — 7.
Как видим, на оптимальном управлении и=ио =—2 функция
Н0(х1, уо, ф^'.фяьи) достигает своего абсолютного минимума, в
то время как ее максимальное значение при |и|^5 достигается
в точке и=Ъ.
Таким образом, для управляемых систем с дискретным време-
нем принцип максимума, вообще говоря, не имеет места.
Другие необходимые условия оптимальности для дискретных
управляемых систем см. в работах [26, 59, 196] и др.; связь между
необходимыми условиями для непрерывных систем и их разност-
ных аналогов изучалась в работе [58J.

282 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. б
4. Рассмотрим задачу оптимального управления линейными
дискретными системами: минимизировать функционал (1) при ус-
ловиях (2), (3), если
Ft (хи Щ) = А& + В^ + ft% i = 0, 1, ... ,'N— 1, (24)
где Ait Bif fi — заданные матрицы порядка /гХп, пХг и nXl со-
ответственно.
Теорема 4. Пусть функции F?, Ф удовлетворяют услови-
ям теоремы 1. Тогда функционал (1) при условиях (2), (3), (24)
дифференцируем в Li2)[09 N] и его градиент /'([и*]) в точке [щ]
вычисляется по формуле
/4N) = {af?(^"f) -Д'|»1. i = 0, 1, , N-l), (25)
где [Х{]=*(Хо, ..., Xn) — решение задачи (2), соответствующее вы-
бранному управлению [щ], a [i|)*}—(t|)_i, ...» фл-i) определяется из
условий
%_, = А\Ъ- ^'^ » '-0. 1 ЛГ—1. (26)
ОХ
дФ(х„)
матрицы Ль 5 < получены транспонированием матриц Ai% Bt.
дФ dF* dF\
Если, кроме того, -г—, ——, —— удовлетворяют условию
-Липшица по совокупности (xt и)^ЕпХЕг, то градиент 1'([щ])
удовлетворяет условию Липшица на всем пространстве W[0> N].
Формулы (25), (26) вытекают из теоремы 1; условие Липшица
для градиента доказывается аналогично тому, как это делалось
в теореме 3.4.
Укажем достаточные условия выпуклости и сильной выпуклос-
ти функционала (1) при условиях (2), (3), (24).
Теорема 5. Пусть выполнены условия (24), функция
Ф(х) выпукла по х на Еп> а /*(*, и) выпуклы по совокупности
переменных (х, и)у т. е.
.Р](ах + (1-а)у,аи+ (1—а)1>) <aF?(x, и) + (1 — a)F?(y, v) (27)
лри любых ху у^Еп, и, t><=£r, ае[0, 1] и i=0, 1, ЛГ—1. Тогда

§ 4] Градиент функционала дискретной системы. Условия оптимальности 283
функционал (1) выпуклый на Ц[О, N].
Если при этом функции Ф, F°i удовлетворяют условиям
теоремы 1, множества К*, i=0, 1, ..., N—1, выпуклы, то для опти-
мальности управления [и]] необходимо и достаточно, чтобы
/ dFUx*,, и\) , , Л
у —^ Btfy, щ-иЛ>0, uteVh t = 0, 1, ... ,N—l.
(28)
Если же вместо (27) имеет место неравенство
F°i(ax + (l— а)у, au + (l — a)v)<aF°l(x,u) +
+ (l—a)F°i(y,v) — a(l—a)K\u — v\29 x = const>0 (29>
при любых х, у^Еп> и, и&Ег, ае[0, 1] и i=0, 1, ..., N—lf то функ-
ционал (1) сильно выпуклый на W[OfN] и задача (1) — (3)„
(24) имеет и притом единственное решение на любом замкнутом
выпуклом множестве £/CZL2r)[0, N].
Доказательство. Решение задачи (2), (24), очевидно, об-
ладает свойством
*i №t] + (1 — а) Ы) = «| ([щ]) + (1 — a)xt ([Vi\), i = 0, 1, ... Nr
при любых а и любых [Ui]9[Vi] в L2r)[09 N]. Тогда выпуклость
[сильная выпуклость] функционала (1) на /ir)[0, N] является
простым следствием выпуклости Ф(*) и условия (27) [условия-
(29)]. Условие оптимальности (28) вытекает из теоремы 2.1.3 и
формулы (25). Последнее утверждение является следствием теоре-
мы 2.1.7.
Упражнения. 1. Доказать, что функционал
/(Ы)-а £ |И;|2 + Р £ l**l2+ Y*& («. Р> Y = const)
при условиях (2), (24) дважды дифференцируем в 1$\ [О, N]^
Доказать, что если при этом а, 0, у^О» то H[ui]) выпуклый,
а если а>0, р, Y^0> то сильно выпуклый на £гг)[0, //].
2. Пусть выполнены все условия теоремы 5 (кроме, быть мо-
жет, условия (29)). Доказать, что тогда условие максимума (23)
является необходимым и достаточным условием оптимальности:
в задаче (1) —(3), (24).

284 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
§ 5. МИНИМИЗАЦИЯ КВАДРАТИЧНОГО ФУНКЦИОНАЛА. ПРИМЕРЫ
1. Пусть В — некоторое банахово пространство, X — гильбер-
тово пространство. Пусть х(и) — отображение пространства В в X,
причем х(и) представимо в виде
х(и) = х(0) + Ки9 иеВ9 (1)
где К — линейный ограниченный оператор из В в X:
\КиЬ<1К\\иЬ. *ев, ||*|1= *ф\Ки\х.
IWK1
Пусть U — заданное выпуклое замкнутое множество из В, у —
некоторый заданный элемент из X.
Рассмотрим следующую задачу: минимизировать функционал
J{ti) = \\x{u)-yfx пщиеи. (2)
Как увидим ниже, ряд важных прикладных задач оптималь-
ного управления, связанных с линейными системами обыкновенных
дифференциальных уравнений или уравнений с частными произ-
водными, являются частным случаем задачи (2).
Функционал (2) в литературе также принято называть квадра-
тичным, поскольку главный его член Ц*(а)11*» соответствующий
<лучаю #=0, является квадратичным в смысле определения § 6.1.
♦Сразу же заметим, что нам будет важен сам факт существования
представления (1); ниже при описании алгоритмов оператор К не
будет использован:
Из представления (1) вытекает
jc(au + (l—a)v) = <zx(u) + (l— a)x(v) при всех к,и6В иаб^
(3)
Отсюда и из выпуклости [* — yfx по переменной х следует выпук-
лость функционала J (и). Кроме того, из (1) имеем
kx(u, h)==x(u + h) — x(u)^Kh,
IM<U)U<|*I|A|b, u>h£B- w
Приращение функционала J (и) тогда можно представить в виде
J(u + h)-J(u) = \\x(u + h)-yf-lx(u)-yr =
= 2(x(u)-y,bx(uth))x + \\\x(u9h)fx =
= 2(х (и) - у, Щх]+ № Щх, и, he В. (5)
Из этого представления и из (4) следует, что J (и) — дважды не-

# 5] Минимизация квадратичного функционала. Примеры 285
прерывно-дифференцируемый функционал на В. Первый диффе-
ренциал / (и) имеет вид
(J'(u),h)^2(x{u)—y9x(u+.h)—x(u))x, u,heB (6)
или если воспользоваться оператором /С*, сопряженным с К (см.
[131], стр. 279), то (/'(и), h)=2(K*(x(u)—y)f Л). Следовательно,
градиент Г (и) выражается формулой
Г{и)шш2КГ{х(щ—у),и£В9 (7)
а второй дифференциал представим в виде
±(J"(u)h,h) = (KhtKh)x = (ICKh9h), т. е. Г{и)=2КГК.
Поскольку /С* также является линейным и ограниченным операто-
ром, действующим из Х*=Х в £*, причем ||/С*11 = ||/СИ ([131],
стр. 279), то из (7) следует, что J'(u) удовлетворяет условию
Липшица
| J' (и) - J* (v) fj* < 21 JCp I и - 0|»
Из теоремы 2.1.3 и формулы (6) следует, что для достижения
функционалом (2) своей нижней грани на выпуклом множестве U
в точке u*eU необходимо и достаточно, чтобы
2(х (и0) — у,х(и)—х (и*)) X=(J' (и*), и — и*)>0 при всех и б U. (8)
Если В — рефлексивное банахово пространство (в частности, В —
гильбертово пространство), U — выпуклое замкнутое ограничен-
ное множество из В, то J (и) достигает на U своей нижней грани
хотя бы в одной точке и*е£/. Это следует из теоремы 1.4.
Справедлива формула
g{a)==J(u + ah) = J (и) + 2а(х(и) — у, Ьх(и, h)) +
+ а2|Дл;(и,А)||*, и, А6В, -оо<а< + оо, (9)
которая получается из (5) при замене h на аЛ. Если ||Д#(и, К) 11=5^0,
то g (а) представляет собой квадратный трехчлен переменной а,
—оо<а< + оо, и достигает своего минимума в точке
• •/ 1Л (*(и)-У.х(и + Ь)-х(и))х (J'(u),h)}
а = а ш, Л) = 5 = о—.
V ' М(« + А)-*(«)6 2||Д*(а,Л)|&
(10)
2. Для приближенного решения задачи (2) могут быть ис-
пользованы методы, описанные в § 2, причем некоторые из этих
методов здесь получают более простой и завершенный вид. Напри-
мер, если В=Н — гильбертово пространство, то метод скорейшего

286 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ \Гл. 6
спуска для минимизации J (и) =11* (и)—д\\2 на Я приводит к после-
довательности
ип+1 = ип — ап^(ип), п = 0, 1, (11)
причем параметр ап^0, определяемый из условия
min gn (а) = gn (ап), gn (а) = J(un — aJf (ип)),
здесь может быть выписан в явном виде. А именно, если
Ьх(ип, —J'(un))==x(un — J'(un))—x(un)^Ot
то согласно формулам (9), (10) £п(а) достигает своего минимума
на числовой оси при
а = ап = a (unt -J> (ип)) = \ \\J' (un)f \Ьх(иП9 - J' (ип))\\~*> 6.
Еслиая = 0, то J'(un)=0 и в силу (8) ип = и* есть точка
минимума J (и) на Я, и процесс (11) на этом заканчивается.
Если жеал>{0, то в О*) принимаем а„ = <хл, и процесс про-
должаем дальше. Наконец, если hx(un,—J(un)) =0, то из (9)
при и=*иПу h=—J'(un) имеем gn(a)=J(u)=const при всех а,
—оо<а<+°°. С учетом формулы (2.1.4) тогда
gn (а) = (/' (ип -*]' (иа))9 - Г (ип)) = 0
при всех а: В частности,
£я (0) = -1| J' К) f = 0 или /' (ип) = 0,
что в силу (8) приводит к оптимальности ип = и*. Таким образом,
если при некотором п
или Д х (иП9 — J' (ип)) = 0, или ап = а* (цп, — J' (ип)) = 0,
то ип = и* — точка минимума J (и) на Я, и процесс (11) заканчи-
вается; если же аЛ>0, то в (41) принимается аЛ = ая, и процесс
продолжается дальше. Сходимость метода следует из теоремы 2.1,
если предположить, что множество М(и0) = {и: J(u)^J(u0)}
ограничено.
Если же U — выпуклое замкнутое множество из гильбертова
пространства Я, то для решения задачи «(2) может быть применен
метод проекции градиента из § 2 (см. п. 2). Как было показано
выше, градиент функционала (2) удовлетворяет условию Липши-
ца, причем в качестве константы Липшица может быть взято
любое число L^2||/C||2. На практике явный вид оператора К и ве-
личина* нормы Ц/CII часто бывают неизвестны, но зато во многих

§ 5] Минимизация квадратичного функционала. Примеры 287
задачах (см. ниже примеры) удается получить оценку вида (4)
||Д*(и, Ь)\\х^С\\к\\в с известной константой С>0. Тогда можно
принять L=2C2, и при выборе параметра ап в формуле (2.2) исхо-
дить из условия
Ч < ап <
L + 2& С* + ъ '
8ь е — положительные постоянные, ех< ; например, мож-
СТ2 + е
но взять ап = ——, п = 0, 1, Сходимость метода проекции
2С2
градиента (2.2) при таком выборе ап следует из теоремы 2.2. Если
£/=#, то этот метод превращается в один из вариантов градиент-
ного метода из § 2 (см. п. 1,6).
3. Остановимся на одном варианте метода условного градиен-
та для задачи (2), когда U — выпуклое замкнутое ограниченное
множество в рефлексивном банаховом пространстве В. В этом
случае из теоремы 1.4 вытекает существование хотя бы одного
элемента u*^U, для которого J (и*) = inf J (и) = J*.
_и
Пусть йп(п^0) известно. Тогда un^U определяем из условия
(2.3), которое с учетом (6) перепишется в виде
-у (J' ("л), йя — ип) = (х (ип) — уух (йп) — х (ип)) х =
= mm(x(un) — y,x(ti) — x(un))x,
или короче
(х(Ип) — У, x(un))x=min(x(un)—yt х(и))х. (12)
и ест
Существование такогоjin следует из теоремы 1.4. После этого
полагаем ып+1 =и>п + о.п(ип—ип)»где аЛ, 0<|ап^1, выбирается из
условия
min gn (а) = gn (ая), gn (а) m J (ип + а (йп — ип)).
0<а<1
Пользуясь формулами (9), (10), выпишем явное выражение
для ап. Если Д*(ип, ип—ип)=х(ип) —*(ап)¥=,0, то согласно (9),
(10) gn(d) достигает своего минимума на числовой оси при
а = ап = а(«я, ип — ип) = L (/>(Ufi)9 ип — ип) \\х(ип) — х{ип)\\~* =
= -т\<Гп(йп)\\\х(йп)-х(ип)\Г>0.

288 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
Если с£ = 0, та /n(ttn)=0^(/'(an), и—ип) при всех ие(/,
и в силу (8) ап = а* есть точка минимума J (и) на £/, т. е. про-
цесс на этом заканчивается. Если о^>0, то квадратный трехчлен
gn(o) достигает своего минимума на O^a^ll, очевидно, при
а = аЛ = min (1, о£). Это и есть искомое явное выражение для <хп.
Наконец, если х(ип) =х(ип)у то в силу (12) снова /п("п)=0^
^{J'{u>n)> и—Ип) при всех u^U, что в силу (8) означает опти-
мальность ип = н*, и процесс на этом заканчивается. Из теоремы
2.3 следует, что \imJ(un) = J*. Неравенство (2.6.6), которое для
Л-ЮО
рассматриваемой задачи запишется в виде
0<J(un)-r<\JnCun)\^2(x(un)-ytx(un)-x(un))^0(n^oo)t
является удобной апостериорной оценкой при практическом
использовании метода условного градиента.
Для иллюстрации вышеизложенного рассмотрим две часто
встречающиеся на практике задачи, являющиеся частным случаем
задачи (3.39—41) (другие приложения см. в § 6, 7).
4. Пусть требуется минимизировать функционал [94, 97,
135, 161]
J{u) = \x(T,u)-y\ln (13)
при условиях
*x=A(t)x + B(t)u + f(t), t0<t<T; x(t0) = x09 (14)
« = tt(06(/C4r,[<oJ], (15)
где x=(xii ..., xn)f w=(w4, ..., ur)\ U— заданное выпуклое множе-
ство из Lp[t0f Т]\ A(t), B(i) — заданные матрицы порядка пХп
и пХг соответственно с кусочно-непрерывными элементами; f(t) —
известная кусочно-непрерывная вектор-функция; моменты *о, Т и
точки х0, у^Еп заданы.
При любом u = u(t)£L<[) [£0, Т] [соответствующее решение за-
дачи (14) представимо в виде
x(t9U)=X(t9 0) + y(t9u)9 tb<t<T, (16)
где x(t, 0) — решение (14) при asO, y{t, и) —« решение (14)
при/(0=0, а:о=0. Пользуясь неравенством (3.26) при Axsj/,
h(t)^u(t), получим оценку
sup \y(t,u)\<Ct \\и(Ща<СгУТ=й \\u{t)\\<r)u „. (17)

§ 5] Минимизация квадратичного функционала. Примеры 289
Равенство х(Т9 и)=х(Т, 0)+у(Т, и) можно рассматривать
как представление (1) при
B = Lir)[t0iTlX=En, Ku = y(Ttuhx(0) = x(T90)t
х(и) = х(Т9 и).
Очевидно, Ки=у(Т9 и) — линейный оператор из L{2r)[t09T] в £п>
ограниченность которого следует из неравенства (17). Как видим,
задача (13) — (15) является частным случаем задачи (2).
Далее, задача (13) — (15) удовлетворяет всем условиям тео-
ремы 3.4. Поэтому выражение для градиента здесь расшифровы-
вается так:
J'(u) = -Br{t)*(t9u), t,<t<T, (18)
где г|? (t, и) является решением задачи
♦ = -Л*(0*. t0<t<T9 Ъ(Т) = -2[х(Т,и)-у]. (19)
Первый дифференциал в силу (6), (18) представим в BHAej
(J' (и), h) = 2(x (7\ u)~y9x(T9u + h)-x (Г, и))Вп =
= - \(B*(t)y(t,u),h(t))Erdt. (20)
Функционал (13) при условиях (14) является выпуклым, поэтому
задача (13) — (15) имеет хотя бы одно решение u=u*(t) на любом
выпуклом замкнутом ограниченном множестве U из W [t0i Т],
причем для оптимальности u*(t) необходимо и достаточно выпол-
нения неравенства
г
- J (*•(<)*<'. и*)9 и (t)-u*(t))Erdt =
= 2(х (Т, «•) — у,х (Т, и) — х(Т, иГ))Вя > 0, и (t) 6 U,
Метод скорейшего спуска для задачи (13)—(15) при £/ =
— L2r) [t0, Т] имеет вид
un+i (t) = ы„ (t) — <х„ J' (и„), п = 0, 1,
j,{Un) = _ВТ(0 *(t, и,*), t0<t<T, (21)
гДе $(t, ип) — решение задачи (19) при и = ип(t), <хп = а„>0,
т
Г \B*W(t,un)\2E dt
ая = Ь =
2\х(Т, Un-J'(u„))-x(T,un)[2E

290 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
(х(Т, ип)- у.х(Т,ип —У («„))-х(Т, ип))д
Е=-, =2- >0
\х(Т, un-J'(un))-x(Tt ип)\%п
(если а„ = 0 или х(Т, un—J'(un))=x(T, ип), то un(t)=u*(t) оп-
тимальное решение задачи (13) — (15), и итерационный процесс
на этом заканчивается).
Метод проекции градиента для задачи (13)—(15) в случае
выпуклого замкнутого множества U имеет вид un+\=Pu(un(t) +
+anB*(t)ty(t9Un)),n=0, 1, 2, ..., где ty(t, ип) — решение задачи
(19) при u = Un(t), а параметр ап может выбираться из условия
где С\ взято из оценки (17), еь е — положительные константы,
ei< с!+г (например, ая =—•).
Если un+\(t)=un{t), то Un(t)**u* (t) —оптимальное решение за-
дачи (13) — (15) (см. доказательство теоремы 2.3.2). Если множест-
во U имеет вид (3.28), то проектирование на U осуществляется по
формулам (3.29).
Метод условного градиента в задаче (13)—(15) для выпукло-
го ограниченного замкнутого множества U из L% [t0, Т] осуществ-
ляется так: зная un(t) (п^0)9 определяем un(t) из условия
- Г(ВЧ9♦('.*<«), un{t))Erdt=
и
= min Г- \{BT(t) *(*, ип), u(t))Ba]9 " (22)
что эквивалентно условию
(х(Т, ип) — уу х(Т, Лп))Еп = min (х(Т, ип) — у9 х(Т, и))вП9
вытекающему из равенства (20) при замене u(t) на un(t)t h(t)
на u(t)—un(t)\ В частности, если множество U имеет вид (3.28)г
то явное выражение для un{t) дается формулой (3.30). Имея
un(t), далее полагаем
un+x(t) = un{t) + an[un{t)-un{t)], t0<t<T, an = min{a;, 1}>0
(23)

§ 5} Минимизация квадратичного функционала. Примеры 291
г _
f (B'(W(t, и„), «„(О -ипЩ)Е dt
«С--* : = г-1—-
2|ж(7\ия)-ж(Г, а„)&
(*(7\ un)-yt *(7\ ал)-х(7\ ал))£
= з^ — >0
|*(7\ия) — х(Т9 ип)\2Еп
(если а„ = О или х(Т, йп) =х(Т9 ип)9 то un(t) = #*(/) — оптималь-
ное решение задачи (13) — (15), и итерационный процесс на этом
заканчивается).
5. Остановимся еще на одном частном случае задачи (2):
минимизировать функционал [93, 97, 161]
Ли)- Ux{t,u)-y(t)\2Bndt (24)
С
при условиях (14), (15); y(t) .— заданная функция из L^ [t0t Т].
Представление (1) для этой задачи вытекает из равенства
(16), если взять
Вшш4РЦШ9Т\9 Х-1*% п *{0) = x(t90)9
Ku=y(t, и), х(и) =*(*, и). Очевидно, Ku=y(t, и), to^t^T, — ли-
нейный оператор из W [t09 Т] Ъ 4Л) [/0, Т], ограниченность которо-
го следует из оценки (17). Как было доказано выше, тогда функ-
ционал (24) при условиях (14) является выпуклым и дэаждЫ
непрерывно дифференцируемым в № [t0f Т]. В силу теоремы 3.4
градиент этого функционала имеет тот же вид (18), т. е. /'(и)—'
=— fi*(/)t|>(f, и), t0^\t^T, однако t|)(f, и) здесь является реше-
нием задачи
* = +2[x(t, u)-y(t)]-A*(t)№> t0<t<T9 1|?(Г)-0. (25)
Первый дифференциал с учетом представления (6) тогда запи*
шется в виде
т
(J>(u)9 h)^2 Г (x(t9 u)-y(t)9 x(t9 u + h)-x(t9 u))Bndt =
T
= - \(Br(t)l(t9u)th(t))B,dt.
С
Если U выпукло в L&r)[t0,T], то, для того, чтобы u*(t)<=U

292 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
было оптимальным решением задачи (24), (14), (15), необходимо
и достаточно выполнения условия
- ]{В* (t) я|> (/, if), и (t) - и* (t))Er dt ^
и
т
е=2 j (*(*, if)—у, x(t, u) — x(t, u*))Endt >09u(t)€EU.
и
Метод скорейшего спуска для задачи (24), (14), (15) при
U = Lir)[t0i Т] заключается в построении последовательности
{un(t)}^U по закону (21), где ^(t, ип)—решение задачи (25)
при u=un(t)t ал = а*>0,
т
l\B*(t)4it,un)\\rdt
а! = Ь =
2\\x(tfun-r(un))-x(t,un)\2E dt
U п
т
l(x(t,un)--y{f),x(ttun--y(tin))-x{t,un))E dt
\\x(ttun-J'(tin))-x(t,un)\2E dt
и п
(если ад = 0 или x(t, un—J'(un))=x(t, ап), to^t^.Tt то un(t)*=>
= #*(/) — оптимальное решение задачи (24), (14), (15), и итера-
ции на этом заканчиваются).
Метод проекции градиента для задачи (24), (14), (15) в слу-
чае выпуклого множества U имеет вид
ип+1 = Pu{un{t) + anBT(t)^(t9 ип))9 п = 0, 1, 2, ...,
где ф(^, ип)—решение задачи (25) при u=un(t)9 а параметр ап
может выбираться из условия
гг<ап<—±—, С = СХУТ=Г.,
с -+- е.,
где С\>0 постоянная из оценки (17), ei, е — положительные кон-
станты, »! < (например, ап = —— \. Если ип+х(t) =un(t),
то un(t)=u*(t) — оптимальное решение задачи (24), (14), (15),
и итерации на этом заканчиваются. Если множество U имеет вид
(3.28), то проектирование на U осуществляется по формулам
(3.29).

§ 5] Минимизация квадратичного функционала. Примеры 293
Метод условного градиента для задачи (24), (14), (15) в слу-
чае выпуклого замкнутого ограниченного множества V из
1% [^о» Т] заключается в построении последовательности
{un(t)}^U по закону (23), где un(t) определяется из (22) или
эквивалентного условия
т _ г
f (* (t, ип) — y(t),x (t, ип))щп dt = min Г (x(t, un) — y(t),x (t, u))E dt,
У ы€С/у
где t|>(£, un) — решение задачи (25) при u = un(t)y a
T ^
*(t)W.Un),tln(f)-Un(t))Erdt
J(B*<
ctf=-^
т _
2$\x(t9un)-x(t,un)\*dt
U
т „ _
$(x(t,un)-y(f)9x(t,un)-x(t,un))E dt
= --<* — >0
]lx(ttun)-x(ttun)\*dt
и
(если a«=0 или x(t, an) = x(t9 un), то un(t) = u*(t) — оптимальное
решение задачи (24), (14), {15), и итерации на этом заканчиваются).
Упражнения. 1. Применить метод сопряженных градиентов
для решения задачи (2) при U=B. Полученные формулы распи-
сать применительно к задачам (13) — (15) и (24), (14), (15) при
U = Lp (t„T).
2. Описать методы скорейшего спуска, проекции градиента,
условного градиента и сопряженных градиентов для минимизации
функционала J (и) = — (А и, и) — (Ь,и) из примера 1.1 в предполо-
жении положительности оператора А: (Аи, и)^к\\и\\2 при всех
«еЯ, x = const>0.
3. Описать методы § 2 для решения задачи минимизации
функционала
т т
J(u) = a1^\u(t)\^dt + a2^\x(tyu)-y(t)\2dt+a9\x(Ttu)-y\^
при условиях (14), (15). Здесь числа <хг^0, y(t) — заданная
функция из L^[t09 Т], у — заданный вектор из Еп.%
4. Пусть требуется решить задачу (24), (14), (15) при допол-
нительном условии х(Т, и)=уу где у — заданный вектор из Еп.

294 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. $
Указать примеры штрафных функционалов на условие х(Т, и)=у.
Рассмотреть случай Ph(u)=k\x(Ty и)—у\2 и указать методы мини-
мизации функционала Jh(u)=J(u) +Pk(u), k=lf 2, ..., при усло-
виях (14), (15). Как ввести в задаче (24), (14), (15) штрафы на
ограничение
sup х1 (tt и) < 1? SUplAT(t, «)|<1?
U<t<T t^U^T
Можно ли принять
т
Pk(u) = k f ImaxfA;1^ и)— 1; 0}\2dt,
t
т т
Р*(и) =£ j" max {х1 (',")- l;0}dff Pk(u) =k§ (\x(tt u)\—l)dt,
to t0
T
Pk(u) = k f|max{|*(/, a)|— l;0}|2d»
(u) = k\\
§ 6. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПРОЦЕССОМ
НАГРЕВА СТЕРЖНЯ
Рассмотрим часто встречающуюся на практике задачу опти-
мального управления, которая в теплофизических терминах имеет
следующий смысл. Пусть дан однородный стержень Oz^s^l, ле-
вый конец 5 = 0 которого теплоизолирован, а на правом конце s = l
происходит теплообмен с внешней средой. Требуется, управляя
температурой внешней среды, к заданному моменту времени Т
привести температурный режим в стержне, как можно ближе
к заданному режиму [35, 40, 104, 107, 162, 183, 227].
Математическая формулировка этой задачи: минимизировать
функционал
J(u) = $\x(s,T)-y(s)\*ds (1)
при условиях
-fjr = -|jr. (M)6Q = {0<s</, 0<*<Г}, (2)
dxft] =0, 0<г<Г; jc(s,0) = 0, 0<s</, (3)
ds
WL!L = v[u(t)-x(ltt)]f 0<t<T, (4)
OS

§ 6] Оптимальное управление процессом нагрева стероюня 295
и = u(t)e U= {и = u(t)6 L2[0, Г], \u(t)\ < 1
почти всюду при 0<f<7,}f (5)
где /, Г, v — заданные положительные константы, #(s) — задан-
ная непрерывная функция на отрезке O^s^!/.
Решением задачи (2)—(4), соответствующим управлению
u=zu(t)&U, называется функция x(s, t)=x(s, ty и), которая удов-
летворяет условиям (2), (3) в обычном, классическом смысле
[107], а условие (4) выполняется в слабом смысле, т. е.
т
lim ГГ <>x(stt) _v(UQ)±.x(s9t))]<p(t)dt = 0
-*/—о J L &s J
о
для любой функции q>(t)£L2[0, f]. Можно доказать [107], что ре-
шение задачи (2) — (4) при любом u=[u(t)£U существует и единст-
венно. Кроме того, справедлива оценка [35, 125]
i т
§\x(s9T)\*ds<±^\u(t)\*dt. (6)
о о
Для получения этой оценки умножим уравнение (2) на х (s, t) и
проинтегрируем по прямоугольнику Q. С учетом условий (3), (4)
будем иметь
Q 0
т
О Q О
Т Т
+ Jil"^^^!2^^4" v^2(Л 0^ —v Гл:(/, ^)f/(0^. (7)
Q
Откуда следует, что
l-[xHstT)ds + v^xHl,t)dt<v^x(lt t)u(t)dt. (8)
2
о
Если воспользуемся очевидным неравенством |а6|<аа + —, то
4
правая часть (8) оценится так:

296 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. $
v Г*(/, t)u(t)dt^v £x4lt t)dt + —f u?(t)dt.
О 0 0
Подставляя это неравенство в (8), сразу придем к требуемой
оценке (6).
Задача (1) — (5) является частным случаем задачи (5.2). Что-
бы убедиться в этом, достаточно в (5.1) положить
В-М0,7Ъ X=L2[0,l],x(u) = x(s9T9u)9x(0) =
= x(s9T9Q) = 0> Ku^x(sfT9u)9
причем оператор К, действующий из L2[0t Т] вХ2[0, /], очевидно,
линеен, а его ограниченность равносильна оценке (6) с ||/С||< у -—•
Из результатов § 5 тогда вытекает, что функционал (1) при усло-
виях (2) — (5) является выпуклым и дважды непрерывно диффе-
ренцируемым на {/, причем градиент его удовлетворяет условию
Липшица с константой L=2|[/C||2^v. Градиент этого функцио-
нала в точке u=u(t)^U может быть представлен в виде
/'(*)==**</,'). 0<*<7\ (9)
где *ф(5, t)=ty(s9 t, и) является решением следующей краевой
задачи:
-2—2-.Ь0€«. <"»
af<°-') gp, *«•»> =_уф(;,(), 0<t<T, (11),
ds ds
yi>(s9T) = c(s)9 0<s</, (13f
где c(s)==2[x(s, Ty u)—y(s)], O^s^l. Можно доказать существ
вование и единственность решения t|)(s, t)=ty(s, /, и) задачи
(10) — (12), которое удовлетворяет условиям (10), (12) в классик
ческом смысле, а условиям (11) — в слабом смысле, причем
имеет смысл говорить о значениях ф(/, t)^L2[09 Г], являющихся
пределом в L2[09 Т] значений t|?(s, t):
т
s-W—о
lim Uty(s9t) — y(l9t)\2dt = 0.
-W—0 У
Выведем формулу (9)-для градиента. Пусть u(t)9 v(t)=u(t) +
+ h(i)^U9 и пусть х(s, t9 u)=x(s9 t), x(s9t9v)=x(sJ)+Ax(s9t)^

§ 6] Оптимальное управление процессом нагрева стержня 2§7
соответствующие этим управлениям решения краевой задачи
(2)—(4). Приращение функционала (1) тогда запишется в виде
\
о
J {и + h) — J(u) = 2 J [x(s, Т) —y(s)]bx~(sr T)ds J- j | Ax(s, T) \2ds.
о
(13)
Заметим, что функция Ax(s, t) является решением краевой задачи
(2) — (4) при u(t)=sh(t), и, следовательно, справедлива оценка
/ т
jlA*(s,7)|2^<^j|ft(0|2d*, (14)
о о
вытекающая из (6)
Учитывая это обстоятельство и условия (10) — (12), имеем
/ i IT
^c(s)bx(sfT)ds= {ty(stT)bx(s,T)ds= f(f — fl>A*) <*Л ds =
Q Q
0 0
T
+ ty(l,t)v[h(t) — bx(l1t)]}dt=v{ty(l,t)h(t)dt. {IS)
0
Так как c(s)=2[x(s9 Г, и)— y(s)]f то формула (13) с учетом
(14), (15) запишется в виде
j (и + h)-J\u) = J vt|>(/, t)h(t)dt + O(||A||t[0>r]).
о
Сравнивая полученное выражение для приращения функционала
с (1.1), находим, что "градиент Г (и) выражается формулой (9),
а дифференциал (/'(и), ft) имеет вид
т I
(J'(u), A)L,[o.n = v J4(U, u)h(t)dt = 2 §[x(s,T9u)-y(3)]bx(sfT)ds.
(16)

298 МЕТОДЫ МИНИМИЗАЦИИ, В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
Таким образом, для вычисления градиента функционала (1) при
условиях (2)—(5) требуется последовательно решить краевые
задачи (2) —(4) и (10) — (12). Для решения этих краевых задач
можно использовать различные приближенные методы, в част-
ности расчеты можно вести по неявной разностной схеме [20, 207,
227]; интегралы (1), (16) вычисляют с помощью квадратурных
формул [19].
Заметим, что приведенное выше доказательство равенств (7),
(15) носит формальный характер, поскольку законность всех про-
деланных при выводе (7), (15) операций осталась необоснованной;
строгий вывод (7), (15) см. в работе [35].
В силу теоремы 1.4 оптимальное решение а=и*(/) задачи
(1) —(5) существует, а согласно теореме 2.1.3 и формуле (16) для
оптимальности и* (t) необходимо и достаточно, чтобы
т
^(lJ,^)[u{n-ur(t)\dt>Oy
о
j (х (s, Г, и*) - у (s)) (х (s, Т, и) - х (s, Г, iO) ds >0
о
при всех u=u(t)^U.
Опираясь на результаты § 5, опишем метод условного гради-
ента для приближенного решения задачи (1)—(5). Пусть un(t),
0^t^\T(n^0) известно. Определим un(t) из условия
т _ т
Г 4j5(/, /, ил) un it) dt = min f ty (/, /, un) и (t) dty
i ^u i
где \|)(5, tf un) — решение задачи (10)—(12) при u=un. В рас-
сматриваемом случае un(t) легко выписывается в явном виде
или
*»-{_;;
1, если i|)(/, t, и„)<0,
если *(/, t, «„)>;о,-.о:<*<7\
Далее, Г полагаем un+i (t) = ип (t) + ап [ип (t) — ип (t)\, 0 < t < Т, где
a„ = min{l;a;}>0,
т _
„•_ __Ь
2 J \x(s, Т, un) — x(s, Т, и„) \*ds

§ 6] Оптимальное управление процессом нагрева стержня 299
J [х (s, 7\ ип) - у (s)] [х (s, Tt ип) — x(sfT, ип)\ ds
]\x(s,T.un)-x(s, T,un)\2ds
о
>0'
0>слиад = 0 или x(s, 7\ un) = x(s9 Т9 ип)9 то un(t) = um(t)t *0<*<Г,
— оптимальное решение задачи (1)—(5), и итерации на этом закан-
чиваются). Сходимость этого метода следует из теоремы 2.3.
Кратко остановимся также на одном из вариантов метода
проекции градиента. Предварительно заметим, что в качестве кон-
станты Липшица L для градиента J'(u) здесь можно взять
L=v. Тогда метод проекции градиента для задачи (1)—(5)
будет заключаться в построении последовательности {un(t)}czU
по правилу
Ин-1 (0 = Ри (ип (0 - anv$ (U, ип)) =
"п{t) — <Wt|>(/, t9 ип)9 если |ип(t) — anvty(lf t9 un)|< 1,
_ И, если un(t) — anv^[(l9 t9 un)>\9
— 1, если un(t) — anvty(l9 t9 un)<— 1,
2
где^ая выбирается из условия е1<а„< ; е19 г —параметры
v —j~k*e
о
алгоритма, выбираемые вычислителем, 0 < гг < , е > 0.
В частности, возможно е = ——, гх = ап = .
Более общие задачи оптимального управления для параболи-
ческих уравнений и формулы для градиентов см. в работе [35].
Упражнения. 1. Пусть дан функционал
J(u) = $j\u(t)\*dt + 6l\x(stT)-y(s)\*ds
о о
при условиях (2) — (4), где р, б=constat), у(s) — заданная не-
прерывная функция. Требуется:
а) доказать, что при Р>0 функционал J (и) сильно выпуклый
в МО, Т];
б) убедиться, что градиент этого функционала в L2[0, Т] име-
ет вид
J'(u) = 2$u(t) + vty(l,t9u)9 tp<t<T9
где \J)(s, /, и) — решение задачи (10) —(12) при c(s) =
= 26[*(s, Т9 и)— y(s)]9 O^s^l;

300 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. б
в) дать описание метода скорейшего спуска для минимизации
J (и) при условиях (2) —(4), t/=L2[0, Г];
г) дать описание методов условного градиента, проекции гра-
диента для минимизации J (и) при условиях (2) — (5);
д) доказать, что точка u*(t) минимизирует J (и) при условиях
(2) —(5) тогда и только тогда, когда
Я(Ч>(/, U а*), а*(0) = пйпЯ(*(/,, tf) а)
iei<i
где
Указание. Заметить, что Я(^, и) выпукла по щ
/ (и) = —iLL4L2L-11t и воспользоваться теоремой 2.1.3 (ср.
ди
с работой [105]).
2. Пусть требуется минимизировать функционал /(а) =
т
= \u2(t)dt при условиях (2) —(5), и, кроме того, *(s, Г, a) =y(s)>
о
0^5^|/, где # (5) — заданная функция. Укажите примеры штраф-
ных функционалов на условие x(s9 Г, u) = y(s), O^s^1/. Рассмот-
рите случай
Pk(u) = k§\x(s,T,u)-y(s)\*ds
о
и укажите методы минимизации функционала /&(и) =/(w) +Pft(a)
при условиях (2) — (5).
3. Как ввести в задаче (1) — (5) штрафной функционал на огра-
ничение sup|jc(s, /)|< 1? Рассмотрите
Q
Pk(u) = k[[\max{x(stt)—l;0}\2dsdt.
§ 7. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПРОЦЕССОМ
г КОЛЕБАНИЯ СТРУНЫ
Пусть имеется однородная упругая гибкая струна O^s^i/
длины / с закрепленными концами, на которую действует внешняя
сила u=.u(s9 t). Требуется, управляя внешними силами, к задан-
ному моменту Т привести струну в состояние, как можно мало
отличающееся от заданного состояния (например, состояния по-
коя) [35,40, 162,227,270].
Математическая формулировка этой задачи: минимизировать
функционал

§ Т\ Оптимальное управление процессом колебания струны 301
J(u) = Pi$\xt(s,T,u)-y0(s)\*ds + p0§\x(s,T,u)-y1(s)\*ds,(l)
о о
при условиях
*« = *„ + "(М); (s,/)€Q = {0<s</, 0<t<T}, (2>
x(Ott) = *(l,t) = 0, 0<t<T, (3)
х (s, 0) = ф0 (s), xt (s, 0) = (ft (s), 0 <s < /, (4>
u = u(s,t)eu, (5)
где t/ — заданное выпуклое ограниченное замкнутое множество из
Wil)(Q); <Pi(s), yt(s) (i=0, 1) —заданные функции на 0<></,
Фо (*), У* (*) 6 WP [0, /]; ф1 (s), У1 (s) 6 W? [0, /], Ф, (0) = % (/) =
= ^(0)=^(/) = о (t = o,i); ^=-1-,^ = -^-,
*.. = "ff; Ро, Рх = const >о, pg + р?>о.
OS2
Здесь n4p)(G) пространство Соболева [210} функций 2 = 2 (%,..»
..., sm), определенных на множестве G cz £m, обладающих всеми
обобщенными частными производными до порядка р включительно
и имеющих конечную норму
G 0<r1+r,+...+rm<p m
Пространство W?2P)(G) является гильбертовым со скалярным произве-
дением
<*• %><*> = J ( L ,*...*'« ' а* ...ал. J *'
В частности, в .UTj1* (Q) норма имеет вид
i"(«,0llw(.)<Q)=(ll"«f,(Q) + ll"sl!,(Q) + l"<l,(Q))V*
В
^} [0. Л : II Фа (5) 11^2»[0(Ч = (И Фо (S) 11ю.ч + В Фо <^> ^.to./l +" < (^ t.[o.i] )V^
Заметим также, что согласно теоремам вложения Соболева [210]
пространство Wip)[0,1] состоит из (р— 1) раз непрерывно лиффе-

302 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
ренцируемых функций <p(s), у которых производная ф^"1)^)
абсолютно непрерывна, a qt&(s)^L2[0t I].
Итак, будем рассматривать задачу (1) — (5). Отметим, что в
частном случае, когда j/o(5)=J/i(s)=0 на [0, /], р0=р1 = 1 мы име-
ем дело с задачей о наилучшем успокоении струны к моменту Т;
если же при этом inf J(u) = 0f то можно говорить о полном
успокоении струны в момент 7\
Под обобщенным решением задачи (2) — (4), соответствующим
управлению и= u(s,t)(i Wil) (Q), будем понимать функцию
x(s, t)=x(s9 t9 и), такую, что:
1) x(s,t)ewll)(Q);
2) граничные условия (3) удовлетворяются в среднем, т. е.
г
f*2(s, t)dt-*0 при s-> + 0 и s-W —0;
о
3) начальное условие x(st 0) = q>o(s) также удовлетворяется в
среднем, т. е. t\x(sft) — <po(s)|2ds-*0 при /->• + ();
о
4) справедливо интегральное тоэвдество
JФх(5) л (5, 0)ds + f J[xti\t—xsr\s+ui\]dsdt = 0
о Q
при всех Ti = т] (s, t) € Wix) (Q), л (0, t) = r\ (/, t) - t| & T) = 0.
Пользуясь методикой, используемой в работе [150], можно
доказать, что при всех
"(M)6MQ), <Pi(s)€I2[0,/], ФоООб^'Чо,/], Фо(0) = Ф0(0 = 0
решение задачи (2) — (4) существует, единственно и удовлетворяет
неравенству
sup (( |x(s, t)\*ds)4' + \\x\\w{{) <C0(|Mk,(Q) +
+}bl^yJM + totkjM); c0=!const>o. (6)
А если же функция и (s, t) 6 Iff (Q),>o (*) 6 Wf [0, /J, 9i (s) € Wl" [0,1]
<рД0) = <р< (/) =o (i = 0, 1), то можно показать, что x(s, t) непрерыв-
на в Q, принадлежит W%* (Q), при каждом t определены значения
xt(s, t) почти всюду на [0,1], *,€М°> I], и x(s,t) непрерывна по t
в норме LJ0, /]; кроме того, справедлива оценка

§ 7] Оптимальное управление процессом колебания струны 303
0^Pr[Po JI^,OliA+PiJk(s.OliA]i/' + Nw«o(Q)<
Ci = const>0, независимая от и, <р0, <рь
Задача (1) — (5) является частным случаем задачи (5.2). Что-
бы убедиться в этом, достаточно в (5.1) положить
Х=Ь2[09 1]XL2[0, /] — пространство пар функций
z(s) = (z0(s); z^s)); y(s) - (y0(s); yt(s))f ... ;
*i(«). yds)eL2[0,l] (1 = 0, 1)
со скалярным произведением l
i i
(*,y)x = $o§y0(s)z0(s)ds + $1§y1(s)z1(s)ds
о 0
и с нормой
далее:
x (и) = (х (s, Г, и); xt (s, Г, а)) € Х\ х (0) = (х (s, Г, 0); *, (s, Г, 0)),
где x(s, Г, 0) — решение задачи (2) —(4) при и(s, t)=0\ Ки=
= (y(s9 Г, и); yt(s, T9u))f где г/(5, *, и) —решение задачи (2) —(4)
при (p0(s)ss<pi(s)s=0, причем оператор К, действующий из Щ (Q)
в X=L2[0t l]XL2[Q, /], очевидно, линеен, а его ограниченность
вытекает из оценки (7). С использованием нормы в X и принятых
обозначений функционал (1) запишется в виде J(u) = \\x(u) — у||£,
.пе y=>(yi(s); yo(s)).
Из результатов § 5 тогда вытекает, что функционал (1) при
условиях (2) — (5) выпуклый и дважды непрерывно дифференци-
руемый на (/, причем градиент его удовлетворяет условию Лип-
шица с константой L=2||/CH2<2C2.
Пусть
и=й(М)ио= v(s, t) = u (s, t) + h(s, t) e W{2] (Q),
и пусть
x(s, t, u), x(s, t, v) = x(s, t, u) + Ax(s, 0—
1 Здесь считаем po>0, Pi>0. О случаях Po=0 или pi=0 см. замечание в
конце параграфа.

304 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. 6
соответствующие этим управлениям решения краевой задачи
(2) —(4). Приращение функционала тогда запишется в виде
J(u + h)-J(u) = 2V0§[x(s,T,u)-yi(s)]/Sjc(sfT)ds +
о
+ 2РХ j [Xt («, t, и) - y0 (8)] Д*, (89 T)ds +
0
+ P# j|Ax(s,7')|2dS + pi||^(s,r)|2ds. (8)
о _p
Так как функция Ддс($, f) является решением краевой задачи
(2)—(4) при q>o(s)sscp^s)s=0, a=A(s, t)y то к &x(s9 t) применима
оценке (7) и поэтому
P0J|Aa:(s, m^rfs + P^ j |А^(^ ^)12^ = 1|Л^(^^)йлг<:С?11Л||^с1)(С).
0 0 2
Это значит, что первый дифференциал функционала (1) при усло-
виях (2) — (4) имеет вид
(/' (и), К) = 2(х(и) — у9 x(u+h)-x(u))x =
i
= 2р0 J [х (в, Т,и)-У1 (8)] Ах (8, T)ds +
о
I
+ 2рх J [xt (st 7, к) - у0 (s)] Д*, (5, T) ds. (9)
о
На практике может оказаться более удобным следующее вы-
ражение для первого дифференциала:
(/' (и), А) = f f *(s, *, a)fc(sf *)**. (Ю)
где ty(s, /, «) = ^J)(5, t) является обобщенным решением краевой за-
дачи
bt = bs, (M)€Q, (И)
№ 0 = 4>(U) = 0, 0<*<7\ (12)
^(s,T) = cJs),-^s,T) = -c0(s), 0<s</, (13)
где
c0(s) = 2p0[*(s, Г, и) — уг(8)]9 cl(s) = 2$l[xt(st 7\и) —ye(s)l,
0<5</. (14)

§ 7] Оптимальное управление процессом колебания струны 305
В самом деле, учитывая условия для Аде (5, t) и (11) — (14), из (9)
имеем
(Г (к), К) = [ c0(s)bx(s, T)ds+ [c^lbXiis, T)ds =
о 0
= j [- * («, T) A* (s9 T) + г|> (s, 7) Аде, (s,"J)] Л =
о
/ T
= fds f —(— ^A* + i|>A*,)# = ff(—ф^л: + фАл:«)й^ =
0 0 Q
T
= fJ (- 4>ssA* + №*ss + Wdsdt = J (- t|>sA* + фАлГз) IД dt +
+ Cf#<&# = ff*(*. t,u)h(s, t)dsdt. (15)
Таким образом, для вычисления дифференциала функционала
(1) в точке w=a(s,/)6l^21,(Q) при условиях (2) — (4) требуется
последовательно решить краевые задачи (2) — (4) и (11) — (14).
Для приближенного решения этих краевых задач обычно применя-
ют какие-либо разностные методы [20,* 207, 227], для вычисления
интегралов (1), (10) можно пользоваться квадратурными форму-
лами [19].
Заметим, что приведенное выше доказательство равенства
(15) носит формальный характер: строгий вывод (15) может быть
осуществлен, например, с помощью методики, используемой в ра-
боте [150].
В силу теоремы 1.4 решение u=u*(t) задачи (1) —(5) суще-
ствует, и согласно теореме 2.1.3 и формулам (9) — (10) для опти-
мальности u*(t) необходимо и достаточно, чтобы
fj*(s,U*)["(s,/)-w*(s, t)]dsdt = 2(x(u*)~y, x(u) — x(u*))x>0
u(s,t)eu.
Опираясь,на результаты § 5, опишем метод условного гради-
ента для приближенного решения задачи (1) — (5). Пусть нп(з, 0»
(s, /)eQ (Л^0) известно. Определим un(s, t) из условия
f f i|> (s, t, un) un (s, t) dsdt = min f Г -ф (s, t, un) и (s, t) dsdt, (16)

306 МЕТОДЫ МИНИМИЗАЦИИ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [Гл. б
где i|)(s, t, ип) — решение задачи (11) —(14) при u = un(s9t). Далее
полагаем
«п+1 (s, t) = ыл (s, t) + art К (s, t) —un (s, *)], (s, t) € Q,
где an = min{l,a;}>0, с£ =
-H*(s, *> Цц)[ия (0- un(f)]dsdt
^2Р0Я I *(*. *; «fa)-*(«. t, tiu) \2dsdt+2h Я| *,(s.', u*)-**(s, *, tt||) |2d*tf ""
Q Q
2\\x(un)-x(un)\\2x
(если a* = 0 или x(sy t, un)=x(s, t,Un), то un(s, t)=u*(s, t) —
оптимальное решение задачи (1) — (5), и итерации на этом закан-
чиваются). Сходимость этого метода следует из теоремы 2.3.
Заметим, что из формулы (10) можно получить формулу, бо-
лее удобную для использования в пространстве W^HQ)-
ww.4-jj[*»+-5-5-+-«{-^-]*«-(..v«-<l7>
где g=g(s9 t) — решение задачи Неймана для эллиптического
уравнения
-3" + -|г— *—*(*.'). (S>')€Q, (18)
*g(0.0 = dg(l,t) 0<f<T; dg(s'0) = W-V = 0, Q<«/.
ds ds dt dt
(19)
Формальное доказательство равенства (17) легко получается под-
становкой выражения ip(s, t) из (18) в (10) с последующим инте-
грированием по частям с учетом граничных условий (19). Если,
например,
l/={«-«(e,0€l^I>(Q):|«lwii)W)<l>,
то для определения un(s9 t) вместо (16) удобнее использовать
формулу (17), откуда с помощью неравенства Коши — Буняков-
ского легко получаем un(s, t) = g(s, t)\g(s, 0i^(i)(Q)-

§ 7] Оптимальное управление процессом колебания струны 307
Замечание. Все изложение этого параграфа велось для
случая р0>0, pi>0. Если р0=0 или Pi = 0, ро + Р?>0, то в (5.1)
надо принять В — W^iQ), X=L2[0, /]; причем
x(u) = x(s9 7\ и), *(0) = *(s, 7,0), Ku = y(s9T,u)
при pi = 0, Ро=1, а если же Pi = l, ро=0, то x(u)=xt(st Г, и)г
x(0)=xt(st Г, 0), Ku=yt(s9 Tt и). Здесь y(s9 Г, и) —решение за-
дачи (2) —(4) npircpo(s)=<Pi(s)sO, u=u(s, t); x(s9 t% 0) — реше-
ние (2) — (4) при u=0. Заметим также, что если Pi=0, Ро=1, то
в (1) — (5) достаточно требовать
t/c=L2(Q), ФхФбМО,/], Фо(5)€^°[0,/], Фо(0) = Фо(0 = 0,
а вместо (7) пользоваться оценкой (6). Предлагаем читателю
подробно рассмотреть эти случаи самостоятельно.
Формулы для градиентов функционалов, определенных на
решениях более общих гиперболических уравнений, а также других
классов уравнений и систем, приведены в работах [35, 102]. Раз-
личные аспекты задач оптимального управления системами, опи-
сываемыми уравнениями с частными производными, рассмотрены
в работах [35, 37, 38, 40—43, 49—51, 53, 62, 71, 72, 76—78, 90—
92, 102, 104—108, 121, 122, 124, 135, 136,151, 158, 159, 162, 163,
173, 183—185, 202, 203, 208, 209, 237, 270] и др.
Упражнения. 1. Описать метод условного градиента для зада-
чи (1) — (5) для случаев а) Ро=1, Pi=0 и б) Ро=0, Pi = l.
2. Пусть ЛИ = ^(") + М<Ф, 0ll^(i)(Q), где p2 = const>0, J(u)
взят из (1). Доказать, что функционал J\(u) при условиях (2) —
(5) является сильно выпуклым в W^iQ). Описать метод услов-
ного градиента для минимизации J\(u) при условиях (2) — (5).

Глава 7
Методы решения задач быстродействия
Задача быстродействия заключается в переводе управляемого
объекта или процесса из некоторого множества начальных состоя-
ний в заданное множество конечных состояний за минимальный
промежуток времени. К таким задачам относятся задачи о быст-
рейшем перелете из одной точки пространства в другую точку,
о быстрейшем нагреве стержня, о быстрейшем успокоении струны
и др. Эти и многие другие прикладные задачи быстродействия мо-
гут трактоваться как частный случай более общей задачи быстро-
действия, когда управления и траектории представляют собой эле-
менты некоторых подходящим образом выбранных функциональ-
ных пространств.
Одна из таких достаточно общих моделей задачи быстродейст-
вия, связанная с линейными системами, будет предложена и иссле-
дована ниже в § 1—3; приложения к конкретным задачам быстро-
действия, связанными с линейными системами обыкновенных диф-
ференциальных уравнений и некоторыми уравнениями с частными
производными, будут рассмотрены в § 4. Литература, посвященная
задачам быстродействия, обширна; упомянем работы [5, 8, 11, 24,
27, 35, 40—44, 50—53, 57, 59, 62, 75, 80, 94, 107, 108, ИЗ, 115,
121—123, 135, 136, 139, 140, 142, 157— 162, 171, 176, 180, 183, 195,
197, 198, 200, 202, 206, 234, 236, 238, 263, 264, 268, 270], в которых
содержатся методы решения таких задач или рассматриваются
другие важные вопросы, такие, как существование и единствен-
ность решения, необходимые и достаточные условия оптимальности
и др. Систематическое исследование методов решения достаточно
широкого класса задач быстродействия, когда имеются фазовые
ограничения и само фазовое пространство является бесконечно-
мерным (в частности, задач, связанных с уравнениями в частных
производных) проведено в работах [50, 51, 53, 121, 122]; краткий
обзор методов см. в конце § 3.
§ 1. ПОСТАНОВКА ЗАДАЧИ
1. Для иллюстрации последующих более общих постановок
задач сначала приведем задачу быстродействия, связанную с ли-
нейными системами обыкновенных дифференциальных уравнений.
А именно, пусть движение управляемого объекта описывается
уравнениями

§ п
Постановка задачи
309
x = A(x)x + B(x)u + f(x)9 x>t0t x(t0) = xQ, (1)
где х=(х\ ..., хп)9 и=(и\ ..., иг); А(х)9 Я(т), /(т) — заданные
матрицы порядка пХп9 пХг и nXl соответственно, элементы ко-
торых определены при x^to и кусочно-непр.ерывны на каждом
конечном отрезке to^x^lt; х — время; начальный момент t0 и
начальная точка х0 предполагаются известными.
Пусть заданы функции аг(т), Рг(т), t=l, 2, ..., г, стределенные
при всех x^t0 и на каждом конечном отрезке /о^т^^<оо, удов-
летворяющие неравенству аг(т)^Рг(т) почти всюду и принадлежа-
щие W[t0i t] (например, аг(т)=—1, р*(т) = + 1, T>tf0,t=l,2,...,r).
Для каждого t9 t0^t<+ оо, рассмотрим множество
и, = {и = и (т) 6 LV ft,, t]: щ (т) < и* (х) < р< (т), i = 1, 2, г,.
почти всюду при *0<т</}. (2)
Нетрудно видеть, что Ut выпукло, замкнуто, ограничено и, следо-
вательно, слабо компактно в Li [tQJ i].
Каждому u=u(x)^Ut соответствует и притом единственная
траектория х=х(х9 и), /о^т^#, системы (1). Напоминаем, что
траектория или решение х(х, и) задачи (1) представляет собой
абсолютно непрерывную вектор-функцию на [t0> t]9 удовлетворяю-
щую интегральному уравнению
т
х(х)= f [A(s)x{s) + B(s)u(s) + f(s)]ds + x0, fe <т «. (3)
Пусть в пространстве En задана точка у. Задача быстродей-
ствия заключается в том, чтобы найти такие Т* и u* = u*(x)^UT*,
чтобы х(Т*, и*)=у9 причем для любых других Т и u = u(x)^UT,
для которых
х(Т9и)=у (4)
было справедливо неравенство Т^Т*.
Отметим следующие свойства траекторий системы (1), когда
u = u(x)^Ut.
1. Имеет место представление
х (т, и) = х (т, и0) + у{х9и — и0)9 t0 < т <*, (5)
где х(х9 и0) — решение задачи (1) при некотором u0=u0{x)^Ut
(например, u0(x) = (ai(x)9 ..., Мт)), ^о^т^О» а У(х> и—щ) —
решение (1), когда f(t)=0, х0=0 и вместо и взято и(х)—и0(х).
При желании можно воспользоваться известной формулой Коши
и выписать явное выражение для х(х9 и0) и у{х9 и—Uq)

310 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ [Гл. 7
V
х (т, щ) = Ф (т, *0) *0 + f Ф (т, s) [В (s) u0 (s) + / (s)] ds,
х
у(х,и — и0) = §<b(x,s)B(s)[u(s) — u0(s)]dst *0<т<*,
и
где матрица Ф(т, s) определяется из условий
d<b{x, s)
dx
= Л(Т)Ф(Т,5), 0>(s,S) = £,
Е — единичная матрица, sy x^to. Однако матрица Ф(т, s) лишь
в редких случаях может быть найдена в явном виде, и поэтому
указанными представлениями для дс(т, и0) и у(х, и—tio) не будем
пользоваться — здесь нам важен сам факт существования пред-
ставления (5).
2. Справедлива оценка
sup \x(xtu)\<Ct(u), (6)
где
Cdu) = [\x0\+sup\\B(x)\\ \\u(x)\dx +
+ Uf(r)\dx]exp{ sup \A(x)\\(t-t0)}9
*•
которая легко получается из выражения (3) с помощью
леммы 6.3.1. В частности, для у(х, и—щ) из представления (5)
имеем
sup \y(x,u-u0)\<Kt ( \\u(x)-u0(x)\*dx)tf\ (7)
где
Kt= sup \\B(x)\\(t-toy/*-exp{ sup \\A(x)\\(t-t0)}
U<x<t t^x<t
не зависит от и, и0 6 Ut.
3. Справедлива оценка
sup\x(xlt и) — х(х2, и)\<£\хг — х2\Ч*М0 (8)
u£Ut
где
Af, = U —*0|V. sup ||Л(т)|| sup Ct(u) +

§ п
Постановка эадаяи
3U
+ sup |В(т)| sup ||и,иг) _ + |/Ы„ п<«>.
Для получения этой оценки достаточно выразить разность
х(х\, и)—x(f2, и) с помощью (3) и затем воспользоваться нера-
венством Коши — Буняковского, оценкой (6) и ограниченностью
Ut в Lir)[t0ft].
4. Если uk(x)€Utt k= 1, 2, ... , и uk(x) слабо в L^I'o» *] схо"
дится к и = и (т) 6£/*, то
sup \x(x,uk) — x(xtu)\-+0(k-+oo). (9)
В самом деле, из оценок (6), (8) следует равномерная ограничен-
ность и равностепенная непрерывность семейства функций
{*(т, uh)} на t^x^t, й=1, 2, ... По теореме Арцела [137] тогда
существует последовательность {x(xt ukfi)}t сходящаяся равномер-
но на [*о, t] к непрерывной функции х(х). Переходя к пределу
при п-^оо в тождестве
*(т, ц^)- hA(s)x(s,ukn) + B(s)ukn(s) + f(s)]ds + x0, t0<x<t,
С
придем к тождеству (3), т. е. х(х)=х(х, и) — решение задачи (1)
при и=и(х). В силу единственности решения задачи (1) получа-
ем, что вся последовательность {х(х9 uk)} сходится к х(х, и) рав-
номерно на [t0, t].
2. Оказывается, перечисленные свойства множеств управле-
ний и траекторий задачи (1) — (4) в том или ином виде присущи
многим другим важнейшим классам задач быстродействия, свя-
занным с линейными уравнениями с частными производными,
интегро-дифференциальными уравнениями и др. Такие задачи мо-
гут быть истолкованы как задачи быстродействия в подходящим
образом выбранных функциональных пространствах и допускают
изучение с общей точки зрения, отвлекаясь от природы управляе-
мого объекта. Здесь мы предложим одну модель задачи быстро-
действия, охватывающую ряд важных прикладных задач быстро-
действия; более общие модели с учетом фазовых ограничений рас-
смотрены \в работах [50, 53, 121, 122].
Пусть / — время, tQ — некоторое заданное начало отсчета
времени t^t0. Пусть при каждом t, и<Л,< + <х>, задано множество
Ut функций и=и(т), определенных при to^x^t и являющихся
элементами некоторого банахова пространства Ви причем сами
значения и(х) при каждом те[^0, Ц принадлежат некоторому ли-
нейному пространству. Множества Ut будем называть множества-
ми управлений, элемент и=и(х) из Ut — управлением. Будем

312
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ
[Гл. 7
предполагать, что множества Ut удовлетворяют следующим усло-
виям I—III.
I. Множество Ut выпукло и слабо компактно в Bt при каж-
дом t, t0<i<+ 00.
II. Если u=u(x)^Utt то управление и(х), рассмотренное на
отрезке ^о^т^'5 при любом 5, t0<s^tt является элементом из Us,
т. е. «сужение» управления и(х) из Ut на отрезок [/о, s]^[^o, ^]
является управлением из Us.
III. Существует число Д>0, такое, что при всех /, *<><*<+ °°.
любое управление u(x)^Ut можно доопределить на отрезке
[t9 t+A] так, чтобы продолженное управление было элемен-
том Ut+A.
Очевидно, множество Ut из (2) удовлетворяет всем условиям
I—III, а именно, здесь Bt = Li [t0, t], всякое управление и(т)е
^Ut может быть продолжено при всех x>t, например, так: и{х) =
■'{ot(r), ..., аг(т)}, и в качестве А можно взять любое положи-
тельное число.
Другим примером множества Ut со свойствами I—III является
шар в Zjr) [А» П при любом конечном t>t0:
Ut = {u = u (т) 64Р [t0, t]: || и (т) - и0 (т) \\^)[ип < #}, (10)
где и0(х) — заданная функция из Lir)[t09 t], R>0 — заданная
константа; всякое u(x)^Ut здесь может быть продолжено при
x>t< например, так: и(х)?=щ(х).
Возможно, что пространства Bt и множества Ut не зависят
от t. Такая ситуация возникает, когда управлением служат какие-
либо параметры, которые в начале движения должны быть как-то
выбраны из некоторого множества Ut=U и в процессе движения
остаются неизменными. Условия II, III здесь, очевидно, выполня-
ются всегда.
Итак, пусть пространства Bt и множества Ut со свойствами
I—III заданы при каждом t>t0. Далее, пусть при каждом t9 t0<
</< + оо, задано линейное пространство Lt функций х(т), опреде-
ленных при t0^x^t, причем для каждого фиксированного
tg[4 t] значение этих функций является элементом некоторого
гильбертова пространства X (пространство X не зависит от t, т).
Пространство Lt будем называть пространством траекторий, а
функции х(х) из Lt — траекториями.
Пусть Хо — некоторая заданная точка из X, и пусть при
каждом t>t0 любому управлению u^Ut и точке х0 поставлена
в соответствие некоторая траектория х(х)=х(х, u)^~Lu удовлетво-
ряющая начальному условию x(t0> и)=х0. Будем предполагать,
что выполнены следующие условия IV—VII.

§ п
Постановка задачи
313
IV. Если u=u(t)^Uu v = v(x)^U8> причем u(x)==v(%) при
<o^T^la=min{/, s}, то дг(т, и)=х(ху v) при to^x^a для любых
t, s>t0.
V. Для любого /, to<t< + oo, существует управление Uq-=
= Uo(x)^Uu такое, что при всех u = u(x)^Ut справедливо пред-
ставление
х(х, и) = х(х, и0) + К(х)(и — u0)t t0<Ci<t, (11)
где x(t0i и0)=хо, К(х) — однопараметрическое семейство линей-
ных операторов, действующих из Ux в LTt t0<x<Ct, причем
\\K(t)(u-u0)\\x<Kt\\u-u0\\Bt
для любого u^Uu Kt>0 — постоянная, не зависящая от u^Ut
(ср. с (5), (7)). Сразу же заметим, что нам будет важен сам факт
существования представления (11); при описании и исследовании
алгоритмов оператор К(х) не будет использован.
VI. Если uh^Uu k=l, 2, ..., и {uk} сходится к u^Ut слабо в
В и то х(т, uk)-+x(x, и) слабо в X при всех те[/о, t] и всех t>t0
(ср. с (9)).
VII..Траектории х(х, u)^Lt непрерывны по те[^о, t] равно-
мерно по u^Uty т. е.
sup||x(x + Дт, и) — гх(%, ы)|| = е, (|Дт|, т)-*0 при
ueut
Лт-^0; x,z + bx£[t0,t]
(ср. с (8)).
Как видим, траектории системы (1) на множестве (2) или
(10) удовлетворяют всем условиям IV—VII (и даже несколько
более сильным условиям), если принять за Lt линейное простран-
ство абсолютно-непрерывных функций на |70, t], Х=Еп. Это сле-
дует из соотношений (5), (7) — (9). Примеры других управляемых
объектов со свойствами I—VIT см. ниже в § 4.
Итак, пусть имеется управляемый объект (процесс) {х(х, и)9
u&Ut, t>t0} со свойствами I—VII. Пусть в пространстве X задана
точка у. Задача быстродействия заключается в том, чтобы найти
такие Г* и и* = а*(т)е£/г*, что х(Т*, и*)=у, причем для любых
других Т и u^UT, для которых х(Т, и)=у справедливо неравенст-
во Г^Т1*. Такие Т* и u*(x)£U[t* будем называть оптимальным
решением задачи быстродействия, ~Т* — оптимальным временем,
и*(х) — оптимальным управлением, х(х, и*) — оптимальной тра-
екторией. Прежде чем переходить к исследованию поставленной
задачи быстродействия, сделаем
Замечание. В сформулированной задаче быстродействия
начальное условие x(t0, и) =xq мы считали заданным. Однако

314
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ
\Гл. Т
встречаются задачи быстродействия, в которых начальное усло-
вие хо заранее неизвестно и подлежит выбору из некоторого за-
данного множества Х/,СХ. В таких зада_чах в качестве управле-
ния следует взять_лару (#(т), *о)=и(т), to^x^t, вместо
множества Ut взятьUt = UtxXt0, вместо Bt — пространство Bt =
= BtxX. Если множество Xt0 выпукло, замкнуто и ограничена
в Ху a Ut удовлетворяет условиям I—III, то Ut также будет удов-
летворять условиям I—III в Bt. В этом случае в условиях IV—VII
всюду вместо Uu естественно, надо писать Ut. Результаты §§ 2, 3
останутся в силе и для такой задачи.
Упражнение. Пусть управляемый объект описывается условия-
ми (1), где м=ш=(ш1, ..., wr) является параметром, выбираемым
из некоторого множества WczEr в начале движения и в дальней-
шем не меняющийся. Показать, что если W — выпуклое замкнутое
ограниченное множество из Ег, то все условия I—VII для такого
управляемого объекта выполнены.
Указание. Принять Ut=W, Bt=Er, при всех t>t0, Х=Еп —
линейное пространство непрерывных кусочно-гладких на отрезке
[/о, t] траекторий.
§ 2. ВСПОМОГАТЕЛЬНЫЙ АППАРАТ. КРИТЕРИИ УПРАВЛЯЕМОСТИ
И ОПТИМАЛЬНОСТИ
Для исследования поставленной задачи быстродействия полез-
но рассмотреть множество Xt правых концов x(t, а), всевозмож-
ных траекторий *(т, и), to^i^t, когда и=и(т) пробегает все
множество Ut, т. е* Xt=x(t, Ut), t>t0. При t=t0 естественно при-
нять Xt0 = {х0} — это множество в данном случае состоит из
одной начальной точки Хо.
Лемма I. Если выполнены условия I, V, VI, то множество
Xt выпукло, замкнуто, ограничено в X и, следовательно, слабо
компактно в X.
Доказательство. Нетрудно видеть, что из представления
(1.11) вытекает* тождество х(%> сш+(1—a)v)=ax(xy и) +
+ (1—а)х(гу v), to^iT^t, справедливое при всех и, v^Uu t>t0, и
любых вещественных а. Отсюда и из выпуклости Ut следует вы-
пуклость Xt. Ограниченность множества Xt является следствием
ограниченности Ut и свойства V:
И/, u)\\x<£\\x(ty и0)\\х+ Kt\\u — u0\\Bt<\\x(ty uJh + KtD,
где
D= sup ||и — 1>|л— диаметр множества Ut.
u,vSUt
Докажем замкнутость Xt. Пусть Xk^Xt и Х\ сходится к х по нор-
ме X. Покажем, что x^Xt. По определению х^ существуют u^^Uu

#2}
Критерии управляемости и оптимальности,
315
такие, что Xk=x(tt ик), k=l, 2, Так как Ut слабо компактно, то
существует подпоследовательность {ukn}> слабо сходящаяся к не-
которому u^Ut. Однако по условию VI xkn =x(tt ukn)-+x(t, u)^Xt
слабо в X. Следовательно, x(t, u)=x^Xt, что и требовалось. Сла-
бая компактность Xt следует из теоремы 6.1.2. J^
При изучении задачи быстродействия большую роль играет
функционал
М (с, t) = min (с, х — у)х = min (с, х (t, и) — у)х =
x£xt ueut
= mln(ctx)x — (cyy)x, (1)
x£Xt
где с — некоторый -элемент из X. Сразу же заметим., что опреде-
ление M(ct t) корректно, так как функционал (с, х—у) слабо*
непрерывен в X по х и в силу теоремы 6.1.1 на слабо компактном
множестве Xt достигает своей нижней грани на некотором элемен-
те х = xCtt 6 Хи соответствующем управлению
и = uCtt 6 Ut: xc%i = х(t, uCii), t >tQ.
При t=t0 естественно принять M(c, t0\='(c, xo—у).
С помощью функционала М(су t) нетрудно сформулировать
один изящный критерий управляемости и оптимальности.
Определение 1. Описанный выше управляемый объект
{х(т, и), u^Uu t>t0} будем называть (у, Г)-управляемым, если
существует управление m = w(t)g(/t, такое, что соответствующая
траектория дс(т, и), /о^т^Г, удовлетворйет условию х(Т, и)=у,
или, иначе говоря, у^Хт.
Теорема 1. Пусть выполнены условия I, V, VI.. Тогда для
(У, Т)-управляемости объекта {х(т, u)t u^Uu t>t0) необходимо
и достаточно, чтобы М(с, Г)^0 при всех сеЯ", или в эквивалент-
ной форме min (с, х) < (с, у) для любого cgX Для того чтобы
x£Xj*
jT* было оптимальным временем, необходимо и достаточно, чтобы
М(су Г*)<;0 при любом с^Х и для любого t, t0^f<T*y сущест-
вовал элемент qgX, такой, что M(ct, t)>0. Иначе говоря, Т* —
минимальное время среди всех T>t0y для которых объект (у, Т)-
управляем.
Доказательство. Условия оптимальности Г* являются
прямым следствием условия (у, Г)-управляемости, поэтому доста-
точно доказать первое утверждение теоремы.
Необходимость. Пусть объект (у> Т)-управляем. Тогда
уеХт и М{су Т)= min (с, х — у)<(с, у — у) = 0
х£ХТ
при любом С^Х.

316 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ \Гл. Т
Достаточность. Пусть при некотором Т имеем М(с, Т)^.0
при любом с^Х. Покажем, что j/eXt. Предположим противное,,
т. е. y&LXT. Так как Хт замкнуто и выпукло в X, то множество
Хт и точка у строго разделимы, и согласно теореме 6.1.6 сущест-
вует такой элемент с^Ху сФО, что min (с, лг)>(с, у). Последнее
неравенство означает, что М(с, Т)>0, а это противоречит усло-
вию. А
Выясним некоторые свойства функционала M(cf t).
Лемма 2. Пусть выполнены условия I, V, VI. Тогда
М(асу t)=zaM(c, t) при любых а^О, t^t0y с^Х. (2)
При каждом фиксированном t^t0 функционал М(су t) слабо-
полунепрерывен сверху по переменной с^Х и достигает своей
верхней грани на единичном шаре G={c.:||c||^il} хотя бы в одной:
точке ct^G. *
Доказательство. Соотношение (2) следует непосредст-
венно из определения (1) М(с, t). Пусть последовательность
{съ}-+с слабо в X. Пусть М(с, t) = (cy xCtt—y), где xc,t^Xt. Тогда
M(ckyt) = mm(ckyx — y)<£(ckyxCtt — y)y k = 1, 2, ...
x£X{
Отсюда при fc-M» имеем UmM(cky tf)<Af(c, t). Таким образом,
fe-*oo
М(с, t) слабо полунепрерывен сверху по с. Тогда функционал
[—М(с9 t)] слабо полунепрерывен снизу. Поскольку шар G слабо
компактен в А", то в силу теоремы 6.1.1 функционал [—А!(с, t)]
достигает своей нижней грани G хотя бы в одной точке с*е(/.
Тогда
M(ctt t)= sup М(су t). А
Положим р(t) = max М(с, t). Так как О 6 б, М(О, t) = О, то
c£G
р(*) >0 при всех t > t0.
С помощью функции р(/) критериям (уу Г)-управляемости и
оптимальности можно придать простой вид.
Теорема 2. Пусть выполнены условия I, V, VI. Тогда для
(у, Г)-управляемости объекта {дг(т, и)у u^Uu t>t0} необходимо
и достаточно, чтобы р(Г)=0. Для оптимальности Г* необходимо
и достаточно, чтобы р(7,*)=0 и р(/)>0 при всех ty U^.t<T*y
т. е. иначе говоря, оптимальное время есть наименьший при
t^t0 корень уравнения p(t) = 0.
Доказательство. Условие оптимальности Т* является
прямым следствием условия (уу Г)-управляемости, поэтому доста-
точно доказать первое утверждение теоремы.

§ 2)
Критерии управляемости и оптимальности
317
Необходимость. Если объект (у9 Г)-управляем, то соглас-
но теореме 1 М(с, Т)^.0 при любых с^Х и, следовательно,
р (Г)= maxAf(с, Г)<0. Однако, как было замечено выше,
сев
p(t)^0 при всех t^t0. Поэтому р(Г)=0.
Достаточность. Если р(Г)=0, то М(с9 Г)^р(Г)=0 при
всех c^G. В силу соотношения (2) тогда М(с, Т)^0 при всех
с^Х. По теореме 1 этого достаточно для (у, Г)-управляемости. А
Таким образом, для решения задачи быстродействия надо
уметь находить наименьший нуль функции p(t) при t^t0. С этой
целью полезно выяснить некоторые свойства функции
р (t) = max min (с, х—у)у дать по возможности простые способы
сев xext
вычисления ее значений.
Теорема 3. Пусть выполнены условия I, V, VI. Тогда зна-
чение функции p(t) при любом t^t0 выражает собой расстояние
от точки у до множества Xt и представимо в виде
р(0 = inf \\х-у\\ = \\xt — у| = (ci9 xt — y) = M(ch t)9 (3)
x€Xt
где xt = PXt(y)—проекция точки у на множество Xtt
ct = ^*Z.y\\ при у&Х* и с* = ° ПРИ Уеxf
Если у&Хи то М(су t) достигает своего максимума на G в един-
ственной точке ct.
Доказательство. Существование'проекции xt точки у на
множество Xt следует из теоремы 2.3.1. Покажем, что пара
(cti xt)^GxXt образует седловую точку функционала (с, х—у)
переменных (с, x)eGxXt в следующем смысле:
(с, xt—y)^(cu xt—y)^(ct, х—у) при любых х^Хи c^G. (4)
Если y^Xty то xt=y, ct = Q, и неравенства (4), очевидно, выполне-
ны. Поэтому пусть y£Xt. Тогда ct=(xt—у) II**—t/lh1, и справедли-
вость левого неравенства (4) следует из неравенства Коши — Бу-
няковского:
(*, **-0)<М-11*<—#11<К—у|1 = (*<•**—у)
при всех c^G. Правое неравенство (4) равносильно (с*, х—xt)^0y
или (xt—у, х—xt)^0, x^Xt9 и является прямым следствием
свойств проекции из теоремы 2.3.1. Соотношения (4) доказаны.
Из правого неравенства (4) сразу следует
К — У\\ = (**. */ — У) = min (си х — у) = M(cti t).
xext
Из левого неравенства (4) тогда имеем

318 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ \Гл. 7
М(с, 0 = min(c, х — у)<(с, xt — y)<M(ct, t)
x£'Xf
при любом с 6 G, поэтому
p(t) = maxM(c, t) = М(си t).
cSG
Равенства (3) доказаны.
Наконец, покажем, что если у£Хи то max М (с, t) = p.(t) реа-
лизуется в единственной точке c=ct=(xt—y)\\*t—J/lh1 (это обстоя-
тельство может оказаться полезным при практическом вычислении
р(/)). В самом деле, если c^G и p(t)=M(c, t)>0, то с помощью
неравенства Коши — Буняковского имеем
0<p(t) = M(c,t) <(c,xt-y) <Й\\Ъ-У\\<МЪ-У\\ =
= (ctfxt — y) = (>(t).
Отсюда следует
(c,xt-y)=\\c\\\\xt-y\\>Oy £gfcO,
что возможно тогда и только тогда, когда c~a(xt—у)У а=const.
Но, очевидно, ||с|| = 1, поэтому a=\\xt—ylh1 и c=ct. А
Полученная ъ этой теореме формула (3) позволяет использо-
вать при вычислении р(/) методы из .§ 6.5. В самом деле, функ-
ционалы \\x(t, и)—у\\ и ||х(t, и)—у\\2 достигают своего минимума
на Ut на одном и том же элементе, поэтому
9Ht) = tnin\\x(tiu)-yf.
ueut
Тем самым задача вычисления p2(t) при каждом фиксированном
t>t0 совпадает с основной задачей § 6.5, и здесь применимы ме-
тоды § 6.5.
Полезно заметить, что теоремы 1—3 и лемма 2 остаются вер-
ными для любых выпуклых замкнутых ограниченных множеств
Xt из гильбертова пространства X, поскольку при доказательстве
этих утверждений происхождение множества Xt по существу не
использовалось. В частности, теоремы 1, 2 дают интересные крите-
рии принадлежности той или иной точки у^Х множеству Хи а
лемма 2 и теорема 3 позволяют получить формулу
р (t) = max min (с, х — у)
сев xext
для расстояния от точки у до множества Xt.

$ 2}
Критерии управляемости и оптимальности
319
Теперь перейдем к исследованию непрерывности М(с, t)> p(t)
по переменной t. Здесь уже существенно будет использована связь
множества Xt с управляемым объектом
{х(т, и), u£Ut, t>t0},
удовлетворяющим условиям I—VII. •
Теорема 4. Пусть управляемый объект
{х(%, и), u£Utt t>Q
удовлетворяет условиям I—VII. Тогда функционалы Af(c, /), p(t)
непрерывны по t при всех t^t0.
Доказательство. Возьмем произвольное t>t0 и условимся
рассматривать лишь те т>£0, для которых \t — т|<—, где А =
= const > 0 взята из условия III. Пусть
М (£, t) = (с, х(t, uCtt) — у), М (с, т) = (с, х(т, исл) — у).
Согласно условию III управления uCtt 6 Ut и uCtX 6 Ux можем продол-
жить на отрезок \t0, t -f I и, сохраняя за продолженными управ-
лениями их прежние обозначения с учетом условия IV, можем
считать, что х(х9 uCtt)€Xx, x(t, uCtX)£Xt. Тогда
[М(с, /)< (с, х(t, uCfX) — у), М(с, т)<(с, х(т, uCtt)—y),
поэтому
(с, х (/, uCt t) — х (т, uCt t)) <M(ct t) — M (с, т) <
< {с, X (t, UCtT) — X (T, lie*)).
С учетом условия VII отсюда имеем
\М(с, 0—М(с, т)|<||с||. sup \\x(ttu) — x(xru)\\<
<||ф,+д/2(|/-т|,0-*0
при %-+t. Непрерывность M(cf t) по t при каждом t>t0 доказана.
Если же t = to, то сразу имеем
\М(с, t0)—M(c, т)| = \(с, x0 — x(tt uCfX)\<£\\c\\\\x(t0, Uc.%) —
— Xfa^%)\\<№utv+A/2(\'t — t0\9t0)-+0 ПрИ Т-^0 + 0.
Теперь докажем непрерывность р(/) при t^t0. Пусть сначала
t>t0. Воспользуемся формулой (3) p(t) = \\xt—у\\9 где xt=x(t, щ) —
проекция у на Xt. Продолжая при необходимости управление

320 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ \Гл. 7
ut=ut{x)^Ut на [t, Н-Л]> можем считать, что *(т, щ)^Хх при
всех т, 11—т| ^ А/2. Тогда
<р(0 + ец.д/2(|< —т|,0,
и поэтому
Итр(т)<р(/).
С другой стороны, пусть p(t)=M(cu 0» cfeG. Тогда р(т)^
^М(си т) и, пользуясь непрерывностью M(ct t) по £, отсюда
имеем
limp(T)>Al(c,ff) = p(0.
Таким образом,
ИпГр (т) = lim р (т) = р (t),
что равносильно непрерывности p(t) при t>t0. Если же t=t0f
то Р(дн1*о-#ЫИ'о, ««>—iri и |P(o-p(gi =
= I \x(t., ut)-y\\-\\x(t, щ)-у\\ | <|*(f, a,) -x (t0f ut)\\ <
<8^+д/2(К —/0|,g^0 при t->to + 0. A
Теорема 5. Пусть управляемый объект {дс(т, и), u^Uu f>tQ}
удовлетворяет условиям I—VII и (у> Г)-управляем при каком-либо
Г, t0<T< + oo. Тогда задача быстродействия имеет решение.
Доказательство. При выполнении условий теоремы p(t)
непрерывна на отрезке t0^.t^.T и р(7,)=0. Тогда найдется един-
ственная точка Г*, t0<T*^DT9 такая, что р(Г*)=0, p(t)>0 при
to^t<T*. В силу теоремы 2 тогда Г* — оптимальное время,
а управление а*е£/т*, для которого \\х(Т*9 и*)—у\\=р(Т*)=09
будет оптимальным. А
При отыскании Г*^ можно использовать различные методы ре-
шения нелинейных уравнений, как например, метод деления отрез-
ка пополам, метод хорд, метод Ньютона и др. '[19]. На одном ин-
тересном обобщении метода Ньютона {66], приспособленном для
отыскания ближайшего к начальной точке нуля функции, остано-
вимся в § 4. В следующем параграфе будет изложен другой метод
нахождения оптимального времени Г*.
Упражнения. 1. Выяснить геометрический смысл теорем 1, 2,
считая Х=Е2.
2. Если выполнены условия I, V, VI, то функционал [—М (cyt)]
является выпуклым по с при любом t^t0 и для любого 1^Х су-
ществует

§*l
р-Метод
321
JM^JL^ lim *(c + e*.Q-M(c,Q = ^ ^_
где XCt t — множество всех тех xCt и для которых М (ct t) = (с, л;с, t—
—у). Доказать.
3. Пусть требуется наибыстрейшим образом перевести точку
х=(х\ х2) из положения (1, 0) в начало координат (0, 0) при ус-
ловии, что движение точки подчиняется уравнениям xl=x2t х2=иу
т^О и управление
и = и(т)€{/< = {й(т)6М°. *]:И*)|<1, 0<т<0.
Проверить выполнение условий I—VII для этой задачи; вычислить
явное выражение для функций М(с, /), р(/).
§ 3. р-МЕТОД
1. В излагаемом ниже методе важную роль играет функция
р(*), введенная в предыдущем параграфе. Поэтому этот метод бу-
дем называть р-методом.
Будем предполагать, что управляемый объект {х(т, и), u^Uu
t>t0) удовлетворяет всем условиям I—VII и (#, Г)-управляем при
каком-либо Г, t0<T< + oo. Тогда согласно теореме 2.5 задача
быстродействия имеет решение. Для отыскания ее решения пред-
лагается следующий итерационный процесс.
В качестве начального приближения возьмем t0, #о, с0=
=\(х<т-у) \\хо—у\\~1 (естественно считать, что Хофу, иначе /0 —оп-
тимальное время); р(*о) = И#о—*/У>0. Пусть известно {k— 1)-е при-
ближение (й^1), т. е.
4-ь **-i 6 Xtk_x\ ck-i = (xk-i — у) \хь-\ —у\\-\
такие, что
p(fc-i) = Aifak_lf tk-x) = \\xk-x-yl р(0>0
при
t0<t<tk-u *0<'i<..-<'ft-i<^
Так как функционал М(сь-\У t) непрерывен по t, причем
р(^1) = М(сЛ.ь 4-i)>0, М(с^и Т)<6
•(см. теорему 2.1), то найдется момент tk> такой, что
t^<tk<Ty M(Ck-u tk) = Q9 M(c^ut)>0
при ^-i</<4- Далее вычисляется
р(^) = тахЛ1(с, tk)
ceo

322 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ * (Гл. 7
и определяются такие
и* 6 Uth, хк = х (tt, ик) б Xtk, ck 6 G,
что
р(**)=Л!(сь /fe) = ll**-</ll.
.Так как р(/)>0 при /0 </</*_! по предположению,
р(0>Л«(с*-ь *)>° ПРИ **-i<*<**
в силу выбора ^, то р(/)>0 при t0^t<th. Может случиться,
что р(4)=0. В силу теоремы 2.2 тогда 4=Г* — оптимальное вре-
мя, u,h=u* — оптимальное управление, и итерационный процесс на
этом заканчивается. Если же p(th) = \\xh—#||>0, то, имея
tk,XktXtk> ck = (xk-y)\\xk-y\\-\ p{th) = M(ckftk)t р(0>0
при to^t^tk<.Tt ^о<I^i<С...<СtЛ<СУ, процесс продолжаем дальше.
р-Метод описан полностью.
Теорема 1. Пусть управляемый объект {*(т, и), u<=Uu t>
>U) удовлетворяет всем условиям I—VII и (у> Г)-управляем при
каком-либо Г, *о<7,<+°°- Тогда решение задачи быстродействия
может быть получено как предел последовательностей, полученных
с помощью описанного выще р-метода, а именно: 1) lifntk=Tm —
оптимальное время; 2) любая слабая предельная точка и* после-
довательности {ик}, uk£Utk9 является оптимальным управлением, а
х(т, и*)у to^x^T* — оптимальной траекторией.
Доказательство. Так как последовательность {/^моно-
тонна возрастает и ограничена сверху величиной Г, то существует
limtk = T* (здесь, естественно, предполагаем, что итерационный
процесс не заканчивается за конечное число шагов, иначе теорема
становится тривиальной). Из непрерывности р(/) следует, что
Р(Ь)-*Р(Г*) (А-оо).
Покажем, что р(Г*)=0. В дальнейшем нам будет достаточно
рассмотреть только такие k^ko, для которых Г*—/*^Д, где Д=
= const>0 взята из условия III. Можем считать, что все управ-
ления u=u(T)^Ut при' 0<Г*—£^Д продолжены на отрезок
[/о, 71*], и за продолженными управлениями сохраним их прежние
обозначения. Пусть управление ик+\ 6 Utk+\ такое, что
М(ск9 4+1)=(сЛ, x(tk+u Uk+\) — y).
Тогда в силу условий II, IV x(tk, uk+\)^Xtk и с учетом равен-
ства M(ck, /ft+1)=0 и условия VII имеем
Q<p(tk) = M(ck, th) — M(cht tk+{)<(ckt x(th, йк+х) — у) —

§3]
р-Метдд
323
—&k9 х(4+i, Uk+i) — y) = (ck, x(tk, Uk+x)—x(tk+u Uk+\)<
<\\x{tk9 ^+1)-x(4+i),^+1)||<2er*(|^-r|, Г)-*0, (k-+bo).
Таким образом, р(Г*)=0, а так как р(/)>0 при to^t^tk, k=
=0, 1, 2, , то р(/)>0 при •*<></< Г*. Следовательно, Г* — оп-
тимальное время.
Пусть #* = и*(т)^£/т* — произвольная слабая предельная точ-
ка последовательности {иъ) в Вт* (напоминаем, что Uk=Uk(x)
предполагаются продолженными на [t0i Г*]). Тогда существует под-
последовательность {ukn}, сходящаяся слабо в Вт* к«*. В силу
условия VI дс(т, Uk )->х(%9 и*) слабо в X при. всех т, /о<;т<;Г*.
Покажем, что х(Т*, и*)=у. Возьмем произвольное eel Очевид-
но, справедливо неравенство
(с, х(Т\ и*)-у)<(с9 х(Г, и*)-х(Т\ ukn)) +
+ ||с||.||*(Г, ukn)-x(tkny ukn)\\ + \\c\\\\x(tkn, икп)-у\\.
Первое слагаемое в правой части этого неравенства стремится к 0,
так как х(Т*9 tikfl)-+x(T*9 и*) слабо в Х\ второе слагаемое стре-
мится к 0 в силу условия VII; третье слагаемое стремится к 0, по-
скольку
И'*ц. Ukn) — У\\ = Р(*кп)-+°
при л-м». Левая^ часть этрго неравенства не зависит от п9 поэтб-
му при п-+оо получим (с, х(Т*9 и*)—у)^0 при всех cgX Взяв,
в частности, с=х(Т*9 м*)—у9 отсюда будем иметь х(Т*9 и*)=у.
Это значит, что и* — оптимальное управление, а х(х9 и*) —опти-
мальная траектория. А
2. Выше мы предполагали, что величины th9 Xk> ck при каждом
k=09 1, 2,... определяются совершенно точно. Однако на практике
эти величины могут быть найдены, вообще говоря, лишь прибли-
женно, и каждый шаг итерационного процесса будет реализован с
некоторыми погрешностями. Опишем такую модификацию р-метода,
для сходимости которой достаточно определить величины tk, Хъ9 Ck
приближенно, лишь бы погрешность вычисления этих величин с
ростом номера k уменьшалась в определяемом ниже смысле.
А именно пусть задача последовательность {6&}, 6&^0 &=>
= 0, 1, ..., 6/г-И) (k-+oo) и функция а(р), определенная и непрерыв-
ная при р^О, 0<а(р)^р при р>0 (например, bk =—г—,
k +1
&=0, 1, ..., а(р)=0,5р или а(р)=0,9р). В качестве начального
приближения, как и выше, возьмем t0t x0t с0= (х0—у)\\х0—у\\~К
считая р(£0) = ||л;о—у\\>0. Пусть известно (k— 1)-е приближение
(k>l): tH_u Xk-\ 6 Xtk^\ ck-x ф 0, съ-i 6 G

324 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ [Гл. 7
такое, что
М(сь-и M>a(|*-i-»I), Р(0>0
при
0</<4-i, ^o<^i<-- <^-1<^Г.
В качестве следующего момента h возьмем произвольное число,
лишь бы
fc_,<fft<7\ M(ck-ut)>0 при <*-|«</Л, M(ck-U th)<bk.
(1)
Существование такого tk следует из непрерывности М(сь-\9 t) и су-
ществования нуля этой функции на отрезке fo-i-<£<T, (напоми-
наем, что M(cft_i, th-i)^a(Uk-i—y\\)>0 из-за \\xh-i—у\\^
^p(tk-\) >0, а М(сЛ_ь Л^О в силу теоремы 2.1). Так как p{t) >
>0 при to^t^tk-i по предположению, a p(/)^Af(Cfe-i, 0>0 при
tk-i^t<.tk в силу выбора 4, то р(*)Х) при t(^t<th. Далее вы-
берем такие cfeeG, uk<=Utk> x(tk, uh)=xk^Xtk, чтобы
*(|**-*У)<А!(*ь У. (2)
В частности, если взять такие ck^Gt xk 6 Xik, для которых р(^) =
=M(ck, tk) = \\xk—у\\, то условие (2), конечно, будет выполнено,
ибо у нас 0<^а(р)<;р по условию. В то же время получение таких
точных ck£G\ xk£Xtk с условием p(tk)=M(ck, tk) = \\Xk—y\\ для
выполнения (2) необязательно. Заметим, что если p(th)>0 и а(р)
монотонно возрастает ((например, а(р)=0,9р), то неравенство
0сх tt(pfa)) ^g(U*fe—у\\) ^ M(ckt tk) ^
9(h) х p(tk) Х pVk)
вытекающее из (2), можно рассматривать как условие на относи-
тельную погрешность, возникающую при замене р(^) на М(ску h)-
Итак, пусть с* €G, tiktUik, x(tkf uk) = xk£Xtk, удовлетворяю-
щие условию (2), найдены. Может случиться, что M(Ck, th)=0.
Тогда из (2) следует а(\\хк—у\\)=0. Однако а(р) =0 тогда и толь-
ко тогда, когда р=0. Следовательно, xk = y£Xik. Тогда р(^)=0
и в силу теоремы 2.2 tk=T* — оптимальное время, Uk=u* — опти-
мальное управление; итерационный процесс на этом заканчивается.
Если же M(ckt tk)>0t то
^¥=0, p(tk)>M(ckt tk)>0y хкфу9 и, имея tht хк£Х<к
скфЬу ckeG, 0<a(\\xk-y\\)<M(ckl tk), p(t)>0
при
t0<t<tk, *.<*1<...<ъ<7\

**1
р-Метод
325
лроцесс продолжаем дальше. Модифицированный р-метод описан
лолностью.
Как видим, в отличие от р-метода п. 1 задача определения
минимального корня уравнения M(ck-u t)=0 при tk-i<t^T здесь
может решаться приближенно: достаточно ограничиться нахожде-
нием такого t^ лишь бы выполнялись условия (1); значение
р(У = тахЛ1(с, tk)=M\\x — y\\
также может быть заменено приближенным М(с^ th), удовлетво-
ряющим (2).
Теорема 2. Пусть выполнены условия теоремы 1. Тогда ре-
шение задачи быстродействия может быть получено как предел
лоследовательностей, полученных с помощью модифицированного
р-метода, а именно: 1) \imtk = T* —оптимальное время; 2) лю-
А-»оо
«бая слабая предельная точка и* последовательности {uh}czUtk яв-
ляется оптимальным управлением, а лй(т, w*), to^x-^T*, — опти-
мальной траекторией.
Д оказ а те ль ств о.* Последовательность {tk} монотонно воз-
растает и ограничена сверху величиной Г, поэтому существует
lim 4 = Т*. Из непрерывности p(t) следует, что p(tk)-+v(T*)
i^-^oo). Покажем, что р(Г*)=0. Как и при доказательстве теоре-
мы 1, будем считать, что все управления u^Ut при 0<Г*—*<;Д
продолжены на отрезок [to,'T*]9 и условимся рассматривать только
такие tk9 для которых Г*—4<1А. Из (1), (2) имеем
0<a(\\xk-y\\)<M(ck, tk)<M(ck,%)-M(ck, tk+x)+ 6*+,
Поэтому a{\\xk—#Н)-*-0 (£-^оо), так как б^->0 по условию, а соот-
ношение
lim [М(ск9 tk)~M(ckt tk+l)]=0
доказывается так же, как в предыдущей теореме. Но а(р)->0 тог-
да и только тогда, когда р->0. Поэтому \\xk—у||-М) (&->оо), а тогда
и 0<р(^)<;||л;А—г/И—МЭ (£->оо), следовательно, р(Т*)=0. Кроме
того, так как р(*)>0 при t<^t^tk, k=0, 1, 2, ..., то р(*)>0 при
to^t<C.T*. Таким образом, Г*—оптимальное время. Утверждение
2) доказывается точно так же, как и аналогичное утверждение в
теореме 1. А-
Полезно заметить, что для практической реализации описан-
ных выше двух вариантов р-метода необязательно иметь числен-
ное значение момента Г; при котором объект (у, Т) -управляем»
Здесь важен лишь сам факт (у, Т) -управляемости при каком-либо
конечном T>tQ. Кстати, если объект не является (у, ^-управляв-

326 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ [Гл. 7
мым ни при каких Г, ^о<7,< + °°, то задача быстродействия не'
имеет решения. При решении конкретных физических задач в (1)
в качестве Т обычно берут либо максимальное Г, допустимое раз-
рядной сеткой ЭВМ, либо какое-нибудь физически «разумное» для
данной задачи время Т. Если при этом выяснится, что р(/)>0 при
to^t^T, то в первом случае остается признать, что рассматривае-
мая задача не может быть решена с помощью данной ЭВМ, а во
втором* случае — объект не может быть переведен из начальной
точки Хо в точку у за физически «разумное» время.
В заключение заметим, что описанный выше р-метод своими
основами восходит к работе [263}; различные модификации р-мето-
да позднее рассматривались для конечномерных 1 задач быстродей-
ствия без фазовых ограничений, например, в работах [57], [200],.
[264]; при наличии фазовых ограничений и запаздывания в работе
[52]; на бесконечномерные1 задачи р-метод был обобщен и иссле-
дован в работах [50], [51], [53].
Аналогично р-методу можно построить так называемый х-ме-
тод [121], связанный с функцией х(^) = sup М(с, t). Оказывает-
(c,i/)= 1
ся, что х-метод является естественным обобщением известного ме-
тода моментов. Метод моментов для конечномерных задач впервые
был предложен и исследован Н. Н. Красовским и подробно-изло-
жен в его книге [139]; применение этого метода к исследованию
задач быстродействия, связанных с некоторыми типами уравнений
с частными производными, см. в работах [40]—(43], [62]. Обобщение
метода моментов с анализом его сходимости для бесконечномер-
ных задач быстродействия в весьма общей постановке проведено
в [121].
Заслуживает внимания и так называемый а-метод [122], свя-
занный с функцией o(t)= supfi(c, t), где |i(c, t) представляет co-
бой нижнюю грань всех тех т среди %^ty для которых М(с,т)^0-
Внешне а-метод очень прост и заключается в построении последо-
вательности {tk} по закону tk+\ = o(tb), k=0, 1, 2, ..., однако вы-
числение значений функции o(t) далеко не всегда просто. Методы,
близкие к а-методу, для конечномерных задач были предложены
еще в работах [135], [197], [268] и др. Для бесконечномерных задач
быстродействия а-метод был предложен и исследован в работе
[122].
Подавляющее большинство описанных до сих пор в литерату-
ре итерационных методов решения задач быстродействия явно или
неявно связаны с функционалом М (с, t) и получающимися из него
функциями p(t),K(t) или a(t) и являются теми или иными моди-
фикациями упомянутых выше р-, х-, а-методов. Это обстоятельство
Здесь имеется в виду размерность фазового пространства X.

§4]
Приложения
327
подчеркивает важную роль величин М(с, t), p(t), к (t), a(i) при
изучении задач быстродействия. Систематическое изучение этих
величин для линейных задач быстродействия в весьма общей по-
становке проведено в работах [51], [53], [121], [122].
Упражнения. 1. Выяснить геометрический смысл р-метода и его
модификации в случае Х=Е2.
2. Пусть управляемый объект {х(т, и), u^Utt t>t0} удовлет-
воряет условиям I—VII, и пусть Y — выпуклое замкнутое ограни-
ченное множество из X.
а) Положив
М(с9 f)= rnin min(c, x — y)t p(t) = maxM(c, /),
x£Xt yeY c£G
показать корректность этих определений; сформулировать и дока-
зать аналоги теорем 2.1—5 для этого случая.
б) Дать описание р-метода для задачи быстрейшего попада-
ния из точки Хо на множество Y и доказать его сходимость.
§ 4. ПРИЛОЖЕНИЯ
Мы здесь ограничимся рассмотрением задач быстродействия,
связанных с системой i(l.l) и с уравнениями теплопроводности и
колебания струны.
1. Начнем с задачи (1.1—4)., которая удовлетворяет всем ус-
ловиям I—VII,из § 1. Вместо множества (1.2) здесь можно взять
X1-Ю) или любое другое множество Ut из L%[to, t] (f>t0), удовлет-
воряющее условиям I—III. Для приближенного решения получаю-
щихся при этом задач быстродействия можно воспользоваться р-
методом (§ 3).
Для функционала
М(су /)=min(c, x{ty и)—у)Е
u£Ut п
здесь можно получить более удобное для практики выражение
t
М(с, n = min \(В*(х)Ц(т), u(x))Edx +
ueut J
+ |(^(т),/(т))£^т + (г|)(д, х0)Еп-(су у)Е< (1)
to
где я|)(т)—решение задачи Коши:
^(т)=_Л*(т)1|>(т), *0<т<*; ^(t) = c. (2)

328 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ [Гл. 7
В самом деле, с учетом условий (1.1), (2) имеем
t
(с, х (/, и))Вя - (*(*), х(t, и)) = J -£- («(т), х(х,и)) dx + ft(У, х0)=*
to
i i
I
+ (ЪЛ* + А* + Я]Л + №(*в), x0) = Jrt(T)f Я(т)и(т) +
+ /(*))* + «('#). *0).
Отсюда и из определения Л1 (с, *) сразу получаем (1).
В частности, если Ut имеет вид (1.2), то минимум в 1-м ела»
гаемом (1) достигается на управлении и(х) = {и1(х), ..., цг(х)} с
компонентами
I pf(T)t если (В«(*)*(*))|<0; t0<x<t,
и, следовательно,
А*(*. 0=2[J (Вф(т)*(т))|0,Гт)А+ j (Вф(т)*(т))|(1|(т)Л1 +
t
где (B*$)i — t-тая компонента вектора £*ф, Л$" — множество тех
тб 1^о» *]» Аля которых (В*(т)Ф(т))*>0> а #Г —дополнение ко мно-
жеству Nt до отрезка [*0, t].
Аналогично, если Ut имеет вид (1.10), то минимум в (1) до-
стигается при
и{х) = и0(х) + «В* W*(t)|B*(T)*(T)fjf)Biffb
поэтому
М(с, 0 = «I^Wt(t)^,.fl + J(B,(T)*(T), «,(*))*+•
+ f 0|?(т), /(*))* 4- Wo). *.)-(с, у).

§ 4]
Приложения
32£
Для ряда других практически часто встречающихся множеств Ut
также удается получить явное выражение для минимума в правой
части (1).
Далее, при вычислении функции р (t) = тахМ (с, t) = inf \x(tt и)—
c€G u£Ut
— y\9 где G = {c:c£ En> |с|ял<1} удобнее всего воспользоваться
соотношением
p2(0=inf|*('> ti)-y\\
ueut
При каждом фиксированном t>U функционал /(и) = |л:(^ и)—у\2г
определенный на множестве Ut при условиях i(l.l), был изучен в
§ 6.5 (см. задачу (6.5.13—15)), где были выведены формула гра-
диента, условия оптимальности, а также обсуждены некоторые ме-
тоды минимизации J (и).
При нахождении минимального корня уравнения
М(с, т) = 0, t>s, (3>
можно воспользоваться известными методами решения нелинейных
уравнений [19]. Например, если отрезок [s, Г], содержащий корень
уравнения (3), известен, то возможно применение метода деления
отрезка пополам, метода хорд, а в случае гладкости М(с, х) па
т метода Ньютона. Если при этом М(с, т) строго монотонна при:
t^s, то эти методы приведут к искомому корню (3); в противном
случае требуется провести дополнительное и, вообще говоря, не-
простое исследование для выяснения того, будет ли найденный
корень наименьшим среди всех корней ^s. Если известно, что
М(с, т) на отрезке [s, Т] обладает левыми и правыми производ-
ными по т, причем
inf Ш(У±0) >g, £ = const<0,
s<t<r дх
то можно воспользоваться модифицированным методом Ньютона*
описанным в работе [66]:
тп+1 = тл+ тт^^ тл)(/г = 0, 1, ...)> t0 = s, М{су s)>0.
(4>
Следуя этой работе, можно доказать, что {тп}, монотонно возра-
стая, стремятся к минимальному корню уравнения (3) на отрезке
[s9 Т], а в том случае, когда это уравнение не имеет корней на
[st Т], то хп>Т при некотором л^О.

330
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ
\Гл. 7
Отдельно остановимся на одном важном частном случае, когда
JJt = {u = u(T)£L2)[t0y t]:u(x)£V почти всюду на [/0, *]}, t>t0,
(5)
где V — выпуклое замкнутое ограниченное множество из Ег. Оче-
видно, такие множества Vu t>to, удовлетворяют условиям I—III
§ 1. Можно показать, что в этом случае функционал М(с, т) при
всех n^to имеет левые и правые производные,'причем [95]
дМ(е9 *-0) = maxmin(c>i4(T — 0)x + B(x — 0)u+f(x — 0)), т>/0;
дХ x£XCtX uSV
дМ(с, х + 0) = m.n min^ А(т + 0)х + в(т + Q)u +f (т + о», t >L,
дХ xbXCtXu€V
где Хс,х = {х: д:еХт, М(с, х) = (с, х—у)}, V взято из (5). Поль-
зуясь этими формулами, с учетом кусочной непрерывности А{х)у
£(т)> f СО» ограниченности V и оценки (1.6) имеем
inf ЭЛ1(С^±0) >g(S, Т)>-оо,
5<Т<Г ОХ
где
cr(s, Г) = — [ sup IIЛ (т) ||- super (а) + sup ||В(т)||тах|м|+
s<x<r a£C/r s<x<r u£V
+ sup|/(tH]-kl<0. (6)
s<t<T
Тогда для поиска минимального корня уравнения (3) на отрезке
[s, Т] можно воспользоваться методом (4) с g=g(s, Т).
Замечание. Согласно теореме 2.2 оптимальное время Г*
является минимальным корнем уравнения p(t)=0 при t^t0. Еслш
известно, что р(/) на некотором отрезке [to, Т] обладает левой и
правой производными по t [95], причем
inf d9([f0) >g>-oo, £ = const<0,
U<t<T at
то для поиска Г* на {^о, Т] можно также воспользоваться мето*
дом из работы [66]: tn+\ = tn Н p(tn), я = 0, 1, 2.... Если
T*^[t0, Г], то последовательность {/п}, монотонно возрастая, стре
мится к Т*. Если же Т*>ТУ то tn>T при некотором п, и тогД*
этот же метод можно применить на некотором отрезке [Г, Г+/5
где Н=const>0. Вместо функции р(/) здесь можно использовать
например, функцию р2(0> которая может оказаться более гладкой»
чем p(t). Это замечание носит общий характер и применимо, я*
пример, ко всем задачам быстродействия с условиями I—VII.

§ 4]
Приложения
331
2. Рассмотрим задачу о быстрейшем нагреве однородного
стержня длиной />0. Пусть один конец стержня теплоизолирован,
а на другом конце происходит теплообмен с внешней средой. Тре-
буется, управляя температурой внешней среды, наибыстрейшим
образом довести температурный режим стержня до заданного ре-
жима.
Сформулируем математическую постановку этой задачи. Пусть
управляемый процесс описывается условиями
дХ дН (s,T)6Qt={0<s<l, 0<т<*}; (7)
дх ds*
дх(0,х)
ds
дх(1, х)
= 0, 0<т<*( x(s, 0) = 0, 0<s</; (8)
= v[«(t)-*(/, т)], 0<т</; (9).
ds
и = и (т) 6 Ut = {и (т) 6 L2 [0, t]: | и (т) | < 1 почти всюду на [0, t]},
(10)
где /, v — заданные положительные постоянные; Л>0. Каж-
дому u=u(i)<=Ut при каждом *>0 соответствует единст-
венное решение, или, как будем говорить, траектория х=
=x(s, т, и) задачи (7) — (9) (определение решения этой
задачи дано в § 6.6). Пусть y=y(s) —заданная функция на отрез-
ке ft<;s<;/ и пусть существуют такие Г>0 и u(x)^Uu что соот-
ветствующее решение x(s, т, и) задачи (7) — (9) удовлетворяет ус-
ловию
x(st 7, u) = y(s)9 0<s</. (11)
Требуется среди всех Т9 для которых выполнено (11) хотя бы при
одном и=и(%)^ит, найти наименьшее.
Сформулированная задача быстродействия (7) — (11) удовлет-
воряет_всем условиям I—VII § 1, если принять Bt=LdQ, t\ Lt=
^L2(Qt), X=L£0, l]. В самом деле, условия I—IV очевидны; об
условии V уже говорилось в § 6.6 (в представлении (1.11) можем
взять ыо(т)—Oel/f при всех t>0). Пользуясь методикой статей
[107, 125, 178] (схему рассуждений см. в [50]), можно доказать, что
x(st т, Wfc)-Ht(s, т, и) в Lj[0, I] при каждом фиксированном те[0, /]„
если только ик=ик(т)->и=и(т) слабо в L2[0, t] (fc-^oo), а также
получить соотношение
sup [\x(st т+Дт, а) —лф, т, u)\2ds-+0
u£Ut J
при Ат->0, 0<т, т + Дт<Х

332- МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ \Гл. 7
Таким образом, условия VI, VII также будут выполнены, и к за-
даче быстродействия (7) — (11) применимы все результаты §§ 2, 3,
в частности, для ее решения можно применить р-метод.
Для функционала
М
(с, t)=; min fc(s)[*(s, /, и) — y(s)]ds
uGUu J
ищ j
здесь можно получить более удобное для практики выражение
t i
М(с, t)= min v Ы(1, %)u(T)dx— [c(s)y(s)ds, (12)
где t|)(5, t) —решение задачи (6.6.10—12) (с заменой t на т, Т на
/). Эта формула следует из равенства
{c(s)x(s, ty u)ds='y fife(/, %)u(x)d%,
которое доказывается точно так же, как равенство (6.6Л5). В ча-
стности, если множество Ut имеет вид (10), то минимум в (12) до-
стигается при и=и(%)=—sigm|)(/, т) и, следовательно,
t i
М(с, 0 = — v f Ж'. *)\d%—$c(8)y(s)d8.
о о
При вычислении значений функции
p(t) = maxM(c, t)= inf (f|*(s, t, u) — y(s)\2ds)4t,
ceo ueut \J /
G={c = t:(s):c(s)6La[0,ZJ,jc2(s)ds<l}
о
удобнее всего воспользоваться соотношением
Pf(0=Jrf (J|*(s, t, u)-y(s)\*dsy
При каждом фиксированном f>0 функционал
J(u)= $\x(s,.t, u) — y(s)\*ds

£ 4]
Приложения
333
при условиях (7) — (10) был изучен в § 6.6 (см. задачу ((6.6.1—5))Г
где были выведены формула градиента, условия оптимальности, а
также обсуждены некоторые методы минимизации J (и).
Поиск минимальных нулей функций M(ct t), p(t) при t^tk^0
может быть осуществлен, например, методами, о которых говори-
лось выше, в п. 1. Сходимость р-метода для задачи (7)—(11) сле-
дует из теорем 3.1—2. Методы решения других более общих задач
быстродействия, связанных с параболическими уравнениями с одной
или несколькими пространственными переменными, рассмотрены в
работах [35, 50, 51, 53, 121, 122, 158] и др.
3. Рассмотрим задачу быстродействия, связанную с уравнени-
ем колебания струны. Пусть имеется однородная упругая гибкая
струна 0^5^:/ с закрепленными концами, на которую действует
внешняя сила u=u(s> It). Требуется, управляя внешней силой, наи-
быстрейшим образом привести струну в заданное состояние (на-
лример в состояние полного покоя).
Математическая постановка этой задачи: пусть управляемый
процесс описывается условиями
-Sr = -7ir + "(*• т); <«• *)е& = {0<5</, о<т<0; (13)
*(0, т) = ж(/, т) = 0, 0<т<*; (14)
х(8, О) = уо00. дХ(°' 0) =<Pi(*)> 0<s</. (15)
OX
u = u(s,x)£Ut = {и(s, т)6 W$](Qt): \\и(s, /)Ц,, < 1}, (16)
где ф0(5), 9x(s) — заданные функции на 0<s</; ф0 (s) € И7?* [&• 'L
<Pi(s) 6 WW [0, /I, фДО) = ъ(1) = 0(t = 0, 1) (обозначения см. в § 6.7).
Каждому u=u(s, т) ^Ut при каждом t>0 соответствует единст-
венное решениех = x(s, т, и)6 W{2(Qt) задачи (13) —(15). (опреде-
ление решения этой задачи дано в § 6.7).
Пусть на отрезке O^s^Z заданы функции yo(s), у\ (s) .такие,
что
y0(s)ew^[ot /], ^(5)6^10, /], yt(o) = yt(t) = o(i = of l).
Пусть существуют такие Т и u(st т)е£/т, что соответствующее ре-
шение x(s, т, u)t задачи (13) — (15) удовлетворяет условиям
x(s, Т, u) = yi(s),dx(s'J'u) =y0(s), 0<s</. (17)
OX
Требуется среди всех Г, для которых выполнено (lj7) хотя бы при
одном u=u(s, t)^Ut, найти наименьшее. В частности, если в (17)

334 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ [Гл. 7
r/!(5)^i/o(5)^0, то получаем задачу о быстрейшем успокоении
струны.
Сформулированная задача быстродействия (13) — (17) удов-
летворяет всем условиям I—VII из § 1, если принять
B^WpiQt), LtmWPiQt), X^L2[0, 1]XL2[0, /].
В самом деле, условия I—IV очевидны; об условии V уже говори-
лось в § 6.7 (в представлении (1.11) можем взять u0(sy x)=0^Ut
при всех />0). Пользуясь методикой, используемой в работе (150^
можно доказать, что если Uk\sy t)->w(s, т) слабо в W$ (Qt), то
i
jU(s, т, uk) — x(s, т, u)\2ds-+0y
о
о
при каждом фиксированном т^[0, t] и, кроме того,
sup (Y|*(s, т + Дт, u) — x(sy т, и)\2 +
-у* J \
dx(s, т, и} |2
о
dx(s, т + Ат, и)
дт
дт
')<fc + 0
при Дт-^0, 0<;т, т+Дт<;£ Таким образом, условия VI, VII также
будут выполнены, и к задаче быстродействия (13)—1(17) примени-
мы все результаты §§ 2, 3, в частности, для ее приближенного ре-
шения можно применить р-метод.
Для функционала
М(с, t)=min [U(8)[X(8, t, и)-У1(8)] + ъ($\ *l8'*> и) -
u€Ut J I l дх
T 0
-y0(s)]\ds, c = {c0(s), ct(s)}cL2[0, /]xL2[0, /],
справедливо представление
M(c, t)= min Г f г|ф, %)u(s, x)dsd%+ f U(s, OJq^s) —
1 Qt 0
-Щ^Ъ(8)-С0(8)У1{8)-Сг(8)Уо(8)]<189 (18)

Sfl
Приложения
335
где \J)(s, т) —решение задачи (6.7.11—13) (с заменой t на т, Т
на t). Формула (18) следует из равенства
\lc0(s)x(sy t, и) + сг(8) dX(S^fU) ]ds= Г Г у(8, %)u(s, x)dsdx +
« Qt
I
+ jj^_(pu(s)ii^. + <Pl(s)^(S( 0)jrfs,
которое доказывается аналогично равенству (6.7.15). Из (18) мож-
но получить более удобную для использования в пространстве
Wil} (Qt) формулу
Щс, 0-rain Г fU + ^^ + i?LJ£-W +
+ J[*(s, 0)Vl(s)-i4^q),(e)-ce(e)y1(s)-cl(s)y,(s)]ds,
0
(19)
где g=g(s, T) —решение задачи (6.7.18—19) (с заменой t на т,
Г на О-
Для множества Ut из (16) в соответствии с формулой (19) те-
лерь имеем
Щс, t) = -\\g(s, *)Ц1>(<,,+ $[*<*. 0><M«)-
о
причем минимум в (19) достигается при u = g(s, t)||g(s, T)l£(i)(Q)-
При вычислении значений функции
p(0 = maxM(c, /)*=inf rf(lx(sf t9 u) — y1(s)\2 +
сев ueut l J \
о
Ь^Й.-.Л(Я)|')Л],Л.
+
d*(s,

336 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЫСТРОДЕЙСТВИЯ [Гл. 7
G = {с = (с,(8), ci(s))€ L2 [0, /] х 1,10, I]: J(| с0 (s) Р +
о
+ \c1(s)\a)ds<l\
удобнее всего воспользоваться выражением
p»(*)=infJ(«),
ueut
где
J(") = §(\x(s,t,u)-yi(s)\* + \ dxis^'u) -y0(s)^ds.
о
При каждом фиксированном />0 функционал J {и) при условиях
(13)—(16) был изучен в § 6.7;(см. задачу (6.7.1—5) при p0=Pi =
= 1), где были выведены формула градиента, условия оптималь-
ности, а также обсуждены некоторые методы минимизации J (и).
Поиск минимальных нулей М(с> t), p(t) при t^tk^0 может
быть осуществлен методами, упомянутыми в п. 1. Сходимость р-
метода для задачи (13) —(17) следует из теорем 3.1—2. Методы
решения других более общих задач быстродействия, связанных с
гиперболическими уравнениями с несколькими пространственными
переменными, рассмотрены в работах [40—43, 51, 53, 121, 122}.
По поводу приближенного решения встречающихся в этом пара-
графе задач Коши и краевых задач см., например, работы [20,.
207].
Упражнения. 1. Рассмотреть задачу быстродействия (1.1),.
(1.4) при условии, когда u=w=(wlt ..., wr) является параметром,
который выбирается из некоторого заданного выпуклого замкнуто-
го ограниченного множества W из Ег в начале движения и в даль-
нейшем не меняется. Указать способы вычисления функций М(с, t)r
p(t). Дать описание р-метода для этой задачи, доказать его схо-
димость.
2. Пусть У— некоторое выпуклое замкнутое ограниченное мно-
жество из L$), I]. Рассмотреть задачу быстрейшего попадания во
множество У при условиях (7) — (10). Описать р-метод для этой,
задачи и доказать его сходимость [50].
Указание. Воспользоваться результатами упражнения 3.2~

Глава 8
Регуляризация некорректно поставленных
экстремальных задач
§ 1. О НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧАХ МИНИМИЗАЦИИ
Пусть функционал J (и) определен и непрерывен на множестве
U из некоторого банахова пространства Я, и требуется минимизи-
ровать J (и) на U. Пусть существует единственный элемент и*е£/,
на котором J (и) достигает своей нижней грани на U: J(u*) =
= inf J {и) — J*. Предположим, что с помощью какого-либо ите-
рационного метода нам удалось построить минимизирующую по-
следовательность {Uk}^U: J(Uk)-+J* (&->оо). Возникает вопрос,
будет ли иъг+и* в 5? Иначе говоря, можно ли из близости значений
J(uh) к /* сделать вывод о близости ик к и* в норме В и затем,
как это иногда делают на практике, в качестве приближения к оп-
тимальному элементу и* взять элемент Uh с достаточно большим
номером? Если элемент и*, на котором достигается нижняя грань
J {и) на [/, не единственный, то и здесь возникает аналогичный
вопрос: можно ли по близости значений J(tik) к /* судить о близо-
сти uh к множеству U*={u: u^U, J(u)=J*} в норме 5?
Оказывается, в общем случае ответ на поставленные вопросы
является отрицательным. Покажем это на двух простых примерах.
Пример 1. Пусть J (и) = —-—, и >0. Очевидно, J* =
= inf J (и) — 0 и достигается в единственной точке и*=0. По-
следовательность tik=K k=\y 2, ..., является минимизирующей, но
тем не менее \и*—Uk\=k-f+6 (£-*оо), точнее даже |и*—ик\^<*>
(fe->oo).
Пример 2. Пусть требуется минимизировать функционал
J(u)= §x2(t)dt при условиях х=и, 0<*<1, *(0)=0,
о
Us=t u(t) € U = {u(t)e L2[0, 1]:|а(01<1 почти всюду на [0, 1]}.
Очевидно, Г *= inf J (и) = О
иеи
и Достигается на единственном управлении и* (0=0. Рассмотрим
последовательность Uh(t)=sinkty 0<^<:1, которой соответствуют
траектории

338 РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ [Гл. 8
xk(ty=— (I— coskt) = — sin2— 0</<1, k= 1,2,
k k 2
Поскольку
1
о
то {tyj — минимизирующая последовательность. В то же время
К — "*llL[o.i]= fsin2&<#=- Lsil,2A->-^ (£-*оо).
о
Как видим, значения J(Uh) и /* при достаточно больших k будут
сколь угодно близки, и тем не менее управления Uk(t) не будут
близки к и*=0 в норме Ь£0, 1].
Определение 1. Задача минимизации функционала J (и}
на множестве U банахова пространства В называется корректно
поставленной, если: 1) множество
1Г = {и:иеи, J(u)=iniJ(u) = J*}
непусто; 2) любая минимизирующая последовательность {^}ef/
такова, что
р(иь{/*)= inf \\uk — u\\-+0 (fe-*oo).
u€U*
Если нарушено хотя бы одно из условий 1) или 2), то задача
минимизации называется некорректно поставленной.
Примером корректно поставленной задачи является задача
минимизации сильно выпуклого функционала J (и) на выпуклом
замкнутом множестве гильбертова пространства Я. В самом деле,,
существование и единственность минимизирующего элемента ит
следует из теоремы 2.1.7, а сходимость минимизирующей последо-
вательности {uk} к и* в Н вытекает из равенства
IK-«T< — [Huk)-J{u*)\
теоремы 2Л.6. Если U компактно в В и J (и) полунепрерывен снизу
на [/, то, очевидно, задача минимизации такого функционала
J (и) на 0 также поставлена корректно. " ;;•
Для корректно поставленной задачи минимизации приближен-
ное нахождение какого-либо из минимизирующих элементов и*&
^[/* облегчается: в качестве приближения к ы* можно взять оди*
из членов минимизирующей последовательности с достаточна
большим номером.

§ 2] Метод регуляризации Л. Н. Тихонова 339
Однако имеются целые классы практически важных задач ми-
нимизации, являющиеся некорректно поставленными. К таким за-
дачам относятся многие задачи минимизации функций конечного
числа переменных, задачи оптимального управления, связанные с
системами обыкновенных дифференциальных уравнений или урав-
нениями с частными производными, а также ряд других экстре-
мальных задач. Возникает практически важный вопрос: как пре-
одолеть трудности решения некорректно поставленных задач мини-
мизации в тех случаях, когда U* непусто и требуется найти не
только минимальное значение функционала, но и какой-либо ми-
нимизирующий элемент с нужной точностью в той или иной нор-
ме? Или, точнее говоря, как строить в таких задачах минимизи-
рующие последовательности {и&}е£/, для которых расстояние
p(uky С/*)->0 (&->-оо) или же \\uk—и*||-*0 (k—>оо), где и* — неко-
торый элемент из U* с определенными свойствами. Ответ на эти
вопросы дает излагаемый в следующем параграфе метод регуляри-
зации некорректно поставленных экстремальных задач, разрабо-
танный А. Н. Тихоновым и оказавшийся весьма гибким и удоб-
ным инструментом для теоретического исследования и численного
решения таких, а также других более широких классов некоррект-
но поставленных задач, возникающих в различных областях науки
и техники [151, 217, 222, 225]. Из обширной литературы по теории
и методам решения некорректно поставленных задач здесь упомя-
нем еще работы {12, 28, 30, 31 „ 33, 36, 37, 53, 98, 151, 156, 162,
172, 218—226, 247—250], непосредственно связанные с экстремаль-
ными задачами (библиографию*см. в работах [222, 225]). По пово-
ду достаточных условий корректности постановки экстремальных
задач см. работы [153, 156, 186].
§ 2. МЕТОД РЕГУЛЯРИЗАЦИИ А. Н. ТИХОНОВА
1. Пусть U — некоторое множество банахова пространства В.
Пусть функционал J (и) определен на множестве £/, причем
U* = {u:ueUyJ(u)= inf 7(a) = 7*}
непусто. Метод регуляризации некорректно поставленных экстре-
мальных задач, разработанный А. Н. Тихоновым [218—221], заклю-
чается в том, что сначала исходную задачу минимизации J (и) на
U заменяют семейством задач минимизации специальным образом
подбираемых функционалов /а(и), зависящих от числового пара-
метра а^О и определенных на множествах Ual^U, причем /0(m)s=
zz=J(u), U0=U. После чего, используя какие-либо приближенные
методы, задачу минимизации 7а (и) на Ua при каждом фиксиро-
ванном а>0 решают с некоторой точностью е=е(а)>0 в сле-
дующем смысле: определяют элемент иа £ Ua такой, что

340 РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ [Гл. 8
/*= inf Ja(u)<Ja(Ua)<Ja + e(a)t Ua£Ua. (1)
иеиа
Говорят, что задача минимизации J (и) на U регуляризована по
Тихонову, если
р(и<х, U*)= inf ||«ос — и|-»0 при <х-* + 0.
иеи*
Для регуляризации экстремальных задач чаще всего исполь-
зуются функционалы А. Н. Тихонова
Ja(u) = J(u) + a&(u), (2)
где а > 0 — числовой параметр, Q (и) — некоторый функционал с
непустой областью определения Uq a U, причем Q (и) > 0 при и 6 Uq.
Функционал Я (и) называется регуляризатором% если можно указать
функцию е = е (а) > 0Z lim е (а) = 0, такую, что иа, определяемые
а-Н-0
из (1) при Ja (и) из (2) и (/« = (/0, обладают свойством
р(иа,(/*) + 0 (а-^ + 0).
2. Ниже будут доказаны теоремы, из которых следует суще-
ствование регуляризаторов для широкого класса некорректно по-
ставленных экстремальных задач, а также указаны примеры регу-
ляризаторов в ряде важных для практики функциональных про-
странств.
Теорема 1. Пусть выполнены следующие условия: 1) U —
заданное множество банахова1 пространства 5, функционал /(и)
определен и ограничен снизу на £/, множество
U* = {и :ueU, J (и) = inf J (и) = /*> — ос}
непусто; 2) функционал Q(u) определен на непустом множестве
Uq^U, Q(u)^0 на Uq , и существует хотя бы один элемент н*е
е£/*, который также принадлежит Uq\ 3) последовательности
W}, {вн} таковы, что aft>0, е&>0, ft=l, 2, ..., a*->0, е&-Я) (k-+-
->оо); 4) последовательность {ик}> k=\, 2, определена из ус-
ловия
J*k<Jk(Uk)<fk + *k> ^€^a> (3)
где
h(и) = J(u) + akQ (и), fk = inf Jk(и).
U^Q
1 Теоремы 1, 2 сохраняют силу, когда В — метрическое пространство.

§ 2]
Метод регуляризации А. Я. Тихонова
341
Тогда последовательность {uk} будет минимизировать функционал
J (и) на U: V\mJ(uk) = J*
k -»оо
Доказательство. Прежде всего заметим, что Jh(u) =
=/(и)+ал Q(u)^J(u)^J*>—оо при любом u^Uq^U, поэтому
inf Jk(u) = fk> — оо.
Далее по условию теоремы существует элемент а*6^*П^о* По-
этому можем написать следующую очевидную цепочку неравенств,
вытекающую из определения J*, h, неотрицательности Q(u),
a*>0 и условия (3):
J* =J{u*)<J(uk)<J(uk) + akQ(uk)= Jk(uk)<Jl + ek<
<Jk(u*) + 4 = J(u*)+akQ(u-) + ek <
<J(uk)+akQ(u*) + ekt *=1,2, (4>
Отсюда имеем
r = J(u>)<J(uk)<J(u*) + *kQ(u') + Bk (ft=l,2, ...), (5)
и поэтому J(uk)-+J*(k-*oo). ±
Теорема 2. Пусть выполнены все условия 1—4 теоремы 1 и,
кроме того, 5) J (и) полунепрерывен снизу на U; 6) Вк/аы+О (£-*-
->оо)
(например, ak = —, гк = —, А = 1, 2, \
7) множество Sc={u: u^Uq, Q(u)^C} компактно в В при лю-
бом C=const^0 (разумеется, речь идет о случаях, когда Sc не-
пусто). Тогда р(ил, £/*)-*0 (Л-^оо), т. е. Q(u) является регуляри-
затором для задачи минимизации J (и) на U.
Наконец, если наряду с условиями 1)—7) имеет место усло-
вие 8) Uq==eU и Q(u) полунепрерывен снизу на U, то любая пре-
дельная точка и* последовательности {иъ} принадлежит мно-
жеству
U" = {и:ие U\ Q(и) = inf Q(«)},
u£U*
причем если U** состоит из единственной точки и*, то р(а^, и*)-+-0
(*->оо).
Доказательство. Из цепочки неравенств (4) имеем
J(tih)+akQ(uk)^J(uk)+akQ{u*)+Bkt или
О(ц0<^(«0 + — *=1,2, ифе1£№ (6)

342 РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ [Гл. *
По условию 6 —=-->- 0 (£-*оо), поэтому
а*
Q(tffe)<C = Q(a*) + sup-^<oo, k = 1, 2,
Следовательно, {uA}eSc, &=1, 2, По условию 7 множество 5С
компактно, поэтому из {#&} можно выбрать хотя бы одну подпосле-
довательность {Wfem}, которая сходится по норме В к некоторому
элементу ^*6Sc£(/qC £/. Покажем, что й*е(/*. В самом деле;
лользуясь полунепрерывностью снизу функционала J{u)9 из (5)
при k=km-*°° имеем
J(u*)<J(a*)<\imJ(uhm)<J(um)t
т. е. /(#*)=/*, или tt*et/*. В силу произвольности предельной
трчки й* отсюда получаем р(и&, £/*)-Ю (к-+оо)..щ
Наконец, пусть выполнены все условия 1—8, Тогда (6) имеет
место при всех u*^U*ciUq=U, и, пользуясь полунепр.ерывностью
снизу Щи), из (6) при k=kryr+oo получим
Q(tt')<limQ(iQ<Q(iQ
для любого м*е1/*. По доказанному й*е£/*. Следовательно,
Q(u*)= inf Щи), т. е. й*е£/**. Если I/** состоит из единственной
«ее/*
точки и*, то вся последовательность {ин}-+и* (&-»-оо) в норме
в. А
Приведем примеры функционалов Q (и) в различных функцио-
нальных пространствах, которые удовлетворяют условиям теорем
1, 2 и при выполнении остальных условий этих теорем могут слу-
жить регулярйзатором для некорректно поставленных экстремаль-
ных задач в соответствующих пространствах.
Пример 1. Пусть требуется минимизировать полунепрерыв-
ную снизу -функцию J (и) на замкнутом множестве U^Em, пусть
ir = {u:ueU9J(u)=iniJ(u)> — oo}
непусто. Положим Q (и) = \ и—й0 |2, где йо — некоторая заданная
точка из ьщ- Согласно теоремам 1, 2, как нетрудно видеть, Q(u)
является регулярйзатором. Поскольку Q(a) непрерывен в ЕШу то
любая последовательность {и,к}, удовлетворяющая условиям тео-
рем 1, 2, будет иметь предельные точки £*<=£/*, наименее удалён-
ные от йо среди точек U*. В частности, если U* выпукло, то на С/*
строго (точнее,*сильно) выпуклая функция £i(u) = \u—й0[2 будет

§ 2] Метод регуляризации А. Н. Тихонова 343
достигать минимума в единственной точке и* и последовательность
{ик}-+и*.
Пример 2. Рассмотрим пространство Саг) [^о, Л непрерывных
вектор-функций и (t) = (и1 (/), , иг (/)), t0 < Г< Г, удовлетворяю-
щих условию Гельдера:
\u(t)-u(x)\<L\t-%p (7)
при всех /, те[<о, Г], где показатель а, 0<а^1, не зависит от
функции u(t)t а константа L>0 может зависеть от u(t). Линейное
пространство C^r) [/0, Т] с естественно определенными операциями
сложения вектор-функций и умножения их на число становится*
очевидно, банаховым, если ввести норму следующим образом:
\\u(t)\\ir)= max \u(t)\+ sup lu®-"£)l .
Пусть U — некоторое замкнутое множество из С£г) [/0, Г], J (и)
полунепрерывен снизу на U9 причем множество
U* = {u:ueU, J(u)= infJ(u)> — oo}
«ее/
непусто. Тогда в качестве регуляризатора можно взять функцио-
нал Q (и) = \\и\\1(г).
Докажем, что множество
Sc={u:ueU, \\и\\{г)<С}
компактно при любом C=const^0. В самом деле, для всех функ-
ций u=u(t)^Sc в неравенстве (7) можно взять одну и ту же кон-
станту L=C. Кроме того,
max I и (t) \ < С
при всех u=u(t)^Sc. Таким образом, множество Sc равномерно
ограничено и равностепенно непрерывно, и по теореме Арцела [137}
из любой последовательности {Ukj^Sc можно выбрать подпосле-
Дова^льность {Ukm}> равномерно сходящуюся к непрерывной функ-
ции u(t). Тогда в неравенствах
\uk(t)-uk(x)\<C\t-T\«

344 РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ [Гл. 8
можно перейти к пределу при т-^оо и убедиться, что
u(t)6C$[t0,T],
а также Кт(0 — й(0Ис<г)-^0 (т-*оо).
Из замкнутости U и непрерывности Q(u) следует, что u(/)&Sc.
Компактность Sc доказана. Таким образом, согласно теореме 2
12 (и) = || и|| tr) является регуляризатором. В качестве регуляри-
затора здесь можно взять также
Q(u) = \\u(t)~u0(t)\Uh или Q(u)= \\u(t)-u0(tf{r)t
хде й0 (t) — заданная функция из СаГ)[^о» Ti-
ll р им ер 3. Пусть U — некоторое замкнутое множество из
&r\to> Т\ — пространства непрерывных вектор-функций u(t) =
= (ul(t), ur(t)), t0^t^T, с нормой \\u(,t)\\c(r)=max\u(t)\Erf
«функционал J (и) полунепрерывен снизу на £/, причем множество
U* = {u:ueU, J(u)=M J(u)> — оо}
непусто. Рассмотрим функционал
т
to
•определенный на пространстве wY [*0, Т] абсолютно непрерывных
лектор-функций w(/) = (m1(^), ,ur(t)) с производной
at
Покажем, что множество
Sc = {« = u(t):Q(u)<С, u(t)£U[)Wl/[t0i T]} _
компактно в Clr)[t0, Т} при любом C = const>0.
Из Q(a)<C следует, что
хотя бы в одной точке т€ [/0, Г]. Тогда
t
|«(OI = |p(s)ds+K(T)|<-i/_C +

§ 2]
Метод регуляризации А. И. Тихонова
345
+ VT-U ( $1«Ф) 12^)1/а<Т/ ^ + КС(Г-^0) = const
и
для любой функции из Sc. Далее
|«(0-в(т)| = ||-^Й_л[<
t
to
для любого u=u(t)^Sc- Таким образом, множество Sc равномер-
но ограничено и равностепенно непрерывно. Из теоремы Арцела
[137] тогда следует компактность Sc в норме пространства С<фо, Т\.
Таким образом, если функционал J (и) достигает своего минимума
на U при
u = u*(t)eU()Wl2r[t0,T],
то согласно теореме 2 функционал Q(u) является регуляризатором.
Если заранее известно, что U ограничено в C<r\t0, 7], то в качестве
т
регуляризатора можно взять Q(u)= V dt.
to
Пример 4. Пусть U — некоторое замкнутое множество в
L{2r)[t0, Т]9 J (и) полунепрерывен снизу на £/, множество
1Г = {и:иеи, J (и) = inf J (и)> — оо}
непусто. Если, кроме того,
W(\Wl2'rlt09T]
также непусто, то в качестве регуляризатора здесь можно взять
функционал Q(u) из примера 3. Это следует из того, что множест-
во 5С, компактное в C^r\t0t Т\, тем более компактно в Lir) [t0, Т]
при любом С=const^0.
Пример 5. Пусть U — некоторое замкнутое множество из
банахова пространства L\r) [t0, Т] вектор-функций u(t) = (и1 (t)f...,
->ur\(t)) с нормой
\H(r)= \\"(t)\dt<oo,
1 U

346 РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ [Гл. s
a J (и) —полунепрерывный снизу функционал на U с непустым
U* = {u:ueU, J(u) = J*> — оо}.
Рассмотрим функционал
т
й(ы)= \\u(t)\dt+\/(u),
ti <•
определенный на линейном пространстве Vtyto, Т] вектор-функций
u(t) = (ul(t), ..., W(t)), t^t-^T, с ограниченной вариацией [137]
гг». Я
VH^sup £|и&) — r/(^-i)l<oo,
где верхняя грань берется по всевозможным to<.t\<Ct2< <tn=
= Т при всех /1=1, 2, Заметим, что V<r)[/o, Л является подпрост-
ранством L^f^o» Л-
Покажем, что множество Sc = {и = и (0 :и (t) 6 £/ f| V(r) [*0, Л'
Q (и) < С} компактно в L\r) [t0, Т]. Из й (и) < С следует, что
|| и\\ (г) < С. Тогда для каждой функции и (t) 6 Sc найдется точка т 6
Li
6 [*о» Т\ такая, что |и(т)|< — . Следовательно,
\'u(t)\<\u(T)\ + \u(t)-u(r)\<
<\и(х)\+\/(и)<-£— + С = М<оо
при всех t, *<></< Г, и всех u(t)£Sc. 1Тогда, считая для опреде.
ленности и (t) 5= 0 вне отрезка t0 < t < Г, имеем
т '+т , ? г '+*
f|"(/ + T)-a(OI<#< f V («)* = f f V (и)-у(и)]
tl tl * С L <° '• J
г+т t т t
= f \/{u)dt— \\/{u)dt =
T+t t f.+т f
= f V(u)dt— f V(")*<2(C + AI)t
при всех т>0 и всех h(*)^Sc.
Таким образом, множество Sc равномерно ограничено и рав-
ностепенно непрерывно в норме L[r)[tQt Г], следовательно, Sc ком-

§ 2] Метод регуляризации А. Н. Тихонова 347
пактно в L\r}[t0,T] ([88], стр. 324—325). Если U* содержит хотя
бы одну функцию u=u*(t)^VW{to9 Т\ то согласно теореме 2
функционал Q(u) является регуляризатором для рассматриваемой
задачи. Более того,- утверждение теоремы 2 здесь можно усилить
следующим предложением: из последовательности {tik(t)}, полу-
ченной согласно (3), можно выбрать подпоследовательность
{Ukm (0)> которая всюду на fo<;^Т сходится к некоторому и* (t) е
е£/*, — этот результат вытекает из теорем Хелли [137]. Заметим,
что если заранее известно, что множество U ограничено BL\r[t0i Г],
г
то в качестве регуляризатора здесь можно взять Q(u) = V (и)-
3. В теореме 2 от множества Sc требовалась компактность в
смысле нормы 5. Кроме того, в теоремах 1, 2 предполагалось су-
ществование минимизирующего элемента и*> принадлежащего об-
ласти определения Q(u)> которая, вообще говоря, может быть бо-
лее узкой, чем область определения функционала J (и) (см. при-
меры 3—5). Эти ограничения для ряда экстремальных задач могут
оказаться слишком стеснительными. Тогда при построении регу-
ляризаторов может оказаться полезной теорема 3. Для ее фор-
мулировки нам понадобится
Определение 1. Функционал Q(u) называется равномерно
выпуклым на выпуклом множестве U банахова пространства В,
если существует функция &(т), определенная при т^О, такая, что:
1) 6(т)>0 при всех т>0, 8(0) =0; 2) б(т)-Я) тогда и только тог-
да, когда т-^+0; 3) Q(au+ (l—a)v)^aQ(u) + (l—a)Q(v) —
—a(l —<х,)6(\\и—v\\) при всех и, v^U; 0<;а<1.
Очевидно, равномерно выпуклый функционал является строго
выпуклым, и согласно теореме 2.1.1 такие функционалы могут до-
стигать своей нижней грани на выпуклом множестве-не более чем
в одной точке. Примером равномерно выпуклого функционала мо-
жет служить любой сильно выпуклый функционал с 8(т)=хт2,
к=const>0; другие примеры см. ниже.
Теорема 3. Пусть U — выпуклое множество, выполнены все
условия 1—4 теоремы 1, и, кроме того, 5) J (и) слабополунепреры-
вен снизу на Uу и U* — выпуклое множество; 6) ел/аь-^О (k-+oo)-f
7) функционал Q(u) определен на U, слабополунепрерывен снизу
и равномерно выпуклый на U; 8) множествоSc={u : ие£/, Й{и)^
<:С} слабокомпактно в В при любом С=const^0 (разумеется,
речь идет о случаях, когда Sc непусто). Тогда последовательность
{uu} сходится по норме В к тому элементу Й*е £/*',_ на котором
достигается нижняя грань Q(u) на £/*:Q(w*) = inf Q(#).
u€U*
Доказательство. Очевидно, цепочка неравенств (4) и вы-
текающие из нее неравенства (5), (6) сохраняют силу и здесь при

348 РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ [Гл. 8
любом u*^U*. Из (5) следует, что последовательность {uk} мини-
мизирует J (и) на U. Из (6) имеем
{uk}eSc, C=Q(tf) + sup-S*-.
По условию 5) множество Sc слабокомпактно. Поэтому из {иь}
можно выбрать хотя бы одну подпоследовательность {иьт}, кото-
рая слабо сходится к некоторому элементу U*^SC^U. Пользуясь
слабой полунепрерывностью снизу функционала J (и), из (5) при
&=£m-voo имеем
J(u*)<J(u*) < lim /(iQ <J(iQ, т. е. J(?) = /(iT), и*6£Л
Так как Q(u) слабополунепрерывен снизу, то из (6) при
k=krrr^oo следует
Q(^)<UmQ(a*J<Q(£0
т-*оо
при любом ы*е£/*. Но й* также е£/*, следовательно,
Q(u*)= inf Q(a).
«ее/*
Однако Q(u) —равномерно выпуклый функционал и на выпуклом
множестве U* достигает своей нижней 1фани в единственной точке,
совпадающей с й*. Поэтому вся последовательность {ин} сходится
к й*- слабо в В. Далее из определения равномерно выпуклого функ-
ционала имеем
0<6a^-^<2[Q(i^) + Q^)]-4Q(i2^)f *=1,2,
Отсюда при &-voo следует 6(\\иъ,-^й*\\)-+0, что возможно только
при \\uk—й*|Ы). А
Пример 6. Пусть J (и) —полунепрерывный снизу выпуклый
функционал на выпуклом замкнутом множестве U гильбертова про-
странства Я, пусть
U* = {u:ueU, J(u) = MJ(u)>—oo}
непусто. Положим Q(u) = \\u—й0||2, где й0— заданный элемент Н.
Функционал,Q(и) непрерывен и сильновыпуклый в Н. Слабая по-
лунепрерывность снизу Q(u) тогда вытекает из теоремы 6.1.3, сла-
бая компактность множества Sc — из теорем 6.1.2, 6.1.10. Следо-
вательно, Q(u) = \\u—Soil2 является регуляризатором для задачи
минимизации J (и) на £/, и любая последовательность {ик} из (3)

§ 3] Регуляризация при вычислении с погрешностями 349
будет сходиться в норме Н к элементу й*е£/*, наименее удален-
ному от й0. Задавая й0 по-разному, можно получить приближения
к различным элементам из U*.
Таким образом, в задачах оптимального управления из § 6.5
в качестве регуляризатора можно взять
Q(it)= |и*)12<#;
'о
в задаче о нагреве стержня из § 6.6 —
т
Q(u)=\\u(t)\2dt;
о
в задаче о колебании струны из § 6.7 —
q(«)=ii«(S(oii;o)W).
Пример 7. Пусть J (и) — полунепрерывный снизу выпуклый
функционал на выпуклом замкнутом множестве U пространства
Lp][t0, Т] вектор-функций u(t) = (а1 (0» » иГ(*)У с нормой
ll^llL(r) = (J>(Oler^)1/P, 1<р< + °о;
пусть
U* = {u:ueU> J(u)=inU{u)> — oo}
непусто. В качестве регуляризатора тогда можно взять
О(и) =!«£(* при 1<р<2,
р
QH = JttfcD прир>2 ± + ± = L
LP Р я
Равномерная выпуклость Q(u) следует из неравенств Кларк-
сона [210]; слабая полунепрерывность снизу Q(u) и слабая ком-
пактность множества Sc вытекает из теорем 6.1.2, 6.1.3 и из рефлек-
сивности пространства L{p[t0t Т], 1 <р< + оо.
§ 3. РЕГУЛЯРИЗАЦИЯ ПРИ ВЫЧИСЛЕНИИ С ПОГРЕШНОСТЯМИ
До сих пор при изложении метода регуляризации мы предпо-
лагали, что значения функционала J (и) при каждом u^U вычис-
ляются точно. Однако на практике вычисления обычно проводятся
приближенно и вместо точного значения J (и) получают приближен-

350
РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ [Гл 8
ное значение 7б (и) с погрешностью \J(u)—Jb(u)\. Оказывается,
если эту погрешность согласовать с регуляризатором Q(u)\ то и в
этом случае задача минимизации J (и) на U может быть регуляри-
зована [221]. А именно, пусть погрешность
\J(u)-J6(u)\<[l+Q(u)]8t б>0. (1)
Тогда для рассматриваемой задачи функционал А. Н. Тихонова
имеет вид
Ja(u) = Jb(u) + aQ(u)9 a = const>0.
Теоремы 2.1—3 остаются справедливыми, если в (2.3) при-
нять
Jk(u) = 76k(u) + akQ(u)tk=lt21 (2)
где последовательность {6&} такова, что ал>бА>0.
8*->0, -*>*—>0(ft-*oo).
а*
В самом деле, неравенства (2.4), игравшие основную роль
при доказательстве теорем 2.1—3, здесь следует заменить цепочкой
неравенств
J (и*) < J (uk) < J (uk) + щ Q (uk) <7*ft (uk) + a* Q (uk) +
+ S* [1 +Q(uk)]=Jk(uk) + 6,[1 + Q(uk)] <
<Jl + 4 + 8* [1 + Q(uk)] <Jk(u*) + zk + 6, + bkQ{uk)< (3)
< J (u*) + 26, + (a, + 6,) Q (u*) + ek +Д Q (uk) <
<J(uk) + 2(6k + sk) + (ak + 8k)Q(u*) + 8kQ(uk)y u^U^Uq.
Отсюда имеем
ak Q(uk)<2(bk + sk) + (ak + 6,)Q(*0 + 6, Q(uk),
или
Так как
то
ОЫ<^ЙМ+2-^-, * =1,2, (4)
a,— Ok a, —о,
ak ak
JijdJi.^1, A±^_^0 (ft-*oo).
<*ft — h <*ft — Oft

§ 4] • Регуляризация с помощью аппроксимации множества 351
Поэтому
&(w*)<C=const, Aj= 1, 2, и TimQ(^)<Q(w*).
fe-*oo
Тогда из (3) следует
J(u')<J(uk)<J(u*) + 2bk+Bk +
+ (о» +бЛ)Q Ю+ б, С, ft = 1, 2, (5)
Теперь ясно, что если в (2.3) принять Jh (и) из (1), i(2), то тео-
ремы 2.1—3 сохраняют силу, причем доказательства также ос-
таются прежними, если неравенства (2.4—6) заменить на (3), (5),
(4) соответственно.
§ 4. РЕГУЛЯРИЗАЦИЯ С ПОМОЩЬЮ АППРОКСИМАЦИИ
МНОЖЕСТВА
В §§ 2, 3 для регуляризации экстремальных задач производи-
лась замена исходного функционала J (и) новым функционалом
Ja(w)=/(a)+aQ(a), который затем приближенно минимизиро-
вался на Uq^U. Однако можно строить минимизирующие после-
довательности и несколько иначе: не меияя исходный функционал
/(a), минимизировать его на подходящим образом выбранных под-
множествах множества U. Мы здесь ограничимся следующей тео-
ремой.
Теорема 1. Пусть выполнены такие условия: 1) U — замкну-
тое, выпуклое и ограниченное множество из рефлексивного банахо-
ва пространства В; 2) J (и) —слабополунепрерывный снизу выпук-
лый функционал на £/; 3) функционал Q(a) определен на С/, слабо-
полунепрерывен снизу и равномерно выпуклый на U, причем мно-
жество Sc={u: u^U, Q(u)<^C} слабокомпактно в В при любом
С=const, для которых &сФ0\ 4) последовательности {6&}, {/&}
таковы, что
6*>0, Jk>J*=inlJ(u), 8^0, 4-W* (*>оо);
5) последовательность {и*}, £=1, 2, определяется из условия
Q;= inf a(u)<Q(uk)<Ql+bkt ukeUk, £=1,2, (1)
ueuk
где Uk = {u:u£U9 J(u)^Jk}. Тогда {uk} минимизирует J (и) на U я
\uk — a*|-*0 (fc-^oo), где и* — элемент из (/*, на котором &(и) дос-
тигает своей нижней грани на U* = {u:u£U, J (и) — J*}.
Доказательство. Из теоремы 6.1.4 следует, что и*Ф0.
Кроме того, U* выпукло, замкнуто и ограничено, и на нем слабо-
полунепрерывный снизу равномерно выпуклый функционал Q(u)

352 РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ [Гл. 8
достигает своей нижней грани в единственной точке a*et/*. Это
вытекает из теорем 6.1.2, 6.1.4? 2.1.1.
Так как /&-»-/* и J*^I(uh)^Jky k=l, 2, ..., то {Uk} миними-
зирует J (и) на U. Далее из (1) с учетом u*^Uht k=lf 2,
имеем
Ql<Q(uk)<Q(u') + 8k<Q(u*) + sup6k = C, *=1,2, ..,, (2)
т. е. {iib}^Sc. В силу слабой компактности Sc из {ик} можно выб-
рать подпоследовательность {и*т}, слабо в В сходящуюся к неко-
торому элементу a*eSc. Покажем, что й*=и*е£/*. Так как {#&}
и тем более {ukm} минимизируют J (и) на U, то из слабой полу-
непрерывности снизу J (и) вытекает, что
J* = limJ(ukm)>J&)>r,
m-юо N
*
т. е. /(£*)=/* и й*е£/*. Далее Q(u) слабополунепрерывен снизу,
и из (2) при k=krrr-^oo имеем
Й(и*) < HmQ (ukJ < Q (и*).
Но Й(и*) = inf Q(u), и из того, что u*£U* и Q(u) на Um достигает
иеи*
минимума в единственной точке, следует, что й* = и*. Это означа-
ет, что {tik} имеет единственную слабую предельную точку и*, т. е.
Uk-+u* слабо в В при &-м». Кроме того, из неравенства
й(uk) <й(и*) + bk имеем lim Й (щ) = Й(и*).
Ле-юо
Далее из определения равномерно выпуклрго функционала сле-
дует
0<8(Ц-к1)<2[Й(^ + ^ *=i,2,...
Отсюда при Л-^оо с учетом соотношений
lim Й (|^) = й(иф), ИшЙ f Uk + U* } > Й (а*) имеем б (||ик — и* \\) ->0,
Что возможно только при \\tik—а*||->0 (А-^оо). ^
При определении последовательности {/а}, /*>/*, /*->■/*, й-*-
-мх>) можно воспользоваться любыми удобными методами мини-
мизации /(и) на £/. Если задача определения {и*} из (1) может
быть решена достаточно просто, то метод регуляризации из теоре-
мы 1 позволяет эффективно строить минимизирующие последова-
тельности, сходящиеся к точке минимума в норме В.

§5]
Усиленная регуляризация
353
О регуляризации некорректно поставленных задач с помощью
аппроксимации множеств см. в работах (36, 37, 98, 247—250].
§ 5. УСИЛЕННАЯ РЕГУЛЯРИЗАЦИЯ
Наконец, кратко остановимся на одной интересной возможно-
сти дополнительной регуляризации задач минимизации функцио-
налов на множествах из р[) [/0, Т] (в частности, задач оптималь-
ного управления). Допустим, что с помощью какого-либо метода
(например, пользуясь регуляризацией из §§ 2—4) построена по-
следовательность {u>k(t)}y минимизирующая J (и) на UczL2r)[t0t Т]
и сходящаяся в Lir) [t0> Т] к некоторому оптимальному и*(t)^U*.
Возникает вопрос, нельзя ли подправить, сгладить эту последова-
тельность {uk(t)} так, чтобы новая сглаженная последовательность
сходилась к u*(t) равномерно на любых замкнутых множествах
из интервалов непрерывности а*(0? Оказывается, можно. На эту
возможность указывает
Теорема 1. Пусть последовательность {uk(t)} минимизирует
непрерывный на £,2Г)[/0, Т] функционал J (и) на Множестве (/с:
S=:Lir)[t0,T] и сходится в L{2 [t0JT] к некоторой кусочно-непрерыв-
ной функции и*(/)€£/* = {u:u£Ut J (и) = inf J(u)> — oo}. Построим
«ее/
новую последовательность {vk(t)} так:
где
__L
h>o, |IM0-"*(0IIl<dP* 2 ^-o (*-oo).
Тогда:
1) \\u-(t)-vk(t)lL(r)->0(k-+oo);
2
2) t»ft(0-»yK('-0) + u*(' + 0)] при t0<t<T,
vkHo)-*• Y"*Co + 0), vk(T) + ±-u'(T-0);
3) vk(t)-+W{t)
равномерно на любом замкнутом множестве, принадлежащем ин-
тервалу непрерывности u*(t). Доказательство этой теоремы см. в
работе [31]. По поводу согласования метода регуляризации с ко-

354 РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ [Гл. 8
нечно-разностными и другими аппроксимациями экстремальных за-
дач см. работы [28, 30, 31, 33, 36, 37]; примеры конкретных при-
кладных экстремальных задач, решенных с помощью регуляриза-
ции, см., например, в работах [37, 143, 151, 222, 224, 226].
В заключение заметим, что метод регуляризации широко при-
меняется для решения самых различных классов некорректно по-
ставленных задач науки и техники, как, например, многих обрат-
ных задач математической физики, задачи численного дифференци-
рования, интегрального уравнения Фредгольма первого рода, вы-
рожденной системы линейных алгебраических уравнений, суммиро-
вания рядов Фурье, и др.
Упражнения. 1. Пусть требуется минимизировать функцию
J (и) = | Аи — Ь\еп при ие£т, где А — заданная матрица порядка
nxm, Ъ — заданный вектор из Еп. Будет ли корректно поставлена
эта задача, если система Аи=Ь имеет решение и притом единст-
венное? Имеет бесконечно много решений? Не имеет решения?
Можно ли в качестве регуляризатора этой задачи взять функцию
Q(u) = \u—й0|2, где uq — заданный вектор из Ет? Как регуляри-
зовать эту задачу, если вместо точных А и Ъ известны ^ишь при-
ближенные А и 6, ||Л—Л[|<6, \Ъ—6|<:б?
2. Привести пример некорректно поставленной задачи линей-
ного программирования. Кая регуляризовать задачу: минимизи-
ровать /(и)=.(с, и) при условиях Аи=Ь, и^0> где «Е£т, Ь&ЕПу
А — матрица порядка nXm, с^Ет [226].
3. Пусть требуется минимизировать функционал
т т
J(u)= j| |tf(s, t)u(s)ds — f(t)\2dt при u = ujt)6L2[0, T]9
о о
где K(s,t), f(t) — заданные функции при 0<^s<7\
/t(M)6L2(Q), Q = {(s,/):0<s,^<r}, /(06L2[0,r].
Привести примеры K(s, t)y когда такая задача поставлена некор-
ректно. Можно ли здесь в качестве регуляризатора взять функцио-
налы Q(u) из примеров 2.2—7?
4..Можно ли в задачах оптимального управления из §§ 6.5—7
в качестве регуляризатора взять функционалы Q(u) из примеров
2.2—7?
5. Указать методы определения элементов Uk из (2.3) для
только что сформулированных упражнений vl—4.

Глава 9
Разностные аппроксимации задач
оптимального управления
Численная реализация многих методов решения задач опти-
мального управления, связанных с системами обыкновенных диф-
ференциальных уравнений или уравнениями в частных производ-
ных, требует применения тех или иных методов приближенного
вычисления встречающихся при этом интегралов, решений задач
Коши, краевых задач. При этом часто исходная задача заменяет-
ся разностной задачей (например, так мы поступили в гл. 4), и
возникает вопрос о сходимости решений разностной задачи оптими-
зации к решению исходной задачи. Вопросам изучения поведения
разностных аппроксимаций для различных задач оптимального уп-
равления посвящены, например, работы {22, 28—30, 32, 33, 58, 77,
78, 112, 259, 261]. Здесь мы ограничимся рассмотрением разност-
ных аппроксимаций для двух задач, изучавшихся в гл. 6.
§ 1. РАЗНОСТНАЯ АППРОКСИМАЦИЯ ДЛЯ ОДНОЙ ЗАДАЧИ
МИНИМИЗАЦИИ КВАДРАТИЧНОГО ФУНКЦИОНАЛА
Пусть требуется минимизировать функционал
J(u)=\x(Tyu)-y\* (1)
при условиях
x = A(t)x+B(t)u + f(t), /0<*<Г; x(t0) = xot (2)
u = u(t)e L{{] [t0, 7J, и(/)6 V почти всюду на t0 <t <7\ (3)
где x=(x\ ..., xn), u=(ul, ..., ur); V — заданное выпуклое замкну-
тое ограниченное множество из Ет\ A,(t), B(t), f\t)—заданные
матрицы порядка пХп, пХг, пХ1 соответственно с кусочно-непре-*
рывными элементами при fo^t^T; моменты to, Т и точки дго, У^Еп
предполагаются известными (см. § 6.5).
Для приближенного решения этой задачи разобьем отрезок
^С^Г на N частей точками *о<*1< ... <txr=T и, приняв эти
точки в качестве узловых, уравнения (2) заменим разностными
уравнениями с помощью простейшей явной схемы Эйлера. Тогда
придем к следующей задаче: минимизировать функционал
ЫМ = 1**-*/|2
(4)

2&6РАЗНОСТНЫЕ АППРОКСИМАЦИИ ЗАДАЧ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [Гл. 9
при условиях
xt+l = xt + Mt[AtxL + Btut + ft], i = 0, 1, 9N—U (5)
k] = (^o»"i» .илг-i), "i€V, t = 0, 1, ... ,N— 1, (6)
где
Af, = ti+l -th Л = A(tt + 0), B, = B(tt + 0), /, = f(tt + 0).
При каждом фиксированном N^A задача (4) —(6) может
быть решена, например, с помощью метода динамического про-
граммирования (гл. 4). Предположим, что при каждом N^A и за-
данном разбиении {U}, t0<.t\<i <tN=T получено дискретное
управление [ufN] = {u*N, , и^), дающее приближенное реше-
ние задачи (4) — (6) в следующем смысле:
Ги<1и№ы\)<Гы + *н> (7)
где /#—нижняя грань функционала (4) при условиях (5), (6), а
последовательность {е^} такова, что е^>0, е*г-*-0 (Af-^oo).
Теорема 1. Пусть при всех достаточно больших N точки
разрыва матриц А (/), B(t), f(t) принадлежат множеству узловых
точек {U} и пусть
max Mt = dN < —, С = const >0, N = 1, 2, ...
Тогда lim /# = «/*, где Г — нижняя грань функционала (1) при ус-
ЛГ-юо
ловиях (2) — (3). Кроме того, последовательность кусочно-постоян-
ных управлений u*N(t), N = 1, 2,... , получаемых с помощью дис-
кретных управлений [u*N] из '(7) по правилу иен (t) = u?N при
'*<<<*Н-1| ' = 0, 1,_ ,N— 1, минимизирует J{u), т. е.
lim J(u'N»(t)) = J\
N-*oo
Для доказательства этой теоремы прежде всего заметим, что:
1) верна оценка
И',и)|<Сь t0<t<£Tt (8)
где Ci=const>0 не зависит от t и выбора u(t). из (3). Эта оцен-
ка вытекает из неравенства (7.1.6) с учетом ограниченности
И (Oil, \\B(t)\\y \f(t)\ и множества V;
2) верна оценка
\x(t9u)—x(x,u)\<C%\t — %\9 t0<t,x<T, (9)
где С2=const>0 не зависит от t, те(^0, Т\ и выбора u(t) из (3).

§ 1] Разностная аппроксимация для одной квадратичной задачи 357
Для получения этой оценки достаточно почленно проинтегрировать
уравнение (2) на отрезке [t, т]:л
\x(t9u) — x(x, и)| = К [A(s)x(s,u) + B(s)u(s) + f(s)]ds\
и дальше воспользоваться неравенством треугольника, ограничен-
ностью ||Л(0Н, ||5(011, 1/(01 и множества V, оценкой (8);
3) верна оценка
\x(t,u)-x(t,v)\<CM\u(t)-v(t)\*dty*, t.<t<T9 (Ю)
где C3=const>0 не зависит от t и выбора u(t), v(t) из (3). В са-
мом деле, функция y(t)=x(t, u)—x(t, v) является решением за-
дачи (2) при /(/)s=0, л;0=0 с заменой и на u(t)—v(t), и оценка
(10) является следствием (7.1.6) (ср. с (7.1.7));
4) функционал J (и) из \(1) при условиях (2) — (3) удовлетво-
ряет условию Липшица
\J(u)-J(v)\<CJu(t)-v(t)\\Lirh (11)
где C4=const>0 не зависит от u(t), v(t) из (3). Неравенство (11)
является простым следствием оценки (10) и вида (функционала (1).
Впрочем, вместо (11) нам для дальнейшего достаточно было бы
непрерывности J (и) в L(2r)[tQ, Т].
Лемма 1. При выполнении условий теоремы 1 для любого
управления u(t) из (3) и любого числа б>0 найдется такой номер
Nu что на всех сетках с номером N^.N\ существует дискретное
управление [щ] из (6), для которого
|/(K)-/„(N)I<6.
Доказательство. Прежде всего покажем, что для любого
управления u(t) из (3) и любого числа у>0 можно указать непре-
рывное управление v(t) из (3), для которого \\u(t) — v(0llL(r) <Y-
Для этого воспользуемся теоремой Лузина {137], согласно которой
для любого т)>0 существует такое замкнутое множество Л1ле
e[fo, Т\ меры мЛГть что Т—10—juuWti<ti и u(t) непрерывна на М^.
Возьмем ti>0 столь малым, чтобы r\D2^y2t где D= sup \и — v\—
u,v€V
диаметр множества V. Положим v(t)=u(t) при /еМп, а на каж-
дом дополнительном интервале, из которых составлено открытое
множество CMn=[t0, Г]\Мл, функцию v(t) доопределим линейно
между значениями функции u(t) на концах рассматриваемого ин-
тервала. Очевидно, функция v(t) непрерывна и, кроме того, удов-

358РАЗНОСТНЫЕ АППРОКСИМАЦИИ ЗАДАЧ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [Гл. 9
летворяет условиям (3) в силу определения v(t) и выпуклости V.
Далее
\\u(t)-v(t)fL{r)= J \u(t)-v(t)\*dt<D*-i\<y*.
2 смп
В силу условия ((11) можем y>0 считать столь малой, что
\J(u)-J(v)\<±.
Возьмем произвольное разбиение {U} отрезка [*о, Л» удовлет-
воряющее условиям теоремы 1, и положим [иЦ=(ио, щ, ..., Un-\)
с Ui=v(U), t=0, 1, ..., N—l. Пусть [*i]=(*0, ..., *jv)—решение
задачи (5), соответствующее выбранному [и<], x(t, v)—решение
задачи (2) при u=v(t). Покажем, что
^max \xt — x(thv)\^0
при N-*~oo. Из (2), (5) имеем
i *k+l
x(ti+Xiv) = x0 + y£ f [A(x)x(%iv) + B(%)v(%) + f(x)]d>x,
k=otk
хт = х0 + £ J [Akxk + Bkv(tk) + fk]d%, * = 0, 1 JV—1. (12)
Отсюда
f^otk
ixft+bio-*+lK2; j (|Л(т)^(т,^-v*i +
*=0*ft
+ |B(t)t;(T)-^(g| + |/(T)-/,|)dT.
Пользуясь неравенством треугольника, ограниченностью и ку-
сочной непрерывностью 4(f), B(t)> f(t), определением Ait Ви fu
непрерывностью v(t) и оценками (8) —(9), из предыдущего нера-
венства нетрудно получить
t
\x{ti+u V) — Xf+l|<
Ч/vAnax
V\x(tk9v)-xk\ + oN(l), (13)
*=o
где Anax= SUP M(f)l. Ojv(1)>0 не зависит от i и о#(1)-*-0 (N-+oc).
u<t<T

§ 1] Разностная аппроксимация для одной квадратичной задачи 359
Из (13) и леммы 6.4.1 при cpfesss \x{tk, v)— xh\, a=Ojv(l), b=dNAm8iX
имеем оценку
\x(ti,v)-xi\<£oN(l)(l+dNAmaxy, / = 0, 1, 9N.
Ho dN < — по условию, поэтому (1 + dNAm^i < exp (СДпах) и
N
\x(th v)-xt\ <о„(1) exp {СЛгаах}( f = 0, 1, • • •-,N, (14)
так что max |л:(*,, v) — хЛ-+0 ,[(JV-»-oo). Из (1), (4) следует, что
0<t<N
J(v) — 1ы([щ])-*0 при #-»-oo, поэтому \J(v) — 1к([щ])\<— при
всех #>Л^. Окончательно с учетом оценки |У(и) — J(v)\ <— име"
ем | J (и) — /# ([щ]) | < б при всех N^NX. А
Лемма 2. Пусть выполнены условия теоремы 1, пусть [wj=
= (но, ..., Un-i) удовлетворяет условиям (6) и и&Ц)=щ при /*<;
^/<**+ь /=0, 1, ..., N— 1. Тогда для любого 6>0 найдется такой
номер N2i что
|/(илг(0)-/лг(Ы)1<в
при всех N^N2.
Доказательство. Пусть (**!= (*о, ..., Xn) —решение зада-
чи (5), соответствующее [щ], x(t, uN)—решение задачи (2) при
u=UN(t). Из (2) и определения u^it) имеем
x(ti+uuN)=x0 + £ J [A(x)x(x, uN) + B(x)uk + f(x)]dx.
k=otk
Вычтем отсюда почленно равенство (12) и после простых преобра-
зований по аналогии с (14) получим
\x(thuN)-xi\^oN(l)exp(CAmax), * = 0, 1, ,N, (15)
где oN(l)-+ + 0 (N-+oo).
В частности, огсюда при i=N имеем, что \х(Ту un)—Xn\->-
-^0 (N-^oo), а тогда из (1), (4) следует \J(uN(t))—IN([Ui])\^8
при всех N^N2. А
Доказательство теоремы 1. Возьмем произвольное
е>0. По определению /* — нижней грани J (и) при условиях (2),
(3)—найдется ue(t), удовлетворяющее условиям (3) и /*<;
<;/(ие(*))<;/*+е/2 (здесь, например, можно взять иг (/)=м*(*),
на котором J(u*(t))=J*; существование оптимального u*(t) см.

ЗвОРАЗИОСТИЫЕ АППРОКСИМАЦИИ ЗАДАЧ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [Гл. 9
в § 6.5). В силу леммы 1 существует такое число N\ и дискретное
управление [щ\ что
|/(И0)-/*(М)1<-§-« N>NX.
Поэтому
In < In (Ы) < /(и* (*)) + -± < У + е,
или I*N < J* + е при всех N > Л^. Следовательно, lim /# < J* + е,
или в силу произвольности e>0:lim/#<,/*.
N-+00
С другой стороны, по определению I*N для любого е>0 и .лю-
бого N>1 найдется такое дискретное управление [uf] из (6), что
lN<lN([u4])<lN+f.
По лемме 2 для управления
и&(0в«№<'<*+ь ' = 0, 1, ,ЛГ—1,
имеет место
\J(u%(t))^IN([u*])\<±
при всех W>N2. Так как и^(0 удовлетворяет условиям (3), то
J*<J(u%{t))<lN([u?])+Y<I» + B> или ^<'*+~
при всех W >#2. Поэтому lim/jv >/* — е или в силу произвольнос-
ти е>0: Нт/#>,/*. Выше было доказано, что lim/#</*. Срав-
нивая последние два неравенства, заключаем, что lim/^ =J*. На-
N-юо
конец, если [u*N] удовлетворяет условиям (6), (7), то для
и* (t)see up, tt <t<ti+u i = 0, ... , N- 1,
будем иметь
0<J(u^(t))-r<\J(uB/(t))-IN([up])\ +

§ 2] Разностная аппроксимация задачи о нагреве стержня 361
Небольшим видоизменением приведенных выше рассуждений
можно убедиться в справедливости утверждений теоремы 1 для
более общего функционала
/(a)- $Р(х9и^)Л + Ф(х(Т))
to
при условиях (2), (3), если Ф(х), f°(x;u, t) непрерывны,
\f°(x,uJ)-P(x + bx,u+Jiutt)\<L(\bx\ + \bu\)
при любых |*|<С1э )х + Д*|<С1э и, u + kueV, t0<t<^T9 а вмес-
то (4) берется
JV— 1
*» (М) = 2 &tJ4*l, Щг 0 + Ф (*N).
При доказательстве теоремы 1 выше использовалась методика
работ [32, 33}. Сходимость разностных аппроксимаций более общих
задач оптимального управления для нелинейных систем обыкновен-
ных дифференциальных уравнений при наличии фазовых ограни-
чений, подвижных крнцов и других факторов и вопросы согласова-
ния разностных аппроксимаций с регуляризацией исследованы в
работах [22, 28, 30, 32, 33, 112, 259, 261].
§ 2. РАЗНОСТНАЯ АППРОКСИМАЦИЯ ЗАДАЧИ ОБ ОПТИМАЛЬНОМ
НАГРЕВЕ СТЕРЖНЯ
Рассмотрим задачу из § 6.6: минимизировать функционал
J(u)=$\]x{stT,u)-y(s)\*ds (1)
при условиях
-£- = -ГГ. (M)€Q = {0<s</, 0<t<T}, (2)
ot 0SZ
dx(0,t) =0) 0<;<Г; X{s,0) = 0, 0<s</, (3)
ds
d*<V> =v[u(t)-x(l,t)],0<t<T, (4)
OS
u(t)£L2[0,T]9 |а(/)|<1 почти всюду на 0<*<7\ (5)
где /, Г, v — заданные положительные константы, у(s) —заданная
непрерывная функция на отрезке 0<;s^/.

362РАЗНОСТНЫЕ АППРОКСИМАЦИИ ЗАДАЧ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [Гл. $.
Для приближенного решения этой задачи в прямоугольнике Q
введем сетку точек ($*, fj), Si=ih, tj=j%, t=0, 1, ..., N; /=0, 1, ..,
..., M, где ft, т—шаги сетки, Nh=l, хМ=Т. Интеграл в ,(!1) за-
меним суммой по формуле прямоугольников, уравнение (2) -— раз-
„ дх . 0 ч
ностными уравнениями по неявной схеме, производные -т— в (3),
OS
(4) — их разностными отношениями. В результате придем к задаче
минимизации функционала -
'м(М)= %h[x{M-y(Si)Y (6)
при условиях
ХИ~Х{"'-1 = X^-'-2xhrXi-U!, I = 1, ■ ■ ■ ,N- 1; /, 1,... ,M, (7)
*•/ = *!/(/= 1. 2, .....Ai), *£o = 0, < = 0, 1,... ,iV, (8)
= v[u,-xNi], j=l,2,...,M, (9)
[«<] = («i, "2. • •••»"m). I"/1< 1, /=1,2 M. (10)
Пусть /* — нижняя грань функционала (1) при условиях
(2)—(5), //t,T —нижняя грань функционала (6) при условиях
(7)—i(10), пусть [uf] представляет собой приближенное решение
задачи (6) — (10) в следующем смысле:
/м</*т([^</м + в, (И)
где е=е(А, т)-^0 при ft, т-^оо.
Теорема 1. Имеет место равенство lim/ft,T = «/\ Управления
uB(t), полученные кусочно-постоянным продолжением [и*] из (11):
u?(t) = и*, tL </<^+i, i = 0, 1, ... , М— 1, минимизируют функцио-
нал J (и), т. е. lim J (ue(t))= J*
ft.T-»0
Доказательство этой теоремы опирается на следующие две лем-
мы,^ аналогичные леммам 1.1—2.
Лемма 1. Для любого управления u(t) из (5) и любого чис-
ла 6>0 существуют ft(&), т(6) такие, что при всех ft, т, 0<ft<
<А(6), 0<т<т(6) можно указать дискретное управление [щ] из
(10), для которого \J(u(t))—Ih,T ([щ]) | <6.
Л ем м а 2. Пусть [щ]= (щ, ..., им) удовлетворяет условию (10)
и uT(t)=uiy tt^t<ti+u i=0, 1, ..., Af— 1. Тогда для любого &>0

§ 2] Разностная аппроксимация задачи о нагреве стержня 363
найдутся такие А(б), т(6)>0, что \J(ux(t))—Ih)T ([щ]) | <бпривсех
Л, т, 0<Д<А(6), 0<т<т(6).
Доказательства этих лемм проводятся с помощью методики,
используемой в работах [107, 125] и в § 42 книги [181], и довольно
громоздки, поэтому здесь их не приводим. Доказательство теоре-
мы 1 проводится с помощью лемм 1, 2 в точности так же, как и
теорема 1.1 с помощью лемм 1.1—2.
При каждом фиксированном Л, т для приближенного решения
задачи (6) —(10) могут быть использованы методы гл. 2 или §6.2.
Решение краевой задачи (7) — (9) при заданном [щ] из (10) удоб-
нее всего получить методом прогонки [20, 207].
Сходимость разностных аппроксимаций для задач оптималь-
ного управления, связанных с другими классами уравнений с част-
ными производными, исследована в работах [77, 78]; общие вопро-
сы аппроксимации экстремальных задач рассмотрены в рабо-
те [30].

ЛИТЕРАТУРА
1. Аббасов Т. М. Метод решения некоторых неустойчивых задач синтеза оп-
тимального управления. ЖВМ и МФ, 12, № 6, 1579—-1584, 1972. -
2. А б р а м о в А. А. О'переносе граничных условий для систем линейных обык-
новенных дифференциальных уравнений (вариант метода прогонки). ЖВМ
и МФ, 1, № 3, 542—545, 1961.
3. Альбер Я. И. К задаче минимизации гладких функционалов градиентны-
ми методами. ЖВМ и МФ, И, № 3, 752—757, 1971.
4. Альбер Я. И. Непрерывные процессы Ньютоновского типа. «Дифференц.
уравнения», 7, № 11, 1931—1945, 1971.
5. А н о р о в В. П. Принцип максимума для процессов с ограничениями общего
вида, I, II. «Автоматика и телемеханика», Jsfe 3, 5—15, 1967; № 4, 5—17,
1967.
6. Ар и с Р. Дискретное динамическое программирование. М., «Мир», 1969.
7. Аркин В. И., Левин В. Л. Выпуклость значений векторных интегралов,
теоремы измеримого выбора и вариационные задачи. «Успехи матем. наук»,
27, вып. 3 (165), 21—77, 1972.
8. А т а н с М., Ф а л^б П. Оптимальное управление. М., «Машиностроение»,
1968.
9. Бабич М. Д. Оценка полной погрешности при минимизации квадратик
ного функционала в шаре. «Укр. матем. журн.», 22, № 3, 308—319, 1970.
10. Бабич М. Д., Иванов В. В. Исследование полной погрешности в зада-
чах минимизации функционалов при наличии ограничений. «Укр. матем.
журн.», 21, № 1, 3—14, 1969.
11. БабунашвилиТ. Г. Синтез линейных оптимальных систем. ДАН СССР,
155, № 2, 295—298, 1964.
12. Бакушинский А. Б. Регуляризующие алгоритмы для решения некор-
ректных экстремальных задач. Сб. «Методы управления большими систе-
мами», т. 1. Иркутск, 1970, стр. 223—235.
13. Б а х и т о Р. У., К р а п ч е т о в Н. И., К р о т о в В. Ф. Синтез приближенно-
оптимального управления для одного класса управляемых систем. «Авто-
матика и телемеханика», № 10, 33—43, 1972.
14. Беллман Р. Динамическое программирование. М., ИЛ, 1960.
15. Беллман Р., ГликсбёрИ., Гросс О. Некоторые вопросы матема-
тической теории процессов управления. М., ИЛ, 1962.
16. Беллман Р. Процессы регулирования с адаптацией. М., «Наука», 1964.
17. Беллман Р., Дрейфус С. Прикладные задачи динамического програм-
мирования. М., «Наука», 1965.
18. Б е л л м а н Р., К а л а б а Р. Динамическое программирование и современ-
ная теория управления. М., «Наука», 1969.
19. Бе резин И. С, Жидков Н. П. Методы вычислений, т. I. М., «Нау-
ка», 1966.
20. Бе резин И. С, Жидков Н. П. Методы вычислений, т. II. М., Физмат-
гиз, 1962. i
21. БерковичЕ. М. О теоремах существования в двухэтапных.задачах сто-
хастического оптимального управления. «Вестн. Моск. ун-та», матем., механ.,
№ 2, 64—69, 1972.
22. Б е р к о в и ч Е. М. Разностные аппроксимации для двухэтапных задач сто-
хастического оптимального управления. «Вестн. Моск. ун-та», матем., ме-
хан., № 3, 43—51, 1972.
23. Б о л т ян с к и й В. Г. Достаточные условия оптимальности и обоснование
метода динамического программирования. «Изв. АН СССР», сер. матем.,
28, № 3, 481—514, 1964.
24. Б о Л1ЛЛ с кий В. Г. Математические методы оптимального управления.
М., «Наука», 1969.

ЛИТЕРАТУРА
365
25. Болтянский В. Г. - Необходимые условия экстремума функции. «Диф-
ферент уравнения», 8, № 9, 1553—1559, 1972.
26. Болтянский В. Г. Оптимальное управление дискретными системами.
М., «Наука», 1973.
27. Б р а й с о н А., X о Ю-Ш и. Прикладная теория оптимального управления.
М., «Мир», 1972.
28. Будак Б. М., Беркович Е. М. Разностные аппроксимации для задач
оптимального управления с подвижными концами при наличии фазовых ог-
раничений, I, II, III. «Вестн. Моск. ун-та», матем. механ., № 6, 59—68,
1969; N° 1, 39—47, 1970; № 3, 23—33, 1970.
29. Будак Б. М., Беркович Е. М. О задачах оптимального управления
для дифференциальных уравнений с разрывными правыми частями. ЖВМ
и МФ, 11, № 1, 51—64, 1971.
30. Б у,д а к Б. М., Б е р кф в и ч Е. М. Об аппроксимации экстремальных за-
дач, I, И. ЖВМ и МФ, И, № 3, 580—596; N° 4, 870-884, 1971.
31. Будак Б. М., Б ерков ич Е. М., Г а поненко Ю. Л. О построении
сильно сходящейся минимизирующей последовательности для непрерывного
выпуклого функционала. ЖВМ и МФ, 9, № 2, 286—299, 1969.
32. Будак Б. М., Беркович Е. М., Соловьева Е. Н. О разностных
аппроксимациях в задачах оптимального управления. «Вестн. Моск. ун-та»,
матем. механ., № 2, 41—55, 1968.
33. Б у д а к Б. М., Беркович Е. М., Соловьева Е. Н. О сходимости
разностных аппроксимаций для задач оптимального управления. ЖВМ и
МФ, 9, N° 3, 522—547, 1969.
34. Будак Б. М., Васильев Ф. П. Приближенные методы решения задач
оптимального управления (тексты лекций), вып. 1. Изд-во МГУ, 1968.
35. Будак Б. М., Васильев Ф. П. Приближенные методы решения задач
оптимального управления (тексты лекций), вып. 2. Изд-во МГУ, 1969.
36. Б у д а к Б. М., В и н ь о л и А., Г а п о н е н к о Ю. Л. Об одном способе ре-
гуляризации для непрерывного выпуклого функционала. ЖВМ и МФ, 9,
№ 5, 1046—1056, 1969.
37л Будак Б. М., Гапоненко Ю. Л., Сидорович В. Г. О прямом ме-
тоде решения некоторой некорректной обратной задачи. В сб. трудов
ВЦ МГУ «Решения задач Стефана». Изд-во МГУ, 1971, стр. 226—234.
38. Будак Б. М., Гольдман Н. Л. Оптимальная задача Стефана для ква-
зилинейного параболического уравнения. В сб. трудов ВЦ МГУ «Решения
задач Стефана». Изд-во МГУ, 1971, стр. 155—179.
39. Буземан Г. Выпуклые поверхности. М., «Наука», 1964.
40. Б у т к о в с к и й А. Г. Теория оптимального управления системами с рас-
пределенными параметрами. М., «Наука», 1965.
41. БутковскийА. Г., Полтавский Л. Н. Оптимальное управление рас-
пределенной колебательной системой. «Автоматика и телемеханика», 26,
N° И, 1900—1914, 1965.
42. Б утков ск и й А. Г., Полтавский Л. Н. Оптимальное управление
двухмерной распределенной колебательной системой. «Автоматика и теле-
механика», N° 4, 32-41, 1966. л
43. Бутковский А. Г., Полтавский Л. Н. Оптимальное управление
волновыми процессами. «Автоматика и телемеханика», № 9, 48—53, 1966.
44. БутковскийА. Г., Ч е р к а ш и н А. Ю. Оптимальное управление элек-
тромеханическими устройствами постоянного тока. М., «Энергия», 1972.
45. В а з а н М. Стохастическая аппроксимация. М., «Мир», 1972.
46. В а й н б е р г М. М. Вариационный метод и метод монотонных операторов.
М., «Наука», 1972.
47. Васильев О. В. Градиентный метод решения одного класса задач оп-
тимального регулирования. ЖВМ и МФ, 7, № 1, 52—61, 1967.
48. Васильев Ф. П. Условия оптимальности для некоторых классов систем,

366
ЛИТЕРАТУРА
не разрешенных относительно производной. ДАН СССР, 184, № 6, 1267—
1270, 1969.
49. В а с и л ь е в Ф. П. О существовании решения одной оптимальной задачи
Стефана. "В сб.: «Вычисл. методы и программирование», вып. 12. Изд-во
МГУ, 1969, стр. 110-114.
50. В а с и л ь е в Ф. П. Об итерационных методах решения задач быстродейст-
вия, связанных с параболическими уравнениями. ЖВМ и МФ, 10, № 4,
942—957, 1970.
51. Васильев Ф. П., Иванов Р. П. Некоторые приближенные методы ре-
шения задач быстродействия в банаховых пространствах при наличии фа-
зовых ограничений. ДАН СССР, 195, № 3, 526—529, 1970.
52. В а с и л ь е в Ф. П., Иванов Р. П. О приближенном решении задачу
быстродействия с запаздыванием. ЖВМ и МФ, 1Q, № 5, 1124—1140, 1970.
53. В а с и л ь е в Ф. П., Иванов Р. П. О приближенном решении задачи
быстродействия в банаховых пространствах при наличии ограничений на
фазовые координаты. ЖВМ и МФ, И, № 2, 328—347, 1971.
54. Вентцель Е. С. Исследование операций. М., «Советское радио», 1972.
55. Воробьев Л. М., Воробьева Т. М. Нелинейные преобразования в
прикладных вариационных задачах. М., «Энергия», 1972.
56. В о р о б ь е в Н. Н. Числа Фибоначчи. М., «Наука», 1969.
57. Г а б а с о в Р., Кириллова Ф. М. Построение последовательных при-
ближений для некоторых задач, оптимального управления. «Автоматика и
телемеханика», № 2, 5—17, 1966.
58. Г а б а с о в Р., Кириллова Ф. М. К вопросу о распространении прин-
ципа максимума» Л. С. Понтрягина на дискретные системы. «Автоматика и
телемеханика», № 11, 46—51, 1966. .
59. Габасов Р., Кириллова Ф. Качественная теория оптимальных про-
цессов. М., «Наука», 1971.
60. Габасов Р., Кириллова Ф. М. Современное состояние теории опти-
мальных процессов. «Автоматика и телемеханика», № 9, 31—62, 1972.
61. Габасов Р., Кириллова Ф. М., СрочкоВ. А., ТарасенкоН. В.
Условия оптимальности высокого порядка. I. Вычисление особых управлений
(обзор). «Автоматика и телемеханика», № 5, 5—21, 1971. II. Необходимые
условия оптимальности высокого порядка (обзор). «Автоматика и телеме-
ханика», № 6, 5—24, 1971. III. Достаточные условия оптимальности высо-
кого порядка. Дискретные системы (обзор). «Автоматика и телемеханика»,
№ 7, 5—34, 1971.
62. Г а л ь ч у к Л. И. О некоторых задачах на оптимальное управление система-
ми, описываемыми параболическим уравнением. «Вестн. Моск. ун-та», ма-
тем. механ., № 3, 21—33, 1968.
63. ГамкрелидзеР. В. О скользящих оптимальных режимах. ДАН СССР,
143, № 6, 1243—1245, 1962.
64. Гамкрелидзе Р. В., Харатишвили Г. Л. Экстремальные задачи
в линейных топологических пространствах. «Изв. АН СССР», сер. матем.
33, № 4, 781—839,1969. '
65. Гамкрелидзе Р. В. Необходимые условия первого порядка и аксио-
матика экстремальных задач. «Тр. МИАН СССР», СХИ, 1971, стр. 152—180.
66. Ганшин Г. С. Расширение области сходимости метода Ньютона. ЖВМ и
МФ, 11, № 5, 1294—1296, 1971.
67. Гельфанд И. М., Вул Е. Б., Гинзбург С. Л., Федоров Ю. Г.
Метод оврагов в задачах ©ентгеноструктурного анализа. М., «Наука», 1966.
68. Гельфанд И. М., Фомин С. В. Вариационное исчисление. М., Физмат-
гиз, 1961.
69. Г е р м е й е р Ю. Б. Введение в теорию исследования операций. М., «Нау-
ка», 1971.
70. Г о л е н к 6 Д. И. Статистические методы сетевого планирования и управ-
ления. М., «Наука», 1968.

ЛИТЕРАТУРА
367
71. Голубь Н. Н. Оптимальное управление линейными и нелинейными систе-
мами с распределенными параметрами. «Автоматика и телемеханика», № 9,
15—28, 1969.
72. Голубь Н. Н. Оптимальное управление нелинейными системами с распре-
деленными параметрами. «Автоматика и телемеханика», № 10, 35—44, 1969.
73. Гольштейн Е. Г. Теория двойственности в математическом программиро-
вании и ее приложения. М., «Наука», 1971.
74. Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования
транспортного, типа. М., «Наука», 1969.
75. Г р о д з о в с к и и Г. Л., Иванов Ю.Н., Т о к j р е в В. В. Механика кос-
мического полета с малой тягой. М., «Наука», 1966.
76. Г у л е н к о В. П., Е р м о л ь е в Ю. М. О некоторых задачах оптимального
управления с уравнениями эллиптического типа. Тр. семинара «Теория оп-
тимальных решений», вып. 1. Киев, 1968.
77. Гул ен ко В. П., Ермольев Ю. М. Конечноразностный метод в задачах
оптимального управления с уравнениями Дарбу. Тр. семинара «Теория оп-
тимальных решений», вып. 2. лиев, Изд-во АН УССР, 1968.
78. Гуленко В. П.* Ермольев Ю. М. О конечноразностном методе в
задачах управления системами с распределенными параметрами. «Ки-
бернетика», № 5, 81—83, 1970.
79. Г у р и н Л. С, Д ы м а р с к и й Я. С, М е р к у л о в А. Д. Задачи и ме-
тоды оптимального распределения ресурсов. М., «Советское радио», 1968.
80. Д а й о в и ч С. К теории оптимальных процессов в линейных . системах.
«Дифференц. уравнения», 8, № 9, 1687—1690, 1972.
81. Данилин Ю. М. Минимизация нелинейных функционалов в задачах с
ограничениями. «Кибернетика», № 3, ПО—117, 1970.
82. Д а н и л и н Ю. М. Методы минимизации, основанные на аппроксимации
исходного функционала выпуклым. ЖВМ и МФ, 10, № 5, 1067—1080, 1970.
83. Данилин Ю. М. Оценка эффективности одного алгоритма отыскания аб-
солютного минимума. ЖВМ и МФ, 11, №4, 1026—1031, 1971.
84. Д а н и л и и Ю. М. Методы сопряженных направлений для решения задач
минимизации. «Кибернетика», № 5, 122—136, 1971.
85. Данилин Ю. М., П и я в с к и й С. А. Об одном алгоритме отыскания аб-
солютного минимума. Тр. семинара «Теория оптимальных решений», вып. 2.
Киев, Изд-во АН УССР, 1967, стр. 25—37.
86. Данилин Ю. М., Пшеничный Б. Н. О методах минимизации с уско-
ренной сходимостью. ЖВМ и МФ, 10, № 6, 1341—1354, 1970.
87. Данилин Ю. М., Пшеничный Б. Н. Метод минимизации без вычис-
ления производных. ЖВМ и МФ, 11, № 1, 12—21, 1971.
88. Данфорд Н., Шварц Дж. Т. Линейные операторы. Общая теория. М.,
ИЛ, 1962.
89. Д а ф ф и н Р., Питерсон Э., 3 е н е р К. Геометрическое программиро-
вание. М., «Мир», 1972.
90. Дегтярев Г. Л., Сиразетдинов Т. К. Об одной задаче оптимального
управления системами с распределенными параметрами. «Изв. АН СССР»,
сер. техн. киберн., № 1, 151—160, 1967.
91. Дегтя р ев Г. Л., Сир а зет д и н ов Т. К. Об оптимальном управлении
одномерными процессами с распределенными параметрами. «Автоматика и
телемеханика», № 11, 29—38, 1967.
92. Д е г т я р е в Г. Л. Об оптимальном управлении распределенными процесса-
ми с движущейся границей. «Автоматика и телемеханика», № 10, 44—56.
1972.
93. Демьянов В. Ф. Построение программного управления, оптимальногс
в интегральном смысле. «Прикл. матем. и механ.», 27, вып. 3, 554—558, 1963
94. Д е м ь я н о в В. Ф. К построению оптимальной программы в линейное
системе. «Автоматика и телемеханика»- 25, № 1, 3—11, 1964.

368
ЛИТЕРАТУРА
95. Д е м ь я н о в В. Ф. Об одной нелинейной экстремальной задаче. ЖВМ и
МФ, 7, № 1,33—51, 1967.
96. Демьянов В. Ф., МалоземовВ. Н. .Введение в минимакс. М., «Нау-
ка», 1972.
97. Д е м ь я н о в В. Ф., Рубинов А. М. Приближенные методы решения
экстремальных задач. Изд-во ЛГУ, «1968.
98. Д м и т р и е в М. Г., П о л е щ у к В. С. О регуляризации одного класса не-
устойчивых экстремальных задач. ЖВМ и МФ, 12, № 5, 1316—1318, 1972.
99. Дубовицкий А. Я., Милютин А. А. Задачи на экстремум при нали-
чии ограничений. ЖВМ и МФ, 5, № 3, 395—453, 1965.
100. Дубовицкий А. Я., Милютин А. А. Необходимые условия слабого
экстремума в задачах оптимального управления со смешанными ограниче-
ниями типа неравенства. ЖВМ и МФ, 8, № 4, 725—779, 1968.
101. Дубовицкий А. Я., Милютин А. А. Необходимые условия слабого
экстремума в общей задаче оптимального управления. М., «Наука», 1971.
102. Дышин О. А. Градиентный метод решения оптимальной задачи для си-
стемы телеграфных уравнений ЖМВ и МФ, 12, № 6, 1465—1477, 1972.
103. Е в т у ш е н к о Ю. Г. Численный метод поиска глобального экстремума
функций (перебор на неравномерной сетке). ЖВМ и МФ, 11, № 6, 1390—
1373, 1971.
104. Егоров А. И. Оптимальные процессы в системах с распределенными
параметрами и некоторые задачи теории инвариантности. «Изв. АН СССР»,
сер. матем., 29, № 6, 1205—1260, 1965.
105. Егоров А. И. Об условиях оптимальности в одной задаче управления
процессом теплопередачи. ЖВМ и МФ, 12, № 3, 791—799, 1972.
106. Егоров А. И., РафатовР. О приближенном решении одной задачи
оптимального управления. ЖВМ и МФ, 12, № 4, 943—959, 1972.
107. Егоров Ю. В. Некоторые задачи теории оптимального управления. ЖВМ
и МФ, 3, № 5, 887—904, 1963.
108. Егоров Ю. В. Необходимые,условия оптимальности управления в банахо-
вых пространствах. «Матем. сб.», 64 (106), № (1, 79—101, 1964.
109. Ермольев Ю. М. Методы решения нелинейных экстремальных задач.
«Кибернетика», № 4, 1—>17, 1966.
ПО. Ер мо лье в Ю. М. О методе обобщенных стохастических градиентов и
стохастических квазифейеровских последовательностях. «Кибернетика», №2,
73—83, >1969. V
111. Е р м о л ь е в Ю. М., Г у л е н к о В. П. О численных методах решения за-
дач оптимального управления. «Кибернетика», № 1, 72—78, 1966.
112. Ермольев Ю. М., Г у л е н к о В. П. Конечно-разностный метод в зада-
чах оптимального управления. «Кибернетика», № 3, 1—20, 1967.
ИЗ. Захаров Г. К., Плотников В. И. Линейные оптимальные быстро-
действия с двумя группами управляющих параметров. ЖВМ и МФ, 8, № 6,
1196—1207, 1968.
114. Зойтендейк Г. Методы возможных направлений. М., ИЛ, 1963.
115. Зубов В. И. Теория оптимального управления судном и другими подвиж-
ными объектами. Л., «Судостроение», 1966.
116. Зуховицкий С. И., Авдеева Л. И. Линейное и выпуклое программи-
рование. М., «Наука», 1967.
117. 3 у х о в и ц к и й С. И., П о л я к Р. А., П р и м а к М. Е. Численный метод
для решения задачи выпуклого программирования в гильбертовом простран-
стве. ДАН СССР, 163, № 2, 282—284, 1965. \
118. Зуховицкий С. И., Радчик И. А. Математические методы сетевого
планирования. М., «Наука», 1965.
119. И в а н и л о в Ю. П., Пропой А. И. Задачи динамического выпуклого
программирования. ЖВМ и МФ, 12, № 3, 571—581, 1972.
120. Иванов В. В. Об оптимальных алгоритмах минимизации функций некото-
рых классов. «Кибернетика», № 4, 81—94, 1972.

ЛИТЕРАТУРА
369
121. Иванов Р. П. Об одном критерии оптимальности и связанном с ним
итерационном методе решения задачи быстродействия. ЖВМ и МФ, 11, №3,
597—610, 197L
122. Ива но в Р. П. Об одном итерационном методе решения задачи быстро-
действия. ЖВМ и МФ< И, № 4, 1031—1037, 1971.
123. И в а н о в а Г. П. О теоремах существования в вариационном исчислении.
ДАН СССР, 170, № 2, 253—256, il966.
124. Иванова Т. П., ~П о л я к Б. Т., Пухова Г. В. Численные методы ре-
шения некоторых экстремальных задач с частными производными. В сб.:
«Вычисл. методы и программирование», вып. 9. Изд-во МГУ, 1967,
стр. 194—203.
125. Ильин А. М., Калашников А. С, Олейник О. А. Линейные урав-
нения второго порядка параболического типа. «Успехи матем. наук», 17,
вып. 3 (105), 3-446, 1962.
126. Ильин В. А., Поз н як Э. П Основы математического анализа, ч. 1. М.,
«Наука», 1971.
127. И о с и д а К. Функциональный анализ. М., «Мир», 1967.
128. Иоффе А. Д., Тихомиров В. М. Двойственность выпуклых функций
и экстремальные задачи. «Успехи матем. наук», 2*, вып. 6 (144), 51—116,
1968.
129. Иоффе А. Д., Тихомиров В. М. Расширения вариационных задач.
«Тр. Моск. матем. об-ва», т. 18. Изд-во МГУ, U968, стр. 187—246.
130. Исаев В. К., Сонин В. В. Вычислительные аспекты задачи об опти-
мальном перелете как краевой задачи. ЖВМ и МФ, 5, № 2, 252—261, 1965.
131. Канторович Л. В., Акилов Г. П. Функциональный анализ в норми-
рованных пространствах. М., Физматгйз, 1959.
132. Канторович Л. В., Горстко А. Б. Оптимальные решения в экономи-
ке. М., «Наука», 1972.
133. Карлин С. Математические методы в теории игр, программирования и
экономике. М., «Мир», 1964.
134. Карманов В. Г. Математическое программирование, ч. 1. Изд-во МГУ,
1968.
J35. К и р и н Н. Е. Вычислительные методы теории оптимального управления.
Изд-во ЛГУ, 11968.
136. Клестов Е. А., СиразетдиновТ. К. Оптимальное по быстродействию
управление угловыми движениями и крутильными колебаниями упругого
летающего крыла. «Автоматика и телемеханика», № 10, 57—66, 1972.
137. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функ-
ционального анализа. М., «Наука», 1972.
138. Корбут А. А., Финкельщтейн Ю. Ю. Дискретное программирова-
ние. М., «Наука», 1969.
139. К р а с о в с к и й Н. Н. Теория управления движением. М., «Наука», 1968.
140. Красовский Н. Н. Теория оптимальных управляемых систем. Механика
в СССР за 50 лет, т. 1. Общая и прикладная механика. М., «Наука», 1968.
141. Кривенков Ю. П. Математические и вычислительные вопросы линейного
динамического программирования. Тр. Вычисл. центра АН СССР. М., Изд-во
ВЦ АН СССР, 1969.
142. К р о т о в В. Ф., Б у к р е е в В. 3., Г у р м а н В. И. Новые методы вариа-
ционного исчисления в динамике полета. М., «Машиностроение», '1969.
143. Крылов И. А. Численное решение задачи об оптимальной стабилизации
спутника. ЖВМ и МФ, 8, № 1, 203—208, 1968.
144. Крылов И. А., ЧерноуськоФ. Л. О методе последовательных при-
ближений для решения задач оптимального управления. ЖВМ и МФ, 2,
№6, 1132—1139, 1962.
145. Крылов И. А., Черноусько Ф. Л. Решение задач оптимального уп-
равления методом локальных вариаций. ЖВМ и МФ, 6, № 2, 203—217,1966.
146. Крылов И. А., Черноусько Ф. Л. Алгоритм метода последовательных

370
ЛИТЕРАТУРА
приближений для задач оптимального управления. ЖВМ и МФ, 12, № 1,
14—34, 1972.
147. КубичекМ., БубникА. Численное решение одной оптимальной зада-
чи. ЖВМ и МФ, 10, № 6, 1541—1647, 1970.
148. Куликовский Р. Оптимальные и адаптивные процессы в системах ав-
томатического регулирования. М., «Наука», 1967.
149. К ю н ц и Г. П., К р е л л е В. Нелинейное программирование. М., «Советское
радио», 1965.
150. Ладыженская О. А. Смешанная задача для гиперболического уравне-
ния. М., Гостехтеориздат, 1953.
151. Латтес Р., Лионе Ж-Л. Метод квазиобращения и его приложения.
М., «Мир», 1970.
152. Лебедев В. Н. Вариационная задача и взлет космического аппарата с
круговой орбиты. ЖВМ и МФ, 3, № 6, 1126—1129, 1963.
153. Л е в и т и н Е. С. О корректности ограничений и устойчивости в экстре-
мальных задачах, I, II. «Вестн.- Моск. ун-та», матем. и механ., № 1, 24—
34; № 2, 8—22, 1968.
154. Левитин Е. С. Об одном общем методе минимизации для негладких
экстремальных задач. ЖВМ и МФ, 9, № 4, 783—806, 1969.
156. Левитин Е. С, Поляк Б. Т. Методы минимизации при наличии огра-
ничений. ЖВМ и МФ, 6, № 5, 787—823, 1966.
156. Л ев и-тин Е. С, Поляк Б. Т. О сходимости минимизирующих последо-
вательностей в задачах на условный экстремум. ДАН СССР, 168, № 5,
997—1000, 1966.
157. Л е й т м а и Дж. Введение в теорию оптимального управления. М., «Нау-
ка», 1968.
158. ЛеончукМ. П. О численном решении задач оптимальных процессов с
распределенными параметрами. ЖВМ и МФ, 4, № 6, 1112—1117, 1964.
159. ЛеончукМ. П., Трофимов А. С, Курбатов И. М. О численном
решении одной задачи оптимального управления ядерным реактором. ЖВМ
и МФ, 5, № 3, 558—561, 1965.
160. Лето в А. М. Динамика полета и управление. М., «Наука», 1969.
161. Ли Э. Б., Маркус Л. Основы теорий оптимального управления. _M.t
«Наука», 1972.
162. Лионе Ж.-Л. Оптимальное управление системами, описываемыми урав-
нениями с частными производными. М., «Мир», 1972. ,
163. Лурье К. А. Оптимальное управление проводимостью жидкости, движу*
щейся по каналу в магнитном поле. «Прикл. матем. и механ.», 28, вып. 2,
258—267, 1964.
164. Любич Ю. И., Майстровский Г. Д. Общая теория релаксационных
процессов для, выпуклых функционалов. «Успехи матем. наук», 25f
вып. 1 (161), 57—112, 1970.
165. Люстернил Л. А., Соболев В. И. Элементы функционального ана-
лиза. М., «Наука», 1965.
166. Майстровский Г. Д. О сходимости метода сопряженных градиентов.
ЖВМ и МФ, 11, № 5, 1291—1293, 1971.
167. Моисеев Н. Н. Методы динамического программирования в теории оп-
тимальных управлений, I, II. ЖВМ и МФ, 4, № 3, 485—494, 1964; 5, № 1,
44—56, 1965.
168. Моисеев Н. Н. О применении методов теории оптимальных управлений
к задаче оптимального планирования. «Кибернетика», № 2, 41—48, 1966.
169. Моисеев Н. Н. Численные методы теории оптимальных управлений, ис-
пользующие вариации в пространстве состояний. «Кибернетика», № 3, 1—
29, 1966.
170. Моисеев Н. Н. Методы оптимизации, гл. I. М., Изд. ВЦ АН СССР (ро-
тапринт), 1968.
171. Моисеев Н. Н. Численные методы в теории оптимальных систем. М.,
«Наука», 1971.

ЛИТЕРАТУРА
371
172. Морозов В. А. О регуляризации некоторых классов экстремальных задач.
В сб.: «Вычисл. методы и программирование», вып. 12. Изд-во МГУ, 1969,
стр. 24—37. {
173. Морозов С. Ф., Сумин В. И. Об одной задаче оптимального управ-
ления нестационарными процессами переноса. «Дифференц. уравнения», 8,
№ 12, 2235—2243, 1972.
174. Моцкус И. Б. Многоэкстремальные задачи в проектировании. М., «Нау-
ка», 1967.
475. Нейштадт Л. Абстрактная вариационная теория с приложениями к ши-
рокому классу задач оптимизации. I. Общая теория. «Кибернетика», №"1,
77—91, 1967. II. Приложения. «J. SIAM Control», 5, No. 1, 90—137, 1967.
176. Непомящий П. А. Об одном из способов решения задачи на быстро-
действие. ЖВМ и МФ, 11, № 1, 79—95, 1971.
177. Hyp минский Е. А. Условия сходимости алгоритмов нелинейного про-
граммирования. «Кибернетика», № 6, 79—81, 1972.
178. Олей ник О. А. Краевые задачи для линейных уравнений эллиптического
и параболического типа с разрывными коэффициентами. «Изв. АН СССР»,
сер. матем., 25, N° 1, 3—20, 1961.
179. О р л о в В. С, П о л я к Б. Т., Р е б р и й В. А., Т р е т ь я к о в Н. В. Опыт
решения задач оптимальдого управления. В сб.: «Вычисл. методы и про-
граммирование», вып. 9. Изд-во МГУ, 1967, стр. 179—192.
180. Павлов А. А. Синтез релейных систем, оптимальных по быстродействию.
М., «Наука», 1966.
181. Петровский И. Г. Лекции об уравнениях_с частными производными.
М., Физматгиз, 1961.
182. Пиявский С. А. Один алгоритм отыскания абсолютного экстремума
функции. ЖВМ и МФ, 12, N° 4, 888—896, 1972.
183. П л отн и ков В. И. О сходимости конечномерных приближений (В задаче
об оптимальном нагреве неоднородного тела произвольной формы). ЖВМ
иМФ„8, № 1, 136—157, 1968.
184. Плотников В. .И., Сумин В. И. Оптимизация объектов с распреде-
ленными параметрами, описываемых системами Гурса—Дарбу. ЖВМ и МФ,
12, N° 1, 61—77, 1972.
185. Плотников В. И. Необходимые и достаточные условия оптимальности и
условия единственности оптимизирующих функций для управляемых систем
общего вида. «Изв. АН СССР», сер. матем., 36, N° 6, 652—679, 1972.
186. Поляк Б. Т. Теоремы существования и сходимость минимизирующих по-
следовательностей для задач на экстремум при наличии ограничений. ДАН
СССР, 166, N° 2, 287—290, 1966.
187. Поляк Б. Т. Один общий метод решения экстремальных задач. ДАН
, СССР, 174, № 1, 33—36, 1967.
188. Поляк Б. Т. Методы минимизации функций многих переменных. «Эконо-
мика и матем. методы», 3, N° 6, 86—107, 1967.
189. Поляк Б. Т. Минимизация негладких функционалов. ЖВМ и МФ, 9, № 3,
509-521, 1969.
190. Поляк Б. Т. Метод сопряженных градиентов в задачах на экстремум.
ЖЬМ и МФ, 9, N° 4, 807—821, 1969.
191. Поляк Б. Т. Итерационные методы, использующие множители Лагранжа,
для решения экстремальных задач с ограничениями типа равенства. ЖВМ
и МФ, 10, N° 5, 1098—1106, 1970.
192. Пол як Б. Т. О скорости сходимости метода штрафных функций. ЖВМ и
МФ,119№ 1,3—11, 1971.
193. Поляк Б. Т. Сходимость метода возможных направлений в экстремальных
задачах. ЖВМ и МФ, 11, N° 4, 855—869, 1971.
194. Понтрягин Л. С. Обыкновенные дифференциальные уравнения. М.,
«Наука», 1965.
195. Понтрягин Л. С, Болтянский В. Г., Гамкрелидзе Р. В., Ми-

372
ЛИТЕРАТУРА
щ е н к о Е. Ф. Математическая теория оптимальных процессов. М., «Нау-
ка», 1969.
196. Пропой А. И. Задачи дискретного управления с фазовыми ограничения-
ми. ЖВМ и МФ, 12, № 5, 1128—1144, 1972.
197. Пшеничный Б. Н. Численный метод расчета оптимального по быстро-
действию управления для линейных систем. ЖВМ и МФ, 4, № 1, 52—60,
1964. i
198. Пшеничный Б. Н., Соболенко Л. А. Ускоренный метод решения за-
дачи линейного быстродействия. ЖВМ и МФ, 8, № 6, 1345—1351, 1968.
199. Пшеничный Б. Н. Необходимые условия экстремума. М., «Наука», 1969.
200. Рабинович А. Б. Об одном классе методов итерационного решения за-
дач быстродействия. ЖВМ и МФ, 6, № 3, 433—445, 1966.
201. Раз инков а Т. Л. Об одном алгоритме машинного поиска экстремума
функции. ЖВМ и МФ, 5, № 4,737—742, 1965.
202. Распопов Б. М. Задача оптимального быстродействия для процессов
несвязанного тепло- и массопереноса. «Автоматика и телемеханика», 26,
№ 10, 1965.
203. Распопов Б. М. Некоторые задачи оптимального управления процесса-
ми тепло- и массопереноса при сушке. «Автоматика и телемеханика», № 2,
185—192, 1968.
204. Растрыгин Л. А. Статистические методы поиска. М., «Наука», 1968.
205. Розоноэр Л. И. Принцип максимума Л. С. Понтрягина в теории опти-
мальных систем, I—III. «Автоматика и телемеханика», 20, № 10—12, 1320—
1334, 1441—1458, 1561—1578, 1959.
206. Ройтенберг Я. Н. Автоматическое управление. М., «Наука», 1971.
207. Самарский А. А. Введение в теорию разностных схем. М., «Наука», 1971.
208. СиразетдиновТ. К. К теории оптимальных процессов с распределенны-
ми параметрами. «Автоматика и телемеханика», 25, № 4, 463—472, 1964.
209. Сиразетдино.в Т. К. Методы функций Ляпунова в задачах управле-
ния системами с распределенными параметрами. «Автоматика и телемехани-
ка», № 7, 5—21, 1972. /
210. Соболев С. Л. Некоторые применения функционального анализа в ма-
тематической физике. Новосибирск, Изд-во СО АН СССР, 1962.
211. Старосельский Л. А., Шелудько Г. А., Кантор Б. Я. Об одной
реализации метода оврагов с адаптацией величины овражного шага по экс-
поненциальному закону. ЖВМ и МФ, 8, № 5, 1161—1167, 1968.
212. Стронгин Р. Г. Об одном алгоритме глобальной минимизации. «Изь.
вузов», радиофизика, 13, № 4, 539—546, 1970.
213. Стронгин Р. Г. Алгоритмы для поиска абсолютного минимума. В сб.:
«Задачи статистической оптимизации». Рига, «Зинатне», 1971.
214. Стронгин Р. Г. Минимизация многоэкстремальных функций нескольких
переменных. «Изв. АН СССР», сер. технич. кибернетика, № 6, 39—46, 1971.
215. Сухарев А. Г. Об оптимальных стратегиях поиска экстремума. ЖВМ и
МФ, И, № 4, 910—924, 1971.
216. Сухарев А. Г. Наилучшие стратегии последовательного поиска экстрему-
ма. ЖВМ и МФ, 12, № 1, 35—50, 1972.
217. Тихонов А. Н. О решении некорректно поставленных задач и методе
регуляризации. ДАН СССР, 151, № 3, 501—504, 1963.
218. Тихонов А. Н. О методах регуляризации задач оптимального управле-
ния. ДАН СССР, 162, № 4, 763—766, 1965.
219. ТихоновА. Н. О некорректных задачах оптимального нланирования и
устойчивых методах их решения. ДАН СССР, 164, № 3, 507—510, 1965.
220. Тихонов А. Н. О некорректных задачах оптимального планирования.
ЖВМ и МФ, 6, № 1, 81—89, 1966.
221. Тихонов А. Н. Об устойчивости задачи оптимизации функционалов.
ЖВМ и МФ, 6, № 4, 631—634, 1966.

ЛИТЕРАТУРА
373
222. Тихонов А/Н. О некорректно поставленных задачах. В сб.: «Вычисл.
методы и программирование», вып. 8» Изд-во МГУ, 1967, стр. 3—33.
223. ТихоновА. Н., Васильев Ф. П. Методы решения некорректных задач
оптимального управления. Тез. докл. Всес. конф. «Математическая теория
оптимального управления». Баку, 1972.
224. Т и х о н о в А. Н., Г а л к и н В. Я., 3 а и к и н П. Н. О поямых методах ре-
шения задач оптимального управления. ЖВМ и МФ, 7, N° 2, 416*—423, 1967.
225. Тихонов А. Н., И в а н о в В. К., Лаврентьев М. М. Некорректно
поставленные задачи. Тр. симпозиума «Дифференц. уравнения с частными
производными». М., «Наука», 1970, стр. 224—239.
226. Тихонов А. Н., Карманов В. Г., Руднева Т. Л. Об устойчивости
задач линейного программирования. В сб.: «Вычисл. методы и программи-
рование», вып. 12. Изд-во МГУ, 1969, стр. 3—9.
227. Т и х о н о в А.. Н., С а м а р с к и й А. А. Уравнения математической физики.
М., «Наука», 1966.
228. Троицкий В. А. О вариационных задачах оптимизации процессов управ-
ления. «Прикл. матем. и механ.», 26, вып. 1, 29—38, 1962.
229. Трухаев Р. И., Хоменюк В. В. Теория неклассических вариационных
задач. Изд-во ЛГУ, 1971.
230. У айлд Д. Дж. Методы поиска экстремума. М., «Наука», 1967.
231. Фан Л я н ь-ц е н ь, В а н ь Ч у-с е н. Дискретный принцип максимума. М.,
«Мир», 1967. \
232. Федоренко Р. П. Приближенное решение некоторых задач оптималь-
ного управления. ЖВМ и МФ, 4, № 6, 1046—1064, 1964.
233. Федоренко Р. П. К задаче Коши для уравнения динамического програм-
мирования Беллмаиа. ЖВМ и МФ, 9, N» 2, 426—431, 1969.
234. Фельдбаум А. А. Основы теории оптимальных автоматических систем.
М., «Наука», 1966.
235. Ф и а к к о А.," М а к-К о р м и к Г. Нелинейное программирование. Методы
последовательной безусловной минимизации. М., «Мир», 1972.
236. Филиппов А. Ф. О некоторых вопросах теории оптимального регулиро-
вания. «Вестн. Моск. ун-та», матем., механ., № 2, 25-^32, 1959.
237. Халилов 3. И., Асланов Э. Дж. Об одной вариационной задаче в
гильбертовом пространстве и ее применении к уравнениям с частными про-
изводными. ДАН СССР, 169, JSfe 5, 1020—1023, 1966.
238. Харатишвили Г. Л. Оптимальные процессы с запаздыванием. Тбилиси,
«Мецниереба», 1966.
239. Хедл и Дж. Нелинейное и динамическое программирование. М., «Мир», .1967.
240. Черноусько Ф. Л. Метод локальных вариаций для численного решения
вариационных задач. ЖВМ и МФ, 5, № 4, 749—754, 1965.
241. Черноусько Ф. Л. Об оптимальном поиске экстремума унимодальных
функций. ЖВМ и МФ, 10, № 4, 922—933, 1970.
242. Черноусько Ф. Л. Об оптимальном поиске минимума выпуклых функ-
ций. ЖВМ и МФ, 10, № 6, 1355—1366, 1970.
243. Чупрун Б. Е. К решению оптимальных задач с использованием принци-
па максимума. «Автоматика и телемеханика», № 9, 21—29, 1967.
244. ШатровскийЛ. И. Об одном численном методе решения задач опти-
мального управления. ЖВМ и МФ, 2, № 3, 488—491, 1962.
245. Шефер X. Топологические векторные пространства. М., «Мир», 1971.
246. ШкадовЛ. М., Б у х а н о в а Р. С, Илларионов В. Ф., Пло-
хих В. П. Механика оптимального пространственного движения летатель-
ных аппаратов в атмосфере. М., «Машиностроение», 1972.
247. Шолохович В. Ф. О неустойчивых экстремальных задачах. «Матем. зап.
Уральского гос. ун-та», 7, тетрадь 2, .103—111, 1969.
248. Шолохович В. Ф. О приближенном решении неустойчивых экстремаль-
ных задач. «Изв. вузов», матем., № 5, 101—108, 1971.

374
ЛИТЕРАТУРА
249. Шолохович В. Ф. Об одном способе численного решения неустойчивых
экстремальных задач. «Изв. вузов», № 6, 92—100, 1972.
250. Шолохович В. Ф. О численном решении неустойчивых экстремальных
задач. «Изв. вузов», матем., № 8, 105—113, 1972.
251. Шор Н. 3. О скорости сходимости метода обобщенного градиентного спуска
с растяжением пространства. «Кибернетика», № 2, 80—85, 1970.
252. Шор Н. 3., Журбенко Н. Г. Метод минимизации, использующий опе-
рацию растяжения пространства в направлении разности двух последова-
тельных градиентов. «Кибернетика», № 3, 51—59, 1971.
253. Шор Н. 3., Г а м б у р д П. Р. Некоторые вопросы сходимости обобщен-
ного градиентного спуска. «Кибернетика», № 6, 82—84, 1971.
254. Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчис-
ление. М., «Наука», 1965.
255. Энеев Т. М. О применении градиентного метода в задачах теории опти-
мального управления. «Космич. исслед.», IV, вып. 5, 651—669, 1966.
256. Э р р о у К. Дж., Г у р в и ц Л., У д з а в а X. Исследования по линейному
и нелинейному программированию. М., ИЛ, 1962.
257. Юдин Д. Б., Г о л ь ш т е й н Е. Г. Линейное программирование. Теория,
методы и приложения. М., «Наука», 1969.
258. IB a s s R. A rank two algorithm for unconstrained minimization. «Math. Com-
putation», 26, No. 117, 12&-144, 1972.
259. Bauer N., Neumann K. Berechnung optimaler Steuerungen. Maximum-
prinzip und dynamische Optimierung. Berlin—Heidelberg—New York, Sprin-
ger-Verlag, 1969.
260. CanonM. D., Сu 11 um С D., P о 1 ak E. Theory of Optimal Control and
Mathematical Programming. Mc Graw-Hill Series in Systems Science, 1970.
261. С u 11 u m J. -Discrete approximations to continuous optimal control problems.
«J. SIAM. Control.», 7, No. 1, 32—49, 1969.
262. Cullum J. An algorithm for minimizing a differentiable function that uses
only function values. Thechnigue of optimization. New York2 London, Academic
Press, 1972, p. 117—rl27.
263. Eaton J. H. An iterative solution to time-optimal control. «J. Math. Anal,
and Appl.», 5, No. 2, 329—344, 1962.
264. FujisawaT., YasudaY. An iterative procedure for solving the time-
optimal regulator problem. «J. SIAM. Control.», 5, No. 4, 501—512, 1967.
265. GreenstadtJ. A quasi-Newton method with no derivatives. «Math. Com-
putation», 26, No. 117, 145—166, 1972.
266. К1 e s s i g R., P о 1 a k E. Efficient implementations of the Polak—Ribiere
conjugate gradient algorithm. «J. SIAM. Control.», 10, No. 3, 1972.
267. Mc С о г m i с k G. P., T a p i a R. A. The gradient projection method under
mild differentiability conditions. «J. SIAM. Control», 10, No. 1, 93—98, 1972.
268. Neustadt L. W. Sinthesiring time-optimal control systems. UL Math.
Anal, and Appl., 1, No. 4, 484—493, 1960.
269. Rockafellar R. T. Convex Analysis. Prinseton University Press, 1070 (см.
русский перевод: Рокафеллер Р. Выпуклый анализ. М., «Мир», 1973).
270. R u s s е 1 D. L. Control Theory of hyperbolic equations related to certain ques-
tions in harmonic analysis and spectral theory. «J. Math. Anal, and Appl.»,
40, No. 2, 336—368, 1972.

УДК
Книга написана по материалам лекций, прочи-
танных автором студентам факультета вычисли-
тельной математики и кибернетики, и содержит
основы наиболее часто используемых на практи-
ке • методов приближенного решения задач мини-
мизации функций и функционалов, теоретическое
исследование и краткую характеристику вычисли-
тельных аспектов этих методов. В первой части
книги рассматриваются методы минимизации
функций одной и нескольких переменных, во вто-
рой — методы минимизации функционалов, опре-
деленных на решениях систем обыкновенных
дифференциальных уравнений, разностных урав-
нений, а также уравнений с частными производ-
ными. Большая часть материалов ранее в учеб-
ной литературе не излагалась и встречается лишь
в журнальных статьях и монографиях, трудных
для восприятия при первом знакомстве с пред-
метом.
Книга рассчитана на студентов, аспирантов, спе-
циализирующихся по вычислительной и приклад-
ной математике, на научных сотрудников и инже-
неров, которым, приходится иметь дело с вопро-
сами минимизации функций и различными зада-
чами оптимального управления.
Печатается по постановлению
Редакционно-издательского совета
Московского университета
Рецензенты:
Кандидаты физ.-матем. наук В. Г. Карманов,
М. С. Никольский, Н. X. Розов
„ 20204-077
В 123—74
007 (02)-74
(5) Издательство Московского университета, 1974 г.

Федор Павлович Васильев
Лекции
по методам решения
экстремальных задач
Тематический План 1974 г. № 123
Редактор Л. И. Лукиных
Переплет художника С. Б. Г енкиной
Технический редактор 3. С. Ко ндрашо в а
Корректоры
С. С. Мазурская, А. А. Алексеева
Сдано в набор 19/XI 1973 г. Подписано к печа-
ти 5/VII 1974 г. Л-50376 Формат 60y90/ie Бума-
га тип. N° 3 Физ. печ. л. 23,5 Уч.-изд., л. 24,71
Изд. №■ 2179 Зак. 330 Тираж 11000 экз.
Цена 96 коп.
Издательство Московского университета.
Москва, К-9, ул. Герцена, 5)7.
Типография Изд-ва МГУ.
Москва, Ленинские горы