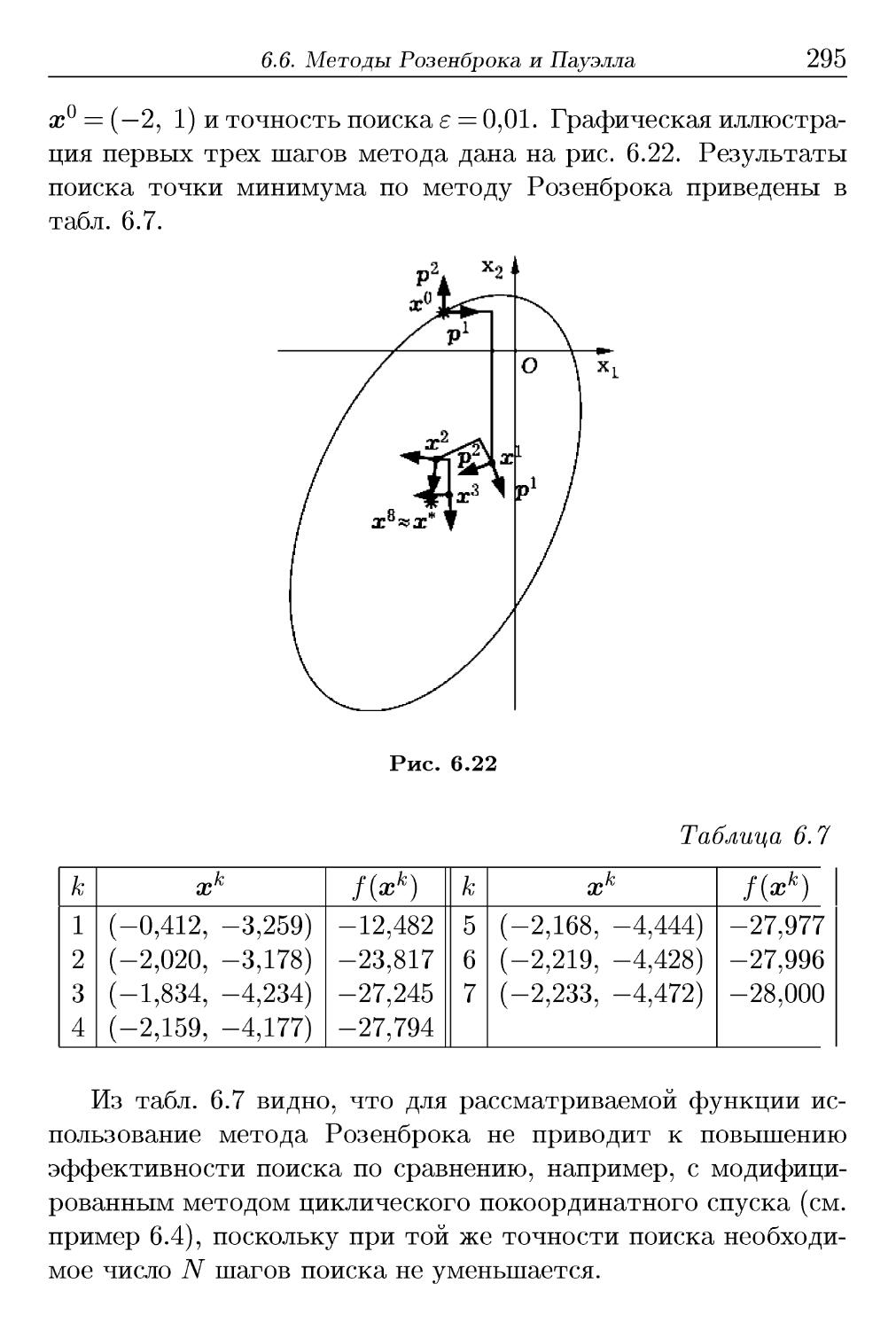
Автор: Аттетков А.В. Галкин С.В. Зарубин B.C.
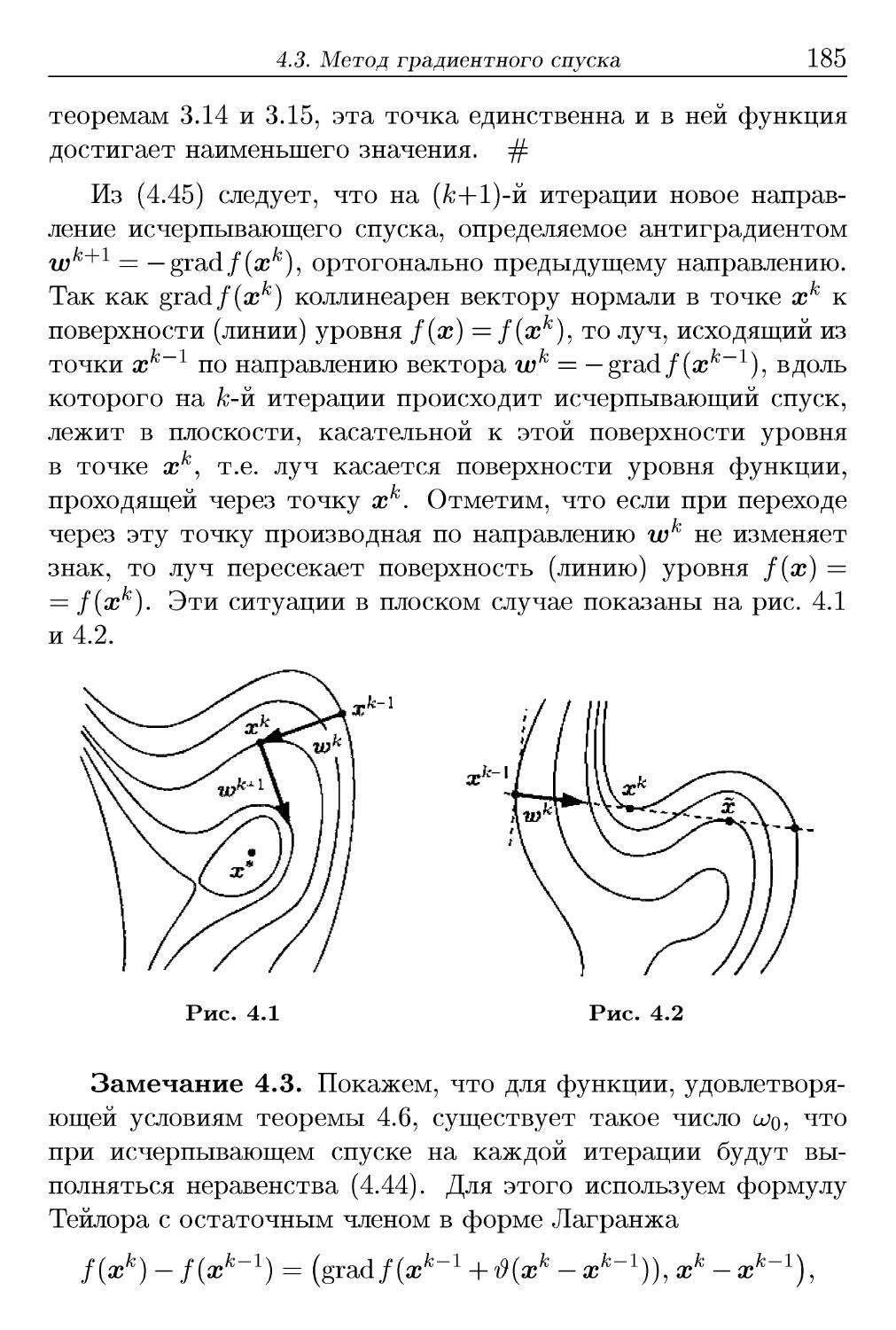
Теги: анализ математический анализ функциональный анализ математика
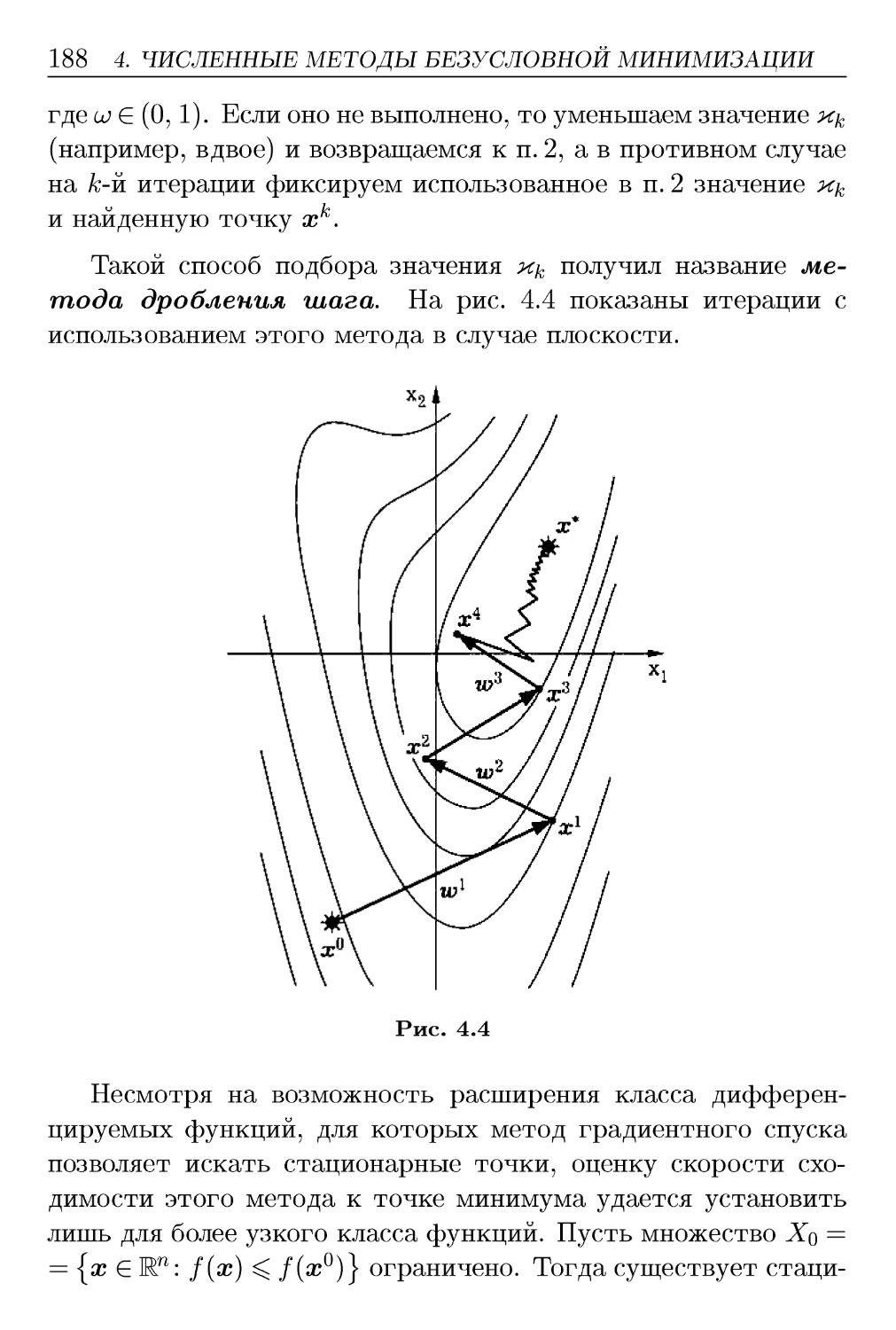
ISBN: 5-7038-1770-6
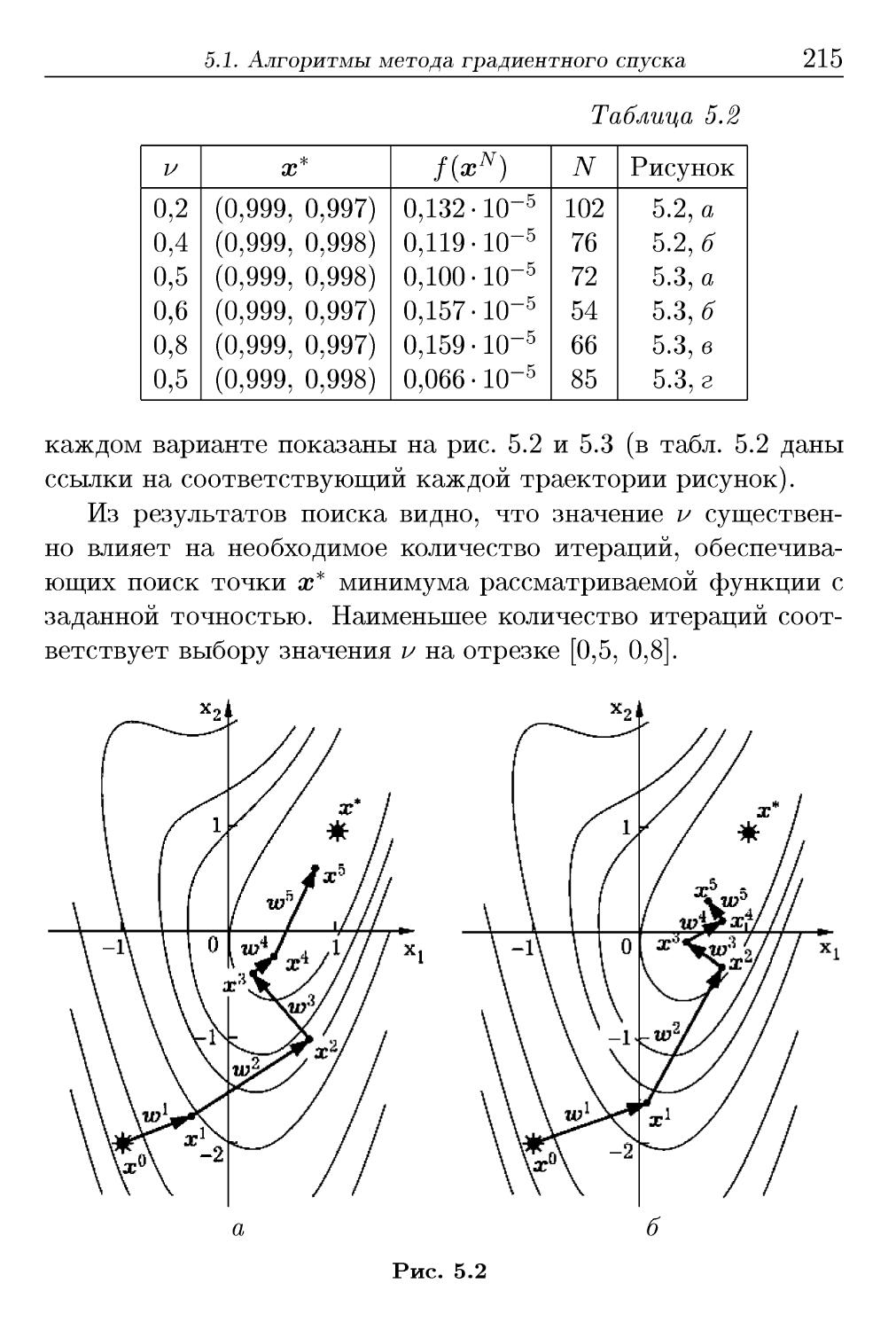
Год: 2003
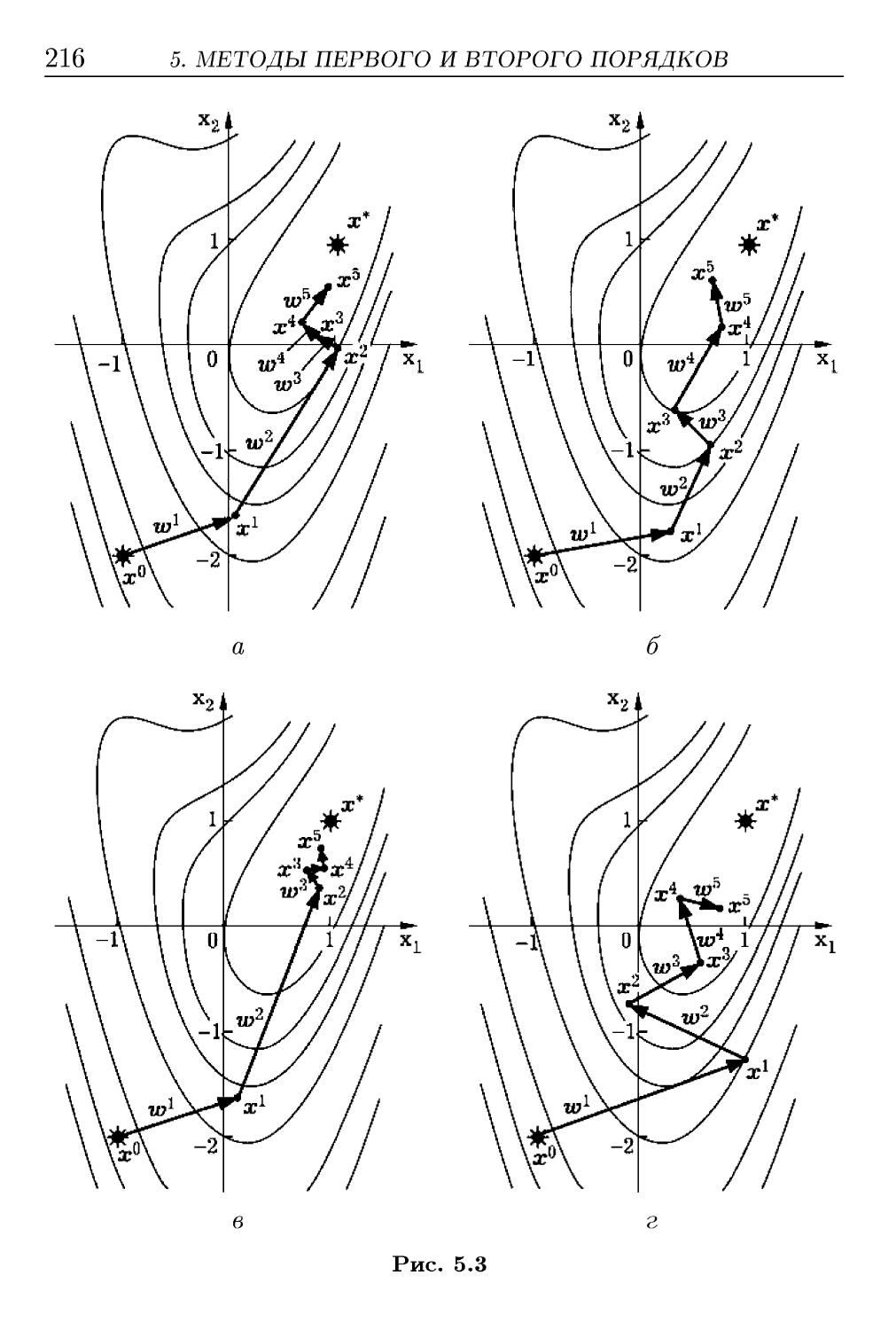
Текст
МАТЕМАТИКА
В ТЕХНИЧЕСКОМ УНИВЕРСИТЕТЕ
f(x) ->> min, х G П С IRn
XIV
А.В. Аттетков, СВ. Галкин, B.C. Зарубин
МЕТОДЫ
ОПТИМИЗАЦИИ
Издательство МГТУ им. Н. Э. Баумана
Математика в техническом
университете
Выпуск XIV
Комплекс учебников из 21 выпуска
Под редакцией В. С. Зарубина и А. П. Крищенко
I. Введение в анализ
П. Дифференциальное исчисление функций
одного переменного
III. Аналитическая геометрия
IV. Линейная алгебра
V. Дифференциальное исчисление функций
многих переменных
VI. Интегральное исчисление функций
одного переменного
VII. Кратные и криволинейные интегралы.
Элементы теории поля
VIII. Дифференциальные уравнения
IX. Ряды
X. Теория функций комплексного переменного
XI. Интегральные преобразования
и операционное исчисление
XII. Дифференциальные уравнения
математической физики
XIII. Приближенные методы математической физики
XIV. Методы оптимизации
XV. Вариационное исчисление и оптимальное управление
XVI. Теория вероятностей
XVII. Математическая статистика
XVIII. Случайные процессы
XIX. Дискретная математика
XX. Исследование операций
XXI. Математическое моделирование в технике
А.В. Аттетков, СВ. Галкин,
B.C. Зарубин
МЕТОДЫ
ОПТИМИЗАЦИИ
Под редакцией
д-ра техн. наук, профессора B.C. Зарубина
и д-ра физ.-мат. наук, профессора А.П. Крищенко
Издание второе, стереотипное
Рекомендовано
Министерством образования
Российской Федерации
в качестве учебника для студентов
высших технических учебных заведений
Москва
Издательство МГТУ им. Н. Э. Баумана
2003
УДК 517.51@75.8)
ББК 22.161
А92
Рецензенты: проф. В.Т. Сергованцев, проф. А.В. Манжиров
А92 А.В. Аттетков, СВ. Галкин, B.C. Зарубин.
Методы оптимизации: Учеб. для вузов / Под ред. B.C. Зарубина,
А.П. Крищенко. - 2-е изд., стереотип. - М.: Изд-во МГТУ
им. Н.Э. Баумана, 2003. -440 с. (Сер. Математика в
техническом университете; Вып. XIV).
ISBN 5-7038-1770-6 (Вып. XIV)
ISBN 5-7038-1270-4
Книга посвящена одному из важнейших направлений подготовки
выпускника технического университета — математической теории
оптимизации. Рассмотрены теоретические, вычислительные и прикладные аспекты
методов конечномерной оптимизации. Много внимания уделено описанию
алгоритмов численного решения задач безусловной минимизации функций
одного и нескольких переменных, изложены методы условной оптимизации.
Приведены примеры решения конкретных задач, дана наглядная
интерпретация полученных результатов, что будет способствовать выработке у
студентов практических навыков применения методов оптимизации.
Содержание учебника соответствует курсу лекций, который авторы
читают в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Может быть полезен
преподавателям, аспирантам и инженерам.
Ил. 100. Табл. 29. Библиогр. 91 назв.
Выпуск книги финансировал
Московский государственный технический
университет им. Н.Э. Баумана
УДК 517.51@75.8)
ББК 22.161
© А.В. Аттетков, СВ. Галкин,
B.C. Зарубин, 2001
© Московский государственный
технический университет
им. Н.Э. Баумана, 2001
ISBN 5-7038-1770-6 (Вып. XIV) © издательство МГТУ
ISBN 5-7038-1270-4 им. Н.Э. Баумана, 2001
ПРЕДИСЛОВИЕ
Предлагаемая читателю книга является одним из учебников
серии „Математика в техническом университете" и
учитывает специфику математической подготовки студентов высших
технических учебных заведений.
В основу учебника положен курс лекций по методам
оптимизации, который читается на протяжении ряда лет студентам
различных специальностей МГТУ им. Н.Э. Баумана, а также
опыт проведения семинарских и лабораторных занятий по
этому курсу.
Этот выпуск серии целиком посвящен конечномерным
задачам оптимизации. Основное внимание уделено прикладным
и вычислительным аспектам оптимизации, связанным с
разработкой численных методов решения задач оптимизации и
построением алгоритмов их реализации. В книге отсутствуют
доказательства сходимости методов (исключение сделано лишь
для некоторых методов). Существует обширная литература по
этим вопросам, и „математические тонкости" доказательств
сходимости можно изучить самостоятельно с использованием
рекомендуемой литературы. В инженерной практике важнее
понимание сути методов и алгоритмов их реализации,
знание условий их применения, примеры и иллюстрации решения
типовых инженерных задач оптимизации. Наличие
большого количества примеров и задач, поясняемых графическими
иллюстрациями и интерпретацией полученных результатов,
позволяет использовать данную книгу не только как учебник, но
и как задачник при проведении семинарских и лабораторных
занятий.
Содержание учебника относится к специальным разделам
высшей математики и для работы с ним требуется хорошее
знание базового курса. В частности, предполагается, что читатель
6
ПРЕДИСЛОВИЕ
умеет оперировать основными понятиями линейной алгебры,
аналитической геометрии, теории матриц и математического
анализа.
В конце книги приведен список рекомендуемой литературы,
в который включены все цитированные источники. Ссылки в
тексте на литературу даны в виде подстрочных сносок, в
которых указаны фамилии авторов соответствующего издания. В
предметный указатель входят в алфавитном порядке (по
существительному в именительном падеже) все выделенные в тексте
полужирным курсивом термины с указанием страниц, на
которых они строго определены или описаны. Выделение
термина светлым курсивом означает, что в данном параграфе он
является одним из ключевых слов и читателю должно быть
известно значение этого термина (его можно уточнить, найдя при
помощи предметного указателя необходимую страницу).
Ссылки в тексте на номера формул, рисунков и таблиц
набраны обычным шрифтом (например, A.5) — пятая формула в
главе 1, рис. 3.1 — первый рисунок в главе 3, табл. 3.2 — вторая
таблица в главе 3), а на параграфы — полужирным (например,
1.3 — третий параграф в главе 1). В квадратных скобках
даны ссылки на другие выпуски данной серии (например, [XV] —
ссылка на пятнадцатый выпуск).
Для самоконтроля предлагаем читателю ознакомиться с
заданиями для самопроверки. В этих заданиях понятия и
термины, которые нужно знать, выделены прямым полужирным
шрифтом. После заданий для самопроверки помещен
список основных обозначений, содержащий часто встречающиеся
в тексте символы и их расшифровку.
Задания для самопроверки
1. Какие множества называют: замкнутыми,
открытыми, ограниченными, компактными? Что такое диаметр
и внутренность множества? [I]
7
2. Что такое центр и радиус окрестности точки? Что
называют отрезком, вложенным в данный отрезок? [I]
3. Из каких этапов состоят доказательства от
противного и по методу математической индукции? [I]
4. Что называют монотонной, строго монотонной,
возрастающей, убывающей, неубывающей и невозраста-
ющей последовательностями? Что такое
подпоследовательность и предельная точка последовательности? [I]
5. Что называют функцией, убывающей,
возрастающей, неубывающей и невозрастающей в промежутке
числовой прямой? Приведите примеры функций,
непрерывных в интервале (а, Ь) или в полуинтервале [а, 6), но не
являющихся непрерывными на отрезке [а, Ь]. Перечислите
свойства функции, непрерывной на отрезке. В чем различие
между точками разрыва первого и второго рода? [I]
6. Дайте определение точной верхней (нижней) грани
функции многих переменных (одного переменного) на
открытом, замкнутом множестве. В чем различие между min/(i)
Hinf/Oc)? [I], [V]
7. Каков смысл символов по малое" и пО большое"? [I]
8. Сформулируйте теоремы Ферма и Лагранжа,
напишите формулу конечных приращений. Что называют
точкой строгого локального экстремума функции одного
переменного? Сформулируйте необходимые и достаточные
условия экстремума такой функции. В чем различие между
локальным экстремумом и наибольшим (наименьшим)
значением этой функции на отрезке? [II]
9. Как проверить, является ли функция одного
действительного переменного выпуклой (строго выпуклой) вниз
(вверх) функцией? Сколько экстремумов может иметь
выпуклая (строго выпуклая) функция одного переменного на
отрезке? [II]
10. В каких точках отрезка линейная функция достигает
своих наибольшего и наименьшего значений? Как найти
точку экстремума квадратного трехчлена в интервале? [II]
8
ПРЕДИСЛОВИЕ
11. Что называют сходимостью метода вычислений и
порядком его сходимости? Запишите условия, при выполнении
которых скорость сходимости метода является линейной,
сверхлинейной, квадратичной, кубической. [II]
12. Какую матрицу называют диагональной,
единичной, симметрической, нулевой, блочной,
транспонированной по отношению к данной? Что называют
определителем квадратной матрицы, ее угловыми минорами,
невырожденной (вырожденной) матрицей? Каковы правила
разложения определителя по строке (по столбцу)?
Сформулируйте необходимое и достаточное условия существования
у квадратной матрицы обратной матрицы. Как связаны
между собой определители этих матриц? Что называют
рангом матрицы, базисным минором матрицы? Что такое
нетривиальная линейная комбинация строк (столбцов)
матрицы? [Ш], [IV]
13. В чем различие между координатной, векторной и
матричной записью системы линейных алгебраических
уравнений (СЛАУ)? Какую СЛАУ называют совместной,
неопределенной, квадратной? Чем отличаются прямые
методы решения СЛАУ от итерационных? [III]
14. Что такое линейное, линейное арифметическое,
евклидово, метрическое и нормированное пространства?
Перечислите аксиомы скалярного умножения. Как
связаны между собой скалярное произведение, норма и
метрика? Запишите неравенство Коши — Буняковского. [IV]
15. Что такое линейный оператор, матрица
линейного оператора? Как записать матрицу линейного оператора в
различных базисах? Что такое ортонормированный базис,
ортогональный и самосопряженный операторы? Какие
матрицы соответствуют этим операторам? Каковы свойства
собственных векторов и собственных значений этих
операторов в конечномерном линейном пространстве? Что
такое характеристическое уравнение матрицы и ее
собственные значения? [IV]
9
16. Что такое линейная и квадратичная формы,
матрица квадратичной формы? Обоснуйте процесс
приведения квадратичной формы к каноническому виду ссылкой
на соответствующие теоремы линейной алгебры. Какую
квадратичную форму и какую матрицу называют положительно
(отрицательно) определенной? Сформулируйте критерий
Сильвестра. Какую квадратичную форму называют
неположительно (неотрицательно) определенной,
знакопеременной? [IV]
17. Напишите формулу Тейлора с остаточным
членом в форме Лагранжа и Пеано для функции одного
действительного переменного и для функции многих
переменных. [II], [V]
18. Какую функцию многих переменных называют
непрерывной по совокупности переменных и непрерывной по
части переменных? Что такое линия (или поверхность)
уровня такой функции? Что называют координатными
функциями векторной функции многих переменных и ее
матрицей Якоби по всем или по части переменных? [V]
19. Что такое градиент функции многих переменных,
матрица Гессе? Запишите приращения дифференцируемой и
дважды дифференцируемой функции, используя эти понятия.
Сформулируйте теорему о неявной функции и теорему
об обратной функции. [V]
20. Что такое производная функции многих
переменных по направлению вектора и как она связана с
градиентом функции? Имеет ли дифференцируемая функция многих
переменных производные по всем направлениям? Верно ли
обратное? [V]
21. Какие условия надо наложить на производную
функции многих переменных по направлению, чтобы можно было
утверждать, что: а) функция непрерывна; б) функция
дифференцируема? Приведите примеры. [V]
22. В чем различие между точкой экстремума и
критической или стационарной точками скалярной функции
10
ПРЕДИСЛОВИЕ
многих переменных? Что называют строгим (нестрогим)
локальным экстремумом такой функции? [V]
23. Сформулируйте необходимые условия экстремума
скалярной функции многих переменных: а) с использованием
частных производных функции; б) с использованием градиента
функции. [V]
24. Сформулируйте достаточные условия экстремума
функции многих переменных с использованием: а) понятия
знакоопределенности второго дифференциала функции; б)
главных миноров матрицы Гессе; в) собственных чисел матрицы
Гессе. Приведите примеры. [V]
25. Может ли линейная функция многих переменных
достигать экстремума внутри замкнутой области? Может ли
квадратичная функция многих переменных достигать
экстремума внутри замкнутой области, как найти точку
экстремума? Приведите пример. [V]
26. Что называют условным экстремумом функции
многих переменных и уравнениями связи? Как найти точки
условного экстремума? Что такое множители Лагранжа
и функция Лагранжа? [V]
27. Напишите формулу Ньютона — Лейбница. [VI]
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
<4 и > — начало и окончание доказательства
Ф — окончание примера, замечания
a G А — элемент а принадлежит множеству А 1-1.1
а ^ В — элемент а не принадлежит множеству В 1-1.1
{аг}^=1 — множество из элементов ai, a2, ..., a/v 1-1.1
AG В — множество А является подмножеством множества В
1-1.2
N — множество натуральных чисел 1-1.2
Z — множество целых чисел 1-1.3
Ш — множество действительных чисел 1-1.3
1R+ — множество положительных действительных чисел
1.5
R* — множество неотрицательных действительных чисел
1.5
W1 — (декартово) произведение п множеств
действительных чисел или n-мерное евклидово арифметическое
пространство 1-2.5, IV
]Щ_ — (декартово) произведение п множеств IR+
положительных действительных чисел 1.5
Щ — (декартово) произведение п множеств R*
неотрицательных действительных чисел 1.5
[а, Ь] и (а, Ь) — отрезок и интервал с концами в точках а и b
1-1.3
[a, 6), (a, b] — полуинтервалы с концами в точках а и b 1-1.3
V и 3 — квантор всеобщности (\/ж — для любого х) и
квантор существования (Зх — существует х) 1-1.5
/: X —)> Y — отображение / множества X в множество Y
1-2.1
12
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
/(a), f(x)\ _ — значение функции f(x) в точке а 1-2.1
D(f) и R(f) — область определения и область значений
функции f(x) 1-2.1
п
^2 о-к — сумма п слагаемых ах, a2, ..., an 1-2.6
N
Y\ dm — произведение n сомножителей 1-2.6
m=l
к = 1, N — число к принимает последовательно все значения
из множества натуральных чисел от 1 до N
включительно 1-2.6
sgnrr — функция знака числа жЕ1 1-3.2
diamX — диаметр ограниченного множества X 1-5.2
дХ — граница множества X 1-5.3
sup f{x) и inf f(x) — точная верхняя и точная нижняя грани
хех хех
функции f(x) на множестве X 1-5.7
{хп} — последовательность элементов хп 1-6.2
lim хп — предел последовательности {хп\ при п —>> оо 1-6.3
п—)>оо
lim f(x) — предел функции f(x) одного действительного пе-
ременного ж в точке а (при ж —>> а) 1-7.1
/(а + 0), /(а — 0) — предел справа и слева функции /(ж) одного
действительного переменного в точке а 1-7.2
/7(а), /7(ж)| _ — производная функции f(x) одного
действительного переменного в точке а II
АВ и \АВ\ — отрезок, соединяющий точки А и В, и его длина
III
т
х = {х\ ... жп) — вектор из W1 с координатами жх, ..., хп
IV
|ж| — длина (модуль) вектора х III, IV
0П — нулевой вектор из W1 III, IV
(а, Ь) — скалярное произведение векторов а и Ь IV
А — матрица, транспонированная к матрице А III
13
Kg А — ранг матрицы А III
detA — определитель матрицы А III
А~г — матрица, обратная к матрице А III
1п — единичная матрица порядка п III
®т,п — нулевая матрица размера т х п III
ь
f f(x)dx — определенный интеграл от функции f(x) по
отрезку [а, Ь] VI
f(x) —>> min, х Е О, — задача минимизации функции f(x) на
множестве О 1.5
f(x) —>> inf, жЕО, — задача нахождения точной нижней грани
функции f(x) на множестве О 1.5
а^Ъ^Ъ^а — каждая координата вектора а Е Кп не меньше
соответствующей координаты вектора b Е Rn 3.1
п
Ах ^Ъ — система из т неравенств ^ aijxj ^ ^ь i = 1,т,
определяемая матрицей А = (а^) размера ттг х п и
т
столбцом b = (&i ... Ьп) высоты п 3.1
ехр(ж), еж — экспоненциальная функция 3.2
14
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Буквы латинского алфавита
Начертание
А а
В b
С с
D d
Е е
F f
G g
Н h
I i
Jj
К k
L 1
M m
A a
В b
С с
D d
E e
F f
G g
H h
I i
J 3
К к
L I
M m
Произношение
a
бэ
цэ
ДЭ
e
эф
же
аш
и
йот
ка
эль
эм
Начертание
N п
О о
Р р
Q q
R г
S s
Т t
U и
V v
W w
X х
Y у
Z z
N п
О о
Р р
Q q
R г
S s
Т t
U и
V v
W w
X х
Y у
Z z
Произношение
эн
о
пэ
ку
эр
эс
тэ
У
вэ
дубль-вэ
икс
игрек
зэт
Представлен наиболее употребительный (но не
единственный) вариант произношения (в частности, вместо „йот" иногда
говорят 55жи").
Буквы греческого алфавита
Начертание
А а
В /3
Г 7
A S
Е е
z С
Н г/
е $в
Произношение
альфа
бета
гамма
дельта
эпсилон
дзета
эта
тэта
Начертание
I L
К Ж
А А
М /i
N v
Е z
О о
П 7Г
Произношение
йота
каппа
ламбда
ми
ни
кси
омикрон
пи
Начертание
Р р
S а
Т т
Т v
Ф ip
X х
ф ф
О L0
Произношение
ро
сигма
тау
ипсилон
фи
хи
пси
омега
Наряду с указанным произношением также говорят
„лямбда", „мю" и „ню".
1. ЗАДАЧИ ОПТИМИЗАЦИИ
В своей жизни человек часто сталкивается с ситуацией,
когда ему из некоторой совокупности возможных вариантов
своего поведения или принятия решения в какой-либо области
деятельности необходимо выбрать один вариант. Наилучший
вариант поведения (принятие наилучшего решения) можно
выбирать по-разному. Если такой выбор предусматривает
проведение количественного анализа ситуации путем сравнения
различных вариантов с помощью какой-либо количественной
оценки этих вариантов, то говорят о необходимости решения
задачи оптимизации (по латыни optimus — наилучший).
Ясно, что задача оптимизации имеет смысл, если есть
несколько возможных вариантов ее решения. Эти варианты обычно
называют альтернативами.
По содержанию задачи оптимизации весьма
разнообразны. Они могут быть связаны с проектированием
технических устройств и технологических процессов, с распределением
ограниченных ресурсов и планированием работы предприятий,
наконец, с решением проблем, возникающих в повседневной
жизни человека. Всевозможные устройства, процессы и
ситуации, применительно к которым предстоит решать задачу
оптимизации, объединим общим названием объект
оптимизации.
В этой главе сформулированы некоторые основные
определения и понятия, играющие важную роль в дальнейшем
изложении материала, даны постановки известных и достаточно
простых задач поиска экстремума из геометрии, алгебры и
других разделов математики, приведены примеры прикладных
задач оптимального проектирования и планирования, а также
перечислены классы задач оптимизации.
16
1. ЗАДАЧИ ОПТИМИЗАЦИИ
1.1. Основные понятия
Обычно человек хочет сделать „как лучше", но, чтобы не
получить плохой результат при самых хороших намерениях,
для решения задачи оптимизации нужно прежде всего найти
ответы на следующие вопросы:
- Что значит „лучше"?
- Что конкретно нужно улучшить?
- За счет чего можно добиться улучшения, что можно
изменить?
- В каких пределах можно производить изменения?
Отвечая на первый вопрос, необходимо сформулировать
критерий оптимальности, т.е. определить те признаки и
предпочтения, по которым следует провести сравнительную
оценку альтернатив и выбрать среди них наилучшую с точки
зрения поставленной цели оптимизации. Именно с этой точки
зрения можно ответить на второй вопрос: что конкретно
нужно улучшить? Это может быть повышение производительности
станка или срока службы технического устройства, снижение
массы конструкции летательного аппарата или затрат на его
производство и т.п.
Для ответа на два последних вопроса необходимо
располагать математической моделью объекта оптимизации. Эта
модель описывает объект при помощи соотношений между
величинами, характеризующими его свойства. Обычно хотя бы
часть этих величин можно изменять в некоторых пределах,
что и порождает множество альтернатив, среди которых и
предстоит выбрать наилучшую. Изменяемые при
оптимизации величины, входящие в математическую модель объекта
оптимизации, называют параметрами оптимизации, а
соотношения, устанавливающие пределы возможного изменения
этих параметров, — ограничениями. Эти ограничения могут
быть заданы в форме равенств или неравенств. Их называют
соответственно ограничениями типа равенства или
ограничениями типа неравенства.
1.2. Некоторые простые примеры
17
Если множество параметров оптимизации является
подмножеством конечномерного линейного пространства, то говорят
о конечномерной задаче оптимизации в отличие от
бесконечномерных задач, которые рассматривают в вариационном
исчислении и оптимальном управлении [XV]. При этом
критерием оптимальности может быть требование достижения
наибольшего или наименьшего значения одной или несколькими
действительными (скалярными) функциями параметров
оптимизации, выражающими количественно меру достижения цели
оптимизации рассматриваемого объекта. Каждую из таких
функций принято называть целевой. Если целевая функция
единственная, то задачу конечномерной оптимизации
называют задачей математического программирования, а в
противном случае — задачей многокритериальной (векторной)
оптимизации [XX]. В дальнейшем ограничимся
рассмотрением задач математического программирования и методов их
решения.
Если целевая функция и ограничения являются линейными
относительно параметров оптимизации, то говорят о задаче
линейного программирования. Одну из первых таких задач
сформулировал и решил Л.В. Канторович*. Задача
Канторовича была связана с выбором оптимальной производственной
программы, что и объясняет появление в названии этого класса
задач слова „программирование". При нелинейной зависимости
целевой функции или ограничений от параметров оптимизации
говорят о задаче нелинейного программирования.
1.2. Некоторые простые примеры
Начнем с рассмотрения достаточно простых задач
оптимизации из геометрии, алгебры и некоторых других разделов
математики. Эти задачи обычно можно решить геометрическим
*Л.В. Канторович A912-1986) — отечественный математик и
экономист, лауреат Нобелевской премии A975 г.).
18
1. ЗАДАЧИ ОПТИМИЗАЦИИ
или алгебраическим путем, а также при помощи необходимых и
достаточных условий экстремума действительной (скалярной)
функции одного переменного [II]. Включение таких примеров
в эту книгу важно по нескольким причинам. Во-первых, эти
задачи тесно связаны с историей развития методов
оптимизации и позволяют наглядно продемонстрировать многообразие
объектов оптимизации. Во-вторых, на простой задаче можно
более четко выявить особенности построения математических
моделей таких объектов с точки зрения выбранного критерия
оптимальности и проследить этапы процесса формулировки
задачи математического программирования. В-третьих,
знание способов и результатов решения многих из этих задач
помогает при решении более сложных задач оптимизации,
например задач оптимального проектирования (см. 1.3).
Пример 1.1. Найдем стороны прямоугольника, вписанного
в окружность радиуса R и имеющего наибольшую площадь S
(рис. 1.1).
Эта задача известна с глубокой
древности, и ее нетрудно решить
геометрическим путем. Диагональ
вписанного в окружность
прямоугольника является диаметром
окружности и имеет фиксированную
длину. Площадь S прямоугольника
равна половине произведения его
Рис. 1.1
диагоналей на синус угла ср между
диагоналями, т.е. S = 2R2 sirup. Ясно, что эта площадь будет
наибольшей при s'mcp = 1, или при ср = 7г/2. В этом случае
диагонали прямоугольника перпендикулярны, а сам прямоугольник
представляет собой квадрат. Таким образом,
прямоугольником наибольшей площади, вписанным в окружность, является
квадрат со стороной R\f2 и площадью 2R2.
Если в качестве параметров оптимизации выбрать
длины й^О и Ь^О сторон прямоугольника, то получим целевую
1.2. Некоторые простые примеры
19
функцию S = ab и ограничение \/а? + Ъ2 = 2R типа равенства,
нелинейные по отношению к этим параметрам. Поэтому
рассматриваемую задачу оптимизации следует отнести к задачам
нелинейного программирования. Ее математическую
формулировку можно представить в виде
{S = ab—> max;
а2 + 62 = 4Д2, а>0, b > 0.
Эту задачу можно решить одним из известных стандартных
путей: либо использовать формальную процедуру поиска
условного экстремума функции S = ab двух переменных с одним
уравнением связи, построив функцию Лагранжа, либо
выразить при помощи ограничения одно переменное через другое
и перейти к поиску экстремума функции одного переменного.
Отметим, что в данном случае возможен и нестандартный
способ решения, связанный с построением вспомогательного
соотношения 4R2 - 2S = а2 + Ъ2 - 2аЪ = (а - бJ, или S = 2R2- Ц^.
Отсюда следует, что S достигает наибольшего значения 5* =
= 2R2 при условии а = 6, т.е. когда прямоугольник является
квадратом, причем a = b = R\/2.
Пример 1.2 {задача Евклида). В заданный треугольник
ABC с высотой Н и основанием b вписать параллелограмм
наибольшей площади, стороны
которого параллельны двум сторонам
треугольника (рис. 1.2).
Критерием оптимальности в
этой задаче является достижение
площадью параллелограмма
наибольшего значения, а ограничения
¦Л, и Л.
связаны с условиями
параллельности сторон и размещения паралле- ис' '
лограмма в пределах заданного треугольника.
Выберем прямоугольную систему координат, совместив ее
начало с общей вершиной параллелограмма и треугольника
20
1. ЗАДАЧИ ОПТИМИЗАЦИИ
(вершина А на рис. 1.2), а ось абсцисс — с одной из сторон
треугольника. В качестве параметров оптимизации выберем
основание х параллелограмма и его высоту h. Тогда площадь
S параллелограмма можно записать в виде S = hx, а условие,
что параллелограмм вписан в треугольник, — как ограничение
типа равенства (Н — h)/H = ж/Ь, которое вытекает из подобия
треугольников DBE и ABC. Итак, имеем задачу оптимизации
[ S = hx —>> max;
Я
h х
х>0.
Эту задачу также можно решить стандартными
способами (см. пример 1.1). Ее решением является параллелограмм с
основанием х* = 6/2 и высотой h* = A — х*/Ъ)Н = Н/2.
Отметим, что выбор вершины треугольника, с которой совпадает
вершина параллелограмма, не является существенным, так как
в любом из трех вариантов выбора вершины треугольника
площадь параллелограмма максимальной площади равна половине
площади треугольника ABC.
Пример 1.3. В прямой круговой конус вписан прямой
круговой цилиндр так, что основания конуса и цилиндра лежат
в одной плоскости (рис. 1.3). Найдем наибольшую возможную
часть объема конуса, занятую таким цилиндром.
Как и задача Евклида, эта задача известна тысячи лет. Ее
можно решить, используя неравенство средних, известное еще
Пифагору, согласно которому среднее
геометрическое не превышает
среднего арифметического, т.е.
ab <
а + Ь
зг~г / а + Ь + с
vabc <
Рис. 1.3
2 7 ^3
и т.п., причем среднее
геометрическое равно среднему
арифметическому только в том случае, когда все
числа равны между собой.
1.2. Некоторые простые примеры
21
Обозначим высоту и радиус основания цилиндра через h и
г, а высоту и радиус основания конуса через Н и R. Запишем
отношение их объемов
7гг2/г r2h
v= ttr2h/3= Wh'
Это равенство задает целевую функцию, в которой в качестве
параметров оптимизации можно взять отношения г / R и h/H.
Из условия задачи (цилиндр вписан в конус) вытекает
ограничение r/R= (Н — h)/H. Подставляя его в целевую функцию,
получаем
{ h\ ( h\2 h h , . /ч
<hX1-h)w я6*0-1»' <l1>
Ясно, что функция rj(h/H) достигает максимума при том
же значении отношения h/H, что и любая положительная
степень правой части этого равенства, в частности степень 1/3.
Используем неравенство для среднего геометрического таких
трех величин, чтобы правая часть этого неравенства оказалась
константой:
Максимум левой части в этом неравенстве будет достигнут при
его переходе в равенство, т.е. - — —— = —. Отсюда находим
2 2Н Н
h/H = 1/3 и, подставляя в A.1), вычисляем г/A/3) = 4/9. При
этом отношение радиусов оснований цилиндра и конуса будет
г/Д = 2/3.
Несложно проверить, что к тому же результату можно
прийти и стандартным путем поиска экстремума функции
Ф/н) при h/He [0,1].
22
1. ЗАДАЧИ ОПТИМИЗАЦИИ
Пример 1.4. Найдем значение параметра а, при котором
достигает максимума функция f(a) = expf — - (х\ + #!)) •> гДе ЖЬ
Х2 — корни квадратного уравнения х2 + ах + За — 1 = 0.
По теореме Виета* [1-4.4] имеем х\ + Х2 = — а и ж^ = За — 1.
Отсюда находим
Хл ~т~ Хп
(xi + х2J - 2xix2 = а2 - 6а + 2 = (а - ЗJ - 7,
и в итоге /(а) = ехрC,5 — 0,5(а — ЗJ). Так как (а — ЗJ > 0, a
ехр(—0,5(а — ЗJ) убывает с возрастанием (а —ЗJ, то функция
/(а) достигает своего максимума при а* = 3 и этот максимум
равен /(а*) = ехрC,5) « 33,115.
Применение теоремы Виета позволило в данном случае
упростить задачу и даже избежать использования
дифференциального исчисления для поиска экстремума функции /(а),
заданной как композиция функций.
Пример 1.5. Луч света, переходя из одной однородной
среды в другую, падает на границу раздела этих сред под углом а\
к направлению нормали и
после преломления на этой
границе составляет с нормалью угол
OL2 (рис. 1.4). Требуется найти
соотношение между этими
углами.
Из курса физики известно,
что в соответствии с принципом
Ферма** геометрической
оптики свет при прохождении через среду с различными свойствами
выбирает такую траекторию, время прохождения которой
минимально.
Пусть t\ — время прохождения световым лучом отрезка
AM со скоростью с\ в среде i, х — абсцисса точки М падения
Рис. 1.4
*Ф. Виёт A540-1603) — французский математик и юрист.
**П. Ферма A601-1665) — французский математик.
1.3. Задачи оптимального проектирования 23
светового луча на границу двух сред, t<i — время прохождения
световым лучом отрезка MB со скоростью c<i в среде 2. Тогда
время прохождения света из точки А в точку В будет равно
ФО=t1+t2 = ^Э±^5 + у/ън«-х)\ (L2)
С\ С<2
Из необходимого условия экстремума функции ?(ж), который
по физическому смыслу задачи является минимумом, получаем
х
с\ л/bl + х2 sinai
С2 a~X Sin «2
у/Ъ1 + {а-х)*
Это равенство выражает закон преломления света,
установленный В. Снеллиусом*.
1.3. Задачи оптимального проектирования
При создании технического устройства различного
назначения обычно часть его параметров можно изменять в
определенных пределах. Это приводит к тому, что при
проектировании появляется некоторое множество вариантов создаваемого
устройства. В результате возникает проблема выбора из
этого множества альтернатив наилучшей альтернативы с точки
зрения критерия оптимальности. Соответствующие такому
выбору задачи оптимизации часто называют задачами
оптимального проектирования.
Пример 1.6. Одной из наиболее простых задач
оптимального проектирования является выбор размеров емкости
определенной формы, имеющей наибольший объем при
заданной площади поверхности или же наименьшую площадь при
заданном объеме.
*В. Снеллиус A580-1626) — нидерландский астроном и математик.
A.3)
24
1. ЗАДАЧИ ОПТИМИЗАЦИИ
Пусть требуется спроектировать бак горючего в виде
прямого кругового цилиндра заданного объема V, на
изготовление которого будет затрачено наименьшее количество листовой
стали. В качестве параметров оптимизации выберем радиус R
и высоту Н цилиндра. Тогда затраты материала на
изготовление бака будет определять суммарная площадь S его боковой
поверхности и двух плоских днищ. Таким образом, необходимо
минимизировать целевую функцию S = 2пR(H + R) при
ограничении типа равенства ttR2H = V, т.е. решить задачу
нелинейного программирования.
Если из целевой функции при помощи ограничения
исключить Н и записать ее в виде
V V о
ЗД = - + - + 2тгД2,
то произведение слагаемых не будет зависеть от i?, и для
нахождения ее минимального значения удобно использовать
то же неравенство между геометрическим и арифметическим
средними, что и в примере 1.3:
S(R) = \ + \ + 2тгД2 > з{/^27гД2 = 3^2тгУ2 = Я.
R R \ R R
Равенство имеет место только при равенстве слагаемых, т.е.
ПРИ ~б = 27гЛ2, тогда Д* = у —. Учитывая ограничение,
получаем
Д* =
ТгД2
т.е. высота оптимального бака равна его диаметру.
При изготовлении одного бака нужно учитывать, что для
заготовки круглого днища площадью ttR2 придется взять
квадратный лист площадью 4i?2, причем после раскроя
оставшуюся часть листа использовать будет практически невозможно.
Поэтому более обоснованно в качестве целевой минимизировать
функцию S = 2ttRH + 8R2 при прежнем ограничении ttR2H = V.
1.3. Задачи оптимального проектирования
25
Тогда в результате процедуры, аналогичной рассмотренной,
получим R* = - VV, S* = 6vl^2, if* = -i?*. Если предстоит из-
готовить крупную партию баков, то раскрой листовой стали
при заготовке днищ можно провести более рационально,
располагая соседние центры днищ в вершинах правильных
треугольников со стороной 2R. Тогда расход листа на каждое днище
будет соответствовать площади 2\/ЗЛ2 правильного
шестиугольника, описанного около окружности радиуса R. При этом
следует минимизировать целевую функцию S = 27ri?if + 4v3i?2
при том же ограничении. В итоге получим
Отметим, что при постановке задач оптимального
проектирования важно, чтобы математическая модель объекта
оптимизации достаточно полно отражала именно те свойства
объекта, улучшение которых является целью оптимизации.
Разработка такой модели обычно требует использования сведений
из соответствующих инженерных дисциплин или областей
техники.
Пример 1.7. Из курса сопротивления материалов
известно*, что допустимая нагрузка, воспринимаемая
прямолинейным стержнем, работающим на растяжение или сжатие (без
потери устойчивости прямолинейной формы равновесия),
пропорциональна площади F его поперечного сечения. При сжатии
стержень может потерять устойчивость, изгибаясь в некоторой
плоскости. Сжимающая сила, вызывающая потерю
устойчивости стержня, пропорциональна геометрическому моменту
инерции I его сечения относительно центральной оси тела,
перпендикулярной плоскости изгиба. От значения I также
зависит прогиб стержня, изгибаемого в этой плоскости, но
зависимость эта обратно пропорциональная. Допустимая нагрузка
*См.: Феодосъев В.И.
26
1. ЗАДАЧИ ОПТИМИЗАЦИИ
при изгибе стержня пропорциональна моменту сопротивления
W = I/ут его сечения, где ут — расстояние до наиболее
удаленной от центральной оси точки сечения. Эти сведения важны
для выбора критерия оптимальности при проектировании
отдельных элементов конструкций, воспринимающих нагрузку.
Предположим, что из круглого бревна радиуса R
необходимо выпилить балку с прямоугольным поперечным сечением
(рис. 1.5) так, чтобы ее можно было наиболее эффективно
использовать в строительной
конструкции. Если балка будет использована в
качестве стойки, работающей на
сжатие без опасности потери
устойчивости, то целесообразно
максимизировать площадь F ее сечения, выбрав
его в виде квадрата со стороной i?y2,
вписанного в окружность радиуса R.
Максимальное значение площади
сечения будет F* = 2R2 (см. пример 1.1).
Таким же должно быть сечение стойки, если возможна
потеря ее устойчивости в любой плоскости, проходящей через
ее ось. Действительно, нетрудно показать, что в этом
случае момент инерции сечения относительно любой оси, лежащей
в плоскости квадрата и проходящей через его центр,
постоянен и равен I = R4/3. Если же плоскость изгиба стойки при
возможной потере устойчивости предопределена условиями ее
крепления, то целесообразно выбрать такое отношение сторон
прямоугольника, чтобы момент инерции сечения относительно
его центральной оси, перпендикулярной этой плоскости, был
максимальным. Обозначим через b ширину сечения вдоль этой
оси, а через h его высоту (см. рис. 1.5). Тогда получим [VI]
Рис. 1.5
h/2
y2dy = by-
-h/2
h/2
-h/2
bh3
~\2'
A.4)
1.3. Задачи оптимального проектирования 27
Но стороны прямоугольника должны удовлетворять
ограничению Ъ2 + h2 ^ 4Д2. Таким образом, приходим к задаче
нелинейного программирования
<
т bh3
I = — -> max;
62 + /i2<4i?2, 6>0, h>0.
Несложно установить, что максимальное значение
будет достигнуто при оптимальных высоте h* = Л\/3 и ширине
b* = R сечения балки.
Такое же поперечное сечение балки следует выбрать,
если она нагружена в рассматриваемой плоскости изгибающей
нагрузкой. При таком выборе жесткость балки будет
максимальной, а ее прогиб — минимальным. Поскольку для
рассматриваемого прямоугольного сечения балки ут = /г/2, то для
момента сопротивления получим W = I/ут = bh2/6. В данном
случае задача нелинейного программирования принимает вид
ш bh*
W = —; > max;
о
62 + /i2^4i?2, 6^0, h^O.
Ее решением будет W* = —^= i?3, h* = —= R = у/2 Ъ*.
9л/3 л/3
Пример 1.8. Из курса физики и термодинамики известно,
что работа, затрачиваемая в компрессоре на сжатие 1 кг
воздуха от начального давления ро до давления р> ро, равна
А
jRTo
Ш)*-*)> <->
7 - -L V v.Po
где 7 — коэффициент, характеризующий процесс сжатия (при
адиабатическом процессе для воздуха 7~1,4); R — газовая
постоянная воздуха; Tq — его температура до сжатия. Чтобы
28
1. ЗАДАЧИ ОПТИМИЗАЦИИ
уменьшить затрачиваемую работу в случае высокой степени
сжатия х = р/ро, проектируют многоступенчатые
компрессорные установки, состоящие из нескольких последовательно
соединенных компрессоров (ступеней) с промежуточными
холодильными устройствами между ступенями, в которых
охлаждают воздух, нагревшийся при сжатии.
Пусть требуется спроектировать компрессорную установку
из га ступеней в предположении, что воздух, поступающий в г-ю
ступень, г = 1, га, охлажден до одинаковой температуры То и
имеет давление Рг-ъ равное давлению на выходе из предыдущей
ступени. Необходимо при заданной общей степени сжатия х
так выбрать степени сжатия отдельных ступеней щ =р^/Рг-ъ
г = 1, га, рт =р, чтобы работа, затрачиваемая на весь процесс
сжатия воздуха, была минимальной.
В соответствии с A.5) работа, затрачиваемая на сжатие в
г-й ступени, равна
7-1 \yp,-J ) 1-1\ '
а работа, затрачиваемая на весь процесс сжатия,
т- -i=i
Так как число га ступеней задано, то минимизируемую целевую
функцию можно представить в виде
7-1
А А*,7
+i = E—> A-е)
Aora Г—' 771
г=1
где Aq = jRTo/(j — 1). Правая часть этого равенства является
7-1
средним арифметическим неизвестных чисел щ = х^ 7 , г =
= 1, га. Геометрическое среднее этих чисел равно
т 7~1 тп 7~1 , „ v 7~1 -у—1
Va!a2...am = n^m7 = П(^)т7 =(~)
т7 _хт7 >
1.3. Задачи оптимального проектирования
29
Используя неравенство между геометрическим и
арифметическим средними (см. пример 1.3), получаем
А 1 Ах^~^ 2=1
hi = > — > X m7 .
Aqtu t—' m
г=1
Отсюда следует, что наименьшее значение работы при
заданной степени х сжатия 1 кг воздуха в m-ступенчатой
компрессорной установке равно
и может быть достигнуто лишь при равенстве всех слагаемых
в правой части A.6), т.е. при щ = const, i = 1, га. Это
возможно только при выборе одинаковой для всех ступеней степени
- 1 / / v \ 1/т
сжатия, равной х= х /т = — . Таким образом, затрачи-
\ро/
ваемая работа минимальна, если значения давлений на выходе
из ступеней образуют геометрическую прогрессию со
знаменателем х: pi = хро, Р2 = xpi и т.д. #
Некоторые параметры оптимизации могут принимать лишь
дискретные значения (например, целочисленные). В этом
случае дифференцирование по таким параметрам при поиске
экстремума целевой функции носит условный характер. После
формального нахождения точки экстремума в предположении
непрерывного изменения этих параметров для них следует
принять ближайшие к найденным дискретные значения. Ясно, что
это повлияет на экстремальное значение целевой функции.
Пример 1.9. Пусть требуется соединить N одинаковых
источников постоянного электрического тока в батарею
таким образом, чтобы батарея имела наибольшую электрическую
мощность, выделяемую на внешней нагрузке с сопротивлением
R. Предполагается, что каждый источник имеет
электродвижущую силу Е и внутреннее сопротивление г.
30
1. ЗАДАЧИ ОПТИМИЗАЦИИ
Если эти источники соединить последовательно, то
получим батарею с электродвижущей силой NE и внутренним
сопротивлением Nr. Тогда при подключении внешней нагрузки
сила тока J\ = — -, а передаваемая мощность W\ = J{К =
т\т2 тр2 гу
= -— —-. При параллельном соединении получим батарею с
электродвижущей силой Е и внутренним сопротивлением r/N.
В этом случае при подключении внешней нагрузки имеем J% =
Е NE тхг N2E2R
/*г ~ *.~ и Wo = 7 ттт^т- В частном случае г = R
r/N + R r + NR z (r + NRJ J
обе батареи дадут одинаковый результат, но при г < R
получим VF2 < Wi, и наоборот (естественно, считал, что N > 1).
Можно использовать комбинированную схему соединения
источников тока. Предположим, что N допустимо изменять
так, чтобы для некоторого натурального числа п число N/n
также было натуральным и больше единицы. Тогда можно
параллельно соединить N/n ветвей, каждая из которых будет
состоять из п последовательно соединенных источников тока и
иметь электродвижущую силу пЕ и внутреннее сопротивление
-п о _. пг п2г
пг. Внутреннее сопротивление такой батареи равно ——— = ——,
а электродвижущая сила равна п. При подключении внешней
7 пЕ
нагрузки сила тока составит J = 2 —-, а передаваемая
мощность будет равна
w = j2r_ (nNEfR
(n2r + NRJ'
Фиксируя N и предполагая, что п изменяется непрерывно,
попытаемся найти максимум передаваемой мощности. Если
точка п* максимума существует, то в ней достигает максимума
и сила тока, которую представим функцией
т/ ч nNE /-. ^
J(n) = —о ^ (!-7)
v } n2r + NR v )
одного переменного п. Из необходимого условия Jf(n) = 0
максимума этой функции получаем при п > 0 ее единственную
1.3. Задачи оптимального проектирования
31
стационарную точку n* = y/NR/r. Проверка достаточного
условия показывает, что, действительно, п* — точка
локального максимума функции J(n). Этой точке соответствуют
максимальные значения
Е NE2
J* = —= и W* = ——.
9 rR Аг
zVlv
Сравним силу тока батарей в зависимости от способа
соединения источников тока. Сначала рассмотрим случай г = R.
Наименьшее значение 7V, при котором имеет смысл
комбинированная схема соединения, равно 4. Тогда п* = 2 (две
параллельные ветви по два последовательно соединенных источника
тока) и^ = E/R > jD). Следующее значение 7V, позволяющее
осуществить комбинированное соединение, равно 6 (три ветви
по два источника или две ветви по три источника), но
формальное вычисление дает для п* иррациональное число между
натуральными числами 2 и 3. Если принять п = 2 или п = 3, то
из A.7) получим J = - — > jF). При N = 8 формальное
вычисление п* также приведет к иррациональному числу, но в этом
случае имеют смысл значения п = 2 или п = 4, для которых из
A.7) найдем J = - — > j(8'. Сравнение ограничим выбором зна-
3 R
чения N = 9, для которого п* = 3 и J* = - —, т.е. сила тока при
2 К
комбинированной схеме более чем в 1,5 раза превышает
значение j(9).
Так как при г < R выполняется неравенство J2 < J\, то
комбинированную схему соединения источников тока достаточно
сравнить с их последовательным соединением. Представим
отношение сил токов в следующем виде:
J* _Nr + R _ Nr + R
Л " VNrR ~ 2у/NrR
32
1. ЗАДАЧИ ОПТИМИЗАЦИИ
В правой части этого равенства стоит удвоенное отношение
среднего арифметического к среднему геометрическому двух
чисел Nr и R. Известно, что это отношение не меньше единицы,
причем оно равно единице только при Nr = R (см. пример 1.3).
Следовательно, J* ^ 2 J\ для всех приемлемых значений 7V, при
которых возможна комбинированная схема соединения.
Аналогично можно показать, что при г > R для всех приемлемых
значений N справедливо J* ^ 2J% > 2J\. #
Математическая модель объекта оптимизации может
оказаться столь сложной, что решение задачи оптимизации с
использованием такой модели потребует слишком много времени.
В таком случае следует попытаться упростить модель, но так,
чтобы в упрощенном виде она отражала свойства объекта,
существенные с точки зрения цели оптимизации, выражаемой
критерием оптимальности. После выбора значений
параметров оптимизации целесообразно провести поверочный расчет
с использованием более полной модели и оценить погрешность,
связанную с ее упрощением.
Пример 1.10. Для интенсификации теплообмена между
нагретой поверхностью и охлаждающей средой увеличивают
площадь поверхности путем ее оребрения. Рассмотрим
плоскую стенку, к которой присоединено достаточно длинное ребро
прямоугольного профиля высотой / и толщиной 2/i (рис. 1.6).
Рис. 1.6
1.3. Задачи оптимального проектирования
33
Помимо передачи теплоты охлаждающей среде с известной
температурой Тс непосредственно с поверхности стенки, имеющей
температуру То > Тс, некоторая часть теплоты
распространяется путем теплопроводности от основания ребра к его вершине
и переходит в охлаждающую среду через боковые поверхности.
Целесообразно так подобрать материал ребра и размеры / и
h его профиля, чтобы тепловой поток Q (количество теплоты
в единицу времени), передаваемый охлаждающей среде через
участок ребра единичной длины, был максимальным.
Для изготовления ребер желательно использовать
материал с достаточно большим коэффициентом теплопроводности Л.
Тогда температура боковой поверхности ребра будет в меньшей
степени отличаться от температуры его основания, что
повысит эффективность использования этой поверхности. Масса
ребра, приходящаяся на единицу его длины, пропорциональна
площади F = 2lh его сечения. Следовательно, один из
вариантов постановки задачи оптимального проектирования ребра,
изготавливаемого из выбранного материала, может быть
таким: критерием оптимальности является максимум
передаваемого через ребро теплового потока Q, а ограничением типа
неравенства будет 21 h ^ Fq, где Fq — заданное значение
площади. Параметрами оптимизации в этом случае являются / и
h. Поэтому необходимо установить связь этих параметров с
величиной Q, т.е. построить целевую функцию. Это
потребует использования математической модели
процесса передачи теплоты от стенки
через ребро охлаждающей среде.
Если условия теплообмена с
охлаждающей средой постоянны вдоль
достаточно длинного ребра, то режим
теплообмена будет установившимся во времени, а
температурное поле в ребре — плоским,
определяемым функцией Т(ж,у), х Е [0, /],
у Е [—/i, h] (рис. 1.7). Известно [XII], что
т
с
a
-
Xj
г
X
k о
[ а
%
i
т
с
a
г У
Рис. 1.7
34
1. ЗАДАЧИ ОПТИМИЗАЦИИ
эта функция при Л = const удовлетворяет двумерному
уравнению Лапласа
д2Т(х,у) , д2Т(х,у)
+
= 0.
A.8)
дх2 ду2
Вследствие симметричности сечения ребра относительно оси
Ох можно рассматривать лишь половину этого сечения и
задавать граничные условия в виде
Т@,у) = Т0, А
дТ(х,у)
дТ(х,у)
ду
у=0
о, Л
дх
дТ(х,у)
Х — 1
+ аТA,у) = 5Тс, !/е[0,Л]; A.9)
дх
y=h
+ aT(x,h)=aTc, жЕ[0Д A.10)
где а ж а — коэффициенты теплообмена с охлаждающей средой
на боковой поверхности ребра и на поверхности его торца
соответственно. Решение краевой задачи A.8)-A.10), записанное в
виде двойного ряда по ортогональной системе функций [IX],
может быть найдено одним из известных методов, например
методом Фурье [XII] или с помощью интегральных
преобразований [XI]. После ее решения для теплового потока,
передаваемого через ребро охлаждающей среде и равного тепловому
потоку, проходящему через его основание, получим
д = 2
-Л
дТ(х,у)
дх
х=0
dy = -2А
п
/
дТ(х,у)
дх
х=0
dy. A.11)
Рассмотренная математическая модель является
достаточно сложной и не позволяет представить зависимость Q от
параметров оптимизации 1иЛв удобном виде. Эту модель можно
упростить, сохранив точность, достаточную для инженерных
приложений. Дело в том, что из соображений качественного
характера при ограниченной площади F = 2lh сечения ребра
целесообразно увеличить его высоту /, чтобы увеличить
площадь боковой поверхности. При этом ребро станет достаточно
1.3. Задачи оптимального проектирования
35
тонким и по его толщине 2Л, = F/l ^ Fq/1, т.е. в направлении
оси Оу, температуру можно принять практически неизменной.
Интегрируя A.8) по у в пределах от 0 до h и учитывая A.10),
находим
д2Т(х,у) | d2T(x,y)Uy
дх2
h
-!
0
ду2
д2Т(х,у) ^ЭТ(х,у)
dy +
дх2
ду
дТ(х,у)
x—h
п
I
д2Т(х,у)
дх2
dy + a
ду
х=0
¦T(x,h)
А
0.
Отсюда, полагая температурное поле в ребре одномерным,
т.е. определяемым функцией Т(ж), приходим к обыкновенному
дифференциальному уравнению (ОДУ)
d2T{x) | aTc-T(x,h) =Q
dx2 Xh
При этом граничные условия A.9) примут вид
дТ(х)
Т@)=Т0, А-
дх
Х — 1
+ aT(l) = аТс
A.12)
A.13)
Но передачей теплоты с поверхности торца ребра чаще
всего можно пренебречь по сравнению с передачей через боковую
поверхность, т.е. положить в A.13) а = 0. Это будет
соответствовать идеально теплоизолированному торцу и приведет к
несколько заниженной оценке для передаваемого через ребро
теплового потока, для которого вместо A.11) теперь получим
Q = -2A/i
dT{x)
dx
1ж=0
A.14)
36
1. ЗАДАЧИ ОПТИМИЗАЦИИ
Краевая задача A.12), A.13) при а = 0 имеет решение
Отсюда, используя A.14), находим
^ ^ЛТ/_ ^ч shra(Z — х) \ Л /——-/т тЧ , / ск 7
Q = 2\h(T0-Tc га / 7 ; = 2VaXh Т0 -Тс thW — /.
сига/ ' w х^
ж=о Y v и w" У Xh
Таким образом, мы имеем целевую функцию, зависящую от
двух параметров оптимизации / и /г, и ограничение 2lh ^ Fq.
Подставляя верхнюю оценку / = F$/Bh) для высоты ребра в
целевую функцию, получаем функцию
Fq / а
Q(h) = 2V^Xh(T()-Tc)th-2 з
одного переменного h. Необходимое условие Q'(h) = 0
максимума этой функции дает трансцендентное уравнение
которое при ( > 0 имеет единственное решение ?* « 2,8384.
Несложно проверить, что соответствующее этому решению
значение
Л. = 13М «0,4994^^
АС| ' V Л
удовлетворяет достаточному условию максимума функции Q(h).
Из ограничения получаем верхнюю оценку для оптимальной
высоты ребра
J* =\!ЫЯю1Лвир1Ы
2h* 2 V а V а
1.4. Задачи оптимального планирования
37
При этом отношение оптимальных значений высоты ребра к
толщине примет вид
а максимальное значение теплового потока —
Q, = Q(h*) = 2П«2—^ (Т0 -Тс) th^ « 1,2563^ВД(То-Тс).
1.4. Задачи оптимального планирования
Задачи математического программирования часто
возникают в экономике, при планировании производственных
процессов и количественной оценке альтернатив, связанных с
принятием управленческих решений. Постановка этих задач
обычно основана на анализе и сопоставлении расходуемых ресурсов
и полученного результата. Такой подход принято называть
методом „затраты — эффективность". Применение этого
подхода приводит, как правило, к двум связанным между собой
типам задач: либо максимизировать эффективность при
ограниченных затратах, либо обеспечивать эффективность не ниже
заданной при минимальных затратах. Таким образом,
критерием оптимальности может быть количественное выражение
затрат или эффективности. Рассмотрим несколько примеров
такого подхода.
Пример 1.11. Предположим, что предприятие может
выпускать продукцию п наименований, для производства которой
требуется т видов ресурсов (сырья, энергии, оборудования и
т.п.). Обозначим через ац затраты i-го вида ресурсов, г =
= 1, т, на производство единицы продукции j-ro наименования,
j = 1, п, а через Ь{ и Xj полные объемы располагаемых
ресурсов и планируемые объемы выпуска продукции соответственно.
Если к тому же по каждому наименованию продукции заданы
38
1. ЗАДАЧИ ОПТИМИЗАЦИИ
нижняя dj и верхняя Aj границы объема выпуска продукции,
то можно записать ограничения типа неравенства
п
2_]aijxj ^ ^Ь ^ = 1, га, aj < Xj < A/, j = 1, п.
i=i
Если эффективность производства продукции
характеризовать суммарной выручкой от продажи продукции, то
оптимальный план х = (#i, #2, •••? #п) выпуска продукции должен
удовлетворять этим ограничениям и обеспечивать максимум
целевой функции
п
S = / jdjXj,
j=i
где rfj — цена единицы продукции j-ro наименования. В данном
случае и целевая функция, и ограничения линейны
относительно параметров оптимизации х^ j = 1, п. Поэтому
рассмотренная задача оптимального планирования выпуска продукции
является задачей линейного программирования.
Пример 1.12 (транспортная задача). Пусть
необходимо составить план перевозок некоторого товара с га складов
в п магазинов так, чтобы затраты на эти перевозки были
минимальными. Предположим, что на г-м складе, г = 1, га, имеется щ
единиц товара, а j-й магазин, j = 1, п, сделал заказ на bj единиц
этого товара, причем стоимость его перевозки с i-го склада в
j-й магазин равна сц. Обозначим через хц планируемое
количество товара, перевозимое с i-го склада в j-й магазин, тогда
стоимость его перевозки составит с^хц. Общие затраты на
перевозки — это сумма затрат на перевозки со всех складов во
все магазины. Поэтому оптимальный план перевозок
соответствует минимуму целевой функции
т п
S = ^2 ^2 CiiXii ~^ min'
i=l j=l
1.4. Задачи оптимального планирования
39
что должно быть достигнуто выбором mn значений хц ^ О,
которые в данном случае являются параметрами оптимизации.
Но при этом необходимо обеспечить потребности магазинов,
т.е. должны быть выполнены ограничения типа равенства
m
г=1
Однако с любого склада нельзя вывезти товара больше, чем
там его находится. Следовательно, должны быть выполнены
ограничения типа неравенства
п
2_\xij ^ аь i — 1? m-
J=l
Отметим, что сформулированная задача оптимизации,
относящаяся к классу задач линейного программирования, имеет
решение, если сумма заказов магазинов не превышает
суммарного запаса товара на всех складах, т.е.
n m
3=1 г=1
Пример 1.13 {задача о диете). Рассмотрим задачу
построения оптимального рациона питания. Обозначим: п —
число видов пищевых продуктов; т — число видов
питательных веществ; ац — число единиц i-го питательного вещества
в единице j-ro продукта; Ъ{ — ежегодная потребность в г-м
питательном веществе; Cj — стоимость единицы j-ro
продукта. Выясним, сколько единиц каждого пищевого продукта
нужно употребить за рассматриваемый период (в данном
случае за год) таким образом, чтобы, обеспечив потребности в
каждом питательном веществе, затратить минимальное
количество денег.
40
1. ЗАДАЧИ ОПТИМИЗАЦИИ
Назовем рационом вектор х = [х\ х^ ... хп) , где Xj —
ежегодное потребление j-ro пищевого продукта. Речь идет,
таким образом, о построении рациона минимальной стоимости.
Математически эта задача может быть сформулирована
следующим образом: минимизировать целевую функцию
п
S = ^2Cjx3 A.15)
з
при ограничениях
п
> dijXj ^ bi. г = 1, га;
j A.16)
Xj>0, j = l,n-
Пример 1.14. Предположим, что предприятие может
производить п изделий, причем затраты на производство Х{
единиц г-то изделия составляют S{x\) =а^% гДе а% — затраты
на производство одного i-го изделия (при мелкосерийном или
индивидуальном производстве обычно к{ ^ 1, а при
крупносерийном — ki < 1). Предположим также, что должно быть
выполнено так называемое условие на ассортимент:
предприятие должно выпустить не менее bi единиц i-го изделия, т.е.
имеем п ограничений типа неравенства Х{^Ь{^ г = 1, п. Если
эффективность производства изделий определить как
суммарную выручку от их продажи, то получим еще одно ограничение
типа неравенства
п
^d%x%>b, A.17)
г=1
где dj, г = 1, п, — цена единицы i-го изделия, a b — заданный
нижний уровень эффективности. При этих ограничениях
необходимо минимизировать нелинейную целевую функцию
п
г=1
1.4. Задачи оптимального планирования
41
характеризующую суммарные затраты на производство
изделий. Следовательно, сформулированная задача является
задачей нелинейного программирования.
Пример 1.15. Пусть сеть газопроводов связывает между
собой га месторождений А^ г = 1, га, газа и п пунктов В^ j =
= 1, п, его потребления с известными значениями pj ^ 0 расхода
газа в единицу времени. Производительность gi i-ro
месторождения, г = 1,га, ограничена заданным значением G^, т.е.
заданы ограничения типа неравенства 0 ^ gi ^Gi. Затраты на
добычу газа на г-м месторождении, г = 1, га, являются
функцией (pi(gi) производительности д{. Сеть состоит из К участков,
причем стоимость подачи газа по к-му участку, к = 1, К,
является функцией fk(qk) расхода q^ через этот участок. В пунктах
потребления газа имеем ограничения типа равенства
кев+ кев~
где В^~ и В^ — множества участков сети с входящими в j-й
пункт и выходящими из него потоками газа соответственно.
Аналогично для месторождений газа получаем ограничения
типа равенства
9i= 5Z ^' г = 1,т.
кел-
Оптимальным планом добычи газа на месторождениях и
распределения потоков газа по участкам сети газопроводов будет
план, который удовлетворяет указанным ограничениям и
обеспечивает минимум общих затрат
m К
S = ^2(Pi(gi) + ^2fk(qk)
г=1 к=1
на добычу и подачу газа. Все ограничения в сформулированной
задаче линейные. Поэтому в частном случае линейных функций
(fi(gi) и fk(Qk) она будет задачей линейного программирования,
но в общем случае — задачей нелинейного программирования.
42
1. ЗАДАЧИ ОПТИМИЗАЦИИ
1.5. Классы задач оптимизации
Как и в любой классификации, разделение задач
оптимизации на отдельные классы достаточно условно. Отметим, что
одна и та же прикладная задача может приводить к разным
задачам оптимизации в зависимости от того, какая
математическая модель используется при рассмотрении реального
объекта оптимизации. Ясно, что желательно применять более
простые модели, но в то же время достаточно полно
отражающие свойства объекта, существенные с точки зрения
поставленной цели, выраженной в критерии оптимальности. Поэтому
при выборе либо разработке математической модели или же
при обосновании ее упрощения необходимо достаточно четко
представлять, к какому классу будет относиться поставленная
задача оптимизации и какие методы применимы для ее
решения.
Пусть /о (ж) — целевая функция, количественно
выражающая некоторый критерий оптимальности и зависящая от
координат Xj, j' = 1, п, точки х Е W1. Эти координаты являются
параметрами оптимизации (иногда их называют также
переменными задачи оптимизации или просто переменными
задачи).
При математической формулировке задачи оптимизации
целевую функцию выбирают с таким знаком, чтобы
решение задачи соответствовало поиску минимума этой функции.
Поэтому формулировку общей задачи математического
программирования обычно записывают так:
/о(ж) —>> min, х Е О, A.18)
где ficRn — множество возможных альтернатив,
рассматриваемых при поиске решения задачи.
Любую точку х Е О называют допустимым решением
задачи математического программирования, а само множество —
множеством допустимых решений или, короче, допустимым
1.5. Классы задач оптимизации
43
множеством. Точку ж* Е О, в которой функция /о (ж)
достигает своего наименьшего значения, называют оптимальным
решением задачи.
При отсутствии ограничений множество О совпадает с
областью определения D(fo) С W1 целевой функции. Если же
рассматриваемые альтернативы должны удовлетворять
некоторым ограничениям, то множество допустимых решений
сужается.
Задачу A.18) в дальнейшем будем называть задачей
минимизации целевой функции на множестве О, понимая под этим
нахождение наименьшего значения функции fo(x) на О и точек
ж Е О, в которых оно достигается. Но целевая функция может и
не достигать на О наименьшего значения. Тогда говорят о
точной нижней грани inf fo(x) функции fo(x) на этом множестве
и вместо A.18) используют запись
/0(aO->inf, жЕО. A.19)
Отличие A.18) от A.19) в том, что в первом случае
предполагают существование точки ж* Е О, в которой целевая функция
достигает своего наименьшего значения на множестве О, а во
втором случае такая точка может и не существовать.
Поэтому решение общей задачи математического программирования
состоит в том, чтобы в первом случае найти точные (или с
некоторой заданной точностью) значения координат Xj, j = 1, n,
точки ж* Е О и значение целевой функции fo(x*) — min/o(aO,
а во втором случае построить такую последовательность {хп}
точек хп Е О, которой бы соответствовала последовательность
{/о(жп)}, сходящаяся к значению inf fo(x), и вычислить это
значение с заданной точностью. Отметим, что в большинстве
прикладных задач имеет место первый случай, поэтому
использование записи вида A.19) будем оговаривать особо.
Если fo(x) — линейная функция, то ее область определения
совпадает cW1. BRn такую функцию с помощью стандартного
44
1. ЗАДАЧИ ОПТИМИЗАЦИИ
скалярного произведения можно представить в виде fo(x) =
= (с, ж), где с— (ci, ..., сп) Е Мп — известный вектор. Ясно,
что целевая функция
п
fo(x) = (c,x) = ^2cjxj
i=i
может достигать наименьшего значения /о(ж*) на множестве
О лишь в точках границы <90 этого множества. Если в задаче
нет ограничений, то О = Rn и точная нижняя грань линейной
функции равна — оо. Поэтому в случае линейной целевой
функции задача оптимизации
(с, ж)-яшп, жЕМп, A.20)
имеет смысл лишь при наличии ограничений.
В частном случае, когда заданы линейные ограничения
типа равенства
Bx = d, жеГ, A.21)
где d ЕШк, В — матрица размера к х п, а параметры
оптимизации могут принимать лишь неотрицательные значения, т.е.
Xj>0, j=I~^, A.22)
соотношения A.20)-A.22) составляют стандартную задачу
линейного программирования, или задачу линейного
программирования в стандартной форме (в литературе ее часто
называют канонической задачей линейного
программирования, или задачей линейного программирования в канонической
форме).
Условия A.22) можно представить в виде х Е Щ, где К^ —
декартово произведение п множеств R* неотрицательных
действительных чисел, называемое иногда неотрицательным
ортантом размерности п. Если к A.20)-A.22) добавить т
1.5. Классы задач оптимизации
45
ограничении типа неравенства
п
^ctijXj <6m, A.23)
где a,ij (Е М, г = 1, га, то соотношения A.20)-A.23) приведут к
формулировке общей задачи линейного
программирования. При этом ограничения A.22) могут относиться не ко всем
п параметрам оптимизации, а лишь к некоторым из них. При
отсутствии ограничений типа равенства соотношения A.20),
A.22) и A.23) составляют формулировку основной задачи
линейного программирования (иногда ее называют
естественной задачей линейного программирования).
Неравенства Xj ^ aj, Xj ^ bj и aj ^ Xj ^ bj, j = 1, п,
называют прямыми ограничениями на переменные задачи, причем
последнее относят к двусторонним, а первые два — к од-
носторонним. Таким образом, ограничения A.22) являются
прямыми односторонними. Методы решения задач
линейного программирования подробно рассмотрены и обоснованы
в [XX].
Если при линейных ограничениях минимизируемая целевая
функция помимо линейной комбинации вида A.20) включает
положительно определенную квадратичную форму, т.е.
(с, х) + - (Qx, х) ->> min, A-24)
где Q — положительно определенная матрица порядка п, то
говорят о задаче квадратичного программирования, а
функцию вида A.24) называют квадратичной. В случае,
когда целевая функция является отношением двух линейных
функций, а ограничения линейны, имеем задачу дробно-
линейного программирования. Ее формулировка включает
ограничения A.21)-A.23) и условие минимума функции
(q,x)+a .
--ишп, A-25)
(г,х)+Р
46
1. ЗАДАЧИ ОПТИМИЗАЦИИ
где g Е Mn, rGRn, ckGMh/^gM заданы. Соотношения
( п
/о (ж) = ^/ij(zj) ->> min;
j=i
J n
I 9i(x) = J^&jfaj) < 7b « = 1, m;
Uj>0, j = l,n,
где 7^ E R заданы, определяют задачу сепарабелъного
программирования. В этой задаче целевая функция fo(x) и
функции gi(x) в левой части ограничений являются суммой
функций, каждая из которых зависит только от одного параметра
оптимизации. В этом случае функции fo(x) и gi{x) называют
сепарабелъными.
В прикладных задачах целевая функция нередко имеет вид
т
у(х) = ^СгРг(х), A.27)
г=1
где х = (жх, ..., хп) Е R+, с^ Е 1R+, a R™ — декартово
произведение п множеств IR+ положительных действительных чисел,
называемое иногда положительным ортантом. При этом
функции^(ж) имеют вид
п
Рг(х) = Цх?, A.28)
J = l
где dij Е R. Требование положительности коэффициентов с^,
г = 1,771, послужило причиной того, что такой вид целевой
функции стали называть позиномом в отличие от полинома
(многочлена), в котором коэффициенты могут быть и
неположительными. Кроме того, в многочлене показатели степени
аргументов являются целыми неотрицательными числами, а в
позиноме благодаря положительности параметров оптимизации
A.26)
1.5. Классы задач оптимизации
47
выражение x-lj определено для любых действительных чисел
ctij. Если целевая функция и левые части ограничений типа
равенства и (или) неравенства в задаче минимизации являются
позиномами, то такую задачу называют задачей
геометрического программирования.
В задаче нелинейного программирования ограничения
могут быть заданы в неявном виде. Тогда множество О
возможных альтернатив приходится строить путем количественного
анализа математической модели объекта оптимизации (см.
пример 1.10). Если ограничения принадлежат к типам равенства и
(или) неравенства
Мх)=0, l = T7k; 9i(x)^0, г = Т^, A.29)
но хотя бы одна из функций fi(x), gi(x) или целевая функция не
является линейной, то говорят об общей задаче нелинейного
программирования. Ясно, что такая формулировка
включает задачи квадратичного, дробно-линейного, сепарабельного и
геометрического программирования.
Среди целевых функций достаточно широкий класс
составляют выпуклые функции. Во многих прикладных задачах
оптимизации область допустимых значений параметров
оптимизации оказывается выпуклым множеством. В такой области
целевая функция может сохранять одно и то же
направление выпуклости, т.е. выпукла либо вниз (выпукла), либо вверх
(вогнута). Например, зависимость эффективности
технического устройства от параметров оптимизации является вогнутой
функцией. Дело в том, что чем выше технические
характеристики устройства, тем труднее добиться его дальнейшего
совершенствования и существенного приращения эффективности.
Наоборот, целевые функции, выражающие массу, габариты или
стоимость технического устройства, по тем же причинам
обычно выпуклы.
Аналогичная ситуация характерна и для функций,
описывающих экономические системы. Например, рост объема
выпускаемой продукции происходит не прямо пропорционально
48
1. ЗАДАЧИ ОПТИМИЗАЦИИ
капиталовложениям или количеству используемых ресурсов, а
с замедлением, причем это замедление часто тем больше, чем
больше объем производства. Это приводит к вогнутости так
называемых производственных функций, выражающих
зависимость объема выпускаемой продукции от израсходованных
ресурсов. Наоборот, при фиксированном объеме производства
дальнейшее снижение производственных затрат и стоимости
единицы продукции по сравнению с достигнутым уровнем
также происходит с замедлением, что приводит к выпуклости
целевых функций, описывающих стоимостные характеристики
производства.
Ясно, что любую вогнутую целевую функцию, изменив знак,
можно сделать выпуклой. Задачи оптимизации, в которых
необходимо найти наименьшее значение выпуклой целевой
функции, рассматриваемой на выпуклом множестве, относят к
задачам выпуклого программирования. Частными случаями
таких задач являются задачи квадратичного и линейного
программирования. Задачи геометрического программирования
при некоторых дополнительных условиях также являются
задачами выпуклого программирования.
Если множество О допустимых решений оказывается
конечным множеством, то мы имеем задачу дискретного
программирования, а если к тому же координаты этих точек —
целые числа, то — задачу целочисленного
программирования. Такие задачи (в том числе для линейной целевой
функции) рассмотрены в [XX].
Вопросы и задачи
1.1. Решите задачи, рассмотренные в примерах 1.1 и 1.2,
как путем построения функции Лагранжа, так и исключением
из целевой функции одного из параметров оптимизации.
1.2. Получите A.3) из необходимого условия экстремума
функции A.2).
Вопросы и задачи
49
1.3. Найдите решение задач, рассмотренных в примерах 1.6
и 1.7, как путем построения функции Лагранжа, так и
исключением из целевой функции одного из параметров оптимизации.
1.4. Классифицируйте рассмотренные в 1.2-1.4 задачи,
отнеся каждую из них к тому или иному (или нескольким
сразу) классу задач оптимизации и к одному или нескольким
вариантам формулировок, рассмотренных в 1.5.
1.5. Найдите максимальное и минимальное значения
функции r](h/H) A.1) при h/H Е [0, 1] и сравните результат с
полученным в примере 1.3.
1.6. Используя необходимые и достаточные условия
экстремума функции одного переменного, убедитесь, что функция
/(а), рассмотренная в примере 1.4, достигает максимума в
точке а* = 3.
1.7. Решите задачу оптимального проектирования бака
горючего, аналогичную рассмотренной в примере 1.6, но при
заданной площади S расходуемого листового материала
максимизируйте объем бака.
1.8. Как из прямоугольной листовой заготовки с
отношением сторон 1 : 2 вырезать круговой сектор, из которого можно
было бы изготовить коническую воронку наибольшего объема?
1.9. Покажите, что геометрический момент инерции
квадратного сечения относительно любой оси, лежащей в
плоскости квадрата со стороной R\f2 и проходящей через его центр,
постоянен и равен J = i?4/3 (см. пример 1.7).
2. МЕТОДЫ ОДНОМЕРНОЙ
МИНИМИЗАЦИИ
2.1. Предварительные замечания
В некоторых случаях ограничения в задаче оптимизации
позволяют через один из параметров оптимизации выразить
остальные и исключить их из целевой функции. В результате
задача будет сведена к поиску наибольшего или
наименьшего (в зависимости от цели оптимизации) значения скалярной
действительной функции /(ж), х Е D(f) С R, выражающей
критерий оптимальности. Выбирая тот или иной знак перед этой
функцией, всегда можно ограничиться лишь поиском ее
наименьшего значения в области определения D(f), заданной с
учетом ограничений на параметр оптимизации х. Поэтому
далее в этой главе будем рассматривать задачу
f(x) -> min, х Е D(f) С R, B.1)
поиска наименьшего значения /* = f(x*) функции f(x) и точки
х* Е D(f), в которой f(x) принимает это значение. Для
краткости будем говорить об одномерной минимизации, имея в
виду нахождение наименьшего значения функции f(x) на
множестве D(f) и точек, в которых это значение достигается.
Изучение методов одномерной минимизации важно не
только для решения задачи B.1), имеющей самостоятельное
значение. Эти методы являются также существенной составной
частью методов многомерной минимизации, при помощи
которых находят наименьшее значение действительных функций
многих переменных.
Пусть область определения D(f) функции f(x) есть
промежуток числовой прямой. Напомним [II], что если D(f) —
2.1. Предварительные замечания
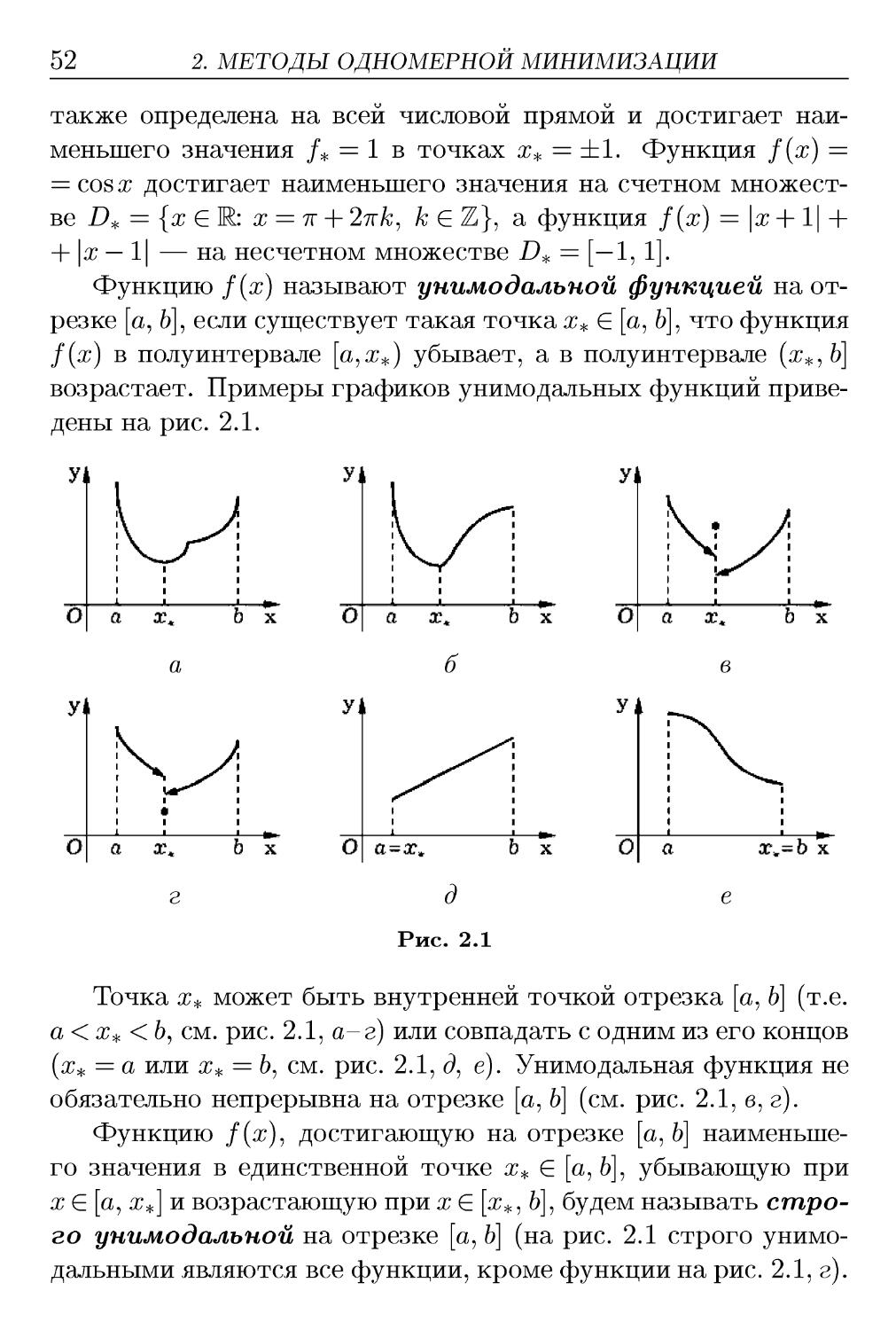
51
отрезок и f{x) непрерывна на нем, то она имеет на этом
отрезке наименьшее значение. Но при наличии на отрезке точек
разрыва функции она может не иметь на нем наименьшего
значения. Оно может не существовать и в том случае, когда D(f)
является интервалом или полуинтервалом.
Если функция f(x) не имеет на множестве D(f)
наименьшего значения, то B.1) следует заменить формулировкой задачи
в виде (см. 1.5)
/(z)->inf, xeD(f)GR. B.2)
Тогда под решением задачи минимизации такой функции на
D(f) следует понимать построение последовательности {хп}
точек из D(f), для которой существует предел
lim f(xn) = inf /(х) = Д, B.3)
™^°° xneD(f)
и нахождение этого предела. Если функция f(x) достигает на
множестве D(f) своего наименьшего значения /*, то /* = /*.
Например, функция f(x) = 1/х на множестве D(f) = [1, 2)
не достигает наименьшего значения, хотя и ограничена снизу.
Точная нижняя грань /* функции в данном случае равна 1/2. В
качестве последовательности {хп} точек в полуинтервале [1, 2),
для которой справедливо B.3), можно выбрать {2 — 1/п}. Тогда
fix )- — - 1 --?-
П п}~ хп~ 2-1/п~ 2п-Г
и последовательность {f(xn)} сходится к числу 1/2 = Д.
Функция может достигать наименьшего значения как в
единственной точке, так и на некотором множестве точек,
конечном, счетном или несчетном. Например, функция f(x) = хА
определена на всей числовой прямой и достигает своего
наименьшего значения /* = 0 в единственной точке х* = 0, которая
является ее точкой минимума. Функция f(x) = ж4 — 2х2 + 2
52 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
также определена на всей числовой прямой и достигает
наименьшего значения /* = 1 в точках х* = ±1. Функция f(x) =
= cos ж достигает наименьшего значения на счетном
множестве D* = {х Е R: х = 7Г + 27г/с, к Е Z}, а функция f(x) = \х + 1\ +
+ \х — 1\ — на несчетном множестве D* = [— 1, 1].
Функцию /(ж) называют унимодальной функцией на
отрезке [а, Ь], если существует такая точка х* Е [а, Ь], что функция
/(ж) в полуинтервале [а,ж*) убывает, а в полуинтервале (ж*,Ь]
возрастает. Примеры графиков унимодальных функций
приведены на рис. 2.1.
У*
У|
о
i
V
i
i
а х* Ь х
У*
У*
х*=Ь х
Рис. 2.1
Точка ж* может быть внутренней точкой отрезка [а, Ь] (т.е.
а < ж* < &, см. рис. 2.1, а-г) или совпадать с одним из его концов
(ж* = а или ж* = 6, см. рис. 2.1, д, е). Унимодальная функция не
обязательно непрерывна на отрезке [а, Ь] (см. рис. 2.1, в, г).
Функцию /(ж), достигающую на отрезке [а, Ь]
наименьшего значения в единственной точке х* Е [а, 6], убывающую при
ж Е [а, ж*] и возрастающую при х Е [ж*, 6], будем называть
строго унимодальной на отрезке [а, 6] (на рис. 2.1 строго
унимодальными являются все функции, кроме функции на рис. 2.1, г).
2.2. Пассивный и последовательный поиск
53
Область определения D(f) минимизируемой функции f(x)
может состоять из нескольких промежутков, не имеющих
общих граничных точек. В этом случае, чтобы найти наименьшее
значение функции на множестве D(f), достаточно определить
наименьшее значение функции в каждом из промежутков,
составляющих D(f), а затем, сравнивая, выбрать среди этих
значений минимальное.
Если функция дифференцируема в промежутке, то
возможно использование необходимого и достаточного условий
локального минимума [II]. Однако в прикладных задачах нередки
ситуации, когда трудно вычислить производные функции
(например, если функция не задана в аналитическом виде). Более
того, не исключено, что значения функции известны или
могут быть вычислены только в отдельных точках. В таких
ситуациях использование необходимого и достаточного условий
локального минимума невозможно и следует применять другие
методы решения задачи оптимизации. Методы минимизации
функции одного переменного, в которых используют значения
функции в точках рассматриваемого промежутка и не
используют значения ее производных, называют методами
прямого поиска.
2.2. Пассивный и последовательный поиск
Пусть требуется найти наименьшее значение или точную
нижнюю грань /* скалярной действительной функции f(x)
одного переменного на отрезке [а, Ь]. Предположим, что
задан алгоритм вычисления значения функции для любой точки
ж ? [а, Ь]. Можно выделить две группы методов прямого
поиска, соответствующие двум принципиально различным
ситуациям:
1) все N точек жд., к = 1, 7V, в которых будут вычислены
значения функции, выбирают заранее (до вычисления функции
в этих точках);
54 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
2) точки Хк выбирают последовательно (для выбора
последующей точки используют значения функции, вычисленные в
предыдущих точках).
В первом случае поиск значения /* называют пассивным,
а во втором — последовательным. Естественно ожидать,
что последовательный поиск лучше пассивного. В этом можно
убедиться, вспомнив детскую игру, в которой надо найти
спрятанную вещь, задавая вопросы и получая на них ответы „да"
или „нет". Задавая вопросы последовательно с учетом
предыдущих ответов, можно найти спрятанную вещь за меньшее
число вопросов (итераций), чем, задав определенное количество
заранее подготовленных вопросов сразу.
Так как в прикладных задачах вычисление каждого
значения функции может быть достаточно трудоемким, то
целесообразно выбрать такую стратегию поиска, чтобы значение /* с
заданной точностью было найдено наиболее экономным путем.
Будем считать, что стратегия поиска определена, если:
- определен алгоритм выбора точек жд., к = 1, N;
- определено условие прекращения поиска, т.е. условие, при
выполнении которого значение /* считают найденным с
заданной точностью.
Для методов пассивного поиска алгоритм выбора точек ж&,
к = 1, 7V, — это правило, по которому заранее определяют все
N точек жд., к = 1, 7V, в которых затем будут вычислены
значения функции f(x). Для методов последовательного поиска
алгоритм выбора точек х^ — это правило, по которому
последовательно определяют каждую следующую точку х^ по
информации о расположении точек ^,i = l,fc-l,HO вычисленных
значениях f(xi) функции f(x) в этих точках. Выбор очередной
точки Хк и вычисление значения /(#&) называют шагом
последовательного поиска.
В методах последовательного поиска количество точек х^
обычно не задают заранее. Однако объективное сравнение
различных методов прямого поиска нужно проводить при одинако-
2.2. Пассивный и последовательный поиск
55
вом количестве п вычисленных значений функции f(x). После
п вычислений обычно указывают интервал (или отрезок)
длины Zn, называемый интервалом неопределенности, в
котором гарантированно находится точка ж*, соответствующая
значению /*. Условие прекращения вычислений в случае
пассивного или последовательного поиска примем одинаковым —
выполнение неравенства 1п ^ е*, где е* — заданная наибольшая
допустимая длина интервала неопределенности.
Длина 1п зависит как от самого метода прямого поиска Р,
так и от минимизируемой функции f(x), т.е. 1п = /П(Р, /).
Зависимость 1п от п дает оценку скорости сходимости конкретного
метода прямого поиска Р к искомому значению /* заданной
функции f(x). Различные методы из некоторого множества
V методов прямого поиска сравнивают обычно при
выбранном фиксированном значении п = N на некотором достаточно
широком классе функций. В качестве такого класса можно
выбрать множество Т унимодальных функций, определенных на
фиксированном отрезке IcK. Для метода прямого поиска
Р Е V примем наихудшую оценку
lN(P)=maxlN(PJ).
Если наихудшей" унимодальной функции не найдется, то
оценку принимаем в виде
lN(P) = 8VLplN(PJ).
Значение /дг(Р) представляет собой оценку сверху
погрешности вычисления точки ^Gl, соответствующей искомому
значению /* произвольной функции / Е Т, которая получена
методом прямого поиска Р Е V по N вычисленным значениям
этой функции. Метод прямого поиска Р* считаем наилучшим,
если
l]Sf(P*) = тттах/дг(Р, /), или /дг(Р*) = minsup/7v(P, /).
56 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Этот критерий сравнения методов поиска определяет
минимаксный метод поиска. Такой метод является наилучшим
для всего множества Т унимодальных функций на отрезке
IcRb том смысле, что он дает наименьшую погрешность
вычисления точки ж*, соответствующей значению /* любой из
рассматриваемых функций / Е Т. Хотя вполне возможно, что
существует некоторый конкретный метод, который для
определенной специально подобранной унимодальной функции из
множества Т обеспечит еще меньшую погрешность.
Все методы прямого поиска можно строить и сравнивать
между собой на отрезке X = [0, 1]. Полученные результаты
при необходимости нетрудно перенести на случай
произвольного отрезка [а, 6], так как любую точку отрезка [0, 1] можно
перевести в соответствующую ей точку отрезка [а, Ь]
растяжением в Ъ — а раз и сдвигом на а.
Если минимизируемая функция f(x) не является
унимодальной на отрезке [а, Ь] (такую функцию называют мулыпимо-
дальной функцией на этом отрезке), то, даже если она
непрерывна на [а, &]), при поиске наименьшего значения /* функции
на отрезке может возникнуть ошибка: будет найдена точка
локального минимума, в которой значение функции не /*, а
другое, большее. Чтобы избежать такой ошибки, в процесс
минимизации включают предварительный этап, на котором отрезок
минимизации разделяют на несколько отрезков, на каждом из
которых минимизируемая функция унимодальна*.
Сравнительный анализ наименьших значений функции на этих отрезках
позволяет найти искомое наименьшее значение /* на всем
отрезке минимизации.
Пример 2.1. Рассмотрим один из возможных подходов
к выделению из промежутка X в области определения D(f)
минимизируемой функции f(x) отрезка [а, 6], на котором эта
функция является унимодальной. Пусть известна такая точка
*См.: Васильев Ф.П., а также: Лесин В.В., Лисовец Ю.П.
2.2. Пассивный и последовательный поиск
57
xq ? X, что при х ^ xq функция f(x) сначала убывает, а затем
начиная с пока неизвестного значения х = х* Е X возрастает,
хотя далее в промежутке X могут быть расположены и другие
участки немонотонного поведения этой функции. Выберем
начальное значение h > 0 приращения аргумента х функции
/(ж), в несколько раз меньшее предполагаемого расстояния
между точками xq и ж*, и вычислим значения f(xo) и /(#].),
где х\ — xq + h.
Может оказаться, что f(xo) ^ f(x\). Тогда за искомый
отрезок [а, Ь] можно сразу принять отрезок [хо, х\\. Но можно
продолжить вычисления и, используя последовательный поиск,
определять значения /(#&) в точках х^ = xq + h/2k~l, k = 2, 3 ...,
до тех пор, пока не будет выполнено неравенство /(#&) < /(жо)-
Тогда следует принять [а, 6] = [жо, #fc-i] (на Рис- 2.2 [а, 6] =
= [жо,Ж2], поскольку точка ж* должна быть либо на отрезке
[жо,жз], либо на отрезке [жз?#2])- Надо сказать, что при этом
можно не заметить" по крайней мере еще один отрезок, на
котором функция унимодальна (штриховая линия на рис. 2.2).
Рис. 2.2 Рис. 2.3
Если /(жо) > f{xi)-> TOi используя последовательный поиск,
вычисляем значения f{x'k), где x'k = xq + (к — l)/i, к = 2, 3 ...,
пока не будет выполнено неравенство f{x'k_l) ^ /0*4), нто
позволяет принять [а, 6] = [ж^._2, ж^] (на рис. 2.3 [а, Ь] = [V2, a^L
так как точка ж* должна быть либо на отрезке [ж2, ж'3], либо на
отрезке [х'3, х±]).
58 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Отметим, что описанный подход не гарантирует
нахождения отрезка унимодальности функции. Например, на рис. 2.3
штриховой линией показан график функции, для которой этот
подход не позволяет обнаружить искомый отрезок.
2.3. Оптимальный пассивный поиск
Пусть требуется путем пассивного поиска найти точку х* Е
Е [0, 1], в которой унимодальная на отрезке [0, 1] функция f(x)
достигает наименьшего значения /* = f(x*). Минимаксный
метод поиска, в котором информация о значениях функции,
вычисленных в предшествующих точках, не может быть
использована, называют оптимальным пассивным поиском.
Рассмотрим алгоритм такого поиска при различном числе N точек,
выбираемых на отрезке [0, 1].
Если N= 1, то единственную точ-
Т ку целесообразно выбрать в середи-
Л1'2) * не отрезка, т.е. принять х\ = 1/2
! (рис. 2.4). В этом случае вследствие
»-¦-« *' унимодальности функции f(x) име-
I J * ем /* ^ /A/2). Поэтому наименьшая
01 1/2 1 х возможная длина интервала неопре-
_> Л Л деленности равна Ц = 1 и можно га-
Рис. 2.4 ^ 1
рантировать, что выбор в качестве
точки х* Е [0, 1] точки х\ = 1/2 приведет к погрешности не
более Д^ = 1\/2 = 1/2. При любом ином положении точки х\
погрешность при выборе х* = х\ будет Ai > А*, так как в
действительности точка х* может лежать на большей части
отрезка [0, 1].
Если при N = 2 (рис. 2.5) две точки расположить на отрезке
[0, 1] так, чтобы они делили его на равные части, т.е. выбрать
х\ = 1/3 иж2 = 2/3, то точка ж* Е [0, 1] будет найдена с
точностью Д^ = 1/3, а наименьшая длина интервала
неопределенности составит Щ = 2А2 = 2/3. В самом деле, если /A/3) < /B/3)
(рис. 2.5, а), то в силу унимодальности функции f(x) отрезок
2.3. Оптимальный пассивный поиск
59
у*
/B/3)
/Ц/з)
1/3 2/3 1 х
/A/3)
/B/3) I-
1/3 2/3 1 х
Рис. 2.5
[2/3, 1] можно исключить и считать, что х* Е [0, 2/3]. Тогда
при выборе х* = 1/3 наибольшая погрешность равна А2 = 1/3 и
/* « /A/3). Если же окажется, что /A/3) > /B/3) (рис. 2.5, 6),
то можно исключить отрезок [0, 1/3] и считать, что х* Е [1/3, 1].
И в этом случае выбор х* = 2/3 приведет к погрешности не
более А2 = 1/3, а /* « /B/3). Заметим, что при /A/3) = /B/3)
можно исключить любой из указанных отрезков, гарантируя
ту же точность нахождения точки х* Е [0, 1]. При ином
делении отрезка [0, 1] на части двумя точками длина какой-то из
его частей будет больше 1/3 и в действительности точка х*
может принадлежать именно этой части, так что получим
погрешность А2 > А2 = 1/3.
Рассуждая аналогично, можно заключить, что при N = 3
нужно также выбирать точки равномерно на отрезке [0, 1]:
х\ = 1/4, Х2 = 2/4, хз = 3/4, обеспечив точность А| = 1/4
нахождения точки ж* Е [0, 1] и наименьшую длину /3 = 1/2
интервала неопределенности. В случае произвольного N Е N
по тем же соображениям надо выбирать точки
Хк = ivTT е [0'1]' fc = I^' <2-4)
обеспечивая точность A*N = 1/(N + 1) нахождения точки х* и
наименьшую возможную длину
if
LN
7V + 1
B.5)
60 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
интервала неопределенности. Таким образом, оптимальный
пассивный поиск состоит в выборе точек, равномерно
расположенных на отрезке. При этом B.5) дает оценку скорости
сходимости пассивного поиска с ростом числа N точек, так
как скорость сходимости любого метода прямого поиска можно
характеризовать скоростью уменьшения интервала
неопределенности с возрастанием N.
Пример 2.2. При заданной наибольшей допустимой длине
е* = 0,2 интервала неопределенности, используя оптимальный
пассивный поиск, найдем точку х* Е [0, 1], в которой
унимодальная на отрезке [0, 1] функция f(x) = х3 — х + е~х достигает
наименьшего на этом отрезке значения*. Из B.5) следует, что
для этого необходимо принять N = 9 и в соответствии с B.4)
вычислить значения функции f(x) в точках х^ = к/10, А; = 1, 9:
х I ОД 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
f(x) | 0,81 0,63 0,47 0,33 0,23 0,17 0,14 0,16 0,18
Из представленных результатов вычислений можно сделать
вывод, что интервалом неопределенности является интервал
@,6, 0,8), а х* = 0,7 ±0,1. Отметим, что при е* = 0,01
потребуется принять N = 199. #
Рассуждения, проведенные выше, попутно обосновывают
процедуру исключения отрезка, которую используют во
всех методах прямого поиска точки минимума унимодальной
функции одного переменного. Эта процедура состоит в
следующем. Пусть на отрезке [а, Ь] числовой прямой расположены
две точки си о?, а < с < d <Ь, и известны (или вычислены)
значения f(c) и f(d) унимодальной на [а, Ь] функции f(x). Если
f(c) < f(d) (рис. 2.6, а), то в силу унимодальности функции f(x)
имеем х* Е [a, d], а отрезок [d, Ь] можно исключить из
дальнейшего рассмотрения. Наоборот, если f(c) ^ f(d) (рис. 2.6, 6), то
ж* Е [с, 6], а отрезок [а, с] далее можно не рассматривать.
*См.: Амосов А.А., Дудинский Ю.А., Копченова Н.В.
2.4. Методы последовательного поиска
6i
У,
fid)
/(с)
О
; л
^ ^ <
i i i
а с d Ь
> X
У,
№
№)
о
. *
—i +—
i i
а с
d 1
X
б
Рис. 2.6
Таким образом, в результате применения процедуры
исключения отрезка получаем новый отрезок, вложенный в
рассматриваемый и заведомо содержащий искомую точку х*. В
методах пассивного поиска применение этой процедуры
позволяет оценить наибольшую возможную погрешность нахождения
точки х*. Все рассмотренные далее методы последовательного
поиска используют процедуру исключения отрезка для выбора
нового отрезка на каждом очередном шаге такого поиска.
2.4. Методы последовательного поиска
Метод дихотомии. Рассмотрим последовательный
поиск точки х* Е [0, 1], в которой унимодальная на отрезке [0, 1]
функция f(x) достигает наименьшего значения /* = f(x*).
Метод прямого поиска, основанный на делении пополам отрезка,
на котором находится точка ж*, называют методом
дихотомии (от греческих слов Slxol — на две части и to\it) — сечение).
Опишем алгоритм этого метода.
Пусть известно, что на k-м
шаге последовательного поиска х* Е
? [ak->hk] С [0, 1] (на первом шаге
при к = 1 имеем а\ = 0 и Ъ\ = 1).
На отрезке [а&, Ьк] длиной 1к
выберем две точки Xki = (ак + Ьк)/2 — 6
кхк2 = (ак + Ьк)/2 + 6 (рис. 2.7), где
У;
№к2)
П*кхУ
о\
t
! Jfe+i
j~*
V
.2<3
s
1к !
аА- xkl Як2 Ьк х
Рис.
2/
г
62 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
8 > 0 — некоторое достаточно малое число. Вычислим
значения f(xki) и f(xk2) функции f(x) в этих точках и выполним
процедуру исключения отрезка. В результате получим новый
отрезок [afc+i,bfc+i] С [afc,ftfc]. Если длина /&+1 нового отрезка
больше заданной наибольшей допустимой длины е* интервала
неопределенности, то алгоритм метода дихотомии переходит
к (к + 1)-му шагу, повторяя все описанные для А;-го шага
действия. Если же Zfc+i ^ ?*, то вычисления прекращают и
полагают ж* = (a/b+i + bfc+i)/2.
Так как Z^+i = Z&/2 + 5, или /&+1 — 25 = (/& — 25)/2, то
Из этого равенства выводим следующую формулу длины /&
отрезка [а&, &&], получаемого на к-м шаге метода дихотомии:
Из B.6) следует, что /& —>> 25 при к —>> оо, но при этом /& > 25.
Поэтому выполнение неравенства /&+1 < ?*, означающее
достижение заданной точности нахождения точки ж*, возможно лишь
при условии выбора 25 < ?*. Кроме того, нужно учитывать
неизбежную погрешность, возникающую при вычислении
приближенных значений f(x) функции f(x). Это приводит к
дополнительной погрешности А* при нахождении точки х* (см. 2.7).
Поэтому выбор значения 5 ограничен и снизу, т.е.
Д*<25<?*. B.7)
Если эти неравенства нарушаются, то знак разности /(x^i) —
— f{xk2) может не совпадать со знаком разности f{x^\) — /(ж^),
что приводит к ошибочному выполнению процедуры
исключения отрезка.
Итак, метод дихотомии — это последовательное
построение на каждом к-м шаге поиска точек х^\ = (а& + Ь^)/2 — 8
2.4. Методы последовательного поиска
63
и хк2 — {p>k + Ь&)/2 + #, симметричных относительно середины
отрезка [а&, 6&] длины /&. После выполнения fc-ro шага будет
выделен отрезок [a^+i, 6/c+i] длины Z^+i и вычислено N = 2к
значений функции. Используя формулу B.6) для длины отрезка
(интервала неопределенности) и полагая /i = 1, получаем
& = '*+1 = ^ + 2* = ^Г + 2*. B-8)
Сравнивая B.8) с B.5), видим, что скорость сходимости метода
дихотомии значительно выше скорости сходимости
оптимального пассивного поиска.
Отметим, что после исключения отрезка на k-м шаге
описанного алгоритма точки х^\ и х^ принадлежат новому
отрезку [а&_|_1, bfc+i], причем одна из них является внутренней для
этого отрезка. Но вычисленное в этой точке значение
функции f(x) в методе дихотомии не используют для исключения
отрезка на следующем шаге, а проводят вычисления в двух
новых точках. Существуют методы последовательного поиска, в
которых на каждом k-м шаге начиная с к = 2 вычисляют лишь
одно новое значение функции в точке, принадлежащей отрезку
[afc+ъ fr/c+i]- Это значение вместе с уже вычисленным на
предыдущем шаге значением функции во внутренней точке отрезка
[ак-) bk] используют при выполнении процедуры исключения
отрезка на следующем шаге последовательного поиска.
Метод золотого сечения. Как известно*, золотым
сечением отрезка называют такое его деление на две неравные
части, при котором отношение длины всего отрезка к длине его
большей части равно равно отношению длины большей части к
длине меньшей.
Термин 55золотое сечение" ввел Леонардо да Винчи**.
Золотое сечение широко применяли при композиционном постро-
*См.: Васютинский Я., а также: Коробко В. И.
**Леонардо да Винчи A452-1519) — итальянский живописец, скульптор,
архитектор, ученый и инженер.
64 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
ении многих произведении мирового искусства, в том числе в
античной архитектуре и в эпоху Возрождения.
Рассмотрим к-тк шаг последовательного поиска. Чтобы
выполнить процедуру исключения отрезка на этом шаге,
отрезок [ak,bk] необходимо двумя внутренними точками Xki, хк2-)
xki < хк2-> разделить на три ча-
f(xk2)
*fe+i
сти. Эти точки выберем
симметрично относительно середины
отрезка [а&, bk] (рис. 2.8) и так,
чтобы каждая из них
производила золотое сечение отрезка
х [а/с, bk]. В этом случае
отрезок [ак+\, Ьк+\] внутри будет
содержать одну из точек Xki, Xk2
(другая будет одним из концов отрезка), причем эта точка
будет производить золотое сечение отрезка [a^+i, ftfc+i]. Это
вытекает из равенства длин отрезков [а&, Xki] и [ж^2, bk]. Таким
образом, на (к + 1)-м шаге в одной из точек ж&+1д, ж/с+1,2
значение функции вычислять не нужно. При этом отношение
1к/1к+1 длин отрезков сохраняется от шага к шагу, т.е.
Рис. 2.8
Jfc+2
h-\
const.
B.9)
Число т называют отношением золотого сечения.
Последовательный поиск, в котором на к-м шаге каждая из
симметрично выбранных на отрезке [а&, bk] точек Xki, xk2
осуществляет золотое сечение этого отрезка, называют методом
золотого сечения. В этом методе каждое исключение
отрезка уменьшает оставшийся отрезок в г раз.
Выясним, чему равно отношение золотого сечения. Так как
точки Xki и Xk2-> хк\ < хк2-> выбраны симметрично относительно
середины отрезка [a&, bk], то
Ьк - хк2 = Xki — o>k = h — h+Ъ
2.4. Методы последовательного поиска
65
(см. рис. 2.8). Для определенности будем считать, что на к-м
шаге выбран отрезок [а/^ж/^]. Тогда на (к + 1)-м шаге одной
из точек деления (а именно правой) будет точка х^\. Значит,
длина lk+2 отрезка, выбираемого на (& + 1)-м шаге, совпадает
с длиной отрезка [a, x^i] и верно равенство /&+2 = h ~ ^+1-
Подставляя найденное выражение для /&+2 в уравнение B.9),
получаем
или т = 1/(т — 1). Преобразуя это соотношение, приходим к
квадратному уравнению т2 — т — 1 = 0, имеющему единственное
положительное решение т = « 1,618034.
Предположим, что отрезком минимизации унимодальной
функции f{x) является [0, 1], т.е. а\ = 0, 6i = 1 и /i = 1. На
первом шаге последовательного поиска (к = 1) на отрезке [0, 1]
выбираем две точки хц = а\ + A — 1/т)Ь\ = 1 — 1/т и Ж12 =
= а\+ Ъ\/т = 1/т, осуществляющие золотое сечение отрезка
[0, 1]. Вычисляем значения минимизируемой функции в этих
точках и выполняем процедуру исключения отрезка. Если
/(хц) < /(#12), то выбираем отрезок [ai,#i2], т.е. полагаем
^2 = ^1= 0, &2 = #12; в противном случае выбираем отрезок
[#п, bi], т-е- полагаем а2 = жц, 62 = Ь\ = 1. Кроме того, в
первом случае принимаем 2?2 = жц, а во втором случае —
#2 = Ж12- Точка 2?2 — одна из точек, осуществляющих золотое
сечение отрезка [а2, 62]? меньшая в первом случая и большая
во втором. Если длина вновь полученного отрезка больше
заданной допустимой длины е* интервала неопределенности,
то следует перейти ко второму шагу алгоритма, на котором
одна из точек Ж21, #22 есть точка Ж2, а вторую можно найти,
например, по формуле а2 + 62 — #2- На втором шаге алгоритма
вычисляем лишь одно значение функции в точке, симметричной
2?2 относительно середины отрезка [02,62]. Если же длина 1^
отрезка [02,62], полученного после первого шага алгоритма,
66 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
оказалась меньше е*, то поиск прекращают и полагают х* «
~(а2 + Ь2)/2.
Пусть на к-м шаге, к ^ 2, последовательного поиска по
методу золотого сечения выбран отрезок [а&, Ь&] и в нем точка
Xk, осуществляющая золотое сечение этого отрезка. Значение
f(xk) функции в этой точке уже вычислено на предыдущем
шаге. Находим вторую точку хк золотого сечения по формуле
хк = ак + Ьк- хк
и вычисляем в ней значение функции. Если хк <хк, то хк\ = хк
и хк2 = хк, иначе хкг = хк и хк2 = хк.
Пусть для определенности хк < хк (см. рис. 2.8) и хк\ = ж&,
^/с2 = #*• Если f(xki) < f(xk2), то выбираем отрезок [а^ждя],
т.е. полагаем a^+i = ак, Ък+\ = ж^2, #fc+i = #fci, иначе выбираем
отрезок [ж/ь1,Ьа;], т.е. полагаем afc+i = ж/ц, Ьк+г = Ьк, хк+г =
= хк2. Длину /&+1 нового отрезка [a^+i, 6/c+i] сравниваем с е*
и принимаем решение, продолжать поиск (при lk+i ^ ?*) или
нет (при Zfc+i < ?*). В случае прекращения поиска полагаем
ж* « (а/с + Ь/с)/2.
Согласно описанию алгоритма, на первом шаге значение
функции вычисляют в двух точках, а на каждом из
последующих шагов вычисляют лишь одно значение функции. Поэтому
после к шагов алгоритма значение функции будет вычислено в
N = к -\-1 точках. Поскольку после каждого шага интервал
неопределенности уменьшается в т раз, то для длины 1к+\ отрезка
[afc+ъ fr/c+i] получаем lk+i — h/т — 1/т •> а зависимость lzN
длины интервала неопределенности от количества N вычисленных
значений функции выражается формулой
Алгоритмы методов золотого сечения и дихотомии
аналогичны. Различие состоит лишь в том, что в методе дихотомии
расстояние 26 между внутренними точками хк\, хк2 отрезка
2.4. Методы последовательного поиска
67
[cLk,bk] на каждом k-м шаге остается неизменным, а в методе
золотого сечения оно зависит от номера шага поиска и
уменьшается с уменьшением длины /& отрезка по мере возрастания
номера шага. Действительно, в методе золотого сечения на к-м
шаге поиска внутренними точками отрезка [а&, Ь&] будут x^i =
= dk + A — 1/т)/& и Xk2 = &к + 1к/т-> a расстояние между ними
равно Xk2 — хк\ — B/т — l)lk = (л/5 — 2)/^ « 0,236068/^.
Метод Фибоначчи. Пусть при поиске точки х* Е [0, 1],
в которой унимодальная на отрезке [0, 1] функция f(x)
принимает наименьшее на этом отрезке значение, можно вычислить
ее значения только в двух точках. Тогда предпочтение
следует отдать методу дихотомии при S <С 1, так как он позволит
уменьшить интервал неопределенности почти вдвое, а метод
золотого сечения — лишь в т « 1,618 раз. Сравнение B.8) и
B.10) показывает, что при количестве вычисляемых значений
функции N ^ 4 эффективность метода золотого сечения
становится выше, чем метода дихотомии.
Однако при любом заданном общем числе N > 2
вычисляемых значений функции можно построить еще более
эффективный метод, состоящий из N — 1 шагов. Он сочетает
преимущество симметричного расположения внутренних точек х^ъ х^2
на отрезке [а&, Ь&] относительно его середины, реализованное
в методах дихотомии и золотого сечения, с возможностью на
каждом шаге изменять отношение lk/h+i длин сокращаемого и
нового отрезков. Как показано при обсуждении метода
золотого сечения, в случае выбора внутренних точек симметрично
относительно середины отрезка для трех последовательных
шагов этого метода выполняется соотношение
lk-i = lk + h+u к = 2,3,... B.11)
Построение алгоритма такого метода удобнее начать с
последнего шага, но предварительно уточним задачу. Располагая
возможностью вычислить в N точках х^ Е [0, 1], к = 1, 7V,
значения унимодальной на отрезке функции /(ж), необходимо как
68 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
можно точнее, т.е. с наименее возможной длиной интервала
неопределенности, отыскать точку х* наименьшего значения этой
функции на отрезке [0, 1].
При выполнении процедуры исключения отрезка на
последнем, (N — 1)-м шаге имеем отрезок [a/v-i, b/v-i] длины In-i с
двумя внутренними точками xn-\ и ждг, симметрично
расположенными относительно середины отрезка на достаточно
малом расстоянии 25 друг от друга
(рис. 2.9). В этих точках
вычислены значения f(xjsr-i) и f(xjsr)
функции f(x). Пусть для
определенности f(xjsf) < f(xjsf-i),
тогда для нового отрезка [адг, Ь/у]
длины /дг — ^/v-i/2 + S внутренней
будет точка ждг, а точка xjy-i
совпадет с одним из его концов.
В такой ситуации при выборе
ж* = xjsi длина интервала неопределенности равна пока
неизвестной длине In отрезка [адг, Ь/у]. Через /дг можно выразить
длину In-i = 2/дг — 2E отрезка [a/v_i, ft/v-i]. Далее в
соответствии с B.11) получаем
Рис. 2.9
2E,
-6E,
Ins = In-2 + In-i = 5/дг — 4E,
Ins = In-4 + Ins = 13/дг — 10E
/дг_2 = In-1 +In = 3/дг -
^7V-4 = ^V-3 + ^V-2 = 81N
и в общем виде
lN-K = FK+2lN-2FK6, K = 0jf=l, B.12)
где коэффициенты Fm определены рекуррентным
соотношением
B.13)
771—1
+ F„
т ¦
3, ЛГ-1, F1=F2 = 1.
Так как при К = N — 1 длина /дг_к = /i = 1 отрезка [0, 1]
известна, то из B.12) можно найти длину интервала неопределенности
А
7N+1
+ 2E
Fn-i
Fn+i
B.14)
2.4. Методы последовательного поиска
69
Существует алгоритм метода прямого поиска,
удовлетворяющий соотношению B.14).
Все коэффициенты Fm принадлежат множеству N
натуральных чисел, и их называют числами Фибоначчи*. В табл. 2.1
представлены эти числа до номера m = 25.
Таблица 2.1
m
1
2
3
4
5
-Тщ
1
1
2
3
5
m
6
7
8
9
10
¦Тщ
8
13
21
34
55
m
11
12
13
14
15
^m
89
144
233
377
610
m
16
17
18
19
20
^m
987
1597
2584
4181
6765
m
21
22
23
24
25
^m
10946
17711
28657
46368
75025
Метод, использующий числа Фибоначчи для выбора длин
отрезков /&, а значит, и точек х^ Е [0, 1], к = 1, 7V, в которых
вычисляют значения минимизируемой функции, называют
методом Фибоначчи (иногда — оптимальным
последовательным поиском). Если на первом шаге поиска (А; = 1, К = N — 1)
интервал неопределенности имеет длину /i, то в соответствии
с B.12) и B.14) длина /2 нового отрезка [а2, 62] равна
¦ FnFn-2
h = ^./v^v — 28Fn_2
Fn , . ^.FnFn-
— /1 + zo
"N+l
Fn+i
^+ (_1)"+i. 25
Fn+i Fn+i
Опишем алгоритм метода, пренебрегая малой величиной 5,
т.е. принимая
1±
h
4N+l
B.15)
Несложно проверить, что в этом случае выполнение процедуры
исключения отрезка на последнем, (N — 1)-м шаге поиска
приводит к совпадению внутренних точек ждг-i и xjy (см. рис. 2.9).
* Фибоначчи, или Леонардо Пизанский A180-1240)
тематик.
итальянский ма-
70 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Отметим, что уже при N = 11 имеем F^/Fn = 144/89 ~
« 1,617978, а при TV = 21 получаем F22/F21 = 17711/10946 «
« 1,618034, что совпадает с отношением т золотого сечения
с точностью до 10_6. Таким образом, на первом шаге длина
исходного отрезка уменьшается практически так же, как и в
методе золотого сечения.
При 1\ = 1 из B.15) находим 1^ = Fn/Fn+i. Таким образом,
учитывая B.13), заключаем, что на первом шаге выбор точек,
симметричных относительно середины отрезка [0, 1], можно
определить по формулам
7 F]\r 17 1^ Fn-1
x\=h = -^ , ж2 = 1-/2 = 1-^ = ^ , х2<хъ
причем расстояние между ними будет равно
Fn Fn-1 Fjy_2
d\ = X\ — X2 =
Fn+i Fn+i Ftv+i
После выполнения на этом шаге процедуры исключения
отрезка одна из точек жх, ж 2 будет граничной точкой нового отрезка
[а2, «xL a ДРУгая — его внутренней точкой, которую
обозначим х'2. Вторая внутренняя точка на этом отрезке должна
быть выбрана симметрично точке х'2 относительно его
середины. Аналогично происходит выбор второй внутренней точки
нового отрезка на всех последующих шагах поиска.
На к-м шаге в соответствии с равенством B.12), в котором
следует положить К = N — к, и равенством B.14) длина отрезка
\р>к-> bk] равна 1к = Fw+2-k/FN+i и происходит ее уменьшение в
Ih/lk+i — Fjy+2-k/Fjy+i-k Раз- Если внутренние точки на этом
отрезке обозначить ^ и ft, то проведенные рассуждения
позволяют написать
Fiv-k „ . F)
N-k о , rN+l-
ак = ак + -^ , Рк = ак + —^ > oik<f3k, k = l,N-l.
Подчеркнем, что реализация метода Фибоначчи
предполагает априорное задание требуемого количества N вычисляемых
2.5. Сравнение методов последовательного поиска 71
значений функции (или количества шагов поиска). Этот
параметр необходим для реализации первого шага алгоритма при
выборе точек хц и х\2 деления отрезка [ai,&i]. Если
параметр N по каким-либо причинам не может быть задан заранее,
следует использовать другие методы, например дихотомии или
золотого сечения.
2.5. Сравнение методов
последовательного поиска
В качестве оценки скорости сходимости методов прямого
поиска можно использовать скорость убывания длины
интервала неопределенности в зависимости от числа п вычисленных
значений минимизируемой функции в различных методах. Для
метода дихотомии, пренебрегая в B.8) малой величиной 5,
находим
^ = Iz|^ + 2?«-L B.16)
п 2П/2 2П/2
а для метода золотого сечения и метода Фибоначчи, согласно
B.10) и B.14), получаем
п т»' п Fn+1 Fn+1 Fn+1 у }
соответственно, где г « 1,618034 — отношение золотого
сечения, Fm, т Е N, — числа Фибоначчи.
Используя формулу Бине*
Тп _ (_т)-(п+1)
т? — 1 L
сравним два последних метода при п —> оо:
lim % = lim ^±i = lim [—^- = ^— « 1,17082.
*См.: Воробьев H.H.
72 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Таким образом, скорость сходимости метода Фибоначчи при
больших значениях п всего примерно на 17% выше, чем
скорость сходимости метода золотого сечения.
Сравнивая при больших значениях п методы золотого
сечения и дихотомии, получаем
lim|=lim^l = Tlim(^)" = 0.
Таким образом, метод золотого сечения качественно „лучше"
метода дихотомии. Но из B.5) и B.16) следует
г In г 1/2П/2 г П+1 п
lim — = ИГЛ —77 7Т = lini —г;-— = U,
n^oo/* га-кхJ/(п+1) n^oo2n/2+1
т.е. скорость сходимости метода дихотомии при больших
значениях п выше, чем скорость сходимости метода оптимального
пассивного поиска.
Итак, метод золотого сечения уступает по скорости
сходимости лучшему методу — методу Фибоначчи — примерно
в 1,17 раза, но является более гибким, поскольку не требует
выбора заранее определенного числа точек, в которых
предстоит вычислить значения минимизируемой функции. В табл. 2.2
приведены значения длины интервалов неопределенности для
рассмотренных методов в зависимости от числа N
вычисленных значений функции.
Пример 2.3. Используя методы дихотомии, золотого
сечения и Фибоначчи, при заданном значении е* =0,1 наибольшей
допустимой длины интервала неопределенности найдем
интервал, в котором расположена точка х* минимума унимодальной
на отрезке [0, 1] функции f(x) = 100(ж - 0,24J. График этой
функции показан на рис. 2.10.
Для данной функции f"(x) = 200 = const. Поэтому в
соответствии с формулой B.20) (см. 2.7) при вычислении
значений функции с точностью Aj = Ю-5 имеем нижнюю оценку
2.5. Сравнение методов последовательного поиска 73
Таблица 2.2
N
г~
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*
1,0
0,667
0,500
0,400
0,333
0,286
0,250
0,222
0,200
0,182
0,167
0,154
0,143
0,133
0,125
0,118
0,111
0,105
0,100
0,095
id
1,0
0,500
-
0,250
-
0,125
-
0,0625
-
0,0312
-
0,0156
-
0,00781
-
0,00391
-
0,00195
-
0,000976
lz
1,0
0,618
0,382
0,236
0,146
0,090
0,056
0,0345
0,0213
0,0132
0,00813
0,00502
0,00311
0,00192
0,00119
0,000733
0,000453
0,000280
0,000173
0,000107
lf
1,0
0,500
0,333
0,200
0,125
0,077
0,048
0,0294
0,0182
0,0112
0,00694
0,00429
0,00265
0,00164
0,00101
0,000626
0,000387
0,000239
0,000148
0,0000913
0,25 0,5 0/?5 x
Рис. 2.10
74 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Д* = 2y/Af/f"(x*) « 0,447 • 10_3 для абсолютной погрешности
нахождения точки х* минимума этой функции любым методом
прямого поиска. Поэтому границы интервалов
неопределенности достаточно вычислять с тремя знаками после запятой, а
в методе дихотомии из условия B.7) можно выбрать 25 = 10_3.
Такое же значение 5 примем и на последнем шаге метода Фибо-
наччи, причем в нем для выполнения условия VN ^ г* достаточно
в соответствии с табл. 2.2 взять N = 6, т.е. ограничиться
числами Фибоначчи до i^v+i = ^7 = 13 включительно.
Применение метода дихотомии потребовало вычисления
значений минимизируемой функции в восьми точках (табл. 2.3),
что согласуется с табл. 2.2, а в методе золотого сечения
(табл. 2.4) оказалось достаточным вычислить шесть значений
этой функции, т.е. столько же, сколько и в методе Фибоначчи
(табл. 2.5), что также согласуется с табл. 2.2. Отметим, что
Таблица 2.3
к
1
2
3
4
5
Интервал
неопределенности
@,000, 1,000)
@,000, 0,501)
@,000, 0,252)
@,125, 0,252)
@,187, 0,252)
Xkl
0,499
0,250
0,125
0,187
f(Xkl)
6,7081
0,0090
1,3283
0,2796
Ж/с2
0,501
0,252
0,127
0,189
f{Xk2)
6,8121
0,0132
1,2826
0,2588
Таблица 2.4
к
1
2
3
4
5
6
Интервал
неопределенности
@,000, 1,000)
@,000, 0,618)
@,000, 0,382)
@,146, 0,382)
@,146, 0,292)
@,202, 0,292)
Xkl
0,382
0,236
0,146
0,236
0,202
f(Xkl)
2,0154
0,0015
0,8855
0,0015
0,1473
Xk2
0,618
0,382
0,236
0,292
0,236
/fe)
14,2910
2,0154
0,0015
0,2683
0,0015
2.6. Методы полиномиальной аппроксимации 75
Таблица 2.5
к
1
2
3
4
5
6
Интервал
неопределенности
@,000, 0,000)
@,000, 0,615)
@,000, 0,385)
@,154, 0,385)
@,154, 0,308)
@,231, 0,308)
Xkl
0,385
0,231
0,154
0,231
0,231
f{Xkl)
2,0125
0,0081
0,7396
0,0081
0,0081
Xk2
0,615
0,385
0,231
0,308
0,232
f{xk2)
14,0625
2,0125
0,0081
0,4624
0,0064
применение оптимального пассивного поиска в данном случае
потребовало бы вычисления этой функции в 19 точках.
Из приведенных таблиц видно, что результаты расчетов
подтверждают теоретические выводы о скорости сходимости
различных методов.
2.6. Методы полиномиальной аппроксимации
В методах прямого поиска мы не имели никакой
информации о минимизируемой функции за исключением ее
значений в выбранных нами точках и предположения, что она
непрерывна и является унимодальной функцией на
рассматриваемом отрезке. Если функцию в некоторой окрестности
точки ее минимума можно достаточно точно заменить
(аппроксимировать) многочленом, то для ее минимизации
целесообразно использовать так называемые методы полиномиальной
аппроксимации. Их общая особенность состоит в
вычислении коэффициентов многочлена по известным значениям
функции в отдельных точках и последующем нахождении минимума
этого многочлена с использованием необходимых и
достаточных условий экстремума. Ограничимся рассмотрением
метода квадратичной аппроксимации минимизируемой
функции /(ж), в котором график этой функции приближенно
заменяют параболой, проходящей через три известные точки (ж^, /^),
г = 1,2,3, где f{ = f(Xi).
76 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Известно [II], что через три различные точки, не лежащие
на одной прямой, можно провести только одну параболу у =
= ах2 + Ъх + с, а/0. Коэффициенты а, Ъ, с удовлетворяют
системе линейных алгебраических уравнений (СЛАУ)
ax2 + bxi + c = fi,
Определитель этой СЛАУ
1,2,3.
Хл
Хг*
XI
х2
х3
= (х\ - х2)(х1 - х3)(х2 - х3)
представляет собой определитель Вандермонда* и отличен от
нуля, когда #1, х2, х% попарно различны. В этом случае СЛАУ
имеет решение, и притом единственное. Его можно записать в
виде
а =
л
+
+
1
(х2
J
(х2
h
-хг)(х2-
f2(xs+Xi)
-xi)(xs-
f2X3Xi
хз)
x2)
(x1-x2)(x1 -Хз)
b= fljX2+X3)
(xi-x2)(x3-xi)
fix2x3
с = i i
(xi - x2)(xi - хз) (x2 - xi)(x2 - хз) (хз - xi)(x3 - x2)'
Если найденные выражения для коэффициентов а и b
подставить в необходимое условие у1 = 2ах + 6 = 0 экстремума
функции, то получим ее единственную стационарную точку
1
(хз
1 J
(хз
1
/з
-xi)(x3-
f3(xi+x2)
-х1)(х2-
hx\x2
х2У
хзУ
х± —
Ь_ _ 1 /1Г23 + /2Г31 + 1зП2
2а 2 fis23 + /2S31 + /з«12 '
B.18)
где гц = х,
Xа И Sij — Xi
xj, h J — 1? 2, 3. Так как у" = 2а =
= const, то в точке 2* при а > 0 имеем минимум функции у (ж),
а при а < 0 — максимум.
*А.Т. Вандермонд A735-1796) — французский математик.
2.6. Методы полиномиальной аппроксимации 77
Если известен отрезок, на котором минимизируемая
функция унимодальна, то нет необходимости вычислять значение
коэффициента а. Достаточно этот отрезок принять в качестве
отрезка [жх, жз], а точку ж2 Е (жх, жз) выбрать произвольно в
интервале (жх, жз). В этом случае имеем /i ) /2 и /з ) /2, откуда
ж* Е [жх,ж3].
На первом шаге метода квадратичной аппроксимации при
помощи B.18) вычисляют ж* и затем /* = f(x* )• Для
~A)
вычислении на втором шаге из четырех точек ж* ' и ж^, % =
B)
= 1, 2, 3, выбирают новую тройку точек х\ по следующему
правилу:
\ Ч1) г- Г 1 7A) / * B) B) B)
а) если х\ Е [ж2, ж3] и /*v ^ /2, то х\ = ж2, ж^ = ж3, а^ =
_41).
*\ 41) л- Г 1 7A) ^ t B) B) 41) B)
б) если х\ Е [ж2, жз] и /* > /2, тож^ = жх, Ж3 =ж; , ж;> =
= ж2;
\ 41) г- Г 1 7A) ^ { B) B) B)
в) если xl ' Е |жх, ж2] и /* ^ /2? то х\ ' = Жх, #з ж2, ^2 =
_41).
\ 41) г- Г 1 7A) ^ t B) 41) B) B)
г) если ж; Е [жх, ж2] и /*v >/2, то ж^ = ж; , х\ = ж3, ж^ =
= ж2.
Далее из B.18) находят ж* , а затем описанную процедуру
повторяют на третьем шаге и так далее до тех пор, пока длина
интервала неопределенности, в котором гарантированно
лежит искомая точка ж* минимума функции /(ж), не станет
меньше заданного наибольшего допустимого значения ?*. Отметим,
что подтверждением приближения к точке ж* и правильности
вычислений может служить уменьшение значения функции у(х)
в найденной точке ж* по сравнению со значением у\х* ) на
предыдущем шаге.
Пример 2.4. Найдем методом квадратичной
аппроксимации минимум функции /(ж) = ж2 + 16/ж, унимодальной на
отрезке [1, 4]. График этой функции приведен на рис. 2.11.
78 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Рис. 2.11
Выберем три точки Ж1 = 1, Ж2 = 3, жз = 4 и вычислим в них
значения функции f(x): Д = f(x\) = 17, /2 = /(#2) ~ 14,333,
/(жз) — /(жз) = 20. Из B.18) на первом шаге метода
квадратичной аппроксимации найдем ж* « 2,286 и затем вычислим
значение ДA) = /(ж!1)) « 12,225.
Так как ж* Е [ж1, Х2] и /* < /2, то по указанному выше
B) B) B) ~A) ^ -
правилу Ж]/ = Ж1, Ж3 = Ж2 и ж;> = ж* . Выбранным точкам со-
рB)
ответствуют значения /| ; = /(ж^ ) = 17, fy — f(x2 ) ~ 12,225
B)ч
fB)
,B)>
рC)
,B)
B)
и /2V°; = /D ) « 14,333. Используя B.18), получим х\} « 2,200
и ДB)=/(ж?2))« 12,113.
ХB)
Д2) B)п
ГB) ^ ,B)
Поскольку ж* Е [х\ , ж;> ] и /* < /2 , то на третьем шаге
C) B) C) B) C) ~B) C) л C) _ 0 опп
имеем ж| -ж| ,Жз -^ и^ =4 , т.е. х\ ' = 1, х\ ~ 2,200
^з ~ 2,286. Этим точкам соответствуют значения Д = 17,
И Жо
/2C) « 12,113 и /3C)
~Сз1 ~
ж*; и 2,087 и затем /,
12,225. В соответствии с B.18) находим
'C)
¦f(x
х(з)
(ЗК
12,022.
C) „C)i
г(з) / -(з)
Снова оказалось, что ж* € [ж^ , х2 ] и /* < /2 . Поэтому
D) C) D)
для вычислении на четвертом шаге получаем х\ = х\ , х3 =
= 43) и х{2} = ж!3), т.е. 44) = 1, ж^4) и 2,087, ж^4) и 2,200 и
/^ = 17, /|4) и 12,022, /;J4) и 12,113. В соответствии с B.18)
имеем Ji4) и 2,054 и /*D) и 12,009.
2.6. Методы полиномиальной аппроксимации 79
Из проведенных расчетов вытекает, что искомая точка
х* минимума функции f(x) лежит в интервале (S?* , S?* ) =
= A, 2,054). Дальнейшие вычисления приводят к
незначительному уменьшению интервала неопределенности, так как
каждая очередная точка будет правее точки 2.
Используя необходимое условие экстремума функции f'(x) =
= 0, заключаем, что х* = 2 и f(x*) = 12. Таким образом, в
данном случае последовательность точек х* ' приближается к
точке минимума ж*, монотонно убывая.
Степень приближения текущей точки к точке минимума
можно оценить следующим образом. Согласно формуле
Тейлора, в окрестности точки минимума х* целевой функции имеем
Вычисляя разность двух приближенных равенств, находим:
f(xi)-f(x2) ~ —-^(xi-x2)(xi+x2-2x*) «
« f"(x*)(xi -x2)(xi -ж*).
В результате получаем приближенную формулу
\f(xi)-f(x2)\
\Х\ х%
\xi-x2\f"(x*y
В данном случае при выборе х\ = х\ , х2 = х\ имеем
|~C)_ ¦ „ 12,022-12,009 _
|Ж* Ж*! B,087-2,054)-6" U'Ubb'
что согласуется с полученными результатами. #
Метод квадратичной аппроксимации удобно применять
после локализации точки минимума методом золотого сечения
или методом Фибоначчи. Это объясняется тем, что для
дважды дифференцируемой функции многочлен второго порядка
80 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
достаточно хорошо аппроксимирует функцию в окрестности
точки минимума.
В одной из модификаций метода квадратичной
аппроксимации на к-м шаге, к > 1, в тройку точек х\ , г = 1, 2, 3, включают
наиденную на предыдущем шаге точку ж* у (как точку х2 ),
С А; — 1) о ~(& —1)
одну из точек жг- , ближайшую к4 , и точку, симметрич-
(к-1) ~(к-1) т-т
ную включенной точке х\ относительно х\ '. Последняя
~{к)
точка новая, и в ней перед вычислением х\ необходимо
определять значение минимизируемой функции.
(к) (к)
Такой выбор тройки точек х\ приводит к равенству х2 —
— х\ — Жз — х2 — Д&, что упрощает B.18):
4*0 _ (/с) , Afc f(x[ })-f(x{s
2 /D*))-2/D*)) + /D*))"
~W _ Л*) , ^ j v^i ; j v^3 ; /o ! Q4
Процесс последовательных приближений к искомой точке ж*
минимума унимодальной функции f(x) прекращают, если по-
лученные на двух последовательных шагах значения jyx* )
и /(ж* ) близки или если проведенные расчеты позволяют
указать интервал неопределенности, длина которого меньше
заданного наибольшего допустимого значения ?*.
ГЛ ~(*0 " 7
Отметим, что в данном случае точка х* , наиденная на к-м
Г (к) (к),
шаге, может оказаться за пределами отрезка [х\ \х^ J, в то
время как в методе квадратичной аппроксимации принадлеж-
~(к)
ность точки х* указанному отрезку гарантирована.
Пример 2.5. Применим описанную модификацию метода
квадратичной аппроксимации для нахождения минимума
функции
f(x) = (x-lJ(x-3J
на отрезке [2, 8]. График этой функции приведен на рис. 2.12.
Процесс итераций закончим, если длина интервала
неопределенности не будет превышать 0,15. На первом шаге выберем
2.6. Методы полиномиальной аппроксимации 81
,Ш
B)
ч
м
x\J ='?•> х\ ' =5 и xy^J =8. Результаты вычислений с учетом
B.19) сведены в табл. 2.6.
После выполнения пятого шага приходим к заключению,
что точка х* минимума функции f(x) расположена в интервале
B,949, 3,076) длины 0,127. Точное значение х* = 3
соответствует минимальному значению f(x*) = 0.
4 х
Рис. 2.12
Таблица 2.6
к
*<*>
Я*Р)
т(*)
я4})
х3
/Dfc))
~(*)
^ь*
/E#°)
1
2
1
5
64
8
1225
3,328
0,583
2
2
1
3,328
0,583
4,656
36,655
2,679
0,290
3
2,030
0,998
2,679
0,290
3,328
0,583
2,814
0,114
4
2,679
0,290
2,814
0,114
2,949
0,010
3,076
0,025
5
2,949
0,010
3,076
0,025
3,203
0,200
3,001
0,000
82 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
2.7. Методы с использованием производных
В методах прямого поиска при вычислении значений
минимизируемой функции f(x) неизбежно возникают погрешности,
к которым чувствительны алгоритмы прямого поиска,
основанные на сравнении значений функции в отдельных точках.
Пусть f(x) — дважды непрерывно дифференцируемая
функция в окрестности точки х* строгого локального минимума,
значения которой вычисляются с абсолютной погрешностью,
не превышающей Ду\ Оценим абсолютную погрешность А*, с
которой может быть найдена точка х* с применением метода
прямого поиска. Для представления функции f(x) в
окрестности точки х* воспользуемся формулой Тейлора [II] с учетом
равенства /(ж*) = 0:
где ? — точка, лежащая между точками ж* и ж. Имея в виду,
что вычисления проводятся в достаточно малой окрестности
точки ж*, положим /"(?) ~ fff(x*). Тогда для приближенно
вычисляемых значений f(x) получим
f{x)-f(x*) = f(x)-f(x,) + (f(x)-f(x))-(f(x,)-f(x.))>
> f(x) - /Ы - 2А/ « f»(x.)?^? - 2Д,.
Из этих неравенств вытекает, что можно гарантировать
выполнение неравенства f(x) > /(ж*), если f"(x*)(x — х*J > 2Aj.
Это приводит к приближенной оценке абсолютной погрешности
нахождения точки х* методом прямого поиска:
Заданная точность е* нахождения точки х* не должна быть
меньше А*, так как иначе эту точность нельзя достичь методом
прямого поиска. Из B.20) также следует, что при нахожде-
2.7. Методы с использованием производных 83
нии точки х* происходит потеря примерно половины верных
значащих цифр, с которыми можно вычислить приближенное
значение минимизируемой функции [II].
Если унимодальная функция f(x) непрерывно
дифференцируема на отрезке минимизации, то точку х* наименьшего
значения функции можно вычислять как корень уравнения f'(x) = О
с помощью тех или иных методов численного решения
нелинейных уравнений [II]. В этом случае на точность решения задачи
решающее влияние оказывает погрешность вычисления
производной функции.
Если абсолютная погрешность вычисления производной не
превышает Aj/, то для нижней оценки абсолютной
погрешности вычисления корня х* уравнения f(x) = 0 имеем [II]
Таким образом, при нахождении этого корня можно сохранить
все верные значащие цифры, с которыми можно вычислить
значение производной f'(x).
Рассмотрим некоторые методы одномерной минимизации,
основанные на использовании производной минимизируемой
функции.
Метод средней точки. Будем искать минимум
функции /(ж), непрерывно дифференцируемой и строго
унимодальной на отрезке [ai,&i]. В этом случае единственной точкой
х* G [ai, &i] минимума будет стационарная точка, в которой
/'(ж*) = 0- Отметим, что непрерывно дифференцируемая
унимодальная на отрезке функция может иметь на нем более одной
стационарной точки.
В методе средней точки используют простую идею:
вычисляют производную f'ixi) = К\ в средней точке х\ =
= (ai+bi)/2 исходного отрезка и, если К\ > 0, то отрезок
[xi,bi] отбрасывают, так как на нем строго унимодальная
функция только возрастает, а если К\ < 0, то отбрасывают
B.21)
84 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
отрезок [ai,^i], поскольку на нем строго унимодальная
функция лишь убывает. В данном случае отбрасывание половины
исходного отрезка [ai,fti] аналогично процедуре исключения
отрезка. Ясно, что в случае К = 0 имеем х* = х.
Оставшуюся после отбрасывания половину отрезка
обозначим [а2, Ьг] и, вычислив производную f'ix^) = К<2 в его средней
точке Х2 = (fl2 + &2)/2, повторим процедуру отбрасывания
половины отрезка и т.д. Условием прекращения вычислений на к-м
шаге может быть выполнение неравенства lk+i < ?*, где lk+i —
= bk+i — a^i — длина отрезка [a^+i, ft/c+i] после отбрасывания
половины отрезка [а&, Ь^]; в* — наибольшая допустимая длина
интервала неопределенности.
Метод средней точки напоминает метод дихотомии, но
сходится к искомому значению х* быстрее, поскольку в отличие
от B.8) для метода средней точки после вычисления п значений
производной минимизируемой на отрезке [0, 1] функции f(x)
для длины интервала неопределенности получаем
In = ^- B.22)
Таким образом, для одинакового уменьшения значения 1п в
методе средней точки нужно вычислить вдвое меньше значений
производной функции по сравнению с числом значений самой
функции в методе дихотомии.
Метод Ньютона. Если строго унимодальная на
отрезке [a, ft] функция f(x) дважды непрерывно дифференцируема
на этом отрезке, то точку х* Е [a, ft] минимума этой
функции можно найти путем решения уравнения f'(x) = 0 методом
Ньютона, иногда называемым методом касательных. Пусть
xq Е [a, ft] — нулевое приближение к искомой точке ж*,
называемое обычно начальной точкой. Линеаризуем функцию
f'{x) в окрестности начальной точки, приближенно заменив
дугу графика этой функции касательной в точке (жо, f'(xo)):
f(x) и /'(*„) + Г'Ы)(х - х0). B.23)
2.7. Методы с использованием производных 85
Рис. 2.13
Выберем в качестве следующего приближения к х* точку
х\ пересечения касательной с осью абсцисс (рис. 2.13).
Приравнивая нулю правую часть B.23), получаем первый элемент
гы
итерационной последовательности {х^}. На
Х1 = Х0 /"(*»)
(к -\- 1)-м шаге по найденной на предыдущем шаге точке х^
можно найти точку
*«=*-?ет B'24)
Для квадратичной функции f(x) функция ff(x) линейна.
Поэтому в B.23) равенство будет точным, а метод Ньютона будет
сходиться за один шаг при любом выборе точки xq из области
определения этой функции.
В общем случае сходимость метода Ньютона существенно
зависит от выбора начальной точки xq. Для надежной
работы этого метода необходимо, чтобы вторая производная fff(x)
в окрестности искомой точки х* сохраняла знак, а
начальная точка xq выбиралась из такой окрестности. В противном
случае второе слагаемое в правой части B.24) может стать
неограниченным. Поскольку для дважды непрерывно
дифференцируемой функции в точке минимума fff(x*) > 0, то должно
быть и f"(xo) > 0. Поэтому говорят, что метод Ньютона
обладает локальной сходимостью в том смысле, что надо выбрать
86 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
хорошее начальное приближение, попадающее в такую
окрестность точки ж*, где f"(x) > 0. Однако проверка выполнения
этого условия не всегда возможна.
Достаточное условие надежной работы метода Ньютона
при нахождении точки х* Е [а, Ь] минимума функции f(x)
можно установить в случае, если эта функция трижды непрерывно
дифференцируема на отрезке [а, Ь]. Ясно, что итерационная
последовательность {х^} будет сходиться к пределу х* монотонно,
если 0< х* Хк+1 < 1. в соответствии с формулой Тейлора с
X* Xk
остаточным членом в форме Лагранжа имеем
/'(**) = 0 = !'{хк) + f"(xk)(x, - хк) + f'"(x)ix* " Хк?
2
где точка х лежит между хк и ж*. Поэтому с учетом B.24)
имеем
х*-хк+1_Х* k + f"(xk)_1_ 2
X* Xfc X* Xfc о _|_ J yXjyX* Xk)
+ 7Щ
Таким образом, последовательность {х^} является монотонной,
f'"(x)
если Р , i > 0, т.е. достаточным условием монотонной сходи-
/ Лхк)
мости метода Ньютона будут постоянство в интервале между
точками xq и ж* знака производной f'"(x) и совпадение его
со знаком ff(xo). Оказывается [II], что в этом случае метод
Ньютона обладает квадратичной скоростью сходимости в
некоторой 5-окрестности и(ж*,#) точки ж*, причем
I | ^ \Х* Xfc — \)
\Х% ^/с| ^ —
С
где
°" тах|/'"(Ж)|' [2-2Ь)
минимум и максимум вычисляются по множеству XJ(x*,S).
2.7. Методы с использованием производных 87
Если радиус E-окрестности U(#*,?) не превосходит С, а
точка Xk попадает в окрестность \J(x*,5/2), то и следующая точка
оказывается в этой окрестности, т.е. итерационная
последовательность не выходит за пределы окрестности U(a;*,tf/2). В
этом случае верна оценка [II]
\хк-х*\ < \хк-1-хк\, B.26)
которую можно использовать для оценки точности
найденного решения уравнения f'{x) = 0 (точки локального минимума
функции).
Пример 2.6. Найдем точку х* наименьшего значения
функции f(x) = х2 + 16/ж на отрезке [1,4].
Вычислим f(x) =2х- 16/ж2, f"(x) = 2 + 32/ж3 и f"(x) =
= —96/ж4. Всюду на отрезке [1, 4] имеем f"(x) > 0, f'"(x) < 0.
Поэтому, если начальную точку xq выбрать исходя из условия
f'(xo) < 0, то построенная итерационная последовательность
будет монотонной.
Выберем хо = 1 и вычислим f'(xo) = —14, f"(xo) = 34, а
затем, используя B.24) при к = 0, получим
^-Т^Г1-^1'4118-
Далее при помощи B.24) последовательно находим Х2 ~ 1,8010,
х3 « 1,9790, ж4 « 1,9998.
Предположим, что верна оценка B.26). Тогда |ж4 —ж*| ^
^ |жз ~~ ж4| ~ 0,0208 и, в силу того что последовательность
{хк} возрастает, искомая точка х* должна лежать в
интервале (ж4, ж4 +0,0208) = A,9998, 2,0206). Так как /'A,9998) «
« -0,0012 < 0, /'B,0206) « 0,1223 > 0, то, действительно,
уравнение f'(x) =0 в интервале A,9998, 2,0206) имеет корень,
который в силу условия fff(x) > 0, х Е [1,4], является точкой
минимума функции f(x). Отметим, что функция f(x) была
рассмотрена в примере 2.4, где получено точное значение х* = 2
точки, в которой функция достигает наименьшего значения.
88 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Модификации метода Ньютона. Вычисление второй
производной fff(xk) минимизируемой функции f(x) на каждом
к-м шаге метода Ньютона может оказаться достаточно
трудоемким. В этом случае целесообразно использовать упрощенный
метод Ньютона, положив в B.24) fn(xk) = fn(xo) = const:
XM=xt~9wY B'27)
Оказывается, что этот метод имеет линейную скорость
сходимости. При этом если в интервале между точками х* и
xq выполнено условие ff(xo)ffff(x) > О, то последовательность
{ж/с}, построенная в соответствии с B.27), сходится к точке х*
монотонно.
Можно избежать вычисления второй производной
минимизируемой на отрезке [а, Ь] функции /(ж), если располагать
двумя приближениями жо, х\ Е [а, Ь] к искомой точке х* Е [а, Ь]
минимума этой функции. Заменяя в B.24) при к = 1
производную f"{x\) выражением
/;(*1)-/Ы
получаем
х\-хъ ,
х2 = хг- ——— jrr^J ж1 ,
а в случае произвольного номера к Е N приходим к формуле
хм=щ-nZ~-nL/{xt)- B28)
Метод решения нелинейного уравнения f'(x) = 0 с применением
рекуррентного соотношения B.28) обычно называют методом
секущих. Геометрическая интерпретация этого метода состоит
в том, что в качестве очередного приближения x^+i выбирают
точку пересечения с осью абсцисс не касательной к графику
функции f'{x), как это делают в методе Ньютона, а секущей,
2.7. Методы с использованием производных 89
проходящей через две точки этого графика, найденные при
выполнении двух предыдущих шагов метода.
Выбор начальной точки х$ в B.28) при к = 1 проводят
следующим образом. Если на отрезке [а, Ь] функция f(x) имеет
знакопостоянную третью производную f'"(x), то в качестве хо
выбирают тот конец отрезка [а, Ь], на котором совпадают знаки
f'(x) и f'"(x), а в качестве
XI
af'(b)-bf'(a)
f'(b)-f'(a)
B.29)
точку пересечения с осью абсцисс хорды, стягивающей дугу
графика функции f'(x) на отрезке [а, Ь] (рис. 2.14). Таким
образом, первый шаг метода секущих выполняют согласно
методу хорд, а последующие шаги — в соответствии с B.28).
Этот метод имеет сверхлинейную скорость сходимости [II],
причем |ж* — Xk\ ^ С(х* — Xk-iO', где С = const, а г = —-— «
« 1,618 — отношение золотого сечения.
ХКГЪ
Рис. 2.14
Модификации метода Ньютона обладают только локальной
сходимостью, т.е. сходятся, если начальная точка выбрана в
некоторой окрестности точки минимума функции. Если же
начальная точка расположена слишком далеко от точки
минимума, то подобный метод может расходиться или ^зацикливать-
90 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
ся". В некоторых случаях целесообразно сочетать различные
модификации метода Ньютона, чередуя их применение в
зависимости от номера шага [II].
Метод кубической аппроксимации. В методах
полиномиальной аппроксимации при построении многочлена,
аппроксимирующего минимизируемую функцию в окрестности
искомой точки х* минимума, помимо значений функции в
отдельных точках могут быть использованы и значения ее
производных.
Пусть для непрерывно дифференцируемой функции /(ж),
строго выпуклой на отрезке [жх5#2]5 известны значения Д =
= f(xi), /2 = /(^2), Л = f'(xi) и /2 = f'{x2). Для строго
выпуклой функции производная ff(x) возрастает на отрезке [II].
Поэтому если значения /{ и f2 одного знака, т.е. f[f2 > 0, то
дифференцируемая функция f(x) не имеет стационарных
точек на отрезке [х\, х2] и, следовательно, не имеет на нем точки
минимума. Если f[f2 = 0, то один из концов отрезка
является стационарной точкой функции /(ж), в которой эта функция
имеет минимум. Наконец, если f[f2 < 0, то для строго
выпуклой функции /х < 0 и f2 > 0. Следовательно, лишь единственная
точка х* Е (х±, х2) будет стационарной, и в ней функция f(x)
достигнет минимума. Таким образом, если f[f2 < 0 на отрезке
[жх,^2], то рассматриваемая функция строго унимодальна на
этом отрезке.
Рассмотрим метод поиска точки х* Е {х\,х2) при условии
f[f2 < 0, называемый методом кубической
аппроксимации, поскольку в этом случае на отрезке [жх5#2] можно
построить единственный многочлен третьей степени, располагая
значениями /х, /2, /{, /2 на концах этого отрезка [II]. Этот
многочлен, называемый кубическим интерполяционным
многочленом Эрмита*, можно преобразовать к виду
Нз(х) =fi+ai(x- xi) + а2(х - х\)(х - х2) + а3(х - xiJ(x - х2)
*Ш. Эрмит A822-1901) — французский математик.
2.7. Методы с использованием производных 91
с коэффициентами
а\
CL2 =
/2-/1
а3
Х2 - Xi '
/2-/1
(x2-xiJ
л+л
л
X<2-Xi
о h~h
B.30)
(rr2-?iJ (Ж2-Ж1)
Несложно проверить, что Н^(х\) = /i, Н$(х2) = /2? Н'3(х\) = /{
иН'3(х2) = &.
Производная Н'3(х) является квадратичной функцией,
непрерывной на отрезке [жх,Ж2] и имеющей на его концах
различные знаки. Поэтому в интервале она может изменить знак
лишь один раз в точке 2*, которая является стационарной
точкой многочлена Нз(х), а именно точкой его минимума, так как
производная меняет знак с минуса на плюс.
Из необходимого условия Н'3(х) = 0 экстремума этого
многочлена получаем с учетом B.30) квадратное уравнение
Заз(х — х\J — 2
2/{ + ^-3«!
Ж2-Ж1
(x-Xl) + f[ = 0.
Его решение, принадлежащее интервалу {х\, х2), представим в
виде ж* =х\ + ц{х2 -х\), где
М:
u + z-fj
*=/l+/2-3
/2-/1
Х2-Х\
^=\А2-Л/2, B-31)
и покажем, что \i Е @, 1). Действительно, поскольку /{ < 0 и
f2 > 0, имеем ш > \z\, uj + z — f[ > 0, 2cj — f[ + /2 > 0.
Следовательно,
0</i =
ш + 2 - /{ cj + г - /{ + (ш - z) _ 2u)-f[
2^-/{ + Л
и ж* E (ж1,ж2).
<
2^-/{ + Л
2^-/{ + Л
<1
92 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Если /'(ж*) = 0, то ж* = ж* — искомая точка минимума
функции /(ж) на отрезке [жх, 2:2]. Если же fix*) ф О, то в
случае f[ff(x*) < 0 можно отбросить отрезок [5?, ?2] и продолжать
описанным выше способом поиск точки минимума на отрезке
[жх, 5?*], и наоборот. После каждого приближения правильность
вычислений подтверждается уменьшением минимального
значения многочлена по сравнению с его минимальным значением
на предыдущем шаге. Вычисления можно прекратить, когда
длина интервала неопределенности, в котором гарантированно
находится искомая точка ж*, станет меньше заданной
наибольшей допустимой величины е*.
Пример 2.7. Рассмотрим ту же функцию f(x) = х2 + 16/ж,
что и в примерах 2.4 и 2.6, и найдем точку ее минимума ж* на
отрезке [жх, жг] = [1,4].
Вычисляем Д = 12, /2 = 20 и по формуле /'(ж) = 2ж — 16/ж2
получаем /{ = —14, f'2 = 7. Используя B.31), находим z = —10,
w = л/198 « 14,0712, /i « 0,3677 и ж* = жх + /Дж2 - жх) « 2,1031.
Так как /'(ж*) ~ 0,5888 > 0, то поиск точки ж* продолжаем на
отрезке [ж^ , х2 ], где х[ — жх = 1 и ж;> = ж* « 2,1031, причем
/(ж^)» 12,0308.
После аналогичных вычислений имеем г'1' « 0,1303, а/1' ~
« 2,9333, /Z1) « 0,8342, ^1} = ж^1} + /iA)(^(lJ - 4^) « 1,9202,
/'(я!4) ~ -0,4990 < 0 и /(ж!1}) « 12,0196. Теперь искомая точка
( B) B)ч B) ~A) 1 попо
ж* находится в интервале (ж^ , х\ у), где ж^ J = ж* J « 1,9202 и
ж?2)= ж* «2,1031.
В итоге аналогичной серии вычислений получаем
?B) « -0,0939, ш^ « 0,5501, /iB) « 0,4365, г12) « 2,0000.
Итак, пришли к значению ж* , у которого четыре верных
знака после запятой совпадают с точным значением ж* = 2
(см. пример 2.4).
Вопросы и задачи
93
Вопросы и задачи
2.1. Имеет ли функция f(x) = хе~х экстремум в интервале
(О, 3)? Если имеет, то в какой точке? Имеет ли она минимум
в том же интервале, минимум на отрезке [0, 3], и если да, то в
какой точке?
2.2. Проверьте, являются ли унимодальными следующие
функции:
а) f(x) = х2 — 2х — 1 на отрезках [0, 2], [1,5, 2];
б) f(x) = ||ж-1|-1| на отрезках [-3,3], [-3,1], [1,3], [0,2].
2.3. Имеются утверждения относительно функции /(ж),
определенной на отрезке [а, Ь]:
а) f(x) возрастает;
б) f(x) не убывает;
в) f(x) имеет локальный минимум на интервале (а, Ъ) в
некоторой точке ж*;
г) 3xE(a,b): f'(x)=0;
д) Эх Е (а, b): f'(x) не существует;
е) f'(x) > 0 на отрезке [а, Ь];
ж) Зе > 0: f'{x) < 0 при х\ — е < х < х\ и f{x) > 0 при
х\ < х < х\ +6;
з) ЗжЕ(а,Ь): f"(x) = 0;
и)Г(ж)=0, жЕ(а,6).
Какие из указанных утверждений вытекают из перечисленных?
2.4. Имеет ли функция
{ж4 sin-, ж^О;
х
0, ж = 0,
минимум в точке х = 0, выполняется ли в этой точке
необходимое, достаточное условия экстремума?
2.5. Для каких унимодальных функций метод золотого
сечения приводит к цели за меньшее количество итераций, чем
метод Ньютона?
94 2. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
2.6. Какой из методов: золотого сечения, Ньютона,
кубической интерполяции — окажется более эффективным, если
производные вычисляются приближенно через разность
значений функции в близких точках?
2.7. Минимизируйте функции
f(x) = (x — l) , у(х) = (х — 1) sinrr
на отрезке [—2, 3] с помощью метода золотого сечения.
2.8. Минимизируйте функцию
f(x) = xarctgx — -ln(l -\-х2)
на отрезке [—6,6] методом Ньютона. Выбирая различные
начальные приближения, найдите какое-либо значение жо, при
котором метод начнет расходиться.
2.9. Минимизируйте функцию f(x) = (х — IL на отрезке
[0,5, 2] и функцию д(х) =xs'm(l/x) на отрезке [0,2, 1] методами
дихотомии и золотого сечения, а также с помощью
оптимального последовательного поиска, градиентного метода и метода
Ньютона. Сравните эти методы.
3. МИНИМИЗАЦИЯ
ВЫПУКЛЫХ ФУНКЦИЙ
Широкий класс задач математического программирования
связан с минимизацией выпуклых функций многих переменных,
определенных на выпуклом множестве. Такие задачи относят
к задачам выпуклого программирования. В этой главе
рассмотрены основные свойства выпуклых множеств и функций
и описаны некоторые методы минимизации выпуклой целевой
функции в случае, когда на область изменения параметров
оптимизации не наложено ограничений.
3.1. Выпуклые множества
Пусть С — конечномерное линейное пространство и ж1,
ж2 — произвольные элементы в С. Множество Е С С вида
Е = {ж Е С: ж = Аж1 + A - А)ж2, А Е [0, 1] С Ш}
будем называть отрезком с концами х1 и ж2 и обозначать
[ж1, ж2].
Определение 3.1. Подмножество О линейного
пространства С называют выпуклым множеством, если оно вместе с
любыми двумя точками ж1, х1 Е О содержит и отрезок [ж1, ж2],
т.е. для любых ж1, ж2 Е О и А Е [0, 1] выполняется соотношение
Аж1 + A — А)ж2 Е О. Пустое множество считаем выпуклым по
определению.
Пример 3.1. а. Линейное подпространство % в линейном
пространстве С является выпуклым множеством. В самом деле,
для любых элементов ж1, ж2 Е % линейному подпространству 7/,
согласно определению, принадлежит и любая линейная комби-
96 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
нация a\xl + о^ж2 этих элементов. В частности, это верно и
при ol\ — А, «2 = 1 — А, где Л Е [0, 1].
б. Отрезок Е = [ж1, ж2] в линейном пространстве С
является выпуклым множеством. Чтобы показать это, выберем две
точки у1, у2 Е Е. Тогда, согласно определению отрезка,
существуют такие значения ti, ^2 Е [0, 1], что
у1 = hx1 + A - h)x2, у2 = t2xl + A - ?2)ж2.
Пусть Л Е [0, 1] выбрано произвольно. Тогда
Ху1 + A - \)у2 = Л^ж1 + A - *1)ж2) +
+ A - Л)(^2ж1 + A - t2)x2) = (Ati + A - Л)*2)ж1 +
+ (A(l-t1) + (l-A)(l-t2))*2.
Положив /?1 = Ati + A - Л)*2 и #2 = ЛA - ti) + A - Л)A - *2),
нетрудно показать, что C\ ^ 0, /?2 ^ 0 и C\ + /?2 = 1. Таким
образом, 0 ^ /?i ^ 1, /?2 = 1 — /?i и
Лу1 + A - Л)у2 = /?1Ж1 + A - /?1)ж2 € Е.
Отметим, что одноточечное множество, как частный случай
отрезка, является выпуклым множеством.
в. Рассмотрим систему линейных алгебраических
уравнений (СЛАУ) Ах = Ь, где А — матрица размера т х п, ж —
матрица-столбец высоты п, составленная из неизвестных
системы, а Ъ — матрица-столбец высоты т, составленная из
правых частей уравнений. Множество решений
рассматриваемой системы есть подмножество линейного арифметического
пространства W1. Это подмножество является выпуклым. В
самом деле, если ж1 и ж2 — решения рассматриваемой
системы, а Л Е [0, 1], то в силу свойств решений СЛАУ (или свойств
матричных операций)
^(Аж1 + A - А)ж2) = ХАх1 + A - Х)Ах2 = ХЬ + A - \)Ь = Ь,
т.е. столбец Аж1 + A — А)ж2 является решением СЛАУ Ах = Ъ.
Рассмотренному примеру можно придать более широкое
толкование. Допустим, что А — линейный оператор, действу-
3.1. Выпуклые множества
97
ющий в линейном пространстве С. Тогда прообраз А-1 (у) =
= {ж Е С: Ах = у} произвольного элемента у Е С есть выпуклое
множество в С. Доказательство этого аналогично тому,
которое было проведено для множества решений СЛАУ.
Подмножество Е в линейном пространстве С назовем
аффинным многообразием, если оно вместе с любыми своими
элементами ж1 и ж2 содержит и любую их линейную
комбинацию вида Аж1 + A — А)ж2, где А Е Ш — любое число. Ясно,
что аффинное многообразие — частный случай выпуклого
множества. Нетрудно показать, что множество решений СЛАУ,
а также прообраз А-1 (у) элемента у для линейного
оператора А являются аффинными многообразиями. Другой способ
получения аффинного многообразия — образовать множество
ж0 + % = {у Е С: у = ж0 + у0, у0 Е И}, где ж0 — произвольный
элемент в ?, а И С С — произвольное линейное
подпространство. Это множество является аффинным многообразием.
Действительно, если ж1, ж2 Е ж0 + И, то хг = ж0 + уг, где уг Е И,
г = 1, 2. Поэтому для любого числа А
Аж1 + A - А)ж2 = А(ж° + у1) + A - А)(ж° + у2) =
= ж0 + (Ху1 + A - Х)у2) Е ж0 + ft.
Отметим без доказательства, что любое аффинное
многообразие может быть представлено в виде ж0 + %. Поэтому в W1
понятие аффинного многообразия равнозначно m-мерной
плоскости.
Пример 3.2. Пусть С — нормированное пространство.
Тогда любое множество Е вида Е = {ж Е ?: ||ж — ж°|| ^ г}, где
||ж|| — норма элемента ж в ?, является выпуклым. Докажем
это. Для любых элементов ж1, ж2 Е Е и любого числа А Е [0, 1]
имеем
|| (Аж1 + A - А)ж2) - ж01| = ||Х(хг - ж0) + A - А)(ж2 - ж0) || ^
< АЦж1 - ж°|| + A - А)||ж2 - ж°|| ^ Хг + A - Х)г = г,
т.е. Ажх + A-А)ж2 еЕ.
98 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Пример 3.3. Пусть С — евклидово пространство, в
котором скалярное произведение элементов ж ж у будем обозначать
(ж, у). Для любого вектора а Е С и любого числа с G М
множество Е = {х ? С: (ж, а) = с} является аффинным многообразием
и, в частности, выпуклым множеством. Чтобы показать это,
выберем произвольные элементы ж1, ж2 Е Е и число Л Е М.
Тогда (ж1, а) = (ж2, а) = с. Следовательно, с учетом свойств
скалярного произведения
(Лж1 + A-Л)ж2,а) =
= Л (ж1, а) + A - Л) (ж2, а) = Лс+ A - Л)с = с,
что означает выполнение соотношения Аж1 + A — А)ж2 Е ?7.
Множество Е указанного вида в дальнейшем будем называть
гиперплоскостью. Отметим, что термин ^гиперплоскость"
в 1R3 означает плоскость, ав!2 — прямую.
Нетрудно показать, что множество Е = {ж Е С: (ж, а) ^ с}
выпуклое, но аффинным многообразием не является. Это
утверждение остается в силе, если в определении множества Е
знак 95^" заменить знаком „^": по существу, это
равносильно замене вектора а вектором —а. Утверждение также будет
справедливым, если знак неравенства заменить строгим
неравенством. Множество Е в дальнейшем будем называть
полупространством. #
Пусть ж1, ..., хк — произвольные элементы в линейном
пространстве С. Их линейную комбинацию \\х1 + ... + А&ж^
назовем выпуклой комбинацией, если все коэффициенты
А^, г = 1, /с, неотрицательны, а их сумма равна единице, т.е.
к
^ А^ = 1. Отметим, что линейная комбинация Аж1 + A — А)ж2,
г=1
участвующая в определении отрезка, при А Е [0, 1] является
выпуклой.
Теорема 3.1. Для того чтобы множество Е С С было
выпуклым, необходимо и достаточно, чтобы любая выпуклая
комбинация элементов Е принадлежала этому множеству.
3.1. Выпуклые множества
99
Ч Достаточность утверждения теоремы очевидна, и мы
остановимся на доказательстве его необходимости, следуя методу
математической индукции по количеству слагаемых в
выпуклой комбинации.
Пусть множество Е С С выпукло. Для выпуклой
комбинации с к = 2 слагаемыми утверждение теоремы верно (оно
равносильно определению выпуклого множества). Пусть
утверждение теоремы верно для любой выпуклой комбинации,
содержащей к слагаемых. Выберем в Е элементы ж1, ..., хк, хк+1
и произвольные неотрицательные числа ai, ..., а&, a^+i,
сумма которых равна единице. Отметим, что если ак+\ = 1, то все
остальные числа а.{ равны нулю и выпуклая комбинация
рассматриваемых элементов совпадает с ж^+1, так что утверждение
теоремы в этом случае тривиально и его справедливость
очевидна. Пусть ак+\ < 1. Положим А = 1 — ак+\ и Д = —-, г = 1, к.
л
Тогда /3i > 0, г = 1, /с, и
Е 1 ^ 1 - ак+1
г=1 г=1
Поэтому, согласно предположению, у = А ж1 + ... + (Зкхк ЕЕ.
Отсюда заключаем, что
агх1 + ... + акхк + ак+гхк+1 =
= А^ж1 + ... + /Зкхк) + A - А)^+1 =
= \у + A-\)хк+1 ЕЕ.
Таким образом, произвольная выпуклая комбинация элементов
множества Е, содержащая к + 1 слагаемых, принадлежит Е.
Согласно принципу математической индукции, любая выпуклая
комбинация элементов множества Е принадлежит Е. >
Теорема 3.2. Пересечение любого числа выпуклых
множеств является выпуклым множеством.
100 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
-4 Пусть А — некоторое семейство выпуклых множеств в
линейном пространстве С. Рассмотрим множество
Е= П К
Пусть ж1 и ж2 принадлежат Е. Тогда они принадлежат любому
множеству F (Е А. Поскольку по условию множество F выпукло,
для любого Л (Е [0, 1] элемент Аж1 + A — А)ж2 принадлежит F. А
так как F GA выбрано произвольно, то
Лж1 + A-Л)ж2Е f]F = E.
FeA
Значит, множество Е выпукло. >
Пример 3.4. Рассмотрим в W1 множество Е элементов
ж = (жх, ..., жп), координаты которых удовлетворяют системе
неравенств
( ацх\ + а\2х2 + ... + а\пхп ^ 6Ь
I а2\х\ + а22х2 + • • • + а2пхп ^ &2, ,^ ^
[ ат\х\ + ат2х2 + ... + атпхп ^ Ьт.
Множество Е является выпуклым. Чтобы доказать это
утверждение, изменим представление множества. Введем
векторы щ = (a^i, ..., CLin). Тогда с помощью стандартного
скалярного произведения в W1 систему неравенств C.1) можно
записать следующим образом: (ж, щ) ^ 6^, г = 1, п. Другими
словами, множество Е представляет собой пересечение т
полупространств. Поскольку любое полупространство является
выпуклым множеством, то и множество Е выпукло. #
Множество ?cRn, заданное системой неравенств C.1), а
также любое конечное пересечение полупространств в
евклидовом пространстве будем называть выпуклым многогранным
множеством.
3.1. Выпуклые множества
101
Выпуклую комбинацию а\х + ... + а^х элементов
линейного пространства назовем строго выпуклой комбинацией,
если все ее коэффициенты положительны. В частности,
выпуклая комбинация Аж1 + A — А)ж2 строго выпукла, если Л Е @, 1).
Элемент х Е Е называют крайней точкой множества
Е С С (или его вершиной), если этот элемент не может быть
представлен в виде строго выпуклой комбинации двух
различных элементов из Е. Иначе говоря, если х = Лж1 + A — Л)ж2, где
ж1, ж2 Е Е, Л Е @, 1), то ж1 = ж2 = ж. Если выпуклое множество
не имеет крайних точек, то его называют строго выпуклым
множеством.
Пример 3.5. У отрезка [ж1, ж2] е? крайними точками
являются элементы ж1 и ж2, и других крайних точек у
отрезка нет. BR2 у выпуклого многоугольника крайними точками
являются его вершины. У круга ?cf2, заданного
уравнением х\-\-х\ ^ 1, множество крайних точек представляет собой
окружность х\ + х\ = 1. #
Никакая внутренняя точка множества Е С W1 не может
быть крайней точкой этого множества. Действительно, если
ж0 Е Е — внутренняя точка Е, то существует окрестность*
[/={жЕКп: |ж — ж°| < б}, целиком принадлежащая Е. Значит,
множеству Е принадлежат элементы ж1 = ж0 + еа и ж2 = ж0 — ?а,
где а — произвольный вектор, для которого \а\ < 1. Очевидно,
что ж° = 0,5ж1+0,5ж2.
Все линейное пространство — выпуклое множество. Но, как
следует из доказанного, в этом множестве нет крайних точек.
Крайних точек также не имеет аффинное многообразие.
Выпуклой оболочкой произвольного подмножества Е
линейного пространства С называют пересечение всех выпуклых
множеств в ?, которые содержат в себе множество Е.
*3десь и далее |ж| обозначает стандартную норму в R77, элемента х.
102 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Теорема 3.3. Выпуклая оболочка множества Е совпадает
с множеством всех выпуклых комбинаций элементов
множества Е.
А Покажем, что множество Е всех выпуклых комбинаций
элементов множества Е является выпуклым. Выберем в Е
произвольные элементы у1 и у2 и рассмотрим их выпуклую
комбинацию у = ау1 + A—а)у2, а Е [0, 1]. Поскольку у1 и у1
принадлежат Е^ их можно представить как выпуклые комбинации
элементов множества Е:
где
fiij^O, г = 1,2, j = l,ki, ^/ijj = l, г = 1,2.
Подставим эти представления в выражение у = ау1 + A — а)у2:
к\ к\
У = ^2a/JijXlj + ^A - a)/j2jx2j.
В правой части равенства линейная комбинация элементов
xlJ, г = 1, 2, j = 1, ki, принадлежащих множеству Е, является
выпуклой комбинацией, так как все коэффициенты линейной
комбинации неотрицательны, а их сумма равна единице:
к\ к±
J^a/iii + J3(l - a)n2j =
3=1 j=i
к\ к\
= aV^/iij + A — a) /_^/i2j = «• 1 + A — «) • 1 = 1.
Следовательно, элемент у можно представить в виде выпуклой
комбинации элементов множества Е, а потому он будет
принадлежать Е. В силу того что элементы у1, у2 и число а Е [0, 1]
выбирались произвольно, множество Е выпукло.
3.1. Выпуклые множества
103
Пусть выпуклое множество F включает в себя Е. Тогда,
согласно условию выпуклости, множество F содержит любую
выпуклую комбинацию своих элементов, в частности элементов
множества Е. Следовательно, множество F включает в себя
множество Е. Таким образом, множество Е является
подмножеством пересечения всех выпуклых множеств, содержащих в
себе Е. Но поскольку множество Е само является выпуклым
множеством, содержащим Е, то оно совпадает с указанным
пересечением. >
Выпуклую оболочку конечного множества ScRn,
содержащего т-\-\ различных точек жг, называют выпуклым
многогранником. Если т = п и элементы жг, г = 1, п+1, не
принадлежат какой-либо гиперплоскости, то выпуклую оболочку
множества Е= {ж1, ..., жп+1} называют симплексом, а
точки хг — вершинами симплекса. Отметим, что условие,
согласно которому элементы жг, г = 1, п+1, не принадлежат
какой-либо гиперплоскости, равносильно линейной
независимости векторов хг — ж1, г = 2, п+1.
Согласно теореме 3.3, любую точку симплекса можно
представить в виде выпуклой комбинации его вершин. Отметим,
что такое представление единственно. Действительно, если
ж1, ..., жп+1 — вершины симплекса и имеют место
представления
1 2 k -4-1
х = а\х +«2Ж +... + а/с+1Ж ^ ,
х = C1х1+C2х2 + ... + (Зк+1хк+\
то, вычитая из первого равенства второе, получаем
71Ж1 + 72ж2 + ... + Jk+ixk+1 = О,
где коэффициенты 7г = <^г — А? ^ = 1, ^+1? удовлетворяют
равенствам
п+1 п+1 п+1
г=1 г=1 г=1
104 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Предположим, что один из коэффициентов 7ь например 7п+ъ
п
отличен от нуля. Тогда 7/с+1 — — X) 7г и
г=1
1 2 /т-1-1
71» +72Ж +... + jk+iX ^ =
= Ъ(х1-хк+1) + ...+1п(хп-хк+1) = 0. C.2)
Так как 7/с+1 7^ 0, то и один из коэффициентов 7г? я = 1,п,
отличен от нуля. Значит, в силу равенства C.2) элементы
х1 — жп+1, г = 1, п, линейно зависимы. Отсюда заключаем, что
существует вектор а, ортогональный всем этим векторам, т.е.
(а, жг — жп+1) = 0, г = 1, п, или
(а, жг) = (а, жп+1), г = Т~п.
Положим с = (а, жп+1). Тогда все элементы жг, г = 1, п+1,
удовлетворяют уравнению (а, ж) = с, а значит, принадлежат одной
гиперплоскости. Но это противоречит предположению,
согласно которому эти элементы являются вершинами симплекса.
Пример 3.6. В R1 симплексом является отрезок
(одномерный симплекс), bR2 — треугольник (двумерный симплекс), в
R3 — тетраэдр (трехмерный симплекс).
Теорема 3.4 {теорема Каратеодори*). Любую точку х
выпуклой оболочки О произвольного множества Е CW1 можно
представить выпуклой комбинацией элементов из Е,
количество слагаемых в которой не превышает п + 1.
А Каждую точку х Е О можно представить в виде выпуклой
комбинации \\х1 + ... + \тхт элементов хг Е Е, г = 1, га. Мы
можем считать, что число га — это наименьшее число
слагаемых в выпуклой комбинации элементов множества Е, равной
заданному элементу х. Если га ^ п + 1, то утверждение
теоремы верно. Поэтому предположим, что га > п + 1. Тогда
векторы хг — ж1, г = 2, га, линейно зависимы, поскольку их
*К. Каратеодори A873-1950) — немецкий математик.
3.1. Выпуклые множества
105
количество превышает размерность линейного пространства.
Следовательно, верно равенство
m
Y,^(xl-x1) = 0, C.3)
г=2
в котором хотя бы один из коэффициентов /jLi отличен от нуля.
m
Положим /ii = — ^2 №г- Тогда с учетом равенства C.3) получим
5>i^ = 0, 5>i = 0. C.4)
г=1 г=1
Поскольку сумма всех коэффициентов \i{ равна нулю, а среди
них есть коэффициенты, отличные от нуля, то \i{ > 0 хотя бы
для одного номера г.
Введем параметр а^Мис учетом равенств C.4) запишем
х = \^XiXl = У_\ \х% — a 2_1^х1 = Z-/^* ~~ afii)xl. C.5)
г=1 г=1 г=1 г=1
При этом
п п п
^(Aj-a/ij) = ^A^-a^/ii = 1-0 = 1.
г=1 г=1 г=1
Подберем такое значение параметра а, при котором
линейная комбинация с коэффициентами А^ — ot\ii будет выпуклой, а
хотя бы один из коэффициентов будет равен нулю. Для этого
достаточно выбрать а равным наименьшему отношению \/ Hi
среди тех, для которых /^ > 0. Обозначим номер выбранного
отношения через /с, т.е. полагаем a = Xk/j^k- Тогда А^ — оцц ^ 0,
% = 1, га. Действительно, если для фиксированного номера г
имеем \ii ^ 0, то число А^ — ol\1{ положительно как разность
положительного и неположительного чисел. Если же \i{ > 0, то
Xi - a/Ji = Xi /ii = fjLi[ — J > 0,
Hk v№ VkJ
106 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
так как разность в скобках неотрицательна в силу выбора
номера /с, а /^ > 0.
Таким образом, в линейной комбинации C.5) все
коэффициенты неотрицательные, их сумма равна единице. Значит,
эта линейная комбинация является выпуклой. Отметим, что в
соответствии с выбором параметра а имеем А& — аць = 0.
Следовательно, выпуклая комбинация C.5) имеет не га слагаемых,
а не более га — 1.
Итак, представив элемент ж выпуклой комбинацией из га
слагаемых, мы при га > п + 1 построили для ж новую выпуклую
комбинацию, в которой не более га — 1 слагаемых. Однако число
га есть наименьшее число слагаемых в выпуклой комбинации.
Полученное противоречие указывает на то, что предположение
га > п -\-1 неверно. >
3.2. Выпуклые функции
Определение 3.2. Функцию /: О —>> R, определенную на
выпуклом множестве О С Rn, называют выпуклой функцией
на этом множестве, если для любых точек ж1, ж2 Е О и любого
А Е [0, 1] выполнено неравенство
f(Xxl + A - Х)х2) < Xfix1) + A - X)f(x2). C.6)
Функцию / называют строго выпуклой, если для любых
ж1, ж2 Е О при А Е @, 1) и ж1 / ж2 выполнено строгое
неравенство
f(Xxl + A - Л)ж2) < Xfix1) + A - Л)/(ж2). C.7)
Понятия выпуклой (строго выпуклой) функции многих
переменных на выпуклом множестве аналогично понятию
выпуклой вниз (строго выпуклой вниз) в интервале функции одного
переменного [II].
3.2. Выпуклые функции
107
Пример 3.7. а. Выпуклой на множестве О = W1 является
линейная функция
п
f(x) = ^2ajxji (з-8)
где ж = (#1, ..., xn), aj ЕМ, J = 1, п. Действительно, для про-
1 / A) A)\ 2 / B) B)\
извольных точек ж1 = [х\ , ..., я^ ;) и ж -^ , ..., я^ ') и
произвольного Л Е [0, 1] имеем
/(А*1 + A - А)Ж2) = J>(Лж^ + A - X)xf]) =
n п
= a^ajxf + A-а)^2a3xf = af(xl) + A - a)f(x2).
б. Рассмотрим в W1 какую-либо норму ||ж||. Функция f(x) =
= || а? || является выпуклой на множестве Rn, поскольку для
любых точек ж1, х2 Е W1 и любого числа А Е [0, 1], согласно
определению нормы, верно неравенство
ЦЛж1 + A - А)ж2|| ^ АЦж1!! + A - А)||ж2||.
В частности, выпуклыми являются функции
№) =
\\^2ХЬ f2(x) = ^2\xi\, /з(ж) = max |жг|,
\ г=1
. -. i=l,n
г=1 '
где ж = (жх, ..., хп). Эти функции соответствуют евклидовой,
октаэдрической и кубической нормам в W1. #
Пусть функция /: О —>> R определена на множестве ficRn.
Множество G(f) = {(ж, у) Е Mn+1: /(ж) ^ у} называют надгра-
фиком функции /(ж). Неравенство C.6) равносильно
утверждению, что надграфик функции является выпуклым множеством.
Действительно, если точки (ж1, у1) и (ж2, у2) принадлежат
108 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
G(/), то выполняются неравенства /(ж1) ^ у1 и /(ж2) ^ у2. Из
неравенства C.6) заключаем, что
/(Ля.1 + A - Л)Ж2) < Л/(ж1) + A - Л)/(Ж2) < Лу1 + A - Х)у\
Следовательно, точка Л(ж1, у1) + A — Л)(ж2, у2) принадлежит
надграфику функции. Наоборот, если надграфик функции
является выпуклым множеством, то вместе с точками (ж1, у1)
и (ж2, у2), где ж1, ж2 Е О, у1 = /(ж1), у2 = /(ж2), надграфику
принадлежит и их выпуклая комбинация (ж, у), где ж = Лж1 +
+ A — Л)ж2, у = Лу1 + A — \)у2. Но если точка (ж, у)
принадлежит надграфику функции /(ж), то /(ж) ^ у, а это равносильно
неравенству C.6).
Повторяя эти рассуждения для произвольных выпуклых
комбинаций и используя теорему 3.1, приходим к следующему
заключению.
Теорема 3.5. Для того чтобы функция /: О —>> R,
определенная на выпуклом множестве ficRn, была выпуклой,
необходимо и достаточно, чтобы для любых элементов х1 Е О, г = 1, /с,
п
и любых чисел с^ ^ 0, г = 1, п, ^ с^ = 1, выполнялось неравен-
г=1
ство Иенсена*
п п
г=1 г=1
Аналогичное утверждение имеет место и для строго
выпуклых функций.
Теорема 3.6. Для того чтобы функция /: О —>> R,
определенная на выпуклом множестве ficMn, была строго выпуклой,
необходимо и достаточно, чтобы для любых попарно
различных элементов хг Е О, г = 1, /с, и любых чисел с^ > 0, г = 1, п,
*И.Л. Иёнсен A859-1925) — датский математик.
3.2. Выпуклые функции
109
П
^2 ai — 1? выполнялось строгое неравенство
г=1
п п
/(^агжг) <^аг/(жг).
г=1 г=1
Пусть О — выпуклое множество. Выберем в О две
точки ж1 и ж2 и рассмотрим числовое множество ? = 5@, ж1, ж2)
тех значений ?, для которых точка txl + A — ?)ж2 принадлежит
О. Нетрудно показать, что множество 5@, ж1, ж2) является
выпуклым подмножеством числовой прямой, т.е.
промежутком. Пусть /(ж) — произвольная функция, определенная на
выпуклом множестве О. Функцию (p(t) = /(tx1 + A — ?)ж2)
одного действительного переменного, заданную на промежутке
5@,ж1,ж2), будем называть сечением функции /(ж).
Теорема 3.7. Для того чтобы функция /(ж), определенная
на выпуклом множестве О С Rn, была выпуклой (строго
выпуклой), необходимо и достаточно, чтобы любое сечение этой
функции было выпуклой вниз (строго выпуклой вниз)
функцией.
<4 Для произвольных точек ж1 и ж2 в О рассмотрим сечение
(p(t) = f(txl + A — ?)ж2) функции /(ж), представив его в виде
(p(t) = /(ж2 + ?р), где р = ж1 — ж2. Предположим, что функция
(p(t) определена для значений t\ и #2, т.е. точки у1 = ж2 +t\p и
у2 = х2 -\-t2P принадлежат О. Тогда для произвольного А Е [0, 1]
и /i = 1 — А имеем
Ay1 + fiy2 = А(ж2 + tip) + /Дж2 + t2p) = ж2 + (Ati + /it2)p,
откуда заключаем, что
<p(\ti+nt2) = f(\y1+w2).
Если функция /(ж) выпукла, то
p(A*i + 1л12) = /(Ay1 + //у2) < А/(у1) + ///(у2) = \фг) + n<p(t2).
ПО 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Так как значения t\ и t<i из области определения ??(?), а также
Л Е [0, 1] можно выбирать произвольно, заключаем, что ip(t)
выпукла.
Допустим, что каждое сечение функции /(ж) является
выпуклой функцией. Тогда для произвольных точек ж1 и ж2 в Q
и любого А Е [0, 1] имеем
/(Лж1 + /лж2) = <р(А) = <р(А • 1 + // • 0)<
<А(^A)+М0)=А/(ж1)+^(ж2),
где /i = 1 — А.
Доказательство теоремы в случае строго выпуклой функции
аналогично. >
Теорема 3.8. Если функции fi(ж), г = 1, га, определенные
на выпуклом множестве О С Rn, являются выпуклыми на О, то
для любых чисел а^ 0, г = 1, п, функция
т
/(ж) = ^аг/г(ж), ж GO, C.9)
г=1
выпукла на множестве О. Если к тому же одна из функций
fi(x) строго выпукла, а соответствующее этой функции число
ai положительно, то функция f(x) строго выпукла.
-4 Поскольку все функции fi (ж) выпуклы, в силу
определения выпуклости для любых точек ж1, ж2 Е О и любого А Е [0, 1]
выполнены неравенства
fi(Xx1 + (l-X)x2)^Xfi(x1) + (l-X)fi(x2), t = l~^. C.10)
Умножая эти неравенства на неотрицательные числа щ и
складывая, получаем
т т
г=1 г=1
т
+ A - Л) J2 aifi(x2) = Л/(ж1) + A - А)/(ж2). C.11)
г=1
3.2. Выпуклые функции
111
Тем самым доказано, что функция f(x) является выпуклой на
множестве О.
Если функции fi(x) являются выпуклыми на О, причем
среди них хотя бы одна функция строго выпукла на О, то при
х1 ф х2 и A Е @, 1) хотя бы одно из неравенств C.10) является
строгим. В этом случае в C.11) неравенство является строгим,
а функция f(x) — строго выпуклой. >
Следствие 3.1. Сумма выпуклой (строго выпуклой) и
линейной функций является выпуклой (строго выпуклой)
функцией.
-4 Согласно примеру 3.7, линейная функция является
выпуклой в IRn, а значит, и на любом выпуклом множестве. В силу
теоремы 3.8 сумма линейной и выпуклой функций, как
сумма двух выпуклых функций, является выпуклой. Аналогично
сумма строго выпуклой и линейной функций является строго
выпуклой. >
Теорема 3.9. Если (р(х) — выпуклая функция на
выпуклом множестве О С Rn, a h(t) — выпуклая неубывающая
функция одного действительного переменного, определенная,
по крайней мере, на множестве <p(fi), то сложная функция
ф(х) = h{if{x)) является выпуклой на множестве О. Если к
тому же (f(x) — строго выпуклая функция, а функция h(t)
возрастающая на множестве R, то функция ф(х) строго выпукла
на множестве ft.
-4 Для произвольных точек ж1 и ж2 из О и любого числа А Е [0, 1]
имеем
^(Лж1 + A - Х)х2) = h((p(\xl + A - А)ж2)) ^
< h(Xip(x1) + A - ХЫх2)) ^ \h((p(x1)) +
+ A - X)h(ip(x2)) = Хф(х1) + A - Х)ф(х2). C.12)
В этой цепочке соотношений первое неравенство справедливо,
поскольку функция h(t) неубывающая, а функция (р(х)
выпуклая. Второе неравенство справедливо в силу выпуклости
112 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
функции h(i). Эти неравенства показывают, что функция ф(х)
является выпуклой на множестве О.
Если дополнительно функция h(t) возрастает, а функция
(р(х) строго выпукла, то при х1 ф х2 и а Е @, 1) в соотношениях
C.12) первое неравенство является строгим, а это означает,
что функция ф(х) в этом случае будет строго выпуклой на
множестве Q. >
Пример 3.8. Функция е1 является возрастающей и строго
выпуклой на множестве IBL Поэтому если функция /(ж),
определенная на выпуклом множестве О С W1, является выпуклой
(строго выпуклой), то и функция e*(z' также является
выпуклой (строго выпуклой) на О. #
Из примера 3.8 вытекает следующее достаточное условие
выпуклости (строгой выпуклости) функции многих
переменных: если функция д(х) на выпуклом множестве О принимает
только положительные значения, то для ее выпуклости
(строгой выпуклости) достаточно, чтобы выпуклой (строго
выпуклой) была функция \пд(х).
Согласно примеру 3.7, выпуклой является линейная
функция, определяемая равенством C.8). Поэтому функция
п
ф(х) = exp[y^ajXj ], C.13)
i=i
где х = (жх, ..., жп), a exp(t) = ег — экспоненциальная функция,
также является выпуклой.
Обратим внимание на то, что функция ф(х) не
является строго выпуклой, так как она на любой гиперплоскости
а\Х\ + ... + апхп = с принимает постоянные значения. Это
говорит о том, что во втором утверждении теоремы 3.9 условие
строгой выпуклости f(x) нельзя заменить условием строгой
выпуклости h(t).
Теорема 3.9 допускает обобщение. Введем для векторов х =
= C?1, ..., хп)
и У = 0/ъ • • • ? Уп) обозначение х ^ у (векторное
3.2. Выпуклые функции
113
неравенство), если выполняются неравенства Xi ^гц, г = 1,п.
Как обычно, строгое неравенство ж < у означает, что ж^р
ж ф у, т.е. хотя бы одно из неравенств Х{ ^ у^% — 1, п, является
строгим.
Теорема ЗЛО. Если (fi(x), г = 1, т, — выпуклые функции
на выпуклом множестве ficKn, a h(y) — скалярная
функция многих переменных, выпуклая на множестве W71 и
неубывающая по каждому своему аргументу, то сложная функция
ф(х) = /i((/?i(a?),... ,(/?т(ж)) является выпуклой на множестве О.
Если к тому же хотя бы одна из функций (pi(x), г = 1, га, строго
выпукла на множестве ficln, а функция h(y) возрастает по
каждому своему аргументу, то функция ф(х) является строго
выпуклой на ft.
-4 Рассмотрим векторную функцию многих переменных ср(х) =
= (<pi(a), ..., <рш(ж)). Тогда ф(х) = h(cp(x)), а для функции
<р(ж) при любых ж1, ж2 Е О и А Е [0, 1] выполняется векторное
неравенство
(fiXx1 + A - А)ж2) ^ А^ж1) + A - А)(^(ж2), C.14)
каждая составляющая которого означает выпуклость
соответствующей координатной функции (fi(x) векторной функции
(f(x). Условие неубывания функции h(y) по каждому
аргументу означает, что h(y1) ^ h(y2) при у1 ^ у2. С учетом этих
соображений цепочка соотношений C.12) из доказательства
предыдущей теоремы воспроизводится практически без
изменений. Действительно, для любых ж1, ж2 Е О и А Е [0, 1] имеем
^(Аж1 + A - А)ж2) = h((p(\xl + A - А)ж2)) ^
< h(XiP(x1) + A - АМж2)) ^ \h(ip{x1)) +
+ A - \)h(ip(x2)) = Хф(х1) + A - Х)ф(х2). C.15)
Дополнительное условие строгой выпуклости одной из
функций (fi(x) означает, что при ж1 ф ж2 и А Е @, 1) векторное
неравенство C.14) становится строгим. А дополнительное уело-
114 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
вие возрастания h(y) по каждому аргументу означает, что
h{yx) < h(y2) при у1 < у2. Поэтому, как и в теореме 3.9, эти
два дополнительных условия гарантируют, что в
соотношениях C.15) первое неравенство будет строгим, а сложная функция
ф(х) — строго выпуклой. >
Пример 3.9. Рассмотрим функцию
т п
ф(х) = J^CiJJea^',
г=1 j=l
где х = (ж1, ..., жп) Е Kn; а^/ ЕК, г = 1, га, j = 1, п; с^ > 0, г =
= 1, га. Эта функция определена на всем линейном
пространстве W1. Представим ее в виде
т
ф(х) = ^2ъщ(х), C.16)
г=1
где
п
(Pi(x) =exp(^2aijxjj- C-17)
Каждая из функций (fi(x) является выпуклой на множестве
W1 (см. пример 3.8). Поэтому, согласно теореме 3.8, функция
ф(х) также выпукла на W1.
Если га < п, то функция ф(х) не является строго выпуклой,
так как она постоянна на каждом аффинном многообразии,
определяемом системой уравнений
( ацхх + а12х2 + ... + а1пхп = 6Ь
I a2\xi + a22^2 + ... + а2пхп = &2,
где 6i, ..., Ьш — некоторые числа, которые всегда можно
подобрать так, что эта система будет совместной. Рассмотрим
случай га = п и предположим, что матрица А записанной системы
3.2. Выпуклые функции
115
уравнений является невырожденной. Тогда систему равенств
f 2/1 = Q>l\Xl + «12^2 + • • • + CLinXn,
у2 = a2lXi + а22%2 + •••+ ^n^n,
I Уп = ctnixi + an2X2 + ... + annxri
можно трактовать как замену старых координат х\, ..., хп
новыми координатами yi, ..., уп. В новом базисе функция ф(х)
имеет вид
ф(у) =cieyi +с2еУ2 + ... + спеУп.
Выберем в W1 произвольным образом несовпадающие точки
У1 ~ (у I? •••? Уп )? i — 1? 2, заданные своими координатами в
новом базисе. Тогда для произвольного А Е @, 1) и /i = 1 - Л
с учетом выпуклости экспоненциальной функции ехр(ж) = ех
имеем
ф(Ху1 + (лу2) = 5>ехр(АугA) + цуЮ) <:
г=1
п
^^с^(Аехр(уга))+//ехр(^2))) =
г=1
= A^czexp(yfV^E^exP^2)) = ^(y1)+^B/2). C.18)
г=1 г=1
Так как у1 ф у2, то для некоторого номера г выполняется
A) / B) о
неравенство уг- фу\ - В силу строгой выпуклости
экспоненциальной функции для указанного номера г выполняется строгое
неравенство
exp(AyJ1} +iiyf}) < Aexp(yJ1}) +/iexp(yf}).
Поэтому в соотношениях C.18) неравенство является строгим,
а функция ф(у) — строго выпуклой.
Если т ^ п и ранг матрицы А равен п, то в
представлении функции ф(х) можно выделить п слагаемых, отвечающих
116 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
базисным строкам матрицы Айв сумме дающих строго
выпуклую функцию. Следовательно, в этом случае ф(х), как
сумма строго выпуклой функции и нескольких выпуклых
функций, является строго выпуклой.
3.3. Дифференцируемые выпуклые функции
Дифференцируемость функции позволяет сформулировать
простые признаки, с помощью которых можно выяснить,
является ли она выпуклой функцией.
Напомним [II], что дифференцируемая на промежутке (а, Ь)
действительная функция h(t) одного действительного
переменного является выпуклой (строго выпуклой) на (а, Ь) тогда и
только тогда, когда ее производная hf(t) на этом промежутке
не убывает (возрастает). Отсюда с помощью формулы
конечных приращений легко заключить, что для выпуклой функции
h(t) при любых t\ и ^2, a <t\ <t2 <Ъ, выполняется двойное
неравенство
Л;(*1)(*2 - *i) ^ h(t2)-h(h) <: ti(t2)(t2-h). C.19)
Действительно, в силу формулы конечных приращений h(t2) —
— h(t\) = hf(^)(t2 — ?1), где ? Е (ti,t2), а в СИЛУ выпуклости
функции h'{ti) ^ h'(?) ^ h'(t2).
Двойное неравенство C.19) является не только необходимым
условием выпуклости функции /i(t), но и достаточным,
поскольку из него вытекает неравенство hf(ti) ^ h'{t2)^ означающее,
что производная функции h(t) не убывает.
Соотношения C.19) записаны в предположении, что t\ <t2.
Однако это требование не существенно. В самом деле,
умножим неравенства C.19) на число —1. В результате придем к
эквивалентным неравенствам
ti{t2){h - h) ^ h(h)-h(t2) ^ ti{tl){tl-t2),
которые сводятся к C.19), если в них поменять местами t\ vit2.
3.3. Дифференцируемые выпуклые функции 117
Нетрудно показать, что замена неравенств C.19) строгими
неравенствами дает критерий строгой выпуклости
дифференцируемой функции h(t).
Критерий C.19) выпуклости функции одного переменного
не лучше традиционного критерия монотонности производной,
но обладает важным преимуществом: его можно обобщить на
случай функции многих переменных.
Теорема 3.11. Пусть скалярная функция f(x)
дифференцируема* на выпуклом множестве Ocln. Тогда для
выпуклости функции f(x) на О необходимо и достаточно, чтобы для
любых двух точек ж1, ж2 Е О было выполнено неравенство
(gvadf(x2),h)^f(xl)-f(x2) < (grad/Oz1),^), C.20)
где h = х1 — х2 и grad/(sc) — градиент функции f(x) в точке х.
А Необходимость. Пусть функция f(x) выпукла на О.
Рассмотрим сечение cp(t) = f(txl + A — t)x2) функции /(ж),
заданное произвольными точками ж1, ж2 Е О. Функция cp(t)
определена и дифференцируема по крайней мере на отрезке
[0, 1]. Согласно теореме 3.7, функция (p(t) выпукла на [0, 1],
а потому для нее справедливы неравенства
?>'(())< ?>A)-р@К ?>'(!)• C-21)
В силу правила дифференцирования сложной функции
ip'(t) = (grad/(a;), h), ж = tx1 + A - t)x2. C.22)
Поэтому (p'@) = (grad/(sc2), h) и (p'(l) = (grad/^2), h).
Подставляя найденные выражения для производных в неравенства
C.21), получаем неравенства C.20).
*Дифференцируемость функции в какой-либо граничной точке
множества ft предполагает, что функция определена в некоторой окрестности
этой точки.
118 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Достаточность. Пусть для произвольных точек ж1 и ж2
множества О выполняются неравенства C.20). Возьмем
произвольные точки у1, у2 Е О и рассмотрим соответствующее
сечение ip(t) = f{tyl + A — t)y2). Выберем произвольные значения
*1 и *2 из области определения i/i(t). Точки хг = ^З/1 + A — U)y2,
г = 1, 2, принадлежат О, и для них выполняются неравенства
C.20). Из равенств C.22) при t — t\ и t<2 получаем
^(ti) = {gvadf(xi),y1-y2), г = 1,2.
Поскольку h = ж1 — ж2 = (*2 — iiXy1 — 2/2)> т0
(grad/(**), Л) = (grad Дж*), у1 - у2) (t2 - *х) =
= ^;(*i)(*2-ti), г = 1, 2,
и неравенства C.20) равносильны следующим:
^Ч*2)(*2 - *l) ^ ^(*2) - ^(*l) ^ ^4*l)(*2 - *l).
Значения t\ и t^ из области определения ip(t) выбирались
произвольно. Следовательно, функция i/j(t) является выпуклой.
Итак, мы показали, что при выполнении неравенств C.20)
любое сечение дифференцируемой функции /(ж) является
выпуклой функцией. Значит, согласно теореме 3.7, /(ж) —
выпуклая функция на О. >
Замечание 3.1. Повторяя ход доказательства теоремы
3.11, несложно установить, что для строгой выпуклости
функции /(ж), ж Е Г?, непрерывно дифференцируемой на выпуклом
множестве OcRn, необходимо и достаточно, чтобы для любых
двух различных точек ж1, ж2 Е О было выполнено неравенство
(gvadf(x2),h)<f(x1)-f(x2)<{gvadf(x1),h). # C.23)
Проверить выпуклость или строгую выпуклость функции
/(ж) с помощью критериев C.20) и C.23) можно, но
практически довольно сложно. Задача упрощается, если функция /(ж)
3.3. Дифференцируемые выпуклые функции 119
дважды дифференцируема. В этом случае ответ можно
получить, исследуя матрицу Гессе функции /(ж).
Напомним, что симметрическую матрицу А называют
положительно (отрицательно) определенной, если она является
матрицей положительно (отрицательно) определенной
квадратичной формы (эту квадратичную форму можно записать в
виде ж Ах, где х Е W1 — вектор-столбец, или с помощью
стандартного скалярного произведения в виде (Ах,х)). Введем
аналогичные понятия неотрицательно (неположительно)
определенной матрицы как матрицы неотрицательно
(неположительно) определенной квадратичной формы, а также
знаконеопределенной матрицы как матрицы знаконеопре-
деленной квадратичной формы.
Сначала рассмотрим одномерный случай. Как уже было
отмечено, критерием выпуклости функции (p(t) одного
переменного является неубывание ее производной. Если функция
ip(t) дважды дифференцируема, то из условия неубывания (f'(t)
вытекает, что (f"(t) неотрицательна. Верно и
противоположное утверждение. Если српf(t) ^ 0, то функция (f'(t) не убывает,
а функция (f(t) выпукла.
Теорема 3.12. Для того чтобы дважды дифференцируемая
на открытом выпуклом множестве ficRn функция f(x) была
выпуклой, необходимо и достаточно, чтобы ее матрица Гессе
Н(х) была неотрицательно определена в любой точке х Е О.
А Необходимость. Выберем в О две произвольные точки
ж1 и ж2 и рассмотрим сечение cp(t) = f(txl + A — t)x2)
функции /(ж), заданное этими точками. Функция cp(t) определена в
окрестности точки 0 (при t = 0), так как функция /(ж)
определена в окрестности точки ж2. Как сложная функция, (p(t)
дважды дифференцируема при t = 0, и
tp"@) = {H(x2)h,h),
где h = ж1 — ж2. Если функция /(ж) выпукла на О, то ее
сечение (f(t) является выпуклой функцией одного переменного.
120 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Поэтому (р"@) ^ 0. В силу произвольного выбора ж1 и ж2
заключаем, что
(H(x2)h,h) >0
для любого вектора /iGRn. Но это и означает, что
матрица Гессе Н(х2) в произвольной точке ж2 Е О неотрицательно
определена.
Достаточность. Пусть матрица Гессе Н(х)
неотрицательно определена в каждой точке ж ? О, т.е.
(Я(ж)Л, h) ^ 0, /iGRn.
Выберем произвольные точки ж1, ж2 Е О и соответствующее им
сечение tp(t) = f(txl + A — ?)ж2). Так как
<p"(t) = (H(x)h,h),
где ж = txl + A — ?)ж2, a fo = ж1 — ж2, для всех значений t из
области определения cp(t) выполняется неравенство (p"(t) ^ 0.
Следовательно, функция (p(t) выпукла, а в силу теоремы 3.7
выпукла и функция /(ж). >
Замечание 3.2. Можно было бы предположить, что
критерием строгой выпуклости на множестве О дважды
дифференцируемой функции является положительная определенность
в О ее матрицы Гессе. Действительно, нетрудно показать, что,
как и в теореме 3.12, положительная определенность
матрицы Гессе на всем множестве является достаточным условием
строгой выпуклости. Однако это условие не является
необходимым. Соответствующий контрпример можно привести уже
в одномерном случае. Функция у = ж4 строго выпуклая,
однако ее вторая производная у" = 12ж2 обращается в нуль в точке
х = 0. Аналогичный пример можно построить при любой
размерности. Так, в двумерном случае функция f{x\,X2) = х\ + х\
является строго выпуклой в!2, но ее матрица Гессе в точке
@, 0) является нулевой. #
3.3. Дифференцируемые выпуклые функции V2\
Проверку свойств матрицы Гессе можно строить на основе
ее собственных значений. Для неотрицательно определенной
матрицы все собственные значения неотрицательны, а для
положительно определенной матрицы все собственные значения
положительны [IV]. Для проверки положительной
определенности матрицы Гессе можно также использовать критерий
Сильвестра. Если функция является квадратичной, то
элементы матрицы Гессе этой функции постоянны. В этом случае
проверка выпуклости или строгой выпуклости такой функции
существенно упрощается.
Пример ЗЛО. Проверим, является ли выпуклой
квадратичная фуНКЦИЯ f(x\1X2) = Зх\ — 4:Х\Х2 + 2ж| +Х\ — 1X2-
Найдем матрицу Гессе этой функции:
„_/ ?х\ fxix2\ _ ( 6 -4\
Угловые (или главные) миноры этой матрицы положительны:
Аг = 6 > 0 и А2 = detff = 6 • 4 - (-4) • (-4) = 8 > 0. Поэтому,
согласно критерию Сильвестра, матрица Н положительно
определенная, и в соответствии с замечанием 3.2 рассматриваемая
функция строго выпуклая. #
Проверка положительной определенности матрицы
небольшого размера (второго или третьего порядков) с помощью
критерия Сильвестра, как правило, проще, чем аналогичная
проверка путем анализа собственных значений. Вполне
естественно в таких ситуациях исследование на неотрицательную
определенность (если матрица не является положительно
определенной) также проводить без вычисления собственных
значений. Существует критерий неотрицательной определенности
матрицы, аналогичный критерию Сильвестра.
Минор матрицы А назовем диагональным минором, если
строки и столбцы, входящие в этот минор, имеют одинаковые
номера.
122 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Теорема 3.13. Необходимым и достаточным условием
неотрицательной определенности симметрической матрицы
является неотрицательность ее диагональных миноров.
<4 Пусть А — симметрическая неотрицательно определенная
матрица, т.е. (Ах, х) > 0, х Е W1. Рассмотрим квадратичную
форму
f?(x) = (Ах, х)+е (х, х) = ((А + el)x, х),
где / — единичная матрица соответствующего порядка, а
е > О — параметр. Ясно, что f?(x) —>> (Ах, х) при е —>> +0.
Для любого числа е > 0 квадратичная форма f? и ее матрица
А + el являются положительно определенными, так как при
х^О
f?(x) = (Ах,х)+е\\х\\2 ^е\\х\\2 > 0.
Любой диагональный минор матрицы А + el путем изменения
номеров ее пар строк и столбцов можно превратить в ее
угловой минор. Такое изменение соответствует изменению порядка
переменных квадратичной формы и сохраняет условие
положительной определенности квадратичной формы и матрицы. В
силу критерия Сильвестра заключаем, что диагональные (не
только угловые) миноры матрицы А + el положительны. При
е —> +0 все миноры матрицы А + el стремятся к
соответствующим минорам матрицы А. Значит, все диагональные миноры
неотрицательно определенной матрицы А неотрицательны.
Теперь предположим, что все диагональные миноры
матрицы А неотрицательны. Можно показать, что определитель
матрицы A + el есть многочлен от переменного е, причем старший
коэффициент этого многочлена (при степени еп) равен единице,
а коэффициент многочлена при степени е , к = 0,п—1, —
сумме всех диагональных миноров матрицы А порядка п — к. Так
как все диагональные миноры матрицы А неотрицательны, то
и коэффициенты многочлена неотрицательны. Следовательно,
det(a + el) > 0 при е > 0.
Сказанное относится не только к самой матрице А, но
и к любому ее диагональному минору: диагональный минор
3.3. Дифференцируемые выпуклые функции 123
Dfr + elk (Ik — единичная матрица порядка к) матрицы А + е1
порядка к есть многочлен переменного е степени /с, причем
старший коэффициент многочлена равен единице, а остальные
коэффициенты равны сумме диагональных миноров матрицы
А соответствующего порядка, входящих в минор D^, и,
следовательно, неотрицательны. Это означает, что минор D^ + el
при е > 0 является положительным.
Итак, у матрицы А + el при е > 0 все диагональные (в том
числе и угловые) миноры положительны. Согласно критерию
Сильвестра, матрица А + el является положительно
определенной. Отсюда вытекает, что квадратичная форма fe(x) =
= (Ах, х) с матрицей А + eI при е > 0 положительно определена,
т.е. f?(x) > 0, если х ^ 0. Но тогда для квадратичной формы
f(x) = (Ах, х) при любом векторе х Е Кп, х ^ 0, имеем
f(x)= limf?(x)>0,
а это означает, что квадратичная форма fx и ее матрица А
являются неотрицательно определенными. >
Исследование симметрической матрицы А на
неотрицательную или положительную определенность рационально начинать
с вычисления ее определителя det А. Если detA = 0 и
диагональные элементы матрицы А неотрицательны, то можно
рассчитывать на неотрицательную определенность матрицы А.
В этом случае проверяются диагональные миноры, причем
проверку диагональных миноров на знак можно прекратить, как
только один из них окажется отрицательным. Это будет
означать, что матрица знаконеопределенная.
Если det А > 0 и все диагональные элементы матрицы А
положительны, то можно ожидать, что эта матрица
положительно определена. Поэтому следует проверить на знак все угловые
миноры матрицы. Проверку можно прекратить, как только
очередной угловой минор окажется отрицательным, что
означает знаконеопределейность матрицы. Если очередной угловой
124 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
минор окажется нулевым, то матрица не будет положительно
определенной, и в этом случае следует перейти к проверке всех
диагональных миноров, чтобы определить, является ли
матрица неотрицательно определенной.
Пример 3.11. Проверим, является ли выпуклой
квадратичная функция
f(xi,X2,Xs) =х\+х\ + х\- Х\Х2 - Х2Хз — Х^Х\ + Х\ + Х2 + Х3 + 1.
Для этой функции запишем матрицу Гессе
/ 2 -1 -1\
-1 2 -1 .
\-1 -1 2)
Непосредственным вычислением убеждаемся, что detH = 0.
Это значит, что матрица Гессе не может быть
положительно определенной. Неотрицательность диагональных элементов
не позволяет сразу же сделать заключение о том, что
матрица Н знаконеопределенная. Поэтому необходимо проверить на
знак все диагональные миноры. В данном случае речь идет о
проверке трех диагональных миноров второго порядка.
Непосредственно из вида матрицы Н заключаем, что все три
диагональных минора одинаковы и равны
I 2 _11-з
|-1 2\~6-
Следовательно, матрица Н неотрицательно определенная, а
квадратичная функция выпуклая вК3. #
Отметим, что для квадратичной функции положительная
определенность матрицы Гессе Н является не только
достаточным, но и необходимым условием строгой выпуклости.
Действительно, если матрица Н неотрицательно определена, но
Н
( ^1
f"
J Х2Х\
\Jxsxi
f
J XiX2
JT2
f"
J X3X2
f" \
JX1X3 1
f"
JX2X3
f'xl J
=
3.3. Дифференцируемые выпуклые функции 125
не является положительно определенной, то эта матрица
вырождена. Значит, существует хотя бы одномерное линейное
подпространство, на котором квадратичная форма функции
равна нулю. На этом подпространстве сама квадратичная
функция линейна, а потому не является строго выпуклой.
Пример 3.12. Выясним, существует ли выпуклое
множество flcR2, на котором функция
/(Ж1,Ж2) =х\+х\ —Х\Х2 + 1
является строго выпуклой.
Запишем матрицу Гессе этой функции
Н
?11 ?11
J rr2 J ХЛ
Х\Х2
?11 ?11
Jx2X! Jx2
м,
Q*
Для положительного ответа на
поставленный вопрос достаточно
указать множество, на котором
матрица Гессе положительно
определена. Согласно критерию
Сильвестра, для этого требуется
выполнение двух условий: Ai = 6х\ > О
и A2=detH = 36x1x2-l > 0.
Соответствующее множество О,
ограниченное гиперболой х±Х2 = 1/36,
представлено на рис. 3.1.
Поскольку при х\Х2 < 1/36 определитель матрицы Гессе
отрицателен, в области ft2 между двумя ветвями гиперболы
матрица Гессе является знаконеопределенной. В области Оз
в третьем квадранте Ai < 0 и А2 > 0, т.е. матрица Гессе
отрицательно определена. Таким образом, область О является
максимальной областью строгой выпуклости рассматриваемой
функции.
Рис. 3.1
126 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
3.4. Условия минимума выпуклых функций
Поиск наименьшего значения функции многих
переменных — сложная задача. Напомним некоторые факты,
относящиеся к этой задаче.
Точка, в которой функция достигает своего наименьшего
значения, является точкой локального минимума этой функции.
Поэтому для определения наименьшего значения функции, если
функция достигает его, достаточно найти все точки
локального минимума этой функции и среди них выбрать ту (или те),
в которой функция имеет наименьшее значение. Такой
подход возможен, если функция имеет конечное (и относительно
небольшое) число точек локального минимума.
Точки локального минимума функции, являющиеся
внутренними точками области определения функции, можно
искать, опираясь на необходимое условие экстремума функции.
Если внутренняя точка ж* Е О множества О С W1 есть
точка локального минимума функции /(ж), определенной на О,
и функция f(x) дифференцируема в точке ж*, то эта точка
является стационарной точкой функции /(ж), т.е. в этой точке
выполняется условие
grad/0z*) = O, C.24)
где grad/^*) — градиент функции в точке ж*. Таким образом,
точки локального минимума внутри области определения — это
либо стационарные точки, либо точки недифференцируемости
функции (критические точки). Поэтому точку наименьшего
значения функции, если она существует, можно искать,
сравнивая значения функции во всех стационарных и критических
точках функции. Выяснять, какие из этих точек являются
точками локального минимума, не нужно.
Проверить, является ли стационарная точка точкой
локального минимума, можно с помощью достаточного условия
экстремума. Если функция /(ж) дважды непрерывно дифференци-
3.4. Условия минимума выпуклых функций 127
руема в стационарной точке ж* и матрица Гессе Н(х*) функции
/(ж) в этой точке положительно определена, то ж* является
точкой строгого локального минимума.
Функция может достигать наименьшего значения в
граничной точке области определения. Дифференциальные свойства
функции многих переменных можно в этом случае
использовать, если границей области определения является гладкая
кривая или поверхность. В этом случае можно поставить задачу
на условный экстремум, в которой уравнения связи описывают
границу области, и определить точку, в которой функция
достигает наименьшего значения, как точку условного
локального минимума. В остальных случаях необходимо
непосредственное исследование функции на границе области определения, а
ее дифференциальные свойства не могут помочь в решении
задачи.
Необходимые и достаточные условия экстремума функции
многих переменных далеко не всегда обеспечивают решение
задачи минимизации. Использование необходимого условия
локального экстремума приводит к необходимости решать
систему нелинейных уравнений, что само по себе является сложной
задачей. Функция может иметь большое (или даже
бесконечное) число стационарных и критических точек, и тогда
выбрать точку наименьшего значения функции среди них сложно.
Наконец, трудности возникают, если точка наименьшего
значения находится на границе области определения функции.
Достаточные условия экстремума могут помочь выделить
среди стационарных точек те, которые являются точками
локального минимума. Тем самым сокращается общее число
точек, „подозрительных на наименьшее значение". Однако даже
если стационарная точка определена, функция дважды
непрерывно дифференцируема в ней, матрица Гессе в этой точке
вычислена, то это еще не гарантирует определенного ответа,
является ли исследуемая точка точкой локального минимума.
Дело в том, что матрица Гессе может оказаться неотрица-
128 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
тельно определенной. А в этом случае на поведение функции
в окрестности стационарной точки оказывают влияние
дифференциалы высших порядков (если такие, конечно, существуют).
Все указанные трудности можно преодолевать с помощью
методов, в которых не используются дифференциальные
свойства функции. И в этом случае важную роль могут играть
другие, не связанные с дифференцируемостью, свойства функции.
Некоторые выводы о существовании и единственности точек
локального минимума можно сделать для выпуклых функций.
Теорема 3.14. Если функция /(ж), определенная на
выпуклом множестве ficRn, является выпуклой, то эта функция
в любой точке локального минимума достигает наименьшего
в Q значения. Множество всех точек локального минимума
функции выпукло. Функция, строго выпуклая на выпуклом
множестве, имеет не более одной точки локального минимума.
-4 Пусть ж*ЕЙ — точка локального минимума функции f(x).
Предположим, что в этой точке значение функции не
является наименьшим на множестве О, т.е. существует точка у* Е О,
для которой /(у*) < /(ж*). Рассмотрим сечение функции /(ж),
соответствующее паре точек у* и ж*, т.е. функцию одного
переменного (p(t) = f(ty* + A — t)x*). Эта функция в силу
выпуклости множества О определена по крайней мере на отрезке
[О, 1]. Покажем, что в точке t = 0 функция cp(t) достигает на
[О, 1] наибольшего значения. Действительно, с учетом неравен-
ства f(y*) < f{x*) при t G @, 1)
?>(*) = /(V + A " t)x*) < tf(y*) + A - t)f(x*) <
<tf(x*) + (l-t)f(x*) = f(x*) = <p@).
Для произвольной окрестности U точки ж* существует
настолько малое число t > 0, что ж = ty* + A — t)x* Е U. Тогда
f(x) = <p(t)<<p@) = f(x*),
3.4. Условия минимума, выпуклых функций 129
а это противоречит тому, что точка ж есть точка локального
минимума. Таким образом, предположение о том, что в точке
локального минимума ж* функция не достигает наименьшего
значения, неверно.
Из доказанного следует, что во всех точках локального
минимума выпуклая функция /(ж) имеет одно и то же значение,
равное наименьшему значению rrif этой функции. Очевидно,
что каждая точка, в которой функция принимает значение га/,
является точкой локального минимума функции.
Следовательно, множество точек локального минимума функции совпадает
с множеством f~l{rrif) — прообразом значения rrif при
отображении у = fix).
Теперь покажем, что множество f~l{rrif) точек локального
минимума функции f(x) является выпуклым. Это утверждение
очевидно, если множество пустое или содержит лишь одну
точку. Поэтому будем считать, что оно содержит не менее
двух точек.
Рассмотрим две точки ж1, ж2 Е /_1(raj), в которых функция
f(x) принимает одно и то же значение rrif. Тогда в каждой
точке х = tx1 + A — ?)ж2, t Е [0, 1], имеем f(x) ^ га/, так как
rrif — наименьшее значение функции в О. В то же время в
силу выпуклости функции f(x)
f(x) = f(tx1 + (l-t)x2)^
^ tf{xl) + A - t)f(x2) = tmf + A - t)mf = rrif.
Таким образом, во всех точках отрезка [ж1, ж2] функция /(ж)
принимает постоянное значение rrif. Следовательно, для любых
точек ж1, ж2 Е f~l{rrif) имеем [ж1, ж2] С /_1(mj), т.е. множество
f~1(rrif) является выпуклым.
Наконец, покажем, что в случае строго выпуклой функции
множество f~1(rrif) не может содержать более одной точки.
Если функция /(ж) строго выпуклая, то для любых различных
точек ж1, ж2 Е О и любого числа t Е @, 1) выполняется строгое
130 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
неравенство
f(txl + A - t)x2) < tf(Xl) + A - t)f(x2).
Предположим, что ж1, ж2 Е /_1(mj) — точки локального
минимума. Тогда в этих точках /(ж) достигает наименьшего
значения rrif. При этом для любого t Е @, 1) имеем
/(ж) = /(te1 + A - ?)ж2) < tmf + A - t)m/ = га/,
а это невозможно, так как га/ — наименьшее значение
функции. Противоречие показывает, что строго выпуклая функция
может иметь не более одной точки локального минимума. >
Теорема 3.15. Пусть функция /(ж) выпукла на выпуклом
множестве ficRnn дифференцируема в точке ж* Е О. Для того
чтобы точка ж* была точкой локального минимума функции
/(ж), необходимо и достаточно, чтобы для любой точки ж Е О
выполнялось неравенство
^гас1/(ж*),ж-ж*) >0. C.25)
А Необходимость. Пусть ж* Е О — точка локального
минимума функции /(ж) и функция дифференцируема в этой
точке. Выберем произвольную точку ж Е О и рассмотрим
сечение cp(t) = f(tx + A — t)x*). Функция cp(t) определена на отрезке
[0, 1], имеет в точке t = 0 локальный минимум и
дифференцируема в этой точке. Следовательно, ^'@) ^ 0. По правилу
дифференцирования сложной функции
= ^гас!/(ж*),ж-ж*),
откуда получаем неравенство C.25).
Достаточность. Пусть в точке ж* выполнено
неравенство C.25). Выберем произвольную точку ж Е О и рассмотрим
сечение tp(t) = f(tx + A — t)x*). Так как /(ж) выпукла, то и ее
<p'@) = -f(tx + (l-t)x*)
3.4. Условия минимума, выпуклых функций 131
сечение (p(t) выпукло. Из неравенства C.25) заключаем, что
(ff@) ^ 0. Следовательно, (p(t) — неубывающая функция на
отрезке [0, 1] и (р@) ^ ^A). Последнее неравенство равносильно
неравенству /(ж*) ^ /(ж). Таким образом, в точке ж* функция
/(ж) принимает наименьшее в О значение. >
Замечание 3.3. Во внутренней точке ж* множества Q
неравенство C.25) равносильно равенству grad/^*) = 0.
Действительно, в этом случае для любого вектора /iGKn для
достаточно малого числа е > 0 имеем ж* + eh Е О и ж* — eh Е О.
Следовательно, одновременно выполняются неравенства
(grad/(aj*), eh) > 0, (grad/(aj*), -eh) > 0.
Отсюда заключаем, что (grad/^*), h) = 0 для любого вектора
heW1 Hgrad/(a;*) = 0.
Таким образом, неравенство C.25) можно рассматривать
как обобщение необходимого условия grad/^*) = 0 локального
минимума функции на случай, когда точка не является
внутренней точкой области определения функции. При этом
следует учитывать, что неравенство C.25) дает не только
необходимое условие локального минимума, как равенство grad/^*) =
= 0, но и достаточное. Такое обобщение стало возможным
благодаря дополнительному условию выпуклости функции.
Заметим, что условие C.25) при ж = ж* переходит в равенство, и
поэтому это условие можно записать в эквивалентной форме
min(grad Дж*), ж - ж*) = 0. C.26)
Замечание 3.4. Предположим, что внутренняя точка ж*
множества ft является стационарной точкой функции /(ж),
определенной на множестве О. Если функция /(ж) дважды
непрерывно дифференцируема в некоторой окрестности U точки
ж*, а ее матрица Гессе неотрицательно определена в каждой
точке окрестности J7, то эту окрестность можно уменьшить
132 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
так, что она станет выпуклым множеством (любая е-окрест-
ность — выпуклое множество), и тогда, согласно теореме
3.12, функция f(x) выпукла в U. Для такой функции условие
grad/(x*) = 0 является не только необходимым, но и
достаточным условием локального минимума.
Отметим, что выпуклая функция может иметь более одной
точки локального минимума. Например, квадратичная
функция /(жх,Ж2) = (х\ +Х2J достигает в точке @, 0) наименьшего
значения, равного нулю. Но точками локального минимума
являются также и все точки вида (?, — ?), t Е R.
3.5. Сильно выпуклые функции
Определение 3.3. Функцию /(ж), определенную на
выпуклом множестве О С Rn, называют сильно выпуклой, если
существует такая константа 7 > 0, называемая параметром
сильной выпуклости, что для любых точек ж1, ж2 Е О и
любого а Е [0, 1] справедливо неравенство
f(ax1 + (l-a)x2) ^
< af(xl) + A - a)f(x2) - аA - а)фг - х2\2. C.27)
Всякая сильно выпуклая функция является строго выпуклой
функцией, но не наоборот. Действительно, при х1 ^ х2 и
а Е @, 1) из неравенства C.27) вытекает строгое неравенство
C.6). Однако выполнение этого неравенства не означает, что
справедливо неравенство C.27). Например, функция f(x\,X2) =
= х\-\-х\ является строго выпуклой и для нее верно неравенство
C.6). Однако неравенство C.27) при х1 = (р, q) и х2 = @, 0)
равносильно неравенству
«V + qA) ^ «(Р4 + qA) ~ «A - «O(Р2 + Ч2),
или
7(р2 + д2КA + « + а2)(р4 + д4),
3.5. Сильно выпуклые функции
133
Рис. 3.2
причем это неравенство должно быть верно при некотором
фиксированном значении 7 и любых р, q и а Е @, 1). Ясно,
что при соответствующем выборе р, q и а оно нарушается
(например, при р = q < 1/2 и любом а Е @, 1)).
Дадим геометрическую интерпретацию определения 3.3,
рассмотрев функцию у = f(x) одного переменного.
Зафиксировав х\ и Х2 из области определения функции и
обозначив х(а) = ш?1 + A — a)^2,
будем изменять а от 0 до 1.
Ясно, что тогда значение х (а)
будет изменяться от Х2 до #i, а
точка (ж, /(ж)) пройдет по
графику функции у = /(ж) от
точки В = (Ж2, /(#2)) Д° точки ^4- —
= (ж1, /fai)) (рис. 3.2).
Уравнения
{х = ж(а),
у = а/(ж1) + A-а)/(ж2)
в плоскости хОу описывают прямую L (секущую),
соединяющую точки А и Р, а уравнения
{ж = ж(а),
у = a/(^i) + A - a)f(x2) - аA - аO(^1 - ж2J
задают параболу Р вида у = аж2 + Ъх + с, а = 7(^1 ~~ х2J•> которая
проходит через точки А ж В. Неравенство C.27) в этом случае
означает, что график функции у = f(x) на плоскости хОу
расположен ниже не только секущей, соединяющей точки А и
Р, но и параболы Р, прогиб которой определяется параметром
7, и его можно выбрать сколь угодно малым. Другими словами,
в области, ограниченной секущей и графиком функции, можно
построить параболу, соединяющую точки А ж В.
Пример 3.13. Убедимся, что квадратичная функция вида
f(x) = (Qsc, х) +2 (с, ж), с,х ? Rn, где Q — положительно
134 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
определенная симметрическая матрица порядка п, является
сильно выпуклой на множестве W1.
В силу тождеств
а2 = а — аA — а) и A — аJ = A — а) — аA — а)
заключаем, что
(Q(ax1 + A - а)х2), ах1 + A - а)х2) =
= a2 (Qx\ х1) + аA - a) ((Qx\ х2) + (Qx2, ж1)) +
+ A - aJ (Qx2, х2) = a (Qx\ х1) + A - a) (Qx2, х2) -
- аA - a) (Q(xl - ж2), х1 - х2).
Поэтому
/ {ах1 + A - а)х2) = Q (ах1 + A - а)х2, аж1 + A - а)х2) +
+ (с, аж1 + A - а)ж2) = a (Qx1, ж1) + A - a) (Qx2, ж2) +
+ а(с, ж1) + A - а) (с, ж2) - аA - a) (Qix1 - ж2), ж1 - ж2) =
= afix1) + A - а)/(ж2) - аA - a) (Qix1 - ж2), ж1 - ж2).
Учитывая, что для положительно определенной матрицы Q
справедливо неравенство (Qix1 —ж2), ж1 —ж2) ^ А|жх — ж2|2, где
А — ее наименьшее собственное значение, приходим к
выводу, что рассматриваемая функция удовлетворяет неравенству
C.27) при 7^Аи, значит, является сильно выпуклой.
Теорема 3.16. Для того чтобы функция /(ж),
дифференцируемая на выпуклом множестве О, была сильно выпуклой,
необходимо и достаточно, чтобы существовала константа \i > О,
для которой при любых ж1, ж2 Е О выполняется неравенство
(grad/fc1) - grad Дж2), ж1 - ж2) > ^х1 - ж2|2. C.28)
3.5. Сильно выпуклые функции
135
Ч Необходимость. Пусть выполнено неравенство C.27).
Тогда выполнено и неравенство C.20). Используя оба
неравенства в случае а = 0,5 и полагая h = ж1 — ж2, получаем
0,257|^|2^0,5(/(Ж1) + /(Ж2))-/@,5(Ж1+Ж2)) =
= 0,5(/(Ж1)-/@,5(Ж1+Ж2)))+0,5(/(Ж2)-/@,5(Ж1+Ж2)))<
<0,5(grad/(a;1),0,5^) -0,5(grad/(a;2), 0,5/г) =
= 0,25{g™df(x1)-g™df(x2),h).
Таким образом, пришли к неравенству C.28) с параметром
Достаточность. Покажем, что если верно C.28), то
верно и неравенство C.27). Полагая h = ж1 — ж2, можем
записать ах1 + A — а)х2 = ж2 + ah и
«/(ж1) + A - а)/(х2) - /{ах1 + A - а)Ж2) =
= a{f{xl) - f(x2)) - f(x2 + ah) + f(x2).
Это позволяет представить неравенство C.27) в эквивалентной
форме
a(f(x2+h) - f(x2)) -f(x2+ah) + f(x2) > ja(l-a)\h\2. C.29)
Рассмотрим функцию
<p{t) = a{f(x2 + th) - f{x2)) - {f{x2 + ath) - f{x2)),
непрерывно дифференцируемую на отрезке [0, 1]. Запишем для
производной <pr(t) этой функции формулу Ньютона — Лейбница
1
ip(l)-ip@)=Jtp'(t)dt.
о
136 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Согласно правилу дифференцирования сложной функции,
<p'(t) = a (grad/(ж2 + th), h) - (grad/(ж2 + ath), ah) =
= a (grad f(x2 + th)- grad / (ж2 + ath), h) =
где у1 = x2 + th и у2 = ж2 + ath. Используя неравенство C.28)
для пары точек у1 и у2, получаем оценку
?>'(*) > М "М V " У2|2 = ««A " «)м|^|2.
гA — а)
Таким образом,
1 1
<рA)-<р@) = (pf(t)dt^a(l-a)fi\h\2 tdt =-аA - а)ф\2.
о о
Непосредственным подсчетом убеждаемся, что <р@) = 0 и
у>A) = «(/(^2 + Л) - /(*2)) " (f(x2 + «Л) " fix2)),
т.е. разность <рA) — <р{0) совпадает с левой частью неравенства
C.29). Тем самым доказано, что это неравенство выполняется
с параметром 7 = 0,5/i. >
Теорема 3.17. Для того чтобы функция /(ж), дважды
непрерывно дифференцируемая на открытом выпуклом
множестве ficKn, была сильно выпуклой, необходимо и достаточно,
чтобы существовала константа \i > 0, для которой при любых
ж G fi и /i Е Rn верно неравенство
(H(x)h,h) >/i|h|2, C.30)
где Н(х) — матрица Гессе функции f(x) в точке х.
3.5. Сильно выпуклые функции 137
-4 Необходимость. Пусть х — точка открытого
выпуклого множества On/iGRn. Тогда при достаточно малом ?о > О
имеем х + eh Е О при |б| < sq и функция
^(t) = (grad/(a + th),h)
определена и дифференцируема на некотором отрезке [0, т],
т > 0. К этой функции можно применить формулу конечных
приращений:
Ф(т) - ф(о) = ф'($т)т, $ е (о, 1).
Непосредственным вычислением с помощью правила
дифференцирования сложной функции получаем
/// ч d f^dfix + th), \
чг=1 7
= ±± ^Ш^нь¦ = №*.*).
J=lг=1 J г
где h = (/ii, ..., /in). Таким образом,
(grad/(^ + T^)-grad/(^),^) = (H(x + $Th)rh,h), C.31)
где$ Е@, 1).
Если функция f(x) сильно выпукла, то для нее выполняется
неравенство C.28). Используя это неравенство для точек х1 =
= х -\- rh, х2 = ж, находим
(H(x + $rh)h,h) = ^(gididf (x + rh) -grad/\x),rh) ^ц\Н\2.
Переходя в этом неравенстве к пределу при т —>> 0, получаем
неравенство C.30),
Достаточность. Покажем, что если для произвольных
х Е О и h Е W1 верно неравенство C.30), то для произвольных
138 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
точек ж1, ж2 ЕО верно неравенство C.28). Согласно теореме
3.16, это и будет означать, что функция /(ж) сильно выпукла.
Выберем произвольные точки ж1, ж2 Е О. Тогда, преобразуя
равенство C.31), которое выполняется для любой функции
/(ж), дважды дифференцируемой на отрезке [ж, ж + rh], можем
записать
(grad/^-grad/^2),/*) = (H(x2 + $h)h,h), C.32)
где в данном случае h = ж1 — ж2. Используя неравенство C.30)
при ж = ж2 + #h и h = ж1 — ж2, заключаем, что
(grad/^1) - grad/^2), ж1 - ж2) > /^ж1 - ж|2,
т.е. выполняется неравенство C.28). >
Пример 3.14. Убедимся в том, что функция /(ж) = |ж — у\2
является сильно выпуклой на множестве W1 (здесь у Е W1 —
произвольная фиксированная точка).
Вычислим градиент функции /(ж) = (ж — у, ж — у):
grad/(a;) = 2{х-у).
Используя это выражение, можем записать
(grad/^1) - grad/(a;2), ж1 - ж2) =
= B(жх - у) - 2(ж2 - у), ж1 - ж2) = 2\х1
2|2
Ж .
Отсюда видно, что неравенство C.28) будет выполнено, если
выбрать параметр \i из интервала @, 2).
К тому же выводу можно прийти, если вычислить матрицу
Гессе функции и применить теорему 3.17.
Теорема 3.18. Пусть функция /(ж) сильно выпукла на
выпуклом множестве О С W1. Если ж* Е О — точка локального
минимума функции /(ж), то для любого ж Е О справедливо
неравенство
\х-х*\2^2Пх)~Пх*\ C.33)
7
3.5. Сильно выпуклые функции
139
где 7 — параметр сильной выпуклости. Если к тому же
функция f(x) непрерывно дифференцируема на О, то для любого
ж Е О выполнены неравенства
Г7|ж-ж*|2 < (gradf(x),x-x*),
J Т|ж — ж*| <|grad/(a>)|, C.34)
(К/(ж)-Дж*К-^Дж)|2.
^ 7
А Отметим, что точка локального минимума выпуклой
функции является точкой ее наименьшего значения (см. теорему
3.14). Поэтому для любой точки х Е О выполняется
неравенство /(ж) > /(ж*). Из неравенства C.27) при х1 = ж, ж2 = ж* и
а = 1/2 имеем
/Ос/2 + х*/2) < /(Ж) У (Ж*} - ^1» - ш*|2.
Отсюда, учитывая, что /(ж*) ^ /(ж/2 + ж*/2), приходим к
неравенству C.33).
Если функция /(ж) дифференцируема на О и сильно
выпукла, то для ее точки ж* локального минимума, согласно
теореме 3.15, справедливо неравенство (grad Дж*), ж — ж*) ^ 0.
С учетом этого неравенства из соотношения C.28), в котором,
согласно доказательству теоремы 3.16, можно положить \i = 7,
при h = ж — ж* находим
7|ж — ж*|2 < (grad/(sc) — grad/(sc*), ж — ж*) =
= (gcadf(x),x-x*) - (grad/(a5*),a5-a5*) ^ (grad/(a;),a5-a5*),
что равносильно первому неравенству в C.34). Применяя к его
правой части неравенство Коши — Буняковского, получаем
7|ж — ж*|2 ^ (grad Дж), ж — ж*) ^ |grad/(sc)| |ж — ж*|. C.35)
140 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Это приводит ко второму неравенству в C.34). Наконец,
используя неравенства C.20) и C.35), заключаем, что
f(x)-f(x*)<(&adf(x),x-x*)<
< |grad/(sc)| |ж — ж*| < — |grad/(sc)|2.
7
Записанные неравенства в сочетании с неравенством 0 ^ /(ж) —
— /(ж*) дают третье неравенство в C.34). >
Теорема 3.19. Функция /(ж), сильно выпуклая и
непрерывная на замкнутом выпуклом множестве OcRn, достигает
своего наименьшего значения на О.
<4 Выберем произвольную точку ж0 Е О и рассмотрим
множество Xq = {ж Е О: f(x) ^ /(ж0)}. Если функция /(ж) достигает
на Xq наименьшего значения в некоторой точке ж*, то эта
точка будет и точкой наименьшего значения функции на
множестве Q, так как для любой точки ж Е О \ Xq выполняются
неравенства /(ж*) ^ f(x°) < /(ж). Чтобы доказать, что на Xq
функция /(ж) достигает наименьшего значения, достаточно (с
учетом непрерывности функции) доказать, что множество Xq
замкнуто и ограничено, т.е. компактно [V].
Множество Xq замкнуто в силу непрерывности функции
/(ж) на множестве О. Действительно, пусть ж — предельная
точка множества Xq. Поскольку Xq С О, а О — замкнутое
множество, то ж Е О и функция /(ж) непрерывна в точке ж.
Выберем последовательность {хп} точек множества Xq,
сходящуюся к точке ж. В силу определения множества Xq верно
неравенство f(xn) ^ /(ж0). Переходя в этом неравенстве к
пределу при п —> ос, получаем
f(x)= \imf(xn)^f(x°),
что равносильно соотношению ж Е Xq.
3.5. Сильно выпуклые функции
141
Множество Xq является выпуклым. В самом деле, выберем
произвольные точки ж1, ж2 Е Xq. Тогда для любого а Е [0, 1]
точка ах1 + A — а)х2 принадлежит О и
f(axl + A - а)х2) < «/(ж1) + A - a)f(x2) <
^а/(Ж°) + A-а)/(Ж°) = /(Ж0),
т.е. аж1 + A — а)ж2 G Хо.
Докажем, что множество Хо ограничено. Используя
неравенство C.27) для точки ж0 и произвольной точки ж1 из
выпуклого множества Хо, заключаем, что
аA-аO|ж1-ж°|2^
< «/(ж1) + A - a)f(x°) - /(аж1 + A - а)х°) <
< а/(ж0) + A - а)/(ж°) - /(аж1 + A - а)ж°) =
= /(ж°)-/(аж1 + A-а)ж°). C.36)
Так как функция /(ж) непрерывна, то можно указать такую
окрестность точки ж0, что в пересечении этой окрестности с Q
функция будет ограниченной. Следовательно, для некоторого
числа 6 > 0 и некоторого М Е Ш выполняется неравенство
/(ж) ^ М при |ж —ж°| < E, ж Е О. Предполагая, что 6 < \хг — ж°|,
выберем а = -— —. Тогда для точки ж = ах1 + A — а) х°
имеем |ж —ж°| = а\х1 — ж°| < 8 и /(ж) ^ М. Из неравенств C.36)
получаем
аA - «hl^1 - ж°|2 ^ /(ж0) - М.
Так как при 5 < 1Ж1 — ж°| выполняются соотношения
аA _ «O|ж1 _ ж0|2 j> * . I . ф _ ш0|2 = h | _ 0|
v ,п ' 2|ж-ж°| 2 " ' 4 ' "
заключаем, что
ж-ж U max< S.
Г ЦПх°)-М)\
142 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Это означает, что множество Xq целиком попадает в п-мерный
шар с центром в точке ж0 и радиусом
R = max I 8, w v J - \,
т.е. оно ограничено.
На замкнутом ограниченном множестве Xq непрерывная
функция f(x) достигает своего наименьшего значения [V] в
некоторой точке ж*. Так как при х Е 0\Хо выполняются
соотношения f(x) > f(x°) ^ /(ж*), точка ж* является точкой
наименьшего значения функции и в пределах множества О. >
Замечание 3.5. Теорема 3.19 перестает быть верной, если
в ней условие сильной выпуклости заменить условием
выпуклости или строгой выпуклости: строго выпуклая (в частности,
выпуклая) функция может и не достигать своего наименьшего
значения на замкнутом множестве. Такова, например, функция
f(x) = ех одного действительного переменного. Вторая
производная этой функции положительна: f"(x) = ех. Поэтому она
является строго выпуклой. В то же время функция f(x)
возрастающая и не имеет точек локального минимума, т.е. она не
достигает наименьшего значения.
3.6. Примеры минимизации
квадратичных функций
Использование необходимого и достаточного условий
локального минимума выпуклой функции рассмотрим на
примерах минимизации квадратичных функций. Любая
квадратичная функция f(x) может быть представлена в виде суммы
f(x) = (Qx, х) + (с, х) квадратичной (Qsc, х) и линейной (с, х)
форм, при этом матрица Гессе Н{х) этой функции постоянна
и связана с матрицей Q квадратичной формы
соотношением Я = 2Q.
3.6. Примеры минимизации квадратичных функций 143
Рассмотрим квадратичную функцию
f(x) = ±(Hx,x) + (c,x) C.37)
с положительно определенной матрицей Гессе Н порядка п
и фиксированным вектором cGln. Градиент этой функции
равен
grad/(a>)=ffa> + c. C.38)
Так как матрица Н положительно определена, то она имеет
обратную матрицу Н~1. Из необходимого условия grad/(#*) =
= 0 локального минимума функции с учетом C.38) находим,
что функция имеет единственную стационарную точку ж* =
= -Н~1с.
Рассматриваемая функция сильно выпуклая на выпуклом
множестве W1 (см. пример 3.13). Значит, эта функция строго
выпуклая (см. 3.5). Поэтому, согласно теоремам 3.14 и 3.15,
необходимое условие локального минимума является и
достаточным условием. В стационарной точке ж* функция C.37)
принимает значение
f(x*) = -1- (НН-'с, Н-1с) + (с, Н-1с) = \ (с, Н-1с). C.39)
Отметим, что если матрица Н квадратичной функции не
является положительно определенной, то она может быть
вырожденной. В этом случае либо функция не имеет стационарных
точек, либо стационарных точек бесконечно много.
Пример 3.15. Исследуем на минимум функцию f{x\,X2) =
= х\ + 2Х\Х2 + 4ж|.
Рассматриваемая функция представляет собой
квадратичную функцию с матрицей Гессе
144 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Нетрудно проверить (например, с помощью критерия
Сильвестра), что матрица Н положительно определенная.
Значит, функция имеет единственную стационарную точку ж* =
= —Н~1с = —Н~10 = 0, в которой принимает наименьшее
значение.
Пример 3.16. Квадратичная функция f{x\,x<2) =х\ + 2х\х<2
также представляет собой квадратичную форму и имеет
матрицу Гессе
-О i)-
Эта матрица знаконеопределенная, но является
невырожденной. Поэтому функция имеет единственную стационарную
точку ж* = — Н~10 = 0. Но поскольку функция не выпуклая
(матрица не является неотрицательно определенной), делать
какие-либо заключения о наличии экстремума в точке ж*
нельзя. И действительно, точка 0 не является ни точкой локального
минимума, ни точкой локального максимума, так как ее
матрица Гессе в этой точке знаконеопределенная [V].
Нетрудно убедиться, приведя квадратичную форму к
каноническому виду, что график рассматриваемой функции
представляет собой гиперболический параболоид с седловой точкой
(О, 0). Функция cp(t) = /(t,0) = t2 (сечение функции f(x\,X2)
при Х2 = 0) имеет при t = 0 строгий локальный минимум, в
то время как функция ip(t) = /(?,—?) = —t2 (сечение функции
f(x\,X2) при х\ = — x<i) при t = 0 имеет строгий локальный
максимум.
Пример 3.17. Квадратичную функцию f(x\,X2)=x\ +
+ 2x\x<i + х\ можно записать в виде f(x\1X2) = {х\ + Х2) •
Отсюда сразу следует, что она достигает наименьшего значения,
равного нулю, в каждой точке прямой х\ + Х2 = 0. Матрица
Гессе этой функции имеет вид
3.6. Примеры минимизации квадратичных функций 145
и является неотрицательно определенной. Значит, функция
выпуклая, а каждая стационарная точка является точкой
наименьшего значения функции. Необходимое условие локального
минимума приводит к системе уравнений
2ж1 + 2ж2 = 0,
2ж1 + 2ж2 = 0,
из которой заключаем, что стационарной является любая точка
вида (?, — ?), t Е М, т.е. точка, лежащая на прямой х\ + х2 = 0.
Приведя квадратичную форму f(x\1x2) = (х\ + х2J к
каноническому виду, легко убедиться, что график функции
представляет собой параболический цилиндр [III].
Пример 3.18. Квадратичная функция
f(xux2) = Ьх\ - Ахгх2 + 3x1 + 4л/5(ж1 + 2х2) + 22 C.40)
далее используется в качестве базовой при сравнительном
анализе различных численных методов безусловной минимизации
и выявлении достоинств и недостатков их вычислительных
свойств. Поэтому представляет интерес подробное
аналитическое исследование свойств этой функции.
Функцию f(xi,x2) можно представить в виде
/(ж) = (Ах, х) + (Ь, х) + с,
где х = (жх, х2) Е М2,
л=(-2 !)• »=ЙЭ- с=22-
Матрица А положительно определенная, так как имеет угловые
миноры Ai = 6>0hA2 = 6-3 — (—2J = 14 > 0. Значит,
рассматриваемая функция сильно выпуклая в R2 и имеет
единственную стационарную точку ж*, являющуюся точкой наименьшего
3.41
146 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
значения. Эту точку можно найти по формуле ж* = —Н 1Ь, где
Н = 2А — матрица Гессе функции. Так как
А ~и{2 6
ТО
X =
В этой точке функция принимает значение /(ж*) = — 28.
Приведем квадратичную форму (Ах, х) функции к
каноническому виду. Для этого найдем собственные значения
матрицы А, составив ее характеристическое уравнение det(A — XI) =
= 0, где / — единичная матрица второго порядка. В данном
случае это уравнение имеет вид
6-А -2
-2 3-А
= 0.
Раскрывая определитель в левой части уравнения, получаем
F - А) C - А) - 4 = 0, или А2 - 9А + 14 = 0. Это квадратное
уравнение имеет корни Ai=2 и А2 = 7, которые и являются
собственными значениями матрицы А. Поскольку собственные
значения различны, а матрица А симметрическая, то
соответствующие этим собственным значениям собственные векторы
ортогональны [V].
Координаты собственных векторов найдем, решая СЛАУ
(А — Х1)е = 0, которая при A = Ai = 2 и А = А2 = 7 сводится к
соответствующим системам
{4^1 - 2х2 = 0, J -xi - 1х2 = 0,
-2^1 + х2 = 0, | -2^1 - 4ж2 = 0.
Решением первой системы является вектор A 2) , а второй —
т
вектор (—2 1) . Нормируя эти векторы, получаем единичные
т т
векторы е\ = A/л/5 2/л/б) и е°2 = (—2/л/б 1/л/б) ,
образующие в IR2 ортонормированный базис. В этом базисе матрицей
3.6. Примеры минимизации квадратичных функций 147
квадратичной формы является диагональная матрица Л с
диагональными элементами, совпадающими с собственными
значениями, а квадратичная форма (Ах, х) примет канонический
вид (Лу, у) = \1У\ + \2у\ = 2у\ + 7у1, у = (уъ у2).
Координаты собственных векторов е\ и е2, записанные по
столбцам, формируют матрицу перехода U к новому,
каноническому базису, которая в данном случае имеет вид
U =
Поскольку матрица U определяет переход от одного ортонор-
мированного базиса к другому, она является ортогональной
[IV]. Поэтому обратную матрицу U~l можно найти с помощью
транспонирования: U~l = U . С помощью матрицы перехода
можно найти координаты вектора Ь в новом базисе по формуле
Ь° = U~1b, что в рассматриваемом случае дает
Таким образом, квадратичная функция в новой системе
координат принимает вид
/i(yby2) = 2y2 + 7y| + 20yi + 22.
С помощью выделения полных квадратов проводим дальнейшее
упрощение вида функции:
/1(у1,у2) = 2(у1 + 5J + 7у22-28,
или /2(^1,^2) = 2z\ + 7zf - 28, где z\ = у\ + 5 и z2 = 2/2• Из
найденного представления функции вытекает, что график
рассматриваемой функции представляет собой эллиптический
параболоид [III].
148 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Преобразование функции проведено за два шага: сначала
переход к переменным yi, у25 а затем — к переменным z\,
Z2- Формулы связи исходных переменных х\, Х2 с конечными
переменными z\ и Z2 имеют вид
Z\ - 2Z2
Xi =
Х2 =
2zi + Z2
л/5,
¦2л/5.
Рис. 3.3
Началом конечной системы
координат является точка 0\, которая в
исходной системе координат имеет
координаты х\ = — v5, Х2 = — 2у5.
Все три системы координат
показаны на рис. 3.3.
Линиями уровня функции f{x\,X2) являются подобные
эллипсы (см. рис. 3.3). Найдем, например, уравнение линии уровня,
проходящей через точку ж0 = (—2, 1). Подстановка координат
этой точки в C.40) дает значение функции /(ж0) = 57.
Следовательно, эта точка расположена на линии уровня f{x\,X2) = 57.
Переходя к конечной системе координат 0]_ziZ2, получаем
уравнение f(zi,Z2) = 2z\ + lz\ — 28 = 57, или
+ ¦
= 1.
85/2 85/7
Таким образом, искомая линия уровня — эллипс с полуосями
а = д/85/2 « 6,52 и b = л/85/7 « 3,48. Найденная линия уровня
показана на рис. 3.3 жирной линией.
3.7. Минимизация позиномов
В прикладных задачах минимизации целевая функция часто
имеет вид
y(x) = ^2CiPi^
C.42)
3.7. Минимизация позиномов
149
Ci > О, г = 1, га, а функции
п
Pl(x) = l[xa;\ C.43)
a^j G R, i = 1, m, j = 1, n, определены на множестве
R™ = {(жь ...xn) еШп: Xi>0, i=l~n}
точек с положительными координатами. Функцию вида C.42)
называют позиномом.
Позином при определенных значениях показателей степени
ctij может не быть выпуклой функцией. Однако с помощью
замены переменных
Xj = eb, j=T^i, C.44)
он преобразуется в выпуклую функцию в W1. Это показано в
примере 3.9. Там же показано, что эта функция является
строго выпуклой функцией в том случае, когда матрица А= (а^)
имеет ранг, равный п.
Поскольку функция y(?i,...,?n) выпукла в Rn, любая точка
ее локального минимума является точкой наименьшего
значения функции (см. теорему 3.14). Более того, так как эта
функция дифференцируема в W1, множество ее точек
наименьшего значения совпадает с множеством стационарных точек
(см. замечание 3.3). В случае строгой выпуклости функция
имеет не более одной точки локального минимума. Поскольку
якобиан замены переменных C.44) при любых значениях ?i, ...,
?п отличен от нуля, любой стационарной точке (?*, ..., ?*)
функции y(?i,...,?n) соответствует стационарная точка ж* =
= (ж*, ..., ж*), ж* = е^ , г = 1, п, и наоборот. Таким образом,
минимизация позинома сводится к поиску его стационарных
точек, причем для определения наименьшего значения
позинома достаточно найти хотя бы одну стационарную точку.
150 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Для строго выпуклой функции exp(t) = ег верно неравенство
Иенсена
ехр($^™г*г) ^5^гУгвхр(*г),
г=1 г=1
m
где Wi ^ 0, г = 1, га, и ^ г^ = 1. Преобразуем левую часть этого
г=1
равенства:
т
U\Wi
i—1 i—1 i—1
Выполнив замену переменных eli = щ, г = 1, га, получим
неравенство взвешенных средних
т т
^тщ^Цщ\ C.45)
г=1 г=1
где щ,У01> 0, г = 1, га, и ^1^ = 1. Неотрицательные коэффи-
г=1
циенты Wi в этом неравенстве, в сумме составляющие единицу,
называют нормированными весами.
Выполнив в неравенстве C.45) замену yi = \и{Щ, г = 1,га,
получим
5»П(*Г-
г=1 г=1 г
Пусть у^ = CiPi(x), г = 1,771, т.е. сумма в левой части
последнего неравенства есть позином у(х) вида C.42). Тогда
у(х) ^v(x,w), C.46)
где w = (г^1, 1^2, ..., wm), а правая часть г>(ж,го) неравенства с
учетом вида функций Pi(x) равна
ТГЬ ть тп ть
«<«.«>=nn©,V"'=n(?№-
z=lj=l г=1 j=l
3.7. Минимизация позиномов
151
Здесь
т
Ъ3 = ^aijwi, 3 = 1^п-
г=1
Подберем нормированные веса w\ таким образом, чтобы
функция v(x,w) не зависела от ж. Для этого необходимо и
достаточно, чтобы выполнялись равенства bj =0. Другими
словами, нормированные веса должны удовлетворять системе
линейных уравнений
т
^2aijWi = 0, ,7 = 1, п. C.47)
г=1
Такой выбор нормированных весов не всегда возможен. Для
существования нормированных весов, удовлетворяющих
системе линейных уравнений C.47), необходимо, чтобы эта система
имела ненулевые решения. Однако даже если система C.47)
и имеет ненулевые решения, то среди них может не оказаться
решений с положительными (или хотя бы неотрицательными)
значениями неизвестных wf. так будет, например, в случае,
когда все коэффициенты ац являются положительными.
Если нормированные веса W{ выбраны в соответствии с
равенствами C.47), то
т
г=1
и неравенство C.46) преобразуется к виду
т n т
*(*) = Е« П*Г >ЩттТ=d{w)- C-48)
г=1 j = l г=1 *
Функцию d(w) называют двойственной к позиному
у (ж), а равенства C.47) — условиями ортогональности
(вектор с координатами W{, г = 1, га, ортогонален каждому из
п столбцов матрицы (а^) размера тхп).
152 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
В Мш рассмотрим множество
т
W = {(wu ..., wm)?Rm:wi>0, г = T7m, ^^ = l}. C.49)
г=1
Нетрудно показать, что это множество представляет собой
выпуклую оболочку элементов wiei EMm, г = 1,га, где ei, ...,
еш — стандартный базис в IRm. Другими словами, VF —
m-мерный выпуклый многогранник. Для двойственной функции
d(w) верна следующая теорема.
Теорема 3.20. Двойственная функция d(w) на
множестве W достигает наибольшего значения d* = с\ + С2 + ... + ст
в точке го* = (ci/d*, С2/сГ, ..., cm/d*) Е VK, и эта точка
единственная.
^ Несложно, вычислив вторую производную, убедиться в том,
что каждая из функций (fi(wi) = —Wi\n(ci/wi) является строго
выпуклой при Wi > 0. Значит, и функция
т
— lnd(w) = — У^^ In —,
г=1
как сумма строго выпуклых функций, является строго
выпуклой (см. теорему 3.8). Если эта функция достигает на W
наименьшего значения, то точка, в которой достигается
наименьшее значение, согласно теореме 3.14, единственная. Значит,
функция d(w) может достигать наибольшего значения только
в одной точке.
Согласно неравенству взвешенных средних,
т т т
ад = ?(-Г<Е«*-- = Е« = <л
г=1 г=1 г=1
причем это неравенство превращается в равенство в точке го*
с координатами w* = с^/сГ, г = 1, т. Следовательно, d(w) ^
^ d(w*), го Е W, и в точке го* функция d(w) достигает
наибольшего значения. >
3.7. Минимизация позиномов
153
Пусть VK* — множество точек w = (w\, ..., wm) в
выпуклом многограннике W, которые удовлетворяют условию
C.47). Множество VK* может быть и пустым, т.е. VK* = 0.
Но если W* ф 0, то позином у (ж) имеет двойственную
функцию d{w\ причем для любых w Е VF* и ж Е М+ выполняется
неравенство d(w) ^ у (ж). Следовательно, позином у (ж)
ограничен снизу положительным числом, в качестве которого можно
взять значение d(w) в любой точке w Е W*. Можно показать,
что в этом случае позином достигает наименьшего значения.
При этом число d(w) можно рассматривать как оценку
снизу наименьшего значения позинома. Отметим, что в
некоторых случаях множество W* может состоять из единственной
точки.
Позином может не достигать наименьшего значения, хотя
он и ограничен снизу нулем (например, функция 1/х{). Как
показывает предыдущее рассуждение, это возможно лишь в
случае, когда множество W* пусто.
Пример 3.19. Выясним, достигает ли наименьшего
значения позином
4
у(х) = \-XiX2~\-2x2Xs + 4Ж1Ж3, ж = (xi, ж2, жз).
xix2x3
Если позином достигает наименьшего значения, то оценим его.
Запишем для этого позинома систему, включающую условие
т
нормировки ^Wi = 1 и условия ортогональности C.47):
г=1
( W\ + W2 + Ws + W4 = 1,
— W\ + W2 + ^4 = 0,
<
- гух + гУ2 + ws = 0,
t — w\ + г(;з + w^ = 0.
Решая эту систему линейных алгебраических уравнений,
находим ее единственное решение w\ = 2/5, W2 = w% = w^ = 1/5.
154 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Таким образом, множество VK* не пустое и содержит
единственную точку й = B/5, 1/5, 1/5, 1/5). Значит,
рассматриваемый позином на Rj_ достигает наименьшего значения.
Поскольку W* ф 0, позином имеет двойственную функцию,
которая в соответствии с C.48) принимает вид
/4\W1/1\W2/2\W3/4\W4
d(w)=( — ) ( — ) ( — ) ( — ) . 3.50
\Wi/ \W2S \W3/ \W±J
В точке w значение двойственной функции равно
Поэтому наименьшее значение позинома у(х) не меньше 10. #
Позином C.42) называют регулярным, если выполнены п
равенств
т
Qj = ^2aijCi = 0, ,7 = 1, п. C.51)
г=1
Если позином регулярный, то координаты W{ = Ci/d* точки
го* G W, в которой, согласно теореме 3.20, двойственная
функция d(w) достигает на m-мерном выпуклом многограннике W
наибольшего значения сГ, равного d* = с\ + ... + ст,
удовлетворяют условиям ортогональности C.47). Действительно,
т т
t=i t=i
Это означает, что для регулярного позинома у(ж) верны
неравенства
d*^M^y(x), же!![. C.52)
Теорема 3.21. Регулярный позином у (ж) достигает в Ж"
своего наименьшего значения у* = у(ж*) = d* = ci + С2 +... + с^
в точке ж* = A, 1, ..., 1)еГС2..
3.7. Минимизация позиномов
155
-4 Поскольку для регулярного позинома верны неравенства
C.52), достаточно показать, что в точке ж* позином
принимает значение й*. С помощью непосредственных вычислений
получаем
у(**) = Ес*П
ran. га
Х-" '
?^(Ч = d .
J
i=l j=l ' J i=l
Итак, поиск наименьшего значения регулярного позинома
не составляет труда: оно достигается в точке ж* с единичными
координатами. Нерегулярный позином у (ж) может не
достигать наименьшего значения, но если известно, что наименьшее
значение этим позиномом достигается, то значение d* = у (ж*)
может рассматриваться как оценка сверху для наименьшего
значения позинома.
Как отмечено выше, если позином достигает наименьшего
значения, то все точки наименьшего значения есть
стационарные точки позинома. Поэтому задачу минимизации позинома
можно решать, определяя его стационарные точки.
Используя представления C.42) и C.43), получаем
уравнения для стационарных точек позинома:
гл ^ га п
ду_
dxj х,
J J г=1 j=l
Эти уравнения сложные. Установить по ним существование
стационарных точек, а тем более найти их не так просто,
особенно при большом числе т слагаемых в C.42) и дробных
показателях степеней.
Введем дополнительные переменные
=z—^2aaijY[x^l3=0, j = l, п. C.53)
=«п
ж-и, i = 1,га, Zj=\nxj, j = 1, п.
Тогда
п
In — = 2_\ aij ln^j 5
Со
1 j=i
156 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
и условия C.53) можно записать в виде двух систем линейных
уравнений
т п
/Ja^z —0, j = l,n, Y^a^j = ln —, г = 1,га. C.54)
г=1 j=l Ci
Теорема 3.22. Если позином у(х) достигает в точке
ж* = (х\, ..., ж*) ? М+ наименьшего значения у* = у(ж*), то
двойственная функция с?(ги) достигает на множестве W*
наибольшего значения d(w*) = у* в точке го* ? VF* с координатами
го* = щ/у*, где ^ = еда (ж*), г = 1, га.
^ Покажем сначала, что точка го* принадлежит множеству
W*, т.е. ее координаты го* = г^/у* удовлетворяют равенству
т
^2 w* = 1 и равенствам C.47). Так как в точке ж* позином
г=1
у (ж) достигает наименьшего значения, эта точка для позинома
является стационарной. Следовательно, выполняются
равенства C.54), в которых
п
Щ = Ci Д(ж*)й^ = (нр{(х*), i = I~m,
и ^ = 1пж*, j = 1, п. Используя первую группу этих равенств,
заключаем, что
т т л т
Щ 1
Кроме того,
г=1 г=1 У* У* г=1
С^(Ж*)
г=1 г=1
Поэтому го* G W*.
3.7. Минимизация позиномов
157
Теперь вычислим значение двойственной функции в точке
го*. Поскольку w* = щ/у* = CiPi(x*)/y*, то
^г У*
< Рг(ж*)'
Используя представление двойственной фунции, находим
т * т / \ w* / тп \ —w* тп
г=1 г г=1 Vjrn у/ 4=1 7 г=1
Во втором произведении все показатели степени складываются,
причем в сумме получаем
т
г=1
Следовательно, это произведение равно у*. Первое
произведение преобразуем, учитывая вид функций^(ж):
(т \ — w* т n п
г=1 ' z=lj=l j=l
где
kj = -^2aijw*=0.
г=1
Значит,
(Пл(**)) =1
и ^(го*) = у*.
Так как d(w) ^ у* для любой точки w Е VK*, то у* = d(w*)
является наибольшим значением d(w) на VK*. >
158 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
Теорема 3.23. Пусть двойственная позиному у(х) функция
d(w) достигает в точке го* = (ги*..., w^) Е VK* наибольшего
значения и щ = w*d(w*), г = 1, т. Позином у(ж) достигает в
IR™ наименьшего значения тогда и только тогда, когда система
га уравнений
п
V^a^-?j = ln —, г = 1,га, C.55)
i=i Сг
где 2j = ln^j, j = 1,п, имеет решения, принадлежащие R™.
При этом любое решение (г*, ..., ?*) системы определяет точку
ж* = {х\, ..., ж*), где z* = 1пж*, j = 1,п, которая является
точкой наименьшего значения позинома.
-4 Пусть позином у(х) достигает в 1Щ_ наименьшего
значения у* в некоторой точке ж*. Тогда, согласно теореме 3.22,
двойственная функция d(w) достигает на множестве W*
наибольшего значения в точке го* с координатами w* = щ/у*, где
щ = CiPi(x*), г = 1, га. Кроме того, d(w*) = у*, и мы можем
записать щ = го*б?(ги*), i = l, т.
Отметим, что функция с/(го) достигает наибольшего
значения в единственной точке. Действительно, множество VK*
есть пересечение выпуклого многогранника W с линейным
многообразием, заданным системой линейных уравнений C.47).
Значит, W* — выпуклое множество. Как было отмечено выше
(см. доказательство теоремы 3.20), функция — lnd(x)
является строго выпуклой. Поэтому она на W* имеет единственную
точку минимума, а функция d(w) — единственную точку
максимума.
Для точки ж* наименьшего значения позинома
выполняются равенства C.54), а так как щ = w*d(w*), г = 1, га, то вторая
группа этих равенств совпадает с C.55). Следовательно,
значения Zj¦ = ж*, j = 1, п, дают решение системы C.55).
Пусть теперь система C.55) имеет решение (z*, ..., z*)
и ж* = (ж*, ..., ж*) — соответствующая точка, для которой
3.7. Минимизация позиномов
159
1пж| — Zp j — 1, п. Тогда из системы C.55) находим
щ w*d(w*)
рг(х*) = П(*рву = expjV^lnx*) = ^ =
j=i 3=1
Поэтому
y(x*) = J2<WiW = d(w*)J2w;=d(w*).
г=1 г=1
В данном случае W* т^ 0 и, значит, верны неравенства C.52),
в которых d* = d(w*). Отсюда делаем вывод, что значение
у (ж*) = d(w*) является наименьшим значением позинома у (ж*)
bR^. >
Теоремы 3.22 и 3.23 позволяют задачу поиска
стационарных точек позинома, т.е. решение системы уравнений 3.54,
заменить задачей исследования на условный максимум
двойственной функции, ограничения в которой являются
линейными. Такая задача может оказаться более простой, а решив ее,
можно найти решение исходной задачи минимизации позинома.
Пример 3.20. Позином
4 о
у(х) = Yx\%2 + 2ж2ж3 +4ж1Ж3, х = (жь ж2, ж3) G М. ,
xix2x3
рассмотренный в примере 3.19, не является регулярным, так
как для этого позинома не выполнено ни одно из условий C.47):
-4 + 1 + 4 = 1^0, -4 + 1 + 2 = -1^0, -4 + 2 + 4 = 2^0.
Однако для него множество W* не пусто (см. пример 3.19), и
поэтому в R^_ он достигает наименьшего значения. В качестве
оценки сверху наименьшего значения этого позинома можно
взять значение уA,1,1) = 11, которое, отметим, является
наименьшим значением любого регулярного позинома с теми же
160 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
коэффициентами q, но соответствующим образом
измененными коэффициентами ац.
Поскольку множество VK* состоит всего из одной точки й,
то найденное в примере 3.19 значение двойственной функции
d(w) = 10 является наибольшим ее значением в W*.
Следовательно, наименьшее значение позинома у(х) равно у* = 10.
Найдем координаты x*j, j = 1, 2, 3, точки ж*, в которой пози-
ном у(х) принимает значение у* = 10.
Используя вычисленные в примере 3.19 координаты w* =
= 2/5, го| = г^| = го| = 1/5 точки w и наибольшее значение
d(w) = 10 двойственной функции, в соответствии с C.55)
получаем систему уравнений:
w\d{w*) B/5) • 10
-zi-z2-z3 = m —- = In = 0,
ci 4
л wXd(w*) л A/5) -10 л 0
Zl+z2 = ln-^ - = ln^-^ = 1п2,
С2 1
л wtd(w*) л A/5)-10 Л
с3 2
, пЯфи*) , A/5)-10 л о
21+г3 = 1п-^ - =1п^Ч = -1п2.
С4 4
Решая эту систему линейных уравнений, находим z\ = 0, z| =
= 1п2, 2:3 = — 1п2, откуда х\ = 1, ж^ = 2, ж| = 1/2.
Непосредственной проверкой можно убедиться, что у* = 10.
Вопросы и задачи
3.1. Установите, являются ли выпуклыми множества:
а) П={(хи х2) ЕМ2: 2ж1+ж2^2, 2хх-х2^-2, х2^0};
б) 0= {(жь ж2) GR2: Ж1-ж2 ^2, ж? + ж| ^4};
в) 0= {(жь ж2, хз) ^К3: ж3 >ж2 + ж2};
г) 0= {(жь ж2, ж3) GIR3: ж3 ^ж2 + ж2}.
Вопросы и задачи
161
3.2. Проверьте, какие из указанных функций являются
выпуклыми в W1:
а) /(xi,x2) = х\ + 2х\Х2 - 10ж1 + 5ж2;
б) f(xi,x2) = х\ + х\ + х\ + х\ + х\х\\
в) f(xi,X2) = xie~(Xl+X2^;
г) f(xi,X2,xs) = 2xl + xiX2 + x'r> + '2xl -6Ж1Ж3;
д) /(ж1,ж2,я3) =ехр(ж? + ж| + ж|).
3.3. Проверьте, является ли функция f{x\,X2) = х\ + х\ +
+ (х\ +Х2)~1 выпуклой на множестве
0 = {Oi, х2) eR2: хх+х2 >0, Ж1+ж2 < -^2}.
3.4. Докажите, что если /^(ж),г = 1,га, — выпуклые (строго
выпуклые) функции на выпуклом множестве О С W1, то
функция
д(х) = max .ft (я?)
г=1,т
выпукла (строго выпукла) на О.
3.5. Докажите, что если д(х) — выпуклая скалярная
функция в IRn, то функция f(x) = —1/д(х) является выпуклой на
множестве ft = {х Е W1: д(х) > 0}.
3.6. Покажите, что произведение выпуклых функций
необязательно выпукло. Существуют ли подклассы выпуклых
функций, замкнутые по отношению к умножению?
3.7. Пусть OcRn — выпуклое множество. Докажите, что
функция f(x)= inf ||ж — у|| выпукла на О. Запишите функцию
yen
f(x) в явном виде, если О = {(#1, х2) Е К2: х\ + х\ ^ l}.
3.8. Пусть f(x) — выпуклая (строго выпуклая) функция в
W1 и f(x + кр) > /(ж) при х Е W1 и к Е [(О, (У], где E > 0.
Покажите, что функция ^(х) = }{х + кр) является неубывающей
(возрастающей) функцией переменного х.
162 3. МИНИМИЗАЦИЯ ВЫПУКЛЫХ ФУНКЦИЙ
3.9. Покажите, что если функция f(x) выпукла вР, то
функция д(у) = inf /(ж), где А — матрица размера гахп,
Ах—у
выпукла в Мш.
3.10. С помощью необходимых и достаточных условий
экстремума выделите среди стационарных точек заданных
функцией те, которые являются точками локального максимума
или локального минимума: a) f{x\,X2) = {х\ — х^)*2 + (х\ — IJ;
6)f(x1,x2) = (x1-x22J + (x1-lJ.
3.11. Найдите и классифицируйте стационарные точки
следующих функций:
а) /(Ж1,Ж2) = х\ — Х\Х2 + х\ — 2х\ +3^2 — 4;
б) /(ж1,Ж2) = 2х\ + 4ж1^2 ~~ 10^1^2 + ж|;
в) f(x\,X2) = 2х\ +4Ж1^2 ~~ 10^1^2 + х\\
г) f(x\,X2) = 2х\ + ^Х\х\ ~~ 10^1^2 +Х<2\
д) f(xi,x2) = 2х\ + 4Ж1^2 ~~ 10x1X2 + ^2-
Графически проиллюстрируйте полученный результат.
Установите, какие из указанных функций являются унимодальными
выпуклыми (сильно выпуклыми) функциями.
3.12. Запишите функции, двойственные позиномам 2х\х2-\-
+ х2/х± -ЬЗДжхЖз) и Ж1Ж3/Bж2)+2ж2/ж1+xi/Dx3)+2ж3.
Укажите дополнительные условия, которым должны удовлетворять
аргументы этих функций.
3.13. Решая двойственную задачу, найдите точки
локального минимума и наименьшее значение следующих позиномов
(коэффициенты a, Ъ и с положительны):
а) ах2/х\ + Ьх1 + 0/(^1^2);
б) ax\jx\ + Ъх\х2 + с/(х\х2)]
в) ах\/х\-\-Ъх^ х2 +c/(#i#2).
4. ЧИСЛЕННЫЕ МЕТОДЫ
БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
Численное решение задач безусловной минимизации
функций многих переменных, как правило, значительно сложнее,
чем решение задач минимизации функций одного переменного.
В самом деле, с ростом числа переменных возрастают объемы
вычислений и усложняются конструкции вычислительных
алгоритмов, а также более сложным становится анализ поведения
целевой фунции.
Методы численного решения задач многомерной
безусловной минимизации многочисленны и разнообразны. Условно их
можно разделить на три больших класса в зависимости от
информации, используемой при реализации метода.
1. Методы нулевого порядка, или прямого поиска,
стратегия которых основана на использовании информации
только о свойствах целевой функции.
2. Методы первого порядка, в которых при
построении итерационной процедуры наряду с информацией о целевой
функции используется информация о значениях первых
производных этой функции.
3. Методы второго порядка, в которых наряду с
информацией о значениях целевой функции и ее производных
первого порядка используется информация о вторых
производных функции.
Методы первого и второго порядков хорошо разработаны.
Для большинства из них имеется строгое обоснование,
проведено аналитическое исследование их свойств, доказана
сходимость, получены оценки скорости сходимости для некоторых
классов целевых функций. Описание алгоритмов этих
методов и иллюстрирующие эти алгоритмы примеры представлены
164 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ниже (см. 5). Методы прямого поиска (см. 6) менее изучены,
большинство из них носят эвристический характер и не имеют
теоретического обоснования. В то же время, они достаточно
просты в реализации, что предопределяет их широкое
применение при решении прикладных задач оптимизации.
В настоящее время не существует универсального метода,
применимость которого была бы оправдана и эффективна во
всех случаях. Выбор того или иного метода, его программная
реализация должны быть согласованы с конкретными
условиями, вытекающими из специфики решаемой задачи безусловной
минимизации. В этой главе изложены некоторые общие
свойства численных методов безусловной минимизации.
4.1. Релаксационная последовательность
Пусть требуется найти точку ж* Е W1, в которой
ограниченная снизу целевая функция /(ж), определенная в Rn, достигает
своего наименьшего значения. Будем считать, что эта точка
существует, так что задачу оптимизации можно представить
в виде
/(ж)-ишп, жеГ. D.1)
Отметим, что такая точка может быть и не единственной.
Общей чертой всех численных методов решения этой задачи
является последовательный переход от точки xk~l к точке ж^,
k Е N, начиная с некоторой начальной точки х° Е Rn, причем
на каждой итерации с номером к выполняется условие
fk = f(xk)^f(xk-1) = fk.b кеК D.2)
Так как целевая функция ограничена снизу, то в силу признака
Вейерштрасса [I] невозрастающая последовательность {/&}
сходится к некоторому пределу. Однако из этого в общем случае
еще не следует, что итерационная последовательность {хк}
4.1. Релаксационная последовательность
165
точек ж Gin, соответствующих значениям /&, сходится, а если
она и сходится, то ее пределом является точка ж* Е Мп
минимума функции /(ж), удовлетворяющая D.1).
Последовательность {ж^}, элементы ж^ Е Мп которой
удовлетворяют неравенству D.2), называют релаксационной.
Численные методы, применяемые для построения такой
последовательности, относят к классу методов спуска. Это
название можно связать с тем, что, например, при минимизации
функции f(x\,X2) двух переменных уменьшение ее значения
при переходе от точки (я^-1,^-1) к точке (х^х^)
означает спуск с линии уровня f(xi,X2) = fk-i на линию уровня
f(xi,x2) = fk <fk-l-
При анализе сходимости релаксационной
последовательности удобно рассматривать невозрастающую последовательность
{(fk}, где (fk = fk - Д > 0 (при (fk =0 принимаем ж* = хк).
Для оценки сходимости этой последовательности используют
следующие утверждения*.
Лемма 4.1. Если для элементов последовательности {(fk}
выполнены условия
<Pk-i ~4>к> 1кЧ>1-ъ Ч>к-\ > 0, 7/с > 0, к Е N, D.3)
то справедлива оценка
?>т< ^^t—> rneK D.4)
1 + <Ро Е 7fc
к=1
-4 После почленного деления первого неравенства в D.3) на
(fk-i<Pk находим
> 1к > 1к-
?к Ч>к-\ Ук
*См.: Карманов В.Г.
166 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
Суммируя это неравенство по А; от 1 до га, получаем
т / 1 1
Е'1 х
1 1 а
fc=1 ?k Vk-\> 4>т Щ к=1
откуда следует D.4). >
Теорема 4.1. Пусть минимизируемая функция f(x)
выпукла и дифференцируема на множестве W1, а
последовательность {ж } является релаксационной. Если
7/г=^гаё/(^-1)|2|^-1-ж*|2' fcGN' D5)
то справедлива оценка D.4).
-4 С учетом D.10) запишем
Ч>к-\ —Рк= fk-1 — fk =
Jk — l~Jk / л?( к — 1\ к — 1 *\2 ^
— (grad/(a5 ),ж — ж ) >
2
(grad/(a3fc 1),хк г —ж*)
^ /fc-l ~ Jk 2 _ 2
^ |grad/^)|2 las* - ж*|2</?fc " 7fe^-1"
Согласно лемме 4.1, получаем оценку D.4). >
Чтобы использовать теорему 4.1, необходимо располагать
оценками для значений 7ь определяемых равенствами D.5). В
общем случае получить такие оценки до проведения численного
решения задачи достаточно сложно, а в процессе этого
решения остается неизвестной разность хк~1 — ж*. Однако для
некоторых численных методов безусловной минимизации удается
установить, что 7/с ^ const > 0 начиная с некоторого номера к.
Тогда в соответствии с D.4) величина (рт имеет порядок
малости 1/га при га —>> оо.
Если для дифференцируемой в W1 функции f(x)
множество Xq = {ж EW1: f(x) ^ /(ж0)} ограничено, т.е. его диаметр
4.1. Релаксационная последовательность
167
diamXo = rj(x0) = ц конечен, то \хк г — х*\ ^ г/, и поэтому в
условиях теоремы 4.1 с учетом D.5) имеем
1к >
fk-l - fk
r/2|grad/(x/c_1)|2'
В итоге оценка D.4) принимает вид
<Pm = fm-f*<: ^-^ : . meN. D.6)
Щ V^ Jk-1 - Jk
'+??
V2 f^1\gr^df(xk-1)\2
Сумма в правой части полученной оценки имеет нулевое
значение, если последовательность {fk} постоянна.
Предположим, что эта последовательность не является постоянной и для
некоторого номера га выполнено неравенство ffh-i ~ ffh > 0-
Тогда при га > га
V~^ Jk — 1 ~ Jk ^ Jrh—1 ~ Jrh гл
^ \gididf(xk~1)\2 ^ |grad/(a?/c_1)|2
и, отбрасывая в знаменателе правой части D.6) единицу,
получаем оценку
г/2
<Pm = fm-f*< -^ , m > га. D.7)
V^ fk-l — fk
^ |grad/(#
к-1\\2
Оценку D.7) легко вычислить, и ее использование в процессе
численного решения задачи минимизации не вызывает
затруднений.
Лемма 4.2. Если для элементов последовательности {(fk}
выполнены условия
4>k-i ~Рк^ ткфк-ъ (рк-i > 0, тк > 0, к е N, D.8)
168 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
то справедлива оценка
т
4>т ^^oexp^-^r/.J, m<EN. D.9)
k=i
А Из неравенств в D.8) следует, что Т& Е @, 1) и
т
^т < A-Тш)<рш_1 <^oJJA_T^)-
Отсюда, учитывая, что 1 — Т& ^ ехр(—т^), приходим к D.9). >
Пусть минимизируемая целевая функция f(x) является
выпуклой и дифференцируемой на множестве W1. Тогда, согласно
теореме 3.11 и неравенству Коши — Буняковского, для любого
к Е N получаем
О < tpk-i = fk-i ~ /* < (grad/(^-1), хк~1 - х*) <
^ |grad/(x/c-1)||x/c-1-x*|. D.10)
Теорема 4.2. Пусть функция f(x) выпукла и
дифференцируема в IRn, множество Xq = {х Е Rn: /(ж) ^ /(ж0)}
ограничено, а последовательность {х } является релаксационной. Если
т^= | ^{-ni» fcGN' D11)
r/|grad/(a^ !)|
где 7/ = diamXo — диаметр множества Xq, to справедлива
оценка D.9).
<4 Используя D.10) и учитывая, что \х — х*\ ^ г/, находим
г г ^ (Л-1 - fkL>k-\ ^
grad/(ar_i) \хК~1 — ж*
(/fc-1 — fk)<Pk-l
r]\grdL,df(x
Согласно лемме 4.2, получаем оценку D.9). >
4.1. Релаксационная последовательность
169
При выполнении условий теоремы 4.2 оценка D.9) имеет вид
Я*та)-Л**)<ИфМу- Д-1-Д A meN D12)
Теорема 4.3. Для сильно выпуклой и дифференцируемой
в W1 функции f(x) при
Tfr=7, fkr}rtUw ^N, D.13)
|grad j(ar i)|^
где 7 — параметр сильной выпуклости функции /(ж),
справедливы оценки D.9) и
|жт - ж*|2 ^ -<рт, т Е N. D.14)
7
^ В силу теоремы 3.18 при k Е N имеем
,г ? ^ \ л ?( к\\2 \ к *\2^nJk~J*
7 7 7
Последнее неравенство равносильно оценке D.14), а из первого
неравенства вытекает, что
Ч>к-\ ~4>к = fk-i ~fk> igrad/^-i)^^-1 = Т^к'
Согласно лемме 4.2, получаем оценку D.9). >
Заменяя в оценке D.9) величины т^ их выражениями по
формулам D.13), а также величины щ = /д. — /*, приходим к
следующей оценке:
f(xm)-f(x*) (_ А /*-!-/* \
га- meN- DЛ5)
170 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
Используя D.14) и D.9), а затем заменяя величины Т& по
формулам D.13), получаем оценку
7gz?JjL<2a4>(^g_^A_i), m6K D.16)
Эти две оценки позволяют в процессе численного решения
задачи минимизации накапливать информацию о приближении
значений Д к значению Д, а в случае сильно выпуклой
минимизируемой функции — и о приближении точки ж к искомой
точке ж* минимума этой функции.
Практически можно задать некоторое число е > 0, связанное
с выбранной точностью вычислений, и проводить итерации до
тех пор, пока не будет нарушено неравенство
|grad j(ar l)\z
а затем либо повысить точность вычислений, либо перейти к
другому методу спуска.
Поиск точки ж* обычно прекращают при выполнении на к-й
итерации одного или обоих неравенств:
\хк -хк~х\ < еи \f(xk) - /(х*-1)] < е2, D.18)
где Е\ и 82 — заданные достаточно малые положительные
числа, называемые параметрами точности поиска. В
случае минимизации дифференцируемой функции необходимым
условием того, что ж* Е W1 — точка ее минимума, является
равенство grad/(sc*) = 0. При этом условием прекращения поиска
на k-ik итерации может быть выполнение неравенства
Igrad/taj*)!^, ?з>0. D.19)
Если при проведении итераций к значению /* = /(ж*)
сходится последовательность {fk} значений /д. = f(xk)
минимизируемой функции /(ж), то говорят о слабой сходимости
применяемого метода (или соответствующего алгоритма), а
если сходится к точке ж* и последовательность {ж }, то о
сильной сходимости этого метода (или алгоритма).
4.2. Методы спуска
171
4.2. Методы спуска
Пусть существует точка ж* Е W1, в которой целевая функция
f(x) достигает минимума. Процедуру поиска этой точки в
методах спуска обычно описывают (после выбора начальной
точки ж0) рекуррентным соотношением
xk = xk-1+0kuk, ?;EN, D.20)
где uk GW1 — единичный вектор, определяющий направление
спуска на А:-й итерации, а /?& ^ 0 — длина шага спуска,
к —Л
т.е. расстояние в этом направлении, отделяющее точку х
от новой точки хк. Методы спуска различаются способами
выбора направления и шага спуска.
Если на А;-й итерации выбран вектор и , то один из способов
выбора значения /3^ базируется на требовании, чтобы
выполнялось неравенство*
/(хк~1 + /Зкик) < A -A^/^-^ + Afc min f{xk-l + Cuk), D.21)
р?К*
где A& E [0, 1]. Отметим, что выбор значения /?& в соответствии
с условием D.21) обеспечивает выполнение неравенства D.2),
так что последовательность {хк}, построенная в соответствии
с D.20), будет релаксационной.
При А& = 1 неравенство в D.21) переходит в равенство, а
значение /3& соответствует минимальному значению функции
f(x) при изменении х вдоль луча, исходящего из точки х в
направлении вектора и , т.е. на множестве
{xeRn:x = xk-1+Cuk, /ЗеМ*}-
В этом случае для нахождения /3^ необходимо решить задачу
одномерной минимизации (см. 2). При этом значение /?& может
быть не единственным (в таком случае выбирают наименьшее
значение).
*См.: Карманов В.Г.
172 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
При \к = О D.21) переходит в неравенство
/(я^-Ч/^КД**-1). D-22)
Необходимость в решении задачи одномерной минимизации
отпадает, а для выбора значения /?& можно использовать
различные эвристические приемы.
Рассмотрим промежуточный случай А& Е @, 1). Для C Е М*
из D.20) и D.21) получаем
f(xk-1)-f(xk)^Xk{f(xk-1)-mmf(xk-1+Cuk))^
р?К*
^(/(^-/(а^-Ч/Зи*)). D.23)
Тогда при выполнении условий теоремы 4.3 оценка D.15)
примет вид
f(xQ)-f(x*) V ^ \gradf(xk !)|2 у
где 7 — параметр сильной выпуклости функции /(ж). Эта
оценка позволяет установить роль параметра* А&. Пока
отношение
f{xk-l)-f{xk)
|grad/(#A
остается достаточно большим, значение А& следует выбирать
таким, чтобы произведение Хкфк оставалось на каждой А;-й
итерации примерно постоянным. Тогда при сравнительно малом
значении А& нет необходимости в высокой точности
вычислений значений /3^ и решения задачи одномерной оптимизации
функции f(xk~l -\- (Зик) по аргументу C и можно выбрать /?&
просто из условия D.22). Однако по мере приближения к точке
ж* минимума целевой функции необходимо увеличивать
значение \к вплоть до единицы и выбирать значение /3^ из более
*=',kij.j:»0'. *6N
*См.: Карманов В. Г.
4.2. Методы спуска
173
точного решения задачи одномерной минимизации функции
f(x + (Зи ) по аргументу /3, обеспечивая тем самым
выполнение условия D.17).
Высказанные соображения качественного характера
справедливы не только для сильно выпуклых функций, но и для
выпуклых функций, удовлетворяющих условиям теоремы 4.1.
При некоторых дополнительных ограничениях эти
соображения можно распространить на невыпуклые дифференцируемые
функции*.
Перед рассмотрением вопроса о выборе направления спуска
докажем вспомогательные утверждения.
Лемма 4.3. Если функция f(x) непрерывно
дифференцируема во всех точках х = у + тр, т Е [0, 1], то справедливо
равенство
1
f(y + p) = f(y) + J{g™df(y + TP),p)dT. D.24)
о
-4 Функция h(r) = /{у + тр) действительного переменного т,
как сложная функция, непрерывно дифференцируема на
отрезке [0, 1], и ее производную для произвольного т Е [0, 1], согласно
правилу дифференцирования сложной функции, можно
записать в виде
Ы{т) = (grad / (у+ тр),р).
Для этой функции верна формула Ньютона — Лейбница
1
fh,(r)dr = h(l)-h@).
о
Поскольку /г@) = /(у), h(l) = /(у+р), то записанная формула
равносильна равенству D.24). >
*См.: Карманов В.Г.
174 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
Лемма 4.4. Пусть функция f(x) непрерывно
дифференцируема на выпуклом множестве X С W1 и существует такая
константа L > О, что для любых ж, у Е X выполнено
неравенство
|grad/(«)-grad/(j/)| ^L\x-y\. D.25)
Тогда для любых ж, у Е X справедливо неравенство
/(Ж) - /(у) ^ (grad/И, я - у) - ||ю - у|2. D.26)
^ Полагая р = х — у, согласно лемме 4.3 и свойствам скалярного
умножения, получаем
1
f(x)-f(y)= / (grad/(y + Tp),p)dT =
о
1
= (grad/(«),p)+ / (grad/(y + Tp)-grad/(#),p)d-r.
о
Используя неравенство Коши — Буняковского и D.25),
заключаем, что для интеграла / в правой части записанного
равенства верны соотношения
1
1> ~ / |grad/(y + Tp)-grad/(#)||p|dT>
о
1
^ — L / |у+ т(ж — у) — х\ \х — y\dr =
о
1
= -L\x-y\2 / A-т)^т = --|ж-у|2.
о
В итоге приходим к D.26). >
4.2. Методы спуска
175
Вектор, противоположный градиенту функции, называют
антиградиентом. Антиградиент функции f(x) в точке х
будем обозначать w(x) = — grad/(sc). Если градиент
определяет направление наибольшего возрастания функции [V], то
антиградиент, наоборот, задает направление наибольшего
убывания этой функции. Для k-ik итерации используем обозначения
wk = — grad/(a?/c_1) для антиградиента в точке xk~l и
_ (wk, uk) _ (grad/(a?/c~1), uk)
°^k — \ Jc\ ~ I Л?( h-A\\ V^'^4
\w^\ |grad/(ar l)\
для косинуса угла между направлениями спуска и
антиградиента.
Теорема 4.4. Если выпуклая и непрерывно
дифференцируемая в W1 функция f(x) удовлетворяет на множестве Xq =
= {х EW1: f(x) ^ /(ж0)} условиям леммы 4.4, множество Xq
ограничено, а последовательность {х }, построенная в
соответствии с D.20) и D.21), является релаксационной, то справедлива
оценка
ДЖ™)-/(**)/ f(x°)-f(x*)^ Л-1 ^щ
/(*«)-/(*•) Ч +—2W—h )
где L — константа в условии D.25), a r\ = diamXo — диаметр
множества Xq.
<4 Используя D.23), D.26), D.27) и учитывая, что \ик\ = 1,
заключаем, что
f^-1) -/(**)> А* (/(х*-1) - fix*-1 + Eик)) >
> Xki&adfix"-1), хк~1 - ixk-l+Cuk)) -
для любых значений /3^0. Из условия максимума правой
части полученного неравенства выберем C = a^\w \/L и после
176 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
подстановки этого значения, обозначив ср^ = f(xk) — /(ж*),
запишем
Ч>к-\~Ч>к -J\x )- J\x ) ^ ~2J~\W I ~~
= ^|grad/(x/c-1)|2>0. D.29)
Отсюда, используя D.10) и учитывая, что \х — х*\ ^ г/, находим
хк<4
2Lr]2
(рк-! -(рк> WT2 Ч>к-Ъ кеК
Сопоставляя это неравенство с первым неравенством в D.3)
и обозначая 7fc = A^ck^/BZ/?72), согласно лемме 4.1, получаем
оценку D.28). >
Оценку D.28), доказанную в теореме 4.4, при некоторых
дополнительных условиях можно упростить, а именно если для
некоторого номера итерации т коэффициент а^ ненулевой, то
сумма в D.28) отлична от нуля и мы можем, немного ухудшив
эту оценку, опустить в ней единицу. В результате получаем
f(xm)-f(x*)< lLT]2 , т^т. D.30)
k=l
Теорема 4.5. Если сильно выпуклая и непрерывно
дифференцируемая в W1 функция f(x) удовлетворяет в W1 условиям
леммы 4.4, а последовательность {х }, построенная в
соответствии с D.20) и D.21), является релаксационной, то
справедливы оценки
\хт — х*\2 2 / т J^ \
/U-/(L,)Sexp(-2i^A^)' mGN' D32)
k=i
4.2. Методы спуска
177
где L — константа в условии D.25), а 7 — параметр сильной
выпуклости функции /(ж).
А Согласно теореме 3.18, имеем |grad/(x/c_1)|2 > 7^/c-i и?
подставляя это неравенство в D.29), находим
<рк-г -<рк = f(xk-1) - f(xh) > 7^№-ъ к G N.
Сопоставляя это неравенство с первым неравенством в D.8)
и обозначая т& = 7^А^/BЬ), согласно лемме 4.2, получаем
оценку D.31). Оценка D.32) следует из D.31), если принять во
внимание доказанное в теореме 3.18 неравенство \хк~1 — ж*|2 ^
<l{f&-x)-№)).>
Если на каждой итерации направление спуска выбирать так,
чтобы для всех к Е N в D.27) 0<а^а^1иО<А^А^1, то
вместо D.30) получим
f(xm)-f(x*)<^^, meN, D.33)
а из D.31) и D.32) следуют оценки
/<.-)-/<«•) _, ^ml meN_ D34)
f(*°)
\xm-
-/(**) ^
-ж*|2
^ ^
2
7
:лр|
exp(-
2L "
j\a2
2L
raj, mGR D.35)
Из D.33), D.34) видно, что при выборе |а&| = а = А = 1 можно
ожидать наиболее быстрой слабой сходимости используемого
метода спуска, а в случае сильно выпуклой минимизируемой
функции — и наиболее быстрой сильной сходимости.
Отметим, что при а& = 1 единичный вектор и , задающий
направление спуска на А;-й итерации, сонаправлен
антиградиенту wix1*-1) в точке хк~г, т.е. ик = , ,ж, ,,,. Такой выбор векто-
ра г^ на каждой итерации характерен для метода
градиентного спуска (хотя его точнее надо было бы назвать методом
178 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
антиградиентного спуска). Если при этом на каждой итерации
\к = Л = 1, то это означает, что в направлении
антиградиента проводят одномерную минимизацию функции f(x + /Зи )
по аргументу C. Такой вариант метода называют методом
наискорейшего спуска.
4.3. Метод градиентного спуска
Пусть целевая функция f(x) ограничена снизу и непрерывно
дифференцируема в W1. Предположим, что существует точка
ж*е!п,в которой эта функция достигает локального
минимума. Рассмотрим некоторые особенности применения метода
градиентного спуска для поиска этой точки.
В этом методе элементы релаксационной
последовательности {хк} удовлетворяют рекуррентному соотношению вида
D.20)
к
хк = хк~1 + ркик = хк~1 + PkT^-Гм к Е N, D.36)
|гиЛ|
где /3^ > 0 — шаг спуска на fc-й итерации, а направление спуска
задано единичным вектором ик = wk/\wk\, сонаправленным
антиградиенту wk = — gra,d f (хк~1) в точке хк~1. Тогда из
D.27) следует, что а& = 1 для всех к Е N.
Если f(x) является выпуклой функцией и удовлетворяет
условиям теоремы 4.4, то градиентный метод обладает слабой
сходимостью, причем справедлива оценка
—^—h
<A+A2f S*4> т^ <437>
М + А2 + ... + Ат тА
где L — константа в условии D.25), r\ = diamXo —
диаметр ограниченного множества Xq = {ж Е Rn: /(ж) ^ /(ж0)}, а
4.3. Метод градиентного спуска
179
А/с ^ А > 0 — параметр в условии D.21), которому подчинен на
k-ik итерации выбор шага спуска /?&. Если же /(ж) является
сильно выпуклой функцией и удовлетворяет условиям
теоремы 4.5, то этот метод обладает сильной сходимостью. При
этом для любого т Е N имеем
f(xm)-f(x*) ^ ( 7А \ ,,„.
f(X*)-f{x*)^\-2Lmh D38)
'о, V* < -ехр(-^ш), D.39)
/(ж0)-/(ж*) 7 V 2L У
где 7 — параметр сильной выпуклости функции /(ж).
Возникает естественный вопрос, при каких условиях
сходится метод градиентного спуска в случае дифференцируемой
невыпуклой функции /(ж). Рассмотрим один из вариантов
этого метода, когда в D.36) /?& = ?c\wk\, где н = const > 0, т.е. шаг
спуска на каждой fc-й итерации пропорционален длине
вектора антиградиента в точке xk~l. Таким образом, вместо D.36)
получим рекуррентное соотношение
xk = xk~1 + Kwk, х>0, кеК D.40)
Теорема 4.6. Пусть функция /(ж) ограничена снизу и
непрерывно дифференцируема в Rn, причем для любых ж, у Е W1
выполнено неравенство
|grad/(aj)-grad/(y)|<L|a;-y|, D.41)
где L > 0 — некоторая константа. Тогда последовательность
{ж }, определяемая рекуррентным соотношением D.40) с к Е
Е @, 2/L), является релаксационной. При этом справедлива
оценка
/(**)</(я*)-*r(l-*r|) Igrad/^)!2 D.42)
и Igrad/^^)! —>> 0 при fc —>> оо.
180 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
< Положив в D.24) у = хк~1 и р = KWk, с учетом D.40),
равенства \wk\2 = (wk,wk) = — (grad/(x/c_1), wk) и свойства
линейности скалярного произведения находим
1
f(xk) - fix1"-1) = [(gicidfix1*-1 + TKWk), KWk) dr =
0
1
с / {gr&&f{xk-l + TKWk)-gT&&f{xk~l),wk)dT.
= —K\wk\2 + K
Оценим интеграл в правой части этого равенства, приняв во
внимание неравенство Коши — Буняковского и D.41):
1
/ (grad/(a?/c_1 + r>cwk) - grad/(a?/c_1), wk) dr ^
о
l
< f\ (grad/(a?/c-1 + r>cwk) - grad/^), wk) \ dr ^
о
l l
<L / \хк~г-\-r^wk-xk~1\\wk\dr = KL\wk\2 / rdr =
-\wk\2.
2 ' '
о о
В итоге получим f(xk) — f{xk~l) ^ —x(l — nL/2)\wk\2, что с
учетом равенства \wk\2 = |grad/(a?/c_1)|2 равносильно D.42).
Представив D.42) в виде
Igrad/Or*-1)!^
fc-ix-a^/^*-1) "/(**)
и просуммировав по /г от 1 до т, запишем
^|grad/(ar
A-iM2^/(«0)-/(«r
<
*r(l-*rL/2)
4.3. Метод градиентного спуска
181
Отсюда в силу ограниченности снизу функции /(ж) следует,
что при m —> оо сумма в левой части будет конечна, т.е.
\gr&df(xk)\ —> О при m —> оо. >
Замечание 4.1. Из теоремы 4.6 не следует сходимость
метода градиентного спуска, в котором используется D.40), к
какой-либо точке. Например, функция /(ж) = 1/A + |ж|2)
удовлетворяет условиям теоремы, но при любом выборе начальной
точки ж0 Е W1 имеем \хк\ —>> оо при к —>> оо.
Приведенный пример показывает, что функция вообще
может не достигать наименьшего значения. Однако если к
условиям теоремы 4.6 добавить требование ограниченности
множества Xq = {ж Е W1: f(x) ^ /(ж0)}, то, согласно теореме 7.1
в случае 0 = Rn, функция /(ж) будет достигать наименьшего
значения. Можно показать, что при этом последовательность
{ж } будет сходиться к какой-либо стационарной точке
функции, ф
Некоторые особенности рассматриваемого варианта метода
градиентного спуска можно выявить, если допустить
нарушение отдельных условий теоремы 4.6. Так, если функция /(ж)
не является ограниченной снизу, то нельзя утверждать, что
\gr&df(xk)\ —> 0 при m —>> оо. Действительно, для линейной
функции /(ж) = (с, ж) при с т^ 0 имеем |grad/(sc)| = \с\ > 0.
Если выбрать к ^ 2/L, то в процессе итераций минимизируемая
функция может не убывать. В самом деле, для ограниченной
снизу функции f(x) = Lx2/2, жЕ1, выполнено условие D.41), а
D.40) принимает вид хк = хк~1 — >cf'(xk~l) = A — >cL)xk~l, но
при выборе к ^ 2/L получим
/(**) = \ (A - xL)^J > \{x^f = f{xk~\
т.е. последовательность {ж } не является релаксационной.
Наконец, рассмотрим последствия нарушения условия D.41).
Функция /(ж) = |ж|1+ , где 6 Е @, 1), имеет точку минимума
182 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ж* = 0, дифференцируема в!п,но ее градиент не
удовлетворяет условию D.41), поскольку
Igrad f (ж) — grad f @I l + S . .
— ^V—n ^^ = г-пгпг-> °o при ж ->0.
|ж-0| {х^-6 F ' '
Для этой функции
^ = -ёгаа/(^-1) = -A + ^)|ж^|^ = -^_ж
Поэтому при достаточно малых значениях |ж 1|,
соответствующих приближению к точке ж* минимума, из D.40) имеем
1**1 =
к_х x(l + f) ^_!| = I _ X(l + f)
Ж |ж/с-1|1-?
|Ж/с-1|1-(^
|ж* 1\ > \хк г\
и f(xk) > f(xk х), т.е. последовательность Цж^Ц не сходится
к нулю. Можно показать, что предел этой последовательности
1
равен ( к ) . Не удовлетворяет условию D.41) и
дифференцируемая на W1 функция /(ж) = |ж|2+?, е > 0, имеющая ту
же точку ж* = 0 минимума, так как
Igrad f (ж) —grad f @I Ч| ._
|ж-0|
В этом случае wk = — B + б)|ж/с_1|?ж/с_1 ив соответствии с D.40)
находим
\хк\ = \хк-1-хB + ?)\хк-1\?хк-1\ = \1-хB + ?)\хк-1\?\\хк-1\.
Отсюда видно, что последовательность {ж } сходится лишь при
условии |l — жB + б)^-1^ < 1, т.е. если начальная точка ж0
удовлетворяет неравенству хB + б)|ж°|? < 2.
Один из недостатков метода градиентного спуска с
фиксированным значением ж в D.40) состоит в том, что в
окрестности стационарной точки ж дифференцируемой функции /(ж)
4.3. Метод градиентного спуска
183
шаг спуска на некоторой k-k итерации может оказаться больше
расстояния х — xk~l, т.е. при этом алгоритм „проскакивает"
искомую точку. Более того, этот шаг может быть
настолько большим, что f(xk) > f(xk~l) и последовательность {хк}
перестанет быть релаксационной. Избежать такой ситуации
позволяет выполнение условия D.41), существенно
ограничивающее класс рассматриваемых функций, а также выбор х Е
Е (О, 2/L) (см. теорему 4.6), который порождает второй
недостаток этого метода: по мере приближения к стационарной
точке шаг спуска x|grad/(# )| уменьшается, что сильно
замедляет сходимость последовательности {х } к этой точке.
Из оценки D.42) следует, что можно избежать „проскаки-
вания" искомой стационарной точки, если выбрать х= 1/L из
условия максимума выражения хA — xL/2). Однако в
прикладных задачах проверить выполнение условия D.41) и найти
константу L обычно не удается. Поэтому вместо D.40)
используют рекуррентное соотношение
хк = ж^-1 + Hkwk = хк~1 - кк grad/^-1), к Е N, D.43)
и подбирают значение х& > 0 на каждой к-тк итерации из
условия, которое в меньшей степени, чем D.41), ограничивает
класс минимизируемых функций. В случае ограниченной снизу
функции f(x) для обеспечения сходимости последовательности
{| grad / (ж ) |} к нулю достаточно, чтобы на каждой к-тк
итерации для некоторого числа с^о > 0 выполнялись неравенства
fix1"'1) - f(xk) ^ ou0\wk\2 = ои0\ grad/^-1)!2, к E N. D.44)
В самом деле, суммируя неравенства D.44) для к = 1, га,
получаем
m
/(^°)-/(^)>o;o^|grad/(^-1)|2.
k=l
оо
Поэтому знакоположительный ряд ^ |grad/(a?/c_1)|2 сходится,
к=1
а в силу необходимого признака сходимости его общий член
стремится к нулю, т.е. |grad/(a?/c)| —>> 0 при к —>> оо.
184 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
Следовательно, условие D.44) в сочетании с D.43) можно
использовать для выбора значения х&. Существуют разные
способы такого выбора*. Ограничимся рассмотрением двух из них.
Если функция f(x) непрерывно дифференцируема вР, то
скалярное произведение
(grad f(x),wk) =-(gYdLdf(x),gYdidf(xk-1))
ее градиента на антиградиент wk = — grad/(x/c_1) является
непрерывной функцией. В точке хк~1 оно равно — \wk\2 ^ О,
причем равенство нулю возможно лишь в случае, когда х —
стационарная точка. Ясно, что функция f(x) убывает в
направлении антиградиента до тех пор, пока это произведение
остается отрицательным. Поэтому один из способов выбора
значения Кк на /с-й итерации состоит в том, чтобы в D.43) х была
ближайшей к хк~1 точкой, в которой производная функции
f(x) по направлению антиградиента обращается в нуль, т.е.
(grad Да^), wk) = О, к е N. D.45)
Указанный способ называют исчерпывающим спуском
(движение в направлении антиградиента wk происходит до тех
пор, пока не будут исчерпаны ^подряд идущие"
отрицательные значения производной функции f(x) по направлению этого
вектора).
Замечание 4.2. Отметим, что точка хк, найденная при
помощи исчерпывающего спуска, может не совпадать с
соответствующей точкой, найденной по методу наискорейшего
спуска. Показано (см. 4.4), что в случае квадратичной
функции эти точки совпадают на каждой итерации. Если функция
f(x) строго выпукла в Rn, то в силу теоремы 3.7 функция
Фк(ж) = f (хк~г-\-KWk) также строго выпукла. Поэтому, если
стационарная точка функции ipkfa) существует, то, согласно
*См.: Полак Э., а также: Пшеничный Б.Н., Данилин Ю.М.
4.3. Метод градиентного спуска
185
теоремам 3.14 и 3.15, эта точка единственна и в ней функция
достигает наименьшего значения, ф
Из D.45) следует, что на (&+1)-й итерации новое
направление исчерпывающего спуска, определяемое антиградиентом
wkJrl = — grad/(a^), ортогонально предыдущему направлению.
Так как grad/(a^) коллинеарен вектору нормали в точке хк к
поверхности (линии) уровня f(x) = f(xk), то луч, исходящий из
точки хк~1 по направлению вектора wk = — grad/(a^_1), вдоль
которого на k-ik итерации происходит исчерпывающий спуск,
лежит в плоскости, касательной к этой поверхности уровня
в точке х , т.е. луч касается поверхности уровня функции,
проходящей через точку хк. Отметим, что если при переходе
через эту точку производная по направлению wk не изменяет
знак, то луч пересекает поверхность (линию) уровня f(x) =
= f(xk). Эти ситуации в плоском случае показаны на рис. 4.1
Рис. 4.1 Рис. 4.2
Замечание 4.3. Покажем, что для функции,
удовлетворяющей условиям теоремы 4.6, существует такое число с^о, что
при исчерпывающем спуске на каждой итерации будут
выполняться неравенства D.44). Для этого используем формулу
Тейлора с остаточным членом в форме Лагранжа
f(xk) - f{xk~l) = (grad/^-1 + ${хк - хк~1)), хк - хк~1),
186 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
где $ Е (О, 1). Отсюда, учитывал D.43), получаем
f{xk~l) - f{xk) = -кк(ётA/{хк-1+Цхк - хк~1)), wk).
Точка хк~1 +,д(хк — хк~1) на прямой исчерпывающего спуска
является промежуточной между хк~1 и хк. Производная по
направлению wk в этой точке отрицательна, и поэтому
(grad Дж^-1 + Цхк - хк~1)), wk) =
= \wk\2^gmdf(xk-1 + ^(xk-xk-1)),^)<().
Следовательно, выбор
со0 > -хи (grad/O^ + Цхк - ж*)), Jj?L) > О
обеспечивает выполнение неравенства D.44). На рис. 4.3
изображены итерации исчерпывающего спуска в случае R2.
Так как при использовании наискорейшего спуска значение
функции ф(к) = f(x + hw ) в точке ее наименьшего значе-
Рис. 4.3
4.3. Метод градиентного спуска
187
ния не превышает величины f(xk) при исчерпывающем спуске,
то неравенство D.44) будет выполнено и в этом случае, что
гарантирует сходимость последовательности {w } к нулю. #
Нетрудно проверить, что при минимизации функций |ж|1+<^,
S Е @, 1), и |ж|2+?, е > 0, для которых нарушено условие D.41),
при любом выборе начальной точки исчерпывающий спуск
приводит в точку наименьшего значения за одну итерацию. Это
указывает на то, что исчерпывающий спуск может дать
положительный результат при минимизации тех функций, к
которым не применим метод градиентного спуска с х = const.
Исчерпывающий спуск сходится к стационарной точке х Е Xq
функции /(ж), непрерывно дифференцируемой на выпуклом
множестве О D Xq, если множество Xq = {ж Е W1: f(x) ^ /(ж0)}
ограничено. Однако за расширение класса функций по
сравнению с рассмотренным в теореме 4.6 приходится расплачиваться
заметным усложнением алгоритма, так как теперь на каждой
итерации необходимо решать достаточно трудоемкую задачу
одномерной оптимизации при поиске точки хк и
соответствующего значения х&.
Выполнение условия D.44) можно обеспечить более простым
путем.
1. В точке хк~1 определяем направление wk = — gi&d f (хк~х)
спуска, вычисляем производную (grad/^^-1), wk) = — \wk\2 по
этому направлению (если |ги^| = 0, то хк~1 — искомая
стационарная точка), полагаем х& = xq, где xq > 0 — некоторое
произвольное значение, одинаковое на всех итерациях, и
переходим к п. 2.
2. Находим с помощью D.43) точку хк = хк~1 + х/сго/с,
вычисляем значение f(xk) и переходим к п. 3.
3. Проверяем выполнение неравенства*
f(xk) < f(xk-l)-uk\wk\2 < /(х'-1) -u>*k\wk\2,
*См.: Пшеничный Б.Н., Данилин Ю.М.
188 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
где L0 ? (О, 1). Если оно не выполнено, то уменьшаем значение х&
(например, вдвое) и возвращаемся к п. 2, а в противном случае
на /с-й итерации фиксируем использованное в п. 2 значение х&
и найденную точку х .
Такой способ подбора значения х& получил название
метода дробления шага. На рис. 4.4 показаны итерации с
использованием этого метода в случае плоскости.
Рис. 4.4
Несмотря на возможность расширения класса
дифференцируемых функций, для которых метод градиентного спуска
позволяет искать стационарные точки, оценку скорости
сходимости этого метода к точке минимума удается установить
лишь для более узкого класса функций. Пусть множество Xq =
= {х EW1: f(x) ^ /(ж0)} ограничено. Тогда существует стаци-
4.3. Метод градиентного спуска
189
онарная точка ж*, в которой дифференцируемая функция /(ж)
достигает наименьшего значения /(ж*) (см. замечание 4.1).
Теорема 4.7. Пусть дифференцируемая в W1 функция /(ж)
достигает своего наименьшего значения /(ж*) в точке ж*. Если
множество Хо = {ж Е W1: /(ж) < /(ж0)} ограничено и для любой
точки ж выполнено неравенство
\gmdf(x)\2>a0{f(x)-f(x*)), D.46)
где сто > 0, то для релаксационной последовательности {ж^},
построенной при помощи D.43) и D.44) и сходящейся к точке
ж*, справедливы оценки
/(ж^)-/(ж*)^^(/(ж°)-/(ж*)), |**-**|<Сд*/2, D.47)
где С>0и<?Е@, 1).
<4 Так как при построении последовательности {ж } на каждой
/с-й итерации выполнено неравенство D.44), то с учетом D.46)
имеем
/(^-^-/(x^^^lgrad/^-^l^wolgrad/^-1)!2^
ИЛИ
fix") - f{x*) < A - а;0а0) (Да^-1) - /(х*)).
Отсюда, выбирая значене ао > 0 так, чтобы q = A — своего),
получаем первое неравенство в D.47). Используя это
неравенство, а также неравенства D.43), D.44) и учитывая, что
релаксационная последовательность {ж } удовлетворяет
условию f(xk~l) - f(xk) ^ f{xk~l) - /(ж*), находим
|ж^-ж^1|2 = ^|ёгаA/(ж^1)|Ч^(/(^-1)-/(ж^))^
ми
< ^(/(а,*)-/(**)) < ^qk-l(f(x°)-f(x*)),
^0 ^0
190 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
где хо — наибольшее из значений параметра х& (со значения
хо на каждой к-к итерации начинают при необходимости
дробление шага спуска). В результате имеем
\хк+1 - хк\ < ciqk'\ с, = /Яж°)-Яж*).
Тогда для любого т > к получим
т~1 m~l 1k/2_qm/2
yl/2 *
\хт -хк\ < Yl i®*+1 - ®i <ci^2 <ii/2 = Ci—
=k
По условию теоремы последовательность {хт} сходится к
точке ж*. Поэтому из последнего неравенства, обозначая С =
с1
= -—1—, приходим при 777, —>> оо ко второй оценке в D.47). >
1 — уЯ.
Отметим, что условию D.46) удовлетворяет, в
частности, сильно выпуклая дифференцируемая функция (см.
теорему 3.18). Кроме того, этому условию удовлетворяет любая
квадратичная функция с положительно определенной
матрицей, поскольку она также является сильно выпуклой
функцией (см. пример 3.13).
4.4. Минимизация квадратичной функции
В теории численных методов многомерной оптимизации
большое внимание уделено поиску минимума квадратичных
функций. Применение численных методов к решению задачи
оптимизации, в которой целевая функция является
квадратичной, представляет интерес по нескольким причинам.
Во-первых, эта задача имеет решение в аналитическом
виде (см. 3.6), которое можно использовать в качестве
эталона при оценке погрешности численного метода и при
сравнении различных методов между собой. Во-вторых,
квадратичная функция служит своеобразным испытательным полигоном,
4.4. Минимизация квадратичной функции 191
на котором можно проверить работоспособность численного
метода (если метод малопригоден для минимизации
квадратичной функции, то, скорее всего, он будет неработоспособен,
когда целевая функция является более сложной). Наконец, при
представлении в окрестности некоторой точки произвольной
дважды дифференцируемой функции формулой Тейлора
можно ограничиться членами второго порядка, т.е.
аппроксимировать эту функцию квадратичной. Тогда задачу минимизации
исходной функции удается свести к последовательности задач
для аппроксимирующих квадратичных функций. Такой подход
особенно эффективен применительно к функциям, имеющим в
окрестности искомой точки минимума положительно
определенную матрицу Гессе и поэтому достаточно хорошо
аппроксимируемым сильно выпуклой квадратичной функцией.
Некоторые алгоритмы, разработанные с учетом свойств
квадратичных функций, позволяют найти точку минимума за конечное
число итераций.
Особое место в теории многомерной оптимизации
занимают задачи безусловной минимизации выпуклых квадратичных
функций двух переменных, или двумерные задачи
безусловной минимизации. Изучение идей конструирования
вычислительных алгоритмов на примере решения задач двумерной
минимизации позволяет наглядно, с помощью геометрических
построений на плоскости, представить отличительные черты
каждого метода, выявить их вычислительные свойства,
обсудить достоинства и недостатки, а также на основе результатов
вычислительного эксперимента получить представление о
сравнительных характеристиках различных методов.
В общем случае квадратичная целевая функция имеет вид
(см. 1.5)
F(z) = ^{Qz,z) + (c,z), zeRn, D.48)
где Q — симметрическая матрица порядка п, а с Е W1 —
заданный вектор. Пусть Q — положительно определенная матрица,
192 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
имеющая обратную матрицу Q~l. Тогда функция F(z)
является сильно выпуклой и достигает наименьшего значения в точке
z* = -Q_1c (см. 3.6), причем F(z*) = i(c, Q~lc).
Для упрощения выкладок далее будем рассматривать в
качестве целевой функции положительно определенную
квадратичную форму
f(x) = ^{Qx,x), xGRn, D.49)
которую можно получить из D.48) параллельным переносом
прямоугольной системы координат [IV]. Функция D.49)
неотрицательна при всех ж и достигает наименьшего значения О
в единственной точке ж* = 0.
Для минимизации функции D.49) используем метод
градиентного спуска. Найдем в произвольной начальной точке
ж0 т^ ж* градиент grad/(sc0) = Qx° этой функции и выберем на
первой итерации (к = 1) в качестве направления спуска
антиградиент w1 = — grad/(sc°) = —Qx°. Тогда в соответствии с
D.43) для следующей точки получим
х1 = ж0 + xiw1 = ж0 - xiQx® = (In - xiQ)x®, D.50)
где 1п — единичная матрица порядка п.
Из D.50) можно сделать важный вывод, в значительной
степени определяющий стратегию построения эффективных
численных методов безусловной минимизации: можно достичь
точки ж* наименьшего значения квадратичной функции D.49)
за одну итерацию, если ж0 — один из собственных векторов
yJ, j = 1,п, матрицы Q. Тогда при выборе >q = 1/Aj, где
Xj > 0 — собственное значение этой матрицы,
соответствующее собственному вектору у^, из D.50), согласно определению
собственных значений и собственных векторов матрицы [IV],
получим
х1 = (/„ - ^.0)у' = -Y.(QyJ ~ х^ = ° = ж*-
4.4. Минимизация квадратичной функции 193
Рис. 4.5
В двумерном случае
графиком функции f(x) = -(Qx,x)
является эллиптический
параболоид, а ее линиями уровня —
подобные эллипсы с общим
центром (рис. 4.5). Метод
градиентного спуска в этом случае
может привести в точку @, 0)
наименьшего значения за одну
итерацию лишь при выборе
начальной точки на одной из осей
эллипсов: в этом случае радиус-вектор точки является
собственным вектором положительно определенной матрицы Q
второго порядка. При одинаковых значениях собственных
значений матрицы Q графиком функции f(x) будет параболоид
вращения, а линиями уровня этой функции — окружности.
Здесь радиус-вектор любой точки ж0 ^ х* является
собственным, а точка наименьшего значения достигается за одну
итерацию при любом выборе начальной точки ж0.
Последняя геометрическая иллюстрация подсказывает,
казалось бы, простой с теоретической точки зрения путь
повышения эффективности метода градиентного спуска в случае
произвольной положительно определенной матрицы Q. Для
этого сначала поворотом системы координат квадратичную
форму D.49) нужно привести к каноническому виду, а затем
изменением масштабов по осям новой системы координат,
базисом которой будет система собственных векторов матрицы
Q, обеспечить равенство всех диагональных элементов
преобразованной матрицы. После ортогонального преобразования
функция D.49) в новой системе координат с осями 0?j, j = 1, n,
примет вид
Л@ = ?>??, ? = (?ь-.?«),
194 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
а после изменения масштабов путем замены (j = ^/Aj?j, j = 1, п,
получим
п
/2@ = Е^ с = (Сь...,Сп),
т.е. квадратичную форму /2(C) = (^С? С) с единичной матрицей
1п порядка п.
Минимизация функции /2(C) методом градиентного спуска
реализуется за один шаг (х = 1), но это упрощение не
оправдывает большой трудоемкости решения задачи на собственные
значения матрицы Q (особенно в случае достаточно высокого
порядка п). Тем не менее такой прием полезно использовать,
если график исходной квадратичной функции имеет так
называемую овражную структуру, когда убывание функции
по одному или нескольким направлениям существенно больше,
чем по остальным. В двумерном случае график такой функции
в окрестности точки минимума напоминает овраг с
крутыми склонами и пологим дном, а линии уровня оказываются
сильно вытянутыми (рис. 4.6). В этом случае преобразование,
состоящее в изменении масштабов переменных и называемое
масштабированием, превращает график минимизируемой
квадратичной функции двух переменных в параболоид
вращения, а линии уровня — в окружности.
Рис. 4.6
4.4. Минимизация квадратичной функции 195
Вернемся к случаю поиска минимума квадратичной
функции f(x) = - (Qx, х) с произвольным выбором начальной точки
и используем вариант метода градиентного спуска с
постоянным значением х& = к = const на всех итерациях. Тогда в
соответствии с D.40) на k-ж итерации получим
х
к
хк l + KWk
X
к-1
-xgrad/(ar L)
= х
k-i
kQxk = (In - kQ)x
k-i
keK D.51)
Последовательность {x } будет сходиться к точке ж* = 0,
если линейный оператор у = (In — kQ)x является сжимающим
отображением, для чего достаточно выполнения неравенства
\\1п~ kQ\\ = q(?c) < 1. Это условие зависит от выбора нормы
линейного оператора (нормы матрицы). В W1 часто используют
спектральную норму матрицы. Для этой нормы имеем [IV]
\\In — xQ\\ =тах{|1 - xAi|, |1 - ж\п\} = q(x),
где Ai, Хп — наименьшее и наибольшее собственные значения
матрицы Q соответственно.
Таким образом, при выборе значения ус нужно обеспечить
одновременное выполнение неравенств 11 — ж\\ | < 1 и 11 — ус\п \ <
< 1. Если выбрать ж Е @, 2/Хп) в соответствии со вторым
неравенством, то первое неравенство также будет выполнено,
поскольку 0 < Ai ^ Ап. Для сжимающего отображения верна
оценка \хк - ж*| ^ qk\x° - х*\ [I].
Поэтому для уменьшения
количества итераций, обеспечивающих
заданную точность, желательно
выбрать значение ж так,
чтобы знаменатель q(?c)
геометрической прогрессии был
наименьшим. На рис. 4.7 показаны
зависимости |1 — хА]_|, |1 —хАп| и
q(?c) от ж при Ai < Ап. Ясно, что
наименьшее значение q(?c) соот-
Рис. 4.7
196 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ветствует равенству |1 — к\\\ = |1 — хАп|, из которого при
Ai < Ап заключаем, что 1 — к\\ = — A — хАп). В результате
2 2
приходим к оптимальным значениям х* = — ^ — и
Ai + An An
An + Ai с(У) + 1
где c(Q) = An/Ai — число обусловленности матрицы Q. Для
единичной матрицы /п все собственные значения одинаковы
и равны единице, так что сAп) = 1 и ^ = 0. Это говорит о
том, что, как уже было отмечено, точка ж* достигается за
одну итерацию при любом выборе начальной точки ж0. Если
же Q плохо обусловлена, т.е. c(Q) 3> 1, то значение q* мало
отличается от единицы и поэтому последовательность {хк}
сходится медленно.
Покажем, что оценку
\xk-x*\^<f\x0-x*\ = (^^)k\x°-x*L fcGN, D.53)
1 '^ ' ' VAn + Ai/ ' "' v J
нельзя улучшить. Для этого достаточно привести пример, в
котором эта оценка окажется точной. Положим ж0 = ж* + у1 + уп,
где у1 и уп — единичные собственные векторы матрицы Q,
отвечающие собственным значениям Ai и Ап. Тогда с учетом
D.51) имеем хк — х* = Aп — >cQ)(xk~l — ж*), откуда, используя
свойства собственных векторов [IV], получаем
хк-х* = Aп - xQ)k(x° -x*) = (In- *Q)k{yl + Уп) =
= (l-xA1)V + (l-^An)V-
Следовательно,
\xk _x*\2= (A _ HXlJk + A _ xAnJfc) |*°-^f D.54)
поскольку с учетом ортонормированности собственных
векторов |ж° — ж*|2 = \у1 + уп\2 = 2. Правая часть соотношения D.54)
4.4. Минимизация квадратичной функции 197
при ж = к*
9fc I П * |9
принимает значение д* |ж — ж | , что при-
Ai + Лп
водит к точному равенству в D.53).
На рис. 4.8 приведена графическая иллюстрация процесса
сходимости метода градиентного спуска в плоскости к
точке минимума ж* = 0 для квадратичной функции /(ж) = х\ +
+ 10ж| при использовании D.51) и различных значениях ж\ на
рис. 4.8, а ж — 0,01, на рис. 4.8, б ж — 0,09.
'6,4 х1 -ЖЛ
Рис. 4.8
Отметим, что собственные значения для соответствующей
квадратичной формы (Qsc, х) = х\ + Юж^ равны Ai = 2 и А2 = 20.
Поэтому условием сходимости метода градиентного спуска с
постоянным значением ж = const является выбор ж Е @, 2/А2) =
= @, 0,1). Если ж ^ 0,1, то последовательность {хк} не является
релаксационной. При использовании D.51) это приводит к
расходимости метода или к его „зацикливанию". На рис. 4.9
представлена графическая иллюстрация этих ситуаций: a —
„зацикливание" при ж = 0,10 ж б— расходимость при ж = 0,11.
2
-6^
0
^21
6Д xL
-6Д
Рис. 4.9
198 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
Для пояснения полученных результатов подробнее
рассмотрим первые три итерации, выполненные в соответствии с
D.51) и с выбором начальной точки х° = A, 2):
1 B\ 1 о^ 1 /1-2х
W =-Uo-800xJ' Ж =Ж +Хад = (,2-80х + 800х2 ''
3_ / 2-8х + 8х2
™ I 20-1600х + 16000^2 ''
3_ 2 з_/ 1-6х+12х2-8х3
ж -ж + хю " ^2-120^ + 2400х2-16000х3
Отсюда при >с= 0,10 получаем
•¦=<'°S). -*=(Т> -*=(^2
т.е. для к = 1, 2, 3 имеем ^Ц = 2 — эффект ^зацикливания"
метода. При ^г = 0Д1 находим
х = / 0,7818 \ 2 / 0,6112 \ з = ( 0,4779 \
1 -2,3636 7' V2'7934/ V'3013/
/(ж1) = 56,479 < /(ж2) = 78,404 < /(ж3) = 109,213,
что свидетельствует о тенденции к расходимости метода.
Наконец, при к = 0,09 имеем
д / 0,8182 \ 2 / 0,6694 \ з = ( 0,5477 \
-1,6364 у' V, 1,3388 у' ^-1,0954 У
и
/(ж1) = 27,446 > /(ж2) = 18,373 > /(ж3) = 12,299,
т.е. можно ожидать, что последовательность {ж } является
релаксационной, а метод градиентного спуска сходится.
4.5. Сопряженные направления спуска
199
Рис. 4.10
Отметим, что применение исчерпывающего спуска при
минимизации рассматриваемой функции приводит к аналогичным
результатам (рис. 4.10). Покажем, что в общем случае целевой
функции f(x) = - (Qx, х) , х Е W1, метод наискорейшего спуска
на каждой /с-й итерации и исчерпывающий спуск эквивалентны,
т.е. точка х при спуске из произвольной точки х ф0 по
направлению антиградиента wk = — grad/(a?/c_1) = —Qxk~l ф 0n
будет одна и та же. Для доказательства этого сначала
вычислим градиент функции в точке х = х -\- z€kw :
gradf(xk) = Qxk = Qxk~l + xkQwk = -wk + xkQwk.
Умножим это равенство скалярно на вектор w is. учтем
условие D.45) исчерпывающего спуска. В результате получим
(grad/(a?/c), wk) = — (wk, wk) + Kk(Qwk, wk) = 0. Отсюда
находим единственное значение
\w
k\2
Xk
(wk,wk)
(Qwk, wk) (Qwk, wk)'
A; EN.
D.55)
4.5. Сопряженные направления спуска
Продолжим рассмотрение методов минимизации на
примере квадратичной формы D.49). Обратимся к более общему
рекуррентному соотношению D.20), записав его в виде
хк = хк~
1 + *крк,
A;EN,
D.56)
200 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
где Xfc > 0, к Е N; рк Е Мп — вектор, определяющий направление
спуска на ?>й итерации; щ\рк\ — шаг спуска. Пусть снова
выбрана произвольная начальная точка ж0 Е W1, в которой для
функции D.49) имеем антиградиент w1 = — grad/(x°) = —Qx°.
Для первой итерации (fc = 1) в соответствии с D.56) запишем
ж1 = ж0 + м\р1- Отсюда видно, что точки ж* = 0 минимума
квадратичной формы D.49) можно достичь из произвольной
точки ж0 за одну итерацию (т.е. ж1 = ж*), если выбрать ж\р1 =
= —ж0 = Q~1w1. При этом направление спуска, вообще говоря,
не совпадает с направлением антиградиента (совпадение имеет
место, например, в случае единичной матрицы Q).
Отметим, что для функции /(ж) = -(Qx, ж) матрица Гессе
Н постоянна и совпадает с матрицей Q. Поэтому при >с\р1 =
= Q~1w1 = —Q~lgidi>df(x{)) можно написать
х1 = х° + к1Р1 = ж0 + Q~lwl = ж0 - H~l grad/^0).
Это равенство представляет собой запись первой итерации
метода Ньютона решения системы уравнений grad/^) = 0, т.е.
нахождения стационарной точки функции /(ж). В данном
случае в силу положительной определенности матрицы Гессе Н = Q
в стационарной точке функция /(ж) достигает наименьшего
значения.
Таким образом, исчерпывающий спуск в направлении,
определяемом вектором —Q~1gra,df(x°) = Q~1w1 и обычно
называемом ньютоновским направлением спуска, эквивалентен
итерации метода Ньютона. При этом точка минимума
положительно определенной квадратичной формы может быть найдена
за одну итерацию, однако для этого нужно располагать
матрицей H~l = Q-1, обратной к матрице Q квадратичной формы.
Поскольку обращение матрицы (особенно высокого порядка п)
является трудоемкой задачей, представляет интерес попытка
сохранить преимущество изложенного подхода, но избежать
обращения матрицы Q.
4.5. Сопряженные направления спуска
201
Возвращаясь к рис. 4.10 (см. также рис. 4.3), обратим
внимание на то, что последовательность исчерпывающих спусков в
направлении антиградиента образует зигзагообразную
траекторию приближения к точке минимума, причем все соседние
звенья ломаной ортогональны. Это закономерно, поскольку
прямая в направлении антиградиента го на k-ik итерации
является касательной к линии уровня f(x) = f(xk), а направление
антиградиента w +1 на (к + 1)-й итерации перпендикулярно
этой касательной. Но исчерпывающий спуск в направлении
любого вектора р , приводящий в точку х , даст аналогичный
результат: антиградиент wk+1 = — grad/(a^) в этой точке
будет ортогонален вектору р , т.е.
(wk+\Pk) = -(grcidf(xk),pk) =0, кек
D.57)
Это равносильно условию завершения исчерпывающего спуска
в точке, в которой производная функции f(x) по направлению
вектора рк равна нулю. Для функции f(x) = -(Qx, х)
соотношение D.57) принимает вид
(grad/(a;*), рк) = (Qxk, рк) =0, к Е N. D.58)
Если известны собственные векторы у1 ж у2 матрицы Q
второго порядка, то при произвольной начальной точке ж0 =
= (ж^ х®) Е IR2 любая последовательность всего двух
исчерпывающих спусков в направлениях, коллинеарных этим
векторам, приводит в точку ж* минимума функции f(x) двух
переменных, т.е. зигзагообразная
траектория состоит всего из двух звеньев.
В самом деле, пусть сначала
исчерпывающий спуск коллинеарен вектору
у1 (рис. 4.11), который соответствует
меньшему собственному значению Ai
матрицы Q (поэтому вектор у1
параллелен оси, проходящей через фокусы
Рис. 4.11
202 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
эллипсов, являющихся линиями уровня функции f(x)). При
этом точка касания прямой спуска и линии уровня /(ж) = /(ж1)
будет лежать на оси симметрии, параллельной вектору у2.
Поэтому второй исчерпывающий спуск вдоль этой оси приведет в
точку ж*.
Ясно, что такой способ нахождения точки минимума
нетрудно обобщить на n-мерный случай, хотя для реализации
этого способа сначала нужно будет решить громоздкую
задачу на собственные значения матрицы Q порядка п. Естествен
вопрос: нельзя ли избежать нахождения собственных векторов
матрицы Q, но все же сократить количество итераций при
поиске точки минимума?
Рассмотрим этот вопрос снова на примере двумерной
задачи для квадратичной формы f(x) = -(Qx, х). Выберем
начальную точку ж0 и произвольное направление спуска,
определяемое вектором р1, не обязательно сонаправленным
антиградиенту w1 = —Qx° функции f(x) в этой точке, но
составляющее с ним острый угол, т.е.
(Qa?°, р1) < 0. Проведя из точки
ж0 в этом направлении
исчерпывающий спуск, получим
точку х1 на линии уровня f(x) =
= /(ж1) (рис. 4.12). Затем
выберем точку ж0, не лежащую на
прямой, проходящей через ж0 и
ж1, но такую, что (Qx®,pl) <0,
и проведем исчерпывающий спуск из точки ж0 в том же
направлении р1. В результате получим точку касания ж1 на линии
уровня /(ж) = /(ж1). Оказывается, что для получения искомой
точки минимума достаточно провести исчерпывающий спуск
из точки ж1 (или из точки ж1) в направлении р2, коллинеарном
вектору ж1 —ж1 (см. рис. 4.12).
Убедимся в этом, показав, что точки ж* = 0, ж1 и ж1 лежат
на одной прямой, т.е. векторы ж1 —ж* и ж1 —ж* коллинеарны.
4.5. Сопряженные направления спуска
203
Умножим каждый из них скалярно на ненулевой вектор Qp1 и,
учитывая, что матрица Q симметрическая, получим (Qx1,^1)
и (Q21, р1). Каждое из этих скалярных произведений является
производной функции /(ж) по направлению вектора р1 в точках
завершения исчерпывающего спуска и поэтому в соответствии
с D.58) равно нулю. Так как эти векторы порознь
ортогональны ненулевому вектору, то они коллинеарны.
Итак, два исчерпывающих спуска по несовпадающим
параллельным прямым позволяют найти направление,
исчерпывающий спуск по которому приводит в двумерном случае к
искомой точке минимума. Описанный способ можно немного
видоизменить. Выберем направление р1 исчерпывающего
спуска, совпадающее с одним из векторов стандартного базиса в
R2, например с е1, и такую начальную точку ж0 Е К2 на линии
уровня /(ж) = /(ж0) = С0, что (Q#°, е1) < 0 (рис. 4.13). В
результате исчерпывающего спуска получим точку ж1 на линии
уровня /(ж) = /(ж1) = С\ < Со. Затем положим ж0 = ж1 + те2,
т ф 0. Точка ж0 линии уровня /(ж) = /(ж0) = Со не лежит на
прямой проведенного исчерпывающего спуска в силу
ортогональности векторов е1 и е2, но число г следует выбрать так,
чтобы (Q5°, е1) ф 0 (иначе из этой точки не удастся
провести второй исчерпывающий спуск в направлении, параллельном
первому направлению). После проведения такого спуска при-
Рис. 4.13
204 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
дем в точку ж1 на линии уровня /(ж) = /(ж1) = С\ < Cq. Теперь
для нахождения точки ж* достаточно выполнить
исчерпывающий спуск из точки х1 (либо из точки ж1) в направлении
р2, коллинеарном вектору ж1 — ж1 (см. рис. 4.13). Проверку
этого утверждения можно провести аналогично предыдущему
случаю.
Таким образом, точку минимума в двумерном случае можно
найти, выполнив всего три итерации. Есть ли еще
возможность уменьшить число итераций? Такая возможность
основана на существующей зависимости между направлением р2
завершающего исчерпывающего спуска в точку ж* минимума и
параллельными направлениями двух предшествующих спусков,
коллинеарными вектору р1. Эту зависимость можно выразить
соотношением
{Qp\p2)=0, D.59)
верным в силу того, что
(Qp2,P1)=±{Qx1,P1)t(Qx\p1)
при р2 = ±(ж1 — ж1), а каждое из скалярных произведений в
правой части этого равенства в соответствии с D.58) равно
нулю.
Следовательно, при помощи D.59) точку минимума ж*
функции /(ж) = -(Eж,ж) можно найти за две итерации. Сначала
выполним исчерпывающий спуск в произвольном направлении,
определяемом вектором р1, из такой точки ж0, что (Qx®,p1^ <
< 0, и найдем точку ж1. Затем из D.59) определим вектор р2 и
в направлении, коллинеарном этому вектору, из точки ж1
осуществим исчерпывающий спуск в искомую точку минимума.
Подробнее остановимся на процедуре нахождения вектора
р2. Прежде всего вычислим Qx1. Если Qx1 = 0, то ж1 —
искомая точка минимума. При Qx1 ф О, полагая р2 = 71Р1 ~~ Qx1,
умножая это равенство скалярно на вектор Qp1 и используя
4.5. Сопряженные направления спуска
205
D.59), получаем (Qp1, jip1 — Qx1) — 0, откуда
= {Qp\Qx1)
71 {QpKp1) '
В частном случае может быть 71 — 0, и тогда р2 = —Qx1 ф 0.
Отметим, что р2/0и при 71 7^ 0- Иначе Qx1 = 71Р1 и с учетом
D.58) мы имели бы IQa?1]2 = 71 (Qx1, р1) = 0, что противоречит
принятому условию Qx1 ф 0. Направление исчерпывающего
спуска, коллинеарное вектору р2, зависит от знака производной
жх,р2) минимизируемой функции в точке ж1 по
направлению этого вектора. Если (Qx1, р2) < 0, то спуск происходит по
направлению вектора р2, а если (Qx1^2) > 0, то в
противоположном направлении.
Векторы р1 и р2, удовлетворяющие условию D.59),
называют сопряженными относительно матрицы Q (или Q-ортого-
нальными), а направления, определяемые такими векторами,
сопряженными направлениями. Понятие сопряженности
векторов является обобщением понятия их ортогональности.
Действительно, если Q = /2, то D.59) переходит в условие
ортогональности векторов р1 и р2. Дадим соответствующее
определение для системы векторов в n-мерном евклидовом
арифметическом пространстве W1.
Определение 4.1. Ненулевые векторы pJ Е W1, j = 1, га,
называют сопряженными относительно симметрической матрицы
Q порядка п (или Q-ортогональными), если справедливы
равенства
{Qp\pj)=0, i,j = T^i, гфз- D.60)
Лемма 4.5. Система га векторов pJ Е Rn, j = 1, га,
сопряженных относительно положительно определенной матрицы Q
порядка п, линейно независима.
Q
206 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
Л Предположим обратное. Тогда существует нетривиальная
линейная комбинация этих векторов:
т
5>У = 0, D.61)
3 = 1
в которой среди коэффициентов clj есть ненулевые, например
d{ ф 0. Умножим обе части D.61) скалярно на Qpl и с учетом
D.60) получим сц(С}рг,рг) =0. Но положительно
определенная квадратичная форма (Qp, р) для ненулевого вектора р — р%
имеет положительное значение. Следовательно, сц = 0, что
приводит к противоречию и доказывает лемму. >
Замечание 4.4. Ясно, что изменение направления
некоторых из векторов, сопряженных относительно матрицы Q, на
противоположное, не нарушает условия D.61). Поэтому если
система п векторов pJ Е Kn, j = 1, п, является сопряженной
относительно матрицы Q, то сопряженной является и система
^Р1 •> J = 1? п? ПРИ любом сочетании знаков перед векторами.
При проведении исчерпывающего спуска в направлении, кол-
линеарном некоторому вектору р из системы сопряженных
векторов, выбор конкретного направления, как и в случае
минимизации квадратичной функции двух переменных, зависит
от знака производной этой функции в начальной точке спуска
по направлению этого вектора. Далее для определенности
примем, что это конкретное направление исчерпывающего спуска
из двух возможных векторов ±р всегда задает вектор р .
Отметим, что для произвольной системы линейно
независимых векторов pJ Е Rn, j = 1, п, можно построить,
используя процесс, аналогичный процессу ортогонализации Грама —
Шмидта, систему векторов, сопряженных относительно
положительно определенной матрицы Q (систему Q-ортогональных
векторов). Выбирая разные системы Q-ортогональных
векторов, мы получаем разные методы сопряженных направлений.
Теорема 4.8. Точку минимума функции f(x) = - (Qsc, х) с
положительно определенной матрицей Q можно найти не более
4.5. Сопряженные направления спуска
207
чем за п итерации, определяемых рекуррентным соотношением
хк = хк~г + KkPk, к = 1, п, где рк ?ШП — векторы,
сопряженные относительно матрицы Q, если на ?>й итерации задавать
значение х& по формуле исчерпывающего спуска
Х* = ""@^У' ,п' ( 6)
Ц Из рекуррентного соотношения для хк получим
к
= ж° + ^хгр*. D.63)
г=1
ж*
Вычислим градиент grad/(a?) = Q# минимизируемой функции
f(x) в точке хк:
к
Qxk = Qx* + Y;^QPl-
г=1
Умножая обе части последнего равенства скалярно на вектор
рк и учитывая D.60), находим
к
(Qx\ рк) = (Qx°, р*) + ^ щ (Qp\ рк) = (Qx°, р*) + х, (Qp*, р*).
г=1
Отсюда следует равенство D.62), поскольку в случае
исчерпывающего спуска в направлении рк в соответствии с D.58) имеем
(Qxk,pk)=0.
Согласно лемме 4.5, векторы рг Е Кп, г = 1, п, линейно
независимы и их количество равно размерности линейного
пространства. Поэтому они образуют базис в W1. Значит, любой
вектор в W1 можно разложить по системе векторов рг, г = 1, п.
В частности, имеет место представление
п
x*-x° = ^2bipi D.64)
г=1
208 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
с некоторыми коэффициентами Ь{. Так как функция f(x)
сильно выпуклая, то необходимым и достаточным условием
достижения ею наименьшего значения в точке ж* является
равенство grad/(x*) = Qx* = 0. Тогда из D.64) имеем
п
Qx* - Qx° = -Qx° = Y,kQpl.
i=l
Умножая это равенство скалярно на вектор рк и учитывая
D.60), получаем — (Qx®,pk) =bk(Qpk,pk). Отсюда следует,
что bk = х&, к = 1, п. Таким образом, коэффициенты
разложения в D.64) совпадают со значениями ж^ на первых п
итерациях. Поэтому точку ж* можно найти не более чем за п итераций
вида хк = хк~1 + Мкрк, к = 1, п, что равносильно D.64). >
Замечание 4.5. Число итераций при поиске точки ж*
может быть меньше п. Дело в том, что при выборе начальной
точки возможна такая ситуация, что {Qx®,p ) = 0 для одного
или нескольких номеров к. В этом случае из D.62) следует, что
на к-й итерации х^=0и поэтому х = х , т.е. к-я итерация,
по существу, не проводится.
Замечание 4.6. Используя D.64) при Ь{ = щ, i = 1, п, и
D.62), с учетом равенства Q = Q и правил выполнения
матричных операций можно написать
^ (Qp\p1) \^(Qp\p1)J
Поскольку в рассматриваемом случае ж* = 0, то при
произвольном выборе точки ж0 приходим к выводу, что
^[{Qp\pl)
т.е. система векторов рг, г = 1, п, сопряженных относительно
положительно определенной матрицы Q, позволяет
достаточно просто построить матрицу Q-1, обратную к Q. В данном
Вопросы и задачи
209
случае Qx® = grad/(x°) и поэтому можно заключить, что п
итераций, проводимых при помощи D.62) и D.63), эквивалентны
одной итерации ж* = ж0 — Q_1grad/^°) метода Ньютона, но
требующей предварительного нахождения матрицы Q-1,
например, используя D.65). Однако система сопряженных
векторов рг, г = 1, п, заранее обычно не известна, и ее строят тем
или иным способом последовательно в процессе проведения
итераций (см. 5 и 6). В частности, такой путь используют при
решении системы линейных алгебраических уравнений Qz = —с
с положительно определенной матрицей Q, поскольку эта
задача эквивалентна задаче минимизации квадратичной функции
F(z) вида D.48). #
Рассмотренные выше подходы к решению задачи
минимизации квадратичной функции служат основой для построения
многочисленных итерационных алгоритмов безусловной
минимизации неквадратичных целевых функций. Наиболее
употребительные из этих алгоритмов рассмотрены ниже (см. 5 и 6).
Вопросы и задачи
4.1. Перечислите методы численного решения задач
многомерной безусловной минимизации в зависимости от
наибольшего порядка производных целевой функции, вычисление которых
предусмотрено в этих методах.
4.2. Дайте определение релаксационной последовательности
{ж^} точек хк Е W1. Каковы особенности методов спуска, что
является характеристикой их скорости сходимости? Как
проводить оценку эффективности методов спуска? Перечислите
алгоритмы, обладающие свойством квадратичной сходимости,
на примере решения задачи минимизации сильно выпуклой
квадратичной функции.
4.3. Дайте определение векторов р7 Gln, j = 1, п,
сопряженных относительно симметрической матрицы Q порядка п.
210 4. ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
Покажите, что если Q — положительно определенная матрица,
имеющая п различных собственных значений, то собственные
векторы этой матрицы, отвечающие различным собственным
значениям, являются сопряженными относительно Q.
4.4. Проанализируйте на примере поиска минимума
квадратичной функции с положительно определенной матрицей
Q, имеет ли значение тот порядок, в котором выбираются
направления исчерпывающего спуска в методе сопряженных
направлений. Можно ли осуществлять поиск минимума
квадратичной функции в одном и том же направлении более одного
раза?
4.5. Решите задачу минимизации функции f(x\1X2) = х\ -\-
+ х\ — 8(х\ +Ж2), используя различные стратегии поиска по
сопряженным направлениям, описанные в 4.5, и выбирая в
качестве начальной точки @, 1) и @, 0). Установите, влияет ли
выбор начальной точки на количество итераций при поиске
точки минимума. Сравните полученные результаты с
вычислениями по методу наискорейшего спуска и методу Ньютона.
Можно ли с применением этих методов получить точку
минимума при указанных начальных точках за конечное число
итераций? Если да, то чему равно это число итераций? Дайте
графическую иллюстрацию полученных результатов.
5. АЛГОРИТМЫ МЕТОДОВ
ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
Если ограниченная снизу целевая функция /(ж), х Е Мп,
является дифференцируемой на множестве Мп, то алгоритм
поиска точки ж* ее минимума можно построить, используя
информацию, по крайней мере, о градиенте этой функции. Более
широкие возможности построения таких алгоритмов
возникают в случае, когда целевая функция дважды дифференцируема,
что позволяет использовать ее матрицу Гессе. В этой главе
применительно к минимизации дифференцируемых и дважды
дифференцируемых функций рассмотрены алгоритмы
методов первого и второго порядков соответственно. Общей чертой
этих алгоритмов является построение релаксационной
последовательности {хк} точек хк Е Rn, получаемых при выполнении
каждой к-й итерации, а различие состоит в используемой
информации о целевой функции и ее производных.
5.1. Алгоритмы метода градиентного спуска
Направление спуска в методе градиентного спуска
совпадает с направлением антиградиента минимизируемой целевой
функции /(ж), дифференцируемой в Rn, а элементы
релаксационной последовательности {хк} строят при помощи
рекуррентного соотношения вида D.43)
хк = xk~1 + xkwk = хк~1 - xkgT&df(xk~l), >ск>0, к EN,
где wk = — gididf(xk~1) — антиградиент целевой функции в
точке хк_1. При этом говорят, что из точки хк на А;-й итерации
алгоритма происходит спуск с шагом спуска xk\w \. На
первой итерации (к = 1) спуск начинают из выбранной начальной
212 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
точки ж . Различие алгоритмов метода градиентного спуска
состоит в способе выбора значения х&.
Сначала рассмотрим способ выбора этого значения,
характерный для метода дробления шага и обеспечивающий
выполнение на каждой k-ik итерации неравенства
f{xk-l)-f{xk)>uKk\wk\\ E.1)
где и Е @, 1), гарантирующего сходимость последовательности
Цгу^Ц к нулю (см. 4.3). Если на к-к итерации не выполнено
это неравенство при некотором начальном значении х& = хо,
то процедуру дробления шага проводят в соответствии с
формулой Жк = z/^o? гДе v ? @, 1) — заданный постоянный
коэффициент дробления, шага, а г — номер этапа дробления, на
котором неравенство E.1) будет выполнено.
В целом алгоритм с использованием дробления шага можно
представить следующим образом. Выбираем начальную точку
ж0 и параметр точности поиска ?з > 0 в условии |ги^| < вз
прекращения итераций, а также значения v и щ. В неравенстве
E.1) обычно принимают ш = 1/2. Вычисляем значение /(ж0)
целевой функции f(x) в точке ж0, полагаем к = 1 и переходим
к основной части алгоритма.
1. В точке xk~l Е Кп, найденной на (к—1)-й итерации (на
первой итерации в точке ж0), вычисляем антиградиент w =
= —grdidf(xk~1). При выполнении неравенства |ги^| < ?з
прекращаем дальнейшие итерации и полагаем ж* « ж , /(ж*) ~
~ /(ж ). В противном случае переходим к п. 2.
2. Определяем точку хк = xk~l + yc^wk и значение f(xk)
целевой функции в этой точке. Если неравенство E.1) (ш = 1/2)
выполнено, то полагаем* х& = хо, А; := А; + 1 и возвращаемся к
п. 1. В противном случае переходим к п. 3.
3. Полагаем х& := vyc^ и возвращаемся к п. 2.
* Здесь и далее при описании алгоритмов используем символ
присваивания :=, который указывает, что значение величины в правой части
формулы нужно присвоить величине, записанной слева от него. Например,
запись к : = к +1 означает увеличение номера итерации на единицу.
5.1. Алгоритмы метода градиентного спуска 213
Пример 5.1. При помощи описанного алгоритма найдем
решение задачи безусловной минимизации функции f(x\,X2) —
= Qx\ — 4:Х\Х2 + 3^2 + 4л/5(^1 + 2^2)+ 22 (см. пример 3.18).
Выберем начальную точку ж0 = (—2, 1), при этом /(ж0) = 57. Кроме
того, фиксируем ?% = 0,01, щ = 0,1 и v — 0,5.
Воспользуемся тем, что функция квадратичная и имеет положительно
определенную матрицу с собственными значениями Ai = 4 и
А2 = 14. Поэтому выбранное
значение хо = ОД G @, 2/А2)
обеспечивает (сильную) сходимость метода
градиентного спуска с постоянным
на всех итерациях значением ус^ =
= ж§ (см- 4.4). При этом в
соответствии с D.53) справедлива оценка
ж
ж
^
-_5_\*
,12/
ж
ж
fceN,
и последовательность {ж }
сходится к искомой точке ж* Е К2 со
скоростью геометрической прогрессии, Рис. 5.1
имеющей знаменатель q = 5/12.
На рис. 5.1 представлена траектория поиска точки ж* =
= (—V5, — 2у5) минимума этой функции, а в табл. 5.1
приведены результаты вычислений (отметим, что у/5 ~ 2,2361 с
точностью 5 • Ю-5).
Характерной особенностью процесса поиска в данном
случае является то, что на первых итерациях спуск в направлении
антиградиента приводит к существенному убыванию значения
минимизируемой функции по сравнению с ее значением в
начальной точке ж0. Затем темп убывания значений функции
замедляется. Эта особенность, уже отмеченная ранее (см. 4.3),
снижает эффективность используемого алгоритма на
завершающей стадии поиска (для выполнения условия \w \ < ?з
потребовалось 15 итераций). #
214 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
Таблица 5.1
к
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
хк
(-2,000, 1,000)
(-1,047, -0,594)
(-0,923, -2,446)
(-1,688, —3,136)
(-1,811, -3,719)
(-2,020, -4,001)
(-2,091, -4,197)
(-2,155, -4,304)
(-2,185, -4,372)
(-2,206, -4,412)
(-2,218, -4,436)
(-2,225, -4,450)
(-2,230, -4,459)
(-2,232, -4,464)
(-2,234, -4,467)
(-2,235, -4,469)
(-2,235, -4,470)
f(xk)
57,000
7,150
-15,976
-23,772
-26,494
-27,460
-27,806
-27,930
-27,975
-27,991
-27,997
-27,999
-28,000
-28,000
-28,000
-28,000
-28,000
\gra,df(xk)\
37,148
18,553
10,309
5,953
3,508
2,087
1,248
0,747
0,448
0,269
0,161
0,097
0,058
0,035
0,021
0,013
0,008
Рассмотрим еще один пример реализации описанного
алгоритма, иллюстрирующий влияние выбранного значения v Е
Е @, 1) коэффициента дробления шага на количество итераций,
обеспечивающих достижение заданной точности поиска точки
ж* минимума целевой функции f(x).
Пример 5.2. Рассмотрим задачу минимизации функции
/(ж1,Ж2) = (х\ — x<iJ + (х\ — IJ, выбрав начальную точку ж0 =
= (—1, —2), в которой /(ж0) = 13, и параметры ?з = Ю-3, xq = 1.
Результаты поиска точки минимума ж* = A, 1)
рассматриваемой функции при различных значениях коэффициента
дробления шага v Е @, 1) (приближенное значение точки
минимума, значение функции в этой точке и количество итераций N)
приведены в табл. 5.2. Траектории поиска точки минимума в
5.1. Алгоритмы метода градиентного спуска 215
Таблица 5.2
и
0,2
0,4
0,5
0,6
0,8
0,5
X*
@,999, 0,997)
@,999, 0,998)
@,999, 0,998)
@,999, 0,997)
@,999, 0,997)
@,999, 0,998)
f(xN)
0,132-Ю
0,119-Ю-5
0,100-ю-5
0,157-Ю
0,159-Ю-5
0,066-Ю
N
102
76
72
54
66
85
Рисунок
5.2, а
5.2,5
5.3, а
5.3,5
5.3, в
5.3, г
каждом варианте показаны на рис. 5.2 и 5.3 (в табл. 5.2 даны
ссылки на соответствующий каждой траектории рисунок).
Из результатов поиска видно, что значение v
существенно влияет на необходимое количество итераций,
обеспечивающих поиск точки ж* минимума рассматриваемой функции с
заданной точностью. Наименьшее количество итераций
соответствует выбору значения v на отрезке [0,5, 0,8].
а б
Рис. 5.2
216 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
Рис. 5.3
5.1. Алгоритмы метода градиентного спуска 217
Отметим, что на практике значение х& на k-ik итерации
выбирают так, чтобы выполнялось неравенство f(xk~l) — f(xk) >
> 0. Это равносильно выполнению неравенства E.1) при си = 0.
На рис. 5.3, г показан именно этот вариант алгоритма
градиентного спуска при хо = 1и^ = 0,5. #
Эффективность алгоритма, использующего спуск в
направлении антиградиента, можно несколько повысить, если
значение Жк на каждой k-ж итерации выбирать путем минимизации
функции
M*) = f(xk-1 + xwk), х>0, E.2)
т.е. применить метод наискорейшего спуска. Напомним, что
для строго выпуклой функции f(x) это равносильно
процедуре исчерпывающего спуска, но в общем случае значение х,
соответствующее наименьшему значению функции ^(х), не
совпадает со значением, получаемым при помощи
исчерпывающего спуска (см. замечание 4.2). Отметим, что поиск минимума
функции ipkfa) может оказаться довольно трудоемкой
самостоятельной задачей, требующей применения методов одномерной
минимизации (см. 2), но для сильно выпуклой квадратичной
целевой функции значение ж^ определено однозначно формулой
D.55).
Выбор значения ус^ как при помощи исчерпывающего
спуска, так и методом наискорейшего спуска гарантирует
сходимость последовательности {w } к нулю (см. замечание 4.3).
Поэтому в качестве условия прекращения итераций и при этом
варианте выбора значения ус^ целесообразно использовать
неравенство \wk\ < ?з-
Опишем алгоритм наискорейшего спуска в случае
произвольной дифференцируемой целевой функции /(ж), х Е W1.
Предварительно выберем начальную точку ж0 и параметр
точности поиска ?з? положим к = 1 и перейдем к основной части
алгоритма.
1. В точке хк~1, найденной на (к—1)-й итерации (в точке х°
на первой итерации), находим значение f(xk~l) целевой функ-
218 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
ции и ее антиградиент wk = — gra,df(xk~1). При выполнении
неравенства \wk\ < ?з дальнейшие итерации прекращаем и
полагаем ж* «ж^-1, /(ж*) « f(xk~l). В противном случае переходим
к п. 2.
2. Минимизируя функцию фк(к) E.2), находим значение х&
и точку хк = ж^-1 + KfrWk, полагаем к : = к + 1 и возвращаемся
к п. 1.
Пример 5.3. Применим рассмотренный алгоритм к поиску
минимума той же квадратичной функции, что и в примере 5.1,
приняв ж0 = (—2, 1) и вз = 0,01. Так как эта функция
является сильно выпуклой (см.
пример 3.18), то значения ус^
выбираем в соответствии с D.55). В
табл. 5.3 приведены результаты
вычислений, а на рис. 5.4
иллюстрируется процесс поиска
точки ж* = (—л/5, —2у5) минимума
этой функции и выполнение
условия D.45) ортогональности
направлений спуска на двух следующих
друг за другом итерациях.
При том же значении еч = 0,01
Рис. 5.4
параметра точности для
завершения вычислений в данном примере потребовалось на две
итерации меньше, чем в примере 5.1. #
Примеры 5.1 и 5.3 показывают, что алгоритм метода
наискорейшего спуска в случае квадратичной функции не дает
заметного выигрыша по количеству итераций по сравнению с
алгоритмом, использующим метод дробления шага.
Минимизация же неквадратичной функции при сопоставимом количестве
итераций, необходимых для достижения заданной точности
при помощи этих алгоритмов, может потребовать существенно
большего общего объема вычислений по методу наискорейшего
5.2. Метод сопряженных направлений
219
Таблица 5.3
к
0
1
2
3
4
5
6
7
8
9
10
11
12
13
хк
(-2,000, 1,000)
(-0,283, -1,872)
(-2,173, -3,001)
(-1,711, -3,773)
(-2,219, -4,077)
(-2,095, -4,284)
(-2,231, -4,366)
(-2,198, -4,422)
(-2,235, -4,444)
(-2,226, -4,459)
(-2,236, -4,464)
(-2,233, -4,468)
(-2,236, -4,470)
(-2,235, -4,471)
f(xk)
57,000
-5,154
-21,860
-26,350
-27,556
-27,881
-27,968
-27,991
-27,998
-27,999
-28,000
-28,000
-28,000
-28,000
Щ
—
0,090
0,145
0,090
0,145
0,090
0,145
0,090
0,145
0,090
0,145
0,090
0,145
0,090
|grad/(a;fc)|
37,148
15,182
9,985
4,081
2,684
1,097
0,721
0,295
0,194
0,079
0,052
0,021
0,014
0,006
спуска вследствие поиска на каждой итерации минимума
функции ipkfa) E.2). Поэтому необходимое количество итераций
еще не является критерием эффективности того или иного
алгоритма.
5.2. Метод сопряженных направлений
Среди методов первого порядка поиска минимума
целевой функции /(ж), ж?Р, особое место занимает метод
сопряженных направлений, основанный на свойствах
векторов, сопряженных относительно некоторой квадратной
матрицы (см. 4.5). Этот метод по сравнению с методом
наискорейшего спуска требует, как правило, заметно меньшего
количества итераций для достижения той же точности поиска при
сопоставимом объеме вычислений на каждой итерации.
Различие в способах построения системы сопряженных векторов,
220 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
определяющих сопряженные направления спуска, порождает
несколько алгоритмов метода сопряженных направлений.
Сначала рассмотрим алгоритм, предназначенный для
поиска точки ж* минимума сильно выпуклой на выпуклом
множестве W1 квадратичной функции вида C.37)
f{x) = \ (Qx, х) + (с,х), жеГ, E.3)
где Q — положительно определенная матрица порядка n, а
с Е Мп — заданный вектор. Напомним, что эта функция имеет
единственную точку ж* = —Q_1c, в которой она достигает
наименьшего значения. Выше (см. 4.5) показано, что, располагая
произвольной системой векторов р1 Е Кп, г = 1, п, сопряженных
относительно матрицы Q, обратную к ней матрицу Q~l можно
вычислить при помощи соотношения D.65)
1 = ^рУ)т
^(Qp^p'Y
Но построение системы сопряженных векторов
представляет собой самостоятельную и в общем случае достаточно
сложную и трудоемкую в вычислительном отношении
задачу*. Особенность алгоритмов метода сопряженных
направлений состоит в том, что систему сопряженных векторов строят
последовательно в процессе выполнения итераций, причем
найденный на очередной, А;-й итерации вектор р Е W1 определяет
на этой итерации направление спуска. Выше (см. 4.5)
изложена элементарная процедура построения системы из двух
сопряженных векторов в R2, используемых при минимизации
квадратичной функции двух переменных. Обобщим эту
процедуру применительно к минимизации функции E.3).
Выберем начальную точку ж0 Е W1, найдем в этой точке
антиградиент w1 = — gr&d f (х°) = —Qx° — с и положим р1 = w1.
Ясно, что если Ip1] ф 0, то вектор р1 определяет на первой
*См.: Пшеничный Б.Н., Данилин Ю.М.
5.2. Метод сопряженных направлений
221
(к = 1) итерации направление спуска (в противном случае
точка ж0 удовлетворяет необходимому условию минимума, а это в
случае функции E.3) равносильно тому, что ж0 = ж* —
единственная точка наименьшего значения этой функции). Считая,
что \рг\ ф О, и проводя исчерпывающий спуск, при помощи
D.55) находим значение
I 1 12 I 1 12
\wl\l |py ,n
Xl (Qw\w^) (Qp1,p1)^U
и точку ж1 = ж0 + я\р1. Таким образом, первая итерация
полностью совпадает с итерацией алгоритма наискорейшего спуска.
На второй итерации (к = 2) вычислим антиградиент го2 =
= — gra>df(x1) = —Qx1 —ев найденной точке ж1. Пусть |го2| фО,
так как в противном случае ж1 = ж*. Положим
p2 = j1p1 + w2 E.4)
и, умножив это равенство скалярно на вектор Qp1 ф 0,
запишем (Qpl,p2) = (Qp1, Jip1 + w2). Потребуем, чтобы
векторы р1 и р2 были сопряженными относительно матрицы Q,
т.е. чтобы выполнялось равенство (Qp1^2) =0. Тогда 71 —
— ~~ (ЯР1? w2) I (Qpl^Pl)• Убедимся, что \р2\ ф 0. В самом деле,
при \р2\ = 0 имеем w2 = — 71Р1 и после умножения скалярно на
вектор w2 ф 0П приходим к противоречию:
(го2, w2) = |го2|2 = -71 (го2, р1) = (го2, го1) = 0,
поскольку при исчерпывающем спуске в соответствии с D.45)
антиградиенты на двух следующих друг за другом итерациях
ортогональны. Вектор р2 задает направление спуска из точки
ж1, так как с учетом E.4)
(grad/^1), р2) = - (w2, 71Р1 + w2) =
= -71 (го2, р1) - (го2, го2) = -|го2|2 < 0.
222 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
Если в направлении вектора р2 провести исчерпывающий
спуск, то теперь при нахождении точки ж2 = ж1 + х2р2 для
вычисления значения Х2 нельзя использовать D.55), так как
в общем случае 71 Ф О и поэтому направление спуска из точки
ж1 не совпадает с направлением антиградиента в этой точке.
Вычислим в точке ж2 антиградиент
w3 = -gra,df(x2) = -Qx2 - с = -Qx1 - x^Qp2 -c = w2 - x^Qp2
и после умножения скалярно на вектор р2 с учетом D.57)
получим (го3, р2) = (го2 — K2QP2:, р2) = 0, откуда
Ж2
(w2,p2) _ (gi^df(x1),p2)
(Qp2,P2)
(Qp2,P2)
E.5)
Так как го3 — w2 = — (^ж2 — с + (^ж1 + с = —Q(x2 — ж1) =
= —^^Qp2-, то с учетом го1 =р1 имеем
(го3, го1) = (го2 - >c2Qp2, го1) = (го2, го1) - х2 (Qp2, р1) = О,
поскольку при исчерпывающем спуске на первой итерации
(го2, го1) = 0, a (Qp2, р1) = (Qp1, р2) = 0 в силу симметричности
матрицы Q и Q-ортогональности векторов р1 и р2.
Следовательно, при исчерпывающем спуске в пространстве Rn, п > 2,
антиградиенты ортогональны на первых трех итерациях.
Продолжая описанную процедуру построения сопряженных
векторов, с помощью метода математической индукции можно
показать*, что на любой А;-й итерации при к = 1, п—1
У+1 =
7fe = -
«>fe+1 =
--1кРк
{Qp\
{Qp
= wk -
(Q/+1,p*):
, {wk+1
«,*) =
+™fc+\
to*+1)
/c,pfc)
¦ xkQpk,
= 0,
= 0, i =
l,k,
E.6)
*См.: Васильев Ф.П., а также: Базара M., Шетти К.
5.2. Метод сопряженных направлений
223
и при этом к^ = (wk, рк) / (Qpk, рк) и хк = xk~l + XkPk-
Таким образом, эта процедура за п итераций позволяет построить
систему векторов рг Е Мп, г = 1, п, сопряженных относительно
матрицы Q и в силу леммы 4.5 линейно независимых.
Антиградиенты wn = — grad/(ar :), fc Е N, в соответствии с E.6)
не
Ьх\ - Axix2 + Ъх\ + 4л/5(ж1 + 2ж2) + 22 двух пе-
образуют ортогональную систему векторов. Так как в W1
может быть более п ненулевых ортогональных векторов, то
один из антиградиентов wk, к = 1,п+1, с номером г должен
быть нулевым вектором, т.е. wl = — grad/(xz_1) = 0П.
Поэтому точка ж* = жг_1 минимума функции f(x) будет найдена не
более чем за п итераций.
Пример 5.4. Описанную процедуру построения
сопряженных векторов используем для поиска точки ж* минимума
функции f(xi,x2)
ременных, рассмотренной в
примерах 5.1 и 5.3, приняв в
качестве начальной точку ж0 = (—2, 1).
На рис. 5.5 представлены две
итерации поиска, причем первая из
них полностью совпадает с первой
итерацией в примере 5.3,
проведенной по методу наискорейшего
спуска. На второй итерации
исчерпывающий спуск из точки х1 =
= (—0,283, —1,872) в направлении
вектора р2, сопряженного с
вектором р1, приводит в искомую точку
ж* = (-л/5, -2у/Е). #
Чтобы использовать метод сопряженных направлений для
поиска минимума неквадратичной дифференцируемой
функции, предварительно необходимо привести систему E.6) к виду,
не содержащему матрицу Q. Это можно сделать, если в
итерационном процессе
Рис. 5.5
X
¦ хк 1 + хкрк,
fcEN,
224 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
с выбором значения х& > 0 на каждой к-к итерации путем
минимизации функции
Ы*) = 1{хк~1 + *Рк), х>0,
в основу построения сопряженных направлений pk+l = j^pk +
+ wkJrl положить свойство ортогональности антиградиентов (а
значит, и градиентов) минимизируемой функции
(ги*+1,ги*) =0, г = ТД.
Такой способ построения сопряженных направлений спуска в
литературе получил название метода сопряженных
градиентов.
Используя последнее уравнение E.6) при г = /с, третье
уравнение, а также равенство D.57), числитель и знаменатель
второго уравнения E.6) можно представить в виде
= („*+*-«,*,«,*+*) = _ J_ к
^к ^к
(^,/)=К-+'-<^=±(ц,>,/).
* к ^к
Таким образом, вместо второго уравнения E.6) имеем 7/с —
= \wkJrl\2 / (wk, рк). Это выражение можно преобразовать, если
учесть первое уравнение E.6), заменив в нем к на к — 1:
1к =
\?1) \ I?// I
(wk,jk-ipk 1-\-wk) jk_i(wk,pk 1) + \wk\2
Но если и в D.57) заменить к на к — 1, то получим (wk, рк г) =
= 0. Следовательно,
\wK\z
5.2. Метод сопряженных направлений
225
Если преобразования в первом равенстве E.7) не доводить до
конца, то вместо E.8) получим
С^ -»'¦«¦»') ,6N. (м)
В случае дважды дифференцируемой целевой функции
можно получить еще одно выражение для 7/с- Так как матрица Гессе
функции (Qsc, ж) /2 + (с, ж) совпадает с матрицей Q, то во
втором равенстве E.6) можно заменить Q матрицей Гессе Н(хк)
неквадратичной целевой функции:
(Н(хк)рк, wk+1)
(Н(хк)рк,рк)
Теперь с помощью одной из формул E.8)-E.10) из первого
равенства E.6), записанного в виде
pk+1=<ykpk + wk+1, кеЦ pr = w\ E.11)
на любой к-тк итерации можно найти вектор, определяющий
направление спуска из точки хк на (&+1)-й итерации. Для
квадратичной функции результат вычислений по каждой из
формул E.8)-E.10) будет одинаковым, но для неквадратичной
функции значения 7/с будут, вообще говоря, различными.
Поэтому использование каждой из этих формул при минимизации
неквадратичной функции f(x) может привести к построению
своей системы направлений спуска. При этом в отличие от
квадратичной функции точка минимума в общем случае не будет
найдена за конечное число итераций.
Более того, при выборе значения уск > 0 на каждой к-й
итерации в рекуррентном соотношении х — х -\- хкР
приходится минимизировать функцию
фк(х) = /(хк-1 + хрк), х>0, кеК E.12)
Это приводит к неизбежным погрешностям на каждой
итерации, которые могут вызвать нарушение сходимости алгоритма.
Чтобы ослабить влияние погрешностей, используют процедуру
226 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
„обновления" алгоритма, состояющую в том, что в E.11)
периодически через заданное число итераций полагают 7/с — 0.
Соответствующий номер итерации называют моментом
обновления алгоритма, или рестартом. Обычно при
минимизации целевой функции в W1 множество таких номеров имеет
вид Хо = {п, 2п, ..., ran, ...}, га Е N. Использование в
алгоритме рестартов позволяет избежать накопления вычислительных
погрешностей и уменьшить вероятность построения после
каждых п итераций линейно зависимых направлений спуска, но
приводит к росту общего числа итераций, необходимых для
достижения заданной точности поиска.
Опишем алгоритм минимизации дифференцируемой
неквадратичной целевой функции f(x). Выбираем параметр ?з > 0
точности поиска и начальную точку х° Е W1, в которой
вычисляем антиградиент w1 = — grad/(a?°). Убедившись, что
(го1] > 6з? формируем множество Iq моментов обновления
алгоритма, полагаем к = 1, принимаем р1 = w1 и переходим к
основной части алгоритма.
1. Минимизируя функцию фк{К) E-12), находим значение
Жк и точку х = х + Ккр . В этой точке вычисляем
антиградиент wk+1 = — gr&d f (хк) и проверяем выполнение неравенства
\w +1| < ?з- Если оно выполнено, то итерации прекращаем и
полагаем ж* « хк~1, /(ж*) « f(xk~l). В противном случае
переходим к п. 2.
2. Если к Е Хо, то полагаем р/с+1 = wk+1, fc : = к + 1 и
возвращаемся к п. 1. В противном случае переходим к п. 3.
3. При помощи E.8) или E.9) вычисляем значение 7/с и?
используя E.11), находим вектор pk+l. Полагаем к := к + 1 и
возвращаемся к п. 1.
Пример 5.5. Используем описанный алгоритм для
поиска минимума функции /(ж 1,^2) = (х\ — хъJ + (х\ — IJ,
рассмотренной в примере 5.2. Зададим параметр точности поиска
бз = Ю-3 и начальную точку ж0 = (—1, —2), в которой /(ж0) =
= 13.
5.2. Метод сопряженных направлений
227
Таблица 5.4
к
1
2
3
4
5
6
7
8
9
10
11
12
13
хк
@,379, -1,483)
@,158, -0,103)
@,792, 0,375)
@,746, 0,494)
@,978, 0,881)
@,965, 0,924)
@,974, 0,930)
@,978, 0,960)
@,999, 0,995)
@,998, 0,996)
@,999, 0,997)
@,999, 0,999)
A,000, 1,000)
f(xk)
3,031
0,726
0,107
0,068
0,006
0,001
0,001
0,000
0,000
0,000
0,000
0,000
0,000
Хк
0,086
0,394
0,432
0,194
1,028
0,114
0,232
0,519
0,286
0,098
0,525
0,398
0,166
|grad/(a;fc)|
3,475
1,624
0,631
0,346
0,828
0,047
0,045
0,058
0,012
0,001
0,002
0,001
0,000
Таблица 5.5
к
1
2
3
4
5
6
7
8
хк
@,379, -1,483)
@,192, -0,064)
@,893, 0,655)
@,901, 0,818)
@,936, 0,927)
@,999, 0,997)
A,000, 1,000)
A,000, 1,000)
f(xk)
3,031
0,663
0,032
0,001
0,000
0,000
0,000
0,000
Хк
0,086
0,401
0,508
0,265
0,133
0,116
0,377
0,088
|grad/(ccfe)|
3,475
1,551
0,406
0,219
0,334
0,003
0,001
0,000
Таблица 5.6
к
1
2
3
4
5
хк
@,379, -1,483)
@,531, 0,326)
@,899, 0,686)
@,990, 0,988)
A,000, 1,000)
/(**)
3,031
0,222
0,025
0,000
0,000
Хк
0,086
0,472
0,325
0,443
0,115
|grad/(a;fc)|
3,475
1,034
0,344
0,050
0,000
228 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
\ -l\ \
\\\^
\\\
х2;
и
0
V1
-$
1
/ / я*
/ PJx5/
/ X\P*/J
fpy*
Хх2
>=1/
*///
\1
/ 1
/1
Л]
t
Рис. 5.6
5.3. Метод Ньютона
229
Результаты вычислений, в которых параметр 7ь входящий
в E.11), определялся в соответствии с формулой E.8),
приведены в табл. 5.4, а аналогичные результаты, в которых параметр
7/с определялся в соответствии с E.9), — в табл. 5.5. Для
сравнения также даны результаты вычислений, в которых параметр
7/с определялся в соответствии с формулой E.10) (табл. 5.6).
Траектории поиска точки минимума ж* = A, 1) для всех трех
вариантов вычислений показаны на рис. 5.6: a — вариант с
формулой E.8); б— вариант с формулой E.9); в — вариант с
формулой E.10).
Из приведенных результатов видно, что необходимое
количество итераций N при поиске точки минимума является
наименьшим в случае, когда используется формула E.10), а
наихудшим оказался вариант с формулой E.8). Для сравнения
отметим, что для достижения той же точности при
использовании метода наискорейшего спуска требуется N = 96 итераций.
5.3. Метод Ньютона
Если целевая функция f(x) является дважды
дифференцируемой в IRn, то эффективность процесса поиска точки ж* ее
минимума можно повысить, используя информацию не
только о градиенте grad/(a?) этой функции, но и о ее матрице
Гессе Н(х). Алгоритмы такого поиска обычно относят к
методу Ньютона. В простейшем варианте алгоритма на каждой
/с-й итерации целевая функция аппроксимируется в
окрестности точки хк~г (на первой итерации в окрестности начальной
точки ж0) квадратичной функцией (fk(x) и затем
определяется точка хк минимума функции (р^(х). На следующей, (/с+1)-й
итерации строится новая квадратичная аппроксимация уже в
окрестности точки хк.
При помощи формулы Тейлора с остаточным членом в
форме Пеано представим целевую функцию в окрестности точки
230 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
х в виде
f{x) = fix*'1) + (grad Да^1), х - хк~1) +
+ ]- (Н{хк-1){х - хк-г), х - хк~1) + о(\х - ж*]2).
Пренебрегая последним слагаемым в правой части, получаем
квадратичную функцию
ipk{x) = f^1) + (grad Д^-1), х - ж*) +
+ \(Н{хк-1){х - хк-г), х - xk~l).
Если матрица Гессе Н(хк~1) целевой функции, вычисленная в
точке х , является положительно определенной, то точка х
минимума функции <pk{x) единственна и может быть найдена
из условия, что ее градиент равен нулевому вектору:
&ad<pk(x) = grad/O^) + H{xk~l){x - хк~1) = 0п.
Отсюда получаем
хк = хк-1 _ tf-^-^grad/^-1), к е N. E.13)
Отметим, что E.13) можно трактовать как рекуррентное
соотношение итерационной процедуры метода Ньютона,
предназначенного для решения системы gra,df(x) = 0П нелинейных
уравнений [V]. Этим можно объяснить и название метода,
применяемого для минимизации целевой функции f(x).
Если размерность п пространства W1 велика, то
вычисление на каждой к-тк итерации матрицы Н~1(х ), обратной к
матрице Гессе целевой функции, может оказаться весьма
трудоемкой процедурой. В таком случае точку х целесообразнее
искать путем минимизации функции <^(ж), например методом
сопряженных направлений или методом градиентов.
Подробнее этот вопрос рассмотрен ниже.
5.3. Метод Ньютона
231
Точку минимума функции (fk(x) можно считать лишь
вспомогательным приближением и, обозначив эту точку х , для
построения релаксационной последовательности {хк}
использовать рекуррентное соотношение
хк = хк-1 + Кк(~к _ д.Л-1) = хк-1 + Ккрк^ к е м? EЛ4^
в котором значение х& > 0 можно выбрать различными
способами. Вектор рк = хк — хк~1 задает на к-к итерации направление
спуска. Если матрица Н(хк~1) положительно определенная, то
это ньютоновское направление спуска. Действительно, с
учетом E.13) и E.14) этот вектор можно представить в виде
рк = -tf-^-^grad/^-1), к е N, E.15)
так что
(grad/(^-1),p^) =
= -(grad/(^/c-1)^-1(^/c-1)grad/(^/c-1)) <0.
Геометрически это означает, что вектор рк образует тупой
угол с градиентом целевой функции, вычисленным в точке
хк~г (рис. 5.7).
Ясно, что если в E.14) выбрать ж^ = 1, то E.13) и E.14)
будут равносильны. Однако значение ус^ > 0 можно найти как
*mdf(xk~l)
pfc = _н-1 {хк-1 j grad f( хк- v j
Рис. 5.7
232 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
точку наименьшего значения функции фк(^) = f(xk~l + крк)
или же при помощи исчерпывающего спуска в направлении
вектора р (согласно замечанию 4.2, эти значения могут не
совпадать). Для выбора значения щ можно также использовать
метод дробления шага.
Если целевая функция является квадратичной вида E.3) с
положительно определенной матрицей Q, то исчерпывающий
спуск из произвольной начальной точки ж0 ? W1 в
ньютоновском направлении приводит в точку ж* минимума этой функции
за одну итерацию (см. 4.5). Для неквадратичной функции
ньютоновское направление в общем случае не проходит через точку
ее минимума, хотя часто оказывается к этой точке ближе, чем
направление антиградиента. Если это так, то спуск в
ньютоновском направлении за одну итерацию позволяет достичь
более существенного убывания минимизируемой
неквадратичной функции и получить более близкое приближение к искомой
точке ж* минимума по сравнению со спуском в направлении
антиградиента.
Если график целевой функции имеет овражную структуру,
то вектор р E.15) может составлять с осью оврага меньший
угол, чем антиградиент. Эта особенность при минимизации
таких функций делает алгоритмы метода Ньютона более
эффективными, чем алгоритмы метода градиентного спуска.
Пример 5.6. На примере минимизации функции f(x\,X2) =
= {х\ — Х2J + [х\ — IJ сравним алгоритмы метода Ньютона
при х^ = 1в E.14) (рис. 5.8, а) и метода наискорейшего спуска
(рис. 5.8, б). Выбраны начальная точка ж0 = (—1, —2), в
которой /(ж0) = 13, и параметр точности поиска ?з = Ю-3.
В случае метода Ньютона (см. рис. 5.8, а) получено
приближенное значение точки минимума ж* « @,999, 0,999) за N = 5
итераций, в то время как в случае метода наискорейшего
спуска (см. рис. 5.8, б) приближенное значение точки минимума
ж* « @,999, 0,998) достигнуто за N = 96 итераций. Из резуль-
5.3. Метод Ньютона
233
а б
Рис. 5.8
татов вычислений видно, что метод Ньютона по сравнению с
методом наискорейшего спуска дает значительное уменьшение
количества итераций и быстрее обеспечивает заданную
точность решения задачи.
Обратим внимание на то, что в методе Ньютона /(ж1) <
< f(x2) (см. рис. 5.8, а), т.е. метод Ньютона привел к
последовательности, не являющейся релаксационной. Такое может
происходить при х^ = 1и при больших отклонениях начальной
точки от точки минимума. #
Сходимость метода Ньютона существенно зависит от
выбора начального приближения. Можно показать*, что если
целевая функция сильно выпуклая и для любых точек ж, у Е W1
относительно матрицы Гессе Н(х) целевой функции выполнено
неравенство ||i?(a?) — Н(у)\\ ^ L\x — у|, L > 0, а начальное
приближение выбрано удачно (точка ж0 расположена достаточно
*См.: Васильев Ф.П.
234 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
близко к точке ж* минимума), то алгоритм метода Ньютона
при значении х^ = 1в E.14) обладает квадратичной скоростью
сходимости, т.е. справедлива оценка
\хк - ж*|< С\хк~1 - ж*|2, к е N, С = const.
Это позволяет для такой функции использовать в качестве
условия прекращения итераций выполнение первого
неравенства D.18) \хк — xk~l\ < si, где е\ —заданное достаточно малое
положительное число. Но в случае, когда целевая функция не
является сильно выпуклой или же начальное приближение
находится далеко от искомой точки ж*, метод Ньютона может
расходиться.
Квадратичная скорость сходимости, а также возможность
контроля за соблюдением достаточного условия минимума
целевой функции f(x) на каждой к-ж итерации при помощи
матрицы Гессе Н(хк~1) этой функции способствуют высокой
эффективности рассматриваемого алгоритма. Однако при его
практической реализации возникают две проблемы.
Первая из них — это сохранение положительной
определенности матрицы Гессе Н(хк~1) целевой функции на каждой к-й
итерации, так как иначе вектор рк = — H~1(xk~1)gra>df(xk~1)
может не соответствовать направлению спуска, вдоль которого
эта функция убывает. Более того, матрица Н(хк~1) может
быть вырожденной и не иметь обратной матрицы. Эту
проблему можно решить, если направление спуска задавать вектором
рк = —(щ1п + Н(хк~1)) grad/(a?/c_1), где 1п — единичная
матрица порядка п, а щ ^ 0 — параметр, выбираемый так, чтобы
в точке хк~г матрица
Нк = щ1п + Н(хк-1), fcGN, E.16)
была положительно определена*.
В связи с этим более серьезной проблемой является
необходимость вычисления и обращения на каждой итерации матрицы
*См.: Базара М., Шетти К., а также: Реклейтис Г., Рейвиндран А.,
Рэгсдел К.
5.3. Метод Ньютона
235
порядка п, что в случае большой размерности пространства
W1 является достаточно трудоемкой операцией. На
практике обычно не вычисляют матрицу, обратную к положительно
определенной матрице ?Г&, а вектор рк находят из решения
системы линейных алгебраических уравнений (СЛАУ)
Нкрк = -gradДа^), к Е N. E.17)
Эту СЛАУ можно решить различными численными
методами, например прямыми и итерационными [III], [IV]. Можно
также решать СЛАУ путем минимизации квадратичной
функции {НкРк,рк)/2 + (grad/(a?/c_1),p/c) методами сопряженных
направлений или градиентов, поскольку выполнение E.17)
является необходимым и достаточным условием минимума такой
функции.
Опишем алгоритм варианта метода Ньютона поиска точки
ж* минимума дважды дифференцируемой целевой функции
/(ж), ж Е Мп, в котором направление спуска определяется путем
решения СЛАУ E.17). Предварительно выбираем начальную
точку ж°ЕКп и значение ?з > 0 в условии \gra>df(xk~1)\ < е%
прекращения итераций. Полагаем к = 1 и переходим к основной
части алгоритма.
1. В точке хк~1 находим grad/(a?/c_1) и матрицу Гессе
Н(хк~1) целевой функции. Если \gra>df(xk~1)\ < ?3, то
итерации прекращаем, принимая ж* « хк~1 и /(ж*) « f(xk~l).
Если при этом матрица Н(х ) положительно определенная, то
ж* — точка минимума целевой функции, а иначе необходимо
провести дополнительное исследование поведения функции в
окрестности точки ж*. При \gra,df(xk~1)\ ^ ?3 и положительно
определенной матрице Н(хк~1) полагаем Н^ = Н(хк~1) и
переходим к п. 3. В противном случае переходим к п. 2.
2. Подбираем значение щ > 0, при котором матрица Н^
E.16) будет положительно определенной, и переходим к п. 3.
3. Из решения СЛАУ E.17) находим вектор рк и затем
точку хк = хк~1 +рк. Полагаем к : = к + 1 и возвращаемся к п. 1.
236 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
5.4. Модификации метода Ньютона
Напомним, что в методе Ньютона для построения
релаксационной последовательности {хк} при поиске минимума
дважды непрерывно дифференцируемой и ограниченной снизу в
W1 целевой функции f(x) используют рекуррентное
соотношение вида E.14)
xk = хк~г + ккрк,
где рк — вектор, задающий на А;-й итерации ньютоновское
направление спуска из точки хк~1 (на первой итерации из
начальной точки ж0). Выше (см. 5.3) перечислены некоторые способы
выбора значения х&. Обычно собственно метод Ньютона
связывают с таким вариантом выбора этого значения, когда на
/с-й итерации принимают >с^рк = —H~l(xk~l)grdAf(xk~l), где
Н(х ) — матрица Гессе целевой функции с элементами,
вычисленными в точке хк~1. Если принять во внимание E.15), то
следует считать, что в методе Ньютона н^ = 1.
Одна из модификаций метода Ньютона поиска точки ж*
минимума функции f(x) связана с применением для выбора
значения н^ метода дробления шага, при котором на каждой
итерации выполняется неравенство*
f(xk-l)-f{xk)>-UKk{gvb&f{xk-l),pk), кеП, E.18)
где и Е @, 1/2). Если на А;-й итерации это неравенство не
выполнено при начальном значении ус^ = xq = 1, то процедуру
дробления шага проводят в соответствии с формулой ж^ = z/,
где v Е @, 1) — выбранный постоянный коэффициент
дробления шага, а г — номер этапа дробления, на котором будет
выполнено E.18).
Алгоритм с дроблением шага и нахождением направления
спуска путем решения системы линейных алгебраических
уравнений (СЛАУ) E.17) можно представить следующим образом.
*См.: Полак Э., а также: Пшеничный Б.Н., Данилин Ю.М.
5.4. Модификации метода Ньютона
237
На предварительном этапе выбираем начальную точку ж Е W1,
параметр ?з > 0 точности поиска в условии |grad/(x/c_1)| < ?3
прекращения итераций, коэффициент v дробления шага и
значение оо Е @, 1/2) в E.18). Вычисляем значение /(ж0) целевой
функции f(x) в точке ж0, полагаем А; = 1, х& = 1 и переходим к
основной части алгоритма.
1. В точке х , найденной на (А;—1)-й итерации (на
первой итерации в точке ж0), вычисляем градиент grad f (хк~г) и
матрицу Гессе H(xk~l) целевой функции. Если \gT&df(xk~l)\ <
< 63, то итерации прекращаем, принимая ж* « ж^-1 и /(ж*) «
~ /(ж ). В противном случае переходим к п. 2.
2. Из решения СЛАУ E.17) находим вектор рк, точку хк =
= хк~х -\- XkPk и значение f(xk) в этой точке. Если при этом
выполнено неравенство E.18), то полагаем ^ = 1, к := к -\-1 и
возвращаемся к п. 1. В противном случае переходим к п. 3.
3. Полагаем ж^ := vh^ и возвращаемся к п. 2.
Другой способ выбора значения х& в E.14) основан на
применении на каждой к-ж итерации исчерпывающего спуска в
направлении, определяемом вектором рк, т.е. связан с
минимизацией функции *фк(к) = f{xk~l + крк). Общая трудоемкость
этого способа может оказаться значительной вследствие
необходимости на каждой итерации для поиска минимума этой
функции использовать один из методов одномерной
минимизации (см. 2). Алгоритм, в котором реализуется такой способ
выбора значения х&, отличается от описанного выше тем, что
во втором пункте алгоритма после нахождения вектора рк
минимизируется функция ф(к), а затем полученное значение х&
используется для вычисления точки хк = хк~1 + ус^рк. После
этого осуществляется переход к первому пункту алгоритма.
Отметим, что на предварительном этапе нет необходимости
задавать значения ^, ш и ^ = 1.
Пример 5.7. Используем рассмотренный алгоритм для
поиска минимума той же функции f(x\1X2) = (х\ — Х2J + {х\ — IJ,
238 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
что и в примере 5.6, выбрав начальную точку ж0 = (—1, —2) и
задавшись значением ?з = Ю-3 параметра точности поиска.
Процесс поиска точки минимума ж* = A, 1) этой функции
для двух различных алгоритмов показан рис. 5.9: а — алгоритм
с дроблением шага (у = 0,5, си = 0,25); б— алгоритм с выбором
параметра х&, входящего в формулу E.14), с помощью
исчерпывающего спуска. Результаты вычислений приведены в табл. 5.7,
в которой колонки а и б соответствуют двум указанным
алгоритмам, а в колонке в содержатся результаты расчетов по
методу Ньютона с выбором х^ = 1в формуле E.14).
Из результатов расчетов видно, что спуск в ньютоновском
направлении уже на первой итерации приводит к значительно
большему убыванию целевой функции и дает более точное
приближение к искомой точке минимума. При одном и том
же значении бз = Ю-3 в вариантах б и в требуется всего пять
итераций, в то время как в варианте а — семь итераций. #
5.4. Модификации метода Ньютона
239
Таблица 5.7
к
1
2
3
4
5
6
7
а
(-0,7143
@,0226,
@,4735,
@,8478,
@,9667,
@,9991,
A,0000,
, 0,4286)
-0,5832)
0,0209)
0,5786)
0,9203)
0,9971)
1,0000)
б
(-0,6888
@,1152,
@,9260,
@,9821,
A,0000,
, 0,6455)
-0,5155)
0,6683)
0,9697)
1,0000)
в
(-0,7143
@,7594,
@,8044,
@,9992,
A,0000,
, 0,4286)
-1,5951)
0,6451)
0,9605)
1,0000)
Отметим, что рассмотренные модификации метода
Ньютона менее чувствительны к выбору начальной точки ж0 по
сравнению с ^классическим" вариантом этого метода,
соответствующим значению х^ = 1 в E.14). Можно показать*, что если
целевая функция является сильно выпуклой и ее матрица Гессе
Н{х) для любых точек ж, у Е W1 удовлетворяет неравенству
\\Н(х)-Н(у)\\^Цх-у\, E.19)
то при произвольном выборе начальной точки обе
рассмотренные выше модификации метода Ньютона обладают
квадратичной скоростью сходимости. При этом справедлива оценка
\хк - ж*| ^ ^\хк~1 - ж*|2, к Е N, E.20)
Ai
где Ai — оценка снизу наименьшего из собственных значений
матрицы Гессе Н{х) целевой функции в окрестности точки ж*,
содержащей точку х , если в этой окрестности матрица Гессе
является положительно определенной, т.е. Ai|#|2 ^ (Н(х)х1 х)
для всех точек х из этой окрестности.
Ясно, что попытка реализовать рассмотренные алгоритмы
наталкивается на те же проблемы, что и при выборе х^ = 1 в
*См.: Пшеничный Б.Н., Данилин Ю.М.
240 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
E.14) (см. 5.3). Главная из них состоит в том, что на каждой
к-ж итерации необходимо вычислять и обращать матрицу
Гессе Н(хк~1) целевой функции или же искать направление спуска
путем решения СЛАУ E.17), где матрица Н^ определяется
равенством E.16). Один из способов разрешения этой проблемы
заключается в использовании для выбора направления спуска
вместо E.15) соотношения
рк = -ff-^Jgrad/fc*-1), к е N. E.21)
Если в начальной точке ж0 матрица Гессе Н(х°) целевой
функции не является положительно определенной, то в E.21) вместо
Н(х°) можно использовать матрицу Hi = r\\ln + Н(х°),
вычисленную в соответствии с E.16) при к = 1.
Оказывается, что использование E.21) приводит к линейной
скорости локальной сходимости, причем справедлива оценка
\хк-х*\ t^q\xk~l -х*\, ?;<EN, q = const. E.22)
Выбор начальной точки ж0 влияет на знаменатель q
геометрической прогрессии: чем ближе ж0 к искомой точке ж*, тем
меньше значение q.
Другой способ разрешения указанной выше проблемы
состоит в периодическом „обновлении" матрицы Гессе в E.21).
В этом случае на первых К итерациях в E.21) используют
матрицу Н(х°) (или Н\, если матрица Н(х°) не является
положительно определенной), а на (К+1)-и итерации ее заменяют
матрицей Н(хк) (или Нк+ъ если матрица Н(хк) не окажется
положительно определенной матрицей) и т.д. Выбор значения
К зависит от целевой функции. Если целевая функция сильно
выпукла и удовлетворяет условию E.19), то алгоритм с
„обновлением" матрицы Гессе при произвольном выборе начальной
точки будет обладать сверхлинейной скоростью сходимости".
*См.: Пшеничный Б.Н., Данилин Ю.М.
5.5. Квазиньютоновские методы
241
При этом для любого из рассмотренных выше способов выбора
в E.14) значения х& справедлива оценка
\хкк - ж*|< С\х^~^к - ж*|к+1, k е N, С = const.
При К = 1, т.е. при „обновлении" матрицы Гессе на каждой
итерации, эта оценка равносильна E.20), а при довольно редком
„обновлении", т.е. при больших значения X, она приближается
к E.22).
5.5. Квазиньютоновские методы
Среди алгоритмов многомерной минимизации следует
выделить группу алгоритмов, которые объединяют достоинства
метода наискорейшего спуска и метода Ньютона. Такие
алгоритмы принято относить к так называемым квазинъюто-
новским методам. Особенность этих алгоритмов состоит в
том, что при их применении нет необходимости вычислять и
обращать матрицу Гессе целевой функции f(x) и в то же время
удается сохранить высокую скорость сходимости алгоритмов,
присущую методу Ньютона и его модификациям (см. 5.3 и 5.4).
Элементы релаксационной последовательности {хк} в
алгоритмах квазиньютоновских методов минимизации
непрерывно дифференцируемой в W1 целевой функции f(x) строят в
соответствии с рекуррентным соотношением хк = хк~1 + МкРк•>
но направление спуска на каждой А;-й итерации задают в виде
pk = -Akgid.df(xk-1) = Akwk, кеК E.23)
Здесь wk = — grdidf(xk~1) — антиградиент целевой функции в
точке х , & Ак — положительно определенная матрица
порядка п, обновляемая на к-ж итерации. Отметим, что направление,
задаваемое на каждой к-ж итерации вектором р E.23),
является направлением спуска, так как с учетом E.23)
{&adf(xk-1),pk)=-{wk,Akwk)<0.
242 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
Матрицы {Ак} определяют таким образом, чтобы
последовательность {Ак} при к —>> оо имела предел, равный if-1 (ж*),
где Н(х*) — матрица Гессе целевой функции, вычисленная в
точке минимума ж* этой функции.
На k-jk итерации алгоритма поиска точки минимума
происходит спуск из точки хк~1 с шагом спуска щ\рк\, причем
значение кк выбирают путем исчерпывающего спуска в
направлении вектора рк. На первой итерации (к = 1) спуск начинают
из выбранной начальной точки ж0 и при этом обычно в
качестве А\ берут единичную матрицу 1п порядка п. Отметим,
что в этом случае р1 = w1 = — grad/(sc0), т.е. первая итерация
алгоритма квазиньютоновского метода полностью совпадает с
итерацией метода наискорейшего спуска (см. 5.1). Если
принять Ah = H~1(xk~1) в E.23) и уск = 1 в E.14), то придем к
классическому" методу Ньютона (см. 5.3).
Как было отмечено выше (см. 5.3), если целевая функция
является сильно выпуклой, то алгоритмы метода Ньютона
обладают квадратичной скоростью сходимости. Поэтому можно
ожидать, что алгоритмы квазиньютоновских методов будут
иметь достаточно высокую скорость сходимости, если на
каждой к-& итерации матрица Ак выбрана близкой к матрице
Н~1(хк~1) в точке xk~l Е W1. Используя при конструировании
матрицы Ак аппроксимацию матрицы Н~1(хк~1) с учетом
информации о градиенте целевой функции в той же точке ж ,
можно существенно упростить процедуру нахождения
направления спуска на к-тк итерации. Именно эти соображения лежат
в основе построения алгоритмов квазиньютоновских методов.
Остановимся на вопросе построения последовательности
матриц Ак. Эти матрицы строят в соответствии с
рекуррентным соотношением
Ак+г = Ак + ААк, fcEN, E.24)
где ААк — положительно определенная матрица порядка п,
называемая поправочной. Способ ее выбора определяет вариант
5.5. Квазиньютоновские методы
243
алгоритма квазиньютоновского метода. На первой итерации,
как уже отмечалось, обычно принимают А\ = 1п.
Предположим, что f(x) = - (Qx, х) + (с, х) — квадратичная
функция с положительно определенной матрицей Q. В этом
случае функция f(x) сильно выпукла, grad/(x) = Qx + c (см. 3.6),
Awk = grad/(x/c_1) - gradf(xk) = Q(xk~l - xk),
и мы можем записать
Q~1Awk = -Axk, fceN, E.25)
где матрица Q совпадает с матрицей Гессе Н(х) функции f(x).
В общем случае, проводя аналогию с E.25), потребуем,
чтобы матрица А^+х в E.24) удовлетворяла так называемому
квазинъютоновскому условию
Ak+lAwk = -ДаД fcEN, E.26)
а поправочную матрицу ААк в E.24) выберем, исходя из
условия
lim||,4fe+1-tf-V)||=0,
/с—^оо
т.е. так, чтобы последовательность {Ак} имела при к —>> оо
предел, равный Н~1(х").
Подставляя E.24) в E.26), получаем AAkAwk = —Ахк —
— AfrAw . Непосредственной подстановкой можно убедиться,
что для любого к Е N одним из решений этого уравнения будет
матрица
Л Л АхкуТ AkAwkzT
A Ah = - -
(Awk, у) (Awk, z)
где у, z Е W1 — произвольные элементы из W1. Полагая у = Ахк
и z = Akw\ получаем с учетом E.24) формулу
_ А^(А^)т AkAwk(AwkfATk
Ак+1-Ак {Aw^Axk) {AkAwk^Awk) ' fcG^> E-27)
244 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
для выбора элементов последовательности {А&}. Такой способ
выбора матриц Ак приводит к одному из алгоритмов
квазиньютоновского типа, известного в литературе как метод Давидо-
на — Флетчера — Пауэлла, или ДФП-метод.
Рассмотренный способ „обновления" матрицы Ak+i
сохраняет ее свойство положительной определенности на каждой А;-й
итерации. Для того чтобы убедиться в этом, воспользуемся
методом математической индукции. Очевидно, что матрица А\
положительно определенная, если принять А\ = 1п.
Предположим, что при к > 1 матрица Ак также положительно
определенная, и докажем, что матрица Ак+\ в E.27) положительно
определенная.
Выберем ненулевой вектор у Е W1. Тогда с учетом E.27)
можно записать
ч , ч (Ахк(Ахк)ту,у)
(M+iV, У) = (АкУ, У) ~
(Awk, Ахк)
(AkAwk(Awk)TATky,y)
(AkAwk, Awk)
E.28)
Из курса линейной алгебры известно [IV], что любая
положительно определенная матрица Ак порядка п может быть
представлена в виде Ак = СкСк, где Ск — невырожденная нижняя
треугольная матрица порядка п. Обозначив и = Ску и v =
= CkAwk, перепишем E.28) в виде
(Л+и/, у)
(и, и) ¦
{Ахк,уJ (и, уJ _
(Awk,Axk) (v,v)
\u\2\v\2 - (и, vJ (Ахк,у)
\v\2 (Awk,Axk)
E.29)
Покажем, что знаменатель второго слагаемого в правой
части E.29) отрицателен. В самом деле, учитывая, что Ах =
— Жкрк, а направление спуска рк на А;-й итерации определяется
5.5. Квазиньютоновские методы 245
согласно E.23), получаем
(Aw\ Axk) = (grad/^) - grad/(a;*), xk - xk~l) =
= -x^(grad/(x/c-1),^grad/(x/c-1)) - xk(g?adf(xk),pk) <
<-Kk(gmdf(xk),pk),
поскольку по предположению индукции матрица Ak
положительно определенная. Так как точку хк находим при помощи
исчерпывающего спуска из точки хк~1 в направлении
вектора р^, то в соответствии со свойством D.57) исчерпывающего
спуска правая часть последнего соотношения равна нулю, т.е.
(Лги*, Ахк) < 0.
В силу неравенства Коши — Буняковского имеем |-гх|2|-L712 ^
^ (гх, v) , причем равенство возможно лишь при u = v, что с
учетом невырожденности матрицы Ск эквивалентно равенству
у = Awk. Но тогда (Дж^, у) = (Дж^, Awk) < 0 и в итоге при
любом ненулевом векторе у Е W1 из E.29) следует, что
u\2\v\2-(u,vJ (Ахк,уJ
\v\2 (Awk,Axk)
т.е. матрица Ак+\ положительно определенная.
К соотношению E.23) можно прийти и из других
соображений. Пусть А — положительно определенная матрица порядка
п. Введем в W1 наряду со стандартным скалярным
произведением (ж, у) скалярное произведение
(х,у)А = (Ах,у). E.30)
Из представления
f(x + h) - f{x) = {АА-1 grad/Ou), h) + o{\h\) =
= (A-1 grad f(x),h)A + o(\h\)
заключаем, что в евклидовом пространстве W1 со скалярным
произведением E.30) градиент целевой функции принимает вид
gYa,dAf(x) = А~гgididf(x). Отсюда следует, что алгоритм
квазиньютоновского метода, в котором используется E.23), можно
(Ак+1У, У)
246 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
рассматривать как алгоритм наискорейшего спуска в
меняющейся на каждой k-ik итерации метрике р(х,у) = [А^ ж, у) при
условии, что Ак — положительно определенная матрица.
Поэтому квазиньютоновские методы иногда называют методами
переменной метрики*.
Можно показать**, что если
{wk,pk) —
[Qpk,Pk)
то при минимизации квадратичной функции с положительно
определенной матрицей Q алгоритм ДФП-метода позволяет
получить точку минимума не более чем за п итераций. Векторы
рк, к = 1, п, определяющие направления спуска, являются
сопряженными относительно матрицы Q и связаны сооношениями
AkQpl=pl-) i = 1, fc, A; = l,n.
При к = п эти соотношения означают, что симметрическая
матрица Aj~Q имеет п собственных значений, равных единице,
а такая матрица является единичной, т.е. AnQ = In. Отсюда
Ап = Q1, и, следовательно, матрица Ап является обратной к
матрице Гессе Н(х*) = Q квадратичной функции, вычисленной
в точке минимума ж*.
Отметим, что если в алгоритме ДФП-метода А\ = /п, то
для квадратичной функции траектория поиска совпадает с
траекторией, полученной по методу сопряженных направлений.
Например, при минимизации квадратичной функции,
рассмотренной в примерах 5.1 и 5.3, алгоритм ДФП-метода приводит
к точке ж* = (—л/5, —2д/б) минимума этой функции из
начальной точки (—2, 1) за две итерации, причем траектория поиска
при выборе А\ = /2 полностью совпадает с полученной в
примере 5.3 методом сопряженных направлений (см. рис. 5.4).
При минимизации целевой функции, не являющейся
квадратичной, использование ДФП-метода в общем случае не
позволяем.: Поляк Б. Т.
**См.: Аоки М., а также: Базара М., Шетти К.
5.5. Квазиньютоновские методы
247
ет найти точку минимума за конечное число итераций. Как и
в методе сопряженных направлений, чтобы ослабить влияние
накапливаемых погрешностей на сходимость ДФП-метода и
уменьшить вероятность появления после очередных п итераций
линейно зависимых направлений спуска, применяют
процедуру „обновления" алгоритма, в соответствии с которой через
каждые п итераций в качестве матрицы А^ используют
единичную матрицу, т.е. полагают Amn+i = А\ = /n, m Е N.
Опишем алгоритм ДФП-метода в случае, когда (не
квадратичная) целевая функция f(x) дифференцируема в Rn. На
предварительном этапе задаем значение ?з параметра
точности поиска в условии прекращения итераций |ги^| < ?з и
выбираем начальную точку ж0. Принимаем А\ = /п, формируем
множество Хо = {п, 2п, ...} моментов обновления алгоритма,
полагаем fe = l и переходим к основной части алгоритма.
1. На /с-й итерации в точке х вычисляем антиградиент
w = — gra,df(x ) целевой функции и проверяем выполнение
неравенства \wk\ < ?3- Если оно выполнено, то итерации
прекращаем и полагаем ж* « ж^-1, /(ж*) « f(xk~l). В противном
случае переходим к п. 2.
2. Используя E.23), вычисляем вектор pk = A^w^,
определяющий направление спуска из точки ж^-1, и, минимизируя
функцию фк(^) = f (х -\- >ф ), находим значение х^ и точку
ж/с _ хк-1 _^_ Ккрк% Если к Е Xq, то принимаем A^+i = /п,
полагаем к := к -\-1 и возвращаемся к п. 1. В противном случае
переходим к п. 3.
3. Полагаем Ахк = хк — xk~l, Awk = wk+l — wk, по формуле
E.27) вычисляем матрицу А&+1, полагаем к := к + 1 и
возвращаемся к п. 1.
Как отмечено выше (см. 5.2), применение процедуры
„обновления" алгоритма увеличивает общее число итераций,
необходимых для достижения заданной точности поиска. Поэтому на
практике используют варианты ДФП-метода, в которых (как
и в случае метода сопряженных направлений) не используется
248 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
„обновление" алгоритма через фиксированное число итераций*.
Поясним суть такого подхода на конкретном примере.
Пример 5.8. Применив ДФП-метод, найдем минимум
функции f(x\,X2) = {х\ — х^J + {х\ — IJ (см. примеры 5.2, 5.5-5.7).
Зададим параметр точности поиска е% = 10_3 и выберем в
качестве начальной точку ж0 = (—1, —2), в которой /(ж0) = 13.
Графическая иллюстрация процесса поиска точки
минимума ж* = A, 1) представлена на рис. 5.10. Здесь первая
итерация совпадает с первой итерацией в примере 5.5, проведенной
как по методу сопряженных направлений (см. рис. 5.6, а, б\
так и по методу наискорейшего спуска. В табл. 5.8
приведены координаты точек хк, найденных при помощи алгоритма
ДФП-метода, значений f(xk) целевой функции в этих точках,
а также матрицы А^ и матрицы, обратные к матрицам Гессе
Н(х ) целевой функции.
Рис. 5.10
* Подробнее см.: Пшеничный Б.Н., Данилин Ю.М.
5.5. Квазиньютоновские методы
249
Таблица 5.8
к
1
2
3
4
5
6
7
хк
@,3787, -1,4830)
@,1584, -0,1027)
@,8593, 0,5572)
@,8707, 0,7660)
@,9942, 0,9708)
@,9980, 0,9964)
@,9999, 0,9999)
/(**)
3,0312
0,7246
0,0526
0,0168
3,4-ПГ4
4,3-10
3,3-100
Ак
(!!)
/ 0,100 -0,127\
V-0,127 0,98бу
/ 0,073 -0,005\
\-0,005 0,456/
/0,382 0,382 \
V 0,382 0,782 J
/0,272 0,481 \
V 0,481 1,351 J
/0,494 0,914 \
V 0,914 2,160/
/0,512 1,01б\
V 1,016 2,51бу
Н~1(хк)
( 0,071 -0,143\
\-0,143 0,78бу
/0,118 0,089\
V 0,089 0,5677
/0,398 0,12бЛ
\ 0,126 0,540 J
/0,367 0,631 \
V0,631 1,584 у
/0,508 0,885 \
V 0,885 2,040 у
/0,483 0,960 \
V 0,960 2,410 J
/0,500 0,999 \
V 0,999 2,494 у
Из результатов вычислений видно, что заданная точность
поиска минимума достигнута за 7 итераций, матрицы Aj и
Н~1(х7) на конечном, седьмом шаге поиска близки друг к
другу. Матрица i7-1(a?*), вычисленная в точке минимума ж*,
имеет вид
^1,0 2,5)
и также мало отличается от А^ и Н~1(х7). Отметим, что для
достижения той же точности в методе наискорейшего спуска
потребовалось 96 итераций. #
Возможны и другие способы построения
последовательности {Ак} матриц с применением E.24). Так, например, в
алгоритме квазиньютоновского метода, называемого в литературе
методом Бройдена — Флетчера — Шенно, или БФШ-методом,
250 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
используют соотношение
^4/c+i = Ак ¦
Дж*(Д
х
к\т
(Awk,Axk)
AkAwk{Awk)rA
к(Л„.МтАт
t + Pkrk(rk)T, ?;EN, E.31)
Рк
где
к _ AkAwk Ахк
(Ахк,Аг»кУ Pk = (AkAw\Awk),
Рк
в алгоритме метода Пауэлла —
Ахк(Ахк)т 1 ^
Л+1 = Ак- ——i Алч, кеК
{Awk,AxkY
где Ах = Ах + Ak Aw , А; Е N, а в алгоритме метода Мак-Кор-
мика —
(Axk + AkAwk)(Axk)T
(Awk,Axk)
Ак+1 = Ак-^ Tr.*7A.Z J , ken,
причем, как и в случае ДФП-метода, обычно полагают А\ = 1п.
Можно показать, что любой из рассмотренных способов
„обновления" матрицы Ак+\ сохраняет ее свойство
положительной определенности, а последовательность {Ак} при к —>> оо
сходится к Н~1(х:?).
Пример 5.9. Сравним различные алгоритмы на примере
минимизации функции f{x\,X2) = {х\ — Х2J + (xi — IJ,
рассмотренной в ряде предыдущих примеров. Выберем начальную
точку ж0 = (—1, —2), в которой /(ж0) = 13 и параметр точности
поиска ?з — Ю-3. Как и в примере 5.8, в применяемых
алгоритмах не будем использовать „обновление" через фиксированное
число шагов.
5.5. Квазиньютоновские методы
251
Рис. 5.11
252 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
В табл. 5.9 приведены координаты точек хк, найденных при
помощи трех алгоритмов квазиньютоновских методов.
Траектории поиска точки минимума для этих алгоритмов показаны
на рис. 5.11 (а — БФШ-метод; б— метод Пауэлла; в — метод
Мак-Кормика).
Таблица 5.9
N
1
2
3
4
5
6
7
8
9
10
БФШ-метод
@,379, -1,483)
@,158, -0,103)
@,859, 0,557)
@,871, 0,766)
@,994, 0,971)
@,998, 0,996)
@,999, 0,999)
Метод
Пауэлла
@,379, -1,483)
@,158, -0,103)
@,859, 0,557)
@,871, 0,766)
@,934, 0,871)
@,998, 0,989)
@,999, 0,999)
@,999, 0,999)
Метод
Мак-Кормика
@,379, -1,483)
(-0,030, -0,394)
(-0,011, 0,043)
@,726, 0,398)
@,966, 0,801)
@,921, 0,810)
@,932, 0,883)
@,995, 1,019)
@,995, 0,990)
@,999, 0,999)
Сравнительный анализ результатов показывает, что для
рассматриваемой функции наилучший результат по количеству
итераций, требуемых для достижения заданной точности, дают
ДФП-метод и БФШ-метод. Метод Мак-Кормика по этому
критерию эффективности им заметно уступает. #
Отметим, что сравнение эффективности алгоритмов
минимизации принято проводить на специально сконструированных
функциях. Графики этих функций имеют четко выраженную
овражную структуру. На рис. 5.12 представлены линии уровня
унимодальной функции Розенброка
f(xbx2) = 100(Ж2 - х\J + A - хгJ, E.32)
а на рис. 5.13 — функции Химмельблау
/(жьж2) = {х\ + Х2- ИJ + (Ж1 +х\- 7J, E.33)
5.5. Квазиньютоновские методы
253
Рис. 5.12
Рис. 5.13
254 5. МЕТОДЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
имеющей четыре точки минимума. Для испытания алгоритмов
используют также унимодальную функцию Пауэлла
/(ж) = (x1+Wx2J + 5(х3-хАJ + (х2-2х3)А + Щхг-хА)\ E.34)
достигающую минимума в точке ж* = @, 0, 0, 0).
Вопросы и задачи
5.1. Покажите, что функция Розенброка E.32) и функция
Пауэлла E.34) являются унимодальными.
5.2. Решите задачу
—хг — х2 + х\х2 — х\ + 2^2 —> min,
выбрав начальную точку @, 0). Используйте алгоритмы
метода сопряженных направлений и метода Давидона — Флетче-
ра — Пауэлла. Покажите, что реализуемые алгоритмы
приводят к одной и той же траектории поиска точки минимума, если
в алгоритме ДФП-метода направление спуска из начальной
точки совпадает с направлением антиградиента. Графически
проиллюстрируйте полученные результаты.
5.3. Решите задачу
/(ж1,Ж2) = Юх2 — 4:Х\Х2 + 7^2 — 4v5E^i -\-Х2) — 16 —>> min,
выбрав в качестве начальной точку ж0 = @, — л/б).
Найдите уравнение линии уровня целевой функции,
проходящей через точку ж0. Ортогональным преобразованием
приведите найденное уравнение к каноническому виду и постройте
линию уровня в исходной системе координат.
Проведите поиск минимума целевой функции из заданной
начальной точки с точностью е = 0,01, применяя алгоритмы
метода градиентного спуска, метода сопряженных направлений,
метода Ньютона и метода Давидона — Флетчера — Пауэлла.
Вопросы и задачи
255
Сравните полученные результаты по количеству итераций,
необходимых для достижения заданной точности, дайте
графическую иллюстрацию процесса поиска точки минимума.
Перечислите методы, гарантированно приводящие к точке минимума
целевой функции за конечное число шагов при удачно
выбранной начальной точке. Является ли таковой точка @, — л/5)?
5.4. Решите задачу
xi + 1х\ + еж?+ж2 ->> min,
выбрав в качестве начальной точку A, 0) и параметр точности
поиска е = Ю-3. Проведите сравнительный анализ различных
методов первого и второго порядков, дайте графическую
иллюстрацию полученных результатов.
5.5. Решите задачу
Щх\ - x2f + (xi - IJ ->> min,
выбрав в качестве начальной точку (—1, 1) и параметр
точности поиска е = Ю-3. Для решения задачи используйте метод
Ньютона и его модификации, метод сопряженных направлений,
один из квазиньютоновских методов. В алгоритмах,
включающих одномерную минимизацию для выбора шага
исчерпывающего спуска, используйте различные методы одномерной
минимизации: дихотомии, золотого сечения, квадратичной и
кубической интерполяции. Установите, какой из
использованных алгоритмов самый эффективный по количеству итераций.
Дайте графическую иллюстрацию полученных результатов.
6. АЛГОРИТМЫ
ПРЯМОГО ПОИСКА
В методах прямого поиска минимума целевой функции (или
методах нулевого порядка) используют информацию только о
значениях этой функции. Многие из этих методов не имеют
строгого теоретического обоснования и построены на основе
эвристических соображений. Поэтому вопросы сходимости
методов прямого поиска еще мало изучены, а оценки скорости
сходимости обычно отсутствуют. Вместе с тем эти методы
идейно связаны с методами первого и второго порядков, что
в ряде случаев позволяет оценивать эффективность
алгоритмов прямого поиска применительно к минимизации некоторых
классов функций.
Распространенным способом оценки эффективности
методов прямого поиска являются вычислительные эксперименты и
сравнительный анализ методов по результатам таких
экспериментов. Однако следует учитывать, что этот анализ не во всех
случаях может приводить к однозначным выводам о
преимуществах одного метода перед другим.
Во-первых, это связано с тем, что сравнению обычно
подвергаются не только методы, но и программные реализации
соответствующих алгоритмов. Хороший метод можно „загубить"
плохим программированием, неудачным выбором параметров
алгоритма. Во-вторых, методы могут вести себя по-разному
на различных этапах процесса минимизации.
Удовлетворительного способа преодоления указанных трудностей не
существует. Единственное, что можно сделать в подобной ситуации, —
привести данные о результатах вычислений в развернутой
форме, позволяющей сравнивать методы по различным критериям.
Кроме того, не следует забывать, что поиск решения всегда
6.1. Особенности прямого поиска минимума 257
остается искусством, которому можно научиться лишь путем
проб и ошибок, применяя различные методы при решении
конкретных задач.
6.1. Особенности прямого поиска минимума
Для применения методов прямого поиска минимума целевой
функции достаточно располагать лишь возможностью
вычисления значения функции в любой точке ее области определения.
Это обстоятельство существенно расширяет сферу
практического применения таких методов.
Опишем один из наиболее простых алгоритмов
минимизации функции /(ж), определенной в W1. Выберем в W1 точку
ж0, называемую обычно базовой. Вычислим в ней значение
/(ж0) функции /(ж), а затем построим n-мерный куб с
центром в этой точке и с ребрами длиной /, параллельными ортам
базиса. Множество вершин этого куба вместе с точкой ж0
составляют так называемый шаблон (или образец). Вычислив
значения функции в вершинах куба, выберем в качестве
новой базовой точки ту из вершин, в которой значение функции
меньше /(ж0), и повторим описанную процедуру построения
шаблона и выбора следующей
базовой точки. Если же такой
вершины не оказалось, то оставим
прежнюю базовую точку ж0 и построим
шаблон с уменьшенной (например,
вдвое) длиной ребер куба.
Процесс поиска закончим, когда длина
ребра куба станет меньше
заданного числа е > 0. Геометрическая
иллюстрация описанного
алгоритма, называемого обычно поиском
при помощи шаблона (или
образца), представлена на рис. 6.1 в
двумерном случае.
Рис. 6.1
258
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Основной недостаток поиска при помощи шаблона
состоит в резком росте количества вычислений значений целевой
функции при увеличении размерности п (порядка 2П), а
главное преимущество — в простоте алгоритма. Эффективность
этого алгоритма можно повысить за счет использования
информации о ранее вычисленных значениях функции, что позволяет
уменьшить число рассматриваемых точек путем отбрасывания
тех точек, в которых значения функции не существенны для
выбора следующей базовой точки. Геометрически это
соответствует процедуре построения вокруг базовой точки в качестве
шаблона не n-мерного куба, а конфигурации с меньшим
количеством вершин, в которых вычисляют значения функции.
Реализация этой идеи привела к разработке методов
симплексного поиска, получивших к началу 1970-х годов
широкое распространение. Симплекс (от латинского слова simplex —
простой) — это простейший выпуклый многогранник в W1 с
п+1 вершинами (в R2 — треугольник, в R3 — тетраэдр).
Каждую вершину этого многогранника называют вершиной
симплекса. Идея построения алгоритма симплексного поиска
состоит в следующем: в вершинах симплекса вычисляют
значения минимизируемой функции, наихудшую из вершин — ту, в
которой значение функции наибольшее, — заменяют по
определенному правилу новой вершиной, образуя тем самым новый
симплекс. Затем эту процедуру повторяют.
В одном из первых разработанных вариантов симплексного
поиска был использован регулярный симплекс, у которого
все вершины равноудалены друг от друга (в R2 —
равносторонний треугольник, bR3 — правильный тетраэдр). Дж. Нелдер
и Р. Мид* в 1965 году впервые рассмотрели произвольный
(нерегулярный) симплекс и предложили способ изменения
скорости его движения путем расширения или сжатия симплекса
в зависимости от того, удачно ли был выбран шаг поиска в
направлении убывания функции или нет. Позднее в исходные
*См.: Базара М., Шетти К.
6.2. Использование регулярного симплекса 259
варианты методов симплексного поиска были введены
различные способы изменения размеров и формы симплекса. Это
привело к разработке метода управляемого прямого
поиска, под которым понимают выбор по определенному правилу
направления смещения центра используемой конфигурации и
величины этого смещения, приводящего к убыванию значений
функции в вершинах или центре симплекса. Метод, в котором в
процессе поиска осуществляют управление изменением формы
симплекса, обычно называют методом деформируемых
конфигураций*. Изменение формы симплекса позволяет улучшить
процесс адаптации используемой конфигурации к рельефу
графика минимизируемой функции.
6.2. Использование регулярного симплекса
Сначала рассмотрим простейший алгоритм симплексного
поиска минимума ограниченной снизу целевой функции /(ж),
xEW1, с использованием регулярного симплекса постоянных
размеров. На первом шаге поиска строим регулярный симплекс
с вершинами х1,г, г = 1, п+1, который обозначаем S\.
Построение симплекса можно провести различными способами.
1. Если ж1'1 Е Si — заданная базовая точка, то координаты
х -'г (г = 2, п+1, j = 1, п) остальных п вершин х1,г Е Si
регулярного симплекса Si, имеющего ребра длиной /, можно вычислить
по формулам**
1,г
хз =
где а^'1, j = 1, п, — координаты вершины ж1'1 Е Si. Например,
если в IR2 выбрана базовая точка ж1'1 = @, 0), то при / = 2
1,1 , л/п + 1
Ха +
л/2
:j + i;
1,1 . \/п + 1 + П - 1 7 • / • , 1
F.1)
*См.: Рыков А.С.
**См.: Реклейтис Г., Рейвиндран А., Рэгсдел К.
260
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
остальные две вершины ж1'2 и ж1'3 имеют координаты х{ =
= 1,932, х1/ = 0,518 и х1/ = 0,518, х1/ = 1,932. На рис. 6.2, а
приведен построенный симплекс.
x2j
2
X1'1
0
i
1 '
\*и
i ^
2 xt
1 У
-1 /
X1-1
х2*
0
-1
X1'3
i ^
\ 1 kL
Ж1-2
Рис. 6.2
2. Если ж°еКп — заданная базовая точка, определяемая
как центр регулярного симплекса Si, имеющего ребра длиной
/, то координаты х -'г (г = 1, n+1, j = 1, п) всех вершин жг'г Е Si
находят по формулам*
Л* _
*? +
ж^
20'+ 1)
1
j < % - 1;
F.2)
где ж^, j = 1, n, — координаты точки ж0. Например, если
в 1R2 задана точка ж0 = @, 0) и / = 2, то вершинами
правильного симплекса будут точки ж1'1 = (—1,000, —0,578), ж1'2 =
= A,000, -0,578), ж1'3 = @,000, 1,156). На рис. 6.2, б приведен
построенный симплекс.
*См.: Дамбраускас А.П.
6.2. Использование регулярного симплекса 261
После построения симплекса S\ на первом шаге поиска в
вершинах х1,г Е Si, г = 1,п+1, вычисляют значения
минимизируемой функции. По результатам вычислений выбирают
вершину, в которой значение функции является наибольшим
(пусть для определенности это будет вершина ж1,п+1; если
таких вершин несколько, то может быть взята любая из них), и
по формуле
ж2,п+1 = 2х1 _ ж1,п+1 = _^ х1* ~ Х1^1 F.3)
г=1
находят точку ж2'п+1, симметричную вершине ж1'п+1
относительно гиперплоскости, в которой лежат остальные вершины
симплекса Si. Точка х\ равноудалена от вершин ж1'*, г = 1, п,
т.е. является центром регулярного симплекса с п вершинами,
или, иначе говоря, центром масс системы материальных точек,
расположенных в вершинах симплекса и имеющих одинаковую
массу.
Нахождение точки ж2'п+1
называют отражением вершины. В
результате получают новый
регулярный симплекс #2, образованный
новой вершиной ж2'п+1 и п вершинами
ж1'2, г = 1, п, принадлежавшими
симплексу Si. На рис. 6.3 представлена
процедура построения нового регу-
г) JrHC. О.о
лярного симплекса в случае Ш .
На втором шаге поиска в новой вершине ж2'п+1 Е S2
симплекса S2 вычисляют значение /(ж2'п+1), и если /(ж2'п+1) <
< /(ж1,п+1), то описанную выше процедуру повторяют. При
построении алгоритма удобно на каждом k-м шаге поиска
отражаемой вершине симплекса S& присваивать номер п + 1, т.е.
обозначать ее xk,n+1 Е S&. Нумерацию вершин симплекса S&
назовем правильной, если выполнены неравенства
/(ж*'1) ^ ... ^ Дж^) ^ ... ^ f(xk>n+1).
262
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Если на fc-м шаге после отражения вершины xk,n+1 Е Sk в
точку хк+1,п+1 и вычисления значения /(ж/с+1'п+1) окажется,
что /(ж/с+1'п+1) > f(xk,n+1), то следует вернуться к
симплексу Sfc, считая отражение вершины ж 'n+1 неудачным. После
этого, предполагая нумерацию вершин симплекса Sk
правильной, проводят отражение вершины ж 'n Е S&, получают
точку ж/с+1'п и сравнивают значения f(xk+1,n) и f(xk,n+1). Если
f(xk^1,n) ^ f(xk,n+1), то отражение и этой вершины считают
неудачным и проводят отражение вершины хк,п~1 Е^и т.д.
При фиксированной длине ребра симплекса поиск
прекращают на шаге с номером К, если отражения всех вершин
симплекса Sk оказались неудачными. Тогда в качестве
оценки искомого наименьшего значения /* минимизируемой
функции /(ж) можно принять наименьшее из вычисленных значений
/(ж^), хК,г Е Sk, i = 1, п+1. Полученной в процессе поиска
конечной последовательности {вь}к построенных симплексов
Sk, к = 1, К, соответствует невозрастающая конечная
последовательность {/(хк,1)}к минимизируемой функции.
Исследование свойств последовательности {/(ж '1)}к
весьма затруднено. Поэтому на практике вместо нее изучают
свойства последовательности {fk} значений fk = f(x)
минимизируемой функции, каждое из которых вычислено в центре хк
симплекса S&, к = 1, К. Процедуру поиска точки ж* Е Rn, в
которой функция /(ж) достигает наименьшего значения, в этом
случае проводят в соответствии с рекуррентным соотношением
„А;+1 _ „к , „, „к
жл+1 = хк + акрк^ k = l,K,
где рк — единичный n-мерный вектор, определяющий
направление смещения центра симплекса на к-м шаге; а& > 0 — смещение
центра симплекса в направлении вектора рк при переходе от хк
к ж +1. Геометрическая иллюстрация процедуры такого поиска
в случае IR2 представлена на рис. 6.4.
Рассмотрим некоторые подходы к построению алгоритмов,
позволяющих повысить эффективность процесса поиска при
6.2. Использование регулярного симплекса 263
Рис. 6.4 Рис. 6.5
помощи регулярного симплекса*. В общем случае управление
процессом поиска можно осуществлять, выбирая как
направление смещения центра симплекса, так и значение а&. При
этом выбор вектора рк из множества возможных направлений
должен быть связан с определенным правилом, допускающим
отражение сразу нескольких вершин симплекса, а изменение а^
при выбранном векторе р предполагает изменение длины
ребра регулярного симплекса при сохранении его формы.
На рис. 6.5 приведен пример построения регулярного
симплекса в пространстве R2 по правилу, допускающему
отражение всех тех вершин правильного треугольника, в которых
значения минимизируемой функции больше, чем в центре
треугольника. Если значения этой функции во всех вершинах
симплекса превышают ее значение в центре, то процесс поиска
прекращают.
Иной путь построения эффективных алгоритмов связан с
идеей изменения размера регулярного симплекса в процессе
поиска. Введение правил такого изменения является одним из
существенных элементов построения алгоритмов управляемого
*См.: Дамбраускас А.П., а также: Рыков А.С.
264
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
прямого поиска. Это особенно важно в тех случаях, когда
наименьшее значение функции /(ж) необходимо найти с высокой
точностью. Действительно, чем меньше размер симплекса, тем
точнее можно локализовать точку ж*, в которой эта функция
достигает наименьшего значения. При этом, однако, малый
размер симплекса приводит к его замедленному смещению в
направлении точки ж*, т.е. к росту числа шагов поиска,
связанному с увеличением вычислительных затрат. Большой размер
симплекса, наоборот, позволяет за каждый шаг поиска
осуществлять большое смещение центра симплекса, но обеспечивает
лишь грубую локализацию точки ж*. Поэтому возможность
изменения размера симплекса наделяет алгоритм поиска
высокими адаптивными свойствами.
Выделим два основных подхода к построению алгоритма,
предусматривающего изменение размера симплекса в процессе
поиска. В первом из них это изменение происходит лишь при
выполнении определенного условия, проверяемого на каждом
шаге поиска, а во втором — на каждом шаге поиска по заранее
заданному закону. Простейшая схема алгоритма, построенного
на основе первого подхода, такова.
Пусть ^СР — регулярный симплекс на k-м шаге
поиска, имеющий правильную нумерацию вершин. Процедура
отыскания вершины ж/с+1'п+1 (= ?^+1 нового симплекса S&+1, в
которой функция /(ж) имеет меньшее значение, чем в вершине
ж/с'п+1, включает два этапа — отражение вершины ж/с'п+1 ^^и
уменьшение размера симплекса S& при сохранении его формы,
называемое редукцией симплекса.
1. Отражение вершины х ,n+1 Е S& осуществляют в
соответствии с формулой, аналогичной F.3):
xk+i,n+i = 2хк _ жЛ,п+1 = _^хк'1 - Ж*'П+\ F.4)
г=1
где хс — точка, равноудаленная от вершин ж 'г, г = 1, п. Затем
вычисляют значение /(ж +1'n+1) функции /(ж) в найденной
точке хк+1'п+1.
6.2. Использование регулярного симплекса 265
2. Редукцию симплекса Sfc проводят только при выполнении
неравенства f(xk+1,n+1) ^ f(xk,n+1). При этом длину всех ребер
симплекса уменьшают в 1/5 раз, где 5 Е @, 1) — заданный
коэффициент редукции, и находят вершины нового симплекса
Sk+i по формуле
Ж
/с+1,г
:ЖМ + ^_ЖМM г = 2,п+1,
сжимая симплекс в 1/8 раз к вершине ж^'1, в которой значение
целевой функции меньше, чем в других вершинах симплекса.
Затем осуществляют переход к этапу 1 при к : = к + 1.
Если же /(ж/с+1'п+1) < /(ж/с'п+1), то редукцию симплекса S&
не проводят и далее рассматривают симплекс Sk+i с новой
вершиной хк+1,п+1 и п вершинами ж^'г, % = 1, п, симплекса S&,
переходя к этапу 1 при к := к + 1.
Эту схему алгоритма следует дополнить условием
прекращения поиска, зависящим от конкретной постановки задачи
минимизации. Например, поиск можно вести до тех пор, пока
длина ребер регулярного симплекса не станет меньше заранее
выбранного значения или же не будет выполнено заданное
число шагов. Одним из возможных условий прекращения поиска
является выполнение неравенства
, 1 п+1 ч 1/2
(^E(/(^)-/(*fe)J) <е' F-5)
^ г=1 '
где е > 0 — заданное достаточно малое число.
Пример 6.1. Используя поиск при помощи регулярного
симплекса, найдем решение задачи минимизации функции
f(xux2) = 6x1 - 4ж1Ж2 + Ъх\ + 4л/5(ж1 + 2х2) + 22,
рассмотренной в примере 3.18. Выберем базовую точку ж0 =
= (—2, 1) и положим е = 0,01 в условии F.5) прекращения
поиска. На рис. 6.6 дана графическая иллюстрация процесса
поиска при коэффициенте редукции E = 1/2 и трех значениях
начальной длины / ребра симплекса, указанных в табл. 6.1.
266 6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
в
Рис. 6.6
6.2. Использование регулярного симплекса 267
Таблица 6.1
1
0,5
1,0
2,0
X*
(-2,233, -4,470)
(-2,233, -4,470)
(-2,233, -4,470)
/(**)
-28,0
-28,0
-28,0
N
32
19
18
Построение исходного симплекса с начальным значением I
было проведено по формулам F.1) с выбором в качестве
базовой точки ж1'1 = ж0. Приближения точки ж* и значения /(ж*)
функции в этой точке, указанные в табл. 6.1, соответствуют
той вершине симплекса Sn на последнем, N-м шаге поиска, в
которой значение функции оказалось меньше, чем в других
вершинах, т.е.
/(ж*)« min f(xN>{). F.6)
г=1,п+1
Увеличение значения / в 4 раза в данном случае не повлияло на
точность нахождения точки ж* и значения /(ж*), но привело к
заметному снижению необходимого числа N шагов поиска. #
Некоторые возможные варианты уменьшения размера
симплекса по заданному закону при втором подходе к построению
алгоритма поиска в случае R2 показаны на рис. 6.7.
По-прежнему считаем, что нумерация вершин симплекса S& на каждом
k-м шаге поиска является правильной.
В первом варианте (рис. 6.7, а) уменьшение размеров
симплекса на каждом k-м шаге поиска осуществляют относительно
найденной отражением вершины х ,n+1 Е S& (в данном случае
п = 2). Ее считают неподвижной, а расстояния до остальных
п вершин изменяют в ^ ' раз. Изменение параметра 5(к) Е
Е @, 1] можно проводить, например, по закону 5(к) = е~^к~г\
где \i > 0 — заданный коэффициент. Этот закон обычно
применяют в тех случаях, когда для достижения достаточно
хорошего приближения к точке наименьшего значения ж* необходимо
268
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Рис. 6.7
значительное число шагов поиска. Возможны и другие
варианты задания закона изменения параметра* 5(к).
Во втором варианте (рис. 6.7, б) неподвижной считают
вершину ж^'1 Е Sk симплекса S& с наименьшим значением /(ж^'1)
функции f(x) и изменяют в ^ раз расстояния от нее
до остальных п вершин. В третьем варианте (рис. 6.7, в)
уменьшение размеров симплекса S& на каждом к-м шаге поиска
осуществляют относительно центра х этого симплекса. При
этом центр симплекса считают неподвижным, а в
8{к-1)
раз
изменяют расстояния от центра х до всех вершин симплекса.
* Подробнее см.: Дамбраускас А. П. или Рыков А. С.
6.3. Поиск при помощи нерегулярного симплекса 269
6.3. Поиск при помощи
нерегулярного симплекса
Стандартные симплексные процедуры безусловной
минимизации, в которых используются регулярные симплексы,
эффективны лишь в тех случаях, когда топография поверхностей
уровня ограниченной снизу целевой функции достаточно
проста. В противном случае эффективность применения
симплексного поиска минимума функции значительно снижается. В
частности, это характерно для функции, скорость убывания
которой по одному или нескольким направлениям значительно
больше, чем по остальным. О графике такой функции говорят,
что он имеет овражную структуру.
Примером функции, график которой обладает овражной
структурой, является функция
f(x1,x2) = l0(xi-x2J + (x1-lJ
с минимумом в точке ж* = A, 1). Топография линий уровня
/(ж1,Ж2) = С этой функции приведена на рис. 6.8.
Препятствием для успешного поиска минимума f(x) является в этом
случае форма симплекса: регулярный симплекс нельзя изменить
так, чтобы он ^вытянулся" вдоль ^оврага", а это не
позволяет успешно продолжить поиск минимума. Естественной в этих
Рис. 6.8
270
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
условиях выглядит идея деформирования симплекса в процессе
поиска, т.е. изменения его формы и размера.
Существует много вычислительных конструкций прямого
поиска с деформируемыми симплексами, различающихся по
способам изменения размеров и формы симплекса. Общим для
всех них является то, что в качестве основной геометрической
конфигурации на каждом шаге поиска выступает симплекс.
Информацию о значениях /(ж) в вершинах симплекса
используют для принятия решения о смещении в область меньших
значений функции.
Рассмотрим простейшую схему алгоритма прямого поиска
по деформируемому симплексу — конструкцию
вычислительного алгоритма Нелдера — Мида. Она предусматривает
возможность отражения только одной вершины симплекса на каждом
шаге поиска.
Пусть 5fcCln — заданный произвольный симплекс на к-м
шаге поиска, имеющий правильную нумерацию вершин.
Процедура отыскания вершины вновь генерируемого симплекса S^+i,
в которой функция имеет меньшее значение, чем в вершине
ж/с,п+1 ? g^ включает несколько этапов: отражение вершины
хк,п+1. изменение размера и формы симплекса, полученного в
результате отражения этой вершины, путем растяжения или
сжатия в направлении новой вершины в зависимости от того,
удачным был шаг поиска в направлении убывания функции f(x)
или нет, и редукция симплекса S& в случае неудачного шага
поиска.
1. Отражение вершины xk'n+1 Е S& осуществляют в
соответствии с формулой, аналогичной F.3):
xk+i,n+i = xk + a{xk _ aAn+i) = L+?L ?y,» _ „дЛп+i,
г=1
где а > 0 — заданный коэффициент отражения; хк =
-, п
= — У^ хк">г — центр грани симплекса с вершинами хк,г. г = 1, п.
ni=i
6.3. Поиск при помощи нерегулярного симплекса 271
В результате получают новый симплекс S^+i, образованный
новой вершиной xk+1,n+1 и п вершинами xk">% G^, г = 1, п. На
рис. 6.9, а представлена процедура построения нового
симплекса в пространстве IR2 при a = 1.
¦fc+1,3
к+\
if+1,3
if+ 1,3
Л-+1Л
if. I
I
Рис. 6.9
В новой вершине вычисляют значение /(ж^+1'п+1) функции
/(ж). Если /(ж/с+1'п+1) < /(ж^'1), то шаг поиска считают
удачным: получен новый симплекс S&+1 с наименьшим значением
/(ж/с+1'п+1) функции f(x) в новой вершине хк+1'п+1. При этом
переходят к этапу 2 растяжения симплекса Sk+i- При
выполнении неравенства f(xk,n) ^ /(ж/с+1'п+1) ^ f(xk'1) далее
используют полученный симплекс S&+1 с новой вершиной ж/с+1'п+1
и п вершинами ж 'г Е5^, г = 1, п, и переходят к этапу 1 при
к := к + 1. Если же /(ж/с+1'п+1) > f(xk'n) > f(xk^), то
переходят к этапу 3 сжатия симплекса Sfc+i.
2. При выполнении неравенства /(ж/с+1'п+1) < f(xk'1)
растяжение симплекса S&+1 осуществляют в соответствии с форму-
272
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
лои
1 -Я п
ж/с+1,п+1 _ хк _^_ д*хк+1,п+1 _ хк\ _ ± 1± \^ х^,г _^_ дхк+1,п+1
г=1
где /3 > 1 — заданный коэффициент растяжения.
Геометрически это можно интерпретировать как увеличение длины
вектора xk+1,n+1 — xk в /3 раз. После растяжения вычисляют
значение /(ж* 'п ) функции /(ж) в найденной точке ж* 'п .
Если /(ж*+ 'п+ ) < /(ж^'1), то далее рассматривают
симплекс S/c+i с вершиной ж* 'п и п вершинами ж^'г ? ?&, г = 1, п,
и переходят к этапу 1 при А; := к + 1. На рис. 6.9, б построен
симплекс Sfc+i в R2 с применением операции растяжения при
/3 = 2. При Дж*+ 'n+ ) ^ f(xk^) растянутый симплекс не
используют, а далее рассматривают симплекс S&+1 с вершиной
xk+i,n+i и п вершинами хк">г Е S&, г = 1, п, и переходят к этапу 1
при /с: = /с Ч- 1.
3. Сжатие симплекса S&+1 проводят различными
способами в зависимости от результатов сравнения значений
функции /(ж) в вершинах xk,n+1 Е Sk и ж^+1^+1 ^ Sfc+1. Если
/(ж/с+1'п+1) ^ /(ж/с'п+1), то сжатие осуществляют в
соответствии с формулой
1 _ п
хк+г>п+1 = хкс+ jix^1^1 -хкс) = —^- J2 ^ + 7**+1,п+\
1=1
где 7 ? @, 1) — заданный коэффициент сжатия. Рис. 6.9, в
иллюстрирует нахождение вершины ж** 'п в R2 при 7 = 1/2-
Если же /(ж/с+1'п+1) > /(ж/с'п+1), то новую вершину определяют
по формуле
1 — п
ж/с+1,п+1 _ хк +^(хк,п+1 _хк\ _ i 1\^ хк,г +^хк,п+1^
г=1
На рис. 6.9, г представлена процедура нахождения вершины
к-\-1,п-\-1 -1 /о
ж** в этом случае при 7 = \ L.
6.3. Поиск при помощи нерегулярного симплекса 273
После сжатия симплекса вычисляют значение /(ж** 'п )
функции /(ж) в найденной вершине ж** 'п и сравнивают его
со значением f{xk^1). Если /(ж*^1,п+1) < J^'n+1), то далее
используют симплекс *b&+i с найденной вершиной ж** и
п вершинами хк,г Е S&, г = 1,п, и переходят к этапу 1 при
fc := к + 1. В противном случае этап сжатия не приводит к
уменьшению значения функции в найденной вершине. Поэтому
далее рассматривают симплекс S& и переходят к этапу 4 —
редукции этого симплекса.
4. Редукция симплекса S^ состоит в уменьшении длин всех
его ребер в 1/5 раз, где 6 Е @, 1) — заданный коэффициент
редукции. Вершины нового симплекса S&+1 находят по формуле
xk+i,i = ЖМ + S(xk,i _ ЖМ)? i = 2^+Т.
Симплексы S& и S&+1 до и после редукции при E = 1/2
изображены на рис. 6.9, д. После вычисления значений /(ж +1'г) функции
/(ж) в найденных вершинах ж^+1'г, г = 2, п+1, переходят к
этапу 1 при к := к + 1.
Помимо описанных этапов периодически (после N шагов
поиска) следует проводить так называемую операцию
восстановления симплекса. Она состоит в следующем: сохраняют
две ^лучшие" точки текущего симплекса S&, расстояние между
которыми принимают за длину ребра вновь генерируемого
симплекса. Это позволяет ликвидировать излишние деформации
симплекса, накопившиеся за предшествующие N шагов поиска.
Рассмотренную схему алгоритма Нелдера — Мида следует
дополнить условием прекращения поиска. Выбор этого условия
диктуют те же правила, что и в методах поиска при помощи
регулярного симплекса (см. 6.2).
Построение начального симплекса в методах поиска при
помощи нерегулярного симплекса проводят различными
способами. Один из способов состоит в выборе в качестве начального
регулярного симплекса Si, координаты вершин которого
вычисляют при помощи F.1) или F.2). Другой способ заключается
274
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
в выборе некоторой базовой точки ж°ЕКп, которую
принимают за вершину ж1'1 начального симплекса Si, а остальные п
вершин находят по формуле
ж1,г+1=ж0+/е.^ 2 = 17^, F.7)
где ei — векторы стандартного базиса вМи; / — заданное
число. Ясно, что в этом случае начальный симплекс Si будет
нерегулярным (например, в М2 получим равнобедренный
треугольник) .
С теоретической точки зрения методы поиска при помощи
нерегулярного симплекса изучены недостаточно полно, однако
практические вычисления указывают на их работоспособность.
В задачах безусловной минимизации рекомендуют выбирать
а = 1, /3 = 2, 7 = 1/2 или « = 2, C = 5/2, 7 = 1/4. Вопрос
выбора оптимальных параметров для каждой конкретной целевой
функции может быть решен после дополнительного
исследования свойств метода с помощью вычислительного эксперимента.
Пример 6.2. Используя поиск при помощи
нерегулярного симплекса, найдем решение задачи минимизации из
примера 6.1. В качестве базовой возьмем точку ж0 = (—2, 1), а
в условии F.5) прекращения поиска положим е = 0,01.
Выберем также коэффициенты отражения а = 1, растяжения /3 = 2,
сжатия 7=1/2 и редукции 6 = 1/2. Результаты приведены в
табл. 6.2, номер варианта соответствует способу построения
начального симплекса Si: 1 — при помощи F.1); 2 — при
помощи F.7) с выбором базовой точки ж0 = ж1'1. Графическая
иллюстрация процесса поиска в обоих вариантах для
каждого из трех значений параметра / — начальной длины ребра
симплекса — приведена на рис. 6.10 и 6.11 соответственно.
Координаты точки ж* и значение /(ж*) функции C.40) в этой
точке, приведенные в табл. 6.2, найдены при помощи формулы
F.6) и соответствуют той вершине симплекса Sn на последнем,
N-м шаге поиска, в которой значение этой функции оказалось
меньше, чем в других вершинах.
6.3. Поиск при помощи нерегулярного симплекса 275
а б
в
Рис. 6.10
276 6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
в
Рис. 6.11
6.3. Поиск при помощи нерегулярного симплекса 277
Таблица 6.2
Номер
варианта
1
2
/
0,5
1,0
2,0
0,5
1,0
2,0
X*
(-2,216, -4,443)
(-2,222, -4,416)
(-2,233, -4,457)
(-2,263, -4,511)
(-2,261, -4,450)
(-2,228, -4,404)
/(**)
-27,997
-27,993
-27,999
-27,995
-27,993
-27,998
N
20
15
17
18
18
14
Из табл. 6.2 видно, что на точность нахождения точки ж*
и значения /(ж*), как и на необходимое число N шагов поиска
влияют и значение параметра /, и форма начального симплекса.
Наилучшим при значении / = 2 является вариант 2, в котором
заданная точность нахождения точки ж* достигнута за N = 14
шагов. Этот вариант далее принят в качестве базового при
установлении влияния параметров алгоритма на необходимое
число N шагов поиска при помощи нерегулярного симплекса.
Вычислительный эксперимент показывает, что изменение
коэффициентов отражения а и растяжения C не приводит к
значительному изменению необходимого числа шагов N
поиска. Так, например, увеличение а от 1 до 2 изменяет N от 14
до 16, а увеличение /3 от 1 до 3 приводит к изменению N от 14
до 15.
Наибольший интерес представляют результаты расчетов,
иллюстрирующие влияние коэффициента сжатия 7 на процесс
поиска (рис. 6.12). Расчет проведен при / = 2, а = 1, /3 = 3 и
различных значениях j: а — j = 1/4 (N = 18); б — 7 = 1/2
(N = 15); в — 7 = 3/4 (N = 29). Из этих результатов видно,
что оптимальным по числу шагов является вариант при 7 —
= 1/2. Выбор других значений 7 приводит к избыточному
числу шагов поиска, причем при 0^7^1/2 процесс поиска
может сопровождаться вырождением симплекса.
278 6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
а б
в
Рис. 6.12
6.3. Поиск при помощи нерегулярного симплекса 279
Результаты расчетов позволяют сравнить эффективность
алгоритмов поиска при помощи регулярного и нерегулярного
симплексов. Сравнение этих алгоритмов по необходимому
числу N шагов поиска показывает (см. табл. 6.1 и 6.2), что в
случае правильного выбора параметров алгоритма метод поиска
с использованием нерегулярного симплекса более эффективен,
чем метод поиска при помощи регулярного симплекса. В то
же время неудачный выбор параметров алгоритма может
привести не только к избыточному числу шагов поиска, но и к
преждевременному окончанию процесса поиска, ф
Ситуации, которые приводят к преждевременному
окончанию процесса поиска, наиболее типичны в тех случаях, когда
целевая функция имеет овражную структуру. Покажем это на
конкретном примере.
Пример 6.3. Используя поиск при помощи нерегулярного
симплекса, найдем решение задачи минимизации
/(ж1,ж2) = 10(ж2 - ж2J + (х\ - IJ ->> min.
График функции f(x\,X2) и топография ее линий уровня
показаны на рис. 6.8. Минимальное значение функции
достигается в точке ж* = A, 1). В качестве начальной выберем точку
ж0 = (—1, 1), а в условии F.5) прекращения поиска положим
е = Ю-2. Графическая иллюстрация процесса поиска при
коэффициентах отражения a = 1, растяжения /3 = 2, сжатия 7 — 1/2
и редукции 5 = 1/2 и различных значениях параметра /
представлена на рис. 6.13: a — в случае / = 0,5; б— в случае / = 0,75.
Построение исходного симплекса S\ с начальной длиной I
ребра было проведено по формуле F.2). Точка ж* и значение
/(ж*) приближенно вычислены на последнем, N-м шаге
поиска в соответствии с формулой F.6). Полученные результаты
показывают, что при заданном значении е = 0,01 параметра
точности поиска и начальной длине / = 0,5 ребра симплекса
алгоритм приводит к минимуму целевой функции за N = 22 шагов
(см. рис. 6.13, а), при этом ж* « @,990, 0,978), /(ж*) « 2,10 • 10~4.
280
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
б
Рис. 6.13
6.4. Циклический покоординатный спуск 281
Для сравнения укажем, что при / = 1,0 поиск с помощью
нерегулярного симплекса приводит к минимуму за N = 25 шагов,
причем ж* « @,999, 1,005), /(ж*) « 5,85 • 10. В то же
время при / = 1,75 симплекс не в состоянии изменить свою форму
так, чтобы, „вытянувшись" вдоль оврага, успешно продолжить
поиск точки минимума (см. рис. 6.13, б). Поиск
заканчивается за N = 14 шагов в точке ж14 = @,237, —0,017), в которой
/(ж14) = 0,635. Аналогичная ситуация наблюдается и в случае
I = 0,4, причем преждевременное окончание поиска после N = 24
шагов приводит в точку ж24 = @,645, 0,404) со значением
целевой функции /(ж24) = 0,127.
К преждевременному окончанию процесса поиска может
приводить изменение других параметров алгоритма.
Например, это происходит при е = 0,01, / = 1,0, если выбрать
коэффициент сжатия 7 — 0,25. Поиск завершается за N = 26 шагов
в точке ж26 = @,671, 0,409) со значением целевой фукнкции
/(ж26) =0,125.
6.4. Циклический покоординатный спуск
Поиск точки ж*, в которой функция /(ж) достигает
наименьшего значения, можно описать рекуррентным
соотношением
xk = xk~1 + akuk, fceN, F.8)
где ж0 — начальная точка] uk — единичный вектор,
определяющий направление спуска на k-м шаге; а& > 0 — длина шага
спуска, т.е. расстояние в направлении вектора uk, отделяющее
точку ж^-1 от новой точки хк. Различные методы отличаются
друг от друга способом выбора направления спуска и
значения а&.
Поиск точки ж* обычно прекращают при выполнении
одного или обоих неравенств:
\хк -хк~г\ =ак< eu \f(xk) - f(xk-l)\ < е2, F.9)
где Е\ и ?2 — заданные параметры точности поиска.
282
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
В одном из алгоритмов прямого поиска, базирующихся на
идее методов спуска, на каждом k-м шаге поиска проводят
одномерную минимизацию целевой функции последовательно по
каждой из п координат ее аргумента ж Е W1. Такой метод
называют обычно методом циклического покоординатного
спуска. Рассмотрим алгоритм этого метода.
Пусть е^ г = 1,п, — стандартный базис в W1. Выберем
начальную точку ж0. Поиск точки минимума функции в
методе циклического покоординатного спуска проводят в
соответствии с рекуррентным соотношением
х)=х)~1+а), кеЦ j=I~n. F.10)
Значение a^GK находят из решения задачи одномерной
минимизации (см. 2)
<pj(a) -unin, (рк(а) = f{xk~l + aej). F.11)
Подчеркнем, что индекс j изменяется циклически, пробегая на
каждом шаге покоординатного спуска все значения от 1 до
п, причем значение on в отличие от значения а& в F.8) может
быть как положительным, так и отрицательным.
Пусть выбраны значения е\ и (или) е% в F.9) и перед к-м
шагом циклического покоординатного спуска по найденной
на предыдущем шаге точке х вычислено значение f(x )
целевой функции (на первом шаге значение /(ж0) вычисляют в
выбранной начальной точке ж0). Тогда для каждого значения
j = 1, п из решения задачи F.11) находят значение а- и затем
вычисляют
п
xk = xk~1 + ^2alJeJ F-12)
и значение f(xk). Далее проверяют выполнение условий F.9)
или того из них, которое выбрано в качестве условия
прекращения поиска. При положительном результате поиск точки ж*
6.4. Циклический покоординатный спуск 283
минимума функции /(ж) прекращают на k-м шаге и
принимают ж* « хк и /(ж*) « f{xk). В противном случае переходят к
следующему шагу метода, полагая к := к + 1.
Рассмотренный алгоритм прост в реализации, но
эффективен лишь в случаях, когда минимизируемая функция является
сепарабелънощ т.е. представляет собой сумму функций, каждая
из которых зависит лишь от одной координаты:
п
В этом случае решение задачи минимизации можно получить
за один шаг поиска.
В самом деле, так как
п п
f(x*) = min fix) = V^ шткАхЛ = >^/г7(ж*),
то достаточно на первом шаге поиска последовательно решить
п задач одномерной минимизации функций hj(xj), j = 1, п, что
позволит найти все п координат ж* искомой точки ж*.
Для функций более общего вида может нарушаться
даже условие релаксационности последовательности {ж^}, т.е.
/(ж^-1) — f(xk) > 0 для некоторых номеров к. Поэтому обычно
используют модификацию этого метода, состоящую в
следующем. На каждом шаге при спуске по очередной координате Xj
учитывают результаты, полученные на этом шаге для
координат ж/, I = 1, j—1. В этом случае значение а- находят из
решения задачи F.11), в которой полагают <^-(а) = f{xk-l +aej),
где
j-i
x)_1 = xk~1 + Y,^i-
1=1
После перебора всех п координат вычисляют хк = х^1_1 + а^еп.
Рис. 6.14 иллюстрируют этапы покоординатного спуска для
первых двух шагов метода в случае функции двух переменных.
284
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Рис. 6.14 Рис. 6.15
Пример 6.4. С помощью модифицированного метода
циклического покоординатного спуска найдем решение задачи
минимизации функции
f(xux2) = 6x1 - AXlX2 + 3x1 + 4л/5 (xi + 2х2) + 22,
рассмотренной в примерах 6.1 и 6.2. В качестве начальной
выберем точку х° = (—2, 1), в которой f(x°) = 57, а в первом
из условий F.8) прекращения поиска положим е\ =0,01.
На рис. 6.15 дана графическая иллюстрация первых двух
шагов процесса поиска точки минимума ж* = (—л/5, —2у5)
этой функции, а в табл. 6.3 приведены результаты вычислений
(заметим, что у5 ^ 2,2361). Из этих результатов видно, что
при заданной точности поиска решение задачи получается за
шесть шагов. #
6.5. Метод Хука — Дживса
285
Таблица 6.3
к
1
2
3
хк
(-0,412, -3,259)
(-1,833, -4,206)
(-2,149, -4,416)
/(**)
-12,482
-27,243
-27,965
\к
4
5
6
хк
(-2,218, -4,462)
(-2,232, -4,470)
(-2,238, -4,476)
/(**)
-27,998
-27,999
-28,000
6.5. Метод Хука — Дживса
Эффективность прямого поиска точки минимума
ограниченной снизу целевой функции можно повысить, если на
каждом k-м шаге поиска соответствующим образом выбирать
направление спуска. Для этого на каждом k-м шаге выделяют
предварительный этап исследующего поиска. Целью этого
этапа является выбор направления спуска путем исследования
поведения целевой функции f(x) в окрестности точки ж^-1,
найденной на предыдущем шаге. В результате выполнения
этапа исследующего поиска находится точка ж , для которой
f(xk) < f{xk~l). Направление спуска, завершающего А;-й шаг
поиска, определяется вектором ж — х . Такая стратегия
поиска, предложенная в 1961 году, получила название метода
Хука — Дживса*.
Опишем один из алгоритмов исследующего поиска. Пусть
выбрана начальная точка ж0 и вектор Ъ = (Ь\ ... Ъп) ,
удовлетворяющий условию \Ь\ ^ ?, где е > 0 — заданный параметр
точности исследующего поиска. Координаты вектора Ь,
называемого вектором перемещений, определяют приращения
координат точки ж0 на этапе исследующего поиска.
Полагаем k = j = 1, хк- = хк = ж0, fj= f(x°) и переходим к основной
части алгоритма исследующего поиска.
1. Вычисляем
fXj = tt*) + bjei) и t0 = j{x)-b3e3),
*См.: Базара М., Шетти К.
286
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
где ei, ..., еп — стандартный базис в Мп, находим точку
j+i - ^ -j " "jcj> /-j < fj и /-j < /+j!
во всех остальных случаях,
полагаем /^+1 = /(й+1) и переходим к п. 2.
2. Если j < п, то принимаем j : = j + 1 и переходим к п. 1. В
противном случае переходим к п. 3.
3. Если Хп+1 фяк, то переходим к п. 4. В противном случае
уменьшаем длину вектора Ь, полагал Ъ : = Ь/7, где 7 > 1 —
коэффициент дробления шага исследующего поиска, и, полагал
j = 1, 2$ = ж^, /j2 = f(xk), возвращаемсл к п. 1.
4. Если |ж^+1 — ж | < ?, то дальнейший поиск точки
минимума прекращаем, полагал ж* « ж^-1 и /(ж*) « f(xk~l). В
противном случае полагаем ж +1 = ж^+1 и переходим на к-м
шаге поиска к этапу спуска в направлении вектора ж ^ — ж ,
имел при этом /(ж/с+1) < /(ж*) ^ f(xk~l).
На этапе спуска по формуле
хк = хк + ак(хк+1-хк), F.13)
подбирал так называемый ускоряющий множитель а& > О,
находим такую точку хк, чтобы f(xk) ^ f(xk+1). С увели-
чением а& увеличиваетсл длина а&|ж ^ — ж | шага спуска в
направлении вектора ж^+1 — хк. Значение а& можно подобрать
из условил минимума функции /(ж) при смещении точки ж в
направлении этого вектора. Может оказатьсл, что а& Е @, 1].
После нахождения точки хк переходим к следующему шагу
поиска (к п. 1 этапа исследующего поиска), полагал j = 1, ж + =
= xk+1 = хк, fk+1 = f(xk) и затем к : = к + 1.
В простейшем варианте метода Хука — Дживса значение а&
в F.13) не подбирают, а задают постоянным, причем обычно
полагают а& = 2. На рис. 6.16 иллюстрируютсл этапы исследу-
6.5. Метод Хука — Дживса 287
Рис. 6.16 Рис. 6.17
ющего поиска и спуска для первых двух шагов поиска точки ж*
минимума целевой функции двух переменных при a\ = а2 = 2,
7 = 2 и начальной точке ж0.
Известно много модификаций метода Хука — Дживса.
Одна из модификаций связана с введением дополнительных правил
выбора точки ж на каждом k-м шаге при проведении этапа
исследующего поиска. Например, координаты этой точки можно
выбирать, используя модифицированный метод циклического
покоординатного спуска". На рис. 6.17 иллюстрируется первый
шаг поиска точки ж* минимума целевой функции двух
переменных с применением на этапе исследующего поиска
модифицированного метода циклического покоординатного спуска, а на
этапе спуска — процедуры подбора ускоряющего множителя
&к — ai > 0 в формуле F.13), исходя из условия минимума
целевой функции в направлении вектора ж2 — ж1.
Для определения точки хк на к-м шаге при проведении этапа
исследующего поиска можно также использовать процедуры
случайного поиска**.
*См.: Базара М., Шетти К.
**См.: Васильев Ф.П.
288
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Другой путь повышения эффективности поиска точки
минимума функции состоит в выполнении на каждом шаге
повторного этапа исследующего поиска*. В случае
квадратичной целевой функции f(x) = - (Qx, х) + (с, х) с положительно
определенной матрицей Q порядка п эта модификация метода
Хука — Дживса позволяет получить точку минимума за один
шаг, если на этапах исследующего поиска использовать
модифицированный метод циклического покоординатного спуска, а
выбор ускоряющего множителя на этапе спуска осуществлять
исходя из условия минимума целевой функции в установленном
направлении спуска.
Пример 6.5. Используем метод Хука — Дживса для
минимизации функции из примера 6.1. Выберем начальную точку
ж0 = (—2, 1) и положим е = 0,01, а& = 2, 7 = 2. На рис. 6.18
представлена графическая иллюстрация процесса поиска точки
минимума этой функции для различных начальных векторов Ь.
Результаты поиска приведены в табл. 6.4.
Таблица 6.4
Вариант
а
б
в
г
Ь
A,1)
A, 0,5)
@,5, 1)
@,5, 0,5)
X*
(-2,234, -4,473)
(-2,234, -4,469)
(-2,234, -4,473)
(-2,234, -4,433)
/(«*)
-28,0
-28,0
-28,0
-28,0
N
16
20
17
18
Из табл. 6.4 видно, что изменение начальной длины вектора
Ь в два раза практически не повлияло на точность нахождения
точки ж* и значения /(ж*), но привело к уменьшению
необходимого числа N шагов поиска. При заданной начальной длине
вектора Ъ уменьшения необходимого числа N шагов поиска
можно также достичь, изменив коэффициент дробления
шага 7 > 1 на этапе исследующего поиска. Так, например, при
*См.: Лесин В.В., Лисовец Ю.П.
6.5. Метод Хука — Дживса
289
Рис. 6.18
290
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Ь = A, 1) (вариант а) наименьшее количество шагов N = 11
достигается при 7 = 5, в то время как при 7 = 4 и 7 = 20 имеем
N = 12, а при 7 = Ю имеем N = 15.
Рассмотрим некоторые модификации метода Хука — Джи-
вса, позволяющие повысить эффективность поиска. В табл. 6.5
приведены результаты поиска, в котором на каждом fc-м шаге
используется не постоянное значение ускоряющего множителя,
равное двум, а переменное, выбираемое из условия минимума
целевой функции в направлении вектора хк+1 — хк.
Таблица 6.5
Вариант
а
б
в
г
ь1
A,1)
A, 0,5)
@,5, 1)
@,5, 0,5)
X*
(-2,235, -4,468)
(-2,236, -4,471)
(-2,239, -4,474)
(-2,234, -4,468)
/(«*)
-28,0
-28,0
-28,0
-28,0
N
14
19
16
16
Из табл. 6.5 видно, что рассмотренный способ выбора
ускоряющего множителя позволяет уменьшить необходимое число
N шагов поиска.
На рис. 6.19 дана графическая иллюстрация первых двух
шагов поиска точки минимума функции, в котором на этапе
исследующего поиска использован модифицированный метод
циклического покоординатного спуска, а ускоряющий
множитель на этапе спуска выбирался двумя способами: в варианте
а он постоянный и равен двум, а в варианте б он определяется
исходя из условия минимума целевой функции в направлении
вектора х +1 — х . Соответствующие результаты приведены в
табл. 6.6.
Таблица 6.6
Вариант
а
б
X*
(-2,238, -4,476)
(-2,236, -4,473)
/(**)
-28,0
-28,0
iV
6
6
6.5. Метод Хука — Дживса
291
Рис. 6.19
Рис. 6.20
292
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Из табл. 6.6 видно, что рассмотренные варианты метода
Хука — Дживса приводят к заметному уменьшению количества
шагов поиска, практически не изменяя точности нахождения
точки минимума и значения функции в этой точке.
Отметим еще одну модификацию метода Хука —
Дживса, позволяющую определить точку минимума целевой функции
двух переменных за один шаг поиска. Графическая
иллюстрация этого метода дана на рис. 6.20. Обратим внимание на то,
что процесс поиска точки ж1 в этом варианте совпадает с
процессом ее поиска в варианте, представленном на рис. 6.19, б.
Проводя исследующий поиск в точке ж1 с помощью метода
циклического покоординатного спуска и выбирая на этапе спуска
ускоряющий множитель по условию минимума целевой
функции в установленном направлении спуска, получим точку ж2,
совпадающую с точкой минимума рассматриваемой функции.
6.6. Методы Розенброка и Пауэлла
Рассмотрим еще одну стратегию поиска точки минимума
ограниченной снизу целевой функции /(ж), ж Е W1. Метод,
реализующий эту стратегию поиска, также предусматривает
проведение исследующего поиска на каждом к-м шаге. Целью
исследующего поиска является выбор текущего направления
спуска с учетом информации о поведении целевой функции в
окрестности точки ж^-1, найденной на предыдущем шаге.
Отличие этого метода от метода Хука — Дживса
состоит в способе выбора направлений исследующего поиска. Если в
методе Хука — Дживса они фиксированы и коллинеарны
направлениям векторов стандартного базиса вР, то в
рассматриваемом методе выбор этих направлений проводят в процессе
минимизации целевой функции путем построения на каждом
к-м шаге поиска нового ортонормированного базиса в W1.
Итогом выполнения этого этапа является нахождение точки хк, для
которой f(xk) < f(xk~l). Тогда вектор хк — хк~1 определит
направление спуска на к-м шаге.
6.6. Методы Розенброка и Пауэлла
293
Такая стратегия поиска впервые была реализована в 1960
году и получила название метода Розенброка*. В
первоначальном варианте метода Розенброка процедура нахождения точки
хк (как и в методе Хука — Дживса) была основана на
дискретных шагах исследующего поиска по выбранным направлениям.
Опишем модификацию этого метода, в которой на каждом А;-м
шаге поиска выбор координат точки ж проводят методом
модифицированного циклического покоординатного спуска.
Пусть выбраны начальная точка ж0 Е Мп и параметр е > 0
точности поиска. Возьмем в качестве векторов р^ j = 1,п,
определяющих направления исследующего поиска на первом
шаге, векторы ej стандартного базиса в W1. Полагаем k = j = 1,
х\ = ж0 и переходим к основной части алгоритма.
1. Минимизируя функцию щ )(к) = f{xk- + хр^), находим
значение >с- ) Е К, вычисляем Й+1 = хк- + >г- рк, и переходим к
п. 2.
2. Если j < п, то принимаем j : = j + 1 и возвращаемся к п. 1.
В противном случае полагаем ж^ = ж^+1 и переходим к п. 3.
3. Если \хк — хк~1\ < ?, где е > 0 — достаточно малое
число, характеризующее точность выполнения этапа
исследующего поиска, то дальнейший поиск точки минимума прекращаем,
принимая ж* « хк и /(ж*) « f(xk). В противном случае
переходим к п. 4.
4. На /с-м шаге поиска строим новый ортонормированный
базис, векторы р -+ , j = 1, п, которого задают направления
исследующего поиска на (к+1)-м шаге. При построении этого
базиса используем процесс ортогонализации Грама — Шмидта
и проводим его следующим образом. Полагаем
тк ъ№ — П-
V^ (к) к (Ю , п ^ = 1,П'
*См.: Базара М., Шетти К.
294
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Далее вычисляем
Lfc + l
а
к+1
Pi
ak+l
аз '
1c(aJ+1,P?+1)P?+1,
г=1
bk3+1 ¦ т—
_i|Jb+l|' J-1»™-
1 i 1
j = i;
i = 27",
/c+1
После вычисления векторов p,-^1, j = 1, n, переходим к п. 1,
полагая j : = 1, ж + = ж^ и затем fc : = fc + 1.
На рис. 6.21 иллюстрируются этапы одного шага поиска
точки минимума целевой функции двух переменных из
начальной точки ж0. Отметим, что рассмотренный алгоритм можно
модифицировать, вводя дополнительные правила выбора
точки х на каждом к-м шаге при проведении этапа исследующего
поиска (см. 6.4).
Рис. 6.21
Пример 6.6. Используем метод Розенброка для
минимизации функции из примеров 6.4 и 6.5. Выберем начальную точку
6.6. Методы Розенброка и Пауэлла
295
ж0 = (—2, 1)и точность поиска е = 0,01. Графическая
иллюстрация первых трех шагов метода дана на рис. 6.22. Результаты
поиска точки минимума по методу Розенброка приведены в
табл. 6.7.
Рис. 6.22
Таблица 6.1
к
1
2
3
4
хк
(-0,412, -3,259)
(-2,020, -3,178)
(-1,834, -4,234)
(-2,159, -4,177)
/(**)
-12,482
-23,817
-27,245
-27,794
\к
5
6
7
хк
(-2,168, -4,444)
(-2,219, -4,428)
(-2,233, -4,472)
/(**)
-27,977
-27,996
-28,000
Из табл. 6.7 видно, что для рассматриваемой функции
использование метода Розенброка не приводит к повышению
эффективности поиска по сравнению, например, с
модифицированным методом циклического покоординатного спуска (см.
пример 6.4), поскольку при той же точности поиска
необходимое число N шагов поиска не уменьшается.
296
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Рассмотрим еще один алгоритм прямого поиска,
предложенный в 1964 году и называемый обычно методом Пауэлла*
Предварительный этап и первые два пункта основной части
этого алгоритма практически совпадают с алгоритмом метода
Розенброка. Отличие состоит в построении системы векторов,
определяющих направления спуска на каждом последующем
шаге поиска и проявляется начиная с п. 3 описанного выше
алгоритма метода Розенброка. В методе Пауэлла вычисления в п. 3
носят итерационный характер. Поэтому на предварительном
этапе для номера г итерации принимают г = 1.
1. Минимизируя функцию гр)- (к) = f{xk- + хр^), находим
значение >с- ' Е К, вычисляем ж^+1 = Щ + уг- 'рк и переходим
к п. 2.
2. Если j < п, то полагаем j : = j + 1 и возвращаемся к п. 1.
В противном случае переходим к п. 3.
3. Полагаем р = ж^+1 — хк и находим значение х,
минимизируя функцию ф{>с) = /(ж^+1 + хр), а затем вычисляем 2^ =
= 2^+1 + хр. Если г < п, то для всех j = 1, п—1 заменяем р^
на Pj+i, полагаем р^=р, х\ = zi, j = 1, г : = г + 1 и переходим
к п. 1 рассматриваемого алгоритма. В противном случае, т.е.
при г = п, переходим к п. 4.
4. Принимаем ж^ = zn. Если |ж^ — ж^-1] < ?, то вычисления
прекращаем и полагаем ж* « ж^ и /(ж*) « f(xk). В противном
случае считаем, что жх-1 = ж^, г = 1, j = 1, А; := А; + 1, и
возвращаемся к п. 1 рассматриваемого алгоритма.
Рис. 6.23 иллюстрирует один шаг поиска точки
минимума целевой функции двух переменных из начальной точки ж0.
Можно доказать, что в случае квадратичной целевой функции
/(ж) = (Qx, ж)/2 + (с, ж) с положительно определенной
матрицей Q с помощью алгоритма метода Пауэлла за один шаг поиска
строится система векторов pj, j = 1, п, сопряженных
относительно этой матрицы. При этом точка ж1, полученная в конце
*См.: Базара М., Шетти К.
6.6. Методы Розенброка и Пауэлла
297
Рис. 6.23
первого шага, совпадает с искомой точкой ж* минимума такой
целевой функции. Покажем это на конкретном примере.
Пример 6.7. Используем метод Пауэлла для минимизации
ранее рассмотренной функции (см. примеры 6.1, 6.4-6.6).
Выберем начальную точку ж0 = (—2, 1) и точность поиска е = 0,01.
Графическая иллюстрация метода представлена на рис. 6.24.
На рисунке видно, что точка ж* минимума целевой функции
достигается за один шаг поиска. В результате этого поиска
получаем ж* « (-2,236, -4,472) и /(ж*) « -28,0, что с точностью
5 • Ю-5 совпадает с точным решением (—л/5, —2д/5) задачи. #
Известно много модификаций метода Пауэлла. На рис. 6.25
представлена одна из таких модификаций в применении к
функции из примеров 6.1, 6.4-6.7. В качестве начальной
выбрана точка ж0 = A, 1). Алгоритм, реализующий этот вариант
метода Пауэлла, включает проведение на каждом k-м шаге
поиска одной дополнительной итерации циклического
покоординатного спуска в направлении вектора* рп. При минимизации
*См.: Реклейтис Р., Рейвиндран Л., Рэгсдел К., а также: Химмелъ-
блау Д.
298
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Рис. 6.24 Рис. 6.25
функции, не являющейся квадратичной, дополнительная
итерация гарантирует линейную независимость векторов,
определяющих направление спуска на каждом к-м шаге поиска.
Вопросы и задачи
6.1. Перечислите методы прямого поиска, выделите те из
них, в которых поиск точки минимума целевой функции
проводится в соответствии с рекуррентным соотношением F.8).
Объясните, почему при построении алгоритмов таких
методов направления поиска должны быть линейно независимыми.
Графически проиллюстрируйте на примере решения двумерной
задачи минимизации возможные подходы к построению таких
направлений поиска.
6.2. В задаче
/(ж1,Ж2) = ll^i + §х\Х2 + 3^2 — 2л/10(ж1 — 3^2) — 22 —>> min,
Вопросы и задачи
299
выбрав в качестве начальной точку ж0 = (\Лб, 0), найдите
уравнение линии уровня целевой функции, проходящей через
точку ж0. При помощи ортогонального преобразования
приведите уравнение, описывающее эту линию уровня, к
каноническому виду и постройте эту кривую в исходной системе
координат.
6.3. Проведите поиск минимума целевой функции в
задаче 6.2 из заданной начальной точки ж0 с точностью ? = 0,01
методами поиска при помощи регулярного и нерегулярного
симплексов, циклического покоординатного спуска, методами
Хука — Дживса, Розенброка и Пауэлла. Оптимизируйте
процесс поиска при реализации алгоритма метода Нелдера — Ми-
да путем изменения параметров алгоритма: выбора способа
построения исходного симплекса и его размеров,
коэффициентов отражения, растяжения, сжатия и редукции симплекса;
при реализации алгоритма метода Хука — Дживса
изменением вектора перемещений и коэффициента дробления шага на
этапе исследующего поиска, а также подбором ускоряющего
множителя на этапе спуска. Проведите сравнительный анализ
результатов, дайте их графическую интерпретацию.
Перечислите методы, гарантированно приводящие к минимуму
целевой функции за конечное число шагов поиска.
6.4. Решите задачу
/(ж1,ж2) = 10(ж2 - ж2J + (х\ - IJ ->> min,
выбрав в качестве начальной точку ж0 = ( —1, 1) и задав
значение параметра точности поиска е = Ю-3. Примените методы
циклического покоординатного спуска, Розенброка и Пауэлла.
Оптимизируйте процесс поиска точки A, 1) минимума целевой
функции, используя различные алгоритмы одномерной
минимизации на каждом шаге покоординатного спуска: дихотомии,
золотого сечения, квадратичной и кубической интерполяции.
300
6. АЛГОРИТМЫ ПРЯМОГО ПОИСКА
Проведите сравнительный анализ алгоритмов по числу N
шагов поиска. Дайте графическую интерпретацию полученных
результатов.
6.5. Используя методы прямого поиска, минимизируйте
функцию Розенброка
f{xl,x2) = l№{x{-x2f + {x1-lf
с точностью е = 10_3, выбрав начальную точку ж0 = (—1, 1).
Установите, какие из примененных алгоритмов не позволяют
при заданной точности поиска получить точку минимума A, 1)
вследствие преждевременного окончания процесса поиска.
6.6. Используя различные модификации метода Хука —
Дживса, минимизируйте функцию Химмельблау
f(xux2) = {х\ + х2- IIJ + (ах +х\- 7J
с точностью е = Ю-3, выбирая различные начальные точки:
а) E, 5); б) E, -5); в) @, 0); г) (-5, -5); д) E, 0).
Оптимизируйте процесс поиска путем изменения параметров алгоритма.
Дайте графическую иллюстрацию полученных результатов.
6.7. Минимизируйте функцию Пауэлла
/(Ж1,Ж2,ЖЗ,Ж4) =
= (ах + 10ж2J + 5(х3 - ж4J + (х2 - 2ж3L + 10(a;i - ж4L,
выбрав параметр точности поиска е = Ю-3 и начальную
точку х° = C, —1, 0, 1). Для этого используйте метод Нелдера —
Мида, оптимизируя процесс поиска подбором параметров
алгоритма. Установите, можно ли получить точку минимума
ж* = @, 0, 0, 0) целевой функции, используя поиск с помощью
регулярного симплекса.
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
НЕЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Общая задача нелинейного программирования может
включать ограничения типа равенства или ограничения типа
неравенства, а также оба вида ограничений одновременно. В этой
главе сначала кратко обсудим задачу нелинейного
программирования, в которую входят только ограничения типа равенства,
а затем перейдем к общему случаю.
7.1. Минимизация целевой функции
на заданном множестве
Рассмотрим общую задачу математического
программирования
/о(ж) —>> min, х Е О, G.1)
где Q — допустимое множество, входящее в область
определения D(fo) С W1 целевой функции /о (ж). Пока не будем уточнять,
каким способом задано множество О, но будем считать, что оно
не пусто.
Если множество О компактное, то существует хотя бы одна
точка ж* Е О, в которой непрерывная на этом множестве
функция fo(x) достигает своего наименьшего значения [V].
Следовательно, задача G.1) в случае непрерывной целевой функции
и компактного допустимого множества имеет решение.
Теорема 7.1. Если функция fo(x) непрерывна на
замкнутом множестве О С W1 и для некоторого «ЕМ множество X =
= {х Е О: fo(x) ^ а} не пустое и ограниченное вКп, то задача
G.1) имеет решение.
302
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
-4 Так как функция fo(x) непрерывна в О, множество X,
определенное нестрогим неравенством /о (ж) ^ а, является
замкнутым. Действительно, если ж0 Е О — предельная точка
множества X, то в любой окрестности этой точки можно
указать точки множества X. Возьмем произвольное число е > 0
и, согласно условию непрерывности функции /о (ж) в точке ж0,
выберем окрестность и(ж°,5), для которой \fo(x) — /о(ж°)| < ?
при х Е и(ж°,5) П О. В этой окрестности существует точка ж1,
принадлежащая множеству X, т.е. для этой точки выполняется
неравенство foix1) < а. Значит, /о(ж°) < fofa1) + ? ^а + е.
Поскольку записанное неравенство верно для любого числа е > 0,
то fo(x°) ^ а и ж0 Е X. Итак, множество X содержит все свои
предельные точки, а потому замкнуто.
Функция fo(x), непрерывная на замкнутом ограниченном
множестве X, достигает на этом множестве наименьшего
значения в некоторой точке ж*. Из условия ж* Е X вытекает, что
/о(ж*) ^ а. Если ж Е О \Х, то в соответствии с определением
множества X выполняется неравенство fo(x) > а. Поэтому
fo(x)>a>f0(x*), хеП\Х,
и значение целевой функции в точке ж* является наименьшим
на всем множестве О. >
Рассмотрим произвольную точку ж Е О. Будем говорить,
что единичный вектор е Е W1 задает допустимое
направление в точке ж, если для некоторого числа 8 > 0 каждая точка
ж + ?е, ?Е @,5), принадлежит множеству О. Множество С{х)
всех единичных векторов, каждый из которых задает в точке
ж Е О допустимое направление, называют конусом
допустимых направлений в точке ж.
Если множество О выпуклое, то допустимое направление
в точке х Е ft можно задать любым вектором ж — ж,
определяемым произвольной точкой ж Е О, не совпадающей с ж.
Действительно, в этом случае для е = -^ г в качестве 8 > 0
можно выбрать 8 = | ж — ж |.
7.1. Минимизация целевой функции на заданном множестве 303
Теорема 7.2. Пусть функция fo(x) дифференцируема* в
точке ж*ЕКп. Если ж* является точкой наименьшего значения
функции /о (ж) на множестве О, то
(grad/0(a:*),e)>0, е е С(х*). G.2)
^ Выберем вектор е Е С (ж*) и соответствующее этому вектору
число S > 0, так что ж* +?е Е О при t Е @,5). Функция (^e(t) =
= fo(x*+te) определена на полуинтервале [0,5) и достигает
наименьшего значения при t = 0, так как </?е@) = /о(ж*) ^
< /о(ж) = ??(*), где ж = ж* + te Е О, ? Е @, S). Отсюда вытекает,
что
Ы*)-Ув(о)>0> te@)J)_
Так как функция fo(x) дифференцируема в точке ж*, то
сложная функция (fe(t) дифференцируема в точке t = 0. Поэтому
существует предел
VM=limy«(*)-y«@)>0.
Производная функции <ре(?) в точке ? = 0 представляет собой
производную функции fo(x) в точке ж* по направлению вектора
е, которую с помощью градиента функции можно записать в
виде (grad/o(a;*), е) [V]. Таким образом, неравенство (р'е@) ^ 0
равносильно неравенству G.2). >
Утверждение теоремы 7.2 можно рассматривать как
обобщение необходимого условия локального экстремума. Чтобы
придать такой трактовке более точный смысл, введем
следующее понятие. Будем говорить, что функция fo(x), определенная
на множестве О, имеет в точке ж* Е О локальный
минимум на множестве О, если существует такая окрестность
*Дифференцируемость функции в точке предполагает, что функция
определена в некоторой окрестности этой точки, т.е. все точки диф-
ференцируемости функции являются внутренними точками ее области
определения.
304
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
U точки ж*, что /о(ж) ^ /о(ж*) при ж Е ?7ПО. Если последнее
неравенство в случае х ф х* является строгим, то будем
говорить о строгом локальном минимуме на множестве Q.
Введенные понятия расширяют понятия локального минимума
и строгого локального минимума: согласно определению,
точка локального (строгого локального) минимума должна быть
внутренней точкой множества О.
Повторяя почти дословно доказательство теоремы 7.2,
можно показать, что если ж* ? О — точка локального минимума
функции /о (ж) на множестве О, а функция /о (ж)
дифференцируема в точке ж*, то имеет место условие G.2).
Если точка ж* является внутренней точкой множества О, то
конус допустимых направлений С (ж*) содержит все п-мерные
единичные векторы, а условие G.2) легко преобразовать в
обычное условие локального экстремума функции, записанное
в виде (grad/o(#*), e)=0,eGRn. Действительно, в этом случае
условие G.2) выполняется для любой пары единичных векторов
е и — е, а потому в этом условии знак нестрогого неравенства
можно заменить знаком равенства. Кроме того, условие |е| = 1
не является существенным, так как множитель, равный длине
вектора е, можно вынести за знак скалярного произведения.
Отметим, что условие (grad/o(^*), е) = 0, eGRn,
эквивалентно условию grad/o(^*) =0- В самом деле первое условие
непосредственно вытекает из второго. Наоборот, если верно
первое условие, то равенство (grad/o(^*), е) =0 верно и при
е = grad/o(#*), т.е. |grad/o(^*)|2 = 0, что равносильно
равенству grad/o(#*) = 0 — обычной формулировке необходимого
условия локального минимума [V].
Теорема 7.3. Пусть функция fo(x) определена на
выпуклом множестве О и дифференцируема в точке ж* Е О. Если для
некоторого числа а > 0 выполнено условие
(grad/0(a;*),e)>a, ееС(х*), G.3)
то ж* — точка строгого локального минимума этой функции
на множестве ft.
7.1. Минимизация целевой функции на заданном множестве 305
-4 Условие дифференцируемостифункции fo(x) в точке ж*
означает, что функция /о (ж) определена в некоторой окрестности
и(ж*,5) точки ж* и в этой окрестности имеет место
представление
fo(x) - f0(x*) = (grad/o(a;*), А*) +о(Ах),
где Аж = ж — ж*, а °/. х' — бесконечно малая при Аж —»> 0.
Уменьшим, если необходимо, радиус окрестности 5 настолько,
чтобы в этой окрестности выполнялось неравенство |о(Аж)| <
<||Д*1-
Пусть ж Е ft П и(ж*,?), ж/ж*. Тогда вектор е = —
задает допустимое направление. Следовательно,
fo(x)-Mx*) = (grad/oOr*), Ах)+о(Ах) >
^ |Ax|(grad/0(cc*),e) -^\Ах\ ^ |Аж|а-^|Аж| = ^|Аж| > 0.
Но это и означает, что в точке ж* функция fo(x) имеет
локальный минимум на множестве О. >
Отметим, что условие G.3) теоремы 7.3 может
выполняться лишь в граничной точке множества О. Действительно, если
бы это условие выполнялось во внутренней точке ж* множества
О, то точка ж* была бы точкой локального минимума
функции fo(x) и, значит, в этой точке выполнялось бы равенство
(grad/o(#*), е) = 0, е Е W1. Но это противоречит условию G.3).
Доказанные необходимое и достаточное условия локального
минимума функции на множестве можно использовать при
решении задач минимизации функции на заданном множестве
О. Если целевая функция достигает наименьшего значения на
О, то для определения точки минимума можно придерживаться
следующего порядка действий.
1. Находим все стационарные точки функции, являющиеся
внутренними точками множества О.
306
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
2. С помощью необходимого условия (см. теорему 7.2)
находим все точки на границе множества О, в которых функция
может иметь локальный минимум на О.
3. Сравнивая значения минимизируемой функции в
найденных точках, находим ту точку, в которой функция имеет
наименьшее значение.
При решении задачи выпуклого программирования, в
которой выпуклая функция минимизируется на выпуклом
множестве, достаточно найти любую точку ее локального минимума,
так как, согласно теореме 3.14, в любой точке локального
минимума эта функция достигает наименьшего значения. В этом
случае уместно использовать достаточное условие локального
минимума на множестве (см. теорему 7.3), которое не
требует вычисления частных производных второго порядка и легко
проверяется.
Узким местом предложенной схемы является применение
необходимого условия локального минимума на множестве. Если
необходимое условие экстремума функции записывается в виде
системы уравнений, то необходимое условие локального
минимума на множестве представлено в виде системы неравенств, в
которых варьируется не только неизвестная точка, но и вектор
е допустимого направления. Выделить с помощью теоремы 7.2
точки, ^подозрительные" на локальный минимум, можно лишь
в случае, когда допустимое множество О имеет границу
простой структуры.
7.2. Минимизация
при ограничениях типа равенства
Задачу нелинейного программирования с ограничениями
типа равенства можно записать следующим образом:
{/о (ж) —>> min;
К J G.4)
Д(*)=0, l = hk.
7.2. Минимизация при ограничениях тина равенства 307
В данном случае допустимое множество О имеет вид
П = {хеШп: Л(ж)=0, / = ТД}-
Сформулированную задачу в случае дифференцируемых
функций fi (ж) можно связать с задачей исследования целевой
функции на условный экстремум [V]. Если точка ж* есть
решение задачи G.4), т.е. если целевая функция /о (ж) достигает
в этой точке наименьшего значения на множестве О, то точка
ж* является точкой условного локального минимума функции
/о(ж) при условиях fi(x) = 0, I = 1, к (эти уравнения называют
уравнениями связи). Поэтому решать задачу G.4) можно
следующим образом. Найти все точки, в которых функция может
иметь условный локальный минимум, а затем путем сравнения
значений функции выбрать из этих точек ту, в которой
функция имеет наименьшее значение. Если задача имеет решение
(т.е. целевая функция при заданных ограничениях достигает
наименьшего значения), то этим решением будет найденная
точка.
Поиск точек, ^подозрительных" на условный экстремум,
выполняют с помощью необходимого условия условного
локального экстремума, суть которого в следующем. Если точка ж*
является точкой условного экстремума функции fo(x) при
условиях fi(x) =0, / = 1, /с, причем функции /г (ж), I = 0, /с,
непрерывно дифференцируемы в окрестности точки ж* и матрица
Якоби J{x) векторной функции /(ж) = (fi(x) ... /&(ж)) в
точке ж* имеет ранг к (максимальный ранг, равный количеству
строк), то существуют такие множители Лагранжа Ai, ..., А&,
что для функции Лагранжа
к
ВД = /о(ж) + 5>Жж) G.5)
i=i
в точке ж* выполняется необходимое условие экстремума
gradL(#*) = О,
308
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
или
дЦх*) _ дЦх*) _ _<9?(ж*) _
Поиск стационарных точек функции Лагранжа сводится к
решению системы п + к уравнений [V]
(fi(x) = 0, 1 = 1, к,
содержащей п + к неизвестных х\, ..., жп, Ai, ..., А&.
Таким образом, исследование функции на условный
экстремум состоит в выделении некоторого набора точек,
^подозрительных" на экстремум, и в проверке каждой точки, является
ли она в действительности точкой условного экстремума.
Набор точек, „подозрительных" на экстремум, можно разделить
на три группы:
1) точки, в которых хотя бы одна из функций fi(x), I = 0, /с,
не дифференцируема или одна из ее частных производных
разрывна;
2) точки, в которых ранг матрицы Якоби J (ж) системы
уравнений связи меньше количества к уравнений связи;
3) стационарные точки функции Лагранжа.
Отличие задачи минимизации при ограничениях типа
равенства от задачи исследования на условный экстремум состоит
в том, что в задаче минимизации нет необходимости проверять,
является ли точка, „подозрительная" на экстремум, точкой
условного локального минимума. Можно просто сравнить
значения минимизируемой функции в этих точках и выбрать ту, в
которой значение функции наименьшее. Эта точка и будет
решением задачи минимизации. Правда, последнее утверждение
верно лишь в случае, когда задача минимизации имеет
решение. В действительности возможна ситуация, когда целевая
функция имеет точки условного локального минимума, но не
достигает наименьшего значения.
7.2. Минимизация при ограничениях тина равенства 309
Необходимое условие условного локального экстремума
можно модифицировать так, что определение стационарных точек
функции Лагранжа будет включать в себя и поиск точек, в
которых нарушается условие на ранг матрицы Якоби системы
уравнений связи (необходимое условие условного локального
экстремума формулируется в предположении, что ранг
системы уравнений связи максимален и совпадает с числом
уравнений связи). Для этого изменим понятие функции Лагранжа,
используя вместо G.5) формулу
~ к
ВД = А0/о(ж) + 5>гЖаО, G.6)
в которую добавлен еще один множитель Лагранжа Ао-
Следующее утверждение называют обобщенным правилом
множителей Лагранжа.
Теорема 7.4. Если ж*?Йп — точка условного
экстремума функции /о (ж) при условиях /г(ж)=0, / = 1, /с, причем
функции fi(ж), / = 0, /с, непрерывно дифференцируемы в
некоторой окрестности точки ж*, то существуют такие множители
Лагранжа А;, / = 0, /с, не все равные нулю, что для функции
Лагранжа L(x) точка ж* является стационарной, т.е.
gradZ(#*) = 0. G.7)
-4 Если ранг матрицы Якоби J(x*) системы функций /г (ж),
I = 1, /с, в точке ж* равен их количеству /с, то достаточно
положить Ао = 1. Тогда утверждение теоремы будет вытекать
из необходимого условия условного экстремума [V].
Предположим, что Rg</(ж*) < к. Тогда строки матрицы J{x*) линейно
зависимы, например, в силу теоремы о базисном миноре [III].
Это означает, что для некоторых значений Ai, ..., А&,
одновременно не равных нулю, выполняется равенство
Ai grad/i(#*) + A2grad/2(^*) + ... + A/cgrad//c(a?*) = 0.
310
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
Положив Ло = 0, запишем
к
A0grad/0(«*) +J^A|grad/i(«*) = 0,
1=1
что в силу G.6) совпадает с G.7). >
Нетрудно увидеть, что множители Лагранжа,
существование которых вытекает из теоремы 7.4, определяются
неоднозначно: их можно, не нарушая утверждения теоремы,
умножить на любой постоянный множитель. Поэтому для
определения к + 1 множителя Лагранжа Ао, ..., А& и п координат точки
ж* достаточно к + п уравнений. Такое количество дают
условие G.7) (это п уравнений) и совокупность уравнений связи (их
количество равно к).
7.3. Общая задача
нелинейного программирования
Общую задачу нелинейного программирования можно
сформулировать следующим образом:
G.8)
1,/с; 3г(я)^0, г = 1,га.
При этом предполагается, что одна из фигурирующих в
задаче функций не является линейной. Считаем, что все функции
fi(x), I = 0, /с, и gi{x), г = 1, га, определены на некотором
открытом множестве X CW1. Упрощая изложение, мы далее
ограничимся случаем X = W1. В конкретной ситуации
можно добиться выполнения этого ограничения, доопределив все
функции вне множества X, например, большим постоянным
значением, которое не повлияет на процесс минимизации
целевой функции.
Сформулированная задача представляет собой частный
случай общей задачи математического программирования, за-
7.3. Общая задача нелинейного программирования 311
ключающейся в определении наименьшего значения целевой
функции /о(ж) на допустимом множестве
П = {хеХ: /|(ж) = 0, / = 1Л #г(жК0, г = 1дп}. G.9)
Отметим, что если все функции fi(ж), / = 1, fc, и gi(x),
% — 1, m, непрерывны в!п, то множество О замкнуто. В
самом деле, это множество можно представить как пересечение
конечного числа множеств вида {ж ? Мп: <р(ж) ^ а},
образованных непрерывной в W1 функцией (р(х). В данном случае в
качестве (р(х) используются функции //(ж), —//(ж), I = 1, /с, и
gi(x), i = 1, га, а а = 0. Такие множества являются
замкнутыми (см. доказательство теоремы 7.1). Поэтому и множество О,
как пересечение конечного числа замкнутых множеств,
является замкнутым.
Большинство известных методов решения задачи
нелинейного программирования позволяют найти лишь точки
локального минимума целевой функции на заданном множестве. В
этой связи важную роль играет априорная информация о
существовании решения задачи, т.е. информация о том, достигает
ли целевая функция наименьшего значения на допустимом
множестве. Если допустимое множество О в задаче нелинейного
программирования замкнуто, то доказательство
существования решения в этой задаче можно строить с помощью теоремы
7.1, проверяя непрерывность целевой функции fo(x) и
ограниченность при некотором а множества fta = {ж Е О: fo(x) ^ а}.
В частности, если множество О ограничено, а целевая функция
непрерывна на О, то задача нелинейного программирования
имеет решение.
Однако проверить ограниченность множества О (или fta) не
просто. Поэтому интересны другие условия, налагаемые на
целевую функцию и ограничения и позволяющие делать
заключение о существовании решения без использования
ограниченности допустимого множества. В задаче выпуклого
программирования, в которой целевая функция выпукла и допустимое
312
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
множество О выпукло, любая точка локального минимума
целевой функции, согласно теореме 3.14, является решением этой
задачи.
Теорема 7.5. Если функции gi(x), г = 1, га, выпуклы в Мп,
то множество
О = {жЕМп:#г(ж)<0, % = 177^} G.10)
является выпуклым.
М Утверждение теоремы очевидно, если множество О пусто или
содержит всего лишь одну точку. Поэтому ограничимся
случаем, когда это множество содержит по крайней мере две точки.
Выберем в нем произвольные точки ж1 и ж2. Тогда gi(xl) ^ 0 и
gi(x2) ^ 0, i = 1, га. В силу определения 3.2 выпуклости функции
для любого числа а Е @, 1) имеем
gi(axi + (l-a)x2) ^ agi(xi) + A - a)gi(x2) ^ 0, г = 1, га.
Поэтому точка ажх + A — а)х2 также принадлежит множеству
О, а это означает, согласно определению 3.1, что О является
выпуклым множеством. >
Замечание 7.1. Из теоремы 7.5 следует, что если
допустимое множество О определяется только ограничениями типа
неравенства gi(x) ^ 0, г = 1, га, причем все функции <7г(#)
выпуклые в IRn, то множество О выпукло. Наличие ограничений
типа равенства усложняет проверку допустимого множества на
выпуклость. Однако если функции fi(x) во всех
ограничениях типа равенства являются линейными, а все функции gi(x) в
ограничениях типа неравенства — выпуклыми, то допустимое
множество выпукло. Действительно, в этом случае допустимое
множество О является пересечением множества О вида G.10)
с гиперплоскостями fi(x) =0, г = 1, га. Множество О выпукло
в силу теоремы 7.5, гиперплоскости также являются
выпуклыми множествами (см. пример 3.3). Поэтому множество О, как
пересечение выпуклых множеств, выпукло. #
7.3. Общая задача нелинейного программирования 313
Ограничения типа неравенства в задаче нелинейного
программирования введением дополнительных переменных можно
преобразовать в ограничения типа равенства. Например,
ограничения gi(x) ^ О, % — 1,га, с помощью дополнительных
переменных Zi можно записать в виде
#г(ж) + ^2 = 0, г = 1~^. G.11)
Таким образом, общую задачу нелинейного программирования
можно свести к частному случаю, когда в задаче нет
ограничений типа неравенства. Это позволяет в решении задачи
использовать технику исследования целевой функции на
условный экстремум (см. 7.2).
Впрочем, техника исследования функции на условный
экстремум может использоваться и непосредственно в задаче,
имеющей ограничения типа неравенства [V].
Пример 7.1. Рассмотрим задачу нелинейного
программирования
f(xi,x2) -^min;
gi(xux2)^0, 52(^1,^2)^0, дз(я1,ж2) ^0,
в которой функции /(ж1,ж2), gi(xi,x2), g2(xi,x2), gs(xi,x2)
непрерывно дифференцируемы в R2. Предположим, что
множество О, которое определяется тремя неравенствами, ограничено
и имеет вид, изображенный на рис. 7.1.
В этой задаче наименьшее значение функции f(xi,x2)
может достигаться либо во внутренней точке множества О, т.е. в
точке множества
Пс = {(хъ х2): gi(xi,x2) < 0, i = 1,2, 3},
либо на границе множества О на одной из дуг АВ, АС\ ВС,
либо в угловых точках границы А, В, С. Поэтому решение
задачи можно строить по следующей схеме.
314
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
5^2 #
д^(хрх2)=0
g1(x1,ac2)=0
д2(хрх2)=0
Рис. 7.1
1. Определяем все стационарные точки целевой функции в
области Ос.
2. Решаем три задачи на условный экстремум
f(xi,x2) -^extr,
9i(xux2)=0;
f(xux2) -^extr,
g2(xux2) =0;
f(xi,x2) -^extr,
дз{хъх2) = 0.
Среди найденных точек отбираем те, которые попадают на
соответствующую дугу АВ, АС', ВС. Например, из решений
первой задачи нужно оставить такие точки (жх, х2), которые
удовлетворяют условиям д2{х\,х2) < 0, дз{х\')х2) < 0.
3. К точкам, отобранным в первых двух пунктах,
добавляем угловые точки A, i?, С, которые находятся из систем
(gi(xux2) =0,
I д2(хъх2) <0,
[дз(хих2)=0;
[д\{хъх2) <0,
32(жх,ж2) = 0,
[дз(хъх2) = 0;
Г^х(жх,ж2) =0,
32(жх,ж2) =0,
[дз(хъх2) <0.
4. Во всех отобранных точках вычисляем значение целевой
функции и отбираем ту (или те), в которой значение функции
наименьшее. #
Описанный в примере 7.1 процесс анализа внутренних точек
допустимого множества и различных частей границы можно
7.3. Общая задача нелинейного программирования 315
объединить в одну формальную процедуру. Рассмотрим общую
задачу нелинейного программирования G.8).
Теорема 7.6. Если точка ж* Е О является точкой
локального минимума функции /о (ж) на множестве О вида G.9), причем
функции fi(ж), / = О, А;, и gi(x), % — 1, m, непрерывно
дифференцируемы в окрестности точки ж*, то существуют такие числа
А/, I = 0, /с, и /ij ^ 0, % — 1, т, одновременно не равные нулю, что
для функции
к т
ВД = А0/о(аО+ ?>/,(*)+ Е
1=1 г=1
выполняется необходимое условие экстремума
gradZ(a;*)=0
и, кроме того, выполняются условия дополняющей не-
жесткости
/Здг(я*)=0, г = 1,гс. #
Теорему 7.6 принято называть теоремой Куна — Так-
кера*, а функцию Ь(ж) — функцией Лагранжа. Хотя
функция Лагранжа определена для любых значений параметров А/,
/ = 0, /с, и /i^, г = 1,771, мы, учитывая утверждение теоремы
Куна — Таккера, будем рассматривать ее лишь при \i^ 0, г = 1, п.
Отметим особую роль в этой теореме условий дополняющей
нежесткости. В рассматриваемой точке ж* локального
минимума функции fo(x) на множестве О каждое из ограничений
gi(x) ^ О, г = 1,771, выполняется либо в виде равенства, gi(x*) =
0, либо в виде строгого неравенства, #г(ж*) < 0. Ограничения
первого вида называют активными ограничениями, в то
время как остальные — неактивными ограничениями. Для
активных ограничений соответствующее условие дополняющей
*См.: Алексеев В.М., Тихомиров В.М., Фомин СВ.
316
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
нежесткости выполнено. Неактивные ограничения в силу
непрерывности фигурирующих в задаче функций выполняются в
виде строгого неравенства не только в точке ж*, но и в
некоторой окрестности этой точки. Поэтому после удаления этих
ограничений из задачи точка ж* останется точкой локального
минимума. Полагая для таких ограничений \i{ — О, мы, с одной
стороны, обеспечиваем выполнение условия дополняющей
нежесткости, а с другой — удаляем соответствующее слагаемое
из функции Лагранжа. В конечном счете утверждение теоремы
Куна — Таккера сводится к обобщенному принципу Лагранжа.
Вернемся к примеру 7.1 и поясним, как работает
сформулированная теорема. В данном случае ограничений типа
равенства нет, а есть три ограничения типа неравенства. Если точка
ж* находится внутри множества О, то утверждение теоремы
будет верно при ц\ = \i2 = /^з = 0, Ао = 1. Если точка ж*
находится на одной из дуг, например на дуге АВ, то в этой точке
дз = 0. Утверждение теоремы вытекает из обобщенного
принципа Лагранжа для задачи с ограничениями типа равенства
при ц\ = \i2 = 0. Наконец, в угловой точке, например в точке
А, выполняются два равенства д\ = 0 и д% = 0. Чтобы
обеспечить условия дополняющей нежесткости, полагаем \i2 = 0. При
этом необходимое условие экстремума для функции Лагранжа
состоит из двух уравнений, в которых неизвестны три
параметра Ао, \i\ и //з, причем относительно этих параметров система
уравнений является линейной и однородной. Ясно, что такая
система имеет ненулевые решения.
Пример 7.2. Рассмотрим задачу нелинейного
программирования
fo(xi,x2) = (xi - ЗJ + (х2 - ЗJ ->> min;
— #1^0, —Х2 ^ 0, Ж1+ж2-4^0.
В этой задаче допустимое множество представляет собой
замкнутую треугольную область на плоскости (рис. 7.2), в
7.3. Общая задача нелинейного программирования 317
которой непрерывная целевая
функция достигает наименьшего
значения. Кроме того, нетрудно увидеть,
что ограничения задачи линейные, а
целевая функция, как квадратичная
функция с положительно
определенной матрицей, строго выпукла.
Поэтому рассматриваемая задача
относится к задачам выпуклого
программирования.
Проследим на примере этой простейшей задачи, как
работает теорема Куна — Таккера. В этой задаче нет ограничений
типа равенства, функция Лагранжа имеет вид
Ь(хЪХ2) = А0 ({Xi - ЗJ + (Х2 - ЗJ) - /JLiXi - /i2?2 + /i3(zi + ж2 - 4).
Записываем систему уравнений, включающую необходимое
условие экстремума функции Лагранжа и условия дополняющей
нежесткости:
BА0(ж1 -3)-/ii+/i3 = 0,
2A0(x2-3)-/i2 + /i3 = 0,
fjLlXi =0,
/i2x2 = 0,
[/i3(xi+x2-4) =0.
В случае Ао = 0 из двух первых уравнений находим ц\ =
= /i2 = /J>3i причем общее значение этих трех коэффициентов
ненулевое, так как по теореме Куна — Таккера хотя бы один из
множителей Лагранжа должен быть ненулевым. Из последних
трех уравнений заключаем, что х\ = ж2 = 0, х\ + ж2 = 4, а это
невозможно. Поэтому решений системы с Ао = 0 нет.
Пусть Ао т^ 0- В этом случае мы можем взять для Ао любое
ненулевое значение. Положим Ао = 1/2. Тогда из первых двух
уравнений можно выразить х\ и ж2 и подставить в остальные.
318
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
Получим систему трех уравнений
/iiC + /ii-/i3) =0,
/i2C + /i2-M3) =0,
/i3B + /ii+/i2-2/i3) = 0.
Рассматривая различные варианты, находим семь решений
системы (табл. 7.1).
Таблица 7.1
Номер решения
Х2
12 3 4 5 6 7
0 0-3-3 0 0-4
0-3 0-3 0-4 0
0 0 0 0 1-1-1
3 3 0 0 2 4 0
3 0 3 0 2 0 4
Первое решение соответствует точке локального минимума
целевой функции, причем эта точка не попадает в
допустимое множество О. Второе, третье и пятое решения
соответствуют точкам условного локального минимума на сторонах
треугольника, ограничивающего допустимое множество.
Наконец, четвертое, шестое и седьмое решения соответствуют
трем угловым точкам множества (вершинам треугольника).
Сравнение значений функции показывает, что единственным
решением рассматриваемой задачи является точка А$ с
координатами х\ = Х2 = 2. К этим выводам легко прийти, если учесть,
что значением целевой функции в точке (жх, Х2) является
квадрат расстояния от этой точки до точки C, 3). #
7.4. Седловая точка функции Лагранжа
Рассмотрим задачу нелинейного программирования
Г/о (ж) -^min;
1^(ж)^0, г = 1,га,
G.12)
7.4. Седловая точка функции Лагранжа
319
в которой нет ограничений типа равенства. Предполагаем, что
функции fo(x) и gi{x), % — 1,га, определенные в Rn, могут быть
недифференцируемыми. Как и выше, сформируем функцию
Лагранжа
m
L{x,ii) = fo(x) + ^2/Jigi(x), G.13)
г=1
где /л = (/ii, ..., /im) E M^, M^ — неотрицательный ортант
в Km. Мы будем рассматривать функцию Лагранжа как
функцию всей совокупности переменных х и /х. Отметим, что в
данном случае в функцию Лагранжа не включен множитель Ао-
Определение 7.1. Точку (ж*, /х*), где ж* Е О, /х Е К^,
называют седловой точкой функции Лагранжа L(sc,/i), если
Ь(ж*,д)<Ь(ж*,/х*)^Ь(ж,/х*), ЖЕ О, /xGC- G.14)
Теорема 7.7. Если (ж*, /х*) — седловая точка функции
Лагранжа Ь(ж,/х), то ж* — точка наименьшего значения функции
/о (ж) на множестве
tt={xeRn: gi(x) ^ О, г = ±7га}.
^ Из определения функции Лагранжа вытекает, что для любых
ж Е О и /i Е К?^ выполняется неравенство Ь(ж,/х) ^ /о(ж), так
как Higi{x) ^ 0, г = 1, га, ж Е О. При этом указанное неравенство
превращается в равенство, если /х = О, т.е. Ь(ж,0) = /о (ж).
Поэтому если (ж*, /х*) — седловая точка функции Лагранжа,
то для любой точки ж Е О
Mx*)=L(x*,0)^L(x*vl*)^L(x,vl*)<M*)- >
Доказанная теорема указывает метод решения задачи
нелинейного программирования G.12). Достаточно определить
седловую точку функции Лагранжа, чтобы прийти к
решению задачи нелинейного программирования. Следующая
теорема устанавливает критерий для седловых точек функции
Лагранжа.
320
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
Теорема 7.8. Точка (ж*,/х*), ж* Е О, ц* = (^ь ..., //ш) Е
Е Щ^, является седловой для функции Лагранжа L(x,/i) в том
и только в том случае, если выполнены условия
L(x*,/i*) = minL(x,/i*), G.15)
/4^(ж*) = 0, г = ±7га. G.16)
Ц Если (ж*, /1*) — седловая точка функции Лагранжа, причем
ж* Е О, /i* ЕIR^1, то соотношение G.15) верно в силу определения
седловой точки. Кроме того, согласно этому определению,
L(sc*,/i*) ^ Ь(ж*,0), что равносильно неравенству
т
fo(x*) + Y,№i(x*)>fo(x*)-
г=1
Таким образом,
т
Y,ti9i(**)>0. G.17)
г=1
Но из условия ж* Е О вытекает, что gi(x*) ^ 0, а условие /х* Е К^
означает, что //* ^ 0, г = 1, га. Следовательно, каждое слагаемое
суммы в неравенстве G.17) неположительно. Поэтому и сумма,
и каждое ее слагаемое равны нулю, т.е. верны соотношения
G.16).
Теперь предположим, что выполнены условия G.15) и G.16).
Тогда L(sc*,/i*) = /о (ж*) и в то же время L(#*,/i) ^ /о(#*) Для
любого /i Е К?^, откуда ?(ж*,/х) ^ ?(ж*,/х*). Это вместе с
G.15) приводит к неравенствам G.14), т.е. к утверждению, что
(ж*, /х*) — седловая точка функции Лагранжа. >
Теорему 7.7 можно использовать в широком круге задач
нелинейного программирования. При этом на функции fo(x) и
gi(x), г = 1, га, не накладываются никакие ограничения.
Однако следует иметь в виду, что достаточное условие, которое
устанавливается теоремой 7.7, лишь заменяет одну задачу
минимизации другой, которая в некоторых случаях может быть
7.5. Двойственная функция
321
проще исходной. Действительно, поиск седловой точки
функции Лагранжа в соответствии с G.15) означает минимизацию
функции Лагранжа по переменным х.
7.5. Двойственная функция
Рассмотрим задачу нелинейного программирования G.12),
не имеющую ограничений типа равенства, предполагая, что
целевая функция /о(ж), а также функции gi(x), г = 1, га,
определены в W1. Как и выше (см. 7.4), сформируем функцию
Лагранжа 1/(ж,/х) в виде G.13), определенную при х Е W1 и
/л Е М^, где М^1 — неотрицательный ортант в Rm.
На множестве К^ определим функцию
w(jx)= inf L{x,ti). G.18)
Функции /о (ж) и ^(аО связаны соотношением
»(м)</оИ, деС1, жеп. G.19)
Действительно, функция Лагранжа удовлетворяет неравенству
L(x,ijl) ^ /о(ж), ж Е О, {л Е К^. Из этого неравенства вытекает,
что
гу(/х) = inf L(x,ijl) ^ inf /0(ж) ^ /о(ж).
Теорема 7.9. Если для некоторых ж* Е О и /х* Е К^
верно равенство /о(ж*) = ги(/1*), то функция /о(ж) в точке ж*
достигает наименьшего значения на множестве О, а функция
w(jjl) в точке /х* — наибольшего значения на множестве К^.
^ Из неравенства G.19) для х = ж* с учетом равенства /о(ж*) =
= ги(/1*) заключаем, что
Это и означает, что значение функции ги(/х) в точке /х* является
наибольшим на множестве К^.
322
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
Аналогично, полагал в неравенстве G.19) /л = /л* и
учитывая, что w(/j,*) = /о(ж*), находим
fo(x)>f0(x*), Х?П,
т.е. в точке ж* функция f(x) достигает наименьшего
значения. >
Любая точка локального максимума функции w(fi) на
множестве Ш^1 является точкой ее наибольшего значения на этом
множестве. Чтобы доказать это свойство функции w(/j,),
достаточно показать, что функция —w(fjb) выпукла на выпуклом
множестве Ж^. Выберем произвольные несовпадающие
точки /i1, /л2 в Щ1 и произвольное число а Е [0, 1]. Пусть /л =
= а/л1 -\- A — а)/л2. В соответствии с определением функции
w(fjL) для произвольного числа е > 0 существует такая точка
х Е О, что гу(/х) ^ LEj,/i) — ?. Из определения функции Лагран-
жа (она линейна по множителям Лагранжа) следует равенство
L(aj,/i) = Ь(ж,а/х1 + A — а)/л2) = аЬ(х^1лг) + A — а)Ь(х^/л2).
С учетом этого равенства имеем
ги(/х) ^ аЬ(х,1л1) + A — а)Ь(х,1л2) — е ^
^ «^(/х1) + A — a)w(fx2) — е.
Ввиду того, что число ? > 0 выбрано произвольно, заключаем,
что
w(fx) ^ aw(iil) + A — a)i(;(/x2),
а это равносильно выпуклости функции —гп(/л).
Теорема 7.10. Функция Лагранжа G.13) имеет седловую
точку (ж*, /1*) тогда и только тогда, когда
w(fi*) = f0(x*). G.20)
^ Пусть (ж*, /х*) — седловая точка функции Лагранжа.
Тогда, согласно определению седловой точки, Ь(ж*,/х*) ^ Ь(ж,/х*),
7.5. Двойственная функция
323
ж Е О, т.е. при заданном /л = /л* функция Лагранжа достигает
на множестве О наименьшего значения в точке ж*. Поэтому
w(/jl*) = Ь(ж*,/х*). Далее, снова используя определение седло-
вой точки, заключаем, что L(sc*,/x*) > L(x*,0) = /о(ж*), откуда
/о(ж*) ^ w(fji*). Сопоставляя последнее неравенство с
неравенством G.19), получаем равенство /о(ж*) = /ш(/х*).
Пусть для ж* Е О и /х* Е М^ верно равенство G.20). Тогда,
согласно теореме 7.9, точка ж* является точкой наименьшего
значения функции /о (ж) на О, а точка /х* — точкой
наибольшего значения функции w(fjb) на Щ1. При этом
Ц/i*) = inf L(*,aO ^ Ь(ж*,/х*) ^ /0(ж*) = Ц/х*).
Следовательно,
?(ж*,/х*) = inf ?(ж,/х*).
Кроме того, Ь(ж*,/х*) = /о(ж*), откуда, используя равенство
G.13), определяющее функцию Лагранжа, заключаем, что
m
г=1
где /х* = (/i*, ..., /ij^). Так как все слагаемые в этом равенстве
слева неотрицательны, то они все равны нулю, т.е. выполняется
условие G.16). Согласно теореме 7.8, точка (ж, /х) является
седловой точкой функции Лагранжа. >
Функцию w(/i), определенную на 1Щ1 соотношением G.18),
называют двойственной функцией по отношению к
целевой функции /о(ж)- Задачу поиска точки /х* Е 'Щ1 наибольшего
значения этой функции называют двойственной задачей по
отношению к задаче минимизации функции fo(x) на множестве
О, а теорему 7.10 — теоремой двойственности.
Установленные свойства функции ги(/х) дают возможность вместо
задачи поиска точки наименьшего значения целевой функции
324
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
решать двойственную задачу, которая может быть проще
исходной. Найденное решение двойственной задачи далее можно
использовать в качестве набора множителей Лагранжа и затем
решать задачу минимизации функции Лагранжа.
Пример 7.3. В задаче
х\+х\^ min;
2ж1+ж2 + 4<0
найдем функцию w(/i), двойственную по отношению к целевой
функции /о (х) = х\+х\.
В данном случае допустимое множество О представляет
собой полуплоскость 2х\ + Х2 + 4 ^ 0. Чтобы найти двойственную
функцию, нужно определить наименьшее значение функции
Лагранжа
L(xi,X2,lJ.) =х\ + х% + fJLBxi +ж2 + 4)
при ограничении 2х\ + Х2 + 4 ^ 0. Такую задачу можно решить,
используя теорему Куна — Таккера: для функции L(xi,X2,/i),
считая \i фиксированным, построить функцию Лагранжа (т.е.
функцию Лагранжа для функции Лагранжа), для чего
необходимо ввести параметры Ао и /I; затем на основании теоремы
Куна — Таккера записать систему четырех уравнений
относительно неизвестных жх, #2, ^о и/1 и решить ее; среди
найденных точек путем сравнения выбрать ту, в которой функция
L(xi,X2->Ij) принимает наименьшее значение. Учитывая, что
функция L(xi,X2,Ij) при фиксированном \i является
квадратичной с положительно определенной матрицей, а значит, сильно
выпуклой функцией (см. пример 3.13), можно утверждать, что
она достигает на полуплоскости 2х\ + Х2 + 4 ^ 0 (это выпуклое
множество) наименьшего значения (см. теорему 3.19).
Следовательно, выбранная точка будет точкой наименьшего значения
функции L(x\,X2->lJ>)- Значение функции Ь(жх,Ж2,/-0 в
выбранной точке, зависящее от /i, и есть значение функции w(/j) при
фиксированном \i.
7.5. Двойственная функция
325
Мы, однако, отступим от этой стандартной
последовательности действий и учтем специфику рассматриваемой задачи.
В выражении для функции Лагранжа L(^i,^2,/i) выделим
полные квадраты по переменным х\ и х2 и запишем эту функцию
следующим образом:
5
?(ж1,ж2,а0 = (xi +/iJ + (х2 + /i/2J +4/i - -/А
Из этого представления вытекает, что значением функции
Лагранжа является квадрат расстояния от точки (—/i, —/i/2)
до точки (#i, х2) плюс величина 4/i — -\i , не зависящая от
точки (жх, Ж2). Следовательно, наименьшее значение функции
Лагранжа (т.е. значение двойственной функции w(/j) ) равно
квадрату расстояния от точки (—/i, — /i/2) до полуплоскости
5 9
О плюс 4/i— -/i . Если точка (—/i, —/i/2) попадает в О, то
расстояние от нее до О равно нулю. Если же (—/i, — /i/2) ^ О,
то это расстояние есть расстояние от точки (—/i, —11/2) до
границы множества О — прямой 2х\ + ж 2 + 4 = 0. Условие
(—/i, — /i/2) Е О означает, что
2(-/х) + (-|)+4<0,
или \i ^ 8/5. Расстояние p(/i) от точки (—/i, —ц/2) до прямой
2^1 + ж2 + 4 = 0 равно [III]
Н^-р/2 + 41
л/5
Следовательно,
2, . D-5/i/2J 16 5 2
В результате получаем
Мм) =
4//--//2, /i^-.
326
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
7.6. Геометрическое программирование
В общей задаче геометрического программирования
(уо{х) H^min;
[yk(x)^l, k = l,K,
и целевая функция уо(х), и левые части ограничений у/Дж),
к = 1, К, являются позиномамщ определенными на
положительном ортанте ~Щ_. Поэтому мы можем записать
у0(х) = ^Сог^Ог(ж), G.21)
где с0г GM+, г = 1,т0,
JL а(?)
Рог(ж) = Пя/', г = 1,га0, G.22)
агу Gl,i = 1,т0, J = 1,гс.
Аналогично
тк
Ук(х) = ^2сыры(х), к = 1,К, G.23)
г=1
где сы е М+, А; = 1, К, г = 1, т0,
™ (fe)
а) у
№(ж) = JJx/' , к = 1,К, г = 1, тЛ, G.24)
(/с)
аг- — некоторые действительные числа.
Особенность сформулированной задачи оптимизации в том,
что целевая функция и левые части ограничений определены
не на всем n-мерном линейном арифметическом пространстве.
7.6. Геометрическое программирование
327
Поэтому непосредственное использование приемов решения
общей задачи нелинейного программирования (см. 7.3-7.5) в
данном случае невозможно. Выходом из положения может быть
замена переменных Xj = е^, j = 1, п, преобразующая позином
в функцию, определенную на всем линейном арифметическом
пространстве. Однако в задачах геометрического
программирования проще использовать другой подход, базирующийся на
неравенстве взвешенных средних
т т
г=1 г=1 г
где yi > 0, Wi > 0, г = 1, га, и
771
г=1
В данном случае удобно преобразовать неравенство таким
образом, чтобы в нем не использовались нормированные веса.
Для этого выполним замену W{ = А^/А, % = 1, га, где А = Ai + ...
... +АШ. Тогда неравенство взвешенных средних можно
записать в виде
г=1 г=1 г=1 г
Используем это неравенство для оценки позиномов у^(х).
Выберем в качестве весов произвольные числа А/^ ^ 0, г = 1, га&,
А; = О, К, и положим
А/с = ^А/сЬ k = 0,K.
г=1
Тогда, учитывая запись позиномов у&(ж) в виде суммы функций
ckiPki(x) специального вида, из неравенства G.25) получаем
у/с(ж)>А/с|Д———J , А; = 0, К. G.26)
328
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
Все части этих неравенств положительны. Поэтому, возведя
обе части неравенства для позинома у&(ж), к = 1, К, в степень
Xk и перемножив левые и правые части всех полученных
неравенств, получим новое неравенство
к=1 к=1 г=1 Ь
Для точек ж допустимого множества ft выполняются
неравенства yk (х) ^ 1, k = 1, К. Значит, левая часть записанного
неравенства не превышает единицы и
К тк
СкгРкг{х)\Хк1
1гПлА,П(?«М22)
к=1 г=1
Умножая это неравенство на неравенство G.26) для целевой
функции уо(х) (т.е. при к = 0), возведенное в степень Ао,
заключаем, что
К тк
УоЛои>ПЛМ1(^т^)ЛЫ- G-27)
'CkiPki(x)\Xk
к=0 г=1 Xki
Напомним, что последнее неравенство верно при произвольном
выборе чисел А/^ ^ 0, г = 1, ттг^, fc = 0, К.
Пусть числа Аог, i = 1, mo, связаны равенством
Ао = 5>0г = 1. G.28)
г=1
Тогда, используя выражения G.22) и G.24) дляр^(ж), г = 1, т&,
А; = 0, К, неравенство G.27) можно преобразовать к виду
У0
г=0 иг 7 /с=1 г=1 ^г г=1
7.6. Геометрическое программирование
329
где
К mk
aJ = ^2^2aifX^ 3 =T7n. G.30)
fc=0i=l
Пусть числа A^, k = 1, К, г = 1,га&, выбраны так, что
выполняются условия ортогональности, т.е. оу =0, j = 1, п. Тогда
правая часть в G.29) не будет зависеть от переменных Xj и мы
придем к соотношению
/то л ч К тк ,
чг=1 7 /с=1 г=1
где го Е М^ — точка с неотрицательными координатами А/^ ^ 0,
к = 0, К, г = 1, ттг^, ттг = ?тго + mi + • • • + тк- Функцию d(w),
как и в случае задачи минимизации позинома без ограничений,
называют двойственной функцией по отношению к позиному
Уо(ж).
Если множество VK* точек w Е К^, координаты которых
удовлетворяют равенству G.28) и равенствам G.30) с оу = 0,
j = 1,п, не пусто, то целевая функция уо(х) на W*, согласно
G.31), ограничена снизу и имеет конечную точную нижнюю
грань М > 0, причем М ^ с/(го) для любого w Е VK*. Выбрав
произвольную точку w Е VK*, можно использовать значение
d(w) в качестве оценки снизу точной нижней грани целевой
функции.
Очевидно, что если уо(ж*) — d(w*) для некоторых точек
ж* Е О и w* Е VK*, то в точке ж* целевая функция достигает
наименьшего значения в О, а в точке го* двойственная функция
достигает наибольшего значения в W*. Можно показать*, что
верно и обратное: если целевая функция достигает в О
наименьшего значения в точке ж*, а двойственная функция достигает в
W* наибольшего значения в точке го*, то уо(#*) = d(w*). Таким
*См.: Евдокимов А.Г.
330
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
образом, решение задачи минимизации функции уо(х) в О
можно искать, решал задачу поиска точки максимума двойственной
функции.
Точку го* и максимальное значение d* = d(w*) двойственной
функции d(w) находят как решение задачи
(d(w) —»> max;
mo
2^А0г = 1,
< i=l
К тк
\ k=0i=l
Значение d* является наименьшим значением функции уо(х),
которое она принимает в точке ж*. Эту точку можно найти,
исходя из равенства уо(х*) = d*.
Отметим, что неравенство уо(х) ^ d(w) получено путем
многократного применения неравенства взвешенных средних
G.25), которое обращается в равенство при выполнении
условий yiX/Xi = 1, г = 1, т. Следовательно, равенство уо(х*) =
= d(w*) означает, что все неравенства G.26) превращаются в
равенства, причем у&(ж*) = 1, к = 1, К. А это возможно лишь
при выполнении условий
>4cCkiPki(x*) . ——
_ = i? г = 1,т/,, к = 0,К.
Таким образом, точку ж* можно найти как решение системы
уравнений
\Poi(x)
<
\Pki(x)
где учтено, что в соответствии с G.28) Ао = 1. Заменой Xj =
= е^, j = 1, п, и последующим логарифмированием система
Л,
0г
СОг
^ксЬ
\ г = 1,га0;
G.32)
, г = 1,771/,, к = 1,К,
7.6. Геометрическое программирование
331
G.32) преобразуется в систему m линейных алгебраических
уравнений относительно п неизвестных ?j, j = 1, п.
К задаче геометрического программирования сводятся
некоторые задачи оптимизации, в которых целевая функция не
является позиномом. Например, функция
Мх) = У1(х) + у2(х)(у3(х)У, хеЩ., G.33)
где yi(x), i = 1, 2, 3, — позиномы, а /3 ^ 0, в общем случае не
является позиномом (она будет позиномом либо в случае, когда
Уз(х) состоит лишь из одного слагаемого, либо в случае
натурального /3). Покажем, что задача минимизации функции fo(x)
в W1 равносильна задаче геометрического программирования
y(z) = У1(х) + у2(х)х^+1 -+ min,
, ч Уъ{х) G.34)
где z = (ж, xn+i) = (жь ж2, ..., xn+i) еК![.
Отметим, что если ж* Е К+ — точка минимума функции
/о(ж), то точка z* = (ж*, <+1) Е К?+1, где <+1 = у3(х*),
удовлетворяет ограничению задачи G.34). Поэтому эта точка
принадлежит допустимому множеству О задачи G.34) и
f0(x*) = yi(x*) + y2(x*){y3(x*)f =
= Ух(х*) + y2{x*){x*n+lf = y(z*) > mmy(z). G.35)
В то же время из ограничения задачи вытекает, что для
любой точки z = (ж, ?n+i) Е О верно неравенство жп+1 ^ уз(х).
Следовательно,
y(z)=yi(x)+y2(x)x%+1 >
> I/i(x) +i/2(x) Ы*))* = /о(ж) > /0(ж*)
и наименьшее значение функции y(z) на множестве О не может
быть меньше fo(x*).
332
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
Таким образом, задача минимизации функции fo(x) в Ш+
и задача геометрического программирования G.34)
эквивалентны.
Пример 7.4. Найдем минимум функции
Х{Х2 V
предполагая, что коэффициенты a, b положительны.
Целевая функция рассматриваемой задачи имеет вид G.33),
где ух (ж) = al(x\x2), У2{х) = 6, у3(ж) = ж? + х\, /3 = 1/2, ж =
— (#ъ х2)- В соответствии с изложенным выше
сформулированная задача равносильна задаче геометрического
программирования
y(z) = -^ Ь б^з -^ min,
Х\Х2
х* х* G-36)
х3 х3
где 2 = (хъ х2, хз) eR\.
Сопоставляя вид целевой функции y(z) с представлениями
G.21) и G.22), а вид левой части ограничения с
представлениями G.23) и G.24), определяем, что в данном случае п = 3, то = 2,
coi = а, с02 = Ь, а^у = -2, a\2J = -1, а^3 = <% = а22 = °> а23 =
= 1/2, К = 1, mi = 2, cff = с$ = 1, аи = «и = 2? а12 = 4? = °
и а13 -а23 --1.
Перейдем к задаче максимизации двойственной функции
d(w). Так как то = mi = 2, то
w = (Aoi, А02, An, Ai2) <ЕК^.
Для упрощения выкладок введем обозначения Aoi = w\, А02 =
= W2, Ац = ^3 и A12 = ^4. Тогда условие нормировки G.28)
и условия ортогональности — уравнения G.30) при aj = 0 —
7.6. Геометрическое программирование
333
приводят к системе уравнении
(W\ +W2 = 1,
- 2wi + 2w3 = О,
— w\ + 2^4 = О,
1,0,5^2 — 'Шз — ^4 = О-
Множество решений этой системы есть множество W*, на
котором необходимо найти наибольшее значение двойственной
функции. В системе четыре уравнения и четыре
неизвестных. Несложно убедиться в том, что система имеет
единственное решение w\ = ws = 1/4, u>2 = 3/4, w^ = 1/8. Таким
образом, множество W* содержит единственную точку го* =
= A/4, 3/4, 1/4, 1/8), а задача поиска максимального значения
двойственной функции оказывается тривиальной. В
соответствии с G.31) двойственная функция d(w) имеет вид
Ъ
<W\/ \W2'
Ее значение d* в точке го* равно
d(w)=(—) (—) (w3 + w4r
\го1 / \wo/
+W4 ( _
\w3
Ws / 1 \ WA
\VU4J
„ (a \l/4/ b \3/4/3\3/8/ 1 xl/4/ 1 xl/
d=lijd C74) (s) A74) (its)
'a266\i/8
,T08~J '
Чтобы найти координаты точки z* = (ж*, ж*,, ж|), в которой
функция y(z) достигает на множестве О наименьшего
значения, решим систему уравнений G.32), в данном случае
принимающую следующий вид:
-$— =w1i
Ьх
Хл
х3
Х<~)
1/2
:W%d*
Wo
wl+wl'
[x3 w%+ w\
334
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
Эту систему можно решить и не преобразовывал ее в
систему линейных уравнений с помощью соответствующей замены
переменных. В результате будем иметь
46 ' ~z 46 ' ~d ~ V^b"J "
Таким образом, исходная функция /0(^1^2) достигает
наименьшего значения точке ж* Е IR2 с координатами
*-4^, x*2=t4l *
Xl w~v ~ь' ~^ у 2 ь
В рассмотренном примере множество VK* содержало
всего одну точку, которая и была искомой точкой максимума
двойственной функции. В общем случае это множество,
определяемое линейными ограничениями, представляет собой
аффинное многообразие, и задача определения наибольшего значения
двойственной функции на этом множестве может оказаться
сложной.
Продемонстрируем использование неравенства взвешенных
средних в одном частном случае, когда задача геометрического
программирования имеет лишь одно ограничение типа
равенства.
Теорема 7.11. Функция
п
y(x) = ^2CiXi, х = (хи ж2, ..., хп)еЩ, G.37)
г=1
где /3{ > 0, г = 1, п, рассматриваемая при ограничении
п
Цх?=А G-38)
г=1
А > 0, 7г > О, г = 1, п, достигает наименьшего значения /i,
равного
Ч-п(|)") • (М9>
Вопросы и задачи
335
где 7 = 71 + 72 + • • • + 1т в единственной точке х с координа-
тами х,
1 А 7
< Согласно неравенству взвешенных средних в форме G.25),
примененному при Л^ = 7ь имеем
»(.) = ? а* ^П^Г1
г=1 г=1 Гг
4=1 г=1 /г 7 V г=1
1/7 / _^//3л7г\1/7
7»'
Неравенство взвешенных средних G.25) превращается в
равенство тогда и только тогда, когда попарно равны основания
степеней под знаком произведения, т.е. когда равны
величины Щ-. При этом обе части равенства равны общему значению
величин ^—. В рассматриваемом случае неравенство превра-
Аг
щается в равенство, когда
ъ
:/i, г = 1,П,
откуда получаем
_ Jj_ /? • _ 1
Xi — —, 2 — 1, 77-.
А 7
Вопросы и задачи
7.1. Минимизируйте функцию /(ж 1,^2) = жх — я?2 при
ограничении х\+х\ = 1. Найдите стационарные точки и точки
минимума. Проанализируйте поведение функции Лагранжа в
окрестностях найденных точек. Классифицируйте найденные
точки (точки минимума, максимума, седловые точки для
функции Лагранжа по переменным ж, А).
336
7. АНАЛИТИЧЕСКИЕ МЕТОДЫ
7.2. Решите задачу
(id + IJ + (ж2 - ЗJ-> min;
I Хл ~\~ %о — J-
и проверьте решение графически.
7.3. Решите задачу
f(^i + lJ + (^2-3J^min;
и проверьте решение графически.
7.4. Решите задачу
Г(ж1 + 1J + (ж2-3J^тт;
\х\ -\-ax2 + /3^0
и проверьте решение графически при значениях: а) а = 1, C = 0;
б) а = -1, /3 = 1; в) а = 0, /3 = 0.
7.5. Путем перехода к задаче геометрического
программирования минимизируйте функцию f(x\,X2) = + bJx + у.
Х\Х2
8. ЧИСЛЕННЫЕ
МЕТОДЫ НЕЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Известно достаточно много численных методов решения
сформулированной в 7.1 общей задачи нелинейного
программирования. Во многих из них использованы идеи, реализованные в
численных методах безусловной минимизации (см. 4-6).
Главное отличие состоит в том, что при решении задачи
нелинейного программирования необходимо учитывать ограничения,
задающие допустимое множество OcRn, на котором нужно
найти точку ж* Е О минимума целевой функции /о (ж). В этой
главе рассмотрены наиболее часто применяемые на практике
численные методы решения такой задачи.
8.1. Метод условного градиента
Для численного решения общей задачи нелинейного
программирования
/oW^min, жеОсМп, (8.1)
где /о(ж) — целевая функция, определенная на допустимом
множестве О, можно применить модификацию одного из
методов спуска. Однако непосредственное использование
методов спуска может привести к тому, что точка хк, найденная
на некоторой к-ж итерации, например, при помощи
рекуррентных соотношений вида D.20) или D.36), выйдет за пределы
допустимого множества, т.е. хк ^ О. Избежать этого в случае
замкнутого ограниченного выпуклого множества О и
непрерывно дифференцируемой на нем выпуклой целевой функции
можно следующим образом.
338
8. ЧИСЛЕННЫЕ МЕТОДЫ
Пусть на k-ik итерации известна точка xk~l Е О (на первой
итерации [к = 1) выбрана начальная точка х° Е О). Используем
главную линейную часть
fk(x) = (grad/oCaj*), х - х^1) (8.2)
приращения
A/fc = /o(a!)-/o(aJ*-1) = (grad/o(a!fc-1),a!-aJ*-1)+0(|a!-aJ*-1|)
целевой функции /о (ж) в точке хк~1 для нахождения
вспомогательного приближения хк из условия
fk(xk) =mm(g™df0(xk-1),x-xk-1). (8.3)
В силу замкнутости и ограниченности множества О и
непрерывности линейной функции fk{x) такая точка хк всегда
существует и лежит на границе <90 этого множества (если таких
точек несколько, то можно выбрать любую из них).
Для некоторых множеств, имеющих достаточно простую
структуру, решение задачи (8.3) удается представить в
явном виде. Например, если множество О является п-мерным
замкнутым шаром радиуса R с центром в точке xq Е Rn, т.е.
О = {х Е W1: \х — xq\ ^ i?}, то, используя неравенство Коши —
Буняковского в виде
(grad/ofc*-1),»-^) >
>-|grad/o(^-1)||^-^o|^-|grad/o(^-1)|i?
и учитывая (8.2), находим
fk(x) = (grad/o^-1), х - хо) + (grad/oO^-1), х0 - хк~1) >
^-\gi^h{xk-l)\R+{gv^f0{xk-l),x0-xk-1).
Правая часть этого неравенства равна наименьшему
возможному значению /&(ж) в искомой точке хк. Таким образом, имеем
fk{xk) = (grad/0(^-1), хк - хк~1) =
= -\gv^h{xk-l)\R+{gx&dh{xk-l),x0-xk-1),
8.1. Метод условного градиента
339
или
(grad/0(a;fc-1),ifc-a;o) = -|grad/o(a;fc-1)|JR.
Это равенство можно удовлетворить, если принять
s* _ n п grad/o^-1)
жк = жи-Д,
fc-n
grad/0(a;
В случае Q = {(х\, ..., хп) ? W1: Xj G [aj, 6j], j = 1, n}
координаты точки ж*, которая расположена на границе сЮ
n-мерного параллелепипеда Оив которой функция (8.2)
dXj
примет минимальное значение, равны
dfo{xk-1)
х)> =
dxj
>0;
&J' dXj '
i = 1, n, (8.4)
а при -^^- = 0 можно выбрать любое значение х^ Е [aj, bj].
Если 0={жЕКп: (di, х) ^bi, i = l,m} — многогранное
множество, то (8.3) может быть сведено к решению основной
задачи линейного программирования. Если же
Q = {ж Е Rn: (сц, ж) ^ Ь^, г = 1, га, 5ж = d} ,
где i? — матрица размера / х п и d Е Кг, то для нахождения
ж получим общую задачу линейного программирования. Для
решения обеих этих задач после их приведения к стандартной
задаче линейного программирования обычно используют сим-
плекс-метод.
Предположим, что задача (8.3) решена и точка ж найдена.
Если хк = ж^-1, т.е. fk(xk) = 0, то из (8.3) для любых ж Е О
имеем (grad/o(^/c_1), ж — ж^-1) ^ 0. Тогда, согласно теореме 3.15,
340
8. ЧИСЛЕННЫЕ МЕТОДЫ
хк~х = ж* — искомая точка минимума выпуклой функции /о (ж)
на множестве й, так что итерации прекращаем. В противном
случае из (8.3) получаем fk{xk) = (grad/of^-1), хк — хк~1) < 0
и полагаем
хк = хк-1 + Кк(~к _ хк-1^ Кк е ^ ^ ^
Ясно, что хк Е О, поскольку множество О выпукло.
Таким образом, вспомогательное приближение хк на
каждой &-й итерации задает вектор рк = хк — хк~1,
определяющий на этой итерации допустимое направление. Оно является
направлением спуска, в общем случае не совпадающим с
направлением антиградиента wk = — grad/o(^/c_1) функции /о(ж) в
точке xk_1 (рис. 8.1). Поэтому нахождение точки хк путем
выбора в (8.5) значения ус^ отличается от соответствующей
итерации метода градиентного спуска. Это отличие
послужило основанием для того, чтобы метод, связанный с решением
задачи (8.3) и использованием (8.5), назвать методом
условного градиента.
Рис. 8.1
Определение 8.1. Допустимое направление, определяемое
вектором рк, назовем возможным направлением спуска
для функции fo(x) из точки х ЕЙ на множестве ЙС1П,
если существует такое число ж^ > 0, что xk~l + мрк Е О при
х Е @, Кк\ и выполнено неравенство f$(xk~l + нрк) < f$(xk~l).
8.1. Метод условного градиента
341
Спуск в возможном направлении из точки xk~l Е О
позволяет на каждой k-ik итерации продолжить построение
релаксационной последовательности {хк}, для которой
последовательность {fo(xk)} является невозрастающей.
Рассмотрим теперь вопрос о выборе значения х& Е @, 1] в
(8.5). Один из возможных вариантов — это поиск минимума
функции
Фк{х) = М*к-1 + хрк), рк = хк-хк-\ (8.6)
по аргументу х в полуинтервале @, 1].
Для квадратичной целевой функции fo(x), имеющей вид
fo(x) = - (Qsc, х) + (с, ж), где Q — положительно
определенная матрица порядка п, точка х^ Е @, 1] минимума функции
<^fc(x) единственна и может быть представлена в явном
виде. Действительно, пусть р — возможное направление
спуска. Подставляя х = xk~l + жрк в квадратичную функцию и
учитывая, что матрица Q симметрическая и в данном
случае [Qxk~x + с,рк) = (grad/o(^/c_1),p/c) = — (wk,pk), где wk =
= —grad/(a?/c_1), получаем
М") = ^{Qp\pk) ~ *{wk,pk) + \{Qxk~\ xk~l) + (с, xk~l).
Случай {Qp\ p ) = 0 для положительно определенной матрицы
соответствует равенству рк = хк — хк~1 = 0 и уже рассмотрен
выше. При (Qpk,pk) >0 имеем относительно х квадратный
трехчлен, достигающий минимума при значении
(wk, рк)
н! = ;„ Iй ' >о, (8.7)
к (Qpk,pk) у }
поскольку для направления спуска р
(wk,pk) = -(grad/0(a;fe-1), xk-xk~l) > О
342
8. ЧИСЛЕННЫЕ МЕТОДЫ
и в данном случае gia>dfo(xk~1) и рк не являются
ортогональными векторами. Если х^ > 1, то точка минимума лежит за
пределами множества О и в (8.5) следует принять к^ = 1, т.е.
ж/с _ ~/^ -g противном случае в (8.5) принимаем х& = х?.
Для произвольной выпуклой функции fo(x) выбор значения
щ из условия минимума функции фк(^) потребует
применения методов одномерной минимизации (см. 2). Отметим, что
если целевая функция fo(x) выпукла, то и функция фк(^)
выпукла (см. теорему 3.7) и в любой стационарной точке х* этой
функции в силу теорем 3.14 и 3.15 она достигает наименьшего
значения. Если fo(x) — строго выпуклая функция, то, согласно
теореме 3.7, и функция (8.6) строго выпукла на отрезке [0, 1]. В
этом случае, согласно теоремам 3.14 и 3.15, стационарная
точка функции фк(к), если она существует, единственна и в этой
точке функция достигает наименьшего значения.
Можно избежать минимизации функции фк{к) (8.6),
выбирая значение ж^ Е @, 1] в (8.5) так, чтобы fo(xk) ^ fo(xk~1), т.е.
чтобы последовательность {хк} была релаксационной. Тогда,
согласно теореме 4.2, справедлива оценка вида D.12)
Мхт)-Мх*) ( lA/o^-VJoH
Mx°)-fo(x*) "eXI\ r,^ Igrad/o^)!
где г/ = diamfi — диаметр ограниченного множества О.
Условием прекращения итераций может быть выполнение
одного или всех неравенств D.18) и D.19). При некоторых
ограничениях метод условного градиента работоспособен и в
случае, когда целевая функция не является выпуклой*.
Пример 8.1. Найдем решение задачи квадратичного
программирования на множестве
П={(хъ x2)eR2:x1e[0, 1], ж2Е[0,2]}
*См.: Васильев Ф.П., а также: Пшеничный Б.Н., Данилин Ю.М.
ТП EN,
8.1. Метод условного градиента
343
для целевой функции /0(^1^2) — х\ — \х\ + х\ — 2х2, которую
представим в виде /о (ж) = - (Qsc, ж) + (с, ж), где вектор с =
т
= (—4 — 2) и матрица
Q =
2 о
О 2
В качестве начальной точки возьмем ж0 = @, 0), а условие
прекращения итераций примем в виде | Ахк\ = \хк — хк_1\ < е =
= 0,1.
Рассмотрим подробнее первую (к = 1) итерацию при
решении этой задачи методом условного градиента.
1. Вычислим в начальной точке ж0 = (х\ , х2 ) = @, 0)
градиент grad/o(a;0) = Qx° + с = с= (—4 — 2) целевой функции и
найдем в соответствии с (8.2) главную линейную часть
приращения этой функции в указанной точке:
fi(x) = (grad/0(^°), х - ж0) = (с, ж) = -Ахг - 2х2.
Функция fi(x) является линейным приближением к целевой
функции в окрестности точки ж0.
2. Вспомогательное приближение ж1
найдем, минимизируя функцию fi(x) на
заданном множестве О, являющемся
прямоугольником (рис. 8.2), причем в (8.4) а\ = а2 =
= 0, 6i = l и Ь2 = 2. Так как производные
0/о(ж°)
dxi
-4 и
0/о(ж°)
0X2
в соответствии с (8.4) имеем ж^ = Ъ\ =
~B) L О
х\ = 02 = ?•> так что ж
—2 отрицательны, то
1 и
1 = A, 2).
х2\
2
х{)
0
к
Q У
X1/
/р1
J
,?!
L х,
Рис. 8.2
3. На первой итерации направление спуска определяется
вектором р
хх-х°
антиградиента w
г.0
= A 2)\
grad/0(^°)
Учитывая выражение для
т
= D2) целевой функции
в точке ж и используя формулу (8.7), находим точку м\
344
8. ЧИСЛЕННЫЕ МЕТОДЫ
минимума функции <^i(x) (8.6):
(иЛр1) _ D 2)A 2)П
УСл =
(Qp\p1)
A 2)
2 О
О 2
= ш=ад-
Поскольку к\ ^ 1, принимаем xi = xj = 0,8 и при помощи (8.5)
находим точку ж1 = ж0 + к\р1 = 0,8A 2) = @,8 1,6) . Ясно,
что ж1 G О (см. рис. 8.2).
4. Проверяя условие прекращения итераций, убеждаемся,
что |жх - ж°| = л/@,8J + A,6J « 1,790 > е = 0,1, т.е. требуемая
точность еще не достигнута и поиск точки ж* Е О минимума
целевой функции fo(x) на множестве О следует продолжить,
заменив в п. 1 точку ж0 на найденную на первой итерации точку
х1 = @,8, 1,6).
Результаты расчетов на первой и
последующих итерациях приведены в
табл. 8.1, а графическая
иллюстрация решения задачи методом
условного градиента представлена на рис. 8.3.
Описанный алгоритм за восемь
итераций с заданной точностью
приводит к точке ж* = A, 1), являющейся
точным решением задачи. В точке
ж8 = @,957, 0,953) значение f0(x8) «
~ —3,910 отличается от
минимального значения /о(ж*) — — 4 менее чем
на 0,1.
Таблица 8.1
^2 i
2
1
Х\
о1
Q
/
/
X1
/ ш
1 f
ж2
L*
L ~.s^«*
F X ^X
*,
Рис. 8.3
k
1
2
3
4
xk
@,800, 1,600)
@,892, 0,861)
@,915, 1,103)
@,929, 0,917)
|A«fe|
1,790
0,745
0,243
0,187
k
5
6
7
8
xk
@,939, 1,069)
@,947, 0,940)
@,952, 1,053)
@,957, 0,953)
|A«fe|
0,152
0,129
0,113
0,100
8.2. Использование приведенного градиента 345
Характерное зигзагообразное движение на рис. 8.3 в
направлении искомой точки ж* связано с тем, что в данном случае при
решении задачи (8.3) минимизации линейной функции fk{x)
на выпуклом множестве О вспомогательными приближениями
поочередно являются крайние точки A, 2) и A, 0) этого
множества, ф
Поиск вспомогательного приближения х Е О на к-ik
итерации метода условного градиента можно вести не только на
основе линеаризации целевой функции /о (ж) в окрестности
точки х Е О. Если fo(x) — выпуклая функция, дважды
дифференцируемая на выпуклом ограниченном замкнутом множестве
О, то ее приращение в окрестности точки х приближенно
можно представить квадратичной функцией
fk(x) = (grad/o^), х-х*-1) + {Н{хк-1){х-хк-1), х-х^1),
где Н(хк~1) — матрица Гессе функции fo(x), вычисленная в
точке х . Такое представление приводит к необходимости
вместо решения задачи (8.3) минимизации линейной функции
на допустимом множестве О решать на том же множестве
задачу минимизации квадратичной функции. Это существенно
усложняет поиск точки х , но благодаря более точной
аппроксимации целевой функции в окрестности точки хк~1 может
уменьшить общее число итераций.
8.2. Использование приведенного градиента
Если допустимое множество ЙСР задано при помощи
линейных ограничений, то для минимизации на нем
дифференцируемой целевой функции fo(x), х Е Кп, можно использовать
подход, аналогичный покоординатному спуску в случае
безусловной минимизации. При этом ограничения удобно
привести к форме, соответствующей стандартной задаче линейного
программирования и содержащей ограничения типа равенства
346
8. ЧИСЛЕННЫЕ МЕТОДЫ
в виде Ах = Ъ с известными матрицей А размера га х п и
вектором Ь е Мш и условие неотрицательности параметров
оптимизации в виде ж (Е 1RJ?, где Ж^ — неотрицательный ортант
размерности п.
Итак, необходимо минимизировать дифференцируемую
целевую функцию /о(ж)? х ? Жп, на множестве
П = {х?1^:Ах = Ь}. (8.8)
Без ограничения общности можно считать, что ранг матрицы
А в (8.8) равен числу га ее строк и меньше числа п ее столбцов,
т.е. RgА = т<п. В самом деле, если RgА = г < га, то в
матрице можно выделить г линейно независимых строк. Остальные
строки матрицы будут линейными комбинациями этих г строк
[III]. В этом случае либо система Ах = Ь несовместна и задача
оптимизации не представляет интереса (допустимое множество
пусто), либо из системы можно удалить п — г уравнений, не
меняя множества ее решений. В результате удаления мы
приходим к аналогичной задаче, в которой ранг матрицы равен
количеству ее строк. Если Rg А = га = п, то система линейных
уравнений Ах = Ь имеет единственное решение, которое можно
записать в виде х = А~1Ъ. Значит, допустимое множество
рассматриваемой задачи оптимизации состоит из одного элемента,
а сама задача не представляет интереса.
Итак, полагаем, что RgA = га < п. Выберем в матрице А
базисный минор В. Для удобства будем считать, что этот
минор расположен в первых га столбцах матрицы А (этого можно
добиться, изменив при необходимости порядок переменных х^
г = 1, п). Тогда матрицу А можно записать как блочную
матрицу (В 7V), где В — квадратная матрица, составленная из
первых га столбцов матрицы А, а матрица N объединяет
оставшиеся п — т столбцов. Матрица i?, соответствующая
базисному минору, является невырожденной. Выбор базисного минора
в системе линейных алгебраических уравнений (СЛАУ) Ах = Ь
приводит к разделению неизвестных Х{, г = 1, п, на базисные
8.2. Использование приведенного градиента 347
неизвестные х\, ..., хт и свободные неизвестные жш+1, ..., хп.
Первую группу неизвестных сгруппируем в вектор-столбец хв',
а вторую — в вектор-столбец xN. Введем также множества
индексов JB = {1, 2, ..., га} и JN = {га + 1, ..., п}.
С учетом введенных обозначений СЛАУ Ах = Ъ можно
записать в виде матричного уравнения Вхв + NxN = Ь. Поскольку
матрица В невырождена, то это матричное уравнение можно
преобразовать к виду
xB = b-NxN, (8.9)
где Ъ = ??_1Ь, N = B~lN. Параметры оптимизации,
составляющие векторы хв и xN, называют обычно базисными и
свободными переменными соответственно.
Матрицу Якоби целевой функции в некоторой точке ж0 Е О
представим в виде блочной матрицы-строки [gB gN), где дв
и gN — матрицы-строки длины га и п — га. Элементами этих
Я/о • I
матриц-строк являются частные производные -^—, j = 1, п, по
базисным и свободным переменным соответственно (д5 и gr^
называют матрицами Якоби функции /о (ж) по части
переменных). Тогда, используя (8.9), для полного дифференциала
целевой функции получаем
d/o(aj°) = (grad/o^0), dx) =gBdxB+gNdxN =
= -gBNdxN+gNdxN = (gN-gBN)dxN = udxN, (8.10)
где и = gN — gBN — матрица-строка длины n — га, называемая
приведенным градиентом целевой функции /о(ж)
относительно свободных переменных в точке ж0 Е О.
Возможны разные стратегии поиска точки минимума в
задаче оптимизации с линейными ограничениями, основанного на
использовании приведенного градиента. Простейшая из них
базируется на методе покоординатного спуска в пространстве
свободных переменных. Последовательный перебор этих пере-
348
8. ЧИСЛЕННЫЕ МЕТОДЫ
менных проводят по тем же правилам, что и при решении
задачи линейного программирования симплекс-методом, а метод,
основанный на этой стратегии, называют выпуклым
симплекс-методом.
Рассмотрим другую стратегию поиска точки минимума с
использованием приведенного градиента. На каждой итерации
процесса минимизации будем изменять все свободные
переменные. Метод, основанный на подобной стратегии, называют
методом приведенного градиента.
Из (8.10) следует, что значение целевой функции быстрее
всего уменьшается при изменении свободных переменных в
направлении, противоположном приведенному градиенту. Но
при этом может быть нарушено условие их неотрицательности.
Чтобы этого избежать, приведенный градиент можно
спроектировать на неотрицательный ортант К^_т — допустимое
множество для этих переменных. Поскольку К^_т является
достаточно простым по структуре множеством, проектирование
на него выполнить несложно. Это позволяет сформировать
возможное направление спуска, т.е. найти координаты pj, j Е J,
вектора р Е W1, определяющего это направление. При Uj ^ 0,
j Е JN, увеличение свободного переменного Xj в окрестности
рассматриваемой точки ж0 Е О приведет к уменьшению
значения целевой функции. Поэтому для этого индекса принимаем
Pj = —Uj. Если же Uj > 0, j Е JN, то увеличение
свободного переменного Xj в окрестности рассматриваемой точки
может привести к ее возрастанию. В этом случае положим
Pj = —UjXj К Таким образом, для координат вектора р Е Rn,
соответствующих свободным переменным и составляющих
вектор рдг ? Мп_ш, имеем
{—Uj, Uj ^ 0;
@) ^n 3*JN. (8.П)
—Ujx)j \ Uj > 0,
Чтобы при движении точки
ж = ж° + хр, х>0, (8.12)
8.2. Использование приведенного градиента 349
в направлении, которое задано вектором pGMn, не были
нарушены ограничения Ах = Ь, определяющие допустимое
множество О вида (8.8), необходимо, чтобы выполнялось условие
Ах = Ах° + к(В N)p = Ь, или Врв = —Л/рдг, поскольку Ах° =
= Ь. Отсюда находим вектор
рв = -B~lNpN = -NpN (8.13)
с координатами pj, j Е JB = J \ JN (здесь J = {1, ..., n}),
соответствующими базисным переменным. Значение к в (8.12)
выбираем, минимизируя функцию ф(>с) = /о(ж° + >ф)? >^ > 0, но
при выполнении условия х Е К^, приводящего с учетом (8.12)
для всех j Е ^7 к соотношениям 0 ^ ж^ = яА + xpj, где ж^ и
х- — координаты точек жиж0 соответственно. Отсюда, если
множество X* = {j ? J: pj < 0} не пусто, получаем ограничение
на максимально возможное значение ус в виде
/ xW\
х ^ х = min J—). (8.14)
jgx*V Pj )
Если же X* = 0, то допустимо значение х Е @, +оо).
Покажем, что если в некоторой точке ж* Е О выполнено
равенство рдг = 0, то это равносильно выполнению необходимого
условия того, что ж* Е О — точка минимума функции fo(x) на
множестве О. Для рассматриваемой задачи оптимизации
запишем функцию Лагранжа
?(ж,А,/х) = /о(ж) + (Л, Ах - Ь) - (/х, ж),
где Л Е W71 и/хЕ1п — векторы множителей Лагранжа,
соответствующие ограничениям Ах — Ь = 0 типа равенства и — ж ^ О
типа неравенства (последнее неравенство означает, что —Xj ^ 0
для всех j = 1, п, т.е. ж Е Щ). Согласно теореме 7.6 и
замечанию 4.1, если ж* Е О — стационарная точка этой функции, то
существуют такие координаты А^, i = 1, m, и /i^ ^ 0, j = 1, n,
350
8. ЧИСЛЕННЫЕ МЕТОДЫ
векторов Аид соответственно, что справедливы равенства
gradL(x*,A,/x) = grad/0(x*) + ATA-/x = O, (/х,ж*) = 0. (8.15)
Эти равенства при рдг = 0 будут выполнены, если положить
\т- „вп-1 ,,т-(,,в ,,N\ //Б-ПТ
Л — -д В , /х — [fi /х J, /х — и , /х
N-u.
В самом деле, в соответствии с (8.11) из равенства рдг = О
следует Uj ^ 0 для всех j Е JN, откуда /jj ^ 0, j = 1, п. Наоборот,
в тех случаях, когда i/j ^ 0, для всех j Е J^ имеем pj = —ujx*a =
= —/jjx*a = 0. Так как /хБ = 0 , то /ij?j = 0 для всех j Е ^7Б,
т.е. второе равенство (8.15) справедливо. С учетом выражений
для А и /х , а также равенств B~lB = /m, B~lN = TV и и =
= д^ — #5Af получаем для матрицы Якоби целевой функции в
стационарной точке ж* Е О тождество
(grad/o(^*))T=(^ 9N)=9B(lm ЛО + @Т gN-gBN) =
= двВ~1 (В N) + @Т и) = -ХТА + /хт.
Следовательно, рдг — 0 равносильно выполнению обоих
равенств (8.15). Это позволяет построить алгоритм поиска точки
ж* Е О минимума целевой функции fo(x) на множестве О с
использованием приведенного градиента. На начальном этапе
задаем параметр ?з > 0 точности поиска, полагаем к = 1,
выбираем начальную точку хк~1 = ж0 Е О, формируем множества
,/дР и ^7^ индексов (например, располагаем координаты точки
ж0 в порядке убывания и выбираем из них в качестве базисных
переменных т первых*), а затем записываем матрицу А в
блочном виде А = (Вк Nk). Вычисляем матрицу В^ и переходим к
основной части этого алгоритма.
1. На к-й итерации находим матрицу 7V& = В^ N^ и в точке
ж^-1 Е О вычисляем матрицы Якоби д^ и д^ целевой функции
по части переменных с элементами -^—k при j Е j? и
OXj
*См.: Реклейтис Г., Рейвиндран А., Рэгсдел К.
8.2. Использование приведенного градиента 351
j Е J^ соответственно, а затем — приведенный градиент ик =
— 9к ~9к^к- По формулам
р*М -?'е^> (8.16)
аналогичным (8.11), находим координаты вектора pkN Е Шп~т.
Если \р%\ < ?з> то итерации прекращаем, полагая ж* « ж^-1 и
/о(ж*) « /o(a;fc_1). В противном случае переходим к п. 2.
2. Используя (8.13), вычисляем вектор ркв = — NkP% Е Мт
и формируем вектор р^ = ((р#) (Рдг) ) , определяющий
возможное направление спуска из точки хк~1. Формируем
множество Ifc = {j Е J: Pa < 0} и вычисляем значение
/ ж(.0)\
x/c = min —^- >0 (8.17)
1?Ц\ Pj J
(в случае 1^ = 0 значение Х& можно принять сколь угодно
большим) и, минимизируя в полуинтервале @, х&] функцию
Фк(м) = fo(xk~1 + xpfc), находим значение х^ Е @, х&] и новую
точку ж^ = хк~1 + х^р^ Е О. Если х^ = хд., то переходим к п. 3.
В противном случае полагаем к : = к + 1 и возвращаемся к п. 1.
3. Устанавливаем индекс i Е ^7, для которого —x^k~l)i/p\ ' =
= х&. Таких индексов может быть несколько. Если все они
принадлежат множеству j?*, то полагаем к := к + 1 и
возвращаемся к п. 1. В противном случае равно нулю хотя бы одно
(к) • я
базисное переменное х\ , г Е J , и мы переходим к п. 4.
4. Индекс г Е ^7/f (если их несколько, то один из них)
переводим из множества J® в множество J^\ заменяя индексом
I Е J^ наибольшего по значению свободного переменного х\.
Для новых множеств индексов J® и J^ разделяем матрицу А
на блоки В к и Nk, вычисляем обратную матрицу i?_1, используя
рекуррентные соотношения, связывающие ее с прежней
обратной матрицей (см. Д.8.1), и, полагая к : = к + 1, переходим к п. 1.
352
8. ЧИСЛЕННЫЕ МЕТОДЫ
Если в течение нескольких итераций состав базисных
переменных не изменяется, то это означает, что достигнута
достаточно близкая окрестность искомой точки ж* Е О, причем
в отличие от задачи линейного программирования ж* может
быть и внутренней точкой множества О. В этом случае для
ускорения сходимости можно применить спуск по сопряженным
направлениям в пространстве IRn_m свободных переменных*.
Пример 8.2. Минимизируем функцию /о(#ъ#2?#з) = х\ ~
— 2х\Х2 + х*2 + х\ при ограничениях х\ + 2^2 + х% = 3 и Xj ^ О,
j = 1, 3. Сначала используем модифицированный алгоритм
метода приведенного градиента, выполняя спуск по сопряженным
направлениям в двумерном пространстве свободных
переменных.
Представим целевую функцию в виде fo(x) = - (Qx, ж), где
/ 2 -2 0\
Q= -2 2 0 —
\ 0 0 2/
неотрицательно определенная матрица. Примем ?з — 0,1 и
выберем удовлетворяющую ограничениям начальную точку ж0 =
= A, 1/2, 1) и х\ в качестве базисного переменного, т.е. J^ =
= {1}, Jx = {2, 3}, Bl = 1, Щ = B 1).
Первая итерация. 1. Вычисляем N\ = В± ~N\ = B 1)
и приведенный градиент в точке ж0:
= (-2ж1 + 2ж2 2ж3)-Bж1-2ж2)Л^1 = (-1 2) - B 1) = (-3 1).
Так как и2 — — 3 и и3 = 1, то в соответствии с (8.16) име-
(!) (!) о (!) (!) @) 1 1 /о 1\т
ем _Р2 = —и\ =3 и ^3 = —г^з ^з = —1, т.е. pjy = C — 1) .
Переходим к п. 2 алгоритма, поскольку \plN\ = л/10 > ?з = 0,1.
*См.: Реклейтис Г., Рейвиндран А., Рэгсдел К.
8.2. Использование приведенного градиента 353
2. Из (8.13) находим р\ = -NlPxN = -B 1)C - 1) = -5 и
формируем вектор р1 = {{р1в) (р]у) ) =(—53 — 1) ,
задающий возможное направление спуска из точки ж0. При помощи
(8.17) на множестве If = I j Е J\ Pj < О У = {1, 3} вычисляем
- • ( ^\ ¦ I ^ 40)\ • /1 А 1
Xl=^l-^J=I^r^'-^))=n,mU'1} = 5-
Минимизируя в полуинтервале @, ~я\\ = @, 1/5] функцию
= \ (Qx°, х°) + х (Qx°, р1) + ^ (Qp\ р1),
находим
,_ {Qx°,pl) 1 _1
Я1-~ТОрХ?)-Гз<Я1-^
вычисляем точку ж1 = ж0 + ^Jp1 = (8/13, 19/26, 12/13) и
переходим ко второй итерации, возвращаясь к п. 1 алгоритма.
Вторая итерация. 1. Множества индексов JB и JN
не изменились, и поэтому N2 = N\ = B 1). Вычисляем
приведенный градиент в новой точке ж1:
Поскольку базисное переменное осталось прежним, то вектор
p2N найдем как сопряженный с вектором plN:
1 212
2 О €Л -1
pN = -u +—PiV =
9 /^1\ (9/13JA2 + 32)/' 3\ _ 18 ( 7
13 V 3 У 32 + 12 V-1/ 169 V -24
Переходим к п. 2, так как Ip2^ = 450/169 > ?3 = ОД-
354
8. ЧИСЛЕННЫЕ МЕТОДЫ
2. При помощи (8.13) находим вектор
р\ =
---Nip%
и формируем вектор
р2-
определяющий
- ш
=-?<21><7-
<*>*)* = ?(*
24)Т
7 -
направление спуска из точки
_ 180
~ 169
¦24)т,
х1. Длина
это-
го вектора для дальнейших вычислении на этой итерации не
имеет значения. Поэтому примем р2 = A0 7 — 24) .
Используя (8.17), на множестве Х| = {j Е ^7: Pj < 0} = {3} вычисляем
- • ( *?\ 4" 1
Минимизируя в полуинтервале @, ~Й2[ = @, 1/26] функцию
М") = МхЧхр2) = l- {Qx\ x1)+k(Qx\P2) + ^- {Qp\p2),
находим
„_ {Qx\p>) _ 1 __
и вычисляем точку х2 = ж1 + ^Р1 = (^ ^ 0)- Поскольку х| =
= >?27 то переходим к п. 3.
3. Так как индекс г = 3 Е J^- принадлежит множеству J^ —
= J-y = {2, 3}, т.е. обратилось в нуль свободное переменное
жз, то переходим к третьей итерации, возвращаясь к п. 1
алгоритма.
Третья итерация. 1. Снова множества индексов JB
и JN остались прежними, и поэтому N% = N\ = B 1). Находим
приведенный градиент в новой точке х2: и3 = д% — д% N% =
= @ 0) — 0-B 1) = @ 0). В соответствии с (8.16) будет нулевым
и вектор р\. Так как |p^| = 0 < ?3 — 0,1, то дальнейшие
8.2. Использование приведенного градиента 355
вычисления прекращаем и полагаем ж* = ж3 = A, 1, 0), /о(ж*) =
= Мх3) = 0.
Функция /о (ж) является выпуклой. Поэтому ж* — точка
наименьшего значения этой функции на множестве О,
определяемом заданными ограничениями. Применение сопряженных
направлений позволило найти точку ж* за две итерации,
поскольку минимизируемая функция является квадратичной, а
свободных переменных всего два. Выполним вторую
итерацию по основному алгоритму метода приведенного градиента
и убедимся, что для достижения точки ж* потребуется большее
число итераций.
Согласно п. 1 этого алгоритма, используя координаты
вычисленного в точке ж1 = (8/13, 19/26, 12/13) приведенного
градиента и2 = (9/13 27/13), в соответствии с (8.16) находим
координаты р2B) = -42L1} = -171/328 и ?зB) = ~42L1} = -324/169
вектора р% = (9/328)( —19 -72)Т. Ясно, что \р%\ > ?3 = 0,1.
Поэтому переходим к п. 2 алгоритма.
Вычислив вектор р2в = —N2P% = т—г (в данном случае этот
вектор — число), сформируем вектор р2 = A10 —19 —72) ,
опуская множитель 9/328. На множестве Х| = {2, 3} находим
Д1)-
Функция 1р2{*с) = /о(ж1 + хр2) достигает минимума при
/ 41}\ Г 19 12 ч 1
(Qxl,p2) 4230
Итак, получаем точку ж2 = ж1 + >с^р2 = A,0333, 0,6596, 0,6535).
Сравнение расстояний \хх — ж*| « 1,0356 и |ж2 — ж*| « 0,7376
показывает, что вторая итерация, выполненная по основному
алгоритму метода приведенного градиента, привела лишь к
некоторому приближению к точке ж*.
356
8. ЧИСЛЕННЫЕ МЕТОДЫ
8.3. Проектирование точки на множество
Выше (см. 8.1) отмечено, что непосредственное применение
к численному решению общей задачи (8.1) нелинейного
программирования одного из методов спуска может привести к
тому, что точка х , найденная на некоторой k-ik итерации,
выйдет за пределы допустимого множества О. Чтобы этого
избежать, можно полученный при помощи рекуррентных
соотношений D.20) или D.36) результат подвергнуть операции
проектирования точки на множество О.
Определение 8.2. Проекцией точки ж^1п на
множество ficRn называют ближайшую к х точку у Е О этого
множества и обозначают ее Р^(ж), т.е. такую точку у = Р^(ж),
что
\у — х\= inf \z — х\ = р(ж,0), (8.18)
где уо(ж,0) — расстояние от точки {элемента) х до
множества О.
На рис. 8.4 дана геометрическая
интерпретация определения 8.2 в случае
плоскости. Если х Е О, то в соответствии с
(8.18) Pq(x) = х. Проекция точки х ^ О
на множество О может и не
существовать вовсе. Например, в случае, когда
О = {ж Е Rn: |ж| < 1} — открытый
единичный шар в R71, для любой точки х (? О имеем р(ж,0) = \х\ — 1,
но не существует точки у Е О, для которой было бы
выполнено (8.18), т.е. \у — х\ = |ж| — 1. Следовательно, не существует и
проекции точки х (? О на открытый шар О.
Перечислим основные свойства операции проектирования*
точки на множество.
1. Если х Е О, то Р^(ж) = ж.
*См.: Васильев Ф.П.
8.3. Проектирование точки на множество 357
2. Если О — замкнутое множество, то любая точка х
имеет проекцию у = Рп(х) на множество О. Если при этом О —
выпуклое множество, то проекция точки ж на О единственна.
На рис. 8.5 точка х имеет две проекции у\ и у2 на невыпуклое
множество О и единственную проекцию у на выпуклое
множество Q.
Рис. 8.5 Рис. 8.6
3. Точка у является проекцией точки жЕР на замкнутое
выпуклое множество О тогда и только тогда, когда для любой
точки 2 Е О выполнено неравенство
(z-y,aj-y)<0, (8.19)
т.е. угол (р между векторами z — у ж х — у не является острым
(рис. 8.6).
4. Если О — выпуклое замкнутое множество, у\ = Pq(xi) и
2/2 — Pq(x2) — проекции точек х\ и Х2 на О, то
\У\~Уъ\ ^ |Ж1-Ж2|,
т.е. длина проекции отрезка на выпуклое
множество не превосходит длины самого
отрезка (рис. 8.7).
Эти свойства важны для обоснования
Рис. 8.7
и анализа сходимости методов,
использующих операцию проектирования точки на допустимое
множество О. Докажем наиболее часто применяемое неравенство
(8.19). Для этого рассмотрим функцию Ф(г) = \z — ж|2, z Е О,
при произвольной фиксированной точке х Е W1. Эта функция
358
8. ЧИСЛЕННЫЕ МЕТОДЫ
является сильно выпуклой на замкнутом выпуклом множестве
Ocln (см. пример 3.14), а значит, и просто выпуклой. Так
как она определяет квадрат расстояния между точками z и ж,
то, согласно определению 8.2, проекция точки х Е W1 на
множество Q должна быть точкой минимума этой функции. В силу
теоремы 3.15 выпуклая функция Ф(^) достигает минимума в
точке у Е О тогда и только тогда, когда выполнено неравенство
(grad<3>(y), z — у) > 0. В данном случае grad<fr(z) = 2(z — х) и,
следовательно,
0 < (grad<?(y), z-y)=2(y-x,z-y) = -2(z-y,x-y),
что равносильно (8.19) для любых z Е О.
Из проведенного доказательства следует, что проекцию
фиксированной точки х Е W1 на замкнутое выпуклое множество
(]СМП можно найти путем решения задачи минимизации
ф(г) = |z - ж|2 ->> min, z Е О, (8.20)
квадратичной функции на множестве О, что согласуется и с
определением 8.2. Однако трудность решения этой задачи
непосредственно связана с формой задания множества О.
Рассмотрим примеры множеств, проектирование точки на которые не
представляет особых затруднений.
Пример 8.3. Если f] = {zGln: \z — х$\ ^ 1} — замкнутый
единичный шар с центром в точке xq Е W1, то, согласно
определению 8.2 проекции точки на множество, для точки х (? Q
имеем
\у — х\= inf \z — х\ = \х — xq\ — 1.
\z-x0\^l
Нетрудно проверить, что этому равенству удовлетворяет точка
у = Рп(х) = Хо + -^^-. (8.21)
\Х — Xq\
Используя неравенство Коши — Буняковского, убеждаемся,
что она для любой точки z выпуклого замкнутого множества
8.3. Проектирование точки на множество 359
О удовлетворяет неравенству (8.19):
/ X-XQ X-XQ \
(z-y,x-y)=[z-xo- ] г, х-хо- ] г =
V \X — Xq\ \X — Xq\/
= ( 1- г ) (z - Xq, X - Xq) - \х - Xq\ + 1 ^
V \x — Xq\/ к
< ( 1 — : г ) |z — жо||ж — Xq\ — \x — Жо| + 1 =
V \X — Xq\/
= (l-\x-x0\){l-\z-x0\)<:0,
поскольку \x — xo\ > 1 при ж ^ Q и |z — жо|^1 при z E О.
Множество fi = {zGln: |z — жо| = 1} замкнутое, но не
выпуклое. Для точки xq (? О существует бесконечное множество
проекций на О, а для всех других точек х такая проекция
единственна и может быть найдена при помощи (8.21).
Пример 8.4. Гиперплоскость
n = {zeRn: (n,z) = b}, (8.22)
где п GW1 — единичный нормальный вектор этой
гиперплоскости, а & — постоянное число, является замкнутым выпуклым
множеством (см. 3.1). Проекцию точки х (? О на множество
О будем искать в виде у = Pq(x) = х + An, А = const. Найдем
число А из условия у Е О, т.е. (п, у) = (п, ж + An) = b. Отсюда
А = Ъ— (п, ж), поскольку (п, п) = |п|2 = 1, и
у = Рп(х) = х + (Ъ - (п, х))п. (8.23)
Убедимся, что точка у, определяемая соотношением (8.23),
удовлетворяет неравенству (8.19) при любых z Е О, т.е. при
(п, *) = &
(z — у,х — у) = {z — х — (b — (п, ж))п, х — х — (b— (п, ж))п) =
= —(&—(п,ж)) (z,n) + (b— (п,ж)) (ж,п) + (&—(п,ж)) |п|2 =
= -&2 + &(п, ж) + &(ж,п)-(ж,пJ + (&-(п, ж)J = 0.
360
8. ЧИСЛЕННЫЕ МЕТОДЫ
Несложно проверить, что точка у = Рп(х) является
проекцией точки х (? О* на полупространство
0* = {zEMn: (n,z)^b}5 (8.24)
так как она для всех z Е О* удовлетворяет неравенству (8.19).
Лемма 8.1. Если ранг матрицы А равен количеству ее
строк, то квадратная матрица АА невырожденная.
М Предположим противное: матрица АА вырожденная и
существует такой ненулевой вектор у Е Rm, что А А у = 0. Тогда
получим у АА у = (А у) А у=(А у, А у) = \А у|2 = 0,
откуда А у = 0. Но система линейных уравнений А у = 0 не имеет
ненулевых решении, поскольку ранг матрицы А системы равен
количеству столбцов матрицы [III]. >
Пример 8.5. Найдем проекцию точки х Е W1 на множество
О = {^GRn: (щ, z) = bi, г = 1, m }, которое является
замкнутым и выпуклым (см. 3.1). Примем, что единичные
нормальные векторы щ линейно независимы, причем т<п (если т = п,
то множество ft состоит из одной точки). Искомую проекцию
представим в виде
т
y = PQ(x)=x + Y^ А*п*> А* G R' (8-25)
г=1
Из условия у Е О получим систему линейных алгебраических
уравнений (СЛАУ)
т
У^Хк (rik, щ) = bi- (щ, ж), г = 1, га, (8.26)
/с=1
для нахождения коэффициентов А&, к = 1, т. При линейно
независимых векторах п^ определитель этой СЛАУ отличен
8.3. Проектирование точки на множество 361
от нуля, так что она однозначно разрешима относительно
коэффициентов Л^. Для этого решения подстановка (8.25) в
(8.19) с учетом (8.26) дает
m mm
(z-y,x-y) = -^\i(z-x,rii) + ^2\i^2 Xk (™Ь Щ) =
г=1 г=1 к=1
m m
= -^2xi(bi- (ж, щ)) + ^2 xi ibi - (пь ^)) = о,
г=1 г=1
т.е. неравенство (8.19) выполнено для любых z Е О.
Пусть векторы щ, г = 1, га, являются строками
прямоугольной матрицы А размера га х п. Тогда систему (8.26) можно
записать в виде АА А = Ъ — Ах, где Л = (Ai ... Am) , Ъ =
т
= (Ъ\ ... bm) . Так как строки матрицы А линейно
независимы, то, согласно лемме 8.1, матрица А А невырождена.
Поэтому Л = (ААТ)_1(Ь- Ах), а
у = рп(х) =х- Ат(ААт)-1(Ах - Ъ). (8.27)
Пример 8.6. Если допустимое множество является п-мер-
ным параллелепипедом О = {х Е W1: aj ^ хj ^ bj, j = 1, п }, где
aj и bj — заданные числа, то координаты проекции у =
= (yi, ..., уп) Е О точки х = (#i, ..., хп) Е Rn на множество О
можно представить в виде
Уз= \
aj:
Xj,
bj,
X П ^\ (Jj n ,
a j < ж j < bj;
Xj ^ 6j,
j = l,n.
Тогда для координат любой точки z = (z±, ..., 2n) E О
справедливы неравенства (;?j — Vj)(xj — yj) ^ 0, j = 1, п. Суммируя эти
неравенства no j от 1 до п и учитывая формулу для
стандартного скалярного произведения в Rn, приходим к (8.19).
362
8. ЧИСЛЕННЫЕ МЕТОДЫ
8.4. Метод проекции точки на множество
Сочетание метода градиентного спуска, используемого при
безусловной минимизации целевой функции, и операции
проектирования точки на допустимое множество ft составляет
существо метода проекции точки на множество,
применяемого для решения общей задачи (8.18) нелинейного
программирования. Такое сочетание позволяет на каждой k-ж итерации
обеспечивать соблюдение ограничений, задающих множество
ft. При этом элементы релаксационной последовательности
{х } находят из рекуррентного соотношения
xk = Pn{xk~l + j€kwk) = Рп(хк), keN, хк>0, (8.28)
где хк = xk_1 + yckwk — точка, используемая в обычном
методе градиентного спуска, wk = — grad/o(^/c_1) — вычисленный
в точке х Е ft (на первой итерации — в выбранной
начальной точке ж0 Е ft) антиградиент целевой функции fo(x),
х Е D(f), дифференцируемой в ее области определения D(f), а
выбор значения жк определен используемым вариантом метода
градиентного спуска. Таким образом, на каждой к-ж
итерации в качестве следующего приближения к точке ж* минимума
целевой функции в соответствии с (8.28) берут проекцию хк =
= Р$}(хк) Е ft точки хк на допустимое множество ft.
Если ft — замкнутое выпуклое множество, то проекцию
х = Рп(х ) Е ft можно найти непосредственно минимизацией
на множестве ft квадратичной функции
I у грК 1 \Л
®k(z) = g -*k{z- xk~\ wk), ze ft.
В самом деле, эта функция является сильно выпуклой (см.
пример 3.14), а значит, и просто выпуклой. Она, согласно
теореме 3.15, достигает минимума в точке xk Е ft тогда и только
тогда, когда выполнено неравенство (grad*^^), z — хк) ^ 0.
8.4. Метод проекции точки на множество 363
В данном случае gracKfr/^z) = z — xk г — Kkwk и поэтому
О < (&саЛФк(хк), z - хк) = (хк - хк~1 - Kkwk, z - хк) =
= -(xk-xk,z-xk). (8.29)
Сравнивая с (8.19), убеждаемся, что точка ж минимума
функции Фк(%) на множестве О является проекцией точки ж =
= хк~х + >ckwk на это множество.
Различные варианты метода проекции градиента связаны
со способами выбора значения як в (8.28),
пропорционального шагу спуска в направлении антиградиента wk. Например,
этот выбор можно провести, исходя из условия
исчерпывающего спуска в направлении вектора wk или же, задавшись
некоторым исходным значением щ > 0, при необходимости на
каждой k-ik итерации уменьшать его до приемлемого значения
Xfc, гарантирующего сходимость последовательности {х } к
искомому решению, т.е. использовать метод дробления шага.
Критерием прекращения поиска точки ж* Е О минимума
целевой функции на допустимом множестве ficRn при
применении метода проекции градиента служат те же условия вида
D.18) и D.19), что и в случае безусловной минимизации.
На примере решения задачи (8.1) опишем подробнее
последовательность действий при выполнении k-ж итерации
варианта этого метода, в котором используется исчерпывающий спуск
в направлении антиградиента w . Примем, что допустимое
множество О задано ограничением д(х) = 0 типа равенства,
где д(х) — функция, дифференцируемая на множестве W1.
Графическая иллюстрация k-ж итерации в двумерном случае
представлена на рис. 8.8. Здесь О есть множество точек
плоской гладкой кривой Г, заданной уравнением д(х) =0.
Пусть ж Е О — точка, найденная на предшествующей,
(к — 1)-й итерации (на первой итерации, к = 1, она является
выбранной начальной точкой ж0 Е О). После вычисления
антиградиента wk = — grad/o(^/c_1) в точке хк~1, ортогонального
линии уровня /о(ж) = f${xk~l) целевой функции /о(ж), проведем
364
8. ЧИСЛЕННЫЕ МЕТОДЫ
Рис. 8.8
исчерпывающий спуск в направлении антиградиента до
точки х касания прямой спуска с линией уровня fo(x) = fo(x )
(см. рис. 8.8). Поскольку д(хк) =d^0, то ограничение типа
равенства, задающее допустимое множество О, нарушено. Для
завершения k-ik итерации и нахождения точки хк необходимо
спроектировать точку х на множество О. В данном случае это
означает, что нужно найти точку плоской кривой Г, наименее
удаленную от точки х . Так как функция д(х)
дифференцируема, то можно доказать, что точка хк будет основанием
кратчайшего перпендикуляра, опущенного из точки хк на
кривую Г (см. рис. 8.8). Отметим, что проекция точки х на
кривую Г в общем случае может быть не единственной.
Аналогичную последовательность действий можно выбрать
и в случае, когда допустимое множество О задано ограничением
типа неравенства д(х) ^ 0, где функция д(х)
дифференцируема в W1. На рис. 8.8 это множество — часть плоскости,
ограниченная кривой Г, которая описывается уравнением д(х) = 0.
При д(хк) = d > 0 имеем хк ^ О, так что геометрически
проекция точки хк на множество О снова является основанием
кратчайшего перпендикуляра, опущенного из этой точки на
кривую Г.
Рассмотрим условия сходимости последовательности {х }.
Теорема 8.1. Если О — замкнутое выпуклое множество,
а целевая функция fo(x) на этом множестве ограничена снизу,
непрерывно дифференцируема и для любых ж, у Е О удовлетво-
8.4. Метод проекции точки на множество 365
ряет условию
|grad/o(aj)-grad/o(y)|<L|»-y|, L > О, (8.30)
то при любой начальной точке ж0 Е О для релаксационной
последовательности {ж^}, построенной по формуле (8.28), где
0 < ?о < Х? < -——, ? > 0, верно равенство lim \хк~1 — хк\ =
= 0. Если при этом множество Хо = {ж Е О: /о(ж) < /о(#0)}
ограничено, то такая последовательность имеет хотя бы одну
предельную точку ж*, в которой для любых ж Е О выполнено
неравенство
(gradf0(x*),x-x*)^0. (8.31)
<4 В силу леммы 4.4 из неравенства D.26) при ж = хк~1 и у = хк
имеем
/о^-1) - /0(хЛ) > (grad/o^1), ж^1 - хЛ) -
--\хк~1-хк\2, кеК (8.32)
Из равенства (8.28) при wk = — grad/o(^/c_1) и свойств операции
проектирования точки на множество (см. 8.3) вытекает, что
для любой точки ж Е О
(ёгас1/о(ж/с),ж-ж/с)>— (хк-1-хк,х-хк), кеК (8.33)
жк
Отсюда при ж = хк~1 и х& < 2/(L + 2б) получим
*к
Подставляя это неравенство в (8.32), находим
fo{xk~l) - f0(xk) ^ six1"'1 - хк\\ хк Е О, к Е N. (8.34)
Так как последовательность {ж^} является релаксационной,
т.е. fo(xk) < f$(xk~l), то последовательность {fo(xk)} невоз-
растающая и ограничена снизу в силу ограниченности снизу
функции fo(x) на множестве О. Согласно признаку Вейер-
(grad/o^-1), хк~1 - хк) > ^ ^ > (| + е) I**
•**|2.
366
8. ЧИСЛЕННЫЕ МЕТОДЫ
штрасса сходимости монотонной ограниченной
последовательности [I], последовательность {fo(xk)} сходится к некоторому
конечному пределу /* > — оо. Поэтому после суммирования
обеих частей (8.34) по к Е N получим
оо
к=1
Это неравенство означает, что ряд в его правой части сходится
[IX]. Следовательно, так как е > 0, то
lim \хк-1-хк\=0. (8.35)
/с—^оо
Если множество Xq ограничено, то все элементы хк
релаксационной последовательности {хк} принадлежат этому
множеству, т.е. {хк} является ограниченной последовательностью и,
согласно теореме Больцано — Вейерштрасса [I], имеет хотя бы
одну предельную точку ж*, которая будет пределом при к{ —>> оо
некоторой подпоследовательности {xki}, выделенной из {хк}.
Тот же предел в силу (8.35) имеет и подпоследовательность
{ж^-1}. Поэтому, переходя в (8.33) к пределу при к = к{ —>> оо,
с учетом непрерывности gradjo(^) приходим к (8.31). >
Можно показать*, что если выполнены все условия
теоремы 8.1 и, кроме того, функция fo(x) выпукла на допустимом
множестве О, то справедлива оценка 0 ^ fo(xk) — /* ^ С/к,
к Е N, С = const > 0. Если же при этом целевая функция
сильно выпукла и при построении при помощи (8.28)
релаксационной последовательности {х } выполнено условие 0 < ?о ^
^ Кк = % < 2j/L2, где 7 ^ L — параметр сильной
выпуклости функции fo(x), то последовательность {х } сходится к
точке ж* минимума целевой функции на множестве О и
справедлива оценка \хк — ж*| ^ qk\x° — ж*|, к Е N, причем 0 < q =
= A — 2^fH-\- k2L2I'2 < 1. Отметим, что при выборе н = j/L2
знаменатель геометрической прогрессии принимает
минимальное значение q = A — 72/L2I'2.
*См.: Васильев Ф.П.
8.4. Метод проекции точки на множество 367
Проиллюстрируем возможности метода проекции точки на
множество на конкретном примере.
Пример 8.7. Минимизируем квадратичную целевую
функцию
/о (#1,0:2) = Юж1 ~~ ^xix^ + 7х2 — 4\/5Erz:i — х2) — 16
на допустимом множестве
0={(жь х2)еШ2
: xi
-Ж2-75 = 0}.
В качестве начальной точки выберем ж0 = @, — л/б) и
используем два правила выбора значения ус^ в (8.28): постоянные
значения х = 0,1 (рис. 8.9, а) и х = 0,05 (рис. 8.9, б') и выбор
нк — ^к в процессе исчерпывающего спуска (рис. 8.9, в).
На каждой к-тк итерации проектирование точки хк на
множество О выполняем в соответствии с (8.23) по формуле
хк = Рп(хк)=хк + (Ь-(п,хк))п,
где Ь = лД/2 и п = A/л/2, -1/л/2)
(8.36)
— нормальный вектор
прямой, заданной уравнением х\ — х2 — л/5 = 0. Условием
прекращения поиска точки ж* = (ж*, ж^) минимума целевой функции
является выполнение неравенства |ж — х | < ?i = 0,01, после
чего принимаем ж* « ж^ и /(ж*) « f(xk).
Точное решение рассматриваемой задачи дает ж* = (л/5, 0)
и /(ж*) = —66, причем л/5 ~ 2,2361 с точностью 5 • Ю-5.
Результаты численного решения, представленные в табл. 8.2,
показывают, что по числу N
итераций и достигнутому Таблица 8.2
приближению к точке ж* в
данном примере
предпочтение следует отдать
варианту метода проекции точки
с использованием
исчерпывающего спуска.
Хк
ж = 0,10
х = 0,05
*к
N
6
7
4
xN
B,234, -0,002)
B,235, -0,001)
B,236, 0,000)
368
8. ЧИСЛЕННЫЕ МЕТОДЫ
Обратим внимание на различие в траекториях поиска точки
ж* при постоянных значениях х (см. рис. 8.9, а и б). Видно, что
при большем из двух значений (при н — 0,1) точка минимума
целевой функции достигнута за меньшее число итераций.
в
Рис. 8.9
8.5. Метод проекции антиградиента
369
8.5. Метод проекции антиградиента
Результатом проектирования точки ж Е W1 на замкнутое
множество ficMn является точка у Е О, либо совпадающая с
ж, если ж Е О, либо лежащая на его границе <ЭО (см. 8.3). Это
свойство операции проектирования позволяет при численном
решении задачи оптимизации с ограничениями на каждой А;-й
итерации использовать обычный метод градиентного спуска
в направлении антиградиента из точки xk~l в точку ж^, а
затем находить проекцию xk Е О точки хк на множество О
(см. 8.4). Если при этом хк ф. Q, то операция проектирования
как бы возвращает ее обратно в допустимое множество О.
Естествен вопрос: нельзя ли предварительно найти такое
направление спуска, движение точки по которому при
определенных ограничениях вообще не выводило бы ее за пределы
допустимого множества О? Сначала рассмотрим случай, когда
множество ft задано при помощи линейных ограничений типа
равенства в виде
П={х?Шп: (аьж)=6ь г = ±7га}, (8.37)
где а^Е1п иб^ЕК — заданные векторы и числа
соответственно. Отметим, что в силу линейности ограничений множество
О является выпуклым.
т
Составим вектор Ъ=(Ъ\ ... Ът) и матрицу А размера га х
х п, строками которой являются матрицы-строки ai , г = 1, га.
Без ограничения общности можно принять, что Rg А = га <п
(см. 8.2). В этом случае векторы а^, г = 1, га, линейно
независимы.
Отметим, что для любой матрицы А матрица АА
является симметрической, поскольку (АА ) = (А ) А = АА . Если
векторы щ Е IRn, г = 1, га, линейно независимы, то, согласно
лемме 8.1, матрица АА невырождена и имеет обратную матрицу
(АА )-1, причем симметрическую, так как матрица А А
симметрическая.
370
8. ЧИСЛЕННЫЕ МЕТОДЫ
Квадратная матрица
Р = АТ(ААТ)~1А (8.38)
порядка п является симметрической, поскольку
Рт = (АТ(ААТ)~1А)Т = АТ(А\ААТУ1)Т =
= АТ((ААТ)-1)Т(АТ)Т = АТ(ААТ)-1А = Р.
Кроме того,
РР= (АТ(ААТ)-1А)АТ(ААТ)-1А =
= АТ(ААТ)-1(ААТ)(ААТ)-1А = АТ(ААТ)~1А = Р,
т.е. Р2 = Р.
Квадратную матрицу М, удовлетворяющую соотношению
М2 = М, называют идемпотпентной матрицей, а
симметрическую идемпотентную матрицу — проекционной.
Отметим, что проекционная матрица является неотрицательно
определенной, так как
(Мги, w) = (М2го, го) = (Мгн, Мго) = \Mw\2 > 0.
Собственными значениями идемпотентной матрицы могут
быть только числа 0 и 1. В самом деле, если ж^О —
собственный вектор идемпотентной матрицы М с собственным
значением Л, то
Аж = Мх = М2х = М(Хх) = Х2х.
Следовательно, (А2 — А)ж = 0 и А2 — А = 0, так как х ф 0.
Уравнению Л2-Л = 0 удовлетворяют только числа 0 и 1. Очевидно,
что собственными значениями проекционной матрицы также
могут быть только числа 0 и 1.
Нетрудно показать, что если Р — проекционная матрица,
то и Р* = 1п — Р — также проекционная матрица. Действи-
8.5. Метод проекции антиградиента
371
тельно,
(Р*J = (/„ - РJ = 1П - 2Р + Р2 = 1П - Р = Р* (8.39)
и
(P*f = (In-Pf = In-P = P*. (8.40)
При помощи матрицы Р любой вектор w Е W1 можно
представить в виде суммы w = Pw + (In — P)w, в которой слагаемые
Pw и (In — P)w ортогональны. Ортогональность слагаемых
вытекает из равенств РAП — Р) = Р — Р2 = в, в соответствии
с которыми
(Pw, (In - P)w) = [w, P(In - P)w) = 0. (8.41)
Вектор Pw является проекцией вектора w на линейное
подпространство Ср = {х Е W1: х = Pw}. Если матрица Р имеет
вид (8.38), то базисом в пространстве Ср являются векторы
di, i = 1,га, так как в этом случае для любого вектора у Е Ср
имеем
m
y = pw = AT(AAT)-1Aw = ATd = J^rfiOi, (8.42)
г=1
где d = (AA )_1Аго, a d{, % = 1, га, — координаты вектора d.
Обозначим Р* = /п — Р. Линейное подпространство ?р*
всех векторов вида Р*го, го Е Rn, является ортогональным
дополнением линейного подпространства ?р, так как для любых
wuw2 eW1
(Pwu P*w2) = (wu P(In - P)w2) = 0.
Поэтому вектор w^~ = Р*го ортогонален каждому вектору а^,
г = 1, га. Таким образом, вектор w ортогонален нормальному
вектору щ Е W1 каждой гиперплоскости (а^, х) = 6^, г = 1, га,
ограничивающей множество О (8.37). Следовательно,
направление, задаваемое вектором го^, параллельно этим
гиперплоскостям и движение в этом направлении из любой точки ж0 Е О
не выводит за пределы множества О.
372
8. ЧИСЛЕННЫЕ МЕТОДЫ
Линейные ограничения типа равенства. Пусть в
задаче оптимизации допустимое множество О определено
ограничениями типа равенства, т.е. имеет вид (8.37), а целевая функция
fo(x) дифференцируема в W1. Предположим, что известна
точка ж0 Е О. Рассмотрим функцию
(р(у)=Мх° + Р*у), у?Шп, (8.43)
где матрица Р определена соотношением (8.38). Для этой
функции в силу правила дифференцирования сложной функции и
симметричности матрицы Р справедливо равенство*
gracMy)=P*grad,fo(*), (8.44)
где ж и у связаны соотношением
ж = ж° + Р*у, ж,уЕМп. (8.45)
Теорема 8.2. Если у* — стационарная точка функции
<р(у), то соответствующая ей точка
ж* = ж° + Р*у* (8.46)
удовлетворяет необходимому условию минимума целевой
функции fo(x) на допустимом множестве О вида (8.37).
-4 Прежде всего убедимся, что ж* Е О. Используя представление
(8.46) и условие ж0 Е О, заключаем, что
(Oj, Ж*) = (аг, Ж°) + (щ, Р*У*) = (щ, Ж°) = bj, г = 1, Ш,
поскольку вектор Р*у* ортогонален каждому вектору
линейного подпространства ?р, в том числе и векторам а^.
Следовательно, ж* Е О.
* Здесь и далее градиент функции трактуется как вектор-столбец.
8.5. Метод проекции антиградиента
373
Так как у* является стационарной точкой функции (р(у), то
grad(^(y*) = 0, и поэтому, учитывая (8.38) и (8.44) при у = у* и
ж = ж*, находим
Р*§гас1/о(Ж*) = grad/0(a:*) - AT(AAT)-1Agradfo(x*) =
m
= grad/0(^*) + АТХ = grad/0(^*) + ^ Агаг = 0, (8.47)
г=1
где Л = — (АА )_1Agrad/o(^*), а Л^ — координаты вектора
Л ? Мш. Представив ограничения (8.37) в виде fi(x) = (а^ ж) —
— Ъ{ = 0, г = 1,771, и учитывая равенства grad/Дж*) = а^,
заключаем, что точка ж* является стационарной точкой функции
Лагранжа
m
Ь(ж,А) = /0(ж) + ^Аг((аг,ж)-6г), (8.48)
г=1
т.е. удовлетворяет необходимому условию минимума целевой
функции fo(x) на множестве О (8.37). >
В соответствии с теоремой 8.2 стационарные точки
целевой функции fo(x) на допустимом множестве можно
определять, решая задачу безусловной минимизации функции <р(у).
В общем случае функция <р(у) может иметь несколько
стационарных точек, причем каждой ее стационарной точке у*
будет соответствовать стационарная точка ж* (8.46) функции
Лагранжа (8.48). При этом теорема 8.2 не гарантирует, что
через минимизацию функции <р(у) можно найти все стационарные
точки целевой функции. Однако если целевая функция является
выпуклой функцией на выпуклом множестве О, то для решения
задачи минимизации такой функции достаточно найти хотя бы
одну стационарную точку целевой функции в О, поскольку в
любой стационарной точке выпуклая функция достигает
наименьшего значения (см. 3.4). Отметим, что строго выпуклая
функция может иметь лишь одну стационарную точку, так как
374
8. ЧИСЛЕННЫЕ МЕТОДЫ
она может достигать наименьшего значения на выпуклом
множестве только в одной точке.
Пример 8.8. Применим теорему 8.2 для поиска минимума
квадратичной функции /о (ж) = - (Qx, х) с положительно
определенной матрицей Q порядка п на множестве О вида (8.37).
Так как в данном случае grad/o(#) = Q#, то в соответствии
с (8.44) и (8.45) можно записать
&ad(p(y)=P*Q(x° + P*y).
Из условия grad(p(y*) = 0 получим СЛАУ
P*QP*y = -P*Q#0, (8.49)
которой должна удовлетворять стационарная точка у*
функции <р(у) (8.43).
Остановимся на частном случае функции двух переменных.
Пусть fo(x) = /о(жъЖ2) = х1 + х\-> а допустимое множество
задано одним ограничением %2 = 2. Тогда
т
а в (8.37) га = 1, а\ = @ 1) и &i = 2. Ограничению типа
равенства удовлетворяет, например, точка ж0 = B, 2), лежащая
на прямой, задаваемой уравнением (ai, ж) = 2, или %2 = 2. В
данном случае имеем А = а1 = @ 1), АА = а1а\ = |«i|2 = 1 и
Р = АТ(ААТ)-1А= Г*Л -1.@ 1
0\ н ,„ ., /0 0
0 1
— <S! -S? =(SS
P*QP* =
1 0\/2 OUl °\-B °
0 0/Ц 2 До 0/ V0 0
^-ii «о mint
8.5. Метод проекции антиградиента
375
Тогда СЛАУ (8.49) относительно координат точки у* = (у*, у|)
принимает вид
'2 0\/уП = (-4'
,о оДу2*; v о,
или 2у| + 0 • yl = — 4 и 0 • у\ + 0 • Уз = 0. Из первого уравнения
находим yl = —2, а второму уравнению удовлетворяет
произвольное значение у\. Используя (8.46), получаем
1 -
х
@)
+ р*
+
2 0
0 0
-2
2/2*
Таким образом, ж* = @, 2) и /о(ж*) = 4. Эта точка минимума
функции fo(x) на множестве О точек прямой с уравнением х% =
= 2, так как функция строго
выпуклая. Полученный результат
очевиден с геометрической точки
зрения: ж* = @, 2) является
точкой касания прямой ж 2 = 2 и
линии урОВНЯ /о(ж1,Ж2) =Ж1 +Ж2 =4
целевой функции (рис. 8.10). #
я,-2=0
Рис. 8.10
Для поиска стационарной
точки у* Е О функции (/2(у) можно
использовать численные методы
(см. 4-6). В частности, можно применить один из вариантов
метода градиентного спуска. Однако при решении
прикладных задач иногда удобнее минимизировать исходную целевую
функцию fo(x), поскольку координаты точки ж Е W1
являются параметрами оптимизации и имеют вполне определенную
содержательную интерпретацию.
Рассмотрим процедуру поиска минимума
дифференцируемой целевой функции fo(x) на множестве О (8.37). Выберем
начальную точку ж0 Е О, вычислим в этой точке антиградиент
w1 = — grad/o(a?°) и антиградиент р1 = Р*гиг функции (р(у) в
376
8. ЧИСЛЕННЫЕ МЕТОДЫ
точке у = w1. Если р1 = 0, то градиент функции <р(у) в
точке w1 равен нулевому вектору, т.е. w1 = у* — стационарная
точка этой функции, а в силу теоремы 8.2 ж0 — точка,
удовлетворяющая необходимому условию минимума целевой функции
на множестве ft (для выпуклой целевой функции ж0 — точка ее
наименьшего значения на О).
При численном решении целесообразно считать у = w1
стационарной точкой функции (р(у) при выполнении условия,
аналогичного D.19): \р1\ < 63, где вз > 0 — параметр точности
поиска. Если \pl\ ^ вз, то вектор р1 определяет направление
спуска для функции (р(у) при ее безусловной минимизации. Но
этот же вектор задает возможное направление спуска для
целевой функции, если в соответствии с (8.45) для первой (к = 1)
итерации записать
ж1 = ж0 + xiP*™1 = ж0 + xip1, xi > 0. (8.50)
Действительно, точка ж1 принадлежит множеству О при любом
значении >q, так как, учитывая равенства (сц, Р*го) = 0, г =
1, га, для любого вектора го1 имеем
(ai5 ж1) = (аг, ж0) + (аг, Р*™1) = (аг, ж0) = Ьг, г = 1, га.
Поскольку с учетом равенств (8.39) и (8.40)
(р1, ёгаа/0(ж0)) = - (Р*™1, w1) = - ((Р*) V, w1) =
= -(p*w1, р*™1) = -ip1!2 < о,
вектор р1 задает направление спуска и для целевой функции, в
котором ее значение уменьшается.
Значение ж\ в (8.50) можно найти при помощи
исчерпывающего спуска в направлении р1 или методом дробления шага,
задаваясь некоторым первоначальным значением xq и при
необходимости уменьшая его так, чтобы добиться выполнения
неравенства /о(ж1) < fo(x°). Это позволит начать
формировать релаксационную последовательность {хк}.
8.5. Метод проекции антиградиента
377
После нахождения при помощи (8.50) точки ж1 переходим
ко второй итерации и т.д. Пусть на ?>й итерации известна
точка х Е О. Вычисляя в этой точке антиградиент w =
= — grad/of^-1), находим возможное направление спуска рк =
_ p*wk^ ПрИ дВИЖении в котором (если \рк\ ^ ?%) ищем точку
хк = xk~l + HkP*wk = хк~1 + ккрк, кк > 0, (8.51)
подбирая соответствующим образом значение кк. Как и в
случае ж1, можно показать, что хк Е О при любом значении кк.
Поэтому можно переходить к следующей, (А; + 1)-й итерации.
Если же \рк\ < ?з, то итерации прекращаем, полагая го* « го^ и
ж* ^ж^-1.
Поскольку на каждой к-тк итерации вектор р является
проекцией антиградиента w целевой функции на ортогональное
дополнение подпространства ?р, то описанную процедуру
поиска минимума этой функции на множестве О назовем
методом проекции антиградиента.
Общий случай линейных ограничений. Пусть задача
оптимизации содержит линейные ограничения типа
неравенства и равенства. В этом случае допустимое множество можно
записать в виде
tt = {x?Rn: (аьж) ^ &ь iel~, (аьж)=6ь гЕХ0}, (8.52)
где Х~ и Х° — конечные множества индексов. Множество Q
(8.52), согласно замечанию 7.1, является выпуклым.
Предположим, что на /с-й итерации точка ж удовлетворяет mk Е N
равенствам (а^, ж^-1) — Ъ{ = 0, г Е Jk, где Jk С X = Х- UI0 —
некоторое подмножество множества I индексов всех векторов
ai Е Шп в (8.52), причем 1° С Jk.
Составим матрицу А& размера mk х п, строками которой
служат матрицы-строки ai , i ? Jk. Если RgA^ = ттг^ ^ п, то в
силу леммы 8.1 матрица АкАк невырожденная и можно
определить квадратные проекционные матрицы Рк = Ак(АкАк)~1 Ак
и Р* = 1п- Рк порядка п.
378
8. ЧИСЛЕННЫЕ МЕТОДЫ
После вычисления антиградиента wk = — gra,dfo(xk г)
целевой функции fo(x) в точке х Е О находим
Р
P?wk.
(8.53)
Отметим, что в частном случае в (8.52) могут отсутствовать
ограничения типа равенства, т.е. множество Х° индексов пусто.
Тогда возможна ситуация, при которой на к-ik итерации все
ограничения типа неравенства не являются активными. При
этом rrik = 0, т.е. пусто и множество ^, а х — внутренняя
точка множества О, для которой (а^, х ) < Ъ{ при всех г ЕХ~.
В этом случае полагаем, что Р? совпадает с единичной
матрицей 1п порядка п, а в (8.53)
рк = wk. Для внутренней
точки антиградиент w задает
возможное направление спуска, по
которому на этой итерации
можно двигаться вплоть до границы
<90 выпуклого множества О (на
рис. 8.11 такая ситуация
показана на плоскости). Чтобы найти
точку жЕ <90, в выражения для
ограничений типа неравенства в
(8.52) подставим ж = хк из (8.51)
приР^*=/п:
Рис. 8.11
bi^(ahxk 1 + xkwk) = (ai,xk l) + щ(щ, wk), г el .
Отсюда видно, что при (а^, w ) > 0 выбор х^ > 0 ограничен
значением {pi — (а^, ж^-1))/ (а^, wk), иначе ограничение с этим
индексом будет нарушено. С учетом всех ограничений типа
неравенства, для которых (а^, wk) > 0, получим
"к
¦ mm
ZGX+
bj- (сд,хк г)
(ahwk)
l+ = {iel-: (ai,wk)>0]. (8.54)
8.5. Метод проекции антиградиента
379
После вычисления x& следует выбрать такое значение х& Е
? @, Xfc], которому соответствует точка хк = ж^-1 + щгик,
обеспечивающая возможно меньшее значение fo(xk) < fo(xk~1)
целевой функции. Отметим, что можно выбрать щ = х&, т.е.
на пересечении направления антиградиента го и
гиперплоскостей, для которых отношение
bj- (aj,xk г)
(ahwk)
в (8.54) оказалось наименьшим. В результате найдем точку
хк = хк~г -\- >c^wk Е О (см. рис. 8.11). Но при этом возможно,
что/0(ж/с)>/о(ж/с).
Пусть Jk ф 0. Если \рк\ ^ ?з > 0, то вектор рк определяет
возможное направление спуска. При движении в этом
направлении не будут нарушены
ограничения типа равенства и
активные ограничения типа
неравенства, но опять возникает
опасность нарушения ограничений,
которые в точке хк~1 не
являются активными (на рис. 8.12 эта
ситуация изображена на
плоскости IR2 при одном активном и
двух неактивных ограничениях
в точке х ). Поэтому
аналогично (8.54) вычисляем
предельно допустимое для ус^ значение
Рис. 8.12
Мк — mm
bj - (щ, хк 1)
J+ = {iel~: (а*,р*)>0}, (8.55)
и затем в (8.51) подбираем ус^ Е @, х&] так, чтобы получить
возможно меньшее значение fo(x ) < fo(x ) целевой функции.
После выбора значения ж^ и нахождения точки хк можно
переходить к следующей, (к + 1)-й итерации.
380
8. ЧИСЛЕННЫЕ МЕТОДЫ
Если \рк\ < ?з? то при Jk — 0 итерации прекращаем и
полагаем ж* « ж , а при Ji-ф 0 вычисляем вектор
А* = (А*^)-1^™* Е Mmfc, (8.56)
г Е с7, kotoj
гранжа в функции Лагранжа
(к)
координаты А^ , г Е ^7, которого являются множителями Ла-
^(ж,Л) = /оИ+^Л^((аг,ж)-6г). (8.57)
Если А^ ^ 0 для всех г Е Jk \2"°, т.е. для всех активных
ограничений типа неравенства, то, согласно теореме 7.6, это означает,
что точку ж можно приближенно считать стационарной
точкой функции Лагранжа (8.57) и можно положить ж* « хк~1. Но
если найдутся индексы г Е ^ \Х°, для которых Аг- ' < 0, то один
из них (обозначим его j) следует удалить из множества »У^ и для
нового множества Jk — Jk\ {j} индексов найти проекционную
матрицу Рк размера (га& — 1) х п. Если при этом Jk = 0, т.е.
77^-1 = 0, то Р*=1п.
Покажем, что новый вектор рк = Pkwk ф О и определяет
возможное направление спуска на А;-й итерации. Этот вектор
можно представить в виде рк = wk — Ак А^, где А^ = (А^Ак )~lA^Wk
и Ак — матрица размера (га& — 1) х п, состоящая из матриц-
строк ai ^ i ^ Jk. Аналогично для вектора рк = 0 с учетом (8.56)
имеем
р* = p*w* = wk- АткХк = wk- \f]a3 - Y, >ч }«г = 0. (8.58)
Предположим, что рк = 0, откуда wk = АкХк = ^ Аг- 'щ. Под-
ставляя w в (8.58), находим
? Х^аг - Af а,- - ? Af )аг = -А<% + ? (А<*> - А?')* = О,
ieJk i?Jk i^Jk
8.5. Метод проекции антиградиента
381
т.е. нетривиальная (поскольку Л^ ' ф 0) линейная комбинация
линейно независимых векторов а^, % Е Jk, равна нулевому
вектору. Это противоречие доказывает, что р ф 0.
Спуск в направлении вектора р не нарушит ограничение
(а^, ж) ^ bj, которое при построении матрицы Р? уже не
рассматривается как активное, если (а^, р ) ^ 0. Убедимся в этом,
для чего умножим (8.58) скалярно на вектор P^clj и запишем
(P*ka3, wk) - Af (P,*aJ5 а,) - Y, Ak) (Pk«v <**) = °- (8«59)
Поскольку (P^dj, clj) =0, i G c7/c, то сумма в левой части (8.59)
равна нулю. Поэтому, учитывая, что матрица Р?
симметрическая и неотрицательно определенная, из (8.59) получаем
(Pfa, wk) = (aj, P*kwk) = {a„pk) = \f {P*ka3, aj) < 0,
поскольку Ay < 0. Следовательно, вектор pk задает возможное
направление спуска.
Если \р \ < ?з5 то предстоит новая проверка условия
прекращения последующих итераций, приводящая либо к завершению
решения задачи, либо к удалению из множества J^ еще одно-
го индекса j, для которого множитель Лагранжа А~ < 0, и
построению очередной проекционной матрицы и т.д. Если же
\рк\ ^ ?з> то Для определения направления спуска, которое
задано вектором р, при помощи (8.51) и (8.55) проводим описанную
выше процедуру выбора значения ж^ и нахождения точки ж^,
что позволяет затем перейти к (к + 1)-й итерации.
Пример 8.9. Решим методом проекции антиградиента
задачу квадратичного программирования
{/о(ж1,Ж2) = 2#i + 2^2 — 2ж1^2 — 4жх — 6^2 —> min;
Ж1+Ж2 —2^0, Ж1 + 5^2 — 5^0, — х\ ^ 0, —^2 ^ 0.
382
8. ЧИСЛЕННЫЕ МЕТОДЫ
Целевую функцию представим в виде /о(ж) = -(Qx,x) +
+ (с, ж), х еМ2, где
«=(- ")•
т
с = (—4 — 6) . Вычислим антиградиент этой функции
w = — grad/o(sc) = — Qx — с —
-(-t-i)(z)-(-t)=(tz+-iO ^>
т
и в соответствии с (8.52) обозначим а\ = A 1) , Ъ\ = 2, с&2 =
= A 5)Т, Ъ2 = 5, а3 = (-1 0)Т, а4 = @ - 1)Т и 63 = &4 = 0.
В качестве начальной точки возьмем ж0 = @, 0), а параметр
точности поиска ?з = 0,1.
Первая итерация. В точке ж0 в соответствии с (8.60)
1 т
имеем w = D 6) . В этой точке активны лишь ограничения
неотрицательности параметров оптимизации х\ и #2, т.е. ^71 =
= {3, 4}. Поэтому
Ai = (a3 a4)T= Г ~J JM, Л1Л1 = П JV
Так как p1 = P^w1 = @ 0) , то, используя (8.56), вычисляем
v=(^,-^=(j;)(-j_?)(j)=(-).
В данной задаче ограничения типа равенства отсутствуют, так
что отрицательными оказались оба множителя Лагранжа при
активных ограничениях типа неравенства. Удалим из множе-
8.5. Метод проекции антиградиента
383
ства J\ индекс % = 4 и для нового множества J\ = {3} найдем
М = (-1 0), А±А? = (-1 0)(-1 0)Т = 1,
*Тч_1
Р1=А^{А1А^)-уА1 =
Р* = 12-Р1 =
Теперь получим
i-(-i о)
о о
0 1
1 о
о о
причем \рг\ = 6 > ?з = ОД, так что вектор р1 определяет
возможное направление спуска.
Для неактивных в точке ж0 = @, 0) ограничений вычислим
(ai, р1) = 6 > 0, (а2, р1) = 30 > 0. При этом
bi-(ai,g°) _ 1 Ь2-(о2,ж°) _ 1
(оьР1) 3' (аг,?1) 6"
Поэтому в соответствии с (8.55) ~к\ = 1/6, при спуске в
направлении вектора р1 первым будет нарушено ограничение с
индексом i = 2 (рис. 8.13).
Рис. 8.13
Подставим х = ж0 + ^р1 в матричное представление целевой
функции:
/o(aj) = Y(Qp1,p1)+x(c,p1)=^1(x).
384
8. ЧИСЛЕННЫЕ МЕТОДЫ
Функция ф\(к) принимает минимальное значение при
{сЗ1) _1
кх
{Qp\pl) 4"
Так как к\ > *с\, то в (8.46) полагаем *с\ = *с\ = 1/6 и находим
х1 = ж0 + xip1 = @, 1) (см. рис. 8.13).
Вторая итерация. В точке х1 = @, 1) из (8.60)
находим w1 = F 2) .В этой точке активными являются
ограничения с индексами г = 2 и г = 3, т.е. J2 — {2, 3},
^2 = (a2,a3)T=(_j jj), Р2*=/2-4(А24)-1А2 = в2
2
и р2 = 0. При помощи (8.56) вычислим Л2 = (А2А2) 1A2w
т
= B/5 — 28/5) . Из множества J2 удаляем индекс г = 3,
соответствующий отрицательному множителю Лагранжа, и
получаем А2 = A 5), А2А2 = A 5)A 5)Т = 26,
^ = h-A2\A2A^A2 = l6^l "J)
и р2 = Р*ги2 = A4/13)E - 1)Т, причем |р2| = л/26 > ?3 = ОД.
Следовательно, вектор р2 определяет возможное направление
спуска. Так как для дальнейших вычислений на этой итерации
длина вектора р2 не имеет значения, то для упрощения примем
р2 = E -1)Т.
Для неактивных в точке х1 = @, 1) ограничений вычисляем
{аър2) = 4 > 0, (а4, р2) = 1 > 0. При этом
fti- (аьж2) _ 1 &4- (а^х1) _
{аър2) 4' («4,Р2)
Таким образом, в соответствии с (8.55) х2 = 1/4, т.е. при спуске
в направлении вектора р2 первым будет нарушено ограничение
с индексом г = 1 (см. рис. 8.13).
8.5. Метод проекции антиградиента
385
Подставляя х = х1 + кр2 в матричное выражение для
целевой функции и учитывая симметричность матрицы Q, находим
ЛИ = у(ОР2,Р2) + *{{Qx\p2) + (с,р2) + (с, ж1)) = V2W-
Функция 1р2(>с) достигает минимального значения при
„_ (QXl,p2) + (c,p2) _ 7 ^ 1__
Поэтому в (8.46) принимаем x<i = 7/31 и получаем х2 = х1 +
+ к2р2 = C5/31, 24/31).
Третья итерация. В точке ж2 в соответствии с (8.60)
вычисляем гу3 = C2/31) A 5) и устанавливаем, что активным
является лишь ограничение с индексом % = 2, т.е. J$ = {2}.
Поэтому Л3 = а\ = A 5) = А2, (^з^з) = 26> рз = ^2 и
з „* з 1 ^ 25 -5\ 32/1Л
Так как |р3| = 0 < ?з = 0,1, то, используя (8.56), находим Л3 =
= (AsA^A^w3 = A/26)A 5)C2/31)A 5)Т = 32/31 > 0.
Таким образом, единственный множитель Лагранжа в функции
Лагранжа (8.57), имеющей в данном случае вид
32
Ь3(ж, А) = /0(ж) + — ((а2, х) - 62),
положителен. Поскольку на этой итерации р3 = О, то точка
х1 = C5/31, 24/31) является стационарной для функции
Лагранжа. Квадратичная целевая функция fo(x) с положительно
определенной матрицей Q сильно выпуклая. Поэтому х1 = ж* —
точка наименьшего значения целевой функции при заданных
ограничениях (см. рис. 8.13). В этой точке целевая функция
принимает значение /о(ж*) = 6882/961 « 7,1613.
386
8. ЧИСЛЕННЫЕ МЕТОДЫ
Нелинейные ограничения. Если среди ограничений в
задаче оптимизации есть нелинейные, то поиск минимума
целевой функции fo(x) на допустимом множестве
усложняется. Пусть для определенности О = {ж Е W1: gi(x) ^ О, г = 1, т },
где ^г(ж) — дифференцируемые функции, и на fc-й итерации
известна точка xk~l Е О, для которой активными являются
ограничения с индексами г Е Х& = {гЕМ: ^г(ж/с)=0}.
Составим матрицу Afc, строками которой являются матрицы-строки
(grad^^a?^-1)) , г ЕХ&, предполагая, что они линейно
независимы. Тогда проекционная матрица Р? = 1п — Ак(А^Ак)~1А^
спроектирует антиградиент wk = — grad/o(^/c_1) целевой
функции в точке хк~1 на направление, ортогональное градиентам
всех функций gi{x), г EI&, задающих в этой точке активные
ограничения. Но в общем случае может оказаться, что это
направление не будет направлением спуска, поскольку оно может
лишь касаться в точке xk~l Е dft границы dft множества О (на
рис. 8.14 эта ситуация представлена на плоскости при одном
активном ограничении в точке х ). Ясно, что любое
продвижение точки в найденном направлении спуска может вывести
ее из допустимого множества, так что х ^ О. Поэтому шаг
спуска на каждой к-ж итерации обычно приходится сочетать с
последующим проектированием точки х на множество О.
gxlx)=Q
g2(x)=0
едено
Рис. 8.14
8.5. Метод проекции антиградиента
387
Рассмотрим на конкретном примере некоторые
особенности поиска точки минимума целевой функции в случае, когда
допустимое множество О задано одним нелинейным
ограничением типа неравенства, т.е. О = {х Е W1: g(x) ^ 0}.
Пример 8.10. Решим задачу выпуклого программирования
{fo(xi,X2) = 2х\ — ^х\ +х\ — 2x2 —> niin;
х\ + х2 — 2x2 ^ 0.
В данном случае целевая функция является квадратичной и
ее можно записать в виде /о (ж) = - (Qx, х) + (с, ж), где
Q={t 2)' С=(-2
Единственное ограничение задачи имеет вид g(x) ^ 0, где
g(xi,X2) = х\ + х?> — 2^2- В качестве начальной возьмем точку
х° = @, 0), а в условии прекращения поиска \хк — хк~1\ < е\
положим е = 0,01.
Вычислим антиградиент целевой функции
w = — grad/o(#) = —Qx — с =
'4 0\ /яЛ_/-4\ = /4-4x1
0 2) \Х2) \-2) V2-2x2
и градиент левой части ограничения
grad#(aO = (l 2ж2-2)Т. (8.61)
Рассмотрим подробнее первую (к = 1) итерацию при решении
этой задачи методом проекции антиградиента.
1. Поскольку (го1, gradg(#0)) = 0, то антиградиент w1 =
= D 2) и градиент gradg(#°) = A — 2) в начальной точке х°
ортогональны. Следовательно, нет необходимости вычислять
проекционную матрицу Р*, которая в данном случае является
единичной, а р1 = P^w1 = w1 = D 2) .
388
8. ЧИСЛЕННЫЕ МЕТОДЫ
2. При помощи исчерпывающего спуска из точки ж0 в
направлении вектора р1 находим значение
(w\pl) 5
Xl {Qp\p1) 18
-1 0 , 1 ПО 5\ ст
и точку ж = ж + xip = I —, - 1. Ясно, что продвижение из
точки ж0 Е О в направлении вектора р1 выводит за пределы
допустимого множества, т.е. ж1 ^ О, так как д(х1) = 25/81 >
> 0. Точка ж1 лежит на касательной к кривой Г, заданной
уравнением д{х) = 0, в точке ж0.
3. Спроектируем точку ж1 ^ О на допустимое множество
О, т.е. найдем точку ж1 Е О кривой Г, наименее удаленную
от точки ж1. Так как функция д(х) дифференцируемая, то
точка ж1 будет основанием кратчайшего перпендикуляра,
опущенного из ж1 на кривую Г (см. 8.4). Эту точку можно найти,
решая задачу (8.20) методом последовательных приближений*
я] = х]_г - ff(?j_i) r^i2 > «EN, где as = grad^(^_1). В каче-
\CLS\
стве нулевого приближения (при 5 = 1) можно принять ж J = ж0,
а условием прекращения последовательных приближений
можно считать выполнение неравенства |ж* — х\_х\ < ?, где 5 > 0 —
заданный параметр точности. При выполнении этого
неравенства полагаем ж1 = ж* и /(ж1) = f(x\). Выбирая 6 = 0,01,
получаем ж = @,9211, 0,7191), при этом ^(ж1)^ 0,0003.
4. Проверяем условие прекращения итераций: \хг — ж°| =
= v/@,9211J + @,7191J « 1,168 > е = 0,01. Так как требуемая
точность еще не достигнута, поиск точки ж* Е О минимума
целевой функции /(ж) на множестве О следует продолжить.
Для этого переходим к п. 1, заменив точку ж0 на найденную
на первой итерации точку ж1.
Результаты расчетов на первой и последующих трех
итерациях приведены в табл. 8.3, траектория поиска точки ж*
представлена на рис. 8.15.
*См.: Реклейтис Г., Рейвиндран А., Рэгсдел К.
8.6. Другие методы проектирования
389
Таблица 8.3
к
1
2
3
4
хк
@,9211, 0,7191)
@,9976, 0,9512)
A,0000, 0,9995)
A,0000, 1,0000)
f(xk)
-2,9086
-2,9976
-3,0000
-3,0000
1 h h — \ 1
\хК — хК l\
1,168
0,244
0,048
0,0005
Рис. 8.15
Таким образом, результат четвертой итерации с заданной
точностью совпал с точным решением задачи ж* = A, 1). #
При реализации изложенного алгоритма может оказаться,
что в точке хк Е О, найденной на А;-й итерации, fo(xk) ^
^ fo(x ). В этом случае следует использовать
модифицированный алгоритм, в котором выбор значения ус^ проводится с
помощью метода дробления шага, а не с помощью
исчерпывающего спуска.
8.6. Другие методы проектирования
Помимо метода проекции антиградиента для минимизации
целевой функции существуют близкие по своей идее методы, в
которых также используется операция проектирования векто-
390
8. ЧИСЛЕННЫЕ МЕТОДЫ
pa на некоторое подпространство. Кратко рассмотрим
некоторые из них.
Проектирование сопряженных направлений.
Эффективность поиска точки ж* Е О минимума дифференцируемой
целевой функции /о(ж), жЕМп, на допустимом множестве
О можно повысить, если на каждой к-й итерации возможное
направление спуска определять не по антиградиенту wk =
= — grad/of^-1) в точке xk~l Е О, а по одному из сопряженных
направлений. При этом сопряженные направления удобно
находить последовательно в процессе итераций.
Рассмотрим допустимое множество вида
ft = {ж eRn: (щ,х) =bj, г =Т~т},
где векторы щ Е W1 линейно независимы. Согласно теореме 8.2,
для поиска точки минимума функции fo(x) на множестве Q
можно использовать задачу безусловной минимизации функции
<p(y)=fo(x0 + P*y), yeRn,
где ж0 Е О — начальная точка; Р* = In — А (АА )~1А —
проекционная матрица порядка п; 1п — единичная матрица того же
порядка; А — матрица размера га х п, составленная из матриц-
строк ai, г = 1, га. Опишем алгоритм метода сопряженных
направлений применительно к поиску минимума функции <р(у)
(см. 5.2).
На первой итерации (к = 1) полагаем, что у0 = 0 и р1 =
= — grad(^(y°), а на любой fc-й итерации по точке у^-1 находим
точку
ук = ук-1 + якр\ ken, (8.62)
причем для направления спуска при к > 1 имеем
|grad(/9(y/c 1>u2
|grad(^(y*
р* = -gracMy*"!) + !g!;a^-2 У- (8-63)
8.6. Другие методы проектирования
391
Значение х& в (8.62) на каждой k-ж итерации подбираем
либо при помощи исчерпывающего спуска в направлении вектора
р^, либо из условия (p(yk) < tp{yk~l) методом дробления шага.
Условием прекращения итераций может быть выполнение
неравенства \рк\ < ?%, где ?з > 0 — параметр точности поиска.
Теперь перейдем в описании алгоритма к исходному
аргументу х = х° + Р*у целевой функции /о (ж). На первой (к = 1)
итерации по известной начальной точке ж0 GRn, учитывая
(8.44), находим р1 = — P*grad/o(#°). На (к — 1)-й и к-ж
итерациях в соответствии с (8.45) имеем хк~1 = х° + Р*ук~1 и
хк = xQ + Р*у . Вычитая из второго равенства первое,
получаем хк — хк~1 = Р*(ук — ук~1). Отсюда с учетом (8.62) имеем
хк = хк~1 + XfePV, fcGN, (8.64)
причем теперь для направления спуска при к > 1, используя
(8.44), можно написать
рк = -P^grad/o^-1) + 'р^^^К"^/- (8-65)
|P*grad/o(ar ^)р
Правила выбора значения ус^ в (8.64) на каждой к-ж итерации
и условие прекращения итераций остаются прежними.
Подход, в котором используется проектирование
сопряженных направлений, можно обобщить на случай, когда
допустимое множество Йс1п задано в виде (8.52), т.е. линейными
ограничениями типа неравенства и линейными ограничениями
типа равенства. В этом случае для поиска точки минимума
квадратичной функции требуется не более п итераций*.
Обобщенный приведенный градиент. Если
объединить идею метода приведенного градиента с линеаризацией
нелинейных ограничений, то можно построить алгоритм,
позволяющий искать решение общей задачи нелинейного програм-
*См.: Пшеничный Б.Н., Данилин Ю.М.
392
8. ЧИСЛЕННЫЕ МЕТОДЫ
жирования. Пусть требуется минимизировать непрерывно
дифференцируемую целевую функцию /о (ж), ж^1п, на множестве
fi = {ajeK?:/(aj) = 0}, (8.66)
где /(ж) — непрерывно дифференцируемая векторная функция
с координатными функциями /г(ж), г = 1, га, причем га < п.
Пусть в любой точке ж Е О матрица Якоби функции /(ж)
имеет ранг, равный га. Обозначим J — {1, ..., п} и выделим
подмножество ^7^ С J таких га индексов, что в некоторой
точке ж^ЕЙ квадратная матрица Якоби В* этой функции по
части переменных Xj, j Е сТ*8, будет являться невырожденной
и иметь обратную матрицу i?. Как и в методе приведенного
градиента, переменные х^ j Е J* , являющиеся координатами
точки хв Е Мш, назовем базисными, а остальные переменные
Xj, j Е J7^ — J\ jf-> являющиеся координатами точки xN Е
Е Мп_ш, — свободными. Тогда функции /г(ж), г = 1, га, можно
представить в виде /^ (жБ, ж^), г EXq.
Согласно теореме о неявной функции [V], существует такая
окрестность и(ж^) точки х^ Е Rn_m, что в этой окрестности
система га уравнений fi (жБ, xN) = 0, г = 1, га, задает
непрерывно дифференцируемую функцию xB(xN), xN Е и(ж^), причем
жБ(ж^) = хв. Из этой же теоремы следует, что матрицу Якоби
функции xB(xN) в точке х^ по всем свободным переменным
ж^, j Е с7^, можно найти по формуле N(x^) = — B^N*, где
7V* — матрица Якоби функции /(ж) в точке ж* по свободным
переменным.
Используя представление целевой функции в виде /о (ж) =
= /о(жБ(ждг), ж^) = cp(xN) и правило дифференцирования
сложной функции, вычисляем ее градиент в точке х^ Е Rn_m:
и(х?) = grad <р(х?) = 0?#(а^) + gf, (8.67)
где #^р и д^ — матрицы Якоби целевой функции по
свободным и базисным переменным. Матрицу-строку и(х^) длины
8.7. Метод возможных направлений
393
п —га в (8.67) называют обобщенным приведенным
градиентом целевой функции относительно свободных переменных
в точке х^ (Е Mn_m. Сравнивая его с приведенным градиентом
и в (8.10), видим, что элементы матрицы N(x^) зависят от
координат точки ж^, тогда как элементы матрицы N
остаются неизменными при фиксированном наборе свободных
переменных.
Алгоритм минимизации целевой функции на множестве Q
(8.66) с использованием обобщенного приведенного градиента
аналогичен описанному выше алгоритму метода приведенного
градиента, но требует пересчета матрицы N(x^) на каждой
итерации даже при неизменном наборе свободных переменных.
Кроме того, на каждой А;-й итерации вновь полученная точка
хк G Мп может и не принадлежать множеству О в силу
линеаризации нелинейных ограничений типа равенства в (8.66) в
окрестности точки х . Поэтому дополнительно приходится
находить проекцию полученной точки хк на множество О и
лишь затем переходить к следующей итерации.
Обобщенный приведенный градиент можно применить для
поиска минимума целевой функции на множестве, заданном в
неотрицательном ортанте К^ при помощи нелинейных
ограничений не только типа равенства, но и типа неравенства, в том
числе с использованием нелинейных функций, значения
которых ограничены и сверху, и снизу*.
8.7. Метод возможных направлений
Метод проекции антиградиента, а также проектирование
сопряженных направлений и приведенного градиента
эффективны только в том случае, когда в задаче оптимизации
присутствуют лишь линейные ограничения (см. 8.5, 8.6). Однако в
случае нелинейных ограничений алгоритм решения
оптимизационной задачи усложняется. Главный недостаток рассмотрен-
*См.: Реклейтис Г., Рейвиндран А., Рэгсдел К.
394
8. ЧИСЛЕННЫЕ МЕТОДЫ
ных методов состоит в том, что на к-к итерации при движении
из точки ж G О нелинейные ограничения, как правило,
нарушаются. Тем не менее и в этом случае можно построить такой
алгоритм выбора возможного направления спуска, что
перемещение точки по этому направлению на некоторое расстояние
не будет приводить к нарушению ограничений задачи.
Сначала рассмотрим задачу оптимизации, в которой
целевая функция /о(ж) непрерывно дифференцируема и ограничена
снизу на допустимом множестве О, заданном ограничениями
типа неравенства. Пусть множество О имеет вид
П={х?Шп: gi(x) ^ О, г = 1~т}, (8.68)
где gi(x) — непрерывно дифференцируемые функции. На /с-й
итерации известна точка xk~l Е О. Обозначим через Z&
множество индексов активных ограничений, т.е. тех индексов г, для
которых gi(xk~l) = 0. Отметим, что если Z& = 0, то xk~l —
внутренняя точка множества О.
Рассмотрим вспомогательную задачу оптимизации: найти
минимальное значение
r/ = max{(grad/0(^/c-1),p), (grad^a^1), р), ielk} (8.69)
т
на множестве векторов р = (р\ ... рп) Е W1, удовлетворяющих
ограничениям \pj\ ^ 1, j = 1, п. Эту задачу можно представить
как задачу линейного программирования
(rj —>> min;
I (grad/o(aj/c-1),p) ^r/;
j (grad^(^_1),p) ^r/, iEX/,;
Uj ^ 1, J = 1, rc; -Pj ^ 1, j = l,n
Ясно, что допустимое множество У\4 сформулированной
задачи оптимизации не пусто, поскольку содержит нулевой
вектор. На этом векторе значение г\ целевой функции равно нулю,
(8.70)
8.7. Метод возможных направлений
395
поэтому точная нижняя грань т\ на множестве W& не превышает
нуля. Рассматриваемая задача оптимизации состоит в
минимизации непрерывной функции (8.69) на замкнутом ограниченном
множестве векторов р Е W1, удовлетворяющих условиям \pj\ ^ 1,
j = 1, п. Следовательно, она имеет решение, т.е. в задаче (8.70)
целевая функция т\ достигает наименьшего значения в
некоторой точке Zk = (p*S%)? причем щ ^ 0. Это решение можно
найти, например, при помощи симплекс-метод а.
Предположим, что эта задача решена, причем получена
такая точка zk = (р^, rjk) Е V\4, что щ < 0. Тогда вектор рк задает
возможное направление спуска из точки х Е О.
Действительно, поскольку zk удовлетворяет ограничениям задачи (8.70),
имеем
(grad/o(a;fc-1),pfc)^r;ib<0, (grad^a^1),^) ^щ <0, ielk.
Следовательно, рк ф 0. Кроме того, согласно формуле Тейлора
с остаточным членом в форме Пеано и равенству gi(xk~l) = 0,
для любого индекса г Е 1к найдется такое а.{ > 0, что при
а Е @, с^)
gt(xk-1+apk)=gl(xk-1+apk)-gl(xk-1) =
= (grad^a;*-1), о^/) +о(а) ^ ащ +о(а) < 0.
Так как gi(xk~l) < 0 при любом / ^ Z&, то благодаря
непрерывности функции gi{x) найдется такое оц > 0, что для всех а Е @, оц)
будет выполнено неравенство gi(xk~l + арк) < 0. Таким
образом, имеем
gi{xk~l -\-арк) < 0, г = 1, га, а Е @, «о), «о = min olj > 0,
г=1,т
т.е. вектор р определяет допустимое направление в точке
ж Е О относительно множества О. При необходимости число
«о > 0 можно выбрать еще меньшим, чтобы при а Е @, ао) было
396
8. ЧИСЛЕННЫЕ МЕТОДЫ
выполнено и неравенство
Mxk-1 + apk)-f0(xk-1) =
= (grad/o^-1), арк) +о(а) < ащ + о(а) < 0.
В итоге получаем, что вектор р задает, согласно
определению 8.1, возможное направление спуска из точки х Е О на
множестве Q.
Перемещение в этом направлении приводит на к-ik итерации
в точку
хк = хк~1 + ккрк, кк Е @, йк), (8.71)
где х& > 0 — это наибольшее значение х, при котором верно
соотношение хк~1 + трк Е О, т Е @, х]. Если О — выпуклое
множество, параметр х& > 0 можно определить формулой
х/ь = max{x > 0: xk~l + хр^ Е О}. (8.72)
Отметим, что в случае неограниченного множества О (в том
числе и выпуклого) для некоторых направлений спуска значение
х& может быть бесконечно.
Различные способы выбора значения х& в (8.71) приводят к
различным вариантам алгоритмов, реализующих спуск в
найденном на каждой итерации возможном направлении. Эти
алгоритмы обычно объединяют общим названием метод
возможных направлений. Один из способов выбора х& состоит
в минимизации функции фк(н) — fo(x + хр ) в
полуинтервале @, Xfc], для чего можно использовать методы одномерной
оптимизации (см. 2). Для целевой функции, удовлетворяющей
условию
|grad/0(^) - grad/0(y)| ^L\x-y\, ж, у Е О,
где L > 0, полагают* х& = mini х&, J-^- >. Наконец, если оценка
значения х& затруднена, то можно применить метод дробления
*См.: Васильев Ф.П.
8.7. Метод возможных направлений
397
шага: выбрать некоторое исходное значение хо, найти при х& =
= хо, используя (8.71), точку х , и если х ^ О, то дроблением
значения х& добиться выполнения условия ж^О. После этого
следует вычислить значение fo(xk), и если fo(xk) > /of^-1),
то продолжить дробление значения х& до тех пор, пока не
будет выполнено неравенство fo(xk) < f$(xk~l). При этом в
случае множества О, не являющегося выпуклым, необходимо
проверить, не нарушено ли при последующем дроблении условие
xk еп.
Вернемся к задаче линейного программирования (8.70) и
рассмотрим случай, когда ее решением является точка z^ =
— {рк> О) ? IRn+1, т.е. rjk = г/* = 0. Покажем, что это равносильно
выполнению в точке х = ж* Е О необходимого условия
минимума функции fo(x) на множестве О (8.68), т.е. существованию
неотрицательных и не всех равных нулю множителей Лагранжа
Ао и Hi, iGlfc, для которых выполнено равенство
A0grad/o(^*) + ^/iigradgi(a*) = 0. (8.73)
iexk
Для любого решения z^ = (р , %) этой задачи выполнены
неравенства, задающие допустимое множество У\4- Первое из
них умножим на Ао ^ 0, а каждое из неравенств для индексов
iGlfc — на /ii ^ 0 и после сложения полученных произведений
с учетом (8.73) и линейности скалярного умножения запишем
A0(grad/0(a;*),p*) + ^^(gradffi(«*),pfc) =
ieik
= (A0grad/o(#*) + ^/iigradgi(a*), p^J = 0 ^ гЦАо + ^ wj.
zGXfc iexk
Так как коэффициент при щ положителен, то щ ^ 0. Но выше
установлено, что щ ^ 0. Следовательно, выполнение
необходимого условия минимума в точке х Е О равносильно
выполнению равенства щ = 0. Можно доказать*, что если функции
*См.: Васильев Ф.П.
398
8. ЧИСЛЕННЫЕ МЕТОДЫ
fo(x) и gi(x), г = 1, m, являются выпуклыми, а множество О
имеет внутренность, то для того, чтобы в точке х достигался
минимум функции fo(x) на О, достаточно выполнения
равенства щ = 0.
Таким образом, в качестве условия прекращения итераций в
методе возможных направлений можно принять выполнение
неравенства \щ\ < ?v, где ?v > 0 — заданный параметр точности
поиска. Рассмотрим особенности применения этого метода
к минимизации квадратичной целевой функции при линейных
ограничениях.
Пример 8.11. Решим методом возможных направлений
задачу квадратичного программирования, уже рассмотренную в
примере 8.9:
/0(^1,^2) = 2х± + 2х2 — 1х\Х2 — 4^1 — 6^2 —>> min;
х\ + х2 — 2 ^ 0, х\ + 5x2 — 5^0, —х\ ^ 0, — Х2 ^ 0.
Как и в примере 8.9, целевую функцию представим в виде
/о(ж) = - (Qx, х) + (с, ж), х е R2, где
В соответствии с (8.60) ее градиент имеет вид
grad/0(aO= '/ Л (8.74)
Обозначим левые части неравенств gi(x) = жх -\-Х2 — 2, д2(х) =
= жх + 5^2 — 5, ^з (ж) — —ж1 ^ #4 (х) = —^2 и запишем их градиенты
grad#x = A 1)Т, grad#2 = A 5)Т, grad#3 = (-1 0)Т и grad#4 =
т
= @ — 1) . Так как множество О задано линейными
ограничениями, то оно является выпуклым. Его представление в
плоскости ххОх2 показывает, что оно ограничено (рис. 8.16).
8.7. Метод возможных направлений
399
x2f
1
Х°
0
Р1/
х1
Q
2
х.
Рис. 8.16
В качестве начальной выберем точку ж0 = @, 0), в которой
fo(x°) = 0, и примем ev = 0,01.
Первая итерация. В точке ж0 в соответствии с (8.74)
имеем grad/o(^°) — (—4 — 6) , а активными являются лишь
ограничения неотрицательности переменных х\ иж2, т.е.
множество индексов Х\ = {3, 4}. Поэтому для поиска направления
т
спуска из точки ж0, определяемого вектором р1 = (р[ Р2 ) •>
следует решить задачу (8.70), т.е. минимизировать переменное
г/ на множестве Wi, заданном неравенствами
-4pi-6p2^?7, —pi^r/, -P2<,r), bi|^l, |р2|^1. (8.75)
Наименьшее возможное значение т\ ограничено в (8.75) вторым
и третьим неравенствами —р\ ^ т\ и —р2 ^ т\ при максимально
допустимых значениях р\ = Р2 = 1, т.е. т\ = — 1. При этом первое
неравенство в (8.75) также будет выполнено. Таким образом,
р = A 1) , причем этот вектор определен однозначно.
Ясно, что при движении точки ж = ж0 + ^р1 в направлении
вектора р1 ограничения дз(х) ^ 0 и д±{х) ^ 0
неотрицательности переменных не будут нарушены. Найдем, при каких
значениях ж станут активными ограничения д\{х) ^0и д2 (х) ^ 0,
т.е.
,(°)
31 (ж) = х\ } + хр\ } + х\ } + >ф2
(!) , „@)
Л1)
^2 (ж) = ж^ + уср\ ' + 5^2 + 5x^2
-2 = 2х-2 = 0,
5 = 6х-5 = 0.
Отсюда следует, что к ^ к\ = 5/6.
400
8. ЧИСЛЕННЫЕ МЕТОДЫ
Значение к\ выберем, минимизируя функцию ?/>i(x),
заданную равенством Va(x) = fo(x° + кР1)-> или
фг(ж) = I (Q(x° + хр1), ж0 + хр1) + (с, ж0 + хр1) = 2х2 - 10х
на отрезке [0, xi]. Отсюда получаем xi = ~к\ — 5/6, а затем
вычисляем ж1 = ж0 + xip1 = E/6, 5/6) и foix1) = —125/18 «
^6,9444 (см. рис. 8.16).
Вторая итерация. В точке ж1 при помощи (8.74)
находим grad/o(a?1) = (—7/3 —13/3) . Активным является лишь
ограничение #2 (ж) ^ 0, т.е. множество индексов I2 = {2}. Следо-
2 / B) B)чТ
вательно, для нахождения вектора р = [р\ р\ ) ->
определяющего направление спуска из точки ж1, следует минимизировать
переменное т\ на множестве W2, заданном неравенствами
7 13
oPi~^-P2^?7, Pi + 5j92^r/, bi|^l, b2|^l. (8.76)
Умножив второе неравенство на 7/3 и сложив с первым
неравенством, получим т\ ^ ~гР2- Так как т\ ^ 0, то и ^ ^ 0. Те-
о
перь умножим второе неравенство на 13/15 и после сложения
с первым найдем р\ ^ — тт7/? т-е- Pi ^ 0- Отсюда следует, что
наибольшему возможному значению р\ = 1 соответствуют наи-
11 5 т-г
меньшее возможное значение т] = — — ж р2 = — —. При этом
все неравенства в (8.76) выполнены. Таким образом, получаем
р2 = A -5/14)Т.
При движении точки ж = ж1 + хр2 в направлении вектора
р2 ограничение #2 (ж) ^ 0 не будет нарушено, так как оно
является активным в точке ж1. Ограничение дз(х) ^ 0 также не
нарушается, так как оно означает, что х\ ^ 0, а в точке ж1 + хр2
для первой координаты имеем х\ + нр\ = - + х ^ 0. Выясним,
при каких значениях х выполняются ограничения gi(x) ^0 и
8.7. Метод возможных направлений
401
д±(х) ^ 0, т.е. когда
<7i (ж) = х^] + кр^] + 41} + хр? -2 = ^-х-^<0,
/ \ (!) B) 5 5 / п
#4(ж) = -х\ - кр\ = YlK~ б ^ °-
Отсюда следует, что Х2 = 14/27.
Функция ф2{к) = /о(ж1 + ^Р2) с учетом симметричности
матрицы Q имеет вид
М") = ^Я{р\р2) + *{{Ях\р2) + (с,р2)) +
1 („ 1 i\ / п 291 2 11 125
77
На отрезке [О, Х2] точкой ее минимума будет К2 = —-. Поэтому
OoZ
х2 = х^^р2 = (§}, ^) и f0(x2) « -7,0850 (см. рис. 8.16).
Третья итерация. Используя (8.74), вычисляем
А, , 2\ ( Ю15 1373 \
grad/o(o.) = (-— -—) .
Так как в точке ж2 нет активных ограничений, то Хз = 0,
и переменное т\ следует минимизировать на множестве УУз,
заданном неравенствами
1015 1373 <Г I 1^1 I 1^1
Иначе говоря, нужно найти минимальное значение левой части
первого неравенства при условии, что выполнены два других
неравенства. Ясно, что минимальное значение достигается при
Р\—Р2 — 1? т»е. р3 = A 1) , и минимальным значением г/ будет
^=-!Н-6'4622-
При движении точки х = х2 + >ф3 в направлении вектора
р3 ограничения дз(х) ^ 0 и д±{х) ^ 0, означающие
неотрицательность переменных х\ и #2, выполняются при любом ^г.
402
8. ЧИСЛЕННЫЕ МЕТОДЫ
Выполнение ограничений д\{х) ^0и д^ (х) ^ 0 означает, что
<71(Ж)=42) + ^13)+42) + ^23)-2 = 2х-^^0,
д2 (ж) = х{р + KPf] + 5х{2] + Ьхр?] - 5 = 6х - -^— < 0.
Отсюда устанавливаем, что хз = —^ ~ 0,0030.
2328
Функция фз(я) = /о(ж2 + хр3) на отрезке [0, хз] достигает
наименьшего значения при хз = хз. Поэтому
ж3 = *2 + -ЗР3 = (Ц, ||) « @,9686, 0,8063)
и /о(ж3) и -7,0975.
Рассматриваемая задача с квадратичной функцией не
является сложной, и ее решение нетрудно найти
аналитическими методами. Наименьшего значения на допустимом
множестве целевая функция /о (ж) достигает в точке ж* = ( —, —
« A,1290, 0,7742), при этом /0(ж*) = -^ « -7,1613 (см.
пример 8.9). Для приближения к точке ж* с заданной точностью
e^ потребуется еще довольно много итераций. #
Случай линейных ограничений. Остановимся на
частном случае, когда в задаче оптимизации допустимое множество
О задано при помощи линейных ограничений gi{x) = (а^, х) ^ 6^,
г = 1, га. В этом случае задачу поиска возможного направления
спуска можно упростить, видоизменив следующим образом. На
каждой к-й итерации вектор рк Е W1, определяющий это
направление, можно искать из условия минимума функции С/с(р) —
= (grad/o(^/c_1),p) на множестве
Wk = {peRn:(al,p)^0, ielk; |р^1, j = M}, (8-77)
где Ik — по-прежнему множество индексов, соответствующих
активным ограничениям в точке xk~l Е О. Можно показать*,
*См.: Базара М., Шетти К.
8.7. Метод возможных направлений
403
что если минимальное значение функции Ск(р) на множестве
Wk равно нулю, то точка хк~1 удовлетворяет необходимому
условию минимума целевой функции fo(x) на множестве О.
Пример 8.12. Вернемся к задаче из примера 8.11 и решим
ее, выбирая возможное направление спуска путем минимизации
функции Ck(p) на множестве (8.77). Отметим, что теперь щ =
= grad#i(#), i = 1, 4, причем Ь\ = 2, Ъ<2 = 5, &з = Ы = 0.
Нетрудно установить, что результат выполнения первой
итерации останется прежним. В самом деле, если выбрать
начальную точку ж0 = @, 0), то получим (i(p) = (grad/o(#°), р) =
= — 4pi — Qp2, а множество Wi будет задано неравенствами
—pi ^ 0, — р2 ^ 0, \pi\ ^ 1 и |р2| ^ 1- Отсюда находим
минимальное значение ((р1) = —10 при р1 = A 1) и затем точку
х1 = х° + ^р1 = E/6, 5/6) (см. рис. 8.16).
На второй итерации в точке х1 = E/6, 5/6) имеем С2(р) =
= (grad/o(^1), р) = —7pi/3 — 13^2/3. Эту функцию необходимо
минимизировать на множестве W2, заданном неравенствами
Pi + 5^2^0, bi|^l, Ы ^ i,
(8.78)
поскольку в точке х активно лишь ограничение с индексом г =
= 2. Множество W2 ограничено трапецией ABCD (рис. 8.17), а
линиями уровня функции ^{р) являются прямые, параллельные
прямой 7pi + 13]92 = 0 (прямая B = 0 на рис. 8.17), на которой
эта функция имеет нулевое значение. Из геометрических
соображений ясно, что функция ^{р) принимает на множестве
Рис. 8.17
404
8. ЧИСЛЕННЫЕ МЕТОДЫ
W<i наименьшее значение в точке р2 = A —1/5) и это значение
равно —22/15.
При движении точки ж = ж1 + >ф2 в направлении вектора
р2 ограничение д<2 (ж) ^ 0, оставаясь активным, не
нарушается. Поэтому необходимо убедиться в выполнении ограничений
9i(x) ^0и #4 (ж) ^ 0. Это означает выполнение условий
дг(х) = 41} + *V? +41} + "V? ~ 2 = \к- \ < 0,
О о
( \ (!) B) 1 5 ^ п
Отсюда заключаем, что >?2 = 5/12.
Поскольку
/м ,М| 2, 62 2 22 125
ф2{Ю=Ых +хр ) = 25^ ~15Х~1Г'
функция ф2(к) достигает наименьшего значения на отрезке
55 55 о
[0, 3?2] = [0, 5/12] при х = —-. Следовательно, УС2 — т^ и ж =
186 186
'35 24'
,31' 31,
В точке ж2 по-прежнему активно лишь ограничение с
индексом г = 2. В этой точке в соответствии с (8.74) grad/o(^2) —
= (—— — —] . Поэтому на третьей итерации необходимо
минимизировать функцию
л ( \ ( л t ( 2ч Ч 32 160
Сз(р) = (grad/0(^ ),р) = -g^Pi - -^Р2
на множестве УУз = УУ2, заданном теми же неравенствами (8.78).
Линии уровня функции Сз(р) — прямые, параллельные прямой
pi -\- 5р2 = 0, на которой функция принимает нулевое значение.
Но прямая pi -\- 5р2 = 0 проходит по стороне DC трапеции,
ограничивающей множество УУз (см. рис. 8.17). Значения функции
в точках трапеции, не лежащих на стороне ВС', положительны.
Таким образом, минимальное значение функции Сз(р) равно
1 i 2 (^
= xl + x2pz= (j
8.7. Метод возможных направлений
405
нулю. Поэтому точка ж* = ж2 = ( —, —) удовлетворяет
необходимому условию минимума функции fo(x) на допустимом
множестве. А так как функция fo(x) является выпуклой и
допустимое множество О является выпуклым, то в точке ж* функция
fo(x) достигает наименьшего значения на множестве О. ф
Случай нелинейных ограничений. На практике при
наличии нелинейных ограничений обычно применяют
несколько модифицированные варианты метода возможных
направлений. Дело в том, что при малых значениях \щ\ направление
спуска, задаваемое вектором р^, который находят из
решения задачи линейного программирования (8.70), хотя и
является допустимым с теоретической точки зрения, может быть
неприемлемым с практической точки зрения, так как оно
может оказаться почти ортогональным направлению
антиградиента wk = —grad/o(^/c_1) целевой функции. При близких к
нулю значениях (w , р ) направление спуска р почти
^касается" границы dft множества О. Поэтому значения к^ в (8.71),
а следовательно и значения х&, будут весьма малыми, а
сходимость процесса поиска минимума — очень медленной. Более
того, возможно ^зацикливание" алгоритма или же сходимость
последовательности {ж^} к такой точке ж Е О, в которой не
выполнены необходимые условия минимума*.
Один из способов ускорения сходимости метода возможных
направлений заключается в том, чтобы при выборе возможного
направления спуска учитывать все ограничения, а не только
активные в точке хк~1. Для этого направление спуска рк на
к-й итерации находят как решение задачи минимизации
(т\ —>> min;
I (grad/o^-1),^) ^r/;
|^(ж/c) + (grad^(ж/c-1),p) ^Ar/, i = ±7^;
[\Pj\ < 1, j = hn,
*См.: Полак Э.
406
8. ЧИСЛЕННЫЕ МЕТОДЫ
где /3i > 0 — некоторые весовые коэффициенты. Так как в
задании допустимого множества W& этой задачи оптимизации
участвуют все ограничения типа неравенства исходной
задачи, то направление спуска не испытывает резких изменений,
когда от итерации к итерации изменяется множество
индексов активных ограничений. Это позволяет избежать
зигзагообразной траектории поиска точки ж* и уменьшает опасность
??зацикливания" алгоритма. Можно показать*, что и для этой
модификации метода возможных направлений равенство щ = 0
равносильно выполнению в точке хк~1 необходимого условия
минимума целевой функции на множестве О.
Недостаток описанной модификации метода возможных
направлений состоит в том, что задача линейного
программирования, на основе которой определяется направление спуска,
усложняется, так как в нее включаются все т ограничений.
Существует промежуточная модификация метода, в которой
учитываются лишь так называемые е-активные ограничения в
окрестности точки ж^-1, т.е. такие ограничения, для которых
в точке хк~1 выполняется неравенство —?& ^ gi(xk~l) ^ 0. В
этой модификации вместо множества индексов Z& используют
множество
Ц = {%€{!, ...,m}:-ek^gi(xk-1)^}. (8.79)
Значение е^ > 0 следует выбирать так, чтобы оно было
существенно больше значения е^. Оно может меняться от
итерации к итерации, но можно также считать, что е^ = ?о — const.
Множество Xj? включает в себя множество Z&, но при этом с
помощью выбора подходящего значения е^ число е-активных
ограничений можно заметно уменьшить по сравнению с общим
числом ограничений.
Поясним смысл введения е-активных ограничений на
примере минимизации целевой функции fo(x) двух переменных при
трех ограничениях gi{x) ^ 0, г = 1, 2, 3 (рис. 8.18, а). Пусть в
*См.: Мину М.
8.7. Метод возможных направлений
407
а б
Рис. 8.18
точке xk_1 GO активно лишь первое ограничение, т.е. Z& = {1}.
Тогда из решения задачи линейного программирования (8.70)
получим направление спуска, задаваемое вектором рк и
являющееся промежуточным между направлениями в точке ж
антиградиентов Wq = — grad/o(^/c_1) и wk = — grad^i(a?/c_1)
целевой функции и функции gi(x) соответственно. Но выбор
значения н^ в (8.71) будет существенно ограничен, так как это
направление спуска пересекает границу множества О,
определяемую ограничением с индексом г = 2, на малом расстоянии от
точки хк_1. Если же учесть ^-активные в этой точке
ограничения (рис. 8.18, 6), то будем иметь 1^ = {1, 2}. Тогда решением
задачи (8.70), в которой Z& заменено на 1^ и учтено влияние
антиградиента wk = — grad^2(^/c_1), можно получить вектор рк ^
задающий более удачное направление спуска. Это направление
позволяет на к-ж итерации сделать более длинный шаг на пути
к точке ж* минимума целевой функции на множестве О.
В общем случае решение zk = (р^, %) задачи линейного
программирования (8.70), в которой множество индексов Z&
заменено множеством Х^, будет удовлетворять одному из двух
условий: щ ^ —8к или — е^ < Щ ^ 0. Если выполнено первое
условие, считают, что соответствующий значению щ вектор
р задает достаточно удачное направление спуска, и этот век-
/0(яг) = const
408
8. ЧИСЛЕННЫЕ МЕТОДЫ
тор используют для нахождения очередной точки х . Если же
выполнено второе условие, то полагают, что найденное
направление спуска неудачно, и ищут другое направление спуска,
уменьшая в (8.79), например вдвое, значение ?&. Уменьшение
Sk приводит, вообще говоря, к сужению множества индексов
Zj?, в результате чего во вспомогательной задаче линейного
программирования часть ограничений снимается, а
допустимое множество расширяется. Поэтому можно ожидать, что
на более широком множестве У\4 можно найти более
удачное направление спуска, которое будет удовлетворять первому
условию. Процедура дробления е^ может и не дать
положительного результата вплоть до выполнения неравенства \е^\ < ???,
что равносильно условию \щ\ < е^ прекращения последующих
итераций.
Если множество О задано при помощи не только
ограничений типа неравенства, но и q линейных ограничений типа
равенства, т.е.
П = {х <ERn: gi(x) ^ О, г = 1, га; Ах = Ь} ,
где А — матрица размера gxn, Ъ Е W, то это следует учесть
во вспомогательной задаче линейного программирования,
добавив в нее ограничение Ар = 0. Тогда при спуске в направлении,
определяемом вектором р , удовлетворяющим последнему
ограничению, точка хк не выйдет за пределы допустимого
множества Q. Действительно, учитывая (8.71), для любого значения
Ж}~ находим
Ахк = Ахк~1 + жкАрк = Ь,
поскольку Ар =0, а точка х по условию принадлежит
множеству О и поэтому Ах = Ъ.
При наличии г нелинейных ограничений вида fi(x) = 0, / =
= 1, г, метод возможных направлений можно применить,
если на каждой А;-й итерации линеаризовать эти ограничения
в окрестности точки хк~1. Но тогда спуск в направлении,
найденном этим методом, при любом значении уск > 0 может
8.8. Методы последовательной безусловной минимизации 409
выводить точку х за пределы О. Это нарушение можно
скорректировать, заменяя найденную точку ее проекцией на
множество О. Другой подход состоит в том, чтобы ослабить
нелинейные ограничения типа равенства, для чего полагают
|/г(ж)| ^ ?&, I = 1,г. По мере приближения к искомой точке
ж* ? О минимума целевой функции на множестве О значение
5к > 0 можно уменьшать*.
8.8. Методы последовательной
безусловной минимизации
Один из подходов к решению общей задачи (8.1)
нелинейного программирования состоит в преобразовании ее в
последовательность задач безусловной минимизации для
сконструированных специальным образом вспомогательных функций.
Алгоритмы, использующие такой подход, принято называть
методами последовательной безусловной минимизации.
Рассмотрим общую схему построения алгоритмов этих
методов на примере решения задачи (8.1) для целевой функции
/(ж), жЕ1п. Формально эта задача эквивалентна задаче
безусловной минимизации
mm (/(*) + &(*)), (8.80)
где 6п(х) — так называемая индикаторная функция
допустимого множества О,:
*"(*) = \+оо, хфП.
Точки минимума функций f(x) в (8.1) и f(x) + Sq(x) в
(8.80) совпадают, но индикаторная функция имеет точки
разрыва второго рода на границе dft допустимого множества О.
Это не позволяет применять известные методы безусловной
*См.: Полак Э., а также: Реклейтис Р., Рейвиндран Л., Рэгсдел К.
410
8. ЧИСЛЕННЫЕ МЕТОДЫ
минимизации к задаче (8.80). Но в случае, когда множество
О задано ограничениями типа равенства и неравенства,
используя фигурирующие в них функции, можно построить такие
непрерывные функции штрафа 5к(х), что в каждой
фиксированной точке х Е W1
]im{Sk(x)} = lim 5k(x) = 5ф). (8.81)
/с—юо
Тогда задача, эквивалентная (8.80), принимает вид
min (f(x) + lim 6k(xj). (8.82)
Если при этом операции вычисления минимума и предела
являются коммутативными, т.е.
то вместо (8.82) получим
fk(x) = f(x) + Sk(x) -> min, x E Mn, fcEN, (8.83)
т.е. исходная задача (8.1) нелинейного программирования
переходит в последовательность задач безусловной минимизации
вспомогательных функций fk(x), которые называют
штрафными. Тогда в качестве решения ж* Е О задачи (8.1) следует
рассматривать предел (если он существует)
последовательности {х^} решений х\ задач (8.83).
Можно указать два основных подхода к построению
штрафных функций и соответственно два типа методов штрафных
функций. Эти типы различают по способу учета ограничений.
Если все точки х\ последовательности {х^} принадлежат
допустимому множеству О, то говорят о методе внутренних
штрафных функций (иногда — о методе внутренней точки).
Если же Хи Ф О, то говорят о методе внешних штрафных
функций (иногда — о методе внешней точки).
8.8. Методы последовательной безусловной минимизации 411
Рассмотрим вычислительные конструкции методов
штрафных функций, наиболее широко применяемых в приложениях
при задании допустимого множества при помощи ограничений
типа неравенства в виде
n = {xeRn: дг(х) < О, г = ±7га}, (8.84)
где gi(x), ж^Мп, — непрерывные функции.
Метод внутренних штрафных функций. Пусть
допустимое множество О вида (8.84) содержит внутренние точки,
т.е. точки, в которых все ограничения выполнены как строгие
неравенства. Функцию 6к(х), определенную во всех внутренних
точках допустимого множества О, назовем функцией
внутреннего штрафа этого множества, если
, u/>0, xett\dQ;
dk[X)~\+oo, х?П\дП.
Ее роль состоит в создании ^барьера" с крутыми склонами
вдоль границы dft допустимого множества О. Чаще всего в
качестве такой функции принимают
т ..
5k(x) = -rk'S^—?—, хеП\дП, кеП, (8.85)
ИЛИ
т
Sk(x) = -rk ^ln ( - gi(x)), x e О \ дП, k e N, (8.86)
i=l
где r& > 0 — коэффициент, называемый параметром
штрафа. Если г& —>> +0 при к —>> оо, то последовательность {5к(х)}
функций, определенных с помощью (8.85) или (8.86), сходится
поточечно к индикаторной функции Sq(x), т.е. удовлетворяет
равенству (8.81).
412
8. ЧИСЛЕННЫЕ МЕТОДЫ
Можно показать*, что последовательность {ж^} решений
ж^О\<90 задачи безусловной минимизации штрафных
функций fk(ж) = /(ж) + 5k(x), к Е N, при использовании
представления функций 5k(x) внутреннего штрафа в виде (8.85) или (8.86)
сходится к точке наименьшего значения целевой функции /(ж)
на замкнутом ограниченном множестве О вида (8.84), если
каждая точка ж*,, к Е N, является точкой наименьшего значения
соответствующей функции //Дж). Если функции /(ж) в (8.1)
и gi(x) в (8.84) являются выпуклыми, то функции /&(ж)
также выпуклы (см. 3.2). Поэтому из приведенного утверждения
следует, что для имеющей решение задачи выпуклого
программирования рассматриваемый метод сходится, поскольку в этом
случае каждая из функций //с (ж) достигает на множестве W1
лишь наименьшего значения.
Опишем алгоритм метода внутренних штрафных функций
решения задачи (8.1) на множестве О (8.84) при
использовании представления (8.85). На предварительном этапе выбираем
начальную точку ж0 Е О \ <90, сходящуюся к нулю
последовательность {r&l положительных чисел т^ и параметр точности
поиска е в условии \fk{x%) ~ fk{x%-i)\ < е прекращения
вычислений, а затем, принимая к = 1 и ж^_1 = ж0, переходим к основной
части алгоритма.
1. Полагая ж^ = ж0, одним из методов безусловной
минимизации (см. 4-6) находим точку ж*, Е О \ <90 минимума штрафной
функции
т .<
fk{x) = f(x) + Sk(x) = f(x) ~гкУ2 —r^,
используя в качестве первого приближения точку х^. Далее
переходим к п. 2.
2. Если \fk{xX) ~ fk(xk-i)\ < е-> то вычисления прекращаем
и принимаем ж* « х\ и /(ж*) « f(xt)- В противном случае
полагаем А;: = А; + 1 и возвращаемся к п. 1.
*См.: Фиакко А., Мак-Кормик Г, а также: Гроссман К., Каплан А.А.
8.8. Методы последовательной безусловной минимизации 413
Эффективность реализуемого алгоритма в значительной
степени зависит от выбора начального значения г$ параметра
штрафа г. Общих рекомендаций здесь не существует. Выбор
„подходящего" значения г о связан со спецификой решаемой
задачи и способом задания функции штрафа. Например, если
штрафная функция имеет вид
m Л
Дж,г) = f(x) -r^—т-т = f(x) -rh(x),
i=l9i[X)
т.е. использует функции штрафа вида (8.85), то в качестве
начального значения параметра штрафа можно принять*
_ (grad/(ag),gradfr(ag))
|grad/i(#)|2
Возможны и другие способы выбора „подходящего" значения**
г. Если начальное значение г о параметра штрафа выбрано, то
элементы последовательности {г^}, удовлетворяющей условию
lim Гк = +0, обычно задают рекуррентным соотношением т^ =
/с—too
= r^-i/7, fc^N, где 7 = const > 1.
Условие прекращения поиска точки ж? безусловного
минимума штрафной функции /д. (ж) зависит от используемого
алгоритма безусловной минимизации. Например, в случае
применения алгоритмов первого или второго порядков (см. 5)
в качестве этого условия обычно используют выполнение
неравенства |grad/fc(sc)| < ?&, где е^ > 0 — заданный параметр
точности поиска. Однако применение этого условия может
приводить к трудностям вычислительного характера и не всегда
практически возможно. В основном эти трудности связаны с
тем, что при больших значениях к значение |grad/fc(sc)| может
быть большим даже в малой окрестности точки ж*,. Это
обстоятельство может оказаться препятствием и при реализации
метода внутренних штрафных функций.
*См.: Фиакко Л., Мак-Кормик Г.
**См.: Гроссман К., Каплан А.А.
414
8. ЧИСЛЕННЫЕ МЕТОДЫ
Эффективность алгоритма рассматриваемого метода
может зависеть и от способа задания функции штрафа.
Универсальных рекомендаций в этом вопросе также не существует. В
одних случаях способ задания этой функции не оказывает
существенного влияния, а в других — его влияние оказывается
решающим. Покажем это на конкретных примерах.
Пример 8.13. Методом внутренних штрафных функций
решим задачу оптимизации
{/(#ъ#2) = Ю^1 — 4^i^2 + 7х2 — 4v5E#i — х2) — 16 —)> min;
(Ж1-1J + (ж2-3J-4<0.
Допустимое множество О в этой задаче представляет собой
замкнутый круг с радиусом 2 и центром в точке A, 3). Вводя
функцию штрафа в соответствии с (8.85) или (8.86), получим
два варианта вспомогательных функций:
fk(x) = f(xUX2) - —г^ г
д{хъх2)
или
fk(x) = f(xux2)-rkln(-g(xux2).
Параметры штрафа Г& определим соотношениями г о = 32, тк =
= r^-i/2, к Е N. На рис. 8.19, а изображены линии уровня
вспомогательной функции fk(x) при значении параметра штрафа
г к = 32, а на рис. 8.19, б — линии уровня функции /д. (ж) при
Решение вспомогательных задач безусловной минимизации
было проведено численно с применением метода Ньютона при
выборе в качестве начальной точки ж0 = A, 3). Поиск точки
минимума ж* Е О прекращался при выполнении неравенства
\fk(x%) - AK-i)l <е или \7к(К) -Mxl-i)\ < ?> где е =10_3-
Результаты проведенных расчетов приведены в табл. 8.4,
где N — число вспомогательных задач минимизации
штрафных функций, решение которых привело к выполнению условия
8.8. Методы последовательной безусловной минимизации 415
Рис. 8.19
Таблица 8.4
Штрафная функция
Мх)
fk{x)
N
17
16
XN
A,970, 1,254)
A,970, 1,251)
In(x*n)
-52,932
-52,997
f(**N)
-52,957
-53,004
прекращения вычислений. Числа в двух последних колонках
таблицы позволяют сравнить значения N-и штрафной функции в
точке x*N ~ ж* и целевой функции f(x) в этой же точке. Из
таблицы видно, что в данном случае способ задания функции
штрафа практически не влияет на эффективность
реализуемого алгоритма. #
Пример 8.14. Найдем решение задачи квадратичного
программирования
{f(x\,X2) = Юж1 — 4:Х\Х2 + 7х2 — 4v5Exi — х2) — 16 —>> min;
Граница допустимого множества О для этой задачи
изображена на рис. 8.20. Используя функции штрафа (8.85) и (8.86),
416
8. ЧИСЛЕННЫЕ МЕТОДЫ
Я*)=-1
Рис. 8.20
получаем вспомогательные функции
Гк
fk(x) = f(xux2)
Гк
Х\—2 Х\ + Х2 — 1
fk(x) = f(xux2) - rk ^ln(-(a;i - 2)) + ln(-(a;i + х2 - 1)) J.
Параметры штрафа г к определим, как и в примере 8.13,
соотношениями го = 32, Гк = rfc_i/2, к Е N.
На рис. 8.21, а показаны линии уровня вспомогательной
функции fk(x) при г к = 32, а на рис. 8.21, б — линии уровня
вспомогательной функции /д. (ж) при г^ = 1. Все расчеты
проведены так же, как и в примере 8.13, их результаты представлены
в табл. 8.5 (обозначения в ней те же, что и в табл. 8.4).
В данном случае способ задания штрафной функции
оказывает существенное влияние на эффективность
реализуемого алгоритма. Предпочтительней является штрафная функция
/(ж), применение которой позволяет найти точку ж* с той же
8.8. Методы последовательной безусловной минимизации 417
Таблица 8.5
Штрафная функция
fk(x)
fk(x)
N
25
11
XN
A,706, -0,706)
A,704, -0,704)
In(x*n)
-61,193
-60,796
f(x%)
-61,19.
—61,194
точностью путем решения значительно меньшего числа
вспомогательных задач минимизации штрафной функции.
Метод внешних штрафных функций. Отличие метода
внешних штрафных функций от метода внутренних штрафных
функций состоит прежде всего в форме задания функции
( = 0, ж <ЕО;
*(х) = |>о, ,*„, *е«
называемой функцией внешнего штрафа. При этом
должно быть выполнено условие (8.81). Как и в методе
внутренних штрафных функций, обычно полагают 5^(х) = г/сФ(ж), где
Гк > 0 — параметр штрафа, но Ф(ж) — функция, определенная
на всем множестве W1, равная нулю на допустимом множестве
О и положительная за его пределами.
418
8. ЧИСЛЕННЫЕ МЕТОДЫ
Если множество О имеет вид (8.84), т.е. задано при помощи
ограничений типа неравенства, то в качестве функции штрафа
обычно используют квадратичную функцию
т
h(x) = rkY,{9t(*)f, (8-87)
г=1
где gf(x) — так называемая „срезка" функции gi(x):
+ м= Г 0, дг(х)^0;
9г[Х) \gi(x), дг(х)>0,
т.е. gf{x) = тах{0,^(ж)} = (gi(x) + \д{(х)\)/2.
Последовательность {6^(х)} функций штрафа, задаваемых в
виде (8.87), сходится к индикаторной функции Sq(x), т.е.
удовлетворяет равенству (8.81), если т^ —>> +оо при к —>> оо. Если
допустимое множество О задано не только при помощи
ограничений типа неравенства gi{x) ^ О, г = 1, га, но и ограничений
типа равенства gi{x) =0, г = га + 1, р, то функцию штрафа
задают в виде
т V
8k{x)=rk^(gj{x)f + rk Y1 Ых)J-
г=1 г=т+1
Опишем алгоритм метода внешних штрафных функций в
случае, когда решается общая задача нелинейного
программирования (8.1) на множестве О (8.84), а функция штрафа
задана в виде (8.87). На предварительном этапе выбираем
произвольную начальную точку ж0, параметр е точности поиска
точки ж* минимума целевой функции f(x) на множестве О в
условии \/к(х%) ~ fk(xk-i)\ < е прекращения вычислений и
возрастающую последовательность {г^} положительных чисел г&.
Принимаем А: = 1, ж^_1=ж°и переходим к основной части
алгоритма.
8.8. Методы последовательной безусловной минимизации 419
1. Полагая хк = ж , одним из методов безусловной
минимизации (см. 4-6) находим точку ж^ минимума штрафной
функции
m
fk(x) = f(x) + 6k(x) = f(x) + rkYt{9t(*)J,
г=1
используя в качестве первого приближения точку х®. Далее
переходим к п. 2.
2. Если |/&(#?) — fk(xk-i)\ < ?? т0 вычисления прекращаем
и принимаем ж* « ж? и /(ж*) « f(xt)- В противном случае
полагаем А;: = к + 1 и возвращаемся к п. 1.
В рассмотренном алгоритме возможны и другие условия
прекращения вычислений. Например, в качестве условия
останова можно использовать неравенство |ж? — х^_г\ < ?, где е —
заданный параметр точности поиска.
Проиллюстрируем работу этого алгоритма на конкретном
примере.
Пример 8.15. Решим методом внешних штрафных
функций задачу из примера 8.13, выбрав в качестве начальной точку
ж0 = @, — у/5) и условие останова |ж? — х^_х\ < е с параметром
точности поиска е = Ю-3. В данном случае штрафные функции
имеют вид
fk(xux2) = /(хъх2)+гк(д+(хъх2)) ,
где g+(xi,x2) = «(flf(^i,X2) + \g(xi,x2)\). Минимизация этих
функций проведена численно с применением того же алгоритма
метода Ньютона, что и в примере 8.13. Параметры тк
определены рекуррентным соотношением тк = гк-\ + 2, к Е N, го = 2.
Результаты расчетов приведены в табл. 8.6, а траектория
поиска точки минимума целевой функции изображена на рис. 8.22
сплошной линией. #
Методы штрафных функций выгодно отличаются от
рассмотренных выше методов проектирования и спуска простотой
420
8. ЧИСЛЕННЫЕ МЕТОДЫ
Рис. 8.22
Таблица 8.6
к
1
2
3
4
5
6
7
К
@,386, -0,672)
@,652, 0,270)
@,899, 0,755)
A,263, 0,928)
A,694, 1,041)
A,852, 1,150)
A,954, 1,212)
/К)
-33,568
-38,698
-40,109
-46,877
-53,222
-53,501
-53,551
к
8
9
10
11
12
13
14
4
A,974, 1,230)
A,976, 1,234)
A,976, 1,236)
A,975, 1,237)
A,975, 1,238)
A,975, 1,239)
A,974, 1,240)
/К)
-53,434
-53,384
-53,348
-53,318
-53,292
-53,271
-53,252
реализации и ^сильными" свойствами сходимости. Поэтому на
их разработку и совершенствование и до сих пор затрачиваются
значительные усилия. В то же время практическая реализация
методов штрафных функций может приводить к трудностям
Д.8.1. Некоторые приемы обращения матрицы 421
принципиального характера. В основном они связаны с
топографией поверхностей уровня штрафных функций fk{x): при
больших к (больших значениях параметра штрафа г&) графики
этих функций приобретают все более выраженную овражную
структуру. Это может приводить к большим вычислительным
затратам при решении вспомогательных задач безусловной
минимизации и даже к прерыванию процесса вычислений ввиду
потери точности. Для преодоления этих трудностей развиты
модификации метода штрафных функций, свободные от
указанных недостатков: метод штрафных оценок, метод
модифицированных функций Лагранжа, метод штрафов с
регуляризацией и др*.
Дополнение 8.1. Некоторые приемы
обращения матрицы
Некоторые алгоритмы численного решения задач
нелинейного программирования включают процедуру замены в
невырожденной матрице В одного столбца с последующим обращением
вновь полученной матрицы В. Если матрица i?-1, обратная к
В, известна, то процесс обращения матрицы В можно
значительно упростить.
Пусть В — невырожденная матрица порядка п. Столбцы
этой матрицы обозначим Ь^, г = 1, п, а строки обратной к ней
матрицы В-1 обозначим ci . Тогда равенство В~1В = Е можно
записать в виде
(buCj) = 5t] = ^ *"?
где 6ij — символ Кронекера.
Предположим, что матрица В получена из матрицы В в
результате замены столбца Ь^ столбцом Ь^. Тогда векторы с^,
*См.: Гроссман К., Каплан А.А.
422
8. ЧИСЛЕННЫЕ МЕТОДЫ
определяющие строки матрицы В 1, можно вычислить по
формулам
(bk-bk,Ci) . —
Ci = Ci -~ —с/ь, г = 1,п. (8.88)
\ок,ск)
Действительно,
(bk,Ci) = (bk,Ci) '—р? ' l (bk,ck) = (bk,Ci),
ybk,ck)
откуда заключаем, что (bk, Cj) = 8к%- Если j ф /с, то (bj, с&) = О
и для любого номера г = 1, п имеем
\Ьк,ск)
Следовательно, (foj, с^) = Sji.
Заметим, что в формуле (8.88) (bk,ck) ф 0. В самом деле,
если это скалярное произведение равно нулю, то вектор ск
ортогонален всем столбцам матрицы В. Но поскольку с + к ф О,
то это возможно лишь в случае, когда столбцы матрицы В
линейно зависимы, а матрица В вырождена. В этой ситуации
матрица ??, разумеется, не имеет обратной матрицы.
В алгоритме, реализующем метод проекции
антиградиента, при построении проекционной матрицы используется
процедура обращения симметрической матрицы D = АА , где А —
прямоугольная матрица размера т х п, соответствующая в
задаче ограничениям типа равенства и активным ограничениям
типа неравенства. При переходе от итерации к итерации эта
матрица может меняться, причем в некоторых случаях новая
матрица А образуется из уже использовавшейся матрицы А
вычеркиванием одной из строк. В этом случае при
обращении матрицы D = АА можно использовать известную матрицу
Д-1, тем самым существенно сокращая объем вычислений.
Д.8.1. Некоторые приемы обращения матрицы 423
Из смысла задачи ясно, что порядок строк в матрице А не
является существенным*, и мы можем считать, что матрица
А получается из матрицы А вычеркиванием последней строки.
При этом предположении матрицу D удобно записать как
блочную матрицу
тл ( G S\
где G — симметрическая матрица порядка m — 1, S — блок
размера (га — 1) х 1, a g — элемент матрицы ?), расположенный
в ее нижнем правом углу. Аналогичным образом запишем и
обратную матрицу
--ft *)¦
где Q — симметрическая матрица порядка га — 1, R — блок
размера (га — 1) х 1, q — элемент матрицы D~l в левом
нижнем углу. При вычеркивании в матрице А последней строки
матрица D = АА преобразуется в матрицу G. Таким
образом, задача состоит в том, чтобы, зная блоки матриц D и Д-1,
определить матрицу G~l.
В соответствии с правилами перемножения блочных
матриц [III] находим
_ (GQ + SR1 GR + Sq \ _ (lm-x е\
~ \STQ + gRT STR + gq)~\ в l)'
* Можно показать, что если в матрице А переставить строки, то в
матрице АА произойдет одновременная перестановка строк и столбцов
с теми же номерами и точно так же преобразуется матрица (ААТ)-1.
424
8. ЧИСЛЕННЫЕ МЕТОДЫ
где 0 обозначает нулевые блоки соответствующего размера. В
результате получаем систему матричных уравнений
[ GQ + SR — Im-i,
GR + Sq = S,
т т (8.89)
SQ + gR=Q,
[STR + gq = l.
Из второго равенства (8.89) находим S = —-GR, с помощью
этого соотношения заменяем S в первом равенстве. В резуль-
1 т
тате получаем GQ — -GRR = /m-i, или
g(q--rrt) =1,
771—1*
Q J
Следовательно,
G~1 = Q--RRT.
С помощью уравнений (8.89) можно решить и
противоположную задачу: пересчитать матрицу D~l в случае, когда к
матрице А добавляется новая строка. В обозначениях,
введенных выше, это означает, что необходимо вычислить матрицу
D_1 при известных G, G-1, S и д.
Из второго равенства (8.89) находим R= —qG~lS, откуда,
учитывая симметричность матрицы G-1, заключаем, что R =
= — qS G~l. Заменяя R в четвертом равенстве (8.89), получаем
qS G_1S = gq — 1, что позволяет найти q:
(8.90)
g-STG~1S
Первое равенство заменой R = — qS G 1 преобразуется к
виду GQ — qSS G~l = /m-i, что позволяет найти матрицу Q:
Q = G-1 + qG~1SSTG-1.
Вопросы и задачи
425
С помощью найденных выражений для Д, q и Q можно
записать матрицу D-1:
! _(G~l + qG~1SSTG-1 -qG~lS
где q определено равенством (8.90).
Вопросы и задачи
8.1. Приведите классификацию численных методов
нелинейного программирования на примере решения задачи
минимизации выпуклой функции, непрерывно дифференцируемой на
замкнутом выпуклом множестве ficRn. Укажите достоинства и
недостатки каждого метода, целесообразность применения при
различных способах задания допустимого множества О: при
помощи ограничений типа равенства и (или) неравенства,
линейных и нелинейных. В чем состоит принципиальное различие
метода условного градиента и метода проекции
антиградиента? На каких множествах целесообразно применять каждый из
указанных методов нелинейного программирования?
8.2. Дайте определение проекции точки на множество. Как
найти проекцию точки на замкнутое выпуклое множество?
Покажите, что проекцию точки ж / жо на замкнутое множество
О = {х Е W1: \х — Xq | = 1} можно найти с помощью соотношения
(8.21).
8.3. Докажите, что точка, определяемая равенством (8.23),
принадлежит полупространству О* (8.24) и при любых z Е О*
удовлетворяет неравенству (8.19).
8.4. Докажите, что точка, заданная равенством (8.27),
принадлежит множеству О из примера 8.5 и при любых z Е О
удовлетворяет неравенству (8.19).
(8.91)
426
8. ЧИСЛЕННЫЕ МЕТОДЫ
8.5. Используя метод условного градиента, найдите
решение задачи квадратичного программирования с целевой
функцией f(x\,X2) = 5x1 + 2х — \х2 + 5^2 — 4л/2Eж1 +Х2) —8 на
множестве 0 ^ х — 1^1, 0^^2^2, выбирая различные начальные
точки: @, 0), @, 1), A, 2). В условии прекращения
итераций \хк — хк~1\ < е положить е = Ю-2. Проверьте полученный
результат, применив метод проекции точки на множество и
выбрав начальную точку @, 0). Результаты расчетов
проиллюстрируйте графически.
8.6. Решите задачу на условный экстремум
2х\ +х\ — 4жх — 2^2 —> min;
у/Ъх\ +х\ — 5 = 0,
выбрав начальную точку ж0 = @, — л/б), с помощью метода
проекции точки на множество и метода проекции
антиградиента. Используйте значение параметра точности е = Ю-2. Дайте
сравнительный анализ этих алгоритмов по числу шагов
итерационного процесса, необходимых для достижения минимума
целевой функции с заданной точностью. Покажите различие
процессов минимизации этими методами в случае ограничений
у/Ъх\ + х\ — 5 = 0 и \Jbx\ + х\ — 5 ^ 0. Дайте графическую
иллюстрацию полученных результатов.
8.7. Решите задачу нелинейного программирования
( 4ж2 + х\ + 2^2 —> min;
< х\ + х\-\х2 ^0,
[-Ж1+ж2-2^0
методом возможных направлений. Полученные результаты
проиллюстрируйте графически.
8.8. Используя метод проекции антиградиента и метод
возможных направлений, решите задачу квадратичного програм-
Вопросы и задачи
427
мирования
' х\ + 2х\ + З^з + х\Х2 — 2х\х% + Х2Х3 — 4xi — 6^2 —>> min;
хъхъхъ >0,
выбрав начальную точку @, 0, 0).
8.9. Методом внутренних штрафных функций решите
задачу квадратичного программирования
{ (xi - 5J + (х2 - ЗJ ->> min;
^1+^2^ 3,
k -хг + 2х2 ^4,
выбрав начальную точку @, 0). Графически проиллюстрируйте
полученный результат.
8.10. Используя метод внешних штрафных функций,
найдите решение задачи нелинейного программирования
{4х\ — Ъх\Х2 + х\ -Л min;
ж2-ж2 + 2^0, Ж1+ж2-6^0, жьЖг^О,
выбрав начальную точку @, 0). Графически проиллюстрируйте
полученный результат.
СПИСОК РЕКОМЕНДУЕМОЙ
ЛИТЕРАТУРЫ
Учебники и учебные пособил
Алексеев В.М., Тихомиров В.М., Фомин СВ. Оптимальное управление.
М.: Наука, 1979. 429 с.
Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные
методы для инженеров: Учеб. пособ. М.: Высш. шк., 1994. 554 с.
Белоусов А.И., Галкин СВ., Герман А.Д. и др. Методы оптимизации
в инжерных задачах / Под ред. СВ. Галкина. М.: Изд-во МГТУ
им. Н.Э. Баумана, 1991. 160 с.
Васильев Ф.П. Численные методы решения экстремальных задач. М.:
Наука, 1988. 552 с.
Волков И.К., Загоруйко Е.А., Фаликова И.Д. Псевдообращение и
линейные системы: Учеб. пособ. М.: Изд-во МГТУ им. Н.Э. Баумана,
1980. 26 с.
Галкин СВ. Методы решения экстремальных задач. М.: Изд-во МГТУ
им. Н.Э. Баумана, 1986. 52 с.
Грешилов А.А. Прикладные задачи математического
программирования. М.: Изд-во МГТУ им. Н.Э. Баумана, 1990. 189 с.
Дамбраускас А.П., Кащеев В.А., Кошаев Д.В. Алгоритмы и
программы симплексного поиска. Красноярск: Изд-во Краснояр. ун-та, 1993. 160 с.
Карманов В.Г. Математическое программирование. М.: Наука, 1975.
272 с.
Лесин В.В., Лисовец Ю.П. Основы методов оптимизации. М.: Изд-во
МАИ, 1995. 341 с.
Линейное и нелинейное программирование / Под ред. И.Н. Ляшенко.
Киев: Выща шк., 1975. 372 с.
Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации.
М.: Наука, 1978. 351 с.
Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации.
М.: Наука, 1986. 328 с.
Феодосъев В.И. Сопротивление материалов / Отв. ред. К. С.
Колесников. М.: Изд-во МГТУ им. Н.Э. Баумана, 1999. 592 с. (Сер. Механика в
техническом университете; Т. 2).
429
Дополнительная литература
Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание:
Пер. с англ. М.: Наука, 1977. 224 с.
Аоки М. Введение в методы оптимизации. Основы и приложения
нелинейного программирования: Пер. с англ. М.: Наука, 1977. 344 с.
Базара М., Шетти К. Нелинейное программирование. Теория и
алгоритмы: Пер. с англ. М.: Мир, 1982. 584 с.
Банди Б. Методы оптимизации. Вводный курс: Пер. с англ. М.: Радио
и связь, 1988. 128 с.
Батищев Д. И. Методы оптимального проектирования. М.: Радио и
связь, 1984. 248 с.
Бекишев Г.А., Кратко М.И. Элементарное введение в геометрическое
программирование. М.: Наука, 1980. 144 с.
Бертсекас Д. Условная оптимизация и методы множителей Лагранжа:
Пер. с англ. М.: Радио и связь, 1987. 400 с.
Брайсон А., Хо Ю-Ши. Прикладная теория оптимального управления:
Пер. с англ. М.: Мир, 1972. 515 с.
Васютинский Н. Золотая пропорция. М.: Молодая гвардия, 1990. 235 с.
Введение в нелинейное программирование / Под ред. К.Х. Эль стера:
Пер. с англ. М.: Наука, 1985. 264 с.
Воробьев Н.Н. Числа Фибоначчи. М.: Наука, 1978. 144 с.
Галеев Э.М., Тихомиров В.М. Краткий курс теории экстремальных
задач. М.: Изд-во Моск. ун-та, 1985. 201 с.
Галкин СВ. Целенаправленные системы в физическо-духовном мире
(Мир, жизнь, разум). М., 1999. 284 с.
Геминтерн В.И., Каган В.М. Методы оптимального проектирования.
М.: Энергия, 1980. 160 с.
Билл Ф., Мюррей У., Райт М. Практическая оптимизация: Пер. с англ.
М.: Мир, 1985. 510 с.
Голъштейн Е.Г. Выпуклое программирование (элементы теории). М.:
Наука, 1970. 268 с.
Гроссман К., Каплан А.А. Нелинейное программирование на основе
безусловной минимизации. Новосибирск: Наука. Сиб. отд-ние, 1981. 183 с.
Дамбраускас А.П. Симплексный поиск. М.: Энергия, 1979. 176 с.
Данциг Дж. Линейное программирование: Пер. с англ. М.: Прогресс,
1966. 600 с.
Даффин Р., Питерсон Э., Зенер К. Геометрическое программирование:
Пер. с англ. М.: Мир, 1972. 312 с.
Демьянов В.Ф., Васильев Л.В. Недифференцируемая оптимизация. М.:
Наука, 1981. 384 с.
430 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРА ТУРЫ
Демьянов В.Ф., Малоземов В.Н. Введение в минимакс. М.: Наука,
1972. 368 с.
Дикин И.И., Зоркалъцев В. И. Итеративное решение задач
математического программирования: Алгоритмы метода внутренних точек.
Новосибирск: Наука. Сиб. отд-ние, 1980. 144 с.
Дэннис Дж., Шнабелъ Р. Численные методы безусловной оптимизации
и решения нелинейных уравнений: Пер. с англ. М.: Мир, 1988. 440 с.
Евдокимов А.Г. Минимизация функций. Харьков: Выща шк., 1977.
160 с.
Евтушенко Ю.Г. Методы решения экстремальных задач и их
применение в системах оптимизации. М.: Наука, 1982. 432 с.
Еремин И.И., Астафьев Н.Н. Введение в теорию линейного и
выпуклого программирования. М.: Наука, 1976. 192 с.
Ермольев Ю.М. Методы стохастического программирования. М.:
Наука, 1976. 240 с.
Зангвилл У.И. Нелинейное программирование. Единый подход: Пер. с
англ. М.: Сов. радио, 1973. 312 с.
Зенер К. Геометрическое программирование и техническое
проектирование: Пер. с англ. М.: Мир, 1973. 112 с.
Зойтендейк Е. Методы возможных направлений: Пер. с англ. М.: Изд-
во иностр. лит., 1963. 176 с.
Зуховицкий И.И., Авдеева Л. И. Линейное и выпуклое
программирование. М.: Наука, 1970. 264 с.
Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М.: Наука,
1974. 480 с.
Коробко В.И. Золотая пропорция и проблемы гармонии систем. М.:
Изд-во Ассоциации строительных вузов стран СНГ, 1998. 374 с.
Лейхтвейс К. Выпуклые множества. М.: Наука, 1985. 336 с.
Линейное и нелинейное программирование / Под ред. И.Н. Ляшенко.
Киев: Выща шк., 1975. 372 с.
Мину М. Математическое программирование. Теория и алгоритмы:
Пер. с франц. М.: Наука, 1990. 487 с.
Муртаф Б. Современное линейное программирование: Пер. с англ. М.:
Мир, 1984. 224 с.
Ногин В.Д., Протодьяконов И.О., Евлампиев И.И. Основы теории
оптимизации. М.: Высш. шк., 1986. 384 с.
О бен Ж.-П., Экланд И. Прикладной нелинейный анализ: Пер. с англ.
М.: Мир, 1988. 512 с.
Пападимитриу X, Стайглиц К. Комбинаторная оптимизация: Пер. с
англ. М.: Мир, 1984. 512 с.
431
Полак Э. Численные методы оптимизации. Единый подход: Пер. с
англ. М.: Мир, 1974. 376 с.
Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983. 384 с.
Пшеничный В.П. Метод линеаризации. М.: Наука, 1983. 136 с.
Пшеничный Б.Н., Данилин Ю.М. Численные методы в экстремальных
задачах. М.: Наука, 1975. 320 с.
Растригин Л. А. Статистические методы поиска. М.: Наука, 1968.
376 с.
Реклейтис Г., Рейвиндран Л., Рэгсдел К. Оптимизация в технике: В 2
кн.: Пер. с англ. М.: Мир, 1986.
Рокафеллар Р.Т. Выпуклый анализ: Пер. с англ. М.: Мир, 1973. 468 с.
Романовский И.В. Алгоритмы решения экстремальных задач. М.:
Наука, 1977. 352 с.
Рыков А.С. Поисковая оптимизация. Методы деформируемых
конфигураций. М.: Физматлит, 1993. 216 с.
Сеа Ж. Оптимизация. Теория и алгоритмы: Пер. с англ. М.: Мир,
1973. 244 с.
Соболь И.М., Статников Р. Б. Выбор оптимальных параметров в
задачах со многими критериями. М.: Наука, 1981. 111 с.
Стронгин Р.Г. Численные методы в многоэкстремальных задачах
(информационно-статистические алгоритмы). М.: Наука, 1978. 240 с.
Уайлд Д. Оптимальное проектирование: Пер. с англ. М.: Мир, 1981.
272 с.
Федоров В.В. Численные методы максимина. М.: Наука, 1979. 279 с.
Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы
последовательной безусловной минимизации: Пер. с англ. М.: Мир, 1972.
240 с.
Филиппов П.В., Королев Н.Т., Чистая И.В. Начертательная геометрия
многомерного пространства в линейном программировании. Л.: Изд-во
Ленингр. ун-та, 1986. 136 с.
Хедли Дж. Нелинейное и динамическое программирование: Пер. с
англ. М.: Мир, 1967. 506 с.
Химмелъблау Д. Прикладное нелинейное программирование: Пер. с
англ. М.: Мир, 1975. 534 с.
Хог Э., Арора Я. Прикладное оптимальное проектирование: Пер. с
англ. М.: Мир, 1967. 480 с.
Чичинадзе В.К. Решение невыпуклых нелинейных задач оптимизации.
М.: Наука, 1983. 256 с.
Шор Н.З. Методы минимизации недифференцируемых функций и их
приложения. Киев: Наук, думка, 1979. 199 с.
432 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРА ТУРЫ
Шор Н.Э., Стеценко СИ. Квадратичные экстремальные задачи и
недифференцируемая оптимизация. Киев: Наук, думка, 1989. 203 с.
Щуп Т.Е. Прикладные численные методы в физике и технике: Пер. с
англ. М.: Высш. шк., 1990. 256 с.
Щедрин Н.И., Кархов А.И. Математические методы
программирования в экономике. М.: Статистика, 1974. 144 с.
Юдин Д.Б., Голъштейн Е.Г.. Линейное программирование. Теория,
методы, приложения. М.: Наука, 1969. 424 с.
Задачники
Акулич И.Л. Математическое программирование в примерах и
задачах. М.: Высш. шк., 1986. 320 с.
Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по
оптимизации. М.: Наука, 1984. 287 с.
Ашманов С.А., Тимохов А.В. Теория оптимизации в задачах и
упражнениях. М.: Наука, 1991. 448 с.
Калихман И. Л. Сборник задач по математическому
программированию. М.: Высш. шк., 1975. 272 с.
Капустин В. Ф. Практические занятия по курсу математического
программирования. Л.: Изд-во Ленингр. ун-та, 1976. 192 с.
Михайленко В.М., Антонюк Р.А. Сборник прикладных задач по
высшей математике. Киев: Выща шк., 1990. 168 с.
Сборник задач по математике для втузов. Ч. 4. Методы оптимизации.
Уравнения в частных производных. Интегральные уравнения: Учеб.
пособ. / Под ред. А.В.Ефимова. 2-е изд., перераб. М.: Наука, 1990. 304 с.
Справочные издания
Александрова Н.В. Математические термины: Справочник. М.: Высш.
шк., 1978. 190 с.
Бронштейн И.Н., Семендяев К.А. Справочник по математике для
инженеров и учащихся втузов. 13-е изд., испр. М.: Наука, 1986. 544 с.
Корн Г., Корн Т. Справочник по математике: Для научных работников
и инженеров: Пер. с англ. М.: Наука, 1973. 832 с.
Математический энциклопедический словарь / Гл. ред. Ю.В. Прохоров.
М.: Сов. энцикл., 1988. 848 с.
предметный указатель
Альтернатива 15
Антиградиент 175
Вектор перемещений 285
Векторы сопряженные 205
Вершина симплекса 103
Веса нормированные 150
Гиперплоскость 98
Градиент приведенный 347
- обобщенный 393
Дополнение ортогональное IV
Задача выпуклого
программирования 48
- геометрического
программирования 47
- двойственная 323
- дискретного программирования
48
- дробно-линейного
программирования 45
- Евклида 19
- квадратичного
программирования 45
- линейного программирования
XX, 17
в стандартной форме XX, 44
естественная 45
общая 45
основная 45
стандартная 44
- математического
программирования XX, 17
общая 42
- минимизации 43
- нелинейного программирования
XX, 17
общая 47
- о диете XX, 39
- оптимизации 15
- конечномерная 17
- сепарабельного
программирования 46
- транспортная XX, 38
- целочисленного
программирования 48
.Интервал неопределенности 55
.Комбинация выпуклая 98
- строго выпуклая 101
Конус допустимых направлений 302
Коэффициент дробления шага 212
- отражения 270
- растяжения 272
- редукции 265
- сжатия 272
Критерий оптимальности XX, 16
Масштабирование 194
Матрица знаконеопределенная 119
- идемпотентная 370
- неотрицательно определенная 119
- неположительно определенная 119
434
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Матрица отрицательно
определенная IV, 119
- положительно определенная IV,
119
- поправочная 242
- проекционная 370
- Якоби функции по части
переменных V, 347
Метод возможных направлений 396
- градиентного спуска 177
- дихотомии 61
- дробления шага 188
- золотого сечения 64
- квадратичной аппроксимации 75
- кубической аппроксимации 90
- наискорейшего спуска 178
- Ньютона V, 200
- (касательных) II, 84
- упрощенный II, 88
- поиска минимаксный 56
- покоординатного циклического
спуска 282
- приведенного градиента 348
- проекции антиградиента 377
- точки на множество 362
- прямого поиска 53
- секущих II, 88
- сопряженных градиентов 224
- направлений 219
- средней точки 83
- условного градиента 340
- Фибоначчи 69
- хорд I- 348, 89
- штрафных функций внешних 410
внутренних 410
Методы второго порядка 163
- квазиньютоновские 241
- нулевого порядка 163
- первого порядка 163
Методы полиномиальной
аппроксимации 75
- прямого поиска 163
- спуска 165
Минимизация одномерная 50
Минимум локальный на множестве
303
строгий 304
Минор диагональный 121
Многогранник выпуклый 103
Многообразие аффинное 97
Многочлен интерполяционный
Эрмита кубический II, 90
Множество выпуклое IX, 95
- многогранное 100
- допустимое 42
- строго выпуклое 101
Множитель ускоряющий 286
Модель математическая XX, 16
Момент инерции геометрический
VI
- обновления алгоритма 226
.Направление допустимое 302
- спуска 171
- возможное 340
- ньютоновское 200
Направления сопряженные 205
Неизвестное базисное IV, 346
- свободное IV, 347
Неравенство взвешенных средних
150
- Иенсена 108
Норма евклидова IV, 107
- кубическая IV, 107
- октаэдрическая IV, 107
- спектральная IV, 195
Нумерация вершин правильная 261
Оболочка выпуклая 101
Объект оптимизации 15
435
Ограничение 16
- активное 315
- неактивное 315
- прямое 45
- двустороннее 45
- одностороннее 45
- типа неравенства 16
- равенства 16
Операция восстановления
симплекса 273
Определитель Вандермонда III, 76
Ортант неотрицательный 44
- положительный 46
Ось тела центральная VII
Отношение золотого сечения 64
Отображение сжимающее I- 315, IV,
195
Отражение вершины 261
Отрезок I- 47, IX, 95
Параметр оптимизации 16
- сильной выпуклости 132
- точности поиска 170
- штрафа 411
Переменное базисное XX, 347
- задачи 42
- свободное XX, 347
Плоскость т-мерная V, 97
Позином 46
- регулярный 154
Поиск исследующий 285
- пассивный 54
- оптимальный 58
- последовательный 54
- прямой управляемый 259
- симплексный 258
Полупространство 98
Последовательность
релаксационная 165
Правило множителей Лагранжа
обобщенное 309
Проекция точки на множество 356
Процедура исключения отрезка 60
-Расстояние от точки (элемента) до
множества IX, 356
Редукция симплекса 264
Рестарт 226
Решение допустимое XX, 42
- оптимальное XX, 43
Стечение отрезка золотое 63
- функции 109
Символ Кронекера IV, 421
Симплекс 103
- регулярный 258
Симплекс-метод XX, 348
- выпуклый 348
Скорость сходимости квадратичная
II, 86
- сверхлинейная II, 89
Спуск исчерпывающий 184
Структура овражная 194, 269
Сходимость локальная II, 85
- сильная 170
- слабая 170
X еорема двойственности 323
- Каратеодори 104
- Куна — Таккера 315
Тетраэдр VII, 104
Точка базовая 257
- множества крайняя 101
- начальная 84
- седловая 319
Уравнение связи V, 307
Условие квазиньютоновское 243
436
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Условия дополняющей нежесткости
315
- ортогональности 151
Формула конечных приращений II
Функция выпуклая 106
- двойственная 323
- к позиному 151
- индикаторная 409
- квадратичная 45
- Лагранжа 315
- мультимодальная 56
- сепарабельная 46
- сильно выпуклая 132
- строго выпуклая 106
Функция строго унимодальная 52
- унимодальная 52
- целевая V, XX, 17
- штрафа 410
- внешнего 417
- внутреннего 411
- штрафная 410
Числа Фибоначчи 69
Число обусловленности матрицы
IV, 196
Шаблон 257
Шаг поиска 54
- покоординатного спуска 282
- спуска 171
ОГЛАВЛЕНИЕ
Предисловие 5
Основные обозначения 11
1. Задачи оптимизации 15
1.1. Основные понятия 16
1.2. Некоторые простые примеры 17
1.3. Задачи оптимального проектирования 23
1.4. Задачи оптимального планирования 37
1.5. Классы задач оптимизации 42
Вопросы и задачи 48
2. Методы одномерной минимизации 50
2.1. Предварительные замечания 50
2.2. Пассивный и последовательный поиск 53
2.3. Оптимальный пассивный поиск 58
2.4. Методы последовательного поиска 61
2.5. Сравнение методов последовательного поиска .... 71
2.6. Методы полиномиальной аппроксимации 75
2.7. Методы с использованием производных 81
Вопросы и задачи 93
3. Минимизация выпуклых функции 95
3.1. Выпуклые множества 95
3.2. Выпуклые функции 106
3.3. Дифференцируемые выпуклые функции 116
3.4. Условия минимума выпуклых функций 126
3.5. Сильно выпуклые функции 132
3.6. Примеры минимизации квадратичных функций . . . 142
3.7. Минимизация позиномов 148
Вопросы и задачи 160
438 ОГЛАВЛЕНИЕ
4. Численные методы безусловной минимизации 163
4.1. Релаксационная последовательность 164
4.2. Методы спуска 171
4.3. Метод градиентного спуска 178
4.4. Минимизация квадратичной функции 190
4.5. Сопряженные направления спуска 199
Вопросы и задачи 209
5. Алгоритмы методов первого и второго порядков 211
5.1. Алгоритмы метода градиентного спуска 211
5.2. Метод сопряженных направлений 219
5.3. Метод Ньютона 229
5.4. Модификации метода Ньютона 236
5.5. Квазиньютоновские методы 241
Вопросы и задачи 254
6. Алгоритмы прямого поиска 256
6.1. Особенности прямого поиска минимума 257
6.2. Использование регулярного симплекса 259
6.3. Поиск при помощи нерегулярного симплекса 269
6.4. Циклический покоординатный спуск 281
6.5. Метод Хука — Дживса 285
6.6. Методы Розенброка и Пауэлла 292
Вопросы и задачи 298
7. Аналитические методы нелинейного
программирования 301
7.1. Минимизация целевой функции на заданном множестве 301
7.2. Минимизация при ограничениях типа равенства . . . 306
7.3. Общая задача нелинейного программирования .... 310
7.4. Седловая точка функции Лагранжа 318
7.5. Двойственная функция 321
7.6. Геометрическое программирование 326
Вопросы и задачи 335
439
8. Численные методы нелинейного программирования 337
8.1. Метод условного градиента 337
8.2. Использование приведенного градиента 345
8.3. Проектирование точки на множество 356
8.4. Метод проекции точки на множество 362
8.5. Метод проекции антиградиента 369
8.6. Другие методы проектирования 389
8.7. Метод возможных направлений 393
8.8. Методы последовательной безусловной минимизации 409
Д.8.1. Некоторые приемы обращения матрицы 421
Вопросы и задачи 425
Список рекомендуемой литературы 428
Предметный указатель 433
Учебное издание
Математика в техническом университете
Выпуск XIV
Аттетков Александр Владимирович
Галкин Сергей Владимирович
Зарубин Владимир Степанович
МЕТОДЫ ОПТИМИЗАЦИИ
Редактор Н.Г. Ковалевская
Художник С. С. Водчиц
Корректор Е.В. Авалова
Оригинал-макет подготовлен
в Издательстве МГТУ им. Н.Э. Баумана
под руководством А. Н. Канатников а
Подписано в печать 19.05.2003. Формат 60x88 1/16.
Печать офсетная. Бумага офсетная.
Усл. печ. л. 27,5. Уч.-изд. л. 25,86.
Тираж 3000 экз. Заказ №
Издательство МГТУ им. Н.Э. Баумана.
105005, Москва, 2-я Бауманская, 5.
Отпечатано в ГУП ППП «Типография «Наука».
121099, г. Москва, Шубинский пер., 6.