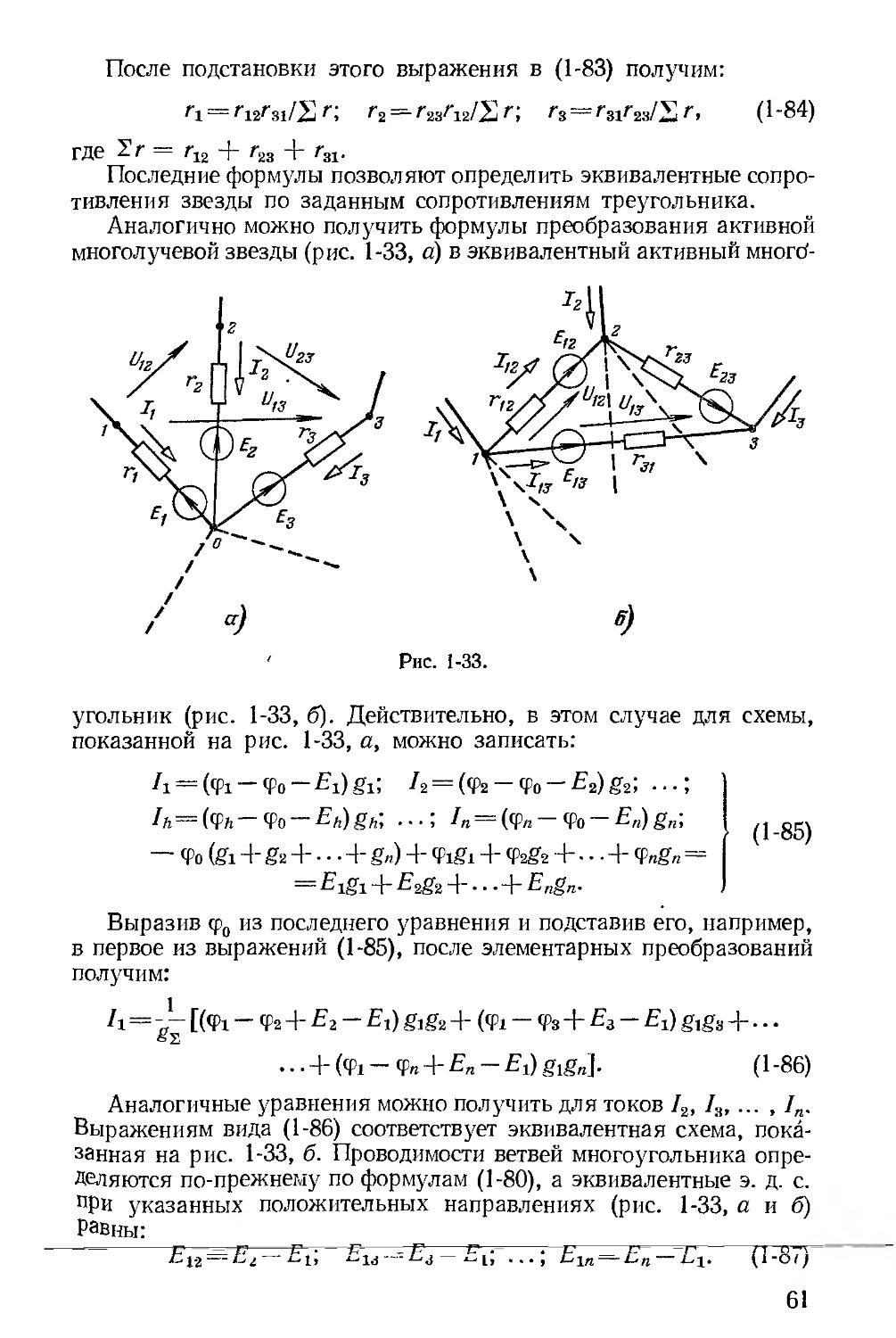
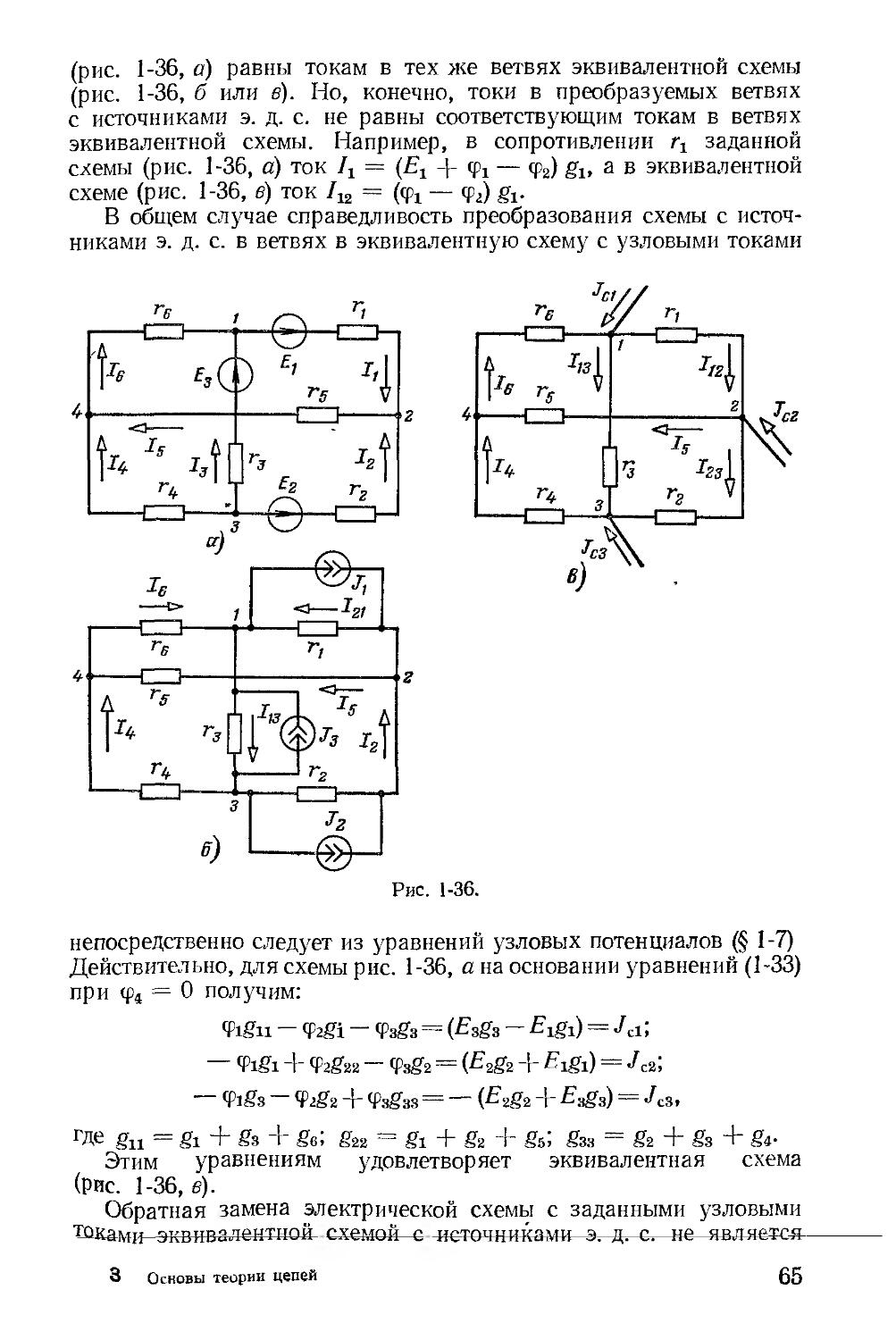
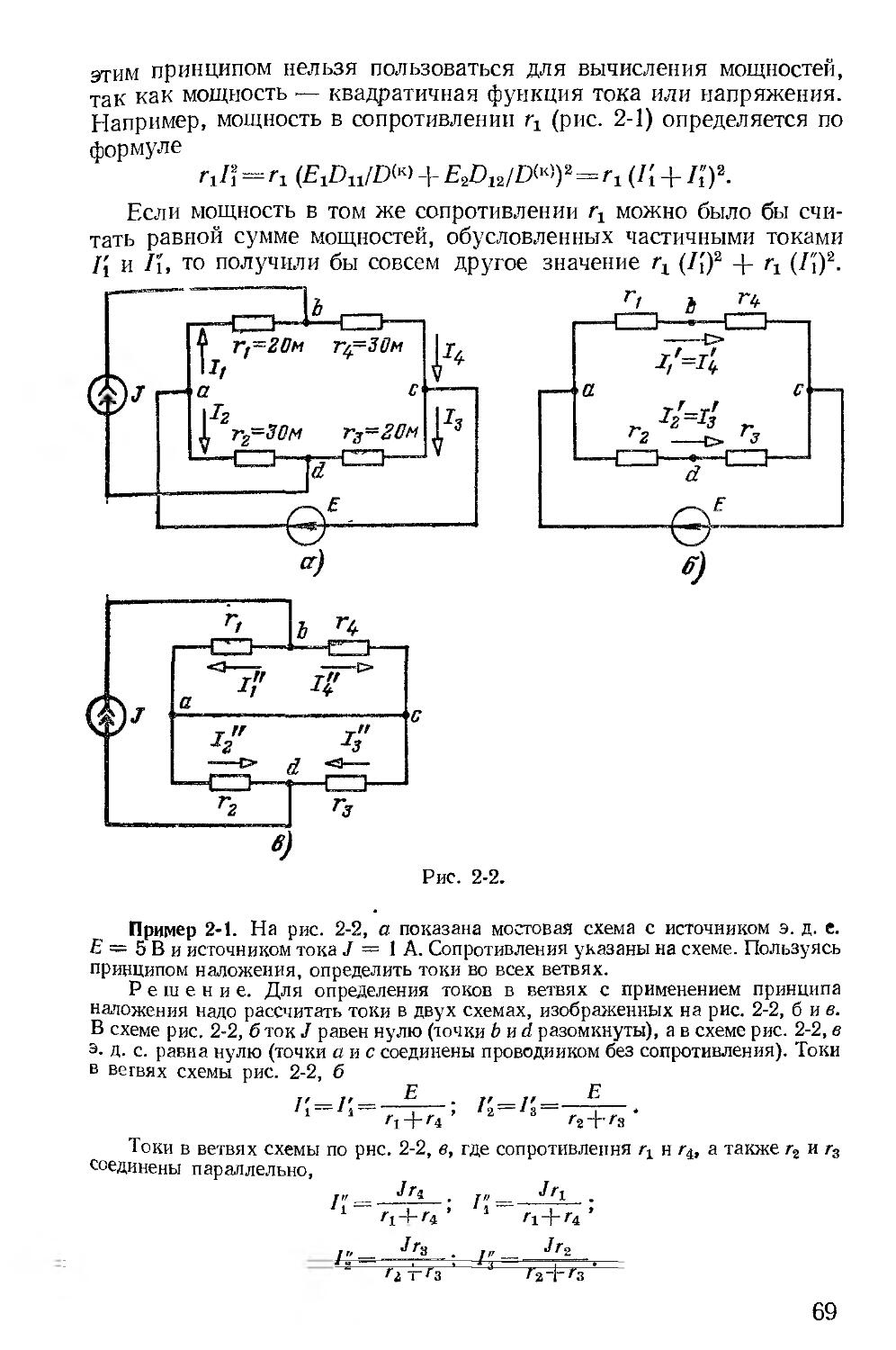
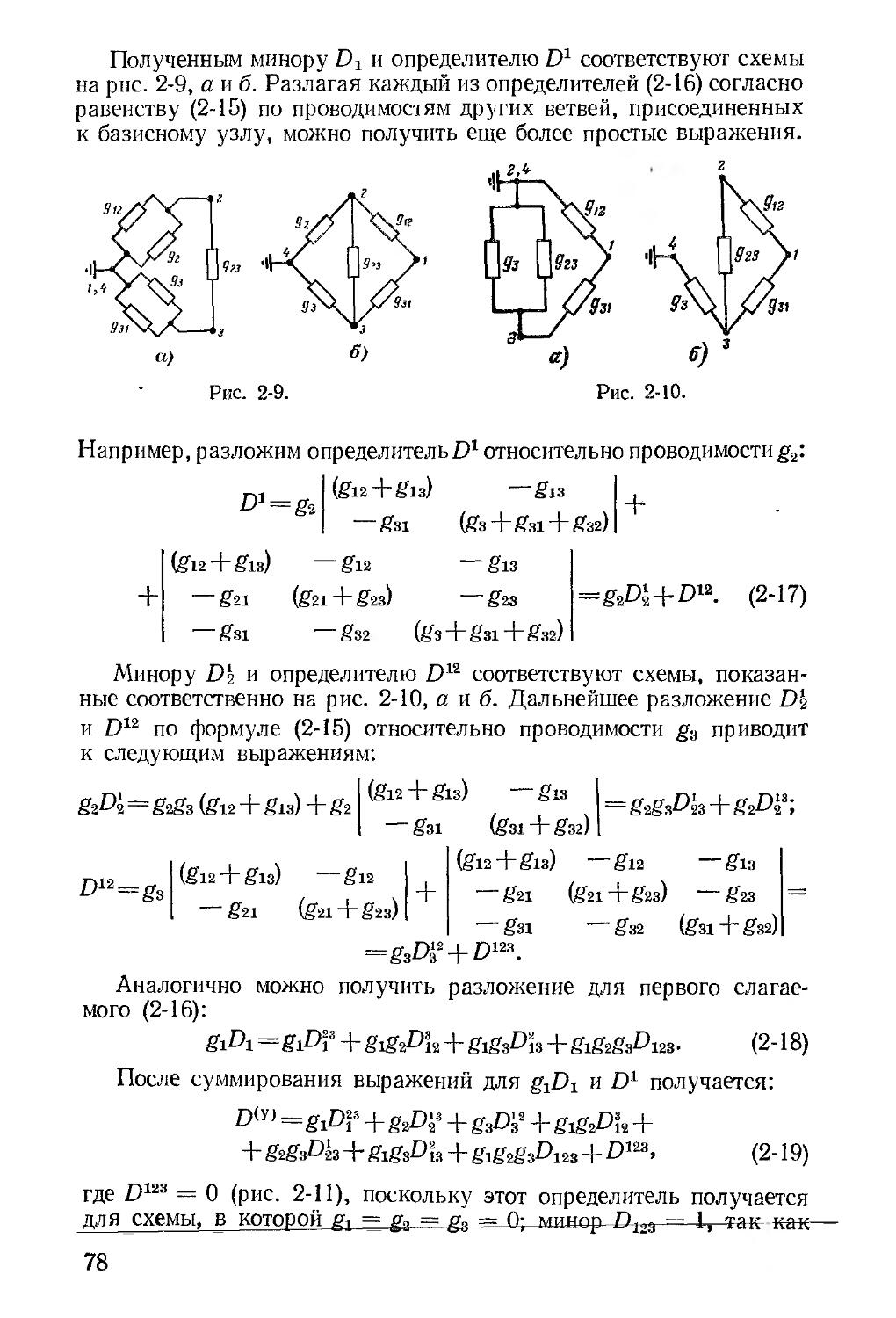
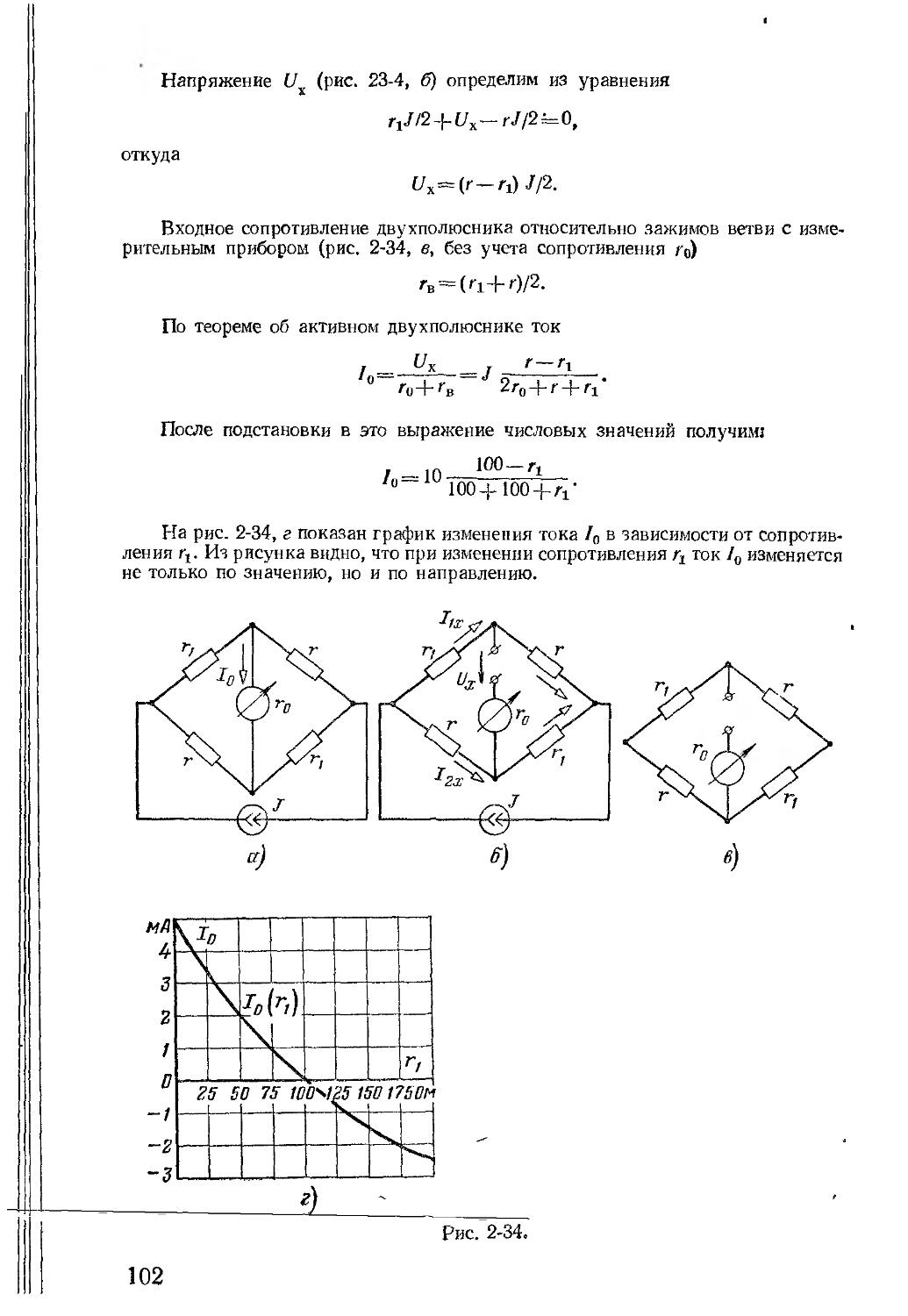
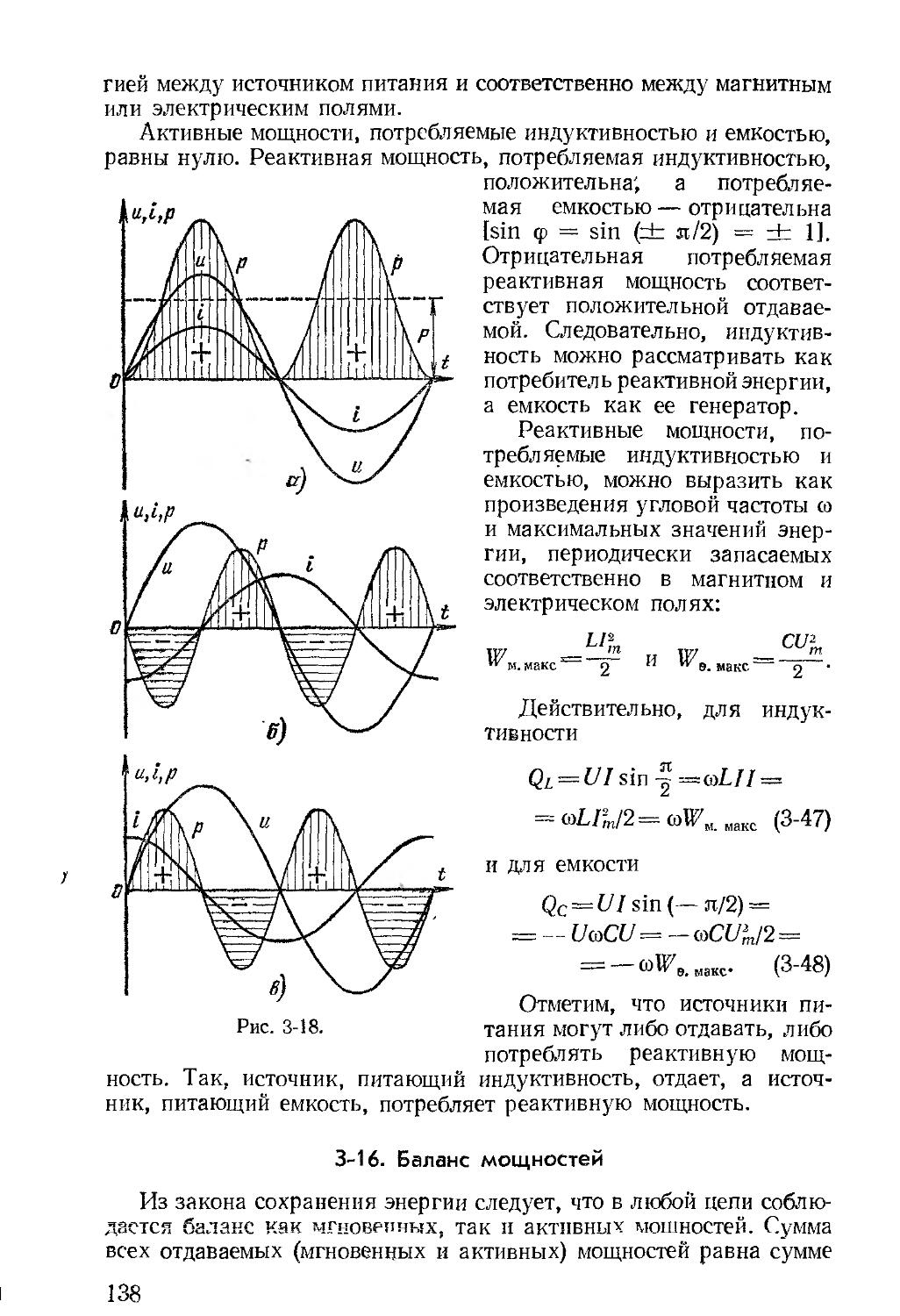
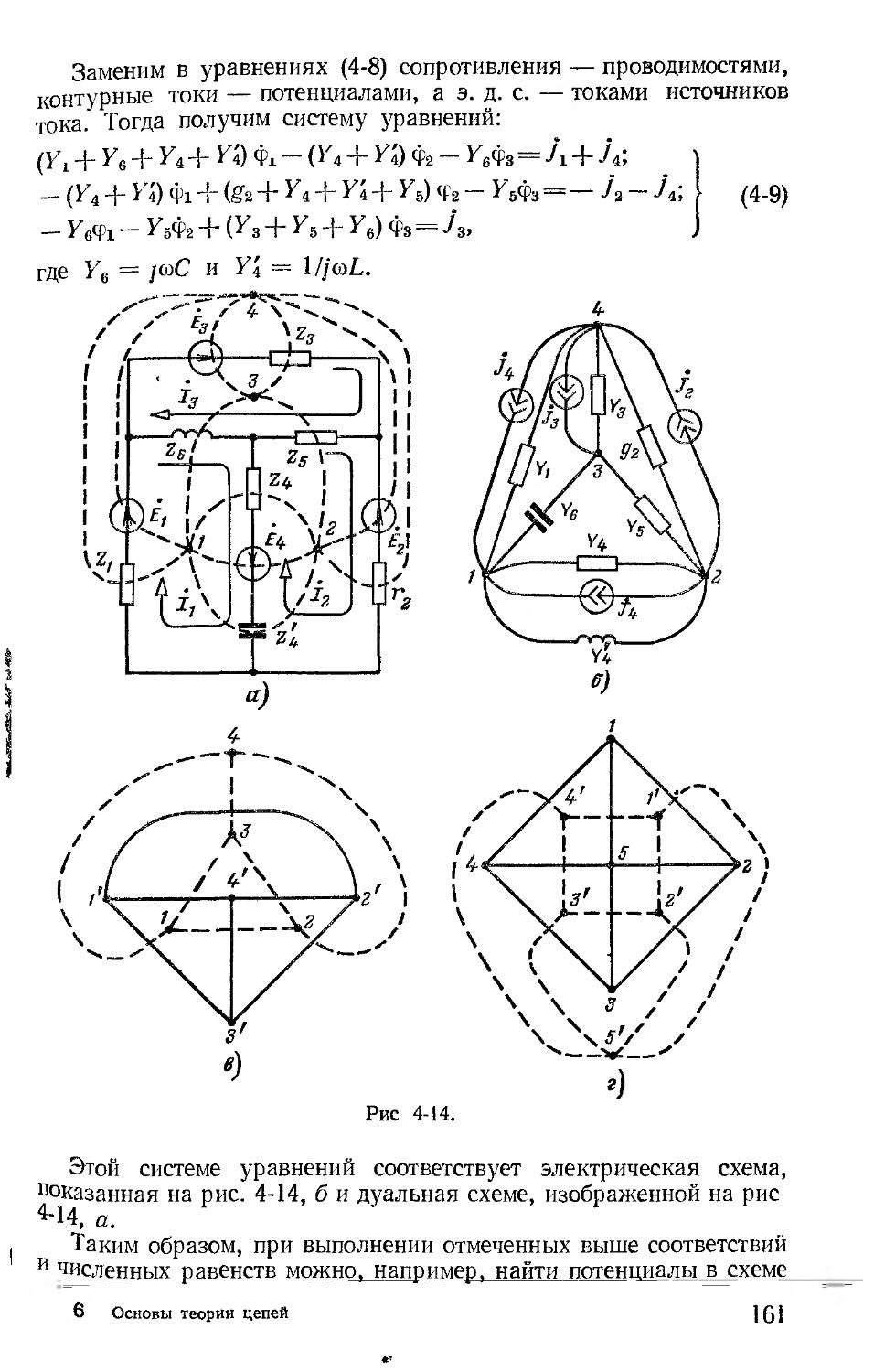
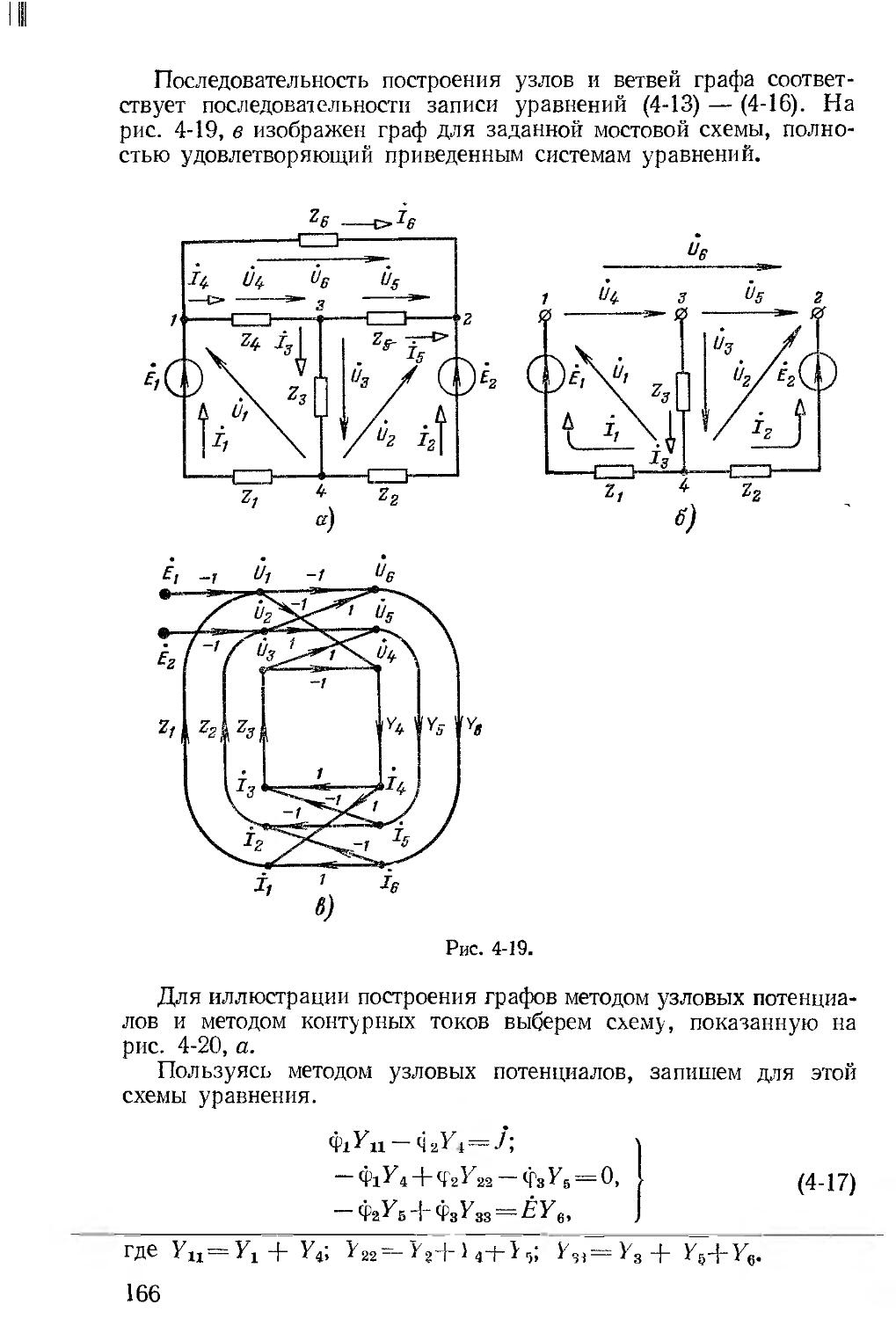
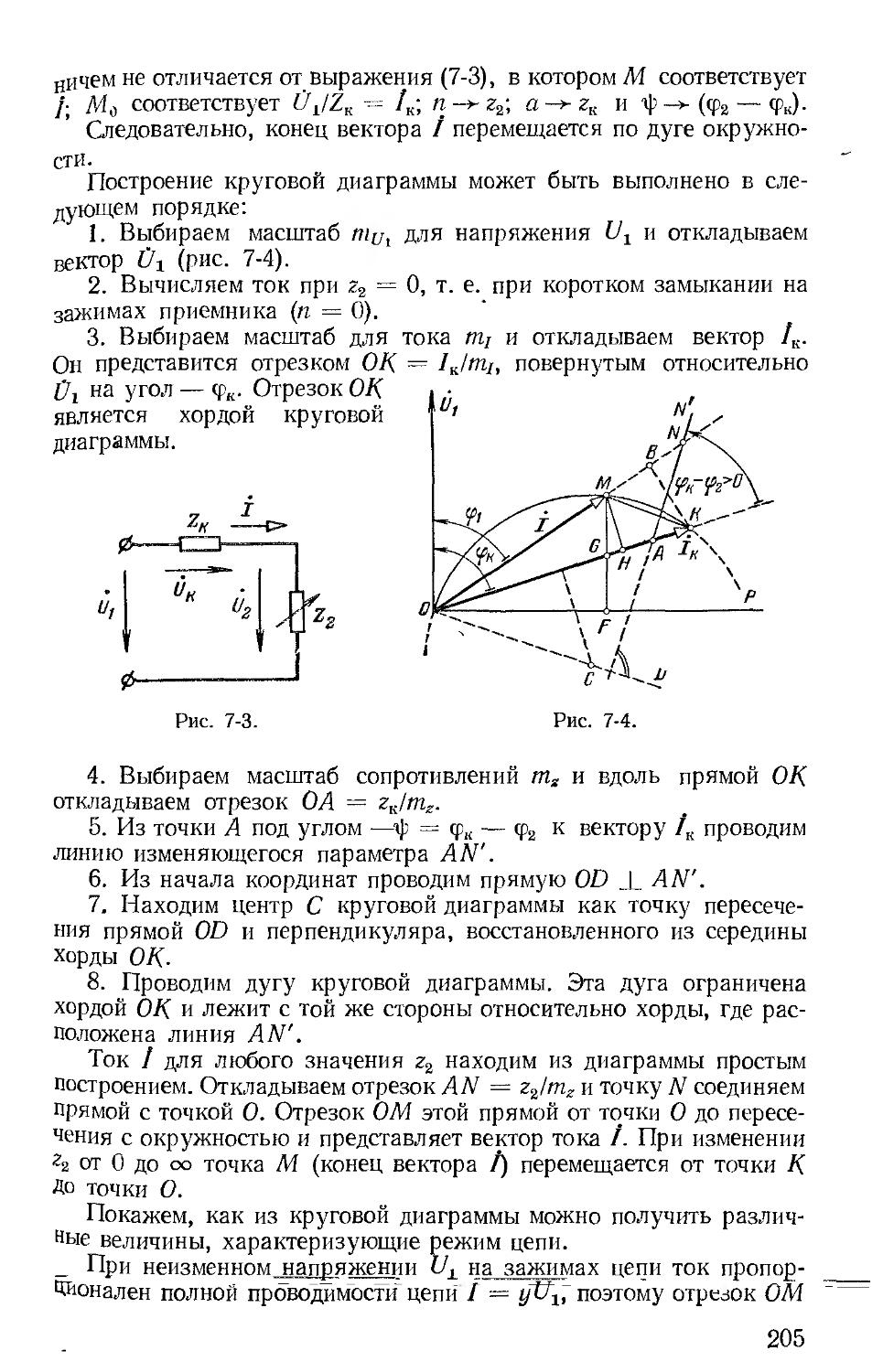
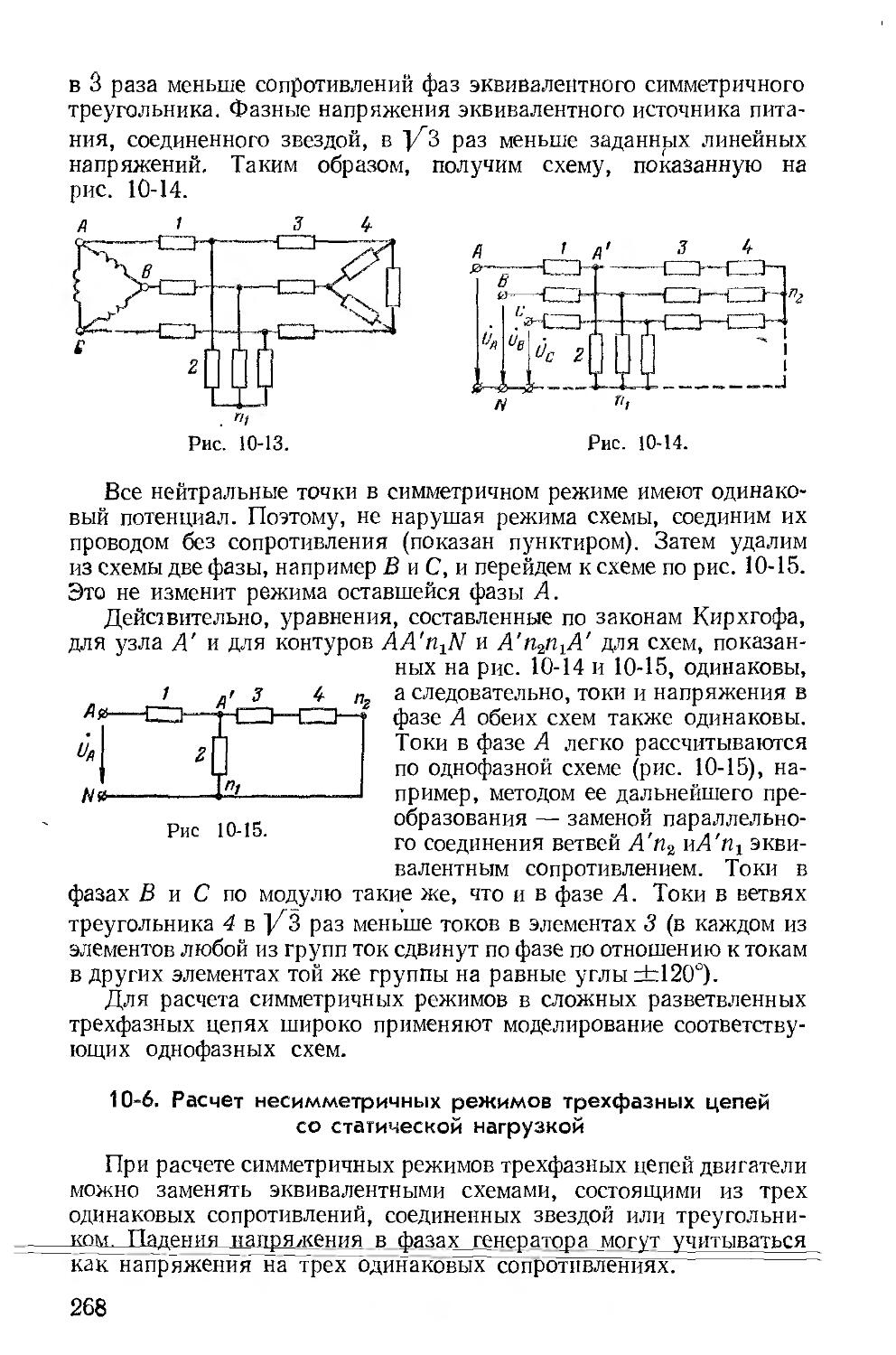
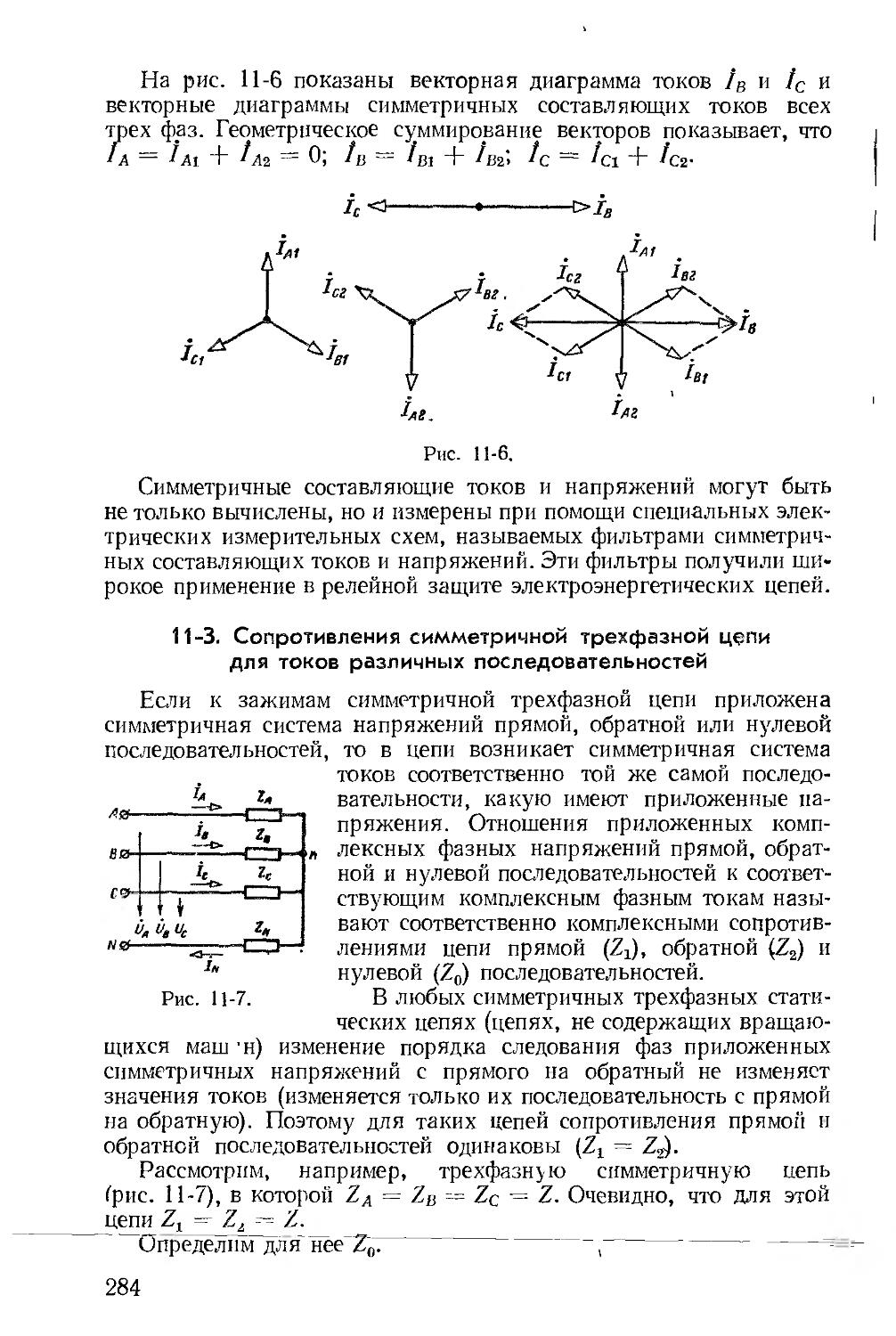
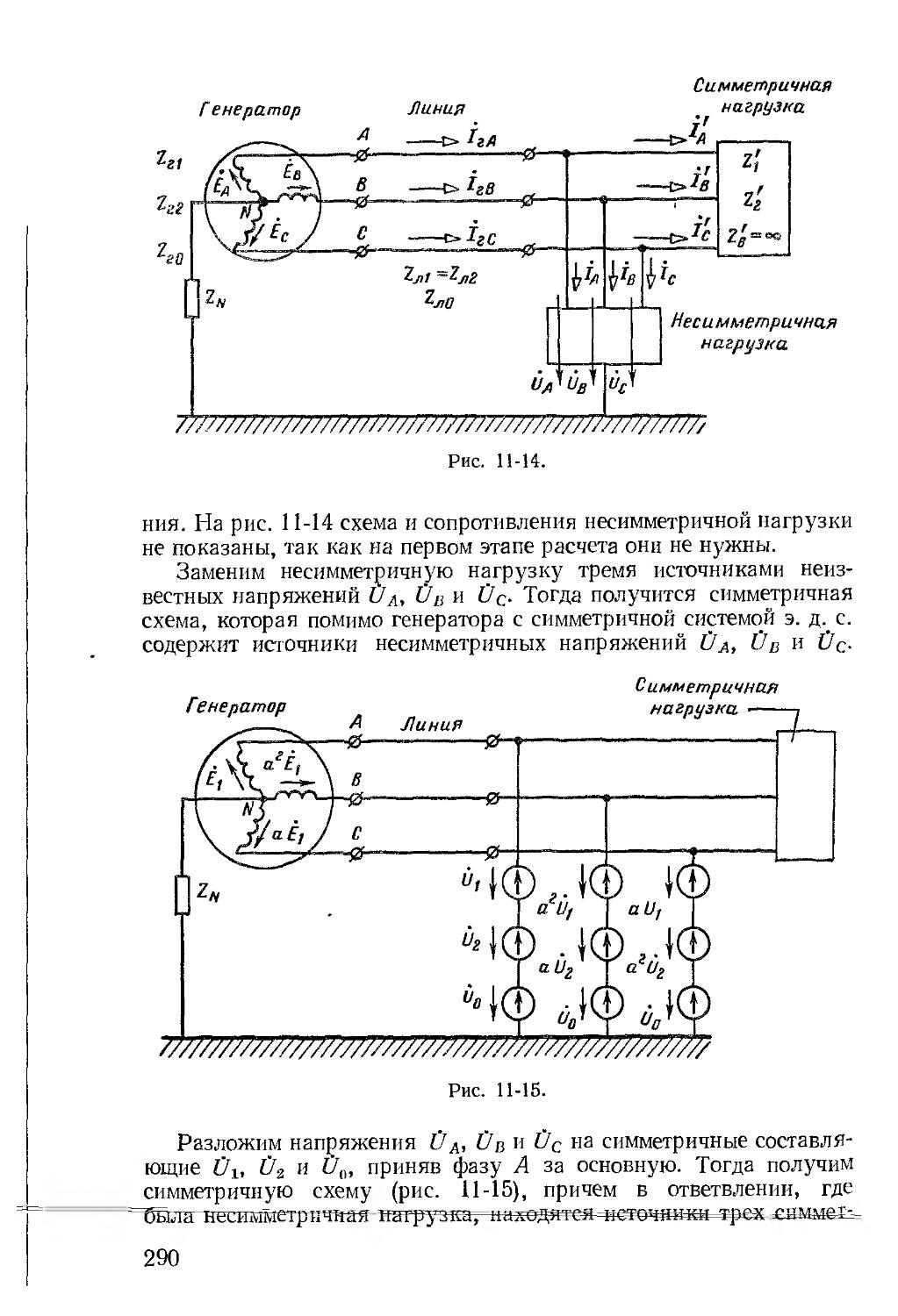
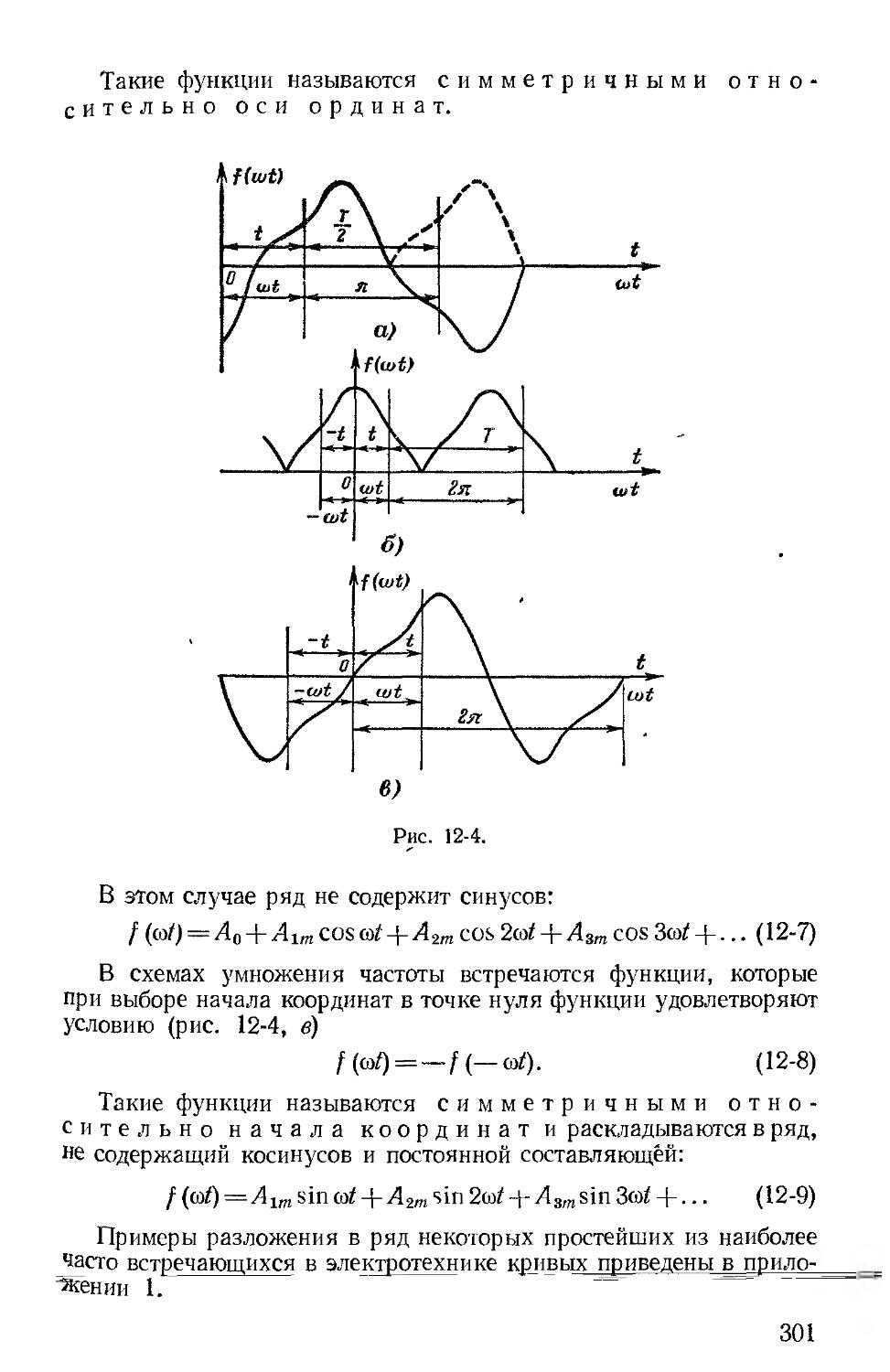
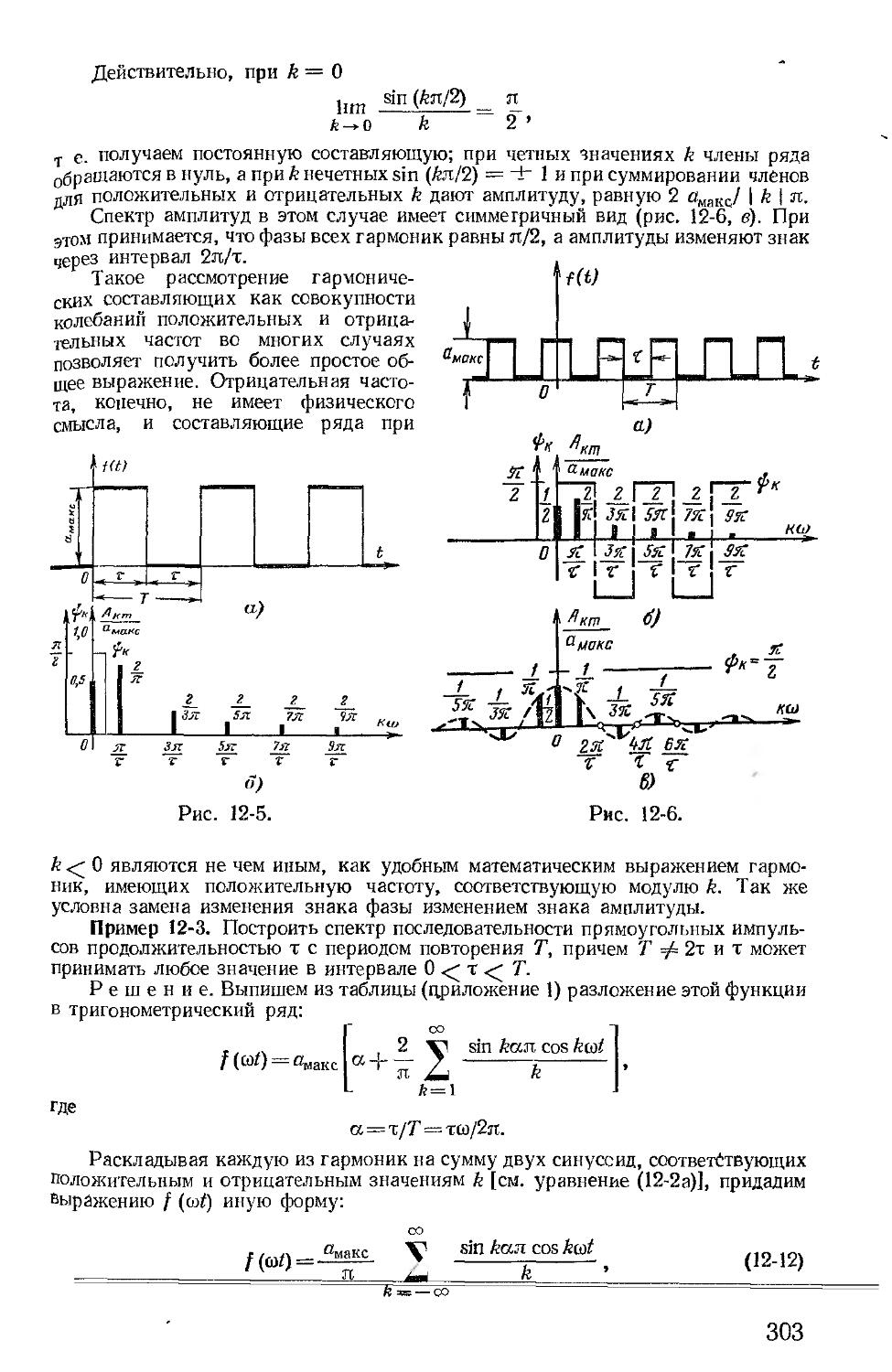
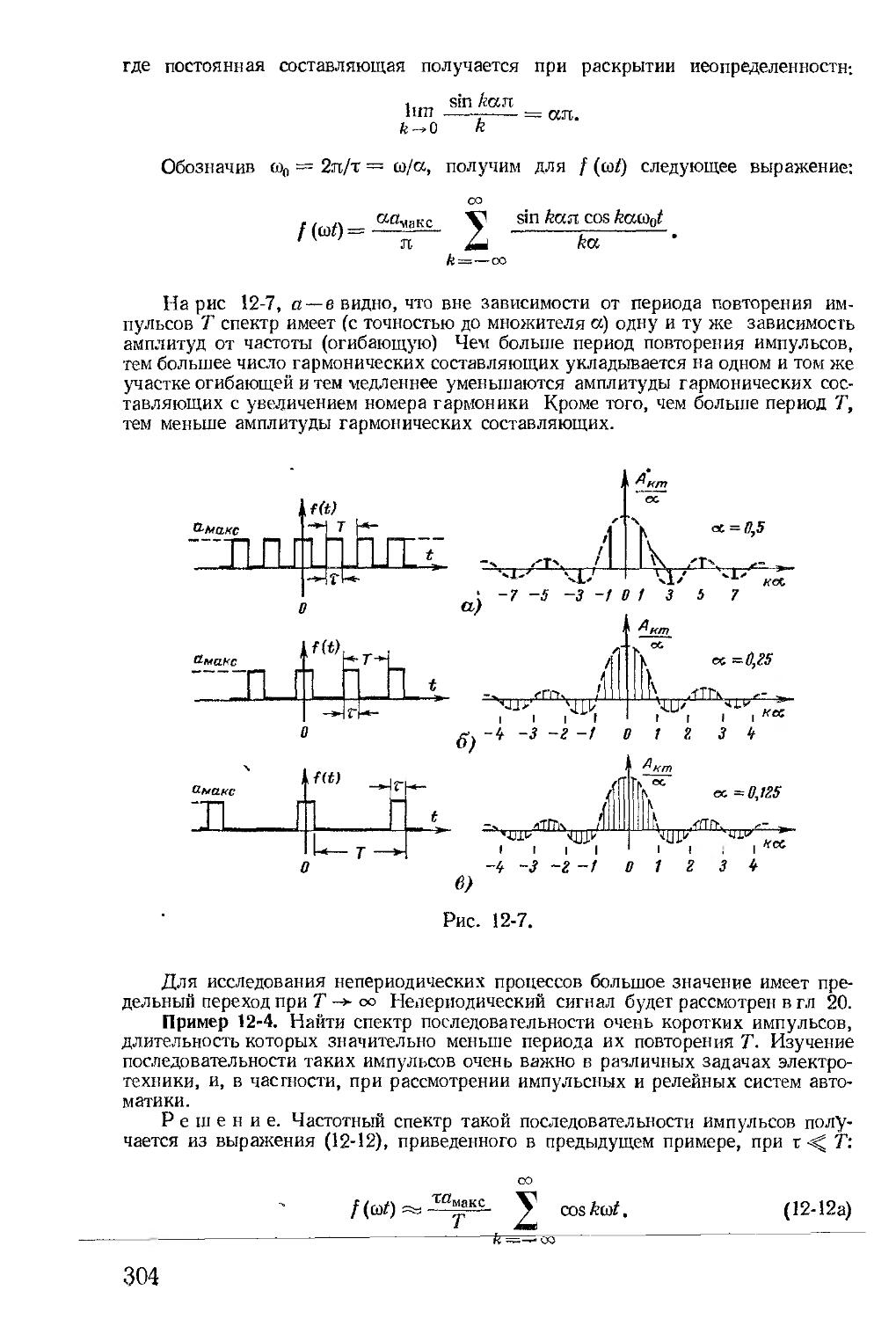
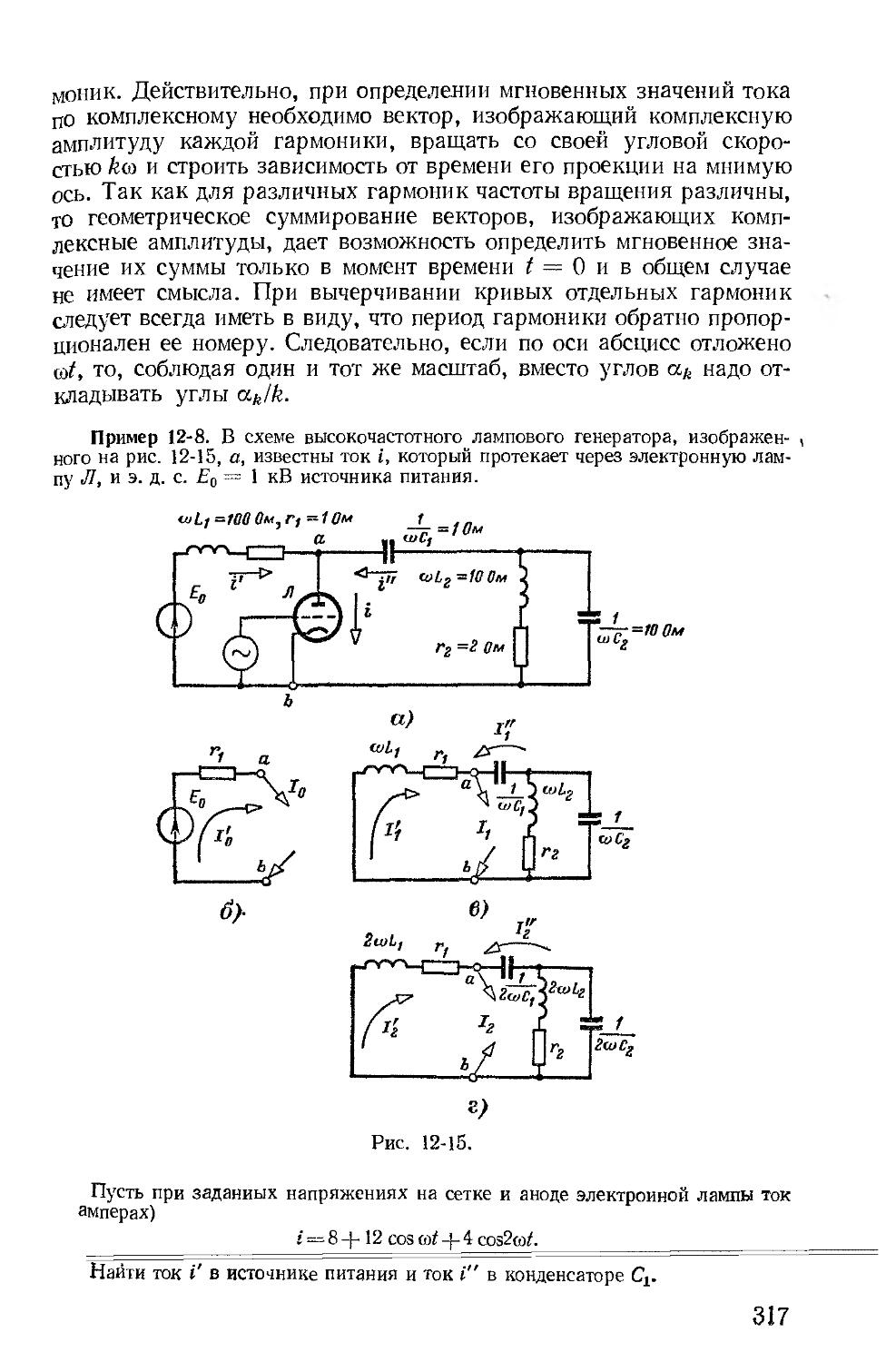
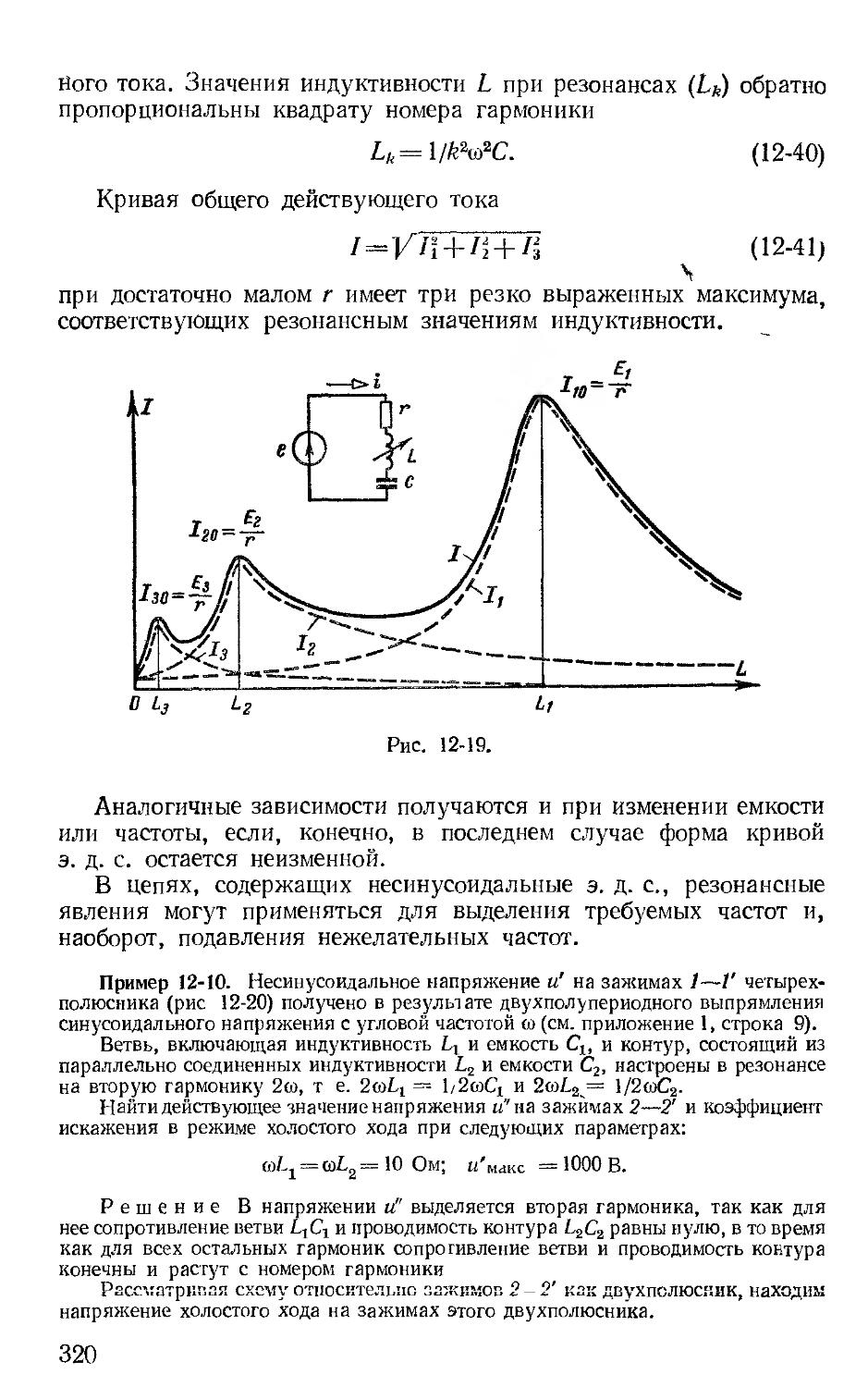
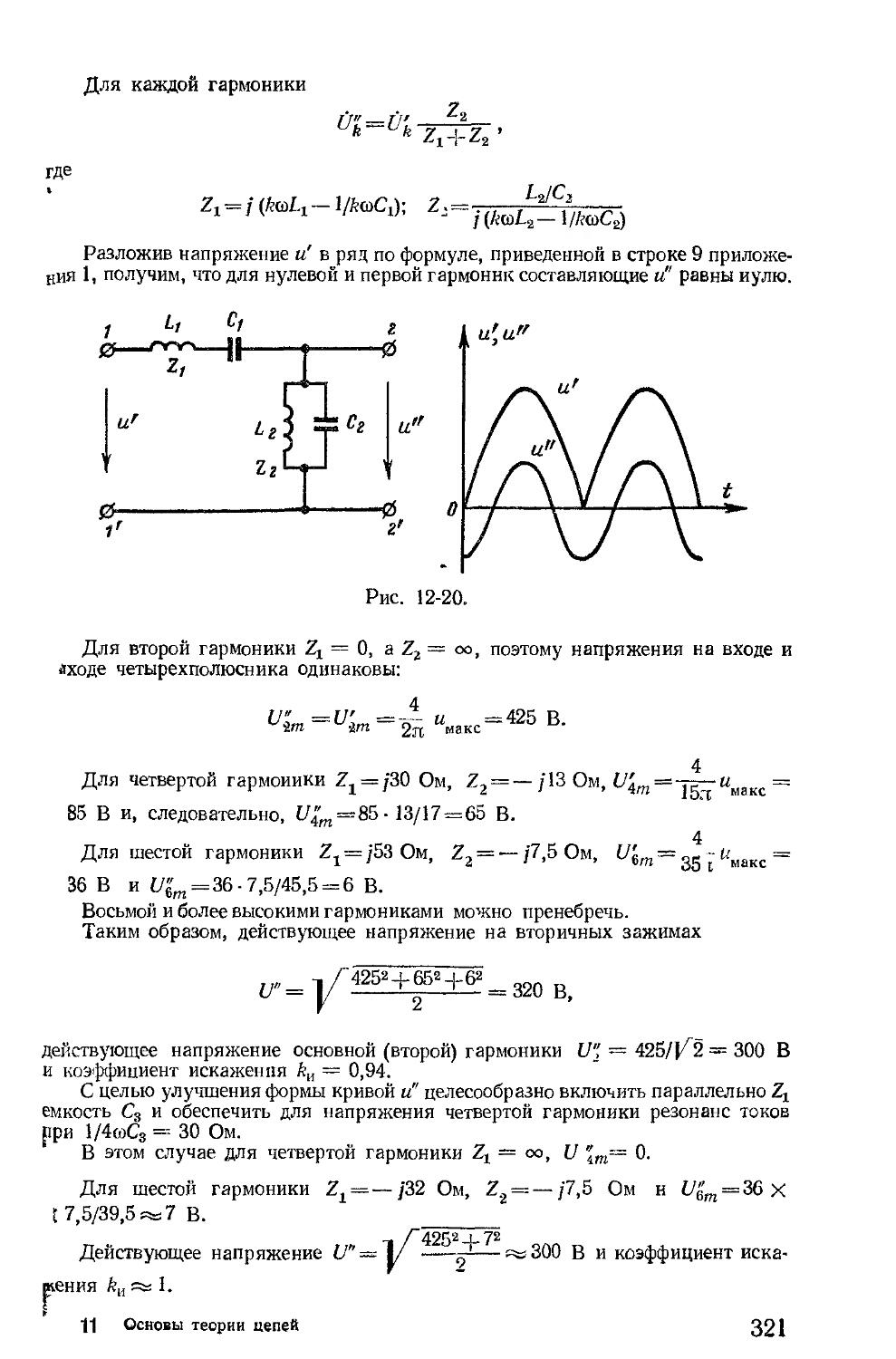
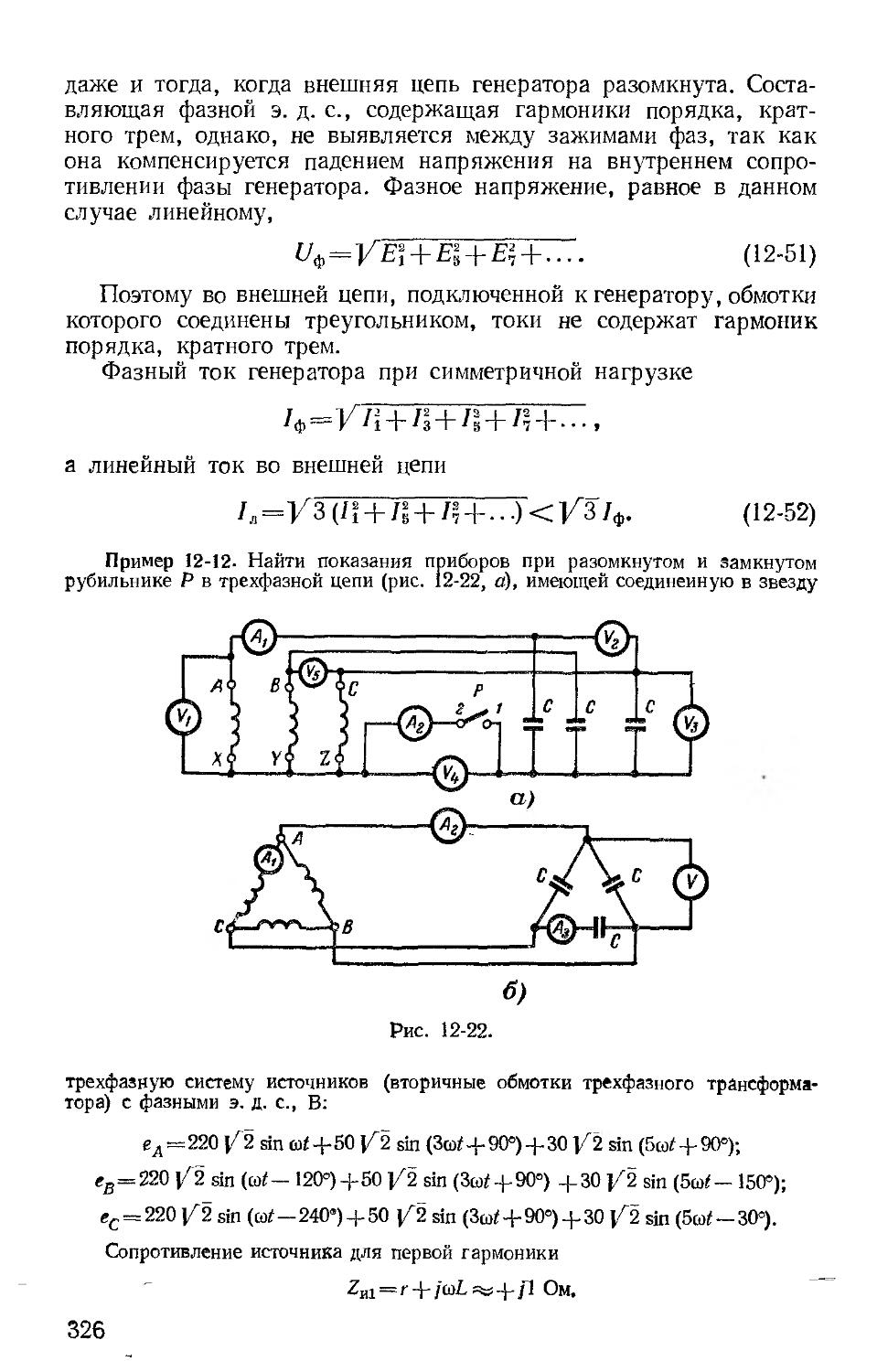
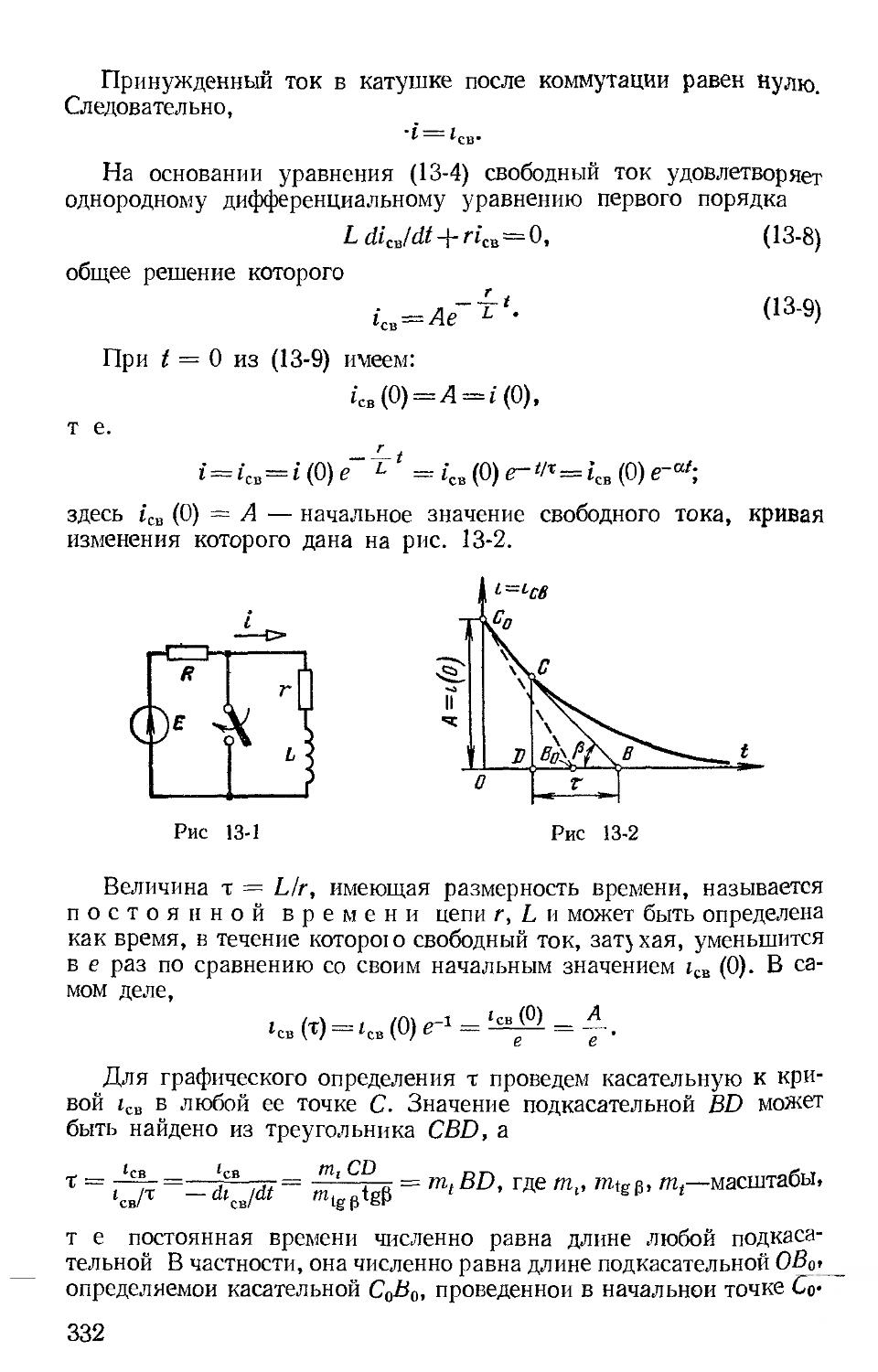
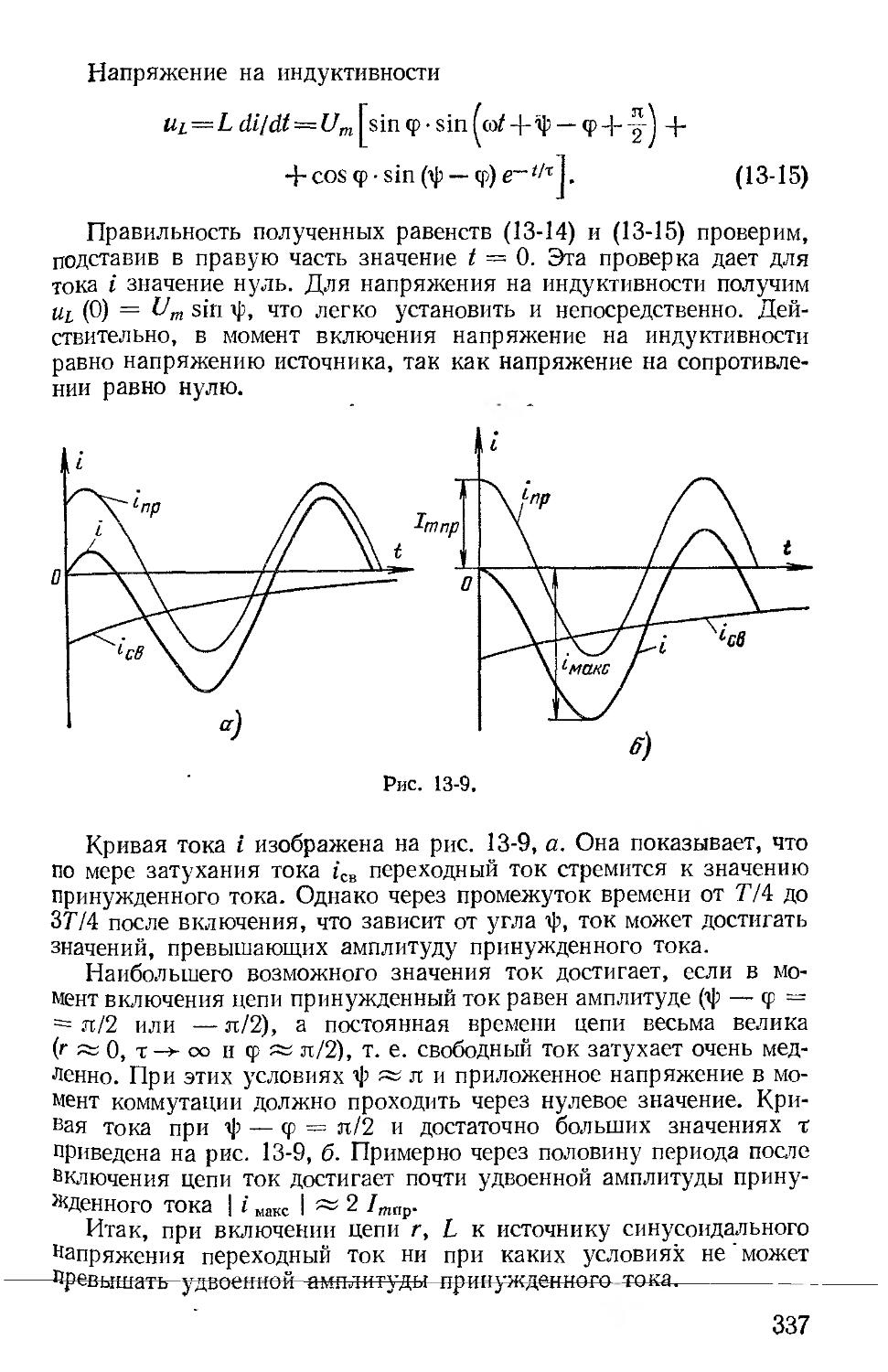
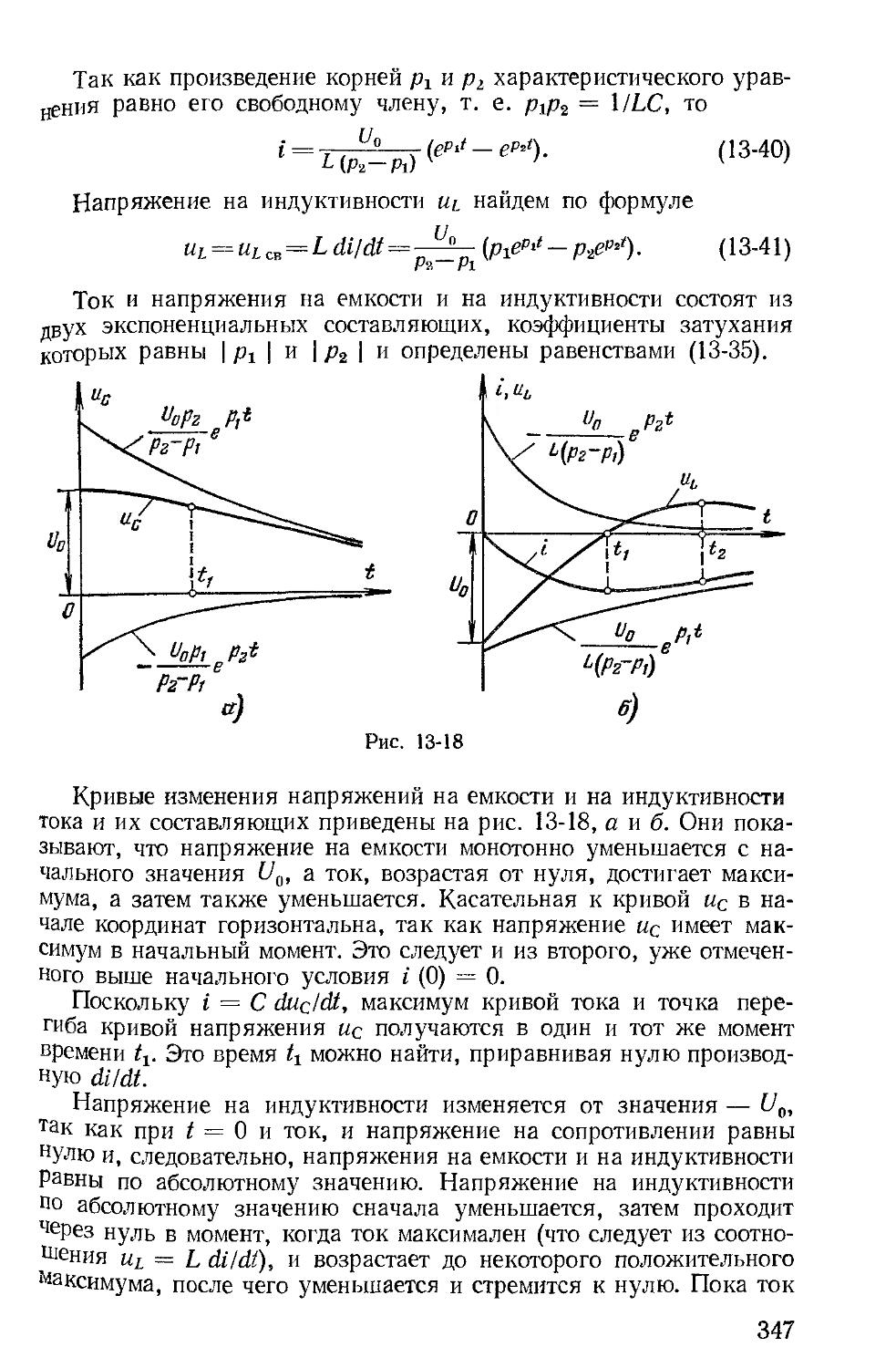
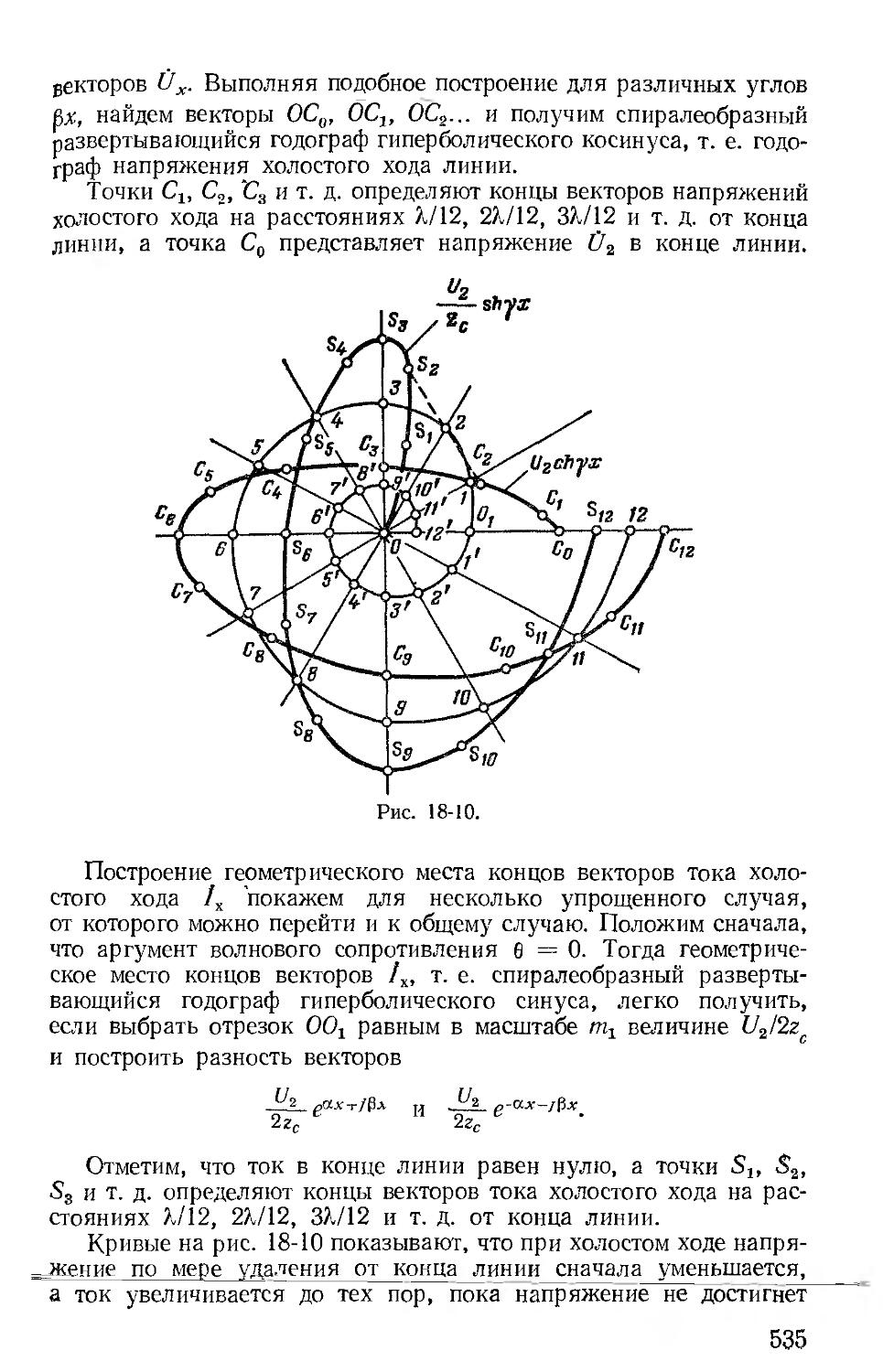
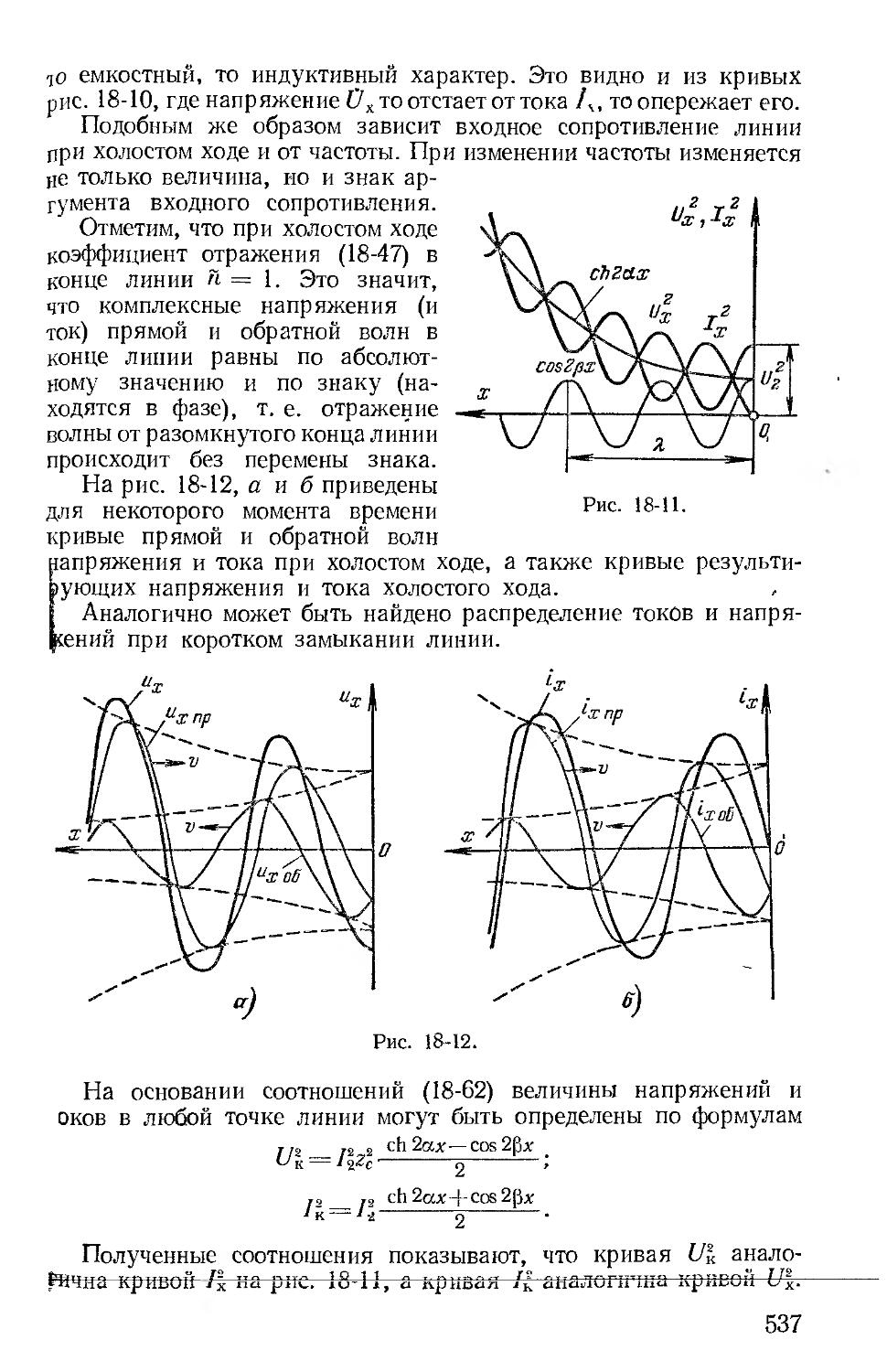
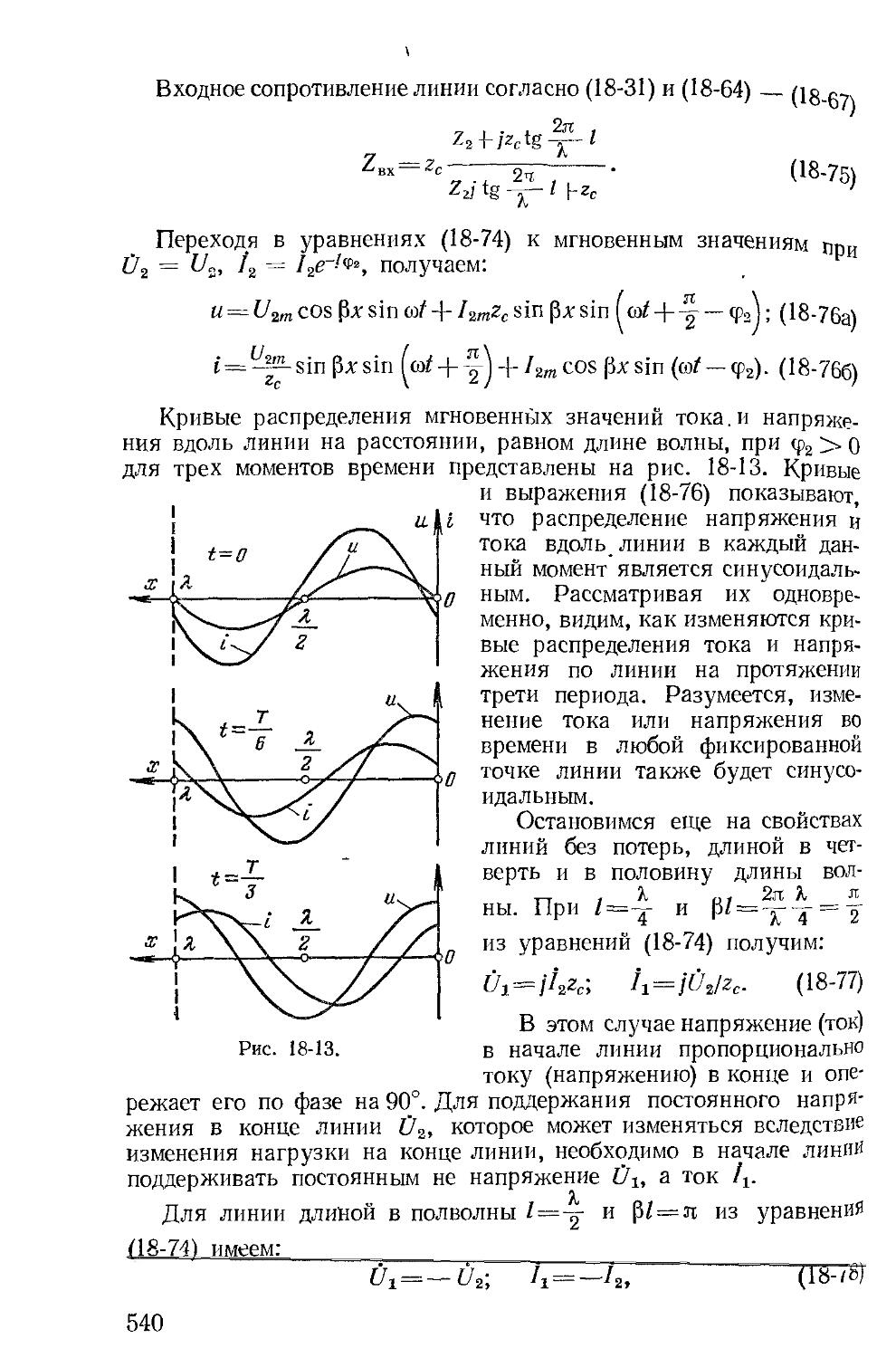
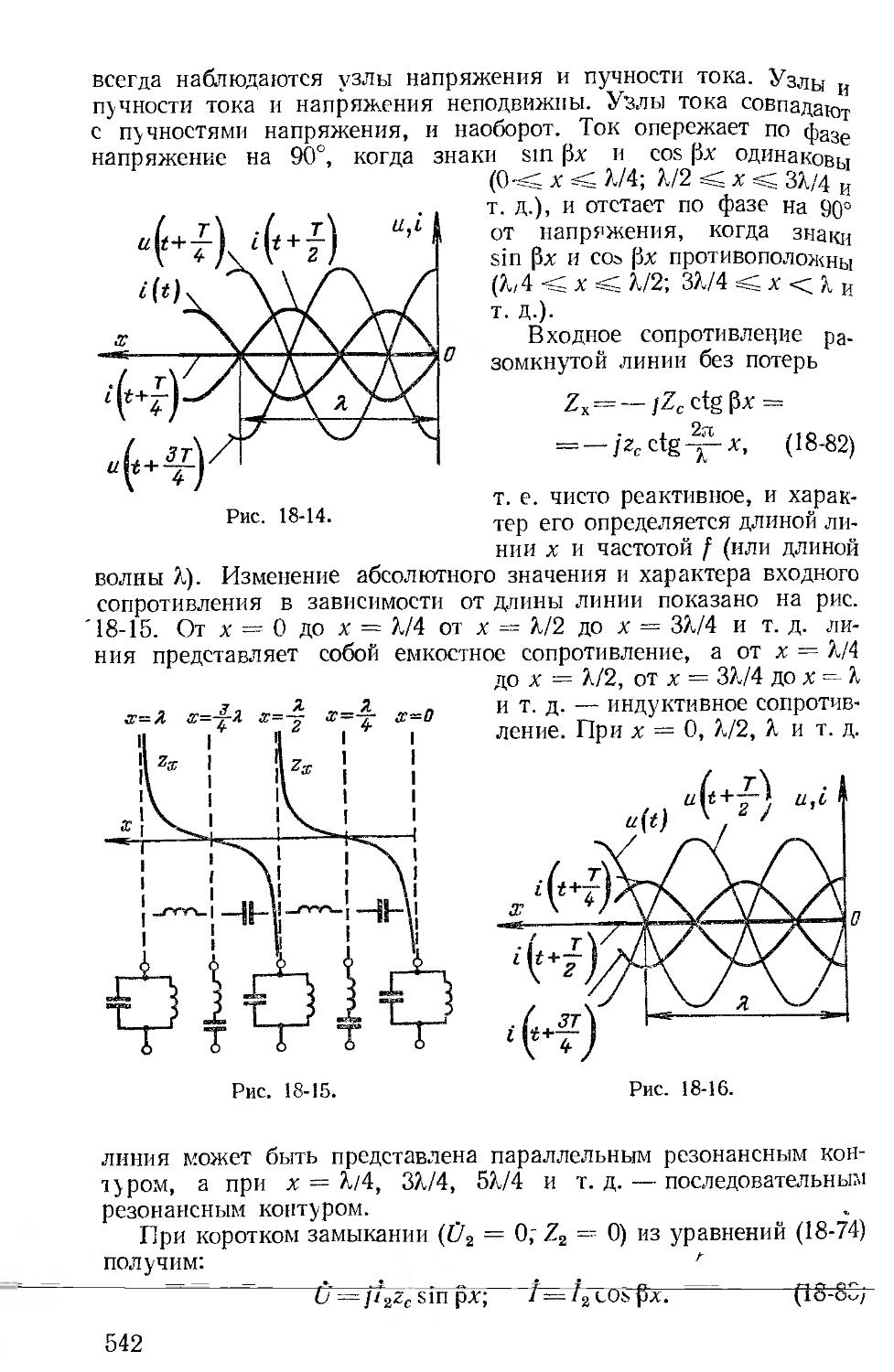
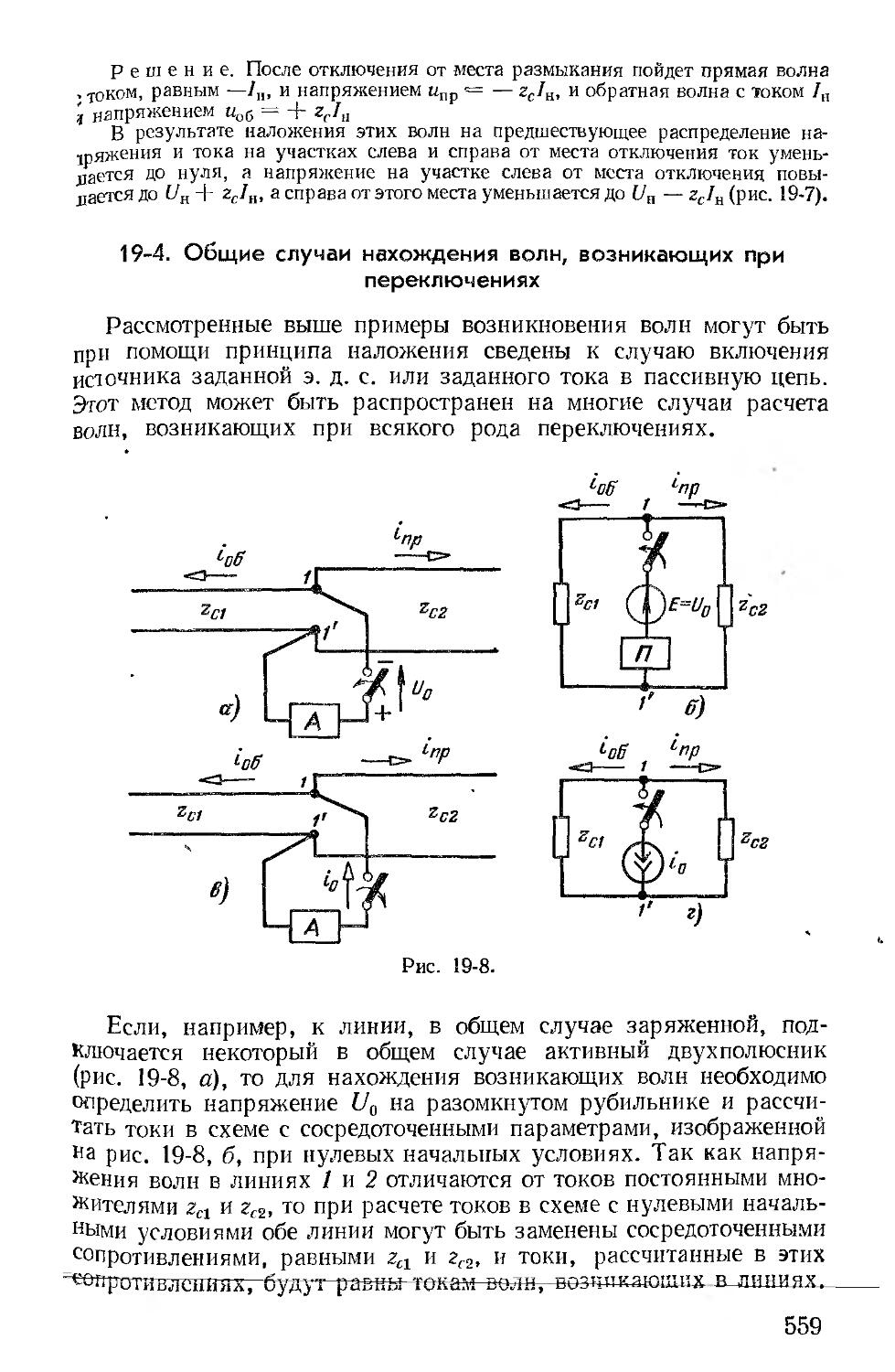
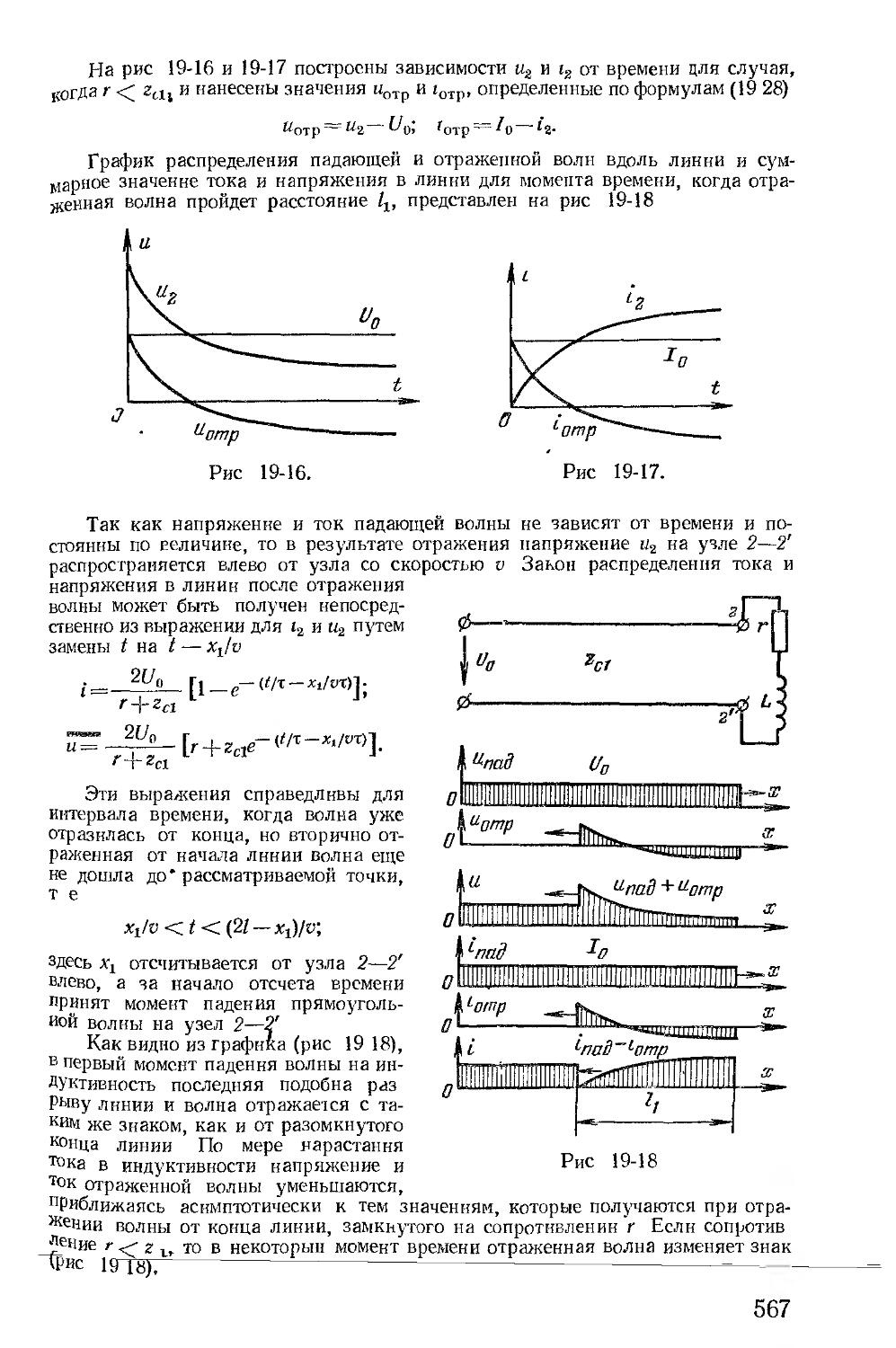
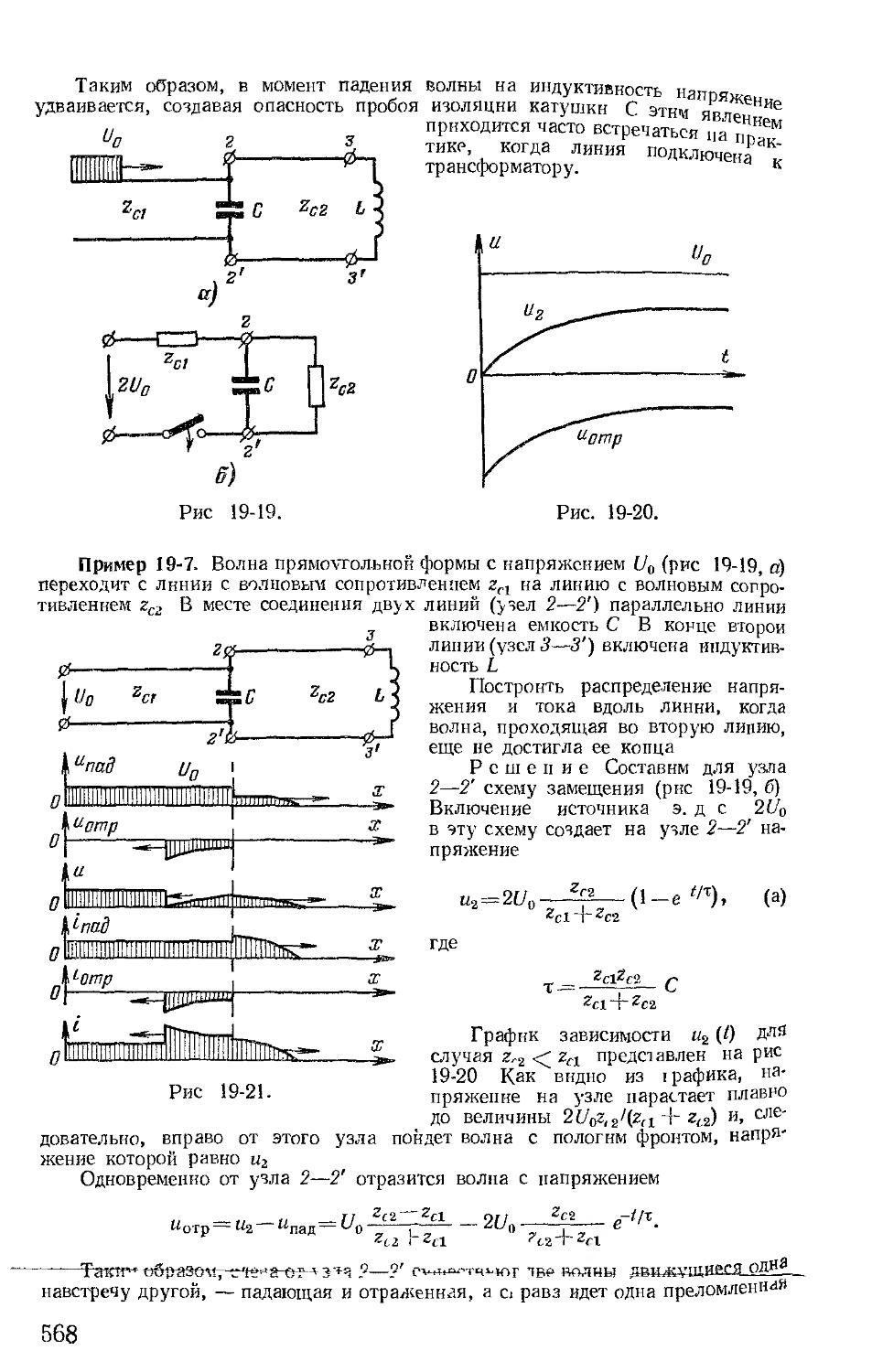
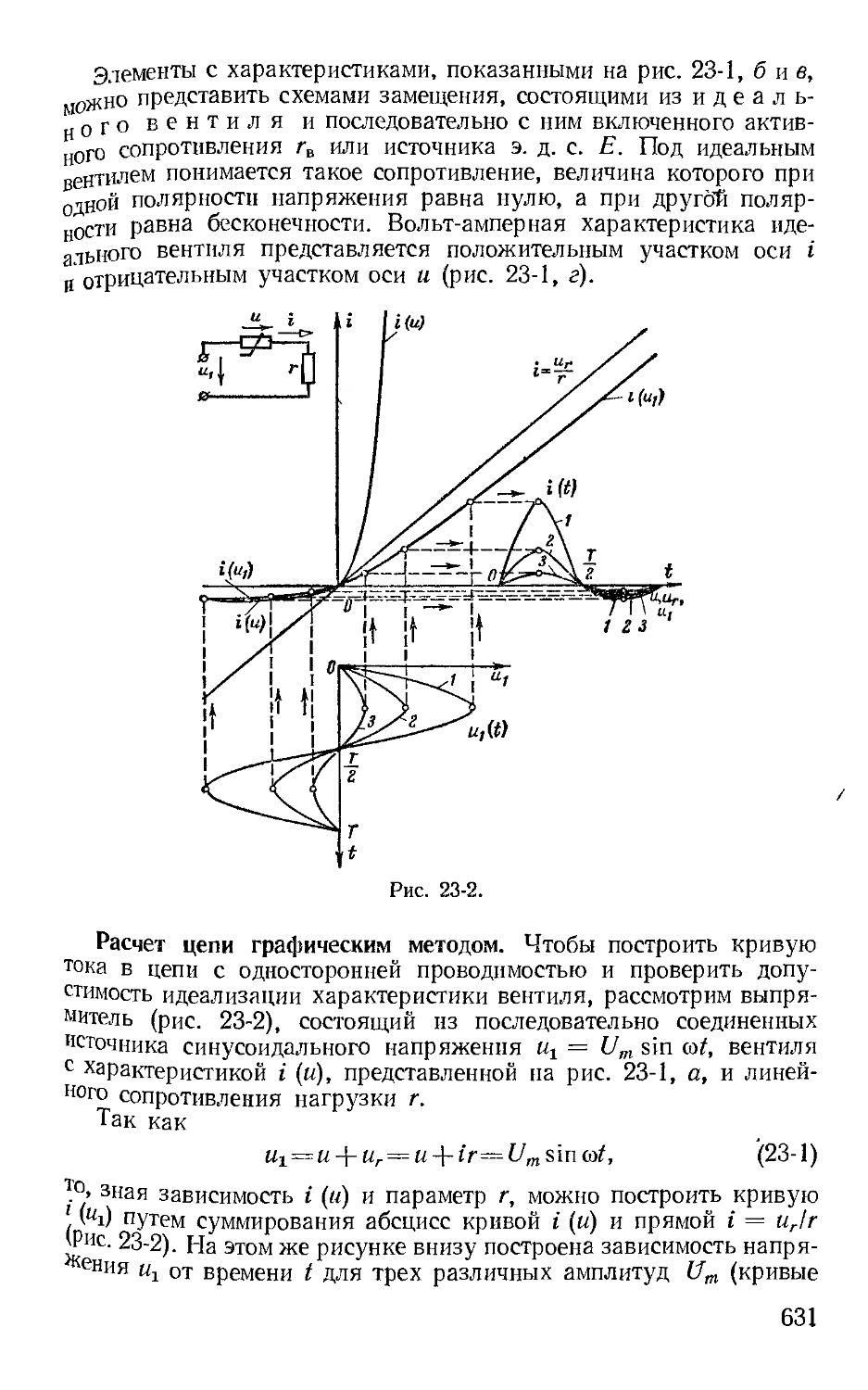
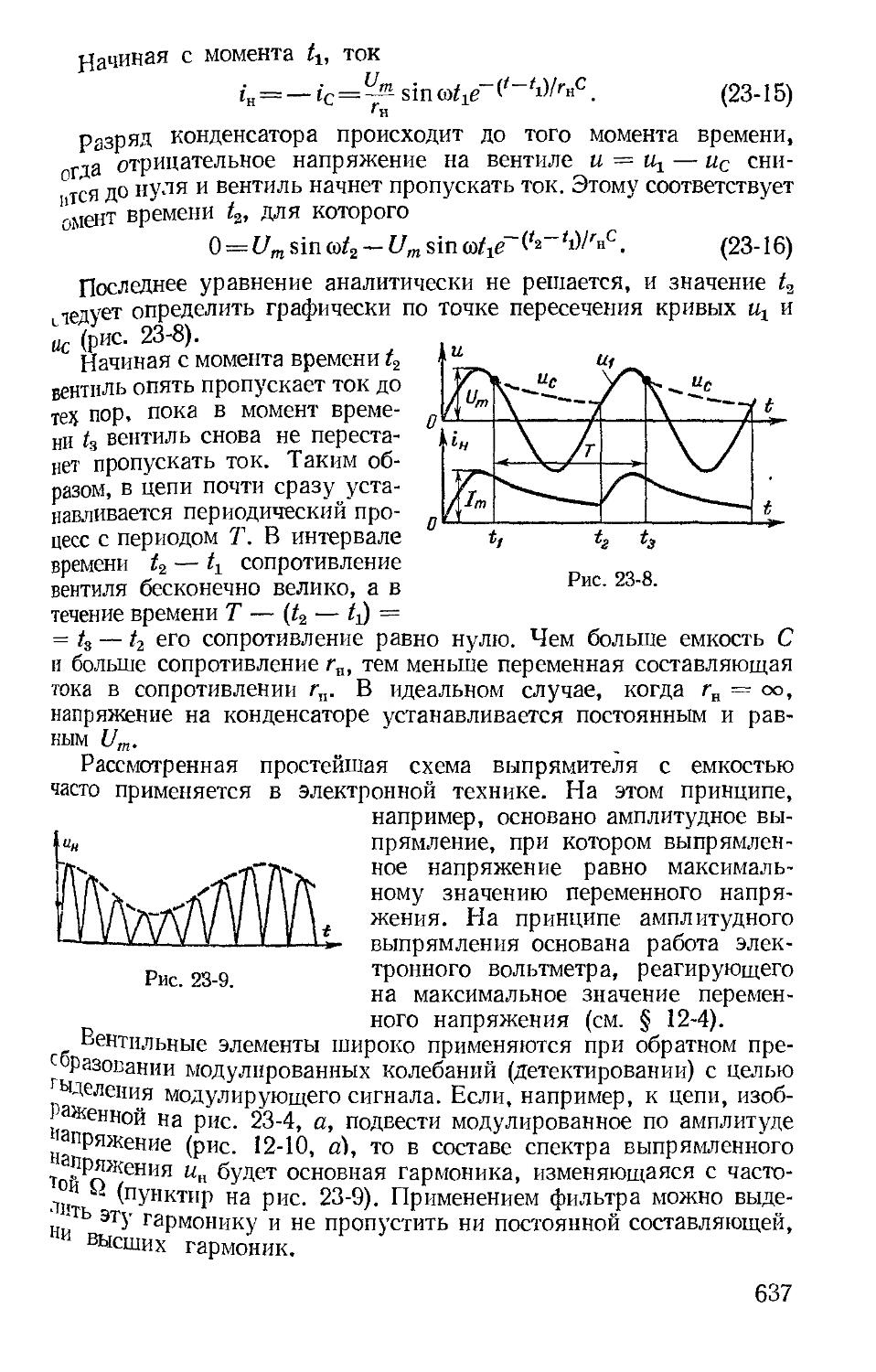
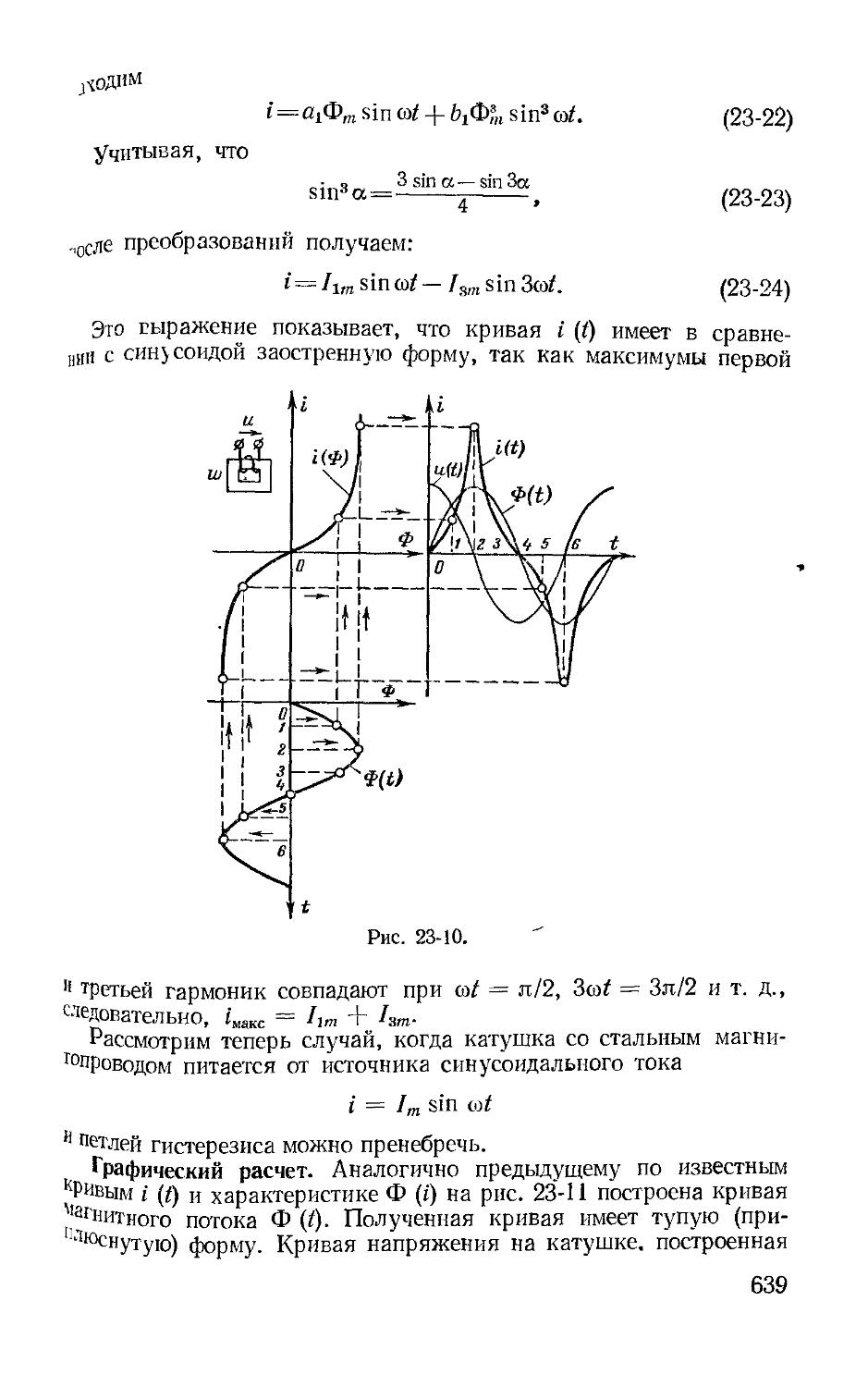
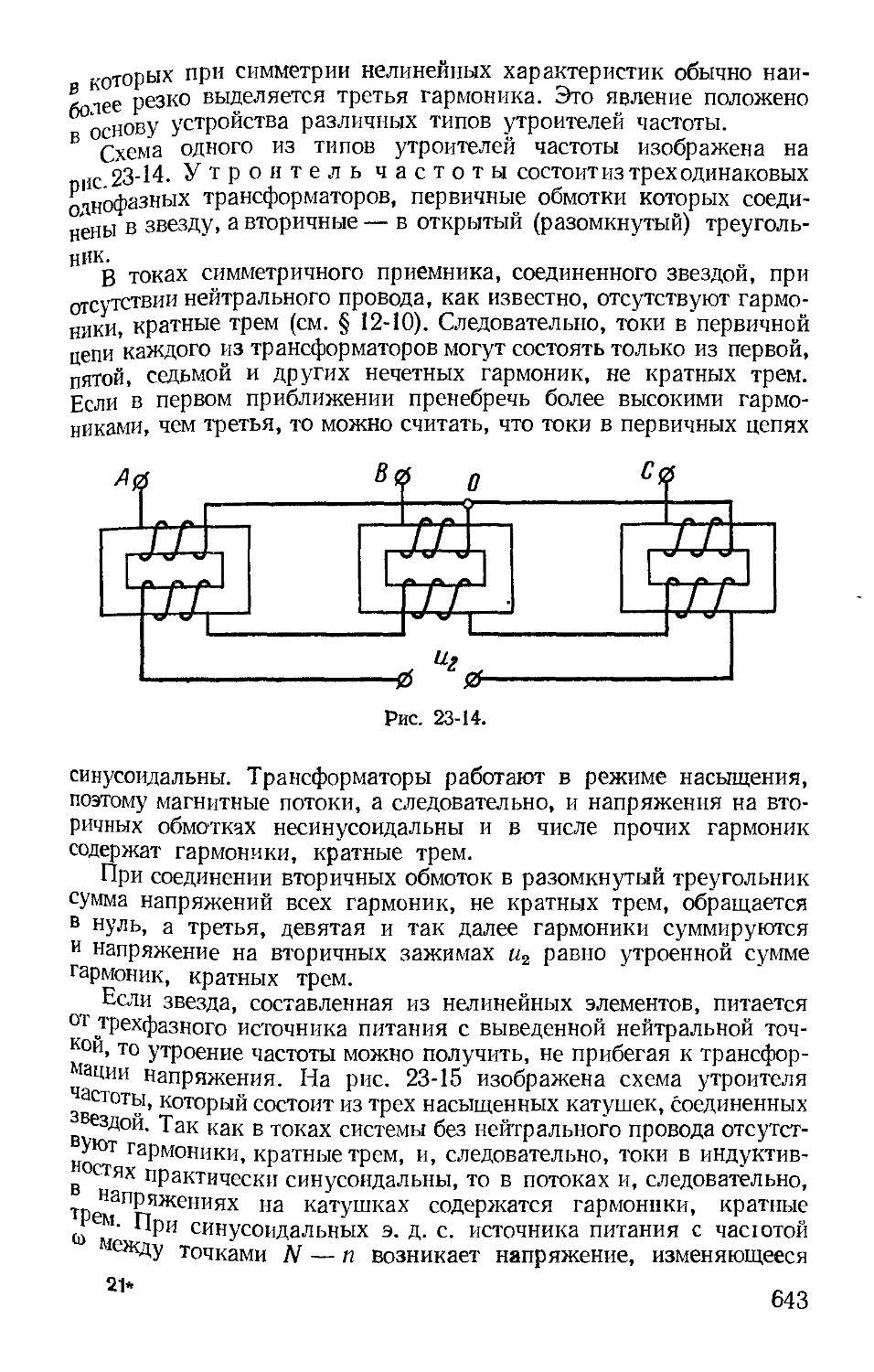
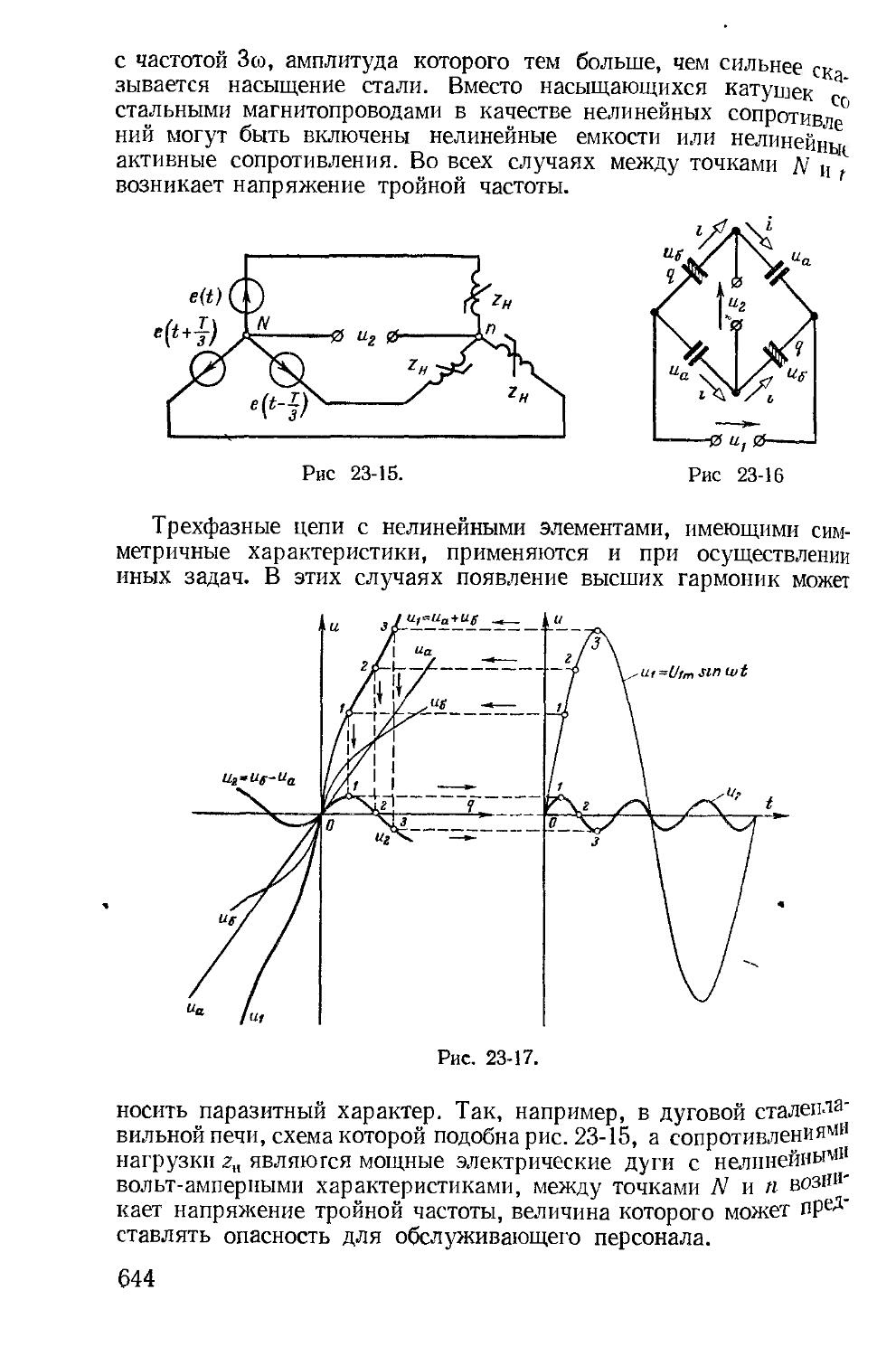
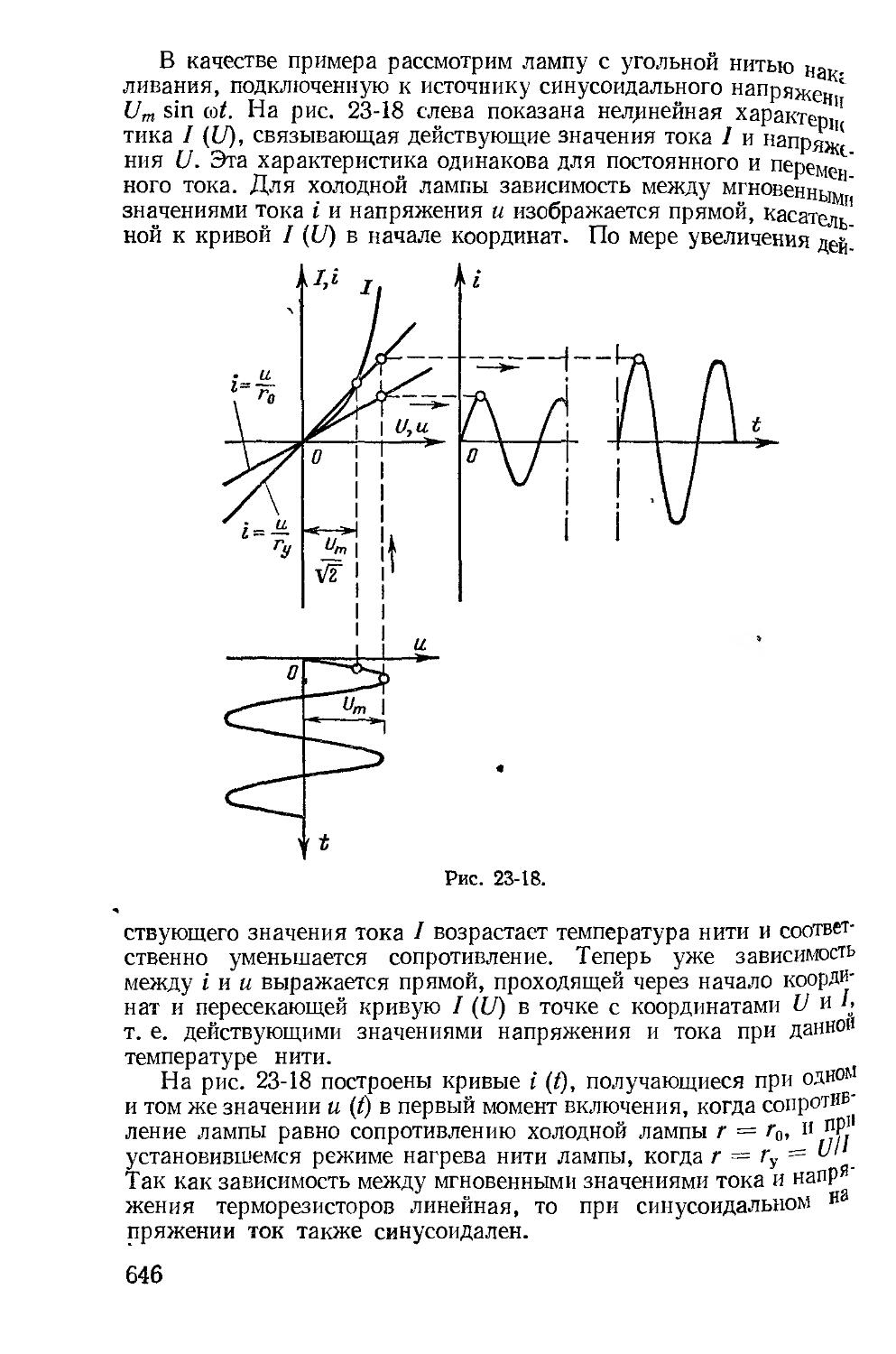
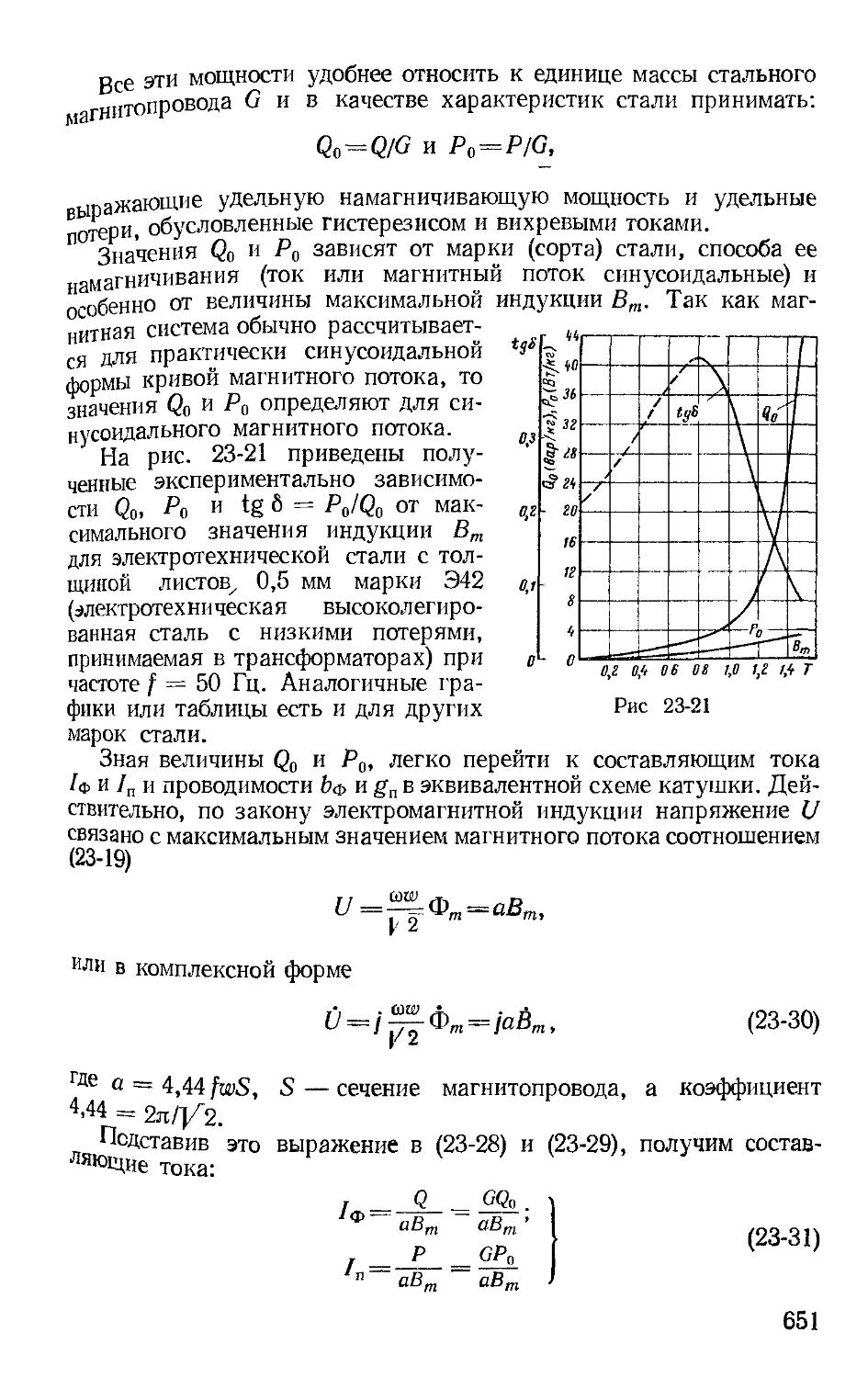
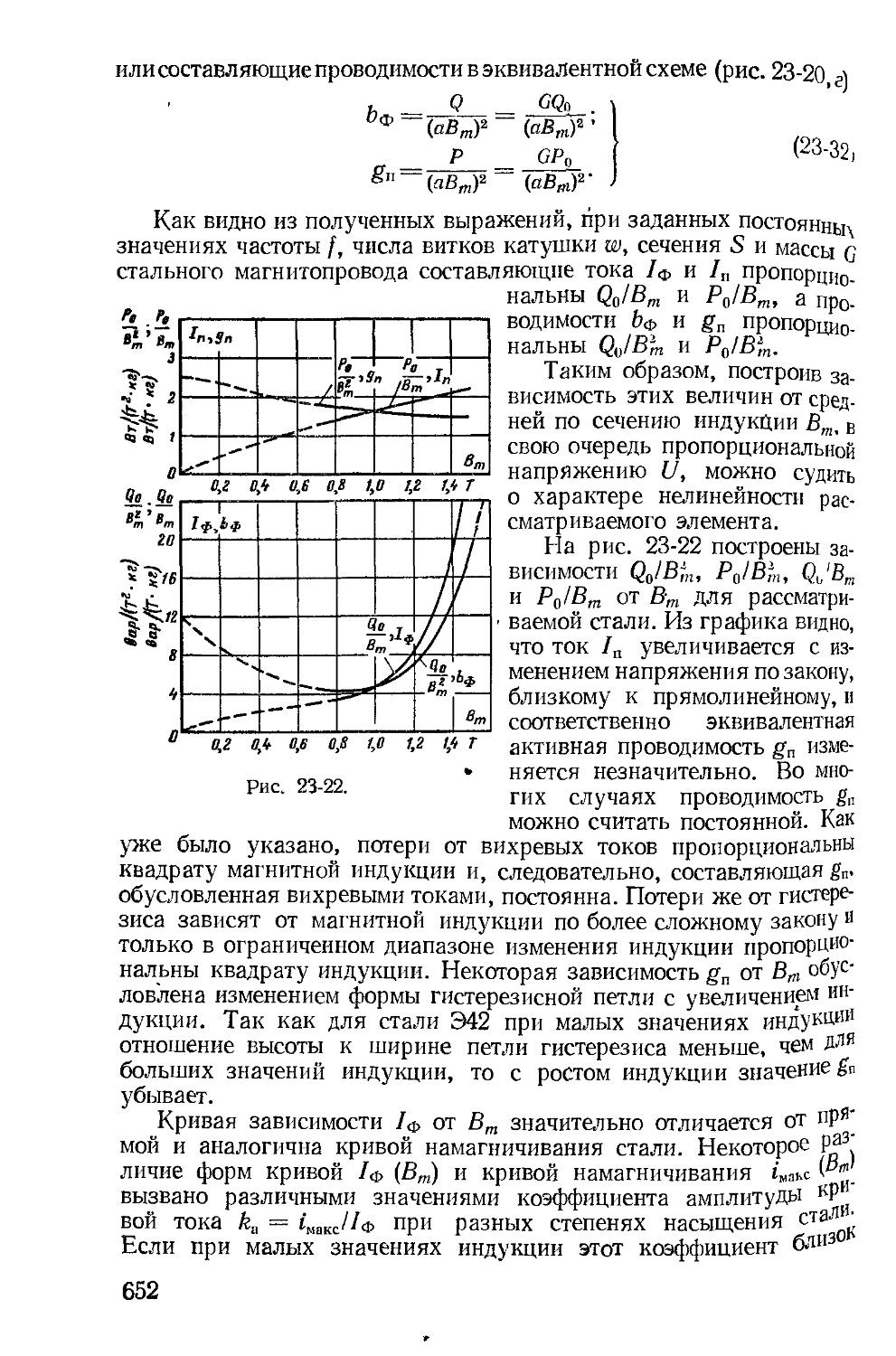
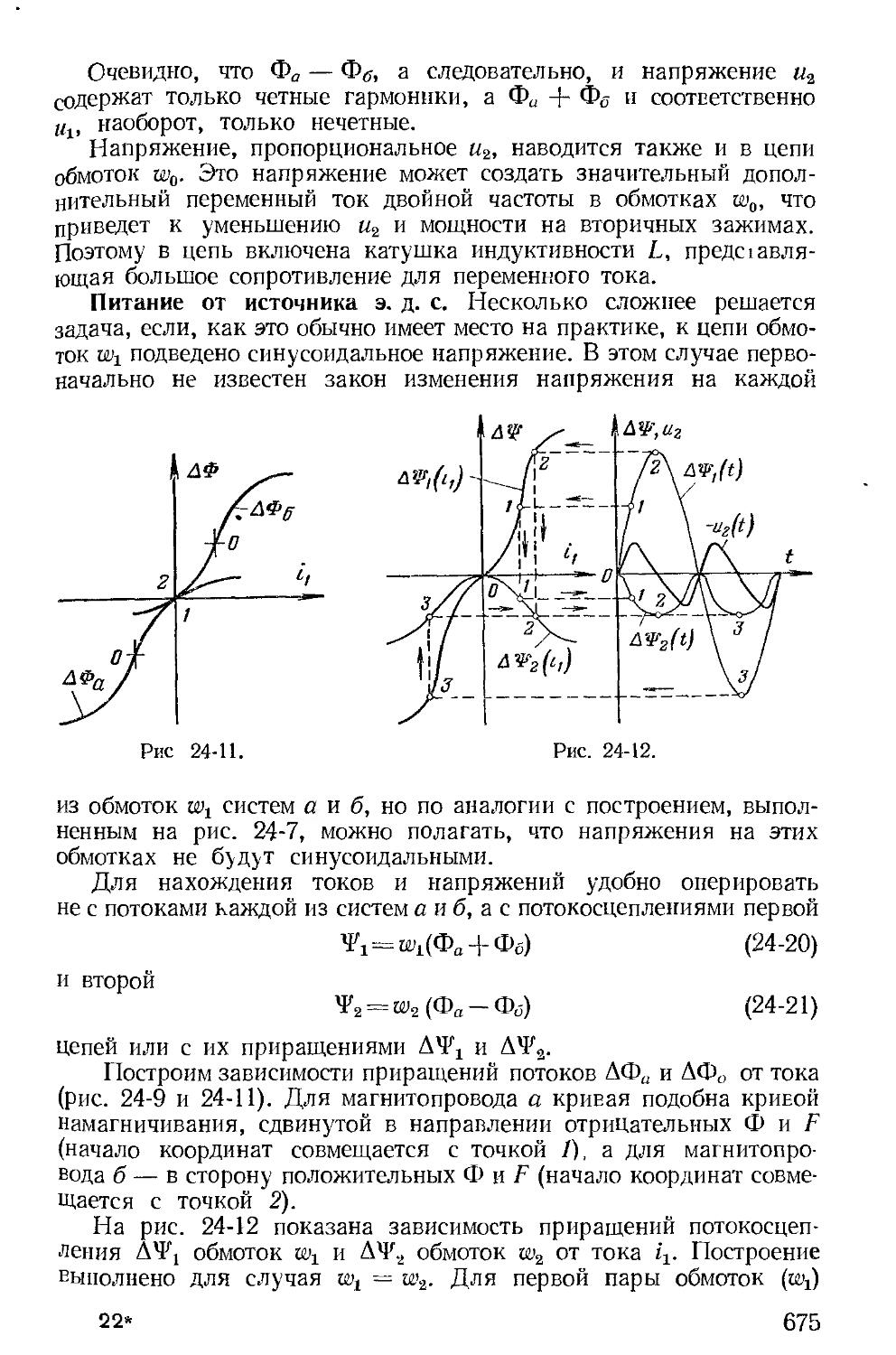
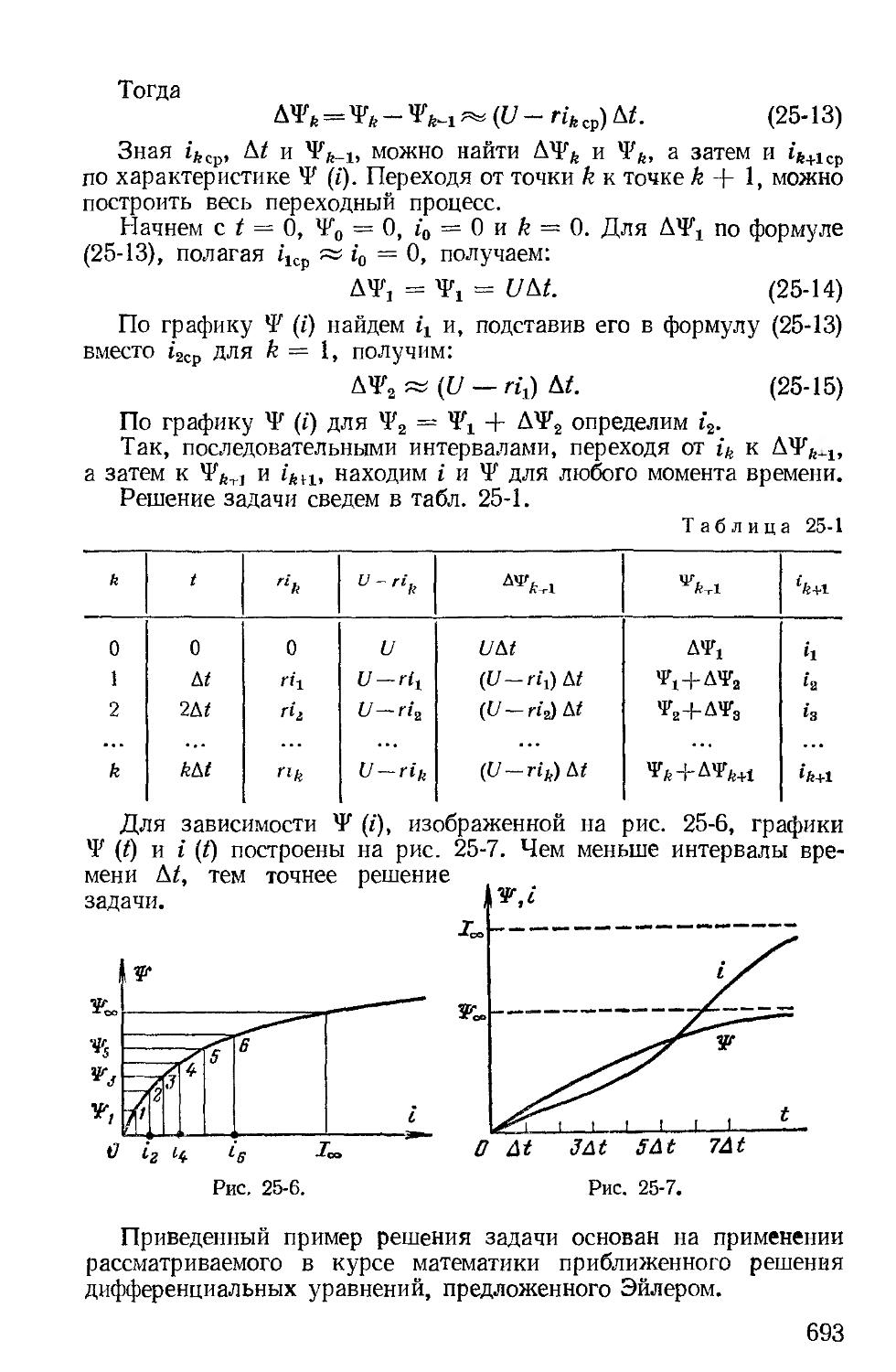
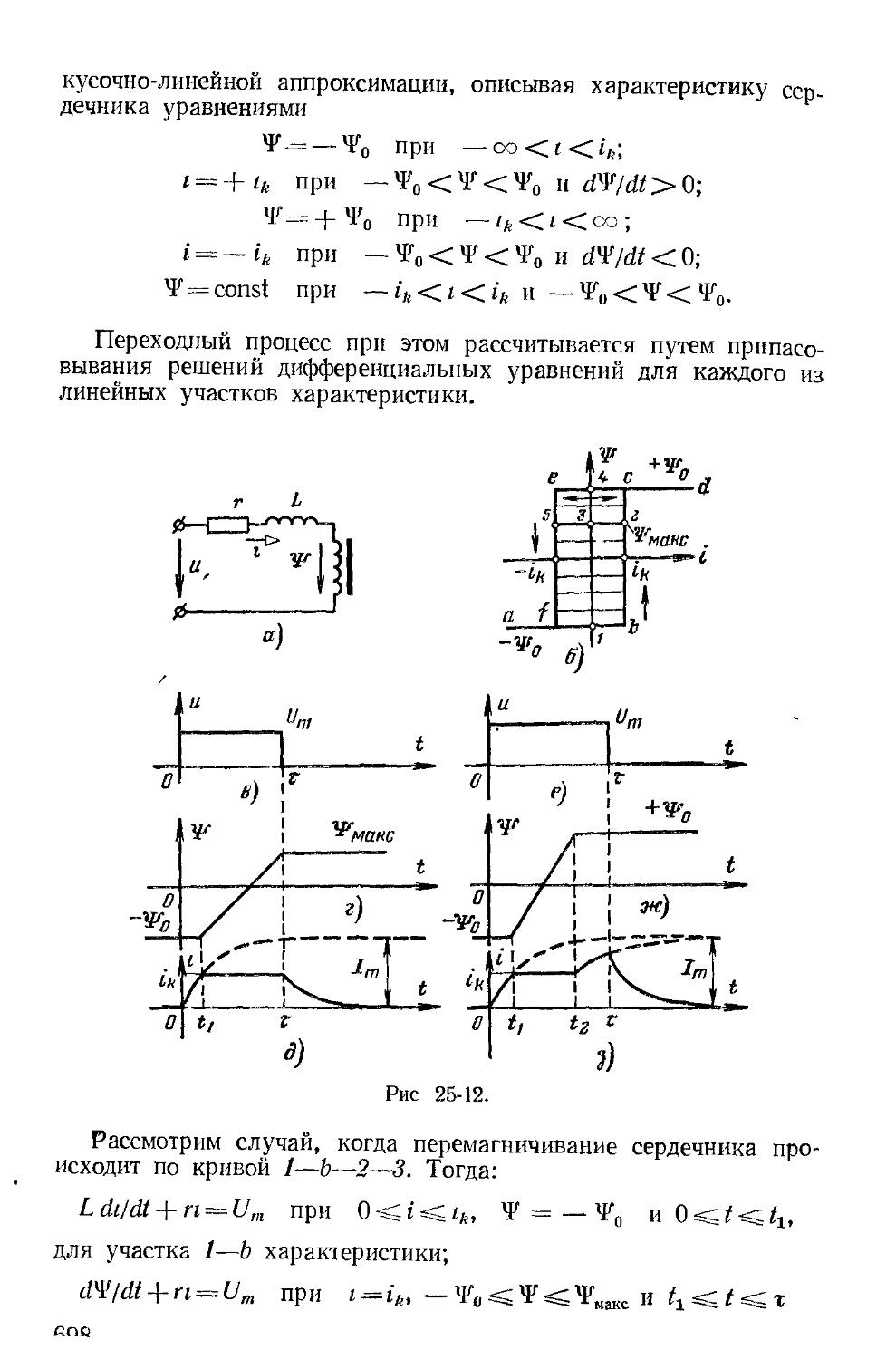
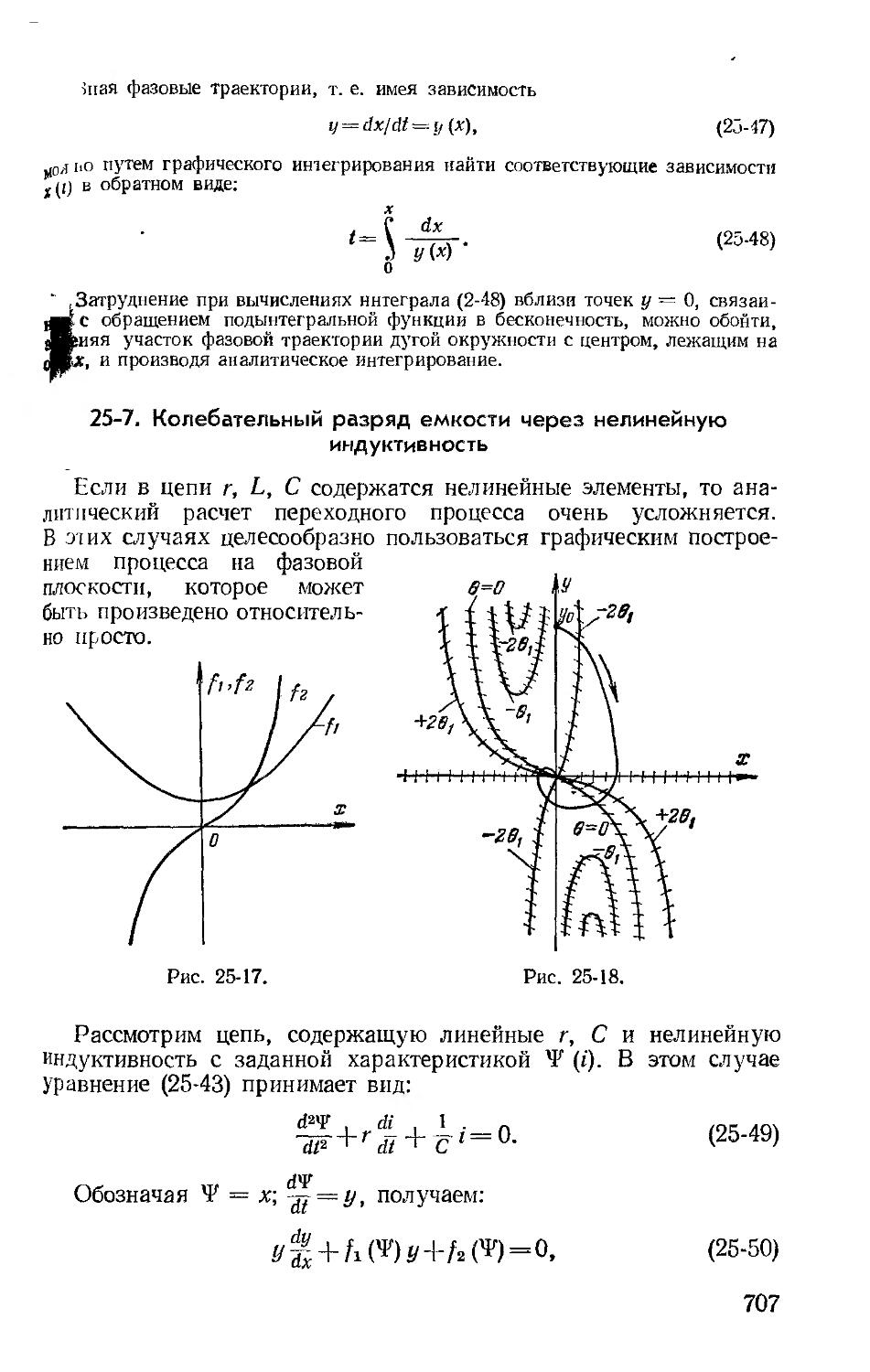
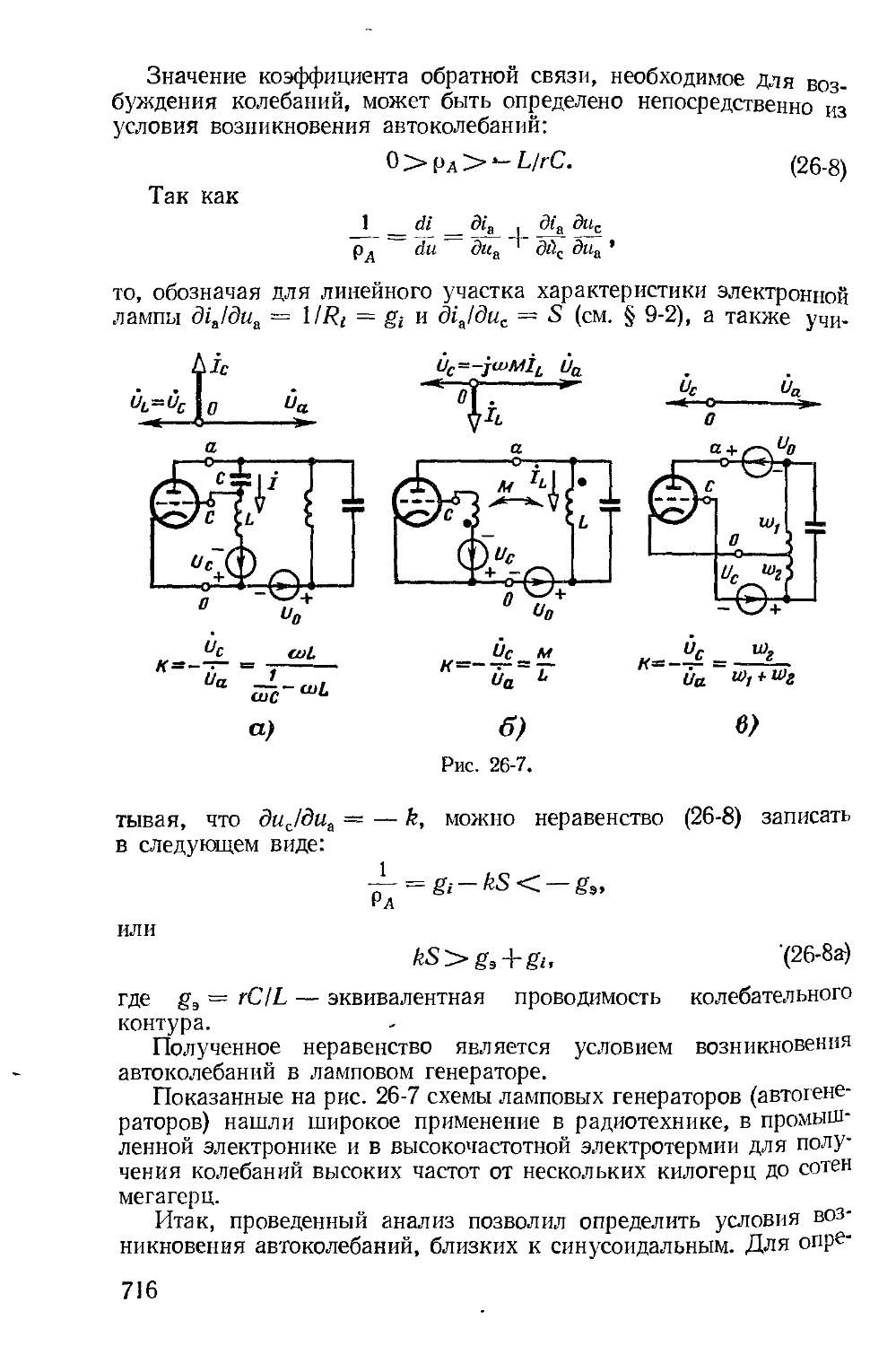
Основы теории цепей. Издание четвертое - Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В.

Автор: Зевеке Г.В. Ионкин П.А. Нетушил А.В. Страхов С.В.

Теги: электротехника теория электрических цепей

Год: 1975

Похожие

Основы теории цепей

Текст

основы т е о р и и ЦЕПЕЙ
ИЗДАНИЕ ЧЕТВЕРТОЕ, ПЕРЕРАБОТАННОЕ
Допущено Министерством высшего и среднего специального образования СССР в качестве учебника для студентов электоотехнических и энергетических специальностей вузов
6П2.1
0-75
УДК 621.3(075)
Авт.: Г. В. Зевеке, П. А. Ионкин, А. В. Нетушил С. В. Страхов
0-76 Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
752 с. с ил.
На обороте тит. л. авт.: Зевеке Г. В., Ионкин П. А., Нетушил А. В., Страхов С. В.
В книге излагаются общие методы анализа и синтеза и описание свойств линейных электрических цепей с сосредоточенными и распределенными параметрами при постоянных, переменных, периодических и переходных токах и напряжениях Рассматриваются свойства и методы расчета установившихся и переходных процессов в нелинейных электрических и магнитных цепях постоянного и переменного тока Все положения теории иллюстрируются практическими примерами
Третье издание книги выпущено в 1965 г
Книга является учебником для студентов электротехнических специальностей вузов.
о
30306-551
051(01)-75
142-75
6П2.1
—Издательство «Энергия», 1975 г.
Светлой памяти основателя московской электротехнической школы Карла Адольфовича Круга и столетию со дня его рождения посвящается эта книга.
ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
Новое, переработанное издание учебника по курсу теоретических основ электротехники (основы теории цепей) подготовлено к печати на основе материала третьего издания, выпущенного в свет в 1965 г. При переработке учебника для четвертого издания авторами была поставлена цель привести содержание учебника в соответствие с црвой программой и дать по возможности краткое и ясное изложение основных свойств и методов расчета цепей с иллюстрацией примерами наиболее важных вопросов теории.
В сравнении с предыдущим изданием учебника в книгу внесен ряд изменений.
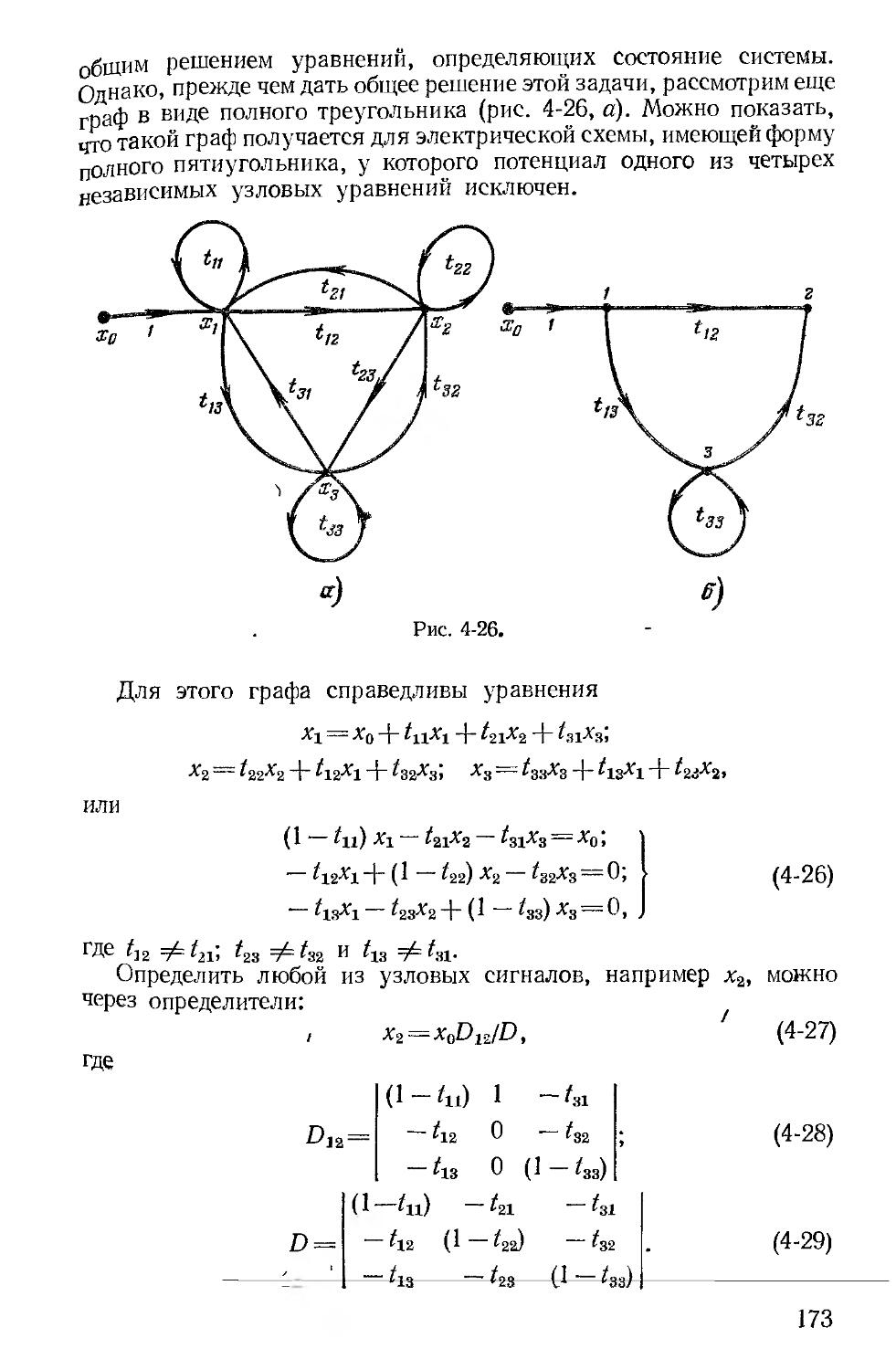
Проведено деление материала книги на три раздела, два из которых посвящены линейным цепям, соответственно с сосредоточенными и распределенными параметрами, а третий раздел объединяет вопросы теории нелинейных цепей.
Учитывая пожелания большого числа преподавателей курса ТОЭ в периферийных вузах, авторы нашли возможным сохранить изложение основных методов расчета линейных электрических цепей и их свойств на примерах цепей с постоянными токами и напряжениями. При этом в качестве дополнений все классические методы расчета линейных цепей сопровождаются матричной формой записи уравнений состояния электрических цепей и их решений. Кроме того, в гл. 2 помещен материал о топологических методах расчета линейных цепей.
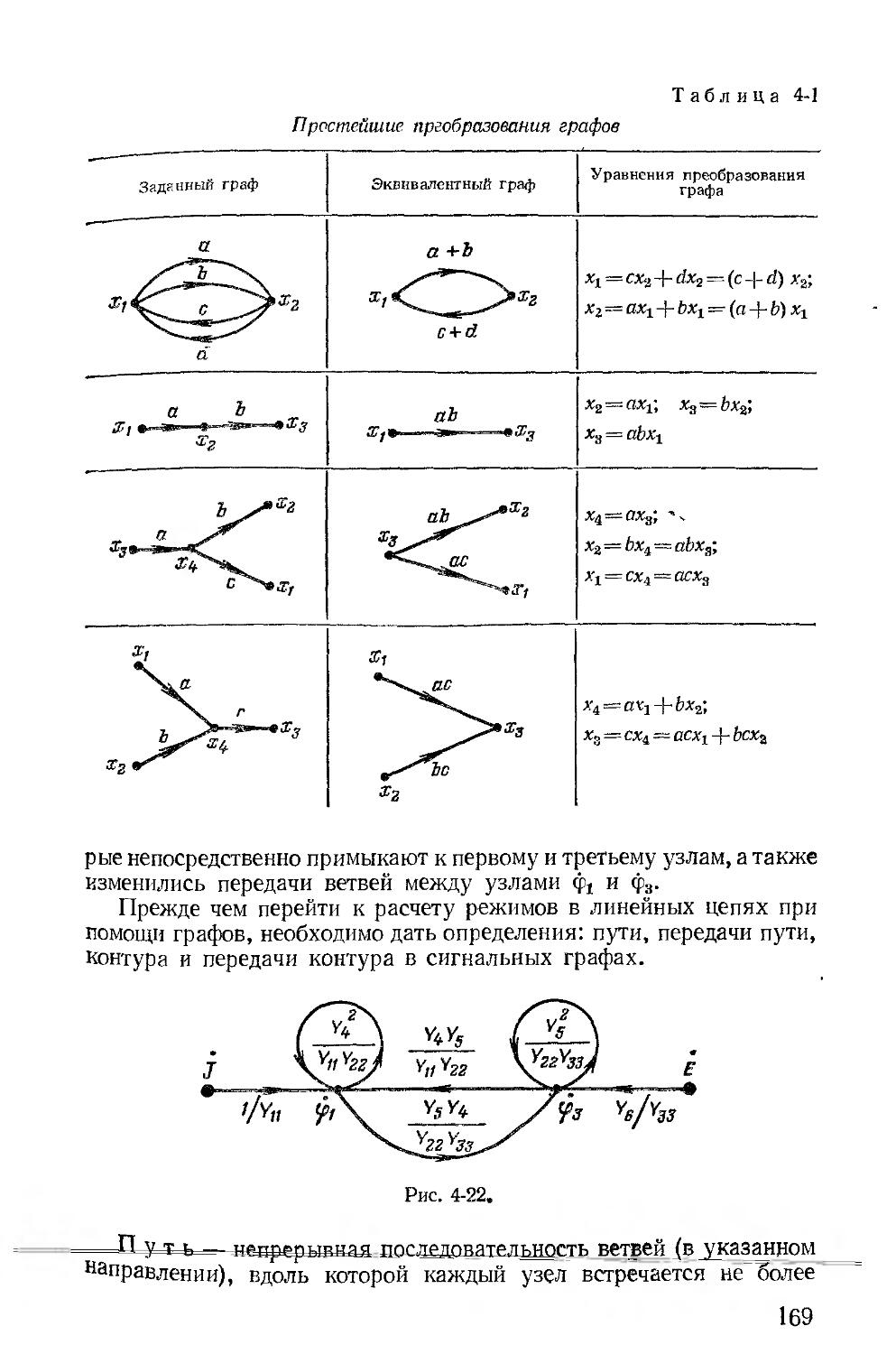
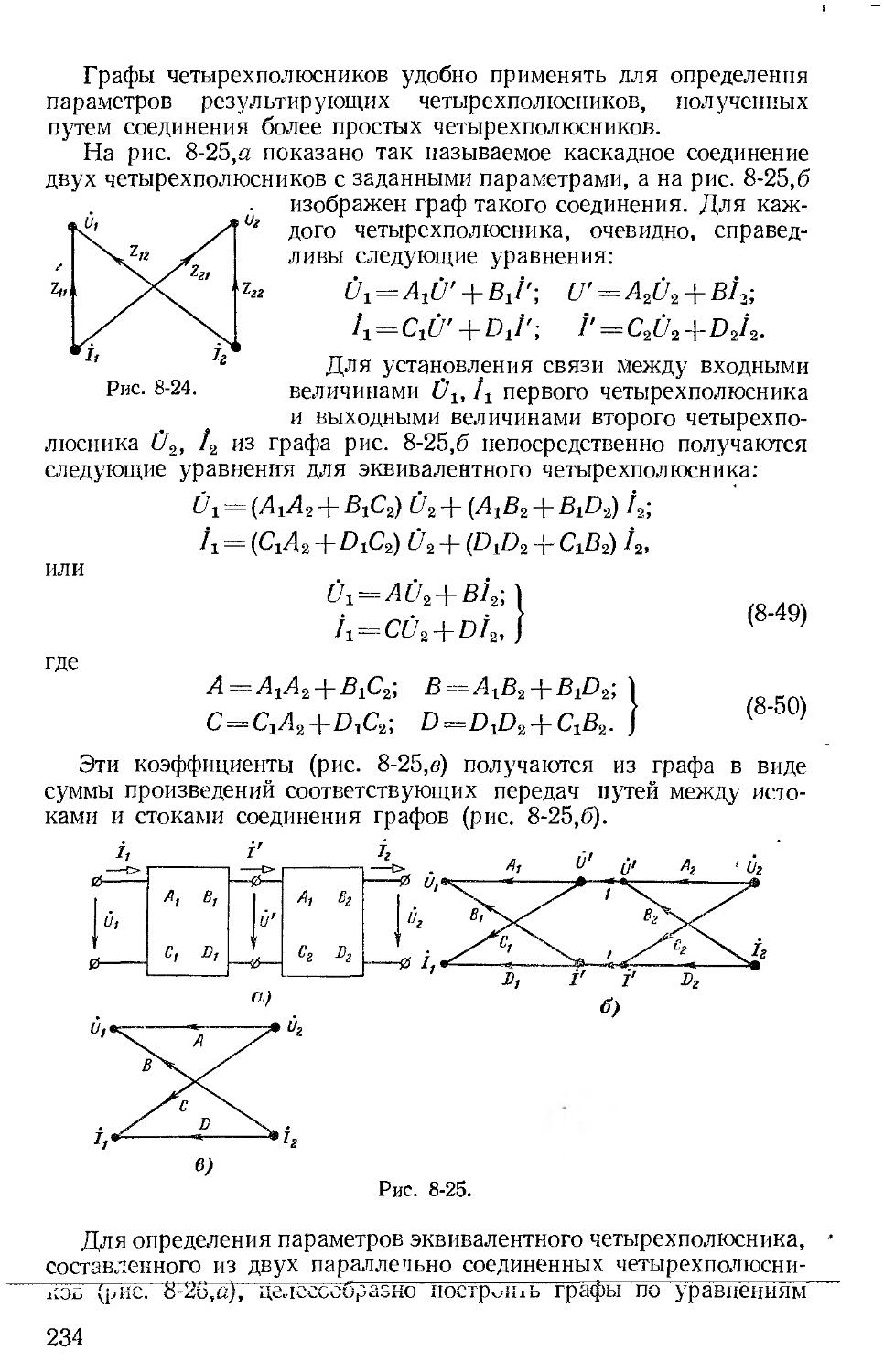
Принцип дуальности изложен в более общей форме в гл. 4, посвященной расчету цепей при синусоидальных токах и напряжениях. В этой же главе введены элементы теории сигнальных графов и показано ее применение.
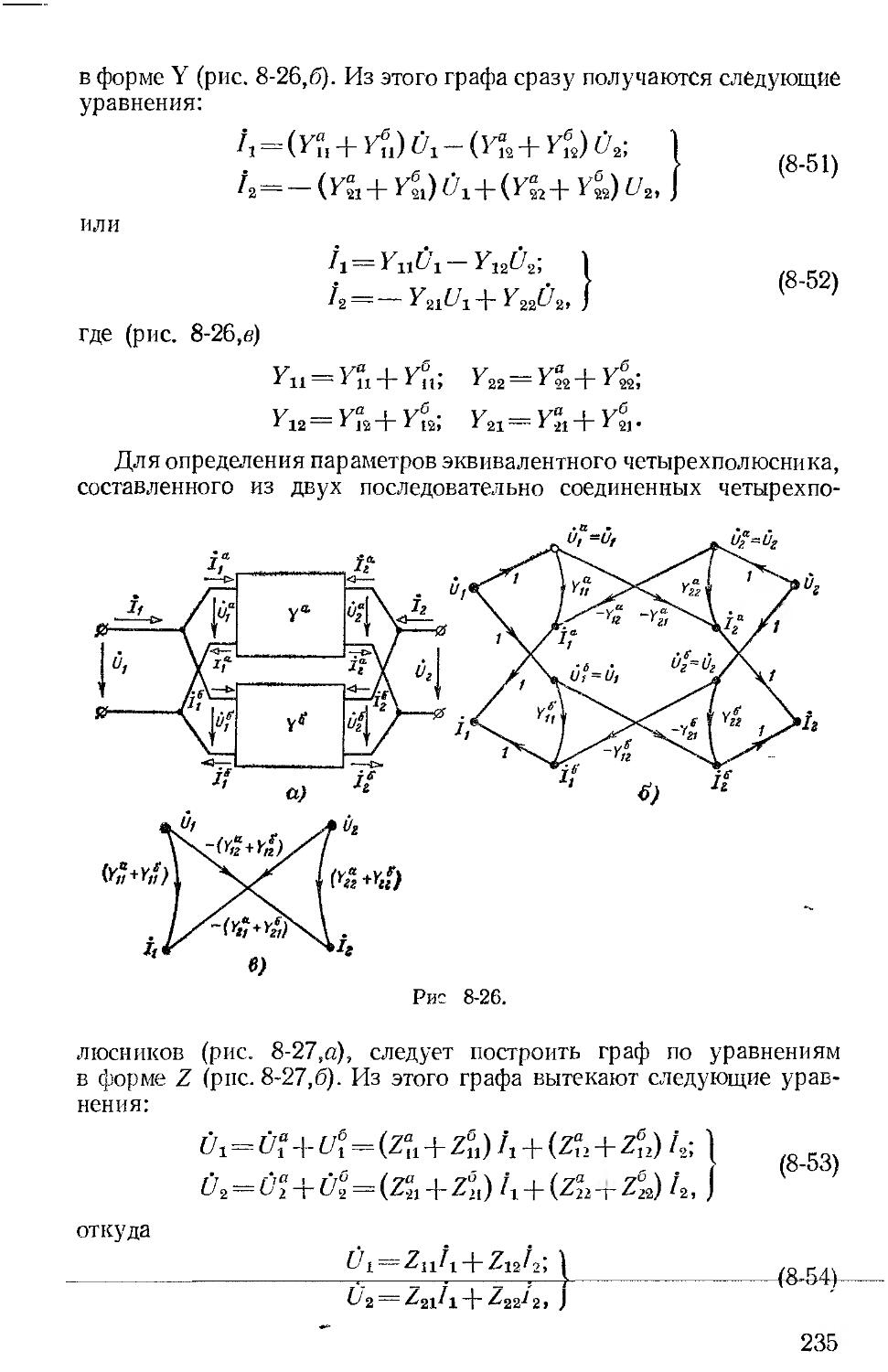
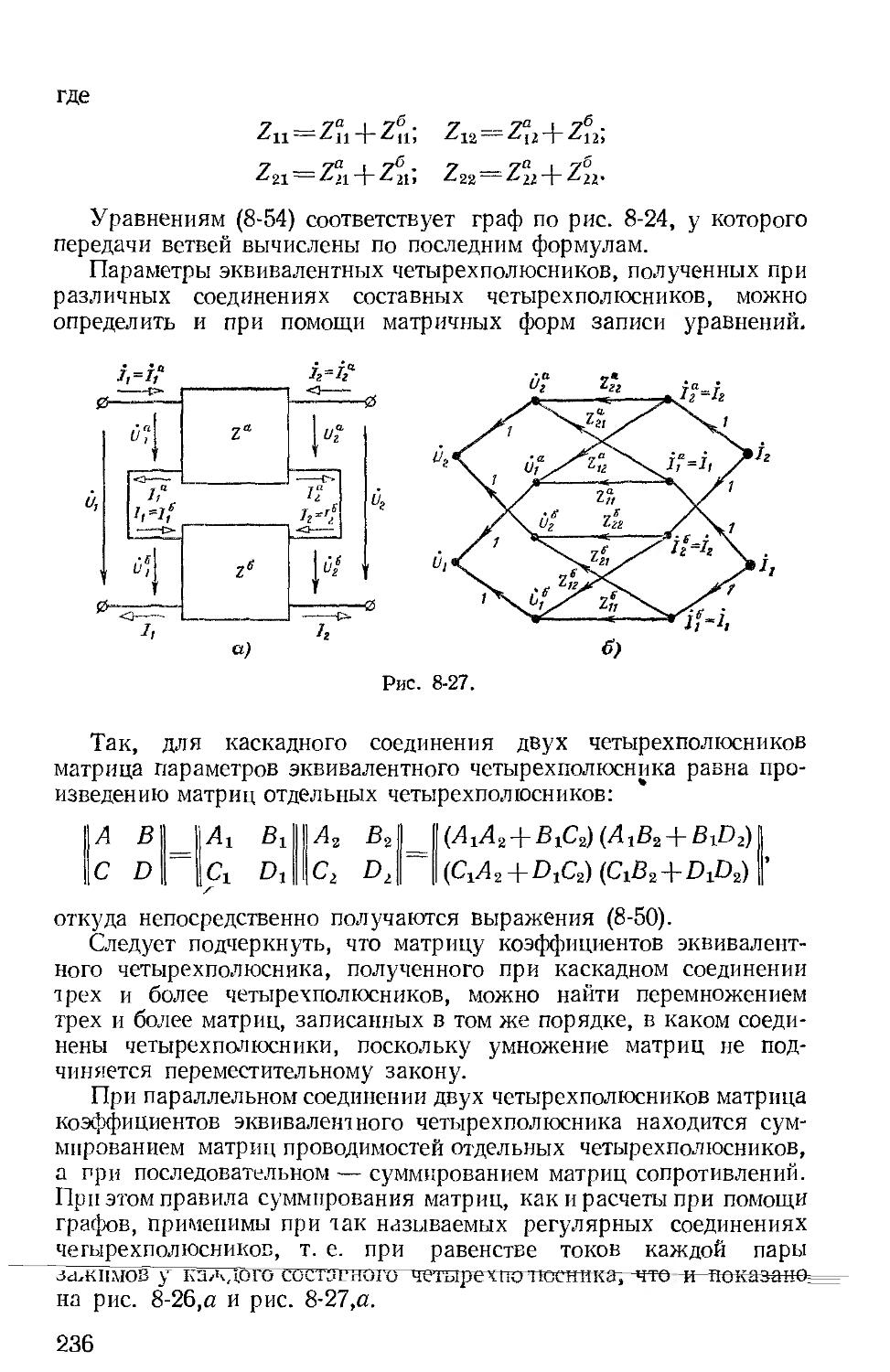
Общие вопросы теории четырехполюсников изложены в одной главе (гл. 8) применительно к цепям с синусоидальными токами и напряжениями. В этой же главе рассмотрены различные виды соединений четырехполюсников и при помощи графов показано определение параметров таких эквивалентных соединений.
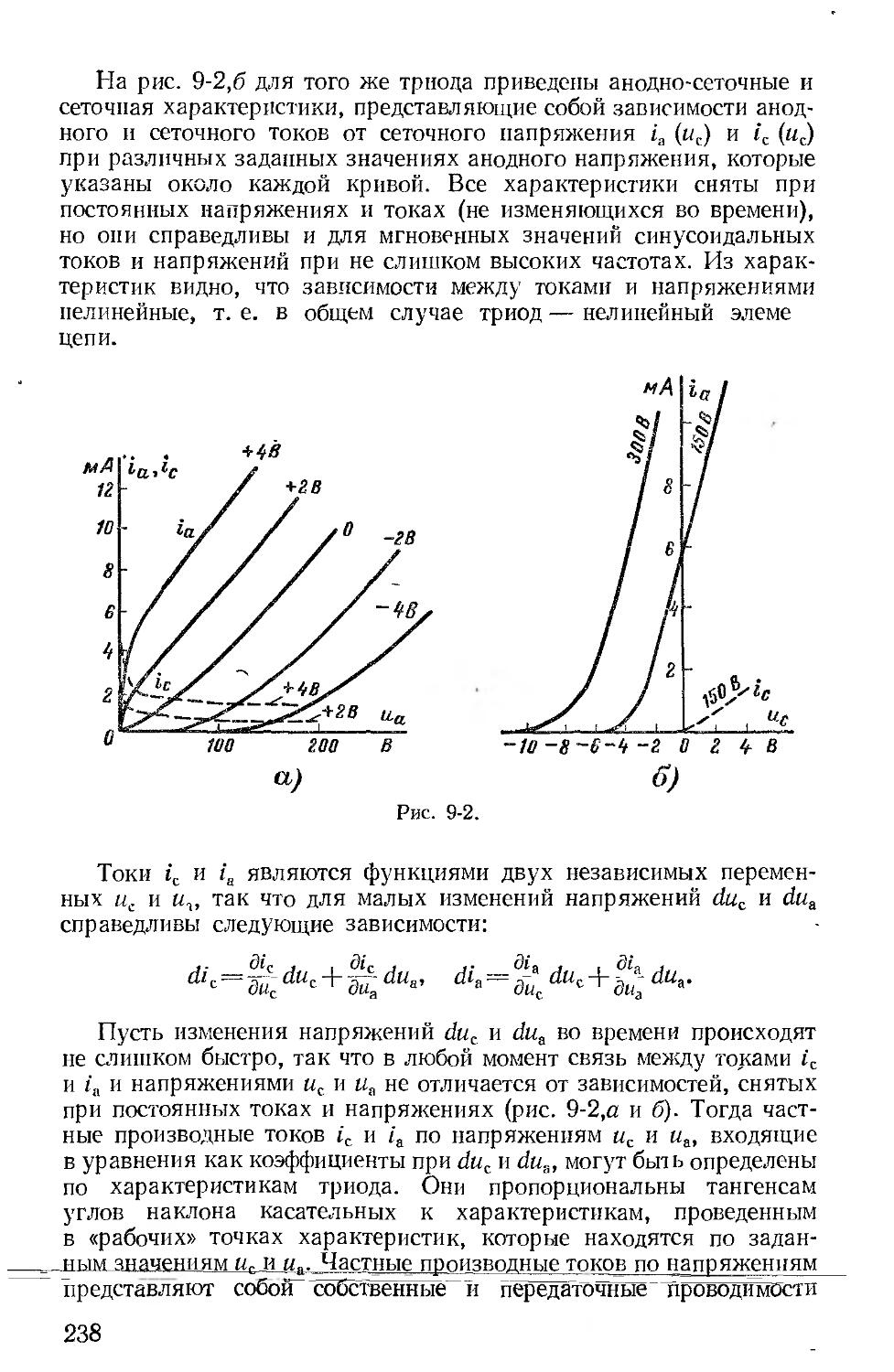
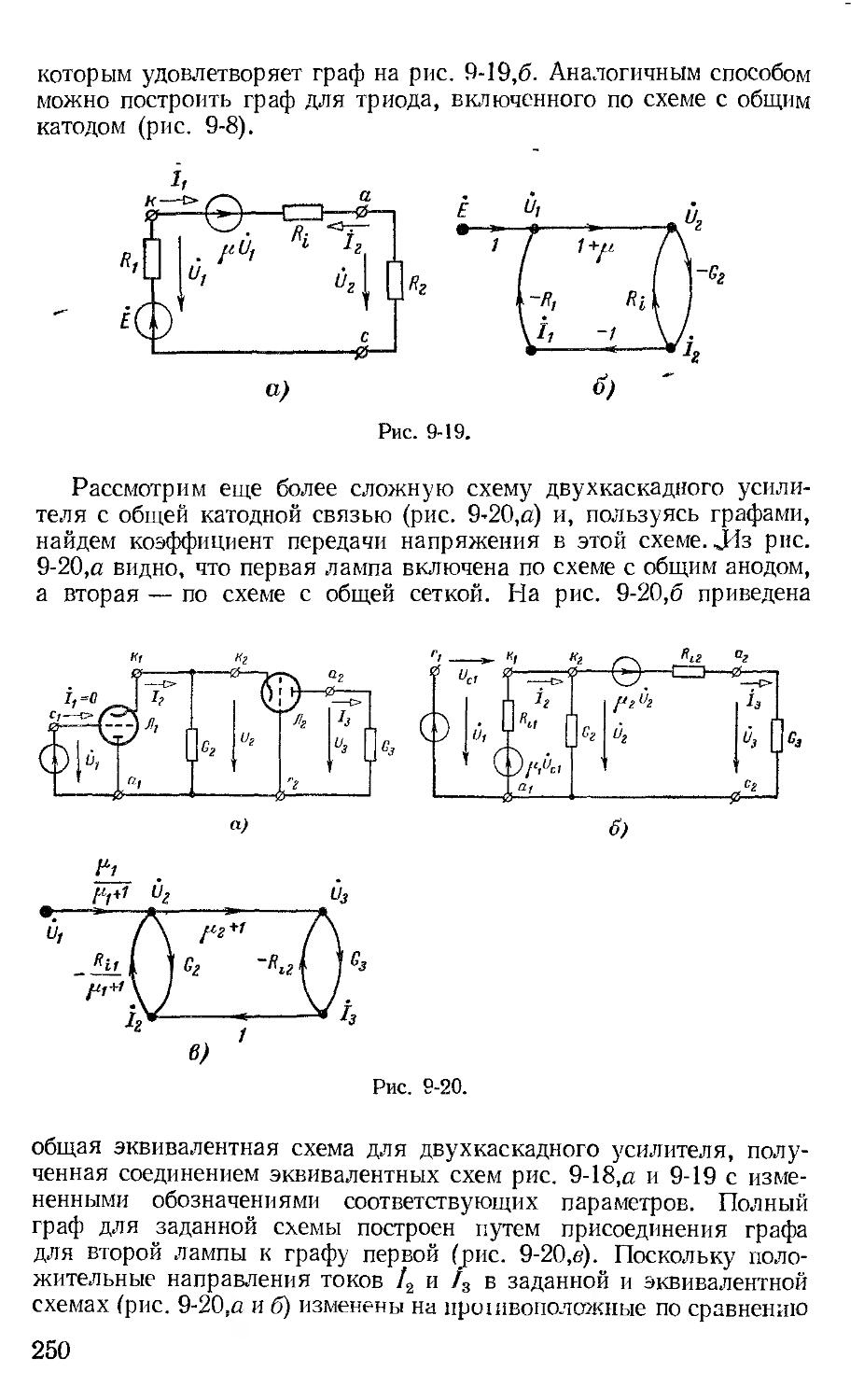
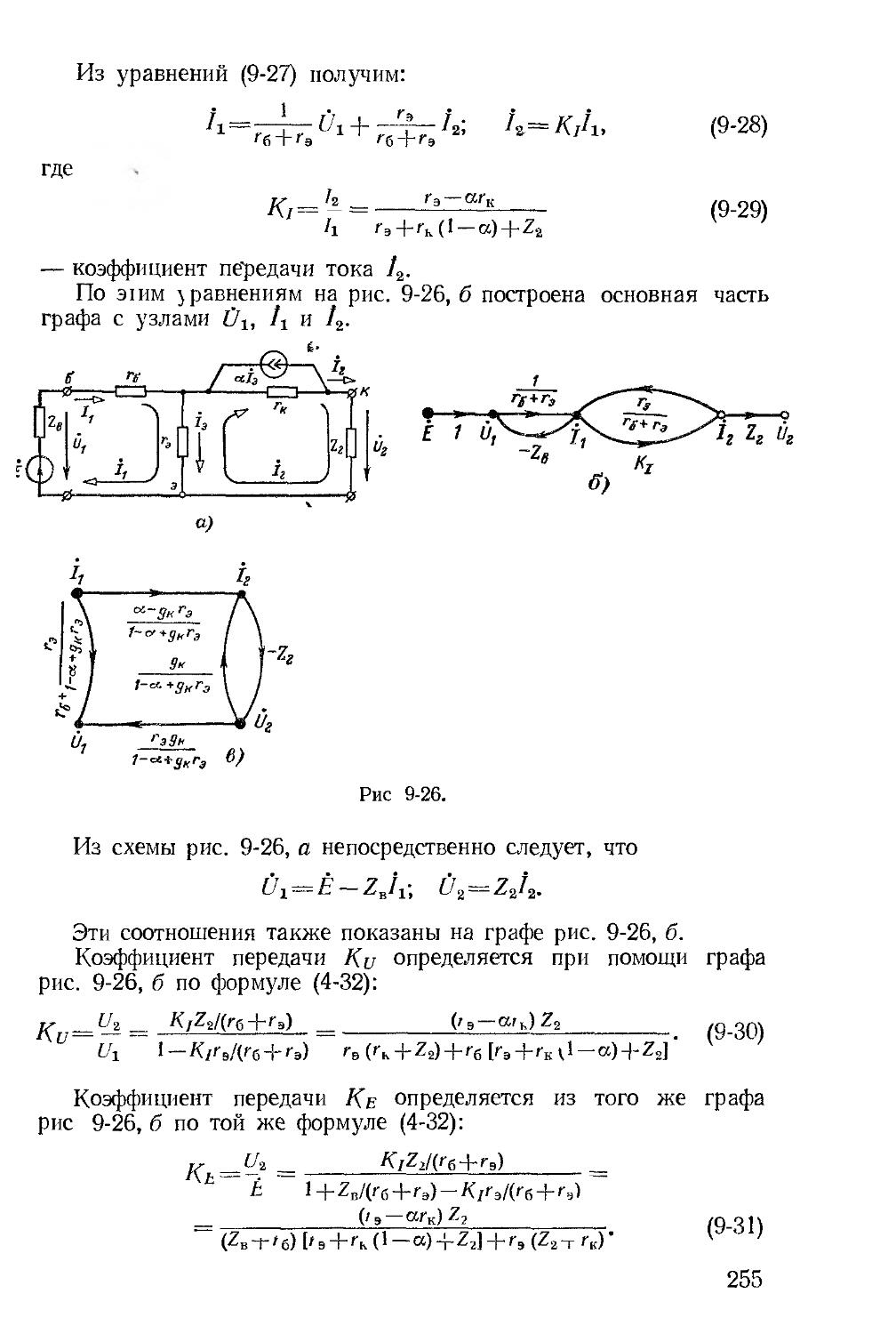
В гл. 9 более подробно, чем в предыдущем издании, рассмотрены простейшие электронные цепи с невзаимными элементами.
В гл. 1’3, где рассмотрен классический метод расчета переходных процессов, введен параграф об их расчете при скачкообразных изменениях параметров цепей; введены временная и импульсная переходные характеристики и методика составления уравнений переходных процессов при помощи прошранства состояний.
Из гл. 14, посвященной операторному методу расчета переходных процессов, исключено несколько параграфов, относящихся
3
к теории преобразования Лапласа и выводу теоремы разложения, поскольку эти вопросы излагаются в курсе математики. По той же причине из гл. 15, где изложен частотный метод расчета переходных процессов, исключен материал об основных свойствах преобразования Фурье.
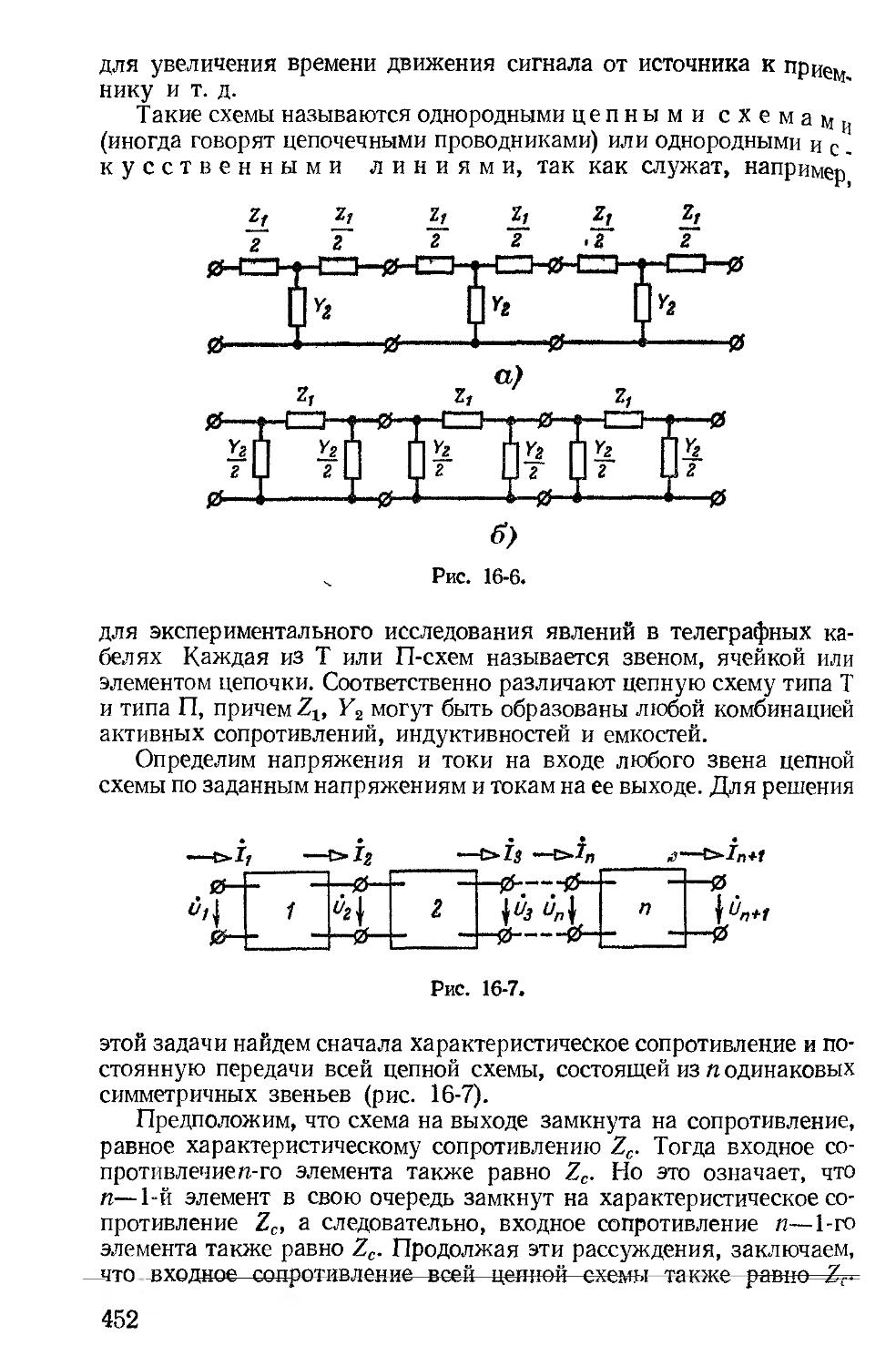
В отдельную главу (гл. 16) выделены все вопросы о вторичных параметрах симметричных п несимметричных четырехполюсников, цепочечные схемы и частотные электрические фильтры.
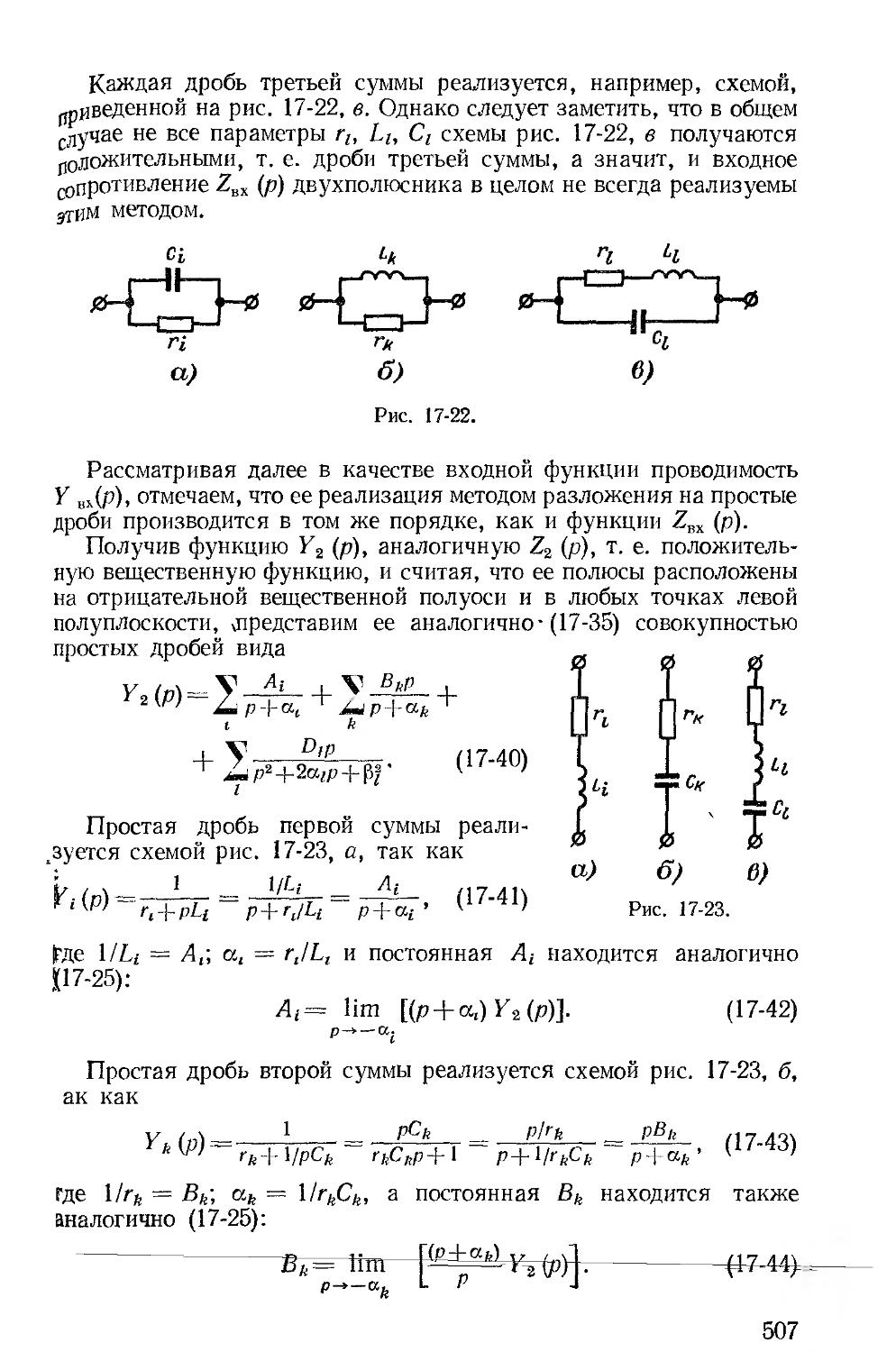
В состав новой гл. 17, где рассмотрены задачи синтеза электрических цепей, включены вопросы, касающиеся цепей минимальной фазы, вопросы синтеза двухполюсников по функции входного сопротивления, представленной в виде простых и цепных дробей, и введен параграф о синтезе четырехполюсников.
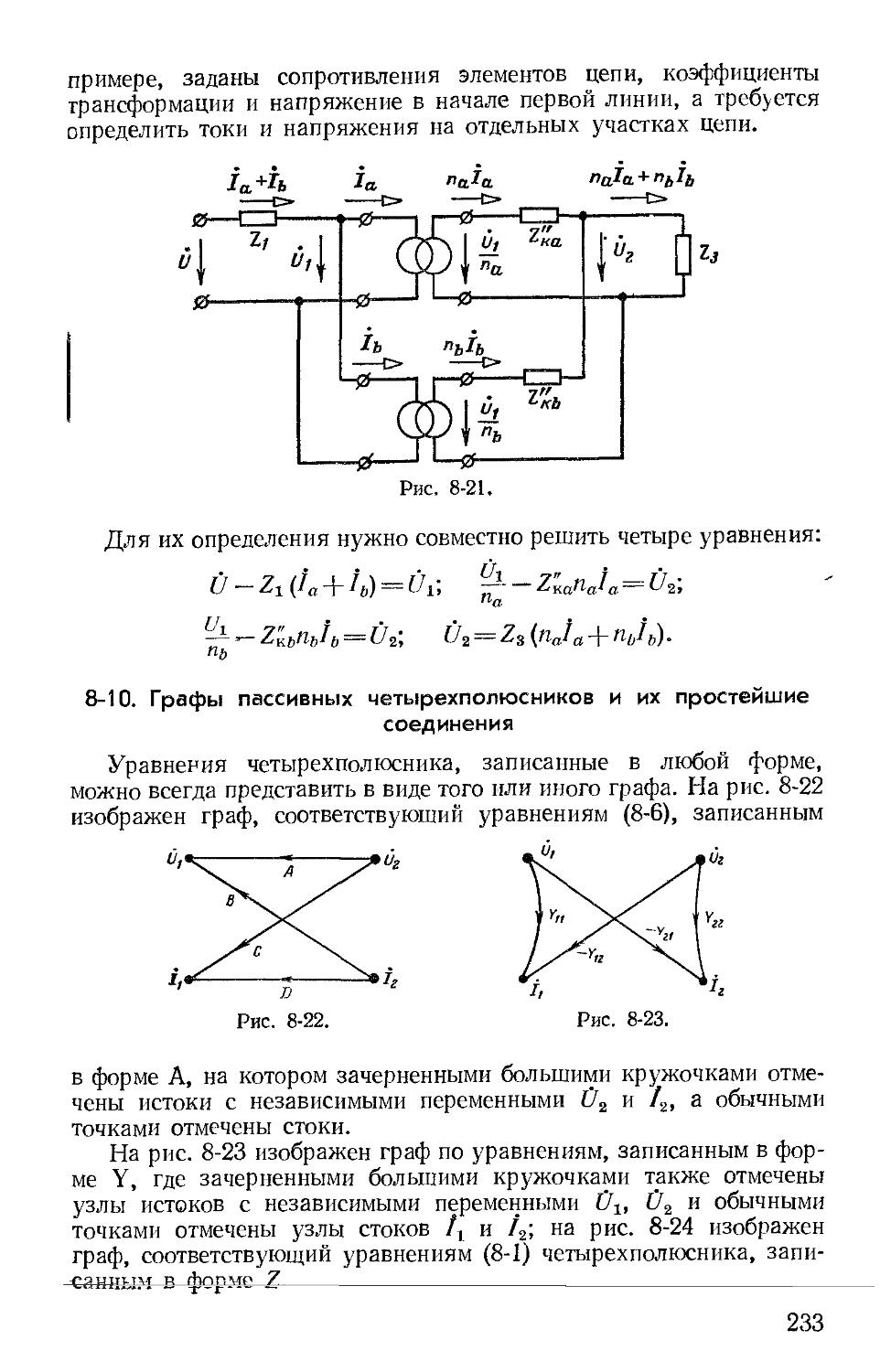
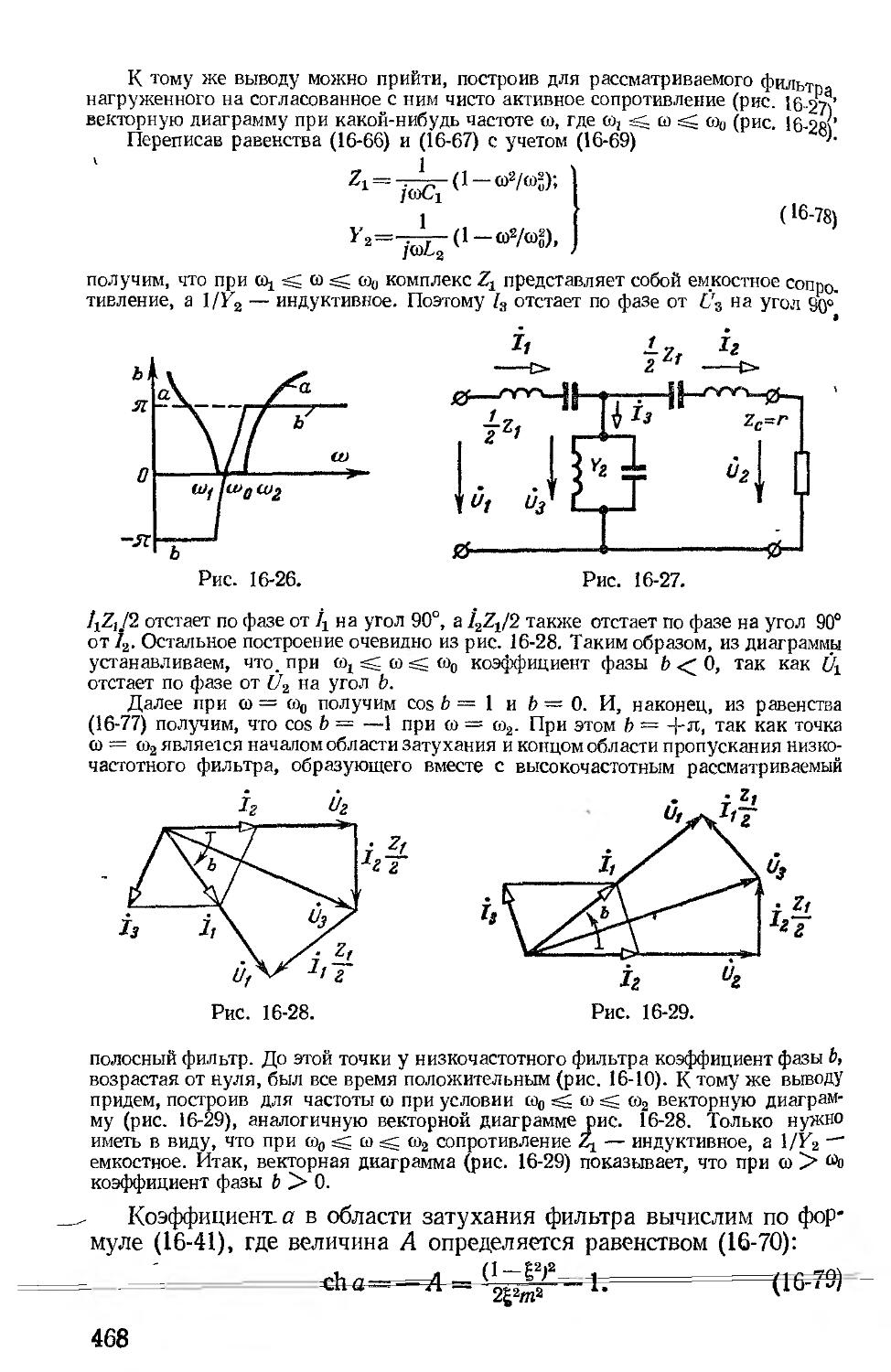
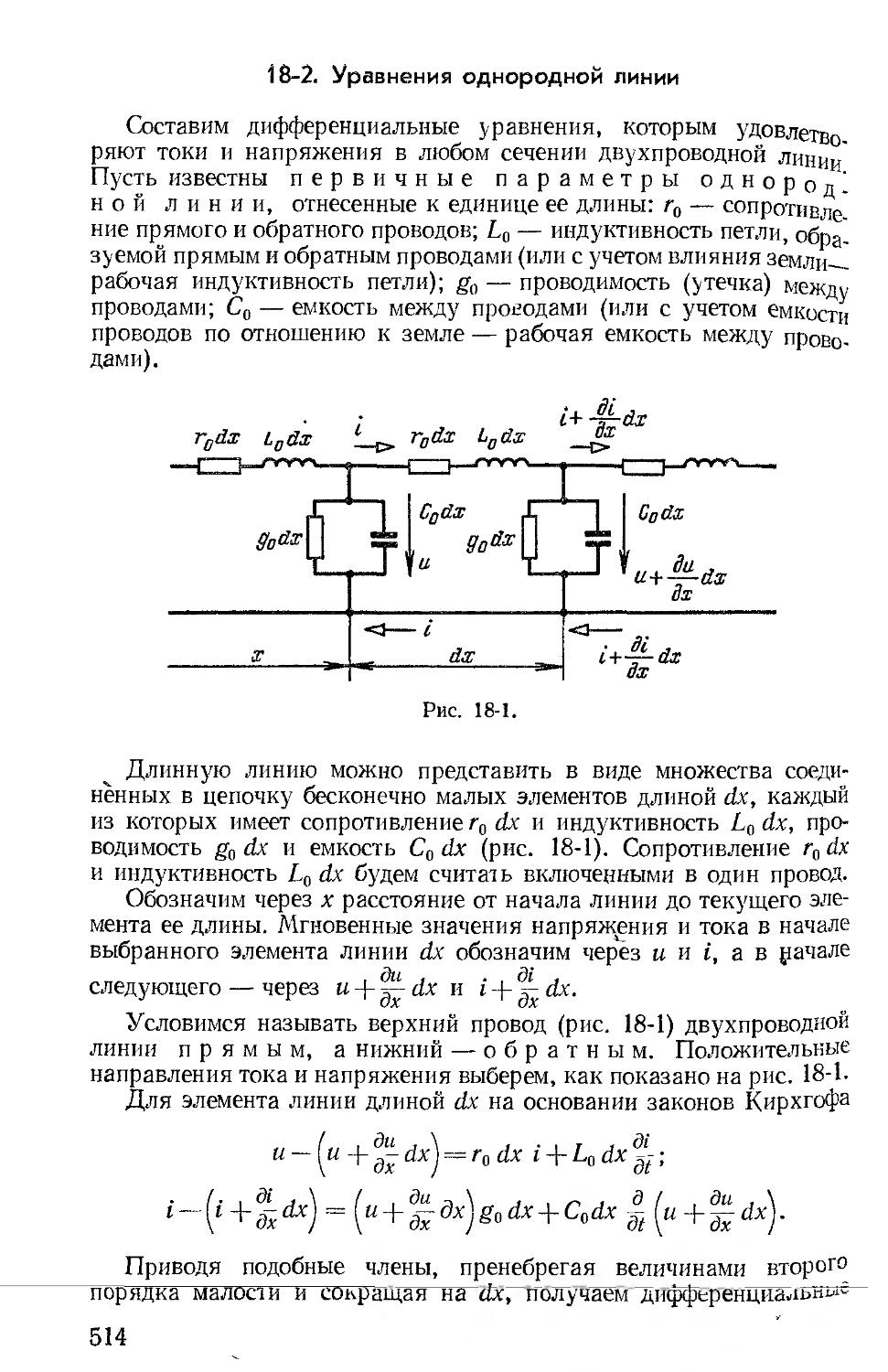
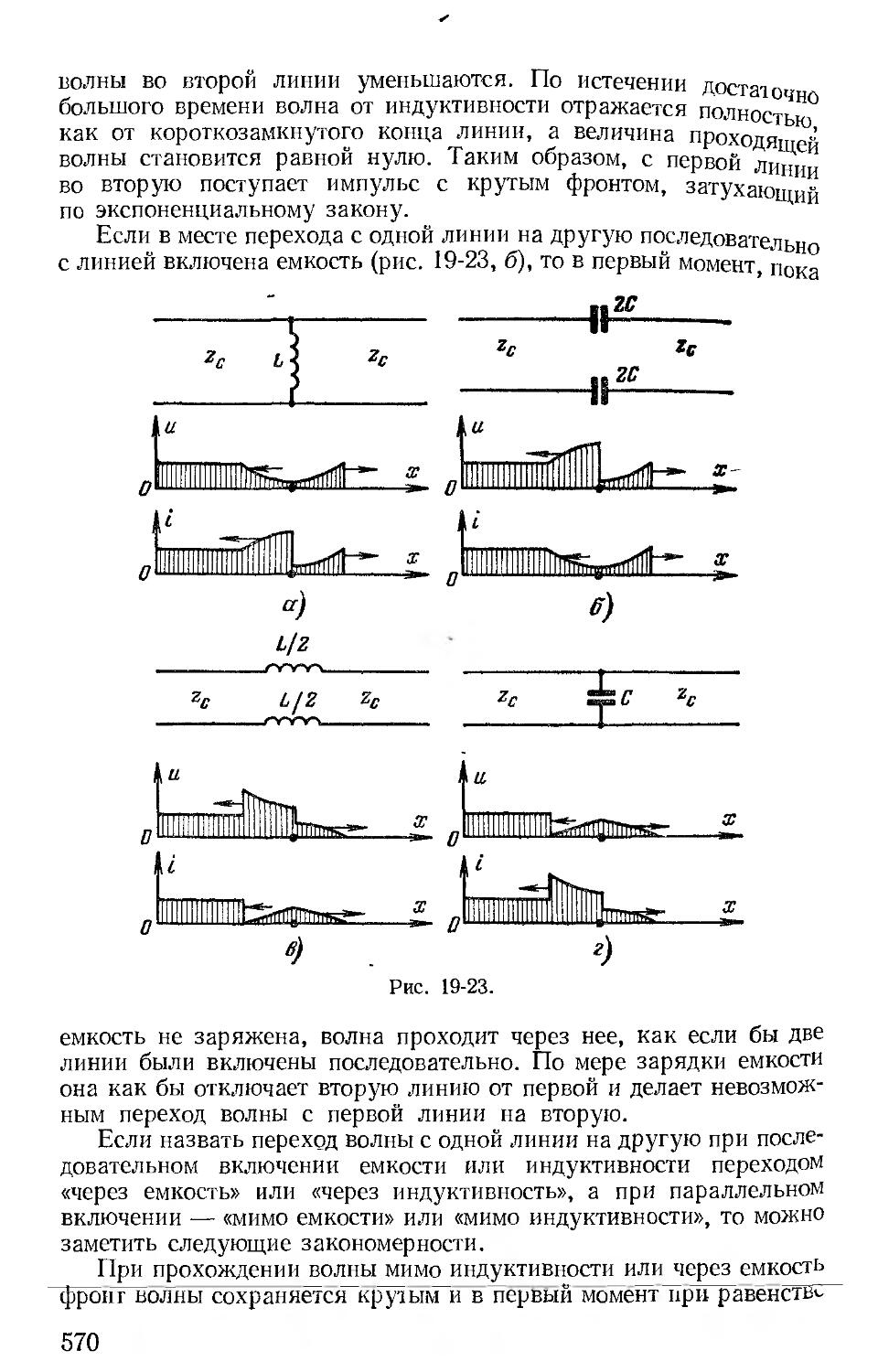
Второй раздел книги — «Линейные цепи с распределенными параметрами» начинается с гл. 18, в основном содержащей материал главы «Цепи с распределенными параметрами» учебника издания 1965 г., из которой по указанным выше соображениям исключены параграфы, посвященные параметрам симметричных и несимметричных четырехполюсников и цепочечным схемам. Рассм------
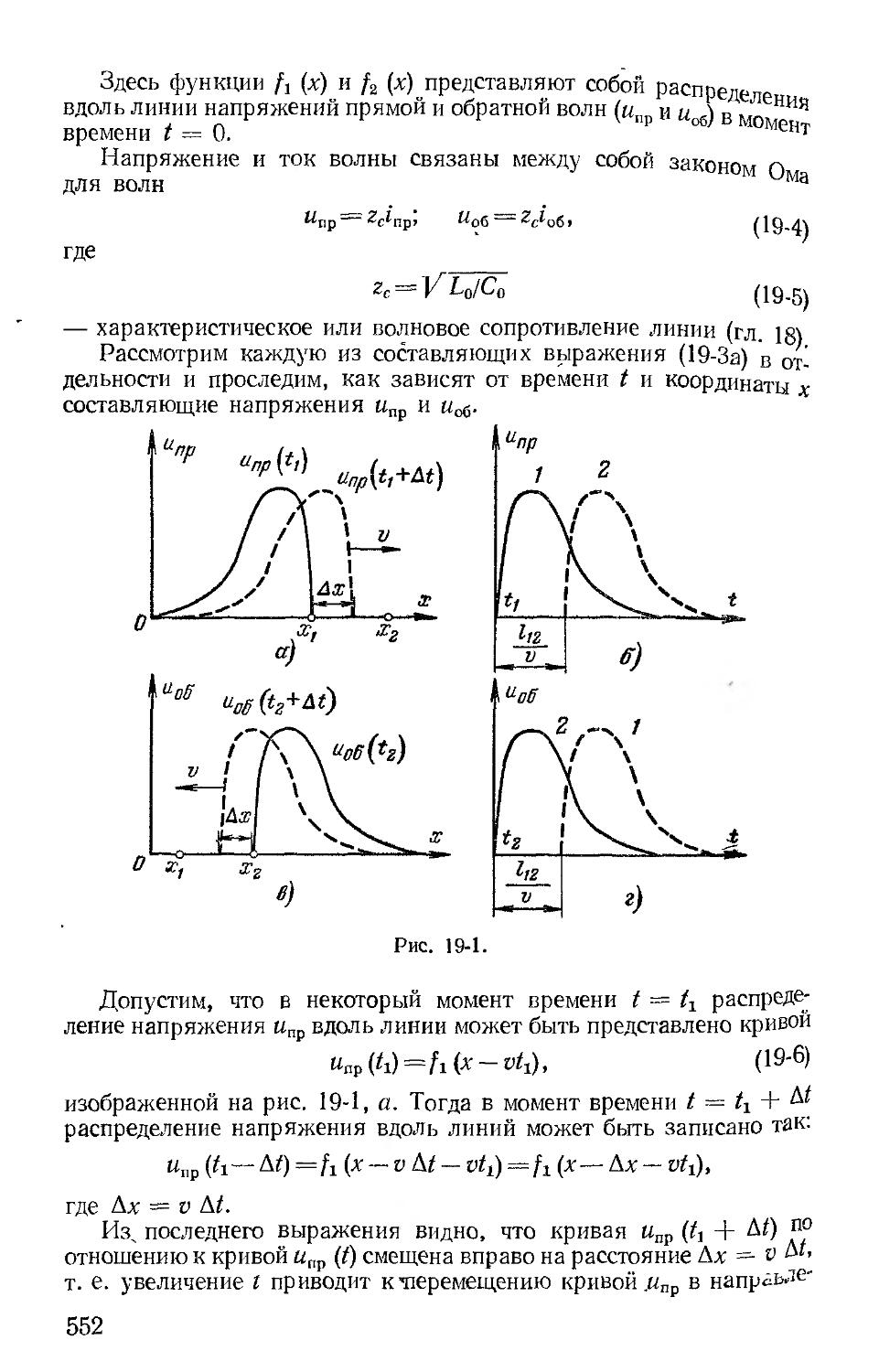
ние переходных процессов (гл. 19) следует в этом разделе непо ственно за изложением гармонических процессов.
Третий раздел книги начинается с изложения методов ра электрических и магнитных цепей при постоянных токах (г. и 21).
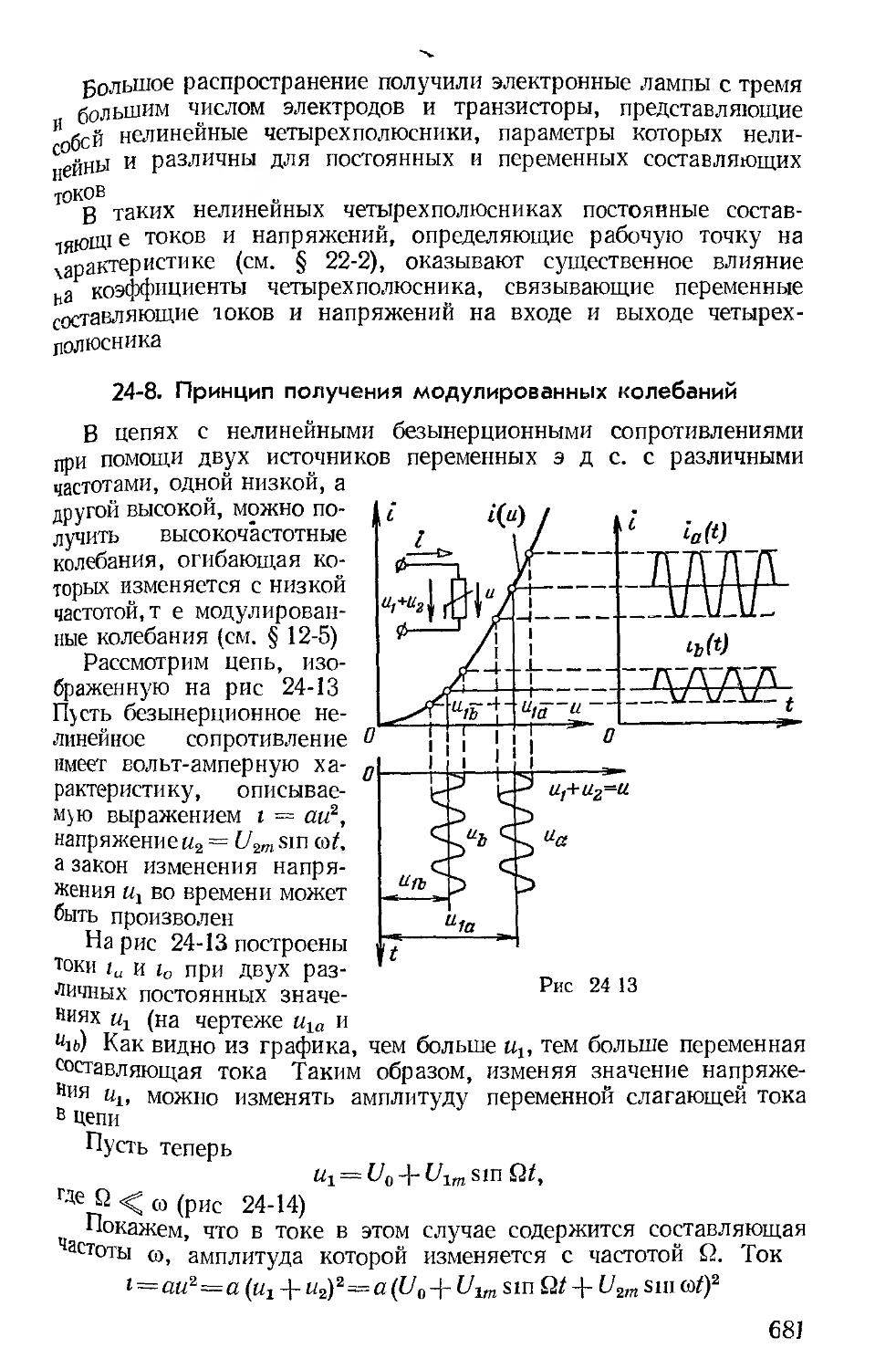
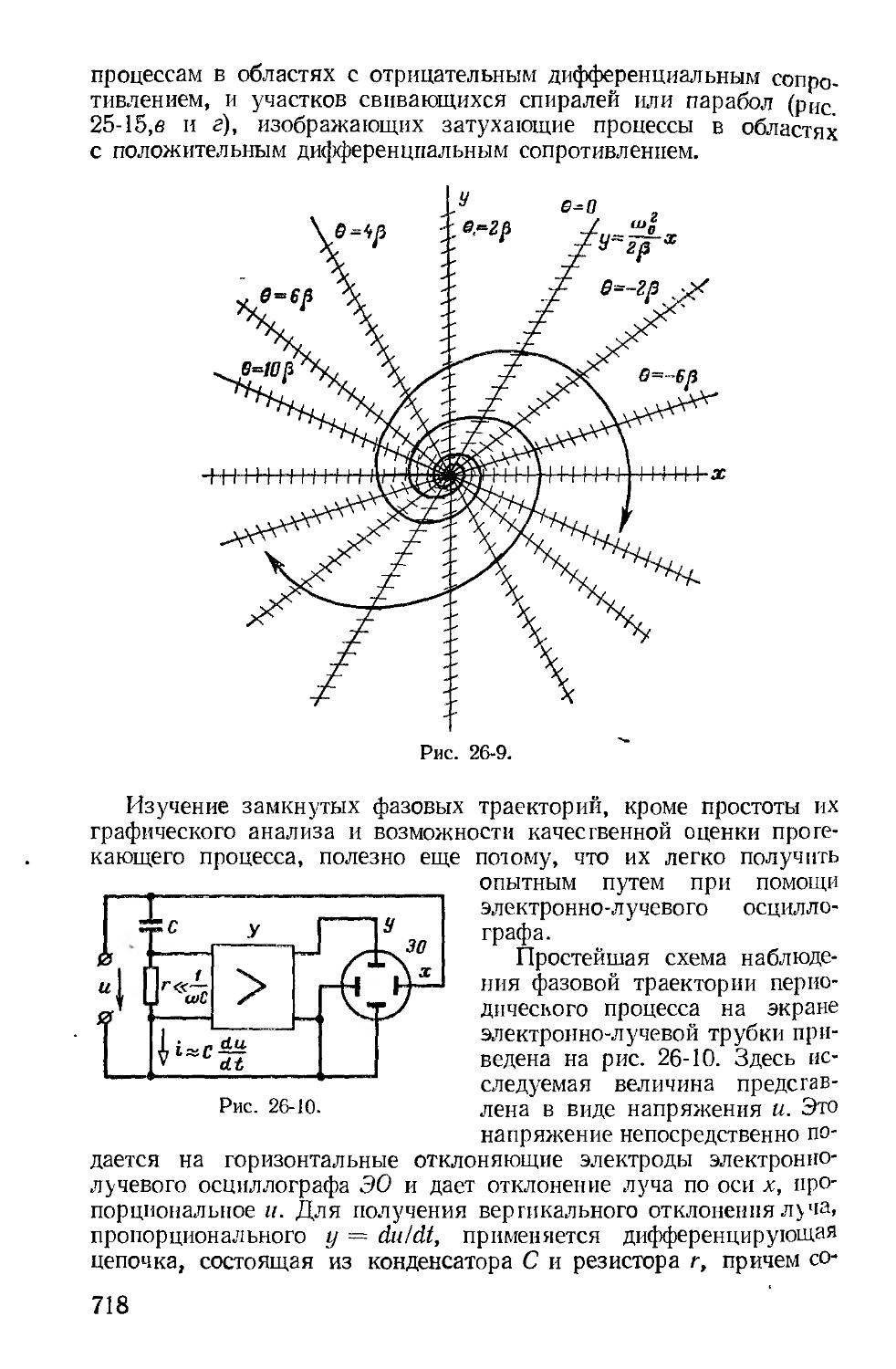
Теория нелинейных цепей переменного тока (гл. 22—26) иллюстрируется различными практическими задачами. В новом издании дополнительно рассмотрены процессы в преобразователях постоянного тока в переменный и в простейших запоминающих устройствах. Фазовая плоскость рассматривается на основе более общего определения пространства состояний.
Работа над учебником между авторами распределялась следующим образом: введение, гл. 1 и 2, § 4-7 — 4-8, гл. 8 (за исключением § 8-6 — 8-9), § 9-5 и гл. 20, 21 написаны проф. П. А. Ионкиным; гл. 3 и 4 (за исключением § 4-7 и 4-8), гл. 5—7, § 8-6 — 8-9, гл. 9 (за исключением § 9-5) и гл. 10, 11 написаны проф. Г. В. Зевеке; гл. 13—18 проф. С. В. Страховым и гл. 12, 19, 22—26 — проф. А. В. Нетушилом.
Авторский коллектив считает своим приятным долгом выразить благодарность рецензенту проф. В. М. Лаврову, внимательно просмотревшему рукопись четвертого издания учебника и сделавшему ряд весьма полезных замечаний.
Выражаем также сердечную благодарность и глубокую признательность доц. Б. Я. Жуховицкому за большую помощь в редактировании и подготовке рукописи к печати.
Все замечания, пожелания и отзывы о книге просим направлять в издательство «Энергия» по адресу: 113114, Москва, М-114, Шлюзовая наб., 10.
Авторы
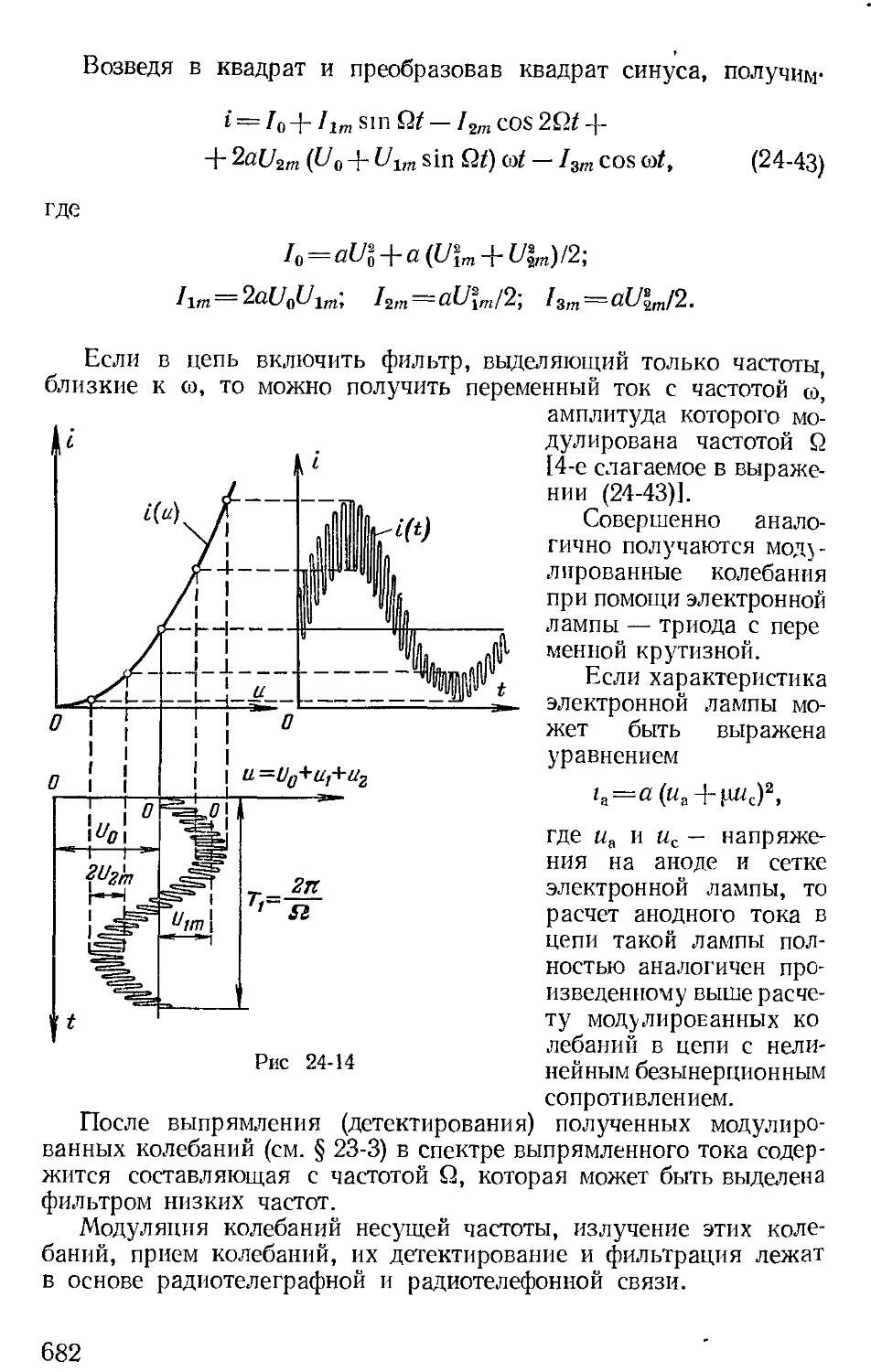
4
ВВЕДЕНИЕ
Электрическая энергия, как известно, широко применяется во всех отраслях промышленности, на транспорте, в сельском хозяйстве и в быту.
Гениальный создатель Советского государства Владимир Ильич Ленин говорил: «Коммунизм — это есть Советская власть плюс электрификация всей страны... Только тогда, когда страна будет электрифицирована, когда под промышленность, сельское хозяйство и транспорт будет подведена техническая база современной крупной промышленности, только тогда мы победим окончательно» (В. И. Ленин. Поли. собр. соч. Изд. 5-е, т. 42, с. 159).
Электротехникой в широком смысле слова называется обширная область практического применения электромагнитных явлений.
Поскольку все отрасли электротехники связаны между собой, то в системе высшего электротехнического образования возникла необходимость создания курса «Теоретические основы электротехники», являющегося базой для изучения различных электротехнических дисциплин.
В настоящее время специальные электротехнические дисциплины ставят перед курсом теоретических основ электротехники задачи расчета и исследования процессов, характеризуемых токами, напряжениями, мощностями, магнитными потоками и т. д., а также-задачи расчета и исследования явлений, которые характеризуются напряженностью электрического и индукцией магнитного полей, потоком мощности и т. д. Задачи первого вида относятся к расчету и исследованию цепей, а задачи второго вида — к расчету и исследованию электромагнитных полей.
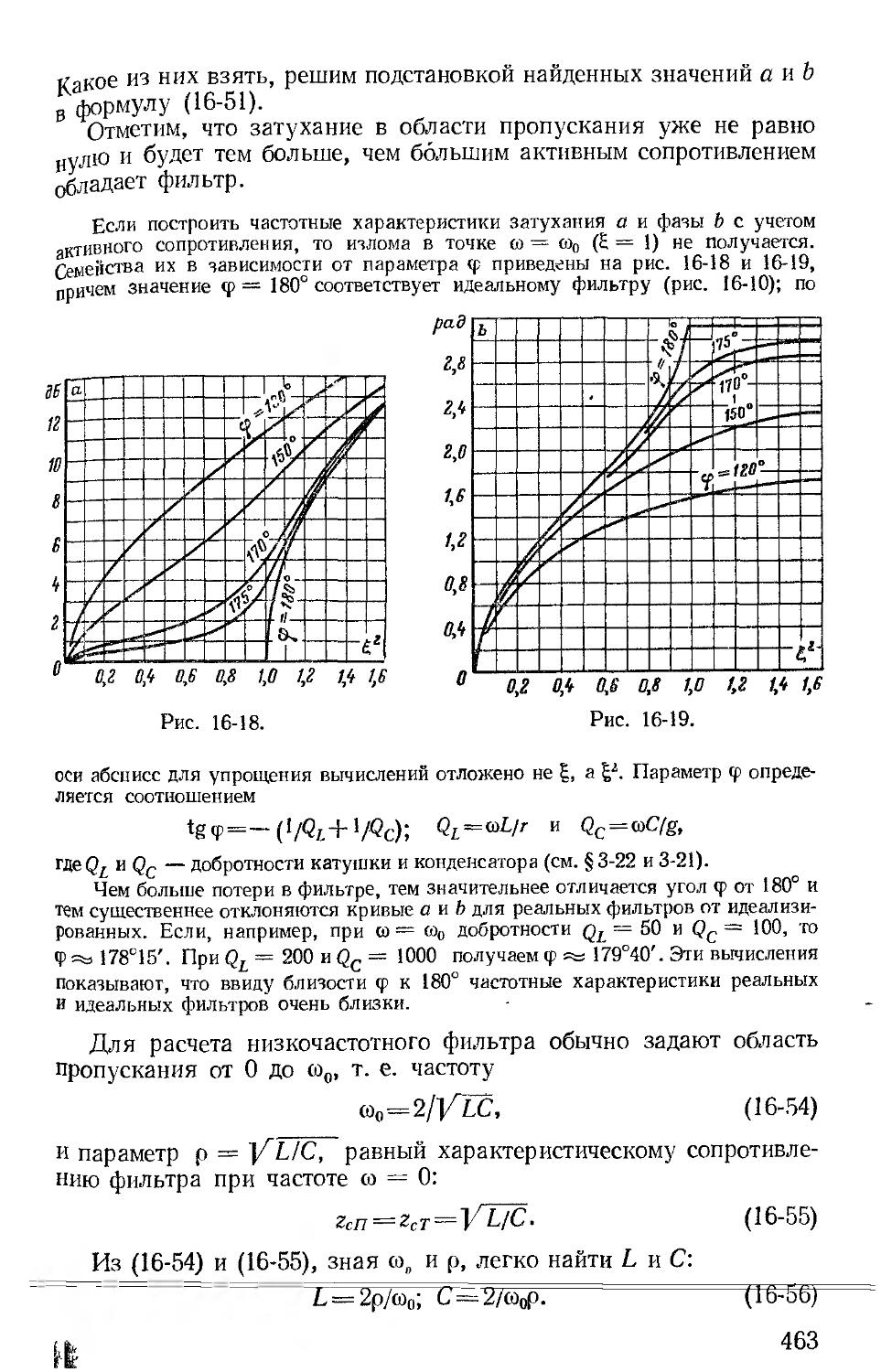
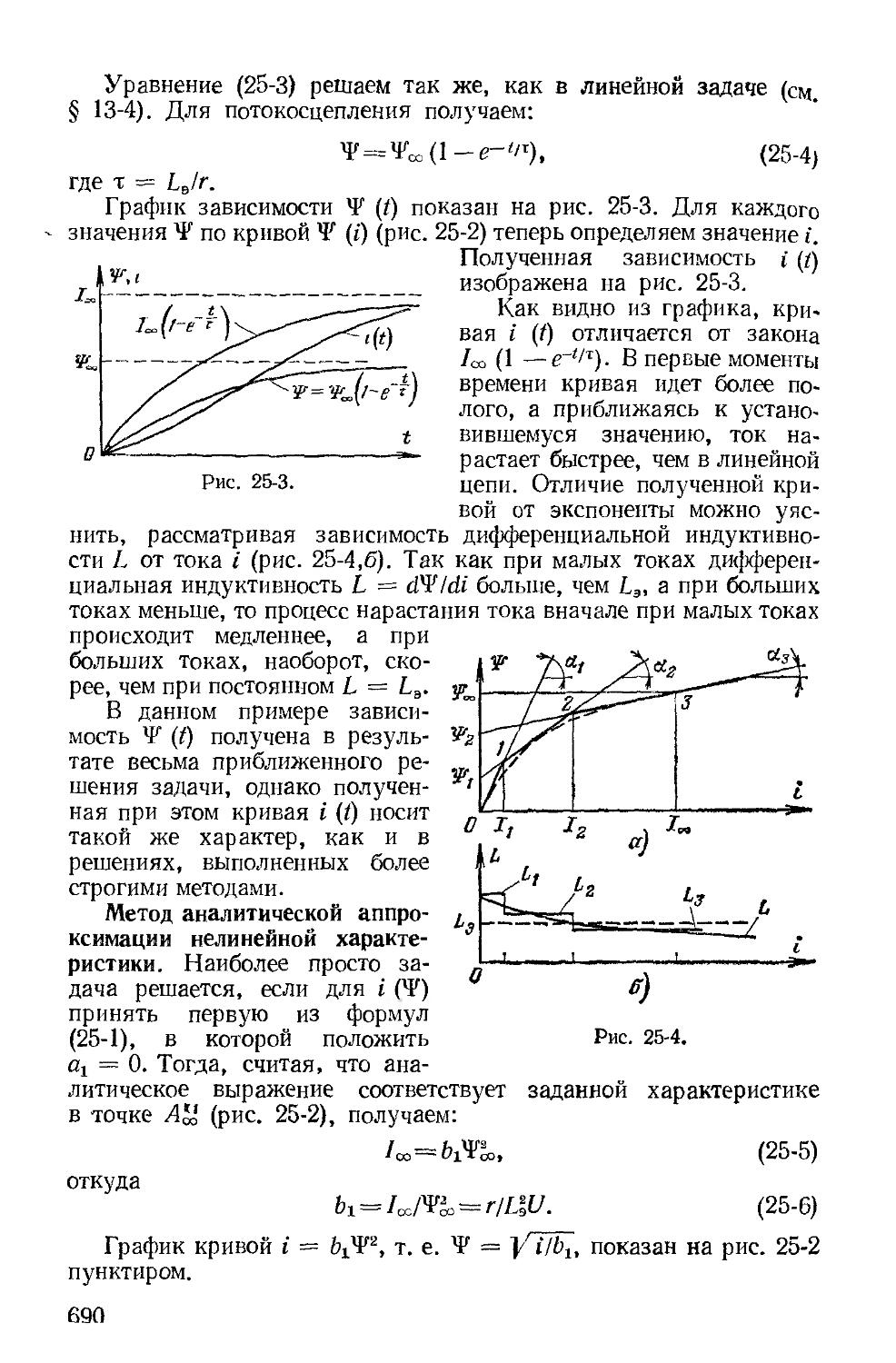
Я* ❖ Я*
Развитие электротехники потребовало больших работ в области изучения и разработки электромагнитных явлений и их практического приложения.
Много открытий и изобретений приходится на долю русских ученых и инженеров, которые совместно с выдающимися иностранными учеными положили начало важнейшим отраслям электротехники.
М. В. Ломоносов создал оригинальную теорию атмосферного электричества, открыл закон сохранения массы и движения.
После изобретения А. Вольта гальванического столба появилась возможность получать электрический ток. Исследуя процессы в электрической цепи, В. В. Петров открыл (1602 г.) электрическую
5
Дугу и указал на возможность практического применения ее для освещения, плавки и сварки металлов.
Весьма важную роль в развитии учения об элекфомагнитных явлениях сыграл английский ученый М. Фарадей, который в 1831 г. открыл явление и закон электромагнитной индукшш.
В 1833 г. русский академик Э X. Ленц открыл закон, устанавливающий связь между направлениями индукционных токов и их электромагнитными и электродинамическими взаимодействиями. В частности, им был установлен принцип электромагнитной инерции. В 1844 г. Э. X. Ленц независимо от английского исследователя Джоуля установил, что количество тепла, выделяющегося в проводнике при прохождении тока, прямо пропорционально сопротивлению проводника и квадрату тока.
Первый в мире электромагнитный телеграф был построен в 1832 г. в России П. Л. Шиллингом.
В 1845 г. немецким физиком Г. Кирхгофом были сформулированы основные законы разветвленных электрических цепей, которые названы его именем и имеют огромное значение для развития теоретической и практической электротехники.
Изобретенная русским ученым П. Н. Яблочковым электрическая свеча (1876 г.) положила начало электрическому освещению.
Первая лампа накаливания с угольным стерженьком была создана русским инженером А. Н. Лодыгиным.
Из других русских ученых второй половины XIX столетия необходимо отметить А. Г. Столетова, который впервые подробно исследовал магнитные свойства железа, и И. А. Умова, заложившего основы для вывода уравнений движения электромагнитной энергии в телах.
Таким образом, за период с 1800 по 1880 г. в тесной связи с развитием прикладной электротехники и, в частности, с телеграфией, гальванопластикой и техникой электрического освещения развивалась теория цепей постоянного гока. За этот период были установлены основные понятия теории электрических цепей и разработаны первые методы их расчета.
Начало применению переменных токов положил в 1876 г. П. Н. Яблочков. Переменный ток обеспечил равномерность сгорания углей в свече Яблочкова и позволил легко осуществить питание многих ламп от одного источника электрической энергии.
Расширение пофебления электрической энергии выдвинуло проблему передачи ее на значительные расстояния. Решение этой проблемы требовало применения различных напряжений для передачи и распределения электрической энергии. Эта задача была решена для переменного тока при помощи трансформаторов, изобретенных также П. Н. Яблочковым.
Переменный ток получил всеобщее признание и широчайшее применение в электроэнергетике благодаря изобретениям русского инженера и ученого М. О. Доливо-Добровольского. Им была разработана 1 рехфазная система, получившая повсеместное распростра-
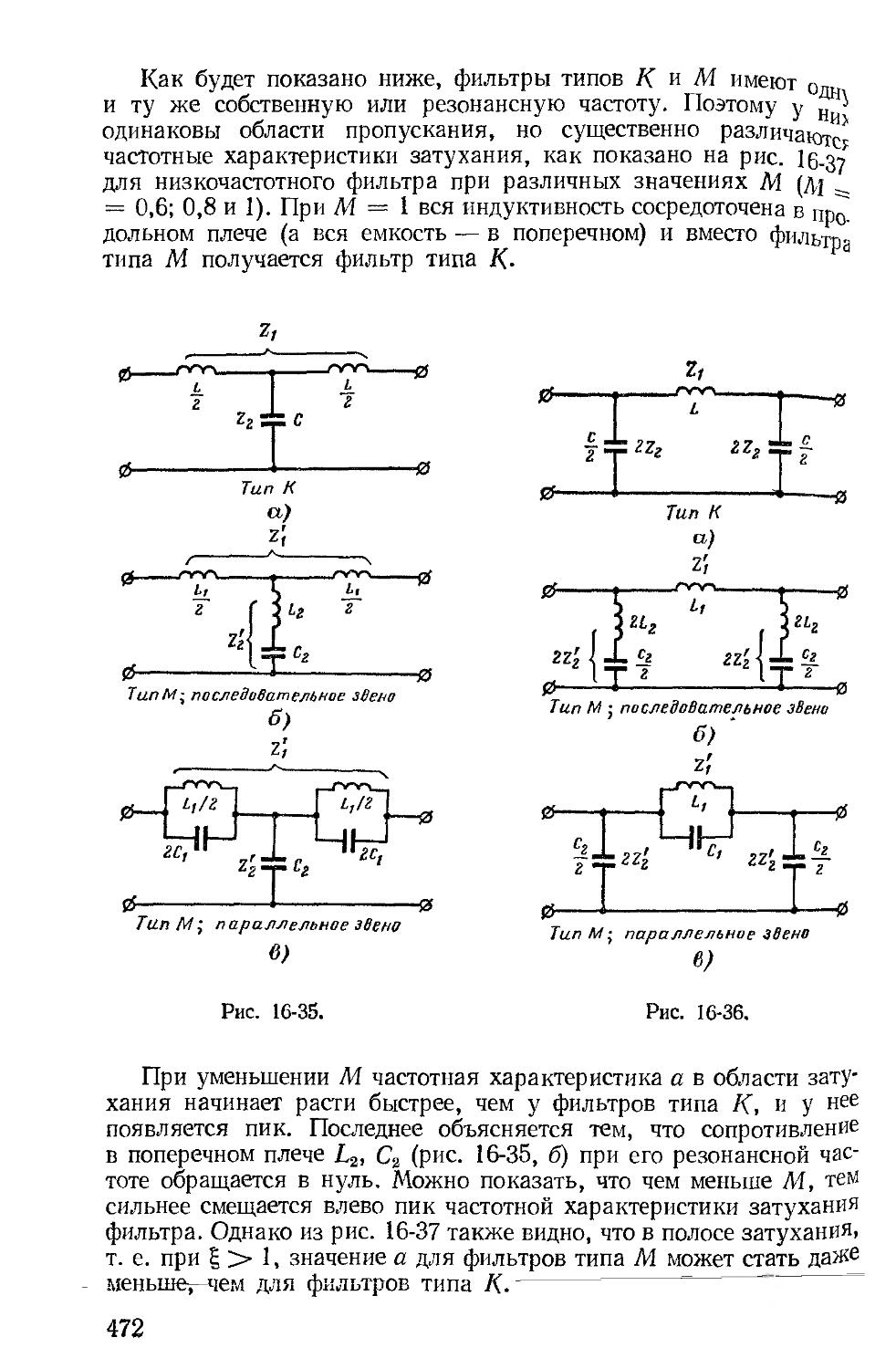
6
некие. В 1889 г. он построил первый трехфазный двигатель, разработал все остальные звенья трехфазной цепи и в 1891 г. осуществил передачу электрической энергии тре(хфазным током на расстояние 175 км.
Применение переменного тока потребовало решения многих теоретических вопросов и практических задач, что послужило основанием для разработки целой области теоретических основ электротехники, получившей в начале XX столетия название теории переменных токов. Особенно значительным в развитии переменных токов было введение американским инженером Ч. П. Штейнмет-цем метода комплексных величин для расчетов цепей.
Наряду с необходимостью решения теоретических задач, относящихся к электрическим и магнитным цепям, практическая электротехника поставила задачи по расчету электромагнитных полей. Конструирование электрических машин и электромагнитных аппаратов потребовало расчета магнитных полей; создание надежной изоляции токоведущих частей выдвинуло задачу расчета электрических полей. Учет распределения переменного тока по сечению проводов потребовал решения задач по расчету электромагнитного поля.
В 1873 г. английский ученый Д. К- Максвелл в классическом труд3 «Трактат об электричестве и магнетизме» изложил в математической форме основы теории электромагнитною поля, представляющей расширение и дальнейшее развитие идей Фарадея о физической реальности электромагнитного поля. Экспериментальное подтверждение и развитие теории электромагнитного поля, разработанной Максвеллом, было осуществлено немецким физиком Г. Герцем в 1887—1889 гг. в его опытах по получению и передаче электромагнитных волн, а также в работах русского физика П. Н. Лебедева, доказавшего наличие давления световых волн.
В 1895 г. А. С. Попов изобрел радиосвязь, открывшую новую эру в Культурной жизни человечества. Развитие радиотехники послужило мощным толчком к разработке как теории электрических цепей, так и теории электромагншного поля.
В 1904 г. в Петербургском политехническом институте проф. В. Ф. Миткевич начал читать курс «Теория электрических и магнитных явлений». В 1905 г. в Московском высшем техническом училище проф. К- А. Круг начал читать курс «Теория переменных токов», который был издан в 1906 г. Первой книгой в России, охватывающей основные вопросы курса теоретических основ электротехники, явилась напечатанная в 1916 г. книга К- А. Круга «Основы электротехники».
Следовательно, в развитии электротехники можно отметить второй этап (1880—1917 гг.), когда формировалась самостоятельная дисциплина «Теоретические основы электротехники».
Несмотря на работы выдающихся русских ученых и изобретателей, внесших крупнейший вклад в мировую электротехнику, электротехническая промышленность России вследствие ее экономиче_______
7
ской отсталости в дореволюционное время не получила должного развития. Лишь после Великой Октябрьской социалистической революции наша страна под руководством Коммунистической партии и Советского правительства создала мощную электротехническую промышленность, которая позволила отказаться от импорта электротехнического оборудования.
После успешного перевыполнения плана ГОЭЛРО применение электричества в годы довоенных и послевоенных пятилеток достигло огромного размаха во всех областях народного хозяйства. В настоящее время продолжаются гигантские работы по строительству величайших в мире электрических станций. Создаются невиданные по размерам и техническим данным машины. Широко внедряется автоматизация во все технологические процессы. Во всех областях народного хозяйства применяется новейшая техника.
Выполнение таких грандиозных задач возможно только при наличии глубокой теоретической базы, стоящей на высоком научном уровне.
* * *
Во всех современных электротехнических устройствах, предназначенных для различных технических целей, происходят те или иные энергетические преобразования. Электрические генераторы и двигатели служат для взаимного преобразования механической и электрической энергии. При помощи трансформаторов электрическая энергия одного напряжения преобразуется в электрическую энергию другого напряжения. В электрической лампе происходит процесс преобразования электрической энергии в световую. Во многих электротехнических устройствах электрическая энергия перераспределяется между отдельными элементами этих устройств.
Для канализации электрической энергии в заданных направлениях широко применяются проводниковые материалы с высокой удельной проводимостью, которые без значительных потерь электрической энергии проводят электрический ток. Концентрации энергии и уменьшения объема электрического поля обычно добиваются при помощи конденсаторов, заполненных диэлектриком с высокой диэлектрической проницаемостью. Для концентрации энергии и уменьшения объема магнитного поля, как правило, пользуются ферромагнитными материалами с высокой магнитной проницаемостью.
Применение указанных материалов для концентрации электромагнитной энергии в очень малых объемах позволяет во многих случаях исследовать протекающие в них физические процессы при помощи известных интегральных понятий: электрического тока, напряжения, э. д. с., магнитного потока, магнитодвижущей силы и т. п.
________Исследования электромагнитных явлений и процессов, протекающих при различных энергётическшГпрёббразбваниях в электро
8
технических устройствах, привели, начиная с 20-х годов текущего столетия, к стремительному развитию курса теоретических основ электротехники. В частности, чрезвычайно широкое развитие получили общие вопросы теории электрических цепей, имеющие большое значение почти для всех прикладных отраслей электротехники.
Предметом курса «Теоретические основы электротехники» является изучение как с качественной, так и с количественной стороны электромагнитных явлений и процессов, происходящих в различных электротехнических устройствах.
Курс теоретических основ электротехники дает учащемуся по возможности в достаточно общей форме знание качественных и количественных соотношений для электромагнитных явлений и процессов и намечает основные пути для решения задач, которые ставят специальные электротехнические дисциплины.
Качественные и количественные стороны исследуемых электромагнитных явлений и процессов находятся в неразрывной связи. Поэтому изучение курса теоретических основ электротехники в высшей школе основывается на знаниях, полученных из курсов физики и математики. Эти знания в курсе теоретических основ электротехники расширяются и развиваются в направлении разработки методов анализа, расчета и экспериментального исследования явлений и процессов, протекающих в электрических и магнитных цепях и в электромагнитных полях.
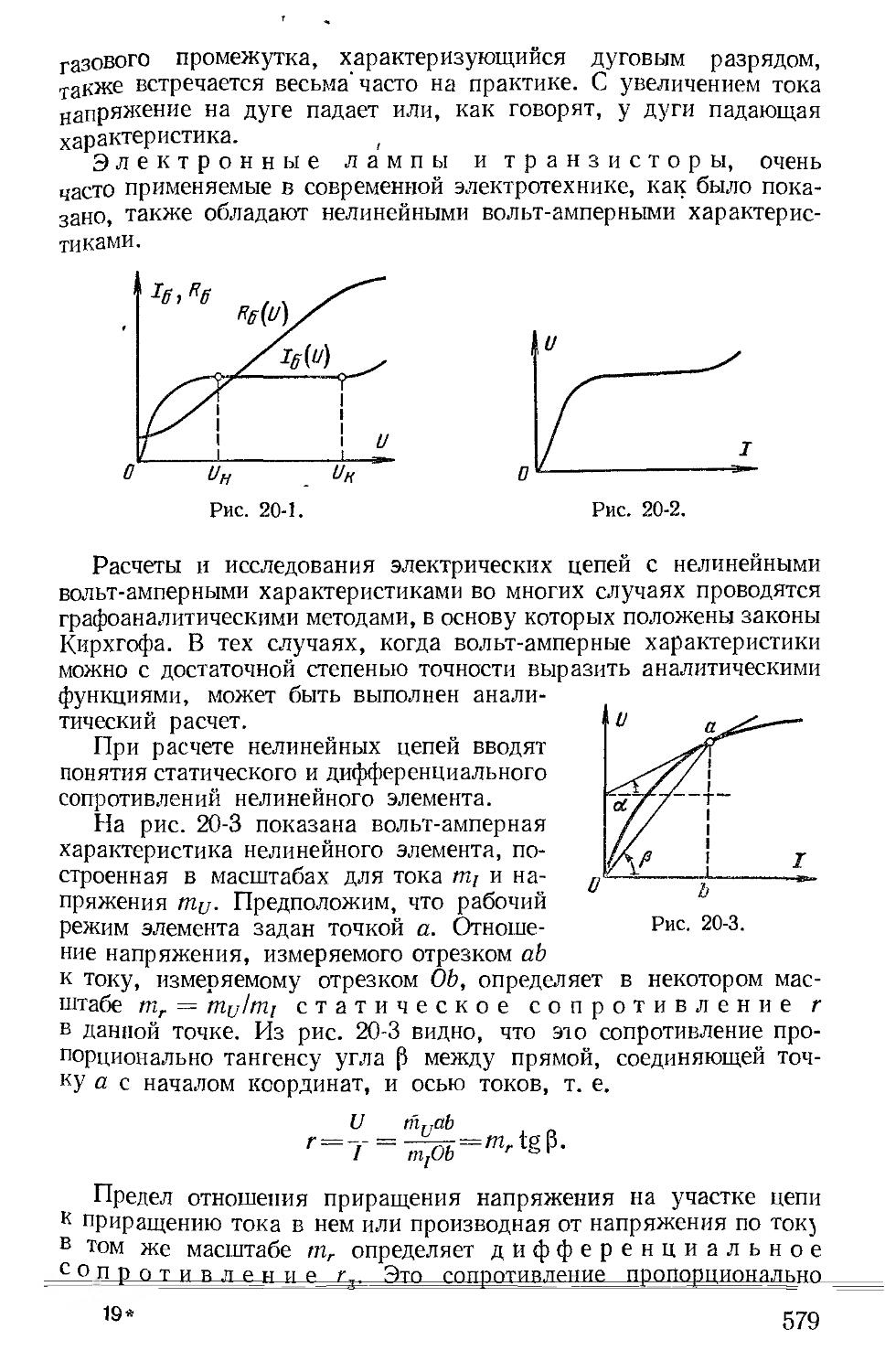
В практической деятельности инженера основная трудность часто возникает на стадии составления математической модели для исследуемой электротехнической, установки, поскольку одна и та же установка может иметь разные математические описания в зависимости от задачи исследования. Так, резко различными могут быть математические модели, применяемые для анализа работы изоляции электрической установки и оценки экономичности ее рабочих режимов. В значительной мере выбор подходящей математической модели связан с требуемой степенью точности выполнения исследований и расчетов. При этом понятие «точность» приходится считать в известной мере условным; оно более определенным оказывается при уже выбранной модели, с которой связано соответствующее математическое описание исследуемых процессов и явлений. Только при наличии уравнений можно говорить о точности их решения.
Существенно подчеркнуть, что теория электромагнитного поля оперирует с дифференциальными понятиями, которыми являются напряженности электрического и магнитного полей, индукция магнитного поля, плотность тока, плотность энергии и т. п. Эти величины относятся к отдельным точкам среды или к конструктивным деталям; они могут быть как постоянными, так и переменными во времени. Для исследования процессов и получения необходимых представлений часто пользуются картиной поля.
Наряду с этим значительное число электротехнических задач, как это уже отмечено, решается при помощи интегральных понятий, к которым относятся; напряжение, э. д. с , электрический ток, маг—
9
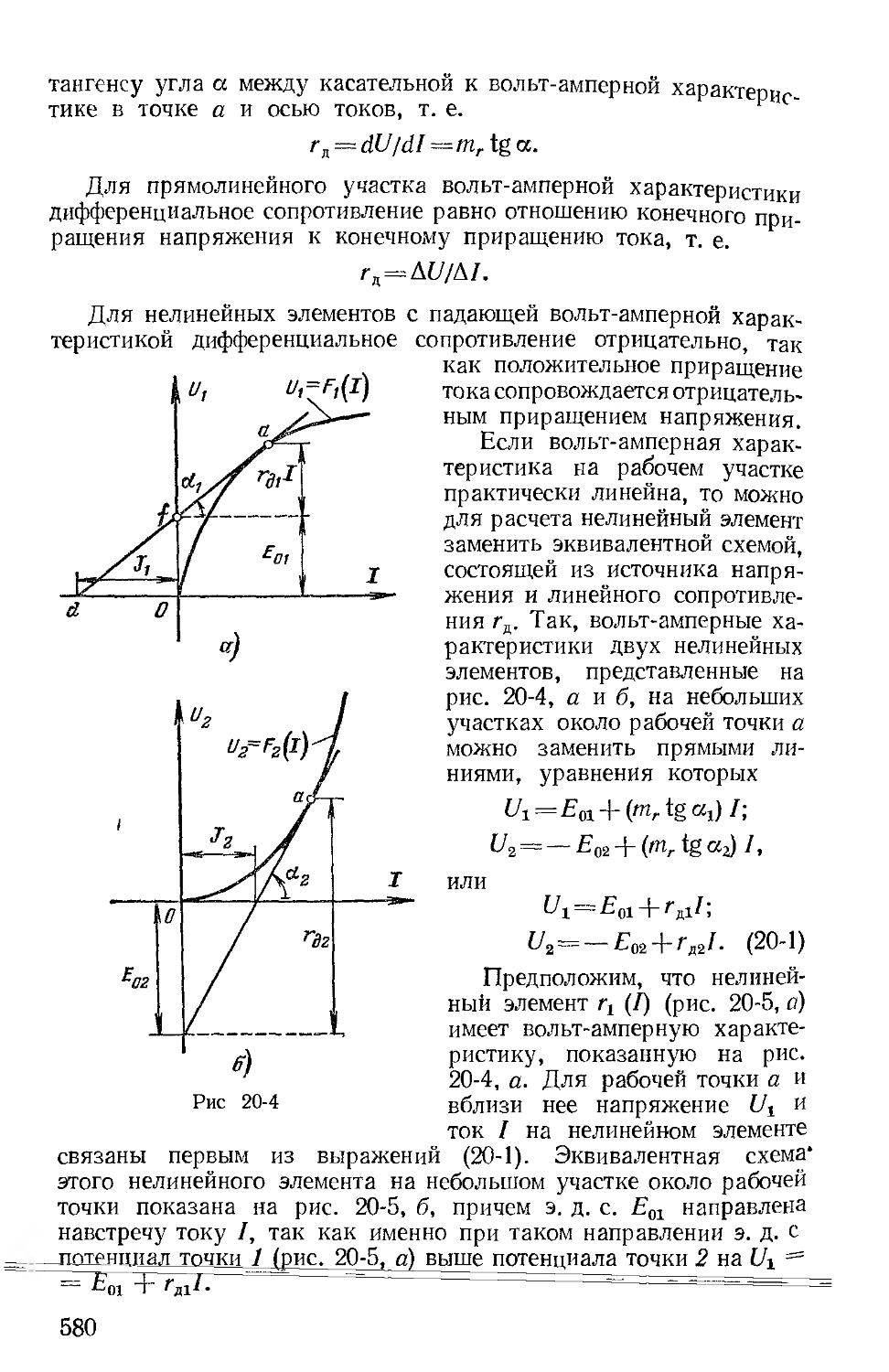
нитный поток, мощность, энергия, сопротивление, емкость, индуктивность и т п. При этом следует иметь в виду, что интегральные величины являются не менее обоснованными и показательными, чем дифференциальные. Так, они легче контролируются в конкретных установках, их применение значительно упрощает экспериментальные проверки Сравнительно просто могут быть определены и допустимые значения по тем или иным условиям. В качестве основы математического описания цепей применяются законы Ома и Кирхгофа.
Как при исследовании физических процессов в цепях, так и при изучении электромагнитных полей различных устройств единственным научным методом познания является диалектический метод: «От живого созерцания, — говорит Ленин, — к абстрактному мышлению и от него к практике— таков диалектический путь познания истины, познания объективной реальности» (В. И. Ленин. Поли. собр. соч. Изд. 5-е, т. 29, с. 151 — 153).
Это основное положение теории познания лежит в основе всего курса теории цепей, содержание которого и изложено в данной книге.
Раздел первый
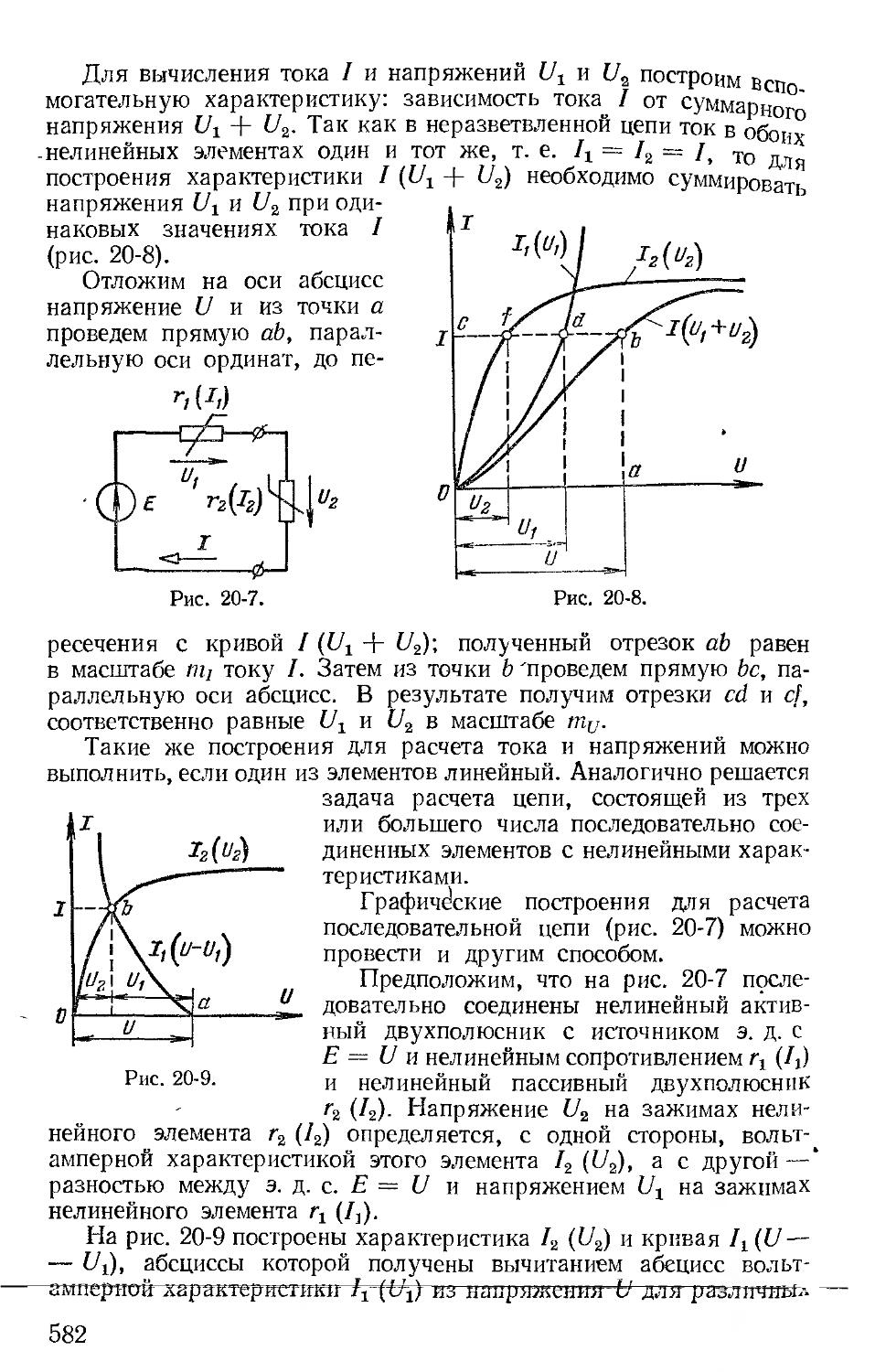
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
Глава первая
ОСНОВНЫЕ ЗАКОНЫ И МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
1-1. Элементы электрических цепей и электрических схем
Электрической цепью называется совокупность устройств, предназначенных для передачи, распределения и взаимного преобразования электрической (электромагнитной) и других видов энергии и информации, если процессы, протекающие в устройствах, могут быть описаны при помощи понятий об электродвижущей силе (э д с ), токе и напряжении
Основными элементами электрической цепи являются источники и приемники электрической энергии (и информации), которые соединяются между собой проводами
В источниках электрической энергии (гальванические элементы, аккумуляторы, элекгромашинные генераторы и т и ) химическая, механическая, тепловая энергия или энергия других видов превращается в электрическую, ав приемниках электрической энергии (электротермические устройства, электрические лампы, резисторы, электрические двигатели и т п ), наоборот, электрическая энергия преобразуется в тепловую, световую, механическую и др
Электрические цепи, в которых получение электрической энергии в источниках, ее передача и преобразование в приемниках происходят при неизменных во времени токах и напряжениях, обычно называют цепями постоянного тока
При постоянных токах и напряжениях магнитные и электрические поля электрических установок также не изменяются во времени Вследствие этого в цепях постоянного тока не возникают э д с самоиндукции и отсутствуют токи смещения в диэлектриках, окружающих проводники
Вместо термина «приемник электрической энергии» в дальнейшем будем применять более краткие и равнозначные термины — приемник или потребитель, а вместо термина «источник электрической энергии» — источник энергии, источник питания или источник
На рис 1-1 условно изображена простейшая электрическая установка с источником энергии — аккумуляторной батареей и с приемником - группой электрических ламщ-Зажимы источника и прием-
11
длектрические
Рис 1-1.
между положи-
ника энергии соединены между собой двумя проводами. Источник энергии, провода и приемник образуют замкнутый проводящий контур. В этом контуре под действием э. д. с. источника энергии происходит непрерывное н односюронне направленное упорядоченное движение электрических зарядов.
Совокупность этих трех элементов — источника энергии, двух проводов и приемника — представляет собой простейшую электрическую цепь постоянного тока. Практически чаще встречаются более сложные элешрпческие цепи с большим числом источников и приемников энергии.
Чтобы облегчить изучение процессов в электрической цепи, ее заменяют расчетной схемой
замещения, т. е. идеализированной цепью, которая служит расчетной моделью реальной цепи. При этом пользуются понятиями двух основных элементов схемы: источника энергии с э. д с. Е и внутренним сопротивлением га (рис 1-2, а) и сопротивления приемников и проводов г (рис. 1-2, б). Таким образом, применяя в дальнейшем термин «схема замещения» или, короче, «схема», будем всегда подразумевать и соответствующую цепь.
Электродвижущая сила Е (рис. 1-2, а) численно равна разности потенциалов <р или напряжению тельным и отрицательным зажимами 1 и 2 источника энергии при отсутствии в нем тока независимо от физической природы ее возникновения (контактная э. д. с., термо-э. д. с и т. д):
£' = Ф1 — Ф2 = П12. (1-1)
Электродвижущую силу Е можно определить Как работу сторонних (неэлектрических) сил, присущих источнику, затрачиваемую на
перемещение единицы положительного заряда внутри источника от зажима с меньшим потенциалом к зажиму с большим потенциалом.
Направление действия э. д с. (от отрицательного зажима к положительному) указывается на схеме стрелкой.
Если к зажимам источника энергии присоединить приемник (нагрузить), то в замкнутом контуре этой простейшей цепи возникает ток I (рис. 1-3) При этом напряжение или разность потенциалов на зажимах 1 и 2 уже не будет равна э. д. с. вследствие падения напряжения 17 в внутри источника энергии, т. е. на его внутреннем сопротивлении гв:
~ = rj.------------------
Рис 1-2.
12
Рис 1-3.
На рис. 1-4 представлена одна из наиболее типичных, так называемых внешних характеристик U12 (/) = U (/), т. е. зависимость напряжения на зажимах нагруженного источника энергии от тока. Как показано на рисунке, при увеличении тока от нуля до I ж 4 напряжение на зажимах источника энергии убывает практически по линейному закону.
V^U^E-VB^E-rBl.
Иначе говоря, при Е = const падение напряжения внутри источника энергии UB в указанных пределах растет пропорционально току. При дальнейшем росте тока нарушается пропорциональность между его
напряжения внутри источника энергии — внешняя характеристика не остается линейной. Такое уменьшение напряжения вызвано у одних источников энергии уменьшением э. Д с., у других — увеличением внутреннего
значением и падением
сопротивления, а у третьих — одновременным уменьшением э. д с. и увеличением внутреннего сопротивления.
Развиваемая источником энергии мощность определяется равенством
РК = Е1. (1-2)
Здесь следует отметить установившееся в электротехнике неточное применение термина «мощность» Так, например, говорят о генерируемой, отдаваемой, потребляемой, передаваемой, теряемой мощности В действительности генерируется, отдается, потребляется^ передается, теряется не мощность, а энертия Мощность характеризует интенсивность энергетического процесса и измеряется количеством генерируемой, отдаваемой, передаваемой и других видов энергии в единицу
времени Поэтому правильно было бы говорить о мощности генерирования энергии, о мощности передачи энергии и т д Следуя традициям электротехники, будем применять приведенные выше краткие выражения
Сопротивление приемника г (рис. 1-2, б) как элемент схемы или идеализированной цепи характеризует потребление электрической энергии, т. е. превращение электрической энергии в другие виды, при мощности
Р = гР. (1-3)
В общем случае сопротивление приемника зависит от тока в этом приемнике г (/).
По закону Ома напряжение на сопротивлении
V=--rI. (1-4)
Отметим, что к открытию этого закона довольно близко подошел еще в 1801—1802 гг. акад В. В. Петров. Позднее, в 182б г., этот закон был сформулирован Омом--------------------------------------
13
Наряду с сопротивлением для расчета цепей вводят понятие проводимости
g=l/r.
На практике часто бывает задана не зависимость сопротивления от тока г (I), а зависимость напряжения на сопротивлении от тока Uab (/) — П (/) или обратная зависимость тока от напряжения / (U) Характеристики U (/) и / (U) получили распространенное, хотя и не совсем точное, название вольт-амперных.
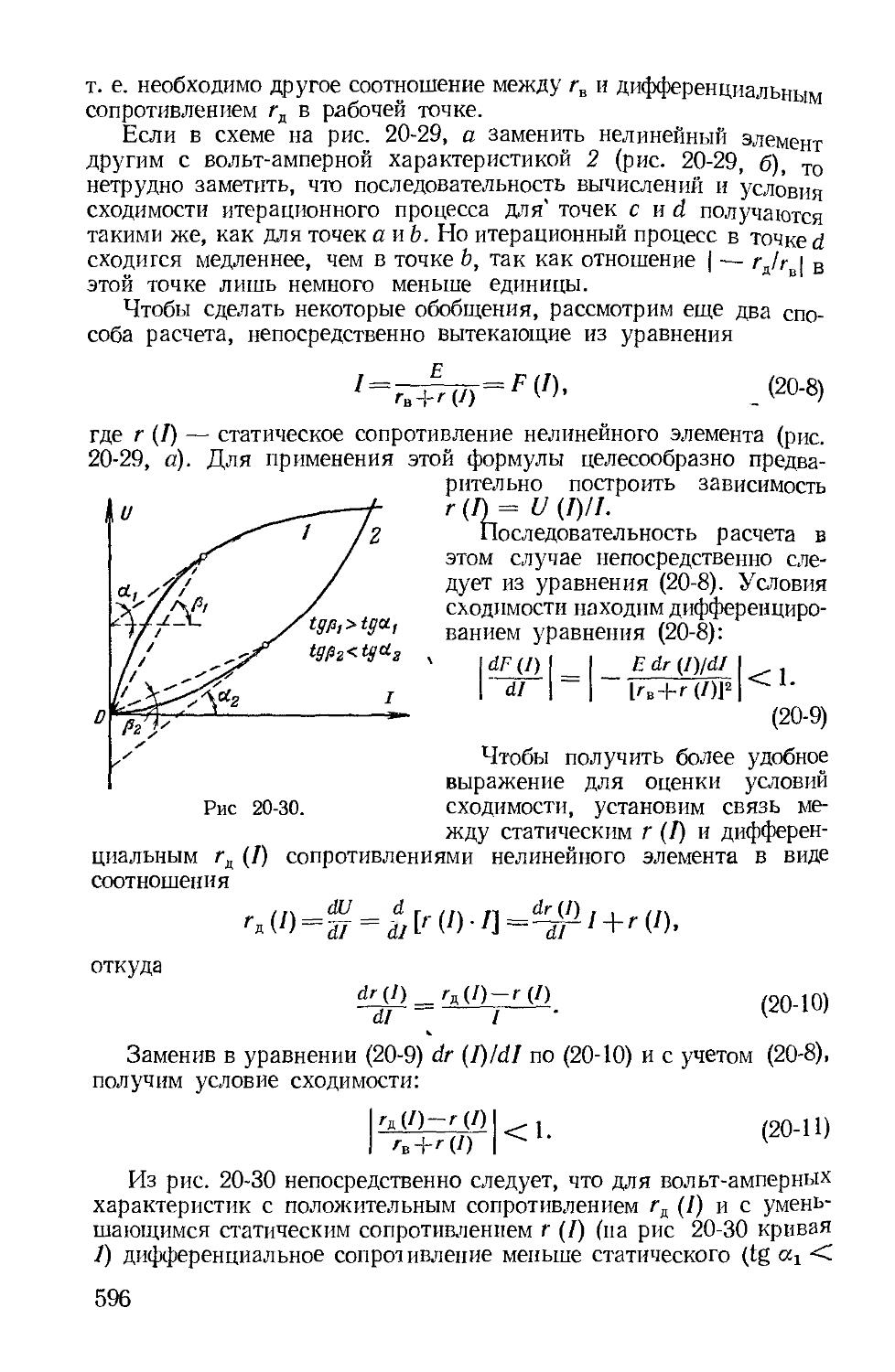
На рис 1-5 представлены вольт-амперные характеристики для лампы с металлической нитью 6/, (/) и для лампы с угольной нитью U2 (/) Как показано на рисунке, связь между напряжением и током каждой лампы — нелинейная. Сопротивление лампы с металлической нитью растет с увеличением тока, а сопротивление лампы с угольной нитью с увеличением тока падает.
Электрические цепи, содержащие элементы с нелинейными характеристиками, называются нелинейными.
Если принять э д с источников энергии, их внутренние сопротивления и сопротивления приемников не зависящими от токов и напряжений, то внешние характеристики источников энергии t/12 (П ~ U (0 11 вольт-амперные характеристики приемников Uab (7) = U (J) будут линейными (рис 1-6)
Электрические цепи, состоящие только из элементов с линейными характеристиками, называют л ине й н ы м и.
Большое число реальных электрических цепей можно отнести к линейным Поэтому изучение свойств и методов расчета линейных электрических цепей представляет не только теоретический, но и значительный практический интерес.
1-2. Эквивалентные схемы для источников энергии
Простейшая электрическая цепь и ее схема замещения, как указывалось, состоят из одного источника энергии с э д с Ей внутренним сопротивлением гк и одного приемника с сопротивлением г (рис. 1-3), где сопротивление соединяющих проводов не показано, если для этой цепи им можно пренебречь Ток во внешней по отношению к источнику энергии части цепи, т с—в прием
14
нике или сопротивлении г, принимается направленным от точки а с большим потенциалом <ря — <рх к точке Ъ с меньшим потенциалом <Рь = ЧЪ-
Направление тока будем обозначать на схеме стрелкой с просветом ичи указывать двумя индексами у буквы I, связанными с соответствующими индексами на схеме. Так, для схемы рис. 1-3 ток в приемнике / — 1аЬ, где индексы а и b обозначают направление тока от точки а к точке Ь.
Покажем, что источник энергии с известными э. д. с. Е и внутренним сопротивлением гв может быть представлен двумя основными эквивалентными схемами.
Как уже указывалось, напряжение на зажимах источника энергии меньше э. д. с. на падение напряжения внутри источника:
U — Ф1 — fPi = E — UB = E — гв1. (1-3)
С другой стороны, напряжение на сопротивлении г
U=q>a-q>b = rl. (1-6)
Ввиду равенства = (ра и <р2 = <рь из (1-5) и (1-6) следует, что Е — rB I = г! или
_ E~rBI-\-rI (1-7)
и
Отсюда видно, что внутреннее сопротивление гв источника
энергии, так же как сопротивление приемника, ограничивает ток.
На эквивалентной схеме можно показать внутреннее сопротивление гв соединенным последовательно с сопротивлением приемника г,
и в зависимости от соотношения между напряжениями на этих сопротивлениях получим две разновидности первой эквивалентной схемы для источника энергии (рис. 1-7).
На эквивалентной схеме рис. 1-7, а с источником э. д. с. Е напряжение U зависит от тока приемника и равно разности между э д с. Е источника энергии и
Рис 1-7.
падением напряжения UB. Если гв г и при одном и том же чоке в этих сопротивлениях напряжение UB U, т. е. источник электрической энергии находится в режиме, близком к так называемому «холостому ходу», то можно практически пренебречь его внутренним падением напряжения, принять Un = rBI т О и получить эквивалентную схему рис. 1-7, б. Такой источник энергии без внутреннего сопротивления (гв = 0), обозначенный кружком со стрелкой внутри и буквой Е~,—называют—и д е
15
а л ь н ы м источником э. д. с. (источником напряжения или источником с заданным напряжением). Напряжение на зажимах такого источника не зависит от сопротивления приемника и всегда равно э. д. с. Е. Его внешняя характеристика — прямая, параллельная оси абсцисс (пунктирная прямая ab на рис. 1-4).
Источник энергии может быть представлен и одной из двух эквивалентных схем по рис. 1-8. Чтобы обосновать эту возможность, разделим правую и левую части уравнения (1-7) на гв.
В результате получим:
— = / + —=I + Ug„ 'в 'в
где £в = 1"в — внутренняя проводимость источника энергии,
или
/ = / + (1-8)
где J = E/rs — ток при коротком замыкании источника энергии (т. е. ток при сопротивлении г = 0);
/в = UlrB= UgK— некоторый ток, равный отношению напряжения на зажимах источника энергии к его внутреннему сопротивлению;
I — U!r= Ug—ток приемника;
g = иг — проводимое Полученному уравнению (1-8) с источником тока (рис. 1-8, а),
Рис. 1-8.
т ь приемника, удовлетворяет эквивалентная схема при этом внутреннее сопротивление гв включено параллельно сопротивлению приемника г.
Если gK -С g или гв^> г и при одном и том же напряжении U на зажимах сопротивлений гв и г ток /в /, т. е. источник энергии находится в режиме, близком к так называемому «короткому замыканию», то можно принять ток /в=^в^0
и получить другую разновидность второй эквивалентной схемы (рис. 1-8, б).
Такой источник с внутренней проводимостью gB — 0 (гк = оо), обозначенный кружком с двойной стрелкой с разрывом внутри и буквой J, называют идеальным источником тока (источником с заданным током). Ток источника тока J не зависит от сопротивления приемника г. Его внешняя характеристика прямая, параллельная оси ординат (пунктирная прямая cd на рис. 1-4).
Таким образом, в зависимости от соотношения между внутрен-
ника г реальные источники электрической энергии могут быть во многих случаях отнесены либо к источникам напряжения, либо к источникам тока. Однако источник энергии при расчетах цепей можно заменить источником напряжения или источником тока и в тех случаях, когда внутреннее сопротивление гв источника энергии соизмеримо с сопротивлением г приемника. Для этого необходимо сопротивление гв вынести из источника энергии и объединить с сопротивлением г приемника.
Источники э. д. с. и источники тока называют активными элементами электрических схем, а сопротивления и проводимости — пассивными.
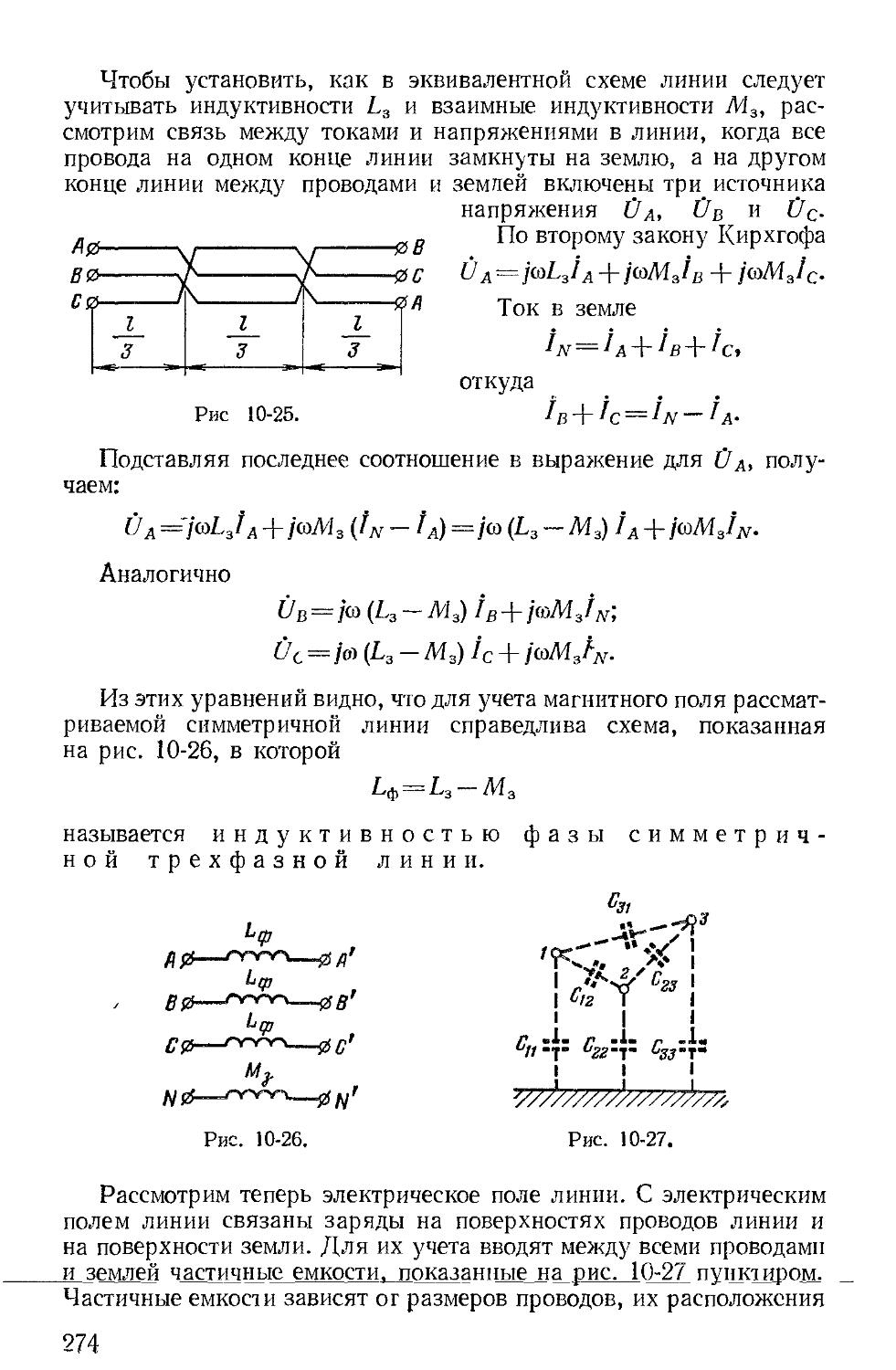
При составлении электрической схемы замещения для той или иной реальной цепи стремятся по возможности учесть известные электрические свойства как каждого участка, так и в целом всей цепи.
Составим, например, эквивалентную схему двухпроводной линии передачи электрической энергии длиной I, схематически изображенной на рис. 1-9, а. В начале линии включен источник энергии с э. д. с. Е и внутренним сопротивлением гв, а в конце линии присоединен приемник энергии, сопротивление которого равно г2.
Напряжение на приемнике, очевидно, меньше напряжения в начале линии на падение напряжения в сопротивлении проводов линии. Ток в конце линии меньше тока источника на ток утечки между проводами линии (из-за несовершенства изоляции).
Пусть каждый провод линии обладает сопротивлением г0'2 и проводимостью между проводами gQ на единицу длины линии.
Разобьем линию на элементы длины dx Грис. 1-9, а). Каждый элемент такой линии обладает суммарным сопротивлением прямого и обратного проводов ro dx — (r,j/2) dx + (r0/2) dx и проводимостью dx.
Поэтому всю линию можно представить электрической схемой из соединенных между собой элементов с сопротивлением r0 dx и проводимостью g0 dx каждый (рис. 1-9, б). Источник энергии на этой эквивалентной электрической схеме представлен в виде источника э. д. с. Е и сопротивления гЕ.
Пользуясь полученной электрической схемой (рис. 1-9, б), легко найти по заданному напряжению и известному току в начале или в конце линии напряже-_____
—япе-н-ток в-любои точке линии (§ 18-4). ~—------------------
17
Если ток утечки линии значите 1ьно меньше тока приемника, то им можно пренебречь и удалить из электрической схемы (рис 1-9, б) все проводимости g0 dx. В результате получится простая (неразветвленная) схема с одним и тем же током во всех элементах, изображенная на рис 1-10, где сопротивление линии гл = г01 показано последовательно соединенным с сопротивлениями гв и г2
В зависимости ог электрических свойств пепи и условий поставленной задачи надо уметь правильно выбирать электрические схемы замещения и пользоваться ими для исследования режимов в реальных электрических цепях.
1-3. Закон Ома для участка цепи с э. д. с.
Для однозначного определения потенциала любой точки электрической цепи необходимо произвольно выбрать потенциал какой-нибудь одной точки. Так, если для схемы, представленной на рис. 1-7, а, положить, например, <р2 = const = С, то по определению потенциал точки Г больше <р2 на значение э. д. с.:
(рг =(р24-£=С4-£. (1-9)
Ток во внешней части простейшей электрической цепи, а в общем случае — в любом пассивном элементе цепи направлен, как
Рис. 1-11.
указывалось, от точки с более высоким потенциалом (п) к точке с более низким (Ь). Поэтому потенциал = <ро первой точки 1 больше потенциала <р2 — <рй второй точки 2:
<Pi=--<p2 + rB/.
Также
Ф1'=ф1 + гв/. (1-Ю)
Из равенств (1-9) и (1-10) имеем:
<ра+£=ф14-М, откуда ток
J <fe~<Pl + g (1-11)
Гв
Аналогично можно написать формулу для тока неразветвлен-ного участка сложной электрической схемы с произвольным числом э. д. с. и сопротивлений и заданной разностью потенциалов на концах этого участка (рис. 1-11).
---Ток / на участке схемы, содержащем э. Д. с., может быть иа-правлен от точки а к точке b или наоборот. Если направление тока
18
заранее не известно, то для составления выражений, подобных (1-11), нужно выбрать направление тока произвольно. Такое произвольно выбранное направление тока условились называть п о-лож и тельным направлением и обозначать так же, как действительное направление, стрелкой с просветом или огме-чать индексами у буквы /.
Если принять за положительное направление тока / на участке (рис. 1-11) направление от точки а к точке Ь, то потенциал <рй определяется через потенциал выражением
фй = фа — ril + Е1 — Гг1 + E2 — r3I — E3 — rJ.
Из этого равенства следует:
ь
r Vab+^E , Ь .
=-----ГГ-----== + W-
rl~rr2~rr3-rz4 rab \ I
\ я /
(1-12)
где гаЬ = г у + г2 + г3 + ri—суммарное сопротивление участка схемы;
Фа — фь = Е)аЬ — разность потенциалов или напряжение между зажимами рассматриваемого участка, взятые по выбранному направлению тока;
ь
^Е ~ Е± + Е2 — Е3 — алгебраическая сумма э. д. с., действую-а
щих на том же участке, причем каждая э. д. с., совпадающая по направлению с положительным направлением тока, записывается с положительным знаком, а не совпадающая — с отрицательным.
Формула (1-12) представляет собой закон Ома для участка цепи (схемы) с э. д. с.
Если в результате расчета по формуле (1-12) для тока / получится отрицательное значенйе, то это значит, что действительное направление тока не совпадает с выбранным положительным направлением (противоположно произвольно выбранному направлению).
Для напряжения между любыми точками цепи также может быть произвольно выбрано положительное направление. Положительное направление напряжения указывается индексами у буквы V или обозначается на схемах стрелкой, которую, например, для напряжений V„b = (рис. 1-11) будем в дальнейшем
ставить от точки а к точке Ь, если потенциал точки а принят (произвольно) выше, чем потенциал точки Ь. Таким образом,, напряжение, как и ток, при расчетах надо рассматривать как алгебраическую величину.
Для э. д. с. источников напряжения и токов источников тока, когда их действительные направления неизвестны, также выбира
19
ются произвольные положительные направления, которые указывают двойными индексами или обозначают стрелками.
На участках схемы с пассивными элементами положительные направления напряжения и тока будем выбирать всегда совпадающими. В этом случае отдельной стрелки для напряжения можно и не ставить.
1-4. Распределение потенциала вдоль неразветвленной электрической цепи
Распределение потенциала вдоль неразветвленной электриче-
ской цепи можно наглядно представить при помощи графика.
Рис. 1-12.
(заземление на
На рис. 1-12 изображена схема простейшей неразветвленной цепи с двумя э. д. с. Е± и Е2 и внутренними сопротивлениями гв1 и гв2 и двумя сопротивлениями г\ и г2.
Пусть э. д. с. Ег больше э. д. с. Е2. В этом случае аналогично (1-7а) действительный ток
Е!~Е2 Г1 + ГВ1 + г2 4* 'в2
(М3)
и совпадает по направлению с э. д. с. £1.-Для однозначного определения потенциала каждой
остальных точек.
точки рассматриваемой цепи можно положить, например, потенциал <ра точки а равным нулю рис. 1-12). Теперь легко найти потенциалы
Потенциал точки b меньше потенциала точки а'.
Ч>Ь = Ч>а-~Г11 = — Til.
При переходе через первый источник энергии потенциал повышается на значение э. д. с. Ег и понижается на внутреннее падение напряжения, так что потенциал точки с
Фе—ф» ~Ь £i — =—ri^ 4~ — гв11 •
Для определения потенциала (ра точки d надо из потенциала <рс вычесть падение напряжения г2/, т. е.
Фй == Фс — г2/ = — t\I + £i — rslI — rJ.
Наконец, при переходе через второй источник энергии потенциал понижается не только на значение э. д. с. £2 (по определению понятия э. д. с. (pd > qv), но и на внутреннее падение напряжения, причем потенциал точки а должен быть равен нулю:
q>a = q>d~£2 — гв2/ = — rj + £j-rB1Z-r2I-E2~ rvSJ = 0.
Отметим, что последнее выражение, конечно, не противоречит (М3). =
20
Если по оси абсцисс отложить в выбранном масштабе сопротивления участков в той последовательности, в которой они включены в цепь, а по оси ординат потенциалы соответствующих точек (рис. 1-13), то получится график распределения потенциала вдоль неразветвленной цепи. Пользуясь этим графиком, можно определить напряжение между любыми точками цепи. В частности, из графика следует, что напряжение на зажимах
первого источника энергии
Ucb = фс — (Рь = Ег — га11
меньше его э. д. с. Ег на внутреннее падение напряжения, а напряжение Eda на зажимах второго источника энергии, наоборот, больше э. д. с. Е2 на внутреннее падение напряжения, т. е.
Eda — (Pif~(Pa — Е2 4- ГВ2^•
Рис. 1-13.
Отношение напряжения к сопротивлению любого пассивного участка цепи равно току участка и на графике потенциала определяется в некотором масштабе тангенсом угла наклона соответствующей прямой к оси абсцисс. Поэтому одинаков наклон прямых (например, ab и cd на рис. 1-13)
определяющих изменение потенциала вдоль всех пассивных участков нфазветвленной цепи с одним и тем же током.
Графики распределения потенциала внутри источника энергии могут иметь разный вид. В простейшем случае при равномерном распределении сопротивления гв и э. д. с. Е в источнике изменение потенциала внутри источника энергии иногда изображают прямой, показывающей или непрерывный рост (в источнике с э. д. с. Ех пунктирная прямая Ьс), или непрерывное уменьшение потенциала (в источнике с э. д. с. Е2 пунктирная прямая da).
1-5. Баланс мощностей для простейшей неразветвленной цепи
Рассмотрим энергетические соотношения для электрической цепи, состоящей, например, из одной машины постоянного тока с э. д. с. Ej и внутренним сопротивлением гв1 и аккумуляторной батареи с э. д. с. Е2 и внутренним сопротивлением гв2 (рис. 1-14). Электродвижущие силы машины и аккумуляторной батареи направлены навстречу друг другу. Пусть э. д. с. машины больше э. д. с. Е2 аккумуляторной батареи. При этом условии действительное направление тока I совпадает с направлением э. д. с. Ег. Напряжение Е на зажимах обоих источников меньше э. д. с. Ег на внутреннее падение напряжения гв11 в машине и больше э. д. с. Е2 на падение напряжения гЪ21 а ба 1 арее, как это было показано в предыдущем
21
параграфе:
V-Ex-rJ (1-14)
или б/~=£2-|-гв27. (1-15)
После умножения обеих частей выражения (1-14) на / и перестановки слагаемых получаем:
EJ^r^ + UI. (1-16)
Левая часть этого уравнения представляет собой мощность, развиваемую машиной, первое слагаемое правой части определяет мощность тепловых потерь (в обмотке машины), а второе слагаемое правой части — мощность, отдаваемую машиной и, следовательно, потребляемую аккумуляторной батареей.
Рис. 1-14.
Если умножим правую и левую части выражения (1-15) на ток I, то получим:
П/-г1)2/2-|-Е2/. (1-17)
Из этого уравнения непосредственно вытекает, что мощность VI, потребляемая аккумуляторной батареей, расходуется на тепловые потери (гв2/2) и на зарядку аккумуляторов (Е2Г).
Полученные соотношения для баланса мощностей применимы не только к цепи зарядки аккумуляторов, но и к любым другим цепям. Отличие состоит лишь в том, что в приемниках другого рода энергия расходуется не на зарядку аккумуляторов, а на другие процессы, например, в электрических двигателях — на механическую работу, в резисторах — только на тепловые потери.
Если представить источник энергии другой эквивалентной схемой (рис. 1-15), то окажется, что мощность, развиваемая источником тока, не равна мощности, развиваемой источником э. д. с.
Действительно, мощность, развиваемая источником тока, определяется произведением тока Д на напряжение V на зажимах источника тока, т. е. равна J^V. Так как Jx = /В1 + /, а /В1 -= то после замены тока ./х и простых преобразований получим:
ЛИ = + О U = + VI. (1-18)
- 22
Из сравнения выражений (1-18) и (1-16) непосредственно следует, что при одинаковом напряжении на зажимах обоих источников и одинаковом гоке I тепловые потерн гк1/2 в схеме рис. 1-14 не равны в общем случае тепловым потерям U2/rKl в схеме рис. 1-15, вследствие чего и мощность, развиваемая источником э. д. с. EJ, не равна мощности, развиваемой источником тока Это следует
имщь в виду при замене реального источника энергии источником э. д. с. или источником тока.
Пример 1-1. К зажимам двух последовательно соединенных источников энергии (э. д. с. Er = 12 В и Д2 = 48 В, внутренние сопротивления г, t — 0,4 Ом и гв2 == 0,6 Ом) подключен приемник-резистор с изменяющимся сопротивлением г (рис. 1-16) Определить значение сопротивления t, при котором мощность резистора
Д/ Дг
Рис. 1-16.
максимальна. Найти мощность
приемника и источников энергии при этом значении сопротивления.
Решение. Для определения сопротивления г, при котором мощность резистора максимальна, ~Воспользуемся выражением мощности Р = "гР.
Так как ток
Д1 + Дг
гв1 + гв2-}-г ’
(гвт + гца + г)2
Вычислив производную от Р по г и приравняв ее нулю, найдем искомое сопротивление
г = гв1 + гв2=1 Ом.
Это соотношение показывает, что мощность приемника максимальна при равенстве суммарного внутреннего сопротивления источников и сопротивления приемника.
Значения остальных величин определяются по формулам: ток
/ = (Д1 + £г)/2г=(12 + 48)/2 = 30 А;
мощности первого и второго источников э. д. с.
Р(11 = £л/= 12• 30 = 360 Вт; Ри2=£а/=48 • 30= 1440 Вт; мощность приемника
P = iP = 1-302 = 900 Вт.
Тепловые потери в обоих источниках
АД = (г„г + бД Р = Рм + Р ,2 - Р = 900 Вт, т. е. мощность приемника равна мощности тепловых потерь в обоих источниках.
1-6. Применение законов Кирхгофа для расчета разветвленных цепей
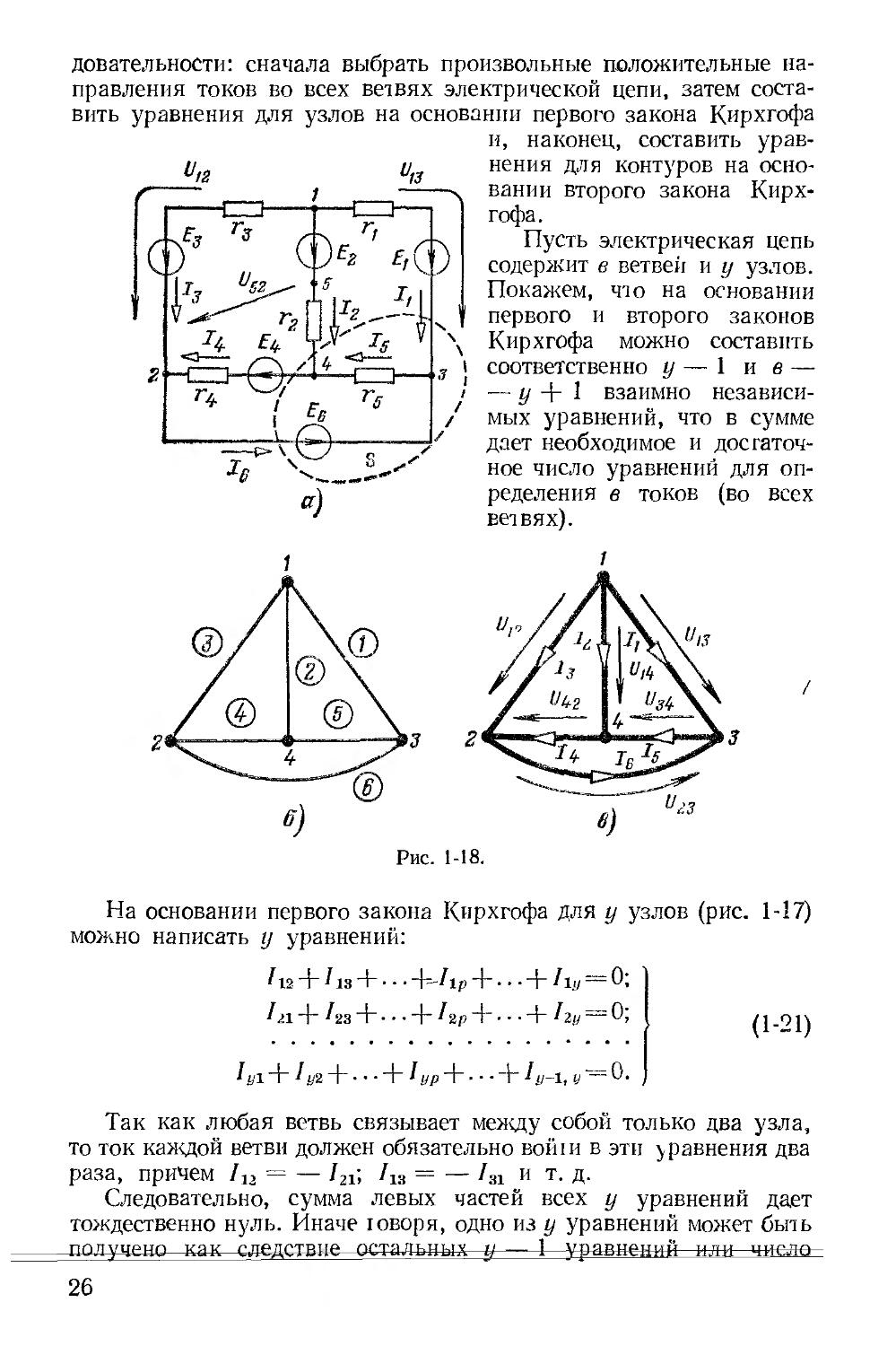
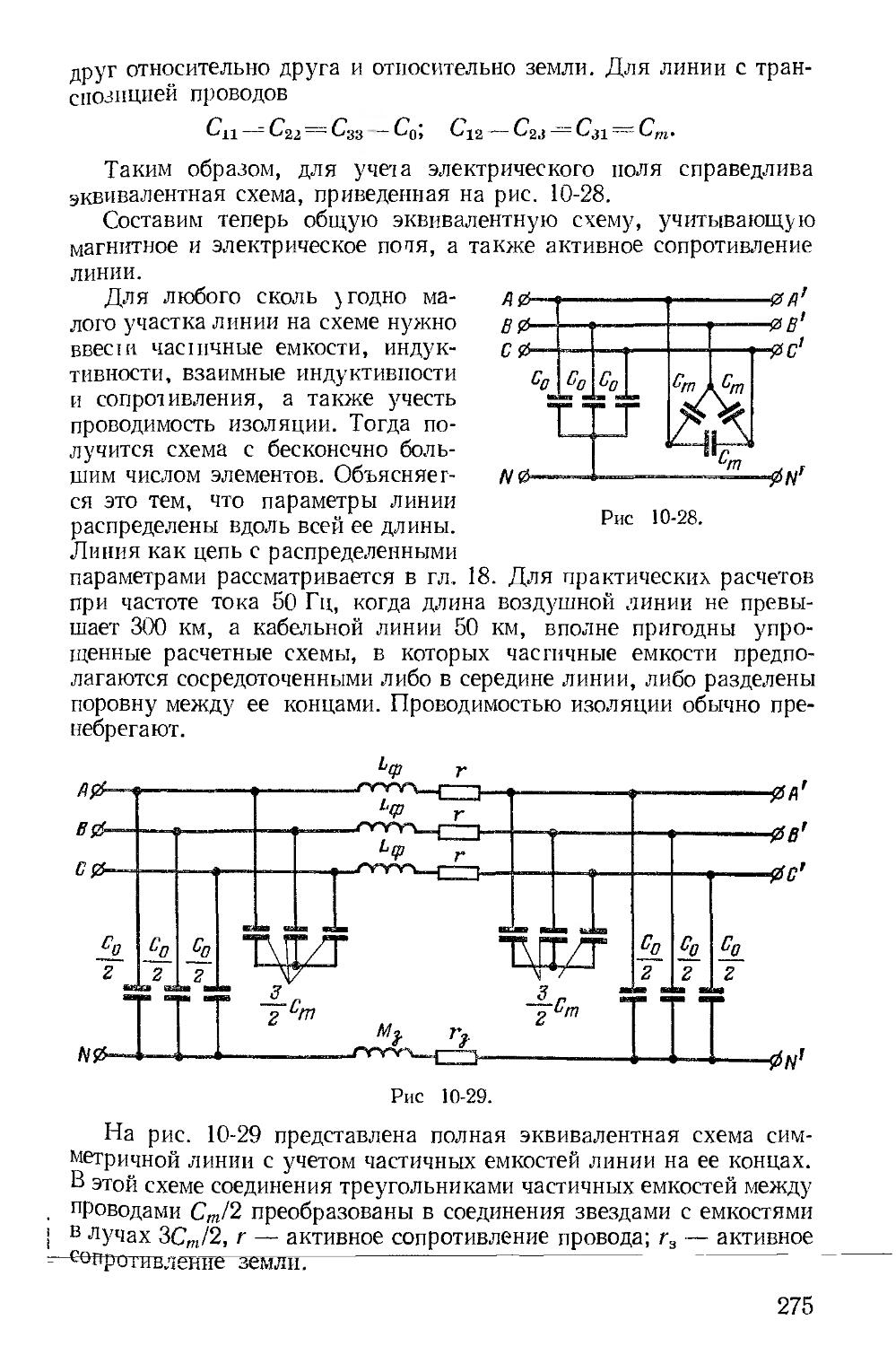
Для расчета разветвленной электрической цепи произвольного вида существенное значение имеет число ветвей и узлов.
Ветвью электрической цепи называется такой ее участок, который состоит только из последовательно включенных источников
23
э. д. с. и сопротивлений и вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трех и более ветвей. Узлом электрической цепи иногда называется точка соединения двух и более ветвей. Однако, как
видно из приведенного выше определения ветви, каждая узловая точка, к которой присоединены только две ветви (она и образует их последовательное соединение), всегда может быть устранена (такие узлы иногда называют устранимыми); в результате в схеме остаются узлы только с тремя и более ветвями.
При обходе по соединенным в узлах ветвям можно получить замкнутый контур электрической цепи; каждый контур
Рис 1-17.
представляет собой замкнутый путь, проходящий по нескольким ветвям; при этом каждый узел в рассматриваемом контуре встречается не более одного раза.
На рис. 1-17 в качестве примера показана электрическая цепь с пятью узлами и девятью ветвями. В частных случаях встречаются ветви только с сопротивлениями, без э. д. с. (ветвь 1 — у) и с сопротивлениями, практически равными нулю (ветвь 2 — р). Так
как напряжение на зажимах ветви 2 — р равно нулю (сопротивление равно нулю), то потенциалы точек 2 и р одинаковы и оба узла можно объединить в один. Режим электрической цепи произвольной конфигурации пол-
ностью определяется первым и вторым законами Кирхгофа.
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов
в узле равна нулю, т. е.
S/ = 0.
(1-19)
В этом уравнении одинаковые знаки должны быть взяты для токов, имеющих одинаковые положительные направления относительно узловой точки. В дальнейшем будем в уравнениях, составленных по первому закону Кирхгофа, записывать токи, которые направлены к узлу, с отрицательными знаками, а направленные от узла — с положительными К
Если к данному узлу присоединен источник тока, то ток этого источника также должен быть учтен. В дальнейшем будет показано, что в ряде случаев целесообразно писать в одной части равенства
1 Такие знаки согласуются с аналитическим выражением для тока через вектор ппотиости тока 6 сквозь замкнутую поверхность S по формуле ф 6 d S — О Так как положительная нормаль к каждому элементу dS замкнутой поверхности выбирается наружу, то токи, направленные внутрь поверхности получаются с отрицательными знаками, а токи, направленные наружу, — с положительными.
24
(1-19) алгебраическую сумму токов в ветвях, а в другой части — алгебраическую сумму токов, обусловленных источниками токов:
(1-19а)
где I — ток одной из ветвей, присоединенной к рассматриваемому узлу, a J — ток одного из источников тока, присоединенного к тому же самому узлу; этот ток входит в уравнение (1-19а) с положительным знаком, если направлен к узлу, и с отрицательным, если направлен от узла.
Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме э. д. с., т. е.
= (1-20)
В этом уравнении положительные знаки принимаются для токов и э. д. с., положительные направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.
Часто применяется другая формулировка второго закона Кирхгофа: в любом контуре алгебраическая сумма напряжений на зажимах ветвей, входящих в этот контур, равна нулю:
W = 0. (1-20а)
При этом положительные направления для напряжений на зажимах ветвей выбираются произвольно; в ) равнении (1-20а) положительные знаки принимаются для тех напряжений, положительные направления которых совпадают с произвольно выбранным направлением обхода контура.
В теории электрических цепей решаются задачи двух типов. К первому типу относятся задачи анализа электрических цепей, когда, например, известны конфигурация и элементы цепи, а требуется определить токи, напряжения и мощности тех или иных участков. Ко второму типу относятся обратные задачи, в которых, например, заданы токи и напряжения, а требуется найти конфигурацию цепи и выбрать ее элементы. Такие задачи называются задачами синтеза электрических цепей. Отметим, что решение задач анализа намного проще решения задач синтеза.
В практической электротехнике довольно часто встречаются задачи анализа. Кроме того, для овладения приемами синтеза цепей необходимо предварительно изучить методы их анализа, которые преимущественно и будут в дальнейшем рассматриваться.
Задачи анализа могут быть решены при помощи законов Кирхгофа. Если известны параметры всех элементов цепи и ее конфигурация, а требуется определить токи, то при составлении уравнений Tro~3aKOH5№b4^HpjmM^-pfeKQMeHAyeica придерживаться такой после
25
довательности: сначала выбрать произвольные положительные направления токов во всех ветвях электрической цепи, затем составить уравнения для узлов на основании первого закона Кирхгофа
и, наконец, составить уравнения для контуров на основании второго закона Кирхгофа.
Пусть электрическая цепь содержит в ветвей и у узлов. Покажем, что на основании первого и второго законов Кирхгофа можно составить соответственно у — 1 не — — у + 1 взаимно независимых уравнений, что в сумме дает необходимое и достаточное число уравнений для определения в токов (во всех ветвях).
1-18.
На основании первого закона Кирхгофа для у узлов (рис. 1-17) можно написать у уравнений:
Кг4-lie+• • • 4=-/ip+• • •+/11/—0;
/л 4" /гз 4~ • • • 4" /гр4" • • + = 0;
/pi 4~ 1ц2 4- • • • 4~ I ур 4~ • • + / р-1, у = 0.
(1-21)
Так как любая ветвь связывает между собой только два узла, то ток каждой ветви должен обязательно войт в эти уравнения два раза, причем /12 = — /21; /13 = — /31 и т. д.
Следовательно, сумма левых частей всех у уравнений дает тождественно нуль. Иначе говоря, одно из у уравнений может быть -получено как следствие остальных у — 1 уравнений илть-чиеле-
26
взаимно независимых уравнении, составленных на основании первого закона Кирхгофа, равно у — 1, т. е. на единицу меньше числа узлов. Например, в случае цепи по рис. 1-18, а с четырьмя узлами
для узла 1
для узла 2 - 13-/4+/6 = 0;
для узла 3 -/i-/6 + /5 = 0;
для узла 4 —/г+Л /5 = 0. .
(1-21а)
Суммируя эти уравнения, получим тождество 0 = 0, следовательно, из этих четырех уравнений только три независимые.
Так как беспредельное накопление электрических зарядов не может происходить как в отдельных узлах электрической цепи, так и в любых ее частях, ограниченных замкнутыми поверхностями, то первый закон Кирхгофа можно применить не только к какому-либо узлу, но и к любой замкнутой поверхности (что уже было отмечено выше).
Например, для поверхности 5 (рис. 1-18, а), как бы рассекающей электрическую схему на две части, справедливо уравнение /4 — /г — /2 — /6 = 0, что можно также получить из уравнений (1-21а) для узлов 3 и 4.
Что%1 установить число взаимно независимых уравнений, вытекающих из второго закона Кирхгофа, напишем для всех в ветвей схемы (рис. 1-17) в уравнений на основании закона Ома:
Ф1 — ф 1 Г 21^ 21
Фз Ф1 = Oi^3i E3i,
Фр Ф1 г pi Е11,
(1-22)
Фр Фи гри1ри Еру,
где гри = Гур — сопротивление ветви, соединяющей узлы р и у, Еру — суммарная э. д. с , действующая в ветви р — у в направлении от р к у,
фр и <рр — потенциалы узлов р и у.
В этих уравнениях суммарное число неизвестных токов в ветвей и потенциалов у узлов равняется в + у.
Не изменяя условий задачи, можно принять потенциал одного из узлов равным любой величине и, в частности, нулю. Если теперь из системы в уравнений (1-22) исключить оставшиеся неизвестными У — 1 потенциалов, то число уравнений уменьшится до в — у 4- 1. Но исключение потенциалов из уравнений (1-22) приводит к уравнениям, связывающим э. д. с. источников с напряжениями на сопротивлениях, т. е. к уравнениям, сосгавленным на основании второго закона Кирхгофа.
27
Таким образом, число взаимно независимых уравнений, которые можно составить на основании второго закона Кирхгофа, равно в — у 4- 1.
В качестве примера напишем уравнения, связывающие потенциалы узлов с токами и э. д. с. для схемы рис. 1-18, о:
Ф1-ф2=^з-£,3; <Р1 —Тз=''1Л-£'1;
<Р1 — Е%, —<Р2~ — Ei,
<f>a — <f>e=r5I5; ф2 —фз= —£«•
(1-22а)
<Р2 — <Рз = — Ее.
Складывая третье и четвертое уравнения и вычитая полученную сумму из первого, получаем:
riE fgj3— E2-YE1 — Е3.
(1-23)
Если применим второй закон Кирхгофа (1-20) к контуру 1-4-2-1 (при обходе вдоль контура по направлению движения часовой стрелки), то получим это же уравнение.
Аналогичным путем можно получить уравнения для остальных контуров:
для контура Т-5-2-/
rJi - г313 — Ei — Ее — Е3‘,
для контура 2-3-4-2
rJi — Eg-\- Ei-
(1-24)
Совместное решение любых трех уравнений (1-21а) и уравнений (1-23) и (1-24) дает значения токов во всех ветвях электрической цепи, показанной на рис. 1-18, а. Если в результате решения этих уравнений получится отрицательное значение для какого-либо тока, то это значит, что действительное направление противоположно принятому за положительное.
При записи уравнений по второму закону Кирхгофа следует обращать особое внимание на то, чтобы составленные уравнения были взаимно независимы. Контуры необходимо выбрать так, чтобы в них вошли все ветви схемы, а в каждый из контуров — возможно меньшее число ветвей. Контуры взаимно независимы, если каждый последующий контур, для которого составляется уравнение, имеет не меньше одной новой ветви и не получается из контуров, для которых уже написаны уравнения, путем удаления из этих контуров общих ветвей.
Например, контур 1-3-4-2-1 (рис. 1-18, а) можно получить из контуров 1-3-2-1 и 2-3-4-2 путем удаления ветви 2-3. Поэтому уравнение для контура 1-3-4-2-1 является следствием уравнений (1-24) и получается путем их суммирования.
Вторым законом Кирхгофа можно пользоваться для определения напряжения между двумя произвольными точками схемы. В этом случае необходимо ввести в левую часть уравнений (1-20) искомое напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого. Например, для определения напряжения
28
и5„ (рис. 1-18, а) можно написать уравнение для контура 2-1-5-2 U52 Г3/3 = 7?2 Ез
или для контура 5-4-2S
г2^2~\~ r&Ii — £4'2 = £4»
откуда легко найти искомое напряжение.
При изложении методов расчета электрических цепей иногда целесообразно применять некоторые топологические понятия, к числу которых относятся, в частности, неориентированный и ориентированный графы.
Как следует из первого закона Кирхгофа (1-19), вид уравнений зависит не от элементов ветвей, соединенных в узлах, а от геометрической структуры самих соединений. Аналогичный смысл имеет уравнение (1-20а), выражающее второй закон Кирхгофа, поскольку в эти уравнения в отличие от уравнений (1-20) элементы ветвей (э. д. с., сопротивления) не входят. Однако сами токи и напряжения зависят не только от геометрической структуры цепи, но и от элементов соответствующих ветвей, что непосредственно следует из закона Ома для участка цепи с э. д. с. (1-12).
Таким образом, для характеристики геометрической структуры схемы электрической цепи можно воспользоваться графом, линейные отрезки которого, часто называемые ветвями (ребрами), изображает ветви схемы электрической цепи. На рис. 1-18, б показан ненаправленный (неориентированный) граф для электрической схемы, изображенной на рис. 1-18, а. При этом каждый из отрезков — ветвей этого графа (рис. 1-18, б) соответствует определенной ветви электрической схемы (рис. 1-18, а).
Направленным (ориентированным) графом называется такой, у которого каждая ветвь имеет определенное направление (ориентацию). Для графов электрических схем направление (ориентация) ветвей, как правило, совпадает с положительными направлениями токов и напряжений, которые выбраны при составлении уравнений состояния электрических цепей.
Для той же электрической схемы (рис. 1-18, а) показан направленный граф на рис. 1-18, в, у которого направления ветвей совпадают с положительными направлениями токов и напряжений.
Для направленного графа рис. 1-18, в можно написать уравнения на основании первого (1-19) и второго (1-20а) законов Кирхгофа в следующем виде:
Л + /2 + /3 = 0; /6 —/3 —/4 = 0; /6-Д-/6 = 0;
и
П12 = 0; Ui3 — U2з ^12==0; ДДг — О.
При этом первые четыре уравнения совпадают с уравнениями (1-21а), а последние три уравнения можно преобразовать в уравнения (1-23) и (1-24) при помощи закона Ома для участка цепи с э- Д. с. (1-12).------------------------------------------
29
Например, из схемы (рис. 1-18, а) следует, что
f7i4== — £2+^2; U42 — — £4 + U12 — —
после замены напряжений Uu, Ui2 и U12 в уравнении для контура 1-4-2-1 (рис. 1-18, в) их правыми частями получается выражение, совпадающее с уравнением (1-23).
Отметим, что концевые точки ветвей графа называются узлами (вершинами).
Для полной характеристики электрического состояния цепи надо знать не только токи и напряжения, но также мощности источников и приемников энергии.
В соответствии с законом сохранения энергии развиваемая источниками энергия равна энергии, потребляемой приемниками. Из этого положения следует, что для любой электрической цепи с источниками э. д. с. алгебраическая сумма мощностей, развиваемых источниками э. д. с., равна сумме мощностей, потребляемых всеми сопротивлениями (в том числе внутренними сопротивлениями источников энергии):
^EhIh= %rhn. (1-25)
h = I h = l
Если действительные направления э. д. с. и тока в некоторой ветви совпадают, то мощность такого источника э. д. с. входит в уравнение (1-25) с положительным знаком и источник отдает энергию в цепь (работает в режиме генератора). Если направления э. д. с. и тока в ветви противоположны, то мощность источника э. д. с. записывается в уравнении (1-25) с отрицательным знаком и такой источник работает в режиме приемника, потребляя энергию.
Отметим, что уравнение (1-25) может быть получено также из законов Кирхгофа (1-19) и (1-20).
Матричная форма записи уравнений Кирхгофа. Если электрическая цепь состоит из в ветвей, то на основании (1-19а) и (1-20) можно в общем случае записать в независимых алгебраических уравнений электрического состояния цепи в следующем виде:
011/1 + ^12/2 + - • -+016/е —Fi;
О21Л + О22Л + • • • + а2еЕ = F2, (1-26)
Oti/i+ Обг/ 2 + • • • 4- о6в/о= Fb.
Поскольку эти уравнения получены на основании двух разных законов, то они не однотипны. В узловых уравнениях, вытекающих из первого закона Кирхгофа (1-19а), коэффициенты a[t не имеют размерности и, очевидно, могут принимать только значения ±1 или 0. Правые части в этих уравнениях F} = SJ имеют размерность тока и равны нулю, если к соответствующему узлу не подключены источники тока.
В контурных уравнениях, вытекающих из второго закона Кирхгофа (1-20), коэффициенты а1} имеют размерность сопротивления, 30
а величины Ft = ^E — размерность потенциала и равны нулю, если в контуре нет э. д. с. Если /-я ветвь входит в г-й кон гур, для которого составляется уравнение, то, очевидно, должно быть а = ± ri;, а если не входит — at) = 0. Здесь гч сопротивление /-Й ветви, входящей в f-й контур.
Уравнения (1-26) можно записать в более общей матричной форме: aI = F, (1-27)
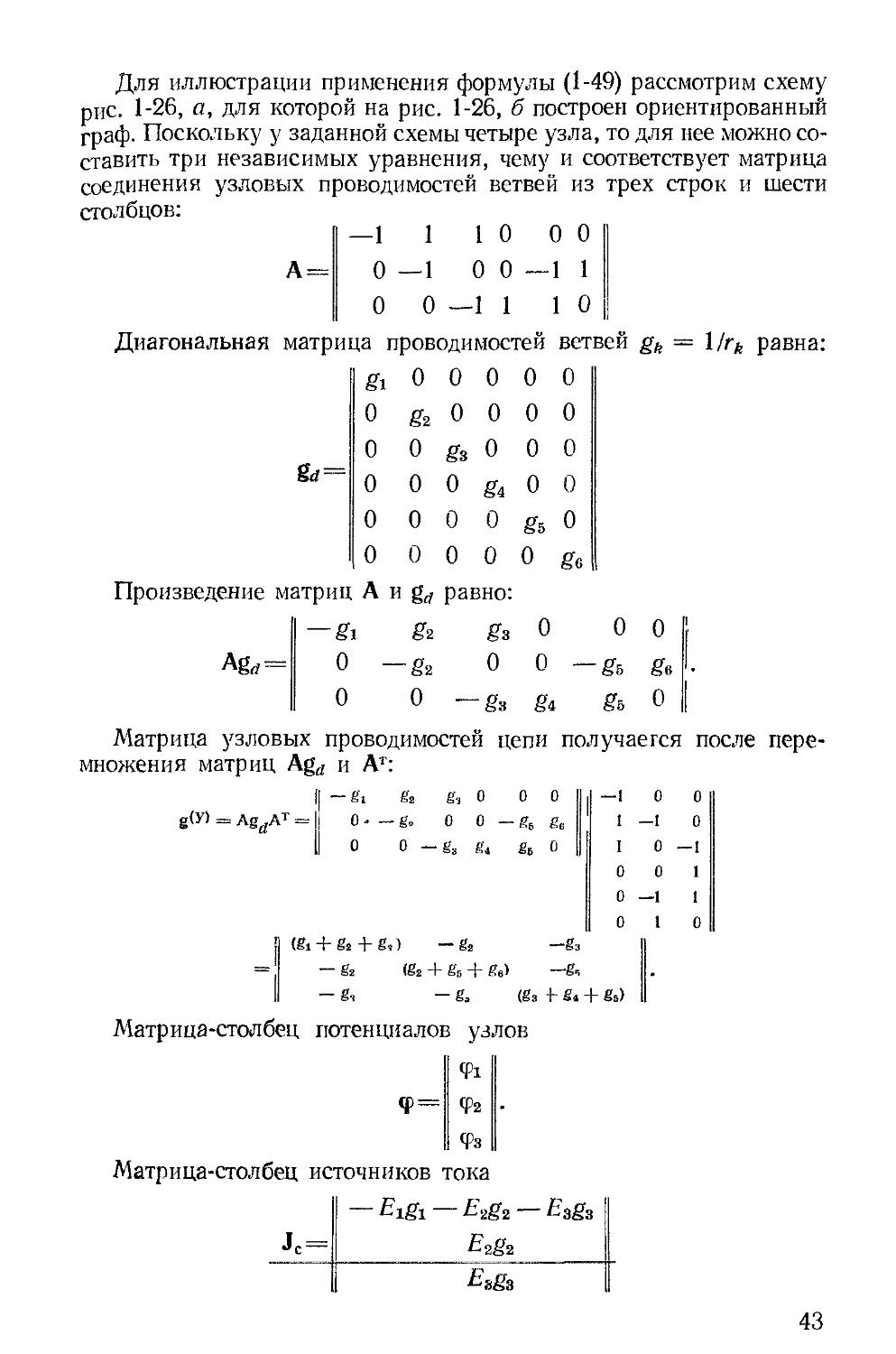
где а — квадратная матрица коэффициентов, т. е.
Оц 012 • • • о1в
„ __ О21 °22 • • • а2е .
I — матрица-столбец токов ветвей, т. е.
/1
1» .'.2..
4 и F — матрица-столбец активных параметров, т. е.
F _ ^2
Fe
Например, для схемы рис. 1-18, а первые три уравнения (1-21а), а также уравнения (1-23) и (1-24) можно записать в матричной форме, если принять:
110 0 0
0—1—10 1
0 0 01—1
г2 ~г3 П 0. 0 ’
0 —rs 0 0 0
0 0 г4 гъ 0
0
0
0
Г Е2-$-Е4 — Е3
Ei Е3 Ев
Е4-\-Е6
31
Справедливость приведенной записи легко проверить, подставив матрицы а, I и F в уравнение (1-27).
Пример 1-2. Пользуясь законами Кирхгофа, написагь два выражения для тока /0 в ветви с гальванометром (рис. 1-19), принимая в одном случае из-
вестным гок /, а в другом — напряжение U.
Решение На основании законов Кирхгофа напишем для заданной схемы с шестью неизвестными токами уравнения:
А + /3 — 1 ~ 0 (для узла /);
4 + /0 — /1=0 (для узла 2);
1 — /2 — /4 = 0 (для узла 3);
rih + — г313 = 0 (для контура 1-2-4-1)-,
г212 — rJs — r0I0 = 0 (для контура 2-3-4-2)-,
г31з + rJi = Е — rj = U
(для контура 1-4-3-1).
Решая совместно эти уравнения, получаем выражение для тока /0 через напряжение U:
{ =________________(^з—U_____________________
° го (гг + га) (/'з + /'4) + /'1г2 (''з + лй + ПЛ (н + Ог)
и через ток 1:
, =___________(г2г3—ггг^ I__________
0 П) (/'1+/'2+/'з+г4) + (/т+/'з) (/2+Ц1)
1-7. Метод узловых потенциалов
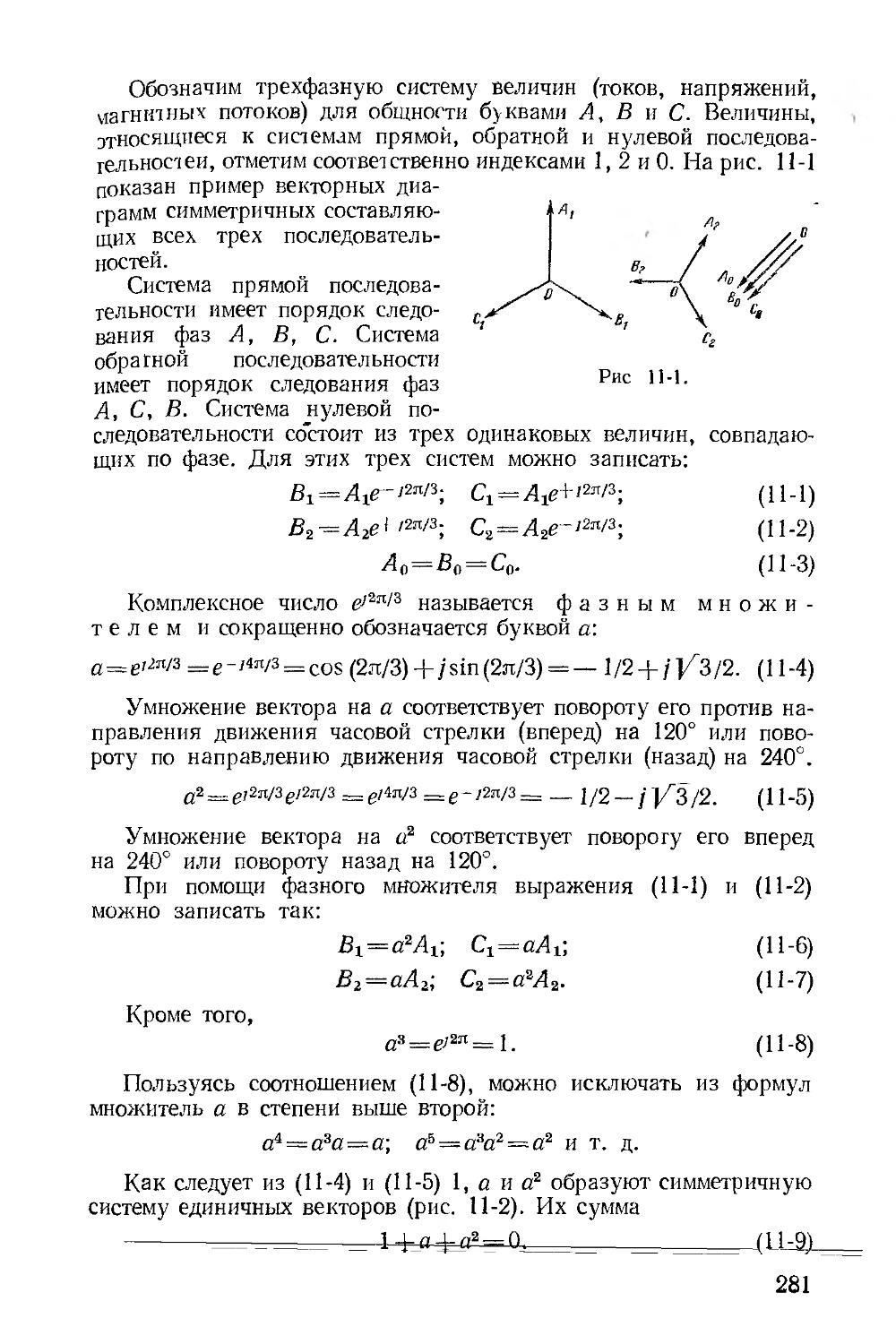
Как было показано, режим любой цепи полностью характеризуется уравнениями, составленными на основании первого и второго законов Кирхгофа, причем для определения токов во всех в ветвях необходимо составить и решить систему уравнений с в неизвестными.
Число уравнений, подлежащих решению, можно сократить, если пользоваться методом узловых потенциалов, основанным на применении первого закона Кирхгофа и закона Ома (М2).
Для выяснения сущности этого метода рассмотрим, например, электрическую схему, показанную на рис. 1-20.
Пусть потенциал одного из узлов, например узла 3, принят равным нулю, т. е. ср3 = 0. Такое допущение не изменяет условий задачи, так как ток в каждой ветви зависит не от абсолютных значений потенциалов узлов, к которым присоединена ветвь, а от разности потенциалов на зажимах ветви.--------------------------
32
На основании первого закона Кирхгофа для узлов 1 и 2 этой схемы при выбранных положительных направлениях токов получаем:
Л — Л — А + /в = 0; 1
—^2 + ^3 = 0. J
Токи в ветвях на основании закона Ома (1-12)
/в== («Pi — ф2) g’e; Л=(—
Л—~Ф1й; Л=гХ(Р1 — (Р2 + ^5)
/г = (—ТгН- Е2) g2, Лз 17-т (ф'2 +-^з) gs>
где <р! и <р2 — потенциалы узлов 1 и 2.
После подстановки (1-29) в (1-28) и группировки членов получим:
ФТ (gi + g& + gi + gi) — Ф 2 (gi + gi) = Еigi — EBgs;
—- Ф i (ge + gi) + Фг (gi + g& + gi + gi) — EBgB -\-E2g2 — E3g3,
(1-28)
(1-29)
или
giiqi-guVi^^Eg-, 1
— Й1Ф1 + g‘224‘2 = У( Eg. 2
(1-30)
В этих уравнениях gn = ge + gB + gt + gp, g22 =ge + g-a + + gi + ge — суммы проводимостей ветвей, присоединенных соответственно к узлам 1 и 2; gJ2 = g>\ = gs + ge — сумма проводимостей ветвей, соединяющих эти узлы.
Правая часть каждого из уравнений (1-30) равна алгебраической сумме произведений э. д. с. источника на проводимость для каждой из ветвей, которая присоединена к рассматриваемому узлу. Произведение вида Eg записывается с положительным знаком в том * случае, кегда э. д. с. направлена к рассматриваемому узлу, и с отрицательным, когда э. д. с. направлена от узла.
Уравнения (1-30) не зависят от выбранных положительных направлений токов в ветвях.
Чтобы подтвердить это положение, рассмотрим опять схему, показанную на рис. 1-20, и для ка;кдого узла примем положительные направления токов от узла.
Для узлов 1 и 2 справедливы уравнения
К+Л' + /5+/в=0; j
/^/з+/М=0. J (ldl)
Принимая, как и раньше, ф3 = 0, напишем выражения для токов ветвей: для узла 1
K = (<Pi-£'i)ft: )
^5 = (ф1—+ (ф1— фг) 1
для узла 2
/г = (ф2—^г) ^з = (ф2 + ^з) ga', 1
/в=(ф2—фх)й; К=(ф2—<Р1—£б)£6. J 1 )
После подстановки (1-32) в (1-31) и группировки слагаемых получаются урав-Нййия, совпадающие с (1-30).
2 Основы теории цепей
33
Таким образом, можно написать уравнения для определения потенциалов узлов произвольной электрической цепи, не задаваясь положительными направлениями токов в ветвях; при этом потенциал одного из узлов надо принять равным нулю.
Если электрическая схема содержит не только источники э д. с., но и источники тока, то в уравнения, составленные по первому закону Кирхгофа, войдут и токи источников тока. При составлении уравнений вида (1-30) токи заданных источников тока учитываются для каждого узла в виде слагаемых в правой части, причем, как было отмечено выше, с положительными знаками должны быть взяты токи источников тока, направленные к узлу, а с отрицательными — от узла.
Например, для узлов 1, 2 и 3 схемы, показанной на рис. 1-21, при = 0 получим соответственно следующие уравнения:
£иф1 - £12<Р2 - £1з<Рз -= J +
ёТлфт 4" g22(P2 g23(Ps — ^2^2’
~~ £з1Ф1 — £з2<Р2 + й'ззЧ’з = Eigz, где
gll ~gl + g& 4“g3,’ g22 =g2 4-^3 -r_S'e>'
ЙЗЗ “ + Й5 + ge! gl2 = g21=g3;
gl3 —g31==g5; g23==g32=ge И gk~^/rk’
Если электрическая схема имеет в своем составе (//+1) узлов (у—любое целое число), а потенциал, например, у + 1-го узла принят равным нулю, то для определения у потенциалов остальных узлов получается у уравнений:
у 1-1
~ £12Ср2 — ... — glptyp — ... — glyCPy — J1 + 2 Eljglj ~ J cl,
7 = 2
— g21<Pl + g22<P2 - ... - g2pVp — ... — g2lMy =
y + 1
= 42+2 E2jg2]— jc2,
7 = 1
7*2
gpiSPi gp2fP2 •••~\~Spp(Pp
gpiWy —
(1-33)
~ gplWl — gp2<fl2 — ... — gppCPp — . • • + gyy<Py--------
у H-1
— •fy-3!- 2 Eyjgyj= Jcy
—-----------------------------------------________------ 7 = 1 --------_
tj=b
34
или в более общей форме для любого узла1р при ф^ — О
у +1 У -г 1 1/ + I
S §Р1^Р ~ 2 £и(Р;==^рН- S ^Р]§Р] = ^Р‘
7 = 1 ; = 1 /=1
г/р l^P i-rP
(l-33a)
В этих уравнениях, так же как и в уравнениях (1-30), проводимость %gPJ = gpp (с двумя одинаковыми индексами) представляет собой суммарную проводимость ветвей, присоединенных к узлу р, и называется собственной узловой проводи-м’о с т ь ю этого узла; проводимость gJP = gP] с двумя различными индексами равна сумме проводимостей ветвей, соединяющих между собой рассматриваемые узлы / и р, и называется общей узловой проводимостью этих узлов. Правая часть каждого из уравнений содержит алгебраические суммы произведений э. д. с. на соответствующие проводимости для всех ветвей, присоединенных к узлу р, и узловой ток Jp, равный алгебраической сумме токов всех источников тока, присоединенных к тому же узлу.
В свою очередь ток Jcf) равен алгеб-раическойг сумме Jp и токов, определяемых источниками э. д. с., которые присоединены к узлу р.
При этом следует иметь в виду, что для замкнутых поверхностей сумма всех узловых токов, как это
вытекает из первого закона Кирхгофа, равна нулю. К узловым токам можно отнести и уже известные в каких-либо ветвях гоки. Проводимости таких ветвей в выражения вида gpp и g]p не входят.
Решив уравнения (1-33), можно определить потенциалы узлов, а зная потенциалы, легко найти токи во всех ветвях по закону Ома (1-12).
Некоторые замечания о составлении узловых уравнений. Выше было показано, что уравнения (1-33) справедливы соответственно для пстенциалов узлов 1, ..., у схемы при фу+1 = 0. При этом узловой определитель, составленный из коэффициентов системы уравнении (1-33),
ЙП ~ gl2 • • • gly
D{y) =
--§21 §22 --§2у
(Ь34)
gyl §y2 • • gyy
симметричен относительно главной диагонали, поскольку проводимости ветвей между каждой парой узлов связаны соотноше-ииями g]p = gpI.
Каждая диагональная проводимость gpp в определителе (1-34) равна сумме проводимостей всех ветвей, присоединенных к соог-
2*
35
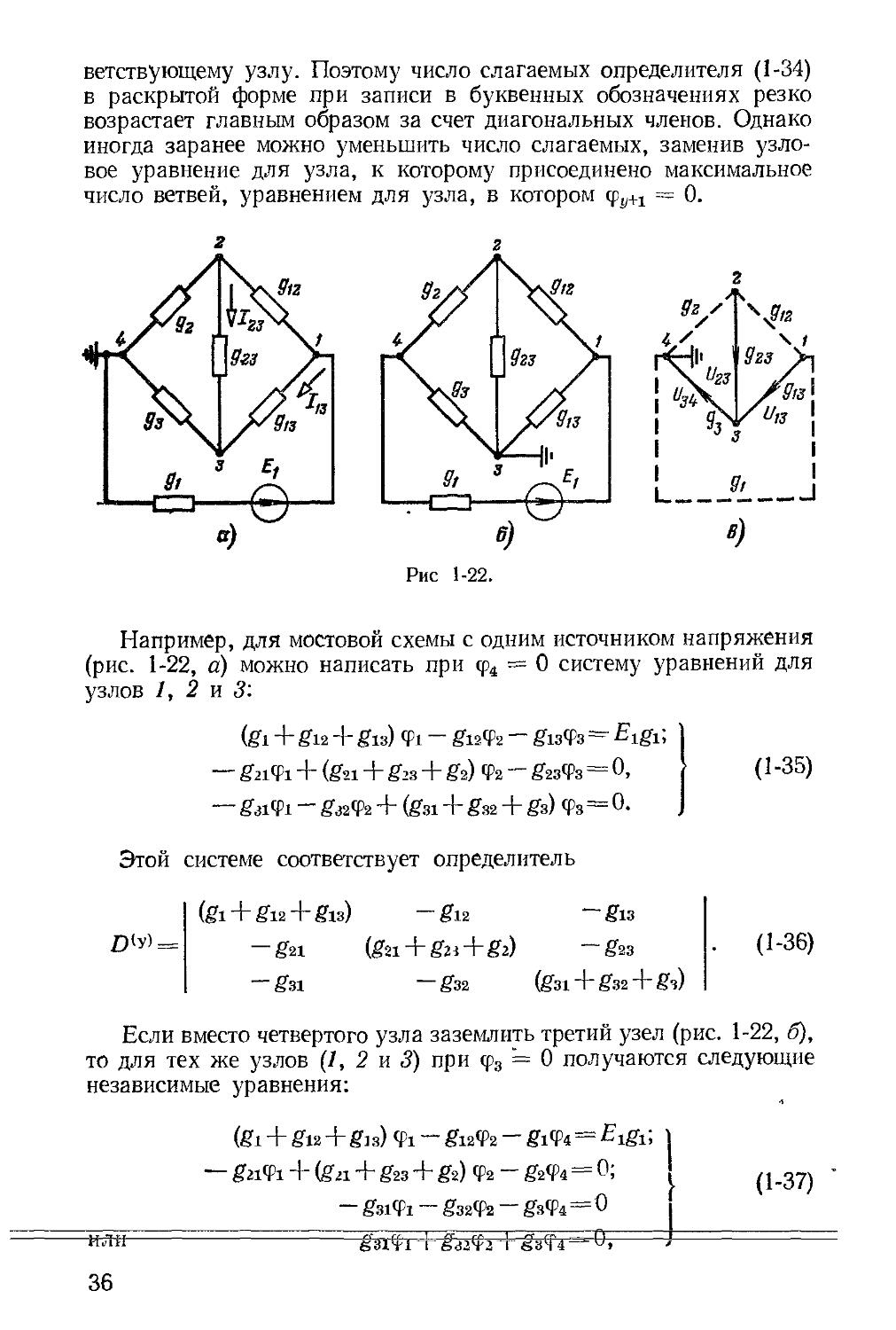
ветствующему узлу. Поэтому число слагаемых определителя (1-34) в раскрытой форме при записи в буквенных обозначениях резко возрастает главным образом за счет диагональных членов. Однако иногда заранее можно уменьшить число слагаемых, заменив узловое уравнение для узла, к которому присоединено максимальное число ветвей, уравнением для узла, в котором = 0.
в)
Например, для мостовой схемы с одним источником напряжения (рис. 1-22, а) можно написать при ф4 = 0 систему уравнений для узлов 1, 2 и 3:
(Si 4-£12 + Sis) Ф1 — Sn(k £1зФз — Eigi, — Sirti Ч- (Szi 4“ Sis 4“ Sz) Фг — £гзФз = 0, --£з1ф1 — £з2ф2 4“ (£з1 4" £з2 4“ £з) фз^О.
(1-35)
Этой системе соответствует определитель
£)(у) =
(S1 4“ £12 4- £1з) ~ £12
— £21 (£214-£214-£г)
— £з1 — £32
~ £1з
— £23
(£314- £32 4- £з)
(1-36)
Если вместо четвертого узла заземлить третий узел (рис. 1-22, б), то для тех же узлов (7, 2 и 3) при <р3 = 0 получаются следующие
независимые уравнения:
ИЛИ
(£14_£12 4_£1з) Ф1--£12фг — Si4i~Eigi'< 1
—£г1ф14-(£214-£23 4-£2) фг — £2*7'4 = 6; I
— £з1ф1 — £згфг — £зф4—0 |
——£ЗТфТ"Г_£з2Ф2 4-“£з(Г 4 —*
(1-37) ’
36
где вместо потенциала <р3 входит неизвестный потенциал <р4. Определитель последней системы уравнений
Z)‘y) =
(gl + £12 + £1з)
— £21
£31
~£12
(g21 + £23 + £2)
£.32
~gl
“£2
£3
(1-38)
Сравним выражения (1-36) и (1-38). В определителе (1-36) только произведение диагональных членов дает 27 слагаемых, а из общего числа, равного 38 слагаемым, 22 члена попарно равны по абсолютному значению и обратны по знаку и поэтому сокращаются. В определителе (1-38) всего 18 слагаемых, из которых два равны по абсолютному значению и имеют противоположные знаки и сокращаются. Оставшаяся сумма 16 слагаемых, естественно, равна определителю, найденному по уравнению (1-36).
Отметим еще, что уравнения (1-38) позволяют проще, чем уравнения (1-36), определить напряжения 1/13 = (рь U23 = <р2 и 534 = — — ф4. Действительно, числители выражений для этих напряжений получаются сразу с несокращающимися членами из определителя (1-38) путем замены соответствующих столбцов правыми частями уравнений (1-37):
Д1з= Ф1 — Фз — Eigi [£з (£214- £23 + gi) + £2£з2] ;
Д>з— фз— фз— Д1£х (£з£г1 — £з£з1);
(1-39)
^34— фз~ ф«— — — -^^[£21£з2 4-£з1(£21 + £2з4-£2)1 >
где алгебраические дополнения Du, Д12 и D13 получаются из (1-38) вычеркиванием первой строки и соответственно первого, второго и третьего столбцов и-умножением полученных миноров соответственно на (—1)1+1, (—1)1+2 и (—1)1+3.
Здесь следует подчеркнуть, что уравнения (1-37) при <р3 = О (рис. 1-22, б) можно получить из уравнений (1-35) при <р4 = О (рис. 1-22, а) путем замены потенциалов <р3, <р2 и <р3 через напряжения U13, U23 и соответствующие ветвям с проводимостями £1з, £23 п £з (Рнс- 1-22, в). Действительно, если в уравнениях (1-35) заменить дц = U13 + U3i, <р2 = U23 + U3i, <р3 = U3i (при <р4 = 0), то получится:
(£1 + £12 + £13) Е13 — £12523 + g-JJ34 = Eigi,
—£21^13 4- (£21+£23+£2) б^з 4- £2 Д34—0;
£.31^13— £з2^2з + £з^34==0.
Эти уравнения полностью совпадают с уравнениями (1-37), в которых, как уже отмечено, при <р3 = 0 надо заменить фх = 513, -Ф> = U23 и Ф1 ~ Е ,-------- ,
37
Таким образом, уравнения, составленные относительно неизвестных напряжений на зажимах ветвей, не зависят от того, какой узел в схеме заземлен
Аналогичные соотношения справедливы и для узловых уравнений в случае более сложных схем. Действительно, например, для
узлов 1,2, 3 п4 схемы рис. 1-23, а и б при <р5 = 0 запишем следующие уравнения:
(ё1 4- Sa 4- ёи) Ti— йДТг—ёлЧ’л—Е1ё1== А;
— Й21Ф1 (& "I’fi'ai-г’й'гч) 4'2 й'гяФ.з—; 0;
— ёз2(Р14 (£32 + ёзi + £з) Тз — £з4<Р4 — о,
~ £11^1 —‘ £43<Рз + fell 4~ ё$3 + £4) Ч>4
Этим уравнениям соответствует определитель узловых проводимостей
(£i + £12 + £14) ~ £12 0 — gu
ЕР ~ £21 (£2 4~ £214~ £23) £23 0
0 ~£з2 (£32 4~ £34 4~ £з) — £.н
“£41 0 —£43 (£414-£43 4~ £4)
(1-41)
Для той же схемы и при том же заземленном узле <р5 = 0 можно составить независимые узловые уравнения для других узлов, например для 2, 3, 4 и 5, в следующем виде:
—ftiVi+(ft+fti+fts) ф2 - ЩлД.!=°;
---Й2Ф2 + (ft + Ёз-Z 1 ft 1) <Рз — ft )4 I — 0: ,, .
„ С1'42)
— Й41Ф1 — Й4зфз + (Й4 + Й41 + йи) ф4 — 0,
— ЙНР, — дафа йзФз — Й4ф4=-^Е1Й^=—Л—------:
38
Полученным уравнениям соответствует определитель
— Й21 (gl + gll + giz) — gll 0
р(У)=- 0 ga — gll 0 (gl + gll + gll) —gts tei -gn Дп + gis) (1-43)
-gi -gl -g3 -gi
Определители (1-41) и (1-43) в раскрытой форме равны между собой и содержат по 45 слагаемых. Однако в определителе (1-41) окончательный результат получается после сокращения 76 попарно
равных по абсолютному значению и противоположных по знаку членов, а в определителе (1-43) только 16 таких слагаемых Иначе говоря, если в определителе (1-41) общее число членов (до сокращения) равно 121, го в определителе (1-43) таких членов 61
Особо подчеркнем, что определители (1-41) и (1-43) легко получаются из определителя, составленного для зависимой системы уравнений, т е записанной для всех узлов схемы Действительно, для схемы рис 1-23 определитель системы узловых уравнений для
всех пяти узлов
(Й12 Lgu + gl)
Д(У)= н
— Й21
О
-g4I
-gl
- gl2 0 - g14 - g,
(g2i + g2J + g2) — g.s o - g,
— g32 <g32+g3> + gS) — g34 — g3
0 — g43 (g41 1 g43 + g4) -g4
— g2 — g3 — g4 (gl + g2 + g3 + g4)
(1 44)
Этот определитель соответствует неопределенной узловой матрице (отмечено индексом «н»), т е полной системе уравнений с пятью неизвестными узловыми потенциалами, сумма элементов такого определителя по строкам и столбцам равна нулю Определитель (1-41), соответствующий системе независимых уравнении (1-40), получается из (1-44) вычеркиванием пятой строки и пятого стотбца, а определитель (1-43), соответствующий уравнениям (1-42), получается из (1-44) вычеркиванием первой строки и пятого столбца Все это и определяет основные соотношения между параметрами схемы, узловыми уравнениями н соответствующими определителями, которые следует учитывать при анализе цепей методом узловых потенциалов
Если в цепи имеются ветви с идеальными источниками э д с , а сопротивлениями этих ветвей можно пренебречь, то при составлении уравнений (1-33) получается неопределенность, поскольку проводимости таких ветвей бесконечно большие Такое затруднение преодолевается путем переноса заданной э д с из ветви с нулевым сопротивлением через соответствующий узел в другие ветви, присоединенные к тому же узлу и имеющие конечные значения сопротивлений В результате такого преобразования токи во всех ветвях заданной схемы не изменяются
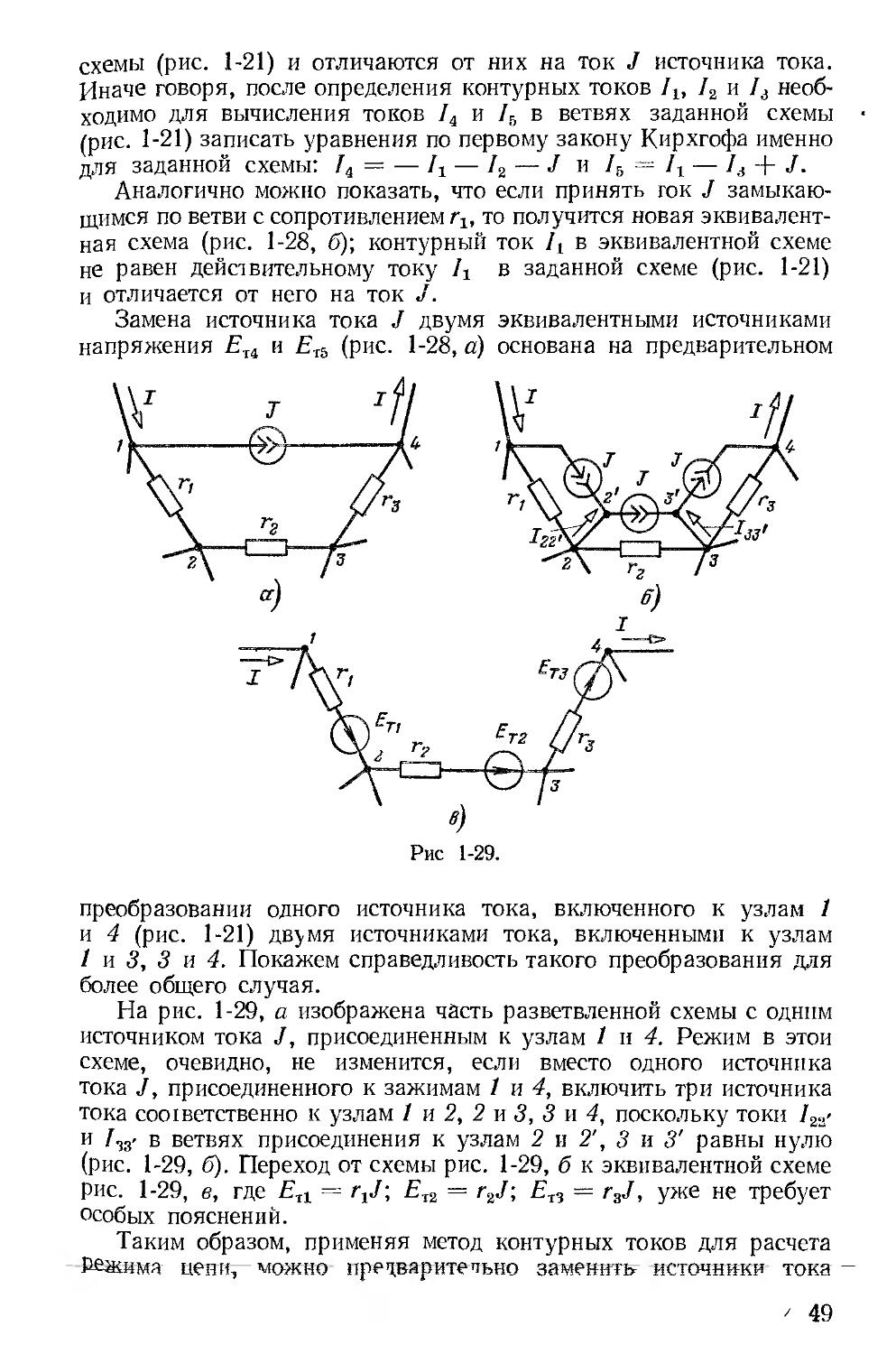
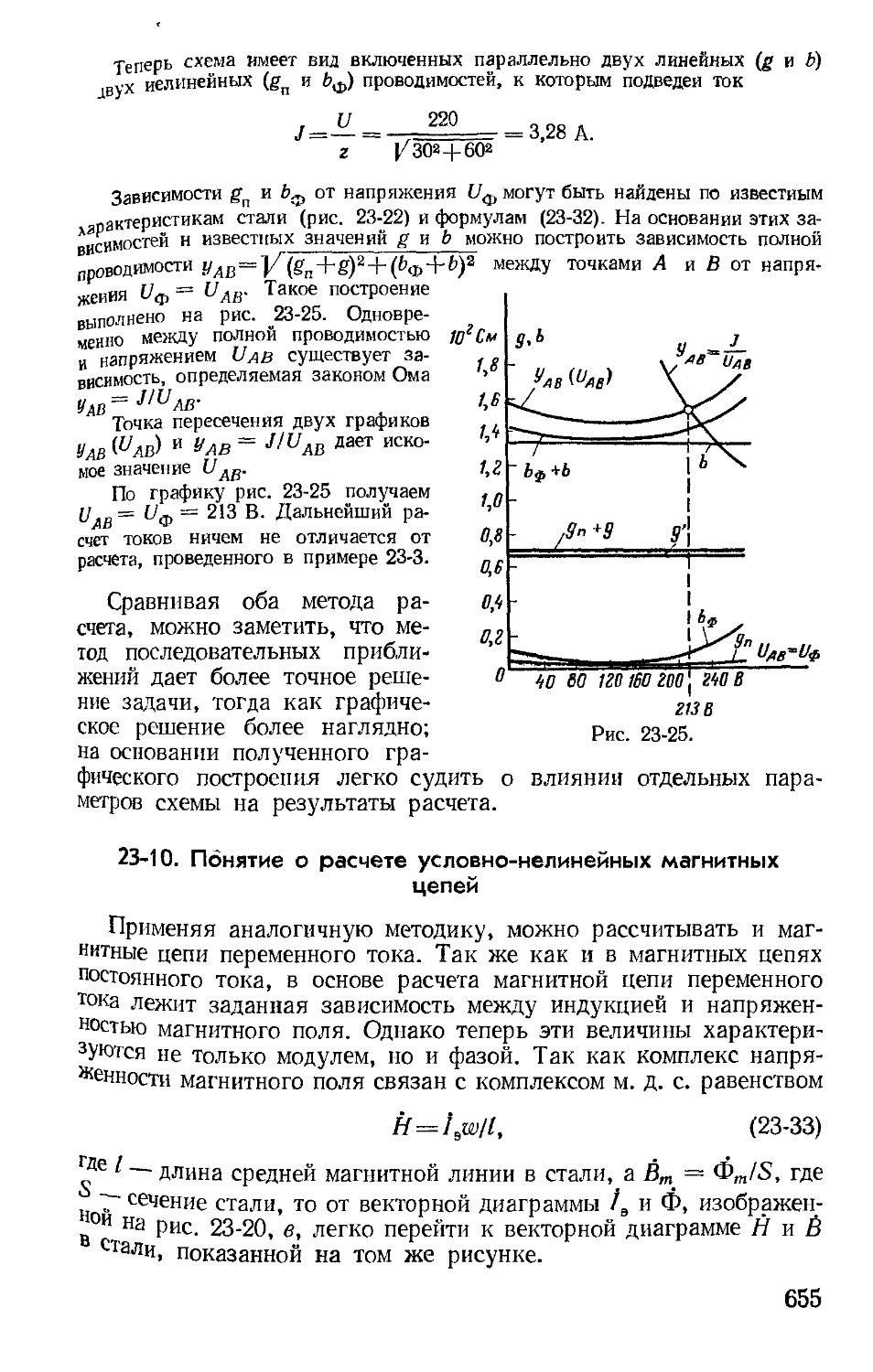
Для иллюстрации рассмотрим схему (рис 1-24, а), у которой в ветви 2-4 сопротивление равно нулю, а э д с равна Е Если Е кюкдую ветвь, присоединенную, например, к узлу 2, включив
39
Рис. 1-24.
источник напряжения с э. д. с., равной Е и направленной от узла 2 (на рис. 1-24, а эти э. д. с. изображены пунктиром), то токи во всех ветвях останутся без изменения, поскольку разности потенциалов между точками'/', 3', 4' будут, так же как в заданной схеме, равны нулю. Теперь потенциалы узлов 2 и 4, очевидно, одинаковы и их можно объединить в одну точку (рис. 1-24, б). Для полученной схемы с тремя узлами (вместо четырех) можно составить два независимых уравнения вида (1-33), из которых определяются искомые потенциалы двух узлов, а затем по закону Ома токи во всех ветвях схемы (рис. 1-24, б), после чего
легко найти ток в ветви с сопротивлением г = 0 (рис. 1-23, а) по первому закону Кирхгофа.
Рассмотренную и аналогичные ей задачи можно решить и без
предварительного переноса э. д. с. через узел схемы в другие ветви
Действительно, если принять в заданной схеме (рис. 1-24, а) <р4 = О, то потенциал <р2 узла 2, очевидно, будет равен Е. Для определения двух неизвестных потенциалов срт и <рз нужно составить уравнения (1-33), которые полностью совпадут с уравнениями, составленными для тех же узлов эквивалентной схемы (рис. 1-23, б).
Полезно еще рассмотреть применение уравнений (1-33) для частного случая схемы с двумя узлами и произвольным числом активных
Рис 1-25.
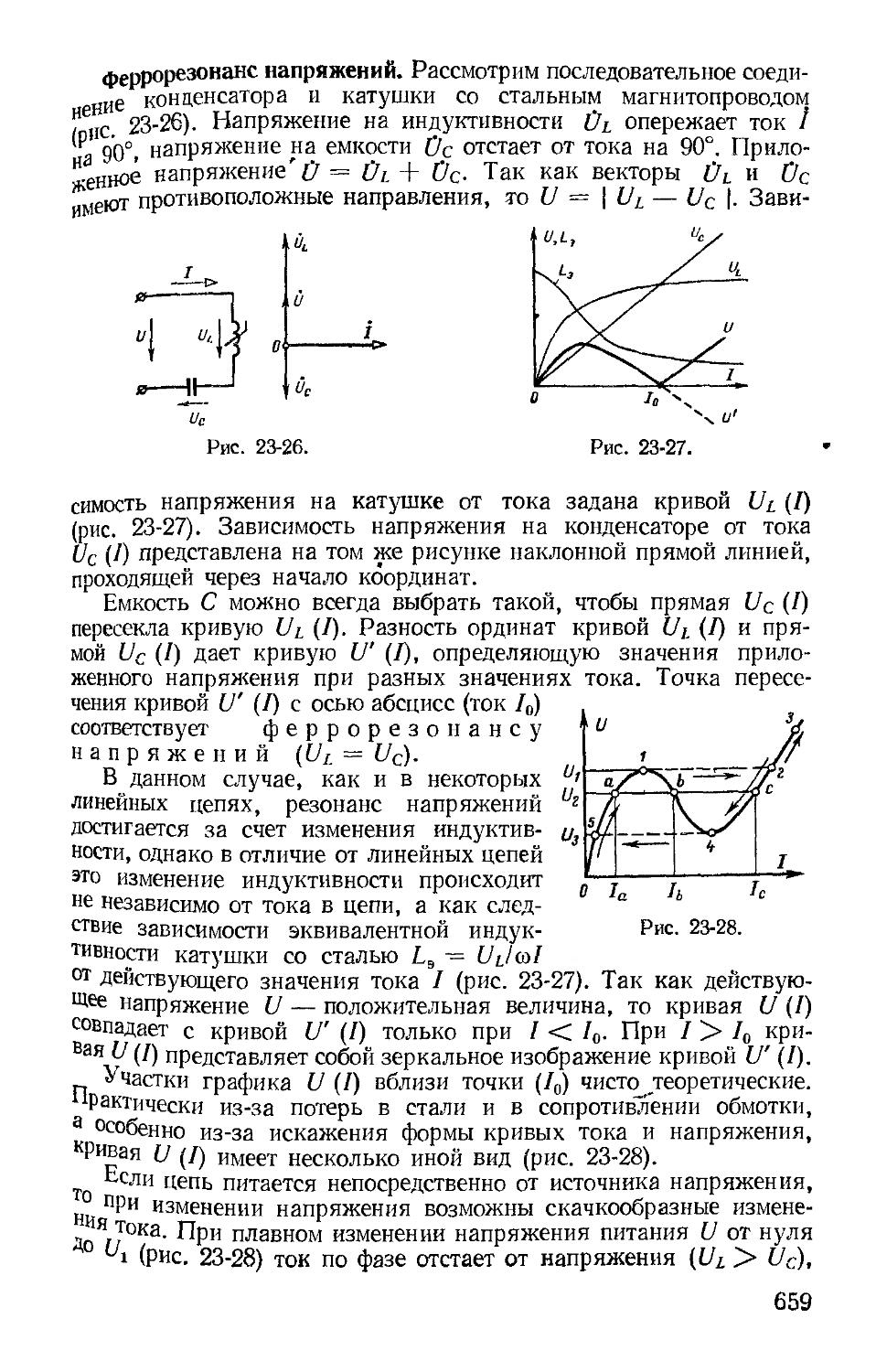
ветвей, когда требуется опре-
делить напряжение между этими узлами.
Пусть между узлами 1 и 2 включено т ветвей (рис. 1-25). Найдем напряжение U12, записав уравнение (1-33) для первого узла
(gi + gz + gs + • • • + gh + • • • 4- gm) —
h~ m
~ (gl + & +ga + • • • ~T gh + • • • + gm) ф2 = 2 Ehghi (1-45)
1
откуда
h — m
2 Ehgh
П12 = ф1-ф2 = -^-----------, (1-46)
_____ _______________._______________g.__________________________
Л = 1
40
где числитель представляет собой алгебраическую сумму произведений э. д. с. на проводимость для всех ветвей, содержащих э. д. с. (С положительным знаком берутся э. д. с. направленные к узлу /), а знаменатель — арифметическую сумму проводимостей всех ветвей, включенных между узлами.
Пример 1-3. На рис. 1-26, а изображена электрическая схема с шестью неизвестными токами; э. д.с. источников: Е( = 6 В, Е2 = 12 В и Е3 = 18 В; сопротивления ветвей: i\ — г2 = г? = 2 Ом и - г5 = г6 = 6 Ом. Пользуясь методом узловых потенциалов, определить токи во всех ветвях.
Рис. 1-26.
Решение. Пусть потенциал точки О равен нулю. Запишем уравнения для узлов с потенциалами фх, <р2 и <р3:
(й 4-й ~hga) Ф1—йфа — бзфз = — Еigi — E2g2 — E3g3;
— &Ф1 4" (gz+g~,4"gr>) <рг—£зфз — Ezgz,
— g:i4-i — Sofi 4- tes 4- gi 4“ gs) фз = Eggz, или после подстановки числовых значений проводимостей и э. д. с.
3 1 1 ,с 1 , 5 1 „
уф!—2~<₽2—2 фз = —I8; — 2"Ф14-6~фг—6 Фз==6;
1 1 , 5 _о
— 2 41— £ ’Рз+'б 4з —9-
Решая совместно эти уравнения, находим искомые потенциалы: <pt = — 9 В; ф2 = 3 В; <(3 = 6 В. Для определения токов в ветвях следует задаться их положительными направлениями. При выбранных положительных направлениях токов (рис. 1-26, а)
Л=(фо—Ф1—£i)£i=1>5 A; l2= (<pi—(р2~[-Е2) g2=0;
Рз=(ф1—фз4~£з)£з= 1,5 А; /4=(фз—фо)&=1 А;
/5 = (фз—ф2)§5 = °,5 А; /6 = (ф2 — фо)£в = °,5 А.
Матричные уравнения узловых потенциалов. Уравнения узловых потенциалов (1-33) можно записать в матричной форме:
— —------- -Л, ---------- - -fW-
41
где
§11 — £12 — • • • — giy — §21 §22-..-^
--& 1 — Sy 2 — •• + gy у
— квадратная матрица узловых
проводимостей схемы;
— матрица-столбец потенциалов узлов и матрица-столбец токов источников тока в узлах, где по (l-33a) Jct = Jt + ^Eijg^', при этом алгебраическое суммирование, выполняемое с учетом знаков, распространяется на все ветви с источниками токов и с источниками напряжений, присоединенные к /-му узлу.
Умножая слева уравнение (1-47) на -1, получим выражение для определения потенциалов узлов схемы в виде
Him,
(1-48)
где ||ё(у)||л — матрица, обратная матрице ||g(y>|L
Ниже показано, что матрицу узловых проводимостей цепи можно составить непосредственно по соответствующей схеме, применяя формулу
g<y) = AgdAT,
(1-49)
где А — матрица соединения узловых проводимостей ветвей схемы или ее ориентированного графа,
gri — диагональная матрица проводимостей ветвей;
Ат — транспонированная матрица соединения узловых проводимостей ветвей схемы или ее ориентированного графа.
Матрица А составляется следующим образом' столбцы матрицы соответствуют ветвям схемы, а ее строки — узлам, на пересечении строки и столбца записывается ±1 или 0 (пробел) в зависимости от того, присоединена данная ветвь к соответствующему узлу или нет; положительный знак записывается в том случае, когда ветвь направлена от узла, а отрицательный — к узлу; при этом направление ветви обычно совмещается с положительным направлением тока в пеиг
42
Для иллюстрации применения формулы (1-49) рассмотрим схему рис. 1-26, а, для которой на рис. 1-26, б построен ориентированный граф. Поскольку у заданной схемы четыре узла, то для нее можно составить три независимых уравнения, чему и соответствует матрица
соединения узловых проводимостей ветвей из трех строк и шести
столбцов:
—1 1 10 00
А = 0—1 0 0—11
0 0—11 10
Диагональная матрица проводимостей ветвей gk ~ \/rk равна:
й 0 0 0 0 0
0 g2 0 0 0 0
0 0 g3 0 0 0
grf= 0 0 0 gi 0 0
0 0 0 0 g5 0
0 0 0 0 0 ge
Произведение матриц А и gfZ равно:
— g 1 g'2 g3 0 0 0
Agrf = 0 — g2 0 0 — g:> ge
0 0 — gs gi gb 0
Матрица узловых проводимостей цепи получается после перемножения матриц Agd и Ат:
—10 0
1 -1 о
I о -1 о о 1
О -1 1
о 1 о
-gl g2 g3 0 0 0 I1
g(y) = AgdAT = 1 0- — g» 0 0 -g6 ge ।
1 0 0 g3 g4 g6 о II
I (gi + gj+g,) — g2 —g3
. ’ Яг (ёг Ч~ ёъ Ч- —ёч
I — ёз - ёя (ёз +- + ё5)
Матрица-столбец потенциалов узлов

Ф1
<Рз
Матрица-столбец источников тока
~~ E2g2 — Еэёз
E?gi Езёз
43
Пользуясь выражением (1-47), легко получить систему уравнений, приведенную в примере 1-3. Если матрицу А дополнить четвертой строкой, соответствующей узлу О, то по формуле (1-49) получится неопределенная матрица узловых проводимостей цепи, для которой сумма элементов по всем четырем строкам и четырем столбцам равна нулю; определитель такой матрицы также равен нулю. После вычеркивания любой строки и соответствующего этой строке столбца, например четвертой строки и четвертого столбца, получается определенная квадратная матрица третьего порядка.
Определитель такой матрицы симметричен относительно главной диагонали. Если вычеркнутая строка не соответствует вычеркнутому столбцу, то и в этом случае получается определенная квадратная матрица, соответствующая независимой системе уравнений. Однако определитель такой матрицы уже не имеет симметрии относительно главной диагонали [см., например, (1-38) и (1-43)1.
Здесь следует особо подчеркнуть, что если принять равным нулю потенциал того же узла схемы, который соответствует вычеркнутой строке матрицы А, то напряжения на всех ветвях схемы определяются через потенциалы узлов по формуле
Ue=ATq>, (1-50)
где положительное направление Ue совпадает с положительным направлением тока в ветви. Это непосредственно получается из формул для напряжения на каждой ветви. Например, для схемы по рис. 1-26
—1 0 0 — «Pl
и. 1 —1 0 <Р1 - <Р2
1 0 -и <Р1 <Р1— <Рз
и. 0 0 1 <Рг «Рз
0 —1 1 Чз — «Рз + tPs
0 1 0 «Рг
Из этого выражения следует:
t/^= <PiJ = (pi <р3; i74~(f>3; б/6 = <р3 <р2;
Ц> = <И-
1-8. Метод контурных токов I
Для расчета режима сложной электрической цепи можно ограничиться совместным решением лишь к = (в — у + 1) независимых уравнений, составленных на основании второго закона Кирхгофа, воспользовавшись методом контурных токов; здесь в — число вет-вей и у — число узлов. При этом первый закон Кирхгофа, конечно,_
всегда удовлетворяется.
44
Для иллюстраций применения метода контурных токов рассмотрим схему на рис. 1-27, а с шестью ветвями и четырьмя узлами. Прежде чем составлять уравнения по второму закону Кирхгофа, надо выбрать взаимно независимые контуры так, чтобы одна из ветвей каждого контура входила только в этот контур. Например, в схеме рис. 1-27, а первая, вторая и третья ветви входят соответственно только в контуры 1-2-4-1, 2-3-4-2 и 1-4-3-1.
Для правильного выбора независимых контуров введем еще дополнительные понятия. Деревом графа (схемы) называется
совокупность ветвей, соединяющих все узлы, но не образующих ни одного контура. Между любыми двумя узлами дерева существует только один путь графа — непрерывная последовательность ветвей между заданными двумя узлами при условии, что каждый узел встречается не более одного раза. Наличие хотя бы двух разных путей между двумя узлами дерева, очевидно, приводит к образованию контура. Если число узлов схемы и ее графа у, то число ветвей дерева равно у—1, так как из у ветвей можно всегда составить контур. Ветвью связи (связью, главной ветвью или дополнением дерева) называется любая ветвь, не входящая в состав дерева. В дальнейшем будем пользоваться преимущественно термином «ветвь связи». Все ветви схемы, не входящие в состав дерева и называемые ветвями связи, дополняют соответствующее дерево до полной - схемы-----: =
45
Взаимно независимые контуры получатся, если в каждый кон тур войдет одна ветвь связи, действительный ток которой буде-равен соответствующему контурному току. Ветви с идеальным! источниками э. д. с. и без сопротивлений обычно включают в состш дерева, а ветви с источниками тока относят к ветвям связи. Вегвт с идеальными источниками э. д. с. и сопротивлениями (соединен нымн между собой последовательно) могут входить как в состаг ветвей дерева, так и в состав ветвей связи. Например, для схемь рис. 1-27, а ветви с токами /4, /Е и /в, соединяющие узлы 1, 2, 3, 4 выбраны в качестве ветвей дерева; тогда ветви с токами /1э /2 и 7; будут ветвями связи. На рис. 1-27, б элементы ветвей дерева изображены сплошными линиями, а элементы ветвей связи — пунктирными. Из приведенной схемы видно, что при выбранном дереве токи в ветвях связи (71, 72, 73), совпадающие с контурными токами равны действительным токам этих ветвей. Это правило распространяется на любую схему.
Для схемы рис. 1-27, а по первому закону Кирхгофа
Zi —Л —73 = 0; 7&4-/2 —71 = 0; 16 + 73 - 72 = 0. (1-51)
На основании второго закона Кирхгофа
riK + г бЛ + — Е$,
f2^2~\~reE —--- Е2,
Г3/3 Г4/4 — г Jg — Ei -|- Е3.
(1-52)
Пользуясь уравнениями (1-51), исключим из уравнений (1-52) токи /4, 7& и /6 всех ветвей дерева, общих для нескольких контуров; в результате получим:
(ГI + Г4 Д Гб) Л — 2 — Г\1?,^Ех — Е4,
— (г2 + гв~\~ гь) 72 — г е7з = — Е2,
i гвЛ + (гз + 4~F- re) 7з=-'7?3 -j-TEY
(1-53)
В соответствии с уравнениями (1-53) можно принять, что каждый из токов /lt /2 и,/3 замыкается через соответствующую ветвь связи в одном из контуров (рис. 1-27, а и б) и назвать такие токи контурными. Напряжения на сопротивлениях любого контура равны алгебраической сумме напряжений, обусловленных токами своего и смежных контуров. Например, в контуре из сопротивлений г1( г5 и г4 разность э. д. с. Ег — Eti равняется сумме трех напряжений: от собственного контурного тока на всех сопротивлениях этого контура и от токов /2 и 73 соответственно на сопротивлениях г5 и г4. Действительные токи в ветвях дерева, общих для нескольких контуров, равны алгебраическим суммам контурных токов:
/4 — 71 4g', 76— 71 — 72; 7в — 72 — 73.
(1-54)
46
Для этой же схемы можно получить и другие взаимно независимые уравнения. Например, выберем другое дерево из первой, пятой и шестой ветвей (рис. 1-27, в); тогда вторая, третья и четвертая ветви будут ветвями связи, действительные токи в которых совпадают с контурными. Применив в этом случае второй закон Кирхгофа для контуров 2-3-4-2, 3-1-2-4-3 и 2-4-1-2, получим уравнения с контурными токами /2, /8 и /4, замыкающимися через ветви деревьев по ветвям связи. Токи в ветвях дерева однозначно определяются через токи ветвей связи (совпадающие с контурными) по формулам
Л=Л — Л и /6=/з4~Д I4.
Выражение для тока /Б получено по первому закону Кирхгофа для действительных токов, примененному к поверхности 5а, след которой показан на рис. 1-27, в пунктиром.
Таким образом, система взаимно независимых уравнений определяется структурой выбранного дерева и соответствующими ветвями связи.
Ниже будет показано, что мостовая схема рис. 1-27, а имеет 16 деревьев; поэтому для такой схемы можно написать 16 систем независимых уравнений, каждая из которых содержит в качестве неизвестных три тока, замыкающиеся по ветвям связи через ветви выбранного дерева.
Из 'приведенных примеров следует, что для определения токов в ветвях этим методом нужно ввести в расчет контурные токи и решить совместно систему уравнений, составленных по второму закону Кирхгофа; число этих уравнений меньше числа неизвестных токов ветвей на число узлов схемы без одного (у — 1). При замене токов в ветвях контурными токами первый закон Кирхгофа всегда удовлетворяется, так как каждый контурный ток в одной из ветвей контура направлен к узлу, а в другой — от того же узла. Например, для узла 4 (рис. 1-27, гй по первому закону Кирхгофа для токов ветвей получим:
Л-/8-/в=о,
или для контурных токов
(Л — /3) (Л — /2) — U2 — Л) = 0.
Если схема содержит не только источники э. д. с., но и источники тока, то можно принять ток каждого из источников тока замыкающимся по любым ветвям дерева, составляющим с ветвью источника тока — ветвью связи замкнутый контур. Падение напряжения, вызванное током такого источника на каждом из сопротивлений контура, учитывается при записи левой части уравнений по второму закону Кирхгофа. Однако эти напряжения можно также учесть С обратным знаком в_правой части уравнений.
47
В качестве примера рассмотрим схему на рис. 1-21. На основании второго закона Кирхгофа
Г1/1 4-г5/б — г4/i—Ex — Е^, r2^2 — ге^в — r$I 4 = Е2 — Eq, гз^з — rele — ^5^6 — 0-
(1-55)
Пользуясь первым законом Кирхгофа, исключим из этих уравнений токи /5, /4 и /6; в результате после группировки слагаемых получим:
(П-|-гБ4-r«) Ii — г51а-^-г^2-}-г^ 4-r&J = £г — £4; (Г2 + Гв +Г«) 12~\-Ге1з~]-Г411 ~\~r iJ = Е2 — Е/р, (гз + гв + гъ) Is-]-feI2 — r&Ii — r&J = 0.
(1-56)
Из этих уравнений следует, что в рассматриваемом случае ток J как бы замыкается по ветвям с сопротивлениями г5 и г4, дополняющими ветвь с источником тока J до замкнутого контура.
Обозначив в уравнениях (1-56) составляющие напряжений rtJ и r5J соответственно через £т4 и £т&, можно переписать их иначе:
(rl~\-r5-\-r4)Il~\~r4l2 — ГЪ13 — Е1 — — Е1Л — Eia,
f4Л + (rr1) 12<K rtJ 3 = E2 — E4 E-xl,
--r&Il + rel2 + (Г3 + re + ^5) 73 = £r&.
(1-57)
Здесь следует отметить, что перенос слагаемых г4./ и r6J из левой в правую часть уравнений (1-57) и замена эт, х напряжений на схеме э. д. с. £т4 и £т& иллюстрирует применение так называемой теоремы о компенсации, изложенной более подробно в § 2-6.
Уравнениям (1-57) соответствует эквивалентная схема (рис. 1-28, а), на которой источник тока J заменен источниками э. д с. £т4 = г4./ и £т5 = r5J, при этом токи в ветвях с сопротивлениями г, и не равны соответствующим токам в ветвях заданной-
48
схемы (рис. 1-21) и отличаются от них на ток J источника тока. Иначе говоря, после определения контурных токов /ъ /2 и /3 необходимо для вычисления токов Ц и 1Ъ в ветвях заданной схемы (рис. 1-21) записать уравнения по первому закону Кирхгофа именно для заданной схемы: Ц = — /х — I2 — J и /Б = /, — /3 + J.
Аналогично можно показать, что если принять гок J замыкающимся по ветви с сопротивлением rlt то получится новая эквивалентная схема (рис. 1-28, б); контурный ток IL в эквивалентной схеме не равен действительному току /х в заданной схеме (рис. 1-21) и отличается от него на ток J.
Замена источника тока J двумя эквивалентными источниками напряжения £т4 и £т5 (рис. 1-28, а) основана на предварительном
преобразовании одного источника тока, включенного к узлам 1 и 4 (рис. 1-21) двумя источниками тока, включенными к узлам 1 и 3, 3 и 4. Покажем справедливость такого преобразования для более общего случая.
На рис. 1-29, а изображена часть разветвленной схемы с одним источником тока J, присоединенным к узлам 1 и 4. Режим в этой схеме, очевидно, не изменится, если вместо одного источника тока J, присоединенного к зажимам / и 4, включить три источника тока соогветственно к узлам / и 2, 2 и 3, 3 и 4, поскольку токи 122> и /ад- в ветвях присоединения к узлам 2 и 2', 3 и 3' равны нулю (рис. 1-29, б). Переход от схемы рис. 1-29, б к эквивалентной схеме рис. 1-29, в, где £Т1 = t\J\ Е.[2 = r2J; El3 = raJ, уже не требует особых пояснений.
Таким образом, применяя метод контурных токов для расчета - Режима ценщ- можно предваритепыто заменить источники тока -
' 49
эквивалентными источниками э. д. с., а затем ввести контурные токи и на основании второго закона Кирхгофа составить систему уравнений для их определения. Действительные токи в ветвях без эквивалентных источников э. д. с., заменяющих источники тока, определяются по первому закону Кирхгофа суммированием контурных токов; в ветвях заданной схемы, в которых на эквивалентной схеме включены источники э. д. с., учитываются и токи источников тока.
При расчете электрических цепей изложенным методом всегда стремятся к тому, чтобы число контурных токов, замыкающихся через каждую из ветвей, было по возможности минимальным. С этой целью обычно выбирают каждый контур в виде ячейки (на рис. 1-27, а три ячейки с контурными токами /1( /2 и /3), руководствуясь указанным выше правилом выбора независимых контуров (дерева и ветвей связи) при составлении уравнений на основании второго закона Кирхгофа.
Положительные направления контурных токов можно выбирать и произвольно, т. е. независимо от положительных направлений токов в ветвях.
Установим теперь более общие, необходимые для дальнейших выводов соотношения между контурными токами, сопротивлениями и э. д. с. цепи произвольной конфигурации. Для схемы, имеющей к независимых контуров, уравнения, аналогичные (1-53), запишутся в виде
(1-58)
В этих уравнениях сопротивление вида га (с двумя одинаковыми индексами) называется собственным сопротивлением контура I, а сопротивление вида г1к = гы (с двумя различными индексами) называется общим сопротивлением контуров Ink. Правые части уравнений (1-58) называются контурными э. д. с. Каждая из контурных э. д. с. вида Ei равна алгебраической сумме э. д. с. всех источников в ветвях контура /. Положительные знаки в каждом уравнении (1-58) должны быть взяты для токов и э. д. с., положительные направления которых совпадают с произвольно выбранным направлением обхода соответствующего контура.
В более общем случае, цогда электрическая цепь содержит как источники э. д. с., так и источники тока, контурное уравнение для /-го контура записывается в виде
'а, (1-58а)
i
50
где riij обозначает собственное сопротивление контура /;
rl} — общее сопротивление двух контуров I и /;
Jij — ток источника тока, замыкающийся по сопротивле-НИЮ Гу.
Решая систему уравнений (1-58) при помощи определителей относительно любого из токов, например /z, получаем:
;<=£.^+^;Й+-+£'> + - +
, ®1д q
р1к
£>(><) ’
(1-59)
где DlK) — определитель системы уравнений (1-58), т. е.
D<& =
rll rVi ... г и ... rLi
Г21 ... Г 21 ... г 2К
Гц г 12 ... Гц ... г{к
(1-60)
Г к! Г к-2 • • • Г к1 • • • Г кк
Dn, Dl2, ... , Dtq, ... , D!k — алгебраические дополнения определителя D(k), причем Dl9 получается из £>(к) путем вычеркивания /-го столбца и q-ii строки и умножения полученного определителя на (—l)z+®. Необходимо отметить, что сопротивления вида ги и rkl нужно записывать в выражении (1-60) с тем знаком, который стоит перед соответствующим напряжением в уравнениях (1-58).
Подчеркнем, что при соответствующем выборе контуров получится такая система контурных уравнений, определитель которой имеет аналогично определителю D60 минимальное число слагаемых с отрицательными знаками (которые сокращаются с соответствующими положительными членами).
Для иллюстрации отмеченных положений рассмотрим схему на рис. 1-27, а, для которой справедлива, например, следующая система уравнений:
(Г1 +г5 + ri) fi — — г4,1з~Е1. —
— Г5/1 + (г2 + Г5-(-Гв) 1> — Гй13~ Е2',
—Г4Л — Гв/а + Дз + ^ + гв) /3=£3 + £4;
Г1/1 + г2^2 + г3/3 = £'1 — Е2 -\-Е3,
(1-61)
где последнее уравнение получено простым суммированием первых трех; оно справедливо для внешнего контура, проходящего через ветви связи с сопротивлениями гъ г2 и гз- Совместное решение любых трех уравнений системы (1-61) определяет неизвестные контурные токи
51
Покажем, что система из первых трех уравнений дает определитель с большим числом слагаемых (до сокращения), чем система, например, из первых двух и четвертого уравнений. Для первых трех уравнений определитель
D(»>=
(Г J + ri + гъ) ГЪ Г4
— гъ (г2 + гъ + ге) — гв
— Г 4 — г 6 (г 3 + Г4 + г в)
(1-62)
Этот определитель после раскрытия имеет 38 слагаемых (до сокращения), из которых 22 попарно равны по абсолютному значению, но по знаку противоположны и сокращаются.
Для первых двух и четвертого уравнений определитель
(Г1 + г4 + гБ) —r5 —ri
/>> =
ГЪ (Г2 + ГЪ + Г(>) ---------------------ГС
— (г 1 + г 4 + Гб) (г2 + Г в) rS +
Г2
rs
+ (Г1 + rt) r5r3 + rlrs + Г2Га (r, + r4 + r5) - rs&r3 + r5r6rx +
+ г^5г2 + r4r. (r2 + r5 + r6). (1-63)
В этом определителе только два слагаемых равны по абсолютной величине, но противоположны по знаку и сокращаются.
Для решения общей задачи расчета неизвестных токов во всех ветвях линейной электрической цепи можно выбрать один из двух основных методов расчета: узловых потенциалов или контурных токов.
Методом узловых потенциалов целесообразно пользоваться, когда число узлов схемы, уменьшенное на единицу, меньше числа независимых контуров у — 1 <; к, а методом контурных токов при У — 1 > к.
Матричные уравнения контурных токов. Уравнения контурных токов (1-58) с учетом (1-58а) можно записать в матричной форме:
г(к>1<к)==ЕсК>» (1-64)
где г1к) — квадратная матрица контурных сопротивлений;
Цк) — матрица-столбец контурных токов;
{(к) — матрица-столбец контурных э. д. с., учитывающая источники э. д. с. и эквивалентные э. д. с. от источников тока.
После умножения уравнения (1-64) слева на || г1к) Ц"1 получим:
1(К) = ||Г(К)Ц-1Е(К)_ (П65)
Покажем, что матрицу контурных сопротивлений г(к> можно получить непосредственно по схеме при помощи матрицы соединения контурных сопротивлений В:
rw —BrdBT, (1-66)
52
де гг! — диагональная матрица сопротивлений ветвей;
Вт — транспонированная матрица соединения контурных сопротивлений.
Матрица соединения контурных сопротивлений В составляется ак, что ее строки соответствуют независимым контурам, а столбцы — ютвям. На пересечении строки и столбца записывается ±1 или О пробел) в зависимости от того, входит или не входит данная ветвь 1 соответствующий контур; положительный знак принимается в том шучае, если направление ветви совпадает с направлением обхода сонтура, а отрицательный знак — если не совпадает. При этом управление обхода каждого контура примем совпадающим с поло-кительным направлением соответствующего контурного тока, а набавления ветвей — с положительными направлениями токов в вет-1ЯХ.
Для получения независимых контуров следует сначала выбрать херево схемы, что в свою очередь определяет вётви связи, а следовательно, и контурные токи.
Для иллюстрации рассмотрим схему на рис. 1-27, а с выбран-тым деревом из четвертой, пятой и шестой ветвей (рис. 1-27, б). В этом случае независимые контуры содержат контурные то-си Д, Д и Д. что соответствует первой, второй и третьей ветвям :вязи.
Л1атрица соединения контурных сопротивлений В состоит из грех сгрок и шести столбцов:
О
0 0 110
10 0—1 1
0 1—1 0—1
Диагональная матрица сопротивлений
rd =
Г1
0
0
0
0
0
0 0 0 0 0
г2 0 0 0 0
0 rs 0 0 0
0 0 г4 0 0
0 0 0 г5 0
0 0 0 0 г6
Произведение матриц В и га равно:
Г1
Brd= 0
0 0 г4 гъ 0
г2 0 0 — гъ г в
0 г3 — г4 0 —,”ь
53
Квадратная матрица по формуле (1-66):
контурных сопротивлений определяется
г<к) = BrdBT =
О Г1 О
О 0 — гъ га
Гз —Г4 0 — Г6
1 О О
О 1 О
О О 1
И 0—1
1 —1 О
О
О» 1—1
(Щ 4“ ri + rs) Г5 Г4
---r5 (r2 + ГЬ + Гв) ГС
— — r6 (r3 -f- ri -f- rc)
Матрица-столбец контурных токов
I(K) =
h
1г l з
E'K) =
Матрица-столбец контурных э. д. с.
Ei —Е4
-е2
Ез4-Е4
Пользуясь уравнением (1-64), матрицами г(к), 1(к) и Е<ск), легко получить уравнения (1-53).
Подчеркнем, что матрица токов ветвей 1в легко определяется через матрицу контурных токов 1(к) по формуле
= ВТ1<К>. (1-67)
Например, для схемы рис. 1-27, а
Ла 1 0 0
Ла 1 Зв 0 0 1 0 0 1 11К
lie 1ьв 1 1 0 —1 —1 0 Лк 1 зк •
1&В 0 1 —1
Из этого матричного уравнения сразу получаем равенства, определяющие токи ветвей через контурные токи:
Лк, /га Лк, 13в — Iзк', lie — Лк 1 зк',
Л» — Лк 1 ?.к\--------------1вв~ liK — 1Зк*-------------------------
54
В дальнейшем индексы в у токов ветвей и индексы k у контурных токов в алгебраических выражениях, как правило, будем опускать,
В заключение подчеркнем, что все соотношения между токами ветвей и контурными токами для схем, показанных на рис. 1-27, а—в,
легко получить из графов, построенных соответственно для этих схем на рис. 1-30, а—в. При этом деревья графа изображены на рис. 1-30,6 и в сплошными линиями, а ветви связи — пунктирными.
1-9. Уравнения состояния цепи в матричной форме
Пользуясь матрицей соединения узловых проводимостей ветвей А и матрицей соединения контурных сопротивлений В, а также законами Кирхгофа, можно получить узловые и контурные уравнения, определяющие электрическое состояние цепи в матричной форме; при этом попутно получаются выражения для определения матрицы узловых проводимостей (1-49) и матрицы контурных сопротивлений (1-66).
Первый и второй законы Кирхгофа запишем в матричной форме:
АЬ = 0; 1 вие=о, J
'де 1в — матрица-столбец токов ветвей схемы;
Ue — матрица-столбец напряжений на зажимах ветвей той же схемы.
Пользуясь уравнением (1-67), представим первое из выражений (1-68) в следующем виде:
АВт1<к> = 0. (1-69)
Полученное выражение справедливо при всех значениях 1<к>, Поэтому АВТ = 0 для любой заданной электрической цепи.____________
55
На основании закона Ома для ветви с э. д. с. при выбранных положительных направлениях тока 1в, напряжении Ue и э. д. с. Ев, очевидно, справедливо равенство
г a!e — Ee-\-Uе,
где га = гв — сопротивления ветвей, или в матричной форме
rrfIe = Ee + Ue и rrfBTIW = Ее + Ue, (1 -70)
где г а — диагональная матрица сопротивлений ветвей.
После умножения обеих частей уравнения (1-70) слева на В получим:
Br(/BTI<K> = BEe-J-BUe. (1-71)
Из этого выражения следует, что произведение Вгг/Вт равно, как уже было отмечено, матрице контурных сопротивлений г<к> (1-66), произведение BE, определяет матрицу контурных э. д. с. Е<к> и, наконец, В11й = 0. Таким образом, из (1-71) следует:
Г(К)1(К> = Е'к). (1-72)
Если в ветвях заданной схемы кроме источников э. д. с. имеются эквивалентные э. д. с. от источников тока, то они войдут в (1-72) в качестве слагаемых; в результате получится уравнение, совпадающее с (1-58а).
Аналогично получается матричное уравнение для узловых потенциалов.
Из уравнения (1-70) непосредственно следует, что
Ie=rd‘(Ee+Ue). (1-73)
Обозначив rdl = ga из первого уравнения (1-68) с учетом (1-73), получим:
Al, Aguila -J- Ag,;E„ = 0.
Из этого уравнения с учетом (1-50) следует, что
Ag^A^p == — Ag(/EB = J, (1-74)
где произведение Agf/AT равно матрице узловых проводимостей схемы g<v> (1-49), а произведение Agf/Ec = — J определяет матрицу узловых токов той же схемы. Если в заданной схеме имеются кроме источников напряжения источники тока, то в правой части уравнения (1-74) входят дополнительные слагаемые и оно в раскрытой форме совпадет с (1-ЗЗа).
1-10. Преобразование линейных электрических схем
Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядными путем преобразования электрических схем од-ного вида в схемы другого вида. Целесообразное преобпазоваиид^
56
электрической схемы приводит к уменьшению числа ее ветвей или узлов, а следовательно, и числа уравнений, определяющих ее электрическое состояние.
Рассмотрим, например, схему трехпроводной линии (рис. 1-31, о). Пусть заданы э. д. с. £1, £2 и внутренние сопротивления гв] и гв2 источников энергии, сопротивления проводов линии г, г0 и сопротивления приемников г12, г23 и г31.
Для определения токов в шести ветвях этой схемы необходимо по методу контурных токов или узловых потенциалов решить систему уравнений с тремя неизвестными.
Однако можно упростить схему, например, так, чтобы она содержала только три ветви с тремя неизвестными токами и всего два узла. Новая схема получится, если три сопротивления г12, г23 и га1,
Рис 1-31.
присоединенные к узлам 1, 2 и 3, заменить тремя другими сопротивлениями г1; г2, г3 (рис. 1-31, б), включенными соответственно между точками 1, 2 и 3 заданной схемы и новой узловой точкой О'. После такой замены токи Д, Д, /3 в ветвях, не затронутых преобразованием, и напряжения U12, U23 и US1 между точками /, 2 и 3 должны быть такими же, как в заданной схеме.
В новой, эквивалентной схеме с двумя узлами О и О' можно сразу найти напряжение между узловыми точками по формуле (1-46), а затем определить токи Д, Д и Д по закону Ома. После этого можно вычислить напряжения U12, U23 и U31 между точками 1, 2 и 3 и токи Д2, Д3 и /31 в сопротивлениях г12, г23 и г31 заданной схемы, т. е. решить задачу достаточно просто.
Во всех случаях замены заданных электрических схем эквивалентными схемами другого вида необходимо выполнять условия неизменности токов и напряжений в тех частях схемы, которые не затронуты преобразованиями.
Если преобразуется часть электрической схемы, не содержащая щеточников энергии, то, как будет видгюГГз^даЛПГёйГи'его, дензмен-
57
ность токов и напряжений в остальной части схемы обеспечивает и неизменность мощностей, потребляемых ветвями. В случае преобразования электрических схем, содержащих источники энергии, суммарные мощности источников и приемников в исходной схеме не равны в общем случае соответствующим мощностям в эквивалентной схеме.
Рассмотрим теперь наиболее характерные, чаще всего встречающиеся на практике случаи преобразования электрических схем как при отсутствии в преобразуемых ветвях источников э. д. с. и тока, так и при их наличии.
Рис. 1-32.
Преобразование соединения сопротивлений многолучевой звездой в многоугольник; преобразование треугольника в звезду. Рассмотрим сначала преобразование соединения сопротивлений многолучевой звездой (с числом лучей больше трех) в эквивалентный многоугольник. Покажем, что соединение сопротивлений /г-лучевой звездой преобразуется в эквивалентную схему многоугольника с числом ветвей, равным п (п — 1)/2.
На рис. 1-32, а изображено соединение сопротивлений в виде «-лучевой звезды. Уравнения электрического состояния для этой схемы:
А=(ф1—<po)gi; 4=(ф? - фо)
Ih~(SPli Фо) Shy •••» 7П—Фо) Ёп'г
+ + + — (ф1 Фо) S1 4~
+ (ф2-фо)£2 + ... + (фл-фо)£л + ...+ (фп-фо)ёгл = 0» (1-75)
где ф1, <р2, ... , <рл, ... , <р„ — потенциалы соответствующих точек схемы. '
58
Из последнего уравнения найдем потенциал точки О:
<Plgl + VS2 + • • + VhBh + • • + 4>ngn (1-76) °__________________________________________gl+g2“F-- +gft +”-+gzi
После подстановки <p0 в первое из выражений (1-75) получим:
7 ф1£1 + фг&+--- + фй£Гй+--- + <Мп \ „ _
11 = Ф1--------------------------------- gl —
\ ss /
— [(ф1 ~ tP2)glft+ (ф1 — (Ps)glg3 4-- • +
+ (<pl ~ фй) gig* + • • • + (ф1 — фга) glg/J> где
S £>h'
Л=1
В полученном выражении разности потенциалов между точками 1, 2, 3, ... , Л, ... , п заменим через напряжения по формуле hi фй ~~~ Фг*
h=--U12^~ + Ul3^ + ... + Uu-^ + ... + ULn^. (1-77)
Аналогично для любого тока
7 7/ ghgl 177 8hg2 1 1 r r ghgh-l 1 1 77 KhKn zj 7c\
lh = fJhl—--1-Ы/12-Т----(-••• + ЫЛ,Л 1—---F----\-Uhn— • U-/C)
gs gs gs £s
Из этих уравнений видно, что ток каждой ветви /г-лучевой звезды можно представить в виде суммы п — 1 частичных токов, пропорциональных напряжениям между соответствующими точками звезды. Например, ток
11— 712 + Лз + *- • + Лй + - + 11т
где
j ___ т 7 gl&2 , j _ т j
/12—С/12~Т , /13—° 13 ~ '
и аналогично для любой ветви
lh~ lhl~\- I hi +• • • + lh, h-1 +• • •+ 1 hn*
Покажем, что выражениям (1-78) удовлетворяет эквивалентная схема в виде полного многоугольника (рис. 1-32, б) с числом ветвей, равным п (п — 1)/2.
Действительно, для схемы рис. 1-32, б
11 — ^12gl2 + ^13gl3 + • • --^-41hglh~V • • -4-^lragln;
^2 = ^21g21 + ^23g23 + - • •+ ^ihgzh + • • •+
.............................................................. (1-79)
lh ~ Uhlghl + Uhighi + • • - + Uh, h-lgh, h-1 + • • • + Uhnghn, I
........................................................ J
59
Для того чтобы схема, показанная на рис. 1-32, б, была эквивалентна схеме рис. 1-32, а, необходимо равенство токов (7Ъ /2, /3 и т. д.) в обеих схемах при одинаковых напряжениях (U12, U13, Ulh и т. д.), что выполняется при
giz=g^/g^=£21; £13=£1£з/£е=£з1 • • • (1-80)
Поскольку число узлов многоугольника равно п, число токов, связанных с каждым узлом, равно п — 1 и каждая ветвь присоединена к двум узлам многоугольника, то число его ветвей как раз равно п (п — 1 )/2.
Из приведенного доказательства следует, что простая математическая операция исключения потенциала <р0 из системы уравнений электрического состояния схемы, имеющей форму /г-лучевой звезды, приводит к эквивалентной схеме в виде многоугольника. Обратная задача о преобразовании многоугольника в эквивалентную /г-луче-вую звезду в общем случае при п > 3 неразрешима, так как число искомых сопротивлений (или проводимостей) ветвей эквивалентной звп’.ды меньше числа п (п— 1)/2 условий, которым они должны у ювлетворять. При п = 3 число условий п (п— 1)/2 = 3 и, следовательно, треугольник сопротивлений всегда можно преобразовать в эквивалентную звезду.
Из формул (1-80) при /г = 3 сразу получаются формулы для преобразования трехлучевой звезды в эквивалентный треугольник в следующем виде:
для эквивалентных проводимостей
„ ___ glgi . __ gigs . __ gsgl z ] on
^12 gl + gi + gs ’ ^2S gl+gl+gs' ^S1 gl^gi + gs' ' ’ ’
или для эквивалентных сопротивлений
r12— ^/gl2 = rl-\~r2-\~rlr2ilrs} Г23 = Г2 + Гз + Г2Гз//'1; 1 ,
, 7 (1-82)
Г31--rs~\~ rl~\~ l3rl/>2- J
Чтобы получить формулы преобразования треугольника с заданными сопротивлениями г12, г23 и г31 в эквивалентную звезду, примем в уравнениях (1-82) в качестве неизвестных сопротивления гъ г2 и г3. В результате получим:
ri = b/r2S; r2=b/rsl; rs = b/r12, (1-83)
где b = /уг2 + r2rs + ГдГр
Выразив попарные произведения искомых сопротивлений в виде г1г2 = Ь2/г23гл; r2rs = b2/rslr12; г3гг = b2/r12r23
и подставив полученные выражения в формулу для Ь, имеем:
£> = ft2 fГ12-)''/’2з+/'з1\ \ Г12Г23Г31 / ’
откуда
— Г12Г23Г31
= = —“ f и 1—Г 2"—Г1---------------------- = “ “ ——
60
После подстановки этого выражения в (1-83) получим:
Г1 = Г12Гз1/^г; г2=-г23г12/2г; г3 = rslr2s/^ г, (1-84) где 2г = г12 + г23 + г31.
Последние формулы позволяют определить эквивалентные сопротивления звезды по заданным сопротивлениям треугольника.
Аналогично можно получить формулы преобразования активной многолучевой звезды (рис. 1-33, а) в эквивалентный активный многб-
Рис. 1-33.
угольник (рис. 1-33, б). Действительно, в этом случае для схемы, показанной на рис. 1-33, а, можно записать:
(<Р1 — Фо—^i)Л=(<Р2-<Ро--£,2)ё'2; •••;
^й==(фй фо Eh)gh, •••! Лг = (фя фо Еп) gn', (j 85)
-- Фо (gl 4~ §2 4~ • • • Ч- gn) + tPlgl + (P2g2 + • • • + tyngn = I
E2g2~[-.. .-\-Engn. )
Выразив <p0 из последнего уравнения и подставив его, например, в первое из выражений (1-85), после элементарных преобразований получим:
[(ф1 — Фгф- Ег — Ei) gig2~\- (<Pi — Фз4~ Е3 — Ei) gig3-\-.. •
...ф-(Ф1— <рп-\-Еп— E^gign]. (1-86)
Аналогичные уравнения можно получить для токов /2, /3,... , /„. Выражениям вида (1-86) соответствует эквивалентная схема, показанная на рис. 1-33, б. Проводимости ветвей многоугольника определяются по-прежнему по формулам (1-80), а эквивалентные э. д. с. при указанных положительных направлениях (рис. 1-33, а и б) Равны:
61
Преобразование параллельного соединения ветвей с источниками э. д. с. и источниками тока. Если сложная электрическая схема имеет одну или несколько групп параллельно соединенных ветвей с источниками э. д. с., то расчет и исследование такой схемы можно значительно облегчить, заменив каждую группу параллельных ветвей одним источником с эквивалентной э. д. с. и эквивалентным внутренним сопротивлением. В частности, так можно преобразовать схемы со смешанным соединением активных и пассивных элементов в схемы с последовательным соединением.
На рис. 1-34, а показана группа из т параллельно соединенных ветвей, выделенная в электрической схеме. Остальная часть схемы условно обозначена прямоугольником. Требуется заменить т параллельных ветвей (рис. 1-34, а) одной эквивалентной ветвью
Рис. 1-34.
(рис. 1-34, б) так, чтобы ток I и напряжение U в эквивалентной схеме, а значит все токи и напряжения в остальной части схемы были такими же,-как в заданной.
Согласно (1-12) для токов ветвей и суммарного тока / схемы рис. 1-34, а справедливо следующее выражение:
/ — ЕД- IhA~ - А~ —
=--(EA-U)glE(~E2~-U)g2-\-...-\-(Eh-U)gh^-...-\-(E,n-U)gm^ — ELgi E2g>-\-. Efigh~\- -Д-Emgm—
~ U (gl4~£r2 + - • •+§* + • • (1-88)
где gk = l/rft.
В схеме рис. 1-34, б ток
I — (E — U)g, (1-89)
где g = 1/r.
Так как условия эквивалентности должны быть выполнены при любых токе I и напряжении U, то, приравнивая правые части выражений (1-88) и (1-89), нужно положить:
U (gi +ёг +• • •+йгл4-. • -Дг gm) = Eg-, -------Ergi —- Eg2 +... Е
62
откуда
g— gl + §2 + • • - + gft + . • -Л-grn, (1'90)
p Elgl E2gi-]-.. -\-Ehgfl-\-...-^-Erngm £ V p /I nn
gi+g24—. + gft + ...+gm g L Lhgh‘ U’yl)
h~ 1
При вычислении эквивалентной э. д. с. Е с положительным знаком записываются те э. д. с. Eh, которые направлены к тому же узлу, что и эквивалентная э. д. с. £, и с отрицательным знаком — направленные к другому узлу. Если какая-либо из параллельных ветвей, например третья, не содержит источника э. д. с. £3, то в выражении (1-91) слагаемого £3g3 не будет, но в состав проводимости g входит проводимость этой ветви g3.
Из выражения (1-90) следует, что эквивалентная проводимость g не зависит от э. д. с., в то время как эквивалентная э. д. с. £ (1-91) зависит не только от э. д. с. ветвей, но и от их проводимостей.
Выше было отмечено, что энергия, потребляемая сопротивлениями ветвей до преобразования схемы с активными элементами, не равна энергии, потребляемой эквивалентными сопротивлениями ветвей после преобразования.
Для иллюстрации этого положения сравним, например, мощности источников и потребителей заданной схемы (рис. 1-34, а) и схемы после преобразования (рис. 1-34, б), когда ветвь с током I разомкнута. В схеме рис. 1-34, а при / = 0 токи /1; /2 ... могут и не быть равными нулю. В результате суммарная энергия источников э. д. с. будет расходоваться на покрытие тепловых потерь в сопротивлениях ветвей. В схеме рис. 1-34, б при 1 = 0 потери в эквивалентном сопротивлении отсутствуют.
Следовательно, несмотря на неизменность токов и напряжений в той части схемы, которая не затронута преобразованием, мощность, развиваемая источниками э. д. с. до преобразования, не равна мощности, развиваемой эквивалентным источником э. д. с. после преобразования схемы.
Однако это обстоятельство не мешает широко пользоваться понятием эквивалентной э. д. с. для расчета электрических цепей, так как после определения тока / в эквивалентной схеме можно вернуться к исходной и найти токи и мощности во всех ее ветвях.
Если к узлам 1 и 2 (рис. 1-34, а) присоединены кроме т ветвей с источниками э. д. с. еще п ветвей с источниками тока, то при вычислении эквивалентной э. д. с. (1-91) нужно учесть токи заданных источников тока:
h — m р—п
£=т 2 £»««+т2 h — 1 р = 1
пРичем с положительным знаком берутся токи, направленные к тому >Ке узлу, что и эквивалентная э. д. с. £, а с отрицательным знаком — Оправленные кгщругому узлу.
63
Преобразование схемы с источниками э. д. с. в эквивалентную схему с узловыми токами (источниками тока). Выше (§ 1-2) было показано, что источник энергии с известным значением э. д. с. и заданным внутренним сопротивлением можно представить источником тока, причем режим приемника энергии останется неизменным. Такую замену можно произвести и в том случае, когда ветвь с источником э. д. с. и внутренним сопротивлением имеет добавочное сопротивление, включенное последовательно с внутренним сопро
тивлением.
Пусть к зажимам 1 и 2 (рис. 1-35, а) присоединена ветвь с источником э. д. с. Е и сопротивлением г, которое включает и внутрен
нее сопротивление источника энергии.
Если напряжение между первым и вторым зажимами равняется U, то по (1-11) ток , __ Е и J U
1 — ~ г' -
г ГТ г ’
(1-93) где E/r = J.
Из этого выражения следует, что ток / источника э. д. с. может
быть представлен в виде разности тока J источника тока, который определяется только параметрами ветви с источником э. д. с., и тока /12 = Ulr. Уравнению (1-93) соответствует эквивалентная схема, показанная на рис. 1-35, б, в которой напряжение U и ток / те же, что и в схеме на рис. 1-35, а. Ток J источника тока направлен так же, как э. д. с. Е (от зажима 2 к зажиму 1).
Такую замену можно провести в схеме как для одного, так и для всех или части источников э. д. с.
Рассмотрим, например, схему, показанную на рис. 1-36, а, с источниками э. д. с. в трех ветвях. Эквивалентная схема с источниками тока приведена на рис. 1-36, б, где
j L--Elglt ^2--------E^gz", Ja------Eaga.
На схеме рис. 1-36, б ветви с источниками тока Jlt J2 и Ja присоединены попарно к одним и тем же узлам 1, 2 и 3, Поэтому целесообразно объединить в каждом узле два тока источников в один (рис. 1-36, в). Суммарные или узловые токи Jcl, Jc2 и Jc3 определяются по первому закону Кирхгофа:
JQ1~=Ja — Ji~Eaga — Exgi', JC2~ Ji + Jz = Eigt_-\-E2g>',
J a —— J3— J 2 = — Eaga — Eag2-
Следовательно, электрическая схема с источниками э. д. с. в ветвях можеъ быть заменена эквивалентной схемой с узловыми токами, причем потенциалы узлов и токи в непреобразованных вет-вях остаются неизменными. Так. токи /j, /5 и 7в заданной схемы
64
(рис. 1-36, а) равны токам в тех же ветвях эквивалентной схемы (рис. 1-36, б или в). Но, конечно, токи в преобразуемых ветвях с источниками э. д. с. не равны соответствующим токам в ветвях эквивалентной схемы. Например, в сопротивлении t\ заданной схемы (рис. 1-36, а) ток 1г = (£4 — Ч’г) gi> а в эквивалентной
схеме (рис. 1-36, в) ток /12 = (срх — <р2) gy.
В общем случае справедливость преобразования схемы с источниками э. д. с. в ветвях в эквивалентную схему с узловыми токами
Рис. 1-36.
непосредственно следует из уравнений узловых потенциалов (§ 1-7) Действительно, для схемы рис. 1-36, а на основании уравнений (1-33) при <р4 = 0 получим:
4i£n — фг£1 — Чз£з = (Езёз — Elgl) = Jcl;
4 iSi 4" Ча£г2 — Ч’з£г = (^г£г Jr £i£i) = JC21
Ч1£з Ч)2^2 4~ Ч>зЯзЗ = (Е2Ц‘2-\- = JcS,
где £и ~ £i т & т £ei £22 ~ £1 + £2 + £5! £зз = £2 + £з + gt-Этим уравнениям удовлетворяет эквивалентная схема
(рис. 1-36, в).
Обратная замена электрической схемы с заданными узловыми таками-эквивалентной схемой с источниками э. д. с. не является
3 Основы теории цепей
65
однозначной. Это объясняется тем, что число узловых токов или число узлов всегда меньше числа ветвей, т. е. количество уравнений, которое можно составить на основании первого закона Кирхгофа, меньше числа искомых э. д. с. Поэтому можно задаться произвольными значениями э. д. с. источников в любых ветвях в количестве, равном числу недостающих уравнений. Остальные неизвестные э. д. с. могут быть определены после совместного решения независимых уравнений, составленных по первому закону Кирхгофа.
Пример 1-4. Определить токи во всех ветвях и составить уравнения баланса мощностей для схемы рис 1-37, а, если Ег = 48 В, £2 ~ 24 В, £3 = 12 В, Е = = 12 В, г4 = 3 Ом, г2 = 6 Ом, гз = г4 = 2 Ом, г = 6 Ом.
Решение Для определения токов /4 и /3 (эти токи одинаковы) заменим каждую группу параллельно соединенных ветвей одной эквивалентной Эквивалентную э д с. Е12 для первой и второй параллельных ветвей и эквивалентное сопротивление г12 определим по формулам (1-91) и (1-90):
£ ^£2^ = 24 В;
gl+gt
5 , 1 , 1 'T'z „ ~
gl2 = — = gl + g2 = —+— ИЛИ Г12 = —1— =2 Ом.
г12 Г1 Г2 Г1~^-Г2
Аналогично находим эквивалентное сопротивление и эквивалентную э. д. с. для трех параллельных ветвей, присоединенных к третьему и четвертому узлам:
£43=^-= Е =12 В; g43 = 3g или г43=г/3 = 2 Ом.
В результате таких преобразований получается схема, показанная на рис 1-37, б.
В этой схеме ток
г _ j £з + £1а — Ем о «
4 гз + '12+П1-|-г43 и напряжения на участках
t/2i=£i2 г12/з=18 В; t/34 = £43-|-r43/3= 18 В.
Токи в ветвях заданной схемы
-------------Л=(^1—^81) £1 = Ю А;---/2=(^2~Ь^21) Й2 —А.---------------
66
Токи в ветвях с одинаковыми э. д. с. Е равны друг другу и направлены навстречу э. д- с.:
/ = (Г/31 —E)g= 1 А.
Суммарная мощность всех источников э. д. с.
E1/1 + E2/2+£3Zs-3£/=648 Вт.
Мощность в сопротивлениях, конечно, равна суммарной мощности источников э. д. с.:
Г1^1 + гг^2 + (гз+г4) + Зг/2 = 648 Вт.
Отметим, что источники с э д. с. Е работают в режиме приемников, потребляя энергию от других источников.
Глава вторая
ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
2-1. Принцип наложения
Каждая э. д. с. Е{ в уравнении (1-59) представляет собой алгебраическую сумму э. д. с. во всех ветвях контура /. Если в уравнении (1-59) заменить все контурные э. д. с. алгебраическими суммами э. д. с. ветвей, то после группиров-
ки слагаемых получится выражение для контурного тока Ц в виде алгебраической суммы составляющих токов, вызванных каждой из э. д. с. ветвей в отдельности.
При этом каждая составляющая тока равна произведению э. д. с. ветви на алгебраическую сумму коэффициентов вида Dlk/D'-K>, входящих в уравнение (1-59).
Это чрезвычайно важное свойство носит название п р и н ц и п а наложения и непосредственно следует из линейности уравне-
ний электрического состояния для цепей с линейными элементами. Принцип наложения справедлив не только для контурных токов !{,
но и для токов Ih ветвей, так как систему независимых контуров можно всегда выбрать так, что рассматриваемая ветвь войдет только в один контур, т. е. контурный ток It будет равен действительному току Ih.
В качестве примера, иллюстрирующего принцип наложения, рассмотрим электрическую схему, показанную на рис. 2-1, для
которой, пользуясь методом контурных токов, запишем следующие
3*
67
уравнения:
ГцА— Г12/2— Г1з1з = Е1', 1
-- Г21Е “4~ ^22 Д Г23^3 — Еъ, ( (2'1)
--Гд1Д— Г32^2 4“ Г33^3 ~ О» J
где
Гц = г1-(-г5г4; r12 = r2i==r5; г13 = г31 = г4;
г22~ г2 + гв + г5; г2з —г32 —г6; г33 — r3-[-r,j-[-r6;
£'i = £'i2 — Ем, Е,2 = £'23Ц-£'42-
Из уравнений (2-1) вытекает:
+ (2-2)
где
DM =
Гц — г12 — г13
О1 Г22 — Г23
Гз1 Г32 г33
Г22 Г23
г32 г33
DVi--=(-1)1-'2
— г12 — г1а
г32 rS3
I'^EiDu/DM- Ii=E2Dm!D^.
Аналогично определяются токи /2 и /8.
Если в выражении (2-2) контурные э. д. с. заменить через э. д. с. ветвей, то получим:
т __р Ди р Дц Руг 1 р Рц
1 э. * * * * * * * * 12 D<K^ 42 D<& ' 23 ’
откуда и следует, что контурный ток /4 равен алгебраической сумме составляющих токов, вызываемых каждой из э. д. с. в отдельности. Кроме того, этот контурный ток равен действительному току ветви с сопротивлением i\ и э. д. с. Е12, так как по этой ветви
другие контурные токи не замыкаются.
Таким образом, при определении токов ветвей при помощи принципа наложения можно поочередно оставлять в схеме по одной
э. д. с., считая все остальные э. д. с. источников равными нулю, но
сохраняя в схеме их внутренние сопротивления. Действительные
токи ветвей определятся как алгебраические суммы токов, вызы-
ваемых каждой э. д. с. Если схема содержит не только источники
э. д. с., но и источники тока, то следует найти составляющие токов,
вызываемые каждой э. д. с. и каждым источником тока, после чего
определить действительные токи ветвей путем алгебраического сум-
мирования этих составляющих.
Так как принцип наложения следует из общих свойств линейных уравнений, то его можно применять для определения любых физических величин, которые связаны между собой линейной зависимостью. В применении к электрическим цепям можно определять не только токи по заданным э. д. с. и сопротивлениям, но и напря-
-жепия по заданным токапг -ц известным сопротивлениям. Однако :
68
этим принципом нельзя пользоваться для вычисления мощностей, так как мощность — квадратичная функция тока или напряжения. Например, мощность в сопротивлении и (рис. 2-1) определяется по формуле
г Л=Г1 (Emd® 4- E2D12/D^Y=г, (/;+ц у.
Если мощность в том же сопротивлении г\ можно было бы считать равной сумме мощностей, обусловленных частичными токами и Л, то получили бы совсем другое значение q (/[)2 4- f\
Пример 2-1. На рис. 2-2, а показана мостовая схема с источником э. д. е. Е = 5 В и источником тока J = 1 А. Сопротивления указаны на схеме. Пользуясь принципом наложения, определить токи во всех ветвях.
Решение. Для определения токов в ветвях с применением принципа наложения надо рассчитать токи в двух схемах, изображенных на рис. 2-2, б и е. В схеме рис. 2-2, б ток J равен нулю (точки bud разомкнуты), а в схеме рис. 2-2, в э- Д. с. равна нулю (точки а и с соединены проводником без сопротивления). Токи в вегвях схемы рис. 2-2, б
/' = /'= Е Г = Г =
1 1 Н4-/-4 ’ 3 гг4тз •
Токи в ветвях схемы по рнс. 2-2, в, где сопротивления гх и г4, а также г2 и г3 соединены параллельно,
1 ’ 1 С14"г4 ’
y,,^ Jr3 . Jr2
69
Токи в ветвях заданной схемы (рис. 2-2, а) равны алгебраическим суммам токов в соответствующих ветвях схем рис. 2-2, б и е:
/!=/(-/?= = 04 А.
Г1+/4
Аналогично
/г=Л + /-'= = 1,4 A; fs=/;-/J=-0,4A; Д=Д + Д = 1,4 А.
2-2. Свойство взаимности
Пользуясь методом контурных токов, установим еще одно важное свойство линейных электрических цепей — свойство взаимности или, как его иногда называют, принцип взаимно с т и.
Сущность этого свойства заключается в следующем. Пусть в схеме произвольной конфигурации единственный источник э. д. с. Eq действует в ветви с сопротивлением rq в направлении от точки Ъ
Рис. 2-3.
к точке а (рис. 2-3, о) и создает в ветви с сопротивлением rt ток /Л направленный от точки d к точке с. Тогда такой же единственный источник э. д. с. £г = Eq, включенный в ветвь с сопротивлением rt и действующий в направлении от d к с (рис. 2-3, б), создаст в ветви с сопротивлением rq ток Iq, направленный от b к а и равный току It.
На рис. 2-3, а изображены ветви ab и cd с сопротивлениями rq и гь а остальная часть схемы, не содержащая источников энергии, условно показана в виде прямоугольника с буквой П (пассивная).
Для доказательства свойства взаимности обратимся к выражению (1-59), определяющему ток в любом контуре. Пусть ветвь cd является частью контура I, а ветвь ab входит в состав другого контура q (рис. 2-3, а) и, как указано, других источников э. д. с., кроме Eq, эта цепь не содержит. Контуры выберем так, чтобы ветви ab и cd вошли каждая в один контур, соответственно q и I.
Тогда ток Ц в контуре I, равный току ветви de, определится выражением
I^EqD^D^. (2-3)
Если источник э. д. с. Eq переставить в ветвь cd контура / (рис. 2-3, б), то после этого ток Iq в контуре q, т. е. ток в ветви ab, определится выражением
70
Алгебраическое дополнение вида Dlq получается из определителя £>(к) путем вычеркивания в нем столбца I и строки q и умножения получаемого определителя на (—1)/ъ?, а алгебраическое дополнение вида Dqi — вычеркиванием столбца q и строки I и умножением получаемого определителя на (—1)«+г. Так как в контурных уравнениях общие сопротивления rql и rtq равны друг другу, т. е. г = г21, Аз = Г32 и т. д., то и Dtq — Dqi (отличаются только тем, что строки Dtq являются столбцамиDqh и наоборот). Следовательно, при равенстве э. д. с. Eq = Et токи в ветвях cd (рис. 2-3, а) и ab (рис. 2-3, б) равны друг другу.
Отметим, что свойство взаимности справедливо не только для токов, но и для напряжений, и его можно также обосновать, пользуясь законами Кирхгофа или методом узловых потенциалов.
2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов
Пользуясь принципом наложения, напишем уравнение для тока в любой ветви, например h, линейной электрической цепи в виде
I h = ghi.E-i.A~ ShzEz-^-.. •'YShhEh-\- -A-ghmEm- (2‘5)
В этом уравнении, составленном согласно указаниям в § 2-1, ток Ih в отличие от уравнения (1-59) обозначает ток ветви h, a Еъ Б2 и т. д. — э. д. с. соответственно в первой, второй и так далее ветвях. При этом, если положительное направление для тока Ih выбрано совпадающим с направлением э. д. с. Eh, то составляющие токов в той же ветви вида ghiEt, создаваемые э. д. с. других ветвей, могут иметь отрицательные знаки.
В уравнении (2-5) множители при э. д. с. имеют размерность проводимости. Поэтому каждый из множителей с двумя одинаковыми индексами вида ghh называется входной проводимостью ветви h, а величина, обратная входной проводимости, — входным сопротивлением гЛЛ той же ветви. Любой из множителей с двумя различными индексами ghm называется взаимной проводимостью ветвей hum, а величина, обратная взаимной проводимости, — взаимным сопротивлением ,rhm тех же ветвей.
Численные значения входных и взаимных проводимостей и сопротивлений ветвей могут быть определены следующим путем. Приравняем в рассматриваемой схеме все э. д. с., кроме Eh, нулю. Тогда ток- Ih = Ehghh, откуда
ghh— 1hJEh=^/r hh- (2-6)
Следовательно, входная проводимость любой ветви определяется отношением тока к э. д. с. в этой ветви при равных нулю э. д. с. ^остальныхветвях, а входное сопротивление ветви обратно входной провидимости. ---------------— ----
71

Рис. 2-4.
определяется отношением тока
Электродвижущая сила Eh, включенная в ветвь h, вызывает в общем случае токи во всех ветвях и, в частности, в ветви т. Ток в ветви т определяется по уравнению, аналогичному (2-5), при равных нулю,всех э. д. с., кроме Eh, т. е.
I т E)gmf„ откуда
gmh~ т/Е^—Х/Гmh. (2-7)
Отметим, что ghm = gmtl, как это непосредственно следует из свойства взаимности.
Таким образом, взаимная проводимость двух любых ветвей в одной ветви к э. д. с. в другой
при равных нулю э. д. с. в остальных ветвях, а взаимное сопротивление двух ветвей обратно взаимной проводимости тех же ветвей. Входные и взаимные проводимости и сопротивления ветвей можно рассчитать или определить экспериментально. Определение входных и взаимных проводимостей и сопротивлений ветвей расчетом покажем на примере схемы рис. 2-4, а.
Приравняем э. д. с. Е2 и Б3 нулю (рис. 2-4, б). Тогда токи в ветвях
j’ ___________Ei_ __ £^1 (Гг4~Тз) __ д. е2-}-г3 .
1 /'14-Г2Гз/(Г2 + ,'з) 7'1Г> + ,’2Гз+,'зг1 1 Р ’
/2 = Б1Г3/р; /з = Б1О/р,
(2-8)
где
Р = Г1Г2 + Г2Г3 + Г3Г1‘
Из выражений (2-8) определим:
gn = Ц/Ei = (О + Гз)/Р = ^/rii, £21 = 7 а/Ei = r3/p— 1/^21! £з1 = EjEi — r^'p— l/r3i.
Аналогично рассчитываются входные и взаимные проводимости и сопротивления второй и третьей ветвей:
1
“; £зз
' 22
gi2
Р гзз ’
Р
£23-----Г1/Р------g32----- Х/Г2з'< £12--------£21----- I/O2; £13----------£з!------1/Оз-
Из полученных выражений следует, что для схемы рис. 2-4 входные и взаимные проводимости ветвей связаны между собой соотношениями
gll--£21+£зЬ g22------gl2~}-g32', £зЗ---£1з+£23-
Если взаимные проводимости найдены, то легко определить токи во всех ветвях npir Любых значениях э. д. с; Так, для схемы
72
рис. 2-4, а
A —fea+gsi) Ei~\- g±2E2 ё1зЕ3', A—feu + S?-) Е2 +&1А1+§2зАд;
А = (ёхз + йгз) A3 + gsiFi gszE2.
Часто взаимные проводимости считают алгебраическими величинами. В этом случае в уравнениях, записанных по принципу наложения, отрицательные знаки получаются у тех слагаемых, для которых взаимные проводимости имеют отрицательный знак.
В общем случае входная проводимость некоторой ветви равна сумме взаимных проводимостей данной ветви и каждой из остальных ветвей, присоединенных к одному из двух узлов, к когорым присоединена эта ветвь.
Рис. 2-6.
Рис. 2-5.
Например, входная проводимость первой ветви (рис. 2-5) равняется сумме проводимостей g13 и g^ или gis, gu и g15, т. е. '
gll---gl3 4" 512---gl3 + 514 gl5-
Эти соотношения непосредственно следуют из первого закона Кирхгофа и свойства взаимности и могут быть применены для расчета электрических цепей.
Например, для определения токов A, 12 и /3 (рис. 2-5) достаточно знать взаимные проводимости g12, g2S и g31 так как
А— feis+gta) At — giiE2,
А — (б12 + 53з) Е2 guE^, 13 = g3iEi~\- g23E2.
Знаки у составляющих каждого из токов учитываются по принципу наложения.
Экспериментальное определение входных и взаимных проводимостей и сопротивлений рассмотрим на примере произвольной цепи, из которой предварительно исключены все источники э. д. с. и источники тока (рис. 2-6). Три ветви этой цепи выделены, а остальная часть условно показана в виде прямоугольника. В каждую ветвь включен амперметр. Чтобы определить входную проводимость первой ветви gu и взаимные проводимости второй и первой g21 и треть-
еи и первой g31 ветвей.
73
э д с Ех Измерив вольтметром напряжение = Ех на зажимах источника э д с и амперметрами токи /х, /2 и /3 в трех ветвях, нетрудно вычислить входную и взаимные проводимости и сопротивления ветвей по формулам
£11 — Л/^1 = §21 = 12,1^1— 1/Г21! £’з1 = /з/^1= 1/Г31-
Аналогично определяются входные и взаимные проводимости и сопротивления других ветвей
Пример 2-2. Определить входные и взаимные проводимости ветвей схемы рис 2 7, а, если гх = г2 = г4 = г6 = 4 Ом, г3 = 2 Ом
Решение Для определения входной проводимости gu и взаимных проводимостей между первой и остальными ветвями положим э д с £3 и £6 равными нулю (рис 2 7,6) Затем можно задаться э д с £х и найти все токи Однако для данной схемы проще задать ток в ветви с сопротивлением г4 или г6, например /' = 1 А, и найти необходимую э Д с £х и токи в остальных ветвях
Рис 2 7
Так как сопротивление г4 = гъ, то Д = 7' и /' = 7' + /' = 2 А Напряжение на зажимах сопротивления г2
{7>г,Д + ^ = 4-1-4=8 В,
ток 7' = U's/r2 = 8/4 = 2 А, ток 7J = /2 + 7( = 2 + 2 = 4 А иэ д с, при действии которой ток Г = 1 А, а остальные токи равны найденным значениям, £х = Щ + ПЛ = 8 + 4 4 = 24 В
Входная проводимость первой ветви равна отношению тока к э д с. £ь т е
gu = 7(/£х = 4/24 = 1/6 См
Взаимные проводимости между первой и остальными ветвями
gi2==g2i =/2/^1= 1'12 См, £1з=&1—/з/Ех= 1/12 См,
&14=£41=Л7£1=1/24 Cm, g16=£5i = /7£i=1/24 См
Аналогично определяются входные и взаимные проводимости остальных ветвей
£22 = &3 = g44 = £o.= 1/6 См,
g23 = g32=g24 = £42 = g25 = g52 = g45 = g54= 1/12 См
Пример 2-3 В условиях предыдущей задачи (пример 2 2) определить токи во всех ветвях, если э д с £j = 24 В, £3 = 12 В и £6 = 24 В
Решение Зная входные и взаимные проводимости ветвей, легко определить в них токи, пользуясь принципом наложения
А = £1А-£1зЕ3-£1А = (1/6) 24-(1/12) 12—(1/24) 24 = 2 А;
^2=£21£1 + &>3£з-|-£25Е5=4 А
74
Входные и взаимные проводимости и сопротивления ветвей в общем случае для более сложных схем целесообразно представить в виде отношений узловых или контурных определителей и их соответствующих алгебраических дополнений.
Для мостовой схемы (рис. 1-22, а) взаимные проводимости между ветвями, например с проводимостями g± и gls, gr и g23, определяются при помощи выражений (2-7) и (1-39) соответственно по формулам
Лз___ Uisgia __ EigiSis Е)ц
Ei ~ Et DM ё1ё13 П'У’ ’
^23__ б^гз&з __ £'1й"1&з D12 _ „ D12
Et~ E1 — E1 Dty> ~ ё1Й23 p(y) ,
(2-9)
где Dn получается, как отмечено выше, из (1-38) путем вычеркивания первой строки и первого столбца, а Р12 находится из того же определителя (1-38) вычеркиванием первой строки и второго столбца и умножением полученного выражения на (—1)1+2 = —1.
Важными параметрами, характеризующими режим электрической цепи, являются коэффициенты передачи напряжения и тока. Эти параметры чаще всего применяются для характеристики цепей с одним источником э. д. с. или с одним источником тока при передаче сигналов. Коэффициент передачи напряжения определяется отношением напряжения на зажимах приемника к напряжению источника э. д. с., действующего в цепи; коэффициент передачи тока определяется отношением тока в приемнике к току источника тока в цепи. Эти величины также могут быть выражены через узловые или контурные определители и их соответствующие алгебраические дополнения.
Например, для схемы рис. 1-23, а, пользуясь уравнениями (1-42), легко определим напряжение U2 = Чг по формуле
^2 = <р2=^г-^2, (2-Ю)
где алгебраическое дополнение D42 = — g21 (g4 -J- g41) (ga + g32 -|-+ gsi) — g^gis (g3 + gsz) — gagzzgzi получается из (1-43) путем вычеркивания четвертой строки и второго столбца.
Коэффициент передачи напряжения
д- ___ Uz ( Eigi) г» —giDiz
1X1/2 Ei EtD<y> DW
(2-П)
Если в схеме рис. 1-22, а источник э. д. с. заменить эквивалентным источником тока = Erg± (рис. 1-22, б), то, пользуясь этой эквивалентной схемой и уравнением (2-10), можно определить коэффициент передачи тока во вторую ветвь по формуле
Uygz —gzDjz
^igi----
(2-12)
75
2-4. Применение топологических методов для расчета цепей
Ранее было показано, что для определения входных и взаимных сопротивлений и проводимостей схемы, а также коэффициентов передачи напряжений и токов приходится в общем случае вычислять определители системы узловых уравнений.
Такие определители для разветвленных цепей обычно содержат, как уже было отмечено, большое число одинаковых членов с разными знаками, которые выявляются, как правило, только в конце преобразований и сокращаются.
Таким образом, представляет’ не только теоретический, но и большой практический интерес знакомство с некоторыми способами разложения узловых и контурных определителей при полном или частичном отсутствии лишних отрицательных и равных им положительных слагаемых. Рассмотрим несколько способов такого разложения и установим между ними связь.
Для электрической схемы, имеющей у + 1 узлов, при tpv+1 = О, запишем определитель узловой проводимости:
gll gll gi) • glu
gll gll gi) • gly
р(У) = (2-13)
gll gn gi; • • giy
gyl gyi • gyi • • • gliy
Пусть проводимость между узлами i и / равна сумме проводимостей двух вегвей
gij=g4 4- ёч •
Тогда определитель (2-13) можно
представить в виде суммы
gu gll . 0 • • • gly gll gll • glj • gly
gn gll . 0 • gly gll gll • gl) • • gly
£)(У) = gii gll • gll • • giy 4- gll gll • • gll • • giy
gyl gyl . 0 gljy —glfllj 4-1 gyl y>. gyl • • gyj • gyy (2-14)
В этом выражении алгебраическое дополнение Dl} получается из (2-13) вычеркиванием i-и строки и /-го столбца и умножением на (—1) 1+1. Оно соответствует электрической схеме, в которой ветвь с проводимостью gf, закорочена; определитель D1’ получается из (2-13) при g'f = 0, что соответствует схеме, в которой ветвь с проводимостью g'4 разомкнута. Очевидно, что разложение
76
вида (2-14) вообще можно выполнить относительно любого элемента gtJ, выраженного в виде некоторой с^ммы проводимостей. Элемент главной диагонали определителя узловой проводимости (2-13), как правило, равны суммам проводимостей соответствующих ветвей. Поэтому разложение (2-14) выполняется обычно относительно ветви, присоединенной между /-м и базисным (заземлен-
ным) узлами, с проводимостью, входящей в элемент главной диагонали (соответствующей /-й строке и /-му столбцу), которую обоз-
начим в дальнейшем g/Q = gr При этом ёч ~gl + gill
где ветвь с проводимостью g^ в общем случае остается по-прежнему присоединенной между /-м и i-м (не базисным) узлами.
В этом случае вместо равенства (2-14) нужно записать:
D™=g,D}+D>, (2-15)
где нижний индекс у минора первого слагаемого обозначает, что /-я ветвь закорочена, а верхний индекс у второго слагаемого указывает, что та же ветвь в той же схеме разом-
Рис 2-8.
кнута, при этом D} — положительное, так как проводимость g} входит в элемент, стоящий на главной диагонали (алгебраическое дополнение равно минору).
Для иллюстрации применения формулы разложения (2-15) рас-
смотрим схему на рис. 1-22, а, для которой была записана система уравнений (1-35) относительно потенциалов <р2 и <р3 при <р4 = О
и определитель (1-36):

(£1 + £12 + £1з) ~ £12
— gil (£2+£21 + 623)
£з1 g32
— gl3
— 623
(£з + £31+632)
Разложим этот определитель относительно ветвей glt g2 и g3 (рис. 2-8), присоединенных к базисному узлу 4. Проводимости 61. £2 11 £з в приведенном определителе (подчеркнуты) представляют собой избыточные члены соответствующих строк или столбцов. Это означает, что при удалении такой проводимости из диагонального элемента сумма всех остальных элементов соответствующей строки и столбца равна пулю.
По формуле (2-15) получим:
П<У> = £1
(£2+ £21 +£23) —£23
£32 (£з + £з1+£з2)
(£1г + £1з) —£12
— £21 (£2 + £21 + £23)
— £31 — £32
— £1з
£гз
(£з + £з1 + £зг)
— £1^1 + D1.
(2-16)
77
Полученным минору Dr и определителю D1 соответствуют схемы на рис. 2-9, а и б. Разлагая каждый из определителей (2-16) согласно равенству (2-15) по проводимостям других ветвей, присоединенных к базисному узлу, можно получить еще более простые выражения.
Рис. 2-10.
Например, разложим определитель/)1 относительно проводимости g2:
Я1=£2
(gl2 + £1з) — Sa -----£з1
(£1г+£1з) — £з1
--£12
(8и 4~ £гз)
£з2
-~£1з
(£з+£з1 + £32)
— £1з
— £23 (£э + £з1+£32)
=g2D‘4-£)12. (2-17)
Минору £Д и определителю £)12 соответствуют схемы, показанные соответственно на рис. 2-10, а и б. Дальнейшее разложение £)| и D12 по формуле (2-15) относительно проводимости gs приводит к следующим выражениям:
£2О2 — g2g3 (gt2 + gi3) + £2
(£12 + £13) £31
— £1з (£31 + £32)
— £2£гЛ‘23 + gzD™;
D™=g3
(£12 + £13) £21
— £12 (£21 + £23)
=£з^2 + £)123.
(£12+£13) —£12 —£13
£21 (£21+£23) —£23
— £31 — £32 (£31 + £32)
Аналогично можно получить разложение для первого слагаемого (2-16):
£1^1=£1^53 4~£1£2^’12 4~£1£з£^1з4~£1£2£з^12з- (2-18)
После суммирования выражений для g^Pr и D1 получается:
— £i^i3 + £2^ + £з£)за + £1£г^12 +
+ £г£з£)23 + £1£з^1з + £1£г£з^12з + ^123’ (2-19)
где £)123 — 0 (рис. 2-11), поскольку этот определитель получается
для схемы, в которой —минор В123 —лзк кйк——
78
его значение находится при = g2 = gs = со (короткое замыкание этих ветвей).
Таким образом, каждому слагаемому (2-19) соответствует определенная схема, которая легко получается из основной схемы путем наложения условий на проводимости ветвей, присоединенных к базисному узлу.
Структура полученной формулы разложения определителя узловой проводимости (2-19) позволяет применить ее для разложения определителя, составленного для более сложной цепи.
Например, определитель (1-41) для схемы рис. 1-23, б
может быть разложен по избыточным элементам главной диаго-
нали (по проводимостям glt g2, g3 и gj в виде
р(у) = S1D^ + g2D2si + g3D32i + SiD^ + glg2D^ + glg3Dn + ~r g'ig'4^14 + gvg-jPw + ~r gsgiD^ 4- gig2g3Dya +
4" + glgigsgiDlSBi + D1234, (2-20)
где D1234 = 1 и £)1234 = 0.
Каждому слагаемому этого определителя соответствует схема, полученная из рис. 1-23, б при Д = 0 наложением условий на значения проводимостей ветвей, присоединенных к базисному узлу. Например, £)234 находится для схемы рис. 2-12, полученной из заданной схемы при gr — со и g2 = gs = gt = 0:
(gil -l -g'2.3) —g23 0
— gs2 (§32 + gai) gst
0 — gi3 (Й414~Й4з)
Обобщая выражения (2-19) и (2-20), составим общее выражение для разложения узлового определителя по ветвям glt g2, ... , gtJ, присоединенным к базисному у + 1-му узлу:
= + 'LgigjDi; + ZgiggkD.jk + . • . + gig2 • • .gy, (2-21)
где верхние индексы, указывающие на номера разомкнутых ветвей, опущены, поскольку одни нижние индексы определяют как закороченные, так и разомкнутые ветви. Например, слагаемое вида gtDt соответствует схеме с i-й закороченной ветвью и с разомкнутыми остальными ветвями; число таких слагаемых, очевидно, равно числу ветвей, присоединенных к базисному узлу. Слагаемые вида gig,Dij соответствуют схемам с двумя закороченными ветвями gt и gj и остальными разомкнутыми, причем число таких слагаемых равно числу сочртяний по дня из у проводимостей.
79
Аналогичный смысл имеют остальные слагаемые. Разложение определителя D<y> по формуле (2-21) называется разложением по узлу или по избыточным членам главной диагонали (по избыткам), а разложение по формуле (2-15) называется разложением по ветви.
Как указывалось, для определения входных или взаимных сопротивлений, проводимостей или коэффициентов передачи токов и напряжений можно пользоваться не только узловыми, но и контурными уравнениями. В последнем случае приходится вычислять определитель контурных сопротивлений £)<к>.
Покажем, что структура контурных уравнений позволяет во многих случаях пользоваться для разложения определителя D (к> формулами, аналогичными (2-15) и (2-21).
В определителе £)<к> системы независимых контурных уравнений
Гц Г 21 Г12 г 22 • • ги . г21 . • Г1к Г1к
D<K> = Гц Г{2 • • Гц . rtK (2-22)
Гк1 Гк2 • . Га Гкк
— ri + rt, где rt — сопротивление одной литель D<K> можно представить в виде
Hi Г12 • . 0 . • г1к Гц
Г21 г22 • . 0 . г2к Гл
Гц Г12 - г, . rth + Гц
гК1 Гк2 • .. 0 . • гкк Гк1
собственное сопротивление г и каждого контура записывается на главной диагонали и всегда равно сумме сопротивлений ветвей, входящих в соответствующий контур. Представим ги в виде г и = из ветвей, тогда опреде-
ли ... ги ... г1к
г22 ... г21 ... г2к
г12 ... r't ... rlK
Г к2 • • • ... Гкк

(2-23)
где минор Di получается из (2-22) вычеркиванием /-й строки и /-го столбца и соответствует электрической схеме, в которой ветвь с сопротивлением rt разомкнута; определитель D1 получается из (2-22) при сопротивлении rt = 0, что соответствует схеме, в которой ветвь с сопротивлением rt закорочена. Поскольку /-й элемент находится на главной диагонали, то минор Di всегда имеет положительный знак.
Для иллюстрации применения формулы (2-23) рассмотрим разложение определителя схемы, показанной на рис. 2-1:
(Г1 + Г j 4- г5) — гъ
-г6 (г2-|-гв-|-г6)
-Гл
— Гл
-гв
(f з 4~
(2-24)
80
В этом определителе сопротивления г1, г2 и г3 входят в диагональные элементы в качестве избыточных слагаемых. Следовательно, в соответствии с уравнением (2-23) разложение определителя можно выполнить по формуле (2-19) после простой замены проводимостей соответствующими сопротивлениями:
£)(к) — гjD;8 + г2D'2 -\-r3D\ -\-Г1ГiD[o -J- г2г3О23 4~
4~ r3riD~i\ + г1г2гз^12з 4~Д123> (2-25)
где О123 = 0, поскольку этот определитель получается для схемы при ri = г2 = г3 -= О, Е>133 = 1, так как значение этого определителя находится при г2 — г2 = г3 = оо (размыкание ветвей с сопротивлениями гъ г2 и г3).
Каждому слагаемому (2-25) соогветствует определенная схема, которая легко получается из основной путем наложения условий
Рис 2 13
на сопротивления ветвей связи, входящих в независимые контуры. Например, минору О~л соответствует схема, полученная из схемы рис. 2-1 при г2 = оои г2 — г3 = 0 (рис. 2=13), для которой получается:
(гв + гв) — ге
— Гв (Г4 4 Гб)
— rir5 + r5re + rart-
Минору О'3, соответствует схема, на рис. 2-14, полученная из схемы рис. 2-1 при г3 = г2 = оо, г3 = 0. Для этой схемы Dl2 = = (г4 + ге). Аналогично находим остальные составляющие выражения (2-25); в результате получим:
— (^1 -|- Г2 -|- Г3) (Г4Г5 4- Г5Гв 4- ГвГ4) 4“ г1г2 (гь + ri) 4~
4- r2r3 (r4 4- гъ) 4- r3t\ (r5 4- re) 4- r2r2r3. (2-26)
Выражения, определяющие разложения определителей £)(у’ и D(K\ связаны между собой довольно простым соотношением:
D(K’ = E>(y’W3...re;
(2-27а)
или
D<') = DWg1g2g3...ge
(2-276)
гДе проводимость каждой ветви g, = 1/г(; в — число ветвей. Например, чтобы получить разложение определителя О(у> для схемы Рнс 2-1, достаточно умножить уравнение (2-26; на произведение
81
проводимостей всех шести ветвей:
О(у) = = [(ri + r2 + r3) (r4r5 + r5r6 + rert) +
+ Г1Г2 (Г«+Гб) + r2rS Дд + чО + Г3Г1 (Гб + Гв) + Г1Г2Гslglgsgsglgsgli”
= (Si + gs + ge) (gigs + gsgs + gsgi) + gigs (gs + g3) +
+ gsge (gs + gi) + geg4 (gi + gs) + gig^Se • (2-28)
Подчеркнем, что число слагаемых в определителях £)(у> и £)<к> для одной и той же схемы одинаково.
К числу топологических понятий, которыми пользуются при анализе цепей, относится дерево. Для количественной характеристики дерева удобно применять произведение проводимостей его ветвей.
1 Определитель определенной матрицы узло-J вых проводимостей £)(у) равен сумме произ-г ведений проводимостей ветвей каждого дерева. Например, определитель схемы рис. 2-15 состоит из 16 слагаемых: g^g^ gig2g&\ gigzge, ёгёзёь и т. Д- Для схемы, имеющей форму полного многоугольника с у узлами, число деревьев d = уь~2. Например, для схемы пол-
ного пятиугольника d = 53 = 125, а для мостовой схемы (рис. 2-15) j _ 42 _ J6 Если схема имеет вид неполного многоугольника, то для определения числа деревьев надо найти численное значение определителя/) <у>, каждый элемент которого принят равным единице. Например, для схемы, показанной на рис. 2-16, определитель
/)(у| =
(gi + g«) — gi О
— gi о (gl+gs+gs) ----gs
— g2 (gl+gs)
(2-29)
где вершины 1 и 3 приняты в отличие от приведенного ранее определения узла за узлы схемы, что не нарушает общности полученных
выводов. Приняв проводимость каждой ветви равной единице, найдем число деревьев:
2 —1
— 1 3
О —1
= 8.
Рис 2-16.
Действительно, количественная характеристика каждого дерева равна произведению проводимостей одинакового числа ветвей, или по-
рядку определителя. Это произведение численно
равно единице, так как проводимость каждой ветви принята равной единице и число деревьев в указанной схеме равно 8 *. Деревья
* Число деревьев в схеме можно найти также, зная узловую матрицу сое-динепияветвей А; определитель произведения матриц ААТ равен числу деревьев (см. например, [ЛПК, с. 135J):
82
можно изобразить в виде неориентированных подграфов (рис. 2-17), где каждая ветвь обозначена конечным отрезком.
Несмотря на то что разложение определителя на сумму произведений проводимостей ветвей деревьев дает лишь положительные члены, число математических операций при вычислении такого определителя остается еще значительным. Можно уменьшить число операций суммирования и умножения, разложив определитель по другим топологическим величинам. Например, можно пользоваться понятием пути (§ 1-8), численное значение которого ПА равно произведению проводимостей ветвей k-ro пути, и понятием минора пути Dk, представляющего собой значение
определителя определенной матрицы узловых проводимостей схемы, остающейся после того, как все ветви /г-го пути замкнуты накоротко; минор пути равен единице, если путь содержит все узлы схемы.
Разложение определителя £)<у> по путям (по узловым парам) по существу получается из (2-21) при помощи простой группировки слагаемых и в общем случае может быть выполнено по формуле
D(y) = SnADfc. (2-30)
Для иллюстрации отмеченных положений сгруппируем в определителе (2-28) все слагаемые, например, следующим образом:
£)(у) __ [(g4g2 -j-g2g3 + gegi) +
(g2 + g'.j) + g’e (gl + gi) + gfigfi] + +gigs (gi + gs +ge) + gage (gi +
+g2 + g5)+glg2g6+g2g3g5. (2-31)
Рис. 2-17.
Это выражение можно представить в виде
= П1О1 + П2О2 + П3Е>3 + П4Г>4 + П5Д5, (2-32)
где ITj — g4; Dj = (g,g2-(-gig's+g3gi)+g5(gi+gs)+gefei H-g^+giige; n2==£fig’5; D2=g2 + ga + ge; n3=gsg6; D3 = gi + g2 + g5; n4=gig2ge; D4=l; n5 = g2g3g5; O5=l.
Такая группировка слагаемых соответствует разложению определителя по всем пяти путям между узлами 1 и 4 (рис. 2-15).
Каждому минору соответствует схема, которая получается из -?аДанной при коротком-замыкании-соответствующего-пути. Напри
83
мер, при Пг = gi минор Dj получается из уравнений для трехузловой схемы, приведенной на рис. 2-18:
jj _ (£г + ёз Ч-ge) — gi (2 33)
gz (gi + £2 + gs)
Если П2 = gAg-a, то D2 = (g2 + g3 + ge), что соответствует схеме (рис. 2-15), в которой ветви с проводимостями gx и g5 закоро-
Чь Sz ffi
Рис. 2-18.
Рис. 2-19.
чены (рис. 2-19). Если путь проходит через все узлы схемы, например при П4 = gigig^ то Di = 1. Аналогичный смысл имеют остальные слагаемые в определителе (2-32).
Для разложения определителя £)<у> по формуле (2-30) можно выбрать и любую другую пару узлов. Например, при разложении того же определителя относительно узлов / и 2 имеются пути со следующими значениями: Пг = gx; П2 = g4g5; П3 = g2g3; П4 = gsg&ge; П5 = gigeg2- Этим путям соответствуют миноры: Dr = (g2 + g3) (g4+ + gs + ge) + glge + gsge, D2 = g2 + + gs + ge', Ds = gi + g5 + g6; Di = = 1; D5 = 1, значения которых легко находятся из схем, получающихся при наложении соответствующих условий на заданную схему (рис. 2-15).
В качестве примера, иллюстрирующего непосредственное применение формулы (2-30), рассмотрим двойной Т-образный мост (рис. 2-20).
Для разложения определителя выберем, например, узлы 1 и 2 и
разомкнем источник тока. Между этими узлами имеются три пути со значениями: = g4g2; П2 = g3g4; П3 = g5ga. При коротком
замыкании ветвей пути со значением ITi = gtg2 минор D± = (g3 + + gi) (ga + ge); при коротком замыкании ветвей пути со значением П2 = gsgi минор О2 = (gi + g2) (g& + ge) и, наконец, при коротком замыкании ветвей пути со значением П3 = g6g6 минор D3 = (g4 ф-+ gz) (ge + gi)- Узловой определитель по фюрмуле (2-30)
D{y) =-gig2 (gs + gi) (g5+ge) + g3gi (gi + g2) (g5+ge) + + gsge (gi+g2) (gs + gi) • (2-34)
Определитель контурных сопротивлений £)<к) можно найти, например, по формуле (2-27а)
D(K) — £)1У1Г1Г2г5г4г5г6 = Д1 | г2) (/'з + г4 + г6 + гв)4-(/’з + г4) (г64-г6).-“
84
Подчеркнем, что каждое слагаемое £><к) представляет собой произведение сопротивлений ветвей, которые как бы дополняют соответствующее дерево, полученное из определителя для заданной схемы. Например, для дерева, состоящего из проводимостей glt g2> ёз> соответствующее слагаемое определителя £)<к> равно г4г6, а для дерева glt git git g6 — r3r& и т. д. Отсюда следует, что число слагаемых в определителях D&> и £)<к> одинаково.
Поскольку порядок определителя DW в данном примере выше порядка определителя О<к> в 2 раза (порядок каждого из определителей Г><у> и £)<к> определяется числом независимых соответственно узловых, включая устранимые узлы, и контурных уравнений), то число элементов в каждом слагаемом узлового определителя (которые входят в виде сомножителей) в 2 раза больше, чем в каждом слагаемом О<к>. Отсюда также следует, что в данном примере число операций умножения в контурном определителе £)<к> значительно меньше числа операций в определителе О<у>.
2-5. Топологические формулы и правила для определения передачи электрической цепи
Для определения входных и взаимных сопротивлений, проводимостей и коэффициентов передачи токов и напряжений по существу, как уже было показано, приходится в каждом случае вычислить отношение тока или напряжения, измеряемых соответствующими приборами, к напряжению или току источника. Для расчета часто целесообразно пользоваться соответствующими разложениями (2-21) или (2-30), причем можно установить связь между значениями этих определителей и условиями, налагаемыми приборами и источниками на режимы цепей в зависимости от определяемых величин. С этой целью следует ввести в схему вегвь с источником И и ветвь с измерительным прибором Пр. Если в рассматриваемой цепи имеется несколько источников и приемников, то сначала рассматривается только одна пара (Ilf и Пр^, а затем поочередно все другие возможные сочетания; для определения соответствующих величин можно пользоваться принципом наложения.
Предварительно введем некоторые дополнительные понятия.
Передача Н (коэффициент передачи, взаимное сопротивление или проводимость) — отношение показания измерительного прибора Пр к напряжению или току источника И; путь пере-Д а ч и — путь, состоящий из двух узлов источника (ветви с источником), ветвей схемы и ветви с измерительным прибором (при определении входного сопротивления или входной проводимости в путь передачи ветви схемы не входят); значение пути передачи Щ равно произведению проводимостей /г-го пути передачи, при этом проводимость измерительного прибора считается равной единице; знак Щ принимается положительным (отрицательным), когда ток в ветви измерительного прибора /г-го пути, обусловленный заданным направле-Ц1,6м тока илкнапряжения источника, стремится ьызватъ положптель-
85
ное (отрицательное) отклонение прибора с известной полярностью. Минор пути передачи Dk равен определителю цепи, остающейся после короткого замыкания k-ro пути передачи, включая ветвь измерительного прибора Пр.
Таким образом, передача Н может быть выражена при помощи топологического закона передачи в виде отношения определителей, разложенных по соответствующим путям:
D' _ UTikDk DW ~ £nltDk ’
(2-35)
где DM — определитель определенной матрицы узловой проводимости цепи, в которой э. д. с. источника и ток источника тока приравниваются нулю, что равносильно короткому замыканию идеального источника э. д. с. и размыканию идеального источника
Рис. 2-21.
тока; сопротивление амперметра принимается равным нулю, а сопротивление вольтметра — бесконечности.
Алгебраическое дополнение D' получается из О,у> вычеркиванием строки и столбца, соответствующих определяемой величине, и умножением полученного выражения на (—1)'+/, где i и / — номера вычеркиваемых строки и столбца. Предполагается, что определитель DM составлен из коэффициентов системы уравнений, определяющих напряжения на зажимах ветвей (в общем случае не совпадающие с потенциалами узлов). К такому виду, как было показано, можно преобразовать любую систему узловых уравнений (стр. 37).
Изложенные правила, как будет показано, по существу непосредственно вытекают из аналитических выражений, определяющих соответствующие величины.
На рис. 2-21, а изображена схема, ранее показанная на рис. 1-23, после замены источника э. д. с. Ег источником тока J1 — Е^. Требуется определить напряжения Ui — <р4, Ua = <р3 и U3i — = <р3 — <р4, а также найти коэффициент передачи тока в одну из указанных ветвей, =
86
Напряжение Uit как следует из ранее составленных уравнений (1-40), определяется по формуле
(2-36)
где 0<у> — определитель узловой проводимости для заданной схемы, определяемый по формуле (2-30), a Du получается из О(у) заменой четвертого столбца правой частью узловых уравнений (1-40); при этом ток J1 вынесен из определителя, т. е.
J 1^14 —
(£1 4“£12 4~£14) ---£12 0
---£21 (§2+й21 + й2з) -----------£23
0 — £зг (g-л 4“ £32 4“ £34)
--£41 0 --giS
g 21 (£2 + £2! + (?2з) — g‘23
—1
о о о
~ £з2 (gs - gs2 “1“ £34)
£11 0
— £43
= Ji {£12£гз£з4 "г- £41 [(£з 4“ £34) (£2 + £214~ £23) + £32 (£2 + £21)]} • (2-37)
Остановимся на разложении определителя О(у> по формуле (2-30). Разложение можно произвести относительно путей между любой парой узлов, например узлов 2 и 3. Между этими узлами имеются' восемь путей со значениями: Пх = £23; П2 = g2g3; П3 = £12£41£34; Щ = £12£1£4£з4‘> Щ = £12£1£з! П6 = g^g^g-M, П7 = £34£4i£i£2; П8 = = £21£п£4£з. при этом каждый из миноров Dit D7 nDs равен единице, поскольку пути со значениями П4, П7 и П8 проходят через все узлы схемы. Сравнительно сложное выражение получается для минора Dlt определяемого из схемы рис. 2-21, б, которая получается из основной схемы при £23 = оо:
Di — £14 [(£1 + £4) (£12 + £2 + £з + £34) + (£i2 + £43) (£2 + £з)] +
+ £.м£12 (£1 - £2 + £з + £4) + £i£4 (£12 + £34 + £2 + £з) +
+ £34 (£гт£з)£гг£4 (£2 4“£з) £12- (2-38)
Однако это выражение легко получается пугем повторного применения формулы разложения (2-30) к схеме рис. 2-21, б; например, при разложении Dr по путям между узлами 1 и 4 (рис. 2-21, б)
= £14; D'{ = (£42 4- g3i + £2 + £з) (£1 + £4) + (£i2 + £43) (£2 + + £3) (получающееся из схемы рис. 2-21, в); П2 = £34£J2; Z)2 = X,(£i + £а + £з + £4); П3 = g^; D3 = (£i2 4- £34 + £2 4- £3);
~~ £34 (£2 4~ £3) £i! D'l = 1; Щ = £4 (g2 4- gs) g12, D'i, = 1.
Остальные миноры узлового определителя находятся по Формулам
D2 = (£12 4- £14~ £14) (£4 4- £43) + £41 (£12 4~ £1);
D 3 = (£14~ £2 4- £з 4- £4); D5=(g3 4- £4 4- g-34);
4- £2 4“ £12)
87
и узловой определитель
Г>(« = ВД + П2Г>2 + П3Г>3 + П4Г>4 + II5D5 +
+ П6£)6 + П7О7 + П8Г>8. (2-39)
Теперь рассмотрим разложение (2-37). Это выражение можно представить в виде разложения по замкнутым путям относительно узлов той ветви, на зажимах которой определяется напряжение Г/4 = Поскольку в выражении (2-37) отсутствует проводимость^, то к зажимам узлов О и 4 присоединяется вольтметр, через который и проходят пути разложения. Кроме того, определитель умножается на ток J, источника тока; поэтому пути разложения определителя должны проходить через источник тока, т. е. от его зажимов через ветви цепи и через вольтметр, измеряющий напряжение U4. Первый путь со значением П{ = ' 1 проходит
через все узлы схемы, следовательно, при коротком замыкании этого пути минор D\ — 1. Второй путь со значением Щ — gy4-l; при коротком замыкании пути со значением ГК (включая вольтметр) определитель
= (g‘2 + g‘21 + §2з) (ga 4“ gsi) + g32 (§2 + §21) •
Напряжение на зажимах третьей ветви
(2-40)
где О(у) — определитель узловой проводимости (2-39) и
j 1^13 J1
---g-л (§2 + §21 4- §2з) о §32
о
§34
---§41
0 (§41+§43+ §<)
-А Г§21§32 (§4 + §41 + §4з) + §41§34 (§2 +§21+§2з).
(2-41)
Полученное выражение легко представить, так же как JjPm, в виде суммы произведений значений путей, проходящих от зажимов источника тока через ветви схемы и вольтметр U3, на соответствующие миноры: П, = §32§21-1; D'{ = (g4 4 §ц + §43); Ш = §и§34-1; D2 = (§21 4- §2 + §23).
Напряжение П34 — ср3 — ср4 можно найти непосредственно по потенциалам ф3 и <р4:
^31 £ЙуГ [§21§32§4 ~ §41§3 (§г + §2з + §21) "~§41§32§2]- (2-42)
Однако это же выражение можно получить при помощи разложения по путям, проходящим от зажимов источника тока через вольтметр П34. Значение пути П{ =§12§2з' 1 ’§4, поэтому минор D\— 1; значение пути Щ = — §41-1 -g-,; Di = (§3 + §23 + §21) и значение пуги Пз = — §41 • 1 •§2з§2’. Из == 1. Пути со значениями Щ и П3 направлены противоположно направлению обхода пути со значением П{ и эти два значения отрицательные. Для определения токов п вствя'< достаточпо у^мЖ)гг<и'Г1) iraiiir/raietfifTTra-зж-т-нм^ ветвен кт
88
их проводимости. Например, ^34 = =
= ртут [ёз4§21ёз2§4 — gsigilge (g> 4-gzs + gn) — gsigugxzgs]- (2-43)
Из этого выражения следует, что для определения тока в соответствующей ветви необходимо проходить пути через ветвь, в которой определяется ток, и проводимость этой ветви входит сомножителем в значение пути. Учитывая это соотношение, при определении тока в соответствующую ветвь можно включить амперметр (на рис. 2-21, а показан в ветви 3—4), принимая в значении пути его проводимость равной единице.
Рис. 2-22.
Рассмотрим еще схему с идеальным источником э. д. с. Е (рис. 2-22, а).
Поскольку ветвь с источником не имеет сопротивления, то для получения узловых уравнений типа (1-33) переведем э. д. с. через третий узел в первую и вторую ветви. После переноса э. д. с. Е узловые точки 3 и 5 объединяются в один узел. Для полученной схемы напишем три независимых узловых уравнения (для узлов /, 2 и 4), решив которые, найдем потенциалы узлов.
Найти напряжения на ветвях и, в частности, по известному напряжению П2 определить коэффициент передачи Ки2 можно при помощи формулы (2-35). При вычислении знаменателя и числителя этой формулы следует пользоваться изложенными топологическими правилами.
Чтобы найти определитель Е>(у>, нужно закоротить источник э- Д- с., т. е. соединить узлы 3 и 5 в одну точку (рис. 2-22, б). Получить выражение для определителя О(у> можно разложением, например, по путям между узлами 1 и 2:
П1 = (£14-£р5) (gg+ge); H1 = (g3 + g4);
: —D, (gx 1 g. | gu) =
' 89
Следовательно, узловой определитель
D^ = (gi~\-g5) (ga4~ge) (gs + go) + g3gd (gi + ga+gs + ge)- (2-44)
Определитель D' находим по формуле
г>'=п;г>;+п'г)',
где nj~g1g’3; D'i— fe+ga + ge); Щ—gaga’. Е>% — (giЦ-^з + gs)> т. e.
O' —gigs (gi + gi + ge) + gzgt (gi+gs+gs)- (2-45)
Коэффициент передачи
к _ D’ - gigs (Si+gt + ge) + g^i (gl + ga+gs)
Us D<V> (gl + ga) fc+ge) (g3+g4)+g3g4 (gl+g2 + ga + ge)
Таким образом, пользуясь топологическими формулами и правилами, можно сразу написать выражение для коэффициента передачи, без составления и решения соответствующих уравнений.
2-6. Теорема о компенсации
В электрической схеме, показанной на рис. 2-23, а, выделена ветвь с сопротивлением t\ и током /х.
Включим в эту ветвь два источника с э. д. с. £[ и Ет (рис. 2-23, б), численно равными напряжению U± = 1\1Г и направленными навстречу друг другу; токи во всех ветвях схемы, очевидно, останутся ,
Рис. 2-23.
без изменения. При переходе из точки d (рис. 2-23, б) в точку с потенциал повышается на величину э. д. с. Е\ — Ut, а при переходе из точки с в точку b понижается на ту же величину, вследствие чего потенциалы точек dub равны. Эти точки можно соединить проводником (закоротить), как показано на рис. 2-23, б пунктиром, т. е. источник э. д. с. — иъ и сопротивление i\ удалить из схемы, не изменив токов во всех ветвях (рис. 2-23, в).
Из сравнения схем рис. 2-23, в и а непосредственно следует, что любое сопротивление можно заменить источником с э. д. с., направленной навстречу току и равной напряжению на этом сопротивлении. Это положение называют теоремой о компенса-Ц И И. = ==-===- = __ - - — —
90
2-7. Линейные соотношения между напряжениями и токами
В эквивалентных схемах рис.2-23 кроме ветви с сопротивлением i\ выделена еще ветвь с источником э. д. с. Е2 и сопротивлением г2. Пользуясь принципом наложения, напишем выражения для токов А и /2 в ветвях схемы рис. 2-23, в в виде
Л==— + | (2 46)
^2 —--gil^l gz2E2-}-g2sEa -j-. . . f
Пусть в схеме рис. 2-23, в э. д. с. первого источника Et может изменяться, а э. д. с. остальных источников Е2, Es и т. д. неизменны. Так как входные (ghh) и взаимные (g/,m) проводимости не зависят от э. д. с. Е1( то, обозначив
g12E2+EisE3 -4-...=const = Or g22E2 -4-g2aEa -4-...=const=а2,
получим:
/1— £цЕ1+°Ь 4—~~ Е21Еу.-\~а21 (2’47)
или, заменив в (2-47) э. д. с. Ег через иг:
А =— gnEi-j-oi; I2 — — S21U v~\-а2- (2-48)
По теореме о компенсации изменение э. д. с. Ег в схеме рис. 2-23, в равносильно изменению напряжения иг при изменении сопротивления Г! в эквивалентной схеме рис. 2-23, а. При этом входная gu и взаимная g21 проводимости остаются неизменными, так как они определены в схеме рис. 2-23, в (при сопротивлении t\ = 0).
Следовательно, при изменении сопротивления гг токи и /2 связаны с напряжением линейными соотношениям и.
Для определения постоянных alt а2, gu и g21 расчетом или опытным путем необходимо, как следует из (2-48), рассчитать или измерить токи Д, /2 и напряжение при двух режимах первой ветви (двух значениях сопротивления гД Наиболее наглядно и просто эти постоянные определяются из режимов короткого замыкания (ri = 0) и режима холостого хода (^ = оо).
При коротком замыкании = 0, токи Д = Дк = аг и /2 = ~ Дк = «Яг- При размыкании первой ветви ток Д = 0. Обозначив разность потенциалов между точками разрыва через Ulx, а ток 4 = 12х, получим согласно (2-48):
0 = Лк — ёиЕ\х, Дх = 72к gziUlx, откуда входная проводимость
= Дк/СД
и взаимная проводимость
- £-21 — 7о?)/П
91
После замены постоянных в первом из уравнений (2-48) получается:
Z1 = Z1K(1 — ZA/ZV^)- (2-49)
Отметим, что изменение напряжения Ur в пределах от Ur = 0 до Z/r ~ соответствует изменению сопротивления t\ от нуля до бесконечности.
Токи Zj и Z2 рассматриваемых ветвей также связаны линейными соотношениями. Действительно, исключив из уравнений (2-48) напряжение Ц, получим:
Z2 = 0-2 — (2-50)
Su gn где
Ь1 —g2l/gll И fl2 — algzl/gll
— постоянные, которые определяются из двух любых режимов первой ветви или вычисляются при известных значениях входных и взаимных проводимостей.
Аналогично можно показать, что при одновременном изменении сопротивлений в двух ветвях напряжения и токи любых трех ветвей связаны линейным соотношением вида
z = a-\-bx-\-cy, где а, b и с — постоянные, определяемые опытным или расчетным путем;
z, х и у — изменяющиеся токи или напряжения.
Пример 2-4. На рнс. 2-24, а изображена схема с сопротивлением г, изменяющимся от нуля до бесконечности Найти зависимость тока в каждой ветви от напряжения U на зажимах сопротивления г, если г4 = га = г3 — г4 = 4 Ом и Ех — Е3 — = Е4 = 100 в.
Решение. Сначала найдем предельные значения напряжения U и тока / при коротком замыкании (г = 0) и холостом ходе (г = оо) рассматриваемой ветви.
При г — оо ток /х = 0, а напряжение U = 1/х. Для схемы рис. 2-24, б
Е з = Гз^ЗХ + + ЛДх,
откуда
Uy = Е3 — г31зк — лДх-
Так как токи
Zix==Z,i/(ri'br2)= 100/8 = 12,5 A; Z3X = (E3 то
Для определения тока на зажимах параллельных
(7Х= ЮО —50 = 50 В.
fK (рис. 2-24, в) предварительно найдем напряжение ветвей по формуле
Eigi + E3g3 -р Ел[>„ ТЭ
а затем токи в ветвях
/1к = (Е1 Uab)gi =6,25 A; Izn — Uabgz~ 18,75 А;
Е&И—УРз—^аЬ) ёз—/4К— (i~i— =“0,2о А
92
и ток
К----Лк 4“ Лк-------Лк — Лк--------- А..
Зависимость тока / в сопротивлении г от напряжения I/ на его зажимах определяется линейным уравнением типа (2-48): / = а + bU. Коэффициенты а и b найдем по результатам расчета режимов холостого хода и короткого замыкания. При г = 0 напряжение U = 0, а ток I = /к = а — 12,5 А При г = оо ток / = О, напряжение U = UK и 0=/K+fet/x, откуда b =— /К/(7Х = — 12,5/50 = = — 0,25 См. В результате получаем: 1 = 12,5 — 0,25 U.
Зависимость тока /4 в первой ветви от напряжения U определяется уравнением прямой Л = аг + bfU. Для того чтобы наити коэффициенты аг и Л, целесообразно и в этом случае пользоваться результатами расчета режимов холостого
Рис. 2-24.
хода и короткого замыкания ветви с переменным сопротивлением г. При г — 0 напряжение (7=0, ток Д = а± = /1к = 6,25 А; при г = оо (рис. 2-24, б) /1Х = /2У = 12,5 А.
С другой стороны, /1х = /1к + ht Uх,откуда bL — (/1Х — ДК)/(7Х= 0,125 См.
Следовательно, Л — 6,25 + 0,125 U.
Аналогично определяются токи /2 = 18,75 — 0,125 U; /3 = /4 = 6,25 — — 0,125 U.
Пример 2-5. В схеме, показанной на рис. 2-25, а, сопротивление г4 изменяется в пределах от г4 = 0 (короткое замыкание) до г4 = оо (размыкание ветви). Пользуясь законами Кирхгофа, выразить токи /4, /2, /3 и /4 через параметры схемы и напряжение (74 и построить найденные зависимости.
Решение. Из уравнения Е = г44 +Д4 непосредственно находим ток 4 = Е/г, — (74/г4 = 2,5 - 0,5 (74.
Ток /4 определим по первому закону Кирхгофа:
/} = 44 7 = 2,5 —0,5 144-1 = 3,5-0,514.
Для определения токов Д и /3 запишем уравнения
и—7 ——
93
Из этих уравнений
/ = , ]25 A=const. / [iLJL = _ 0,125 A=const.
'Ы-'з О 4 г3
Оказалось, что токи /2 и /3 не зависят от сопротивления г4 (при любых его значениях остаются неизменными).
Для построения найденных зависимостей определим предельные значения напряжения t/4 при изменении сопротивления г4. При г4 = 0 напряжение 1/4 = 0; при т4 = оо напряжение l/4 = UiK. Это напряжение найдем из уравнения Е = = г/1х + Uix, откуда l/4x = Е — г,Цк. Так как при т4 = оо (при размыкании ветви с сопротивлением г4) /1х = — 7, то напряжение Д4х = Е + rtJ = 5 + 2 -1 = = 7В. Таким образом, при изменении сопротивления г4 от нуля до бесконечности напряжение 1/4 увеличивается от 0 до 7 В. На рис. 2-25, б показаны искомые зависимости.
2-8. Теорема о взаимных приращениях токов и напряжений
Пользуясь уравнениями (2-48) и (2-49), установим связь между приращениями токов А7Ь А72 11 приращением напряжения (рис. 2-23, а) при изменении сопротивления первой ветви в пределах от нуля до Arv
Если г4 = 0, то напряжение = 0 и согласно (2-48) ток 74 = = аг — 71к; при сопротивлении первой ветви, равном Агъ напряжение на ее зажимах Л £7, = Агг7ъ а ток = —А(У;£П 71к.
Следовательно, при изменении сопротивления первой ветви на Агу изменение тока этой ветви
А/j — 71к — It — At/Jg’jj — Ar! Iign-
(2-51)
Аналогично можно показать, что при изменении сопротивления первой ветви на Агг изменение тока во второй
- А/2—Айjg-2i^iggv = - _ (2-52)
94
Из выражений (2-51) и (2-52) легко найти входную и взаимную проводимости ветвей через отношение приращений:
gu —A/i/AHj; g2i — АЛ/АСЛ.
Согласно уравнению (2-49), где иг при новых обозначениях надо заменить на AUlt получим:
Л = Лк (1 - = Лк (1 - = Лк - л = Лк - Агг gll/lf
откуда
После подстановки этого выражения в уравнения (2-51) и (2-52) получаются формулы для определения приращений токов:
<М4>
<2-55’
Выражения (2-54), (2-55) для приращений токов называют теоремой вариации или теоремой о взаимных приращениях. Если сопротивление первой ветви изменяется не от нуля до Агъ а от гг до Л = ту + Агъ то для определения приращений токов АД и А/2 можно пользоваться теми же формулами (2-54) и (2-55). При этом входная gL1 и взаимная g21 проводимости, а также ток Лк имеют другие значения, определяемые, как и раньше, при А^ = 0.
2-9. Общие замечания о двухполюсниках
При исследовании процессов в сложных электрических цепях часто интересуются током, напряжением и мощностью только одной ветви. Однако отдельные ветви могут быть выделены из сложной цепи не только для исследования процессов именно в этих ветвях, но и для установления связи, например, между одной частью цепи с источниками электрической энергии и другой — с приемниками. Во всех этих случаях выделяют ветвь, присоединенную к сложной цепи в двух точках (двумя зажимами). Часть электрической цепи произвольной конфигурации с двумя выделенными зажимами, именуемыми полюсами, называется двухполюсником.
Двухполюсники, содержащие источники электрической энергии, называются активными, а двухполюсники, не содержащие источников электрической энергии, — пассивными. Всякий пассивный двухполюсник является потребителем электрической энергии и характеризуется одной величиной — сопротивлением^. Поэтому на эквивалентной схеме пассивный двухполюсник мо-Жет быть представлен одним элементом — сопротивлением гв, называемым внутренним или входным сопротивле-_н и е м пассивного двухполюсника.
95
Если известна схема пассивного двухполюсника, то для определения входного сопротивления гв нужно тем или иным способом ее «свернуть» относительно двух заданных зажимов.
Рис. 2-26.
Рассмотрим, например, схему на рис. 2-26, а. Если выделить в этой схеме ветвь с источником э. д. с. Ег и сопротивлением гъ
то остальную часть схемы (обведенную пунктиром) можно рассматривать относительно зажимов 2—2' как
пассивный двухполюсник (без источников энергии). Часть той же схемы относительно зажимов /—Г ветви с сопротивлением г2 (рис. 2-26, б) можно рассматривать как активный двухполюсник (обведен пунктиром).
Рис. 2-27. В дальнейшем активные двухполюс-
ники (рис. 2-27, а) будем обозначать прямоугольниками с буквой Д (активный), а пассивные (рис. 2-27, б) — прямоугольниками с буквой П (пассивный).
2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей
Выделим в электрической цепи одну ветвь 2—2' с сопротивлением г, присоединенную в точках /—Г к активному двухполюснику
(рис. 2-28). Покажем, что для расчета тока / в ветви 2—2' активный двухполюсник можно заменить источником э. д. с. и пассивным двухполюсником. Чтобы найти э. д. с. источника, разомкнем цепь между точками 1 и 2 (рис. 2-29, о) и определим разность потенциалов L\ опытным или расчетным путем. Затем подключим к точкам 1 и 2 источник с
Рис. 2-28.
э. д. с. Ех = Ех, направленной навстречу 7/х
(рис. 2-29, б); ток в ветви 2—2' останется равным нулю, так как при этом разность потенциалов любых двух точек не изменилась. Схема, показа иная 11 а р ис. 2-29, -б, отличается отзадаииой (рис. 2-28) тем,
96
что в ней между точками 1 и 2 включен источник э. д. с. Е'х и ток в ветви 2—2' равен нулю. Эта схема будет эквивалентна заданной, если между точками 1 и 2 ввести еще одну э. д. с. £х — £х, противоположно направленную э. д. с. £х (рис. 2-29, в).
По принципу наложения ток I в ветви 2—2' эквивалентной схемы (рис. 2-29, в), а значит и заданной (рис. 2-28), найдем как алгебраическую сумму токов, создаваемых каждым из источников. Но все источники, находящиеся внутри активного двухполюсника, совместно с источником э. д. с. £х не вызывают тока в ветви 2—2'
Рис. 2-29.
(рис. 2-29, б). Поэтому ток в ветви 2—2', создаваемый одним источником э. д. с. £х (рис. 2-29, г), равен действительному току в этой ветви (рис. 2-28):
(2-56)
, Е* и--
г + гв Г +
где гв — входное сопротивление пассивного двухполюсника, получающегося из заданного активного после того, как все э. д. с. источников напряжения и все токи источников тока приняты равными нулю.
В частности, при г = 0, т. е. при коротком замыкании ветви 2—2', /к = UJrB, т. е. входное сопротивление активного двухполюсника можно определить как отношение напряжения холостого Хода к току короткого замыкания:
=== ПХ/7К.
Формулу (2-56) можно еще записать так:
, ; Ох
Последнее выражение легко получить и из (2-49). Действительно, Пуская индексы у напряжения и тока, запишсм-это уравнение-
4 Основы теории цепей 97
(2-56а)
в следующем виде:
откуда и получается (2-56а).
Сопротивление г в общем случае может быть входным сопротивлением пассивного двухполюсника, присоединенного к зажимам 1—1’ заданного активного двухполюсника.
Уравнение (2-56) представляет собой математическое выражение теоремы об активном двухполюснике, называемой также теоремой об эквивалентном генераторе или теоремой Гельмгольца и Тевенена. Эту теорему можно формулировать следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с э. д. с. равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным вход' ному сопротивлению активной цепи, то ток в этой ветви не из~ менится.
Уравнению (2-56) соответствует эквивалентная схема, показанная на рис. 2-29, д, где активный двухполюсник представлен в простейшей форме, в виде неразветвленной цепи с источником э. д. с. Ех = Ех и сопротивлением гк. Таким образом, активный двухполюсник по отношению к присоединенной ветви с сопротивлением г можно рассматривать как источник с внутренним сопротивлением гв и э. д. с. £х, равной напряжению Ux между зажимами двухполюсника при разомкнутой ветви 2—2'.
Активный двухполюсник можно также представить в виде источника тока J = Ех/гв и параллельно ему присоединенного сопротивления гв, как это показано в § 1-2.
Если рассматриваемая ветвь содержит не только сопротивление г, но и э. д. с. Е, то ток в этой ветви
Р Hr Р
(2-57)
гв Г '
где э. д. с. Е берется с положительным знаком, когда обе э. д. с. Ех и Е действуют в одном и том же направлении (рис. 2-29, е), и с отрицательным, когда э. д. с. Е направлена навстречу £х.
В дальнейшем будем называть эту теорему только теоремой об активном двухполюснике, так как при £ > £х и отрицательном знаке в формуле (2-57) двухполюсник будет не отдавать, а потреблять энергию (от источника с э. д. с. £).
Подчеркнем, что в эквивалентной схеме активного двухполюсника (рис. 2-29, д), так же как при любых других преобразованиях схем с источниками энергии, мощность источника с эквивалентной э. д. с. и потери в сопротивлении гв в общем случае не равны соответственно суммарной мощности источников энергии в реальной цепи и потерям в сопротивлениях ветвей активного двухполюсника.
Остановимся теперь на применении теоремы об активном двухполюснике и принципа наложения для расчета разветвленных электрических цепей. =================--------=
98
Расчет токов в заданной электрической цепи, которую можно рассматривать относительно одной из ветвей в виде активного двухполюсника (рис. 2-28), может быть упрощен, если пользоваться принципом наложения. Действительно, ток в каждой ветви активного двухполюсника можно определить путем алгебраического
Рис. 2-30.
суммирования токов, возникающих в этой ветви при холостом ходе (рис. 2-29, а или б) и при действии одного источника с э. д. с. Ех = Ux (рис. 2-29, г). Удачный выбор размыкаемой ветви (режим холостого хода) может значительно упростить расчетные схемы.
Рассмотрим, например, схему на рис. 2-30, в которой требуется определить токи во всех ветвях при заданных э. д. с. источников, напряжении U и сопротивлениях ветвей.
Разомкнем ветвь с сопротивлением г5 (рис. 2-31, а) и определим ток /1Х = /2х из уравнения
— (гj-)- r2) Ilx — U
и ток /Зх = /4х из уравнения
Д4= (Г3 + Г4) /Зх — U.
Зная токи /1х и /2х, вычислим напряжение U5x по формуле Arix ~ гзДх — Г1 Ах + £1>
Затем положим э. д. с. Ег и Ei и напряжение U равными нулю и включим в ветвь с сопротивлением гъ источник с э. д. с. Ех = U5x
Рис. 2-31.
(Рис 2-31, б) и найдем токи во всех ветвях. Входное сопротивление двухполюсника гв на зажимах 1 и 3 (ветви с сопротивлением г5)
...1. Г-A. J. J- гЛ------------------------------------------
4*
99
Ток
Ек — Е — L!bJ(r в + гя)-Токи в остальных ветвях
___ J Г2 .Г _________ Г Г1 .Г ________ ЕГ1 . J ______ ЕГ
1к 25r_L~ » 2 2к 2 5 г \ г » г 1 r > 2 4к r_Lr *
Г1ГГ2 '1П~Г2 Г3“ГГ4 Г3-ТГ4
Токи в ветвях заданной схемы (рис. 2-30) определяются при помощи принципа наложения:
Л — Лх 4“ Лк! Е— Ех Лк! Е—Ех ^2к!
Е—Лх+Лк! Е—Ех+Ек—0-j-Е; I—Е + Е-
Таким образом, шесть неизвестных токов в ветвях разветвленной схемы рис. 2-30 определены путем наложения частичных токов, найденных для простых схем (рис. 2-31, а и б).
Рассмотрим еще один прием расчета разветвленных цепей, базирующийся на принципе наложения и на своеобразном применении теоремы об активном двухполюснике.
Пусть в схеме (рис 2-32, а) заданы э. д. с. источников и сопротивления; требуется определить токи во всех ветвях.
При одновременном размыкании первой и второй ветвей (рис. 2-32, б) токи /х, /Зк, Ех и напряжения t/lx, U2x в полученной схеме определяются очень просто:
Г __ /__J ___ Е ^4
* х _ 2 Зх 2 4л ——— —
X ЗХ ах r-rrs^lt’
Е1х = Е1 + Г3/3х; Е2х =-Е4-(-Г4Ех*
При одновременном включении в первую и вторую ветви источников сэ. д. с. Ец гг Е'2х, равными напряжениям Uu и tE,
100
(рис. 2-32, в), токи в первой и во второй ветвях будут, так же как и в схеме рис. 2-32, б, равны нулю. Если теперь в первую и вторую ветви включить еще по одному источнику с э. д. с. Е1Х и £2Х, направленными противоположно э. д. с. Е[х и Е'2х (рис. 2-33, а), то токи во всех ветвях будут такими же, как и в заданной схеме. Так как при совместном действии источников э. д. с. Е, £1( £4, £(ч, Е2х токи в первой и второй ветвях (рис. 2-32, в) равны нулю, а схема, изображенная на рис. 2-33, а, тождественна заданной, то для расчета токов в этих ветвях достаточно учесть действие источников э. д. с. £1Х = Ulx и £2Х = U2x (рис. 2-33, б), что непосредственно следует из принципа наложения.
Отметим, что, поскольку в схеме на рис. 2-32, в 11х = 0 и /2х = = 0, то и ток 15х также равен нулю, т. е. в схеме рис. 2-33, б ток 15к равен току /5 в заданной схеме. Следовательно, для определения
токов /1( /2 и /5 достаточно произвести расчет схемы, показанной на рис. 2-33, б, например, предварительно преобразовав треугольник сопротивлений rs, г и г4 в эквивалентную звезду. Зная токи /1( /2 и /5, легко найти токи /Зк, /4к и /к в схеме рис. 2-33, б и по принципу наложения определить токи /3, /4 и I:
/з — Лзх'Г /зк; Л= Лх'Г Лк! 7 = /х+4.
Таким образом, и в этом случае все неизвестные токи (рис. 2-32, а) определены путем наложения частичных токов, найденных для более простых схем (рис. 2-32, б и 2-33, б).
По найденным значениям токов 11г I, и /5 нетрудно рассчитать остальные токи и прямо по схеме на рис. 2-32, а.
Пример 2-6. По теореме об активном двухполюснике найти выражение для тока /0 в ветви с измерительным прибором (рис. 2-34, а), если ток источника тока J = 10 мА, сопротивление г = 100 Ом, сопротивление измерительного прибора г0 — 50 Ом, а сопротивления гх двух противоположных плеч моста изменяются одновременно от пулч до 2 г; построить график изменения тока /0 в зависимости от сопротивления
Решение Разомкнем ветвь с измерительным прибором (рис. 2-34, б) и Найдем равные токи:
°--------------------------Лх=Да=7/2-----------------------------
101
Напряжение U (рис. 23-4, б) определим из уравнения nJft+U*— rJ/2~0t
откуда
Ux^(r~ri)J/2.
Входное сопротивление двухполюсника относительно зажимов ветви с измерительным прибором (рис. 2-34, е, без учета сопротивления /0)
гв = (4+^/2.
По теореме об активном двухполюснике ток
Ux r—r-i
го+гв 2г0 + т + Г1
После подстановки в это выражение числовых значений получим:
/ _in . 1
0 100+100+rf
На рис. 2-34, г показан график изменения тока /0 в зависимости от сопротивления гх. Из рисунка видно, что при изменении сопротивления ток /0 изменяется не только по значению, но и по направлению.
102
2-11. Передача энергии от активного двухполюсника к пассивному
Для исследования передачи энергии от активного двухполюсника к пассивному вернемся к эквивалентной схеме, показанной на рис. 2-29, д, и будем считать, что гв — входное сопротивление активного двухполюсника (источника энергии) и Ех = Ux — эквивалентная э. д. с. остаются постоянными, аг — входное сопротивление пассивного двухполюсника может принимать любое значение.
Прежде всего установим соотношение между сопротивлениями гв и г, при выполнении которого мощность пассивного двухполюсника максимальна.
Мощность пассивного двухполюсника определяется выражениями
P = ExI-rBP = UxI-rBF (2-58)
Р = гР, - (2-59)
где UXI — мощность, развиваемая эквивалентным активным двухполюсником;
гв/2 — мощность потерь в сопротивлении гв.
Для определения тока I, при котором мощность Р максимальна, найдем производную от Р по / из уравнения (2-58) и приравняем ее нулю:
dP[dI = Ux — 2rBl = 0,
откуда искомый ток
I = Uj2rn
[уравнением (2-59) пользоваться нельзя, так как его правая часть содержит две переменные: г и /]. Но в общем случае (рис. 2-29, д) ток I = Uxt(r 4- гв). Значит, мощность максимальна при
г = гв, (2-60)
т. е. при равенстве входных сопротивлений пассивного и активного двухполюсников.
По формуле (2-59) при г = гв мощность
Лшкс = *Л/4гв.
Отношение мощности Р пассивного двухполюсника к мощности Ра = UXI, развиваемой эквивалентным активным двухполюсником, называется к. п. д. эквивалентного активного Двухполюсника
д-f /7/—-1-?/- г ------------------------(e-w
1 РА UxI и* rB-t-r
103
Из выражения (2-61) следует, что при максимальной мощности пассивного двухполюсника к. п. д. равен 0,5. Более высокие значения к. п. д. будут при г> га.
Коэффициент полезного действия реального активного двухполюсника равен к. п. д. эквивалентного только при выполнении определенного условия. Если при отключении пассивного двухполюсника от реального активного в ветвях последнего не будет
Рис 2-35.
токов и потерь, так же как в эквивалентной схеме на рис. 2-29, д, то к. п. д. реального и эквива
лентного активных двухполюсников равны. При невыполнении этого условия к. п. д. реального активного двухполюсника всегда меньше к. п. д. эквивалентного двухполюсника.
Полученные результаты применим, например, для характеристики режима линии передачи и электрической энергии небольшой длины, у которой утечкой тока можно пренебречь.
Пусть в начале линии передачи напряжение U± поддерживается неизменным (рис. 2-35, а).
Тогда линию можно представить в виде последовательного соединения активного двухполюсника с источником э. д. с. £х = 7/j и сопротивлением проводов г, и
пассивного двухполюсника — приемника с сопротивлением г2 (рис. 2-35, а). По формулам (2-58) и (2-61) найдем мощность Рг приемника и к. п. д. ц линии передачи
P^UJ-r^-,
1 U1 гл + г2-
(2-62)
Мощность, развиваемая источником, Л = ^7,
а напряжение на зажимах приемника

По полученным уравнениям на рис. 2-35, б построены завнси-
ЛИНИН.
104
При r2 = оо (холостой ход линии) ток / равен нулю (на рис. 2-35, б — точка в начале координат), при г2 = гл ток определяется отрезком Оа и при г2 = 0 (короткое замыкание линии) значение тока максимально и равно /к. Кроме того, при г2 = гл мощность Р1г определяемая отрезком ас, равна удвоенной мощности приемника (ас = 2аЬ = 2Ьс) и к. п. д. я = ОД
По эквивалентной схеме (рис. 2-35, а) установим еще связь между потерями в проводах линии (в сопротивлении гл) и мощностью приемника Р2:
9/ /Р \2
= , (2-63)
где I — длина линии; S — сечение каждого провода.
Из выражения (2-63), в частности, следует, что при Р2 — const повышение напряжения U2 вызывает уменьшение тока / и, следовательно, уменьшение потерь в проводах, что в свою очередь позволяет уменьшить сечение проводов. Конечно, при этом надо усилить изоляцию проводов линии.
В случае передачи по линии электрической энергии при большой мощности стремятся получить возможно больший к. п. д., для чего необходимо, как непосредственно следует из (2-62), иметь г1 г2- При передаче сигналов по линии связи стремятся получить максимальную мощность в приемнике, что приводит к низкому значению к. п. д.
Первые опыты передачи электрической энергии при постоянном токе осуществил русский инженер Ф. А. Пироцкий В 1874 г. вблизи Петербурга Ф. А. Пироцкий создал линию передачи энергии при мощности около 6 л. с. на расстояние до 1 км. Затем Пироцкий проводил опыты передачи электрической энергии по рельсам конно-железной дороги. На основании своих опытов Ф. А. Пироцкий установил, что можно передавать электрическую энергию при большой мощности на большие расстояния. В качестве источников энергии для первичных двигателей он предложил пользоваться энэргией водных потоков.
Теоретические основы передачи электрической энергии по линии разработал Д. А. Лачинов. В 1880 г. он опубликовал в первом номере журнала «Электричество» свой труд «Электромеханическая работа».
Опыты Пироцкого остались совершенно незамеченными. И лишь этим можно объяснить, что инициатором передачи электрической энергии считался Марсель Депре. В своем докладе в Парижской академии наук (1881 г.) он провозгласил тезис, установленный почти за год до этого Д. А. Лачиновым, а именно: повышая напряжение, можно передавать электрическую энергию при любой мощности на большое расстояние с минимальными потерями (2-63). В следующем, 1882 г., Депре осуществил на постоянном токе передачу энергии при мощности в 2 л. с. на расстояние 57 км (при напряжении^! 500-2000 В). _____________________________________
105
Глава третья
ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
3-1. Переменные токи
Широкое применение переменного тока в электротехнике началось со времени решения задачи централизованного производства электрической энергии и ее передачи на значительные расстояния.
Передача и распределение энергии требуют по экономическим соображениям и по условиям безопасности применения различных напряжений: высокого — для передачи энергии и сравнительно4 низкого — для ее распределения потребителям.
Преобразование напряжения переменного тока возможно при помощи относительно простого аппарата — трансформатора, который в 1876 г. изобрел П. Н. Яблочков. В 1889 г. М. О. Доливо-Добровольский изобрел трехфазный асинхронный двигатель и разработал все звенья передачи и распределения энергии трехфазным током (см. гл. 10). После этого переменный ток получил преимущесг-венное распространение.
Познакомимся с основными понятиями, относящимися к переменным токам.
Переменным током называют ток, изменяющийся во времени. Значение тока в любой данный момент времени называют мгновенным током i. Для одного из двух возможных направлений тока через поперечное сечение проводника мгновенный ток i считают положительным, а для противоположного направления — отрицательным. Направление тока, для которого его мгновенные значения положительны, называют положительным направлением тока. Ток определен, если известна зависимость мгновенного тока от времени i — F (f) и указано его положительное направление.
Токи, мгновенные значения которых повторяются через равные промежутки времени в той же самой последовательности, называют периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока
i=F(t) = F(t+T).
На рис. 3-1 показан участок АВ электрической цепи и дан пример зависимости i = F (t) для периодического тока. Стрелка на схеме указывает положительное направление тока. Пунктирными стрелками показаны действительные направления тока в моменты времени, когда i > 0 и когда i <z 0. Отрезки кривой между точками а и b или О и с охватывают один полный цикл изменения тока за один период.
Величина, обратная периоду, называется частотой / = = 1/Г, Частота измеряется в герцах. Частота периодического тока равна 1 Гц, если период равен Г с, т. е^1 Гц — 1 с ’•-
106
Постоянный ток можно рассматривать как частный случаи периодического тока, период изменения которого бесконечно велик, т. е. частота равна нулю.
Термин переменный ток часто употребляют в узком смысле, применяя его для такого периодического тока, у которого постоянная составляющая равна нулю, т. е.
г
~ J idt = O.
о
Диапазон частот переменных токов, применяемых в электротехнике, весьма широк — от десятков до миллиардов герц.В элек-
троэнергетике в СССР и в Европе 50 Гц, в США 60 Гц. В различных областях промышленного применения переменных токов встречаются частоты от 10 до 2,5-109 Гц. В радиотехнике и электронике применяются частоты до 3 • 1010 Гц.
Все определения, введенные выше для токов, и те новые определения, которые будут введены в дальнейшем, применимы и для напряжений и, э. д. с. е магнитных потоков, а также любых других электрических и магнитных величин, изменяющихся во времени. Некоторые
принята стандартная частота
Рис. 3-1.
пояснения требуются лишь в отношении знака переменных напряжений и э. д. с.
У переменного напряжения и между двумя точками А и В, определяемого по заданному пути I, знак периодически изменяется. При этом, если в данный момент времени напряжение между А и В, определяемое в направлении от Л к В, т. е. иАВ, положительно, то
в тот же момент времени напряжение иВА, определяемое в обратном направлении от В к А, — отрицательно. Поэтому для однозначного суждения о напряжении необходимо указать направление пути, которое принято для его определения. Это направление назовем положительным направлением напряжения и будем отмечать либо стрелкой на схеме, либо порядком индексов у буквы и.
Аналогично вводится понятие о положительном направлении
ДЛЯ э. д. с.
В электроэнергетике применяются простые гармонические или синусоидальные токи, т. е. токи, являющиеся синусоидальными функциями времени. Объясняется это тем, что при несинусоидальных токах могут возникнуть нежелательные Явления, как-то: увеличение потерь энергии, появление на отдельных
107
участках цепи значительных напряжений и возникновение мешающих влияний на работу электросвязи.
Для передачи информации (связь, радиовещание, телемеханика) также широко применяются синусоидальные токи. Передаваемая информация (сигнал) изменяет амплитуду, частоту или фазу тока.
Периодические несинусоидальные токи могут рассматриваться как совокупность синусоидальных токов различных частот.
Все это обусловливает первоочередную необходимость основательного изучения цепей синусоидального тока.
3-2. Понятие о генераторах переменного тока
Рис. 3-2.
Познакомимся с устройством генераторов переменного тока, применяемых в электроэнергетике. Генератор состоит из неподвижной части — статора и подвижной части — ротора. Обычно на роторе располагаются электромагниты (рис. 3-2). Их обмотка, называемая обмоткой возбуждения, питается через кольца и щетки от источника постоянного тока. В пазах статора, собранного из стальных листов, находятся проводники обмотки статора. Они соединены друг с другом последовательно поочередно с передней и с задней сторон статора (эти соединения показаны на рис. 3-2 соответственно сплошными и пунктирными линиями).
Рисунок3-2 дает лишь схематическое представление об устройстве генератора. В действительности на статоре имеются еще две анало-
гичные обмотки (см. § 10-1) и каждая из трех обмоток располагается в большем числе пазов, чем это показано на рисунке.
При вращении ротора изменяется магнитный поток, сцепленный с обмоткой статора, и в ней наводится э. д. с. Генераторы конструируют таким образом, чтобы э. д. с. была близка к синусоидальной.
За один оборот ротора происходит р полных циклов изменения э. д. с., где р — число пар полюсов. Если частота вращения ротора равна п оборотов в минуту, то получается рп периодов в минуту, следовательно, частота э. д. с.
f=pnffi).
При частоте f — 50 Гц ротор генератора с одной парой полюсов должен вращаться с частотой 3000 об/мин, а с двумя парами полюсов 1500 об/мин. Для обеспечения механической прочности ротора при таких больших частотах вращения его выполняют без выступа----ю!!Ц1Х !!олюсов. Еще сушествеппее отличаются по конструкции высо-кочастотные машинные генераторы. Они изготовляются для частот
108
от 800 до 8000 Гц и применяются наряду с Ламповыми Генераторами в электротермических установках. Переменные токи еще более высоких частот получают исключительно от электронных генераторов (генераторов с электронными лампами, полупроводниковыми приборами и др.).
3-3. Синусоидальный ток
Мгновенное значение синусоидального тока определяется выражением
i = /msin(y /4-ф), (3-1)
где 1т — максимальное значение или амплитуда тока. Аргу-
мент синуса у 14- ф называется в начальный момент времени начальной фазой. Фаза растет. После ее увеличения на 2л весь цикл изменения тока повторяется. Поэтому, когда говорят о фазе для какого-либо момента времени, обычно отбрасывают целое число 2л так, чтобы значение фазы находилось в пределах ±л или в пределах от 0 до 2л. В течение периода Т фаза увеличивается на 2л. Величина 2л/Т измеряет скорость изменения фазы и обозначается буквой со. Принимая во внимание, что f = МТ, можно написать:
со=2л/Т=2 л/. (3-2)
фазой. Угол ф равен фазе (/ = 0) и поэтому называется с течением времени непрерывно
Это выражение, связывающее со и /, послужило основанием называть со угловой частотой. Измеряется со числом радианов, на которое увеличивается фаза в секунду. Так, например, при f = 50 Гц имеем со = 314 рад/с. Вводя в (3-1) обозначение со Цля угловой частоты, получаем:
i = Im sin (со/4-гр).
На рис. 3-3 дан график синусоидальных токов одинаковой час-, готы, но с различными амплитудами и начальными фазами:
h = /misin (co/4-rpi); i2=/m2sin(co/4-rp2).
По оси абсцисс отложены время t и пропорциональная времени величина со/.
109
Начальный фазный угол отсчитывается всегда от момента, соответствующего началу синусоиды (нулевое значение синусоидальной величины при переходе ее от отрицательных к положительным значениям), до момента начала отсчета времени t = 0 (начало координат). При фт >• 0 начало синусоиды (it) сдвинуто влево, а при
<; 0 —(t2) вправо от начала координат.
Мгновенное значение синусоидального тока можно представить и в виде косинусоидальной функции времени
t = /mcos (со/ ф- й),
где
& == ф — п/2.
Если у нескольких синусоидальных функций, изменяющихся с одинаковой частотой, начала синусоид не совпадают, то говорят, что они сдвинуты друг относительно друга по фазе. Сдвиг фаз измеряется разностью фаз, которая, очевидно, равна разности начальных фаз. На рис. 3-3, например, фг — ф2 >» О, т. е. ток ij опережает по фазе ток г2 на угол ф\ — ф2, или, что то же самое, ток /2 отстает по фазе от тока на угол фг — ф2.
Если у синусоидальных функций одной частоты одинаковые начальные фазы, то говорят, что они совпадают по фазе, если разность их фаз равна ±зт, то говорят, что они противоположны по фазе, и, наконец, если разность их фаз равна ±л/2, то говорят, что они находятся в квадратуре.
3-4. Действующие ток, э. д. с. и напряжение
Для суждения о периодическом токе вводят понятие о среднем квадратичном значении тока за период, которое называется действующим током:
У 51-2 dt-
(3-3)
За один период переменного тока в проводнике с сопротивлением г выделяется тепловая энергия:
J ri2dt^rTy J i2dt=rI2T.
Отсюда следует, что действующий ток численно равен такому
— - постоянному току+ который за один период выделяет в том же сопро-
тивлении такое же количество тепла, как п ток переменный. 110
Установим связь между действующим током I и амплитудой 1т синусоидального тока:
j У 7
Z2=y i2dt — ~ § sin2 (coZ-J-ty) =
6 б
T
= 2^ [1 —cos (2coZ + 2чр)] dt = ~?г-о
Следовательно,
7=/т//2. (3-4)
Среднеквадратичные значения любых других периодических величин за один период тоже называются действующими. Так, например, действующие э. д. с. и напряжение
г т ' г т
£=]/ 67= j/ ~^u2dt.
О о
В частности, для синусоидальных э. д. с. и напряжения
£ = £m//2; U = Um/V2.
Когда речь идет о периодических напряжениях и токах, обычно подразумевают действующие напряжения и токи и ради краткости просто говорят: напряжение столько-то вольт, ток столько-то ампер.
В электротехнике приходится встречаться как с очень малыми, так и с очень большими напряжениями и токами. Напряжение на входных зажимах радиоприемника, при котором еще возможен прием радиосигналов, бывает порядка микровольт. Напряжение между проводами линий электропередачи Волгоград — Москва 500 кВ. Токи в электроплавильных печах достигают десятков тысяч ампер, а в электронных лампах могут быть меньше 1 мкА.
\
3-5. Изображение синусоидальных функций времени векторами и комплексными числами
Расчет цепей переменного тока облегчается, если изображать синусоидально изменяющиеся токи, напряжения, э. д. с. и т. д. векторами или комплексными числами.
Пусть некоторая величина (ток, напряжение, магнитный поток й т. п.) изменяется по синусоидальному закону:
t)=Vwsin (o)/-p^).
Возьмем прямоугольную систему осей M0N (рис. 3-4). Расположим под углом яр относительно горизонтальной оси ОМ вектор Vm, Длина которого в выбранном масштабе равна амплитуде Vm (положительные углы $ откладываются против^ а-отрицательные — по на-
Ш
правлению движения часовой стрелки). Представим себе, что вектор Vm с момента t = 0 начинает вращаться вокруг начала координат О против направления движения часовой стрелки с постоянной угловой скоростью, равной угловой частоте со. В момент времени t вектор составит с осью ОМ угол at + ф. Его проекция на ось ATM как раз равна в выбранном масштабе мгновенному значению рассматриваемой величины v.
Мгновенные значения v как проекции вектора на ось N'N
можно получить и другим путем, оставляя вектор Vm неподвижным и вращая, начиная с момента t = 0, ось N'N по направлению дви-
жения часовой стрелки с
угловой скоростью со. В этом случае вращающуюся ось N'N называют линией времени.
Таким образом, между мгновенным значением v и вектором Vm можно установить однозначную связь. На этом основании вектор Vm называют вектором, изображающим синусоидальную функцию времени, или кратко вектором величины v. Так, например, говорят о векторах напряжения, э. д. с., тока, магнитного потока и т. д. Конечно, эти векторы имеют смысл, отличный от смысла векторов, определяющих физические
величины в пространстве, к которым
относятся векторы скорости, силы, ускорения, напряженности электрического поля и т. п.
Векторы, изображающие синусоидальные функции времени, будем обозначать большими буквами с точкой наверху. Совокупносгь векторов, изображающих рассматриваемые синусоидальные функции времени, называется векторной диаграммой.
Если считать оси ММ' и NN' осями вещественных (действительных) и мнимых величин на комплексной плоскости, то вектор Vm соответствует комплексному числу, модуль которого равен Vm, а аргумент — углу ф. Это комплексное число Vm называется комплексной амплитудой рассматриваемой величины.
Комплексную амплитуду можно записать в полярной, показательной, тригонометрической и алгебраической формах:
Vm L ф = 14^®= Vm(cos^ + /sinip) = Vm4-/Vm, (3-5)
где /=К— 1.
Если вектор Vm, начиная с момента времени t = 0, вращается против направления движения часовой стрелки с угловой скоростью <о,ю емусоо1встс1в>еткомплскспа51
112
называется комплексной мгновенной величиной:
v = = V,n cos (со/ ф- гр) ф- jVm sin (со/ ф- гр).
Значение ее мнимой части (без /) равно рассматриваемой синусоидально изменяющейся величине v.
Таким образом, величина v и ее изображение — комплексная амплитуда однозначно связаны следующим равенством:
v — Im [Уте} 1 ’] = I m { Vme^'eja/] = Im [Ёте^ю/], (3-6)
где символ Im обозначает, что от комплексной функции времени, записанной в квадратных скобках, берется только значение мнимой части.
Заметим, что только комплексные величины, изображающие синусоидальные функции времени,'обозначают большими буквами с точкой наверху. Все остальные комплексные величины, которые встречаются при расчетах цепей синусоидального тока, принято обозначать большими буквами без точек.
Если гармонически изменяющуюся величину представить в виде косинусоидальной функции времени, то ее мгновенное значение
v— Vm cos (со/ф-й) — Re [Vm cos (со/ф-й) ф- jVm sin (со/ф-й)] = = Re [ (и/+в)] = Re [ Vmeja']> (3-7)
где символ Re обозначает вещественную часть комплексной функции времени, записанной в скобках.В этом случае мгновенное значение v определяется графически как проекция вращающегося вектора Vme,a>t на ось вещественных величин.
Мстог расчета цепей синусоидального тока, основанный на изображении гармонических функций времени комплексными числами, называется методом комплексных величин, методом комплексных амплитуд или комплексным методом расчета.
Комплексный метод был введен в электротехнику американским ученым и инженером Штейнметцем.
Пример 3-1. Написать комплексную амплитуду тока t — 10 sin (со/ — л/6) А.
Решение Комплексная амплитуда /т == 10 z — л/6 А
Заданный ток равен мнимой части (без /) комплексной функции времени:
/теуи/ = /теУ(™-л/б>=10 z (со/-л/6) А.
Пример 3-2. Комплексная амплитуда напряжения йт = — 100 4- / 100 В, частота f = 1 кГц Написать выражение для мгновенного напряжения
Решение Угловая частота со = 2л/ = 2л-103 = 6280 с1, амплитуда Vm = /ЁФ0бЁ“ф~Тб()2 = 100|/2 В, tgip= Ю0/(—100) = — 1; так как вещественная часть комплексной амплитуды отрицательна, а мнимая часть положительна, то вектор лежит во второй четверти и, следоватольно, ф — Зл/4.
Таким образом, мгновенное напряжение
и 100 lz2 sin (6280/ 4- Зл/4) В
113
Illi
3-6. Сложение синусоидальных функций времени
При исследовании цепей синусоидального тока приходится алгебраически суммировать гармонические функции времени одинаковой частоты, но с различными амплитудами и с различными начальными фазами. Непосредственное суммирование гармонических функций времени связано с трудоемкими и громоздкими тригонометрическими преобразованиями. Значительно проще эта задача решается графически при помощи векторной диаграммы или аналитически путем суммирования комплексных амплитуд.
Пусть требуется найти сумму двух гармонических функций времени = Vlm sin (coz' + фх) и v2 = V2m sin (со/ + ф2).
Сначала рассмотрим решение, выполняемое при помощи векторной диаграммы.
Отложим векторы Vlm = Vlm Z Фс и V2m — V2m Z Фг и графически определим вектор Vm = Vm Z Ф, равный геометрической сумме векторов Vlm и V2in (рис. 3-5). Эта векторная диаграмма построена для случая, когда фл > 0 и ф2 < 0.
Представим себе, что векторы Vlm, V2m и Vm с момента t = 0 начинают вращаться вокруг начала координат О против направления движения часовой стрелки с постоянной угловой скоростью со. Проекция вращающегося вектора Vm Z (coz' + ф) на вертикальную ось N'N в любой момент времени равна сумме проекций на эту же ось вращающихся векторов Vlm Z (coz' + фх) и V2mZ(co/ + ф2), т. е. мгновенных величин Ул и v2. Следовательно, проекция вертикальную ось равна искомой сумме
Vi + v2, а вектор Vm = У„^Ф изображает искомую синусоидальную функцию времени v = vt + v2.
Таким образом, определив из диаграммы длину вектора Vm и угол ф, можем написать выражение искомой величины v = = Vm sin (со/ + ф).
Теперь перейдем к аналитическому методу. Рассматривая векторы как комплексные амплитуды, на основании выполненного построения (рис. 3-5) можно написать:
на
Vlm-J- Уят— Упь
Чтобы произвести суммирование комплексных чисел, их надо представить в алгебраической форме:

114
Осуществляя суммирование, получаем:
+ /VlmH- jV'2m= + jV m~ Vmt
где <
V'm = Vl,n + V^m; Vm = Vim + V^m-
Отсюда находим:
Vm = V(Vmy + (Vm)2, tg^ = V'^V'm.
Так как tg ф = tg (ф± л), то для определения ф нужно еще знать, 4 в какой четверти располагается вектор Vm. Это легко устанавливается по знакам вещественной и мнимой частей Vm. В расчетах для удобства начальную фазу ф выражают не в радианах, а в градусах.
Рассмотренные способы можно применить для сложения любого числа синусоидальных функций времени одинаковой частоты.
Обычно при расчетах цепей синусоидального тока необходимо знать только действующие величины для синусоидальных функций времени и их сдвиг по фазе друг относительно друга. В этих случаях при построении векторных диаграмм нужно точно соблюдать углы сдвига фаз между векторами, а положение осей координат можно выбрать произвольно или оси совсем не изображать. Кроме того, длины векторов часто берут равными не амплитудным, а действующим величинам.
Соответственно при аналитическом расчете начальные фазы можно изменить на один и тот же угол, например так, чтобы начальная фаза одной из рассматриваемых функций стала равной нулю. Вместо комплексных амплитуд часто берут значения в ]/2 раз меньшие, так называемые комплексные действующие величины:
V=Vm/V2.
Пример 3-3. Даны токи ц = 6 sin CcoZ + 120°) А и i2 = 1,5 sin (w/+ 30°) А.
Определить ток i, равный разности токов ц — i2
Решение. 11т = 6 2.120° = — 3 + j 5,2 A; lim = 1,5 2.30° = 1,3 + + /0,75 А;
1зт = 1гт — 1?т — —4,3+ /4,45 = 6,19 2 134° А.
Следовательно, i = 6,19 sin (ш/+ 134°) А.
3-7. Электрическая цепь и ее схема
Электрический ток неразрывно связан с магнитным и электрическим полями. При переменном токе эти поля изменяются во времени. Изменяющееся магнитное поле наводит э. д. с., изменение электрического поля сопровождается изменением зарядов на проводниках. В проводниках, в резисторах, а часто и в окружающей их __среде электромагнитная энергия преобразуется в тепло. В ряде устройств электромагнитная энергия преобразуется и в другие —
115
Рис 3-6
Виды энергии (в механическую, химическую и т. д), часть электромагнитной энергии излучается. В электрической цепи нельзя выделить какого-либо участка, с которым не бцли бы связаны эти явления.
Для того чтобы упростить исследование процессов в реальной электрической цепи переменного тока, ее, как и цепь посюянного тока, заменяют схемой замещения или, короче, просто схемой, составленной из элементов, каждый из которых учитывает одно из этих явлений.
К пассивным элементам схемы при переменных токах относятся сопротивление г, собственная индуктивность или короче индуктивность L и емкость С. Их условные обозначения показаны на рис. 3-6, а, б, в.
Наименования элементов схемы совпадают с наименованиями параметров цепи, которые эти элементы характеризуют.
Взаимная индуктивность между отдельными частями электрических устройств учитывается, как взаимная индуктивность А! между индуктивностями на схеме (рис. 3-6, г). Таким образом, взаимная индуктивность не является самостоятельным элементом схемы.
В этом разделе рассматриваются линейные цепи, т. е. такие цепи, сопротивления, индуктивности и емкости которых не зависят от тока или напряжения.
В сопротивлении г электромагнитная энергия преобразуется в тепло. Мощность преобразования энергии в тепло равна rt2. Сопротивления часто вводят в схему также и для учета преоб-
разования электромагнитной энергии в другие формы энергии (например, в механическую) и для учета излучаемой энергии.
Напряжение между зажимами сопротивления и ток в сопротивлении (рис. 3-6, а) связаны законом Ома:
ur—ri. (3-8)
Элемент схемы — индуктивность L (рис 3-6, б) учитывает энергию £i2/2 магнитного поля и явление самоиндукции. При изменении тока в индуктивности возникает э. д. с. самоиндукции щ. По закону Ленца она препятствует изменению тока. Поэтому при выборе положительных направлений для тока t и э. д. с. ei. одинаковыми (как это обычно принято делать) знаки еь и dddt противоположны и et = —Ldi/dt. Для того чтобы через индуктивность проходил переменный ток, на ее зажимах должно быть напряжение, равное и противоположное наведенной э. д. с. При одинаковых положительных направлениях напряжения и э. д. с. они противоположны — по _знаку: _________ __________________________________________
ul——eT~L diidt~~‘=====“=:^^ (3-Л)
116
(элементы цепи и элементы схемы, обладающие взаимной индуктивностью, рассматриваются в гл. 6).
Элемент схемы — емкость С (рис. 3-6, е) учитывает энергию Си2/2 электрического поля. На электродах емкости заряды равны и противоположны по знаку: qA = —дБ, причем
9д = С((рл — <рв); дв=С((рв~ <Рд)-
Для указанных на рис. 3-6, в положительных направлений тока i и напряжения на емкости tie заряд qA и напряжение ис = (рА — <рв имеют одинаковые знаки, т. е. qA — Cue.
Ток в ветви с емкостью равен скорости изменения заряда на электродах, и при указанном положительном направлении тока знак тока совпадает со знаком производной по времени от заряда qA. Действительно, приросту заряда qA соответствует положительное значение тока, убыли заряда qA — отрицательное значение тока. Поэтому, обозначая qA = q, можем' написать:
i — dq! di=С duddt, (3-10)
или
Uc — ^^idt. (3-11)
Расчетная схема зависит от частоты переменного тока. Так, при достаточно низкой частоте резистор может быть представлен сопротивлением, индуктивная катушка — йоследовательным соединением индуктивности и сопротивления, а конденсатор при хорошей изоляции между электродами—емкостью.
С ростом частоты, как будет показано в следующих параграфах, увеличиваются э. д. с., обусловленные индуктивностями, и токи, обусловленные емкостями. Поэтому при высоких частотах приходится учитывать индуктивность проволочных резисторов и меж-витковую емкость катушек. Кроме того, с увеличением частоты растут потери в изоляции конденсаторов. Для учета всех этих явлений приходится резисторы, индуктивные катушки и конденсаторы заменять более сложными схемами (подробнее см. § 3-21 и 3-22).
При высоких частотах приходится также учитывать емкости между проводами, соединяющими различные элементы реальной электрической цепи, и вводить их в расчетную схему.
В тех случаях, когда схема получается с ограниченным (конечным) числом элементов, говорят, что реальная цепь рассматривается как цепь с сосредоточенными параметрами. В тех же случаях, когда приходится пользоваться схемой, содержащей неограниченно большое (бесконечное) число элементов, говорят, что цепь рассматривается как цепь с распределенными параметрами.
Теперь рассмотрим вопрос о применимости к схемам для перемен-лых токов и нанрижений-законов Кирхгофа» — ----------------=
117
На проводах и в узлах схемы не могут накапливаться заряды (единственными накопителями зарядов являются емкости). Поэтому для любого узла схемы справедлив первый закон Кирхгофа:
Алгебраическая сумма мгновенных токов в проводах, соединенных в узел, равна нулю.
Напряжение между двумя точками цепи переменного тока в общем случае зависит от пути, вдоль которого оно определяется. Выясним, например, каково различие в напряжениях между точками А и В двух проводов цепи переменного тока (рис. 3-7), определяемых по двум различным путям. Между точками А и В включены два вольтметра для измерения напряжения. Соединительные провода от первого вольтметра идут по пути АтВ, от & второго вольтметра — по пути АпВ.
Согласно закону электромагнитной ин-т дукции напряжение вдоль замкнутого кон-
тУРа АпВтА равно э. д. с., индуктирован-ной в этом контуре магнитным потоком Ф, 1 z пронизывающим поверхность, ограничен-
ную контуром:
В ^АпВтА==^== 6Ф/(И.
Рис. 3-7. Заметим, что знак минус перед t/Ф fdt
ставится в том случае, когда положительное направление магнитного потока и положительное направление э. д. с. (направление обхода контура) согласованы по правилу правого винта. В рассматриваемом случае положительное направление Ф выбрано от читателя за плоскость чертежа.
и АпВтА ~ иАпвА-иВтА ~ ^АпВ ~ ^AmB-
Подставив это равенство в предыдущее выражение, получим: и-Апв — иАтв ~е=— ddo/dt.
Следовательно, напряжения между двумя точками, определенные вдоль двух различных путей, отличаются друг от друга на э. д. с., индуктированную в замкнутом контуре, образованном этими двумя путями.
Напряжения, определяемые вдоль различных путей, будут одинаковы только в том случае, если замкнутые контуры, образованные этими путями, не пронизываются переменным магнитным потоком.
В расчетной схеме напряжения между различными ее точками от пути не зависят, а зависят только от свойств ее элементов. Так, напряжения на зажимах элементов схемы г, L и С связаны с током приведенными выше соотношениями (3-8) — (3-11) вне зависимости от путей (взятых вне элементов), по которым эти напряжения опреде-ляются. Поэтому точки схемы переменного тока можно, так же как и точки цепи постоянного тока, характеризовать потенциалами,~ТГ 118
напряжения рассматривать как разности потенциалов. Имея это в виду, говорят, что расчетные схемы или идеализированные цепи потенциальны. Изменение потенциала по любому замкнутому контуру такой цепи равно нулю. Поэтому справедлива следующая формулировка второго закона Кирхгофа:
Алгебраическая сумма мгновенных э. д. с. всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура или, иначе, алгебраическая сумма мгновенных напряжений на всех элементах любого замкнутого контура схемы равна нулю.
В этом разделе рассматриваются линейные цепи, содержащие источники энергии с синусоидальными э. д. с. Если в цепи действуют несколько источников энергии, то рассматриваются только те случаи, когда частоты э. д. с. всех источников одинаковы. Заметим, что именно этот случай имеет место при нормальном режиме в электрических цепях энергетических систем.
Наконец, здесь рассматриваются так называемые установившиеся режимы цепей, которые наступают после некоторого промежутка времени (обычно от долей секунды до нескольких секунд) после окончания всех переключений в цепи. При установившемся режиме токи и напряжения во всех ветвях и участках линейных цепей также синусоидальны и изменяются с той же частотой, что и э. д. с. источников энергии.
Таким образом, в уравнения, выражающие законы Кирхгофа, входят алгебраические суммы синусоидальных функций времени, суммирование которых, как указывалось, целесообразно заменить суммированием изображающих их комплексных величин.
После такой замены получаются законы Кирхгофа для комплексных амплитуд или для комплексных действующих токов, напряжений и э. д. с.:
Алгебраическая сумма комплексных токов в проводниках, соединенных в узел, равна нулю. Алгебраическая сумма комплексных э. д. с. всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме комплексных напряжений на всех остальных элементах того же контура или, иначе, алгебраическая сумма комплексных напряжений на всех элементах любого замкнутого контура схемы равна нулю.
3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости
Пусть в схеме (рис. 3-8), состоящей из последовательно соединенных сопротивления г, индуктивности L ц емкости С, известен ток
== Lcoj-ЕФ,). (3-12)
119
Выясним, каковы напряжения на отдельных элементах и на входных зажимах.
На основании второго закона Кирхгофа
4~ ис —
(3-13)
где
ur = ri = rlm sin (со/ -|-ф,); (3-14)
ul=L di/dt=aLIm cos (co/4-ip() = coL/msin (со/ + ф-л/2); (3-15)
ис = ^ J idt = — ^с08(со/4-ф1)==^51п(со/4-фг-уУ (3-16)
ис
Рис. 3-8.
тивности (йЫт ифг
(отставание). Таким
Постоянная интегрирования в выражении для ис принята равной нулю, так как в установившемся режиме, как уже указывалось, напряжение на любом участке цепи синусоидально.
Из полученных выражений для ur, Ul и ис видно, что напряжение на сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает ток по фазе на угол л/2, а напряжение на емкости отстает ' по фазе от тока на угол л/2.
На рис. 3-9 показаны кривые мгновенных значений тока и напряжений для частного случая, когда амплитуда напряжения на индук-больше амплитуды напряжения на емкости Iт1 соС
0. Синусоида иг совпадает по фазе с синусоидой тока, а синусоиды uL и ис сдвинуты относительно синусоиды тока на угол л/2 соответственно влево (опережение) и вправо ' -
образом, напряжения на индуктивности и на емкости сдвинуты друг относительно друга по фазе на угол л (находятся в противофазе).
Ординаты кривой напряжения
u = Um sin (со/ + ф„) согласно (3-13) равны алгебраической сумме ординат кривых ur, Ul и Uc-
Определение напряжения и сводится к вычислению Um и ф„, которые могут быть найдены непосредственным суммированием трех синусоидальных функций времени иг, иь и ис с последующими тригонометрическими преобразованиями. Однако, как указывалось,- проще всего задача решается комплексным методом^
120
Запишем комплексный ток и комплексные напряжения на основании выражений для мгновенного тока и мгновенных напря-
жений: г
1 = 1е^ц (3-17)
Ur=rle^i=ri-, (3-18)
UL = аЫе’^+л/2) = aLIe^e^2 = /®L/; (3-19)
= -я/2) = 1 A~W2 = -j ' = (3-20)
с cdC соС s соС /соС ’ v 7
U = Ue'^. (3-21)
В выражениях для OL и Uc учтено, что
е;л/2 — cos 2 -J- / Slf| -2
а
е-M/2 = cos у sin = _ j = 1//.
Сопоставляя выражения для мгновенных напряжений uL и ис (3-15), (3-16) с комплексными напряжениями UL и Uc (3-19), (3-20), можно установить простое правило перехода от производной и интеграла синусоидальной функции времени к изображающим их комплексным величинам: синусоидальная функция заменяется изображающей ее комплексной величиной, дифференцирование заменяется умножением на ja, а интегрирование делением на ja.
Сумме синусоидальных напряжений (3-13) соответствует сумма изображающих их векторов или комплексных действующих напряжений:
Ur + UL + Uc = U. (3-22)
Это соотношение представляет собой Рис. 3-10.
уравнение по второму закону Кирхгофа, записанное в комплексной или векторной форме. Представим его на векторной диаграмме (рис. 3-10).
Напряжение иг совпадает по фазе с током i, поэтому вектор йг изобразим одинаково направленным с вектором I. Напряжение uL опережает по. фазе i на л/2, поэтому вектор Ul сдвинем относительно вектора I на угол л/2 «вперед» (против направления движения часовой стрелки). Напряжение tzc отстает по фазе от i на я, 2, поэтому вектор йс сдвинем относительно вектора / на угол л/2 «назад» (по направлению движения часовой стрелки).
Эти соображения о взаимном расположении векторов напряжения и тока непосредственно, следуют и из записи выражений комплексных напряжений Ur, UL и йс.
121
Действительно, вектор Ur (3-18) получается умножением / на вещественную величину г. Аргумент комплексной величины г! такой же, как и комплексного тока /, поэтому направление вектора Ur совпадает с направлением вектора /. Вектор Ul (3-19) получается умножением I на /coL. Умножение тока / на вещественную величину <о£ не изменяет аргумента, а умножение на / = е>л/2 увеличивает аргумент на л/2. Следовательно, вектор UL повернут относительно вектора / на угол л/2 «вперед». Вектор йс (3-20) получается делением / на /соС. Деление комплексной величины на соС не изменяет аргумента, а деление на /, что равносильно умножению на —j = £>-/л/2, уменьшает аргумент на л/2. Следовательно, вектор йс повернут относительно вектора / на угол л/2 «назад».
Так как умножение и деление вектора на / приводит к повороту вектора на л/2 соответственно «вперед» и «назад», то множитель / часто называют оператором поворота на л/2.
Сложив векторы Ur, Cl и йс, получим вектор С. Его длина определяет действующее напряжение U = UmFV 2, а положение относительно координатных осей — начальную фазу ф„.
Решим ту же задачу аналитически. Теперь уравнение (3-22) будем рассматривать кш< соотношение между комплексными числами. Подставив в него значения комплексных напряжений, получим: ri+jabi -j- i/jaC=й,
или
й=[г+j (<oL - 1 /соС)] /. (3-23)
Это соотношение между комплексными напряжением и током называют законом Ома в комплексной форме. Записав комплексные величины в показательной форме, получим:
Ue^» = у г2 + \aL — j2e^Iе'\ где , <s>L—\!<лС <p = arctg-------------------------,
t/='Kr2 + (coL—1/coQ2/; фи = ф» + ф.
Так как Um = '\/'2U и Im — 02/, то
Um=/г2 + (coL-l/coQ2 Im.
Таким образом, амплитуда Um и начальная фаза ф„ напряжения на зажимах цепи определены и можно записать выражение для мгновенного напряжения:
u = U,n sin (со/ + + ср). (3-24)
В заключение заметим, что уравнение для комплексных токов и напряжений и векторные диаграммы взаимно связаны Уравнения можно рассматривать как запись геометрических суммирований
122
векторов, выполняемых на векторной диаграмме, и наоборот, векторную диаграмму можно рассматривать как графическое представление соотношении между комплексными величинами в уравнении.
3-9. Сопротивления
Введем теперь ряд величин, характеризующих цепь синусоидального тока.
Отношение' комплексного напряжения к комплексному току называется комплексным сопротивлением
Z = ^- = ^=ze^ = z (3-25)
где z = UU = — отношение действующего или амплитуд-
ного напряжения соответственно к действующему или амплитудному току называется полным сопротивлением. Полное сопротивление равно модулю комплексного сопротивления. Аргумент комплексного сопротивления равен разности фаз напряжения и тока, т. е. <р = фи — ф/.
Комплексное сопротивление можно представить в виде
Z = ze№ = г cos <р -j- jz sin <р = г -|- jx, (3-26)
где г = z cos <р — вещественная часть комплексного сопротивления, называется активным сопротивлением; х = z sin <р — значение мнимой части комплексного сопротивления, называется реактивным сопротивлением.
Очевидно, что
z = ]/rr2-\-x2; <p=arctgy.
В технической литературе встречались также следующие наименования для сопротивлений: вместо полного сопротивления — кажущееся сопротивление, импеданс; вместо комплексного сопротивления — комплексный импеданс, вместо реактивного сопротивления — реактанс.
Из выражения (3-23) следует, что для схемы,' представленной на рис. 3-8, комплексное сопротивление
Z=r-\-jx = r-\-j (coL— 1/соС), причем реактивное сопротивление
х=coL — 1 /соС=xL — хс, (3-27)
Где
xL = aL; хс=1/юС
называются соответствен по индуктивным и емкост-Н~Ъ1 5Г-Т_итгр_(5 Т И В Л СТ; is я“мТК
123
Из выражения (3-15) видно, что индуктивное сопротивление связывает между собой амплитуды напряжения на индуктивности и тока:
U Ltn = т, XL = ™L = ULmlIm = UlJl-
Индуктивное сопротивление прямо пропорционально частоте тока. Это объясняется тем, что напряжение на индуктивности пропорционально скорости изменения тока: ul = L di/dt.
Емкостное сопротивление, как следует из выражения (3-16), связывает между собой амплитуды напряжения на емкости и тока:
Ucm= Хс= 1 /<оС = UСт/1т — Uс/1.
Емкостное сопротивление обратно пропорционально частоте тока. Эту зависимость от частоты легко пояснить, если считать заданным напряжение на зажимах емкости, а искомой величиной ток: i = dqldt = Cdiicldt. Ток прямо пропорционален скорости изменения напряжения на зажимах емкости и, следовательно, емкостное сопротивление обратно пропорционально частоте напряжения.
Напряжения на последовательно соединенных индуктивности и емкости противоположны по фазе; поэтому в выражение (3-27) для реактивного сопротивления х сопротивления xl и хс входят с различными знаками. Напряжения на индуктивности и на емкости сдвинуты по фазе относительно напряжения на сопротивлении соответственно на л/2 и —л/2. Поэтому эти сопротивления входят в Z как г, jxl и —jxc.
Следует обратить внимание на то, что индуктивное и емкостное сопротивления являются величинами арифметическими — положительными, а реактивное сопротивление х = Xi —хс — величина алгебраическая и может быть как больше, так и меньше нуля.
Для ветви, содержащей только индуктивность, реактивное сопротивление х равно индуктивному сопротивлению xi, а реактивное сопротивление х ветви, содержащей только емкость, равно емкостному сопротивлению, взятому со знаком минус, т. е. —хс.
Заметим также, что для ветвей, каждая из которых содержит только сопротивление г, только индуктивность L или только емкость С, комплексные сопротивления соответственно равны:
Zr = r; ZL = jaL; Zc=^ — j^.
3-10. Разность фаз напряжения и тока
Условимся под разностью фаз ср напряжения и тока всегда понимать разность начальных фаз напряжения фи и тока фг (а не наоборот):
<Р==Ф« —фо (3-28)
Поэтому на векторной диаграмме угол <р отсчитывается в направ-'лснпибгвсктора I к векторутЛДшс, 3-10). Именно при гаком оцре-124
делении разности фаз угол <р равен аргументу комплексного сопротивления. Угол <р положителен при отстающем токе (ф„ > ф,) и отрицателен при опережающем токе (фи <ф,).
Разность фаз между напряжением и током зависит от соотношения индуктивного и емкостного сопротивлений. При xl > хс имеем х = xl — Хс > 0 и ток отстает по фазе от напряжения, <р = = arctg (х/г) > 0. При xL = хс имеем х = 0, <р = 0, г = г, ток совпадает по фазе с напряжением, цепь в целом проявляет себя как активное сопротивление. Это случай так называемого резонанса, который подробно рассматривается в § 5-1. Наконец, при xl <хс имеем х < 0, < 0, ток опережает по фазе напряжение.
г>0
а)
т!
-j^ci
х=0
е)
Рис. 3-11.

Векторные диаграммы для трех возможных соотношений xl и Хс даны на рис. 3-11. При построении этих диаграмм начальная фаза тока ф, принята равной нулю. Поэтому <р и ф„ равны друг другу.
Рассматривая при заданной частоте цепь по рис. 3-8 в целом как пассивный двухполюсник, можно ее представить одной из трех эквивалентных схем: при х, > хс как последовательное соединение сопротивления и индуктивности (г и x'l = xL — хс), при xL = хс как сопротивление г и при X/ <; хс как последовательное соединение сопротивления и емкости (г и х'с = Хс — х;). При заданных L и С соотношение между Ху. и Хс зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
Выше, в §3-8, было принято, что задан ток, а определялись напряжения на элементах и на зажимах цепи. Однако часто бывает задано напряжение на зажимах, а ищется ток. Решение такой задачи не представляет труда. Записав по заданным величинам комплексное напряжение U и комплексное сопротивление Z, определим комплексный ток
и тем самым действующий ток и начальную фазу тока.
Часто равной нулю принимается начальная фаза заданного напряжения: ф>„ — П. Тогда, как следует из (3-28), начальная фаза_____
125
тока ф, равна и противоположна по знаку разности фаз <р, т Ф» = —ф.
Установленные выше соотношения между амплитудами или д ствующими токами и напряжениями, а также выражение для сдв фаз ф позволяет вычислить ток и не прибегая к записи закона С в комплексной форме. Подробно этот путь решения показан в п мере 3-4.
Пример 3-4. К цепи, состоящей из последовательно соединенных конденсат и катушки, приложено напряжение и = 100 sin 5000 t В. Емкость конденсат С — 5 мкФ, сопротивление катушки г~ 15 Ом, индуктивность L — 12 Найти мгновенный ток в цепи и мгновенные напряжения на конденсаторе т катушке.
Решение. Схема замещения цепи показана на рис. 3-8.
^=0)1=5000- 12.10-з=60 Ом; хс == 1/соС= 1/5000 - 5 - 10~в=40 Ом;
л:=л:£—л:с=60— 40 = 20 Ом; z==j/г2-р*2==]/' 152 + 202 = 25 Ом!
г ит 100 л . л 20 7«=^=25=4А; ^=15;
<р=53°08'; i = 4 sin (5000/—53°08') А;
t7cm-Vm=40-4=i60 в-
Напряжение на емкости отстает от тока по фазе на 90°, следовательно, ис= 160 sin (5000/— 143°08') В.
Комплексное сопротивление катушки
ZKaT = г+/x£= 15-р/60=61,8 Z 75с58' Ом.
Комплексная амплитуда напряжения на зажимах катушки
б,катт = 2кат/т = 61,8 Z 75°58'• 4 Z — 53°08' = 247,2 z 22°50' В.
Мгновенное напряжение на катушке
MKaT = 247,2 sin (5000/22°50') В.
Пример 3-5. В цепи, состоящей из последовательно соединенных конге тора и катушки, ток I = 2 А, его частота f — 50 Гц. Напряжение на зажг цепи U = 100 В, на зажимах катушки 17кат = 150 В и на зажимах конденсат Uc = 200 В. Определить сопротивление и индуктивность катушки и емкость , деисатора.
Решение. to = 2л/ — 2л-50 = 314с-1;
хс=1/с/7=100 Ом и С— 1/солс = 31,8 мкФ.
Полное сопротивление цепи
z = 17// = 5О Ом.
Полное сопротивление катушки
zKaT б^кат/7 = 75 Ом;
z2=r2-p (^/ — хс)2=г24-х£ — ^xLxc~^~xhi
гкат = г2 + 4; z2-*KaT==-4*c + *C;
гкат + хЕ~г2
~—=65,6 Ом; А = л:£/ш = 0,209 Г,
126
3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости
Пусть к схеме, состоящей из параллельного соединения элементов г, L и С (рис. 3-12), приложено напряжение и = Um sin (со/ + + 'Фи)-
Определим токи во всех ветвях.
По первому закону Кирхгофа или
Л + 4 + /с = ^- Рис. 3-12.
Вводя для заданного синусоидального напряжения изображающее его комплексное напряжение
U=Ue®“,
применим,для каждой ветви закон Ома в комплексной форме. Тогда получим:
/ = £ Л- Л =-£- = -
' г г ’ /со/. coL ’
/с = = j^cu==aCUe' ^»+п/2'>.
Из полученных выражений видно, что ток в сопротивлении совпадает по фазе с напряжением, ток в индуктивности отстает по фазе от напряжения на угол л/2,
а ток в емкости опережает напряжение по фазе на угол л/2. Векторная диаграмма напряжения и токов показана на рис. 3-13, где принято, что
< 0 и IL > Л>
Подставив выражения комплексных токов в уравнение первого закона Кирхгофа, найдем, что
U [г -J- UЦаЬ 4- ]а>Сй=I
или
[1/г —/(l/coL —®С)] t7==/.
(3-29)
От значения аргумента комплексной величины в квадратных скобках, на которую умножается комплексное напряжение, зависит разность фаз напряжения и тока. Так как под разностью фаз понимается величина ср = — фг и, следовательно, — ср, то
аргумент комплексной величины- в квадратньнг-скобках следует—
127
обозначить —<р:
/('У + = (3-30)
где , / 1/gjL—соС\ — Ч> = arctg - —---------------------------j,
или , 1/coL — шС <p=arctg -— ---------------------------.
Из (3-30) следует, что
/ = ]/Г(7)2 + (^-®С)2^/;
На основании этих данных
t = 7CTsin (coZ' + 'фи —<р).
3-12. Проводимости
Продолжим рассмотрение величин, характеризующих цепь синусоидального тока.
Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению
Y=l/U = \/Z — \!ге^=уе^=у Z — <Р> (3-31)
где у = 1/г—величина, обратная полному сопротивлению, называется полной проводимостью.
Комплексная проводимость и комплексное сопротивление взаимно обратны. Комплексную проводимость можно представить в виде
Y=уе~>ч ~у cos <р — jy sin <p=g — jb, (3-32)
где g = у cos <р — вещественная часть комплексной проводимости, называется активной проводимостью; Ь — у sin <р — значение мнимой части комплексной проводимости, называется реактивной проводимостью;
y = Vg2-Yb2-, <p = arctgj.
Наряду с принятой в этой книге алгебраической формой записи комплексной проводимости (3-32) в зарубежной технической литературе встречается и такая запись: Y = g + jb. При этом b = = — у sin <р, а не b = у sin <р, как было написано выше.
В технической литературе встречались также следующие наименования для проводимостей: вместо полной проводимости — кажу-—шаяся проводимость, адмитанц; вместо комплексной проводимости — комплексный адмитан ц; —:
128
Из выражений (3-30) и (3-29) следует, что для схемы, представленной на рис. 3-12, комплексная проводимость
И== 1/г — / (1/со£ — aC) = g — j (bL —bc),
ГДе g=l/r; bL = l/&L=l/xL; fec = coC=l/xc
и называются соответственно активной, индуктивной и емкостной проводимостями.
Реактивная проводимость
b=bL-bc. (3-33)
Индуктивная (bL) и емкостная (Ьс) проводимости — арифметические величины, а реактивная проводимость (Ь) — алгебраическая величина и может быть как больше, так и меньше нуля. Реактивная проводимость b ветви, содержащей только индуктивность, равна индуктивной проводимости Ьс, а реактивная проводимость b ветви,
содержащей только емкость, равна емкостной проводимости с обратным знаком, т. е. —Ьс.
Сдвиг по фазе между напряжением и током зависит от соотношения индуктивной и емкостной проводимостей цепи. На рис. 3-14
представлены векторные диаграммы для трех случаев, а именно bL > bc, Ьс = Ъс и Ьс < Ьс. При построении этих диаграмм начальная фаза напряжения принята равной нулю, поэтому q> и фг, как это следует из (3-28), равны и противоположны по знаку (ф/ = —<р).
Рассматривая схему по рис. 3-12 в целом как пассивный двухполюсник, можно заметить, что при заданной частоте она эквива-
лентна в первом случае параллельному соединению сопротивления и индуктивности, во втором — сопротивлению и в третьем — параллельному соединению сопротивления и емкости. Второй случай называется резонансом и рассматривается в гл. 5. При заданных L и С соотношение между bL и Ьс зависит от частоты, а поэтому J от частоты зависит и вид эквивалентной схемы.
Обратим внимание на то, что в схеме рис. 3-12 каждая из параллельных ветвей содержит по одному элементу. Поэтому получилось |гакое простое выражение для Y, в которое проводимости элементов Входят как отдельные слагаемые.---------------—----------------
б Основы теории цепей
129
В общем случае
т/ 1 1 __ Т JX Г . X -t /о о и \
= Z ~ r + ix ~ Г2+Х~ ~ 2*— 1 ~ (3-34)
откуда
g = r/z2; b =x/z2 (3-35)
и, наоборот,
r-=gz2 = g!y2-, x=bz2 — b/y2. (3-36)
Из полученных соотношений видно, что b и х всегда имеют одинаковый знак.
Например, для схемы по рис. 3-8 получаем для g и b довольно сложные выражения, причем не только Ь, но ng зависят от частоты:
г . t, - coL—1/соС — r2 + (coL- 1/соС)2’ 1/ыС)2’
Наоборот, для схемы на рис. 3-12, состоящей из параллельного соединения элементов, получаются простые выражения для проводимостей, но относительно сложные выражения для сопротивлений, причем и эквивалентное активное сопротивление зависит от частоты. По формулам (3-36)
S .. IfaL—шС
r~g2 + (l/coT —соС)2’ Х~~g2+(l/coL-coC?‘
Переход от сопротивления Z = г ф- jx к проводимости Y — = g — jb и обратно соответствует замене схемы цепи с последовательным соединением элементов г и х эквивалентной схемой с параллельным соединением элементов g и b и обратно.
Заметим, что обозначения Z, Y, г, х, Xl, хс, g, b, bL и Ьс применяются не только для сопротивлений и проводимостей, но и для элементов схемы, характеризуемых этими величинами. В таких случаях элементам схемы дают те же самые наименования, какие присвоены величинам, которые обозначаются этими буквами. Комплексные сопротивления или проводимости как элементы схемы имеют условное обозначение в виде прямоугольника (рис. 3-1). Точно так же обозначают реактивные сопротивления или проводимости, если хотят отметить, что они могут быть как индуктивными, так и емкостными сопротивлениями или проводимостями.
Пример 3-6. Цепь состоит из конденсатора емкостью 6=10 мкФ и резистора с сопротивлением г = 100 Ом, включенных параллельно. Определить, каковы должны быть емкость конденсатора и сопротивление резистора, чтобы при их последовательном соединении получилась цепь, эквивалентная данной при со = = 103 с-1.
Решение. Проводимости данной цепи
1/г== Ю-a см; Ь = — Ьс = — соС= — 105- ю. 10-в=_ю-2 См;
I/2 = g2_|_fc2==2 • 1О’« См2.
Сопротивления данной цепи
r=g/zy2=50 Ом; х = Ь/у2—~50 Ом.
Эквивалентная цепь должна иметь такие же сопротивления. Таким образом, искомое сопротивление резистора 50 Ом, а емкость конденсатора С = — 1 /сох *= — 20 мкФ,----------------------------------------------------------
130
3-13. Пассивный двухполюсник
Ток и напряжение на входе любого пассивного двухполюсника (рис. 3-15) связаны законом Ома
й=zi и I=yu,
где Z и Y — входные комплексные сопротивление и проводимость
двухполюсника.
Входному комплексному сопротивлению 2 = г + jx соответствует эквивалентная схема двухполюсника, состоящая из последовательного соединения активного сопротивления г и реактивного сопротивления х.
Последнее в зависимости от знака следует рассматривать либо как индуктивное, либо Рис. 3-15. как емкостное сопротивление. Поэтому на эквивалентной схеме (рис. 3-16, а) сопротивление х показано
условно прямоугольником.
Напряжение U можно разложить на составляющие:
и=zi=(г+jx) i=гi+jxi=us+йр,
где Йа = rl — составляющая, совпадающая по фазе с током, называется активной составляющей н а -пр я ж е н и я;
Йр = jxl — составляющая, сдвинутая по фазе относительно тока на угол л/2, называется реактивной составляющей напряжения.
Составляющие Йа и Йр можно рассматривать как напряжения на элементах г и х эквивалентной схемы.
На рис. 3-16, в представлена векторная диаграмма двухполюсника для случая, когда <р > 0, т. е. х — индуктивное сопротивление. Треугольник, образованный векторами О, U., и Йр со сторонами, пропорциональными z, г и | х |, называется треугольником напряжений. Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны сопротивлениям г, г и I х |, называется треугольником сопротивлений. Из треугольника напряжений следует, что
t/a=£/cos<p; t/p=t/|sin<p|; U ~ У Ul -р 6/p .
Входной комплексной проводимости Y = g — jb соответствует эквивалентная схема двухполюсника, состоящая из параллельного соединения проводимостей g и Ь. Последняя в зависимости от знака либо индуктивная, либо емкостная. Поэтому на эквивалентной схеме Фис. 3-16, б) проводимость показана условно прямоугольником. Ток на входе двухполюсника можно разложить на составляющие: s____ i^YU^fg-ibW^gU-ibU^ + y
б*
131
где Д =gU — составляющая, совпадающая по фазе с напряжением, называется активной составляющей тока;
/р = —jbO — составляющая, сдвинутая по фазе относительно напряжения на угол л/2, называется реактивной составляющей тока.
Составляющие /а и 1р можно рассматривать как токи в элементах g и b эквивалентной схемы.
Треугольник, образованный векторами /, /а и /р, со сторонами, пропорциональными у, g, | fe|, называется треугольником
Рис. 3-16.
токов. Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны проводимостям у, g и | b |, называется треугольником проводимостей.
Из треугольника токов имеем:
/a = /cos<p; 7р= Г | sin <р |; I Ра + Рр .
Пример 3-7. Напряжение и ток на входе пассивного двухполюсника (рис. 3-.15) и = 100 sin (314 t — 15°) В, i = 10 sin (314 t + 45°) A.
Определить параметры двух эквивалентных схем двухполюсника, активные и реактивные составляющие напряжения и тока.
Решение.
йт = 100 z. -15° В; 1т = 10 z. 45° А;
Z= 7^ = -Т02'^~= ‘° Z ~60°=5-/5 Ом;
F=l/Z=l/10 Z—60°=0,l Z 60°=0,05+ /0,05 /3 См;
г=5 Ом; х=— 5 /3 Ом; g — 0,05 См; 6 = — 0,05/3 См;
<p = argZ = i|:;z—1|>;=— 15 — 45 = —60°;
Ham==t/m cos <p = 100cos z. —60°=50 B;
Upm = Um s>n <P— 100 | sin Z —60° | =50 /3 B;
Zam =/m cos (p= 10 cos Z — 60®=5 A;
/pm=Zm | sin qj |= 10 I sin z—60®|=5/3 A;
tza = 50 sin (314/+ 45°) B; up = 50 /3 sin (314/ — 45°) B;
ja = 5 sin (314/— 15°)A;
tp = 5/5 sin (314/+ 75°) A.
132
3-14. Мощности
Перейдем к рассмотрению энергетических соотношений в цепи синусоидального тока.
Положим, что за элементарный промежуток времени dt через
оперечное сечение провода в направлении, принятом за положи-тельное для тока i (рис. 3-15), проходит электрический заряд dq. Перемещение заряда в направлении, совпадающем с положительным направлением э. д. с. источника, сопровождается элементарной рабо-той dA = edq источника э. д. с. Такая электромагнитная энергия отдается источником во внешнюю цепь и затрачивается на работу
dA = udq по перемещению заряда dq в положительном направлении напряжения и через пассивный двухполюсник.
Мгновенная мощность, производимая и отдаваемая источником э. д. с. и потребляемая двухполюсником, равна скорости совершения работы в данный момент времени: p=dAjdt—ui.
Напряжение и ток на входе пассивного двухполюсника в общем случае сдвинуты по фазе на угол ср. Примем начальную фазу напряжения = 0, тогда
—ср. При таком условии мгно-
из (3-28) начальная фаза тока фг
венные значения напряжения и тока
u = t/msinco/; i — Im sin (coz' — ср).
Мгновенная мощность
p = ui = UmIm sin cot sin (co/ — <p) — 5 [cos <p — cos (2coZ — cp)] =
= UIcoscp — UIcos(2cot — cp). (3-37)
Мгновенная мощность имеет постоянную составляющую и гармо-
ническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока (рис. 3-17). Мгновенная мощ
ность, потребляемая двухполюсником и отдаваемая источником
э- Д. с., положительна, когда у напряжения и и тока i одинаковые знаки, т. е. когда действительные направления напряжения и тока в двухполюснике одинаковы, а в источнике э. д. с. противоположны (рис. 3-15); она отрицательна, когда у напряжения и и тока i разные знаки, т. е. когда действительные направления напряжения и тока ^Двухполюснике противоположны, а в источнике э. д. с. одинаковы.
133
Действительные направления и и i в течение отдельных интервалов времени показаны нй рис. 3-17 пунктирными стрелками.
Когда мгновенная мощность отрицательна, энергия поступает не в двухполюсник, а возвращается из двухполюсника источнику э. д. с. Такой возврат энергии источнику питания возможен, так как энергия периодически запасается в магнитных и электрических полях элементов цепи, входящих в состав двухполюсника. Энергия, отдаваемая источником и поступающая в двухполюсник в течение времени t
t, равна § р dt. На графике она соответствует площади, ограниченной о
кривой р и осью абсцисс на интервале времени t. Знаками плюс и минус отмечены заштрихованные площади, соответствующие энергии, поступающей в двухполюсник и возвращаемой источнику.
Если двухполюсник состоит только из активных сопротивлений, энергия накопляться в нем не может. В этом случае нет сдвига фаз между напряжением и током (ср = 0). Ток i и напряжение и всегда одного знака, р 0 (см. далее рис. 3-18, а) и нет таких моментов времени, когда энергия возвращалась бы из двухполюсника источнику питания.
Среднее значение мгновенной мощности за период называется активной мощностью или иногда просто мощностью
т
Р = i р dt = UI coscp. (3-38)
о /
Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник не потреблял бы энергию, а генерировал бы ее), поэтому всегда cos ф 0, т. е. на входе пассивного двухполюсника —л/2 sg <р sg п/2. Случай Р — 0, Ф = | л/2 | теоретически возможен для двухполюсника, не имеющего активных сопротивлений и содержащего только индуктивности и емкости.
Электрические машины и аппараты конструируют для работы при определенных значениях напряжения и тока. Поэтому их характеризуют не активной мощностью, зависящей от сдвига фаз ср между напряжением и током, а полной мощностью
S = UI, (3-39)
равной произведению действующих напряжения и тока (раньше полная мощность обычно называлась кажущейся).
Очевидно, полная мощность равна наибольшему значению активной мощности при заданных напряжении и токе. Отметим также, что амплитуда гармонической составляющей мгновенной мощности (3-37) численно равна полной мощности. Размерность полной и активной мощностей одинаковая, однако единицу измерения мощности в применении к полной мощности называют вольт-ампер (В-А), Это позволяет при численном выражении полной мощности—
134
патко говорить: мощность столько-то вольт-ампер, так как наименование единицы (вольт-ампер) сразу указывает, что речь идет о полной мощности.
Отношение активной мощности к полной, равное косинусу ла сдвига фаз между напряжением и током, называется коэффициентом мощности: Р U/ cos <в S =-^ = 0054).
(3-40)
Для лучшего использования электрических машин и аппаратов желательно иметь возможно более высокий коэффициент мощности или возможно меньший сдвиг по фазе тока относительно напряжения, т. е. стремиться получить cos ср — 1. Так, например, для питания приемника мощностью 10 000 кВт при cos <р = 0,7 источник питания должен быть рассчитан на мощность 14 300 кВ-А, а при cos <р = 1 на 10 000 кВ-А.
Высокий коэффициент мощности желателен также для уменьшения потерь при передаче энергии по линиям. При данной активной мощности Р приемника ток в линии тем меньше, чем больше значение cos <р:
I = PjU cos ср.
При расчетах электрических цепей находит применение так называемая реактивная мощность Q=UI sin ср.
(3-41)
Она положительна при отстающем токе (<р > 0) и отрицательна при опережающем токе (ср <; 0). Единицу мощности в применении к измерению реактивной мощности называют вар х. Это отдельное наименование позволяет говорить вместо реактивная мощность просто мощность, равная стольким-то вар.
Активная, реактивная и полная мощности связаны соотношениями
X2 = Р2 4- Q2; S = У Р2 + Q2; Q/P = tg <р. (3-42)
Для увеличения коэффициента мощности (cos <р) приемника нужно, очевидно, уменьшать его реактивную мощность.
В то время как активная мощность определяет (в среднем) совершаемую работу или передаваемую энергию в единицу времени, полная и реактивная мощности не определяют ни совершаемой Работы, ни передаваемой энергии за единицу времени. Однако в электроэнергетике по аналогии с понятием активной мощности приписывают реактивной мощности аналогичный смысл, а именно, ее рассматривают как мощность генерирования, потребления или передачи некоторой величины, которую хотя она и не является энергией, условно называют реактивной энергией
__________ Wp—Qt.
^Название происходит от сокращения слов: волы, ампер и реактивный.
135
Размерность этой величины одинакова с размерностью энергии. Единицу измерения реактивной энергии называют вар-ч; напомним, что энергия в электроэнергетике обычно измеряется в ватт-часах. Если наряду с энергией нужно рассматривать и реактивную энергию, то во избежание путаницы для внесения четкого различия этих двух понятий энергию называют активной энергией.
На практике реактивная энергия, как и активная, измеряется счетчиками. При изменяющейся с течением времени нагрузке по показаниям счетчиков можно определить средний коэффициент мощности (cos <р)ср предварительно вычислив
rp CM Qcp
(tg<p)cp = -^=|^= (3-43)
w а * ср ь г ср
где Wz — активная энергия; Рср и Qcp— средние значения активной и реактивной мощностей.
Рассмотрим теперь простой прием, позволяющий найти активную и реактивную мощности по комплексному напряжению и комплексному току. Он заключается в том, что нужно взять произведение комплексного напряжения U и комплекса /, сопряженного с комплексным током I. Это произведение называют комплексной мощностью, которую будем обозначать 5.
Пусть 0 = 0 Z. ф,„ 1 = I тогда I = I Z — ф, и 5 = 01 = = О = 01 Z. Ч’/г — "Ф/ '= 01 Z. <Р = 01 cos ф +
4- jOI sin ф, т. е.
S = UI = P+jQ. (3-44)
Отсюда видно, что вещественная часть комплексной мощности равна активной мощности, а мнимая часть (без /) — реактивной. Модуль комплексной мощности равен полной мощности S.
Иногда (в зарубежной литературе) комплексную мощность опре-деляют как произведение комплекса О, сопряженного с комплексным напряжением О, и комплексного тока /. При этом получается комплексная величина S', сопряженная с S:
S' = t// = S=P-/Q
и, следовательно, реактивная мощность равна мнимой части (без /) комплексной мощности, взятой с обратным знаком.
Из приведенных выше основных выражений для мощности 5, S, Р и Q получается ряд других выражений, в которые входят параметры пассивного двухполюсника или активные и реактивные составляющие тока и напряжения:
S = 0l = Zil=ZI2, S = ui==UYO=YO2-, S = OI = zI2 = yO2-,
P = OI cos ф — U J = UIa = zl2 cos ф =- rI2 = yU2 cos ф=gU2: = Q = OI sin (f—zl2 sin (p~xl2 — yU2 sm M2. =
136
Ппя абсолютного значения реактивной мощности справедливы та«5е выражен.,»
|Q| = Z7pZ==C7Zp.
Из равенств 5 = Ul, Р = UJ = UIa и | Q | = U?I = UI сдетует, что стороны треугольников напряжений и токов (см. § 3-13) пропорциональны мощностям S, Р и | Q Подобный им треугольник, стороны которого в произвольно выбранном масштабе равны мощностям S, Р и | Q |, называется треугольником мощностей.
3-15. Мощности в сопротивлении, индуктивности и емкости
Вся энергия, поступающая в активное сопротивление, преобразуется в тепло. Принимая во внимание, что u = ri, мгновенную мощность можно представить в следующем виде:
p = ui = ri2.
Ток совпадает по фазе с напряжением, <р = 0, cos <р = 1 и в соответствии с (3-37)
p = H/(l-cos2co/). (3-45)
Мгновенная мощность колеблется в пределах от 0 до 2UI и не бывает отрицательной (рис. 3-18, а). Активная мощность равна полной мощности, а реактивная мощность равна нулю (sin <р = 0).
Мгновенные мощности поступления энергии в индуктивность и в емкость равны скоростям прироста энергии соответственно магнитного и электрического полей.
Действительно, для индуктивности
т di . d
’Li2\
2 )
и для емкости
p = ui = uC
du d ( Cu2\
dt dt \ 2 / ‘
Так как для индуктивности <р = л/2, а для емкости <р = — л/2, то для обоих случаев из (3-37) получаем:
р = — Ul cos f 2<о/ zjz ~ = zjz UI sin 2со/. (3-46)
Здесь верхние знаки относятся к индуктивности, а нижние — к емкости.
Площади, ограниченные кривыми мгновенных мощностей и осями абсцисс (рис. 3-18, б и в), пропорциональны энергии, которая Поступает в индуктивность или емкость (отмечены знаком плюс) и возвращается источнику питания (отмечены знаком минус); эти Рлощади равны друг другу. Происходит непрерывньпГЬбмен эпер-
137
гией между источником питания и соответственно между магнитным
или электрическим полями.
Активные мощности, потребляемые индуктивностью и емкостью,
равны нулю. Реактивная мощность, потребляемая индуктивностью,
ность. Так, источник, питающий
положительна; а потребляемая емкостью — отрицательна [sin <р = sin (± л/2) = ± 1]. Отрицательная потребляемая реактивная мощность соответствует положительной отдаваемой. Следовательно, индуктивность можно рассматривать как потребитель реактивной энергии, а емкость как ее генератор.
Реактивные мощности, потребляемые индуктивностью и емкостью, можно выразить как произведения угловой частоты со и максимальных значений энергии, периодически запасаемых соответственно в магнитном и электрическом полях:
L/s CU2
FM.MaKC = -f И ^В.макс = -~
Действительно, для индуктивности
Qi/= UI sin I =
= coL/m/2 = coIFM накс (3-47) и для емкости
Qc = UI sin (— л/2) ==
— — UuCU = — (S)CU2ml2 =
= -®IFB.MaKc. (3-48)
Отметим, что источники питания могут либо отдавать, либо потреблять реактивную мощ-индуктивность, отдает, а источ-
ник, питающий емкость, потребляет реактивную мощность.
3-16. Баланс мощностей
Из закона сохранения энергии следует, что в любой цепи соблюдается баланс как мгновенных, так и активных мощностей. Сумма всех отдаваемых (мгновенных и активных) мощностей равна сумме
138
всех потребляемых (соответственно мгновенных или активных) мощностей- Покажем, что соблюдается баланс и для комплексный и, следовательно, для реактивных мощностей.
Пусть общее число узлов схемы равно п. Здесь в отличие от обычных определений терминов узел и ветвь будем под узлом понимать имеете соединения любых двух элементов схемы (источников и приемников), а под ветвью — каждый участок схемы, содержащий один из ее элементов.
Напишем для каждого из п узлов уравнения по первому закону Кирхгофа для комплексов, сопряженных с комплексными токами:
/12 + {1з +...+ А„ = 0;
А1 + ^2.3 +...+ А/; — Di
1щ 'Г Л12 +...'Г In, п-1 — 0.
Эти.уравнения записаны в общей форме в предположении, что каждый узел связан со всеми остальными (п — 1) узлами. При отсутствии тех или иных ветвей соответствующие слагаемые в уравнениях выпадают. При наличии между какой-либо парой узлов нескольких ветвей число слагаемых соответственно увеличивается. Так, Например, если между узлами 1 и 2 включены двеяветви,до вместо /12 и /21 в уравнения войдут суммы Гк + пг и + /гь
Умножим каждое из уравнений на комплексный потенциал узла, для которого составлено уравнение, и затем все уравнения просуммируем. Учтем, что комплексы, сопряженные с комплексными токами, входят в эти уравнения дважды (для двух различных направлений), причем /21 = — /12, /31 = — /13 и т. д. В результате получим:
(Ф1 Фг) ^12 4~ (Ф1 Фз) 113 + • • •+ (Фи-i Ф«) I п-1, « = 0,
т. е. сумма комплексных потребляемых мощностей во. всех ветвях цепи равна нулю. Здесь все слагаемые представляют комплексные потребляемые мощности, потому что они вычисляются для одинаковых положительных направлений напряжений (разностей потенциалов) и токов.
Полученное равенство выражает баланс комплексных мощностей. Из него следует равенство нулю в отдельности суммы потребляемых активных мощностей и суммы потребляемых реактивных мощностей. Так как отрицательные потребляемые мощности представляют собой мощности отдаваемые, то можно утверждать, что суммы всех отдаваемых и всех потребляемых реактивных мощностей равны Друг другу.
Аналогичную формулировку можно придать и балансу комплексных мощностей. Перенеся часть слагаемых в правую часть уравнения с противоположным знаком, т. е. рассматривая их как мощности отдаваемые, мы получим равенство сумм комплексных потреб
139
ляемых и отдаваемых мощностей:
У "^потр
—
При равенстве сумм комплексных величин суммы их модулей в общем случае не равны друг другу. Отсюда следует, что для полных мощностей 5 баланс не соблюдается.
Потребляемая реактивная мощность на входе любого пассивного двухполюсника должна равняться сумме реактивных мощностей, потребляемых индуктивностями и емкостями, которые входят в его схему:
Пользуясь соотношениями (3-47) и (3-48), получаем:
FH.HaKc-2re.HaKc).
(3-49)
Заметим, что положения этого параграфа могут быть распространены и на цепи, между элементами которых имеются взаимные индуктивности, так как подобные цепи, как будет показано, можно свести путем преобразования к схемам, не содержащим взаимных индуктивностей.
Рис. 3-19.
3-17. Знаки мощностей и направление передачи энергии
Пусть два активных двухполюсника Aj и Л2 соединены друг с другом (рис. 3-19, а). Предположим, что передача энергии в зависимости от режима работы может происходить в любом направлении — и от At к А2 и от А2 к Аъ
Выбранные положительные направления напряжения и тока (рис. 3-19, а) совпадают друг с другом в двухполюснике А2 и противоположны друг другу в двухполюснике Аг. Поэтому мощности ,
p = ui и S — Gl = P + iQ
являются мощностями, потребляемыми двухполюсником А2 и отдаваемыми двухполюсником Л1. Если р > 0, то в данный момент времени энергия передается от двухполюсника Л1 к двухполюснику А.,. Если Р > 0, то за каждый период Т двухполюсник А2 принимает,
140
а двухполюсник Ai отдает энергию, равную РТ. При Q > 0 двухполюсник Аг отдает, а двухполюсник А2 потребляет реактивную энергию. При р < 0 энергия в данный момент передается в обрат-ном направлении, при Р < 0 энергия за каждый период поступает из двухполюсника Л2 в двухполюсник Дх. При Q < 0 реактивную энергию отдает двухполюсник А2.
Для рассматриваемой цепи на рис. 3-19, б приведена векторная диаграмма напряжения и тока. При выбранном направлении вектора О в зависимости от режима цепи- вектор тока 1 может лежать в любом квадранте диаграммы. На диаграмме различными направлениями штриховки отмечены области расположения вектора /, соответствующие положительным значениям активной и реактивной мощностей. Так, для положения вектора /, показанного на диаграмме пунктиром, Р > 0 и Q < 0. В этом режиме работы активная мощность передается от Аг к А2, .а реактивная — от А2 к
Рассмотрим теперь, как определяется направление передачи энергии по кривым мгновенных значений напряжения и тока, полученным экспериментально. На рис. 3-20, а показана схема включения осциллографа — прибора, на экране которого наблюдают эти кривые. Ординаты кривых пропорциональны мгновенным значениям напряжений, подводимых к зажимам осциллографа с надписями «напр.» и «ток». Ток в цепи между двухполюсниками Аг и А2 регистрируется осциллографом косвенно, как напряжение на небольшом актив
ном сопротивлении г, которое включено в соединительные провода. Напряжение на этом сопротивлении пропорционально току и совпадает с ним по фазе. Знаками «+» и «—» отмечена полярность зажимов осциллографа, при которой ординаты кривых положительны.
Пусть наблюдаются кривые или, как их называют, осциллограммы и и ur = ri, показанные на рис. 3-20, б.
Для решения вопроса о направлении передачи энергии укажем на схеме положительные направления напряжения и тока в соответствии с разметкой «+» и «—» зажимов осциллографа. Положительные направления напряжения и тока, удовлетворяющие этому Условию, совпадают для двухполюсника Аг и противоположны для Двухполюсника А2. Следовательно, по кривым тока и напряжения, показанным на рис. 3-20, б, определяется мощность, потребляемая Двухполюсником Alt или мощность, отдаваемая двухполюсником А2. ё те, промежутки времени, когда ординаты- кривых «- и иг одного Зйака, энергия передается от Л2 к Аи когда же знаки и и иг раз
141
личны, энергия передается от Ат к А2. Из осциллограммы видно, что Ф л .2л/3, следовательно, Р = Ul cos ср <; 0 и Q — Ul sin <р > 0. Таким образом, активная мощность передается от к А2, а реактивная — от Д2 к Аг. Ясно, что направление передачи энергии может быть установлено по осциллограммам тока и напряжения только в том случае, если известна полярность зажимов осциллографа и
схема его подключения к цепи.
Активная мощность измеряется ваттметром, который имеет две
[ть, две обмотки — напряжения и тока. Два зажима, один — обмотки напряжения и один — обмотки тока, обозначают одинаковыми значками, обычно звездочками (рис. 3-21, а).
Ваттметр устроен так, что измеряет величину
^вДв-rCOS (Д 77 вт, 4т), где Двт и /вт — действующие напряжение и ток, подведенные к ваттметру, а Д Т7вт, /вт — угол сдвига фаз между ними, который соответствует одинаковым положительным направлениям Olf( и /вт
относительно зажимов, отмеченных звездочкой (например, на рис. 3-21, а — от зажимов, отмеченных звездочкой, к зажимам, не отмеченным звездочкой). Стрелка ваттметра отклоняется по шкале в том случае, когда | Д Двт, 4т I < л/2, т. е. когда cos (Д Двт, 4т) > 0_. Если же | Д Двт, 4т I > л/2 и, следовательно, cos (Д Т7вт, /В1) < 0, то стрелка
отклоняется не по шкале, а в противоположную сторону.
На рис. 3-21, б показаны два ваттметра, у которых обмотки тока включены различно. У ваттметра 1 зажим токовой обмотки, отмеченный звездочкой, находится слева, а у ваттметра 2 — справа. Как уже отмечено, ваттметры дают показания (стрелки отклоняются по шкале), когда | Д Д,.т, 4т, I < л/2. Для ваттметра 1 это будет в том случае, когда энергия передается от At к А2, а для ваттметра 2 в том случае, когда энергия передается от А2 к АТ. Таким образом,
по показаниям ваттметра можно определить не только мощность, но и направление передаваемой энергии, нужно только знать раз-метку зажимов ваттметра и как он включен в цепь.
3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра
Существуют различные экспериментальные методы определения параметров пассивных двухполюсников. Рассмотрим метод, основан-пый на измерении-тока, напряжения и активной мощности на входе двухполюсника.
142
Определив по приборам U, I и Р, найдем:
z=UH\ у=Ци-, г=Р/Р-, g=P[U2.
Затем вычислим абсолютные значения реактивных сопротивления и проводимости
\b\ = + Vy^-b2.
Для определения знака х и b необходимо провести дополнительные измерения в измененных условиях. Можно, например, последовательно с двухполюсником включить конденсатор с емкостным сопротивлением хс и, проведя заново измерения, определить по приведенным выше формулам новое абсолютное значение реактивного сопротивления | х — л< |. Если реактивное сопротивление двухполюсника положительно и емкостное сопротивление конденсатора Хс < | 2х |, то очевидно, что | х — хс | < | х |; если же реактивное сопротивление х двухполюсника отрицательно, то | х — хс | > | х|. Таким образом, выбирая хс < 12х | и сопоставляя абсолютные значения х и (х — л<), можно определить знак х (знак b совпадает со знаком х).
Можно включить конденсатор параллельно двухполюснику и, проведя измерения, вычислить новое значение | b — Ьс |. Если выбрать Ьс < | 2Ь |, то при | b — bc | < | b | проводимость b > О, а при | Ъ — bc | > | b | проводимость Ь < 0.
Во многих случаях последовательное или параллельное включение конденсатора практически не изменяет активного сопротивления или активной проводимости цепи. Поэтому увеличение или уменьшение абсолютного значения реактивного сопротивления или проводимости приводит соответственно к увеличению или уменьшению полного сопротивления или проводимости и по изменениям их значений можно судить о знаке х или Ь.
Надо твердо помнить, что параметры реальных цепей зависят от частоты и, будучи определены при одной частоте, не могут применяться для расчетов при других частотах.
3-19. Условия передачи максимальной мощности от источника энергии к приемнику
Представим источник энергии р э. д. с. Ё и внутренним сопротивлением ZB = rB + jxs схемой замещения (рис. 3-22). Выясним, каково должно быть сопротивление Z = г ф- jx приемника, чтобы передаваемая ему активная мощность была максимальной.
Мощность приемника
п 12 гЕ2
p-rl ~ (г+гвУ+(Х+хвГ
Очевидно, при любом г мощность достигает наибольшей величины при х = — хв. В этом случае
ТУ Г ~ --
Г /V -
143
Взяв от полученного выражения производную по г и приравняв ее нулю, найдем, что Р имеет наибольшее значение при г = гв (см. также § 2-11).
Таким образом, приемник получает от источника наибольшую активную мощность, когда его комплексное сопротивление является сопряженным с комплексным внутренним сопротивлением источника:
Z = ZB. " (3-50)
При этом условии
Рмакс = £2/4/-в. (3-51)
Коэффициент полезного действия
"-(та?-0'5' <3'52>
В электроэнергетических установках режим передачи максимальной мощности невыгоден вследствие значительных потерь энергии. В различного рода устройствах автоматики
Рис. 3-22.
и связи мощности сигналов весьма малы, поэтому часто приходится специально создавать условия передачи приемнику максимально возможной мощности. Снижение к. п. д. обычно никакого значения не имеет, так как количество передаваемой энергии незначительно.
Согласование сопротивлений приемника и источника питания в соответствии с (3-50) можно получить и добавлением в цепь эле-
ментов, обладающих реактивными сопротивлениями (см. далее
пример 4-6).
Иногда сопротивление приемника можно изменять не произ-
вольно, а только с сохранением соотношения между активным и реактивным сопротивлениями, т. е. = const. Анализ, который здесь не приводится, показывает, что в этом случае мощность Р
максимальна, когда равны друг другу полные сопротивления приемника и источника (г = гв). При этом
Р'—
Согласования полных сопротивлений приемника и источника питания можно добиться, включая приемник через трансформатор (см. § 8-8).
3-20. Понятие о поверхностном эффекте и эффекте близости
Познакомимся с некоторыми явлениями, оказ'ывающими влияние на параметры электрической цепи.
На рис. 3-23 схематически показана картина магнитного пол я в плоскости поперечного сечения уединенного проводника с током. ~
144
Представим себе этот провод в виде совокупности нитей, параллельных его оси. Чем ближе нить расположена к оси проводника, тем с большим числом магнитных линий она сцеплена.
При периодическом изменении тока изменяется магнитное поле н в нитях проводника наводятся э. д. с., противодействующие изменениям тока. Это противодействие тем значительнее, чем больше э. д. с. (чем больше магнитных линий сцеплено с нитью), т. е. чем ближе нить проводника расположена к оси провода. В результате плотность тока в различных точках поперечного сечения получается неодинаковой: наибольшая на периферии провода и наименьшая на его оси.
Рассмотренное явление концентрации переменного тока в поверхностном слое проводника называют поверхностным эффектом. Резкость проявления его возрастает с увеличением частоты /, диаметра провода d, магнитной проницаемости р и удельной проводимости о материала провода. Это объясняется тем, что увеличение р приводит к возрастанию магнитного поля внутри провода, увеличение d создает большую разницу в сцеплениях с магнитными линиями осевых и периферийных нитей провода, а повышение /ио увеличивает роль наводимых
в нитях э. д. с., противодействующих из- рис. 3-23.
менению тока в них. Так, в предельном случае о = оо весь ток должен концентрироваться на поверхности провода в бесконечном тонком слое.
Вследствие поверхностного эффекта поперечное сечение провода при переменном токе используется хуже, чем при постоянном токе. При одинаковых значениях переменного и постоянного токов (равенстве значения постоянного тока и действующего значения переменного тока) тепловые потери больше при переменном токе. Поэтому сопротивление провода переменному току (активное сопротивление) выше, чем сопротивление провода постоянному току.
Другим следствием поверхностного эффекта является некоторое уменьшение индуктивности цепи ввиду ослабления магнитного поля во внутренней части провода. В предельном теоретическом случае, когда ток концентрируется на поверхности провода в бесконечно тонком слое, магнитное поле внутри провода отсутствует.
При высоких частотах переменного тока внутренняя часть провода практически не используется, поэтому часто применяют пустотелые провода в форме труб. Применяют также высокочастотные многожильные провода. Они состоят из тонких изолированных друг от друга жил, перевитых таким образом, чтобы каждая из жил поочередно занимала в поперечном сечении провода различные положения от его осп до периферии. При такой конструкции каждая Из жил находится в одинаковых условиях и токи в жилах равны
145
друг другу. Кроме того, в пределах каждой жилы вследствие малого ее диаметра поверхностный эффект проявляется не резко и плотность тока по сечению жилы различается незначительно. При очень больших частотах емкостная проводимость между жилами становится настолько значительной, что жилы оказываются как бы зам-
кнутыми между собой и поверхностный эффект проявляется, как в сплошном проводе. Кроме того, становятся весьма заметными потери энергии в изоляции между жилами. Поэтому при частотах выше 10® Гц многожильные провода не применяются. При частоте 50 Гц поверхностный эффект заметен только в проводах (шинах) достаточно большого поперечного
сечения. В медных проводах с диаметром меньше 1 см при частоте 50 Гц увеличением сопротивления вследствие поверхностного эффекта практически можно пренебречь.
На распределение переменного тока в проводе оказывают влияние токи соседних проводов. Это явление называют эффектом близости. Как показано на схематических картинах магнитных полей двух проводов с токами (рис. 3-24), различные части сечений
проводов сцеплены с неодинаковым числом магнитных линий. На
основании рассуждений, аналогичных приведенным для уединенного провода, можно прийти к заключению, что наибольшая плотность тока будет в тех частях сечения проводов, которые сцеплены с наименьшим числом магнитных линий.
Если токи в проводах направлены одинаково (рис. 3-24, а), наибольшая плотность тока наблюдается в наиболее удаленных друг от друга частях сечений; при различных направлениях токов (рис. 3-24, б) наибольшая плотность тока получается в наиболее близких друг к другу частях сечений проводов. Области наибольших плотностей тока отмечены на рис. 3-24 толстыми линиями. Вызываемая эффектом близости неравномерность распределения тока по
сечению проводов приводит к увеличению потерь энергии, к увеличению разницы в сопротивлениях проводов переменному и постоянному токам. Расчеты распределения тока по сечению проводника с учетом поверхностного эффекта или эффекта близости и сопротивления проводника относятся к задачам теории поля.
3-21. Параметры и эквивалентные схемы конденсаторов
При низких частотах конденсаторы можно рассматривать как емкости. При высоких частотах играют существенную роль потери энергии в изоляции. Эти потери растут с увеличением частоты тока гГзависят от”материала изоляции. Например; "бумажная"изоляция,
J46
которая применяется для конденсаторов, устанавливаемых в цепях низких и звуковых частот, оказывается непригодной при высоких частотах, так как потери энергии в ней приводят к недопустимому нагреву.
Энергия, преобразуемая в тепло в изоляции конденсаторов, подводится от источника питания, поэтому ток в конденсаторе опережает по фазе напряжение на его зажимах на угол | ср |, меньший л/2 (рис. 3-25). Угол, дополняющий | | до л/2, обозначают буквой
6 и называют углом потерь.
Для конденсатора, как для любого двухполюсника, можно составить две схемы замещения (рис. 3-26), в которых g и г учитывают потери энергии в диэлектрике.
Рис. 3-26.
Обычно угол потерь 6 очень мал. Величина tgS для различных частот и диэлектриков лежит в пределах от 10“4 до КУ4. При таких условиях g соС и г 1/coCj. Поэтому практически можно считать
У = (йС И 2=1/иС1 и так как
уг = 1, то
С = СЪ
т. е. емкости О и Сг обеих схем практически одинаковы.
Связь между г и g найдем из общих соотношений между сопротивлениями и проводимостями (3-36):
r==gly2^g/®2C2.
На практике конденсатор характеризуют параметрами 0 и tg 6. Для эквивалентной схемы (рис. 3-26, а)
g=bc |ctg<р | = соС tg6.
Отношение емкостной проводимости конденсатора к активной называют добротностью конденсатора
-------л -1 - , г г________________________________
VC“T - tie ‘S’*-!*
147
3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов
При низкой частоте, например при 50 Гц, эквивалентная схема индуктивной катушки состоит из последовательно соединенных сопротивления г и индуктивности L (эту схему можно, конечно, заменить схемой, состоящей из параллельно соединенных активной и реактивной проводимостей). Сопротивление обмотки катушки увеличивается с ростом частоты вследствие поверхностного эффекта и главным образом — эффекта близости. Поэтому величина QL =aL/r, называемая добротностью катушки, не пропорциональна частоте. В некотором диапазоне изменения частот величина QL остается почти постоянной.
При высоких частотах нельзя пренебрегать емкостями между витками. Эти так называемые межвитковые емкости условно показаны на рис. 3-27 пунктиром. Чем выше частота, тем меньше емкостные сопротивле
ния между витками. Токи в витках катушки получаются неодинаковыми. Найти распределение тока в катушке при высокой частоте нелегко. При достаточно высоких частотах из-за межвитковых емкостей эквивалентное реактивное сопротивление катушки может даже стать емкостным.
Применяемые на практике проволочные резисторы обладают всегда некоторой индуктивностью, и, кроме того, между отдельными витками имеется емкость. При низких частотах индуктивности и емкости практически никакого влияния не имеют и в расчетах не учитываются.
Рис. 3-27.
Глава четвертая
РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ
4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока
Уравнения, выражающие законы Кирхгофа в комплексной форме для цепей синусоидального тока (§ 3-7), имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока:
1У=0; (4-1)
У и=О или (4-2)
Только токи, напряжения, э. д. с. и сопротивления входят в уравнения (4-1), (4-2) в виде комплексных величин.
Все методы расчета цепей постоянного тока получены ня основе законов Кирхгофа. Вели повторить все рассуждения и выводы,
148
взяв за основу уравнения Кирхгофа в комплексной форме, то Для цепей синусоидального тока можно обосновать те же методы, которые были получены для цепей постоянного тока (такая полная аналогия расчетов цепей постоянного и синусоидальных токов имеется только при отсутствии взаимной индуктивности, см. гл. 6).
Для того чтобы установить связь между токами и напряжениями (э. д. с.), нужно на схеме указать положительные направления заданных и выбрать положительные направления для искомых токов, напряжений или э. д. с. При расчетах цепей постоянного тока искомые токи и напряжения получаются отрицательными, когда действительные направления тока или напряжения не соответствуют выбранным для них положительным направлениям. При расчетах цепей синусоидального тока действительные направления токов и напряжения периодически изменяются, поэтому произвольность выбора положительных направлений отражается только на их фазах. Изменение выбранного положительного направления на противоположное меняет фазу на л, что соответствует изменению знака комплексного тока или напряжения и изменению направления вектора на векторной диаграмме на 180°.
Несмотря на общность методов расчета цепей синусоидального и постоянного токов, расчеты цепей синусоидального тока значительно сложнее и обладают рядом особенностей. Показать специфику расчетов цепей синусоидального тока проще всего на конкретных примерах, которые и приводятся в последующих параграфах этой главы. Конечно, они не исчерпывают всего многообразия задач, которые могут встретиться на практике.
4-2. Последовательное соединение приемников
При последовательном соединении п приемников энергии с комплексными сопротивлениями Zr ,Z2, ••• , Zn эквивалентное или общее комплексное сопротивление цепи
п
Z=r + ix = ^Zk, (4-За)
1
причем
г=^гк; x=^xk. (4-36)
i i
Порядок расчета цепи с последовательным соединением элементов зависит от того, какие величины заданы и какие нужно найти.
Пример 4-1. На рис 4-1, а показана расчетная схема линии электропередачи с присоединенным к ней приемником Линия представлена последовательным соединением активного и реактивного сопротивлений гл и хл, а приемник — пассивным двухполюсником Индексами «1» и «2» обозначены величины, относящиеся сиответственно-к-началу и концу линии. Дано. г т = х7 — 6 0мщ1Д= 5500 В; _ *2 — бои кВт, cos q>2 — 0,91, <р2 > 0 Определить напряжение в начале линии Ut.
149
Решение. Представим пассивный двухполюсник эквивалентной схемой, состоящей из последовательного соединения сопротивлений г2 и х2 (рис. 4-1, б).
Ток в двухполюснике (и в линии)
/ = P2JIJ2 cos <р2= 100 А,
Сопротивления
г2=(72// = 55 Ом; r2= PJI-—-50 Ом;
x2~Vz‘i — г1 = 22г9 Ом; r1=r2-]-rJI = 56 Ом;
х1 = х2-|-х1 = 28,9 Ом; z1=j/r^ + %i = 63 Ом.
Искомое напряжение U, = г±1 = 6300 В.
На рис. 4-1, в показана векторная диаграмма напряжений и тока (заметим, что в курсе электрических сетей приводятся удобные для расчета формулы, позволяющие просто определять разность lj± — U2 = ДО' и находить IJX = U2 + + ДН).
Рис. 4-1.
Пример 4-2. Для той же цепи, что и в примере 4-1, дано: Ur = 6300 В, Рг = 560 кВт, U2 = 5500 В, Р2 = 500 кВт; I = 100 A; «ft > 0; <р2 > 0. Определить гл и хя.
Решение. Сопротивление
G = (Pi-^)№ = 6 Ом
Сопротивление хп определяется по аналогичной формуле, но предварительно надо найти и Q2.
S1=t/1Z = 630 кВ • A; S2 = (72/ = 550 кВ-А;
Qx = УSf — Pf = 288 квар; Q2 = — Pi = 228 квар; хл = (Q, — = 6 Ом.
Пример 4-3. Для той же цепи, что и в примере 4-1, дано: г„ = х„ = 6 Ом; иг = 6300 В; U2 = 5500 В; Р2 = 500 кВт; <р2 > 0. Определить ток в линии I.
Решение. Для решения задачи составим уравнение
L/i=£/2 + ZJ. (а)
Примем начальную фазу напряжения О2 равной нулю, тогда U2 == 5500 В.* Начальная фаза тока ф; = ф„2 — <р2 = — <р2 и, следовательно, / — I — ф2. Комплексное напряжение й± = 6300 Z фи1.
Подставим в уравнение (а) известные величины
6300 £, фит= 5500+(64-/6) / Z—<р2
150
или
6300 cos фй14-/6300 sin фи1 =5500 4-6/ cos фг 4- 6/ sin ф2+/6/ cos <p2 — /6/ sin <p2.
Из этого уравнения с комплексными величинами получаем два уравнения (для вещественных и мнимых величин):
6300 сов фй1=5500 4- 6/ cos ф2+6/ Ч-'2> (б)
6300 sin = 6/ cos ф2 — 6/ sin ф2. (в)
Эти два уравнения с геометрической точки зрения представляют равенства проекций вектора й1 суммам проекции векторов Л2 и ZJ на две взаимно перпендикулярные оси (ось вещественных и ось мнимых величин).
Находим:
/соЭф2=/а = Р2/{/2=91 А.
Подставляя значение / cos ф2 в уравнения (б) и (в), получаем:
1050 cos фй1 = 1008 4* I sin ф2; 1050 sin фй1 = 91 — I sm ф5 или
10502=(1008 + / sin ф2)2 + (91 — 1 sin ф2)2, откуда
/япф2 = 7р^42 А; / = У Z|+^=V 912 4- 422 100 А.
4-3. Параллельное соединение приемников
При параллельном соединении п приемников энергии с комплексными проводимостями Fj, Y2, , Y„, эквивалентная или
общая комплексная проводимость
(4-4а) 1
причем
Я = 2^: & = (4-46)
1 1
В случае двух параллельных ветвей их эквивалентное или общее комплексное сопротивление определяется по формуле
7 — Л — 1 — 1 — ^1^2 /д с\
V ~ *44*4 ~ 1/ZX41/Z3 - Zx4Z2 • I*
Пример 4-4. Резистор с сопротивлением и катушка с сопротивлением г2 и индуктивностью А2 соединены параллельно (рис. 4-2, а). В цепь включены амперметры. Дано: = 20 Ом, показания амперметров /х = 2 А, /а = 3 А, / = ~ 4 А. Определить параметры катушки г2 и х2 = <лЬ2.
Сопротивлением амперметров пренебречь.
Решение. Сначала рассмотрим графический способ.
Найдем напряжение, приложенное к цепи, U — = 40 В. Выберем масш-
табы для напряжения т^, В/мм, и для тока mh А/мм. Отложим векторы [! и /х (рис. 4-2, б). Они совпадают по направлению, так как ток /х совпадает по фазе с напряжением (]. Построение векторов 1 и /2 основывается на том, что / = /t 4 4 и что ток /2 отстает по фазе от напряжения С. Проводим из начала и-конца вектора 4 дуги, радиусы которых в выбранном масштабе равны токам I и /2. Точка В Пересечения этих дуг определяет положение концов векторов 7 и /2.
151
Отметим, что существует еще одна точка пересечения этих дуг— выше вектора U (на рис. 4-2, б эта точка не показана) Она не может служить для определения положения концов векторов / и /2> так как вектор /2, проведенный в эгу точку, опережал бы вектор напряжения U, в действительности же он отстает от вектора U.
Разложим вектор напряжения (J на два составляющих вектора, один из которых, Ua, совпадает по направлению с вектором 7,, а другой, 7/р, ему перпендикулярен Это—векторы активной и реактивной составляющих напряжения на катушке
Находим действующие значения — m( OD н Up — m^DG и, наконец, | вычисляем:
Г2~^а/^2! ^2 = ^p/^2‘
Теперь рассмотрим аналитический способ решения на основе векторной диаграммы.
Рис. 4-2.
Векторную диаграмму (рис. 4-2, 6) строим качественно — не в масштабе. Она нужна только для того, чтобы наглядно представлять тригонометрические соотношения между ее отрезками. Из треугольников ОАВ имеем:
/2 = 7f -j- 7= — 27jZ2 cos (180=* — ф2),
или
42 = 22-р32-}-2 • 2 • 3cos <р2,
откуда
cos =0,25; ф2 = 75°32'; sin ф2 = 0,969;
г2=^5-==^212Я-=3,3 Ом; x2 = Up/I2 = U sin ф2/72= 12,9 Ом.
*2 '2
4-4. Смешанное соединение приемников
Токи в цепях со смешанным соединением приемников проще всего рассчитываются путем преобразования схем или методом подобия (методом пропорциональных величин). Ниже иллюстрируется первый метод. Второй метод поясняется в § 4-6.
Пусть заданы сопротивления всех элементов схемы (рис. 4-3) • и напряжение О на ее входе; требуется определить токи во всех ветвях.
Заменим параллельно соединенные приемники энергии одним_^^ эквивалентным с проводимостью Y' = У? + Ys + У4 или сопро-152
тивлением Z' = 1/V'. После этого преобразования схема состоит из двух последовательно соединенных сопротивлений Zv и Z'. Ее эквивалентное сопротивление ZB = ZY + Z'.
Ток в неразветвленной части цепи
Напряжение на разветвлении
U' — Z'ii.
Токи в параллельно соединенных приемниках 72 = /7'/Z2; 13 = U','Z3,
На практике встречаются задачи и по расчету параметров цепи, удовлетворяющих различным поставленным условиям.
Рис. 4-3.
Рис. 4-4.
Пример 4-5. Даны сопротивления (рис. 4-4) Zx = 200 + j 1000 Ом и Z2 = = 500 + j 1500 Ом. Каково должно быть сопротивление г3, чтобы ток /2 отставал от напряжения U по фазе на л/2?
Решение. Сначала наметим ход решения.
Положим начальную фазу напряжения Uравной нулю,тогда U=U. Затем методом, указанным в начале параграфа, найдем в общем вцд,е выражение для тока /2. Ток /2 будет отставать по фазе на л/2 от напряжения U = U в том случае, если комплекс /, будет отрицательной мнимой величиной. Это и является условием для определения сопротивления г3.
В соответствии с намеченным планом решения находим эквивалентное сопротивление цепи
Z = Zi+Z2r3/(Z2 г3),
ток в неразветвленной части цепи
A=i//z, напряжение на разветвлении
и, наконец, ток
, __ Ubc __ гз , г,л _________77___________
Z2 Z2-|-r3 1 Z2—z3 Zi-]-Z2r3/(Z24-r3)
= rsC
700r3 — 1 400 000+j (800 000 + 2500r3) ‘
Числитель этого выражения — вещественный. Комплекс /2 будет отрицатель-Д^Д-'чтимым. сети з тамсиатслъ—= недащительный-йгнилтын,' те. при у^човни-гз — 1 400 000 = 0 или при г3 = 2000 Ом.
153
Пример 4-6. Определить реактивные сопротивления х3 и х4 (рис 4-5, а и б), при которых приемник с сопротивлением Z2 = r2 + jx2 получает максимальную мощность от источника с внутренним сопротивлением Zx = + jXt
Решение. Вся активная мощность, отдаваемая источником, потребляется в приемнике (в сопротивлении г2), так как остальные сопротивления — реактивные. Поэтому необходимо (см. § 3-19), чтобы входное сопротивление каждого пассивного двухполюсника (на рис. 4-5 обведены пунктиром) было равно сопряженному *
комплексному внутреннему сопротивлению источника Zt = — jxlt т. е. для
схемы рис. 4-5, а нужно, чтобы
№4
/44(^ + №) _ _
Га+У (^a + ^i)
и для схемы рис. 4-5, б
1Г2 У (Х2 *з)1 jx4 _ г .
Г2 + У (*2 + Х3 + Xi) 1 1
Каждое из полученных уравнений для комплексных величин можно записать в виде двух уравнений — для вещественных и для мнимых величин, из которых и определяются х3 н л:4.
Реальные элементы цепи обладают не только реактивными, но и активными сопротивлениями, поэтому приведенный расчет согласования сопротивлений
Рис. 4-5.
приемника и источника питания является приближенным.
Пример 4-7. Какое соотношение должно быть между сопротивлениями Zlt Z2, Zs н Z4 мостовой схемы (рис, 4-6),
Рис. 4-6.
чтобы мост находился в равновесии, т. е. чтобы ток /0 в диагонали моста был равен нулю? Заметим, что в качестве индикатора, по которому судят об отсу i-ствии тока в диагонали моста, применяют: телефон, вибрационный гальванометр н различные электронные приборы.
Решение. Ток в диагонали моста отсутствует, если = 0, т. е. когда Zili=zjz и z3i4—z4i2e
Разделив эти равенства друг на друга, имеем:
Z^Z^ZJZt,
или
21 , , , г2, . ч
—- Z Iф!----И— —------------фрт
г3 г4
154
или
г1/гя=?2/г4; <Р1+ф4=ф2+<Рз.
Зная три комплексных сопротивления, при которых наблюдается равновесие моста, можно определить четвертое комплексное сопротивление.
4-5. Сложные разветвленные цепи
Выбор наиболее рационального метода расчета сложной разветвленной цепи основан на учете особенностей схемы и поставленной задачи. Все соображения по выбору расчетных методов для цепей постоянного тока применимы и к выбору расчетных методов для цепей синусоидального тока.
Следует иметь в виду, что после преобразования соединения пассивных элементов треугольником в эквивалентное соединение звездой или обратно комплексные сопротивления преобразованной схемы могут получиться с отрицательными вещественными частями, т. е. отрицательными активными сопротивлениями. Эти сопротивления имеют чисто расчетный смысл. Активная мощность г/2 такого сопротивления отрицательна и, следовательно, электромагнитная энергия в нем не поглощается, а генерируется. Суммарная активная мощность во всех ветвях преобразованной схемы пассивной цепи, конечно, не отрицательна и равна активной мощности в исходной схеме.
Пример 4-8. На рис 4-7, а показана часть разветвленной цепи, в которой две одинаковые катушки и конденсатор соединены треугольником Дано: г = =
Решение. Комплексные сопротивления звезды
^12^31 __ 0 +/) (1 -Н)
^12 + ^23+^з1 2—/
0,4_|_/0,8 Ом;
__ — /3(1 -ру)
2 + ^23 + ^31 2 — /
2,25 — /0,6 Ом;
155
Эквивалентная схема представлена на рис. 4-7, б, в которой rt = — 0,4 Ом; г2 = г3 ~ 2,25 Ом; = 0,8 Ом и л:2 = хв = — 0,6 Ом.
Пример 4-9. На рис. 4-8 представлена эквивалентная схема цепи, встречающейся в релейной защите (фильтр-реле обратной последовательности) Дано: xCi = xC4 = 260 Ом; г2 = 450 Ом; г5=150Ом; г3=173 0м; xi3 = 300 Ом.
К зажимам а—J) и с — d приложены напряжения UаЬ = Ucb~ Ю В, причем напряжение йсЬ отстает по фазе от напряжения Uab на л/3 Определить
напряжение jjde (напряжение на зажимах реле)
Решение Рассмотрим ветвь de как приемник, а остальную цепь как активный двухполюсник.
Рис. 4-9,
Рис. 4-8.
Входное сопротивление активного двухполюсника
ZBx = - /ХС1Г2/(Г2 - ^С1) - / Ws - lxd) = 225 “ /260 Ом-
Определим напряжение холостого хода Udex.
Udbx=rJlx=~^-=7,5+j4,33 В;
Г2~~‘ХС1
гг > ~~1XcJJcb .о ес „
^4бх — — /*cJbx = r _jx--/8’66 В’
ГЪ ‘ХС4
Ude^Odbx-Uebx = 7,b+i\^\Z Z 60е В.
Искомое напряжение (по теореме об активном двухполюснике) ^=('-з+/х£3)/з=-^^^- = 12,96 4 114=50' в.
Пример4-10. На рис. 4-9 представлена схема цепи, встречающаяся в релейной защите (фильтр-реле обратной последовательности). Дано: /у = г4 = 185 Ом; xL2 “ хСз ~ 32®®м’XU = *С4‘ Кзажимам a — cnb —dприложены напряжения Vac =г Ubd ~ Ю В, но йас отстает по фазе от Ubd на л/3 Определить напряжение Ucd.
Решение.. Проще всего задача решается методом узловых потенциалов» Полагаем Ubd = Е6= Uba = 10 В, тогда йас_ = £в = 10 Д — 60° В Принимаем фа = 0, тот да фа = 10 В, tpa = фс + £в = фс + 10 Z — 60°. Нужно составить одно уравнение для определения фс
Будем исходить из следующего уравнения для токов
-------=--------- ---Л——-------------------=-----------
156
или
Ф^ —Ф<? , Фс" Ф^ Фб"Фс , Фб —Фа 1XL2 'l+ 1 (xU~XCl) -1XC3 rl ’
или фс+10£-№ фг 10—фс 10—(tpc-|-10 /. —60°) 7320 |" 185 — /320 185
откуда искомое напряжение
{7сй=фс= 10 / 60° В.
4-6. Топографические диаграммы
Для суждения о значениях напряжений между различными точками схемы и их фазах удобны топографические диаграммы. Они представляют собой диаграммы комплексных потенциалов, причем каждой точке схемы соответствует определенная точка на топографической диаграмме. Точке отсчета, потенциал которой принят равным нулю, на топографической диаграмме соответствует начало координат.
Рнс. 4-10.
Рис. 4-11.
Построим качественно топографическую диаграмму для схемы, представленной на рис. 4-10. Отложим вектор тока I в произвольно выбранном направлении (рис. 4-11, о). Примем потенциал точки g равным нулю (сре — 0) и определим потенциалы остальных точек.
Будем обходить схему, начиная от точки g, навстречу положительному направлению тока. Потенциал точки f больше потенциала точки g на величину напряжения на индуктивности: Ф/ = +
4- Так как <fg = 0, то потенциал <р/ изобразим вектором foLI. Конец этого вектора обозначим буквой f, так как он определяет потенциал точки [. Потенциал точки d выше потенциала точки f на величину напряжения на сопротивлении г: cpd — фу Д- rt. Откладываем от конца вектора ф/ вектор rt. Конец вектора rl обозначим буквой d, так как он определяет потенциал точки d. Действительно, если провести вектор из начала координат к концу вектора /1, то он будет равен сумме векторов j®Ll + rl, а эта сумма
-равна ф;(-. = =----------~ =---- =
157
Аналогично находим фй = фй — /7/соС. В соответствии с этим равенством проводим из конца вектора ri (точка d) вектор — ji/(nC. Конец вектора — ji/caC обозначим буквой Ь, так как он определяет потенциал точки Ь. От конца вектора — ji/aC откладываем вектор К/ и получаем последнюю точку а топографической диаграммы, определяющую потенциал фо = Ф» + Ri или напряжение C/ag = = Фа — Фд = Фа- Электродвижущая сила источника Ega = Cag.
Необходимо обратить особое внимание на направления векторов напряжений на топографических диаграммах. Векторы напряжений направлены относительно точек топографической диаграммы противоположно положительным направлениям напряжений относительно соответствующих точек схемы. Так, например, вектор напряжения C/af (положительное направление на рис. 4-10 от d к f) направлен на топографической диаграмме (рис. 4-11, б) от точки / к точке d, а вектор напряжения Дуй (положительное направление от f к d) направлен на топографической диаграмме (рис. 4-11 ,б, пунктир) от точки d к точке f. Это соответствует известному правилу вычитания векторов, согласно которому вектор Odf, представляющий разность векторов ф^ — фу, направлен от конца вектора фу к концу вектора ф^, а вектор Ofa, представляющий разность векторов фу — фй, направлен от конца вектора к концу вектора фу. Учитывая сказанное, на топографической диаграмме можно не указывать направлений векторов напряжений, а ограничиться только обозначением точек.
По топографической диаграмме можно определить напряжение между любыми точками схемы. Для этого достаточно соединить соответствующие точки топографической диаграммы отрезком прямой и придать этому отрезку надлежащее направление. Так, вектор напряжения tfbf представлен на топографической диаграмме (рис. 441, а) отрезком прямой между точками f и Ь, взятыми в направлении от [ к Ь.
В отличие от векторов напряжений векторы э. д. с. направлены относительно точек топографической диаграммы одинаково с положительными направлениями э. д. с. относительно соответствующих точек схемы. Так, вектор э. д. с. Ega (положительное направление на рис. 4-10 от точки g к точке а) направлен на топографической диаграмме (рис. 4-11, а) тоже от точки g к точке а.
Рассмотрим еще один пример. Пусть даны все параметры схемы рис. 4-12 и напряжение С на ее зажимах. Требуется найти токи в ветвях и построить топографическую диаграмму.
Эта задача может быть решена аналитически обычным путем: сначала схема преобразуется к простейшему виду, затем определяется ток /3, потом находятся токи 1г и /2 и, наконец, вычисляются потенциалы всех точек и строится топографическая диаграмма. Однако расчет значительно упрощается, если воспользоваться методом подобия.
Задавшись произвольным значением комплексного тока Д, -^например, положив — И вычислим напряжения пД и ЫЕЕ.—
158
Затем отложим на диаграмме векторы Д, гуД и /со/^Д (рис. 4-13). Сумма векторов гЛД + равна вектору напряжения Оьа. Затем найдем ток Д = f76d//coL2. Вектор Д отстает от вектора Сы на угол л/2. Ток Д — Д + Д определим или аналитически, или графически. Из точки b диаграммы проводим вектор напряжения __j!-j<вС2 под углом л/2 к вектору Д в сторону отставания. Конец этого вектора определяет на топографической диаграмме точку а.
Рис. 4-12. Рис. 4-13.
Проводим из точки d вектор — г3Д, его конец определяет на топографической диаграмме точку Д так как фу = фй — г3Д. Вектор напряжения 17 af может не совпадать по значению с заданным напряжением 17. Чтобы привести в соответствие построенную диаграмму с заданным напряжением, достаточно изменить масштабы напряжений и токов в отношении U/Uaj.
4-7. Дуальность электрических цепей
Если сравнить между собой структуры и методы решения уравнений узловых потенциалов и контурных токов, то обнаружится много общего. В частности, это видно при сравнении операций по преобразованию схем путем уменьшения числа узлов и числа контуров. Все математические выражения получаются сходными по форме записи, причем проводимостям в уравнениях узловых потенциалов соответствуют сопротивления в уравнениях контурных токов.. Отмеченное сходство можно обобщить и применить, например, для Целесообразной замены схем при расчетах режимов сложных электрических цепей.
Пусть электрическая схема произвольной конфигурации планарного вида (без пересекающихся ветвей, расположенных на плоскости) имеет в своем составе у узлов и к независимых контуров и пусть Положительные направления контурных токов выбраны так, что Падения напряжений в общих ветвях входят в контурные уравнения с отрицательными знаками \ Предположим, что число независимых
1 Если контурные токи в общих ветвях имеют одинаковые направления, то соответствующие составляющие напряжений входят я контурные уравнения ° положительными знаками.
159
узлов (у — 1) равно числу независимых контуров к, и сравним комплексное уравнение контурных токов для любого s-ro контура
2 zSJis- 2 zSJi}zSJjSJt's, (4-6)
7 = 1 ; = 1 7 = 1
/ r-s K.
где У, ZSJ — собственное контурное сопротивление s-ro контура 1 1
с уравнением узловых потенциалов для любого s-ro узла
у у . у .
У КуФз I 5Zsy<P/ = A+ У YSJES} = J s, (4-7)
7 = 1 7=1 7 = 1
]^S f^S
У
где У Y SJ — сумма проводимостей всех ветвей, прнсоединен-(7 = 1
7/'-S
ных к s-му узлу.
Легко установить полное сходство в записи уравнений (4-6) и (4-7). Из сходства уравнений следует, что для любой заданной планарной схемы можно составить другую электрическую схему, для которой узловые уравнения типа (4-7) будут идентичны контурным уравнениям (4-6) первой схемы. Такие две схемы называются дуальными. Контурные токи для первой схемы идентичны потенциалам соответствующих узлов второй схемы; общие сопротивления контуров первой схемы идентичны проводимостям ветвей, включенных между соответствующими узлами второй; суммарные э. д. с. в контурах первой схемы идентичны узловым токам второй; токи в ветвях, обусловленные источниками тока первой схемы, идентичны э. д. с. в соответствующих ветвях второй. Иначе говоря, справедливы следующие взаимные соответствия:
Д- —zsj Кз^; Es<=-Js, JSJ^ESJ.
При этом общее число узлов второй дуальной схемы на единицу больше числа независимых контуров первой схемы.
Поскольку возможности преобразования «узловой» схемы несколько большие, чем для «контурной» (например, можно преобразовать многолучевую звезду в эквивалентный многоугольник, но не наоборот), то иногда проще произвести расчет режима узловой схемы, а затем полученное решение представить через режим (токи, напряжения) контурной схемы.
Рассмотрим в качестве примера схему на рис. 4-14, а. Для этой схемы при выбранных положительных направлениях контурных
токов запишем уравнения:
(Л + Z6 + Z, + Z'4) Л - (Z4 + ZJ) /, - Z6/3 = + £4;
—• (Zi-]-Zi) /j-f-(r2 + Z4 + Z4 -|-ZB) /2 —- Z5IS^— Ё2 —
— ZeIi- Z5l2-{- (Za -j- Z5-|-'Z6) —
(4-8)
_ гдёД2^"= /wL h Z4 — 1//cuC.
160
Заменим в уравнениях (4-8) сопротивления — проводимостями,
контурные токи — потенциалами, а э. д. с. — токами источников тока. Тогда получим систему уравнений:
(izj У6 У4) Ф± — (У4 + А) Ф2 — УбФз=-^ 1 + А;
— (У4 + y'i) Ф1 + (§2 + У 4 + У 4 + У5) Ч 2 — УбФз ~- А — j
— УвФ1 ~~ АФгА (^з + У в) Фз = -^ 3>
(4-9)
Этой системе уравнений соответствует электрическая схема, показанная на рис. 4-14, б и дуальная схеме, изображенной на рис
Таким образом, при выполнении отмеченных выше соответствий и численных равенств можно, например, найти потенциалы в схеме
6 Основы теории цепей
161
с проводимостями, которые будут равны контурным токам в схеме с сопрртивлениями и наоборот. Кроме того, соответствие У Z означает, что если у первой схемы сопротивление некоторой ветви Z = г + jxt, причем г и xt включены последовательно, то соответствующая проводимость второй ветви У g jbc, причем g и be включены параллельно и емкостная проводимость Ьс численно равна индуктивному сопротивлению xl (рис. 4-15, а и б).
Для построения дуальной схемы (например, для показанной на рис. 4-14, а) можно пользоваться графическим способом. Внутри каждого независимого контура отмечается узловая точка дуальной схемы (на рис. 4-14, а отмечены узлы 1, 2 и 5), общее число которых
равно числу независимых контуров. Зависимый узел указывается во внешней (по отношению к заданной схеме) области (на рис. 4-14, а узел 4). Затем между узлами проводятся линии (пунктирные на рис. 4-14, а), каждая из которых пересекает один элемент заданной схемы. Например, на рис. 4-14, а четвертая ветвь состоит из последовательно соединенных двух со-
противлений и одного источника э. д. с., поэтому между узлами 1 и 2 проведены три пунктирные линии.
Для определения направлений токов источников тока дуальной схемы обратимся к уравнениям (4-8) и (4-9). Из сопоставления уравнений видно, что если при обходе контура заданной схемы (рис. 4-14, а) по направлению контурного тока э. д. с. входит в уравнение (4-8) с положительным знаком, то ток источника тока в соответствии с уравнением (4-9) в дуальной схеме (рис. 4-14, б) будет
направлен к узлу, отмеченному внутри этого контура.
Следует особо подчеркнуть, что после графического преобразования полученной дуальной схемы (рис. 4-14, б) должна получиться исходная схема (рис. 4-14, а); это позволяет проверить правильность построения дуальной схемы (рис. 4-14, б).
Изобразим для большей наглядности все ветви заданной мостовой схемы (рис. 4-14, а) отрезками линий (рис. 4-14, в); дуальная схема, изображенная на рис. 4-14, в пунктирными линиями, получилась такой же конфигурации. Такие схемы называются само-дуальными. На рис. 4-14, г изображены две самодуальные схемы
с восемью ветвями, для которых можно написать четыре независимых контурных и четыре независимых узловых уравнений.
Пример 4-11. Составить схему, дуальную показанной на рис. 4-16, а. Векторы Ё1г E,nJ совпадают по фазе.
Решение. При выбранных положительных направлениях контурных токов /j и /2 запишем контурные уравнения (4-6):
(Г1 + Гв. + Гз) 4 — — —rsj у
~—ге4.'Т(Г2-)-Г1-{~Ге) 4 = — Ёо — Гjjy =_
162
Им соответствуют узловые уравнения
tei + ft+gs) Ф1— &'р2= Л — Д— j3;
— ёаФ1 + (& +^4+^5) ф2= — А — giE — — j?— Ji-
После подстановки в обе системы уравнений числовых значений получим: lO/j —5/2 = 25, —5/1+10/2=~35;
Юф! — 5ф2=25; —5ф1-|-10ф2 =—35 при фз = 0.
Последним двум уравнениям соответствует дуальная схема на рис. 4-16, б. Заменив узловые токи соответствующими э. д. с., получим неразветвленную
Рис. 4-16.
схему (рис. 4-16, в) с током I = 20 А и с потенциалами узлов -гг = 1 В, о2 = — ЗВ (при ф3 = 0), что при переходе к заданной схеме дает контурные токи Д = 1 А и /2 = — 3 А.
4-8. Сигнальные графы и их применение для расчета цепей
Для исследования сложных электрических цепей и систем, в особенности с обратной связью, полезно наглядное изображение уравнений состояния с учетом влияния всех параметров цепи. Такую наглядность дает сигнальный (направленный) граф, представляющий собой графическое изображение соотношений между переменными величинами заданной системы уравнений. Однако достоинство таких графов состоит не только в их наглядности; применение сигнальных графов во многих случаях позволяет определить зависимость любой переменной величины — сигнала через остальные переменные непосредственно по конфигурации графа.
Рассмотрим примеры построения сигнальных графов для электрической схемы рис. 4-17, а. Пользуясь методом контурных токов, запишем для этой схемы уравнения:
ДпА—д^2==Д1> 1
-Z/.+Z.4—z»/.}<4'10>
где Zu = Zr + Z; Z22 = Z + Z3 + Z3.
6*
163
Ill
Из уравнений (4-10) следует, что j _ I z f .
У1—у Г ’у '2,
Z11 Z11
/ ______ Z3 : Z j
7 J + 7 ^22 ^22
(4-11)
Последним уравнениям соответствует сигнальный граф (рис. 4-17, б), представляющий собой совокупность узлов и направленных ветвей (имеющих определенное направление).
Пользуясь методом узловых потенциалов и принимая ф3 = 0, получаем для той же схемы (рис. 4-17, а) выражения, определяющие потенциалы фх и ф2 узлов 1 и 2 в виде
Ф1==^1 JZ + y2 Ф2; Ф2 = у~/+^Ф1. (4-12)
1 11 1 11 1 22 1 22
где Уи = Ух + У + У2 и У22 = У2 + У3.
Этим уравнениям удовлетворяет сигнальный граф, изображенный на рис. 4-17,в. Легко заметить, что уравнения (4-11) и (4-12), представленные на рис. 4-17 сигнальными графами, записаны в форме «причинно-следственных» отношений, когда каждая переменная выражена в явном виде через другие переменные.
Введем дополнительные термины, применяемые для сигнальных графов.
Истоком сигнального графа (истоком) называется узел, от которого направлены все примыкающие ветви. Истоку (обозначен жирной точкой) соответствует независимая переменная, представляющая обычно фйзиче-скую причину. На рис. 4-17, бив изображены истоки для источника э. д. с. Ёг и источника тока J.
Стоком сигнального графа называется узел, к которому на-
правлены все примыкающие ветви и который изображает зависимую переменную (сигнал электрической цепи).
Ветвью сигнального графа называется топологическое изображение направленным отрезком элемента схемы или зависимости между переменными (токами, э. д. с., потенциалами и т. д.). Например, на рис. 4-18 показано, что между узлами k и / существует передача сигнала от узла k к узлу j. На рис. 4-17, б и в показаны направленные графы, каждый из которых имеет четыре ветви.
164 .
Коэффициент передачи ветви графа, или, короче, передача ветви характеризует интенсивность передачи сигнала по этой ветви и в общем случае выражается в виде ajk = х}1хк или Xj = ctjkXk (рис. 4-18), где хк и х} — сигналы в узлах k и /, а а — передача сигнала из узла k в узел /.
Истоки содержат только выходящие ветви, а стоки — только входящие. Любой другой узел, кроме истоков и стоков, соответствует, как уже отмечено, одной из зависимых переменных системы уравнений и может быть назван промежуточным узлом. Передача ветви может быть размерной или безразмерной величиной. Например, в сигнальном графе на рис. 4-17, б передача от источника э. д. с. имеет размерность проводимости; все остальные передачи безразмерные. В сигнальном графе на рис. 4-17, в передача от источника тока j а.
имеет размерность сопротивления, а осталь-ные передачи безразмерные.
Узловой сигнал в любом узле, кроме Рис 4 18
узлов истока, равен сумме сигналов, поступающих по ветвям, направленным к этому узлу. Ветви, направленные от узла, не влияют непосредственно на его узловой сигнал, но создают сигналы в других узлах, к которым они направлены.
В дальнейшем будем пользоваться без специальных оговорок более кратким термином «граф» вместо сигнальный граф.
Применение законов Кирхгофа, контурных и узловых уравнений для построения сигнальных графов. Для построения графа на основании законов Кирхгофа следует придерживаться определенной последовательности. Сначала выбирается дерево, содержащее ветви с источниками э. д. с. схемы и без источников э.д.с., но не содержащее источников тока. Так, на рис. 4-19, а показана мостовая схема и для построения графа этой схемы выбрано дерево из трех ветвей (рис. 4-19,6) с произвольными положительными направлениями напряжений Ог, О2 и Os. Затем напряжения ветвей связи выражаются через напряжения ветвей дерева, а токи ветвей дерева — через токи ветвей связи; в результате получаются уравнения
= £>5=б?24-^3; б’6=-г\ + {72; (4-13)
токи ветвей связи
Л = h = U&Y&- = (4-14)
11 токи ветвей дерева
А = Л"ЬЛ>; Л = —Л—7е; 73 = /4— 75. (4-15)
Наконец, напряжения на ветвях дерева выражаются через сопротивления, токи и э. д. с. ветвей:
= — bi, 12 — Zj2—L 2, ^3~Y.gis’ (4-16)
165
Последовательность построения узлов и ветвей графа соответствует последовательности записи уравнений (4-13) — (4-16). На рис. 4-19, в изображен граф для заданной мостовой схемы, полностью удовлетворяющий приведенным системам уравнений.
Для иллюстрации построения графов методом узловых потенциалов и методом контурных токов выберем схему, показанную на рис. 4-20, а.
Пользуясь методом узловых потенциалов, запишем для этой схемы уравнения.
Ф1Л1-42^1=7;
— ФгУа + ^гУгг ~~ Ф3У5 —0, -ф2УБ+Ф3У33-ДУ6,
(4-17)
где Уи=У1 + У4; У22=-У?+ Ь+b; Г3т=У3 + УБ+У6.
166
Цз уравнений (4-17) находим:
Ф1=у--/ + уАФ2: ф2= уФ14~/ф3; Г 11 1 11 1 22 1 22
У6 Л . У5 •
Ф3=у7~£ + у-ф2.
г 33 ' 1 33
(4-18)
Уравнениям (4-18) удовлетворяет граф, показанный на рис. 4-20, б.
Пользуясь методом контурных токов, запишем для схемы рис. 4-20, а уравнения
244/4 Z275 = J Z^‘
4~ 25575 Zj§ — 0; z3i3 -j- z№i\=— ь,
(4-19)
где Z44— Z, -|- Z4 4 Z2; Z55 — Z2 Z5 4- Z3; Z66 — Z3 4- Z§. Из этих уравнений получим:
j __ j 1 j . j ________ j 1 Zs f .
'4— 7 J “Г 7 J5, /5—-7~'4"i 7
^44 ^44 ^55 ^55
/е=--71-£4-Э-/5.
^66 Л66
(4-20)
На рис. 4-20, в построен граф, удовлетворяющий уравнениям (4-20).
Таким образом, в зависимости от применяемого метода для составления уравнений получаются различные графы для одной и той же схемы. При этом легко убедиться в том, что графы, построенные на основании законов Кирхгофа, сложней графов, построенных на основании уравнений Для контурных токов или узловых потенциалов.
Преобразования графов и их связь с преобразованиями электрических схем. Для получения правил преобразо-вания графов рассмотрим ряд примеров.
Исключим из системы
Уравнений (4-11) ток /2, а из-т - —I -. т
системы уравнений (4-12)— z3/zss Ig
потенциал ф2; в результате е>
после__элементарных пре- -----Рис. 4-20.
167
образований получим:
/ __ Z2 / I Ё ZZ3 J.
11 — 7 7 11 ' 7 7 7 ’
^11^22 ^11 ^11а22
Y* . , a Yt . Y2
<Рх = ‘Pl + Е Y + Y~Y~
1 11* 22 * 11 * ll1 22
(4-21)
Полученным уравнениям соответствуют графы, показанные на рис. 4-21. Из сравнения первых из уравнений (4-11) и (4-21), а также сопоставления графа, приведенного на рис. 4-17, б, с показанным на рис. 4-21, а следует, что операция исключения контурного тока /2 из системы контурных уравнений приводит к устранению контура в заданной схеме (рис. 4-17, а) и узла с током /2 в графе рис. 4-17, б. В результате исключения этого узла получается в графе (рис. 4-21,а) простейший контур, состоящий из петли с передачей, равной произведению передач ветвей Z/Zn и Z/Z22, и ветви от источника тока
Рис. 4-21.
J с передачей, равной произведению передач ветвей — Z3/Z22 и ZIZU. Исключение потенциала ф2 в графе на рис. 4-17, в приводит к аналогичному результату, что непосредственно следует из сравнения графов рис. 4-17, в и рис. 4-21, б. ч
Таким образом, решение уравнений соответствует преобразованию соответствующих графов. Такие простейшие преобразования уравнений и графов показаны в табл. 4-1. Исключение неизвестных из системы уравнений автоматически приводит к исключению соответствующих узлов в графе.
Например, исключив из системы уравнений (4-17) или (4-18) для схемы рис. 4-20, а и графа, показанного на рис. 4-20, б, потенциал фа, получим:
Ф1 у J у у Ф1 Ч у у Фз>
1 11 1 111 22 1 11г 22
/« Л , , /5/4 •
срз^гв-Е +
1 33 1 22 1 33 * 22 1 33
Этим уравнениям соответствует граф, изображенный на рис. 4-22, не имеющий узла с потенциалом ф2. При этом исключение второго узла привело к тому, что в узлах с потенциалами ф4 и ф3 появились пеТли с перёдачаТшГравньши произведениям передач ветвей, кото
168
Простейшие преобразования графов
Таблица 4-1
Заданный граф Эквивалентный граф Уравнения преобразования графа
га Н 1 * а +Ъ c + d %! — сх.> + dx$ — (с -|- d) а-2; х2=ах-i+bxt = (а + Ь) xt
а & -»хз '‘-г аЪ 'в3!3 Л-2 —’ Л-g bx^i Xg —— CtbX-^
ъ У*3* аЬ-^я3'г £ £ II II II л о* q £ II II " © а ,
*s'nc Хд CZVj —р Ьх2^ х3=сх& ~ acxi + Ьсх%
рые непосредственно примыкают к первому и третьему узлам, а также изменились передачи ветвей между узлами ф( и ф3.
Прежде чем перейти к расчету режимов в линейных цепях при помощи графов, необходимо дать определения: пути, передачи пути, контура и передачи контура в сигнальных графах.
Путь непрерывная последовательность ветвей (в указанном направлении), вдоль которой каждый узел встречается не более
169
одного раза; передача пути П — произведение передач ветвей вдоль этого пути (имеющего определенное направление); контур — простой замкнутый путь (имеющий определенное направление), который начинается и заканчивается в одном и том же узле и вдоль которого любой другой узел этого контура встречается не более одного раза за один обход контура; передача контура L — произведение передач ветвей в этом контуре.
В приведенных выше примерах были показаны некоторые преобразования графов, вытекающие преимущественно из простых преобразований системы контурных и узловых уравнений схемы. Поскольку метод графов может быть применен для анализа и других систем (не электрических), то рассмотрим еще один случай преобразования в более общей форме.
На рис. 4-23, а изображен граф с четырьмя ветвями и одним контуром. Исключая из этого графа узел с сигналом х2 при помощи равенства х2 = aXi + сх3, получаем для узлов х3 и х4 уравнения х3—bx2=abx1 -ф bcxs; х4=dxg. (4-22)
Этим уравнениям соответствует граф, приведенный на рис. 4-23,6. После подстановки значения х3 из первого уравнения системы (4-22) во второе определяется сигнал
(4-23)
Таким образом, исключение петли приводит к графу (рис. 4-23, в) с одной ветвью, передача которой равна йЫ/(1 — Ьс), где произведение abd равно передаче пути П14 между узлами с сигналами X} и х4, а произведение Ьс равно передаче контура L.
Расчет коэффициента передачи при помощи графов. Прежде чем подучить общую формулу. для определения коэффициента передачи линейной электрической цепи произвольной конфигурации при по
170
мощи графов, рассмотрим несколько достаточно общих примеров на' определение коэффициента передачи.
На рис. 4-24 изображен четырехконтурный граф, часть узлов которого для упрощения обозначена цифрами, с контурными передачами: L] =• bi, L2 = ch; Ls = dg и L4 = ef. Сигнал распространяется из узла х0. Требуется определить коэффициент передачи х6/х0.
Для узлов 1, 2, 3, 4, 5, 6 справедливы уравнения
х4 — cixq -|- ix2;
xs = cx2 + gxi; х-о — ех4;
х2 — Ьхг -J- hxs; x4=dxs-\-fx5; xa—kxt.
Рис. 4-24.
Искомый коэффициент передачи определим, постепенно исключив остальные неизвестные, начиная с х5, из системы уравнений.
Иначе говоря,
х4 = dx3 -Т fx5 = dxs -J- fex4,
откуда
x4 = dx3/(l — Ц).
Затем из уравнения gdx3 . ЬяХз
Хз—сх^+ — сх2 +
определим
х3 = с (1 Т4) х2/(1 h3 Lj
и т. д. В результате получим связь между х4 и х0 в виде „ 1 ----------- (^1 + h2 + ^3 + ^4) + ^1^3 + ^-1^-4 +
1 1-Д2 + ^ + ^)+^4 ~ахо,
откуда
Х1 __ _____а [1 ~ С'2 ~Н^З~Ь^4) ~Н^2^-4]_
Xo 1 — (^-1+h2 L3 -}- L4) -р L^Lg ~р L4L4 -р L2L4
Искомый коэффициент передачи
хв __ kxi afe [ 1 — (L2 -р Z-з -р -р ^2^-4] (4-24)
171
Числитель этого выражения равен произведению передачи пути Пх = ak на определитель DL = 1 — (£2 + L3 + £4) + £2£4, который получается вычитанием из единицы передачи всех контуров, не касающихся пути с передачей П1( и суммированием произведения контурных передач не касающихся друг друга контуров £2 и £4 и пути с передачей Пх. Знаменатель в этом случае равен определи-
О • W q ................Эи»1 У Jan -У ж...........................V — •*№ Т
а г Ъ з с 4 d 5 е w6
Рис. 4-25.
телю графа рис. 4-24, который получается вычитанием из единицы всех передач контуров графа и суммированием с полученной разностью попарных произведений передач всех не соприкасающихся друг с другом контуров.
В качестве второго примера рассмотрим граф, показанный на рис. 4-25, для которого нужно найти коэффициент передачи сигнала из первого узла в шестой, т. е. найти отношение хъ]хг.
Запишем уравнения для узлов 2, 3, 4, 5 и х2 = ахх + hx3, х3 = bx2 + gXi, х4 = сх3 + /х5; х5 = dx^, х6 = ех5. Исключив из этих уравнений неизвестные сигналы в узлах графа, начиная от его конца, получим:
Х2 _ П (1 £2 £3)
Х1 1—(^-1 + ^2 “и£-з)+Н/-3
Поскольку хв — edx4 и х4 = сх3 + fdx4, то edcx3 edcb (1—L3) edcbx2
Хб~- (!-£,) ~ l—L2—L3
Наконец, abcdexj 6__________________1 — (Н + ^-г + ^ + Н^-з
или окончательно
хв__________abcdeDj_______
1—U-1 + £г+£з) + £1^з
(4-25)
Числитель полученного выражения (4-25) равен произведению передачи пути от узла xt к узлу хв на определитель Dlt т. е. Пх = = abcde на D4. Поскольку путь с передачей Пх проходит через все узлы схемы, то определитель числителя получается равным единице (£\ = 1). Знаменатель выражения (4-25) определяется аналогично знаменателю (4-24) и получается вычитанием передач всех трех контуров из единицы и суммированием с полученным выражением произведения передач двух несоприкасающихся контуров (£х и£3).
При определении передачи от источника к любому узлу графа можно, не применяя преобразований, непосредственно пользоваться-
172
общим решением уравнений, определяющих состояние системы. Однако, прежде чем дать общее решение этой задачи, рассмотрим еще граф в виде полного треугольника (рис. 4-26, а). Можно показать, ЧТо такой граф получается для электрической схемы, имеющей форму полного пятиугольника, у которого потенциал одного из четырех независимых узловых уравнений исключен.
Для этого графа справедливы уравнения xi=л'о+41-^1 4- 4~ 4л;
х2 — ti2X2 4~ ^12-^1 4~ ^з! Х3 — ?33Х3 4“ ДЛ т ^2ЛХ21
ИЛИ
(1 — Д1) Х1 — ^21Х2 — ^31Х3 ~ Х0;
^12-^1 Ф(1 “ ^22) Х2 — ^32Х3 — 0;
Дз-М — ^23-^2 4~ (1 ^зз) -^3 — 0,
(4-26)
Где =/= ^23 ^32 И ^13 tgy.
Определить любой из узловых сигналов, например х2, можно через определители:
/ x2 = x0D12/D, ' (4-27)
где
(l-/u) 1 -/31
— ^12 0 ^32 ; (4-28)
^13 0 (^ ^зз)
(1-Дх) ^21 ^31
D = G.2 (1-^22) 1з2 (4-29)
у 1 — ^13— — ^23 (1-*зз)
173
В раскрытой форме определитель
D----1 — ^22 — ^33 ~~ ^12^21 ' ^23^32 ' ^1,'4з1 ~~ ^12^23“31 ^13^32^21 4~
4" tц^22 4“ 4г^33 4" 6)3'11 + ^13^31^22 4" ^12^21^33 4" ^23^32^11 41^22^33- (4-30)
Из полученного выражения следует, что второе — девятое слагаемые представляют собой передачи всех восьми контуров, имеющихся в графе; остальные слагаемые (за исключением единицы) состоят из произведений передач контуров, не соприкасающихся друг с другом, т. е. не имеющих общих точек в графе. Отметим, что передачи всех контуров входят в выражение (4-30) с отрицательными знаками, а их попарные произведения — с положительными знаками. Последнее слагаемое, равное произведению передач трех несоприкасающихся контуров, имеет отрицательный знак. Особо подчеркнем, что произведения четного числа контурных передач всегда входит в определитель с положительными знаками, а нечетного — с отрицательными.
Определитель
П12---^12 (1 — 4“ 6з^32--П1Р1 4“ П,О2, (4-31)
где П'1 = /]2 и Щ — /13^32 — передачи путей от источника сигнала в узел 2 (рис. 4-26, б); D\ = (1 — tR3) — определитель части графа, не касающейся пути с передачей П[; £>2 = 1, поскольку путь с передачей П2 проходит через все узлы схемы.
Обобщив результаты приведенных примеров, получим, что в общем случае коэффициент передачи графа определяется по формуле (Мезона)
о i-S41,4-S42)-S43)+-’
k k k
(4-32)
где
D = (4-32a)
k k k
Lty — произведение передач контуров /г-й возможной комбинации г несоприкасающихся контуров при г > 1. При этом формула разложения определителя D (4-32а) может быть применена и для разложения миноров числителя (4-32) D'K, что, в частности, непосредственно следует из (4-31) и подтверждается выражениями (4-24), (4-25).
Пример 4-12. Пользуясь графом (рис. 4-20, б), определить ток в сопротивлении Z3 схемы, показанной на рис 4-20, а.
Решение. Так как в схеме два источника (э. д. с. Ё и тока j), то для определения тока /3 найдем потенциал ф3 = !':t, пользуясь принципом наложения. Потенциал фд, создаваемый э. д. с. £', определяется по формуле (4-32);
_______________Фз =
(Гв/^зз) (1 — М) р
1-£4—’
174
где передачи контуров графа Ъ=У}/УиУ^ Ц=У1/У^У33. .
В числитель полученного выражения входит передача li контура, не касающегося пути УК!УЯЗ-
Потенциал фЛ, создаваемый источником тока J, находится по той же формуле (4-32):
где передача пути П(, = У\Уа/УпУг2Узз и D't = 1.
Потенциал ф3, создаваемый обоими источниками,
гУ п ri' J-зз) Ё (1 — /_4) -j-(l/Vn) JY^^/Y^Yss
о3=<Рз —Фз -гЧ’з--------------j ""_ £---------------’•
Ток в сопротивлении Zs, очевидно, равен:
1 r’y V 0 з/^зз) Ё (1—Lq) +(У з/Уц) ^У^Уъ/У^УзЗ IS-USYS-
В заключение полезно подчеркнуть, что, пользуясь графами и формулой (4-32), можно во многих случаях сразу определить искомые величины, не решая совместно системы заданных уравнений электрического состояния тон или иной цепи.
Глава пятая
РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
5-1. Резонанс в неразветвленной цепи
Резонансом называется такой режим пассивной цепи, содержащей катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением.
Рассмотрим последовательное соединение сопротивления, индуктивности и емкости (рис. 3-8). Такую цепь часто называет п о-следовательным контуром. Для нее наступает резонанс, когда х = xl — хс = 0 или хь = *с> т. е.
соТ==1/(оС. (5-1)
При xl = Хс значения противоположных по фазе напряжений на индуктивности и емкости равны (рис. 3-11, б), поэтому резонанс в рассматриваемой цепи называют резонансом напряжений.
Напряжения на индуктивности и емкости при резонансе могут значительно превышать напряжение на зажимах цепи, которое равно напряжению на активном сопротивлении. Полное сопротивление Цепи z при х — 0 минимально: г = ]/г2 -г х~ = г, а ток / при задан
175
ном напряжении U достигает наибольшего значения U/г. В теоретическом случае при г — 0 полное сопротивление цепи в режиме резонанса также равно нулю, а ток при любом конечном значении напряжения U бесконечно велик. Точно так же бесконечно велики напряжения на индуктивности и емкости.
Из условия coL = 1/соС следует, что резонанса можно достичь, изменяя либо частоту напряжения источника, либо параметры цепи — индуктивность или емкость. Угловая частота, при которой наступает резонанс, называется резонансной угловой частотой
(л0 = 1/УЬС. (5-2)
Индуктивное и емкостное сопротивления при резонансе
cooL = 1/со0С=VL/C = р. (5-3)
Величина р называется характеристическим с о-п-рот явлением цепи или контура.
Отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи, при резонансе
называют добротностью контура или коэффициентом резонанса. Коэффициент резонанса указывает, во сколько раз напряжение на индуктивности или на емкости при резонансе больше, чем напряжение, приложенное к цепи: Q> 1, если р > г. Наименование «добротность» контура будет разъяснено в следующем параграфе.
Для уяснения энергетических процессов при резонансе определим сумму энергий магнитного и электрического полей цепи w = WM + шэ. Пусть ток в контуре i Im sin со0/. Тогда напряжение на емкости
Ис = UCm sin (<0(/ — л/2) = — UCm cos о0/.
Суммарная энергия
Li2 Си} Lf2 CU}„
w = wK + wa=^~ + -J- = -g- sin2 соо/ -I-g— cos2 coo/.
Ho
= Im^VL/C Im,
откуда
CU°cm/2^Ll2m/2
и, следовательно,
LI* CU}m
—“o- — —=2—“Const,
176
т е. сумма энергий магнитного и электрического полей с течением времени не изменяется. Уменьшение энергии электрического поля сопровождается увеличением энергии магнитного поля и наоборот. Таким образом, наблюдается непрерывный переход энергии из электрического поля в магнитное поле и обратно.
Энергия, поступающая в цепь от источника питания, в любой момент времени целиком переходит в тепло. Поэтому для источника питания вся цепь эквивалентна одному активному сопротивлению.
Наименование «резонанс» для рассмотренного режима цепи заимствовано из теории колебаний. Как известно, резонансом называется процесс вынужденных колебаний с такой частотой, при которой интенсивность колебаний при прочих равных условиях максимальна. Но характеризовать интенсивность колебательного процесса можно по различным проявлениям, максимумы которых наблюдаются при различных частотах. Поэтому нужно условиться о критерии резонанса.
В электрической цепи колеблются заряды. Можно было бы взять за критерий резонанса максимум амплитудного значения заряда на емкости, что соответствует максимальной амплитуде напряжения на емкости. Этот критерий определяет амплитудный резонанс. Для принятого в начале параграфа критерия резонанса ток при резонансе совпадает по фазе с приложенным напряжением, это так называемый фазовый резонанс. В рассматриваемой схеме (рис. 3-8) фазовый резонанс наступает при максимальной скорости движения колеблющихся зарядов или максимуме тока.
Если заряженный конденсатор замкнуть на катушку индуктивности, то в такой цепи при достаточно малом сопротивлении катушки наблюдается процесс затухающих колебаний напряжений и тока. Частота этих колебаний называется частотой собственных или свободных колебаний. Отметим, что частоты, при которых наблюдаются фазовый и амплитудный резонансы, не совпадают с частотой собственных колебаний (они совпадают только в теоретическом случае, когда сопротивление цепи равно нулю). Принятый здесь критерий резонанса применим и в том случае, когда в цепи вследствие большого сопротивления собственные колебания невозможны.
5-2. Частотные характеристики неразветвленной цепи
Пусть к цепи (рис. 3-8) приложено синусоидальное напряжение и = Um sin со(, амплитуда которого неизменна, а частота может изменяться в пределах от 0 до оо.
Изменение частоты приводит к изменению параметров цепи. Меняется ее реактивное, а следовательно, и полное сопротивление, а также угол ср (аргумент комплексного сопротивления). Зависимости от частоты параметров цепи назовем частотными характеристиками цепи, зависимости действующих или амплитудных значений тока и напряжения от частоты — резонансными кривыми.
На рис. 5-1 даны частотные характеристики xL, — хс и х = х{ — ~~ хс. Изменение реактивного сопротивления приводит к изменению режима цепи. На рис. 5-2 приведен примерный вид резонансных кривых I (со), UL (о), Uc (со) и кривой ср (со) для цепи, добротность которой Q = 1,25. При со = 0 напряжение, приложенное к цепи, во времени не изменяется, поэтому ток в цепи отсутствует. При из-менении частоты от* 0 до со» реактивное сопротивление х = хт — хс ?1чеет емкостный характер и изменяется от — оо до 0 (рис. 5-1).
177
Вследствие этого ток возрастает от 0 до наибольшего значения U/г, а угол сдвига фаз между напряжением и током изменяется от — л/2 до 0. При изменении частоты от со0 до оо результирующее реактивное сопротивление возрастает от 0 до оо и имеет индуктивный характер. Вследствие этого ток уменьшается от наибольшего
значения до 0, а угол <р возрастает от 0 до л/2. Напряжение rl изменяется пропорционально току.
В выражении напряжения на индуктивности UL = xfI оба сомножителя зависят от частоты. При со = 0 сопротивление xL = 0, ток / = 0 и, следовательно, UL = 0. При изменении частоты от 0 до соо оба сомножителя увеличиваются и UL возрастает. При дальнейшем увеличении частоты (со > соо) ток I уменьшается, но за счет роста со£ напряжение Uf продолжает возрастать. Анализ, который здесь не приводится, показывает, что для цепи с добротностью Q <; < 1/]/2 это возрастание UL продолжается непрерывно до значения U, а для цепи с добротностью Q2> 1 /р2 напряжение UL при некоторой частоте 5> соо достигает максимума 7Л.,,,акс U, а затем уменьшается. При со = оо и coL = оо, следовательно, UL = U.
Теперь рассмотрим зависимость напряжения на емкости Uc = = хс1 от частоты. При со = 0 тока в цепи нет, поэтому Uc = U. При возрастании со, начиная от нуля, хс непрерывно уменьшается. Анализ показывает, чго для цепи с добротностью Q <; 1/^/ 2 напряжение Uс непрерывно уменьшается, а при 1/|/2 напряжение сначала из-за возрастания тока I увеличивается, достигает при некотором значении частоты сос < со0 максимума 7/Смакс > U, а затем уменьшается.
Уменьшение напряжения Uc = хс/ с ростом частоты начинается ---при частоте а,:, меньшей со0, вследствие непрерывного уменьшения хс. При со — оо как /, так и хс равны нулю, поэтому Uc = 0. За
178
Рис 5-3.
метим, ЧТО t/смакс = ^Ьмакс. При со -= й0, как было отмечено, и = Uj — QU-
Граф™ зависимости тока от частоты показывает, что рассмат-иваемая цепь обладает «избирательными свойствами». Цепь облапает наименьшим сопротивлением для тока той частоты, которая наиболее близка к ее резонансной частоте.
Избирательными свойствами таких цепей широко пользуются в электросвязи и радиотехнике. При этом режим резонанса является нормальным режимом работы. Наоборот, в устройствах, где резонансный режим не предусмотрен, появление резонанса нежелательно, так как возникающие значительные напряжения на катушке и конденсаторе могут оказаться опасными для изоляции.
Выясним влияние параметров цепи на форму резонансной кри
вой I (со). Для удобства сравнения резонансных кривых друг с другом будем их рассматривать в виде зависимостей
///0==Л (®/и0),
где Io = U/г — действующий ток при резонансе.
Преобразуем выражение полного сопротивления цепи:
г = |Л2 + - Jc-)2 = ]/r2 + <оД2
= гЦ 1 + Q2(co/coo- <o0/co)2.
Ток в цепи
I== u = U _ l0
z r Kl+Q2(co/<uo—wo/ы)2 I' 1J-Q2 (w/w0— Wo/w)2
Выражение (5-5) показывает, что влияние параметров цепи на вид резонансной кривой полностью учитывается величиной Q.
На рис. 5-3 представлен ряд резонансных кривых. Чем больше Q, тем острее резонансная кривая, тем лучше «избирательные свойства» Цепи, что и послужило одной из причин назвать Q добротностью к°нтура. Заметим, что наибольшие достигаемые на практике значения Q контуров, состоящих из катушек индуктивности и конденсаторов, лежат в пределах 200—500.
Для оценки избирательных свойств цепи вводят условное понятие ширины резонансной кривой или полосы пропускания контура, которую определяют как разность частот, между которыми отно-Шбние 1//0 превышает 1/]/2.___________________________________
179
На рис. 5-3 проведена горизонтальная линия, соответствующая ///0 = 1/^2. Ее пересечение с резонансными кривыми определяет граничные частоты (в относительном масштабе), между которыми расположены полосы пропускания контуров. Из рисунка видно, что чем выше добротность, тем уже полоса пропускания контура.
5-3. Резонанс в цепи с двумя параллельными ветвями
I
Рис. 5-4.
резонанса токов.
Рис. 5-5.
Рассмотрим цепь с двумя параллельными ветвями: одной —с сопротивлением и индуктивностью, а другой — с сопротивлением и емкостью (рис. 5-4). Такую цепь часто называют параллельным контуром. Резонанс наступает, когда входная реактивная проводимость
Ь — Ьг + Ь2 = 0 или Ь2=—Ьъ (5-6)
где Ьг и Ь2 — реактивные проводимости ветвей.
При Ь2 = — Ь± противоположные по фазе реактивные составляющие токов равны (рис. 5-5), поэтому резонанс в рассматриваемой цепи получил название Из векторной диаграммы видно, что при
резонансе ток I на входе цепи может быть значительно меньше токов в ветвях. В теоретическом случае при 1\ = г2 = 0 токи Д и /2 сдвинуты по фазе относительно напряжения на углы + л/2 и —л/2 (рис. 5-6) и суммарный ток / = Д + /2 = 0. Входное сопротивление цепи при этом бесконечно велико.
Подставив в соотношение (5-6), т. е. в условие резонанса, значения Ъ± и Ь2, выраженные через параметры цепи и частоту, получим:
_____________l/МС р /Г уч ^4-(coL)2 4 + (1/соС)2_' ’
Изменением одной из величин (со, L, С, г1г г2) при остальных четырех постоянных не всегда может быть достигнут резонанс. Резонанс отсутствует, если значение изменяемой величины при ее определении из уравнения (5-7) получается мнимым или комплексным. Для L или С могут получаться и по два различных вещественных значения, удовлетворяющих уравнению (5-7)
изменением L или С можно достичь двух различных резонансных
В таких
режимов. .
180
Решая уравнение (5-7) относительно и, находим следующее значение для резонансной угловой частоты:
®о =
L/C-rl
Vlc V цс~г\
(5-8)
Резонанс возможен, если’сопротивления гх и г2 оба больше или оба меньше р. Если же это условие не выполнено, получается мнимая частота «о, т. е. не существует такой частоты, при которой имел бы место резонанс. д/2
При = r2 ¥= Р резонансная частота со' = соо, т. е. такая же, как и при резонансе в последовательном контуре.
При Н = г2 = Р резонансная частота ©о = 0/0 •
имеет любое значение, т. е. резонанс наблюдается на любой частоте. Действительно, при t\ = г2 — р х~0 эквивалентное сопротивление
_ ад л
Zi + Z2 2r+/(wZ.-l/wC) Р’ V 1
т. е. эквивалентное сопротивление цепи — актив- Рис. 5-6. ное и не зависит от частоты. Следовательно, ток
совпадает по фазе с напряжением при любой частоте и его действующее значение равно U!p.
Заметим, что в радиотехнике и электросвязи применяются контуры с малыми потерями, т. е. в них t\ и г2 малы по сравнению с р. В таких условиях резонансную частоту можно вычислять по формуле
«о = 1 V LC—со0.
Анализ, который здесь не приводится, показывает, что в общем случае сумма энергий электрического и магнитного полей при резонансе не остается постоянной. Эта сумма постоянна только в теоретическом случае, при t\ — г2 = 0.
Рис. 5-7.
Пример 5-1. Угловая частота со и действующее значение / синусоидального ?°Ка> подводимого к цепи (рис. 5-7, а), поддерживаются неизменными. Емкость Ко,|Денсатора без потерь изменяется до тех пор, пока при некотором значении С
181
Напряжение U, измеряемое вольтметром, не достигнет максимального значения 1/макс. По известным величинам со, /, С, С/макс и R требуется определить иг катушки, присоединенной к зажимам J и 2
Решен и е. Проще всего задача решается путем преобразования схемы в эквивалентную, состоящую из переменной емкости и двух параллельно соединенных элементов — активной g и индуктивной bL проводимостей (рис. 5-7, в) — с источником тока Jt, подсоединенным к зажимам 3 и 4.
В этой схеме при неизменном действующем токе и изменении емкости максимум напряжения, измеряемого вольтметром, будет наблюдаться при резонансе токов, так как входное сопротивление цепи при этом максимально.
В соответствии с намеченным путем решения приступаем к преобразованию схемы Питание цепи (рис 5-7, а) заданным током 1 может рассматриваться как питание от источника тока J = I (показан пунктиром). Заменим источник тока источником э д. с. Е = RI (рис. 5-7, 6), а от источника э д. с перейдем к новому источнику тока, подключенному к зажимам 3 и 4 Ток этого источника
J1 = E/z = RI /г, где
г =4 (г + й)2 + (со£)2.
Последовательное соединение элементов R, г и L заменим параллельным (рис. 5-7, в) с проводимостями
g = (г + Я)/г2; bL == wL/г2. (а)
Л1аксимум напряжения между зажимами 3 и 4 наблюдается при резонансе токов, когда
bL = bc — аС (б)
и
^M8KC“(V^) А ~
Из последнего равенства найдем связь между неизвестными g и г:
(в)
где для сокращения записи отношение известных величин UmKC/R/ обозначено а. Подставив (б) и (в) в выражение g2 + b£ — 1 /г®, получим.
g2+(<uQ2=g2a2,
откуда
соС „1 а2 — 1 g= —==-; г2=—- =----------------.
| «--1 д'-с/Л (coC)2a2
Наконец, из (а) найдем, что
шТ = Ь,г2=-^— . г==рг2_о= 1 _ р
L шС а2 ’ Г 8 К аСа2 Л
5-4. Частотные характеристики параллельного контура
Построим резонансную кривую тока / (со) в неразветвленной части параллельного контура при постоянном напряжении U источника питания для идеального случая /у = г2 — 0 (рис. 5-8, «).—=—
182
На рис. 5-8, б показаны частотные характеристики проводимостей ветвей Ъх = bL = 1/aL и b2 = — Ьс = — соС и входной проводимости цепи b = br + b2 = 1/coL — аС. Ток I = | b | U, поэтому кривая | b | = F (и) в соответствующем масштабе и есть резонансная кривая тока /(и). __
При изменении частоты от 0 до соо = l/p^LC эквивалентная проводимость b > 0, т. е. индуктивная, и изменяется от оо до 0. При ю = <в0 наступает резонанс токов, b = 0, / = 0, Ц = UI&0L = — (j/р и /2 = ®0СЙ = U!p. При возрастании частоты от соо дооо
входная проводимость b < 0, т. е. емкостная, и изменяется от 0 до — оо.
В общем случае при сопротивлениях t\ и г2, не равных нулю (рис. 5-4), входная активная проводимость цепи отлична от нуля при любой частоте, поэтому ток / ни при одном значении частоты не равен нулю. Анализ, который здесь не приводится, показывает, что при условии П < Р и < р зависимость I = F (со) при U = const имеет, минимум, причем этот минимум наблюдается при частоте, отличающейся от резонансной частоты. Последнее объясняется тем, что максимум полного входного сопротивления получается при частоте, для которой дх/ды = 0, а резонанс имеет место при частоте, для которой b = 0 или х = 0. Чем меньше t\ и г2,
тем меньше
минимальное значение тока /, тем ближе значение
частоты, при которой наблюдается минимум тока, к резонансной частоте и тем больше график / = F (со) похож на кривую / (со) при t\ = г2 = 0 (рис. 5-8).
При условии t\ — г2 = р и U — const ток /, как было показано в § 5-3, при любой частоте одинаков. Зависимость / = F (со) не имеет ни максимума, ни минимума и графически представляется прямой, параллельной оси абсцисс.
Анализ показывает, что при условии гу > р и г2 > р кривая / = F(co) при некотором значении частоты достигает максимума.
5-5. Понятие о резонансе в сложных цепях
Условия резонанса Ъ = 0 или х — 0 для разветвленной цепи с несколькими индуктивностями и емкостями дают для частоты со уравнения, которые могут иметь несколько вещественных корней Другими словами, у разветвленной цепи Может быть несколько резонансных частот
Рассмотрим, например, цепь рис 5-9, а, потерями в которой можно пренебречь Входное сопротивление цепи реактивное
--- —— 1-------( /' собу---------F г — ----1 —Р — --—
7. = jaL3 -j--=----—-=— - j ни « — —^т~7=,-г — jx.
/со/-! — //(оС2 L a>-‘L1C2— 1J
183
Резонанс наступает при b = 0 или х — О, причем если х = 0, то b = <», и, наоборот, если b = 0, то х ~ <х Это справедливо всегда, если пренебречь активными сопротивлениями в ветвях. Следовательно, резонансными нуль или в случае х = оо
будут частоты, обращающие х в бесконечность. В рассматриваемом при co2L1C2 — 1 = 0 или
со= 1/К^1С2=сот.
При этой в параллельных ветвях с Lj иС2 получаем:
частоте наступает резонанс токов Полагая х — О,
“н—I зС2-
При этой частоте имеет место резонанс напряжений в последовательном контуре, состоящем из индуктивности и емкости, эквивалентной двум параллельным ветвям. Таким! образом, у рассматриваемой цепи две резонансные частоты: сог и сон.
На рис 5-9, б приведены частотные характеристики проводимостей и сопротивления рассматриваемой цепн. Кривые bt = 1/соТ* и А2 = — «>С2 представляют характеристики проводимостей ветвей 1 и 2. Суммируя ординаты этих кривых, получаем характеристику эквивалентной проводимости Ь' двух параллельных ветвей 1 и 2. Кривая х' = i/b' представляет эквивалентное сопро-ветвей Суммируя ординаты кривых х' и
тивление параллельных
построгм характеристику входного сопротивления цепи х. Эта характеристика имеет две особые точки при со = сот и со — сон.
Глава шестая
ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
6-1. Индуктивно связанные элементы цепи
В том случае, когда изменение тока в одном из элементов цепи приводит к появлению э. д. с. в другом элементе цепн, говорят, что эти два элемента индуктивно связаны, а возникающую э. д. с. называют э. д. с. взаимной индукции.
Степень индуктивной связи двух элементов цепи характеризуют коэффициентом связи k, под которым понимают отношение
k = M/V^L2, (6-1)
где М — взаимная индуктивность элементов цепи;
и L2 — индуктивности элементов цепи.
Покажем на частном примере, что коэффициент связи всегда меньше единицы, и выясним, при каких условиях он мог бы быть равен единице.
Пусть две катушки намотаны в виде тонких колец большого -диаметра, При указанной форме—катушек с большой степенью, точности можно считать, что все витки каждой катушки сцепляются
184
с одинаковым магнитным потоком. На рис. 6-1 показана схематически картина магнитного поля при наличии тока в первой катушке. Витки первой катушки сцепляются с магнитным потоком самоиндукции Фц, а витки второй катушки — с магнитным потоком взаимной индукции Ф21. Потокосцепления самоиндукции и взаимной индукции первой и второй катушек
^11 = ^21 “ ^2^21-
По определению индуктивность первой катушки и взаимная индуктивность между катушками
L = Ш1Фц •
м=м21
По поводу этих отношений сделаем некоторые пояснения.
Положительные направления тока и магнитного потока самоиндукции условились всегда выбирать согласованными по правилу правого винта, поэтому, когда > 0, то Ч\г > 0, а когда < О, то и < 0 и, следовательно, отношение всегда положительно.
Что же касается положительного направления для потока взаимной индукции Ф21, то его выбор произволен, поэтому отношение 4f21/t1
может иметь любой знак. Так как в этой книге взаимная индуктивность считается положительной величиной, то выражение для М записано как абсолютное значение | 4f21/t1 |.
На рис. 6-2 показана схематическая картина поля при наличии тока только во второй катушке. По определению
Рис. 6-2.
____^22 __ ^гФга .
2 12 12 ’
I »2 I I «2
Равенство М12 = M2l ~ М может быть доказано исходя из условия независимости энергии магнитного поля токов и i2 от порядка их возрастания от нуля до своих конечных значений.
Составим отношение
М 12^21 I ЦДа^ФцФ.д I Аг
£1^2 I I
Так как | Ф12 | < | Ф22 | и | Ф21 | < | Фи |, iok2 < 1. Коэффициент связи двух катушек мог бы равняться единице, если бы [ Ф12 | =
I Ф22 I и | Ф21 | = | Фи |, т. е. весь поток, создаваемый током -Д-Одной катушке, полностью (без рассеяния) сцеплялся бьгс витками
185
другой катушки, что возможно лишь при совмещении катушек. Практически витки двух катушек, так же как и различные витки одной и той же катушки, пронизываются неодинаковыми магнитными потоками и поэтому всегда k < 1.
Изменения индуктивной связи между двумя катушками можно достигнуть перемещением одной катушки относительно другой. Приборы, состоящие их двух взаимно перемещающихся катушек, называются вариометрами.
6-2. Электродвижущая сила взаимной индукции
При изменении тока в одном из индуктивно связанных элементов цепи (рис. 6-1 и 6-2) в другом элементе возникает э. д. с. взаимной индукции и между его разомкнутыми зажимами появляется напряжение. Абсолютные значения э. д. с. и напряжений, обусловленных взаимной индукцией (закон электромагнитной индукции):
1“™1=1<’ш1 —= |м $|-
Для облегчения решения вопроса о знаке этих величин прибегают к специальной разметке зажимов индуктивно связанных элементов цепи.
Два зажима, принадлежащих двум разным индуктивно связанным элементам цепи, называют одноименными и обозначают одинаковыми значками, руководствуясь следующим правилом: при одинаковом направлении токов относительно одноименных зажимов магнитные потоки самоиндукции и взаимной индукции в каждом элементе должны суммироваться.
Применим это правило для разметки зажимов катушек, показанных на рис. 6-3, а. При направлении тока от зажима а к зажиму b и тока i2 от зажима с к зажиму d магнитные потоки самоиндукции Фи (или Ф22) и взаимной индукции суммируются. Поэтому зажим а одноименен с зажимом с и аналогично зажим b одноименен с зажимом d. Для катушек, показанных на рис. 6-3, б, одноименными являются зажимы аг и dlt а также Ь± и сг. Разница с предыдущим случаем обусловлена другим направлением намотки витков второй катушки.
Одну из двух пар одноименных зажимов обозначают специальными значками, например точками, звездочками, треугольниками и т. и.
Установить взаимное расположение катушек и направление намотки их витков так просто, как на рис. 6-3, не всегда представляется возможным. Но найти одноименные зажимы можно на основании простого опыта, для которого требуются гальванический элемент (или аккумулятор) и гальванометр. Одна из катушек соединяется с гальванометром, другая подключается к гальваническому
186
элементу (рис. 6-4). При замыкании ключа К кратковременно возникает ток i2, ослабляющий магнитное поле, созданное током i2. Следовательно, в момент включения источника питания токи л i направлены относительно одноименных зажимов противоположно. Направление тока определяется полярностью источника питания. О направлении тока i2 судят по кратковременному отклонению стрелки гальванометра. Если стрелка отклоняется в сторону шкалы (имеется в виду гальванометр с односторонней шкалой),
Рис. б'-З.
Рис. 6-4.
то ток i2 направлен к положительному зажиму гальванометра (рис. 6-4). При этом зажимы катушек, присоединенные к положительным зажимам гальванометра и источника питания, одноименны, точно так же одноименны зажимы катушек, присоединенныс\к отри-
цательным зажимам гальванометра и источника питания; заметим,
что в момент отключения источника питания стрелка гальванометра
вновь отклоняется, но уже в обратном направлении, так как ток
противодействует уменьшению магнитного поля.
Перейдем теперь к решению вопроса о знаке в выражениях для э. д. с. и напряжения, обусловленных взаимной индукцией.
Рассмотрим две катушки (рис. 6-5). Пусть первая катушка разомкнута, а во второй протекает синусоидальный ток i2. Выберем положительные направления для
э- Д. с. еьи и напряжения и1Л1 в первой катушке и для тока t2 во вгорои катушке относительно одноименных зажимов одинаковыми, например от а к b и соответственно от с к d.
Прежде всего отметим, что при одинаковых положительных направлениях напряжения и1М и э. д. с. величины и е1М Равны и противоположны по знаку: и1М - — е1Л1. Действительно, к°гда е1Л1 _> 0, потенциал зажима b больше потенциала зажима а и, СлеДовательно, и1Л1 < 0.
Электродвижущая сила е1И на основании закона Ленца должна Иеть такое направление, при котором вызываемый ею ток преият-
187
ствовал бы изменению магнитного потока взаимной индукции. Поэтому, если di2ldt >» 0, то э. д. с. е1М должна иметь действительное направление от Ъ к а, т. е. е1М < 0. Если di2ldt <; 0, то э. д. с.
должна иметь действительное направление от а к Ь, т. е. > 0.
Таким образом, при выбранных положительных направлениях (рис. 6-5) знаки е1М и di2/dt всегда противоположны, поэтому
^1Л1== — е1М = М
Для комплексных величин получим:
UiM — — E1M=j&Mi2. (6-2)
Если бы положительные направления для е1Л1 и и1М в первой катушке и тока i2 во второй катушке относительно одноименных зажимов были выбраны различными, то аналогичные рассуждения показали бы, что знаки е1М и dijdt всегда были бы одинаковы:
Л /Г 2
«1М = — etM = — М ;
(6-3)
Из выражений (6-2) и (6-3) видно, что напряжение обусловленное взаимной индукцией, сдвинуто по фазе относительно тока /2 на угол л/2 или — л/2. Знак этого угла зависит от выбора положительных направлений О1М и /2 относительно одноименных за
жимов.
сопротивлением
Величина со/И имеет размерность сопротивления, называется
взаимной индукции и обозначается хм. Величина /со/И называется
остальных элементов. При бегать к разным условным
комплексным сопротивлением взаимной индукции и обозначается ZM. Таким образом,
ZM=jaM = jxM.
Если индуктивно связаны между собой не два, а несколько элементов цепи, надо у каждого из них отметить зажимы, одноименные с зажимами этом в общем случае приходится прп-обозначениям. Поясним это на при
мере трех катушек, расположенных, как указано на рис. 6-6.
Верхний зажим первой катушки одноименен с нижними зажимами второй и третьей катушек, но эти последние не являются одноименными по отношению друг к другу, поэтому их нельзя обозначить одинаковыми значками. На рис. 6-6 одноименные зажимы первой и второй катушек обозначены звездочками, первой и третьей — треугольниками, а второй и третьей — точками. В частных случаях
для разметки одноименных зажимов нескольких катушек можно обойтись одним условным обозначением. Убедиться в эюм можно
188
на примере нескольких катушек, расположенных вдоль одной оси (аналогично рис. 6-3).
При большом числе индуктивно связанных элементов цепи указанная выше система разметки одноименных зажимов получается недостаточно наглядной, так как приходится вводить много различных обозначений В таких случаях удобнее ДРУгая система разметки, при которой взаимные индуктивности считают алгебраическими величинами
Сначала совершенно произвольно указываются направления обхода каждого индуктивно связанного элемента цепи, например, ставится буква н у зажима, от которого начинается обход, и буква к у другого зажима. Затем указываются знаки взаимных индуктивностей, руководствуясь следующим правилом. Если при совпадении направлений токов с выбранными направлениями обходов потоки взаимной индукции и потоки самоиндукции суммируются,то соответствующая взаимная индуктивность положительна, если же они вычитаются, то соответствующая взаимная индуктивность отрицательна
Примем, например, для катушек, показанных на рис 6-6, за начала обхода верхние зажимы и за концы обхода — нижние зажимы, тогда все взаимные индуктивности будут отрицательны (Л112 < О, ТИ23 < 0 и Л131 < 0).
Знаки в выражениях для напряжений, обусловленных взаимной индуктивностью, получаются, конечно, такими же, как и при первой системе разметки зажимов; при совпадении положительных направлений и г'2 с принятыми направлениями обходов получаем при несовпадении получаем
= — jcoAf12/2. При-этом взаимная индуктивность считается величиной алгебраической и берется с тем знаком, который для нее указан при разметке зажимов
Вторая система разметки при наличии только двух индуктивно связанных элементов менее удобна, так как требует не только маркировки зажимов, но и указания знака взаимной индуктивности В дальнейшем применяется только первая система разметки.
6-3. Последовательное соединение индуктивно связанных элементов цепи
б)
Рис. 6-7.
Предположим, что два приемника энергии, обладающие сопротивлениями гг и г2, индуктивностями и £, и взаимной индуктивностью М, соединены последовательно. Возможны два вида их включения — согласное (рис. 6-7, а) и встречное (рис. 6-7, б). При согласном включении токи в обоих элементах цепи в любой момент времени направлены одинаково относительно одноименных зажимов, поэтому магнитные потоки самоиндукции Фп (или Ф22) и взаимной индукции Фп (или Ф21), сцепленные с каждый элементом, складываются. При встречном включении токи в обоих элементах цепи в любой _____
тивоположно относительно одноименных ные потоки самоиндукции и взаимной "а'Мым элементом, вычитаюгся.
момент
времени направлены прозажимов, поэтому магнит-индукции, сцепленные
189
Индуктивность двух последовательно соединенных индуктивно связанных элементов
и]-5?6. ((М)
где Ч\ и 4L — потокосцепления первого и второго элементов, причем Ч\ — L±i± Mt; — L2t ± Ml. Знак плюс относится к coi-ласному, а знак минус к встречному включению. Следовательно, L=L1+L2±2M. (6-5)
В предельном случае идеальной связи (при k = 1) имеем L — = Lj + L2 ± 2 l/LjLg = (]/Li ± ]/L2)2. Если, кроме того, = = L2, то при согласном включении L = (2 УLt)2 — 4Llt а при встречном L = 0 (при k < 1 всегда L > 0).
Полное сопротивление при согласном включении больше, чем при встречном. Этим можно пользоваться для определения опытным путем одноименных зажимов индуктивно связанных элементов цепи.
Напряжения на элементах имеют по три составляющих:
Ui = + J«L,/ ± jcoM 1; 1
Й2 = Г2! + jcoL27 ± ]<£>М 1. J
Если индуктивность одного из элементов меньше взаимной индуктивности, то при встречном включении наблюдается своеобраз-
но
[{Ь1Й «емкостный» эффект. Пусть, например, L2 < М, тогда в выражении
{72 = г2/ 4- /со (L2 — Л1) 7
имеем со (£2 — М.) <z 0 и, следовательно, напряжение О> отстает по фазе от тока 1, как в случае емкостного сопротивления. Конечно, реактивное сопротивление всей цепи в целом индуктивное, так как д = + L2 — 2М > 0 и ток / отстает по фазе от напряжения О.
На рис 6-8 показаны векторные диаграммы для согласного и встречного включений при одинаковом значении тока в обоих случаях.
Входное комплексное сопротивление цепи получим, учитывая (6-6): ...............
Z=UH=(6\ + U2)/I = Zj + Z2 ± 2Z/M, (6-7)
где Zj = + jtoLi, Z2 = r2 + jcoL2 ; ZM — jaM.
6-4. Параллельное соединение индуктивно связанных элементов цепи
одноименные зажимы
Рис. 6-9.
Предположим, что два приемника энергии, обладающие сопротивлениями и г2, индуктивностями и L2 и взаимной индуктивностью М, соединены параллельно, причем присоединены к одному и тому же узлу (рис. 6-9).
При выбранных положительных направлениях токов и напряжения
/=А+4; (6-8)
U^ZxA + Z^; (6-9)
О=--zMit+ z,2i (6-Ю)
где Zj == -j- jtuLi, Z2 = г2 -f- /со£2;
ZAI = ](йМ.
В этих уравнениях комплексные напряжения ZJ4/2 и ZMf2 взяты со знаком плюс, так как положительные направления этих напряжений (выбранные сверху вниз) и тех токов, от которых эти напряжения зависят, ориентированы относительно одноименных зажимов одинаково.
Решая уравнения, получаем:
/ = Ъ.....Ьф Z7; / = у
ZrZ 2-Zm ZxZ2-Zm
ZjZ2 — Zm
(6-11)
откуда следует, что входное комплексное сопротивление рассматриваемой цепи
7__<7 _ ZtZ2 — Zm
Г ^i + Z2~2Zm
(6-12)
191
При Z/4 = 0, т. е. нри отсутствии индуктивной связи между ветвями, это выражение принимает знакомый вид:
V__ ZjZ2
Zi+Z2‘
Рассмотрим теперь случай включения, когда одноименные зажимы присоединены к разным узлам, т. е. и L2 присоединены к узлу разноименными зажимами, а не как указано на рис. 6-9. Тогда положительные направления напряжений взаимной индукции (выбранные сверху вниз) и тех токов, от которых они зависят, ориентированы относительно одноименных зажимов неодинаково и комплексные напряжения Z.Mf, и ZMf2 войдут в уравнения (6-9) и (6-10) со знаком минус. Для Д, Д и / получатся выражения, аналогичные (6-11), с тем отличием, что ZM заменяется на — ZM и входное
сопротивление цепи
ZjZi—Zm Z1+Z2^2Zm‘
(6-13)
6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности
Расчеты разветвленных цепей можно вести, составляя уравнения по первому и второму законам Кирхгофа или методом контурных
токов. Метод узловых потенциалов непосредственно непригоден. Объясняется это тем, что ток в любой ветви зависит не только от э. д. с находящегося в ней источника и от потенциалов тех узлов, к которым ветвь присоединена, но и от токов других ветвей, которые наводят э. д. с. взаимной индукции. Поэтому нельзя простым путем выразить токи ветвей через потенциалы узлов и э. д. с. источников, как в цепях без индуктивно связанных элементов.
Применение метода узловых потенциалов требует особых приемов и здесь не рассматривается.
Теорему об активном двухполюснике можно применять, если внешняя по отношению к двухполюснику часть цепи не имеег индуктивных связей с той частью цепи, которая входит в состав
двухполюсника. Разумеется, что нельзя пользоваться выведенными ранее формулами для преобразования треугольника сопротивлений в эквивалентную звезду и обратно. _
192
Чтобы обойти указанные выше ограничения в применении расчетных методов, в ряде случаев целесообразно исключить индуктивные связи, перейдя к эквивалентным схемам без индуктивных связей (см. следующий параграф).
При составлении уравнения по второму закону Кирхгофа э. д с. взаимной индукции обычно учитываются как соответствующие напряжения. Знак комплексного напряжения ± j&Mks/s на элементе k определяется на основании сопоставления направления обхода элемента k и положительного направления тока в элементе s. Если эти направления относительно одноименных зажимов одинаковы, то напряжение равно i&Mks/s. В противном случае напряжение равно — joMllsis. Это правило знаков вытекает из обоснований, приведенных в § 6-2.
В качестве примера запишем уравнения по законам Кирхгофа для схемы, представленной на рис. 6-10. Для большей ясности напряжения в уравнениях выпишем в порядке расположения элементов контура без приведения подобных членов:
Лг + Л> +Д? = 0;
raia4-i^Ja—acIc - jtoM.aaid—rbfb+ji b/aCb - jaLbib^
== Ea Eb',
foEbIb b/(fiCb -]- rbIb jaLcic -ф- jcoAf a d rcI c
= Eb + Ec-
riji!<? + a — ф- jCf>Mcdic — Etj.
Приведем также уравнения, составленные по второму закону Кирхгофа для контурных токов:
[fa Л~ГЬ 4~/ 4" — 1 4 ф-
4~[— rb ф- j (— a>Lb -ф- l/coCj, ф- toAloc)] 4 ~ №M.udIs = Ea — Е ь,
[— f ь 4~ / (— + 1/®Сй + соМас)] 4 4~
4 [гь + Гс+i (®ЕЬ -ф-(£>ЬС — 1/соСф)] 4 — /<оЛ1с^4 = Еь -ф- Ес;
— + (f d 4“ 4 ==£<?•
Сокращенно последние уравнения можно записать так:
£ц4 4" ^1г4+£»4=е1' z214+^2й4+£гз4=е2,
•^314 4“ ^зг4 4" ^зз4 — Ез,
гДе Zu, Z22, Zd3 — комплексные сопротивления контуров 1, 2 и 3;
•Z12 = Zgl, Z23 = ZS2, £31 =£13
7- комплексные взаимные (общие) сопротивления контуров 1 и 2, 2 иЗ, 3 и 1;
7 Основы теории цепей
193
Ёи Ё2, Es — комплексные контурные э. д. с. Например,
%и = ^а + гь~\~] — 1/соСг,);
Z12 = — г 64- / (— <лЕь + 1/coCj + <вЛ1ас);
21з== — Ei — Ea — Eb.
Заметим, что в комплексные сопротивления контуров и в комп-лексные взаимные сопротивления двух контуров слагаемые j(t)Mks входят со знаком плюс или минус в зависимости от того, совпадай? или не совпадают по отношению к одноименным зажимам элементов цепи k и s направление обхода контура через элемент k и положительное направление тока через элемент s.
Для цепей, содержащих индуктивно связанные элементы, справедливо свойство взаимности. Доказательство этого положения ничем не отличается от приведенного для цепей постоянного тока.
Пример 6-1. К зажимам/—/'цепи (рис 6-11) подведено питание Определить напряжение между разомкнутыми зажимами 2—2'. Дано, г, = г3 = 3 Ом; «Щ, = = coL3 = 4 Ом; иЛ1 = 2 Ом; Ц = 10 В.
Рис. 6-11.
Решение. Полагаем (jr = = 10 В Находим:
Л =----^T- = -q-^-r=l,2-/l,6 А.
сзЧ/и^-з 3-|-/4
Напряжение Д2 определяем, обходя схему от зажима 2 к зажиму 2'; (
Д2=/(оЛ4/1+Д1=13,4 д 10’18' В.
Если бы нижний конец индуктивности Д был одноименным с верхним концом индуктивности L.t, то направление обхода элемента Д> и направление тока в элементе L3 относительно одноименных зажимов были бы различными. Тогда перед слагаемым j(oM/1 следовало бы поставить знак минус и напряжение Оъ было бы равно 7,21 д —19° 26' В.
Пример 6-2. Определить входное сопротивление цепи, показанной на
194
Р е_ш е н и е. Зададимся напряжением Ut, подсчитаем ток и затем найдем
= Ujlx- Заметим, что если бы не было взаимной индуктивности, то ток /а был бы равен нулю, ток /2 равнялся току и ZBX было бы равно гг + jaL^.
Для контура 1—3—2—2'—1'
(rjt+jwLi) l1+jaM!s=U1. (а)
Для контура 3—3'—2'—2—3
Оз+4+/1=0, (б)
откуда
/8=— 7(о.М/1/^з+/шЛз). (в)
Подставив (в) в (а), получим:
^1+/Co£1 + 7-p}5E-j/1_t/1,
откуда
ZBX = —- = Г1 + /О)/,! ---— (г)
А Гз + /0)£3
(см. также пример 6-3).
6-6. Эквивалентная замена индуктивных связей
Анализ и расчет электрических цепей в ряде случаев упрощаются, если часть схемы, содержащую индуктивные связи, заменить эквивалентной схемой без индуктивных связей. Этот прием называют эквивалентной заменой, устранением или развязкой индуктивных связей.
Рис. 643.
Найдем схему без индуктивных связей, эквивалентную двум индуктивно связанным элементам цепи, присоединенным к общему Узлу 3 (рис. 6-13, а). При этом учтем два возможных случая: когда в общем узле элементы цепи соединены одноименными зажимами и когда разноименными.
Введем дополнительную ветвь без сопротивления, соединяющую Индуктивно связанные элементы цепи с узлом 3 (рис. 6-13, б). В том случае, когда в узле 3 соединены только три ветви, введение такой Дополнител иной ветви не требуется._______________
7»
195
I,
Рис 6-14.
Напишем выражения для напряжений между зажимами 1,3 и 2,3: U 1з = ZytZU23 = Z^iZmIi.
Верхние знаки относятся к первому случаю (когда в узле элементы цепи соединены одноименными зажимами), а нижние — ко второму случаю. Этого порядка расположения знаков будем придерживаться и во всех последующих выражениях.
Пользуясь соотношением Д + /2 — /3 = = 0, исключим из первого уравнения ток /2, а из второго уравнения ток Д, тогда получим.
U 1з = (Zt zp ZM) ii± ZnJs’, и2й = (Z,2 Zp Zy|j) 12 Z«/3.
Кроме того, имеем:
U12 = (Z.i zp Z,u) Ii — (Z2 zp ZM) f2.

Эти три уравнения справедливы и для схемы, показанной на рис 6-14, которая, является искомой эквивалентной схемой без
И
таким образом, индуктивных связей.
Итак, при устранении индуктивной связи к сопротивлениям Zi и Z2 добавляется zp ZM, зажим 3 перестает быть узлом для ветвей 1 и 2, а между зажимом 3 и новым узлом 3' появляется элемент ± ZM.
Если индуктивно связанные элементы соединены трехлучевой звездой или треугольником, то, применяя последовательно рассмотренный способ эквивалентной замены, можно перейти к схемам без индуктивных связей.
Развязка индуктивных связей в четырехлучевой звезде труднее, так как на промежуточном этапе получается схема, в которой индуктивно связанные элементы расположены в ветвях, не имеющих общего узла.
Две любые индуктивно связанные ветви, не присоединенные к общему узл*у, также без до-ею
можно заменить эквивалентной схемой индуктивной связи, однако эта схема в статочной мере сложна и пользоваться нецелесообразно.
Пример 6-3. Найти входное сопротивление цепи (рис. 6-12), применив при решении эквивалентную замену индуктивных связей
Решение Учитывая, что индуктивно связанные элементы присоединены к узлу 3 разноименными зажимами, получаем эквивалентную схему, представленную на рис 6-15, для которой
ZBx = n + /o (L1+M) + -^±AL(4±l^(~ = ^+/^+-4^-.
196
6-7. Передача энергии между индуктивно связанными элементами цепи
Рассмотрим, как передается энергия между двумя индуктивно связанными
элементами разветвленной цепи Всю цепь, за исключением этих двух элементов, представим в виде активного четырехполюсника (рис 6-16)
р В течение каждого полупериода изменения токов tx и i2 энергия, поступающая в магнитное поле индуктивно связанных элементов, возвращается обратно
Однако это не означает, что равны количества энергии, поступающей в поле и возвращаемой из поля обратно для каждого элемента в отдельности Покажем, что при сдвиге фаз между токами tt и t2, отличающимися от 0 и л, от одного из элементов в магнитное поле поступает больше энергии, чем возвращается, а от другого элемента, наоборот, в магнитное поле поступает меньше энергии, чем возвращается В результате энергия передается от одного элемента к другому
Пусть известны токи
и 12 = 12е'^.
Составим выражения для комплексных мощностей первого и второго элементов, обусловленных взаимной индукцией.
= — u>MI2Ir sin (ф2—'ф1) + /«>Л4/2/1 cos (ф2 — фл),
откуда
Р1Л1=- Р2Л1=wMziZ2sm (M’l - Фа); <?! Л1=<22Л1 = соЛ4//2 cos (Ф1 - ф2).
При указанных на схеме положительных направлениях токов и напряжений положительные значения мощностей соответствуют притоку энергии к рассматриваемым элементам от активного четырехполюсника, а отрицательные значения мощностей — передаче энергии из рассматриваемых элементов в четырехполюсник
Суммарная активная мощность, обусловленная взаимной индукцией и поступающая в оба элемента, равна нулю, т е Р1М + Р9М — 0, суммарная реактивная мощность, обусловленная взаимной индукцией, в общем случае отлична от нуля И может быть как положительной, так и отрицательной.
Если я>ф1—ф2 > 0, то Р1ЛЛ>0, аР2Л1<0. В этом случае энергия передается из активного четырехполюсника в магнитное поле через первый эле мент и возвращается через второй элемент Если л > ф2 —i('t > 0, то Р2Д[ > О, а < О В этом случае энергия поступает через второй элемент и возвращается обратно через первый.
Пример 6-4. Цепь состоит из двух индуктивно связанных катушек, включенных параллельно (рис 6-17, а) Дано = 20 Ом, = 80 Ом; г2 = 30 Ом, xL‘z ~ 50 Ом, соД4 = 40 Ом; U = 120 + /20 В Требуется определить мощности, Дяемые ваттметрами, и провести анализ энергетических процессов
197
Решение Подставляя числовые данные Zx = 20 + /80 Ом, Z2 = 30 {-+ /50 Ом, ZM — /40 Ом и U — 120 4 /20 В в (6-11), получаем:
4=~------Z7=-/l = l Z-90° А;
z.—ZM .
HZ7= 1 -/1 = K2 z -45г A;
/=4+4=1—/2 A.
Схемы включения ваттметров таковы, что они измеряют поступающие мощности Р, Рх и Р2 во всю рассматриваемую цепь и в каждую катушку в отдельности.
Р = Re [W] = Re [(120 + /20) (1 + /2)] = 80 Вт;
P1 = Re[[71] = Re [(120+/20) (+ /1)] = —20 Вт;
Р2= Re [[7/2] = Re [(120+ /20) (1 + /1)] = 100 Вт .
Результаты подсчета показывают, что поступающая от источника питания мощность Р меньше мощности Р2, поступающей в одну вторую катушку. Зато
первая катушка отдает мощность (Р, < 0). Стрелка первого ваттметра должна отклониться в обратную сторону — не по шкале Чтобы измерить мощность, отдаваемую первой катушкой, надо изменить схему включения ваттметра Wy. Можно, например, изменить у него подключение цепи напряжения, присоединив зажим со звездочкой к нижнему проводу, а зажим без звездочки к верхнему проводу, так как это показано на рис. 6-17, б Тогда он будет измерять мощность, отдаваемую катушкой.
Р1 = t/BT/BT COS Z (^ВТ, 4т),
где
[4т=- [7= - 120 - /20 В, /вт=А, или
Ру = Re [— Wil = Re [(— 120-/20) (+ /Т)] = 20 Вт.
Сумма мощностей, отдаваемых источником питания и первой катушкой, равна мощности, поступающей во вторую катушку Из всей мощности Р2 = 100 Вт, поступающей во вторую катушку, часть ее, равная
— гг/|=30-(|/2)2= 60Вт,
198
Преобразуется в тепло. Оставшаяся часть
Р2-г2/| = 100—60 = 40 Вт, очевидно, поступает в магнитное поле и затем из магнитного поля в первую катушку. Покажем это:
=jыМ12 = /40 (1 - /1) = 40 + /40 В;
Тг2Л1 = /шЛ4/1=/40(-/1) = 40 В.
Мощность, отдаваемая второй катушкой в магнитное поле,
P2M = Re[7/2M/2] = Re[4()(1+/1)]=40 Вт,
Т,е' Р =Р-гР
2Л1 2 2 2-
Мощность, отдаваемая первой катушкой в магнитное поле, Р1Л1 = Re PwA] = Re К40+У40) (+ / >)1 = ~ 40 Вт.
Таким образом, Р1Л/] 0, т. е. эта мощность не отдается, а подводится из
магнитного поля и численно равна мощности Р2Л1, поступающей в магнитное поле от второй катушки. Часть поступившей мощное!и преобразуется в тепло в первой катушке
ГЛ = 20.12=20 Вт, а остальная часть
(-р1Л1)~^ = 20 Вт возвращается в цепь.
Мощность, поступающая в цепь от источника питания, равна мощности, преобразующей в тепло,
Р = nil+nil = 20 + 60 = 80 Вт.
Для рассматриваемой цепи на рис. 6-17, в приведена векторная диаграмма, токов и напряжений.
Сдвиг фаз U и Д превышает л/2, поэтому Pt 0. На диаграмме показаны активные составляющие напряжений, обусловленные взаимной индукцией 7/1Л1 и 02Мя. Составляющая Д9Л1а совпадает по фазе с /2, а составляющая Д1Д1а находится в противофазе с 71, поэтому Р%м > 0, а ₽1Л{ 0.
6-8. Трансформатор без стального сердечника (воздушный трансформатор)
В электротехнике широко применяется передача энергии из одного контура цепи в другой при помощи трансформаторов. Они мсгут иметь различные назначения, но чаще всего предназначаются Для преобразования переменного напряжения. Отсюда возникло и само название аппарата, происходящее от латинского слова trans-formare — преобразовывать. Такое преобразование необходимо, например, в том случае, когда напряжение источника энергии отличается от напряжения, которое требуется для приемника энергии.
Трансформаторы состоят из двух или нескольких индуктивно связаннных катушек или обмоток. Ограничимся здесь рассмотрением простейшего двухобмоточного трансформатора без ферромагнитного сердечника. Такие трансформаторы применяются при высо
199
ких частотах, а в ряде специальных измерительных устройств и при низких частотах переменного тока.
Обмотка трансформатора, к которой подводится питание, называется первичной, обмотка, к которой присоединяется приемник энергии, — вторичной. Напряжения между зажимами обмоток и токи в этих обмотках называют соответственно первичными и вторичными напряжениями и токами трансформатора. Цепи, в состав которых входят пер
вичная и вторичная обмотки трансформатора, называются соответственно первичной и вторичной цепями трансформатора.
Если пренебречь распределенной емкостью между витками
Рис. 6-19.
Рис. 6-18.
обмоток трансформатора, то цепь, состоящая из двухобмоточного трансформатора и приемника (нагрузка), имеет схему, представленную на рис. 6-18.
Введем обозначения:
<oLi—Xi, г2-)-гн— г22, coL2-J-хн—х22,
где га и ха — активное и реактивное сопротивления приемника, г22 и х22 — активное и реактивное сопротивления вторичного контура.
Запишем уравнения по второму закону Кирхгофа для первичного и вторичного контуров: '
ЛтА —)оМ12=й1;
^22^2 4" 1^22^2 — ](&М 11 = 0.
(6-14)
Построим векторную диаграмму токов и напряжений для первичной и вторичной цепей. Для этого зададимся током и отложим векторы /2, гн/2, /хн/2, г2/2 и /coL2/2 (рис. 6-19, где принято хн > 0). Соединив конец вектора j&L2t2 с началом векторной диаграммы, получим, как следует из второго уравнения (6-14), вектор — jtaMit Разделив на пряжен ие ш /И /j на те М, определим значение тока Д.
200
Вектор Л отложим под углом л/2 (в сторону опережения) к вектору—/со ИД. Затем построим векторы rJA, jaiL-Jy и —/соЛ1/2. gx сумма равна вектору напряжения Оу.
Решая уравнения (6-14) относительно тока Д, получаем:
^ = (Г1+гвн) + /(^ + ^н)’ (6'15)
со22И2
где обозначено гвк= (6-16)
'23 —Г Л22
(02М2 —
^*ВН ~ г2 I у2~ ^22- (6-17)
* 22 ~I Л22
Сопротивления гвн и Л'в„ называют вносимыми (из второго контура в первый) активным и реактивным сопротивлениями. Из структуры выражения (6-15) следует, что со стороны первичной
обмотки вся схема может рассматриваться как двухполюсник с со-
противлениями Гу + Гв„ И Д + хвн.
Вносимое активное сопротивление всегда больше нуля. В нем поглощается энергия, которая в реальной цепи передается из первичной цепи во вторичную. Вносимое реактивное сопротивление имеет знак, противоположный знаку Д2.
Пользуясь схемой эквивалентного двухполюсника, решим вопрос об усло-
Рис. 6-20.
виях передачи максимальной активной
мощности во вторичную цепь, т. е. передачи максимальной мощ-
ности в сопротивление г,,„. Для этого (см. §3-19) должны удовле-
творяться следующие соотношения между сопротивлениями:
ГВН = Г1 и д + дн = 0,
или
а»
__ w2Af2
Х1--Г2 1У2 Х22-
1 22 ~ГЛ22
(6-18)
(6-19)
Последние соотношения можно получить, если предусмотреть возможность изменения параметров контуров. Для изменения Д и х22 в первичный и вторичный контуры можно включить конденсаторы переменной емкости (рис. 6-20), для изменения М применить трансформатор с подвижными обмотками (вариометр) или трансформатор с подвижной магнитной системой. Отметим, что для выполнения соотношений (6-18) и (6-19) достаточно предусмотреть изменение только двух из трех параметров Ху, х22 и М.
Все приведенные выше выражения справедливы для схемы по Рис. 6-20, если положить
• Ху—cof^y — 1/coOj, Л22со/.2—р — 1/оС2.
201
Из соотношения (6-18) получаем:
*22
j/" Ю2^2Г22 —
х22 имеет вещественное значение при условии, что со/И 2з Уrrr^.
Если Л4 < У t\r22J(£>, то ни при каких значениях х22 и хг не может быть получена максимальная мощность.
Схема двух контуров с индуктивной связью (рис. 6-18) может быть заменена эквивалентной схемой без индуктивной связи. Для этого соединим между собой два нижних зажима схемы (режим при этом не изменится). Части контуров с элементами rlt и r2, L2 рассмотрим как две индуктивно связанные ветви, присоединенные к одному узлу своими одноименными зажимами, и применим для них эквивалентную схему (рис.
6-14). В результате для рассматриваемой цепи получим эквивалентную схему по рис. 6-21.
Глава седьмая
КРУГОВЫЕ ДИАГРАММЫ
7-1. Комплексные уравнения прямой и окружности
Многие практические задачи требуют исследования зависимости цепи от различных факторов. Для таких исследований наряду с аналитическими методами прибегают к графическому методу — к построению геометрических мест концов векторов, изображающих различные величины. Эти геометрические места, называемые диаграммами (годографами), могут иметь сложную форму. В простейших случаях получаются прямые линии и дуги окружности, которые и называют соответственно линейными и круговыми диаграммами.
При исследовании электрических цепей часто какая-нибудь комплексная величина определяется уравнением вида
L = A+N, (7-1)
где А = ае>а = const, a N = tieiv — изменяющаяся комплексная величина с неизменным аргументом v и переменным в пределах от 0 до оо модулем п. Геометрически L представляет собой сумму двух векторов (рис. 7-1), один из которых А неизменяем, а другой, N сохраняет неизменное направление (v = const), но изменяется по длине. Конец вектора L совпадает с концом переменного вектора N
Следовательно? гебмшрическим мёссшГ^кЗйца вок гор a tr служит
202
полупрямая, проходящая через конец вектора А. Таким образом, Арп указанных условиях уравнение (7-1) является комплексным уравнением полупрямой. Если же п рассматривать не как модуль комплексной величины (который всегда положителен), а как вещественное число, изменяющееся от — оо до + то уравнение (7-1)
будет представлять комплексное уравнение прямой, проходящей через конец вектора А. Часть прямой, соответствующая отрицательным значениям п, показана на рис. 7-1 пунктиром.
Теперь рассмотрим другой тип уравнения, который очень часто встречается при анализе электрических цепей:
,, В
M~A + N’
(7-2)
где А — ае'а = const, В = = const, a N — neiv — комплекс-
ная величина с неизменным аргументом v = const и модулем п, изменяющимся в пределах от 0 до оо.
Покажем, что геометрическим местом концов векторов М
Для этого разделим числитель и знаменатель выражения (7-2) на А\
является дуга окружности.
Рис. 7-2.
М — - В/А..... = М° (7-3)
M-l + N/A пе?ф> (73)
1 а
где Мо — В!А (Мо = М при
п = 0), = v—а, и перепишем
выражение (7-3) в следующем виде:
(7-4)
При всех значениях п сумма двух изменяющихся векторов М и М (п/а)е!^ равна неизменному вектору Л40. На рис. 7-2 векторы показаны для одного частного
значения п при условии яр > 0.
При всех значениях п от 0 до оо вектор М (п/а)е№ повернут относительно вектора М на угод яр, а угол при вершине М треугольника 0Л4/С равен постоянной величине л — гр.
Отсюда следует, что конец вектора М лежит на дуге ОМК окружности, для которой вектор Мо является хордой. Ниже будет дан простой способ построения этой окружности, а сейчас покажем, как найти вектор М для любого значения п.
Отложим от точки О по направлению хорды ОК отрезок ОА,
Равный в некотором (произвольном) масштабе, а. Затем через точку — ^проведем прямую AN' под углом — чр = а — v к вектору Л40
203
и продолжим линию ОМ до пересечения в точке N с линией AN'. Получились два подобных треугольника OAN и ОМК (Z. КОМ ~ ~ /_ AON, £ ОМК = Д AON = п —ip). Из подобия следует, что
А N/OA —МК/ОМ~п/а. (7-5)
Таким образом, если отрезок ОА соответствует а, то отрезок AN в том же масштабе определяет модель п изменяющейся комплексной величины N. Линия AN' называется линией изменяющегося параметра. Откладывая на ней отрезки AN, соответствующие различным значениям п, и соединяя их концы с точкой О, можно для любого значения п определить положение вектора М. При увеличении п точка М приближается к точке О. В пределе при п — оо длина вектора М должна согласно (7-3) равняться нулю, следовательно, точка М сольется с точкой О, т. е. секущая ON станет касательной ОТ, и так как точка N уйдет в бесконечность, то прямая ОТ будет параллельна линии изменяющегося параметра AN', поэтому перпендикуляр 0D к линии изменяющегося параметра является вместе с тем перпендикуляром к касательной точке О и, следовательно, совпадает по направлению с диаметром окружности, проведенным через точку О. Отсюда вытекает следующий прием построения круговой диаграммы:
1) откладывается вектор Мо — это хорда ON окружности;
2) от начала вектора Мо по его направлению откладываем отрезок ОА, равный в произвольном масштабе а;
3) под углом —1|) = а — v к вектору Мо проводим линию изменяющегося параметра AN';
4) проводим прямую OD перпендикулярно линии AN'; прямая 0D проходит через центр окружности;
5) из середины вектора Мо восстанавливаем перпендикуляр и продолжаем его до пересечения в точке С с линией 0D. Точка С — центр искомой окружности.
Заметим, что «рабочая часть» окружности, т. е. та дуга, по которой перемещается точка М, расположена относительно хорды ОК с той же стороны, где находится линия изменяющегося параметра.
7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника
Рассмотрим схему неразветвленной цепи (рис. 7-3), состоящую из последовательно соединенных неизменного сопротивления ZK = гкеЮк и сопротивления Z2 = с неизменным аргументом <р2 и модулем г2, изменяющимся в пределах от 0 до оо. Положим для определенности, что <рк > <р2 > 0. Найдем геометрическое место конца вектора тока при неизменном напряжении
Выражение для тока
- Z1; + , г2 j ftp*—
Zk
ничем не отличается от выражения (7-3), в котором М соответствует /; соответствует UJZK — /к; п -> г2; а гк и гр -> (<р2 — <рк). Следовательно, конец вектора / перемещается по дуге окружности.
Построение круговой диаграммы может быть выполнено в следующем порядке:
1. Выбираем масштаб mUl для напряжения и откладываем вектор (рис. 7-4).
2. Вычисляем ток при г2 = 0, т. е. при коротком замыкании на зажимах приемника (и = 0).
3. Выбираем масштаб для тока nij и откладываем вектор /к. Он представится отрезком ОК = IJmt, повернутым относительно
Рис. 7-4.
Рис. 7-3.
4. Выбираем масштаб сопротивлений ms и вдоль прямой ОК откладываем отрезок ОА = zKlmz.
5. Из точки А под углом —чр = <рк — <р2 к вектору /к проводим линию изменяющегося параметра AN'.
6. Из начала координат проводим прямую OD I AN'.
7. Находим центр С круговой диаграммы как точку пересечения прямой OD и перпендикуляра, восстановленного из середины хорды ОК-
8. Проводим дугу круговой диаграммы. Эта дуга ограничена хордой ОК и лежит с той же стороны относительно хорды, где расположена линия AN'.
Ток / для любого значения г2 находим из диаграммы простым построением. Откладываем отрезок AN = z2lmz и точку N соединяем прямой с точкой О. Отрезок ОМ этой прямой от точки О до пересечения с окружностью и представляет вектор тока /. При изменении г2 от 0 до оо точка М (конец вектора /) перемещается от точки К До точки О.
Покажем, как из круговой диаграммы можно получить различные величины, характеризующие режим цепи.
_ При неизменном напряжении U± на зажимах цепи ток пропор-нзюнален полной проводимости цепи / = yU^; поэтому отрезок ОМ
205
может Служить мерой полной проводимости цепи. Масштаб д,зд проводимости определим по режиму короткого замыкания, при котором проводимость измеряется отрезком ОК- ту—^~. В этом же масштабе можно определить активную и реактивную проводи-мости цепи, как проекции отрезка ОМ на ось, совпадающую с вектором и ось ОР, ей перпендикулярную.
Если т. е. считается вещественным числом, и вектор
Or направлен по осп вещественных величин (на рис. 7-4 вещественная ось направлена вверх), то / и У имеют одинаковые аргументы и круговая диаграмма для тока в масштабе ту является круговой диаграммой комплексной проводимости цепи.
Из диаграммы имеем:
где ОК—йг/т^, OM — U^mjZ^, MK=O2lmi^K-
Длины отрезков ОК, ОМ и МК пропорциональны напряжениям l/j, 0к и О2. Напряжения UK и U2 можно определять по отрезкам ОМ и МК, пользуясь масштабом
tnUK^mU2 = UrlOK,
Направления векторов Ок и О2 (на диаграмме не показаны) отличаются от направлений векторов ОМ и МК на угол фк.
Длина перпендикуляра MF, опущенного из точки М на линию ОР, определяет активную мощность Рг на входе цепи. Действительно,
Pi ~ U J cos <pr = UjtnfiM cos <pi == Vr^i-iMF=mpxMF,
где тп = Uxmi — масштаб мощности Рх.
Отрезок OF прямой ОР пропорционален реактивной мощности на входе цепи. Действительно,
Qr=Uil sin<pi = U rtrtjOM s in <pi = Vrm-iOF—mP1OF.
Покажем еще, что полную (Х2), активную (Р2) и реактивную (Q2) мощности можно определить отрезком MG перпендикуляра MF к линии ОР или длиной перпендикуляра МН, опущенного из точки М на хорду ОК-
Опустим из точки К перпендикуляр КВ на прямую ON. Площадь треугольника ОМК равна:
^0М-КВ = -^0М-МК$1п(/ КМВ) = ^—sin(Z КМВ)^
£ & & ^£/2
— sin (4. КМВ) g
~ 2mimU2 2'
Угол О. КМВ = | 'Ф I = | ф2 — фк | не зависит от положения -гочкшлМ. В полученном выражении для п л ощадитреу гольи и ка _ ОМК все сомножители, кроме S2, постоянны. Следовательно,
206
режима и разделив полученные отмеченного на диаграмме точ-т,,МКт,ОМ
лошадь треугольника пропорциональна S2. Так как ср2 = const, то лошадь треугольника пропорциональна также Р2 = S2 cos q>2 и n = S2 sin <p2. У треугольника ОМК сторона ОК постоянна, поэ-^5му его площадь пропорциональна высоте МН (ОК принята за оСнование треугольника) или отрезку MG, который пропорционален мн.
Масштабы т$2, т.р2 и то2 можно определить, вычислив мощности 5„, Р2 и <2г для любого частного значения на длину отрезка MG.
Например, исходя из режима, кой М, имеем:
_ «2 _U2I _ _ mS2 — MG — MG — MG ;
So cos ср» So sin cp,
mP2=-^5^ = ms2 cos <p2; mQ2 = -^^==mS2sinq2.
Пользуясь круговой диаграммой, можно определить зависимости I, UК, ^2. <Pi, Pl, р2, Qi и <2г от г2.
Для этого, задавшись значением г2, отложим соответствующий отрезок AN и определим положения точки М — конца вектора /. Затем проведем отрезки МК, MF и MG и замерим их длины; наконец, пользуясь масштабами, вычислим соответствующие этим отрезкам величины. Вообще же по круговой диаграмме можно найти зависимость всех перечисленных выше величин от любой из них, принятой за независимую переменную. Вычер- 5
чивая ряд отрезков, изображающих величину, которая принята за независимую переменную, нетрудно построить отрезки, определяющие Рис- 7-5-остальные величины.
Рассмотренная круговая диаграмма для неразветвленной цепи применима к любому активному двухполюснику, сопротивление нагрузки которого изменяется так, что угол <р2 = const. Это утверждение следует из теоремы об активном двухполюснике, согласно которой можно активный двухполюсник с сопротивлением нагрузки hZ2 представить схемой по рис. 7-3, в которой ZK —входное сопротивление активного двухполюсника, а LA - Пх — напряжение на зажимах двухполюсника при холостом ходе.
Пример 7-1. Построить диаграмму для тока / в неразветвленной части цепи РИс 7-5 При изменении емкости С, считая, что остальные параметры цепи /у, и L, а также частота и напряжение питания неизменны.
Решение Ток I = I + /2. Ток = 7//(г1 + /хД неизменный, а ток 4 = & (г2 — jxc) изменяется по круговой диаграмме. Заметим, что г2 и — jxc ® схеме на рис. 7-5 соответствуют сопротивлениям ZK и Z2 в схеме на рис. 7-3 и комплексным величинам А и N в выражении (7-2).
Выбрав масштабы и ms, отложим векторы U и (рис. 7-6). Конец век-й примем за начало Ot для построения круговой диаграммы тока 12. Вычис-ИЛ! ток /2 при коротком замыкании изменяющегося сопротивления, т. ёГ при
207
хс~ 0, получим /Зк = U/r^. Ток / совпадает по фазе с напряжением U- Отложив вектор 72к из конца вектора /1( получим хорду С//( круговой, диаграммы /2. Выбрав масштаб тг, отложим отрезок 0}А — r2/mz. Затем из точки А под углом
— ф = <х — v = 0 — (— л/2) = л/2 п AN'. Перпендикуляр 0}D, проведеннь няющегося параметра AN', совпадает восстановленный из середины хорды
Рис. 7-6.
роведем линию изменяющегося параметра ,тй из начала диаграммы к линии изме- с хордой О]К'. Поэтому перпендикуляр, (показан пунктиром), пересекается с OtD в середине хорды. Эта точка пересечения — центр С круговой диаграммы. Таким образом, в рассматриваемом случае хорда ОХА является диаметром окружности. Круговая диаграмма тока /2 представляется половиной дуги окружности, лежащей слева от OtK (на той стороне, где находится линия изменяющегося параметра). На круговой диаграмме по-
Рис. 7-7.
казано положение вектора f2 для некоторого частного значения хс. Так как I — It + /?, то, как видно из построения, конец вектора / перемещается по той же полуокружности, по которой перемещается конец вектора /2.
На диаграмме отмечены два резонансных режима (когда ток / = /J и/ = /J совпадает по фазе с. напряжением Z7): первый резонансный режим (/') —при хс — х'с и второй (!") — при хс = х”(.. Из круговой диаграммы следует, что минимум тока /мпн получается вблизи первого резонансного режима, но не при резонансе.
Если lt sin = Ul^, то круговая диаграмма расположится, как указано на рис. 7-7, а, и, очевидно, возможен только один резонансный режим. При A sin > U(рис. 7-7, б) резонанс не получается ни при каком значении емкости С.
7-3. Круговые диаграммы для любой разветвленной цепи
Если в разветвленной цепи сопротивление одной из ветвей, например сопротивление второй ветви, изменяется, а все остальные сопротивления и э. д. с. (токи) источников энергии неизменны, то, как было показано в § 2-7, токи и напряжения любых ветвей связаны линейными зависимостями. Это справедливо и для цепей синусоидального тока, если неизменны амплитуды э. д. с. В частности, для тока Д в первой ветви и тока Д во второй справедливо соотношение
(7-6)
где А и В — комплексные^числа. ” " ~
208
Рис. 7-8.
Д в b раз и к повороту его на
Рис. 7-9.
На рис. 7-8 показана разветвленная цепь, в которой выделены источник напряжения LK в первой ветви и одно из сопротивлений Z2, входящее в состав второй ветви. Остальная часть цепи, которая может содержать источники питания (активная цепь) показана в виде прямоугольника А.
Пусть г2 (модуль сопротивления Z2) изменяется, а аргумент <р2 остается неизменным; тогда, рассматривая всю цепь относительно сопротивления Z2 как активный двухполюсник, придем к заключению, что конец вектора /2 перемешается по дуге окружности. Покажем, что в этом случае диаграммой тока Д также является дуга окружности.
Пусть дуга ОК2 (рис. 7-9) представляет круговую диаграмму тока Д. Умножение Д на В = ЪеК‘ приводит к изменению длины вектора угол р. Поэтому диаграмма вектора ВД представляется дугой окружности ОК', проходящей через точку О, повернутой относительно дуги ОК2 на угол Р и имеющей радиус, в b раз больший радиуса дуги ОК2- Перенеся дугу ОК' параллельно вектору А на отрезок, равный длине вектора А, получим дугу O^Ki- Конец вектора Д = А + ВД, как это следует из построения, находится на дуге окружности (Д/Д, т. е. дуга OrKi — круговая диаграмма тока д.
Итак, если в какой-либо ветви разветвленной цепи изменяется только модуль одного из сопротивлений и остаются неизменными амплитуды э. д. с. (токов) всех источников питания, то конец вектора тока любой из ветвей описывает круговую диаграмму. Так как напряжения и токи любых ветвей связаны линейными зависимостями, то и для всех изменяющихся напряжений получаются круговые диаграммы.
Чтобы определить комплексы А и В линейного соотношения (7-6), нужно знать токи Д и /2 для каких-либо двух режимов, при двух различных значениях г2, например при г2 = 0 и г2 = оо.
При г2 = оо (т. е. при разомкнутой ветви 2) Д = 0. Пусть при этом Д = Дх, тогда из написанного соотношения имеем: Дх = == А 4- В -0, откуда А = Дх, т. е. коэффициент А равен току в ветви 1 при разомкнутой ветви 2. _ Пусть при г2 = 0 (т. е. при ~корогком_замыкании веши /2 ^Дк и Д — Дк, тогда, ггодстав-
209
ляя эти значения в (7-6), получаем:
Лк—71 + + ^Лк>
откуда
В
и, следовательно,
/1==д+в/2=/1х+Ц-^/2.
у2К
(7-7)
Обозначим через О2х напряжение на зажимах ветви 2, когда она разомкнута, и через Z2K — входное сопротивление всей остальной
цепи, рассматриваемой как активный двухполюсник относительно зажимов ветви 2. Тогда по теореме об активном двухполюснике
! ___ — _______________^2Х____________
2 Z2K -j- Z2 Z2K (1 -|- Z2/Z2K)
=------, (7-8)
1_Ь_±2_еЛ1?
Z2K
где -ф = <р2 -— <р2к.
Подставляя (7-8) в (7-7), получаем:
йк In.
z2K
(7-9)
Второе слагаемое имеет такой же вид, как выражение (7-3), и, следовательно, графически может быть представлено круговой диаграммой с хордой /1К — /1Х.
Для построения .круговой диаграммы тока 7Х нужно предварительно определить 71х, 71к и Z2K.
Построение круговой диаграммы выполняем в следующем порядке:
1) выбира.ем масштаб mV1 и откладываем вектор (рис.7-10);
2) выбираем масштаб и откладываем векторы /1х (отрезок OOj) и /1к (отрезок ОК). Построение круговой диаграммы приводится для случая, когда <р1х <0 и <р1к > 0;
3) соединяем точки Ох и N, получаем хорду ОгК,
4) выбираем масштаб тг и откладываем на хорде ОгК отрезок ОХА = z2Jmz\
5) проводим прямую изменяющегося параметра AN' под углом — Ф = <Ргк — <Рг к хорде OiK рассматриваемой как отрезок, имеющий направление от точки О, к точке К (построение круговой лиа-граммы приведено для случая, когда угол <р2к — <р2 > 0, и поэтому
210
на рис. 7-10 этот угол отложен относительно ОХК против направления движения часовой стрелки);
6) проводим прямую OJ7) I AN'-,
7) на пересечении перпендикуляра к середине хорды с линией OyD находим центр С круговой диаграммы.
Для любого значения г2 можно отложить отрезок AN = z2lmz и на пересечении линии ОХА'Г с круговой диаграммой в точке М найти положение конца вектора тока Д.
рис. /-с, за исключением
Рис. 7-11.
Из сказанного выше следует, что дуга ОгМК, рассматриваемая относительно точки Ог, представляет пропорционально измененную и повернутую на некоторый угол круговую диаграмму активного двухполюсника. Под активным двухполюсником здесь подразумевается вся цепь, представленная i сопротивления Z2. Поэтому ток /2, напряжение U2, мощности S2, Р2 и Q2 определяются теми же отрезками прямых, которые служили для этой цели в круговой диаграмме двухполюсника. Ток /2 определяется отрезком ОгМ, напряжение U2 — отрезком МК, а мощности Х2, Р2 и Q2 — отрезком МН, или, что удобнее, пропорциональным ему отрез-
ком MG.
Для определения масштабов U2, 12, Р2 и Q2 нужно вычислить значения этих величин для каких-либо частных режимов и затем
разделить эти значения на длины соответствующих им отрезков диаграммы. Например, вычислим /2К и U2x. На диаграмме току /2к и напряжению Й2х соответствует хорда О±К. Следовательно, масштаб пг12 = Рк/ОхК и масштаб mU2 = U2XIO±K.
Пример 7-2. В цепи, показанной на рис. 7-11, Ё = 10 В, Zt = 10s Ом; Zs = = /Ю3Ом; хс изменяется от 0 до оо. Построить круговую диаграмму для тока 1г и определить по ней значения Iv /2, U2 и хс в двух режимах, когда /2 = ' Смаке и когда U2 б^2макс.
Решение. Находим величины, необходимые для построения круговой Диаграммы и для определения масштабов:
Ё
Ёх = Сх = -7-Г7~ = 7>07 - 45° мА;
Z1"TZ 3
7 7
Im = = E/Zt = 10 мА; Z2K = = 707 д 4f? Ом;
(zi + zs)
C2x = Z3/3x=7,07 z. 45° В; -ф=<p2K-<p2 = 45°-(- 90°)= 135°.
Выбираем масштаб и откладываем векторы /1х и / (рис. 7-12). Обратим внимание, что на рис. 7-12 система координатных осей повернута на 90° против часовой стрелки по сравнению с ее обычным расположением. Ось положительных Вещественных величин направлена вверх, а ось положительных мнимых — влево. Такое расположение осей применяют часто, желая направить вектор напряжения или э д, с. вертикально при нулевой начальной фазе. Заметим, что такое расположен ие вектора напряжения было и на рис. 7-4 и 7-10 На рис. 7-12 вектор э- Д. с. ие изображен, поскольку он не нужен для решения задачи.
211
Проводим хорду Oj/C Выбираем масштаб тг и откладываем о i резок 0,А = ~ zaJmz~ 7$7/тг. Из точки А под углом —ф = 135° проводим линию изменяющегося параметра AN'. Опускаем перпендикуляр 0J) на линию AN' и восстанавливаем перпендикуляр к середине хорды Получаем точку С — центр круговой диаграммы.
Ток /, измеряется отрезком ОМ, ток /2 — отрезком 0,М, напряжение 07™ — отрезком Л7И, сопротивление хс —отрезком AN. Масштабы т{1 и т были выбраны, масштабы mJ2 = = мА/см, и mU2 = ОуО^К =7,07/0^0
В,см. Ток 1г = /2макс, когда отрезок 0tM имеет наибольшую длину, т е. когда точка 7И занимает положение 7ИХ. Напряжение 072 = t72Makc, koi да отрезок КМ
имеет наибольшую длину, т е когда точка 7И занимает положение ТИ2, совпадающее с точкой О Значения переменных величин, соответствующих точке Mlt обозначим одним штрихом, а точке ТИ2 — двумя штрихами.
7J —тлОЛ11 = т/1ОО1=71х=7,07 мА,
7; = т,„О17И1 = 7Д^О^1Л2=10|/2 мА;
7 07
O',-=mU2KM1 = -~-O1K=7fi7 В;
- 1 огк
Х‘\ = т AN, = т = — 500 Ом.
с Z 1 г |/2 J<2
В проведенном подсчете учтены следующие соотношения между длинами отрезков, очевидные из рассмотрения диаграммы.
O7W1 = OO1; ATW^OjA и AN, = O,A]V2.
Ток /;' = 0;
Д'=т/2О1Л72 = ^О1Л72=Ю мА;
7 07
07" = тЬ2КМ2 КМ2 = 7,07 р' 2 = 10 В;
= mzAN2 = тгОгА У 2 = г?к]/2 = 1000 Ом.
Точка М2 соответствует резонансу токов Так как рассматривается теоре-тический случай, когда в-ветвях 2 иЗ нет активпого-сопротивлсния, то Г'=-0л U2 = Е.
212
Пример 7-3. Для той же цепи (рис 7-11) построить при изменении л'с круговую диаграмму для тока Л> и отметить на ней точки Alj и Л12, соответствующие /2мэКГ и ^амакс Найти для этих режимов значения тока /3
Решение При хс = 0 имеем 7 = 0 Все остальные параметры, необходимые для построения круговой диаграммы для /3, 'вычислены в предыдущем примере
Выбрав масштаб т/3, откладываем вектор / = /1х (рис 7-13) Таккак/Зк = = 0, то конец вектора /зк — точка К совпадает с точкой О Выбрав масштаб тг, откладываем отрезок OtA = = 7,07/ тг Из точки А под углом —тр = 135°
проводим линию переменного параметра AN' Затем определяем центр С окружности и строим круговую диаграмму Отрезками ОМ, ОгМ, КМ и AN измеряются соответственно 7 /2, и х, Масштабы m,s и тг были выбраны, масштабы m/2 = liJOyK и mU2 = Н2х/О1Д Ток /2 = /2макс в точке Mt Напряжение О = Н2макс в точке М2 Из дна! раммы находим 12 = 7ЗХ = 7,07 мА и 73 — ) 273х = = 10 мА
Глава восьмая
МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ Й НАПРЯЖЕНИЯХ
8-1. Четырехполюсники и их основные уравнения
Исследование режима работы сложной электрической цепи часто сводится к установлению связи между токами, напряжениями и мощностями различных ее участков или ветвей. При этом режим остальной части цепи может оставаться неизвестным, хотя все ее параметры учитываются при решении задачи. В таких условиях
Рис 8-1.
Рис 8-2.
Рис 8-3.
рассматриваемая цепь может определяться обобщенными параметрами на соответствующих зажимах, относительно которых параметры заданы или должны быть найдены.
Часть цепи, которая характеризуется обобщенными параметрами, необходимыми и достаточными для составления уравнений связи между токами и потенциалами на ее зажимах, называется многополюсником. Число полюсов многополюсника равно числу зажимов на границе данной части цепи. Многополюсники часто условно изображаются в виде прямоугольников с соответствующим числом зажимов-полюсов. Так, на рис. 8-1 показано условное изображение пассивного двухполюсника, на рис. 8-2 изображен трех-полюсник, а на рис. 8-3 — четырехполюсник.
---Практически при исследовании электрических цепей чаще приходится пользоваться двухполюсниками, трехполюсниками и четы
213
Рис. 8-4.
ления токов в этих ветвях
рехполюсниками с фиксированными зажимами для присоединения источников электрической энергии и приемников. Четырехполюсники, не содержащие в своих ветвях источников энергии, называются п а с с и в н ы м и, к числу которых относятся, например, линии передачи электрической энергии и трансформаторы. Четырехполюсники, содержащие в своих ветвях источники энергии, называются активными.
Для изучения теории и методов расчета режимов пассивных четырехполюсников рассмотрим схему с двумя источниками энергии.
Выделим две ветви с источниками э. д. с. Ег и Ё2 (рис. 8-4). Тогда остальную часть схемы можно рассматривать как пассивный четырехполюсник с первичными — входными зажимами 1 — I' и вторичными — выходными зажимами 2 — 2'; при этом внутренние сопротивления источников энергии отнесены внутрь четырехполюсника. Положительные направ-и напряжений на их зажимах выбраны
в соответствии с направлениями э. д. с. (рис. 8-4).
Пользуясь методом контурных токов (при выбранных положительных направлениях токов Д, /2 и напряжений 1У2), напишем следующие уравнения:
£1=Й1=Zili1 -j- z124; £2 = ^2 — 4" ^22^2.
где Zu = £Д/Д и Z21 — Cjli при Д = 0 (питание четырехполюсника со стороны первичных зажимов и разомкнутые вторичные); Z22 = и Z12 = С\П2 при Д = О (питание четырехполюсника со стороны вторичных зажимов и разомкнутые первичные).
Форма записи уравнений (8-1) называется формой Z. Эти уравнения можно записать и
£Д
(8-1)
матричной ^11 ^12
форме:
1
Z21 222
(8-1а)
2
Если из уравнений (8-1) выразить токи Д и Д через напряжения и f72, то получаются следующие уравнения:
А— ^21^4 + У22^2, /
где
У11==______?22___. у __________Z12
ZnZas Z12Z21’ 12 ZUZ?2— Zi2Z2i ’
V - 1 -
Z11Z22 ZlaZ21 ’ 22 ZUZ22—Zl2Z21
214
Уравнения (8-2) могут быть получены и непосредственно из схемы рис. 8-4 методом узловых потенциалов. Форма записи уравнений (8-2) называется формой Y; эти уравнения можно записать также в матричной форме:
Л
4
/Л
и2
(8-2а)
Для анализа четырехполюсника с транзисторами (см. гл. 9) часто применяются уравнения с так называемыми смешанными (гибридными) параметрами, в которых независимыми переменными являются напряжение О2 и ток Д, а зависимыми — напряжение и ток /2. Эти уравнения легко получаются из (8-1) в следующем виде:
/А=//и4 Ч- и 12^2;
(8-3)
где и ZiiZ2z Z12Z21 rj z12 Z711 — 7 П12 7 A22 *^22 rr — — ^21 . EJ 1 /721 7 у П 22 7 • ^22 ^22
Аналогично (8-1 а) и (8-2а) уравнения (8-3), которые называются формой Н, можно записать в матричной форме:
Ui
4
//и
#21
(8-4)
Для исследования режимов четырехполюсников при их каскадном соединении целесообразно иметь такую форму уравнений, в которой напряжение и ток Д выражены через напряжение О2 и ток Д. С этой целью по теореме о компенсации заменим э. д. с. Е2 падением напряжения в сопротивлении Z2 от тока Д, направленного навстречу £2 (рис. 8-5). Эту схему смежно рассматривать и как
четырехполюсник с источником э д. с. на входных зажимах и сопротивлением нагрузки Z2 на выходных.
В связи с изменением положительного 'рис. 8-5) в уравнениях (8-2) для этой схемы тэком Д:
Рис. 8-5.
направления тока /2 изменится знак перед
4— |
у2= * 21L'l “Г Т 22°'2- J
18-5)
215
В результате совместного решения уравнений (8-5) относительно йг и получим:
U1=AU2~\-Bi2; }
K = CLJ2 + Di2, / ( ‘6)
где А = У22/Уг1 — безразмерная величина;
В = 1/У21 имеет размерность сопротивления;
С = (УПК22 - У]2Г21)/У21 имеет размерность проводимости;
D = Уп/У21 — безразмерная величина.
Форма записи уравнений (8-6) называется формой А*.
Коэффициенты четырехполюсника А, В, С и D связаны между собой соотношением
Поскольку для взаимных цепей У12 = У21, то, рассматривая далее четырехполюсники, для которых выполняется принцип взаимности (взаимные), получим:
AD-BC=1.
(8-7)
Подчеркнем, что комплексные коэффициенты четырехполюсника А, В, С и D, как и другие коэффициенты и параметры зависят от сопротивлений, проводимостей, конфигурации схемы и от частоты э. д. с. или тока источника.
Уравнения (8-6) можно записать в матричной форме:
А В
С D
Л
(8-8)
Если, у четырехполюсника рис. 8-5 присоединить источник э. д. с. /2 к вторичным зажимам, а к зажимам 1—Г присоединить
Рис. 8-6.
сопротивление нагрузки Z± (рис. 8-6) и изменить положительные направления токов Д и Ц (по сравнению с рис. 8-5) на обратные, то уравнения (8-6) примут вид:
и^Ай^-вЦ-,)
-Л-сС.-с/,.} <м>
Из этих уравнений с учетом (8-7) получим:
772=M+B/i: |
(8-10)
----* Такое наименование объясняется тем, нт иногда все коэффициенты в уравнениях (8-6) обозначают буквой А с различными индексами;
216
Сравнивая эти уравнения с (8-6), легко заметить, что при обратном питании коэффициенты А и D меняются местами.
Четырехполюсник называется симметричным, если при перемене местами источника питания и приемника токи источника энергии и приемника не изменяются. Уравнения симметричного четырехполюсника должны осгаться неизменными при взаимной замене первичных и вторичных зажимов. Поэтому А = D и разметка первичных и вторичных зажимов для симметричного четырехполюсника необязательна. Все четырехполюсники, не удовлетворяющие этому условию, называются н е с и м м е г р и ч н ы м и.
8-2. Определение коэффициентов четырехполюсников
Комплексные коэффициенты несимметричного пассивного четырехполюсника определяются опытным путем или расчетом, причем в последнем случае должны быть известны величины сопротивлений или проводимостей ветвей, составляющих четырехполюсник, и схема их соединения.
Из выражений для коэффициентов А, В, С и D следует, что их значения определяются различным сочетанием трех постоянных величин: Уи (входной проводимости со стороны зажимов 1—Г при закороченных зажимах 2—2'), У22 (входной проводимости со стороны зажимов 2—2' при закороченных зажимах 1—Г) и У12 — ^21 (взаимной проводимости). Следовательно, для экспериментального определения этих коэффициентов достаточно иметь данные опытов, в той или иной форме определяющих три комплексные величины: У1Ъ У22 и У12 = У21. Если можно измерить одновременно как первичные ток и напряжение Д и С/ъ так и вторичные /2, С/2, то для определения коэффициентов А, В, С и D достаточно иметь данные только двух опытов.
Наиболее просто значения этих коэффициентов вычисляются по данным опытов холостого хода и короткого замыкания.
При разомкнутых вторичных зажимах, т. е. когда /2 = 0, из уравнений (8-6) первичные напряжение и ток
£71х = Л[/2; iix = CU2, откуда
А=и^/и2, C = ilxlU.z. (8-11)
Входное сопротивление со стороны первичных зажимов при разомкнутых вторичных
Zix==C\x/Ax — А/С. (8-12)
При этом должны быть измерены не только модули соответствующих величин, но и их фазы.
При коротком замыкании на вторичных зажимах, т. е. когда #2 = 0, из уравнений (8-6)
217
откуда
B-f7iK/4; D=hKii2. (8-13)
Входное сопротивление со стороны первичных зажимов при коротком замыкании вторичных
ZiK=U1K/l1K=B/D. (8-14)
Следовательно, измерив модули и фазы О1Х, /1х и С/2 при холостом ходе и й1к, /1к и 12 при коротком замыкании, легко определить все четыре коэффициента четырехполюсника.
Коэффициенты четырехполюсника можно также рассчитать по данным опытов, измеряя в каждом опыте только первичные или только вторичные ток и напряжение. В этом случае необходимо иметь данные трех опытов, из которых два опыта, описанных выше, проводятся при питании четырехполюсника со стороны первичных зажимов и один опыт — при питании со стороны вторичных, или наоборот. Наиболее простые выражения получаются для коэффициентов Л, В, С и D по данным опытов холостого хода и короткого замыкания при питании четырехполюсника со стороны вторичных зажимов и опыта холостого хода при питании со стороны первичных зажимов.
При питании четырехполюсника со стороны вторичных зажимов и при = О из уравнений (8-10)
откуда входное сопротивление со стороны вторичных зажимов при коротком замыкании первичных
^2К = U2vjI2K—В/А. (8-15)
При.питании четырехполюсника со стороны вторичных зажимов и при /х = 0 из уравнений (8-10)
(8-16) откуда входное сопротивление со стороны вторичных зажимов при холостом ходе на первичных
Z2x = U2xli2x=D/C. (8-17)
Решая совместно уравнения (8-12), (8-15) и (8-17) и учитывая (8-7), получаем:
Так как сопротивления комплексные, расчет по данным опытов дает два значения коэффициента А, а следовательно, и два значения каждого из остальных коэффициентов, поскольку они выражаются через А по формулам
£ = Л£2к; С=Л/71Х; D=AZ2x/Z1K. (8-19)
Такая двузначность объясняется тем, что коэффициенты зависят не только от элементов схемы четырехполюсника, но и от выбора
218
положительных направлений напряжений и токов относительно зажимов четырехполюсника. Однозначное опредение коэффициентов возможно при помощи опыта, позволяющего определить, как это было указано, сдвиг по фазе напряжения или тока на входе четырехполюсника по отношению к напряжению или току на выходе.
Здесь следует также отметить, что возможная ошибка в определении коэффициентов, возникающая вследствие неучета связи между значениями коэффициентов и положительными направлениями токов и напряжений, может привести к ошибочному определению только фазы на угол, равный л. Такая ошибка во многих случаях исследования четырехполюсника не имеет значения. Однако в ряде случаев неправильное определение фазы может иметь существенное значение, например при параллельном соединении четырехполюсников.
Необходимо подчеркнуть, что сопротивления Zlx, Z2x, Z1K и Z2K связаны между собой соотношениями ZtJZ2& = ZlyJZ2y = AID, причем для симметричного четырехполюсника эти отношения равны единице (А = D). Из уравнений (8-18) и (8-19) следует, что для определения коэффициентов симметричного четырехполюсника при А = D достаточно иметь данные двух опытов, например холостого хода и короткого замыкания.
8-3. Режим четырехполюсника при нагрузке
Уравнения (8-6) показывают, что как напряжение Съ так и ток /( на первичных зажимах состоят из двух слагающих, из которых одна пропорциональна напряжению приемника С2, а другая — току 12.
Пусть заданы напряжение С2 и ток 12. Если при разомкнутых вторичных зажимах (/2 = 0) установить напряжение С2 равным напряжению при нагрузке, то напряжение и ток на входных зажимах должны быть равны:
Й1х = Л£/2; Лх = СЙ2.
Если при коротком замыкании на вторичных зажимах (Й2 = 0) установить ток /2 равным току нагрузки, то напряжение и ток на первичных зажимах должны быть равны:
UiK=BI2, /1к=О/2.
Следовательно, напряжение Ur и ток Д при нагрузке равны суммам соответственно напряжений и токов в режимах холостого хОДа и короткого замыкания четырехполюсника. Действительно,
Uг —АС2А~В12 = U |
^г=€Д2Н-П/2 = /и + Дк. J }
219
Эти уравнения выражают принцип наложения. Иначе говоря, для того, чтобы получить на вторичных зажимах четырехполюсника напряжение О2 и ток /2, необходимо установить на первичных зажимах напряжение ОЛх и ток /1Х, пропорциональные О2, а также напряжение, О1к и ток /1К, пропорциональные току /2.
Для характеристики рабочего режима четырехполюсника часто пользуются понятием входного сопротивления со стороны первичных зажимов 1—Г при сопротивлении нагрузки Z2 (рис. 8-5) и понятием входного сопротивления со стороны вторичных зажимов 2—2' при сопротивлении нагрузки Z, (рис. 8-6).
Для определения входного сопротивления схемы рис. 8-5 достаточно разделить первое из уравнений (8-6) на второе; в результате получим:
Z = £4 = М+.В/2 = А^+В . (8-21)
4 c//2-|-d/2 cz2+d
В частности, при коротком замыкании (Z2 = 0) получаем Z1K = В/D, при холостом ходе (Z2 = оо) имеем Zlx = A/C.
Аналогично при обратной передаче (рис. 8-6) на основании уравнений (8-10) имеем:
В2 _ DBi + B/t = DZ1 + B /2 ~ Ct/i+Д/х ~ CZ1+4 '
(8-22)
На практике часто применяются и другие выражения для Z1BX и Z2bx. Например, вместо коэффициентов четырехполюсника А, В, С и D в формулы (8-21) и (8-22) вводят сопротивления холостого хода и короткого замыкания при прямом и обратном питании, т. е.
7 _А В/A 4‘Z2_у ^2к + ^2
1ВХ~ с n/c+z2”z'1’tz2X+z2:
7 ____DB/D-j-Zj___у ZjK-j-Zt
2вх “ С А/С 4- Zj ~ 2х Zlx+Zj ‘
(8-23)
Полученные выражения (8-23) показывают, что четырехполюсники могут быть применены для преобразования сопротивлений.
8-4. Эквивалентные схемы четырехполюсников
Выше было показано, что любой пассивный взаимный четырехполюсник с заданными первичными и вторичными зажимами характеризуется тремя независимыми постоянными коэффициентами. Следовательно, можно представить пассивный четырехполюсник в виде трехэлементной эквивалентной П-образной схемы,
220
или П-схемы (рис. 8-7), и эквивалентной Т-образной схемы, или Т-схемы (рис. 8-8).
Определим параметры П-образной схемы.
Если в правой части первого уравнения (8-2), определяющего ток /’1, прибавить и вычесть Y12Ult а в правой части второго урав-
Рнс. 8 7. ___ Рис. 8-8.
нения для /2 прибавить и вычесть Y21U2, то после преобразований получим:
К —(Yn — У!2) (71 + У12 (Ui — (72) =/ц + 712J 1 (8 24)
/2 = ^21 ((71 — U2) + (Y 22 — Y21) U2 —122 Al- J
Полученным уравнениям (при У12 = У21) удовлетворяет схема, показанная на рис. 8-7. Элементы этой схемы:
ZS=J-: Z1= *— = (8-25)
1 12 1 11 — 2ГЗ * 22 1 12
Пользуясь уравнениями (8-6) и (8-7), можно выразить параметры П образной схемы через коэффициенты четырехполюсника:
ZS = B; Л = = (8‘26>
Элементы Т-образной схемы можно найти по формулам преобразования треугольника сопротивлений (рис. 8-7) в эквивалентную звезду (рцс. 8-8):
у___ "Z-YZ-l . у/ ___ 7372 . у___ 7.^7.2 ,q пух
Zl"“Z3 + Z1H Z2 ’ 73 + 7! + 72' Z.,+Zr | Z2 '
После замены в этих уравнениях Za, Zx и Z2 согласно (8-26) получим:
= = (8-28)
Здесь следует подчеркнуть, что изменение положительного направления тока /2 (на рис. 8-7 и 8-8 указаны пунктирной стрелкой) не влияет на параметры эквивалентных схем, что легко проверить.
Если для четырехполюсника не выполняется свойство взаимности, т. е. Z12 Ф Z21 или У12 Ф У21, то это можно учесть в каждой из эквивалентных схем (рис. 8-7 и 8-8), например, при помощи Дополнительного зависимого активного параметра.
Для иллюстрации отмеченного положения применительно к эквивалентной схеме рис. 8-7 обратимся опять к уравнениям (8-2).—’------
221
В правой части уравнения, определяющего ток Д, надо прибавить и вычесть слагаемое а в правой части уравнения для тока /2 соответственно а также Й12(72; после простейших преобразований получим:
Л=уnt/1—у 12й 2=(У и — У12) -}-
+ ^12(^1 —1/2) = Л1 + Аг! (8-29)
А== У21U У22й2—(Ур, ^12)^2
— ^12 КА — ^А) 4* (^12 — ^21) ^1 = ^22 Аг4- J 12-
Этим уравнениям удовлетворяет эквивалентная схема, показанная на рис. 8-9, в которой источник тока 712 = (К12 — П21)
Рис. 8-9.
является активным параметром, зависящим от входного напряжения С±\ Zr = 1/(Уп— У12);
= 1/(Г22-Г12); Z=l/K12.
Полученная эквивалентная схема для невзаимного четырехполюсника не является единственной. Например, преобразованием тех же уравнений (8-2) можно, аналогично предыдущему, полу-
чить эквивалентную схему с источником тока, зависящим от напряжения (72 и присоединенным к первичным зажимам 1—Г четырехполюсника.
Эквивалентную схему для невзаимного четырехполюсника при Z12 Ф Z21 можно получить путем преобразования уравнения (8-1)
к следующему виду:
Й1 = Zu^i + Z12Z2 — (Zu — Z12) -J- Z12 (Zx -J- /2);
U2 = ^21^14*^22^2— (^22 — Zi2) A 4*
4- (Z21 — /к) A 4- Z12 (A 4- A)-
(8-30)
Этим уравнениям удовлетворяет эквивалентная схема рис. 8-10, где э. д. с. Ё21 = (Z2X — ZX2) /х является активным параметром, зависящим от тока Эквивалент-
ные схемы невзаимных четырехполюсников применяются для анализа и расчета электрических цепей, содержащих электронные лампы и транзисторы.
Четырехполюсники с взаимными параметрами, у которых не заданы парные зажимы для при-
-Ае» Ыг1-71г) (ггг~г/Р
0------CZI-------Г—----------------0
й, а,+4)|[]гв йг 0“---------------1----------------г-0
Рис. 8-10.
соединения источников электриче-
ской энергии и приемников, характеризуются в общем случае шестью коэффициентами, поэтому эквивалентные схемы для таких
хадержат-диесть-элементоа.
222
Для иллюстрации этого положения выделим из сложной схемы некоторую ее часть, не содержащую источников э. д. с. или источников токов, с числом полюсов, равным четырем. Каждый полюс можно характеризовать током и потенциалом по отношению к некоторой произвольной, но общей для всех полюсов точке О (рис. 8-11, а).
Не изменяя режима внутри пассивного четырехполюсника и на его зажимах, дополним рассматриваемую систему до замкнутой, включив между каждым полюсом и общей точкой источник с э. д. с.,
равной потенциалу соответствующего полюса (рис. 8-11, а). Пользуясь принципом наложения, напишем выражения для токов четырехполюсника в виде
Ё = Ё1Уц — — Ё3У13 — Ё4У44;
Ё — ^1^21 + ^2^22 — £з^23—Ё^У^', ('8-311
А — — £1 Кз1 — Ё2У32Ё3У33 — Ё4У34,
Ё— Ё4У41 — Ё<У— Ё~У43 4~ Ёу44.
Пользуясь вторым законом Кирхгофа, можно заменить в этих уравнениях все э. д. с. напряжениями между тем полюсом, для которого определяется ток, и остальными полюсами. Например, в выражении для тока /^заменим э. д. с. Ё4,. Ё2, Ё3 и £4 на основании равенств Ёг = 6%; Ё2 = —+ tf10; Ё3 = — й1я + Д10; £4 = ~ —й14 + О10. В результате получим:
А~ Ё10 (Уи — У12 — У13 — Уц) + Й12У12 + Й13У 1з + Ё14Уi4. (8-32)
Аналогичные уравнения получаются для токов /2, 13 и /4:
А = U20 (У22 ^21 ^23 ^24) 4" Ё21У21 4~ Ё 23У23 4~ +24У24J 1 Ц~Ё30(У33—У31 — Уз2 — + Hsi^si + Й32Уз2 + Й34У34; । (8-33)
А Ё40 (У44 — У41 — У42 — У43) + Ё41У41 4~ ЁуУ42 4~ Ё43 У4S. J
В этих уравнениях напряжения между полюсами связаны РяВеНСТВЙМИ ^”12 "—"* ' ~ ^21 > ^23 ' £^32
223
Так как сумма токов А + 4 + 4 + 4 — 0 при любых £ь Ё2, Ё8 л £4, то из уравнений (8-33) и (8-32) при их суммировании непосредственно следует:
- У12 - У13 - У14 = 0; - У21 + У22 - У23 - У24 —0; )
-- ^31 И32-|-У33 У34 — О; Yil 42 У43+У44 —0- J
Следовательно,
А ~Ё12У12 + С'13У13 + 4==СГ215Л21 + СГ23^Л2з + СГ24^245 1 ,g 35
Д = Й31У31 + Й32У32 + Й34У34; МЛ+^+^Дз. J
Полученным уравнениям удовлетворяет эквивалентная схема, имеющая вид полного четырехугольника (рис. 8-11, б) с сопротивлениями ветвей
Z12 — 1/У12; 713=1/У13; ^£з~ 1/^2з и т. д.
При этом очевидно, что такая эквивалентная схема справедлива для пассивного взаимного четырехполюсника.
Аналогичным путем можно определить параметры эквивалентной схемы для пассивного многополюсника с числом полюсов больше четырех. В общем случае число параметров эквивалентной схемы для пассивного многополюсника равно числу ветвей полною многоугольника, т. е. п (п — 1 )/2, где п — число полюсов.
8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника
На рис 8-12 условно изображен активный четырехполюсник, к входным зажимам которого присоединен источник э. д. с. £ь а к выходным — сопротивление нагрузки Z2
Пользуясь теоремой о компенсации, заменим сопротивление Z2 источником э д с £2 == Z24 и по принципу наложения напишем выражения для токов А и Д:
А — £1Уц — £2^12 + £3У13 + £4Уы+
. ) (8-ЗЬ)
4 — £1И21 t.2Y22-\- £3И23 + £4^4 + -. j
После замены в этих уравнениях э д с £4 и Ё2 соответствующими напряжениями и замены составляющих токов, вызываемых всеми остальными э д с (£3, £4 и т. д), находящимися внутри четырехполюсника, через
Ла==£з^/13 + £4^i4 + - • •! | ("8 37)
/2а=£3И23 + £4У24 + ... J 1 '
получаются следующие выражения:
4=Гп£1-Г12£2 + Да; 1
АуА-+.Д-! 4. h
(8-38)
224
Из уравнений (8-38) непосредственно следует, что при напряжениях йл = 0 и U, = 0 токи короткого замыкания Дк = /ь и /,к = /2а. В отличие от режимов для пассивного четырехполюсника эти токи определяются при одновременном коротком замыкании первичных и вторичных зажимов активного четырехполюсника.
В результате совместного решения уравнений (8-38) относительно первичных напряжения и тока Д получаются следующие уравнения четырехполюсника в форме А:
или
— AU2-\-B (12 —
(Л — Лк)== сй2 -ф d (12—12к) >
где величины А, В, С и D — коэффициенты четырехполюсника, удовлетворяющие, так же как для пассивного (взаимного) четырехполюсника, условию AD — ВС = 1.
Из уравнений (8-39) следует, что любой активный четырехпо-
люсник с заданными первичными и вторичными зажимами харак-
теризуется пятью независимыми параметрами (тремя коэффициентами и токами У1к = Дк = Да; Лк = Лк — Ла) - Поэтому его можно представить в виде пятиэлементной эквивалентной схемы.
Для определения параметров, например, П-образной схемы обратимся к уравнениям (8-38) и
Рис 8-12.
(так же как в случае пассивного
четырехполюсника) в правой части выражения для тока Д прибавим и вычтем а в правой части выражения для /2 прибавим и вычтем в результате получим:
Л — (^и — ^12) + ^12 (Hj — Й2) 4- J iE;
Л = У21 (Й1 — Й2) — (^22 — Д>1) и2 4“ Лк-
(8-40)
Уравнениям (8-40) удовлетворяет эквивалентная схема, показанная на рис. 8-13. Источники энергии, находящиеся внутри четырехполюсника, представлены на эквивалентной схеме источниками тока Угк иУ2к- Пассивную часть схемы (П-образную) можно заменить Т-образной (рис. 8-14) так же, как это было сделано при переходе от схемы рис. 8-7 к схеме рис. 8-8.
Источники тока можно также представить на эквивалентной Т-образной схеме (или П-образной) источниками с э д с Zlx = = Д1Х и /Дх = (рис 8-15), определяемыми-при одновременном
8 Основы теории цепей
225
Рис 8-13.
Рис. 8-14.
размыкании ветвей, присоединенных к первичным и вторичным зажимам активного четырехполюсника.
Установим связь между э д. с. Г1х и Ё2х и токами J1K и J2K. Для этого запишем уравнения (8-39) при одновременном размыкании первичных и вторичных зажимов (токи Д = 0 и /2 — 0), т. е.
£Лх=AU2x — BJ2к и —J^ — CU2x DJ2vi.
Из этих уравнений
^Х Ё1Х Q
Ё2х=и2х = Q
_Ai 2К Q J 1К,
2к~ с
(8-41)
Эквивалентная схема на рис. 8-15 может, быть получена из схемы рис. 8-14 и путем замены источников тока J1K и ./2К источниками
э. д. с., так же как это делалось в методе контурных токов.
Полезно подчеркнуть, что коэффициенты активного четырехполюсника (Л, В, С и£>) и параметры пассивных частей эквивалентных схем не зависят от э. д. с. источников энергии и равны соответствующим коэффициентам и пара-
Рис. 8-15.
метрам пассивного четырехполюсника. При этом, конечно, должны учитываться внутренние сопротивления источников энергии. Вместе с тем активные параметры эквивалентных схем /1К, J2K, Ё1Х и Е2х зависят как от активных,
так и от пассивных элементов заданного четырехполюсника.
8-6. Идеальный трансформатор как четырехполюсник
Идеальный трансформатор представляет собой пассивный взаимный четырехполюсник (рис. 8-16), которому приписывается следующее свойство: при любых условиях отношение первичного и вторичного комплексных напряжений и отношение вторичного и
226
первичного комплексных токов равны друг другу и равны постоянному комплексному числу:
(8-42)
^2 Л
Это комплексное число п называется коэффициентом трансформации идеального трансформатора.
При расчетах идеальный трансформатор часто применяется в качестве составного элемента эквивалентных схем трансформаторов и автотрансформаторов со стальными магнитопроводами, а также в задачах синтеза электрических цепей.
Познакомимся с другими свойствами идеального трансформатора.
Пусть к вторичным (выходным) зажимам идеального трансформатора присоединен приемник с комплексным сопротивлением Z2. Тогда входное сопротивление со стороны первичных зажимов • • 1гТТ
10----1 ।--0----1
,мз) *1 ©4^
т. е. оно в п2 раз больше сопротивления Z2. /0--1 <--0^—>
Если к первичным зажимам присоединен
приемник с комплексным сопротивлением Zb рис 8-16. а питание осуществляется со стороны вто-
ричных зажимов, то аналогичным путем можно показать, что
Z^Z^n2. (8-44)
Эти соотношения характеризуют трансформацию сопротивлении. Если вторичные зажимы разомкнуты, то Z1BX = 00, если они короткозамкнуты, то Z1BX = 0.
’ Установим связь между комплексными мощностями на входе и выходе идеального трансформатора. Комплексная мощность на входе
Sj—и i,ii—пй ziz/n-, где
п V п
п Z. —V
и, следовательно,
S1=e/2VS2.
(8-45)
В том случае, когда коэффициент трансформации вещественное число, т. е. п = п 0°, получаем: = S2 и, следовательно,
73! = Р2 11 Qi = Qi- При комплексном коэффициенте трансформации Рj Р2 и Qi =0= Q2.
Выясним, каковы должны быть параметры реального трансформатора
8*
227
Покажем, что отношение первичного и вторичного комплексных напряжений при любых нагрузках трансформатора будет постоянным, если:
1) сопротивления обмоток равны нулю: гг = г2 = 0;
2) коэффициент магнитной связи между обмотками равен единице: k— 1.
Действительно, при = г2 = 0 напряжения щ и иг равны и противоположны по знаку э д. с е, и е2, наводимым в обмотках трансформатора (Для напряжений
и э. д. с. приняты одинаковые положительные направления относительно одно-
именных зажимов). При k = 1 все витки обеих обмоток трансформатора пронизываются одинаковым магнитным потоком Ф и поэтому
t/Ф t/Ф
U1 = -ei=W14r- U2=^e2==W2_ri
или
Z7X = /сои^Ф; й2=/wu’/Ь, (8-46)
откуда
UilU2=u^/u>2=const.
Определим, какие требования надо предъявить к параметрам трансформатора, чтобы обеспечить
постоянство отношения вторичного и первичного токов. Для указанных на рис. 8-17 положительных направлений токов
= ЯМФ,
где rcv'i — wzt2 — результирующая магнитодвижущая сила (м. д. с ); 7?м — магнитное сопротивление для магнитного потока, или
ю1/1-ю24=ДмФ.
Подставив из (8-46) значение Ф = получим:
wrii — wj2 = Rjji/jawi, откуда
А =
4 W? jMWiW2l'i ’
Отношение 72//( будет постоянным, если
1) либо 7?м = 0;
2) либо uij и w2 стремятся к бесконечности, причем их отношение остается неизменным.
Если бы все перечисленные условия были выполнены, то реальный трансформатор стал бы трансформатором идеальным, коэффициент трансформации которого п = п = Wi/w2. Идеальный трансформатор создать нельзя, но проведенный анализ показывает, как следует выбирать параметры реального трансформатора, чтобы его свойства приблизились к свойствам идеального трансформатора.
8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника
Как известно, пассивный взаимный несимметричный четырехполюсник с двумя парами зажимов характеризуется тремя независимыми параметрами, поэтому для него можно составить эквивалентные схемы из трех элементов. Раньше уже приводились П-и Т-образные эквивалентные схемы. Теперь введем новые эквивалентные схемы (рис. 8-18), содержащие в качестве одного из элементов идеальный трансформатор. Эти схемы применяются для
—и автотрансформаторов со стальными магнито—=
228
проводами. Сопротивления элементов Zlx, Z1K, Z2x и Z2K — это входные сопротивления схем при холостом ходе и при коротком замыкании при питании с первичной (Zlx, Z1K) и при питании с вторичной стороны (Z2X, Z2K).
Действительно, при холостом ходе ток /1х проходит только через сопротивление Zlx, когда схема , (рис. 8-18, а) питается со стороны первичных зажимов, а ток /2х проходит только через сопротивление Z2x, когда схема (рис. 8-18, б) питается со стороны вторичных зажимов. При коротком замыкании ток /2к ограничивается только сопротивлением Z2K, когда схема (рис. 8-18, а) питается со стороны вторичных зажимов, а ток /1к ограничивается только сопротивлением Z1K, когда схема (рис. 8-18,6) питается со стороны первичных зажимов. Рассматриваемые схемы эквивалентны данному четырехполюснику, если сопротивления Zlx, Z1K, Z2x и Z2K в схемах равны соответствующим входным сопротивлениям данного четырехполюсника. Что касается коэффициентов трансформации идеальных трансформаторов, то необходимо иметь:
п' = А; n"=i/D,
где А и D — коэффициенты данного четырехполюсника.
Действительно, эти коэффициенты трансформации равны отношению комплексных напряжений при холостом ходе,
причем для схемы (рис. 8-18,о) — при питании с первичной стороны, а для схемы (рис. 8-18,6) — при питании с вторичной стороны, как и должно быть по уравнениям четырехполюсника (8-6) и (8-10).
Из двух эквивалентных схем четырехполюсника (рис. 8-18) можно получить еще четыре эквивалентные схемы, перемещая идеальный трансформатор либо на вход, либо на выход. При этом для сохранения эквивалентности нужно изменить значения тех сопротивлений, которые переходят с одной стороны, идеального трансформатора на его другую сторону. Если сопротивление переходит с вторичной стороны на первичную, то его следует увеличить в п'2 или п"2 раз, если же оно переходит с первичной стороны на вторичную, то его следует уменьшить в п2 или п"2 раз. Необходимость такого изменения сопротивлений вытекает из соотношений (8-43) и (8-44).
8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом
Стальной магнитопровод у трансформатора уменьшает магнитное сопротивление и увеличивает коэффициент магнитной связи —между обмотками.- Это-дриближает свойства трансформатора к свой
229
ствам идеального трансформатора, но в магнитопроводе трансформатора наблюдаются потери энергии, обусловленные вихревыми токами и гистерезисом Вследствие нелинейной зависимости между магнитной индукцией и напряженностью магнитного поля ток в трансформаторе при синусоидальном приложенном напряжении может быть и несинусоидальным Все эти явления подробно рассматриваются в гл 23 Сейчас важно отметить, что заметное отклонение формы кривых тока в трансформаторе от синусоидальной наблюдается только в режимах, близких к холостому ходу В нагрузочных режимах эти отклонения настолько незначительны, что ими можно пренебречь и считать трансформатор со стальным магнитопроводом линейным элементом цепи
Эквивалентную схему трансформатора можно получить, подробно анализируя все происходящие в нем явления Именно 1акой способ ее получения приводится в курсах электрических машин и трансформаторов или в специальных монографиях, посвященных трансформаторам Здесь рассмотрим трансформатор как четырехполюсник и применим для него эквивалентные схемы, рассмотренные в предыдущем параграфе
Опыты показывают, что при холостом ходе трансформатора со стальным магнитопроводом отношение комплексных первичного и вторичного напряжений практически одинаково независимо от того, осуществляется ли питание трансформатора со стороны первичных или со стороны вторичных зажимов Опыты показывают также, что отношение этих комплексных напряжений практически можно считать вещественным числом, равным отношению их действующих значений и равным отношению чисел витков обмоток трансформатора.
Cjx Uj
С2 l/2x w2 ’
где и С2х — соответственно напряжения на первичных и вторичных зажимах в режимах холостого хода при прямом и обратном питании
Отношение действующих значений первичного и вторичного напряжений трансформатора при холостом ходе называется его коэффициентом трансформации п
Таким образом, рассматривая трансформатор как четырехполюсник, можно считать
А = 1 /D = w-^/w2, (8-47)
следовательно, в обеих эквивалентных схемах (рис 8-18) коэффициенты трансформации идеальных трансформаторов практически одинаковы и равны коэффициенту трансформации реального трансформатора
п' = п" = п = w-Jw2.
При холостом ходе ток в трансформаторе существенно отли-чается от синусоидального Сопротивления Zlx и Z^ определяются —
230
как комплексные сопротивления для эквивалентных синусоидальных токов, которые эквивалентны несинусоидальным токам z]x и г2х в том смысле, что имеют одинаковые с токами г1х и /2х действующие значения и тем, что при этих токах получаются те же активные мощности
Экспериментальное определение сопротивлений Zlx и Z2X может быть проведено так, как описано в § 3-18, в предположении что измеряемое амперметром действующее значение несинусоидального тока является действующим значением эквивалентного синусоидального тока.
Из соотношений (8-14), (8-15) и (8-12), (8-17) имеем:
Z1k/Z2k=A/D, Z1x/Z2x=A/D.
Из соотношения (8-47)
Л/D = =-- и2.
Следовательно,
Z1K/Z2lt=Zlx/Z2x=n2. (8-48)
Для трансформаторов сопротивления Zlx, Z1K, Z2x и Z2K принято обозначать соответственно Z'x, Z'K, Zx и Z^ Эти сопротивления называют сопротивлениями холостого хода и короткого замыкания трансформатора, приведенными к первичной обмотке (Zx и Zk) и приведенными к вторичной обмотке (Zx и Z').
Обычно у трансформаторов' полные сопротивления холостого хода намного больше полных сопротивлений короткого замыкания г'х = (180 — 500) 2к Поэтому во многих случаях можно применять упрощенные схемы без ветвей, содержащих сопротивления Z'x и Zx В ориентировочных расчетах пренебрегают иногда и сопротивлениями Z' и Z,", г е рассматривают реальные трансформаторы как трансформаторы идеальные
Трансформаторы помимо преобразования значений переменных токов и напряжений применяются для согласования полных сопротивлений источников питания и приемников (для обеспечения условия передачи максимальной мощности, см § 3-19) Расчет входных сопротивлений обычно выполняется по формулам (8-43) и (8-44), справедливым для идеального трансформатора Более точный расчет может быть сделан с учетом всех параметров эквивалентной схемы трансформатора.
8-9. Расчеты электрических цепей с трансформаторами
Приведем два примера, иллюстрирующих применение эквивалентных схем трансформаторов в расчетах электрических цепей В обоих примерах будем пользоваться упрощенными эквивалентными схемами, не содержащими ветвей с сопротивлениями Zx или Zx.
231
Цепь с каскадным соединением трансформаторов. Рассмотрим цепь, состоящую из линии 1, трансформатора а, линии 2, трансформатора b и приемника. На рис. 8-19 линии и приемник учтены комплексными сопротивлениями Z2 и Za, а трансформаторы — простейшими эквивалентными схемами, содержащими сопротивления Zk« и Zub и идеальные трансформаторы с коэффициентами
Рис. 8-19.
трансформации па и пь. Пусть заданы сопротивления всех элементов схемы, коэффициенты трансформации и напряжение О в начале первой линии, а требуется определить токи и напряжения на отдельных участках цепи.
Перейдем к схеме без идеальных трансформаторов, сохраняя входное сопротивление всей схемы неизменным (рис. 8-20). Для этого все сопротивления, которые раньще находились за идеальными трансформаторами -(считая от входа схемы), следует изменить,
умножив их на квадраты коэффициентов трансформации тех трансформаторов, которые находились между сопротивлениями и входом схемы. Так, сопротивления Z2 и Z^ следует умножить на п2а, а сопротивление Z3 на nlnl.
Ток Д в этой схеме определить легко. Затем по схеме рис. 8-19 находим Д = п„Д и Д = 11Ь12 = и рассчитываем напряжения на ее отдельных участках.
Параллельное соединение трансформаторов. Рассмотрим цепь (рис. 8-21), состоящую из линии Д двух параллельно соединенных трансформаторов а и b и приемника. На практике, как правило, параллельно включаются трансформаторы с одинаковыми коэффициентами трансформации, однако для общности будем считать, что коэффициенты трансформацииразличные. Пусть, как и в нервом
232
примере, заданы сопротивления элементов цепи, коэффициенты трансформации и напряжение в начале первой линии, а требуется определить токи и напряжения на отдельных участках цепи.
Для их определения нужно совместно решить четыре уравнения:
и - Zr (Ia + 4) = йг, £ - Z"Kanala = В2;
па
Zv.^tib!'b — Ui, Ui = Z^ (nJ} a-\-nJь)-
8-10. Графы пассивных четырехполюсников и их простейшие соединения
Уравнения четырехполюсника, записанные в любой форме, можно всегда представить в виде того пли иного графа. На рис. 8-22 изображен граф, соответствующий уравнениям (8-6), записанным
в форме А, на котором зачерненными большими кружочками отмечены истоки с независимыми переменными Д2 и /2, а обычными точками отмечены стоки.
На рис. 8-23 изображен граф по уравнениям, записанным в форме Y, где зачерненными большими кружочками также отмечены узлы истоков с независимыми переменными Ои и обычными точками отмечены узлы стоков /г и /2; на рис. 8-24 изображен граф, соответствующий уравнениям (8-1) четырехполюсника, запи-свиным в форме 7.________________________
233
Графы четырехполюсников удобно применять для определения параметров результирующих четырехполюсников, полученных путем соединения более простых четырехполюсников.
На рис. 8-25,а показано так называемое каскадное соединение двух четырехполюсников с заданными параметрами, а на рис. 8-25,6 изображен граф такого соединения. Для каждого четырехполюсника, очевидно, справедливы следующие уравнения:
LJ^AtU' + Bj'; U'=A2U2 + Bl2;
I^CrU'+dJ'-, i'=c2u2+D2i2.
Для установления связи между входными величинами первого четырехполюсника и выходными величинами второго четырехпо-
из графа рис. 8-25,6 непосредственно получаются
люсника /2
следующие уравнения для эквивалентного четырехполюсника:
02 = (Л, -J- BjC2) и2 (AtB2 -J-B]D2) 12; А=(С1Д2 -\-DiC2) й2 -j- (d1d2 CiB2) 12,
й1 = Ай2 + В12;
i^cu2+Di2,
или
(8-49)
где
А — AjA2 -J- В2С2,
С — С2А2 -}-DiC2',
B=AxB2+B2D2-, | D—DxD2-\~С1В2. J
(8-50)
Эти коэффициенты (рис. 8-25,в) получаются из графа в виде суммы произведений соответствующих передач путей между истоками и стоками соединения графов (рис. 8-25,6).
Рис. 8-25.
Для определения параметров эквивалентного четырехполюсника, -составленного из двух параллетьно соединенных четырехполюсни-кэг> ^рнс. 8-26,и), целесообразно постройi ь графы по уравнениям
234
в форме Y (рис. 8-26,6). Из этого графа сразу получаются следующие уравнения:
Л = (К?1 + У?1)^1-(^2 + У®)^2; 1
, , > (8-51)
А = (^21 + У41) 6^1+ (^22+ У22) ^?2> J
или
j^YnUr- У1Д; )
1- Y U +Y U (8'52)
У2---- I 21и1~Г Г 22U2> )
где (рис. 8-26,в)
V ___Vй I V6 • v __va । v6 •
1 11 — 1 11 "Г 1 II, Г 22- Г 22 Т Г 221
V ___va 1 V6 • V __Vй 1 V6
г 12 — Г 12 -j- Г 12, Г 21 — г 21 -Г г 21
Для определения параметров эквивалентного четырехполюсника, составленного из двух последовательно соединенных четырехпо-
Рис 8-26.
люсников (рис. 8-27,с), следует построить граф по уравнениям в форме Z (рис. 8-27,6). Из этого графа вытекают следующие уравнения:
Д1 = Ul + U6i = (Zatl + Z?,) A + (Z?2 + Z?2)
Д2 = U“ + = (Za2i 4-ZJ,,) к + (zb -r Z22) /2 J
откуда
Д1--ZhA + Z12A; | (8-541
6'2 = Z2i/i4-Z22r2> J
235
где
Zu— Zii-^-Zn', Z12— Z12 + Zn;
Z21 = Zji + Z21; Z22 = Z2i-\- Zi2.
Уравнениям (8-54) соответствует граф по рис. 8-24, у которого передачи ветвей вычислены по последним формулам.
Параметры эквивалентных четырехполюсников, полученных при различных соединениях составных четырехполюсников, можно определить и при помощи матричных форм записи уравнений.
Рис. 8-27.
Так, для каскадного соединения двух четырехполюсников матрица параметров эквивалентного четырехполюсника равна произведению матриц отдельных четырехполюсников:
^1
Bi А2 в2
Di С2 D2
А В
С D
(Л1Л2 + BiC2) (AiB2-\~BiD2) (С1Л2 + £)1С2) (CiB2 + DiD2)
откуда непосредственно получаются выражения (8-50).
Следует подчеркнуть, что матрицу коэффициентов эквивалентного четырехполюсника, полученного при каскадном соединении трех и более четырехполюсников, можно найти перемножением трех и более матриц, записанных в том же порядке, в каком соединены четырехполюсники, поскольку умножение матриц не подчиняется переместительному закону.
При параллельном соединении двух четырехполюсников матрица коэффициентов эквивалентного четырехполюсника находится суммированием матриц проводимостей отдельных четырехполюсников, а при последовательном — суммированием матриц сопротивлений. При этом правила суммирования матриц, как и расчеты при помощи графов, применимы при так называемых регулярных соединениях четырехполюсников, т. е. при равенстве токов каждой пары Зажимов у кэ/кдого состзгного четыре к питюсникаг-чте и показано на рис. 8-26,о и рис. 8-27,о.
236
Глава девятая
ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ
9-1. Ламповый триод и его параметры
В различных областях современной техники широко применяются управляемые элементы электрической цепи. В настоящей главе рассматриваются цепи, содержащие в качестве управляемых элементов электронные лампы и полупроводниковые приборы. Анализ ограничивается линейным режимом, т. е. такими областями значений токов и напряжений, при которых между изменениями токов и напряжений сохраняются линейные зависимости. При таком ограничении цепи линейны, однако, как будет показано в дальнейшем, они не обладают свойством взаимности, а в их расчетные схемы приходится вводить зависимые источники тока и на пр я- с . жения.
Трехэлектродная электронная лампа или и триод имеет три электрода: катод (к), j анод (с) и сетку (с), которые находятся $----------
в стеклянном, металлическом или керамическом
баллоне, откачанном до высокого вакуума Рис 9-1. (рис. 9-1). Катод нагревается до высокой тем-
пературы, в результате чего возникает термоэлектронная эмиссия. Поток электронов направляется от катода через промежутки сетки к аноду, которому сообщается по отношению к катоду положительный потенциал. Так как за направление тока принимается на-
правление движения положительных зарядов, то говорят, что \ ток внутри лампы направлен от анода к катоду.
Ток ta анодной цепи зависит не только от анодного напряжения па (между анодом и катодом), но в значительно большей мере от сеточного напряжения щ (между сеткой и катодом). Сильное влияние сеточного напряжения на анодный ток объясняется тем, что сетка экранирует анод от катода. Поэтому электрическое поле, действующее между катодом и сеткой на движущиеся электроны, значительно больше зависит от сеточного напряжения, чем от анодного. При положительном сеточном напряжении часть электронов, испускаемых катодом, притягивается сеткой и возникает сеточный ток tc.
На рис. 9-2,о в качестве примера приведены анодная и сеточноанодная характеристики для одного из типов триода. Они представляют собой зависимости анодного и сеточного токов от анодного напряжения ta (иа) и tc (щ) при различных заданных значениях сеточного напряжения ис. Кривые анодного тока показаны сплошными линиями, кривые сеточного тока — пунктирными. Цифры, стоящие около кривых ta и i^, указывают значения постоянного сеточного напряжения.
237
На рис. 9-2,6 для того же триода приведены анодно-сеточные и сеточная характеристики, представляющие собой зависимости анодного и сеточного токов от сеточного напряжения ц (щ.) и zc (z/c) при различных заданных значениях анодного напряжения, которые указаны около каждой кривой. Все характеристики сняты при постоянных напряжениях и токах (не изменяющихся во времени), но они справедливы и для мгновенных значений синусоидальных токов и напряжений при не слишком высоких частотах. Из характеристик видно, что зависимости между токами и напряжениями нелинейные, т. е. в общем случае триод — нелинейный элеме цепи.
Рис. 9-2.
Токи ic и ц являются функциями двух независимых переменных ис и гц, так что для малых изменений напряжений duc и dua справедливы следующие зависимости:
di,. —dtic + dua, diR = <a duz + - dua. c йис c 1 dua a’ 8 du, c 1 dti-, a
Пусть изменения напряжений du, и du, во времени происходят не слишком быстро, так что в любой момент связь между токами ц и /а и напряжениями пс и иа не отличается от зависимостей, снятых при постоянных токах и напряжениях (рис. 9-2,о и б). Тогда частные производные токов ic и /а по напряжениям и, и на, входящие в уравнения как коэффициенты при du, и dus, могут быть определены по характеристикам триода. Они пропорциональны тангенсам углов наклона касательных к характеристикам, проведенным в «рабочих» точках характеристик, которые находятся по заданным значениям щ и Частные производные токов по напряжениям представляют собойГ собственные-и передаточные проводимости
238
сеточной и анодной цепей в рабочей точке: д/с/дпс=£сс; dijdua=g^ dia/duc = ^ас» Saa*
Ведя эти обозначения, получаем:
^Й*с == See Ф" ё^са С^"1)
dia ~ gae du, -J- gSa ^^a- (9"2)
Проводимость gs, = dia/dua называют крутизной анодно-сеточ-ной характеристики анодного тока и обозначают буквой S. Величина, обратная собственной анодной проводимости l/gaa = duJdi.., называется внутренним сопротивлением лампы (в анодной цепи) и обозначается Rt.
Введя эти обозначения, имеем:
dia = S du, + dua~-^(SRtdua-\- dua). (9-3)
Из этого выражения видно, что приращение сеточного напряжения вызывает в 57?г раз большее изменение анодного тока, чем равное ему изменение анодного напряжения, которое в качестве слагаемого входит в (9-3). Величина SR,- называется коэффициентом усиления и обозначается р.. Полагая в уравнении (9-3) dia = 0, получаем:
|т = ST?,- = (dujduc) = сопЦ,
т. е. коэффициент усиления можно рассматривать как предел отношения уменьшения анодного напряжения (dua < 0) к компенсирующему его увеличению сеточного напряжения (du, > 0).
Электрические цепи, содержащие триоды, в большинстве случаев имеют источники питания постоянного напряжения (аккумуляторные батареи или выпрямители). Поэтому токи и напряжения в этих цепях содержат постоянные составляющие. Однако основной интерес представляют переменные составляющие токов и напряжений, так как обычно именно от них зависит работа того или иного устройства, содержащего триод.
В этой главе рассматриваются только переменные составляющие токов и напряжений и принято, что их значения изменяются в области, для которой справедливы линейные соотношения (9-1) и (9-2). Эта область изменения напряжений может быть достаточно широка, если постоянные составляющие сеточного и анодного напряжений таковы, что рабочие точки триода лежат в области прямолинейных участков характеристик. При таких ограничениях для переменных составляющих токов и напряжений триод представляет собой линейный элемент.
Цепи, содержащие триоды в линейном режиме работы, сущест-вепно отличаются от ранее рассмотренных ценеш-в-том отношении,
239
что для них несправедлив принцип взаимности. Действительно, gca так как эти передаточные проводимости определяются разными характеристиками триода.
9-2. Эквивалентные схемы лампового триода
Пусть переменные составляющие токов и напряжений изменяются по синусоидальному закону. Изобразив их комплексными величинами, получим уравнения для переменных составляющих сеточного и анодного токов в комплексной форме:
U г -4- п U я:
L olt V 1 ova а»
Za = Si7c + gaat7a.
Этим уравнениям удовлетворяет эквивалентная схема (рис. 9-3), содержащая два источника тока.
В большинстве случаев практического применения триодов сеточное напряжение имеет отрицательную постоянную составляющую, так называемое отрицательное сеточное смещение, такой величины, что при всех значениях сеточного напряжения потенциал сетки меньше потенциала катода. При этих условиях ток сетки равен нулю (триод работает в той области сеточных характеристик,
а) б)
Рис. 9-4.
которые находятся на рис. 9-2,6 слева от оси ординат) и эквивалентная схема триода упрощается. Цепь сетки состоит только из изолированного зажима с, а проводимости g№ и источника тока gzaCJa в схеме нет (рис. 9-4,а). Путем преобразования источника тока в источник э. д. с.
-1-5Дс = Д,.5Дс = рДс saa
получаем другую эквивалентную схему триода (рис. 9-4,6).
До сих пор предполагалось, что изменения напряжений происходят не слишком быстро и токи определяются по характеристикам триода, снятым при постоянных напряжениях и токах. Это справедливо только при относительно низких частотах. При более высоких
240
частотах нужно учитывать емкости между сеткой и катодом, сеткой и анодом и анодом и катодом (рис. 9-5). Эквивалентная схема (рис. 9-4,о) соответственно усложняется и принимает вид, показанный на рнс. 9-6. Эта схема справедлива при достаточном отрицательном
Рис. 9-5.
Рис. 9-7.
сеточном смещении, которое устраняет замыкание через сетку части тока, обусловленной термоэлектронной эмиссией катода. Однако ток в цепи сетки все же не равен нулю вследствие ее емкостной связи с анодом и катодом (емкости Сск и Сса).
При еще более высоких частотах приходится учитывать ряд дополнительных факторов: индуктивность и взаимную индуктивность вводов к электродам лампы; время пролета электронов между электродами; диэлектрические потери в изоляторах. Иногда для учета этих факторов в схему рис. 9-6 вводят дополнительные индуктивности, взаимные индуктивности и т. д. Однако практическая ценность подобной усложненной схемы невелика, так как не представляется возможным определить экспериментально параметры многочисленных дополнительно вводимых элементов схемы.
При любых частотах триод можно рассматривать как четырехполюсник, два полюса которого соединены проводом, не имеющим гсопротпвленпя (рис. 9-7). Токи определяются через напряжения, щапример уравнениями в форме Y:
Л = ЛА7к12й2; 1
Л = — } 21^14" 226'2, J
где передаточные проводимости У12 и У21, как и следует ожидать, не равны друг другу. Этим уравнениям, как было показано, удовлетворяет эквивалентная схема, приведенная на рис. 8-9, которая по структуре не отличается от схемы, приведенной на рис. 9-6. В диапазоне высоких частот (рис. 8-9) Zx = 1//ыСск; Уз = 1//соСса; 1/Z2 = MRi + /юСак; 7j2 = SOC.
При сверхвысоких частотах параметры Уи, У12, У21 и У22 должны определяться экспериментально, как параметры четырехполюсника при той частоте, при которой работает триод.
241
С точки зрения общей теории цепей для переменных составляющих токов и напряжений триод представляет собой активный трехполюсник или четырехполюсник с закороченной стороной. В состав его эквивалентной схемы входят так называемые зависимые источники тока или напряжения, так как создаваемые ими ток или напряжение |л(7с зависят от напряжения Ос, подводимого между сеткой и катодом.
Ранее такие четырехполюсники были названы невзаимными.
Применяя для ламп эквивалентные схемы, можно рассчитывать линейные режимы в любых цепях, содержащих электронные лампы с тремя пли даже с большим числом электродов, известными методами расчета линейных цепей.
Пример 9-1. На рис. 9-8 представлена схема одного каскада усилителя переменны о напряжения В этой схеме бат арея с э. д с. Е питает анодную цепь, а батарея с э. д. с. £с создает отрицательное сеточное смешение. Источник напряже
ния и2 учитывает напряжение сигнала, подводимого к усилителю. Сопротивление R2 — сопротивление нагрузки, на котором нужно получить усиленное (увеличенное) напряже-
Рис. 9-9.
ние сигнала. Цепь накала катода на схеме не показана. Даны параметры триода S, R,, Сск, Сса, Сак и сопротивление нагрузки R2 Определить коэффициент усиления напряжения Kv = f/2/Z7r Внутренними сопротивлениями источников питания пренебречь.
Решение. Составляем эквивалентную схему усилительного каскада (рис. 9-9). На этой схеме КС|( = faCcx, Уак = l/R£+/wCaK и б2 =
= 1/К2.
Расчет проще всего выполняется методом узловых потенциалов. Записываем для узла а уравнение по первому закону Кирхгофа
са (62 6't) V акIJ2 SUt = О,
из этого уравнения находим отношение
К Y™~S
U1 У са + ^ак +
, Для низких частот можно полагать:
5/ск = 5/са = ° и raK=W
При этом
& _ S R,SR2 jiR2
и i/Rt+4R2 Ri+Ri R1 + R2'
Знак минус указывает на противоположность фаз Л'2 и £/v Коэффициент усиления напряжения (по модулю) меньше коэффициента усиления лампы р. Очевидно, что Ку Д только—при R = ------------- '------=—=------ ~
242
Схема включения триода (рис. 9-1), принятая в основу проведенного выше теоретического анализа и встретившаяся в примере (рис. 9-8), называется схемой с общим катодом (зажим катода является общим и для цепи сетки и для цепи анода). Наряду с этой,
Рис. 9-10.
Рис. 9-11.
наиболее часто применяемой схемой встречаются две другие схемы включения триода: с общей сеткой (рис. 9-10) и с общим анодом (рис. 9-11). На приведенных рисунках показано подсоединение нагрузочного сопротивления R2. Отметим, что эквивалентная схема триода (рис. 9-6) может быть применена и для этих схем включения.
9-3. Транзисторы (полупроводниковые триоды)
Транзисторы (или полупроводниковые триоды) обычно изготовляются из германия и по своему конструктивному выполнению ^подразделяются на точечно-контактные и плоскостные. Ограничимся рассмотрением плоскостного транзистора, который представляет*собой кристалл германия, содержащий минимум три области % с различными типами электропроводности. Область полупроводника, в которой электропроводность в основном обусловлена свободными электронами, называется «-областью (от слова negative — отрицательный). Она получается путем добавления к германию примесей других элементов (фосфора, сурьмы, мышьяка), атомы которых имеют на один валентный электрон больше, чем атом германия.
Область полупроводника, в которой электропроводность в основном обусловлена дырками, называется p-областью (от слова positive — положительный). Она получается путем добавления к германию примесей других элементов (индия, бора, алюминия или галлия), атомы которых имеют на один валентный электрон меньше, чем германий (дыркой называется незаполненная ковалентная связь атомов). Дырка может перемещаться по кристаллической решетке, причем ее перемещение равносильно перемещению положительного заряда, равного по абсолютной величине заряду электрона:--------------------------=-----------=-----------------
243
Транзисторы с тремя областями электропроводности бывают двух типов: р-п-р и п-р-п.
Транзистор типа р-п-р состоит из двух p-областей, отделенных друг от друга тонким слоем (порядка тысячных долей миллиметра) //-области (рис. 9-12,а). В триоде типа п-р-п чередование слоев обратное. Средняя область транзистора называется базой (б) или основанием. Одна крайняя область называется эмиттером (э), другая — коллектором (к).
Детальное рассмотрение явлений в транзисторе требует привлечения современных квантовых представлений и выходит за рамки данной книги.
Ниже проводятся упрощенные пояснения.
Вследствие диффузии положительные заряды (дырки) из p-области направляются в «-область, а свободные электроны движутся в обратном направлении. В результате у границ раздела областей (у р-п-переходов) появляются объемные заряды — положительные в «-области и отрицательные в p-областях (на рис. 9-12, а показаны знаками «+» и «—»). Объемные заряды создают электрические поля, и между р и «-областями появляются разности потенциалов или потенциальные барьеры, которые препятствуют дальнейшей диффузии зарядов. В конечном счете ток через границы раздела р и «-областей прекращается. На рис. 9-12, б показано распределение потенциала, которое устанавливается вдоль транзистора, когда он не присоединен к внешней цепи. Рассмотрим, что произойдет, если к транзистору подключить два источника постоянной э. д. с. t736 и l/gK, как показано на рис. 9-13, а.
Напряжение Usc} — прямое, оно снижает потенциальный барьер между эмиттером и базой. Напряжение П6к — об
ратное, оно увеличивает потенциальный барьер между базой и коллектором. Получающееся распределение потенциала показано на рис. 9-13, б.
Снижение потенциального барьера между эмиттером и базой облегчает процесс диффузии дырок из эмиттера в базу и элекгронов из базы в эмиттер. Дырки, попадающие в базу, стремясь равномерно заполнить ее объем, попадают в область база — коллектор и здесь под действием электрического поля увлекаются в коллектор. В результате в цепи коллекюра возникает электрический ток. Он меньше тока эмиттера, так как не все дырки, попавшие в базу, переходят в коллектор. Часть дырок рекомбинирует в базе с электронами. Кроме того, ток эмиттера больше тока коллектора за счет того, что он обусловлен не только диффузией дырок из эмиттера в базу, но и диффузией элекгронов из базы в эмиттер. Эта последняя составляющая тока эмиттера идет целиком мимо коллектора.
Схема включения транзистора, представленная на рис. 9-13,6/, называется схемой с общей базой (так как база входит в цепь эмиттера и в цепь коллектора). Цепь эмиттера называется входной цепью, а коллектора — выходной.
На рис. 9-14 представлено семейство статистических выходных характеристик одного из типов плоскостного транзистора типа р-п-р, включенного по схеме с общей базой. Выходные характери
244
стики представляют собой зависимость тока iK в цепи коллектора от напряжения между базой и коллектором при заданном значении тока iB эмиттера. Значения iB написаны около каждой кривой. В линейной части характеристики сопротивление цепи коллектора Анбк/А/к для приращений тока в коллекторе очень велико (достигает сотен тысяч и миллионов ом). Из тех же характеристик видна почти линейная зависимость тока цепи коллектора от тока цепи эмиттера. Изменяя ток эмиттера, можно пропорцио-
нально изменять ток коллектора, причем отношение А/к/А/в = а, коюрое называется коэффициентом усиления по току, достигает значений 0,8— 0,97. Для плоскостных триодов с гремя областями а < 1, так как часть тока эмиттера ответвляется в базу. В других типах транзисторов коэффициент усиления по току может быть больше единицы.
Транзистор, включенный по схеме с общей базой, при а < 1 не может работать как усилитель тока, но он может работать как
-0,2-0,1 О
3 мА
2,5 мА
2 мА
1,5 мА
1мА
0,5 мА
! О ! U5k
10 20 В
Рис. 9-14.
усилитель напряжения и мощности. Поясним это следующими простыми рассуждениями. Пусть в цепь коллектора последовательно
с источником питания включено высокоомное нагрузочное сопротивление R2 (одного порядка с величиной Au6k/Aik) и пусть напряжения сигнала Аивб, подведенное с цепи эмиттера, изменило ток эмиттера на величину AiB. Тогда почти на такую же величину изменится ток коллектора AiK = aAiB. Изменение напряжения на нагрузочном сопротивлении будет во много раз больше изменения напряжения сигнала, так как R2 много больше сопротивления цепи эмиттера, работающей в прямом (в проводящем) направлении. По этой же причине приращение мощности R2 А.ГК будет много больше мощности сигнала Аив6 AiB.
9-4. Эквивалентные схемы транзисторов
На рис. 9-15 показано условное обозначение транзистора типа j-n-р, включенного по схеме с общей базой (условное обозначение (фиода типа п-р-п имеет то отличие, что стрелка у эмиттера делается i обратном направлении). На рисунке указаны положительные 1аправления для приращений токов и напряжений. Они выбраны ючно такими же, как и при рассмотрении ламповых триодов.
Для бесконечно малых приращений токов и напряжений можно Записать:
^U1 = аф ^2 ~^2‘
245
Если токи и напряжения изменяются во времени не слишком быстро, то значения частных производных в этих уравнениях от времени не зависят, могут рассматриваться как активные сопротивления и определяться по статическим характеристикам транзистора (снятым при постоянных токах и напряжениях):
711 ~ (^«i/dz1)is=con4tj 7'12= (^i/^l2)11 = const;
r21 — (du2/dii)l2 — const j 7"22 = (^W2/5l2)i1 = const,
причем rlz #=r21. Поэтому цепи с транзисторами (так же как и с ламповыми триодами) невзаимны.
При работе транзистора в линейной части характеристик приведенные уравнения справедливы и для конечных приращений.
Рис. 9-16.
Пусть приращения токов и напряжений изменяются во времени по синусоидальному закону. Изобразив их комплексными величинами и1г О2, Ц и /2, получим следующие уравнения:
Й1=г нА г 12/2; (9'5)
Й2 = Г21А + 7"22Д- (9'6)
Эти уравнения справедливы для эквивалентной схемы транзистора, приведенной на рис. 9-16 (без емкости Скб), если положить:
т'э + т'б — гп 1 т'6 = г12; Т'т4-7'б = 7'21; т'к-|- Г(,~г22, откуда
т'б'==7'12; т'э = Г]1 г12; т'к = г22 — Г12; Гщ — r2i ту2.
Уравнения (9-5) и (9-6) и эквивалентная схема (рис. 9-16) справедливы для транзистора при низких частотах переменных составляющих токов и напряжений. С ростом частоты начинает сказываться емкость Сьб перехода коллектор — база; эквивалентную схему следует дополнить емкостным элементом (изображен пунктиром на рис. 9-16) Емкость р-и-перехода эмиттер — база почти не сказывается, так как параллельно ей включено сравнительно малое сопротивление гэ и в эквивалентной схеме она не учитывается. При высоких частотах параметры становятся комплексными и сопротивления ru, г12, г21, г22 должны быть заменены комплексным^ сопротивлениями Zu, Z12, Z21 и Z22.
246
Помимо рассмотренной схемы включения транзистора с общей базой применяются еще две усилительные схемы с общим эмиттером (рис. 9-17,а) и с общим коллектором (рис. 9-17,6). На приведенных схемах помимо транзисторов показаны источники питания входной и выходной цепей, источники напряжения (Д (поступающего
.сигнала) и нагрузочные сопротивления ₽2. Если проводить аналогию между полупроводниковыми и ламповыми триодами, то эмиттер ‘следует считать аналогичным катоду, коллектор — аноду, а базу — ^етке. Эквивалентная схема транзистора по рис. 9-16 применима (и для схем включения транзистора с общим эмиттером и с общим коллектором.
9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы
Расчет электрических цепей с невзаимными элементами в виде электронных ламп или полупроводниковых приборов часто выполняется матричным способом или при помощи графов. Покажем на простых примерах, как рассчитываются такие цепи указанными методами.
Прежде всего рассмотрим методику построения неопределенной и определенных матриц по уравнениям, составленным для эквивалентных схем с невзаимными элементами.
На рис. 9-6 изображена эквивалентная схема триода, в которой в общем случае учитываются все три емкости между сеткой, анодом п катодом (рис. 9-5). Пользуясь методом узловых потенциалов, напишем для этой схемы следующие уравнения:
О са ^ск) Фс УСкФк Iс,
0 са *^) Фс+ (ЕСа~5 Еак "ф- ^faa) Фа (1^ак Ч- Ч~ ^аа) Фк
0Лск + >3)Фс ~ (Кпк + йаа)Фа 4“ (Еск Ч~ Yак + S + gaa) Фк = 4 > .
(9-7)
где /к — ток катода, причем сумма токов сетки, анода и катода в сошветствип с выбранными положительными направлениями
247
(рис. 9-1) равна нулю, т. е. /с 4- /а + /к = 0; Уса = /юСса; Уск = /СоСск, Уак /^Сак» Фс Фк
На основании уравнений (9-7) запишем неопределенную матрицу узловых проводимостей триода:
v (У) I и — (Уса+Уск) -(Уса-5) (Ус - (Кск+5) - -Гса а + Уак + gaa) -Уск — (Уак + 5 -J- gaa) . (9-8)
'(* а к 4” Saa) (Ус к-У Уак+ gaa + 5)
Сумма элементов матрицы (9-8) столбцу равна нулю. по любой строке и любому
Эту мат рицу можно (Уса+Уск) представить — у 1 са в виде суммы двух _ у 1 СК матриц:
v<y) I н -Уса -Пек (У + са + Уак + gaa) - (Уак + gaa) 0 0 0 5 0—5 — 5 0 S (Уак + gaa) (Уск-У Уак + gaa) + ' (9-9)
Из сравнения (9-8) и (9-9) видно, что матрица YM не имеет симметрии относительно главной диагонали, причем нарушение симметрии вызвано наличием второй матрицы, отличные от нуля элементы которой равны крутизне 5 характеристики триода. Следовательно, и нарушение свойства взаимности обусловлено тем же элементом 5.
Заметим, что проводимости каждого элемента схемы записываются в соответствующие строки и столбцы неопределенной матрицы 4 раза, из них 2 раза с положительными знаками и 2 — с отрицательными. Поскольку сумма проводимостей по всем строкам и столбцам, как уже отмечено, равна нулю, то этим свойством можно пользоваться для проверки правильности составления матриц.
Чтобы получить три определенные матрицы для трех схем включения триода: с общим катодом, с общей сеткой и с общим анодом — необходимо из матрицы (9-8) вычеркнуть соответственно третьи столбец и строку, первые столбец и строку и вторые столбец и строку. В результате получается:
v<y>___
1к —
(Уса + Уск)
-(Уса-5)
(Иса+ Уак + gas) ||
Y<y> =
(Уса + Уак + gaa) (Уак “У gaa)
— (Уак + + gaa)
(Иск 4~ Уак + gaa + 5)
у(У)____
I а —
(Уса+Уск)
-(Гск + 5)
(Уак + Уск + 5 + gaa)
(9-10)
(9-П)
(9-12)
При низких частотах емкостные проводимости Уса, Уск и Уак имеют очень малые значения и ими можно пренебречь. В результате
248
матрицы (9-10), (9-11) и (9-12) получаются очень простыми. Такими матрицами обычно и пользуются при расчетах цепей на низких частотах.
Для расчета цепей с электронными лампами иногда целесообразно пользоваться графами, которые получаются различными не только в зависимости от соединения элементов схемы, но в и зависимости от структуры уравнений для одной и той же схемы.
В качестве иллюстрации применения графов к расчету схем с электронными лампами построим графы сначала для простейших схем.
Рис. 9-18.
Для схемы включения триода с общим анодом (рис. 9-11) эквивалентная схема без учета емкостных проводимостей показана 'на рис. 9-18,о. Для этой схемы справедливы уравнения
ДС = Д!-Д2; = + (9-13а)
Уравнениям (9-13а) удовлетворяет граф, показанный на рис. 9-18,6.
Приравнивая Йс из первого и второго уравнений (9-13а), получаем;
<9'136)
из схемы рис. 9-18,о
/2 = — G2U2. (9-13в)
Этим уравнениям соответствует граф на рис. 9-18,в, у которого отсутствует узел с напряжением Дс.
Построим граф для схемы включения с общей сеткой (рис. 9-10). Эквивалентная схема для этого случая изображена на рис. 9-19,а с учетом внутреннего сопротивления источника.
Для нее справедливы следующие уравнения:
Й2 = Д1 + цД1 + 7?г/2; 1 (9-14)
. £/1 = Ь ЛЗН5 yi —— 4=б2ь2, J
249
которым удовлетворяет граф на рис. 9-19,6. Аналогичным способом можно построить граф для триода, включенного по схеме с общим катодом (рис. 9-8).
Рис. 9-19.
Рассмотрим еще более сложную схему двухкаскадного усилителя с общей катодной связью (рис. 9-20,а) и, пользуясь графами, найдем коэффициент передачи напряжения в этой схеме. Лз рис. 9-20,о видно, что первая лампа включена по схеме с общим анодом, а вторая — по схеме с общей сеткой. На рис. 9-20,6 приведена
Рис. 9-20.
общая эквивалентная схема для двухкаскадного усилителя, полученная соединением эквивалентных схем рис. 9-18,о и 9-19 с измененными обозначениями соответствующих параметров. Полный граф для заданной схемы построен путем присоединения графа для второй лампы к графу первой (jpuc. 9-20,в). Поскольку положительные направления токов /2 и /3 в заданной и эквивалентной схемах (рис. 9-20.« и 6) изменены на нрошвоположные по сравнению
250
с рис. 9-19,й и б, то»у графа (рис. 9-20,в) изменены знаки параметров, связывающих соответствующие токи и напряжения.
Пользуясь формулой (4-32), можно сразу записать выражение для коэффициента передачи напряжения К и — ^з/^i в следующем виде:
д- _________________Щ (Иг Ч~ 0/(И1+1)_____________
1++ R^ + Rl2°3 + щ-Rf Rl*Gs
(9-15)
или
Hl (H2+1)
(H14- 1) (1 +^?120з) + (1 +^263) ^11^2+(Н2+ 1) Rnfis
(9-16)
Числитель выражения (9-15) получен перемножением передач ветвей для пути графа (рис. 9-20,в) между узлами и Ол. В знаменателе передачи контуров записаны с положительными знаками,
Рис. 9-21.
Ьак как передачи контуров в графе (рис. 9-20,в) имеют отрицатель-тые знаки; последнее слагаемое представляет собой произведение передач двух несоприкасающихся контуров.
Если в схеме усилителя (рис. 9-20,с) применяются две одинаковые лампы (с одинаковыми параметрами), т. е. щ = ц2 = ц и Rn == R12 = Яь то выражение для коэффициента передачи напряжения (9-16) значительно упрощается:
Ки
________________И________________
(l+/?(G3)(l+j~p-J+^G3’
Перейдем к расчету простейших схем с транзисторами.
Пользуясь эквивалентной схемой транзистора с общей базой, сначала составим определенную матрицу узловых проводимостей и построим граф для этой схемы. На рис. 9-21,а изображена эквивалентная схема транзистора с общей базой, отличающаяся от схемы Jia рис. 9-16 тем, что ветвь с невзаимным элементом изображена Виде параллельного соединения источника тока а/э и проводимости «Ьллектора
251
Напишем для всех четырех узлов схемы уравнения для узловых потенциалов:
£эФэ — й'эФо= 41 £б,Фб — йбФо = 4;
— “§ЭФВ+£кФк—(ё* — аёь) Фо= 4;
— (gB - аёэ) фв - £ГбФб - £кФк + (g, +g&+gK- ag9) Фо = 0.
(9-17)
Пользуясь этими узловыми уравнениями, составим неопределенную матрицу (сумма элементов по любой строке и любому столбцу равна нулю) узловых проводимостей:
ёь 0 0 , ёэ
у(У) 1 н ~— 0 ёб 0 — ёб . (9-18)
-а^э 0 ё« — (§к-“^э)
— (£в-“£э) —ёб — ёк gs+ёб+ёк - ^ёь
Чтобы получить определенную матрицу, достаточно из матрицы (9-18) вычеркнуть один столбец и соответствующую строку. При вычеркивании четвертого стобца и четвертой строки определенная матрица узловых проводимостей имеет наиболее простой вид:
УбУ>==
0 0 ёб о
0 gs
(9-19)
0
У этой матрицы, так же как у матрицы (9-10), отсутствует диагональная симметрия, что отражает нарушение принципа взаимности.
1 Аналогично можно получить определенные матрицы для транзисторов с общим эмиттером и с общим коллектором.
Чтобы построить граф для схемы рис. 9-21, я, запишем уравнения по законам Кирхгофа:
— G>4 —гб41 U&—£4 + гб4;1 4=йк§’к—«4; 4=—4—4- j
(9-20)
Этим уравнениям удовлетворяет граф на рис. 9-21, б.
Для эквивалентной схемы транзистора с общим эмиттером (рис. 9-22, а) по уравнениям
—гб4+?‘э4>
4=4+4; 4—а4 + ёк^к
(9-21)
построен граф на рис. 9-22, б, у которого, так же как у графа
рис.'О-^Г/ б^ напряжснттс 'б'! и ток /2 зависшшегперетепнж;—=
252
Аналогичным путем построен на рис. 9-23, б граф для схемы транзистора с общим коллектором (рис. 9-23, а) по уравнениям ^х = ГбЛ+ук; UK — U2 — rJ2, 1 (9 22)
/2 = Сх/2— А"Г“(?к^к- )
Эквивалентные схемы для транзисторов можно рассматривать и как невзаимные четырехполюсники относительно входных и
Рис. 9-22.
выходных токов и напряжений. В этом случае графы на рис. 9-21, б, 9-22, б и 9-23, б нужно преобразовать так, чтобы напряжения l7lt О2 и токи Д, /2 были связаны между собой непосредственно через соответствующие коэффициенты. С этой целью исключим из указанных графов промежуточные узлы. Так, если в первое и третье уравнения системы (9-20) подставить напряжение и ток /б из
Рис. 9-23.
второго и четвертого уравнений той же системы, то после преобразований получим уравнения в форме Н:
—н иЛ+
Д—H2i Л+Н2%и~
2>
(9-23)
где
Гб(1-ос). „ _ Гб£к 12-1 + ^к
___
"U“'eT l+f6gK .
и __ а + гб£к и
— 22
(9-24)
1 Т-гвйк"''----—
253
Рис 9-24.
Рис 9-25
Полученным уравнениям (9-23) соответствует эквивалентная схема по рис. 9-24 и граф, показанный на рис. 9-25.
Такой же граф получается и для схемы по рис. 9-22, а с общим эмиттером (при исключении узлов /в и у графа рис. 9-22, б), но, конечно, значения коэффициентов HL1-, Hl2; Н21", Н22 получаются другими:
//и^Гб+(Г=^)+§?э:
гт __ ОС , tj __ Sk_______
21~ (!— «)+§кгэ’ 22“(1—а)+£кгэ’
(9-25)
Аналогично для схемы по рис. 9-23, а с общим коллектором (при исключении узла Ок и петли с передачей а у узла 12 на рис. 9-23, б) получим граф по рис. 9-25 с передачами ветвей:
Г4 _ г I_______{j____. ТГ _ (*~~к) .
11 б + (1— a)+ghr9’ 12 (1— а)п-§Егэ ’
14________~~~1 . 14________
21 (1— а)+£кгв’ 22 (1— а)+£кгэ’
(9-26)
Рассмотрим несколько примеров на определение коэффициента передачи при помощи графов.
На рис. 9-26, а изображена эквивалентная схема транзистора с общим эмиттером. Выходные зажимы замкнуты на сопротивле.-ние Z2, транзистор питается от источника с синусоидальной э. д. с Е и внутренним сопротивлением ZB. Требуется определить коэффициенты передачи
Ku^O^Ur, Ke=ieje
и входное сопротивление схемы по отношению к зажимам с напряжением 0^.
Запишем для схемы рис. 9-26, а уравнения с контурными токами: (гбН-гв)/х-Гэ/^671; . |
“(гэ-агк) A+(^+^K + Z2-arh)72 = 0, J '
где второе уравнение получено после подстановки
^«/э = о:/-ь(/х-72).
254
Из уравнений (9-27) получим:
i* — Гй_|_г + т:К^ъ (9-28)
'бТ'Э 'б ' 'Э
где
Ki = ------- (9-29)
Л /'э+/'к(1 СС) + ^2
— коэффициент передачи тока /2.
Рис 9-26.
Из схемы рис. 9-26, а непосредственно следует, что й^Ё-zJr, u2=z2i2.
Эти соотношения также показаны на графе рис. 9-26, б.
Коэффициент передачи Ки определяется при помощи графа рис. 9-26, б по формуле (4-32):
Д- __ ~рГэ) (Z Э |) zg 204
1—КЛэ/Кб + Гэ) rB (rh +^2) + гб [г9-J-rK (.1 a)-|-Z2]
Коэффициент передачи Ке определяется из того же графа рис 9-26, б по той же формуле (4-32):
__Ui, _ э)________
Ь 1 +2в/(Гб+гэ) — К/Гэ/(Гб + г9)
____________(/э —«гк) Z?________ (ZB-r/6) Р9+Гк(1—a)+ZJ + r9 (Z.21 rKy
255
Отличие выражения для коэффициента от Ки состоит в том, что в знаменатель входит дополнительное слагаемое — передача контура, состоящего из ветвей 1/(гэ + гс) и —ZB.
Для определения входного сопротивления схемы по отношению к зажимам с напряжением (рис. 9-26, а) можно пользоваться формулой (4-32), применяя ее к графу, показанному на рис. 9-26, в. Этот граф получен из графа рис. 9-25 при известных Нп, Н12, Н21, Н22 чз (9-25) с добавлением ветви с сопротивлением Z2, причем отрицательный знак у сопротивления Z2 учитывает, что положительное направление тока /2 в схеме рис. 9-26, а противоположно направлению того же тока на рис. 9-22, а.
На основании формулы (4-32) имеем из графа рис. 9-26, в следующее выражение:
^вх дир 1 —Lj ’
где
Щ=гб+т—1 — 1 + т—;
1 6 I 1—а+екгэ 1 1— а+§кгд
П' == fagK (— ?>) _ — (a—gKr3) ragKza.
2 (1 — a+gKr»)(l--a+giJ's) (1— «+gKra)a ’
D'2=l.
После подстановки значений передач путей и определителей в выражение (9-32) и некоторых преобразований получим:
+ (9-33)
rK(i—a)-f-r9-pz2
Глава десятая
ТРЕХФАЗНЫЕ ЦЕПИ
10-1. Понятие о многофазных источниках питания и о многофазных цепях
На рис. 10-1 схематично показано устройство генератора переменного тока с тремя обмотками на статоре Ради упрощения каждая обмотка показана состоящей только из двух проводов, заложенных в диаметрально противоположные пазы статора. Эти провода на заднем торце статора соединены друг с другом (соединения показаны пунктиром). На переднем торце статора они оканчиваются зажимами А, X, В, Y, С, Z, которые служат для подсоединения внешней цепи.
Наводимые в обмотках э. д. с. максимальны, когда ось полюсов ротора пересекает проводники статора. Для разных обмоток это ___происходит в различные моменты времени. Поэтому наводимые э. д. с. не совпадаю! но фазе.
256
питания называется
р и ч е с к и х цепей.
многофазной системой Отдельные ее части называются
Л
\ 1
Рис 10-1.
I
Генераторы с несколькими обмотками, в которых наводятся э д. с. одинаковой частоты, но сдвинутые относительно друг друга по фазе, называются многофазными генераторами. Соответственно любые источники питания, имеющие несколько зажимов (полюсов), между которыми создаются напряжения одной и той же частоты, сдвинутые относительно друг друга по фазе, называются многофазными источниками п и т а -н и я. Совокупность электрических цепей с многофазными источниками э л е к т фазами, например, отдельные обмотки генератора называют фазными обмотками или, кратко, фазами генератора. Таким образом, в электротехнике термин «фаза» имеет два различных значения: он является понятием, характеризующим стадию периодического процесса и, с другой стороны, наименованием составной части многофазной системы электрических цепей.
По числу фаз многофазные источники питания и системы цепей подразделяются на двух-, трех-, четырехфазные и т. д. В соответствии с этой классификацией генератор с тремя обмотками (рис. 10-1) — трехфазный, а цепи переменного тока, рассмотренные в предыдущих главах,
Впервые многофазные системы цепей и многофазные генераторы были применены на практике П. Н. Яблочковым для питания изобретенных им электрических свечей. В его установках обмотки многофазных генераторов присоединялись к электрически не соединенным друг с другом линиям, питавшим отдельные группы свечей. Такого рода многофазные системы цепей получили название несвязанных. В настоящее время вследствие существенных преимуществ применяются многофазные системы цепей, гальванически соединенные друг с другом. Такие многофазные системы цепей называются связанными. Способы соединения или связывания цепей рассматриваются ниже (§ 10-2). Связанная многофазная система цепей по существу образует одну сложную разветвленную цепь, поэтому обычно она называется просто многофазной цепью.
В электроэнергетике вследствие наибольшей экономичности и технического совершенства применяются почти исключительно трехфазные цепи. Все звенья трехфазной цепи, начиная от генера-
9 Основы теории цепей 257
можно назвать однофазными.
тора и кончая двигателем, были изобретены и разработаны известным русским инженером и ученым М. О. Доливо-Добровольским.
В установках, преобразующих переменный ток в постоянный, встречаются шести- и реже двенадцатифазные цепи. В автоматике и телемеханике применяются двухфазные цепи.
Крайним точкам фазных обмоток генераторов дают наименования «начало» и «конец». В трехфазных генераторах «начала» обозначим первыми буквами латинского алфавита А, В и С, а «концы» — последними буквами X, Y и Z (более сложные обозначения по ГОСТ здесь не рассматриваются.). При разметке руководству-
ются следующим условием: при одинаковых положительных направлениях э. д. с. во всех обмотках от «концов» к «началам» (или
от «начал» к «концам») э. д. с. должны быть сдвинуты по фазе друг огносительно друга симметрично. Исключение в этом отношении
составляют двухфазные генераторы (см. ниже). Поясним сказанное на примере трехфазного генератора.
Покажем, что разметка концов фазных обмоток на рис. 10-1 удовлетворяет принятому условию, т. е. что э. д. с. в фазах А, В и С сдвинуты друг относительно друга симметрично на 1/3 периода. Выберем положительные направления э. д. с. во
всех обмотках от концов к началам. В момент времени, соответствующий положению ротора, показанному на рис. 10-1, э. д. с. в обмотке А
максимальна и имеет направление, которое принято положительным, т. е. в этот момент э. д. с. в обмотке А достигает положительного максимума. Положительный максимум э. д. с. в обмотке В наступит позже, когда ротор повернется на 1/3 оборота. Так как один оборот ротора двухполюсного генератора соответствует одному периоду изменения э. д. с. в любой обмотке, то поворот ротора на 1/3 оборота соответствует 1 /3 периода и, следовательно, э. д. с. в обмотке В отстает по фазе от э. д. с. в обмотке А на 1/3 периода. Рассуждая аналогично, можно убедиться, что э. д. с. в обмотке С отстает по фазе от э. д. с. в обмотке В также на 1/3 периода.
На рис. 10-2 показаны векторная диаграмма и график мгновенных э. д. с. трехфазного генератора.
Порядок, в котором э. д. с. в фазных обмотках генератора проходят через одинаковые значения, например через положительные максимумы, называют последовательностью фаз или порядком чередования фаз. При указанном на рис. 10-1 направлении вращения ротора получаем последовательность фаз АВС и т. д. Если изменить направление вращения ротора на противоположное, то последовательность фаз получится обратной. У генераторов роторы—вращаютсяг лсееда-в одном-лаправленищ.
258
поэтому последовательность фаз никогда не изменяется и может быть раз навсегда установлена и обозначена. Ее обозначение связывают с наименованием фаз. Наименования устанавливаются
первыми буквами латинского алфавита, причем таким образом, чтобы нормальный порядок букв (А, В и С) соответствовал после-
довательности фаз.
Рассмотренная совокупность э. д. с. в обмотках трехфазного генератора называется трехфазной системой э. д. с. Совокупности э. д. с. (напряжений, токов) в многофазных цепях называют многофазными системами э. д. с. (напряжений, токов). Эти системы называют симметричными, если все э. Д. с. (напряжения, токи) равны по величине и если каждая э. д. с.
Рис. 10-3.
(напряжение, ток) отстает по фазе от предыдущей э. д. с. (напряжения, тока) на один и тот же фазный угол, равный 2эт/т, где
т — число фаз.
На рис. 10-3, а в качестве примера приведена векторная диа-
грамма симметричной системы э. д. с. шестифазного генератора.
Двухфазные генераторы изготовляются таким образом, чтобы э. д. с. в одной из обмоюк была сдвинута по фазе относительно э. д. с. другой обмотки на 1/4 периода. Векторная диаграмма системы э. д. с. двухфазного генератора приведена на рис. 10-3, б, эта система э. д. с.
несимметрична.
10-2. Соединения звездой и многоугольником
Существуют два основных способа соединения обмоток генераторов, трансформаторов и приемников в многофазных цепях: соединение звездой и соединение многоугольником. Например, соединение генератора и приемника звездой показано на рис. 10-4, а соединение треугольником — на рис. 10-5.
При соединении звездой (рис. 10-4) все «концы» фазных обмоток генератора соединяют в одну общую точку. Общие точки обмоток
Рис. 10-4;------------- ---------------------------ГнС. 10-5.
9*
259
генератора и ветвей звезды приемника называют нейтральными или нулевыми точками, а соединяющий их провод — нейтральным или нулевым проводом. Остальные провода, соединяющие обмотки генератора с приемником, называют линейными.
При соединении треугольником (рис. 10-5) или многоугольником фазные обмотки генератора соединяются последовательно таким образом, чтобы «начало» одной обмотки соединялось с «концом» другой обмотки. Общие точки каждой пары фазных обмоток генератора и общие точки каждой пары ветвей приемника соединяются проводами, носящими название линейных проводов. На первый взгляд может показаться, что соединение обмоток генератора в треугольник (многоугольник) равносильно короткому замыканию, как это было бы при подобном соединении, например, гальванических
элементов. На самом деле, при симметричной системе э. д. с. сумма э. д. с., действующих в контуре треугольника (многоугольника), в любой момент времени равна нулю. Убедиться в этом можно хотя бы из рассмотрения векторной диаграммы и кривых мгновенных значений э. д. с. для трехфазного генератора (рис. 10-2).
Заметим, что схемы рис. 10-4 и 10-5 можно представить получающимися из схем несвязанных трехфазных цепей, показанных на рис. 10-6, путем объединения друг с другом проводов, вычерченных рядом.
Схемы соединения обмоток источников питания и приемников не зависят друг от друга. В одной и той же цепи могут быть источники питания и приемники с разными схемами соединений. Лучи звезды или ветви многоугольника приемника называют фазами приемника, а сопротивления фаз приемника — фазными сопротивлениями. Электродвижущие силы, наводимые в фазных обмотках генератора или трансформатора, напряжения на их зажимах, напряжения на фазах приемниках и токи в них называют соответственно фазными э. д. с , н а п р я ж е н и -_ __g м_и и токами (Z^, t/ф, /)ф. Напряжения между линейными проводами и токТГв них называют л итГеТГн ы м и н ап ряже
260
ниями и токами (U„, 1Л). При соединении фаз звездой линейные токи равны фазным /л = /ф. При соединении фаз многоугольником линейное напряжение между проводами, присоединенными к одной и той же фазе приемника или источника питания, равно соответствующему фазному напряжению Uл = £/ф.
Положительные направления токов во всех линейных проводах выберем одинаковыми от источника питания к приемнику, а в нейтральном проводе — от нейтральной точки приемника к нейтральной точке источника питания. Положительные направления э. д. с. ' и токов в ветвях треугольника источника питания будем обычно выбирать в направлении АСВА, а напряжений и токов в ветвях треугольника приемника — в направлении АВСА (рис. 10-5).
Многофазную цепь и многофазный приемнцк называют симметричными, если комплексные сопротивления всех фаз одинаковы. В противном случае их называют несимметрич-н ы м и.
Если к симметричной трехфазной цепи приложена симметричная система напряжений, то получается симметричная система токов. Режим многофазной цепи, при котором многофазные системы напряжений и юков симметричны, называется симметричным режимом.
10-3. Симметричный режим трехфазной цепи
На рис. 10-7 приведены топографическая диаграмма и векторная диаграмма токов при симметричном режиме для схемы по рис. 10-4 и индуктивном характере нагрузки (<р > 0).
Ток в нейтральном проводе отсутствует:
Лг=Да+^в + Л? = О.
Поэтому при симметричном приемнике нейтральный провод не применяют. Линейные напряжения оп фазных напряжений:
йАв = йА — U в; йвс = йв~йс,
йСА=йс-иА. (ю-1)
Из равнобедренного треугольника AN В имеем:
U AB — 2U Acos /_ NAB— 2UА cos 3Q°, или
^ = /ЗПф. (10-2)
На рис. 10-8 приведены векторные Диаграммы напряжений и токов при
симметричном режиме и<р > 0 для схемы рис. 10-5. Линейные токи определяются как разности фазных токов:
I А~1 АВ~ Ica", I В = 1 BC~~ I АВ", СА— hiCt (10-3)
261
причем
/Л=ГЗ/Ф. (Ю-4)
Активная мощность симметричного трехфазного приемника
Р = 3^7ф/ф cos <р. (Ю-5)
Принимая во внимание, что при соединении ветвей приемника звездой = Пл/]/3 и /ф = /л, а при соединении ветвей приемника треугольником Пф = 7/„ и /ф = 1Л/У3,
получим независимо от вида соединения: Р = /ЗПл/лсо8(р. (10-6) Следует помнить, что в этом выражении <р — сдвиг по фазе между фазным напряжением и фазным током.
Аналогично для реактивной и полной мощностей симметричного трехфазного приемника имеем:
С==ЗПф/ф8ш<р= КЗ П,/Л51п<р; (10-7) 5=ЗПФ/Ф = ГЗПЛ/Л. (10-8)
Определим суммарную мгновенную мощность трехфазного приемника при симметричном режиме. Запишем мгновенные знамения фазных напряжений и токов, приняв начальную фазу напряжения равной нулю:
;;л = иф]/2 sin at; 1д = /ф]/'2 sin (at—<р);
/ 2 \ { 2 \
2 sin 3 nj i 1в=Л1> V2 sin з Л —<pj ;
(2 \ r- / 2 \
co/-f-g nj; 1с = /фр 2 sin (co/-|-g-л — <pj
и выражения для мгновенных значений мощностей каждой фазы приемника:
Ра = иА1 А = cos Ф - ифгф cos (2<’)Z - Ф):
Рв =11У в~ иУ ф cos Ф ~ и У ф cos (2cof - 3 л - ;
/ 4 \
Рс = “с1 с=иф}ф cos ф - ф cos ^2coZ+-3- Л - ср) -
При суммировании мгновенных значений мощностей отдельных фаз вторые слагаемые в сумме дадут нуль. Поэтому суммарная М1новенная мощность
Р = Р А + Рв + РС = 3Ч/ф C0S Ф = Р
не зависит от времени и равна активной мощности.
Многофазные цепй, в которых мгновенное значение мощности постоянно, называются уравновешенными.
Заметим, что в двухфазной симметричней цепи (рис 10-9) с несимметричной системой э. д с. источника питания (рис 10-3, б) система токов также несиммет^ рична, однако цепь являеюя уравновешенной, так как сумма мгновенных значе
262
Рис. 10-9.
ний мощностей в фазах постоянна. Это можно показать тем же путем, каким была показана уравновешенность симметричной трехфазной цепи.
Постоянство мтовенных значений мощности создает благоприятные условия для работы генераторов и двигателей с точки зрения их механической нагрузки, так как отсутствуют пульсации вращающего момента, наблюдающиеся у однофазных генераторов и двигателей.
Рассматривая симметричные режимы трехфазных цепей, легко показать их преимущество в экономическом отношении по сравнению с несвязанными трехфазными системами цепей.
У несвязанной трехфазной системы цепей шесть проводов с
токами /л = /ф. Трехфазная цепь без нейтрального провода, которая питает те же самые приемники, соединенные звездой, имеет только три провода с теми же токами 1Л = /ф и линейными напряжениями, в УЗ раз большими линейных напряжений в несвязанной трехфазной системе цепей, для которой 1УЛ = U$. В случае соединения приемников треугольником также получается вдвое меньше проводов, чем в несвязанной трехфазной системе цепей (три вместо шести), при этом токи в линейных проводах больше фазных токов не в 2 раза, а только в Уз раз. Это позволяет уменьшить затраты материала на провода.
10«4. Некоторые свойства трехфазных цепей с различными схемами соединений
В трехфазных цепях, питающих однофазные приемники (электросварочные аппараты, однофазные двигатели, электрические лампы и различные бытовые электроприборы), при изменении числа включенных приемников напряжение на их зажимах не должно по возможности изменяться.
Это условие выполняется как при соединении приемников звездой с нейтральным проводом, так и при соединении их треугольником. На рис. 10-10 в качестве примера приведены соответствующие схемы включения электрических ламп. Если принять, что напряжения на зажимах источника питания (Л, В, С и N) поддерживаются неизменными, и пренебречь падением напряжения в проводах, то в обеих схемах напряжения на лампах не отличаются от напряжений на зажимах источника питания и неизменны независимо от числа и мощности включенных в каждой группе ламп. Если оборвать нейтральный провод в схеме по рис. 10-10,а, то между нейтральной точкой п приемника и нейтральной точкой N источника питания появится напряжение. Фазные напряжения на лампах будут зависеть от соотношения их сопротивлений во всех трех группах и будут изменяться при изменениях числа ламп, включенных
263
в какой-либо группе. Поэтому соединение групп ламп звездой без нейтрального провода не применяется. При наличии нейтрального провода в случае перегорания предохранителя в одном из проводов магистральной линии, например в проводе А (рис. 10-10, а), гаснут лампы, присоединенные только в этому проводу, остальные лампы имеют нормальный накал. В этом же случае в схеме треугольника (рис. 10-10, б) под нормальным напряжением Останется только одна группа ламп в ветви ВС. Две другие ветви треугольника окажутся соединенными последовательно, питаются эти ветви по-прежнему от магистральных проводов В и С. Лампы в этих ветвях треугольника будут иметь неполный накал. Напряжения
Рис. 10-10.
между ветвями АВ и СА распределятся пропорционально их сопротивлениям. Чем больше включено ламп в одну из ветвей, например в АВ, тем ярче будут светить лампы в другой ветви СА (увеличение числа включенных ламп уменьшает сопротивление ветви).
Трехфазная цепь с нейтральным проводом обладает тем преимуществом, что может питать приемники, рассчитанные для работы при различных напряжениях. Приемники в такой цепи можно включать между линейными проводами на линейное напряжение и между линейными проводами и нейтральным проводом на фазное напряжение. На практике обычно встречаются низковольтные трехфазные цепи с нейтральными проводами и напряжениями
Пл = 380 В; Пф = 220 В
или
Пл = 220 В; Пф = 127 В.
Пример 10-1. Источник питания и приемник, состоящий из трех одинаковых —__резисторов с сопротивлениями гл = rs ~ гс, соединены по схеме звезда с ней-
тральным проводом (рис 10-11, а). Фазные напряжения источника ншання сим
264
метричны и не меняются при переключениях рубильников и изменениях нагрузки, указанных в задании.
Дано: Ult — 220 В и IА = IB — Ic — 1 А. Требуется построить топографические диаграммы цени и векторные диаграммы токов для следующих режимов-
1. Симметричный режим (рубильники 1 и 3 замкнуты, рубильник 2 разомкнут)
2. Положение рубильников то же, что и в п. 1, но активное сопротивление гА заменено на равное по величине емкостное сопротивление.
3 Рубильники 1 и 2 разомкнуты, а рубильник 3 замкнут.
4. Все рубильники (/, 2 и 3) разомкнуты.
5 Рубильники 1 и 2 замкнуты, а рубильник 3 разомкнут.
Решение. 1. Для симметричного режима цепи ее топографическая диаграмма и векторная диаграмма токов показаны на рис. 10-11, бив, фазные напряжения приемника и источника питания одинаковы и равны 220//3 = 127 В. Векторы фазных токов имеют одинаковые направления с векторами фазных напряжений (активная нагрузка). Ток в нейтральном проводе отсутствует.
2. При замене сопротивления г А равным емкостным сопротивлением напряжения на фазах приемника не изменяются. Токи и 1С остаются прежними, а у тока 1А сохраняется прежнее действующее значение 1 А, но он теперь опережает по фазе напряжение UАп на угол л/2. Топографическая диаграмма цепи для этого случая прежняя (рис. 10-11, б), а векторная диаграмма токов показана на рис. 10-11, а. Ток в нейтральном проводе равен сумме фазных токов IN~lA +
+ Д + /с, причем IN = У2 А.
Заметим, что если дополнительно разомкнуть рубильник 3, то ток /Л, будет равен нулю, однако, при этом потенциалы точек N и п станут различными. Фазные напряжения UАп, UBn и UCn не будут равны соответствующим фазным напряжениям источника питания UAN и UCN- Действующие значения токов во всех
фазах изменятся Рассчитать их для этого режима проще всего методом узловых потенциалов, как указано дальше, в § 10-6.
----3._При рятиыкянии рубильника 1 потенциал точки а становится равным----------- Потенциалу точки п. Других изменений в топографической диаграмме (рис. 10 11,0/ -
265
не происходит Векторная диаграмма токов для этого случая приведена на рис 10-11, д Из нее находим IN = 1 А
4 Если дополнительно разомкнуть рубильник 3, то потенциалы точек п и N становятся различными Сопротивления в фазах В и С получаются соединенными последовательно На каждое из этих сопротивлений приходится половина линейного напряжения йвс На топографической диаграмме точки и и о располагаются на середине отрезка ВС (рис 10-11, е)
Из топографической диаграммы находим напряжения между нейтральными точками N и п между разомкнутыми концами фазы А
UNn-^- - 63-5 В- иАп = 2 190,5 В.
U /(3
Напряжения на резисторах гв и гс уменьшаются в —2--------Рач> 130
столько же раз уменьшаются токи в этих сопротивлениях lfi = /с = Г 3/2 А. Векторная диаграмма токов для этого случая показана на рис. 10-11, ж.
5 При замкнутых рубильниках 1 и 2 разомкнутом рубильнике 3 потенциалы точек А, а и п одинаковы (рис 10-11, з) Напряжения на резисторах гв и гс равны линейным напряжениям UBfl = 0ВА и UCn = йСА- Вследствие этого токи 1 в и 7С в КЗ раз больше, чем в симметричном режиме, т е 1В— 1С — |/3 А Ток 1А находим из векторной диаграммы (рис 10-12, и) 1А ——
Пример 10-2. Три одинаковых резистора соединены треугольником (рис 10-12, а) К зажимам А, В n С приложены симметричные линейные напряжения, равные 220 В, которые не меняются при отключении рубильников 1 и 2 и изменении нагрузки При замкнутых рубильниках 1 и 2 линейные токи /л = 1 А
Требуется построить топографические диаграммы цепи и векторные диаграммы токов для следующих режимов t
1 -Симметричный режим (рубильник 1 и 2 замкнуты)._____________
2 Рубильник 1 разомкнут, а рубильник 2 замкнут.
266
3 Рубильник 2 разомкнут, а рубильник 1 замкнут
4 Рубильники 1 и 2 замкнуты и активное сопротивление в фазе Ьс заменено равным по ветчине емкостным сопротивлением
F Решение 1 Для симметричного режима топографическая диат рамма цени и векторная диаграмма токов показаны на рис 10-12, б и е Гоки в фазах приемника в Jz3 раз меньше линейных токов 1аъ = 1ьс~ Ica~ 1/1'3 А Векторы фазных токов 1аЬ, 1Ьс 1са совпадают по направлению с векторами напряжений bt L'bc и (Jca (активная нагрузка) Линейные токи определяются как разности фазных токов
hib ^13 ^Ьс ^са ^Ьс
2 При разомкнутом рубильнике 1 ток Ц,,. = 0 Потенциал точки Ь’ одинаков с потенциалом точки С Токи 1аЬ и 1са остаются без изменения, поэтому прежнее значение имеет и ток 1А= I — 1са Токи и /с изменяются 1В =---------1аЬ
и гс= !са
Векторная диаграмма токов приведена на рис 10 12, г
3 При разомкнутом рубильнике 2 и замкнутом рубильнике 1 сопротивления в ветвях са и ab соединены последовательно На каждое из этих сопротивлении приходится половина линейного напряжения На топографической диаграмме (рис 10 42 б) точка а располагается на середине отрезка Ьс Напряжение между разомкнутыми концами фазы А
U. = 77.ncos30° = 220 1/'3/2= 190,5 Б. /1(2- AIj т
Напряжения на сопротивлениях ветвей са и ab по сравнению с симметричным режимом уменьшаются в 2 раза Во столько же раз уменьшают токи в этих ветвях 7 = 1аЬ ~ 0,5 (1/J/3) = 0,289 А Токи I в и /снаходим по векторной диаграмме (рис 10-12, е)
Lc^ca-tbc', 1Б = ’ь-1аЬ; 7С = = 0,866 А.
4 Топографическая диаграмма цепи та же, что и в первом случае Векторная диаграмма токов приведена на рис 10-2, ж Из нее находим IА = 1 А, 1В =
= 2/6ccos75°-=2(l/K3) 0,259=0,299 А, /с=2/со cos 15°=2( 1/^3) 0,966= 1,15 А
Пример 10-3. Определить, во сколько раз изменятся линейные токи, если резисторы предыдущего примера (рис 10-12, а) соединить звездой и включить на те же линейные напряжения (схема звезды без нейтрального провода)
Решение В схеме треугольника резисторы находились под линейным напряжением ил и токи в них были 7.,/J 3 В схеме звезды резисторы находятся под напряжением U,t/\'3 и, следовательно, токи в них уменьшаются в J- 3 раз и станут равными 7 ,/3, где 7,, — прежнее значение линейного тока В схеме звезды токи в линии и фазах приемника одинаковы, таким образом, линейные токи в схеме звезды в 3 раза меньше линейных токов в схеме треугольника
10-5. Расчет симметричных режимов трехфазных цепей
Для ознакомления с расчетами симметричных режимов рассмотрим порядок расчета токов в симметричной цепи рис. 10-13 Пусть напряжения на зажимах источника питания симметричны и заданы и пусть известны сопротивления всех элементов цепи 1,2,3 и 4 Для выполнения расчета проще всего преобразовать схему, заменив соединения треугольниками источника питания и элементов 4 на соединения звездами. Сопротивления фаз симметричной звезды
267
в 3 раза меньше сопротивлений фаз эквивалентного симметричного треугольника. Фазные напряжения эквивалентного источника питания, соединенного звездой, в ]/3 раз меньше заданных линейных напряжений. Таким образом, получим схему, показанную на рис. 10-14.
Все нейтральные точки в симметричном режиме имеют одинаковый потенциал. Поэтому, не нарушая режима схемы, соединим их проводом без сопротивления (показан пунктиром). Затем удалим из схемы две фазы, например В и С, и перейдем к схеме по рис. 10-15. Это не изменит режима оставшейся фазы А.
Действительно, уравнения, составленные по законам Кирхгофа, для узла А' и для контуров и А’п^А' для схем, показан-
ных на рис. 10-14 и 10-15, одинаковы,
а следовательно, токи и напряжения в фазе А обеих схем также одинаковы. Токи в фазе А легко рассчитываются по однофазной схеме (рис. 10-15), например, методом ее дальнейшего преобразования — заменой параллельного соединения ветвей А'п2 иА'п1 экви-
Рис 10-15.
валентным сопротивлением. Токи в фазах В и С по модулю такие же, что и в фазе А. Токи в ветвях треугольника 4 в ]/3 раз меньше токов в элементах 3 (в каждом из элементов любой из групп ток сдвинут по фазе по отношению к токам в других элементах той же группы на равные углы ±120°).
Для расчета симметричных режимов в сложных разветвленных трехфазных цепях широко применяют моделирование соответствующих однофазных схем.
10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
При расчете симметричных режимов трехфазных цепей двигатели можно заменять эквивалентными схемами, состоящими из трех одинаковых сопротивлений, соединенных звездой или треугольни-ком. Падения напряжения в фаза^ценератора могут учитываться как напряженияна трех одинаковых сопротивлениях.
268
Такие простые эквивалентные схемы для двигателей и такой простой учет падений напряжения в генераторах оказываются непригодными для расчета несимметричных режимов. Анализ процессов в трехфазных электрических машинах (двигателях и генераторах) при несимметричных режимах показывает, что для них справедливы более сложные эквивалентные схемы, не удовлетворяющие принципу взаимности. В настоящее время для расчета несимметричных режимов в трехфазных цепях с трехфазными двигателями почти исключительно пользуются специальным методом расчета — мето-
дом симметричных составляющих, который рассмотрен в следующей главе.
В этом параграфе ограничимся исследованием несимметричных режимов цепей при следующих двух
условиях:
1) имеется только статическая нагрузка (нет электродвигателей);
2) падения напряжения в гене-
Рис. 10-16.
раторах не учитываются.
При двух указанных ограничениях расчеты несимметричных режимов трехфазных цепей не содержат ничего принципиально нового и могут выполняться лю-
быми методами,известными из предыдущих глав. Последующее содержание параграфа иллюстрирует это положение на ряде частных
примеров.
Пусть заданы несимметричные фазные напряжения О а, О в и [7С на зажимах несимметричного приемника (рис. 10-16). Определим токи. Заданные напряжения можно всегда приписать источникам э. д. с. (показаны пунктиром)
£д=йд; Ёв~йв и Ёс=ис.
В схеме два узла, поэтому целесообразно применить для расчета
метод узловых потенциалов.
Обозначая напряжение между нейтральными точками ника и источника питания через получаем:
прием-
ОnN —
YaUa+ybUb+ycUc ya + yb+yc+yn
(Ю-9)
где УА, У в, Ус, У n — проводимости ветвей;
4==Гл((7л-ад; /в= Ув (йв -UnN), |
Ё:-У С (Uc ~ йпМЁ, ^N — УN^nN— iд+ Л) + k- J
В предельном случае при yN = оо, т. е. ZN = 0, имеем On!V = 0 следовалепьно, напряжения па фазах приемника равны фазным
269
напряжениям источника питания. При этом условии ток в каждой фазе может быть подсчшан по закону Ома независимо от токов остальных фаз.
При отсутствии нейтрального провода расчет можно вести в таком же порядке. Изменится лишь выражение для напряжения ОnN, поскольку Yn = 0, а именно
О nN
Уа^а±ХЛ±Х<£с
(10-11)
Л Уя
I----------0----:-------4ZZJ—]
j В YB
./..-ди, , ' 1 • • ' | I I
} С Ар Jr
Рис. 10-17.
Однако обычно при отсутствии нейтрального провода бывают заданы не фазные, а линейные напряжения на зажимах цепи. Сумма линейных напряжений равна нулю, как сумма напряжений вдоль замкнутого контура, соединяющего зажимы А, В и С:
Одв + Ас + Йса = 0-
Учитывая эту связь, достаточно задать два линейных напряжения. Можно, например,
их задать двумя источниками напряжения (рис. 10-17) с э. д. с. Ёв — О ва и Ёс = Оса-
Тогда, принимая во внимание, что потенциалы точек N и А оди-
каковы, имеем:
О nN —
В^ВА + O'CA УА+Ув+Ус
(10-12)
IА = — 'О aU pN; 1b=YВ (Ё в — UnN) — Y в (О в А — йцк)', 1с = ¥с (Ёс — OnN) = Yc (Оса — ОпА)~— IА — 1В.
Рассмотрим простейшую схему с несимметричным приемником, соединенным треугольником (рис. 10-18). Если известны линейные напряжения между зажимами А', В', С', к которым присоединены сопротивления приемника, то задача определения токов элементарно проста. Ток в каждой ветви треугольника определяется по закону Ома, а затем находятся токи в проводах питающей линии.
Однако обычно бывают известны напряжения не на зажимах приемника, а на зажимах Л, В, С источника питания, поэтому расчет несколько усложняется. Проще всего его провести, заменяя треугольник сопротивлений эквивалентной звездой. Тогда получается схема по рис. 10-17 и токи в ней рассчитываются, как указано выше. По найденным токам определяются напряжения на зажимах треугольника в исходной схеме (рис. 10-18) и затем токи в ветвях треуголь
ника.
К преобразованию схемы следует прибегать и в случае цепи с несколькими приемниками, имеющими различные схемы соедине--иt-а. Тяк, например, при расчете токов в негда^-нредетавленней—на^-^
270
рис 10-19, звезду 2 следует преобразовать в эквивалентный треугольник, ветви которого будут параллельны ветвям треугольника 3. После замены каждой пары параллельных ветвей треугольников одной ветвью получается рассмотренная выше схема (рис. 10-18).
Заметим, что преобразование треугольника 3 в звезду не дало бы возможности продолжить упрощение схемы. Потенциалы нейтраль-
Рис 10-19.
ных точек получившейся звезды и звезды 2 в общем случае различны и нейтральные точки этих звезд нельзя соединять друг с другом
В том случае, когда элементы цепи индуктивно связаны друг с другом, расчет может быть всегда произведен путем решения уравнений Кирхгофа, составленных для токов в ветвях или же для контурных токов. В ряде случаев целесообразно исключить индуктивные связи, перейдя к эквивалентным схемам (§ 6-6).
10-7. Напряжения на фазах приемника в некоторых частных случаях
л
Рис 10-20
Пусть приемник соединен звездой (рис 10-17) Проводимости фаз !/гл Фа = ^а ~ Фд> * в~Ув — Фв! ^с~Ус —Фс-
Фазные напряжения при заданных линейных напряжениях определяются на топографической диаграмме положением нейтральной точки, для определения положения которой обратимся к выражению (10-12)
Рассмотрим некоторые частные случаи
Симметричный приемник при несимметричных линейных напряжениях При У А = У'в — Y( вектор напряжения
УРва+УсРса ^ва + ^са
Уа+У» + УС 3
равен одной трети диагонали параллелограмма (рис 10-20) Отсюда следует, что нейтральной точке на топографической диаграмме соответствует центр тяжести треугольника линейных напряжений
Приемник с однородными сопротивлениями фаз (ср , = фв= <рс), одно из которых изменяется При проводимости уА, изменяющейся от 0 до оо, получим
УiPba У Ус1'с а_______________
Уа + Ув+Ус
271
сохраняется, а длина его
Рис 10-21
В этом выражении все величины постоянны, кроме у А. При изменении уА аргумент UnA остается неизменным, следовательно, направление вектора 1гпА изменяется. Конец вектора йпА описывает прямую линию (получается линейная диаграмма). Для построения этой прямой достаточно найти любые две точки, через которые она проходит При уА~ = о°(2д = 0) имеем йпА = 0 и точка п совпадает на топографической диаграмме с точкой А (рис 10-21) При уА = 0 (гА = оо) получим 1А = 0; 1В= — 1С. Поэтому
^Вп 7в'в гЯ
UCn 7С?С ZC
Отсюда видно, что URn и UCr, отличаются по фазе на 180°, следовательно, точка п находится I точки В и С. Ее положение на этом отрезке
определяется отношениемг^/г^ (на рис 10-21 положение точки п при уА — 0 показано для случая, когда zBlzc = 2). Прямая, соединяющая точки Ann (уА = 0), представляет геометрическое место, описываемое точкой п при изменении уА от оо до 0.
Приемник с неоднородными сопротивлениями фаз, одно из которых изменяется Пусть YB = Y( = g, YА — jbc, причем bc изменяется от 0 до оо. Тогда
.у — = !!РА
пА~ 2s+lbc ^+!bc/2g'
где
Up а = (йВА+UCA)P.
Выражение для йпА совпадает по своей структуре с выражением
Л4 =----,
Рис. 10-22.
па отрезке,
которое рассматривалось в § 7-1 Там было показано, что при изменении п конец вектора М описывает дугу окружности Следовательно, геометрическим местом, описываемым точкой п при изменении Ь(., будет круговая диаграмма Выполним се построение при симметричных линейных напряжениях
На топографической диаграмме (рис 10-22) эти напряжения представлены равносторонним треугольником АВС. Отложим хорду диаграммы [) А Началом круговой диаграммы является точка А, она соответствует Ьс = оо, при этом вектор ЙпА обращается в нуль. Конец хорды находится в точке D. Хорда AD соответствует вектору U Л при значении переменного параметра Ьс = 0 аналогично тому, как вектор Мо представляет собой М при п = 0 Выбрав масштаб для проводимостей тх, отложим от начала хорды (точка Л) по направлению к ее концу (точка О) отрезок AF, равный 2g, и затем из точки F под углом — ф = — 90° к хорде AD проведем линию изменяющегося параметра FL Перпендикуляр, опущенный из начала диаграммы (из точки /1) на линию изменяющегося параметра, совпадает с хордой и пересекается с перпендикуляром, восстановленным к ссре-дине хорды, в середине хорды. Таким образом, центр круговой диаграммы нахо-
272
дится в середине хорды, которая в данном случае является диаметром. На топо- графической диаграмме показано положение точки п в частном случае, когда —g.
Напряжения UBtl и UCn на од паковых сопротивлениях в фазах В и С
получаются неодинаковыми. Если в качестве сопротивлений лампа в фазе В будет светить ярче, чем
в фазе С. Поэтому две лампы и конденсатор, включенные по схеме рис. 10-23, о, применяют как указатель последовательности фаз. Напряжение на лампе, которая светит ярко, опережает по фазе напряжение на лампе, которая светит тускло.
Можно вместо конденсатора включить катушку (рис. 10-23, б). Накал ламп будет также неодинаков. Однако в этом случае
Рис.
взять лампы, то
10-23.
больший накал наблюдается у лампы, на коюрой напряжение отстает по фазе
от напряжения на лампе, светящейся
тускло. Показать это можно, заменив в фазе А (рис. 10-17) переменною емкость переменной индуктивностью. Геометрическим местом потенциала точки п будет дуга окружности, показанная на диаграмме (рис. 10-22) пунктиром.
10-8. Эквивалентные схемы трехфазных линий

Рис. 10-24.
Чтобы упростить задачу составления эквивалентной схемы линии, рассмотрим отдельно различные стороны электромагнитного процесса. Сначала обратим внимание только на магнитное поле, а поле электрическое и преобразование электромагнитной энергии в тепло учитывать не будем (примем активные сопротивления проводов линии равными нулю).
На рис. 10-24 представлен поперечный разрез трехфазной линии. Роль нейтрального провода выполняет земля. Ток в земле обычно учитывают токами в трех фиктивных проводах, оси которых находятся на расстоянии DB от осей проводов линии. Это расстояние называют эквивалентной глубиной протекания обратного тока. Оно зависит от частоты переменного тока и от
удельной проводимости грунта. В качестве среднего значения при частоте / = 50 Гц принимают DB = 1000 м.
При таком учете тока в земле получаются три петли, каждая из которых состоит из реального и из фиктивного проводов. Индуктивности петель провод — земля одинаковы LA = Lb = Lc = L3, а взаимные индуктивности петель МАВ, МВс и МСА различны. Для того чтобы линии были симметричными элементами трехфазной цепи и не обусловливали несимметричного режима, их выполняют с круговой перестановкой или с так называемой транспозицией проводов. Вся длина линии делится на кратные трем равные части (на рис. 10-25 длина линии разделена на три части). Каждый провод на трех участках занимает три различных возможных положения и. таким образом, все провода находятся в одинаковых условиях. При этом МАВ = Мвс = МСА = Л13.
273
Чтобы установить, как в эквивалентной схеме линии следует учитывать индуктивности L3 и взаимные индуктивности 7И3, рассмотрим связь между токами и напряжениями в линии, когда все
провода на одном конце линии конце линии между проводами г
Рис 10-25.
замкнуты на землю, а на другом землей включены три источника напряжения О А, и Ос.
По второму закону Кирхгофа
U а~ а~\~ в + /СйМ3/о Ток в земле
In — ^А + + ^С»
откуда
In~~I А-
Подставляя последнее соотношение в выражение для О А> получаем:
UA~j<aL3l+ /соТИз (In — (L3 — M3) 1 дЦ-/соЛ43/дг.
Аналогично
ив — ]<й (L3 — A-i 3) 1в + j(oM3i
U с ==/й (L3 — М3) /с + j&M3lк.
Из этих уравнений видно, что для учета магнитного поля рассматриваемой симметричной линии справедлива схема, показанная на рис. 10-26, в которой
Аф = L3 М 3
называется индуктивностью фазы симметричной трехфазной линии.
Рис. 10-26.
I । /* л
Ч/-Т- 6гг-т ‘агт"
I I ।
Рис. 10-27.
Рассмотрим теперь электрическое поле линии. С электрическим полем линии связаны заряды на поверхностях проводов линии и на поверхности земли. Для их учета вводят между всеми проводами и землей частичные емкости, показанные на рис. 10-27 пунктиром. Частичные емкости зависят ог размеров проводов, их расположения
274
друг относительно друга и относительно земли. Для линии с транспозицией проводов
СД — С22— С33 -Со; С12 — С2з — Сл — Ст.
Таким образом, для учета электрического поля справедлива эквивалентная схема, приведенная на рис. 10-28.
Составим теперь общую эквивалентную схему, учитывающую магнитное и электрическое потя, а также активное сопротивление
линии.
Для любого сколь угодно малого участка линии на схеме нужно ввесш часшчные емкости, индуктивности, взаимные индуктивности и сопротивления, а также учесть проводимость изоляции. Тогда получится схема с бесконечно большим числом элементов. Объясняет-
ся это тем, что параметры линии распределены вдоль всей ее длины. °-
Линия как цепь с распределенными
параметрами рассматривается в гл. 18. Для практических расчетов при частоте тока 50 Гц, когда длина воздушной линии не превышает 300 км, а кабельной линии 50 км, вполне пригодны упро-
щенные расчетные схемы, в которых частичные емкости предполагаются сосредоточенными либо в середине линии, либо разделены поровну между ее концами. Проводимостью изоляции обычно пренебрегают.
На рис. 10-29 представлена полная эквивалентная схема симметричной линии с учетом частичных емкостей линии на ее концах. В этой схеме соединения треугольниками частичных емкостей между . проводами Ст/2 преобразованы в соединения звездами с емкостями | в лучах ЗСт/2, г — активное сопротивление провода; г3 — активное _ сопротивление земли.
275
Для симметричных режимов можно пользоваться эквивалентной схемой для одной фазы 1рис. 10-30). Если считать все частичные емкости сосредоточенными в середине линии, то для симметричного режима получается схема, показанная на рис. 10-31.
В этих схемах в проводах NN' элементы г3 и 7И3 отсутствуют, так как в симметричном режиме ток через землю не проходит. Емкость Сф = Со + ЗСт называется емкостью фазы лини и.
В воздушных линиях электропередачи с напряжением ниже 35 кВ влияйие емкостей линии на режим цепи невелико и их обычно не учитывают.
В некоторых типах линий низкого напряжения можно ограничиться учетом только активного сопротивления проводов.
10-9. Измерение мощности в трехфазных цепях
Выясним, сколько ваттметров нужно включить для измерения акшвноп мощности в трехфазной цепи при любом несимметричном режиме.
На рис. 10-32 прямоугольником условно показана сколь угодно сложная цепь, питаемая трехфазной линией с нейтральным прово
Рис. 10-33.
дом. Фазные напряжения на входе линии с нейтральным проводом всегда можно приписать трем источникам напряжения (показаны пунктиром). Из этого следует, что для измерения активной мощности в трехфазной линии с нейтральным проводом нужно включить три ваттметра, как показано на рис. 10-32 (ваттме1ры измеряют активные мощности источников напряжения).
В цепи без нейтрального провода (рис. 10-33) линейные напряжения иа входных зажимах всегда можно фГассмагривать получи1--
276
при которых стрелка
Рис 10 34
ющимися or двух источников напряжения, например включенных так, как показано пунктиром на рис. 10-33. Следовательно, активная мощность передачи энергии по линии без нейтрального провода может быть измерена двумя ваттметрами. Следует иметь в виду, что возможны такие режимы работы цепи, того или иного ваттметра отклоняется в обратную сторону, несмотря на правильное включение ваттметра в цепь. Тогда, чтобы сделать отсчет по шкале, нужно изменить подключение обмотки напряжения или обмотки тока соответствующего ваттметра на противоположное. Измеренную после этого -
мощность следует считать отрицатель-ной. Пример подобного случая при-водится ниже. Ci
Выясним зависимость мощности, измеряемой каждым из ваттметров в схеме рис 10-33, от сдвига фаз между напряжениями и токами в частном случае симметричного
режима На рис 10-34 показана векторная диаграмма токов и напряжений. Линии, соединяющие центр тяжести треугольника напряжений с его вершинами, можно рассматривать как фазные напряжения эквивалентного приемника, соединенного звездой.
На основании схемы включения одноименных зажимов ваттметров и руководствуясь векторной диаграммой, можно записать:
Р^Ас'а™ ^ас 1А = ил1яСОз(Ю-ч),
Р‘2 = UcJ В cos Р ВС, ^В~ Р Jл C0S ф)’
Pi -|- Р2 = 2 cos 30°. cos <р — jT-З ил 15 cos ф.
Как следует из этих выражений, показания ваттметров одинаковы только при <р = 0 При Ф = 60° получаем Р2 — 0, а при ф = — 60° имеем Рх = 0 При ф > > 60° имеем Р2 < 0, а при <р < — 60° получаем < 0 При ф = ± 90° имеем Р2~ — Pi Таким образом, при | ф | > 60° стрелка одного из ваттметров отклоняется в обратную сторону
10-10. Вращающееся магнитное поле
Одним из основных преимуществ многофазных токов является возможность получения вращающихся магнитных полей, лежащих в основе принципа действия наиболее распространенных типов двигателей переменного тока. Вращающееся магнитное поле было получено физиком Г. Феррарисом в 1884 г., однако он пришел к ошибочному заключению о невыгодности его применения для создания электродвигателей.
В 1887—1888 гг. физик-инженер Н. Тесла сконструировал двухфазный асинхронный двигатель (наименование «асинхронный» . будет пояснено в следующем параграфе), а в 1889 г. М. О. Доливо-Добровольский изобрел и построил трехфазный асинхронный дви-“
277
гатель. Н. Тесла в последующие годы вел работы по внедрению двухфазных двигателей, генераторов и электропередач в США. Одновременно М. О. Доливо-Добровольский разрабатывал все звенья трехфазной системы и внедрял ее в Европе. Подлинным три
умфом трехфазного тока явилась установка по передаче энергии на расстояние 175 Км от Лауфенского водопада до Франкфурта-на-Майне, осуществленная М. О. Доливо-Добровольским в 1891 г. Преимущества трехфазного тока были несомненны, и он быстро получил общее признание и повсеместное применение.
Ознакомимся на простейшем примере с получением вращающегося магнитного поля посредством трехфазной системы токов. Расположим три одинаковые катушки 1, 2 и 3 под углом 120° друг относительно друга. На рис. 10-35,а
они показаны в поперечном разрезе.
Подключим катушки /, 2 и 3 соответственно к фазам А, В и С источника питания таким образом, чтобы токи были симметричны (рис. 10-35, б) при показанных на рис. 10-35, а положительных направлениях токов. Рассмотрим
Рис 10-35 схематические картины магнитного
поля для различных моментов времени, следующих друг за другом. Пусть первый из рассматриваемых моментов времени соответствует совпадению линии времени с вектором Д. При этом Д > 0, Д < 0 и Д < 0. Направления токов в катушках и схематическая картина магнитного -поля показаны на рис. 10-36, а, где пунктиром изображены две магнитные линии. Для момента времени, соответствующего положению линии времени, отмеченному цифрой 2, Д > 0, Д = 0 и Д < 0. Направления токов в катушках и схематическая картина поля даны на рис. 10-36, б. Далее на рис. 10-36, в и г показаны на
правления токов и схематические картины поля для моментов времени, соответствующих положениям линии времени 3 и 4. Сопостав-
ление схематических картин магнитного поля, приведенных для различных, следующих друг за другом моментов времени, наглядно показывает вращение магнитного поля. Продолжив анализ, можно убедиться, что в течение одного периода переменного тока магнитное поле таких катушек совершает один полный оборот.
Направление вращения магнитного поля зависит исключительно от последовательности фаз токов в катушках. Если сохранить подключение катушки 1 к фазе А источника питания, катушку 2 подключить к фазе С, а катушку 3 — к фазе В, то направление вращения поля изменится на противоположное. В этом можно убедиться, построив схематические картины магнитного поля для различных моментов времени, аналогично тому, как это было показано выше. ~ ~
278
Движущиеся в пространстве магнитные поля, частным случаем которых является рассмотренный пример, широко применяются
в различных областях электротехники. Для получения движущегося магнитного поля нужно иметь минимум две пространственно смещенные обмотки с несовпадающими по фазе токами.
10-11. Принципы действия асинхронного и синхронного двигателей
Поместим между неподвижными катушками (рис. 10-37) в области вращающегося магнитного поля укрепленный на оси подвижный металлический барабан. Если магнитное поле вращается по направлению движения часовой стрелки, то барабан относительно поля вращается в обратном направлении. Принимая это во внимание, по правилу правой руки найдем направление наведенных в барабане токов (на рис. 10-37 указаны крестиками и точками). Затем, применяя правило левой руки, убедимся, что взаимодействие этих токов с магнитным полем дает силы, приводящие в движение барабан в том же направлении, в каком вращается магнитное поле. Частота вращения барабана меньше частоты вращения магнитного поля относительно катушек, так как при одинаковых угловых скоростях прекратилось бы наведение токов в барабане и, следовательно, не было бы сил, создающих вращающий момент.
Рассмотренное простейшее устройство поясняет принцип действия трехфазных асинхронных двигателей. Слово асинхронный заимствовано из греческого языка и означает неодновременный Этим словом подчерки--Дается различие в- частотах вращающеюся поля и ротора подвижной части—= Двигателя.
279
Поместим между неподвижными катушками (рис. 10-38) в область вращающегося магнитного поля укрепленный на оси подвижный электромагнит, питаемый постоянным током На э пек грома! нит действует вращающий момент, направление которого изменяется 2 раза за каждый оборот магнитного поля Вследствие периодическою изменения направления вращающегося момента и инерции подвижной системы электромагнит останется неподвижным Однако, если его привести во вращение посредством какого-либо приспособления с угловой скоростью, близкой к угловой скорости вращающегося поля, то он будет продолжать вращаться и достигнет частоты вращения, одинаковой с частотой вращения поля.
Рис 10-37.
Рис. 10-38.
Рассмотренное устройство поясняет принцип действия трехфазных синхронных двигателей Греческое слово синхронный означает одновременный. Этим словом подчеркивается одинаковая частота вращения вращающегося поля и ротора
В электрических машинах для вращающегося магнитного поля создается магнитная цепь Статор — неподвижная часть машины, выполняется в виде полого цилиндра, собранного из отдельных изолированных друг от друга стальных листов Ротор — подвижная часть машины — в асинхронных двигателях выполняется в виде стального цилиндра, обычно также собранного из стальных листов с обмоткой, размещенной в пазах на его поверхности.
Глава одиннадцатая
МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
11-1. Симметричные составляющие трехфазной системы величин
Для анализа и расчетов несимметричных режимов в трехфазных цепях широко применяется метод симметричных составляющих. Он основан на представлении любой трехфазной несимметричной системы величин (токов, напряжений, магнитных потоков) в виде суммы в общем случае трех симметричных систем величин. Эти симметричные системы, которые в совокупности образуют несимметричную систему величин, называются ее симметричными составляющими. Симметричные составляющие отличаются друг от друга порядком следования фаз, т. е. порядком, в котором фазные величины проходят через максимум, —и называются системами п-р- я м о й,—обратной и нуле-вой последовательностей.
280
Обозначим трехфазную систему величин (токов, напряжений, магнитных потоков) для общности буквами А, В и С. Величины, этносящпеся к системам прямой, обратной и нулевой последовательностей, отметим соответственно индексами 1, 2 и 0. На рис. 11-1
показан пример векторных диаграмм симметричных составляющих всех трех последователь-
Рис 11-1.
совпадаю-
ностеи.
Система прямой последовательности имеет порядок следования фаз А, В, С. Система обратной последовательности имеет порядок следования фаз А, С, В. Система нулевой последовательности состоит из трех одинаковых величин, щих по фазе. Для этих трех систем можно записать:
С1 = Д1е+'2гт/3; (11-1)
В2^=Д2е1/2л/з. С2 = Д2е~72л/3; (11-2)
До==^О = ^О- (11'3)
Комплексное число е}2п/3 называется фазным множителем и сокращенно обозначается буквой а:
fi===e;2n/3==e-/4n/3 = COS(2n/3) + /sin(2n/3) = — 1/2+ //3/2. (11-4)
Умножение вектора на а соответствует повороту его против направления движения часовой стрелки (вперед) на 120° или повороту по направлению движения часовой стрелки (назад) на 240°.
а2 = е?2"/з е^3 = е'4л'3 = е - '2л/3 = — 1 /2 - j Уз /2. (И -5)
Умножение вектора на а2 соответствует поворогу его вперед на 240° или повороту назад на 120°.
При помощи фазного множителя выражения (11-1) и (11-2) можно записать так:
В1 = о2Д1; С^аАй (11-6)
Д2=оД2; С2 = оМ2. (11-7)
Кроме того,
а3=е^2л = 1.
(Н-8)
Пользуясь соотношением (11-8), можно исключать из формул множитель а в степени выше второй:
а4 — а3а=а; а5 = а3а2 = а2 и т. д.
Как следует из (11-4) и (11-5) 1, а и а2 образуют симметричную систему единичных векторов (рис. 11-2). Их сумма
1 + а _ ДЩ
281
Докажем теперь, что любую несимметричную систему векторов А, В и С можно разложить на симметричные системы прямой, обратной и нулевой последовательностей. Если это имеет место, то
А = Л1 +Лй +Ло; (11-10)
В^ + Вг + В», (11-11)
С=Ci -J- С2 + Со- (11-12)
Выразим в этих предполагаемых равенствах все векторы симметричных систем через векторы Аъ А2 и Ло, пользуясь соотношениями (11-3), (11-6) и (11-7):
Л=Д1 + Лг+Д0; (11-13)
В = а2А1 + аА2 + А0; (П-14)
С=аЛ1 + агЛг + Л0. (11-15)
Получены три уравнения, из которых однозначно можно определить векторы Аъ А2 и Ло, что и доказывает возможность разложения заданной несимметричной системы векторов Л, В и С на три симметричные системы.
Складывая уравнения (11-13) — (11-15), получаем:
А +В + С=(1+с2 + о) Лг +
+ (1 Д^Д^2) Л2 -рЗЛо-
Принимая во внимание (П-9), находим, что Ло~ | (Л+в+ Q- (П-16)
Рис 11-2.
Умножая уравнение (11-14) на а и (11-15) на а2 и затем складывая уравнения (11-13) — (11-15), находим, что
Л1=у(Л+«В + о2С). (11-17) -
Умножая уравнение (14-14) на а2 и (11-15) на а и затем складывая уравнения (11-13) — (11-15), получаем:
Л2=у(Л+с2В + йС). ’ (11-18)
11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
В нейтральном проводе ток равен сумме линейных токов и, следовательно, тройному значению составляющей тока нулевой последовательности [см. выражение (11-16)].
Сумма линейных напряжений равна нулю, поэтому линейные напряжения не содержат составляющих нулевой последовательности.
Симметричные составляющие прямой и обратной последовательностей фазных напряжений приемника, соединенного звездой, -однозначно связаны с соответствующими—енмметричными состав*
282
ляющими подведенных к нему линейных напряжений. Отсюда следует, что фазные напряжения различных приемников, соединенных звездой, при одних и тех же линейных напряжениях имеют одина-
ковые симметричные составляющие прямой п обратной последовательностей и могут отличаться друг от друга только за счет симметричных составляющих нулевой последовательности.
В том случае, когда при несимметричном режиме ток в од
ной пли двух фазах цепи отсутствует, сумма симметричных составляющих токов в этих фазах равна нулю. Поясним сказанное примерами.
В схеме, показанной на рис. 11-3, фазы В it С разомкнуты, 1В = /с = 0. Применяя формулы (11-16) — (11-18), получаем:
/дт = g- (Jа + с0 -j- с20) = -g Iа',
iА2~ 3 (^аФ~°20 + и0) = g/д', ^АО— 3 (^л + О-Г’О)-- з~ /д.
На рис. 11-4 изображен вектор тока fA и построены векторные
диаграммы для систем симметричных трех фаз. Там же проведено геометрическое суммирование векторов симметричных составляющих токов, показывающее, что
I Al + ^А2 "Т I А0~1 А’<
т>2 + /га — 0;
/щ Н' А.г + А?.о = 0.
составляющих токов всех
В схеме рис. 11-5 токи 1А = 0; /в = —/с.
По формулам (11-16) — (11-18) получим:
/до—О; /д1= з (и/в+с)= (а — a2) — jiB/\/ 3;
-----| НэW-c) - 'l («2 о)-^//,<3
283
На рис. 11-6 показаны векторная диаграмма токов /в и /с и векторные диаграммы симметричных составляющих токов всех трех фаз. Геометрическое суммирование векторов показывает, что
= iAl + 1 Аг = 0; /в = Ли + h’rZ 1с ~ ?С1 + 1сг-
Симметричные составляющие токов и напряжений могут быть не только вычислены, но и измерены при помощи специальных электрических измерительных схем, называемых фильтрами симметричных составляющих токов и напряжений. Эти фильтры получили широкое применение в релейной защите электроэнергетических цепей.
11-3. Сопротивления симметричной трехфазной цопи для токов различных последовательностей
Если к зажимам симметричной трехфазной цепи приложена симметричная система напряжений прямой, обратной или нулевой последовательностей, то в цепи возникает симметричная система
Рис. 11-7.
токов соответственно той же самой последовательности, какую имеют приложенные напряжения. Отношения приложенных комплексных фазных напряжений прямой, обратной и нулевой последовательностей к соответствующим комплексным фазным токам называют соответственно комплексными сопротивлениями цепи прямой (ZJ, обратной (Z2) и нулевой (Zo) последовательностей.
В любых симметричных трехфазных статических цепях (цепях, не содержащих вращаю-
щихся маш ’н) изменение порядка следования фаз приложенных
симметричных напряжений с прямого на обратный не изменяет значения токов (изменяется только их последовательность с прямой
на обратную). Поэтому для таких цепей сопротивления прямой и обратной последовательностей одинаковы (Zy = Z2).
Рассмотрим, например, трехфазную симметричную цепь (рис. 11-7), в которой ZA^ZB-Zc- Z. Очевидно, что для этой цепи = ZL — Z.
Определимом я нееТ0. , -----=
284
Пусть к зажимам цепи приложена симметричная система фазных напряжений нулевой последовательности С а = О в ~ &с = == С/о. Тогда система, токов также симметрична и имеет нулевую j последовательность IА = /в = /с = 4- Ток в нейтральном про-| воде /Л= 370.
Составим для контура AnNA уравнение 0 А~ Z aI аА- N
и подставим U А = #0; Л = 4; 1N = 3/0 и ZA = Z..
Тогда получим: '
о — (7 - j- 3Zjy) 4, отку да
Zo — U 0/1(| = Z+3Z/V-
При отсутствии нейтрального провода .токи нулевой последовательности протекать не могут: Zo = оо и 4 = 0.
При расчетах цепей методом симметричных составляющих рассматривают отдельно схемы для токов и напряжений различных последовательностей. Сопротивление в нейтральном проводе не оказывает влияния на симметричные системы токов прямой и обратной последовательностей, поэтому в схемах для токов этих последовательностей сопротивления л в нейтральном проводе не I ‘ указывают (рис. 11-8). В схеме
।' для симметричных токов и напряжений нулевой последовательности вместо сопротивления ZN в нейтральном проводе вводят утроенные значения этого сопротивления в каждую фазу (рис. 11-9). Легко проверить, что сопротивления нулевой последовательности для схем, представленных на рис. 11-7 и 11-9, одинаковы.
Все расчеты ведут для одной фазы, которую называют основной. Обычно за основную фазу принимают фазу А, и в этом случае для сокращения записи в обозначениях токов и напряжений различных последовательностей индекс А не пишут. Так, для рассматриваемого примера (рис. 11-7) на рис. 11-10 показаны три однофазные схемы для токов и напряжений различных последовательностей. Эти схемы сокращенно называются схемами прямой, обратной и нулевой последовательностей.
В качестве схем прямой и обратной последовательностей для трехфазных линий можно применять любую из двух схем, показанных на рис. 10-30 и 10-31. В схему нулевой последовательности сопротивление г3 и индуктивность М. (рис. 10-29) должны быть введены утроенной величиной в каждую фазу. В зависимости от того, разнесены ли частичные емкости поровну по концам линии или сосре-~“^док)ченьПВ середине,-получатся две разновидности схсм-нулевой
285
последовательности для трехфазной линии, не отличающиеся по структуре от схем, показанных на рис 10-30 и 10-31 Только в этих схемах вместо г, и Сй следует взять г0 — г 4- Зг3, £0 = Ьф + ЗЛ'13 = L3 + 2Л43 и Со (через частичные емкости Ст токи нулевой последовательности протекать не могут)
В электрических машинах не только Zo отличается от Zj, но Z2 не равно Zr.
Рис 11-10
Причину этого поясним на примере асинхронного двигателя В нормальном режиме работы, когда к обмоткам статора двигателя приложена симметричная система напряжений прямой последовательности, магнитное поле и ротор двигателя вращаются в одну и ту же сторону (см § 10 11) Частота вращения ротора обычно всего на 1,5—4% меньше частоты вращения магнитного поля Иные условия получаются в симметричном режиме для токов и напряжений обратной последовательности Обеспечим вращение ротора двигателя с той же скоростью и в том же направлении, какие были в нормальном режиме работы (например, вращая его посредством другого двигателя), но изменим последовательность фаз напряжений, подведенных к обмоткам статора, с прямой на обратную Тогда в обмотках двигателя будет симметричная система токов обратной последовательности, которая создаст магнитное поле, вращающееся с той же скоростью, как и в нормальном режиме работы, но только в обратную сторону (навстречу движению ротора) В результате вращающееся магнитное поле относительно ротора будет иметь скорость, почти в 2 раза превышающую скорость движения поля относительно статора и во много раз превышающую скорость поля относительно ротора при нормальном режиме работы По сравнению с нормальным режимом резко возрастут токи, индуктированные в роторе По закону Ленца они будут ослаблять наводящее их магнитное поле в большей мере, чем в условиях нормального режима Это приведет к уменьшению э д с , наводимых магнитным полем в обмотках статора А так как приложенные к обмоткам статора напряжения в основном уравновешиваются этими э д с , то их уменьшение вызовет увеличение токов в статоре
Таким образом, при одинаковых значениях приложенных симметричных напряжений прямой и обратной последовательностей и при неизменных частоте н направлении вращения ротора токи обратной последовательности получаются больше токов прямой последовательности Следовательно, полное сопротивление двигателя для токов обратной последовательности меньше его сопротивления для токов прямой последовательности z2 <
Токи нулевой последовательности не создают вращающегося магнитного поля (длч получения движущегося магнитною поля, как было указано в § 10 10, нужно иметь не только пространственно смещенные обмотки, но и сдвинутые в них по фазе токи) Значит, условия протекания в двигателе токов нулевой последовательности отличаются от условий протекания токов прямой и обратной последовательностей, поэтому Zx 4= 70 =/- 22
В расчетах методом симметричных составляющих двигатели, как и статические цепи, представляют тремя отдельными схемами прямой, обратной и нулевой последовательностей, состоящими соответственно из сопротивлении Zb Z2 и Za Гёнёраторы имеют’
286
такие же схемы с тем отличием, что в схеме прямой последовательности, кроме сопротивлений включены источники фазных э. д. с.
генератора.
Отметим, что неравенство сопротивлений Zj и Z2 приводит к тому, что трехфазные цепи, содержащие вращающиеся машины, не обладают свойством взаимности (см. конец этого параграфа).
Расчеты несимметричных режимов трехфазных цепей, содержащих машины, для которых Z2 =/-= можно проводить и не прибегая к методу симметричных составляющих. Однако для этого приходится пользоваться особыми расчетными схемами, имею-
щими по два неодинаковых комплексных
сопротивления взаимной индукции для каждой пары фаз. Так, для двигателя справедлива схема, показанная на рис. 11-11, где
2АВ“ 2ВС — ^СА ~ ZM> ZI1A ZAC — Zm,
причем =/-= Zm.
Значения Z, Zai и Zm должны быть выбраны такими, чтобы сопротивления схемы для токов прямой, обратной и нулевой последовательностей были равны сопротивлениям Zb Z2 и Zo двигателя.
Можно показать, что это будет соблюдаться, если
2—“б (Zi + Z24-Z0); О
Zm = -g-IcZj-pa^a-J-Zo);
% М = 3~ (^1 + й^2 "Ь ^о) •
(И-19)
Для генератора схема аналогична, но в каждой фазе содержится источник фазной э. д. с. (предполагается, что обмотки соединены звездой).
Расчетная схема (рис. 11-11) не может быть осуществлена в виде модели, состоящей из сопротивлений, конденсаторов и катушек, так как комплексные сопротивления взаимной индукции между двумя реальными элементами цепи обладают тем свойством, что ZAB = ZBA, и представляют собой чисто мнимую величину. Между тем в расчетной схеме ZM =£ Zffl и, кроме того, как видно из (11-19), Zm и Zm могут содержать и вещественные части.
Неравенство комплексных сопротивлений взаимной индукции ZM и Zm свидетельствует о том, что трехфазные цепи с вращающимися машинами не обладают свойством взаимности.
11-4. Определение токов в симметричной цепи
Для того чтобы определить токи в симметричной цепи (рис. 11-12), к которой приложена несимметричная система напряжений, прежде всего найдем по формулам (11-16) — (11-18) симметричные состав-
287
юков определим на основании закона Ома:
i^Uz[- (П-20)
Затем по формулам (11-13) — (11-15) находим токи 1А, /в и 7С.
Итак, расчеты методом симметричных составляющих основываются на применении принципа наложения. Поэтому этот метод можно применять только к линейным цепям или к цепям, которые приближенно рассматриваются как линейные.
Рис 11-12.
Пример 11-1. Линейные напряжения на зажимах двигателя UAB = ^са~ = 365 В и U/jC = 312 В, сопротивления двигателя (в рассматриваемом режиме): /1 = 3,6+ /3,6 0м и Z2=0,15 I /0,5 Ом Нейтральный провод отсутствует. Требуется определить линейные токи
Решение Фазные напряжения источника питания могут быть взяты любыми, лишь бы их разности были равны заданным линейным напряжениям Для расчетов удобно выбрать фазные напряжения, как показано, на рис 11-13, где вектор U А направлен под прямым углом к векторам UB и Uq
Напомним, что указанный произвол в выборе фазных напряжений не отражается на их симметричных составляющих прямой и обратной последовательностей "(см § 11-2), а сказывается лишь тга симметричных составляющих нулевой последовательности, которые в данной задаче для расчета не нужны, так как токи нулевой последовательности протекать не могут.
Из треугольника АВС (рис 11-13) находим
[7с = Пв = 312/2=156 В, С/л = 330 В.
Положим, что UA = 330 В, тогда 0в = — /156 В и Uc = /156 В.
По формулам (11-17) и (11-18) определим.
= X ^uA+aUB+<fiUc)= у [330 l/ 156 (_ й+й2)] = 200 В;
^2 = 4 (^а + ^В + ^с)=20 В-
Находим симметричные составляющие токов по закону Ома:
А = = 39,3 Z - 45° А, /2 = +2/Z2 = 38,3 д - 73° 18' А.
По наиденным симметричным составляющим токов и формулам (11 -13) —(11-15) находим линейные токи
za = zi + 4 = 38>8-/64-5 А-
/в = й2/1 + с/2==_ц,7+/17(7 а> /с=_/л_/в=_27,1+/46,8 А.
Действующие токи +/г— 75 2 А: +. — 21,2 Ан/,.- 54,1 А.
288
11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи
Рассмотрим пример трехфазной несимметричной цепи (рис. 11-7), у которой =^= ZR =Z=ZC. Если к такой цепи приложить симметричную систему напряжений любой последовательности, то в ней возникнет несимметричная система токов, которая в общем случае содержит симметричные составляющие всех трех последовательностей. Справедливо и обратное положение: симметричная система токов любой последовательности вызывает в такой цепи систему напряжений, которая в общем случае содержит составляющие всех трех последовательностей. Если к цепи приложена несимметричная система напряжений, то симметричные составляющие токов любой последовательности оказываются зависящими от симметричных составляющих напряжений всех трех последовательностей.
11-6. Расчет цепи с несимметричной нагрузкой
В нормальных условиях несимметричные режимы в высоковольтных трехфазных цепях встречаются относительно редко (преимущественно в цепях с дуговыми электроплавильными печами и однофазными электротяговыми двигателями) Обычно несимметричные режимы получаются в аварийных условиях, когда в какой-либо Цепи появляется несимметрия.
Различают два вида несимметрии — поперечную и продольную. Поперечная несимметрия возникает при подключении к симметричной трехфазной цепи несимметричной нагрузки. К ней, в частности, относятся различные виды несимметричных коротких замыканий (замыкания между фазами, замыкание одной или двух фаз на землю). Продольная несимметрия возникает, когда в рассечку фаз линии включаются неодинаковые сопротивления или когда один или два провода обрываются (несимметричный участок линии).
Для расчетов несимметричных режимов трехфазных цепей удобно пользоваться принципом компенсации, заменяя несимметричную нагрузку или несимметричный участок в линии источниками напряжений, значения которых до окончания всего расчета остаются неизвестными. Целесообразность этого приема заключается в том, что после такой замены вся цепь становится симметричной и для нее разноименные симметричные составляющие токов и напряжений не зависят друг от друга. Связи же между симметричными составляющими токов и напряжений различных последовательностей, обусловленных несимметрией, вводятся позднее.
Рассмотрим метод расчета на примере схемы рис. 11-14, содержащей симметричную динамическую (Z[, Z%, Z6 = °°) и несимметричную статическую нагрузки. Пусть заданы э. д. с. генераторов и сопротивления- элементов схемы.Требуется найти токи инапряже-
10 Основы теории цепей 289
Симметричная
Несимметри чная нагрузка
777777777777777777777777777777777777777777777777777777/
Рис. 11-14.
ния. На рис. 11-14 схема и сопротивления несимметричной нагрузки не показаны, так как на первом этапе расчета они не нужны.
Заменим несимметричную нагрузку тремя источниками неизвестных напряжений ОА, Ов и Ос- Тогда получится симметричная схема, которая помимо генератора с симметричной системой э. д. с. содержит источники несимметричных напряжений Од, 0в и Ос-
Рис. 11-15.
Разложим напряжения О А, Ов и Ос на симметричные составляющие Оъ 0% и О0, приняв фазу А за основную. Тогда получим симметричную схему (рис. 11-15), причем в ответвлении, где =был а несгимметрт чн а я иагр у з ка, наяедятся и сточннjarтрех щшме г - =
290
рнчных систем напряжений прямой, обратной и нулевой последовательностей.
В симметричной цепи симметричная система напряжений какой-либо последовательности вызывает симметричную систему токов той же самой последовательности.Следовательно, можно составить три независимые схемы, показанные на рис. 11-16. Для упрощения в этих схемах не учтены частичные емкости линии (см. § 10-8).
б)
Рис. 11-16.
б)
Рис. 11-17.
Режим фазы А исходной схемы (рис. 11-14) определим путём наложения режимов этих трех схем.
Конфигурации схем прямой и обратной последовательностей всегда одинаковы. Схема нулевой последовательности обычно существенно отличается. В данном примере она не имеет разветвления, так как в правой части трехфазной цепи (рис. 11-14) токов нулевой последовательности быть не может. Следует обратить особое внимание на то, что сопротивление в нейтральном проводе вводится в схему нулевой последовательности утроенной величиной (см. § 11-3).
Из рассмотрения составленных схем видно, что наибольшие значения симметричных составляющих напряжений обратной и нулевой последовательностей наблюдаются в месте подключения несимметричного приемника, так как в схемах именно там находятся источники э. д. с. обратной и нулевой последовательностей.
Для дальнейшего расчета целесообразно преобразовать схемы отдельных последовательностей к простейшему виду, не затрагивая при этом ветвей с источниками неизвестных напряжений С/2 и О0.
В схеме прямой последовательности заменим ветви генератора и симметричного приемника эквивалентным генератором (рис. 11 -17, а):
с ___ 1 1^1 , V V I V'

10*
291
где
у1=т4^; = F
Лл1 Т Лг1 ^1
ЁХ=ЁА.
В схеме обратной последовательности объединяем ветви генератора и симметричного приемника (рис. 11-17, б):
7 _ (^Г2~Р^Л2) ^2
Э2 ^гг+^лг+^в
Схема нулевой последовательности в данном примере в преобразовании не нуждается, так как она имеет простейший вид.
777777777777777777
Для каждой из трех схем напишем уравнения по второму закону Кирхгофа:
Z3i4 + ^i = 4i; ZB24 + ^2 = 0; ZsJ0-\- Uo — Q, (11-21) где ZM = Z.0 + Zr0 + 3ZA..
В этих трех уравнениях шесть неизвестных: /ъ 4, /0, Ои С2, О0. Дополнительные три уравнения, связывающие эти шесть неизвестных величин, могут быть составлены на основании заданной схемы и параметров несимметричной нагрузки.
Составим дополнительные уравнения для некоторых видов несимметричных нагрузок. Для нагрузки, представленной на рис. 11-18, а,
UA=ZAIA; 4=0; 4 = 0, или
+и 2+uo—zA (li 4- 4+4);
я24 4~®4 4~ 4=0; я4 4-®г4 4~ 4=о»
Для нагрузки, показанной на рис. 11-18, б,
‘А—0; &B=zBiB, u-Q—Z^tc,
292
или
Л+А+Д=О;
o2t7i-\~ ай 2-\~ й q = (a2^i 4"аЛ Ч- й)> ай! + а2йг + йо = Zc (air -j- a2I2 Ч~ й)
При отсутствии соединения несимметричного приемника с землей, например, для схемы, приведенной на рис. 11-18, в, симметричные составляющие токов нулевой последовательности равны нулю и составление схемы цепи нулевой последовательности на предыдущих этапах расчета выпадает. Получаются два основных уравнения с четырьмя неизвестными и нужно составить только два дополнительных уравнения, а именно:
1д=0; nB-t7c=z/B
или
Л 4-4 = 0; а2й1А~ай2 — (fl(714-fl2(?2) = Z (a2f1-\-ai2).
Аналогично составляют дополнительные уравнения и при других видах статической несимметричной нагрузки. При совместном решении уравнений Кирхгофа для схем различных последовательностей с дополнительными уравнениями определяются симметричные составляющие тока фазы А в ответвлении к несимметричному приемнику. Затем находят распределение этих составляющих по отдельным ветвям схем прямой, обратной и нулевой последовательностей.
Зная составляющие токов в любой ветви, подсчитывают действительный ток в каждой фазе и составляющие падений напряжения различных последовательностей, а затем и фазные напряжения на отдельных участках схемы.
Приведем расчет режима схемы (рис. 11-14) для случая несимметричной нагрузки, представленной на рис. 11-18, а, при условии, что 7.^ = 0 (однофазное замыкание на землю). Составим дополнительные уравнения:
6/д = Ц+£/2 + £/о = О; (11-22)
/в=а2/1-|-а/2-|-/о = 0; (11-23)
/c = a/1+a2/2 + /0 = °. (11-24)
Вычитая (11-24) из (11-23), получаем:
(а2— а) /1+(а — а2) — 0 или /3 = 4.
Подставляя этот результат в (11-23), имеем:
(а2+с)/1+/о=0,
откуда /0 = /1а
Заменяем в уравнениях (11-21) /2 и /0 на /, и затем их суммируем. Тогда с учетом (11-22) получим.
(^эг + ^эа-^^эо) fi = Esl, Откуда
293
Симметричные составляющие напряжений (в месте замыкания на землю) определяются из (11-21)
Fi=£9i—^э1Л> Уъ= Z32I2i UB— Z3Bfa.
Для схемы рис 11-16, а
l'i=Ui/Z'i и /ri = A+/i-
Для схемы рис 11 16, б
Для схемы рис 11-16, в
Ло=Ai-
Симметричные составляющие напряжении на зажимах генератора могут быть найдены по тем же схемам (рис 11-16)
£/ri=-Ei— 2rl/rl = 6'1-|-Zril/rl, t/r2= — Zr2/r2 = t/a-i-Z^r2;
^r0=- (3za’+M irO=uo+zMirO.
11-7. Расчет цепи с несимметричным участком в линии
Рассмотрим метод расчета на примере цепи, представленной на рис. 11-19 Пусть заданы э. д с. генератора и все сопротивления элементов схемы. Требуется найти токи и напряжения.
Рис. 11-19.
Заменим несимметричный участок схемы тремя источниками неизвестных напряжений Оа’А’, О в-в1 и #сс"- Разложим неизвестные напряжения на симметричные составляющие Й2 и Йо, приняв фазу А за основную, и составим три независимые схемы (рис. 11-20, а, б, в) прямой, обратной и нулевой последовательностей. Напишем для этих схем уравнения по второму закону Кирхгофа:
(Zri + 2Л1 + ZI) А + ГД = Fi; (Zr2 + Z,2 + Z'2} /2 + U2 = 0;
(3Zjy -J- Zr0 -J- Z ,0 -j- Zc') /о -j- Uo — 0.
В этих трех уравнениях шесть неизвестных. Дополнительные три уравнения составляются, исходя из схемы н-паряметров не-сим-метричного участка цепи.
294
Составим дополнительные уравнения для некоторых видов несимметричных участков цепи.
Для схемы, представленной на рис. 11-21, а:
U a’A" = Za1 д; = t/c'C'=0.
Для схемы, представленной на рис. 11-21, б:
/д = 0; Дв'Н" = 0; Йс'С"=0.
То же для рис. 11-21, в:
Ua’A"=Za1 а', Uв-В" = Z Jв; ()с'С"==0.
В этих дополнительных уравнениях нужно напряжения и токи выразить через нх симметричные составляющие.
----О > ^А ..
Afgh-4ZJ—.—0fi" А0—-0 А'ф--CZD—т~0А
Bf0—--— 5™0 B,r Вг0-- —-Т—0 в" в'0------7—0 в"
с'0--- 1с—0СГГ с'0------ 7с..0 с" с'0-------0/;"
а) б) в)
Рис. 11-21.
Решив совместно основные и дополнительные уравнения, найдем симметричные составляющие токов, а затем определим и все остальные искомые величины.
В специальных курсах, в которых рассматривают несимметричные режимы трехфазных цепей, дают обоснования комплексным расчетным схемам. При этом схемы отдельных последовательностей соединяют друг с другом в одну сложную (комплексную) схему таким ибразом7~чтобы-удовлетворялись усло
295
вия, вытекающие из особенностей того или иного вида поперечной или продольной несимметрии. Расчет ведут непосредственно по этим схемам, без привлечения дополнительных уравнений, зависящих от вида несимметрии, так как условия несимметрия учитываются особыми способами соединения схем различных последовательностей друг с другом. Для расчета несимметричных режимов сложных разветвленных цепей широко применяется моделирование схем.
Пример 11-2. Провод фазы А линии, питающей трехфазный асинхронный двигатель, оборвался (рис. 11-22, а) При определенных условиях, рассмотрение которых выходит за рамки данного курса, двигатель может продолжать работать, получая питание по двум фазам.
Рис 11-22.
Пусть в рассматриваемом режиме линейные напряжения UAB = Uf,c — = UCA = 380 В и двигатель работает, имея сопротивления Zx = 3,6 + /3,6 Ом и Z2 = 0,15 +, /0,5 Ом. Определить токи в питающих проводах и напряжения А А’’ йА'п’ ^П'п’ йс-n И ^Nn-
Решение. Примем, что линейные напряжения между зажимами А, В и С создаются тремя источниками симметричных фазных э. д. с. £х = 380/1 3 = 220 В.
Заменим несимметричный участок схемы (обведенный на рис. 11-22, а пунктиром) источниками э д.с. и составим схемы прямой, обратной и нулевой последовательностей (рис. 11-22,6). Схема нулевой последовательности разомкнута, так как отсутствует четвертый провод.
Запишем основные уравнения для схем прямой и обратной последовательностей:
(а)
— ® (б)
и добавочные уравнения
/д=0; ^сс,==®-
Выражая в этих уравнениях гоки и напряжения через их симметричные составляющие, получаем:
4+4 = 0 или /2 = —/г; (в)
c2t71+a/72+t7o = 0; (г)
яЕц (PU2 +77^и/ (д)
296
Решив уравнения (г) и (д), найдем, что
L 2=Ui = UQ.
Подставив Uz= Ui и /2 = — 4 в (б), получим:
. Z„J1 -j- U i = 0.
Затем вычтем последнее уравнение из (а) и получим:
(Zx4-Z2) /х —Ёх.
Следовательно,
р
Г1= = 39,6 Z — 47’33 А;
Zl + Z2
IB = aif!L-]-aI2 = (a2~a) ^ = 68,5 z— 137'33' А;
7/.,=—Z2/2=20,67 д 25'45' В;
^ал- = ^1 + ^2 + ^о=3,72 = 62 25C45' B;
^A',r~=zA + Z2f2 = (zi ~ Z2) /j= 183,5 z -5 36' B;
7B,„ = c=Z171+oZ/2 = (c2Z1-aZ2) ^=203,5 Z - 116'43' B;
Uc, =aZ.L-}-a‘-Z9l9 = (aZ.—a2Z9) /,=219 Z 114'26' B;
Т/Л,г = /70 = 20,67 Z 25’45' B.
Глава двенадцатая
НЕСИНУСОИДАЛЬНЫЕ ТОКИ
12-1. Несинусоидальные э. д. с., напряжения и токи
В предшествующих главах рассматривались линейные цепн с неизменными параметрами г, L, С и М при действии источников постоянных или синусоидальных э. д. с. или токов.
На практике кривые э. д. с., напряжений и токов бывают обычно в большей или меньшей степени отличны от постоянных или синусоидальных. Зависимость тока
или напряжения от времени |г . « р
.может быть периодической, / / рч /-ч
почти периодической и не- J j . \ \
периодической.
В машинных генераторах переменного тока
вследствие отличия кривой а> и
распределения магнитной
индукции вдоль зазора от Рпс- 12-1 •
синусоиды кривые наводи-
мых в обмотках э. д. с. отличаются от синусоидальных. В цепях, содержащих нелинейные сопротивления, индуктивности или емкости (например, вентиль, электрическую дугу, катушку со стальным магнитопроводом), даже при синусоидальных э. д. с. возникают Несинусоидальнме^=токи и- -не^ивусбняалвнае^ганряження7===^кн==^ Рис. 12-1 показаны примеры кривых тока в цепи с насыщающимся
297
реактором (рис. 12-1, а) и в цепи управляемого вентиля (рис. 12-1,6).
Генераторы периодических импульсов применяются в различных устройствах радиотехники, автоматики, телемеханики, вычислительной техники, обработки данных, в автоматизированных системах управления. Форма импульсов может быть самой различной: пило-
Рис. 12-2.
образной (рис. 12-2, а и б), ступенчатой (рис. 12-3, а) и прямоугольной (рис. 12-3, б). При прохождении этих импульсов через различные электрические цепи их форма существенно изменяется.
На рис. 12-1 — 12-3 все кривые строго периодичны (период повторения Т) и представляют собой примеры н е с и н у с о и -дальных периодических токов.
При передаче, например, радиотелеграфных и телефонных сигналов встречаются кривые тока, которые не строго периодичны,
Рис. 12-3.
но имеют периодически изменяющуюся огибающую с периодом То и на малом интервале времени могут считаться синусоидальными с периодом Тк.
При несоизмеримости То и Тн нет такого периода Т, через который эти кривые в точности повторяются. Поэтому их нельзя назвать периодическими, но они очень близки по своим свойствам к периодическим кривым и могут быть названы почти периодическими (в частном случае, когда То = kTH, где k — целое число, эти кривые периодические с периодом 70). Примером почти периоди-----ческой кривой- является токг протекающий дерез лрпь репродук--тора при передаче периодически изменяющегося звука.
298
Кроме указанных типов несинусоидальных кривых с явно выраженным периодом повторения мгновенных значений или огибающей часто приходится иметь дело с непериодическими кривыми, т. е. кривыми, у которых нет периода повторения. Эти кривые могут быть вполне определенными, как, например, при передаче одиночных импульсов, но могут быть и случайными, например, в случае шумов и помех.
Во всех задачах, где приходится иметь дело со сложными несинусоидальными кривыми токов и напряжений, очень важно уметь свести сложную задачу к более простой и применить методы расчета более простых задач. В настоящей главе рассматриваются методы расчета линейных цепей при несинусоидальных периодических или почти периодических токах и напряжениях, которые можно разложить на гармонические составляющие.
12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд
Явления, происходящие в линейных цепях при периодических, но несинусоидальных э. д. с., напряжениях и токах, проще всего поддаются исследованию, если кривую э. д. с., напряжения или тока разложить в тригонометрический ряд Эйлера — Фурье.
Как известно, всякая периодическая функция / (оз/), удовлетворяющая условиям Дирихле, т. е. имеющая на всяком конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометрический ряд:
f (со/)=Ао + Almsin (со/ -фф^ -J- А2тsin (2со/ + ф2) + • • •=
= У, Ат8Ш(£со/ + фй), - (12-1)
k = 0
где при k = О
ф/г ===фо== л/2.
Первый член ряда Ао называется постоянной составляющей или нулевой гармоникой, второй член Alm sin (со/ + + "Ф1) — основной синусоидой или первой гармони к о й, . а все остальные члены вида Altm sin (kat + фА.) при k >• 1 носят название высших гармоник; со = 2л/Т — основная частота; Т — период несинусоидальной периодической функции.
Тригонометрический ряд после раскрытия синуса суммы для каждой из гармонических составляющих или, короче, гармоник записывается и в иной форме:
f (со/) = Aq -|- Вsin со/ В2т sin 2со/ -|-...-|- В/гт sin /ссо/-|-...
•.. Cijn COS Со/ -J- С2т COS 2со/ ... -J- С km COS /то/ .. . =
= = Л» + У (Вь,„ sin/гсо/+ Сь,и cos До/). (12-2)
t=i
299
ЗдеСЬ Bkm A km COS Cpni A km sin ф/г.
Коэффициенты Ao, Bkm и Ckm могут быть вычислены при помощи следующих интегралов:
7/2 Я
Л0 =4 $ Н0<*/=^- $/И)<*И);
— Т/2 -л
л
В km=/ (и/) s in k&t d (at);
— Л
л
Ckm == 4 / (со/) COS kat d (co/).
— Л
(12-3)
Постоянная составляющая Ao равна среднему значению функции f (/) за ее период Т — 2л/со.
Зная коэффициенты ряда (12-2), легко перейти к форме (12-1), подсчитывая
Akm~V BkmA-Ckm И ф* = arctg
Dkm
Вводя условно отрицательные частоты, т. е. переходя к суммированию пой от —оо до + оо, можно ряду (12-2) придать более компактный вид (где по существу каждая гармоника, кроме нулевой, входит под знак суммы дважды):
ОО
/(со/)=2 У, (Bkm sin kat 4- Ckm coskat). (12-2a)
k — —co
Постоянная составляющая в этом выражении получается при k ~ 0, что соответствует выражению (12-3), так как Ао = С0т/2.
Значительное число непериодических функций времени, с которыми приходится встречаться в электротехнике (рис. 12-4, а), удовлетворяет условию
f(at) =— /(со/4-л). (12-4)
Функции, удовлетворяющие этому условию, называются симметричными относительно оси абсцисс. Они раскладываются в ряд, который не содержит четных гармоник и постоянной составляющей:
/ (со/) = Alm sin (со/ 4“Ф1) 4~ Аз,п sin (Зсо/ 4-ф3) 4-
+ ^вт sin (5со/4-ф5) 4-... (12-5)
При выпрямлении переменного тока или напряжения часто приходится встречаться с функциями, которые при соответствующем выборе начала координат удовлетворяют условию (рис. 12-4, б)
-- ———°- /(co/J=/(—со/). — = (12-6)
300
Такие функции называются симметричными относительно оси ординат.
Рис. 12-4.
В этом случае ряд не содержит синусов:
f (at) = А0 + Аlm cos (ot + А2т cos 2ot + ASm cos Зсо/ -ф... (12-7)
В схемах умножения частоты встречаются функции, которые при выборе начала координат в точке нуля функции удовлетворяют условию (рис. 12-4, в)
= (12-8)
Такие функции называются симметричными относительно начала координат и раскладываются в ряд, не содержащий косинусов и постоянной составляющей:
/ =Аlm sin со/ -|- А2т sin 2со/ -f- Asm sin Зсо/ +... (12-9)
Примеры разложения в ряд некоторых простейших из наиболее часто встречающихся в электротехнике кривых приведены в приложении 1.
301
Если начало отсчета времени сдвигается, то соответственно изменяется вид ряда, в котором амплитуды гармоник остаются прежними, но изменяются их начальные фазы Например, если перейти от функции / (со/), выражаемой рядом (12-1), кД (со/) == / [со (/ — /0)], т е сместить начало отсчета времени на /0, то получим ряд
fl (Со/)=/[и(/ — /())] = Д о^4 lm Sill (со/ф-ф})-)-
~|~ Д am sin (2со/ф^)У Д^т sin ф/?)> (12-10) где
ф£=ф/г — k(Dt0. (12-11)
Совокупность гармонических составляющих несинусоидальной периодической функции называется ее дискретным частотным спектром
Спектр можно характеризовать некоторой зависимостью Akm (спектр а м п л и т у д) и ф^ (спектр фаз) от частоты /гео.
Пример 12-1. Построить спектр для несинусоидальной функции в виде ряда прямоугольных импульсов продолжительностью т с высотой омлкс, следую щих один за другим через интервалы времени Т = 2т (рис 12-5) Напряжения такой формы встречаются в различных схемах телеграфии, телемеханики и авто матики
Решение Найдя коэффициенты разложения по формулам (12 3) или выписав их из таблицы (приложение 1), представим рассматриваемую функцию в виде ряда
f («/) = gb”KC + ——а— (Sin со/ + q Sin Зсо/ + ~ Sin 5со/ + Zi JT \ о О
где со = л/т
Дискретный спектр амплитуд этих импульсов представлен на рис 12 5, б Там же показан спектр фаз, изображенный в виде непрерывной функции Эта функция реально существует только в тех точках, где Акт =/~ 0
Пример 12-2. Построить спектр той же кривой, что и в примере 12 1, при начале отсчета времени, сдвинутом на /0 = т/2 (рис 12 6, а)
Решение Эта функция симметрична относительно оси ординат и ее разложение в тригонометрический ряд имеет вид
fi (со/)=/ ^со/—со
(cos со/— 1 COS Зсо/+ л \ 3
г \ ,
2)~ 2 ф
1 г . 1
5 cosbco/— у cos/со/-|-
Спектры амплитуд и фаз этой функции показаны на рис 12-6, б Естественно, что спектр амплитуд остался прежним
Рассматривая каждую гармонику как сумму членов ряда для k = ± | k | и переходя от записи (12 2) к (12-2а), можно этому выражению придать следующий вид.
4- оо
7г(<о/)^-^Ф У -^Ц^созсо/.-^-
/?= —со
302
Действительно, при k = О
lim sin (fejT'/2) "
л—о k 2’
т е. получаем постоянную составляющую; при четных значениях k члены ряда обращаются в нуль, а при k нечетных sin (Ьт/2) = тЬ 1 и при суммировании членов для положительных и отрицательных k дают амплитуду, равную 2 ом;1КС/ | k | л.
Спектр амплитуд в этом случае имеет симметричный вид (рис. 12-6, в). При этом принимается, что фазы всех гармоник равны л/2, а амплитуды изменяют знак через интервал 2л/т.
Такое рассмотрение гармонических составляющих как совокупности колебании положительных и отрицательных частот во многих случаях позволяет получить более простое общее выражение. Отрицательная частота, конечно, не имеет физического
Рис. 12-6.
Рис. 12-5.
/г< О являются не чем иным, как удобным математическим выражением гармоник, имеющих положительную частоту, соответствующую модулю k. Так же условна замена изменения знака фазы изменением знака амплитуды.
Пример 12-3. Построить спектр последовательности прямоугольных импульсов продолжительностью т с периодом повторения Т, причем 7’ =/- 2т и т может принимать любое значение в интервале 0 < т < Т.
Решение. Выпишем из таблицы (приложение 1) разложение этой функции в тригонометрический ряд:
/(CO/)
— ймакс
sin katn cos kul
k
где
fe=i
a = i/T=хы/2п.
Раскладывая каждую из гармоник на сумму двух синусоид, соответствующих положительным и отрицательным значениям k [см. уравнение (12-2a)j, придадим выражению f (со/) иную форму:
/И)=-^-
sin kan cos kut
(12-12)
— CO
k
303
где постоянная составляющая получается при раскрытии неопределенности-.
1пп
k---0
sin kart
—г------= ал,
k
Обозначив (rtf, = 2л/т = ш/а, получим для f (at) следующее выражение:
СО
г I л аомакс V1 sin ton cos kaa^t
L ----------to-------
fe=—oo
На рис 12-7, a — e видно, что вне зависимости от периода повторения импульсов Т спектр имеет (с точностью до множителя а) одну и ту же зависимость амплитуд от частоты (огибающую) Чем больше период повторения импульсов, тем большее число гармонических составляющих укладывается на одном и том же участке огибающей и тем медленнее уменьшаются амплитуды гармонических составляющих с увеличением номера гармоники Кроме того, чем больше период Т, тем меньше амплитуды гармонических составляющих.
Рис. 12-7.
Для исследования непериодических процессов большое значение имеет предельный переход при Т -► оо Непериодический сигнал будет рассмотрен в гл 20.
Пример 12-4. Найти спектр последовательности очень коротких импульсов, длительность которых значительно меньше периода их повторения Т. Изучение последовательности таких импульсов очень важно в различных задачах электротехники, и, в частности, при рассмотрении импульсных и релейных систем автоматики.
Решение. Частотный спектр такой последовательности импульсов получается из выражения (12-12), приведенного в предыдущем примере, при г •<; Т:
cos kat.
--------------------о.;---------------
(12-12a)
304
Таким образом, спектр периодической последовательности кратковременных импульсов приближенно может быть выражен бесконечным множеством равных по 'амплитуде гармоник с частотами, кратными основной частоте импульсов со = 2л/Т. Амплитуда гармоник в Т/т раз меньше, чем высота импульсов. Это соответствует среднему участку спектра, представленного на рис 12-7, при стремлении периода огибающей, которая изображена на этом рисунке пунктиром, к бесконечности (когда а -> 0), если, конечно, по оси абсцисс откладывать не ka, а просто k или feco.
12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов
Периодически изменяющаяся несинусоидальная величина / (со/) помимо своих гармонических составляющих характеризуется тремя величинами:
максимальным значением за период сгмакС) средним квадратичным за период или действующим значением
Л = j/' т Р (со/) dt о
(12-13)
и средним по модулю значением
т
Лср = т § |/ (®/) I dt. о
(12-14)
Если кривая f (cot) симметрична относительно оси абсцисс и в течение половины периода функция f (со/) ни разу не изменяет знака, то среднее по модулю значение равно среднему значению за половину периода:
Т/2
2 С Лср = г- J f (со/) dt, о
(12-14а)
причем в последнем выражении начало отсчета времени должно быть выбрано так, чтобы f (0) = 0. В тех случаях, когда за весь период функция ни разу не изменяет знака (см., например, рис. 12-4, б), среднее по модулю значение равно постоянной составляющей Ао.
При несинусоидальных периодических процессах, как и при синусоидальных, обычно под значением э. д. с., тока или напряжения понимают действующее значение.
Если кривая периодически изменяющейся величины разложена в тригономстрический ряд, го действующее значение может быть
305
найдено следующим образом:
Т г оо 2
У Aftm sin (W-|-ipA)
6 lfe = 0
t#==
со Т
= | 2 $ A/;msin2(W+iy dt +
k = 0 о
со Т
+ 7 2 J ^<m^*msm(ico/ + il3z)sin(^ + ^)dz'
( = 0 6
k = 0
t tk
(12-15)
(такое возведение ряда в квадрат вполне допустимо, так как ряд абсолютно сходится при любом значении со).
Каждый из интегралов в последней сумме равен нулю, и, следовательно, равно нулю среднее за период значение от произведений мгновенных величин различных гармоник. Учитывая это, для действующего значения получим:
со Т
А2= У -1Д Afemsina(feco/ + ^) dt =
k = 0 о
со со со
=Л2+ ф = 2 &1 = У А1 (12-16)
= l fe = l fe = 0
(12-17)
Таким образом, действующее значение периодической несинусоидальной величины зависит только от действующих значений ее гармоник и не зависит от их фаз 'ф*.
Если, например, напряжение и состоит из ряда гармоник Uo, щ, и2 и т. д , действующие значения которых Uo, иъ U2 и т. д., то действующее напряжение
U^=VUl + Ul + Ul + ...- (12-18)
Аналогично для тока i
/=]//о + Л + /5+
(12-19)
Часто среднее по модулю и действующее значения несинусоидальных величин могут быть рассчитаны непосредственно на основании интегральных соотношений (12-14) и (12-13). В этих случаях нет необходимости в предварительном разложении функции на гармонические составляющие. ~
306
Пример 12-5. Найти средние по модулю и изображенных на рис 12 8
и решение В случае, изображенном на определения действующего и среднего по нодулю значений следует, что
А = Аср — Смакс*
В случае рис 12-8, б по формуле (12-13)
и по формуле (12-14) 7/4
. ___ 4 С Щ-,акс
Л ср — р 1 ымакс р ш g О
В случае 12 8, в по формуле (12 13)
и по формуле (12-14)
АСр— Смакс®*
действующие значения функций, рис 12-8, а, непосредственно из
Рис 12 8
Расчет действующего значения по формуле (12-17) приводит к тем же резуль тагам.
12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых
При оценке несинусоидальных периодических кривых в электроэнергетике, где кривые преимущественно симметричны относительно оси абсцисс, пользуются коэффициентом формы кривой /гф, коэффициентом амплитуды /гй, коэффициентом искажения kK.
Коэффициент формы определяется как отношение действующего к среднему по модулю значению
£Ф = Д/Лср. (12 20)
Для синусоиды = л/2]/2 = 1,11.
Коэффициент амплитуды равен отношению максимального к действующему значению:
йа = амаКсМ- (12-21)
Для синусоиды k.& = ]/2 = 1,41.
Коэффициент искажения определяется как отношение действующего значения основной гармоники к действующему значению всей кривой:
k^AjA. (12-22)
~ Для синусоиды kB =1. — ---
307
В электронике и радиотехнике для оценки искажений пользуются коэффициентом гармоник, который определяется как отношение действующего значения высших гармоник к действующему значению основной гармоники:
При отсутствии постоянной составляющей
Й = (12-23)
«И
Для синусоиды k = 0.
Пример 12-6. Определить коэффициенты кг, k,Auk для кривых, изображенных на рис. 12-8, о и б
Решение. В случае 12-8, а по известным действующему и среднему по модулю значениям находим:
7’ф ~ ‘ 1 ,
и по разложению функции на гармоники (приложение 1, п. 4)
fe„ = 2/2/л = 0,9 и й=-^- 1Л1-^=0,49.
Кц
Аналогично в случае 12-8, б
= 2/1^3^1,15; йа = КЗ«=1,73;
/г[1==4 j/6/л2^ 0,995 и &я=0,1.
Кривые напряжения промышленных сетей обычно отличаются от идеальной синусоиды. В электроэнергетике вводят понятие о практически синусоидальной кривой. По стандарту напряжение промышленной сети считается практически синусоидальным, если действующее значение всех высших гармоник не превышает 5% действующего значения напряжения основной частоты. Коэффициент искажения такой кривой с точностью до долей процента равен единице.
Значения /гф, ks и kK простейших кривых приведены в приложении 1. Сопоставляя значения коэффициентов первых четырех кривых, можно установить, что чем острее кривая, тем больше значения 1гф и /га.
Измерение несинусоидальных токов и напряжений приборами различных систем может давать неодинаковые результаты.
Приборы электродинамической, электромагнитной и тепловой систем реагируют на действующее значение измеряемой величины.-Магнитоэлектрические приборы сами по себе измеряют постоянную составляющую, а с выпрямителями — среднее по модулю значение. Амплитудные электронные вольтметры реагируют на максимальные значения. Так как обычно этими приборами пользуются для пзмерешш дег'ютвующих -значений -синусоидальных величин, то
308
шкалы их градуируют на U — 1,11 £/срв приборе выпрямительной системы и на U = пмакс/|/2 в амплитудном электронном.
Отношения U к Псри имакс при несинусоидальных токах нередко сильно отличаются от коэффициентов 1,11 и 1/]/2, и соответственно приборы выпрямительной системы и амплитудные электронные приборы дают большую погрешность при измерении действующих значений таких несинусоидальных величин.
Пример 12-7. Найти показания вольтметров различных систем, подключенных к источнику э д с с максимальным значением напряжения 100 В, для различных случаев формы кривой, представленных на рис 12-8
Решение В первых двух случаях магнитоэлектрический прибор, реагирующий на постоянную составляющую, покажет нуль Показания же приборов остальных систем будут различными
В случае рис 12-8, а электродинамический прибор покажет 100 В, прибор выпрямительной системы 111 В, а амплитудный электронный прибор 100/1' 2 = = 71 В
В случае рис 12 8, б электродинамический прибор покажет 100/1'3 = 58 В, прибор выпрямительной системы 50-1,11 = 55,5 В, а амплитудный электронный прибор 100/|'2=71 В
В случае рис 12 8, в при т = 0,2 Т электродинамический прибор покажет 100 1'0,2 = 45 В, прибор выпрямительной системы 20-1,11 = 22,2 В, а амплитудный электронный прибор 71 В Магнитоэлектрический прибор покажет постоянную составляющую Uo = 20 В.
Таким образом, вольтметры разных систем могут показывать совершенно различные значения напряжений и зависимости от формы кривой напряжения.
12-5. Несинусоидальные кривые с периодической огибающей
Кроме несинусоидальных периодических функций, разлагаемых в тригонометрический ряд на гармонические составляющие с частотами, кратными основной частоте, в электротехнике встречаются несинусоидальные кривые с периодическими или почти периодическими огибающими (см. § 12-1), также разлагаемые на гармонические составляющие.
Период напряжений или токов, описываемых такими кривыми, обычно во много раз превышает период любой из составляющих и может стремиться к бесконечности К числу явлений, характеризуемых такими кривыми, относятся биения и модуляция.
Биения. Простейший случай биений получается в результате сложения двух синусоид с равными амплитудами и близкими, но не равными частотами со3 и со2, причем сщ > со2:
/ (t) = Am (sin©^4-sin©20. (12-24)
Преобразуя сумму синусов, получаем:
f(0=2/lmcos25p/
Будем считать, что кривая f (/) представляет собой синусоиду угловой частотой (n^+ б>2)/2. амплитула которой изменяется по
309
косинусоиде со значительно меньшей угловой частотой Q =- (сщ — —со2)/2:
/ (/) = 2.-4mcosn/-sinco/. (12-25)
Частотой биений называется частота /б = О/зт, равная числу максимумов огибающей кривой в единицу времени (рис. 12-9).
Период биений Тб = зт/62 в общем случае не равен периоду кривой / (/). Действительно,
f(t + Т6) = 2Am cos (П/ + зт) sin (со/ зт
(12-26)
Очевидно, что только при со/й = 2 k — 1 (целое нечетное число)
период биений совпадает с периодом кривой f (t). Во всех остальных случаях кривая / (/) на участках двух соседних периодов
Рис. 12-9.
биений не повторяется и период кривой / (/) превышает период биений. При несоизмеримости угловых частот со и й отношение этих величин является иррациональным числом, т. е. не существует такой частоты, на которую без остатка делятся частоты со и 9. Следовательно, период функции / (/) равен бесконечности и кривая f (/) не периодическая, хотя она и разлагается на две синусоиды.
Модулированные колебания. Си-
нусоидально (гармонически) изменяющаяся величина f (/) = Ат sin (со/ + ф) задается тремя параметрами: амплитудой Ат, угловой частотой со и фазой ф. Все эти
величины постоянны и не зависят от времени.
Однако для передачи различного рода сигналов применяются
генераторы, в которых одна из этих величин сравнительно медленно изменяется по некоторому заданному закону. Изменение во времени одного из параметров Ат, со или ф называют модуляцией. Изменение амплитуды Ат называется амплитудной модуляцией, изменение частоты со — частотной модуляцией, изменение фазы ф — фазовой модуляцией (последние два вида модуляции в книге не рассмотрены).
Рассмотрим простейший пример функции, изменяющейся с частотой соо и с амплитудой, модулированной по косинусоиде (1 + + т cos Q/) АОт (рис. 12-10, а):
f (/) = Ат (/) sinco0/ = АОт (1 ф-m cos й/) sin со0/. (12-27)
Частота со0 называется несущей частотой, частота й — модулирующей частотой, а т — коэффи-——ц ке н т о м кто дул я ц й и. Коэффициент модуляции харак
310
теризует степень отличия максимальной и минимальной амплитуд оТ некоторого среднего значения Аот. Обычно т меньше единицы.
Амплитудная модуляция широко применяется в радиовещании й радиосвязи, где несущая частота <в0 — это частота радиосвязи, а модулирующей Q служат звуковые частоты передаваемой речи дли музыки.
При определении токов или напряжений в цепях, схемы которых содержат источники э. д. с., модулированных по амплитуде, последние могут быть разложены на синусоидальные составляющие. Действительно, преобразуя выражение (12-27), получаем:
f — sin A3m (sin соД-J-sin <»2Z), (12-28)
где A 2m == tnAf,m/2., ft>i=roo П и -}-(}.
Начальная фаза каждой из трех гармонических составляющих Ф* = О-
Таким образом, простейшие модулированные по амплитуде колебания могут быть представлены в виде суммы трех синусоидальных колебаний с постоянными амплитудами и с частотами со0, СЩ и со2. Частоты сщ и со2 называют боковыми частотами.
Дискретный спектр амплитуд модулированной по амплитуде функции представлен на рис. 12-10, б.
При иррациональности отношения несущей (й0 и модулирующей Q частот они несоизмеримы, а следовательно, кривая f (() не периодическая. Тем не менее эта кривая совершенно точно может быть представлена в виде суммы трех синусоидальных составляющих различных частот.
Представляет интерес сопоставить спектр модулированных колебаний со спектром огибающей колебаний (рис. 12-11, а):
Ат Авт (1 4~ т COS QZ).
Спектр огибающей содержит постоянную составляющую Айт и первую гармонику с амплитудой Alm = тАоот.
Учитывая, что cos = + cos (—П(), запишем огибающую (по аналогии с примером 12-2) в следующем виде:
311
и представим спектр в виде трех спектральных линий: на нулевой частоте (постоянная составляющая) и на частогах — Q и й, расположенных симметрично относительно постоянной составляющей (рис. 12-11,6). Сопоставляя спектр модулированных колебании (рис. 12-10, б) и симметричный спектр огибающей Ат (f), легко заметить что они отличаются только сдвигом по оси частот на интервал, равный несущей частоте со0.
Это соотношение между частотными спектрами огибающей и модулированных колебаний имеет большое значение, когда рассмат-
Рис 12-11.
ривают различные случаи амплитудной модуляции.
Модулированные импульсы. Передача сигналов может производиться как при помощи изменения параметров синусоиды, так и путем изменения параметров последовательности импульсов (см. пример 12-3).
Изменение во времени амплитуды импульсов носит название амплитудно-импульсной модуляции (АИМ), изменение продолжительности импульсов т — широтно-импульсной модуляции (ШИМ), изменение частоты
импульсов о)о =- 2л/7—частогно-импульсной модуляции (ЧИМ), а
изменение фазы импульсов — фазоимпульсной модуляции (ФИМ).
Рассмотрим простейший пример амплитудно-импульсной модуляции при т То (пример 12-4), если амплитуда импульсов изменяется во времени (рис. 12-12с) по закону
«макс (0=А от (1 -|- т cos Qf).
(12-29)
Согласно выражению (12-12а) спектр модулированных импульсов приближенно описывается уравнением
f (at)= ХТ АОщ (1 4-mcos Ш) coska)0t. (12-30) k = — оо 4
Преобразуя произведение косинусов
cos a cosP=cos-'(;-~P-)+cos(a + p)> *8
получаем: It
f (at) = АОту [cos cos (/e<oo — fi) 14- cos (Лсо0 -]- Q) .
k ~ — со
(12-31)
Таким образом, спектр модулированных импульсов (рис. 12-12,6) представляет собой периодическую функцию, повторяющую с пе
312
риодом <в0 симметричный спектр модулирующей огибающей (рис. 12-11, б). Чтобы спектр модулированных колебаний на каждом из интервалов частот (k — 0,5) со0 < to < (k + 0,5) <в0 без пска-
Рис. 12-12.
жений воспроизводил спектр модулирующей огибающей, необходимо выполнить условие 2Q < со0.
Это очень важное в практике радиотехники, телемеханики и автоматики неравенство было получено акад. В. А. Котельниковым.
12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими
Несинусоидальные функции, получающиеся в результате биений и модуляции, являются либо периодическими, либо при несоизмеримости частот — почти периодическими. Хотя в последнем случае период кривой возрастает до бесконечности и говорить о действующем значении не имеет смысла, формула (12-17) Дает значение, близкое к действующему за период огибающей функции.
Строго говоря, действующие значения за различные периоды огибающей при несоизмеримости частот оказываются различными, так как одной и той же фазе огибающей всегда соответствуют различные фазы несущей частоты. Однако при ю0 Q это различие настолько ничтожно, что им можно пренебречь.
Под действующим значением колебаний с периодической огибающей, описываемых функцией
-------------------f(Z/=2\Fff2tysino(/,--------------------
313
обычно понимают действующее значение огибающей, деленное на /2: ______________
Г т
(12-32)
где Т — 2л/£2.
Соответственно для модулированных по амплитуде импульсов действующее значение огибающей умножается на j/a.
Выражением (12-32) можно пользоваться, когда исследуется непериодический процесс в электрической цепи за достаточно большой промежуток времени.
Покажем, что для рассмотренных случаев биений и модуляции расчет по формулам (12-17) и (12-32) дает одинаковые результаты. Действительно, в случае биений получим по формуле (12-17)
А =У(Ат/У2 )2 + (Дт/Г2 )2 = Ат
и по формуле (12-32)
-4=2Дт
J/2 т
_L-—д
J2 т
В случае амплитудной модуляции получим по формуле (12-17)
то же получается и по формуле (12-32).
12-7. Расчет цепей с несинусоидальными периодическими э. д»х. и токами
Если в линейной цепи действует один или несколько источников несинусоидальных периодических э. д. с. или токов, то расчет такой цепи распадается на три этапа:
1. Разложение э. д. с. или токов источников на постоянную и синусоидальные составляющие (получение дискретного спектра).
2. Применение принципа наложения и расчет токов и напряжений в цепи для каждой из составляющих в отдельности.
3. Совместное рассмотрение решений, полученных для каждой из составляющих.
Суммирование составляющих в общем виде часто бывает затруднительно и далеко не всегда необходимо, так как уже на основании дискретного спектра можно судить о форме кривой и об основных величинах, ее характеризующих.
Рассмотрим второй этап, представляющий собой основную часть расчета цепей с несинусоидальными э. д. с. и токами.
Если, например, несинусоидальная э, д. с. представлена в виде суммы постоянной и синусоидальных составляющих, то источник
314
несинусоидальной э. д. с. можно рассматривать как последовательное соединение источника постоянной э. д. с. и источников синусоидальных э. д. с. с различными частотами. Так, если э. д. с. (рис. 12-13, а)
е=Ео + Elm sin (а>К -f-+ E2m sin (&2t + ф2). (12-33)
то действие источника такой э. д. с. аналогично действию трех последовательно соединенных источников э. д. с. (рис. 12-13, б):
е0 = £0; e! = £lmsin (cOiZ-T'Q’i);
Сг — Е2т sin -]—фг)•
(12-34)
Применяя принцип наложения и рассматривая действие каждой из составляющих э. д. с. в отдельности, можно найти составляющие токов во всех участках цепи.
fo «7 ег
0----@-------Q------0------0
0
Рис. 12-13.
Мгновенное значение тока в цепи равно сумме мгновенных значений составляющих токов. Если, например, в какой-либо ветви токи, создаваемые э. д. с. £0, и е2, соответственно равны 70, А и 12, то общий ток
i — Iq + й + 12-
Таким образом, расчет линейной цепи с несинусоидальными э. д. с. сводится к решению п задач с синусоидальными э. д. с., где п — число синусоидальных составляющих э. д. с. различных частот, и одной задачи с постоянными э. д. с.
При решении каждой из этих задач необходимо учитывать, что для различных частот индуктивные и емкостные сопротивления неодинаковы. Индуктивное сопротивление для k-й гармоники в k раз больше, а емкостное, наоборот, в k раз меньше, чем для первой:
xLk = kaL=kxL1; xCk = 1/kaC=xa/k.
Активное сопротивление также зависит от частоты, возрастая с ростом последней вследствие поверхностного эффекта. Когда расчет ведется для невысоких частот и относительно малых сечений проводов, можно не учитывать изменения сопротивления с частотой и считать, что при всех частотах активное сопротивление равно сопротивлению при постоянном токе.
Если источник несинусоидальной э. д. с. подключен непосредственно к зажимам емкости, то для k-й гармоники тока
+ ф + (12-35)
е xk = 1/&<вС.
315
Чем больше k, тем меньше по величине реактивное сопротивление емкости для этой гармоники. Следовательно, высшая гармоника э. д. с. или напряжения, даже если ее амплитуда составляет незначительную долю амплитуды основной гармоники, может вызвать ток в емкости, соизмеримый с током основной гармоники и даже его превышающий. Поэтому при напряжении, близком к синусоидальному, ток в емкости может быть резко несинусоидален из-за высших гармоник.
При подключении источника синусоидальной э. д. с. к индуктивности ток k-ii гармоники
tfe==^sin(^ + ^-|), (12-36)
токи несинусоидальных источников, остается тем же.
где хк — kaL.
С увеличением порядка k гармоники индуктивное сопротивле-Поэтому в токе через индуктивность высшие гармоники всегда имеют относительно меньшее значение, чем в напряжении на ее зажимах; даже при резко несинусоидальной кривой напряжения форма кривой тока нередко приближается к синусоиде.
Если задача поставлена иначе, заданы не э. д. с., а то принцип решения задачи
Источник несинусоидального тока всегда можно представить в виде параллельного соединения ряда источников, синусоидальный ток каждого из которых равен соответствующей составляющей несинусоидального тока.
Так, если к узлам ветви или двухполюсника подводится несинусоидальный ток (рис. 12-И, о):
t = 4 +/to sin (со^ + (Xi) +/2яг (sinciV + a2), (12-37)
то источник такого тока действует подобно параллельному соединению трех источников (рис. 12-14, б):
й —А; й — Аш sin (o^-J-oii);
Й 2т Sin (©2/ ОС2).
Рассчитав напряжения на сопротивлении Z от каждой из составляющих тока, легко найти мгновенное значение полного напряжения как сумму отдельных составляющих.
При расчете каждой из гармоник можно пользоваться комплексным методом и строить векторные диаграммы для каждой из гар-„моник вот дел ы-юстп. Однако щеданустимы суммирование нсктл-ров и сложение комплексных напряжений и токов различных гар
(12-38)
316
моник. Действительно, при определении мгновенных значений тока по комплексному необходимо вектор, изображающий комплексную амплитуду каждой гармоники, вращать со своей угловой скоростью 1гы и строить зависимость от времени его проекции на мнимую ось. Так как для различных гармоник частоты вращения различны, то геометрическое суммирование векторов, изображающих комплексные амплитуды, дает возможность определить мгновенное значение их суммы только в момент времени t = 0 и в общем случае не имеет смысла. При вычерчивании кривых отдельных гармоник следует всегда иметь в виду, что период гармоники обратно пропорционален ее номеру. Следовательно, если по оси абсцисс отложено то, соблюдая один и тот же масштаб, вместо углов а* надо откладывать углы а*/&.
Пример 12-8. В схеме высокочастотного лампового генератора, изображен- , ного на рис. 12-15, а, известны ток I, который протекает через электронную лампу Л, и э. д. с. Ео = 1 кВ источника питания.
г?
Рис. 12-15.
Пусть при заданных напряжениях на сетке и аноде электронной лампы ток амперах)
i — 8 + 12 cos at 4 соз2ы/.
Найти ток I' в источнике питания и ток i" в конденсаторе С±.
317
Решение Для определения токов и напряжений необходимо независимо рассчитать три схемы, изображенные на рис 12 15, б—г На схемах показаны э д с Ео, токи источников различных частот /0 = 8 А, Д = 12/[2 А; Д = 4/|/ 2 А и значения параметров
Рассчитав токи в каждой из схем, получаем округленно: для постоянной составляющей
/;=8А и 7^0;
для первой гармоники
6 12
/{ = —— Z. 17° А и /[' =----z. 120° А;
|/2 [2
для второй гармоники
ОК 4 14
7' = Д^-Z-~88° А и Д = ДДД£90°А.
/2 J/2
Просуммировав мгновенные значения различных гармонических составляющих, получим.
«' = [8 + 6 sin (со/Д- 17")-|-0,15 sin (2щ/ —88°)] А;
i" = [12 sin (со/Д- 120°) + 4,15 sin (2и/-|-90°)] А.
На рис 12-16 построен график составляющих и результирующего тока i". Так как по оси абсцисс отложено at, то при построении синусоиды второй гармоники начальная фаза (90°) разделена на номер гармоники (9072 — 45°).
Пример 12-9. Определить напряжение и" (Z) на вторичных зажимах четырехполюсника в режиме холостого хода при известном напряжении на первичных зажимах и’ (7) (рис 12-17)
Для четырехполюсника теоретически или экспериментально получена зависимость от частоты
U"IU' = N(jalt) = ne,fPk,
где п и ф — модуль и аргумент комплексного числа А'
Напряжение на первичных зажимах предшавляет собой сигнал, модулированный по амплитуде, спектр которого задан уравнением (12-28)
Решение Зная напряжение и' на первичных зажимах четырехполюсника, разложим его на гармонические составляющие .... ...............
k
318
и будем искать напряжение на вторичных зажимах в виде ряда
k
где
u'im = n(^k)u'km; + *₽(“*)•
Для рассматриваемою четырехполюсника при холостом ходе

= пе’П ыкт—/1
где т = гС.
На рис. 12-18 построены графики п (ak) и <р (йа).
Чтобы рассматриваемый сигнал проходил через четырехполюсник без существенных искажений, т е и" мало отличалось от и', необходимо выбрать пара
метры четырехполюсника, удовлетворяющие условию и,? > 10
Как следует из рис 12-10 и 12-18, при этом условии напряжения на входе и выходе четырехполюсника практически не будут отличаться, так как для всех трех составляющих частот сигнала И 1, а 0.
Рис. 12-18.
Рис. 12-17.
12-8. Резонанс при несинусоидальных э. д. с. и токах ।
При несинусоидальных э. д. с. и токах явление резонанса усложняется, так как возможны отдельные резонансы гармонических составляющих.
Предположим, что источник несинусоидальной э. д. с., состоящей из трех гармоник, подключен к последовательно соединенным сопротивлению г, индуктивности L и емкости С (рис. 12-19).
Ток каждой из гармоник
Ik = г....... (12-39)
//-2 + (toL— 1/fewC)2 ’
Если индуктивность L изменять от нуля до бесконечности, то действующее значение каждой из составляющих тока будет изменяться по резонансной кривой от/м^=-^—- ___ при L — 0 до
Г г2 -|- 1/£2со2С2
Ek/r при L = Lk = 1//г2о2С и далее — снижаться до нуля при L — оо.
На рис. 12-19 пунктиром построены резонансные. кривые для трех гармонических составляющих периодического несинусоидаль
319
Ного тока. Значения индуктивности L при резонансах (L*) обратно пропорциональны квадрату номера гармоники
Lk= l/k%>2C.
(12-40)
Кривая общего действующего тока
(12-41)
X
при достаточно малом г имеет три резко выраженных максимума, соответствующих резонансным значениям индуктивности.
Аналогичные зависимости получаются и при изменении емкости или частоты, если, конечно, в последнем случае форма кривой э. д. с. остается неизменной.
В цепях, содержащих несинусоидальные э. д. с., резонансные явления могут применяться для выделения требуемых частот и, наоборот, подавления нежелательных частот.
Пример 12-10. Несинусоидальное напряжение и’ на зажимах 1—Г четырехполюсника (рис 12-20) получено в результате двухполупериодного выпрямления синусоидального напряжения с угловой частотой со (см. приложение 1, строка 9).
Ветвь, включающая индуктивность 1Ч и емкость Съ и контур, состоящий из параллельно соединенных индуктивности L2 и емкости С2, настроены в резонансе на вторую гармонику 2(0, т е. 2(0/^ ~ 1/2(оС! и 2(oL2 = 1/2(оС2.
Найти действующее значение напряжения «’на зажимах 2—2' и коэффициент искажения в режиме холостого хода при следующих параметрах:
(oLj = со£2= 10 Ом; и' макс == 1000 в.
Решение В напряжении и" выделяется вторая гармоника, так как для нее сопротивление ветви ЦС-, и проводимость контура L2C2 равны нулю, в то время как для всех остальных гармоник сопротивление ветви и проводимость контура конечны и растут с номером гармоники
Рассматривая схему относительно зажимов 2-2' как двухполюсник, находим напряжение холостого хода на зажимах этого двухполюсника.
320
Для каждой гармоники
, . 7
где
Zt = j (fecoLj- 1/fecoCj); Z.= ](k®L2—\/li<£>C2)
Разложив напряжение и' в ряд по формуле, приведенной в строке 9 приложения 1, получим, что для нулевой и первой гармоник составляющие и" равны нулю.
Рис. 12-20.
Для второй гармоники Zx = 0, a Z2 = оо, поэтому напряжения на входе и лходе четырехполюсника одинаковы:
4
^т=^т = 2Й%акс = 425 В-
4
Для четвертой гармоники Z1 = /30 Ом, Z2 =— /13 Ом, =
85 В и, следовательно, Д4"т=85 13/17 = 65 В.
4
Для шестой гармоники Z1 = /53 0m, Z2 =— /7,5 0м, (Дт — gg - <-'макс =
36 В и Щт = 36 - 7,5/45,5 = 6 В.
Восьмой и более высокими гармониками можно пренебречь.
Таким образом, действующее напряжение на вторичных зажимах
действующее напряжение основной (второй) гармоники U" — 425/(2 = 300 В и коэффициент искажения ka = 0,94.
С целью улучшения формы кривой и" целесообразно включить параллельно Zx емкость С3 и обеспечить для напряжения четвертой гармоники резонанс токов [фи 1/4соС3 = 30 Ом.
В этом случае для четвертой гармоники Z, = оо, U "1т~ 0.
Для шестой гармоники Z2 = —/32 Ом, Z.2 = — /7,5 Ом н Z7gm = 36 X 1 7,5/39,5 «а 7 В.
Действующее напряжение U" = гения fc„»l.
у/~42^ 9^—-- 300 В и коэффициент иска-
11 Основы теории цепей
321
Такая схема представляет собой частный случай полосового фильтра и может быть применена для увеличения частоты вдвое (\множитель частоты) На аналогичном принципе основываются утроители частоты и частотные умножители большей кратности
12-9. Мощность периодических несинусоидальных токов
Активная мощность периодического тока произвольной формы определяется как средняя мощность за период
г
P=^uidt. (12-42)
о
Если мгновенные значения напряжения и тока выразить в виде тригонометрических рядов, то получим:
Т Г co I Г оо
^ = 7 § У £4msin (kut + tytik) У Ikmsin (Адаг'+Ф,*) dt.
о Щ = о

Так как среднее за период значение произведения мгновенных значений синусоид различной частоты равно нулю (см. § 12-3) и тригонометрические ряды абсолютно сходятся при любых частотах со, то
Т со
= у У ^fem/femsin(W + 4:„ft)sin(^+4)lft) dt,
О 4-0
или после интегрирования
со оэ
Р = и010+ 2 = 2 ^cos<pft) (12-43)
k—1 k—0
где
*Pfe---Ф/Zfe
Из этого выражения следует очень важный вывод, что средняя мощность несинусоидального тока равна сумме средних мощностей отдельных гармоник (постоянная составляющая рассматривается как нулевая гармоника с ср0 = 0):
р-хр-
fe = 0
(12-44)
Полученная таким образом мощность представляет собой активную мощность или энергию, необратимо преобразуемую в единицу времени в данном участке цепи в тепловую, механическую или какую-либо иную форму энергии.
322
Кроме понятия активной мощности Р по аналогии с синусоидальными токами вводится понятие полной мощности S, определяемой как произведение действующих значений тока и напряжения:
/СО со
(12-45)
fe = 0 fe = 0
Активная мощность меньше полной; исключение составляет только мощность в цепи, имеющей чисто активное сопротивление, когда Uk = rlk, и, следовательно, S = Р.
Отношение активной мощности к полной называют коэффициентом мощности и иногда приравнивают косинусу некоторого условного угла й:
% = P/S = cos й. (12-46)
Можно дать геометрическую интерпретацию углу й, пользуясь понятием эквивалентных синусоид тока и напряжения, действующие значения которых равны действующим значениям несинусоидальных величин. Если между эквивалентными синусоидами напряжения и тока установить такой угол сдвига фаз, чтобы мощность, выделяемая в цепи, равнялась мощности несинусоидального тока, то этот угол сдвига и будет равен условному углу й.
Формально можно ввести понятие реактивной мощности, определяемой как сумма реактивных мощностей отдельных гармоник:
СО со
Q= 2 sin У*- (12-47)
*=1 6=1
Для несинусоидальных токов в отличие от синусоидальных квадрат полной мощности обычно больше суммы квадратов активной и реактивной мощностей:
S2S&P2 + Q2.
Пример 12-11. Вычислить Р, Q и S, если напряжение и ток состоят из двух гармоник, первой и третьей Известны действующие значения гармоник напряжения ({7Х и t/3) и тока (Д и /3), а также углы сдвига фаз между гармониками напряжения и тока (фх и <р3).
Решение. В этом случае активная, реактивная и полная мощности
P = U1Il cos ф!+t/3/3 cos ф3;
Q = UJi sin ф!+173/3 sin ф3; S = + (4 +Л)!
Si—(P2+Q2) = UlIl + UlI2l—2U1l1U3ls (cos фх cos ф3-р sin фх- sin ф3) =
= Wilз)2—2иг1 iU3l3 cos (фх — ф3) ф- (USIx)2.
Очевидно, что S2 = P2 + Q2 только при условиях фх = ф3 и = t/3//3. Оба эти условия выполняются в тех случаях, когда сопротивление приемника чисто активное, линейное, не зависящее от времени, т. е. форма кривой тока в точности совпадает с формой кривой напряжения.
11я
323
12-10. Высшие гармоники в трехфазных цепях
В трехфазных цепях кривые напряжения во второй и третьей фазах со сдвигом на треть периода обычно в точности воспроизводят форму кривой напряжения в первой фазе. Так, например, если напряжение ид в фазе А может быть представлено некоторой функцией времени
то
uB=7(/-773); uc=f(t + T/3),
где Т — период основной частоты.
Рассмотрим гармонику порядка k функции f (t) во всех трех фазах. Пусть
HAk = km SIH (W 4- ф*).
Тогда, учитывая, что соТ = 2л и подставляя вместо t соответственно t — Т/3 и t + Т/3, получаем:
uBk = и km S i П (knit + Ij)fe — 2kn/3);
Uck = Ukm sin (kat 4-Ф* 4- 2&ЗТ/3).
Сравнивая полученные выражения для различных значений k, можно заметить, что напряжения гармоник порядка, кратного трем (k — Зп), где п — любое целое число, во всех фазах в любой момент времени имеют одно и то же значение и направление При k = Зп 4-1 гармоники трех фаз образуют симметричную систему напряжений, последовательность которой совпадает с последовательностью фаз первой гармоники. При k = Зп 4- 2 гармоники образуют симметричную систему напряжений с последовательностью, обратной основной.
Таким образом, гармоники порядка 1, 4, 7, 10, 13 и т. д. образуют системы напряжений прямой последовательности, гармоники 2, 5, 8, 11, 14 и т. д. образуют системы напряжений обратной последовательности. Наконец, гармоники 3, 6, 9, 12 и т. д. образуют системы напряжений нулевой последовательности. При наличии постоянной составляющей в напряжении каждой из фаз она может рассматриваться как нулевая гармоника порядка, кратного трем (k — 0), т. е. образующая нулевую последовательность.
В большинстве практически важных случаев в напряжениях отсутствуют как постоянная составляющая, так и все четные гармоники, поэтому в дальнейшем ограничимся исследованием только нечетных гармоник.
Рассмотрим различные схемы соединения трехфазных цепей.
Если фазы генератора соединены в звезду, то при несинусоидальном фазном напряжении линейные напряжения, равные разностям напряжений двух смежных фаз, не содержат гармоник напряжений порядка, кратного трем, так как последние образуют ____системы нулевой последовательное!и.----------------------------
324
Отсутствие гармоник порядка, кратного трем, в линейных напряжениях приводит к тому, что при несинусоидальных напряжениях отношение линейного напряжения к фазному меньше /3. Действительно, фазное напряжение
f/ф=| £4 4- 4- U i -j- U'i 4-..., а линейное напряжение
ил=Гз yui+ui+^+~.
Отсюда следует, что
Г</зб/ф.
(12-48)
При симметричной нагрузке фазные токи основной частоты и
все высшие гармоники, за исключением высших кратного трем, образуют системы прямой и обратной последовательностей и дают в сумме нуль. Гармоники же порядка, кратного трем, образуют систему нулевой последовательности, т. е. имеют в любой момент времени одинаковые значения и направления. Поэтому ток в нейтральном проводе равен утроенной сумме токов высших гармоник нулевой последовательности:
In = 3 V Р3 +11 +Цк + .... (12-49)
гармоник г орядка,
Рис. 12-21.
При отсутствии нейтрального провода токи в каждой из фаз не могут содержать высших гармоник порядка, кратного трем, так как в этой схеме сумма токов в любой момент времени должна равняться нулю, что невозможно при наличии высших гармоник порядка, кратного трем. Поэтому в приемнике нет напряжений от токов нулевой последовательности и между нейтральными точками генератора и симметричного приемника может появиться значительное напряжение, содержащее только гармоники, кратные трем.
Если фазы генератора соединены треугольником, то при несинусоидальных э. д с. в фазах сумма э. д с., действующих в замкнутом контуре генератора, не равна нулю, как при синусоидальных э. д. с., а равна тройной сумме высших гармоник порядка, кратного трем. Если включить вольтметр в рассечку треугольника (рис. 12-21), то вольтметр измерит гармоники э. д. с. порядка, кратного трем, так как остальные в сумме дадут нуль:
U = 3Г^4-^4-£1з + -~ (12-50)
Открытый треугольник с э. д. с., содержащими высшие гармоники, применяется как утроптель частоты (см. гл. 24).
Если фазы соединены в замкнутый треугольник, то э. д. с. гар-лоник порядка, кратного трем, вызывают внутренний ток в гене-шIоре. Эют ток~протекает в замкнутом треугольнике генератора
325
даже и тогда, когда внешняя цепь генератора разомкнута. Составляющая фазной э. д. с., содержащая гармоники порядка, кратного трем, однако, не выявляется между зажимами фаз, так как она компенсируется падением напряжения на внутреннем сопротивлении фазы генератора. Фазное напряжение, равное в данном случае линейному,
иф=УЁ1 + Е1 + Е^ + .... (12-51)
Поэтому во внешней цепи, подключенной к генератору, обмотки которого соединены треугольником, токи не содержат гармоник порядка, кратного трем.
Фазный ток генератора при симметричной нагрузке
/ф==Г/1+/1+/|+Л+...,
а линейный ток во внешней цепи
/л=Гз (/1 + Л+/?+...)<Кз/ф,
(12-52)
Пример 12-12. Найти показания приборов при разомкнутом и замкнутом рубильнике Р в трехфазной цепи (рис. 12-22, а), имеющей соединенную в звезду
0
Рис. 12-22.
трехфазную систему источников (вторичные обмотки трехфазного трансформатора) с фазными э. д. с., В:
еА=220 /2 sin at+50 /2 sin (Зсо/+90°) + 30 /2 sin (ScoZ + 90°); eB=220 /2 sin (co/ — 120°)+50 /2 sin (3coZ -p90°) +30 /2 sin (5coZ — 150®); ec = 220/2 sin (со/—240’)+50/2 sin (Зсо/+90°) + 30 /2 sin (5coZ — 30°). Сопротивление источника для первой гармоники
2и1=г + /шГ«=!+Л Ом.
326
Приемником служит трехфазная система конденсаторов, соединенных в звезду. Для первой гармоники
Znl= 1//шС=—/10 Ом.
Решение Найдем показания приборов (индексы токов и напряжений соответствуют обозначениям приборов в схеме)
Для случая звезды без нейтрального провода (рубильник Р разомкнут)
А = /ф=А = К (ДгАт)2+(А/А)2 = /24,4^+ 10-' =26,2 А;
1/3 = /(24,4- 10)2 + (10-2)2«=244 В; 1/4 = 50 В;
(/1 = )/-^ + ^ = 250 В; 1/2 = Д5 = /31/3 = 423 В.
Для случая звезды с нейтральным проводом (рубильник Р замкнут)
А= /ф=А = I ' + (£з/г3)2 + (£5/А)2=К24.42 + 150‘2 + № = 152 А;
l/s=l/1 = /(24,4- 10)2+(150 • 3,33)2 + (10 2)2 = 556 В;
U2 = I/, = 423 В; /2 = 3 (50/0,33) = 450 А.
Близость к резонансу на третьей гармонике привела к очень большому значению тока третьей гармоники в нейтрали В этом случае оказалось, что линейное напряжение, которое не содержит третьей гармоники, меньше фазного, так как вследствие резонанса напряжений третья гармоника фазного напряжения больше основной
Пример 12-13. Найти показания приборов при тех же фазных э. д с. и сопротивлениях, что и в примере 12-12, но при соединении источника и приемника треугольником (рис 12-22, б)
Решение. В этом случае третья гармоника замыкается в контуре генератора и
Д 3 = 50/3= 16,7 А
Так как остальные составляющие те же, что и в примере 12-12, то
А = I7 A.i + А.з + А.» = /24,42 + 16,72 + IO2 = 31 А;
/3=//2 1 + /2 .=/24,42 4-102 = 26,6 А;
А = /3 /3 = 45,5 А; 1/л = = 244 В.
Таким образом, третья гармоника влияет только на внутренние токи источника и не сказывается на распределении токов и напряжений приемника.
Глава тринадцатая
КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
13-1. Возникновение переходных процессов и законы коммутации В
В электрических цепях могут происходить включения и отключения пассивных или активных ветвей, короткие замыкания отдельных участков, различного рода переключения, внезапные изменения параметров и т. д. В результате таких изменений, называемых часто коммутационными или просто коммутациями, которые будем считать происходящими мгновенно, в цепи возникают
327
переходные процессы, заканчивающиеся спустя некоторое (теоретически бесконечно большое) время после коммутации.
Сформулируем два закона коммутации:
1. В любой ветви с индуктивностью ток и магнитный поток в момент коммутации сохраняют те значения, которые они имели непосредственно перед коммутацией, и дальше начинают изменяться именно с этих значений. Так, при включении ветви с катушкой, в которой не было тока, ток в этой ветви в момент коммутации равен нулю. Если для такой ветви допустить, что в момент коммутации ток изменяется скачком, то напряжение на индуктивности (L dildt)~ — Ul будет равно бесконечности и в цепи не будет соблюдаться второй закон Кирхгофа.
В случае двух и большего числа цепей, связанных взаимной индуктивностью, но при отсутствии в каждой из них магнитных потоков рассеяния формулировка первого закона коммутации изменяется в том смысле, что в момент коммутации общий магнитный поток этих цепей не может, а токи в каждой из них в отдельности могут изменяться скачком.
2. В любой ветви напряжение и заряд на емкости сохраняют в момент коммутации те значения, которые они имели непосредственно перед коммутацией, и в дальнейшем изменяются, начиная именно с этих значений.
Так, при включении ветви с конденсатором, который не был заряжен, напряжение на конденсаторе в момент коммутации равно нулю. Если для ветви с емкостью допустить, что в момент коммутации напряжение на емкости изменяется скачком, то ток i = — (Cdu(idt) будет равен бесконечности и в цепи, всегда имеющей сопротивление, опять-таки не будет соблюдаться второй закон Кирхгофа.
С энергетической точки зрения невозможность мгновенного изменения тока в индуктивности и напряжения на емкости объясняется невозможностью скачкообразного изменения запасенной в них энергии (энергии магнитного поля катушки, равной Li2/2, и энергии электрического поля конденсатора, равной СиЧЧ). Действительно, скачкообразное изменение энергии требует бесконечно больших мощностей в индуктивностях и емкостях, что лишено физического смысла, так как реальные источники питания не обладают бесконечно большой мощностью.
В этой главе рассмотрены переходные процессы в линейных электрических цепях. Поэтому исключается из рассмотрения нелинейный элемент — электрическая дуга, которая возникает при включении или отключении. Чтобы исключить влияние дуги при коммутациях, предположим, что длительность коммутации по сравнению с продолжительностью переходного процесса очень мала. В этом случае при расчетах можно считать, что переключатель, осуществляющий коммутацию, включается или отключается мгновенно. Если нет специального указания, будем считать момент коммутации за начало отсчета времени и принимать, что в момент t = О
328
или точнее t = 0 + коммутация уже произошла. Отключение отдельных ветвей будем рассматривать, если в отключаемой ветви шт индуктивности и если ее отключение не приводит к необходимости скачкообразного изменения тока в других ветвях с индуктивностями.
13-2. Переходный, принужденный и свободный процессы
Рассмотрим сначала некоторые общие вопросы расчета переходных процессов на примере включения неразветвленной цепи с сопротивлением, индуктивностью и емкостью (последовательного контура) к источнику э. д. с. е, которая изменяется во времени непрерывно и задана каким-нибудь аналитическим выражением.
Запишем второй закон Кирхгофа для любого момента времени: ri + Ld~+^^idt=e, (13-1)
где i — ток переходного процесса, который в дальнейшем будем называть переходным током или просто током i.
Когда с переходным процессом можно уже не считаться, наступает принужденный режим. Принужденный режим, создаваемый источником произвольной периодически изменяющейся э. д. с. (или тока), называют еще установившимся режимом. После окончания переходного процесса источник э. д. с., изменяющейся, например, по экспоненциальному закону, создает принужденный режим, а источник постоянной э. д. с. или э д. с., изменяющейся по гармоническому закону, создает принужденный или установившийся режим.
Когда наступит принужденный режим, уравнение (13-1) примет вид:
dlnn 1 (*
п’пр + L ~аГ + с J 1”рdt = е’ (13-2)
где /пр — ток принужденного режима или просто принужденный ток.
Вычитая почленно уравнение (13-2) из уравнения (13-1) и обозначая
t 1пр ^св> (13-3)
получаем: nCB + L-^+ JiCB^=0, (13-4)
или св Ч- св Ч~ св (13-4а)
Разности токов и напряжений переходного процесса и принужденного режимов называются соответственно током и напряжением свободного процесса или просто Свободными током и напряжением.
329
(13-5)
Уравнение (13-4) показывает, что при переходе цепи от одного принужденного состояния к другому напряжения на всех элементах, создаваемые свободными составляющими токов, взаимно уравновешиваются, но свободные напряжения зависят, конечно, от э. д. с. е источника.
Уравнение (13-3) показывает, что процесс, происходящий в цепи, можно рассматривать состоящим из двух накладывающихся друг на друга процессов — принужденного, который как бы наступил сразу, и свободного, имеющего место только во время переходного процесса. Благодаря свободным составляющим и достигается в переходном процессе непрерывное приближение к принужденному режиму. Следовательно, во время переходною процесса токи и напряжения могут быть разложены на слагающие принужденного режима и свободного процесса:
I ^пр “1“ Св» === пр "Ь св,
И/, И/. Пр Н- У-L св» «С «С пр "4" «С св*
Так как принцип наложения применим лишь к линейным цепям, то это разложение допустимо для линейных цепей Конечно, физически существуют только переходные токи и напряжения и разложение их на принужденные и свободные составляющие является удобным математическим приемом, облегчающим расчет переходных процессов в линейных цепях.
Разложение переходных токов и напряжений соответствует правилу решения линейных неоднородных дифференциальных уравнений, согласно которому общее решение таких уравнений равно сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Действительно, свободный ток представляет собой общее решение однородного дифференциального уравнения (13-4) и, следовательно, в его выражении должны быть постоянные интегрирования, число которых равно порядку дифференциального уравнения.
Принужденный ток представляет собой частное решение неоднородного дифференциального уравнения (13-1), а именно такое, которое получается из общего решения неоднородного дифференциального уравнения при равных нулю постоянных интегрирования. Иными словами, в составе принужденного тока не должно быть слагающих свободного тока. Тогда переходный ток i, равный сумме inp и iCK (13-5), и будет общим решением того же самого неоднородного дифференциального уравнения.
При помощи законов коммутации нетрудно найти начальные значения свободного тока в ветви с индуктивностью i‘£cB (0) и свободного напряжения на емкости иСсв (0), что необходимо для определения постоянных интегрирования.
Пусть цепь до коммутации находилась в произвольном режиме. Обозначим ток и напряжение этого режима ii~ (t) и ис- (t). В момент коммутации-/-^ 0 ток /'/- (0) и напряжение ис- (0) режимащо_
330
коммутации будем считать известными. Так как переходный ток в индуктивности и переходное напряжение на емкости в момент коммутации не могут изменяться скачком, то на основании (13-5) имеем:
i£_ (0) = 1£пр (O)-J-t'icB (0); ис-(0)-«Спр(0) + «сев(0), (13-6)
Или
iieB(O) = tr-(O)-iznp(O); исев(0) = «с-(0)-«Спр(0). (13-6а)
Если цепь до коммутации находилась в принужденном режиме, то, обозначая ток и напряжение этого режима i£np_ (t) и icnp~ получаем:
h св (0) = iinp-(0)-ii пр (0); иссв(0) = Цспр-(0)-Испр(0). (13-66)
!i В частном случае, когда до коммутации цепь была отключена и на емкости не было заряда, т. е. /тпр-(0) = 0 и испрД0) = 0, имеем:
»тсв(0) = —iinP(0); «Ссв(о) = — «спр(О). (13-7)
Начнем изучение переходных процессов с исследования процессов в простейших цепях так называемым классическим методом. Этот метод заключается в интегрировании дифференциальных уравнений, связывающих токи и напряжения цепи, в результате чего появляются постоянные, и в определении постоянных из начальных условий, вытекающих из законов коммутации.
Начальными условиями назовем значения переходных токов в индуктивностях и напряжений на емкостях, при t = 0, т. е. те величины, которые в момент коммутации не изменяются скачком. Иногда эти условия называются еще независи-. мыми начальными условиями. В отличие от них начальные значения всех остальных токов и напряжений называют зависимыми начальными условиями. Зависимые начальные условия определяются по ’независимым начальным условиям при помощи уравнений, составленных по первому и второму законам Кирхгофа. Отметим, что эсновная трудность классического метода исследования переходных процессов в сложных цепях как раз и состоит в определении зависимых начальных условий.
13-3. Короткое замыкание цепи г, L
Ветвь с сопротивлением и индуктивностью (в дальнейшем сокращенно называемая цепью г, £), иначе говоря, реальная катушка внезапно замыкается рубильником накоротко (рис. 13-1). Ток в катушке до коммутации был постоянным
Е
tnP-—
Найдем закон изменения тока в катушке.
331
Принужденный ток в катушке после коммутации равен Нулю. Следовательно,
На основании уравнения (13-4) свободный ток удовлетворяет однородному дифференциальному уравнению первого порядка
L dizJdt -f- riCB— 0, (13-8)
общее решение которого
<>М)
При t = 0 из (13-9) имеем:
»св(0) = Л = »(0). т е.
i = iCB = i (0) е~ * = iCB (0) е~ =гсв (0) е~а(;
здесь tCB (0) = А — начальное значение свободного тока, кривая изменения которого дана на рис. 13-2.
Рис 13-1
Рис 13-2
Величина т = Ыг, имеющая размерность времени, называется постоянной времени цепи г, L и может быть определена как время, в течение которою свободный ток, затихая, уменьшится в е раз по сравнению со своим начальным значением iCB (0). В самом деле,
iCB(T)^/CB(0)e-^^> = А.
Для графического определения т проведем касательную к кривой iCB в любой ее точке С. Значение подкасательной BD может быть найдено из треугольника CBD, а
г = = = mtBD, где m(, mtg|3> /^-масштабы,
т е постоянная времени численно равна длине любой подкасательной В частности, она численно равна длине подкасательной ОВо>_
определяемой касательной С0В0, проведенной в начальной точке Со-
332
Величина, обратная постоянной времени, а= \/x = rlL
называется коэффициентом затухания цепи г, L. Свободный ток затухает тем медленнее и, следовательно, новый принужденный режим не устанавливается тем дольше, чем больше постоянная времени т или чем меньше коэффициент затухания а, т. е. чем больше индуктивность L и чем меньше сопротивление г.
Значение тока iCB (0), т. е. постоянной интегрирования А, определим из начальных условий. В ветви с индуктивностью переходный ток в момент коммутации t — 0 не может измениться скачком. Поэтому
«св (0) = i (0) = 1пр_ (0)
и для тока i катушки получим:
« = ^=7^7^. (13-Ю)
Электродвижущая сила- самоиндукции
с‘=-г-Л=£ЯТ7с“'/,=-“1 (13-П)
равна при t = 0 напряжению на сопротивлении г и в момент коммутации поддерживает значение тока на начальном уровне.
С энергетической точки зрения процесс короткого замыкания цепи г, L характеризуется тем, что вся энергия, запасенная до коммутации в магнитном поле катушки,
IFH = LisP_(0)/2 = Li2(0)/2
в течение переходного процесса превращается в сопротивлении г в тепло:
оо оо 2г_ ,
§ i2r dt=i2 (0) г § е г dt — Li2 (0)/2. о о
Заметим, что теоретически процесс исчезновения тока в короткозамкнутой катушке длится бесконечно долго, чем и объясняется необходимость в качестве верхнего предела у интеграла взять бесконечность. Однако практически для многих катушек этот переходный процесс закончится весьма быстро. Постоянная времени Цепи г, L обычно лежит в пределах от нескольких микросекунд До долей секунды. Последнее значение относится к большим катушкам со стальным магнитопроводом и значительным числом Житков.
Если до короткого замыкания в катушке был переменный ток, о характер переходного процесса нисколько не изменится, но i (0) авдо значению тока в катушке в момент короткого замыкания.
333
Рис 13-3.
С переходным процессом в цепи г, L приходится считаться во многих случаях электротехнической практики, например при измерении сопротивления г обмотки трансформатора с большой индуктивностью (рис. 13-3), которая питается от источника постоянной э д. с. Б через дополнительный резистор с сопротивлением R. Напряжение на обмотке измеряется милливольтметром. Если после отсчета показаний амперметра и милливольтметра отключить обмотку трансформатора от источника напряжения, то ее ток замкнется через милливольтметр. Так как ток обмотки трансформатора может быть до-момент отключения рубильника не изме-
статочно большим и в
няется скачком, то, пройдя через милливольтметр, ток может его
сжечь.
Обмотку возбуждения мощной электрической 0--------------1
машины при необходимости быстро снять воз- П
буждение не отключают от цепи питания (по- I Ц
стоянное напряжение), а замыкают на разрядное Л Т
сопротивление, в котором энергия магнитного И ^5
поля превращается в тепло (рис. 13-4). Если Т э
просто разомкнуть цепь обмотки возбуждения, 0 J-----J
то даже при наличии электрической дуги ток
очень быстро уменьшится до нуля (— di/di будет Рис 13-4 очень велико). Так как обмотка возбуждения
имеет большую индуктивность Бв, то в ней возникает весьма значительная э. д. с. самоиндукции щ. = — L^di/dt, которая может пробить изоляцию на корпус машины или изоляцию между витками.
13-4. Включение цепи г, L на постоянное напряжение
При включении цепи г, L на постоянное напряжение (рис 13-5) ток в первый момент равен нулю. Поэтому
i (0) = in₽ (0) + iCB (0)=-0.
А так как
inp = inP(0) = H/r,
то
iCB (О) = л=-Б/Щ
Поэтому ток переходного процесса
____=____i = inP+1^=—+ (I -*~^), . _(U42>
334
где
т = L/r.
Напряжение на индуктивности
ui == uL св =- L & = Ue~ W.
(13-13)
Поскольку до включения напряжение на индуктивности было равно нулю, а в момент коммутации uL = U, то переходное и свободное напряжения на индук-
тивности изменяются скачком. Кривые изменения i, /пр, zcb 11 Ul приведены на рис. 13-6. Как и следовало ожи
i
Рис 13-5.
дать, они показывают, что ток в цепи не устанавливается мгновенно и что требуется известное время (теоретически бесконечное) до наступления принужденного режима со значением тока U/r. Ток i возрастает тем медленнее, чем больше постоянная врем&ни цепи т, т. е. чем медленнее затухает свободный ток.
Энергия, получаемая от источника, идет частью на увеличение энергии магнитного поля катушки, а частью переходит в тепло в ее сопротивлении г.
Пример 13-1. В цепи /у = 20 Ом, L = 0,6 Г, подключенной к источнику постоянной э д с с напряжением U — 220 В (рис 13 7), происходит внезапное уменьшение сопротивления от значения rL до г2 — 12 Ом (рубильник замыкает некоторую часть сопротивления гх, равную гх — <2 = 8 Ом) Найти Закон изменения тока в цепи
Решение На основании формул (13-9) и (13-5) напишем сразу выражение для свободного тока
____*—
1св = Ле L = Де °'05
и для переходного тока
‘ = ‘пР + ‘ср = -^ + Ае~^= 18,3 + Ае~^ 05 .
Из условия отсутствия скачка тока i при t = 0 получаем:
‘пр- (0) = I///! = 11 = i (0) = 18,3 + 4, откуда
-------- —=------------7,3.----------------------=______=
335
Следовательно,
i= 18,3- 7,3е~Z/C105 А.
Отметим, что постоянная времени цепи после коммутации определяется пара, метрами L и г2. Кривые токов i и iCB показаны на рис. 13-8 Из них видно, что i0K ) постепенно возрастает от меньшего значения 1//гх = 11 А до большего »= 18,3 А. 2
Переходный процесс при внезапном увеличении сопротивления аналогичен рассмотренному. Только ток будет постепенно уменьшаться.
13-5. Включение цепи г, L на синусоидальное напряжение
При включении цепи г, L (рис. 13-5) на синусоидальное напряжение
и — Um sin (coZ + ’f) принужденный ток
inp=^- sin (со/ 4-ф - ф),
где
г=1^г2 + (со£)2; tgcp = coL/r,
а свободный ток определяется равенством (13-9), т. е.
i’cb = Ае L — Ае т.
Для переходного тока i получим:
i = i'np + tCBsin (со/ + if - ф) 4- Ае-'/*.
В рассматриваемой цепи до включения тока не было. Поэтому / = 0 при / = 0. Отсюда
/св (0) = А = — sin (if- ср).
Окончательно получаем:
j sin (со/-4-if — <р) — sin (if — ф) e~^x (13-14)
— _______________Z------------------z-----«
336
Напряжение на индуктивности
Ul — L di/dt = Un in <p • sin -j- Ф — ф + у J +
cos ф sin (ф — ф) e~‘lr .
(13-15)
Правильность полученных равенств (13-14) и (13-15) проверим, подставив в правую часть значение t = 0. Эта проверка дает для тока i значение нуль. Для напряжения на индуктивности получим Ul (0) = Um sin if, что легко установить и непосредственно. Действительно, в момент включения напряжение на индуктивности равно напряжению источника, так как напряжение на сопротивлении равно нулю.
Кривая тока i изображена на рис. 13-9, а. Она показывает, что по мере затухания тока iCB переходный ток стремится к значению принужденного тока. Однако через промежуток времени от 774 до 3774 после включения, что зависит от угла ф, ток может достигать значений, превышающих амплитуду принужденного тока.
Наибольшего возможного значения ток достигает, если в момент включения цепи принужденный ток равен амплитуде (ф — Ф — = зт/2 пли — л/2), а постоянная времени цепи весьма велика (г ~ 0, т -> оо и ф ~ л/2), т. е. свободный ток затухает очень медленно. При этих условиях ф ~ л и приложенное напряжение в момент коммутации должно проходить через нулевое значение. Кривая тока при ф — ф = л/2 и достаточно больших значениях т приведена на рис. 13-9, б. Примерно через половину периода после включения цепи ток достигает почти удвоенной амплитуды принужденного тока | i макс | « 2 /тпр.
Итак, при включении цепи г, L к источнику синусоидального Напряжения переходный ток ни при каких условиях не' может -Превышать удвоенной амплитуды принужденного тока.---------
337
Начальное значение свободного тока равно по величине и противоположно по знаку начальному значению принужденного тока. Поэтому, если в момент включения принужденный ток проходит через нуль, то начальное значение свободного тока также равно нулю. Свободный ток вообще не возникает, и в цепи сразу устанавливается принужденный режим Это будет, как показывает фор. мула (13-14), при ф — <р = 0 или ф — <р = л.
В разветвленной цепи с одной индуктивностью (рис 13-10, о) постоянная времени свободной составляющей любого из токов определяется по формуле
где гвх — входное сопротивление цепи по отношению к зажимам ветви с индуктивностью.
Рис 13-10.
Чтобы получить гвх в формуле (13-16), составим схему для свободных токов, т е исходную схему, из которой изъяты источники (рис 13-10, б). Из этой схемы следует, что поскольку внешняя (по отношению к ветви г, L) цепь состоит из однородных элементов — в данном случае сопротивлений, то она может быть для расчета постоянной времени заменена одним эквивалентным сопротивлением
1_______
Гвх~ 1Л1+1/г2+1/гз ‘
Составим теперь простую формулу для непосредственного определения переходного тока в ветви с индуктивностью L произвольной цепи, содержащей источники э д с любого вида и кроме индуктивности L — только активные сопротивления (например, цепи по рис 13-10, а) Ток
= ‘‘tup (0 + Чсв (0 = Чпр (0 + Ае~tl .
где т определяется согласно (13-16) При I = 0
lL (°) = Qnp- (°) = 1£пр (°) + Л> откуда
Л = гЛпр„(0)-г£пр(0).
Следовательно, ток в индуктивности
- ----------------«>)-%₽ -------------------------------------------<^17)
338
Если до коммутации (t <; 0) режим был не принужденный, то ток i/.np- (0) нужно заменить током iL_ (0) предшествующего режима, т е.
lL (0=«inp (O+Pz- (0)-‘inp (0)] e~tlx
(13-18)
Подчеркнем, что приведенные формулы (13-17) и (13-18) применимы только для ветеи с индуктивностью
13-6. Короткое замыкание цепи г, С
Предположим, что конденсатор емкостью С был заряжен от источника постоянного напряжения (рис. 13-11) до напряжения Uo = Е, а затем замыкается рубильник и конденсатор разряжается
через сопротивление г.
Ветвь с сопротивлением и емкостью в дальнейшем будем называть сокращенно цепью г, С.
Исследуем возникающий переходный процесс.
Принужденное напряжение на емкости и принужденный ток в цепи равны нулю. Найдем свободные составляющие тока и напряжения. Выберем положительные направления напряжения на емкости и тока
Рис 13-11.
совпадающими (как и
при расчете установившихся режимов в цепях переменного тока).
Тогда
гсв dqBB! dt С duCB/ dt.
(13-19)
Запишем уравнение второго закона Кирхгофа для свободных составляющих:
riCB + «ccB=0- (13-20)
На основании выражений (13-19) и (13-20) составим однородное дифференциальное уравнение (первого порядка) для свободного напряжения:
- гС^ + иСсв = 0. (13-21)
Общее решение последнего уравнения _______________________t_ uCQB=uc=Ae гС = uCzB (0) (0) e~at,
где цСсв (0) = A — начальное значение свободного напряжения на емкости.
Величина т = гС, имеющая размерность времени, называется постоянной времени цепи г, С. Обратная ей величина а = 1/т = 1/гС называется коэффициентом затухания цепи г, С. Постоянная времени т тем больше, чем больше емкость и сопротивление. Рледовательно, чем больше емкость С и сопротивление г, тем медленнее в цепи затухают свободные токи и напряжения, тем медленнее происходит разряд конденсатора. -
339
Значение Uc (0) (т. е. постоянной интегрирования А) определим из начальных условий. Для любой ветви с емкостью они сводятся к тому, что напряжение на емкости в момент коммутации (т. е. при t — 0) не может измениться скачком. Поэтому при t = О
Нс (0) — А = tic св (0) = Е = Uq.
Для напряжения на конденсаторе получим:
uc = Uoe~t/'T,
и ток согласно (13-20)
I = г'св
ЫС св __ _ L'o Г г
(13-22)
(13-23)
Кривые изменения ис и i приведены на рис. 13-12.
С энергетической точки зрения процесс короткого замыкания цепи г, С характеризуется переходом энергии, запасенной до ком-
мутации в электрическом поле конденсатора, в тепло в сопротивлении г'.
ОО
С Г/2
\ Er dt——
J г
о
dt=
CUI
2 •
Отметим, что практически ветвь с сопротивлением и емкостью всегда имеет и какую-то индуктивность, хотя бы и очень малую. Поэтому и в данном слу-
чае ток начнется с нуля (т. е. не изменится скачком), но очень быстро достигнет значения, весьма близкого к Uolr, и затем будет уменьшаться практически экспоненциально (13-23).
Если конденсатор в цепи рис. 13-11 до включения рубильника питался от источника синусоидальной э. д. с., то ис (0) будет зна-
чением напряжения на емкости в момент коммутации.
Если положительное направление тока i (рис. 13-11) выбрать
противоположным положительному направлению напряжения ис, то знаки в формулах (13-19) и (13-23) изменятся на обратные.
13-7. Включение цепи г, С на постоянное напряжение
Рассмотрим переходный процесс при включении цепи г, С на постоянное напряжение U (рис. 13-13).
Уравнение, составленное по второму закону Кирхгофа для свободного процесса, совпадает с (13-21). Поэтому свободное напряжение на емкости
uc^Ae-t/^^Ae-UT, - "
340
Переходное напряжение на емкости
Ис = «с Пр + «с св = U 4~ //т-
Так как конденсатор не был заряжен, т. е. при t = 0 напряже-
ние ис (0) = 0, то А = —U и iic = U (1 —
Для тока получим:
i = C-£ = — at г
(13-24)
(13-25)
Начальное значение тока i (0) может быть рис. 13-13. получено и непосредственно. Так как tzc (0) — 0, то все напряжение источника U при t = 0 оказывается прило-
СПВ
иСсв
Рис 13-14.
женным к сопротивлению г.
Кривые изменения ис, испр< uCc« и i (рис. 13-14) показывают, что напряжение на емкости и ток в цепи не устанавливаются мгновенно. Напряжение возрастает и ток спадает тем медленнее, чем больше постоянная времени цепи т, т. е. чем медленнее затухает свободное напряжение tzc СЕ.
Отметим аналогию законов изменения тока Д в цепи г, L и напряжения ис в цепи г, С при включении их на постоянное напряжение. Она следует из сравнения равенств (13-12) и (13-24) и кривых на рис. 13-6 и 13-14. Аналогично также изменение величин ui и i в тех же цепях. Аналогия распро-
страняется и на случаи включения цепей г, L и г, С на синусоидальное напряжение.
К исследованию процессов зарядки и разрядки конденсатора через резистор сводятся многие важные пракгические задачи, воз-
никающие при расчете переходных процессов и в цепях автоматики, телемеханики, электро- 1 ники и связи.
Как будет показано ниже, энергия, пере-ходящая в тепло при включении цепи г, С, I
не зависит от г. “ j
' ,ь
Пример 13-2. В цепи, показанной на рис. 13-15, замыкается рубильник. Найти напряжения на конденсаторах и ток, если конденсаторы были заряжены до напряжений 1/10 = 100 В, L/2n = 25 В; Q = 1 мкФ; fca = 2 мкФ; г = 75 Ом.
Решен и е. Имберг-м попожителпиые направления тока t и напряжений на энденсаторах и и2 (рис. 13-15).
341
В установившемся режиме ток будет равен нулю. Поэтому потенциалы точек а и b сравняются, т. е.
Ы1Пр И2пр = О»
ИЛИ
‘Угпр/Сг, (а)
где <?! и q2 — заряды на конденсаторах.
Согласно закону сохранения заряда
91пр + ‘/2пр = 9ю + ?20> (б)
где
9ю=С11/10; q2o=C2U2O.
Решив совместно уравнения (а) и (б), получим:
?1пр — р + О2С2-.) = СтНгпр»
F Li-j-C2
Ст
?2Пр = £ (^1^10 + C2U20) = C2U2np»
откуда
Тогда
ui = t|inp+-^e— </т = 50-рАе~*/г, (в)
где т = г 7^7^- = 50 • 1О-6 с,
С1~ГС2 поскольку конденсаторы соединены последовательно.
По второму закону коммутации при t = 0 получим «1 (0) = Ul0 и из формулы (в) их (0) = 50 + А, откуда
А = цх(0) — 50 = 50 В и и1 = 504-50е—В.
Аналогично находим:
и2 = 50 - 25е~1/х В
И ток
> —С, -------С 2 —______ \ё~^х А
. <-L1 dt ~ dt ~ Ё A‘
Устремляя г к нулю и решая задачу в этом случае, получим, что суммарная энергия конденсаторов по окончании переходного режима меньше их суммарной первоначальной энергии. Это указывает на неточность постановки задачи при
СО
г= 0. В самом деле, при г 0 ток i — оои интеграл J i2r d/может быть конечным, о
13-8. Включение цепи г, С на синусоидальное напряжение
Пусть цепь г, С (рис. 13-13) включается на синусоидальное напряжение
и = Um sin (oV 4- ip).
Принужденное напряжение на емкости
„ ... ,
Иг пп = ~SIH - ПР гшС ’ al 4- ф - гр — ' »
342
где
г=]/г2 + (1/ыС)2; tg<p=—1/coCr.
Изменение свободного напряжения на емкости по-прежнему определяется соотношением
Переходное напряжение на емкости
«с = «с пР + «с св = sin (at + ф - <р - л/2) + Аег-*
Начальные условия дают: ис = 0 при t = 0. Отсюда
л = —Й^МЧ’-ф-л/2)
и напряжение на емкости
пс=^8ш(«/ + ф-ф —л/2) —^sin^ —ф-^е-б^, (13-26)
где постоянная времени цепи т = гС. Ток
Лд. I/
. z-> С т
t = C -тг- =--------
at г
cos <р • sin (at-f-ф — ф) — sin ф • sin (ф — ф —
2 J J’
(13-27)
Проверка для t = 0 дает для напряжения ис значение нуль, а для тока i (0) = Um sin ty/r. Действительно, в момент включе
ния цепи емкость как бы закорочена [ис (0) = 0] и все напряжение питания приложено к зажимам сопротивления.
Полученное выражение для тока объясняет возникновение больших толчков тока при включении ненагружен-ной кабельной сети, т. е. сети, в которой распределение энергии происходит по кабелям. На рис. 13-16 приведена эквивалентная схема ненагр уженной кабельной сети, где С — эквивалентная
Рис. 13-16.
емкость, учитывающая емкость каждой
фазы на землю и емкость между фазами. Если сеть достаточно мощная, то поперечные сечения кабелей значительны и сопротивления г малы. Поэтому при включении сети в момент, когда напряжение одной из фаз проходит через амплитудное значение, наблюдаются весьма значительные толчки тока.
Кривая изменения напряжения ис аналогична кривой тока на рис. 13-9, а. Спустя время от 7/4 до 3 7/4 после включения, ^пряжение ис может достигать значений, превышающих ампли-?ДУ ^принужденного режима. Максимальное значение ис полу
343
чается, если в момент включения цепи принужденное напряжение ргвио амплитудному значению (ф — <р = л или 0), а постоянная вге лени цепи т -> оо. Кривая ис для ф — <р = л аналогична кривой тока на рис. 13-9, б. Примерно через половину периода после включения цепи напряжение на емкости достигает почти удвоенной амплитуды принужденного режима исмакс ~2(7Стпр.
Итак, в этом случае переходное напряжение на емкости ни при каких условиях не может превышать удвоенной амплитуды принужденного режима.
Если в момент включения принужденное напряжение на емкости проходит через нуль, то начальное значение его свободной составляющей также равно нулю, т. е. свободного напряжения на емкости вообще нет и в цепи сразу возникает принужденный режим.
Совершенно так же, как и для цепи на рис 13-10, а, но заменяя индуктивность емкостью, можно показать, что в разветвленной цепи из активных сопротивлений с одной емкостью постоянная времени
т = (г + гвх)С. (13-28)
Можно дать простую формулу для непосредственного определения переходного напряжения на емкости для цепи с активными сопротивлениями и одним конденсатором.
Напряжение на емкости
«С (0 = “Спр <0 + “Сев <0 = “Спр + Ае~ '/Т»
где т определяется согласно (13-28). При £ = 0
“с (°) = “спр-(0) = «Спр(0)+Л, откуда
А = иг (0) —(0)
Спр-v J Спр' 7
и окончательно
«с (0=«Спр (0+[«Спр-(°) - “Спр (°)]'</т- (,3'29)
Если до коммутации (t < 0) режим не был принужденным, то напряжение “с пр- нужно заменить напряжением ис_ (0) предшествующего режима. Тогда получим:
“С (0 = “сПр (0 + [«С- (°)-«спр (°)] e~tlx- О3’30*
Подчеркнем, что приведенные формулы (13-29) и (13-30) действительны только для напряжения на емкости.
13-9. Переходные процессы в неразветвленной цепи г, L, С
По второму закону Кирхгофа свободные напряжения на всех элементах неразветвленной цепи взаимно уравновешиваются. Поэтому для цепи (рис. 13-17), состоящей из последовательно соединенных сопротивления, индуктивности и емкости (цепи г, L, С или последовательного контура), имеем:
псв + £^- + «ссв=0, - (13-31)
344
где
iCB — dq^Jdt == C duc св/dt. (13-32)
Подставляя значение iCB в уравнение (13-31), после дифференцирования получим для иСсв дифференциальное уравнение второго порядка:
d2u~ „„ г dur 1
~df? 1" L ~~di Ь ££ «с св = 0 • (13-33)
Свободный заряд на конденсаторе удовлетворяет такому же дифференциальному уравнению: ^2?св । r . £ ___q
dt2 L dt ' LC ^CB
Дифференцируя это уравнение по времени, с учетом равенства (13-32) получим аналогичное дифференциальное уравнение для iCB:
</2<ев । r diCB । 1 • _q
dt2 L dt LC св~ •
Тождественность дифференциальных уравнений указывает на одинаковый закон изменения ИСсв, <7св и 1СВ.
Для решения любого из этих дифференциальных уравнений составим характеристическое уравнение
p2+tp+vc-q- (13-34)
Характер свободного процесса зависит только от параметров цепи г, L, С, т. е., иначе говоря, от вида корней характеристического уравнения. Так как эти корни определяются равенством
Р1,2~— 2L— — LC ’ (13-35)
то характер свободного процесса зависит от знака подкоренного выражения, который и определяет, будут ли корни вещественными или комплексными.
13-10. Апериодический разряд конденсатора
Апериодическим разрядом конденсатора, заряженного до напряжения (70, через резистор и катушку индуктивности называется разряд, при котором напряжение на конденсаторе монотонно спадает от значения (70 до нуля, т. е. не происходит перезарядки конденсатора. С энергетической точки зрения это означает, что црц разряде конденсатора отдаваемая им энергия лишь в малой Доле переходит в энергию магнитного поля катушки, а большая ее часть поглощается в резисторе. Начиная с некоторого момента ь₽емени, в тепло переходит не только оставшаяся энергия электри
345
ческого поля конденсатора, но и энергия, которая запаслась в магнитном поле катушки.
Апериодическое решение однородного дифференциального уравнения, т. е. в нашем случае апериодический характер свободного процесса (разряда конденсатора), имеет место, если корни характеристического уравнения (13-35) вещественны, т. е. если
г2/4Л2 > 1/LC
или
r>2VL/C. (13-36)
Назовем критическим сопротивлением контура такое наименьшее его сопротивление, когда свободный процесс имеет еще апериодический характер:
rKp = 2’j/L/C. (13-37)
Корни рт и вещественные и различные, если выполняется неравенство г > гкр.
Общее решение однородного дифференциального уравнения второго порядка и в частности (13-33) при различных корнях представляется в виде
ис св = А^ + А^, (13-38)
где при условии (13-36) Аг и — вещественные постоянные интегрирования, определяемые из начальных условий, а рх и р2 — вещественные и различные корни характеристического уравнения. Заметим, что корни обязательно отрицательны, так как свободный процесс должен быть затухающим во времени.
Согласно (13-32) ток
КВ = С^=С (А1Р1е^+ А2р2е^). (13-39)
При разряде конденсатора принужденное напряжение на емкости и ток равны нулю, поэтому их переходные значения равны свободным:
св» Кв-
Из начальных условий uc = Uo и i = 0 при t = 0 определим значения постоянных интегрирования. Подставляя начальные условия в равенства (13-38) и (13-39), получаем:
^о=^1+Л2; 0 = AiPi -j-А2р2, откуда
1 Р2—Р1’ 2 ' Р2-Р1'
При этих значениях постоянных интегрирования напряжение (13-38) и ток (13-39)
«с = «с (p^Plt =Лл.еР^ j {eVit - eM-==
346
Так как произведение корней р± и характеристического уравнения равно его свободному члену, т. е. prp2 — 1/LC, то
<,3'40>
Напряжение на индуктивности ul найдем по формуле
ul = uL св = L di/dt=—- р.^). (13-41)
Ря Р1
Ток и напряжения на емкости и на индуктивности состоят из двух экспоненциальных составляющих, коэффициенты затухания которых равны |pi | и |р2 | и определены равенствами (13-35).
Кривые изменения напряжений на емкости и на индуктивности тока и их составляющих приведены на рис. 13-18, а и б. Они показывают, что напряжение на емкости монотонно уменьшается с начального значения (70, а ток, возрастая от нуля, достигает максимума, а затем также уменьшается. Касательная к кривой ис в начале координат горизонтальна, так как напряжение tzc имеет максимум в начальный момент. Это следует и из второго, уже отмеченного выше начального условия i (0) = 0.
Поскольку i = С duc/dt, максимум кривой тока и точка перегиба кривой напряжения ис получаются в один и тот же момент времени tv Это время 4 можно найти, приравнивая нулю производную di/dt.
Напряжение на индуктивности изменяется от значения — (70, так как при t — 0 и ток, и напряжение на сопротивлении равны нулю и, следовательно, напряжения на емкости и на индуктивности Равны по абсолютному значению. Напряжение на индуктивности по абсолютному значению сначала уменьшается, затем проходит через нуль в момент, когда ток максимален (что следует из соотношения uL — L di/df), и возрастает до некоторого положительного Максимума, после чего уменьшается и стремится к нулю. Пока ток
347
алгебраически уменьшается (в интервале от нуля до tr), э. д. с. самоиндукции, поддерживая его, будет по закону Ленца положительной, а напряжение на индуктивности отрицательным. Когда ток начинает алгебраически возрастать, э. д. с. самоиндукции противодействует ему и будет отрицательной, а напряжение на индуктивности — положительным.
Максимум кривой ul и точка перегиба кривой i получаются в один и тот же момент времени t2, что следует в свою очередь из равенства ul = L dildt. Этот момент времени t2 можно найти, приравнивая нулю производную diiiJdt.
Отметим также влияние индуктивности на протекание процесса. Из выражений (13-35) следует, что увеличение индуктивности £ приводит к уменьшению абсолютных значений рг и р2 и, стало быть, к замедлению нарастания тока и спада напряжения на зажимах конденсатора. Наоборот, при малой индуктивности L ток растет быстро и быстро спадает напряжение на зажимах конденсатора. Такой случай фактически получается при разряде конденсатора через резистор (см. § 13-6).
13-11. Предельный случай апериодического разряда конденсатора
Предельный случай апериодического разряда конденсатора имеет место, если сопротивление контура г равно критическому гкр, т. е. корни характеристического уравнения (13-34) вещественные и равные:
Р1 = Рг = Р = — r/2L. (13-42)
Общее решение однородного дифференциального уравнения (13-33) дается в этом случае формулой
иСсв==ис = 014-^2О ept- (13-43)
На основании (13-32) для свободного тока tCB получим:
iCB = i = С (А2 +pAi + pA2t) ept. (13-44)
-При начальных условиях tzc (0) = Uo и i (0) = 0 находим постоянные интегрирования Аг = Uo, А2 = — рий. Подставляя значения и А2 в соотношения (13-43) и (13-44), получаем ток и напряжение на емкости:
«с = По (1 — pt) ept-, (13-45)
i = — Cp2Ubtepi — — tepi. (13-46)
Определим также напряжение на индуктивности:
ц£ = £^=-[/о(1+дОер£ (13-47)
Кривые изменения I, ис и ut по форме не отличаются от приве-денных на рис. 13-18, а и б. =
348
13-12. Периодический (колебательный) разряд конденсатора
Разряд будет периодическим или колебательным, если сопро-гивление контура меньше критического г < гкр, т. е. корни харак-герлогического уравнения (13-34) комплексные и сопряженные.
Обозначим в (13-35)
a = r/2L; (13-48)
®° ~ LC — 4L2 = fo ’ (13-49)
гак что
/а2 + ю2 = \/V LC, (13-50)
4 назовем ю0 — угловой частотой собственных колебаний контура, i То — периодом его собственных колебаний.
Для корней Pi и р2 получим:
Pi, 2 = — а±/ю0. (13-51)
Решение дифференциального уравнения (13-33) при комплексных корнях его характеристического уравнения удобно записать з виде
uc св = AraZ sin (юс/4-х). (13-52)
Тогда ток
tCB=CAe~at [— a sin (со0/ 4- х) + и0 cos (oV4- X)]- (13-53)
Так как переходное напряжение на емкости и ток по-прежнему равны их свободным значениям и начальные условия такие же, как в двух предыдущих случаях, то по формулам (13-52) и (13-53) получим:
t/0 = Asinx; 0 = СД (— asinx+ra0cosx).
Из последних соотношений находим:
A cosx=~(70;
ш0
tg х=®о/«; А = [/о/®о VLC;
СОо GC
sin х= “г___cosy^—д .
]/a24-cog 1 а2 + к>В
Подставляя значения A, sin х и cos х в выражения (13-52) и (13-53) и обозначая для краткости
Дсm — ULn — ~\АLC — [Д/sin х; Im = По/ГОоД
получим окончательные выражения:
ис = Uс те-ш sin (oi0t + 7.y, (13-54)
i = /mC“a* sin (nV 4-л); (13-55)
ui = UL me~al sin (<o0/ — 7J- = =(13-56)
349
Кривые изменения tzc и I даны на рис. 13-19. Ток и напряжения на емкости и на индуктивности представляются затухающими синусоидальными функциями с угловой частотой собственных колебаний контура ы0 и коэффициен-
том затухания а, причем как со0, так и а определяются только параметрами контура г, L и С. Начальная фаза х зависит также только от параметров контура, в то время как UCm, и 1т зависят и от параметров контура, и от начального напряжения на емкости. Пользуясь и для затухающих гармонических процессов понятием сдвига фаз, отметим, что ток опережает пофазе напряжение на емкости на угол л — х „ отстает от напряжения на индуктивности на угол л — х-
Кривые ис и i касаются
огибающих (на рис. 13-19
изображены пунктиром), когда синус равен единице. Строго говоря,
кривые ис и i не являются синусоидами, а только похожи на сину
соиды и максимумы их не лежат посередине между точками пере
сечения ими оси абсцисс (в пределах каждой половины периода зона возрастания ординат занимает меньше, а зона их убывания — больше четверти периода. Это объясняется тем, что в формулы входит множитель затухания е~а9-
При изучении синусоидальных (переменных) токов мгновенные значения получают, проектируя на мнимую ось векторы, длины которых равны амплитудам, и вращающиеся против направления движения стрелки часов с угловой скоростью со. Также и мгновенные значения ис, i и tz£ [формулы (13-54) — (13-56)] можно найти как
проекции на вертикальную линию
векторов Ucme~at, Im^ и ULme вращающихся с угловой скоростью соо, длины которых уменьшаются пропорционально КоН' цы этих векторов описывают не окружности, как при синусоидальных токах, а логарифмические спирали. Таким образом, ДЛЯ
350
затухающих синусоидальных колебаний может быть построена векторная диаграмма, приведенная на рис. 13-20. Эта диаграмма наглядно показывает, что напряжение на емкости отстает от тока на угол зт — %, а напряжение на индуктивности опережает ток на угол л — %. При этом радиусы-векторы Uim, lmf и ^Cm> складываясь геометрически, образуют равнобедренный треугольник не только в начальный момент времени
лв+во+од=о,
но и в любой следующий момент
Л^+ЖО4-ОЛ = 0.
Полученные равенства, естественно, вытекают из второго закона Кирхгофа для мгновенных значений
И/. св Ч- Ф" «С св 0*
Быстроту затухания рассматриваемых колебаний характеризуют отношением напряжений в моменты времени tn t + То:
«с('+го) t/cwe_a<' + r°)sin[%(;+ro)+x]
Это отношение, называемое декрементом колебания, — постоянная величина, не зависящая от времени t, а зави-
сящая лишь от параметров цепи г, L, С.
Часто быстроту затухания колебаний характеризуют натуральным логарифмом этого отношения
. иг (0
4-|"дат=“!'> (13-57>
который называется логарифмическим декрементом колебания. Если кривая затухает медленно, то отношение ее значений, отстоящих на время То друг от Друга, близко к единице, лога-
Рис. 13-21.
рифмический декремент близок к нулю и логарифмическая спираль закручивается медленно. Если же затухание значительное,то логарифмическая спираль закручивается весьма быстро.
На рис. 13-21 представлены кривые изменения отношения амплитуд колебаний в конце 1, 2, 3-го и т. д. периодов к начальной амплитуде, построенные для разных значений логарифмического Декремента Д.
351
Сопротивление г оказывает существенное влияние на скорость затухания колебательного разряда емкости. Кроме того, как показывает равенство (13-49), по мере увеличения сопротивления г уменьшается частота собственных колебаний соо и увеличивается их период То. Когда г достигнет значения гкр, частота собственных колебаний будет равна нулю, период То — бесконечности, что соответствует апериодическому разряду.
При колебательном разряде конденсатора через идеальную катушку (г — 0) получим:
®о=1/К^С'; tgx = oo; х = л/2; а=0, (13-58)
т. е. затухание процесса равно нулю, а частота собственных колебаний имеет наибольшее возможное значение и равна резонансной частоте последовательного контура.
Из равенств (13-54) — (13-56) следует, что ис, I и ид будут изменяться гармонически с угловой частотой соо:
нс == Uо sin (со0/ + л/2);
~^sin(6V + jr);
Uz = £/0 sin (ft>(/--л/2).
i
Ток i отстает по фазе на л/2 от напряжения на индуктивности
и опережает на л/2 напряжение на емкости. Поскольку сопротивле-
ние отсутствует, первоначальный запас энергии остается неизменным и энергия попеременно переходит из электрического поля в магнитное, и наоборот.
13-13. Включение цепи г, L, С на постоянное напряжение
Рис. 13-22. Условимся называть контур г, L, С (рис.
13-22) апериодическим, если каждая из со-
ставляющих его свободного тока изменяется по экспоненциаль-
ному закону.
Сравнивая включение апериодического контура г, L, С на постоянное напряжение U с апериодическим разрядом емкости (§ 13-10), заключаем, что принужденный ток по-прежнему равен нулю, а принужденное напряжение на емкости теперь равно не нулю, a U-Поэтому в отличие от апериодического разряда емкости теперь пссв (0) = — U, т. е. знаки коэффициентов Лх и А2 изменяются на обратные. Переходные напряжение на емкости, ток и напряжение на индуктивности
ис = U+~~ <№Р1( - р^);
Pl Pi
i и— iePit — epst);
O(Pi—p2)v 7
UL = ^ePj ~ P^-
Pl Рч
(13-59)
(13-60)
(13-6П
352
Кривые Uc, i и Ul даны на рис. 13-23. Напряжение на емкости монотонно возрастает от нуля до напряжения источника U, причем точка перегиба кривой при t = получается в момент, когда ток достигает максимального значения. Касательная к кривой Uc в начальный момент 1 = 0 горизонтальна, так как ток в начальный момент равен нулю. Кривые тока i и напряжения и^ по характеру такие же, как и в § 13-10.
Включение цепи г, L, С на постоянное напряжение при г = гкР исследуется аналогично рассмотренному в § 13-11.
Будем называть колебательным контуром цепь г, L, С, свободный ток которой изменяется по затухающему синусоидальному закону.
Сравнивая включение колебательного контура г, L, С с колебательным разрядом емкости, заключаем, что свободные напряжения и ток в рассматриваемом случае изменяются так же, как
при колебательном разряде, только теперь иСсв (0) = —U и знак коэффициента А изменяется на обратный. Поэтому, как было показано выше, знаки свободных напряжений на емкости (13-54) и на индуктивности (13-56) и тока (13-55) тоже изменяются на обратные:
«с = ис пР + ис св=U----e~af sin (соо/ -ф х); (13-62)
(0q у
i=tCB=—4-e-01* sin ©о/; (13-63)
(Ооь
«£= — UL св=erat s in (aot - x). (13-64)
Кривые тока и напряжения на емкости даны на рис. 13-24. Ток совершает затухающие колебания относительного нулевого значения. Напряжение на емкости колеблется около своего принужденного значения U и не может превзойти 2U. Оно достигает наибольшего значения примерно через половину периода после включения цепи. Этим пользуются в импульсной технике для получения напряжения на конденсаторе, равного двойному значению напряжения источника питания. Колебательный контур г, L, С с определенной частотой включают на постоянное напряжение и отключают. Соответственно с той же частотой на зажимах конденсатора образуются импульсы напряжения, величина которых почти вдвое больше напряжения источника питания.
Так же как и при колебательном разряде емкости, заслуживает внимания случай включения на постоянное напряжение идеаль-
12 Основы теории цепей
353
кого колебательного контура (г = 0). В этом случае выполняются равенства (13-58). Поэтому из (13-62) — (13-64) для тока и напряжений на емкости и индуктивности имеем:
процесса, перейдет в„тепло, а
ис = и — U c.os eV;
и .
t = 77=,smcooZ; uL = U cos &ot.
Ток и напряжение на емкости изменяются гармонически с частотой свободных колебаний <в0. При этом напряжение на емкости колеблется от 0 до 2U.
С энергетической точки зрения процесс включения цепи г, L, С на постоянное напряжение интересен тем, что при любых г, L, С половина энергии, полученной от источника за время переходного другая половина запасется в элек-
трическом поле конденсатора.
Действительно, энергия, поступающая от источника:
оо со оо 0 U
^Uidt = ^ (uri + Uii 4- uci) dt=\ ri2 dt + § Li di + § Cue due oo ooo
или
U oo
с г Cl]
U \ Cduc=CU2= ri2dt + ^
о 0
т. e.
C *2 CU* \ ri2 dt = -^~.
о
Как частный случай, из доказанного следует, что те же самые энергетические соотношения будут иметь место и при L = 0, т. е. при включении цепи г, С на постоянное напряжение.
Аналогично рассматриваются явления, возникающие при включении апериодического и колебательного контуров г, L, С на синусоидальное напряжение и = Um sin (coz' + ty).
13-14. Общий случай расчета переходных процессов классическим методом
Рассмотрим общую методику расчета переходного процесса на примере разветвленной цепи, в состав которой входят хотя бы по одному разу элементы г, L, С и источники постоянной или гармони-
354
Рис. 13-25.
ческой э. д. с. или тока (рис. 13-25). Рассчитаем токи во всех ветвях и напряжения на всех ее элементах в переходном процессе при включении рубильника Ps.
Для этого прежде всего определим принужденные токи и напряжения до и после коммутации. Поскольку Э. Д. С. ИЛИ ТОКИ ИСТОЧНИКОВ предполагаются постоянными или гармоническими, расчет принужденных режимов до и после коммутации выполним одним из известных методов.
Определение свободных токов и напряжений начнем с составления характеристического уравнения.
Для этой цели (разумеется, при замкнутом рубильнике Р3) воспользуемся, например, методом контурных токов применительно к мгновенным значениям свободных составляющих:
(О + Гз)Йсв + ^ Йсв^ —^2св==0;
— гзйсв + (Г2 + rs) hzs + ^2 i-2VB dt=O.
Введем обозначения ru, r22, L22 и Сц, С22 — сопротивления, индуктивности и емкости каждого из контуров: г12 — общее сопротивление двух соседних контуров.
С учетом этих обозначений последние уравнения примут вид:
гИ11св 4
1
Сц
Пев dt 4" ^*12^*2св 6>
r21/1СВ 4" Г22*2св + ^22 Д/Д
^2св dt 0.
(13-65а)
(13-656)
£ С22
Решение системы уравнений (13-65а) и (13-656) для любого из токов z1CB или z2cB представляется в общем случае в виде суммы экспоненциальных функций, каждая пара которых, имеющая одинаковые показатели, должна удовлетворять этим уравнениям. Поэтому дальнейшие рассуждения проведем для любой из пар:
iiCB = 4'e^; 12СЕ = Л"еД,
Тогда
%"==Р4'^ = я1СЕ; ^ = р/2св; $Йсв^ = |Л'^ = ^;
2*
355
Подставляя значения производных и интегралов токов ilc t2CB в уравнение (13-65), получаем: Е’
(гп + 1 /рСц) Ьсв + г121'гсв = 0; (13-66а)
r2111СВ 4~ ^22 4“ Р^22 + рС22_) 1'2св ~ (13-666)
Дифференциальные уравнения (13-65а) и (13-656) относительно функций i1CB, /2СВ превратились в алгебраические [(13-66а) и (13-666)] относительно этих же функций. Такое преобразование называется алгебра и зац и ей системы дифференциальных уравнений.
Полученная система двух однородных уравнений (13-66) с двумя неизвестными i1CB, i2CB имеет решение, отличное от нулевого, если определитель системы равен нулю:
Д(/7) =
Г22 4- Р^22 4
1
РС22
(13-67а)
(нулевое решение iJCB = i2CE = 0 означает отсутствие свободного процесса, что возможно в частном случае и притом только в цепях, описываемых дифференциальными уравнениями первого порядка).
Из (13-67а) следует, что р является корнем уравнения Д (р) = 0. Само же уравнение
Д(р)=0 (13-676)
представляет собой характеристическое уравнение для данной системы дифференциальных уравнений. В рассматриваемом примере получаем характеристическое уравнение третьей степени.
Решение уравнения Д (р) = 0 (точное или приближенное) производится по обычным правилам алгебры. Поэтому его корни pi, р2 и Pi в дальнейшем будем считать известными.
Выбор контуров при расчете методом контурных токов здесь целесообразно делать так, чтобы для каждого из контуров порядок дифференциального уравнения был наименьшим В качестве таких контуров нужно выбирать по возможности контуры, содержащие только сопротивления, только индуктивности, только емкости, только сопротивления и индуктивности или только сопротивления и емкости В самом деле, уравнение второго закона Кирхгофа для свободных токов в контуре с одними сопротивлениями является алгебраическим Для контура с одними индуктивностями оно хотя и дифференциальное, но интегрированием легко приводится к алгебраическому В контуре с одними емкостями оно интегральное, но дифференцированием приводится к алгебраическому Наконец, для контуров с сопротивлениями и индуктивностями или с сопротивлениями и емкостями получаем дифференциальные уравнения первого порядка Кроме того, контуры, конечно, надо выбирать так, чтобы уравнения по второму закону Кирхгофа были независимыми Тогда порядок дифференциального уравнения относительно одной неизвестной функции и степень характеристического уравнения цепи будут равны сумме порядков дифференциальных уравнений отдельных контуров.
Степень характеристического уравнения цепи можно нанги/не составляя и не раскрывая определитель системы дифференциальных уравнении Например, тля кепи рис 13-25 выберем контуры так. чтобы второй включал индуктивность Т2 и емкость С2, а первый — только емкость Сх 1огда порядок дифф6'
356
енЦиального уравнения для второго контура равен двум, а для первого — единице Следовательно, степень характеристического уравнения цепи равна трем 11 В общем случае, когда цепь разбивается указанным выше способом на п контуров и каждый контур содержит в своем составе индуктивность и емкость, степень характеристического уравнения цепи будет 2 п
Составить определитель Д (р) в общем случае можно следующим образом Рассматривая коэффициенты при свободных контурных токах Исе 11 j2cb в равенствах (13-66а) и (13-666), видим, что они записаны как комплексные сопротивления тех же контуров, но с заменой /и на р Например, комплексное сопротивление второго контура ^22 Г22 ф- Z.22 4~ ^ //
заменяется величиной
^22 (р) — Г22 "Г“ Р^22 4" МрС22.
Следовательно, определитель системы может быть составлен подобно тому, как это делается при расчете цепей переменного тока методом контурных токов.
Как будет показано ниже (§14-3), можно записать в зависимости от р входное сопротивление цепи (рис 13-25) для любой из ветвей, например первой
7 (пХ____.7 (пХ I ^2 (Р) (Р)
/1Бх(р) А(Р)+ z2(p)+zs(p)
и, приравняв его нулю, сразу получить характеристическое уравнение цепи При этом легко убедиться, что числители входных сопротивлений любой из ветвей будут одинаковы. Поэтому для получения характеристического уравнения можно составить любое из входных сопротивлений Z1EX (р), Z2BX (р) или Z3BX (р).
Найдя корни характеристического уравнения системы, напишем общие выражения для каждого из контурных токов.
Рассмотрим несколько случаев.
а) корни ръ р2 и ра вещественные и различные:
Йсв = + А^ + А
б) корни pi, р2 и ра вещественные и равные, т е. р2 — р2 — р3 — = р
йсв = (414- A2t 4- 43/2) ept‘,
в) корень рг — вещественный, а корни р2 и р3 — комплексные и сопряженные, т е. р2 = —а ф- /со, ра = —а — /со,
lie == Агер^ ф- (Л2 cos at ф- А3 sin со/) е~а/.
Поскольку порядок расчета не зависит от вида корней характеристического уравнения, рассмотрим в дальнейшем первый случай.
Выберем произвольно положительные направления свободных токов в ветвях схемы (рис. 13-25) Целесообразно (но, разумеется, нс обязательно), когда это возможно, выбрать их совпадающими с принятыми ранее положительными направлениями контурных Токов (например, токи 11сз и i2CB в ветвях 1 и 2).
357
Далее запишем выражение переходного тока, например, ветви 1:
h = imp + iicB = iinP + Л iepit + A + A (13-68)
и покажем, как определить постоянные интегрирования Alt А2 и А3 Для этого дважды продифференцируем (13-68) и подставим t = 0 в (13-68) и в полученные дифференцированием выражения:
i'i (0) — z11Ip (0) -J- Ai Ц- А2 -p-Zlg;
t'i (0) = finp (0) + р1Л1 + /?2Л2 + /7зЛ3;
ii (0) = iwP (OJ + P^ + plAz + p^.
(13-69)
Так как значения принужденного тока zlnp и его производных при t — 0, а также корни характеристического уравнения рг и р3 известны, то из уравнений (13-69) можно найти Alt А2, А3, если известны значения тока 1г и его производных t( и при t — 0. Для вычисления /ДО), z{ (0) и t’{ (0) запишем уравнения первого и второго законов Кирхгофа для токов ветвей:
z’i — ^*2 4“ is» (13-70а)
fiZi 4-Wei 4" = (13-706)
где == C^dticJdP,
r2,l2-\~L2 4~ иС2 — rsis — 0, (13-70в)
где i2 = С2 duC2/dt.
По законам коммутации токи в ветвях с индуктивностью и напряжения на емкостях в момент коммутации скачком не изменяются. Следовательно, в системе (13-70а)—(13-70в) при t = 0 значения z2(0), zzC1(O) 11 «С2 (0) известны. Тогда из первых двух уравнений (13-70) находим zx (0) и z3 (0).
Затем продифференцируем уравнения (13-70а) и (13-706) и перепишем уравнение (13-70в):
di^dt ~ dijdt 4- di3ldt\ (13-71a)
dt + Ct + dt dt ’ (13-716)
r2ia 4“ ^2 4" — rah ~ 0- (13-71B)
Рассматривая систему уравнений (13-71а)—(13-71в) для t = 0 и учитывая, что в ней известны начальные значения всех токов, а также ei (0) и иС2(0), из уравнения (13-71в) находим t'2 (0), а из первых двух t'i (0) и 1з (0).
Дифференцируя еще раз эту систему, получаем:
d2ti ____d2i2 d2l3
"dt2
d2i, 1 dZ, ri~dP+c^ + r.
din . r d2t2 , ij dt +Z'2 'di2 + C2
(13-72a)
(13-726)
(13-72b)
d2ia _d2e1
~d& ~ 'dF’
-r -s л
dt~-V-
358
рассматривая систему (13-72а)—(13-72в) для t = 0 и зная начальные значения всех токов и их первых производных, из уравнения /13-72в) находим % (0), а из первых двух (0) и 1'3 (0).
' "Теперь легко найти постоянные интегрирования А1г А2, А3 й3 системы уравнений (13-69).
В общем случае для дифференциальных уравнений, определитель Л (р) которых п-го порядка, при вычислении постоянных
интегрирования нужно предварительно определить начальные значения искомой величины и ее п — 1 производных.
Из подобных же уравнений определяются постоянные интегрирования, например, для тока i2, если его нельзя найти из уравнений Кирхгофа по найденному току i\. Впро-
Рис. 13-26.
чем, часто это можно сделать.
Например, для схемы, изображенной на рис. 13-25, следует после определения тока найти напряжение на зажимах ветви 1 и по нему ток ia. Затем по первому закону Кирхгофа легко найти ток /а.
Пример 13-3. Найти токи i, i, и i2 в цепи (рис 13-26) после выключения рубильника, если известны R = 30 Ом, г = 10 Ом, L — 9-10~2 Г, С = 9- 10-4 Ф, и = 180 sin (300 t+ 45°) В.
Решение. Найдем ток i и напряжение uL на индуктивности в принужденном режиме до коммутации
/пр_=-----= 3> 14+/°>40 А>
z+ Z-J+Z,
где
Z=R + /coL; Z1=l//coC; Z2=r/2;
inp_ = 4,48sin(300(+7o20') A;
Hip- (°) = 4,48 sin 7°20' = 0,574 A;
^р- = 'п»-т|&-6’5-'6'8
(7C
4np-=—7^— = 1 >3 — /1,36 A;
^np- = 4p-/“L = - 10,9+j85 B;
«inp_= 121,3 sin (300?+97°20')B; uinp_(0) = 120,3 B.
Найдем все токи в принужденном режиме после коммутации:
/пр=-----^7-= 3,21 + /0,44 А,
z+^+ir
359
где Z; = г;
Ч=/пр7^ё=-3,04 28°48' Ь
U = ’.65^-63^05' А;
»пр = 4,58 sin (300;ф- 7°45') A; inp (0) = 4,58 sin 7'-45' =0,618 А.
Переходим к расчету переходных токов.
Разбйв схему на контуры, как показано на рис. 13-26, составим уравнения для свободных контурных токов:
(Я+О ^асв + L dieCB/^+rt6cB — 0;
^*асв~1~г1*&свЧ dt=Q.
Алгебраизуя эту систему дифференциальных уравнений, получаем:
(40ф-9 • 10 sp) iOCB+ 10ibCB = 0; 10ieCE-}-^10-}-^—g—^-j^ ibCE = 0.
Характеристическое уравнение составим, приравняв нулю определитель этой системы однородных алгебраических уравнений:
40+9-10-2р 10
или
81 • 10-вр2 + Зб. 10-3рф-4=0.
Корни его
Pi = Pz==P=— 222 с'1.
Напишем сначала выражение для тока i:
i = I пр + iCB = 4,58 sin (300;ф-7°45') ф- (Atф-Аф) e~^.
В момент коммутации (t = 0) ток в индуктивности не изменяется скачком. Поэтому
i (0) = »пр_ (0) = 0,574=0,618+Л, откуда
Aj = —0,044 А.
Так как при t= 0 не изменяется скачком напряжение на конденсаторе ис, то, как видно из схемы рис. 13-26, не изменится скачком и напряжение на индуктивности Ид, что позволяет сразу найти (L dildt)t=Q.
uL (0) = нХпр_ (0) = 120,3 = (L dildt)t_0 = = 9 • 10-2 (4,58 • 300 cos 7°45' ф- 0,044 - 222 ф- A2),
откуда A2 — — 35, 76 A/c.
Окончательно для i получаем:
i = 4,58 sin (300;ф-7°45') — (0,044 ф- 35,760 e~^f A.
Составив для внешнего контура схемы рис. 13-26 уравнение второго закона Кирхгофа для свободных токов
0=PiСЕ ф- L di^fdt ф- п*2СЕ,
360
найдем, что
«2св = -°>1 (30iCB + 9.10-2*-CB/<ft) = (0,366+35,76/) А.
Тогда
Йсв=*св-«'2св=-(0,41+71,52/)е-222' А.
Теперь запишем переходные токи i2 и ц:
12=»2пр+»2св= 1,65 Sin (300/—63°05') + (0,366 + 35,760 е“222/ А;
i1=ilnp+i1CB = 4,325 sin (300/+28°48') — (0,41 +71,52/) е~^ А.
13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля)
Пусть к источнику непрерывно изменяющегося напряжения и (/) (рис. 13-27) подключается произвольный пассивный линейный двухполюсник (рис. 13-28). Требуется найти ток i (t) или напряже-
ние в любой ветви ив (/) двухполюсника после включения рубильника.
Рис. 13-28.
Рис. 13-27.
Задачу решим в два приема. Сначала найдем искомую величину при включении двухполюсника на единичный скачок напряжения (т. е. когда включаемое напряжение постоянно и по величине равно единице). Эти ток /х (f) или напряжение «В1 (/) могут быть выражены так:
’М0=г^(0=^(0; (13.73)
«bi (0 = 1 • y(t) =у (0-
Функция g (/), численно равная току, называется переходной проводимостью, а функция у (t), численно равная напряжению, называется переходной функцией напряжения.
Обе эти функции называются временными функция-м и или временными характеристиками и часто обозначаются через h (t).
Например, для цепи г, L переходная проводимость
i • ^(0==+(1-е_г/)
к для цепи г, С переходная функция напряжения на емкости
361
Переходную проводимость g (t) и переходную функцию напр» жения у (/) при любой схеме пассивного двухполюсника можно най" ти классическим методом (или операторным методом, или методом интеграла Фурье — см. ниже). Таким образом, в дальнейших рас четах g (0 и у (/) будем считать известными.
Так как включается пассивный двухполюсник, то при t g токи и напряжения в любой ветви равны нулю. Поэтому при t g следует считать любую переходную проводимость g (t) = 0 и любую переходную функцию напряжения у (t) = 0.
Все дальнейшие рассуждения проведем для случая, когда нужно рассчитать ток.
Непрерывно изменяющееся напряжение и (f) заменим ступенчатой функцией с элементарными прямоугольными скачками Ди. Тогда процесс изменения напряжения можно представить как включение при t = 0 постоянного напряжения и (0), а затем как включение элементарных постоянных напряжений Ди, смещенных друГ относительно друга на интервалы времени Дт и имеющих знак плюс или минус, смотря по тому, рассматривается возрастающая или падающая ветвь заданной кривой напряжения.
Составляющая искомого тока в момент t от постоянного напряжения и (0) равна и (0) g (t). Составляющая тока в момент t от элементарного скачка напряжения Ди, включаемого в момент времени т (рнс. 13-27), равна Ди g (t — т). Здесь аргументом переходной проводимости служит время (t — т), поскольку элементарный скачок напряжения Ди начинает действовать на время т позднее включения рубильника или, иначе говоря, поскольку промежуток времени между моментом т начала действия этого скачка и моментом времени t равен t — т.
Элементарный скачок напряжения Ди может быть выражен следующим образом (рис. 13-27):
Дм?=^Дт tga—Дт и' (т).
Поэтому искомая составляющая тока
Ди g (Z — т) = и' (т) Дт g (t — т).
Элементарные скачки напряжения включаются на интервале времени от t — 0 до момента t, для которого определяется искомый ток. Поэтому, суммируя составляющие тока от всех скачков, переходя к пределу при Дт -> 0 и учитывая составляющую тока от начального скачка напряжения и (0), получаем:
t
i (/) =и (0)g (0 + §«' (T)g (t — T)dr. (13-74)
о
Последняя формула для определения тока при непрерывном изменении приложенного напряжения называется формулой или интегралом Дюамепя Выражение (13-74) называют первой формой записи формулы Дюамеля. ~
362
(13-75)
Из теории определенных интегралов известно, что для любых двух функций (/) и f2 Й существует соотношение " t t
j fi (<—I) f2 (?) dt = Д (т) Ъ (i—t) dr, b b
pOe легко проверить заменой переменной интегрирования.
К На основании (13-75) перепишем выражение (13-74) и получим вторую форму записи формулы Дюамеля:
i (0=и (0) g (/) Д- j и' (t—т) g (т) dt, b
где и' — г) — производная функция и (t — т) по ее аргументу t — т или, что то Же самое, ее производная по t.
Интегрируя по частям в правой части равенства (13-74), получаем:
(g (^—т) и' (т) dt—g (0) и (t)—g (t) и (0) +j g' (i—t) и (т) dt, о о
где g’ (i — г) — производная функция g (t — т) по ее аргументу I — т или, что тоже самое, ее производная по I
Подставляя значение полученного интеграла в правую часть равенства (13-74), получаем третью форму записи формулы Дюамеля:
t
i (°) “ (0 + $ g' (t-x) и СО dx. о
Применяя формулу (13-75) к интегралу правой части последнего выражения, получим четвертую форму записи формулы Дюамеля:
i (/)=g (0) »(/) +J g' (т) и (t—t) dt.
о
Далее легко видеть, что выполнением дифференцирования выражение t
u(t-t)g(t)dr
б
приводится к первой или второй формам Оно представляет собой пятую форму записи формулы Дюамеля. Наконец, шестая форма записи формулы Дюамеля
t
о
выполнением дифференцирования приводится к третьей или четвертой формам.
Ту или иную из полученных первых четырех форм выбирают, руководствуясь Удобством и простотой выполнения вычислений. Следует отдать предпочтение той из первых четырех форм записи формулы Дюамеля, для которой будет проще подынтегральное выражение и которая имеет меньше слагаемых, что зависит от Условий конкретной задачи.
Кроме того, если напряжение, воздействующее на цепь, изменяется с нуля, е и (0) = 0, то первые слагаемые в первой и второй формах записи формулы мюамеля равны нулю и их выражения несколько упрощаются. Если в ветви, которой определяется ток, последний не может изменяться скачком, то g (0) — 0. f Ри этом первое слагаемое в третьей и четвертой формах записи формулы Дюамеля Р вно нулю, поэтому они также несколько упрощаются.
fa 4ЯТая и шестая формы представляют собой сокращенную запись первой- или . Рои и соответственно третьей или четвертой форм.
363
13-16. Включение пассивного двухполюсника на напряжение любой формы
В дальнейшем под любой формой напряжения будем понимать
его изменение, определяемое кусочно-аналитической функцией, т. е.
функцией, аналитически заданной на каждом конечном интервале
и имеющей в точках стыка интервалов разрывы непрерывности первого рода.
Пусть произвольный пассивный двухполюсник подключается к источнику напряжения, кривая изменения которого дана на рис.13-29. Для вычисления тока определим, как и выше, переходную проводимость g (Z).
Так как в промежутке О t - включаемое напряжение
задано функцией (t), то, воспользовавшись первой формой записи формулы Дюамеля (13-74), можем написать для этого промежутка
времени:
t
i (t) = tzi (0) g (0 4- $ u'i (t) g (t - t) dx. о
(13-76)
В следующем промежутке t t2 напряжение задано другой функцией и2 (t), причем в момент 1\ оно изменяется скачком от величины u-l (/,) до величины и2 (Zt). Для учета скачка напряжения в точке t = будем считать, что в этот момент к двухполюснику прикладывается отрицательное постоянное напряжение, равное u3 (Zj) —щ (lt). Кроме того, учтем составляющие тока от начального скачка напряжения (0) и от элементарных скачков напряжения, определяемого кривой (/) и действующего от t = 0 до t = tt.
Тогда получим:
ti
i (t) = Ut (0) g (t) + u[ (t) g (t - t) dx +
0
t
+ [«2 (ti) - «1 (4)] g (t - ti) + (t) g (t - t) dx. (13-77)
it
В этом равенстве в третьем члене аргументом переходной проводимости служит величина t — tr, так как напряжение и2 (4) — ui включается в момент Аргумент t — х переходной проводимости g в обоих интегралах один и тот же, поскольку он имеет смысл промежутка времени, прошедшего от включения элементарного скачка напряжения Ли до рассматриваемого момента времени t (рис. 13-27). Однако, разумеется. пределы изменепия Z в обоих интегралах раз-личны.
364
(13-79)
Если скачок тока принципиально возможен, то g (0) #= 0. Тогда скачок напряжения в момент t = tL от величины щ (/х) до величины w2 (^i) вь130вет’ разумеется, и скачок тока
(Ai)/=Z1 = [u2 (tj- U1 (MW). (13-78)
Если скачка чока быть не может, то g (0) = 0 и по формуле (13-78) в момент времени t =tr также и (At)/ = /, = 0, несмотря на на-дачие в этот момент скачка напряжения.
Наконец, для промежутка времени /2 t < оо учтем, что в момент t = /2 включается постоянное напряжение —tz2 (^2) и что элементарные скачки, определяемые кривой напряжения tz2 (t), действуют до момента времени t = t2. Поэтому
i (/) = tii (0) g (0 + $ «I (т) g (t - т) dx + [tz2 (M - tzi (0] g (t - ti) +
0
^2
+ 5 Ui(x)g(t-x)dx — u2 (t2)g(t-t2).
Рациональнее, однако, воспользоваться для решения этой задачи третьей формой записи формулы Дюамеля. Для промежутка времени 0 sg t согласно третьей форме записи формулы Дюамеля имеем:
t
i (0 = g (°) «1 (0 + j S' (t—т) Ul (Т) dx. b
Сравнивая последнее равенство с (13-76), заключаем, что для этого промежутка времени третья форма записи преимуществ не дает.
Для следующего промежутка времени /х t t2 сначала преобразуем интегрированием по частям входящие в (13-77) интегралы:
Л 4
\ (г) g (/ — т) dx=g (t — td ut (id—g (t) ut (0) + ) g' (t—t) ux (r) dx-,
b b
t r
j «2 (?) g (t—x) dx = g(O) u2 (l)—g (t—td u2 (td + )' g' (i—T) u2 (t) dx.
4 4
Подставляя полученные значения интегралов в (13-77), будем иметь после простых преобразований для промежутка t2:
4 t
i (t)=g (0) и2 (0+J g' (i—i) Ui (т) t/т 4- J g' (i—x) u2 (t) dx. 0 4
Здесь внеинтегральный член и интегралы записаны согласно третьей форме записи формулы Дюамеля. Легко видеть, что расчет тока i (/) по последней формуле несколько проще его расчета по формуле (13-77), так как в (13-77) нужно учитывать еще одно дополнительное слагаемое [и2 (/х) — их (4)] g (/ — 4)- Разумеется, эти выводы будут правильны, если подынтегральные выражения в (13-77) и в последнем выражении примерно одинаковой сложности.
Аналогично для промежутка /2 sg: / < оо
G h
/ (0=J g’ (t—i) «1(T) dx+ J g' (t—x) u2 (t) dx. о ti
z.n Легко видеть, что расчет тока i (f) по этой формуле проще, чем по формуле '*“'9), так как в последней нужно учитывать три дополнительных слагаемых,— ^словленных скачками приложенного напряжения в моменты t = 0, /х, t2.
365
Преимущества третьей формы Записи формулы Дюамеля тем более ощутимы чем больше разрывов непрерывности первого рода у приложенного напряжения’ на заданном промежутке его действия.
О
Рис. 13-30.
Рассмотрим, наконец, переходные процессы при включении произвольного активного двухполюсника к напряжению любой формы.
Найдем ток i в любой ветви активного двухполюсника (в частности, и в ветви рубильника). Расчет проведем по принципу наложе-. , ния. Сначала будем считать двухполюс-
-1 v ник пассивным, т. е. учтем только
включаемое напряжение и (I). Расчет t тока при этом проведем по формулам Дюамеля. Затем учтем только источники активного двухполюсника, т. е. найдем ток в той же ветви при замыкании накоротко зажимов источника напряжения и ((). Расчет тока в этом случае
выполним, например, классическим методом (см. § 13-14). Суммируя найденные составляющие токи, получаем искомый ток.
Отметим еще, что при подаче на вход активного двухполюсника ряда импульсов напряжения (рис. 13-30) расчет токов в любой ветви также можно провести при помощи формулы Дюамеля.
При действии последовательности прямоугольных импульсов расчет можно вести и без применения формулы Дюамеля. В самом деле, для учета действия любого прямоугольного импульса можно считать, что в момент начала его действия включается постоянное напряжение, равное по величине напряжению импульса, а в момент окончания действия импульса включается такое же постоянное напряжение, но противоположное по знаку.
Пример 13-4. Найти ток в индуктивности (рис. 13-31) для промежутков времени 0 sg t 2,5 мс и / 2,5 мс, если гх = 2 Ом, г2 = 5 Ом, L = 4 мГ. Форма
кривой приложенного напряжения задана (рис. 13-32),
Рис. 13-31.
Решение. Переходную проводимость для ветви с индуктивностью найдем по формуле (13-17)
&(0=Дпр+[дпр-(0)-Дпр(0)]е-//т, .
гДе ДпР=°’6 А- Дпр-=ДпР-(°)=и- ”
366
Постоянную времени т найдем по формуле (13-16):
V2_______
гх + г2 357
Тогда
g (И = 0,5 (l — e-ss’O См.
Уравнение приложенного напряжения (рис. 13-32)
«(0=100(1—8000 В.
Применяя первую форму записи формулы Дюамеля для промежутка 0 sg t 2,5 мс, получаем: t
iL (t) = u(O) g(0 + jg(^-T) и' (т) dT= 162-4 104/- 162г-357Г д. О
Проверяя, убеждаемся, что iL (0) = 0..
Для промежутка времени = 2,5 мс t оо -записываем:
4
i£(O = «(O)g(O+j g(t—x)u'(x)dx — u{tl)g{t — t1) (а)
о
и получаем:
iL(0=—Не-35’< А.
При 1= /, ток iL измениться не должен, несмотря на скачок приложенного напряжения. Проверяя, убеждаемся, что
‘1С1-°) = Т(^1+0) = -4.5 А.
Кривая тока iL приведена на рис. 13-33.
Заметим, что попытка применить для вычисления тока i£ (0 в промежутке 2,5 мс sg t < оо вторую форму записи формулы Дюамеля, когда интеграл
^£(/—т) и'(т) с/т в правой части равенства (а) был бы заменен интегралом о г,
\ g(x) и’(t—x) dx, дает неправильный результат. Действительно, из ра-b
вепства (13-75) следует, что эти интегралы равны только при верхних пределах t. если же верхний предел равен то
/, t
\ g (i—t) и' (т) dx — \ S (т) и' dx, b - t — tt
откуда и следует для промежутка 2,5 мс < оо выражение тока iL (f) по второй Форме записи формулы Дюамеля:
t
J/(0 = н(0)я(/)+ g(r)u' (/ — т)с/т — H(A)g(/ — /,)
t-h
367
13-17. Временная и импульсная переходные характеристики
В линейной теории автоматического управления и в других дисциплинах часто пользуются понятиями временной и импульсной переходной характеристики какой-либо системы или цепи. Первая из них введена в § 13-15 для двухполюсника. Последняя называется иначе весовой функцией системы или цепи.
!—• Временной характер ист и-
к о й, например, четырехполюсника назы-t вается реакция (напряжение или ток) на вы-д -* ходе при приложении ко входу единичного ступенчатого воздействия.
Рис 13-34. Единичный скачок (или единичное ступен-
чатое воздействие) задается единичной функцией 1 (f), изображенной на рис. 13-34, и представляет собой с точки зрения теории электрических цепей единичное постоянное напряжение или ток, включаемые на вход цепи или системы в момент t = 0, так что
О при t < 0;
1 при 0.
(13-80)
Если определяется ток, то в соответствии с § 13-15 временная функция h (t) совпадает с переходной проводимостью g (/), т. е.
h(t)=g(t),
(13-81)
а если определяется напряжение, то она совпадает с переходной функцией напряжения у (I), т. е.
- (13-82)
Понятие временной характеристики, как реакции системы (или как выходной величины, за которую может быть принята любая из функций системы) на единичное ступенчатое воздействие, приложенное к ее входу (причем, за вход системы может быть принята любая точка, ветвь или два ее зажима), применимо не только к электрическим цепям, но и к любым физическим системам — механическим, пневматическим, гидравлическим, электромеханическим и т. д.
Таким образом, временные характеристики цепей г, L; г, С', г, L, С, если, например, в качестве выходной величины выбраны токи, даются формулами (13-12), (13-25), (13-60), (13-63) при U = 1, а если выбраны напряжения на емкостях, то формулами (13-24), (13-59), (13-62) также при U = 1.
Временная характеристика введена в основном по двум причинам:
1. Единичное ступенчатое воздействие 1 (t)—скачкообразное и поэтому довольно тяжелое для любой системы внешнее воздействие. Следовательно, важно знать реакцию системы именно при та
368
ком воздействии. Ийые, например, всевозможные плавные воздействия будут для системы легче.
2. Если определена характеристика h (/), то при помощи интеграла Дюамеля (см. § 13-15 и 13-16) с учетом равенств (13-81) и (13-82) можно определить реакцию системы при любой форме внешних воздействий.
Выше были определены переходные процессы в цепях г, L и г, С также при гармонических внешних воздействиях. Это делалось потому, что гармонические воздействия очень часто встречаются в электротехнике. Но, разумеется, реакции любых цепей на приложенные к их входу гармонические внешние воздействия можно найти и по известным временным характеристикам h (f) при помощи интеграла Дюамеля.
Существует еще один вид внешнего воздействия, называемый единичным импульсом, дельта-функцией 6 (t) или функцией Дирака, которое определяется как производная по времени единичной функции
' 8 (t) — dl(t)/dt (13-83)
i представляет собой предельный случай импульса зчень большой величины и очень малой продолжительности (рис. 13-35), когда его длительность стремиться к нулю, но площадь сохраняется равной единице.
Действительно, оставляя сейчас в стороне вопрос о законности операций дифференцирования разрывной функции 1(f), hq отметив, что в теории обобщен-
ных функций эти операции достаточно строго обоснованы, найдем площадь единичного импульса:
№
t
О
Рис 13-35.
J 6(0^= 5 dl(t)—l(t) fzt“ = /(oo)-/(— m)== 1-0^1.
(13-84)
Импульсной переходной характеристикой или весовой функцией системы (например четырехполюсника) называется реакция на выходе, если к входу приложено внешнее возмущение в виде единичного импульса 6 (f). Эту реакцию обозначим как k (f). Поскольку внешние возмущения 1 (f) и 6 (/) связаны равенством (13-83), а также полагая, что h (0 +) = 0, получаем, что подобным же равенством связаны и их реакции на выходе системы, т. е.
k(f) — dh(f)/dt. (13-85)
В справедливости (13-85) можно убедиться непосредственно, вычислив h(t), k(t)} и dh(t)/dt, что особенно удобно сделать операторным методом (см. гл. 14).
Если же h (0 +) #=0, то соотношение (13-85) обобщается:
^(0 = ^г + А(0 + )6(0- (13-85а)
369
Например, если при включении цепи г, С на единичный импульс в качестве выходной величины рассматривается ток, то
= = и й(0 + )==1.
Так как при t = 0 в составе приложенного напряжения имеется дельта-функция и в этот момент по второму закону коммутации ис (0 +) = 0, то дельта-функция должна быть и в составе тока, что и объясняет наличие второго слагаемого в правой части (13-85а).
В задачах теории автоматического управления часто нужно бывает знать импульсную переходную характеристику k (f). Она введена по тем же двум причинам, что и h (f):
1. Единичный импульс — скачкообразное и поэтому довольно тяжелое возмущение для системы или цепи; оно тяжелее, чем плавное возмущение. Следовательно, важно знать реакцию системы или цепи на это возмущение.
2. При помощи некоторого видоизменения интеграла Дюамеля можно, зная k (f), вычислить реакцию системы или цепи на любое внешнее возмущение (см. § 13-18).
Реализацию внешнего воздействия в виде единичного импульса 6 (I) обычно представляют как экспоненциальное воздействие с очень большой начальной ординатой (Uu) и очень малой постоянной времени т, так что
6(0 = Нт (1/от)=1, (13-86)
Uo-*со т—>0
где 670т — площадь, ограничиваемая экспоненциальным импульсом, т. е.
lim § Uoe— ilxdt~Uox. (13-87)
о
Отметим еще, что если в теории электрических цепей типовыми внешними воздействиями считаются ступенчатое и гармоническое, то в теории автоматического управления и в других дисциплинах — единичное ступенчатое 1 (I), единичный импульс 6 (0 и гармоническое внешние воздействия.
13-18. Запись теоремы свертки при помощи импульсной переходной характеристики
Пусть на вход пассивной системы или цепи действует источник напряжения иг (t) или тока 1г it). Для того чтобы охватить оба случая, будем говорить о действии внешнего возмущения xL (0 (рис. 13-36). Определим реакцию на выходе в момент времени t-
Разобьем кривую хл (/) на отдельные импульсы шириной dx и высотой х± (т) для момента времени t т. Для единичного импуль-са, действующего в момент времени реакция на выходе по опреде~_
лению равна импульсной переходной характеристике k (t — х),
370
e f — х — промежуток времени от момента т действия импульса 0 момента t. Но плошадь рассматриваемого импульса не равна единице, а равна лу (т) dx. Поэтому реакция от него на выходе в момент t будет равна k (t — т) хл (т) dx. Суммируя действия всех импульсов, каждый из которых имеет бесконечно малую площадь, от т = 0 до
= t, получим реакцию на выходе
t
x2(t) = \k(t-t)x1(x)dx = о
t
= (т) Ху (t — х) dt. (13-88)
о
Эта запись, применяющая им-
пульсную переходную функцию,
более удобна, чем запись, определяемая пятой или шестой формами
интеграла Дюамеля, использующая переходную проводимость g (/), так как здесь от интеграла не нужно брать производную, и называется она теоремой свертки двух функций k (t) и xt (t).
Представляет интерес случай, когда внешнее воздействие было приложено к входу задолго до начала счета времени, т. е при t = — оо, и действует далее непрерывно (рис 13-37)
Тогда вместо (13-88) можем написать
i
x^(t)= k (I— x)x1(x)dx. (13-89)
— оо
Осуществив в (13-89) замену переменных I — т = Tt, получим.
х2 (О = J k (tj) xt (t — Т]) dxt. (13-90)
о
При этом легко видеть, что новая переменная интегрирования т, изменяется в пределах от т, — 0 (импульс, примыкающий слева к точке f) до т, = со (им пульс, расположенный в начале действия возмущения A', (t), т. е при t — — со)
Предположим, что внешнее воздействие, приложенное к входу системы или Цепи продолжается и правее точки /, вплоть до t = Д оо Ясно, что все импуль-сы, действующие в моменты времени, большие /, не могут дать никакой реакции на выходе в момент t, им предшествующий, так как следствие (реакция на выходе) не может возникнуть раньше причины (возмущение на входе) Иначе говоря, физически не осуществимым является возникновение следствия раньше причины Наоборот, физически осуществимым яв ляется только такое положение, когда следствие возникает одновременно или позже появления причины
Однако при рассмотрении систем автоматического управления, находящихся
под воздействием стационарных случайных возмущений (статистическая динамика) ₽Риходи1ся иногда рассматривать идеальный случай При этом с целью получения Йиболее простых соотношений (так называемые задачи Шеннона — Боде и Винера) В считаются с положением о физической осуществимости, принимая,что в составе
371
реакции на выходе в момент времени t участвуют абсолютно все элементарные импульсы, возникающие на всем промежутке времени от t = — оо до t ~
Тогда в теореме свертки соотношения (13-89) и (13-90) будут записываться следующим образом:
4-00 4- со
х2(0= J k (t-~т) Xi (т) j k{Ti)Xi(t—Ti)dTv (I3-90a)
— oo — oo
13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах
4—Ll
До сих пор рассматривались такие цепи и режимы их работы, для которых удовлетворялись законы коммутации
ii(O + ) = i£(O-); Нс(0 + ) = нс(0-), (13-91)
где t = (0—) — момент времени непосредственно перед коммутацией, a t ~ (0 -|-) — момент времени сразу после коммутации.
Рассмотрим теперь такие цепи и их режимы, для которых законы коммутации (13-91) не соблюдаются, и прежде всего процессы при отключении ветвей в некоторых цепях с индуктивностями. Например, пусть в цепи, питаемой от источника постоянной э. д. с. с напряжением U (рис. 13-38), мгновенно отключается ветвь с сопротивлением г3.
Токи во всех ветвях непосредственно перед коммутацией £ (0—), t2 (0—) и i3 (0—) легко определяются. После коммутации ток i в контуре, составленном [из первой
(гх, £,) и второй (r2, £2) ветвей, может быть определен из дифференциального уравнения
(Г1 + Г2) i -|- (£14- £2) di/dt = и, (13-92)
решение которого известно:
i = i 4-^6-^=—^-4-Де-//т, (13-93)
ПР 1 Г14-Г2 1
где т = 4- £2)/(Н + г2).
Для определения постоянной А нельзя воспользоваться первой из формул (13-91), ибо до отключения ветви с сопротивлением г3 токи
Рис. 13-38.
к
Й(О-)
— LJ(r3-[-r3) и . /Q _ \ __________________LIr3
Г1Г2 + г?Гз+ГзГ1 2' ' rir2-\-r2r3 + r3ri
были различны, а после ее отключения они, очевидно, одинаковы, и частности, в пер в ый—момент__после коммутации_ц (0 4~) _____
= t2 (0 4-) = i (0 +)• Значит, токи и Z2 в момент отключения ру-
372
- ,льНика должны измениться скачком, что приведет к возникновению бесконечно больших напряжений на индуктивностях. Но так как гоки во всех ветвях схемы рис. 13-38 конечны, то для промежутка коммутации (от t = 0— до t = 0+) алгебраическая сумма бесконечно больших напряжений на индуктивностях и напряжений на сопротивлениях должна уравновеситься приложенным напряжением
Uli + ~ dif1 + dt “ ~ i ^Г1 + ПРН 0 4~ •
Интегрируя это равенство за промежуток коммутации, т. е. от f = 0— до t — 0+, и учитывая, что ввиду конечности правой части при t = 0 и стремления промежутка интегрирования к нулю интеграл от правой части равен нулю, получим:
/ = о+ . 11(0+) ( = 04- 12(0+)
Ц t ( di^-L2 ^Л = -£2 di2.
1 Lit 1 . j HL j
( = 0— 1'1(0—) ( = 0— 12(0—)
(13-94)
Перепишем (13-94) так:
Li [й (0 +) —(0 —)] = Li [i (0 -|-) —1\ (0 —)] —
= - L2 [z2 (0 4-) - i2 (0 - )]=- £2 [i (0 +) - i2 (0 -)], (13-95) I
или
£1Ai1-|-£2Az2 = 0, или АЧ\4-A4f2 = 0, (13-96a)
или
(£i 4~ £2) i (0 4~) =£i»i (0 —) 4- £2^’2 (0 — )• (13-966)
Из равенства (13-966) следует, что потокосцепление контура Ч;, составленного из первой и второй катушек (иначе говоря, сумма потокосцеплений с обеими катушками), до и после отключения ветви осталось неизменным:
(0 4-) = (£х 4- £2) г (0 4-) = ^ (0—) = £хг 1 (0—) 4- L2i2 (0—). (13-97) Отсюда находим:
t-(0 4-)=Llt'1(0-)+4H°-)> . (13-98)
Ъ1 -j- /-2
Далее из (13-93) — постоянную
л —_________U (71Г2 — 72Г1) г2_____ /13-991
(Г14т2) (7i4-72) (Г1/'24-/'2/'з4-г3/'1)
Следует иметь в виду, что бесконечно большие напряжения на катушках иц (0 +) и uL2 (0 +) противоположных знаков (Рис. 13-39
построен в предположений, что А >0) появились вследствие предположения о том, • что коммутация произошла за бесконечно малый промежуток времени А^->0. Эти им-пульсы напряжения Имеют бесконечно малую длительность. Но
373
интегралы от этих импульсов (13-94) имеют конечные значения и равны приращениям и А'1Г2 потокосцеплений каждой из катушек. На том же рис. 13-39 показано, что токи в катушках при t ~ g изменяются скачком и ток i, протекающий в обеих катушках после отключения ветви с сопротивлением rs, изменяется в соответствии с постоянной времени т и стремится к величине i (оо) = U/(Г1
Подчеркнем, что разность энергий, запасенных в магнитных полях обеих катушек до коммутации,
U7(0-)=^t^=J. + ^lJ=) (13.100)
и после коммутации
UZ(0 + ) = (L1 + L2)^t), (13-101)
т. е.
АГ = Г (0—) и/ (0 +) ~г-(11+Ла) Vl). С*. (13-102)
положительна и расходуется на выделение тепла в сопротивлении искры или дуги, которая появится между контактами выключателя,
и на возможное здесь излучение. При решении задачи была принята идеализация процесса выключения, т. е. мгновенная коммутация. На самом деле она происходит хотя и весьма быстро, по за конечное время ДА При этом в сопротивлении возникающей между контактами выключателя электрической искре и расходуется часть энергии A W. Кроме того, катушки L2 и Li обладают распределенной емкостью между витками и между расходящимися контактами выключателя существует емкость, что приводит к образованию сложного колебательного контура, который может излучать энергию (на высокой ча
стоте), па что расходуется другая часть энергии AW. Если учесть все эти процессы, то никакие бесконечно большие напряжения на катушках не возникнут и токи в них не будут изменяться скачком, т. е. будут справедливы законы коммутации (13-91), сформулированные выше, в § 13-1.
Интересно отметить, что при учете сопротивлений катушек закон коммутации для токов получается из более общего закона о неизменности е момент коммутации потокосцеплений контуров. Покажем это на примере схемы рис. 13-40.
374
Токи до коммутации:
G(0 —) = f2 (0 —)==-^—-; i3(0-) = 0. (13-103)
ЧТ'2
Потокосцепления первого контура:
а) до коммутации
¥хх (0 ~) = Iiti (0 -) + L2i2 (0 -) = (^ + L2) (13-104)
б) в момент коммутации
¥xx (0 +)=Mil (0+) + L2i2 (0 -|-). (13-105)
Приравнивая их, получаем:
¥ji (0 —) = ¥ii (0 +) — Mh (0 +) + Lziz (0 ~r) = (^-i + L2) , .
'1~Г'2
(13-106)
Потокосцепления второго контура:
а) до коммутации (полагаем, что в состав второго контура до коммутации входит рубильник, сопротивление которого равно бесконечности, а индуктивность равна
нулю)
¥22(0-)==-L2/2(0-) +
+ L3t3 (0 —) — — L2 —; (13-107)
'1~Г'2
б) в момент коммутации
¥22 (0 +) — — L2i2 (0 +) L3i3 (0 ).
(13-108)
Приравнивая их, получаем:
¥22(0-)=.¥22(0 + ) = -L2/2(0 + ) + L3is(0 + ) = -L27^-.
(13-109)
Первый закон Кирхгофа для узла А в момент коммутации
ii(0 + ) = /2(0 + ) + t3(0 + ). (13-110)
Решаем совместно уравнения (13-106), (13-109) и (13-110) относительно токов i’i (0 +), i2 (0 -J-) и 13 (0 +):
й (0 +) = 1г (0 +) = П/(Г1-|-r2); is (0 -|-) = 0; (13-111)
Учитывая (13-103), получаем:
Й(О+) = Гх (0 —); i2 (0 + ) = i2 (0-); i3 (0 + ) = i3 (0-), (13-112)
’ e. именно те же соотношения, которые дал бы закон коммутации 13-91), сформулированный выше, в § 13-1.
Легко проверить (рекомендуется читателю), что тот же резуль-'ат получается для схемы рис. 13-41 и для любых схем с ветвями г, ' при подключении к ним новых ветвей г, L.
Понимая под потокосцеплением контура алгебраическую сумму |угокосцеплен11Й всех входящих в него катушек, первый закон рммугации будем формулировать как обобщенный закон комму
375
тации: потокосцепление любого замкнутого контура в момент коммутации (t = 044 равно алгебраической сумме потокосцеплений всех входящих в него катушек, которые последние имели непосредственно до коммутации (t = 0—). Некоторые из этих катушек перед коммутацией могли одного замкнутого контура и не составлять, а образовали его лишь после коммутации.
Например, если в рассмотренной выше схеме рис. 13-40 считать что в катушке r3, Ls до коммутации был ток, то при подключении ее в момент t = 0 к контуру, образованному катушками гг и r2L2, нужно считать, что в этот момент рубильник РА мгновенно включается, рубильник Р2 мгновенно отключается (рис. 13-42).
Рис. 13-41.
Докажем применительно к рассматриваемой схеме (рис. 13-42) первый обобщенный закон коммутации. Для этого рассмотрим контур 2, образованный катушками Lj и L3 в момент 0 — +S / =С 04-, т. е. в момент его образования. Так как второй закон Кирхгофа справедлив для любого момента времени, то имеем:
Vi + Li^ + М12 + М13 + t3r3 L3 44 м-J + 4482 =ei
или
• • т di-t , ж г diet । »г dio г dto . > , di. »< dig
01 - Vi - 44 = Li ~df + M12 j/4~ 44ls + L3 2t+ 443i & + M32 •
Интегрируя последнее равенство от t = 0— до t = 04~> на осно вании сказанного выше получаем:
<=о+ ..
(ei — h.ri-~i3r3) dt = 0= +
/ = 0 — /=0 —
и(0+)
+ Ls^ + A481^ + M32djl^ = L1 ( +
Lit lit Lit J
4(0-) z
«,(»+) Ц(0+) 4(0+) 4(0+)
•ф Л112 <41’2 4“ 44ig <4<з ~T Дз di344f3i d('i4“
4(0-) 4(0—) 4(b—) 4(0—)
h (0~b)
4- ^32 Л’2=(Т14~Л431) [4(04’) — ii(0 —)] 4"
is (0—)
4- (Л112 4- Л432) [Д (0 4-) — 12 (0 —)] 4- (ЛДз 4- Ls) [13 (0 4-) — г'з ~~ /+
376
Перенося все токи для момента t = 0— в левую часть равенства и учитывая, что t2(0—) = 1\(0—), будем иметь:
(0 — ) +4412*1 (0 —) + Mis/j (0 —) + A3Z3 (0 —) + 443i*i (0 —) 4* + 4432*1 (0 —) —£<iii (0 + ) + 44J2Z2 (0 +) + 4fi3ts (0 + ) +
+ 13*3 (0 +) + 44з|+ (0 +) + 44з2*2 (0 + )•
Легко видеть, что левая часть последнего равенства представляет собой результирующее потокосцепление рассматриваемого контура 2 до коммутации, как если бы в этот контур входила катушка г3, что и доказывает приведенный выше первый обобщенный закон коммутации.
Решим задачу об определении значений токов в катушках в момент коммутации (t = 0+), учитывая в общем случае, что все они связаны взаимными индуктивностями (рис. 13-42).
Запишем потокосцепления 1-го и 2-го контуров перед коммутацией (Z = О —), считая, как обычно, Mif- = Mfi и понимая под ¥2 (0 —) в соответствии с данным выше определением алгебраическую сумму потокосцеплений катушек 1 и 3, которые непосредственно образуют замкнутый контур 2 после коммутации:
(0 -) - (£х + L2 + 2М12) Zj (0 -) + (4413 + М23) i3 (0 -); (13-113)
(0 ) = (Z-i + 4412 + 4431) (0—) + (Lg + 44i3) Z3 (0—) + 4432Zi (0—).
(13-114)
Токи it (0—) и ia (0 —) в случае любых э. д. с. ег и е3 (постоянных, гармонических и т. д.) находятся из уравнений второго закона Кирхгофа:
й (Г1 + г2) + (Li + L2 + 2441г) j^ + (44is + 4423) (13-115)
й^з + ^-з + (44si + 4432) ^~ез- (13-116)
Далее запишем потокосцепления контуров 1 и 2 в момент комму-ации (Z = 0 +), учитывая, что для узла А по первому закону Кирх-эфа t2 = jx _ i8;
(0 +) = Ljix (0 +) + 44i2 [1’1 (0 +) — Z3 (0 +)] + 44i3is (0 +) +
+ l-г [Zi (0 + ) — ig (0 + )] + 442iZi (0 + ) + 442з*з (0 +); (13-117)
4 (0 +) = Li?i (0 +) + 4412 [Zi (0 +) — Z3 (0 +)] + 441з/3 (0+) +
+ I-3Z3 (0+) + 443ii’i (0+) + 4432 [Zi (0+) — *з (0 + )]• (13-118)
377
Токи (0+) и is (0 +) находятся из уравнения 2-го закона Кирхгофа:
iiri +М + -ЛТ12 (ij— is) + Мз + (ii ~ is) ^2 + ^2 (ti — /3)
+ M21^ + M2S^=ei; (13-119)
hr 14- £1 + Mi2 & (1’1 — i3) 4- M13 4- isr3 4-
+ L? t+ Мз1^ + ~ t^==ei- (13-120)
Приравнивая потокосцепления
(04-) = ^!(0-), 1F2(0 + )=1F2(0-), (13-121)
получаем два уравнения для определения t\ (0+) и i3 (0 +).
Отметим, что значения iL (0 +) и i3 (0 +), которые получаются решением уравнений (13-121), |не изменятся, если вместо контура 2 взять контур 3, образованный катушками 2 и 3. Для доказательства запишем потокосцепления третьего кош ура (рис. 13-42) до и в момент коммутации.
Ч'з (0—) = L2/! (0—) + М211х (0—) + Л123/3 (0—) -- L3i3 (0—) - (М31 + М32) tl (0—);
Ч-з (04-) = Т2 Ь (0+) -13 (0+)] + М211Х (0+) 4-
4- 442sis (0+) — L3i3 (0-|-) M31ii (0-|-)
— Л1з2 [h (0+) ~ is (0+)]-
(13-122)
Теперь придется для определения ij (0 4-) и Ч (0 4~) решить совместно два следующих уравнения:
ч\(04-)=ч\(0-); ^3(о+)=^3(о-)- (В-123)
Легко видеть, что на основании (13-122), (13-117) и (13-118) получаем:
Чгз(0Д) = 1К1(0+)-1К2(0+) (13-124)
и соответственно на основании (13-122), (13-113) и (13-114) имеем 4*3 (0-) = (0-) - ¥2 (0-), (13-125)
так что система уравнений (13-123) приводится к системе уравнений
t1(04-)=’F1(0-);
(0+) - 4^2 (04-) = ^ (0-)-^2 (0-),
(13-126)
которая в силу первого из уравнений (13-126) тождественна системе уравнений (13-121), что и доказывает сделанное выше утверждение
Рассмотрим процессы, возникающие при одновременном включении двух заряженных до разных напряжений конденсаторов С2 и Са к заряженному до напряжения Д конденсатору Ci (рис. 13-43;.
378
Полагаем, что сопротивления ru r2, rs проводов, соединяющих кон-енсаторы Ci, С2, Cs, пренебрежимо малы. Поэтому постоянные времени, обусловленные ими, также ничтожны. При этих условиях напряжения на всех трех конденсаторах в момент включения рубильника могут изменяться скачком и через них могут проходить бесконечно большие токи. Все три конденсатора до включения рубильника были заряжены до различных напряжений tzci (0 —) =
U; исг (0 —«сз (0 —) и имели заряды qci (0 —) = CttZci (0 —); QC2 (° —) = C2fZc2 (0 —9сз (° =
= Слисз (0 —)• Токи конденсаторов будут существовать только в течение бесконечно малого промежутка времени от t = 0 — до ^ = 04- Так как напряжение источника U и сопротивление последовательного участка цепи г ко
нечны, то суммарный ток i должен оставаться конечным и импульсы токов в трех параллельно соединенных конденсаторах должны взаимно уравновешиваться, т. е,
+ = 0-^/<0 + . (13-127)
Интегрируя это равенство по времени от ? = 0 — до / = 0 4-
/ = о+ < = 0+ /.--0J
г* аи,.л р darej г* аиГг}
Сг -^-dt + C2 J -^dt + Cs -^dt^O, 1=0 — / = 0— 1 = 0—
или
“Ci <°+) “с-2 <°+> “сз
Ci § duci-}~C2 § dtic2~\~C3 diics = 0,
“C2<0—) «Сз<°—>
или
Ci [t/ci (0+) ~ uci (0—)] + C2 [пег (0+) -- ^C2 (0—)] 4-
4- Cs [пСз (0 4-) «сз (0—)] = 0, (13-128)
или
Cj Atta -|- C2 Awc2 4" C3 Дпсз =0> (13-129)
приходим к равенству
Л<71 + Л<72 + Л<73 = О. (13-130)
Отсюда следует, что изменение зарядов на всех параллельно включенных конденсаторах за время коммутации равно нулю, т. е. сумма зарядов конденсаторов перед коммутацией (t = 0 —) равна сумме их зарядов непосредственно после коммутации (t = 0 +) — закон сохранения заряда. Этот же результат получается и из (13-127),
379
если учесть, что после коммутации (/ = 0 +) напряжения на всех параллельно включенных конденсаторах равны:
Uci (0+) = Мег (0+) = «сз (0-Ь) —Wc (О4-). (13-131)
На основании (13-128) и (13-131) получаем:
Ciuci (0—) 4~ C^Ucz (0—) 4- С3иСз (0—) = (Сх 4- С2 4- Сз) ис (0+), (13-132) откуда
S (0—)
Wc (04-) = ~~~з-----(13-133)
%С,
1=1
При этом все три конденсатора заменяются одним с емкостью С = Ci 4- С2 4- С3 и напряжение wc на нем после коммутации определяется дифференциальным уравнением
du,, rC-^- + uc = U, (13-134)
решение которого известно:
uc = U + Ae-^, (13-135)
где
т=гС.
На основании сказанного выше ис (0 +) — U + А и А = ис (0 4-) - U.
Тогда из (13-135) получаем
Мс=.£/4-[нс(04-)-£/]е-^ (13-136)
и ток
U—ur U—ur (О-}-)
1 = ——£ =-------(13-137)
Легко показать, что энергия, запасенная в конденсаторах до коммутации,
W (0—) = 2 (0-)/2 (13-138)
;=1
больше энергии электрического поля эквивалентного конденсатора С после коммутации
W (0+)--Cut (0+)/2, (13-139)
а избыток ее
AlF=№(0—)-№(0+) (13-140)
перейдет в 1епло в сопротивлениях контактов рубильника, сопро' тивлениях проводов и в энергию излучения сложного колебатель*
380
контура, который получится, если учесть, что соединительные Н°овода всегда имеют индуктивность, хотя и очень малую.
ПР Подчеркнем, что при наличии сопротивлений во всех трех вет-с конденсаторами напряжения на них в момент 'коммутации БЯдчком не изменяются, токи в них остаются конечными, т. е. выпол-сяется второй закон коммутации, сформулированный выше, в § 13-1.
13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока
Для определения переходных процессов и установившихся режимов в линейных цепях при воздействии периодических импульсов напряжения или тока известно много методов. Некоторые из них основаны на суммировании токов или напряжений, созданных отдельными импульсами. В других методах для этой цели вводится
Рис. 13-44.
периодическая импульсная реакция цепи. Третьи методы для той же цели вводят другую специальную характеристику цепи,' так называемую эшелонную функцию.
Рассмотрим метод, основанный на непосредственном суммировании токов или напряжений, созданных отдельными импульсами, что реализуется учетом запаздывания последующих импульсов относительно предыдущих.
Поясним метод на примере расчета тока i в простейшей цепи г, о (рис. 13-44), которая в момент t — 0 подключается к источнику, создающему бесконечную последовательность импульсов напряже-Ния « = е, представленную на рис. 13-45.
Найдем сначала ток в цепи от воздействия первого импульса спряжения uL = U (1—t/t0) при 0 «С t sC и = 0 при
Переходная проводимость цепи находится известными методами:
g(0 = 1
(13-141)
381
Применяя интеграл Дюамеля при 0 t t0, имеем: t
i=Ug (f) + § и{ (т)g(t-т) dT= Ur e~wc-0
t
- S ^-(i-xVrC (13-142)
о
Для t t0 получаем:
to to
i^Ug (t) + «I 0)g (t — T) di;=~e-grC — 77Д e~(/-'Wrc ^T==
6 0
=Ke~~t!rCy (13-143)
где
K=^0-HC-rCW'c). (13-144)
Переходя к поставленной задаче, напишем формулу для тока i в промежутке времени, когда действует п 4- 1-й импульс напряжения, т. е. при пТ-^t -^ пТ 4-10.
Как было указано выше, ток i представим в виде суммы токов, каждый из которых создается одним отдельно взятым импульсом напряжения. Первый импульс напряжения дает составляющую тока, определяемую формулой (13-143). Второй импульс запаздывает по отношению к первому на время Т и ток от него равен ge-(t—T)irc. Для учета составляющей тока от третьего импульса напряжения нужно в (13-143) вместо t подставить t — 2Т и т. д.
/-(п—1)Т
Составляющая тока от п-го импульса равна Ке гС . Кроме того, следует учесть действие п-\- 1-го импульса напряжения, который на рассматриваемом промежутке времени еще не закончился. Созданную им составляющую тока найдем по формуле (13-142) с учетом запаздывания во времени на пТ, т. е. вместо t подставим в (13-142) t — пТ.
Результирующий ток
t t- Т t~(n — l) т
i = Ke 'Сф-Ке гС 4-...4-Ке гС 4-
4-^-[-гС4-(^о4-гОе'’^.
(13-145)
Суммируя первые п слагаемых, представляющих собой геометру ческую прогрессию со знаменателем еТ1гС, для интервала пТ — ^пТ 4- t0 получаем:
пТ/гС_ j ртГсДД
t — nT I
/1Ч 146)
382
Ля нее запишем ток в промежутке времени, соответствующем паузе, т. е. при пТ + t0 t (п + 1) Т:
t t T t-пТ <р+Г)Т!гС ) *
i^Ke^c+Ke 'с Л-.-.+Ке 'с = К e-^T1Vc~~е~'с ,
(13-147)
Для определения тока установившегося режима преобразуем /13-146) и (13-147), вводя замену t = пТ + f, где t' — время, отсчитываемое от начала действия п + 1-го импульса напряжения.
для (13-146) получим: „nT/rC_t riT + f t = -е +urrC+{to + rC)r-^rc]. (13-148)
Для (13-147) будем иметь: еТ/гС -пТ/гС i = (13'149)
Полагая в (13-148) и (13-149), что п -> оо, находим установившийся ток. В течение действия импульса
^-^^^t,/rC+^[->-c + (t0 + rC)e-f,rC]-, (13-150) е 1 —1 rt0
в течение паузы
, = Х-^се'е‘'гС- (13-151)
Если источник э. д. с., начиная с момента t = 0, создает бесконечную последовательность импульсов без пауз, т. е. tn = Т, то ток и для этого случая получим из формул (13-142), (13-143), (13-144), (13-146) и (13-150), положив в них t0 = Т.
При более сложной форме э. д. с. источника иногда целесообразнее рассматривать его как наложение импульсов на некоторое постоянное или какое-либо иное напряжение.
Глава четырнадцатая ££ 45
ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
14-1. Применение преобразования Лапласа к расчету • переходных процессов
5 Классический метод расчета переходных процессов требует общем случае многократного решения систем алгебраических
^Равнений для определения постоянных интегрирования по началь-м условиям и для нахождения начальных значений функции и ее
э-ги113Воднь1х’ что и представляет собой основную трудность расчета 1 им методом.---------------------------------------------------
383
Так как дифференциальные уравнения переходных процессов в линейных цепях с сосредоточенными параметрами представляют собой линейные уравнения с постоянными коэффициентами, т0 цх можно интегрировать также операторным методом, основанным ца преобразовании Лапласа. Это было впервые показано русским математиком М. Е. Ващенко-Захарченко в его монографии «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений» (Киев, 1862). В конце XIX в. английский ученый О. Хевисайд независимо пришел к операторному методу и впервые применил его к расчету электромагнитных переход, ных процессов. Однако Хевисайд не приводил математических обоснований метода. Дальнейшему развитию операторного исчисления способствовали своими трудами советские и зарубежные ученые В. С. Игнатовский, Д. Р. Карсон, Б. Ван-дер-Поль, А. М. Эфрос, А. М. Даниловский, К. А. Круг, А. И. Лурье и др.
М. Е. Ващенко-Захарченко показал также, что операторный метод применим не только к обыкновенным линейным дифференциальным уравнениям с постоянными коэффициентами и их системами, но также к линейным уравнениям с переменными коэффициентами и к линейным уравнениям с постоянными коэффициентами в частных производных, т. е. говоря на языке электротехники, к расчету переходных процессов в цепях с распределенными параметрами.
Сущность операторного метода заключается в том, что некоторой заданной однозначной ограниченной функции f (t) вещественной переменной (например, времени /), называемой оригиналом, удовлетворяющей условиям Дирихле на любом конечном промежутке времени и равной нулю при t < 0, сопоставляется другая функция F (р) комплексного переменного р = s + /со, называемая и з о б р а ж е л и е м.
Напомним, что условия Дирихле заключаются в том, что на любом конечном промежутке функция f (t) должна быть или непрерывной, или иметь конечное число разрывов непрерывности первого рода, и, кроме того, должна иметь на этом же промежутке конечное число максимумов и минимумов.
Это сопоставление производится по формуле
F(p) = \ О4'1)
О
которая представляет собой прямое преобразование Лапласа над функцией / (i) и обозначается так:
E(p) = L{/(0} или Е(р) =/(/),
где F (р) называется Лапласовым изображением функции / (0;, Обратно, если нужно по имеющемуся изображению F (р) найта оригинал f (f), то это может быть выполнено в общем случае пр1
384
ПОМОПШ
обратного преобразования Лапласа (интеграла Бромвича)
О Р/СО
/(0 = 21/ $ eP‘F(p)dp, G —/со
(14-2)
опое представляет собой решение интегрального уравнения
1) относительно неизвестной функции f (f) и может быть получено годами теории функций комплексного переменного. Интеграл л4-2) вычисляется по прямой на плоскости комплексного перемен-нОГ0 р = s + /®, параллельной мнимой оси и расположенной правее всех особенностей (в частности, простых и кратных полюсов) функции F (р).
Интеграл (14-2) обозначается еще так:
/(0=L-1{F(p)} или f(t) = F(p).
Иногда изображение функции f (t) определяется несколько иначе:
СО
У(р) = р\ e~ptf (f) dt. о
Последнее выражение называется прямым преобразованием Карсона — Хевисайда.
Очевидно,
(р(р) = рК(р).
Основным преимуществом изображения функции по Лапласу является очень простая связь его с частотным спектром функции (см. гл. 15). В случае применения преобразования Карсона — Хевисайда эта связь сложнее, но изображением постоянной величины является она сама, так что с точки зрения физики оригинал и изображение имеют одинаковые размерности.
В дальнейшем будем пользоваться преобразованием Лапласа.
Переходные процессы, как было показано в гл. 13,“описываются системой интегродифференциальных уравнений с постоянными коэффициентами. Для преобразования их по Лапласу в соответствии с формулой (14-1) приходится находить изображения производных и интегралов от оригинала. При этом оказывается, что изображения производных и интегралов от оригинала выражаются алгебраическими функциями от изображения и начальных значений самой Функции, ее производных и интегралов. Поэтому система интегродифференциальных уравнений относительно оригиналов заменяется системой алгебраических уравнений относительно их изображений, т- с. производится алгебраизация исходной системы интегродифференциальных уравнений.
При решении полученной системы алгебраических уравнений определяются изображения искомых функций, а затем при помощи Обратного преобразования, вытекающих из него формул или спе-ральных таблиц — оригиналы, т. е. искомые функции времени.
13 Основы теории цепей 385
Ряд таких функций и их изображений приведен в приложении 2 Подробные таблицы оригиналов и соответствующих им изображений приводятся в справочниках. В наиболее полном из них, составлен ном В. А. Диткиным и П. И. Кузнецовым, содержится свыше 1500 оригиналов и изображений по Карсону — Хевисайду.
Необходимость вычисления постоянных интегрирования по начальным условиям отпадает, поскольку все начальные условия учи-тываюгся при переходе от системы ишегродифференциальных уравнений к системе алгебраических уравнений.
Приведем (без вывода) формулы для изображений производных и интегралов от оригинала. Если
L{/(/)}=F(p), (14-3)
то
= + (14-4)
l {Г «)}=р* [к (р) - _ qo±)j (14.5)
и т. д.
Отметим, что если функция / (t) и ее производные /' (/), /" (?)... при t = 0 изменяются скачком, то в (14-4) и (14-5) нужно подставлять их значения с учетом этих скачков, т. е. справа от нуля, что и отмечено в их аргументах знаком 0 4-.
Если начальные значения функции и ее производных при t = 0 + равны нулю, то изображения первой и последующих производных находятся особенно просто:
Ь{Г (0}=рЕ(р);1
Ь{Г(0} = р2Е(р) J 1 J
И т. д.
Изображения интегралов от оригинала имеют вид:
L^/(/)^J = ^ (14-7)
' й<0. (14-8)
а
0 +
Если интеграл J /(/) tf/ при ^=0 изменяется скачком, то нужно а
брать его значение справа от нуля, что и обозначено в его верхнем пределе знаком Оф-.
Итак, если начальные (т. е. при t — 0 или в случае скачков при t — 0 +) значения функции, ее производных и интегралов равны нулю, то величину р можно рассматривать как оператор; умножая на оператор изображение данной функции, получаем изображение ее производной (14-6), деля на оператор изображение этой функций, получаем изображение ее mneiрала (14-7);--------------------
386
Нужно всегда иметь в виду, что при расчете переходных процес-оператоРНЬ1М мет°Л°м необходимо не только находить пзображе-с0Б функции, их производных и интегралов, но и решать обратную нйЯачу — находить функции (оригиналы) по их изображениям. Для заД как указывалось, можно пользоваться таблицей, приведен-эТ0„ в’ приложении 2, или справочником. Однако могут встретиться И°ображения, для которых оригиналы неизвестны и само их отыска-11 те является весьма трудной задачей. В таких случаях можно пользоваться приближенными (численными) методами отыскания оригинала по изображению.
Часто изображение имеет вид рациональной дроби
Fi (р) __ bt!pm\-btpm 1-р Fbm Л 4-9)
МИ aopn + a1pn~1 + ап ' ’
при т < п, причем дробь Ft (p)/F2 (/?) = F (р) несократимая, т. е. многочлены /4 (р) и F2 (р) общих корней не имеют, и ak, bk — вещественные числа.
Оригинал / (0 изображения (14-9) можно найти по формуле, называемой теоремой разложения:
(14-10)
(р)1 ' ' ’ F , (.Pk) v ’
k= 1
которая представляет собой сумму вычетов подынтегральной функции F (р) ept выражения (14-2) относительно всех ее полюсов pk, здесь pk — простые корни характеристического уравнения F2 (р) — = 0, причем один из них может равняться нулю.
Часто встречается другая форма записи разложения, применяющаяся в том случае, кшда в составе знаменателя (14-9) есть множитель/?, г. е. знаменатель (14-9) имеет один нулевой корень. Необходимо найти оригинал для изображения Fr (p)/pF2 (р), где в составе f2 (Р) уже нет множителя р. Предполагая, что уравнение F2 (р) = О имеет различных и не равных нулю корней pk (k = 1,2,...,«), получим другую форму теоремы разложения:
L1
—f Н (0) I V (Р&\е k /14 in
* = i
Если уравнение F2 (р) = 0 имеет комплексные сопряженные корнн, то нет необходимости вычислять слагаемые суммы, стоящей в правых частях равенств (14-10) или (14-11) для каждого из комплексных сопряженных корней в отдельности. Известно, что функции с вещественными коэффициентами от комплексных сопряжен-Ь1Х значений независимого переменною — сами комплексно сопря-*енпые. Поэтому, если корни pk и pl — комплексные и сопряжен-Ые> то достаточно вычислить слагаемое сумм (14-10) или (14-11) »га.ЬКо ДЛя К0Рня Pk, а для корня р^, взягь значение, сопряженное o'lIj слагаемому.
13*
387
Если среди корней многочлена F2 (р) есть кратные, то можно записать теорему разложения аналогично формулам (14-10) или (14-11), но с двойной суммой в правой части (одна сумма по числу корней, а вторая — для каждого корня по порядку его кратности) Однако эта формула довольно сложна и здесь не приводится.
Если изображение F (р) наряду с п простыми полюсами в точках Pi, , Pk, ••• , рп имеет, например, еще один полюс кратности « в точке рп+1, т. е.
F (р} —----Т-^-------
то, применяя формулу вычета в кратном полюсе, получаем:
f /А _ V (Рл) ePkt 1 d<« [fi (р) 1
(14-12)
Это соотношение позволяет учесть кратные корни характеристического уравнения. Если кратных корней несколько, то для каждого из них нужно записать слагаемое, аналогичное второму слагаемому в правой части последнего равенства.
Если нужно вычислить начальное (при t = 0 +) и установившееся (при t = оо) значения оригинала, т. е. f (0 +) и f (оо), то можно, конечно, пользоваться формулами (14-10) или (14-11). Однако начальное и установившееся значения оригинала в случае, когда установившийся процесс непериодический, определяются гораздо проще по так называемым предельным соотношениям:
f (0 + ) = Uni pF(p) (14-13)
р ->со
и
/ (оо) = lim pF (р). (14-14)
Р-0
Дополнительно отметим, что теорема разложения применима не только к рациональным дробям, но и когда (р) и F2 (р) содержат трансцендентные, например экспоненциальные, круговые и гиперболические функции.
14-2. Законы Ома и Кирхгофа в операторной форме
Рассмотрим пепь г, L, С (рис. 14-1), которая была подключена к источнику э. д. с. et (/) и в момент t = 0 переключается к источнику э. д. с. е (t).
Закон Ома для мгновенных значений после переключения запишется так:
i
--------------------пс i (14-15) — CO
388
j Я(НИЙ предел интеграла, равный — оо, берется в том случае, -к моменту переключения рубильника (t = 0) режим в цепи
пгпЯ К MUivivxiAj ------ rj
Становился, т. е к источнику
уС с Ci (0 цепь была включена tМомент1 времени t = — оо (только этих условиях режим к моменту переключения рубильника теоретн-пески мог установиться).
Если к моменту переключения режим не установился, то в качестве нижнего предела нужно брать —4, где \ — время, прошедшее с момента включения источника Э. д- С. б! (о до момента t = 0.
Постановка у интеграла ниж-
него предела, равного — оо или —имеет целью подчеркнуть, что в момент коммутации конденсатор уже был заряжен, т. е.
t о t t
-с idt=£ idt=uc(O) idt, (14-16)
—*<х> — оо 0 0
где ис (0) — напряжение на емкости в момент переключения, т. е. при 1 = 0.
Чтобы перейти от закона Ома, записанного для мгновенных значений (оригиналов), к его выражению в операторной форме, нужно в соответствии с формулой (14-1) поступить так: умножить обе части равенства (14-15) на e-p/dt и проинтегрировать от нуля до оо. Тогда получим:
со со со t со
г J e-pli dt + L \e~ptjtdt+c е -pt jj i dt dt = ( e~pte (t) dt.
0 0 0 —co 0
Полагая, что
7(p) = L{i(0}; £(p) = L{6(0}
и учитывая формулы (14-4), (14-7) и (14-16), получаем следующее алгебраическое уравнение:
иг (0) I (/')
ri (p)+LpI (р) - Li (0) + + W = E (р),
откуда получается закон Ома в операторной форме для цепи г, L, С E(p)+Li(0)-u (0)/р
HP)-------r+pL+Wi-------• (14‘17)
Последнее равенство справедливо, и в том случае, когда процесс До переключения рубильника еще не был установившимся.В обоих ^Учаях под i (0) и ис (0) надо понимать ток в индуктивности и на-Цряжение на емкости в момент переключения рубильника. Заметим,
889
что в соответствии со сказанным выше нужно было бы писать i (0 -j \ и ис (0+). Но так как ток в индуктивности и напряжение на ем-кости не изменяются скачком при t =- 0, будем писать короче-i (0) и ис (0).
Выражение, стоящее в знаменателе, назовем полным сопротивлением цепи г, L, С в операторной форме или операторным сопротивлением
Z(p) = r + pL+l/pC. (14-18)
Сопротивление в операторной форме уже встречалось в § 13-ц н теперь получено вполне строго. Напомним, что сопротивление цепи г, L, С в операторной форме построено так же, как ее комплексное сопротивление, если в последнем заменить ]ы через р. Величина, обратная операторному сопротивлению, называется о п е р а [ о р -ной проводимостью:
У (р)^= 1/Z(p).
Операторная э. д. с. цепи, стоящая в числителе (14-17), состоит не только нз операторного выражения внешней э. д. с., г. е. £ (р), но и еще из двух слагаемых, которые определяются начальными условиями, т. е. током в индуктивности i (0) = £ (0) и напряжением на емкости ис (0). Иными словами, наличие двух дополнительных э. д. с. Li (0) и —ис (0)/р, которые можно назвать внутренними или расчетными э. д. с., указывает на то, что в магииiном поле катушки и в электрическом поле конденсатора в момент коммутации была запасена энергия. Положительные направления этих э. д. с. выбраны совпадающими с положительным направлением тока ветви.
Заметим, что, как и ранее, положительные направления тока и напряжения на конденсаторе считаются совпадающими. Если же до коммутации конденсатор был заряжен и, стало быть, положительное направление напряжения на нем до коммутации «с- было задано, а положительное направление тока через конденсатор выбрано противоположным положительному направлению «с, т0 внутренняя или расчетная э. д. с., обусловленная емкостью, должна быть взята с обратным знаком, т. е. +«с (0)/р.
Особенно просто выглядит выражение (14-17) при нулевых на чальных условиях, т. е. при II (0) =- 0 и ис (0) = 0,
/(p)^£(p)/Z(p). (14-19)
Тогда оно полностью аналогично закону Ома в комплексной форме.
Для любого узла разветвленной цепи
h + £ + • • • + in=0,
поэтому, обозначив изображения токов Ik (р) z± ik (t), на основании (14-1) получим первый закон Кирхгофа в о п е -
390
т О р н О й форме: р а т ° р п
/1(р)4 /2(р) + ...+ 4(р)= Ц 4(Р) = 0. (14-20)
*-=-1
Для
любого замкнутого контура, состоящего из п ветвей,
2 r"ifc+2L,t £ + 2 ск §ikdt 2 ек~
/(Ч А 1 А-I —со А = I
Полагая
Ik(p) = L\ik(t)}- Ek(p) — L{ek(t)}
и повторяя все рассуждения, которые были сделаны при записи закона Ома в операторной форме, получаем второй закон Кирхгофа в операторной форме:
2 r*;*(P)+2 Lk[ph(P)~ik(ty] + ki
А = 1 k=\ k- \
что можно переписать так:
2 2Ир)/Ир)=2 [^(р) + ^а4(0)-^Д]. (14-21) "
A=I k=l L
В последних выражениях ik (0) и ис к (0) — начальные значения токов в катушках индуктивности и напряжений на конденсаторах в соответствующих ветвях.
Особенно просто запишется второй закон Кирхгофа при нулевых начальных условиях, т. е. при ik (0) = 0 и uck (0) = 0:
п п
YiZk(p)lk{p)=^iEk{p). (14-22)
А-1
В такой записи он полностью аналогичен второму закону Кирхгофа в комплексной форме.
Итак, закон Ома, первый и второй законы Кирхгофа в операторной форме аналогичны по форме своей записи тем же законам комплексной форме для цепи гармонического тока. Нужно только меть в виду, во-первых, что в каждой k-\i ветви при ненулевых начальных условиях, т. е. при ik (0) ^0 и иСк (0) ^=0, действует ная °ЛЬКо Внешняя э. д. с. Ек (р), но еще и внутренняя или расчет-р0„ Д- с. Lkik (0) — иСк (0)/р, положительное направление кото-в ч Выбрано совпадающим с положительным направлением тока рРт„°и ветви, и, во-вторых, что в качестве сопротивления ветви бе-операторное сопротивление.
391
Найдем, например, ток при переключении ветви г, I ,С (рис 14 1) от источник синусоидальной э д с q (/) = Elirl sin (со/ I ф) к источнику постоянной э п Ка е (0 = Е с
На основании закона Ома в операторной форме имеем
E/p+Lt(0)-uc(0)p C[E+pLi(0)-uc(0)] Fgp)
I(P}~ r + pL+l/pC \ -iCp--\-LCp2 F„(p)'
где i (0) и u(. (0) надо найти, рассчитав цепь в установившемся режиме до коммута ции
Оригинал для ! (р), т е ток t, определим при помощи теоремы разложения
Сначала вычислим корни pt и р2 уравнения F2 (р) = 0, которые примем для определенности вещественными и различ
Рис 14 2
ными
_ г l/"/5 Г~
Pi 2- 2£ + у 4L> Yc~
Затем найдем
FjpJ^CfF + p^i (O)-uc(O)J, (F2) = С[£ + р/1 (0) — ис (0)], Н (р) =- rC + 2/ Ср, Г’_ (рх) = (г+2£р,) С, F’, (Pi) = (r+2LpJC
формулу (14-10)

Подставим эти результаты в
Ft (Pit) сРк Е + PJ1 (0) ~ ис (0)
1= 2; -
1
или после
Р1< £+Рг£( (°)~ цс(°) г + 21 р2
F2 (Pk)
простых преобразований F — иг (0) , . ,
Li (0)
_______, । .= -г (pteP1 — р^1'1^)-
J^2 —4L/C ) r2—4L/C
Как и следовало ожидать, принужденной составляющей в составе тока t иет, а свободный ток состоит из двух экспонент с коэффициентами затухания | Р1 I и I р2 I Для цепи с нулевыми начальными условиями во всех ветвях (рис 14 2) изо бражение тока, например, во второй ветви найдем из очевидного соотношения , Zi(P) _ £(Р) (Р) у (п}Е(о)
i(p} ri^ZAp}+z.(p) Z2(p)Z3(p) Z2(p)+Z3(p) 21(p)
Z1(p)+^)+W)
Здесь У21 (p) — взаимная операторная проводимость ветвей 2 w 1
Изображение гармонической э д с е = Ет sin (aot + ф) (см приложение 2)
{ ряпф |-С00СО5ф
ц (Р) — Ст
— довольно сложное Зная, что эта э д с представляет собой мнимую часть комплекса e = Im [Ете! (“°* + ,’W], можно оперировать с мгновенной комплексной э Д с
e(t)=Fm [cos (и,/+ф) + / sin (coof + ф)] = Eme> (t"o/ + = Emel&ot, изображение которой E (p) хотя и является комплексной функцией р, все будет значительно более простым
Е (p)=L {е (/)} =—. С4 231
'-i'' 1 р — ]ш0
392
пояснения расчетов с такими изображениями рассмотрим сначала ие-тгеннтю цепь с нулевыми начальными условиями, в которой после коммута-РаЗБ№Йствует один источник э д с е (t) иии ДР закону Ома в операторной форме комплексное изображение тока
/(p) = E(p)/Z(p), лексный оригинал переходного тока К°МП i(t)=Lr{I(p)}
(14-24)
(14-24а)
й переходный ток
i(f) = Imp (01
Если в этой цепи после коммутации кроме источника
(14-246)
_________________ , _ , с гармонической э д с ействует, например, еще источник с постоянной Е и апериодической Еое-а* э д с й если начальные условия были ненулевые, что учитывается введением расчетных э д с 1л (0) и — ис (0)/р, то все э д с , кроме е (/), должны быть введены в числитель формулы (14 24) с множителей /, т е
„ч £(р)+Д-1(0)-/к (0)/р
/(р)-
Z(p)
(14-25)
где
р Р Г
Е (р) = + / — + .
Только в этом случае они будут учтены при определении переходного тока как мнимой части комплексного оригинала t (/) Необходимость умножения изображении всех внешних э д с (кроме синусоидальных) и внутренних дополнительных э д с ветвей на / распространяется также и на уравнения второго закона Кирхгофа для разветвленных цепей, если синусоидальные внешние э д с заменяются их мгновенными комплексными значениями е (/)
В случае включения пепи по рис 14-2 к источнику тока / (р) = = L{i (/)} при ус новин z (0) =Л 0 необходимо, чтобы ветвь Z, (р) и хотя бы одна из ветвей Z2 (р) или Z.( (р) не имели индуктивностей. В ветви Zx (р) сразу будет принужденный режим с током (t) — = i <i)
Составим уравнение по второму закону Кирхгофа для контура, образованного ветвями Z2 (рУи Z3 (р), и уравнение по первому закону Кирхгофа на точки разветвления Переписав их для изображений и учитывая, что Д (р) = I (р), решим два уравнения с двумя неизвестными 1г (р) и /3 (р), т е найдем их изображения. Токи t2 (t) и С (0 определим по теореме разложения или при помощи таблицы соответствий
Достаточно найти один из токов /2 (р) или Is (р) и соответственно l2 (О или !3 ((), так как другой ток сразу определяется по первому закону Кирхгофа.
14-3. Эквивалентные операторные схемы
При расчете переходного процесса операторным методом полезно q^TaBI1Tb для заданной цепи эквивалентную операторную схему. т°бы показать, как составтяется эквивчтентная операторная ема в достаточно общем случае при ненучевых начальных j с то
393
виях, запишем для схемы (рис. 14-3) уравнения Кирхгофа в опеп торной форме, опуская для кратности аргумент р у изображений'
Л ~г Л + А — 0;
Li [pli — h (0)] — г212 — L2 [pl2 —12 (0)] с2р ~ ^2,
/„ иг, (0)
г2/2 + А [р!2 — А (0)] + гл; 4* ‘ ,, ~~ гз1з Lspls —
-Л+^=£^£а. ।
СзР ' р
Переписав их в виде
А 4~ А 4- А=0‘.
Lipli — Р^2 A—£14* АА (0) — ^E2-]~L2i2(0)-----------~р~~
[г2 + pL2 + p-cJ 12 - (г3 + pL3 + -JJ А -=
=£2 + АА(0)------£34--—
составим по ним эквивалентную операторную схему, представлен ную на рис. 14-4 Из рисунка ясно, что, вводя операюрные реактив
ные сопротивления pL и 1/рС, заменив заданные э д с. их изображениями и включив в каждую ветвь с индуктивностью и емкостью дополнительные внут
Рис 14-4.
Рис 14-3
ренние э. д. с. Li (0) и — ис (0)/р, причем положительные нг правления этих дополнительных внутренних э. л с. принт совпадающими с положительным направлением тока в данно ветви, получим уравнения Кирхгофа для изображении, аналоги1 ные уравнениям цепн гармонического юка Л так так и''П-ме'оД расчета цепей выводятся из уравнений Кирхгофа, то для расчет
394
бпажений какого-либо тока или напряжения в схеме (рис. 14-4) 1,30 но пользоваться методами контурных токов, узловых потен-МО/*пов, активного двухполюсника, преобразований и т. д.
циа^аКйм образом, операторный метод позволяет использовать
определения изображений токов и напряжений весь аппарат Счислении, применяемый для расчета установившихся токов и напр«жен11Й
Составим теперь характеристическое уравнение, например, пиравнивая нулю числитель входного сопротивления для источника э д с > включенного в первую ветвь Z1BX (рис. 14-3):
2-=^+zSr=0-
Такая возможность вытекает из теоремы разложения, когда для получения характеристического уравнения приравниваем нулю знаменатель изображения
В общем ел \ чае оно будет четвертой степени Однако, если параметры ка-; кои либо паны параллельных ветвей, например второй и третьей, удовлетворяют соотношению
Г 2/Гз = ^2^ 3~С^С2,
то характеристическое уравнение будет только второй степени
В самом 1еле, выражая из последнего уравнения и С3 через сопротивления г„ и /•,, и С, и подставляя их значения в выражение 2tBX, после преобразований полу чаем
7 _ [(г2-р ?з) / ! 4 Г;/11 /'О/У З Г '-i _„
1вх” (г.+гз)рс;
Таким образом, возможность преобразовывать операторные сопротивления, так же как и комплексные, позволяет очень просто установить слу чаи, когда из-за пропорциональности параметров ветвей г, L и 1/С степень характеристического уравнения понижается Ск.Ланиое относится гакже к параллельным ветвям г, L и параллельным ве1вям г, С, еспи пх параметры соответственно пропорциональны.
Пример 14-1. Нзптп ток в индуктивно!тн (рис 14-5) после включения рубильника, если дано U 200 В, ис (0) = 100 В, гг = 30 Ом, г2 = 10 Ом, Л - 0,1 Г, С ~ 1000 мкФ
Решение Составим уравнения для ( изображений по методу контурных токов. —о д
^i+O.lp/j-0,hi (0)- 10/,=
1000 ur (0)
-10/1+ ю/2+— /,—Lil=o, p p
где
‘г (°) = ‘inp- (0/=200/40 = 5 A.
Решив эти уравнения, найдем /А-
Рис 14-5.
200/р+0,5 —10
100/р IQ-LlOOQ/p
395
где
Отсюда
40+OJp —10
—10 10 + 1000/р '
, _5Р , 300 .
1~ \р + р^+400/7+40 000
Оригинал первого слагаемого равен 5 Корни знаменателя второго слагаемого Pi = Рг ~ Р ~ — 200 Гак как корнй кратные, то теорема разложения в виде (14-10) неприменима Представив второе слагаемое в виде
5 300 1500
/?2 +400/7+ 40 000 — (р + 200)2 »
найдем его оригинал по таблице (приложение 2):
L 1
1500 ) (/7 + 200)2 )
= 1500/Р-2^.
Оригинал того же слагаемого можно найти и по формуле (14-12):
(1500е₽Л = 1500/e~2Oof;
(2—l)t dp v ₽1
для ij окончательно получаем:
t-1==5+ 1500te“20«z А.
В частности, при t = 0, как и должно быть, (0) = ilnp_ (0) = 5 А.
Пример 14-2. Определить напряжение на индуктивности (рис 14-6, а) после включения рубильника, если гх = 10 Ом, L = 0,15 Г, г2 = 10 Ом, С = 25= 10 Г| Ф, И= 150 sin (314/+ 60°) В.
Рис. 14-6.
Решение. Изображение тока /t найдем по методу активного двухпопюс ника Составим для цепи (рис. 14-6, а) эквивалентную операторную схем' (рис 14-6, б) и определим расчетные э. д. с. Из расчета режима до коммутаии найдем:
/1пр_ = 4,2 sin (314’'— 13'45') А;
==53,5 sin (314/ — 103°45') В
и, следовательно,
й (0) —йпр_ (0) = 4,2 sin (—13'45') —— 1 А;
и,. (0)—н.. (0) — —52 1 В.
С ' z С11р“ ' ' ’
396
jjo методу
активного двухполюсника
И руб
Z + Zb ’
«е r.JpC _ 37,5- 10-Sp2_|_0,175pJ 20
Z + Zb-Tj + p/- , r2+i/pC ~ 25 10«p+l
Найдем далее напряжение l/ba при отключенной ветви с индуктивностью
— «с(0) 0,1305
Uba = I'i = р (/,2+ j/pQ- Г2 = 25 10-4p+i •
Напряжение на рубильнике
,, .РмПМ -37,5-10-5^+0,3055^+152^+21650
1/р}б = <7ьа-НЕ +^1 00- (25 • 10 *р+1) (р2+3142)
Ток в ветвн с индуктивностью
, —р3 + 815р2+405 • 10+ + 578 105
11 = (р2 + 3142) (р2 + 467р + 534 Гб2Г'
Поскольку в момент коммутации в индуктивности был ток, изображение напряжения на индуктивности представится разностью изображений потенциалов точек d и с:
lJL==4d~4c==I-iPL~Lil (°) =
_ 192,2р3+836 • 102р2+ 155,6 • 105р + 79 10’ _ ГА (р)
~ (p° + 3142)(p2 + 467p + 534. 102) ~ F2(p)'
Находим корни характеристического уравнения /дО-) —0
Pi ——267; р? = —200; р3— /314; р4 =—/314.
Далее находим:
Д' (р) = 2р (р2 + 467р + 534 • 102) + (р2 + 3142) (2р + 467);
(Pi) = — 113,5 • IO3; F's (р2) = 93 • IO3;
Д' (р3)=— (92+/28,3) 106; р' (р4) = —(92-/28,3) 106. *
Аналогично находим F} (рк).
Применяя теорему разложения (14-10), учитывая, что в теореме разложения слагаемое от корня р4, сопряженного ръ получается сопряженным слагаемому от корня ръ сумму обоих слагаемых найдем сразу как удвоенную вещественную масть слагаемого от корня р3:
4
и, (Л = у FM = -b-OSJO9 е-м _ А3-10! е-2оо/ +
17 Li F'ztPk) —113,5 103 е 93 105 -Г Л ~ 1
+2 Re ’°^5)' 109е/зиЛ = 157 sin (3141 + 81с) + 92,6е-2б’*-57е-2«й В.
бильниИМеР *4’3' Найти напряжение на конденсаторе ис после включения ру-вели^ е ш е н и е Представим заданную гармоническую э д с комплексной чиной ё (t) и составим эквивалентную операторную схему (рис. 14-7, б). Обозначим
Гэ = /-)--:—; Т=Г=С
Г1 + г2
397
й найдем напряжение на конденсаторе до коммутации'
иСпр- (0 = — £i + хс sin М 4- Ф—Ф — 90°)>
где
г = |Чл+л,Г+(1/ШС)\ хс~; tg<p=—(од(/+Г1)-.
Следовательно,
ис = — £i 4—хс sin (Ф — Ф — "°)-
Найдем по методу двух узлов комплексное изображение напряжения йаЬ-£1 1 I (0) I ’
г г — — ;ргГ + Ь —/Ц> ! Р ] г+'/рС
аЬ 1 1 , 1
И + г I- VpC + г2
Зная его, находим комплексное изображение тока /:
__ ис (°) _ п
! 1 р аЬ ' г+ЦрС
Далее, поскольку конденсатор в момент коммутации был заряжен, найдем комплексное изображение напряжения па конденсаторе йс как разность комплек-
сных операторных потенциалов <р/ и тс,; в эквивалентной операторной схеме (рис 14-7, б)
цс (0) 1
—+ /_.
Подставляя значение Uab в формулу для /, а значение 1 в формулу Для пвсле ряда алгебраических преобразовании получаем - -----fir___________________________rjgi
с (Р —/«) (14-тр) pin |-г2)(14 ?Р) 14-тр
се (°) т
398
гт именив теорему разложения (14-10), найдем комплексный оригинал иско-апряжения на конденсаторе:
М0Г0.И -Ё^ I rth г-"Ч , ^e~t>X
ис + Ч-т/со +/ с() +/Г1 + с> 1+т/й*
q учетом приведенного выше значения ис (0) найдем напряжение
(fl = Im [йс (/)] =— хс sin (ft>(+if-<j>1-90’) +
С ГI -f- Г 2
+ Г £t+ ХС sin (ф— ф—90") + хс sin (ф - Ф1 - 90°)j е~ 4х ,
где
21==]/"^+ (l/соС)2; tg<pi = —1/соСгэ.
В частности, при /= О получаем для ис (0) приведенный выше результат.
14-4. Переходные процессы в цепях с взаимной индуктивностью
катушках Кирхгофа
(14-26)
Рассмотрим переходные процессы в цепи (рис. 14-8), у которой две катушки с сопротивлениями rt, г2 и индуктивностями Lt, L., связаны взаимной индуктивностью М, причем вторая катушка замкнута накоротко, а первая включается на постоянное напряжение U.
Токи ц и й в обеих связаны уравнениями
'ч+Ц*' +м * “°-
Отметим, принципиально важное обстоятельство, что учет взаимной индуктивности между катушками не повышает порядка
Перепишем уравнения (14-26) и
(14-27)
дифференциальных уравнений. (14-27) для изображений
(riH“ pLj) Ii -j- рМ12 — —; pMh -J- (r2 -j-pL2) Л —0.
Решая их, находим:
Т _________и О+ртг)________ = т 1 (р) .
1 k2) (p^+ap + b) pF2(P)’
г ______________MU____________ F3 (p)
3 OK (1— k2) (p2 + ap + b) F2(pY
Ji® Ti = Li/rp, t2 = L2/r2 — постоянные времени каждой из кату-> когда другая разомкнута;
___1 /1 , Н , 1
а 1 — k2 (Tj ' Т2 / ’ (1 — k2) TjT2
Л1/]/ LiL2 — коэффициент связи.
399
Решая характеристическое уравнение системы
Р2 (p) = P2 + ap + b = Q,
находим его корни:
„ _________ [ 1 , 1 _ I /?1 , iy 4(1-^)]
2 2 (1 — k2) | т, "I” т2 у \т1'*'т2/ ТЛ Г
Применив к выражению для тока Д теорему разложения в вице (14-11), а к выражению для тока /2 — в виде (14-10), найдем после некоторых преобразований с учетом равенств
+ № = (т=^у^; F'Ap)=2p-P1~p2
оригиналы токов it и i2:
= £ Г1 + ePlt _ 1±/ДД ef,j 1.
1 П L flPl-P2 J’
k4J
12 = (P2 —Pi) (1 —/e2) Af ~ еР^-
Для лучшего уяснения процесса рассмотрим простейший случай, когда обе катушки одинаковы:
Г1 = г2==г; £1==£2=L; k = M/L.
Тогда постоянные времени каждой из катушек в отдельности равны между собой:
Ti = т2 = т=Д/щ = L2/r.2=L/r.
Коэффициенты затухания и а2 также упростятся:
~ 1 г 1 г
«1==—Р1=(1+Й)т — Л+Л1 ; “2 = —р2 = (1_£)т — £-Л)'
и токи катушек
rt Г/ \ г г f rt rt
(14-28)
На рис. 14-9 построены кривые изменения токов Д и Д. Одна из свободных составляющих токов затухает медленно, т. е. имеет большую постоянную времени, определяемую суммой индуктивности L и взаимной индуктивности М, а вторая затухает быстро, так как ее постоянная времени определяется разностью L и М._Дл” сравнения на рис. 14-9 показано, как изменялся бы ток первой катушки при ее включении, если бы вторая была разомкнута (пунктир’ ная кривая). В первые моменты после включения ток первой катуШкй увеличивается быстрее, чем он возрастал бы при разомкнутой в10' рой катушке. В этом можно у-бедитьс;1,, Г1о,ч<'чита1?. iia'ia.ibiibie siia'1'/ ния производных dijdt в обоих случаях. При замкнутой вторично”
АЛЛ
каТушке
из первого выражения (14-28) получим fdii \ _ U
\ di (1 —k2) L ’
и разомкнутой вторичной катушке (см. § 13-4)
3 /dq\ _£
\ di )t.=o L '
В первом случае производная больше, поэтому ток ц растет бы-
При t> tr ток z2 по абсолютному значению уменьшается и знак его производной изменяется на обратный. Кроме того, как показано на рис. 14-9, ток q, начиная с некоторого момента времени, растет медленнее, чем при разомкнутой второй катушке.
Попутно отметим, что, поскольку при включении токи катушек имеют противоположные направления, механические силы их взаимодействия стремятся оттолкнуть катушки друг от друга.
Рис. 14-9.
Рассмотрим энергетические со-
отношения.
Для этого умножим на ^dt обе части уравнения (14-26) и на i^dt обе части уравнения (14-27) и представим их в виде
Г] q dt + Li/'i dix + Mq di2 = rxq dt 4- d +
4- Add (qq) — Mi2 di\ = 7/q dt't
— Mi2 dir = r2il dt + L2i2 di2 = r2q dt + d ).
Подставляя — Mi2 dit в предыдущее уравнение, получаем:
qtj dt + r2i‘i dt + d 4- d + Md = Uit dt.
Проинтегрировав в пределах от 0 до t, будем иметь:
t t t
q/f dt 4- r2ii dt 4- + ^r + Mqq == Uii dt.
0 0 0
Отсюда следует, что получаемая от источника энергия преобразуется частично в тепло, выделяемое в сопротивлениях обеих кату-ек (первые два слагаемых левой части последнего равенства), а .Этично запасается в магнитном поле, обеих катушек (три послед-Их слагаемых левой части этого равенства). Так как знаки токов
401
ij и z2 различны (рис 14-9), ю последний член + Afz1z2 отрицателе Более подробный анализ показывает, однако, что знак суммы тпр последних членов всегда положителен, так что за любой промежутс) времени от 0 до t энергия источника частью переходит в 1епло а частью расходуется на увеличение энергии магнитного поля кату шек. у'
Рассмотрим еще случаи включения первой кагушки на постоянное напряге ние, если вюрая катушка замкнута на резистор с сопротивлением г
При этом будем считать, что числа витков катушек wt и а>2 различны, а магнитные потоки рассеяния, а следовательно, и индуктивности рассеяния катушек равны н\лю (потоками рассеяния катушек называются потоки, сцепляющиеся только с каждой из них в отдельности, индуктивности рассеяния соответствуют этим потокам)
ф51=ф52 = 0 и Lsl = Lsi—0.
Учитывая равенства
L=LS1+WW\M, L2 = LS2+^M,
запишем уравнения закона Кирхгофа для каждой из катушек:
11Г1+ - М л, +М Т7 = V1+ ('1К’1+/2“'2) = ^>
1 ' w, dt dt у dt
м (14 29)
L (г + /-г) + - ~dl ('1^1-НдО = 0
Здесь для слсая двух катушек, намотанных на стальной тороид с длиной I средней магнитной линии и сечением S, М равно
,, ,, ,, W,W HLlnS
м = Ми = Л-1 л = 1 у °-.
По закону полного тока, полагая для простоты воздушный зазор в стальном сердечнике отсутствующим, имеем
& Hdl = Hl= ——1 =—~ё7Г = liwi (14 30)
J цро UPoS/Z
Но магнитный поток Ф скачком измениться в момент коммутации не может, так как это вызвало бы появление в каждой из обмоток бесконечно большой э Д с , пропорциональной и оба уравнения (14-29) перестали бы соблю-
даться для момента коммутации (/ = 0)
Поэтому
Ф(0) = 0
и
wdi (°) + wdi (0) == 0. (14 31)
Вместе с тем в отличие от ранее рассмотренных задач каждый из токов ц и t2 в отдельности мо?кет в момент включения измениться скачком
Подчеркнем физический смысл задачи, заключающийся в том, что при вкЛЮ" чении катушек, связанных взаимной индуктивностью, именно наличие потоков рассеяния (а следовательно, и индуктивностей рассеяния LS1 и Lsi) не позволяет токам изменяться ь мо еат включения скачком, так как иначе э Д с — LS1 dtjdl и — Z.iS2 di-Jdt обратились бы в бесконечность.
402
ом (14-31) перепишем уравнения (14-29) для изображений С учети
/л+ — р(М’1Ч-Лк'2)=-—;
Р
_ м
/2 (г + г,) + — Р (4^1 + /2®г) = 0.
решая их относительно 4 и /2, получаем
==_________(r + 'j)+^aWl_________________= Л(Р) .
p{Mp{w{ (/+r2) + r1ayfJ+ay1w2r1(/- + r2)} рР2(Р)’
. ___________________им________________________ Г3.р)
2 Мр [wj (r+riJ+n^l + ^Z! (' I O' Л>(Р)’
Применяя к току 4 теорему разложения в форме (14-11), а к току /2 в форме
(14 Ю), найдем токи
^Le-at

UaM
; «2= гп—ге . ' г. (г 1 М •
где
Wi п — —;
nM (гЧ-Гг + н/п2)
Отсюда видно, что ток q в момент включения изменяется скачком от нуля до значения
li (0) —
U
'гпр = U4 Ток 4 в момент вклю-
Рис
14-10
1Л0) =
^ч(о) pL, Mi2(0)
и затем постепенно увеличивается до значения чения также изменяется скачком от пуля до значения
Un /Л\ К’1
'2 (Г-^Г2) ~ 11 ( ) ш2 ’
а затем постепенно спадает до нуля
Магнитный поток Ф найдем из (14-30):
ф = 2!1^(1_е-аТ).
Поток Ф нарастает постепенно, начиная с нуля
Отметим, что именно из-за отсутствия индуктивностей рассеяния катушек у
таков и потока получилась только одна свободная составляющая (процесс вклю-чения в этом случае описывается дифференциальным уравнением первого порядка) и™етим, наконец, что если в цепи (рис 14-8), действовал источник переменного напряжения и затем в момент t — 0 первая катушка замыкается накоротко, то Уравнения в изображениях с учетом индуктивностей рассеяния будут [см уравне-ния (14-26) и (14-27)|.
/•j/j pLJ ! — 7-i<i (0) -|- рМ1, — Mi, (0)=0; Г2^22 — ^-2'2 (0) ~^-pMI 1* — Mil (0) — 0
(rj-4-pLi) -}-pMI., = Lli1 (0)-[-Л41, (0); pMI 1 + (г2 +р/-2) 12 = Z-2i2 (0) -j-Mii (0).
403
Этим уравнениям соответствует эквивалентная операторная схема, ппинр» ная на рис. 14-10. йен'
Подобным же образом рассматриваются переходные процессы и при дтп коммутациях в цепи по рис. 14-8. ня их
14-5. Сведение расчетов переходных процессов к нулевым начальным условиям
При изучении переходных процессов в электрических машинах в схемах автоматического регулирования и в других случаях часто сводят их расчет при ненулевых начальных условиях к расчету при нулевых начальных условиях следующим приемом.
Пусть к зажимам 1—2 активного двухполюсника рубильником Р подключается ветвь с операторным сопротивлением Z12 (р) (рис. 14-11, а). Если в подключаемой ветви есть источники э. д. с. или заряженные конденсаторы, то их можно включить в состав активного двухполюсника.
Для расчета тока в подключаемой ветви (в’ ветви рубильника) или в какой-либо иной ветви активного двухполюсника определим прежде всего напряжение и12 (/) на зажимах 1—2 рубильника до его включения, обусловленное всеми э. д. с. активного двухполюсника. Затем включим (рис. 14-11, б) в ветвь рубильника два источника с противоположно направленными э. д. с. е (I), равными по величине «12 (f). При этом режим в цепи не изменится.
Теперь рассмотрим включение рубильника. Так как система линейна, то будем вести расчет по принципу наложения. ПреЖДе всего найдем токи при действии всех э. д. с. активного двухполюсника и той э. д. с., которая действует противоположно напряжению п12 (t) (рис. 14-11, в). В этой схеме рубильник включает ветвь с источником э. д. с. е (f), равной и противоположной по направлению эквивалентной э. д. с. активного двухполюсника. Поэтому в этой схеме ток в ветви рубильника равен нулю, а значит, для всей схемы в целом это будет режим до коммутации. Остается учесть последнюю
404
действующую в ветви рубильника в том же направлении, э. д- с апр’яжеиве на его зажимах до коммутации (рис. 14-11, г), как иассчитать переходный процесс при включении ветви с источ-т. е- Р g д с. е (/) к пассивному двухполюснику или, иначе говоря, нйК°нулевых начальных условиях.
пРи У прП включении рубильника определяется ток в какой-ни-
11 ветви активного двухполюсника, то нужно в соответствии со бранным учесть, что он состоит из тока, существовавшего в этой сКа3и д0 коммутации, и тока, который возникает в этой ветви после ВеТ точения источника э. д. с. е (/) к пассивному двухполюснику. Р в частности, рассчитывается ток в ветви рубильника, равный ю’ до коммутации, достаточно рассчитать режим в схеме по рис. 14-П, г.
1 Свести расчет переходных процессов в цепи с ненулевыми начальными условиями к расчету при нулевых начальных условиях можно, применяя как классический, так и операторный метод. Сопротивление Z12 (р) может быть в общем случае входным сопротивлением другого пассивного двухполюсника, подключаемого к зажимам 1—2.
Аналогично можно показать, что отключение любой ветви, не содержащей индуктивности, можно свести к включению в нее источника тока с током, равным и противоположным по направлению току в этой ветви до коммутации.
Пример 14-4. Найти ток в конденсаторе (рис. 14-12) после включения рубиль-
ника, если г, = г2 = г = 10 Ом; L = 0,1 Г; С = 1000 мкФ; U = 200 В; ис (0) = = 100 В.
Решение. Выбрав положительное направление напряжения на рубильнике, как указано на рис. 14-12, найдем это напряжение:
и ,= <р— ср, =щ (0) |---—г2=200 В.
руб та т/, С с ' 1 Г1 _|_ р2 z
Собственное операторное сопротивление ветви 3 z
7 =- _ 1 , О (О + ДС) = р2|-200р(-20 000
рС Tj+rj-j-pL 0,1/?2{-20р
(14 ^ображение искомого тока / найдем по закону Ома в операторной форме 1/ру6 200 (0,1р + 20) Fx(p)
1 - Z “ р24-200р + 20000 ~ Д2(р) ’
^Приравнивая F2 (р) = 0, находим корни характеристического уравнения: 4," —• 100 + /100; р2 = — 100 — /100. Оригинал (ток i) найдем по теореме раз-Pa^iT1151 (14-10). В соответствии с замечаниями, сделанными при решении приме-14-2, имеем:
200ePl< (O.Ipi-4-20) I
2pt + 200 J
= 20 |/ 2 e"looZ sin (100; + 45е) A.
U
11
L
u.PUB
Рис. 14-12.
Hi (Pi) ePii
1 2RelP'(Pi)
405
14-6. Определение свободных токов по их изображениям
Пусть, например, требуется найти переходные токи в цепи рис. 14-13, а после включения рубильника Р2. В первой и третье" ветвях действуют источники гармонических э. д. с. ег и еа разны частот coj и <в3, а во второй ветви действует источник постоянной э. д. с. е2.
Найдем принужденные токи и напряжение на конденсаторе От всех трех одновременно действующих э. д. с. как до коммутации так и после коммутации. Тогда для определения токов переходного процесса нужно еще найти только свободные токи во всех ветвях.
Рис. 14-13.
Для этого сначала вычислим значения свободного тока в индуктивности i1CB (0 +) и свободного напряжения на емкости tzCcB (0 +) в момент t — 0. Это легко сделать по формулам (13-66). Составим далее уравнения по первому и второму законам Кирхгофа для свободных токов, считая пх положительные направления такими же, как и у переходных токов ils i2, :8:
Сев Т" Сев Т" Сев
ПСсв + L — г 2Ссв — 0;
1
ССсв Т" ПЛсв Т" Q Сев dt -|- Г/Ссв (Q 4” ) 0.
о
Перейдем в этих уравнениях от оригиналов к изображениям, опуская у изображений обозначение их аргумента р:
^1св 4” 2св 4“ ^ЗСВ 0,
r1Асв4“ f_Pl 1св — Сев (0 4- )] г2^2св = 0;
-------- I _____________и„_(0-М
~~ 1"2 /гсв + ГзЛсв + 4--;------= 0.
р^ р
406
я операторные сопротивления ветвей, перепишем сокра-нно полученные алгебраические уравнения:
полученные алгебраические уравнения:
/ 1св “Ь Н- Дев О,
Z1/ 1св гДсв 7л*1св (0 “Г" ) Д"1св’ иг (О р) — Г2^2св + ^Зсв =----------------— Дзсв»
(14-32)
я которые, легко найти изображения всех трех свободных Р ов_ Затем по теореме разложения найдем их оригиналы, т. е. свободные токи, а следовательно, и токи переходного процесса i3. Свободное напряжение на конденсаторе по свободному току
можно найти, например, интегрированием
^Ссв £ ^Зсв d-t9
причем постоянная интегрирования принята равной нулю,так как постоянной составляющей в составе свободного напряжения быть не может. Зная пСсв. легко найти напряжение на конденсаторе ис в переходном процессе.
Разумеется, на основании уравнений (14-32) можно составить эквивалентную операторную схему (рис. 14-13, б) и для определения изображений свободных токов применить любой из методов расчета электрических цепей при установившихся режимах.
Рассмотренный метод проще, чем непосредственный расчет токов переходного процесса по теореме разложения в тех случаях, когда внешние э. д. с. имеют простые формы, например синусоидальную или постоянную, т. е. когда легко вычислить принужденные токи. В тех случаях, когда заданы э. д. с. относительно сложной формы или когда э. д. с. представлены в виде кусочно-аналитических функций, этот метод теряет свои преимущества и рациональнее пользоваться формулами Дюамеля.
14-7. Формулы включения
При включении источника экспоненциального, постоянного или гармонического напряжения к пассивному двухполюснику с входным операторным сопротивлением Z (р) можно на основании теоремы Разложения (14-10) и с учетом для гармонического напряжения формул (14-24), (14-24а) и (14-246) получить простые расчетные форму-называемые формулами включения.
Для случая экспоненциального напряжения Ueat, изображение за2°^° = U/(p ~ <см- приложение 2) получим, применяя
(14°д^ма в операторной форме при нулевых начальных условиях
Т(р] —л________
W Zip) (р —a)Z(p)’
(14-33)
407
Определяя оригинал (14-33) по теореме разложения (14-1о\ получим формулу включения для экспоненциального напряжений
I (О -L {/ (р)} - + 2 , (14.34)
k=i '
предполагая, что Z (р) = О имеет п простых корней, и учитывая Чт
Z (pk) = 0. Здесь Z (а) = Z (р) при р = а и Z' (pk) = dZ/dp ’Пр° Р = Pk-
Первое слагаемое (14-34) представляет собой принужденный ток а сумма всех остальных слагаемых — свободный ток. ’
Формулу включения для постоянного напряжения U получаем из (14-34), полагая а = 0:
<(о=—+ У —
Z(0)+ L PkZ'(PkY
(14-35)
При включении гармонического напряжения и ~ Im{ =
= 1гп{Йте,ы% полагая в (14-34) а = /со и заменяя U комплексной амплитудой Um = U получаем из (14-34) ток i (t) как мнимую часть комплексного оригинала:
i (f)= Im
Ume!ai z (/w)
у
Li (Pk — /со) Z' (рк)
т. e. формулу включения для гармонического напряжения.
14-8. Расчет переходных процессов методом переменных состояния
Метод переменных состояния (называемый иначе методом пространства состояний) основывается на двух уравнениях, записываемых в матричной форме.
Структура первого уравнения определяется тем, что оно связывает матрицу первых производных по времени переменных состояния х(1> с матрицами самих переменных состояния х и внешних воздействий и, в качестве которых рассматриваются э. д. с. и токи источников.
Второе уравнение по своей структуре является алгебраическим и связывает матрицу выходных величин у с матрицами переменных состояния х и внешних воздействий и.
Определяя переменные состояния, отметим следующие их свойства:
1. В качестве переменных состояния в электрических цепя следует выбирать токи iL в индуктивностях и напряжения ис н емкостях, причем не во всех индуктивностях и не на всех емкостях, а только для независимых, т. е. таких, которые определяют обши порядок системы дифференциальных уравнений цепи.
408
ПиФференцналнные уравнения цепи относительно перемен-2- ^ояния записываются в канонической форме, т. е. представ-пых с° решеннымп относительно первых производных переменных ЛХяния по времени.
с°Сп метим, что только при выборе в качестве переменных состоя-токов it в независимых индуктивностях и напряжений tzc на
ЯИЯ висимых емкостях первое уравнение метода переменных состоя-не3яабуДет иметь указанную выше структуру.
1511 ^с?чИ в качестве переменных состояния выбрать токи 1С в ветвях мкостями или токи ir в ветвях с сопротивлениями, а также напря-с я ul на индуктивностях или напряжения иг на сопротивлениях то первое уравнение метода переменных состояния также представить в канонической форме, т. е. решенным относительно первых производных по времени этих величин. Однако структура их правых частей не будет соответствовать данному выше определению, так как в них будет еще входить матрица первых производных от внешних воздействий и'1'.
3. Число переменных состояния равно порядку системы дифференциальных уравнений исследуемой электрической цепи.
4. Выбор в качестве переменных состояния токов iL и напряжений ис удобен еще и потому, что именно эти величины согласно законам коммутации (§ 13-1) няются скачком, т. е. одинаковы для моментов времени t — 0 + и М-.
Рис. 14-14.
в момент коммутации не изме-
5. Переменные состояния iL и ис потому так и называются, что в каждый момент времени задают энергетическое состояние электрической цепи, так как последнее определяется суммой выражений
6. Представление уравнений в канонической форме очень удобно при их решении на аналоговых вычислительных машинах и для программирования при их решении на цифровых вычислительных машинах. Поэтому такое представление имеет очень важное значение при решении этих уравнений с помощью средств современной Еьиислительной техники.
Покажем на примере цепи рис. 14-14, как составляются уравне-НИя по методу переменных состояния.
'-начала получим систему дифференциальных уравнений, соот-®Тствующую первому матричному уравнению метода, а затем запи-ем ее в матричной форме. Алгоритм составления этих уравнений я любой электрической цепи следующий. Сначала записываются Равнения по законам Кирхгофа или по методу контурных токов; (1 ем выбираются переменные состояния и путем дифференцирова------я исходных уравнений и исключения других переменных полу-
409
чаются уравнения метода переменных состояния. Этот алгоп очень напоминает применяемый в классическом методе расчета п>1ТМ ходных процессов для получения одного результирующего диск?0' ренциалыюго уравнения относительно одного из переменных <е'
В частных случаях, когда в цепи нет емкостных контуров т контуров, все ветви которых содержат емкости, и нет узлов с шЛ соединенными ветвями, в каждой из которых включены индуКт, ' ности, может быть указан и другой алгоритм. Не останавливая на нем, отметим лишь, что он основан на замене емкостей источни” ками э. д. с., индуктивностей—источниками тока и — метода наложения.
Для цепи рис. 14-14 по законам Кирхгофа
применении
—j (0 — Тс + + i-c — О, rii + L dii/dt + rir — e (/); uc — rir = 0.
(14-36)
Определяя ir из первого уравнения, подставляя в третье, заменяя ic = С ducldt и представляя полученное дифференциальное уравнение в канонической форме относительно ducldt, получаем:
duc 11 1
и с ~ Q it rfj ис + q 1 (0- (14-37)
Решая второе уравнение (14-36) относительно L dijdt, заменяя ir согласно первому уравнению (14-36) и подставляя ic — С ducldt, получаем:
L diL/dt = — 2п7 + rC duc/dt -j-e (t) — ri (f). (14-38)
Складывая почленно (14-38) с умноженным на гС уравнением (14-37) и определяя из полученного результата diiJdt, получаем:
(14-39)
Перепишем уравнения (14-39) и (14-37) в матричной форме:
д г 1 L L 1 j II + 1 0 1 e(f) (14-40)
Ис с ~ Тс ис 0 с i(t)
х<р = Ах-]-Ви, (14-41)
или
где для рассматриваемой цепи имеем:
Х<1' = -r'l1' xl ~ 1 IL и С ; х = \х2 ir ис . (14-42а)
А = г ~~L 1 1 " L 5 в= 1 L О 0 1 ; и — J е(0| ; их II (14-426)
С гС “ С 1 и II \ / И
410
ем случае первое уравнение метода переменных состояния В ,,лИ (Ьопме запишется в виде
Гтоичнои фоРме запишется м<нр
= Ax + Bu. (14-43)
, т011Цы А и В в линейных цепях зависят только от параметров с, т е являются постоянными величинами. При этом цсПП квадратная матРиЦа порядка п и называется основной матри-А цепи, матрица В — в общем случае прямоугольная, размера цеН /и и называется матрицей связи между входом цепи и перемен-П ми состояния, матрицы х и и — матрицы столбцы или векторы переменных состояния (размера п \ 1) и внешних возмущений (размера т /. 1)
В рассматриваемом примере матрица В получилась квадратной второго порядка, так как число переменных состояния (tL, щ) равно числу внешних возмущении (е (/), t (/))
Перейдем к составлению второго уравнения метода В качестве выходных можно выбрать любые из величин Возьмем, например, в качестве выходных три величины ir, ic и iti
Значения их запишутся через переменные состояния (t£, ис) и внешние возмущения (е (/), i (/)) непосредственно из уравнений (14 36)
ir—0 i[ -5rtidr 4-0 е (/) }- 0 i(Z), ic = «(04-k-ir==iT-«с/^Ч-О е(П4-1 uL = — rtL — UC+ 1 е(04-0 i(t),
(14-44)
или в матричной форме
tr
ic
uL
I г
1 г
-1
0
0
1
(14-45)
И
Вди сокращенно
у —Cx + Du, (14-46)
ДЛя Рассматриваемой цепи
II о 1 1° 0
|у’ =- zt C=~-5 1 - 1/r , D |o 1 (14-47)
1 Уб ul !-/ -i ПГГ 0
411
а в общем случае второе уравнение метода переменных
COCTOHHU5J
(14-48)
Cx)-Dti.
Матрицы С и D зависят только от параметров цепи г, L, С. В об щем случае — это прямоугольные матрицы соответственно размеип k X п и k X т, причем С называется матрицей связи переменны состояния с выходом цепи, a D — матрицей непосредственной связи входа и выхода цепи (или системы).
Для ряда физических систем D является нулевой матрицей и второй член Du в (14-48) обращается в нуль, так как нет непосред. ственной связи между входом и выходом системы.
Если в качестве переменных состояния взять, например, ток i и напряжение uL и представить дифференциальные уравнения относительно них в канонической форме, то (опуская все промежуточные преобразования) первое из уравнений метода в матричной форме будет иметь вид:
х(1) = Ах 4- Ви + Еи(1),
(14-49)
где
(14-50)

Таким образом, действительно, первое уравнение метода переменных состояния будет в матричной форме иметь вид (14-43) только при выборе в качестве переменных состояния тока iL и напряжения ис.
Переходя к решению матричного дифференциального уравнения (14-43), прежде всего отметим, что оно особенно упрощается, если квадратная основная матрица А порядка п является диагональной-Тогда все п линейных дифференциальных уравнений (14-43) развя заны, т. е. производные переменных состояния зависят каждая только от своей переменной состояния.
Рассмотрим сначала решение линейного неоднородного матри^ ного дифференциального уравнения (14-43) операторным методе' Для этого преобразуем его по Лапласу:
рХ (р) - х (0) — АХ (р) 4-BU (р), (14’5))
1
X (р) = L {х (0}; U (р) = L {и (0}гТоТ)=х (0 -)=що), Т1
412

х (о) — матрица-столбец начальных значений переменных
*х(0) (0)
(14-53)
х(0) =
х„(0)
которые в момент равны их значени Перепншем (14
коммутации не изменяются скачком, заданы и ям в момент t = 0 —.
-51):
(р —А) X (p) = (pl — А) X (p)=x(O)-f-BU (р), (14-54)
е ।__единичная матрица порядка п.
Для получения матрицы изображений переменных состояния X (п) умножим слева обе части (14-54) на обратную матрицу (pl — — А)'1:
(р 1 - A)-1 (pl - А) X (р) = X (р) = (pl - А)-1 х (0) +
+ (pl-A)-1BU(p). (14-55)
Переходя обратно к оригиналам при помощи обратного преобразования Лапласа, получаем:
L-i {X (р)} = х (0 = L~4(pl - А)-1} х (0) +
+ L*1 {(pl — А) 1BU (р)}. (14-56)
Из операторного метода известно, что
L“1{/-^} = L 4(/’-“)“1} = L-»{(p-l-a) = (14-57)
По аналогии, записывая обратное преобразование Лапласа в матричной форме, будем иметь:
L”1 {(pl — А)-1} = еА/, (14-58)
гдееА< — переходная матрица состояния системы, называемая иначе фундаментальной.
Таким образом, находим оригинал первого слагаемого правой части (14-56)
L"1 {(pl — А)-1} х (0) = еА/х (0). (14-59)
Обратная матрица определяется делением присоединенной или Зацмной мафицы на определитель основной матрицы:
(pl-A^ffifri-A) (14-60)
v ’ det (pl —A)’ v '
Где Уравнение
det (pl - A) = 0 (14-61)
непрСТавляет собой характеристическое уравнение исследуемой
413
Оригинал второго слагаемого правой части (14-56) нахОп при помощи теоремы свертки в матричной форме Дится
L-1 {Fi (р) F2 (р)} = fi (t -т) f2 (т) dt, (l4
о ' DZ)
если положить
F1(p) = (pl-A)-1B = L{f1 (/)} = L {еА/В} (14
F2(p)=U(p) = L{f2(/)} = L{u(O}. (14-64)
Тогда на основании (14-62)—(14-64)
L-1 {(pl - A)-1 BU (p)} = jBu (t) dr (i4.65) и общее решение дифференциального неоднородного матричного уравнения (14-43) на основании (14-56), (14-59) и (14-65) будет иметь вид: z
х(/) = еА'х(0) -{-§ eA<z~T>Bu (т) dt. (14-66)
о
Первое слагаемое правой части (14-66) представляет собой значения переменных состояния или реакцию цепи при нулевом входе, т. е. и = 0. Иначе говоря, оно представляет первую составляющую свободных процессов в цепи хсв (/)/„ = 0, обусловленную ненулевыми начальными значениями переменных состояния цепи, и поэтому является решением уравнения х(1) = Ах. Второе слагаемое представляет собой составляющую реакции цепи при х (0) = 0, т. е. при нулевом состоянии цепи.
Нулевым состоянием цепи назовем такое ее состояние, когда начальные значения всех переменных состояния равны нулю. Иначе говоря, второе слагаемое (14-66) представляет собой сумму при принужденной реакции цепи хпр (/), возникающей под влиянием внешних воздействий и (/) и второй составляющей свободных процессов хсв(0/х(0)=О •
Равенство (14-66) означает, что реакция цепи равна сумме реакций при нулевом входе и нулевом состоянии.
На основании (14-48) и (14-66) для выходных величин имеем.
у (t) = CeMx (0) +С § eA<z~T)Bu (т) dt-j- Du (t). (14-6/)
о
Если состояние цепи задано не в момент t = 0, а в момент 0 — sg t «С t, то равенства (14-66) и (14-67) обобщаются:
x(0=eA<<-'t>x(T)+JeA«-т>Ви(т)с/т; О4'68) т
у (/) = СеА (* - *) х (т) + С $ еА Ч Ви (т) dt + Du (0 - - (14'б9)
v
414
14-5 Для разветвленной цепи второго порядка составлены уравне-Ттояния
ЦИ”С х/ X,1 =Зл1-4х2-2р(/)
ых начальных условиях xt (0) = 1, х2 (0) = 2 и при единственном при 1,еНУ^ в ней источнике э д с
e(0 = sin+=«(0.
Пойти переменные состояния х, (t) и х2 (t).
р е ш е н и е. Перепишем уравнения состояния в матричной форме
где
1—2 1 Л II
; х(0)--= I; В = 3—4 V ’ 2 ।
Найдем сначала первые свободные составляющие переменных состояния при нулевом входе Для этого составим матрицу
II 1 0 (pl~A)=p Г }
1 —2
3 —4
Р-1
—3
2
Р + 4
Для нахождения присоединенной или взаимной матрицы заменим в предыдущей матрице каждый элемент его алгебраическим дополнением Получим матрицу
I р + 4 4- 3
I .—2 р — 1
Транспонируем ее, найдя присоединенную или взаимную матрицу:
р + 4
3
—2 р-1
Найдем определитель матрицы (pl — А).
2
Р + 4
det (pl —А) =
Р-1
—3
—Р2+Зр + 2— (р+1) (р+2).
На основании (14-60) обратная матрица будет равна:
Г Р + 4 —2 -[
(р + 1)(Р + 2) (р + 1)(р{-2) 3 р— 1
L(p + D(p + 2) (p+l)(p + 2)J
(pl-A)-i =
Повергнем ее обратному преобразованию Лапласа с учетом того, что для На о Нужно подвергнуть обратному преобразованию Лапласа каждый ее элемент.
счовании (14-73) получим переходную матрицу состояния цепи
^L^pl-A)1}-
Например,
L4W^}-3‘_'-2r“ “т-«•
415
Для переходной матрицы состояния системы получим: Зе-< —2е“2< + 2e~2t
Зе-/_ 3r2Z
еА' =
-2е-%Зе~2МГ (14 70)
Для первых свободных составляющих переменных\:остояния 6vn₽» у дем иметь
хсв (О |ц-(Г^
*1CB (О
*2CB (О
= <’Azx(0) =
Зе' —2e~2t —2e-< + 2e-2''
Зе-*— 3e~2t — 2t-<4-3e-2/ — e“f+2e 2* I — e-*-|-3e~2* j ’
т. e.
*1CB(0 |u-0 = - e-f + 2e-^;
*2cb (0 |u,0 = — e^ + 3e^.
Далее на основании (14-66) найдем сумму принужденных и вторых свободны составляющих переменных состояния:
рЛи-т)Ви о
о
Зе-</-т>_2е-2(/-т> 3g- </-T)_3g-2</-TI
7
—ге-'^Т’ + Зе-а^-т,
—Зе-'^’ + Зе-г^-г)
7g- < t~Т)_Qe~2<f~r>
•’ j 7е~'*~х' — 9е“21Г~Т1
sin т dr =
7е“* ех sin т dr — бе’2* j е2Т sin т dr 0 О
t t »
7Р-/ j Рт sjn -j- cZt — 9e“2/ e2T sin r dr о 0
Суммируя полученные результаты, находим искомые значения переменных состояния:
7 6 И . ± 23
_g-/__g-2/4._slnZ__[_cos/
7 , 9 1 . 17 ,
-^е t — ~re — —TKcosi
2 5 10 10
7 6 11 23
Xi(Q = — е~*Н-2е~2*4- — e~f—г е~2*-|—sin t — - ^c№t— 2 5 10 10
И . 2 23 2 5 4
= Т0 SmZ~ 10 COS/+2 е+ДГ;
х2(1) = — е-'+Зе~^+ ? e~f— | е~*—— sin t— -j(j cos/=
1 f 17 , ,5 , , 6
== - До sffl l~ To cos/+¥ e +~5 e
Так как решение уравнения (14-43) было получено выше и. дан° формулой (14-66), то для проверки правильности решения (И' и вычисления с его помощью матрицы переменных состояния х и можно сначала непосредственной подстановкой (14-66) в (14' убедиться, что последнее при этом обращается в тождество. Д этого нужно только сначала вычислить х(1) (/), дифференйиР" (14-66). При этом получаем:
xd’ (I) = АеА*х (0) + $ АеАР-т)Ви(т) dx + Ви (/)• (14'71>
о ----
416
нетрудно непосредственно убедиться, что (14-66) действи-ТепеРдЛяется решением матричного дифференциального уравпе-те51’й-43)- А,
нцЯ I1 ' что переходная матрица состояния системы ем поз-^'найт'и в пространстве состояний, т. е. в пространстве, число воляет которого равно числу компонент вектора переменных измер011 х перемещение, начинающееся из некоторого началь-соСГ°подожения (при t = 0 или при t = т), причем вектор х (/) н°г° т значительную информацию, так как одновременно описы-с°'^Рвсе переменные состояния, т. е. функции времени лу (/), х2 (/),...
. *п (О- .
••• ’Пля того чтобы непосредственно воспользоваться решением /14-66) и вычислить матричную экспоненциальную функцию
прибегая к обратному преобразованию Лапласа, следует, например, выполнить ее разложение в ряд:
/>а/=1 + д+ДА^+ААА^+.
/2 /3
= 1 ф- А 4- A2 gi + А3 Ц-.,.
(14-72)
При этом правую часть (14-72) нужно представить в замкнутой форме, чтобы се вычисление могло быть произведено путем выполнения конечного числа операций, как, например, в формуле (14-70).
Вычисление переходной матрицы состояния может производиться различными методами — методом разложения в бесконечный ряд, методом, основанным на критерии Сильвестра, методом Кэйли — Гамильтона, методом частотной области, методом передаточной функции и др.
Рассмотрим кратко два первых метода. Сначала рассмотрим первый метод (разложение в бесконечный ряд) на числовом примере.
Найдем переходную матрицу состояний по заданной основной матрице А системы
Степени А получим последовательным умножением на А:
-2 6|| II6 - 14
А2 — А3=
-3 7 Г II7 -15
На основании (14-72)
(эА/ ZZZZ- 1 0 11° -2L -2 6/2 16 -14 /3
0 1 + |1 -з| + -3 7[|21 +7 -15 31 +••••
Складывая матрицы правой части, -получаем:
__2/Д б/з _ 6/2 14/3
21 + 31 + 3! 1 3!
1 _ 3/4-7/2-'--4-2! 1 3/1 ш о! 3! ‘
Основы теории цепей
417
Далее следует найти в замкнутом виде каждый элемент грицы. Для данного примера нетрудно убедиться в том, что из элеменюв матрицы можно представить в замкнутом виде ность двух экспонент:
Э1°й Мг.
КаЖДЫц как раз.
---
2е 1 — е2' е~* — e2i
2 (е 2t — ef\ 2е 2< — е1
(14-73)
что и решает поставленную задачу.
По методу, основанному на критерии Сильвестра,
где
еА<= 2 еР^Ф*, (14-74)
k — 1 '
и (А —pzl)
/=1’2........."• (14-75>
I фк
Здесь pk, pi — собственные
значения или характеристические числа матрицы А, т. е. простые корни характеристического уравнения цепи (число их равно п).
Пример 14-6. Для цепи рис 14-15 при г = „ Ом, С = 1Ф, L = * Г рас считать ток ic при включении ее к ис точнику тока i (t) при условии, что в момент включения (t = 0) даны ток в индук тивности iL (0) и напряжение на конденсаторе ис (0), что обеспечивается одновременной и мгновенной коммутацией всех трех рубильников цепи.
Решение В качестве переменных состояния выбираем «с и iL, а выходной величиной у считаем ток в емкости i‘c.
На основании законов Кирхгофа составим уравнения состояния цепи и урав-некие для выходной величины.
Рис 14-15.
ur dur di, dur
i =-----p i r C : L = Пгт} у -- irr — C r — i
r 1 L 1 dt ’ dt c H c dt
“C-ir (14-76) r
откуда
duc 1 11 diL 1
“c = ~dt = " rc uc т *1 +у '> lL = = 7Г «с-
(14-77)
418
Характеристическое
уравнение цепи
det{A-pl} = det|
— 1/гС — р — 1/С
1/ь -р
Р* + rC Р+ LC °’
(14-79)
3 , Тр 4 12=0, откуда рг = — Зср2 = — 4с”1.
1,1Й Основная матрица цепи А и матрица связи В равны:
А =
—7 —1
12 0
1 о
0 II
01Г
В =
По (14-74) найдем матрицы и Ф2:
1 0 д+4 0 ! Ф1— -34-4
II 1 О II
А+3||о 1| ф2- —44 з
л _7 —J II з '• | 12 0 +|| О
1—3 —1 ;
= | 12 4
° lh 4 1II
3 ||/~ —12 3 И’
По (14-73) найдем переходную матрицу состояний:
—1
4
еА/ = eDlt фх 4- еГг/ Ф2=е~ st
—3
12
4-е“«
4
— 12
—3t>--z|4eT/ 12е~зт_ 12e“4f
— е st 4 е
4е 3t — Зе 4Z
(14-80)
1
—3
На основании (14-66) найдем матрицу
переменных состояний:
t
цс (О lL (О
_Зе~зр4£,-4С 12е-зт— 12г4/
— е зре-4/ 4е-зт — 3e~4Z
|| ис (°) II
II li (°) II
+S о
__Зе-з (т-т) 4 4,9-4 < /т; 12е~з</ г>___12е 4<Т-т>
___е-.5 </ Т) 4 е“4 it т> II || 4g-a </-т>______зе к /-Т1 || I
i (т) dx =
1
О
—Зе 3r_[_4g-4/ 12е 3/- 12е4'
— e-at-^e-u 4е-зТ—3e~4Z
__3g-3 </“T) |_ 4g“4 <Г-Т) 12e 3(/-r>_ I2e-4'T-T>
«С (°) II
'НО) Г
i (r) dx.
(14-81)
Раскрывая матрицы (14-81), находим:
«С (0 = (-Зе^ + 4е '0 чс (°) + +е~Л/) 'г (°) +
t
4 J [—Зе-- (Т-п 44е~4«-г)] i (Т) dx; (14-82)
О
iL (0 = (12е-^— Т2е -^) ис (0)+ (4е~^—3^/) t
-7 j [1-с "" r" л'' 1 j г (ь) dr. ’ (l-i-бЗ;
о
419
На основании (14-76), (14-82) и (14-83) наймем выходною величину-
У (0 - 1С (0 - с = I (0 + (9а з/_ 16a-«0 «с (°) +
I
+ (_3е-з^ — 4е~«') i£ (0) + )' [Эе-з<«-т>_ 16е~4 <<“*>] (
Полученные результаты легко проверить непосредственно для установив гося режима, если источник тока i (/) — единичный, те i (t) — t (т) ~ [ р16' средственно из схемы рис 14-15 следует, "то пои этих условиях ток едичичн*10' источника тока замкнется через индуктивность, т е tL (оо) — 1, источник тока будет ею закорочен, т е. ис(оо) _= 0, и ток в конденсаторе 6j дет равен цуЛ|0 т е (оо) = 0 ’
По формулам (14 83), (14-82) и (14 87) получаем, выполняя интегрировани и полагая t= оо е
(L(co)=l; ис (со)=ь0, (со) = у (оэ)=0.
14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения
Как известно, решение этой задачи можно получить в вице ряда Фурье (суммы бесконечного числа гармоник). Здесь будет дано иное решение, основанное на возможности найти изображения периодического воздействия при помощи применения теоремы запаздывания. Согласно этой теореме, если
F(p) L {/(/)}, 1
то > (14-85)
L — т)} = е pZF(p). J
Теорема показывает, что изображение функции f (t — т), запаздывающей на время т по отношению к исходной f (/) (рис 14-16), получается умножением изобра
f(t г) ) жения F яа е РХ вреМЯ
' v запаздывания)
—"V Поэтому, если и (/) — перио-
V । днческое несинусоидальное на-
пряжение, подключаемое к цепи
_________________________ ___в момент I = 0, иг (0 — ег° / 0_________________________f_аналитическое выражение в те-
чение первого периода измене-
Рис. 14-16. ния (0 Т) и его изобра-
жен не U1 (р) - [.{щ (/)}, то изображение напряжения U (р) = L{u (^} для любого момента вре' мени (0 t оо) на основании (14 85) запишется так:
у , , , гг- (п\ /1 4
(Р)=-С1(Р) (1-|-е - - Ч-е - J
420
йзображение искомои величины
Х(р) = [/(р)К(р)=?^7-К(р), (14-87)
пгинал может быть найден на основании (14-2) как сумма вы-
jr ^j\_передаточная функция цепи, определяемая как отноше-
где лапласовых изображений выходной и входной величин при ну-0йе х начальных значениях переменных состояния цепи.
^Искомая величина х (f) равна сумме ее принужденного хпр (/) свободного хсв (0 значений, причем хпр (/) равно сумме вычетов 'тносительно полюсов приложенного напряжения U (р) в выражении (14-87), a xLB (0 — сумме вычетов относительно полюсов передаточной функции К (р) для того же выражения (14-87). Указанные соображения следуют непосредственно из закона Ома в операторной форме (14-19) и были подтверждены вышерассмотренными примерами 14-2 и 14-3. Из (14-86) следует, что число полюсов приложенного напряжения U (р), которые находяшя из уравнения 1 _ е riI = 0 и равны pk — 'ftkn/T, бесконечно велико. Поэтому находить
хпр (0 по изображению X (р) из (14-87) нецелесообразно, так как это приведет к бесконечно большому числу слагаемых (к ряду Фурье).
Но х (/) можно определить как разность
хпр(0=х(0-хсв(/). (14-88)
Величину хсв (0 найти по (14-87) нетрудно, так как число полюсов передаточной функции цепи К (р) конечно. Аналитическое выражение для х (/) надо найти для каждого периода изменения приложенного напряжения и (/) отдельно, что нетрудно для первых периодов. Но тогда по (14-88) находится и аналитическое выражение для
(0, не одинаковое для каждого из периодов. Проверить полученное значение дтя хпр (/) можно из тех соображений, что значения однь В начале 11 в К0НЦе рассматриваемого периода должны быть
Пусть к цепи г, L в момент t — 0 подключается периодически из-^няющееся напряжение и (I) пилообразной формы (рис. 14-17). Пе Ппло°бразное напряжение и (/) можно получить наложением и Р «одическим повторением трех функций, рассматриваемых с мо-еНтов начала их действия: прямой другой прямой
А (/) „
Т \1 — Т) и iicciOMHiioi’f величины /3 (/) — - - U (t - Т}.
421
Применив теорему запаздывания (14-85), найдем изображе первого зубца пилы (рис. 14-17): Н11е
.. , ч U U т U т Ui(P)=T?~T^e~P ~ Ре ' •
(И-89)
Заметим, что тот же самый результат получится непосредствен ным интегрированием по формуле (14-1):
Ui (Р) = § 7 te pt dt=^^ te~pt dt. о b
Изображение всей пилообразной функции и (t) получится в виде суммы изображений одинаковых зубцов, смещенных на время т друг относительно друга:
(14-90)
Изображение тока в цепи
/ (p) = U (р)К (р) = 2/ м Ue~p’’T (14-91)
Тр {r-^pL) р (1 — е Р')(г-рр£)
Свободный ток iCB на всем промежутке времени (О Сг: ос) найдем как вычет функции / (р) ер( в полюсе передаточной функции Рх = —r/L, т. е.
iCB = Res
Uept
Тр2 (r + pL)
Ц(Р^ г> р (\—е~рТ) (г +pL)
P = — r/L
Fi(Pi)^ Le L i'APi) >2T +
~~<f -T) e b
(14-92)
где Fx (p) и F2 (p) — числитель и знаменатель изображения тока ^св (Р)•
На промежутке времени О ==S t Т (первый зубец пилы) полный ток цепи i найдем как результат воздействия только напряжений fx (О = Ut!T = L-1{t//Tp2} в виде суммы вычетов выражения
V Рез г UpPt 1 = I ^nt 1 Г
Г1 = —г/Ь,
р- = 0
(// t/L
1Г 1 Гр2
(-1+е
(14-93)
i
422
Принужденный
__ и
— lev тг2
hip
ток найдем согласно (14-88):
/ -ГД ——t
rt-\-L\— 1 - j- с L j —Le L
(14-94)
Указанная выше проверка выполняется, так как
Гг
/п\ • /'ТЧ ГГ — 4" Й- — Г Т) б
гПр (0) = гпр (Т) = U-------ТД\~'
Tr2\l — eL I
(14-95)
Аналогично находится изображение при периодическом знакопеременном прямоугольном напряжении и (/) (рис. 14-18):
щр)^и (1-2е рП2+2е-рг_...) = ^ (14-96)
р pl +е '
так как бесконечный ряд в скобках, как легко проверить, представляется делением двучленов числителя и знаменателя правой части.
В самом деле, постоянное напряжение + U, включенное в момент = 0, действует бесконечно долго. Изменение знака напряжения в момент t — TI2 реализуется включением в этот момент постоянного напряжения — 2U, действующего также бесконечно долго. Далее в момент t Т включается напряжение + 217 и т. д , что и учтено Формулой (14-96).
Подобным же образом можно найти изображение напряжения ® виДе трс'5 гольной кривой (рис. 14-19). Рисунок 14-19 показывает, То треугольная функция и (/) = f (f) получается наложением и периодическим повторением трех прямых Д (I) = 2Ut/T, f2 = := ._ 41/ / 2U
~T\~ 2/ 11 /з = у (1 — 7), рассматриваемых с моментов на-Чада их действия до t оо.
Ра>к ИМенпв теоРемУ запаздывания (14-85), найдем лапласово изоб-ение первого треугольника функции и (f):
t-i (P) ~ ppz
423
Разумеется тот же результат получится непосредственным вц< лением интеграла прямого преобразования Лапласа на промеж» "с от 0 до Т;
Т 2 Т
U1(p) = J § (2U— t^e~pt dt.
О Тг'
Глава пятнадцатая
ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
15-1. Преобразование Фурье и его основные свойства
В § 12-2 было дано разложение периодической функции с перио. дом Т, удовлетворяющей условиям Дирихле, в ряд Фурье:
/(0 = Лоф- У, (XfcmcoswA/-l-BfcmbinoV), (15-1) где
Ч 7 /2
— 7/2
2 +С/2
Akm \ f (т) COS COfcT df,
— Т/2
2+f/2
= y \ f (T) sin M/Д dt
- T/2
и ak = k2n/T принимает дискретные значения: и1 = 1-2л/71;
а>2 = 2-2п1Т и т. д.
Подставляя значения Ло, Akm и Вк1П в (15-1) и обозначая интер« вал между соседними частотами
сод.+1 — mk — (k + 1) 2njT — k • 2л/Т = 2njT=Дш, получаем:
+ Z/2 оо + 7/2
f (0 = § f (т) dt -|- 2 f J / (т) (cos cos wfcT +
-772 k 1 -772
4- sin bijit sin wat) dt =
+ T/2 oo + T/2
— y f (t! dt 4- -i- У Дю f (t) cos [c'7; (t —
-T/2 ' —T/2
424
Здесь |coso^~ т) I'-1, поэтому
T,2
f (t) cos ak (t — x) dx -<
T/2
7 к бесконечности, заключаем, что если функция ^солютно интегрируема в бесконечных пределах (т. е. если интеграл § |/(т)' cfxj, то конечное значение имеет также
f (т) cos ak (t — т) dx при любых ak и t. При этом же
\f(x)\dx.
- Т/2
устремляя Мт)ас.
конечен
интеграл условии
т. е. приближенно
/(О
f Т/2
lim 4 /(т)с/т = 0,
7 — Л/2
СО 4~С°
’ У Доз U (т) cos wfe (t — т) dr. (15-2)
J b х&ЯЯ ,)
fe=l —oo

Но так как Лоз — 2л/7—>• 0 при Т -> оо, сумма в правой части (15-2) переходит в интеграл, а приближенное равенство (15-2) — в точное (при этом Лоз заменяется на da, а дискретные значения частоты оз^ — на непрерывно изменяющуюся частоту оз):
о
-|-со
da f (х) cos оз (t — т) dx. (15-3)
—СО
Поскольку Т -> оо, то функция f (t), заданная на промежутке
— оо t ф сю, является уже непериодической функцией. Поэтому можно утверждать, что формула (15-3) представляет собой сумму бесконечно большого числа гармонических функций с непрерывно изменяющимися частотами оз и бесконечно малыми амплитудами. В самом деле, выражение
я da f (т) cos оз (t — т) dx
—со
представляет собой бесконечно малую по амплитуде гармонику частоты оз Конечно, эта бесконечно малая гармоника частоты оз может бить найдена только по заданной функции / (f). Суммируя тем гармонические составляющие (внешний интеграл по оз) ^ри изменении оз or 0 до оо (т. е. учитывая все бесконечное множест-гармоник с непрерывно изменяющимися частотами оз),получаем
Данную функцию / (/).
п г^пыми. стонами, непериодическая функция характеризуется непрерывным спектпом частот, в то время как периодическая функ-1 я дискрешым,
425
Формула (15-3) называется интегралом Фурье в тр!1Г неметрической форме. Отметим, что абсолютная интегрируемос° функции f (/) в бесконечных пределах является для вывода форму?1 (15-3) достаточным условием, но не необходимым. Ь|
Ввиду четности cos оз (I— т) относительно со формулу (15-3) йе репишем еще в виде
4-оэ 4~со
f(t) — Доз f (т) cos оз (t — т) dr.
—оо —оо
(15-4)
Подчеркнем, что при решении электротехнических задач ran. моники с отрицательными частотами физического смысла не имеют (см. также гл. 12). Однако введение их позволяет представить функ. цию f (f) вместо формулы (15-3) более симметричной формулой (15-4)
Далее в силу нечетности функции sin оз (t— т) относительно а аналогично (15-4) найдем, что
4 со 4 00
0 = ^~. da f (т) sin оз (/ — т) dr. (15-5)
—со —оо
Умножая (15-5) на / и складывая с (15-4), получаем интеграл Фурье в комплексной форме, который часто значительно удобнее для расчетов:
/(O = gt S do) f (г) dr. (15-6)
—00 •—00
Если функция / (f) задана на промежутке от 0 до оо, а на промежутке от — оо до 0 равна нулю, то соответственно
/(О—2Д § ^°з § f (т) cos оз (t — т) dr; (15-7)
—со О
J da J (т) dr. (15-8)
—со О
Внутренний интеграл с заменой т на t (значение определенного интеграла не зависит от того, как обозначена переменная интегрирования) может быть переписан так:
F (ja) =_ $° е (0 dt—F (оз) ^0(“’. (15‘9)
О
Комплексная функция частоты F (/оз) дает закон изменения комплексных амплитуд гармоник в зависимости от частоты оз и н зывается частотным спектром (спектральной плотность ’ спектральной, частотной пли амплитудно-фазовой характеристик? заданноп фупкции f (I). Само соотношение (15-9) называется пр
426
преобразованием Фурье и обозначается еще •"Лн.
F '^уЧетом (15-9) перепишем (15-8) так:
4-со
/(0=^ $
(15-10)
Таким образом, функция F (/оз) по модулю и фазе характеризует армонику частоты оз, а выражение F (/оз) с;С1/ йоз представляет бой гармонику с частотой оз функции f (t). Эта гармоника выражена в комплексной форме, имеет бесконечно малую амплитуду и взывается элементарной. Соотношение (15-10) называется обрат-11 ы м преобразованием Фурье и обозначается F 1 {/(/оз)}. Н Сравнивая формулы прямого и обратного преобразований Лапласа (14-1) и (14-2) с формулами прямого (15-9) и обратного (15-Ю) преобразований Фурье (см. также приложение 3), заключаем, что преобразование Фурье является частным случаем преобразования Лапласа, получается из него при р = /оз и применимо для более узкого класса функций [ (/), что и было отмечено выше. Следовательно, частотный спектр F (/оз) функции f (Z) получается из ее лапласова изображения F (р) по формуле
Г(/оз)=Г(р)^/Щ.
(15-Н)
Поэтому установленные в гл. 14 свойства преобразования Лапласа справедливы и для преобразования Фурье.
Выше было показано, что операторный метод, основанный на преобразованиях Лапласа, применим для расчета переходных процессов Поэтому и частотный метод, основанный на преобразованиях Фурье, может быть как частный случай операторного метода применен для тех же целей.
15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров
Рассмотрим цепь г, L, С (рис. 14-1), которая была подключена к источнику э. д. с. ег (/) и в момент t = 0 переключается к источ- , НикУ э. д. с. е (t).
Найдем согласно (15-9) частотный спектр э. д. с. е (Z):
ОО
Е (}ы) = J е~'Ые (0 dt = E (p)p_ja.
О
(15-12) *
уСп^акон Ома для частотных спектров при ненулевых начальных °виях получим из (14-17) при р = /оз:
Е (]ы) + Ы (0) — ис (0)//со у (/“) ~ г -р /сой +1 /ушС
(is-i3)
427
Знаменатель этого выражения
Z (/со) = Z (р)р /а=г + /(oL +
представляет собой комплексное сопротивление цепи г, L, С, пп нявшееся ранее для расчета установившихся (гармонических) цессов. Как показывает (15-13), оно находит применение и для °' счета переходных процессов, когда токи и напряжения могут ич?3' няться во времени не гармонически, а по самым различным закона16'
В самом деле, при помощи Z (/и) по формуле (15-13) найл ' частотный спектр тока / (/оз). А далее по формуле, аналогично1”' (15-10), и ток переходного процесса
= i < /(/оз)е^Лз.
(15-14)
Как следует из и токи ограничены,
более подробных исследований, если э. д. с но не удовлетворяют условию абсолютной интегрируемости в бесконечных пределах, то при вычислении интеграла (15-14) полюсы подынтегральной функции при интегрировании по вещественной оси нужно обходить снизу.
Из (15-14) заключаем, что ток также может быть представлен в виде суммы элементарных гармоник с частотами, непрерывно изменяющимися от—оо до + оо, а величина -L представляет собой элемен-
тарную гармонику с частотой со функции i (t).
Аналогично изложенному в § 14-3 и на основании соотношения (15-13) может быть составлена эквивалентная комплексная (для частотных спектров) схема (рис. 15-1). По-
этому при расчете переходных процессов частотным методом можно сначала составить эквивалентную комплексную схему и по ней прямо находить частотные спектры токов и напряжений.
Из (15-13) получим закон Ома для частотных спектров при нуле'
вых начальных условиях
1^=^-, (15-15)
v ’ Z(jco)’
а из равенств (14-20) и (14-21) при р = /оз — уравнения первого и второго законов Кирхгофа для частотных спектров
п
У, 7ft (/оэ)=0;
*== 1
(15-15)
Ш)Ш = 2 [£fe(/«) + ^(0)-~~J- (15'17)
ч ь=1 fe=iL
428
м образом, в общем случае вычисление токов или напря-“ меюДОИ интеграла Фурье выполняется следующим образом »<еН1111аданнои Цепи составляется эквивалентная комплексная схема. Ц-пЯ 3 е определяются частотные спектры токов или напряжений По с' мощи любого из известных методов расчета линейных цепей ПРЙ с.1аНовившемся режиме (методы контурных токов, узловых ПР11 цццалов и т д ) Расчет можно также свести, применяя принцип П°Тожения, к нулевым начальным условиям (см § 14-5) Для нахож-НаЛ{Я оригинала можно пользоваться таблицами (см приложение 3) А6” применять теорему разложения, формула для которой получается из (14-10) при р = /оз Поэтому, если
/(/ю)
(15-18)
то
р 1 (]ык) iaht Д'(/03,()
(15-19)
где (/со) — производная от Fz (pF) по /оз, а /оц — простые корни характер истического уравнения
^2 (/“)-= 0.
Заметим, что при комплексных и сопряженных корнях /оз характеристического уравнения частоты оц получаются также комплексными, но сопряженными относительно вещественных частей.
Пример 15-1. Найти ток и напряжение на конденсаторе при включении цепн г, С на экспоненциальное напряжение
J t/e at при t X О, ) I 0 при t О, где а. > О
Решение Прежде всего х бед имея, что функция и (t) представима интегралом Фур'е Деист ните тьно, функция и (/) абсолютно интегрируема в бесконечных пределах, гак как интеграл
со О со оо
\ | « (г) 1 dt— f и (С) । dtp- ? и (t) | dt = O-r f Ue dt — —
.) a — co — co 0 о
конечен при любом a =/ О
Но таблицам функций и их частотных спектров (см приложение 3) или по -весгному лапласову изображению функции и (О запишем ее частотный спектр.
,, / U \ U 11Р~1 агс1" (“/«)
^(/оз)=-------=--------------= U (со) |М> = -----------—,
\Р+а/р)а а г/“ ра-фш2
полу чаем амплитудпо- и <1 азочастогную характеристики приложенного
,, . . U со
с'(со) ——ф (со) —— arctg г и--1-ш- и
429
Отсюда следует, что включение апериодического напряжения и (/) Мо сматривать как включение бесконечно большою числа элеметарных i ап^Н0 ких колебаний, частот которых изменяюich непрерывно oi минус ^1,И'1£(-бесконечности. * “лкх.
Рис 15-2.
Рис 15-3.
На рис 15-2 даны амплитудно- и фазочастотная характеристики U (от) иф (м)
На рис. 15-3 построена частотная характеристика U (/со), т. е., иначе говоря годограф комплексной функции U (/от) при изменении со от 0 до оо, которая представляет собой полуокружность, что следует из выражения для U (/от).
Комплексное сопротивление цепи
-(/со)- r+ jaC - .ыС .
Так как начальные условия нулевые, то на основании закона Ома для частотных спектров
/ = UlaC
4 ’ Z(ja) (/со+«) (/со/Сф-1) ‘
Применяя для вычисления тока t (/) теорему разложения (15-19), обозначим
Л (/co) = /coCt/; F2 (/со) = (jaф-а) (/согСф-1)
и найдем корни характеристического уравнения F2 (/со) = 0:
/со! = — а и /со> =—1/гС.
Вычислив значения множителей обоих слагаемых теоремы разложения К1(/со1) = —«СП; F\ (/со2) = — U/г;
F'2 (Jai) = 1 — rCa; F', (/со2) = — 1 + гСи,
после простых преобразований получим:
«(0 =
UC агС — 1
_L е-1/гС гС
ае^
Напряжение на конденсаторе ис (0 находим, интегрируя ток и полагая по стоянную интегрирования равной нулю. Эю ясно из физических соображении (никакой постоянной составляющей в составе напряжения ис (f) в данном случа быть не может);
ис^ = ^с $ Z (°Л=мСпр+иСсв=^л(-е’ОД+е гС)-
Найдем напряжение ис (/) несколько иначе и притом для случая одинаков# затухания иСпр и и Ссв, когда а = \/гС, г. е. в случае равных корней зна',е1
430
и (/<о) Так как
уеЛ" ь
ис (/W)
U 1//соС a-}-/to г+ 1//соС
Ua (a + /to)^ ’
,ая лля вычисления ur (/) формулу вычета в кратном полюсе (14-14), ТО, примеНЯИ " получи
1
«С V) 53 2л
Uc (/to) eJai i’r (/“) eJai (a + /“)2]
, d
= Ua~r,—-d (/to)
(p/®^) =Uate
l/to — — a
/со —— a
Пример 15-2. Найти ток в ветви с сопротивлением г1 после включения ру-бИЛЬПано (^1OoL(314/ + 6O-) В, г3=200е~в< В, г1=ЮОм, 6 = 300 мГ; г ^20 Ом, С=Ю0 мкФ, г3 = ЗО Ом.
Рис 15-5.
Рис 15-6
Решение Рассчитываем режим до коммутации (рис 15-5).
г2пр- = <1пр-= 1.01 яп (314/— 1220') А, «хгпр- (0= ЮЛ sm (314/— 12°20') В.
Задачу решим методом приведения к пулевым начальным условиям Для этого найдем напряжение на зажимах рубильника
«руб (0 = «12пр-(0-^3 (0=10,1 sm (314/—12°20') —200е-5^ В.
Частотный спектр напряжения па зажимах рубильника
,, . v о u -/to+1435 200
^Р> б (/to)-2,16 3142+(/ш)г 5 + /и-
Рассчитаем переходный процесс в схеме рис 15-6 Для этого найдем сначала заимную комплексную проводимость первой и третьей ветвей для любой частоты
у 7-i /to (0,3/со + 20)
13~ Z1Z2+Z,Z3+Z3Z1 - 12 (/(о-]-105,8) (/со + 236,2) ‘
Частотный спектр тока ц (/) в схеме рис 15-6
/; (/to) = у13 (/to) др1 б (/to)=
JCO (0,3/(0 + 20) {2,16 (— /ю+1435) (5-}-/со) — 200 [(/to)2 + 314з]}
(5 + /W) (314-to) (314+gt)12 (/to |-105,8) (/со | 236,2)
^гинал тока t, (/) на основании теоремы разложения (15-19) равен
Т(0 = 0,1942 sin (314/4-31°) | 0,0661e->'+l,685'-u».8'_ь,Ь7е А.
431
Пользуясь методом наложения, находим ток переходного процесса с сопротивлением гр ‘ ь ВеТЕц
ц(/) = —11пр_ (0 + »; (0=-—0,88 sin (314/—21°02')4
4- 0,0661с"5' + 1,685с" ’о">,8х f;,87f 236,2 д.
Примеры показывают, что расчеты переходных процессов раторным методом и методом интеграла Фурье весьма похо^ друг па друга. Преимущества метода интеграла Фурье сказывают^ при расчете переходных процессов приближенными способами. Ся
15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций)
Для любой линейной электрической цепи по законам Кирхгофа можно составить систему иитегро-дифферепцпальных уравнений описывающих процессы в этой цени. То же самое можно сделать для любой динамической системы: электромагнитной, механической или электромеханической. В электрических цепях и динамических
Д’, (/)=?(«)
Рис. 15-8.
системах любую величину можно рассматривать как входную и считать ее изменение во времени заданным. Любую другую величину можно рассматривать как выходную и определять ее изменение. Переходя в уравнениях, характеризующих эти системы, от оригиналов к изображениям, можно исключить изображения всех остальных величии, кроме входной X, (р) и выходной Х2 (р). Как уже было указано выше, отношение переменных состояния цепн при нулевых начальных значениях называется передаточной функцией электрической цепи или системы
К(Р)=Н4 о5-20’
Л1 {Р)
Например, легко найти передаточную функцию четырехполюсника, приведенного на рпс. 15-7:
ил<Р1 ___?__
бДр) 14,Ср’
Пусть входная величина xt (I) задана в виде единичного скачь3 %! (/) = 1 (/) (рпс. 15-8). Тогда ____________________.. . . 1 , , ,, Л1\Р)—р — 1 (О'
/1Г..91)
I1 '
432
гцпгл выходной величины (называемый, как было указано временно1"1 функцией или временной характеристикой) для этого случая через h (t):
x,(')-h(l)^X2(p)=K(p)j. (15-22)
рассматривая здесь такие системы, для которых h (0) = 0, цолУчаем: h' = рХ2 (р) = К (р). (15-23)
Таким образом, изображением производной от временной харак-сгпки системы является передаточная функция последней. П^агаяв правой части (15-23) р jo, получаем, что h' (f) связана с/((/со) формулой обратного преобразования Фурье (15-10):
h' (t) = 2ф К (/со) e’al do,
(15-24)
гче К (/со) = К (со)е'е<(О) — частотная характеристика или спектральная функция системы; К (со) — амплитудно-частотная и 6 (со) — фазочастотная характеристики системы.
Разлагая По формуле Эйлера, получаем:
'4-СО +со
h' (0 --=2^ X (w) cos [со/ ф- 6 (со)] do ф- К (со) sin [со/ ф- 6 (o>) j do.
Модуль частотной характеристики системы или ее амплитудно-частотная характеристика /( (со) — всегда четная функция, а фазочастотная характеристика 6 (со) — всегда нечетная функция частоты со.
Так, для цепи рис. 15-7
/((/0))-=.-^^- = 7--?______^-e-i^rc^
' 7 1ф-/гСсо j/1-рг-’С-со2 откуда
Я = ./rr-^V; 6 (f0) =- — arctfi гСы-
|/ 1 J- г2С3(03
Докажем это для более общего случая, когда К (р) представляет обой частное от деления двух многочленов. Полагая р — jo, j еждаемся, что вещественные части числителя и знаменателя будут Поэт ЖаТЬ только четные, а мйимые — только нечетные степени со. сумТомУ (°’)> равная частному от деления квадратных корней из ме„Мы кваДРатов вещественных и мнимых частей числителя и зна-таиг^151’ бУдет чотной функцией со, ч 8 /со), равная разности арк-цСоенсов от отношений мнимой к вещественной части числителя твсгственио знаменателя, будет нечетной функцией частоты со. фуцка Осповании сказанного заключаем, что подынтегральная
Ищ^?''\ВтоРого интеграла — нечетная, а так как пределы этого 1'с*ла равны по величине и противоположны по знаку, то этот
433
интеграл равен нулю. Подынтегральная функция первого ннт ла — четная. Поэтому ‘ егРа-
ОО
h' (t) = ± J /С (со) cos [со/4-6 (co)]dco. (15_25)
Но, во-первых, до момента t = 0 в цепи не была запасена э., гия и не действовали источники. Во-вторых, функция h' (/) оцпеЛ ляется, как оригинал, формулами обратного преобразования Ла ' ласа (15-23) или Фурье (15-24) и в силу условий этих преобразован^ как было указано выше, равна нулю при t < 0. Следовательно’ заменяя / на — /, из (15-25) получаем:
0=— К. (со) cos [0 (со) — со/] фк>. о Обозначим
К (со) cos 0 (со) = В (со); К (<о) sin 0 (со) — М (со),
(15-26)
следовательно,
К(/со)==В(со)4-/А4(®).
где В (со) — вещественная, а М (со) — мнимая частотные характеристики системы. Заметим, что вещественная частотйая характеристика В (со) — четная функция со, а мнимая М (со) — нечетная. Из последнего соотношения следует, что передаточная функция К (ja) может быть найдена, если задана какая-либо пара частотных характеристик: амплитудная и фазовая или вещественная и мнимая, Перепишем теперь (15-25) и (15-26):
й' (/) — ^ ^ [В (со) cos со/ — М (со) sin со/] й'со; о
СО
0 = ~ [В (со) cos со/ -ф М (со) sin со/] da. (15-27) 6
Складывая почленно последние равенства, получаем:
ОО 2 с h' (t) = — \ В (со) cos со/ da.
о
Наконец, интегрируя по / и учитывая условие/г (0) = 0, находим что t со t
е 2 с с
h (/) = \ h' (/) dt — -n \ В (со) da \ cos со/ dt = О 0 0
2 С В(«) • у/15-28) — ----—— \“ sin at da. ____________
si J co о
434
ценное соотношение позволяет по вещественной частотной мешке системы В (ы) определить ее временную xapaKie-характе^ /а -г. е. переходный процесс при воздействии на систему Р11СТ1'Хго скачка напряжения.
еД0Л0Жим теперь, что электрическая цепь при нулевых ных условиях подключается к единичному напряжению и началь 'цедить юк в какой-нибудь ее ветви. Тогда, принимая за нУ^®0 величину единичное напряжение, а за выходную — ток, вХ°Дючаем из (15-20), что передаточной функцией системы будет закЛ я операторная проводимость между включаемой ветвью и взаи ю где ищется ток. Соответствующую комплексную проводить Y (/®) = Y (“)e/<f(“> можно .......™..............
риментально, определяя порознь
рассчитать или получить экспе-амплитудную Y (со) и фазовую
B(w)
—J В,
Рис. 15-9.

----
1
I Гг(ш)
1 I I
вг \в4 Ве и> f(w) ! ( 1
—ч
Рис. 15-10.
ф (со) характеристики. Зная Y (со) и ср (со), можно найти им соответствующие вещественную и мнимую частотные характеристики В (со) и М (со).
В случае сложной цепи, естественно, сложными функциями частоты со будут В (со) и М (со). Поэтому рассмотрим приближенные метод определения тока i (f) = h (/) при графически заданной вещественной частотной характеристике В (со) по формуле (15-28).
llycTb вещественная частотная характеристика В (со) имеет юбую форму, но с ограниченным интервалом пропускания частот Jo, т. е. В (со) о при со 3s w0. Заменим заданную кривую В (со) Ругой кривой В (со), достаточно мало отличающейся от первой и (рис30^^)10^ пРямолпнеяными отрезками, которые ограничены Тог^Р°ведам через эти точки прямые, параллельные оси абсцисс. Те да КР11вая в (®) будет заменена суммой трапецеидальных харак-(рис. 15-10) (со) — трех для кривой на рис. 15-9.
пр0 кая замена позволяет составить таблицы расчета переходных * №им С°В Для Ряда тпповых трапеций, что существенно облегчает енение приближенного метода.
435
h
Так как В(со) = У, тл, (со), то
k= 1
7... ' 2 Г В(И) , , 2
h (t) —— \ —— sin wt da = -
' ' Л J to л
о
СО
С tk (со) . , ,
—-— Sin (lit d(£>, о
(!5-29)
где h (/) достаточно мало отличается от h (t).
Выражение (15-29) показывает, что определение Ъ (f) сводит к расчету ряда временных характеристик для отдельных ,ПСЯ пеций. ₽а‘
Покажем, как найти оригинал
СО
/л 2 С т (со) . , ,
s (t) = — \ —— sin ot do
' ’ л J to о
(15-30)
по трапецеидальной частотной характеристике т (со), определяемой следующими параметрами (рис. 15-11): начальной ординатой т (0), z , интервалом пропускания или областью
1 ' существенности частот со0 'и коэффициен-
том наклона
Ф)———и = со/со0, (15-31)
1\
I w где сор — интервал равномерного пропус-О " ...и)п w0 кания частот, на котором функция
р т (со) — постоянна.
Рис. 15-11. Рассмотрим единичные трапецеидаль-
ные характеристики, для которых т (0) == 1; соо = 1, а коэффициент наклона находится в пределах 0 я 1-Временная характеристика, соответствующая единичной ipa‘ пецеидальной частотной характеристике с наклоном и, опреде
ляется так:
^(O=^rn4j[Si W-xSi (х0+-^-^1. (15'32)
В таблице (см. приложение 4) даны функции йх, вычислен^6 по формуле (15-32) для ряда значений х в пределах от 0 до 1.
Формула (15-32) может быть выведена, например, следующим
Заменим вещественную частотную характеристику В (со) прямыми ли’вСаТЬ и вычислим интеграл (15-28) по участкам. Для участка (tox, to2) можем на (рис. 15-12):
------------------------В^) = В1 ] (СП М1).--------------- (02 — (01
436
<,5-2S)
2 i* A^sin то/ dro= -\ co r
Jt J
(01
(Ог
2 (*
я '
«1
В2-В1
“d0) =
(О
(02
tot
то2- то,
(02
I* sin то/ , ^---dT0 +
2 Bi-B1 c л то3—«I '
Ml
2 B2—cosro2/ — cosco,/
2 гс / л О’/ Д1
[Sl (£°2Z)-S1 (CDiOl -
Я С) 2—TOj
(15-33)
й)2 —• (i)j
I
Здесь Si (то/) означает функцию, называемую интегральным синусом: (at
с . .. С sin со/
Si (то/) = \---cltot,
о
'(15-34)
как сумму
которая табулирована и может быть легко вычислена. Г. - ------------------------------- -----------------
отрезков, можно вычислить переходный процесс (15-33). Применяя формулу (15-33) к единичной трапецеидальной характеристике, у которой т(0) = 1, со„-= 1 и коэффициент наклона и, получим равенство (15-32). В самом деле, для этого достаточно для горизонтального участка единичной трапецеидальной характеристики (рис. 15-11) положить В, = В2 ~ 1, с»! — О, 1%= (ос — ксоо ~~ х, а для наклонного участка принять В, -= 1, — 0, roj = ир -= и, w3 = 1
в результаты вычисления для обоих участков сложить
Для трапецеидальной характеристики с любыми т (01 и и0 нужно взять функцию йи по значению и — с),Ло0 (приложение 4), умно-лить на т (0) и* построить ее графически, приняв во внимание теорему подобия пли теорему изменения масштаба вре-ени, т е. учитывая, что значению функции йЛ в момент времени т соответствует печение искомого оригинала s (I) в момент времени t = т/тоо-
“ самом деле, если (15-28)
Разбивая вещественную частотную характеристику на ряд прямолинейных интегралов вида
0 По теореме подобия
Р В (то) .
\ —sin тог dro,
J и о
h
о
В (иго) . , ,
—1—— sin то/ dro.
то
(15-35)
jHa'^n-r—h2.‘^i4,‘ -p, при " ЛТ-'-Т-Т'-бд КГИ?'1'"| В t(f>) ВИЛЛ*:
n Раз масштаб кривой ft (/) вдоль оси / уменьшается в п раз, и наоборот.
437
Для доказательства заменим в (15 28) t па t'n
/ to/ \ dt\>
\ п )
В последнем интеграле сделаем замену переменных, введя новую ™ ную
£|)„ — Ю/П.
Тогда
В №>п) is
——— sin to„/aton,
откуда сразу следует рассматриваемая теорема, если заменить снова ы на что всегда возможно, так как значение определенного интеграла не зависит п обозначения переменной интегрирования 1 2
Например, для трапецеидальной частотной характеристики, имеющей т (0) == = 3, ы0 = 60 рад/с йр — 36 рад с, коэффициент наклона и = wp/oo0 = Об Из таблицы (см приложение 4) для и = 0,6 и, например т = 2,5, находим hy~ = 1,01, что соответствует времени / = т/щ, = 2,5/60 = 0,0417 с
В этот момент искомый оригинал s (/) — т (0) hK =3 1,01 = 3,03 Подобны» же образом определяются оригиналы s (Л для всех трапецеидальных характерно тик, на которые разлагается вещественная частотная характеристика В (®) Суммируя графически оригиналы s (/), получаем временную характеристику сне темы
Пример 15-3. На вход четырехполюсника (рис 15 7) включается постоянн напряжение = 100 В Вещественная частотная характеристика передаточн функции четырехполюсника В (to) = К (to) cos 0 (to) построена по получен® экспериментально К (to) и cos 6 (to) на рис 15 13 Найти методом трапеций напр жение и2 (/) на выходе четырехполюсника е
Решение Разложение В (to) на две характеристики первую — б угольную и вторую — трапецеидальную показано на том же рис 15 13, а характеристики приведены отдельно на рис 15 14
Каждая из них характеризуется следующими данными
1) Т1(0) = В) = 86, tonl ~ 0, to0i = 190 рад/с, ^ = 0,_____________ д
2) t2(0) = B2=14, t0p2= 190 рад/с, to02 = 667 рад/с, = 190/667==° “
438
йгице ( 4 приложение 4) находим функции йЛ для двух трапеций
П° м‘и х и пересчитываем их и время т, как было указано выше (табл 15-1) сразЛИ
Таблица 15-1
t — Х.с tool ,lKt Si (0 = 86ЛК), В tz = , с (002 йиа s2 (t) = В
о 0,00 0 0 0,00 0
0 000264 0,138 11,87 0,000752 0,2054 2,88
OP 000523 0,310 26,7 0,001504 0,3988 5,6
1,0 0,00792 0,449 38,6 0,002256 0,5872 8,23
1,^ 00132 0,674 58 0,00376 0,8562 12
25 Л а 0,0209 0,856 73,5 0,006016 1,0606 14,85
4,и 0,0523 0,939 80,8 0,01504 1,0198 14,26
iUtv 0,1046 0,967 83.3 0,03008 0,9934 13,89
ZU," 26,0 0,1368 0,975 83,9 0,0390 1,0022 14,30
На рис 15-15 построены для каждой из двух трапеций характеристику процесса, т пряжение и2 (0 на выходе четырехполюсника (рис 15-15)
Приближенный метод рассматривался при действии на входе системы единичного возмущения. Если же на входе системы действует возмущение, изображение которого Xt (р), то согласно (15-20)
х2^)^Х2(р)= К(р) Х^р).
т е функции времени % (/) и s2 (/) Сложив кривые (/) и s2 (/), получим временную
оригиналы,
е на-
Рис. 15-15.
Тогда в соответствии с равенствами (15-23) и (15-24) имеем:
(f) рХг(р)=рК (р) Х^р)-,
х'2 (/) = 2~ /со/< (/со) (/со) e'at с/со.
—СО
Введем обобщенную частотную характеристику системы:
® 0ю) = /соХ (/со) Хд (/со) = /соХ (/со) Хд (со) с1*1 = Ф (со) ,
Так°РаЯ ^ЧИТЬ1вает как саму систему, так и внешнее воздействие. тотнКаК Вне111Нее воздействие х2 (f) известно, то известна и его часами^'4 характеристика X, (/со). Поэтому можно найти обобщенные ” ЦтУДную и фазовую характеристики системы:
Ф (со) = соХ (со) X] (со); ф (со) = 6 (со) -ф- <р, (со) -ф- л/2.
439
15-4. О переходе от преобразований Фурье к преобразованиям Лапласа
Выше было показано, что если оригинал — функция [(f) абсо. лютно интегрируемая в бесконечных пределах, то существует пря. мое и обратное преобразования Фурье
F(/co) \ е >atf(t)dt^F{f(t)};
о
Г -°
f (t) — e’atF (j®) da-= F 1 {F (/co)}.
(1-36)
(15 37)
Но если функция f (t) не является абсолютно интегрируемой в бесконечных пределах, го интегралы (15-36) и (15 37) не существуют и преобразованиями Фурье или нельзя пользоваться, или можно пользоваться с очень большой осторожностью, производя все время проверку результатов, формально полученных с их помощью
В этом случае целесообразно перейти от функции / (/), не интегрируемой абсолютно, к другой функции (f), интегрируемой абсолютно в бесконечных пределах при помощи соотношения
А (0=7 (0^-4 (15-38)
где о0 > 0 и t > 0
К функции А (/) можно применять преобразования Фурье (15-36)
Fi (/со) $ е ,at fi (0 di - § е~‘ Jb)>(f (t) dt — F (<r0 -|- /о). (15-39)
о 0
Полагая в (15-39) p o0 + /со, т e вводя новое комплексное переменное р, будем иметь
F(p)-\e ptf(t)dt=-L {/(/)}, Л (15-40)
о
т е прямое преобразование Лапласа для функции f (/).
Применив к функции Д (f) обратное преобразование Фурье и учитывая соотношения (15 38) и (15-39), получаем
1 с° 1 V°
А (ОМ (0^°”/ = 97 \ eJia/F1(]a) da- \ е'о/Г(<т04 /со) da, откуда
e(go + /b>)Cf £гг^Ц-до) гйо. (15-41)
—от
440
Произведя в (15-41) ту же, что и выше, замену переменных, т. е. = сг0 4 » dp = получаем:
<?о+/со
/(0=24/ J e&F (р) dp—Lr1 {F (р)}, (15-42)
а0 — /со
т е обратное преобразование Лапласа для функции / (f).
Таким образом, если функция f (t) не интегрируема абсолютно Б бесконечных пределах и не может быть преобразована по Фурье, следует перейти к преобразованиям Лапласа, которое применимо к функции f (/), не интегрируемой абсолютно в бесконечных пределах.
Это позволяет рассматривать преобразования Лапласа как обобщение преобразований Фурье.
15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях
Сопоставим достоинства и недостатки расчета переходных процессов классическим методом, различными вариантами операторною метода и методом интеграла Фурье.
В цепях с характеристическим уравнением первой или второй степени трудности расчета невелики и примерно одинаковы, каким бы методом ни производить расчет Классический метод в этих случаях даже несколько проще Чем выше степень характеристического уравнения, тем больше уравнений нужно решать совместно при определении постоянных интегрирования и тем больше возрастают трудности расчета при пользовании классическим методом. Для разветвленной цепи с характеристическим уравнением выше четвертой или пятой степени расчет классическим методом представляет известные трудности из-за сложности определения четырех и более постоянных интегрирования
Отметим, что если цепь представляет собой полный многоугольник, т е каждый узел связан ветвью со всеми остальными узлами, то трудности определения постоянных интегрирования, свойственные классическому методу, возрастают с увеличением числа узлов и степени характеристического уравнения. В более простых цепях, когда не все узлы связаны друг с другом, часто можно значительно уменьшить число уравнений, которые нужно решать совместно В особенности это касается цепей с двумя узлами В последнем случае, как и в ряде других, разумно ввести в рассмотрение потенциалы узлов.
Таким образом, если степень характеристического уравнения выше четвертой — пятой, классическим методом пользоваться менее целесообразно, а нужно пользоваться одним из вариантов операторного метода
Переходя к операторному методу, сравним два варианта — расчет переходных токов по теореме раздожепня и расчет свободных токов но их изображениям
При расчете операторным методом не нужно определять постоянные интегрирования из начальных условии решением какой-либсг-системы уравнений Кроме того, при расчете изображений в эквивалентных операторных схемах ЧОЖно пользоваться всеми ранее известными методами расчета цепей при установившихся режимах. Эти два момента и определяют достоинства операторного Метода К недостаткам операторного метода надо отнести утомительность вычнс-ЛеВДя слагаемых сумм в теореме разложения. Если при расчете по теореме раз-л°Женцн_тхтязу_я- срчзу переходные токи, то из-за наличия внешних э. ч с (гармонических с разными частотами и экспоненциальных с разными коэффици-
441
впсппл но край сче! внутренних я форма теорему
ентами затухания) усложняются многочлены (р) и Ц (р) в составе изобра>1{ нпя какого-либо тока / (р) = Ft (p)/F2 (р) илн напряжения Если, нацр11Че.е' цепь содержит три гармонические э д с разной частоты, то число слагаему в теореме разложения больше степени характеристического yp?-”-'--" х ней мере на три Кроме того, все изображения усложняются за (расчетных) э д с Li (0) и —«с (0)/р Отметим также, что обычн;
разложения (14-10) неприменима при наличии кратных корней
Подчеркнем, что расчет по теореме разложения возможен и для всех таких внешних э д с, изображения которых являются отношением двух целых трансцендентных функций
Расчет операторным методом только свободных токов по их изображениям целесообразен тот да, когда действует ряд различных по характеру внешних э д с (гармонических с разными частотами, экспоненциальных с разными коэффици, ентами затухания и т д) В эквивалентную операторную схему для свободных токов внешние э д с не входят, что существенно упрощает изображения токов и напряжений Однако для определения внутренних (расчетных) э д с необходимо знать режим до коммутации и принужденный режим после коммута-ции. Поэтому рассматриваемый вариант операторного метода применим в тех случаях, когда внешние э д с имеют простую форму изменения (гармоническую экспоненциальную, постоянную) и принужденные токи сравнительно легко найти.
Расчет переходных процессов методом интеграла Фурье очень близок к расчету операторным методом и характеризуется теми же достоинствами и недостатками Метод интеграла Фурье целесообразно применять для расчета переходных процессов в заданной системе в том случае, если для исследования каких-либо дру-гих процессов в ней уже применяются частотные методы, аналитическим аппаратом которых являются преобразования Фурье К таким системам относятся, например, линейные системы автоматического регулирования, для которых необходимо исследовать устойчивость при помощи одного из геометрических критериев, исследовать качество регулирования и полностью рассчитать какие-нибудь переходные процессы Этот метод целесообразно применять при приближенном расчете переходных процессов по вещественной частотной характеристике, особенно когда амплитудная и фазовая частотные характеристики входного сопротивления или проводимости получены экспериментально В этих случаях метод интеграла Фурье имеет преимущества перед операторным Заметим, что пользуясь операторным методом, входные или взаимные операторные проводимости можно только рассчитать и нельзя получить опытным путем Проводя же расчет методом интеграла Фурье, получив экспериментально характеристики входных или взаимных проводимостей, имея э д с е (/) и найдя частотный спектр Е можно графически найти частотный спектр тока 1 (/со) и построить его вещественную или мнимую частотные характеристики Далее, применяя метод трапеций, можно приближенно рассчитать переходный процесс
Если напряжение на зажимах пассивного двухполюсника дано кусочно-аналитической кривой, имеющей разрывы, расчет целесообразно вести при помощи формул Дюамеля При этом переходная проводимость g (t) или переходная функция у (/) находятся одним из известных методов
Отметим также, что при пользовании любым из указанных методов можно задачу расчета переходных процессов с ненулевыми начальными условиями свести к задаче с нулевыми начальными условиями (см § 14 5) Целесообразность этого приема нужно выяснить в каждом конкретном случае с точки зрения максимально возможного упрощения расчета
В заключение укажем, что операторный метод и метод интеграла Фурье весьма широко применяются в теории автоматического регулирования и пр11 расчете переходных процессов в электрических машинах, а операторный метод и в некоторой мере метод интеграла Фурье — еще при расчете переходных процессов в цепях с распределенными параметрами, в то время как классический метод во всех этих случаях почти не находит применения.
442
Глава шестнадцатая
ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
16-1. Характеристические сопротивления и постоянная передачи несимметричного четырехполюсника
"По определению характеристическими сопротивлениями несимметричного четырехполюсника со стороны входа ZC1 и со стороны выхода Zc2 называется такая пара сопротивлений, когда при сопротивлении нагрузки на выходе Zc2 входное сопротивление со стороны входных зажимов равно ZC1 (рис. 16-1, а) и, наоборот, при сопротивлении нагрузки на входе ZC1 входное сопротивление со стороны выходных зажимов равно Zc2 (рис. 16-1, б).
Рис. 16-1.
Из основных уравнений четырехполюсника (§ 8-1) u1=au2-\-b12, 1 '
A=си2 -f- d12 J
(16-1)
в соответствии с данным выше определением найдем входное сопротивление четырехполюсника со стороны первичных зажимов при сопротивлении нагрузки Z(2: *
__ 6'1____ЛЦ2 , В/2 _ _ АВ^/Ц+В_AZc2-\-B (16-2)
1ВХ“~ 11~ с1~~cu2+di~CL’2/I2+D~ CZc2+D' 1 ’
Аналогично при обратном питании четырехполюсника
____^2__В ___ DZa }- В (16-3) 2вХ”йГ“ с2“С6\ + AА ~ CZcl + A ‘ '
Решая эти уравнения относительно ZC1 и Zc2 и учитывая, что из Уравнений (16-1) легко найти сопротивления холостого хода и короткого замыкания Zlx = А/С и Z1K = BID и аналогично определить те же сопротивления при обратном питании Z2x = D/С и Ак = В/А, получаем:
ZC1 = У AB/CD У Z^Z~; (16-4)
Z( 2 = ) BD/AC=VZ^ • (16-5)
В двух последних формулах перед квадратными корнями остав--ны только знаки плюс. Знаки минус отброшены как не отвечаю-.ие физическому смыслу сопротивлений Z ; и Zc3.
443
Действительно, до сих пор предполагалось, что к выходцу, зажимам четырехполюсника подключается приемник энергии (Пд' требнтель). Поэтому вещественная часть его комплексного сопротцв ления, т. e.Zc2, должна быть положительной. При обратном питащ." тот же вывод следует и для Zcl. Однако из равенств (16-4) и (ig.r-! получаем для Ztl = zclefl' и для Zc2 = гс2е'е2 по два значения д^ каждого из аргументов, которые разнятся на л, т. е. ех; бх + л 6 2; б 2 Д ’
Так как 61 и 62 — аргументы комплексных сопротивленец ZC1 и Zf2, то они всегда лежат в пределах — л/2 6Х «S + л,2 — л/2 ==; 62 -sj + л/2. Поэтому rcl = г.л cos Gp> 0 и rc2 — гс2 cos 6 2 > 0.
Отсюда также следует, чго г'а zfl cos (бх + л) < 0 и г’г2 ~ — zc2 cos (g2 + л) < 0 и углы 6Х + л, g2 + л должны быть отброшены. А так как изменение 6 х, 62 на л как раз и означает изменение знаков у комплексов Zclii Zc2, то, следовательно, перед квадратными корнями равенств (16-4) и (16-5) должны быть оставлены только знаки плюс.
Отметим, что, поскольку несимметричный четырехполюсник имеет различные характеристические сопротивления со стороны входа и выхода, его можно применять для согласования источнике (генератора) и приемника (рис. 16-2, а), двух линий (гл. 18) с раз личными характеристическими сопротивлениями (например, воздуш ной и кабельной линий), линии и приемника (рис. 16-2, б) и т. Д
Согласованным режимом работы несимметричногс четырехполюсника, включенного между генератором и приемник® (рис. 16-2, а) или линией и ттриемнпком (рис. 16-2, б) называете? режим при Zc2 = ZH, ZC1 = Zr для схемы рис. 16-2, а и Zc2 =- Ъ и ZC1 = Zc для схемы рис. 16-2, б. При этом в месте включения че тырехполюсника не будет возникать отраженных волн (§ 18-8) или говоря иначе, в цепи не будет возникать добавочного затухания Само упоминание о волнах (в данном случае — отраженных) в че тырехполюспике станет понятным позднее, если учесть возмог дюсть замены его эквивалентной лщидей (§ 18-13), К согласованной режиму с точки зрения отсутствия отражения волн очень часп
444
емятся в цепях слабого тока (радио, телефон, телеграф, телеме-cTLlKa), так как появление отраженных сигналов (напряжения или накладывающихся на падающие (основные) сигналы, мешает
Давильной работе аппаратуры.
рщаче говоря, несимметричный четырехполюсник может приняться для трансформации характеристических сопротивлений. Поэтому он называется иногда трансформатором сопро-*и в лен ий.
Как было показано выше (§ 3-19), условием передачи максимальной активной мощности от генератора к приемнику является равенство Zn = Zr. Если равенство не соблюдается, то для его выполнения можно включить между ними несимметричный четырехполюсник. Другим определением для согласованного режима несимметричного четырехполюсника, включенного в место соединения генератора и приемника (рис. 16-2, а), служит такой режим, когда 7 = Za и ZC1 = ZT. При этом входное сопротивление со стороны зажимов 1 — Г четырехполюсника должно быть равно Zr, т. е. г = гг п хс1 = — хг, а значит, в эквивалентном приемнике, состоящем из несимметричного четырехполюсника и приемника, будет выделяться максимальная активная мощность. В этом случае нужно так выбрать характеристические сопротивления несимметричного t*
четырехполюсника, чтобы Zr2 = Z„ и Zrl = Zr.
Подчеркнем, что в цепях постоянного тока условия согласованного режима несимметричного четырехполюсника по отсутствию отраженных волн и по выделению максимальной мощности в эквивалентном приемнике будут одинаковы.
Третьим параметром, характеризующим четырехполюсник с точки зрения изменения полной мощности и угла комплексного числа U1 при передаче через него электромагнитной энергии является п о -моя н на я передачи g, представляющая собой комплексную величину, определяемую при нагрузке четырехполюсника на выходе или на входе на сопротивления, равные характеристическим, и при питании его соответственно со стороны входа или выхода.
При питании со стороны первичных зажимов и согласованной нагрузке ZH = Zc2 на вторичных постоянная передачи определяется По формуле
g = a+jb= (16-6)
Z < J2 ш
Вещественная частьgназывается коэффициентом за-т У х а н и я
й = |1п^1= ‘in'J, (16-7)
т; е- ие может быть выражена через отношения только напряжений ’ЭДи только доков на входе иди выхте четыпрхпппк>сника. что бу'ют-“иеть место (см. § 16-2) для симметричного четырехполюсника.
445
Мнимая часть g называется коэффициентом фазы и при # = U1e^,a> 4 = /^, определяется ВЬ1р^
жением
Ь— 2"[(Фи1 — ф/<2) + ('Ф|1 — Ф12)] (16-8)
и не является сдвигом фаз между напряжениями и токами на входе и на выходе.
Согласно определению характеристических сопротивлений, ес,^
U 2 == 72^и == ^2^с2 >
ТО
= АЛВХ =
поэтому
«=?|п^‘"1пй/? !'И
2 t>2ZCl ^2 F ZC1
ИЛИ
g=lln^=lnW^. (16-10)
b 2 PSZC2 /2 V Zc! V 1
На основании (16-1) имеем:
71=сй2+Р72=Л(сгс2+Р) и g=in(CZf2+D)vZ^;.
Подставляя значения ZC1 (16-4) и Zc2 (16-5), получаем:
g = In (УЛП-[-У ВС) (16-11)
или
eg = VAD +У ВС.
(16-Па,
Можно показать, что постоянная передачи имеет то же самое значение при питании четырехполюсника со стороны вторичны' зажимов и при сопротивлении нагрузки четырехполюсника на пе| вичных зажимах, равном характеристическому сопротивлению 4 Следовательно, постоянная передачи не зависит от направлен)! передачи энергии через четырехполюсник.
Величины g, Zfl и Zf2 называются вторичными пара метрами четырехполюсника. Их число равно трем, так как пр любой форме записи уравнений пассивного взаимного несимметрич ного четырехполюсника число его независимых коэффициенте равно трем.
Уравнения несимметричного четырехполюсника могут бы1 записаны с гиперболическими функциями.
В самом деле, на основании (16-Па) имеем:
1 I'AD 1'вс l/AD + VBC АР-ВС
УЛВ - У ВС- = =
446
0ТСЮДа
shg= J (^-е 8)=^УВС; chg-=4(eff + e^=^yAD\
Кроме того, из уравнений (16-4) и (16-5) получим: — В/С, zclizc^ A/D.
решая поставленные четыре уравнения относительной, В, ChD,
будем иметь:
Л = |/Г|^сЬ^; B = VZblZc2shg;
C= J______
J/ ZciZc2
^chg. Cl
(16-12)
Подставляя значения А, В, C, D в уравнения (16-1), получаем:
Ul = |Z{йг ch g 4- Z2ZC2 sh g);
A = ]/~ j^(|j-shg-|-/2chg).
(16-13)
Последние уравнения, особенно упрощаются при согласованной нагрузке (U2 = /2ZH = t2Zc2):
U! = U2 j/lge8;
(16-13a)
Разумеется, они непосредственно следуют из (16-9) и (16-10).
При пользовании формулами (16-13) необходимо находить значения гиперболических функций ch g и sh g от комплексного аргумента g Это следует делать, пользуясь таблицами гиперболических функций от комплексного аргумента или с известным приб-шжением определяя их значения по специально построенным лмограммам.
16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника
Для симметричного четырехполюсника А = D и характеристическое сопротивление Zc будет одним и тем же как со стороны Первичных, так и со стороны вторичных зажимов, что следует 113 (16-4) и (16-5). Оно определится как входное сопротивление со Стороны первичных зажимов, если вторичные замкнуты на сопротивление Zc (рис 16-3), или, наоборот, как входное сопротивление со стороны вторичных зажимов, если первичные замкнуты на-сопротив-'’Cinie-ДГ(рис 16-4). = = =
447
На основании (16-4) и (16-5)
Zti = Zc2“-2c==]/ В/С.
(16-1
Согласованный режим работы симметричного четырехполюсны будет при ZH = Zc. Если этот четырехполюсник представляет соб( линию или кабель любой длины, то, поскольку у них Zc не завис от длины (§ 18-5), входное сопротивление на зажимах 1 — 1' чет рехполюсника (эквивалентного линии или кабелю) будет равно; В результате приемник с ZH = Zc оказывается как бы нелосредс венно присоединенным к зажимам 1 — Г, а в месте присоединен! четырехполюсника к приемнику отраженных волн возникать JIt будет.
Максимальная активная мощность будет выделяться в эквив^ лентном приемнике, состоящем из четырехполюсника и приемника *
при Zc — Za = Zr.
Рис. 16-4.
Постоянная передачи симметричного четырехполюсника (иногт называемая в литературе его собственной постоянной передачи1 определится из формул (16-9), (16-10) или (16-11):
1п^- = 1п -- =1п(Л + ф/^6?). (16-1
£4 4
Так как в данном случае =A=Z_=zre/0, (16-1
4 4
то из (16-7), учитывая, что сдвиг по фазе между напряжение*’ током на входе и на выходе один и тот же (ZBX = Zc = ZH), получи для коэффициента затухания а (который иногда еще назывы собственным коэффициентом затухания четырехполюсника):
1 ил , й=1гЧ=1п4
1 Ir, cos0
2 IHf/2/2cose
<161:
или
V-jUz — — s'2.
(16-17:
Подчеркнем, что для симметричного четырехполюсника g и могут быть выражены через отношение только напряжений 1Ы юлько токов четырстпслкзснпка;
448
Коэффициент затухания характеризует изменение абсолютного ачения напряжения (или тока) на выходе по сравнению с его зна-3ениеМ..Яа входе. А так как отношение U-JU2 (или /г//а) может быть ^ень большим и к тому же сильно зависеть от частоты, то, следуя °акону Вебера — Фехнера (зависимость восприятия от влияния Зо3действия логарифмическая), здесь для а также вводят логарифм. Поэтому коэффициент затухания а и был впервые определен в телефонии как натуральный логарифм этого отношения (16-17).
Для коэффициента затухания а ранее была введена единица измерения, называя непером Нп. Полагают, что а = 1 Нп, если в режиме согласованной нагрузки симметричного четырехполюсника имеем 14/1/2 = е = 2,718.
В настоящее время принято определять коэффициент затухания а как десятичный логарифм отношения Р^Р^.
a = lg^-. (16-18)
г 2
При таком определении а получается другая единица измерения, называемая белом (Б). Очевидно, что а= 1Б, если PJP^ = Ю. Бел —большая и поэтому не всегда удобная единица. Чаще пользуются в десять раз меньшей единицей — децибелом (дБ). Тогда с учетом (16-17) и (16-18) получаем:
а = Ю 1g = 20 1g = 20 1g (ДБ). (16-19)
"2 и2 >2
Соотношение между непером и децибелом легко устанавливается из равенств (16-17) и (16-19);
1 , Рг 2,303 . 11К
«Нп = у,п К = -2П0“ ’° lg К = °’115йДб,
откуда
1 дБ = 0,115 Нп и 1 Б=1,15 Нп. (16-20)
Для коэффициента фазы Ь (который также иногда называется собственным коэффициентом фазы четырехполюсника) из (16-15) имеем:
6=Ф«1-ф«2=Ф/1-Фг2. (16-21)
Он выражает сдвиг фаз между напряжениями (или токами) симметричного четырехполюсника при согласованной нагрузке.
Выражения коэффициентов А = D, В, С симметричного четырехполюсника через два его вторичных параметра Zc и g получаем из равенств (16-12):
A =D — chg-, B—Zcshg; C=~~shg, (16-22)
1 из формул (16-13) получаем уравнения симметричного четырех-Юлюсника с гиперболическими функциями
(7i = (/2chg4- shg;)
( <16‘23)
15 Основы теории цепей
449
Эти уравнения особенно упрощаются при согласованной нагру3
(^2 = 4zh = /2Zc): .... Ке
Ui = U2eg; Ir = 12eg. (16.24
Разумеется, они непосредственно следуют из (16-15).
16-3. Вносимая и рабочая постоянные передачи
В действительных условиях работы трудно согласовать сопротивления входе и выходе несимметричного четырехполюсника с его характеристическими сопротивлениями во всей полосе частот передаваемых сигналов. Отсутствие согл^ сования приводит к появлению отраженных волн напряжения и тока, т. е. к иска^
Рис. 16-5.
жению передаваемых сигналов, и к д0. полнительным потерям мощности. Поэтому собственная постоянная передачи (cog. ственное затухание и собственный коэф, фициент фазы) могут служить в этих ус. ловиях лишь приближенными оценками действительного режима работы.
В качестве общего критерия оценки работы четырехполюсника приняты так называемые вносимая и рабочая постоянные передачи.
Вносимая постоянная передачи определяется из соотношения
gi=ai+/fcf=4 1п ~7Г- (16‘25) ^2'2
Здесь й[ и 1[ определяются из .режима, когда приемник ZH непосредственно присоединен к генератору с э д. с. Ё и внутренним сопротивлением Zr (рис. 16-5).
При этом
Ё(=Ё-/;гг; /;=E/(zr+zH); (16-26)
U2 и /2 определяются из режима, когда приемник ZH присоединен к генератору через несимметричный четырехполюсник с вторичными параметрами g, Zci Zc2 (рис 16-5), причем U± = Ё — IrZt-, U2 = 4ZH, a (71,4 связаны c U2J2 уравпе ниями (16-13).
Из сказанного следует, что вносимая постоянная передачи характеризуе соотношение между напряжениями и токами приемника при непосредственны его включении к зажимам генератора (переключатель рис. 16-5 в положении 1—1 и при включении его через четырехполюсник (переключатель в положении 2—2) Таким образом, вносимая постоянная передачи дает возможность оценить измене ння режима приемника при его включении к генератору через несимметричны, четырехполюсник.
Выражая все токи и напряжения через параметры четырехполюсника g Zel, ZL2, генератора Zr и приемника ZH) после преобразования получаем:
§,=§+1п
2\'Z^~i
, ZH4-Zr2 , ln-V -4 2Kz„Zc2
ln(l—pip2e 2g) —In
(16-27)
2 K"ZA
Здесь Pi и p2 — коэффициенты отражения на входе и на выходе четырех-полюсника,
(16-28)
z-r“rz-ci '-irides
обращающиеся в нуль при отсутствии отряженных волн (71 = ZLl и Zd
450
Вносимое затухание «( найдется как вещественная часть (16-27):
Ci==a-|-ati+flt2+ai3—ait — я+ln
Zri ^ci
+ In I 1 — P1P2C 2g | — In
Мп
^гЧ~^н 2 Jz Z;ZH
^h4~^C2 2 j/ ZHZe2
(16-29)
+
Таким образом, вносимое затухание состоит из пяти слагаемых. Первое сла-емое равно собственному затуханию четырехполюсника, второе а(1 и третье а,2 взываются затуханием из-за отраженных волн (или, иначе говоря, отсутствием ИпГласования) на входе и на выходе четырехполюсника. Четвертое слагаемое al3 взывается затуханием вследствие взаимодействия отражений на входе и выходе четырехполюсника Пятое слагаемое fl;4 называется затуханием вследствие несогласованности внутреннего сопротивления Zr генератора и сопротивления Z„ приемника при непосредственном подключении приемника к генератору Если четырехполюсник согласован на входе (Zr = Zcl, /д = 0) и на выходе (Zc2 = ZH> = 0), то аа — а12 = а,3 = 0. Если к тому же Zr = ZH, то = 0 и вносимое затухание равно собственному.
3 Частным случаем вносимой постоянной передачи gt (и соответственно вносимого затухания а,) является рабочая постоянная передачи £р (и соответственно рабочее затухание ар). Рабочая постоянная передачи получается, если при положении 1—1 переключателя (рис. 16-5) сопротивление приемника выбирается равным сопротивлению генератора.
Вывод выражения для gp аналогичен выводу выражения для glt за исключением того, что вторая формула (16-26) теперь имеет вид.
7( = £/2Zr. (16-30)
Для рабочего затухания ар имеем:
ар = a + all + ai2~b ai3~ ai +
Zr+ZH
(16-31)
Вносимое затухание меньше рабочего на a,4 Но при определении вносимого затухания нужно учитывать, что приемник не согласован с генератором ZH Zr, поэтому и появляется слагаемое atl В то же время при расчете рабочего затухания в соответствии с его определением, т. е. при ZH = Zr,

a/4=ln
(16-32)
При расчетах электрических цепей связи в качестве критерия оценки четырехполюсника в зависимости от условий постановки задачи могут быть приняты вносимая или рабочая постоянная передачи(или соответственно вносимое или рабочее затухание).
Для симметричного четырехполюсника получим все необходимые соотношения из (16-25)—(16-32), полагая ZC1 = Zc2 = Zc.
16-4. Цепные схемы
При решении различных практических задач и исследовании линий в лабораторных условиях встречаются схемы, состоящие из ряда тождественных и симметричных Т или П-схем или четырехполюсников, соединенных в каскад, как показано на рис. 16-6, а и б. К подобным практическим задачам относится, например, расчет Распределения напряжений в гирлянде изоляторов, в обмотках Машин и трансформаторов при высокой частоте, расчет «линий задержки», состоящих из одинаковых четырехполюсников и служащих
451
для увеличения времени движения сигнала от источника к прием нику и т. д.
Такие схемы называются однородными цепными схемам {1 (иногда говорят цепочечными проводниками) или однородными и с. кусственными линиями, так как служат, например
Zf Z; h Z; Z; Z, г г г г .st г
Рис. 16-6.
для экспериментального исследования явлений в телеграфных кабелях Каждая из Т или П-схем называется звеном, ячейкой или элементом цепочки. Соответственно различают цепную схему типа Т и типа П, причем Zx, Y2 могут быть образованы любой комбинацией активных сопротивлений, индуктивностей и емкостей.
Определим напряжения и токи на входе любого звена цепной схемы по заданным напряжениям и токам на ее выходе. Для решения
——t>Z, —t*Z^ —0Z3 —-t*Zn g—
Рис. 16-7.
этой задачи найдем сначала характеристическое сопротивление и постоянную передачи всей цепной схемы, состоящей из п одинаковых симметричных звеньев (рис. 16-7).
Предположим, что схема на выходе замкнута на сопротивление, равное характеристическому сопротивлению Zc. Тогда входное сопротивление и-го элемента также равно Zc. Но это означает, что и—1-й элемент в свою очередь замкнут на характеристическое сопротивление Zc, а следовательно, входное сопротивление п—1-го элемента также равно Zc. Продолжая эти рассуждения, заключаем, —что входное сопротивление всей цепной схемы также равно Д--
452
Следовательно, характеристическое сопротивление всей цепной схемы равно характеристическому сопротивлению одного звена. Для определения постоянной передачи всей цепной схемы ее дудсно выразить через постоянную передачи одного звена.
У По формуле (16-15) для одного звена
рассматривая далее всю цепную схему как некоторый четырехполюсник, можем написать:
где gn — постоянная передачи всей цепной схемы.
Так как каждый элемент схемы замкнут на характеристическое сопротивление, то
— = —= &п ее
4 й3 йп+i
Следовательно,
gu=ln(^^.. = = (16-33)
Wa Us ип+1/
Итак, постоянная передачи цепной схемы, а значит, и ее коэффициенты затухания и фазы пропорциональны числу звеньев схемы.
В соответствии с обозначениями рис. 16-7 запишем для всей цепной схемы:
41=4-Вц4+1>
4 ~ Сцйп+1 + Ац/п+1.
Коэффициенты Дц, Вц, Сц выразим через Zc и согласно равенствам (16-22) с заменой в них g через £ц:
Лц=Рц=с11£ц; BIX=ZcshgIK; С
Тогда с учетом (16-33) получим:
Ui = 4я+1 ch ng 4- 4+i4 sh ng\
k=^sh ng+ ln+1 ch ng,
(16-34)
(16-35)
причем счет звеньев схемы ведется от ее начала.
Для напряжения и тока на входе й-го звена имеем: Uk = йпЪ. ch (п - k + 1) g + 4+i4 sh (п - k + 1) g’, 4=^sh (и — й 4~ 1) g 4-4+i ch (n-k+ l)g.
При включении ряда несимметричных четырехполюсников в
453
сопротивлений (рис. 16-8) будем иметь, что характеристическое сопротивление со стороны вторичных зажимов Z^’ У k-ro четырехполюсника равно характеристическому сопротивлению со стороны первичных зажимов Z(/i+1> f(k + 1) четырехполюсника. НагрузКа на вторичных зажимах последнего («-го) четырехполюсника согласованная, т. е. Z1? = ZH, а входное сопротивление со стороны первичных зажимов первого четырехполюсника Z1BX = Z//. Таким образом, вся цепная схема представляется несимметричным четырехполюсником с характеристическими сопротивлениями zVi и Z’?.
Рис. 16-8.
Постоянную передачу для всей цепной схемы найдем по формуле (16-6), учитывая, что и = f[k)-
ё<\ П ц 4~ /Ьц g

'lntt+llnw -...

1 [)W ^n)
... 4- у In =gi + ёг + • • • + ёп,
(16-36)
т. e. равна сумме постоянных передачи всех включенных в каскад несимметричных четырехполюсников.
При каскадном включении четырехполюсников и несоблюдении принципа согласования их характеристических сопротивлений вычисление параметров эквивалентного четырехполюсника по вторичным параметрам отдельных четырехполюсников становится более трудным.
Проще найти коэффициенты А, В, С, D эквивалентного четырехполюсника. При других соединениях четырехполюсников находят параметры эквивалентного четырехполюсника, пользуясь другими их коэффициентами (см. § 8-10).
16-5. Частотные электрические фильтры
Электрическими фильтрами называются четырехполюсники, обычно составленные из катушек индуктивности и конденсаторов, которые пропускают к-нриечникути всего спектра
454
частот источника один или несколько заданных диапазонов частот.
Электрические фильтры широко применяются в проводной связи, В радиотехнике и технике сильных токов. Впервые применил электрический фильтр для одновременного телеграфирования и телефонирования по одному проводу русский военный связист упитан Г. Г. Игнатьев в 1880 году.
Принцип работы электрических фильтров основывается на известных положениях: во-первых, что индуктивное сопротивление прямо пропорционально, а емкостное — обратно пропорционально частоте, и, во-вторых, что в индуктивности ток на угол л/2 отстает от напряжения, а в емкости — на столько же опережает. Различные комбинации катушек индуктивности и конденсаторов дают фильтры, различные по своему действию.
Назовем идеальными фильтры, состоящие из чисто реактивных элементов, и будем рассматривать симметричные фильтры следующих типов: низкочастотные, высокочастотные, полосные, многополосные и заграждающие.
Приведенная классификация фильтров — не единственная. Фильтры разделяются еще на следующие типы: фильтры постоянной К, фильтры постоянной М, мостиковые фильтры, фильтры, образованные индуктивно связанными цепями, кварцевые фильтры, гС-фильтры и др.
Низкочастотные фильтры пропускают токи с частотами от 0 до соо, высокочастотные — токи с частотами от соо до ОО.
Полосные фильтры пропускают токи, частоты которых лежат в пределах от сщ до со2, а м н о г о п о л о с н ы е фильтры — токи одновременно нескольких диапазонов частот — от оц до со2, от со3 до со4 и т. д. Заграждаю щ и е фильтры пропускают токи с частотами от 0 до <»! и от <в2 до оо.
Поскольку фильтр — частный случай четырехполюсника, то его свойства определяются вторичными параметрами: характеристическим сопротивлением Zc и постоянной передачи g, причем g — ~ а + jb, где а — постоянная или коэффициент затухания и b — постоянная или коэффициент фазы.
Областью пропускания идеального фильтра называют Диапазон частот, в котором коэффициент затухания фильтра а равен нулю, а областью затухания (не -пропускания) — диапазон частот, в котором коэффициент затухания а отличен от нуля.
В области пропускания токи и напряжения на входе и на выходе фильтра должны быть одинаковыми по абсолютному значению. Это было бы возможно, если бы фильтр был согласован с сопротивлением нагрузки, т. е. Za = Zc во всем диапазоне частот области пропускания, что, однако, как будет показано в § 16-6, принципиально недостижимо.
Действительно, при. согласовании фильтра с нагрузкой токи и напряжения входа /Д и выхода Д, щ связаны соотноше-
455
нием (16-15)
W=eWZ (16-37)
1/2 ‘2 1
Тогда очевидно, что при а = 0 будем иметь:
^1 = ^2>’ (16-38)
Если же оба условия ZH = Zc и а = 0 одновременно выполнены
не будут, то величины токов и напряжений на входе и выходе уже не будут одинаковы.
Таким образом, в области пропускания фильтра (а = 0) равен-ство величин токов и напряжений на входе и выходе получается только для одной или нескольких таких частот этой области, для которых фильтр окажется согласованным с сопротивлением нагрузки.
При практическом выполнении фильтров всегда стремятся по возможности добиться согласованной нагрузки и уменьшить затухание в полосе пропускания. Например, потери в элементах фильтра можно часто уменьшить настолько, что станет допустимым рассматривать его как чисто реактивный. Однако характеристические сопротивления П- и Т-образных схем четырехполюсников и, в частности, фильтров зависят от частоты. Поэтому нельзя обеспечить согласование фильтра с заданным постоянным сопротивлением нагрузки во всей области пропускания. А это и означает, что, кроме одной или нескольких частот, принадлежащих области пропускания, для которых согласование будет иметь место, при всех остальных частотах токи и напряжения на входе и выходе не будут равны.
Даже для идеальных фильтров коэффициент а в области затухания не равен бесконечности. Практически в области затухания для одних фильтров а постепенно возрастает от нуля, у других сначала возрастает, затем уменьшается и т. д. Для получения резкого увеличения коэффициента а в области затухания, начиная от границ этой области, пользуются многозвенными фильтрами, состоящими из нескольких включенных в каскад П- и Т-звеньев, или фильтрами с более сложными схемами (например, типа М),
16-6. Низкочастотные фильтры
Определение фильтрационных свойств тех или иных четырехполюсников сводится к исследованию зависимости их коэффициентов затухания и фазы и характеристического сопротивления ог частоты. Рассмотрим, как рассчитываются эти зависимости для фильтров, собранных по Т- или П-образным схемам, из чисто реактивных элементов.
Как показано в § 16-2 и § 8-1, для симметричного четырехполюсника и, в частности, фильтра
£1_____________A^h^ch-(a+j&)^l [ Z12r\-----------------(16-39)
456
(16-41)
Так как исследуемый фильтр состоит из чисто реактивных элементов, то Zb V2 — величины чисто мнимые и, следовательно, д — положительное или отрицательное вещественное число. При этИх условиях уравнение
Л = ch (а 4- jb) — ch a cos b 4* j sh a sin b (16-40)
распадается на два:
Л =ch с cosh;
0 = shasinh.
Рассмотрим сначала низкочастотный П-образный фильтр (рис. 16-9), у которого
Zt=i(aL; Y2=jaC (16-42)
и по (16-39)
Л = 14-^=1-^. (16-43)
Границы области пропускания (о = 0, ch а = 1) определим согласно (16-41) неравенством — 1 -С cos b = Л 4-1, так как cos b изменяется в пределах от — 1 до 4- 1, т. е. 0.
—1^ l-~^sS4-l. (16-44)
Следовательно, фильтр пропускает без затухания (о = 0) токи с частотами от со = 0
до соо = 2/]ЛLC. Из схемы, приведенной на Рис. 16-9. рис. 16-9, легко установить, что соо — соб-
ственная частота контура, состоящего из индуктивности L и двух последовательно соединенных емкостей С/2 и С/2.
Изменение коэффициента фазы b в области пропускания фильтра (с = 0) найдем из равенств (16-41) и (16-43):
cos b—Л = 1 — со2СС/2.
Обозначив g=co/a>o, получим:
со8&=Л = 1-2g2. (16-45)
На рис. 16-10 приведены кривые a (g) и b (g). Они показывают, что в области пропускания фильтра (а = 0), когда g увеличивается от 0 до 1, cos b изменяется от 1 до — 1, что следует из равенства (16-45). При этом b может изменяться от 0 до л или от 0 до — л.
В необходимости выбрать для b положительный знак можно Убедиться, построив векторную диаграмму при любой частоте в области пропускания этого фильтра, согласованного с нагрузкой (рис. 16-11). Такая векторная диаграмма дана на рис. 16-12. Поскольку фильтр на выходе согласован с нагрузкой, а характеристическое сопротивление его в области пропускания — чисто активное (см. ниже), то сопротивление нагрузки также активное и ток /2
457
совпадает по фазе с О2. После построения токов/3 и /4и напряжения на сопротивлении coL найдем напряжение которое опережает напряжение П.2 на угол b > 0. При со = 0 из схемы, (рис. 16-1 о ясно, что иг = U2. При возрастании частоты вектор О1 опережает вектор на все больший угол b < л. Поэтому из диаграммы ясно что коэффициент фазы Ь, т. е. угол между векторами и П2, будет при всех значениях со положительным.
Рис. 16-11.
В области затухания фильтра, когда g изменяется от 1 до оо, а =£ 0 и, как следует из второго равенства (16-41), b остается равными. Из первого равенства (16-41) получим в области затухания: chcz=—-71 = 2g2—1, (16-46)
откуда и находим затухание а.
Отметим, что именно для чисто реактивных фильтров левая часть второго из равенств (16-41) равна нулю при любых частотах со.
Рис. 16-12.
Рис. 16-13.
Это и определяет вид частотных зависимостей затухания а и фазы Ь, приведенных на рис. 16-10. Так как второе уравнение (16-41) удовлетворяется либо при а = 0, либо при Ъ = л (или 0), то точки излома частотных характеристик а и Ъ получаются как раз при со = = ®0 (g = 1).
Итак, кривая b в области пропускания строится по уравнению (16-45); в области затухания b = л. В области пропускания а = О, а в области затухания кривая а строится по уравнению (16-46).
Как было показано выше, при согласованной нагрузке в области пропускания (а = 0) величины входных и выходных напряжений и 458
соответственно токов одинаковы. Отличие а от нуля в полосе затухания означает неравенство иг и U2, Ц и /2, точнее — уменьшение выгодных величин по сравнению с входными, т. е. U2 < Ui, I2 < Д.
Подчеркнем, что для фильтра в отличие от линий (гл. 18) затухание в области непропускания не связано с потерями в его элемен-тах (фильтр чисто реактивный). Сказанное иллюстрирует векторная диаграмма, построенная для схемы рис. 16-13, где L = 0,64 Г, Q = 0,16 мкФ, U2 = 200 В. На этом рисунке изображен тот же П-образ-ный низкочастотный фильтр, работающий в режиме согласования с нагрузкой при одной из частот в области затухания (со = 2со0), когда характеристическое сопротивление его — емкостное (см. ниже). Из диаграммы рис. 16-14 видно, что U2 < иъ 1г < А и что сдвиг фаз между векторами и О2, а также /х и /2 равен 180°, как это и следует из частотной характеристики b (рис. 16-10).
Так как равенство (16-39) справедливо не только для П-, но и для Т-схем, то все сказанное выше о за-
висимостях а и Ь от частоты относится и к Т-фильтру низких частот (рис. 16-15). Иными словами, частотные характеристики коэффициентов затухания и фазы и граничная частота со0 для П- и Т-фильт-ров одинаковы. Легко убедиться, рассматривая схему (рис. 16-15), чтосо0для Т-фильтра является собственной частотой контура, получаемого коротким замыканием входных и выходных зажимов. Не одинаковы для И- и Т-схем только характеристические сопротивления. Приведенные выше частотные зависимости затухания а и фазы b могут быть качественно получены из физических соображений, если исходить из известных графиков характеристических сопротивлений Zc (рис. 16-16) и считать фильтр согласованным с нагрузкой во всем диапазоне частот. В области пропускания характеристическое сопротивление Zc — активное, т. е.
* Zc = zc. Поэтому при согласованной нагрузке входное сопротивление фильтра со стороны первичных зажимов (рис. 16-9 и 16-15), равное характеристическому сопротивлению, также чисто активное (т. е. напряжение Сг совпадает по фазе с током Д). Следовательно,
L
0
Рис. 16-15.
Й1=/Хгс и U2 — i2zc.
(16-47)
А это означает, что при согласованной нагрузке фильтр работает в режиме резонанса для всех частот в области пропускания.
459
Кроме того, для чисто реактивного фильтра одинаковы первичные и вторичные активные мощности, т. е.
Л = ^/1= ^2=^/2.
(16-48)
Из соотношений (16-47) и (16-48) в порядке проверки получаем U±— О2 и Д = /2 и на основании (16-37) заключаем, что при этом о=0.
Далее из схем рис. 16-9 и 16-15 очевидно, что при со -> О коэффи. циент фазы b -> 0. С увеличением частоты в пределах области пропускания вектор Ог (Д) опережает вектор О2 (Д) на все больший угол, что следует из векторной диаграммы рис. 16-12. Если построить векторные диаграммы для Т-схемы при г = гс = 0 или для П-схемы при г = гс = оо, то можно убедиться, что б\(Д) опережает по фазе О2 (Д) на 180°.
В области затухания для П-схемы Zcn — емкостное. Поскольку схема (рис. 16-13) содержит только индуктивности и емкости, очевидно, что Ох (Д) может находиться либо в фазе, либо в противофазе с О2 (Д). Построением векторной диаграммы при любой частоте со >со0, аналогичным приведенному на рис. 16-14, можно убедиться, что Ох (Д) находится в противофазе с О2 (Д) и что Ох > U2 и Д > 12. Построив векторные диаграммы для двух каких-либо
значений со > со0, легко убедиться, что с возрастанием со отношения ОхЮ2 и Д/Д растут, т. е., как следует из равенства (16-37), растет затухание а. Из схем рис. 16-9 и 16-15 непосредственно видно, что при со — оо напряжение О2 на выходных зажимах равно нулю, т. е. затухание а равно бесконечности.
Найдем теперь частотные зависимости характеристических сопротивлений П- и Т-фильтров низких частот.
На основании (16-22), (16-23), (16-39) и опыта короткого замыкания для П-схемы получаем для Zcn'-
Zcr
Zcn
Zcn
ZCT
s>
£
J

ZcT
$
о
1

] / Zcn
Рис. 16-16.
460
Из тех же формул и опыта холостого хода для Т-схемы имеем
ДЛЯ ZcT-
<1М0>
Частотные характеристики сопротивлений гсп и гст приведены на рис. 16-16. В области пропускания характеристическое сопротивление — активное. При очень малых частотах оно мало изменяется с ростом частоты и близко к значению ]/L/C. По мере увеличения частоты и приближения ее к ы0 характеристическое сопротивление П-фильтра стремится к бесконечности, а Т-фильтра — к нулю.
В области затухания при достаточно большой величине £ в формулах (16-49) и (16-50) можно пренебречь под корнем единицей по сравнению с В2.
Тогда получим:
Отсюда следует, что при достаточно высоких частотах для П-фильтра индуктивное сопротивление катушки возрастает настолько, что характеристическое сопротивление определяется только емкостным сопротивлением входного конденсатора С/2. Аналогично для Т-фильтра при достаточно высоких частотах характеристическое сопротивление стремится к величине индуктивного сопротивления катушки L/2.
Применение той или иной схемы фильтра определяется условиями его работа и предъявляемыми к нему требованиями.
Например, пусть к линии, представляющей собой одновременно два канала
связи — канал низкой и канал высокой частот, — нужно подключить какой-нибудь аппарат низкой частоты. Это можно сделать, как показано на рис. 16-17, при помощи низкочастотного фильтра, включаемого между линией и аппаратом. Низкочастотный фильтр пропустит в аппарат токи низкой частоты и не пропустит токи высокой частоты. Фильтр может быть собран по Т- и П-схемам. Однако в данном случае целесообразнее выбрать Т-схему, так как для П-схемы токи высокой частоты без всякой необходимости за-__мыкаются через входной конденсатор С/2, что может ухудшить работу канала высокой частоты.
461
Соединение в каскад ряда П- или Т-схем дает многозвенный фильтр.
Как общее свойство всех фильтров, отметим, что включение в каскад ряда звеньев увеличивает крутизну кривой затухания фильтра. При соединении в каскад звеньев с одинаковым характеристическим сопротивлением общее затухание фильтра равно сумме затуханий отдельных звеньев. Однако, как показывает более подробное исследование, из-за активных сопротивлений затухание всего фильтра растет не пропорционально числу звеньев, а несколько медленнее. Например, если затухание одного звена равно а, то двухзвенного фильтра — 1,65 а, а трехзвенного — 2,6 а.
При учете активного сопротивления звеньев зависимости затухания а и фазы b от частоты определяются следующим путем.
На основании (16-39) для Т- и П-схем
ch(o + /b) = M + /W=l+^. (16-51)
Так как в общем случае и У2 — комплексные, то левую часть равенства (16-51) можно представить в виде
ch (a -j-]b) = ch a cos b 4- j sh a sin b — М + jN.
Приравнивая в отдельности вещественные и мнимые части, получаем:
chacosb = M; shosinh=./V.
Возводя последние равенства в квадрат и заменяя во втором из них синусы через косинусы, будем иметь:
№ = sh2Gsin2h = (ch2a— 1) (1 —cos2Ь) = ch2 о 4-cos2 Ь — 1 — М2,
или
ch2 a -j- cos2 b — М2 1 + №.
Прибавляя к обеим частям последнего равенства ± 2ch a cos Ъ = == ± 2М и извлекая квадратный корень, получаем:
cho4~cos & = ±]/(Л14-1)2+A'2; ch a — cos Ь=±]/(Л1 — 1)24-№.
Здесь знаки минус должны быть отброшены, ибо ch а всегда больше плюс единицы, и формулы должны быть верны при любых по модулю значениях а и Ь.
Решая эти два уравнения, найдем ch а и cos b:
ch а= ~ [4- К(М+ 1)24-Л'24-]/(М- 1)24-7V2]; (16-52)
cosb = |[4- |/(М41)24№-]Л(Л1-1)24-№]. (16-53)
Полученные выражения позволяют по заданным параметрам _П- или Т-схем найти М и IV, затем ch а и cos b и по ним коэффициент тьгшатухания^й^и фазы Ь. Но cos b найдем два значения фазы »•
462
Какое из них взять, решим подстановкой найденных значений а и b в формулу (16-51).
Отметим, что затухание в области пропускания уже не равно
нулю и будет тем больше, чем большим активным сопротивлением обладает фильтр.
Если построить частотные характеристики затухания а и фазы b с учетом активного сопротивления, то излома в точке to = <оо (£ = 1) не получается. Семейства их в зависимости от параметра <р приведены на рис. 16-18 и 16-19, причем значение <р — 180° соответствует идеальному фильтру (рис. 16-10); по
Рис. 16-18.
оси абсцисс для упрощения вычислений отложено не Е, а V- Параметр <р определяется соотношением
tg<p = — (l/Qi+l/Qc); = и Qc = coQg, гдефЛ и Qc — добротности катушки и конденсатора (см. §3-22 и 3-21).
Чем больше потери в фильтре, тем значительнее отличается угол ср от 180° и тем существеннее отклоняются кривые а и b для реальных фильтров от идеализированных. Если, например, при со — ыв добротности ql = 50 и Qc = 100, то <Р =» 178°15'. При Ql = 200 и Qc = 1000 получаем <р «а 179°40'. Эти вычисления показывают, что ввиду близости <р к 180° частотные характеристики реальных и идеальных фильтров очень близки.
Для расчета низкочастотного фильтра обычно задают область пропускания от 0 до <оо, т. е. частоту
со0=2/]/ТС, (16-54)
и параметр р = рДДС, равный характеристическому сопротивлению фильтра при частоте = 0:
Zcn = zcT=V L/C. (16-55)
Из (16-54) и (16-55), зная со0 и р, легко найти L и С:
ЧГ=2р/<»0; С— 2/сОор. (16^567
463
и параметр р = ]/£/£, равныйхарактеристическомусопротивление фильтра при со = оо,
Zcn = ZiT = V L/C.
Из (16-63) и (16-64) найдем:
L = р/2со0; С = 1 /2со0р.
(16-64)
(16-65)
16-8. Полосные фильтры
Путем каскадного соединения низкочастотного фильтра, который пропускает токи с частотами до со2, и высокочастотного фильтра, пропускающего токи с частотами выше причем со2 > со1, можно получить фильтрующую систему, пропускающую токи с частотами ОТ О»! ДО С02.
2 С,
2С7
Рис. 16-24.
Рис. 16-25.
Эту же задачу выполняют специальные полосные фильтры, собираемые по Т-схеме (рис. 16-24) или П-схеме (рис. 16-25).
Продольное сопротивление и поперечная проводимость длй этих Т- и П-схем
Zx = /(coLj — l/coCi)=—V (1 — cfl^Ci); (16-66)
Уг=/©С2+ l//®£2=-L- (1 — co2£2C2). (16-67)
/СОА-2
Если выбрано
ЦСХ = L2C2, (16-68)
то для частоты
со0= l/V^Ci = \!VLfi2 (16-69)
продольное сопротивление Zx и поперечная проводимость У2 равны нулю. Стало быть, в продольной ветви наступает резонанс напряжений, а в поперечной — резонанс токов. Поэтому = Uz и /х == /2> т. е. частота со0 принадлежит полосе пропускания этих фильтров.
С учетом (16-66), (16-67) и (16-69) вычислим коэффициент

(1-coW
- 2a>2LtCf ---
4L6JQ)
466
Аналогично изложенному в § 16-6 заключаем, что границы полосы Пропускания полосного фильтра определяются из неравенства
(16-71)
Рассматривая верхний предел неравенства а + 1, получаем со = == соо, т. е., что со0 принадлежит полосе пропускания. Рассматривая нижний предел неравенства, будем иметь:
(16-72)
Извлекая корень, находим
1 — со2/соо = ± 2<о | А2Сх
и ____
со2± 2a0]/L2C1 со — а>о = О, (16-73)
или с учетом (16-69)
со2 ± 2со0 VLjLi со — со^ = 0.
Решая квадратное уравнение, получаем:
co=co0(±m±]/m2 +1), (16-74)
где
tri^LjL-i. (16-75)
Так как со может быть только положительной величиной, то отсюда получаем границы полосы пропускания полосного фильтра:
ощ2 = «0(/т2+1 (16-76)
Перемножая почленно два последних равенства, получаем важное соотношение, связывающее граничные частоты с резонансной:
C0jC02 = C0q.
Для полосы пропускания {а = 0) из первого равенства (16-41) найдем соотношение, позволяющее определить изменение коэффициента фазы д:
cOS ь — — j _ ~ ю2/юо)2 __ । _ 0 — Е2)2 (16-77)
COSO —/с — 1 2to2L2Ci — 1 2S2m2 ’
Из равенства (16-77) следует, что cos Ь = — 1 при со = сор При этом для b должно быть взято значение — л, так как точка со — coj является концом области затухания и началом области пропускания высокочастотного фильтра, образующего вместе с низкочастотным рассматриваемый полосный фильтр. Для такой точки 6 = — л и далее b уменьшается по абсолютному значению, оставаясь все время отрицательным (рис. 16-26). ------
467
К тому же выводу можно прийти, построив для рассматриваемого фильтп нагруженного на согласованное с ним чисто активное сопротивление (рис. I6-2A векторную диаграмму при какой-нибудь частоте со, где с», со sg со0 (рис. 16-2RV Переписав равенства (16-66) и (16-67) с учетом (16-69)

(*6-78)
получим, что при cOj аа со ag комплекс представляет собой емкостное сопр0 тивление, а 1/У2 — индуктивное. Поэтому 13 отстает по фазе от L’s на угол 90°'
Рис. 16-27.
тетает по фазе от 4 на угол 90°, а 4^/2 также отстает по фазе на угол 90° от 4- Остальное построение очевидно из рис. 16-28. Таким образом, из диаграммы устанавливаем, что. при сох аа со ag со0 коэффициент фазы b < 0, так как йх отстает по фазе от 7/2 на угол Ь.
Далее при со = со0 получим cos b = 1 и b — 0. И, наконец, из равенства (16-77) получим, что cos Ь = —1 при со = со2. При этом b — так как точка со = со2 является началом области затухания и концом области пропускания низкочастотного фильтра, образующего вместе с высокочастотным рассматриваемый
полосный фильтр. До этой точки у низкочастотного фильтра коэффициент фазы Ь, возрастая от нуля, был все время положительным (рис. 16-10). К тому же выводу придем, построив для частоты со при условии со0 ag со ag со2 векторную диаграмму (рис. 16-29), аналогичную векторной диаграмме рис. 16-28. Только нужно иметь в виду, что при со0 ag со ag со2 сопротивление Zj — индуктивное, а 1/И2 — емкостное. Итак, векторная диаграмма (рис. 16-29) показывает, что при со > <Яо коэффициент фазы b > 0.
Коэффициент, а в области затухания фильтра вычислим по фор* муле (16-41), где величина А определяется равенством (16-70):
- -= +1Ы . 1- (а-а;
468
Частотная характеристика а построена на рис. 16'26. Отметим, qTo частотные характеристики а и b одинаковы для Т- и П-полосных фильтров по тем же соображениям, что и для низко- и высокочастотных.
На основании равенства (16-50) получим:
(>мо>
Частотная характеристика гст построена по выражению (16-80) на рис. 16-30.
Для полосного П-фильтра на основании выражения (16-49) будем иметь:
j Г gJ .!. —_
V y^i+z^/4
(16-81)
Частотная характеристика zcn построена по выражению (16-81) на том же рис. 16-30. Не производя подробного анализа, отметим,
что при 0 --С « coj характеристическое сопротивление 4л — индуктивное, a Zct — емкостное, а при <в2 =С со sC sg оо — наоборот. В области пропускания характеристическое сопротивление полосных Т- и П-фильтров — чисто активное.
Характеристические сопротивления гст и гсп не остаются постоянными в полосе пропускания. Поэтому, как было указано в § 16-5, согла
сование фильтра принципиально невозможно для всех частот полосы пропускания. Однако, как видно из кривых рис. 16-30,
вблизи резонансной частоты со0 сопротивления гст и гсп медленно изменяются и остаются почти постоянными и равными УЬ2! Сг. Поэтому если у фильтра согласованная нагрузка при частоте со0, то это согласование распространяется и на некоторые области частот, прилегающие к ней справа и слева.
Для расчета полосного фильтра задают границы полосы пропускания W1 — 2лД и п)2 = 2л/2 и параметр р = VL.JCi, причем при со == соо == 1 / УLjCt = 1 /УL2C2 сопротивления
ZcII = 2CT = У L2/Qi = Р-
469
Как будет показано ниже, фильтры типов К и М имеют Одн и ту же собственную или резонансную частоту. Поэтому у н одинаковы области пропускания, но существенно различают^ частотные характеристики затухания, как показано на рис. I6.37 для низкочастотного фильтра при различных значениях М (Д| = 0,6; 0,8 и 1). При М — 1 вся индуктивность сосредоточена в пр^ дольном плече (а вся емкость — " ---------—' ” ------ ’
типа М. получается фильтр типа
в поперечном) и вместо фильтра к.
Рис. 16-35.
0------------
Тип К
а)
Тип /И ; последовательное звено
б)
Zr'
0--------------------L—0
Тип М параллельное звено
6)
Рис. 16-36.
При уменьшении М. частотная характеристика а в области затухания начинает расти быстрее, чем у фильтров типа К, и У нее появляется пик. Последнее объясняется тем, что сопротивление в поперечном плече L2, С2 (рис. 16-35, б) при его резонансной частоте обращается в нуль. Можно показать, что чем меньше М, тем сильнее смещается влево пик частотной характеристики затухания фильтра. Однако из рис. 16-37 также видно, что в полосе затухания, т. е. при £ > 1, значение а для фильтров типа М может стать даже - меньше, чем для фильтров типа К. “
472
Диализируя частотную зависимость характеристического сопро-,йБления для низкочастотного фильтра типа М можно показать, . „„„„ . созданного по Т-схеме,
Tl.
' она для последовательного звена, зависит от М и остается такой же, ®к и для фильтров типа /< (рис. 16-38), а для последовательного звена, собранного по П-схеме, Zcn существенно зави-сйт от М, а именно: при уменьшении М кривая zcn с возрастанием частоты зна-чительно менее отклоняется от постоянной величины, равной VL/C. Из кри-вЫх рис. 16-38 видно, что при М ~ 0,6 и при 0 0,88 величина Zcn от-
клоняется от VL/C не более чем на 5%.
Иными словами, гсп остается почти постоянным и равным У L/C в значительно большем диапазоне частот, чем для фильтра типа К.
Для параллельных звеньев низкочастотного фильтра типа М наоборот: у П-схемы Zcn не зависит от М и остается таким же, как для фильтров типа К, у Т-схемы Zct зависит от М и с уменьшением М кривая гст выравнивается, т. е. гст остается почти постоянным и равным У L/C в большем диапазоне частот, начиная с со = 0, чем для фильтров типа /( (рис.
16-39).
Рис. 16-38.
Рис. 16-39.
Более подробные исследования показывают, что характеристическое сопротивление фильтра в области пропускания (при
£ sC 0,88) будет практически почти постоянным при М = 0,6 ’ 6,62. Таким образом, при этом значении М получается наиболее
473
НаГРУЗКц
совершенное согласование фильтра с сопротивлением (т. е. приключаемыми к нему устройствами).
Покажем на примере последовательного звена фильтра типа как определяются его продольное (Zj) и поперечное (Zj) сопротив’ ления (рис. 16-35, б и 16-36, б) по заданным сопротивлениям фильтра типа Л (рис. 16-35, а и 16-36, а) и величине М.
В соответствии с принципом построения последовательного звена и равенством (16-83)
— (16-85)
Вообще говоря, далее можно проводить исследование двумя путями. Идя первым путем из равенства характеристических сопротивлений фильтров Л и М для их Т-схем можно определить Z2 и исследовать, какие получаются при этом частотные зависимости Z’cn для П-образной схемы фильтра типа М.
В соответствии со сказанным преобразуем выражение (16-80) для Zct. Полагая
1/1/2=='^2> (16-86)
получаем:
= + ад + (^)2. (16-87)
Аналогично запишем выражение для Zc? фильтра типа М:
Zc'r = '|/z;Z^ + (^y. (16-88)
Приравняв
Za = Z'cr (16-89)
и решив полученное уравнение относительно Z2, найдем:
+ <16-ад
На основании равенств (16-85) и (16-90) по заданным L и С для Т-фильтра можно найти параметры Llt L2 и С2 у М-фильтра:
LX = MU С2 = МС; L2^^L. (16-91)
Если теперь построить частотные зависимости характеристического сопротивления Zcn при разных М для последовательного звена П-схемы с параметрами, определяемыми соотношениями (16-91)> то получим кривые, приведенные на рис. 16-38.
Если же идти вторым путем и в вышеприведенном исследовании исходить из равенства характеристических сопротивлений длЯ П-схем низкочастотных фильтров типа К и М и равенства (16-85)» то для Za получим [сравнить с формулой (16-90)]:
y,_2Zj ± V4Zf+M2(4Z2+ZjZgI______________л6-92)
^Hfiz2+z\) — 1 —
474
Более подробное исследование частотных зависимостей характе-сТического сопротивления Т-схемы последовательного звена оказывает?- что при полученном значении Z'2 коррекции (т. е. Плучшения) их в указанном выше смысле с изменением величины М У происходит. Таким образом, второй путь исследования отпадает.
Аналогично производится исследование параллельных звеньев низкочастотного фильтра, а также высокочастотного, полосного й заграждающего фильтров типа М.
Ограничимся лишь приведением расчетных формул для определения параметров параллельного звена низкочастотного фильтра Л1: (16-93) (16-94)
y;=l/Z' = My2=M/Z2;
У’_У__ Y* ! *~М2 у 1 ZJ М 4М 2
или прямо для параметров Llt С2, Сб
L1 = ML; С2 = МС;
(16-95)
Отметим, что полученные выше результаты позволяют рассматривать фильтр типа К как частный случай фильтра типа М при М = 1.
Далее запишем, например для схемы рис. 16-35, б, значения Zi и У2:
Z1—jaML; (16-96)
1 „ . 1—r , 1 . (1— MyaPLC-4 zl„n_.
Y2 ~ Z2~1 4M + jaMC ШНС ’ (16-97)
Убедимся, что отношение Zi/K2 зависит от частоты:
_ L[4-(l-M)2g>2LC]
Y2~ 4С ' (16-98)
И, наконец, убедимся также и в том, что собственная частота фильтров типа /С и М одна и та же и не зависит от М. Например, для схемы рис. 16-35, б, замкнув накоротко входные и выходные зажимы (см. § 16-6), при учете соотношений (16-91) найдем, что
= bit.MC + ®о -^ = ®0 [ 4М Д + "4 Allj, (16-99) откуда получаем:
соо = 2/УСС> (16-100)
т- е. то же значение, что и для фильтра типа К (§ 16-6).
Для получения оптимальных результатов в смысле затухания 11 меньшей зависимости характеристических сопротивлений от час-!оты применяется каскадное включение фильтров типа К и М. *1усть, например, включены в каскад три звена фильтра типа М с° значениями М = 1, М = 0,8 и М = 0,6, что часто и осуществляется на практике. Суммируя частотные характеристики отдельных звеньев, получаем результирующую кривую затухания=
475
(рис. 16-40) с лучшей частотной зависимостью затухания, чем Пп каскадном включении трех одинаковых звеньев типа К (пунктип на рис. 16-40). Из рис. 16-40 заключаем, что кривая затухани?
1Я каскадного соединения трех различных звеньев фильтра типа М растет быстрее при переходе в область затухания^ и обеспечивает в этой области бдльщИе значения затухания а, чем кривая за. тухания трехзвенного фильтра типа Д Отдельные звенья и полная схема та^ кого фильтра приведены на рис_ 16-41, а и б.
Более подробный анализ показывает что звено М — 1 (или Д) дает фильтру в целом значительное затухание при частотах, значительно больших резонансной. Параллельное звено при М = 0,8 повышает крутизну кривой затухания и создает в ней пик. Два параллельных полузвена типа М при М = 0,6 (иначе называемых Г-образными несимметричными фильтрами) также повышают крутизну кривой затухания фильтра и обеспечивают появление дополнительного пика в составе этой кривой. Но основная
0
Рис. 16-41.
цель разделения звена М = 0,6 на два полузвена заключается в выравнивании частотной зависимости характеристического с0 противления фильтра в полосе его пропускания, т. е. в улучшени11 условий его согласования е~ согцзотпвлеиием нагрузки.
476
Отметим также, что структура всех звеньев (рис. 16-41, а) такова, уменьшается число элементов, из которых состоит каскадное Единение. В самом деле, поскольку все звенья начинаются и окан-сйВаются конденсаторами, то для каскадного соединения нужно ’LjbKO объединить емкости соответствующих поперечно включений конденсаторов.
16-11- Г-образный фильтр как пример несимметричного фильтра
Наряду с рассмотренными симметричными Т- и П-образными фильтрами широкое распространение на практике нашли также фильтры, в состав которых входят г-образные несимметричные схемы.
При рассмотрении фильтров постоянной К их симметричные П- и Т-схемы ложно считать образованными каскадным соединением Г-образных схем. Например, соединив два Г-образных полузвена низкочастотного фильтра (рис. 16-42) в точках 2—2', получим симметричный Т-образный низкочастотный фильтр (рис. 16-15).
Соединив же их в точках 1—1', получим симметричный П-образный низкочастотный фильтр (рис. 16-9).
На рис. 16-43 приведено Г-образное полузвено высокочастотного фильтра. Со-
10-
L/г
0 г
4л
2L
Рис. 16-42.
0 г'
/'#----------*------02'
Рис. 16-43.
ответствующим каскадным
соединением двух таких полузвеньев можно получить симметричный Т- или П-образный высокочастотный фильтр (рис. 16-20 и 16-22). Легко убедиться, что сказанное относится также к симметричным Т- и П-образным полосным и заграждающим фильтрам, которые можно получить соответствующим каскадным соединением Г-образных полузвеньев.
Однако в полной мере целесообразность рассмотрения Г-образных полузвень-евобнаруживается при исследовании фильтров постоянной М. На рис. 16-44, fl и б даны Г-образные полузвенья фильтров типа К и типа М, которые как несим-
1 Тип к г
°).
Рис. 16-45.
Рис. 16-44.
' 2С
10-----1|-
ф с/г
Устричные четырехполюсники имеют различные характеристические сопротивления со стороны зажимов 1—Г и 2—2'. Поэтому при соединении Г-звеньев "Ужно различать, со стороны каких зажимов выбираются одинаковые характеристические сопротивления Г-полузвеньев фильтров типов Д и М.
В самом деле, выше было указано, что при образовании фильтров типа М /’Фильтров типа К принимают ZJ = MZ} (16-85). Далее, если исходить из равен-Ва^сГ = Z’lT, т. е. применительно к схемам рис. 16-44, а и б полагать одинаковыми характеристические сопротивления со стороны зажимов 1—Г, то Zj 5^т определяться равенством (16-90) При этом получается последовательное -£8афилътра типа М. Здесь, как и выше для фильтров типа Д', соединив зажимами
477
1—1' (рис. 16-44, б) два последовательных Г-полузвена типа М, получим симм₽ ричное П-образное последовательное звено типа М (рис. 16-36, б) с характер]?' тическим сопротивлением Z‘cll. с'
Значение Z’cn найдем из формулы (16-81):
(16.101)
если подставим сюда Z[ и Z'2 из соотношений (16-85) и (16-90). После преобраэо. ваний получим:
тда;['+<'-"’>4]=
Соединив же два последовательных Г-полузвена типа М зажимами 2—2' получим симметричное Т-образное последовательное звено типа М (рис. 16-35, б) с характеристическим сопротивлением Z’cT.
Поскольку у последовательного звена фильтров типа М сопротивления Z'cT = ZcT, то можно соединять в каскад Г-образные полузвенья фильтров типов /< и Д) зажимами 1—Г, соблюдая правило согласования характеристических сопротивлений. Получается несимметричный П-образ-ный фильтр типа М с характеристическими сопротивлениями Zcn и Z'c{1 (рис. 16-45). При соединении Г-образных фильтров типа К и М в каскад зажимами 2—2' не соблюдается правило согласования характеристических сопротивлений. При этом получается Т-образный несимметричный фильтр, имеющий совсем иные свойства в полосе пропускания.
Если же выбрать ¥'2 = М¥2 (16-93) и исходить из равенства характеристических сопротивлений Г-образных фильтров типа К
и М (рис. 16-44, а и б) со стороны зажимов 2—2', т. е. принять Zcn = Z'cn, то можно соединить в каскад эти Г-схемы зажимами 2—2', соблюдая правило согласования характеристических сопротивлений. При этом получим для Z) равенство (16-94), т. е. придем, как было показано выше, к параллельному звену фильтра типа М.
Соединив Г-образные схемы рис. 16-44, б зажимами 2—2', получим симметричное Т-образное параллельное звено фильтра типа М (рис. 16-35, в) с характеристическим сопротивлением Z'(T, которое найдем из формулы (16-80):
z;z-=pAzJ'Z'(i+^i (16-юз)
если Z; и Zg заменить их значениями согласно (16-94) и (16-93).
После преобразований получим:
1 1 ’
гг> гг'
Рис. 16-46.
/<=]/" Z1Zi 1 _ Z‘T П6-104)
сТ Г 1 + Z1/4Z21 + (1-^)Z1/4Z2 \ + {\-M^Z^Z2- 1
Любопытно отметить, что произведения характеристических сопротивлений фильтров типа К (ZcT и Zcn) и М (Z’cT и Z'n) одинаковы и не зависят от частоты
7' 7' _______ 7 7 _ В _____ 7 7 _____ ^1
‘JcT ^сП~~ -~Q — '-Ч'-з —--
(16-105)
Соединив Г-образные схемы рис. 16-44, б зажимами 1—Г, получим симметрий' ное П-образное параллельное звено фильтра типа М (рис. 16-35, в) с характерна тическим сопротивлением Zcn. Если же, соблюдая правило согласования хар-я-к,г
478
тиЧеских сопротивлении, соединить Г-образные полузвенья фильтров К и М Рамами 2—2', получим несимметричный Т-образный фильтр типа М с характе-Зи'тическими сопротивлениями ZcT и ZcT (рис. 16-46).
Подобным же образом можно получить Г-образные схемы типа М для полосах и заграждающих фильтров. Затем, соединив в каскад Г-образные схемы
Рис. 16-47.
типа М, можно получить симметричные, а схемы типа К и М — несимметричные полосные и заграждающие фильтры типа М, При этрм также улучшаются частотные зависимости характеристических сопротивлений, которые приведены на рис 16-47 для полосного Т-образного симметричного фильтра типа М, а на рис 16-48 — для полосного П-образного симметричного фильтра типа М.
16-12. Безындукционные (или г, С) фильтры
Чтобы построить низкочастотный фильтр L, С с узкой полосой пропускания нужно, в частности, применять катушки с большой индуктивностью (<в0 = 2/]/LQ. Увеличиватьиндуктивность катуш-кивведением магнитопровода нецелесообразно, так как индуктивность будет зависеть от тока. Для получения большой индуктивности увеличением числа витков катушки при одновременном требовании высокой добротности пришлось бы увеличивать сечение проводов катушки, ее массу и габариты, что также нецелесообразно.
Поэтому часто применяют безындукционные (или г, С) фильтры, которые, как показывает само их название, не содержат катушек индуктивности и состоят из конденсаторов и резисторов.
На рис. 16-49, а — в показаны Г-, Т- и П-схемы низкочастотного г> С-фнльтра. При низких частотах, когда емкостные сопротивления поперечных ветвей фильтра велики, токи через активные сопротивления малы, падения напряжения на активных сопротивлениях также малы и напряжение на выходе фильтра лишь немногим меньше Напряжения на его входе. Поэтому при низких частотах коэффициент затухания фильтра невелик. Отметим также, что ток через нктивное сопротивление /, С-фильгра мал и потому, что обычно
479
нагрузкой фильтра служит усилитель с большим по сравиецП1о с г входным сопротивлением.
При увеличении частоты емкостное сопротивление уменьшается ток через активное сопротивление увеличивается, напряжение на выходе уменьшается и коэффициент затухания фильтра растет
В соответствии с тем, как это было сделано выше для L, С-фильт-ров, рассмотрим частотные характеристики коэффициентов затухания а и фазы b для низкочастотного г, С-фильтра, для которого Zj = г и Z2 = 1/jcoC.
На основании (16-56) имеем:
ch g=ch (а 4- jb) = ch a • cos b + j sh a • sin b ~
= 1 + Zj/2Z2 = 1 + jrcoC/2, (16-106)
откуда
ch a- cos 6 — 1; shn-sinh = rcoC/2. (16-107)
Подчеркнем, что для постоянного тока (со = 0) эти равенства удовлетворяются при а = Ъ = 0. Для переменного тока любой
г/г
а)

частоты со 0 и ги>С12 > 0 они могут удовлетворяться лишь при sh а > 0 и sin Ь > 0, а значит, при а > 0 и b > 0. Таким образом, г, С-фильтр принципиально не имеет такого диапазона частот, в котором коэффициент затухания а равен нулю.
Совместное решение уравнений (16-106) относительно а и b позволяет получить частотные характеристики.
Для коэффициента затухания получим:
sho=|<!£!^l + ^j/l+^y. (16-103)
Рассматривая область достаточно малых частот, для которой г<»С12 < 1, приближенно имеем:
sh а а - "j/” г-~- (16-109)
и более точно
a=Arsh]/rcoC/2. (16-110)
В качестве граничной частоты полосы пропускания, называемой иначе частотой среза сос, принимают частоту^ для которой равяй
480
д-ивиое и емкостное сопротивления Г-образного полузвена низкочастотного rC-фильтра, т. е. г/2 = 2/<»сС или
<вс=4/гС.
(16-111)
Рис. 16-50.
0з (16-108) можно вычислить затухание, соответствующее частоте еза если учесть, что ги>сС/4 = 1. Получаем sh а == 2,2 и а = X 1,54 Нп = 13,4 дБ.
На рис. 16-50 приведена частотная характеристика коэффициента затухания а, построенная по формуле (16-108). Применительно ко всем типам г, С-фильтров следует отметить, что ввиду малой крутизны этой кривой в полосе затухания для ее увеличения соединяют в каскад 2— 3 звена. Однако при этом неизбежно увеличивается затухание и в полосе пропускания. Обычно г, С-фильтры работают совместно
В этом случае в полосе пропускания может даже иметь место
с усилителями.
усиление.
На рис. 16-51, а — в приведены Г-, Т- и П-схемы высокочастотного г, С-фильтра. При низких частотах, когда емкостные сопротивления велики, падения напряжения на них также велики и напряжение на выходе фильтра мало (при постоянном токе оно равно нулю), т. е. коэффициент затухания фильтра большой. При увеличении частоты емкостное сопротивление уменьшается, напряжение на выходе фильтра растет и коэффициент затухания убывает.
0-Н1-П II—0 гс п гс
0.----..4 0
б)
Рис. 16-51.
Для высокочастотного г, С-фильтра = 1//юС и Z2 = г, и на основании (16-106) имеем:
ch п-cos& + /sh о-sin й== 1 —(16-112) и
cha-cosh = l и shosinfe = —(16-113)
Совместное решение уравнений (16-113) дает:
sllG=]///'2^С-У' 1 + (4гйС)-2 ’ (16-Ш2
16 Основы теории цепей
481
1—Г (рис. 16-44, б) два последовательных Г-полузвена типа М, получим Сим
ричное П-образное последовательное звено типа М (рис. 16-36, 6) с характ’ег'
тическим сопротивлением Z'cn. J,1c-
Значение Z'cn найдем из формулы (16-81):
если подставим сюда Z\ и Z'2 из соотношений (16-85) и (16-90). После преобразо, ваний получим:
Соединив же два последовательных Г-полузвена типа М зажимами 2—2' получим симметричное Т-образпое последовательное звено типа М (рис. 16-35 б) с характеристическим сопротивлением Z'cT. ’ '
Поскольку у последовательного звена фильтров типа М сопротивления Z'cr =, — ZcT, то можно соединять в каскад Г-образные полузвенья фильтров типов /< и Л1 зажимами 1—Г, соблюдая правило согласования характеристических сопротивлений. Получается несимметричный П-образ-ный фильтр типа М с характеристическими сопротивлениями Zcn и Z'cn (рис. 16-45). При соединении Г-образных фильтров типа и Л; в каскад зажимами 2—2' не соблюдается правило согласования характеристических сопротивлений. При этом получается Т-образный несимметричный фильтр, имеющий совсем иные свойства в полосе пропускания.
Если же выбрать = MY2 (16-93) и исходить из равенства характеристических сопротивлений Г-образных фильтров типа К.
и М (рис. 16-44, а и 6) со стороны зажимов 2—2', т. е. принять Zcn — Z'tn, то можно соединить в каскад эти Г-схемы зажимами 2—2', соблюдая правило согласования характеристических сопротивлений. При этом получим для Z, равенство (16-94), т. е. придем, как было показано выше, к параллельному звену фильтра типа М.
Соединив Г-образные схемы рис. 16-44, б зажимами 2—2', получим симметричное Т-образное параллельное звено фильтра типа М (рис. 16-35, в) с характеристическим сопротивлением Z’cT, которое найдем из формулы (16-80):
ZcT=y (16-103)
если Zj и Z' заменить их значениями согласно (16-94) и (16-93).
После преобразований получим:
Рис. 16-46.
—tJlz"2____________________=______________________ (16-104)
1+ Zj/4Z2 1+ (1—Af2)Z1/4Z2 1 + (1-Л42)гх/4г2 • 1
Любопытно отметить, что произведения характеристических сопротивлений фильтров типа К (ZcT и Zcn) и М (Z'cT и 7/сП) одинаковы и не зависят от частоты-
Zc'r^ = Zc7.Zc77 = A= ZxZ2=b-. (16-105)
Соединив Г-образные схемы рис. 16-44, б зажимами 1—1', получим симметри4' ное П-образное параллельное звено фильтра типа М (рис. 16-35, в) с характер^' =тическим сопротивлением Z'cn. Если же, соблюдая правило согласования
478
тических сопротивлений, соединить Г-образные полузвенья фильтров К и М Рамами 2—2', получим несимметричный Т-образный фильтр типа М с характе-3®сГцческими сопротивлениями ZcT v,7.lT (рис. 16-46).
Р Подобным же образом можно получить Г-образные схемы типа М для полос-яИх и заграждающих фильтров Затем, соединив в каскад Г-образные схемы
Рис. 16-48.
типа М, можно получить симметричные, а схемы типа К и М — несимметричные полосные и заграждающие фильтры типа М, При этом также улучшаются частотные зависимости характеристических сопротивлений, которые приведены на рис 16-47 для полосного Т-образного симметричного фильтра типа М, а на рис. 16-48 — для полосного П-образного симметричного фильтра типа М,
16-12. Безындукционные (или г, С) фильтры
Чтобы построить низкочастотный фильтр L, С с узкой полосой пропускания нужно, в частности, применять катушки с большой индуктивностью (соо = 2/]/LC). Увеличивать индуктивность катуш-кивведением магнитопровода нецелесообразно, так как индуктивность будет зависеть от тока. Для получения большой индуктивности увеличением числа витков катушки при одновременном требовании высокой добротности пришлось бы увеличивать сечение проводов катушки, ее массу и габариты, что также нецелесообразно.
Поэтому часто применяют безындукционные (или г, С) фильтры, которые, как показывает само их название, не содержат катушек индуктивности и состоят из конденсаторов и резисторов.
На рис. 16-49, а — в показаны Г-, Т- и П-схемы низкочастотного 9 С-фильтра. При низких частотах, когда емкостные сопротивления Поперечных ветвей фильтра велики, токи через активные сопротивления малы, падения напряжения на активных сопротивлениях также малы и напряжение на выходе фильтра лишь немногим меньше Напряжения на его входе. Поэтому при низких частотах коэффициент затухания фильтра невелик. Отметим также, что ток через -Активное сопротивление /, С-фильтра мал и потому, что обычно
479
нагрузкой фильтра служит усилитель с большим по сравнению с г входным сопротивлением.
При увеличении частоты емкостное сопротивление уменьшается ток через активное сопротивление увеличивается, напряжение на выходе уменьшается и коэффициент затухания фильтра растет
В соответствии с тем, как это было сделано выше для L, С-фильт1 ров, рассмотрим частотные характеристики коэффициентов затухания а и фазы b для низкочастотного г, С-фильтра, для которого Zj = г и Z2 = 1/jcoC.
На основании (16-56) имеем:
chg = ch (а4- jb) — ch a- cos b + j sh a• sinb =
= 1 ~b Zi/2Z2= 1 -4-уУсоС/2, (16-106)
откуда
chc-cosh=l; she-sinh —rcoC/2. (16-107)
Подчеркнем, что для постоянного тока (со = 0) эти равенства удовлетворяются при а = b = 0. Для переменного тока любой
0 1 4"...... £ "i-m 11М0
в)
г/г г/г г/г
а) б)
Рис. 16-49.
частоты со > 0 и гсоС/2 > 0 они могут удовлетворяться лишь при sh а > 0 и sin b > 0, а значит, при а > 0 и b > 0. Таким образом, г, С-фильтр принципиально не имеет такого диапазона частот, в котором коэффициент затухания а равен нулю.
Совместное решение уравнений (16-106) относительно а и b позволяет получить частотные характеристики.
Для коэффициента затухания получим:
+ <16-108)
Рассматривая область достаточно малых частот, для которой rcoC/2 < 1, приближенно имеем:
sha^a = ~]f~- (16-109)
и более точно
сг=Аг811/Дд?/2. (16-11°)
В качестве граничной частоты полосы пропускания, называемо® иначе частотой среза сос, принимают частоту, для которой равй^
480
активное и емкостное сопротивления Г-образного полузвена низко-цастогного rC-фильтра, т. е. г/2 = 2/сосС или
сос=4/гС. (16-111)
Из (16-108) можно вычислить затухание, соответствующее частоте гРеза, если учесть, что гюсС/4 = 1. Получаем sh а = 2,2 и а = X 1,54 Нп = 13,4 дБ.
Па рпс. 16-50 приведена частотная характеристика коэффициента затухания а, построенная по формуле (16-108). Применительно ко всем типам г, С-фильтров следует отметить, что ввиду малой крутизны этой кривой в полосе затухания для ее увеличения соединяют в каскад 2— 3 звена. Однако при этом неизбежно увели-
чивается затухание и в полосе пропуска
ния. Обычно г, С-фильтры работают совместно с усилителями.
В этом случае в полосе пропускания может даже иметь место
усиление.
На рис. 16-51, а — в приведены Г-, Т- и П-схемы высокочастотного г, С-фильтра. При низких частотах, когда емкостные сопротивления велики, падения напряжения на них также велики и напряжение на выходе фильтра мало (при постоянном токе оно равно нулю), т. е. коэффициент затухания фильтра большой. При увеличении частоты емкостное сопротивление уменьшается, напряжение на выходе фильтра растет и коэффициент затухания убывает.
0 IF г—II—0
гс п гс
I I г 0.——„—0 б)
Рис. 16-51.
Для высокочастотного г, С-фильтра = 1//соС и Z2 = г, и на основании (16-106) имеем:
cha-cosh4-/shfi-sinh = l — j (16-112)
и
chc-cosfe = l и shfl-sinb = —(16-113)
Совместное решение уравнений (16-113) дает:
shfl===]/"8(t-(oC)a + + (4г®С)2 ’ (16-114)
16 Основы теории цепей
481
Рассматривая область достаточно высоких частот, для котопп-1/2гсоС< 1, приближенно получаем: 11
и более точно
n=Arsh]/’27Sc. (1б-116)
В качестве частоты среза <ос принимают частоту, для которой равны активное и емкостное сопротивления Г-образного полузвена-юс=1/4гС. (16-117)
На этой частоте а = 13,4 дБ.
На рис. 16-52 приведена частотная характеристика коэффициента затухания а, построенная по формуле (16-114).
Рис. 16-52.
Рис. 16-53.
Одна из возможных схем полосного г,С-фильтра приведена на рис. 16-53. Первое Г-полузвено (высокочастотный фильтр) обеспечивает затухание низких частот, а второе Г-полузвено (низкочастотный фильтр) — высоких частот. Некоторая частота ю0 в полосе
пропускания, при которой коэффициент затухания фильтра наименьший (рис. 16-54), вычисляется по приближенной формуле
С00 1Z(0cl(IJc2 = 1 iVryCyr2С2, (16-118)
где cdc1 и <ос2 — частоты среза низко- и высокочастотного фильтров определяемые формулами (16-111) и (16-117).
В качестве одной из возможных схем заграждающего г, С-фильтря на рис. 16-55 приведено параллельное соединение Т-образны^ высоко- ц |щ-зко!!астот1юго г, Офильтроь^ Подбирая параметра
482
эТОй схемы, можно получить на некоторой частоте равный нулю тОк нагрузки. Коэффициент затухания фильтра на этой частоте будет равен бесконечности (рис. 16-56).
Отметим в заключение, что индуктивно-связанные цепи тоже представляют собой фильтр. На практике применяются также мостиковые и кварцевые фильтры.
Глава семнадцатая
СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
17-1. Общая характеристика задачи синтеза
В предыдущих главах рассматривались методы анализа электрических цепей, когда при заданной структуре цепи и параметрам определялись различные свойства и процессы в .цепи.
Однако часто приходится решать и обратную задачу: для линейной пассивной цепи так подобрать структуру и параметры, чтобы при заданном законе изменения во времени входной величины xBX (t) получить заданный закон изменения во времени выходной величины хвых (0- Переходя к лапласовым изображениям Хвх (/;) = = L (хвх (/)} и Хвых (р) = L{xBblx (0}> получим, что задана передаточная функция цепи К (р) = Хвых (р)/Хвх (р). Тогда задачу синтеза цепи можно поставить так: по заданной передаточной функции цепи К (р) или (переходя к преобразованиям Фурье) по заданной частотной характеристике цепи Д' (/ю) нужно найти структуру цепи и ее параметры.
Рассмотрим сначала общие соображения о синтезе двухпопюс-ников. В качестве входной величины возьмем напряжение на зажимах двухполюсника UL (/со), а в качестве выходной — ток на входе Л (/со). Тогда
№) = T^=Z(M- (17-1)
Таким образом, для двухполюсника в качестве передаточной функции можно выбрать входное сопротивление Z (/со) или обратную ему величину — входную проводимость Y (/со), которые часто называют входными функциями цепи. Они могут быть заданы аналитически или графически (в виде частотных характеристик).
Легко проверить, пользуясь рис. 17-1, а и б, что приведенные на нем различные по структуре так называемые дифференцирующие Цепи могут иметь одинаковые передаточные функции
1__________ _____________
|е для цепи рис. 17-1,ц 7’= £/г, а для цепи рис.~~Г/-1,& Т = гС7
16*
483
Этот пример показывает, что одну и ту же передаточную функци или частотную характеристику могут иметь различные цепи, т задача синтеза цепи по заданным К (р) или К (/ю) имеет неодно значное решение. В некоторых случаях она вообще может не иметь решения, когда для цепей, состоящих из резисторов, катущек и конденсаторов, параметры г, L или С получаются отрицательными Поэтому решение задачи синтеза распадается обычно на два этапа.
На первом этапе следует установить, реализуема ли физически цепь, заданная своей передаточной функцией К (р) или входными функциями Z (р) и Y (р) при помощи пассивных линейных элементов г, L и С Если же для цепи за
даны графически частотные- характеристики К (/и), Z (/со) или Y (/со), то их следует с достаточной точностью аппроксимировать функциями, которые заведомо допускают физическую реализацию цепи.
На втором этапе следует реализовать функции цепи мето-
дами, разработанными в теории синтеза цепей, т е. определить ее
структуру и параметры, причем часто стремятся к уменьшению числа элементов синтезируемой цепи. При этом выбирается метод синтеза, учитывающий неоднозначность решения в смысле структуры синтезируемой цепи.
Важно отметить, что функции цепи К (р), Z (р) и Y (р) являются функциями комплексного переменного или комплексной частоты р = s + /со Как известно из теории функций комплексного переменного, функции цепи однозначно определяются распределением их нулей и полюсов.
17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы
Для четырехполюсника передаточная функция может быть например, задана как отношение лапласовых изображений выходного и входного напряжений,
/<(Г) = (Л(р)М(р).
Полагая р = /со, получаем передаточную функцию в комплексной форме, т е частотную характеристику четырехполюсника, которая равна отношению частотных спектров выходного и входного напряжений.
К (/со) = иг (]ы). (17 3)
Составим отношение напряжений Т/2 и 74 четырехполюсника Из второго урав ненит^(8 2) при положшельном направлении тока 1г, как на рис 17-1, имеем 12-y^i+y^-
При сопротивлении нагрузки Za
484
таК как U2 = ДА. откуда определяем:
U2 У21А
U\ 1 — Y22ZH
В гл 14 было показано, что сопротивления ветвей, а также входные и взаимные проводимости в операторной форме представляют собой отношения многочленов относительно р (иначе говоря, рациональные дроби). Поэтому передаточная функция К (р) также представляется отношением многочленов
fe„Pm + fe1pw"1 + + П7.4)
а0Рп+а1Рп~1 + ... +й„ ’
где тип — целые положительные числа, причем т < п.
Обозначим полюсы Д (р), г. е. корни знаменателя (17-4), через р 1ю, р2 с, ...
Р„со> а НУЛИ К (Р)> т- е- корни ее числителя, через р10, p2Q, pmQ и перепишем К. (р) так:
Д (г)-. = fco(P~Рю)(Р —Рао) (Р — Рто)
U ЫР) a0(p-Pico)(p—Рас») (Р—Р«со) ’
Для частотной характеристики К (j<£i) будем иметь:
Д (;Ю) = Mfo —Ри) (fo—Рао) (/to — Pmo) U 3 а0 (/со — р1со) — р2с< ) ... (/со — р„оо)
Вводя амплитудно-частотную Д (со) и фазочастотную характеристики четырехполюсника, получаем для Д (/со):
Д (/со) = Д (<в) ej(l I//03 MJ--
а0 I (/to-pj.cc) | ...
I (До —Pmo) I
I (/«0-рясо) |
v / (arg (/и - Р1о)+ • • - + arg (/со + Рто) - arg (/со - Р1Ю) - ... - arg (/со -Р„то)].
А г
Выясним свойства передаточной функции Д (р) по расположению ее полюсов и нулей на комплексной плоскости.
Отметим, что при учете активных сопротивлений четырехполюсника или приемника все корни знаменателя Р2 (р) [т. е. все полюсы Д (р)| лежат в левой полуплоскости Выше уже обращалось внимание на то, что при учете активных сопротивлений все корни характеристического уравнения вещественные и отрицательные или, если они комплексные, то у них отрицательные вещественные части. Только при этих условиях все свободные составляющие токов и напряжений затухают. При отсутствии активных сопротивлений все корни знаменателя будут чисто мнимыми.
Иначе обстоит дело с нулями Д (р), т. е. с корнями его числителя (р). При учете активных сопротивлений они могут располагаться в любой части комплексной плоскости (их положение никак не связано с характером изменения во времени свободных составляющих токов и напряжений). При отсутствии активных сопротивлений все корни числителя (как и знаменателя) Д (р) расположатся на мнимой оси.
Рассмотрим амплитудно-частотную Д (со) и фазочастотиую 6 (со) характеристики при изменении частоты со от —оо до +°о. Это удобно сделать при помощи Рис 17-2, на котором показаны пара нулей и пара полюсов передаточной функции, Расположенных в левой полуплоскости. Модули выражений | (/со— Рт0)| и I (/со — р | геометрически представляют собой расстояния от нулей и полюсов Ю точки М, перемещающейся по мнимой оси снизу вверх, что соответствует Вменению частоты со от —оо до +°о. Аргументы выражений (/со — р ) и (/со — ~ Рпо) обозначены соответственно иа рис. 17-2 буквами ср/я0 и <рясо.
=—Рисунок 17 2 ждсдзыдает, что ес-ти ни один из н-тл-й не лг.ьит иа мнимой >си, г е. если четырехполюсник имеет активные сопротивления, то ни один из
485
модулей (/со — рт0) I, а значит и К (со), не обращается в нуль при изменении со от —оо до +°о, так как
К (со) = 1в'ш—I К/'(°-Рсто)1
1 ’ «о |(/Ш —Р1сю)| ... | (/СО — Р„оо)|
Физически это означает, что если на вход четырехполюсника подано напряге-ние, то при любой частоте со на выходе будет какое-то напряжение Это утверждение справедливо, если ни одна ветвь между зажимами выхода не является чисто реактивной.
Рисунок 17-2 показывает также, что если ни один из полюсов не лежит на мнимой оси, то К (со) ни при какой частоте не обращается в бесконечность Как следует из (17-3), обращение К (со) в бесконечность означало бы, что при входном напряжении, равном нулю, на выходе могло бы быть некоторое конечное напря-женне. Но при учете активных сопротивлений четырехполюсника и при отсутствии напряжения на его входе не будет напряжения и на его выходе.
Вообще говоря, если корни числителя и знаменателя 1< (/со) расположены в левой или правой полуплоскости, но вблизи мнимой оси (рис. 17-2), то при прохождении точки Л/ вблизи нулей функция К (со) будет иметь минимумы, а при прохождении М вблизи полюсов функция К (со) будет иметь максимумы.
Вблизи точек, где расположены минимумы (максимумы) К (от), фазовая характеристика увеличивается (уменьшается) на г я. В самом деле, рис 17-2 показывает, что если точка L — нуль К. (со), то при движении из точки М' в М" аргумент 6 (со) увеличится почти на +л.
Если же L — полюс К (со), то, поскольку двучлен (/со — рпа) относится к знаменателю К (р), приращение 6 (со) будет равно —л, т е. при прохождении точки М вблизи максимума К (со) аргумент 6 (от) уменьшится на л.
При перемещении хотя бы одного нуля из левой в правую полуплоскость в симметричное положение относительно мнимой оси (из точки L в точку L') амплитудно-пе изменится, а фазочасто гная изменится,
так как теперь при прохождении точки М вблизи L' приращение аргумента 6 (со) будет равно не +л, а —л. Значит, одной и той же амплитудно-частотной характеристике К. (со) соответствуют две различные фазочастотные характеристики 6 (со). Так как в общем случае, например для цепей с распределенными параметрами, число нулей у функции К (со) может быть бесконечно велико, то при поочередном перемещении всех нх из левой полуплоскости в симметричное положение на правой полуплоскости амплитудно-частотная характеристика будет оставаться неизменной, а фа.зочасготная характеристика при перемещении каждого из нулей будет иной Следовательно, одной и той >|(С амплитудно-частотной характеристике в общем случае может соответствовать бесконечное число фазочастотных характеристик.
Рисунок 17-3 показывает, что при переходе любого нуля из левой полуплоскости в правую аргумент двучлена (/со — р10) увеличивается при положительном значении частоты со (см. последовательные положения точек N, N', N”, N"f N””). Следовательно, при со > 0 сумма аргументов двучленов (/со — ри0)> —когда они лежат в правой полунлоскосш, -больше, чем при расположе-Щ'1 иулей в левой полуплоскости. Более подробное исследование показывает,
486
из бесконечного числа фазочастотных характеристик, соответствующих Чяной заданной амплитудно-частотной характеристике, минимальное значение пгумента 0 (со) при любом выбранном положительном значении частоты со Ждет в том случае, koi да все нули К (w) расположены в левой полуплоскости 0 В соответствии с этим электрические цепи, все нули передаточной функции которых лежат в левой полуплоскости и, значит, аргумент 6 (со) имеет
шее возможное значение, называются лннималыю фазовыми цепями Если хотя бы один нуль передаточной функции электрической цепи расположен в правой полуплоскости, она называется не минимально фазовой цепью
Из сказанного вытекает, что для не минимально-фазовых цепей однозначной связи между К (со) и 0 (со) не существует Как было указано, причиной этого является ''расположение хотя бы одного нуля функции К (ы) в правой полуплоскости А так как все нули функции К (со) для минимально фазовых цепей располо-
наимень-
жены в левой полуплоскости, то для них фазочастотная характеристика может быть однозначно определена по амплитудно-частотной
Выше (см § 15-3) были получены соотношения (15-26) и (15-27) Они косвенно подтверждают, что между амплитудно-частотной К. (со) и фазочастотной б (со), а также между вещественной В (со) и мнимой М (со) частотными характеристиками электрической цепи при некоторых условиях может быть определенная связь, так что, зная одну из них, можно найти другую, и наоборот Выражения (15-26) и (15-27) можно рассматривать как особого рода интегральные уравнения, из которых, зная К (со), можно найти б (со), а также, зная В (ы), можно найти М (со), и наоборот
Наконец, из сказанного вытекает, что две электрические минимально-фазовые цепи, имеющие одинаковые
амплитудно-частотные характеристики, имеют одинаковые фазочастотные характеристики Такого утверждения нельзя сделать для не минимально-фазовых цепей
Пример 17-1. Определить передаточную функцию цепи рис 17-4.
Решение Составим изображения тока I (опуская аргу мент р)
/=____41___
rl + r2+VpC
И напряжения на выходе
^=7h^Wc^+VpC).
Передаточная функция
К _ 'а+УрС ~ Г1 + г2+1/рС-
Функция К (р) имеет нуль при р = —\/г2С, т е он лежит в левой полуплоскости, поэтому цепь рис 17-4 минимально-фазовая.
Пример 17-2. Определить передаточную функцию цепи рис. 17-5, называемой фазовращателем на том основании, что при изменении частоты входного ,1аг!ряжы;ия и неизменной его амплитуде величина выходного напряжения остает-Ся неизменной, а фаза изменяется.
487
Решение. Найтем изображения токов и /2:
, _ UiPC
1 2 r-\-l/pC rCp-±-l
Определим изображения потенциалов точек end: , 1 Ui
Л ус - ^-ус^+Т ’ г . UirCp
— Ча f.Qp । j •
Найдем изображение выходного напряжения
f/2=<pt — <pd=—ур- UCp -1).
Тогда
к = гСр — 1 = р — 1/rC = р~а
W Ut rCp+\ p^-l/rC р + а'
Функция К (р) имеет нуль при р = с = 1 /гС, т е в правой полуплоскости, и фазовращатель является примером не минимально-фазовой цепи.
Далее , joi~a ... . | /со — а | .
Л (/со) = -—:— ; К (со) = —г—т = * ’ /соф-с ' I /м[-а |
и ,, , . ! ® \ , 7 со \ г 2иа
fi (со) = arctg - arctg ) = arctg ,
т. е. цепь по рис. 17-5 действительно фазовращатель- ее амплитудно-частотная характеристика не зависит от частоты, а фазочастотная характеристика от частоты зависит.
Пример 17-3. Найти передаточную функцию цепи рис. 17-6.
Решение. Найдем изображения токов Ц и /3-
/ _ . /_ Ui
1 ’ 3 Гз+Gi'
Определим изображения потенциалов точек cud ф<~Уа--1зГз, <Pd = <Pa —ЛЛ и изображение выходного напряжения
=фс-фй=7 л - isr3=и\ (уу^-с;
488
Тогда
iz __ ^2 _ Priri — r-‘JC2 _ p
(r3+ri)(pri+l/C2) 4 (Гз+г4)(р+1/'-1С2) •
Нуль К (p) расположен в точке р = г^г^С^, т. е в правой полуплоскости, рассматриваемая цепь не минимально-фазовая
F Упомянем, наконец, о цепи, которая являе1ся так называемым запаздывающим звеном, встречающимся, например, в системах автоматического управления. Ее передаточная функция
К (р) = ke~,,x и К (/со) =
Амплитудно-частотная характеристика цепи постоянна К (со) = k и никак не зависит от фазочастотной в (ой = —сот. Таким образом, запаздывающее звено также является примером не мннимально-фазовой цепи.
17-3. Входные функции цепей. Положительные вещественные функции
Как известно из предыдущего (§ 14-3, 14-5 и др.) входные операторные сопротивления Z (/;) и проводимости Y (р) двухполюсников представляются рациональными дробями, т. е. отношением двух многочленов
Н(р) ~'b^+bipm 1 р... + Ьга
и обладают четырьмя важными свойствами.
1. При вещественных значениях р (р = s) функции Z (р) и Y (р) — вещественные, так как коэффициенты полиномов G (р) иН(р),т. е. ak и bk, — вещественные. Действительно, коэффициенты ак и Ьк при определении Z (р) по сопротивлениям отдельных ветвей получаются суммированием, умножением или делением параметров ветвей г, L, М и С, которые вещественны.
2. Синтез будем проводить для пассивных двухполюсников, у которых все нули if полюсы входных функций Z (/;) и Y (р) расположены в левой полуплоскости комплексного переменного р или на мнимой оси этой плоскости, причем в последнем случае все полюсы и нули простые.
В отношении последнего свойства следует отметить, что если при расположении корней характеристического уравнения на мнимой оси корень р = ± /со был бы, например, кратности т, то соответствующее ему решение характеристического уравнения имело бы вид:
хсв = (С0 + С1/ + С^2 + ... + Сот jF-^sino)^. (17-6)
Это приводило бы к нарастающему свободному процессу, что невозможно в пассивном двухполюснике.
При сформулированных выше условиях оказывается, что все коэффициенты дл и Ь„ полиномов G (р) и Н (р) должны быть положительными. . ==—----
489
Убедиться в этом можно представив, например, полином G (Г1\ в следующем виде: '
G (р) = аорп + а^-14-... + ап=а0 (р - рг) (р - р2)... (р - рп). (17.7^ Для каждой пары комплексных и сопряженных корней pk = sk + /со* и pk+1 = sfe — /cofe будем иметь:
(P~Pk) (р- Pk+i) =
= {p — sk— jak) (p-sk + jak) = (p-SA)2 4- < (17-8)
Для вещественных корней pi будем иметь множители р — р.
— р — st. Следовательно, при sk 2 0 и s(- 2 0 все коэффициенты при р в множителях (р — slt)2 4- полинома G (р) неотрицательны, а поэтому, выполнив в (17-7) перемножение всех множителей, получим, что все коэффициенты й0, alt ..., а„ будут положительными.
3. Вещественные части входных функций Z (р) и Y (р) положительны или равны
нулю, т. е. Re Z (р) 2 0 или Re Y (р) 2 0, при условии, что Re /з — Re (s i /ю) = s 2 0.
Докажем это свойство, т. е. что Re Z (р) 2 0, если s 2 0 для чисто реактивной цепи. Например, для чисто реактивной цепи L, С имеем:
2 (Р) = pL + = (s 4- /“) L + (s-'rja) C = sL + sC4-/coC ‘ 17'9^
Рис. 17-7.
Это выражение для Z (/;) по форме полностью совпадает с комплексным сопротивлением цепи, приведенной на рис. 17-7:
Z(/tt) = r + /ttL + ?^.- (17-10)
Очевидно, что Re Z (/со) 2 0 при г 2 0 и g 2 0. Таким образом, для любой чисто реактивной цепи, состоящей из L и С элеменюв, может быть при р = s + /ю построена аналогичная цепь, но уже содержащая активные элементы г и g. Так как для аналогичной цепи Re Z (/со) 2 0, что ясно из физических соображений, то получаем, что и для исходной чисто реактивной цепи Re Z (р) 2 0 при s 2 0-Сказанное тем более справедливо, если исходная цепь содержит активные сопротивления и проводимости.
4. Степени п и т полиномов G (р) и Н (р) числителя и знаменателя не должны отличаться друг от друга больше чем на единицу-
Нетрудно убедиться непосредственно, что для любого двухполюсника это правило будет выполняться.
Функции, обладающие первыми тремя указанными свойствами, относятся к положительным вещественным функциям.
Таким образом, для того, чтобы рациональная дробь (17-5) была операторпым выражением входных функций Z (р) или Y (р) и, следовательно, могла бы быть реализованной в виде электриче-
490
зой цепи, она должна быть положительной вещественной функцией обладать четвертым свойством.
Сказанное относится к любым пассивным двухполюсникам, содержащим не только реактивные, но и активные сопротивления.
17-4. Реактивные двухполюсники
В частном случае реактивных двухполюсников входные функции Z (р) и Y (р) — положительные вещественные и обладают рядом дополнительных свойств.
1. В соответствии со сказанным выше степени п и т полиномов б (р) и Н (р) числителя и знаменателя в (17-5) не должны разниться больше чем на единицу. Но в данном частном случае, кроме того, степень р каждого из последующих членов G (р) и Н (р) меньше степени предыдущего на две единицы.
Для доказательства этого положения выразим .входной ток 4 реактивного двухполюсника через его входное напряжение £4 = пользуясь методом контурных токов (§ 1-8):
Zu=f~, (17-12)
ли .
где ZBX = Zn — входное сопротивление двухполюсника! D — определитель цепи, состоящей из п контуров (и, следовательно, имеющий п строк и п столбцов), а Ап — его алгебраическое дополнение, т. е. определитель п — 1 порядка.
В каждом элементе О и Дп содержатся (в случае реактивного двухполюсника) реактивные сопротивления вида
Zkk=iXkk=iaLkk+Ттос^ = 4 )
И
Z kn — lxkn = ~ 75 ),
т е. в каждом элементе определителя есть мнимый множитель //со и вещественный (записан в скобке) Вынесем //со за скобки из всех элементов определителей D и Ап; тогда получим:
7 -D = <'/со)" D° i Jh-вх ' вх Аи Дно со Д110 ’
или
где О(, и Д11(1 — вещественные.
Элементы этих определителей имеют вид:
^2^kk —^l^iik и GCkn..
Раскрывая определители Do и Auo и группируя в них члены с одинаковыми степенями со, получаем в числителе и знаменателе хвх (со) полиномы вида

± а(,со2« 1 а2со2" 2 ± ... + о2^2со2 а2я
со ( г fenco8* а с Ь2'
£17-14)
491
откуда ii следует утверждение, что для реактивного двухполюсника, в ка,кд0,-ветви которого имеются L и С, наивысшие степени полиномов числителя и зНаи менателя разнятся на единицу (2и и 2п — 1) и что степень со у каждого из поС/1е'. дующих членов полиномов числителя и знаменателя меньше, чем у предыд/ щего, на две единицы.
Переписывая (17-14) в операторной форме и вводя ZBX (р), вместо хвХ (со) получаем:
z („\ - - д0р2л+«2Р2"~2+----1-а2«-гР2+Д2Я /]7
ff(p) p(bop2n'-2+b2p2n~i + ...+bi„^p2 + b2n-2) ‘ [
Находя корни полиномов числителя и знаменателя хвх относительно со2 и обозначая их со2, соз, C02„_j для числителя и col, ... С02П-2 Для знамейателя, получаем:
.. ± (ц2~ю1) (ю2~и1)- (ц2-ю1» -х) ,, 7
вх(> Ьо ш(^-Ш|)(^-Ш|)...(со2-со|„_2) •
Полагая Н = а01Ь0, получаем формулу, известную под названием теоремы Фостера. При значениях со2, равных корням знаменателя, будем иметь полюсы входной функции лвх (со) (аналогично резонансу токов в простейшей цепи), а при значениях со2, равных корням числителя, — нули входной функции л'вХ (со) (аналогично резонансу напряжений в простейшей цепи).
Переписывая (17-15) в операторной форме и вводя ZBX (р) вместо хт (со), получаем: /
7 <г\ _ °° (р2+Ю*) (р2 + ^) - +
вх ьв р (р2 + ш2) (р2 + со|) ... (р2 + ь4„2) ‘
2. Для реактивных двухполюсников хвх (со) всегда возрастает с ростом частоты, т. е.
dxBJda > О,
откуда вытекает свойство чередования полюсов и нулей хвК (со). Простейший пример чередования был уже получен в § 5-5 для кривой х (со): вслед за полюсом (при со = сот) следовал нуль (при со — сов); кроме того, для всех со (О со оо) выполнялось неравенство dx/dca > 0. Для всех схем, которые рассматриваются ниже, это положение будет подтверждено.
Сопротивление хвх, увеличиваясь, например, от — оо (полюс функции), проходит через нуль (нуль функции) и, продолжая увеличиваться возрастает до + оо (снова полюс функции). Затем ,гвХ скачком изменяется от + оо до — оо и процесс повторяется так, что dxBX/da > 0. Те же рассуждения остаются справедливыми, если хвх начинает увеличиваться с нуля. Отметим, что хвх меняет знак при каждом переходе через нуль и через полюс.
Таким образом, в силу чередования нулей и полюсов функции хвх для корней ее числителя и знаменателя имеем:
0 ‘Ч • • W2«-2 W2z!-V
492
Для доказательства этого положения в общем случае предположим, что в, хполюсник имеет п реактивных ветвей Для любой i-й ветви, содержащей инД5 ктивность L, и емкость С\, имеем
х, = — 1 /шС, и dxjda =Lt+ > °-
Но входное сопротивление двухполюсника хвх (со) зависит от сопротивлений
* (ю) всех ветвей Поэтому
п
dxBX (И) __ V дхвх (И) dxl (17-16)
dco ~ dxt dto ’
1=1
.. (to) .
Для доказательства нужно еще показать, что —gp— > 0 Пусть ко входу
двухполюсника подключена э д с (рис применяя теорему компенсации, заменим ее сопротивление /х, э д с £, = —/х(/, (знак минус объясняется совпадением положительных направлений э д с Е, и тока /,) На основании принципа наложения определим токи /х и Г,
Д—УцЁх+УпЁ.,) . . 1 (17-17)
Л=Ги£1+У„£г, J 1 7
где все проводимости Yllt Уй, Ylt и Yц
17 8) Выделим любую i-ю ветвь и,
Рис 17-8
не зависят от сопротивления jxt, т е
остаются постоянными при его изменении Подставляя вместо Et его значение — jxji и исключая из уравнения (17-17) ток получаем
откуда
lYuY,lX, \ 1 +/У»Л/
Ёъ
Ё1 _____14 / Yt[xi_
4 ^11+/^1») xi
дхвх _ ______Y?,________
dxt [Уц+/(УцУ„-У?1)х,р •
(17 18)
(17 19)
(17 20)

и
Так как рассматривается реактивный двухполюсник, то все собственные и взаимные проводимости чисто мнимые, т е Y = —]Ь
Окончательно получаем
-д*ву. =_________------------> 0. (17 21)
dxt [41 +(ЬцЬц — ftft) xj2
что и доказывает высказанное положение
17-5. Частотные характеристики реактивных двухполюсников
В зависимости от расположения нулей и полюсов возможны четыре типа частотной характеристики многоэлементного реактивного двухполюсника.
1. Частотная характеристика с двумя внешними полюсами (рис. 17-9), называемая характеристикой оо — со. В этом случае
493
при со = юо — 0 и © = со входное сопротивление двухполюсник бесконечно велико, т. е. через пего пе может проходить ни посюяц9 ный ток (со = 0), ни переменный ток бесконечно большой частоты'
Рис. 17-9. Рис. 17-10.
2. Частотная характеристика с двумя внешними нулями (рис. 17-10), называемая характеристикой 0 — 0. В этом случае при со = 6^ = 0 и со = со2п-с = оо входное сопротивление двухполюсника равно нулю, т. е. через него могут проходить как постоянный ток, так и переменный ток бесконечно большой частоты.
3. Частотная характеристика с внешним нулем при со = cot = ° и внешним полюсом при со = оо (рис. 17-11), называемая характеристикой 0 — оо. В этом случае через двухполюсник может проходить постоянный ток и не может проходить переменный ток бесконечно .большой частоты.
4. Частотная характеристика с внешним полюсом при со — ©о = 0 и внешним нулем при © = ©2n-i = °° (рис. 17-12), называем34
494
характеристикой оо — 0. В этом случае через двухполюсник не моЖет проходить постоянный ток и может проходить переменный ток бесконечно большой частоты.
На рис. 17-9 — 17-12 частоты, соответствующие нулям функции
(со), обозначены нечетными индексами, а соответствующие полюсам—четными. На тех же рисунках частоты, соответствующие нулям функции хвх (со), обозначены на оси абсцисс кружками, а соответствующие полюсам — крестиками. Значения хвх (со) при й — 0 и со = оо непосредственно следуют из рассмотрения схем, приведенных на тех же рисунках.
Из тех же рисунков следует, что общее число нулей и полюсов на единицу больше общего числа элементов L и С реактивного двухполюсника или, что то же самое, общее число частот последовательного и параллельного резонансов на единицу меньше числа последних. Это правило не выполняется, если все ветви, сходящиеся в каком-либо узле схемы двухполюсника, имеют индуктивности или емкости. Тогда число частот резонансов может быть меньше, чем число элементов двухполюсника без одного.
И, наконец, следует отметить, что чем больше нулей и полюсов имеет частотная характеристика хвх (ю), тем все более многочисленной будет группа реактивных двухполюсников с различными схемами, но с одинаковыми по виду частотными характеристиками Хвх (со).
17-6. Синтез реактивных двухполюсников. Метод Фостера
Входная функция реактивного двухполюсника, например Zin (р) или ZBX (/со), дана выражениями (17-15а) и (17-15). Требуется найти его схему и параметры, т. е., как говорят, реализовать двухполюсник по частотной характеристике ZBX (/со) = jxBK (со).
Рис. 17-13. Рис. 17-14.
Как было указано выше, задачи синтеза неоднозначны, т. е. целый ряд схем могут иметь один и тот же вид частотной характеристики хвх (со). Поэтому обычно выбирают типовые схемы, к которым прежде всего относятся так называемые канонические схемы, реализуемые по методу Фостера.
Различают два вида канонических схем реактивных двухполюсников.
Первая каноническая схема составляется из последовательно включенных параллельных L, С-контуров, причем один или два йз них могут быть неполными из-за отсутствия в них либо индуктивности, либо емкости. На рис. 17-13 приведена схема с двумя непол-
495
ними контурами и Со. Вторая каноническая схема составляете из параллельно включенных последовательных контуров, приче один или два из них могут быть неполными. На рис. 17-14 приведена схема с двумя неполными контурами Lo и Сю.
Для синтеза первой канонической схемы запишем комплексное сопротивление /-го контура схемы (рис. 17-13):
7 jaLil/jaCi _ /со
' /(coLj-l/coC,) СДсо?-^)’ (17~22)
где со, = 1/ LtCi — резонансная частота /-го контура.
В операторной форме для Zt (р) имеем:
(17-23)
где At = 1/С,. Заметим, что полюсы Z,- комплексно-сопряженные, равны Azj&i и лежат на мнимой оси.
Таким образом, для синтеза первой канонической схемы нужно представить ZBJi (р) в виде суммы простых дробей вида (17-23), дополненной слагаемым /соЕго = pLm = рАт, если схема имеет в виде первого неполного контура индуктивность £ю, и дополненной еще слагаемым 1//соС0 = 1/рС0 = Ай!р, если схема имеет в виде второго неполного контура емкость Со. Иными словами, для синтеза первой канонической схемы заданную равенством (17-14а) функцию ZBX (р) следует представить в виде
(р) = Moo + ^ + 2 , (17-24)
причем число слагаемых суммы равно числу точек параллельного резонанса у частотной характеристики хвХ (со) или, что то же самое, числу пар полюсов у сопротивления ZBX (р), не считая полюсов' при со = 0 и со = оо.
Первое слагаемое рА^, будет в формуле (17-24), если в выражении (17-14а) для ZBX (р) коэффициент а0 отличен от нуля. В этом случае до разложения ZBX (р) на простые дроби из него нужно выделить целую часть рАх. Второе слагаемое А0/р будет в формуле (17-24), если в знаменателе ZBX (р) множитель р выходит за скобки.
Если в схеме рис. 17-13 есть неполный контур с индуктивностью Lm, то это обеспечивает условие хвх оо при со -* 0 для характеристик типа оо — 0 и оо — оо. Если в схеме рис. 17-13 есть неполный контур с емкостью Со, то это обеспечивает условие хвх — оо при со —> О для характеристики типа оо — 0 и оо — оо.
Значения всех коэффициентов А находятся при помощи интегральных вычетов или из простых соотношений:
lim
Г — Р
Л о = limpZBX (р);
Р-0
(17-25)
496
Отсюда следует, что для определения А, следует предварительно найти все корни знаменателя относительно со2, т. е. представить его ” виде (17-15).
Переходя ко второй канонической схеме, записываем комплексное сопротивление i-ro контура (рис. 17-14):
1 со’—со2
Zi (/и) = /со£,- - / —= Lt , (17-26)
где со, = l/V^LiCi — резонансная частота i-ro контура.
Поскольку все ветви в схеме рис. 17-14 соединены параллельно, проще иметь дело с входной проводимостью Увх (р) = 1/ZSX (р). Запишем Yt (р) в операторной форме:
Yi(P)=^p (17-27)
где Ai = 1/£г. Как и для первой схемы, нули Zt (р), т. е. полюсы У, (р), — комплексно-сопряженные, равны ± /со, и лежат на мнимой оси.
Для синтеза второй канонической схемы нужно проводимость УяХ (р) разложить на простые дроби вида (17-27), дополнив разложение слагаемым /соСоо = рСт — рАт, если степень многочлена числителя Увх (р) на единицу больше степени его знаменателя, и дополнив результат еще слагаемым l//coLo ~ UpL0 = AJp, если знаменатель дроби УвХ (р) имеет корень р = 0. Формула для У„х (р) совпадает с формулой (17-24), а значения коэффициентов А находятся по формулам, аналогичным соотношениям (17-25).
Пример 17-4. Дана входная функция ZBX (р) реактивного двухполюсника (Р)= р4_р37."1о^4^бЛб^- ПостРоить частотную характеристику и синтезировать (реализовать) двухполюсник в виде первой и второй канонических схем.
Решение. Поскольку решение проводится методом Фостера, находим корни р; и pl знаменателя ZBX (р) В данном случае их легко найти, решив биквадратное уравнение р4 + 37-1012р2 + 36-1024 = 0, откуда р% =—1012; pj = = —36-1012.
Сопротивление ZBX (р) представим в виде
7 М 10ср(р2+16-№2) 1 ’ (р2+1 • кд2) (р2+зб • ю12) •
Подставляя р = /со и обозначая со] = 1-Ю12, от] = 16- 10й, со| = 36-1012, будем иметь:
7 /со10» (со;—со2) .
(/со) - (ю| _ и2) (ю, __ и2) - (СО).
По выражению xBX (от) на рис. 17-10 построена частотная характеристика реак-•ивного двухполюсника, относящаяся к типу 0—0. В самом деле легко видеть, что три о> —> 0 и о> —> оо сопротивление хвх -> 0, т. е. характеристика хих (от) имеет (ва внешних пуля Кроме того, хвх (от) имеет две точки параллельного резонанса при в— о>2 в от — 4jj к ому точку послерез-овдися при нт — от, 5азу меется, все полюсы и нули ZBX (р) лежат на мнимой оси.
497
Отметим, что задачу можно было бы поставить несколько иначе. Реактив ный двухполюсник можно было бы прямо задать частотной характеристикоГ вида
, К <»(<») — ш2 *)
*ВХ (W) - _ и2) _ и2) ,
где со?, со] и со] определены данными выше значениями, а К. может быть найдено если задано значение хвх (со) для одной из нерезонансных частот. Например’ при со = 0,3- 10ес 1 задано хвх = 146 Ом, откуда получаем К = 10»Ф-1. ’
Реализовав двухполюсник в виде первой канонической схемы, что задает структуру искомой схемы (рис. 17-10), представим ZBX (Р) в виде
7 i ____, РАь
™(р) р2+ы2, + p2+coj ’
откуда
Л2=2- = lim ZBX (р) ^±^1 = | • 10» Ф-i; С2 = 4 нФ и р2-> —(1)2 р I о
г 1 з „
Li~~C2m-2 ~ 7 мГ’
Аналогично находим остальные параметры:
Л4= ^= hm zBX(p)^±^l&^ . Ю» Ф-i; С4=^нФ и Ь.1 р2->—Ь>а р / Ч
Li=г~>=мГ-
С4со| 63
Реализуя далее двухполюсник в виде второй канонической схемы, что > акже
задает его искомую структуру (рис. 17-15), представим
Рнс. 17-15.
7ВХ (р) в виде
Гвх (₽) =Р^со4-210- +
Из схемы рис. 17-15 следует, что Увх (р) имеет два внешних полюса (при р = 0 и р = оо) и один внутренний полюс (при р2 = —со]). Тогда в силу ранее доказанного свойства, что dxBX/dco > 0 для
всех частот, между тремя полюсами входной функции УБХ (р) должны располагайся два ее нуля, что и приводит к тому же виду частотной характеристики хпХ (со), которая приведена на рис. 17-10.
Найдем постоянные Асо, Ао и А3:
А№ = Ст= hm Увх-(р)- = 1 нФ, Ло= lim рУвх(р)=_ $ . 10* Г-1; р -> со р Lq р -> О Ф
Lo=~ мГ; As=.-= Пт = IL . юз p-i;
° 9 Ls рг-^~а2 p 4
j 4 „ „ 1 75 ,
Ls^15 МГ: Cs==£^T = '64 НФ-
17-7. Синтез реактивных двухполюсников. Метод Кауэра
Метод Кауэра выгодно отличается от метода Фостера тем, что для его применения не требуется отыскания корней знаменателя Н (р) дроби, представляющей собой входные функции ZBX G”' или Увх (р). По методу Кауэра реактивный двухполюсник реали-
49Я
уется в виде так называемых первой или второй цепных схем. Первая из них составляйся из продольных индуктивностей и поперечных емкостен (рис. 17-16), вторая, наоборот, — из продольных
Рис 17-16
емкостей и поперечных индуктивностей (рис. 17-17). Первая цепная схема может начинаться с индуктивности, причем в последней (самой правой) ветви могут быть либо индуктивность и емкость, включенные последовательно (рис. 17-16, а и б), либо только одна индуктивность (рис. 17-16, в и г). То же касается и второй цепной схемы (рис. 17-17, а, б, в и г).
Рис 17-17.
Алгоритм метода Кауэра заключается в постепенном выделении слагаемых вида Ар или В/p сначала из входной функции ZBX (р) или Увх (р), а затем из всех последующих остатков, получающихся после выделения предыдущей части и проводимой реализации выде
499
ляемых частей при помощи индуктивностей или емкостей. Алгорцт, применяется до тех пор, пока остаток не будет равен нулю.
Переходя к реализации первой цепной схемы, выбираем сначал в качестве входной функции ZBX (р) такую, которая имеет полюс при р — оо. Это означает, что степень числителя G (р) на единицу больше степени знаменателя Н (р) [см. (17- 14а)]. Разделив числитель G (р) на знаменатель И (р), выделяем целую часть Агр, соответствующую полюсу Z вХ(р) при р = оо. Получим (рис. 17-18, а):
ZBX(p)=A1p+Z1(p), ' (17-28)
где Zj (р) — остаток от деления, представляющий собой правильную дробь, степень числителя которой на единицу меньше степени знаменателя. Это следует из отмеченного выше свойства полиномов G (р) и Н (р), у которых степень р каждого из последующих членов
Рис. 17-18.
на две единицы меньше степени предыдущего (§ 17-4). Рассматривая проводимость Уг (р) = 1/Zi (р), у которой, как и у ZBX (р), степень числителя на единицу выше степени знаменателя, произведем с ней аналогичную операцию выделения целой части (рис. 17-18, б):
У1(Р) = А2р+У2(р). (17-29)
Аналогично поступим с Z2 (р) (рис. 17-18, в):
+ <17'30)
Г 2 {Р)
и так продолжаем до тех пор, пока остаток не будет равен нулю.
Легко видеть, что описанный выше алгоритм реализуется в виде цепной дроби
Ях (р) = Агр+------------Ц------------ (17-31)
Л2р +-----------j-----
АзРН----—------—
Л;~1Р+дяго •
Отсюда следует, что входная функция ZBX (р) реализуется в виде схемы, у которой первый продольно включенный элемент — индуктивность = Alt второй поперечно включенный — емкость С2 -
Я2, трегийпродольный — сноьа пндуктпвноыь А3 Л3 и т. д-
500
, йс. 17-16, а). Если число i — нечетное, то последним элементом справа б^дет индуктивность L; — А„ а если четное, то емкость G А‘-
Так как составляется первая цепная схема, то при делении слагаемые полиномов числителя и знаменателя следует располагать й0 убывающим степеням р, т. е. выделяемые целые части А,р получаются в результате деления члена с наивысшей степенью р в числителе на такой же член в знаменателе.
Если ZBK (/;) имеет нуль при р = оо, т. е. степень его числителя меньше степени знаменателя на единицу, то нужно применить вышеприведенный алгоритм по отношению к обратной величине l/ZBx (р) ~ VBX (р). Тогда в результате деления в качестве первого
6)
а)
Я
Рис. 17-19.
члена получилась бы поперечная емкостная проводимость Агр = — Сгр, в качестве второго •— продольная индуктивность и т. д., т. е. в этом случае схема начиналась бы с поперечной емкости С\ (рис. 17-16, г и б) и заканчивалась бы либо индуктивностью Д = = Alt либо емкостью С; = Дг.
Перейдем к реализации второй цепной схемы. Рассматривая в качестве входной функции операторную проводимость Увх (/?), предположим сначала, что степень многочлена ее знаменателя будет нечетной, т. е. входная функция имеет полюс при р = 0. В этом случае Увх (р) представляется также в виде цепной дроби, но последовательным делением выделяются части, имеющие полюсы при р = 0, т. е. члены вида AJp. При этом получаем Увх (р) = AJp + + У1 (р); (р) = Л2/р + Z2(p); У2 (р) = А3/р + Z3 (р) и т. д.
до тех пор, пока остаток не будет равен нулю. Этот алгоритм показан на рис. 17-19. Соответствующая ему цепная дробь имеет вид:
УВх (Р)^ + ------------Ц----------- (17-32)
Р + Лз 1
р ............
Р ^-+0 р
Для построения цепной дроби (17-32) следует расположить слагаемые полиномов числителя и знаменателя по возрастающим степеням р. ---------
501
Рис. 17-20.
Если же степень знаменателя входной проводимости у i . четная (а степень числителя — нечетная), то вышеуказанный ад^ ритм построения цепной дроби нужц" 4 применить к обратной его величине, г е° от входной проводимости Увх (р) перейти к входному сопротивлению ZBX (р).
Пример 17-5. По тем же данным, что и примере 17-4, применяя метод Кауэра, синтезировать (реализовать) двухполюсник в виде первой и второй цепных схем
Решение. Представим в виде первой цепной схемы входную операторную проводимость Увх (р):
р«+37- 1012 p2-p 36- 1024 Гвх(Р)— 10»рЗ+16. 1021р
и выделим первое слагаемое рСг делением числителя Увх (р) на знаменатель:
р4-|-37. 1012p2_)_36.1()24 | 10Чрч-}-16. 102ip р4 +- 16 • 1012р2 10 »р
21 • 10!2р2-|-36.1024
Первым элементом первой цепной схемы будет поперечная емкость = = Ю“9 Ф = 1 нФ (рис 17-20). В соответствии с ранее введенными обозначениями запишем:
Далее
Ю9рЗ+ 16. Ю21р
Z1(p) 21 • 1012р2_рзб. 1024 - PLt + Z2(P)-
При этом слагаемое pL2 выделяем делением числителя Z± (р) на знаменатель, иначе говоря, делителя первой операции на остаток:
10»рз+ 16 • 102ip | 21 • 1012р2+36 • 1024
___ 12 i
Ю»р»+у 102ip ± . Ю-зр
Вторым элементом схемы рис. 17-20 будет продольная индуктивность
£2=±.10-Г = ±мГ,
поэтому
_1 _ ^°-Ю21р J
zi(p) —21 10 SP + 21.1012р2-|-36- 1024 “ 21 " 10 3p + z2^-
Далее
„ , . 21 • 1012р2_Г.36. Ю24
^2 (P)-— pCs -f- У3 (p) .
Адг . IQztp=-------------------
502
При этом слагаемое рС3 выделяем делением числителя У2 (р) на знаменатель, *гче говоря, делителя второй операции на остаток:
21.1012р2 4- 36 • 1024 1199.10в1р
21'1012Р2 foo’10^
36 . 1024
Третьим элементом схемы рис. 17-20 будет поперечная емкость
147
Cs=To6’lo“8 ф=1>47 нф>
>тому
147 36-1024 147
У2 (Р) = Гбб • 10-р + 1^-— = Гоо -10- 8р + YS (р).
-у- Ю21р
Далее
^•1021Р 25
Zs = 36 1024 =63 10 3Р = LiP •
Четвертым и последним элементом схемы рис. 17-20 будет продольная индук-ивность
, 25 25
Li~63' ° Г-63мГ‘
Реализуя далее двухполюсник в виде второй цепной схемы, располагаем полиномы числителя и знаменателя Y (р) по возрастающим степеням р и, выполняя деление, будем выделять слагаемые вида А/р:
9 1
4. юз А
4 р
36 - 1024 + 37 • 1012р2+ pi | 16 • 1021/3 + 1№рЗ 9
36-1024+4 Ю12р2
139
-ДГ. Ю12р2+р4
Первым элементом второй цепной схемы будет поперечная индуктивность 4 4
= • 10~3 Г — g мГ (рис. 17-21). В соответствии с введенными выше обозначениями запишем:
139
J _^.Ю13р2 + р4 }
У (р) = "ЯГ + 1бТ1021р+Ю»рЗ = 4 10_3^ + V1
Далее
16 1021p+10»p3 1
Zi(p)- 139 , рсЛ^’
_ _ . 1012p2+pl--------------
503
При этом слагаемое 1/рС2 выделяем делением числителя Z, (р) на знам тель, иначе говоря, делителя первой операции на остаток: еНа-
16 - 102ip I-1 Оврз | 1®- • 10i2p2 + р1 .
— 64 “64 1
^Р+Т^.10^ ГЗГЮ4
7 г;
139-10^3
Вторым элементом схемы рис. 17-21 будет продольная емкость „ 139 in о Л 139 Л
С2 = -64 10 8 Ф-= 64 НФ‘
Поэтому
75
• Ю»рЗ

139 1
139 139 +z2(Ph
'•Ю72+р* 64-1°-9/^
Далее
139
Ю12р2+р4
4
V2(p)=----75------
ras "r”’

Как и выше, слагаемое 1/pL3 выделяем делением числителя К, (р) на знаменатель, иначе говоря, делителя второп операции на остаток:
75
Т39 '"‘Г’
1QQ I
l4--io12p2+p1|
~ 139 Ш12 2 ~139S ~T .
4” W pi *300 '10 7
P4
Третьим элементом схемы рис. 17-21 будет поперечная индуктивность т 300 кь,г 300 г La 1392 ' ° Г~ 1392 мГ-
Согласно предыдущему запишем:
1 р4 1
^2 (Р) = "TV 1" 7g = gpp F 7 (р).
PLs -L2 . ios„3 217.10~з„
139 р 1392 ш Р
Далее 75 1 1
^>=139-108 7 = Z7-
Четвертым и последним элементом схемы рис 17-21 будет продольная емкость
_ 139 |П „ Л 139 Л
С4=75-Ю»Ф=7^ нФ.
Отметим в заключение, что все четыре схемы, изображенные
на рис. 17-10, 17-15, 17-20 и 17-21, имеют одинаковые частотны^
504
^ктеристики, подобные приведенной на рис. 17-10, и реализуют 0Му и ТУ же ВХ°ДНУЮ функцию, заданную в виде операторного сопротивления ZBX(р) или операторной проводимости Увх (р) = i^y/ZBX (р)- У всех схем одинаковое (минимально необходимое) цйРло элементов, равно четырем (две индуктивности и две емкости), для всех четырех схем ZBX (0) — 0 и ZBX (оо) = 0 или, что то же самое, Увх (оо) — оо и Увх (0) = оо. Однако структура этих схем й их параметры различны, что и подтверждает отмеченную выше многозначность решения задачи синтеза. Выбор той или др угон схемы определяется удобством реализации ее индуктивностей и емкостей: в одних схемах индуктивности получаются больше, в других соответственно — емкости.
17 8. Синтез двухполюсников с потерями. Метод Фостера
В § 17-3 было указано, что для реализации входных функций двухполюсника с потерями ZBX (р) или Увх (р) они должны быть заданы как положительные вещественные функции. Там же были сформулированы четыре свойства, которым должны удовлетворять функции ZBX (р) и Увх (р).
Первое свойство проверяется легко и обеспечивается тем, что коэффициенты многочленов G (р) и 77 (р) в (17-5) задаются вещественными.
Второе свойство проверяется применением, например, критериев Гурвица или Рауса к каждому из многочленов G (р) и 77 (р) в отдельности. Эти критерии рассматриваются в курсе высшей математики (в разделе «Линейная алгебра»). Они позволяют установить отсутствие или наличие хотя бы одного нуля у этих многочленов в правой полуплоскости.
Третье свойство, сводящееся к положительности функции Re ZBX (р) Ss 0 или Re Увх (р) 0 при Re р — s 0, проверяется
применением теоремы Штурма, которая сводится к установлению наличия или отсутствия нулей у вспомогательных функций при изменении со2 от нуля до бесконечности. Теорема Штурма рассматривается в курсе высшей алгебры.
Четвертое свойство устанавливается непосредственно, поскольку полиномы G (р) и 77 (р) задаются.
В дальнейшем будем считать, что входные функции ZBX (р) или Увх (р) — положительные вещественные.
Рассматривая сначала в качестве входной функции сопротивление ZBX (р), отмечаем, что корни многочлена И (р) могут лежать на мнимой оси, на отрицательной вещественной полуоси и в любых точках левой полуплоскости. Здесь обращается внимание на корни знаменателя ZBX (р) потому, что метод Фостера основывается на разложении ZBX (р) на простейшие дроби.
Для реализации ZBX (р) выделим сначала все слагаемые, соответствующие корням 77 (р), расположенным на мнимой оси, т. е. реактивнойсопротивление Zlp (р). Учитывая разложение, сделанное
505
в § 17-6, получим:
Л (р) = ZBX (р) - Zlp (р) = Znx (р) -
(17-33)
I
причем Z± (р) — положительная вещественная функция, все полюсы которой лежат на отрицательной вещественной полуоси и в любых точках левой полуплоскости.
Далее найдем частоту со' при которой Re [Zr (/со')] = д имеет минимум, определим Дшш и вычтем Лыин из Zr (р), т. е. составим выражение
Z2 (р) = Zi (р) - Амин. (17-34)
Эта операция называется приведением функции Zx (р) к виду минимального активного сопротивления, т. е. к такой функции Z2 для которой при частоте со' получаем Re [Z2 (/со')] = о. Подчеркнем, что приводя Zr (р) к виду минимального активного сопротивления, нельзя вычитать произвольное А. Если, например, взять А > Дмин, то Re [Z2 (/со')] <0 и не будет соблюдено условие положительности вещественной части функции Z2 (jco).
Таким образом, приведение к виду минимального активного сопротивления вытекает из требования, чтобы рассматриваемые функции были положительными вещественными.
У положительной вещественной функции Z2 (р) в общем случае полюсы лежат на отрицательной вещественной полуоси и в любых точках левой полуплоскости. Поэтому она может быть разложена на совокупность дробей вида
Z2(p) = y-^ + У ^^4-У-§Е±£т_. (17-35)
p-'rat ^p + ak 1 а-(р +а/)2+<-),- v 1
i k I
Каждая простая дробь первой суммы реализуется схемой из параллельно соединенных С, и rL (рис. 17-22, а). В самом деле,
Z. (р\ = , (17-36)
’ rt+\/pCi р+1/rfit p+at ’ v '
где lICi — At; = l/rtCt и постоянная А, находится аналогично (17-25):
A=lim[(p + a,)Z2(p)]. (17-37)
р-> —at
Каждая простая дробь второй суммы реализуется схемой из параллельно соединенных Lk и rk (рис. 17-22, б):
Zk (р) = -pLk2 = ~£г-.т- = -^k-, (17-38)
v/ pT-fe + a P~!rrklLii P-\-Uk ' ’
где rk = Bk\ ak = rkILk, а постоянная Bk находится также аналогично (17-25):
Bk= lim [<£±g*)z2(p)l.(17-39)
506
Каждая дробь третьей суммы реализуется, например, схемой, приведенной на рис. 17-22, в. Однако следует заметить, что в общем случае не все параметры rh Ц, Ct схемы рис. 17-22, в получаются положительными, т. е. дроби третьей суммы, а значит, и входное сопротивление ZBX (р) двухполюсника в целом не всегда реализуемы 57ИМ методом.
Рис. 17-22.
Рассматривая далее в качестве входной функции проводимость Y вх(р), отмечаем, что ее реализация методом разложения на простые дроби производится в том же порядке, как и функции ZBX (р).
Получив функцию У2 (р), аналогичную Z2 (р), т. е. положительную вещественную функцию, и считая, что ее полюсы расположены на отрицательной вещественной полуоси и в любых точках левой полуплоскости, представим ее аналогично-(17-35) совокупностью простых дробей вида
I k
+ 11^+$Г (17-40>
Простая дробь первой суммы реализуется схемой рис. 17-23, а, так как
= (17’41) Рис. 17-23.
(где 1/Lt = Ар, = rJLt и постоянная А, находится аналогично £17-25):
lira [(р + «() У2 (р)]. (17-42)
Простая дробь второй суммы реализуется схемой рис. 17-23, б, ак как
у _________1________P^k ___ p!rk _____ pB/i /17 лох
rk+\/pCk r^Cfp+l p+l/rkCk p + ak’ 1 >
Где \lrk = By, ak — l/rkCk, а постоянная Bk находится также аналогично (17-25):
----------------lim р^-У2н1.----------------------(17-44)
507
Дробь третьей суммы реализуется схемой рис. 17-23, в, так как у ?__________________Р^1_____ -
1 W rt + pLt + 1/рСг p^LtCt + rtCtp + 1
PlLl = PDi /, 7 л
L'Z
Однако и здесь в общем случае не все параметры rt, Lh q (рис. 17-23, в) получаются положительными, т. е. дроби третьей L суммы, а значит, и входная про-
/.«, Со __г~Ч-] водимость Увх (р) двухполюсника
0—||' | I—-| в целом не всегда реализуемы этим
1—II— Д методом.
с 11
1 U Пример 17-6. Дана положительная
| вещественная функция
1* L 7 . v p5+6p4 p6p3 |-21p2-i-4p |-10 iLK 'ВХР Р4 + бр3 + р2 + 5р =
т. Г - g(p)
р н (р) •
~ * Требуется реализовать ZBX (р) методом
Рис 17-24 Фостера, т е методом разложения на
простые дроби.
Решение Корни уравнения Н (р) = 0 находятся любыми известными методахш pt = 0, р2, 3 = , pi = — 5, т е
#(p) = P(p2+D (Р + 5)
р
р j-. По формулам (17 25) находим
Выделяем слагаемые, соответствующие полюсам ZBX (р), расположенным " л 1 ^4л
на мнимой оси рЛю4—-Р
/00== hm [Ъх(Р)1 = к 40= hm [pZrv(p)] = 2, р->сс L р J о
Поэтому
[2
Р + ~
Р±1 р + 5 ’
Найдем минимальное активное сопротивление Для этого определим
Re Zj (/со) =- Re
/<о+2 /«>+5
10 -p CO2
25+w2
и, приравняв пулю производную
A Re Z, цен) =
d 10 + м2 dco 25-(-со2
найдем, что при частоте <£>' = 0 минимальное активное сопротивление А = R = 2/5 Выделяем R из состава Z, (р)
3
210 (Р) = Zx(Р)-R-| ,
Р ~г о О р-\- о
которое реализуется схемой рис 17 22, б с параметрами г» — — 3/5 и Lfe
- I Kiai 3 2с>
На рис 17-24 представлена полученная схема двухполюсника
508
17-9. Синтез двухполюсников с потерями. Метод Кауэра
Для реализации положительной функции ZBX (р) методом Кауэра, г е. методом разложения в цепную дробь, выделим сначала, как л раньше, совокупность всех слагаемых Zlp, которые соответствуют полюсам, расположенным на мнимой оси рДсо, Ajp, A,pl (р2 + со,). Далее выделим из Z1 (р) = Z (р) — Z 1р (р) минимальную вещественную часть Дмин = г\ и получим функцию Z10 (р) = Zx (р) — которая уже не имеет полюсов на мнимой оси. Но возможно, что они есть у обратной функции F10 (р) = 1/Z1O (р). У проводимости У10 (р) выделим, как и раньше, все слагаемые (р), соответствующие ее полюсам, расположенным на мнимой оси. Далее выделим из У2 (р) —
Ую (р) — К2р (р) минимальную вещественную часть АМШ1 = g2 и получим функцию Y20 (р) = Y2 (р) — g2, которая уже не имеет
г1р(р) г1
Рис 17-25.
%
полюсов на мнимой оси. Однако возможно, что их имеет обратная функция Z2(l(p) = 1/У29 (р) = ^з(р) + £зР (р) и т. д. Продолжая этот процесс, получаем цепную дробь вида
Z(P) = ЛР + И 4------------‘---у----------> (17-46)
Др + Ё2 4 j
Др + Гз |~ • —————jj -
Др + й+/5р + г5+;_.
которой соответствует цепная схема двухполюсника, представленная на рис. 17-25.
Конечно, в процессе построения этой цепной схемы отдельные элементы или даже контуры в ней могут отсутствовать.
Вполне возможно, что на отдельных этапах расчета у рассматриваемых сопротивлений или проводимостей полюса на мнимой оси могут отсутствовать. Тогда, следуя методу Бруне, их можно ввести искусственно, применяя, например, отрицательные индуктивности. Эти индуктивности в окончательную схему двухполюсника не войдут, если их заменить трансформаторами без потерь с надлежащим образом подобранными положительными индуктивностями первичной и вторичноА обмоток и с коэффнциенюм свя-зи, равным единице.
509
17-10. Понятие о синтезе четырехполюсников
Как и для двухполюсников, синтез четырехполюсников прои3 водится по заданной передаточной функции К (р) или частотной ха" рактеристике К (/со) = Д' (и) е/в((й>. При этом вместо К (/<о) могут быть заданы в отдельности амплитудно-частотная К (со) и фазе, частотная 6 (со) характеристики. Как и для двухполюсников, задача синтеза может быть поставлена для реактивных четырехполюсников и для четырехполюсников с потерями. Передаточная функция Д ал четырехполюсника обычно задается (см. 17-4) отношением двух полиномов G (р) и Н (р) с вещественными коэффициентами:
К (п) = -ВЫ-\(Р1 . И 7 47\
Н(р) хвх(р)’ (1Л47)
т. е. отношением лапласовых изображений двух величин, одна из которых принята за выходную, а другая за входную.
Для передаточной функции четырехполюсника необязательно должны выполняться все условия, необходимые для входных функций двухполюсника Z (р) или К (р), а именно:
1) наивысшие степени многочленов G (р) и И (р) могут разниться больше чем на единицу:
2) вещественная часть К (/а) может быть отрицательной;
3) нули К (р), т. е. нули многочлена G (р), могут располагаться не только в левой, но и в правой полуплоскости, если Д' (р) принадлежит системе не минимально-фазового типа.
Вместе с тем полюсы Д (р) могут располагаться, как и у двухполюсников, только в левой полуплоскости. Если бы это было не так, то система была бы неустойчивой.
Любопытно отметить, что у некоторых четырехполюсников не минимально-фазового типа затухание не зависит от частоты. Это получается, если нули функции Д (/со) располагаются в правой полуплоскости и являются зеркальными изображениями относи
тельно мнимой оси полюсов функции Д (/со), расположенных в левой полуплоскости.
Сказанное вытекает из соотношения (17-4а), так как при указанных условиях Д (со) остается постоянной, а 6 (со) зависит от частоты. Например, такими свойствами обладают симметричные мостовые (Х-образные) четырехполюсники (рис. 17-26). Отметим, что эти четырехполюсники применяются в цепях проводной и радиосвязи для коррекции фазы выходных напряжений или токов.
Для синтеза четырехполюсников в ряде случаев могут применяться изложенные выше общие методы синтеза двухполюсников.
Рассмотрим решение задачи реализации реактивного симметричного мостового четырехполюсника по одной из заданных его пере*
Рис. 17-26.
510
даТочных функций К (р) = /2 (p)/^i (р) ~ G (р)1 Н (р) и заданном активном сопротивлении нагрузки.
Разложим полином Н (р) на нечетную HL (р) и четную Н2 (р)
вставляющие:
РГ Л-Л G (р) = g(pVhi (P'i_
#i(p)+#2(p) 1+^2(рЖ(р)‘
(17-48)
Запишем основные уравнения четырехполюсника типа | Y | Б операторной форме, опуская аргументы р у изображений:
/2 = 21^1 4“ 22^2= У21^1 4“ ^22^2Гн-
(17-49)
Из второго уравнения (17-49) найдем:
1 __ Y13G1
2~ 1-^Н
(17-50)

рце для симметричных мостовых четырехполюсников Уц = — У22. Приравнивая правые части (17-48) и (17-50),
получаем:
________= —9.!н..1__ (17-51)
1-1-К1Хгн \ + Н2/НС <1Z
Приравнивая числители и знаменатели (17-51), 5}дем иметь:
ГМ = А; Гп = ^. (17-52)
По Уа1 и Уи найдем Zr и Z2 схемы
рис. 17-26:
Пример 17-7. Дана передаточная функция
к м _ Мр) = G(P) = 1-0,5- 10~12р2
UiAp) Н(р) 0,5 - 10 10р2 + 4 • 10 ;<р+100
)еактивного четырехполюсника. Реализовать его в виде симметричной мостовой :хемы, если сопротивление нагрузки гп = 100 Ом.
Реше и и е. В соответствии с (17-48)
G (р)= 1 — 0,5 • 10_12р2; Д1 = 4.10“Зр; 7/2 = 0,5-10-Юр2+100.
Находим:
G _ 1-0,5-10-т2р2
Xs!1~ ~ 4 - 10 зр
v Н2 _ 1+0,5- 10-12р2
---------4 10~зр---
511
Далее найдем элементы искомой схемы (рис. 17-27):
Л = = 2 10 :‘Р = Lp-, L==2 мГ;
Y 11+ Г21
— • с = 250 пФ. Ср ’
Здесь был рассмотрен только один из простейших методов синтеза реактивных четырехполюсников. Вообще же говоря, синтез четырехполюсников по заданным передаточным функциям или частотным характеристикам представляет собой более трудную задачу, чем синтез двухполюсников.
Синтез цепей применяется для создания фильтров, фазовращателей и всевозможных корректирующих устройств в измерительной технике, проводной и радиосвязи и в системах автоматического управления. Применение синтеза позволяет создавать такие цепи, которые в совокупности с уже заданными цепями должны обеспечить желаемые передаточные функции и частотные характеристики всей системы в целом.
Раздел второй
ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Глава восемнадцатая
ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
18-1. Токи и напряжения в длинных линиях
В предыдущих главах книги уже рассматривались линии электропередачи, при частоте 50 Гц и напряжениях до 35 кВ небольшой длины, в которых можно пренебрегать токами, обусловленными емкостью между проводами (токами смещения) и проводимостью изоляции (токами утечки через гирлянды изоляторов и токами, обусловленными коронным электрическим разрядом вблизи поверхности проводов).
При больших напряжениях, встречающихся в электроэнергетике, и при больших частотах, с которыми имеет дело электросвязь, а также при значительной длине линий пренебрегать токами смещения и утечки недопустимо. Следовательно, ток в проводах не одинаков в разных сечениях линии.
Ток в проводах линии вызывает падение напряжения в активном сопротивлении проводов и создает переменное магнитное поле, которое в свою очередь наводит вдоль всей линии э. д. с. самоиндукции. Поэтому напряжение между проводами также не остается по-постоянным вдоль линии.
Чтобы учесть изменение тока и напряжения вдоль линии, нужно считать, что каждый сколь угодно малый элемент линии обладает сопротивлением и индуктивностью, а между проводами — проводимостью и емкостью, т. е. рассматривать линию как ц е п ь с распределенными параметрами. Такую линию называют длинной.
Будем считать сопротивление, индуктивность, проводимость и емкость равномерно распределенными вдоль линии, что является некоторой идеализацией действительных условий. Такую линию Условимся называть однородной.
Об идеализации надо говорить потому, что в реальной линии утечку тока через гирлянды изоляторов нужно рассматривать как совокупность ряда сосредоточенных процессов. Кроме того, провес проводов на длине пролета линии изменяет равномерность распределения их емкости и индуктивности.-------------------------
17 Основы теории цепей
513
18-2. Уравнения однородной линии
Составим дифференциальные уравнения, которым удовлетв ряют токи и напряжения в любом сечении двухпроводной линии' Пусть известны первичные параметры однород ной лин и и, отнесенные к единице ее длины: г0 — сопротивле" ние прямого и обратного проводов; Lo — индуктивность петли, обра'. зуемой прямым и обратным проводами (или с учетом влияния земли_
рабочая индуктивность петли); g0 — проводимость (утечка) между проводами; Со — емкость между проводами (или с учетом емкости проводов по отношению к земле — рабочая емкость между проводами).
Длинную линию можно представить в виде множества соединенных в цепочку бесконечно малых элементов длиной dx, каждый из которых имеет сопротивление r0 dx и индуктивность Lo dx, проводимость godx и емкость Codx (рис. 18-1). Сопротивление rodx и индуктивность Lodx будем считать включенными в один провод.
Обозначим через х расстояние от начала линии до текущего элемента ее длины. Мгновенные значения напряжения и тока в начале выбранного элемента линии dx обозначим через и и i, а в рачале следующего — через и -ф ~ dx и i -ф dx.
Условимся называть верхний провод (рис. 18-1) двухпроводной линии прямым, а нижний — обратным. Положительные направления тока и напряжения выберем, как показано на рис. 18-1.
Для элемента линии длиной dx на основании законов Кирхгофа
и ~ + дх dx} r°dx 1 + L°dx % '•
= (w + d£dxjgodx + Codx (u+^dx^.
Приводя подобные члены, пренебрегая величинами второго порядка малости и сокращая на г&сДполучаёмдифференциально^
514
равнения:
-£==&«+<“. (18-2)
Решение полученной системы уравнений в частных производных при определенных начальных и граничных условиях дает возможность определить ток и напряжение как функции расстояния от начала линии и времени. Эти уравнения справедливы при любых изменениях тока и напряжения во времени.
18-3. Установившийся режим в однородной линии
Рассмотрим установившийся режим в длинной линии при синусов ильном напряжении источника питания. Переписывая уравнения (18-1 (18-2) для установившегося режима и вводя комплекс-
ные напряжения, токи, сопротивления и проводимости, получаем:
- 37 =-(/-o + /®Lo) / = Z07; (18-3)
- f = feo +/юС0) U = Y0U, (18-4)
где Zo — r0 + /со£0 — комплексное сопротивление;
— go + /®Со — комплексная проводимость единицы длины линии.
Подчеркнем, что Zo и Yo не являются величинами, обратными друг другу.
Продифференцируем уравнения (18-3) и (18-4):
_ _ 7 dL. _d21 _ у
dx2 n dx ’ dx1 0 dx
и заменим dl'dx и dUldx согласно (18-4) и (18-3). Тогда получим:
~^ZgY0U- (18-5)
g=Zoro/. (18-6)
Дифференциальные уравнения (18-5) и (18-6), определяющие изменения комплексных напряжения и тока вдоль линии, одинаковы. Поэтому? достаточно найти, например, закон изменения напряжения О, а ток можно получить из уравнения (18-3).
Решение уравнения (18-5) — линейного дифференциального уравнения второго порядка с постоянными коэффициентами — имеет вид:
й = А1е~^х+ = «ле-/рл_|_ Д2еахе}$х> (18-7)
где ____ _____________________
у = а + /Р Z0Y0^V(r0 + jO)Lo) teo + jwCo); (18-8)
Aj, A2 — комплексные постоянные интегрирования.
17
515
Ток I согласно уравнению (18-3)
1— = (18
Z. Л Z,' 1 ! ’ rz„/vrj 10 9)
Знаменатель формулы (18-9), имеющий размерность сопротивления, называют волновым сопротивлением лини и ZB. Для однородной линии, рассматриваемой как четырех, полюсник, волновое сопротивление совпадает с характеристическим т. е.
ZK=Z,-- = rc 4- jxr = У Z0/Y0 =
= l/~-r°-1 iaL°- = 1 -°+a2L" e’Q = 1A> e?e (18-101
V go + /«Co | gl + ^cy V yoe ’ <18 10)
где
6= ? arctg • (18-11)
Подставляя Zc в формулу (18-9), запишем ее в виде
/ = е-ахе~^х — еахе^х. (18-12)
Выражая комплексы Aj и А2, имеющие размерность напряжения, в показательной форме
Аг = Д^; Д2 = /4 2е'Ч
запишем мгновенные значения напряжения и тока:
и = У2 A^^sin (at — рх-г-1]'() -|-фг2 Л2с'/Л'к1п (at -ф рх -ф ф2)> (18-13)
i = g-ax sin _ g) _
zc
_V2yie^xsin^t+^x+^2_Gy (18-14) zc
Каждое из слагаемых правой части двух последних выражений можно рассматривать как бегущую волну, движущуюся в направлении возрастания или убывания координаты х и затухающую в направлении движения.
В самом деле, каждое из слагаемых в любой фиксированной точке х = х± представляет собой периодическую функцию времени. В любой же фиксированный момент времени t = tr каждое из слагаемых изменяется вдоль линии (т. е. с изменением х) по закону затухающей синусоиды.
Основными характеристиками бегущей волны являются фазовая скорость и длина волны.
Фазовой скоростью волны v называется скорость перемещения фазы колебания, которая в течение времени t и по мере увеличения расстояния х, пройденного волной, остается постоянной, т. е. _ _ ____
~ ~ at — рх -ф ф1 = const. - — - —
516
Тогда
(о^-Рх4-^!) = 0
и
tfx/d/ = n=co/p. (18-15)
Аналогичное исследование второго слагаемого правой части равенства (18-13) дало бы для фазовой скорости такое же значение, но с обратным знаком. Отсюда заключаем, что эти слагаемые могут рассматриваться как волны, движущиеся в противоположных направлениях.
Длиной волны Z, называется расстояние между ближайшими двумя точками, взятое в направлении распространения волны, фазы колебания в которых различаются на 2л. Следовательно, для первого слагаемого равенства (18-13) получим:
со/ —Р (х4-А,)-|-ф1 = со/ — рхф-ф]. — 2л, откуда
^=2л/р (18-16)
и
строят огибающие ± ]/ 2/l1e’“-v.
т. е. за время, равное периоду, волна пробегает расстояние, равное длине волны.
Затухающая синусоидальная волна представлена на рис. 18-2. Для ее изображения сначала Затухающая волна вписывается в область, ограниченную огибающими. '
Условимся волну, движущуюся от начала линии (рис. 18-2), называть прямой, а движущуюся от конца линии — обратной.
Выберем теперь положительные направления напряжений и токов прямой и обратной волн. Так как оба слагаемых в правой части равенства (18-7), определяющие напряжение О, входят с положительными знаками, то
вполне естественно выбрать положительные направления напряжений прямой и обратной волн совпадающими с положительным направлением напряжения О, т. е. от прямого провода линии к обратному (рис. 18-1).
Для тока существуют две возможности. Можно оставить оба слагаемых в правой части равенства (48-12) й^азличными знаками 1
517
или же поставить между слагаемыми знак плюс, а минус включить в состав второго слагаемого. Будем определять ток 1 как разность токов прямой и обратной волн, т. е. положительное направление тока прямой волны выберем совпадающим с положительным направлением тока 1 (рис. 18-1), а положительное направление тока обратной волны — противоположным положительному направлению тока 1.
В соответствии с этим можно записать:
U — ^пр + ^об! ^==ЛР~4б;
где
^C6=--VYv; /Об=-4-^.
'-с '
(18-17)
(18-18)
Из формул (18-18) вытекает, что токи и напряжения как прямой, так и обратной волн связаны между собой законом Ома:
/пр-=£7пр/^с; /о6 = Йоб/7с. (18-19)
Введенные понятия о прямых и обратных волнах в линиях при установившемся синусоидальном режиме облегчают представле
Рис. 18-3.
ние и анализ процессов. Однако нужно иметь в виду, что физически существуют в линии только результирующие ток / и напряжение U и что разложение их на прямые и обратные волны следует считать лишь удобным приемом.
Построим теперь векторную диаграмму распределения напряжения и тока прямой и обратной волн вдоль линии, т. е. их годографы.
На основании первого равенства (18-18) заключаем, что если отложить вектор на комплексной плоскости (рис. 18-3) и затем поворачивать- его по направлению движения с1релкй~ часов, Одно--
518
Еременко умножая на е"“х, то концы векторов напряжений прямой волны расположатся на свертывающейся логарифмической спирали. На расстоянии, равном длине волны Z, аргумент |3х изменяется на 2л. На рис. 18-3 нанесены еще 12 векторов напряжений для точек, расположенных на расстояниях Z./12 (|3х = л/6). На расстоянии от начала линии, равном длине волны (точка 12 на рис. 18-3), напряжение (ток) совпадает по фазе с напряжением (током) в начале линии (точка 0), но амплитуда уменьшается в раз.
Влияние затухания наглядно иллюстрируется сравнением с линией без потерь (см. § 18-11), у которой длина векторов напряжения одинакова и их концы описывают окружность. По расстоянию точек спирали до точек этой окружности можно судить о величине затухания.
На рис. 18-3 справа построена кривая распределения мгновенных значений напряжения прямой волны вдоль линии для фиксированного момента времени t — tr. Ординаты этой кривой получены вращением с угловой скоростью Р вектора {7пр, длина которого определяется логарифмической спиралью, и проектированием его на ось ординат, т. е. выполнением операции, известной из теории переменных токов.
Аналогично из третьего равенства (18-18) следует, что если отложить вектор А2 на комплексной плоскости (рис. 18-3) и затем поворачивать его против направления движения стрелки часов, одновременно умножая на еах, то концы векторов напряжений обратной волны расположатся на развертывающейся логарифмической спирали. Вращая вектор £7об и проектируя его концы на ось ординат, получим (рис. 18-3) кривую распределения мгновенных значений напряжения обратной волны вдоль линии.
Совершенно так же строятся годографы и кривые распределения мгновенных значений токов прямой и обратной волн. Чтобы изобразить распределение мгновенных значений тока i и напряжения и вдоль линии, необходимо согласно равенствам (18-17) построить сумму мгновенных значений напряжений (рис. 18-3) и разность мгновенных значений токов прямой и обратной волн.
Кривые распределения мгновенных значений напряжений и токов также имеют волнообразный характер. Они показывают, что в каждый данный момент времени как результирующие токи и напряжения, так и токи и напряжения прямой и обратной волн в различных точках линии могут отличаться не только по величине, но и по знаку.
Отметим, наконец, что все полученные результаты применимы и к трехфазным симметричным или несимметричным, но транспонированным линиям. В этом случае напряжение С и ток 1 — это фазное напряжение и ток, а параметры г0, £0, Со и g0 должны быть отнесены к одной фазе.
Пример 18-1. Трехфазная линия передачи электроэнергии Куйбышев — Москва длиной I = 900 км .в начальном периоде ее эксплуатации работала при напряжении 400 кН и чаыи.е/ —иОГц. Сшласно одниму из вариантов-
519
проекта первичные параметры линии имеют следующие значения: г0 ~ 0,08 Ом/ • Lq = 1,336-IO-8 Г/км; Со = 8,6-10-8 Ф/км; потери Ро в изоляции и на коро*1’ составляют 2000 Вт/км на одну фазу.
Определить характеристики линии гс, 0, а и р, называемые ее вторичным параметрами, а также длину волны 2. и фазовую скорость V. и
Решение. Из формулы
Pq = 1/ф®°
найдем:
So= =------------°-4----- = з 75 10-е См/км.
ё £7ф (400/рЗ)2- 106
Комплексные сопротивление и проводимость на 1 км:
Zo = ro-)-/(oZ,o = 0,427 2. 79°13' Ом/км;
Го=go+/coCo = 2,7 - 10“в 2.-90° См/км.
Характеристики линии:
ZC = K^/To=397 2,- 5°23' Ом;
Y = J/ZX= 1,073- Ю-з д 84°37' км~1;
««=8,7-10'4 дБ/км (см. § 16-1); р= 1,068 • 10 3 рад/км;
Х=2л/Р = 5880 км; с, = 7/ —294000 км/с.
18-4. Уравнения однородной линии с гиперболическими функциями
В формулах (18-7) и (18-12) постоянные и А2 можно опреде лить, если известны граничные условия.
Пусть заданы напряжение С\ и ток Д в начале линии (х — 0) Отметим, что выбрать произвольно и и Д—значит задать опре деленное сопротивление нагрузки Z2 в конце линии. Если же наоборот, задано сопротивление нагрузки Z2, то выбрана може быть только одна из величин 1У1 или Д.
Из (18-7) и (18-12) при х = 0 получим:
— А^ Л2; — — А2,
откуда
242 = -g-(t71 AZe).
(18-2(
Подставив Ат и Д2 в (18-7) и (18-12), для напряжения # и тока в любой точке линии (на расстоянии х от ее начала) получим:
й =4 + А^) г-^ + 4 - А^) еух;
f 1 ! V, . ; \ 1 / ГР
2 ('zr + /1Je '
7 \
520
Группируя члены в правой части и вводя гиперболические функции ch у х и sh у х, будем иметь:
еУх+е~Ух г еУх—еУх .
и = иг —--------I1ZC-----2---=t/j ch ух - IjZf sh yx;
} й1еУх—ё~Ух , ; еУхА-е~Ух Ux , , ; , (18-21)
----2----ЬЛ—^2-------= ~ -^shyx +Achyx.
Эти формулы позволяют определить ток и напряжение в любой точке линии по их значениям в начале линии.
Пусть теперь заданы значения напряжения О2 и тока Д в конце линии, т. е. задан режим приемника, а значит, и сопротивление Z2 ~ ^Д/Д-
В этом случае целесообразно отсчитывать расстояние текущей точки от конца линии. Обозначая его через х', получаем х = I — х', где I — длина всей линии.
Тогда из (18-7) и (18-12) найдем:
Й== ф- А2еУ1е~Ух'-, fZ^A^y^' — А^'е-у*’.
Обозначим . .
Л3 = Л1е у1\ А4 = А2еУ/
и условимся, отсчитывая расстояния от конца линии, обозначать их не через х', а снова через х. При этом никакой путаницы внесено не будет, так как в каждом конкретном случае по заданным напряжениям и токам или й2, Д видно, откуда отсчитываются расстояния. Тогда
й = А3еУх + А4е~Ух- IZC = АаеУх ~ А4е ух, (18-22)
где АаеУх — прямая волна напряжения, а А1е~Ух — обратная волна. Из формул (18-22) при х = 0 получим:
и2—л3 -j- А4> i2zc—As А4,
откуда
A=^(^+AZ); A=’((72-/2Zc). (18-23)
Подставляя (18-23) в (18-22), группируя члены и вводя гиперболические функции ch ух и sh ух, получаем:
U = U2 ch ух + 12ZC sh ух; ‘
; и2 , } , (18-24)
/ = sh ух Д ch ух.
zc
К формулам (18-24) относятся все замечания, сделанные выше относительно формул (18-21).
Соотношения для линий постоянного тока, у которых сопротивление проводов и утечка между проводами, обусловленная Несовершенством изоляции, равномерно распределены вдоль линии, когут быть получены как частный случай из выведенных соотношений (18-24) при со = 0. В самом деле, со = 0 означает, что при
521
постоянных во времени токах и напряжениях отсутствуют э. д самоиндукции (но не магнитное поле между проводами) и Токс смещения между проводами (но не электрическое поле между ними? Поэтому, полагая в формулах (18-8) и (18-10) со = 0, получаем для линий постоянного тока:
? = а='|/7^; ^-c~rc~V г о/g0. (18-25)
Кроме того, для линий постоянного тока не приходится говорить ни о каких фазовых соотношениях, т. е. ни о каких сдвигах по фазе между токами и напряжениями. Поэтому, нацример, фор. мулы (18-24) для линии постоянного тока перепишутся так:
U = U2 ch ахI2rc sh ax', sh ахф- /2 ch ах. (18-26)
Пример 18-2. По результатам примера 18-1 определить 1) ток в Москве (конец линии), 2) напряжение и ток на Волжской ГЭС имени В И Ленина в Куйбышеве (начало линии); 3) сдвиг фаз между напряжениями в начале и в конце линии; 4) к п д линии, 5) составляющие напряжения и тока в начале линии при холостом ходе (если [/2Х = U2) и корогком замыкании (при /2К = /2), если в конце линии (в Москве) известны-
Р2 = 300 МВт! U21 = Г'З • 220 кВ; cos <р2 = !•
Решение Положим й2 = М2ф = С 2ф = 220 кВ
Ток в Москве при активном сопротивлении нагрузки (cos <р3 — 1)
/2=/2 = о,, ₽2 „ ~ = 455 А.
3[/2фС03ф2
Значения гиперболических функций от комплексного аргумента yl — 0,0906ф ф j 0,962 можно найти по таблицам Но можно пользоваться формулами
shVZ=-|<eTi-e-V)==A 1,0947z55’—у0,914 Z-55°=0,824 z 86°23',
ch yl = (М7 4- е~У1) = 0,581 z 7°22' .
Напряжение и ток на ГЭС найдем по формулам (18-24):
f/1 = t/2chyZ+/2ZcshyZ = 222 z 47 30' кВ;
h = sh yl +I2 ch yl = 548 Z 63° 10' A, £-c
т e ток в начале линии опережает по фазе напряжение на угол 15®40'.
Так как L 2 = U2, то сдвиг фаз между напряжениями в начале и в КОицё линии равен 47°30'
Активная мощность, отдаваемая ГЭС в линию,
/ф = ЗГфф cos Ф1 = 3 222 • 548 cos (47°30' — 63°10') = 352 МВт
и к п Д линии
Т] = Р2/Рг = 300/352 = 0,853.
Составляющие напряжения Ur
Z/lx = f.'2 chyZ= 126,7ф-/16,4 кВ; Z71K = /2Z(;sh-vZ = 23,3 + /147,l кВ.
Составляющие тока.
71х = -у" sh yl = —14,5 4-/456 A, ZlK = /2ch yZ = 262 ф/33,9 АГ
522
18-5. Характеристики однородной линии
В связи с тем, что напряжения и токи в линиях можно получить наложением прямых и обратных волн, принимают определенные наименования введенные выше величины. Комплексная величина у называется коэффициентом распространения, а — коэффициентом затухания, |3 — коэффициентом фазы (иногда добавляют на единицу длины). В самом деле, из формул (18-13), (18-14) и последующих видно, что а характеризует затухание амплитуд прямой и обратной волн, а р, входящее в аргумент синуса, характеризует изменение фазы волны в зависимости от координаты х точки линии. Коэффициент затухания определяют в децибелах (или неперах) на единицу длины (см. пример 18-1 и § 16-1), а коэффициент фазы— в радианах на единицу длины.
Для подсчета а и |3 и для построения их частотных характеристик можно обратиться к формулам
а—2 (гоУо~\~ro8o~~
Р = 1/ ~2 (гоУо + ^>2L0C0 г(,§(,),
(18-27)
которые получены из (18-8). В частности, в отношении коэффициента фазы надо сделать вывод, что он монотонно возрастает
с увеличением частоты.
Сопротивление Zc определяет токи прямой и обратной волн по соответствующим напряжениям (18-19). Средние значения модуля Zc для воздушных линий 300—400 Ом, а для кабелей 60—80 Ом. Для кабелей емкость Со значительно больше, а индуктивность Lo меньше, чем для воздушных линий, так как провода у них расположены ближе друг к другу, а отно
сительная диэлектрическая проницае-
мость изоляции порядка 4—5. Поэтому' гс для кабелей в 6— 8 раз меньше, чем для воздушных линий.
В табл. 18-1 приведены значения первичных и вторичных пара
метров воздушных и кабельных силовых линий и линий связи.
Построение частотных характеристик для гс и е может быть выполнено по формулам (18-10) и (18-11). На рис. 18-4 даны кривые
изменения модуля гс и аргумента е волнового сопротивления для воздушных и кабельных линий. Из выражения (18-10) видно, что при со = 0
= V r0/g0, (18-28)
а при со = оо
zc — г Cq/Cq»
(18-29)
523
Первичные и вторичные параметры линий
Таблица 18-1
Наиме но- Воздушные лн- Силовые кабели Воздушные двухпроводные линии связи Кабели Воздушные двухпроводные ЛИНИИ связи Кабели Медный коаксиалы-
ванне параметра иа пряжей ня ИО—400 кВ напряжением 10 кВ Медные и веские биметалли-провода Стальные провода СВЯЗИ Медные провода Стальные провода связи ныи кабель»
/ 50 Гц 50 Гц 0,2— 30 кГц 30- 300 кГц 0,2— 10 кГц 300- 5000 Гц 800 Гц телефонна средняя я частота) 1 МГц
г0, Ом/км 0,08—0,2 0,5 — — — — 2,84 42,2 22,6 27
go См/км (0,038-0,5) 10“« — — — — • 0,7 • 10-е 0,7 • 10-6 0,7 IO”0 32,5 10-е
Llt, Г/км (1,27-1,43) 10-з — — — — — 1,94- 10'3 8,96 • IO”3 0,6 IO’3 0,256 10-з
хс Ом/км 0,4—0,45 0,1 — — — — — __ — —
Со, Ф/км (8,3—9) 10-» — — — — — 6,35- 10’» 6,32-10-° 35,5- IO’9 52 10’°
Ьп, См/км (2,6—2,8) 10-е 54,0 • 10~в — — — — — — — —
а, дБ/км (8,7-61) 10’4 26,1 • 10-з 0,0174— 0,140 0,140-0,445 0,043-0,87 0,22-1,30 — — — ' 1,69
Р, рад/км (1,05-1,12) 10"з 410"3 0,005— 0,66 0,66-6,6 0,00112— 0,299 0,015-0,37 — — — 22,9
1 Диаметр внутренней трубы d = 4 мм. Внутренний диаметр внешней трубы D — 14,4 мм, zc — 70 Ом.
Как для воздушной, так и для кабельной линии всегда r0/g0 >
Lo/Co, что объясняется в отношении всех линий незначительной величиной утечки go и дополнительно в отношении кабельных линий довольно большой емкостью Со.
Поскольку практически <оСо > g0, аргумент комплексаg0 + /соС0 в знаменателе выражения (18-16) близок к 90° и больше аргумента комплекса r0 Д /соГо в числителе. Поэтому аргумент 6 волнового сопротивления обычно отрицателен.
Из выражения 0 следует, что 6 = 0. при со = 0 и со = оо.
Фазовая скорость волн в линиях определяется, как следует 1ИЗ (18-15), коэффициентом фазы (J.
Ниже (см. § 18-9 и 18-11) будет показано, что для линий без ^искажений (r0/g0 = Lo/Co) и для линий без потерь (г0 = 0; g0 = 0)
v = = -4—, (18-30)
/L0C0 У ер.
где с — скорость света в вакууме;
е и ц — относительные диэлектрическая и магнитная проницаемости диэлектрика, окружающего провода.
В воздушных линиях 8» 1 и р ~ 1 и при отсутствии потерь скорость волн v практически равна скорости света в вакууме. Для кабелей с относительной диэлектрической проницаемостью изоляции е » 4-7-5 скорость волн в 2—2,5 раза меньше скорости света в вакууме. Фазовая скорость в линиях с потерями, хотя и немного, но все же меньше скорости света в вакууме.
На рис. 18-5 показаны зависимости фазовой скорости от частоты для однородных воздушных и кабельных линий связи. Из них видно, что при 1000 Гц фазовая скорость в воздушных линиях с медными и биметаллическими проводами почти достигает скорости света в вакууме, в то время как в линиях со стальными проводами и кабельных линиях она при f х 1500 Гц еще примерно вдвое меньше скорости света в вакууме.
Длина волны Z в воздушных линиях сильного тока, для которых скорость v близка к скорости света, при частоте / = 50 Гц составляет:
K=vT «=<с// = 6000 км.
525
Например, строительство Волжских гидростанций потребовало сооружения линий длиной около 1000 км для передачи энергцц этих гидростанций в Москву. Даже на таких линиях укладывается сравнительно небольшая доля длины волны и нельзя наблюдать волнообразного изменения тока или напряжения по длине, а можно наблюдать лишь их монотонное изменение.
Волнообразное изменение напряжения и тока вдоль линии можно наблюдать в устройствах связи, где линии соединяют, например, радиопередатчик с антенной. Для передатчиков, работающих в диапазоне коротких волн, длина линии может быть во много раз больше длины волны.
18-6. Входное сопротивление линии
l'2 ch у1 + цгс sh yZ „ Z,+Ze th yZ С., cZ2thyZ + Zc’
^-shyZ + Z2chyZ
(18-31)
При исследовании процессов в линии часто важно знать входное сопротивление линии. Под входным сопротивлением линии ZBX понимают сосредоточенное сопротивление, которым можно заменить линию вместе с приемником на ее конце при расчете режима в начале линии. По определению и с учетом равенств (18-24) получим:
7 __
™ 11
Входное сопротивление при любом сопротивлении нагрузки Z2 можно выразить через входные сопротивления линии при холостом ходе Zx и коротком замыкании ZK. Из (18-31) находим при холостом ходе (Z2 = оо, /„ = 0):
Zx=-^ = -^^-=Z,cthy/—(18-32) Zlx (-2 . , thyZ v '
-% sh г
и при коротком замыкании (Z2 = 0; /72 = 0)
ZK = = Zc th у/. (18-33)
/1к Z2 ch yZ
Разделив числитель и знаменатель правой части (18-31) на th у/, с учетом (18-32) и (18-33) получим:
= (18-34)
Этой формулой удобно пользоваться, если известны Zx и ZK, которые могут быть определены, например, из опытов холостого хода и короткого замыкания линии.
Однако для построения частотных характеристик гвх и <рЕХ лучше выразить ZBX в другой форме.
Обозначив_____________________________________________
Z2/Zc = th m
(18-35)
526
и разделив числитель и знаменатель правой части (18-31) на Zc, перепишем (18-31) с учетом (18-35):
th (m+vO- (18-36)
Формулой (18-36) удобно пользоваться при заданных Z2 и Zc. Тогда из (18-35) можно найти пг.
,, ет — е~т _ 1—e-2m ' Z2
tn/7/— — ]_|_е-2га — 2^-
Отсюда
т = ~ In = «h + (18-37)
m -j- yl = тг -f- al ф j (m2 -f- p/) = x -J- jy, (18-38)
где
x=m1-{-al; y~m2-\-$l. (18-39)
Так как pt+jy------------------------------p-ix+fiji
th (x + jy) =---------——;
v 1 gX+jy^g-ix+jyi
exyjy — ex (c0S у Ц-ysin z/); e (x~^,y>=e x (cos у — j siny),
то, обозначая
th (x + jy) = Te,(ft, (18-40)
посте преобразований получим:
?BX = zcT=zc]/ 1'?7СО5? ; (18-41)
вх с с у cn2x-pcos2j/ ’ ' '
Tax=S + T/ = 6 + arctg-|^7 (18-42)
Более подробный анализ соотношений (18-41) и (18-42) показы вает, что поскольку — 1 _ cos 2п . т-,
С „ -< 4- 1, то Т и <т7, а зна-sin 2у 1 ’ ‘
Рис. 18-6.
чит, гвх и <Рвх изменяются волнообразно при одновременном изменении хи у. В свою очередь из соотношений (18-38) и (18-39) следует, что при изменении длины / линии х и у изменяются линейно в функции от I. Величины х и у изменяются и с ростом частоты, поскольку от нее зависят а, р, т1 и т2. В конечном итоге оказывается, что гвх и <рвх изменяются волнообразно
как при изменении длины ли-
нии I, так и при изменении частоты f. Сказанное иллюстрируют рис. 18-6 — 18-8.
___Ня пис 1816 показано лзменение ?,._и zv для медной двухпро-водной воздушной линии связи при диаметре проводов 3 мм и пр~и
527
частоте / = 800 Гц (X = 375 км) в зависимости от длины линии / На рис. 18-7 дано изменение гвх, а на рис. 18-8 изменение медной линии связи в функции частоты при г2 = zt./2 и при г2 = 2zc (в обоих случаях <р2 = 6).
Отметим также, что через входные сопротивления линии при холостом ходе и коротком замыкании легко выразить Zf и у. Перемножив, а затем разделив почленно (18-32) и (18-33) и извлекая корень, получим:
Zc = yrZxZK = '/zxzKe 2 ; (18-43)
th yl=ZK/ZX = У zjz^e = te'x, (18-44)
где
1=-^У*., (18-45)
откуда
th2a/ = -^i; tg2p/=-^i (18-46)
При помощи таблиц круговых и гиперболических функций можно найти а, р и по ним у.
18-7. Коэффициент отражения волны
В § 18-4 было показано, что при произвольном сопротивлении нагрузки Z2 в конце линии коэффициент Л4 не равен нулю (18-23), т. е. в линии возникает обратная волна. Это можно учесть, введя так называемый комплексный коэффициент отражения волны или, короче, коэффициент отражения ii, определив его в общем случае как отношение комплексов напряжений или токов обратной и прямой волн в любой точке линии:
U2 + hZc Z2+Zc~ ' U0-/
528
В более узком смысле слова коэффициент отражения определяется в точках, где есть какая-либо неоднородность (конец или начато линии)
Зная, например, прямую волну напряжения и коэффициент отражения п, легко можно вычислить обратную волну напряжения Так, если
Йпр = А^, то
Йо6 = Л4с у'с = пА^х.
Отсутствие обратной волны имеет то преимущество, что вся мощность, переносимая прямой волной к концу линии, поглощается сопротивлением нагрузки При наличии обратной волны часть мощности прямой волны возвращается источнику обратной волной. Поэтому мощность, выделяющаяся в сопротивлении нагрузки, будет меньше, если считать, что мощность источника Рг остается неизменной.
18-8. Согласованная нагрузка линии
Если в конце линии включено сопротивление нагрузки, равное волновому:
Z2 = Zc=t72//2,
то, обращаясь к формулам (18-23), находим, что
Л3 = Й2; Л4 = 0, (18-48)
т е отраженная волна не возникает Такую нагрузку называют согласованной нагрузкой или нагрузкой без отражения.
При этом, как следует из (18-47), коэффициент отражения п = 0.
Из написанных выше соотношений с учетом (18-48) получим: Й=Ппр=Й^; = (18-49)
Отсюда следует:
(18-51) ' /г h
т е для любой точки линии отношение комплексов О и / равно волновому сопротивлению Zc Поэтому режим работы генератора, питающего такую линию, не изменится, если в любом сечении линии ее разрезать и вместо отрезанной части линии включить волновое сопротивление. Режим работы оставшегося участка линии также не изменится.
Из соотношения (18-31) следует, что для согласованной линии (Z2 = Zc) входное сопротивление равно волновому ZBX = Zc.
529
Полагая начальную фазу напряжения в конце линии равной нулю, т. е. О2 = U2, запишем на основании (18-49) и (18-50) мГНо венные значения напряжения и тока в любой точке линии:
и — sin (со/ ф- рх); i sin (со/ ф- Рх — 6). (18-52)
Полученные соотношения изображены на рис. 18-9. Точки пересечения оси абсцисс с кривыми напряжения и тока сдвинуты на расстояние 6 /р, причем согласно сказанному в § 18-5 величина g отрицательна. Поэтому, применяя термины, справедливые, строго говоря, только для синусоидальных величин, можно сказать, что
Рис. 18-9.
ток опережает по фазе напряжение на угол | 6 |. Напряжение и ток в различных точках линии различаются не только по амплитуде, но и по фазе.
Л1ощность, проходящая через какое-нибудь сечение линии,
Р = UI cos 6 = е2ах cos 6.
(18-53)
Эта мощность уменьшается по мере удаления от начала, так как на каждом элементе длины линии поглощается мощность
dP = 2а — е2кх cos 6 dx~ (r0I2 ф- g0U2) dx, (18-54)
zc
равная сумме потерь в сопротивлении проводов и в проводимости изоляции на элементе линии dx. Равенство средней и правой частей соотношения (18-54) можно показать после преобразований. Для этого следует в средней его части заменить U2eax, ё'-х, a, zc, 6 их значениями из равенств (18-49), (18-50), (18-27), (18-10) и (18-11), выразив предварительно cos 6 через cos 2б по известной формуле cos 6 = V (1 + cos 2б)/2.
Мощность, передаваемая по согласованной линии, называется естественной или натуральной мощностью. Режим передачи естественной мощности может иметь место в линиях, если сопротивление нагрузки равно волновому сопротивлению (Z2 = Zt). Средние значения естественной мощности для линий 500, 400, 220, 110 и 35 кВ соответственно равны 600, 360, 120, 30, 3 МВт. Отсюда видно, как сильно увеличивается естественная передаваемая мощность с увеличением напряжения линии.
Мощность, получаемая линией,
Pj=/ДД cos 6.
530
Мощность в конце линии
cose.
На основании равенств (18-49) и (18-50)
Л = t/j/j cos 6 = U2I^1 cos 6 = P2e2aZ (18-55)
к. п. д. линии
Т]= Ррг=е (18-56)
Все сказанное здесь о согласованной линии применимо и кбеско-;чно длинной линии, поскольку в последней не может возникнуть сраженная волна.
Пример 18-3. По результатам примера 18-1 определить- 1) естественную >щиость, передаваемую в Москву при напряжении в Москве 1/2л = р 3-220 кВ; напряжение на ГЭС; 3) токи в начале и в конце линии.
Решение. Естественная мощность, передаваемая в Москву,
Р., = 31/гф/2 cos е -= 3 cos fi = 363,8 МВт.
гс
Ток в Москве
/2 = H2/ZC = 553 Z. 5°23' А.
Фазное напряжение на ГЭС
П1=Е2е«^ = 241 Z. 55° кВ; t/u = 241 1'3 = 417 кВ.
Ток на ГЭС
/1 = (.'1/Zc = 607 Z 60°23' А.
18-9. Линия без искажений
Если токи и напряжения линии электросвязи несинусоидальные, но периодические, то, разлагая их в тригонометрические ряды, можно к каждой гармонике применить полученные результаты. Однако токи и напряжения линий связи, соответствующие передаваемой по ним речи и музыке, — непериодические функции времени. В этом случае наеденные соотношения можно применить, разлагая непериодические токи и напряжения в непрерывный спектр (см. гл. 15)
Подчеркнем некоторые особенности линий связи. Для кабельных линий связи благодаря близкому расположению проводов друг от друга индуктивное сопротивление х0 = (oL0 мало по сравнению с активным г0 и им в первом приближении можно пренебречь Точно так же активной проводимостью g0 между проводами можно пренебречь по сравнению с реактивной проводимостью Ьо = ыС0. Поэтому, полагая Lu = 0 и gu — 0 и, следовательно, Zo = r0, Yo = /отСо, из общих формул (18-27) и (18-10) получим:
Из этих соотношений видно, что коэффициент затухания а и коэффициент фазы р пропорциональны квадратному корню из частоты. Поэтому гармоники более высоких частот затухают сильнее, что приводит к искажению речи, музыки и телеграфных сигналов, т. е. к так называемым амплитудным искажениям. Фазовая скорость также зависит от частоты. Зависимость фазовой скорости от частоты приводит к изменению формы кривых токов и напряжений в конце линии по сравнению с их Формой в начале линии. Эти искажения называются ‘.фазовыми. Амплитудные искажения также изменяют форму кривых. Подчеркнем
531
особо, что при высоких частотах г0 << ы£(|; g„ < ыС\, и согласно (18-27) коэЛж циент фазы Р = ы]-' LyC0 Поэтому фазовая скорость не зависит от частоты* фазовые искажения практически отсутствуют Далее отметим, что из-за амплит’Л ных и фазовых искажений кабельные линии связи без особых йриспособлен^-непригодны для передачи речи и музыки на большие расстояния ‘ Ии
Воздушная или кабельная линии связи, ие снабженные специальными vc лителями, пригодны для передачи речи и музыки, koi да коэффициент затух**" ния a tie зависит от частоты и невелик Так как сохранение тембра звука и пЛ' борчивости речи определяется обертонами в их составе, т е высшими гармони ками токов, то исследование выражения а на минимум как для кабельных, так и для воздушных линий связи надо проводить, полагая частоту и Достаточно большой, а следовательно, выражения r0/wL0 и gB!<JtC0 достаточно малыми.
После некоторых преобразований для а будем иметь.
а— 2 VC0!L0+gb V I о/Со) .
Рассматривая а как функцию отношения z= 10fC0, найдем минимум а в функции г Приравнивая da/dz= 0, получаем значение г, при котором а минимально
Любопытно отметить, что это условие было получено Хевисайдом еще в 1893 г Значение аМ1П1 и коэффициент фазы (3 найдем из общих формул (18-27) для а и р с учетом условия (18-57)
юмин= р = со j/LoCo- (18-58)
Линию, удовлетворяющую условию (18-57), У которой, следовательно, коэффициент затухания не зависит от частоты и минимален, называют линией без искажений
При тех же условиях согласно (18-10) волновое сопротивление
= = 6 = 0. (18-59)
Иначе говоря, волновое сопротивление линии без искажений не зависит от частоты и активное
Фазовая скорость в линиях без искажений также не зависит от частоты
4 о=Ю=-72==-. (I8 60)
Р I ЛА
Отметим дополнительно, что соотношение (18-57) легко вывести, если исходить только из условий независимости Zc, а и v от частоты В самом деле, представив Zc в виде
7 _ l/ + -|/ Lo fo/Z-Q-HCO
г gb + /wCo г Св у fti/AT/01’
заключаем, что Zc не зависит от частоты и равно V L^C,., если выполняется условие (18-57) Учитывая (18-59), находим коэффициент распространения
Т = а + /Р — V(го + /юД>) (йггЛ’А) = (&iH"/o>C(l) 1/" =
= teo+/«co)Zc = (&+/wCo) у = откуда ___
- - a = gol/ = ^= -7-^. ------------
Г 1вс0
532
Как указывалось, у кабельных линий связи Lo/Co мало, a rB/gB, наоборот, досыточно велико. Выполнить условие (18-57) можно, увеличив индуктивность кабеля и тем самым снизив величину затухания.
В 1900 г. был предложен метод увеличения индуктивности цепи путем сосредоточенного включения индуктивности (катушки индуктивности, включаемые в линию примерно через каждые 1,7 км). Такой метод приводил к снижению затухания примерно в 4 раза в звуковом диапазоне частот и тем самым увеличивал дальность связи также в 4 раза Если же очень большого (возможного в то время) увеличения дальности связи (до 300—350 км) не требовалось, то метод сосредоточенного включения индуктивности все же применялся по экономическим соображениям, так как позволял при выполнении равенства (18-57) увеличить активное сопротивление, т. е. снизить диаметр провода, а следовательно, уменьшить расход меди и свинца.
Однако позднее встал вопрос об отказе от дополнительного увеличения индуктивности кабельной линии для дальних передач, так как увеличение индуктивности приводило к уменьшению фазовой скорости. Нормами установлено, что телефонная связь удовлетворительна, если максимальное время распространения сигнала не превышает 0,25 с (при таких условиях спрашивающий может получить ответ через 0,5 с, что и определяет наибольшую дальность связи). Наибольшая дальность телефонной связи по линии с сосредоточенной дополнительной индуктивностью согласно расчету равна 3200 км, а практически составляет 2500—2800 км, что объясняется включением в цепь усилителей и других устройств (в том числе станционных), замедляющих распространение электромагнитной энергии
Для связи на небольшие расстояния увеличение индуктивности и в настоящее время дает существенную экономическую выгоду. Отметим еще, что согласно нормам для получения отчетливой телефонной связи при длине линии I затухание al не должно превосходить 10,5 дБ
Если линия без искажения согласована с нагрузкой, т. е.
Г 2 = I' Eq/Co,
то из формул (18-49) и (18-50), полагая Т/2 = 1/2, получаем:
w = U2те^г,,ё°х sin co (tYLBCB х);
i = elr,&x sin ш (/ + (/ £ с0 х).
VLB/CB
Эти формулы показывают, что ток и напряжение в любой точке линии совпадают по фазе и иа любом элементе длины dx:
L01’2 dx — -% Со«2 dx,
т е энергии магнитного и электрического полей в любой момент времени равны Друг другу В частности, они одновременно достигают максимума и одновременно проходят через нуль
В случае произвольной нагрузки это равенство энергий имеет место для линий без искажений [и для линий без потерь (см. § 18-11)] только отдельно Для прямой и обратной волн.
18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями
Рассмотрим холостой ход линии. Если в нагрузочном режиме напряжение и ток в конце линии были Й2 и /2, то после отключе-_ния приемника (/2 = 0) напряжение на конце ее при неизменном напряжении в начале линии С\ изменится. Изменив напряжение-
533
й начале линии так, чтобы напряжение в конце линии осталось равным из уравнений (18-24) при холостом ходе получим:
Ux = U2chyx; lx=^shyx. (18-61)
Если теперь, не изменяя напряжения в начале линии, закорО-тить ее на конце, ток на конце уже не будет равен /2 и в ряде случаев возрастет. Изменив напряжение в начале линии так, чтобы ток в конце короткозамкнутой линии стал равным /2, из уравнений (18-24) получим:
f7K=/2Zeshyx; /K = /2ch?x. (18-62)
На основании соотношений (18-24), (18-61) и (18-62) можно при этих условиях написать:
Й = ЙХ + ЙК; /=7х-|-/к. (18-63)
Полученные формулы показывают, что действительные ток и напряжение в любой точке линии могут быть разложены на составляющие холостого хода и короткого замыкания, чем иногда удобно пользоваться в расчетах. Например, при расчете распределения тока и напряжения вдоль нагруженной линии с потерями можно сначала найти составляющие напряжений и токов при холостом ходе и коротком замыкании в отдельности, а затем, геометрически суммируя их, получить действительные токи и напряжения.
Покажем, как можно построить векторные диаграммы и графики, дающие распределение величин и фаз токов и напряжений вдоль линии, нагруженной на конце.
Решим сначала эту задачу в режиме холостого хода линии. Из уравнений (18-61), полагая (?2 = U2, имеем:
Йх = (72сЬуХ=
7Х= shух=Л2 e-/6sh ух—~(e'ix'lj'^x — е а*~/Р*).
Геометрическим местом концов векторов, определяемых выра-жением еах+,^х, в полярных координатах является логарифмическая спираль, раскручивающаяся при положительных х и закручивающаяся при отрицательных. Построение ее было дано в § 18-3.
На рис. 18-10 отрезок ООГ в масштабе mv изображает напряжение UJ2. Точки 1, 2, 3, ..., И, 12 спирали соответствуют положительным х, а точки Г, 2', 3', ..., 1Г, 12' отрицательным значениям х. Легко видеть, что вектор Ох для любой точки линии равен сумме двух векторов e“v+yl5x и <**-/₽*, повернутых в противоположные стороны от оси абсцисс на один и тот же угол Р*-Складывая, например, векторы 03 и 03', получаем вектор 0Cs, определяющий точку на годографе гиперболического косинуса от комплексного аргумента, т. с. точку на геометрическом месте
534
ректоров Ux. Выполняя подобное построение для различных углов рх, найдем векторы ОСо, ОС1г 0С2... и получим спиралеобразный развертывающийся годограф гиперболического косинуса, т. е. годограф напряжения холостого хода линии.
Точки Сь С2, С3 и т. д. определяют концы векторов напряжений холостого хода на расстояниях Z/12, 2Z/12, 3V12 и т. д. от конца линии, а точка Со представляет напряжение О2 в конце линии.
Рис. 18-10.
Построение геометрического места концов векторов тока холостого хода /х покажем для несколько упрощенного случая, от которого можно перейти и к общему случаю. Положим сначала, что аргумент волнового сопротивления 6=0. Тогда геометрическое место концов векторов /х, т. е. спиралеобразный развертывающийся годограф гиперболического синуса, легко получить, если выбрать отрезок ООГ равным в масштабе тг величине U2I2zc и построить разность векторов
^2 xza't/Pa 2гс
и е~ах~^х.
2гс
Отметим, что ток в конце линии равен нулю, а точки Slt S2, Ss и т. д. определяют концы векторов тока холостого хода на расстояниях V12, 2V12, 3V12 и т. д. от конца линии.
Кривые на рис. 18-10 показывают, что при холостом ходе напря-_ жение по мере удаления от конца линии сначала уменьшается, а ток увеличивается до тех пор, пока напряжение не достигнет
535
некоторого минимума, а ток — максимума, причем в общем случа в разных точках линии. После этого напряжение начнет возрастать а ток падать, пока напряжение не достигнет максимума, а ток -Z минимума и т. д. Максимумы и минимумы, постепенно сглаживаясь чередуются через интервалы, примерно равные половине длины волны, причем максимумы напряжения сдвинуты на расстояния примерно равные четверти длины волны чгю отношению к максимумам тока.
Таким образом, если длина линии не превышает Z/4, то, как следует из рис. 18-10, напряжение монотонно возрастает по направлению к концу линии (ср. длины отрезков 0С3, ОС2 и ОС/ по сравнению с отрезком ОС0). Это повышение напряжения в конце линии при холостом ходе объясняется влиянием емкостного тока, который в достаточно длинных линиях высокого напряжения может достигать значительной величины. Емкостный ток, опережая по фазе создающее его напряжение, вызывает такое падение напряжения в индуктивности линии, которое и приводит к увеличению напряжения в конце линии по сравнению с напряжением в ее начале.
Кривые рис. 18-10 показывают также, что на протяжении первой четверти длины волны от конца линии ток холостого хода опережает напряжение (векторы 08\, OS2 опережают векторы ОСЪ ОС2). Затем ток отстает по фазе от напряжения (0Х4 и OS5 отстают от ОС4 и 0С5). Начиная с третьей четверти длины волны ток холостого хода опять опережает напряжение и т. д.
Напряжения и токи в любой точке линии можно определить, заменив ch ух и sh ух их модулями:
Ux~\ U2ch (ax + /px)| = 6/2’j/ch2axcos2 ₽x-J-sh2 ах sin2 [5х~
= ^2 ]/"_|_ A. (cos2px - sin2 Рх);
7 /s г 7S ch 2ссх cos 2р% "х —^2 2 \
Ix = sh (ах + /рх) I • Ц=-4 сЬ2с/-а'тсоАЁ£.
лс г гс 2
На рис. 18-11 построены кривые ch2ax и cos2Рх в зависимости от х, а также кривые ch 2ctx ± cos 2Рх, ординаты которых пропорциональны £/* и /(. Эти кривые показывают, что Ux и изменяются с чередующимися максимумами, причем значения их постепенно увеличиваются, а отношение максимума к минимуму стремится к единице. В конце линии ток равен нулю, а напряжение имеет максимум. Характер изменения кривых Ux и 1Х тот же, что и кривых Ux и Д, но с меньшими пульсациями.
Входное сопротивление линии при холостом ходе было найдено выше (18-22). С изменением длины линии I мнимая часть комплекса th yl изменяет знак, т. е. реактивная составляющая Zx имеет
536
io емкостный, то индуктивный характер. Это видно и из кривых рис. 18-10, где напряжение t7x то отстает от тока /х, то опережает его. Подобным же образом зависит входное сопротивление линии при холостом ходе и от частоты. При изменении частоты изменяется
не только величина, но и знак аргумента входного сопротивления.
Отметим, что при холостом ходе коэффициент отражения (18-47) в конце линии n = 1. Это значит, что комплексные напряжения (и ток) прямой и обратной волн в конце линии равны по абсолютному значению и по знаку (находятся в фазе), т. е. отражение волны от разомкнутого конца линии происходит без перемены знака.
На рис. 18-12, а и б приведены для некоторого момента времени кривые прямой и обратной волн
[апряжения и тока при холостом ходе, а также кривые результи-
>ующих напряжения и тока холостого хода.
Аналогично может быть найдено распределение токов и напряжений при коротком замыкании линии.
Рис. 18-12.
На основании соотношений (18-62) величины напряжений и оков в любой точке линии могут быть определены по формулам т,2_____________________,s s ch 2ах—cos 2рх
С/ к — 1’
ch2ax-Lcos2(3x
Ji 2 ‘
Полученные соотношения показывают, что кривая UI аналогична кривот/х на рис. 18-11, а кривая аналогична крнвои 6'х.
537
Входное сопротивление линии при коротком замыкании был найдено выше (18-33). Отметим, что и в этом случае реактивна° составляющая ZK в зависимости от длины линии и от частоты измеЯ няет знак.
Как следует из соотношения (18-47), при коротком замыкании коэффициент отражения в конце линии п — —1. Это означает, что комплексные напряжения (и ток) прямой и обратной волн равны по величине и противоположны по знаку (находятся в противофазе), т. е. отражение волны от короткозамкнутого конца линии происходит с переменой знака. Кривые прямой и обратной волн напряжения и тока, а также кривые результирующих напряжения и тока при коротком замыкании аналогичны соответственно кривым тока и напряжения при холостом ходе.
Пример 18-4. По данным примера 18-2 определить линейное напряжение в конце линии (в Москве) и ток в начале линии (на ГЭС) при сбросе всей нагрузки на конце линии и сохранении фазного напряжения на ГЭС, равного 220 кВ.
Решение
Й2Х = -^- =----- = 382 z —7°22' кВ;
ch у/ 0,581е/7 22
t/2x„ = /3.382 = 661,5 кВ.
Повышение напряжения при холостом ходе
Д1/= ^5=^ 100 = 73,6%; /1Х=-^- sh у/ = 792 /. 84с24' А.
Интересно отметить, что и ток в начале линии при холостом ходе получился на 45% больше того же тока в режиме нагрузки:
792
/1х =5-48 Л = 1,45/х,
хотя напряжение в начале линии во втором случае (t/x = 220 кВ) почти равно напряжению в первом случае (С7± = 222 кВ).
18-11. Линии без потерь
Если положить равными нулю сопротивление проводов линии г0 — 0 и проводимость утечки между проводами g0 = 0, то получим так называемую линию без потерь.
Для коротких высокочастотных линий, применяемых в радиотехнике, часто с достаточно большой точностью можно пренебречь сопротивлением г0 и утечкой g0 по сравнению с и соС0. Поэтому в радиотехнике очень часто рассматривают двухпроводные воздушные линии и коаксиальные кабели как линии без потерь. Вообще же говоря, линию без потерь следует рассматривать как идеализацию действительной линии.
Из соотношений (18-8), (18-10), (18-15) и (18-16) для такой
линии получим: ,____
а=0; ₽ = со/£0С0;
Zc = |/L0/C0 = zt; 0 = 0;
(18-64)
(18-65)
V— —l/р Д)С(Ь
(18-66) (18-С7)
л=2ji/p,
538
|е. у линии без потерь затухание равно нулю, а волновое сопро-(Влснис активное и не зависит от частоты. Точно так же и фазовая Ьрость в линиях без потерь не зависит от частоты. Заметим, цто р, v, Z для линии без потерь такие же, как и для неиска-жающсй линии с потерями.
Преобразуем формулу (18-66) для фазовой скорости к другому виду. Это преобразование проведем, например, для двухпроводной линии. Емкость единицы длины двухпроводной линии, Ф/км,
<18-68)
а индуктивность той же линии, Г/км,
L0=-^ln(d/r0); (18-69)
здесь г0 — радиус провода, a d — расстояние между осями проводов.
Подставляя значения Lo и Со в формулу (18-66) для v, получаем:
t>=—(18-70) | е0р0 ец | Еаца
ж еа и р.а — абсолютные диэлектрическая и магнитная прони-жмости среды между проводами.
Но, как известно, скорость света в вакууме'
с= 4=^- (18-71)
I' еоНо
и для фазовой скорости можно записав:
"“-ГДТ <|8-72>
Для воздушных линий е = р = 1 и фазовая скорость совпадает со скоростью света. Для кабельных линий е > 1 и v < с.
Аргумент волнового сопротивления линии без потерь 0=0, т. е. токи прямой и обратной волн совпадают по фазе с напряжениями.
Уравнения длинной линии с гиперболическими функциями от комплексного аргумента (18-21) и (18-24) для линии без потерь переходят в уравнения с круговыми функциями от вещественного аргумента. Если заданы напряжение Й, и ток Д в начале линии, то получим:
U~U1 cos Рх — /7^ sin рх;
7 —— j L.1 sin рхф- 7( cos рх.
Если заданы напряжение О, и ток /2 в конце линии, то имеем: U = U2 cos рх+ji-,Zc sm рх; '
(18-73)
539
Входное сопротивление линии согласно (18-31) и (18-64)
^2 Ъ 1ZC Ш
^вх ‘ % с' ' •
Нс
— (18-67)
(18-75)
Переходя в уравнениях (18-74) к мгновенным значениям при Д2 = t/2, /2 = получаем:
« = H2mcos Pxsin (o/-]-/2mzcsin рх sin ^co/-J--y — <р2^; (18-76а)
i = ^—sin pxsin (a>/-J--^4-/2mcos |3xsin (at — <p2). (18-766)
Кривые распределения мгновенных значений тока.и напряже
ния вдоль линии на расстоянии, равном длине волны, при <р2 > О для трех моментов времени представлены на рис. 18-13. Кривые и выражения (18-76) показывают,
Рис. 18-13.
что распределение напряжения и тока вдоль_ линии в каждый данный момент является синусоидальным. Рассматривая их одновременно, видим, как изменяются кривые распределения тока и напряжения по линии на протяжении трети периода. Разумеется, изменение тока или напряжения во времени в любой фиксированной точке линии также будет синусоидальным.
Остановимся еще на свойствах линий без потерь, длиной в четверть и в половину длины вол-„ , 7 2л к л
ны. При и р/=-у-у = -%
из уравнений (18-74) получим: 0!=}!^ 11=1й^гс. (18-77)
В этом случае напряжение (ток) в начале линии пропорционально току (напряжению) в конце и опе
режает его по фазе на 90°. Для поддержания постоянного напряжения в конце линии {7а, которое может изменяться вследствие
изменения нагрузки на конце линии, необходимо в начале линии поддерживать постоянным не напряжение Olt а ток
Для линии длиной в полволны 1=~2 и — из уравнения
(18-74) имеем:
f71==—Й2; 4 = —/2, (Т8До7
540
т. e. напряжение и ток в начале линии равны по величине и противоположны по фазе напряжению и току в конце линии. Если не считать поворота векторов на 180°, питание приемника от источника энергии происходит таким образом, как будто бы самой линии передачи нет.
18-12. Стоячиё волны
Рассмотрим случаи, когда активная мощность, поглощаемая приемником в конце линии без потерь, равна нулю. Это может быть при холостом ходе, коротком замыкании и чисто реактивной нагрузке.
При холостом ходе (/2 = 0, Z2 = оо) из уравнений (18-74)
следует:
U = U2 cos Рх;
/=/ -74 sin Рх.
zc
(18-79)
Мгновенные значения напряжения и тока при О2 — равны:
tz = t/2mcospxsinco/; ' /=7421. sin Pxcosco/
zc
(18-80)
и представляют собой уравнения стоячих волн. Математически уравнение стоячей волны представляется произведением двух функций, причем аргумент одной зависит только от времени, а другой — только от координаты.
Стоячей волной называется процесс, получающийся от наложения прямой и обратной волн с одинаковыми амплитудами.
Действительно, при холостом ходе (Z2 = ос) п = 1 и, как следует из (18-47), А3 = Выражение для напряжения (18-80) можно представить в виде суммы (а для тока в виде разности) прямой и обратной волн с одинаковыми амплитудами:
ц —-74—sin (со/-J-рх) +-7412-sin (со/ —рх); (18-81а)
i = in (со/ + рх) sin (со/ - рх). (18-816)
При холостом ходе на конце линии (х = 0) и в точках, отстоящих от конца на расстояниях
x^kJ=k-2>
где k — целое число, имеем в любой момент времени максимумы Напряжения, называемые пучностями, и нули тока, называемые узлами (рис. 18-14). На расстояниях же от конца линии
—--------------х — (2* -(2/? 1 1) 4----------------
541
всегда наблюдаются узлы напряжения и пучности тока. Узды и пучности тока и напряжения неподвижны. Узлы тока совпадают с пучностями напряжения, и наоборот. Ток опережает по фазе напряжение на 90°, когда знаки sin рх и cos рх одинаковы (0-s< х -С Л/4; Л/2 ==£ х ЗЛ/4 и т. д.), и отстает по фазе на 90° от напряжения, когда знаки sin рх и со» рх противоположны (Л/4 - х =С Л/2; ЗЛ/4 х < X, и
Рис. 18-14.
т. д.).
Входное сопротивление разомкнутой линии без потерь
Zx = — /Zc ctgPx =
= — /zc ctg-^-x, (18-82)
т. е. чисто реактивное, и характер его определяется длиной линии х и частотой f (или длиной
волны Л). Изменение абсолютного значения и характера входного
сопротивления в зависимости от длины линии показано на рис. 18-15. От х = 0 до х — № от х = Л/2 до х = 3Z/4 н т. д. ли-
ния представляет собой емкостное сопротивление, а от х = Л/4 до х = Л/2, от х = ЗЛ/4 до х — Л
Рис. 18-15.
и т. д. — индуктивное сопротивление. При х = 0, Л/2, Л и т. д.
Рис. 18-16.
линия может быть представлена параллельным резонансным контуром, а при х = Л/4, ЗЛ/4, 5Л/4 и т. д. — последовательным резонансным контуром.
При коротком замыкании (О2 = 0; Z2 = 0) из уравнений (18-74) получим: Л
U = /'Г2 сsin рх; Т—12<лУъ$х. (18-83;
542
Мгновенные значения
u = kMzc sin Рх cos со/; i~ I2m cos Px sin со/,
Рис 18-17.
т. е. напряжение и ток представляют собой также стоячие волны. Для любого момента времени на конце линии (х = 0) и в точках, отстоящих от него на целое число полуволн (W2), имеем узлы напряжения и пучности тока, а в точках, отстоящих от конца линии на расстояния, равные нечетному числу четвертей длин волн (2/г + 1) Х/4, получаются пучности напряжения* и узлы тока (рис. 18-16). При этом пучности напряжения и пучности тока, а также узлы напряжения и узлы тока сдвинуты на четверть длины волны друг относительно друга. Напряжение опережаег по фазе ток на 90°, когда знаки sin Рх и cos рх одинаковы (0 -С х 7-/4, V2 гС х гС 3Z/4 и т. д.), и отстает на 90е от тока, когда знаки sin рх и cos Рх противоположны (Z/4 •< х Z/2, 3Z/4 - • : х - • : Z и т. д.).
Выходное сопротивление короткозамкнутой линии без потерь 2тт
ZK=/4 tg рх=jzc tg ~ х (18-84)
также чисто реактивное и в зависимости от длины линии / и частоты/ может быть индуктивным или емкостным. Изменение входного со
противления в зависимости от длины короткозамкнутой линии показано на рис. 18-17. Из него видно, чю от х = 0 до х = V4 от х — к/2 до х == 3Z/4 и т. д. линия представляет собой индуктивное сопротивление, а от х = Z/4 до х = Z/2, от х = 3Z/4 до х — к и т. д. — емкостное сопротивление. При х = 0, к/2, к и т. д. линия может быть заменена последовательным резонансным контуром, а при х = к/4, Зк/4, 5Z/4 и т. д. — параллельным резонансным контуром.
При согласовании линии с нагрузкой (см. § 18-8) приходится включать индуктивное или емкостное сопротивление параллельно или последовательно приемнику. В качестве такого сопротивления при высоких частотах может служить короткозамкнутая или разомкнутая линия без потерь. Но, воспользовавшись линией для согласования, разумно взять ее наименьшей длины, т. е. как показывают рис. 18-15 и 18-17, вместо емкостного сопротивления выбирать разомкнутую линию длиной менее к/4, а вместо индуктивного — короткозамкнутую, длиной менее к/4. Длину разомкнутой линии без потерь х можно определить при заданном хс из формулы
___-____(18-8S)
OjC~ -д \ /
543
Величину х можно найти и из кривой гх, приведенной и3 рис. 18-15, если построение выполнено достаточно точно. Длину короткозамкнутой линии без потерь х можно определить при заданном xl из формулы
aL=xL = zctg-^x. (18-86)
Величину х можно также найти прямо из кривой zK, приведенной на рис. 18-17.
При чисто реактивном сопротивлении нагрузки Z2 = ч? Д2 в линии также будут стоячие волны. Действительно, как было только что показано, емкостное л индуктивное сопротивления могут быть заменены отрезками разомкнутой или короткозамкнутой линии. Сле-
довательно, линия с реактивным сопротивлением нагрузки ничем не отличается от разомкнутой или короткозамкнутой линии большей длины. Только в конце линии с реактивным сопротивлением нагрузки не будет ни пучности, ни узла тока или напряжения (рис. 18-18).
В узлах ток или напряжение равны нулю в любой момент времени, поэтому мощность в них
и,1
всегда равна нулю и энергия через
Рис. 18-18. эти точки проходить не может.
Следовательно, передачу энергии по линии осуществляют только бегущие волны. В случае стоячих
волн движение энергии вдоль линии возможно только на участках между двумя смежными узлами тока и напряжения и связано с обменом энергией между электрическим и магнитным полями на каждом из таких участков. В разомкнутой или короткозамкнутой линии длиной несколько меньше четверти волны движение энергии (обмен энергией между генераюром и линией) происходит вдоль всей линии, так как только на конце линии есть узел тока (разомкнутая линия) или узел напряжения (короткозамкнутая линия).
Предположим теперь, что у линии без потерь активное сопротивление нагрузки Z2 = г2. Обозначая
zc/r2=K
и подставляя в выражения (18-74), после простых преобразований получаем:
f/ = f/2[K^ + (l-^cospH; / = ~2 [Ke^ + /(1-K)sinpx]
zc
и при Й2 = U2
u = U2mK sin (at рх) (1 — /<) cos Pxsin со/;
₽*) j Р г sin V—
544
Линия, питающая антенну
Дьтенна
0-
гс
zci Z8z Т
гг
Л
4
0-
Рис 18-19.
В этих уравнениях Напряжение и ток представлены суммами дгл х слагаемых. Первое из них — бегущая волна, а второе — стоячая волна. Таким образом, если линия не согласована с нагрузкой (Д' ф 1), то напряжение и ток в линии можно представить суммой бегущих и стоячих волн. Чем сильнее отличается от единицы в ту или другую сторону, тем резче выявятся стоячие волны. При К = 0 (холостой ход) и 7< = оо (короткое замыкание) в линии наблюдаются только стоячие волны. Чем ближе Д' к единице, тем резче проявляются бегущие волны. Стоячие волны отсутствуют при К = 1 или r2 = Zc, т. е. когда нагрузка согласованная.
Линия без потерь длиной в четверть 1 волны применяется в качестве согласующего элемента между какой-либо линией без потерь и активным сопротивлением нагрузки на ее конце Z2 — г>> не равным волновому сопротивлению линии На
пример (рис. 18-19), при помощи линии длиной в четверть волны можно согласовать линию (без потерь), питающую антенну, с самой антенной, входное сопротивление которой Z2 = г2, т. е чисто активное.
Найдем входное сопротивление четвертьволновой линии I = Л/4, нагруженной на антенну, прн Z2 = г2 = г2 на основании (18-75):
, . , 2л 7.
22 + /^^
7. , •
/zstg +zc
Так как tg л/2 = оо, то
Для согласования питающей линии с антенной необходимо, чтобы
гБх=
г,,? г j — волновое сопротивление питающей линии.
Отсюда
zc = С
В этом случае четвертьволновая линия без потерь называется четвертьволновым трансформатором, так как она как бы приводит (трансформирует) волновое сопротивление питающей линии к сопротивлению нагрузки.
Линия без потерь длиной в четверть волны, замкнутая в конце подогревателем термопары, т. е. практически накоротко, применяется как вольтметр для измерения распределения напряжения в двухпроводной линии, питаемой генератором с длиной волны 7. (рис 18-20). Термопара присоединяется к милливольтметру, измеряющему ее э. д с Кроме того, дается специальная градуировоч- ’ пая кривая, т е. зависимость э д с термопары от тока нагрева ее спая.
Соотношение между напряжением в пучности ил (начало короткозамкнутой линии) и током в пучности /2 (ее конец) определяется из (18-74):
lh = i#cj sin (ЗХ/4, т е. ------------------------------------------------------------------------------
18 Основы теории цепей
545
Определив по показаниям милливольтметра ток в пучности четвертьводп вой линии, при помощи последней формулы вычисляют напряжение в ее начайе' т е напряжение между проводами исследуемой липин Перемещая место при’ соединения четвертьволновой линии вдоль исследуемой линии, можно измерить распределение напряжения вдоль последней
Как видно из рис 18 17, входное сопротивление короткозамкнутой линии без потерь длиной Z./4 бесконечно велико, поэтому ее подключение не влияет на распределение напряжения вдоль исследуемой линии
В сантиметровом и дециметровом диапазонах волн для измерения комплекс ного входного сопротивления какого иибудь приемника применяют так назы ваемую измерительную линию в виде отрезка коаксиальной линии без потерь В коаксиальной линии прорезают щель, в которую вводят зонд, представляющий собой небольшой стерженек (или рамку) Щель вырезается параллельно линиям поверхностного тока, протекающего по оболочке коаксиальной линии Как показывает анализ и опыт, наличие щели изменяет лишь в слабой степени первоначальную конфигурацию поля в измерительной линии Зонд, который
извлекает небольшую часть энергии, проходящей по измерительной линии, соединяется с индикатором Показания индикатора пропорциональны напряженности электрического поля, а следовательно, и напряжению в данном сечении измерительной линии Перемещая зонд вдоль щели, можно исследовать поле внутри измерительной линии В конце линии присоединяют приемник, Комплексное входное сопротивление которого измеряется По распределению напряжений вдоль измерительной линии можно определить 'сопротивление нагрузки (рис 18-21)
Распределение напряжения и тока вдоль линии определяется уравнениями (18-7) и (18-9) При отсчете координаты от начала линии
U=A1e-Jflx+A2eJPx, 7= — (А1е^Рх—А2е^х).
гс
Комплексный коэффициент отражения
A>eJ&x j <2jix-+$2-4>p
n = ~—— =- — ----------= ne ,
Aye-JPx Ale^te~J^x
где n = Л2Мх — его модуль
Модуль коэффициента отражения п можно вычислить, определив коэффициент бегущей волны напряжения
& = мин/Uмакс»
здесь 1/ыин и 17макс — минимальное и максимальное напряжения в линии, измеряемые непосредственно индикатором В точке к = I — х0, где прямая и обратная волны находятся в противофазе, имеем так что
А2,
546
В точке, где они совпадают по фазе напряжение максимально: ^макс — -Л j + Ag.
Следовательно, А —Ла 1—п
Ai~j^A2 1 -|-п ’
откуда
С учетом выражения п перепишем Uni'.
U=Aie-}?,x [1 + пе>
/=Л е-^[1_„е;(2|^1ф2-Ф1>Г гс
Найдем входное сопротивление нагрузки (х = I) v „ U2 i+„e/(2₽^*i) вх г-/2 Zc l_rta/(2P^-W ’
Так как в точке х = I — хв минимума напряжения векторы А2е1$х и Aj^ifix находятся в противофазе, то '
Ф‘2 + Р хо) [ф1 Р (I хо)] ~
и
ф2—ф1=л—2р G—Хо).
Подставляя значение этой разности в выражение для ZBX, получаем: _ 1+пеНл+2рх0) _ 1_ИР/2р>„
hX^Zc 1 _пе1 (л+2₽х0> ~Zc i+rte/2px„ •
Заменяя е/2рл-„ по формуле
„1 гр*» _ * Ы tg Рхо 1—/ tg(Jx0
I выражая п через k, после преобразований находим, что
7 _7 k~П8Р*о вх с 1—/fetgpx0’
Таким образом, для вычисления ZBX необходимо измерить См„и и {7макс, т е гоэффицнент бегущей волны напряжения k, и расстояние х0 от приемника до глижайшего минимума напряжения.
Если обозначить fe = th р,
'о можно представить Zi;v как гиперболический тангенс некоторого комплекс-юго аргумента умноженный на гс,
%вх~гс th (РН-1 Рло)= гс th
Пример 18-5. Найти входное сопротивление короткозамкнутой двухпровод-гой липни длиной / = 35 м для генератора, работающего на волне длиной А. = = 50 м Диаметр проводов линии 2г = 4 мм, расстояние между проводами d = ~ 13,54 см Найти индуктивность катушки, эквивалентной по сопротивлению nc.h ЛИнЧИ.------------------------------------------------------------
18»
547
Решение. Пренебрегая потерями, найдем волновое сопротивление in 1т/що=505 ом
F - Со f П Г 880Я Л Г \ 880 м*
ЛННИЦ
Входное сопротивление
2т
ZK = /гс tg р/ = /гс tg 1 = /1554 Ом.
л
Линия представляет,для генератора индуктивную нагрузку, что ясно vw из того, что л/2 < I < 37./4. у е
Индуктивность эквивалентной катушки
L =
XL
СО
7ГЬ-Х=41 мкГ. 2лс
18-13/ Линия как четырехполюсник
Сравнивая основные уравнения длинной линии (18-24) 7\ = U2 ch yl -|- i2Zc sh yl; Ц ~ sh yl ф- 72 ch yl
с уравнениями четырехполюсника
/7i== Д7724-в72; 1
7х-сС2+1)/2, J
(18-87)
можно заключить, что длинная линия является симметричным четырехполюсником, коэффициенты которого
Д=хсЬу/; В —2cshy/; С=^Д; £)=Д=сЬу/. (18-88)
Условие AD — ВС = 1 выполняется 4 и для линии, так как ch2 yl — sh2 yl = 1.
Но, как известно, всякий симметричный четырехполюсник может быть представлен симметричной схемой замещения, например П- или Т-образной (см. § 8-4).
Определим сначала сопротивление Zr и проводимость У2 симметричной Т-образной схемы (рис. 18-22, а), которой можно заменить длинную линию при заданной частоте.
Симметричная Т-схема является схемой замещения симметричного четырехполюсника, если равны какие-либо два коэффициента (например, А и С) четырехполюсника и Т-схемы. Можно говорить о равенстве именно двух коэффициентов, ибо коэффициенты В и D связаны с первыми двумя А и С соотношениями D — А и Л2 — ВС = 1.
Как следует из формул (18-87) и (18-88), для длинной линии
A = -^ = chyl; = (18-89)
7 i Zc
548
С другой стороны, выше [см. (16-39) и (16-50)] для Т-схемы было получено:
А =-^=1 + ^-; С=-4^=У2. (18-90)
ZTg 2 IJ2
Приравнивая значения А и С для длинной линии (18-89) и для Т-схемы (18-90), цолучаем:
у2=-^-; 1 +b2jL=ch v/; г1==-2/с.Ь’г-1).2 (i8.9i)
Формулы для Zt и У2 можно записать несколько более единообразно. Для этого умножим числитель и знаменатель правых
Рис. 18-22.
частей формул (18-91) на у/ и, учитывая соотношения (18-8) и (18-10), получаем:
¥^У7 ^f=Y^- (18-92) oil у I, H
Введенные коэффициенты и T<2 соответственно равны:
д- 2(ch^-?L. т<2=='±£ (18-93)
1 yZshyZ ’ “ yZ ' '
Подсчитав коэффициенты К\ и /<2, определяем затем по формулам (18-92) сопротивление и проводимость Т-схемы замещения и, таким образом, длинную линию любой длины заменяем симметричной Т-образной схемой замещения.
Теперь найдем сопротивление Zr и проводимость У2 симметричной П-образной схемы, которой также можно заменить длинную линию (рис. 18-22, б). При этом удобно приравнять коэффициенты А и В линии и схемы.
Выше [см. (16-39) и (16-49)] для П-схемы было получено:
Д=-^ = 1+-^|^; B = (18-94)
Приравнивая значения А и В для длинной линии (18-88) и для П-схемы (18-94), получаем:
Z1=Zcshy/; 1+—~- = chy/; У2 = "° (18-95)
Запишем формулы для Zj и Y2 также через коэффициенты и Для этого j множим числитель и знаменатель правых частей
549
формул (18-95) на yl и согласно (18-8) и (18-10) получим:
Z1=t/Zc-^ = Z0/^;
У1
V ___т£_ (с^ 0 __у its „
Y2~ Zc ylshyl yoli\i- (18-96)
Таким образом, длинную линию любой длины I можно также заменить симметричной П-образной схемой замещения.
Полученные схемы замещения пригодны и для линий постоянного тока, если положить ю = 0.
Основное затруднение при вычислении параметров Т- и П-схем (Zi, У2) представляет вычисление коэффициентов и /(2 по фор. мулам (18-93), поскольку приходится находить значения гиперболических функций от комплексного аргумента.
Исходя из выражений (18-93) для /Q и Т<2 и представляя shy/ и ch yl рядами, получаем:
„ _ 2(chyZ— 1) . (yZ)2 , (у/)4
ylshyl 12 120
_sh У1 1 I (VZ)2 । (ТО4 ।
Аг—1 +—g— -j- ..
При анализе этих выражений, естественно, возникает мысль о приближенной замене Ki и К2 единицей. Например, если потребовать, чтобы модуль наибольшего из отбрасываемых членов в выражении /(2, т. е. (у/)2/6, не превышал 0,01, то можно найти предельную длину линии I, удовлетворяющую этому условию. При этом влияние всех остальных отбрасываемых членов будет ничтожно, ибо 0,0001, byJ- -С 0,000001 и, кроме того, знаменатели отбрасываемых членов быстро растут.
Параметры воздушных линий высокого напряжения'(35,110, 220,330 и 500 кВ) при различных напряжениях изменяются незначительно. Взяв для определенности трехфазную воздушную линию ПО кВ с сечением проводов 120 мм2 при частоте f = 50 Гц, с параметрами г„ = 0,15 Ом/км; Lo = 0,0013 Г/км, Со = = 0,009-10~6 Ф/км; g0 = 0,5-10~6 См/км на одну фазу, получим:
| у2/2/6 | = 0,208 • 10-ф.
Из условия | у2Р/6 | = 0,208-10“6 Р sg 0,01 находим: I = 220 км, т. е если длина воздушной линии высокого напряжения не превосходит 220 км (3,5% от длины волны /.), то можно приближенно полагать Kt и равными единице При этом ошибка для будет еще меньше, так как наибольший из отбрасываемых членов в составе /<, вдвое меньше, чем в составе /<2.
Приведем аналогичные данные для силовых кабелей напряжением 3,6 и 10 кВ, поскольку параметры их также мало изменяются с изменением напряжения. Для трехфазного кабеля напряжением 10 кВ с сечением жил 50 мм2 с параметрами г0 = 0,36 Ом/км; Lo = 0,00035 Г/км; Со = 0,185- 10"6Ф/км; g0 = 0,5-10~6 См/км на одну фазу получим при частоте 50 Гц:
уЧ2/& = (~ 1,03-|-73,5). 10-6/2.
Модуль этой величины не превосходит 0,01, когда I 52 км, что составляет 2,2% длины волны Л. Итак, при длине силового кабеля высокого напряжения,
550
Глава девятнадцатая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
19-1. Возникновение переходных процессов в цепях с распределенными параметрами
В цепях с распределенными параметрами, например в длинных линиях, обмотках электрических машин и трансформаторов и т. п., включение и отключение какого-либо участка сопровождаются переходными процессами (так же как и в цепях с сосредоточенными параметрами). При большой протяженности линий изменение внешних электрических и магнитных полей, например при грозовых разрядах, также вызывает переходные процессы. Переходные процессы в линиях возникают и при передаче телеграфных и телефонных сигналов, телемеханических импульсов или специальных импульсов для проверки линий и выявления места их повреждения.
Во всех случаях при анализе переходных процессов в цепях с распределенными параметрами необходимо исходить из общих закономерностей и дифференциальных уравнений, рассмотренных в гл. 18. Так как линия является наиболее распространенным примером цепи с распределенными параметрами, в дальнейшем изложении речь будет идти о переходных процессах в линиях.
19-2. Общее решение уравнений однородной линии
Для изучения переходных процессов в цепях с распределенными параметрами рассмотрим дифференциальные уравнения, выведенные в § 18-1 для однородной линии:
— duldx = r0i-\-L0di/dt-, 1
— dildx—gou-\-Coduldt, J
где r0, Lo, g0 и Со — параметры единицы длины линии, ах — координата выбранной точки, отсчитываемая от начала линии.
Если можно пренебречь потерями в линии, т. е. считать, что го — 0 и g0 — 0, то уравнения (19-1) принимают вид:
dti г di di л*, du /1 о
В общем случае решение этих уравнений для однородной линии (т- е. при Lo и Со, не зависящих от х) записывается так:
и=fl (X — vt) + f2 (X + vf) = Ппр + Моб; (19-За)
‘ f* + t'O]=Ч “ *об, (19-36)
де о = 1 /у L0C0 называется скоростью волны или в о л -1° с ^ц1-п о£, т ь_ю ц численно, равна фазовой скорости
551
Здесь функции Д (х) и Д (х) представляют собой распредели вдоль линии напряжений прямой и обратной волн (ппр и но6) в Мо НИя времени t = 0. ° Мент
Напряжение и ток волны связаны между собой законом О для волн Ма
Ицр = 2Упр, «об = 2,1о6,
где
(19-4)
%с — 'V Lo/C0 (19-5)
— характеристическое или волновое сопротивление линии (гл. 18)
Рассмотрим каждую из составляющих выражения (19-За) в отдельности и проследим, как зависят от времени t и координаты х составляющие напряжения нпр и поб.
Допустим, что в некоторый момент времени t = Д распределение напряжения ипр вдоль линии может быть представлено кривой «пР(Д)=Л(^-цД), (19-6)
изображенной на рис. 19-1, а. Тогда в момент времени t = Д + &t распределение напряжения вдоль линий может быть записано так: ипр (Д—АО {x — vkt — vt^==fx (х— Дх — уД),
где Дх = v kt.
Из. последнего выражения видно, что кривая ипр (Д + ДД отношению к кривой цпр (Д смещена вправо на расстояние Дх =- v kt, т. е. увеличение t приводит к'перемещению кривой .ипр в напраьле-
552
йй возрастания х. Иными словами, tznp выражает напряжение волны, движущейся в сторону возрастания координаты х, т. е. п р я м о й волны. Точка линии с координатой хф, для которой справедливо условие, что ппр = 0 при х > хф и ппр ф 0 при х < хф, называется фронтом прямой волны. Фронт прямой волны движется в сторону возрастания координаты х со скоростью v.
Если в точке х1; совпадающей с фронтом волны хф в момент установить прибор, записывающий мгновенное значение напряжения, то он запишет кривую 1 (рис. 19-1, б). Эта кривая представляет собой зеркальное изображение кривой ппр (х) при соответствующем изменении масштаба вдоль оси абсцисс. Прибор, установленный в точке х2 (рис. 19-1, а), запишет аналогичную кривую 2, которая, однако, смещена в сторону возрастания времени на величину
(х2 — x1)/v = l12/v,
где /12 — расстояние между точками хг и х2-
При исследовании изменения напряжения волны в зависимости от времени целесообразно выражению (19-6) придать следующий вид:
«пр=Ф1(^-^/0. (19-7)
В точке с координатой х + Ах напряжение волны описывается той же функцией (pj, но с запаздыванием во времени на величину Лх/ш
Рассуждая совершенно аналогично, можно показать (рис. 19-1, в и г), что составляющая ио6 представляет собой напряжение волны, движущейся в сторону убывания координаты х, т. е.обратной волн ы:
«об=М* + ^)==:СР*(* + *А’)- (!9-8)
Координата фронта обратной волны характеризуется условием Щ>б = 0 при х < хф и ио6 #= 0 при х > хф. Фронт обратной волны движется в сторону убывания координаты х со скоростью v.
Скорость движения волн в воздушных линиях примерно равна скорости света в вакууме v с 300 000 км/с. В кабелях скорость распространения волн примерно вдвое меньше, чем в воздушных линиях (гл. 18).
Если известны зависимости ппр (/) и цо6 (/) в какой-либо точке линии и волновая скорость v, то по уравнению (19-За) подобно тому, как это сделано на рис. 19-1, легко построить кривые ппр (х) и иоб (t) в любой момент времени.
Так как между напряжением и током волны существует прямая пропорциональность (19-4) и коэффициент пропорциональности (19-5) зависит только ог параметров линии, то в дальнейшем часто бУдем рассматривать только напряжение волны.
При исследовании волн в линиях иногда удобно выражать каждую из волн только в функции времени, находя эту функцию в какой-иибо точке линии, например хх, и принимая за начало отсчета вре-
553
мени момент, когда фронт волны дойдет до этой точки. Так, нал мер, для ппр (/) и ио6 (t), изображенных на рис. 19-1 с"~’~ линиями, такими точками соответственно являются х} и х2 для иоб.
сплошными
-Т ДЛЯ и «пр
Если известны функции ппр (/) и ио6 (/) в точках х, и х2, то пепе ход к общему выражению каждой из волн выполняется согласно (19-За) так:
Цпр(х, 0 = «пр(/-^-' «об(*, 0 = «об(^ + ^у^
(19-9)
В любой момент времени напряжение и ток в линии можно рассматривать как сумму только двух волн, прямой и обратной Каждую из двух волн в свою очередь иногда целесообразно представить на основании принципа наложения в виде суммы отдельных волн более простой формы.
При анализе отражения волн оказывается недостаточным подразделение волн на прямые и обратные. Пусть, например, прямая или обратная волна движется по линии и падает на узел соединения с линией, имеющей другие параметры. В месте соединения двух линий эта волна распадается на две волны, одна из которых проходит из первой линии во вторую, а другая отражается от места соединения двух линий По аналогии с оптикой первую, исходную волну называют падающей (пад), а две другие — соответственно отраженной (отр) и преломленной или проходящей.
При отражении волны от конца линии преломленной волны, естественно, нет.
19-3. Возникновение волн с прямоугольным фронтом
Включение источника. Для выяснения физической стороны возникновения и движения волны рассмотрим незаряженную линию, которая в момент времени t = 0 присоединяется к источнику постоянной э. д. с. с напряжением Uo (внутреннее сопротивление равно нулю). Для источника синусоидального напряжения промышленной частоты (7. = 6000 км) за время прохождения волной расстояния в пределах нескольких сотен километров его напряжение также можно считать постоянным.
После подключения источника к линии возникает волна с напряжением п„р = Uo, которая от одной точки к другой заряжает линию до напряжения Uo. Предположим, что в момейт t волна достигла сечения тп (рис. 19-2). Тогда во всех точках левее сечения между проводами напряжение равно По, а правее этого сечения напряжение равно нулю.
На поверхности верхнего провода происходит накопление поло-жишлбною заряда и левее сечения тп заряд на единицу длипл 554
qo = Co^o. a правее равен нулю. За время dt волна переместится правее сечения тп на расстояние dx = v dt. При этом отрезок линии dx получит заряд dq — q0 dx = C0U0 dx, который должен пройти по верхнему проводу через сечение тп и через любое сечение верхнего провода левее тп. Распространение заряда создает на всем протяжении верхнего провода от источника до сечения тп ток
i = dq/dt = q0 dx/dt = CoUov =?= 10. (19-10)
Одновременно с накоплением положительного заряда на поверхности верхнего провода линии происходит накопление отрицательного заряда на поверхности нижнего провода. Распространение отрицательного заряда вдоль нижнего провода слева направо связано с электрическим током'В нижнем проводе, направленным в противоположную сторону, т. е. справа налево.
Процесс распространения заря-' дов можно представить себе таким образом, что по мере перемещения волны слева направо элементы верхнего провода один за другим приобретают некоторый положительный заряд и такой же положительный заряд отнимается от элементов нижнего провода. Противоположные заряды образуют электрическое поле между проводами на всей длине участка линии,
по которому уже прошла волна. При возникновении электрического поля у фронта волны между вновь заряжаемыми элементами проводов (тр и nq на рис. 19-2) протекает ток смещения. Получается замкнутая цепь тока. От положительного полюса источника ток идет по верхнему проводу, замыкается у фронта волны током смещения между проводами и затем идет по нижнему проводу к отрицательному полюсу источника. По мере движения волны цепь удлиняется, но ток в цепи остается неизменным /0 = CoUov.
В контуре, образуемом этой цепью, возникает магнитный поток, линии которого лежат в плоскостях, перпендикулярных к осям проводов. При перемещении волны на расстояние dx = v dt магнитный поток увеличивается на величину d<l> = L0I0 dx = L0I0vdt. При возникновении потока d(£> в контуре mpqn наводится э. д. с. самоиндукции
dQ/dt = L0I0 dx/dt —Lovlo, (19-11)
Действующая против направления движения стрелки часов. Таким образом, э. д. с. самоиндукции у фронта волны, направленная по линии qpt равна и противоположна напряжению:
~ “ (19-12)
555
откуда
о
ко =Lv==L /о Е L0C0
что соответствует (19-5).
Энергия, отдаваемая в единицу времени источником, равна U j В единицу времени волна перемещается на расстояние, равное° ° На каждом единичном отрезке линии, пройденном волной, зап/ сается энергия C0Hg/2 в электрическом поле и Е0/б/2 в магнитном поле. На основании закона сохранения энергии
и О1 о —v 'у 2 г 2 Г
Подставив в левую часть этого у равнения /0 = CoUov, получим соотношение
_ЗД_= Vk zlqi4.
2 2 ’ (1У-13)
т. е. для волны значения энергии электрического и Магнитного полей па участке линии, пройденном волной, равны между собой.
Рассмотренная волна имеет прямоугольную форму ипр (t — x/v) = 0 при t < x/v, unp (t — x/v) = U0 при t>x/v и обычно называется волной с прямоугольным фрон-т о м.
Если к линии подключается источник с активным внутренним сопротивлением г„, ток и напряжение волны становятся меньше. В этом случае
^пр ^0
и по-прежнему
откуда
(19-14)
^пр Рпр/^< l/oz,
__________ t п₽__zf + r„ ’ 1пР ZL + >
При подключении генератора с индуктивным внутренним сопротивлением фронт волны искажается и волна перестает быть прямоугольной (см. дальше § 19-4).
Включение нагрузки. Волны прямоугольной формы возникают и при подключении к заряженной линии приемника с активным сопротивлением.
Рассмотрим линию с волновым сопротивлением zc, заряженную Д° напряжения Uo. Если в момент времени t = 0 в конце линии вклю-чается__сопротивление шгрузки
гн (рис. 19-3), то в конце ли-
и,
(19-15)
в
о
1иБ
Рис. 19-3.
556
лии возникает обратная волна, движущаяся от конца линии к ее началу.
Напряжение и ток этой волны могут быть легко рассчитаны при помощи уравнений, составленных по закону Ома для волны п для сопротивления нагрузки:
^об ^4об> «Н ~" 1^0 "Е Ноб (Ор Об) Об^*н,
откуда
= 1‘«б = -ТТ7-- (19-16)
*£ 1 ' Н *С Т ' И
На рис, 19-3 показаны прямоугольные волны напряжения и
тока, возникающие в этом случае.
Отключение источника. При отключении линии от источника питания в ней также возникают волны.
Пусть в линии с сопротивлением нагрузки гц установится трк /н = UJr^. Если в момент t = 0 отключить источник энергии (рис. 19-4), то ток в начале линии мгновенно спадет до нуля и воз-
никнет волна с напряжением и током
9ip Al* (19-17)
В результате наложения этой волны на предшествующий режим ток в линии i = /н 4-/пр = О, а напряжение и = Йн + и„р =
Ц, 2’с-^и’
Если ток нагрузки /н меньше зарядного тока /0 при включе-
Рис. 19-4.
нии линии к источнику постоян-
ного напряжения Uo = UK, т. е. /н < Ujzc, то напряжение и — UB — zcIH ‘ будет положительно и на пройденном волной участке сохранится после отключения некоторая доля напряжения того же направления (рис. 19-4). "
1н
иоВ
loS
Рис. 19-5.
Если же /н > Пн<гс, то линия на участке, пройденном волной, зарядится в противоположном направлении.
Отключение приемника. При отключении приемника (рис. 19-5) в линии возникает такая же волна, как и при отключении источника. Разница заключается только в том, что эта волна имеет противоположный знак и распространяется в__обратном на-
правлении.
557
В результате наложения этой волны на предшествующий реж ток в линии /н + io6 = 0, а напряжение и = + иоб = и . и.м
(рис. 19-5). н^2с/н
При отключении приемника обратная волна вызывает повыше ние напряжения в линии, которое тем больше, чем больше водно' вое сопротивление линии. В случае отключения приемника от воздушных линий перенапряжения могут быть весьма значительными.
При помощи аналогичных рассуждений могут быть най-дены волны, возникающие g более сложных случаях.
Рис. 19-6.
Пример 19-1. Найти волны, возникающие при подключении в произвольной точке нагруженной линии дополнительного приемника с сопротивлением гд (рис. 19-6).
Решение. При подключении приемника справа и слева от места подключения пойдут волны с равными значениями напряжений И ЮКОВ. tZnp tzo6, Kip J*o6-
Ток в сопротивлении гд равен сумме токов обеих волн и по закону Кирхюфа
— 2t Пр — 2t06,
а напряжение на гд равно сумме С/н и напряжения этих волн:
Чд — 1*дгд — ^н+инр«
Учитывая, что tzlip = zcinp, из выражений для 1Д и пд получаем: _-и^с
+ ИпР~“об~2гд + гс-
На рис. 19-6 показано распределение тока и напряжения в линии после подключения дополнительного приемника. Справа от места включения ток (пр складывается с током /н> и так как 1по 0, го суммарный ток меньше /й. Слева от места включения ток 1об направлен противоположно гоку /н, г. е. вычитается из тока /н, и так как «об < 0, то суммарный ток больше /и. Напряжение и,1р справа и иоб слева складываются с £7И, и так как ипр = uog < О,
то напряжение на линии уменьшается.
Полученные волны тока и напряжения можно рассматривать как результат наложения на предшествующий режим токов и напряжений, получающихся при подключении к незаряженной линии источника с э. д. с. Е = Ua и внутренним сопротивлением гд. Так как этот источник подключается одновременно к двум одинаковым линиям (справа и слева от места подключения), то при расчете напряжения волны сопротивление гс делится на два.
Пример 19-2. Найти волны, возникающие—.три отключении нагруженной линии посредине (рис. 19-7). -
Рис. 19-7.
558
Решение. После отключения от места размыкания пойдет прямая волна . током, равным —и напряжением ппр = — гс1а, и обратная волна с током /и j напряжением uo6 = + zcIa
В результате наложения этих волн на предшествующее распределение наряжения и тока на участках слева и справа от места отключения ток уменьшается до нуля, а напряжение на участке слева от места отключения повышается до l/H + гс1а, а справа от этого места уменьшается до Ua — гс1н (рис. 19-7).
19-4. Общие случаи нахождения волн, возникающих при переключениях
Рассмотренные выше примеры возникновения волн могут быть при помощи принципа наложения сведены к случаю включения источника заданной э. д. с. или заданного тока в пассивную цепь. Этот метод может быть распространен на многие случаи расчета волн, возникающих при всякого рода переключениях.
Рис. 19-8.
Если, например, к линии, в общем случае заряженной, подключается некоторый в общем случае активный двухполюсник (рпс. 19-8, а), то для нахождения возникающих волн необходимо определить напряжение £/0 на разомкнутом рубильнике и рассчитать токи в схеме с сосредоточенными параметрами, изображенной на рис. 19-8, б, при нулевых начальных условиях. Так как напряжения волн в линиях / и 2 отличаются от токов постоянными множителями гс1 и гг2, то при расчете токов в схеме с нулевыми начальными условиями обе линии могут быть заменены сосредоточенными сопротивлениями, равными гс1 и гс2, и токи, рассчитанные в этих ^сопротивлениях, будут равны токам волн, возникающих в линиях,
559
Если рубильник не включается, а отключается (рис. 19-g то задача решается еще проще. В этом случае, зная ток в "разм каемом рубильнике, необходимо рассчитать токи в линиях ПЬ1' подключении источника тока противоположного знака непосрет^'1 венно к концам отключаемой ветви. Токи в сосредоточенных сопоТ~ тивлениях zcl и гС2 схемы, изображенной на рис. 19-8, г, равн искомым токам волн в линиях. ’ Ь1
Рис 19-9.
Таким образом, расчет волн, возникающих при переключениях, может быть сведен к расчету эквивалентных схем с сосредоточенными параметрами.
Пример 19-3. Найти волну, возникающую в линии с волновым сопротивлением гс при подключении к ней источника с э. д с. е = Ео, внутренними сопротивлением г и индуктивностью L (рис 19-9, а)
Решение Составив эквивалентную схему с сосредоточенными параметрами (рис 19-9, б) и рассчитав токи волн в линии, находим для тока вол® в начале линии (х — 0) выражение, аналогичное (13-12).,
тде т =£/(,' + г4).
г+гс

560
в любой точке линии при t> x’v в соответствии с (19-7) ток прямой волны
Ток волны для этого случая показан на рис 19-9, а
Пример 19-4. Наити волну, возникающую в линии с волновым сопротивлением гс при подключении к ней источника с синусоидальной э д с е ~ =- Ет sin (tot +i]i), внутренними сопротивлением г и индуктивностью L (рис 19-9, в)
Решение Эквивалентная схема та же, что и в предыдущем примере (рис 19-9, б) Рассчитаем ток в этой схеме.
i = -^-[sin (art <p) — sin (ф—ср) e~^r], где
г=^(г+гс)8+со2Л2; v = aictg— f Г гс
В произвольной точке линии с координатой х при t Z> x/v
и F Г t—x/v]
^лр —_ | sin (co/ —сол'/г + ’ф—'ф) — sm (lb—q) e x J-ze
Ток волны показан на рис 19-9, в.
19-5. Отражение волны с прямоугольным фронтом от конца линии
Отражение ст сопротивления. Рассмотрим волну с прямоугольным фронтом
^пад ~~ Ид, 1'пяд 10 (19-18)
движущуюся по однородной линии и падающую на приемник с активным сопротивлением г2 (рис. 19-10, а и б). Когда волна дойдет до конца (рис. 19-10, в), она частично отразится. В рассматриваемом случае падающая волна движется в направлении возрастания х (в прямом направлении ) и может называться прямой. Отраженная волна движется в обратном направлении и может называться обратной. Однако при исследовании отражения волны удобнее пользоваться понятиями «падающая и отраженная» волны, а не «прямая и обратная».
Для определения условий отражения волны найдем ток в сопротивлении г2.
Напряжение в конце линии п2 = «пая + ногг, а ток i2 = —
— imp. Поэтому ток отраженной волны iOTp — — i2 = /0 — i2
и напряжение п0,р -= (отргс = zc (Io — i2) = Uo — zci2.
Тогда
и2 = r2i2 = U о + потр — 2U(I — zci2, (19-19)
откуда
__________________________________________________(19-20)
561
Из выражений (19-20) следует, что ток в сопротивлении г2 рав току, который получился бы в схеме с источником напряжени*1 2t/0 и сопротивлениями г2 и zc, включенными последователь^Я
Напряжение в конце линии н2 зависит от величины и знака отраженной волны (рис. 19-10, г). Из (19-19) и (19-20) находим-«отР = ^о-2Л = ^“По = /гП0; (19-21)
. ^отр Г 2 % С _
1°тР = '7Г = ^+^^==/г/о’ (19’22)
где п = '2 ,гр — коэффициент отражения. га + гс
Тогда
И2 = {^о + Иотр==(1 +/г)
4== Л> готр = (1 Л,-
(19-23) (19 24)
Если линия на конце разомкнута (г2 = оо), то п = 1 (см. также
гл. 18) и потр =
t/0, г'отр = 4» т- е- волна отражается полностью без перемены знака. Напряжение в конце удваивается: п2 = 2(70, а ток i2 = 0.
Если линия на конце короткозамкнута (г2 = 0), то /г = — 1 и u0Tp = — Uo, ьО1р = = — /0, т. е. волна отражается полностью с переменой знака. Напряжение в конце линии ц2 = 0, а ток /2 = 2/0.
Вообще можно сказать, что если сопротивление приемника энергии больше волнового сопротивления линии r2 гс, н > 0, то падающая волна встречает в конце линии большее сопротивление. Ее заряды не успевают стекать через это сопротивление и напряжение в конце линии, обусловленное зарядами, приносимыми волной, возрастает, н2 = (1 + п) Uo > Uo. Отраженная волна имеет тот же знак, что и падающая.
Если же г2 < zc, то, наоборот, через сопротивление г2 стекает большее количество зарядов, чем приносится волной; требуется дополнительное поступление зарядов из заряженной линии, что приводит к снижению напряжения в линии. Отраженная волна имеет знак, про-
тивоположный знаку падающей, и на конце линии напря-
жение понижается.
Если г2 = 2с, то п = 0, иотр = 0, i0Tp = 0 и 'отраженной волны нет. Как только волна дойдет до конца, в цепи сразу установится неизменный ток, и вся энергия, доставляемая падающей (бегущей)
волной, поглощается в сопротивлении г2.
При падении отраженной волны на начало линии она должна
562
Ленин. Волна, отраженная от начала линии, будет прямой. Рассмотрение таких многократных отражении приведено в конце главы.
Отражение от неоднородности. Если в конце линии имеется узел соединения различных линий или разветвление, то этот узел следует рассматривать как неоднородность, аналогичную некоторому сопротивлению г, включенному в конце линии. Если, например, в конце линии с волновым сопротивлением z(1 параллельно подключены две линии с волновыми сопротивлениями zc2 и zfS
(рис. 19-11, а), то по этим линиям пойдут волны, сумма токов которых равна току, притекающему к узлу по первой линии; такой узел подобен сопротивлению
^сг+^сз
Все выводы об отражении волны от сопротивления, сделанные выше, могут быть распространены и на рассматриваемое разветвление линий.
19-6. Общий метод определения отраженных волн
Как видно из рассмотренных примеров, на практике часто однородность линии нарушается — в линию включаются элементы с сосредоточенными параметрами, присоединяются линии с различными волновыми сопротивлениями, причем могут встретиться узлы параллельного включения нескольких линий. Для определения переходных режимов при падении волны на узел, так же как и при переключениях (§ 19-4), разработан общий метод, который применим при любой схеме соединения линий и цепей с сосредоточенными параметрами.
Пусть вдоль линии с волновым сопротивлением zcl движется волна произвольной формы ипад и 1пад, причем цпад = гл111йя. Эта волна может быть и прямоугольной формы (рис. 19-2), и в виде импульса (рис. 19-1), и любой иной формы (например, рис. 19-9). Волна падает па узел 2—2' соединения или разветвления, схема которого может быть также любой (например, рис. 19-11, а и б).
Во всех случаях часть цепи, присоединенную к линии в точках ^~~2' справа, можно рассматривать как пассивный двухполюсник
563
(рис. 19-12, а), напряжение и2 и ток i2 которого иредставл собой некоторые функции времени. Я1ог
Так как зажимы двухполюсника 2—2' относятся и к лини с волновым сопротивлением гс1, то напряжение на этих зажимах равно сумме напряжений падающей и отраженной волн, а ток__________
разности токов волн:
t^2 ~ Идад ИОтр, (19-25)
. . . ^няд" ^отр
г2~ ^пад 1<лр~ ~ • (19-26)
Решив совместно два эти уравнения, получим:
2нпад = н2 + гс112. (19-27)
Последнее выражение является основным расчетным уравнением для определения напряжения и тока в месте отражения волны.
Рис. 19-12.
Из уравнения (19-27) следует, что ток и напряжение в линии в месте отражения волны такие же, как и при замене линии, по которой движется волна, эквивалентной схемой с сосредоточенными параметрами, состоящей из последовательно включенных источника э. д. с. с напряжением 2ипад и сопротивления гс1 (рис. 19-12, б).
Вся часть цепи справа от узла 2—2' может быть также представлена эквивалентной схемой из элементов с сосредоточенными параметрами. Например, при падении волны ипад на узел соединения двух линий справа от узла еше нет зарядов и могут возникнуть только преломленные волны, движущиеся от узла в прямом направлении. Поэтому между токами и напряжениями в линиях справа от узла существует зависимость и = zci. Следовательно, при расчете возникающих отраженных волн каждая линия, примыкающая к узлу, может быть заменена сосредоточенным активным сопротивлением 2С.
Таким образом, решение задачи о переходном режиме в длинной линии при падении волны на узел разветвления может быть сведено к расчету переходного процесса в схеме замещения с сосредоточенными параметрами (рис. 19-12, б) при помощи одного из описанных в предыдущих главах методов (например, классического или опе-___ раторного)._______
НаПУсн75вШкшщказаннбго=мвжно==^^шужревй5ЕЬ—следщоЩЁЁ-правило. При падении на узел волны с напряжением ипад, движущейся

tio линии с волновым сопротивлением ге, напряжение и ток в этом t/зле будут такими же, как и при подключении источника напряжения 2иаал с внутренним сопротивлением гс непосредственно л- рассматриваемому узлу.
Схемы замещения для расчета напряжения и2 и тока i2 в узлах цепей, показанных на рис. 19-11, приведены на рис. 19-13,0 и б.
Зная напряжение и2 и ток i2, легко определить отраженную
волну:
^отр «2 ^пад, ^пад ^2-
(19-28)
По известным значениям напряжений и токов падающей и отраженной волн, а следовательно, прямой и обратной волн можно найти распределение напряжения и тока вдоль линии в любой момент времени при помощи выражений (19-9) и построить графики, аналогичные приведенным на рис. 19-1.
При решении задачи операторным методом зависимость между (р) и 12 (р) представляется в виде
Рис. 19-13.
U2(p) = I2(p)Z2(p),
где Z2 — входное сопротивление пассивного двухполюсника в схеме замещения (рис. 19-12, б).
Уравнение (19-27) и формулы (19-28) принимают вид:
2t7naw (р) = С/2 (р) + гс1/2 (Р)==^2 (Р)Г1 + Ж| (19-29)
И
^отр(р) = ^2(р)-^пад(р). (19-30)
Исключая U2 (р) из этих уравнений, получаем:
=N W <19-31>
V ^2 \Р) ”Г
и соответственно
/отр(р)=|^^/пад(р)=Л((р)7пад(р), (19-32)
гДе N (р~) — коэффициент отражения в опера-1 о р н о й форме:
(19‘33)
Z2 (/’) I 2C1
Пример 19-5. Волна прямоугольной формы, напряжение которой Uo, пере-ЭДит-с липни с волновым сопротивлением^г^^лга-Динню с волновым сопротнвле-Иы,! гс2 (рис. 19-14, а). Найти напряжение и ток отражешюй аоЛнЫ.
565
Решение Составим эквивалентную схему (рис 19-14, б) Наппя и ток i2 определим непосредственно из схемы ’ 1 Жение
(( _ 2f7GZ,2 . ( __ U2 _ 2Ц0 .
^<1 + гс2 ’ 2 гс2 ZC1 + гс?_
волна, которая пойдет по линии гс2 (преломленная волна), имеет напряжен
Как видно из выражения для и2, в случае, если zc2 > zfl, напряжение прел ленной волны больше, чем падающей Такое возрастание напряжения им°М' место при переходе волны с кабельной липин на воздушную Если, наприм^1 волновое сопротивление кабельной ~ ’ Рп
переходе волны с кабельной линии _ / 2zf2
вается почти в 2 раза ----— =
\ ZC1 "T ZC2
к кабельной питающей линии между кабелем и приемником избегают включать
линии он им, а воздушной 600 Ом то пр на воздушную напряжение волны увеличу 1,841 Поэтому при подключении потребителя
Рис 19-14. Рис 19-15.
воздушную линию Наоборот, с целью снижения напряжения волны, приходящей к потребителю по воздушной линии, между линией и приемником можно включить участок кабеля
Волна, отразившаяся от узла 2—2',
г; гС2 гс1 . иотр . ZC2 Zd
итр — ипад= ^cr— J— ; 1отр — ~z = 1пад ~ ~7~Z •
zc2~rza za zc2~rzci
Таким образом, волна отражается от места перехода на линию с другим волновым сопротивлением точно так же, как и от активного сопротивления, включенного в конце линии Если zc2 <7 га, то отраженная волна имеет обратный знак Если zt2 > zcl, то отражение происходит без перемены знака При zc2 za волна переходит с одной линии на другую без отражения
Пример 19-6. Прямоугольная волна с напряжением Uo падает на катушку с инду ктивпостью L и сопротивлением г, включенную в конце линии (рис 19-15, о) Построить распределение напряжения и тока после отражения волны от конца линии
Решение Составим схему замещения для этого случая (рис 19-15, Q) и запишем дифференциальное уравнение по закону Кирхгофа
2t/0=(zcj-|-r)-]-Z.t/i2/t/i.
Его решение дает для t > 0 при нулевых начальных условиях:
_____________________Т+гС1 ____ ___________________________________ ____________ где т = L/(r + ztl), a t отсчитывается с момента прихода волны к концу линии
566
На рис 19-16 и 19-17 построены зависимости и2 и t2 от времени цля случая, когда г < г(11 и нанесены значения иотр и готр, определенные по формулам (19 28)
^Отр~^2 Ц» ГОтр = Л) Ц*
График распределения падающей и отраженной волн вдоль линии и суммарное значение тока и напряжения в линии для момента времени, когда отраженная волна пройдет расстояние /х, представлен на рис 19-18
Так как напряжение и ток падающей волны стоянны по величине, то в результате отражения распространяется влево от узла со скоростью v напряжения в линии после отражения
не зависят от времени и по-папряжение и2 на узле 2—2' Закон распределения тока и
волны может быть получен непосред-
ственно из выражении для i2 и и2 путем 0-----------—
замены t на t — xt/v I
W ^77
= - (t/x - Jex/VT)J. I
r + zcl L 0-----
r + zci ж ,Jmu
Эти выражения справедливы для интервала времени, когда волна уже отразилась от конца, но вторично отраженная от начала линии волна еще
не дошла до* рассматриваемой точки, т е
xt/v <zt < (2/ — xj/v;
здесь л-, отсчитывается от узла 2—2' влево, а за начало отсчета времени принят момент падения прямоугольной волны на узел 2—2'
Как видно из графика (рис 19 18), в первый момент падения волны на индуктивность последняя подобна раз Риву линии и волна отражается с таким же знаком, как и от разомкнутого конца линии По мере нарастания тока в индуктивности напряжение и ток отраженной волны уменьшаются,
приближаясь асимптотически к тем значениям, которые получаются при отражении волны от конца линии, замкнутого на сопротивлении г Если сопротив Дение то в некоторый момент времени отраженная волна изменяет знак
Дрис 1£п«Б----------------------------—---------------------------------

Рис 19-18
567
Таким образом, в момент падения волны на индуктивность напоя удваивается, создавая опасность пробоя изоляции катушки С этим явпЖеНие приходится часто встречаться па тике когда линия подключена J трансформатору. к
“С
*cz
2
б)
Рис 19-19.

пример 19-7. Волна прямоугольной формы с напряжением Uo (рис 19-19, а) переходит с линии с волновым сопротивлением гг1 на линию с волновым сопротивлением гс2 В месте соединения двух линий (узел 2—2'} параллельно линии включена емкость С В конце второй линии (узел 3—3') включена индуктивность L
Построить распределение напряжения и тока вдоль линии, когда волна, проходящая во вторую линию, еще не достигла ее конца
Решение Составим для узла 2—2' схему замещения (рис 19-19, б) Включение в эту схему пряжение
источника э. д с 2(/0 создает на узле 2—2' на-
п2 = 21/0
где
- А?—(1-е ^), гс1 + гС2
zcizf2
(a)
для рис
на-
гС1 + гС2
График зависимости (О случая г,2 < гс1 представлен на 19-20 Как видно из трафика, пряжение на узле нарастает плавно
до величины 2UBzl2/(zrl zc2) и, сле' довательно, вправо от этого узла пойдет волна с пологим фронтом, напряжение которой равно и2
Одновременно от узла 2—2' отразится волна с напряжением
«отр = «2- «пад= Ц) - 2Ц) — г7г—
навстречу другой, — падающая и отраженная, а с, равз идет одна преломленная
568
волна На рис 19-21 представлены в отдельности падающая, преломленная и отраженная волны напряжения н тока, а также результат их наложения
Из приведенного расчета очевидно, что в момент падения волны на емкость
напряжение на емкости остается равным п\лю, а ток равен удвоенному току волны Таким образом, емкость в момент падения волны пронзьодит такое же действие, как и короткое замыкание Только по мере зарядки емкости ее действие уменьшается, и по истечении времени, в несколько раз превышающею постоянную времени т, в узле 2—2' устанавливается
такое же напряжение, как если бы емкости С не было вовсе. Ток слева от узла 2—2' больше, чем справа, На ток зарядки емкости
Как видно из всех приведенных расчетов, индуктивность L, включенная в конце второй линии, не оказывает влияния ни на составление эквивалентен схемы, ни на распределение токов и напряжений Действительно, до тех пор, пока волна не дойдет до конца второй линии, распределение токов и напряжений в линии не зависит от нагрузки в конце второй линии Только после того как волна во второй линии дойдет до узла 3—3', начинает сказываться его
влияние
Отражение волны от узла 3—3' может быть рассмотрено аналогично предыдущему при помощи схемы замещения для этого узла На рис 19-22 изображена схема замещения для определения напряжения на узле 3—3' при падении на него волны, прошедшей уже через узел 2—2' (мимо емкости) В этом случае напряжение источника э д с в схеме замещения уже не постоянно, а плавно нарастает по закону 2и2 Решение задачи производится так же, как и в случае изменения напряжения по произвольному закону в цепи с сосредоточенными параметрами (см § 13-15)
19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости
и индуктивности
Как видно из рассмотренных примеров, конденсатор и катушка, включенные в цепь с распределенными параметрами, производят различное действие.
В момент падения волны индуктивность подобна разрыву в месте ее включения, но по мере нарастания тока ее действие все более соответствует короткому замыканию. Емкость, наоборот, в первый момент оказывает действие, подобное короткому замыканию между точками ее включения. По мере того как емкость заряжается, ток через емкость уменьшается. При полной зарядке емкость аналогична разрыву между точками ее включения.
Основываясь на этих рассуждениях, можно рассмотреть прохождение прямоугольной волны через узлы схемы, в которых емкости и индуктивности включены различным образом.
Пусть в месте перехода с одной линии на другую с такими же параметрами параллельно линии включена индуктивность (рис. 19-23, а). Тогда сначала, пока ток в индуктивности не достиг заметной величины, процессы происходят так, как будто бы индуктивности не было вовсе, и ток и напряжение волны при переходе с одной линии на другую не изменяются. Однако по мере нарастания тока в индуктивности ее влияние становится все больше и ток вннанряжение
569
волны во второй линии уменьшаются. По истечении достаю большого времени волна от индуктивности отражается полностьН° как от короткозамкнутого конца линии, а величина проходяи Р“ волны становится равной нулю. Таким образом, с первой лини во вторую поступает импульс с крутым фронтом, затухающий по экспоненциальному закону.
Если в месте перехода с одной линии на другую последовательно с линией включена емкость (рис. 19-23, б), то в первый момент, пока
MwfBLr- * а) L/Z
. ____
L/2 _———_______
------------------------------------------
ZC Zff
------------------------------------------
1 L
емкость не заряжена, волна проходит через нее, как если бы две линии были включены последовательно. По мере зарядки емкости она как бы отключает вторую линию от первой и делает невозможным переход волны с первой линии на вторую.
Если назвать переход волны с одной линии на другую при последовательном включении емкости или индуктивности переходом «через емкость» или «через индуктивность», а при параллельном включении — «мимо емкости» или «мимо индуктивности», то можно заметить следующие закономерности.
При прохождении волны мимо индуктивности или через емкость фропгПолны сохраняется крутым и в первый момент при равенстве
570
волновых сопротивлений линий максимум напряжения (тока) проводящей волны равен напряжению (току) падающей волны. С течением времени напряжение (ток) проходящей волны убывает, снижаясь до нуля.
При прохождении волны через индуктивность или мимо емкости фронт волны сглаживается и напряжение (ток) волны лишь с течением времени при равенстве волновых сопротивлений линий достигает значения напряжения (тока) падающей волны.
Графики распределения напряжений и токов для двух последних случаев представлены на рис. 19-23, виг.
ff)
Рис. 19-24.
Отраженные волны имеют характер, обратный характеру проходящих волн. Если фронт проходящей волны становится пологим, то фронт* отраженной волны остается крутым и, наоборот, проходящей волне с крутым фронтом соответствует отраженная волна с пологим фронтом.
Если волна прямоугольной формы имеет ограниченную длину 1К (рис. 19-24, а), то ее можно рассматривать как сумму двух волн кпад1 = и «падг — — бесконечной длины, равных по абсолютному значению, но противоположных по знаку, сдвинутых одна по отношению к другой на расстояние 1В.
Прохождение такой волны через индуктивность может рассматриваться как наложение токов и напряжений, подобных изображенным на рис. 19-23, в для положительной и отрицательной волн (рис. 19-24, б). Аналогично можно построить кривые напряжения и тока для прохождения импульса мимо индуктивности или мимо емкости, а также через .емкость.
19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления
Включение источника. Для исследования многократных отражений волн при наличии поглощения энергии на концах линии Рассмотрим включение линии, замкнутой на приемник с активным сопротивлением г2 zz. Пусть -питающий генератор имеет чисто активное внутреннее сопротивление гх и э. д. с. Ео.
Вычислим коэффициенты отражения пг и п2 в начале и конце >инии:
.,l2=S;- - _J19~34)
571
Первая прямая волна в соответствии с § 19-4 имеет напряже «пР1 = EoZrl(zc + fj), а первая отраженная обратная волна в соо^ ветствин с § 19-6 — напряжение поб1 = п2ипр1. г'
Аналогично определяются отраженные волны и,
^2^пр2» ^прЗ ^1^об2 Н Т. Д.
Таким образом, для k-ii волны
пр2~ th Поб1, Поб2 =
^об k (^1^2)^ 1 ^2^пр1»
(19-35)
а для k + 1-й соответственно
Ilnp (fe+1) (^1^2)^ Ипр1‘
(19-36)
Наложение этих волн дает значение напряжений (и токов) в любой момент времени.
Пример 19-8. Найти распределение напряжения и тока в линии с волновым сопротивлением zc, подключаемой к генератору с постоянным напряжением Va (внутреннее сопротивление г, = 0) Сопротивление нагрузки г2 = 4гс.
Решение По формулам (19-34) получаем пг = —1 и п2= 0,6 Рассмотрим систему многократных отражений волн от начала и конца линии и результаты запишем в виде табл. 19-1, где и it обозначают напряжение и ток в начале линии, а и2 и i2 — в конце линии.
„ Таблица 19-1
Промежуток времени ИМо Значения напряжения последующих волн Ma/L/o ч'1.
0 ... l,v 1 1 ^npl “ ^0 0 0
1/V ... 2l/v 1 1 ^061 “ ^2unpl “ 0,6(7q 1,6 0,4
21 v ... 3l/v 1 -0,2 ^np2 = ^1^061 ~ 0,6(7 q 1,6 0,4
3Z/t> ... M/v 1 -0,2 ^об2 == ^2^np2 " "0,060 Q 0,64 0,16
4Z,o ... 51,v 1 0,52 Unp3 = Wl(zo62 — O,36t/o 0,64 0,16
5l/v ... 61/V 1 0,52 ^обЗ" ^2^ПрЗ“ 0,2160/o 1,216 0,304
6l/v ... ll/v 1 0,088 ^np4 “ ^1^063 -0,2l6(7o 1,216 0,304
2kl V (2k '-I) Z V 1 0,25 ^np<fe+l' “0 1 0,25
при k -> co
Пример 19-9. То же, что в предыдущем примере, но сопротивление г2 = = Z./3
Решение. В этом случае нз формул (19-34) получаем nL = —1 и п> =* — ““О’5
Аналогично прелыдзтему, рассматривая систему многократных отражении, можно решение задачи записать в г>,„бл. 19 ------------------—
572
Т а б л и ц а 19-2
Промежуток1 времени U1/UO й/Л> Значения напряжения последующих волн 112^0 1г/ ^0
0 ... l/v 1 1 ^npl — Uq 0 0
l/v ... 21 v 1 I tzo61 — ^2llnpl — “0,5Z7o 0,5 1,5
21 v ... 3l/v 1 2 11П p2 = Щ Uo61 — +0,5t/0 0,5 1,5
3l/v ... 4l/v 1 2 ^062 — ^2^пр2 ~ 0,2э(7о 0,75 2,25
4ljv ... 5l/v 1 2,5 «п гз = «1 “062 = + 0,25t/0 0,75 2,25
Zl/v ... 6l/v 1 2,5 ^обз — Г'2^прз~ ~0,125(70 0,875 2,625
61 V ... ll/v 1 2,75 np4 ~ ft'i ^обз ~0,l 25(7q 0,875 2,625
2kl (2k +-1) /
V V 1 3 ^пр Л+11—0 1 3
При k -> co
На рис. 19-25, а и б показано изменение тока ilt поступающего в линию от источника, в зависимости от времени для двух случаев, рассмотренных в примерах 19-8 и 19-9: a) r2 > zc (г2 = 4г,); б) г2 < < (г2 = гс/3). На тех же рисунках показано тонкими линиями
изменение напряжения и2 в конце линии. Повышение напряжения в сравнении с установившимся значением наблюдается, только когда r2 > zc, и наибольшее значение напряжения получается, когда первая волна дошла до конца линии.
В случае «а» напряжение и ,ток совершают колебания вокруг ^которых установившихся значений напряжения Uo и тока 12 = ППТ.ТмЛн yOGPL Г* РПДМДЦТ1 у STtiM QU QUPTJI^ ПЛТ T~Tt~.ll
573
r2 — оо, что соответствует холостому ходу (п2 = 1)( колебав не затухают. Период таких колебаний Т = 2 - 2l/v. На рис. 1g показано, как при этом изменяются ток в начале линии и напряж ° ние в конце линии.
Время Т называется периодом собственных колебаний длинно? линии, a f = \/Т — ее собственной частотой: 1
4/ ]/ L0C0
В реальных линиях ]7?х | < 1 и колебания всегда затухают
В случае «б» напряжение и ток апериодически нарастают до установившихся значений Uo и /2 = U0lr2.
Если сопротивление г2 равно нулю, то пг — п2 = — 1 и каждая волна, приходящая к началу линии, увеличивает ток на 2/0 == = 2U!zc. График изменения тока в начале линии для этого случая
представлен на рис. 19-27. При Uo = const (т. е. при бесконечно мощном источнике) и при отсутствии потерь ток в линии возрастал
Рис. 19-26.
бы до бесконечности. В реальных линиях скачки тока постепенно уменьшаются, и он приближается к некоторому предельному значению — току короткого замыкания линии.
При приближенном рассмотрении реальных линий с потерями сопротивление проводов гл может быть условно разделено пополам и отнесено: гл/2 — к началу линии; rJ2 — к ее концу. Эти сопротивления могут быть при расчетах включены в у и г2.
Включение нагрузки. Если линия, заряженная до напряжения Uo, разряжается с одного из концов на сопротивление г (рис. 19-28), то изменение напряжения и тока в линии может быть определено аналогично предыдущему.
Так как напряжение на рубильнике перед его включением равно — Uo, то в соответствии с § 19-4
; ______ Up ______т .
bipl— r + zc—
— ----------------Mnpi = — ________________(19-37)
• "Г -
574
Находим коэффициенты отражения для начала и конца линии Б соответствии с (19-34):
г—гс ,
«1=7+^ и "2=1-
Тогда
io6i= Jnpi== — Л; 1цр2 — fhio6i= — I sfht
^обг —1'пр2==—inp3 — /г1/об2 — —1эП21 и т. д.;
^об k ^пр k
Учитывая равенство tnpft = to6A, можно заметить, что каждая последующая обратная волна тока компенсирует предыдущую
прямую волну и ток в начале линии всегда равен току последней прямой волны. Ток в сопротивлении г по абсолютному значению такой же и противоположен по знаку.
Таким образом, ток в сопротивлении
tr=—гПр* = /эп*"1, а напряжение
ur=rir = rl9nkl~1.
На рис. 19-28, а—в показаны кривые изменения иг (или ir) во времени для случаев: а) г > гс; б) г < zc; в) г = гс. В первом случае напряжение и ток уменьшаются скачкообразно через каждые 2//ц секунд, не изменяя знака; во втором случае пг < 0 и эти изменения знакопеременные. Если же г = гс, то первая прямая волна снимает с линии половину напряжения, а’ первая обратная волна —• Бторую половину и процесс заканчивается через 2//п секунд. Все ~ to напоминает случаи апериодического, колебательного и предельно апериодического разрядов конденсатора;----------------
575
Последний случай имеет большое практическое значение та как аналогичный принцип применяется в радиотехнике для полу* чения импульсов прямоугольной формы, продолжительность которых зависит от длины линии.
Выше были рассмотрены некоторые простейшие примеры многократных отражений волн от концов линии. Во всех примерах прямая и обратная волны представлялись как результат наложения многократно отраженных волн. Те же результаты можно получить если рассматривать только результирующие значения прямой и обратной волн непосредственно, анализируя уравнения (19-9) и граничные условия на концах линии. Такой метод позволяет свести задачу к решению уравнений в конечных разностях, что упрощает расчет сложных случаев многократных отражений волн.
19-9. Блуждающие волны
Помимо появления волн при включении, отключении, коротком. замыкании или изменении нагрузки, а также при случайных заземлениях возможны еще волны под действием атмосферных явлений. Соседство грозовых туч, снег, дождь, движение воздуха, особенно во время восхода и заката солнца, — все это может привести к накоплению на изолированных проводах статических зарядов. Значительные заряды могут образоваться, когда по соседству с линией находятся грозовые тучи. Грозовая туча, имеющая, предположим, отрицательный заряд, действует таким образом, что разделяет в проводах на соответствующей длине линии положительные и отрицательные заряды (электростатическая индукция). Положительные заряды в проводах находятся в связанном состоянии с зарядами тучи и могут быть сосредоточены на небольшой длине линии, а свободные отрицательные заряды распространяются по всей длине линии и через несовершенную изоляцию стекают на землю; благодаря малой плотности этих зарядов их влиянием на процессы в линии можно пренебречь.
Когда грозовая туча внезапно разрядится с соседними облаками или с землей, бывшие до этого в связанном состоянии положительные заряды на проводах уже не удерживаются зарядами тучи. Поэтому от места накопления зарядов в ту и другую сторону пойдут волны.
В начальный момент (t = 0), когда заряды неподвижны, ток в линии равен нулю:
“пп °) — “об (х, °) л
и(х, 0) = unp(x, 0) + uo6(x, 0); i(x, 0) =---------------0
и следовательно,
«пр(х, 0) = ноб(х, 0)=^Л
Накопленные заряды в линии после их освобождения (t = 0) от удерживающих сил (от влияния грозовой тучи) распадаются
576
на две одинаковые волны с половинными значениями напряжений. Волны начинают перемещаться в противоположные стороны (рис. 19-29) со скоростью V. Пока волны не разойдутся, напряжения в соответствующих точках складываются и токи вычитаются. В дальнейшем эти половинные волны перемещаются независимо друг от друга к концам линии.
Изучение процессов в электрических цепях при наличии таких блуждающих волн имеет большое практическое значение для расчета и проектирования электрической изоляции машин, аппаратов и линий электропередачи.
имакс

Многократное отражение блуждающих волн происходит аналогично рассмотренным выше многократным отражениям прямоугольных волн. Если, например, линия с обоих концов разомкнута ni = п2 = 1 и отражение у концов линии происходит полностью и без перемены знака, то после отражения волны движутся навстречу друг другу, накладываясь друг на друга при встрече, как показано на рис. 19-29.
В реальных линиях наличие потерь приводит к затуханию волн; Напряжение блуждающих волн постепенно уменьшается, и по израсходовании всей энергии волны исчезают.
19 Основы теории цепей
Раздел Ilf
НЕЛИНЕЙНЫЕ ЦЕПИ
Глава двадцатая
НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
20-1. Элементы и эквивалентные схемы простейших нелинейных цепей
Выше были изложены основные методы расчета и описаны свойства линейных электрических цепей. В этом разделе рассматриваются нелинейные электрические цепи, т. е. цепи, содержащие элементы с нелинейными вольт-амперными характеристиками.
Нелинейные элементы электрических цепей можно разбить в зависимости от их характеристик на две основные группы: симметричные и несимметричные. Симметричными называют нелинейные элементы, у которых вольт-амперные характеристики не зависят от направлений тока в них и напряжения на их зажимах. К числу таких элементов относятся электрические лампы, бареттеры, терморезисторы (термисторы) и т. п. Несимметричными называют нелинейные элементы, у которых вольт-амперные характеристики не одинаковы при различных направлениях тока и напряжения на зажимах. В качестве примеров таких нелинейных элементов можно назвать электрическую дугу с разнородными электродами (медь — уголь, железо — ртуть), триоды (ламповые и полупроводниковые), вентили и т. п.
Рассмотрим вольт-амперные характеристики некоторых нелинейных элементов. Вольт-амперная характеристика бареттера (применяется для стабилизации тока) интересна тем, что при изменении в некоторых пределах напряжения U на его зажимах ток 1б остается практически неизменным (рис. 20-1). Ток в бареттере практически один и тот же при изменении напряжения в пределах от Ua до UK. Сопротивление бареттера /?й растет с увеличением тока.
Для стабилизации напряжения в электрических цепях включают терморезисторы, у которых с повышением температуры сопротивление уменьшается. На рис. 20-2 показана типичная вольт-амперная характеристика терморезистора. Они включаются также в различные схемы для измерения и регулирования температуры, применяются для температурной компенсации И т. д.
Некоторые электрические цепи содержат в качестве нелинейных элементов приборы тлеющего разряда, ^Еджим работу
578
газового промежутка, характеризующийся дуговым разрядом, также встречается весьма' часто на практике. С увеличением тока напряжение на дуге падает или, как говорят, у дуги падающая характеристика.
Электронные лампы и транзисторы, очень часто применяемые в современной электротехнике, как было показано, также обладают нелинейными вольт-амперными характеристиками.
Расчеты и исследования электрических цепей с нелинейными
вольт-амперными характеристиками во многих случаях проводятся
графоаналитическими методами, в основу которых положены законы Кирхгофа. В тех случаях, когда вольт-амперные характеристики можно с достаточной степенью точности выразить аналитическими
функциями, может быть выполнен аналитический расчет.
При расчете нелинейных цепей вводят понятия статического и дифференциального сопротивлений нелинейного элемента.
На рис. 20-3 показана вольт-амперная характеристика нелинейного элемента, построенная в масштабах для тока тч и напряжения mv. Предположим, что рабочий режим элемента задан точкой а. Отноше-
ние напряжения, измеряемого отрезком ab
к току, измеряемому отрезком ОЬ, определяет в некотором масштабе mr = mulmi статическое сопротивление г
в данной точке. Из рис. 20-3 видно, что эю сопротивление пропорционально тангенсу угла [3 между прямой, соединяющей точ-
ку а с началом координат, и осью токов, т. е.
tnvab mflb
=mr tgp.
сопротивление
Предел отношения приращения напряжения на участке цепи к приращению тока в нем или производная от напряжения по tokj 3 том же масштабе тг определяет дифференциальное G- Это сопротивление пропорционально
19*
579
тангенсу угла а между касательной к вольт-амперной характера тике в точке а и осью токов, т. е. н
r7^dU/dI=-=mr tga.
Для прямолинейного участка вольт-амперной характеристики дифференциальное сопротивление равно отношению конечного приращения напряжения к конечному приращению тока, т. е.
гд=Д£//Д7.
Для нелинейных элементов тернстнкой дифференциальное
Рис 20-4
с падающей вольт-амперной харак-сопротивленне отрицательно, так как положительное приращение тока сопровождается отрицательным приращением напряжения.
Если вольт-амперная характеристика на рабочем участке практически линейна, то можно для расчета нелинейный элемент заменить эквивалентной схемой, состоящей из источника напряжения и линейного сопротивления гд. Так, вольт-амперные характеристики двух нелинейных элементов, представленные на рис. 20-4, а и б, на небольших участках около рабочей точки а можно заменить прямыми линиями, уравнения которых
6^1 = Е 01 ф- (mr tg aj) I;
V2 = — Eoi ф- (mr tg <z2) 1 > или
^1 = Е01ф-г д1/;
Е2 = -Е02-Дгя21. (20-1)
Предположим, что нелинейный элемент г± (/) (рис. 20-5, а) имеет вольт-амперную характеристику, показанную на рис. 20-4, а. Для рабочей точки а и вблизи нее напряжение 1Д и ток / на нелинейном элементе
связаны первым из выражений (20-1). Эквивалентная схема* этого нелинейного элемента на небольшом участке около рабочей точки показана на рис. 20-5, б, причем э. д. с. £01 направлена навстречу току 1, так как именно при таком направлении э. д. с тютенпиал точки 1 (рис. 20-5, а) выше потенциала точки 2 на := 7 Е01 ф- гд17. —
580
Разделив последнее выражение на гд1, получим соотношение = Е011гл + I, которому соответствует эквивалентная схема с источником тока (рис. 20-5, в), где 1Я1 = UJr^. Ток равен в масштабе mi отрезку Od (рис. 20-4, а), отсекаемому на оси токов продолжением касательной af, что легко показать при помощи соотношения между катетами треугольника dOf.
Если нелинейный элемент (рис. 20-5, а) имеет вольт-амперную характеристику, показанную на рис. 20-4, б, то при тех же поло-
жительных направлениях для тока и напряжения (рис. 20-5, а) на эквивалентных схемах изменяются направления э. д. с. и тока источника тока на обратные, что следует из второго уравнения (20-1) и нетрудно уяснить из построений на рис. 20-4, б.
Если на некотором участке вольт-амперной характеристики нелинейного элемента напряжение убывает при увеличении тока (рис. 20-6), то дифференциальное сопротивление эквивалентной схемы получается отрицательным. Это означает, что в схеме замещения такое сопротивление можно представить источником э. д. с. или тока.
Следует еще раз подчеркнуть, что все соотношения, которые можно установить при помощи эквивалентных схем, справедливы лишь для таких режимов, когда нелинейные элементы электрической цепи работают на практически прямолинейных участках вольт-амперных характеристик.
20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами
„На рис 20-7 показано последовательное соединение двух нелинейных элементов t\ (/J и г2 (/2), вольт-амперные характеристики которых Ц (L\) и /2 (U2) заданы (рис. 20-8) Пусть требуется определить ток I и напряжения 1/г и U2 на элементах при заданном ~идяря/кеш!И11а зажимах ikuh I'— ---
581
Для вычисления тока I и напряжений и1 и (72 построим вСп могательную характеристику: зависимость тока I от суммарной" напряжения Ur + U2. Так как в неразветвленной цепи ток в обоих нелинейных элементах один и тот же, т. е. 1г= I2 = д То ДДя построения характеристики I (U1 + U2) необходимо суммировать напряжения Ur и U2 при оди-
наковых значениях тока 1 (рис. 20-8).
Отложим на оси абсцисс напряжение U и из точки а проведем прямую ab, параллельную оси ординат, до пе
Рис. 20-8.
тЛЕ)
Рис. 20-7.
ресечения с кривой / (U1 + П2); полученный отрезок ab равен в масштабе Ш] току I. Затем из точки b 'проведем прямую Ьс, параллельную осн абсцисс. В результате получим отрезки cd и cf, соответственно равные и U2 в масштабе mv.
Такие же построения для расчета тока и напряжений можно выполнить, если один из элементов линейный. Аналогично решается задача расчета цепи, состоящей из трех или большего числа последовательно соединенных элементов с нелинейными характеристиками.
Графические построения для расчета последовательной цепи (рис. 20-7) можно провести и другим способом.
Предположим, что на рис. 20-7 последовательно соединены нелинейный активный двухполюсник с источником э. д. с Е = U и нелинейным сопротивлением t\ (Л) и нелинейный пассивный двухполюсник г2 (12). Напряжение U2 на зажимах нелинейного элемента г2 (/2) определяется, с одной стороны, вольт-амперной характеристикой этого элемента /2 (U2), а с другой-—* разностью между э. д. с. Е — U и напряжением на зажимах нелинейного элемента t\ (Ц).
На рис. 20-9 построены характеристика I2 (U2) и кривая 71(П — — иг), абсциссы которой получены вычитанием абсцисс вольт-амперной характеристики A (t- i) из напряжения-Г/ для различны.-.
582
значений тока Из построений на рис. 20-9 непосредственно следует, что в точке b пересечения кривых I2 (U2) и 71 (U — Ur) удовлетворяются равенства U2= U — U1 и Л = /2 — h определяющие режим в рассматриваемой цепи.
20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов
На рис. 20-10 показаны параллельно соединенные нелинейные элементы t\ (7j) и г2 (12), вольт-амперные характеристики которых h (^i) 11 4 (О заданы (рис. 20-11). Пусть напряжение на зажимах цепи равно U-, тогда по вольт-амперным характеристикам (t/J и /2 (^4) легко определить токи и 12 в нелинейных элементах, а на основании уравнения 1Г + I2 = I — ток в неразветвленной
части цепи.
Рнс. 20-10.
Если задан ток I, то для определения напряжения U и токов 4 и 12 в нелинейных элементах t\ (It) и г2 (12) надо построить вспомогательную характеристику (7Х + т. е. зависимость суммарного тока от напряжения U. Так как при параллельном соединении L'x = U2 = U, то для построения этой характеристики в соответствии с уравнением 7=4 + 4 суммируем ординаты кривых 4 (^4) и 4 (74) для одних и тех же значений напряжения 74 = = U2 (рис. 20-11). Затем отложим на оси ординат отрезок Ос, равный в масштабе т7 току I, и проведем из точки с прямую cb, параллельную осн абсцисс, до пересечения с характеристикой (7Х + I2)U\ полученный отрезок сЪ = Оа равен в масштабе mv напряжению U. Наконец, из точки b проведем прямую, параллельную оси ординат, До пересечения с осью абсцисс. В результате получим отрезки °d и af, равные в масштабе т7 токам /х и /2.
Таким же путем можно рассчитать электрическую цепь с любым числом параллельно включенных нелинейных элементов.
20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов
На рис. 20-12 показана схема со смешанным соединением нелинейных и линейных элементов. Пусть заданы напряжение источника U, а также вольт-амперные характеристики нелинейных
583
элементов /х (t/x), /2 (б/2) (рис. 20-13) и сопротивление г3 линейног элемента; требуется найти токи во всех ветвях и напряжения0 на элементах.
Для определения искомых токов и напряжений можно применить так же как при расчете последовательных и параллельных цепей’ графический метод. ’
Рис. 20-12 Рис. 20-13.

Рис. 20-14.
перную характеристику линейного элемента — прямую /3 (Д8), проходящую через начало координат. Затем суммированием ординат кривой /2 (Д2) и прямой 13 (7/3) для одних и тех же значений напряжения U2 = Ua — U2S построим вольт-амперную характеристику параллельного соединения (/2 + /3) U23. Наконец, суммированием абсцисс кривых /х (Г/х) и (/2 + /3) U23 для одних и тех же значений тока /х = /2 + /3 получим вольт-амперную характеристику всей цепи
Л (^1 + ^2з)=Л (^)-
Отложим в масштабе ти на оси абсцисс заданное напряжение U (отрезок Оа) и проведем прямую, параллельную оси ординат, до пересечения с кривой /х (Д); полученный отрезок ab определяет в масштабе trij ток /х. Затем проведем из точки b прямую, параллельную оси абсцисс, до пересечения с кривыми /х (7Д)
и (/2 + /3) U2з в точках с и d и опустим из точки d перпендикуляр dg на ось абсцисс. В соответствии с уравнениями £7 = С7Х -f- U23 и /х — 4 + 4 отрезки db и cb определяют в масштабе mv соответственно напряжение 7/х на первом элементе и напряжение U23 на* разветвлении, а отрезки ge и gf в масштабе т, дают токи /2 и /3-Графические построения для расчета рассматриваемой цепи можно выполнить, так же как при расчете схемы с последователь- ным соединением нелинейных элементов (рис. 20-7), другим спо-" ~сбббМ/Представим сЯему
584
соединения нелинейного активного двухполюсника с источником g д с. Е = U и нелинейным сопротивлением t\ (/t) и нелинейного пассивного двухполюсника г23 (/2 + /3), эквивалентного двум параллельным ветвям с элементами г2 (/2) и г3 (рис. 20-14) и с вольт-амперной характеристикой (/2 + /3) 1/23 (рис. 20-13). Полученная схема (рис. 20-14) не отличается от схемы на рис. 20-7, поэтому расчет режима схемы, показанной на рис. 20-14, может быть выполнен при помощи построений, аналогичных выполненным на рис. 20-9.
20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей
Схема, изображенная на рис. 20-12, может быть применена для стабилизации напряжения U, = Us — U23 на зажимах приемника с сопротивлением r3. JXeii-ствительно, если напряжение U, соответствующее рабочей точке Ь (рис. 20-13), увеличится на Д1/, то напряжение U23 на зажимах сопротивления г3 изменится значительно меньше на Д1/23 (рис. 20-13).
Степень постоянства напряжения на зажимах приемника характеризуют коэффициентом стабилизации. Коэффициентом стабилизации напряжения называют отношение относительного изменения стабилизируемого напряжения U к вызванному им относительному изменению стабилизированного напряже- Ет rSt ния 1/23, т. е. а. ф [——------------
А Д1/ Д(723 Un &U с~~и~ '
или в пределе
U2S dU
с и dU^ •
Очевидно, чем больше коэффициент стабили- р 15
зации, тем меньше относительное изменение ста- ' ' ‘
билизированного напряжения.
Для выяснения стабилизирующих свойств схемы определим коэффициент стабилизации напряжения на сопротивлении г3 в схеме, показанной на рис. 20-12, при помощи эквивалентной схемы.
Заменим вольт-амперные характеристики Д (Uj) и /2 (1/2) на участках pq и тп прямыми линиями qO' и пО". Уравнения этих прямых:
= —UB1 U2—U02-[-гк212,
где гл и гд2 — дифференциальные сопротивления нелинейных элементов.
Этим уравнениям удовлетворяет эквивалентная схема на рис. 20-15, в которой Enl = и Ет = Um.
Для этой схемы по законам Кирхгофа
17-|-£о1 = Гд1/14-143; E02 — U23
7i = /2+73, откуда
rr rr ГД1ГД2 + ГД1Г8 + Гд2/"з
17 — 17 23------------------------------------ .
' Ц2Г3 ' д2
Производная от напряжения U по U2S:
585
После подстановки dlJ/dlJ2S в выражение для fec получим:
Для хорошей стабилизации напряжения (J23 коэффициент 4 должен нмет возможно большее значение. В рассматриваемой схеме это достигается приме нением нелинейных элементов с возрастающим rt (4) и уменьшающимся г статическими сопротивлениями. Дифференциальные сопротивления гл и r^/npo-порциональны соответственно tg а, н tga2 (Рис- 20-13). Так как tgc/., tga то отношение гД1/гл2 1- Таким образом, при определенных соотношениях между сопротивлениями гд1, гА2 и г3 можно получить значение fec, во много раз превышающее единицу.—
Рис. 20-16.
Для стабилизации напряжения можно пользоваться и другими схемами, в частности мостовой схемой, показанной на рис. 20-16, а. Пусть в рассматриваемом режиме вольт-амперные характеристики нелинейных элементов гг (4) = — гв (4) и г2 (/2) = г4 (4) заменены прямыми линиями, уравнения которых
64=—Е01+гд14; =Ео2 4-гд2/2.
На рис. 20-16, б показана эквивалентная схема, на которой нелинейные элементы заменены источниками э. д. с. и дифференциальными сопротивлениями. Так как схема симметрична, то Д = 13 и /2 = 4- Для определения четырех неизвестных токов составим уравнения:
Е -|-Eoi — Ео2==Гд1/14-Гд2/г!
Ео1 + Ео2 = гд14 + го6о— 4=4+4; ^=4+4-
Пусть рд1 = г,2 = гл, что нетрудно получить в реальных условиях. Тогда в результате совместного решения уравнений найдем:
Ерх+Еог Гд+Гр
Из последнего выражения следует, что ток 4 и напряжение Uo ~ г010 на со-—нунтннлении л, ис^авпсят от приложенного напряжения U = £. Следовательно, эта схема может служить стабилизатором напряжения истока. =
586
20-6. Вольт-амперные характеристики нелинейных активных двухполюсников
приходится пользоваться вольт-ампер-
Рис. 20-17.
При графоаналитических расчетах разветвленных цепей с нелинейными элементами часто ными характеристиками активных двухполюсников с нелинейными элементами.
На рис. 20-17, а показана активная ветвь, эквивалентная некоторому нелинейному двухполюснику с источником э. д. с. Е и нелинейным элементом г (/);
вольт-амперная характеристика этого элемента дана на рис. 20-18 в виде кривой / = f (U). Для схемы, изображенной на рис. 20-17, а при выбранных положительных направлениях тока / и напряже-
ния U21, очевидно, справедливо уравнение U21 = Е — U. По
этому уравнению и заданной вольт-амперной характеристике / — ~ f (U) на рис. 20-18 построена вольта-амперная характеристика,
показывающая зависимость тока / от напря-
Рис. 20-20.
жения U21. При изменении тока / в пределах от нуля (точка а) до I = /0 (точка Ь) напряжение U21 уменьшается, изменяясь от значения U21 = Е до значения t/21 = 0 (участок ab кривой). При дальнейшем увеличении тока / напряжение U21 на зажимах двухполюсника становится отрицательным и определяется абсциссами участка кривой Ьс (рис. 20-18). При отрицательных значениях тока / и напряжения U напряжение U21 растет с увеличением
тока / (участок ad).
Если э. д. с. Е (рис. 20-17, б) имеет про-
тивоположное направление, т. е. Е,л =
— Е — U, то получится другая вольт-амперная характери-^Д^л^актчаногцдаухнежосникагвшвделкртгвойI (— Е~ Ц)г=
587
(рис. 20-18). Из рис. 20-18 ясно, что вольт-амперная характеру стика I = f ( — Е — U) получается путем переноса каждой ордц! наты кривой / = / (Е — U) на величину 2Е влево относительно кривой / = f (Е — U).
Вольт-амперные характеристики для активных двухполюсников с источником тока (рис. 20-19, о и б) построены на рис. 20-20 в виде кривых: / = J + Is = f (U) и I = — J + /„ = f (If). Методика построения этих характеристик показана непосредственно на рис. 20-20 и не требует особых пояснений.
20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами
На рис. 20-21, а показана разветвленная схема с тремя известными э. д. с. источников Еъ Е2, Es и тремя нелинейными элементами ri (Л), r2 и rs (/3), вольт-амперные характеристики которых
для упрощения дальнейших графических построений приняты одинаковыми [кривая /2 (U2) на рис. 20-8] и симметричными; требуется определить токи 1Ъ /2 и /3 во всех ветвях.
Выберем положительные направления токов /1( /2 и /3 так, как показано на рис. 20-21, а. Тогда разность потенциалов между точками 2 и 1
(p2 — (Pi==^2i=E1 — U1=E2 — U2 = —E3 + Ua, (20-3)
где Ult U2 и U3 — напряжения на нелинейных элементах.
Пользуясь вольт-амперной характеристикой /2 (U2) (рис. 20-8), построим (рис. 20-21, б) кривые:
LJ^=^dEj~Ur)- = I2 (Е2 -Z/2);
^3 (^21) — Л (---Ез + Ез).
588
Для определения токов в ветвях построим вспомогательную характеристику (Д + Д)£721 суммированием ординат кривых Д (Д21) и Д (^41) Для одних и тех же значений напряжения £/21.
Токи в ветвях должны удовлетворять уравнениям (20-3) и первому закону Кирхгофа: Д + Д = Д. Следовательно, ордината точки а пересечения кривой Д (t/2i) и кривой (Д -ф- Д) £/21 определяет в масштабе искомое значение тока Д, а абсцисса той же точки а в масштабе т1; дает значение напряжения U21. Построив из точки а прямую, параллельную оси ординат, получим отрезки сЬ и cd, определяющие в том же масштабе т{ токи Д и Д. Отметим, что выбранное положительное направление тока Д не совпадает с действительным направлением этого тока (точка d лежит ниже оси абсцисс).
Другим приемом решения поставленной задачи является построение кривой (Д + Д — Д) U21 (пунктирная кривая на рис. 20-21, б). Так как алгебраическая сумма токов Д + Д — Д равна нулю, то точка с пересечения кривой (Д + Д — Д) U21 с осью абсцисс определяет неизвестное напряжение U21.
Рассмотренные приемы расчета можно распространить и на более сложные цепи, состоящие из любого числа активных и пассивных нелинейных элементов со смешанным соединением. Для пояснения прежде всего вернемся к схеме, показанной на рис. 20-21, а и покажем, что графические построения на рис. 20-21, б соответствуют расчету схемы на рис. 20-21, в, состоящей из двух активных нелинейных двухполюсников. В этой схеме один из двухполюсников с источником э. д. с. Ев и нелинейным элементом г6 (Д ф- Д) эквивалентен двум заданным параллельным ветвям с источниками э. д. с. Д и £2 и нелинейными элементами (Д) и г2 (Д).
Действительно, при суммировании ординат кривых Д (U21) и Д (£/21)дляодних и тех же значений напряжения U21 (рис. 20-21, б) устанавливается зависимость (Д -ф- Д) U21 между суммарным током Д ф- Д и напряжением U21 на зажимах двух указанных параллельных ветвей. Если э. д. с. Ев и вольт-амперная характеристика нелинейного элемента гв (Д ф- Д) подобраны так, что зависимость между током (Д ф- Д) и напряжением U21 для этой схемы такая же, как и для схемы на рис. 20-21, а, то полученный двухполюсник эквивалентен двум параллельным ветвям с заданными источниками э. д. с. Ег и Е2 и нелинейными элементами t\ (Д) и h (Д).
Электродвижущая сила Ев эквивалентного активного двухполюсника равна напряжению на его зажимах при токе Д ф- Д = 0, чему соответствует на рис. 20-21, б точка е. Вольт-амперная характеристика (Д ф- Д) UB эквивалентного элемента гв (Д ф- Д) (рис.
_ 41-21, в) может быть найдена в соответствии с уравнением UB = Ев—
^21, т. е. вычитанием абсцисс характеристики (Д + Д) U21 113 э. д. с. Ев.
Для определения тока Д в схеме на рис. 20-21, в можно восполь-З'Даться изложенными выше Д 20 2) вторым сиосоиом расчега-
589

последовательной цепи (рис. 20-9), что полностью совпадает с построениями на рис. 20-21, б.
В сложных цепях со смешанным соединением нелинейных элементов следует заменить параллельно соединенные ветви эквивалентными двухполюсниками, как только что было показано а затем преобразовать всю схему к простому последовательному
Рис. 20-22.
соединению двухполюсников. Например, для расчета схемы, изображенной на рис. 20-22, а, можно первую и четвертую ветви, а также вторую и пятую заменить эквивалентными двухполюсниками и получить неразветвленную цепь из трех активных двухполюсников (рис. 20-22, б), расчет которой не представляет затруднений. Затем следует вернуться к исходной схеме и по законам Кирхгофа определить токи в остальных ветвях.
При расчете разветвленных цепей с линейными элементами иногда можно упростить схему, применяв для линейной части цепи взаимное преобразование треугольника и звезды сопротивлений. Например, схема на рис. 20-23, а содержит звезду из постоянных сопротивлений rit г5 и г3. После преобразования этой звезды в эквивалентный треугольник получится схема (рис. 20-23, б) со смешанным соединением линейных и нелинейных элементов, метод расчета которой уже известен.
590
20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами
Для расчета разветвленных электрических цепей и нелинейными элементами иногда целесообразно теоремой об активном двух-
с линейными пользоваться
полюснике.
На рис. 20-24, а показана схема разветвленной цепи с одним нелинейным элементом rs (73), причем известны э. д. с. источников £х и Е2, сопротивления гь r2, rit г5 и ге и вольт-амперная характеристика нелинейного элемента; требуется определить токи во всех
Рис. 20-24.
ветвях.
По теореме об активном
двухполюснике представим за-
данную схему (рис. 20-24, а) в виде последовательного соединения двух двухполюсников (рис. 20-24, б). В полученной схеме э. д. с. £ =-£х равна напряжению между точками 1 и 2 при отключенном элементе; — входное сопротивление активного двухполюсника по отношению к зажимам 1—2; /3 — искомый ток в нелинейном элементе. Этот ток
Рис. 20-25
в схеме на рис. 20-24, б легко найти ранее изложенным способом. При известном токе /3 токи в остальных ветвях определяются аналитически любым расчетным методом схемы на рис. 20-24, а.
Эквивалентную схему на рис. 20-24, б можно получить, не применяя теоремы об активном двухполюснике. Для этого треугольник сопротивлений rit г& и ге следует преобразо-
вать в эквивалентную звезду, а полученные в результате такого преобразования две параллельные ветви заменить одной ветвью с эквивалентными источником э. д. с. £ и сопротивлением гк.
Применяя теорему об активном двухполюснике к нескольким ветвям, иногда удается довольно просто рассчитать разветвленную пепь с несколькими нелинейными элементами после ее преобразования к более простому виду.
591
На рис. 20-25, а изображена мостовая схема с двумя нелинейных и тремя линейными элементами, для которой заданы вольт-амперны' характеристики нелинейных элементов, а также сопротивленн ветвей г, t\ и г4 и напряжение U; требуется определить токи во всех ветвях.
Рис. 20-26.
Разомкнем одновременно вторую и третью ветви с нелинейными элементами и найдем напряжения Ux2 и Ux3 на зажимах этих ветвей. Затем, так же как при расчете линейной цепи (рис. 2-32), включим в разомкнутые ветви источники э. д. с. £х2 = Ux2 и £хз = £х3 и закоротим зажимы 3 и 4. В результате получится схема (рис. 20-25, б). У этой схемы токи /2 и /3 в ветвях с нелинейными элементами равны действительным токам в тех же ветвях заданной мостовой схемы (рис. 20-25, а). Расчет полученной схемы (рис. 20-25, б) со смешанным соединением линейных и нелинейных элементов выполняется ранее изложенными способами.
Рис. 20-27.
Необходимо отметить, что иногда в результате размыкания ветвей с нелинейными элементами они отсоединяются от остальной активной части схемы; возникает неопределенность при расчете напряжений на зажимах этих ветвей. Например, такая неопределенность появляется при определении напряжений UxS, UXi и и я в схеме на рис. 20-26, а, полученной в результате одновременного
592
размыкания трех ветвей с нелинейными элементами г3 (/8), г4 (/4) и r3 (h)- Эту неопределенность легко устранить. Если положить напряжение на зажимах одной из ветвей, например Ux3, равным нулю и соединить между собой проводником с нулевым сопротивлением точки 1 и Г (изображено пунктиром на схеме рис. 20-26, а), то режим не изменится, так как токи во всех ветвях с нелинейными элементами не возникают. Следовательно, для расчета заданной схемы достаточно определить напряжения Uxi и Ux5. Токи в нелинейных элементах могут быть теперь найдены по схеме рис. 20-26, б, которая после преобразования треугольника сопротивлений rlt г2 и ге в эквивалентную звезду приводится к схеме с двумя узлами.
Таким образом, в случае неопределенности величин напряжений на зажимах ветвей при их размыкании следует разомкнуть не все ветви с нелинейными элементами. При этом токи во всех ветвях с нелинейными элементами должны быть, так же как в разомкнутых ветвях, равны нулю.
В заключение рассмотрим еще один прием расчета любых разветвленных цепей с линейными и двумя нелинейными элементами, основанный на применении эквивалентной Т-образной схемы активного четырехполюсника.
На рис. 20-27, а показан линейный активный четырехполюсник А с двумя присоединенными к нему нелинейными элементами t\ (/4)
11 г2 (Л). Заменим активный четырехполюсник Т-образной схемой (рис. 20-27, б), в которой э. д. с. £Х1 и £х2, как известно, равны напряжениям на зажимах 1—1' и 2—2' при их одновременном размыкании. Пассивные элементы , f2, эквивалентной схемы найдем так же, как в § 8-5.
Зная вольт-амперные характеристики нелинейных элементов и параметры эквивалентной схемы с двумя узлами (рис. 20-27, б), нетрудно определить токи Л и /2 в ветвях с нелинейными элементами одним из ранее изложенных способов.
Аналогичным путем можно произвести расчет сложной разветвленной цепи с тремя нелинейными элементами (рис. 20-28, а). Для 3T0g схемы после одновременного размыкания ветвей с нелинейными элементами и включения э. д. с., равных напряжениям на зажимах разомкнутых ветвей, запишем уравнения, рассматри
593
вая токи А» /2, А как контурные:
Гц11 Г12/2-|- Г 13^3~ЕХ1 — Uь Г21 А 4Г 22^ 2 4“ Г 23/3 = £*2 — Ь'2;
Сз1 А4~ Г32 А 4" Г33^3 — Ехз — U3-
Линейную часть схемы рис. 20-28, а с шестью зажимами, к которым присоединены три нелинейных элемента, заменим эквивалентным шестиполюсником (рис. 20-28, б) в соответствии с уравнениями
(ги4“^12 4~Оз) A4~ri2 (А — А) 4-Пз (А~ А) =ЕХ1~ иг-
r2i (А ~ А) 4~ (^22 4~ r2i 4“ ^гз) А 4“ (А ~ А) = £х2—‘^А;
Гз1 (А — А)4_?'з2 (А ~ А) 4~ (гзз4~ ^з14~гзг) А = £\з-1/3.
На эквивалентной схеме рис. 20-28, б обозначено:
Г1 = Гц4~С12 4~ Нз! Г2 = Г21 4“ Г22 4“ Г23; Г3 — Г31 4“ Г32 4~',33> причем r12 = r21; r23 = г32; г31 = г13.
Полученная эквивалентная схема может быть рассчитана сравнительно просто ранее изложенными способами.
20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений)
При расчете цепей с нелинейными элементами очень часто при
меняют приближенный аналитический способ решения нелиней-
Рис. 20-29.
ных алгебраических уравнений, называемый методом итерации.
Для выяснения сущности этого метода рассмотрим сначала произвольную цепь с одним нелинейным элементом. Схема с одним нелинейным элементом, на которой источник с э. д. с. Е и сопротивлением гв заменяют линейную часть цепи произвольной конфигурации, показана на рис. 20-29, а. Вольт-амперная характеристика нелинейного элемента задана (кривая 1 или 2 на рис. 20-29, б).
Найдем прежде всего условия, при которых сходится итерационный процесс для двух значений сопротивлений гв и для двух типов нелинейных элементов с различными вольт-амперными характеристиками.
Пусть э. д. с. Е и сопротивление гв
имеют такие значения, при которых
внешняя характеристика эквивалентного источника изображается прямой fg (рис. 20-29, б). Очевидно, что графически рабочий режим цепи в случае первого нелинейного элемента определится точкой а-
594
Для того чтобы найти напряжение и ток в цепи методом итераций, зададимся напряжением U, например, равным Е и по кривой 1 найдем ток / (точка р на рис. 20-29, б). Затем по уравнению
U=E-r„/=F(U) (20-4)
определим уточненное значение напряжения (что соответствует на рис. 20-29, б переходу из точки р в точку q). После этого найдем по вольт-амперной характеристике новое значение тока / (точка s), а затем по уравнению (20-4) определим новое уточненное значение напряжения V и т. д. Из рис. 20-29, б непосредственно следует, что при заданных значениях Е, гв и известной вольт-амперной характеристике нелинейного элемента итерационный процесс в этом случае сходится.
Можно показать (в курсе математики это положение доказывается), что условие сходимости требует, чтобы в окрестности искомого корня (точка а) абсолютное значение производной |F' (U) | было меньше единицы, и чем меньше значение |F' (U) |, тем быстрее сходится процесс.
Для исследуемой схемы после дифференцирования (20-4) получим:
dF (U)/dU — — rB dl/dU = — rB/rn>
причем необходимо, чтобы
I гвА"д I 1 •
(20-5)
Так как дифференциальное сопротивление гл определяется в некотором масштабе значением tg а, а сопротивление гв в том же масштабе значением tg |3 < tg а (рис. 20-29, б), то в окрестности точки а условие (20-5) выполняется.
Другой способ вычислений основан на применении уравнения для тока
t = ^^ = F(/). (20-6)
В этом случае зададимся током / и по кривой 1 найдем значение напряжения U, а по формуле (20-6) определим уточненное значение тока. Затем по вольт-амперной характеристике 1 найдем новое значение напряжения и т. д.
При тех же значениях Е, гв и вольт-амперной характеристике нелинейного элемента, т. е. той же рабочей точке а, как показывают расчеты, итерационный процесс расходится.
Однако легко убедиться, что при помощи второго способа вычислений можно найти методом итерации ток и напряжение, соответствующие рабочей точке b (рис. 20-29, б), т. е. при сопротивлении гв> значительно большем, чем в первом случае (внешняя характеристика //г). Это объясняется тем, что условие сходимости при втором способе расчета записывается так:
— — I = I — ^-1 < 1
di rB I j гв |
(20-7)
595
т. е. необходимо другое соотношение между гк и Дифференциальным сопротивлением га в рабочей точке.
Если в схеме на рис. 20-29, а заменить нелинейный элемент другим с вольт-амперной характеристикой 2 (рис. 20-29, б), то нетрудно заметить, что последовательность вычислений и условия сходимости итерационного процесса для' точек cud получаются такими же, как для точек а и Ъ. Но итерационный процесс в точке d сходится медленнее, чем в точке Ь, так как отношение | — гд/гв| в этой точке лишь немного меньше единицы. в
Чтобы сделать некоторые обобщения, рассмотрим еще два способа расчета, непосредственно вытекающие из уравнения
р
J2M)
где г (/) — статическое сопротивление нелинейного элемента (рис. й формулы целесообразно предварительно построить зависимость г (7) = 6/ (7)/7.
Последовательность расчета в этом случае непосредственно следует из уравнения (20-8). Условия сходимости находим дифференцированием уравнения (20-8):
I dF (/) I_I Е dr (I)ldl I .
I ~dT | ~ | “ lrB + r(/)F I < b
(20-9)
Чтобы получить более удобное выражение для оценки условий сходимости, установим связь между статическим г (/) и дифферен
циальным гд (/) сопротивлениями нелинейного элемента в виде соотношения
G = 37 = dl л 1 + г
откуда
dr(l) __ гя(Г) — г (/) di I
(20-Ю)
Заменив в уравнении (20-9) dr (T)/dI по (20-10) и с учетом (20-8), получим условие сходимости:
гД(П~ ' (Л I
Гв -И (Л I
< 1.
(20-П)
Из рис. 20-30 непосредственно следует, что для вольт-амперных характеристик с положительным сопротивлением гл (/) и с уменьшающимся статическим сопротивлением г (/) (па рис 20-30 кривая У) дифференциальное сопротивление меньше статического (tg «i <
596
Pi), T. e. абсолютное значение разности |гд (/) — г (/)| всегда 1еНьше г (/). Поэтому условие сходимости (20-11) выполняется при любом значении сопротивления гв.
Аналогично можно показать, что для вольт-амперных характеристик с возрастающим статическим сопротивлением г (U) (на рис. 20-30 кривая 2) расчетное уравнение нужно составить относительно напряжения на нелинейном элементе, т. е.
<20-12>
При этом условие сходимости имеет вид:
Гв Г (<7)/гд (б/)] — 1 гв + г (^)
<1.
(20-13)
Для вольт-амперных характеристик с положительным сопро тивлением г (U) и с возрастающим сопротивлением г (U) стати
ческое сопротивление меньше дифференциального (tg р2 < tg а2) и их отношение г (U)/rn (U) всегда меньше единицы (рис. 20-30). Поэтому условие сходимости (20-13) выполняется при любом значении сопротивления гв. Конечно, быстрота сходимости итерационного процесса зависит не только от вида вольт-амперных характеристик и
Рис 20-31.
выбора начальных приближений,
но и от значения сопротивления гв. Однако основным фактором,
определяющим решение нелинейных уравнений методом итерации, является способ составления расчетных уравнений.
Поскольку при указанных способах расчета (20-8) и (20-12) итерационный процесс сходится при любом значении сопротивления гв, его можно применить для расчета сложной разветвленной цепи с любым числом нелинейных элементов.
На рис. 20-31, а показан нелинейный элемент г2(/), присоединенный к зажимам разветвленной активной нелинейной цепи (условно обозначенной прямоугольником с буквами АН) с э. д. с., не зависящими от токов. Такую активную нелинейную цепь можно представить в виде активного двухполюсника с эквивалентной э- Д. с. Е и нелинейным элементом гх (/) (рис. 20-31, б). В результате получилась неразветвленная схема с двумя нелинейными элементами, расчет которой можно выполнить изложенным способом.
Для иллюстрации методики расчета рассмотрим примеры.
Пример 20-1. На рис. 20-32 изображены вольт-амперные характеристики единенных элементов, показанных на схеме рис 20-31, б, э д. с Е = 10 В Определить ток / и напряжения на участках итерационным способом, применяя Расчетные уравнения (20-8) и (20-12).
597
Решение. Запишем уравнение (20-8) для схемы рис. 20-31,6:
_________Е 10
Us) lL r2s U s) ris Us) H" r2s Us) ’ где s — порядковый номер приближения.
Расчет по этой формуле при помощи вольт-амперных характеристик (рис. 20-32) приведен в табл. 20-1.
Таблица 20-1
S номер приближения !s- А [/ , В 2S (из характеристики) r2S^ и ' Ом uis- в (из характеристики) и Ом 'й + 'и- Ом г ~— А
0 0,400 5,3 13,25 0,75 2,00 15,25 0,655
1 0,655 6,55 10,00 1,35 2,06 12,06 0,827
2 0,827 7,25 9,СО 1,95 2,36 11,36 0,880
3 0,880 7,40 8,41 2,15 2,44 10,85 0,920
4 0,920 7,50 8,15 2.30 2,50 10,65 0,940
5 0,940 7,55 8,04 2,40 2,56 10,60 0,940
Табл иц а 20-2
/ А £Л В ris ~
номер прибли- U2S- в S’ (из ха-ракте- V2S 1S’ (из ха-ра кте- I ' 'is+r2s-Ом vzsi-в
ристики) Ом ристики) Ом
0 6,00 0,52 11,5 1,05 2,0 13,50 8,55
1 8,55 1,50 5,7 7,00 4,66 10,36 5,50
2 5,50 0,43 12,8 0,80 2,0 14,80 8,65
3 8,65 1,60 5,4 12,0 7,5 12,10 4,18
4 4,18 0,26 16,1 0,4 2,0 18,10 8,90
Таблица 20-3
I . А и , в r2s ~
номер прибли- "и- в S’ (из ха-ракте- Г ’ 2S (из ха-ра кте- 'Т$4-г2$’ Ом В
ристики) Ом ристики) Ом
0 7,0 1,5 4,67 8,50 5,67 10,34 4,50
1 4,5 1,3 3,46 8,25 6,35 9,81 3,53
2 3,53 1,19 2,96 8,10 6,80 9,76 3,04
3 3,04 1,09 2,67 7,90 7,25 9,92 2,69
4 2,69 1,00 2,69 7,70 7,70 10,39 2,59
5 2,52 0,99 2,61 7,65 7,73 10,34 2,52
6 2,52 0,98 2,57 7,60 7,77 10,34 2,49
598
Из этой таблицы видно, что итерационный процесс довольно быстро заканчивается, несмотря на ухудшение условий сходимости вследствие влияния нелинейного сопротивления rls. В результате получены значения тока и напряжений на участках, практически совпадающие с величинами, найденными графически (рис 20-32).
Можно показать, что при расчете напряжения U по формуле _________________Us)_________ rls(/s)^r2s(/s) получается расходящийся процесс, что иллюстрируется табл. 20-2.
Однако, если применить расчетное уравнение (20-12) для определения напряжения L', на нелинейном элементе с возрастающим сопротивлением Г1{1) (рис 20-31, б), то итерационный процесс сойдется. Расчетное уравнение в этом случае ‘
,,_____________Erls (Is)
1<S+D 1\S(I s)-\-r2s(I s)
По этому уравнению и вольт-амперным характеристикам {7Х (/) и U2 (/) составлена табл. 20-3.
Из этой таблицы видно, что итерационный процесс практически заканчивается после шестого приближения
Пример 20-2. На рис 20-33 изображена мостовая схема с двумя нелинейными элементами гх (/х) и г2 (/2). Вольт-амперные характеристики этих нелинейных элементов заданы (рис. 20-34) Пользуясь итерационным методом, определить токи в ветвях с нелинейными элементами и напряжения на их зажимах.
Решение По методу контурных токов, запишем уравнения:
(гз4-гб)Л + ^5^2—(г3 + ГГ>) Л) ~ Hj!
+ (Г4 ~Р 7 2 — (г4 + Гй) =
— (гз + г5)Л — (г4 + г5)Л + (''з + г4+''5+г)^3==^>
где /j, /2 и /3 — контурные токи.
Выразим контурный ток /3 из третьего уравнения и подставим его значение в первое и второе. После преобразований получим:
(гз + га) (п+г) j , у^у —У3У4 / = £ Гз+*> _ jj .
Уз + ^+Гб + г 1 У3 + У4 + У5 + У 2 У3 + Г4 + У5 + У *’
___У-/ —У3У4 I , (У4Ч-У5) (у-. + у) j У4Ч-У5 _ ГЗГ г4 ~Г ГЬ ~Г г 1 Г3-рГ4-j-Гц-p r 2 У3 + У4 + У5 + У 2’
или при заданных числовых значениях сопротивлений и э. д. с.
о о 2 8
угЛ-^/2=16-171; _--/1 + --/2 = 8-t72, О О О <5
откуда
/х = 7,2—0,417!—0,Ш2; /2=4,8—0,Шх—0,4t/2.
599
Так как статическое сопротивление гх (/х) первого нелинейного элемента убывает с увеличением тока, а статическое сопротивление г2 (/„) второго нели нейного элемента возрастает, то для обеспечения сходимости итерационного про" цесса необходимо пользоваться уравнениями для тока Ц и напряжения и Р
Из уравнений, определяющих токи 4 и /2, получим: , ____________7,2-f-2t4rss_________.
115111 1 |-0,4 (т-ls-—J—г2л.) —J—О,15rlsr2s ’
ж г _____Л2/~|6/'2А______________________
21,111 1 + 0,4 T2s) + 0,15rlsr-2S
Результаты расчета сведены в табл 20-4.
Т а б л и ц а 20-4
S номер приближения lis’ А Vis’ в (из характеристики) ~ 'is ’ Ом U2S’ В А (нз характеристики) r2S = ±24. l2S Ом Л <$+!>’ А В
0 1,2 0,7 8,07 8,00 1,86 4,30 1,57 5,57
1 1,57 10,6 6,75 5,57 1,58 3,52 1,81 5,23
2 1,81 11,0 6,07 5,23 1,52 3,44 1,94 5,25
3 1,94 11,3 5,83 5,25 1,53 3,43 2,01 5,2,5
4 2,01 И,4 5,67 5,25 1,53 3,43 2,04 5,25
Из этой таблицы видно, что итерационный процесс практически заканчивается после четвертого приближения.
Глава двадцать первая
МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ
21-1. Основные понятия и законы магнитных цепей
В современных электрических машинах, трансформаторах, электромагнитных аппаратах и приборах для увеличения магнитного потока в определенных частях устройств применяют
600
ферромагнитные материалы. Такие устройства обычно состоят из магнитопроводов и обмоток, изготовляемых из изо-на магН11ТОПрОВОдЫ в за.
лированных проводов и надеваемых висимости от требований, предъявляемых к различным электромагнитным устройствам, их магнитопроводы изготовляются самой разнообразной формы.
На рис. 21-1 показан трехстержневой магнитопровод трехфазного трансформатора. Обмотки трансформатора размещаются на вертикальных стержнях. На р-ис. 21-2 схематично изображено магнето, применяемое в цепи зажигания газовой смеси в двигателях внутреннего сгорания. В пространство мёжду полюсными наконечниками подковообразного постоянного магнита помещен металлический сердечник, изготовляемый, так же как полюсные наконечники, из мягкой стали. В этом
Рис. 21-1.
случае магнитное поле существует вследствие остаточной намагничен
ности.
Совокупность устройств, содержащих ферромагнитные тела и образующих замкнутую систему, в которой при наличии магнитодвижущей силы образуется магнитный поток и вдоль которой
замыкаются линии магнитной индукции, называется магнитной цепью.
Магнитное поле определяют вектором магнитной индукции В, связанным с векторами намагниченности J и напряженности магнитного поля Н для изотропной среды соотношениями
В = |.i0J4-|ЛОН и В = ц|.10Н = раН.
Магнитная индукция В характеризует силовое действие магнитного поля на ток, а также свойство переменного магнитного поля возбуждать электрическое поле; намагниченность J характеризует состояние
Рис. 21-2.
вещества при намагничивании, магнит-Ная постоянная ро = 4л-10~’ Г/м = 4л-10“9 Г/см; ра = ~~ BIH — абсолютная магнитная проницаемость и |л = |ла/рл — относительная магнитная пРоницаемость. Магнитная проницаемость зависит от строе-ния и магнитного состояния вещества и в общем случае изменяется с изменением напряженности магнитного поля.
601
Зависимость между В и Н для ферромагнитных материалов не имеет точного аналитического выражения, поэтому для каждого ферромагнитного материала эту зависимость изображают в виде крй. вой намагничивания В — f (Н), определяемой опытным путем.
Впервые зависимость магнитной проницаемости от напряжен» ности магнитного поля была установлена в 1871 г. русским физиком А. Г. Столетовым и опубликована в его докторской диссертации «Исследование о функции намагничивания мягкого железа» Эта работа послужила основой для расчета электрических машин и сыграла громадную роль в развитии электротехники.
Если ток в обмотке кольцевого сердечника, изготовленного из ферромагнитного материала, плавно изменять в пределах от положительного максимального значения + ^макс Д° отрицательного максимального значения — /накс и от — /накс до + /мако то зависимость индукции в сердечнике от напряженности магнитного поля получается в виде петли, называемой петлей магнитного гистерезиса. Эта петля в первом цикле намагничивания и размагничивания не замкнута. При повторных изменениях тока в тех же самых пределах получается ряд петель, которые сначала отличаются друг от друга. После ряда циклов перемагничивания получается устойчивая симметричная петля (рис. 21-3).
Каждый из отрезков, отсекаемых петлей гистерезиса на оси ординат, определяет остаточную и н д у к-дый отрезок, отсекаемый той же пеглей на оси абсцисс, — коэрцитивную (задерживающую) силу (Нс и —Нс). Часть петли, лежащая во втором квадранте, ограниченная изменением индукции от +ВГ н Н = 0 лр В — Он Н — —Нс, называется кривой размагничивания. Этой кривой пользуются при расчете постоянных магнитов (§ 21-4). Основной кривой намагничивания называют геометрическое место вершин замкнутых симметричных гистерезисных петель при различных максимальных значениях тока /макс.
На рис. 21-4 показаны основные кривые намагничивания В (И) различных марок электротехнических сталей.
Для расчета цепей с постоянными магнитами имеют большое значение так называемые частные гистерезисные цикл ы, одна из вершин которых лежит на кривой размагничивания (рис. 21-3). Обычно петли этих циклов очень узки и в расчетах могут быть заменены прямыми линиями, проходящими через вершины частных гистерезисных циклов. Отношение магнитной
602
ндукции к напряженности АН частного гистерезисного цикла называется коэффициентом возврата
&вз=АВ/ДН.
Между величинами, характеризующими магнитные и электри-нескне цепи, существует формальная аналогия, позволяющая для магнитных цепей ввести ряд понятий, аналогичных понятиям, которые применяются при исследовании’ процессов в электрических цепях. Эта аналогия распространяется и на методы расчета
магнитных цепей.
В электрических цепях постоянные токи возникают под действием э. д. с. источников электрической энергии; в магнитных цепях магнитные потоки чаще всего возбуждаются токами обмОток. Поэтому между э. д. с. в электрической иепи и токами в обмотках, создающими магнитные потоки, существует формальная аналогия.•'Магнитный поток аналогичен току в электрической цепи. Пользуясь законом полного тока, можно ввести для магнитной цепи еще понятия магнитодвижущей силы и разности скалярных магнитных потенциалов, аналогичные понятиям э. д. с. и напряжения для электрической цепи.
По аналогии с сопротивлением электрическому току часто вводят сопротивление магнитному потоку, называемое магнитным сопротивлением цепи, и
Рис. 21-4.
величину, обратную магнитному
сопротивлению, — магнитную проводимость.
В электрических цепях постоянного тока пренебрегают током в изоляции проводников, так как проводимость изоляции очень мала по сравнению с проводимостью материала проводников. Магнитные проницаемости материала магнитной цепи и окружающей среды иногда мало отличаются друг от друга, а обмотки с электрическими токами занимают лишь небольшую часть участков магнитной цепи. При этих условиях приходится считаться с наличием магнитного потока, частично выходящего за пределы магнитной цепи.
Магнитный поток Ф, целиком замыкающийся по магнитной tenn, называется основным потоком, а магнитный от°к, замыкающийся частично по участкам магнитной цепи, а
603
Рис. 21-5.
частично — в окружающей среде, называют потоком рас. сеяния.
В этой главе рассмотрены такие магнитные цепи, которые изготовлены главным образом из ферромагнитных материалов В таких цепях резко отличаются магнитные проницаемости магнитной цепи и окружающей среды и потоками рассеяния во многих случаях можно пренебречь. Поэтому можно считать, что с любым витком одной и тон же катушки с током / сцеплен один и тог поток Ф и что поток на каждом участке магнитной цепи остается одним и тем же по всей длине участка.
Рассмотрим сначала неразветвлен-ную магнитную цепь (рис. 21-5).
Пусть участки и /2 магнитной цепи выполнены каждый из одного и того же ферромагнитного материала и имеют различные поперечные сечения Si и S2. При незначительном потоке рассеяния поток Ф в любом по
перечном сечении магнитной цепи один и тот же. Если длины участков магнитной цепи dx и /2) значительно больше поперечных размеров, то магнитная индукция во всех точках каждого участка может быть принята одинаковой.
На первом участке магнитной цепи индукция Вх — Ф/8Ь втором участке В2 — Ф/82. Напряженности магнитного поля этих участках
на на
/71—Вх/ pi^o — Ф/ РтИо^ь Н2~ Т^г/ргро ~ Ф/РгРо^г.
Применим закон полного тока к контуру, совпадающему со средней магнитной линией длиной I = 1Г + /2. Тогда получим:
F=ф Н d\ = Hili + //2/2 = Iw.
(21-1)
В этом уравнении величина F = Iw называется по аналогии с э. д. с. электрической цепи магнитодвижущей силой (м. д. с.) или иногда намагничивающей силой (н. с.).
После подстановки значений Нг и //2в уравнение (21-1) найдем, что
Р = /да^ф_-А_ + ф-А_ =ФРН1 + Ф^М2, (21-2)
где /?„1 и /?м2 — магнитные сопротивления у ч а с г к о в.
Произведение магнитного потока Ф на магнитное сопротивлм । Д’ы2 или разность скалярных магнитных потенциалов можно н вать по аналогии с электрической цепью магнитным н пряжением, взятым по направлению потока от точки а к то1 b (рис. 21-5), т. е. Нма6 = Ф/?м2.
604
Следовательно, магнитный поток
Ф = . ^»аЬ
^м1 + ^мг Rt/Л Rm2
(21-3)
Это уравнение аналогично закону Ома для электрической цепи.
Если на сердечнике помещено несколько катушек с различными числами витков и различными токами (рис. 21-6), то результирующая м. д. с. равна алгебраической сумме отдельных м. д. с.:
ЕЕ = S/a>=IjWl + /2щ2 — = £/// = £Ф/?М>
откуда
/1W14-/г®’—ftw3_
~ ~ Ж?
(21-4)
Ф
где Е7?м — магнитное сопротивление всей цепн.
Направление м. д. с. связывают с направлением тока в обмотке правилом буравчика (с правой нарезкой). Если буравчик вращать по направлению тока в витках обмотки, то направление м. д. с.
совпадает с поступательным движением буравчика.
Известно, что линии вектора магнитной индукции (магнитные Д1щии) замкнуты, т. е. не имеют начал и концов. Поэтому магнитный поток сквозь любую замкнутую поверхность всегда равен нулю и для узлов магнитных цепей справедливо уравнение
Ф1 + Ф2 + Фз + -.- = ЕФ = 0.
(21-5)
Рис. 21-6.
В этом уравнении положительные знаки принимаются для потоков, имеющих положительное направление от узла, а отрицательные — для потоков, направленных к узлу магнитной цепи (или наоборот), аналогично знакам токов в первом законе Кирхгофа для электрической цепи.
Уравнение (21-5) выражает первый закон Кирхгофа для магнитных цепей: алгебраическая сумма магнитных потоков в узле магнитной цепи равняется нулю.
Пользуясь законом полного тока, получаем для разветвленной магнитной цепи уравнение, аналогичное второму закону Кирх-г°фа для электрической цепи.
На рис. 21-7 показана разветвленная магнитная цепь. Эта Цепь состоит из шести неразветвленных участков с длинами 1Х, J’ •••, 16 и таким же числом различных магнитных потоков Фъ 2> •••, Ф6. Предположим, что каждый участок магнитной цепи из-Готовлен из одного материала с неизменным поперечным сечением по всей длине участка. Вместе с этим разные участки этой цепи
605
могут быть выполнены из различных ферромагнитных материале и могут иметь разные поперечные сечения Slt S2, S6.
Пренебрегая потоками рассеяния и принимая длины участко значительно превышающими их поперечные размеры, определив магнитные индукции на участках:
о _. о ______фа
Sj.’ °2 S2
п
£>в — “с~ •
Напряженности магнитного поля на этих участках магнитной цепи найдем по кривым намагничивания (рис. 21-4) при получен- ных значениях магнитной ин
Рис. 21-7.
дукции.
Применим теперь закон полного тока, например, к замкнутому контуру 1—2—3—1 магнитной цепи (рис. 21-7). Для интегрирования по этому контуру направление обхода выберем, например, по движению часовой стрелки; в результате получим:
EF = SIw = liWi — I3w3 =
— Hili — H3l3— H^. (21-6)
В это выражение составляющие Н313 и H^i входят с отрицательными знаками, так как направление обхода контура не совпадает с выбранными поло-
жительными направлениями магнитных потоков, а следовательно, и напряженностей магнитного
поля на третьем и четвертом участках. Так как
Hi — Ф1/Р1 Н3 — Фз/РзЦо^з! Н^ — ФДрдРо^а»
то после подстановки этих значений напряженностей в уравнение (21-6) получим:
/ /3Щ3 = Ф1 —Фз [ГцЩё Ф4 .Г..' с ' —
F’lJ’o*-5!
= Ф^ - Ф3Дм3 - Ф4/?м4 = ЕФ/?В. (21-7)
Аналогично записывается уравнение для любого контура; например, для контура 1—2—3—4—1 (рис. 21-7):
Kwi — 7 3Щ3 -J- / 2Ц>2 — Ф17?м1 — ФзДмз 4~ Ф5/?мБ + ФзТ?м2 — £Ф7?м-
Обобщая на любой замкнутый контур, можно написать: Е/щ=ГД = ЕФ/?м = ЕЯ/, (21-8)
606
т е. второй закон Кирхгофа для магнитных цепей: алгебраическая сумма м. д. с. в контуре магнитной цепи равна алгебраической сумме магнитных напряжений в том же контуре.
Здесь необходимо особо отметить, что сопротивление любого участка магнитной цепи обычно не может рассматриваться как постоянная величина вследствие зависимости магнитной проницаемости ферромагнетиков от индукции. Следовательно, расчеты магнитных цепей сходны с расчетами электрических цепей с нелинейными вольт-амперными характеристиками.
других — поток по
21-2. Расчет неразветвленных магнитных цепей
При расчете неразветвленных магнитных цепей приходится встречаться с двумя видами задач.
В одних задачах необходимо определить намагничивающий ток по заданному магнитному потоку, а в заданному току или заданной м. д. с. В обоих случаях, как правило, известны геометрические размеры всех участков магнитной цепи, материалы, из которых они изготовлены, основные кривые намагничивания или петли гистерезиса и числа витков катушек. В магнитных цепях из магнитно-мягких материалов гистерезисом можно обычно пренебречь, т. е. считать зависимость индукции от напряженности магнитного поля однозначной и определяемой основной кривой намагничивания (рис. 21-4).
Рассмотрим неразветвленную магнитную цепь (рис. 21-8), состоящую из П-образного сердечника электромагнита и стальной пла
стины, замыкающей его концы. Между концами сердечника электромагнита и пластиной имеется немагнитный, например воздушный, зазор /в. Размеры сердечника электромагнита и пластины, а также материалы, из которых они изготовлены, известны. Необходимо определить намагничивающий ток, при котором магнитный поток Ф в воздушном зазоре имеет заданное значение. Сечение сердечника электромагнита во всех частях одинаково и равно 8Ь а сечение пластины равно S2.
При этих условиях всю магнитную цепь представим в виде' трех последовательно соединенных участков с одинаковым потоком сердечника электромагнита, двух воздушных зазоров и стальной пластины. Для расчета магнитной цепи наметим приближенно среднюю магнитную линию и определим длины ее отдельных участке® li, 21в и /2. При малых размерах поперечных сечений сердечни-°в по сравнению с их длиной небольшие неточности в определе-ии средних длин участков не вносят в расчет существенных по-Решностей. Точный расчет распределения магнитного потока
607
в воздушном зазоре представляет трудную задачу. Однако пгщ малой длине зазора и параллельности плоскостей ферромагнитных тел, ограничивающих зазор, магнитное поле в зазоре можно считать однородным, а его сечение 8В — равным сечению сердечника 8
Неразветвленную магнитную цепь, изображенную на рис. 21-8 представим эквивалентной схемой, составленной из трех последовательно соединенных сопротивлений Rul, RMB и Rm2 (рис. 21-9) и м. д. с. Iw = F. В этой схеме сопротивления RH1 и Rm2 зависят от магнитного потока, а сопротивление R постоянное. 'в
По второму закону Кирхгофа для магнитной цепи м. д. с.
F = /^==//1/1 + //2/2 + //b2/b.
Магнитные индукции определим по заданному значению магнитного потока
Рис. 21-9. В^Ф/Зь В2 = Ф/32; В„ = Ф/8„.
По найденным значениям магнитной индукции ВА и В2 и основным кривым намагничивания для соответствующих материалов определим напряженности магнитного поля Н1 и Н2. Для воздушного зазора Нв = Вв/р0. Намагничивающий ток
w w
Если при расчете магнитный поток задан не в веберах (Вб), а в максвеллах и сечение магнитопровода в квадратных сантиметрах, то магнитная индукция Ва получится не в теслах (Т), а в гауссах (Гс) Тогда напряженность магнитного поля Нв в воздушном зазоре определяется в А/см по формуле
D D 1 Г)~8
Нв (А/см)=-^ = о,8В8 (Гс)=0,8 • 10* Вв (Т) или
Нв (А/м) = 80Вв (Гс) = 80 • 10*Вв (Т).
Рассмотрим теперь ту же -магнитную цепь рис. 21-8, для которой требуется определить магнитный поток по заданному зна чению м. д. с. Эта задача в отличие от предыдущей не имеет «прямоте» решения вследствие нелинейной связи между потоком и намагни чивающим током.
Решение такой задачи можно выполнить, -например, следую щим методом. Сначала зададимся предполагаемым значением маг нитного потока, например Ф', затем, так же как и в предыдуще1' «прямой» задаче, найдем м. д. с. F' = I'w = Л (Hl)’. Еслй полу ченное значение м. д. с. совпадает с заданным F = Iw, то задач i решена. Однако такого совпадения после первой попытки обычн не получается. Поэтому зададим другие значения магнитного пс тока Ф", Ф"' и т. д., найдем соответствующие значения м. д-с F" = I”w, F'" = I"'w и т. д. и построим вспомогательную хараг теристику Ф = f (£Н1) (рис. 21-10). Затем отложим на оси абсцис заданную м. д. с. F = Iw (точка а) и проведем из этой точки пр*
608
ю параллельную оси ординат, до пересечения с кривой Ф (У HI) ^точке b Отрезокопределит искомое значение магнитного потока. В Необходимо подчеркнуть, что в практических расчетах не имеет ысла строить всю кривую Ф (£///), начиная с нулевого значе-‘ я магнитного потока. Для получения первой точки этой кривой надо приравнять заданную м. д с. F = Iw магнитному напряжению на участке с наибольшим магнитным сопротивлением /?МФ' =
iw и из этого уравнения при помощи кривой намагничивания определить максимальный магнитный поток Ф'.
Если в магнитной цепи есть воздушный зазор, то он чаще всего п является участком с наибольшим магнитным сопротивлением
Для воздушного зазора применительно к рис. 21-8 последнее уравненье можно записать в следующем виде: откуда ,
2/в/Ш>^В
Рис 21-10
Так как другие участки той же неразветвленной магнитной цепи, так же
как участок с максимальным магнитным сопротивлением, ограничивают магнитный поток, то его последующие значения, необходимые для построения кривой Ф (^НГ), следует взять меньше Ф'
При решении подобных задач все вычисления целесообразно
свести в табл. 21-1.
Таблица 211
ф Вб = - ?L * т вг~- _ ф ~ s2 • т |!яе|соян 133 II Hi А/м Нъ А'м "в- А/ м Hill А Н212, А Нв21в А 2, HI, А
ф' в\ В1 В'в "'1 И’в Ив21в (£///)'
ф' в; в2 Вв «в Нв21в
Так как магнитный поток во всех участках неразветвленной '•агнитной цепи один и тот же, то характеристика Ф (ZHI) может быть построена и по аналогии с неразветвленной электрической ВДпью графическим суммированием абсцисс прямой Ф (Яв2/В) и кРивых ф (/Д/д и ф (/д/2) для одних и тех же значений магнитно потока.
Характеристика Ф (7/в2/в) — это прямая, проходящая через Начало координат. Ее легко построить, если найти напряженность
20 Основы теории цепей 609
магнитного поля Нв для какого-нибудь значения Ф:
Яв=Ф/Но5в.
Характеристики Ф (Н^) и Ф (Нг12) строятся при помощи основных кривых намагничивания для материалов первого и второго участков магнитной цепи. Для этого нужно умножить ординаты кривых намагничивания соответственно на сечения первого и второго участков (Ф = BS), а абсциссы — на их длины (HI).
21-3. Расчет разветвленных магнитных цепей
Расчеты разветвленных магнитных цепей основаны на применении законов Кирхгофа для магнитных цепей. Вследствие нелинейной связи между индукцией и напряженностью магнитного
поля для ферромагнитных материалов расчеты таких цепей обычно ведутся графоаналитическими методами аналогично методам расчета нелинейных электрических цепей (гл. 20).
При расчете магнитной цепи, как и для расчета электрической цепи, прежде всего нужно указать на схеме направления м. д. с., если известны направления токов и расположение обмоток, или задаться положитель-
ными направлениями м. д. с., если они являются искомыми. Затем необходимо задаться положительными направлениями магнитных
потоков, после чего можно переходит^ к составлению эквивалентной схемы и ее расчету.
На рис. 21-11 приведен пример разветвленной магнитной цепи »с одной м. д. с. На рис. 21-12 показана эквивалентная схема этой магнитной цепи. Для такой магнитной цепи возможен «прямой» расчет, если средний стержень
имеет одинаковое сечение по всей дли- ‘ рис. 21-12. не /2 и выполнен из одного и того' же материала и если требуется определить м. д. с. по заданному значению потока в воздушном зазоре Ф3.
По известному потоку Ф3 вычислим индукцию В3 = Ф3/*5з> по кривой намагничивания найдем напряженность магнитного поля Н3 и по формуле Нв = Ви/ц0 = Фз41о5в—напряженность поля в воздушном зазоре. Магнитное напряжение третьей ветви, т. е. между узлами а и Ь,
икаь=ед/=д3 (/з+/д+Нв1а.
610
Так'как вторая и третья ветви соединены параллельно, то и =^"ИкаЬ. Вычислив Н2 = UMabll2, по кривой намагничивания найдем В2.
Поток Ф2 = B2S2, а поток Фг = Ф2 + Ф3. Определив поток Фъ вычислим магнитную индукцию Вг = ФГ/5Г и по кривой намагничивания найдем напряженность магйитного поля
По второму закону Кирхгофа искомая м. д. с.
F ~ IW — H1l1-\-U.,ab-
Рис. 21-13.
4-Дмп (рис. 21-12) одним
Более общая задача определения всех потоков при заданной м. д. с. может быть решена графическим методом (рис. 21-13) аналогично расчету цепи постоянного тока с нелинейными элементами.
Прежде всего при помощи кривых намагничивания построим кривую Ф2 (UKOb) = ф2 (Н212) и зависимость ф3 (^м«б) — Ф3 (HslB 4~ ВД путем суммирования абсцисс прямой Ф3 (Н„/в) и кривой Ф3 (/Д/3) (где /8 = 13' + /3") для одних и тех же значений магнитного потока Ф3. Суммированием ординат кривых Ф2 (Дно6) и ф3 (Uaab) Для одних и тех же значений магнитного напряжения Uuclb получим кривую (Ф2 + Ф3) Укаь-
Выполненные построения эквивалентны замене двух параллельных ветвей с сопротивлениями Ra2 и R,.
нелинейным сопротивлением, характеристикой которого и является кривая (Ф2 4- Ф3) UKa6.
Дальнейшие построения для полученной неразветвленной цепи можно выполнить или как при расчете цепи на рис. 21-9, или построением характеристики Фг (Iw — Н^) = Фх (Дма6), как при расчете электрической цепи на рис. 20-21, в. На рис. 21-13 расчет произведен последним способом. Точка т1 пересечения кривой Ф1 (^Мсб) с кривой (Ф2 4- Ф3) Диаг> определяет магнитное напряже-Ни^Мог> и поток Фг. Ординаты точек пересечения т2 и т3 вертикальной прямой т1 — тс кривыми Ф2 (Дм'ой) и Ф3 (Дма6) дают соответственно потоки Ф2 и Ф3.
Пример 21-1. На рис. 21-14, а изображен магнитопровод, выполненный из электротехнической стали Э42.
Определить магнитные индукции во всех участках магнитной цепи, если сечения участков = S2 = 5 см2, S3 = 10 см2, длины участков = 30 см, 2 см’ ~ *0 см и м‘ д‘ с‘ = ^1Wl ~ 440 Д = l2w2 ~ 280 А.
Решение. Эквивалентная схема для заданной магнитной цепи предста-°лена на рис. 21-14, б. На основании выражений (21-5) и (21-8) составим для эт°и схемы уравнения:
Ф3 = Ф1 + Ф2; Ilwl=
I^2~B2l2-\-UKai,', UKCIb — HJ.3.
20*
611
Чтобы решить полученную систему уравнений, надо построить характе стики для всех участков магнитной цепи:
—^1/1) — Ф1 (^ма/>); Ф»(/26У2— Т/2/2)— ФеСЦдаб); Фз (^зУ = Фз (1/пг
С этой целью зададимся рядом значений магнитных потоков Фъ Ф21 ф найдем индукции в различных участках ’ 3
Bi—Ф1/51! В 2 — Ф2Д82', &з— Ф.ч/^з,
а затем по кривой намагничивания определим напряженности магнитного пот По известным значениям напряженности магнитного поля вычислим магнитные
Рис. 21-14.
напряжения на участках для различных Чютоков. Результаты вычислений представлены табл. 21-2.
По данным таблицы построим (рис. 21-14, в) кривые Ф, (Пмаб), Ф2 (U^ab) и Ф3 (Пмаг,). Так как значения магнитных потоков должны удовлетворять уравнению Фх + Ф2 — Ф3, то построим еще одну вспомогательную кривую
Таблица 21-2
Ф1, Фг. Вб В^Вг т > II * ? 'll Н1/1. А Л ^2^2> А /гш2— — Я 2^2. А Ф8, Вб В,. Т А/м Н В, А
0 0 0 0 440,0 0 280 0 0 • 0 0
25- 10~« 0,5 55 16,5 423,5 22,0 258 70 • 10-5 0,7 90 9
30 • io-в 0,6 70 21,0 419,0 28,0 252 80 • 10-5 0,8 120 12
35-10 6 0,7 90 27,0 413,0 36,0 244 90-10-5 0,9 155 1т
40 • 10“В 0,8 120 36,0 404,0 48,0 232 100-10-5 1,0 200 23
45-10-6 0,9 155 46,5 393,5 62,0 218 110-10-5 1,1 350 Зз
50-10-в 1,0 200 60,0 380,0 80,0 200 120-10-5 1,2 500
55 10 0 1,1 350 105,0 335,0 140,0 140 130- IO'5 1,3 800
60 -10 1,2 500 150,0 290,0 200,0 80 140-10-5 1,4 1200 1
612
Т аб лица 2.
В £ £ S е с к о о g И < £ S Нн I В1<УЛ=Ф1 »-’° °ЕЗ (из характеристики) v/9a ‘lSl j <<> S || 01 04 В2 S.S2-®2.S.-10 5- В3 (из характеристики) «м2.5,- Вб/А и 1 —U А 3 S) 3 м3($р в, „Я,= Ф„ t -10 6, 1б d .S1 <3 О S (из xapaKiepiiciUMi) V/9S -,s №В V <tj-s,№/7 ъ е» S А <0 со 2
0 2-30 = 60 10,0-5 = 50 0,834 2- 10 = 20 Ю -5 = 50 2,50 5-40 = 200 12- 10=120 0,600 124,8 23,9 276
1 124,8* 11,"). 5 = 57,5 0,465 23,9* 10,6-5 = 53 2,22 276* 12,7-10=127 0,460 131,5 34,6 268
2 131,5 11,6-5 = 58 0,440 34,6 11,0 5 = 55 1,59 268 12,6-10=126 0,480 140 39,8 256
3 140 11,7 • 5 = 58,5 0,418 39,8 11,4-5 = 57 1,43 256 12,55- 10=125 0,490 145 44,8 255
4 145 11,8-5 = 59 0,407 44,8 11,7-5 = 58,5 1,31 255 , 12,5-10=125 0,490 149 48,9 252
5 149 12,0-5=60 0,402 48,9 11,8-5 = 59 1,21 252 12,5- 10=125 0,495 152 52,0 249
6 152 12,2-5 = 61 0,400 52,0 12,0-5 = 60 1,15 249 12,45 10= 124,5 0,496 154 55,4 246
7 154 12,3-5 = 61,5 0,392 55,4 12,2-5 = 61 1,10 246 1? 4-10 = 124 0,504 156 56,1 244
По известному магнитному напряжению и известной длине для каждого участка магнитной цепи определяется напряженность магнитного
W поля, а затем по кривой намагничивания — магнитная индукция.
(Фх 4- Ф2) UKab. Для этого суммируем ординаты кривых Фх (UKab) и Ф2 (U,,nb) д. одних и тех же значений магнитного напряжения Uuab. Ордината точки т3 пер сечения кривых (Фх 4-Ф2) UKab с кривой Ф3 (UKab) определяет поте Ф3 = 130-10~8 Вб, так как для этой точки справедливы уравнения
/1Ш1—Д1/1 = /2^2—И Ф14~Ф2 = Фз*
Чтобы найти потоки Ф, и Ф2, проведем через точку т.л прямую, параллельна оси ординат, до пересечения с кривыми Фх (ЙыаЬ) и Ф2 (17ывЬ) в точках /п-, и ц отрезки и тт2 определяют потоки Ф2 = 70- 10”в ВС^и Ф2 — 60-10-8 В Зная потоки, легко определить магнитные индукции:
В1=Ф1/51=1,4 Т; В2=Ф2/52=1,2 Т; В3=Ф3/53= 1,3 Т.
Пример 21-2. На рис. 21-15, а изображена магнитная система, выполненная из электротехнической стали Э42. Пользуясь методом итерации, определить магнитные индукции во всех участках магнитной цепи, если сечения участков Sx = S2 = 5 см2, S3 = 10 см2; длины участков = 30 см, Z2 = 10 см, 13 = 40 см, м. д. с. Fi — = 400 A, F2 — 300 А.
Рис. 21-15.
Решение. При помощи эквивалентной электрической схемы, показа ной на рис. 21-15, б, получим для магнитных напряжений 17ы1, 1/ы2 и Пма следу! щие расчетные уравнения:
г г F1 (Sm2IS) 4~gM3 IS)) IS') .
~ i „ r ~ »
6M1 (s) “Г6M2 IS) iбМЗ (S)
tt _______, ^2 fold ($) £m3 (S)) Flgwi (S) .
vm2 (s+i)-----~ ZF77——-,
SMl (S) I &m2<S) I &M3<S)
IT _______ ^1 <S)4~ A2gM2 IS)
VM3 (S+l) — ~ Г7г ,
gut IS) T«М2 IS) 'Г6МН IS)
где Skills), Sm2,s) и &3<s) — магнитные проводимости соответствующих участк магнитной цепи, определяемые по формулам
SmI is) =Ф1 (S)/^M1 <S>; guts IS) — <S>/t^M2 is), Smt is)= IS)/^M3 is)-
Все расчеты по этим уравнениям сведены в табл. 21-3.
21-4. Расчет магнитной цепи кольцевого постоянного магнит с воздушным зазором
На рис. 21-16 схематически показан стальной магнитопровс в виде кольца с воздушным зазором. Определим магнитный поте в воздушном зазоре, если магнитопровод предварительно нама
614
законом полного тока.
Рис. 21-16.
ничен до насыщения. Размеры магнитопровода и кривая размагничивания В = / (И) для материала заданы.
Если в магнитопроводе нет воздушного зазора, то после намагничивания магнитная индукция в магнитопроводе равна остаточной индукции Вг, а напряженность магнитного поля равняется нулю, что непосредственно следует из закона полного тока Н dl = 0, поскольку намагничивающий ток отсутствует. На четле гистерезиса это состояние соответствует верхней точке кривой размагничивания (рис. 21-3).
При наличии воздушного зазора напряженность поля не равна нулю, что легко показать, пользуясь нитная цепь в этом случае состоит из двух участков: стального магнитопровода, в котором напряженность поля Нс можно считать одинаковой во всех точках средней линии, и воздушного зазора, напряженность магнитного поля в котором связана . магнитной индукцией известной зависимостью
//в
При незначительной длине воз-зушного зазора можно принять сечение воздушного зазора 5В равным
сечению магнитопровода 5С, т. е. считать индукцию во всех точках магнитной цепи одинаковой:
Вс = Ф/5с==Ф/5в=Вв.
Выбирая путь интегрирования вдоль средней линии по направлению вектора магнитной индукции Вс = Вв, напишем следующее выражение:
откуда
§Hdl = tfc/c + 7/JB = 0,
(21-9)
*с Но Но
1Ж = /Е//с называется размагничивающим коэффициентом по индукции.
Следовательно, в этом случае, несмотря на отсутствие намагничивающих токов, напряженность магнитного поля во всех точ-Ках кольцевого магнитопровода не равна нулю. В воздушном промежутке направление вектора напряженности поля совпадает направлением вектора магнитной индукции, а внутри магнито-Ровода они направлены противоположно (рис. 21-16).
Отрицательное значение напряженности магнитного поля вну-Ри сердечника означает, что при наличии воздушного зазора маг
615
нитная индукция Bz — Ва меньше остаточной индукции Вг — как следует из выражения Вс = ц07 + ц0Яс.
Так как отрицательному значению напряженности магни, поля Нс соответствуют положительные значения индукции Вс -
io магнитное состояние магнитопровода определяется однси
Рис. 21-17.
точек кривой размагничивания рой квадрант петли гистере^
Для расчета рассматрив. магнитной цепи построим за: мость магнитного потока Фс = от магнитного напряжения V ~ ВЗЯТОГО В НЭ!
лении вектора Нс между точ, а и Ь концов магнитопровода, зависимость получается из кр ^o.i размагничивания путем прослго умножения ее ординат на 5С и ..бс-цисс — на /с (рис. 21-17). На том же рисунке построим зависимость магнитного потока в воздухе Фв от магнитного напряжения, взятого
в направлении Нк между теми же точками а и Ь магнитопрого ;а, пользуясь тем же приемом, что и при построении кривойФх (L на рис. 21-13. Это напряжение
U*. в = Uaab = Ды. ЬФв = HJa = “Мв = Фв ,
откуда
Вм. в
и..в '
/в/Мо$с
Из последнего выражения следует, что магнитный поток пропорционален магнитному напряжению UM в (прямая липы рис. 21-17). Отметим, что магнитное сопротивление воздуп зазора в действительности несколько меньше определяемом: формуле RK в = /в/Ро^с, так как магнитный поток в воздун зазоре распределяется по большей площади, чем поперечное <. ние магнитопровода (SB > Sc).
Так как магнитный поток в магнитопроводе равен потоку в душном зазоре, т. е. Фс = Фв, и магнитное напряжение UK с = то магнитный поток определится ординатой точки пересечен^ кривой Фс (Дн с) и прямой Фв = с/м.в/Дм.в (рис. 21-17).
Опустив из точки т1 перпендикуляр тгт на ось абсцисс, получ отрезок От, определяющий магнитное напряжение между точка а и Ь.
Определим теперь магнитный поток в воздушном зазоре в 1 случае, когда после намагничивания стального магнитопрово величина воздушного зазора будет уменьшена введением ферро1*? нитного диска (рис. 21-18) с площадью Sc. Магнитную пронии!
616
сть будем считать такой высокой, что магнитным сопротивлением диска можно пренебречь.
Н в этом случае длина зазора станет меньше, а значит, уменьшитсяего магнитное сопротивление до величины RM в = /в/р05с. Зависимость магнитного потока в воздушном зазоре от напряжения UM в представится прямой Фв = Uu JRM в с большим углом наклона к оси абсцисс, чем прямая Фв = Um B/Ru в (рис 21-17) Но поток в стальном магнитопроводе будет расти не по кривой размагничивания Ф (^ с)> а по кривой частного цикла, т е.
Фс (<4 с), которую можно заменить приближенно прямой линией Точка пересечения т2 с прямой Фв = = {/„ вв и определяет искомое значение потока в воздушном зазоре Фв = Фс
Если сердечник намагнитить при вставленном стальном диске, то магнитный поток будет значительно больше и определится ординатой точки т3 При уда-
чении диска из воздушного зазора сердечник будет Рис 21 18

размагничиваться и поток уменьшится до величины, определяемой ординатой точки При введении стального диска в зазор магнитный поток возрастет только до величины, определяемой ординатой точки т2.
Из графического построения, приведенного на рис. 21-17, видно влияние параметров магнитной цепи на величину магнитного потока. В частности, увеличение длины магнита и применение материала с большей коэрцитивной силой Нс приводит к относительному увеличению абсцисс кривой Фс (Дм), а увеличение сечения магнита Sc и применение материала с большей остаточной индукцией Вг при той же коэрцитивной силе приводит к увеличению ординат кривой Фс (Дм) И увеличение абсцисс, и увеличение ординат приводит к возрастанию магнитного потока Ф.
21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом
На рис 21-19 изображена магнитная цепь, состоящая из постоянного магнита длиной /с и сечением 5С, участка цепи длиной + Г и сечением 5, выполненного из магнитно-мягкого материала (для которого можно пренебречь гистерезисом, т. е. считать, что его магнитное состояние однозначно определяется основной кривой намагничивания), и воздушного зазора длиной /в Определим магнитный поток в воздушном зазоре после намагничивания всей Депи до насыщения
При помощи кривой размагничивания построим, как и в пре-Цьщущем параграфе, зависимость Фс = ВС5С — ФС(Ц< с)> где U„ с = Ф (рис. 21-20) Затем на том же рисунке построим кривую в для остальной части магнитной цепи, включая воздушный 3аз°Р Для построения этой кривой зададимся рядом значений по-ока фв( определим индукции Вв = Фв/8 и найдем напряженности
617
магнитного поля Н на участке длиной /' + /" по кривой нама чивания и в зазоре Нв = Вв/ц0- После этого вычислим магниц10 напряжение U.,nb для каждого значения потока по формуле UM * = Н (Г + Г) + HBts, т. е. составим зависимость Фв (ПнаЬ) "
Поток во всех участках цепи имеет одно и то же значени Фс = Фв, а магнитное напряжение UK с = UKab. Поэтому иском^ значение магнитного потока определится ординатой точки щ пепе. сечения кривых Фв (Пна6) и Фс (Пм.с).
В заключение в виде примера, иллюстрирующего практическое применение постоянных магнитов, рассмотрим качественную сторону явлений, наблюдающихся при вращении якоря магнето (рис. 21-2), и выясним пределы изменения магнитного потока в зазоре. Для упрощения построений магнитные сопротивления сердечника и полюсных наконечников примем равными нулю.
Рис. 21-19.
На рис. 21-17 показана кривая размагничивания постоянного магнита, ординаты которой умножены на сечение магнита, а абсциссы — на среднюю длину.
Пусть вся система магнето была намагничена до состояния насыщения при положении якоря, указанном на рис. 21-2, т. е. при минимальном воздушном зазоре. Магнитный поток в якоре Ф3 определится ординатой точки та (рис. 21-17) пересечения кривой размагничивания с прямой 0т3. При повороте якоря из положения, указанного на рис. 21-2, в положение, при котором воздуш-ный зазор становится максимальным, поток в якоре уменьшается до значения Фь определяемого ординатой точки т1 пересечения кривой размагничивания и прямой 0тг. При дальнейшем повороте якоря до такого положения, при котором воздушный зазор становится минимальным, поток возрастает до значения Ф2, определяемого ординатой точки т2 на кривой частного цикла (рис. 21-17). После следующего поворота якоря до положения» в котором воздушный зазор становится максимальным, магнитный поток уменьшается по спадающей кривой частного цикла до прежнего значения Фх (после нескольких оборотов якоря)-
Таким образом, при вращении якоря магнитный поток из'1е' няется на ЛФ = Ф3 — Фг, что соответствует разности ордннаТ 618
очек гл?, и /7ф При вращении якоря магнето в витках обмотки тавОдится переменная э. д. с. Наибольшее значение этой э. д. с. ваВцспт от числа витков обмотки якоря, максимального значения ротока (Ф2) 11 частоты вращения.
Глава двадцать вторая
ОБЩАЯ характеристика нелинейных цепей переменного тока И МЕТОДОВ ИХ РАСЧЕТА
22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах
В предыдущих главах нелинейные элементы рассматривались только при постоянных токах. Однако большинство электротехнических устройств с различными нелинейными элементами работают на переменном токе.
Если при постоянных токах можно ограничиваться исследованием статических характеристик, т. е. характеристик, полученных для постоянных токов и напряжений: вольт-амперной и (I) для нелинейного активного сопротивления, вебер-амперной Ф (/) для нелинейной индуктивности и кулон-вольтной Q (U) для нелинейной емкости, то при переменных токах это не всегда возможно. Вследствие тепловой инерции в сопротивлениях, магнитной вязкости и вихревых токов в ферромагнитных сердечниках и релаксационных процессов в сегнетодиэлектриках при переменных токах часто нельзя ограничиться рассмотрением только характеристик U (Г), Ф (/) и Q (U), а необходимо учитывать изменение этих характеристик во времени в зависимости от скорости нарастания тока, напряжения, заряда или магнитного потока.
В общем случае для нелинейных элементов при переменном токе необходимо получить характеристики, устанавливающие зависимость между мгновенными значениями и (i), Ф/ (z), q (и), причем вид этих функций зависит от характера изменения аргумента во времени. Так, например, вольт-амперная характеристика германиевого диода для напряжения прямой полярности оказывается разной при постоянном или медленно изменяющемся токе и при его быстрых изменениях. На рис. 22-1 показаны вольт-амперные статическая характеристика германиевого диода при постоянном токе (/) и динамическая характеристика при протекании ви^е3 ДПОД импУльса тока z продолжительностью 1 мкс. Из графика чеЗНо’ что эти характеристики очень сильно различаются. Стати-ф КИе характеристики применимы только при импульсах с пологим Чфонтом продолжительностью не менее нескольких миллисекунд, лам 63КО Разлпчаются статические и динамические характеристики Ров Накалпвания, терморезисторов и других нелинейных резистора ’в КотоРых изменение свойств обусловлено изменением темпе-
УРы. На рис. 22-2 показаны вольт-амперные характеристики -
619
терморезистора, снятые при медленном изменении тока / (Г при быстром изменении тока (прямая) i (и), при котором темпер, гура терморезистора сохраняется, и при совместном протек нии постоянного и переменного токов (кривые вблизи точки /
Рис 22-1
при высокой частоте к ка (сплошная линия) при низкой частоте ц< ременного тока (пуш тир).
Существенно отлич, ются одна от другой х< ракт ернетики магните проводов, снятые при разных частотах. Даже для феррита, структура которого обеспечивает отсутствие влияния вихревых токов, с изменением частоты тока изме-
няется зависимость ме-
жду В и И или между Ф и I. На рис. 22-3 показана половина петли гистерезиса, полученная для феррита при переменном синусоидальном токе различных частот Для диапазона частот 0—250 Гц характеристики практи чески совпадают, однако дальнейшее повышение частоты приводит к большему отставанию индукции от внешнего магнитного поля
и петля гистерезиса заметно расширяется.
Все перечисленные особенности характеристик нелинейных эле ментов при переменных токах крайне затрудняют расчет и исс.в дование нелинейных цепей. При расчете нелинейных цепей пер менного тока необходимо учитывать зависимость характерист! нелинейного элемента от динамики процесса и вводить дннамич ские параметры (сопротивления, индуктивности, емкости). Толы при относительно низких частотах можно пользоваться статич
620
чцми характеристиками и соответственно дифференциальными параметрами и, основываясь на них, производить расчет цепей переменного тока. „
В дальнейшем ограничимся рассмотрением относительно малых скоростей изменения напряжений и токов, при которых характеристики, полученные для постоянных токов, U (/), Ф (/), Q (U) совпадают с характеристиками для мгновенных значений и (i), Ф, (0. <?(«)-
При постоянном токе не имеет принципиального значения, является ли вольт-амперная характеристика нелинейного резистора симметричной или несимметричной. В цепях переменного тока зависимость характеристики от полярности приложенного напряжения или направления тока очень существенна, так как только при несимметрии характеристики можно получить постоянную составляющую и четные гармоники тока при синусоидальных напряжениях источников.
Симметричными характеристиками обладают терморезисторы, некоторые типы газоразрядных приборов, катушки со стальными магнитопроводами при отсутствии постоянного или остаточного подмагничивания, конденсаторы с сегнетодиэлектриками и др. Для нелинейных элементов с симметричными характеристиками справедливы следующие равенства: для сопротивлений и (i) = —и (—i), для индуктивностей Ф/ (i) = —Ф, ( — i) и для емкостей q (и) = —q (—и).
Несимметричными характеристиками обладают электронные лампы, полупроводниковые диоды и транзисторы, многие типы газоразрядных приборов и ряд других нелинейных резисторов. Для резисторов с несимметричными характеристиками и (t)
—и (—i), причем это неравенство обычно весьма существенно. Несимметрия характеристики может быть получена искусственно путем введения в цепь, содержащую элемент с симметричной характеристикой, дополнительного источника постоянной э. д. с.
Все рассмотренные выше нелинейные элементы могут быть представлены в виде нелинейных двухполюсников: электрических и (i), магнитных Ф/ (i) и емкостных q (и).
Если на вход таких двухполюсников поступает сумма постоянной и переменной составляющих и переменная составляющая Достаточно мала, то при гладкой характеристике нелинейного Двухполюсника ее можно линеаризовать, т. е. заменить линейной вблизи рассматриваемой рабочей точки [Ip; V р— и (/p)J. Так, зависимость и (i) можно представить в следующем виде:
и (0 ^ «(/₽) + ( J)l=/p(i-/p), (22-1)
заменив нелинейный элемент линейным, причем эта замена справедлива только при малых отклонениях от точки /р, Up.
Здесь
(ди\
(22-2)
621
представляет собой дифференциальное сопротивление, рассмотрег ное в § 20-1. В этом случае зависимость между отклонениями с рабочей точки Лг = i — /р и Ди = и — Up выражается законе Ома Ли = гдЛг. Аналогично можно линеаризовать характеристик нелинейных магнитных и емкостных двухполюсников.
Таким образом, при малых отклонениях от рабочей точки для переменных составляющих токов, напряжений, магнитных потоков и зарядов в нелинейных цепях могут быть построены эквивалентные линейные схемы, дающие возможность для некоторой области переменных составляющих приближенно провести расчет цепи.
Анализ нелинейной цепи в этом случае распадается на три этапа-1) определение рабочих точек на характеристиках нелинейных элементов, которое проводится для постоянных токов аналогично задачам, рассмотренным в гл. 20 и 21; 2) определение дифференциальных параметров нелинейных элементов, аналогично (22-2), и составление эквивалентной линейной схемы; 3) определение переменных составляющих режима, которое производится методами теории линейных цепей (гл. 1 — 19).
Линеаризация нелинейных цепей при малых отклонениях от рабочей точки применима как для простых, так и для более сложных цепей, содержащих кроме нелинейных двухполюсников нелинейные четырехполюсники, такие, как транзисторы и электровакуумные триоды (см. гл. 9).
22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
Если для нелинейного электрического двухполюсника нелинейная характеристика задается функцией одного переменного i (и), то характеристика нелинейного четырехполюсника описы-
Рис. 22-4.
вается двумя функциями двух переменных. Одна из этих перемен ных обычно является аргументом, а вторая — параметром и функ ция задается семейством кривых, полученных для различных постоянных значений параметра.
Для описания нелинейного четырехполюсника эти две функции и их аргументы и параметры могут быть выбраны различно. Так. для нелинейного четырехполюсника, показанного на рис. 22-4, и,
622
era характеристики можно задать уравнениями для входа иг (и2, i2) л й (и2, i&)> ДЛЯ выхода и2 (ult i\) и i2 (ult ix), для напряжений и (11, 1г) и w2 On 4)» Для токов (и1г и2) и t2 (tzlf tz2).
1 Здесь в скобках первая величина является аргументом, а вторая — параметром. Выбор той или иной пары уравнений и аргументов и параметров обусловлен удобством решения поставленных конкретных задач.
Теория нелинейных четырехполюсников получила наиболее широкое развитие в связи с применением транзисторов, представляющих наиболее общий 'случай нелинейного резистивного четырехполюсника. В качестве характеристик такого четырехполюсника обычно применяются зависимости напряжений от токов для входа и выхода, причем в качестве параметра для характеристик входа принимается напряжение на выходе н2, а для характеристик выхода — ток на входе iP
Такие характеристики
«г) и u2 = tz2(i2, tj)
(22-3)
называются смешанными. При помощи этих характеристик могут быть легко найдены рабочие точки на нелинейных характеристиках в любых схемах включения четырехполюсников и определены параметры их линейных схем замещения (см. гл. 9) при работе вблизи рабочей точки.
Рассмотрим наиболее общий случай включения нелинейного резистивного четырехполюсника (рис. 22-4, б), когда его первичная и вторичная цепи подключены к активным нелинейным двухполюсникам с нелинейными характеристиками (uj и i2 (tz2). При этом характеристики входа и выхода четырехполюсника заданы семействами вольт-амперных характеристик при значениях параметров и°, и* и ис, для входа и ip, i<2> и i<3> для выхода.
Характеристики входа и выхода удобно построить в первом и третьем квадрантах, как показано на рис. 22-5. Четырехполюс-
ник, ко вторичным зажимам которого подключен двухполюсник tl2 (i^), можно со стороны первичных зажимов рассматривать как некоторый двухполюсник, характеристику которого ur (it) получим простым построением.
Для этой цели, начертив в первом квадранте характеристику Двухполюсника i2 (iz2), представляющую собой нагрузочную характеристику выхода четырехполюсника /, найдем токи пересечения /, 2, 3 этой характеристики с соответствующими характери-стиками'четырехполюсника для ip, i<2> и ip. По этим точкам на оси i2 находим токи ip, ip и i<3). По найденным токам во втором квадранте построим вспомогательную характеристику i2 (ij) (кривая /7).
По значениям параметра (и", иь и иу по характеристикам / и И определим соответствующие значения i°, ib и if и для них на входных характеристиках (iJt и2) найдем точки а, b и с. Соединив
623
эти точки, получим входную характеристику /// четырехполк ника, ко вторичным зажимам которого подключен двухполь ник i2 (и2).
Таким образом, четырехполюсник с подсоединенным ко в ричным зажимам двухполюсником эквивалентен двухполюсни с характеристикой ///. Рабочую точку Р определим как тот пересечения характеристики (щ) (кривая IV) двухполюснп подсоединенного к первичным зажимам четырехполюсника, и дв\ полюсника с характеристикой ///.
Зная рабочую точку, можно определить дифференциальные параметры линеаризованного четырехполюсника в этой точке, составить эквивалентную схему для переменной составляющей и решать линейную задачу для малых отклонений от рабочей точки так, как это сделано в гл. 9. При этом на характеристиках рис. 22-Ь процесс изображается некоторой замкнутой кривой или участком прямой, расположенной вблизи точки Р, подобно тому как это показано на рис. 22-2.
Изменяя параметры двухполюсников, подключенных к нелинейному четырехполюснику, можно изменять положение рабочей точки Р на характеристике четырехполюсника и таким образом управлять параметрами эквивалентной линейной цепи, преобр* зующей переменный сигнал, как, например, в различного ро.' электронных усилителях переменного тока.
624
22-3. Явления в нелинейных цепях переменного тока
Относительно редки случаи, когда нелинейность не приводит существенно новым явлениям, отсутствующим в линейных целях, и только усложняет расчет цепи. В большинстве электротехнических устройств с нелинейными элементами не только возникают явления, принципиально не осуществимые в линейных цепях, но на нелинейности цепи основывается принцип действия устройства.
Такие явления, как выпрямление и стабилизация напряжения, умножение и деление частоты, усиление мощности, преобразование различных сигналов, получение модулированных колебаний различной формы, скачкообразное изменение тока при плавном изменении напряжения питания (релейный эффект), основаны на принципиально нелинейных эффектах.
В нелинейных цепях, питаемых только от источников с синусоидальными э. д. с. или токами одной частоты, возникают токи различных частот. Из спектра частот тока можно выделить постоянную составляющую и использовать ее в качестве источника постоянного тока. На этом принципе основано устройство в ы-прямителей. Из спектра частот тока могут быть выделены те или иные высшие гармоники и использованы в качестве источников более высоких частот. Это является основой построения умножителей частоты. Нелинейность характеристики цепи может обеспечить неизменность величины напряжения основной гармоники в одном из участков цепи при значительных изменениях напряжения источника, т. е. дает возможность получить стабилизаторы напряжения.
Еще большие возможности открываются применением нелинейных элементов в цепях, питаемых от источников питания различных частот. Применение источников постоянного тока наряду с источниками переменного синусоидального тока дает возможность управлять переменным током, воздействовать на его величину. В нелинейных цепях можно получить переменный ток значительной мощности за счет энергии источников постоянного тока и, наоборот, получить мощный сигнал постоянного тока за счет энергии переменного тока. Это является основой построения различ-№ усилителей сигналов.
^Включение нескольких источников синусоидальных напряже-ний различных частот в нелинейную цепь приводит к появлению кР°ме гармонических составляющих токов каждой из этих частот еШе ряда боковых частот, т. е. к получению модулирован-н Ь1 х колебаний.
В цепях с нелинейными элементами получают самые различные переходные процессы, которые применяются для формирова-нИя различных импульсов в устройствах автоматики и радиотех-
625
В нелинейных цепях, питаемых только от источников постояв ного тока, возможно возникновение периодических автоколебатель" ных режимов с токами, по форме более или менее близкими к си' нусоидальным. Подобные режимы наблюдаются и в цепях, питаемых от источников переменного тока. В этих случаях амплитуда тока той же частоты, что и напряжение источника, может изме-пяться с некоторой частотой автоколебаний (см. гл. 26)
Все перечисленные явления получили широкое применение в самых различных технических устройствах современной электротехники, и их анализ очень важен, хотя и сопряжен с большим,, математическими трудностями.
22-4. Методы расчета нелинейных цепей переменного тока
В теории линейных электрических цепей с постоянными параметрами весь анализ сводится к решению системы линейных дифференциальных или алгебраических уравнений. Математический аппарат для решения подобных уравнений был полностью разработан еще в начале прошлого века. Задача теории в последнее время сводилась к тому, чтобы найти наиболее экономичный и наглядный метод инженерного расчета, анализа или синтеза цепи. При этом для решения всех задач широко применяются принципы наложения и взаимности.
Значительно сложнее обстоит дело с расчетом нелинейных электрических цепей. Сама теория нелинейных дифференциальных уравнений, описывающих процессы в нелинейных электрических цепях, разработана значительно меньше. Для нелинейных уравнений каждого типа существуют свои методы подхода и решения, причем многие нелинейные уравнения не имеют аналитических решений и требуют построения специальных функций. Особенно усложняется расчет нелинейных цепей тем, что в большинстве задач характеристики нелинейного элемента заданы графически и отсутствует достаточно простое математическое описание этих характеристик.
Однако инженерная практика требует получения хотя бы грубо ориентировочных расчетных соотношений, которые дают количественную оценку процессов, происходящих в нелинейных цепях. Именно поэтому в отличие от теории линейных цепей, где может быть получено решение задачи с любой точностью, основой теории нелинейных цепей является получение приближенных решений, дающих в основном качественную оценку процессов.
Развитие теории нелинейных электрических цепей относится в основном к нынешнему веку. В этой области ведущее значение имеют работы русских и советских ученых А. М. Ляпунова, Л. И. Мандельштама, Н. Д. Папалекси, А. А. Андронова, Н. М. Крь? лова, Н. Н. Боголюбова и многих других. Из зарубежных работ большое значение для развития нелинейной электротехники имел11 исследования Пуанкаре, Ван-дер-Поля, Рюденберга и др.
626
Можно назвать следующие методы приближенного расчета не-инейных цепей переменного тока, получившие преимущественное Распространение в практике инженерных расчетов.
Р 1. Методы малого параметра и условной линеаризации. Одним
из методов расчета нелинейной цепи является такое ее упрощение, основанное на пренебрежении относительно малыми величинами, чтобы можно было применять методы расчета линейных цепей, но при решении «квазилинейной» задачи вводить некоторые коррективы, обусловленные нелинейностью. Например, при расчете нелинейных цепей переменного тока, в которых значение высших гармоник относительно невелико, несинусондальные токи заменяют эквивалентными синусоидами и применяют комплексный метод расчета, но с учетом нелинейной зависимости между действующими значениями и фазами эквивалентных синусоид тока и напряжения.
Разновидностью метода малого параметра является метод гармонического баланса. При расчете цепи этим методом рассматривают амплитуды основных гармонических составляющих токов и напряжений в нелинейной электрической цепи и пренебрегают действием всех высших гармоник. При этом иногда полагают, что
амплитуды гармонических составляющих медленно изменяются, но нет необходимости учитывать спектр гармоник, связанных с из-
менением амплитуды.
Такое упрощение задачи по существу является заменой нелинейной зависимости линейной, справедливой только для определенного значения амплитуд тока или напряжения. Поэтому этот метод иногда называется методом гармонической линеаризации. Он был применен в работах Л. И. Мандельштама и Н. Д. Папалексн, затем в работах Н. М. Крылова и Н. Н. Боголюбова и получил дальнейшее развитие в работах Л. С. Гольдфарба, Е. П. Попова и др. применительно к задачам теории автоматического регулирования.
При расчете переходных процессов метод условной линеаризации основывается на приближенной замене нелинейной функции линейной и применении решений линейного уравнения с последующим уточнением результата введением поправок.
Этот метод дает очень приближенное решение задачи, однако он наиболее прост и поэтому применяется для ориентировочного Расчета процессов, анализ которых более точными методами представляет значительные трудности.
2. Метод аналитической аппроксимации нелинейной характеристики. Сущность метода заключается в приближенном выражении нелинейной характеристики некоторой аналитической функцией такого вида, чтобы достаточно просто решалось нелинейное днф-Фсреццпальное уравнение цепи. Успешное применение метода за-исит от того, насколько точно удалось подобрать аналитическое Сражение для нелинейной характеристики и насколько просто Решается полученное дифференциальное уравнение.
627
При решении дифференциального уравнения иногда прей, гают некоторыми членами ввиду их относительной малости, сматривая их как своего рода малый параметр.
Этот метод при расчете нелинейных цепей переменного применяется в сочетании с методом гармонической линеарнг и дает возможность аналитически найти первую гармонику или напряжения'в нелинейной цепи.
3. Метод кусочно-линейной аппроксимации характеристик припасовывания линейных решений. Сущность метода заключи в замене нелинейной характеристики некоторой ломаной ль-и решении задачи методами линейной электротехники. Реше, полученные для каждого из участков ломаной, «припасовываю одно к другому соответствующим выбором постоянных интегр вания.
Этот метод получил широкое применение для решения самых различных задач.
4. Итерационный метод. Применяя этот метод, сначала находят приближенное решение, а затем его уточняют путем подстановки решения в исходное уравнение цепи. Итерационные методы применяются в сочетании с методами малого параметра.
5. Графический метод. Сущность метода заключается в сведении дифференциальных уравнений цепи к системе нелинейных уравнений и получении решения графическими построениями.
Этим методом просто и точно рассчитывают переходные i цессы в цепях с постоянными э. д с., описываемых днфференци ными уравнениями первого, а в несколько измененном виде — рого порядка. Для установившихся режимов в цепях с переменными э. д. с. этот метод применяется в сочетании с методом малого параметра и условной линеаризации.
Применительно к расчету переходных процессов графические методы качественного анализа процессов получили развитие в работах А. А. Андронова, С. Э. Хайкина и А. А. Витта и известны под названием метода фазового пространства.
6. Метод последовательных интервалов. Сущность метода заключается в замене дифференциального уравнения алгебраическим, содержащим приращения исследуемых величин за соответствующие интервалы времени. Решение задачи получается в результате множества элементарных расчетов, сводимых обычно в таблицу
При помощи этого метода может быть проведено численное решение тех же задач, что и графическим методом. Метод пос к-довательных интервалов менее нагляден, чем графический, и более громоздок, однако он хорошо сочетается с применением цифрой4 вычислительных машин, применение которых делает этот метод все более и более распространенным.
Из перечисленных методов графический метод наиболее nai ден и в то же время дает удовлетворительную точность реик задачи. Однако при помощи графического метода трудно усД‘ вить общие зависимости. Аналитический метод обычно менее на!
628
н иногда громоздок и менее точен, однако при помощи аналитического расчета удается получить общие расчетные зависимости, цпсленные итерационные методы и метод последовательных интервалов при малой наглядности и некоторой громоздкости вычислений позволяют получить наиболее точный результат.
В практических задачах обычно применяют то или иное сочетание различных методов расчета. При решении задач надо иметь в виду приближенный характер задания нелинейных зависимостей, которые могут существенно изменяться с течением времени, а особенно при замене деталей устройства. Поэтому простота и наглядность решения часто более желательны, чем точность математического описания нелинейного элемента и полнота исходных уравнений.
В гл. 23—26 рассматриваются различные технические задачи нелинейной электротехники и для расчета применяются перечисленные выше методы.
Все перечисленные методы приобретают особое значение в связи с применением электронных вычислительных машин (ЭВМ) для решения электротехнических задач. Применение ЭВМ для решения конкретных задач при заданных параметрах и характеристиках электрических цепей дает возможность рассчитывать режим в линейных и нелинейных цепях практически любой сложности и с любой требуемой точностью. При этом методы решения линейных и нелинейных задач различаются значительно меньше, чем при аналитических расчетах.
В связи с этим при рассмотрении явлений в нелинейных электрических цепях предпочтение отдается простоте и наглядности метода расчета и возможности суждения о явлении без его точного количественного анализа, который в случае необходимости всегда может быть произведен при помощи ЭВМ.
Глава двадцать третья
НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ
23-1. Общая характеристика цепей с источниками Э. Д. С. одинаковой частоты
Простейшие электрические нелинейные цепи с источниками Достоянных э. д. с. и токов были рассмотрены в гл. 20, там же были приведены статические характеристики некоторых нелинейных резисторов. При постоянном токе нелинейные резисторы нашли ^Рименение преимущественно в цепях стабилизаторов тока и на-
Применение источников синусоидальной э. д. с. (даже только Дной частоты) в цепях с нелинейными резисторами значительно р СШнряет число практических задач, решаемых при помощи
629
нелинейных резисторов. Во-первых, появляется возможность пг менять в электрических цепях наряду с нелинейными активны^ сопротивлениями также нелинейные реактивные сопротивления-Д индуктивности и емкости — и, во-вторых, к задаче воздействия на значение напряжения или тока добавляется задача изменения формы кривой напряжения или тока.
В цепях с нелинейными активными сопротивлениями, имеющими несимметричные характеристики, можно осуществить выпрям-ление напряжения и тока. В цепях с нелинейными реактивными сопротивлениями, имеющими обычно симметричную характеристику можно получить утроение частоты. В цепях с нелинейными активными и реактивными элементами возможна стабилизация тока или напряжения.
Рассмотрим примеры решения каждой из этих трех задач ц особенности возникающих явлений.
23-2. Форма кривой тока в цепи с вентилями
Нелинейное активное сопротивление с наиболее резко выраженной несимметрией характеристики (относительно начала координат), т. е. сопротивление с односторонней проводимостью, называется электрическим вентилем. Односторонней проводимостью обладают меднозакисные, селеновые, германиевые, кремниевые и другие полупроводниковые вентили, ртутные вентили, газотроны, тиратроны и электронные лампы всех типов.
Рис. 23-1.
Статическая вольт-амперная характеристика для мгновенных значений и и i таких элементов показана на рис. 23-1, а. В зависимости от реальных параметров цепи ее можно приближенно представить в виде ломаных линий, изображенных на рис. 23-L б и в. Характеристики полупроводниковых и электронных (кенотронов) вентилей ближе к кривой, изображенной на рис. 23-1» о, а характеристики ртутных вентилей и газотронов имеют вид кривой на рис. 23-1, в. Ограничимся процессами при таких скоростях изменения тока, для которых можно считать, что динамическая вольт-амперная характеристика сопротивления совпадает со статической. Такие сопротивления будем называть б е ынерционными.
630
Элементы с характеристиками, показанными на рис. 23-1, б и в, можно представить схемами замещения, состоящими из и де а л ь-л 0 г о вентиля и последовательно с ним включенного активного сопротивления гв или источника э. д. с. Е. Под идеальным вентилем понимается такое сопротивление, величина которого при одной полярности напряжения равна нулю, а при другдИ полярности равна бесконечности. Вольт-амперная характеристика идеального вентиля представляется положительным участком оси i и отрицательным участком оси и (рис. 23-1, г).
Рис. 23-2.
Расчет цепи графическим методом. Чтобы построить кривую тока в цепи с односторонней проводимостью и проверить допустимость идеализации характеристики вентиля, рассмотрим выпрямитель (рис. 23-2), состоящий из последовательно соединенных источника синусоидального напряжения ur = Um sin at, вентиля с характеристикой i (и), представленной на рис. 23-1, а, и линейного сопротивления нагрузки г.
Так как
u1 = u + ur = u4-ir=t/msinco^, (23-1)
То. зная зависимость i («) и параметр г, можно построить кривую ' (wi) путем суммирования абсцисс кривой i (и) и прямой i = ur/r Фис. 23-2). На этом же рисунке внизу построена зависимость напря-ения иг от времени t для трех различных амплитуд Um (кривые
631
1, 2, 3). Находя по характеристике i (t/j) для каждого мгновенно! напряжения иг соответствующее значение тока, нетрудно по то кам построить зависимость тока i от времени t (справа на рис. 23-2
Как видно из построения, кривая i (t) состоит из чередуь щнхся положительных и отрицательных полуволн. Так как угс наклона характеристики i (tiL) при положительных значения напряжения иг во много раз больше, чем при отрицательных,! положительные полуволны тока значительно больше отрнцатещ ных. Различие в абсолютных значениях полуволн тока тем замет нее, чем больше амплитуда Um напряжения источника. При достаточно большой амплитуде (например, кривая /) отрицательной полуволной тока можно пренебречь и считать, что кривая тока состоит только из положительных полуволн, каждая из которые имеет форму половины синусоиды (однополупериодное выпрямление). При выпрямлении малых напряжений (например, кривая 3) ток обратной полуволны может оказаться одного порядка с током положительной полуволны. В этом случае выпрямляющее действие вентиля сказывается значительно меньше.
Часто выпрямитель работает в таком режиме, когда ток положительной полуволны много больше тока отрицательной полуволны и последним можно пренебречь. В этом случае с вполне допусти мой для практики точностью характеристику реального вентлт (рис. 21-1, а) можно заменить характеристикой идеального вентиля (рис. 21-1, г) и рассчитывать цепь методом кусочно-линейной аппроксимации.
23-3. Простейшие выпрямители
Рассмотрим теперь простейшие схемы, предназначенные для выпрямления, т. е. преобразования переменного тока в постоянный с/ Расчет проведем методом ку-
g сочно-линейной аппроксима-
И П1“« ции-
г«|| | Для однопол упер иодного
0_______J выпрямителя с активным со-
. противлением нагрузки г„, ли-
,, u,i > таемого от источника синусои
дального напряжения иг (рис. 23-3, о), на рис. 23-3, б построены кривые токи i и напряжения на сопротивлении нагрузки 1/н в предположении, что вентиль идеальный.
Напряжение на сопротивлении нагрузки резко несину сондально и имеет наряду с
постоянной составляющей 170, равной по величине Um!n (прило ’ е-ние 1), еще первую и все четные гармоники. Если схему с веьгч-
632
ieM применяют дчя получения постоянного напряжения, то перед сопротпвпением гн включается фильтр низкой частоты, пропускающий только постоянную составляющую и не пропускающий все гармоники, начиная с первой
Рассмотрим, каковы значения тока, напряжения и мощности источника в цепи (рис 23-3, а) при отсутствии фильтра
Действующее напряжение питания Ur = Um/^2. Действующий ток, как и в цепях синусоидального тока
/"У?
/=у ~y2dt, о
но интеграл, стоящий под знаком корня, в 2 раза меньше его значения при отсутствии вентиля, когда протекает синусоидальный ток Поэтому
Т__Л/ L_______ — и™ __ /оо 9\
1'2 г 2 2 2гв |2гн’ ’2)
т е действующий ток зависит от действующего напряжения источника по линейному закону Действующее напряжение на сопротивлении нагрузки
l/H = /rH=t/,n/2 = t/1/K2. (23-3)
Активная мощность в сопротивлении нагрузки в 2 раза меньше мощности, выделяемой при отсутствии выпрямителя
P = UJ = UmIm/4 (23-4)
Потная мощность источника питания
S==6/1/=Uffl/m (23 5)
р2 2 v
и, следовательно, коэффициент мощности выпрямителя
Х=5 =^2 = °,707. (23-6)
То обстоятельство, что коэффициент мощности не равен единице, объясняется в рассматриваемом случае не наличием реактивных сопротивлений, а искажением формы кривой тока по отношению к форме кривой напряжения источника питания
Для сопротивления нагрузки ги действующее напряжение в |Л2 раз меньше, чем для источника, и, следовательно,
Р/5Н=1. (23-7)
Реактивная мощность источника
tv* sin 0, (238)
633
так как напряжение содержит только основную гармонику, a net вая гармоника тока (см. приложение 1 и рис. 23-3) совпадает по фазе с напряжением.
На аналогичном принципе построены и более сложные схеж, выпрямителей двух, трех и большего числа фаз.
На рис. 23-4, а изображена схема двухполуперподного кенотронного выпрямителя со средней точкой. Токи, проходящие через оба вентиля (кенотрона), в сопротивлении гн совпадают понаправ-лению. В течение одного полупериода ток проходит через верхнюю часть вторичной обмотки трансформатора и первый вентиль по пути О, а, 1, О', О, а в течение другого полупериода — через нижнюю часть обмотки и второй вентиль по пути О, Ь, 2, О', О.
Если принять характеристику вентиля идеальной, то постоянная составляющая напряжения на нагрузке Uo в л/2 раз меньше
Рис. 23-4.
максимального значения напряжения, питающего один вентиль, однако, так же как и в схеме однопол упер иодного выпрямите ri, постоянная составляющая в л раз меньше амплитуды общего напряжения на вторичной обмотке трансформатора (между зажимами а и Ь). Выпрямленное напряжение теперь не содержит основной гармоники — частоты питающего напряжения (рис. 23-4, б). Дейсг-вующее значение выпрямленного напряжения (рис. 23-4, б) равно действующему напряжению одной фазы (между точками а и О или О и Ь).
Фильтр, не пропускающий высшие гармоники, применяемый для сглаживания напряжения ан, в этом случае должен быть рассчитан на частоты, начиная со второй гармоники и выше.
Для двухполуперподного выпрямления широко применяются мостовые схемы. На рис. 23-5, а изображена принципиальная схем3 мостового выпрямителя. К зажимам а — Ъ моста, составление!0 из четырех вентилей, приложено синусоидальное напряжение »i В течение первой половины периода (рис. 23-5, б) напряжение z,i положительно, ток протекает через вентиль 1 в направлении о* а к п, через сопротивление rt, и вентиль 3 в направлении от р к Напряжение на вентилях 1 и 3, пропускающих ток в этом направле- 634
634
ЧП 11'11111
практически равно нулю, и, следовательно, оно полностью tf’L’nTCH на каждый из вентилей 2 и 4, не проводящих ток в направ-л0 от п к b и от а к р. Таким образом, в течение первой половины
а
дении _________ __ ______
пеоиода u,,b ~~ Uap Uab U1’
Jnc. 23-5, б).
Upb — Uan = 0 (пунктир ИЗ
Рис. 23-5.
в)
Во время второй половины периода напряжение иг отрицательное. Теперь проводят ток вентили 2 и 4, а напряжение ложится полностью на непроводящие вентили 1 и 3. Таким образом, во время второй половины периода ипЬ = иар = 0, а ирЬ = иап — иаЬ= и±.
Напряжение на сопротивлении гн нагрузки ии = ипр = ипЬ — — ирЬ ~ | иг |, так как при их положительном ин = ипр = ипЬ, а при щ отрицательном ин = ипр = — ирЬ. Зависимость от вре
мени показана на рис. 23-5, в. Максимальное значение выпрямлен-ного напряжения равно амплитуде переменного напряжения пита-Ння и, следовательно, постоянная составляющая выпрямленного напряжения на сопротивлении нагрузки Uo в л/2 раз меньше мплитуды Um напряжения питания иг.
т „схс'ме трехфазного выпрямителя (рис. 23-6), каждый из вен-лен (кенотронов) пропускает ток только тогда, когда напряже-чем На °^мотке Данной фазы генератора или трансформатора выше, что напРЯЖение каждой из двух других фаз. На рис. 23-6 видно, каждая из фаз пропускает ток в течение одной трети периода.
635
Рис 23-7.
Напряжение на сопротивлении гн содержит постоянную соста ляющую и высшие гармоники, кратные трем (приложение 1) п стоянная составляющая Uo при идеальной характеристике вентцЛе равна где Um — амплитуда фазного напряжения. вь
прямленное напряжение содержит еще меньше высших гармонщ чем в двух рассмотренных ранее сх< мах.
Выше были рассмотрены тольк простейшие выпрямители, нагружен ные на активные сопротивления, Ц практике при рассмотрении цепей выпрямителями обычно необходим учитывать кроме сопротивления г также индуктивность и емкость фильт ра. В этих случаях при расчете токо
можно пользоваться методами расчета переходных процессов j производить «припасовывание» решений, полученных для каждой из линейных участков характеристики вентиля.
Рассмотрим включение цепи, представленной на рис. 23-7 при нулевых начальных условиях. Характеристику вентиля приме: идеальной.
Пусть напряжение
sir: (23-9
и замыкание рубильника происходит при t = 0. Тогда сразу ж, после включения рубильника в сопротивлении гн и в емкости ( возникают токи
= sin coZ; (23-10
ic — С = CUma cos at, (23-11
через вентиль проходит ток
i = tH + ic — Um sin at +®C cos at \rH
(23-12
В некоторый момент времени 4 вентиль перестает пропускал ток (г = 0), так как напряжение на нем становится отрицательным и конденсатор начинает разряжаться на сопротивление нагрузки Для этого момента времени
0 = Ст f -1 sin ati -фaC cos ,
vn /
откуда находим:
Д = ^arctg(— arKC).
(23-13
(23-H
636
Начиная с момента tr, ток
iH = — ic=sin atie~. (23-15)
разряд конденсатора происходит до того момента времени, Гда отрицательное напряжение на вентиле и = иг — ис синится до нуля и вентиль начнет пропускать ток. Этому соответствует омент времени t2, для которого
О = Um sin a>t2 — Um sin co/jo- ,i)/z'hc . (23-16)
Последнее уравнение аналитически не решается, и значение t2 тедует определить графически по точке пересечения кривых иг и нс (рис. 23-8).
Начиная с момента времени г2 вентиль опять пропускает ток до тех пор, пока в момент времени вентиль снова не перестанет пропускать ток. Таким образом, в цепи почти сразу устанавливается периодический процесс с периодом Т. В интервале времени t2 — tt сопротивление вентиля бесконечно велико, а в течение времени Т — (t2 — =
= t3 —12 его сопротивление равно нулю. Чем больше емкость С и больше сопротивление г„, тем меньше переменная составляющая тока в сопротивлении гп. В идеальном случае, когда гн = оо, напряжение на конденсаторе устанавливается постоянным и равным Um.
Рассмотренная простейшая схема выпрямителя с емкостью часто применяется в электронной технике. На этом принципе,
например, основано амплитудное выпрямление, при котором выпрямленное напряжение равно максимальному значению переменного напряжения. На принципе амплитудного выпрямления основана работа элек-
Рис. 23-9.
тронного вольтметра, реагирующего на максимальное значение переменного напряжения (см. § 12-4).
Вентильные элементы широко применяются при обратном преобразовании модулированных колебаний (детектировании) с целью Уделения модулирующего сигнала. Если, например, к цепи, изображенной на рис. 23-4, а, подвести модулированное по амплитуде напряжение (рис. 12-10, о), то в составе спектра выпрямленного •апряжения ип будет основная гармоника, изменяющаяся с часто-л (пунктир на рис. 23-9). Применением фильтра можно выде-и,‘ Эт^ гаРмонику и не пропустить ни постоянной составляющей, высших гармоник.
637
HliMIBI
23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями
В катушках со стальными магнитопроводами при синусоида-ных напряжениях на зажимах токи обычно оказываются неси! соидальными, и, наоборот, при синусоидальных токах«Ь напря/} ниях появляются высшие гармоники.
Рассмотрим форму кривой тока при синусоидальном напрял нии и = Um sin (со£ + л/2) на зажимах катушки со стальш магнитопроводом. Допустим, что сопротивление обмотки катуш ничтожно мало и им, так же как и потоком рассеяния, при расчс напряжения на катушке можно пренебречь. Тогда между поток! в магнитопроводе и напряжением на зажимах катушки существ\ следующая зависимость:
и~f/msin (at + п/2) — ~eL~dW/dt — w dQ/dt, (23-1
где w — число витков обмотки. Отсюда
и •
ф = -™si и coz'. (23-1
соау '
Здесь и в дальнейшем мгновенные значения потока и потокосие ления следовало бы обозначать Ф/ и Ч^. Однако для упрощен! записи будем писать короче: Ф и
Таким образом, при синусоидальном напряжении магнитны поток также синусоидален и отстает по фазе от напряжения ш угол л/2, его амплитуда
Ф»г==^/соа>. (23-1!*)
Первоначально рассмотрим магнитопровод, выполненный из магнитно-мягкой стали с малыми потерями, для которой петлей гистерезиса можно пренебречь и считать, что зависимости Ф (i) и соответственно i (Ф) однозначны. Зная зависимость Ф (/) и имея кривую i (Ф), легко найти зависимость i (i).
Расчет графический. Для рассматриваемого случая кривая i (й построена на рис. 23-10. Как видно из построения, кривая тока имеет заостренную форму. Чем больше амплитуда магнитного потока, тем сильнее сказывается насыщение стали, острее кривая тока и резче в ней выступают в первую очередь третья, а затем и пятая гармоника.
Основная гармоника тока (рис. 23-10) совпадает по фазе с магнитным потоком и отстает от напряжения на четверть периода Активная мощность, потребляемая от источника синусоидально'1 э. д. с., равна нулю.
Расчет аналитический. К тем же выводам можно прийти, выражая характеристику намагничивания, например, в виде
г = О1Ф фбДЫ. (23-20»
Подставляя пП
Ф = Фт8шсо/, (23-21)
638
j4oAHM
i=a^m sin со/ + й1Ф,3„ sin3 co/.
Учитывая, что
sin3a=-sincc~sin3K 4 »
п0Сде преобразований получаем:
/=Лт s in со/ — Ism s in Зсо/.
(23-22)
(23-23)
(23-24)
Это выражение показывает, что кривая i (/) имеет в сравнении с синусоидой заостренную форму, так как максимумы первой
11 третьей гармоник совпадают при со/ = л/2, Зсо/ = Зл/2 и т. д., следовательно, tMaKC = Iim + Ism.
Рассмотрим теперь случай, когда катушка со стальным магни-т°проводом питается от источника синусоидального тока
i = Im sin wt
11 петлей гистерезиса можно пренебречь.
Графический расчет. Аналогично предыдущему по известным кривым i (f) и характеристике Ф (/) на рис. 23-11 построена кривая Магнитного потока Ф (/). Полученная кривая имеет тупую (при-плюснуту10) форму. Кривая напряжения на катушке, построенная
639
путем графического дифференцирования кривой магнитного i < lf t имеет заостренную форму.
Рис. 23-11.
Расчет аналитический. То же можно показать, пользуясь прг. ближенным аналитическим выражением кривой памагничигания
Ф=a2i — b2is. (23-25;
Подставляя
i = 7msinco/, получаем:
Ф = а2/т s in at — b2Im s in3 at
или после преобразований, учитывая (23-23),
Ф = ф1т5Ш(о£4-Фзт5тЗ<»Л (23-201
Выражая напряжение через магнитный поток, получаем: и = w cbl>/dt = шсоФют cos at -ф ЗжоФзт cos Зсо/ =
= Ulm cos at -ф U3m cos 3co7. (23-2
Последнее выражение показывает, что кривая и (7) имеет за< стренную форму, так как максимумы первой и третьей гармон*1 совпадают (пмакс = Ulm + U3m при at = 0), а отношение ампл! туды третьей гармоники к первой для кривой напряжения в 3 ра3 больше, чем для кривой потока. Таким образом, при синусоида-111 ном намагничивающем токе относительно небольшая несин}с°'* дальность кривой магнитного потока приводит к более значШеЛЬ ному отличию от синусоиды кривой напряжения на катушке.
640
Сложнее производится расчет для стали с потерями, когда епьзя пренебречь гистерезисом и необходимо учитывать неоднозначность зависимости между i и Ф. Эта зависимость изображается петлей гистерезиса (рис. 23-12). Графическое построение для расчета катушки выполняется по точкам аналогично рис. 23-10 и для случая питания катушки от источника синусоидальной э. д. с. показано на рис. 23-12. Как видно из построения, максимумы тока и магнитного потока во времени совпадают, но ток проходит через нуль несколько раньше, чем магнитный поток достигает нуля, что обусловлено гистерезисом. При аналитическом решении этой задачи
обычно ток в катушке со сталью представляют в виде суммы двух составляющих. Зависимость одной из них от магнитного потока выражается однозначной функцией, подобной (23-20), а зависимость второй от магнитного потока изображается эллипсом, оси которого соответствуют максимальной индукции в стали и ее коэрцитивной силе.
Все большее применение в технике получают сегнетоэлектрики. Конденсаторы с сегнетоэлектриками имеют нелинейную характеристику Q (и). Эта зависимость ана-
Рис. 23-12.
логична кривой Ф (i) у ка-
тушек со стальным магнитопроводом. Если учесть, что ток в кон-
денсаторе i = dqldt выражается подобно тому, как и напряжение на катушке и (/), то, выполняя построения, аналогичные рис. 23-10 или рис. 23-11, легко установить характер кривых тока и напряжения для конденсатора с сегнетодиэлектриком. При достаточно большом синусоидальном напряжении на конденсаторе кривая тока имеет заостренную форму (аналогично u(t) на рис. 23-11), а при синусоидальном токе в конденсаторе на нем возникает несинусоидаль-ное напряжение заостренной формы [аналогично i (t) на рис. 23-10].
обоих случаях в несинусоидальных кривых наиболее резко выкупает третья гармоника.
При последовательном соединении линейной и нелинейной или ^скольких различных нелинейных индуктивностей и питании такой (1 Пн от источника синусоидальной э. д. с. как ток, так и нарряже-ч”е R3 Различных участках оказываются обычно несинусоидальны-э ' ° этих случаях токи и напряжения можно определять также на °вании графических построений или аналитических расчётов.
21 Основы теории цепей
641
Пример 23-1. Цепь состоит из линейной Lx и нелинейной Ч^ (£) индуктив стей, включенных последовательно на гармоническое напряжение и = и со,Но (рис 23-13, а) Зависимость Т, (i) задана графически (рис 23-13, б) Пости,, <й| зависимости ЧГ1 (/) и Ч^ (/) ИТ|:
Решение Потокосцепление первой катушки Ч^ = Lxi и, следователе общее потокосцепление ‘ но>
Y=¥1+¥2=£1f+^(t).
Так как общее напряжение (TV d
U = = ~dF at,
то кривая потокосцепления V (/) также синусоидальна Ч1, = Чг,„ sin at = Um/a (рис 23-13, б)
Рис 23-13.
На этом же рисунке построены прямая ЧГ1 (i) и суммарная кривая 'F (г) = = ЧГ1 + для положительных значений этих величин
Зная для любого момента времени значение Ч1, (например, точки 1 и 2), гра фически определим соответствующие значения Ч^ и Чг2 и построим графики Ч^ (I) и Ч'з (0 Это построение выполнено на рис 23-13, б Как видно из построения, при данном значении Чг,„ график 'Fj (t) имеет в сравнении с синусоидой заостренную форму, а Чт2 (/), наоборот, притупленную Если теперь определить путем графического дифференцирования ut = d^/di и и2 = d^Jdt, то легко убедиться что оба напряжения несинусоидальны, напряжение их имеет притупленное форму а напряжение и2 — заостренную.
Рассматривая форму несинусоидальных кривых, получаемых в цепях с реактивными нелинейными сопротивлениями, можно заметить, что во всех случаях кривые симметричны относительно оси абсцисс и, следовательно, не содержат четных гармоник. Отсутствие четных гармоник — следствие симметрии нелинейных характеристик реактивных сопротивлений (рис. 23-10, 23-11 и 23-13)
23-5. Утроители частоты
Как было показано выше, при питании цепей с нелинейным11 элементами от источника синусоидального напряжения на отдел ных участках возникают резко несинусоидальные напряжен!
642
„оторых при симметрии нелинейных характеристик обычно наи-Адпее резко выделяется третья гармоника. Это явление положено основу устройства различных типов утроителей частоты.
Б Схема одного из типов утроителей частоты изображена на niic 23-14. Утроитель частоты состоит из трех одинаковых однофазных трансформаторов, первичные обмотки которых соединены в звезду, а вторичные — в открытый (разомкнутый) треугольник.
В токах симметричного приемника, соединенного звездой, при отсутствии нейтрального провода, как известно, отсутствуют гармоники, кратные трем (см. § 12-10). Следовательно, токи в первичной цепи каждого из трансформаторов могут состоять только из первой, пятой, седьмой и других нечетных гармоник, не кратных трем. Если в первом приближении пренебречь более высокими гармониками, чем третья, то можно считать, что токи в первичных цепях
синусоидальны. Трансформаторы работают в режиме насыщения, поэтому магнитные потоки, а следовательно, и напряжения на вторичных обмотках несинусоидальны и в числе прочих гармоник содержат гармоники, кратные трем.
При соединении вторичных обмоток в разомкнутый треугольник сумма напряжений всех гармоник, не кратных трем, обращается в нуль, а третья, девятая и так далее гармоники суммируются и напряжение на вторичных зажимах и2 равно утроенной сумме гармоник, кратных трем.
Если звезда, составленная из нелинейных элементов, питается от трехфазного источника питания с выведенной нейтральной точкой, то утроение частоты можно получить, не прибегая к трансформации напряжения. На рис. 23-15 изображена схема утроителя астоты, который состоит из трех насыщенных катушек, соединенных ездой. Так как в токах системы без нейтрального провода отсутст-н"'Ют гармоники, кратные трем, и, следовательно, токи в индуктив-в стях практически синусоидальны, то в потоках и, следовательно, треНапРяжениях на катушках содержатся гармоники, кратные м. При синусоидальных э. д. с. источника питания с часютой ,СЖДУ точками N — п возникает напряжение, изменяющееся
21*
643
с частотой Зсо, амплитуда которого тем больше, чем сильнее ск зывается насыщение стали. Вместо насыщающихся катушек стальными магнитопроводами в качестве нелинейных сопротив^^ ний могут быть включены нелинейные емкости или нелинейны активные сопротивления. Во всех случаях между точками N и t возникает напряжение тройной частоты.
Рис 23-15.
---0 и, 0—— Рис 23-16
Трехфазные цепи с нелинейными элементами, имеющими симметричные характеристики, применяются и при осуществлении иных задач. В этих случаях появление высших гармоник может
Рис. 23-17.
носить паразитный характер. Так, например, в дуговой сталеплавильной печи, схема которой подобна рис. 23-15, а сопротивлениями нагрузки za являются мощные электрические дуги с нелинейными вольт-амперными характеристиками, между точками N и п возНИ' кает напряжение тройной частоты, величина которого может пре'1 ставлять опасность для обслуживающего персонала.
644
утроенне частоты получают не только в трехфазных, но и в „офазных системах. На рис. 23-16 изображена мостовая схема ^конденсаторами, два из которых имеют одинаковую линейную С пактеристику q = Сиа, а два других — одинаковую нелинейную 'авактеристику q (tzc) сегнетодиэлектрика.
х Если к одной из диагоналей моста подключить источник сину-оидального напряжения = Uim sin cot, то при соответствующем сbIgope параметров цепи на зажимах второй диагонали получится напряжение и2 тройной частоты.
Пример 23-2. Построить график напряжения и2 в цепи по рис. 23-16 при известном синусоидальном напряжении tq и заданных характеристиках q (и) конденсаторов (рис. 23-17).
Решение. Для мгновенных значений напряжений справедливы следующие равенства:
= u2=ug—ua.
Так как при отсутствии тока во второй диагонали заряды обоих включенных последовательно конденсаторов в любой момент времени равны, то, имея характеристику иб (д) и зная, что иа — q/C, построим (q) и п2 (?) как сумму и разность прямой иа (?) и кривой и6 (q) (рис. 23-17). По характеристикам щ (д) и «2 (?) для заданного щ (I) построим зависимость и2 (£) (рис. 23-17).
23-6. Формы кривых тока и напряжения в цепях с терморезисторами
Выше были рассмотрены цепи, в которых нелинейная зависимость связывала мгновенные значения тока и напряжения, тока и магнитного потока или напряжения и заряда. Предполагалось, что нелинейная характеристика не зависит ни от времени, ни от скорости процесса.
Однако существуют сопротивления, для которых эти допущения несправедливы. К их числу в первую очередь относятся т е р мо -резисторы, в которых нелинейность вольт-амперной характеристики обусловлена тепловыми процессами, происходящими достаточно медленно. При частоте 50 Гц и выше за четверть периода (промежуток времени, за который ток нарастает от нуля до наибольшего значения) температура терморезистора вследствие инерционности обычно изменяется так мало, что приближенно можно считать температуру постоянной. Таким образом, в пределах периода тока сопротивление можно рассматривать как неизменное, линейное. При изменении действующего значения тока изменяется температура терморезистора, а следовательно, и сопротивление, оэтому между действующими значениями тока и напряжения суще-твует нелинейная зависимость.
4pJaKIle элементы, как терморезисторы, для которых зависимость «ежду действующими или амплитудными значениями основных НеЛчп? (например, в случае терморезисторов напряжения и тока) вел "Неина> а зависимость между мгновенными значениями этих ичин остается линейной, называют условно-нелинейны м и. J
645
В качестве примера рассмотрим лампу с угольной нитью Нак, ливания, подключенную к источнику синусоидального напряжен г Um sin cot. На рис. 23-18 слева показана нелинейная характер? тика / (С/), связывающая действующие значения тока 1 и напряг ния U. Эта характеристика одинакова для постоянного и переМе,' ного тока. Для холодной лампы зависимость между мгновенным" значениями тока i и напряжения и изображается прямой, касате^' ной к кривой / (U) в начале координат. По мере увеличения деа'
Рис. 23-18.
ствующего значения тока I возрастает температура нити и соответственно уменьшается сопротивление. Теперь уже зависимость между i и и выражается прямой, проходящей через начало координат и пересекающей кривую / ([/) в точке с координатами V и Т т. е. действующими значениями напряжения и тока при данной
температуре нити.
На рис. 23-18 построены кривые i (f), получающиеся при одном и том же значении и (t) в первый момент включения, когда сопротивление лампы равно сопротивлению холодной лампы г = г0, и ПР” установившемся режиме нагрева нити лампы, когда г = гу = "' Так как зависимость между мгновенными значениями тока и напри жения терморезисторов линейная, то при синусоидальном н пряжении ток также синусоидален.
646
Отсутствие высших гармонических в кривых тока и напряжения ьма облегчает расчет цепей с терморезисторами. При отсутствии ве„у111ек индуктивности и конденсаторов расчет схемы с термо-ка3(1СТорами на переменном токе ничем.не отличается от расчета нелинейных цепей при постоянном токе.
23-7. Замена реальных нелинейных элементов условно-нелинейными
у терморезисторов условную нелинейность их характеристик вносит тепловая инерция. В емкостях и индуктивностях условная нелинейность может быть следствием инерционного изменения взаимного расположения пластин конденсаторов или обмоток катушек индуктивности, происходящего под влиянием электростатических или электродинамических сил. Так, некоторые электромеханические системы (например, конденсаторы электростатических вольтметров или катушки электродинамических амперметров) являются условно-нелинейными емкостями или индуктивностями. Для них зависимость между мгновенными значениями заряда q и напряжения и пли потока Ф и тока i остаются линейными при нелинейности характеристик, связывающих действующие значения Q (U) или Фд (/).
Для нелинейных индуктивностей и емкостей, не содержащих движущихся частей, таких примеров нет. Однако простота расчета цепей с терморезисторами и сложность точного расчета нелинейных цепей заставляют искать приближенные методы анализа электрических цепей, содержащих нелинейные L и С, подобные расчету цепей с терморезисторами. Таким приближенным методом является расчет с допущением, что при нелинейной зависимости между действующими значениями / и Фд или U и Q сохраняется прямая пропорциональность между мгновенными значениями i и Ф или « и д. При этих допущениях реальные нелинейные элементы заменяются условно-нелинейными и расчет ведется без учета высших гармоник или с заменой несинусоидальных кривых i (t), Ф (/), и (0 или q [t) эквивалентными синусоидами.
Разумеется, что анализ цепей с условно-нелинейными элементами справедлив только в тех случаях, когда высшие гармоники не играют УЩественной роли, а основное значение имеет нелинейная зави-к Мость между действующими значениями. Такой анализ относится методам условной линеаризации.
23-8. УЧет реальных свойств стальных магнитопроводов
катушШе в большинстве примеров рассматривались характеристики Котор еК С° СТалью без учета потерь в стали, т. е. той части энергии, и вихрЯ РасходУстся на нагрев стали, обусловленный гистерезисом
647
При инженерных расчетах технических устройств, содержат стальные магнитопроводы и работающих при переменном /(Д такое допущение недопустимо, так как именно этими явления/ и обусловлены потери энергии, величина которых опредедя' тепловой режим работы устройств.
Вихревые токи возникают в стальном магнитопровол под влиянием электрического поля, наводимого в магнитопровол переменным магнитным потоком. На рис. 23-19, а распределение вихревых токов в массивном магнитопроводе схематически показано пунктирными линиями.
Кроме потерь энергии вихревое токи производят размагничивающее действие, которое сильнее сказывается в середине магнитопровода и меньше на его поверхности. Это объясняется тем что средние участки магнитопровода охватываются большими вихревыми токами, чем участки, близкие к поверхности магнитопро-
23-19.
Рис
вода. Поэтому распределение магнитного поля по магнитопроводу оказывается неравномерным. Индукция больше на поверхности сердечника и меньше внутри него. Внутренние участки магнитопровода как бы экранируются вихревыми токами.
Для уменьшения потерь энергии от вихревых токов и их экранирующего действия магнитопровод собирают из отдельных электрически изолированных одинтот другого листов (рис. 23-19, б). В таком магнитопроводе вихревые токи уменьшатся, так как будут замыкаться по узким вытянутым путям, представляющим большое сопротивление. Кроме того, уменьшится экранирующее действие, так как весь магнитопровод разделен на отдельные листы, находящиеся в одинаковых условиях. Неравномерность распределения магнитного потока в пределах каждого листа при достаточно малой его толщине незначительна. Применяются также магнитопроводы, собранные из электрически изолированных тонких стальных проволок.
Для уменьшения вихревых токов листы и проволоку, из которых собирается магнитная цепь, изготовляют из специальных сортов электротехнической стали, содержащей различные присадки (примеси), снижающие удельную проводимость. Чтобы потер> энергии от вихревых токов не были чрезмерно велики, тоЛ^Игц листов берут тем меньше, чем выше частота. При частоте f = 5° применяют листы толщиной 0,25—0,5 мм, при звуковых часТг5)Тм порядка сотен и тысяч герц применяют листы толщиной 0,02—0,05 м При более высоких частотах применяют сердечники из более т ких лент. Для частот до 30—50 МГц применяют сердечники, вып
648
ь1е из магнитодиэлектриков — ферритов. Маг-не^одиэлектрнкн состоят из ферромагнитного порошка с размерами частии порядка нескольких микрон и связывающего эти частицы диэлектрика.
расчет распределения магнитного потока в стальных магнитопро-х и подсчет потерь от вихревых токов рассматриваются в В ории электромагнитного поля. В том случае, когда можно предречь неравномерностью распределения магнитного потока в поперечном сечении листов, из которых собран магнитопровод, дЛЯ мощности потерь от вихревых токов получается следующая зависимость:
PB=«G,
где Or — коэффициент, зависящий от сорта стали и размеров стальных листов; Вт — амплитуда магнитной индукции; G — масса рассматриваемой части магнитопровода.
Периодическое перемагничивание стали сопряжено с потерями энергии, обусловленными гистерезисом. Мощность потере от гистерезиса пропорциональна частоте f и определяется по различным эмпирическим формулам, например
Pr = or/CG,
где ог — коэффициент, зависящий от сорта стали; п = 1,6 при значениях Вт в пределах от 0,1 до 1 Т и п = 2 при значениях Вт в пределах от 1 до 1,6 Т.
То обстоятельство, что потери энергии от вихревых токов и от гистерезиса имеют различную зависимость от частоты, позволяет отдельно рассчитать или измерить их, если известны суммарные потери в магнитопроводе для двух (или более) значений частоты, но при одном и том же значении индукции Вт.
Рассмотрим простейшую магнитную цепь, представленную на рис. 23-20, а, допуская, что активным сопротивлением обмотки и индуктивностью рассеяния, обусловленной частью магнитного потока катушки, замыкающейся через воздух, можно пренебречь. Тогда при синусоидальном напряжении магнитный поток в стальном магннтопроводе синусоидален (23-18), а ток в катушке имеет неси-пусоидальную форму (рис. 23-20, б).
На практике при расчете катушки со стальным магнитопроводом целесообразно заменить реальный стальной магнитопровод некоторым условно-нелинейным элементом, в котором синусоидальный магнитный поток возникает под действием также синусоп-ального тока ia (рис. 23-20, б), в известной степени эквивалентного иствительному несинусоидальному току i. Условием эквивалент-t S0.1 является, во-первых, равенство действующих значений токов 3 1 и, во-вторых, равенство потерь, обусловленных токами i9 и i. с о иЭМен? Реальной кривой тока эквивалентной с и н у -мет0Л ° 11 позв°ляет при расчете цепи пользоваться комплексным
Дом и векторными диаграммами. Векторная диаграмма рассмат-
649
риваемой простейшей цепи изображена на рис. 23-20, в, а состве ствующая ей эквивалентная схема — на рис. 23-20, г. 1
Для определения параметров эквивалентной синусоиды ___ дей
ствующего значения /э и угла сдвига по фазе 6 относительно маг' нитного потока Ф или активной /п и реактивной /ф составляющи' (рис. 23-20, в) обычно пользуются реальными характеристиками стального магнитопровода, снятыми при переменном токе заданноп частоты. Значения /п и /ф зависят от числа витков катушки ц> от размеров стального магнитопровода и от максимального значения магнитной индукции в стальном магнитопроводе.
Рис 23-20
При расчете таких цепей в качестве характеристик магнитопровода удобнее пользоваться не непосредственно значениями /п в /ф, а не зависящими от числа витков катушки величинами: РеаК' тивной мощностью
<2 = Д/эсо?б-=Д/ф = Д2йф, (23-28)
которую называют намагничивающей, и активной мой' ностью
P = HZ3sin6 = Z7/n = H2gn, (23-/9)
соответствующей потерям в стали и равной сумме потерь» обусловленных вихревыми токами и гистерезисом:
Р=РВ + РГ.
650
Все эти мощности удобнее относить к единице массы стального агнитопровода Сив качестве характеристик стали принимать:
Q0-=Q/G и P0 = P/G,
сажающие удельную намагничивающую мощность и удельные отери, обусловленные гистерезисом и вихревыми токами.
Значения Qo и Ро зависят от марки (сорта) стали, способа ее намагничивания (ток или магнитный поток синусоидальные) и - —-------------------------индукции Вт. Так как маг-
к составляющим тока
особенно от величины максимальной нитная система обычно рассчитывается для практически синусоидальной формы кривой магнитного потока, то значения Qo и ро определяют для синусоидального магнитного потока.
? На рис. 23-21 приведены полученные экспериментально зависимости Qo. Ро и tg 6 = Po/Qo от максимального значения индукции Вт для электротехнической стали с толщиной листов,, 0,5 мм марки Э42 (электротехническая высоколегированная сталь с низкими потерями, принимаемая в трансформаторах) при частоте f = 50 Гц. Аналогичные графики или таблицы есть и для других марок стали.
Зная величины Qo и Ро, легко перейти
/ф и /п и проводимости Ьф и gn в эквивалентной схеме катушки. Действительно, по закону электромагнитной индукции напряжение U связано с максимальным значением магнитного потока соотношением (23-19)
Д =—= Фт=йВт,
I 2
или в комплексной форме
. Сййу г . а
t7==/pT°m==/fiBm’
(23-30)
где а = 4,44 fwS, S — сечение магнитопровода, а коэффициент 4-44 = 2л/У2.
ЛЯ1^Дставив это выражение в (23-28) и (23-29), получим состав-
I Q — GGn
® аВт аВт
I _ Р GP°
п аВт аВт
(23-31)
651
или составляющие проводимости в эквивалентной схеме (рис. 23-20 г)
< Q _ GQo . Оф-(аВтГ (аВт)ъ ’ ёп (аВтУ (аВп1Г
(23-32,
Как видно из полученных выражений, при заданных постоянных значениях частоты /, числа витков катушки w, сечения 5 и массы с стального магнитопровода составляющие тока /ф и /„ пропорциональны Q0/Bm и Рй1Вт, а пр0. водимости ЬФ и gn пропорциональны QJBm И Р01В“т.
Таким образом, построив зависимость этих величин от средней по сечению индукции Вт, Е свою очередь пропорциональной напряжению U, можно судить о характере нелинейности рассматриваемого элемента.
На рис. 23-22 построены зависимости Q0IBttl, Р0/В;п, и Р0/Вт от Вт для рассматриваемой стали. Из графика видно, что ток /п увеличивается с изменением напряжения по закону, близкому к прямолинейному, и соответственно эквивалентная активная проводимость gn изменяется незначительно. Во многих случаях проводимость g„ можно считать постоянной. Как
уже было указано, потери от вихревых токов пропорциональны квадрату магнитной индукции и, следовательно, составляющая gn. обусловленная вихревыми токами, постоянна. Потери же от гистерезиса зависят от магнитной индукции по более сложному закону и только в ограниченном диапазоне изменения индукции пропорциональны квадрату индукции. Некоторая зависимость gn от Вт обусловлена изменением формы гистерезисной петли с увеличением нн' дукции. Так как для стали Э42 при малых значениях индукции отношение высоты к ширине петли гистерезиса меньше, чем ДДЯ больших значений индукции, то с ростом индукции значение gn убывает.
Кривая зависимости /ф от Вт значительно отличается от прямой и аналогична кривой намагничивания стали. Некоторое Ря3. личие форм кривой /ф (Вт) и кривой намагничивания i„abc (^ вызвано различными значениями коэффициента амплитуды КР вой тока ka = 1макс//ф при разных степенях насыщения стал Если при малых значениях индукции этот коэффициент близ
652
значению, характеризующему синусоиду ka = У 2 = 1,41, то ь и насыщении стали он сначала увеличиваем, я до двух и даже нисколько выше, а при сильном насыщении может несколько синеться. Поскольку зависимость /ф (В,„) нелинейна, то проводи-мость Ьф значительно изменяется с изменением напряжения U. Таким образом, при расчете катушек и трансформаторов со стальными магнитопроводами необходимо считаться с нелинейностью реактивной проводимости в схемах замещения (рис. 23-20, г).
23-9. Расчет тока в катушке со стальным магнитопроводом
Рассмотрим катушку со стальным магнитопроводом при низ-
кой частоте переменного тока, когда емкостью между витками катушки можно пренебречь.
На рис. 23-23, а схематически показана картина магнитного поля катушки. Часть магнитных линий замыкается помимо магнито-
провода, через воздух, и определяет индуктивность рассеяния, индуктивное сопротивление которой хв. Катушка имеет активное сопротивление обмотки г.
б)
Рис. 23-23.
Так как эти сопротивления при синусоидальном токе / вызывают падение напряжения Д(7 = (г + /хв) I, то эквивалентная схема катушки отличается от схемы, рассмотренной в предыдущем параграфе, только наличием последовательно включенного сопротивления Z = г + jxB (рис. 23-23, б). Соответственно векторная Диаграмма (рис. 23-23, в) отличается от диаграммы, изображенной На Рис. 23-20, в, только составляющими падения напряжения А £7.
Если задано напряжение питания С, то из-за падения напря-ения Д{7 непосредственно нельзя найти Вт и эквивалентные елинейные проводимости еп и Ьф, соответствующих данному режиму.
м В этом случае необходимо вести расчет либо итерационным ч °Д°м, произведя последовательно ряд расчетов, либо графики, преобразовав схему к более удобному для расчета виду, ассмотрим примеры расчета этими методами.
653
Пример 23-3. Магнитопровод катушки имеет сечение S — 6 см2, мас G= 1,4 кг и выполнен из стали марки 942-0,5. Число витков обмотки = 120Q Сопротивление Z— г + /*в = 30+ /60 Ом. Напряжение питания U = 220 В рас считать ток в катушке итерационным методом (последовательных приближений!
Решение. Первоначально — в нулевом приближении — задаемся (t/ф) J. — /200 В. Индекс (0) означает нулевое приближение. 0
Тогда
(Вст)0= ХФ-7ё-=1»25 т-
' 4,44ay1/S
По графику рис. 23-21 находим (Ро)0 = 2,2 Вт/кг и (Qo)o = 12 вар/кг (для большей точности следует пользоваться не графиками Ро и Qp, а соответ, ствующими таблицами).
Далее рассчитываем:
W<r (U G/(^)0 = °.°84 А; (7П)О= (Ро)о С/(й/ф)о=О,О154 А и, следовательно,
(/)0 = 0,084+ /0,0154 А.
Тогда
(00) = (Йф)0+(/)0 Z = /200 + (0,084 + /0,0154) (30+/60) =1,6+/205,5 В, т. е. (П)о == 205 В.
Так как действительное значение U отличается от (Uo), то для определения следующего приближения, принимая метод пропорциональных величин, получаем:
m=200S=214 в-
Теперь, задавшись (с7ф)х = /214 В, повторяем аналогичный расчет и получаем:
= 7.34 Т, (Ро)! = 2,4Вт/кг, • (Q0)i = 20 вар/кг, (/ф)1=0,13А, (/п)1 =#0,0157А, (1/)1=223 В.
Следующее приближение
220 (Go)2 = 214-223 = 211 В
Рис. 23-24.
дает еще более близкое решение. Так, после ряда последовательных приближений получаем условие, когда (^ф)п+1= ((/ф)л и, следовательно, итерационный процесс закончен. Для заданного дросселя (7ф = 213 В, В = 1,33 Т, Ро~ = 2,4 Вт/кг, Qo = 18 вар/кг, /ф = 0,177 А, /п = 0,0156 А?
Пример 23-4. Произвести графический расчет катушки примера 23-3.
Решение. Для этой дели преобразуем источник напряжения 220 В в источник тока J, подключенный параллельно нелинейной проводимости g + /Ьф (Р1!С‘ 23-24, а). Кроме того, последовательное соединение г и хв пРсобР зуем в параллельное соединен линейных активной и реактивн проводимостей (рис. 23-24 , 6):
g = гЦг2 + х=) = 0,0066 См:
6 = л:в/(га+х:|) = 0,0133 См'
654
Теперь схема имеет вид включенных параллельно двух линейных (g и Ь) JByx нелинейных (gn и Ьф) проводимостей, к которым подведен ток
J
U г
220 р/302+602
= 3,28 А.
Зависимости gn и Ьф от напряжения иф могут быть найдены по известным рактеристикам стали (рис. 23-22) и формулам (23-32). На основании этих зависимостей н известных значений g и Ь можно построить зависимость полной проводимости t/AB=У(£п+g)2 + (Ьф+6)2 между точками Л и В от напряжения 1/ф = UAB. Такое построение выполнено на рис. 23-25. Одновременно между полной проводимостью и напряжением Uab существует зависимость, определяемая законом Ома yAB=J/UAB-
Точка пересечения двух графиков уАВ (UAB) И уАВ = J/UAB дает искомое значение UАВ.
По графику рис. 23-25 получаем илв — иф= 213 В. Дальнейший расчет токов ничем не отличается от расчета, проведенного в примере 23-3.
Сравнивая оба метода расчета, можно заметить, что метод последовательных приближений дает более точное решение задачи, тогда как графическое решение более наглядно; на основании полученного гра
фического построения легко судить о влиянии отдельных параметров схемы на результаты расчета.
23-10. Понятие о расчете условно-нелинейных магнитных цепей
Применяя аналогичную методику, можно рассчитывать и магнитные цепи переменного тока. Так же как и в магнитных цепях постоянного тока, в основе расчета магнитной цепи переменного тока лежит заданная зависимость между индукцией и напряженностью магнитного поля. Однако теперь эти величины характеризуются не только модулем, но и фазой. Так как комплекс напряженности магнитного поля связан с комплексом м. д. с. равенством
(23-33)
где I — длина средней магнитной линии в стали, а Вт = Фт/5, где сечение стали, то от векторной диаграммы /э и Ф, изображении на рис. 23-20, в, легко перейти к векторной диаграмме Н и В стали, показанной на том же рисунке.
655
Отношение комплексов действующих значений магнитной ипд\ к ции и напряженности магнитного поля представляет собой КгА/ лексное число
~ = рор = р0 (Pi - /р2) = Роре-Л (23-34)
где р называется комплексной относительной магнитной проницаемостью. Понятие комплексной проницаемости было введено профессором Московского универ, ситета В. К. Аркадьевым в 1913 г. и получило широкое применение при расчете магнитных цепей переменного тока.
Величина р может быть непосредственно рассчитана на основании известных удельных мощностей Qo и Ро. Выражая Он/ через Вт и Н, согласно (23-28) — (23-30) и (23-33), получим с учетом (23-34) для комплексной мощности магнитной цепи:’
(23-33) w V 2 Pop
Решая последнее уравнение относительно р и учитывая, что отношение массы стали G к ее объему V представляет собой ее плотность d, получаем:
~ _,, _ _ ^fBm _ nfBm (Q0-7P0) т
P-Pi ^^~-^(Qo+fPo)d
Вещественная часть pj комплексной магнитной проницаемости пропорциональна реактивной мощности намагничивания Qo, а мнимая часть р2 — потерям в стали Ро.
Наряду с комплексной проницаемостью р иногда целесообразно пользоваться понятием комплексного магнитного удельного сопротивления
р=Pi /Рз=~, (23-37)
РРо
где
Р1=-т^-; Р2=-^4-- (23-38)
nfBm Р nfBfn '
При параллельном соединении участков магнитной цепи удобнее пользоваться понятием р, а при последовательном соединении более простые выражения получаются при пользовании Р-Рассмотрим теперь простейшую магнитную цепь, состоящую из стального магнитопровода длиной /м и сечением 8М, с воздуш' ным зазором длиной /в и сечением 8В. Определим магнитный поток в цепи, создаваемый м. д. с. F. Расчет магнитного потока в цепи можно произвести аналогично расчету магнитной цепи постоянного тока:
ф = 21 =_____£_____ (23-39)
7 7 4-7 * '
656
7 =7,11*- (Qo + lpn> . oM nfbmoM
у_________7B
M B~ [XUSB •
(23-40)
14з этого выражения видно, что вещественная составляющая 7 пропорциональна реактивной мощности намагничивания, унимая — потерям в стали. В полученном выражении р зависит от магнитной индукции в стали.
для решения задачи воспользуемся методом последовательных приближений. Задавшись приближением (Вт)0 и определив по графику или по таблице соответствующие ему (Q0)0 и (Р0)0, по формуле (23-38) рассчитаем нулевое приближение (р)0. Подставив полученное значение (р)0 в формулы (23-40) и (23-39), найдем первое приближение магнитного потока (Ф)1э а следовательно, и магнитной индукции (£?т)1 ~ (Фт)1/‘5м>
Основываясь на полученном новом значении Вт, определим по графику или таблице соответствующие ему (Q0)t и (P0)i> по формуле (23-38) получим первое приближение (р)ъ а по формуле (23-39) — второе приближение для магнитного потока. Так, после ряда последовательных приближений можно получить решение задачи с необходимой степенью точности.
Пример 23-5. Магнитопровод катушки выполнен из стали Э42-0.5, характеристики которой приведены на рис 23-21, 23-22 Требуется определить магнитную индукцию в магнитопроводе при м д с F~ 1000 А Размеры 1К = 220 мм, SM = 600 м2, lB — 1 мм, SB = 600 мм2. Частота f = 50 Гц Плотность стали 7,8 103 кг/м3
Решение Для удобства расчета последующего приближения по предыдущему формулы (23-38) — (23-40) преобразуем следующим образом
___________А|2_____________
с I й, (Qp+/fi>) d
ML s^fB2m + posBJft
Направляя вектор F по вещественной оси и подставляя числа, получаем

1,77
1 + 1,36.10-2
\ 13 ni Dm-/k
Вс, этой формуле при помощи графика, изображенного на рис 23-22, произ-Как Расчет Ряда приближений Результаты расчета приведены в табл 23-1 дится'1ДНО И3 Расчета> в данном случае ряд последовательных приближении сходство весьма медленно и потребовалось 17 приближений для получения удов-
Рительной точности результата
нриб ДНако Расчет можно значительно упростить, если, рассмотрев первые два Ження''кения, начать процесс сначала, задавшись в качестве нулевого прибли-прнбЛИ}^Редвим значением индукции, полученным в результате первых двух
657
Так, задавшись вначале (Вт)0 = 1,2 Т и получив (Вт\ = 1,61 Т и (В \ — 1,3 Т (табл. 23-1), можно начать расчет снова, принимая в качестве нулевп приближения г
Bm = 1,45 Т
Ряд последовательных приближений для этого случая совпадает с прибл жениями 16 и 17 предыдущего случая (табл 23-1) Очевидно, что теперь достаточн двух приближений для получения удовлетворительной точности.
Таблица 23-[
номер приближения Т О) ' \ вгп Ik вар/(Т® • кг) (5Х Вт/(Т2 • кг)
0 1,2 7 1,5 — 1,61-/0,03
1 1,61 27 1,5 1,3 -/0,019
2 1,3 9,3 1,5 1,58-/0,028
1ё 1,45 16 1,5 1,455-/0,024
17 1,455 16,3 1,5 1,455-/0,024
Аналогичным путем могут быть рассчитаны и более сложные разветвленные магнитные цепи, содержащие несколько намагничивающих обмоток.
При решении этих задач может быть также применен графический метод.
23-11. Явление феррорезонанса
В цепях с нелинейной катушкой индуктивности, содержащих конденсатор, плавное изменение напряжения может вызывать скачки фазы и амплитуды основной гармоники тока, и, наоборот, плавное изменение тока может сопровождаться скачкообразным изменением фазы и амплитуды основной гармоники напряжения на некоторых участках цепи. Явление изменения знака угла сдвига фаз между основными гармониками напряжения и тока при изменении напряжения или тока источника питания, обусловленное нелинейностью катушек со сталью, носит название ф е р р ° ’ резонанса. В линейных цепях подобные явления принципиально невозможны.
Точный анализ феррорезонанса с учетом несинусоидальности формы кривых представляет значительные трудности. Поэтому в дальнейшем применяется упрощение, при котором напряжение, ток и магнитный поток заменяются эквивалентными синусоидами; а индуктивность принимается условно-нелинейной и зависящей от тока. Кроме юго, предполагается, что катушки со сталью не имеют потерь, т. е. угол сдвига фаз между эквивалентными синусоидами напряжения и тока катушки = л/2, и что зависимость между их действующими значениями задана.
658
феррорезонанс напряжений. Рассмотрим последовательное соеди-ие конденсатора и катушки со стальным магнитопроводом “е с 23-26). Напряжение на индуктивности Ol опережает ток 7 'Р 90°, напряжение на емкости Ос отстает от тока на 90°. Приложенное напряжение' О = Ol + Ос- Так как векторы Ol и Ос имеют противоположные направления, то О — | OL — Ос |. Зави-
симость напряжения на катушке от тока задана кривой Ol (7) (рис. 23-27). Зависимость напряжения на конденсаторе от тока (7С (7) представлена на том же рисунке наклонной прямой линией, проходящей через начало координат.
Емкость С можно всегда выбрать такой, чтобы прямая Ос (7) пересекла кривую OL (7). Разность ординат кривой UL (Г) и прямой Ос (7) дает кривую О' (Г), определяющую значения приложенного напряжения при разных значениях тока. Точка пересечения кривой О' (7) с осью абсцисс (ток 70) соответствует феррорезонансу напряжений (UL = Ос).
В данном случае, как и в некоторых линейных цепях, резонанс напряжений достигается за счет изменения индуктивности, однако в отличие от линейных цепей это изменение индуктивности происходит не независимо от тока в цепи, а как следствие зависимости эквивалентной индуктивности катушки со сталью L5 - 00<л!
от действующего значения тока 7 (рис. 23-27). Так как действующее напряжение О — положительная величина, то кривая О (7) совпадает с кривой О' (7) только при I < /0. При 7 > 70 кривая 7/ (/) представляет собой зеркальное изображение кривой О' (7).
Участки графика О (7) вблизи точки (70) чисто теоретические, фактически из-за потерь в стали и в сопротивлении обмотки, ® особенно из-за искажения формы кривых тока и напряжения, Ривая О (/) имеет несколько иной вид (рис. 23-28).
Если цепь питается непосредственно от источника напряжения, пРи изменении напряжения возможны скачкообразные измене-До^°Ка’ ПРИ плавном изменении напряжения питания О от нуля (рис. 23-28) ток по фазе отстает от напряжения (Ul > Uc),
659
изменение его величины происходит по участку характеристики Q В точке 1 происходит скачок, при котором ток возрастает до 3t' чения /2, соответствующего точке 2; по фазе теперь ток опережа напряжение (Uc > Ul, как видно из рис. 23-27), т. е. происхощ опрокидывание фазы. Дальнейшее возрастание напряжения conn ? вождается плавным увеличением тока. Уменьшение напряжения ч значения Us снова вызывает скачок тока, соответствующий переход, из точки 4 в точку 5.
Угол сдвига фаз между первыми гармониками напряжения и тока в точках 1 и 5 носит индуктивный характер, в точках 2 и 3 — емкостный, а в точке 4 он близок к нулю.
График изменения тока / и напряжений Ul kUc& зависимости от общего напряжения U показан на рис. 23-29. На участке Ц > > U > Us значения /, Ul и Uc различны в зависимости от того происходит ли увеличение напряжения от величины Us или уменьшение от величины иг.
Некоторому значению напряжения источника U2 на характеристике U (/) соответствует три значения тока /о, Ц и 1С (рис. 23-28). Точке а соответствует ток, получающийся в цепн при повышении напряжения от величины, меньшей, чем U3, до значения U2. Точке с соответствует ток, получающийся при величины, большей, чем Ult до значе-
UL,UCJ
о
Рис. 23-29.
снижении напряжения от
ния U2. Точка Ъ, лежащая в промежутке между точками скачкообразного изменения тока (точки 1 и 4), не может быть достигнута при питании цепи от источника напряжения.
Характеристику U (/) при всех значениях тока можно получить в случае питания цепи не от источника заданной э. д.с, а от источника заданного тока. Если, например, последовательно с источником напряжения, намного превышающего UL и Ес, включить переменное сопротивление достаточно большой величины, то, изменяя величину этого сопротивления, можно задавать любое значение тока /. Таким образом, плавно изменяя ток, можно снять всю кривую U (/).
Сравнивая кривые Ul (U) uUc (U), представленные на рис. 23-29, заметим, что при U > иг наклон кривой Ul (U) много меньше, чем наклон кривой Uc(U). Малый наклон характеристики UtW в области больших насыщений стали позволяет осуществить феР' рорезонансные стабилизаторы напряжения (см. § 23-12).
Феррорезонанс токов. Если катушка со стальным магнитопро водом и конденсатор соединены не последовательно, а параллельн (рис. 23-30), то в цепи также могут возникнуть резонансные явл ния. Однако в этом случае при питании цепи от источнн заданного напряжения не происходит скачков тока и, наобор ’ при питании цепи от источника заданного тока возможны ска
660
апряжения’ сопровождающиеся изменением знака угла сдвига ляз между напряжением и током.
Так же как и в предыдущем случае, построим зависимость IL , /с от напряжения источника U (рис. 23-31). Так как при отсут-яйИ потерь ток в конденсаторе опережает напряжение на 90°, а эквивалентная синусоида тока в индуктивности отстает от напряжения на 90°, то общий ток I — \ IL — /с |. Разность абсцисс графиков h (^) 11 1с (U) Дает кривую Г (If), абсциссы которой определяют значения общего тока при различных значениях напряжений (рис. 23-31).
Из построения видно, что при некотором значении напряжения U ток в индуктивности IL компенсирует емкостный ток /с и наступает
феррорезонанс токов.
На рис. 23-32 построена зависимость / (U) (пунктирная кривая). Полученная кривая носит теоретический характер. Практически
из-за потерь в стали и несинусоидальности тока в катушке даже при равенстве действующих значений IL и /с общий ток не равен нулю.
Рис. 23-32.
Рис. 23-30.
Рис. 23-31.
На практике зависимость между общим током и напряжением имеет вид сплошной кривой на рис. 23-32.
Можно подобрать такое значение напряжения U, при котором реактивная составляющая первой гармоники IL равна току 1С. В этом случае общий ток содержит только активную составляющую первой гармоники и высшие гармоники тока в индуктивности. Обычно амплитуда активной составляющей значительно меньше амплитуд высших гармоник, причем наибольшую амплитуду имеет третья, так что общий ток изменяется с тройной частотой.
Если питать цепь не от источника заданной э. д. с., а от источника заданного тока, то наблюдаются скачки напряжения. Плавное увеличение тока от нуля до Д приводит к изменению напряжения по Участку характеристики 01 (рис. 23-32). Дальнейшее увеличение риводит к резкому возрастанию напряжения и изменению знака > ла сдвига фаз между й и 1 (переход из точки 1 в точку 2). При ^алых токах реактивное сопротивление цепи емкостное, а при сопЬЩПХ токах — индуктивное. Последующее увеличение тока ^провождается увеличением напряжения по участку 2—3. Умень-
Ие тока приводит к плавному уменьшению напряжения по
661
участку 3—4. При снижении тока до значения /3 происхот скачкообразное уменьшение напряжения, сопровождающееся из”11 нением знака угла сдвига фаз. 1е"
Явления, аналогичные феррорезонансам тока и напряжен» могут наблюдаться в случае линейной индуктивности и нелинейно” емкости или нелинейных индуктивности и емкости. и
23-12. Стабилизаторы напряжения
Стабилизаторы напряжения представляют собой такие четырех, полюсники, в которых значительное изменение величины напряжения на входе вызывает лишь незначительное изменение напряжения на выходе.
Как указывалось в § 20-5, стабилизаторы характеризуются коэффициентом стабилизации
/, _Д[4. ^2
и/ U2’
(23-41)
где и± — напряжение на входе стабилизатора; U2 — напряжение на выходе (на приемнике); Д64 и Д6/2 — изменения напряжения на входе и выходе.
Чем больше коэффициент стабилизации /гс, тем выше стабилизирующие свойства цепи. Стабилизация возможна только в нелинейных цепях, так как в линейных пас-I i(uay 1(и^ сивных цепях между напряжениями
/&и\/ у'' входа и выхода всегда существует пря-
« s' мая пропорциональность (/гс = 1).
Ранее были рассмотрены мостовые
/ / /Al стабилизаторы постоянного тока. Мосто-
/ / ./вые стабилизаторы с терморезисторами /Л'' ли' ^~Ul иб при достаточной инерционности термо------------у——резисторов могут быть применены и для ' стабилизации периодически изменяю-
Рис. 23-33. щихся напряжений. Аналогичные мосто-
вые стабилизирующие цепи могут быть осуществлены и при помощи реактивных сопротивлений (сочетания нелинейных и линейных индуктивностей или емкостей). Так. цепь, изображенная на рис. 23-16, при соответствующем выборе ее параметров является стабилизатором напряжения.
Зависимость между действующими значениями напряжения и тока для нелинейной емкости, рассматриваемой как условнонелинейный элемент, выражается кривой I (Uo) (рис. 23-33), а для линейной емкости — прямой / (£/„)• При этом Ux = Ua + и°' a U2 — Uo — Ua. Построив (при отсутствии нагрузки) зависимость тока в одной из ветвей моста от суммы напряжений Ua и Uo [кривая / (1/1)1, можно, зная Ur и &Ult определить графически 1/2.и
Как видно из рис. 23-33, на параллельных участках кривы / (Ua) и / (Uo) изменение Ut на величину Д//г практически не пр
662
т к изменению (72 н> следовательно, коэффициент стабилизации fe очень велик. Наличие высших гармоник несколько снижает его значение. •
В качестве второго примера стабилизирующего устройства асСмотрим простейший феррорезонансный стабилизатор напряжения (рис. 23-34). В цепи феррорезонанса напряжений (см. § 23-11) он напряжении питания U, большем, чем напряжение опроки-чыванпя фазы (£7г на рис. 23-29), изменение напряжения питания от U' на значительную величину At7 (рис. 23-35) сопровождается незначительным изменением напряжения на индуктивности от U2 д0 у:, -ф Л(Л>. Таким образом, в цепи, представленной на рис. 23-34, получается стабилизация напряжения U2.
Сущность явления стабилизации заключается в таком изменении параметров последовательно включенных элементов нелинейной цепи с изменением напряжения питания, при котором относительное изменение напряжения на одном из участков цепи оказывается
значительно ниже, чем на входных зажимах. Так, в цепи, изображенной на рис. 23-34, с увеличением напряжения питания ток резко
возрастает и его увеличение приводит к уменьшению индуктивности
катушки со стальным магнитопроводом, в то время как емкость остается без изменения. Таким образом, относительное изменение напряжения на индуктивности (зажимы 2—2’) оказывается значительно меньшим, чем на зажимах 1—Г.
Вместо конденсатора С в цепь можно включить и линейный резистор или катушку с линейной характеристикой, однако эффект стабилизации будет меньше, так как изменение тока в катушке со стальным магнитопроводом, а следовательно, и в ее эквивалентной индуктивности при изменении напряжения питания в этих случаях меньше.
Присоединение приемника к вторичным зажимам стабилизатора создает ветвь, параллельную нелинейной катушке, в результате ок в катушке уменьшается. С изменением напряжения питания одное сопротивление между зажимами 2—2’ изменяется меньше, бцМ Г1РН отсутствии нагрузки, а следовательно, ухудшаются ста-“^изирующие свойства цепи. Коэффициент стабилизации нагру-(Шого стабилизатора обычно ниже, чем при холостом ходе.
в с>а счет несинусоидальности форм кривых токов и напряжений Нелинейных цепях напряжение {72 обычно содержит высшие
663
гармоники даже при питании стабилизатора от источника синусов дальней э. д. с. с напряжением U. Из рассмотренных типов с1абц лизаторов напряжения только у мостовых стабилизаторов с тер\10 резисторами напряжение на выходе близко по форме к синусоиде
Глава двадцать четвертая
НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ
24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот
Выше были рассмотрены нелинейные цепи с однородными источниками питания: либо постоянными э. д. с., либо синусоидальными э. д. с. определенной частоты то. Применение наряду с источником э. д. с. частоты со источника постоянной э. д. с., источника переменной э. д. с. другой частотьптли последовательности импульсов расширяет область технического применения цепей с нелинейными параметрами.
Включение источника постоянной э. д. с. в нелинейную цепь позволяет смещать участок характеристики, в пределах которого происходит изменение переменного тока, так называемый рабочий участок характеристики. Изменение рабочего участка характеристики может происходить либо непроизвольно в результате действия постоянных э. д. с., присущих данной цепи, либо специально, например для получения несимметричных зависимостей в цепях с нелинейными элементами, имеющими симметричныехарактеристики. Это дает возможность применять нелинейные элементы с симметричными характеристиками для получения несинусоидальных токов, содержащих четные гармоники.
Изменяя постоянную э. д. с., можно воздействовать на значение переменной составляющей тока, возникающего под действием переменной э. д. с. Таким образом, при помощи напряжения одного источника питания можно воздействовать на ток второго источника питания — управлять этим током.
Рассмотрим явления в цепях с источниками питания различных частот.
24-2. Вентили в цепях с постоянными и переменными э. Д- с'
В цепях с вентильными элементами при наличии постоянных и переменных э. д. с. кривая тока может очень значительно отли чаться от кривых токов простейших выпрямителей. (
Рассмотрим цепь однополупериодного выпрямителя, в которо наряду с переменной э. д. с. е = Ет sin art действует постоянн э. д. с. Ео (рис. 24-1).
664
pja рис. 24-1 построена вольт-амперная характеристика i (и) следовательного соединения идеального вентиля и сопротив-пеВНя г. Внизу показана зависимость и = —Ео + Ет sin cot от времени для двух случаев: £0 = 0 п £0 0. Справа построена
зависимость тока от временй для этих двух случаев. При Ео = 0 кривая тока А ничем не отличается от полученной в § 23-3.
В случае, когда Ео =^= 0, кривая тока В также представляет собой ряд импульсов, однако форма их другая. Аналитически зависимость тока от времени может быть выражена так:
Em sin cot Ео р • j р .
r Н (24-1)
0 при Ет sin со/ <ZE0.
Обычно импульсы тока характеризуются углом отсечки 6, который определим из соотношения
cos 6 = EfjEm. (24-2)
Продолжительность каждого из импульсов 4 найдем из условия - 26, откуда
4 = 26/®. (24-3)
В зависимости от направления и абсолютного значения э. д. с. Ео значение 9 может изменяться в пределах от 0 до л.
Как видно из графика, введение э. д. с. Ей привело к изменению Рабочего участка нелинейной характеристики. Если при Ео = 0 Рабочий участок характеристики был ограничен точками 1 и 2,
РРи Ео 0 он сместился влево и ограничен точками 3 и 4. ств° КачестВе ВТОРОГО примера цепи с вентилями рассмотрим устрой-ф0 0> применяемое для преобразования напряжения синусоидальной
РМы в напряжение трапециевидной формы. На рис. 24-2 представ-
665
лена схема замещения для газоразрядного стабилитрона, подк, ченного к источнику -----------“ - - - т------------*—
Рис. 24-2.
переменной
э. д. с. Такие преобразовав формы кривой Приг няются в устройств электронной автомат р31 Если к цепи пр, жено напряжение
«i = Hmsinco/, то в сопротивлен! ток ц протекает то тогда, когда | иг | > При этом напряж между точками А по абсолютной вел не оказывается рас > Ео (вентили на схеме замещения идеальные). При токе напряжение на зажимах А и В равно ut.
Таким образом, для напряжения а2 может быть записано сл ющее выражение:
( Um sin at при | Um sin со/ | <£0;
2 ( ±£0 при | £msin со/1 >£0.
(2'
Графики зависимости ult и и2 от времени показаны на рис.
справа.
Если Um £0, то кривая напряжения а2 приближается к прямоугольной форме.
Из- рассмотренных примеров видно, что при помощи включения вентилей и постоянных э. д. с. в цепь, состоящую из источников синусоидальных э. д. с. и резисторов, можно получить различные кривые напряжения, имеющие форму отрезков синусоид. Так могут быть получены и кратковременные импульсы (см., например, /г на рис. 24-2) и прямоугольные продолжительностью около
Рис. 24-3
половины периода.
Сложнее решаются задачи при наличии в цепи, содержа®-вентили, реактивных элементов. Предположим, что в схеме, изобр2' женной на рис. 24-1, вместо сопротивления нагрузки г включена®1' дуктивность L. Тогда с момента времени /2, определяемого из уело-вия Ет sin со/2 — £0 = 0, напряжение u = Ет sin со/ — £0 ПРЙ’ кладывается к индуктивности L. Ток в индуктивности определяем из уравнения и = L ditdt и, следовательно, t
/ = (Ет sin со/ — £0) dt = (cos со/2 — cos со/) — (/ — /а)-
(24-5)
666
тТ0к протекает через цепь до момента /3, когда ток равен нулю Фитиль запирается.
” На рис- 24постРоены графики u(f) и i(f). Из построения видно, ппи наличии в цепи индуктивности ток протекает значительно 410 ше, чем при чисто активном сопротивлении (рис. 24-1), и напря-Д0Л ие на индуктивности изменяет знак и в момент ta скачком спадает до нуля-
24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный
Выше (в гл. 23 и § 24-2) рассматривались двухэлектродные неуправляемые вентильные элементы. На практике большое распространение получили трехэлектродные управляемые вентили. К их
числу относятся ртутные вентили с управляющим электродом (игнитроны и экзитроны) и управляемые полупроводниковые приборы — тиристоры.
Упрощенно управляемый вентиль можно представить себе в виде ключа, который замыкается в тот момент, когда на управ-
t
ляющий электрод поступает положительный им-
Рис. 24-4.
пульс (при условии, что в этот момент напряжение на аноде положительно), а размыкается в тот момент, когда ток вентиля снижается до нуля. Изменяя момент поступления управляющего импульса, можно изменять время, в течение которого через вентиль проходит ток, и, следовательно, управлять постоянной составляющей выпрямленного напряжения.
Простейший однополупериодный управляемый выпрямитель с активным сопротивлением нагрузки г показан на рис. 24-4, а. "«меняя фазу а управляющих импульсов иу, можно изменять момент озникновения тока в цепи и, таким образом, управлять выпрямлен-м напряжением. Временная диаграмма процессов в выпрямителе казана на рис. 24-4, б и в. Из графика видно, что в случае одно-н УпеРиодного выпрямления, изменяя фазу а от нуля до л, можно енять выпрямленное напряжение от Um!n (см. § 23-3) до нуля.
Логично можно управлять значением выпрямленного напря-ногп'Я В слУчае двухполу пер иодного, трехфазного и многофаз-
Pj ВЬ1прямления.
3ааченИ Помо1ци управляемых вентилей можно не только изменять яццыйИе спрямленного напряжения, но и преобразовывать посто-ток в переменный.
667
Пример простейшего однофазного преобразователя По янного тока в переменный показан на рис. 24-5, а. Здесь на ляющие электроды вентилей УВ1 и УВ2 попеременно с частоте и сдвигом во времени на т = l/2f поступают положительные пульсы пУ1 и иу2, по очереди отпирающие вентили УВ1 и у В каждый момент отпирания последующего вентиля конденсате» начинает разряжаться через вентиль, ранее проводивший т и снижает его ток до нуля, приводя к отключению вентиля.
Рис. 24-5.
Временная диаграмма поочередной работы вентилей (токи и 1в2)> управляемых импульсами пу1 и tzy2, схематично показа на рис. 24-5, б — е. Если при t < 0 вентиль УВ1 проводит 1 и напряжение на нем £7В, а вентиль УВ2 заперт и напряжение нем примерно равно Ео, то конденсатор С заряжен до напрял ния ис я» Ео — UB. В момент t = 0 на управляющий ' электр вентиля УВ2 поступает отпирающий импульс цу2 (рис. 24-5, Разряд конденсатора С через последовательно включенные в( тили УВ1 и УВ2 практически мгновенно приводит к уменьшен' до нуля тока в вентиле УВ1 и нарастанию тока в вентиле УЕ
По мере перезарядки конденсатора С ток iB2 уменьшается установившегося значения. Переходный процесс изменения т01" 668
1Я УВ2 можно рассчитать по схеме (рис. 24-5, ж), где гя — 5еВТ,,‘1ентное сопротивление отпертого вентиля УВ2.
3bEnocie завершения переходного процесса перезарядки конден-
1 „ с чепез резисторы rlt г2 и вентиль УВ2 напряжение на кон-Тнсаторе «с = (рис. 24-5, е).
16 В момент t = т в цепь управления первого вентиля поступает гльс «У1. вентиль УВ1 отпирается, а вентиль УВ2 запирается.
т'1П^ поочередно с периодом Г = 1// = 2т отпираются и запираются;
т’ипи УВ1 и УВ2 и через резисторы t\ и г2 и вентили УВ1 и УВ2 Беотекают импульсы переменного тока (рис. 24-5, гид).
ПР разность токов и i2 определяется из уравнения ис = гг1г — г i2 (рис. 24-5, о) и при i\ = г2 = г изменяется по тому же закону, 4T02[i напряжение Uc (t\ — i2 = «с/r).
Вместо резисторов t\ и г2 могут быть включены две секции первичной обмотки трансформатора, вторичная обмотка которого может служить источником переменного напряжения с частотой f. В этом случае м. д. с. трансформатора пропорциональна — i2 п вследствие индуктивности обмотки трансформатора и цепи источника £0 имеет кривую, более близкую к синусоиде, чем в цепи рпс. 24-5, а.
Такого рода схемы (инверторы) применяются для получения переменного тока от источника постоянного тока.
На аналогичном принципе основаны трехфазные инверторы, преобразующие постоянный ток источника в трехфазный переменный ток.
24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с.
В цепях с нелинейными катушками смещение рабочего участка характеристики может явиться результатом как появления постоянной составляющей тока в основной обмотке, так и применения добавочной обмотки 'постоянного подмагничивания с постоянным током /0.
Питание от источника тока. Рассмотрим замкнутый стальной магнитопровод с двумя обмотками и u'j (рис. 24-6). В обмотке протекает постоянный ток /0. Зависимость магнитного потока в стали Ф от м. д. с. F задана кривой намагничивания.
Пусть в обмотке wr протекает синусоидальный переменный к li = sin со/. В таком случае м. д. с.
F—Iowo + i-iWt = Iowo + I,nwr sin со/. (24-6)
гра*3 РИС‘ 24-6 внизу построена зависимость F (/); справа путем Напп1ЧеСК0Г0 постРоения, ясного из рисунка, получена кривая Ф (/). Ровяи Женис ui на обмотке найдено графическим дифференци-а«ием кривой Ф (/):
ы1=ау1 dQ/dt. (24-7)
669
Как видно из построения, кривые Ф (/) и (t) наряду с неч ными гармониками содержат и четные гармоники. Кривая ф имеет постоянную составляющую
г
Ф01 = f § Ф (0 dt. о
(21
Значение создаваемого несимметрии
Ф01 меньше постоянного магнитного потока ( током /0 при = 0, что является результате кривой Ф (F) относительно точки 3. Таким образом переменный ток в обмотке wt изменяет постоян-ную составляющую магнитного потока, оказывая своего рода размагничивающее действие.
Если произвести построения, аналогичные рис. 24-6 для различных значений /0, то можно заметить, что чем больше /0, тем при одном и том же значении /т в меньших пределах изменяется Ф и соответственно меньше щ. Таким образом, постоянная со-
/0 существенно влияет на зависимость между напря-переменной составляющей тока i\.
ставляющая жением щ и
Питание от источника напряжения. Пусть теперь обмотка c'i
подключена не к источнику синусоидального тока, а к источнику
синусоидального напряжения
Wi = Um cos соЛ
(24-9)
Тогда при достаточно малом сопротивлении обмотки uij магнитный поток в стали изменяется по синусоидальному закону, а ток И отличается от синусоиды (рис. 24-7). Интегрируя выражение (24-7), получаем:
Ф = Ф014-Ф1т sin о^, (24-W)
где
Ф1и=1/Лй. (24-П)
Поток Ф01 в данном случае является неопределенной посте янной интегрирования. Очевидно, что чем больше ток подм0ГН чивания /0, тем больше поток Фо1, однако простой зависимое между этими величинами нельзя усмотреть. Если при известнь-
670
ачениях й и /0 поток Ф01 можно было найти путем графического
-троения Ф (0> то ПРИ питании обмотки wt от источника напряжения «1» зная ток ^0> 'затруднительно определить Фо1. Задачу * х0Дится решать обратным путем: задаваться некоторым зна-ПрНИем Фор строить кривую Ф (/) по Ф01 и щ (t) и затем находить 4 к /0, создающий магнитный поток Ф01 при заданном переменном напряжении ux (Г).
для решения этой задачи необходимо учесть, что ток в катушке с0 стальным магнитопроводом при питании цепи от источника напряжения, не содержащего постоянной составляющей, не может иметь постоянной составляющей. Действительно, обмотка катушки с0 стальным магнитопроводом имеет активное а напряжение, ток и магнитный поток связаны уравнением „^r+wicW/dt. (24-12)
Если в напряжении нет постоянной составляющей, а в производной от периодической функции с!Ф/о? 'принципиально не может быть постоянной составляющей, то, следовательно, нет постоянной составляющей и в токе i\, как бы ни мало было сопротивление г.
Эти соображения позволяют, задаваясь величиной Фи, найти соответствующее ’ ~ 24-7
значения Среднее
сопротивление г,
Ф
Фп 3
^1/п
Рис. 24-7.
/
t I
&фл
ut
значение 10. На рис. (24-11), и некоторого строена кривая F (t).
Равно I^w0:
ДЛЯ
«1, т. е. Ф1т рисунка по-
заданной величины Ф01 в нижней части значение F (/) за период как раз
т 1
/о^0 = у
т
(24-13)
. о
Так же как и в предыдущем случае, значение магнитного потока % при том же /0 11 ii — 0 (Pm = 0) больше, чем постоянная составляющая магнитного потока Ф01 при Um ^0.
На рис. 24-7 пунктиром выполнено построение кривых магнитол потока Ф и тока при том же напряжении ut, но для /0 = 0. 3 построения видно, что постоянный ток /0 оказывает существен-сое влияние на максимальное значение переменного тока i1M0KC; ( Уличением постоянного тока /0 может значительно возрасти ПеРеменный ток tx.
671
Влияние постоянного тока /0 на переменный ток имеет бол шое практическое значение, например для построения магнитш усилителей (см. § 24-10).
Все приведенные выше выводы были сделаны на основан! ц графического решения задачи Совершенно аналогичные выводы можно сделать, решая задачу аналитически.
Пример 24-1. Найти закон изменения магнитного потока в сердечнике намагничиваемом током ix = Im sm coZ в обмотке с числом витков оу, при постоям ном подмагничивании /ошо Кривая намагничивания на ограниченном участке вблизи точки /0, Фо (рис 24 6) задана полиномом
Дф=ш1—/ц2. (24-14)
Решение Подставляя ix в выражение (24-14), получаем:
ДФ = а/т sin <£>t—bPm sin2 coZ.
Преобразуя квадрат синуса, находим, что
ДФ — ДФ0 —|- ФХт sm coZ -|- Фо,я cos 2<а/, где
Дф =ф ==Ы~ /2 ф. —а! 0 2m ml ’ “'m-
Таким образом, чем больше /т, тем больше вторая гармоника Ф2т и больше изменение постоянной составляющей магнитного потока Фи = Фо — ДФ0
Этот вывод справедлив только для ограниченного диапазона изменения 1т, в котором справедлива аппроксимация (24-14) Так как действительная зависп мость ДФ (i) не имеет максимума, то 1т должно быть заведомо меньше а/26, что соответствует максимуму функции (24 14)
Пример 24-2. Найти закон изменения магнитного потока в сердечнике, к одной обмогке которого с числом витков шх подведено напряжение щ ~= = Um cos coZ, а по второй (с числом витков w0) протекает постоянный ток 10 Кривая намагничивания на участке вблизи точки 3 (рис 24-7) задана полиномом
И^ДФ + РДФ2 (24-15)
Решение Подставляя в (24-15)
Дф = Дф0 ф1т sin со/, где ®lm = ^m/u’lc0> находим, что
‘1 = /ю + Ilm sm cos 2Ш/,
где
/Ю = йДФо + 6ДФо+2Ф1т;
'1т= Ф1т («+ 26Дфо); ^т = ЬФ-;т/2.
Решив уравнение /10 = 0, получим:
262Ф;т „
Д Фо=- - -----— • (24-16)
Легко заметить, что ДФ0 имеет отрицательный знак и по абсолютной величШ е тем больше, чем больше Ф1т
672
Это решение справедливо только для ограниченного диапазона изменения Um. Действительно, у зависимости (ДФ), определяемой реальной кривой намагничивания, нет точек экстремума, тогда как в уравнении (24-15) имеется экстремум в точке, где dix/d® = а + 2Ь ДФ — 0.
Таким образом, рассмотренный расчет пригоден только для таких пределов •йменения Um, при которых | ДФ | < а/2Ь
24-5. Удвоитель частоты
Рассмотренное в предыдущем параграфе возникновение четных гармоник в магнитном потоке при постоянном подмагничивании положено в основу магнитного удвоения частоты.
Удвоитель частоты состоит из двух стальных магнитопроводов а и б с тремя обмотками каждый. Схема соединения обмоток представлена на рис. 24-8.

Рис. 24-8.
Каждая пара обмоток &у0, се/г и ш2 соединена последовательно, однако, если в цепи обмоток потокосцепления складываются, то в цепях обмоток и w2 они вычитаются. При отсутствии тока в обмотках &у0 и любом напряжении в обмотках w2 наводятся равные и противоположные по знаку э. д. с. и, следовательно, и2 — 0.
Постоянный ток 10 обмоток нарушает симметрию схемы. При /0 =И=0 на зажимах обмоток w2 появляется напряжение и2, изменяющееся с частотой, в 2 раза большей, чем основная частота. Напряжение и2 при постоянном подмагничивании /0 можно определить графически, пользуясь характеристиками стальных магнитопроводов.
Ток /0 в обмотках создает дополнительные м. д. с. Fo = = I0w0. В магнитопроводе а м. д. с. Fo = Iowo складывается с м. д. с. Fj = IjW-l, а в магнитопроводе б вычитается из Fy = ijW^ Таким образом, току соответствуют различные суммарные м. д. с.
в магнитопроводах о и б
/Л+(,».; 1
Fc— —J
22 Основы теории цепей
673
На рис. 24-9 изображена кривая намагничивания стальных магнитопроводов и показаны изменения магнитных потоков ДФа и ДФб при изменении в обмотках от нуля (точки 1 и 2) до +Fj (точки 3 и 4). Как видно из рисунка, из-за нелинейности характеристики равные изменения м. д. с. F1 вызывают различные изменения магнитных потоков ДФО и ДФе в магнитопроводах а и б. Вследствие насыщения стали увеличение м. д. с. вызывает меньшее изменение потока, чем ее уменьшение | ДФ(, | < | ДФб |.
Сложность определения напряжения и2 существенно зависит от того, питается ли цепь обмоток wr от источника синусоидального
Питание от источника тока. В этом случае, зная токи и 1„, найдем закон изменения потока в магнитопроводах а и б, выполнив построения, аналогичные показанным на рис. 24-6. На рис. 24-10 представлены зависимости Фй и Фб от времени. Для определения напряжения
= (24‘18)
на рис. 24-10 построена зависимость Фо — Фб от времени. Графическое дифференцирование этой кривой дает u2 (I). Как видно из построения, напряжение н2 содержит только четные гармоники и, следовательно, основная частота напряжения на вторичных зажимах в 2 раза выше частоты напряжения источника питания.
Последнее можно показать и аналитически, представив потоки Фо и Фе в виде гармонических рядов и учитывая идентичность магнитных систем а и б:
Фо = Фот + Ф1т cos со/ (- Ф2т cos 2со/ -j- Ф3т с os Зсо/ +...; (24- 19а)
Фб= — Фа “Г Т/2) — — Фо1 Ф1т cos Со/ — Ф2т COS 2со/
+ Фзт COS Зсо/ —... (24-196)
674
Очевидно, что Фо — Ф^, а следовательно, и напряжение «2 содержат только четные гармоники, а Фа + Ф6 и соответственно И1, наоборот, только нечетные.
Напряжение, пропорциональное и2, наводится также и в цепи обмоток w0. Это напряжение может создать значительный дополнительный переменный ток двойной частоты в обмотках ьу0, что приведет к уменьшению и2 и мощности на вторичных зажимах. Поэтому в цепь включена катушка индуктивности L, представляющая большое сопротивление для переменного тока.
Питание от источника э. д. с. Несколько сложнее решается задача, если, как это обычно имеет место на практике, к цепи обмоток подведено синусоидальное напряжение. В этом случае первоначально не известен закон изменения напряжения на каждой
из обмоток wx систем о и б, но по аналогии с построением, выполненным на рис. 24-7, можно полагать, что напряжения на этих обмотках не будут синусоидальными.
Для нахождения токов и напряжений удобно оперировать не с потоками каждой из систем с и б, а с потокосцеплениями первой
^-^(Фа + Фб) (24-20)
и второй
Т2 = и>2(Фа-Фо-) (24-21)
цепей или с их приращениями ДЧД и ДЧ;2.
Построим зависимости приращений потоков ДФЙ и ДФО от тока (рис. 24-9 и 24-11). Для магнитопровода а кривая подобна кривой намагничивания, сдвинутой в направлении отрицательных Ф и F (начало координат совмещается с точкой У), а для магнитопро-вода б — в сторону положительных Ф и F (начало координат совмещается с точкой 2).
На рис. 24-12 показана зависимость приращений потокосцепления ДЧ\ обмоток и»! и ДЧ*'.2 обмоток w2 от тока i±. Построение выполнено для случая = w2. Для первой пары обмоток (кд)
22*
675
потокосцепления складываются:
АЧ\ = wt (ДФа 4- АФО), (24 22)
а для второй пары обмоток (ьу2) вычитаются:
АЧ;2=w2 (ДФа — ЛФО). (24-23)
Таким образом, зависимости ДЧ^ (ij и АЧ;2 (it) для обеих цепе? неодинаковы.
Если к цепи обмоток приложено напряжение иъ изменяю щееся по косинусоиде иг = Ulm cos со/, то АЧ^ изменяется синусоп дальне:
ДЧ\ = Ui dt=sin <<>t, (24-24,
а ток ii несинусоидален.
По графику ДЧГ1 (ij и ДЧГ2 (ij) и по известной зависимости АЧ\ (/) на рис. 24-12 построена зависимость АЧ;2 (/). Продифференцировав графически ДЧ^ (/) по времени, определим и и2 (/), так как
u2 = dV2/dt. (24-25)
Как видно из построения, ДЧ/2 и и2 изменяются с двойной частотой, причем кривая ДЧГ2 (/) симметрична относительно оси ординат, а кривая и2 (t) симметрична относительно начала координат.
Рассчитаем напряжение и2, если удвоитель (рис 24-8) питается от источника тока ц = Im cos at при подмагничивании /0, а нелинейная характеристика стального магнитопровода может быть аппроксимирована полиномом
Ф=аР— ЬРЛ (24-26)
Учитывая, что м д с в магнитопроводах а и б выражается уравнениями (24-17), а потокосцепления вторичной цепи
Чг2 = ®2(Фа-Ф0), (24-27)
найдем зависимость от токов ц и /0
чг2=к’2 {2й/ошо-2Н(Ш)3+3/0^^с№2®д}. (2428>
По формуле (24-25) напряжение и2 определяется дифференцированием лиг
= = 12гг>,w w"J FLЬ sin со/ cos co/ = 6ay w w\IJsmb sm 2co/ (24-29)
Интересно заметить, что изменение на л фазы тока и напряжения первичной цепи не изменяет фазы напряжения на зажимах вторичной цепи и2 Это вытекает как из построений, проведенных на рис 24-9 и 24 10, так и из расчета
При расчете по формулам (24-26) — (24-29) следует иметь в виду, что аппроксимация (24-26) пригодна только при ограниченных пределах изменения м д с Легко показать, что м д с в каждом сердечнике не должна превышать значение, соответствующее экстремуму функции (24-26) в точке, где ЛФ/ЛГ — а — 3bF2 = 0 Следовательно, 1т должно быть таким, чтобы максимальное значение м Д с ка/кдого сердечника не превышало У а/ЗЬ
Итак, удвоитель частоты (рис. 24-8) дает возможность преобразовать электрическую энергию при частоте со в энергию при частоте 2со. Поскольку такая трансформация обусловлена нелипеи-676
лестью системы, а для нелинейных систем неприменим принцип взаимности, то, следовательно, это устройство не может быть непосредственно применено для обратной трансформации электроэнергии при частоте 2со, подводимой к вторичным зажимам, в энергию при частоте со на первичных зажимах.
Однако при наличии в первичной цепи резонансного контура колебания во вторичной цепи с частотой 2со могут привести к возникновению в первичной цепи незатухающих колебаний с частотой оз, причем фаза этих колебаний при одном и том же токе 12 в зависимости от начальных условий может изменяться на угол л. Это явление носит название параметрического разонанса, оно было впервые исследовано Л. И. Мандельштамом и Н. Д. Папалекси еще в 1934 г. л получило применение в запоминающих устройствах вычислительной техники, которые называют параметронами.
24-6. Метод гармонического баланса
При анализе периодических процессов в нелинейных цепях широкое распространение получил метод гармонического баланса. Основой этого метода является разложение несинусоидальных величин в нелинейных элементах на гармонические составляющие и рассмотрение уравнений системы для основной гармоники.
Рассмотрим применение метода гармонического баланса на примере анализа установившихся режимов в параметроне.
Простейшая схема индуктивного параметрона может быть получена из удвоителя частоты (рис. 24-8), если его питание производить от цепи 2 — 2', а в цепь 1—Г кроме резистора г включить конденсатор С, емкость которого выбирается так, чтобы в этой цепи возникал ток с частотой в два раза меньшей, чем частота напряжения источника питания. Обозначим частоту напряжения источника питания 2со. Тогда будем искать условия, при которых в цепи 1 — Г может возникнуть ток с частотой со.
Если к зажимам 2 — 2' удвоителя частоты (рис. 24-8) подвести синусоидальный ток с частотой 2со, а цепь обмоток 1 разомкнуть, то в обмотках цепи 1 наведутся равные по величине и противоположные по направлению э. д. с., сумма которых даст напряжение tzlt Равное нулю. Однако при наличии в цепи 1 тока с частотой со влияние цепи 2 на цепь 1 уже начинает сказываться и при определенных условиях может сопровождаться передачей энергии из цепи 2 Е Цепь 1.
Это непосредственно вытекает из уравнения цепи 1, если к зажимам 2 подводится ток, изменяющийся с частотой 2со.
Решим задачу методом аналитической аппроксимации в сочетании с методом гармонического баланса.
При наличии токов во всех трех обмотках м. д. с. магнитопро-БоДов а и б соответственно
Fa = Z’1^1 + Z2^2 + loWo, 1 /o . Qn.
, C (24-30)
4 6 — ^1^1 ~~ ^2^2 0^0* J
677
Зависимость между потоком и м. д. с. выражается уравнение-(24-26). Потокосцепление цепи 1 '
Tj=w-t (Ф,, Фб). (24-3 ।
Составим дифференциальное уравнение цепи 1 по второе закону Кирхгофа ЛЦГ 1 (»
-dT+ij + c yidt = O (24-32)
и будем искать решение для установившегося тока в цепи 1 в вцде й = A sin со/ фВ cos со/ = Ilm sin (со/ 4~ ф), (24-33)
считая, что
/2 = hm sin 2со/ — 2/2m sin оо/ • cos со/. (24-34)
В соответствии с методом гармонического баланса пренебрегаем всеми высшими гармониками в цепи 1.
Выразим в (24-31) Фа и Фб через (24-26) и (24-30). После преобразований получим:
Тх=2wx [aFl - b (Fl 4- ЗВ^)], (24-35)
где = iiWf, F2 = i2w2 + I0w0.
Подставив i, и i2 из (24-33) и (24-34) в уравнение (24-35) и преобразовав степени синуса и косинуса по известным тригонометрическим формулам, для первой гармоники получим:
= [аА — РВ — у А (А2 4- В2)] sin со/ 4-
4- [аВ — рА — уВ (А2 4- В2)] cos со/, /3 3
где а=2®1 (о —3/^6 —у/|шау^); р =^3I0I2mw0w2b; y = ^b-
Подставим и ir в уравнение (24-32). После дифференцирования, приравняв нулю коэффициенты при sin со/ и cos со/, получим:
тА 4- {п _ k) В 4- qA (А2 4- В2) = 0; 1 36)
mB + <n + k) A+qB(A2-YB2)=Q, f (
где
т = 1 — 2С(о2к'1^— 31~bwlb — I~vnw2b 4- aj;
n~3(t>2CI0I2mw0w2b; k—orC-, <7=ЗСсо2Ь/4.
Из уравнений (24-36) находим;
Р1т А2 4- В2 = - 4 >Л»2..-/г-2 (24-37)
и
4 <24-й’
Так как 11т — величина вещественная, то корень в выраж®® (24-37) следует брать со знаком плюс и соответственно со зна минус выражение (24-38).
678
Из выражения (24-37) непосредственно следует, что колебания в цепи 1 возникают при условии
/г2_^>т2. (24-39)
Для уяснения физического смысла отдельных членов уравнения (94-37) преобразуем его к следующему виду:
и2 = /Ф-|-(т4-<7/-1,„)2
и разделив на со2С2, подставим значения т, п и k. Тогда имеем: z2 = г2 + Г-L — 2awr (а — 3Ilw%b — ЗГ^Ь) ф- cofe/| F, (24-40)
где Л и ^2 — действующие токи в цепях 1 и 2.
Величина (а — З/^Ь — З/^Ь) имеет размерность индуктивности и может рассматриваться, как та часть (Lo) собственной индуктивности цепи 7, которая не зависит от тока /1# Величина -b/i есть та часть (Е,) собственной индуктивности цепи 1, которая зависит от тока 1±. В целом z можно рассматривать как эквивалентное полное сопротивление цепи 1:
z2 = r2 + (1/coC_coL)2j
где L Lo Lr.
Чем больший ток требуется получить, тем больше должно быть г, а следовательно, и произведение 1012. Минимальное значение для этого произведения, при котором колебания в цепи 1 прекращаются, находятся из условия = 0. Если обозначить собственную частоту 1/LC = cog, то т = (1 — со2/а>о) и представляет собой расстройку собственной частоты (м0) относительно задающей со, a k является коэффициентом затухания. Коэффициент п выражает связь между контурами 1 и 2, Чем больше п, тем соответственно больше Л-
Расчет в этом примере, так же как и в других случаях аналитической аппроксимации, нуждается в проверке соответствия принятой аппроксимации реальной характеристике магнитной системы. При подстановке 11т, 12т и 10 в формулы (24-30) значения Fa и F6 не должны выходить за пределы применимости формулы (24-26).
Рассмотренный расчет соответствует упрощенной схеме параметрона, в котором под влиянием тока в цепи 2 с частотой 2со в цепи ' возникает ток с частотой со, причем фаза этого тока в зависимости от начальных условий может быть либо гр, либо л ф- ср.
24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениями
Как уже указывалось, к нелинейным цепям неприменим прин-п наложения. Если в нелинейной цепи действуют два источника А- с. с различными частотами, то составляющие тока каждой
679
из частот зависят не только от э. д. с. своей частоты, но и от э д другой частоты с
Рассмотрим, как влияет постоянная э. д. с. на ток, создаваемь переменной э. д. с., если переменная составляющая тока ^Но'и меньше постоянной.
Для решения этой задачи воспользуемся методом линеаризацц нелинейной кривой на определенном ее участке и заменим реальною характеристику касательной в точке, определяемой постоянной составляющей тока или напряжения.
Предположим, что задана характеристика нелинейного активного безынерционного сопротивления (диод, германиевый вентиль и т. д) i = i {и) и известны постоянные составляющие напряжения на нем Uo и тока /0. Тогда, разлагая функцию t (и) в ряд
г । fdi X л । ! d2t \ &и2 , 1=/0 + j-) и 1 \dujo \du2/о 2 1
и обозначая Ди = и — Uo = иг, a Дг = i — Io = ilt получаем-fdi \ , f d2i\ ul ,
ь — К- «1 + hr?) n + • • •
x \dujo 1 \du2 Jo 2
Пренебрегая квадратом и более высокими стенами их, окончательно получаем:
= (24-41)
Таким образом, зависимость между малыми изменениями тока и напряжения может быть принята линейной, аналогичной закону Ома, в котором дифференциальная проводимость^ (Uo) или дифференциальное сопротивление гд == 1/§д представляет собой нелинейную функцию постоянной составляющей напряжения или тока.
Пример 24-3. Нелинейное сопротивление имеет характеристику, приближенно описываемую выражением i = аи2. Последовательно с этим сопротивлением включены источники постоянной э д с £0 и переменной э д с е = ~ Ет sin at, причем Ет Ео Найти амплитуду переменной составляющей тока и дифференциальное сопротивление
Решение Общий ток в цепи
i = a (Etl-'re)2 ^aEl-\-2aE0Em sm at=l0-\-Im sin at (величиной e2 пренебрегаем ввиду ее малости)
Амплитуда переменной составляющей тока
1т = 2аЕ0Ет (24 42)
зависит не только от Ет, но и от £0
Если нелинейную характеристику вблизи точки с координатами Ль 3 ' менить касательной, то амплитуда переменной составляющей тока Im MOiiie быть выражена через дифференциальное сопротивление
I
где согласно (24-42)
гд = (dw/di)0 = 1 /2а£0,
680
большое распространение получили электронные лампы с тремя большим числом электродов и транзисторы, представляющие 1'бей нелинейные четырехполюсники, параметры которых нелинейны и различны для постоянных и переменных составляющих токов
В таких нелинейных четырехполюсниках постоянные состав-тяюШ1 е токов и напряжений, определяющие рабочую точку на характеристике (см. § 22-2), оказывают существенное влияние ha коэффициенты четырехполюсника, связывающие переменные составляющие токов и напряжений на входе и выходе четырехполюсника
24-8. Принцип получения модулированных колебаний
Рис 24 13
В цепях с нелинейными безынерционными сопротивлениями при помощи двух источников переменных э д с. с различными частотами, одной низкой, а другой высокой, можно получить высокочастотные колебания, огибающая которых изменяется с низкой частотой, т е модулированные колебания (см. § 12-5)
Рассмотрим цепь, изображенную на рис 24-13 Пусть безынерционное нелинейное сопротивление имеет вольт-амперную характеристику, описываемую выражением t = аи2, напряжение и2 = U2m sin со Л а закон изменения напряжения щ во времени может быть произволен
На рис 24-13 построены Юки tu и io при двух различных постоянных значениях и1 (на чертеже и1а и
и1ь) Как видно из графика, чем больше ик, тем больше переменная составляющая тока Таким образом, изменяя значение напряжения ик, можно изменять амплитуду переменной слагающей тока Б Цепи
Пусть теперь
«1 = £4 + Ulm sin гДе Q со фИс 24-14)
Покажем, что в токе в этом случае содержится составляющая астоты со, амплитуда которой изменяется с частотой Q. Ток
i = au2=a 4- и2)2—a (Uo-ф Ulm sin £2/ ф- U2m sm (ot)2
681
Возведя в квадрат и преобразовав квадрат синуса, получим-
i = Л) + llm Sin £2/ — l^m cos 2П/ -j-
+ 2at/2m Po + Uim sin Q/) at — Ism cos co/, (24-43)
где
Io — aU% -f- a (Utm + Ulm)/2;
I Im — ^-^U(fj im', I2m — ClUlm/2', l3m = aU2tn/2.
Если в цепь включить фильтр, выделяющий только частоты, близкие к со, то можно получить переменный ток с частотой со,
амплитуда которого модулирована частотой О [4-е слагаемое в выражении (24-43)1.
Совершенно аналогично получаются модулированные колебания при помощи электронной лампы — триода с пере менной крутизной.
Если характеристика электронной лампы может быть выражена уравнением
1а = а(«а + (Шс)2,
где иа и ис — напряжения на аноде и сетке электронной лампы, то расчет анодного тока в цепи такой лампы полностью аналогичен произведенному выше расчету модулированных ко лебаний в цепи с нелинейным безынерционным
сопротивлением.
После выпрямления (детектирования) полученных модулированных колебаний (см. § 23-3) в спектре выпрямленного тока содержится составляющая с частотой Q, которая может быть выделена
фильтром низких частот.
Модуляция колебаний несущей частоты, излучение этих колебаний, прием колебаний, их детектирование и фильтрация лежат в основе радиотелеграфной и радиотелефонной связи.
682
24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями
В цепях с нелинейной индуктивностью при постоянном подмагничивании магнитопровода зависимость между магнитным потоком и током вследствие остаточных явлений носит сложный неоднозначный характер. При расчете таких цепей недостаточно знать только характеристики, снятые при постоянном или переменном токе.
Рассмотрим стальной тороид с двумя обмотками, первая из которых подключена к источнику постоянного тока /0, а вторая — к
источнику переменного тока 1\. Пусть числа витков обеих обмоток равны: w0 = w} =±= w.
При токе г1т равном нулю, зависимость магнитного потока от тока задается кривой первоначального намагничивания 00'А, представленной на рис. 24-15.
Каждой точке на характеристике соответствует определенное значение статической индуктивности
LCT = w®/t (24-44) и дифференциальной индуктивности
£,диф = wdO/dz. (24-45)
Если от магнитного потока перейти к индукции, а от тока к напряженности поля, то статической ностям соответствуют абсолютная проницаемость
_ В _ ЦоЦст уу —
Рис. 24-15.
и дифференциальной индуктив-статическая магнитная
= (24-46)
и абсолютная емость
дифференциальная магнитная проница-
_ dB __ I РоРдиф jyy £диф
(24-47)
где I — длина средней магнитной линии в тороиде;
5 — площадь его поперечного сечения.
Проницаемости рст и рди* пропорциональны тангенсам' углов «j и <х2, показанных на рис. 24-15.
Если теперь включить переменный ток с амплитудой 11т /0,
то при увеличении тока от 0 до +/1т магнитный поток первоначально будет изменяться по характеристике, снятой при посто
683
янном токе (О' — а на рис. 24-15). При уменьшении тока от до —/1т изменение магнитного потока будет происходить уже по верхней петли частного гистерезисного цикла, наклон которой меньше (кривая а — Ь). Следующая положительная полуволна тока приведет к некоторому увеличению магнитного потока (кри-вая Ъ — с) и т. д. В итоге установится некоторый режим, при котором постоянная составляющая магнитного потока увеличится, а наклон характеристики уменьшится (е — f на рис. 24-15).
Переменный ток в намагничивающей обмотке вызывает как бы «встряску» магнитных диполей, при которой большее их число ориентируется соответственно постоянному магнитному полю. Поэтому при включении переменного тока точка О' начальной кривой намагничивания заменяется точкой О". Таким образом, в дейст-„ вительности зависимость постоянной со-
p. ставляющей магнитного потока от пе-
/ \ Рст ременной составляющей сложнее, чем
/ в примерах, рассмотренных выше.
\. Приращение магнитного поля в точ-
.__ ке О" под влиянием переменного тока ix
-------------------------------- н меньше, чем под влиянием постоянного °_______________тока в О' (на начальной кривой намаг-
Рис. 24-16. ничивания), т. е.
< tfO/d/o-
Тангенс угла наклона а3 характеристики, соответствующей установившемуся режиму изменения тока tn выражает так называемую обратимую проницаемость
= (24-48)
которая имеет большое значение при расчете магнитных цепей с малыми значениями переменных составляющих магнитного потока, например магнитных цепей телефонов и громкоговорителей.
Зависимости относительных статической и обратимой магнитных проницаемостей от постоянной напряженности поля представлены на рис. 24-16. Как видно из графика, рст с ростом Н вначале увеличивается, а затем по мере приближения к насыщению — уменьшается, а робр с ростом Н все время убывает.
В тех случаях, когда изменение переменного тока во второй обмотке приводит к незначительному изменению магнитного потока, можно считать, что при синусоидальном напряжении их ток t также синусоидален. В этом случае
Wi=L06p^’i/^ 4-^'1 (24-49
и, следовательно, в комплексной форме
I :
1 Г + /(oi-обр
(24-50
684
Индуктивность Lo6p представляет собой функцию цобр. Например, для тороида
(24-51)
где W1 — число витков обмотки, по которой проходит ТОК lj.
Изменяя постоянный ток в обмотке ю0, можно изменять значение Lo6p, а следовательно, и переменного тока в обмотке
При изменении переменного тока в больших пределах уже нельзя говорить о синусоидальности тока и магнитного потока. Однако и в этом случае, изменяя постоянный ток, можно изменять переменный ток — управлять переменным током.
24-10. Магнитные усилители мощности
В ряде практических задач бывает необходимо при помощи статических устройств, затрачивая небольшую мощность, управлять большими мощностями Такне устройства называются усилителями мощности Принцип действия усилителей мощности может основываться как на линейных, так и на нелинейных явлениях
К нелинейным усилителям относится так называемый магнитный усилитель мощности Схема одного из простейших магнитных усилителен мощности представлена на рис 24-17. Управляющей цепью магнитного усилителя служат две последовательно
Рис 24-17.
Рис 24-18
Рабочая цепь усилителя состоит из двух последовательно соединенных обмоток переменного тока wlt намотанных на тех же магнитопроводах Полярность вклю чення обмоток и такая же, как и в рассмотренном ранее удвоителе частоты
Если ток в управляющей цепи /0 = 0, то зависимость между приращениями потокосцеплений ^Va, ^Vg и A'F, = ДЧ^ -j- A4f^ от тока задается обычнон характеристикой магнитной системы [на рис 24-18 кривая A4rj (ц) при /„ = 0]
Наличие тока в управляющей цепи приводит к изменению кривой А'У, (ц) Так же как и при построении кривой ДЧ^ (ц) на рис 24 12, в рассматриваемом случае A’F, (i,) представляет собой сумму двух кривых &'1га (ц) и A4r(j (iJ, Каждая из которых является характеристикой магнитной системы с началом координат, перенесенным в точку с координатой + для первой кривой и в точку с координатой — /оюо для второй (см построения на рис. 24-9, 24 Н, 21-12).
С85
Таким образом, в зависимости от /0 характеристика A’F, выразится одной из кривых семейства, изображенного на рис 24-18. Чем больше ток памагиичи-вания, тем положе идет характеристика Поэтому с увеличением тока /0 наклон характеристики при = 0 меньше и кривая идет ниже.
Если к обмоткам wt подключить источник напряжения и1г изменяющегося по синусоидальному закону, то, пренебрегая индуктивностью рассеяния, потерями в стали и сопротивлением обмоток wlt можно считать, что и потокосцепление А'р изменяется по синусоидальному закону [кривая A'F, (t) на рис 24-18] В зави симости от тока /0 данной кривой A’FX (/) соответствуют различные кривые it (^ максимумы которых тем больше, чем больше 10. Как видно из построений, ток г, (/) несинусоидален
Если, наоборот, через обмотки пропустить синусоидальный ток ilt то A’F, и = d'Vykll несинусоидальны и максимум напряжения н1 тем больше, чем меньше ток /0.
На практике и ток ilt и напряжение иА песинусоидальны, так как последо-
вательно с источником напряжения и и обмотками ги, в рабочую цепь магнитного
усилителя включают сопротивление нагрузки г. Точный расчет цепи в этом случае представляет значительные трудности Вполне достаточная для практики точ-
ность может быть получена, если, так же как и ранее, обмотку tWj рассматривать
Рис. 24-19.
как условно-нелинейную индуктивность Еэ, значение которой зависит не только от пере менного, но и от постоянного тока.
На рис 24-19 изображены кривые Ux (/*/-) для различных значений /0, где = /jwL, Эти кривые имеют такой же характер, как и AV, (ij) По оси абсцисс отложен не ток /1( а произведение тока 4 на сопротивление па грузки г. При таком построении облегчается определение тока 4 для различных значе ний тока /0 при заданном напряжении источника питания U.
Действительно, считая, что напряже ние L\ сдвинуто по фазе по отношению к току на угол 90°, можно написать:
t/f+(/ir)s=£A
(24-52)
Если известны U и 10, то, выбирая соответствующую кривую (4 (44 и проводя окружность радиуса U с центром в начале координат, найдем U1 и Цг как координаты точки пересечения окружности с кривой (44 (на рис 24-19 такое построение выполнено для /0 = 0)
Таким образом, для каждого значения /0 можно найти соответствующие ток 4 и мощность Р = Zfr, выделяемую в рабочей цепи. Чем больше /0, тем выше значение Р При этом мощность, затрачиваемая в цепи постоянного тока, в десятки и сотни раз меньше мощности Р.
Магнитные усилители применяются в самых различных областях техники, например для плавного автоматического управления двигателями и другими преобразователями энергии, для плавного регулирования освещения
Магнитные усилители являются основным звеном так называемых измерительных трансформаторов постоянного тока Принцип действия этих устройств заключается в следующем Постоянное подмагничивание магнитных систем а и б (рис 24-17) осуществляется шиной постоянного тока, проходящей через обе магнитные системы Соответствующим подбором характеристики стали достигаются условия, при которых ток 4 мало зависит от питающего напряжения U и в достаточной мере точно пропорционален току /0 Коэффициент пропорциональности между токами 4 и /0, так же как и в обычных трансформаторах, зависит от отношения чисел витков wtl/wl
На аналогичном принципе могут быть осуществлены усилители с нелинейными емкостями — диэлектрические усилители мощности.
RRR
Глава двадцать пятая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
25-1. Общая характеристика переходных процессов в нелинейных цепях
Переходные процессы в нелинейных цепях существенно отличаются от переходных процессов в линейных цепях. Нелинейность характеристики какого-либо из элементов электрической цепи может привести как к чисто количественному изменению переходного процесса, так и к качественно новым явлениям.
В первом случае нелинейность характеристики может увеличить скорость процесса в одном из промежутков времени и уменьшить скорость в другом промежутке, при этом может возрасти максимальное значение тока в переходном процессе, однако качественно процесс остается без существенных изменений. Во втором случае в результате нелинейности характеристики возникают новые явления, принципиально недостижимые в линейных цепях.
Если в линейных цепях включение источника постоянной или синусоидальной э. д. с. (или тока) сопровождается некоторым затухающим переходным процессом и переходный процесс переходит в принужденный режим, частота которого равна частоте напряжения источника, то в нелинейных цепях переходный процесс может привести к возникновению колебаний с частотой, отличной от частоты напряжения источника. Такие колебания носят название автоколебании.
Примером автоколебаний могут служить рассмотренные в § 24-6 колебания с частотой со в цепи параметрона, питаемого от источника с частотой 2со. Автоколебания в цепях, питаемых от источника постоянного напряжения, рассматриваются в гл. 26.
Нелинейные цепи с неоднозначными нелинейностями могут быть применимы для запоминания импульсов, поступающих в цепь. В этом случае переходный процесс сопровождается переходом цепи из одного устойчивого состояния в другое.
Если в линейных цепях напряжения и токи переходного процесса обычно можно представить состоящими из двух составляющих: принужденной и свободной, то в нелинейных цепях принцип наложения неприменим и нельзя раскладывать величины на свободные и принужденные составляющие.
В зависимости от вида э. д. с., действующих в цепи, расчеты переходных процессов в нелинейной цепи различны по сложности. Расчет цепей с постоянными э. д. с. значительно проще, чем цепей с переменными э. д. с.
Для переходных процессов в нелинейных цепях нельзя указать общий аналитический метод, позволяющий рассчитать процесс
687
в цепи любой сложности. В зависимости от вида цепи и действующ^ в ней э. д. с. для расчета переходных процессов применяются раз. личные, часто очень приближенные методы. Задача сводится к реше. нию нелинейных дифференциальных уравнений, для которых в математике существует множество различных методов решения. Общая характеристика этих методов была дана в гл. 22. Рассмотрим теперь применение различных методов расчета переходных про-цессов.
25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение
При включении катушки с замкнутым стальным магнитопроводом на постоянное напряжение переходный процесс качественно происходит так же, как и при включении линейной цепи г, L. Однако количественно он несколько иной и уже не может быть точно описан разностью постоянной величины и экспоненты (см. § 13-4).
Если пренебречь гистерезисом и вихревыми токами, возникающими в стали при изменении магнитного потока, то анализ
Рис. 25-1.
процессов при включении катушки со стальным магнитопроводом на постоянное напряжение можно свести к расчету схемы, изображенной на рис. 25-1, где обозначено: 'F — потокосцепление катушки; г — сопротивление катушки; U — напряжение источника.
Зависимость 'F (/) задана кривой, изображенной на рис. 25-2 сплошной линией, которая для любой катушки со стальным магнитопроводом может быть построена, если известна кривая намагничивания стали.
Для выражения нелинейной зависимости Т (/) в цепях со сталью применяется множество различных формул. Некоторые из этих формул уже применялись в гл. 23 и 24. Приведем еще примеры 688
таких формул с указанием пределов допустимых изменений одной из переменных величин:
I—ф- Ь±¥2 при 0<Т<;оо;
i — a^ + при —оо<Т<;оо;
i = а3 sh bjV при —оо<;Т<;оо;
Т = aj. 4- Ь$12+Cii3 при 0<i</f, T=cz6i 4~ bai3 -j-Cgi6 при —Ij. <C i 4* 1 ij
T=ae arctg (b6i 4- cei3) при — сю < i < oo;
(25-1)
здесь /t — некоторое значение, задающее верхний предел изменения тока.
Если в течение рассматриваемого промежутка времени ток изменяет направление, то для выражения кривых намагничивания следует пользоваться нечетными функциями (например, вторая, третья и пятая формулы). Постоянные коэффициенты ог, Ь1 и сг определяются из условия наибольшего соответствия формулы заданному участку характеристики. Если переходный процесс происходит на некоторой ветви частного цикла перемагничивания, то в аналитическое выражение необходимо ввести постоянную составляющую тока или магнитного потока.
Запишем уравнение по второму закону Кирхгофа для схемы по рис. 25-1:
dV/dt-{-ri—’U. (25-2)
В установившемся режиме dW/di = 0 (при t — оо) и, следовательно, i = Iw = Ulr, а Т = Too и определяется в соответствии с /оо по кривой намагничивания (точка на рис. 25-2).
Рассмотрим решение этой задачи при помощи различных методов на ряде примеров.
Метод условной линеаризации. Заменив нелинейную характеристику T (i) прямой линией, проходящей через точку Лоо и выражаемой уравнением Т — LBi, перепишем уравнение (25-2) следующим образом:
f 4-Д-Ч'=-(/. (25-3)
где L3 — некоторая статическая индуктивность, соответствующая точке Лоо.
23 Основы теории цепей
689
Уравнение (25-3) решаем так же, как в линейной задаче (см. § 13-4). Для потокосцепления получаем:
где т = LB/r.
Т=Чгю(1-г'/1),
(25-4)
График зависимости 'Г (/) показан на рис. 25-3. Для каждого значения W по кривой T (i) (рис. 25-2) теперь определяем значение i.
Полученная зависимость i (t) изображена на рис. 25-3.
Как видно из графика, кривая i (0 отличается от закона /ео (1 —В первые моменты времени кривая идет более полого, а приближаясь к установившемуся значению, ток нарастает быстрее, чем в линейной цепи. Отличие полученной кривой от экспоненты можно уяс-
нить, рассматривая зависимость дифференциальной индуктивности L от тока i (рис. 25-4,6). Так как при малых токах дифференциальная индуктивность L = dW /di больше, чем Д, а при больших
токах меньше, то процесс нарастания тока вначале при малых токах
происходит медленнее, а при больших токах, наоборот, скорее, чем при постоянном L = La.
В данном примере зависимость ’К (0 получена в результате весьма приближенного решения задачи, однако полученная при этом кривая i (/) носит такой же характер, как и в решениях, выполненных более строгими методами.
Метод аналитической аппроксимации нелинейной характеристики. Наиболее просто задача решается, если для i (Т) принять первую из формул (25-1), в которой положить аг = 0. Тогда, считая, что ана-
литическое выражение соответствует заданной характеристике в точке (рис. 25-2), получаем:
(25-5) откуда
b^I^^r/LlU. (25-6)
График кривой i = fejT2, т. е. Т = УУ/бц, показан на рис. 25-2 пунктиром.
690
Подставив i в уравнение (25-2), получим:
ИЧГ г2 dt L-JJ
Решая уравнение относительно времени и интегрируя, находим, что
. = Ь Arth—.
и .) г L5U
После преобразования получим:
4^=-*-tlJ- (25-7)
и соответственно
t=^th2l, (25-8)
где
х = Ьэ/г.
Выражения (25-7) и (25-8) приближенно описывают переходный процесс включения катушки со стальным магнитопроводом. Точность решения задачи тем выше, чем ближе аналитическое выражение соответствует нелинейной характеристике.
Применение иных из формул (25-1) позволяет получить более точное аналитическое выражение нелинейной характеристики, однако решение задачи значительно усложняется.
Метод кусочно-линейной аппроксимации нелинейной характеристики. Если характеристику Ф (/) заменить некоторой ломаной линией 0—1—2—3 (рис. 25-4,о), то решение задачи представляется в виде трех различных выражений в соответствии с тремя участками линеаризации.
Для первого' участка 0—1 зависимость между током и потокосцеплением имеет вид:
'F -= Lxi при О < i <. Ii,
для второго участка 1—2
'F = + L2i при Д < i < /2
и для третьего участка 2—3
Т = + Lsi при /2 < i < /ет.
Потокосцепления и Ч;2 находим графически (рис. 25-4,а). Дифференциальную индуктивность L определяем как величину, пропорциональную тангенсу угла наклона ломаной на соответствующем участке: £г : L2 Ls = tg а, : tg a2 : tg cc3. Изменение L при переходе от одного участка ломаной к другому показано на рис. 25-4,6.
Разбивая все время переходного процесса на три промежутка в соответствии с участками ломаной, для различных промежутков
23*
691
времени записываем уравнение (25-2) в виде трех дифференциальных уравнений:
Lydildt-^-ri — U при 0<1<Д и 0</<4;
L2diidtA~ri = U при Д<1</2 и Д</</2; (25-9)
Lsdi!dt-{-ri — lJ при 12<Л<.1т и t2<.t<.<x>.
Обозначив ту = LJr\ т2 = L2/r и т3 = L3/r, запишем решение
этих уравнений для каждого из участков:
t — + при 0<Zt<Zli и
i — + при Д < i < /2 иД<^</2; (25-10)
г==/оо + ^зе~(/~<2>/Тз При /2<1</со и ^2</<оо.
Из условия невозможности изменения тока скачком в точках О, 1 и 2 (припасовка) находим
Af = 1т', ^2==(/l /co)j Дз=(/г /оо).
Значения tlt t2 определяем из условий r(M = /i = /oo(l-r-^);
I (t2) = /2 = /оо + (Д - /оо) ег - й)/ч
Решая первое из уравнений относительно tlf а второе относительно t2, получаем:
/1=тг1пг4г; I
/“_/ (25-П)
/2 = Т21П7^—J- + G.
7 со 7 2 /
На рис. 25-5 построена зависимость i (t) для всех трех участков
характеристики.
Полученная зависимость, так же как и рассмотренное ранее решение, показывает, что нелинейность характеристики стали
Рис 25-5.
замедляет процесс нарастания тока в начале и ускоряет в конце.
Приведенный расчет основан на применении метода припасовывания, предложенного Н. Д. Папалекси в 1912 г.
Метод последовательных интервалов. Разобьем промежуток времени процесса на ряд малых равных интервалов Д/ и для каждого интервала на основании дифференциального уравнения (25-2) запишем равенство
№1;/Ы ъ (dW/dt), = U~ rik ср, (25-12)
где k — номер интервала; Дср — средний ток за время интервала времени с номером k\ №¥к — приращение потокосцепления за время этого интервала.
692
Тогда
ATfc = Т* - (U - rik cp) M. (25-13)
Зная iAcp, Д/ и ЧД_х, можно найти ДТ* и 'Fft, а затем и ife+xcp по характеристике 'F (i). Переходя от точки k к точке k + 1, можно построить весь переходный процесс.
Начнем с f = О, То = 0, i0 = 0 и fe = 0. Для ДЧ^ по формуле (25-13), полагая ilcp « i0 = 0, получаем:
Д'Тх = = ПДА (25-14)
По графику (i) найдем и, подставив его в формулу (25-13) вместо i2cp для k = 1, получим:
ДТ2 « (U — nJ ДА (25-15)
По графику Т (i) для Т2 = Т'х + ДЧТ2 определим t2.
Так, последовательными интервалами, переходя от ik к ЛТДх, а затем к и ikil, находим i и Т для любого момента времени.
Решение задачи сведем в табл. 25-1.
Таблица 25-1
k t rik U-rik *Й-г1
0 0 0 V VM Д^х й
1 м П1 U — п’х (U—rij) M Ч'х+ДЧ',
2 2Д/ U— riz (V — rin) M is
k kM rik U ~rik (U — rik) M ^+д^+1 ik+1
Для зависимости У (г), изображенной на рис. 25-6, графики 'F (0 и i (/) построены на рис. 25-7. Чем меньше интервалы вре-
мени Д/, тем точнее задачи.
решение
ЗР-
Рис. 25-6.
Приведенный пример решения задачи основан на применении рассматриваемого в курсе математики приближенного решения дифференциальных уравнений, предложенного Эйлером.
693
Недостатком данного метода является зависимость дальнейшего
решения от погрешности при вычислении всех предыдущих значений искомой величины и замены ifecp величиной ik^. Так, ошибка в вычислении ЛЧ\ сказывается при вычислении всех АЧ;Л для k > 1.
Метод Эйлера является наиболее простым и наименее точным в группе методов численного интегрирования дифференциальных уравнений, известных как методы Рунге—Кутта. В современных цифровых вычислительных машинах
имеются стандартные программы, основанные на методах Рунге—Кутта, при помощи которых задача может быть решена быстро и точно.
Метод графического интегрирования. Представим уравнение (25-2) в следующем виде:
(25-16)
U—п ' '
Рис. 25-8.
По заданной кривой Чт (i) (рис. 25-2) построим зависимость 4f - f и проинтегрируем графически эту зависимость по Ч;.
На рис. 25-8 по оси абсцисс отложена величина ll(U — ri), а по оси ординат — потокосцепление. Для того чтобы найти время, в течение которого потокосцепление изменится от 0 до Чг, нужно вычислить
'Г
(* rlV
/== \ (25-17)
\ U — ri v '
или на графике определить площадь Soat>'c- Величина этой площади при учете масштабов Чг и 1/и дает время.
Так, определяя t для различных значений Ч;, строим / (4f) или Ч; (/), а зная Ч; (/), по кривой Ч; (i) легко находим и i (t).
Исследование переходных процессов в нелинейных цепях методом графического интегрирования было развито в работах Рюденберга.
Если сопоставить все пять примеров расчета, то надо заметить, что для рассматриваемой задачи наилучшие результаты получаются в двух последних случаях. Метод последовательных интервалов может дать более точное решение, а при помощи графического интегрирования удается при достаточной точности решения получить наглядное представление о влиянии параметров цепи на характер переходного процесса.
25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение
При включении катушки со стальным магнитопроводом на синусоидальное напряжение решение задачи сопряжено со значительно большими трудностями.
Рассмотрим дифференциальное уравнение цепи
№/dt-\-ri = Um sin (coz'4- а). (25-18)
Наличие в правой части уравнения гармонической функции времени значительно затрудняет применение некоторых из рассмотренных методов решения задачи. Так, аналитическое выражение кривой намагничивания приводит к нелинейному дифференциальному уравнению с правой частью, представляющей гармоническую функцию времени, которое не имеет достаточно простого решения. Замена характеристики ломаной приводит к необходимости на протяжении периода изменения напряжения несколько раз (более пяти) сопрягать («припасовывать») решения, получаемые для различных участков ломаной. Так как переходный процесс обычно продолжается несколько периодов, то такое решение сопряжено с очень большими трудностями. Наличие гармонической функции времени затрудняет разделение переменных и решение задачи методом графического интегрирования.
Таким образом, пригодными для решения задачи можно считать только два из рассмотренных методов: метод условной линеаризации и метод последовательных интервалов.
Пример 25-1. Решение методом условной линеаризации В уравнении (25-18) падение напряжения ri обычно значительно меньше, чем (П!кН. В установившемся режиме (см гл. 23) при определении зависимости 'И (Z) обычно пренебрегают падением напряжения ri. В переходном режиме этой величиной пренебречь нельзя, однако ее можно рассматривать как малый параметр и согласно методу условий линеаризации считать, что
п = гЧЩ, (25-19)
где Ьэ = ^тИт —отношение максимальных значений потокосцепления и тока в установившемся режиме.
Тогда уравнение (25-18) приближенно запишется в следующем виде:
d'¥/dt-\-'¥/T — U„l sin (coZ-j-a), (25-20)
где т = L3/r.
Так как в уравнении (25-20) коэффициент 1 /т постоянен, то Y (Z) определим совершенно так же, как и при включении линейной индуктивности на синусоидальное напряжение (см. § 13-5).
Принимая, что остаточного намагничивания нет, т. е. Y (0) = ¥0 = 0, получаем:
Y (Z) = 4rm sin (coZ-j-a — <р)—Ч'т sin (а — ф) e”Z/T, (25-21)
i-где Чт = —; <р = arctg .
' |/ г2+ (ш/-э)2 V г
Обычно aL3 > г и л/2. В этом случае = ит1ы.
Наибольшее значение магнитного потока получается при включении катушки момент времени, соответствующий а = 0. Тогда
(Z) = - cos coZ+='Fnp+'FCB. (25-22)
На рис. 25-9 построен график У (Z), а на рис. 25-10 по кривой намагничивания стали Чг (Z) построена соответствующая зависимосгь i (t). Если при включении линейной индуктивности наибольшее значение тока не может превысить удвоенную амплитуду его принужденного (установившегося) значения, то, как
695
видно из графика, при включении катушки со стальным магнитопроводом наибольшее значение тока iMaKC может во много раз превышать амплитуду его установившегося значения 1т.
Пример 25-2. Решение методом последовательных интервалов. Интегрируя уравнение (25-18) по времени от 0 до t, запишем потокосцепление
t
4r(0=Y0--^!-cos(co<-l-a)+-^-cosa-r idt. (25-23) b
Заменяя интеграл суммой п произведений тока в начале интервала времени на длительность этого интервала Дг“, получаем:
п
¥ (п А/) «= ’Fo—~^"cos (яш д^+а)+~~ cos а — г (23-24)
I
Таким образом, потокосцепление катушки в любой момент времени п Л.1 можно представить в виде суммы четырех величин. Первые три из этих величин определяем непосредственно для любого момента времени, а четвертую находим методом последовательных интервалов по заданной кривой Y (i).
Решение задачи методом последовательных интервалов может дать значительно большую точность, чем при условной линеаризации характеристики. Однако, несмотря на элементарность вычислений, этот метод сопряжен с большой счетной работой.
Применение цифровых вычислительных машин и стандартных программ интегрирования обыкновенных дифференциальных уравнений дает возможность быстро получить решение методом последовательных интегралов с необходимой степенью точности.
Переходный процесс при решении задачи обоими методами был найден без учета гистерезиса. На практике даже при включении катушки с магнитопроводом, выполненным из мягкой стали, приходится считаться с неоднозначностью характеристики Чт (i).
Если остаточный поток в стали имеет обратное направление в сравнении с установившимся значением потока в момент включения, то влияние остаточной намагниченности может привести к еще большему нарастанию тока при включении.
На рис. 25-11 схематически построена зависимость Чт (i) для переходного процесса при включении катушки со стальным магнитопроводом на переменное напряжение. В начальный момент Т (0) = Ч\, (точка 1 на характеристике). С нарастанием тока в течение первой половины периода изменение происходит по участку
характеристики 1—2. Из выражения (25-23), пренебрегая последним членом, при а ~ 0 получаем:
Ш W I 9 nr I 9ЦГ
макс 1 ОТ ~ /тт.
(25-25)
В действительности из-за потерь значение Ч\,акс несколько меньше.
Дальнейший ход зависимости между током и потоком характеризуется графиком 2—3—4— 5—6 и т. д. вплоть до установившегося режима, соответствующего гистерезисной петле A—B—C—D—E—F—A. Так
Рис. 25-11.
как Чгмакс возрастает с увеличением %, то, следовательно, и бросок тока тем больше, чем больше Чг0.
Со значительным возрастанием тока в момент включения (пусковой ток) необходимо считаться при включении ненагру-женных трансформаторов.
25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями
Рассмотрим переходные процессы при импульсном воздействии и (/) на катушку со стальным магнитопроводом, выполненным из жесткой стали с прямоугольной характеристикой намагничивания. Малый постоянный наклон характеристики стали в области насыщения или прямых возврата можно описать некоторой линейной индуктивностью L, объединенной с индуктивностью рассеяния и включенной последовательно с неоднозначным нелинейным индуктивным элементом с прямоугольной характеристикой У (i).
Эквивалентная схема цепи показана на рис. 25-12,а. Здесь г и L — линейные параметры цепи, а V (i) — нелинейная характеристика, изображенная на рис. 25-12, б. Из характеристики видно, что в зависимости от предшествующего режима, задаваемого сигналом и(1), потокосцепление при —ik < i < ik может иметь любое значение, лежащее между —Ч)'п и Ч'д, и ферромагнитный сердечник может запоминать некоторую информацию, которую несет сигнал и (t)-
Пусть напряжение на входе цепи и (t) имеет форму прямоугольного импульса высотой Um и продолжительностью т. Исследование переходного процесса в магнитопроводе, характеристика которого (рис. 25-12,6) имеет прямоугольную форму, проведем методом
697
кусочно-линейной аппроксимации, описывая характеристику сер дечника уравнениями
— % при —cv<t<ik\ i^+tk при — Vo<Чг<То п d4r/d/>0;
V= + Vo при —ik<zt<i<x>-, i~ — ik при — Vo<V<Vo и d^/dtCO-, V = const при — ik < i <Z ik и — Vo < V < Vo.
Переходный процесс при этом рассчитывается путем припасо-вывания решений дифференциальных уравнений для каждого из линейных участков характеристики.
L di/dt -\-rt — Um при OCr-CU*. V =—Vo и 0<^/b для участка 1—b характеристики;
d^ldt-\-ri = Um при i—iki — V0^V^VMaKC и

для участка b—2 характеристики;
L di/dt + ri = 0 при OsCisS ifc, V=4fMaI£c и i (т) = ik и t т для участка 2—3 характеристики.
Решение линейного дифференциального уравнения для каждого из трех участков получим в следующем виде:
i=Im (1 — е~Чт) и V = —То при Osg/ 'CZ1!, (25-26)
где Im=Umlr-, T=L/r\ tr = T ]n-r- m
‘m — Ik
для участка 1—b\
i = — 1Fo+(t/m-nft) (Z-Zx) при /х--С/-<т (25-27)
для участка b — 2;
(/—Т)
i^ike т ; T=YHaKC = -T0 + (t/m-nfc)(T-Z1) (25-28) при / > т для участка 2—3.
Полученное решение соответствует линии 1—b—3—2 характеристики V (i) на рис. 25-12, б для случая, когда Ч;мпкс < Vo, Zx < т и 7,„ > ik. Графики и (Z), V (Z) и i (Z) для этого случая показаны на рис. 25-12, в—д.
Если в полученном решении ’Рмакс > Чг0, то это соответствует выходу на насыщение и линии 1—b—с—d—4 на характеристике. В этом случае нужно рассматривать четыре участка характеристики, для которых имеем следующие уравнения:
Ldi/dt + ri = U,n при O^t^ti и V = — Vo
для участка 1—Ь.
d4!/dt + rt = Um при i = Zfc, —Vo iC V iC Vo и Z t / -С
для участка b—с;
Ldi/dt-\-ri = Um при t2^t^x и V = To
для участка с—d\
L di/dt 4-ri = 0 при tSsO, t>-x и V = Vo для участка d—4.
Решения для этого случая имеют вид:
i=7m(l-e-vr) и V = — Vo при 0 -sS / «S(25-29) для участка 1—Ь\
i-=ik, V = — T04-(t/m — rtk) (t — Zx) при (25-30)
где Z2 = Zx + -г-.—s— дл я участка b—c;
i = ^ + (/m-i\)(l-e-^-Wr) и V = V0 при Z2^Z^t (25-31)
enn
для участка с—d;
i= Ixe-<t~-r>/T и 'F = 4f0 при t^-x, (25-32)
где Л =- ift + (I,„ — ik) (1 — для участка d—4.
Графики и (/), Т (() и i (О для этого случая показаны на рис. 25-12, е—з.
Два случая намагничивания магнитопровода с прямоугольной петлей гистерезиса рассмотрены весьма упрощенно. Здесь не учитывались вязкости ферромагнетика, распределенность обмотки, отличие характеристики от прямоугольной. Однако даже такое упрощенное рассмотрение дает достаточное представление о процессах и позволяет сделать выводы о возможности применения магнитопроводов в качестве запоминающих устройств- вычислительной техники.
25-5. Понятие о простейших запоминающих устройствах
Одним из наиболее распространенных запоминающих устройств автоматики и вычислительной техники являются ферромагнитные тороиды, работающие при импульсных воздействиях. Они применяются для запоминания как аналоговых, так и цифровых значений. В первом случае информация о запоминаемой величине определяется значением Ч'макс, до которого намагничен магнитопровод, а во втором записанная цифра (в двоичной системе) задается сочетанием различных магнитопроводов со значениями Т = —Ч;о или Т = + 4%. Обычно V = — % соответствует записи нуля, а V -= + Tq — единицы. Рассмотренные в §25-4 два случая импульсного воздействия соответствуют этим двум случаям записи в устройствах аналоговой и цифровой памяти.
Так, путем воздействия на магнитопровод с прямоугольной магнитной характеристикой производится магнитная запись, которая может храниться сколь угодно долго.
Если и rik Um, то из уравнения (25-28) можно получить, что
AT=¥0+¥HaKc^t/mr, (25-33)
т. е. изменение Т равно площади прямоугольного импульса. Таким образом, в устройствах аналоговой памяти в магнитопроводе можно записать значение площади, ограниченной кривой импульса напряжения, поступающего в цепь.
Для того чтобы считывать произведенную запись, магнитопровод имеет вторую обмотку. При подаче отрицательного напряжения в первую обмотку, если магнитопровод был намагничен до Ч‘макс, во второй обмотке появляется импульс напряжения и2, пропорциональный dW/dt. Рассуждая так же, как и в примерах, рассмотренных в § 25-4, убедимся, что амплитуда этого импульса задается напряжением в первой обмотке, а его длительность пропорциональна значению ДЧ7, записанному в магнитопроводе.
Таким образом, в магнитопроводе можно записать AV и прочесть, подавая на обмотку в нужный момент времени отрицательное напряжение. При этом в магнитопроводе аналоговой памяти перемагничивание происходит (рис. 25-12, б) по линии 3—5—f—а—1, а в магнитопроводе цифровой памяти по линии 4—e—f—а—1 или 1—а—1, в зависимости от того, что записано в сердечнике: 1 или 0.
На описанном принципе основываются устройства магнитной памяти, применяемые в различных измерительных, автоматических и вычислитепьных системах.
25-6. Изображение переходных процессов на фазовой плоскости
В предыдущих параграфах определялись переходные процессы в нелинейных цепях, описываемых дифференциальным уравнением первого порядка.
С повышением порядка уравнения расчет существенно усложняется. Требуется применение новых методов расчета. Одним из таких методов является изображение переходных процессов в пространстве состояний или в фазовом пространстве.
Переходные процессы можно рассматривать в различных системах координат. До сих пор переходные процессы рассматривались в координатах i и /, Т и t, q и t или и и t. По оси абсцисс откладывалось время, а по оси ординат — исследуемая величина.
Однако те же явления исследуются и в другой системе координат.
Для переходного процесса, описываемого нелинейным дифференциальным уравнением порядка п или п нелинейными дифференциальными уравнениями первого порядка, всегда можно выбрать п таких переменных, называемых координатами состояния, что система уравнений принимает вид:
Л = Л(-Ч, х2, ..., xit ..., хп, ult и2, ..., и„ ..., tzm);
X2 = f2(Xi, Х2, ..., Л’,, ..., Хп, Hi, И2, •••, Hi, •••> ^m):
...........................................................(25-34)
x,---f^Xj, х2, ..., х,, ..., х„, ill, и2, ..., ut, ..., um);
Xn = fn(Xi, x2, ..., x„ ..., xn, Ui, u2, ..., ti„ ..., tim).
Здесь Xt — координата состояния; x, = xf —ее производная по времени; ut — внешнее воздействие на электрическую цепь; Д- — некоторая нелинейная функция, в отличие от линейных цепей, где ft — линейная алгебраическая функция.
Решение уравнений (25-34) для этого случая рассматривалось i § 14-8.
Если электрическая цепь не подвержена каким-либо внешним временным воздействиям, то tq — 0. Для этого случая пространство остояний обычно называется фазовым пространством.
7П1
Наиболее широкое распространение изображения переходных процессов в фазовом пространстве полечило для систем второго порядка. В этом случае переходный процесс изображается на плоскости координат лу и л'2, называемой фазовой плоскостью, некоторой кривой, которая лежит в области, ограниченной по обеим осям координат, а уравнения (25-34) приобретают вид;
Л=Л(*1. *2); x2=f2(Xi, х2). • (25-35)
Исследование переходных процессов в электрических цепях на фазовой плоскости впервые было проведено академиками Л. И. Мандельштамом и Н. Д. Папалекси и получило дальнейшее развитие в работах А. А. Андронова, С. Э. Хайкина, А. А. Витта и их учеников.
Изображение процессов на фазовой плоскости может дать представление о характере процесса без решения дифференциального уравнения в конечном виде.
При выборе фазовых координат хт и х2 для описания переходного процесса возможны различные варианты. Обычно отдается предпочтение такому выбору координат, при котором хг = х2. В этом случае обычно обозначают хг = х; = х2 = у и записывают уравнения (25-35) в виде
dxldt=--y, dy/dt=f (х, у). (25-36)
Каждому состоянию цепи соответствует точка на фазовой плоскости, которую называют изображающей или представляющей точкой. Всякое изменение состояния цепи на фазовой плоскости изображается некоторой кривой, которую называют фазовой траекторией.
Если процесс описывается уравнениями (25-36), то в верхней полуплоскости у = dxldt > 0 и представляющая точка может перемещаться только направо — в направлении возрастающих значений х. Для нижней полуплоскости, наоборот, у < 0 и представляющая точка может перемещаться только влево. Таким образом, движение представляющей точки происходит только по направлению движения часовой стрелки.
Если процесс описывается дифференциальным уравнением первого порядка, то все фазовые траектории лежат на одной кривой и представляющая точка может перемещаться только по этой кривой. Если процесс описывается дифференциальным уравнением второго порядка, то в зависимости от начальных условий представляющая точка может оказаться в любом месте фазовой плоскости.
Рассмотрим фазовые траектории простейших процессов в линейных и нелинейных цепях.
Пусть цепь г, L с током iQ переключается без разрыва тока к источнику постоянной э. д. с. с напряжения U (рис. 25-13, а). Тогда переходный процесс описывается дифференциальным уравнением
L di/dt + ri = U
702
пли при обозначении i через х, a di/dt через у уравнением
[J — гх
У—Е~- (25-37)
На рис. 25-13, б изображена фазовая траектория переходного процесса в виде прямой, проходящей через точки (О, U/L) и (U/r, 0). Для верхней полуплоскости у = dx/dt > 0 и, следовательно, представляющая точка перемещается в направлении возрастающих значений х. Для нижней полуплоскости у < 0 и представляющая точка перемещается в направлении отрицательных значений х. Точка равновесия А лежит на оси х и соответствует установившемуся режиму.
Рис. 25-13.
В зависимости от начального значения тока i0 (в момент t ~ 0) фазовая траектория может начаться в различных точках прямой — в верхней или в нижней полуплоскости. С течением времени (вне зависимости от начальных условий) движение представляющей точки происходит в направлении точки А со скоростью, которая уменьшается по мере приближения к точке А. Если цепь г, L замы-каегся накоротко (U = 0), то фазовая траектория проходит через начало координат (на рис. 25-13, б изображена пунктиром).
Аналогичные фазовые траектории получаются и для переходных процессов в цепях г, С, рассмотренных в § 13-6 и 13-7.
Еспи индуктивность нелинейна и характеризуется графиком Д (t) или i (Д), то, полагая Д = х, а t/ДIdt = у, получаем нелинейное уравнение
y + rHx)^-U, (25-38)
которое выражает на фазовой плоскости все возможные переходные процессы в схеме на рис. 25-1. Фазовые траектории для данного случая показаны на рис. 25-14.
В цепи г, L, С (рис. 25-15, а) фазовые траектории переходных процессов сложнее. Рассмотрим случай, когда г = 0, а индуктивность и емкость соединены последовательно и подключаются к источнику постоянного напряжения U. Начальные значения тока в индуктивности i0 и напряжения на емкости и0 могут быть любые.
703
Дифференциальное уравнение переходного процесса в этом случае известно (§ 13-9):
<Pi । 1 • п
dt2^~ LC (2о-39)
Обозначая i = х, di/dt = у и 1/Z.C — ®20, получаем:
или после интегрирования
f/2 + <4t2=£2,
(25-40)
где к — постоянная интегрирования, зависящая от начальных условий.
Уравнение (25-40) на фазовой плоскости изображается семейст
вом эллипсов (рис. 25-15,6), равны 2k, а горизонтальные 2/гЛоо. Полученные эллипсы соответствуют незатухающим синусоидальным колебаниям. Амплитуда колебаний тока равна полуоси эллипса, на
прячем вертикальные оси эллипсов
Рис. 25-15.
Рис. 25-14.
правленной по оси абсцисс, а частота равна отношению вертикальной полуоси к горизонтальной.
Так как при t = 0 задано i — i0 и ис = и0, то фазовая траектория проходит через точку с координатами х — i0 и у = di/dt = = (U — u0)/L, а амплитуда колебаний тока
(25-41)
В реальном колебательном контуре всегда есть некоторые потери и сопротивлением г нельзя пренебречь. За период колебаний амплитуда тока уменьшается и фазовые траектории имеют вид спиралей, завивающихся вокруг начала координат.
704
Так как за один период колебаний То ~ 2л/<оо » 2л У LC в контуре теряется энергия
т
AF f (Im sin ©оО2 г dt = у PmrT0, о
а общая энергия, запасенная в контуре, W = L/^/2, причем дЦ- W, то отношение радиусов двух соседних витков равно:
Полученное выражение справедливо только при гуУЬ/С, когда при подсчете потерь All7 можно пренебречь уменьшением амплитуды колебаний за один период. В общем случае колебательный процесс описывается уравнениями (13-55) и (13-56), которые являются параметрическими уравнениями спирали. Отношение Im (t + Тв) к Im (f) представляет собой величину, обратную декременту колебания (см. § 13-12).
По мере увеличения сопротивления шаг спирали увеличивается и при г > 2 У L/C = гкр семейство спиралей вырождается в семейство параболических кривых, проходящих через начало координат.
Фазовые траектории при г <z гкр и г > гкр изображены на рнс. 25-15,в и г.
Если сопоставить фазовые траектории для трех различных значений г (рис. 25-15), то можно отметить некоторые общие свойства этих кривых. Все кривые пересекают ось х под прямым углом с переменой знака dyldx. Во всех трех рассмотренных случаях имеется только одна точка равновесия, лежащая в начале координат, однако характер равновесия различный.
При г = 0 равновесие наименее устойчивое. Достаточно бесконечно малого отклонения от точки равновесия, чтобы начался незатухающий колебательный процесс с бесконечно малой амплитудой колебания. При этом представляющая точка совершает периодические движения по орбите с центром в точке равновесия. Точка равновесия такого типа называется центром.
При г < гкр все процессы, возникающие в цепи, — колебательные затухающие и представляющая точка после любого принужденного отклонения от равновесия возвращается в исходное положение равновесия, совершая при этом несколько оборотов вокруг точки равновесия. Такого рода точка равновесия называется устойчивым фокусом.
Если г> гкр, то представляющая точка, возвращаясь апериодически в состояние равновесия, движется по параболе и не совершает более полуоборота вокруг начала координат. Точка равновесия такого типа называется устойчивым узлом.
При построении фазовых траекторий процессов, описываемых Дифференциальным уравнением второй степени, удобно пользо-ваться методом изоклин. Изоклиной называется геометри-
705
ческое место точек, в которых касательные ко всем интегральн кривым (возможным фазовым траекториям) имеют одинаковь” наклон. Если известно семейство изоклин, то фазовые траектоп И могут быть построены геометрическим путем без дополнительно/1 анализа. 0
Пример 25-3. Построить фазовые траектории цепи г, L, С при г (рис 25-15, а) методом изоклин. ГкР
Решение. Дифференциальное уравнение цепи (см. § 13-9)
d2i г di , 1 . п
dt2 ' L dt'*' LC 1
(24-13)
Обозначив r/L = 2Р и применив ранее принятые обозначения i = х, di/dt — у и \/LC ~ cog, получаем:
dy/dZ+2pj/4-cogx=O. (25-44)
г? л /л/ dy dx dy
Если dyldt заменить через --т = ~ у, то, исключив время в уравнении
CLX UL Ил
(25-44), получим:
dy 2р«/+ш=х
-------у-----•
Так как Во всех точках изоклин должно выполняться равенство
dy/dx~coibt = 6,
то уравнением изоклины является
у 6-S-2P
(25-46)
Изоклины представляют собой семейство лучей, проходящих через начало координат. Наклон этих лучей зависит от параметров контура и наклона 6 каса-
Рис. 25-16.
тельных к интегральным кривым в точках их пересечения с данной изоклиной.
Из последнего уравнения следует, что ось х является изоклиной с е = оо, а ось у совпадает с изоклиной 6 — —2р. Уравнение изоклины 6=0, называемой изоклиной горизонтальных касательных, имеет вид: у = — <й;;л'/2р, следовательно, она лежит во втором и четвертом квадрантах.
Полагая 6 = ± 2/г[3, где п — целое число, получим семейство изоклин, представленных на рис. 25-16. Здесь короткими штрихами показан наклон интегральной кривой к изоклинам.
Проводя интегральные кривые так, чтобы они пересекли кажДУ10 изоклину под соответствующим углом, получаем фазовые траектории переходных процессов. На рис-25-16 показаны две фазовые траектории для разных начальных Ус" ловий (точки ах и а2).
706
>пая фазовые траектории, т. е. имея зависимость
ц = dx/ dt=у (х),
(25-47)
доя 1,0 путем графического интегрирования найти соответствующие зависимости f(i) в обратном виде;
X
t=
6
dx
УМ *
(25-48)
Затруднение при вычислениях интеграла (2-48) вблизи точек у = 0, связанно обращением подынтегральной функции в бесконечность, можно обойти, гияя участок фазовой траектории дугой окружности с центром, лежащим на х, и производя аналитическое интегрирование.
25-7. Колебательный разряд емкости через нелинейную индуктивность
Если в цепи г, L, С содержатся нелинейные элементы, то ана литический расчет переходного процесса очень усложняется
В этих случаях целесообразно нием процесса на фазовой плоскости, которое может быть произведено относительно просто.
пользоваться графическим построе-
Рис. 25-18.
Рассмотрим цепь, содержащую линейные г, С и нелинейную индуктивность с заданной характеристикой Т (i). В этом случае Уравнение (25-43) принимает вид:
S+4+lz=°- <25-49)
dT
Обозначая Т = х; -^~yt получаем:
yfx + K^)y+f2^) = 0, (25-50)
707
где
К (Т) = г di/dW и f2 (Т) = I ф)/С —
известные функции Т или х, показанные на рис. 25-17.
Уравнение изоклин получается после замены dyldx постоянной величиной 6 и имеет следующий вид:
/9пп,
e+/iW" (‘5’01)
Семейство изоклин, построенных по этому уравнению, схематически показано на рис. 25-18. Там же построена одна фазовая траектория переходного процесса разряда конденсатора в цепи с нелинейной индуктивностью.
Глава двадцать шестая АВТОКОЛЕБАНИЯ
26-1. Нелинейные резисторы со спадающим участком характеристики
При рассмотрении переходных процессов в нелинейных цепях особый интерес представляют процессы в цепях с сопротивлениями, характеристики, на котором дифференциальное сопротивление отрицательно:
t\ = duldi<ZQ.
/ Все характеристики элементов, обладающих отрица-•° и тельными дифференциальными сопротивлениями, можно разделить на две группы: Рис. 26-1. характеристики типа X и
типа N. Наименование типа соответствует начертанию характеристики при горизонтальном расположении оси напряжения и вертикальном расположении оси тока (рис. 26-1,о и б).
Характеристиками типа X обладают газоразрядные электровакуумные приборы (газотрон, неоновая лампа) и электрическая дуга, у которых спадающий участок характеристики обусловлен ионизацией междуэлектродного пространства.
Характеристики типа W имеют электронные лампы с заметным влиянием вторичной эмиссии с анода, туннельные диоды, а также электронные лампы, на управляющую сетку которых подается дополнительно напряжение Atzc, противоположное по знаку изменению анодного напряжения Аца. Спадающий участок характеристики в этих случаях обусловлен изменением условий эмиссии
имеющими спадающий участок
du. а.ь
г.
di
>n
Тип S
to
/Тип N
du^^o^du di

708
^ектронов анодом лампы или обратным воздействием управляющего напряжения сетки лампы на ее ток.
Малые колебания тока вокруг некоторой точки, лежащей на
задающем участке характеристики, соответствуют отрицательному потреблению или отдаче мощности нелинейным резистором. Эта отдача мощности происходит за счет преобразования энергии
источников постоянного тока в энергию переменного тока, отдавае
мую нелинейным резистором во внешнюю цепь.
В качестве примера искусственного получения спадающей характеристики рассмотрим вольт-амперную характеристику триода, на сетку которого кроме постоянного напряжения £/с0 подается дополнительное напряжение ku&, пропорциональное и противоположное по знаку напряжению между анодом и катодом (рис. 26-2),
tzc — Uc0 — ku&, (26-1) где k = — dujdua называется коэффициентом обратной связи.
При определенных значениях коэффициента обратной связи вольт-амперпая характеристика лампы может иметь значитель-
ный участок с отрицательным Рис. 26-2.
дифференциальным сопротивле-
нием. Для иллюстрации на рис. 26-2 построена вольт-амперная характеристика электронной лампы — триода при напряжении на сетке (в вольтах)
ис = 40 — 0,2иа.
(26-2)
Построение выполнено на основании заданного семейства характеристик ia (tza) при различных uz.
При исследовании процессов, возникающих в цепях с нелинейными резисторами, имеющими спадающий участок характеристики, первоначально будем считать заданной вольт-амперную характеристику нелинейного резистора. Затем, определив частоты тармонических составляющих, возникающих в цепи в переходном и установившемся процессах, будем судить о том, какими средствами может быть получена требуемая нелинейная характеристика (задача синтеза).
709
26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами
В электрических цепях с источниками постоянных э д с нелинейными резисторами, имеющими спадающий участок xapa»8 теристики, при определенных условиях невозможен установившийся режим протекания постоянного тока. Некоторые значения токов найденные при помощи общих методов расчета цепей постоянного тока, не могут быть получены, так как они соответствуют неустойчивому режиму. Достаточно ничтожно малого отклонения от этих значений, чтобы начался переходный процесс, приводящий к новому устойчивому значению постоянного тока или к возникновению переменного тока. Поэтому даже при расчете цепи постоянного тока с нелинейными резисторами типа Suh’ необходимо решить вопрос об устойчивости полученного режима.
Основы математической теории устойчивости были заложены трудами выдающегося русского ученого профессора Харьковского университета А. М. Ляпунова. Исследуя нелинейные задачи небесной механики, А. М. Ляпунов показал, что правильное суждение об устойчивости при малых отклонениях от состояния равновесия может быть получено на основании линеаризации нелинейного уравнения, т. е. замены нелинейной характеристики касательной в точке предполагаемого состояния равновесия.
Предположим, что исследуется состояние равновесия цепи с нелинейным резистором при токе /у и напряжении Ду. Раскладывая характеристику i в ряд вблизи точки равновесия и пренебрегая высшими степенями, получаем:
“-Ма.')/'-'-)-
Обозначая приращения тока и напряжения относительно Д и Uy через Ai и Atz, дифференциальное сопротивление в точке равновесия (du/di)y через ру, получаем закон Ома для приращения тока и напряжения
Atz = АД
причем на спадающих участках характеристики ру < 0.
Правая часть дифференциального уравнения цепи для Ан или Ai, характеризующая установившийся режим, равна нулю и решение содержит только свободные составляющие. Но в отличие от реальных линейных цепей, для которых все корни характеристически4 уравнений имеют отрицательную вещественную часть и свободные составляющие затухают, в цепях с нелинейными резисторами типа о или W характеристические уравнения могут иметь корни с поло
жительной вещественной частью.
Такие корни свидетельствуют о наличии нарастающих свободны4 составляющих переходного процесса, т. е. о неустойчивом режи'’е-Следовательно, критерием устойчивости состояния равновеси является отсутствие в характеристическом уравнении, составлеН
710
ном при линеаризации нелинейной характеристики в точке равновесия, корней с положительной вещественной частью.
При анализе устойчивости режима большое значение имеют малые паразитные емкости и индуктивности нелинейных элементов, которыми пренебрегают при исследовании линейных цепей Опыт доказал, что при анализе устойчивости цепей, содержащих нелинейные резисторы типа S, необходимо учитывать малую индуктивность, включенную последовательно с сопротивлением. Для резисторов типа N, наоборот, необходимо учитывать малую емкость, включенную параллельно нелинейному резистору.
На значение малых параметров при анализе устойчивости нелинейных цепей впервые обратили внимание А. А. Андронов и С. Э Хайкин.
Пример 26-1. Исследовать устойчивость режима в точке 3 на характеристике неоновой лампы (кривая О—1—3—2—4 на рис 26-3) при включении ее в цепь, рис 26-4, а
изображенную на для двух случаев: г > I ру I;
I р51;
Ру <о, здесь ру — дифференциальное сопротивление неоновой лампы в точке 3, Lo — ничтожно малая паразитная ин-дукшвноегь, аг и С — сопротивление резистора и емкость конденсатора, включен 1ых в цепь В обоих слу чаях точка предполагаемого зрьтате пересечения кривой
б
установившегося режима (ючка 3) получена в ре-
I (и) и прямой I — (Ua — и)/г
Решение Заменяя нелинейное сопротивление отрицательным линейным сопротивлением pv и применяя обычные методы теории переходных процессов, составляем характеристическое уравнение
2И-р>.+Л+7^'£г -0.
или после преобразования
йогСр2+(груС + йо) р + (г+ру)=О,
Р2+2рР + ш*=0,
ИЛИ
где
ФуС 4- Lo Ру ₽='-2L0/-C К=>'2Ц’
г+ру Т^С~-
Рис 26-4.
Корни характеристического уравнения Р12=—Р t ^Р2—COJ-
Так как Lo ничтожно мало, pv < 0, то для обоих случаев (рис 26-3, а и б) Р < 0 Следовательно, по крайней мере один из корней характеристического уравнения положителен
Таким образом, вне зависимости от соотношения между г и Ру режим в точке 3 при Ру < 0 оказывается неусюйчивым.
711
Иной вывод получается, если пренебречь малой индуктивностью L в случае характеристическое уравнение
ЭТО\

имеет единственный корень
Р1 = —(»• +Ру)/»-РуС.
Рассматривая полученное выражение, можно сделать ошибочный вывод ЧТГ| при I ру | > г [вариант рис 26-3, б и соответствующая ему прямая \ =2 — (^ai — и)/' ПРИ == Uzi на Рис 26-3] равновесие будет устойчивым
В неустойчивых цепях с отрицательными дифференциальными сопротивлениями при действии только постоянных э. д. с. могут возникать переходные процессы, приводящие к колебательному режиму — автоколебаниям.
Автоколебания, возникающие в нелинейных цепях, можно подразделить на: а) резко несинусоидальные или релаксационные и б) близкие к синусоидальным или, как их условно называют, синусоидальные, хотя этот термин не совсем соответствует действительности.
Рассмотрим примеры автоколебаний каждого типа.
26-3. Релаксационные колебания в цепи с отрицательным сопротивлением
Возникновение релаксационных колебаний рассмотрим на примере цепи с неоновой лампой (рис. 26-4).
Характеристика неоновой лампы типа S (рис. 26-3) имеет область с отрицательным дифференциальным сопротивлением, лежащую между точками 1 и 2 при напряжении t/2 < « < Ut.
Так как ток в конденсаторе ic = С du/dt, то, пренебрегая паразитной индуктивностью, получаем следующее уравнение
r(i + Cdu/dt) 4- и — Uit или
du 1 i r j ..
dt = rC — u — ir)-
При постоянном токе в цепи dutdt = 0 и ия — и
I — ~.
(26-3)
(26-4)
Если параметры цепи таковы, что прямая, выражаемая этим уравнением, пересекает характеристику неоновой лампы в одно’ точке, для которой дифференциальное сопротивление отрицатель^ (ючка 3 на рис. 26-3), и устойчивое равновесие невозможно, переходный процесс приводит к возникновению незатухаюй” колебаний, значительно отличающихся от синусоидальных.
712
f Рассмотрим последовательно различные этапы возникновения jn-их колебаний.
* После включения цепи до тех пор, пока конденсатор не зарядился до напряжения ток неоновой лампы равен нулю и конденсатор С заряжается через сопротивление г, как и в линейной цепи г, С (см. § 13-7), по закону
uc=UB(l-e~^.
Когда напряжение на конденсаторе в момент t = достигнет значения Ur (рис. 26-3), неоновая лампа зажжется и, так как напряжение на ней из-за параллельно подключенного конденсатора не
может измениться скачком, ток лампы увеличится от нуля до величины Д (точки 1 и Г на рис. 26-3).
С этого момента времени 4 процесс описывается нелинейным дифференциальным уравнением (26-3). Скорость изменения напряжения на неоновой лампе duldt, которая пропорциональна горизонтальному отрезку между прямой i = (Ua — u)!r и кривой i (tz) (на рис. 26-3 эти отрезки показаны штриховкой), становится отрицательной. Конденсатор начинает разряжаться через неоновую
практически мгновенно
лампу. Зависимость на-
пряжения и от времени при разрядке конденсатора может быть найдена графическим ийтегрированием непосредственно из уравнения (26-3)
Ui
rC du
UB — и—ir '
Напряжение на конденсаторе убывает до тех пор, пока не снизится в момент времени /2 до величины U2 и неоновая лампа гаснет (точки 2 и 2' на рис. 26-3).
Дальнейшая зарядка конденсатора от напряжения погасания До напряжения второго зажигания неоновой лампы происходит аналогично первоначальной зарядке.
Итак, в цепи устанавливается периодический процесс попеременной зарядки и разрядки конденсатора; график этого процесса Представлен на рис. 26-5.
Для получения линейного изменения напряжения при зарядке Конденсатора вместо резистора г включают насыщающийся диод, а Для ускорения разрядки конденсатора вместо неоновой лампы применяют тиратроны с большими значениями тока зажигания Д, Которые обеспечивают большую скорость разрядки конденсатора ~ (отрезок Г—1" на рис. 26-3). Так могут быть получены напряжения пилообразной формы, необходимые, например, для развертки лУча на экране электронно-лучевого осциллографа.
713
26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением
Для уяснения условий получения незатухающих синусоида ть них колебаний рассмотрим колебательный контур, подключенный к источнику постоянного напряжения U& (рис. 26-6,а) через нелинейное сопротивление типа W (рис. 26-6,6). При анализе устойчивости этой цепи паразитная емкость может считаться включенной в емкость С.
Так как в рассматриваемой цепи напряжение на конденсаторе ис = И& — и, а ток ic — С duc/dt = — С duldt, то по второму закону Кирхгофа получаем следующее уравнение:
г d2u , ~du , . т di . j,
LC~dP + fC di^u + Ldt+ir~U&- <26’5)
При постоянном токе в цепи все производные должны обратиться
в нуль и
Г
(26-6)
Допустим, что параметры цепи подобраны так, что прямая, описываемая этим выражением, пересекает характеристику нелинейного сопротивления в одной точке (точке равновесия А), для которой дифференциальное сопротивление отрицательно (рис. 26-6,6).
Пусть в момент включения цепи напряжение на конденсаторе и ток в катушке равны нулю. Тогда сразу же после замыкания рубильника напряжение и на нелинейном резисторе равно напряжению источника Да и по мере зарядки конденсатора напряжение и — U & — ис убывает, казалось бы, приближаясь к значению Ua>
соответствующему точке равновесия.
Для анализа переходного процесса рассмотрим условие равновесия, соответствующего точке А. Заменив нелинейный элемент дифференциальным сопротивлением рл в точке А, составим характеристическое уравнение для приращений и и i относительно этой
точки:
Z(p)=r+p£ +
- Ра/Рс Ра+1Дс
О,
714
дои после преобразований
Р3 +2₽р + ^ = 0,.

(26-7)
£орни уравнения (26-7)
Р1,2 = — р±КР2-«о = — Р±/®,
где
Предположим, что корни комплексные cog > р2 и свободные колебания в цепи могут быть выражены формулой (13-54).
Поскольку рд < 0, коэффициент затухания р может быть как толожительным, так и отрицательным. Если 0 > рА > — ЫгС, то Р имеет отрицательный знак, режим в точке А неустойчив и свободные колебания, возникающие в цепи с частотой со, нарастают.
Таким образом, в цепи не устанавливается, как можно было бы предположить, постоянный ток, а возникают автоколебания, амплитуда которых постепенно увеличивается до тех пор, пока значения тока и напряжения в нелинейном сопротивлении не выйдут за пределы спадающего участка характеристики. Переход на участок \аракiepriстики с положительным дифференциальным сопротив-дением ограничивает амплитуду колебаний, в цепи устанавливаются практически синусоидальные колебания с частотой, близкой к со.
Нелинейным элементом при получении синусоидальных колебаний часто является электронная лампа, например триод. Поэтому остановимся па создании обратной связи между напряжением на аноде лампы и напряжением на сетке, обеспечивающей получение спадающего участка характеристики нелинейного сопротивления.
На рис. 26-7, а—в представлены три схемы ламповых генераторов, для когорлх при некоторой частоте со и соответствующем сыборс параметров цепи и напряжений Uo и Uc могут быть выползни условия (26-1), обеспечивающие наличие спадающего участка Шт- ампер ной х а ра ктер исти ки.
Векторные диаграммы переменных составляющих напряжений сражены для каждой из схем над нею. Как видно из диаграмм, ^Ременная составляющая напряжения на сетке Ос находится противофазе с напряжением на аноде лампы С/я. Таким образом, коэффициент обратной связи k в выражении (26-1) получается положительным (его выражение для каждой схемы приведено на рис. ,7). Следовательно, вольт-амперная характеристика участка 'и,и между анодом и катодом лампы при достаточно большом 'Наченпи коэффициента обратной связи имеет спадающий участок we. 26-2).
715
Значение коэффициента обратной связи, необходимое для возбуждения колебаний, может быть определено непосредственно из условия возникновения автоколебаний:
0>Ра>*-Ь/гС. (26-8)
Так как
1 di dis . di& £>tic рл du ди& ’ dt\ диа ’
то, обозначая для линейного участка характеристики электронной лампы dijdu& = \!Rt = gi и dijduc = S (см. § 9-2), а также учи-
б)
Рис. 26-7.
тывая, что dujdua — — k, можно неравенство в следующем виде:
X = g.-kS< — g9,
(26-8) записать
или
kS>g3 + git (26-8а)
где g3 = rCIL — эквивалентная проводимость колебательного контура.
Полученное неравенство является условием возникновения автоколебаний в ламповом генераторе.
Показанные на рис. 26-7 схемы ламповых генераторов (автогенераторов) нашли широкое применение в радиотехнике, в промышленной электронике и в высокочастотной электротермии для получения колебаний высоких частот от нескольких килогерц до сотен мегагерц.
Итак, проведенный анализ позволил определить условия возникновения автоколебаний, близких к синусоидальным. Для опре
716
деления амплитуд и формы кривых тока и напряжения применяют специальные методы анализа нелинейных цепей. Такими методами являются, например:
а) рассмотрение процесса на фазовой плоскости;
б) метод гармонического баланса, основанный на условной линеаризации задачи.
26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением
Если в колебательный контур (рис. 25;15,о) вместо сопротивления г включен нелинейный элемент с отрицательным дифференциальным сопротивлением, который в определенном диапазоне изменения тока может быть заменен источником постоянной э. д. с. и отрицательным сопротивлением г = гд < 0, то коэффициент затухания Р = r/2L оказывается отрицательным. В этом случае переходный процесс не затухает, а нарастает.
На рис. 26-8 представлены фазовые траектории для 0 > г > — гкр______и
гкр, где гкр = 2 ]/ L/C; здесь, так же как и при положительных значениях г (см. § 25-4), точка равновесия одна, однако теперь она неустойчива. При О д> г >• — гКр эта точка называется неустойчивым фокусом, а при гкр—- неус-
тойчивым узлом. В обоих случаях достаточно ничтожного отклонения от положения равновесия для возникновения лавинообразного процесса, уводящего представляющую точку далеко от положения равновесия в область, где дифференциальное сопротивление уже перестает быть отрицательным и переходный процесс затухает.
. Фазовые траектории могут быть построены методом изрклин гак же, как это сделано в § 25-6. На рис. 26-9 показано семейство кзоклин для г > — гкр и нанесены две возможные фазовые траектории. Построение полностью аналогично выполненному на Вис. 25-16.
В цепях с нелинейными резисторами, имеющими спадающие арактеристики, устанавливается режим, изображаемый на фазовой лоскости либо точкой (устойчивый фокус или узел), либо замкну-эй кривой, которую называют предельным циклом. Та замкнутая кривая состоит из участков развивающихся спиралей ли парабол (рис. 26-8,о и б), соответствующих нарастающим
717
процессам в областях с отрицательным дифференциальным сопротивлением, и участков свивающихся спиралей или парабол (рис 25-15,в и г), изображающих затухающие процессы в областях с положительным дифференциальным сопротивлением.
Изучение замкнутых фазовых траекторий, кроме простоты их графического анализа и возможности качественной оценки протекающего процесса, полезно еще
получить помощи осцилло-
наблюде-
потому, что их легко опытным путем при электронно-лучевого графа.
Простейшая схема
ния фазовой траектории периодического процесса на экране электронно-лучевой трубки приведена на рис. 26-10. Здесь исследуемая величина представлена в виде напряжения и. Это напряжение непосредственно по
дается на горизонтальные отклоняющие электроды электроннолучевого осциллографа ЭО и дает отклонение луча по оси х, пропорциональное и. Для получения вертикального отклонения луча, пропорционального у = du/dt, применяется дифференцирующая цепочка, состоящая из конденсатора С и резистора г, причем со
718
противление г выбирается так, чтобы напряжение на нем было много меньше напряжения на конденсаторе. Тогда ток в резисторе г, а следовательно, и напряжение на нем пропорциональны duldt. Это напряжение усиливается при помощи усилителя У и подается на вертикальные отклоняющие электроды электроннолучевого осциллографа ЭО.
Таким образом, оказывается, что горизонтальное отклонение луча пропорционально исследуемому напряжению и, а вертикальное отклонение луча пропорционально du/dt, и кривая, очерченная лучом на экране электронно-лучевой трубки, представляет собой фазовую траекторию изучаемого предельного цикла.
26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний
Рассмотрим на фазовой плоскости процессы, которые возникают в цепи, изображенной на рис. 26-6,а, и применим для анализа метод кусочно-линейной аппроксимации характеристики.
Выразив нелинейную’характеристику i (и) (рис. 26-6,6) в виде четырех прямолинейных участков (рис. 26-11,а) и принимая в качестве координат фазовой плоскости х = и = Ua — исму = du/dt= ~ —duc!dt, можно и фазовую плоскость разбить на четыре области (рис. 26-11,б).
Запишем линейное уравнение участка характеристики i (и) и дифференциальное уравнение (26-5) для каждой из этих областей: область I. i = 0; LC^ + rC1^ -\-u = U& (26-9)
при и < 0;
г т ___и f р .
область И. i = -; LC 4-pt dt2 '
при 0 < и < Ut;
('C+Dt+O+ifK"-<2610)
- nr u — U, тг,(Ри . [ п , L\du /. г\
область ///. 1=-^-; LC d-+(rC + -)d? + (l + -)M =
= + (26-П)
(J2
при < и <; U2;
область IV. i = 0; LCd*“ + rCd“±u = Ua (26-12)
при и > U2.
Здесь для прямой О—1 сопротивление pr = du/di> 0, а для прямой 2—1 сопротивление р2 = duldi <0.
Находя корни характеристического уравнения для каждой из областей, получаем, что для контура с высокой добротностью (г L/C) параметры цепи можно выбрать так, чтобы во всех четырех областях переходные процессы были колебательными.
719
При этом в областях /, // и /V коэффициент затухания 0 всегда положителен и, следовательно, колебания затухают, а в области III он становится отрицательным и при выполнении условия (26-8а) колебания нарастают.
Таким образом, в областях /, // и IV фазовые траектории аналогичны графику на рис. 25-15,в, причем центры спиралей являются устойчивыми фокусами и соответствуют значениям и = UF для областей / и IV и i
* 1 * * А Л Л А л. я. л л л л л. W д
и = р 1[/а/(р! + г) = ив для области // (см. точки о и В на рис. 26-11), что следует из уравнений (26-10) при du/dt — d?u/dt2 = 0.
В области III фазовые траектории аналогичны графику на рис. 26-8,а, центр спиралей является неустойчивым фокусом; его координата соответствует условию
,, Р2^а + ГЧ2 II W =---------= U д
Ра + г А
и он лежит в области III (рис. 26-11).
На границе двух областей должны выполняться условия «припасовывания» или «сшивания» фазовых траекторий соседних областей. Так как пс по закону коммутации не может измениться скачком, то, следовательно, не может измениться скачком и и = Ua — ис. В таком случае не может изменяться скачком и ток i в нелинейном сопротивлении, представляющий собой непрерывную функцию напряжения и. Также остается непрерывным и ток, протекающий через емкость ic — С diicldt, являющийся сум
мой тока i и тока в индуктивности, который по закону коммутации
не может измениться скачком, а следовательно, не может измениться скачком и duldt - — duc!dt. Итак, условием «сшивания» фазовых траекторий является непрерывность и и duldt, т. е. непрерывность движения изображающей точки при переходе из одной области в другую.
На рис. 26-11,6 изображены фазовые траектории процессов в рассматриваемой цепи. Из построения видно, что центр спиралей фазовых траекторий в областях I и IV лежит вне этих областей (ючкаа),также каки центр спиралей фазовых траекторий области // (точка В вне области //). В области III центр развивающихся спиралей соответствует неустойчивой точке равновесия типа фокуса и находится внутри области в точке А. Точка А —единственная точка равновесия рассматриваемой .цепи — неустойчивый фокус, следовательно, в цепи не может установиться постоянный ток.
720
Путем построения ряда фазовых траекторий для различных начальных условий можно убедиться, что при любых начальных условиях включение цепи приводит к периодическим колебаниям, изображаемым на фазовой плоскости в виде предельного цикта. Так, если начальные условия соответствуют точке, лежгщей внутри области, ограниченной предельным циклом (точкам' на рис. 26 11,6), то колебания в цепи нарастают, пока не достигнут значения, соот-
Рис. 26-12.
ветствующего предельному' циклу. Если же точка, характеризующая начальные условия, лежит вне этой области (точка b на рис. 26-11,6), то возникшие колебания затухают до значения, соответствующего предельному циклу. В обоих случаях фазовая траектория как бы наматывается на предельный цикл.
Предельный цикл установившегося колебательного процесса относительно мало отличается от эллипса, т. е. возникают колебания вокруг точки равновесия А, близкие к синусоидальным.
В реальной цепи плавные переходы характеристики вместо изломов в точках О, I и 2, принятых при кусочно-линейной аппроксимации (рис. 26-11,а), еще более приближают действительный предельный цикл к эллипсу.
24 Основы теории цепей
721
На рис. 26-12 дана фотография осциллограммы нарастания колебаний и предельного цикла с экрана электронно-лучевого осциллографа, включенного по схеме на рис. 26-10. Амплитуда напряжения на емкости ис определяется как горизонтальная полуось эллипса, а частота со в соответствующем масштабе равна отношению отрезков вертикальной и горизонтальной осей (рис 26-11,6). ___
У большинства ламповых генераторов г УЫС и | |
L/C', в этом случае со «= 1/УLC.
26-7. Определение амплитуды автоколебаний методом гармонического баланса
Амплитуда и частота установившихся автоколебаний в нелинейной цепи могут быть определены при помощи метода гармонического баланса (см. § 24-6).
Для пояснения этого метода рассмотрим автоколебания, возникающие в цепи, изображенной на рис. 26-7,6.
На рис. 26-13 схема генератора изображена в виде двух звеньев —
нелинейного (/) и линейного (//)
Рис. 26-13.
разомкнутой обратной связью. Каждое из звеньев представляет собой такой четырехполюсник, для которого напряжение или ток на выходе практически не зависит от нагрузки, подключенной к вторичным зажимам. В первом звене это справедливо потому, что внутреннее сопротивление электронной лампы Ri отнесено к второму звену и лампу можно рассматривать как источник тока, значение
которого ta зависит только от напряжения на сетке пс. Сопротивление Rt приближенно принимается постоянным. Нагрузкой второго звена при замыкании обратной связи (соединение зажимов 1—1' а 2—2') является сопротивление между сеткой и катодом электронной лампы, которое весьма велико, а следовательно, напряжение на зажимах 2—2' практически не зависит от нагрузки.
Для первого нелинейного звена по характеристике электронной лампы может быть построена зависимость мгновенного значения тока на выходе от напряжения на входе. Задаваясь различными значениями амплитуды синусоидального напряжения п1с на входе, по нелинейной характеристике электронной лампы можно построить несинусоидальную кривую тока ia и, разлагая ее на гармоники, найти соответствующее напряжению wtc значение первой гармоники
тока tla.
722
В комплексной форме отношение Д1с/Ла=г1 (^1т)
(26-13)
представляет собой вещественную функцию гу амплитуды напряжения на входе Ulm. Пример такой зависимости приведен на рис. 26-14.
Для второго линейного звена отношение к току /1а может быть выражено комплексным сопротивлением, зависящим от частоты 6) и не зависящим от Ulm:
Zx (/со) = %-=jwM (26-14)
/1а /1а
Выражая /1а через /1L:
Ла = Лг [ 1 + f
получаем: Рис. 26-14.
Z1 Ri + (r+jML)(\+jwRlC') • (26'15)
Автоколебания существуют при равенстве амплитуд и фаз первой гармоники напряжений на входе и выходе цепи:
#1с = #с.
Согласно (26-13) и (26-14) в этом случае
Z1(/co) = r1(t/lm) (26-16)
и, следовательно,
ImZiO^O. (26-17)
После подстановки (26-15) в (26-17) получаем:
Дг-ф-г=a>2RiLC, или
<26-|8>
Подставляя значение со в (26-15), на основании (26-16) получаем:
<26-19»
По зависимости г, от (Д1т) (рис. 26-14) при гь рассчитанном по формуле (26-19), графически находят амплитуду напряжения первой гармоники для установившихся колебаний
24*
Разложение периодических функций
й п. График f (at) Разложение в ряд f (cot) A
1 ZX f XjT t” <at_ f (a>t) = Am sin at Am V2
о X Z
2 °, H®t) = ^X X ^sin a sin tot+-i sin 3a X X sin 3w^4-i sin 5a x zb Xsin 5a><+...+ 4- -i- sin ka sin ko)t + ...) R2 j
л <Ц£ l/ 1 ймакс у —
У 1г
3 r 0)t X 1 /(ю0=-8^«£.Х sin at —i- sin 3coZ+ дмакс /3
/Ч I / \ла-\т2з + sin 5w<— ... + fe-1 \ (—1) 2 1 + -1—~ sin kut... I R2 /
"" X/
4 X ^sin at+-sin 3co^ + ( о 1 °макс
'4 амаке ♦ «• 2л аЛ
0 4- -=- sin 5o>t -]-...+ D -{- ~ sin + -1 R /

5 ^_2П -*d X Г «Л X Sin -g— COS (J)t + , 1 . Зал n , . + — Sin —к— cos + О Си , 1 . 5ал - , . 1 4- sin -yj— cos 5cut+ ... 5-2 J Смакс
,1 ph- ~&макс ’ art
#«|
724
Приложение 1 в тригонометрический ряд
*"сР k. Ф fta *и
2Ат Л п 2 12 /2 1
о г я г> 1 а! й - 1 я ® м]л а 1 й 1 2 У2 sin а
-i/" 1_Л^ у Зл аПТ/~1-f OJ V
Смаке 2 2 Кз /3 4 Кб л2
Смаке 1 1 2}'2 Л
аСмакс 1 Va 1 j/a о 1 • Ct Л 2 У 2 sin — л V а
725
№ п п. График f (со/) Разложение в ряд / (о/) A
6 / ((о/) — ^макс | ~2 д X X ^sin coZ4--Г sin 2c>t+ + -у sin Зш<+ ...V| Из
у7*! /аткс/ ' , / t Z 'Л*
гя
7 Г 2 f(wO-=«Mabc а+-л x X ^sm ал cos си?+ ^макс
]_ Чужане 1 <*>*
/7 -гла ’ + ~ sin Зал cos 3arf + ...)] 3 / J
8 лт /'гл ci>t X t 1 S cr ® e 8 СЧ , co 8 ~ — |<N [ X 2
/7 Х_ S / ✓ 1 • 6 — ;Д=- COS 4fl)t + О • 0 1 \ + -z—=- cos 6«rf —... ) 5 • 1 /
9 At / ^/7т\ X—J ’ V/ У 2Л f(coO = ^- X x(2 + 1-3 cos2w< 1 Л , —cos 4o)t+ 0 ’ 0 , 1 a , \ 1 —— COS . 5-7 j И 2
726
Продолжение приложения 1
Лср Ф *а fc«
^макс 2 2 рз Уз рТб" Л
G^uaKc 1 J-'a 1 У а У 2 sm ап л | а
Ат П Ф 2 —
л 1 Л 2 ['2 /2 —
727
Ns п п
График f (со/)
Разложение в ряд f (о/)
11 ^-^?<91^-хсЛгл.г
f (caf\ cos at—cos fi
«макс !_cose
при f>0
№0- 3|/5~л". X 7 п
/1 , 1
X \2 + "2“Г C0S 3orf ~
---COS 6С0^ + О • /
/И) ~"°маьс X
X ( «о+ У КЛ cos kat ।
\ fe=i I
где
1
X (sm 6 — 6 cos 6);
________1
aft—fen(l—cosfi)
[ sin (fe—1)0
X [
sin (fe-|-l) 6 1 i+T J
Приложение 2
Таблица оригиналов и изображений (по Лапласу)
Оригинал Изображение
A л/р 1
eat p — a
l—e-at a p(p+«)
ЬФ) p — /«о
cos u>ot P P2+“u
, sin woi <Qq P2 + «6
sin (со0/ ' ^--) p Sin Ip + Wo COS ip p2+w^
cos(co0H p cos, ip—toc sin ip p2 + wg
728
Продолжение приложения 1
Лр *ф *а
Ат 2л 2 —
•> / 2 1 л 1/ - 4- — V 27 Зл/з Т/2 + 2Й-г Л
^макс^О — — —
Продолжение приложения 2
Оригинал Изображение
е“а/ sin aBt «о
(р + а)2+®о
e'at cos aot (р+а)
(р + «)2 + «о 1
t Р2
tn, где n — целое положительное п!

число te р 1
(рЧ-ар
tne^ai, где n— целое п!
положи т ел ьное число (p + «)nrl
ta-leP^ 1
(а—1)! (Р —Р«)“
729
Приложение 3
730
Таблица функций и их частотных спектров
№ п.п. Функция времени Частотные спектры
F (fra) Амплитуда F (co) Фаза 0 (co)
1 Г О о ’’С Л\ о \.7 || - || -С к о s ci- ех, Ci- ех В Е 1 fl jj # A j<£> A co I
2 /«=• • Ае~& при t 0; л 0 при t A /co+P A jAo^ + p2 . to - arctg у
3 / (0= ' Ame~$f sin при t0; , 0 при r~ €0(5/4^ topyl . 2mP
0 j/7? (/co + p)2 + coj F(P3 + u)2-co2)2 + 4w2P2 r g р2+о)а-ш2
Функция времени
Продолжение приложения 3
Частотные спектры
F (/и) Амплитуда F (со) Фаза 0 (со)
<В<И m 1 Й>(м4 т 1 0 при (0 <о)о;
— со2 4- 1 — W24-O)j | Я при (0^5 (00
[ 1 — е“4<п \ 24 1. сот | sin —— шт
/<° \ J ш 1 2 1 2
1 1 0
Функция времени
О при
А при тг^ ts
О при / 23 ts
О при t s'- О;
40 =
t при О=г /г^т;
О при i>-x
fi(t)
/i(0 = fWcos о)0Л где
О при t s' 0; _ /
А приО^/^т;
О при
Продолжение приложения 3
Частотные спектры
F С/со) Амплитуда F (©) ФИ1 0 (ы)
Д — е-1<ЛГ}Х /со у [j -т,)] 2/ | f т3 — т, \ I — sm СО - -- - ; со 1 \ 2/1 W СЧ-7-т2) 2
л Г е -’"П Д / 1 _ е I тсо- j —Ц- X тсо2 / (со г sm со г — 1 1 / +coscot)3 + ' 1,' + (сот cos сот — “ — sm сот)2 сот cos сот — arctg . coTsmcoT—1 + -j- cos COT
! Л (/и) = Й-777Т-----ТГ {(Ш + Шо) ЯП (со — со0) т + (со — со0) ЧП (со + соп) т +
+ / [—2со + (со4-соо) cos (со — со0)т4-(со — со0) cos (со + соо) т]} =
= F1(co)e/ei<w>
Приложение 4
Таблица h, функций для трапеций*
X. X Т ООО 0 05 0 10 0 15 0 20 0 25 0 30 0 35 0 40 0 45 0 50
00 0 000 0 000 0 000 0 000 0 600 оооо 0 000 0 000 оооо 0(00 оооо
05 0 138 0 1б5 0 176 0 184 О 192 0 199 0 207 0215 0 223 0 231 0 240
1 0 0 310 0 325 0 340 0 356 0 371 0 386 0 402 0417 0 432 0 447 О4Ы
1 5 0 449 0 469 0 494 0 516 0 о38 0 560 0 594 0 603 0617 0 646 0 065
2 0 0 571 0 560 0 628 0 1 55 0 682 0 709 0 732 0 761 0 785 0 810 0 831
30 0 755 0 792 0 828 0813 0 895 0 928 0 958 0 986 1 013 1 038- 1 Ос 1
40 0 85b 0 898 0с37 0 974 1 008 1 039 1 0Ь6 1 090 1 110 1 127 1 141
50 0 895 0 939 0 977 0 012 1 042 I 067 1 087 1 102 1 112 1 117 1 117
60 0 903 0 945 0 981 1 013 1 037 1 054 1 065 0 070 1 068 1 062 1 051
70 0904 0 945 0 978 1 006 1 024 1 034 1 037 1 033 I 023 1 009 0 992
80 0911 0 951 0 983 1 007 1 020 1 024 1 021 1 011 0 998 0 982 0 966
90 0 925 0 966 0 9G6 I 016 1 025 1 025 I 017 0 006 0 992 0 978 0 968
10 0 0 939 0 980 I 009 I U25 I 030 1 027 1 018 1 005 0 994 0 985 0 982
П 0 0 947 0 988 1 015 1 028 1 озо 1 024 I 013 1 002 0 993 0 990 0 993
1J0 0 950 0 990 I 015 I 025 1 024 1 015 I 004 0 994 0 988 0 990 0 997
13 0 0 950 0 989 1 012 1 049 1 015 1 004 0 4)3 0 986 0 981 0 989 0 997
14 0 0 951 0 990 1 010 1 015 1 008 0997 Ои87 0 983 0 985 0 991 0 999
15 0 0 956 0 993 1 012 1 014 1 006 0 995 0 987 0 986 0 991 0 998 1 005
160 0 961 0 998 1 015 I 014 1 006 0 995 0 990 0 992 0 999 1 007 1 010
17 0 0 965 1 001 1 016 1 014 1 005 0 996 0 993 0 998 1 (Оо 1 ОН 1 012
18 0 0 966 I 002 1 015 1 012 1 002 0 994 0 994 1 000 1 007 1 010 1 008
190 0 966 1 002 1 013 1 008 0 998 0 992 0 994 1 001 1 ооь 1 006 1 001
20 0 0 967 1 col 1 011 1 004 0 995 0 991 0 9°4 I (01 1 004 1 001 0ЗД5
21 0 0 9Ь8 1 002 1 010 1 003 0 994 0 991 0 996 1 002 1 003 0 999 0 993
22 0 0 97J 1 004 1 011 1 002 0 994 0 994 1 (ОО 1 005 1 004 0 998 0 995
23 0 0 973 1 006 1 он 1 002 0 995 0 997 1 (03 1 00b I 004 0 998 0 997
24 0 0 975 1 006 1 010 1 001 0 995 0 998 1 0С5 1 006 1 002 0988 0 999
25 0 0 975 1 006 1 008 0 999 0 995 0 999 1 004 1 004 0 999 0 99b 1 ооо
т \ 0 55 0 60 0 65 0 70 0 75 0 80 0 85 0 90 0 95 1 00
00 0 000 о ооо ОООО оооо оооо оооо 0 000 оооо ООСО оооо
05 0 248 0 255 0 259 0 267 0 275 0 282 0 290 0 297 0 304 0 314
1 0 0 476 0 490 0 505 0 519 0 534 0 547 0 561 0 575 0 590 0 602
1 5 0 Ь85 0 70о 0 722 0 740 0 758 0 776 0 794 0813 0 832 0 844
20 0 85b 0 878 0 899 0 919 0 938 0 957 0 974 0 991 1 008 I 022
3 0 0 081 1 100 1 116 1 131 1 143 1 154 1 162 1 169 1 175 1 177
40 I 151 1 158 1 162 1 163 1 161 I 156 I 150 1 141 1 132 1 119
50 1 114 1 107 1 097 1 084 1 069 1 053 I 036 1 019 1 003 0 987
60 1 036 1 020 1 001 0 984 0 956 0 949 0 934 0 992 0914 0 907
70 0 975 0 957 0 941 0 927 0 917 0911 0 909 0 911 0917 0 926
80 0 952 0 941 0 934 0 932 0 936 0 944 0 955 0 970 0 986 1 002
90 0 962 0 961 0 967 0 976 0 990 I 006 1 023 1 038 1 051 I 060
10 0 0 984 0 993 1 006 1 020 1 036 1 019 1 059 1 063 1 062 1 056
11 0 1 001 1 014 1 027 I 039 1 047 1 048 1 044 1 034 1 021 1 005
120 1 007 1 018 1 026 1 029 1 025 1 015 1 000 0 984 0 970 0 958
1зо 1 006 1 012 1 012 1 005 0 993 0 980 0 96э 0 955 0 952 0 955
1,0 1 005 1 005 0 998 0 987 0 975 0 965 0 961 0 965 0 976 0 991
15 0 I 006 1 002 0 994 0 983 0 977 0 978 0 987 1 001 1 018 1 032
16 0 1 008 1 001 0 994 0 990 0 993 1 003 1 018 1 031 I 040 1 039
17 0 1 007 1 000 0 996 0 999 1 008 ] 020 1 030 1 032 1 026 1 012
18 0 1 001 0 997 0 997 1 004 1 014 1 020 1 018 1 608 0 993 0 978
14 0 0 995 0 993 0 997 1 004 1 009 1 006 0 995 0 981 0 970 0 967
20 0 0 991 0 992 0 998 1 003 1 001 0 991 0 980 0 972 0 975 0 986
21 0 0 992 0 996 1 001 1 002 0 996 0 987 0 982 0 989 1 001 1 015
22 0 0 997 1 000 1 004 1 002 0 995 0 991 0 997 I 010 1 024 I 029
23 0 1 002 1 007 1 007 1 002 0 997 1 001 1 011 1 022 1 025 I 016
24 0 1 004 1 007 1 004 0 999 0 999 1 007 1 015 1 016 1 006 0 990
2э 0 1 004 1 004 0 999 0 996 1 000 1 007 1 008 0 938 0 984 0 975
* Перепечатана из журнала «.'Автоматика и телемеханика», 1949, К> 5 с некоторыми исправлениями
733
СПИСОК ЛИТЕРАТУРЫ
1 Нейман Л Р, Демирчян К. С. Теоретические основы электротехники. Т 1 и 2 Л , «Энергия», 1966 522 н 407 с
2 Атабеков Г. И. Теория линейных электрических цепей М , «Советское радио», 1960 712 с
3 Поливанов К- М. Теоретические основы электротехники Т 1 М, «Энергия», 1972. 239 с
4 Жуховицкий Б. Я-, Негневнцкнй И. Б. Теоретические основы электротехники Т 2 М, «Энергия», 1972 200 с
5 Атабеков Г И. Основы теории цепей М , «Энергия», 1969 424 с
6 Бессоиов Л. А. Теоретические основы электротехники М, «Высшая школа», 1973 750 с
7 Атабеков Г. И. Теоретические основы электротехники Ч 1. М, «Энергия», 1970 592 с
8 Атабеков Г. И, Тимофеев А. Б., Хухриков С С Теоретические основы электротехники Ч 2 М, «Энергия», 1970 232 с
9 Теоретические основы электрогехники Ч 1 М, «Высшая школа», 1965 734 с Авг П А Ионкин, Н А Мельников, А И Даревскии, Е С Кухаркин.
10 Гольдин О. Е. Задачник по теории электрических цепей М , «Высшая школа», 1969 312 с
11 Каплянский А. Е., Лысенко А. П , Полотовский Л. С. Теоретические основы электротехники М, «Высшая школа», 1972 447 с
12 Гиллемин Э. А. Синтез пассивных цепей М, «Связь», 1970 720 с
13 Задачник по теоретическим основам электротехники (теория цепей) Под ред проф К М Поливанова М , «Энергия», 1973 304 с
14 Гоноровский И. С. Радиотехнические цепи и сигналы М, «Советское радио», 1971 671 с
15 Поливанов К. М. Ферромагнетики М — Л , Госэнергоиздат,* 1958. 254 с
16 Белецкий А. Ф. Основы теории линейных электрических цепей М, «Связь», 1967 608 с
17 Шебес М. Р. Теория линейных электрических цепей в упражнениях н задачах М , «Высшая школа», 1973. 424 с
18 Основы инженерной электрофизики Под ред докт техн наук, проф П А Ионкина Ч II М , «Высшая школа», 1972, 636 с Авт П А Ионкин, А А Соколов, Ф Е Пашукаиис, В Е Боголюбов, А С Капорский, В Г Миронов
19 Кирпатовский С. И. Периодические процессы в нелинейных цепях. Изд во Львовского политехи ин та, 1973 124 с
20 Андронов А А., Витт А. А., Хайкин С. Э. Теория колебаний. М , Фнзматгиз, 1959, 916 с
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
А
Автоколебания 687, 708
Анализ электрических цепей 25
Анод 237, 709, 715
Анодный ток 237, 709
Активная мощность 134
— проводимость 128
Активное сопротивление 116, 123
Активные составляющие напряжения 131
— — тока 132
Активный двухполюсник 95
— четырехполюсник 591
— шестиполюсиик 591
— элемент 17
Алгсбранзация уравнений 356
Амплитуда 109
— автоколебаний 722
— комплексная 112
Амплитудная модуляция 310
Амплитудно-частотная характеристика 485
Амплитудное выпрямление 637
Амплитудный спектр 302
Аналитический метод расчета 638
Апериодический разряд конденсатора 345
Асинхронный двигатель 279
Б
База (транзистора) 244
Баланс мощности 21, 138
Бареттер 578
Барьер потенциальный 244
Бегущая волна 516
Безынерционный нелинейный элемент 630
Бел 449
Биения 309
Блуждающие волны 576
Боковые частоты 311
В
Вариации теорема 95
Ваттметр 142
Ваттметры в трехфазной цепи 276
Вектор вращающийся ИЗ
Векторная диаграмма 112
— — паралцельного контура 180
— — при параллельном соединении 127
— — — последовательном соединении 121, 190
— — трансформатора 199
Вентиль 630, 664
— Идеальный 631
Вершины (узлы) графа 30
Ветви передача 165
Ветвь дерева 45
— связи 45, 53
— электрической цепи 23
Взаимная индуктивность 184, 399
Взаимности принцип 70
Взаимные проводимости 71
— сопротивления 71
Вихревые токи 648
Включение ваттметра 142
— индуктивностей, встречное и согласное 189
— цепи г, С 340
---г, L 334
---г, L, С 352
Включения формулы 407
Внешняя характеристика 13
Вносимая постоянная передачи 450
Вносимое затухание 451
— сопротивление 201
Внутреннее сопротивление 13, 95, 239
Внутренняя проводимость 16
Волна бегущая 516
— обратная 517, 553
— отраженная 554
— падающая 554
— преломленная (проходящая) 554
— прямая 517, 553
— с прямоугольным фронтом 554
Волновое сопротивление линии 516, 552
Волновые уравнения 514. 551
Волны блуждающие 576
Волны длина 517
— скорость 551
— фронт 553
Вольт-ампер 134
Вольт-амперная характеристика 14, 579,
587
Вращающееся магнитное поле 227
Вращающийся вектор 112
Встречное включение индуктивно связанных элементов 189
Вторичные напряжение и ток трансформатора 200
— обмотка и цепь трансформатора 200
— параметры четырехполюсника 446
Второй закон Кирхгофа 24, 119
Входная проводимость ветви 71
— функция цепи 483
Входное сопротивление ветви 71
— — двухполюсника 95
— — линии 526
— — четырехполюсника 218, 443
Выбор положительных направлений 19, 24
Выпрямитель 632, 667
Выпрямление амплитудное 637
— двухполупернодное 634
— однополупериодное 632
— трехфазного тока 635
Высокочастотный фильтр 464
Высшие гармоники 299
— — в трехфазных цепях 324
Вычет функции 388, 422, 496
Г
Г-образный фильтр 477
Гармоники высшие в трехфазной цепи 324
— периодической функции 299
Гармонические колебания 352
— составляющие 299
Гармонический баланс 722
Гаусс Ь08
Генератор двухфазный 259
— ламповый 715
— многофазный 257
— переменного тока 108
— синусоидальных колебаний 719
— трехфазвый 259
Гиперболические функции 447
Гистерезис 602
Гистерезисная петля 602
Гистерезисныи цикл 602
Граничные условия для линии 520
735
Границы области пропускания фильтра 457, 464, 467
Граф направленный 29, 247
— ненаправленный 29
— пассивного четырехполюсника 233
— сигнальный 163
— цепи с невзаимными элементами 247
Графа ветвь 29, 164
— дерево 45. 165
— исток 164
— преобразование 167
— путь 45. 83, 169
— сток 164
Графический метод расчета 631, 639
Д
Двигатель асинхронный, синхронный 279
Двухполупериодиый выпрямитель 634
Двухполюсник 95
— активный 95, 204, 587. 591
— нелинейный 619
— пассивный 95, 131
— реактивный 491
— с потерями 505
Действующие комплексные величины 115
— несинусоидальные периодические функции 305
— ток, э д с и напряжение 110
Декремент колебаний 351
— — логарифмический 351
Дельта функция 369
Дерево схемы 45, 53, 165
Детектирование (демодуляция) 637
Децибел 449
Диаграмма векторная 112, 121, 190, 200, 261
— круговая 202
— линейная 202
— топографическая 157. 261
Диод полупроводниковый 630
Дирака функция 369
Дирихле условие 299
Дискретный частотный спектр 302
Дифференциальные уравнения линии 514, 551
— — электрической цепн 355
Дифференцирующая цепочка 718
Длина волны 517
Добротность катушки 148
— конденсатора 147
— контура 176
Дробь цепная 500
Дуэльные цепи 159
Дюамеля интеграл 361
Е
Единичная функция 368
— — импульсная 369
Емкостная проводимость 129
— связь 241
Емкостное сопротивление 123
Емкость 116, 539
3
Заграждающий фильтр 470
Зажимы входные и выходные 443
Зазор воздушный 607
Закон Ома 13, 18
— — в операторной форме 388
— — для частотных спектоов 427
— сохранения заряда 379
— — магнитного потокосцепления 376
— электромагнитной индукции 118
Законы Кирхгофа 24, 119 165, 193
— — в операторной форме 388
— — для магнитной цепи 605
— — — частотных спектров 427
— коммутации 328, 376
736
Запоминающее устройство 700
Затухание вносимое 451
— рабочее 451
Затухающие колебания 350
Звезда сопротивлении 58
И
Идеальные источники эдем тока 16
Идеальный трансформатор 226
Измерение мощности 142
— — в трехфазиых цепях 276
Изображающая (представляющая) точка 702
Изображение операторное 384
Изображения по Лапласу и Карсону — Хевисайду 385
— функции, ее производной и интеграла 386
Изоклины 705
Индуктивная катушка 117
— проводимость 129
— связь 184
Индуктивное сопротивление 123
Индуктивно связанные цепи 184
Индуктивность 116
— взаимная 184, 399
— дифференциальная 683 н
— двухпроводной линии 539
— нелинейная 638
— обратимая 684
— рассеяния 653
— статическая 683
Индукция магнитная 601
— остаточная 602
Интеграл Бромвича 385
— Дюамеля 361
— Лапласа 384
— Фурье 426
Искусственная линия 452
Исток сигнального графа 164
Источник идеальный 16
— напряжения 16
— питания многофазный 256
— тока 16. 48 Ь4
— э д с 16. 64
— электрической энергии И 14
Итерационный метод расчета 594
К
Канонические схемы реактивных двухполюсников 495
Карсоиа —Хевисайда преобразование 385
Каскадное соединение трансформаторов
232
— — четырехполюсников 215, 451
Катод 237
Катушка индуктивности 148
— со стальным магнитопроводом 638#
669
Кауэра метод 498. 509
КирхгоФа законы 24, 119, 165, ЮЗ
Классификация двухполюсников 95
— фильтров 455
— четырехполюсников 214
Классический метод расчета переходных процессов 327
Колебания затухающие 350
— модулированные 310, 681
— релаксационные 712
Колебательный контур 353
— разряд 707
Коллектор (транзистора) 244
Коммутация 327
Комплексная амплитуда 112
— действующая величина 115
— магнитная проницаемость 656
— мгновенная величина ИЗ
— мощность 136
— проводимость 128
Комплексная Функция времени 112
Комплексное сопротивление 123
— удельное магнитное сопротивление 656
Комплексный метод расчета цепей переменного тока 113
Конденсатор 146
Конденсатора добротность 147
Контур апериодический 352
— замкнутый 24
— параллельный колебательный 180, 714
— последовательный колебательный 175, 353
Контура добротность 176
Контурные уравнения 1ь5
Контурный ток 44
Короткое замыкание 16
— — лннин 526
— — трансформатора 228
— — цепи г, С 339
— — цепи г. L 331
— — четырехполюсника 217
Коэрцитивная сила 602
Коэффициент амплитуды 307, R52, 725
— бегущей волны 546
— возврата 603
— затухания линии 52з
— — переходного процесса 333
— — четырехполюсника, фильтра 455
— искажения 307 725
— модуляции ЗЮ
— мощности 135. 323, 633
— обратной связи 709. 715
— отражения 528, 546
— передачи 71, 165 251
— — сигнального графа 170
— полезного действия 103, 144
— размагничивания 615
— распространения 523
— связи 184
— стабилизации 585 662
— трансформации 227, 230
— усиления 239. 245
— фазы линии 523
— Формы кривой 307 725
Коэффициенты ряда Фурье 300
— четырехполюсника 214
Кривая намагничивания 602
— резонансная 177
Критерий Сильверста 418
— устойчивости 710
Критическое сопротивление 346
Круговая диаграмма 202
Крутизна характеристики 239
Л
Лампа электронная 579
Ламповые генераторы 715
Лапласа преобразованне 728
Линии входное сопротивление 526
— дифференциальные уравнения 514 551
— короткое замыкание 533
— COI ласованная нагрузка 529
— схема замещения 548
— уравнения с гиперболическими функциями 520
— холостой ход 533
Линия без потерь 538
— возду ш н а я 539
— длинная 513
— измерительная 546
— искусственная 452
— кабельная 539
— как согласующий трансформатор 545
— — четырехполюсник 548
— неискажающая 531
— однородная 513
— передач и 17
— трехфазная 273
Логарифмический декремент колебаний 351
М
Магнит постоянный 614
Магнитная индукция 601
— постоянная 601
— проводимость 603
— проницаем-ють абсолютная 601
— — дифференциальная 683
— — комплексная 656
— — обратимая 684
— — относительная 601
— — статическая 683
— цепь 600
— — неразветвленная 607
— — разветвленная 610
— — условно нелинейная 655
Магнитное напряжение 604
— поле вращающееся 277
— потокосцепление 374
— сопротивление 604
Магнитно мягкий материал 607
Магиитиыи гистерезис 602
— поток 600
— — основной 603
— — рассеяния 604
— усилитель 685
Магнитодвижущая (намагничивающая) сила (м д с ) 604
Магнитодиэлектрик 649
Магнитопровод 614
Матрица контурных сопротивлений 54
— связи переменных состояния 412
— соединении 53
— узловая 39. 248
Матричные уравнения Кирхгофа 30
— — контурных токов 52
— — уззовых потенциалов 41
— — четырехполюсника 236
Мгновенная мощность 133
Мгновенное значение 109
Мезона формула 174
Метод аналитическом аппроксимации 690
— гармонического баланса 677. 722
— графического интегрирования 694
— графоаналитический 610
- — двух узлов 40
— изоклин 705
— итерационный 594
— - Кауэра 498, 509
— комплексных амплитуд (величин) 113
— контурных токов 44, 167
— кусочно линейной аппроксимации 691
— переменных состояния 408
— последовательных интервалов 692, 696
— — приближений 594
— разложения в бесконечный ряд 417
— симметричных составляющих 280
— топологический 76
— трэпецнц 432
— узловых потенцнапов 32. 166
— условной линеаризации 689, 695
— Фостера 495. 505
— частотный расчета переходных процессов 424
Методы синтеза электрических цепей 495
Минимально фазовые цепи 484
Многоугольник 58, 218
Многофазная система цепей 256
Модулированные колебания 310, 681
Модуляция амплитудная ЗЮ
— импульсная 312
— фазовая 310
— частотная 310
Мостовая схема выпрямителя 634
Мостовой четырехполюсник 510
Мощности баланс 21, 138
— измерение 276
Мощность 13, 133 137
— активная 134
— активного двухполюсника 103
— источника 13, 104
737
Мощность комплексная 136
— максимальная 103. 143
— мгновенная 133
— намагничивающая 650
— иесииусоидального тока 322
— полная 134
— потерь в стали 650
— — от вихревых токов 649
— — — гистерезиса 649
— приемника 13, 650
— реактивная 134
— средняя за период 134
— трехфааной цепи 262
Н
Нагрузка согласованная 529
Наложение волн 517, 569
Наложения принцип 67
Намагничивания кривая 602
Наматиичивающая сила (н с) 604
Намагничивающий ток 607
Напряжение анодное 237
— комплексное 121
— линейное 260, 325
— магнитное 604
“ мгновенное 1I8
— несинусоидальное 297
— сеточное 237
— смещения 240
— фазное 260, 325
Напряженность магнитного поля 601
Начальная фаза 109
Начальные условия 331
— — нулевые и ненулевые 404
Неискажающая линия 531
Нейтральная точка 261
Нейтральный провод 261
Нелинейная индуктивность 638
— цепь 578
Нелинейный двухполюсник 619
— четырехполюсник 619
— элемент симметричный и несимметричный 578
Неминимально фазовые цепи 484
Непер 449
Неразветвленная магнитная цепь 607
— электрическая цепь 20
Несвязанная трехфазная цепь 257
Несимметричные трехфазные цепи 268, 289
— фильтры 477
— четырехполюсники 217, 443
Несимметрия поперечная и продольная 289
Несииусоидальные токи 297
Несущая частота 310
Неустойчивые фокус и узел 717
Низкочастотный фильтр 456
Нулевая последовательность 280
О
Области пропускания и непропускания фильтра 455
Обмоткн трансформатора, первичная и вторичная 200
Обратимая магнитная проницаемость 684
Обратная волна 517, 553
— последовательность фаз 258
Обратное преобразование Лапласа 385
— . — Фурье 426
Общая проводимость узла 35
Общее контурное сопротивление 50
Однополупериодное выпрямление 632
Однородная линия 513
Оператор поворота 122
Операторная проводимость 390
— схема 393
Операторное изображение функций времени 384
— сопротивление 390
Операторный метод расчета переходных процессов 383
Опережение по фазе 120
Опыты короткого замыкания и холостого хода 217, 230
Оригинал функции времени 384
Основная кривая намагничивания 602
— синусоида 299
— частота 299
Основной магнитный поток 603
Остаточная индукция 602
Отражение воли 528, 561
Отставание по фазе 120
П
Падающая волна 554
Падение напряжения 12
Параллельное соединение 151
— — трансформаторов 232
— — четырехполюсников 234
Параллельный колебательный контур 180
Параметрон 677
Параметры катушкн 148
— конденсатора I46
— линии 514
— распределенные 513
— резистора 148
— четырехполюсника вторичные 446
Пассивные двухполюсники 95, 131
— четырехполюсники 214
— элементы цепи 17
Первичная обмотка трансформатора 200
Первичные параметры линии 514
Первый закон Кирхгофа 24, 119
Передаточная функция четырехполюсника 484
Передача ветви 165
— контура 170
— максимальной мощности 143
— пути 170
— электрической цепи 85
— энергии 197
Переменные состояния 408
Переменный ток 106
Переход волны 569
— рп 244
Переходная проводимость 361
— функция цепи 361
Переходные процессы 328, 687
— — в линии 551
— — — нелинейной цепи Ь87
Период несинусоидального тока 298
— переменного тока 106
— собственных колебаний 349
Петля гистерезиса 602
Пилообразная функция 421
П образные фильтры 457
— четырехполюсники 221
Поверхностный эффект 145
Поле магнитное вращающееся 227
Полная мощность 134
— проводимость 128
Полное сопротивление 123
Положительная вещественная функция 489
Положительные направления тока, напряжения 19, 107
Полоса пропускания контура 179
Полосный фильтр 466
Полупроводниковый триод (транзистор) 243
Полюс функции 489
Полярная форма записи комплексного числа 112
Поперечная несимметрия 289
Последовательное соединение приемников 149
— — четырехполюсников 236
Последовательности прямая, обратная и
нулевая 280
— фаз 238
Последовательный контур 175
Постоянная времени цепи 332
— магнитная 601
— составляющая 299
738
Постоянная передачи 443, 447
Постоянные передачи, вносимая и рабочая 450
Постоянный магнит 614
— электрический ток 11
Потенциал 12, 20
Потенциальная диаграмма 21
Потери в стали 650
— от вихревых токов 649
— — гистерезиса 649
Поток магнитный 402, 600
— рассеяния 402
Потокосцепление 374
Предельный цикл 717, 721
Преломленная волна 554
Преобразование графа 167
— Карсона —Хевисайда 385
— Лапласа 383, 440, 728
— параллельного соединения ветвей с источниками 62
— соединения звездой и треугольником 58
— схемы с двумя узлами 40
— Фурье 424, 427. 440
Преобразователь постоянного тока в переменный 667
Приемник энергии 11
Принужденный процесс (режим) 329, 420
Принцип взаимности 70
— наложения 67
Провод нейтральный 260
Проводимость 14, 16
— активная 128
— взаимная 71
— внутренняя 16
— входная 71
— единицы длины линии 515
— емкостная 129
— индуктивная 129
— комплексная 128
— общая узловая 35
— операторная 390
— переходная 361
— полная 128
— реактивная 128
— собственная узловая 35
Продольная иесимметрия 289
Проницаемость магнитная 601
— — комплексная 65b
Проходящая волна 554
Процессы принужденный и свободный 328
Прямая волна 517, 553
— последовательность фаз 258
Прямое преобразование Лапласа 384
— — Фурье 426
Прямоугольный фронт волны 554
П схема 451, 549
Путь передачи 85
Пучность стоячей волны 541
Р
Рабочая постоянная передачи 451
Рабочее затухание 451
Разветвленная магнитная непь 6i0
— электрическая цепь 23
Развязка индуктивных связей 195
Разделение потерь в стали 650
Размагничивания кривая 615
Размагничивающий коэффициент 615
Разметка зажимов ваттметра 142
— — взаимной индуктивности 187
Разность фаз напряжения и тока 124
Разряд конденсатора апериодический 345
— — колебательный 349
— линии 574
Распределенные параметры 513
Распространение воли в линии 516, 551
Реактивная мощность 135
— проводимость 128
— составляющая напряжения 131
— — тока 132
Реактивное сопротивление 123
Реактивный двухполюсник 491
— четырехполюсник (фильтр) 455
Режим короткого замыкания и холостого хода трансформатора 227, 230
— — — — — — четырехполюсника 217
— принужденный (установившийся) 329
Резистор нелинейный 708
Резонанс 175
— амплитудный 177
— в сложных цепях 183
— напряжений 175
— при несинусоидальных э д с. и токах 319
— токов 180
— фазовый 177
Резонансная кривая 177
— частота 176, 181
Релаксационные колебания 712
Ряд тригонометрический (Фурье) 724
С
Свободные колебания 349
Свободный процесс 329
Свойства преобразования Лапласа 386
— — Фурье 424
Свойство взаимности 70
Связанная многофазная система 257
Связь емкостная 241
— индуктивная 184
Сдвиг фаз 110
Сегнетоэлектрик 641
Сетка 237
Сигнальный граф 163
Симметричная многофазная (трехфазная) цепь 261
— петля гистерезиса 602
— система э д с 259
Симметричные составляющие трехфазной системы 280
Симметричный фильтр 456
— четырехполюсник 217 447
Синтез двухполюсников без потерь (реак тивных) 495
— — с потерями 505
— четырехполюсников 510
— электрических цепей 23 483
Синусоида эквивалентная 649
Синусоидальный ток 109
Синхронный двигатель 280
Системы прямой, обратной и нулевой последовательностей 280
Скорость волны 551
— света 539
— фазовая 516, 539
Смешанное соединение 152, 583
Собственная проводимость узла 35
Собственные колебания 349
Согласное включение индуктивно связан-*
пых элементов 189
Согласованная нагрузка 529
Согласованный режим 444
Соединение графов 233
— звездой 259
— каскадное 215, 232, 451
— многоугольником 259
— параллельное 151, 191. 232, 583
— последовательное 149, 189. 581
— смешанное 152, 583
— треугольником 259
— четырехполюсников 233
Соотношения линейные 91
Сопротивление активное 116, 123
— взаимное 71
— взаимной индукции 188
-- вносимое 201
— внутреннее 12, 95, 239
— волновое 516, 552
— входное ветви 71
— — двухполюсника 95
739
Сопротивление входное линии 526 '
— — четырехполюсника 218, 443
— дифференциальное 579, 622, 7Ю
— емкостное 123
— индуктивное 123
— комплексное 123
— контурное общее 50
— — собственное 50
— короткого замыкания и холостого хода 218, 526
— критическое 346
— ма! нитное 604
— нелинейное 638
— отрицательное 712
— операторное 390
— полное 123
— приведенное 231
— приемника 13
— реактивное 123
— статическое 579
— характеристическое контура 176
— фазное 260
— — четырехполюсника 443, 447
Сопротивления для токов различных последовательностей 284
Спектр амплитуд 302
— дискретный 302
— непериодической функции 425
— непрерывный 425
— периодической функции 302
— прямоугольных импульсов 302
— частотный 426, 730
Среднее зиачение пеРи°Дическс>й функции
— квадратичное 305
— по модулю 305
Стабилизация напряжения 585, 662
Статическая индуктивность 683
Статическое сопротивление 579
Сток сигнального графа 164
Стоячая волна 541
Схема замещения J2
— мостовая 510
— с двумя узлами 40
— цепная 499
— эквивалентная активного четырехполюсника 222
— — без индуктивных связей 202
— — индуктивной катушки 148
— — катушки со стальным магиитопро-водом 653
— — конденсатора 146
— — лампового триода 240
— — операторная 393
— —gC идеальными трансформаторами
— — — источниками э. д с 585
— — транзистора 245
— — трансформатора со стальным магнитол роводом 229
— — четырехполюсника 220
Схемы прямой, обратной и нулевой последовательностей 285
— эквивалентные источников 14, 22
— — П- и Т образные 220
Т
Таблица оригиналов и изображений 728
Теорема вариации 95
— о взаимных приращениях 94
— — компенсации 90
— об активном двухполюснике 9ь
— — эквивалентном генераторе 98
— разложения 387
— свертки 370
Терморезистор 578, 620, 645
Тесла 608
Тлеющий разряд 578
Т образный фильтр 459
— четырехполюсник 221, 451
Ток анодный 237
— гармонический 107
— действующий 110
— комплексный 125
— контурный 46
— линейный 261
— мгновенный 106
— несинусоидальиый 297
— переменный 106
— переходный 329
— постоянный 11
— принужденный 329
— свободный 329, 406
— сеточный 237
— синусоидальный 107
— фазный 260
Токи вихревые 648
— короткого замыкания и холостого хода 217, 534
Топографические диаграммы 157, 261
Точка нейтральная 260
— рабочая 622
Траектория фазовая 717
Транзистор 243, 579
Трансформатор воздушный 199
— идеальный 226
— сопротивлений 445
— со стальным магнитопроводом 229
— четвертьволновый 545
Треугольник мощностей 137
— напряжений 131
— проводимостей 132
— сопротивлений 58, 131
— токов 132
Трехлучевзя звезда 60, 259
Трехфазная линия 273
— система 259
— цепь несимметричная 267
— — симметричная 268
Трехфазный выпрямитель 635
— генератор 257
Трехэлектродная лампа 237
Тригонометрическая форма комплексного числа 112
Триод ламповый 237
— полупроводниковый (транзистор) 243
Т схема 451, 549
У
Угловая частота 109
— — собственных колебаний 349
Угол потерь конденсатора 147
— сдвига фаз 124
Удвоитель частоты 673
Узел (вершниа) трафа 30
— неустойчивый 717
— устойчивый 705
— электрической цепи 24
Узловая матрица 39
Узловые потенциалы 32
— уравнения 35, 165
Узлы н ветви сигнального графа 164
— стоячих волн 541
Уравнение характеристическое 345
Уравнения дифференциальные 356
— Кирхгофа 24
— — в комплексной форме 148
— — — операторной форме 390
— контурных токов 50, 165
— матричные 42, 52
— однородной линии в дифференциальной форме 514, 551
— — — в комплексной форме 515
— — — с гиперболическими функциями 520
— состояния цепи 55
— трансформатора 200
— узловые 35
— узловых потенциалов 41
— четырехполюсника 214
740
Усилитель мощности магнитный 685
Условие Дирихле 299
Установившийся режим 329
Устойчивость 710
Устойчивые узел и фокус 705
У трои гель частоты 642
Ф
Фаза минимальная 484
— начальная 109
— приемника 260
— тока, напряжения, э д. с 109, 124
Фазное напряжение 260, 325
Фазный множитель 281
— ток 260
Фазовая модуляция 310
— плоскость 701
— скорость 516, 539
— траектория 702, 717
Фазоуказатель 273
Фазочастотная характеристика 485
Феррит 649
Ферромагнитный материал 601
— резонанс напряжений 659
— — токов 660
Феррорезоиансный стабилизатор 663
Фильтр 454
— безындукционный 479
— высокочастотный 464
— Г-образный 477
— заграждающий 470
— идеальный 455
— несимметричный 477
— низкочастотный 456
— П- и Т-образныи 457
— полосный 466
— постоянной М 471
— симметричный 457
— частотный 443
Фокус неустойчивый 717
— устойчивый 705
Формулы включения 407
— Дюамеля 361
— топологические 85
Фостера метод 459, 505
Фронт волны 553
Функция временная 361
— Дирака 369
— единичная 368
— переходная 361
— положительная вещественная 489
Фурье преобразования (прямое и обратное) 427
— ряд 299
X
Характеристика анодная 237
— вебер амперная 619
— внешняя 13
— временная 361. 368
— вольт-амперная 14, 579, 587
— динамическая 619
— импульсная 368
— кулон вольтная 619
— линейная 14
— нелинейная 579
— несимметричная 621
— сеточно анодная 237
— симметричная 621 ,
— статическая 619
— частотная 177, 182, 493
Характеристики типа S и N 708
Характеристические сопротивления четырехполюсника 443, 447
Характеристическое сопротивление контура 176
— уравнение 345
Холостой ход линии 526
— — трансформатора 228
— — четырехполюсника 217
Ц
Центр 705
Цепные схемы 451
Цепочка дифференцирующая 718
Цепь дуальная 159
— линейная 14. 56
— магнитная 660
— многофазная 256
— нелинейная 14
— неразветвленная 581
— переменного тока 106
— постоянного тока 11
— г, С 339
— г, L 331
— г, L, С 344
— с распределенными параметрами 513
— трехфазная 256
Цикл предельный 717, 721
— частный гистерезисный 602
Ч
Частный гистерезисный цикл 602
Частота биении 310
— боковая 310
— модулирующая 310
— несущая 310
— основная 299
— периодического тока 106
— резонансная 176, 181
—- собственных колебаний 349
— угловая 109
Частотные характеристики 432
— — амплитудные 435
— — неразветвлениной цепи 177
— — параллельного контура 182
— — реактивного двухполюсника 493
— — фазовые 435
— — фильтра 458
Частотный метод расчета переходных процессов 424
— спектр 426, 730
— фильтр 443
Чередование фаз 258
Четвертьволновый трансформатор 545
Четырехполюсник 213
— активный 214, 591
— минимальной фазы 484
— мостовой 510
— нелинейный 619
— несимметричный 217. 443
— пассивный 214
— П-образный 220, 452
— симметрич'ный 217, 447
— Т образный 221, 452
Четырехполюсника коэффициенты 214
— синтез 5Ю
— уравнения с гиперболическими функциями 447
Четырехполюсников соединение 233
Э
Электрических схем преобразование 56
Электродвижущая сила 12
— — взаимной индукции 186
— — несинусоидальная 297
— — самоиндукции И6
Электронные лампы 579
Элемент активный 17
— безынерционный 630
— нелинейный 578
— пассивный 17
— условно нелинейный 645
— электрической цепи 11
Эмиттер (транзистора) 244
Энергия активная 13b
— реактивная 133
Эффект близости 144
— поверхностный 144
741
ОГЛАВЛЕНИЕ
Предисловие к четвертому изданию .................................. 3
Введение......................................................... 5
Раздел первый.
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ
ПАРАМЕТРАМИ
Глава первая
Основные законы и методы расчета электрических цепей при постоянных токах и напряжениях
1-1. Элементы электрических цепей и электрических схем............ 11
1-2. Эквивалентные схемы для источников энергии................... 14
1-3. Закрн Ома для участка цепи с э. д. с......................... 18
1-4. Распределение потенциала вдоль неразветвленной электрической цепи.......................................................... 20
1-5. Баланс мощностей для простейшей неразветвленной цепи .... 21
1-6. Применение законов Кирхгофа для расчета разветвленных цепей ........................................................ 23
1-7. Метод узловых потенциалов.................................... 32
1-8. Метод контурных токов........................................ 44
1-9. Уравнения состояния цепи в матричной форме . . ............. 55
1-10. Преобразование линейных электрических схем.................. 56
Глава вторая
Основные свойства электрических цепей при постоянных токах и напряжениях
2-1. Принцип наложения............................................ 67
2-2. Свойство взаимности.......................................... 70
2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов................... 71
2-4. Применение топологических методов для расчета цепей.......... 76
2-5. Топологические формулы и правила для определения передачи электрической цепи ........................................... 85
2-6. Теорема о компенсации........................................ 90
2-7. Линейные соотношения между напряжениями и токами............. 91
2-8. Теорема о взаимных приращениях токов и напряжений............ 94
2-9. Общие замечания о двухполюсниках............................. 95
2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей........................................... 96
2-11. Передача энергии от активного двухполюсника к пассивному . . . ЮЗ
Глава третья
Основные понятия о цепях синусоидального тока
3-1. Переменные токи............................................. 106
3-2. Понятие о генераторах переменного тока..................... 108
3-3. Синусоидальный ток.......................................... 109
3-4. Действующие ток, э. д. с. и напряжение................. . 110
3-5. Изображение синусоидальных функций времени векторами и комплексными числами............................................. 111
3-6. Сложение синусоидальных функций времени..................... 114
742
3-7. Электрическая цепь и ее схема................................ 115
3-8. Ток и напряжения прн последовательном соединении сопротивления, индуктивности и емкости............................... 119
3-9. Сопротивления................................................ 123
3-10. Разность фаз напряжения и тока.............................. 124
3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости...................................... 227
3-12. Проводимости................................................ 128
3-13. Пассивный двухполюсник...................................... 131
3-14. Мощности.................................................... 133
3-15. Мощности в сопротивлении, индуктивности и емкости........... 137
3-16. Баланс мощностей............................................ 138
3-17. Знаки мощностей и направление передачи энергии.............. 140
3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра..............'............ 142
3-19. Условия передачи максимальной мощности от источника энергии к приемнику.................................................. 143
3-20. Понятие о поверхностном эффекте и эффекте близости.......... 144
3-21. Параметры и эквивалентные схемы конденсаторов............... 146
3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов........................................................ 148
Глава четвертая
Расчет цепей при синусоидальных токах
4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока................................... 148
4-2. Последовательное соединение приемников....................... 149
4-3. Параллельное соединение приемников........................... 151
4-4. Смешанное соединение приемников.............................. 152
4-5. Сложные разветвленные цепи................................... 155
4-6. Топографические диаграммы.................................... 157
4-7. Дуальность электрических цепей............................... 159
4-8. Сигнальные графы и их применение для расчета Цепей........... 163
Глава пятая
Резонанс в электрических цепях
5-1. Резонанс в неразветвленной цепи.............................. 175
5-2. Частотные характеристики неразветвленной цепи................ 177
5-3. Резонанс в пепи с двумя параллельными ветвями................ 180
5-4. Частотные характеристики параллельного контура............... 1#2
5-5. Понятие о резонансе в сложных цепях.......................... 183
Глава шестая
Цепи с взаимной индуктивностью
6-1. Индуктивно связанные элементы цепи..................... 184
6-2. Электродвижущая сила взаимной индукции................. 186
6-3. Последовательное соединение индуктивно связанных элементов
цепи.................................................... 189
6-4. Параллельное соединение индуктивно связанных элементов
цепи.................................................... 191
6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности 192
6-6. Эквивалентная замена индуктивных связей................‘195
6-7. Передача энергии между индуктивно связанными элементами
цепи ........................................................ 197
6-8. Трансформатор без стального сердечника (воздушный трансформатор) 199
743
Г лава седьмая
Круговые диаграммы
7 1 Комплексные уравнения прямой и окружности......................... 202
7 2 Круговые-диаграммы для неразветвленной цепи и для активного двухполюсника .............................................. 204
7-3 Круговые диаграммы для любой разветвленной цепи................... 208
Г шва восьмая
Многополюсники и четырехполюсники при синусоидальных токах и напряжениях
8-1 Четырехполюсники и их основные уравнения . . ... 213
8-2 Определение коэффициентов четырехполюсников . ....... 217
8 3 Режим четырехполюсника при нагрузке ....................... . 219
8 4 Эквивалентные схемы четырехполюсников . 220
8 5 Основные уравнения и эквивалентные схемы для активного четырехполюсника ............................................... 224
8 6 Идеальный трансформатор как четырехполюсник ...................... 226
8 7 Эквивалентные схемы с идеальными трансформаторами для четырехполюсника . . 228
8 8 Эквивалентные схемы трансформатора со стальным магнитопроводом 229
8-9 Расчеты электрических цепей с трансформаторами .... 231
8 10 Графы пассивных четырехполюсников и их простейшие соединения ........................................................ 233
Глава девятая
Цепи с электронными и полупроводниковыми приборами в линейном режиме
9 1 Ламповый триод и его параметры ... . . .... 237
9-2 Эквивалентные схемы лампового триода . . . 240
9 1 Транзисторы (полупроводниковые триоды) . 243
0 4 Эквивалентные схемы транзисторов ............................... 245
9-5 Простейшие электрические цепи с невзаимными элементами и их направленные графы ......................................... 217
Г шва десятая
Трехфазные цепи
10 1 Понятие о многофазных источниках питания и о многофазных цепях ............. ..................... . 256
10-2 Соединения звездой и многоугольником . 259
10-3 Симметричный режим трехфазной цепи............................... 261
10-4 Некоторые свойства трехфазных цепей с различными схемами со единений.................................................... 263
10-5 Расчет симметричных режимов трехфазиых цепей ... . 267
10-6 Расчет несимметричных режимов трехфазных цепей со статической нагрузкой .................................................. .... 268
10 7 Напряжения на фазах приемника в некоторых частных случаях . 271
10 8 Эквивалентные схемы трехфазных линий . 273
10 9 Измерение мощности в трехфазных цепях . . . 276
10 10 Вращающееся магнитное поле............................... . 277
10 II Принципы действия асинхронного и синхронного двигателей . . . 279
Г iae I одиннадцатая
Метод симметричных составляющих
11 I Симметричные составляющие трехфазной системы величин . . . 280
11 2 Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений............................. 282
744
11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей ...................................... 284
11 -4. Определение токов в симметричной цепи ...................... 287
11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи........................................... 289
11-6. Расчет цепи с несимметричной нагрузкой....................... 289
11-7. Расчет цепи с несимметричным участком в линии................ 294
Глава двенадцатая
Несинусоидальные токи
12-1. Несинусоидальные э. д. с., напряжения и токи................ 297
12-2 Разложение периодической иесинусоидальной кривой в триюно-метрический ряд............................................. 299
12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов.............. 305
12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых............................................. 307
12-5. Несинусоидальные кривые с периодической огибающей........... 309
12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими............................................ 313
12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами ....................................................... 314
12-8. Резонанс при несинусоидальных э. д. с. и токах.............. 319
12-9. Мощность периодических несинусоидальных токов............. 322
12-10. Высшие гармоники в трехфазных цепях........................ 324
Глава тринадцатая
Классический метод расчета переходных процессов
13-1. Возникновение переходных процессов и законы коммутации . . . 327
13-2. Переходный, принужденный и свободный процессы................ 329
13-3. Короткое замыкание цепи г, L................................. 331
13-4. Включение цепи г, L на постоянное напряжение............. 334
13 5. Включение цепи г, L на синусоидальное напряжение........... 336
13-6. Короткое замыкание цепи г, С................................. 339
13-7. Включение цепи г, С на постоянное напряжение............... 340
13-8. Включение цепи г, С на синусоидальное напряжение........... 342
13-9. Переходные процессы в неразветвленной цепи г, L, С........... 344
13-10. Апериодический разряд конденсатора.......................... 345
13-11. Предельный случай апериодического разряда конденсатора . . . 348
13-12. Периодический (колебательный) разряд конденсатора........... 394
13-13. Включение цепи г, L, С на постоянное напряжение............. 852
13-14. Общий случай расчета переходных процессов классическим методом .......................................................... 354
13-15. Включение пассивного двухполюсника на непрерывно изменяю-
щееся напряжение (формула или интеграл Дюамеля).............. 361
13-16. Включение пассивного двухполюсника на напряжение любой формы 364
13-17. Временная и импульсная переходные характеристики............ 368
13-18. Запись теоремы свертки при помощи импульсной переходной характеристики ................................................. 370
13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах..................................... 372
13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока . . . 381
745
Глава четырнадцатая
Операторный метод расчета переходных процессов
14-1. Применение преобразования Лапласа к расчету переходных процессов .................................................... 383
14-2. Законы Ома и Кирхгофа в операторной форме................ 388
14-3. Эквивалентные операторные схемы .............................. 393
14-4. Переходные процессы в цепях с взаимной индуктивностью .... 399
14-5. Сведение расчетов 'переходных процессов к нулевым начальным условиям................................................... 404
14-6. Определение свободных токов по их изображениям........... 406
14-7. Формулы включения........................................ 407
14-8. Расчет переходных процессов методом переменных состояния . . . 408
14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения................ 420
Глава пятнадцатая
Частотный метод расчета переходных процессов
15-1. Преобразование Фурье и его основные свойства.................. 424
15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров................................................... 427
15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций)...............х....... 432
15-4. О переходе от преобразований Фурье к преобразованиям Лапласа ...................................................... 440
15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях................................... . .441
Глава шестнадцатая ’
Цепные схемы и частотные электрические фильтры
16-1. Характеристические сопротивления и постоянная передачи несимметричного четырехполюсника ............................... 443
16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника ............................... 447
16-3. Вносимая и рабочая постоянные передачи ....................... 450
16-4. Цепные схемы.................................................. 451
16-5. Частотные электрические фильтры............................... 454
16-6. Низкочастотные фильтры...................................... 456
16-7. Высокочастотные фильтры....................................... 464
16-8. Полосные фильтры.............................................. 466
16-9. Заграждающие фильтры.......................................... 470
16-10. Фильтры постоянной М ........................ 471
16-11. Г-образный фильтр как пример несимметричного фильтра .... 477
16-12. Безындукционные (илн г, С) фильтры........................... 479
Глава семнадцатая
Синтез электрических цепей
17-1. Общая характеристика задачи синтеза........................... 483
17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы...............«....................................... 484
17-3. Входные функции цепей. Положительные вещественные функции 489
17-4. Реактивные двухполюсники...................................... 491
17-5. Частотные характеристики реактивных двухполюсников........ 493
17-6. Синтез реактивных двухполюсников. Метод Фостера............... 495
17-7. Синтез реактивных двухполюсников. Метод Кауэра................ 498
17-8. Синтез двухполюсников с потерями. Метод Фостера............... 505
17-9. Синтез двухполюсников с потерями. Метод Кауэра................ 509
17-10. Понятие о синтезе четырехполюсников.......................... 510
746
Раздел второй ЛИНЕЙНЫЕ ЦЕПН С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Глава восемнадцатая
Гармонические процессы в цепях с распределенными параметрами
18-1. Токи и напряжения в длинных линиях........................... 513
18-2. Уравнения однородной линии................................... 514
18-3. Установившийся режим в однородной линии...................... 515
18-4. Уравнения однородной линии с гиперболическими функциями . . . 520
18-5. Характеристики однородной линии.............................. 523
18-6. Входное сопротивление линии.................................. 526
18-7. Коэффициент отражения волны.................................. 528
18-8. Согласованная нагрузка линии................................. 529
18-9. Линия без искажений.......................................... 531
18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями........................................................ 533
18-11. Линии без потерь............................................ 538
18-12. Стоячие волны............................................... 541
18-13. Линия как четырехполюсник................................... 548
Глава девятнадцатая
Переходные процессы в цепях с распределенными параметрами
19-1. Возникновение переходных процессов в цепях с распределенными параметрами ................................................ 551
19-2. Общее решение уравнений однородной линии..................... 551
19-3. Возникновение волн с прямоугольным фронтом................... 554
19-4. Общие случаи нахождения волн, возникающих при переключениях ............................................................. 559
19-5. Отражение волны с прямоугольным фронтом от конца линии . . . 561
19-6. Общий метод определения отраженных волн...................... 563
19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности........... 569
19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления....................................... 571
19-9. Блуждающие волны............................................. 576
Раздел III
Нелинейные цепи
Глава двадцатая
Нелинейные электрические цепи при постоянных токах и напряжениях
20-1. Элементы и эквивалентные схемы простейших нелинейных цепей .............................................................. 578
20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами........................................................ 581
20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов.............................................. 583
20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов................................... 583
20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей............................. 585
747
20-6. Вольт-амперные характеристики нелинейных активных двухполюсников ..................................................,........ 587
20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами..................................................... 588
20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами.................................................... 591
20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений)........................ 594
Глава двадцать первая
Магнитные цепи при постоянных токах
21-1. Основные понятия и законы магнитных цепей...................... 600
21-2. Расчет неразветвленных магнитных цепей......................... 607
21-3. Расчет разветвленных магнитных цепей........................... 610
21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором .................................................. 614
21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом................................................ 617
Г лава двадцать вторая
Общая характеристика нелинейных цепей переменного тока и методов Их расчета
22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах................................................... 619
22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников................................ 622
22-3. Явления в нелинейных цепях переменного тока.................... 625
22-4. Методы расчета нелинейных цепей переменного тока............... 626
Г лава двадцать третья
Нелинейные цепи с источниками э. д. с. и тока одинаковой частоты
23-1. Общая характеристика цепей с источниками э. д. с. одинаковой частоты............................................................. 629
23-2. Форма кривой тока в цепи с вентилями .......................... 630
23-3. Простейшие выпрямители......................................... 632
23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями....................................... 638
23-5. Утроители частоты.............................................. 642
23-6. Формы кривых тока и напряжения в цепях с терморезисторами . . . 645
23-7. Замена реальных нелинейных элементов условно-нелинейными . . . 647
23-8. Учет реальных свойств стальных магнитопроводов................. 647
23-9. Расчет тока в катушке со стальным магнитопроводом.............. 653
23-10. Понятие о расчете условно-нелинейных магнитных цепей........ 655
23-11. Явление феррорезонанса........................................ 658
23-12. Стабилизаторы напряжения ................................... 662
Глава двадцать четвертая
Нелинейные цепи с источниками э. д. с. и' тока различных частот
24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот.............................................. 664
24-2. Вентили в цепях с постоянными и переменными э. д. с............ 664
748
24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный............................... 667
24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с........................................ 669
24-5. Удвоитель частоты........................................... 673
24-6 Метод гармонического баланса................................. 677
24-7. Влияние постоянной э. д. с. на переменную составляющую тока
в цепях с нелинейными безынерционными сопротивлениями .... 679
24-8. Принцип получения модулированных колебаний............... 681
24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями........................................... 683
24-10. Магнитные усилители мощности............................... 685
Глава двадцать пятая
Переходные процессы в нелинейных цепях
25-1. Общая характеристика переходных процессов в нелинейных цепях .............................................................. 687
25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение........................................................ 688
25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение.............................................. 694
25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями ............................................................ 697
25-5. Понятие о простейших запоминающих устройствах....... 700
25-6. Изображение переходных процессов на фазовой плоскости .... 701
25-7. Колебательный разряд емкости через нелинейную индуктивность 707
Глава двадцать шестая
Автоколебания
26-1. Нелинейные резисторы со спадающим участком характеристики . . . 708
26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами ....................................................... 710
26-3. Релаксационные колебания в цепи с отрицательным сопротивлением ......................"...................................... 712
26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением ................................................... 714
26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением ........................................................... 717
26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний .......................................................... 719
26-7. Определение амплитуды автоколебаний методом гармонического баланса..................................................... 722
Приложения..................................................... 724
Список литературы ................................................ 734
Предметный указатель............................................ 735
Уважаемые читатели!
В 1976 году установлена новая форма распространения (продажи) узкоспеци альнон литературы издательства «Энергия»
Эта литература будет продаваться только через специализированный мага зии № 170 «Книга — почтой» Москниги
Ниже помещен список узкоспециальной литературы по электротехнике из плана выпуска литературы на 1976 год для оформления индивидуальных заказов
ПРОИЗВОДСТВЕННО-ТЕХНИЧЕСКАЯ ЛИТЕРАТУРА
Электрические машины и трансформаторы
План № 272
План № 273
План № 274
План № 275
План № 276
План № 277
План № 278
План № 279
План № 280
Аветисян Д А , Соколов В С , Хан В X Оптимальное проектирование электрических машин на ЭВМ J2.5 л 89 к
Алексеев А Е Тяговые электрические машины и преобразователи Изд 2 е, перераб и доп 29,5 л 1 р 72 к
Бочаров В И Беспазовые тяговые электродвигатели постоянного тока 9 л с ил 46 к
Дорожко Л И , Либкинд М С Реакторы с поперечным подмагничиванием 12,5 л с ил 64 к
Копылов И П , Панферов Ю Б Микроэлектродвигатели постоянного тока с коммутаторами на магнитоуправляемых контактах 5 л с ил 26 к
Осин И Л , Колесников В П , Юферов Ф М Синхронные микродвигатели с постоянными магнитами 12,5 л с ил 64 к
Столов Л И , Зыков Б Н Моментные двигатели с постоянными магнитами 7 л с ил 36 к
Талалов И И Параметры и характеристики явнополюсных синхронных машин 16 5 л с ил 1 р 31 к
Шелехов С А , Шелехова Т С Рольганговые двигатели серии АР. 10,5 л с ил 54 к
Серия «трансформаторы»
План № 281 Дубатов Б П Производство трансформаторов I и II габаритов. 7,5 л с ил 39 к
Электротехнические материалы и кабели
План № 282
План № 283
План № 284
План № 285
План № 286
План № 287
План № 288
Бабицкий О Ш , Лехтман Л Я Технология скрутки кабелей 7 л с ил 36 к
Горбенко Л А , Месенжник Я 3 Кабели и провода для геофизических работ 12 5 л с ил 64 к
Гроднев И И Кабели связи Изд 2 е, перераб 16,5 л с ил 98 к Кабыстина Г Ф Обмоточные провода с волокнистой изоляцией и технология их производства Изд 2 е, перераб 8 л с ил 31 к Масленникова Г Н , Харитонов Ф Я Керамика, стойкая к термоударам 14 5 л с ил 88 к
Новиков М Н , Порфиров В А Финкельштейн С И Технология производства изделии из низковольтного фарфора 12,5 л с ил 64 к Шварцман Л Г Муфты силовых кабелей высокого напряжения. 10,5 л с ил 54 к
Преобразовательная техника
План № 289 Забродин Ю С Автономные тиристорные инверторы с широтно-имп\ льсным регулированием 9 л сил 41 к
План № 290 Морговский Ю Я Импульсные системы управляемой структуры с тиристорными преобразователями 12,5 л с нл 64 к
750
Электропривод
План № 291 Аракелян А К , Афанасьев А А , Чиликин М Г В<,,гичьный электропривод с синхронным двигателем и зависимым иьвертором 15,5 л с ил 93 к ' г
План Ks 292 Демидов С В , Полищук Б Б Быстродействующий тиристорный электропривод с питанием от высокочастотного источника 8 л с ил 41 к "
План № 293 Кашкалов В И Конденсаторное торможение асинхронных двигателей 5 л с ил 26 к г
План № 294 Моделирование асинхронных электроприводов с тирИСТОрНым управлением 12,5 л с ил 64 к — Авт Л П Петров, В д Ладен-зон, Р Г Подзолов, А В Яковлев
План № 295 Петров Б И , Полковников В. А Динамические возможности следящих электроприводов 8 л с ил 41 к
План № 296 Сандлер А С , Тарасенко Л М Динамика каскадных асинхронных электроприводов 10,5 л с ил 54 к
План № 297 Тиристорные электроприводы с реверсорами 5 л сил 26 к — Авт Я Ю Солодухо, А П Богословский, С Н Плеханов, А х Шору-КОВ * *
План № 298 Электрические трансмиссии пневмоколесных транспортных средств 14,5 л с ил 88 к — Авт И С Ефремов, А П Г1пплыгин Ю М Андреев, А Б Миндлин ‘ролыгин, Светотехника
План № 299 Розенталь Э С Электроустановочные изделия для светичьников с люминесцентными лампами 5 л 26 к
План № 300 Сапожников Р А Теоретическая фотометрия Изд 3-е, пеОераб и доп 16,5 л 1 р 40 к F F Электротермия
План № 301 Мармер Э Н , Мурованная С Г Электропечи для тера)овакуум. ных процессов 12,5 л с ил 64 к
План № 302 Простяков А А Индукционные печи и миксеры для плавку , 15,5 л сил 93 к ччу1уна
Библиотека электротермиста
План № 303 Васильев С 3*, Маергоиз И И , Пушкарев Л И V экзогаза 7 л 36 к
План № 304 Кувалдин А Б Низкотемпературный индукционный нагрев стали 5 л с ил 26 к р
План № 305 Смоляренко В Д Высокомощные дуговые сталеплавильцые печи 6 л с ил 31 к
План № 306 Электропечи сопротивления с широтно-импульсным УпР,1влением с применением тиристоров 5 л с ил 26 к — Авт М И кг.„.п Я А Полищук, С Г Обухов, В М Яров _ «холкер, С аннотациями на эти книги можно ознакомиться во второй час}и плана выпуска литературы на 1976 год, который направлен во все книжные МагазИ1щ
Магазин № 170 принимает индивидуальные заказы на книг" 1976 года
Заказ оформляется на почтовой открытке в к автор, название книги (книг), количе-
Книги будхт высып >
Адрес маг
Магазин №17
Проезд-
ост. ул.
Георгий Васильевич Зевеке
Петр Афанасьевич Ионкин
Анатолий Владимирович HeiyuiuA
Сергей Владимирович Страхов
ОСНОВЫ ТЕОРИИ ЦЕПЕЙ
Редактор Б Я Жуховицкий
Редактор издательства И В Антик
Переплет художника В И Карпова Технический редактор Л А Молодцова Корректор Г А Полонская
Сдано в набор 20/111 1975 г Подписано к печати 6/Х 1975 г Т 17317, Формат 60_X90*/i6 Бумага типографская Ке 2 Усл печ л 47.
Уч-изд л 51,96 Тираж 70 000 экз Зак 19и0 Цена I р 98 коп
Издательство «Энергия», Москва, М 114, Шлюзовая наб, 10
Ордена Трудового Красного Знамени Ленинградское производственно техническое объединение «Печатный Двор» имени А М. Горького Союзполиграфпрома при Государственном комитете Совета /Министров СССР по делам издательств, полиграфии и книжной торговли, 197136, Ленинград, П-136, Гатчинская ул , 26,