2
Fuzzy Techп%gy
ББК 65.053
Рецензенты:
Академик международной академии компыотерных наук и систем,
заслуженный деятель науки и техники Украины доктор технических
наук, профессор, Б. М. rерасимов.
Доктор технических наук, профессор ю. Н. Минаев.
Доктор технических наук, npофессор А.А. Рось.
Б 77 Бочарников в.п.
Fuzzy....Технолоrия: Математические основы. Практика
моделирования в экономике.  санКт....Петер6урr: «Наука»
РАН, 2001. .... 328 с.
ISBN 966..521..082...3
в книrс рассмотрены КЛlочевые вопросы математических основ
Fuzzу"технолоrии и конкретные при меры их практической
реализации в проrраммных комплексах. РассматриваlОТСЯ подходы и
npимеры формализации нечетки данных на основе нечетких мер.
РазвиваlОТСЯ основы нечетко"интеrральноrо исчисления для обрабоки
нечетких данных. Сформулированы и решены аналитические задачи
оценки состояния, идентификации моделей и оmимизации
управления сложными динамическими системами. Описан ряд
nporpaмMHbIx комплексов, разработанных и успешно применяемых
компанией ИНЭКС (Украина) для решения конкретных
консалтинrовых задач в маркетинrс, лоrистике, валютном дилинre и
т.д. Особое внимание уделяется npактической направленности Fuzzy..
технолоrии, ее математических основ и nporpaMMHoro обеспечения
для решения аналитических зцдач в бизнесе в условиях реальной
неопределенности рынка.
Книra предназначена как для специалистов., занимаlОЩИХСЯ общими
вопросами моделирования и управления сложными динамическими
объектами, так и для практиков, фактически реluаlОЩИХ задачи
лоrистики, м аркетиHra и рекламы, бизнеспланирования, задач
формирования спроса и стимулирования сбыта.
(g Бочарников В.П., 200 l r.
(g Консалтинrовая компания «иизкс».
Запрещается полное или частичное воспроизведение
данноr"о издания Лlобым способом без соrласия
автора.
50чарнuков в.п.

Fuzzy Techп%gy
3
СОДЕРЖАНИЕ
Введение
Стр.
16
1. Анализ подходов к обработке нечетких данных в 21
аналитических задачах поддержки принятия решений
1.1. Аналитические задачи поддержки принятия решения. 22
1.2. Проблема обработки нечетких данных в аналитических 31
задачах поддержки принятия решеНИ}J.
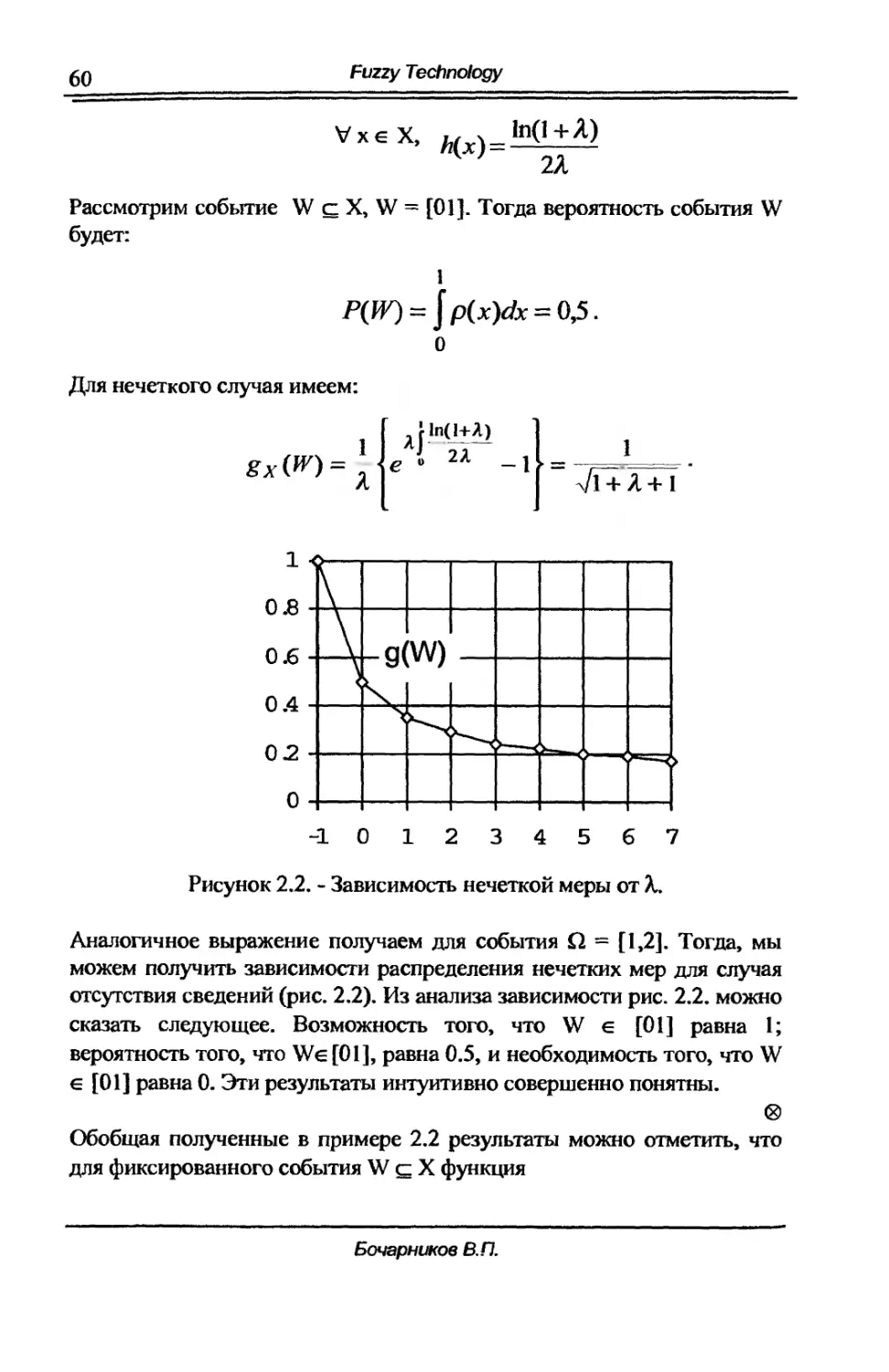
2. Представление нечетких данных на основе теории 43
нечеткой меры.
2.1. Определение и основные свойства нечеткой меры. 44
2.2. Построение нечетких мер. Семантические модальности 46
нечетких мер.
2.3. g А ....меры Суджено и их свойства. Семантические спектры. 55
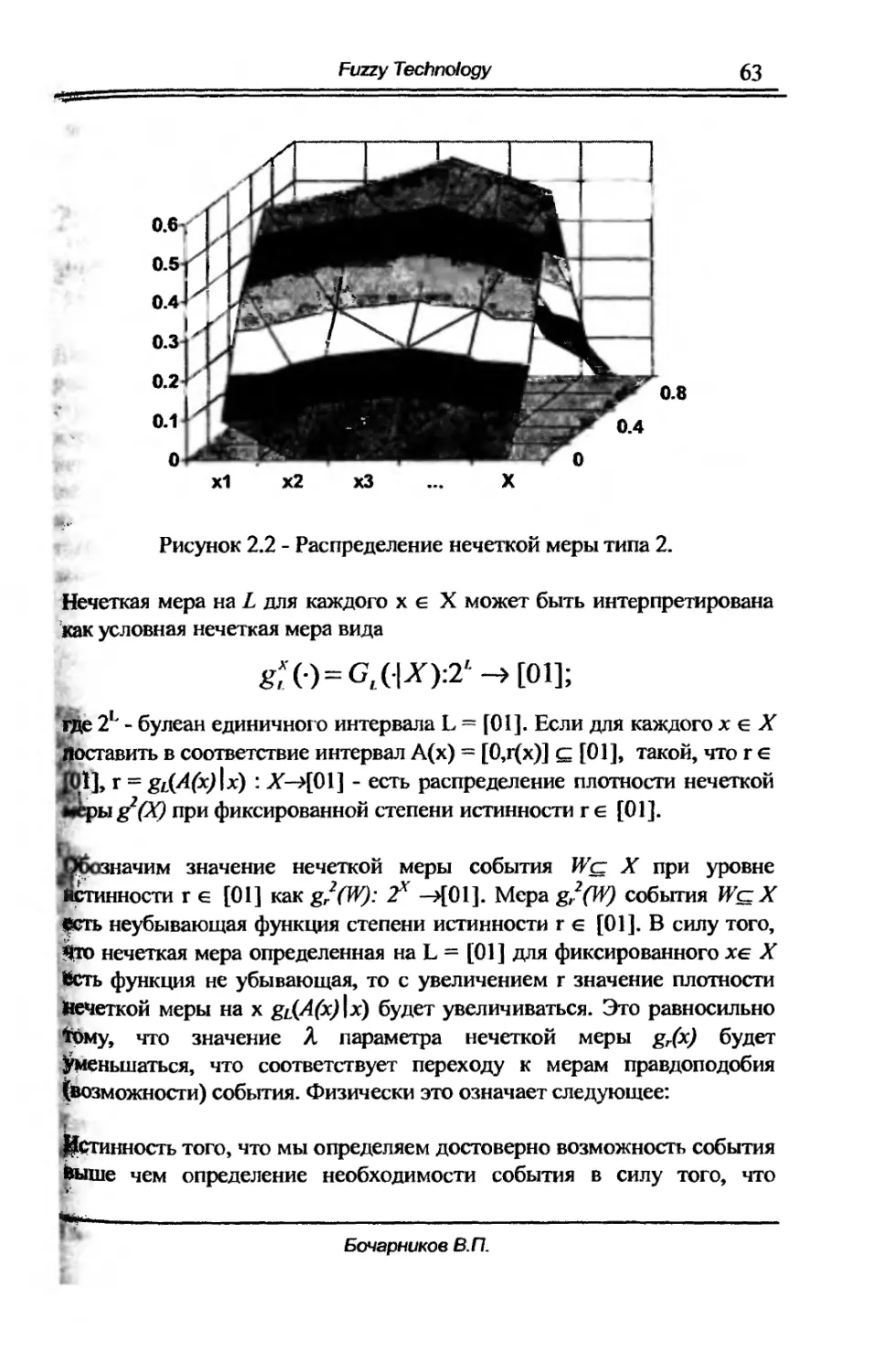
2.4. Нечеткозначные нечеткие меры и их связь с 62
семантическими модальностями.
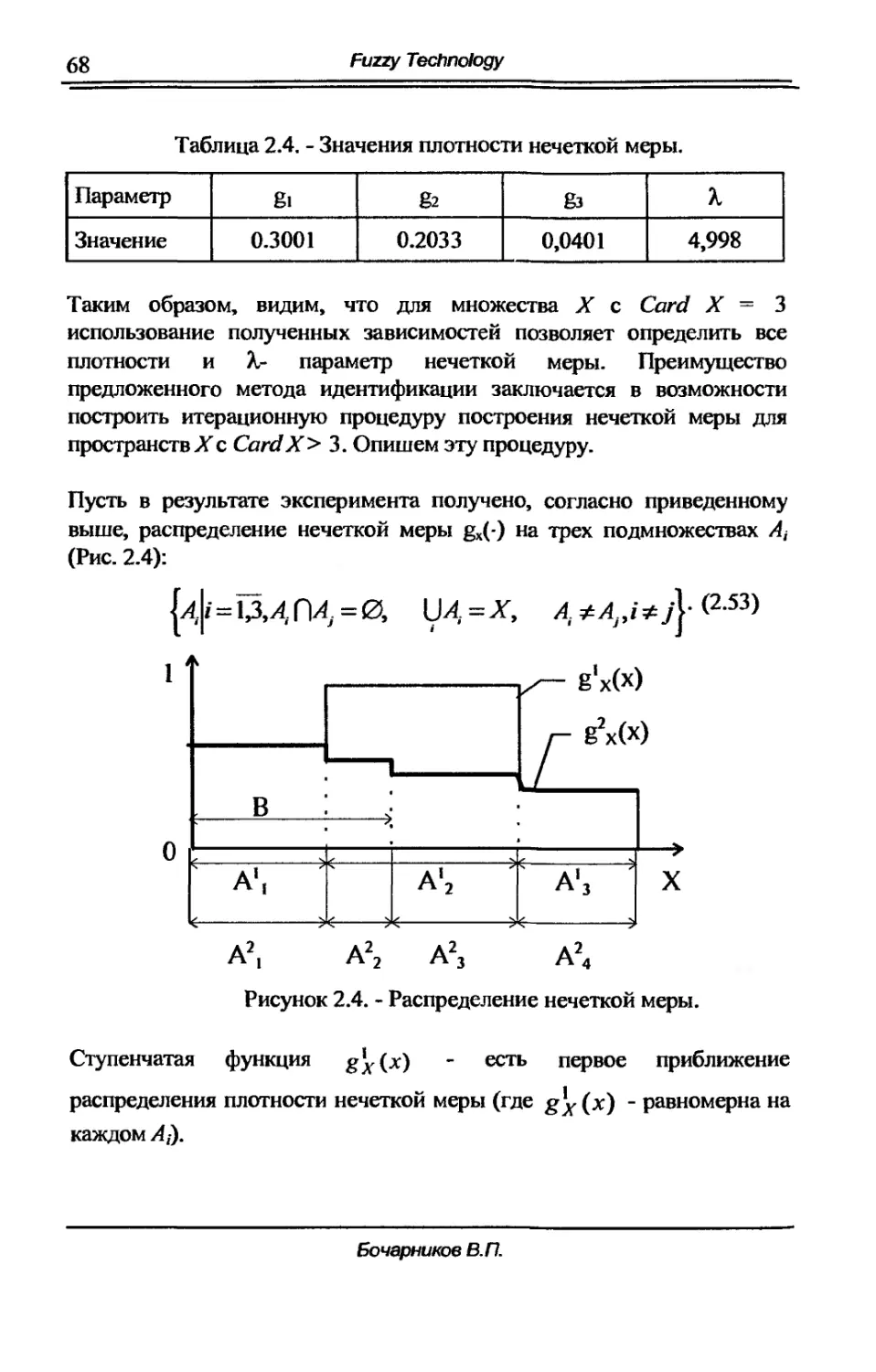
2.5. Идентификация и аппроксимация g А .... нечетких мер. 65
з. Обработка нечетких данных на основе нечетко.... 73
интеrpальноrо исчисления.
3.1. Определение нечеткоrо интеrpала. 74
3.2. Основные свойства нечетких интеrpалов. 82
3.3. Определение расширенной нечеткой меры. 87
3.4. Основная теорема о нечетком интеrpале по расширенной 91
нечеткой мере и ее следствия.
3.5. Свойства нечеткоrо интеrpала по расширенной нечеткой 97
мере.
3.6. Интеrpирование В .. измеримых функций по 102
нечеткозначной нечеткой мере.
4. Преобразования пространств с нечеткими мерами 106
4.1. Условные нечеткие меры и их свойства. 107
4.2. Нечеткие меры на декартовых произведениях 112
пространств.
Бочарнuков в.п.

4 Fuzzy Techп%gy
Стр.
4.3. Н....соответствия. Нечеткие меры доверия и правдоподобия 120
как Н....соответСтвия.
4.4. Н....операции над нечеткими мерами. 127
4.5. Нечетко....интеrpальные зависимости. 146
5. Моделирование нечетких процессов. 154
5.1. Нечеткие процессы и их представление через нечеткий 155
интеrpал по расширенной нечеткой мере.
5.2. Особенность непрерывных нечетких процессов. Нечетко.... 163
дифференциальное представление нечетких процессов.
5.3. Дискретные нечеткие процессы. Композиционные 166
нечеткие уравнения, как частный случай дискретных
нечетко....интеrpальных уравнений.
5.4. Нечетко..интеrpальные уравнения непрерывных 172
управляемых нечетких процессов.
6. Решение аналитических задач оценки состояния нечетких 179
процессов.
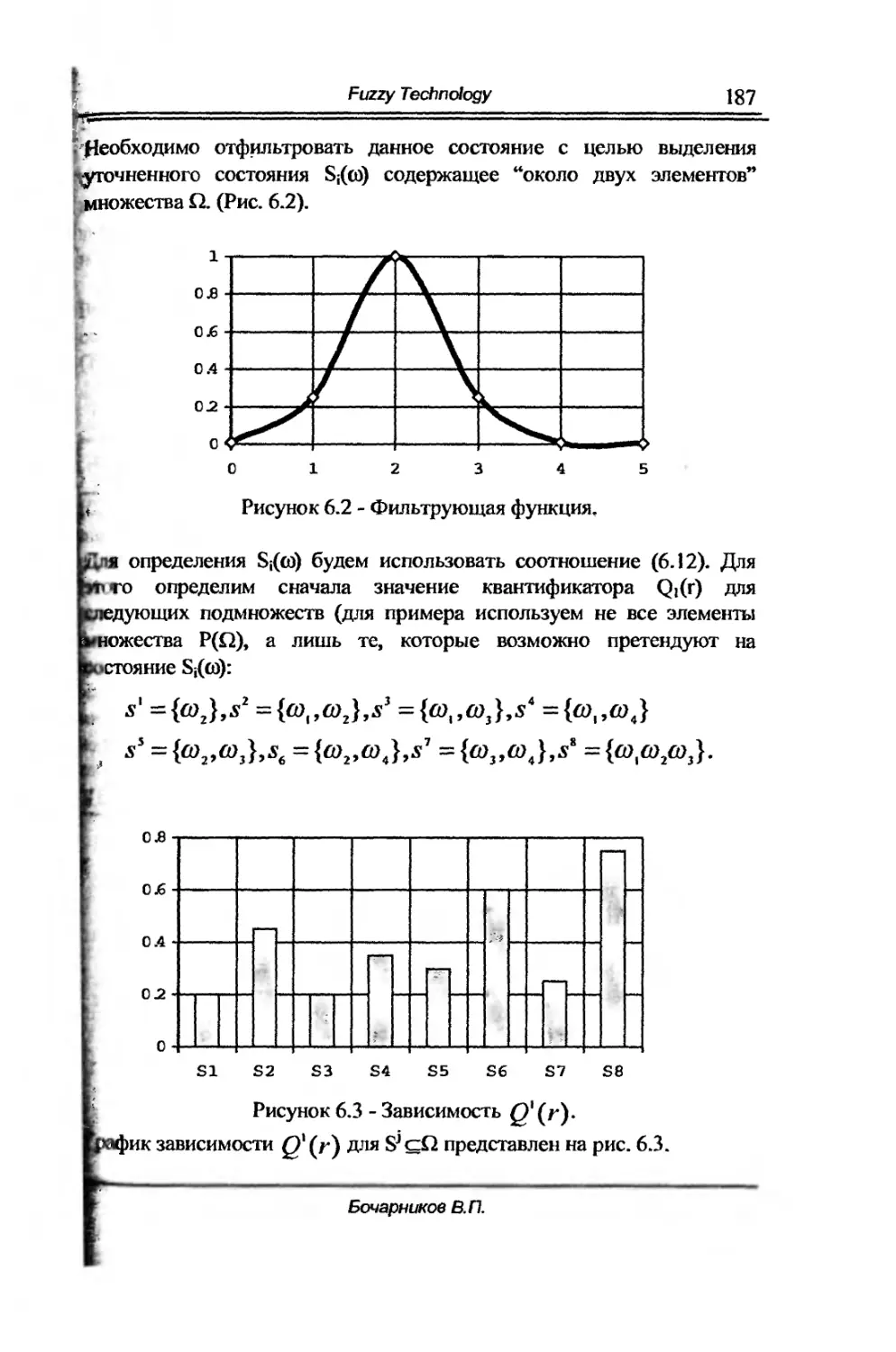
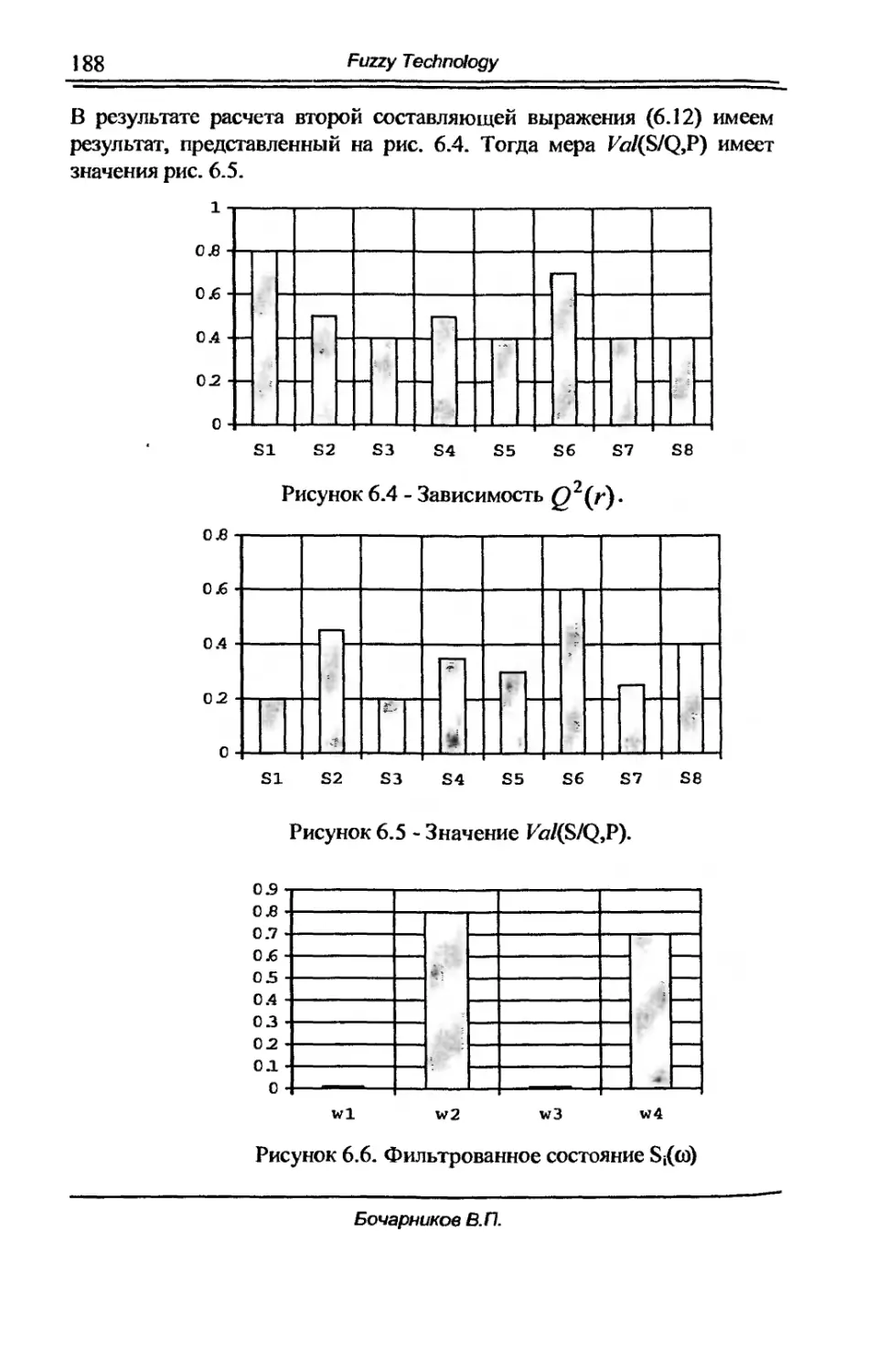
6.1. Понятие нечеткоrо изображения. Оценка статическоrо 180
состояния нечеткоrо процесса.
б.2. Фильтрация статическоrо состояния нечеткоrо процесса 184
на основе квантификации.
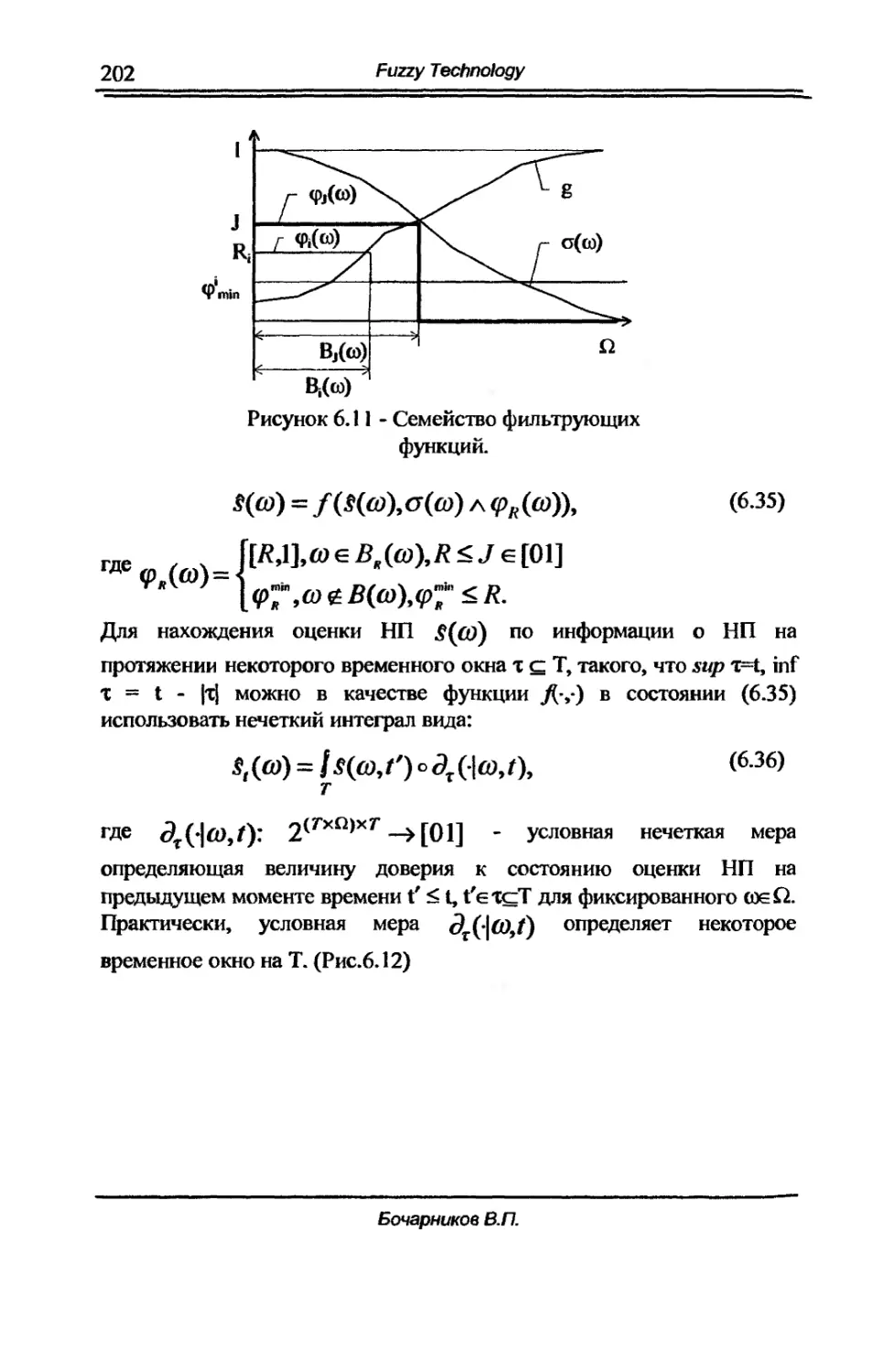
б.3.. Фильтрация нечетких процессов. Нечеткий наблюдатель. 190
б.4. Оптимальный нечетКIIЙ наблюдатель. 206
б.5. Дискретный нечеткий наблюдатель. 213
б.6. Экстраполяция нечетких процессов. 217
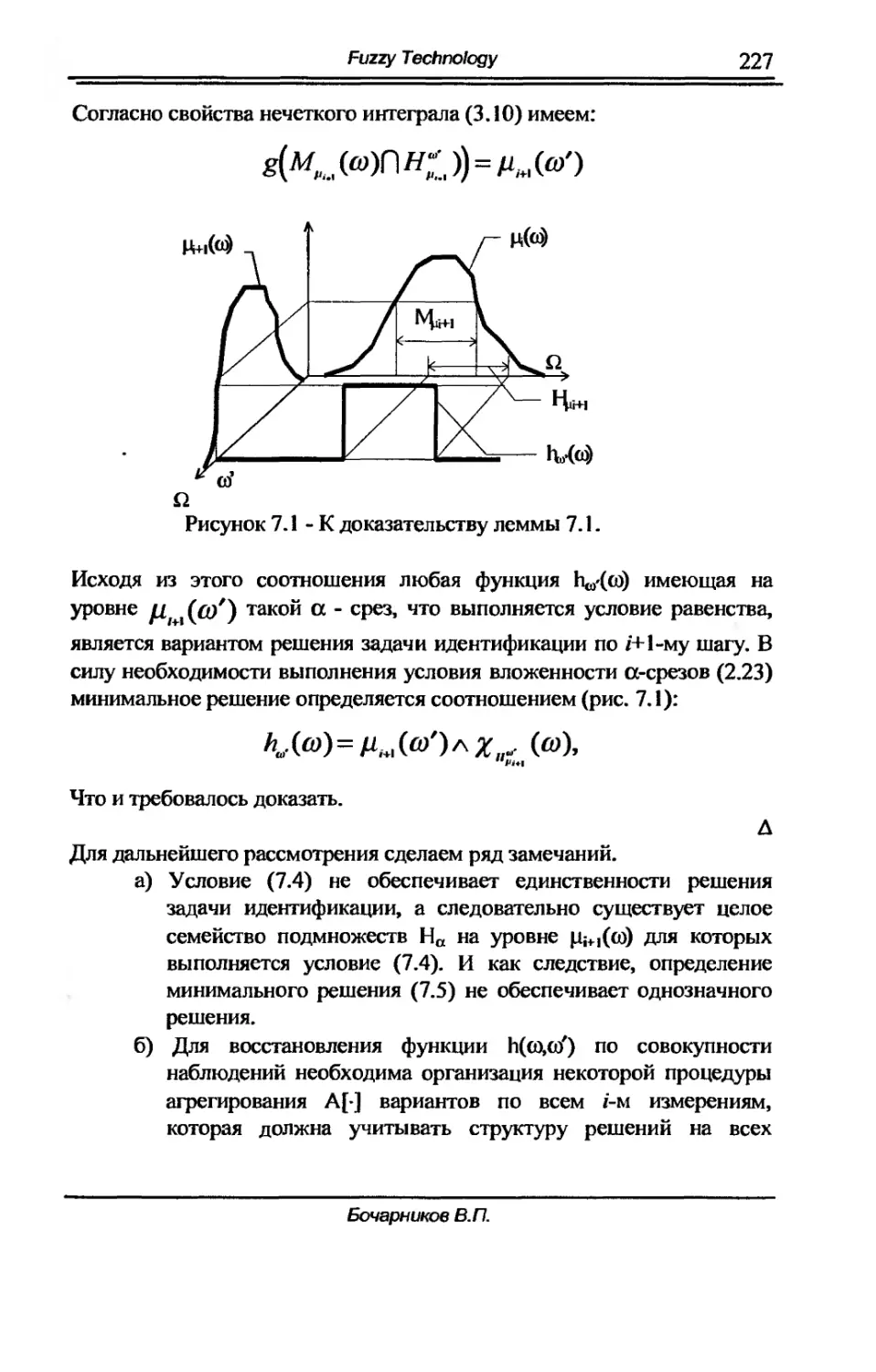
7. Идентификация нечетко....интеrpальных моделей нечетких 223
процессов.
7.1. Задача идентификации моделей нечетких процессов. 224
7.2. Идентификация моделей дискретных нечетких процессов. 226
7.3. Идентификация моделей непрерывных нечетких 240
процессов.
7.4. Оценка качества моделей нечетких процессов на основе 246
нечетко....интеrpальных зависимостей.
Бочарнuков В. п.

Fuzzy Techп%gy 5
Стр.
7.5. Декомпозиция моделей MHorOMepHbIx нечетких процессов. 249
ВекТорно....матричные нечетко..дифференциальные
уравнения мноrомерных нечетких процессов.
8. Оптимизация нечетких процессов и выбор решений. 258
8.1. Задача оптимизации нечетких процессов. 259
8.2. Метод нечеткоrо динамическоrо проrpаммирования для 262
формирования управления непрерывными нечеткими
динамическими системами.
8.3. Определение функции потерь (выиrpыша) при 269
оптимизации управления нечеткими динамическими
системами.
9. Комплекс проrpаммных продуктов 272
Fuzzy..технолоrии для моделирования в экономике.
9.1. Назначение проrpаммных продуктов Fuzzу....технолоrии 273
9.2. Проrpаммируемый нечеткий вычислитель 276
Fuzzy Calculator (FC), версия 2.1.
9.3. Проrpамма Fuzzy for Ехсе' (FE) 282
для работы с нечеткими числами в среде MS Excel, версия
2.0.
9.4. Экспертно....аналитическая система 291
Expert Professional..2000 (ExPro..2000), версия 2.0
9.5. Проrpамма Fuzzy Estimation of Critical Messages (FECM) 298
для нечеткой оценки критических сообщений при
проведении арбитражных валютных операций,
версия 1.1.
9.6. Приложение МаркетЭффект системы FinExpert для поиска 308
эффективных маркетинrовых решений
9.7. Система анализа данных Data Engine, версия 2.1 319
9.8. Консалтинrовая компания ИНЭКС 322
Литература 326
Бочарнuков В. п.

б
Fuzzy Techп%gy
ПРЕДИСЛОВИЕ РЕЦЕНЗЕНТА
Диалектика взаимодействия и взаимовлияния теории и практики
особенно ярко проявляется во взаимном обоrащении и развитии
математики и экономическоrо моделирования, техники. Очередное
яркое свидетельство тому возникновение теории нечетких множеств и
интенсивное применение ее достижений в новых информационных
технолоrиях, лоrистических и маркетинrовых расчетах, решении
друrих прикладных задач.
Родоначальником теории нечетких множеств является американский
ученый л. Заде, опубликовавший в 19б5 rоду в журнале '''Information
and Control" статью, которая называлась "Fuzzy Sets". На русском языке
термин "Fuzzy' переводится как «нечеткий», «пушистый», «размытый»,
<<расплывчатый». Наиболее распространенным узаконенным сеrодня
является первая интерпретация перевода.
Как указывает академик д. А. Поспелов «основная идея Заде состояла в
том, ЧТО человеческий способ рассуждений, опирающиися на
естественный язык, не может быть описан в рамках традиционных
математических формализмов. Этим формализмам присуща строrая
однозначность интерпретации, а все, что связано с использованием
ecтecTBeHHoro языка имеет м ноrозначную интерпретацию....
Последовательно проводя идею нечеткости, по мнению Заде, можно
построить нечеткие аналоrи всех основных математических понятий и
создать необходимый формальный аппарат для моделирования
человеческих рассуждений и человеческоrо способа решения задач».
Комментируя эту же основную идею Заде, профессор А. п. Ротштейн
указывает, что «человек ходит, плавает, водит автомобиль, узнает
знакомые объекты, улавливает закономерности, решает дрyrие
сложнейшие с математическои точки зрения задачи управления и
принятия решений, не прибеraя к строrим количественным
соотношениям.»
Бочарнuков в.п.

Fuzzy Techп%gy
7
Теория нечетких множеств в очередной раз подтвердила еще одну,
извесmую всем исследователям истину: применяе1ЫЙ формальный
аппарат по своим потенциальным возможностям должен быть
адекватным смысловому содержанию и точности исходных данных.
Поэтому методы математическоrо анализа применяются эффективно
при точных исходных данных. Математическая статистика и теория
веРQятностей используют экспериментальные данные, обладающие
cтporo определенной точноcrью. Теория нечетких множеств имеет дело
с «человеческими знаниями», которые принято называть «экспертнои
информацией».
эти ВОЗМОЖНОL'ТИ математическоrо аппарата, развитоrо в рамках
теории нечетких множеств, позволяют решать широкий кpyr сyrубо
прикладных задач, для решения которых единственно возможной
исходной информацией являются экспертные знания. Идеи Заде и ero
последователей находят применение при управлении экономическими,
социальными и техническими системами, при решении задач
планирования в условиях неопределенности, в системах искусственноrо
интеллеКТd, робототехнических системах, системах распознавания и
т.д.
Рецензируемая моноафия занимает свое особое место в развитии
теории нечетких множеств и ее практических приложений.. Автор
развивает важное направление теории, а именно теорию нечетких мер
для представления и обработки плохо определенных, нечетких
исходных данных. Использование нечетких мер позволяет перейти к
единому математическому описанию четких, статистически..
вероятностных и нечетких исходных данных, использовать при
моделировании сложных процессов всю доступную разнородную
информацию, что. несомненно, ПОВЫllJает достоверность и качество
принимаемых реllJений. Автор справедливо считает, что «наиболее
приемлемым для реlllения практических задач в условиях
неопределеНIIОСТИ может быть подход, ба".1ИРУЮЩИЙСЯ на теории
нечетких мер и нечетко..и нтеrpальHoro исчисления, который в
значительной еrепени обобJцает известные подходы к описанию
неопределенности и позволяет создать эфq)ективное приклздное
математическое обеспечение в системах поддержки при нятия
решений».
БочаРНt.JКО6 В.П.

8
Fuzzy Techп%gy
Содержание моноrpафии полностью соответствует этим намерениям
автора. Наряду с приведенными новыми теоретическими результатами
моноrpафия содержит значительное количество практических
примеров.
Книrа на наш взrляд будет весьма полезна как для более rлубокоro
знакомства с современной теорией нечетких множеств, так и для
практическоrо применения в решении прикладных задач.
Рецензент
Академик международной академии компьютерных
наук и систем,
заслуженный деятель науки и техники Украины
доктор технических наук, профессор,
Б. М. rерасимов
27.0б.2000
Бочарнuков в.п.

Fuzzy Techп%gy
9
ПРЕДИСЛОВИЕ РЕЦЕНЗЕНТА
Предлаraемая читателю моноrpафия Бочарникова в.п. представляет
собой яркое выражение Toro уровня и специфики научных
исследований в области теории и применения теории печетких
множеств, нечеткой математики инечеткой лоrики, который был
достиrнут в бывшем СССР и ныне продолжается в России, Украине,
rрузии и друrих странах содружества. Начиная с пионерских работ
Айзенберrа, советская школа (ныне украинская, российская и T.Д)
научных исследований в этой области была ориентирована на cтporoe
и корректное (по возможности) доказательство основных положений,
состаВЛЯlОщих ядро HOBoro направления в науке.
Исторически сложилось так, что Украина, как в прочем и дрyrие
республики бывшеrо СССР, вынуждена была идти в русле научных
исследований, которые вела российская наука. Соответственно
"информационный rолод" удовлетворялся только в той мере, какую
считала возможным допустить "большая" академия (АН СССР).
Существенный толчок к развитию научных исследований в области
нечerких множеств в Украине начинается с 1971 rода, коrда появилась
скромная (по размерам) моноrрафия л. Заде "Понятие
линrвистической переменной и ero применение к принятию
IJриближенных решений", изданная в издательстве "Мир".
в ЭТОЙ связи моноrpафия Бочарникова в.п. представляет счастливое
исключение, коrда выбранная тема исследования не только не
дублирует исследования, начатые "большой" академией, но
практически уникальна. И эта уникальность, прежде Bcero в том плане,
что в условиях "инq)ормационноrо rолода" было выполнено
полноценное научное исследование, показавшее уровень и
возможности украинской науки. Здесь весьма уместно вспомнить М.
rорькоrо о молодом и. Бабеле, что он MHororo не знает, но о MHoroM
доrадывается.
Бочарнuков В.П.

.,..'""V'. .У&.6д".ц...пIVI ll.Y"''''l\.un \ДU 1 I I"одаj и советских научных школ,
автор постарался максимально cтporo представить результаты
 своих
научных исследований. Зто, естественно, не является подарком для
широкоrо читателя, которому, читая КНИI'У, придется буквально
продираться сквозь дебри доказанных теорем (нередко имеющих
вспомоraтельную направленность), для Toro, чтобы увидеть результат.
110, полаrаlО, что эти усилия не будут напрасными и будyr сторицей
вознаrpаждены.
Что же сделано автором и почему моноrрафия заслуживаer такой
высокой оценки? Математический базис теории нечетких множеств
весьма м ноroобразен, и одним из разделов этоrо базиса является
теория нечеткой меры. Здесь я не Mory не отметить еще раз
уникальность этоrо исследования, сравнивая ero с аналоrичными
исследованиями за рубежом. Зарубежные исследования, посвященные
нечеткой мере (кстати, весьма интенсивные в наСТОЯIдее время, о чем
roворит тот факт, что за Последние 5 лет вышли два специальных
выпуска журнала "Fuzzy Sets and Systems") в основном направлены на
определение общих интеrpальных свойств этой меры. Подавляющее
большинство работ в той или иной мере связаны с исследованием
интеrpала 111 оке:) для Koтoporo интеrpал Суджено, рассматриваемый
автором, является частным случаем Но автор поставил задачей
исследование частных (локальных) свойств нечетких мер и здесь
добился заметных успехов, ПОЗВОЛИВIUИХ успешно реализовать мноrие
технические приложения.
Не вдаваясь в подробный пересказ содержания моноrpафии, отмечу,
что предлаrаемая автором концепция обработки нечетких данных на
основе нечеткоинтеrpальноrно исчисления представляет собой новый
подход к принятию решений в условиях неопределенности, что
существенно пополняет арсенал лиц, принимающих решения.
Опуская теоретические особенности предлаraемых автором методов,
не Mory не отметить той особенности предлаraемой идеолоrии, коrда
рассмотрение и анализ локальных свойств объекта (в данном случае
нечетких мер) позволило получить определенные обобщения.
I Jапример, удалось с единых м етодолоrических позиций
проанализировать моделирование недостаточно информационно
определенных процессов ("нечетких" процессов) и представить их как
неI.JеТКI1Й интеrрал по расширенной нечеткой мере. В этом ряду
Бочарнuков В. п.

успешно решенных задач стоят иденти ф
 ИII
моделеи, оценка состояния и оптимизаци ия нечеткоинтеrральных
решений. я Ifечетких процессов, выбор
Весьма отрадныМ является тот факт, что
описание проrpаммных ПРОДУКТов n моноrpафии при водится
,
f,tоделирования сложных задач в том чис.J1 использующихся для
яроrpаммные продукты разработаны Под е и в экономике. Данные
основу положена рассмотренная в моноrpУ1<:оводством автора. В их
нечетких данных. Фии концепция обработки
..
,,-
Возникает законный вопрос, .... есть ли в
Безусловно, есть. Особенно это моноrpафии недостатки?
Kc
математической строroсти излаraемых ко <1ется целесообразности
лучшее .. Bpar хорошеrо. Поэтом у я 1f4епций. Но, как известно,
 ' B
практи чески и и литературный ypoBelft Соко оценивая научный,
возможным опубликовать ее в предстаВIlе моноrpaфии, считаю
:новизна работы, уровень изложения дОсТо.... Iili0М виде, ибо научная
Mor познакомиться широкий читаТCJ!ь. 11lfLI TOro, чтобы с работоii
Рецензент
Доктор технических наук, профессор
1-0. Н. Минаев.
13.07.2000.
Бочарнuков В.П. 

lб
Fuzzy TeChпo/ogy
ВВЕДЕНИЕ
Принятие решения во всех без ИСКЛIО4ения областях деятельности
человека непременно связано со сбором и обработкой инq)ормации.
При этом значительная роль в процессе выработки обоснованных
решений отводится аналитическим задачам, которые позволяют
получить на базе исходной инq)ормации новые знания о ситуации,
обеспечить rлубокое понимание про исходящих процессов и тем самым
правильно принять решение.
Таким образом, достижение необходимоrо уровня эффективности при
принятии решений невозможно без опоры на результаты решения
аналитических задач, которые предполаraIОТ rлубокую оценку
обстановки, точные расчеты., обоснованные решения, тщательное
планирование и достоверную оценку ожидаемых результатов. Чаще
Bcero принятие решения сопряжено с высоким уровнем
ответственности за конечные рзультаты. В тоже время, оно может
осложняется нестереОТИПI-IОСТЬЮ, уникальностью складывающихся
обстоятельств, острым де)ицитом времени на выработку решений. В
ЭТих условиях необходимость.поддержки принятия реlllений очевидно
должна реализовываться на базе компьютерной аналитической
под.а.ержки.
Анализ показал, что для обеспечения эффективности принятия
решений в рамках компы
терныыx систем под.а.ержки принятия
решений должны реlllаться аналитические задачи оценки состояния,
идентификации моделей и формирования управления сложными
динамическими системами, каковыми являются экономика
rосударства, ero БIОДЖет, инвестиционные проекты, коммерческие
операции и друrие объекты.
Адекватные математические модели, эq)q)ективные методики и
расчетные задачи для реlllения указанных аналитических задач
треБУIОТ BcecтopoHHero учета влияния (IJaKTopoB неопределенности
связанных с особенностями:
БочаРНUКО6 в.п.

Fuzzy Techп%gy
17
. целевых условий (м н оrокритериальность, наличие качественно
определенных целей принятия решений" психолоrические аспекты
принятия человеком предлаraемых решений);
. моделируемых объектов и предметных областей (конфликтная
природа; иrровая неопределенность; наличие линrвистической,
экспертной информации, описывающей объект; отсутствие
возможности статистическоrо описания изза уникальности и
нестереотипности ситуаций; имеющиеся оrpаничения на ресурсы
(деньrи, время и т.д.);
. исходной и текущей информации о происходящих процессах
(противоречивость, недоопределенность, неточность, нечеткость"
неоднозначность и др.).
Влияние данных факторов создает серьезную проблему в решении
аналитических задач и осложняет получение необходимых правильных
И обоснованных реlllений. Таким образом, с одной стороны существует
острая потребность, а с дрyrой .... проблема в решении аналитических
задач управления сложными динамическими системами изза наличия
высокой степени неопределенности задач, моделируемых объектов,
предметных областей, нечеткости имеющихся данных. Зто
подчеркивает практическую важность проблемы обработки нечетких
данных и необходимость про ведения соответствующих исследований в
области создания соответствующей технолоrии, опирающейся на
использование прикладноrо математическоrо и проrpаммноrо
обеспечения в автоматизированных систем аналитической поддержки
nринятия решений. При этом данная технолоrия должна эq)фективно
учитывать влияние факторов неопределенности.
Традиционно ддя решения аналитических задач в условиях
неопределенности применялись вероятностно..статистические методы.
Однако, как показала практика, использование только данных методов
для решения практических задач оrраничивается следующими
обстоятельствами:
. необходимостью учета факторов неопределенности, имеющих
не статистическую природу (субъективные оценки, экспертно....
линrвистическая неопределенность, иrровая неопределенность и
т.д.) [1];
. невозможностью получения вероятностно..статистических
данных о складывающихся ситуациях в сложных орrанизационно"
технических системах [2];
Бочарнuков В. п.

18
Fuzzy Techп%gy
. оrраниченностью информации, приводящей к неустойчивости
получаемых распределений вероятности [3];
· необходимостью учета большоrо объема разнородной и
противоречивой информации, приводящей к сложно преодолимым
математическим трудностям при формалИЗ31fOlIi и реlllении
рассматриваемых задач [4];
· психолоrическим неприятием лицом, принимающим решения в
реальных условиях, подсказок и решений, полученных на основе
только вероятностНо....сТатистических методов [5].
Не учет этих оrpаничений приводит к неадекватным, заведомо не
приемлемым решениям. Причинами получения подобноrо рода
неприемлемых решений является не учет влияния разнородных
факторов неопределенности, неадекватная формализация и обработка
имеющихся нечетких данных.
в силу этоrо в трудах зарубежных исследователей Заде, Лукасевича,
Беллмана, Яrера.. Суджено". Прада,. Дюбуа Макнила.. Бездека,
Цукомото, Кофмана, rупта и друrих, а также целоro ряда
отечественных ученых Айзенберrа, Орловскоrо, Поспелова. Мелихова,
Аверкина, Минаева, Батыршина, Алиева, rерасимова, Ротштейна и
друrих была обоснована необходимость использования наряду с
вероятностно....сТатистическими подходами новых математических
подходов к моделированию и обработке нечетких данных на основе
экспертных оценок, нечетких множеств, лоrическоro подхода и т.д.
Последние rоды для решения праКТических задач бьmи предложены
различные подходы, базирующиеся на теории ошибок, субъективных
вероятностях, интервальных средних, МОД33IЬНОЙ лоrики и друrих.
Исследования и опыт практическоrо применения данных подходов
показали, что использование их наталкивается на трудности связанные
с:
· отсутствием достаточной математической строrости и
обоснованности ряда эвристических методов, требующим
значительных дополнительных исследований в каждом конкретном
случае;
· невозможностью учета различных семантических
модальностей нечетких данных;
· невозможностью унифицированноrо описания
неопределенностей различной природы, количественно и
качественно выраженной информаuии и т.д.
Бочарнuков В. п.

Fuzzy Techп%gy
19
. сложностью описания динамических процессов в условиях
неопределенности, имеющей различную природу, особенно в
непрерывном времени и мноrие дрyrие.
Данные трудности осложняют непосредственное использование ранее
предложенных подходов для решения аналитических задач поддержки
принятия решений в условиях неопределенности. Зто предопределило
необходимость разработки и развития технолоrии и специальноro
(специфическоrо) математическоrо аппарата, предназначенноrо для
решения слабо структурированных инеструктурированных
(качественно выраженных) задач) адекватно отражающих реально
про исходящие процессы с учетом объективных и субъективных
характеристик ситуаций при нятиЯ решении, которые бы в
максимальной степени компенсировали недостатки существующих
подходов.
Исследования автора показали, что наиболее приемлемым. для
решения практически задач в условиях неопределенности может
быть подход базирующийся на теории нечетких мер инечетко..
интеrральноrо исчисления, который в значительной степени
обобщает известные подходы к описанию неопределенности и
позволяет создавать эффективное прикладное математическое
обеспечение в системах помержки принятия решений.
Использование данноrо подхода позволяет решать широкий Kpyr
аналитических задач управления. При этом дает возможность с единых
позиций описать как количественно, так и качественно выраженную
информацию об объектах, учитывать семаIПические модальности
информационньiх единиц, нечеткость данных, мультипликативное
влияние факторов неопределенности, синерrетические эффекты,
влияние рисков и субъективных решений и ряд дрyrих моментов
повышающих адекватность получаемых решений.
Приведенные в моноrpафии теоретические положения, методы и
8JIrоритмы обработки нечетких данных являются развитием ранее
известных положении и значительно расширяют представление о
возможностях использования на практике нечетких мер инечетко..
интеrpальноrо исчисления в аналитических задачах поддержки
при нятия решений при управлении сложными динамическими
системами в условиях неопределенности.
Бочарнuков В.П.

20
Fиzzy Techп%gy
Приведенные результаты по теории нечетких мер и нечетко..
Иllтеrpальному исчислению леrли в основу технолоrии обработки нечетких
данных или Fuzzy"технолоrии, которая в настоящее время успешно
применяется ДЛЯ решения широкоrо Kpyra практических задач. Слово
Fuzzy с анrлиискоrо обозначает нечеткий, пушистый, размытый.
Использование нечетких данных значительно расширяет возможности
моделирования сложных предметных областей, объктов и процессов, что
ЯШIЯется весьма аюуальным в реальных условиях при отсyrствии
достоверных данных, непольной статистике и дрyrих случаях.
Fuzzу"технолоrия, как и любая дрyrая технолоrия, включает в себя
концептуальные, орrанизационные, математические и
инструментальные (пр orp ам м ные) основы. В данной моноrpафии
будyr рассмотрены, прежде Bcero, математические основы Fuzzy..
технолоrии, которые во MHorOM определяют подходы к решению
практических задач, требующих аналитической поддержки принятия
решений. В последней rлаве кратко будет представленна информация
по ряду созданных и успешно используемых проrpаммных
комплексов, реализующих математические основы FUZzy....технолоrии.
Автор выражает rлубокую признательность своему наставнику,
Заслуженному деятелю науки и техники Украины, доктору технических
наук, профессору Прокофьеву Вадиму Павловичу, своим KOJUIeraM,
которые оказали существенную помощь при написании моноrpaфии. В
частности кандидату технических наук Свешникову Серrею Викторовичу,
который реализовал предложеЮlые в моноrpафии математические основы
Fuzzy-.технолоrии в виде конкретных проrpаммных комплексов, кандидату
технических наук Цыraнку Александру Владимировичу, Захарову
Константину Валентиновичу.
Особую блаrодарность автор выражает рецензентам работы Академику
международной академии компьютерных наук и систем, заслуженному
деятелю науки _ и техники Украины доктору технических наук,
профеССОРУ9 Борису Михайловичу rерасимову, доктору технических
наук, профессору Юрию Николаевичу Минаеву, доктору технических
наук, профессору Анатолию Александровичу Рось, которые на основе
cBoero опыта и rлубокоrо знания рассматриваемоrо предмета сумели
тщательно разобраться в приведенном материале, дать ценные советы и
рекомендации по ero улучшению и высоко оценили представленные
результаты труда автора.
Бочарников в.п.

Fuzzy Techп%gy
21
r лава 1
АНАЛИЗ ПОДХОДОВ К
ОБРАБОТКЕНЕЧЕТКИХ
ДАННЫХ В АНАЛИТИЧЕСКИХ
ЗАДА ЧАХ по,дцЕРЖКИ
ПРИНЯТИЯ РЕШЕНИЙ
!
..,. . .

Бочарнuков в.п.

22
Fuzzy Techп%gy
1.1. Аналитические задачи поддержки
принятия решения
Принятие решений, направленное на достижение жизненно необходимых
целей, во всех сферах человеческой деятельности связано, прежде Bcero, с
обработкой информации, ДОС1)'пнои для анализа при решении
соответстВУЮЩИХ задач. В этой связи принятое решение выС1)'пает в
качестве упраШIЯющеrо воздействия на некоторый анализируемый объект.
В качестве Taкoro объекта MOryr ВЫCIyпать как масштабные rлобальные
объекты, такие как rосударство, мировая финансовая система, система
международной безопасности, так и более локальные объекты, например
инвестиционный проект, коммерческая операция, структура предприятия и
мноrие друrие объекты.
Очевидно, что достижение целей и принятие обоснованных решений
должно, прежде Bcero, опираться на всесторонний анализ внешних и
внyrренних факторов, определяющих состояние анализируемоrо
объекта и перспективу ero развития на ближайшее будущее. Как
показала практика решение выше указанных задач невозможно без
опоры на новые формы, методы и способы принятия решений и
формирования управления, широко использующие достижения
информатизации и автоматизации процессов управления, то есть
использующие современные компьютерные автоматизированные
системы под.а.ержки принятия решении. Данные системы призваны
обеспечить повышение эффективности управленческой деятельности,
оперативности, полноты, обоснованности принимаемых по
разрешению проблемных ситуаций, требующих коллективноrо
обсуждения.
Следует отметить, что указанные выше задачи, возникающие в
процессе принятия ответственных решений, в основном носят
аналитический характер и направлены на получение оценок некоторых
ситуаций, планов проектов и т.д., а также на выработку предложений
по проведению мероприятий управляющеrо содержания. Значительная
Бочарнuков в.п.

Fuzzy Techп%gy
23
доля этих задач является задачами КОl\1плексными сложными и
требуют всесторонн ero привлечения специалистов....экспертов,
способных решать TaKoro рода аналитические задачи в условиях
высокой степени исходной и текущей неопределенности. В связи с
этим данные задачи следует отнести к классу экспертноаналитических
задач, решение которых должно базироваться на орrаническом
сочетании в рамках системноrо подхода экспертной методолоrии и
перспективных математических методов обработки данных,
предСТ8ВЛЯЮЩИХ собой некоторую Научно....обоснованную технолоrию.
Исходя из сказанноrо, можно сделать вывод о том, что для решения
аналитических задач в процессе принятия решений с использованием
автоматизированных систем необходимо создание соответствующеro
прикладноrо проrpаммноrо обеспечения, выступаЮlцеrо в качестве
инсументальноrо базиса технолоrии решения эксптно""
аналитических задач. Такое обеспечение должно включать в себя
соответствующие математические модели и расчетные задачи, которые
. условно можно разбить на два больших класса:
. информационные модели и задачи;
. аналитические модели и задачи.
К информационным задачам целесообразно omести все задачи которые
treпосреДСТБеННО связаны со сбором, хранением, oroбражением мaCClmOB и
потоков информации. Решение этих задач ЯШIЯСТСЯ весьма важныIM для
обеспечения эффекrивноro приия rnя решения. Однак"О, rлавное lШЗНачение
Математических моделей и методик расчетов все же обеспечение
omимизации принимаемых решений, повышение их обоснованнocrи, чro
осуществляercя решением СО80К)'ПНОС111 аналитических задач оценки,
ftpornозирования, оптимизации и дрyrих Таким образом решение
аналитических задач поддержки принятия решений иrpaет ключевую роль и
Itмеино на них должна ориентироваться соответствующая технолоrия
Опыт разработки прикладноrо проrраl\Iмноrо обеспечения для решения
аналитических задач показывает, что решающим и во MHorOM
определяющим облик и характер будущеrо проrpаММI-Iоrо комплекса
является обоснование и выбор эффективных математических
Подходов, методов и алrоритмов, обеспечивающих приемлемую
формализацию информационных единиц и адекваТНУJО обработку
йнформации. Этап обоснования и выбора математическоrо подхода,
методов, алrоритмов преДll1ествуer разработке конкретных расчетных
процедур задачи или модели. Необоснованный, не правильный выбор
Бочарнuков B{1.

24
Fuzzy Techп%gy
математических методов, как правило, при водит к низкой
эффективности создаваемых задач и математических моделей, их
неадекватности, получению заведомо ложных результатов в процессе
их ПРИ1\.1енения и как следствие недоверие к получеННЫ1\.1 результатам,
иrnорирование получаемых подсказок и рекомендаций.
Обеспечение оптимизации, обоснованности и оперативности
принимаемых решений на основе математических моделей и методик
расчетов можно рассматривать в качестве rлавноrо результата, цели
q)ункционирования автоматизированной системы поддержки принятия
решений и в этой связи данное обеспечение будет является ключевым,
системообразующим фактором целостности всей технолоrии
выработки реlllений. Исходя из этоrо, проrpаммный комплекс и
технолоrия ero использования для решения аналитических задач
поддержки принятия решений можно рассматривать как некоторую
функциональную систему, направленную на получение отмеченноrо
выше rлавноrо результата [б].
Изучение функциональных систем позволило выявить ряд их
важнейших системных свойств, одним из которых является свойство
внутренней и внешней симметрии [б, 7, 8]. Под симметрией
понимается катеrория, которая обозначает сохранение произвольноrо
множества признаков объектов относительно некоторых изменений
[б]. Системное свойство симметрии для функциональных систем (в том
чие и для всей технолоrии реlllения аналитических задач)
про являете я, прежде Bcero, в виде сохранения, как внyrренней
структуры системы, так и сохранения возможных вариаIПОВ
(парадиrм) взаимодействия ее со средой (Табл. 1.1.)[6, 8]. Сохранение
этих свойств наблюдается для всех систем на любом из уровней
управления, что позволяет выявить ряд общих важнейших
особенностей создания прикладноrо проrраммноrо обеспечения для
решения экспертно....аналитических задач принятия решений и
выработки управления.
Бочарнuков В.П.

Fuzzy Techпology
25
Таблица 1.1.. .. Структурные варианты взаимодействия со средой.
'Структура .N Внешняя Обратная Тип
п.п структура связь
1 'F I U  1. (о 0 Без
ин(ормаuии
Х" Ф 2. Х#сХ 0 Частичная
{ .. I информация
2F U
3. Х' == Х 0 Il0лная
ИНфОРf\1ация
 4. 0 Ус!1 Частичная
I I u выходная
2р информация
.,.
у
5. 0 У==!1 Полная
выходная
 информация
Х.. Ф б. Х'сХ Уса Частичная
' 1  I u входная /
выходная
у информация
7. Х' == Х Ус!1 Полная входная
I частичная
выходная
" ;f информация
8. Х'сХ У=:!1 Частичная
 входная I
..
полная
<- выходная
" информация
9. Х' == Х У==!1 Полная входная
" I выходная
информация
"'>
....
Бочарнuков В.П.

26
Fиzzy Techп%gy
в табл. 1.5 приняты следующие обозначения:
IF .. подсистема (элемент) реализующая цель, то есть подсистема,
описывающая конкретные процессы функционирования
анализируеМОIО объекта;
2р .. подсистема (элемент) выбора цели, в качестве которой выступает
теХНОЛОIИЯ решения экспертно..аналитических задач..
Состояния входных переменных во множестве Х определяют так
называемые "ecTeCTBeHHыe состояния' анализируеМОI'О объекта, а
состояния переменных Q представляют выходы, на которых
определена функция ВЫrоды. Iель функционирования есть
макс ИАl изация функиии BbIronbI с помощью выбора решения,
определенноrо состояния переменных U (переменных приияrия
решений).
Проuесс выработки решения происходит в рамках структурь]
функuиональной системы сохраняющей свой вид для всех уровней
управления в силу свойства ее внутренней симметрии.
 1 2  3 .. 4 .
.. н.. O" ..
.4 Т
Рисунок 1.1 ... Структура функциональной системы принятия решений.
На рис.l.) [9], обозначено 1 ... подсистема информационной подrотовки
принятия решения, 2.. подсистема интерпретации по реализации
решений, 3 .... подсистема принятия решениЙ, 4 ... объект действия.
?
Как видно из табл. 1.1 1-1 рис. 1..1 для функционирования элемента "F Б
прикладном проrpаммном обеспечении необходимо использование
информации, прежде Bcero о состояниях подсистемы (элемента IF)
реализующеru цель, ТО есть объеь..73 управления. Учитывая это,
останuвимся на некоторых формальных моментах постановок
аналитических задач для поддержки принятия решения.
Бочарников В.П.

Fuzzy Techп%gy
27
Анализ показывает, что анализируемый объект, как объект управления,
для рассматриваемых аналитических задач может быть формально
описан в виде кортежа:
(О, Х, U, Т, У, р, 1, ),
(1.1)
rде: О .. пространство состояний (объектов, исходов и т.д.), Х ...
множество характеристик, признаков, описывающих состояния из О
объекта управления и принимающих свои значения каждый в своем
множеcrве значений {V j }, U пространство управлений
(ОРI'анизационных мероприятий, решений, пр ое кто в, планов и.д.), Т ..
время (дискретное или непрерывное), У .. пространство выходных
значений (наблюдаемых проявлений, оценок и т.д.),
р: (О х Т) х U х Т  О .. отображение, описывающее динамику
изменения предметной области, состояния объекта, реакцию
динамической системы в конкретном состоянии на управляющие
воздействия, у: О х Т  У .... выходное отображение, описывающее
процесс наблюдения объекта управления (получения оценок, мнений и
tд.),  .. некоторые внешние неуправляемые факторы, условия и т.д.,
оказывающие влияние на динамику объекта управления (иноrда Moryr
е описываться характеристиками из Х).
Для объекта управления (1.1) аналитические задачи, необходимые для
щ>инятия решений, не претендуя на полную общность классификации,
Moryr быть разбиты на три основных класса аналитических задач, как
npиведено на рис. 1.2.
Данные аналитические задачи формально MOI'yr быть представлены в
lЩЦе следующих общих постановок задач:

h 3адачи оценки состояния объекта :
0). Задача оценки теКУЩе20 состояния со Е D (задача фильтрации).
Пусть объект описывается в виде (1.1). Необходимо на основе
Наблюдения динамики состояния объекта и имеющейся eI'o модели в
УСЛовиях воздействия помех  найти такое отображение
i': n х т  О', О = О' при котором оценочное состояние объекта ro'
,.!: Q' по критериям {К} максимально совпадает с истинным
-ТОянием.
. 
,
Бочарнuков В.П

28
Fиzzy Techпology
I Аналитические задачи СМ О I
I
.ь w ....
Задачи идснтификации Задачи оценки состояния Задачи формирования
моделей управления
Структурная 1Кластсризация Задачи выбора
н идентификация 
lКлассификация
Парамстрическая Экстраполяция Лоrический вывод
Н идентификация  ......-i
(проrнозирование)
ч Задачи порожпСIIИЯ Фильтрация I .........) Ранжироваиие
моделеи ал ьтериатив
н Оцеика
чувствительности Оптимизация

Оценка устойчивости
Рисунок 1.2 .. Классы аналитических задач принятия решений
б) Задача разбиения множества состояний D. на классы состояний
(задача кластеризации).
.
Пусть объект описывается в виде (1.1). Каждому состоянию ro Е Q
соответствуют значения характеристик из х. Множество Q J\.10жет бьпь
разбито на некоторое множество классов {К}. Необходимо определить
это множество классов {К} и найти отображение <р: Q """'""7 {К},
разбивающее все множество состояний объекта Q на классы {К}.
в) Задача отнесения произвОЛЬНО20 состояния со Е D. в один из классов
состояний {К} (задача классификации).
Пусть объект описывается в виде (1.1) и пусть определено множество
классов {К} состояний. Каждому классу состояний соответствуют
значения характеристик из х. Необходимо найти отображение а: n 
{К}, позволяющее отнести произвольное состояние ro Е Q,
описывающееся характеристиками х, в один из заданных классов
состояний {К}.
2) Задача nРО2нозuрованuя состояния со Е D. (задача экстраполяции).
Пусть динамика объекта описывается в виде (1.1). Необходимо на
основе наблюдения и имеющейся J\.10дели объекта управления найти
такое отображение р:(!) х Т) х U х T'lp  Q, которое позволяет
определить ПрОI"'нозное состояние объекта, ОПТИJ\.lально совпадающее с
Бочврников В.П.

Fuzzy TechпoJogy
29
истинным состоянием объекта через время ПрОI'ноза с точки зрения
критериев оптимизации {К}.
z. Задачи идентификации математической модели объекта
управления .
Пусть объект описывается в виде (1.1). В результате наблюдения
меется информация о значениях входных и выходных состояний
объекта в течение HeKoToporo промежyrка времени. Необходимо по
имеющейся информации о динамике объекта управления определить
такую elo модель р':(О х Т) х U х Т  Q (дискретную или
непрерывную), которая обеспечивает максимальное совпадение по
некоторым критериям {К} выходных состояний модели и состояний
ИСТИННОI'О процесс а на фиксированном наборе входных воздействий.
3. Задачи формирования vправления и выбора решений .
а) Задача формирования оптималЬНО20 управления.
Пусть объект описывается в виде (1.1) и пусть перевод объекта в
новое состояние оценивается с точки зрения совокупности критериев
{К}. На множестве {К} определена система предпочтений Р: К х К 
L, rде L .. решётка. Необходимо найти такое управление UE U, которое
обеспечит перевод объекта в новое состояние с максимальной оценкой
1Ipедnочтения в решётке L.
) Задача ранжирования альтернатив и выбора решений.
Пусть объект описывается в виде (1.1) и пусть в качестве альтернатив
"ступают элементы множества U, которые приводят к исходам из о.
}lсходы из Q оцениваются с точки зрения множества критериев {К}, на
pOM определена система предJ10чтений Р: К х К --7 L, Iде L ..
:решётка. Необходимо найти отображение "': U  L, позволяющее
:раюкировать элементы из U (альтернативы) с точки зрения системы
.предпочтений Р и осущеcrвить выбор приемлемоrо решения из
:множества и.
tаким образом, рассмотренные выше формальные постановки
аналитических задач позволяют определить Kpyr реальных
Naтeматических подзадач, которые должны решаться прикладным
I!porpaMMHblM обеспечением автоматизированной системы поддержки
"JfНЯТИЯ в рамках соответствующей теХНОЛОIИИ. Однако на практике
ение указанных математических задач наталкивается на реальные
"удности, которые связаны в первую очередь с особенностями
Jil
Бочарнuков В.П.

30
Fиzzy Тесhnо/ову
исследуемых объектов, сложностью их математической фuрмализации,
отсyrствием четкой, достоверной информации о их
функционировании.
в дальнейших разделах моноrpафии в основном будyr
рассматриваться вопросы связанные с математическими основами
теХНОЛОI"'ИИ решения экспертно--аналитических задач в условиях
неопределен, ности получившей название fuzzу....Технолоrии.
Рассмотренные в данной АI0ноrpафии математические основы
послужили фундаментом для разработки и практичеСКОI"'О
использования целой серии проrpаммных комплексов Fuzzy.-
теХНОЛОI"'ИИ, краткое описание которых при водится в последней rлаве.
Бочарнuков в.п.

Fuzzy Techпo/ogy
31

1.2. Проблема обработки нечетких данных в
аналитических задачах поддержки принятия
решения.
в настоящее время существует множество подходов к реluению
аналитических задач, возникающих в процессе формирования
управления сложными объектаJ\.lИ. При этом в рамках данных ПОnXОДОВ
ДЛЯ формализации описания объектов управления и саАIИХ процессов
управления MOryт быть использованы различные математические
одели, которые баЗИРУIОТСЯ на определенных матеАlатических
теориях позволяющих эффективно описывать и решать задачи
управления. l-lаи60лее широко применяемые варианты подходов,
оделей, математических теорий для описания сложных, конфликтных
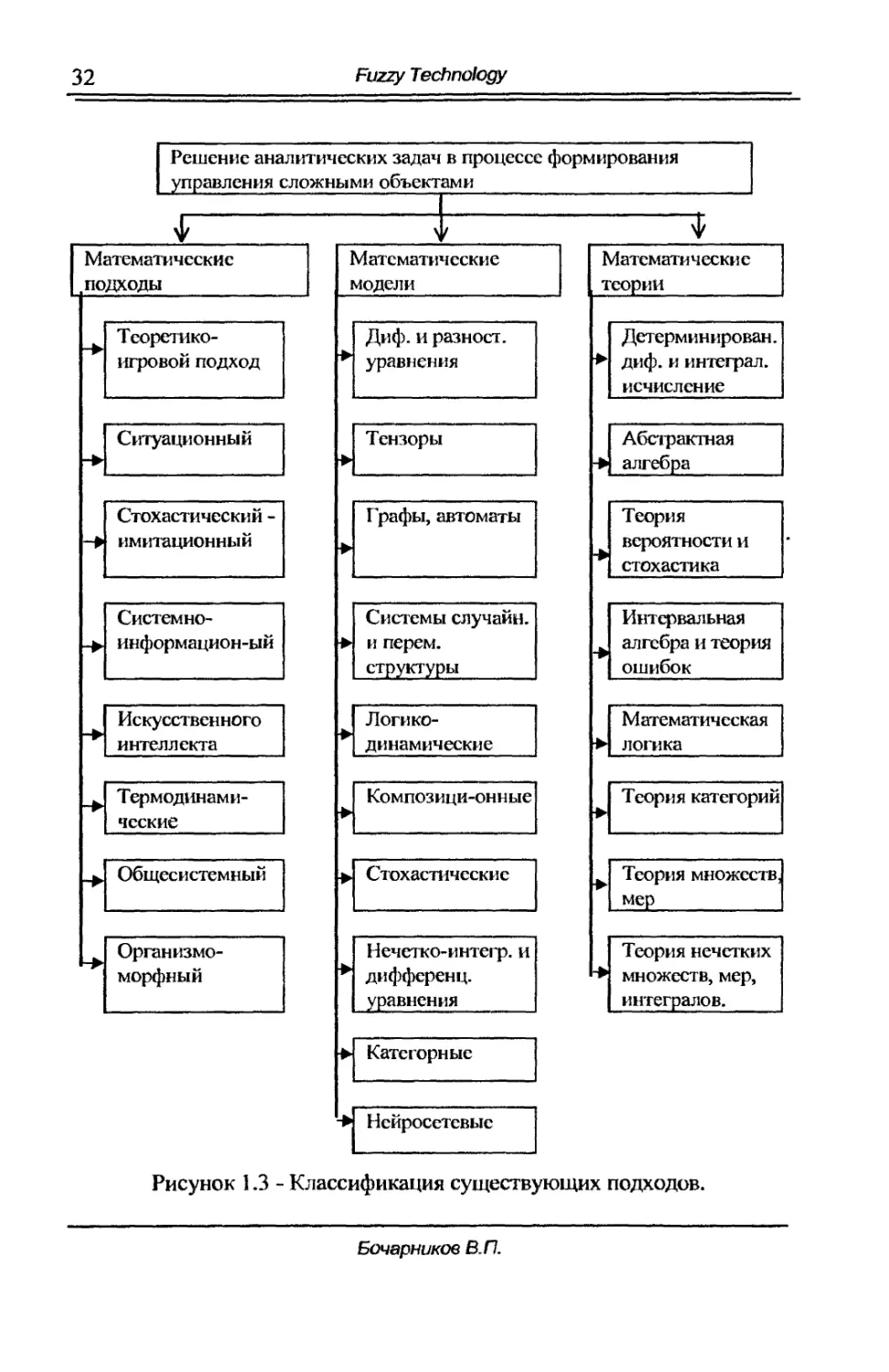
Qбъектов приведены на рис. 1.3.
Каждый из приведенных классов аналитических задач обладает своими
особенностями, сложностью решения, подходами и т.д., однако, как
было отмечено ранее, во всех аналитических задачах для получения
:Р.кРективных результатов их решения необходимо всесторонне
учитывать с войcrва объекта управления или раССАlатриваемой
дмerной области. (Объект 4 рис. 1.2).
ализ свойств объектов и предметных областей, рассматриваемых
при решении аналитических задач принятия решения, а также
lJPактическиЙ опыт создания прикладноrо математическоrо и
nporpaMMHoI'O обеспечения показал, что одним из основных системных
Свойcrв является конфликтная пр ирода существования,
функционирования и раЗБИТИЯ моделируемых объектов. При этом,
КОНФЛИКТУ10ЩИМИ сторонаtvlИ, МОI)1Т выступать не только действия
противоборствующих сил, но и широкий Kpyr ДРYI"'их конфликтующих
факторов, таких как м ноrокритериальность, неопределенность
Исходной и текущей информации, действие случайных, не
учитываемых факторов и TД. приводящих К так называемым
проблемным (КОНфЛИКТНЫl) ситуациям [9].
...............)"" ""..
Бочарников В.П.

32
Fuzzy Techп%gy
Решение аналитических задач в процессе формирования
n авления сложными объектами
Математические
ПОДХОДЫ
+ т еоретико,-
иrровой ПОДХОД
Ситуационный

Стохастический ..
I имитационный
Системно..
..... информацион"ый
f+ Ис кусствен HOro
интеллекта
+ Термодинами..
I.Iеские
+ 06щесистемный
 Орrанизмо,-
морфный
Математические
модели
Диф. и разност.
уравнения
Тензоры
rрафы, автоматы
Математические
тео ии
Детерминирован.
диф. и интеrрал.
исчисление
Теория
вероятности и
стохастика
Интервальная
алreбра и теория
ошибок
Теория катеrорий
Теория нечстких
множеств, мер,
интеr алов.
Рисунок 1.3 .. Классификация существующих подходов.
Системы случайн.
и перем.
сткты
динамические
Композици'-онные
Стохастические
Нечеткоинтеrр.и
дифференц.
авнения
 Нейросетевые
Бочврнuков в.п.

Fuzzy TechпoJogy
зз
в настоящее время изучению конфликтных объектов и
СJ(JIадывающихся в процессе их функционирования конфликтных
ситуаций посвящено большое количество работ [5, 6, и др.]. Одним из
определений конфликтной ситуации является следующее.
Ситуация, возникающая в процесс е управления сложной
орrанизационной или технической системой при рассоrласовании
действительноrо и желаемоrо состояния системы, в силу действия
факторов неопределенности вьпекающих из конфликтной природы
C8Moro объекта и связанной с необходимостью выбора лицом
принимающим решение (ЛПР) конкретной альтернативы управления
при наличии каКой....либо информации о состоянии объекта и системы
управления, критериев, решающих правил, собственной системы
предпочтений.
Естественно, что причины возникновения конфликтных ситуаций при
выработке решений непосредственно связано с конфликтной природой
объекта управления. Данные причины Moryr быть разделены на пять
FJJУПП [9] (рис.l.4).
Причины, порождающие конфликтные ситуации
I
'" \1, .j, '" 
Несовершенство Ненадеж.. Оrрани" М Horo.. Потеря
Ьроцесса управления, ность ченные значность, способности
обусловленная элементов возможности мноrокри" системы
иеопределенностью системы системы териальность управления
информаuии об управления управлеиия возиикающая решать
об-ьекте. (оrраиичеиия в процессе возникшие
иесовершеиСТ80М иа ресурсы) управления задачи
методов и управлеиия
8Лrоритмов,
ошибками персонала
, И т.д.
Рисунок 1.4 Причины порождения конфликтных ситуаций.
Конфликтная природа объектов управления определяет то, что данные
объекты целесообразно рассматривать как сложные системы, имеющие
большое количество взаимосвязанных различных частей, структур или
элементов, аспектов, деталей понятий затрудняющих не только их
изучение и моделирование., но и в целом понимание про исходящих в
них процессов.
23ак 771
Бочарников В.П.

34
Fuzzy Techп%gy
Сложные объекты, как объекты управления обладают рядом
отличительных особенностей [4]:
1. Не все цели выбора управляющих решений и условия,
влияющие на этот выбор, Moryr быть выражены в виде
количественных соотношений. С точки зрения приведенных
формальных постановок задач плохо определенными,
нечеткими MOryт быть множество критериев {К} и заданная на
них система предпочтений Р, нечетко MOryr быть определены
также характеристики классов при решении задач
классификации.
2. Отсуоствует либо является неприемлемо сложным
формализованное описание объекта управления. То есть имеет
место сложность построения функции р, описывающей
динамику объекта управления и определения значений
переменных, входящих в неё. Формально функuия р может
предcrавлять собой нечеткое отображения входных
переменных в ВЫХОДНЫе. .
3. Значительная часть информации, необходимая для
математическоrо описания объекта существует в форме
представлений и пожеланий специалистов--экспертов,
имеющих опыт работы с данным объектом. Это чаще Bcero
приводит к нечеткости описания элементов формальноrо
представления объекта управления (1.1). В чаcrности нечетким
может бьпь описание состояния объекта Q и ero
характеристик Х, описание времени (например, нечеткость
запаздывания действия управления, момента начала
воздействия внешнеrо фактора и т.д.), нечеткость процесс а
наблюдения за объектом 'у и сами оценки ero состояния У
(например, выrодность сложившейся обстановки, степень
удовлетворения проекта целям и задачам проrpаммы, плана и
Т.Д.), а также Moryr наблюдаться различные сочетания
нечеткости в описании составляющих аналитических задач.
Таким образом, неопределенность, про водящая к значительным
трудностям в решении задач и моделировании объектов и процессов
управления сложными динамическими объектами, порождается
множеством факторов. В том числе кроме указанных факторов следует
учитывать неопределенность из....за мноrокритериальности задач,
невозможности учета всех взаимно влияющих факторов "природы" ,
Бочврнuков В.П..

Fuzzy Т echп%gy
35
"";""".JII
статистической неопределенности, наличия конфликтующих сторон,
npиводящеro к иrpовой неопределенности хода и исхода (иноrда
вазывающеrося стратеrической неопределенностью), оrpаниченности
и недостаточной достоверности исходной и текущей информации и
МfJоrие Др)'I"'Ие факторы.
l.
едования последних лет показали, что неопределенность
npнсущая аналитическим задачам принятия решения имеет более
о6щую природу, а не только статистическую. Основные виды
иеопределенности приведены в виде дерева на рис.l.5. Некоторые
ВOiснения относительно классификации видов неопределенности
рассмотрены в работе [1].
-!
Неопределеииость
Недостовсрность (неполнота, недостаточность
недоопрсдслснность.нсадскватность)
../
Линrвистичсская нсопрсдслснность
Нсопредслснность
значений слов
Неодиозначность
смысла фраз

V __,
l.!
f'"
Рисунок 1.5.... Основные виды неопределенности.
G-T.
Qq>.мление к решению указанных аналитических задач в условиях
пределенности на основе традиuионных подходов заставляет
QtCсматривать две альтернативы.
!.
Первая .... постараться учесть все возможные факторы, влияющие на
IIf,>ведение объекта. К сожалению, в силу специфики сложных
9бъектов, это попытка "объять необъятное". Если и можно построить
 модель, используя традиционные методы, то она будет
IPoмоздкой и неприемлемой для практическоrо использования, что
;:  но как с функциональными, так и экономическими аспектами.

Бочврнuков В.П.

36
Fиzzy Techп%gy
Вторая альтернатива .. упрощение модели в рамках традиционных
методов, что неминуемо приведет к неадекватности получаемых
управленческих решений в следствие недостаточно полноrо учета
факторов неопределенности.
Таким образом построение точных математических моделей сложных
объектов, приrодных для реализации в прикладном проrpаммном
обеспечении при решении аналитических задач принятия решения, на
основе использования традиционных, широко распространенных
вариантов формализации и представления объектов (см. рис. 1.3) либо
затруднительно, либо вообще невозможно. Более Toro в [5]
доказывается, что свести подобные аналитические задачи с
неопределенностями к точно поставленным (хорошо
структурированным, хорошо формализованным) математическими
задачами, использующим классические пuдходы, нельзя в при нципе,
поскольку это требует "снятия" неопределенности.
При решении подобноrо класса задач мы неминуемо сталкиваемся с
проблемой выбора альтернатив, формализацией неопределенноrо
объекта в слабоструктурированных (плохо формализуемых) ситуациях,
основная особенность которых заключается в том, что их модель
может быть построена на основании дополнительной информации,
получаемой от специалистов, экспертов, лиц принимающих решения в
реальных условиях. Отсюда следует необходимость разработки
специальноrо (специфическоrо) математическоrо аппарата,
предназначенноrо для решения слабо структурированных (смешанных)
и неструктурированных (качественно выраженных) аналитических
задач. Этот аппарат должен адекватно отражать реальную
действительность с учетом характеристик субъекта, принимающеI'О
решение. В противнuм случае рекомендации, предлаrаемые
управляющие решения, полученные с помощью математических
моделей, расчетных задач, Moryr ИI'норироваться либо превратно
пониматься конкретными ЛПР, поскольку часть сведений о
закономерностях развития сложных динамических объектов, которыми
они располаrают, носят характер нечетких описаний на
ЛИНI'вистическом уровне. Именно наличие качественных, нечетких
описаний позволяют ЛПР принимать удачные решения в конкреrnых
слабо структурированных ситуациях и не учет ЭТОI'О, в рамках
математических подходов при решении аналитических задач
помержки принятия решений, не допустим.
Бочарников В. п.

Fиzzy TechпoJogy
37
 -i-l
.. i1
_ьтернативным способом моделирования и работы с очень сложными
стемами, возможно самым важным, являеся допущение нечеткости
ВРИ описании данных [8, 13]. Это yrверждение основывается на
j1pинципе несовместимости. r оворя не формально, суть этоrо
"'):,
1Jpинципа состоит в том, что с ростом сложности систем наша
особность делать точные и содержательные утверждения об их
поведении паДает до определенноrо предела, за которыми такие
характеристики, как точность и содержательность (или реальность),
ciaновится взаимоисключающими. В этом смысле абсолютно точный
количественный анализ реальных сложных объектов управления не
.:слишком подходит для решения.
 ..
rаким образом, подход к решению аналитических задач под.держки
,рнятия решений должен опираться на то, что ключевыми
:;шементами являются не числа, а метки некоторых нечетких множеств,
:10 есть классов объектов, для элементов которых переход от
'Jlринадлежности к не принадлежности классу является не резким, а
,JIостепенным. В самом деле, ..вездесущая.. нечеткость человеческоrо
; 
,ыленияя наводит на мысль, что ЛОIИка рассуждении человека не
'(ШЛяется обычной двухзначной или даже мноrозначной лоrикой, но это
. лоrnка с нечеткими истинами, нечеткими отношениями и правилами
:-Ывoдa. Как ни странно, именно такая нечеткая и не вполне понятная
,hornKa является важнейшим компонентом одной из rлавн ЫХ
бенностей человечеСКОIО мышления, а именно способность
'i>бoбщать информацию, выделять только необходимые данные для
:feшения конкретной задачи.. Эта ключевая способность человеческоrо
'ышления и позволяет принимать удачные решения командирами и
'ачальниками, ЛПР в конкретных конфликтных ситуациях. Не учет
3тoro фактора при создании приклаДНОIО математическоrо и
nporpaMMHoro обеспечения во MHoroM определяет недостатки
'современных теХНОЛОIИЙ и систем под.держки прииятия решений.
Исходя из сказанноrо выше для реализации эффективнurо прикладноrо
математическоrо и проrpаммноrо обеспечения теХНОЛОI ии решения
аналитических задач поддержки принятия решений по управлению
"СЛожными динамическими объектами необходимым условием,
позволяющим получить более или менее адекватные решения, является
всесторонний учет неопределенностей при формализации и обработке
информации. Учет неопределенности информации и ero
Бочарников в.п.

38
Fиzzy Techпology
эффективность на прямую зависят от выбора математическоrо
фундамента, определяеМОI'О математической теорией (рис.l.3)..
На сеrодняшний день можно выделить ряд математических теорий
предназначенных для формализации неопределеннuй информации:
1. МНОIuзначная лоrика;
2. Теория вероятности;
3. Теория ошибок (Интервальные модели);
4. Теория интервальных средних;
5. Теория субъективных вероятностей;
6. Теория нечетких множеств;
7. Теория нечетких мер и интеrpалов.
Результаты сравнения математических теорий, с точки зрения их
применимости для решения рассмотренных выше аналитических
задач, лриведены в табл. 1.2.
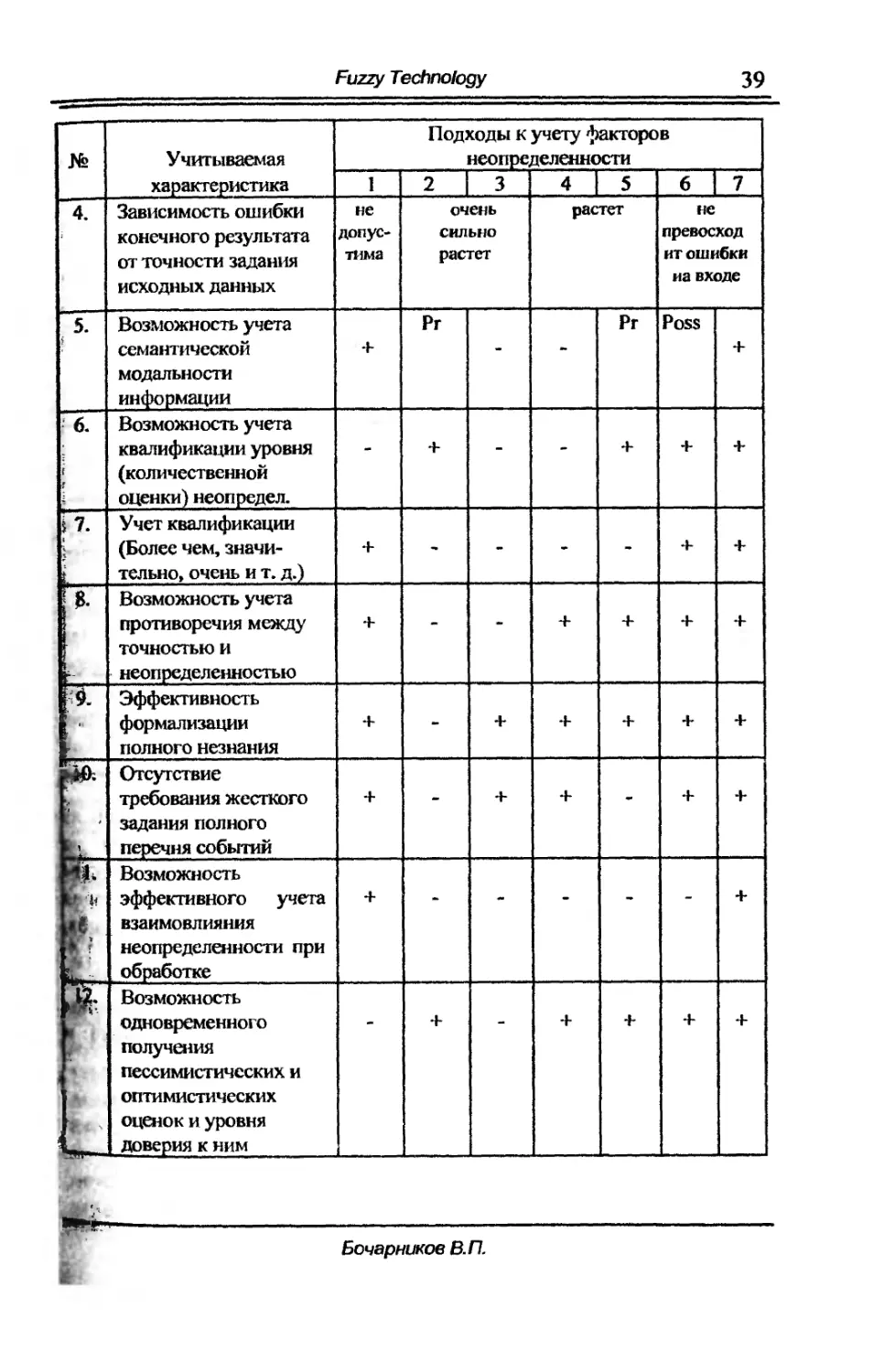
Таблица t.2 ..Сравнительный анализ математических подходов.
Подходы к учету факторов
Н!! Учитываемая неопределенности
характеристика 1 2 3 4 5 6 7
1. Учет физической
числовой .... + + + + + +
неоnределенности
2. Учет физической
нечисловой (событий) + + .. + + + +
неоnределенности
з. Учет нечисловой
линrвистической + .. .. .... + + +
неоnределенности
Бочарников в.п.

Fuzzy Techno/ogy
39

...
ПОДХОДЫ к учету факторов
Н!! Учитываемая неопределенности
характеристика 1 2 3 4 5 6 7
4. Зависимость ошибки I--Je очеl--JЬ растет I--JC
: конечноrо результата допус.. СИЛЬ.,О превосход
от точности задания тима растет ит ошиБКJI
исходных данных иа входе
5. Воз:можность учета Pr Pr Poss
j семантической +
.. .. +
модальности
информации
: 6. Возможность учета
квалификации уровня .. + .. .. + + +
f (количественной
, оценки) неопредел.

 1. Учет квалификации
I (Более чем, значи"
, + .. .. ... .. + +
..
t теЛЬНО t очень и т. д.)
. 8. Возможность учета
противоречия между + .. ... + + + +
точностью и
;;. , неопределенностью
9. Эффективность
>: .
, формализации + .. + + + + +
 полноrо незнания
iJ); Orсyrствие
"".. .
" требования жесткоrо + ... + + .. + +
<,
. задания полноrо
 перечня событий
___ Возможность
'=1 эффективноrо учета + ... .. .. .. .. +
':".5;, взаимовлияния
...
: неопредсленности при
CI '. обработке
,}. Возможность
  ...,
одновремеННОl"'О .. + .. + + + +
получения
пессимистических и
оптимистических
... оценок и уровня
..... доверия к ним
..........
, .i
.... .1
у.............
Бочарников В. П.

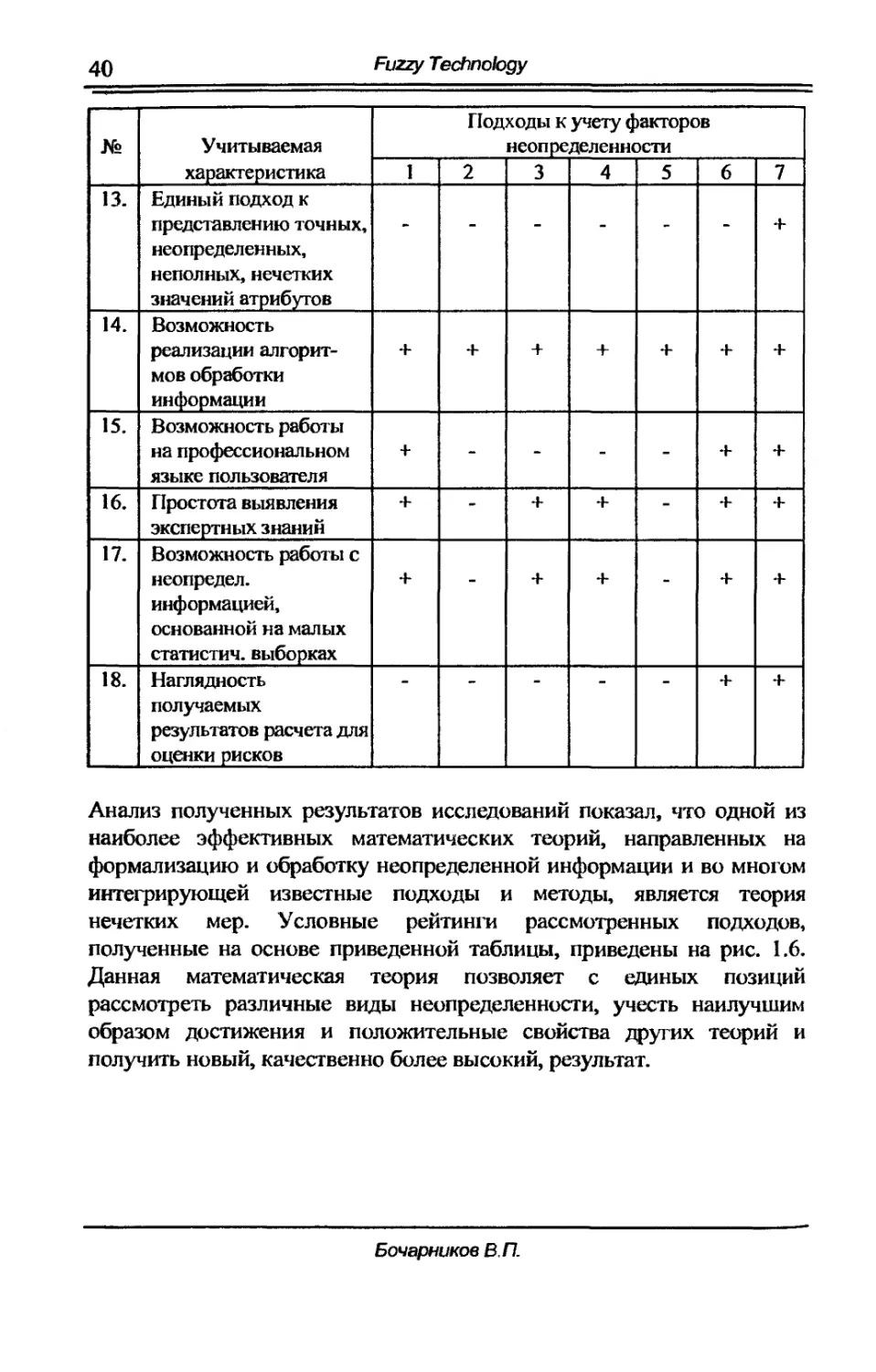
40
Fиzzy Techпo/ogy
Подходы к учету факторов
Н!! Учитываемая неопределенности
характеристика 1 2 3 4 5 6 7
13. Единый подход к
представлению точных,  .. .. .. ..  +
неопределенных,
неПОЛНЫХ,нечетких
значений атрибyrов
14.. Возможность
реализации алrорит" + + + + + + +
мов обработки
информации
15.. Возможность работы
на профессиональном + .. .. .. .. + +
языке пользователя
16. Простота выявления + .. + + .. + +
экспертных знаний
17. Возможность работы с
неопредел. + .. + + .. + +
информацией,
основанной на малых
статистич.выборках
18.. Наrлядность .. .. .. .. .. + +
получаемых
результатов расчета для
оценки рисков
Анализ полученных результатов исследований показал, что одной из
наиболее эффективных математических теорий, направленных на
формализацию и обработку неопределенной информации и во MHOI'OM
интеrpирующей известные подходы и MeTOДЫ является теория
нечетких мер. Условные реЙТИНI'И рассмотренных подходов,
полученные на основе приведенной таблиuы, приведены на рис. 1.6.
Данная математическая теория позволяет с едИных позиций
рассмотреть различные виды неuпределеннuсти, учесть наилучшим
образом достижения и положительные свойства ДРYI"'их теорий и
получить новый, качественно более высокий, результат.
Бочарников В.П.

Fиzzy Techп%gy
41
 :''''
....<tJ'РейТиНr
. <.. 18
16
14
12
10
8
6
4
2
О
.
r
1
2
з
4
5
6
7
t:
Рисунок 1.6.... Условные рейтинrи подходов
.
" м образом, ДЛЯ создания технолоrии решения рассмотренных
ее классов аналитических задач в условиях неопределенности
есообразно применение именно теории нечетких мер. При этом в
..8е представления нечетких данных в виде распределений нечетких
. возникает ряд практических задач обработки TaKoro рода данных,
. ". рые .должны базироваться на сформулированных и доказанных
"". ретических положениях. Несмотря на значительное развитие в
, ледние rоды теории нечетких множеств математические подходы,
ользующие нечеткие меры еще развиты недостаточно и остается
. льшое кuличество вuпрuсuв их практическоrо применения. С
 омента первых публикаций по основам теории нечетких мер [1 О]
iфoшло уже окuло 30 лет. Наибольшее распространение получили
t<
.Jltследования и практическое применение меры возможности и
fIeoбходимости [11, 12 и др..]. Работы по развитию всеЙ теории
четких мер представляют собой в основном статьи которые
f>acкрывают отдеЛьные аспекты применения нечетких мер и не
'nOзволяют решить полностью рассмотренные задачи.
Сследования показали, что наиболее неизученными являются
..оменты, связанные с моделированием, оценкой состояния и
авлением процессами, описывающими нечеткими данными, как в
I:UIcкpenloM, так и в непрерывном времени. В имеющихся подходах
более часто используются для описания неопределенности
: четкие множества (MOryт трактоваться как распределение плотности
четкой меры возможности ... частный случай нечетких мер), что
<Щ>аничивает имеющиеся возможности по моделированию и решению
.
Бочарников в.п.

42
Fиzzy Techп%gy
аналитических задач. Исходя из сказанноro выше, рассмотрение
дал ьнейшеrо материала будет проводиться с точки зрения
последовательноrо решения следующих четырех задач.
1. Развитие унифиuированноrо математичеСI<Оro подхода 1<
представлению нечетких данных на основе теории нечетких мер.
2. Развитие теоретических основ обработки и преобразования
данных в моделях нечетких процессов на основе нечеТl<оrо
интеrpирования.
3. Разработка математических моделей нечетких процессов.
4. Разработка методов и алrоритмов оценки состояния,
идентификauии, моделей, оптимизации управления и выбора
решений в аналитических задачах управления войсками
стратеrическоrо уровня.
Таким образом, прежде Bcero необходимым является систематизация и
развитие теоретических основ нечетких мер, множеств и интеrpалов,
которые MOryт быть эффективно применены для решения
аналитических задач поддержки принятия решений и являются
математической основой Fuzzу"технолоrnи. Именно этим задачам и
будут посвящены следующие три rлавы. Далее будyr рассмотрены
вопросы общих формулировок и решений аналитических задач
поддержки принятия решений в условиях неопределенности (задачи
оценки состояния, идентификации моделей объектов, формирования
управления сложными динамическими объектами)..
Бочарнuков в.п.

Fиzzy Technology
43
.......
. rлава 2
ЦРЕДСТАВЛЕНИЕ НЕЧЕТКИХ
ДAlШЫХ НА ОСНОВЕ ТЕОРИИ
ВЕЧЕТКОЙ МЕРЫ
(,
.
Бочарников В.П.

44
Fиzzy Т echпology
2.1. Определение и основные свойства
"""
нечеткои меры
Нечеткая мера может рассматриваться как обобщение понятия
вероятностной меры, свободное от ряда оrpаничений.
Как известнu, мерой называется функция мнuжества т: Р ( х )  R
удовлетвuряющая следующим трем аксиuмам [14, 15]:
I)А с Х => т(А» о;
2) т (0) == о;
3)А. В Е Р (Х), то т (А u В) == т(А) + т(В)... т (А n В) ==
т(В) + т(А) .. т (В пА).
Здесь Р (Х) .. множество всех подмножеств Х, R .. множество
действительных чисел. При R == [01] эти аксиомы определяют
вероятностную меру. В отличии от вероятностной меры,
рассматриваемая нами в дальнейшем, нечеткая J\.tepa свободна от
весьма оrpаничительноrо требования аддитивности. Приведем
сuответствующее определение нечеткой меры.
ОПDепеление 2.1. Нечеткой мерой, заданной на пространстве (Х,
В), rде В .... а.... алrебра дЛЯ Х, называтся не аддитивная функция
множества g(.): В  [01] удовлетворяющая следующим
свойствам:
1) g (0) == о, g (Х) == 1. (оrpаниченности);
2) Если А, В Е В И А с В, то g (А) < g (В)
(монотонности);
З) Если Fn Е В, n ==ЛJ: {}.. является монотонной
последовательностью множеств (возрастающая или убывающая),
то lim g(F ) == g(lim F ) (непрерывности).
.,.....00 ., .,...... N
Бочарников в.п.

Fиzzy Т етпо/оуу
45
_i
Тройка (Х, В, g) .... называется пространство м с нечеткой мерой. 8
общем случае для нечеткой меры не должно выполняться условие
аддитивности:
g (А u В) * g (А) + g (8), А, В е В, А n В == 0.
Нечеткую меру g(.) можно рассматривать как однопараметрическое
расширение вероятностной меры. С семантической точки зрения
выражение g(A) представляет собой меру, характеризующую степень
нечеткости события А, то есть оценку нечеткости суждения "х е А"
:.'t
Иепосредственно из аксиомы монотоннuсти вытекают следующие
неравенства, характеризующие uбъединение и пересечение множеств:
g (А u В) > mах (g (А), g (В)),
<,"'" g (А n В) < min (g (А), g (В).
(2.1 )
Предельным случаем (1) для нечетких мер оказываются Функuии
множества удовлетворяющие выражениям:
Poss (А u В) == mах (Poss (А), Poss (В),
Ness (А n В) == min (Ness (А), Ness (В»,
(2.2)
(2.3 )
...-де Poss (possibility) .... мера возможности, а Ness (nessesary) .. мера
необходимости.
 аналоrии с функцией распределения вероятности (если Х == R) меру
:а(:) можно определить с помощью непрерывной функции,
У#{овлетворяющей следующим свойствам:
,. 1) Еслих < у,тоh(х) < h(у), х,уе R;
,;
2) lim h(x) = h(a);
Х""""й
3) lim h(x) = О, lim h(x) == 1.
............ ."'..............
Функция h(x) называется нечеткой функцией распределения. Значения
g(x) нечеткой меры, определенные на одноточечных подмножествах х
Е Х называются плотностью нечеткой меры.
.............
Бочарников в.п.

46
Fuzzy Techп%gy
2.2. Построение нечетких мер.
Семантические модальности нечетких мер
Вопросу построения и предcrавления нечетких мер посвящено
большое количество работ [], 1 О, 11, 12, 16] и др_ Однако, наиболее
стройным построением нечетких мер можно считать построение на
основе функции меры фокальных элементов.
Оппелеление 2.2.
Функцией меры фокальных элемеmoв называется функция
определенная на подмножествах Ер, р == 1,N' ; Ер с Х называемых
фокальными элементами и удовлетворяющая условиям:
lт(E р) = 1;
р= I,N
(2.4 )
Ур, т(Ер»О.
Величина m(Е р ) понимается как значение вероятноcrи совокупности
элементарных событий, составляющих Ер, причем здесь не
оrоваривается распределение величины m(Е р ) по элементарным
событиям. Подмножества Ер, р==1, м называются "фокальными
элементами" и Moryr отражать неточность наблюдений. Семантически
величина m(Е р ) соrласно [1] выражает степень уверенности,
отнесенную к множеству А в целом.
На основе функции m(.): Р(х)  [01] Moryr быть построены различные
нечеткие меры.
Опuелеление 2.3.
Мерой доверия (belief measure) называется функция множества
Bel(-): 2 Х  [01], определяемая по распределению уверенности
т(-) как:
Bel(A) ==  т(Е )
";1'(;.4 "
(2.5)
Бочарнuков В. п.

Fuzzy Techп%gy
47
.i><h
и удовлетворяющая следующим свойствам:
а) Bel (0) == О, Bel (Х) == ]
б) V' А.,. . . , А 11 С Х, п > О
 1/1+. (п )
Bel{A.u...UA п » (......1) Веl А;,
/{....п} ;е/
'-.0
(2.6)
rде 111.. мощноcrь множества I (индексной последовательности).
Для двух множеств А, В с Химеем:
Bel(A UB) > Bel(A)+ Bel(B) Bel(A nB) (2.7)
функция Bel семантически определяет тот факт, что crепень доверия к
ВJ,1сказыванию А (А *" 0), которое является истинным, не обязательно
равна 1. Это доказывает, что существует некоторое доверие к
высказыванию А. определяемое внешними или внyrpенними
факторами. В то же время, отсюда следует, что сумма crепеней
доверия к событию А и ero отрицанию A также не обязательно равна
-", а может быть либо равной, либо меньше 1. Из (2.5) вытекает:
J
V'A c X:Bel(A)+Bel(A)=l Lт(E p )e[OlJ
Epg;A
EpA
(2.8)
В работах [1, 12] показано, что если множество фокальных элементов
{Ер} образует последовательность вложенных подмножеств, т.е. если
E1 с Е 2 с ... С E N , то функция доверия Bel(A) может трактоваться как
нечеткая мера необходимости.
Опnеделение 2.4
Мера доверия удовлетворяющая свойствам (2.6) и свойству (2.3)
называется нечеткой мерой необходимости. (Ness (.»
При этом выполняюrся условия:
min [Ness (А), Ness ( А )] == О,
'V А, В с Х, Ness(A u В) > тах [Ness (А), Ness (В)].
(2.9)
(2.1 О)
Мера необходимости Ness(A) определяется фокальными элементами,
образующими вложенную последовательность подмножеств Х,
.
Бочврнuков в.п.

48
Fuzzy Techп%gy
которые делают необходимым появление события А (влекут за собой
событие А).
Опnелеление 2.5
Нечеткой мерой правдоподобия (plausibility measure) называется
функция м ножеcrва PI(.): 2 Х ----+ [01], определяемая по
распределению уверенности m(.) как:
\f А с:х. PI (А) == I. т(Е,.) (2.11)
'-r n'.f#0
и удовлетворяющая следующим свойствам:
а) Pl (0),PI (Х) == 1;
б) VA.,...,A п с Х,п>О,
R(n..,) < I: (.......1)+1H(Ц4)
/{In} leJ
(2.12)
Для двух множеств А, В с Х выполняется:
Рl (А n В) < Рl (А) + РI (В).
Мера Pl(.) выражает степень правдоподобности события А с Х,
которая может быть и больше, чем О даже в случае ложноcrn
высказывания А. Соrласно [1] между мерами доверия и правдоподобия
существует двойственная связь, определяемая следующими
соотношениями:
Рl (А) + Веl (А) == 1.
V А, В с Х. Рl (А) > Веl (А).
(2.1 З)
в том случае, коrда множество фокальных элементов является
вложенной последовательностью подмножеств, нечеткая мера
правдоподобия определяет нечеткую меру возможности.
ОПDелеление 2.6.
Нечеткой мерой возможности называется функция множества,
удовлетворяющая следующим условиям:
а) Poss (0) == О, Poss (Х) == 1.
б) \fieI. А; с Х. Poss (A; )==su Р Poss (А;), (2.14)
,еl ;el
rде 1 .. множество натуральных чисел.
В случае вложенности множества фокальных элементов нечеткая мера
возможности может быть определена с помощью распределения
Бочарнuков в.п.

Fuzzy Techп%gy
49

 
возможности п(х): Х---7 [01] (плотности нечеткой меры возможности)
такоii,что
sup 1t (х) == 1.
ХЕ Х
(2.15)
При этом имеем:
L,щЕ j ), х е Ej,x  Ei1
\;/х е Х, :п(х) == j=i
(2.16)
О, хеХ\Е р
rде E i С Ei+l.
в силу Toro, что меры возможности являются нечеткими мерами
'ПРавдоподобия, а необходимости .... мерами доверия, то для них
справедливо условие двойcrвенности (2.1 З):
v А с Х, Poss (А) == 1 .... Ness (Х\А).
(2.1 7)
тношение (2.17) выражает численное соотношение двойственности
!ежду семантическими модальностями "возможно" и "необходимо" (в
"модальной лоrике), поcryлирующее тот факт, что некоторое событие
необходимо, коrда противоположное событие невозможно. В силу
oтoro всеrда можно построить меру необходимости исходя из
""распределения плотности нечеткой меры возможности с помощью
формулы:
';'
Ness(A) == inf{1  п(х)1 х  А}
(2.18)
't точки зрения теории нечеткой меры возможно и представление
1feчетких множеств, нашедших широкое применение в прикладной
,тематике для описания сложно формализуемых объектов и систем.
:(Iри этом, задание нечеткой меры локализирует значение переменной

,Ж, выражая для каждоrо подмножества А с Х имеющуюся
формацию об отношении х с А. Семейство подмножеств,
:\одходящих для представления переменной х с Х, будет индуцировать
Обобщенную характеристическую функцию нечеткоrо множества. При
ЭТом данное представление cтporo эквивалентно представлению через
tункцию принадлежности Jl(x):   [01] [15] в случае использования
,нечетких мер возможности. Нечеткое множество, в этом случае,
;рассматривается как "след" меры возможности на одноточечных
."ножествах в Х. Если Е с Х достоверное событие, то леrко определить
..
Бочарнuков в.п.

50
Fuzzy Techп%gy
ФУНКЦИЮ П со значениями {0,1}, удовлетворяющую условию (2.2)
ВИда:
{ 1, АПЕ0
ПЕ(А)== О, АПЕ==0;
(2.19)
в этом контексте ПЕ(А) == 1 означает, что событие А возможно, а
следовательно функция П(.) == Poss(.). Если мера возможности
принимает значения в единичном интервале, то функцию плотности
нечеткой меры возможности п(х), определенную на одноточечных
подмножествах Х, можно интерпретировать, как функцию
принадлежности qeтKOrO множества F, рас с матр и вaeMoro как
достоверное событие, на котором сосредоточена мера Poss(.).
Действительно, обозначая F(X) множество нечетких подмножеств
универсума Х, имеем:
\f Poss(.), 3 F Е F (Х), \fxeX., Poss ({х}) == 7t (х) == Ilx (х).
(2.20)
В то же время, задание нечеткоrо множества доcrаточно для описания
функции плотности нечеткой меры возможности при условии, что это
нечеткое множество нормально, то ecrь 3 х е Х, JlF (х) == 1.
Если же считать., что условие Poss (х) == 1 может не выполняться, то
имеем:
\fF е F (Х), 3 Poss (.), \fXE Х., Poss ({х}) == 7t (х) == Ilx (х).
(2.21 )
Величина Poss(x) == sUPllx(X} называется высотой нечеткоrо множества
F и обозначается hgt (Jl). Леrко видеть., что при определении ФУНКЦИИ
плотности нечеткой меры по мере фокальных элементов т(.) сами
фокальные элементы образуют семейство
С(Р) == {РU I Fa == [х е Х I JlF (х) > а Е [01]] }
(2.22)
а.. срезов нечеткоrо множества F. (Множество Fo. содержит все
элементы из Х, дЛЯ которых уровень совместимости F не менvше а Е
[О 1 ]).
Семейство С(Р) всех а....срезов естС монотонная последовательность
множеств, удовлетворяющая условию:
а, 13 Е [0,1], О < а < 13 < 1 =:) F (х :J FJ}
(2.23 )
Бочарнuков в.п.

Fuzzy Techп%gy
51
Тоrда, если Fa совпадают с фокальными элементами Ер (определение
2.2) имеем:
Ер == F ар' rде
ар
L т (Е j)
j = р ... N
(2.24)
тосда:
Vxe Х,
J1F(X)==
L т(F ap )
p.xeF ap
(2.25)
Это так называемый "вероятностный способ" представления нечеткоro
множества.
Для представления четких данных, по которым имеется полная
уверенность в их значении, может использоваться примитивный класс
мер, а именно меры Дирака.
ОПDелеление 2.7 .
Мера Дирака есть функция множества, определяемая
соотношением:
V А с Х,
:{
\
{ 1, ХО Е А;
р(А) =
О, xoA;,
rде хо .... заданный элемент в Х, на котором сосредоточена мера
Дирака.
(2.26)
..
!
,
!
.
:K видно из определения мера Дирака есть частный случай
"оятностной меры, соответствующий детерминированной ситуации
epы полной уверенности).
с JleKoтopbI е наиболее существенные соотношения нечетких мер,
\рссмотренные ранее, приведены в табл. 2.1.
",
:"Р заключение пункта продемонстрируем возможность представления
_,.ечетких данных для решения аналитических задач поддержки
,.ринятия решений на основе нечетких мер на просто м примере
.'ькспертной линrвистической оценки риска при реализации HeKoToporo
"инвестиционноrо проекта.
r
Бочарнuков в.п.

52
Fuzzy Techп%gy
Таблица 2.1 .. Соотношения нечетких мер.
Х2 Условие Соотношения
1. VA c X PI (А) + Hel ( А) == 1.
2. VA c X Pos (А) == 1 .... Nes (Х\А)
Xi А, Nes(A)==inf(l.... Pos ({х}»
з. 'VA c X Pos(A) > Pl(A) > Bel(A) > Nes (А)
4. V Pos (.), Pos ({х}) == Jlf (х).
3Fe Р(Х), sup Pos ({х}) == 1.
V х Е Х, ХЕ Х
Пример 2.1.
Пусть оценка риска оценивается линrвистически На множестве
возможных значений: D == (1 ..риск отсутствует, 2 ... минимальный риск,
3 .. допустимый, 4 .... критический, 5 .. недопустимый, 6 .... неизвестно,
является ли ЭТО риском). В табл. 2.2 приведены варианты
формализации нечетких данных при решении задачи оценки уровня
риска реализации проекта.
Таблица 2.2 .... Пример формализации нечетких данных.
H Описание нечетких Представление нечетких данных на основе
данных НМ
I Неизвестно есть ли риск 1, р(.) = Poss(.);
или нет, но если он есть, JL(d) =  л Е [01], р(-) = Pl(.), Ве/(.);
то неизвестно какой
величины. О, р(.) = Ness(.).
2 Вполне возможно, что л, d < з.
,
риска нет, тем не менее JL(d) =  О, d > з;
есть возможность Л, ЧТО
риск есть и он 1, d == 6.
оценивается не выше
криmческоrо.
3 Есть полная уверенность, p{d) == е, d Е О\ {6};
что риска нет.
1, d = 6.
Бочарнuков в.п.

Fuzzy Techпology
53
Х!! Описание нечетких
данных
4 Вполне правдоподобно..
что есть риск и
достаточно BLIcoKoro
уровня, но имеется и не
нулевая возможность Л..
что эта риска нет
5 Есть полная уверенность..
что риск есть, но тяжело
оценить ero значение.
6 Полная уверенность, что
риск есть, и неполная
ииформация о ero
значении. Однако
известно, что значение
риска от минимальноrо
до допустимоrо.
1 Полная уверенность, что
риск есть инечетко
известно, что он
небольшоrо размера.
8 Полная уверенность, что
есть допустимый риск.
Представление нечетких данных на основе
нм
JL(d) == { PJ, d е D\ {6};
л, d = 6.
Pl .. распределение меры правдоподобия для
понятия «риск BLIcoKoro уровня»
1, р(-) == Pass(.), d:f; 6;
p(d) =  л Е [01], р(.) == Pl(.), Вel(.), d:f; 6;
О, р(-) := Ness(.) v (d == 6).
1) d Е [2,3];
JL(d) =  О, d  [2,3];
О, d = 6.
JL(d) = { lfJ(d), d Е D\ {6};
О, d = 6.
<р( д) .. распределение нечеткости для
понятия «риск небольшоrо размера», рис.
2.1.
JL(d) = { О, d Е D \ {3};
1, d  3.
1
0.8
0.6
0.4
0.2
О
1 2 3 4 5 6
Рисунок 2.1 .... Распределение нечеткой меры оценки уровня риска
понятия «риск небольшоrо размера».
Очевидно, что приведенные в табл. 2.2. примеры формализации
нечетких данных не оrpаничивают Bcero спектра возможностей

Бочарнuков В.П.

54
Fuzzy Techп%gy
ПОДХода на основе нечетких мер. При
конкретной аналитической зцдаче
индивидуальные, наиболее подходящие
нечетких данных.
необходимоcrи в каждой
Moryr использоваться
варианты формализации
Приведенные определение и основные свойства нечеткой меры
позволяют констатировать, что использоваНllе формализма нечетких
мер дает возможность описать более широкий спектр разнородных,
плохо определенных данных, эффективно учеcrь различные
семанrnческие модальности информации о собыrnях, более адекватно
описать реальные аналитические зцдачи поддержки принятия решения.
В частности, нечеткие множества и вероятностная мера Moryт
рассматриваться как частный случай нечетких мер.
Бочарников в.п.

Fuzzy Techп%gy
55
 t d..
2.3. gл ... меры Суджено и их свойства.
Семантические спектры
При решении практических задач нашли широкое распространение
различные конструкции нечетких мер, удовлетворяющие свойствам
определения 2.1. Однако, наиболее широкое распространение нашли
так называемые gA, .... нечеткие меры введенные в рассмотрение в
работах [10, 16] М. Суджено (М. Sugeno)
1 для построения gл... мер используется следующее Л... правило:
v А, В с Х, А n В 0 ,
gл(А u В) == gл(А) + gл(В) + л. gл(А);, gл(В), л е [..1, + 00[. (2.27)
,
. в случае, коrда А u В == Х и gл (А u В) == 1 условие (2.27) является
условием нормировки gл.. меры. Исходя из условия нормировки gл..
меры можно определить меру дополнения A = Х \ А А с Х
, ,
irласно выражения:
gA (:4) = J=- gАJАL ;
1 + л · gл (А)
Формула (2.28) определяет класс лдополнений Суджено,
::Ьripеделяемый reHepaтopOM О'Ipицания (монотонно возрастающий
;.;функцией) t: [01] ----7 R+, t (О) == О, такой, что c(g) =:: [1(t(l) .. t (g» вида
'
j " 1 (2.29)
, ( А (g) = .л1n(1 + Ag).
(2.28)
J3ce рассматриваемые gл"нечеткие меры в зависимости от параметра
)JОРМИровки л Moryт быть разбиты на клссы:
1) супераддитивных нечетких мер (л > О);
2) субцддитивных нечетких мер (.... 1 < л. < О);
$i. 3) вероятноcrных мер (л == О).
:(Для супераддитивных мер справедливо выполнение условия:
L..
v А, В с Х, А n В == 0, gл (А u В) > gл (А) + gл (В). (2.30)
Бочарнuков В. п.

56
Fuzzy Techп%gy
При этом, если h(x) .. есть функция распределения плотности нечеткой
меры, для супераддитивных нечетких gл"" мер, Х есть непрерывное
пространство, то выполняется и следующее условие:
J h(x)dx = N л < l'
х
(2.3 1 )
J  интеrpaл Лебеra.
х
Как нетрудно заметить, что условия (2.30), (2.31) соответствуют
условиям (2.6), (2.7), определяющим нечеткие меры доверия
(определение 2.3). Отсюда следует, что любая gл .. нечеткая мера
является по семантической модальности нечеткой мерой доверия тоrда
и только тоrда, коrда Л. > о.
rде 1
N л == л Iп(1 + А),
it Е [I,+oo[,
для субад.цитивных нечетких мер условия (2.30), (2..31) принимают
следующий вид:
УА,В с Х, АПВ = О, gл(АUВ) < gл(А) + gл(В)'
JЦХ)dx=N л >1'
х
в этом случае выполняются условия (2.12) определения 2.5,
определяющеrо нечеткую меру правдоподобия. Следовательно, по
аналоrии с нечеткими мерами доверия, любая gл .... нечеткая мера
является нечеткой мерой правдоподобия Тоrда и только Тоrда, коrда л.
Е [....1'0[. В случае, коrда л == О мы имеем выполнение следующих
условий:
(2.32)
(2.33)
1) \f А с Х, gл(А) Е [01], gл(0) == О, gл (Х) ==1;
2) \f A j с Х, i Е N, \f i  j, A j п А .i== 0, то
gл(UА;)== I,g.\(A;),
;eN ieN
(2.34)
которые соответствуют аксиомам, определяющим вероятностную
меру.
в табл. 2.3 приведены классификация нечетких мер, их определения по
фокальным элементам, рассмотренные ранее, а таюке наиболее
Бочарнuков В.П.

Fuzzy Techпology
57

характерные зависимоCI'И, условия нормировки и соответствующий л...
парамe'Ip меры.
Таблица 2.3 .. Классификация нечетких мер.
К!! Класс Семант. Определенне Характерные Условия 3 на..
ИМ !модальн по фокал. зависимости нормировки чен
элемент. А
I Супер дове.. Qi}= lrnp) Bel(A) + Bel(A) =
адди" рие Be1QiUB}Be1Qi)+ = 1 I,m fВ p ).
ЕI'!;;А
тив" (belief) +Ве1аз}ВelQiПв) Ep(tA о
Л
ные Ера;А 
Jb<Xk1x=N A <1
 х
 необхо- анолоrично Nes(AuB) > Nes(A) л
ДИМОСТI Вel. > Nes(A)vNes(B). Nes( А)==
,
( nesse.. Е. с Е 2 с ... Nes (АnВ):::: =0 <:>
Л
, ...<
sary) c E N == Nes(A) л Nes(B),
;:
3 Су6 правдо РI (А) == PI(AnB)PI(A)+ PI(A) + PI(A» 1.
адди.. подоби( I,m (Ер +PI(B). Ih(x)dx=N A >1 с:>
(plause.. v
тив-- Ер ПА #0 б 
V
ные bility) .....
.

 ВОЗ мож, анолоrично PI; Pos( U A i ) == sup PoS(xa == 1
ность Е) с  с ._. I
iE/ 
 (posse.. c E N I
'- " == s u р Pos (A i ), 11
bility) 
: ;Е'
Адди.. вероят.... анолоrично Pr(A u В) == Pr (А)  1: Pr( х.) == I
тив" ность Ве' и PI; + Pr (В).. Pr (АnВ): I
; '.1 ные (proba.. Ер == {хр} Pr (А \ В) == Pr (А) .. о
11
bility) .. Pr (В). 
Ди- чет.. .. \:;/Л с Х .. Про
,
рака кость { 1, ХО Е ... из
.;;',,
J-l{ А) = О, Хо f!: А rоль
ное
Представление нечеткой gл .. меры зависит ОТ
rcrM х на roT::::::. Коrда
носителя меры ..
Х есть конечное

58
Fuzzy Techпology
миожество Х == {Xj}, тоrда нечеткая мера gл. алreбры всех подмножеств
(Х, 2 Х ) строится следующим образом [12].
Пусть gx (Xi) == gi Е [01], i== lп . Тоrда условие нормировки будет:
t { "  }
. П(I+лg')1 =1,
л ;I
л Е [l,+oo[
(2.35)
Величина gi определяет нечеткУю меру сосредоточенную на
одноточечном миожестве {Xi} с Х, i == 1, N . и тем самым определяет л...
плотность нечеткой меры по Суджено. Тоrдз, при любом
подмножестве А с Х можно получить удовлетворяющую л...правилу
меру gx (А) по формуле:
gx( А) == } { п (1 + Agi) .....t }
it Х-ЕА
f
(2.36)
Из приведенных выражений следует:
gx( {Xj}) == gi
gx( {Xi, i}) == gi + g' + Л. gi,
i  j.
(2.37)
в случае, коrда пространство Х, изоморфно множеству
действительных чисел R можно задать функцию Н(х) аналоrичную
функции распределения верояrnости (см. п. 2.1). Тоrда с
использованием этой функции можно определить нечетКУIО меру для
люБОI.О интервала [а, Ь] с Х следующим образом:
Н(Ь) ...... Н(а)
gx([a.bD= l+ ii-iw' V'[a.b] c X.
(2.38)
Уравнение (2.38) непосредственно следует из условия л...правила (2..27).
Соrласно Суджено функция Н(х) называется функцией р..
распределения. Как показано в [12] для непрерывноrо Х л."мера
подмножества А с Х может быть определена исходя из следующих
соотношений. Пусть h(x) есть ппоrnость нечеткой меры на х. Тоrда
соrласно (2.31) имеем:
Jh(X}l&=-+). AE[l+oo[.
Х it
Бочарнuков В. П.

Fuzzy Techпology
59

Если мы определяем меру g(A), А с Х, тоrда имеем:
J h(x)dt ==  l + {Х( А22 .
х
Выражая из этоrо равенства g(A) получим:
l { itJh(X)dX }
gx(A)::::  е А .... 1 .
л
(2.39)
Таким образом для определения gл. ... меры в (2.39) используется
"нтеrpал Лебеrа, то есть л. .. нечеткая мера вводится как сумма
бесконечноrо числа интеrpалов Лебеrа функции плотности h(x) по А
{; х. Следует отметить, что соrласно теоремы Лопиталя [12]
веРОЯПlОСПlый случай входит как частный случай в уравнение (2.39).
,Данное уравнение можно предcrавить в эквивалентной форме:
#('
gx(A) = {(1+ л)еР l} i;
pN
gx(A) = J ле}.Jdt;
о
р= ! h(X)dx'{! h(X)dx}' ·
(2.40)
(2.41 )
(2.42)
Леп<о показать, что функция gx(.) удовлетворяет л.....правилу (2.27).
Используя функцию (2.39) можно просмотреть изменение
Семантической модальности нечеткой меры при изменении л.....
_раметра. Рассмотрим пример представления неосведомленности
А:2].
, .
Qpимер 2.2.
,.
!
I:IYCТL Х == [02]. Неосведомленность с вероятностной точки зрения
Рпределяется равномерным распределением: \j х Е Х, Р (х) == 0,5.
{<
в случае F",плотности, тот же случай неосведомленности определяется
выражением:
.., .
Бочарнuков В. п.

60
Fиzzy Techпology
v х Е Х. h(X)= )nO +л)
2л
Рассмотрим событие W с Х, W == [01]. Тоrда вероятность события W
будет:
1
P(W):: J p(x)dx == 0,5.
о
Для нечеткоrо случая имеем:
{ '1 J I Iп(l+л) }
1 л - 2Л  1
gx(W)== А е · l == ,!l+A+. "
1
\
\ g(W)
)
,
 

\..
"'""11\>
0.8
0.6
0.4
02
О
1 О 1 2 3 4 5 6 7
Рисунок 2.2. ... Зависимость нечеткой меры от л..
Аналоrичное выражение получаем для события g == [1,2]. Тоrда, мы
можем получить зависимости распределения нечетких мер для случая
отсyrствия сведений (рис. 2.2). Из анализа зависимости рис. 2.2. можно
сказать следующее. Возможность Toro, что W е [01] равна 1;
вероятность Toro, что We [01], равна 0.5, и необходимость Toro, что W
е [01] равна о. Эти результаты интуитивно совершенно ПОНЯТНЫ.
(8)
Обобщая полученные в примере 2.2 результаты можно отметить, что
для фиксированноrо события W с Х функция
Бочарнuков в.п.

Fuzzy Techпo/ogy
61
 
gx(W) == seт W (л),
(2.43)
еде sетw(л):[I,+ОО[----7 [01], определяет зависимость значения
нечеткой меры от семантической модальности события W с х.
Определение 2.8
Функция sет,J'(л.):[.....I,+оо[ [01], определяющая для
фиксированноro л значения нечerкой меры g(W) события W с Х
называется семантическим спектром события W с х.
Функция seт w (л.) есть функция не возрастающая для любоrо W с Х
Построение, исследование и практическое применение зависимостей
:семантической модальности gл. .. нечетких мер для семантическоrо
спектра события W с Х . является одним из наиболее интересных
направлений исследования нечетких мер и их применения.
Использование введенных понятий в реальных системах подцержки
.ТiPяняrnя решений раскрывает широкие rоризонты для более полноro
учета субъективных особенностей процессов принятия решений.
.Однако, на сеroдняшний день данные исследования еще находятся в
. чальной стадии.
,
'tiТаким образом, сеrодня одним из достаточно эффективных способов
.
оделирования нечетких мер можно считать применение gл .... мер
. tyджено, строящихся на основе л .. правила. Использование
roритмов построения gл. .. нечетких мер как для дискретноrо, так и
.р непрерывноrо пространства Х позволяют сделать эффективные
четные процедуры для прикладноrо проrраммноrо обеспечения при
,,-
шении практических задач поддержки принятия решений в сложных
jptнамических системах.
..
'.:
I
..
\
,
1

Бочарнuков В. п.

62
Fuzzy Techп%gy
2.4. Нечеткозначные нечеткие меры и их
связь с семантическими модальностями.
Аналоmчно тому, как для нечетких множеств существует обобщение
функций принадлежности для их области определения [11, 15, 17]
можно рассмотреть некоторое обобщение и для нечетких мер.
Рассмотрим пространство Х Пусть F(x) определяет множество всех
возможных распределений нечетких gл.... мер на Х, т.е.:
F(X) = {g,,(.g,,(.):2x  [Ol]}. (2.44)
Для любой нечеткой меры gx (-) соответствует плотность
распределения нечеткой мерыg(х): Х  [01]. Тоrда можем переписать
2.44 в виде:
F(X)={g(xg(x):X  [01], \fxeX}
(2.45)
Нечеткозначная мера или нечеткая мера типа 2 может быть задана
рекурсивно следующим образом:
F> (Х) == Х;
рl (Х) == F (РО (Х» == F (Х);
Р. (Х) == P(F 1 (Х» == {g2 (х) I g2 (х) : Р (Х) ---4 [01]}. (2.46)
Нечеткая мера типа 2 может быть интерпретирована как нечеткое
высказывание ВИДа "W есть Jl, есть л'\ т.е. событие W имеет нечеткую
меру Jl с истинностью л.
Практически, для фиксированноrо значения х Е Хнечеткая мера ,(х;
задаем распределение плотности нечеткой меры на единичном
интервале L == [01]. rрафически это представляется в виде (рис.2.3).
Бочарнuков В. п.

Fuzzy Techп%gy
63

.
"
А1
-
0.6  .
::: ",: '< · .'!;
0.3 t
0.2 _
0.1
I I
-,-
..........
 '1-
,
-..


;ar; 't .,-.;),... h......
 .':"
0.8
 '
'о
0.4
о
о
х1
х2
х3
х
.,.
Рисунок 2.2  Распределение нечеткой меры типа 2.
Нечеткая мера на L для каждоrо х Е Х может быть интерпретирована
'как условная нечеткая мера вида
Х l
gl (.) = G L (-IX):2  [01];
rде 2 L .. булеан еДИНИЧНОI'О интервала L == [01]. Если для каждоrо х Е Х
iIocтавить в соответствие интервал А(х) == [O,r(x)] с [О 1], такой, что r Е
JIJ, r == gL(A(x) Ix) : х ......)[01] .... есть распределение плотноcrи нечеткой
- 1
рыg (Х) при фиксированной степени истинности r Е [01].
..... значим значение нечеткой меры события Wc Х при уровне
..;:тинности r Е [01] как gr1(W): r ......)[01]. Мера gr 2 (W) события Wc Х
 неубывающая функция степени ИСТИННОСТJ1 r Е [01]. В силу Toro,
 нечеткая мера определенная на L == [01] для фиксированноrо ХЕ Х
ICТЬ функция не убывающая, то с увеличением r значение плотности
неЧеткой меры на х gL(A(x) Ix) будет увеличиваться. Это равносильно
y, что значение л параметра нечеткой меры gr(X) будет
еньшаться, что соответствует переходу к мерам правдоподобия
Возможноcrи) события. Физически это означает следующее:
_стинность Toro, что мы определяем достоверно возможноcrь события
-Ыше чем определение необходимости события в силу Toro, что
io
} .
Бочарников В.П.

64
Fuzzy Techпo/ogy
определение возможности менее "обременительно", чем определение
необходимости события.
Таким образом, мы получаем некоторую зависимость функции gJ. 2 (И? и
seт w (Л). То есть нечеткозначные нечеткие меры (нечеткие меры типа
2) Moryт быть определены для каждоro собьпия W своим
семантическим спектром seт w (А) в случае определения функции -,"(У) :
[01]  [I,+oo[.

Бочарнuков В.П.

Fuzzy Techпology
65
.,
2.5. Идентификация и аппроксимация
81 ... нечетких мер
для решения практических задач и дальнейшеrо использования в
ичноrо рода алrоритмах обработки нечеткой и слабо
.crpуктурированной информации очень важным является
Jlдeнтификация нечеткой меры. В работе [15] предлаrается следующий
родход к идентификации нечеткой меры. Предполаrается, что
.сперимент должен дать оценки степени важности всех подмножеств
113 пространства х. При этом необходимо иметь субъективные оценки d
'11UCИе, что d : 2 Х ----+ [01]. Torдa идентификация нечеткой меры
-ключается в минимизации функционала вида:
;\
у == + L(dAE) g).y(E)Y,
12 I EE'
(2.47)
.' ,12xl == Card 2 Х .... мощность множества 2 Х , а gAx (Е) .. вычисляется по
> стной формуле для нечетких gA .. мер для подмножеС1Ва Е с Х
. УЛЬТRfОМ решения задачи идентификации является значение
етра л. инечетких плотностей gxl, gx2, ... gxпt п == Card х.
-ако, у данноrо подхода к идентификации нечеткой gл .. мерь]
ествует ряд недocrатков:
1. Этот подход может бьпь использован лишь при не большой
мощности пространства Х, иначе процедура оптимизации
функционала (2.47) оказывается весьма сложной.
2. С практической точки зрения при большом Card Х
значительно осложняется процедура выявления знаний у
эксперта относительно субъективных оценок подмножеств из
2 Х .
. м образом, в реальных задачах использование этоrо метода
: ыаетсяя затруднительным.
. 771
Бочарнuков В.П.

66
Fиzzy Techпology
Однако, использование свойств gA .... меры позволяет упростить
процедуру ее идентификации по ответам экспертов (их субъективным
оценкам). Рассмотрим следующий подход к идентификации нечеткой
gA .. меры.
Разобьем пространство Х на три подмножества {А,}, i = 1.3 таким
образом чтобы А; nAJ == 0, UA; ==Х, А; :/:-А р ;:/:- j. Обозначим
;
меру подмножества A i как gi . Эксперту предлаrается оценить степень
  ........
предпочтения А; над А; (rде А; .. дополнение к А, А; ==.л\ А;), то
есть Toro, что, например, истинное значение нечеткой величины
находится в подмножестве А;, а не Aj. Torдa из условия нормировки
имеем:
g, + G 2З + АgjG 2з = 1;
 ==a;
G 2З
(2.48)
rде G 2з .. мера подмножества А 2 U Аз, а а... степень предпочтения А I над
А 2 U Аз, L Е [0,1]. В данном случае может быть использована
обоснованная Т. Саати [2] шкала субъективной оценки предпочтения
одноrо элемента над друrим.
Преобразуем (2.48). Из BToporo уравнения G 2з == g. a.. l . Представив это
выражение в первое уравнение, имеем:
Ag +g)(l+a)......a =0.
(2.49)
Данное уравнение определяет зависимость меры множества А I от Il"
параметра и субъективной оценки предпочтения. Используя
аналоrичные рассуждения для подмножества А 2 и определяя
gt
экспертное предпочтение А[ над Al в виде .-. = r ,получим
g2
следующую систему уравнений:
Бочарников В.П.

Fиzzy Techпo/ogy
67
...ai
19l + g2 (1 + а)  а == О
19j: + g2 (1 + {З) ....... {З == о
g. == rg2
(2.50)
...,,-
\
t

..
riiы имеем разрешимую систему уравнений относительно g., g2, л. В
J?C3ультате решения (2.50) получим:
 r 2 (3....а
... g2 == r2W )r (a+ 1) '
r
"'.' У 2 Jj ..... а
t.:.
g    
·  у(р+ 1).... (а + 1)'
002 аЬ{r2fЗ+а}+Ь2r{З
l = .  ......  .  .
r(r2fЗа)2 '
(2.51 )
.-1'"
,{".
a=r 2 (f3+1), b=r(u+l).
чение меры подмножества Аз леrко находится из условИJI
, мировки:
}..... G I2 (2.52)
g. == 1 + л.G 12 ;
-де О'2 = g. + g2 + лg.g 2 .
,о.'
.аким образом, в результате обработки трех ответов эксперта
, ительно парноrо сравнения указанных выше подмножеств мы
,_ м возможность определить их меры.
.имер 2.3.
...
 истинное значение нечетких плотностей меры на пространстве
ird х== 3 равны g. == 0.3, fu == 0.2, gз == 0.04 и параметр нормировки
. .  5.8 результате опроса эксперта имеем
;.
:
== 1.07
G 2J
g2 = 0,5
G. J
g. 1 .
= .5
gl
_ пользуя выражения (2.51) мы получаем значения (Табл. 2.4):

Бочарников В. п.

68
Fиzzy Techп%gy
Таблица 2.4. .. Значения плотности нечеткой меры.
Параметр g. g2 g] Л
Значение 0.3001 0.2033 0,0401 4,998
Таким образом, видим, что для множества Х с Card Х == 3
использование полученных зависимостей позволяет определить все
плотности и Л.. параметр нечеткой меры. Преимущество
предложенноrо метода идентификации заключается в возможности
построить итерационную процедуру построения нечеткой меры для
пространств Х с Card Х > 3. Опишем эту процедуру.
Пусть в результате эксперимента получено, соrласно приведенному
выше, распределение нечеткой меры gx(.) на трех подмножествах А;
(Рис. 2.4):
{Aili = 1,3 ,А , n A j = 125,
1
А , =l:-Aj,i =1:- j}. (2.53)
g'x(X)
g2X(X}
UA. == Х,
. ,
,
в
о
А',
А'2
А'з
х
А 2 .
А 2 2
А 2 з
А 2 4
Рисунок 2.4. .... Распределение нечеткой меры.
Ступенчатая функция g(x) есть первое приближение
распределения плотности нечеткой меры (rде g i (х) .... равномерна на
каждом A i ).
Бочарников В.П.

Fиzzy Techп%gy
69

jtaльнейшее уточнение функции gx(x) на 2....м шarе осуществляется
следующим образом. Эксперту предлаrается оценить предпочтение
подмножества В с Х над В=Х\В.. (Желательно, чтобы Vi, В  A i ,
flпаче информации для уточнения gx(x) не будет). 8 результате оценки
имеем уравнение:
A.g(B)+g)(BXl+a)a==O .
(2.54)
При известном л (из предыдущеro шara) с учетом тoro, I.по gх(в) Е [01]
имеем:
 (1+a)+,{(1 )2  4ia
gX<B)== 2A e[Ol].
(2.55)
в результате полученной от эксперта информации функция gx может
быть уточнена следующим образом. На втором шarе получаем
следующее множество подмножеств (см. рис. 2..3):
{Aii==l4, AiПА]== yAi==A: Ai;l:A],i;l:j}- (2.56)
3IIачение функции g( -) на A i , i== 1,4 определяется из соотношений:
g(Al) = g(A 1 1 );
2 gx(B) g(A 1 1 );
g( А 2 ) =     
1 + 19(A)I)
2 g(AJ).... g(Ai)
g( А ) ==      ;
з l+lg(Ai)
g(A]) == g(Al).
(2.57)
r.
If Таким образом мь] имеем возможность уточнить функцию gx(x).
 Обобщая данную процедуру для [....20 шarа будем иметь возможность
yrочнения функции gx(x), при этом для [....20 шarа буде м имет ь значение
gx(A'J на 1+2 непересекающихся подмножествах i = 1,1 + 2. Учитывая
. условия аналоrичные (2.56) в пределе будем иметь при [  00 непрерывную
функцию IU1ОТНОСТИ нечеткой Mepblg){(x): Х  [01].
-pq
Бочарников В.П.

70
Fиzzy Techпology
Однако, не является рациональным увеличивать количество q вопросов
к эксперту. На I....M шarе эксперту будет задано вопросов:
q == 1 + 2.
(2.58)
Поэтому, после получения приближения функции распределения
.
плотности нечеткой мерь] на q подмножествах пространства Х
целесообразно осуществить аппроксимацию функции плотности gxfx}
функцией (L..R)....типа.
Определение 2.9.
Функция, обозначаемая
(L....R) типа тоrда
'Vx Е Х = [О,-+ос[: Ц ....х) = Цх);
на множестве х.
L (или R) является функцией
и только тоrда, коrда
40)=1, L(.) .. монотонно убывает
.
в качестве таких функций MOryr выступать функции вида:
L(x) = max(O.llxPI);
Цх) = exp(lxPI). р > 1
(2.59)
Для функции распределения gA, (-) меры может быть использована такая
L(.) функция для которой:
g([O,x]) = L[(a.... х) I fJ v О], (2.60)
rде а .... параметр, при котором g([Oa]) == 1, р.. коэффициеm
нечеткости.
Таким образом, определив функцию (L....R) типа аппроксимация
нечеткой меры может быть представлена в виде следующей
процедуры. Пусть в результате экспертной оценки имеем значение
нечеткой меры gx(AJ == g; на подмножествах пространсmа Х:
{Alli == 1,1 + 2,А. ПА] = 0,YA 1 == х}
(2.61 )
Будем полаrать, что для любоrо А; с Хнечеткая мера gxf
сосредоточена в точке Xi Е А; с Х, такой, что:
Бочарников в.п.

Fиzzy Tвchпo/ogy
71
А. = [ Х_  141 . х. + 141 ] ,
, , 2" 2
r
фе 'А,1 .. длина интервала А;_ Тоrда мера подмножества А, через (L..R)
Ункцию может быть представлена в виде:
А = L[9'+J1 ]L[9'p '
gx( ;} [ I A.' ]
] + ЛL f{J.... 
2/3
(2.62)
2( о  х. )
fде f{J = ..!,o = inf х. Используя значения gx(A i ), полученные
 2/3
!1t экспертов, задача (L..R) аппроксимация функции распределения
Нечеткости сводится к оценке параметр08 а и р (L..R) функции по
:минимуму функционала качества:
J
I
и= { L<gх(В)gi-(В))2 } 2 min.
Ве2 Х
g:(B)=  [Пв(лgl+l)lJ
(2.63)
(2.64)
аким образом, при минимизации функционала (2.62) мы получаем
довлетворительное представление функции распределения нечеткой
ры (L....R) .. функцией.
. .
рис. 2.5 приведен обобщенный алrоритм идентификации нечетких
на основе предложенноrо выше подхода. Приведенный алrоритм
нтификации по сравнению с подходом, основанным на методе
rи, а также с подходом I1рямоrо рейтинrования являеТСJl более
ктивным. Например, в случае рассмотрения дискретноrо
анства Х размерности CardX == 6, величины поrpешности,
.},о-доемкости и сходимости оценок нечеткой меры приведены в табл.
.,U. , ·
Бочарников В.П.

72
Fиzzy Techпology
Таблица 2.5 .... Оценка эффективности алrоритма
Характеристика Алrор. Саати Алrор. А * Прямое
п и cardx == 6) ейтинr.
Поrpешность, % > 1.5 > 1.7 =10
Т доем кость, кол.с . 14 6 6
Сходимость, кол.ите . 14 4 6
Начало А *
Определ. ПQдмножествв
{Ai l I i == 1,3; 'А}n Ajl == 0;
u Ail==X; i *- j}
Определ. степеней
предпочтения а, В, у
Решение системы
лgI 2 +gl(l+а) .. а == о;
л2+g2(1+f3)" f3 == о;
gl == 'т2.
Определение gз(Аз l )
1== 1 + ]
Задание BL*- ail1
определение
семейства {Ai L }
Расчет g(Ai L )
Конец
Рисунок 2.5 .. Алrоритм идентификации нечетких мер.
Синтезированный новый эффективный алrоритм идентификации
нечетких gA .. мер является важным с практической точки зрения. Он
обеспечивает высокую степень адекватности оценок нечеткой меры,
снижает вычислительные затраты и обеспечивает итерационный
подход, учет внyrpенней структуры меры, снижение наrpузки на
экспертов (в случае их привлечения). Тем самым данный алrоритм
позволяет эффективно осуществлять формализацию нечетких данных
при описании аналитических задач поддержки принятия решений.
Бочарников В.П.

Fиzzy Techпology

r лава 3
.ОБР АБОТКА НЕЧЕТКИХ
.ДАННЫХ НА ОСНОВЕ
ВЕЧЕТКОИНТЕrРАльноrо
ИСЧИСЛЕНИЯ
.}.
.,
:
'"
','{
..
Бочарников В.П.
73

74
Fиzzy Techпology
3.1. Определение нечеткоrо интеrpала
Для исчисления нечетких величин представленных нечеткими мерами
и множествами на пространстве с нечеткой мерой MOryr быть
использованы нечеткие интеrpалы, которые задаются соrласно
следующеrо определения.
Определение 3.1
Нечеткий интеrpал (НИ) от функции Ь(х) : Х ----+ [01], измеримой
на пространстве (Х, В) с нечеткой мерой g: 2 Х ----+ [О 1] на
множестве А с Х по нечеткой мере g(.) определяется
выражением:
J h(x) о g(.) == sup {а л g(АПН а )}. (3.1)
А ae[OI]
rде На == {xl h( х) > а}. J  нечеткий интеrpaл.
в литературе [15, 17] нечеткий интеrpал называется также нечетким
ожидаемым значением (fuzzyexpected value FEV). Кроме определения
нечеткоrо интеrpала (3.1) может быть использовано следующее
выражение, определяющее нечеткий интеrpал.
Теорема 3.1:
Пусть (Х В) измеримое пространство с заданной на нем
нечеткой мерой g(.) и пусть Ь(х) .. в"измеримая функция.
Нечеткий интеrpал ОТ функции Ь(х) на множестве А с Х по
нечеткой мере g(.) определяется выражением:
! h(x)o g.,(-)== r[i!Jf h(x) л g(AnE)] (3.2)
Бочарников В.П.

Fиzzy Techпology
75
, ,...
JlQкззательство.
'Рассмотрим нечеткий интеrpал на А с х. Соrласно (3.1) имеем
'За- Е [01], J h(x) о g(.) = а. л g(AnHa.)== F. Для выражения (3.2)
А
рассмотрим 2 случая:
1. Если Е::> На4', то имеем а. > inf h(x) и
ХЕЕ
g(A (1 Е) > g(A (1 На.).
Тоrдасправедливо: Fi > inf h(x) л g(A nЕ);
хеЕ
2. Если Е с На4', то имеем а. < inf h(x) и
ХЕЕ
g(A (1 Е) < g(A (1 Н а *).
Тоrда справедливо: Fi < inf h(x) л g(A nЕ).
хеЕ
4 _
()тсюда видно. что V ЕсХ p[ i!!f h( х) л g( Е ПА)] = F..
'Следовательно выражение (3.2) справедливо.
fожно показать, что понятие НИ сходно с понятием интеrрала
JIебеrа. Для этоrо рассмотрим разбиение множества Х на
!Jiепересекающиеся подмножества E i следующим образом:
- "
rX=UE i , E,nE j =0, i,j==l,п, i*-j. Представим
'=1
ункцию h(x) в виде ступенчатой функции: h( х ) = L а ;/Е. (х), rде
.
lXi e [О 1], EiE В, hj(X} Е {О 1} .... характеристическая функция множества
. Пусть на пространстве (Х, В) задана мера Лебеra 1(.). Интеrpал
jre{)era от функции h(x} по множеству А с Х определяется выражением:
fh(x)dl='iaJ{AпEJ, a, < ai+"i=l,n. (3.3)
А ;=1
пользовавшись разбиением множества Х на подмножества E i
ункция h(x} может быть переопределена в друroм виде. Пусть
Бочарников В.П.

76
Fиzzy Techп%gy
множество F; определяется как F; == Е, UE;+I U...UE n и а; < U;+I.
Тоrда функция h{x) может быть представлена как:
h(x) == тах min «(Xi, fFi(X»,
;
rде fFi(x) .... характеристическая функция множества F i , определенноrо
выше. Torдa нечеткий интеrpал по аналоrии с интеrpалом Лебеrа
может быть определен в виде:
J h(x) о g == m a min(aj,g(Anfi»). (3.4)
А i=1 7 п
Сравнивая (3.3) и (3.4) можно обнаружить сходство между данными
интеrpалами (операции сложеНИJl и умножения замены для интеrpала
(3.3) на операции тах и min соответственно для НИ).
в случае интеrpирования по вероятностной мере оба интеrpала
Лебеrов инечеткий MOryт быть сравнены.
Теооема 3.2:
Пусть (Х в, Р) .... вероятностное пространство, а Ь(х): X----+[Ol]
есть в .... измеримая функция, то справедливо оrpаничивающее
неравенство:
 ( l  inf h ) 2 < J мр ! h о Р < ( su p h ) 2 (З.5)
2 х .\' 2
rде infh = inf h(x), suph = suph(x).
хеХ хеХ
Доказательство.
Пусть значение нечеткоrо интеrpала будет:
J h о Р == м Е [О]] == м л Р(Н м ) ;
х
rде Н м == {х' h( х ) > М}; Рассмотрим интеrpaл Лебеra от функции
h(x):
J hdP == J hdP+ J hdp.
Х 11м X\11 M
Бочарников В.П.

Fиzzy Теchлоlоgу
77
:.Для нечеткоrо интеrpала определим семейство функций {h, (х )} для
J«YfOpLlX выполняется условие 'rj hj(x ), 1 h j ( х ) о Р == м · Определим
Х
мажоранту и миноранту этоrо семейства функций. Мажорирующая
tyнкция семейства {h; (х )} определяется выражением:
. { suph,x Е НМ
h (х)==
М,х (/. Н лt
Минорирующей функцией будет:
{ М, хеН м
h:(x) == . f 'z.. Н
IЛ т" Х(/. М
.'
'nOдставим значения мажоранты и миноранты в интеrpал Лебеrа. Для
.
ункции h (х) будем иметь:
JhdP== J hdP+ J МР < J suphdP+ J MdP==
Х НМ Х\Н м НМ Х\11 лt
== suph. Р(Н М ) + M(l  Р(Н М » == suph. М + M(l  М).
,IJЯ функции h.(x) имеем:
J hdP== J hdP+ J МР > J MdP+ JinfhdP==
Х 11м X\11 M НМ X\11 M
== М. P(HM)+infh.(1  Р(Н М »== м 2 +inf h.(I  М).
:. ким образом справедливо:
l(
М 2 +inf h(lM) < J hdP < M(l M)+suph.M
.J(
оrда разность интеrpала Лебеrа и НИ будет оrpаничена
l;еравенствами:
t:F; =М +inf 1(1  М)..... м < f ЫP1 hoP<M(1  М)+suphМ м=р;
  
i
Бочарников В.П.

78
Fиzzy Techп%gy
Найдем максимальный диапазон неравенств по М. Для этоro найдем
экстремумы функцией Р;, i == 1,2 по значению НИ М.
dF . dF
d ==2МIПfh1; d ==2M+suph.
Откуда максимальный диапазон неравенств определяется при
М == 1 + inf h ДЛЯ нижнеrо оrpаничения и при М == ! sup h для
2 2
Bepxнero оrpаничения" Тоrда подставим значеНИJl М в функций F;. 1 ==-
1,2:
· F ( 1 +inf h ) 2 · f{1 1 +inf h ) 1 +inf h
mlП = +ln  ..... =
м I 2 2 2
1  2inf h 4 +(inf h)2 == { l  f h J
mахР = SUP ( 1  SUPh ) + (suphY  suph == ( SU P h ) 2
м 22 2 2 2 2
Следовательно справедливо:
( linfh ) 2 J ( SUPh ) 2
 2 < xhdP!hoP < 2
Что и требовалось доказать.
Следствие 3.1
Если (Х, В. Р) .... вероятностное пространство, Ь(х): Х ----+ [01]
.в....измеримая функция то:
1
J hdP.....l hoP < ;
х Х 4
(3.6)
Доказательство следствия тривиально, так как \ixeX, Ь(х) е [01] и
подстановка предельных значений единичноrо интервала в
неравенство (3.5) дает величину по модулю равную 0.25. В противном
случае функции F i , i==1,2 не превосходят по модулю 0.25.

Бочарников В.П.

Fиzzy Techп%gy
79
ta
Определение нечеткоrо множества, фиксирующеrо степень
принадлежности элемента х Е Х подмножеству А Е F(X), rде Р(Х)..
множество всех нечетких подмножеств Х, может быть пред ставлено с
использованием нечеткоrо интеrpала следующим образом.
f
Ib'cTh необходимо оценить степень принадлежности ..элемента х Е Х
 .J.ножеству Е с х. Очевидно, что для пустоrо множества эта степень
ri]>инадлежности равна О, а для х Е F, rne Е с F равна единице, то есть
i-creпень принадлежности для х Е F будет больше, чем дЛЯ ХЕ Е, если
.",
J.EcF.
"".
: t
 степень принадлежности хо Е Е равна g(xo,E), а вместо Е имеем
flечетное множество J1 А Е F(X), тоrда:
g(xo,A) = J РА(Х)О g(xo)= Jlл(Х о )
х
(3.7)
..
r. "
iJPO rоворит, что степень нечеткости суждения xo Е А" равна степени
инадлежности ХО нечеткому подмножеству РА- Таким образом, мы
е раз видим, что понятие степени нечеткости в теории нечетких мер
' ючает в себя понятие степени принадлежности теории нечетких
жеств.
ически нечеткий интеrpал можно представить соrласно рис.3.1.
.....
Ь(х)
f(x)
Рисунок 3.1 ... rрафическое представление нечеткоrо интеrpала
F I2
,
1

F.(a)
fAhOg
r F 2 (a)
. а*
1
Бочарников В.П.

80
Fиzzy Techпology
При этом НИ представлен в следующем виде:
I Цх) о g(.)= sup {F;(a) лF;(а)}'
A aeIOI]
rде F;(a) = а;
F;(a)=g(HJIA) = g({xlh(x) > а} ПА) =  {еХ{ Лн!!(х}dt ]l}
rде!(х).. распределение плотности нечеткой меры.
Рассмотрим пример вычисленИJI нечеткоrо интеrpала ДЛЯ дискретноrо
множества х.
Пример 3.1.
Пусть задано пятиэлементное множество Х = {х,} , i = 1,5 на котором
заданы ФУНКЦИЯ принадлежности нечеткоrо множества h(x) и
распределение плотности нечеткой MepLlg (о) (та6л. 3.1).
Таблица 3.1 .. Исходные данные.
1 1 2 3 4 5
h (х) 0,1 0,3 0.7 0,6 0.2
К; 0.143 0,4 О,26) 0,350 0,1 3 1
Соrласно условия нормировки параметр л. нечеткой меры равен:
л == ..0.51. Тоrда значение S НИ принимает значение:
s = SUp {а л ga },
ae[OI]
(3.8)
ga = 1 ( П(Agi+l)I )
А iee a
Соrласно приведенных формул значение НИ будет: S == 0.5645.
8а = {llh(x;) > а}'
@
Бочарников В.П.

Fиzzy Techп%gy
81
rДля непрерывноro прocrpaнcrва Х "" R вычисление нечеткоro
интеrpала может быть упрощено и сведено к нахождению значения на
MOHorpaMMe (или в таблице). Если h(x} есть отображение функции
принадлежит, то справедливо, что:
Va i , а, < а2' а ; Е [01], i = 1,2 => Ра. :J Fa;. ,{xlh(x) > а;} = F
 этом случае соrласно [12] справедливо следующее. Если f(x} ..
: ttЛ0ТНОСТЬ нечеткой меры, значение НИ от h(x} по нечеткой мере равно
значению а Е [01] для KOToporo справедливо:
ln(l + ал.)
р(Н ) = -- л. Е [....l,+oo[
а In(1 + А) ,
(3.9)
.
тде
Р(Да) == J f(x)tk. [ ! f(X)dx ] 1 ·
110; Х
.
.рравая часть (3.9) зависит только от значений л. и а и может быть
: получена заранее в числовом виде в форме таблицы или rpафика.
Jlевая же часть (3.9) представляет собой отношение области
'рпределяемой уровневым множеством На ко всей области определения
-функции плотности нечеткой MepLIf(x}.
».
:Использование (3.9), таким образом, может облеrчить орrанизацию
 <Вычисления нечеткоro интеrpала.
"
fo
It.
Бочарников В.П.

82
Fиzzy Techпology
3.2. Основные свойства
нечетких интеrpалов
Для дальнейшеrо рассмотрения нечетко..интеrpальноrо исчисления
целесообразно остановиться на основных свойствах нечеткоrо
интеrpала.
Нечеткий интеrpал на непрерывном пространстве Х будет принимать
значение М если будет выполняться условие:
1 h(x)og== M==g(H M ),
Х
rде НМ == {xlh(x) > м Е [Оl]}ПРИ этом выполняется то, что
g(H м) > м > g(H м+{)' rде Н М+{) = {Xlh(x) > м Е [Ol]}. ЕсЛl1
обозначить Н = { X 1 h ( x ) > М( l  ! )} тоrда Н = lim Н. Б
п , М пoa п
п
(3.10)
этом случае, значение нечеткоrо интеrpала может рассматриваться как
"редел:
м == lп1!l g(H,,) == g(HM)-
в том случае, коrда рассматривается интеrpирование постоянной
Функиии Ь(х) == const == а Е [01] нечеткий интеrpал удовлетворяет
соотношению:
1 h(x)og= I aog==a.
х х
(3.11 )
Пусть Ь(х): Х --4 [01], а а Е [01] тоrда соrласно [10] удовлетворяются
следующие соотношения:
J (avh(x»og=av J h(x)og,
Е с Х Е
(3.12)
Бочарников В.П.

Fиzzy Techпology
83
,.,.
J (алh(х»)оg=ал J h(x)og.
Е с Х Е
(3.13 )
_ Аналоrично тому, как для интеrpала Лебеrа существует возможность
. вахождения интеrpала по областям, для НИ справедливо следующее.
. .nусть Е. F е В, а (Х, В. g) .... пространство с нечеткой мерой. Тоrда
'справедливы соrласно [10] следующие соотношения:
1 h( х ) о g > J h( х) о g V J h( х ) о g ,
EUF Е F
(3.14)
J h(x) о g < J h(x) о g Л J h(x) о g .
EnF Е F
(3.15)
Кроме Toro, если Е с F то соrласно [15] выполняется следующее
"'lIepaBeHCTBO:
J h( х) о g < 1 h( х) о g .
Е F
(3.16)
,Если на пространстве (Х В, g) заданы две функции принадлежности
J1i(X), i 1,2 такие, что 'rIx Е Х, Ь.(х) < Ь 2 (х), ТО дЛЯ нечеткоrо ин.теrpала
,Выполняется следующее соотношение [15]:
J h.(x)o g < J h1(x)o g.
(3.17)
Данный результат может быть расширен на случай рассмотрения
рересечения и объединения множества функций h j (х).
.
..
.8Ссмотрим семейство функций Н == { h j (х) I h j (х): Х ----+ [01], i==I,N}.
Цля данноrо семейства функций справедливым оказываются
f
ледующие неравенства [10]:
I m.in h. (х ) о g < m.in I h. ( х ) о g;
Е. " , Е '
I mxh.(x)o g > тxl h.(x)o g;
Е " , Е'
(3.18)
(3.19 )
ь том случае коrда семейство функций Н является монотонной
ледовательностью В .... измеримых функций при увеличении i, то
enpаведливым оказывается следующий предельный переход:
Бочарников В.П.

84
Fuzzy Techп%gy
Ilm h. ( х ) о g = 1m I h. ( х ) о g ·
,oa ' ,oa'
(3.20)
Кроме Toro, если h;(x} .... монотонно возрастающая (убывающая)
последовательность В .. измеримых функций и {йа .... монотонно
убывающая (возрастающая) последовательность вещественных чисел
ai Е [01], то в работе [10] бьшо показано, что выполняется тождество:
1 ;/ a; Лh;(х»]оg== ;I[a; л lh;(x) о g]; (3.21)
в случае интеrpирования нечетких отношений оказывается
возможным установить следующие важные соотношения.
Лемма 3.1
Пусть задано пространство (Х В, g) с нечеткой мерой и
нечеткое отношение h(x,y} :Х х У ----+ [01] тоrда ВЫПОлняются
неравенства:
sup f h(x,y)o g < f suph(x,y)o g,
уеУ Х Х уеУ
(3.22)
inf f h(x,y)o g > f inf h{x,y)o g.
уеУ Х Х уеУ
(3.23)
Доказательство .
Из определения проекции нечеткоrо отношения h(x,y) [18] следует.
что:
V'x,y, Proj Xh(x,y) == suph(x,y) > h(x,y).
уеУ
Для нижней rpани нечеткоrо отношения выполняются условие:
Vx,y, inf h(x,y) < h(x,y).
уеУ
Тоrда, исходя из свойства (3.17) можем записать:
Бочарников B.п

Fиzzy Techпology
85
V'y Е У ,
1 h(x,y) о g < J suph(x,y)o g
х х y
..
..
, \.
'>'
I h(x,y)o g > J inf h(x,y)o g
х  y
. и требовал ось доказать.
А
Соrласно работы [12], если смяrчить условие оrpаничения на значение
иечеткой меры полаrая, ЧТО ДЛЯ Х == R выполняется условие:
lim НА (х) = ! ln(l + А) ·
xoa А
(3.24)
.;rдe н-л(х) .. Функu ия F.. распределения gA (.) меры, то есть что мера
ero множества оrpаничивается нормирующим множителем
1
л = А ln(l + А). то справедлива доказанная в [12] лемма:
Лемма 3 .2
Если функция 1UI0тности нечеткой меры, с помощью которой
строится мера gл одна и та же, то для пары
А А Е [ .....1 +оо [ такой, ЧТО Л, < Л2, справедливо неравенство:
l' 2 ,
J h(X)og1 (-» J h(x)og;.".
х "1 Х 
(3.25)
,1.
or.i.-'!I
.4;
 
. заключении рассмотрения ОСНОВНЫХ своиств нечетких интеrpалов
, . ,BeдeM возможный вариант вычисления нечеткоrо интеrpала для
j' кpeTHoro множества х.
.(.<
'>rласно свойства (3.15) можем записать:
1 h(x)o g > тx(e.)
() "
(3.26)
... ei .. нечеткий интеrpал от функции Ь(х) по подмножеству А; с Х ,
и UA. == Х,А. nA = {о при i =/:. j. Однако, ДЛЯ любой
.' "
,
\  ,купности подмножеств A i условие (3.26) выполняется, что следует
свойства (3.16).
Бочарников В.П.

86
Fиzzy Techпo/ogy
Тоrда, если переопределить Функцию h(x) как не возрастающую, то
есть h(x.» h(x 2 » ...> h(x,,),h(x;) е [01], то множество а..срезов
h(x) будет удовлетворять при уменьшении а следующему условию: A i
=: Ai+IU{Xi}, Ai+.=={Xlt...,Xi...}. ФУНКЦИЯ меры gi == g(A i ) будет функцией
не убывающей (Рис.3.2).
1
0.8
o.
0.4
0.2
о I

.  io-o--
......... у "
"" ,. о io-o-- О h(x)
. ...... ........... io-o-- О g(Ai)
.......  i
. .
"1'--- ' .... ....... ...... ..... 
 . . r
::- ,
, 
х1 х2 х3 х4 Х
.1 ....:
 ,
Аз
Рисунок 3.2.. Определение нечеткоrо интеrpала..
Тоrда, нечеткий интеrpал для К8ЖДоrо подмножества А ё будет
удовлетворять:
е; == min(h(x;),g(A;».
Следовательно, предельное значение последовательности нечетких
инrеrpaлов ei равное нечеткому инrеrpалу от функции Ь(х) может быть
определено в виде:
J== 1 h(x)o g = sp(eJ= sup{ min(h(xJ,g(AJ)}.
х WA 
(3.27)
Формула (3.27) может быть использована для вычисления нечеткоro
инrеrpала при дискретном множестве х.

Бочарников В.П.

Fиzzy Techпology
87
, 
. .. 
3.3. Определение расширенной
...,
:вечеткои меры
Прежде чем приступитъ к рассмотрению расширенной нечеткой меры
дацим определение нечеткоrо интеrpaла на нечетком множестве [15].
Определение 3.2
Нечеткий интеrpaл от функции h(x): Х  [О 1] на нечетком
множестве РА(Х):Х  [01] по нечеткой мере g(.),
определенной на пространстве (Х В) находится как:
J h(x)og= J[,uA(X) л h(x)] о g(.).
J.LA(X) Х
(3.28)
аким образом) рассматривая обычное множество Е с Х ДJIЯ нечеткоro
rpала справедливым будет следующее выражение:
1
J h(x) о g = J {ХЕ(Х) л h(x)} о g,
Е Х
(3.29)
_.де ХЕ(Х) : X{O,I} .. характеристическая функция подмножества
ji 1 b х.
.,;.

)'СТЬ (Х В. g) .. пространство с нечеткой мерой. Обозначим через F(X)
ожество всех нечетких множеств на пространстве Х При этом,
tf
евидно, что В с F(X), так как обычное множество можно
сматривать как частный случай нечеткоrо множества, ДJIЯ KOToporo
КЦИЯ принадлежности совпадает с характеристической функцией
Horo множества. В этом смысле множество F(X) является
ширением множества В. Определим нечеткую меру на Всех
ементах множества F (.х).
i ';
Бочарников В.П.

88
Fиzzy Techпology
Определение 3.3 .
Функция множества g(.) определяемая в виде:
g(J1J == 1 J1Jx) о g
х
(3.30)
ДЛЯ нечеткоro множества А = {(Х'РА(Х»}' РАХ) е F(X)
,...,.
называется расширенной нечеткой мерой на F (.Х).
fрафически определение расширенной нечеткой меры приведено на
рис. 3.3.
1
х(А)
g(Jl(X) )
g(A)
g(.)
 Jl(X)
А
Рисунок 3.3 ... Определение расширенной нечеткой меры.
Расширенная нечеткая мера g(J.l) позволяет определить нечеткую
меру для четких подмножеств Е с Х с учетом оrpаничения заданноrо
нечетким множеством Jl.
:reoneMa 3.3 .
Пусть h(x): Х  [01] .... произвольное нечеткое множество на
пространстве (Х: В, g) с нечеткой мерой. Расширенная нечеткая
мера g,,(h) для нечеткоrо множества h(x) определяет нечеткую
меру на (Х В) для всех ЕсХ и удовлетворяет следующим
свойствам:
а) g,,(0) = о; g"(Х) = ! h(x)o g. оrpaниченность;
б) 'VA с В,=> кь(А) S КЬ(В); монотонность;
в) если АпЕ В и {А,.,}.... монотонная последовательность
множеств, то
lim g (А ) = g (Iim А ), непрерывность.
пoo 1,,, 1, ,.---t.... "
Бочарников В.П.

Fиzzy Technology
89
.,.
J1pказательство.
. 
J'асширенная нечеткая мера gn(.) для нечеткоrо множества h(x) и
ароизвольноro подмножества Е с Х определяется как
i ,
У,
gh(E) == I h(x) о g.
Е
(3.3 1 )
,Проверим выполнение свойств а, б, в..
{, а) g'h(0) = I h(x)o lr xl[X!O Л h(x)] о g= 100 g==O.
o х
g,,(X)== I h(x)og= М,rде M=g(H M ).
х
б) Проверим выполнение свойства монотонности. Пусть
 с В тоrда, соrласно (3.16) имеем соотношение:
1 h(x)o g < I h(x)o g => g/i (А) < g/i (В).
А п "
в) Пусть {AnlA n Е В}" монотонная последовательность
ожеств, а ХЛn: x {Ol} .. характеристическая Функuия множества
 s: х. Тоrда соrласно (3.29) можем записать:
V'A п , gh(A п ) == J h(x) о g = J [ XA (х) л h(x) ] о g.
АХ'}
fJ
 пределим функцию hn(x)  ХА" (х) Л h(x).
монотонной последовательности множеств {An} будем иметь
нотонную последовательность В.... измеримых функций hn(x). Тоrда
g/i(A )= I h (х)о g
, п Х п
 можем записать соrласно свойства (3.20):
· n(A,,) = lim I h,.(x) о g= I limh,.(x) о g= Ilim r ХА (х)лii.. х ) ] о g=
.. п---+ю Х Х п---+ю Х п 11
,
"fii.. х ) лlim Х4 (X) ] og= I 1(x)og==:g"h(limA n )
L " 1 . А п---+ю
. 1т ,"
.
Бочарников В.П.

90
Fuzzy Techпology
Что и требовалось доказать.
[]
Таким образом расширенная не четкая мера g,,(.):2 X  [01]
удовлетворяет свойствам нечеткой меры (см. определение 1.1) с такой
лишь разницей, что в свойстве оrpаниченности верхняя rpaHb значения
нечеткой меры оrpаничивается величиной М Е [01], M==xJ Jl(X) о g.
С учетом (3.27) расширенную нечеткую меру для нечеткоrо множества
h(x) можно рассматривать как сужение нечеткой меры g(.) на
подмножество Е с Х TaKoro, что V Х Е Е с Х, h( х) > I h( х ) о g.
х
То есть расширенная нечеткая мера g,,(.) определяетс.я на множестве
нечетких подмножеств
Fh(X) = {h'(x)lh'(x) = h(x) л ХА (х), V'A С Е}.
Бочврников ап.

Fиzzy Techпo/ogy
91
;'3.4. Основная теорема о нечетком интеrpале
..... .....
'по расширеннои нечеткои мере
.Н ее следствия
Прежде чем приступать к рассмотрению вопроса об интеrpировании
функций вида h(x): Х 4 [01], заданных на измеримом пространстве
напомним, что соrласно определения 3.3 по зависимости (3.30)
нечеткая расширенная мера определяется как:
g (.)= 1 J1(y)o g,
р (.)
(3.32)
. у
Tдe g: 2 4[01] ... нечеткая мера заданная на пространстве У, а J.l (у) .. g..
..измеримая функция вида р(у): У4[01].
..
,оrласно теоремы 3.3 расширенная нечеткая мера gp(.) обладает
:всеми свойствами нечеткой меры: оrpаниченностью, монотонностью,
'мепрерывностью, с той лишь разницей, что gp (У) < 1 и может быть
'определена как:
gi Y ) = I Jl(y) о g.
у
J'еперь рассмотрим следующую теорему.
(3.33)
Теооема 3.4 .
Пусть заданы пространства с нечеткими ерами (х, f{.» и (f:
g(.», связанные между собой отображением qJ: F(.X) 4 F(Y), rде
Р(.) .. множество всех нечетких подмножеств. Тоrда, нечеткий
интеrpaл от f .. измеримой функции h(x): Х 4 [01] по
расширенной нечеткой мере gp(.)' rде р(у) Е F(Y) на
множестве Е с Х определяется выражением:

Бочарников в.п.

92
Fиzzy Techпo/ogy
I h(x) о gll(-) == SUp(r л g(M p nФр(Н а nЕ»). (3.34)
Е r
rде
r==ал/3. a./3E[OI]. На == {xjh(x) > а}
Мр == {YlJl(Y) > /3}. Фр == {J-1qJ( Н а nЕ) > /3}.
lIоказательство.
в силу Toro, что определено отображение qJ расширенную нечеткую
меру можно представить в виде:
g (.)= f р(у)о g(.).
J.l ф(_)
Подставим данное выражение внечеткий интеrpал от функции
h(x) eF(X).
lh(x)ogll(-)==lh(x)o 1 Jl(у)оg(.)==sup { ал I P(X)og(.) } ==
Е Е (1'(-) а (I'(HanE)
== a л p(x) л q>(Ha nЕ)] о g(.)} ==
== a л il/3 л g(Фр(Н а nЕ)n М р )]} ==
== SUp {у лg(Фр(Н а nЕ)n М р )}
r=ал/3
Что и требовалось доказать.
[]
Данная теорема имеет ряд интересных следствий, показывающих более
общий характер нечеткоrо интеrpала по расширенной нечеткой мере.
Следствие 1 .
Если отображение Q): F(X)  F(Y) определяется через
условную нечеткую меру Ox(.1 у), то нечеткий интеrpал по
Бочарников В.П.

Fиzzy Techпology
93

.'"
расширенной нечеткой мере определяется соотношением (3.3),
rде:
Ф/3== { ) ' - ! l(x)oo"(oly» Pe[Ol] } .
Ha flE
(3.35)
Доказательство следствия очевидно и оно следует из доказательства
теоремы.
Следствие 2.
Если отображение  есть тождественное отображение
пространства Х на себя такое, что g() == f(.), то нечеткий
интеrpал по расширенной н е четкой мере определяется
соотношением:
_:
1 h(x) о gp(o) == sup(r лf(М/3 ПНа ПЕ»,
Е у
(3.36)
rде
r==ал/3, a,/3e[Ol], На =={хl h(x» a}
м /3 == {У\ J.l(y) > /3}.
оказательство.
1h(x) о gp(-) == 1 h(x) о (-) == 1 h(x) о 1 J.l(x) о f(-) ==
:Е Е Е Х
i'=sup { a л 1 р(х) о f(.) } = sup { a лsup(/3 лf(Н а ПЕП М/3)] } =
а Ha nE а /3
fi: Sup {У л f(Ha ПЕП М р )}.
у=ал/3
Что и требовалось доказать.
l1
'. lетим, что в следствии 3 используются понятия и соотношения
дставленные в следующей rлаве. Данное следствие приведено здесь
 сохранения общности изложения материала.
 Бочарников В.П.

94
Fиzzy Techпology
Следствие 3 .
Если отображение qJ есть отображение задающее Н....
соответствие между пространствами ( f(..» и (У, g(.», rде
Н С Xx то нечеткий интеrpал по расширенной нечеткой мере
определяется через Hro.... операцию над нечеткими мерами g(.) и
f(.) с бинарной операцией (J) такой, что
Сар== [FaпA]mM p ,
и находится соrласно выражения:
1 h(x)o gp(.) == sup{r АН", {g,f}[CaJI]}
А У
(3.37)
rде r == а л рЕ [01];
Ра == {xlh(x) > а Е [Ol]},
Мр == {ylll(y) > {з Е [Ol]}.
Доказательство .
Соrласно теоремы 3.4. можем записать:
lh(x)og (.)=lh(x)o I p(y)og,
А Jl А ф( Х)
rде q(x) есть функция qJ: Х  [О 1] Н.. соответствующая нечеткой мере
f(.), определяемая соrласно (4.28):
q>(X)(y)== J l(x)of(.).
Е н (у)
Соrласно теоремы 3.3. Н.... соответствия определяет расширенную
нечеткую меру порожденную характеристической функцией Х Е н (у) ·
Исходя из сказанноrо выше, можем записать:
1 h(x) о gp (.)== sup { a л I J1(y)0 g(.) }
А а ф[f;жПА](}')
Соrласно (4.28) будем иметь:
Бочарников в.п.

Fиzzy Techпology
95

'P[FanA]<y)= 1 l(x)ofO =i(EH(y)n(F a ПА».
ti EII(y)n(F a ПА)
rим это выражение в нечеткий инrеrpaл:
4,I(X) ogp(O) = sp{a л l[j.I(y) л q>[Fa ПА](у)] о g(.)} =
.,==suJ а л f J.1(y) о 1 1(у) о g(o) } ==
 а1 у ф[FаПАtу)
:sup { a л J J.1(y) о J q>[Fa ПА y) о g(.) } =
а у у
. .ал{Рл 2 р FanAy)og(o)]}=
"{Y л Jpf(EH(Y)('KPanA»og}= p{Y л Hw{g,[}<Cи/J)}
и 'Ipебовалось доказать
l1
tрафически нечеткий интеrpал по расширенной нечеткой мере может
Iьrrь npОИЛЛЮС'Ipирован, как приведено на рис. 3.5.
(
r <р{ Ha)
/
<... g(.)
!it
,#
{
.!
<р(.)
. Рисунок 3.5 ... Нечеткий интеrpал по расширенной нечеткой мере.
едует отметить, что предложенный в теореме 3.4 нечеткий интеrpал
.. расширенной нечеткой мере очень схож с рассма'Ipиваемым в
чном интеrpальном исчислении интеrpалом Лебеrа .. Стилтьеса.
f
Бочарников В.П.

96
Fиzzy Technology
Ранее мы уже отмечали СХОДСТВО (сравнимость) интеrpала Лебеrа и
нечеткоrо интеrpала по Суджено (теорема 3.2). Далее мы HeMHoro
остановимся на свойствах нечеткоrо инrеrpaла по расширенной
нечеткой мере.
Бочарников В. п.


Fиzzy Techпology
97
'::.5. Свойства нечеткоrо интеrpала по
.' ..., ...,
. ..сширеннои нечеткои мере
..' < приведенноrо ранее материала видно, что основные свойства
. четких интеrpалов во MHorOM определяются свойствами нечеткой
.- ы относительно которой осуществляется интеrpирование.
rlo
iCCМО'Ipенная нами ранее теорема 3.3 позволяет сделать вывод, что в
. 110М, расширенная нечеткая мера обладает всеми основными
,-> йствами нечеткой меры, а именно свойствами непрерывности,
. нотонности, оrpаниченности.. Единственное отличие расширенной
еткой меры от обычной меры, данной в определении 2.1,
ючается в том, что расширенная нечеткая мера gp(.) на всем
· ожестве Х может принимать значения меньше единицы, то есть
,
g,JX) == J р(х) о g(-) < 1,
х
i, <р(х) :Х  [01], g(.) : 2 Х -4 [01].
(3.38)
curnм образом имеем верхнее оrpаничения на значение функции
. .жества gp(.). В дальнейшем будем считать, что функция gp(.)
; аничена величиной Ме [О 1], то есть:
gJl(X) == м Е [01].
(3.39)
-вие (3.39) будет определять некоторые отличия свойств нечеткоro
 .ала по расширенной нечеткой мере от свойств интеrpала
деленных в пункте 3.2
. силу совпадения свойств обычной и расширенной нечетких мер
: йства нечетких интеrpалов не связанные с условием (свойством)
.... ниченности нечеткой меры останyrся без изменений в виде
<дставленном в пункте 3.2. В этом пункте мы рассмо'IpИМ лишь те
. 771
Бочарников В.П.

98
Fиzzy Т echпology
свойства нечетких интеrpaлов, rде условие оrpаниченности (3.39)
может оказать свое воздействие.
Лемма 3.3 .
Нечеткий интеrpал по расширенной нечеткой мере gp (.) от
постоянной функции 'tIXE h(x) == а Е [01] определяется
соотношением:
laog (-)==алМ.
х j.l
(3_40)
Llоказательство .
,
I aog (-)= I ао I J.1(x)og(.)== I ао I 1(x)og= l[алJ.1(х)]о Il(x)og=
х j.l х х х р(х) Х Х
== l[алJ.1(х)]оg==ал I J.1(х)оg=алМ
х х
fJ.
Лемма 3.4.
Для нечетких интеrpалов по расширенной нечеткой мере
справедливы следующие свойства:
I[a л h(x)] о gp(-) == а л 1 h(x) о gp(')' (3.41)
х х
![а vh(x)]ogi o ) =={av ! h(x) о gp(o)} Л М, (3.42)
тде аЕ [01], р(х), h(x): Х---7[ОI], g:2 x ---7 [01].
Llоказательство .
Сначала рассмотрим доказательство соотношения (3.41).

Бочарников В.П.

Fиzzy Techпology
99
Jfалh(х)]оgll(-)== f[алh(х)]о f J1(x)og== f ао f J1(x)og==
..Х'" Х Х Х h(x)
: 1 а о J[h(X) л J1(Х)] о g == а л f[h(x) л J1(Х)] о g ==
'К Х Х
'.0 О'а л f h(x) о f J1(Х) о g == а л f h(x) о Кll(-).
s Х Х Х
"-<
· доказательства соотношения (3.42) рассмО1рИМ ФУНКЦИЮ (а v h(x».
"видно, что при а < а Е [01] а .. уровень функции (а v h(x»
. = {xlav h(x) > а Е [Ol]} = х. Исходя из этоrо можно
ставить следующую зависимость:
("
f[avh(x)]ogll(-)== SUp {алgll(G а )}==
Х aE[OI]
== sup {а лgр(Gа)}v sup {а лgll(G а )};
аЕ[О,а]  aE( l  
А В
,,- ; '!:
и А > В, то:
f[a v h(x)] о gi-) == sup {а л gll(G a )}== а л М;
Х аЕ[О,а]
., A<.В тоrда имеем:

f[a v h(x)]o Кр(.) == sup {а лgll(G а )};
Х aE(a,I]
· G a == {xlh(x) > а Е (a,l]}, а следовательно:
f[avh(x)]ogll(-)== f h(x)ogll(-).
Х Х
;" сюда имеем:
На v h(x)] о Кр(-) == [а л М] v f h(x) о Кр(-) ==
Х Х
=[av !h(х)оgро]л[ Mv !h(X)ogp(-)]
,.нако м > f h( х) о g 11 (-), поэтому:
. Х
Бочарников В.П.

100
Fиzzy Techпo/ogy
J[avh(x)]ogpO=[av J h(x) о gi.)] л М.
х х
8
Рассмотрим следующую лемму, определяющую свойства нечетких
интеrpалов по расширенной нечеткой мере. Если hi(x) .... монотонно
возрастающая (убывающая) последовательность g.. измеримых
функций hi(x): Х  [01], а {ai} .. монотонно убывающая
(возрастающая) последовательность вещественных чисел ai Е [01], то
справедлива лемма.
Лемма 3.5.
При указанных выше свойствах последовательностей функций
hi(x) И чисел ai для нечеткоrо инrеrpaла по расширенной
нечеткой мере справедливо свойства:
f  [ a. л h.(х) ] оg (.)=  [ a. л J h.(x)og (.) ] .(3.43)
. . /, 11 . . 1 1 11
XI= r 1= Х r
Доказательство.
в силу монотонности свойств функций hi(x) для убывающей
последовательности hj(x) справедливо соотношение Fa. cE a., rде:
F: == {xlh2 > а},Еа == {xlh. > а}.
Для простоты будем рассма'IpИВать последовательность из 2..х
функций" Тоrда:
2
f .[ai л(х)]о gp(-) = sup {алоgр(Еа)}v sup {алgр(F а )}.
X'. ае[Оа.] ае(а..а2]
с дрyrой стороны нмеем:

Бочарников В.П.

Fиzzy Techпology
101

f'
f[ л (x)]o ;g',J) v f[йz л hz(x)] о ;g',J) =
х х
= sup {аЛ;g'р(Еа)}v sup {аЛ;g'р(Fа)}v
aE[Oa r J aE[Oa r ]
V sup {а л ;g'p(F a )}.
аЕ[а, ,"2]
O, так как в силу МОНОТОННОСТИ КIl(Е а ) > gll(F a ) имеем

HCTBO:
,,-1. 2
1'у(а; л h;(x)} о КрО = f[a. лh.(х)]gр(-)v f[a 2 л(х)]gр(-),
.х,=1 Х Х
.:,.
1:1-
случая п > 2 доказательство аналоrично. Тоrда имеем:
,.,
00
J V ( а.лh.(х) ) о'lf (.)=su р J[а.лh.(х)]оg (.)=
. 1 I I 6р I I Р
Х ,= i Х
=  [ a; л f h;(x)ogi o ) ] .
,=1 х
". о и 'Ipебовалось дказать.
,,!
. I
А
j
.. .
t.: М образом приведенные свойства нечеткоrо интеrpала по
.. mиренной нечеткой мере позволяют использовать ero на практике
.. ..
. моделировании и расчетах с нечеткими величинами, которые
! ,',дставлены в виде распределения нечетких мер.
.}
.
.{
Бочарников в.n.

102
Fuzzy Techп%gy
3.6. Интеrрирование В ... измеримых
функций по нечеткозначной нечеткой мере
в пункте 2.4. нами было рассмотрено определение нечеткой меры
принимающей нечеткие значения в единичном интервале для
пространства (ХБ). Пусть h(x): X[OI], Б.. измеримая функция.
Рассмотрим возможность применения конструкuии нечеткоro
интеrpала ДЛЯ интеrpирования таких функций.
Ранее отмечал ось, что при фиксированном Vx Е Х мы имеем
нечеткую меру на единичном интервале L [OI]. Обозначим ее
G(.(x), G(.(x): 2 L [Ol], т.е. это нечеткая мера на единичном
инrервале L. Для фиксированноrо уровня аЕ L соответствует
интервал [О,а] с L. Тоrда для Vx Е Химеем: G([Oalx) Е [01].
Если для Vx Е Х зафиксировать степень уверенности r Е [01], тоrда
для Vx Е Х будем иметь значение а(х) Е [01] для KOТOporo
выполняется условие:
G{[Oa(x)]x) == r Е [01].
(3.44)
Функция а(х) для которой выполняется условие (3.44) определяет
распределение плотности нечеткой меры на Х для фиксированноrо
уровня rE [01] уверенности. При этом значение плотности меры
удовлетворяют соотношению:
gr (х) == а(х) == argmax{G([O,a ]х) < r}.
а а
(3.45)
Для непрерывноrо пространства X R нечеткая мера множества
А с Х при фиксированном уровне уверенности r Е [О 1] может быть
определена как:
Бочарников В.П.

Fиzzy Techпo/ogy
103
gr (А) == k [ех{ Ау! gr (х)ш )  I ].
(3.46)
 интеrpал по А понимается в смысле интеrpала Лебеrа, а Ar .. есть л..
.. аметр нечеткой Mepы отражающей семантику индуцированной
>-' еткой меры на Х при фиксированной степени r Е [О 1].
fаким образом для "V А с Хнечеткая мера типа 2 будет порождать
...: кцию F....распределения на L со значениями в единичном интервале.
. ..ис.3.6).
r
.
.. . ... .. .."
r 
I
;
х
А
х
Рисунок 3.6 .... F..распределение порождаемое нечеткой мера типа 2.
.. значим ЭТО F..распределения как F.; (.). При этом выполняется
едующее. Переобозначим функцию gr (А) (3.46) при
иксированном А В функuию:
-!
gr (А) == Р А (r): [01]  [01].
u u
,. а
'-R
:. оrда функция F.: ([ Оа]) является обратной Функuией к функи ии
А (r), Т..е. выполняется:
. ..
F([Oa]) = (P4(r))I,
(3.47)
,!
'-
Бочарников В.П.

104
Fиzzy Technology
rде (.)""1... обратная функция к Р л (r). Исходя из сказанноrо определим
значение нечеткоrо интеrpaла от функции h(x) по нечеткой мере типа 2
в виде:
Jh(X)og;(.)== { r sup ((а л gr(H a ) } =
х ae[OI] (3.48)
= {r I а = gr (На)' На = {x:h(x) > а}} = Fx)([Oa]).
Т.е. нечеткий интеrpал от В .. измеримой функции h(x) есть F ...
распределение на интервале L со значениями r в единичном интервале
(re [01] ). Таким образом:
r;,x)([Oa])=r= 1 h(x) о g;(-),
х
(3.49)
rде а = gr (На)' На = {х Е xlh( х) > а};
Введенная ранее функция F .. распределения Р(.) соответствует
отображению:
F 2 (.): [01] -----) [01]
u u
а r
(3.50)
Тоrда обратная ей функция [p(.)]1 будет соответствовать
отображению:
[F2(.)]I: [01][01]
(3.51 )
u
r
u
а
В пункте 2.4. мы отметили,
f w(r): [О 1] -----) [.....1,+00[, rде Л
u u
r л
нечеткой меры, то существует отображение q> при котором
gw(.) = sетw(л) для фиксированноrо события W с х. Тоrда
что если задана функция
.. есть параметр нормировки
интересным является следующий результат:
Бочарников В. п.

Fиzzy Techп%gy [О5
seтh(x)[/w(Fx)([o.a]))] == [Fx) ([o,a])]1 == а. (3.52)
о есть обратная функция от функции F ... распределения на L,
олученная при интеrpировании В .. измеримой функции h(x)
(нечеткоro собьпия h(x) по нечеткозначной нечеткой мере g2(.)
,npеделяет семантический спектр нечеткоrо события h(x} при
'inвестной функции /w(.):[Ol]  [1;+00[.
J3 заключение отметим, что рассмотренные в данной rлаве вопросы,
g)язанные с понитием нечеткоrо интеrpала и основами нечетко..
'интеrpальноrо исчисления, позволяют увидеть основные механизмы
Обработки нечетких данных представленных с помощью формализма
 ечетких мер. Обоснованные свойства нечетких интеrpалов, позволяют
1<орректно обрабатывать нечеткие данные при моделировании
! альных задач принития решений в условиях неопределенности.
9собо следует отметить предложенный в rлаве нечеткий интеrpал по
расширенной нечеткой мере, который является аналоrом интеrpaла
i ебеra....стилтьеса. Полученный результат раскрывает возможности по
оделированию дискретных и непрерывных процессов
,Iункционирования реальных объектов в задачах принятия решения в
. словиях объективной и субъективной неопределенности.
f .
.......
Бочарников В.П.

106
Fuzzy Techпo/ogy
r лава 4
ПРЕОБРАЗОВАПИЯ
ПРОСТРАПСТВ
С НЕЧЕТКИМИ МЕРАМИ
Бочарнuков в.п.

Fuzzy Techп%gy
107
_*1
'.-4.1. Условные нечеткие меры и их свойства
.<
f1p основе приведенных ранее основных моментов теории нечетких
 инечетких и нтеrрало в, рассмотрим различноrо рода
Цреобразования пространств с нечеткими мерами, необходимые для
моделирования в задачах поддержки принятия решения.
Пусть (А: в , gx) пространство с нечеткой мерой. Если рассмотреть
отображение ер: Х  У, rде У некоторое произвольное пространство, то
'; 'релевская о.... алrебра в и нечеткая мера gx индуцируют на У о..
. 1 -бру ВЧ> и нечеткую меру gy соответственно. При этом, если Fe вЧ>,
JIO :справедливо соотношение:
VF с Y,3!tpI(F)E B,gy(F) = gx(tp1 (F)); (4.1)
. о есть, если пространство У связано с пространством Х с помощью
tпoбражения lp, то на У индуцируется нечеткая мера gy, с помощью
рой измеряется степень нечеткости на У, связанная снечеткой
 рой наХ.

усть Е с Х, F с У. Рассмотрим все множество функций h(y)
Довлетворяющих нечеткоинтеrральному соотношению:
g(E ntp1 (F)} = J h{y)o g), (.).
F
(4.2)
.:,
e функции h(y) удовлетворяющие (4.2) образуют семейство функций
>Y[OI], удовлетворяющих подмножеству Е с Х и условию ср(х) == у.
". значим данное семейство функций через а{ Elq>( х) == у ). т orдa,
{'
fJ8CCMoтpeB для всех множеств Е Е В семейства а{ Elq>( х ) == у ),
ПQлyчим некоторую меру a{-Iq>(x) == у).
Определение 4.1
Функция множества а( .Iq>( х) == у ): 2 Х  [01] для которой
.
Бочарнuков в.п.

108
Fuzzy Т echп%gy
V'E Е В выполняется условие (4.2) называется условной
нечеткой мерой при условии <р (х)::= у.
В дальнейшем для простоты обозначений условную нечеткую меру на
Хпри фиксированном у Е Убудем обозначать как ах (. !у):2Х ---7 [01]-
При Е Е В нечеткая мера ох(Е I у) может быть интерпретирована как
степень нечеткости суждения "один из элементов Е с Х имеет место
при заданном значении у Е У". В том случае, коrда в выражении (Б.42)
пространство у не усекается до F с У будет иметь место следующее
соотношение:
gX<E)== i aX<Ely) о gy.
у
(4.3 )
Выражение (4.3) определяет связь нечеткой меры на Х и
индуцированной отображением <р : xy нечеткой меры gy(.) через
условную нечеткую меру ox(-Iy). Исходя из определения условной
нечеткой меры справедливы ее следующие свойства [15]:
1) Для любоrо фиксированноrо подмножества Е Е В, условная
нечеткая мера (j х (Ely) есть в(Ч» .. измеримой функцией.. То есть
VEE В:
(jx{Ely): У  [О]].
(4.4)
2) Для любоrо фиксированноrо элемента УЕ J: функция ox(.Jy)
является нечеткой мерой для пространства (Х в), то есть
Vy ЕУ,
aA-lу):2 х ---7 [01]-
(4.5)
Рассматривая условную нечеткую меру для подмножества Е Е В ее
можно определить соrласно следующеrо выражения:
а x(Ejy) == i l(х) оа х (-jy),
Е
(4.6)
rде l(х) определяется как функция полной неопределенности, ТО есть:
V ХЕХ, l(x) == 1.
(4.7)
Выражение (4.6) может быть преобразовано соrласно (3.29) к виду:
Бочарнuков в.п.

 Fиzzy Тechrюlogу 109
x(Ely) ==! l(x) о о"х (-1 у) == ![ХЕ(Х) л 1(x)]oO"x(1Y) == (4.8)
.1 ХЕ(Х) о (}x(.ly),
,Х
,
:;
ХЕ(Х):Х""'"7 {O,l}.... характеристическая функция множества
re В.
s том случае коrда вместо четкоrо множества Е Е В рассматривается
[)jюизвольное нечеткое множество J1 Е (х) справедливо выражение
if'лоrичное ( 4.6):
() х(Е!у) == J РЕ(Х) о () x(.jy)' (4.9)
х ,.,.
е Е" обозначает нечеткое подмножество на Х
''фически определение условной нечеткой меры можно представить
,J5иде, представленном на рис. 4.1.
..
Рисунок 4.1 .. Определение условной нечеткой меры.
 этоrо момента мы рассматривали лишь отображение <р : Х  У. Если
этом существует произвольное отображение f: Х  У, то как
азано в [16] существует сопряженная условная нечеткая мера на У
> фиксированных х Е Х такая, что при заданных gx(.), gy(.), ox(.ly)
полняется соотношение:
,
"'.
J(}y(Flx)og ==/(}x{Ely)ogy'
Е F
( 4.1 О)
t
Бочарнuков в.п.

110
Fuzzy Techп%gy
rде oy(.lx) .. сопряженная нечеткая мера. Равенство (4.10) можно
рассматривать как нечеткий аналоr формулы Б8Йеса определения
апостериорной вероятности. В этом смысле gx(.) может
рассматриваться как аПРИ0рная нечеткая мера, а gx(.ly) .... апостериорная
нечеткая мера. Учитывая соотношение (4.9), формула (4.10) может
быть распространена и на нечеткие подмножества Е и F , то есть:
J <Jy(!x)ogx = J <Jx(ly)ogy.
JlE(.Yf) hF(x)
( 4.11 )
Возникает вопрос, каким образом определить апостериорную
нечеткую меру при известных априорных не четки х мерах и
сопряженной условной нечеткой мере.
Лемма 4.1.
Пусть заданы два пространства (Х В, gx) и (1": ц gy) снечеткими
мерами которые связаны между собой условной нечеткой мерой
ox(.Jy). Тоrда сопряженная условная нечеткая мера oy(.lx)
удовлетворяет оrраничениям:
1. Если gx({x;}) > !<JX({xi]y)ogp то
<Jy(FlxJ = ! а х ({ХЕ]У) о gy.
2. Если gx({xJ) = I<JX({Xiy)ogp ТО
F
<J у (Flx,) > ! аА {xJly) о gr'
(4.12)
(4.13)
rде F Е В.
Локазательство.
Соrласно (4.3) VXiE Х справедливо соотношение:
gA {xJ) = I аА {XiY)O grO.
r
в то же время для произвольноrо F Е Е используя (4.1 О) можем
записать:
Бочарнuков В.П.

Fuzzy Techпo/ogy
111

oi
! () А {xi}ly) О gy = {!.} оА J1x)o gx = (}y(J1x.) лgА {xJ)-
Jf;iссматривая полученное выражение получаем два случая:
а) Если gx( {x i }) > () у {FjxJ, ТО ЭТО равносильно ТОМУ. что:
gx{ {X i }) >! () х{ {xi}ly)o g," . а следовательно:
() " ( FI Х; ) = I () х ( {Х;} 'У ) о g}. ·
F
> >. б) Если gx( {х.}) < () r{FlxJ,
'х< {х;}) = ! () х{ {хЕ}lу) о gy.a следовательно:
то
имеем
.
"'J..
() у {FlxJ > ! () А {xi}ly) o g,o'
роо случая доказывают соотношения (4.12), (3.51). Что и следовало
азать.
А
Следствие .
Используя полученные выражения для дискретных множеств Х
и У соотношения (4.12) (4.1 З) Moryr быть представлены в виде:
а) Если gx(X j ) > () x(x;IYj) л gy{Yj)' то
!.
(}J,(y;lx;) == () x(x;ly j ) л gY(Yj).
б) Если gx(Xj)== () х(х;lуj)лgу(у j ), то
(}J' (y;lx;) > (}x(x;ly j ) л gY(Yj).
(4.14)
"' ;

( 4.15)
 ;
этом ДЛЯ вычисления сопряженной условной нечеткой меры в
'''Чае б) можно использовать соотношение:
(J (y _ l x. ) == 1 + (},.\О (x;IY;) .
" ) ' 2'
(4.16)
f.
" 'рое однозначно определяет значение условной нечеткой меры.
!!
1!
Бочарнuков в.п.

112
Fuzzy Techп%gy
4.2. Нечеткие меры на декартовых
произведениях пространств
Пусть имеется два пространства с нечеткими мерами' (Х В, g/) и
(>': В}) gl). Подмножество Н с Х х У декартовоrо про из ведения
пространств Х и У задает бинарное отношение между этими
пространствами. Пусть Z == Х х  тоrда Н с z. Бинарное отношение Н
позволяет сопоставить каждому элементу х Е Х ero образ в У
определяемый соотношением:
iтHx=de/ {у Е YI(x,y) Е н} = F(x)-
(4.1 7)
Аналоmчно (4.17), каждому у Е У сопоставляется про образ в Х в виде:
ае/ { }
coiтHy= х Е XI (у,х) Е Н = Е(у).
( 4.18)
Используя данные соотношеНИЯ 7 можно ввести отображение
индексирования.
Определение 4.2
Для произвольноrо бинарноrо отношения Н с ХхУ отображение
вида:
ind/i: Х  Р(У),
ind//(x) = iт//(x).
(4.19)
rде Р(}') булеан множества У, называется индексированием
подмножеств множества У элементами из х Е .А: порожденным
отношением Н.
Исходя из этоrо определения очевидно, что произвольное отображение
<p:XP(Y) совпадает с индексированием, порожденным подходящИМ
отношением Н rp = {( х, y)1 у Е <р( х) } · СледОБm'eJIЬно, сущecтвyer
биективное соответствие между множествами Р(ХхУ) и Мар(Х,Р(У)) ==={q>},

Бочарнuков в.п.

Fиzzy Т echпology
113

;ДЛЯ любых двух множеств Х и У, rде обозначено: Р(-) .... булеан
.:Nножества, а Мар(-,.) .... множество всех отображений из первоrо
множества во второе.
Используя отображение индексирования леrко расширить ero до
отображения из Р(Х) в Р(У). Для этоrо рассмотрим отображение вида:
J:
.
rH(E) = n indH(x) = n F(x)
ХЕЕ ХЕЕ
r'H (F) = n indH(y) = n Е(у)
уеР уеР
' ДHHыe таким образом отображения, соrласно соответствия rалуа,
еводят произвольные подмножества в замкнyrые и тем самым
.индуцируют отображение между замкнyrыми подмножествами в Р(Х)
Р(}').
. денные в рассмотрение выше понятия, позволяют представить
извольное отношение Н с (Х х У) в виде объединения декартовых
 изведений подмножеств E j и F i , связанных между собой
,'ражениями (4.20) и (4.21).
1"\.: 
 .; Лемма 4.2.
IV
Произвольное бинарное отношение Н с Х х У можно представить
в виде:
.
со
.!""
н == U[E; Х F;],
;=1
(4.21 )
: rде Е ; ЕР(Х), F; ЕР(У),  = rH(E i ).
тель Bt.
.'
t
 отрим отображение <р : Х  Р(}') биективно связанное с
. ением Н такое, что:
ср(Х;) = iт 1J x; = F(x;) Е Р(У).
а · жение q> есть индексирование множества У элементами из Х
ленное отношением Н с Х х 1': Определим отображение:
Бочарников В.П.

114
Fuzzy Techп%gy
( ) ..... { СР(Х j}' i = j;
ер. Х 
/ 0, i:f:. j.
Отображение <р:Х ---7 Р( 1') есть практически покомпонентное
представление отображения <р(х), то есть
tp(X) = {90 tp;(x) I i = 1, ос }.
в силу биективности множеств Р(Хх1') и Мар(Х,Р(У}) отображению <Pi
(х) соответствует отношение вида:
Н. = х. Х iт 1/ x.
I I ,
Тоrда справедливо представление отношения Н в виде:
н = Ql:X i Х im"x.].
Для подмножества E i с Х отображение (4.20) стави"f. в соответствие
подмножество F i r н(Ед. Однако, отображение r и (.), являясь
элементом соответствия rалуа, обращает включения, то есть если
E i с Fj, то r H(E i ) ::> r H(E j ) и следовательно
\;/X k Е E i , F; == rH(E j ) с F(x k ).
Тоrда \;/X k Е Ej, [F; х Е;] с [Xk Х iтHXk]' причем, найдется
такое E j , что будет выполняться равенство отношений. Следовательно
справедли во:
00
Н= .U[E; xF;], F; =r/i(E j ).
1=0
А
Используя полученный результат можно определить нечеткую меру на
декартовом произведении пространств с заданными на них нечеткимИ
мерами. Соrласно [11] нечеткая мера декартовоrо произведения двух
множеств определяется операцией lniп. Следовательно нечеткая мера
произвольноrо отношения Н будет.
Бочарнuков В. п.

Fuzzy TechпoJogy
115

Определение 4.3 .
Нечеткая мера произвольноrо отношения Н с ХхУ заданноrо на
декартовом произведении пространств (Х, ВХ ,gl) и (У, ВУ' g2)
определяется соотношением:
со
g(H)== .v{gl(Е;)лg 2 (F;)},
1=1
(4.23)
rде F i == rи(Е j ), а r н(.) .... отображение вида (4.20) между Е; сх: и Fi с У:
Нечеткая мера произвольноrо отношения Н с ХхУ заданноrо на
цекартовом произведении представляется в виде поверхности, как
flоказано на рис. 4.2.
. -
...
1
g(H)
g({Xi,Yj})
Н с ХхУ
",сунок 4.2  Нечеткая мера на декартовом произведении пространств.
"',ределение 4.3 позволяет связать меры g. и g2 С мерой на декартовом
"'изведении. Однако, непосредственное использование соответствия
7.-, lуа для практическоrо определения нечеткой меры подмножества
 ХхУ затруднительно. Можно по казать, что нечеткая мера g(lf)
. "означно определяется через нечеткий интеrрал Суджено (3..4).
Лемма 4,З
Для подмножества Н с Х хУнечеткая мера может быть
определена через нечеткий интеrpал следующим образом:
t
"" "
g(H) = J gl (Е (у)) о g2(.) = J g2(F(x)) о gl (.), (4.24)
у х
rде g,:2  [Ol],g2:2Y  [01].
Бочарнuков в.п.

116
Fuzzy Techпology
]J.оказательство .
в силу (4.17), (4.18) можем отметить, что F(x) Е Р(У), а E(v) Е Р(х).
Отсюда следует, что g.(E(v» .. является Ву .. измеримой функцией.
Аналоrично g2(E(x» является Вх .. измеримой функцией. В силу этоrо
интеrpал (4.24) существуют.
Для выполнения равенства в (4.24) достаточно доказать, что любой из
интеrpалов соответствует нечеткой мере отношения Н определенной в
(4.23). Для BToporo интеrpала ситуация будет аналоrичной. Интеrрал
Суджено для первоrо из интеrpалов в (4.24) определяется выражением:
1 gl(E(y)) о g2(.) == sup {а л g2(F a )},
у ae[OI]
Fa =={уl g,(E(y)) > a,ae[OlJ}
Рассмотрим более детально определение (Х.... ypoBHeBoro множества Fo..
Если (Х == g.(E n ), то условие g.(E(y» > g.(Е л ) выполняется в случае если
Ел с Е(у), что следует из условия монотонности нечеТI<ОЙ меры. Torдa
(Х.... уровневое множество Fa можно переопределить в виде:
Fa == {у I Е(у) ::J Е п }.
Иначе, данное соотношение можно переписать как:
Fa == {}1 Е (у) == Е п }.
Однако, nE(y)=r(F:)' rде r;(.) есть отображение (4.21).
)'ЕУ
Следовательно (Х .. уровневое множество F (х является прообразом
множества En c X относительно отображения r; (.) соответствия rалуа
и притом максимальным. В силу условия монотонности нечеткой
меры V F с Fa, g2(F) <g 2(F(X). Тоrда g2(F a ) являются максимальным
значением меры g2(.) для подмножества соответствующеrо En, а
следовательно и выбранному (Х.... уровню для функции g.(E(y». ИсхоДЯ
из сказанноrо выше справедливо, что Fa ==  == r;i(E п ). в силу
однозначноrо соответствия (Х == g.(Е л ) каждому En соответствует (1, а
следовательно получаем:

Бочарнuков В.Л.


t
".
\
Fuzzy Techп%gy
117
f gl (Е(у)) о g2 (.) = sup{a л g2 (F a )} =
у а
sup{g.(E n ) л g2(r(En))} == v{gl(E n ) л g2()}'
 n
соответствует определению 4.3. Для BTOpOro интеrpала (4.24)
суждения и результат аналоrичны. Следовательно лемма доказана.
А
дальнейшеrо рассмотрения материала при ведем без
J(азательства теорему СудженоФубинн [15].
'\
(;
Теоnема 4.1 .
Пусть (А: B gy) и (>: Ву, gx) два пространства снечеткими
мерами, и пусть gz == gx Х gv .. нечеткая мера заданная на Z Хх У,.
Тоrда для gz ....изМеримой функции h(x,y): Х х У ---7'[01]
справедливо соотношение:
$ :

J h(x,y) о gz = f [ J h(x,y)o gy ] o gx.
z х у
(4.25)
ная теорема является аналоrом теоремы Фубини для обычных
еrpалов.
"- етим, что доказанная выше лемма 4.3 определяет нечеткую меру
i' четком отношении Н с Х х У. Однако в том случае, коrда на Х х У
: .ано нечеткое отношение, то оно определяет расширенную нечетh.')'lО
I .у наХхУ.
t.
Теорема 4.2 .
Пусть h(x,y) : ХХУ---7'[ОI] .... нечеткое ОТНОIlJение, а на Х и У
заданы нечеткие меры gl и  соответственно. Тоrда нечеткая
мера g на пространстве ХхУ является расширенной нечеткой
мерой, порожденной нечетким отношением h(x,y) и
определяется как:
g(h)= j Ь(х, у) о gH(.) ,
хху
rде gH (.) = f gl (Е (у »0 g-, (-), а Е(у)
у 
соотношением (4.18).
определяется
(4.26)
Бочарнuков В. п.

118
Fuzzy Techп%gy
Доказательство .
Нечеткое отношение h{x,y) может быть представлено через свои а 
срезы в виде:
rде i = 1 00
, ,
Ь(х.у) == j{a j л ХНа; (х. у »),
а Е [01],
ХН (х, у ), .. характеристическая функция
а,
множества На С Х х У а....уровня. Тоrда для фиксированноrо а Е [01]
выполняется условие (4.24) леммы 4.3 и можно записать:
gn. :::! g.(Ea(y »0 g2(-) =! g2(FJx» о g.(-).
rде при этом если а _ < а. то Е ::) Е F::) F . Для BToporo
, J a;......."j , а,  U j
интеrpала формально имеем:
Vx еХ. g2(Fa(x»::: 1 XF a (x)(y)og2'
у
rде XFa{X)(y).... характеристическая функция на У для любоrо
фиксированноrо ХЕК Рассмотрев совокупность всех таких функций
ДЛЯ всех ХЕХ получим характеристическую функцию отношения На:
11 (х, У ) == Х (у ) . Следовательно, подставив это выражение в
АНа Fa(x)
зависимость для g2(F:(X)) получим:
g2(F a (x)) = J ХН (х,у) о g2-
у "
Тоrда нечеткая мера а"уровня определяется соотношением:
gH = 1 [ 1 Хн (X,y)og2 ] og..
а Х у а
Если теперь рассмотреть все а,....уровни нечеткоrо отношения h(x.y), то
нечеткая мера g(h) будет определяться соотношением:
gh(.) =  { a; л gH _ (.) } = '( { а; л J [ J Xli (х,у) о g2(.) ] о gl(-) } -
1 а, , Х у а,

Бочарнuков В.П.

.

спользуя свойства нечеткоrо интеrpала (3.12) (3.13) может
рРеобразовать это выражение к виду:
.
Fuzzy Techпology
119
gh(') == y[r[!(a i л ХНа; (xy»)o g20JO g.O
fсоrласно свойства (3.21) получим:
;
ghO == ![!{у(а; л ХНа; (х,у) )}о g2(')] 0 g. (-) ==
== ![! h(x,y) о g20] о g.O.
оrда соrласно теоремы Суджено4>убини имеем:
 
i;
g"O == xL h(xy)o gH (.) == g,,(')'
" есть нечеткая мера на нечетком отношении пространств есть нечто
.-., как расширенная нечеткая мера на ХхУ порожденная нечетким
ошением h(x,y). Что и требовалось доказать.
о
6очарников в.п.

120
Fuzzy Techп%gy
4.3. Н",соответствия.
Нечеткие меры доверия и правдоподобия
как Н",соответствия
Будем полarать, что на пространстве (Х В) задана нечеткая мера
g:2x[01].
Определение 4.4 .
Если на Х задано отношение Н с ХхХ', Х':= Х, то функция
р(. ): Х  [О 1] называется Н",соответствием по мере g, если
выполняется условие:
р(х) = g(EH(x)),
rде EI/(x)== {x'I(X,X') E Н С Х х Х'}.
( 4.27)
Практически отношение I1 с Х х Х' при известной нечеткой мере g
задает функцию J1(') Н .... соответствующую g, устанавливая
отображение lfJH:g F(X), F(X)  множество всех нечетких
подмножеств множества х. Соотношение (4.27) может быrь
представлено через нечеткий интеrpал Суджено в виде:
р(х) == f XEI/(x) (х') о g(.) == J l(х') о g(-)' (4.28)
х' ЕII (х)
rде ХЕiI(Х)(Х')" характеристическая функция множества
Ен(х) С Х' индексированноrо значением ХЕХ, 1 (х') .. функция
неопределенности:
\;f х' Е Х, 1 ( х' ) =: 1.
fрафически Нсоответствие может быть проиллюстрировано в виде
представленном на рис. 4.3.

Бочарников В.П.

Fuzzy Techп%gy
121

g(EH(P'' _.._.._.ш_Ц(ХJ
Х) Х 2 
. .. х
x-_:::::::::::::  ... j Н с ХхХ
Рисунок 4.3  Определение Нсоответствия.
том случае коrда соответствие нечеткой мере g устанавливается
четким отношением h(x,x'): Х х Х ---7 [О 1 ] Н.... соответствующая
fн кция J1 (х) определяется соотношением:
р(х) == J hx(X') о g(.)'
Х'
( 4.29)
hx(x') = h(x,x').
.. довательно, отображение qJн, определяемое заданным отношением
I  \'ХХ позволяет определить функцию принадлежности (степени
. 'еТкости) Н.. соответствующую нечеткой мере g:2 X ---7[01]. Кроме
, ., при определенных видах отображения qJ можно получить
.,qение функции J.1{x) удовлетворяюшей условиям IШотности
- .. ой меры Н .... соответствующей нечеткой мере g.
,k мотрим следующую теорему, определяющую преобразование
 ределения вероятности в распределение возможности на Х как
, :соответствие.
Теооема 4. 3
Мера возможности, определяемая соотношением [11]:
Jl(X) = LP(x'),
х': p(x')p(x)
(4.30)
является нечеткой мерой на ХН.. соответствующей мере
 вероятности Рх(.): 2 Х ---7[01] с функцией IШотности вероятности
р(х): Х---7[ОI] если отношение Н задается характеристической
Бочарнuков в.п.

122
Fuzzy Techпology
функцией вида:
{ I, р(х) > р(х')
Хн(Х'Х') = О,
р(х) < р(х')
( 4.31 )
n'оказательство .
Прежде Bcero рассмотрим выражение (4.30). Для мерь] вероятности
Рх(.) справедливо соотношение:
Рх(А) = LP(X)"
хеА
Тоrда (4.30) можно переписать в виде:
J1(X) = LP(X')'
х'еА х
rде Ах == {Х'!р(х) > р(х')}."
Следовательно представляя множество Ах ero характеристической
функцией, можем записать:
J1(x)= L р(х')= LXAx(x')-р(х')=Рх(А)==
х'еА х х'еХ'
J ХА (х')оРх(.)= II(x')oP x (.).
Х' х Ах
Данное выражение соответствует выражению (4.28) в случае коrда
VXEX, Ах == Ен(х), rде Ен(х) определяется соrласно (4.18). Данное
условие будет выполняться коrда отношение Н задается
характеристической функuией вида.
{ l, р(х) > р(х')
Хн(Х'Х') = О,
р(х) < р(х')
Что и требовалось доказать.
о
Бочарнuков В. п.

Fuzzy Techпology
123
iJ-
I
Jlpиведенная теорема показывает, что известные соотношения [1, 4]
ывающие нечеткие меры вероятности и возможности являются
l' I 
,-стным случаем полученноrо соотношения для Н....соотвеТствия между
функциями распределения нечетких мер. Более Toro, указанная
. нструкция Н....соотвеТствия нечетких мер на пространстве Х
воляет до некоторой степени обобщить результаты и предложения
f.иейфера о порождении мер на основе так называемой базовой
ятности т(.) определяемой выражениями (2.4):
 .
т:2 Х  [01],
L т (А ) == 1.
АсХ
Напомним, что множества A i с Х для KOToporo т(Аа> О называются
фокальными элементами. Соrласно определений 2.3, 2.5 базовая
t.epоятность т(.) позволяет определить меру доверия и правдоподобия
'rласно следующих соотношений:

,.
j
Bel(A) = "Lт(B),
Br;;;.A
Pl(A)== "Lт(B).
BnA0
(4.32)
ункция т(.) задает адцитивное распределение уверенности на
_ ножестве фокальных элементов, что не всеrда оправдано. В более
бщем случае следует предположить, что мера т(.) обладает
 ойствами нечеткой меры (определение 2.1) заданной на степенном
ожестве Р(Х) == 2 Х . В этом случае можно использовать предлarаемый
подход для построения функций распределения нечеткости
.l....соответствующих заданной "базовой" нечеткой мере g:2 X ---7[01].
. ассмотрим
fJpocтpaHcTBo
остранстве
YXi'X j Е Х,
эту конструкцию более подробно. Пусть задано
(Х в) и нечеткая мера g:2 x ----7[01]. Зададим на
Х отношение Н с ХхХ' такое, что
Х; '* X j =:) со;тнх ; '* coiтH(x j ), то есть для
VE(x;),E(x j ) с Х =:) Е(х;),* E(x j )
(4.33)
Таким образом отношение Н порождает множество подмножеств
{Е(х)} с Х', Е(х) Е Р(Х') индексированные элементами этоrо

Бочарнuков в.п.

124
Fиzzy Techпo/ogy
же множества Х (Х = Х'). При таком задании отношения Н
существует функциональное отношение между множеством Х и ero
crепенным множеством 2 Х Р (Х'), а следовательно на Р(Х')
индуцируется нечеТК8Я мера lpP(x):Pp(X')  [01], rде РР(Х') ....
множество всех подмножеств множеcrва Р(Х'), которая однозначно
соответствует нечеткой fepe g(.). То есть выполняется условие:
lpP{x.) (Е(х» = gx(x)
(4.34)
А кроме тoro справедливо соотношение:
фр(х.)({Е(х)})= f l(x)og(-)'
{х}
rде {Е (х)} с РР'(Х'), {х} с Х.
( 4.35)
в случае выполнения условия (4.33) множества Е(х) Е Р(Х) Moryr
рассматриваться как фокальные элементы на Х == Х' индексированные
элементами х Е Х, а построенная соrласно (4.34), (4.35) мера lpP(x l ) (.)
иrpает ту же роль, что и функция т(.) определенная соrласно (2.4)
базовой вероятности в схеме Шейфера. Тоrда имеется возможность
построить на основании базовой нечеткой меры g(.), выдерживая
лоrику построения мер по Шейферу, меры доверия и правдоподобия
Н.. соответствующие мере g(.), а именно:
BelH(A)= f l(х)о g(.),
{xIE(x);;A}
P1H(A) = J l(x)og(.)'
{хIЕ{х)ПА*0}
(4.36)
(4.37)
rде А с Х' = Х .
Указанные зависимости являются обобщениями конструкций мер
доверия и правдоподобия (4.32). Используя приведенные выше
рассуждения леrко доказывается следующая лемма.
Лемма 4.4
Если g(.):2 x [O 1] есть вероятностная мера и для отношения Н
выполняются условия (4.33), то мера правдоподобия и доверия
Бочарников В.П.

Fиzzy Techп%gy
125
.
.... . ....
I Н....соответствующие мере g(.) удовлетворяют соотношениям
(4.32).
казательство .
Пусть
{ l'
х(х) =
О,
Е(х) с А;
Е(х) ::> А.
Тоrда х(х} есть характеристическая функция множества (х) Е(х) сА } и
fOrласно (4.36) справедливо соотношение:
: "', "t
BeIH(A) = J X(x)og(o)=gx({x/E(x) C A})= Lgx(x) "
х {x)E(X)s;;A}
.Jlo, в силу (4.34) и (4.35) существует однозначное соответствие между
:"ерой g(.) И фр(х)(.) для которой ФР(Х) (Е(х) = g(x) и
.,следовательно мера СРР(Х)(.) является вероятностной и удовлетворяет
'(2.4). Тоrда получаем:
BeIH(A) = LФР(Х)(В)'
Bs;;A
....
де В = Е(х) с Х . Множества В иrpают роль фокальных элементов.
>.
'олученное выражение совпадает с выражением (4.32) для Bel(A). Для
"- еры правдоподобия рассуждения аналоrичны. Следовательно лемма
.:: оказана.
l:'1
заключении этоrо параrpафа отметим, что определение
J,i-соответствия между нечеткими мерами, заданными на пространстве
t{x В) Moryт быть распространены и на случай произвольны" бинарных
i9тношений н с Х х У. В этом случае отображение q>н определяет
IhPеобразование нечеткой меры на Х в нечеткую меру на 1': н ..
оответствующую мере на Х:
t
!
!
qJH:gx(.)  р'у(.),

I
Бочарнuков В.n.

126
Fиzzy Techпo/ogy
rде ру(.):2У  [01]" есть функция Н",соответствия:
ру(у) = gx (Е н (у)).
Фактически рассмотрев семейство М всех Н"соответствий можно
записать М с F (У), rде F( у) .. множество функций распределения
нечеткости заданных на пространстве У. Обозначив p; (у) функцию
НiСООТСТВИЯ можно определить нечеткое отношение Т: Мх Y[Ol]
с функцией определяемой соотношением:
Т(у, Н) == p; (у).
( 4.38)
в этом случае, исходя из результата доказанноrо в лемме 4.3, нечеткую
меру произвольноrо отношения H i Е М можно определить как:
g() = 1 T(y,H j ) о gy(.). (4.39)
у
Таким, образом, используя Н....соответствия можно определить
нечеткую меру отношения Н с Х х }'.

Бочарников в.п.

Fиzzy Techпology
127
;"1
!
ОС.
. :.4. Н...операции над нечеткими мерами
,,:. предыдущем пункте БЬVIО отмечено, что Н...соответствие задает
"'
..БРажение, которое переводиr одну нечеткую меру в друryю заданную

. на том же пространстве .х: либо на ПрОС1ранстве У -:/; х , что зависит
 характера заданноrо отношения Н. В том случае коrда наХ и У заданы
"''И нечеткие меры, то шrrepесно paCCMmpeть случай композицин этих мер,
результатом зафиксированным на множecrве Z , которое может быть либо
,Ь:: Х, либо Z == t: либо Z == Н х 1':
'":<!' , как И раньше зафиксированы два пространства (Х ВХ, g) (1': Ву,
,c нечеткими мерами.
J.'
Лемма 4.5. .
'. ;;. Нечеткая мера g 11 (.) заданная на множестве Х х У,
(Н С Х х У) есть функция, задающая отображение вида:
..
gH(.)= Р(Х) х Р(У)  [01],
(4.40)
rJle Р(Х) .... степенное множество (множество всех подмножеств)
r множества Х, Р( У) .... то же для множества У.
1" c
 
· ательство.
.' еткая мера gi(.)i == 1.2 задается как функция множества
<{.):2 Х  [01],(2 X = Р(Х)). Соrласно определения 4.3.
. :жения (4.23) мера g/1 (.) может быть представлена в виде:
со
g(H) = {gl(Ei) Л g2)}'
1==1
}. F i Е Ву, E i Е Вх. Соrласно этоrо выражения для g(ff) существуют
. fle подмножества Е. Е Вх и F Е Ву. что справедливо:
g(H) = gl(Е.)л g2(F.).
Бочарников в.п.

128
Fиzzy Techпology
НО Е* Е Р(Х), а F* Е Р(У), следовательно для любоrо отношения
Н с Х х У мера g(ffl есть функция удовлетворяющая соотношению
(4.40). Что и требовалось доказать.
д
Лемма 4.5. позволяет рассмотреть ее расширение на случай коrда одно
из множеств Х или У представляет из себя декартово произведение
дрyrих множест4. Тоrда существуют некоторое отношение R с [Хх z]
х У для Koтoporo нечеткая мера
gR(.):[ Р(Х) Х P(Z)] х Р(У)  [01].
(4.41)
Если на декартовом произведении булеанов произвольных множеств
 .... 
Xs,s=l,N s задать отображение ю:Р(Х))х...хХ(Х N )---7Р(Х)
6
представляющее собой N s ....арную операцию, то мы имеем возможность
рассмотреть мноrоосновную алrебру заданную на семействе булеанов
множеств Xs. Рассмотрим этот момент подробнее. Пусть
Р = { Р( Х s )1 s Е s}  произвольное семейство булеанов множеств
 индексированных элементами из S множества сорто4. ОбознаЧИА1
через Ор(Р) множество всех операций вида:
Ю:Р(Х Sа )x..xP(X sN )  P(Xs).
(4.42)
Тем самым определено отображение
[: Ор(Р) SxS.
(4.43)
Если g == {ю} .... множество символов операций то исходя из (4.42)
определяется сиrнатура алrебры над множеством сортов S каК
отображение:
type: g  Sx S.
(4.44)
Теперь дадим определение мноrоосновной (MHoro сортной) алrебрыI
над булеанами множеств P(X s ).
ОПDепеление 4.5 .
Семейство Р булеанов множеств Xs называется MHoro сортной
универсальной алreброй сиrнатуры П, если задано такое
отображение s: g  Ор(Р), которое делает следующуЮ
диаrpамму коммyrативной:

Бочарников в.п.

Fиzzy Techпo/ogy
129

.
Q IJ1JC! > SxS
 01;)
в том смысле, что type = t о Б , rде " О" .. операция композиции.
том случае, коrда множество сортов оснований Q..алrебры
. ,
. ждается до одноrо сорта (например, операции lJ) заданы на
- леане Р(Х), (О: ph (Х)  Р( Х) ) мы рассматриваем одноосновную
бру с сиrнатурой Q.
Jетим, что если на Р(Х) задаНа бинарная операция
. Р(Х) х Р(Х)  Р(Х), то множество Р(Х) называется
. лоидом, а действующая в Р(Х) бинарная операция l1J  законом
. . енней композиции.

Определение 4.6 .
f' Бинарной Н....операцией называется оператор, ставящий в
соответствие нечетким мерам gl:2 X  [01] и g2:2Y  [011
заданным соответственно на пространствах Х и У, нечеткую
меру g:2 Z  [О 1], такую, что выполняется:
'''1 'VC c Z, g(C)=gH(Hn(OI(C)),
I
!
rде gH(.) определяется соrласно (4.23), Н с ХхУ
WI(C)EP(XXY), W:P(X)xP(Y).......:tP(Z) .. бинарная
операция в трехосновной алreбре реализующая такую функцию,
что:
1
. I
'. 1
( А х В с А' >< В' Е Р(Х) х Р(}) => с с С Е P(Z).
<о х }': Z, l1J есть бинарная операция заданная на х. В качестве
Й операции может ВЫС1)'пать операция min mах, или
..;. етические операции исчисления интервальной математики. Если
eCTвe операции lJ) используется операция maх, то нечеткая мера
.. есть результат Но6ъединения нечетких мер gl и . Для
'lepации введем следующие обозначения:
71
Бочарников в.п.

130
Fиzzy Techпo/ogy
g(.) = H{g.ltJg2} = H ro (g.,g2).
(4.45)
rрафически Н....операция над нечеткими мерами может быть
представлена в виде рис 4.4.
g2(Y)
Рисунок 4.4 .... Н..операция над нечеткими мерами
в ТОМ случае коrда l1J определяет бинарную операцию в одноосновной
aлrебре Н..операция представляет собой операТОр вида:
н т: F(X) х F(X)  F(X) ,
(4.46)
rде F(X)  множество всех распределений нечетких мер на
пространстве Х, и выступает в роли закона нечеткой внутренней
композиции.
ОПDелеление U .
)Тпорядоченная пара состояuцая из J7(A) и закона внутренней
нечеткой композиции Н tJ) на F(A) называется нечетким:
rpуппоидом (Р(А), Н tJ) для нечетких мер.
Исходя из определения 4.6. результируюuцая нечеткая мера g(.)
Н ш " операции может быть определена соrласно следуюuцей теоремы.
Теооема 4.4 .
Нечеткая мера подмножества С с Z являющаяся результатом
Н tJ) .. операции над нечеткими мерами g. :2 Х ........) [О 1], и
g2: 2Y  [01], удовлетворяет соотношению:
Бочарнuков В. п.

J
Fиzzy Techпology
131
.'
g(C) == н т(g.,g2) == 1 g.(E(y) ПА) о g2 ==
В
== I g2(F(х)ПВ)оg.
А
(4.47)
 rде уе 1': х E С c Z, Н cXx t: с == l1J (А, В), А с Х, В с 1':
Е(у), F(x) .... определяются по (4.17), (4.18).

казательство.
ласно определения (4.6) нечеткая мера g( С) определяется исходя из
..шжения: g(C) == gH(H Пm'(с)). Так как
...t(c) еР(Х хУ), то на ХхУ существует оrnошение Q с Х хУ ,
; ос. что Q={(x,yx еА,уеВ}. Torдa EQ(y)={XI(x,y)eQ}.
,
.tледовательно 'Vy Е B,EQ(y) == 0, и Vy Е B,EQ(y) == А.
'Jjta, можем записать g(с)==gн(НПQ). Обозначим Н'=НПQ.
еткая мера gH' соrласно (4.24) определяется выражением:
J н' f н'
g(c)= gl(E (y))og2== g.(E (y))og2=
У BU{Y\B)
I{[XH(Y) v ХВ]Л g.(E H ' (У»} о g2'
У
.:'i' Хв, ХН.... характеристические функции множеств В и 8 == У \ В.
" tывая квадраrnые скобки в подынтеrpальном выражении имеем:
. С) = н(хн(у) Л g.(E H ' (y»)v (Хн (у) л g.(E H ' (у» )}о g2'
... мотрим более детально выражение под интеrpалом.
".;
,. I(E H ' (у» == g.(E H (у)ПЕQ(у» == { g.(E H (у)ПА),у е в
f gl(E H (y)n0)=O,yeB.
a хв(у) Л gl(E H ' (у» == О, а следовательно:

Бочарников В.П.

132
Fиzzy Techпo/ogy
g(C)= !{ХВ(У) Л gl(EH'(y»} о g2 = !gl(E H '(y))Og2 =
1 н'
= gl(E (у)ПА) о g2.
В
Что И требовалось доказать.. Для BToporo интеrpала в (4.47)
рассуждения аналоrичны. Следовательно теорема доказана.
[]
Из теоремы 4.4. можно рассмотреть следующие важные следствия.
Следствие 1 .
Если пространства с нечеткими мерами (Х, g.) и (У, g2)
связаны отношением Н с Xxt: а на Р(Х) задана унарная
операция со:Р(Х)  P(Z) со значением в Z, то H(J).... операция
над нечеткими мерами g. и g2 определяет меру g на Z соrласно
зависимости:
g(C) = J g2(F(x)) о gl = i g. (Е (у) ПА) о g2. (4.48)
А у
rде С == l1J ( А) с7..
Доказательство следствия следует из доказательства теоремы 4.4. при
замене множества В на все пространство У.
Следствие 2 .
Если g. и g2 две нечеткие меры на Х, а ro бинарная операция на
Х удовлетворяющая соотношению:
{ 0,т(А,В),В ф. В;
со(А, В) ==
АА==В
,
то результирующая Нт .... операции нечеткая мера есть мера на
Х, определяемая соотношением:
g(A) = f g2(F(х)ПА)оg. = J g.(Е(х)ПА)оg2. (4.49)
А А

Бочарников В. п.


Fuzzy Techпology
133
110казательство.
:оrласно определения Hro .... операции имеем g(A) = gH (Н nQA)' rде
. А С Х х Х .... отношение порожденное бинарной операцией ro на Р(Х).
,..
IpIHoe отношение определяется характеристической функцией:
{ 1, Х"Х 2 Е А;
XQA(X I .X2) = О, (х) Е А) v(x 2 fl А).
,.
.. Ir..'
.
.ледовательно:

g(A) == J gl(E H (x 2 )nE Q " (х 2 » о g2'
f А
.е EQA (х 2 ) == {xlix2 Е А} == А.
юда следует доказательство следствия 2.
l:1
t>cле Toro, как нами была определена возможность нахождния
'четкой меры результирующей Hro  операцию через нечеткие
.' еrpалы мы можем рассмотреть основные свойства нечеткоrо
,"'Уппоида (F(X), Hro) для нечетких мер.
.. ·  ЬСТВО теоремы 4.4. IЮказывают, что Н(J)Операция заданная над
ированной Q  алreбpoй УДОRJ1erворяет операции коммyraтивности:
н {gl2} = Н {gl2}' (4.50)
следовательно нечеткий rpуппоид (F(X), Н (J) является
, ммутативным. Рассмотрим свойство ассоциативности Hro операции.
Теооема 4.5 .
Для нечеткоrо rpуппоида (F(X),H(J) закон нечеткой внутренней
композиции 8 виде H(J) .. операции над фиксированной Q ..
aлrеброй с ассоциативной бинарной операцией
со:Р(Х) х Р(Х)  Р(Х) в Р(Х) является ассоциативным, то
есть
н cd {g.,H Cd{g2' gз}} == н cd {н cd {g.,g2},gз},
(4.51)
Бочарников В.П.

134
Fuzzy Techпology

а следовательно инечеткий rpуппоид (F(X),H ro ) является
ассоциативным.
Локазательство.
Пусть для простоты дальнейшеro рассмотрения будут определены
пространства Х = у == z с фиксированными нечеткими мерами g., g2, gз
На них соответственно. Кроме Toro, обозначим giJ{-) .. нечеткую меру
полученную в результате Н ro .. операции над нечеткими мерами gi , gj, а
g(-) .. нечеткую меру результирующую после двух последовательных
Ню.... операций.
в дальнейшем будем полаraть, что бинарная операция
т: Р(Х) х Р(Х)  Р(Х) является ассоциативной. Обозначим А с Х,
В с У, С с z. Для йJ считаем, что (А l1J В) == D, (В l1J с) Р , к == (D l1J С )==
(А йJ Р). Тоrда имеем:
н со (gj (А)ЩS2(В») == gj2(D).
Соrласно (4.47) можем записать:
gI2(D) == J g (F(х)ПВ) о g. о J (Е(у)ПА)о g2'
А 2 В
rде х Е Х, У Е У, Х = у => D_ Тоrда, для произвольноrо К с Z = Х = у для
результирующей нечеткой меры g(.) справедливо соотношение:
g(K) == н со {gI2(D), gз(С)}.
Нам необходимо доказать, что
g(K) == н (j) {g.(A), g2З(Р)}'
rде g2З(Р) = Н (j) {g2(B), gз(С)}.
Для g(К) можем записать:

Бочарников В. п.

Fuzzy Techпo/ogy
135

,К)==l gз(F(z)пqоg.2 ==ifgз(F(z)пq Л%D]оl l(z)ogI2(.) =
D r' z
<I(F(z)nqol Xv o g.2(.)==1 gз(F(z)пqоg.2(D) =
z z z
.' gз(F(z)Пqо J g.(E(y)nA) о g2 = 1 gj(E(y)nA) о i gз(F(z)ПС)о g2 ==
C(!!:Z В Z B g;{pj 
Jgl(E(y)nA)o g2J(P) = 1 g. (Е(у)ПА) о g2J(.) = H ro {g.(A),g23(P)} =
1'% р
. о 'В т {g,(A), Н т {g2( В),gз( q}}.
.. и требовалось доказать.
,"..,
[J
.. :-доказательства теоремы 4.5. можно сделать вывод о том, что если в а..
 бинарная операция l1J JlВЛЯется ассоциативной, ro есть rpУППОИД
f\X),т) является ассоциативным, то фиксированная IЩД этой aлreброй НfЛ"
IЯ является ассоциаmвной, а следовательно и нечerкий Ipуппоид для
lNeткиx мер (F(X), Hro) является аССОW1ативным.
тресным с практической точки зрения является вопрос
; ествования дистрибутивных Нro..операций в F(X). Раскрывая этот
.. . рос рассмотрим теорему о дистрибyrивности Нro..операций.
'; : Теооема 4 .
}"- ; Пусть в Р(Х) задана Q..алrебра с сиrнатурой
t: '
: Q={w.(2),w 2 (2),} rде Ю/ и IOZ бииариые операции. и IOZ
:, дистрибyrивна относительно ltJ 1. И пусть в F(X) определена
: бинарная Hro'" операция н' с фиксированной в Q...алrебре
; : йJ.
:\
I
: операцией т/. Тоrда:
, 1. Существует такая
н 2 с
йJ.
, фиксированной в Q..алrебре операцией которая дистрибyrивна
к н. операции, то есть выполняются:
йJ.
н m..операция
в
F(X)
H {gl,H (g2,gз)} = H {H. (gl,g2),H (gl,gз)}.
( 4.52)
Бочарников В.П.

136
Fиzzy Techпo/ogy
2. Существует Нro--операция Н. с фиксированной в g..алrебре
Ш 2
операций ll>2 дистрибутивная к операции Н. которая заданна
ш.
на F(X), то есть
H {gl,H2 (g2,gз)} == H2 {H (gl,g2),H (gl,gз)}.
(4.53)
Доказательство.
Как и в доказательстве теоремы 4.5 сохраним обозначения для
результирующих нечетких мер. Для подмножеств из Р(Х) при ведем
следующие соотношения:
Х = Y = Z,A c X,B c Y,C c Z
Для доказательства предположения теоремы 4.6 обозначим:
(В т/ q :::: Р, (А т/ В) :::: L, (А lJJJ С) :::: D, (А (J)/ Р) =: (L т/ D) == К.
Нечеткая результирующая мера множества К для выражения слева в
соотношении (4.52) может быть представлена в виде:
g(K) = f g.((x)nA)o g2З'
l'
rде нечеткая мера g2З(.) для подмножества Р будет определяться
выражением:
g2З(Р) = f g2((x)nB)o gз.
с
Отметим, что индексы i множеств Fj(x) определяJOТ номер отношения
фиксированноrо на ХхУ. Преобразуем эту величину:
Бочарников В. п.

Fиzzy Techпology
137
.1()= f[xi x ) Лgj((Х)ПА)]о! l(x)o &3 = !gj((x)nA)o g23(P) =
, J gj(1';(х)ПА) о !&(Fz(x)nE) о g, = Dgj (F;(x)nА) л gj(1';(x) ПА)]о
 &(Р)
. .&(f';(x)nB)og, =Dgj(F;(Х)()А)лg2(f;(х)nВ)]о!  g, =
- gт
. cJgj((x)nA) л &(f;(x)n в )] о gjзо
мотрим более подробно подынтеrpальное выражение. Обозначим
.:lCaK функцию j{x) == g. (( х)П А) л g2 (( х)П В).
.." пасно условия теоремы подмножества F.(x) являются
. : ированными для Н. ..операции. Рассмотрим вспомоraтельное
, ш.
I ошение:
f g,((x)nA)o g2 = М Е [01]:
F!(x)nп
,а существует такое i еХ, что выполняется соrласно (3.10)
ошение:
м == g. (Р.. (х *)П А) == g2(H a n F;(x*)n),
t 
-. O; с Х: .. множество а"уровня функции g.(F;(X)nA) на уровне
.. g(F;(x")nA)- Torдa, если На С F;(x*). то существует такое
.'. . ение Н 2 дЛЯ KOToporo справедливо:
Jf;(x)nA) л g2(F;(x)nB) = f g,(F'..(x)nA) о g2 =
F 2 {X)nB
:ХР 2 (х) о f g,(F'..(x)nA)o g2 = f XF 2 (x) о g12(L) =
в х
.'X F2 (x) о f X L (х) о gl2 = f[ XF 2 (x) л XL]O gl2 = gI2(F;(x)nL).
. х х
t · вив это выражение в соотношение для g(К) получим:
. =1 gI2(1';(х)nL)оgI30=J'ю. {gI2,gl3} =H {{gl,g2}' {gj,gз}}.
D
I образом., первое утверждение теоремы является доказанным.
Бочарников В.п.

138
Fиzzy Techпology


для доказательства Bl0poro утверждения мы можем воспользоваться
следующими соотношениями в n..алrебре
(В Ю} С) == Р, (А (f)J В) == L, (А lJJJ С) == D, (А Ю/ Р) == (L т} D) == К.
Тоrда, для g(К), исходя из рассуждений приведенных выше, можем
записать выражение:
g(K) == f[gl((x)nA) л g2((x)nB)]o f gl((x)nA) о gз'
х с
Для выражения в квадратных скобках справедливо (исходя из
рассуждений доказательства по пункту 1 теоремы) соотношение:
[g. (F;(x)nA) л g2(F;(x)nB)] == g,2(F; (х)п L).
rде L = А (о В · т оrда с учетом дистрибутивности операций Ю( и ll>2 в
f
n ..алrебре можем записать:
g(К) == H {Н {gl,g2},H {gl,gз}},
что н требовалось доказать в теореме.
[]
Используя основные свойства HtJ)'" операции и ее определения через
нечеткие интеrpалы соrласно теоремы 4.4 и ее следствий мы можем
определить расширенную нечеткую меру. При этом еще раз
подчеркнем необходимость отмеченной в определении 4.6
функциональной зависимости операции (J) в трехосновной алrебре на
которой определена HtJ) ... операция.
Теорема 4.7 .
Расширенная нечеткая мера подмножества С с Z, определяемая
функцией Jl (z) : Z[Ol] и нечеткой мерой g, результирующей
Н ш " операцию нечетких мер g. и g2, заданных на пространствах
Х, у соответственно находится из соотношения:
g()l)[C] == sup па л g2(F(y)nB a )] о g.' (4.54)
ае(ОI J Аа
rде: F{y).. определяется из (4.18), АатВ а = Ма n С,
Мех == {х/р(х) > а Е [Оl]}, Вех с У, Аех с Х.
Бочарников В.П.

Fиzzy Techпo/ogy
139
: Т ьс во.
--wиренная нечеткая мера g соrласно определения (3.30)
< \
деляется через нечеткую меру g(.) на z. Однако, исходя из условия
. емь] g(.) :=: Н(.() {g.mg 2 } . Тоrда можем записать:
.gi c ) == f JL(Z) о Н ш {g\IOg2 } == sup {а л g(M a n С)} ==
. с aE[Ol1
( == sup{a л Н ш {g.IOg2 }[ Ми Пе]}
а
 Ма ПС = АаСОВа тоrда соrласно теоремы (4.4) мы можем
'"!,..
. \ исать:
. !<С) == s а л.! g2(F(x )nBJo g.] == s.![ а л g2 (F(x)n BJ] о gl
'.>
t И тре60валось доказать.
[J
.
, том случае, коrда lJJ определяет унарную операцию вида
;!,: P(X) P(Z) имеет место интересное следствие теоремы 4.7.
;.
.' Следствие 1 .
'1,- Если т.. есть унарная операция такая, что "V А с Х,
щА) == М n С с Z, то расширенная нечеткая мера g J1 (С)
подмножества С с Z определяется через нечеткую меру на Х
g.(A) в виде:

gp(C) == sup f[a л g2(F(x))] о g\(A)-
а Х
(4.55)
. 'казательство следствия непосредственно следует из доказательства
'ремы 4.7. В том случае коrда унарная операция является
ждественным отображением Х в Х == Z следствие 1 при водит к
едующему результату.
I Следствие 2 .
Пусть Х = Z и lJJ .... унарная операция тождественноrо
Бочарников в.п.

140
Fuzzy Techпo/ogy

........
преобразования. Тоrда расширенная нечеткая мера
подмножества С с Z определяется соотношением:
gJJ (С)= a л м!nc g2 (F(х»о g о] =a л&",.... (Ц, ПС)]
(4.56)
Доказательство следствия очевидно следует из доказательства теоремы
4.7.Следcrвие 2 устанавливает интересную взаимосвязь расширенных
нечетких мер, которая порождена H(J) .. операцией над нечеткими
мерами.
Пусть задана Hwl.... операция такая, что lOl есть унарная операция, вида
щ: Р(Х) P(Z) (Имеется ввиду, что Нrol есть операция над нечеткими
мерами gl:2 X  [01], g2:2Y  [01] с результирующей мерой
g:2 Z  [01].) Тоrда соrласно (4.28) может быть определена мера
g:2 Z  [01].. Интересной оказывается возможность задания
сопряженной Н w2'" операции над нечеткими мерами gl и g2, rде ll>2 есть
унарная операция.
Лемма 4.6
Пусть &>1:2z[01] еcrь результирующая нечеткая мера НЮI ..
операции над нечеткими мерами gl и g2, заданными на Х и У
соответственно lOl:Р(Х) P(Z). Тоrда существует такая унарная
операция ll>2: Р(У) P(Z) и такое отображение f Р(Х)  Р(У),
что для результирующей Н W2 "0перации меры gro2 справедливо:
\/C cZ , grol (q == gro2( С).
(4.57)
или
f g2(F(x)) о g, = f g, (Е (у)) о g2'
А В
(4.58)
rде щ(А)=щ(В)= Сс Z.,В с У,А с Х.
Доказательство .
Для доказательства леммы используем тот факт, что если заданы две
функции монотонно убывающие и имеющие одинаковое начальное
Бочарнuков в.п.

Fиzzy Techпo/ogy
141
,. .' ение, ТО всеrда можно задать такие арrументы этих функций, что
'чения их будут равны рис. 4.5.
1(
х)
Х2
.' .
:
f2(Y2) == f I (Х2)
Рисунок 4.5 .. К доказательству леммы 4.6.
\tI
,одя из условия и доказательства леммы 4.3 (4.24) имеем
;f{.) == gcd2. (.) при А Х, В == У. Соrласно, свойства нечеткоrо интеrpала
А; С A i +. выполняются:
f g2(F(x»)og. < f g2(F(x))og..
А; Ан 1
,- едовательно. функция gWI (.) есть убывающая функция для
.Iженной последовательности подмножеств A i . Аналоrично. функция
': (.) также является убывающей для последовательности
. дмножеств В. СВ. I с..с В. , при п  00.
I  J+   J+"
",' rда, исходя из выше приведенной посылки и рис. 4.1. следует что
любоrо Ai c X можно найти такое Bj c t: что будет выполняться
ровие (4.58). Следовательно существует отображение fP(x)P(y)
,. tвлетворяющие лемме 4.6.

,еделенные в этом параrpафе Н ю "" операции над нечеткими мерами
: воляют рассмотреть нечеткий интеrpал Суджено от функции
 (х) : X[OI] по нечеткой мере gx (.) как частный случай
 ш.... операции над нечеткой мерой g и нечеткой мерой возможности
.: ответствующей функции р(х). В этой связи рассмотрим теорему
· навливающую интересную связь между расширенной нечеткой
Бочарнuков в.п.

142
Fuzzy Techп%gy


мерой, соответствующеrо ей интеrpала Суджено и Нro.... операций над
нечеткими мерами.
Теоnема 4.8 .
Расширенная не четкая мера gJ1 (А) подмножества А сХ,
порожденная нормированной функцией р. (х) : X[Ol] и
нечеткой мерой gx (.): 2 Х [Ol], равна нечеткой мере л(А)
подмножества А вида
л А = { H w (1C,g)[A],
() о А=0
, ,
А -:/:. о.
,
(4.59)
rде Нro (1t,g) .. результирующая нечеткая мера полученная в
результате Нro .... операции между нечеткой мерой & (-) и
нечеткой мерой возможности п(.) с функцией плотности
нечеткой меры равной р(х), а Нro.... операция определяется
отношением Н с ХхХ с характеристической функцией вида:
{ l' Р(Х.) > J1(x 2 ), Х.'Х 2 Е Х (4.60)
XH(X 1 ,X 2 ) ==
О, J1(x.) < р(х 2 ).
и бинарной операцией (JJ:
'VA,B с Х,
{ О,
т( А, В) =
А,
А*В.
,
А == В.
(4.61 )
При этом справедливо соотношение:
f Jl(x)ogx =gi A ) = А(А) = f n{EH(y)nA)ogxO=
А А (4.62)
= sup{n(M a ПА) л gx(M а ПА)},
Ма
rде
Ма = {xIJl(X) > а Е [Ol]}, Ы а = (Х \ Ma)UCovM a
Cbvц.... множество rpаничных точек множества Ми, EII(y) ..
определяется соrласно (4.17).
Бочарников в.п.

Fиzzy Techпology
143
тельст ·
ласно теоремы 3.3. функция р(х) определяет расширенную
. еткую меру gll (.) через нечеткий интеrpал Суджено. Для
ьнейшеrо доказательства теоремы рассмотрим Н ro '"* операцию с
. ристиками, указанныl\'!И в условии теоремы над нечеткими
''-:ми gJ...) И мерой возможности кх(-) С плотностью меры,
"1Q'fВeтствующей функции р(х). Соrласно алrебры с операцией ю..
анной как (4.61), множество А сХ образуется в случае щА,А ) А .
довательно отношение Н с ХхХ должно быть рассмотрено
;rласно теоремы 4.4. на усеченном декартовом произведении
. хх) п (АхА)- В этом случае справер.ливо:
;..
А(А) == f 1С(Е,,(у))П А) о gx(.) ,уеХ
А
<!:
, ,
. - значим через Н.... отношение Н == Н п Q, rде Q ь;; ХХХ,
. =={(x.y)1 хеА,уеА}. Тоrда:
А(А) == f 1С(Е н ,(у)) о gx.
А
I .rласно определения (4.3.) нечеткая мера декартовоrо произведения
,- ер определяется по (4.23). Но, для усеченноrо отношения Н'
.' ., веДЛИ80 выражение:
А(А) == sup(1C(E H n А) л gx(E H ПА)),
п
. де Е п == n Е н (у) == r; (F,), r; (. )  оператор преобразования (4.21).
"
'Отношение Н с ХхХ заданное как (4.60) для переупорядоченной по
"Убыванию функции Jl(X), может быть представлено в виде рис. 4.6, rде
)aшrpихованная часть есть область с единичной характеристической
-.+ункцией ХН (XI, Х2) == 1.

Бочарников в.п.

144
Fиzzy TechпoJogy


l
х
l
н
Jl(X)
Мо
х
Рисунок 4.6 .. К доказательству теоремы 4.8.
в силу TOrO, что мера возможности пх(х) для подмножества Еп
определяется в виде: п х(Е,,) = тахр(х), а также в силу
хеЕ"
доказательства леммы 4.3 справедливо:
F" == {ур, Е Х,Е н(у ) :::> Е,,},
а также:
F" == Ma{yIJl(y) > а == п(Е,,)}.
ТОI'да, соrласно заданной характеристической функции (4.60) можем
записать:
Е" = nEII(y)= {х Е XI\fy Е Ma,Jl(y » Jl(X)}.
-'"
Это условие можно переписать в виде:
Е п = { Х Е Х 1 1 min р(у) > р{х> } =
уеМ а
1
хl Х\ Ма U ( X11 , 1 min(p(y» = р(х» = {х Е Х! х Е Ma} Е п = Ма.
! уеМ а
I .   
1 CovM a
Подставив данное соотношение в формулу для л(А) получим:
Бочарников в.п.

L
Fиzzy Techпology
145
J n(Ef/(y)n А)о g == sup(n(M a n А) л gx(M a пА)).
А а
фическое представление этоrо СООТНОlllение изображено на
 ;'с. 4.6. Для доказательства тождества
J p(x)og== Hm(n(A),g(A») == J n(EH(y)nA)og'
А А
таточно доказать, что
р(у) == n(EH(y)n А) = п(М а пА):
 JI меры возможности п:(х) справедливо:
п(Ен(у)ПА) = тах р(х),
хеЕп{у)П А
Е" (У) n А == {х Е А/р(у) > р(х)}. Учитывая отношение Н
! ывается справедливым следующее (см. рис.4.2)
. ах р(х) = тахр(х)= р(у) или
д (у) хеА
iax р( х ) == тах р( х ) == р(у). Отсюда следует, что теорема
. (y)nA хеЕп(у)
азана

[]
..:.аключении отметим, что понятие Н..операции над нечеткими
Jами открывает возможности по обработке нечеткой числовой
. ормации в аналитических задачах поддержки принятия решений.
, сеrодняшний день Н....операции были использованы при создании
.. циальноrо проrpаммноrо обеспечения для обработки нечеткой
'.;повой информации. В частности FC v. 2.1 (Fuzzy Calculator), ExPro..
.. t v.l.O (Expert Professional), FE v.2.0 (Fuzzy Excel). Применение
..Horo nporpaMMHoro обеспечения позволяет уже сейчас на практике
менять возможности Fuzzу"технолоrии для про в еде ни я
I ели ров ан и я и расчетов в условиях неопределенности.
Бочарников в.п.

146
Fиzzy Techп%gy
4.5. Нечетко--интеrpальные зависимости
в данном пункте мы рассмотрим ряд зависимостей между нечеткими
величинами (функциями при надлежнос1И, нечеткими мерами и т.д,,),
связанными через нечеткие интеrpалы. Данные зависимости Moryт
оказаться весьма полезными при решении практических задач. С этой
целью рассмотрим ряд лемм.
Лемма 4.7
Пусть заданы три пространства с фиксированными на них
нечеткими мерами (Х, g.), (У, g2), (Z, gз) и задано отношение
Н. с XxZ. Тоrда сущесmует такое отношение Н 2 с YXZ, что
результирующие нечеткие меры равны:
л(Н.) == q(H 2 ), или
!gl(E" (z))ogJ ==lg2(E" (z))og]- 4.63)
z I z 1
Доказательство .
Рассмотрим подынтеrральную функцию g.(.). В силу определения 4.4.
эта функция является Н.... соответствием по мере g. и определяется
соотношением (4.28).
gl(EH,(z»== f l(x)Ogj(-).
Е". (z)
Аналоrичным образом может быть представлена и функция
g2(E J / z (z)). Если ДЛЯ любоrо z Е Z g.(E".(Z))==g2(E,,;z(z)), ro
(4.63) является справедливым. При фиксированном отношении Н.
VzeZ.. g.(E", (z))E[Ol]. Тоrда в силу монотонности функции
нечеткой мерь] на множества Р(У) может быть определено такое
множество АеР(У), что
Бочарников в.п.

Fиzzy Тесhлоlоgу
147
fi
J l(x)og) == J l(y)og2.
Еl/. (z) А
и теперь положить А == Е Н 2 (z), то для всех zE Z, множества
(z) восстанавливают однозначно отношение Н 2 с Yxz. При этом
....H'l
'. опняется равенство g.(E u .(Z))==g2(E/ll(Z)), а следовательно
 ествует для меры g2 отношение Н 2 дЛЯ KOToporo справедливо
ошение (4.63). Что и требовалось доказать.
д
..
 данной лемме интеrральная зависимость между нечеткими мерами
':g2 и соответствующими им отношениями Н. и Н 2 определялись при
. ком равенстве подынтеrpальных функций. Однако,
-:.1Дынтеrральные функции Moryr быть и не равными между собой, а а
 же время интеrралы от этих функций будyr иметь одинаковое
. цение. Рассмотрим лемму.
{.........
Лемма 4.8
Пусть ( В, g.) .. пространство с нечеткой мерой, a' f ..
измеримая функция, определенная на (Х В,) со значениями в
измеримом пространстве (У, 1;). g2 .. нечеткая мера,
индуцированная на (Y,) функцией
f (g2(A) == g)(f)(A)), А Е с;), тоrда существует g2"
интеrрируемая функция р(у) сопряженная g. .. интеrpируемой
функции h(x) для каждоrо Ае В, в том смысле что:
. i: .
.,.,,;
. '.

Jp(y)og2(.)== 1 h(x)og,.
А fI(A)
(4.64)
,..
i .  . ельст о.
доказательства рассмотрим второй интеrрал соотношения (4.64):
J h(x)og. ==suр(алgl(НаПf.(А))).
f.{A) а
rласно равенства (4.2) существует такая функция t(y): У -----+ [О 1 ]
 'рая удовлетворяет равенству:
Бочарников в.п.

148
Fиzzy Techпo/ogy

g.(Ha nf'(A)) == J ((у) о g2 == SUp {р л g2(An T p )},
А pe[Ol]
Тр == {y)t(y) > р},
и кроме Toro, существует такое fЗ · Е [О 1], что
g.(H a nf'(A))== g2(An T p ')== J l(у)о g2'
АПl р
Для возрастающеro ае [О 1] g. (На n f. (А)) .. есть функция не
возрастающая. Тоrда с увеличением а для сохранения выше
приведенноrо равенства необходимо уменьшение множество т - Если
р
теперь рассмотреть значение BToporo интеrpала (4.64) в виде:
а. = g.(H a . nf.(A)), то любая последовательность множеств 
индексированных значениями а для которой
f * *
j l(у) о g2 == Р == а
Т.ПА
р
задает семейство вложенных подмножеств У, определяющих
соответственно [11] функцию p(y):Y[01] Таким образом, отсюда
следует, что существует функция р(у) для которой соотношение (4.64)
удовлетворяется.
/).
Функцию р(у) по аналоrии с условным математическим ожиданием
случайной величины [19] можно назвать условным нечетким
ожиданием h{x) относительно функции! в силу, Toro что функция р(у)
в общем случае не единственна, то любую функцию на 1':
удовлетворяющую соотношению (4.64), можно назвать вариантом
условноro нечеткоrо ожидания функции h(x) (нечеткой величины h(x».
Для леммы 4.8 существует следствие.
Следствие 1 .
Пусть задано пространство (А: В, g.). Если пространство У
совпадает с  а l; есть а.. подалrебра в и f.. есть тождественное
отображение на .х: то g2 есть сужение меры g. на . Тоrда
условным нечетким ожиданием функции h(x) относительно 
является любая ""измеримая функция р(у), которая для \;/ А Е 
Бочарников в.п.


Fuzzy Techп%gy
149
удовлетворяет равенству
1 h(x) о g, == J р(у) о g2' у,х Е х.
А А
(4.65)
оказательство следствия непосредственно вьпекает из доказательства
. .,
ммы 4.8.
 четко"интеrральные зависимости можно наблюдать и в более
'. ожных случаях. В частности для двойных нечетких интеrpалов
 )l(НО рассмотреть зависимость между функциями заданными на
чных пространствах.
. Ncть заданы два пространства с нечеткими мерами (А: g.) и (У, g2 ) и
. . о нечеткое отношение: h(x) :Хх Y[OI]. И пусть на Хоп ре делена
.. измеримая функция tp(x) :X[Ol]. Тоrда можем рассмотреть
 дующуюлемму.
l:
Лемма 4.9 .
Для фиксированной функции tp(x) CYIleCTByeT такая g2 ...
измеримая функция 1(v):Y[Ol] для которой выполняется
следующее соотношение:
J [ J h(x,y) о g2 ] о g) == J [ J h(x,y) о g2 ] о gl. (4.66)
ср{х) у Х I(y)
, ,. 
j ! ательс тво .
..'
r сть ХхУ == z. Тоrда каждой паре (х, у) соответствует z е z. Для
.jнкций ({J (х) И l(v) определим цилиндрические продолжения как
А' кции
V'yeY, q>(x,y)==q>(x),
V'xex, l(x,y)=l(y).
'rдa соотношение (4.66) можем переписать в виде:
l

![ <р (х,у) л h(x,y )]0 gz == ![l(х,у) л h(x,y >]0 gz'
Бочарников в.п.

150
Fиzzy Techп%gy


rде gz == g.Xg 2 . Соrласно теоремы 4.2. можем записать
J ф(х 7 у) О J h(x,y)ogz == J lp(X,y)ogh(.)"
Z Z Z
и тоrда:
J ф (х,у)о g,,(.) == J 1 (х,у)о gJr(.).
Z 2
в этом случае существование Z(x,y) для функции q5(X,y) следует
из следствия леммы 4.8. А так как цилиндрические продолжения
однозначно определяются исходными функциями можно сделать
вывод, что для функции tp(x) существует l(y) такая, что выполняется
равенство (4.66).
/).
в заключение rлавы отметим, что в приведенном выше материале
рассматриваются вопросы обработки нечетких данных на оснОве
Нечетко....иНтеrpальноrо исчисления. В целом полученные результаты
обобщают существующие понятия нечетко"интеrральноrо исчисления.
Кроме этоrо приведены новые понятия, соотношения и зависимости,
которые расширяют возможности по описанию преобразований
пространств с нечеткими мерами и тем самым позволяют повысить
адекватность и эффективность моделирования процессов "ринятия
решений в условиях неопределенности.
Для более систематическоrо представления приведенных результатов
ниже в таблицах 4.1 и 4.2 даны основные понятия и соотношения
нечетко"интеrральноrо исчисления, которые непосредственно
используются для моделирования и расчетов с неопределенными,
нечеткими величинами.
Бочарников в.п.

L
Fиzzy Techп%gy
151
Таблица 4.1 .. Основные понятия.
Наименов. Определение
Д Нечеткий НИ от h(x):X[OI], по НМ g: 2 Х  [01]
! интеrpал по на А с Х
 ИМ (НИ определяется:
 Суджено) J h(x)ogf)= БUp{а лg(АПн а )},
А аеЮ
На == {xlh(x) а},
р(х) = g(EH (х»)'
 Ьс)={х1 Ьс'х)ЕН с х хх' .
ИМ на Для пространств (X,g.) (Y,) НМ на
. отношении ИсХ хУ есть:
Н==ХхУ 00
gfi)= {glЕi)лg2i)},
=1
== Jg1(E (y»og2)
у
== J g 2 (F (х» о gl f),
х
!. .;
;;r.
расширен....
цая НМ
.

. j
Условная
,.
<:;, НМ
,
1)
.Ф
.

Н..
. >.

соответст",
вие

.;.
f
f1'
:.,
-r
r
Расширенная ИМ есть ИМ на множстве
нечетких подмножеств и определяется:
g(J1A) == J Р А {x)og
Х
емейство НМ на Х ад (. !У) 2 Х  [01]
индексированных
Vy е у, q> (х) == у для KOToporo
выполняется:
gx (Е) == J (J'x (Е Jy) о gy
у
Функция J1 f):X  [о 1] называется
..соответствием по мере g, если
ВЫП01Пlяется:
rде E i  F i == rи(Е j ) с У.,
а r .  отоб жение соответствия rал
Бочарников в.п.
Свойства
Сходимость,
оrpаниченность,
монотонность,
непрерывность,
вынос за знак
интеrpала
постоянных
кций.
Оrpаниченность,
монarониость,
непрерывность
1.\fEX
о"х eьn: у  01].
2.
Vye У,
ах (. [у) 2 Х .... [01].
в зависимости'от
НМgи
отношения Н
определяет все
классы ИМ
Оrpаничен.,
монотонность,
непрерывность

152
Fиzzy Techп%gy

H Наименов. Определение Свойства
6. Н..операции Для (X,g)} и (У, g2) бинарная Н..операция 1. (F(X), Нш}
над нм есть оператор, задаюший нм на Z rруппоид.
такую НМ g, что V'C с z: 2. Нш ..
g t' ) = н ru {gl,g2} =, коммутативна..
=gH UinlOlt» з. Нш 
ассоциативна.
rде Н с ХхУ 4. Нш ..
V' Н; сН.,сХх У =>C ;C C'jEZ. дистрибутив на
ю: Р(Х) х Р( у)  P(Z).
7. Нечеткий Пространства (Х,Л.}) и (Y,g(.}), связаииы Свойства
интеrрал по отображением аналоrичны
расшнрен.. ср: F(X)F(Y), НИ от h(x):X[01] по свойствам НИ
ной НМ расширенной НМ g V1)' rде p(Jt) Е F(Y) Суджено за
исключением
наЕ с Х есть: свойств,
j Ь(Х)О g tu) = БUpС' л связанных с
Е r условием
л gt1 /3 П Ф /3 q{a ПЕ»), оrраниченности
rде расширенной НМ.
r = а л {3'На = {xlh(x)  а}
м р = {J-{Jl {у}  р},
Ф р = {J-{e;o O"-I a ПЕ}  JЗ}.
Ниже приведены некоторые ключевые соотношения нечетко..
интеrpальноro исчисления.
Таблица 4.2 .. Соотношения нечетко"интеrpальноro исчисления.
.N Наимен. Основное выражение Следствия
1. Соотноше е i1fhJ ( hJ . .
J I : 1
иие НИ и   2 5; ! blP  ! h о Р 5; H  1riP  hoPj <
и нтеrрала ,Х х ; 4
Лебеrа
2. Аналоr 1 (J. (F'i x ) о g = 1 (j х Iy) о gy Если Е сХ , F c Y
формулы у I х
I1 Е {Х)  4- L I\» четкие, то
Байеса  
соотношение
выполняется 

Бочарников В.П.

. I Наимен. I
. Теорема
--:: I суджено"
Фубини
: Определен
иеНМ
. через
Н....
.соответст",
"'L
-. Расширен
:' пая ИМ по
"ИМ
. ,
t -
резуIIЬ ти"
. рующей
, Н..
операцию
Сопряжен
ные Н..
оп апни
(Связь
IIOнятий
НИ..
счисле..
1tИЯ
""'вязь
- йных
'JI
Fиzzy Techпology
Основное выражение I
i h(x,y)og.z = i i h{x,y)ogy ogx
z х "
7== 7X и.
 ....,
Be (А) == i l(x)og()
{х IE' (х )A}
P.t(A)= 1 l(x)ogf)
{х Iв (x)nA0}
g (и) t;] = SJP 1 [а лg 2 (F' W)ПВ а >] о gl
аЕ (01] l\x
АаЮВ а = м а Пс I
\:j и 1 (1)1 3 и.l (1)1 .. днстрибутнвная;
3 и' (1)2 .... дистрибутивная;
lJ1(x)ogx =gll(A) = Hru(tr,g)[A =1=0]
А
= Itr(E H (у)п А)о gx(.) ==
А
=sup{rr( M a ПА)лgх(М а ПА)}
Ма
Ма ==(X\Ma)UCovM a
V'qXx),3((y)
1 r lJ(x,y)og2 ] og, ={ I J(X,y)og2 ] O&
x!Y Цп
153
Следствия I
Если g == Pr,
и с ххх для
KOToporo
ЕИ(Хi)  Еи(Хj)
имеем им
Nes(.), Pos(.)
соот ветст в.
Даны
следствия
для случаев
1. (Оунарная
операц.
2. ro ..
унарная,
тождеств.
операцня
Бочарников В п.

154
Fuzzy Techпology
r лава 5
МОДЕЛИРОВАНИЕ
НЕЧЕТКИХ ПРОЦЕССОВ
Бочарников В.П.

Fиzzy TechпoJogy
155
. . '\
,
1. Моделирование нечетких процессов
а основе Heemoro интеrpала
i
'-1' '-1'
 О расширеннои нечеткои мере
,-=,
.fи:;
с._ "t"
ктическое решение аналитических задач предусматривает
.} -
r . ходимость моделирования процессов функционирования сложных
eКТOB их развития. Данные процессы Moryт быть представлены в
. е динамической системы (1.1). OднaKO анализ показал что в силу
. :; причин, рассмотренных paHee при моделировании сложных
.' : .ктов необходимо всесторонний учет влияния факторов
  пределенности, что приводит к наличию нечетких данных в
./и'сании задач. При этом данные объекты MOryr быть представлены в
J е нечетких динамических систем (ИД С). в работе [11]
матривается следующее определение ндс.
k.
ОПDелеление 5. 1
ИДС есть система представляющаяся кортежем:
f! I
(n u, Т, y р, 'Y Jlp Jly),
(5.1 )
rде: n .. пространство состояний, U .. пространство управлений,
I' Т.. время (дискретное или непрерывное), У .. пространство
-" I ВЫХОДНЫХ значений, р: (Q х т) х U х Т  Q  отображение,
I описывающее реакцию ИДС и формализующееся функцией
вида:
Jlp(Щ:"/о,u,I,W): (ЙХ1)хихТхп  [О 1],
1: nхТ ...... у .. нечеткое выходное отображение с функцией:
(5.2)
111: nхТхУ  [01],
(5.3)
как правило характеризующее некоторое нечеткое наблюдение.
I ХОДЯ из определения 5.1. видно, что состояние ИДС в каждый
-мент времени lе Т описывается некоторым распределением
Бочарников В.П.

156
Fиzzy Techпo/ogy
нечеткости J1,(m) е F(Q) (например: распределением меры
вероятности, нечетким множеством, произвольной нечеткой мерой),
rде F (О) .. множество всех функций распределения нечеткости на !2.
Детальный анализ существующих подходов к формализации нечетких
данных (некоторые результаты приведены в табл. 1.6) показал, что
наиболее приемлемым является подход основаннь)й на использовании
теории нечетких мер. Данный подход позволяет с единых позиций
представить разнородные данные о функционировании моделируемых
объектов, до некоторой степени обобщить дрyrие подходы (теории
вероятности, ошибок, интервальных средних, нечетких множеств
субъекrnвных вероятностей и т.д.) к формализации данных в УСЛОвиях
неопределенности.
Для иде, с помощью которой моделируется тот или иной объект
управления в аналитической задаче поддержки принятия решений,
последовательность {Jlt (т)} образует в пространстве F (Q )
некоторый процесс, который называется нечетким процессом (НП).
Опnепеление 5.2 .
Нечетким процесс ом (НП) называется процесс, состояние
Koтoporo в каждый момент времени t Е Т описывается
некоторым распределением нечеткости J1,(m) е F(Q) на
пространстве состояний процесса n.
Таким образом понимая под НП процесс, удовлетворяющий
определению 5.2 определение иде может быть представлено в виде:
Определение 5.3 .
Под нечеткой динамической системой понимается система,
динамика которой описывается нечетким процессом.
Описание систем, моделируемых в виде нде оказывается весьма
полезным, а иноrда и единственно возможным в ряде конкретных
прикладных задач [17]. В частности, целесообразно использование
НДе для описания реальных объектов возникает при решении задач
проrнозирования, принятия решений в крупномасштабных системах,
представления конфликтных систем и в друrих
слабоструктурированных задачах [12].

Бочарников в.п.

Fиzzy Techпology
157
настоящее время для представления нде наибольшее
пространение получили описания, основанные на теории нечетких
:ожеств В виде нечетких композиционных уравнений, нечетких
ностных уравнений, матрично"та6личных представлений,
иентированных на описание нде в дискретном времени [20].
работе [21] бьmо предложено описание непрерывной динамики иде
; виде нечетких дифференциальных включений, то есть
I .', ференциальных включений в правой части соотношения которых
i* ит нечеткое множество. Такой подход к представлению нп еще до
цa не исследован и требует дополнительноrо изучения. Однако, в
';, ' Toro, что изменение функции принадлежности по времени для
, kсированноro roe О не всеrда является дифференцируемой функцией
\ пользование подхода нечетких дифференциальных включений
. яется оrpаничительным и приемлемым лишь для определенноrо
:, ,cca нп.
 ... --:'
-'Приведенных выше подходах нечеткие данные не представлялись с
I
.1 мощью нечетких мер, что оrpаничивало возможность решения
'.нкретных прикладных задач. Для описания и моделирования
.- ьных процессов при управлении сложными объектами на основе
пользования нечетких данных, .представленных распределениями
,)
етких мер, необходимо примене ние нечетко....иНтеrpальноrо
._' "сления [22 23..25, 37, 39], которое позволяет определить
\
. 'уемые зависимости между нечеткими мерами при преобразовании
ветствующих пространств, что было рассмотрено в предыдущих
вах.
'работе [31] автором было предложено описание нп при помощи
'.', етко....интеrpальных уравнений для дискретноro времени. В этом
Iучае динамика нде описывается следующим образом. Если на
;. 11
ранстве состояний О определена нечеткая мера g(.): 2 ------+[01],
'исывающая некоторые оrpаничения на g для нде, J1i(m): 0------+[01]
 ,:rояние иде в i....й момент времени, а преобразование состояния
.'. темы на i + I шаrе определяется оператором h i + l (lO,ro):QxQ------+[ОI],
'состояние иде на i + I шаrе будет описываться уравнением:
11.+1 (т) = 1 hi+1 ( lO, т) о g(.).
JJ.«(JJ)
(5.4)

Бочарников В.п.

158
Fиzzy Т echпology
Представленные в указанных выше работах описания НП
ориентируются в основном на случай нечеткой функции чеТКОrо
apryMeHT8 [1 ], то есть неопределенность состояния процесса
определяется неопределенностью связанной с пространством
состояний, а наблюдение времени является четким. Однако, практика
показывает, что неопределенность состояния НП, который описывает
динамику НДС, может быть вызвана и неопределенностью времени
наблюдения процесса [8, 13]. Исходя из этоro в наиболее общем случае
НП целесообразно рассматривать как нечеткую функцию нечеткоro
apryмeHTa. При этом описание НП непосредственно может быть
представлено при непрерывном изменеиии нечеткоro aprYMeнтa (то
есть при непрерывном изменении нечеткоro времени). Для описания
нечеткости процесса по времени на Т целесообразно рассматривать
некоторую нечеткую меру Ft(.): 2 Т ...... [01] [23]. Обозначим r(t)
произвольный временной интервал, определяющийся функцией
r(t): т  [01]. Отметим, что частным случаем является четкий
временной интервал r(t) == [O,t]. В дальнейшем будем полаraть, что
временное пространство Т и пространство состояний n для НДС
связаны через условную нечеткую меру a,J:lt), Те есть справедливо
следующее соотношение:
g(.) = J а со (.It) о F; (.).
т
Исходя из этоro вытекает следующая лемма для представления
временных интервалов.
(5.5)
Лемма 5.1.
Произвольный четкий или нечеткий временной интервал
reF(r) имеет нечеткое изображение в N, а непрерывная
последовательность интервалов {rпJ порождает в пространстве
n непрерывный НП f(lOlt), соответствующий данной
последовательности.
Доказательство.
Пространства n и т связаны через условную нечеткую меру (1,А: I t).
Соrласно свойства нечеткоrо интеrрала (3.1 1) справедливо
представление:
Бочарников В.П.

Fиzzy Techпo/ogy
159
(1 ю (.ft) = i 1( lO ) о о" ю (-It) ,
n
де 'Vw е Q, 1 (т) == 1. Тоrда, ДЛЯ произвольноrо нечеткоrо множества
OJ), исходя из (4.9), справедливо:
 О"ю(f(lO)lt)= i l(lO)ОСТ ю (-l t ) = 1 [(lO) о O"co(.!t).
f{ю) n .
. етим, что функция a((J(f(m)lt) есть функция распределения
, четкости на Т, то есть G((J(f(m)lt): Т  [01], а следовательно эта
. Ункция может быть сопоставлена с некоторым временным
,' тервалом r(t): Т  [01]_ Таким образом для произвольноrо
'i>eMeHHoro интервала [(t) на пространстве (т, Ft(') существует
некоторое условное нечеткое ожидание Jl(t) такое, что:
,.
V'A с Т, ir(t)oF,(.) = i J1(t)oF,(.).
А А
Ьедовательно, если p{t) ::: а ro ( f( т) I t), то существует нечеткое
1iЗo6ражение 1(т) на Q ДЛЯ BpeMeHHoro интервала r(t), ТО есть для
боrо r(t) можно поставить в соответствие нечеткое множествоfI<.т)..
'еперь рассмотрим последовательности временных интервалов. Пусть
(тп} есть монотонно возрастающая последовательность временных
валов и пусть r(t) есть предел этой последовательности в момент
ремени t Е Т, r ( t) = lim r , то есть {r n } есть непрерывный ИЛ на Т.
п......... п
.окажем, что в этом случае образованная в Q последовательность
'тюке является непрерывным нп. Рассмотрим:
1
I r(t) о F, (.) == i lim r n о F, (.) == Iim i r n о F, (.).
т т пOO IIOO т
Рднако, для r существует такой};,( т), что выполняется:
11
':Ir(t) о F;(.) = lim; l(J;,(m)lt) о F;(-) = i lim(jco(!;l(lO)lt) о F;(.) =
'Jr n...::,оо Т т п
= f ! 1im.f.,(m) о aoJ1t) ] о F;(.) == i (Jco [ limh (lO)1 t ] о F;(.).
;tQ Т п
Однако имеем:
Бочарников в.п.

160
Fиzzy Techпology
I r(t) о F; (.) = j а(.!; (ю)Jt) о F; (.).
т т
Следовательно существует
limf (ю) = f(lO)' то есть
п..,.,..... " I
предел последовательности
непрерывная монотонная
последовательность временных интервалов {r n } порождает в n нп
fn( т) такой, что для r(t) существует t( т). Что и требовалось доказать.
Д
Доказательство леммы 5.1 OTKpbJBaCT возможность представления
непрерывноrо ИЛ, описывающеrо динамику ИДС в аналитических
задачах СМО, на основе нечеткоro интеrpала по расширенной
нечеткой мере.
TeODeMa 5.1 .
Пусть преобразование состояния ИДС описывается нечетким
отношением вида: h'(lO,lOlt):(QxT)xQ[Ol]. Тоrда
ИЛ, описывающий динамику ИДС через каждый интервал
времени r(t) Е F(1) может быть описан нечетко"интеrpальным
уравнением вида:
J1r (lO) = J h( lOJt) о g(f r (lO )), (5.6)
т
rде h(юlt) = I h'(lO,lOJt)o g(.) оператор
Il,(} (ю)
преобразования состояния НДС с учетом начальных условий
J.l ' r(t) .. интервал времени, g(.): 2rJ.  [01] .... нечеткая мера
'и(Ю)
на n, j;( т): n  [О 1]  НЛ на n, порожденный возрастающей
последовательностью временных интервалов.
Доказательство .
Допустим, что на Т определена нечеткая мера F..(-), задающая
нечеткость динамики ИДС по. времени. Тоrда состояние ИЛ можно
представить в виде:
.......
Бочарников в.п.

Fuzzy Т echпology
161
....м
J.lr(ro) = J h(rol/) о F;(.) = 1 h(lOl/) о 11(1) о F;(-) =
r{/} r{t) т
_ _ = lr h(lO(/) л r(/)] о 11(1) о F; (.) = 1 h(rol/) о 1 1(/) о F;(.) =
,s r т т r{/)
= 1 h(rol/) о 1 r(t) о F;(.).
т т
Соrласно леммы 5.1, расширенная нечеткая мера, порожденная
Временным интервалом r(t), может быть заменена расширенной
Jlечеткой мерой порожденной условным нечетким ожиданием
'.. .Ofj)(fJ co)I/), то есть:
1 r(/) о F;(/) == 1 CТco(!r( lO)lt) о F;(.).
т т
Тоrда:
Jlr ( ro) = 1 h( mJ () о 1 (j со (!r ( lO)1 1) о F; (-).
т т
()бозначим через 1JI,(.lro) .. условную нечеткую меру, связывающую
.!lPocтpaHCТBa n и т, и двойственную (сопряженную) мере crro(-It). Torдa
torласно (8_11) справедливо соотношение:

1 (j (f(lO/)oF(.)== ! 1JI:(\{/(lJ)og(.),
v(I) fJJ , f(fJJ) I
:tде \1(1) : Т  [О 1]. В силу этоro можем записать:
-!
:Pr(CO)=a.. л H!,)a..Cfr(CO)lt)oF;O}=
> =:sup { afJJ Л 1 \fI.(Hu(t)lro)o g(.) } = sup { aro л ! !r (lO) о g(.) } ,
alJ) f..(fJJ) U at \II,{lI..{I)Jw)
"rдe нои) = {tlh(l.tJlt) > а.. Е [Ol]}  множество а.уровня при
:-фиксированном (ОЕ о. В силу TOro, что
. 'P,(Ha(/)!lO) = 1 1(1)0 'Р/(.:lO), имеем следующее
На (I)
представление:
Jt.p
б Зак. 771
Бочарников в.п.

162
Fиzzy Techпo/ogy
Jlr(W) == saCJJ лsр(р лЩF р пФр(Н:(f»)))} =
== sup{rCJJ л ЩF р пФр(Н:(t)))}.
Y(JJ
р Е [01], r ru == а ш Л р, Fp == {ltJifr(ltJ) > р},
Ф (J ( Н;(t))== { wll l (f)O'Pt(-:W» р } .
jH::(/)
Таким образом, полученное выражение соответствует выражению
(3.34) нечеткоrо интеrрала по расширенной нечеткой мере и следствию
1 теоремы 3.4. Исходя из этоro можем записать:
J1r(ltJ) == 1 h(lOlt) о g(fr(ltJ)).
т
Что и 1ребовалось доказать.
D
Таким образом, при помощи уравнения (5.6) может бьпь описан
непрерывный нп и определено ero нечеткое состояние через
интересующий нас нечеткий интервал времени. Полученный результат
открывает возможности по моделированию динамики сложных
объектов, рассматриваемых в аналитических задачах. Далее будут
рассмотрены некоторые особенности НП описываемых уравнением
(5.6), а также показано, что представление ИЛ через интеrрал по
расширенной нечеткой мерой является наиболее общим для
представления нп.
Бочарников В.П.

Fиzzy TechпoJogy
163
$.2. Особенность непрерывных нечетких
чРоцессов. Нечеткодифференциальное
рредставление нечетких процессов
,Прежде чем мы перейдем к рассмотрению нечетКо....дифференциальной
иси ИП остановимся HeMHoro на уравнении (5.6) и попробуем
_.отследить некоторые особенности ИЛ описываемых таким
уравнением. В доказательстве теоремы 5.1. присyrcrвует
,<эквивалентная запись для состояния нп в виде:
J1r(ro) == 1 h(ltJlt) о 1 r(t) о F(t).
т т
';Последовательность r; ( t) образует в Т непрерывный возрастающий
apoцecc (r:+I(t) > I;(t)). Соrласно леммы 4.8 существует такая
функция s(t) на Т что:
1 r(t) о F(t) = 1 s(t) о F(t) = S. (5.7)
т т
При этом s(t) может быть отлична от r(t) (Рис 5.1).
I
"-
s
."....,.
,.
"
А Т
Рисунок 5.1 .. К представлению нечетких временных интервалов.
Соотношение (5.7) для функции s(t) будет выполняться если
i \;/( Е А с Т, s(t) > S . Таким образом если приравнять
Бочарников в.п.

164
Fиzzy Techпology
s( t) aJfr(w)lt) можно наблюдать следующее. С увеличением времени
t Е Т величина S интеrpала от функции r(t) увеличивается, а
следовательно увеличивается интервал А  Т, rде функция aJfr(w)lt)
принимает значение не менее S Е [01]. С увеличением r(t) значение
интеrpала определяющеrо J.1..( т) будет увеличиваться. Так как функция
h( щt) описывает степень приращеНИil значения функции
принадлежности р(т) по времени, то в силу наличия
вышеупомянутоrо свойства функции aJfr(w)lt) мы будем наблюдать
следующий эффект. Функция p.(т) с увеличением r(t) будут иметь
возрастающий по времени уровень не9пределенности a.(t) на фоне
KOToporo будет наблюдаться нп. То есть ИЛ р..(т) может быть
представлен в виде двух составляющих изменяющихся по времени:
111(m)==al(m)v I1(т),
(5.8)
rде (1r( т) .. есть постоянная на n ФУНКЦИЯ уровня неопределенности
возрастающая по r и являющаяся "диффузионной" составляющий нп;
11; (т) .. нп отражающий "содержание" изменения состояния
процесса и иrpaющий роль "переносной" составляющей нп. Термины
"диффузионной" и "переносной" составляющих заимствованы из
представления стохастических процессов.
Теперь представим, что нп fr(W) задан на пространстве Q и
удовлетворяет условиям необходимым для представления нп через
уравнение (5.6). По аналоrии с представлением стохастических
процессов определяемых интеrpaлом Ито [26] в виде стохастических
дифференциальных уравнений мы можем рассмотреть символическую
запись "приращений'У составляющих описания нп через, так
называемые, нечеткие дифференuиалы. Будем полаrать, что через
интервал времени r(t) приращение времени определяется состоянием
нечеткоrо процесса fr (т). Пусть fd(.) .. есть обозначение нечеткоrо
дифференциала. Тоrда нечеткое приращение по времени будет
представляться символической записью fd А{ т). По аналоrии с выше
отмеченным, нечеткий дифференциал состояния НП будет
записываться в виде fd J.1(m). Тоrда символическая запись уравнения
(5.6) в виде нечеткоrо дифференциальноrо уравнения примет вид:
fd РС т) == h( щt) fd f{ т).
(5.9)
Бочарников В.Л.

Fиzzy Techпology
165
Уравнение (5.9) является символической записью, как и
tтoхастические дифференциальные уравнения, и отражает тот момент,
то состояние нл может быть найдено при вычислении нечеткоrо
 щеrрала по расширенной нечеткой мере порожденной НП fr{w),
ажающим неопределенность проuесса по времени.
Запись уравнения нп через нечеткие дифференциалы (5.9) несколько
t'"Pощает запись уравнений динамики ндс. В дальнейшем мы будем
использовать как интеrpальной записью уравнений динамики (5.6) так
ее ero дифференциальным аналоrом (5.9).
Бочарников В. п.

166
Fиzzy Techпology
5.3. Дискретные нечеткие процессы.
Композиционные нечеткие уравнения,
.v .v
как частным случаи дискретных
.v
нечетко",интеrpальных уравнении
в ряде практических задач необходимо рассмотрение дискретных нп.
Прежде чем мы будем рассматривать нечетко...интеrральное
представление дискретных ИП целесообразно остановиться на
алrебраической структуре множества нечетких временных интервалов
Временной интервал Т наблюдения ИП можно отождествить с
множеством неотрицательных действительных чисел R+. При этом
произвольный момент времени t е Т представляется неотриuательным
действительным числом. В случае, коrда мы хотим отразить
нечеткость момента времени и определенноrо им интервала времени
наблюдения НП uелесообразно использование нечетких
неотрицательных действительных чисел [12].
Опоепеление 5.4.
Нечеткое неотрицательное действительное число определяется
как отображение р : R+  [О 1], удовлетворяющее условиям:
р(О) ==0, тах{р (r) I reR+ }==l , (оrраниченность),
'\IreR+ :p(r) == тах{р (r') I r'eR+, r' < r} ,(непрерывность слева).
Таким образом, нечеткий момент времени t EF(1) мы отождествляем
снечетким неотрицательным действительным числом. При этом
t ЕF(Т) может быть интерпретировано следующим образом. Функция
p(t) соответствующая t, p(t):T[OI] пони мается как степень
нечеткости принадлежности неясноrо момента времени t четкому
интервалу [О" [. Исходя из этоrо можно видеть, что функция {i..t) есть
Бочарников в.п.

Fиzzy Techпology
167
:
'.
неубывающая функция. А если установить однозначное соответствие
между 1 и [0,1 [, то функция р (/) будет удовлетворять свойствам
:dечеткой меры заданной на Т. Если теперь использовать однозначность
соответствия момента времени t и определенноrо им интервала [О,' [
}JVIЯ случая нечеткоrо момента времени t мы можем определить
<нечеткий интервал f(t}e F(1) фиксированный этим t. Функция r(t)
'-отражает степень нечеткости Toro, что интервал [O,t[ не покрывает
"ечеткий момент времени t определяемый функцией р (t).
Исходя из этоrо функция r(t) может быть определена по функции p(t)
OMeHTa времени t как ее дополнение. При этом если p(t) есть
. нечеткая мера удовлетворяющая правилу нормировки по Суджено, то
. > справедливо:
r(t)== lp(t) Е [01] .
1 + Л-р(t)
(5.1 О)
13 том случае, коrда p(t) есть мера возможности (функция
принадлежности) функция r(t) может быть восстановлена как:
[(t) == ] .. р (t).
(5.11 )
Пусть H(R+) ... множество всех неотрицательных действительных чисел.
рИа H(R+) возможно задание часmчноrо порядка:
Plp <=> Vr Е R+:cp(r) < p(r),
(5.12)
"Jlелсо видеть, что {H(R+)} является решеткой. Следовательно
множество всех нечетких моментов времени Н(Т) обладает свойством
решетки. Если обозначить G(r) множество всех нечетких интервалов
r(rJ, то между G(r) и Н(Т) существует изоморфизм, а следовательно
1) также как и Н(Т) обладает свойством решетки.
На Я(R+) может быть определена естественная алrебраическа'Я
.операция задаваемая соотношением:
{р  lp}(r)== mах{р(р) л lp(s)lp,s Е R+,s + Р == r}. (5.13)
..
Бочарников в.п.

168
Fиzzy Techпology
Тоrда
(H(R+),<, )
образует
частично упорядоченную
коммутативную полуrpуппу. Аналоrично (5.13) на множестве С(1)
возможно задание алrебраической операции ffi и тоrда G(1), будет
наделена структурой частично упорядоченной коммутативной
полуrpуппы. При этом справедливо:
r; --< r 2 <=> Vt Е Т: r;(t) < r 2 (t).
{r; еэr 2 }(t) = max{r;(p) л r 2 (s)1 S,pE T,s+ р= t}.
Определим в С(Т) возрастающую последовательность нечетких
интервалов {ri(t) I i 1,1} определяемую рекуррентно:
ri(t) == ril(t) ЕВ дr(t), (5.16)
При этом лr(t) можно трактовать как нечеткую дискрету по времени, а
ri(t) последовательность нечетких дискретных интервалов времени
через которые наблюдается нп.
в соответствии со структурой множества {ri(t)l i II} мы можем
определить нечеткий дискретный процесс (ндп), как частный случай
непрерывноrо ип, определенноrо уравнением (5.6).
Теооема 5.2
Пусть непрерывный НП, описывающий динамику НДС,
представлен нечетко--интеrpальным уравнением (5.6). Тоrда
ндп относительно последовательности моментов времени I
будет описываться дискретным нечетко"интеrpальным
уравнением вида:
Jli+.(Ю) = 1 h;(ю,ю)о g(Jl,(Ю)).
n
(5.17)
rде g(Jl;(Ю))  расширенная нечеткая мера, а hi(щю) ....
нечеткое отношение на пространстве состояний n в i .. й
дискретный момент времени, отражающее динамические
. характеристики нп.
Доказательство.
Пусть в i .. й дискретный момент времени НП наблюдался в течении
ri(t) нечеткоrо BpeMCHHoro интервала. При этом в конце ri(t) нп имел
Бочарников в.n.

Fиzzy Techпology
169
't'.
.,:;,...
'состояние Jli(Ю): n  [01].. В (i+l)..й момент времени интервал
наблюдения НП будет определяться функцией r i + l (t) задаваемой в
 t'иде:
rj{t) == r il{t) ffi дjr(t),
_ rде .6 i r(t) .. есть нечсткий временной интервал определяющий
t'днскретность наблюдения НЛ в i.. й момент времени.. Таким образом,
на лjr(t) состояние l1i(Ю) можно расценивать как начальное условие
< уравнения (5.6). Тоrда справедливо:
Pr .и(т) = l [ 1 h'(ю,lVlt) о g(.) ] о g(!h-r(I)(lV».
1+ т Р; (т) ,
Соrласно свойств расширенной нечеткой меры и теоремы Суджен{)оо
Фубини можем записать:
Р. (ю) = 1 [ 1 h'(lV,lVlt) о K(!hr ( l ) (ю» ] О g(.).
,+1 11; (т) т
Внутренний интеrpал можно расценивать как интеrpальный оператор
преобразования состояния ИДС на нечстком интервале лir(t), ТО есть:
!h'(m,m1t) о g(!Air(t)(m)) = h;(m,m): QxQ [01]-
. Тоrда выражение для состояния J.li+I(Ю) принимает ВИД:
р.+.(т)= 1 h(m,m)og(.)= 1 h(m,m) о 1 l(m)og(-) =
, 11; ( т) 11; ( т) n
== 1 h;(ю,со) 01 р;(ю) о g(.) == 1 h;(lV,lV) о g(Jl;(lV».
ппп
Что и требовалось доказать..
[]
Следует отметить, что если за нечеткий интервал ri(t) интеrpальный
оператор преобразования системы был h i ( Щ ю), а за ri+l(t) : l, i + l ( са ю)==
hi(щю) для всех ie/, то ДНП будет стационарным.. В этом случае ДИП
будет описываться стаuионарным дискретным нечетко..интеrpальным
уравнением:
Бочарников в.п.

170
Fиzzy Technology
Pi+I«(j) == I h«(j),co) о g(p;«(j)).
12
(5.18)
Полученное дискретное не чстко....интеrральное уравнение
описывающее ДНП включает в себя, как частный случай, известное
нечеткое тax..тiп композиционное уравнение, нашедшее широкое
распространение в решении практических задач управления нечеткими
системами [17]. Напомним, что нечеткое тax..тiп композиционное
уравнение имеет вид:
Pi+ I (т') = тах min{ h( СО, т'), (Р; ( т) }. (5.19)
те12
rде h«(j),co'): Q х Q  [01] .. стационарное нечеткое отношение
реализующее оператор преобразование состояние ндс.
JeODeMa 5.3
Нечеткое тax..тiп композиционное уравнение (5.19) является
частным случаем дискретноrо нечетко"интетральноrо уравнения
(5.18), если а.. множество равновозможных состояний ндс, т.е.
\1ш Е а, g(ю) == 1.
Доказательство .
Рассмотрим более подробно расширенную нечеткую меру в уравнении
(5.30) ДJlЯ А с а:
К(CI)(А)::: 1 р;((О) о g(.).
А
Так как соrласно условия теоремы g(.) есть мера возможности такая,
что \1 ю Е а, g( ю) == 1, то данное выражение можно представить в виде:
,
1 р,(т) о g(.) = sup{a лg(М а nA)}== sup { a л шах g((O)l,
А aeJOIJ aeJOIJ теМиНА 1
rде Ма == {COlpi(CO) > а Е [Ol]}. Тоrда, если Ма ПА * {2), ТО
g(Ma.п А) == 1 и следовательно:
g (А) = 1 р.(т)о g ( . ) = тах р (со)-
р,(ю) А I roEА '
Отсюда исходный интетрал можно представить в виде:
Бочарников в.п.

Fиzzy Techпology
171
. Рн I ( со) == 1 h( со, со) о gJH ш) (-) == max { min h( (J), (J)') л тах р; ( (J) ) } ,
n I EQ тЕЕ тЕЕ
: rде min h( тт') определяет а  уровень нечеткоrо множества h( Щ 01)
roeE
при фиксированном 01 Е о. Следует отметить что для вложенной
последовательности множеств Е. с Е 2 с ... с Ei c ..., 'r;/i E i с n ФУНКЦИЯ
.min h((J),(J)') при фиксированном о1еО является не возрастающей,
ШЕЕ
то есть если: E i с Ej с О, то:
min h( (J), (J)') > min h( (J), (J)').
тEE тЕЕ.
, J
Следовательно, максимум по Е с Q в выражении для Jli+.(ro)
достиrается при рассмотрении всех одноточечных подмножеств
 {щ}. Отсюда получаем:
J1r+l ( т') = max { minh( (J),cd) л max,ui ( (J) ) } == max: {h( CO j , со') л .ц (ю) } ·
Ejd"! ш:=Е j ШЕЕ j ll1eQ
..
Полученное выражение есть ничто иное как тiптax композиционное
'уравнение (5.19) определяющее динамику дискретной ИДС. ЧТО и
f.
требовалось доказать.
[]
Таким образом, из доказательства теоремы 5.3. следует, что
.'полученное нечетко-интеrpальное уравнение (5.30) дЛЯ ДНП
,
. охватывает известное и широко используемое тiп....тax
..l(омпозициоНное уравнение как частный случай для распределения
iнечеткой меры возможности на пространстве состояний НДС. Этот
факт позволяет использовать дискретНQе нечетко....иНТеrpальное
. уравнение (5.18), моделирующие более ШИРОКИЙ спектр
неопределенностей НП от возможности до необходимости появления
\'TOro или иноrо состояния ИДС. При этом использование gл"мер
позволяет учитывать различные семантические модальности
неопределенности в НДС. Исходя из этоrо следует, что использование
уравнений типа (5.17) является более rибким инструментом
моделирования НДС в аналитических задачах, чем ШИРОКО
npименяемые сейчас композиционные уравнения типа (5.19).
Бочарников в.п.

172
Fиzzy Technology
5.4. Нечетко",интеrpальные уравнения
непрерывных управляемых
нечетких процессов
в предыдущих параrpафах мы рассматривали ИП в непрерывном и
дискретном времени, которые не учитывали возможное воздействие
управляющих факторов. При этом предполаrалось, что оператор идс,
определяющий ее динамику, описывается нечетким отношением
h(ro,rolt): ('1 х Т) х '1  [01],
не зависящим от внешних факторов, в том числе и от управляемых.
TaKJ.{e нп Moryr характеризоваться как свободные ип. В наСТоящем
параrрафе МЫ будем рассматривать динамику иде при воздействии на
нее управляющих факторов или короче .. управления. Моделирование
управляемых ндс наиболее актуально при ршении задач
оптимизации управления, которые являются ключевыми для принятия
решений.
Пусть на НДС в каждый момент времени t Е Т действует управляющее
воздействие u Е U, rде U .... множество всех возможных управлений.
Тоrда управление можно рассматривать как функцию времени u(t). В
том случае, коrда мы хотим рассматривать нечеткое управление,
данная нечеткость может выражаться либо как нечеткость на
пространстве управлений U, либо как нечеткость на временном
пространстве Т. Последнее характерно для случая, коrда точно
неизвестно начало действия управляющих факторов на ндс.
Например случай нечеткоrn запаздывания управления. Таким образом,
наиболее общим случаем является управление как нечеткая функция
нечеткоrо арrумента [5]. Исходя из сказанноrо управление может быть
представлено как НП характеризующийся функцией вида:
c(uI t): UxT[Ol].
(5.20)
Бочарников в.п.

Fиzzy Techпology
173
: 
Теперь рассмотрим следующую теорему о
управляемоrо ИП через нечетко--интеrpальное
расширенной нечеткой мере.
представлении
уравнение по
Теооема 5.4.
Пусть на ИДС действует управление c(ult): UxT[OI] и оператор
преобразования состояния ИДС с учетом начальных условий Ilo( ю)
описывается нечетким отношением h(u,юlt): (О х U) х Т  [01]
Тоrда динамика непрерывной НДС с учетом процесса управления
описывается нечетко--интеrpальным уравнением вида:
J.lr( т) == 1 h( ю, ui t ) о glf иr (fr( ю))'
C(lI:')
(5.21 )
rде r(t): т  [01] .. нечеткий временной интервал наблюдения НП,
jr(ю) .... соответствующий r(t) ип на (2,
gн щ (fr(m» = H{V..l.lo:.,)}fr (т)о g(-) 
расширенная нечеткая мера, Н{Vu,'Vt(.lю)} .. Ноперация над
нечеткими мерами: v u (.) .. оrpаничения на управления и 'Vt( I ю),
которая порождена отношением Н с U х Т возникающим при ..
уровнях нечеткоrо отношения h(ro,ult) л c(ult) и фиксированном
roe (2.
lJ.оказательство.
Состояние иде через интервал времени r(/) может быть определен
соrласно теоремы 5.1. следующим нечетКо....интеrральным уравнением:
J.lr(UlO) == f h(u, (J)lt) 014;(.) ==
r(l)
== 1 h(u,(J)II) о 11(1) 014;(.) == f h(u,(J)II) 01 r(t) 014;(.),
т r(l) т т
rде J1T(U, ю).... состояние ИДС зависящие от принятоrо на интервале r(/)
управления. Соrласно леммы 5.1 можем записать:
1 r(t) 014; (t) == 1 а (JJ(fr( ю) / t) о F; (.),
т т
Бочарников в.п.

174
Fиzzy Techпology
fr(ro) .... соответствующий r(l) ил на а, а 0(1)('11) .. условная нечеткая
мера связывающая пространства Т и а. Следовательно:
J.1r(u,m) == 1 h(u,ro) о 1 D"co(fr(m)lt)of;(.).
т т
Для фиксированной на r(l) последовательности управлений C(U,I)
оrpаниченных на U нечеткой мерой VtJ(.): 2 U [Ol], состояние НП JLr(ro)
будет определяться соотношением:
JLr(ro) = I [ 1 h(u,ro,t) о 1 D"co(fr(ro)lt) о f;(t) ] о v u (.).
C(lll) т Т
Соrласно теоремы суджено....фубини можем записать:
J.Lr( ro) == ! [ 1 h(u, ro,t} о V и(.) ] о ! D" со (fr(m )It) о f;(t) =
т ы) Т
= 1 [ 1 [hco (u,t) лс(u,t)]о v u (.) ] О 1 D"co(fr(ro)lt)of;(t).
т U т
Соrласно теоремы 4.2 можем рассмотреть эквивалентное выше
приведенному выражение:
J.lr( ю) = J {hro(u,t) л c(u,t)} о / У и (-) Х J й"ro (fr «(j))lt) о f;O)'
тхи \ т !
r де h(() (ut) = h( u rol t), а
( V и(-) Х 1 й" ro (fr( (j))lt) о f; (о) ) = /(.). -
\ т
декартово произведение нечетких мер заданных на U и на Т, при этом
H c UxT, Р// (.):2 и )(1'  [01]. Соrласно определения 4.3 можем
записать:
P1/(H) = S UP { VII(E;) л 1 D"co(fr(ro)lt)of;(.) } ,
Е; r;;.U r ll (Е;)
rде Е; С и,rll(E;) С Т, rl1 (-) .... отображение (4.20), входящее в
соответствие rалуа. Пусть '1'.(.11) .. условная нечеткая мера
Бочарников в.п.

176
Fиzzy Techпology
J.lr(m) == 1 {hm(u,t) л c(u,t)}o Р н (-) ==
тхи
== т!и {hC1J(u,t) л с(и,t)} о l н{ v", 'Р,(-!т)}о gfr(C1J)(-) ==
== I h(m,ult)o 1 fr(m)og(.)==
с( 11,1) /1 { v" , ЧJ, (.Im)}
== J h(m,ujt)оКиuт(fr(m».
c(u,t)
Что и требовалось доказать.
[]
Теорема 5.4 позволяет описывать динамику управляемых НП дЛЯ НДС,
моделирующих реальные объекты в аналитических задачах поддержки
принятия решений_ Отметим, что практически нечетко....иНТеrpальные
уравнения описывающие управляемые инеуправляемые НП сходны
между собой и являются уравнениями с интеrралом по расширенной
нечеткой мере. Отличием является то, что для управляемоrо ИП связь
между пространства ми n и Т учитывает влияние на НП управляющих
факторов как через последовательность управлений c(u,t), так и через
учет нечетких оrpаничений на управление V u (-): 2 U ---7 [01].
в заключении данной rлавы отметим, что как и для не управляемых
ИП в случае наличия управления возможно рассмотреть нечетко..
дифференциальную запись уравнений в следующем виде:
fdJl( т) == [h( m,ult) л с ( m,u,t)]fdf;( ю),
(5.22)
rде "Vm Е Q, c (m,u,t)== c(u,t) .... цилиндрическое расширение
функции c(u,t);
f;(m)== fr(m)л н{ V.' 'P(-Im)}
(5.23 )
есть функция, учитывающая временную неопределенность (аналоr
броуновскоrо движения в стохастических дифференциальных
уравнениях) НП с учетом влияния управляющих факторов из
множества U.
в заключении rлавы преведем ее основные результаты в виде табл. 5.1.
Бочарников В.П.

Fиzzy Techп%gy
177
Таблица 5..1 .. Описания различных видов нп.
I ь' tи ,СО It) о g  )
po to)
ператор преобразования состояния
П с учетом НУ J1 ' r(t) ..
'11 (ю)
нтервал времени, g{.).... НМ на '1,
r(ltJ): Q  [01] .... НП на '1,
орожденный возрастаюшей
ослед. в менных инте валов.
Непре.... J1 ru) = J h tи и! t) о N ( F tи)\ Дифференциальная
.... r I I ::1Н ит  1}
РЫВНЫИ ii(uJt} запись
управля.... де h(u,rolt) .... аналоr. п.l табл.6, 1дJlto> = [ь ttJ,чt>л с to,u,t>]
емый (ult).... нечеткое управление, fr(ro).... 1дf to),
ИП налоmчно п.l табл.6, \;!{fJ Е (2, С to,u,t) == ct,z,t
H vт ( to» == H{V)«O:CO)}  to) о 9 О to) == f to)ЛН{Vu''Р Ею)}
а Р h {v \11 ( . 1 rO :\ } .. Н .... налоr броуновскоrо
сши енная нм, u,yt 'J
вижения в
перация над НМ: v u (') .. оrpанич.. н
1 тохастических
пр. и 'V.(. (О), на отношении
h с {(u,t) Ih(щult) л C{U It), ифференциальных
 равнениях
(о == const.
Вид ип
Математическая модель
Непре.. I rде
рыБНЫЙ I'т to) = т h to It) о g Щ. to»,
неуправ....
ляемый Ь tи It) ==
нп
Дополнительные
данные
Дифференциальная
запись
fd J1( ltJ)  h( щt) fd f{ ltJ),
rдеfd(.) .. обозначение
нечеткоrо
дифференциала
(аналоr
стохастическоrо
дифференциала)
Бочарников в.п.

178
Fиzzy Techпology
Вид нл
ДИСI(Т" J.1i+l tn) = I ц tn ,т) о 9 Q1i tи»).
ныи n
неупра rде 9 Q1i to).... расширенная НМ, а
ляемый h i ( Щ 0)  нечеткое отношение на n
ип в i  й дискретный момент
времени, отражающий динамич.
харки ил.
J.l i + 1 т) = I h i т,со,и)о
{1хи
о (g tui)X VIJ t:'i»).
h i ( щ Щ и) ... аналоrично п.2, (. х .) ..
декартово произведение НМ.
Дискрет'"
ный
упраВля....
емый
ип
Математическая модель
Дополнительные
данные
mах....mlП
композиционное
уравнение есть
частный случай
модели дискретноrо
неуправляемоrо ил
Аналоrично п.З
табл.5.1
Бочарников Bп.

Fиzzy Techпology
179
r лава 6
, 
ЕШЕНИЕАНАЛИТИЧЕСКИХ
.1АДА Ч ОЦЕНКИ СОСТОЯНИЯ
,НЕЧЕТКИХ ПРОЦЕССОВ
> ,
.. '
10.
..,
'!

!
5,
k
1;
Бочарников В. п.

180
Fиzzy Techпology
6.1. Понятие нечеткоrо изображения.
Оценка статическоrо состояния
нечеткоrо процесса
Для представления нечеткой информации в реальных системах
обработки оказывается полезным использование дискретноrо
пространства состояний Q [3, 7, 8 и др.]. Это связано с удобством
представления сиrналов в вычислительных машинах, сокращение
операций по обработке информации и друrими моментами.
в том случае коrда исходная информация носит четкий характер или
представляется непрерывным распределением нечеткости (например
непрерывной функции принадлежности (ФП) на пространстве
состояний, то для перехода к дискретному представлению
используется отображение в нечеткие изображения.
Под нечетким изображением пони мается в общем случае следующее.
Входной информации u в виде точноrо значения или в виде
распределения нечеткости ставится в соответствие вектор И[1]],
называющийся нечетким изображением, элементы Koтoporo выражают
нечеткую меру соответствия входной информации u некоторой
совокупности заданных априорно нечетких мер Q(Q) c F(Q), сде F(Q) ..
множество всех возможных распределений нечеткости на Q. Каждая
мера q :21>' ---7[01] может определять некоторую нечеткую переменную
[27] .
ОПDелеление 6. 1 .
Под нечеткой переменной понимается тройка (11,Q,QI1)' rде: 11 ..
наименование нечеткой переменной; Q область ее
определения или универсальное множество; QI1:21>' ---7 [01] ....
распределение нечеткой меры на Q, соответствующее понятию
11.
Бочарников В.п.

Fиzzy Techпology
181
:.ДлJl получения нечеткоrо изображения информации u семейство Q(Q)
i'определяется конечным множеством мер ч(.) таких, что:
(VroeQ), 3iEN, qfli (ro»О,
(6. 1 )
rде N == Card Q(Q). ТО есть семейство Q(Q) обеспечивает некоторое
'nокрытие пространства Q и для множества W == {1l} наименований
нечетких переменных определяет условную нечеткую меру qf.>.(.lll).
.
;!Iечеткая или четкая входная информация u может быть
аПпроксимирована в виде не которой функции Jlu( т): Q  [О 1] на
Пространстве состояний. Torдa вектор нечеткоrо изображения может
· быть определен как:
-1
u [11] == I 11. (Ф) о Qf.>.(.lll).
11 I
( 6.2)
4
Если обозначить как U(И/) множество всех возможных векторов И[11]
:,.,ДЛя фиксированноrо семейства мер Q(Q), то интеrpальпая зависимость
':'{6.2) определяет отображение вида:
;.
F[1J]:F(Q) U(W).
(6.З.)
1 Введенное таким образом понятие нечеткоrо изображения сходно с
 рассмотренными в [4.. IЗ] линrвистическими переменными. Если
''ножество W .... есть терммножество нечеткой переменной, а И[11а,
'; Е 1, N есть мера ВОЗ!\.IОЖНОСТИ принадлежности входной информации
... . t
: к нечеткому понятию lli Е W, то нечеткое изображение И[11] есть
иечеткое множество заданное на множестве термов линrвистической
.:еременной. При этом для функции принадлежности термов lli
 линrвистической переменной накладываются дополнительные к (6.1)
.:,оrpаничения [4, 13]. В силу этоrо нечеткое изображение есть более
f .
"широкое понятие, чем линrвистическая переменная, так как включает
' как частный случай.
Если входная информация u есть некоторый вектор признаков,
. описывающих некоторое понятие с lV шкальными оценками, то
возникает проблема оценивания нечеткоrо изображения u[ll]
информации u по всему вектору признаков (характеристик). То есть
. :Rообходимо нахождение TaKoro вектора u[ll], который адекватно
списал бы отнесение входной информации о векторе признаков

Бочарников в.п

182
Fuzzy Techпology
(характерисПfК) к множеству шкальных оцеНОI( рассматриваемоrо
понятия.
Отметим, что если множество нечетких переменных 1]i, i Е 1,N для
каждой переменой входноrо вектора U одно и тоже, то задача оценки
нечсткоrо изображения сходна с задачей мноrокритериальноrо
оценивания объектов [1 1].
Если мы опишем состояние НП в фиксированный момент времени
t Е Т В виде нечеткоrо изображения, то пространство состояний АДе
будет уже не '1, а w. В том случае, ко rда исх одная информация
определена набором характеристик {Uj} j:= I,N j , каждая из КОТОРЫХ
фиксирована на своем пространстве значений !1.i ' то задача оценки
нечеткоrо изображения И(1]), 1] Е W СВОДИТСЯ к нахождению оператора:
F[Т}] : F(Q) х...х F(Qj) U(W).
(6.4)
Таким образом, нахождение оператора (6.4) позволяет найти оценку
статическоrо состояния ИП в случае «сложной» входной информации
и.
Рассмотрим формальное решение этой задачи. Пусть состояние НП
описывается на пространстве W == {1]i}, i = 1,N. Для оценки
статическоrо состояния НП на пространстве n.. компонент вектора U
входной информации должны быть определены семейства Q(Qj)
нечетких мер соответствующих W V'j Card Q('1 j ) == N.
Обозначим qj(.fr1) условную нечеткую Mepy порожденную
семейством Q('1 j ). Все семейство условных нечстких мер {Qj(.lll)} для
всех компонент вектора и ВХОДНОЙ информации будем обозначать как
Ч( '111, Uj), rде Uj Е U, j .. й компонент вектора, а tJ .. множество всех
компонент. Тоrда, нечсткое изображение статическоrо состояния НП
будет определяться соотношением:
И[1]] = J { i Jl j (йJ)oq(.I1J,U j ) } o gu(.),
u n j
(6.5)
rде РJ ( (j) )  функция принадлежности j....й компонент вектора входной
информации, а gu(')  мера важности учетаj  й компонент для оценки
Бочарников в.п.

Fиzzy Techпology
183
по 11 Е w. В более общем случае gu(-) может иметь свое значение для
каждоrо состояния 1}Е w. В этом случае gu(.tr1) .... является условной
I нечеткой мерой и тоrда имеем:
U[1J] = J { J llj(lV) о Q(.I1J,U j ) } о gu(.I1J), (6.6)
и n
J
тде внешний интеrpал берётся для соответствующих компонентами
11 Е w. Интеrpальные операторы (6.5) и (6.6) являются
соответствующими операторами вида Р[11] (6.4).
Таким образом для скалярных и векторных величин преобразования в
нечеткие изображения выполняются в соответствии с табл. 6.1.
Таблица 6.1 .. Определение нечеткоrо изображения.
I Вид входной Отображение Выражение ДЛЯ определения
информации
Скалярная Ф[1}] : F(QI)  U [11]  1 J.lu to) о Qn('I11).
величина F(W). n
и Е а.. четкая 11i Е W.. Q{1(.I1})" условная НМ7
инф.; множество индексированная элементами
Jlu( ю): Q [O 1 ] наименований множества w
... нечеткая инф.. нечетких
переменных
Векторная Ф[11]: F(QI) х...х U]= 1{ 1 PZ to)Oq(Ir1,)}ogи О,
величина x...xF(Qj)F{W). и {1J
и=" {Jl! to)} Е g'/(.).... мера важности учетаj.. й
Е Р(а) )x..xF(Qj) компоненты для оценки по 1}Е W
Бочарников в.п_

184
Fиzzy Techпology
6.2. Фильтрация статическоrо состояния
нечеткоrо процесса
на основе квантификации
в данном пункте будем полаrать, что рассматривается состояние НП,
представленное нечетким изображением Jl(m): 11 [01] на
пространстве 11 дискретных состояний процесса. В том случае, коrда 11
имеет большую мощность возникает необходимость выделения
HeKoToporo подмножества S( т) наиболее значимых состояний НП по
информации о распределении Jl( т). При этом, для математическоrо
моделирования линrвистических термов, определяющих мощнос1Ъ
значимых состояний процесса типа "большинство", .по меньшей мере
половина" и т.д. Moryт применятъся нечеткие квантификаторы.
Нечеткий квантификатор Q на пространстве 11 есть распределение
степеней нечеткости на множестве целых чисел {O,I,....,q,...}== R+.
Нечеткий квантификатор Q может быть задан как нечеткое
кардинальное число I Jl( т) I множества 11( т) с конечным носителем
[11]:
\fne R+, (,Olp(.,JI(n) = Sup{ a,IMJ > п},
rде а Е [01], Ма == {O)I Jl(O) > а}. В этом случае имеем:
CPIII(lIJ) (О) == 1, \;;/ i > О, СР;II(lIJ) (i) > СРР(lIJ) (; + 1).
Функция <р(.) моделирует семантическое высказывание "11(0) содержит
по меньшей мере i элементов". Если же наоборот, мы определяем
нечеткий квантификатор Q как "Jl(O) содержит более р элементов", то
функция Q(i) определяет собой степень необходимости тoro, ЧТО i > р:
Q(i) = i {l  qJ'P(")J(j)} == 1  qJr(",)j(i + 1). (6.8)
Бочарников В.П.

Fиzzy Techпology
185
Для определения наиболее значимоrо подмножества элементов
(возможно нечеткоrо) определяющеrо по информации 11(0) yrочненное
I состояние НП необходимо найти такое подмножество S.(O) Е F(D) дЛЯ
lCoтoporo выполняется:
S'(m):: arg Val(SIQ,J.L(m»), (6.9)
:rде Val(SIQ,p(т» .. есть нечеткая мера истины Toro, что S содержит Q
s.
''':элементов со свойством 11(0). Данную меру будем определять из
," условий:
. в S(O) должно содержаться около Q элементов;
· в S( 0) содержаться не более "O' элементов не
удовлетворяющих свойству Jl(O).
J Для моделирования nepBoro условия будем использовать абсолютный
"квантификатор [11] Q1(r):
QI(r):: Q,(tт(mJ)R+  [01],
( 6.1 О)
'rде т(т) == min(S(т),p(т».
Для определения BTOporo условия запишем функцию:
g(ro) == min(S(lO),lp(lO».
и для нее найдем квантификатор Q2 "более О элементов":
Q2(O) = 1..... tp l (O + ]) == }..... sup { a ll G I > О } == 1  тах g«(JJ) ==
р(ш,,. а (OE'J
:: 1 х[S(m)л(1  J.L(m)}J
(6.11 )
Тоrда мера Val(") определяется соотношением:
Val(51Q,J.L(m»)::Q' л(f =:QI(r)л{Is(m)л(IJL(m»]}=:
=: Q'(r)лffiax[ s (iO}л { Т It (lo)}]:: QI(r) л min[S(m) лр (m)] ::
(J)€Q (f)EQ
== Ql(r) лmi!]S(m) V Jl«(JJ)].
(f)EQ
Окончательно имеем:
Бочарников В.П.

186
Fиzzy Techп%gy
V aZ( SJQ, Jl( lO) ) = QI ( t mjn( S( со; ),р( со;) ) л min[ S(ш) V Jl( lO)].
. I roеа
,
(6.12)
fla основании выражений (6.9), (6.12) можно выделить подмножество
S(m) Е F(,Q) состоящее из Q элеl\1ентов, определяющих состояние нп.
Данные выражения дают возможность фильтраuии стаmческоr'о
состояния проиесса с целью снижения размерности описания
состояния, уточнения состояния и т.д. В заключении отметим, что Е
случае необходимости определения для выделеННОI'О состояния S{ro)
некоторой нечеткой пропорции вида: "по меньшей мере х %"
целесообразно использование пропорuиональноrо квантификатора в
виде нечеткоro числа из интервала [01] такое 7 что: \1'х < у, Q{x) < Q(y),
Q(I) == 1.. При этом квантификатор определяется как функция:
 1J1co }[Ol][Ol], q=CardO..
Для иллюстраuии фильтра статическоrо состояния нп рассмотрим
следующий пример.
ПримеD 6.1 .
Пусть в i..й дискретный момент времени наблюдения нп
реализовалось состояние Ri(ro), описываемое на дискретном
пространстве a Card Q =: 4 следуюшим вектором Ri{ro) == (0.5/0)1,
0.8/, 03/roз, 07/01t), (Рис. 6.1.)
1
0.4

 
-' '" foo-ooooo
.

.. io----- 
.............. -$о
>
.. ...........  
: : <-
>. "
,

0.8
0.6
0.2
о
w1
w2
wЗ
w4
Рисунок 6.1 .. Состояние R i { ю).
Бочарников В.П.


;:flеобходимо отфльтровать данное состояние с целью вьщеления
рчненноrо состояния Si(ro) содержащее "около двух элементов"
множества а. (Рис. 6..2).
Fиzzy Techпology
187
1
0.8
0.6
0.4
02
О
О 1 2 3 4 5
t-
Рисунок 6.2 .. Фильтрующая Функция
я определения Si(ro) будем использовать соотношение (6.12). Для
.ro определим сначала значение квантификатора QI(r) для
едующих подмножеств (для примера используем не все элементы
( ножества Р{а), а лишь те, которые возможно претендуют на
'. стояние Sj(ro):
...
Sl == {m 2 },S2 = {т, ,т 2 } ,S3 == {т. ,т з },S4 = {т"т 4}
}. SS = {т 2 ,т З }'S6 = {т 2 ,т 4},S7 = {т з ,т 4},S8 == {т 1 т 2 т з }.
0.8
,.......
1----
1'""""'"
;"l '"'"'"'"

r:7'"
........
  .... .... .... .....  ..... i--ooo
..
0.6
0.4
02
о
51
52
53
54
55
56
57
58
Рисунок 6.3 .. Зависимость Q' (r).
· фик зависимости QI (r) для sj с а представлен на рис. 6.3.
Бочарников в.п.

188
Fuzzy Techпology
в результате расчета второй составляющей выражения (6..12) имеем
результат, представленный на рис. 6.4. Тоrда мера Val(S/Q,P) имеет
значения рис. 6.5.
1
0.8
......
- ....
...... ......
......  .....
.; .
<
- ....  """"" .... i-oooo r--- ...... .... .... ...... i-oooo ..... r--- ...... ...... ......
, 
о;
0.6
0.4
0.2
О
S1
S3
S7
S8
S2
S6
S4
S5
Рисунок 6.4 .. Зависимость Q2(r).
0.8
....... .....
 >
 ...........
о
......
1:- ...... ...... '""'""  1---- ....... ....  ......
....'
.
..:t .,
0.6
0.4
0.2
о
S1
S8
S2
S3
S6
S7
S4
S5
Рисунок 6.5 .. Значение Val(S/Q,P).
0.9
0.8
0.7
0.6
05
0.4
03
0.2
0.1
О

f-----oo
, 
........
........
,
........
w1
w4
w2
wЗ
Рисунок 6.6. Фильтрованное состояние Si(ro)

Бочарников в.п.

Fиzzy Т echпology
189

-.Таким образом, отфильтрованным состоянием Si(ro) является
-:состояние Si(ro) == Ri(ro) л S6(ro) представленное на рис. 6.6. Как видно
:яз примера в результате фильтрации осуществляется "отсечка" мало
.'значащих состояний на Q определенных в i..й момент времени
Наблюдения нп.
Резюмируя nриведенное выше фильтрация статическоrо состояния на
Основе квантификации может быть представлена в виде aлrоритма
_' абл.6.2).
Таблица 6.2 .. Фильтрация статическоrо состояния.
Задача
айти
-: . енку S( (О)
,- t стояния
11
:- ш):Q[ОI]
f ,-
1 J ержащую
, .кОЛО q
ементов и
,'; СИМ8Ль"
· удовле-
:'зряюших
,-)
)
"
Критерий
Va/(S Q.p( ш» ==
QI(S)лQ2(S)mах
s
Va/(.).. нм истины
удовлетвор.оценки
S( ш) условию задачи.
Q.: S(co) содержит q
элементов.
Q2: S( ш) содержит
не более «О»
элементов не
довл. (о .
Решение
* tu) = ащmахvаslo ,р tu»)
5w)
О1 = {tmi{S foi),Jlfo i »)
О2 = m!I s to > V Jl to)].
roen
Бочарников в.п.

190
Fuzzy Techпology
6.3. Фильтрация нечетких IIроцессов.
Нечеткий наблюдатель
Ранее, в предыдущем параrpафе, мы рассмотрели возможность
уточнения нечеткоrо состояния НП за счет фильтрации одноrо
состояния ("статическая" фильтрация), IIредполarающей выявление
наиболее значимоrо подмножества состоян:яй нп. Однако при этом не
учитывалась предыдущая информация о НП, то есть не учитывались
динамические особенности процесса. В данном парarpафе будет
рассматриваться возможность динамической фильтрации НП.
Из приведенноrо ранее материала извеСТН<J, что НП формально может
быть описан нечетко"интеrpальным (нечетко..дифференциальным)
уравнением вида:
Sи(ro) = ! h'(ro,t) о gfr(Ю)О' (6.13)
rде h'(cot):Q Х Т  [01] .... нечеТК<Jе отношение ДЛЯ НДС,
описывающее ее динамику при фиксированном начальном состоянии
suo(m): Q ---7 [01]. Предполаrаем, что данное нечеткое отношение нам
неизвестно. g(. ): 2{). ---7 [О 1 ]  нечеткая мера на а, fr (со)" НП 
аналоrичный винеровскому процессу, задающий неопределенность НП
по времени. Пусть имеется модель НП с>писывающая динамику НДС
следующим уравнением:
SM(ro) = ! h(ro,t) о gfr (Ю)О,
(6.14)
rде h(щt) .... нечеткое отношение модел... (переходная характеристика
НП) вообще то, отличающееся от h'(щt) &1стинноrо ип. Для истинноrо
НП уравнение (6.13) условно можно пере писать в виде:
Sи(ro) = 1] * J h{ro,t) о ;g'f.--(ю)(-)'
т
(6.15)
Бочарнuков B п.

Fuzzy Т echпology
191
.h
'rде 11 ... не которая составляющая НП, определяющая ero вариацию,
связанную с поrpешностями объекта наблюдения, а (*) - неизвестный
оператор, связывающий 11 и уравнения модели.
.
Истинное пространство состояний Q с заданной на нем нечеткой
lttерой g(.) связано с пространством наблюдений О' == Q через
1Условную нечеткую меру Rs(-Ip). Отображение пространства Q в
npocтpaHcTBo наблюдений (2' определенное мерой Rs(. 'р) индуцирует в
a' нечеткую меру Р, связанную с мерой g соотношением:
Р(.) = J Rp(.S) о g.
12 .
(6.16)
}o.в СШIу Toro, что существует связь пространств {2 и О' истинному
:,Состоянию нп s...( (О) в {2' соответствует образ, определенный
'уравнением:
Р 1, ( со ) = 1 s" (т) о R s (.Ip ) == Rs (s" ( со p ).
а
(6.17)
днaKO, наблюдение НП осуществляется с некоторыми шумами 
ими, что В результате вместо Pu«(O) имеем некоторое состояние вида:
,
РА(СО) == P.,(co}* = * R.,(s,,( ro)lp),
(6.18)
 (*)  неизвестный оператор, определяющий характер влияющих
".rpешностей. В соответствие с описанным выше, структурная схема
,: инноro НП вместе с контуром наблюдения может быть
'. едставлена как на рис. 6.7.
Rs(.J р)
 l  ·
11
, ,
h( ro,t)
Su l
I
Рисунок 6.7 .. Структурная схема истинноrо НП с контуром
наблюдения.
:. зим образом, вместо истинноrо I-IП Su( (О) мы наблюдаем некоторый
цecc рл«(о). Кроме этоr'о, имеется возможность наблюдать
. СТояние SM«(O) нп модели., описываемой уравнением (6.14). Исходя
 ( этоro вообще то r'оворя, необходимо сформировать некоторую
Бочарнuков в.п.

192
Fuzzy Techпology
оценку s(m) нп максимально близкую к истинному состоянию Su(ro)
НП.
Если в качестве критерия совпадения s(m) и Su«(O) выбрать меру
близости, определяемую как нечеткое ожидаемое значение (fazzy
expected value) пересечения s(m) и su((o} то критерий оптимизации
мы можем записать в виде:
J = l[s(m) л Sll(m)] о g(.)  шах.
а s
(6.19)
Критерий (6.19) задает семейство оценок 3=={s(m)} упорядоченных
по вложенности. Множество 3 с оператором -< вложеННОС111
определяет нечеткий rpуппоид (3, --<). Если в качестве решения (оценки
s( т) выбрать нижнюю rpaHb (3, --<), то степень размытости решения
-У(т) будет минимальна. В силу, этоrо наиболее целесообразным Б
качестве оценки s(m) НП выбирать точную нижнюю rpaHb семейства
(3, --<) решений удовлетворяющих критерию оптимальности (6.19).
с физической точки зрения критерий (6.19) определяет степень
соответствия (покрытия) оценки состояния s(m) НП и истинноro
состояния Su(ro). Ранее уже отмечалось, что исходной информации для
формирования состоятельной оценки НП s( т) являются информация
о наблюдаемом состоянии рл(ro), а также состояние, полученное из
модели НП sM(ro). В силу уравнения (6.16) нечеткое состояние модели и
оценки s(m) может быть представлены в следующем виде:
s(w)== R (p(m)ls) = J p(m)oR (.Is)
р а р
S м( т) = R p (p м( m)ls) = J рм(m)о R (.Is)
а р
в силу двойственности условных нечетких мер наблюдение состояния
модели sM( (О) и оценочноrо процесса s( т) может быть представлено Б
виде:
р(ro) == R.(s(ro)lp) == ! Цro)о R.(-Ip)
Рм( ro) == R. (s м( ro)lp) == ! S м( ro)о R, (-Ip)
Бочарников в.п.

Fuzzy Techпology
193
Однако, условная нечеткая мера Rs(- 'р) нам неизвестна. Структурная
схема нечеткоro наблюдателя может быть представлена в виде
приведенном на рис. 6.8.
На данной схеме оператор f{.) обеспечивает получение такой оценки
р(.) в пространстве наблюдений 12' по информации о рм И рА, которая
 при известной условной нечеткой мере Rp(' I s) обеспечивает
, выполнение критерия (6.19).
1)

r
Su
Rs(-J р)
pu
h(ro,t)
h(ro,t)
SM
Rs{.1 р)
Rs*(.1 р)
рм
f(.)
р R р(. , S)
s
Наблюдатель
Рисунок 6.8 .. Структурная схема нечеткоrо наблюдателя.
Практически можем обозначить:
Rs.(.lp) == Rs(.lp) * f{'),
(6.24)
rде Rs*(.Ip) .. некоторая условная нечеткая мера определяемая
композицией меры Rs(.lp) и оператора f{.) и обеспечивающая
выполнение критерия (6.19), (*) .. некоторая композиция.
Условная нечеткая мера Rs.(.Jp) должна обеспечить получение TaKoro
р(.), что определенная с помощью Hero оценка i(ro} стремится к
Su{ ro).. Оказывается, что если обеспечить близость состояния НП
наблюдения истинноrо НП pu{ro) и наблюпения НП оценки р(.), то
критерий (6.19) выполняется. Покажем это.
Лемма 6.1
Если обеспечить выполнение критерия
J p = J(iXro) л рu(ro))оР(.) 4тах,
п 
то критерий (6.19) выполняется.
(6..25)
lal\ 771
Бочарников B.п

194
Fuzzy Techпology
lIоказательство.
Оптимальное значение критерия (6.19) определяется выражением:
J* == тах I[SIl(Ю) л(ю)]о g(-) == тах I[Rp(Pllls) л RAPls) ] о g(.).
J(ю) n -'(ro) n
рассмотрим более детально выражение в квадратных скобках:
RР(Рllls)лRАi\s) == !РIl(Ю) о Rp(-Is) л !JXЮ) oRil s ) >
> J[Ри(lO)лJXlO)]оRр(.ls)
n
Очевидно, что при максимизации прзвоro интеrpала левая часть
выражения также будет увеличиваться. Это следует из свойства
нечеткоrо интеrpала. Следовательно модифицированный критерий
будет иметь вид:
J* = тах J Rp ( JXw) л Ри( w)ls ) о g(.).
ji.ro) N' I
Подставив в это выражение уравнение обратное уравнению (6..16) ДЛЯ
меры g(.) имеем:
J* == тах i R p( ю) л Ри( w)is) о J Rs(.Jp) о Р(.) ==
ro) n а
=тахJRр(m)лрu(m)ls)о J l(w)oP(.)=
ro) n R,s{'lp)
=тах J Rs [ Rp(JXm) л Pu(w)ls)lpl оР(.).
т) n' I ]
Исходя из свойств нечеткоrо интеrpала очевидно, что при увеличении
функции Ри(Ю) л Аю) будет расти значение условной нечеткой меры
Rp(W) л A,(lO)!S), а следовательно подынтеrpальная функция для
критерия J будет увеличиваться, что в целом максимизирует критерий
J.
Исходя из этоrо критерий оптимизации можно представить в виде:
J* = max[plI(w) л Р(lo)] о Р(.) = maxJ .
р(ro) р(ro) р
Следовательно, если обеспечить максимизаиию критерия вида
Бочарников 5.П.

Fuzzy Techпology
195
J p == I[Ри(lO) л Р(lO)] о Р(.)  тах,
О' р(ro)
.то условие максимизации исходноro критерия (6.19) будет
:. выполняться, что И требовалось доказать.
fз.
. Истинное состояние pu( ro) наблюдения нам не известно, однако оно
может быть восстановлено исходя из информации рл(ro) и наблюдения
состояния модели рм(ro). Соrласно структурной схемы 6.8. рл(ro)
отличается от Pu( ro) за счет поrpeшностей наблюдения , а Рм{ ro) .. за
счет поrpешностей объекта 11- В силу Toro, что и рм(ro) и рл(ro) есть
. некоторые npиближения истинноro (без искажений) наблюдения Pu(ro)
наиболее целесообразным предположить, что Pu( ro) находится в
:области близкой к пересечению рл(ro)лрм(ro).
Исходя из приведенных рассуждений критерий (6.25) может быть
1J>ансформирован к виду:
J p = l[Рll(m)лрм(m)лр(m)]оР тах, (6.26).
Q р(ro)
Лемма 6.2.
Критерий (6.26) может быть трансформирован так, что
оценочный НП s( т) удовлетворяющий критерию вида
1 {SM(lO) л Rp(p А (lO)ls) }о f $(lO) о g(.)  тах, (6.27)
Q Q j(ro)
будет оптимальным и обеспечивать максимизацию критерия
(6.26).
. азатель во:
'ассмотрим более подробно критерий (6.26)
l[РА(lO)ЛРм(lO)ЛР(lO)]ОР(-)== f [РА(m)лр(lO)]ОР(.)==
n' р А (ro)
::::: J [RS(SM(m)lp) л Rs ($(m)1 р)] О Р(.)
р А (ro)
силу Toro, что для подынтеrpальноrо выражения справедливо
).
еравенство:
Бочарнuков в.п.

196
Fиzzy Techпology
Rs(s Mlp) л Rs((co)lp) > /[s м(т) Л(lO)]о Rs(.lp),
Q
то дЛЯ максимизации критерия (6.26) достаточно потребовать
максимизацию соотношения:
/ [ 1 {Sм(lO)л(т)}оRs(.lр) ] оР(.)== / Rs(sм(т)л(т)lр)ор(.).
РА(ro) Q Pi'f(ro)
в силу свойств условных нечетких мер можем записать:
f Rs(sм(m)л$(m)lр)оР(-)== f Rp(PA(m)ls)og(o)==
РА(ro) sм(ro)лJ(ro)
= f[s м(т) л $(Ю) л Rp(p А (m)ls)] о g(.) =
Q
= f[s м(ю) л Rp(p А (m)ls) ]0 f $(т) о g(o).
n Q
Полученное выражение соответствует выражению для критерий (6.27).
Что и требовалось доказать.
д
Рассмотрим более подробно полученный результат. Критерий (6.27) с
физической точки зрения отражает необходимость нахождения оценки
состояния НП исходя из оrpаничений связанных со структурой
пространства состояний системы определяемой распределением
нечеткой меры g(.), а также оrpаничений определенных
характеристиками реально наблюдаемоrо нп. Последние связаны в
первую очередь с представлением о самой модели НП, ее точности
определяемой состоянием SM(ro) и свойствами канала наблюдения НП,
то есть реально получаемыми значениями наблюдаемоro НП Рд(ro)..
Таким образом, найденный оценочной НП s( т) в каждый момент
времени удовлетворяющий критерию (6.27) будет учитывать всю
доступную нам информацию о нечетком процессе. При этом, исходя из
доказательств выше приведенных лемм данный оценочный процесс
обеспечивает оптимальную оценку, в смысле нечеткоrо ожидания
совпадения с истинным процессом.
Практически, нахождение оценочноrо НП связано с поиском такой
апостериорной нечеткой меры R:(.lp), которая после получения
Бочарников Bп.

Fuzzy Techп%gy
197
'информации о НП лает максимум совпадает оценочноrо и истинноrо
)Iп по нечеткому ожидаемому значению.
Следует отметить, что доказанное в лемме 6.2. выражение для
'JCPитерия оптимизации оценки истинноrо НЛ включает в себя как
'lJастный случай уже извеС11Iое ранее выражение для алroритма
учения по нечеткой мере в дискретном времени предложенный
Суджено [15]. Покажем это, доказав следующую лемму.
Леммv 6.3.
В случае отсутствия оrраничений в пространстве состояний
НДС, а именно Vще11, g(щ): 11 ---+ [01], g({Щ}) ==1 (мера
возможности), а также оrpаничений на оператор
преобразОВ8НИЯ состояния ндс в пространстве 11 в дискретные
моменты времени: hk(щro) : ОХО---4 [01], hk(щ,щ,) == 1,
'V щ,щ, е 11 критерий оптимальности для получения оценки НП
определяется выражением:
f Rp(p(ro)IS)OK(ro)  шах.
а 
(6.28)
i}оказательство.
rласно доказанной леммы 6.2. оптимальная оценка ИЛ должна
удовлетворять соотношению
I[Rp(pA IS) л S м (lo)] о I (lO) о g(.)  шах.
а а I(ш)
_"'сходя из доказательства теоремы 5.3. состояние дискретноrо
:иечеткоro процесса для модели SM(ro) определяется соотношением:
t
. К I
SM(lOj) = hK(lOj'lOv) о g(.),
а
J'де h k (lOj'lOv) = h (lOj ' lOv) л S:;I (lOv);
аким образом для дискретной иде критерий (6.27) примет вид:
I [ Rp(p (lo )IS) л I h K ( lOj'lOv) о g(.) ] о I K(ro) о g(.).
а а а
ассмотрим более подробно выражение в квадратных скобках:

(
Бочарников В.П.

198
Fиzzy Techпology
F == [ Rp(p(m)ls) л l hK(mj,mJ о g(-)] ==
= Rp(p(m)ls) л sup{a j л g(H oj (mJ)} ==
a j
= Rр(р:(m)ls)л;{аj л g({m})}.
Исходя из TOrO, что 3 <q Е О, hk(<q,щ,) == 1 и tI<q, g({<q})::::::1 имеем:
F == Rp(p(m)ls) л sp{ х(mj'ЩJ л 1( {m j })} ==
J
= Rp(p: (lO)ls) л l(lO) = Rp(P:(lO)ls).
Исходя из этоrо соотношение (6.27) примет вид:
1 Rp(P:(lO)ls) о I K(lO) о g(.) == sup { p л I K(lO) о g(.) } ,
Q Q Р Fp
{'де
Рр ={Rp(p:(m)ls» РЕ[О1З}.
Рассмотрим более детально интеrpал в фиrурных скобках. Соrласно
результата, доказанноrо в теореме 4.8. данный интеrpал примет вид:
[= I K(lO)og(.)= suр(sк(ЕаПFр)лg(ЕаПFр»=
Fp EaO
 sup sK(E a ПРр),
Еа nFp =1=0
{'де Sk(.)" есть мера возможности.
Бочарников В.П.

L
Fuzzy Techпology
199
я данноro выражения зависимость ero от а Е [О 1] может быть
....дсТаВлена rpафиком рис. 6.9, rде <Xmin определяется соотношением:
a min ={supa\EanFp =0}.
t
. -..
1
CXmin
a.uux
1 а
Рисунок 6.9 .... Зависимость 1 от а.
 :
. · оrично можно определить ПХ. Последовательность <EanFp)
ожеств является возрастающей при увеличении а.. Следовательно
t. ествует такое а Е [01], что данная последовательность множеств
 еет предел:
3 ае[Оl] liт Еа nFp = Fp.
11=( €rа)I-4оо
'о Sk(ro) есть неубывающая функция множества. Следовательно, для
. .убывающей последовательности множеств (EanFp) можно
исатъ:
sup sK( E a nF p ) = lil1!1 sK(E a nF p ) ==
Ей nFp0 п={€ra) -400
= SK { li (Ба n Fp) } = sK(F p ) == й.
Il=(aa) 1400
Исходя из этоrо следует, что данный интеrpaл зависит лишь от
ункции Sk(ro) и критерий оптимизации определяется выражением:
f Rp(p(йJ)IS)O$K(йJ)  тах.
n 
.

fJ.
tr
Бочарников В. п.

200
Fиzzy Techпology
Таким образом, на основании критерия (6.27) может быть
сформирован нечеткий наблюдатель, позволяющий вычислять на
основе текушей информации о НП оценочный процесс r (lO) ..
Информацией для данноrо наблюдателя являются измерения p ( lO) и
текущее состояние модели SM(ro). Представим выражение (6.27) в
следующем виде:
1 а(lO) о 1 (lO) о g  шах,
Q Q !(ro)
rде функция а (ro) определяется соотношением:
(6.29)
а(lO) = s М(lO) л Rp(p А (lO)ls) .
( 6.30)
Выражение (6.29) может быть преобразовано к ВИJ.J:у:
J а( lO) о i (lO) о g = 1 а( lO ) л (lO ) о g = i а( lO) о g.
Q Q Q !(ro)
То есть соотношение (6.29) определяет нечеткий интеrpал от функции
а (ro) по мере g, взятый на нечетком множесmе &(lO), определяющем
оценку нп. В случае упорядоченной по убыванию функции 0'(0)
значение нечеткоro интеrрала
1 а( lO ) о g == J ,
(1
(6.31 )
определяется rpафически, как показано на рис.6.1 о.
1
J
<р
о{ (J)
в
n
Рисунок 6 1 О .. rрафическое представление нечеткоrо интеrpала.
Значение интеrpала J определяет некоторое подмножество В(ю) с Q
при которых 0'( ro)  J. Как показано на рис.6.1 О пара (J, В( 0)))
Бочарников B.п

L
Fиzzy Technology
201
рпределяет ФУНКЦИЮ q>(ro), иrpающую роль фильтрующей функции,
lCоторая задается выражением:
{ [J,l], со Е В(со) с П;
ч>Аm)== О, mВ(m).
(6.32)
.Смысл этой функции можно определить следующим образом. Для
:m>ro, чтобы критерий (6.29) был максимальным (а самое большое
значение критерия достиrает величины JE [О 1]) необходимо и
.достаточно, чтобы выIолнялосьь условие:
VroeB(m) c Q, а(со) л (co) > lpJ( со).
(6.33 )
.;Значение функции а(со) л(со) на m Е В(ю) не влияют на значение
. критерия (6.29) и с точки зрения необходимости определения точной
нижней rpани в rpуппоиде (8, --<) значения функции ( йJ ) ,
'> определяющей оценку НП, целесообразно уменьшать от величины
fPJ(m). Таким образом, функция q>J(m) иrpает роль фильтрующей
"функции. Следует отметить что функция (6.32) является "предельной"
.
!.фильтрующей функцией. Можно определить целое семейство
,фильтрующих функций {q>} в некотором смысле вложенных в область,
. .спределенную функцией <р( (О) (см. рис.6.11) <PR( ю) Е {q».
.
,
Для каждой из функций q>R(m) из семейства {q>} необходимо
.выполнение условий, аналоrичных (6.33). Тоrда критерий (6.29) будет
Иметь значение R е[ОI], R < J. Исходя из выше приведенных
 рассуждений, структура нечеткоrо наблюдателя должна определяться
функцией вида:
(co) = f((co),(j(CO),qJR(CO)).
(6.34)
Так как фильтрующая функция l{JR(CO) в основном определяет
подмножество BR(m) с Q значимых состояний в пространстве Q после
получения информации О'(Ю), ТО целесообразно структуру нечеткоro
наблюдателя определить как функциюf(..,.) двух переменных в виде:
Бочарников ВП.

202
Fuzzy Techпology
J
R.
I
g
a(w)
i
<Р min
8 J «(O) n
8 i (w)
Рисунок 6.11 .. Семейство фильтрующих
функций.
.f(ro) = !(.f(ro),a(m) л lfJR(ro»), (6.35)
['де ..... { [R,I],ro Е BR(ro),R < J Е [01]
<1>R(W) <1>';", т fl B(ro},qJ": < R.
Для нахождения оценки НП (ro) по информации о НП на
протяжении HeKoтoporo BpeMeHHoro окна  с Т, тaKoro, что sup  t, inf
1: == t .. l'tl можно в качестве функции f{.,.) в состоянии (6.35)
использовать нечеткий интеrpал вида:
,(m) = / (ro,t') oa,(.lro,f),
т
rде a1'(-lт,t): 2(ТХО)ХТ.......) [01] .. условная нечеткая мера
определяющая величину доверия к состоянию оценки НП на
предыдущем моменте времени t' < t, t' Е 1:СТ дЛЯ фиксированноro (J)E а.
Практически, условная мера a'f(.lro,t) определяет некоторое
временное окно на Т. (Рис..6.12)
( 6.36)
Бочарников в.п.

f
I
Fuzzy Techпology
203
..
(J) == const
I
a(t' O
0.5
о
?
't
Рисунок 6.12.. Временное окно.
В (6.36) в качестве значения (m.,t) выступает измерение в момент
t Е Т, то есть:
(m,t) = й-,(т) лtp(m),
i' ('де а, ( т) определяется (6.30).
. Следует отметить, что момент времени t может быть инечетким
Таким образом, выражение (6.36) определяет нечеткий наблюдатель
построенный на нечетком интеrpале. В каждый момент t Е Т
. реализуется двухмерная фильтрующая функция, определенная
.,декартовым произведением:
w; (т, т) == tp (т) х aT(.lm, ().
(6.37)
Фильтрующая функция Jt: (т, т) определяет в конкретный момент
-tеТ некоторую подобласть в пространстве QxT. В том случае, коrда в
оценке , ( ю) НП учитывается только одно предьщущее значение
функции (т), отстоящее от текущеrо t на некоторый временной
<нтервал 1: с Т, то нечеткий наблюдатель вида (6.36) может бьпь
npеобразован к следующему виду.
,$,(т) = I (m,t') о aT(.lm,t) = {S''''T( (О) л aT(t  Tlm,t)} v
т
'v {[О", (т) л 'P( т)] л JT(tlm,f)} v {$,(т) л [О", (т) л 'P (т)]}.
(6.38)
.в этом случае нечеткий наблюдатель определяется нечетко..
дифференциальным уравнением представленном в следующей
теореме.
Бочарников В.П.

204
Fuzzy Techпology
, Теоnема 6.1.
Нечеткий наблюдатель, определяющий оценочный НП g, (ю) ,
в случае учета одноrо предыдущеf'О значения оценки  ( ю )
'T
описывается нечетко....дифференииальным уравнением вида:
! fd(ю) == {('Т(ю) Л aT(t 1'lю,t)) v h(ю,t')}fd/,F (ю),
(6.39)
['де h(ю,t')-- нечеткое отношение (переходная характеристика)
модели НДС,
f,F (со) == f, (со) л Rp(p,A( co)/s) Л {%( со) л(9,-с( со) Va-c(4co,f»}.
(6.40)
скорректированная нечеткая функция описывающая
,временную неопределенность НДС (аналоr броуновскоrо
I движения).
Доказательство.
Для простоты записи выкладок формульных зависимостей введем
следующее обозначения:
a l = ,т(ю) Л aT(t..... 1'lm,I);
а 2 == qJ(Ю) л aT(tlro,t);
аз == tТ(Ю) Л qJ(Ю).
Тоrда выражение для наблюдателя (6.38) принимает вид:
,(ю)=аl V(G,(ю)ла 2 )V(G,(ю)ла з )=а l v[а t (ю)л(а 2 vа з )].
Рассмотрим более дстально функцию G,(ю), отражающую
имеЮЩУЮСJJ информацию о ИЛ на момент времени t Е Т СОf'ласно
(6.30) имеем:
0", (со) = S,M (со) л Rip,A (co)/s) = ! h( со, (') о gJ, (ш) (-) Л Rp(p,A (CO)/s}
Бочарников в.n.

Fиzzy Techпology
205
На момент времени t е Т переменные Gi, ;=1,3, и R p (p;4(ro»)S)
::ПРИНJ.Iмают определенные значения и не зависят от переменной t'eT
( интеrрирования. Исходя из этоrо справедливы следующие
'. преобразования:
: (lO) = О. V [R p(}1A(lO)/S) л(ll:2 V 0:1) л! h(m, (') о ;g'/,(w)O] =
==0. vl{R р (]I,(lO)IS)Л(ll:2 VO:1) л h(m,t')} о 1 /,(lO')og(.)=
т У', (-Ico')
o. V 1 h(m,t') о I {.(,(lO') л Rip: (lO)ls) л(ll:2 VO:1)}o g(.).
т У', (-Ico')
Рассмотрим подынтеrpальную функцию для BToporo интеrpала:
, /,( lO') л Rp(p,A (lO)ls) л[ (ф( lo) л д т ( tlm,t» v (%( lo) л 9'T( lo»] =
, := /,(ro')л Rp(p:(ro)ls) ЛqJ(ro) Л{,-r(ro) va-r(tlro,t)} = /,F (Щro').
Тоrда для оценки получаем соотношение:
 .  : : ,(ro) = О, v I h(ro,t') о I /,F (rolro') о g(.) =
 т У', ('Iw')
J{{t-r(ro) Л aT(t  Tlro,t» v h(ro,t')}o J /,F (rolro') о g(.).
т У', (.Ico')
-,
Данное выражение в нечетко....дифференциальной записи приобретает
.едующий вид:
.
. fd9,(lO) = {(9'T( lo) л aT(t  Tlm,t» v h( m,t') }fd/,F (lOllO').
Что и требовалось доказать. 11
'!tаким образом, доказанное выражение (6.39) определяет нечеткий
ааблюдатель. Для ero физической реализации необходимо определение
умерной фильтрующей функцией (щ).
'1
Бочарников в.л.

206
Fиzzy Techп%gy

6.4. Оптимальный нечеткий наблюдатель
Оптимальный нечеткий наблюдатель будем рассматривать ДЛЯ случая
учета одноrо предыдущеrо значения оценочноrо процесса. То есть
Card't == 2. Как показано в п. 6.3. нечеткий наблюдатель определяется в
этом случае нечеткодифференциальным уравнением (6.39). Данный
наблюдатель может эффективно применяться для оценки состояния
дискреrnоro нп. В этом случае нечеткодифференциальное уравнение
вырождается в рекуррентное соотношение для наблюдения
Дискретный наблюдатель будет рассмотрен ниже.
в случае Card't == 2 нечеткий наблюдатель построенный на основе
нечеткоro ИlПеrpала (6.36) расписывается соотношением (6.38). В
данном выражении неизвестными являются функции
ar(.lm,t),qJ(m). Для дальнейшеrо изложения рассмотрим
вспомоrательную лемму.
Лемма 6.4.
В случае Korдa CardQ == 2 значение нечеткоrо интеrpала вида:
J == 1 р( (1J ) о д а (.)
(l
определяется величиной lШотности нечеткой меры д а (.) В точке
ЩЕ n для которой Jl( щ) > Jl( €q), j*i, €qE n, то есть:
min(p(ro;),p(m j»' д(ю;) < /1(ro j );
J == д(т;), р(ю j) < J(m j ) < р(ю;);
max(p(roj),p(m j)' a(m j ) > p(ro j ).
(6.41)
Бочарников В.Л.


Fиzzy Techп%gy
207
1Jоказательство.
Распишем интеrpал в следующем виде:
J =!J.1{ (0)0 д no= (J.1{co. )лд( со. »V(J.1{ щ)лд( Щ)V(J.1{ со. )лJ.1{ щ».
Пусть (р((о.» p«(O:z)). Тоrдаимеем:
J = (,и((О.) л д((О.) v (д((О:z)л ,и((О2» v Р«(О2) =
= { (Р«(О.)Л д«(О. )v ,и((О2)' a((O:z) > ,и«(О2);
(р( (О. ) л д( (о. ) ) v р( (о 2 ), д( (о 2) < р( (о 2 ).
Таким образом интеrpал не зависит от значения плотности д(Щz) для
_ОТОрОЙ Jl( Щz) < Jl( ю.).
J == (р«(о.)л д«(О. )v p«(O:z).
Для функции J зависимость от д( (О.) представлена на рис. 6.13.
J.l( (1)2)
J.1( (О.)
J!( (1)2) J.l( (о.) 1 д{ (О.)
Рисунок 6.13.... Зависимость функции J.
Данная зависимость соответствует соотношению (6.41).Что и
; требовалось доказать.
11
Как леrко заметить, функция (6.41) однозначно аппроксимируется
соотношением:
J = (1..... а),и( (0.)+ а,и( (02 ),а Е [01]. (6.42)
Коэффициент а определяет вклад каждой составляющей в значение
интеrpала. Тоrда, исходя из доказанной леммы следует что значения
Бочврников B.п

208
Fиzzy Techпology
плотности меры фильтрующеrо BpeMeHHoro окна в выражении (6.38)
целесообразно принять в следующем виде:
д r(t....... Tlro,l) = д r (/Iro,l) = д,(ro);
(6.4 З)
a l (ro) = (1....... a)/T(ro) + а. [(JI (ro) л q>(ro)].
(6.44)
Таким образом, оценка нечеткоrо состояния НП будет определяться
соотношением (6.39) для KOTOpOro J'l"(.lro,t) является нечеткой мерой
с равномерной плотностью для каждоro (ОЕ Q определенной
соотношением (6.44).
Как видно из соотношения ДЛЯ а,(ro), мера д t"(.lro,t) зависит от ае [01]
и фильтрующей функции q> ( ro).. Для определения этих параметров
необходимо учитывать динамику нечеткоrо процесса. Так как соrласно
критерия (6.29) он должен выполнятся для любоrо t Е Т мы можем
записать:
min 1 (}I'(ro) 01 g,,(ro) о g  шах'
't n n 9,(ш)
(6.44)
rде t' Е '[ с Т.
Для рассматриваемоrо случая Card't == 2 соотношение имеет вид:
1 (Jt(ro) о 1 gt(ro) о g л J (J/(1(ro)o J g'T(ro)o g тах. (6.45)
ппп n 9, (ш)
Оптимальный нечеткий наблюдатель определяется следующей
теоремой..
Теооема 6.2..
Оптимальный нечеткий наблюдатель дЛЯ НП при Card't == 2
определяется нечетко..дифференциальным уравнением (6.39) для
KOTOpOro двухмерная фильтрующая функция (6.37) W,(w,'t)
определяется через функции:
al(ro) = (1  а). 9tT(ro) +а. [(JI(ro) л q>(ro)], (6.46)
Бочарников В. л.

Fиzzy Techпology
209
, { [R,l],ro Е BR(ro) с g
qJR(CO)= О,СО Е BR(co)
(6.47)
rде <Хе [О 1] определяется из соотношения:
I .
, I
J min {(l  a)g'T(ro) + аа,(ro)}  R I  min;
IWEBR(w) а
(6.48)
R = 1 а, (т) о 1 g'T(ro) о g < J Е [01].
n n
(6.49)
1I0казательство.
Для доказательства теоремы определим прежде Bcero характеристики
фильтруюшей функции cp ( ro) при оrраничениях, сложившихся на
предыдущий момент времени, то есть соrласно соотношения (6.45).
Представим нечеткий интеrpал для момента времени teT в следующем
виде:
1 а,(ro) о 1 g'T(ro) о g = [ 1 а,(ro) о 1 g,'C(ro) о g V а ] л [3,
ппп D
rде а, ре [О 1] .... являются неизвестными функциями. Подставим это
выражение в (6..45). Получим:
{ I а,(ro) о J g'T(ro)o g vа } л J а,(ro) о 1 g,'C(ro) о g Л {з  тах.
Q n n Q а,/3
Так как для оптимальности оценки НП необходима максимизация
критерия (6.29) на каждом шarе, то справедливо сооrnошение:
1 а,(ro) о 1 ,т(ro) о g < {З..
n n
Тоrда предыдущее соотношение примет вид:
{ I а,(ю) о 1 /т(ro)оgvа } л 1 a,'C(ro)o 1 gtT(ro)O g тах.
ппп Q а
Преобразуем данное соотношение. Исходя из свойств нечеткоrо
интеrрала (3.12), (3 .18) справедливо:
Бочарников в.п.

210
Fиzzy Techпology
J[a V(Jt(ro)]Л(JtТ(СО) о J tT(ro)O g тах;
Q n а
J[a Л(J,т(ro)]V[(Jt(ro) Л(J,-r(ro)]о I gtT(CO)o g тах.
n n а
Соrласно свойства (3.19) можем преобразовать:
[ 1 q(ro)ol н(ro)оgлаlv/[о;т(ro)лq(ro)]оl g,(ro)ogtmX.
11 n J n Q а
Обозначим: J G ( со ) о 1 g о g == 1 .. значение критерия (6.29) на
t-r 'T ''C
n n
момент 1....'tE Т.
1[а,(ro)л а,т(ro)]о 1 g'T О g = К,.
n n
Данная функция иrрает роль корреляционной функции набnюдаемоrо
нп. Тоrда соотношение примет вид:
р = (1'1 ла)v К,  тах.
а
1
1
к.
к.
ItT
р
11'1
к.
IIt
1
11'1
к.
Рисунок 6.14 .... Значение функции Р для Kt <I,'t .К, >I't .
Как видно из rpафиков рис. 6.14 значение а целесообразно выбирать
из условия:
а > К, == 1[ (Jt(ro) л а,'С(ro)]о J /T о g.
Q n
Если в качестве а принять а == К, тоrда получим:
J а, (со) о I gt о g = 1 а, (ro) о 1 g/1 О g V К,.
Q n Q n
Бочарников В.Л.

Fuzzy Тесhлоlоgy
211
Так как а > К, можем записать:
1 <Jt{lO) 01 gt о g = l[at(lO) v (at(lO) л <Jt1"(lO))]o 1 gtT О g =
ппп n
= 1 а,(lO) о 1 gtT og= R Е [01].
n n
ИСХОДЯ из этоro фильтрующая ФУНКЦИЯ qJ R( т) примет ВИД, как на рис.
6.15 :
{ [R,l], lo Е BR(lO), R < J Е [01];
qJ(lO) =
О, lo е ВR(ш).
I
O't( (О)
J
R
BR«(O) Q
Рисунок 6.15.... Фильтрующая ФУНКЦИЯ.
Для Toro, чтобы выполнялось равенство:
1 <J t ( lo) о J , О g = R '
n n
(*)
необходимо и достаточно выполнение условия:
.
v lo Е BR(lO), S,(lo) > R.
Но, так как соrласно леммы 6.4 имеем:
д, ( lo ) = S, ( lo ) = (1  а ) · S'I ( Ш ) + а[ а I ( lo ) л ф ( ш )],
то для подмножества BR(ro) при qJR(m) == I справедливо:
д, ( lo ) = S, ( lo ) = (1 .... а )S'I ( ш ) + аа, ( lo ) > R .
Отсюда для выполнения условия (*) необходимо а удовлетворяющее
соотношению:
Бочарников В.Л.

212
Fuzzy Techпology
I min {( la ) s(ro)+aa , (ro)lR min.
ЮЕ8 н (ш) I I 1 а
Таким образом, это определяет ОПТИl\fальный нечеткий наблюдатель.
Полученные соотношения соответствуют приведенным в условии
теоремы. Следовательно теорема доказана.
[]
Таким образом, мы получаем возможность осуществить оптимальную
в смысле (6.44) нечеткую фильтрацию. Физически уравнение
оптимал LHoro нечеткоrо наблюдателя может быть пояснено
следующим образом.
Величина коррекции состояния оценочноrо нп определяется в
зависимости от характера ero наблюдения и поведения модели нп.
При этом вариация I (ro) зависит от корреляционной функции К, ИЛ
йi(O)) зависящеrо от динамики наблюдаемоrо нп р,(ы) и модели
s(ro).
Функция К, определяет "степень доверия" к новому измерению и чем
выше корреляция измеряемоrо нп Oi( 0)), тем большее число элементов
I (ro) корректируется в сторону увеличения к Oi( 0)) и на большую
величину R Е [01].
.
Бочарников В.Л.

Fиzzy Techпology
21З
6.5. Дискретный нечеткий наблюдатель
Цель этоrо параrрафа показать.. что те подходы к построению
нечеткоrо наблюдения, которые рассмотрены ранее, полностью
справедливы и для случая дискретных НП. При этом дискретность
может касаться как времени, так и пространства состояний а.
Например, коrда используются для описания состояния НП нечеткие
изображения, рассмотренные в пункте 6.1.
Для дискретноrо I-IП нечеткий наблюдатель также может быть
представлен в виде нечетко"интеrpальной свертки предыдущих
состояний оценочноrо процесса.
gK( ro) = 1 g( йJ, t') о д" (.1 со, (').
т
rде g(ro,t') .. определяется как срез оценочноrо НП в дискретный
момент времени t' == К....nl1 из интервала окна Т, suрт. :=; К, а д r (.1 ro, [) ..
дискретная нечеткая мера на временном интервале Т. В случае учета
только RKI(ro) нечеткий наблюдатель имеет вид:
к(ro) == {KI(ro) л aKI(ro)} v {[ак(ro) л ер: (ro)] л aK(ro)}v
v {SKI(ro) л [О"к(ro) л q>: (ro)]}.
(6.50)
(6.51 )
Теорема 6.З
Дискретный нечеткий наблюдатель, определяющий оценочный
НП  к (со) при Card Т == 2 описывается нечетко....интеrpальныМ
уравнением вида:
RK(co') = (KI (со') Л д(ro') v
(6.52)
v J {hK(ro,ro') л Rp(p:(ro)IS,lO')} о g
КI(w)ла«(j/)
Бочарников В. л.

214
Fиzzy Techпology
rne Rр(Р:(ш)ls,т')" цилиндрическое продолжение
функции Rp(p:(lO)IS)J
а( ю) = {q>: (ю') л д(ю)} v {КI(Ю') Л q>: (ю')}, (6.53)
д(т') = д KI (т) = д А (т).
Локазательство.
Доказательство теоремы во MHOroM сходно с доказательством теоремы
6.1. Введем обозначения:
а.(т) = gK.(ro) л дK.(т);
а 2 (т) = ЧJ: (т) л дк (т);
аз (т) == ЧJ: (т) л gK1 (т).
Исходя из этих обозначений оценочный процесс может быть описан
уравнением вида:
gK(ro') == а.(т') v {й"к(т') л (а 2 (т') v аз (т'»}.
Для дискретноrо НП стк(ro) описывается соотношением:
О"к(ю') = Rр(р(ю)ls)л f h((О,ю') о g(.) ==
gKI(W)
== f [R p(p( ю)ls. ю') л h((O, ю')] о g(.).
gKI(W)
Подставив ЭТО уравнение в соотношение для 9 к (т') получим:
gK(ro') = а. (т') V {а к (ш') л (а 2 (т') v аз (т'»)} =
= {9KI (т') л д(т')} V {й" к (т') л а(т')} = {K. (т') л д(т')} V
V { f [RiР(Ю)ls,Ю') л h(IO,Ю')] о g(-) л а(ю') } .
gK1 (ш)
В силу Toro't что а(o:f) не зависит от g(a) соrласно ишеrрала может
записать:
Бочарников В.Л.

Fиzzy Techп%gy
215
gK1 (ю') = {gK1 (со') Л д(ю')} v
v I [Rp(p:(CO')ls,co') л hK(co,co')] о g(.).
gK1 (w)ла(W')
д( ю') = д KI ( ю) = д к ( ю ) соrласно леммы 6.4. Следовательно
теорема доказана.
[]
Однако, уравнение нечеткоrо наблюдателя для дискретноrо НП при
Card 't == 2 в виде (6.52) получается довольно таки сложным. Исходя из
свойства иечеткоro интеrpала для двухточечных функций (лемма 6.4.)
уравнение нечеткоrо наблюдателя целесообразно представить в виде:
K(CO) = (1  a)KI(co) + а[а к(СО) л ЧJ: (СО)}. (6.54)
в случае отсyrствия оrpаничений в пространстве состояний ндс,
V€qeQ, g{{€q}) == 1 и при отсyrствни модели процесса функция (J к(ю)
определяется лишь измерением, что доказано в лемме 6.3. Тоrда:
K(CO) == (1  a)K1 (со) + a[Rip:(CO)ls) л ЧJ: (СО)!
(6.55)
ae[OI] .... определяет скорость сходимости фильтра. Уравнение (6.55)
можно преобразовать к знакомому по фильтру Калмана
представлению:
.fK(CO) = KI(CO)+a{[Rp(p:(CO)ls) л ч>: (CO)]KI(CO)}. (6.56)
Структурная схема дискретноrо нечеткоrо наблюдателя, реализующеrо
соотношению (6.56) представлена на рис. 6.16.
Rp(pA.(ro) I s) а
min
а
л
Sk( ro)
<pKR(ro)
1
Рисунок 6.16. Структурная схема дискретноrо нечеткоro наблюдателя
Бочарников В. л.

216
Fuzzy Techпology
в заключение отметим, что фильтр (6.55), полученный нами как
чаcrный случай из уравнения нечеткоrо наблюдателя для дискреrnоrо
НП при Card 't == 2 является аналоrом алrоритма обучения
предложенноrо Суджено и описанноrо в книrе [22].
Бочарников В.П.

Fuzzy Techпology
217
6.6. Экстраполяция нечетких процессов
Во мноrих прикладных задачах наибольший интерес представляет
решение задачи проrнозирования состояния KaKoro либо процесса. При
этом на проrноз влияет целая совокупность различных внешних
факторов, пр и водя щих к необходимости постановки задачи
проrнозирования состояния процесса в нечетких терминах. Ниже будет
рассмотрен один из .возможных подходов проrnозирования состояния
динамическоrо процесса в условиях неопределенности на основе
экстраполяции нп.
Допустим, что на пространстве состояний Q необходимо
спроrnозировать состояние HeKoToporo процесса. На процесс действует
совокупность внешних факторов Х {х}  каждый из которых может
привести к определенной динамике процесса. При этом для фактора
XkE Х возможное состояние процесса оrpаничивается HeKOTOpы НП,
описывающимся нечетко",интеrpальным уравнением вида:
ах ( rolt п p ) == 1 hx ( ro,t l1 p ) о 1 /, (ro) о gro(.). (6.57)
k Т k Ч'т (.Iw) "Р
rде tлрЕТ, Т .... временной интервал проrноза. Если в текущий момент
lтek влияние различных факторов определяется функцией важности
р(х):Х .......) [01], то задача проrнозирования состояния процесса
заключается в нахождении TaKoro нечеткоrо процесса, который бы
аrpеrировал НП (6.57) с учетом функции р(х) , то есть:
gt"p (ro) = F(a Х ! (w,t l1p )'p(x»).
(6.58)
Практически проmоз определяется некоторым оператором F
аrpеr ир ования Ф ункций  ( rO t ) В качестве Taкoro оператора
V Х! ' пр .
может выступать нечеткий интеrрал на множестве Х по некоторой
нечеткой мере rnх(.): 2 X .......)[01], отражающей свойства оператора Р.
Леrко показать, что если рассмотреть функцию I:(xlro, lпp) такую, что
Бочарников В.П.

218
Fuzzy Techпo/ogy
L(xklco.f"p)==a Xk (CO,f"p)' то интеrpирование этой функции по
нечеткой мере ш х (.) удовлетворяет свойству:
min1: (xk/co,( l1р ) < I 1:(х А' lco,f"p) о т-к<-) < max1:{x k /co,f"p)'
хеХ Х хеХ
(6.59)
Для этоro докажем следующую вспомоrательную лемму.
Лемма 6.5.
Для функции Ь(х): Х  [01] нечеткий интеrрал по нечеткой
мере ш,,(.):2 х .......)[ОI] является теоретико"множественной
операцией для которой выполняется
l11 in Цх) < I h(x)o(jJ xC-) < mjnh(x).
(6.60)
для любой функции (jJ х (. ).
Доказательство.
Для доказательства леммы переупорядочим функцию h(x) в порядке
убывания, как показано на рис. 6.17.
а;
б
SUPI ei
infX
 х
А Х.
Рисунок 6.17. К доказательству леммы 6.5.
ТоrД8, рассмотрев множество а....срезов ФУНКЦИИ h(x) будем иметь
возрастающую последовательность множеств Ai(X) с Х таКИХ, что 'v ;,
j, <Xi> lXjE [01] А,{х) с А;{х). Нечеткий интеrрал для каждоrо из
подмножеств Ai(X) с Х будет определяться следующей зависимостью:
е; = min(h(x j ),li1 x (Aj».
Бочарников в.п.

Fuzzy Techпology
219
Следовательно интеrрал от всей функции h(x) соrласно (3.27)
удовлетворяет соотношению:
1 h(x) отх(.) = supe; = sup{h(x;) лlU x(A j )}.
Х i i
Рассмотрим более подробно данное выражение. Значение ero зависит
от выбранноrо распределения функции меры тх(Ад.
а) если \1'хеХ х;/; infX тх (х) == О и
х == injX, тх(х) > h(x), (rде Xi > Xj, если h(xj) > h(Xi», ТО
1 h(x)oli1 x =sup(h(x»);
х х
б) если Х == sup Х тх (х) > h(x), \1' х ;f; sup А: тх (х) == О, то
1 h(x)o(jJx = minh(x).
х х
Данное условие иллюстрируются на рис. 6.17. Во всех промежуточных
значениях для интеrрала выполняются условие (6.60).Что и
требовалось доказать.
11
Таким образом, arреrирующие свойства нечеткоrо интеrрала,
определяются распределением меры тх (.) и в зависимости от нее
нечеткий интеrрал может выступать как операция со свойствами либо
объединения, либо пересечения нечетких множеств.
Для определения степени выполнения операции объединения qF можно
использовать следующую меру:
qF = 11](x)oli1 x (.),
х
(6.61 )
rде функция ll(Х) определяется соотношением для непрерывноrо Х:
l1(Х) = s'!pX \
supX
(6.62)
или для дискретноrо Х, Card Х == n в виде:
Бочарников В. п.

220
Fuzzy Techпology
п....j
1](Х j) =  l '
п
XEX
J
(6.63)
Величин обратная q F будет определять меру выполнения операции
пересечения:
rF== 1 .. qF
(6.64)
Исходя из приведенных выше рассуждений для определения
экстраполированноrо нечеткоro процесса  «(О) будем использовать
',1Р
в качестве оператора аrpеrирования НП (1 ( Ш t ) нечеткий
ХА 'пр
интеrpал по мере mл.). Для учета информации о важности
действующих факторов р(х) можно использовать следующие функции:
(1' « (О t ) = (р( х ) л r ) . (J « (О t ) (Р(Хl )vq F) (6.65)
Х! ' пр k F Х! 'пр ·
Тоrда для получения НП g « (О) можем использовать следующее
IIIp
соотношение:
, «(О) = 1 I(X k 1ш, t п p ) о ro х (.1 (О), (6.66)
пр х
rде (J'Jx(.f(O).... условная нечеткая мера оператора F,
I{xklco,t пp ) = а;! (coft пp )' определяемой соотношением (6.65). В
этом случае, проrnозируемый нечеткий процесс будет представлять
собой нечеткую функцию на Q по времени проrноза.
в заключении отметим, что проrнозируемый процесс в виде g, «(О)
1'11'
можно представить некоторой 'рубкой" в пространстве ОхТ. При
этом, наиболее подходящим проmозом процесса являлась бы такая
"трубка" для которой выполнялись два противоречивых условия:
а) в каждый момент tпpE Т размытость состояния НП БЬUIа
бы минимальной;
Ь) реальное значение процесса через время проrноза в
максимальной степени совпало с проrнозированным.
Формально данные критерии можно записать в следующем виде:
Бочарников в.п.

Fuzzy Techпology
221
Sp(, (со)) ---7 шах,
"1'
SUP{lпr «(О)лs;«(О)} шах,
ше!}
(6.67)
rде Sp(.).. мера точности [11], stU(m).... истинное значение процесса через
время проrnоза.
Критерии (6.67) определяют оптимизационную задачу для
экстраполяции нечеткоrо процесса g (со ) , который находится из
1,,1'
соотношения (6.66). При этом управляемым параметром является
функция распределения плотности меры (jJ x(.lco) по времени
проrnоза. Выбор этой функции осуществляется из следующих
соображений.
в начальный момент времени, коrда tпp О выполнение критериев
(6.67) осуществляется при реализации внечетком интеrрале операции
пересечения, то есть r F.......) 1. В процессе увеличения t пp для обеспечения
выполнения критерия б) необходимо «размывание» НП  (со), ЧТО
'",
обеспечивается за счет плавноrо перехода от операции пересечения к
операции объединения. То есть реализуется нечеткий процесс:
fd(iJx(xICO,tпp) = h(x, T)fd/,,,I' (СО),
( 6.68)
rде h(x,t) .. есть Функция характеризующая динамику плотности
нечеткой меры (jJ ( x l (J) t ) по времени проrноза и реализующая
х , пр
такую динамику qF(t пp ), для которой выполняются (6.67) (Рис. 6.18).
1
 t
Рисунок 6.18. Функция qF(t пp ).
Бочарников в.л.

222
Fuzzy Techпology
.
При этом существует оптимальная функция qF (t пp ), которая зависит от
конкретных условий и KOHкpeTHoro проrнозируемоro процесса. Задача
нахождения оптимальноrо (jJ ( x l ro t ) является сложной и чаще
х , пр
Bcero осуществляется экспериментальным путем.
Бочарников В.Л.

Fuzzy Techпology
223
r лава 7
ИДЕНТИФИКАЦИЯ
НЕЧЕТКО..ИНТЕrр АлъныIx
МОДЕЛЕЙ
НЕЧЕТКИХПРОССОВ
Бочарников в.п.

224
Fuzzy Techп%gy
7 .1. Задача идентификации моделей
нечетких процессов
Использование нечетких моделей является одним из вариантов
исследования сложных систем. Использование нечеткости при
моделировании таких систем, позволяет нам, как это не звучит
парадоксально, повысить адекватность получаемых моделей.
Объясняется этот факт "принципом несовместимости" для сложных
систем, сформулированным еще Л. Заде в роботе [28]: "... чем ближе
мы подходим к рассмотрению проблем реальноrо мира, тем очевиднее,
что при увеличении сложности системы наша способность делать
точные и уверенные заключения о ее поведении уменьшаются до
определенноrо nopora, за которым точность и уверенность становятся
почти что взаимоисключающими характеристиками".
в силу этоrо, для использования подходов описания неопределенности
через нечеткие множества и меры.. используются различные алrоритмы
идентификации моделей. Но, все основные подходы, алrоритмы и
методы идентификации, разработанные на сеrодняшний день,
ориентированны на модель НП, представленную в виде нечеткоrо
композиционноrо уравнения типа (5.19) или ero модификаций. Для
идентификации данной модели, а именно нечеткоrо отношения,
связывающеrо пространство входов и выходов НДС, применяются
различные алrоритмы в основном ориентированные на построение
некоторой теоретико"множественной операции, обратной операции
композиции, с последующим сrлаживанием результата [2, З, 15, 27 и
др].
Для идентификации моделей типа нечетких реrрессий в работе [20]
предлаrается итерационно"оптимизационной алrоритм определения
нечетких коэффициентов модели. В силу отсyrствия, на сеrодняшний
день, в широкой практике использования нечетко"интеrpальных и
дифференциальных уравнений описания сложных систем, методы
идентификации таких моделей отсутствуют. Поэтому, в этой rлаве
будут рассмотрены подходы к идентификации моделей в виде нечетко
Бочарников В.П.

Fuzzy Techпology
225
интеrpальных и дифференциальных уравнений для дискретных и
непрерывных нп.
Для описания дискретноrо ИП будем рассматривать уравнение вида:
Jli+l(m) == f h(m,m') о f Jli(m) о g(.),
n l n
(7.1 )
rде р,{ro) .. функция, описывающая состояние нп в j..й момент времени,
h«(i)(J)').... стационарное нечеткое отношение реализующее оператор
вход"выход, g(.).. нечеткая мера на пространстве состояний.
Для описания непрерывноrо ИП в качестве модели рассматривается
нечетко"интеrpальное уравнение вида:
p(m) = J [ f h(m, ml,t) ] о f fc(m) о g(.). (7.2)
т 111'( ro') '1', ( .Iro)
Состояние ИДС изменяется в нечеткие моменты времени 'tEF(1),fl..ro)
.. ИП .. аналоr броуновскоro движения, h( т, т' , t).... нечеткое
отношение, являющееся оператором BXOД"BЫXOД'.
Идентификация нечеткой модели ИП в виде уравнений (7.1}. (7.2.)
предполаrает определение оператора вход",выход (нечеткоrо
отношения) по информации о реализующихся или уже реализованных
пар входа р,{ro) и выхода Р;+t(ro) на некотором временном интервале
так, что6ыI обеспечить некоторое "свойство хорошеrо отображения"
при котором выполняется
N
D = Ld(Jl;(m),j1;(m) min,
;=1
(7.3)
rде d(.,.) .. функция расстояния между истинным состоянием ИП и ero
модели j1;(m) в виде нечетко..интеrpальноrо уравнения (Например
расстояние Хемминrа). Ниже мы более подробно остановимся на
проблеме оценки адекватности модели ип.
lак. 771
Бочарников В.П.

226
Fиzzy Techпology
7.2. Идентификация моделей дискретных
нечетких процессов
Рассмотрим модель дискретноrо ИП (7.1). Данное уравнение может
быть переписано в следующем виде:
l1i+' (т') = I[ Цт,т') л l1i(m)] о g(.).
n
в даниом уравнении неизвестным является нечеткое отношение
h(юm'). Подход к идентификации функции h(тш'):nXn [OI]
строится на основе результатов приведенных в следующей лемме.
, Лемма 7.1
'Функция h(тш') по информации (u,{ro),j1i+l(ro» на i+l....M шаrе
определяется из условия
i g( МII. n НII. ) = 11;+1 (ro') , (7.4)
) "'1+1 "'1+1
'тде +I =={ J.li«(J) > JLн..(ro')}, НА+I =={ hю(ш) > J.li(ro')},
для фиксированноrо Ю е а' и задается минимальной функцией:
h, ( CJXJJ') == /1;+1 ( т') л Х 11-' (т)
"'9-1
(7.5)
rде Х . (ro)" характеристическая функция множества а - среза
II pl ...
, ,
н ro (ro) для фиксированноrо ()) еО, полученноrо из условия
Р;+I
(7.4).
lJоказательство.
Уравнение дискретноrо НП можно записать:
/lж (ш') = ![ h((J)(J)') л р.(ш )]0 g = sp[a л g(Mn«(J) )пн: (ш»].
Бочврников В.П.

Fиzzy Techпology
227
Соrласно свойства нечеткоrо ИlПеrрала (3.1 О) имеем:
g( М",., ((J) )П н :', ») = J1 ;+1 ( (J)')
"+I( ю)
Q
fi.i+1
.(Щ
Q
Рисунок 7.1 .... К доказательству леммы 7.1.
Исходя из этоrо соотношения любая функция h(l)'(W) имеющая на
уровне 11'+1 (lO') такой а .... срез, что выполняется условие равенства,
является вариантом решения задачи идентификации по j+l--MY шаrу. В
силу необходимости выполнения условия вложенности а..срезов (2.23)
минимальное решение определяется соотношением (рис. 7.1):
hw.(lO) = 11;+1 (lO') л Х Id' (lO),
11 Pi+-l
Что и требовалось доказать.
д
Для дальнейшеrо рассмотрения сделаем ряд замечаний.
а) Условие (7.4) не обеспечивает единственности решения
задачи идентификации, а следовательно существует целое
семейство подмножеств На на уровне J.!i+I(W) для которых
выполняется условие (7.4). И как следствие, определение
минимальноrо решения (7.5) не обеспечивает однозначноrо
решения.
б) Для восстановления функции h( щи) по совокупности
наблюдений необходима орrанизация некоторой процедуры
аrpеrирования А[..] вариантов по всем j"M измерениям,
которая должна учитывать структуру решений на всех
Бочарников В.П.

228
Fиzzy Techпology
уровнях Jli+J(ro'), i == 1,1 и для всех наблюдений, даже при
равенстве J1 ;+1 ( т') == J1 ;+, ( т') ·
в) Следует отметить, что условие (7.4) справедливо соrласно
свойства (3.1 О), которое получено для случая непрерывноrо
носителя а. Если же пространство Q является дискретным
условие (3.1 О) должно быть заменено на менее жесткое
условие вида
g( M".Jm)n H,,, (т») > JlI+I(m').
(7.6)

Таким образом, смяrчение условия равенства (7.4.) при водит к еще
более не однозначному решению задачи идентификации и осложняет
поиск оценки функции h( щro'.
Лриведенные выше замечания показывают, что идентификация
функции h( щro') в нечетко",интеrpальном уравнении (7. 1 ) для
дискретных НП есть задача не реryлярная и требует предварительной
реrуляризации, позволяющей найти некоторое квазиоптимальное
решение. Вариант решения задачи идентификаци для дискретноrо Q
может быть получен в результате формирования процедуры аrpеrации
(Х .. уровневых решений по каждой паре вход"выход построеиной по
принципу приближения условия (7.6) к условию (7.4), то есть
обеспечивая минимизацию меры
g( М";., (т )п н:.:, (т »  m in. (7.7)
Нахождение квазиоптимальноrо решения для дискретноrо Q,
построенноrо на основе условия реrуляризации (7.7), определяется
теоремой.
Теооема 7.1
Квазиоптимальное решение задачи идентификации модели
дискретноrо ИП (7.1) определяется по информации о динамике
иде до ;..ro шаrа рекуррентным соотношением при
фиксированном ro' Е П:
111+. (т, т') = [ 11, (т, т') V Рl+' (т')] л h, (т,т'), (7.8)

rде h;( т, т') == h L,nax (т), определяется последовательно,
Бочарников В.П.

Fиzzy Techпology
229
соrласно соотношения:
ii'+1 (т) == ii'(w) V (Р'+I (т) л XIl,., (ю»). (7.9)
ho (т) == Х " ро (т), Р0 > 11;+1 (ro') = Р. > 112 >... > 111.rnp ,
"v ( т ) .. характеристическая функция множества Н/+ /:
л.. 11'+1
N,
Н'+I == Н, U U Р;,. (7.10)
K,I
rде К, = 1,N," количество выходов при которых
Jl'+I(W')== р,. Р;' с М к , =={wIJl(W» Jl,}для KOТOporo
выполняется:
Л l [ H,u U ljl ] nMK' )  min,
к, Бl К,=I
{ р.К, } .. семейство подмножеств р.К, С М для которых
h h  
(7. 11 )
g(:') > 11, (т').
(7.12)
llоказательство.
Пусть на j"M шarе модель ИЛ определялась для фиксированноrо

сечения roе!} функций h,(m). Если полаrать, что на j....M шаrе
реализовать значение J.Li+.(ro'), на выходе, то соrласно (7.6) изменения

оценки h( (.От') MOryr определять лишь те (1.. срезы для которых
(1 < Jli+t(ro') (рис.7.2).
Бочарников в.п.

230
Fиzzy Techпology
1
ro' == const
hi(ro)
Jl1+1 (ro)
, hi+l(lO)
.......'\.
"
Н ро
Q
MJro)
Рисунок 7.2 .... К доказательству теоремы 7.1.
Следовательно, задача состоит в поиске некоторой функции h i ( ro),
#о
которая изменяет оценку h; ( т ) для всех (J) при которых
#о #\
h; ( т) < Р'+I (т'). у словие изменения оценки h; ( т ) < J1 ;+1 (т)
можно представить в виде:
11;+1 (т) = [11;( т) л XHI'i+1 (т)] v h'; (т),
rде h'; (т) некоторая функция. Так как вариации подлежат все
#о
h; ( т ) < J1 ;+1 (т), то функция h'; (т) может быть представлена в
виде:
h;{m) = [h;(m)v Р;+I (т')] л [щ(m) л Pi+1 (т')]
rде {mlh;( т) > Р;н (т')} = {mlщ( т) > Рi+I (т'»'
Подставив это соотношение получим:
Бочарников В.П.

Fuzzy Techпology
231
 (со) = [(CO)v p; (со')] л {[ (co) л Х".... (со)] v[ щ( со) л Ро+' (со')]} =
={[(CO)v Jli+I(со')]Л[(СО)ЛХ".... (со)]} v
v{[ (CO)v .uж (со')] л[ щ( со) лJl; (со')]} = [( со) v РНI (СО')] л
л{[ (co) л Х"..., (со)] v щ( со)} = [( CO)v РНI (ао] л {( (CO)v щ(со») л
л(Х"..., (CO)V щ(со»)}=((со)v p,(co'») л(Х".... (CO)V щ(со)}
Таким образом, если положить искомую функцию в виде:
h;(m) == XH pi + 1 (ш) V т;(т),
то получим, что идентифицируемая функция будет определяться
соотношением (7.8). Для 'V т Е Н Pie. (т), h; ( w ) == х 11",+. (ш )
целесообразно принять }t(co) = Х"..., (со). Функция m;(ю) будет
определяться а",уровнями ДЛЯ a:s; Jli+'(of). Для упорядоченных
J.lo >J.!i+J(W) == Jl. > J.!2> ..е >JlLmax рассмотрим произвольный /"уровень. На
rOO,J
/....1 уровне функция h/1 ( т) имеет множество уровня:
H,, (со) = {col1 (со) > Jl/--I}.
Пусть на / ... м уровне количество выходов иде по координате ro е Q
равно N / . ДЛЯ каждоrо выхода J.!i(ro) при котором J.!i+J(ro') == J.L/
множество уровня Jl/ будет определяться соотношением:
'VK, = 1,N"
М к , = {coIJl;' (со) > р,}.
Для каждоrо КI должно выполняться условие (7.6). Пусть ЛкЛ:Мка ..
есть множество всех подмножеств M K1 . Тоrда существует семейство
подмножеств {P jk K/} С ЛкЛ:М к1 ) такое, что выполняется условие
Kl М P K1 ) ' )
P jk С К/, И g( jk > J.!i+I( (J) .
Для Toro, чтобы выполнялось условие (7.6) для каждоrо КI необходимо
и достаточно выполнеиие (М к, п Нрд е {P jk Kl} то есть пересечение J.!l""
уровня функции h(щro') при фиксированном roеа с Jlr уровнем
Бочарников в.п.

232
Fиzzy Techпology
ВХОДНОЙ функции J.1i(ro) ПРИН8длежал семейству {P jk K /}. Для
восстановления подмножества Н ( ш) с учетом условия вложенности
11,
а .. уровней (2.23) может быть использовано любое подмножество
вида:
N,
Н, == H,, U U p_' ·
К,=I J
в этом случае условие (7.6) выполняется. ОДНако семейство решений
может быть сколь уrодно велико что определяется мощностью
семейств {P jk K /}. С целью получения единственноrо решения
используем условие реryляризации (7.7). Получим:
g( Мк, n Н",)  min;
 М К , П{Н'I U Q. :,}) min.
Примеиив условие реrуляризации ко всем входам rде Jli+I(ro')  11/
получим:
'> g ( м к N { нн U U p-' })  min,
 I  J
rде минимизаЦИЯ осуществляется на множестве наборов P jk для всех К/.
Таким об разом, решив задачу оптимизации приведенную выше для
всех 1 == 1,L функция hi(ro) будет оцениваться в виде функции
тa

h ( ш ) рассчитанной соrласно (7.9), так как выполняется условие
l.rn;ц ,
'""-1
вложенности а..у р авнений и h ..... Х ( r,1 ) Следовательно, теорема
о.... 11 LV.
1',.1
доказана.
[)
Таким образом, доказанная теорема позволяет построить приемлемый
алrоритм идентификации, позволяющий получить квазиоптимальное
решение на основе условия реryляризации (7.7). Структура алrоритма
А I имеет вид:
Бочарников В.П.

Fиzzy Techп%gy
2ЗЗ
АлrОDИТМ А 1.
1. Для фиксированноrо ro е Q определяется убывающая
последовательность а"уровней:
Jlo >JlJ > J.!2> . . . >J.!Lmax, 1 == О L ·
, та"
2. Для каждоrо входа, на каждом '....м уровне определяются
семейства {pK, }, удовлетворяющих условию теоремы 7.1.
JIi.
- 
з. На уровне I множество уровня оценки функции h;(w)
находится соrласно условий (7.1 О), (7.11).

4. На 1+1 уровне вспомоrательная функция h ( т ) находится
'I
соrласно (7.9).
5. Пункты 2..4 выполняются до 1 L тa и уточняющая функция
h i ( ю) определяется как h. (т) == h ( т ) .
I 4na!l
6. Оценка функции нечеткоrо отношения дЛЯ НДС дЛЯ
фtlксированноro ro е Q по информации о i шаrах строится
rласно (7.8).
7. Пункты 1....6 повторяются для всех roеа и восстанавливается
 
оценка функции в виде: 'V т' Е Q h; «(.От') = h,w" (т).
8. При поступлении новой информации на i+ 1 шаrе "ункты 1.. 7
повторяются для уточнения оценки оператора идс.
(8)
Анализ приведенноro aлroриrма идентификации показывает, что данный
anroритм крlПИЧен с точки зрения 'Ipудоемкоcrи определения семейств
{P jk К1} на каждом [..м уровне среза функции h( Щro') и приемлем, в основном,
для иде описывающихея на дискретном пространстве состояний Q с малой
мощностью. В то же время, точность идентификации функции h(щro')
ожидается значительной. Однако, коrда мощность Q более 100 и в пределе
при непрерывном Q данный aлroритм идентификации будет
малоэффекrnвным. для решения задачи идентификации в этом случае
целесообразно использовать упрощенный aлroритм иденrификации.. При
этом основное упрощение касается ПОCIpOeния семейства {P jk Кl }. Так как
существует Bcero 'Ipи варианra пересечения множеств lIa.(w) и MJw), а
именно:
а) На( ю) с MJ ю);
б) На(ю) п Ма(ю) с Ма(ю);
в) HJW) ::J Ма(ю),
Бочарников В.П.

234
Fuzzy Techno/ogy
то справедливо соотношение:
g( М"...<т») > #1,+1"
(7.1 3)
Исходя из этоrО t в качестве наибольшей оценки подмножества Р; в
,
соответствующем семействе можно использовать подмножество J..!i+I"
уровня от входной функции. Тоrда 9 в качестве оценки подмножества 1..
"""-1
уровня для функции h ( m ) можно использовать единственное
L"","
соотношение:
N,
H'+I = H,U I М",
(7.14 )
Условие построения множества (7.14) является условием
реrуляризации максимизирующим меру
g( М "..0 (т)П н :.:, (т»  тах.
(7. 15)
Исходя из данноrо условия реrуляризации алrоритм идентификации
функции h(щro') (f\лrОDИТМ A) имеет вид аналоrический алrоритму
А 1 при изменении пунктов 2 и 3 пунктом:
"""-1
· Множество уровня 1 для функции h, (т ) определяется
соотношением (7.14).
в силу Toro, что выполняется условие
'Vj,k,l,
рК, С { p, }
J ....... J, '
р..К, С М
J ......... р,
спрведливо соотношение:
\:;/ m Е а,
#о #о
h;' (со) < h;2(m),
(7.16)
rде AI, А2 .. соответствует оценкам полученным соответственно по
первому и второму алrоритмам. Исходя из этоrо, получаемые на
выходе модели состояния ИЛ, соrласно свойства нечеткоrо интеrрала
(3.17) будут удовлетворять условно вложенности:
\;;1т еП,
рАI (т) < рА2 (ю).
(7. 17)
Бочарников В.П.

Fиzzy Techп%gy
235
Таким образом, модель идентифицированная по алrоритму А2 будет
обладать больше чем для А l уровнем неопределенности. В силу этоrо,
целесообразно, при использовании модели идентифицированной по
А2, про водить дополнительные исследования на степень адекватности.
В заключении отметим, что идентифицированные модели НП строятся
лишь на определеином наборе входной и выходной информации. В
силу этоrо, на дрyrих исходных входных сиrналах модель может иметь
ошибки на выходе и в силу этоrо проверка адекватности модели для
использования ее в общем случае является обязательным условием.
Для ИJШюстрации работы алrоритмов рассмотрим численные примеры.
ПDимеn 7.1.
Пусть Q .... дискретное пространство состояния ндс Card Q == 5. На Q
задана нечеткая мера g(.) определяемая следующим распределением
плотности:
g(.) == {11 0.1, 21 0.2, 31 0.35, 41 0.25, 51 0.1 }.
Истинное нечеткое отношение h( щro') определяется матрицей
I 0.8 0.5 0.4 0.1
0.7 0.9 0.8 0.4 0.3
h(mm') = 0.5 0.7 0.9 0.6 0.5
0.4 0.6 0.8 1 0.4
0.1 0.4 0.5 0.9 1
На вход НДС были поданы три входных сиrнала:
p (110.9 210,7 310.5 410.3 510.1 ),
p(110.2 210,4 310,8 410,5 510,1 ),
p(110,1 210.3 310,5 410.7 510.8).
При этом выходная информация имела вид:
. '<r
Бочарников В. п.

236 Fuzzy Techпology
Jlblx (1(0,5 2(0,5 3(0,5 4(0,4 5(0,35),
Р;ых (1(0.4 2(0,5 3(0,5 4(0,5 5(0.4),
Jl:bIx(I(0.4 2(0,5 3(0,5 4(0,5 510,45).
Необходимо по информации (pr , Р7 ЫХ ), i = lЗ восстановить
функцию h(щro'). Для решения будем использовать алrоритм A.I.
t 00==1 1,1 ..... 05 112 ...... 04 113 ....... 04 Н...../Л
· r вых..... ., reblX..... , , r вых , I .....)(,..1.
Определяем семейство множеств:
{1J}J5 ==3 = {2,3}, {Ij}.4 = {Р2''Рз}, {Pj}.4 == {Рз,Рз}
I 2 к
H o . s =H1U U Pj ==НIUЗ =р2З; Н О . 4 =HosU U р* ·
К=I К=I
"
Р. будет определяться соrласно условия реrуляризации (7.11) рис.
7.3.
g{(Ho.s UJ; U)nM.4} л g{(Ho.s UJ; U)nM:.4} == 0.6;
g{(Ho.s UJ; U)nM.4} лg{(Н о . s UJ; U)nM:4} == 0.45;
g{(Ho.s U U)nM.4} л g{(Ho.s UJ; UP)nM:.4} = 0.6;
g{(Ho.s U U)n M.4} лg{(Н о . s U U)nM:4} == 0.7
g{(Ho.s UP Up)n м;.4} лg{(Н о . s U UP)nM:4}= 0.6;
g{(Ho.s U U)n М.4}лg{(Но.s Up U)nM:.4} == 0.7;
rде М. {2,3,4}, М 2 {3,4,5}.
0.4 0.4
0.8
0.6
0.4
0.2
О
1 2 3 4 5 6
к
Рисунок 7.3 .. Определение семейства р. соrласно условия
реrуляризации (7. 11 ).
Бочарников В.П.

Fuzzy Techпology
237
На оси абсцисс приведены номера сочетания подмножеств из семейств
{ -К k t 2 С
PJ}O.4' == 1,2 Отсюда Но.4 == Ho.sUP 23 uР зs . ледовательно в
А
сечении ш 1 функция h(rom:)== (1(0 2(0.53'0.5 4(0 5 0.4)
2. Для ш==2 pых == р;ых == р;ых == 0.5
{P}.5 == 1;, {Р}:.5 == , {P}.5 == 
н 0.5 == 0 u  u  u P == 1;) u 4 == 1;34
Это решение единственное. Тоrда для ro 2:
h(юm;)== (1(0 210.53(0:54(0.5510).
3. Для ro3 решение аиалоrично ro 2.
4. Для ro 4 и ro 5. Процедура идентификации аналоrична выше
А
приведенной и полученные значения функции h( (.От') имеют вид:
h(m, т;) == {1(0.4 2(0 3(0.5 4(0.5 5(0},
h(m,m;) == {1(О 2(0.4 3(0.45 4(0 510.45}.
А
При использовании полученной оценки функции h( mm') реакция на
выходе модели для фиксированных входов р:и i == 1,3 имеем:
I М
Рвых == {1105 2(0.5 3(0.5 410.4 5(0.4},
2 М
Рвых == {1(0.4 210.5 310.5 4(0.5 5(0.4},
Р:ЫХ м = {11О.4 210.5 310.5 410.5 5IO.45}.
Как видно решение расходится лишь по первому входу при ro 5. Что
rоворит о хорошей степени адекватности модели на рассматриваемом
семействе реализаций вход"выход.
ПDимеD 7.2.
Рассмотрим пример применения алrоритма А2 идентификации
нечеткой модели дискретноrо нп.
Бочарников В.П.

238
Fuzzy Techпology
Исходные данные для решения задачи аналоrичны исходным данным
приведенным в примере 7.1.
t. Для сечения oJl:
Hos == M;.s =={1,2,3}
НО4 == Hos U М: 4 UM;.4 == НО5 U{2,3,4}U{3,4,5,} == {1,2,3,4,5}.
2. Для сечения ro 2 и ro 3:
Hos == M;.sU M: s UM:. 5 = {1,2 y 3}U{3,4}U{3,4,5}== {1,2,3,4,5}.
3. Для сечения m 4 :
Н05 == M.5 U Mg.s == {3,4}U{3,4} == {3,4}
Н 0.4 == Н 05 UM.4 == {1,2,3}U{3,4} == {1,2,3,4}.
4. Для сечения ш==5:
H O . 4s == M;.4S == {3, 4,5}
НО.4 == НО.45 UM:... == {3,4,5}U{2,3,4} == {2,3, 4, 5}
Н о . зs == НО4 U М.зs ={2, 3, 4,5}U{1,2,3} == {1,2,3, 4, 5}.
5. Оценка модели, в силу этоrо, будет
0.5 0.5 0.5 0.4 035
0.5 0.5 0.5 0.4 0.4
fi( ют') == 0.5 0.5 0.5 0.5 0.45
0.4 0.5 0.5 0.5 0.45
0.4 0.5 0.5 О 0.45
6. На выходе модели для рассмотренных входов будем иметь:
I М
J1вш == {1(0.5 2(0.5 3(0.5 4(0.4 5(0.4},
2 М
Рвых == {1(0.4 2(0.5 3(0.54(0.5 5(0.45},
з м
Р вых == {1(0.4 2(0.5 3(0.5 4(0.5 5(0.45}.
Бочарников В.П.

Fuzzy Techпo/ogy
239
ВЫХОД модели в этом случае близок к ВЫХОДУ реальноrо процесса.
Ошибки в сторону завышения значений наблюдаются в 1 и 2 выходном
множестве при 0)=5. Как видно из результатов при сравнеиии с
алrоритмом AI (пример 7.1) выполняется условие (7.17), однако
вычиспительные затраты при решении задачи идентификации
значительно ниже, что делает использование алrоритма А2 дЛЯ
решения задачи идентификации весьма привлекательным.
Бочарников В.П.

240
Fuzzy Techп%gy
7.3. Идентификация моделей непрерывных
нечетких процессов
Идентификация моделей непрерывных нп яаляетСJl более
затруднительной, в силу значительной сложности разложения
нечеткоrо интеrpала по расширенной нечеткой мере, через который
представляется соответствующая модель. Модель HenpepbIBHoro
процесса описывается уравнением (7.2). Пусть в результате
наблюдения за НП мы имеем i = 1,N измерений реализовавшихся пар
вход"выход. Пока будем считать, что идентификация осуществляется
по дискретным "срезам" нп. Однако, как будет видно дальше данный
алrоритм может быть без труда расширен на случай непрерывноrо
процесса идентификации модели нп. Таким образом, через нечеткий
интервал времени LiEF(1) реализовывается пара
{Jl; (т). Jl;a (т') }. Необходимо по имеющеЙСJl информации о
мере 'Pt(.lro), НП A(ro) и накопившейся информации за i измерений
восстановить функцию h(щro',t), определяющую модель нп. Следует
отметить, что как и для дискретноrо, так и ДЛЯ непрерывноrо случая
задача восстановления нп имеем не однозначное решение. Для
получения приемлемоrо решения необходимо введение условий
реrуляризации получаемых решений. В противном случае получение
единственноrо решения невозможно. Наиболее лоrичным, с точки
зрения nрактики, может являться условие реrуляризации приводящее к
"покрывающему" решению, то есть получению такой оценки модели
НП, использование которой при водит к выполнению условия:
'VPex(т) Е F(D.), Р:Ь,х(m) < Рвых(m) ,
(7.18)
rде р:ых (т)" нечеткое состояние истинноrо НП, Р:ых ( т) .. нечеткое
состояние для модели нп. Исходя из этоrо, по аналоrии с
дискретными НП, может быть использовано условие реrуляризации
типа (7.13), (7.14), при водящее к максимизации оценки и получению
"покрывающеrо" решения.
Бочарников В.П.

Fuzzy Techпo/ogy
241
\
С у\етом условия реrуляризации (7.18) модель HenpepLIBHoro НП
можef быть идентифицирована исходя из применения результатов
слеДУIpщей теоремы:
1еоnема 7.2
Модель HenpepbIBHoro НП на основании i = 1, N измерений
вхЬд"выход определяется с учетом условия реrуляризации
(7.18) соrласно следующеrо соотношения для фиксированноrо
ro' eQ:
N
п(m,t) == ;.[.и:(т') л ХН; (m,t)],
(7.19)
rде H i С NXТ .. четкое отношение на декартовом произведении
пространств ОхТ для i..ro измерения определяемое как:
Н. = E х F. ,
, , ,
(7.20)
rде Е; == MJi...x(m'> == {mlll:a(IO) > .и(т')} c O,
F;* = r(E;*) c T, такое, что
"\1 т Е {wl/'lj (т) > .и:п.х(т')}, 'JI,(F;*lw) > .и(т')'
r(.).. соответствие rалуа (4.20).
Доказательство.
Уравнение описывающее динамику HenpepLIBHoro НП имеет
следующий вид:
Jl;ЫX(IO')==/r 1 h(IO,m',t)og ] o J /(m)og(.).
( H
Лреобразуем это уравнение к виду:
р;ЫХ(m') = 1 [ 1 {h(m,m',t) л p:x < m:t) } о g J o J /(m)o g,
т n 'Р, (.Im)
Бочарников В.П.

242
Fuzzy Techпology
rде \:;/ t Е Т, Р:Х (т, t) p (т) .. цилиндрическое продолжение.
Соrласно теоремы 4.1, являющейся аналоrом теоремы Фубини, можем
записать:
JLrflblX(m') = J [h(m,m' ,1) л р:"(m :t)]ОI \ 1 g(.)x J h(m) о g(-»).
Тха , 'If, (.Jll) /
rде / g(o)X J f:(m)o gO ) .. есть декартово произведение нечетких
\ \If,('Iю)
мер, которое является нечеткой мерой на пространстве ОхТ.
Рассмотрим функцию в квадратных скобках при фиксированном Ш Е Q.
Данная функция является нечетким отношением на декартовом
произведении пространств nxT. Отсюда, для модели иепрерывноrо
нечеткоrо процесса справедливо предcrавление:
rде
р;Х(m') == sup { а Л ( g(.)x J . f-c(m) о g / '<H a ) } ,
ae[OI] 'If, (-Ill)J
(g(o)X Jio>,!.(m)og)<H a )
есть
функция
меры
от
подмножества а..среза нечеткоrо отношения hll),(mt)лр:Х(mt), то
есть:
На = {(йJ,I) I hro,(йJ,I) Л Р:"(йJ,I) > а Е [Оl]}.
Рассматривая полученное выражение для j..ro измерения вход""выход
можем записать следующее условие:
/ g(o)X J fT(m) о g' ) O(Ha) = р:;и(m').
\ 'If, (.Ill)
Соrласно определения 4.3 нечеткая мера отношения На определяется
выражением:
, /g(o)X J fT(m)Og)(H a )= V { g(Е)Л I h(m)og(8) } ,
'Р, ('Ill) I Е n 'If, (r( E)Ill)
Бочарников В.П.

Fuzzy Techпology
243
rде r(E) с т, r(.) .. ФУНКЦИЯ (4.20) из соответствия rалуа,
порожденноrо отношением На. Тоrда для ;..ro измерения должно
выполняться:
v { g(Еi*)Л J t-с«(J)оg(.) } =Р;blХ«(J)').
Е; t,;Q "', ( r( E j $ )(m) ·
Возвратимся к условию реrуляризации (7.18).
Е; = М вых ( ' ) = { (J) I р: (т) > p;X (т') } ,
РТ; (J) , ,
реrуляризации будет выполняться. Тоrда, остается определить такое
подмножество r(E i *) для KOToporo условие для ;..ro измерения будет
выполняться. При выборе E == М имеем g( E: » IIBblX ( m' ) .
I I1/X (ю') I r-c;
Подмножество E х r ( E ) с Q х Т моделирует отношение H i на
I I 
уровне р;':Х ( т') Е [О 1 ]
,
Н ..... Е * r (E * ) то для ;..ro измерения приведенное выше
«ЫХ ( ' ) .... i Х ;'
111:; (J)
условие выполняется. В силу леммы 4.2 Е; х r(E;*) .. определяет
наименьшее решение, в смысле вложенности. Однако, остается
неизвестным из KaKoro множества подмножеств множества g
.
выбирать E j и какое окончательно отношение Н выбирать.
11;?'Х (ю')
.
Если выбрать
то условие
в
том
смысле,
что
если
Тоrда можем записать:
I [,,(т) о g = 1l:::Х (т') = I[t" (т) л 'JI,(r(E;*)lw] o g(.).
", (r( Е;. )I{J) , n
Исходя из условия реrуляризации (7.18) для выполнения приведенноrо
равенства справедливо определить требование:
V'w Е Q, т Е {h( т) > .и;,ых (т')}. 'JI,(r(E;* т) >1l :;Х (т').
Таким образом, для ;..ro измерения вариант функции h(щro',t) при
фиксированном ro' Е g И при выполнении условия реrуляризации может
определяться соотношением:
1i,«(J),t) = р;':Х (т') л Хн. «(J),t),
, .
Бочарников В.П.

244
Fиzzy Techпology
rде Н; = М ; ( ' ) х r( М; ( , » ).
J.l""щ ltJ JlNhI:r; ltJ
Тоrда, соrласно условия реryпяризации (7.18) в качестве оценочноrо
решения может быть принято решение:
N
"fIJ,(w,t) = iJJI.r(т')л Хн, (т,!)}
Таким образом, теорема является доказанной.
[]
Приведенная теорема позволяет определить алroритм идентификации
функции h(щro',t} в модели непрерывноrо нп. Алrоритм будет иметь
следующий вид:
АлrОDИТМ АЗ
1. Для фиксированноrо те!} определяется убывающая
последовательность а"уровней по всем N измерениями
J.LI >J.L2 > .. . > J.Li > .. . > J.LN.
2. Определяется для j..ro среза подмножество E = М
I Р;:""" ( ю')
I
начиная i == 1.
3. Определяется подмножество F;* = r ( м ) .
, pЫ.'( (ю')
4. Строится решение
h;(ro ,t) = р; л Хн. (ro,t) = р; л XE..XF:.(ro,t}.
t t t
Пункты 2....4 выполняются для всех i = 1,N.
5. Строится оценочное решение
А N А
h .(rot) = у h.(rot).
(IJ ,=1 '
6. Пункты 1..5 повторяются для всех fff е Q и восстанавливается
'"
общее решение h(aIOJ't) в качестве оператора вход"выход.
Приведенный алrоритм позволяет получить оценочное решение для
построения модели нп. Наиболее трудоемким в реализации данноrо
Бочарников В.П.

Fиzzy Techпology
245
. .
алrоритма является определение подмножества F i == r(E i ) при котором
выполняется условие
't/ т Е {mlfT ( т) > pых (т') }, 'JI, ( 1';* 1ю) > pых ( т').
Решение данной задачи не является единственным и здеСL также
необходимо вводить условие рeryляризации. При этом целесообразно
осущеcrвлять поиск решения численными методами.
Бочарников в.п.

246
Fиzzy Techпology
7.4. Оценка качества моделей
нечетких процессов на основе
...,
нечетко",интеrpальных зависимостеи
Проверка адекватности идентифицированной Модели является
принципиально важным при практическом использовании. Проблема
заключается в том, что модель должна удовлетворять свойству
"хорошеrо отображения" [12]. Практически это сводиrcя к условию
полноrо равенства функций распределения нечеткости выхода
реальной системы и модели при любом входном воздействии. Ранее
было отмечено, что задача идентификации модели НП является не
рeryлярной. Условие же реryляризации чаще Bcero сводит задачу к
поиску квазиоптимальноro решения. В этом случае оценка модели с
точки зрения выполнения свойства "хорошеrо изображения" является
необходимой.
Рассмотрим пространство состояний идс а. Множество всех
нечетких состояний дЛЯ ИДС обозначим F(Q). На пространстве F(Q)
дЛЯ каждой ero точки (нечеткому состоянию НДС) соответствующей
истинному выходу нечеткой системы реализуется нечеткое состояние
(точка из F(Q» модели нп. Модель обладает свойством "хорошеro
отображения" если в каждой точке F(Q) истинноrо НП наблюдается
полное равенство с моделью нп. В общем случае, Korдa не все
состояния совпадают можно rоворить о мере (степени) выполнения
свойства "хорошеrо отображения". Чем выше значение, меры тем
более адекватно представляется истинный нп своей моделью. Данная
мера ДOJDКHa характеризовать степень удовлетворения своЙства:
"динамика НП во всех точках F(Q) хорошо представляется
моделью ИЛ".
Однако, про верка выполнения свойства "хорошеrо отображения" во
всех точках F(Q) затруднительно по той причине, что реальная
информация о состоянии нп оrраничивается лишь счетныМ
Бочарников В.п.

Fиzzy Techпology
247
количеством измерений N. fIри этом выполнение свойства "хорошеrо
отображения" может быть рассмотрено лишь Uлокальн07 по i....й точке
npocrpaHCТBa F(Q). Общее свойство '.хорошеrо отображения'7 для Bcero
F(Q) не может быть выведено из npOCToro линейноrо объединения
частных (месПIЫХ) оценок модели. Для общей оценки целесообразно
использовать поняrnе нечеткой меры измеряющей степень
адекватности модели.
Если состояние истинноrо НП описывается функцией JlM(ro) е F(Q), а
выход модели JlM(ro) е F(Q) в j..e измерение, то может быть определена
мера соответствия JlM(ro) истинному состоянию НП. При этом для
оптимистической точки зрения степень соответствия \) (J..L U t J.1M)
определяется мерой возможности:
v(PU ,J1N) = sup min{J1 U (Ш),J1 N (ш)},
l.OЕО
(7.21 )
а при песпимистической .... мерой необходимости:
V(Jl U , Р М) = inf тах { Р А' ( т), 1.... р и ( (J) ) } .
юеn
(7.22 )
Если на пространстве (l задано оrpаничение в виде распределения
нечеткой меры g: 2 n  [О 1], то оно может быть продолжено на
пространстве F«(l) с помощью понятия расширенной Нечеткой меры
рассмотренной в пункте 3.3. Тоrда важность выполнения адекваrnости
модели в точке JlU(ro)e F(Q) определяется как;
g(p") = J р"«(О)о g(.). (7.23)
D
Для подмножества точек пространства F(Q) А = {p;f«(O)} c F(!1)
мера будет определяться как
I v р:'«(О) о g(.)==g(A).
о p;'l {(JJ)e А
(7.24)
Используя эти соотношения адекваПIОСТЬ J модели может быть
определена через нечеткий интеrpал вида:
J= .l V(Р;',р)оg(.)=suр { алl у P;«(J))og } , (7.25)
{ii,:I.N} ae(OI] DP.EA
Бочарников в.п.

248
Fиzzy Techпology
rде А = {Jl;(m)lv(Jl: ,Jl) > а}.
Величина J определяет степень выполнения свойства "хорошеrо
отображения" для модели ИЛ учитывая нелинейность оценки
адекватности модели НП на пространстве состояний N.
Бочарников в.п.

Fиzzy Techпology
249
7.5. Декомпозиция моделей мноrомерных
нечетких процессов. Векторно",матричные
нечетко... дифференциальные уравнения
мноrомерных нечетких процессов
До наcrоящеro времени мы рассматривали нечеткие процессы на
унарном пространстве !1. В том случае. коrда пространство состояний
нде описывается как декартово произведение пространетв, на
KOТOpЫ заданы значения компонент вектора состояния, возникают
сложности не только с представлением моделей НП, но и
принципиальные сложносrn при идентификации модели,
моделирование НДС в реальных вычислительных системах,
устройствах и т.д.
Кроме тoro, в некоторых случаях возникают трудноС1И с физической
реализацией вычислительных процедур, использующих модели
MHOroMepHbIX нп. В ЭТОЙ СВЯЗИ'" возникает проблема декомпозиции
моделей мноrомериых нп, решение которой в свою очередь,
открывает новые возможности анализа сложных систем, их синтез [8].
Запишем нечетко..интеrpальное уравнение MHoroMepHoro ИЛ в виде:
J.L T (щ... W J = Q",Jт.) h( щ... W n' Ш:... Ш:, () о (gn, х. ..xgn.)] о Кf,(шJ)'
(7.26)
rде Jlr(CO....CO,,):Q.X...xQIl  [01] мноrомсриое нечеткое
состояние НП, (gn, х...хgц.)  декартово произведение нечетких мер,
g "'" ( . ) .. расширенная нечеткая мера порожденная процессом!-!...ro) на
f,(w)
пространстве Ц которое может совпадать с !1 i , i = 1, п или любым ero
подмножеством. При этом
Бочарников В.п.

250
Fиzzy Techпology
g (.) = 1 1: (ш ) о g(.).
.f..(w) v.(-Iw) r
Отметим, что размерность нечеткоrо отношения Ь(.) в случае, коrда
dim[Ц] == Qi, i = 1, п, n i .. дискретное, составляет величину равную:
dim[ho]==[Uq,J +).
(7.27)
При значительном увеличении размерности модели моделирование
отношения Ь(.) становиrся проблемаrnчным. Однако. модель (7.26)
может быть декомпозирована.
Прежде чем мы перейдем к рассмотрению основной теоремы о
декомпозиции рассмотрим ряд вспомоrательнь положений и
yrверждений. Пусть имеем нечеткое отношение h(ml...щ,) заданное на
декартовом произведении n.x...xQn .
Определение 7.1.
Проекцией нечеткоrо отношения h(ml...) на множество а.,
i = 1, п называется функция вида:
proj; h(m'...(Oп) = SUp...SUp sup...suph(m'...(Oп).
щ ЩI Щ+) 0)11
Если имеем нскоторую функцию Jl(Щ) е р(n.), i= l,n, то ее можно
расширить на универсум n.x...xQn .
Qш>елеление 7.2.
Цилиндрическим продоткением нечеткоrо множества Jl( щ) на
универсум n.х...х!}., называется нечеткое множество
определенное в виде:
v Щ, i = l,n CI...;I,i+J_..п(Jl«(O;»)«(JJI...(Oп) = J.l«(O;), (7.29)
Соrласно [11] справедливы следующие Положения. Декартово
произведение нечетких множеств Jl(щ) .... Jl(щJ может быть
представлено через цилиндрические продолжения этих множеств на
n.x....xQn в следующем виде:
Бочврников в.п.

Fипу Techп%gy
251
п
р( ю;) х.. .хр( Ю п ) = n C....;.,,;+....п(p( Ш; ».
;=.
(7.30)
Кроме этоrо справедливо следующее сооrnошение:
п
h(w....W n ) с .х proj; (h(w....W n ». (7.31)
,=.
Вложенность понимается в смысле вложенности нечетких множеств
[11]. Исходя из определения проекции и цилиндрическоrо
продоnжения нечеткоrо отношения оказываются очевидными
следующие соотношения:
h(w....w п ) < C'...i.,i+'...n (proj; (h(w....w n »)
(7.32)
п
h(w....W п ) < n C....;.,;+....п [proj j (h(w....w n »]. (7.33)
;=.
Пусть h(Щ,ffi2) и Jl(ml,0>2) .. бинарные нечеткие отношения. Докажем
следующую лемму для проекций нечетких отношений.
Лемма 7.2.
Для проекций нечетких отношений h(ml,0>2)
справедливо соотношение:
Vji, i= l,2 рrоj;(h(W.,W 2 )ЛJ1(W.,w 2 » <
< proj; h( Ш. , Ю 2 ) Л proj; J1 ( Ш. , Ю 2 ).
.
и Jl( Щ ,0>2)
(7.34)
Доказательство.
Соrласно определения 7.1 справедливо соотношение:
\;/ j  i, proj; h(.) > h(w;,w j ), proj;Jl(.) > p(W;,W j ).
Соrласно (7.32) имеем:
proj; h{щ"щJлprq; J1(щ.)= proj;[С;[proj;l1(.)]лС;[proj;J1(.)]].
Однако в силу (7.33) можем записать:
Cj[proj;h(.)] л Cj[proj;p(-)] > h(w. ,) л р(ю. ,lJJz).

Бочарников В. п.

252
Fиzzy Techп%gy
Тоrда, в силу определения 7.1 справедливо:
proj;[ C}proj;h(.)] л Cj[proj;JlO]] > proJ[h( lOl ,) Л J1( Щ ,) l
Таким образом исходя из выше отмеченноrо получаем, что отношение
(7.34) справедливо, что и требовал ось доказать.
А
Учитывая сделанные выше замечания и введенные определения"
положения можем отметить, ЧТО MHorOMepHoe нечеткое состояние
иде можем оценивать 8 качестве вектора
М 1 ' (р( ro)) = [р( ro.) р( ro 2 ). .. р( ro,,) ]1' , элементами KOToporo
являются нечеткие множества, заданные на унарных универсумах Ц ,
i = I,п . При этом, если 'V i = l,n J1(ro j ) = proj; р.*(ro... .ro п ), то
имеем оuеночное решение вида:
п
р( ro l . . . ro п ) = n CI..; 1,;+ 1...11 (р( ro;») > J1 * (ro l ... ro п ),
;=1
Ero можно использовать при описании состояния MHorOMepHoro ИЛ в
качестве наибольшеrо оценочноrо решения.Рассмотрим теорему о
декомпозиции модели MHorOMepHoro нп.
Теорема 7.3
Модель ИЛ (7.26) может быть представлена в виде:
р( ro.) == I { 1 h( ro l co;t) о g. (.)л...л 1 h( ro.ro nl)O g'l } О gft (ю)
l' Р«(БО р(ю,,) 
.
.
.
.
.
.
р(ro,,) = J 1 ' { J ) h(rollro,t)o g. л...л J. h{ro"ro:'t)о g,, } o gh(W)(.)
р{ш. р(ю.)
(7.35)
]Jоказательство.
Рассмотрим внyrpенний интеrpал в соотношении (7.26):
Бочврников в.n.

Fиzzy Techпology
253
I 1( щ... (Оп' щ'... (Oп,t) 0(& х.. .xg п ) =
J.lr «(O ...(O)
= J [l(щ...lOп'..lOп,t)лС.ш"АJlr(щ'...)]]о(&х..х&,).
11. x...xn"
Обозначим подытеrpальноеe соотношение в виде функции
"'"
h « (O ...(0 , (O'...m' , t ) . Используя условие (7.32) и свойство
I " . "
нечеткоrо интеrpала (3.17) можем записать:
п
J h(щ ...ltt,щ'...cq:,t) 0(& х..><&} < J j l:;..н.i+1,...п[ РЧ ц (Б(.»] о
nx..xn !1х...xn 
n
о(&х..><&} < j  l:;...Ч;+I,...п[Pti q (h('»] о (&х..><&).
Это условие справедливо для любоrо фиксированноrо набора ml...O\tt.
Рассмотрим более подробно i...й интеrрал. Можем записать:
J CI.H,i+I..п[projni о (п(.»] о (glx...xg п ) =
11. х...х11"
= I [ J CI.iI.;+lp..п[prOjn;h(')]O к; ] о
11. X...X11;1 X11i+1 х...х11" О,
o(g)x...Xg;1 Xg i + 1 X...xg n )
Пусть интеrpал в квадраrnых скобках принимает значение ае [О 1]. При
\;/ j *- i подынтеrpальная функция является константой и corпaCHO (3.11)
можем записать:
п п
; J G..iI.i+I....п[рrojnih(-)]о(glх..хgп)= j J projn;h(.)og;.
01 х...Xn" о;
Учитывая соотношение (7.34), доказанное в лемме 7.2. можем записать
следующее неравенство:
п n
!' J projn;hO о к; < !' J h(.) о к; =
,=) О, ,=1 рrо.hJlr(Щ ..щ,)
п
=!' I Projo;h«(O)...(On(O;...(O;,t) о gj.
,=1 Jlr(cq )
Бочарников в.п.

254
Fиzzy Tвchпology
Напомним что проекция projn'i бралась из учета фиксированноrо
набора щ..., t. Исходя из приведенноro выше можем записать:
Jlт(щ...со п ) < Jr.; J рrojлh(щ".СОп,щ...со;,t)о g; ] o gl' «(0 ) (.).
'=I 111" (t.ц) , J
Рассмотрим проекции состояния MHoroMepHoro нечеткоrо процесса.
Соrласно определения 7.1" справедливо:
Jlт(ltJ j ) = рroj j J1т(щ...ltJ п ) < projo. { Jr. 1 proj(th(.) о & ] 0 gf (а».
J '=IРf(Щ) 1 Jf:
Соrласно свойства (3.22) можем записать:
/lт (соj) < JрrО j л . [ .; 1 рrОjлhооg; ] оgJ;«(t»(.).
т J ,:::: I I1т (а); )' 
Исходя из леммы (7.34) данное соотношение в ВИДе:
J.lr(CO j ) < Jr. рrоjл 1 рrоjл. h (.) о g; ] o gf (а»(') =
'=I J I1т; (а);') I f
=lr.; 1 рrОjл.рrОjл:h(.)оg; ] оg/«(t»(.)==
}l, = I I1т; (а); ') J I Т
п
= J .Л J h«(JJjCO;t) о g; о Kf (О)}(.)'
T,==I рт(а);') . r
Таким образОМ t V j Е 1,п мы получаем соотношение (7.35) при
условии принятия максимизирующеrо решения. Что и требовалось
доказать.
[]
Таким образом, приведенная выше теорема позволяет осуществить
декомпозицию модели MHoroMepHoro нечеткоrо процесса. При этом
модель, декомпозированная в соответствии с приведенными
соотношениями, приводится к композиции бинарных моделей по
каждому входу и каждому выходу. Из доказательства теоремы
очевидно ТО, что разрыв связей между отдельными компонентами
вектора состояния (исключения отдельных перекрестных связей,
Бочарников В.П.

Fиzzy Techпology
255
представляющихся тернарными и более нечеткими отношениями)
приводит к оrpублению модели. Это подтверждается наличием
Hecтpororo неравенства. ОчеВИДНО t что с физической точки зрения это
ecrественный, объективно существующий факт. При этом, если
С&разрывается" значимая для сушноти процесса связь между
компонентами, различие между исходным выходом модели и ero
аппроксимацией после декомпозиции будет больше, чем в случае
&&разрыва" менее значимой связи. Этот факт подтверждается в
результатах исследования в области системноrо анализа Дж. Клира [8]
. по реконструктивному преобразованию систем.
Оценка искажений модели в результате реконструкции (разрыва
: отдельных связей) соrласно [8] целесообразно оценивать используя
понятие информационноrо расстояния.
Пусть h(ml...O\t,ro'l...ro'n) исходное нечеткое отношение, описывающее
. преобразование состояние идс. Если в результате декомпозиции мы
получим множество подсистем h i (.), то объединение их
цилиндрических продолжений на все пространство
: (llx...xQnx!1.'x...x{ln'xT даст нам оценку нечеткоrо отношения
А
системы h ( ro ...со , ro'...W' , t ) . Для оценки качества декомпозиции
I n I п
,.,
: системы информационное расстояние D(h,h) определяется
't
соотношением:
А
D(h,h)== 1 ! log Ic(h,a)1 da. (7.36)
log21CI о 2 'с( h,a)1
rде c(h,a).... множество а....уровня функции h(.), I с I .. мощность
пространства !1.х. . .x!1nxQ I 'х. . .xQn'xT.
Очевидно, если 1 == 1, п множество шаrов, &&разрыва связей" в системе,
. то на 100М шаrе можно разорвать различные, ранее не разорванные
связи. Если обознаЧИTh Х/ .. множество всех вариантов разрыва на
каждом I"M уровне декомпозиции и определить
. А
D,(h,h) =11}nDx, (h, h),
(7.37)

Бочарнuков В. п.

256
Fиzzy Techп%gy
А
rде Dx, (h, h) .... информационное расстояние дЛЯ Х/  варианта
декомпозиции на I"M уровне, то для конкретнОЙ системы функция
,.,
D,(h,h) будет не убывающей (рис.7.4). Выбрав уровень адекватности
в виде пороrа бе [О 1] в качестве наилучшеro варианта декомпозиции
А
системы целесообразно выбрать h(.) для lCоторой выполняется:
kO=arg max{D, (h,h)1 D, (h,h) < б}
(7.38)
1
0.8
0.6
0.4
0.2
О
О
: :.:::  :
':.: ::0. o:::"
 : ... ..: .. .:..
"0 ,:ae<; .;;:O: ;, ".
." :: ;.o':o;::.'.::;r"{ о;.  . ":,:::o""
IDO(.) I
1
2
3 4
,.,
Рисунок 7.4 .... Зависимость D ( h h ) ·
х, '
Приведенное соотношение позволяет выбрать приемлемый вариант
декомпозиции модели MHoroMepHoro ил. В том случае, коrда
декомпозиция осуществляется до уровня представления системы в
виде набора бинарных соотношеНий мы можем упростmъ исходную
запись уравнений модели используя векторно--матричную запись
нечетко"интеrpальных и дифференциальных уравнений. Если
состояние НДС описать нечетким вектором МТ(ro) == [ Jl(ro.), Jl(c:o.z), --.,
Jl()]T, то уравнение модели примет вид:
М,(ю) = t[мJ W 1 Н( ю,ю' ,1)0 GO]o gf.IW)O,
rде G T (_) == [8.(.), g2(.), ..., gn(-)]T ... вектор нечетких мер,
(7.39)
Бочарников В. п.

Fиzzy Techп%gy
257
h( OJ I , OJ I 1 ,1) h( OJ I , OJ 2 ' , {)
h( OJ I , OJ 11 ' , 1)
f h( OJ 2 , OJ I r ,1) h( OJ 2 , OJ 2 ' , 1 )
Н(OJ,OJ ,/) = .
h(OJ 2 ,OJ II ' ,1)
h( OJ " , OJ I r , t) h( OJ" , (J) 2 r , 1)
h( OJ", OJ" I ,1)
lИатрИчная функция системы.
Используя символьную запись для нечеткодифференциальных
уравнений можем записать:
fd М(т) == H((J)t)fdf".),
(7.40)
rде H(йJ,!)  матричная Функция преобразования сОСтояния системы
после учета текущеro состояния (с учетом начальных условий).
Введеное ПОНЯТИе векторно--матричных нечеткоиитеrpальных и
дифференциальных уравнений ДЛЯ описания моделей MHOI'OMepHblx
НП. ПОЗВОЛЯет УПРОСТИTh аналитическую запись математических
Моделей сложных npoцессов и сОкратить ВЫЧислитеЛьные затраты при
реализации aлrОрИТМов В системах ПОJЩержки ПРИНЯТИя решений.

Заk 771
Бочарников В. п.

258
Fиzzy TechпoJogy
r лава 8
ОПТИМИЗАЦИЯ НЕЧЕТКИХ
ПРОЦЕССОВ
И ВЫБОР РЕШЕНИЙ
Бочврнuков В.П.

Fиzzy TechnoIogy
259
8.1 Задача оптимизации нечетких процессов
в данной rлаве рассмотрение задачи оптимизации начнем со случая,
Е)'rда модель НП на пространстве n описывается нечетко..
i
дифференциальным уравнением вида:
!..
fd р(ro) == [h(tou t)л с (ro u t)]f d fT"(m)9
(8.1 )
..де С ( Ш, и, () == с ( u , (), 't;/ (jJ Е Q .... нечеткая функция управления,
.заданная на пространстве U .... значений управляющеrо воздействия
;,-(UE U), h(щu,t) .. оператор управляемой НДС, /;'«(0) .. нп на n,
епредe.mtющий нечеткость П(IOцесса но времени для управляемой ндс,
-э..даваемый соотношеmreм (5.23).
.
. Будем считать, что эффективность управления ЯДС определяется по
f
:JlfНожеству критериев 8{ v} на котором задана нечеткая мера важности
е-
;Юt критериев' ge<.):. 2 Ol,].. В общем случае, потери по каЖДdму из
"Скaзarrе.п.ей ve6 зависят от выбора управления u Е U, В к.онкретный
.1МJМe1iП" времени в KeтHOM состоянии НДС. Обозначим через
:t)yнкцию.l(11,u): f) х U'  [Ojl']. IWтери по показателям VE е при выборе
1mPавленИSJ 11 Е u.
"
, общем случ.ае управление ЫЕ U, как было отмечено выше,
;яетея в. виде функции u(t,ro). Нечеткое отношение l(ro,u) можно
аонимать как распределение меры возможности потерь по VE е при
'выореe управления u Е v. Для меры возможности дополнение [11]:
lt(1t;u) ] ..[ (v,u)
(8.2)
у:,удет f)JIЯТЪ мер}' выrодности выбора управления u Е U для

.kpитерия V Е 8. Сmлаено свойств распределения меры возможности.
>lКaксимально' возмсжНШt выодность по критерию VE е при выборе
упрамения; из подмножества Е с U будет опредеЛSI1:ЬСЯ соотношением:
j == mx f ] .....Z(V,U) ] .
"еЕ
(8.3)
r
Бочврников В.П.

260
Fuzzy Techп%gy
в соответствии с этим минимально возможные потери u будут
вычисляться соrласно выражения:
v = 1  j == 1  тах[1  Z(v,tL)] = 1  max[XE(v,tL) л (1  Z(v,u)],
UЕЕ иеЕ
(8.4)
rде \f v, Х Е (v,lJ)== Х Е{И) .. характеристическая функция множества Е
с u. Минимально возможные потери при выборе управления из
нечеТJ<оrо подмножества <р(и): U  [01], будут соответственно
определяться соотношением:
v(v) = 1  max[qJ(и) л (1  Z(v,и»)]. (8.5)
иеЕ
в основу формирования 'управляющих воздействий для нде положим
принцип оптимальности, который кратко можно сформулировать в
ВИДе:
следует искать всеrда оптимальное продолжение процесса
относительно Toro состояния, которое достиrнуто в данный
мемент.
Как известно данный принцип оптимальности был предложен Р.
Беллманом. На ero базе им был построен метод динамическоrо
. проrраммирования, кс'{ьрый может быть эффективно  nрименен для
широкоrо Kpyra"'CJ.tCTeM (не ТОЛЬК<9 описываемых дифференциальными
:' уравnениями).
НДС (8.1) будем рассматрива;rь на некотором нечетком интервале
времени r(t) ': Т  (01]. Так как функция !'(V,u) определяет выrрыЪ
ш
по критерию. v Е" -8,' то по всем критериям выиrрыш будет
определяться заlйtсймостью:
';(и)==1 ['.(v,u)o ge(.)
е
(8.6)
в текущий момент времени. Исходя из (8.6) и нечеТJ<о..иmеrральноrо
управления ДЛЯ'лредстанления НП (5.18) интеrральный выrръIшш будет
,) Оl1редеJ1ЙТЬci функционалом:
J  .J Z(u) о J ; fr(m) о g(.) , (8.7)
т 1JI, (.Im)
Бочарников в.п.

Fиzzy Techп%gy
261
rде g(.) : 20.  [O,I],.fr :n[OI] .. нечеткий процесс на Q задаIQЩИЙ
> временную нечеТКОС"fЬ динамики ндс.
Таким образом, далее будем рассматривать для объекта (8.1) задачу
формирования оптимальноrо, в смысле максимизации функционала
(8.7), управления в соответствии с пр и няты М принципом
оптимальности БеЛ1IМ8на.
у--
Бочврников В.П.

262
Fиzzy Techпology
8.2. Метод нечеткоrо динамическоrо
проrpаммирования для формирования
управлеНlfЯ непрерывными иде
Прежде чем мы непосредственно приступим к рассмотрению метода
нечеткоrо динамическоrо проrраммирования (НДП) сделаем ряд
вспомоrательных замечаний касающихся нл /1... ro). Формально
функция /1...(0), соответствующая нечеткому интервалу -r(t): Т  [01]
может быть представлена соrласно определения.
Qnpелеление 8.1.
Нечетким моментом остановки, соответствующим нечеткому
интервалу "t(t}, который определяет временной отрезок [О, р], rде
р .. нечеткое положнrельное действкrельное число (определение
5.4) называется нечеткое множество /J..(O) удовлетворяющее
условию:
fc(ro) = v: { J;«(J))' I J;«(J))og < I т(t)оF;О. А с т } .
I ЧJ(Аlro) А
(8.8)
Как видно из определения функция /J..(O) задает некоторую aлrебру
нечетких множеств f,{ro) относительно операции взятия максимума
Соrласно определения 8.1. функция /1...(0) является изоморфной
нечеткому интервалу 1;(/), который оrpаничен нечеткими
действительными числами О и р. В том случае, коrда нам необходимо
определить произвольный нечеткий временной интервал [ро, р] будем
пользоваться следующим определением.
I ОПDепеление 8.2.
Произвольный нечеткий временной интервал определяerся двумя
нечеткими моментами остаНОВКИ/tf) «(О) и/I..(О) соrласно условия:
Бочарников В.П.

Fиzzy Techпology
263
[[д,р](ro):= {(ro)IJj(ro) :J J;(ro),A с Т,
J
l'Co°f;(-)= J f'1(,(ro)og < J [f'1(,(ro)v Jj(ro)]og <
А ЧJ(Аlro) ЧJ(АI(о)
< J fc(ro)og= 1 'Со of;(.) } .
'f(AIro> А
(Индекс i соответствует нечетким множествам из определения
8.1 ).
(8.9)
Соrласно определения и соотношения (8.9) можно сделать вывод, что
функцияfiро. РI (ro) задает подалrебру в алrе6ре определенной функцией
Il...ro). с учетом рассмотренных определений перейдем к выводу
Функциональноrо уравнения для определения оптимальноrо
управления ндс.
Пусть динамика нде рассматривалась на нечетком интервале
: 1i Lpo,PK]" Тоrда функциональное уравнение для определения
; оптимальноrо в смысле максимизации критерия (8.7) управления
. может быть записано в виде:
J*(z() == maxJ(ZI(p.»,
иеи '
(8.1 О)
rДе PiE [Ро,Рк]. Для определения оптимальноrо управления,
удовлетворяющеrо (8.1 О) рассмотрим следующую теорему.
Теоnема 8. 1=
Опrnмальное в смысле максимизации критерия (8.7) управление
находится из Функциональноrо неравенства вида:
J$(u.) > тах/ l'(uv)o ge(.)
иеи е
(8.11 )
(Аналоr уравнения Беллмана).
, Доказательство..
. Рассмотрим функциональное уравнение (8.1 О). В соответствии с
определением 8.1. выражение для критерия J примет вид:
kr
Бочарников В. п.

264
Fuzzy Techпology
J(u)==шахll(u)о 1 h(lO)og(.)==JI(u)o I { ":J;(lO) } о g(.).
llElJ т 'Р( -1ш) т 'Р( -Iw) ,
Будем рассматривать ндс на интервале [р;, P,J. Соrласно
приведенноrо ранее принципа оптимальности на данном интервале ДЛЯ
.
оптимальноrо управления реализуется Функционал J (и) , который
задается соотношением:
J(u*) == шах J l(u) о I f[p',p ]g(.).
llЕи Т 'Р( -Iw) I lr
Допустим., что на нечетком интервале [р; + др, Рк] соrласно принципа
.
оптимальности реализовалось оптимальное управление u Е u.
Тоrда соrласно определения 8.2. и свойств нечеткоrо интеrрала можем
записать:
J(u*)==maxl1(u)o 1 f[-,fJj ](m)og(.)==
lIEU т 'Р{ -Iw) I 1
== maxl1(U)O { J fr [ п п_+л,, ] (lO)оg(.)v I frn.+A.п ] (ro)og(-) } ==
lIеи т 'Р( -1ш) 1', '1"  Ч'(-Iw) w, а..ух,,.,!
==ma J 1(и)о 1 f[A.A+/'yJ](W)ogvJ(u)o 1 f rPJ +tJp,I\I(W)oFf...-) }
lIеиl т 'P{-Iw)' , т Ч'(-Iro)
Соrласно определения 8.2 при lip  о функциа Ji l ]  fr .
Р; +ЩJ'Рlr [P,Pk]
При этом второй иитеrрал, 13 случае реализации принuипа
оптимальности, является величиной не зависящий от u Е U на
нтервале [Р; + др, Рк] и l\Wжет быть вынесен за пределы операции
максимизации по u ( тах ), то есть:
lIеи
J [д _ р ] (u*» max [ ll(U)O J fr [Д  Д .+Аn](lO)оg ] V [ n_+Аnn ] (u*).
" k "Еи Т Ч'(-Iw) l' I  1"', I""""k
с учетом малости Д р можем записать:
J(u*) > тах 1 z:з(u) о 1 f[IH+f>pJ(w)o g(-).
"Еи Т Ч'(-Iw) l' I
Бочарников В_П_

Fuzzy Techn%gy
265
Используя соотношение (8.6) и теорему суджено....фубини (4.1) можем
записать:
J(u*» max { J [ JI'(Ut,V)O J f[A_A.+6pj(OJ)Og(.) ] oge } .
"еи е т '1', (.1 си) '"
Обозначим выиrрыш на интервале [Р; + др, р,]
определяемый как:
как /'(и, v)
l'(и, v) = J ['(и" v) О J fr [ ,, ".+А р] (ro)О g(.).
т '1', (-'си) ,.,,,,.,,
Тоrда функциональное неравенство для определения оптимальноrо
управления примет вид:
J(u.) > maxJ ['(и, v)o ge.
lIе(l в
Что и требовалось доказать.
[]
Рассмотренное в теореме 8.1 функциональное неравенство Иrрает роль
'уравнения Беллмана ДЛЯ метода нечеткоrо динамическоrо
проrраммирования (НДП) дЛЯ непрерывных иде.
Далее рассмотрим решение неравенства (8.1 1) (уравнения Беллмана)
дЛЯ НДС в том случае, коrда Функционал J (8.7) зависит от
выбираемоrо управления UtE U, которое, в свою очередь, не зависит от
состояния ro Е Q иде. Данный случай можно рассматривать как
вариант формирования "nporpaMMHoro" управления.
TeODeMa 8.2
Оптимальное нечеткое управление fl.(U) дЛЯ НДС (8.1) в смысле
максимума функционала (8.7), не зависящеrо от состояния НДС
может определяться нечетко",интеrральным уравнением вида:
р*(и)= J /'(и, v)o ge.
е
(8.12)
!К. 771
Бочарников В.Л.

266
Fиzzy Techпology
110казательство.
Оптимальное управление в данной теореме будем искать в классе
нечетких управлений Jl(U): U  [01]. В силу справедливости
выражения (8.] 1) и используя выражение (8.5) можем записать:
J(J1*(U» = J max [ jl*(u) л I'(и, v) ] o ge > тах 11'(u, v) о ge"
е иеи иеи е
в силу TOro, ЧТО справедливо неравенство
 vee, maxp(и» тах[р 8 (и) л f'(u, v)],
"Еи "Еи
и соrласно (3.17) можем записать:
! n;XJ1"(u)o ge > ! m,.!x[J1" (и) л ['(и. v)]o ge'
Исходя из данносо неравенства с учетом выражения дЛЯ J(J.l.*(U»
справедливо следующее сооrnошение:
J maxjl*(u) о ge > тах ll'(u, v) о ge.
е иеи uеи е
ИЛИ 9 так как в левой части неравенства подъппеrральное уравнение не
зависит от ve е, имеем:
maxjl.(u) > mах 1 I'(и, v)o ge.
I1fi.U "еи е
в случае jl. (и) = 11'( и, v) о g неравенство выполняется, а также
е е
выполняется и условие (8.1] ). Следовательно выражение (8.12)
является вариантом решения неравенства (8.11) и определяет
оптимальное управление, в смысле максимизации (8.7). Теорема
доказана.
[J
Следует отметить" что функцию выиrpыша ((и, v) можно рассматривать
как нечеткий аналоr функции Беллмана.
Теперь рассмотрим более сложный случай, коrда управление зависИТ
не только от времени t е Т, но и от состояния ндс ro е о. Обозначим
как St( ro):U х Q  [О 1]  нечеткую стратеrию управления в момент
te Т.
Бочарников в.n.

Fиzzy Techпology
267
Пусть для каждоrо из критериев v Е енечеткий выиrpыш зависит от
состояния (о Е о. Нечеткий выиrрыш при выборе стратеrии S.((o) будет
определяться нечетким отношением:
l(v, 8,(0))) : е x(UxQ) [OI].
Тоrда справедлива следующая теорема.
Теорема 8.3. ·
Если дЛЯ НДС (8.1) нечеткое управление u зависит от состояния
(о Е О, то ОПтимальное нечеткое управление <p*(u), в смысле
максимизации критерия (8.7) (с учетом зависимости управления
от (О) определяется соотношением:
f/J:(U)== 1 Ь(и,т)о g(.),
J.l r «(())
(8.1 З)
rде J.LJ(O) .. текущее состояние ИДС, а b(u,ffi) нечеткое отношение
определяемое как:
ы..и, т) = 1[1  l(u, v)]o (je(.lm)'
е
(8.14)
(J е (-1т) .. условная нечеткая мера определяющая важность
критериев v Е 8 в состоянии (о Е Q.
· Ыоказательство.
Определим нечеткий выиrpыш !'(v, s) с учетом состояния НДС:
!'(v,S) = 1 1'(v,8(m) о (Jm(.lv).
f!
(8.15)
Условная нечеткая мера (Jm(.lv) учитывает важность состояния (о с
. точки зрения оценки по критерию v Е 8. Тоrда соrласно теоремы 8.2
*
:.оптимальная нечеткая стратеrия S определяется исходя из выражения:
t.'"
1 1'(v,S)o ge == 8,*(т)
е
. .
.Подставив в это равенство (8_] 5) получим:
-s
.>
S"(m)== ![! 1'(v,S(m»o а ..(-1 v)] о ge

Бочарнuков в.п.

L015
,..uzzy I BCппO/ogy
Рассмотрим данное выражение при фиксированном состоянии <.о Е '1.
8 t (<.o) будет определять лишь нечеткое управление, то есть р(и ) SJ.. <.o):
Ux<.o  [О 1 ].
Совокупность р(и) для всех <.о Е '1 обозначим Ь(и, <.о): U х '1  [01].
Тоrда при фиксированном <.о справедливо:
ь(и,(о) = n!Z'(v,S( (0»0 о" ",(-Iv)] о ge = L l'(v,u )0(0" ",(-Iv)x ge)'
rде u =: 8,(<.0) при фиксированном <.о Е '1, а {D"ro(v)x&)'" декартово
произведение нечетких мер. Соrласно леммы (4.3) соотношения (4.24)
при фиксированном (ОЕ '1 можем записать
(D"m(.lv) Х ge) = J D"m«(J)lv) Х ge.
е
А соrласно выражений доказанныIx в лемме 4.1 справедливо
следующее преобразование:
Ь(и,т) = lZ'(v,u) о J D"ю(mllv) Х ge =
е е
= J Z'(vu)OD"m(.llO) == 1[I.......Z(v,u)]oO"m(.lm)
е е
Для определения требуемоro управления в нечеткий момент времени р
( через интервал '[ р ) при условии реализации состояния J.LJ <.о)
необходимо провести интеrpирование по g(.) на нечетком
подмножестве J..Lr{<.o) то есть:
f/J:(U) = J Ь(и,т) о g(.)
Pr(ro)
Следовательно теорема доказана.
D
Таким образом теоремы 8.2 и 8.3 позволяют найти оптимальное 9 в
смысле минимизации ожидаемых нечетких потерь (максимизации
ожидаемоrо выиrpыша), нечеткое управление для случаев, коrда
Функционал качества зависит или не зависит от текущеrо СОСТОЯIlИЯ.
Управление (8.13) реализует принцип управления с обратной связью
по измерению нечетких координат состояния идс.
Бочарников в.п.

Fuzzy Techп%gy
269
8.3. Определение функции потерь
(выиrpыша) при оптимизации
управления иде
ИСХОДЯ из приведенных в предыдущем параrрафе результатов по
, выработке оптимальноrо управления иде видно что это управление
определяется функцией потерь (или выиrрыша) l(v. и). Данная функции
нечеткоrо отношения, определенноrо на ехи является аналоrом
. функции Беллмана в классическом методе динамическоro
проrpaммирования.
Таким образом, необходимо формирование функции I(V Jl и) на основе
обработки имеющейся информации о структуре и характеристиках
идс. Множество е =={v} определяет множество критериальных оценок
. желаемоro состояния Hдe а U .... есть множество ВОЗМО>IЩых
м управляющих воздействий на систему. Для формирования функции
::!(v, и) рассмотрим дополнительно множество Х .... характеристик идс
(например характеристик состояния идс, внешних возмущений
 дополнительных (внешних) оrpаничений и т.д.).
:.

\'>
Каждая характеристика Х; Е Х принимает свои значения во множестве
A;. Множество А; может быть произвольным (числовым, номинальным,
.орядоченным ми нет и т.д.). при этом полаrаем что в конкретный
.MOMeHT времени дЛЯ НДС характеристика Х; может принимать
LiIpоизвольное как четкое, так и нечеткое значение то есть
пределяться функцией Р Х ; (о): А;  [01].
. ..
в качестве характеристик Х целесообразно выбирать такие которые в
максимальной степени определяют оценку по критерию v е е и зависят
 выбранноrо управления. Для определения функции l( V JI и) для
fфиксированных VEe сначала на основе различных методов
Kcnepmoro оценивая, обработки имеющихся наблюдений и друrих)
,
:определяется условная нечеткая мера (j . (.1 v), задающая «степень
 Х,
,
 Hoвaп

270
Fuzzy Techпo/ogy
желаем ости» значения Oi Е А ; характеристики Х; Е Х для критерия v Е е
и нечеткая мера qJ.lv) определяющая важность учета значения
характеристики Х;Е Хпри оценки по критерию v. Функции ах_ (.Iv) и
I
qJ'lv) определяют некоторую базу знаний о предметной области ндс.
Формально база знаний определяется корreжем:
(е,u, Х, {AJ, 0",. (-1 v ),fJ' ..(-Iv»)'
(8.16)
в выражении (8.16) все компоненты описаны ранее. Для определения
функции /J(v, и) В текущий момент необходимо измерить
(спроrнозировать, оценить) возможные значения (четкие или нечеткие)
характерис1ИК из Х при выборе управления ИЕ и. Пусть В результате
измерения мы имеем нечеткую функцию h(x;, а;, и) : Xx{Ai}x U ----7 [О]]
определяющую возможные значения GiE А; дЛЯ характеристики Х; при
выIранномM уравнении u Е и. Тоrда функция потерь (выиrрыша) /'(v.u)
будет определяться двойным нечетким интеrpалом вида:
l'(v,u) = i [ i h(xi,ai,u) о ах. (.,v) ] о ер x(.lv). (8.17)
х А. I
I
После взятия nepBoro интеrрала мы имеем для фиксированноrо
критерия v Е е выrоДНОСТЬ выбора управления u Е U ПО каждой ИЗ
характеристик из х. Второй интеrpал позволяет получить обобщенную
степень выrодности выбора управления u для каждоrо из критериев
VE е.
Функция (8.] 7) может бьпь использована как функция выиrpыша для
выбора оптимальноrо управления соrласно (8. 12) или (8.13), (8.14).
Использование (8.17) в случае (8.] 2) позволяет решать «статические»
задачи выбора в условиях неопределенности. Тоrда характеристики из
Х определяют показатели характеризующие объе выбора в качестве
KOToporo выступают элементы множества u Е и.
Таким образом задача мноrокритериальной е экспертной оценки
объектов из U, описывающихся набором своих характеристик из Х
является частным случаем задачи оптимизации по методу нечеткоro
динамическоrо проrpаммирования для нечетких мер. Если оценки
объектов из U были получены каждым из rpуппы экспертов Р, с
Бочарников В. П.

Fuzzy Techп%gy
271
уровнем компетентности Vp(p), ТО интеrpальная оценка при rрупповой
экспертизе будет определяться соотношением:
",(и) == f JL(u,p)oV p (.)'
р
(8. J 8)
rде Jl{u, р):::: J..Lv(u).. оценка объекта u Е UэкспертомреР..
.
Данный подход был реализован для решения задач поддержки
принятия решений в сложных трудно формализуемых предметных
областях в nporpaMMHOM продукте Expert Professional ExPro2000
(экспертная оболочка оценки альтернаrnв и выбора решений).
описанном в следующей ['лаве и успешно применялся более чем в 30
предметных областях.
lA"
Бочарников В.П.
...

272
Fuzzy Techпo/ogy
r лава 9
КОМПЛЕКС проrрАммныIx
ПРОДУКТОВ
FUZZY.. ТЕхнолоrии
Бочарнuков в.п.

Fuzzy Techп%gy
273
9 .1. Назначение проrpаммных продуктов
Fuzzу",технолоrии
Приведенные в предыдущих rлавах математические основы
обрабротки нечетких данных, которые леrли в основу Fuzzy..
технолоrии, были использованы при создании семейства проrраммных
продуктов, которые в общем случае предназначены для аналитической
обработки информации в том числе и недостаточно определенной,
нечеткой.. Как уже отмечалось ранее «нечеткий» .. это термин, который
соответствует термину fuzzy (анrл.  пушистый, ворсистый, размытый)
и применительно к информации и данным обозначает их
неопределенность, неясность. Примеры нечетких величин: "прибыль
около 2 тыс. rpH.', "температура высокая" и др
Подобноrо рода информация, как было показано ранее возникает при
решении широкоrо Kpyra практических задач и достаточно успешно
может формализовывзться на основе использования нечетких мер. При
этом, в качестве OCHoBHoro инструмента обработки TaKoro рода данных
достаточно эффективно может быть использовано нечетко..
инrеrральное исчисление.
в настоящее время, как у нас так и за рубежом, использование
нечетких множеств, мер и интеrралов давно вышло за пределы (<чистой
науки» и преобрело практическую направленность. При этом мноrие
алrоритмы обработки нечетких данных леrли в основу создания
элементной базы новейших электронных систем оценки и управления.
Значительное практическое распространение алrоритмов Fuzzy....
технолоrии обусловлено применением их в автоматизированных
системах поддержки принятия решений в виде конкретных
проrpаммных средс1В. На принципах использования Fuzzу..технолоrии
создано несколько продуктов зарубежными фирмами Management
Intel1igenter Technologien GmbH; GmbH, Fuzzy Logic 1пс, Fuzzy Systems
Engineering и др.
Бочарнuков в.п.

274
Fuzzy Techп%gy
Настоящая rлава не ставит целью провести всесторонний обзор
проrpаммых продуктов использующих в той ИЛИ иной форме
алrоритмы Fuzzy"технолоrии. Здесь лишь при водится информация по
проrраммным продуктам непосредственно использующим нечеткие
меры для представления нечетких данных в аналитических задачах и
lIечетко....интеrральное исчисление в качестве механизмов обработки
такото рода информации. Данные проrраммные продукты в основном
реализованы специалистами консалrnнroвой компании "ИНЭКС"
(Украина) и широко применяются для решения широкоro кpyra
консалтинrовых лоrистических задач внешнеэкономических операций,
оптимизаЦllИ меропияrnй формирования спроса и стимулирования
сбыта [29..3 1,39].
Областью применения рассматриваемых ниже nporpaмMHbIx продуктов
является проведение расчетов с числовыми данными и словесными
оценками в экономике, финансах, бизнесе, маркетинrе, валютом
дилинrе, везде, rде в процессе поддержки принятия решений
приходится иметь дело с информационной неопределенностью, с
недостатком или недоверием к информации.
Применение комплекса nporpaMMHbIx продуктов наиболее эффективно,
коrда:
. недостаточно статистической информации, либо эта
информация не вызывает должноrо доверия;
· проблематично или дороrо получить достаточный объем и
качество потребной информации;
I
. имеющаяся информация только или в основном словесная
(вербальная, экспертная);
. информация разнородна по источникам и составу (словесная и
числовая);
. необходимо делать проrнозы при недостаточно известных
факторах будущеro;
· предстоит анализировать риски.
в этой rлаве будут рассмотрены проrраммные продукты двух типов.
Продукты nepBoro типа это nporpaMMHbIe продукты универсальноrо
применения, которые можно рассматривать как спеuиализированные
nporpaMMHbIe среды, используя которые имеется возможность
моделирования различных предметных областей, сложных
Бочарнuков в.п.

Fuzzy Techno/ogy
275
динамических объектов и решения широкоrо Kpyra экспертно..
аналитических задач. К данным просраммным продуктам относятся:
О Fuzzy Calculator (FC)  нечеткий вычислитель;
О Fuzzy for Ехсе' (FE)  нечеткие электронные таблиuы;
о Expert Professional (ExPro)  экспертно....аналитическая
система;
О Data Engine (DE)  система анализа сложных данных;
Продукты BTopOro типа это специализированные проrраммные
продукты, предназначенные для применения в конкретных областях и
для решения определенноrо Kpyra экспертноаналитических задач. К
данным проrраммным продуктам относятся:
О Fuzzy Estimation of Critical Messages (FECM) .... nporpaMMa
для нечеткой оценки критических сообщений при
проведении арбитражных валютных операций;
О МаркетЭффект (МЭ) .... приложение из состава системы
учета и управления предприятиями FinExpert,
предназначенное ДЛЯ поиска эффективных маркетинrовых
решений.
Из отмеченных выше nporpaMMHbIX продуктов FC, FE, ExPro и FECM
являются продуктами разработки специалистов консалтинrовой
компании "ИНЭКС" (Украина). Проrpаммный продукт ОЕ является
разработкой партнера компании "ИНЭКС", reрманской фирмы
Management Intelligenter Technologien GmbH. Приложение МЭ
разработано совместно украинской компанией 10М Ltd Со и
компанией "ИНЭКС.
Бочарнuков в.п.

276
Fuzzy Techno/ogy
9.2. Проrpаммируемый нечеткий
вычислитель
Fuzzy Calculator (РС), версия 2.1
Проблема.
В ряде задач, связанных с проведением расчетов, например,
экономической эффективности сделок, их возможных издержек мноrие
числовые показатели MOryr быть определены только приблизительно,
неточно, описательно [35]. При этом количество таких показателей
часто бывает достаточно большим. Для расчетов с такими неточными
нечетко определенными числами предназначен проrpаммируемый
нечеткий вычислитель Fuzzy CaJcuJator (FC). Он позволяет, наряду с
обычными вычислениями над точными, четкими числами,. производить
математические расчеты с размытыми, нечеткими числовыми
величинами.
в теории и в FC под нечетким числом подразумевается функция
распределения уверенности человека в истинности значения числа.
Такая уверенность, как уже ранее было показано, может эффективно
быть формализована в виде распределения нечеткой меры (см. rлаву
2). Само нечеткое число может быть описано словесно. Кроме тоro,
оно может быть представлено rpафически (реже таблично).
rоризонтальная ось TaKoro rрафика  диапазон обычных чисел, а
верrnкальная  степень уверенности в их истинности (от О до 1).
Результирующий rрафик  нечеткое число.
Реальные ситуации изобилуют множеством примеров необходимосrn
использования нечетких чисел, например, таких как: "около 5", "от 3
до 2", "]0, а может быть 15", "ожидаемая прибыль около 250 тыс.
rpH.", "спрос на эТОТ вид напитков резко возрастет к июню месяцу до
800..900 шт.lдень, затем устойчиво продеРЖИТС1l на этом уровне до
осени, после чеro медленно упадет до 60....70 шт./день" и им подобных.
Бочарников в.п.

Fuzzy Techп%gy
277
Очевидно, что вариант, коrда имеется инструментальная возможность
использования нечетких чисел, является более информативным и
соответствующим действительности. В результате расчеты с
использованием таких нечетких чисел дадyr более объективные
результаты, позволят принять более обоснованные, оперативные
решения. Именно в таких ситуациях необходимость использования
предлаraемоrо FC  налицо, а получаемые эффективность и выиrрыш
по сравнению с традиционным расчетом  максимальны.
Назначение.
Проrpаммный продукт Fuzzy Calculator предназначен ДЛ1l выполнения
математических расчетов с числовыми данными, и в первую очередь с
нечеткими и/или смешанными (нечеткими и обычными, четкими)
числами. Он предназначен для пользователей, сталкивающихся на
практике с необходимостью учета числовых величин, точные значеНИ1l
которых не определены или неизвестны, но о которых все же
существуют некоторые соображения относительно их порядка и/или
характера.
Возможные области применения.
Традиционно"нечетки'области:
о анализ инвестиционных проектов, разработка и экспеprиза
бизнес..планов, решение маркетинroвых задач;
О расчеты в бизнеспланировании, оценка выrодности
предстоящих сделок,
О экспеprиза проектов, оптимизация экономических,
коммерческих операций;
О проrнозные расчеты, оценка и анализ рисков.
Исполнение.
FC  это компьютерная nporpaMMa, реализованная как традиционное
Wiпdоws..приложение. На экране компьютера FC имеет вид обычноrо
калькулятора с добавлением некоторых специальных клавиш и
rpафическоro окна отображения результата ввода и вычисления чисел.
Вид rлавноrо окна FC показан на рис. 9.1 НИЖе.
Бочарников в.п.

278 Fuzzy Techпo/ogy
Кнопка Кнопка Кнопка Кнопка Кнопка
установки отмены включения заrрузки включения
уровня последней режима nporpaMMbl режима
уверенности введенной обработки пользователя ручноrо ввода
в значенин цифры нечетких на нечетких
числа чисел трансляцию чисел
,":"uzzy Calclator  None
IJ.lHJOHHO U Н(: i .i i; 1. ){HHHHHН-}e  О;'}
 ОООС/I)(J'з....О1
r'J;:;:Y

i 1.1 7; :P',!.i!;
.
О1
е t-L .. .....
1  ..

.... .
, .....
5
.. "s
J;
??1?:'S.Of
"з OnIlOljCI)..1)1 1 SMO(I )O,.rl.a

U. (IN
I   о
Е.
 LIUJd
. .-,
:i Jfw ,
. :
11n иt
L

 ..
.{

". -:.. ""
.
,.
;4.
.... "'t"""
"'. !
е'
,.
i
.,;
 € -t-
I
.
t .  ....t.....::.."", . ..'
X .,\:..n,. ... ,У..
Кнопка
ввода
результатов
расчета в
ячейки
памяти
Кнопки ввода
чисел в
выполняемую
nporpaMMY и
продолжения
ее выполнения
Кнопки ввода,
извлечения и
сохранения
чисел в
ячейках
памяти
Кнопка
копирования
rрафика в
буфер обмена
Кнопка
перехода к
работе с
текстом
nporpaMMbI
пользователя
Рисунок 9. J  rлавная панель РС.
Функциональные возможности.
В FC обеспечивается возможность ввода пользователем, обработки и
вывода четких и нечетких чисел. Ввод нечетких чисел может
производиться как в автоматическом режиме, при котором числа
"размываются" собственно FC на основе зависимостей, определенных
ранее экспертно"теоретическим путем, так и в ручном режиме в
Бочарников В. п.

Fuzzy Techпology
279
соответствии с индивидуальным представлением сущности чисел
пользователем.
Результат ввода чисел и их обработки отображается на обычном
числовом табло индикации и в rpафическом окне. При этом в качестве
результата используются среднее ожидаемое значение числа, число с
максимальной степенью уверенности и интервал значений числа на
заданном уровне уверенности. В rрафическом окне отображается
также и непосредственно сама функция распределения числа, как это
показано на рисунке выше.
в FC есть возможность построения и анализа рисккривых. Данные
кривые определяются как соотношение нечетких мер превышения
(принижения) HeKoтoporo заданноrо значения числовой величины
значения нечеткоrо числа. Для анализа полученных результатов в FC
предусмотрены: возможность изменения используемоrо уровня
уверенности, возможность работы с памятью.
Расчеты в FC производятся непосредственно с интерфейса nporpaMMbI
а также MOryт быть записаны как nporpaMMa на встроенном, очень
простом и доступном языке проrраммирования FuzzyBasic и
транслированы средствами caMoro FC.
FC оснащен стандартной системой Windоws"помощи. Кроме тoro,
обеспечена выдача пользователю в процессе работы с FC текстовых
подсказок на числовое табло индикации.
Основные достоинства.
FC совмещает простоту обычноrо калькулятора и прекрасные
возможности по обработке приблизительной числовой информации,
нечетких, неточных" неопределенных данных. Ero использование не
требует каких...либо особых знаний нечеткой математики.
Специфические понятия и правила FC скрыты от пользователя.
Необходимо лишь понимание Toro, что такое "нечеткое число" и как
оно может трактоваться. В FC, наряду с новыми возможностями по
вводу и обработке чисел, имеете}) также целы ряд возможностей (по
сравнению с обычными расчетами) в получении дополнительных,
более адекватных результатов, в более корректной интерпретации
(трактовке) полученных результатов.
Бочарников в.п.

280
Fиzzy Techпo/ogy
Использованный подход.
В основу FC положены современные подходы искусственноrо
интеллекта к обработке неопределенной информации и
апробированная методика обработки нечетких чисел на основе теории
нечеткой меры и нечетко--интеrральноrо исчисления
Требования к вычислительной технике:
. РС",компьютер;
. Windows'9x.
Пример.
Применение Fuzzy Calculator ДЛЯ решения задачи планирования и
сравнительноrо анализа эффективности инвестиционных проектов:
.'Разработка золоторудных месторождений Украины" и "Производство
хлеба на базе сети минипекарен". В частности для одной из
важнейших составных частей такой задачи  подзадачи эксперrnой
оценки риска потери ВЮIадываемых средств. Более полробно описание
этой задачи приведено в [32].
в итоrе были получены достаточно детальные результаты,
представленные в табл. 9.1 ниже.
Таблица 9.1  Результаты анализа эффективности инвестиционных
проектов
.. ." . crc;:%: .    . , . . 
-..... -.
Проект Мини.... наиболее средне-- Макси
мальный возможный взвешен",ный мальный
"Разработка 16,4 2829.7 28,3 33
золоторудных
месторождений
Украины"
"Производство 24.7 28,9 32,2 31,5 41,4
хлеба на базе сети
минипекарен"
По имевшейся экспертной информации получено, что степень риска
(риска получения расчетных прибылей по этим проектам) у nepBoro
проекта меньше, чем у Bтoporo. При этом оба проекта находяТСЯ, в

Бочарников В.П.

Fuzzy Techпo/ogy
281
основном, в так называемой зоне повышенноro риска (25..50%).
Абсолютные значения финансовых cpeДCTB планируемых к
инвестициям, и расчетных прибылей этих проектов различны и
определяются спецификой проектов.
Бочарников В.П.

282
Fuzzy Techпology
9.3. Проrрамма Fuzzy for Excel (FE)
ДЛЯ работы с нечеткими числами
в среде MS Excel, версия 2.0
Назначение.
Очень часто при про ведении финансовых расчетов, определении
экономической эффективности сделок используются проrраммы
электронных таблиц типа Мiсrоsоft Excel. Однако далеко не всеrда
числовые показатели MOryт быть определены точно, часто .... только
приблизительно. Для расчетов с такими нечетко определенными
числами может применяться проrpамма Fuzzy Calculator, описанная
ранее. Однако она не обеспечивает работу в среде MS Excel. Для этоrо
предназначена друrая проrрамма .... Fuzzy for Ехсе' (FE).
FE является второй версией nporpaMMHoro продукта Fuzzy for Excel,
разработанноrо фирмой "ИНЭКС" и обеспечивающеrо возможность
простоrо и доступноrо использования технолоrии обработки нечетких
чисел в традиционной для пользователей среде MS Ехсеl [30].
FE реализована в виде надстройки MS Excel, которая подключает к MS
Ехсеl дополнительную панель инструментов Fuzzy Tools и меню Fuzzy
рис. 9.2.
FE, как и Fuzzy Calculator, позволяет, наряду с обычными числами,
работать с числовыми величинами, точные значения которых не
определены или неизвестны, но о которых все же существуют
некоторые соображения хотя бы относительно их порядка и/или
характера. При этом обеспечивается анализ чисел не в одном (что
свойственно традиционным числовым расчетам, в том числе и с
помощью обычных электронных таблиц), а в двух измерениях:
. собственно на числовой оси;
. и на оси уверенности (риска).
Бочарнuков В.П.

Fuzzy Techп%gy
283
 Microsoft Е xeel  F e)(celUemo
. ..:JiI  
.,..,


.
1: .  
?
Arial Су,
Е5
 . .. 
... .I'<
rl0
..
..
."
..,. .
= FuzzvFiqure 1020;1;1)
Q'
'"
[ . '
1 IJРИМЫ nОЛЬЗБI:f фунчий atg)co exc:: .Q...  FIIw tCt  t..
 . ..l. . ....i........ ....J.  ... ............. .............  "
: 3 OP..pl 1:!ЛЬЗОБ НИ f! ФУНК . даI:f ИЯ нечеТI<ИХ чисl'
i  ! Рез .льтат ."'>
 : : I.-=[  1;: .{=  C  . j
:а LI....AJ:' j\J, iI:'!.l'.: > ') ; J;. 
,  DE1"IO L. ,. ..
т.
r
А
Рисунок 9.2  Панель инструментов Fuzzy Tools
FE выполнен в виде обычной надстройки MS Excel'97 и не требует
специальных знаний математики. Ero специфические понятия и
правила скрыты от пользователя, которому требуется лишь понимание
физической при роды неопределенности и навыков интерпретации
нечетких чисел. Простота работы обеспечивается за счет Toro что FE
предоставляет ряд интуитивно понятных функций для задания
нечетких чисел И реализации традиционных арифметических
операций.
Большинство функций работает как с нечеткими, так и с обычными
числами. Правила вызова и использования функций FE традиuионны,
как в Мiсrоsоft Excel. FE также предоставляет пользователю широкие
возможности по визуализации результатов расчетов как с помощью
традиuионных средств Мiсrоsоft Excel, так и собственными,
встроенными средствами..
Попитие нечеткоrо числа в FE.
Если с обычной числовой осью (rоризонтальная ось) связать ось
уверенности в значении числа (вертикальная ось, значение плотности
нечеткой меры) и каждому значению на rоризонтальной оси
(носителю) присвоить некоторое значение уверенности (от О до 1), в
результате получится rрафик, представляющий зависимость
уверенности в том, что рассматриваемая переменная (числовая
величина) примет то или иное значение. Этот rрафик и называется
нечетким числом. Основное отличие числовых величин (например,
дохода или издержек), описываемых нечеткими числами, заключается
Бочарников в.п.

284
Fиzzy Techпology
в том, что величина размыта на числовом интервале. Причинами этоrо
размытия являются факторы неопределенности (например, возможная
потеря/приобретение новых клиентов или ужесточение/ослабление
налоrовоrо пресса и т.д.). Эти факторы и приводят к тому, что
значение величины может оказаться левее или правее наиболее
ожидаемоrо четкоrо числа. Нечеткие числа имеюr несколько
характеристик:
. число с максимальной степенью уверенности;
. число  центр тяжести rpафика нечеткоrо числа;
. максимальное значение числа по заданному уровню
уверенности;
. минимальное значение числа по заданному уровню
уверенности.
Представление нечетких чиел в FE.
В ячейке обычных Мiсrosоft Ехсеl может отображаться только одно
число, а в FE (по выбору пользователя) может использоваться одна из
четырех числовых характеристик нечетких чисел, каждая из которых в
зависимости от ситуации может оказаться наиболее полезной.
Кроме этоrо, имеется возможность npедставления нечетких чисел в
полном объеме .... rpафическом виде. Для каждоro нечеткоrо числа,
одна из характеристик KOToporo отображается в ячейке электронных
таблиц, FE дополнительно npеДОСJaвляет rpафик этоrо числа. Исходя
из соображений рациональной дискретности, lIечеткие числа в FE
npeдставляются в виде двух массивов размерности 21 каждый:
. носителя нечerкоro числа, то есть массива последовательно
возрастающих чисел от минимальноrо до максимальноrо;
. функции уверенности, то есть массива степеней уверенности,
соответствующих каждому из элементов носителя.
Для получения отдельных элементов этих массивов в FE имеются
соответствующие функции.
Обычные числа также Moryr быть npедставлены как нечеткие. Для
этоrо все элементы массива носителя числа npиравниваются к
задаваемому числу, один из элементов функции увереннос"Пf
npиравнивается к 1, а остальные .... о. в таком виде обычные числа
представляются как частный случай нечетких и с ними, как и с
нечеткими числами, работают функции РЕ.
Бочарников в.п.

Fиzzy Techп%gy
285
Использование FE.
Основные компоненты FE, которые определяют возможности
nporpaMMHoro продукта:
Q Функuии задания нечетких чисел;
Q функция расчетов FuzzyFormula;
Q вспомоrательные функции;
Q инструменты FE.
Функции задания нечетких чисел.
FE предоставляет пользователю следующий набор из 14 функций для
задания нечетких чисел различными способами вручную,
полуавтоматически или по внешним статистическим данным. Их
перечень в алфавитном порядке:
FuzzyFigure  задание числа в виде reометрической фиrуры;
FuzzyHand  задание числа из двух строк: последовательности
чисел и их степеней уверенности;
FuzzyHandFromCells  задание числа из двух последовательностей
ячеек, содержащих числа и их степени уверенности;
Fuzzylnterval  задание числа в виде ЮIтервала;
FuzzyLessThan  задание числа типа t;'меньше, чем ....";
FuzzyLessThanT о  задание числа типа 68;меньше у чеrvl... до ... ";
FuzzyMakeFromStatistic  задание числа из набора статистических
реализаций;
FuzzyMoreThan  задание числа типа "больше, чем ...";
FuzzyMoreThanTo  задание числа типа 6'больше, чсм....до ...";
FuzzyNear задание числа типа '8;около ...'1'1;
FuzzyNearAndLessTo  задание числа типа "около...и 1\leHee до ...";
FuzzyNearAndMoreTo  задание числа типа "около ... и более до
".
... ,
FuzzyNearFirstOrSecond  задание числа типа "около (... или ...)";
FuzzyNearFromTo  задание числа типа t;'около (от ... до ...)".
Пример задания нечеткоrо числа с помощью функции FuzzyFigure (в
виде rеометрической фиryры) и представления ero в FE показан на рис
9.3 ниже.
Бочврников в.n.

286
Fиzzy Techп%gy
r
: F иuу N umbers
1 ,...... 
...
ЕЗ
15
5 ...... 1
t .
1
,--'"

r

1\1'
\
i i

[. ... -
I I . , .
n ""  .. r
.. . I . . ,
.  l  & .J  ..... ..
 . . . 1 I . .
'" - I
I 
..
о , ,    t  .
--..
. , I , . \ . I
4 ' . I . ,
о r I
I
. I ,
"', I \ I ... 1 ..
I I
"J ,
О . j ..
 .........
 ,. .
CI   ,.,  .  
... о .. : 4"""  " ... .J Ф ..  ..
.. ... . .. r-
R'" ;'",
!
. !
а
'
.
а
 --:
..
S fj
1(
Рисунок 9.3 .. Задание нечеткоrо числа функцией FuzzyFigure
Автоматическое формирование нечетких чисел.
Некоторые функции FE автоматически формируют нечеткие числа
исходя из значения параметра, передаваемоrо в функцию. Прежде
Bcero это функции задания нечетких чисел типа: "около ..."
(FuzzyNear), "меньше, чем ..." (FuzzyLessThan) и некоторые дрyrие.
Правила автоматическоrо формирования чисел эmми функциями
основаны на те оретически обоснованных и достаточно
апробированных на практике авторских алroритмах
Ф}'нкция FuzzyFormula.
Функция FuzzyFormula выполняет арифметические расчеты с
нечеткими числами, которые предварительно сформированы в
ячейках. Функция имеет один параметр, представляющий собой
арифметическое выражение, которое должно состоять из имен ячеек и
обычных чисел. В ячейках, на которые ссылается функция, Moryr
находиться как нечеткие, так и обычные числа. Функция та.юке
поддерживает тот случай, Коrда все числа в выражении обычные.
Функция поддерживает все традиционные правила выполнения
арифметических операций для обычных чисел. Для нечетких чисел
Бочарников в.п.

Fuzzy Techпology
287
правила выполнения арифметических операций имеют следующие
особенности:
. допускается деление числа на нечеткий ноль;
. допускается возведение в нечеткую степень только целоro
числа.
При успеШНО1 завершении функция фОрIИрует нечеткое число 
результат выполнения заданной последовательности арифметических
операций.
Вспомоraтельные функции.
FE предоставляет пользователю ВОЗIОЖНОСТЬ воспользоваться
мноrими функциями, реаЛИЗУЮIЦИМИ ВСПОl'llоraтельные, но очень
полезные операции с нечеткими числаIИ:
Q обu,teynотребляемые операции: вычисление суммы или
произведения нескольких нечетких чисел; вычисление
среднеrо из нескольких чисел; возведение в заданную степень
и др.;
Q специфические операции над нечетКИJ\1И числами:
В03враlцение значения заданноrо параметра нечеткоrо числа;
возвраu,tение пары обычных чисел, соответствуюu.tИX
заданному УРОВIIЮ уверенности; вычисление пересечения или
объединения нескольких чисел; В03враu,tение координаты
пересечения двух нечетких линий (анало!' возможности,
ПРИСУlцей nporpa1'llMHoMY продукту Маркет Эффект) и т.д.;
D операции над нечеткиМI1 числами для использования в
прикладных областях: вычисление ставки дисконта;
возвращение обычноrо числа, соответствующеrо заданному
уровню риска; возвращение риска Toro, что нечеткое число
окажется меньше или больше заданноrо и мноrие дрyrис.
Перечень вспомоrательных функций в алфавитном порядке:
Fuzzy А \'erage  вычисляет среднее из нескольких чисел;
FuzzyComplementation  обращает функцию уверенности числа;
FU7..zyCon\r ' olution  вычисляет свертку нескольких чисел с учетом
весовых коэффициентов;
FuzzyDegreeFunction  возводит функцию уверенности числа в
заданную степень;
FuzzyGetBearer  возвращает значение носителя числа по ею
номеру;
Fuzz:yGctDiscount  вычисляет ставку дисконта;
Бочарников в.n.

288
Fuzzy Techпology
FuzzyGetLe\Je1  B03BpauJ;aeT значение уверенносш носителя
числа;
FuzzyGetMembership  возвращает значение уверенности носителя
числа по ero номеру;
FuzzyGetNumberForRisk возвращает обычное число,
соответствующее заданному уровню риска;
FuzzyGetNumbers возвращает пару оБычныlx чисел,
соответствующих заданному уровню уверенности;
FuzzyGetParameter  возвращает значение заданноrо параме1ра
нечеткоrо числа;
FuzzyGetRiskLessThan  возвращает риск Toro, что нечеткое число
окажется меньше заданноrо;
FuzzyGetRiskMoreThan  возвращает риск Toro, что нечеткое
число окажется больше заданноrо;
Fuzzylntegral  возвращает значение нечеткоrо интеrpала одноrо
числа 110 дpyrOMY;
Fuzzylntersection  возвращает координаты пересечения двух
нечетких линий;
FuzzyMax  вычисляет объединение нескольких чисел;
FuzzyMin  вычисляет пересечение нескольких чисел;
FuzzyProduct  вычисляет произведение нескольких чисел;
FuzzySum  вычисляет сумму нескольких чисел.
в FE имеется встроенная сиcrема контроля использования функций и
выдачи подсказок.
иllсТр)'МеН....ы FE.
В инструменты FE входит меню "'Fuzzy'" и панель "Fuzzy tools",
которые автоматически подключаются к Мiсrоsоft Ехсе' после
инсталляции FE.
Инструменты FE обеспечивают интерактивное задание, просмотр и
документирование нечетких чисел, а также доступ пользователя до
системы помощи и управление отображением характеристик нечетких
чисел в ячейках Excel.
Состав ИНСТРУ1\'1ентов:
D Show numbers (просмотр чисел);
D SJ)OW зо numbers (просмотр тpexMepHoro изображения чисел);
D Prepare excel diagram (I10дrотовка диarpамм FE);
D Options (опции);
D Help и About (помощь и о I1porpaMMe).
Бочарников в.п.

Fиzzy Т echпology
289
Более детальное описание FE и правила работы с ним изложены во
встроенной системе WindОWS"ПОI'l10ЩИ и соответствующем руководстве
пользователю этоro проrpаммноrо продукта.
Пример.
Один из мноrочисленных возможных ПрИl'llеров  использование Fuzzy
for Excel для npоrнозирования эффективности I'Ilаркетинrовых
мероприятий предприятия. После реализации в FE aBTopcKoro подхода
к моделированию рынка и работы На нем предприятия ввода в FE..
модель исходных данных (зачастую неопределенных) получена
исходная рыночная I'Il0дель, достаточно адекватно описывающая
происходящие на рынке процессы с продвижением товара,
функционирующая в среде FE и rpафически представленная на первом
рис. 9.4.
Данная модель позволила оценивать влияние маркетинrовых
мероприятий предприятия и дрyrих, недостаточно определенных,
внешних факторов на эффективность продвижения продукции этоrо
предприятия на рынке, а также прослеживать динамику продвижения с
течением времени.
в Tore были получены проrнозные cas}) flow, финансово..
экономические показатели работы предприятия и выработана наиболее
оптимальная ero стратеrия (в виде последовательности эффективных
I'Ilероприятий предприятия).
Бочарников В.Л.

290
Fиzzy Techп%gy
"'\: Microsoft Exccl о Market
,.a :
'"" . , 9\ ....,./f, _, '
..
'\.
 :.
I 
f
 I
, - А.;  ':."...

..
.  :'1
.o.I:?..!.9!3. o",.o.j ...
1.. Moдeb PI?. o.O' 
.
    о".....  _  ...
F«J!..' tlJCf :
.1
;....
 .
' 1 50
50
40
..,
:30
::r
2й
10
О
О
Исходная модель рынка
. .:-..
;11-:>
 t
.,.
I .
\
,

\
<.j
""
r' . t
7-
,
t
-, .
'" .
--.
. t
. s:и..t:

200
400 600
kолмчеСТ80
..
800
10Х1 ;...: ':
_"
l y
МИН.лредл. . :
........... Пост. IOд ерж.. 
: .п
11
Мин.сnроса
о 'o."" Макс. nред.л.
.............. Макс. спроса
 Периэдержки
..
o лис !. 
..
o....1 .. ';...;'
,..O;,'\....._...
Рисунок 9.4 .. Исходная модель рынка
Бочарников В. П.

Fuzzy Т echпology
291
9.4. Экспертно...аналитическая система
Expert Professional...2000 (ExPro...2000),
версия 2.0
Проблема.
Деятельность rосударственных opraHoB и учреждений, частных
компаний и отдельных должностных лиц различноrо уровня постоянно
связана с необходимостью решения задач оценки, выбора,
раюкирования и т.п. [36]. При решении задач оценки эффективности
экономических и коммерческих проектов, выбора лриоритетов
деятельности предприятий, проrноза бизнеса или рисков необходимо
анализировать объекты или ситуации, описанные неТQЧНО,
ранжировать их или сопоставлять с идеальным вариантом по целому
ряду критериев и т.д., используя при этом ли нrвистические
(словесные) Оl1Исания и заключения специалистов.
Яркими npимерами здесь Moryr быть задачи управления ресурсами
(запаСШvlИ, закупками), проrнозирования общеro состояния экономики
или предприятия, ero частных составляющих (инвестиционноrо
климата, поступлений в бюджет, маркетинrовой ситуации,
продвижения товаров и т..д.), оценки различных вариантов и схем
(внешнеэкономических операций, коммерческих сделок). Этот
перечень может быть продолжен и далее.
Несмотря на различия перечисленных задач, все они имеют одну
оБI1.{}'Ю черту  это задачи аналиmческие. Для их решения имеющихся
четких данных, как правило, явно недостаточно, однако вместо
отсутствующих данных имеется иеполная, неточная, словесная
информация.. Не вcerna при решении аналитических задач можно
привлечь достаточное количество информации причем требуемоro
качества. Это вызвано, например, или просто отсутствием физических
датчиков для измерения (наПРИlVlер, уровня cтpaHoBoro риска) или
неприемлемой ценой потребной информации. Вместо традиционных
источников информации в таких случаях может быть задействован
компетентный специалист. эксперт. Остается лишь правильно и
корректно обработать такую информацию.
Бочарников В.П.

292
Fиzzy Techпo/ogy
Традиционные системы моделирования, работающие с числовыми
данными, при решении таких задач неэффективны. В этих случаях
весьма кстати оказывается использование экспертно..аналитической
системы Expert Professional..2000.
Назначение.
Система ExPro..2000 предназначена для решения экспертно..
аналитических задач оценки и проrнозирования состояния сложных
систем в условиях неопределенности (отсутствия приоритетов и
терминолоrии, которая устоялась; слабой структуризации решаемых
задач; неточности, недоопределенности, нечеткости исходной
информации). В первую очередь, в области экономики, бизнеса,
финансов, политике и социальной сфере.
ExPro..2000  универсальная система компьютерноrо моделирования
для поддержки принятия решений, которая ориентирована на широкий
кpyr квалифицированных специалистов, исслеДУЮI1.{ИХ состояние и
поведение сложных систем различной природы. Пользователи ExPro..
2000  лица, подrотавливающие и/или принимающие решения:
руководители, аналитики, эксперты, консультанты, советники,
менеджеры и дрyrие специалисты.
ИСllолнение.
Система ExPro..2000  новая, существенно расширенная, Windows...
версия компьютерной DОS"проrpаммы ЕхРrоV.З (версии З), по сyrи 
это новый проrpаммный продукт. Ее интерфейс приведен на рисунках
ниже. ExPro..2000 функционирует на I в М"совместимых РС..
компьютерах под управлением Windows'9x (NТ) и выше.
в основу работы системы положена Fuzzy...технолоrия решения
подобноro рода экспертно..аналитических задач, являющаяся know..how
разработкой и собственностью компании "ИНЭКС". ExPro..2000
является инструментом, который в доступной форме обеспечивает
строryю математическую формализацию решения задачи, выполнение
соответствующих расчетов и анализа получаемых решений.
Система ExPro...2000 по своим возможностям объединяет большинство
дрyrих продуктов  разработок компании "ИНЭКС". Пракrnчески все
задачи, которые решаются ими, в том числе и с использованием
Бочарников В.П.

Fuzzy Т echп%gy
293
одновременно нескольких продуктов, Moryr быть решены с поrvtОЩЬЮ
одной ExPro..2000..
Общая СТРУК1)'ра ExPro..2000.
Общая структура ExPro--2000 показана на рис. 9.5. Она включает в себя
четыре основные составляющие:
Q модель предметной области .прикладной задачи, т.е. базу
знаний (зависимостей, связей, правил и Т.I1.);
Q оценки конкретных объектов из этой предметной области;
Q факторы, действующие на оцениваемые объекты;
Q расчетные алrоритмы, скрытые от обычноro пользователя
системы ExPro--2000.
...
"
- ti J_ 'п-тvaЛkLl!Sа IAf')nA
"  ............. "
n ue r, iit'.
, .  .
{tJ f
с.
.1:
aqpbJ
.будWiеrо:
ФаКТОРbl ;,, :  .' .:
Статистич&-
С'5ИР:ffНые
_....,....."(r.& ..............
;..-:- ::""" -.r;:::.'"::-.-:,'-
· 11 TCfТbI
Я 1
etн 11
э
али
........, .... --, -.' 
'. . :
....a..  .....'r:Wf.:...... .k.
   
Оцнки объеов из
преметной облсти
Рисунок 9.5 .. Общая структура ExPro....2000.
иходные данные.
База знаний является стержнем ExPro--2000. Она является
представлением пользователяаналитика о I1pедметной области, о
понятиях, о структуре задачи, взаимосвязях в ней и предпочтениях.
Совокупностью саrvtЫХ простых понятий пользователь характеризует
аналируемый объект и поэтому они называются характеристиками
,объекта. Характеристики Moryr быть словесными либо числовыми,
последние  в виде нечетких чисел или обычных. Именно эти
характеристики по встроенным алrоритмам подлежат дальнейшей
, обработке в ExPro..2000.
 и база знаний, и оценки объектов находятся под влиянием внешних
факторов, сила и состав которых меняется во времени. Эти факторы
р'
Бочарников в.п.

294
Fuzzy Techпology
по отношению к текущему моменту времени разделяются на факторы
npошлоro и будущеrо. Отображением факторов npошлоrо являются
различноrо рода статистические данные, которые Moryr
использоваться также для задания числовых характеристик объектов.
Факторы будущеrо отражают взrляды аналитика на динамику
процессов и оценок объектов. Факторы будущеrо Moryr иметь
различную физическую природу, но они Moryr быть описаны рядом
общих проrнозных параметров: временем существования, силой
проявления, своей важностью и возможность возникновения. Такое
представление позволяет моделировать достаточно широкий спектр
возможных вариаций факторов будущеro. Таким образом, исходными
данными являются:
. совокупность характеристик оцениваемых объектов;
· система критериев оценки и предпочтений;
. оценки частных характеристик KOHKpeTHoro объекта;
. описание внешних факторов.
Порядок решения зкспертно..аналитических задач.
Решение экспертно..аналитических задач осуществляется на основе
хорошо зарекомендовавших себя авторских алrоритмов представления
и обработки информации, заложенных в ExPro..2000. Их работа в
целом заключается в сведении частных характеристик каждоrо
объекта, оцененноrо пользователем, к системе интеrpальных понятий
базы знаний и получении, таким образом, обобщенных оценок этих
объектов. Если база знаний и оценки объектов статичны (нет факторов
будущеrо), имеем решение задачи оценки.. Если задано влияние
факторов будущеrо на базу знаний или/и оценки объектов, имеем
решение задачи проrноза.
Решение задач и оценки, и проrнозирования осуществляется на единой
основе, по единой технолоrии, что упрощает задачу пользователя по
овладению и пользованию системой. Каждый шаr работы в ситеме
ExPro..2000 документируется и может быть использован для контроля,
анализа и пояснений.
Характеристики ExPro:
t/ характер исходной информации  линrвистическая, неточная,
неполн8Я, а также обычная;
Бочарников в.п.

Fиzzy Techпology
295
 поддерживается процедура rpупповой оценки объекта
несколькими специалистами;
,/ имеется возможность npоведения анализа получаемых
результатов, их зависимосm от исходных данных;
,/ теоретическая база системы перспективный
матемаrnческий аппарат теории нчетких мер и множеств.
Получаемые резуль"rа"rы.
На базе ExPro Moryr быть построены различные npикладные системы,
работоспособные в условиях информационной неопределенности.
Например:
Q экспертные системы анализа инвестиционных и дрyrих
коммерческих npоектов, внешнеэкономических операций,
TOBapHoro MapKem.нra;
Q системы ранжирования и выбора альтернатив;
Q системы расчета инвестиционных качеств ценных бумаr,
банковских кредитных рисков, анализа валютноrо рынка,
рейтинrования банков;
Q системы выявления и расчета рисков в бизнесе, экономической
безопасности в целом;
Q системы классификации в экономике, политике, медицине и
др.
Мноrие из таких прикладных систем уже созданы и эффективно
Функционирую в том числе и в условиях информационной
неоnpеделенности, коrда дрyrnе аналоrичные системы не работают.
Фрarмент интерфейса системы ExPr<r2000 и примера получаемых
результатов, а также структуры использовавшейся базы знаний одной
из уже созданных специализированных систем представлены
соответственно на рис. 9.6 и рис. 9.7 (более темным цветом показаны
характеристики которые числовые, светлым словесные,
линrвистические ).
Экспертно--аналИ1Ическая систеrvtа ExPro--2000 и ее предшественница
ЕхРrоV.З апробированы на решении более чем 40 конкретных задач из
самых различных предметных областей: от экономики до техники.
Использование этоrо универсапьноrоииструмента позволяет не только
получать решения сложных аналитических задач. но и
совершенствовать свой профессиональный уровень специалистам,
Бочарников в.по.

29б
Fuzzy Techп%gy
работаюшим с системой, rлубже I1рОНИКать в I1РИРОДУ анализируемых
I1роцессов.
 ..\ (pc,' ProfrJ Уonв.( ZnU9 - Cop .
 C.,(Ii:"i 41:t1'1.J  :t  -:
. : . . Ii -.,. .":- . . j . :
.;;   .,.  .  ., ..'  .:;;.
f.:,

..
.
:: ... ;.F... ;  . t:'........"\.>
Н6 ft лnaJfl$

RfI О
.х (

...

fI
, ,
. I!
.
.
....,...... ...
 ......:,......t..... L.
" .H.....",..,..ao..;+;rJI'ateJ
-1 T . . .. '*
., i. Co6EТ1' ''f!j , !r
4JL""""",,,,,:Q.,. . .... ",",.. ....".,. .
....у
_" . '!OJ .
..-
.... .... ..  "' .J'. 
...3 
:. . 8$
 , :'';i ..'. 
F иzzy est;mat;on
.:
Фокс
'. . ..
Ф.с
t..."$ '..;,'
 . .
d\S' !>..;:.:
"'I!
l'
:'
j4 i
. . i I
..
.... t..
"J)I

yt:
. .:: i

t t. Cl6bn' ;
:!......""""""'\."Ii:
..at
..
 75 : IIIJ
" ;.;. О!'"!' 1.. ./....
 ,.
l
rJ 2
0.020
. . .
t  Jареziurп
r   ....
I
05
1 
u 
. <

..;,.
..
....
Собыr1

C2
"'..:.
.
П).
O
,".
,
, r
-1
t1: :;
.... ...................... .....................
..;;.0.... \0.--
'...... :;,,:х;.а.:;
7.0-;.
, .
J J
li3
Рисунок 9.б  Фраrмент интерфейса системы ExPro..2000
Бочарнuков В.П.

Fиzzy Techп%gy
297


l'
'#
, ,1
'!
/1
./.t
2
 Knowledge В as-e
." !lr
' ",Т ."t J! .:
I
., ;:'.:. fi :.;, '"
. ,
. ,A'
с
.
1...
.,:'
,;
';! t..  -
Jt ,
.. ,.J '
, , 
...
:' 
Рисунок 9.7  Фраrмент структуры базы знаний.
, . <'
.
9
.]>
.
,.,
,
1-


Зак. 771
""...
'.' .....il
. ' J' 
. . .у t
5;;" -,

tf ...  ...IИ. "'..  (
;.6
1'" ... ..
Бочарников В.П.
.

298
Fиzzy Technology
9.5. Проrрамма Fuzzy Estimation ofCritical
Messages (FECM) дЛЯ нечеткой оценки
критических сообщений при проведении
арбитражных валютных операций,
версия 1.1.
Проблем8.
Любой начинающий трейдер знает, что анализ цен на валютном рынке
FOREX покоится на двух китах: техническом и фундаментальном
анализе. Первый из них более формализован и леrок в интерпретации,
поддерживается развитым проrpаммным обеспечением. В отличие от
технических, фундаментальные по казател и (и их ожидания)
интерпретируются менее определенно, их влияние на динамику цен
носит зачастую непредсказуемый характер, что может приводить к
катастрофически большим денежным потерям и даже к разорению
трейдеров. каждыIй учаСТНИI\ тoprOB интерпретирует фундаментальные
факторы по своему и .'Н3 rлазок, может по..разному смотреть на их
влияние на динамику курса и с разной степенью доверять им. Новостей
Фундамеmзльноrо характера может быть м Horo, они Moryr
наслаиваться, дополнять или отменять дрyr дрyra, между ними
возникают и исчезают мноroчисленные системные взаимосвязи, всю
совокупность которых не в состоянии учесть даже тренированный
человек. Успешный анализ подобной информации возможен с
помощью Fuzzy..технолоrии.
Именно для этих целей специалистами консалтинrовой фирмы
"НИЗКС" на основе современной технолоrии обработки нечетких
данных разработан проrраммный продукт Fuzzy Estimation of Critical
Messages (FECM), позволяющий производить оценки критических
сообщений при проведении арбитражных валЮ1Ных операций. FECM
осуществляет интеrральную о цен К}' влияния сообщений
фундаментальноrо, техническоrо и психолоrичеекоrо характера,
Бочарников В.П.

Fиzzy Techп%gy
299
поrупаюших .8 процессе ToproB, на курсы валют и работает в
режиме близком к режиму реальноrо времени.
Основным вопросом для участников валютных ToproB является вопрос
правильноrо проrноза: Korna в какой момент и насколько
"переломится" курс, чтобы изменить свою тактику или предпринять
меры предостережения. Для решения проrнозной задачи участники
валютноrо рынка (а также участники внешнеэкономической
деятельности) получают из различных источников например, из
информационных финансовых систем типа Reuters Terminal в реальном
масштабе времени информацию двух принципиально различных
типов:
. о кошровках, курсах валют, количестве и суммах сделок по их
npодаже/покупке;
. о событиях и факторах, которые прямо или косвенно Moryr
влиять на курсы валют.
Информация nepвoro типа представляет собой временную
последовательность исключительно цифровых данных. Они Moryr
быть леrко отображены, проанализированы и обработаны
существующими проrраммами финансовоrо техническоrо анализа
типа Тrзdе Station. В содержательном плане они отражают только
предысторию изменения курсов валют и любые попытки
проrнозирования с помощью компьютера по этой информации не
MOryт быть построены по иному при н ципу, чем принцип "прошлое
определяет будущее'.
Однако на практике все происходит rораздо сложнее. Возникают и
исчезают события и фаКТОРЫ t на которые реаrирует мировой рынок.
Сведения о них содержатся в информации BTOpOro тип3, которую
участники ToproB Moryт получать в виде текстовых сообщений. Эти
сообщения Moryr касаться и npошлоrо, и будущеrо. При этом каждый
участник тoproB может по--разному смотреть на их влияние и с разной
степенью доверять им. Сообщений очень MHoro, они наслаиваются,
дополняют или отменяют друr друrа.
Однако человек в состоянии учесть действие Bcero до 5..7 факторов, а
хорошо тренированный  до 12..15. Дальше этоrо пороrа начинаются
ошибки, которые оплачиваются деньrами. К сожалению, большинство
Бочарников В. п.

32б
Fиzzy Techпo/Ogy
ЛИТЕРАТУРА
1. Обработка нечеткой информаuии в системах принятия решений /
А. Н. Борисов, А. В.. Алексеев" r. В. Меркурьева и др. .. М.: Радио и
связь, 1989. .. 304 с.
2. Т. Саати, К. Кернс. Аналитическое планирование. Орrанизация
систем: Пер. с анrл... М.: Радио и связь, 1991.  224 с.
3. Линник А.П." Климов С.А. Инвариантные выводы в статистике.. ..
М.: Радио и связь, 198бr.. .. 408 с.
4.. Мелихов А.Н., Берншейн Л.С., Коровин С.Я. Ситуационные
советующие системы снечеткой лоrикой. ... М.: Наука, 1990. .. 312
с..
5. Понаморев ю.п. Иrpовые модели: математические методы,
психолоrический анализ. .. М.: Наука, 1991. .. 160 с.
6. Павлов В.В. Синтез стратеrий в человеко"машинных системах. ...
К.: Выща шк. rоловное изд"во, 1989. .. lб2 с.
7. Анохин П.К. Принципиальные вопросы общей теории систем. ..
М.: Ун"т дружбы народов им. п. Лумумбы, 1971. .. 40 с.
8. Клир Дж. Системолоrия. Автоматизация решения системных
задач.: Пер. с анrл. .. М.: Радио и связь, 1990... 544 с.
9. Б.М. rерасимов, В.А. Тарасов, И.В. Токарев. Человеко"машинные
системы при няrnя решений с элементами искусственноro
интеллекта.. К.: Наукова думка, 1993 r. 184 с.
10. Sugeno М. Fuzzy Measure and Fuzzy Integral./I Transaction of the
Sosiety ofInstrument and Control Engineers, Tokyo. .. 1972. .... v.8, И!! 2.
.. рр. 218..226
11. Дюбуа д., Прад А. Теория возможностей. Приложения к
представлению знаний в информатике.: Пер. с фр. .. М.: Радио и
связь, 1990... 288 с.
12. Нечеткие множества и теория возможностей. Последние
достижения.: Пер. с анrл.l Под ред.. Р.Р. Яrера. .. М.: Радио и связь,
198б. .. 408 с.
13. Дмитриев А..К., Мальцев П.А... Основы теории построения и
контроля сложных систем. .. Л..: Энерrоатомиздат. Ленинrpадское
отд"ние, 1988. .. 192 с..
14. Турбин А.Ф." Працевитый Н.В. Фрактальные множества, функции
распределения. .... К.: Наукова думка, 1992. .. 207 с.
Бочарнuков В.П.

Fиzzy Techпology
327
15. Нечеткие множества в моделях управления и искусственноrо
интеллекта) ПОД ред. Д.А. Поспелова... М.: Наука, 1986... 396 с.
16. Sugeno М. Fuzzy Oecision Making ProbIems.!/ Transaction of the
Sosiety of Instrument and Control Engineers, Tokyo. .. 1975. .. v.ll, Н!!
б. ... рр. 85..90.
17. Прикладные нечеткие системы: Пер с япон.! К. Асаи, д. Ватада,
с. Иван и др.; Под ред. Т. Терано, К. Асан, М. CyrCHO, .. М.: Мир,
1993 r. .. 38б с.
18. Кофман А. Введение в теорию нечетких множеств: Пер. с франц. ...
М.: Радио и связь, 1982. .... 432 с.
19. Зллиот Р. Стохастический анализ и ero приложения.: Пер. с анrл. ....
М.: Радио и связь.. 1990. .. 324 с.
20. Алиев Р.А., Церковный А.З., Мамедова [.А. Управление
производством при нечеткой исходной информации. .... М..:
Знерroатомиздат, 1991. .. 240 с.
21. Ульянов С.В. Нечеткие модели интеллектуальных промышленных
систем управления.! Известия АН СССР. Техническая
кибернетика. Н!! 3, 1991. .. С 38 - 49.
22. Бочарников В.П., Цыrанок А.В., Свешников С.В. Fuzzу"технолоrия
решения экспертно--аналитических задач оценки военно--
политических ситуаций в условиях неопределенности: Научно..
методическое пособие. ... К.: в/ч А 4000, 1997. .. 68 с.
23. Бочарников В.П. Модель нечеткоrо процесса для задач управления
нечеткими динамическими системами)1 Проблемы управления и
информатики. .. 199б. .. Н!! 3. .. С.61--6б.
24. Бочарников В.П. Обеспечение скрытности информации как
нечerкий динамический процесс.ll 3ап.tита информации. .. К.,
КМУfЛ, 1995... С. 70-74.
25. Бочарников В.П. Дискретная модель нечеткоrо процесса на основе
нечетко..интеrpальноrо уравнения.!1 Прикладные системы
искусственноrо ишеллекта в задачах автоматизации, тестирования
npоrpзмм и управления в технических системах. ... К.: Кf\ЛVfЛ,
1998. С.
26. Корн r., Корн Т. Справочник по математике для научных
работников и инженеров. .. М.: Наука. rлавная редакция физ...
матем. литературы, 1984..... 831 с.
27. Перфильева И.f. Приложение теории иечетких множеств./ Итоrи
науки и техники. Серия: Теория вероятностей. Математическая
статистика. Теоретическая кибернетика. Том 29./1 Под ред.
fамкрелидзе. .. М.: ВИНИТИ, 1990. .... 150 с.
Бочарников В.П.

328 Fиzzy TechпoJogy
28. Zadeh L. А. Toward а theory of. fuzzy systems.l Aspects оп Network
and System TI)eory. Holt, Rinehart, Wiпstоп, N.Y. .. 1971, рр. 209 ..
245.
29. Риски во внешнеэкономической деятельности предприятий.! В.П.
Бочарников, С..М. Репецкий, К.В. Захаров и др. .. К.: 000
«Интер rи Д», 1997. .. 124 с.
30. Бочарников в.п. Свешников С.В. ВознякС.Н. Проrнозные
коммерческие расчеты и анализ рисков на Fuzzy for Excel.  CaHKT
Петербурr: «Наука» РАН, 2000. 159 с.
3 1. Бочарников в.п.. Захаров К.В. ЦыrаНОI< А.В., Лоrистика,
эффективность и риски внешнеэкономических операций. .. Санкт..
Петербурr: «Наука» РАН, 2000. 237 с.
32. Цыrанок А.В. Шампанское без риска. // Бизнес. Бизнес компьютер
.... 1997. .. N2 4 (211). ... С.39.
33. Садовский А.Л. Применение экспертных методов в задачах
принятия решений в условиях нечеткой информации.! Принятие
решений и анализ экспертной информации. Вопросы кибернетики.
.. М.: 1989. .. с. 45..53.
34. З8Йченко ю.п. Исследование операций: Нечеткая Оl1ТИмизация:
Учеб. пособие... К.: Выща шк., 1991. .. 191 с.
35. Если вы не уверены в числах, используйте Fuzzy Calculator./ в. п.
Бочарников, Ю.Н. Минаев, С. В. Свешников и др.. Компьютерное
обозрение N212(3б), 1996. .. с. 20  21.
3б. Бочарников в.п. Свешников С.В. Цыraнок А.В. Компьютер
nOMoraeT принять правильное решение.! Компьютер + nporpaмMbI.
NQ 2 (17), 1995. .. С. 4 .. 6.
37. Bocharniko\r1 У.Р. Modeling of Fuzzy Processes оп the Theoretical
Basis of the Fuzzy Measure and Integral / Proc. EUFIT'98 .. Sixth
European Congress оп Intelligent Techniques and Soft Computing ...
Aachen, Germany: Elite..Foundation. .. 1998. .. Р. 2234..2239.
38. Bochamikov V.P., Tsiganok А. V. Fuzzy Tecl)nology the Analysis and
Risk Menedgment I Proc. EUFIT'98 .. Sixth European Congress оп
Intelligent Techniques and Soft Computing .. Aachen, Germany: Elite..
Foundation. .. 1998. .. Р. 2541..2545.
39. Бочарников в.п. Модель управляемоrо неnpерывноro нечеткоrо
процесс а на основе нечетко..интеrральноrо уравнения.!/ Проблемы
управления и информатики. .... 1998. .. NQ 5. .. С. 72..77.
Бочарников В.П.

Издание ОС1/ществлено при 1/частии
издательстfJа «ААетеЙЯIt (СПб.)
ИЛ М 064366 от 26. 12. 1995 r.
Издательство . Алетейа. :
193019, Санкт..Петербурr, пр. Обуховской обороны, 13
Телефон издательства: (812}5672239
Факс: (812}5672253
E..mail: aletheia@spb.cityline.ru
Сдано в набор 09.0.2000. Подписано в пеЧ8Т. .28.0.2.2001.
Формат 60 х 88/16. 20,5 п. л. Тнраж 1200. 38каз N! 771
Orпечатано с rотоиыx ДИ8ПОЗИТНВОВ в АIC8ДеNИЧКJCОЙ ТRПОrpaфии
.Наука. РАН;. 199034. СаВJ(тПетербурr. 9 пиии.. д. 12
Printed in Russia