и. АЙЗЕНБЕРГ, В. ГРАЙНЕР
МЕХАНИЗМЫ
ВОЗБУЖДЕНИЯ
ЯДРА
6
7
9
ЭЛЕКТРОМАГНИТНОЕ	12
И СЛАБОЕ ВЗАИМОДЕЙСТВИЯ	.. 15
. 15
Перевод с английского	15
канд. физ-мат. наук С. П. Камерджиева	я’ 22
29
33
. 33
 43
48
. 55
. 59
• 59
I
77
83
87
| 90
» 94
101
107
112
123
МОСКВА АТОМИЗДАТ 1973
132
134
3
УДК 539.144
NUCLEAR THEORY
VOLUME 2
EXCITATION MECHANISMS OF THE NUCLEUS
ELECTROMAGNETIC AND WEAK INTERACTIONS
Judah M. Eisenberg, Professor of Physics.
University of Virginia, Charlottesville, Virginia, U. S. A.
Walter Greiner, Professor of Theoretical Physics.
Johann Wolfgang Goethe Universitat, Frankfurt am Main, Germany
1970
NORTH-HOLLAND PUBLISHING COMPANY
AMSTERDAM—LONDON
V
a
Jfexa- *
В.
Айзенберг И., Грайнер
низмы возбуждения ядра. Электромагнитное и" сла-
бое взаимодействия. Перев. с англ. М., Атомиад&Г,
1973 , 348 с.	-
д ’
Книга является вторым томом трехтомнои. мо-
нографии, посвященной современной теории стр'ук-\_
туры ядра. Авторы исходят из основных лринципо^^
теоретической физики, что придает изложению '
стройность и убедительность.
В данном томе рассматривается теория элек-
тромагнитного взаимодействия ядер — взаимодей-
ствие с у-квантами, электронами, р-мезонами, ку-
лоновское возбуждение — и слабое взаимодействие
в ядрах — Р распад, p-захват. Многие из рас-
смотренных вопросов плохо отражены в нашей
учебной и обзорной литературе (рассеяние элек-
тронов, взаимодействие с р-мезонами, реориента-
ционный эффект).
Книга написана на высоком педагогическом
уровне. Авторы не только обсуждают физический
смысл результатов, но и довольно подробно пока-
зывают, как они получены.
Рис. 53, табл. 9, библиографии — 391 назва-
ние.
0237—018
034(01)-73“ 18—73
© Атомиздат, 1973 г.
I
ОГЛАВЛЕНИЕ
Предисловие авторов к русскому изданию	6
Предисловие переводчика ...	7
Предисловие.................................................... 9
Введение...................................................... 12
Часть I. ТЕОРИЯ ИЗЛУЧЕНИЯ И ФОТОВОЗБУЖДЕНИЕ	ЯДЕР ........ 15
Глава 1. Фотоны .............................................. 15
§ 1.1.	Уравнения Максвелла.......... 15
§ 1	2. Взаимодействие электромагнитного поля с заря-
женными частицами и законы	сохранения	22
§ 1.3.	Плоские волны	. .	29
Глава 2. Разложение по мультиполям .................... .	33
§ 2.1.	Вращение и	операторы углового момента .	.	33
§ 2.2.	Сферические	тензоры................ .	.	43
§ 2.3.	Потенциалы	и поля мультиполей	....	48
§ 2.4.	Разложение	по мультиполям для	фотонов	.	55
Глава 3. Вторичное квантование электромагнитного поля ... 59
§ 3.1.	Лагранжианы и гамильтонианы для электромаг-
нетизма ....	................59
§ 3.2.	Вторичное квантование: представление чисел
заполнения.............................. .	77
§ 3.3.	Энергия электромагнитного взаимодействия ... 83
Глава 4. Взаимодействие излучения с веществом..................87
§ 4.1.	Разложение по мультиполям и теорема Зигерта 90
§ 4.2.	Эффективные заряды для электрических переходов 94
§ 4.3.	Правила отбора по изоспину................101
§ 4.4.	Общие свойства электромагнитных переходов в
длинноволновом приближении................	107
§ 4.5.	Рассеяние фотонов; эффект Рамана..........112
§ 4.6.	Фотоядерный гигантский резонанс и правила сумм 123
§ 4.7.	Поглощение фотонов большой энергии и квази-
дейтронный механизм............................. 132
§ 4.8.	Пример; фотопоглощение в 4 Не ............134
3
Часть II. ЭЛЕКТРОВОЗБУЖДЕНИЕ ЯДЕР ............................141
Г л а в а 5. Общие свойства рассеяния электронов ...	141
§ 5.1.	Взаимодействие электрона с ядром......... 144
§ 5.2	Разложение по мультиполям для взаимодейству-
ющих зарядов . .	................150
§ 5.3.	Результаты борновского приближения с плоскими
волнами..........................................153
§ 5.4.	Сравнение процессов электрорасщепления и фото-
расщепления ядра	  164
§	5.5.	Упругое рассеяние........................166
§	5	6.	Выход за рамки борновского приближения с пло-
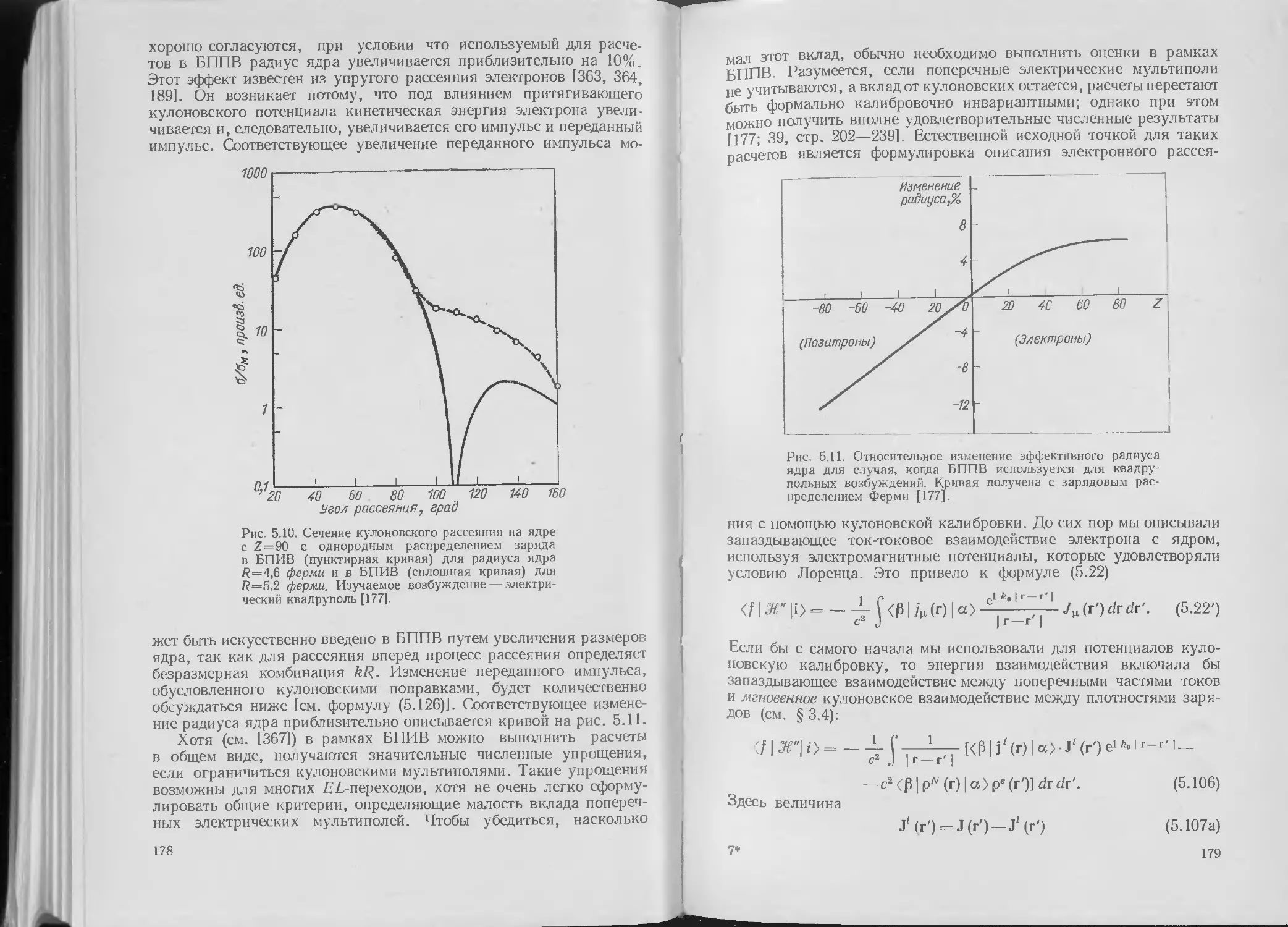
скими волнами . .	.	... 174
§ 5.7	Радиационные поправки для рассеяния электронов 185
Глава 6. Информация о структуре ядра, получаемая из анализа
электровозбуждения ядер................................. .190
§ 6.1.	Оператор электровозбуждения в ядерном про-
странстве: преобразование Фолди—Вутхайзена 190
§ 6.2.	Правила сумм для рассеяния электронов .	. 199
§ 6.3	Модель Хелма...............................204
§ 6.4	Пример: рассеяние электронов на 4Не . .	. 207
Глава 7. Кулоновское возбуждение.............................212
§ 7.1.	Полуклассическое рассмотрение кулоновского
возбуждения..................................... 213
§ 7.2.	Квантовомеханическое рассмотрение кулонов-
ского возбуждения .	 .....................225
§ 7.3.	Многократное кулоновское возбуждение и ре-
ориентационные эффекты...........................232
Гл а в а 8. Мюонные атомы....................................238
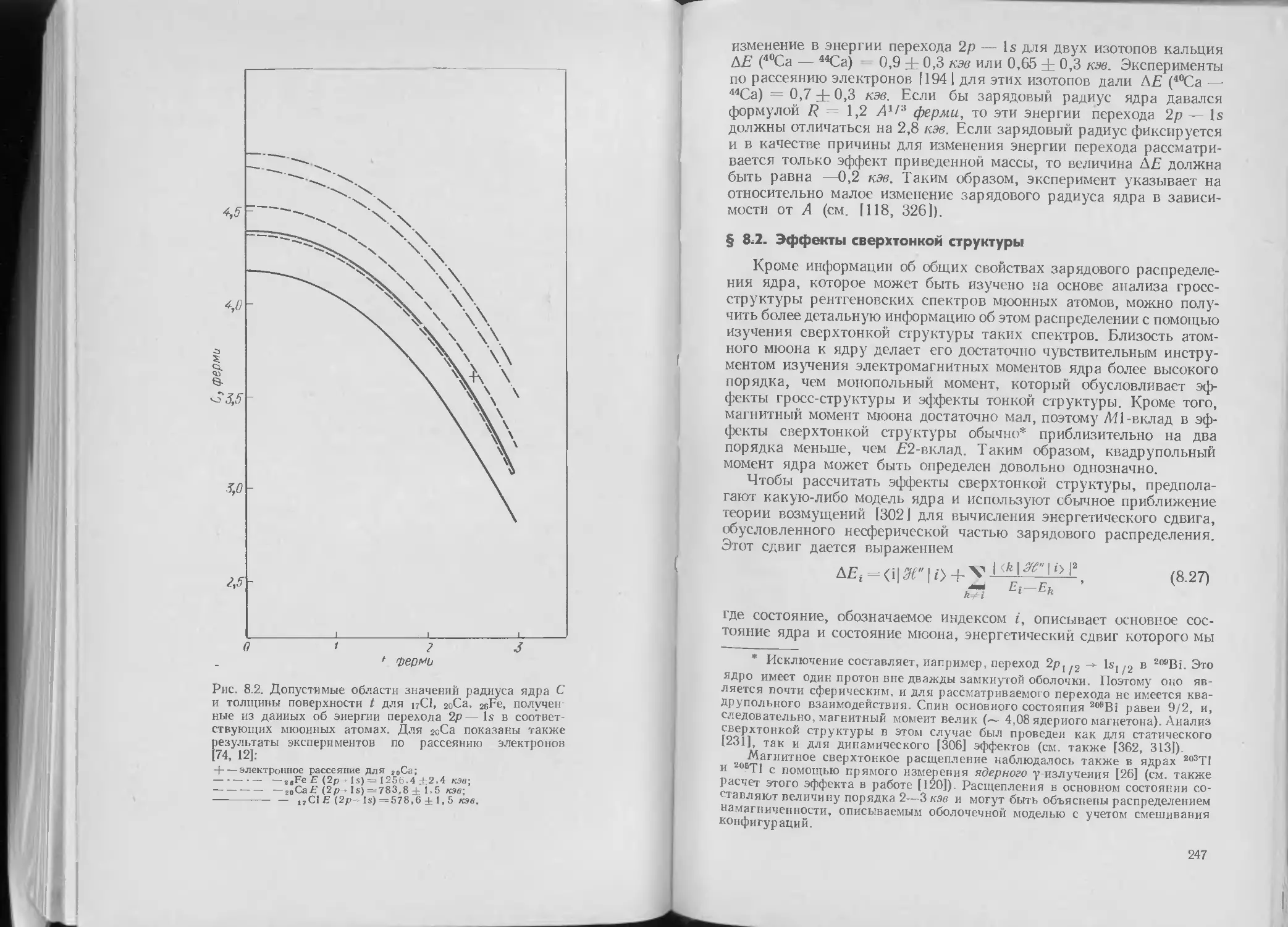
§ 8.1.	Сферическое распределение статического заряда 239
§ 8.2.	Эффекты сверхтонкой	структуры.............247
§ 8.3.	Пионные атомы	....	. 257
Часть III. СЛАБОЕ ВЗАИМОДЕЙСТВИЕ В ЯДРАХ Ч.............. .	260
Глава 9. Универсальное взаимодействие Ферми и бета-распад ядер 260
§ 9.1.	Гамильтониан слабого взаимодействия .... 260
§ 9.2.	Нерелятивистский предел в пространстве ну-
клонов ..........................................270
§ 9.3.	Разложение по мультиполям............... .	273
§ 9.4.	Бета-распад..............................275
§ 9.5.	Гипотеза сохранения	векторного тока . .	286
Глава 10. Захват мюонов......................................292
§ 10.1.	Вероятность захвата.....................293
§ 10.2.	Гипотеза частично сохраняющегося аксиально-
векторного тока..................................302
§ 10.3.	Связь радиационного поглощения пионов с за-
хватом мюонов....................................307
Приложение	А.	Квантовая теория	углового момента.....312
§ ПА.1.	Операторы углового	момента .............312
§ ПА.2.	Сложение угловых моментов. Коэффициенты
Клебша—Гордана	и	З/'-символы..........314
4
§ ПА.З.	Сложение трех угловых моментов, коэффици-
енты Рака и 6/-символы.......................319
§ ПАЛ.	Сложение четырех угловых моментов, 9/-сим-
волы ...................................... -	321
§ ПА.5.	Тензорные операторы и теорема Вигнера —
Эккарта......................................322
§ ПА.6.	Обращение времени в теории угловых моментов 324
П р иложение Б. Теория Дирака .	. .	...	326
§ ПБ.1.	Уравнение Дирака и его трансформационные
свойства .	.........................326
§ ПБ.2.	Решение уравнения Дирака в виде плоских
волн.........................................330
§ ПБ.З.	Уравнение Дирака для центрального потен-
циала	.... 333
Приложение В. Матрицы плотности	.	- 335
§ ПВ.1.	Определение и общие свойства ...	335
§ ПВ.2.	Поляризационная матрица плотности .	. 335
Литература . . ................................... .	. 337
Дополнительная литература ...	.	.	.... 346
ПРЕДИСЛОВИЕ АВТОРОВ К РУССКОМУ ИЗДАНИЮ
Выход в свет русского издания нашей книги, посвященной тео-
рии ядра, — большая радость для нас. Мы надеемся, что книга
будет полезна студентам и специалистам различных профилей.
В прошлом в России, а впоследствии в Советском Союзе был
достигнут высокий уровень работ в области атомной и ядерной
физики. Этот уровень сохраняется и в настоящее время.
Мы будем также очень рады, если перевод этой книги поможет
дальнейшему развитию международных связей и сотрудничества
в деле решения увлекательных проблем физики ядра.
Шарлоттесвилле, Виргиния
Франкфурт на Майне
Сентябрь 1972 г.
И. М. АЙЗЕНБЕРГ
ВАЛЬТЕР ГРАЙНЕР
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
Изучение взаимодействия ядер с полями, слабыми по сравнению
с полями, которые действуют между нуклонами, является важней-
шим методом изучения ядерных свойств. Слабость поля «пробных»
частиц позволяет рассматривать все процессы в рамках теории
возмущений по взаимодействию ядер с такими полями. При прочих
равных условиях это, как правило, значительно увеличивает на-
дежность получаемых результатов и обеспечивает относительную
простоту их интерпретации по сравнению с результатами, которые
получаются с помощью частиц, сильно взаимодействующих с ядром.
О популярности указанного метода изучения ядер свидетельствует,
в частности, непрерывное строительство и совершенствование со-
ответствующих экспериментальных установок. Объем накопленной
информации в этой области огромен и продолжает быстро расти.
Книга Айзенберга и Грайнера посвящена рассмотрению теории
взаимодействия ядер с электромагнитными полями и теории слабого
взаимодействия в ядрах. Она является вторым томом трехтомной
монографии авторов «Теория ядра». Авторы — известные физики,
активно работающие в области теоретической ядерной физики, в ча-
стности в области приложения формализма, описанного во втором
томе. Л1онография написана для читателей, изучивших обычный
одногодичный курс квантовой механики и общий курс ядерной
физики. Авторы поставили перед собой благородную цель — дать
систематическое изложение современной теории ядра исходя,
по возможности, из основных принципов теоретической физики.
В этом смысле они делают все, чтобы теория ядра не выглядела
«набором кулинарных рецептов».
В книге с большим педагогическим мастерством изложен не-
тленный формализм, который необходим для понимания физических
процессов в ядрах, активно исследуемых и теоретиками и экспери-
ментаторами. Значительное внимание в ней также уделяется и фи-
зической стороне рассматриваемых вопросов. В литературе на рус-
ском языке до настоящего времени отсутствовали не только
книги, но и достаточно подробные и доступные обзоры по таким
важнейшим вопросам, как взаимодействие ядер с электронами и
7
ц-мезонами, слабое взаимодействие в ядрах, которые составляют
содержание второй и третьей частей книги Айзенберга и Грайнера.
Поэтому перевод этой книги является весьма своевременным.
Учитывая, что она может быть использована как учебное пособие,
при переводе было решено дополнить библиографию, приведенную
авторами, списком учебной и монографической литературы на рус-
ском языке и в соответствующих местах снабдить текст примеча-
ниями терминологического характера.
Особенностью книги Айзенберга и Грайнера является ясность
и наглядность изложения: примеры и иллюстрации тщательно
подобраны и очень хорошо «работают», материал излагается так,
чтобы всегда был виден физический смысл используемого формализ-
ма, общетеоретический материал максимально приспособлен к це-
лям ядерной физики. Другой особенностью является подробный
вывод многих важных формул, что делает ее полезной в качестве
справочного пособия при расчетах соответствующих процессов
взаимодействия ядер. Книга восполняет разрыв между имеющимися
учебниками, в которых рассматриваемые вопросы излагаются на
довольно элементарном и недостаточном для практического ис-
пользования уровне, и монографиями и обзорами, в которых изла-
гаемые в ней вопросы считаются хорошо известными читателю.
Поэтому книгу Айзенберга и Грайнера можно считать учебником
(или монографией) нового типа, который подготавливает читателя
непосредственно к чтению оригинальной литературы. Несомненно,
что она будет хорошим помощником и преподавателям, которые
теперь в большей степени смогут сосредоточиться на физической
стороне дела, и тем, кто решит самостоятельно разобраться в ин-
тересующем их вопросе. Таким образом, можно надеяться, что
книга Айзенберга и Грайнера будет «долгожителем» в нашей ли-
тературе.
С. КАМЕРДЖИЕВ
ПРЕДИСЛОВИЕ
Теория структуры ядра долгое время была одной из наиболее
трудных для преподавания областей физики. Дело в том, что мето-
ды, применяемые для изучения ядер, весьма разнообразны, и среди
них невозможно выделить достаточно широкие общие темы. Напри-
мер, экспериментально исследовались такие различные явления,
как (d, п)-рсакнии и захват мюонов. Даже те эксперименталь-
ные методы, которые взаимно связаны в силу своей физической
природы (например, кулоновское возбуждение, фотоядерные реак-
ции и мюонные атомы, имеющие в основном электромагнитную
природу), основываются на совершенно разных свойствах ядерной
динамики или статики. Вследствие этого экспериментальная ин-
формация в определенной степени имеет тенденцию к фрагментации,,
а не к интеграции. Подобная же картина наблюдается и в работах
по теории ядра. В попытках описания свойств ядер с помощью
феноменологических моделей привлекалось множество специаль-
ных областей физики, которые часто очень далеки друг от друга:
классическая гидродинамика, вращающиеся молекулы, модель
оболочек, сверхпроводимость, дисперсионные соотношения и т. д.
При таком положении большинство попыток представить физику
ядра в более или менее законченном виде сводилось к написанию
обзоров основных результатов в разных областях ядерной физики.
Читателю же оставлялась тяжелая работа понять, как первоприн-
ципы теории превращаются в детальные количественные предсказа-
ния свойств ядер. Эта работа становится все более трудной по мере
того, как литература по ядерной физике, обширная и хаотическая
уже в настоящее время, увеличивается с устрашающей скоростью,
тогда как некоторые наиболее фундаментальные принципы теории
весьма кратко излагаются лишь в оригинальных журнальных
статьях. Нам кажется, что настало время попытаться представить
накопленный материал в компактном виде и рассмотреть его>
с единой точки зрения.
В соответствии с этим мы попытались дать замкнутое изложе-
ние физики ядерной структуры, которое отражало бы главные до-
стижения теории и развивало бы их разумным образом. Нашей
9
целью было представить материал так, чтобы все результаты, кото-
рые мы рассматриваем, были бы последовательно выведены друг
из друга. Мы полагали, что физик, который хорошо знаком с глав-
ными направлениями развития теоретической мысли, сможет отно-
сительно легко применить основные методы в других областях
ядерной физики. Выполнению указанной программы очень помогли
успехи последних лет, которые привели к большему пониманию
того, как несвязанные на первый взгляд попытки описания свойств
ядер в действительности оказываются тесно связанными, если при
этом систематически применяют первопринципы теории.
Настоящее изложение теории структуры ядра состоит из трех
томов, каждый из которых, как предполагается, является отдельной
книгой, но все вместе дополняют друг друга. Содержание распреде-
ляется по томам следующим образом.
1.	^Мерные модели (коллективные и одночастичные явления).
В этом томе рассматриваются феноменологические способы описания
коллективных вращательных и колебательных свойств ядер, а так-
же эмпирически обоснованные аспекты модели оболочек для сфе-
рических и деформированных ядер.
2.	Механизмы возбуждения ядра (электромагнитное и слабое
взаимодействия). Здесь рассматриваются главные методы исследо-
вания ядра, которые не приводят к усложнениям, связанным с силь-
но взаимодействующими «пробными» частицами.
3.	Микроскопическая теория ядра. Том посвящен описанию
ядердных свойств, исходящему из «затравочного» нуклон-нуклон-
ного взаимодействия. Он включает обсуждения двух- и трехнук-
лонных систем, ядерной материи, приближения Хартри — Фока,
частично-дырочного формализма, спаривания и их связи с более
феноменологическими подходами.
Книги написаны на таком уровне, который делает их полез-
ными для тех, кто прослушал обычный одногодичный курс кван-
товой механики и немного знаком с ядерными явлениями. Они
могут служить учебниками по теории ядра для студентов старших
курсов, причем для изучения каждого тома требуется приблизи-
тельно один семестр. Это предполагает, конечно, что при работе
в аудитории часть материала в каждом томе будет опущена. Мы
думаем, что это должно быть именно так: ведь раньше преподава-
тели ядерной физики несли тяжелую ношу разработки весьма скуд-
ного теоретического материала, даваемого в стандартных учеб-
никах. По нашему мнению, лектору лучше было бы сосредоточить-
ся на физической стороне дела, представляющей интерес в его курсе,
а на долю учебника оставить задачу информирования студентов и
подготовку их к чтению журнальной литературы. Мы надеемся,
что эти книги могут быть также использованы для аналогичных
целей специалистами по ядерной физике, которые найдут в них
дополнительный материал в областях, связанных со сферой прило-
жения их главных интересов. В частности, мы думаем, что многие
экспериментаторы-ядерщики будут себя чувствовать более уверенно
10
с книгой, в которой выполняются промежуточные выкладки, чем
с той книгой, в которой они опущены, — ведь детали опускают-
ся под предлогом простоты, но это обычно приводит лишь к мисти-
фикации читателя.
Настоящий том является вторым в задуманной серии книг. Он
посвящен изложению основ формализма мультипольных полей и
квантования электромагнитного поля, а также последующему при-
менению этой техники к описанию явлений фото- и электровоз-
бужденпя, кулоновского возбуждения и к мюонным атомам. Затем
излагается теория слабого взаимодействия в ядрах, при чем осо-
бенно подчеркивается связь между этой теорией и ядерными элект-
ромагнитными процессами. Таким образом, данный том служит
естественной промежуточной ступенью между квантовой теорией
и ее применением в изучении физики ядра.
Мы очень хорошо знаем, как много людей помогало нам в напи-
сании книг, и хотим воспользоваться этой возможностью, чтобы
выразить им глубокую благодарность. Мы очень обязаны многим
физикам за полезные обсуждения, которые привели к прояснению
и лучшему отбору материала в этой книге и в остальных томах, —
докторам Акеру, Барнхилу, Даносу, Финку, Фриске, Фульчеру,
Гаю, Келли, Ле-Турне, Нильссону, Пичману, Риттеру, Шейду,
Шопперу, Соботке, Спамеру, Спайсеру, Титце, Веберу и Вайтхеду.
Один из нас (В. Г.) хочет поблагодарить доктора Кабрера за госте-
приимство, оказанное им в Университете штата Виргиния. Мы так-
же хотим выразить особую благодарность доктору Вайтхеду,
а через него Центру современных исследований Университета штата
Виргиния за решение многих трудных административных проблем,
которое сделало возможным наше сотрудничество. Мы также бла-
годарим в этой связи Немецкое исследовательское общество, Феде-
ральное министерство научных исследований и Гессенское мини-
стерство по делам культов.
Мы очень признательны редакторам Academic Press, The Physi-
cal Review, Physical Review Letters и Reviews of Modern Physics
за любезное разрешение использовать иллюстрации, которые были
опубликованы в их журналах.
Наша работа по подготовке рукописи к печати была значительно
облегчена благодаря неизменной заботе и терпению многих людей,
которые занимались размножением материала. Это прежде всего
мисс Левлейн, мисс Кнолле, мисс Пауп, мисс Валкер и мисс Вигент.
Миссис Дадакис помогала в получении библиотечных материалов,
а мисс Урбанек и мисс Спрингвальд оформляли рисунки. Мы выра-
жаем здесь нашу искреннюю благодарность за всю эту помощь.
Шарлоттесвилле, Виргиния
Апрель 1969 г
И. АЙЗЕНБЕРГ
В. ГРАЙНЕР
ВВЕДЕНИЕ
Настоящий том посвящен теоретическому описанию различных
механизмов реакций, используемых для изучения структуры ядра.
С теоретической точки зрения, прежде чем выбрать для изучения
ядер какую-либо конкретную реакцию, необходимо рассмотреть
два основных вопроса. Во-первых, необходимо понять степень на-
дежности, с которой современная теория может быть применена для
описания изучаемого процесса; во-вторых, необходимо выяснить
свойства ядерной структуры, к которым чувствительна данная
реакция. В реакциях, которые здесь будут обсуждаться, в основном
не существенны те эффекты сильных взаимодействий, которые еще
недостаточно понятны. Эти реакции будут главным образом связаны
с электромагнитным и слабым взаимодействиями, так что основная
часть обсуждаемых проблем будет относиться к структуре ядра,
а не к механизму реакции. Кроме того, эти реакции часто обладают
тем свойством, что в них возбуждаются ядерные колебания спе-
цифического характера. Соответствующие уровни обычно относят-
ся к возбуждениям, в которых много нуклонов участвует в движе-
нии на равноправной основе. Подобный вид коллективного движе-
ния в ядрах может быть описан с помощью полуфеноменологических
теорий, использующих коллективные параметры для построения
моделей ядра. При этом ядро рассматривается как непрерывное
распределение материи. С другой стороны, и это, быть может,
самое удивительное, коллективное движение может быть удовлет-
ворительно описано в рамках модели оболочек, которая с самого
начала рассматривает ядро как совокупность взаимодействующих
частиц. Изучение и примирение этих двух альтернативных подходов
является одним из основных вопросов теории ядерной структуры.
Поэтому следует ожидать, что реакции, в которых возбуждаются
коллективные колебания, будут играть особенно важную роль
в теории ядра.
Хорошим примером применения двух указанных подходов яв-
ляется описание гигантского резонанса в фотоядерных реакциях.
В 1947 г. было обнаружено [18, 19], что в реакциях, вызываемых
у-квантами, в ядрах наблюдаются сильные резонансы при энергиях
12—20 Мэв. Эти резонансы, как теперь известно, являются общим
свойством, найденным во всех ядрах, и соответствуют возбуждению
ядра электрической дипольной компонентой налетающего фотона.
То, что электрическое дипольное возбуждение электромагнитной
12
волной является предпочтительным в том случае, когда длина волны
больше размеров возбуждаемой системы, — хорошо известный и
весьма общий факт. Следовательно, преобладание этой компоненты
в фотовозбуждении при указанных энергиях в действительности
содержит лишь немного больше информации, чем подтверждение
того, что размеры ядер малы. Но понимание того, что уровни, лучше
всего возбуждаемые в дипольных переходах, все сосредоточены
в одной и той же области энергий, и что эта область в разных ядрах
находится примерно в одном и том же месте энергетического спектра,
является следствием наших знаний о структуре ядра. Оказывается,
что рассматриваемые возбуждения соответствуют колебаниям про-
тонов относительно друг друга, и поэтому они называются изоспино-
выми колебаниями*. Феноменологически такое движение может
рассматриваться как колебания сферы протонов относительно
сферы нейтронов или как колебания во взаимопроникающих про-
тонной и нейтронной жидкостях, находящихся в сферическом или
эллипсоидальном ящике. Однако можно также описать гигантский
дипольный резонанс в рамках модели оболочек. В этом случае при
образовании соответствующих уровней происходит переход час-
тицы из последней заполненной оболочки остова в следующую
оболочку. Связи между этими двумя способами рассмотрения ги-
гантского резонанса могут быть изучены весьма подробно.
Колебания, соответствующие гигантскому фотоядерному резо-
нансу, могут также возбуждаться в неупругом рассеянии электро-
нов. При малых переданных импульсах такой процесс по существу
эквивалентен фотовозбуждению и, следовательно, проявляет ос-
новные свойства тех же самых протон-нейтронных осцилляций. По
мере того как увеличивается импульс, переданный ядру электроном,
начинает играть роль новый вид коллективного движения. Нале-
тающий электрон становится чувствительным к той части ядерного
тока, которая связана с намагниченностью, и в результате воз-
буждаются уровни, которые соответствуют тому, что мы будем
называть спин-изоспиновыми колебаниями. Эти колебания соот-
ветствуют ситуации, когда протоны со спином «вверх» и нейтроны со
спином «вниз» совершают колебания относительно протонов со спи-
ном «вниз» и нейтронов со спином «вверх» (рис. В.1). Как и в случае
фотопоглощения и возбуждения изоспиновых колебаний, нет ничего
удивительного в том, что при подробном рассмотрении механизма
электровозбуждения эти спин-изоспиновые колебания должны появ-
ляться в основном при не очень больших переданных импульсах.
Удивительно то, что в эксперименте соответствующие уровни обна-
руживаются в весьма узкой области энергий возбуждений, и эта
область довольно хорошо совпадает с областью фотоядерного ги-
* Здесь и в дальнейшем авторы используют слово mode для обозначения
конкретного вида колебаний. В русской литературе по ядерной физике это
слово, обычно переводимое как мода, приживается с большим трудом и,
по-видимому, пока не является необходимым. Поэтому оно переводилось как
колебание с тем определением, которое есть в тексте. —- Прим, перев.
13
гантского резонанса. И опять, причины таких специфических свойств
заключаются в ядерной структуре указанных коллективных коле-
баний и, в частности, связаны с тем фактом, чтоядерные силы от-
носительно слабо зависят от спиновых и изоспиновых состояний
взаимодействующих нуклонов.
Возбуждение изоспиновых и спин-изоспиновых колебаний играет
также решающую роль в реакции мюонного захвата. Поэтому данная
реакция может быть использована для изучения таких колеба
и, наоборот, хорошее понимание их свойств особенно важно
выполнения полной программы описания слабого взаимодействия.
Использование мюонного захвата для изучения структуры ядра
несколько затруднено, поскольку нельзя экспериментально на
цасть I.
ТЕОРИЯ ИЗЛУЧЕНИЯ И ФОТОВОЗБУЖДЕНИЕ ЯДЕР
ГЛАВА 1
ФОТОНЫ
Рис. В.1. Графическая иллюстрация изоспиновых (а) и спин-
изоспииовых (б) колебаний ядра. Вертикальные стрелки
показывают направление спина.
блюдать вылетающие нейтрино; чтобы получить спектр возбужде-
ния, необходимо наблюдать нуклоны, испущенные после захвата.
Это в свою очередь приводит ко всем трудностям физики сильных,
взаимодействий в теории ядерных реакций. Ситуация отчасти об-
легчается благодаря тому, что можно связать мюонный захват
с радиационным поглощением пионов. В последнем процессе свя-
занный отрицательный пион поглощается ядром с испусканием вы-
сокоэнергетического фотона, который уносит большую часть энер-
гии, соответствующей массе покоя пиона. При этом очень легко воз-
буждается много спин-изоспиновых колебаний и, так как вылетаю-
щий фотон является наблюдаемым, можно непосредственно изме-
рять распределение энергии возбуждения ядра по спин-изоспи-
новым уровням.
В данном томе в основном обсуждаются лишь те аспекты ядер-
ных взаимодействий, которые можно понять без привлечения слож-
ных моделей ядерной структуры. Несколько примеров очень про-
стых моделей ядра используются для иллюстративных целей; более
подробно модели ядерной структуры рассматриваются в двух других
томах. В частности, в первом томе обсуждаются феноменологи-
ческие модели, описывающие коллективные формы ядерного дви-
жения, а во втором — микроскопические подходы к теории струк-
туры ядра.
Взаимодействие между заряженными частицами и электромаг-
тным полем — наиболее изученное явление в физике. Причин-
*го заключается в том, что, хотя полное описание электа
* магнитных явлений требует применения аппарата квантовой
гханики, можно выполнить классические макроскопические экс-
1срименты в этой области и получить соответствующие физические
законы. Эти законы, а именно уравнения Максвелла, можно затем
относительно просто обобщить на случай учета квантовых эффектов
и объединить с квантовомеханическим описанием систем частиц.
Такое обобщение было сделано в первой половине нашего века.
Сравнение построенной теории с экспериментом привело к самым
замечательным количественным результатам в физике.
При изучении механизмов электромагнитного возбуждения ядер
требуется относительно мало сведений из квантовой электродинами-
ки. Например, обычно мы не учитываем электромагнитные поправ-
ки высокого порядка, поэтому рождение и уничтожение заряжен-
ных частиц может быть описано довольно просто. Кроме того,
обычно не является существенным, выполняем ли мы расчеты с яв-
ным соблюдением требования релятивистской ковариантности или
нет. С другой стороны, нам нужен аппарат для описания рождения
и уничтожения фотонов, и, поскольку состояние ядра характери-
зуется определенным значением углового момента, мы должны
развить формализм для рассмотрения углового момента электро-
магнитного поля.
§ 1.1.	Уравнения Максвелла
Выполнение указанной программы мы начнем с краткого обзора
результатов классической электродинамики. Уравнения Максвелла
в вакууме имеют вид*:
V  Е (г, t) = 4лр (г, I),	(1.1а)
* В этой книге будут использованы гауссовы единицы.
15
(1 ] томатически включающие в себя некоторые из этих ограниче-
Т.й Такими величинами являются потенциалы А и <р. Если
, г'рвый ИЗ них определить соотношением
I	Н(г,1) = ухА(г,0,	(1.4)
^ \о четвертое уравнение Максвелла будет удовлетворяться дл_я
Ампера любого А. Подставляя (1.4) в (1.1в), получаем ---------
j йА \ _п
vxH(r,/) = ^J(r.o+-L
с	с dt
VXE(M)+-L^iA = o,
с dt
V-H(r, t) = 0.
Первые два уравнения — закон Кулона и закон ампера .
связывают электрическое и магнитное поля Е и Н с их источникам
Источниками являются плотность заряда р и плотность тока j, ком
рые должны удовлетворять вспомогательному уравнению, выр!
жающему закон сохранения заряда*:	так что
V-j(r,O + ^-^ = O.	(1.1 ввести 'потенциал <р:	t
у Ф (г, /) = —Е (г, 0 с	•
Последние два уравнения — закон Фарадея и соотношение, выра
жающее тот факт, что свободные магнитные монополи не сущее? .. нона (1 1а) тогда примет вид
вуют, — источников не содержат. Эти уравнения определяют дина Закон КУ • i й	д
мические свойства самого электромагнитного поля. Чтобы з>	V2(P4---—(V А) =	ЛР>
вершить классическое описание взаимодействия между электро	с
магнитными полями и заряженными частицами, необходимо допол	Ампера (1.16) с помощью (1.4) запишет
нить законы Кулона и Ампера вторым вспомогательным соотноше а закон
нием — выражением для силы Лоренца, которое дает силу, деи образом.	4п .	। д
ствующую на распределения заряда и тока р' (г', t) и j' (г', t) в при	v X (V X А) =— j ^~~dt
сутствии электромагнитного поля:
V/f ' С dt
) величина в круглых скобках может быть всегда запи-
видс градиента скалярной функции. Таким образом, можно
c dt
j__ад
с dt
(1.5)
(1.6)
следующим
Е= P'(r', t) E(r', t)dr' j'(r', 0 X H(r', t)dr\
V	с V
Таким образом, взаимодействие между двумя заряженными телами
осуществляется только через поле, которое характеризуете^
напряженностями Е и Н. Это значит, что одно из заряженных
тел можно считать источником электромагнитного поля, которое
затем действует посредством сил Лоренца на другое тело. Ясно,,
что не существует способа, который позволил бы нам выбрать одно
тело в качестве источника, а другое рассматривать как тело, под-
вергаемое воздействию, и фактически на начальной стадии развития-
теории электромагнетизма идея электромагнитного поля была ввод
дена довольно искусственно. В конце концов оно, конечно, «полу-)
чило права гражданства» и объективно существует в форме электро-»
магнитных волн или, если эти волны проквантовать, в форме
фотонов.
Уравнения Максвелла связывают шесть величин Е и Н, описы-
вающих поле, с четырьмя величинами р и j, характеризую-
щими источники. Очевидно, что сами уравнения накладывают не-
которые ограничения на шесть полевых компонент, и естественно
попытаться развить теорию, в которую входили бы величины,
* Уравнение (1.2) называется уравнением непрерывности. В дальней-
шем авторы пользуются этим названием. — Прим, перев.
16
(1.3
Используя тождество
V X (V X А) = —v2 А-|-v (V ‘ А),	(1.7)
получаем
2 .	1 й2 А 4л . . _ / . . 1 dq> \	z i
V2A----=--------------J+V V-АЧ--------У- -	(1-8)
c2 dt2	с \ c dt /
Уравнения	(1.6)	и (1.8) вместе с определениями (1.4) и	(1.5)	пол-
ностью эквивалентны исходным уравнениям Максвелла.	Как хо-
рошо известно, потенциалы А и ф при преобразовании Лоренца
ведут себя как компоненты 4-вектора, при этом ф играет роль
временной компоненты. Этот факт существен для ковариантной
формулировки законов электродинамики, но является второстепен-
ным для применений в теории структуры ядра. В последнем слу-
чае главное в формализме определяется тем, что ядерный гамиль-
тониан инвариантен относительно пространственных вращений,
и поэтому уровни ядра характеризуются квантовыми числами угло-
вого момента. Разумеется, при пространственных вращениях
А преобразуется как обычный 3-вектор, а ф — как скаляр. Это
приводит к несколько неточной терминологии, в которой А назы-
вается векторным потенциалом, а ф — скалярным потенциалом.
Четыре величины А и <р связаны в уравнениях (1.6) и (1.8) с ве-
личинами j и р, характеризующими источники, довольно неудобным
способом. Ыеудрбсгве пр^гвляется из-за того, что эти уравнения
2 Зак.г1ЩЗ '	17
связывают А п ф между собой. Его можно устранить, если вспом-
нить, что при данных плотностях заряда и тока физическая ситуа-
ция может быть описана с помощью многих наборов векторного и
скалярного потенциалов. Если соответствующим образом выбрать
потенциалы, то новые уравнения Максвелла больше не будут свя-
заны. Произвол в выборе А и <р возникает из-за того, что можно
выполнить особый вид преобразования, известный под названием
калибровочного преобразования. Рассмотрим
А' (г, /) = А (г, /) + vA(r, /),	(1.9а)
где А удовлетворяет уравнению (1.4). Тогда
VXA' = VXA = H,
так что А' и А эквивалентны, поскольку они соответствуют одному
и тому же значению напряженности магнитного поля. Если одно-
временно с заменой (1.9а) мы также преобразуем скалярный по-
тенциал ср по формуле
ф'(г,/)=<р(г,о—!- dN(r:t},	(1.9б)
С ot
используя ту же самую скалярную функцию Л, что и в (1.9а),
то будем иметь
Таким образом, калибровочное преобразование не меняет электри-
ческого поля, при условии что преобразования (1.9а) и (1.96) вы-
полняются одновременно.
Мы используем свободу, даваемую калибровочными преобразо-
ваниями, и наложим на наши потенциалы специальное условие,
которое будем называть условием Лоренца:
v.A + _LaL = 0.	(1.10)
с dt
Можно быть уверенным, что всегда существуют потенциалы, которые
подчиняются этому условию, так как, если найдены А и q такие,
что
v.A + -L^- = f(r,/)^O,	(1.П)
с dt
всегда можно выполнить преобразования (1.9) и перейти к новому
набору потенциалов А и ср, которые будут удовлетворять уравне-
нию (1.10). Получаем из (1.11)
д . 1 dq>	9 , , 1 <Др' . 1 й’Л с
V-A + — ^r = V-A ~V2A + ------^-+— -^T=f(r> 0
с dt	с dt С2 dt2
ИЛИ
□ A^v2A-4^A = -/(r,0,	(1.12)
с2 dt2.
18
где оператор Даламбсра определяется следующим образом:
Так как f (г, t) —известная функция, которая выражается согласно
(1.11) через старые потенциалы, можно решить это уравнение отно-
сительно А, накладывая необходимые граничные условия на со-
ответствующие А и ср. Эти новые потенциалы будут тогда удовлет-
ворять условию Лоренца.
Если условие Лоренца для потенциалов выполняется, уравне-
ния Максвелла (1.6) и (1.8) принимают вид
□	ф=-—4лр,	(1.13а)
□	А=——j.	(1.136)
с
Следует отметить, что наложение условия Лоренца еще не означает
однозначного выбора потенциалов. Можно выполнить преобразова-
ния (1.9), в которых как старые А и ср, так и новые А и ср удовлетво-
ряют уравнению (1.10). Как видно из (1.12), в такие преобразо-
вания входит функция, удовлетворяющая условию
□ А = 0.
Можно, конечно, наложить какое-либо другое полезное калиб-
ровочное условие, совершенно отличное от условия Лоренца.Един-
ственная трудность, возникающая при этом, заключается в том,
что, в то время как условие (1.10) ковариантно относительно преоб-
разования Лоренца, другое условие, вообще говоря, не будет обла-
дать этим свойством. Условие Лоренца включает свертывание
4-градиента
с 4-векюром (A.icp), и результирующее выражение будет одним
и тем же в любой системе координат. В то же время, например,
условие
V-A = 0	(1.14)
не является ковариантным. Следовательно, каждый раз, когда мы
рассматриваем нашу физическую систему в другой системе отсчета,
условие, которое накладывается на А и ф, меняется, а вместе с этим
меняется также математическая задача нахождения А и <р. Во
многих случаях это может быть значительным неудобством, по-
скольку приводит к потере изящества и математической простоты
явно ковариантной формулировки. С другой стороны, для наших
целей такие недостатки часто могут компенсироваться специфиче-
скими упрощениями, которые возникают, например, при исполь-
зовании калибровки, определяемой уравнением (1.14).
2*
19
Калибровка, в которой
у-А =0,
называется поперечной, или кулоновской, калибровкой. Если ис-
пользовать эту калибровку, то из уравнения (1.6) получим обычное
уравнение Пуассона для скалярного потенциала
у2<р(г,/) =—4лр(г, t),	(1-15)
решение которого хорошо известно:
<P(r,/) = f-,p(r,’/,) dr'.	(1.16)
J I г—Г I
Происхождение названия «кулоновская калибровка» для условия
(1.14) возникает из последнего результата, из которого видно, что
скалярный потенциал определяется зарядом и мгновенным куло-
новским взаимодействием. Потенциал в момент времени t опреде-
ляется положением заряда в тот же самый момент t. Это противо-
речит требованию специальной теории относительности, которое
гласит, что ни один сигнал не может распространяться быстрее
скорости света. Поскольку уравнения Максвелла обязательно
должны подчиняться специальной теории относительности, проти-
воречие в действительности является кажущимся. Оно возникает
из-за использования условия (1.14), которое не является явно реля-
тивистски ковариантным. Это противоречие можно устранить, если
вспомнить, что <р (г, t) непосредственно не наблюдается, а наблю-
дается только в комбинации
ю . ,,	, ,ч 1 <?А (г, /)
Е (г, 0 = — W (г> 0--------
с dt
В процессе вычисления этой величины устраняется запрещенная
теорией относительности «мгновенная» часть в Е (г, /), порождаемая
слагаемым у<р (г> 0, которое содержит заряд, движущийся в момент
времени t.
Векторный потенциал определяется уравнением (1.8), которое
для кулоновской калибровки записывается в виде
।— л	4л  । 1	. -7,
□ А=---------Н------У-^,	(1-17)
с с at
где <р уже известно из (1.16). Из уравнения непрерывности и выра-
жения (1.16) получаем
(1.18)
dt	J | г—г' |
где штрих у оператора градиента обозначает производную по пере-
менной г'. Используя этот результат, мы увидим (см. стр. 22), что
в уравнение (1.17) войдет лишь поперечный ток р, т. е.
П А(г,0=~ —Р(М)-	(1-19)
С
20
Ток единственным способом разделяется на поперечную и про-
дольную части
j j'+j',	(1.20а)
где
VJ’( =0,	(1.206)
vxj'-o.	(1.20b)
Соотношения (1.19) и (1.206) обеспечивают выполнимость условия
поперечной калибровки (1.14). Разбиение на слагаемые в (1.20)
можно понять, если рассмотреть
j'(r,0 = 4' V ’: V X Г dr'	(1.21а)
Г(М) -^-vf dr'-	<L216)
4 л J | r — r |
Ясно, что эти величины удовлетворяют уравнениям (1.206) и (1.20в)
Кроме того, интеграл в (1.216) можно записать в более удобной
форме. Сначала «проинтегрируем по частям» правую часть (1.216),
написав
г_УЧ(г',0 dr, = (‘	, j(rco_;dr,_
J |r-r'| J V Ir-r'l '
—	(1.22)
J	|r-r |
где использовано векторное тождество для дивергенции от произве-
дения скаляра s на вектор v
V(sv)~v’Vs + sV-v-	(1-23)
В силу теоремы Гаусса первое слагаемое в (1.22) можно преобра-
зовать в поверхностный интеграл
J |г—г'|
S'
dS'.
Поскольку можно считать, что распределение зарядов и токов лока-
лизовано в ограниченной области пространства, этот интеграл будет
исчезающе мал, если поверхность S' достаточно велика и охваты-
вает все пространство, которое содержит источники тока. Таким
образом, мы перенесли действие оператора у на функцию 1/| г — г' |.
Используем далее симметрию этой функции, чтобы заменить про-
изводную по г' производной по г. Тогда второе слагаемое в (1.22)
примет вид
— С j(r', 0-V'---=
J	И—г |
= fj(r,,/)-v	1 dr' = y- С ](r	(1.24)
J	И—г' |	J 1 г—г |	,
21
где последнее равенство получается из-за того, что оператор у не
действует на функции от г', например на j (г', t). Таким образом,
имеем из (1.21а) и (1.24)
jf = — Tv х у X f j(r ’ Р dr'—vv- f J‘(r ’ dr'l
4л [v J |r-r' | vv J |r-r'| J
и, используя тождество
уху xv = y(y-v)-y2v,
(1.25)
получаем
Г + Г = —7- f j (г'. О V2 . 1 , , dr'.
4л J	|r—r I
Этот интеграл легко взять, так как согласно закону Кулона еди-
ничный точечный заряд создает потенциал вида 1 |г — г'|. Ис-
пользуя уравнение Пуассона (1.15), получаем
V2 , 1 ,, = —4л6 (г—г'),
1г—г' |
(1-26)
где 6 (г - г') — трехмерная дельта-функция Дирака. В результате
имеем
j' + j' = $ 1 (г', 0 6 (Г—г') dr' = j (г, t),
что и доказывает правильность разбиения (1,20а) тока j на слагаемые
(1.21). Кроме того, ясно, что из (1.17), (1.18), (1.20а) и (1.21) следует
уравнение (1.19). Следовательно, при поперечной калибровке век-
торный потенциал определяется только поперечной частью источ-
ника.
Поперечная калибровка особенно полезна при рассмотрении
областей, не содержащих источников. В этом случае можно взять
в качестве решения уравнения (1.15) ср = 0, а векторный потенциал
будет удовлетворять уравнению, в которое источники не входят:
□ А = 0.
Пользуясь решением этого уравнения, которое удовлетворяет
соответствующим граничным условиям, можно получить напряжен-
ности электромагнитного поля
Е =
j___ЙА
с dt
Н = у х А.
§ 1.2.	Взаимодействие электромагнитного поля
с заряженными частицами и законы сохранения
Прежде чем дальше рассматривать физические свойства полей,
описываемых уравнениями Максвелла, обсудим, как связаны друг
с другом электромагнитные поля и заряженные частицы в клас-
сической электродинамике. Это означает, что в дополнение к ска-
занному о том, как заряды и токи создают поля [что мы делали
22
в связи с уравнениями (1.1)], следует также рассмотреть, как поля
действуют на заряженные частицы. Это видно из выражения (1.3)
для силы Лоренца, которое мы теперь объединим с законом Ньютона
и запишем в виде
= f Р (Г', О Е (г', 0 dr' +-L f j (г', О X- Н (г', 0 dr', (1.27)
dt J	с J
где полагают, что величина
mv
Р =—/	__
1/1—v2/c2
является релятивистским импульсом распределения заряда, на кото-
рое действует электромагнитное поле. Если мы рассматриваем
частицу с зарядом q, то
р(г,0=?6(г—гр(/)), |
j(r,O = Qv6(r—rp(O), J
где гр (0 — координаты частицы в момент времени t, a v =
= drp(t)/dt—ее скорость. Величины (1.28) удовлетворяют урав-
нению непрерывности, так как
= _qv. V6 (г-Гр (0) = - V• j (г, 0-	(1.29)
dt
Подставляя (1.28) в уравнение (1.27), можно следующим образом
записать уравнение движения для отдельной частицы:
^-=4е(гр(0,0 + —хН(Гр(0,/)] .	(1.30)
«I	с	J
Значения напряженности поля берутся в точке, где находится час-
тица. Кроме того, мы видим, что изменение энергии частицы в еди-
ницу времени дается выражением
dp	d mv
V- —— =v •-—  —	=
dt dt Vl— u2 c2
__ mv
"]/1 —v2lc2
1 m dv2 d me2	..
2 (1—c2)3/2 dt dt Vl^U2?? ’	‘ '
которое является производной по времени от релятивистской энер-
гии U me2/] 1 — о2/с2 частицы. Таким образом, с помощью
выражения (1.30) получаем
d\V
dt
или для распределения заряда
I ](г',/)-Е(г',О^г'.	(1.33)
Г dv	1 v 1	dv2 ।
L dt	2 "с2” 1 — v2/c2 dt J
(1.32)
qv- E,
23
Соотношения (1.27) и (1.33) описывают действие электромагнит-
ного поля на заряженные частицы. Мы можем теперь задать вопрос,
каким образом эти выражения связаны с законами сохранения
энергии и импульса. Очевидно, что поскольку ни dp/dt, ни dWIdt
не равны нулю, то, для того чтобы получить законы сохранения
для системы взаимодействующих частиц и полей, необходимо ввести
энергию и импульс электромагнитного поля. Например, распреде-
ления заряда и тока в (1.27) можно всегда выразить через поля
в этой области с помощью неоднородных уравнений Максвелла
р(г', 0 = 7-V'•£(«•', О,
4л
j (г', 0 = -у-Гсу' х Н (г', 0 — gE ’Z) ]
4я L	dt J
и получить
AL = J-JE(r', 0 у'-Е (г', 0 dr' +
+^- (Tv'xH(r',o LAAA-lxH(r',0dr'.	(1-34)
4л J L	с dt J
Далее
JLxh = A(exH)-Ex^- = ^(ExH)+cEx(v'XE),
dt	dt	dt dt
так что выражение (1-34) можно записать в виде
= _ J- А (' Е (r; 0 х и (Г', 0 dr' +
dt 4лс dt J
+ —С[Еу'.Е—Ex(v'  Е) — Hx(v'xH)]dr'. (1.35)
4л J
Мы попытаемся интерпретировать первый член в (1.35) как ско-
рость изменения импульса поля и преобразовать второй интеграл
в поверхностный интеграл, содержащий поток импульса поля
через границу соответствующего объема интегрирования. Чтобы
выполнить эту работу, начнем с той части подынтегрального выра-
жения, которая относится к электрическому полю:
Еу'-Е—Е х (у' ХЕ)= Еу'-Е+ (Е-у') Е---— V' (Е2). (1.36)
Здесь мы использовали векторное тождество для градиента от ска-
лярного произведения двух векторов. Это выражение в свою очередь
24
может быть записано как дивергенция аффинора*
V'. (ее----Те2),	(1.37)
где/—единичный аффинор, или идемфактор.
Остальная часть подынтегрального выражения второго интегра-
ла в (1.35), относящаяся к магнитному полю, может быть рассмот-
рена по аналогии с (1.36) и (1.37), если вспомнить, что четвертое
уравнение Максвелла позволяет нам добавить равное нулю слагае-
мое Н (v'-H). Тогда эта магнитная часть будет выражаться в той
же самой форме, что и (1.36). Таким образом, выражение (1.36)
может быть в следующем виде записано через вектор рР£М и аф-
финор Т, которые описывают импульс поля:
A(p + pfieW)=fv'.7cfr'.
at	J
С помощью теоремы Гаусса второй член может быть преобразован
в поверхностный интеграл по поверхности S':
4(р+рй^)= С dS'-T.	(1.38)
at	J
S'
Импульс поля определяется следующим образом:
pfieia _ —1— Г £ /г'; /) х н (г', Л dr',	(1.39)
4лс J
т. е. выражается как объемный интеграл от вектора плотности
импульса
N(r',0 = —Е(г',0хН(г',0-	(1-40)
Поток импульса поля через поверхность выражается через поверх-
ностный интеграл от аффинора
Т= —
4л
ЕЕ+НН------1- 7(Е2+Н2)]
(1.41а)
* Аффинором называется линейный оператор, который действует в трех-
мерном пространстве и переводит один вектор в другой. Матрица этого пре-
образования состоит из девяти элементов, совокупность которых образует
тензор второго ранга. Единичный аффинор, или идемфактор, — это тождест-
венное преобразование, матрица которого представляет собой единичную
матрицу 3X3. (Подробнее см. [253, разд. 1.6], а также Рашевский П. К.
Риманова геометрия и тензорный анализ. М., «Наука», 1967.) В русской ли-
тературе по классической электродинамике эта терминология обычно не
применяется. — Прим, перев.
25
или с использованием обозначений тензора второго ранга
TtJ = ХГ£.£. + /7;/7._А_б (F |-№)1 ,	(1.416)
4л I	2	I
где 6;i—символ Кронекера. Тензор (1.41) называется тензором
напряжений Максвелла.
Главный вывод из соотношения (1.38) заключается в том, что
в области, окруженной поверхностью S', на которой исчезает элект-
ромагнитное поле, так что
dS'7 = 0,
S'
сумма импульсов р ф- системы, состоящей из частицы и поля,
сохраняется. Тот факт, что поле обладает импульсом, является
одним из подтверждений его объективного существования, хотя
это еще не является полностью доказанным до тех пор, пока не
рассмотрены электромагнитные волны. Наличие у поля импульса
наводит на мысль, что оно также является носителем энергии. Это
может быть установлено с помощью второго неоднородного уравне-
ния Максвелла (1.16), которое позволяет переписать соотношение
(1.33) в виде
= -L Г Е (г', t). lev' ХН(Г', /)—aE-^°1dr'. (1.42)
dt 4л. J	L	от
Метод рассмотрения подобен нашему методу получения закона
сохранения импульса. Интегрируем первое слагаемое в (1.42) по
частям, используя векторное тождество
V'. (ExH) = H-(v'xE)-E-(v'xH)	(1.43)
и теорему Гаусса. Тогда
= — С|сН- (V' хЕ)—Е — Idr'—
dt 4jt J [	St J
----- f(EX H)-dS'.
4л J
S'
(1-44)
В интеграл по поверхности S' входит подынтегральное выражение,
сходное с выражением (1.40) для плотности импульса поля. Введем
вектор Пойнтинга
S (г', /) = — (Е (г', I) X Н (г', /)) = с2 N (г', f) (1.45)
4л
26
и, используя уравнение (1.1 в), напишем
* =	f [н.	+ Е ldr'~ f s‘ds'
lit 4ix.H Я Л J J
или
— (W + W^ld) = — f S • dS',
dt	J
S'
где величина
Wfield = J- J (E2 + H2) dr’.
(1-46)
(1.47)
определяется как энергия электромагнитного поля. В выражении
(1.46) поверхностный интеграл от вектора Пойнтинга представляет
собой убыль энергии поля через поверхность S' в единицу времени
и связан, согласно (1.45), с поверхностным интегралом от плотности
импульса поля. Если интеграл в (1.46) равен нулю, то, как следует
из (1.46), суммарная энергия частиц и поля сохраняется.
Установив, что электромагнитное поле обладает энергией и
импульсом, можно задать вопрос о том, какие другие физические
величины системы «поле плюс материальные частицы» обладают
такими свойствами, чтобы их сумма сохранялась Важнейшей
сохраняющейся величиной, которую мы можем сконструировать
на данном этапе, является угловой момент. Это будет иметь для
нас особую важность в последующем рассмотрении, так как мы
знаем, что ядра претерпевают электромагнитные переходы, в кото-
рых изменяется спин ядра. Поэтому способность электромагнит-
ного поля нести угловой момент будет существенна, если эта вели-
чина сохраняется. Воспользуемся уравнением (1.30), чтобы рас-
считать скорость изменения во времени углового момента частицы
L — г X р:
-^ = гХ-^- = 7гх|е(г, 0+— хН(г, /)
dt di L	с
(1-48)
или для пространственного распределения заряда
dL (r’ dr = 1 г х Гр (г, t) Е (г, t) +
dt J L
+ -Lj(r>Z)xH(rJ)lrlr.	(1.49)
c	J
Еще раз воспользуемся неоднородными уравнениями Максвелла и
получим
f-^dr =-*- frxfEV-E+(VxH) хН-----------L2LXH|dr,
J dt 4л J L	c dt J
где величины в квадратных скобках фигурируют в подынтеграль-
ном выражении в уравнении (1.34). Вычисляя их подобно тому,
27
как мы делали выше [см. (1.35) — (1.37), (1.40) и (1.41) 1, получаем
Г dL .	I d С /с их j
—-t/r= —  ---- г х (Е X Н) dr +
J dt	4лс dt J
+ -!-Jrx[V- (ЕЕ + НИ--2 7(E* 1 2 3 * * * * + H2)Jpr
или
J(4+^)*=frx<v-n*.	(Г50)
Здесь
Llield (r, f) = r x N (r, /),	(1-51)
где N (r, t) — импульс поля, a T — максвелловский тензор напря-
жений. Объемный интеграл в правой части равенства (1.50) можно
преобразовать в поверхностный интеграл, если воспользоваться
свойством
3	3	3
[V.(Txr)h= 2 2 2 ^цтТыгт] =
1 1 = 1 m=l Ork
2 eilm( ,	2	&ilm ^kl
klm \orh	) klm
-[(V-F)xrjz.
(1.52)
Здесь учтен тот факт, что тензор напряжений Максвелла симметри-
чен, тогда как псевдотензор Леви — Чивита третьего ранга eiZm
полностью антисимметричен*. Наличие дивергенции в левой части
* Этот псевдотензор определяется так:
1 (;7т) = (123). (231), (312).
efZm= - !(//«) = (132). (213), (321),
0 в остальных случаях.
Векторное произведение можно выразить через ецт в виде
з 3
(vxw)j= У, У Eilmvlwm-
1=1 т=1
ецт обладает многими полезными свойствами, например
з
2 eilm Sjkm~$ii $lk
т= 1
3	3
2 У erZm ejlm = j,
I = 1 m= 1
И
3	3
2 У У BilmBilm~ 6.
Z = 1 Z= 1 m= 1
28
равенства (1.52) дает возможность использовать теорему Гаусса
и написать

) dr =
dt
M-dS,
(1.53)
где M — псевдотензор второго ранга с компонентами
з з
М.ц=	Eilm Tji rm.
I =1 m=l
(1-54)
Соотношение (1.53) выражает тот факт, что электромагнитное поле
имеет угловой момент, который в комбинации с угловым моментом
частицы является сохраняющейся величиной. Поток углового мо-
мента через поверхность дается поверхностным интегралом от
тензора М, тогда как плотность углового момента поля выражается
векторным произведением координаты г на плотность импульса
поля
§ 1.3.	Плоские волны
Рассмотрение законов сохранения было проведено для поля,
взаимодействующего с заряженными частицами, но оно касалось
главным образом свойств поля: его энергии, импульса и углового
момента. Теперь мы кратко обсудим некоторые другие свойства
электромагнитного поля в классической физике, а именно природу
полей в отсутствие источников. Для этого используем поперечную
калибровку [см. (1.14) — (1.16), (1.19)]. Тогда скалярный потенциал
равен нулю, а векторный потенциал является решением уравнения
□ A(r, 0=(V2--L-^ А (г, 0=0
\ с2 dt2 )
с калибровочным условием поперечности
V • А (г, 0 = 0.
(1.55)
(1.56)
Решение этих уравнений, например, в декартовых координатах,
конечно, очень хорошо известно. Для данного волнового вектора
к имеем
А (г, 0 = Л^кЕке’ (кт-®*),	(1.57)
а более общее решение является непрерывной суперпозицией таких
векторных функций. Подставляя предполагаемое решение (1.57)
в уравнение (1.55), мы видим, что указанное уравнение удовлетво-
ряется при условии, что величина волнового вектора связана с час-
29
тотой соотношением k = со/с. Условие поперечности будет удовлет-
ворено, если для каждого волнового вектора мы имеем
k-ek = 0.
(1.58)
Мы считаем здесь вектор поляризации ек единичным вектором,
а произвольный нормировочный множитель включаем в Nk.
Поскольку плоские волны составляют полный набор, то супер-
позиция решений
А (г, Л = f Nk Ek'e* (k-r-coi)
7 J	(2л)8
(1.59)
дает общий вид векторного потенциала, удовлетворяющего урав-
нениям (1.55) и (1.56). Таким образом, можно в принципе удовлет-
ворить граничным условиям, которые налагаются на А в силу
наличия источников в области, внешней по отношению к области,
рассматриваемой в уравнении (1.55). Практически обычно исполь-
зуют решение в декартовых координатах только тогда, когда гра-
ничные условия достаточно легко формулируются для этой системы
координат. Обычно накладывается требование периодичности реше-
ния на каждой грани куба с ребром L. Это требование отбирает
волновые векторы, удовлетворяющие условию
к= —
L
(1.60)
где п = (пж, пу, п,) —тройка положительных или отрицательных
целых чисел. Непрерывная суперпозиция (1.59) сводится тогда
к дискретной сумме, которая далее может быть преобразована с по-
мощью требований, накладываемых на А. Учитывая (1.60), полу-
чим число различных значений частоты, содержащихся при данной
поляризации в объеме Is и в интервале от со до со da>:
I з
dn = —— dk	(1.61а)
(2л)8	'	7
или
п2 dn dQ = ——— k2 dk dQ = ——— co2 den dQ,	(1.616)
(2л)8	(2лс)3
где dQ—элемент телесного угла, определенный в направлении
волнового вектора.
Экспоненциальная форма записи для плоских волн в выражениях
(1.57) и (1.59) является более предпочтительной по сравнению
с решениями в виде синуса и косинуса) которые также могут быть
использованы), поскольку экспоненциальная запись дает особенно
простые алгебраические выражения для интересующих нас раз-
30
личных величин. Например, с помощью (1.4) и (1.5) можно получить
выражения для напряженностей. Для заданной частоты имеем
Н (г, /) = V х А (г,t) = iMk (к х Еь) е’(к	(1.62)
и
Е(г, 0=------L_^L = i ДГк/гЕке* (кт-шо.	(1.63)
с dt
Таким образом, напряженности Е и Н в вакууме имеют одинаковую
абсолютную величину и три вектора (k, Е, Н} образуют правовин-
товую систему. В этих выражениях все еще остается неопределен-
ным нормировочный коэффициент для данного волнового век-
тора. Существует много способов, чтобы найти его. Например,
можно подставить выражения (1.62) и (1.63) в (1.47) и вычислить
энергию для данного волнового вектора в объеме L3, а затем каким-
либо удобным способом нормировать ца соответствующие значения
Wfield (к). Вычисление по формуле (1.47) с комплексными зна-
чениями Е и Н тогда дает
W’ield (к) = — С (Е • Е* + Н • Н*) dr =
8л J
Д’
=+<к х £з=	43^  о-64)
откуда
(D [ L3 J	'
I
Импульс, соответствующий компоненте поля с волновым вектором
к в объеме L3, согласно (1.39) имеет вид
рй>и (к) = — С Е X н* dr =
4лс J
L3
= ^-[£ekx(kXek)]L3=^-£3k.	(1.66)
4лс	4лс
Здесь использовано условие (1.58). С помощью выражения (1.64)
можно связать его с соответствующей энергией
plield (к) = W!ield (к) к/с,	(1.67)
где к — единичный вектор в направлении вектора к. Безотноси-
тельно к конкретному виду Wfield (к) соотношение (1.67) является
естественным следствием теории, основанной на уравнениях Мак-
свелла. Однако, как мы увидим в гл. 3, квантовая теория электро-
магнитных волн приводит к конкретному виду этой величины,
а именно
WiieId (k) = Aco,
(1.68)
31
где ti—постоянная Планка, деленная на 2л. Это фиксирует норми-
ровку нашего решения в виде плоских волн:
М^Г"-	(1.69)
L <oL3 J
Импульс поля, конечно, выражается формулой
pf‘eW(k) = Ak.	(1-70)
Выражение для углового момента поля, соответствующее полу'
ценному решению в виде плоских волн в объеме L3, вообще говоря,
мало интересно, так как оно зависит от точки объема, относительно
которой берется момент. Очевидно, что использование декартовой
системы координат не очень удобно для обсуждения свойств углового
момента электромагнитного поля, так как в сферической системе
координат они будут выражаться намного более простым способом
*
* *
Книги Джексона [212], Ландау и Лифшица [226], Мариона
[241 ] и Пановского и Филлипса [265] содержат подробное рассмот-
рение классической электромагнитной теории, включая большую
часть материала, обсуждаемого в этой главе*.
* На русском языке, кроме книги Ландау и Лифшица [226], см. книгу
Тамма [385], учебник Левича [379]. Краткое изложение основных вопросов,
рассматриваемых в этой главе, имеется также в первых главах книг Лхиезера
и Берестецкого [7] и Берестсцкого, Лифшица и Питаевского [370]. — Прим,
перев.
ГЛАВА 2
РАЗЛОЖЕНИЕ
ПО МУЛЬТИПОЛЯМ
Как и в большинстве других областей теоретической физики,
одной из важнейших целей теории структуры ядра является
отчетливое отделение свойств системы, обусловленных особен-
ностями симметрии, от свойств, которые обусловлены специфи-
ческими особенностями динамики. Типичным объектом применения
этого положения для ядер является угловой момент, который играет
в теории решающую роль. Поскольку гамильтониан ядра инва-
риантен относительно вращений, ядерные состояния характери-
зуются определенным значением углового момента. Таким образом,
для каждого конкретного процесса необходимо рассматривать
влияние правил отбора по угловому моменту, а также другие ос-
новные геометрические аспекты физики ядра. Если эти эффекты
можно выделить, то остальные свойства изучаемой проблемы будут
более ясно обнаруживать свойства динамики ядра: сильное корот-
кодействующее взаимодействие, взаимодействие с жестким кором
и т. д. Когда в рассматриваемых процессах участвуют фотоны,
то очень полезно с самого начала уметь использовать те свойства
электромагнитного поля, которые связаны с угловым моментом.
Для того чтобы понять эти свойства, мы будем изучать характери-
стики потенциалов и полей в сферических координатах и их поведе-
ние при пространственных вращениях. В конечном счете мы увидим,
что формализм, который здесь описывается, можно будет легко
обобщить на случай других интересующих нас реакций.
§ 2.1.	Вращение и операторы углового момента
В гл. 1 мы использовали декартовы координаты, чтобы получить
(для векторного потенциала с поперечной калибровкой) решения
волнового уравнения (1.55) в виде плоских волн. Прежде чем при-
ступать к исследованию этого уравнения в сферической системе
координат, полезно изучить решения волнового уравнения для
скалярного поля в сферических координатах. Рассмотрим уравнение
□ «(г,о= V*—LJL.\u(M)==o,	(2.1)
\ с2 dt1 /
33
где и (г, t) — скалярная функция. Если выделить обычную осцил-
ляторную зависимость от времени, то для компоненты с частотою
со можно написать
и (г, t) = и (г) e-‘“f.	(2.2)
Вводя обозначение k — соФ, получаем уравнение Гельмгольца
для функции и (г)
(V2 + /s2)u(r) = 0.
(2-3)
Если ввести сферическую систему координат, в которой г — рас-
стояние от центра, 6 — полярный угол, ср — азимутальный угол,
то уравнение Гельмгольца примет вид
Г 1 д 2 д ,	1 д . .. д .	1 д2 , I , п .	„
-----Г------(	sin6	1-4- /г2 и (г, 0, <р) = 0.
г2 дг дг г2 sin 0 50-----------------------------50 г2 sin2 0 5<р2 J
(2.4)
Регулярное решение этого уравнения, как известно, имеет вид
Щт (г, е, ф) = Nil (kr) Ylm (0, ф),
(2-5)
где h (kr)—сферическая функция Бесселя, Ylm (0, ср) —
сферическая гармоника, N — нормировочная константа. Сфери-
ческие гармоники определяются следующим образом:
Ylm (6, Ф) = Р^Т±(^тГ/2<- 1)т е‘т<Р Р‘т} <COS °)’ <2’6а>
L 4л (/Ц-т)! J
I 0.
Здесь PT (cos0)—присоединенный полином Лежандра:
РГ(cos0) = --у—sinm 0 —-——-(—sin2 0)z.	(2.66)
v 7	2'/!	5(cos0)z+mV	’	V ’
Для—I	m < 0 определение (2.6a) обобщается с помощью
соотношения
Г;_т(0,Ф) = (-1)тЕГт(0,Ф).	(2.7)
Соотношения (2.6) и (2.7) приводят к условию нормировки
$ YI т> (0, ф) Ylm (0, ф) dQ = 6mm- ,
(2-8)
где интегрирование проводится по всей сфере единичного радиуса
с элементом телесного угла dQ = cfcpcf cos 0.
Чтобы понять смысл целых чисел I и т, которые появляются
в сферических гармониках и в решении уравнения Гельмгольца
(2.5), необходимо рассмотреть поведение этого решения в случае,
34
когда система координат вращается*. Поскольку оператор Лапласа
в уравнении (2.3) является скалярным оператором, ясно, что вид
уравнения Гельмгольца в новой координатной системе будет таким
же, как и в старой системе, а соответствующие решения в двух сис-
темах будут тесно связаны между собой. Любое вращение можно
описать с помощью одной из двух схем. Первая из них состоит в па-
раметризации с помощью фиксированного единичного вектора
п, вокруг которого выполняется поворот на угол 0. Вторая схема
основана на использовании углов Эйлера 6t, 62 и е3. Они опреде-
ляют ориентацию новой системы координат с помощью следующей
последовательности поворотов (рис. 2.1):
Рис. 2.1. Углы Эйлера.
Углы Эйлера определяются с помощью трех последовательных поворотов:
на угол Gi вокруг оси z с образованием системы (x't/z') (а), на угол в2 во-
круг оси у' с образованием системы (x"y"z") (б) и поворота на угол в?
вокруг оси z", приводящего к конечной системе (x"'y"'z"') (в).
а)	поворот исходной системы координат (xyz) на угол 6j вокруг
оси z с образованием промежуточной системы с осями х', у', z';
б)	поворот промежуточной системы (х'у'z') на угол 62 вокруг
оси у', приводящий к системе (x"r/"z");
в)	поворот системы (x"y"z") на угол 03 вокруг оси z" для полу-
чения новой системы (x"'y'"z'").
Мы также можем описать вращение, если в данной точке про-
странства укажем связь между старыми координатами г и новыми
координатами г'. Эта связь наиболее просто определяется с помощью
действительной ортогональной матрицы 3x3:
r' = Rr,
или
3
r'i= Rurj, 2, 3.
/=i
(2.9a)
(2.96)
* Мы рассматриваем здесь элементы теории вращений и углового момен-
та, которая, как предполагается, читателю относительно хорошо известна.
(См. в этой связи книги, указанные в конце данной главы.) Сводка основных
результатов квантовомеханической теории углового момента приводится
в Приложении А.
35
Девять элементов матрицы 7? могут зависеть только от трех неза-
висимых величин (пи 0 или 61, 62, 03); остальные степени свободы
исключаются условием ортогональности. Действительно, используя
определенные выше углы Эйлера, можно записать*
tcos61Cos02cose3— sinf^sinOg sin01cosC2cos034 cos0,sinO3 —sin02cos03\
— cos0icos62sin03—sin0icos03 —sin01cos02sinO3+cos61cos03	sin02sin03
cos01sin02	sinOjsinOj	cos02 /
(2.Ю)
Если рассматривается скалярное поле, которое (независимо от
системы координат, используемой для описания точки) каждой
точке пространства ставит в соответствие лишь одно число, то
вращение приводит к изменению функциональной зависимости поля.
Согласно определению скалярного поля, это изменение в соответ-
ствии с соотношением (2.9) в точности компенсируется изменением
радиуса-вектора, т. е.
u'(r')=u(r),
(2.И)
так что одно и то же число сопоставляется данной физической точке
как старой, так и новой функцией безотносительно к тому, к какой
системе координат мы относим точку. Соотношение (2.11) указывает
новый путь для описания вращений. В (2.9) мы рассматривали опе-
ратор (или матрицу) R, который действует в конфигурационном
пространстве; теперь мы можем ввести оператор** Т (R), который
действует в пространстве функций и характеризует вращение R.
Действие Т (R) на и дает новую функцию, которая в соответствии
с (2.11) должна удовлетворять для вращения R соотношению
(Г (7?) ц](7?г)=«(г).
(2.12)
Можно также ввести вектор р = Rr, который действует в том же
пространстве, что и г. Тогда (2.12) принимает вид
[7’(/?)W](p) = u(7?-> р),
* Заметим, что в нашем определении мы поворачиваем систему коорди-
нат в положительном направлении на углы Эйлера 0j, 02 и 03. Это эквивалент-
но повороту векторов в системе на углы Эйлера — 02, —02 и —03. Наше
определение совпадает с определением в [355, 126, 109, 287]; противополож-
ное определение используется в [288, 247, 55]. См. том 1, гл 5, в частности
формулу (5.159).
**, В томе I этот оператор обозначается символом R. Обозначение Т (R)
используется здесь, чтобы различить операцию вращения в пространстве
функций от этой же операции в конфигурационном пространстве.
36
где R-1 — вращение, обратное по отношению к R, получаемое
в силу (2.9) обращением матрицы R. Если мы теперь, устраняя
излишние обозначения, назовем этот новый вектор вектором г вмес-
то р, то будем иметь
[T(R)u](r)=u(R~lr),	(2.13)
где модифицированная функция в левой части уравнения (2.13)
берется в точке г.
Очевидно, что если не выполняется никаких вращений, то R
является единичной матрицей и Т (R) |@г о = 1. Если выполняет-
ся бесконечно малое преобразование, скажем, путем поворота сис-
темы координат на малый угол е вокруг оси п, то Т (R (п, е)) близко
к 1. В этом случае оператор Т (R) можно разложить в ряд Тейлора
и записать в первом порядке по е:
T(R(n, e)) = l+ien-L,	(2.14)
где вид операторов L = (Li, L2, Ls) подлежит определению. (На
этой стадии они могут быть даже равны нулю или линейно зависеть
от е; в последнем случае Т (R) отличалось бы от единицы только во
втором порядке или еще меньше.) Можно легко получить выражение
для L Рассмотрим, например, малый поворот вокруг оси z. Возьмем
п параллельным этой оси и обозначим
или
так что
/1' = Г]-|-еГ2,	Г2 - Г2 — ЕГЪ Г3=Г3
/ 1 е 0\
е 1 О),
\ 0 0 17
7?->г =
Тогда получаем из (2.13)
[(l+ieLgJuKrj, r2, г3) = и (гг—ег2, r2±Erlt г3) =
1 —е
(ri> г3),
(2.15а)
(2.156)
(2.16)
(2-17)
G —ег2
г 2 + е/ j
 rs .
где правая часть (2.13) разложена в ряд Тейлора. Поскольку соот-
ношение (2.17) должно выполняться для любого скалярного поля,
можно получить вид оператора L3:
Ls=-ilri^—r2^ .	(2.18)
( дг2 дгг I
37
Аналогичная процедура с пх, выполняемая последовательно для осей
х и у, дает подобный же результат для двух других компонент, так
что
L=—irxV.	(2.19)
Это стандартный вид для оператора углового момента в квантовой
механике. Таким образом, операторы орбитального углового мо-
мента генерируют бесконечно малые повороты для скалярного поля.
Что касается поворотов на конечный угол 0 вокруг оси п, то о них
мы можем говорить как о поворотах, состоящих из ряда N беско-
нечно малых преобразований на угол е = Q/N. Для таких враще-
ний имеем
Т(Я(п, 0))=lim	п-lV = eie"’L. (2.20)
л'-.оо \ N )
Чтобы упростить обсуждение поведения решений уравнения
Гельмгольца (2.4) при таких преобразованиях, рассмотрим частный
случай k — 0; тогда уравнение Гельмгольца переходит в уравнение
Лапласа
V2n(r)=0	(2.21)
и решения, согласно формуле (2.5), имеют вид
I	Угт(г) = г'Угт(0, <р),	(2.22)
т. е. в соответствующих декартовых координатах они являются од-
нородными полиномами степени I. Рассмотрим далее уравнение
(2.21) в преобразованной системе координат. Поскольку у2 —
скалярный оператор и, следовательно, коммутирует с оператором
Т (R), имеем
Г (R) (V2 vlm (г)] = v2 [Г (7?) vlm (г)] = 0,
так что Т (R)vlm (г) также является решением уравнения Лапласа.
Кроме того, Т (R) действует линейно на координаты, поэтому и
функция Т (R)vlm (г) является однородным полиномом степени I.
Это новое решение может быть, таким образом, записано как
линейная суперпозиция 21 ф- 1 старых решений степени I:
T(R)vlm(r)=vlm(R~' г) = 2 D‘m.m(R)vlm-(f). (2.23а)
m’ = — I
Опустим множитель г1, который должен входить в обе части этого
соотношения; тогда
T(R)YlmCr)=Ylm(R~lf)= 2 Dlm.m(R)Ylm'(r), (2.236)
Щ’ = — I
где единичный вектор г имеет направление радиус-вектора и по-
этому используется как эквивалент величин 6, <р. Коэффициенты
38
Dmm' (R), образующие матрицу (2/ -f- 1) x (2/ + 1), следует счи-
тать функцией величин, описывающих рассматриваемое вращение,
т. е. функций или пи 0, или углов Эйлера 01, 02, 6з- Явный вид
матрицы вращений Dlmm- (0i, 02, 03) можно легко получить
(см. книги по теории углового момента, указанные в конце этой
главы). Из (2.236) получаем также трансформационные свойства
решений, даваемых формулой (2.5):
i
ulm(R~lr) = 2 ^-m(/?)«/m-(r). (2.23в)
т' = — I
Таким образом, как видно из (2.13), (2.14), (2.19) и (2.23), про-
странственная ориентация системы координат для скалярного
поля полностью определяется сферическими гармониками. Для
такого поля вращение является результатом действия оператора
орбитального углового момента и приводит к новому решению
с данным I, которое является суперпозицией старых решений,
имеющих то же самое значение /. Можно ли ожидать, что аналогич-
ный результат сохраняется и для решения векторного уравнения
Гельмгольца (1.55)? Мы можем надеяться выразить решение этого
уравнения через компоненты, каждая из которых имеет вид, опреде-
ляемый формулой (2.5), и суперпозиция которых удовлетворяет
условию поперечности (1.56). Однако ясно, что такое решение
не будет обладать простыми трансформационными свойствами
(2.23в), так как компоненты, составляющие решение, при вращениях
сами должны преобразовываться друг через друга. Необходимо
объединить трансформационные свойства векторов с трансформа-
ционными свойствами сферических гармоник, даваемых формулой
(2.236). Чтобы это выполнить, попытаемся построить оператор,
аналогичный оператору Т (7?) в соотношениях (2.13) и (2.14), кото-
рый генерирует бесконечно малые повороты для скалярного поля.
Определяющим свойством векторного поля является трансформа-
ционный закон
[Т(7?)А](г) = 7?А(/?-’г).	(2.24)
Появление дополнительной по сравнению с (2.13) матрицы R в пра-
вой части является отражением того факта, что компоненты всех
векторов по определению должны преобразовываться по тому же
правилу, что и радиус-вектор [см. (2.9)1.
Попытаемся теперь найти оператор Т (/?), который будет гене-
рировать бесконечно малые преобразования для векторного поля
по аналогии с формулой (2.14) для скалярного поля. Рассмотрим
снова повороты на малый угол е вокруг оси z и напишем
Т (7? (п, е)) = 1 + ien - J = 1 + ieJs.	(2.25)
Пока еще не определенные операторы J = (J i, J2, Jз) должны
быть матрицами 3x3, которые действуют на соответствующие
39
трехмерные векторы, записываемые в виде матриц-столбцов
/А(г)\
А(г)=1Д(г)1.	(2.26)
\Л3 (г) /
После подстановки формул (2.15), (2.16), и (2.25) в (2.24) получаем
/ 1
[(1 +ieJ3)A](r) = l —е
\ О
е 0\ /Д (гх — ег2, г2 + erj, г3)'
1 О Д (/-!—ег2, г2 + ег1( г3)
О 1/ \Л3 (fi—ег2, г2 -НН. га).
А (г), (2.27)
где последнее выражение получено в первом порядке по е. Отсюда
можно определить J3
/1	0	0\ /О	—i	0\
J3 = — i (п — — г2 — И 0	1	0 +| i	О	О I	(2.28а)
\ дг« dri I \	I \	I
\о	0	1/ \0	0	0/
или
J3=L3 + S3,	(2.286)
где L3 является произведением единичной матрицы 3 X 3 на опе-
ратор орбитального углового момента (2.18),
/0	—i	0\
S3=( i	0	О).	(2.28в)
\о	о	о/
Можно еще раз выполнить аналогичные вычисления с п для осей
х и у, в результате получим
J=L + S,	(2.29а)
где L — оператор (2.19), умноженный на единичную матрицу
3 X 3, и
/0	0	0\	/ 0	0	i\
Si=|0 0 —i I, S2 = | 0 0 0 I, (2.296)
\0	i	0/	\—i	О	О/
в S3 дается (2.28р). Из соотношения, аналогичного (2.20), снова
получаем для конечных вращений
T(R(n, 0))=.eie" J.	(2.30)
40
Как хорошо известно из квантовой механики, оператор орби-
тального углового момента L удовлетворяет коммутационным
соотношениям
LxL=iL.	(2.31)
Матрицы S = (Si, S2, S3) удовлетворяют аналогичным соотно-
шениям*:
SxS^iS.	(2.32)
Кроме того, так как L — единичная матрица в пространстве трех-
компонентных векторов-столбцов, то L и S коммутируют и
JxJ=iJ.	(2.33)
Таким образом, из соотношения (2.30) видно, что J генерирует
вращения для векторного поля, а из (2.33) — что он удовлетворяет
коммутационным соотношениям для операторов углового момента.
Следовательно, можно ожидать, что J будет играть роль оператора
углового момента для потенциала электромагнитного поля и что
надо построить решения векторного волнового уравнения (1.55),
которые являются собственными функциями оператора J.
Однако, прежде чем это делать, можно записать J и, в частности,
S в более удобной форме. В квантовой механике удобно рассматри-
вать операторы орбитального углового момента L в представлении,
в котором матрица La диагональна. Фактически мы этим уже поль-
зовались для наших скалярных решений уравнения Гельмгольца,
поскольку хорошо известно, что сферические гармоники (2.6),
(2.7) одновременно со свойствами
L2 Y,m (6, ф) = (L? + £1 + L3) Ylm (6, <р) = / (/ + 1) Ylm (6, Ф) (2.34а)
также удовлетворяют соотношению
L3Ylm&, 4) = tnYlm(Q, <р).	(2.346)
Таким образом, в представлении этих функций La автоматически
будет диагональным. Аналогично мы выберем базис в трехмерном
пространстве векторов-столбцов. В этом базисе будет диагональна
* Соотношения (2.32) можно проверить путем непосредственного пере-
множения матриц или используя следующее свойство: матричные элементы
t й компоненты S могут быть выражены через полностью антисимметричный
тензор третьего ранга (см. сноску в § 1.2):
[St ] дГ — — tetqr-
Тогда матричный элемент векторного произведения, соответствующий пере-
ходу p-q, имеет вид
[(S X S)a]gp = 22 [Sn]gr [S/]rp =
nt r
—	2 8ant engr etrp==eagP== i [Sa]gp.
ntr
41
S3. Тогда, согласно (2.286), матрица J3 будет также диагональной.
Чтобы это получить, следует выполнить унитарное преобразование
S3=-.USsU+	(2.35)
такое, чтобы S'3 была диагональной. Это преобразование имеет
вид
	д=	'-1//2 0 1//Г	i/j/2 0 1//Г	О’ 1 0-	,	(2.36)
что дает новое выражение для S*: /0 1 0\	/0			—i	0\	/1 0	0\
=	1 0 1/2 \0 1	1 , S; 0/	1 1 . /2\ 1 \0	0 - i	-i 1, 0/	s3=|o о о). \0 0 — 1/ (2.37)
При этом коммутационные соотношения (2.32), конечно, выпол-
няются.
Преобразование (2.36) приводит также к новому набору базис-
ных векторов, который заменяет используемую в (2.26) — (2.29)
первоначальную тройку единичных векторов ej, е2, е3, соответст-
вующих осям х, у, 2. Эти новые векторы имеют вид
з
lt = 2
г = 1
(2.38)
Перейдем к более удобным обозначениям: для первого вектора возь-
мем t = 1, для второго t = 0 и для третье: о t = — 1. Тогда
E±i = +-^=(ei±ie2\ Е3 - е3.	(2.39)
V2
Этот набор векторов называется сферическим базисным набором.
Векторы комплексны, и из (2.39) следует, что
^ = (-1)Ч-в	(2.40)
и
=	(2.41)
где греческие индексы’пробегают значения — 1,0,1. Этот комплекс-
ный базисный набор приводит к специальной метрике для векторов,
представляемых в нем. Для действительного вектора V имеем
1 1
Для удобства мы опускаем штрихи в преобразованных матрицах.
42
и из (2.40), (2.41) и (2.42) получаем
^ = ^-¥ = (-1)^^.
(2.43)
Если рассмотрим второй вектор W, то для компонент в сферическом
базисе
V w= s	i (~l)MV_MrM.
Ц=—1	Ц = —1
(2.44)
По определению являются собственными векторами оператора
Ss, так что по аналогии с (2.346)
$з — Elii-
(2.45)
Аналог соотношения (2.34а) получается тривиально, так как из
(2.37) следует
Sa = Sf+Sl+S5 = 2,
(2.46)
где в правой части подразумевается единичная матрица 3 ХЗ.
Поскольку оператор углового момента S удовлетворяет коммута-
ционным соотношениям (2.32), он обладает свойством S2= s(s 1),
где s обозначает собственное значение оператора углового момента.
Из (2.46) получаем, что s = I. Таким образом, соответствует
собственному вектор\ углового момента для спина 1. Это тот
спин, который следует добавить к орбитальному угловому моменту
в (2.29а), чтобы получить полный угловой момент поля фотона.
§ 2.2. Сферические тензоры
Теперь мы должны построить из собственных функций орби-
тального углового момента Ylm и собственных функций соответ-
ствующих спину 1, новые собственные функции для полного угло-
вого момента J = L -)- S. Процедура такого рода хорошо известна
из квантовомеханической теории углового момента, которая кратко
изложена в Приложении А. При сложении величин Jt и J2, соот-
ветствующих угловым моментам двух различных частиц или орби-
тальному и внутреннему угловым моментам одной частицы, необ-
ходимо рассматривать два возможных базисных набора. В одном
из них диагональными являются операторы Ji2 = /1 (/± + 1),
J»2 = /2 (h + 1). (-Ь)з = ffli и (J2)3 = m2. Этот набор называется
несвязанным представлением. В другом, или связанном, представ-
лении диагональными являются величины Jt2, J22, J2 = (J1 +
+ J2)2 = J (J +1), (J)3 = (Ji + J2)3 = M. Матричные элементы
унитарного преобразования, которое осуществляет переход от одного
представления к другому, называются коэффициентами Клебша —
43
Гордана. Мы будем их обозначать* как (j1j2J\ni1m„M). Их свойства
кратко обсуждаются в Приложении А и более подробно — в книгах
по теории углового момента, указанных в конце главы.
Несвязанным представлением для рассматриваемой задачи яв-
ляется'произведение сферических гармоник и векторов сферического
базиса. Эти произведения являются собственными функциями че-
тырех соответствующих операторов несвязанного представления:
L2Fto(r)^ = /(/+l)rZm(r)^, S2KZra(r)|n = 2KZm(r)ln, 7-3 У 1т (Г) Su =	Im (Г) 1ц • S3KZm(r)lw = pyZm(r)|u.	(2.47)
(2.49)
Мы воспользуемся коэффициентами Клебша — Гордана, чтобы
перейти к связанному представлению, определяя новые собствен-
ные функции полного углового момента
Tj/;AI(r) = 2(/lJ|mnAl)yZmfr)^.	(2.48а)
пщ
Эти трехкомпонентные величины называются векторными сфери-
ческими гармониками**. Имеем
J2TJZ;A/(?) = J(J + l)TJz.A((r),
Js Ту/; м (r)= м (г)
и
L2TJZ;AZ (г) = 1(1+1) Тл.м (г),	(2.50)
S2TJZ;A/('r) = 2T/z,A/(r).	(2.51)
Учитывая свойства симметрии коэффициентов Клебша — Гордана
(ПА.206) и соотношения (2.7), (2.40), (2.48), получаем
Ту/;А/ (г) = 2(—l)m+^(/U| /пр.Л()У/_т(г)|_ц =
-(~l)A'S(/U|-m-pAl) KZm (г)§ц =
= (_ 1)лг+г+ 1 +^v (/j j |	-М) Ylm (г)	=
= (__l)M+z+i+JTjz._A,(r).	(2.52)
* Наиболее употребительными обозначениями для коэффициентов Клеб-
ша—Гордана, или коэффициентов векторного сложения, являются
[(/г h т, | jm) = (ц /, mL т2 | ц /2 jm)= С1"1т^тг = С^„,2.
Сводка различных обозначений коэффициентов Клебша—Гордана приведена
в работе [109] — Прим, перев.
** Заметим, что эти величины не являются векторами в смысле трансфор-
мации свойств, описываемых выражением (2.9), или (что эквивалентно) вы-
ражением (2.23) с коэффициентами	Их трансформационные свой-
ства описываются преобразованием (2.54) (см. ниже).
44
Здесь мы воспользовались тем фактом, что при суммировании
в (2.48а) коэффициенты Клебша — Гордана исчезают, если шф р #=
=^=7И, так что двойное суммирование в действительности является
лишь суммированием по одному индексу, т. е.
1
Ъ/:м(г)= 2 (/U|M—щШ)Уш_ц(г)^ (2.486)
и = -1
Можно показать, что величины (2.48) удовлетворяют условир
ортогональности на единичной сфере:
$Т^Г;ар(г)-Т,/;М(г)Ж =
= S (Z'U'I М'— p'p'M')(/lJ|/W — ррА4) х
нк'
X • In S Y*i'M - - ц- (г) Yim_ и (г) dQ. =
= &ir &мм- ^(UJ' | М— рр/И) (/1J | М—ррЛ1)
= &ir $мм' Sjj' 	(2.53)
Здесь мы использовали соотношения (2.8) и (2.41) и свойства орто-
гональности коэффициентов Клебша — Гордана. Величины TJZ; (г)
образуют полный набор в трехмерном пространстве на единичной
сфере, поскольку Еи определены в трехмерном пространстве, а сфе-
рические гармоники образуют полный набор функций от 0 и <р.
В силу определения (2.48) и свойств коэффициентов Клебша —
Гордйна скалярное произведение векторной сферической гар-
моники на вектор V преобразуется при вращении г' = Rr следую-
щим образом:
V’TjZ. AZ(r)= Dm’m (R) V T}z. az- (rz).	(2.54)
A/' — — J
Сравним этот результат с формулами (2.11) — (2.13) и (2.23). Со-
отношение (2.54) обобщает для случая векторного поля результат,
полученный ранее в (2.23) для скалярного поля. Оно указывает,
что на языке теории угловых моментов Рака проекция TjZ;A/(r)
на вектор дает неприводимый тензор ранга J. Поэтому можно при-
менить теорему Вигнера -— Эккарта к матричному элементу этой
величины, взятому между двумя состояниями с хорошими кванто-
выми числами углового момента и его проекции, например, |/imi)
и |/2т2/. Это дает (см. Приложение А)
(A m2|V-TJz.A(|/;/??!>=:
= (/i Jii I Mmz) </21| V-TJZ || A),	(2.55)
где дважды отчеркнутая величина, определяемая как приведенный
матричный элемент, не зависит от всех магнитных квантовых чисел.
Это утверждение в конечном счете будет играть очень существенную
роль в наших теоретических рассмотрениях, так как оно позволит,
45
не обращаясь к деталям ядерной структуры, выполнить всю ту
часть вычислений, которая зависит только от геометрии (т. е. от
магнитных квантовых чисел). Формула (2.55) также дает правила
отбора, заключающиеся в том, что матричный элемент исчезает,
если не выполняется правило треугольника
171—
и соотношение + М = т2.
Одно из самых полезных приложений формализма векторных
сферических гармоник относится к вычислению градиента от произ-
ведения функции от г на сферическую гармонику. Конечная фор-
мула, называемая градиентной формулой, имеет вид
Эта формула значительно упрощает математические выкладки для
полей со спином 1. Чтобы ее доказать, воспользуемся тем, что сфе-
рические гармоники образуют полный набор на единичной сфере,
а базисные векторы сферического базиса определены в трехмерном
пространстве. Тогда, используя (2.8) и (2.41) —(2.43), можно на-
писать
V/(r)KZm(?) =
= t	(2.57)
ц, = — 1 LM
Здесь — p-я компонента оператора градиента, представленного
в сферическом базисе. Этот оператор является векторным операто-
ром, поскольку при вращении 7? он преобразуется с помощью
матрицы вращений Т’цщ (R). Следовательно, для интеграла в фор-
муле (2.57) можно воспользоваться теоремой Вигнера — Эккарта:
$У£м(г)¥[г/(г)У;т(?)Ж =
= (ZlL|mpM)<L||Vf(r)|| /> =
= (/1L | трМ) (l\L 1ООО)—1 $ Ylo (?) VJ (г) Yl0 (r)dQ. (2.58)
Мы увидим, что для соответствующих случаев (/1L|OOO) не исче-
зает. Интеграл в (2.58) можно вычислить непосредственно, так
как для сферических координат
д	дг д	д cos 0 д  дф д 
дг	дг дг дг д cos 0 dz dtp
д г \ д
дг yx2 + y2+z2 j 3 cos 0
= coseA + ^^_,	(2.59)
dr rd cos 0
46
и из (2.6) и (2.7) следует
Ую (0 = 1(2/ + 1)/4л]1/2 pt (cos 0).	(2.60)
Полиномы Лежандра удовлетворяют соотношениям
(1 + 1)PZ+1 (cos 0)—(21 + 1) cos 0Pz(cos 6) +/Л;_1 (cos 6) = 0, (2.61а)
sin2 0 -------- Pt (COS 0) = I [Р/_, (cos 0) — cos 0 P, (cos 0)] =
d cos G
= n1 [Л-! (COS 0)-PZ+l (COS 0)].	(2.616)
Поэтому получаем
Vof (О У10 (r)= I [(21 +1) (21- I)]-"/2	+^‘ /) Уг_io (r) +
+ (1 + 1) [(21 + 1) (21+ 3)]~ i/2 f -L f\Yl+l0 (?). (2.62)
\dr r J
Коэффициент Клебша — Гордана в знаменателе выражения (2.58)
имеет следующие значения (см. табл. ПА.1):
(ПЛ 1000) =
[(l + l)/(21 + l)]i/2,
0,
— [1/(21+I)]’/2,
Л=/ + 1,
L = l,
L=l—1,
(2.63)
Подставляя (2.58), (2.62) и (2.63) в (2.57) и используя (2.8), получаем
W (0KZm(r) = 2 (—1)и§-ц[ — (—Ц-У/2 (111—1 |трт + ц) X
xKz_lm+p(r)(^ + Z±lf] +
V dr г )
+ (Й+У/2<П/+11тНт + р)ГН-1т+ц(г)(-^-----—	. (2.64)
\ 214 3 /	\ dr г ! \
Мы видим, таким образом, что операция деления в (2.58) не приве-
ла к трудностям.] Пользуясь свойством симметрии (ПА.20), по-
лучаем
w(r)yZm(r)= i	4—y/2(z—11/| m+p—pm) Yi— Im |-ц, X
= — 1	|_ \ 2/1 /
/ df . Z+l Л Z/ + 1V/2
X I— +—— f — —(1 + Hl | m + p—pm)Kz+im+u X
\ С*/" Г J \ J-1J
что с учетом определения (2.48) и дает градиентную формулу (2.56).
47
не ot
част!
магн
отбо
если
и сс
(
сфе{
веде
мул
Как видно из выражения (2.5), если f (г) в (2.56) выбрать в виде
сферической функции Бесселя порядка /, то величина
A(m(r; l)=^v/z(MK;m(r)	(2.65)
к
будет удовлетворять векторному уравнению Гельмгольца
(V2 + k2) Alm (г; I) =0. Однако поскольку
V  Alm (г; I) =	V2/, (йг) Ylm (?) = -kj, (kr) Ylm (?) #= 0, (2.66)
то такой потенциал не удовлетворяет условию поперечности (1.56).
Поэтому потенциал (2.65) с индексом [ называется продольным.
Хотя он не годится для описания электромагнитного поля с попе-
речной калибровкой, им полезно пользоваться для других калиб-
ровок. Заметим, что в силу соотношений для сферических функций
Бесселя
Эта
пол
Р1'1
а б
пре
пи<
-у- h (kr) = £/z _ i (kr)——±—~ji (kr),	(2.67a)
ar	r
4 h (*r) =	• (^) + — li (kr) (2.676)
ar	r
градиентная формула (2.56) дает особенно простой результат
(kr) Tzz_1;m(r) +
. { /4-1 V/2 	// хт /Л
+ I h+i (kr)Tn+ii m(r).
\ Al H- * j
(2.68)
Зд
в 1
ро
ма
MJ
Отсюда также следует, что поскольку обе векторные сферические
гармоники в (2.68) при вращении R преобразуются как неприводи-
мые тензоры [в смысле формулы (2.54)1, то и продольный потенциал
обладает этим же свойством.
М
з;
к
§ 2.3. Потенциалы и поля мультиполей
Теперь мы должны вернуться к получению решений для век-
торного уравнения Гельмгольца, удовлетворяющих условию попе-
речности. Результаты предыдущего параграфа позволяют легко
понять, что любой вектор вида
В/Мт(г) = А(^)Т/Л;т(?), |/-1|<Х</ + 1	(2.69)
будет удовлетворять векторному уравнению Гельмгольца
(V2+F)BZX;m(r)=0,	(2.70)
поскольку в В(х. т входит величина Д (kr) У^т-ц (г), которая
удовлетворяет уравнению (2.4). Эти решения для данного I обра-
зуют неприводимые тензоры ранга I. В частном случае I = 0 имеется
48
только одно такое решение, поскольку Л. должно тогда равняться
единице. Однако, подставляя I = 0 в (2.65), (2.66) и (2.68), мы ви-
дим, что такое решение в любом случае не является поперечным и
поэтому сейчас не представляет для нас интереса. Следовательно,
надо рассматривать три решения, а именно случаи 7 = I — 1,
I i 1. Любая суперпозиция из этих трех потенциалов будет
удовлетворять уравнению Гельмгольца и будет преобразовываться
как неприводимый тензор ранга I. Однако, как видно из (2.68),
не все суперпозиции будут удовлетворять условию поперечности.
Необходимо подобрать коэффициенты таким образом, чтобы это
условие выполнялось.
Мы также должны добавить новое требование, которому должны
удовлетворять получаемые потенциалы мультиполей. Подобно
тому как мы раньше требовали, чтобы потенциалы имели определен-
ное значение углового момента, потребуем, чтобы они имели опре-
деленную четность. Это необходимо потому, что рассматриваемые
нами гамильтонианы ядра включают в основном сильное взаимодей-
ствие и, следовательно, инвариантны при инверсии всех трех про-
странственных осей. Собственные функции таких гамильтонианов
одновременно будут собственными функциями оператора четности,
и можно более эффективно изучать взаимодействие электромаг-
нитного поля с ядром, если с самого начала ввести понятие четно-
сти поля.
Чтобы это сделать, рассмотрим пространственную инверсию сис-
темы координат, в результате которой компоненты данного вектора
меняют свой знак на противоположный: г' = —г. Изменение
функции В;?,; т (г) при таком преобразовании обусловлено вектор-
ным характером величин (£ц —— £и) и зависимостью от на-
правления г, которая входит в величины Ухш—р (г)- Для полярного
и азимутального углов сферической системы координат пространст-
венная инверсия записывается в виде
6->л— 6, <р—>Ф±л,
и из (2.6) и (2.7) получаем
Г Хт — р ( Г) = } Хт — р (Л	0, ф + л) =
= (- 1)ХУхт-р(6, ф)=(-1)ХУхт-р(г).
(2.71)
(2.72)
Следовательно, из трех решений BZx;m (г) два с ?. = /±1 должны
иметь одинаковую четность, которая в свою очередь противополож-
на четности решения с X = I. Поэтому попытаемся построить ре-
шение в виде
Ate(r; -n) = jz(^r)TZZ;m(r)	(2.73)
и
AZm(r; e) = cz_ijz_i(^r)Tzz_i;m(r)4-
+ ci +i ji+i (kr)Tu 4-j; m (r),	(2.74)
3 Зак. 1193
49
где потенциал (2.73) имеет четность (—1)г, а потенциал (2.74) —
четность (—l)z+’. В последнем выражении c/±i являются двумя
константами, которые должны быть определены из условия
поперечности. Для разделения обоих типов решений используются
буквы ч1 и е; удобство этих обозначений будет видно ниже. По-
тенциал (2.74) имеет ту же самую четность, что и продольный по-
тенциал (2.68); это фактически соответствует просто неудачному
(в смысле удовлетворения условия поперечности) выбору вели-
чин cz±I.
Теперь надо удовлетворить условию поперечное™ для потенциа-
лов (2.73) и (2.74). Для этого необходимо вычислить
V-(/x (kr) Tz>..,„(r)) =
= 5 (XI/ | m—ppm) V (Д (/гф (r)),	(2.75)
и
где использовано соотношение (2.486). Из (2.65) и (2.68) имеем для
правой части
— ppm)gM-[(	Y/2/\-i (М Пх-ц (г) +
. / 7 + 1 \1/2 .	- -
+ (^~77 I /x-М (МЬл+1;т-ц(Г) =
— &У (— 1)н(XI/ |m—ppm) х
и
X	Д-i	(X—11Х|т—pm—р)Ух-ш(г) +
+ (^?т')1/2/х+1(М(^ + 11л|т—• (2.76)
С учетом свойства симметрии и ортогональности коэффициентов
Клебша — Гордана (ПА.20) и (ПА.17) получаем
V-(A(^)Tzx:m(?)) =
,. ,,	.ч Г/ 1+ 1 ) 1/2 Л	>/ 1 \1/2х	1
= — kh(kr)Ylm(r) ——	б’"-“ + ктГГ fix+,z
(2.77)
Для потенциалов с X = /, определяемых формулой (2.73), правая
часть в (2.77) равна нулю и у- А.1т (г; т) = 0. Для AZm (г; е), опре-
деляемых в (2.74), получаем
V-AZm(r; е) =
= -Ч,(40Г,„(г)	' <2'78>
I \ ZZ "j - 1 /	\ ZZ 1 J	J
Для значений cz+J, которые приводят к продольному потенциалу
(2.68), в силу (2.66) квадратная скобка в выражении (2.78) равна
50
единице. Мы получим поперечный потенциал, если возьмем, на-
пример,
так что
AZm(r; е) =	(^)Тг/_1;т(г) —
\ Zt -f l /
2il+l(kr)Tll+i;m(r).	(2.80)
Потенциалы мультиполей, определенные формулами (2.73) и (2.80),
исчезают для случая I — 0. Это соответствует тому физическому
факту, что поперечный фотон со спином 1 должен переносить по
крайней мере одну единицу углового момента.
Произвольная общая константа в потенциалах (2.68), (2.73) и
(2.80) выбирается из условия нормировки. Используя (2.53),
получаем
$А;'4'(г; a')-AZm(r; o)dr =
со
= бОС1' $11' $тт' 5 1а (г) Г2 dr,
0
(2.81а)
где штрих у первого потенциала указывает, что его аргументом
является fe'r; о и а' обозначают индексы I, ш, е и
О')--
[07-1 ii-i 0 +l)/7'+i/7+11, a—I,
iiji,
TjjfY 10	17-1 ji~ t f 07+i /7+1], a= e.
(2.816)
В (2.816) штрих снова обозначает аргумент k’r. Интегралы (2.81)
легко вычисляются, так как
оо
$ h(k'r) jK(kr) г2 dr = — 6 (k-k'),	(2.82)
0	'г
где правая часть не зависит от X и содержит одномерную 6-функцию
от модулей волновых векторов. Таким образом,
^Apm,(r; a')-A/m(r; a) dr = -7-6 (Л—k’) 6Qn' dtr bmm>.	(2.83)
3*
51
Этот результат также указывает, что А1т (г; I) и AZm (г; е) линейно
независимы, так что полнота системы Т^; т (г) и сферических функ-
ций Бесселя обеспечивает полноту набора потенциалов A(ni (г; I),
AZm (г; m), AZm (г; е).
Вид векторных потенциалов, описываемых формулами (2.68),
(2.73) и (2.80), обладает большим преимуществом. Это связано с тем,
что сразу же можно получить основные свойства потенциалов как
неприводимых тензоров и их трансформационные свойства при вра-
щениях. С другой стороны, выражение (2.68) мы получили рас-
смотрением действия оператора градиента на ji (kr) Ylm (г) [см.
(2.65)1. Можно записать и другие потенциалы с помощью простых
дифференциальных операторов, действующих на указанную
функцию:
AZm (г; пг) =	2— Ljz (kr) Ylm (г),	(2.84a)
У/(Z+l)
AZm (r; e) = —EUz V x (L/z (kr) Ylm (r)),	(2.846)
*V/(Z+1)
где L = — ir X v — оператор орбитального углового момента.
Формула (2.84а) легко получается, если вспомнить, что L -— век-
торный оператор, поэтому в силу теоремы Вигнера — Эккарта
(Гт' | Lv | Im} — (ИГ | mvm') {Г || L II Z) =
= (lU'\mvm’)(lU'\ 101)—’ <Z1|LO[Z1>,	(2.85)
где последнее равенство справедливо для /	1 и Г	1. Из уравне-
ния (2.346) следует
в то время как из табл. ПА. 1
(Zl/| 101)~1 = ]//(/ + !)-
В результате имеем
(Tm'\Lv | /т> = 6/г УI (I + 1) (111 | mvm'). (2.86)
Для случая I = 0 матричный элемент исчезает, что и отражено в вы-
ражении (2.86). Поскольку L коммутирует с функциями от г, правая
часть равенства (2.84а) имеет вид
h (^) 2 (~ Dv (Hl I mvm') Ylm- (r) g_v.
V
Используя свойства симметрии коэффициентов Клебша — Гордана
(ПА.20), получаем, что эта сумма равна TZZ;nl(r), и с помощью
выражения (2.73) приходим к формуле (2.84а).
52
Что касается потенциала, обозначаемого с помощью индекса
е, то из (2.84а), (2.73), (2.65) и (2.68) видно, что правая часть фор-
мулы (2.846) принимает вид
---Г V X ii(kr) Тц.т(г) =
К
= -42(П/|т—V (hikrjYim-»
К |1
= i 2(/l/|m—ррт)|иХ Г( —?—)1/2ii-tTu-
ц	L \ л Н 1 /
1; т—ц
(2.87)
Чтобы вычислить векторное произведение, заметим, что из (2.39)
и табл. ПА.1 можно получить
+	(2.88)
поэтому
i 2 (И/| т—ppm) 1ц X Т/Х: т_м =
и
= —1^2 2(/1/1 т—ццт) (XI/1 т~р—vxm—р) X
(XV
Х(Ш |pvp+v)yXm_p_v|p+v.	(2.89)
Первые два коэффициента Клебша — Гордана могут быть перепи-
саны с помощью (ПА.31) в виде
(XI/ \ т—р—vvm— р) (/1/ \т—ррт) =
= 2£//(11/1 vpp-(-v) (X//1 m—р—vp-f-v/n) 1Г(Х1/1; //), (2.90)
t
где / = |/2/ + 1, a W — коэффициент Рака. Если провести сум-
мирование по р и v, оставляя р р 4 v фиксированным, то свой-
ства ортогональности коэффициентов Клебша —• Гордана дадут
/ — 1 и тогда для (2.89) получим
(-1/+4V6 Г(//11; 1Х)У(Х1/|т-ррщ)Пт_р(£)£р =
р
= (-1)'+ЧУбУ(//11; 1Х)ТгХ:т(?) =
= _1_ /(HU)+2-X(X_+_l) т г}	(2 91а)
2	У/(/+1)
Мы использовали свойства симметрии коэффициентов Рака (ПА.31)
и (ПА.36) и явное выражение для 1Г (//11; 1 X) из ((ПА.39).
В (2.87) мы рассматриваем случаи Х = /=Е1, Для которых выраже-
ние (2.91а) дает
±1/2
*п± 1; т (г).
(2.916)
53
Подставляя (2.916) в (2.87) и учитывая определение (2.80), получаем
Формулы (2.84а) и (2.846), справедливость которых мы только
что показали, удобны для вычисления напряженностей, соответст-
вующих потенциалам мультиполей. Чтобы получить электрическое
поле, следует вспомнить, что все потенциалы имеют зависимость от
времени в виде e~i<w [см. (2.2)], поэтому для поперечной калиб-
ровки
Е(г, /)=Е(г)е-!и(=— gAjr,_4 ^А(г)е-^.	(2.92а)
с dt
В частности, поля, соответствующие индексам I, т, е, имеют вид
EZm (г; а) = ikAlm (г, а), а=1, «, е.	(2.926)
Магнитное поле определяется как
HZni(r; а) = V х AZm(r; а), а= I, т, е.	(2.93)
Из (2.65) имеем
HZm(r;I) = 0,	(2.94)
а из (2.84a) и (2.846)
HZm («*; '") = V X AZm (r; m) = ikAlm (r; e) = EZm (r; e).	(2.95a)
Магнитное поле для е-случая легко вычисляется, если восполь-
зоваться соотношением
VX(VxA) = — V2 А + V (V-A) = й2 А,	(2.96)
которое получается из условия поперечности и уравнения Гельм-
гольца. Тогда
HZm (г; е) = - i- V х (V X AZm(r; m)) =
К
= -ikAlm (г; ш) = - Е/Го (г; т).	(2.956)
Поля, которые удовлетворяют соотношениям (2.95а) между Н (ш) и
Е (п) и (2.956) между Н (п) и Е (nt), обычно называют дуальными
полями. Эти соотношения возникают потому, что замена
Е' = ± Н, Н' = + Е	(2.97)
оставляет инвариантными уравнения Максвелла для свободных
полей, а также величины, представляющие интерес с физической
точки зрения, например вектор Пойнтинга (1.45), энергию поля
(1.47). Из (2.95а) и (2.956) также следует, что электрическое и маг-
нитное поля являются неприводимыми тензорами, преобразую-
щимися с помощью тех же матриц вращения Dlm'm (Я), что и соот-
ветствующие потенциалы.
54
Обратимся, наконец, к вопросу о происхождении обозначений
га и е для потенциалов мультиполей. Они возникают из рассмотре-
ния потенциалов и полей в ближней (или статической) зоне, т. е.
для случая kr 1. В этой области функции Бесселя могут быть
заменены их главными членами*
Ъ(^)га-ЧМ,/(2/ + 1)П.	(2.98)
и тогда нетрудно получить оценки по порядку величины
H;ra (г; е) ~ (kr) HZm (г; га)« HZm (г; т), |
Е;т (г; га) ~ (kr) EZm (г; е) « EZm(r; е). J
Таким образом, индексы га и е соответствуют тому, что га-ком-
понента магнитного поля превосходит е-компоненту магнитного
поля в статической зоне. Аналогично е-компонента электрического
поля в этой зоне значительно больше его га-компоненты. Потен-
циалы и поля, отмеченные индексом га, называют магнитными
мультиполями, а отмеченные индексом е — электрическими муль-
типолями. В частности, потенциал AZm (г; га) описывает магнитный
мультиполь порядка I (сокращенно Ml). Он имеет угловой момент
I, преобразуется с помощью матриц D‘m’m (R) и имеет четность
(—1)'. Аналогично AZm (г; е) описывает электрический мульти-
поль порядка I (сокращенно Е1). Он также несет I единиц углового
момента, но имеет четность (—1)г+1. В электромагнитных пере-
ходах мультиполя порядка Ml четности участвующих уровней
различаются как (—1);+>, в то время как для ЕАпереходов
четность должна меняться в соответствии с фактором (—1)г.
Это происходит потому, что потенциалы мультиполей входят в со-
ответствующие матричные элементы в виде скалярного произведе-
ния на оператор тока, который является векторным оператором и
изменяет знак при пространственной инверсии.
§ 2.4. Разложение по мультиполям для фотонов
В § 1.3 мы рассматривали плоские волны в качестве решений вол-
нового уравнения с поперечной калибровкой. Как видно из (1.57) и
(1.58), они имеют пространственную зависимость вида
^(r) = eeik-r, е-к = 0,	(2.100)
где опущен очевидный индекс к у вектора поляризации е и ис-
пользована рукописная буква Л для обозначения ненормирован-
ного поля. Такая форма векторного потенциала удобна для опи-
сания фотонов, наблюдаемых в лабораторной системе координат
(при условии, что можно не учитывать детали конструкции волно-
вого пакета). С другой стороны, когда в ядре происходит электро-
__ (2*	факториал^определяется следующим образом: (2Z + 1)!! =
55
магнитный переход между состояниями с определенным угловым
моментом, необходимо рассматривать потенциалы мультиполей.
Следовательно, важно знать, как они входят в поперечные плоские
волны Л (г), что означает необходимость выполнить разложение
этого векторного поля но полному набору AZm (г; а) (где а = I,
ш, е). Эта задача значительно упрощается, если взять ось z парал-
лельной к или в сферическом базисе сориентировать £0 вдоль к.
Тогда, так как вектор в перпендикулярен к, он должен лежать в пло-
скости (£i, £_х):
£— _ (—l)^6—ц!ц—	i е—и 1ц-
Ц = ±1	ц=±1
(2.101)
Для {е± = 1, е_х = 0} это соответствует правой круговой поля-
ризации фотонов, в то время как набор = 0, е_х = 1) описы-
вает левую круговую поляризацию
(рис. 2.2). Линейная поляриза-
ция в направлении х и у опреде-
ляется значениями коэффициентов
Рис. 2.2. Вектор электрического по-
ля электромагнитной волны с ле-
вой круговой поляризацией с точки
зрения наблюдателя, стоящего пе-
ред приближающейся волной (век-
тор к параллелей оси z). Для вол-
ны с правой круговой поляризаци-
ей вектор Е вращается в противо-
положном направлении, т, е. по
часовой стрелке.
е±1 = ±1/)л2или е±1 = =р i/ ]/2
соответственно. Конечно, любая
другая поляризация может быть
описана как суперпозиция двух
линейных или двух круговых по-
ляризаций.
Согласно (2.101), достаточно
рассмотреть Л(г) для е, параллель-
ного р = ±1. Так как Л (г)
должно быть суперпозицией муль-
типольных потенциалов, запишем
Лц (г) = 1ц е1 k г = 2 [с1т (О X
1т
^1т (г;0 + ^Im («ОАцДг; т) +
+ czm(e) AZm(r; е)]. (2.102)
Подействовав оператором div на обе части этого равенства, полу-
чим, что cIm (I) = 0, т. е. продольный мультиполь не может давать
вклад в нашу поперечную волну. Чтобы вычислить коэффициенты
с1т (а), для а = т, е применим вначале операцию rot к обеим
частям равенства (2.102); используя в левой части соотношения
(2.88) и (2.95), получаем
V X (1ц е1к•г) = i^|0 X |ц е,к г = Л j/2 (1111 р 0 р) gp, eik •г =
— рЛ|и е|к •г = р/гЛц (г) =
= ik 2 [clm (m) Alm (г; е)-clm (е) AZm (г; т)].	(2.103)
1т
56
Поскольку мультипольные потенциалы ортогональны друг другу
[см. (2.83)] н составляют полный набор, то сравнение (2.102) и
(2.103) дает clm (е) = iuc/m (ш). Чтобы вычислить остальные кон-
станты, подействуем оператором L на обе части равенства (2.102)
и образуем скалярное произведение. Затем, пользуясь разложением
плоской волны с вектором к вдоль оси г
eikz = eikr cos е _ у (214-1) iz jz (kr) Pt (cos 0) =
/
=	2 (21 + 1)' /2 i' jz (kr) Yl0 (0, Ф),	(2.104)
I
и формулами (2.84), (2.80) и (2.86), получаем
/4^-2 [/ (/ + 1) (2/ + 1)11/2 i' Azo (г; пт) =
I
= g с1т (пт) {[/(/ + 1)]- >/2 L2 /г (kr) Ylm(6, ф) + Al.(V х AZm (г; п,))}.
Для второго члена в правой части имеем
L-(V X А) = —i г-(V X V х А) =
= ir-[V2A — V(V-A)] = — i/?2r-A,
так как потенциал поперечен и удовлетворяет уравнению Гель-
мгольца. Кроме того, этот потенциал является потенциалом маг-
нитного мультиполя, для которого из (2.84а) имеем r-AZm (г; пт) = 0.
Пользуясь для второго члена уравнением (2.34а), а для левой части
соотношением (2.73), получаем
-<4^ V [/ (I +1) (21 + l)]i/2 р (kr} (i 111 [г_и0) Yltl (6, ф) =
= 2 [/ (/ + 1)]*/2 с1т (Ш) jz (kr) Ylm (6, ф).
Im
Из условия ортогональности сферических гармоник имеем
с1т (’") = -Ил (21 + l)]i/2 р 6m[i (I 111 и_и0) =
= р [2л(2/1)]1/2 Р6тц, р=±1.
Гаким образом, для волнового вектора к, взятого вдоль оси z, полу-
чаем из (2.102)
А (г) = е1к  г = ,1 (2л)1 /2 2 (21 +1) 42	[AZM (г; in) +
+ i pAZ|1 (г; е)], £ р = ± 1.	(2.105)
Полученный результат легко обобщается на случай произволь-
ного направления вектора к. Если предположить, что к описывается
полярным и азимутальным углами 0 и ф в определенной системе
координат, то эта система получается из той, которая использова-
лась в (2.105) поворотом на углы Эйлера 01 = 0, 02 = — 9,
57
03 = —<Р (рис. 2.3). Поскольку величины А1т являются неприводи-
мыми тензорами, то при таких вращениях они преобразуются
Рис. 2.3. К обобщению формулы
(2.105).
Результат, даваемый формулой (2.105),
действителен для нештпихованиой си-
стемы отсчета, в которой ось г сориен-
тирована вдоль вектора к. Чтобы обоб-
щить этот результат, необходимо рас-
смотреть поворот, который переводит
систему xyz в систему x"y"z". В по-
следней системе направление к зада-
ется полярным и азимутальным углами
6 и ф. Углы Эйлера, описывающие этот
поворот,— 61=0, 62= —6, 03 = — <р.
А(г)=^е'к-г=Л?е1кг = (21
1 К
2, ”з). В данном случае, чтобы из
частного результата (2.105) полу-
чить (г) в произвольной систе-
ме координат, необходимо обра-
тить преобразование, указанное
в (2.54). Поэтому мы используем
(61, 62, Оз)’1 = (-03,- 02, — 01)
и получим
^ll(r) = |(Xeik-r = p(2n)i/2 х
X 2(2/-f-1)1/2	(ф, 0,0) X
lv
X [AZv(r;m)-[-ipAZv(r; е)]. (2.106)
Формулы (2.105) и (2.106) бу-
дут необходимы при изучении ис-
пускания и поглощения попереч-
ных фотонов, описываемых пло-
скими волнами, системой, имеющей
угловой момент в качестве хоро-
шего квантового числа. Чтобы за-
кончить обсуждение этих формул,
рассмотрим также случай р = 0.
Используя (2.104) и (2.65), полу-
чаем для к, параллельного оси z,
)>/22(2Z+l)1/2iz-1Azo(r, О- (2-Ю7)
В этой главе основное внимание обращалось на те свойства по-
лей со спином 1, которые связаны с угловым моментом, и не рас-
сматривались другие результаты теории углового момента. Краткий
очерк последней представлен в Приложении А, а также дается
в большинстве обычных учебников квантовой механики. Более
подробное обсуждение можно найти в книгах Вигнера [355], Фано
и Рака [126], Эдмондса [109], Роуза [288] и Бринка и Сэтчлера
[551. Так же как и в книге [287], в этих книгах представлены и ре-
зультаты, касающиеся электромагнитных мультиполей. Разложе-
ние векторной плоской волны по мультиполям дается в другой
форме в статье Герцеля [1761. Многие из важнейших статей по
теории углового момента перепечатаны в [38]*.
* Кроме указанных книг, часть из которых переведена на русский язык,
м. также [7, 90, 302, 368, 369, 376, 377, 391]. — Прим, перев.
ГЛАВА 3
ВТОРИЧНОЕ КВАНТОВАНИЕ
ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Прежде чем переходить к обсуждению взаимодействия фотонов
с ядром, мы должны тщательно рассмотреть два других вопроса
электромагнитной теории. Первым из них является вычисление
энергии взаимодействия для системы, состоящей из поля и заряжен-
ных частиц. Это будет необходимо, например, в кваптовомехани-
ческих расчетах вероятностей электромагнитных переходов, так
как в них входит квадрат матричного элемента от энергии взаимо-
действия. Вторым вопросом является описание рождения и унич-
тожения фотонов в различных процессах взаимодействия, для чего
необходимо ввести специальный формализм, называемый вторич-
ным квантованием. При введении этого формализма нам будут
очень полезны результаты предыдущей главы, где было установле-
но, что фотоны имеют спин 1. Таким образом, если принять обыч-
ную связь между спином и статистикой 1216 , 352], то можно ожи-
дать, что фотоны подчиняются статистике Бозе — Эйнштейна.
В процессе применения лагранжева и гамильтонова подхода к элект-
ромагнитной теории при обсуждении вторичного квантования поля
можно будет легко рассмотреть и вычисление энергии взаимодейст-
вия поля с частицами.
§ 3.1. Лагранжианы и гамильтонианы для электромагнетизма
В классической механике лагранжиан L для системы частиц
определяется как функция обобщенных координат qa(f) (s = 1,
2, ..., 2V) и соответствующих скоростей qs (t); он может явно зависеть
от времени. Он строится как разность между кинетической энер-
гией и обобщенным или зависящим от времени потенциалом V : L —
~ Т — V. Лагранжиан удовлетворяет уравнению, полученному
из вариационного принципа, т. е. требованию, чтобы действие
/я
S= 5 L(qs, qs, t)dt	(3.1a)
h
59
имело экстремум
6S = 0	(3.16)
при независимых вариациях bqs обобщенных координат. Соотноше-
ния (3.1а) и (3.16), известные как принцип Гамильтона, определяют
движение системы в интервале времени от ti до t2. Поскольку
имеем
6S = V [ [—6^ +
** J U<?5 s a9s dt /sJ
S=1 t,
N t2	N
= V f f—--------- ^-]bqsdt+ V ^6qs ‘‘=0,	(3.2)
-J J dt dgj	dqs tt	'
s= 1 tt	s= 1
где выполнено интегрирование по частям. Последнее слагаемое
здесь исчезает, поскольку при получении уравнения движения
в интервале от момента Н до t2 предполагается, что координаты
фиксируются в конечных точках, так что Sqs (G) = £>qs (G) = О
(s = 1, 2, ..., N). Поскольку вариации Sqs произвольны и незави-
симы, то для момента t, взятого между И и t2, подынтегральное
выражение в (3.2) должно само равняться нулю. Отсюда получаем
уравнения Лагранжа, которые описывают эволюцию системы в ука-
занном интервале времени:
_£^£__^£=о.	(3.3)
dt dqs dqs
Другим способом описания является введение гамильтониана
системы и использование уравнений Гамильтона в качестве урав-
нений движения. Чтобы это сделать, определим канонический им-
пульс, соответствующий координате qs:
ps(t)=d^,	(3.4)
dqs
который, как видно из уравнений Лагранжа, удовлетворяет урав-
нению
Гамильтониан является функцией обобщенных координат, их сопря-
женных импульсов и, возможно, времени. Он определяется следую-
щим образом:
к
ж (ps, qs, Z ps Ps—l (Ps, qs, 0	(3.6)
s = 1
60
и в действительности является функцией только указанных пере-
менных (а не скоростей qs), поскольку с учетом (3.4)
d&i(ps, qs, 0=2 [M'Zs+^s dps -^-dqs—^- d?sl —
s__ j L	dqs dqs J
(3-7>
Таким образом, из (3.7) и (3.5) получаем уравнения Гамильтона
дМ	 дЖ	-	дЖ	dL
—;— — q ----- =—п ------- =-----.
dps	dqs	rs	dt	dt
(3.8)
Еще одним способом описания движения классической системы
является использование скобок Пуассона. Для любых двух функ-
ций динамических переменных F (ps, qs, t) и G (ps, qs, t) имеем
N
IF, G]^ 2
s = 1
t dF dG dG df
\dqs dps dqs dps
(3.9)
Удобство использования скобок Пуассона станет очевидным, если
мы рассмотрим полную производную по времени, например, от F:
dF(ps, qs. t) V t dF dF „ \ dF
----Ji-----= Z-+ Ps I =
dt---------\dqs dps ) dt
V ('dF dW dF d&£ \ . dF	, dF
7,-------------------I -I—т = [F, atЦ-----.
S=1 dps dps dqs ) dt	dt
Частным случаем соотношения (3.10) является
d>J£ (ps. qs. t) (9У] | da J	daF
dt	dt dt
(3.10)
(З.Ц)
откуда следует хорошо известный факт, что если гамильтониан явно
не зависит от времени, то он есть интеграл движения. Другие при-
меры скобок Пуассона:
qs = R7s. 3t\, ps = [ps,	(3.12a)
[<7s(0. 9s'(01=0, [ps(t), Ps'(01 = 0,
[<7s(0. Ps'(01=6ss-	(3.126)
Вместе с соотношениями (3.126) в качестве вспомогательных соотно-
шений, которым должны удовлетворять правильно определенные
координаты и сопряженные импульсы, уравнения (3.12а) дают
уравнения движения системы. Важность скобок Пуассона обус-
ловлена тем, что они инвариантны по отношению к классическому
каноническому преобразованию, и поэтому соотношения, выражае-
61
мне скобками Пуассона, имеют одинаковый вид для любого набора
канонических переменных. Это свойство вместе со многими другими
алгебраическими свойствами скобок Пуассона, общими со свойст-
вами коммутаторов, позволяет построить теоретический базис
квантовой механики с помощью следующего соответствия:
FG — GF=ih[F, G],	(3.13)
где 2лЙ — постоянная Планка.
Таким образом, при построении квантовомеханической теории
для описания динамической системы следует начать с нахождения
лагранжиана такого, чтобы соответствующие уравнения (3.3)
давали правильные уравнения движения для этой системы. Затем
с помощью соотношений (3.4) и (3.6) необходимо получить сопря-
женные импульсы и гамильтониан. Уравнения движения даются
уравнениями (3.12), а применение соотношения (3.13) приводит
к квантовомеханическому варианту теории.
Начнем с получения классического лагранжиана для движения
релятивистской заряженной частицы в электромагнитном поле.
Уравнение движения, которое описывает такую систему и которое
требуется получить с помощью уравнений Лагранжа, имеет вид
[см. (1.30)]
—	-=9/'е + —хнУ	(3.14)
dt 1/1—t)2/c2	4 V с )	'
Мы рассматриваем здесь частицу с массой ти зарядом q, движущую-
ся со скоростью V. Электрические и магнитные поля Е и Н берутся
в точке г ((), где находится частица. Как и в (1.4) и (1.5), введем
векторный и скалярный потенциалы:
H = VxA, Е = — V<p— —	(3.15)
с dt
Тогда из (3.14) получим
-А_^=_Л?<р--1-^+-х(?хА)] =
dt Д/1—v2/c2	L	с dt с	'J
= v( —?(р+9—•а') -1-^- +v-v') А =
\	с f с \ dt	/
= V ( —9ф+? —•а') (3-16)
\	с I с dt
где мы использовали
dA(-J' ° = (4 + V • v ) А (г (0, ()•	(3.17)
at \ at 1
Таким образом, уравнение движения частицы, взаимодействующей
с полем, можно выразить через потенциалы и импульс
р = от// 1 — о2/с2
(3.18)
62
следующим образом:
— ( . ОТУ..=-+—А) +Vfgy —-g-v-A^O.	(3.19)
dt к 1/1 — v2ic2 с I	с /	’
Из уравнения (3.3) следует, что подходящим лагранжианом яв-
ляется величина
L (г, о) = —тс2 У1 —о2/с2 + — v-A (г, t)—qq> (г, t). (3.20)
с
Тогда канонический импульс принимает вид
p = VrL=	+~А(Г> 0 = Р + -А(г, 0-	(3.21)
у 1 —Vе/с2 с	с
Тем самым для нашей системы получено хорошо известное правило,
что включение электромагнитного поля приводит к замене канони-
ческого импульса р на р -ф (<?/с) А (г, t), где р остается, как гово-
рят, «измеряемым» импульсом. Конечно, поскольку в скобки Пуас-
сона (3.126) входит канонический импульс, необходимо, согласно
рецепту квантования (3.13), заменить в классическом гамильтониа-
не р (а не р) на (A't')v Для того, чтобы получить соответствующее
уравнение Шредингера.
Действительно, гамильтониан имеет вид
5^ = p-v—L =	- -|-щр	(3.22а)
l/l-v2/c2 Y	'	7
и является здесь полной энергией. Хотя в (3.22а) мы записали га-
мильтониан как функцию от v, фактически он должен рассматри-
ваться как функция от р; более подробно
Ж (г, р)=с( р-----^А(г, о]2 + (тс)2|'/2 +<7Ф(г> 0> (3.226)
где для квантового случая р = (А/г) V- В случае поля, независящего
от времени,
сШ _ дЖ _ ,
dt ~ dt ~
и полная энергия частицы в поле сохраняется. Для нерелятивистских
частиц имеем
|р|= р-----— А тс,
с
(3.23)
так что гамильтониан принимает вид
Щг, р)=тс2 + { р —-^-АГ/(2т)+щр.	(3.24)
\ с )
Первое слагаемое здесь является просто постоянной массой покоя
частицы. Второе слагаемое содержит величину
(</А)2/(2тс2),
63
которая существенна лишь в процессах с двумя фотонами и поэ-
тому может временно не учитываться (см. § 4.5). Остающиеся члены
имеют вид
3t = q^—q —  А
с
(3.25а)
и описывают взаимодействие заряженной частицы с одним фотоном.
Для системы с плотностью заряда р (г, t) и плотностью тока j (г, t)
формула (3.25а) обобщается:
Ж = С рф---------- j • Al dr.
(3.256)
Выражение (3.256) дает совершенно правильную энергию взаимодей-
ствия плотности заряда и тока с полем. Но наше рассмотрение было
до сих пор довольно ограниченным, поскольку оно относилось
только к нерелятивистским частицам. Мы не будем сейчас обсуж-
дать следствия из формулы (3.226), так как на практике обычно
требуется квантовомеханическое описание системы частиц, и фор-
мула (3.226) не является хорошим исходным пунктом для такого
рассмотрения (см., например, [305, стр. 54—64]). В § 3.3 мы вернем-
ся к рассмотрению энергии взаимодействия частицы и поля, но
исходя из рассмотрения динамики поля.
Поэтому обратимся теперь к изучению другой части нашей сис-
темы, а именно рассмотрим поведение электромагнитного поля для
случая, когда имеются источники заряда. Для этого следует сначала
обобщить для полей анализ лагранжианов, гамильтонианов и схе-
мы квантования. Рассмотрим плотность лагранжиана 5?, которая
является функцией поля* ф (г, t) и его первых производных по
пространственным и временному аргументам, т. е.
Й?(ф, Фф, ф).
Тогда лагранжиан и действие будут выражаться формулами
L = § X (ф, Фф, ф) dr,
v
tz	^2
S = § L dt = § § X (ф, Фф, ф) dr dt,
ti	ti v
(3.26)
(3.27)
где H и t2 являются конечными точками временного интервала,
на котором мы изучаем «траекторию» поля. Рассмотрим вариации
величин ф, такие, что
6ф(г, ^) = 6ф(г, <2)=Ц-	(3.28)
* Для электромагнитного поля ф следует считать кратким обозначением
компонент ф и А.
64
Тогда, поскольку 6 (yip) = y(6ip) и = d/dt (6ip), будем иметь
[как в уравнениях (3.2) и (3.3)]
2
Л V
7^ + 77^ -v W+ 7^ 4(6ФГ^’ (3-29а)
[dip д (Vip)	dip dt J
где
d$t.
d (V1P)
•V(6ip) =
з
у dse — (бф).
d (dip/dxz) dxi
(3.296)
Если рассматривают функцию ip, имеющую несколько полевых ком-
понент, то соотношение (3.29) должно содержать суммирование по
этим компонентам. Воспользуемся теоремой Гаусса в 4-пространст-
ве, чтобы проинтегрировать по частям последние два члена. Тогда
V- ( dSC
\ д (Aip)
\___д_ дЭГ
/ dt dip.

s
d^ , dSS 1 < ,
--------  П -J--— n„ oip.
d(Vip) dip J
(3.30)
где (n, n0) — единичный вектор в 4-пространстве, нормальный
к трехмерной гиперповерхности S. Второй член в интеграле по этой
гиперповерхности вычисляется с помощью (3.28):
dSn0^bty = fd'^6ip I dr— f^-Sip
dip J dip |G J dip
V	г
dr = 0,
(3.31)
так как каждый из
Первый член в
записан в виде
написанных интегралов равен нулю.
интеграле по гиперповерхности X может быть
da --------oip,
d(Vip)
где da — умноженный на единичный нормальный вектор элемент
двумерной граничной поверхности Л, которая охватывает объем V.
Этот интеграл равен нулю, так как мы берем объем V большим и
требуем, чтобы поля исчезали на больших расстояниях, Вариации
произвольны в интервале между ti и /2, поэтому квадратная
скобка в первом интеграле (3.30) должна равняться нулю, и мы
получаем уравнение движения Эйлера — Лагранжа для поля
V-—— — =0.	(3.32)
dip \d(Vip)/ dt dip
Формализм, развитый в (3.4) — (3.8) для построения гамиль-
тониана, применим для любого конечного набора обобщенных
65
координат. В то же время в уравнениях (3.32) имеется бесконечно
много «координат», соответствующих значениям, которые ip (г, t)
могут принимать на бесконечном множестве точек г. Чтобы обойти
эту трудность, введем (см., например, [185]) в трехмерном про-
странстве ячейки 6rs. Эти ячейки должны быть настолько малы,
чтобы поле яр (г, t) заметно не изменялось по г в интервале 6rs.
Затем отождествим qs со средним от яр (г, t) на 6rs, а (д/дг^ яр (г, /)—
с (<7s+i — (Xsh- Наконец, яр (г, t), усредненное по интервалу
6rs, возьмем в качестве qs. Тогда выражение (3.26) заменится сле-
дующим:
25Ж, <7s)6rs.	(3.33)
S
Таким образом, аналогом соотношения (3.4) является
ps(O=^- = ^6rs.	(3.34)
uQs uQs
Определим величину
(3.35а)
ors dqs
которая в пределе очень малых ячеек 6rs->0 переходит в величину
л (г, t) = - 355 - .	(3.356)
Лр (г- t)
Тогда, как и в формуле (3.6),
=	2(ns^s—Ж(?з.4з))бг,	(3.36а)
S	S
ИЛИ
Ж 5 (ляр—Ж) dr.	(3.366)
Это позволяет ввести плотность гамильтониана
Л = ляр—%,	(З.Збв)
такую, что
M=\hdr.	(3.36г)
Как и в (3.7) и (3.8), имеем из (3.366)
О = П л г/яр + яр dn — ~ с?яр —	• d (Vxp) —
J L	дяр d (Vip)
— ^d/ldr.	(3.37)
ap T dt ]	v
Согласно (3.356) первое и пятое слагаемые взаимно уничтожаются.
Четвертое слагаемое можно проинтегрировать по частям, а интег-
еб

рал по поверхности опустить. В результате получим из (3.32) и
(3.356)
—л dtp—^dtjdr.	(3.38)
Но, вообще говоря,^ является функционалом от ф, уф, л и у.п
(how от ф), поэтому
Ж =
— С?ф +	• V(<ty)+ — dn +
дф Y д(Уф)	dn
 ф(^л) + — dt] dr =
d (Ул)	dt J
dh
d (Ул)
dn + — dt I dr.
dt J
(3.39)
Здесь снова выполнено интегрирование по частям. Сравнивая (3.38)
и (3.39), получаем аналог уравнений Гамильтона (3.8)
 д/г „ dh
Ф =--------V • ----- ,
dn \д(Ул))
( dh „	dh \
л = —---------V-------
к дф d (Уф) '
dh
dt dt
(3.40)
Наконец, как и в (3.9), можно ввести скобки Пуассона для F и
G —двух функционалов от ф, уф, л и ул. Они определяются так:
СЯ——v-(-*2-YI
J 1|дф кд (Уф) '] [дл уд (Ул) Ч
Г^_у/'^\1Г^_у
(дф кд(Уф)/Л.дл кд(Ул)/_и
(3-41)
Теперь, проводя обычное интегрирование по частям, мы можем
вычислить полную производную по времени от функции кинемати-
ческих переменных:
dF (ф Уф, л, Ул, t)
dt
С учетом (3.40) и (3.41) получаем
dF (ф. Уф, л, Ул, t) [р	dF
dt
dt
(3-42)
67
К этому уравнению можно добавить соотношения
[9s(0. 9s'(01 = 0, [ps(0, Ps'(01 = 0; [9s(0, Ps'(01= 6ss' (3.43a)
пли в пределе 6rs->0
[ф(г, 0, Ф(г', 01=0, [л (г, 0, л (г', 01 = 0.
[1р(г, 0, л (г', 01 = б(г—г').	(3.436)
Для полей с более чем одной компонентой они принимают вид
[фк (г, 0,	Д', 01 =0, [л“ (г, 0. л₽(г', 01 =0,
[4>“(Г, 0, Л₽(г', 01 = ^а₽6(г—г').	(3.43в)
Как и (3.13), все эти соотношения могут быть переписаны в кван-
товомеханическом виде, при условии что коммутаторы соот-
ветствующих функций динамических переменных заменяются скоб-
ками Пуассона, умноженными на величину 1А. Это завершает для
случая полей цепочку лагранжиан — гамильтониан — скобки Пуас-
сона — квантование.
Теперь мы применим этот аппарат для квантования амплитуд
электромагнитного поля. Физическую причину процедуры кван-
тования легко понять. Она возникает как следствие квантования
механических величин в обычной квантовой механике, поскольку
это квантование приводит к принципу неопределенности, который,
в свою очередь, исключает возможность одновременного измерения
положения и импульса, например, заряженной частицы. Однако
Бором и Розенфельдом [46] было отмечено, что если электромаг-
нитное поле не квантованно, то можно использовать его для того,
чтобы одновременно определить указанные параметры частицы.
Поэтому в последовательной теории напряженности поля должны
подчиняться соотношениям неопределенности, аналогичным соот-
ношениям неопределенности для частиц, а их уравнения движения
должны соответствующим образом квантоваться.
При выполнении этой программы мы обратим основное внимание
на электромагнитное поле в отсутствие источников. Соответствую-
щие рассуждения нетрудно обобщить на случай наличия источников.
Кроме того, фактически все черты механизмов реакций, которые
мы хотим обсудить здесь, можно рассмотреть с помощью резуль-
татов, полученных при квантовании свободного поля. Наконец,
квантование электромагнитного поля при наличии источников, когда
иековариантная поперечная калибровка не является полезной, в дей-
ствительности требует явно ковариантной схемы. Такой подход
служит предметом самостоятельного обсуждения во многих книгах
(см. список литературы в конце главы). Поэтому мы предпочитаем
рассмотреть основные элементы квантования свободного поля,
поскольку это представляет для нас наибольший интерес.
Рассмотрим электромагнитные потенциалы, удовлетворяющие
условию поперечной калибровки в области пространства, в которой
68
Нет источников. Из (1.16) и (1.19) видно, что можно взять скаляр-
ный потенциал <р (г, t) =0, а векторный потенциал будет при этом
удовлетворять уравнению
□ А (г, 0=0.	(3.44)
Поля определяются с помощью этого потенциала следующим об-
разом:
Е= — — H = VxA.	(3.45)
с dt
Условие поперечности имеет вид
V-A = 0.	(3.46)
Попытаемся описать динамические свойства свободного поля с по-
мощью плотности лагранжиана
Ж = — А2 — — У f—(3.47)
8л [ с2 2 "Т? 'дгь дг‘ ' -I
При варьировании компонент А/ (I = 1, 2, 3) временно откажемся
от условия (3.46); впоследствии мы его введем для приемлемых ре-
шений получившегося уравнения движения для А. Имеем из (3.32)
—Г———11=0>	(3.48)
4л ( с2 dt	дгь \ дгь dri /]
так что если воспользоваться уравнением (3.46), то сразу же полу-
чается уравнение (3,44). Из уравнений (3.45) следует, что плот-
ность лагранжиана численно равна
£= — (Е2—Н2)	(3.49)
8л
и исчезает для свободных полей в вакууме. Тем не менее, величина
X (3.47) имеет правильную функциональную зависимость от А, по-
зволяющую получить корректные уравнения движения для поля.
Установив, что (3.47) является надлежащей плотностью лагран-
жиана для электромагнитного поля, продолжим обсуждение вопро-
са о квантовании поля. Сначала, как и в (3.356), введем соответст-
вующий сопряженный импульс поля
л(г,/)= ~ = —1-А-=------— Е.	(3.50)
дК 4лс2	4лс
Тогда, согласно (3.36), гамильтониан примет вид
Я=[(лА — Ж)г/г= — f(E2 + H2)dr.	(3.51)
J	8л J
Как можно видеть из (1.47), в действительности это—энергия
электромагнитного поля. Гамильтониан более удобно записать
69
через компоненты потенциала и их сопряженные импульсы
Ж = у J |4лс2 л2 +	(V X A)2j dr.
(3.52)
Воспользуемся теперь соотношениями (3.13) и (3.43в), чтобы
получить коммутационные соотношения для свободного поля,
а именно
И,- (г, t), At (г', 0] = [л, (г, 0, nt (г', 0] =0,	(3.53а)
[А, (г, t), лг (г', 0] = —	[А,- (г, t), Е, (г', 0] =
4лс
= 1Йбл6(г—г').	(3.536)
Последнее коммутационное соотношение является источником не-
которого противоречия. Из него вытекает
[V-A(r, 0, Е(г', 0] =—4jtificV6(r—г'),	(3.54а)
что нарушает условие поперечной калибровки \7-А = 0, а также
[А(г, 0, V'-E(r', 0] = — 4л i Йс V'6 (г—г'),	(3.546)
что противоречит уравнению Максвелла V’E 0 в области, сво-
бодной от источников. Эта трудность возникает потому, что в со-
отношениях (3.53) мы молчаливо допускали что имеются три неза-
висимые компоненты для А и л, тогда как в действительности усло-
вие поперечное™ ограничивает их число, и полностью независимы-
ми являются лишь две компоненты. Например, если рассмотреть
решения (1.57) для данного волнового вектора к вместе с условием
(1.58), то компоненты Af и А2 могут быть взяты независимыми,
а для третьей компоненты условие поперечности дает
А3 =------- (^ Ах + k2 А,), л3 =-лх + k2 л2). (3.55а)
k3	k3
Поскольку Alt А2 и ль л2 удовлетворяют соотношениям (3.53),
то мы должны иметь
[А3, л3] = (k2/£2 — 1) i ЙЙ(Г-Г'),	(3.556)
что противоречит (3.536). Способ исправления соотношения (3.536)
теперь совершенно ясен. Мы должны заменить правую часть сим-
метричным тензором, дивергенция от которого как по г, так и по
г' равна нулю. Вместо соотношения (3.536) постулируем модифи-
цированное коммутационное соотношение
[А; (г, 0, л, (г', 0] =
= i й (блб(Г-Г')~ — Д	(г-г'). (3.56)
(	4л drj dri | г —г |)
70
Величина 6,-z (г — г') в фигурных скобках в правой части назы-
вается поперечной дельта-функцией, так как она обладает свойст-
вом
V^-6/z(r-r')- /-б(г-г')+ /уб(г-г') = 0.	(3.57)
дг:	дг,	дп
1
Здесь использованы уравнение (1.26) и свойства симметрии дельта-
функций пог и г'. Те же свойства симметрии могут быть исполь-
зованы, чтобы показать:
V^^(r__r') = 0.
Если теперь рассмотреть соотношения (3.54), то с помощью моди-
фицированного коммутационного соотношения (3.56) нетрудно
получить
[V-A(rJ) Е(г',/)] = [А(г,ф V'-E (г',/)] =0,	(3.58)
как и должно быть.
Однако оказывается, что новое коммутационное соотношение
приводит к новой трудности. А именно, мы видим, что А (г, t) и
л (г', t) не коммутируют, даже если точки с координатами г и г' как
угодно далеко удалены друг от друга. Это кажется противореча-
щим принципу причинности, который требует, чтобы измерения,
выполненные в двух точках, разделенных пространственноподоб-
ным интервалом, не влияли друг на друга. Но надо помнить, что
А (г, t) не является наблюдаемой величиной (хотя величина
л — Е (4 лс), разумеется, является таковой), и поэтому мы
должны исследовать коммутаторы для полей; в результате получим
[Е} (г, /), Ek (г', /)) = (4лс)2 [Я; (г, 0,	(г', /)] = 0, (3.59а)
[Hj (г, /), Hk (г', 01 = [(V X А (г, t))j, (V' х А (г', 0)ft] =0 (3.596)
И х
[Hj (г, z), Eh (г', /)] = — 4лс Е/mp (г, 0 nh (г', /)1 =
L тр	J
= — 4л1Ас^еутр-^-[брйб(г—г') — -±-	~ -—Ц-} =
дгт ( р	4л дгр drk | г—г ) J
= 4л1йс8Лт-^-д(г—г').	(3.59в)
ОГт
В силу свойств полностью антисимметричного тензора ejkm в правой
части последнего равенства т может принимать лишь одно значе-
71
ние для данных / и k. Как следует из соотношения (3.59в), измере-
ния напряженностей поля, которые являются действительно на-
блюдаемыми величинами, влияют друг на друга в один и тот же
момент времени только тогда, когда измерения выполняются в од-
ной точке.
Разложим теперь А и л по плоским волнам, которые мы рас-
сматривали в § 1.3. Для этой цели воспользуемся функциями
(1.57):
А (г, t) = 2	2 l<7kK (0 uk, (г) +9+ (0 и*? (г)],
К - U } Л--------- 1 !
Я (Г, 0=2	2 lPkk (0 ukX (г) -bpk+ (0	(Г)],
К (U) Л — 1 , £
где
uk?.= L~3/2ek;.eik-r.
(3.606}
Новый индекс Л обозначает состояние поляризации поперечной
волны и поэтому может принимать два значения. Эти функции нор-
мированы в объеме L8 следующим образом:
5 «к-v (г) -ukX (г) dr = бЬк  6},к-.
(3.61)
Коэффициенты разложения <7kz (t) и ркК ((), которые, вообще го-
воря, могут быть операторами, входят в разложение вместе со
своими эрмитово сопряженными величинами <?кх (t) и ркк (/). Поэ-
тому операторы А и л эрмитовы. Суммирование по к в (3.60а) огра-
ничено одной полусферой в ^-пространстве, так как эрмитово со-
пряженные величины автоматически учитывают вторую полусферу,
поскольку ( — к) включено в ukx. В дальнейшем мы будем это
обозначать с помощью штриха у символа суммирования.
Сами операторы разложения т/к;. и ркг_ могут считаться обоб-
щенными координатами и соответствующими сопряженными им-
пульсами, так как они дают вклад в А и л с данным импульсом
к и данным значением поляризованного состояния X. Поэтому есте-
ственно квантовать их в духе двух соотношений (3.12в) и (3.13).
Рассмотрим
(0> qk^ (01 = [<7kx (0, ?ktv (01 =
= lPkJ0, Pk^(01==lPkx(0. PkV(01=0,	(3.62a)
(9kX(0, Pk<v(01=0	(3-626)
l?kx(0, Р&,- (01 = [pkt (0> pk-x- (01 = i *6kk-	• (3.62b)
72
Вместе с выражениями (3.60) эти коммутационные соотношения*
сразу же приводят к соотношениям
Иу (г, 0, Д; (Г', 0] = [Лу (г, 0, л, (г', 0] = 0	(3.63)
и
[Ду (г, 0, лг (г', 0] =
= X £ !(^(r))i(uk-v(O)/[?+(0, pvv(01 +
kk' ZA/
(uk?. («))/ (uk r (Г0)/ [qk} (0, p+K. (0]| =
X Z (ekA(ekA[eik (r'-r)+e-ik (r--r>].	(3.64)
k X=I,2
Суммирование по состояниям поляризации выполняется так. Рас-
смотрим тройку единичных векторов, таких, что третий вектор на-
правлен вдоль к (он обозначается екз = к | к |), а двумя другими
векторами являются ек1 и ек2. Тогда
з
2 (ekx)y(ekX)z = 2 (ек0у(ек0г —(екз)у(ек3)г буг—kj kt/k\ (3.65)
1=1.2	?.= !
поскольку величины rk> (X = 1, 2, 3) образуют полный базисный
набор в трехмерном пространстве. Этот результат выражает усло-
вие поперечности (3.46) и (1.58). Тогда получаем для коммутатора
[Ду (г, 0, л, (г', /)] =
i h
U
i h V’’ / kt ki \
77 2 (6y,-------— [eik<r'-r>-|~e~ik‘<r'—r)i =
L k \ k2 ) 1	J
2	A^e^-fr'-r).	(3.66)
V k2 dr; dr I ]
В последнем выражении устранено ограничение одной полусферой
при суммировании по к и опущен лишний член, включающий — к.
Первая сумма в (3.66) вычисляется просто:
J_Ve‘k ^_г)лу Л е1к.|(г-г) = б(г_г,)	(3 67)
* Заметим, что написанные коммутаторы являются соответствующими
коммутаторами для комплексных динамических переменных, так как если
мы разложим q и р на эрмитову и антиэрмитову части, каждая из которых
удовлетворяет коммутационным соотношениям, полученным из (3.126) и
(3.13), то будем иметь
? = (<7i+i<7a)//"2. P = (₽iT-i₽2)//2,
I?. ₽+) = у- l4i+i?2- Pi—iPa]= ~ [<7i. Pi] + ~~ [<7a> Pa] = i&-
73
Вторая сумма вычисляется, если учесть, что в пределе большого
объема L3 из (3.67) следует
V2 у 4л eik-<r’-rU_4n6(r_ и_
A k43
С помощью уравнения (1.26) можно, таким образом, отождествить
рассматриваемую сумму с функцией Грина для уравнения Пуассона:
JLy±Leik-
L3^k2
(г-г')
L СО
(3.68)
Тогда равенство (3.66) сведется к правильному «поперечному»
коммутационному соотношению (3.56)
[Л,-(г, /), л7(г', /)] = 1?гбц(г—г').
Такой результат следует из выбора коммутационных соотношений
(3.62) для 9k?. и ркх и из формулы (3.65), выражающей условие
поперечности. Это подтверждает, что модификация коммутацион-
ного соотношения из (3.536) в (3.56) в действительности является
лишь способом правильного учета условия поперечности у-А = О,
а не изменением схемы квантования, описываемой соотношениями
(3.126) или (3.43) и (3.13).
С помощью выражения для потенциала А можно теперь полу-
чить величины, представляющие интерес с физической точки зрения.
Из (3.60) и (3.60а) имеем
Е(г, t)=— 4лс 2 У (Pkx(0ukx(r) + Piik(0u^(r)],	(3.69)
к Х=1,2
а из (3.45) и (3.60)
Н(г, 0 = *Х S [?kx(O(kxUkUr))-^(O(l<XU^(r))]. (3.70)
к Х= 1,2
Тогда из (3.51) и (3.61) получаем гамильтониан
57 = 4- У' У 1(4лс)2 Рк\ (0 Ркк (04- к2 9ki (t)Чкк (/)]•	(3.71)
4л к к
Воспользуемся соотношениями (3.12а), (3.13) и (3.71), чтобы полу-
чить уравнения движения для (0 и Рм. (7). С учетом (3.62в) имеем
для коммутаторов
= тт [?ki, 57] = 4лс2 Ркл	(3.72а)
1П
и
Ркх = -ту- [Pki, 57] = —<7кл-	(3.726)
in	4л
74
Взяв второй раз производную от первого соотношения и подстав-
ляя в него второе, получаем
?кх = ~ ^2c29ki= —	(3.73)
где coft = kc. Решения этого уравнения имеют вид
?kHO = fekxe-i^'+^+ei‘>*',	(3.74а)
где бы и бы —две операторные константы. Из (3.72а) получаем
Рк?.(О =	‘ e'“ft ‘ )	(3.746)
Величины Ьик имеют вид
йк>. = 4- (<7кх +	Pkz )	,	(3.75а)
2 \	<l)k	[t=o
=	РкЛ	(3.756)
2 \	(Oft	Jt=O
и удовлетворяют соотношениям
[бы, b£ ?.-] = [бы, 6k^v] =^- бкк- би- (3.76)
Чтобы избавиться от коэффициентов при дельта-функциях в правой
части этих коммутационных соотношений, определим новые опе-
раторы
ак;. = —1/^т-йы, ^ = -*-1/-^^	(3-77)
с у 2лН	с у 2nh
которые удовлетворяются соотношением
[ак?., ct-к' /.-] =[йы, акы-] = 6кк-6м,-	(3.78)
(все другие пары равны нулю). С помощью этих операторов по-
лучаем
A(r, t) = c^’ v ./-25Я_{[Оьг1е-^Чак^е!“^]иы(г) +
к 1=1,2 У “к
+ [°Й.е'"»'+<1ие-1"»'] иЬ(г)|,	(3.79)
л(г.() = -!-У' V 1/^-([-«11е-'“«' + оИ+е1"*'|и1а(г) +
С	1 Oil-
к Х== 1 .2 г
+ [ййе'^'-аые-1^'] и^(г)[.	(3.80)
75
Отсюда видно, что можно отождествить ам. с a_ki
и написать
а(г,о=с у
к 1=1.2
X (акЛ Uki (г) е '“л' + гц?, (г) е,шь'},
(3.81)
X
X |-«k;.iik;.(r)c-iwkM flkl?.Uk;.(r)ei“^|>	(3.82)
где суммирование по к теперь включает все ^-пространство. Тогда
выражение (3.71) принимает вид
3^ = 2' 2 riak(ak>.akK+aika^) =
к 1=1,2
= 2 2 flMk (aia Gkl + ^kl~ flkl + !)•	(3.83)
к 1=1,2
Здесь мы воспользовались коммутационными соотношениями
(3.78). Устранив ограничение на суммирование по к, получим
^ = 2 2	1/2).	(3.84)
к 1=1,2
Первый член содержит величину Okiaki. которая, как мы увидим,
«.считает» число фотонов с данным волновым вектором к и поляри-
зацией X. Каждый из них дает вклад в полную энергию, равный
энергии Планка = lick. Член
2 2 ~k^k = ^twk
к 1=1,2 2	к
является неудачным результатом теории. Эта бесконечная энергия
обусловлена энергией нулевых колебаний гармонического осцил-
лятора для каждого из бесконечного числа фотонных состояний.
Она не будет представлять для нас каких-либо особых трудностей,
поскольку эта величина является просто общей аддитивной кон-
стантой энергии. Ее можно исключить, если перенормировать энер-
гию поля так, чтобы отсчитывать все энергии относительно этой
величины. Тогда
= 2 2 ^«kGkiaki.	(3.85)
k 1= 1,2
Аналогично из формулы (1.39) можно получить импульс поля.
В соответствии с (3.45), (3.50), (3.81) и (3.82) имеем
рЦ-ezd =_J_Je(i-, /)хН(г, t)dr ——pt(r, 0x(vxA(r, t))dr =
= 2 2 Ak(ab\aki+1) = 2 2 ^ка^ац, (3.86)
k 1=1,2	k 1=1,2
76
где на этот раз постоянный член исчезает без каких-либо предполо-
жений, так как различные противоположно направленные волно-
вые векторы компенсируют друг друга;
^Ак = О.
к
Формула (3.85) приводит к заключению, что каждая компонента
свободного поперечного электромагнитного поля с волновым век-
тором к и состоянием поляризации X обладает энергией huk, что
соответствует квантовым гипотезам Планка и Эйнштейна. При этом,,
как следует из формулы (3.86), каждая компонента будет иметь им-
пульс (йю^/с) к = Ак. В свете квантовых гипотез эти выражения
также наводят на мысль, что роль оператора Пю.Ск?, заключается
в том, чтобы давать число квантов в каждом состоянии (k, X) при
действии на вектор состояния, описывающий поле.
Рассмотрим теперь формализм, который используется для описа-
ния распределения квантов и их рождения и уничтожения.
§ 3.2.	Вторичное квантование: представление чисел
заполнения
Мы закончили обсуждение квантовых свойств свободного попе-
речного электромагнитного поля, выражаемых в основном форму-
лами (3.81) и (3.85). Однако необходимо рассмотреть, как операторы
ак~л, входящие в разложение потенциала А по полному набору сос-
тояний, описывают динамические свойства поля. Эти операторы ком-
мутируют друг с другом, за исключением одного существенного
случая
[а,-, ф+] = бл.	(3.87)
В выражении (3.87) мы используем более компактные обозначения,
чем, например, в соотношениях (3.78), Единственный индекс / обоз-
начает индексы (k, X), которые входят в эти соотношения; в более
общем случае он может обозначать любую комбинацию индексов,
описывающих элементы полного набора состояний, по которым
выполняются необходимые разложения. Введем также билинейные
комбинации операторов Uj, которые будем называть операторами
числа частиц
Nj = a+ а,	(3.88)
и оператором полного числа частиц
N=^Ni=^ai,	(3.89)
/ /
где суммирование проводится по всем состояниям, входящим в наш
полный набор.
77
Из (3.87) и (3.88) легко получить, что
[Лд, at] = [at а}, at] = а/ [а}, aj + [at, ajа} = —а}8jh (3.90а)
[Nj, at] = at [a]t at] + [at, at]aj = at f>n (3.906)
и
[N}, Nt]=at [NJt at]+[N}, at]at =
= (—a/ aj + at aj) 6,y = 0.	(3.90b)
Определим теперь пространство, в котором действуют операторы
aj и Nj. Из соотношения (3.90в) ясно, что можно определить орто-
нормированный базис, в котором одновременно могут быть диаго-
нализованы все операторы Nj, а их собственные значения tij можно
использовать для обозначения этих базисных векторов:
TVj|/7i, п2, п3, ..., п}, ...)=nj\n1, п2, п3, .... nj, ...>.	(3.91а)
Для краткости обозначений будем часто называть набор {«i, ns,
п3, nj, ...,} просто nj, так что
Nj\nj) = nj\nj).	(3.916)
Тогда, если ] nj) —конкретное состояние и мы строим с его по-
мощью состояние at |иу>, то, как следует из (3.906), это соответст-
вует состоянию, в котором j-e собственное значение увеличивается
на единицу, т. е.
Nj (af\nj'>) = (Njat~at Nj)\nj>+af N}\nj> =
= а?\п})+ъа?\п})==(П1+1Ца?\nj>).	(3.92a)
Состояние aJ\nj'> имеет собственное значение nj — 1, так как
Ny aj | iij) = (Nj aj—aj Nj) | ny> +a} Nj | n}> =
= (n}-1)а}\П]>.	(3.926)
Чтобы получить нормировку этих новых состояний, запишем
at |ny> = c+|ny+l>
и заметим, что
| с+12 = («у | aj а/ | ny> = (пу1 (at а,- +1) | п,-> = Пу + 1;
аналогично соотношение
ау'|П;>=С_|Пу—1>
дает
|c_|2 = (ny|af fly|ny>=/iy,
поэтому для данного выбора фаз получаем
at I иу> = 1 «у +11 Пу + 1 >,	(3.93а)
ai I ni> = V aj | nj — 1 >.	(3.936)
78
Собственные значения n.j положительны или равны нулю, так как
nj =	| Nj |	= <п,- | af oj | п;> = (aj | n}))+(a} | n;>) > 0.	(3.94)
Отсюда следует, что и, — целые числа, поскольку если бы они не
были таковыми, то, многократно действуя оператором а} согласно
(3.936), мы каждый раз понижали бы tij на единицу до тех пор,
пока оно не стало бы отрицательным. Целочисленность величин
устраняет это неудобство, так как после /г^-кратного действия опе-
ратором Пу на | n.j) получаем
aj | пь п2, п3, ..., 0,, ...) = 0.	(3.95)
Состояние, для которого действие всех, операторов в соответст-
вии с (3.936) дает нулевой результат, называется вакуумом электро-
магнитного поля и обозначается | 0). Для него
aj 10> = 0, ЛгЦ0> = 0для всех /	(3.96)
С помощью вакуума мы простым образом можем построить про-
странство векторов, в котором действуют операторы aj и of. На-
пример, .состояние
—af 10> = 10ь 02, 03, ..., 1, ...>	(3.97)
является нормированным состоянием, имеющим нулевое собствен-
ное значение для каждого оператора Nj, кроме /-го, для которого
nj = 1. Мы постулируем, что (3.97) соответствует одной частице
в состоянии, описываемом волновой функцией Uj (г). Для операто-
ров, используемых в § 3.1, это состояние имело бы вид
• ‘j-j- flux 10> = | Ok, 0k,x2, Ok2x„ ..., Цх, -•>	(3.98)
и соответствовало бы наличию одного фотона в состоянии с волно-
вым вектором к и поляризацией X. Как видно из (3.85), (3.88) и
(3.916), оно имеет энергию huk = tick, так как
Ж (afo, 10>^= timh (afx | 0>) = tick (ак\ | 0)).	(3.99)
Как следует из (3.86), оно имеет импульс Ак, так как
Р,,м (flk\ 10» = Ak (ай. 10».	(3.100).
В дальнейшем это состояние характеризуется обычными волновыми
функциями цы (г) (3.606).
Разумеется, если бы мы интересовались только одночастичными
или однофотонными состояниями, то операторы а, и af были бы
не очень полезны. Их удобство становится более очевидным, когда
нужен формализм, описывающий изменение числа имеющихся фо-
79.
тонов, или, например, при рассмотрении двухчастичных состояний.
Эти двухчастичные состояния могут быть двух типов:
1 -ну- at at 10) = 10ь 02, 03, ..., 2j, ...)	(3.101)
или
= 10T, 02, 03, ..., ly, 0/+1, 0y+2>... , lz, ...>.	(3.102)
Согласно (3.93a) оба эти состояния нормированы. Они имеют одни
и те же собственные значения оператора полного числа частиц:
N (тт10>)ара^10>=
р
= 2 ( —}= at at 10> V
V 12 '	1 J
N (af at 10»=^ at ap af at 10> = 2 (af at |0».
p
Состояние (3.101) соответствует симметричной двухчастичной нор-
мированной волновой функции
-у- [Uj (rj Uj (r2) + Uj (r2) Uj (fi)] = IZy (rj Uj (r2),
а состояние (3:102)—функции
—= [Uj (rj IZZ (Г2) + Uj (r2) tzz (rj].
I £
Симметрия между двумя частицами, которая подразумевается в фор-
ме записи последнего состояния в рамках аппарата вторичного
квантования или более явно в волновой функции, является необ-
ходимой, поскольку мы имеем дело с системой частиц (или фотонов),
удовлетворяющих статистике Бозе—Эйнштейна. В общем виде
нормированное состояние с собственным значением п = опе-
I
ратора числа частиц строится в виде
П -^-у (Д*Р I °> = I »1, »2, Из, ..., tij, ...).	(3.103)
z 1 ni!
В процессе перехода от вектора, описывающего частиц в /-м
состоянии, к вектору, описывающему tij + 1 частиц в этом состоя-
нии, мы используем оператор а/, который называется оператором
рождения-, так как а} уменьшает на единицу, то называется
оператором уничтожения или оператором аннигиляции. Проис-
хождение названия для Nj оператор числа частиц очевидно, так
как его собственным значением является просто число частиц
в /-м состоянии. Величины пу- называются числами заполнения.
80
Матричное представление для рассмотренных операторов, соответст-
вующих /-му состоянию, имеет вид
	о । Г о о ...		0 0	0 0 ...
	о о ] Г о ...		/Г о	0	0 ...
	0 0	0 /3“ ...	. «г=	0 /2	' 0	0 ...
	0 0	0	0...		0	0	Уз о ...
			Z 	• •
		0 0 0	0 ...'	
		0 1 0	0 ...	
Nj = a'j aj =		0 0 2	0 ...	
		0 0 0	3 ...	
			1	
Соответствующие векторы состояния для чисел заполнения п} = О
1, 2, 3, ... имеют вид
	1		0		0		0
	0		1		0		0
0/> =	0	. 1Ь> =	0	, |2/> =	1	. |3/> =	0
	0		0		0		1
Легко видеть, что оператор потенциала А (г, /) (3.81) в пред-
ставлении чисел заполнения уменьшает или увеличивает числа за-
полнения состояния на единицу. Очень часто требуется знать
матричные элементы оператора А (г, t) между состояниями, в одном
из которых не имеется фотонов (фотонный вакуум), а в другом
имеется один фотон. Из (3.81) и (3.93) следует, что эти матричные
элементы выражаются формулами
<Y|A(r,O|0>=<0klM, Ok,x2, 0klM,..., lkX, ...| A(r,/)|0> =
= cV 2nA/(obrtzkx (r) e°ft fj>	(3.104a)
и
<°|A(r,/)|T>=<0|A(r,'0|0klM> 0klXj, 0кгМ,..., lkx,...> =
= c]/^ 2nti/(nk ukx(r)e !ah‘.	(3.1046)
(Нормировка плоских волн, которая здесь появляется, отличается
от нормировки в выражениях (1.57) и (1.65) на величину 1/2 из-за
того, что мы связываем положительные частоты только с процесса-
ми поглощения, а отрицательные частоты — с процессами испуска-
4 Зак. Ц93	81
ния.) В более общем виде получаем для переходов без участия фо-
тонного вакуума
<nkX+l | А (г, 0|«кх> =
= c|/rnbx + 1 У Ukx(r)e1K,ft< ,	(3.105а)
<«kx— 11 А (г, t) | «кх> =
= с|/ЛПкхрЛ 2nA/o)ft uk?. (г) е |0>ь*,	(3.1056
где величины J/ + 1 и ]Дгк?. суть факторы усиления для вы-
нужденного испускания и поглощения, обусловленные наличием
других фотонов с соответствующим волновым вектором к. Резуль-
таты, даваемые формулами (3.104) и (3.105), выражают главную
цель введения формализма вторичного квантования. Они позволяют
нам описать важнейшее свойство квантованной системы (в данном
случае электромагнитного поля), а именно, что она может отдавать
или получать энергию единичными порциями. Для электромагнит-
ного поля эти порции имеют величину ЛсоЛ, и они появляются в ап-
парате вторичного квантования в результате действия операторов
рождения и уничтожения и Пкх, входящих в А (г, t).
Прежде чем закончить рассмотрение формализма вторичного
квантования, кратко опишем модификацию схемы квантования для
системы частиц, подчиняющихся статистике Ферми—Дирака. В этом
случае формализм должен учитывать антисимметричность многоча-
стичных состояний. Постулируем антикоммутационные соотноше-
ния для операторов рождения и уничтожения:
{щ, аг)={а/’, at} = 0,	(3.106а)
{а}, аг+} = 6Л.	(3.1066)
Фигурные скобки означают антикоммутатор
{Д В}=ЛВ+Д4={В, Л).	(3.107)
Легко видеть, что соотношения (3.106) содержат в себе принцип
исключения Паули для фермионов, так как если мы попытаемся по-
строить многочастичную систему с двумя фермионами в одном и том
же состоянии, то из соотношения (3.106а) получим
а/ at ——а/ at = 0,	(3.108a)
a} ai — — а}а)=0.	(3.1086)
В частности,1
at at |«i, n2, пз, . 0? > •••> = 0-	(3.109)
Антикоммутаторы (3.106) не представляют собой квантового аналога
скобок Пуассона, как это было для соотношений (3.76) и (3.78), полу-
ченных из соотношений (3.536). В действительности они не имеют
классического аналога, и суперпозиция величин п; не может быть
82
наблюдаемой величиной в отличие от соответствующей ситуации
для фотонов, описываемой формулами (3.70), (3.74) и (3.77). Одна-
ко билинейные формы операторов а, дают наблюдаемые величины.
Например, можно ввести оператор числа фермионов
Nj=- dj а},	(3.110)
который в представлении чисел заполнения служит для описания
числа фермионов в различных состояниях. Можно легко найти его
собственные значения. Из соотношений (3.108) следует, что
N* = aj a, a? aj = а/ (1 — af afl а}='а* а} = Nь S (3.111J
так что и/ = tij и п, равны нулю или единице. Это соответствует
правилам заполнения, определяемым принципом исключения Паули.
Явная матричная форма для операторов рождения и уничтоже-
ния фермионов может быть записана по аналогии с формой, полу-
ченной ранее для бозонов. Для /-го состояния она имеет вид
0 0\
0 I/
о 1\	. /о 0\	+
, с+=	, Nj = aj а}=
fl О) 1 U о)
соответствующие векторы состояний для nj = 0, 1 даются матрицами
Мо)'
а> =
В заключение заметим, что при выборе схемы квантования много-
частичной системы, характеризуемой соотношениями (3.87) или
(3.106), мы руководствовались теоремой Паули [267, 325 216],
которая гласит, что для физически разумных случаев частицы с полу-
целым спином должны квантоваться как фермионы, а частицы с це-
лым спином — как бозоны. Предположения, требующие «разумных»
физических свойств, заключаются в том, что энергия не должна
быть отрицательной и что коммутаторы наблюдаемых величин,
принадлежащих точкам пространства—времени, разделенным про-
странственноподобным интервалом, должны обращаться в нуль
(причинность). Поскольку из гл. 2 уже известно, чтофотоны имеют
спин 1, то, не проводя более подробных исследований, мы смогли
выбрать коммутаторы, а не антикоммутаторы в выражениях (3.56),
(3.62), (3.76) и (3.78).
3.3. Энергия электромагнитного взаимодействия
Как следует из формулы (3.20), лагранжиан взаимодействия
заряженной точечной частицы в присутствии электромагнитного
поля имеет вид
К' = ?[— • А (г, t)—<р(г, /)],	(3.112а)
С
4*
83
где г — координата точечного заряда. Если мы рассматриваем
распределение зарядов, лагранжиан принимает вид
L' =	(г, t) dr = J [-1- j (г, /) • А (г, /)—р (г, /) <р (г, t^dr. (3.1126)
Соответствующие гамильтонианы взаимодействия для нерелятивист-
ского случая получены в (3.25); фактически — это лагранжианы
2Г= — Г.	(3.113)
Чтобы убедиться в правильности этих результатов для Ж’, можно
теперь рассмотреть энергию взаимодействия для поля в присутствии
заряженных частиц. Разумеется, следует ожидать, что мы получим
те же самые формулы, что и (3.112) и (3.113). Как видно из (1.16),
для скалярного потенциала с поперечной калибровкой энергия
взаимодействия является обычной кулоновской энергией (для слу-
чая без запаздывания). Поэтому
5^сои1 = § Р (г, О <Р (г, t) dr—
= f р(г,7)----—— р(г', /) р(г', /) drdr'.	(3.114)
J |г —г |
Из (3.1126) и (1.19) видно, что для векторного потенциала в при-
сутствии заряженных частиц мы должны обобщить (3.47):
£n^ = £+--fj'(r.O- А(г, t)dr. (3.115)
С J
Поперечный ток в (3.115) определяется формулой (1.21а) или в эк-
вивалентном виде
з
jk(r,t)= 5 ^6м(г—г') jz(r', f)i/r',	(3.116)
i=i
если воспользоваться поперечной дельта-функцией (3.56); этот
ток удовлетворяет уравнению
V-j'(r, 0 = 0.	(3.117)
С помощью уравнений (3.32) и (3.48) получаем, что новый лагран-
жиан приводит к уравнению движения для потенциала
□ А (г, 0=----— j'(M),	(3.118)
С
это соответствует уравнению (1.19). Далее по аналогии с соотноше-
ниями (3.50) и (3.53) получаем, что сопряженный импульс
anew (г. t) =	= Л <г>	(3-119)
не меняется, и поэтому все результаты §3.1, касающиеся кван-
тования, остаются без изменения. Гамильтониан (3.36) с учетом
84
взаимодействия теперь должен содержать член
Mans=------------------------Lf j'(г, 0-А(г, t)dr.	(3.120)
С J
До тех пор пока мы пользуемся поперечной калибровкой, можно
его записывать в виде
3('trans =---j (Г, t)  А (Г, t)dr.	(3.121)
Это выражение справедливо, поскольку, согласно (1.20) и (1.21),
j(r,/) = j'(r,/) + Vf(r,O,	(3-122)
где [ (г, t) — скалярная функция. Поэтому
$ j • Adr = jj (j' + V f) • Adr = § j *  Adr—jj / V • Adr,
где выполнено интегрирование по частям во втором члене, кото-
рый теперь исчезает, так как в указанной калибровке у • А = 0.
Чтобы получить полную энергию взаимодействия, следует объ-
единить выражения (3.114) и (3.121)
b/k — ^Coul “т" trans—
= Jjp(r,/)ф(г, t)----- j(F, /)-А(г, /)]dr.	(3.123)
Этот результат получен для поперечной калибровки, и если сохра-
няется частный вид величины (р (г, /), использованный в (3.114),
то полученное выражение несправедливо для других калибровок.
Мы часто будем пользоваться формулой (3.123) именно в таком виде,
ограниченном выбором определенной калибровки, поскольку если
имеется только распределение тока, то кулоновская энергия не
играет роли в изменениях состояний, описывающих систему «поле+
+частица». С другой стороны, результат (3.123) для ЗС является
намного более общим, чем может показаться на первый взгляд.
Чтобы в этом убедиться, удобно рассмотреть величину
V — f 3£' dt = СГр (г, I) <р (г, t)-— j (г, t)-A (г, /)1 drdt, (3.124)
J	JI	с	J
которая появляется при изучении эффектов взаимодействия. Со-
гласно (3.1126) и (3.1а), она противоположна по знаку вкладу
взаимодействия в действие S. Матричные элементы от V обычно
используются в квантовомеханических расчетах вероятностей пере-
ходов. При этом осцилляторная зависимость от времени волновых
функций поля и частицы приводит к закону сохранения энергии
благодаря дельта-функции, Дирака, появляющейся после интегри-
рования по времени. Далее, V является лоренц-инвариантной ве-
личиной, поскольку каждый из наборов величин (ср, j) и (<р, А) —
4-вектор, и, следовательно, подынтегральное выражение (3.124)
является скаляром, а элемент объема является инвариантом; V —
также и калибровочно инвариантная величина, так как если приме-
85
нить преобразование (1.9), то получим
V -> (Тр ftp------------L j. (А -|- VA)1 drdt —
J L \ c dt I c	J
= jjp<P---' A+ ~Л +V-j^drd/ =
= §[ptp—j-A]drdC	(3.125)
Здесь выполнено интегрирование по частям и использовано урав-
нение непрерывности для тока. При интегрировании по частям пред-
полагалось, что калибровочная функция Л выбрана равной нулю
в конечных точках интервала интегрирования по времени. В системе
покоя частицы с учетом поперечной калибровки V принимает вид
V = dt— ptpdrdt— §p(r, t) । 1 > । р (r'’ ^r^r'	(3.126)
что представляет собой интеграл по времени от кулоновской энер-
гии в рассматриваемой лоренцевской системе. Поскольку величи-
на V является инвариантом как относительно преобразования Ло-
ренца, так и относительно калибровочного преобразования, то
она должна определять энергию взаимодействия при любом выборе
системы координат и калибровки.
Обратимся теперь к применениям формулы (3.123) или (3.124)
для расчета вероятностей перехода при фото- и электровозбужде-
нии. В частности, мы начнем с обсуждения некоторых вопросов по-
глощения и испускания фотонов, для которых можно использовать
поперечную калибровку и не учитывать кулоновскую энергию, т. е.
использовать формулу (3.121). В дальнейшем мы должны будем ис-
пользовать аппарат вторичного квантования, развитый в предыду-
щих параграфах, особенно формулы (3.104).
*
* *
Квантование электромагнитного поля в рамках приближений,
аналогичных тем же, что и используемые здесь, обсуждается в кни-
гах Гайтлера [186, 187], Шиффа [302] и Бете [30]. Обширное систе-
матическое рассмотрение квантовой электродинамики, особенно ее
ковариантных формулировок, дается во многих книгах, например
в книгах Вентцеля [343], третьем издании книги Гайтлера [187],
Боголюбова и Ширкова 148], Гамильтона [181], Мандла [238],
Фейнмана [133], Ахиезера и Берестецкого [7], Швебера [305], Бьер-
кена и Дрела [42]*. Менее подробные, но интересные обсуждения
имеются в книгах Дирака [99], Бенедетти [90], Газировича [154]**.
Оригинальные статьи в этой области особенно ценны, многие из
них собраны в [304]. Кроме того, следует указать статьи Гейзен-
берга и Паули [185], Ферми [128], Бора и Розенфельда [46].
* Большинство из указанных в этом разделе работ иностранных авторов
переведено на русский язык. См., кроме этого, книги Бете, Швебера, Гофмана
[390], Соколова [384]. — Прим, перев.
** См. также книги Берестецкого, Лифшица, Питаевского [370], Давы-
дова [376], Блохинцева [372]. — Прим, перев.
ГЛАВА 4
ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ
С ВЕЩЕСТВОМ
Знание взаимодействия фотонов с заряженными телами, такими
как, например, ядра, необходимо для расчетов вероятностей пере-
ходов, в процессе которых взаимодействующая система может перей-
ти из некоторого начального состояния в другие разрешенные для
нее состояния. Рассмотрим, например, систему, состоящую из ядра
и электромагнитного поля. В исходном положении она может на-
ходиться в состоянии, в котором ядро возбуждено (чаще всего с по-
мощью какой-либо реакции, механизм которой мы в данный момент
не рассматриваем), но фотонов еще не имеется. В конечном состоя-
нии системы может быть ядро в более низком возбуждении или*в ос-
новном состоянии и фотон с энергией, равной разности энергий
двух состояний ядра. Нас может также интересовать конечное со-
стояние, в котором имеются два или более фотонов. Это соответст-
вует схеме распада ядра, содержащей каскад через одно или более
возбужденных ядерных состояний, или наличию специфического
правила отбора, в силу которого (обычно весьма малая) вероят-
ность испускания двух фотонов становится сравнимой с вероятно-
стью излучения одного фотона. Процесс, обратный процессу одно-
фотонного излучения, предполагает начальное состояние системы,
в котором ядро почти всегда находится в его основном состоянии
и имеется фотон, вызывающий возбуждение ядра. ТЦожно рассмо-
треть также переход, в процессе которого ядро высвечивается через
один из видов фотонного излучения, о котором мы только что гово-
рили. Особенно это необходимо в том случае, когда конечное состоя-
ние ядра для процесса возбуждения расположено ниже самого низ-
кого порога испускания частиц. Однако если конечное состояние
ядра образуется в результате вылета ядерной частицы с ненулевой
массой, то необходимо выполнить расчет сечения и для такого про-
цесса фоторасщепления.
Сначала рассмотрим лишь те процессы, в которых испускается
или поглощается один фотон. Мы не будем также касаться ядерных
реакций, которые предшествуют электромагнитному переходу или
следуют за ним. Эти ограничения означают, что в главном порядке
по константе электромагнитного взаимодействия ^/(Ас) = 1/137,04
можно использовать ядерные матричные элементы, полученные из
87
энергии взаимодействия (3.121) в первом порядке теории возмуще-
ний. Оператор А в формуле (3.121) имеет матричные элементы, да-
ваемые формулами (3.104) для рождения или уничтожения одно-
фотонного состояния.
Вероятность перехода в единицу времени (скорость перехода)
дается «золотым правилом» зависящей от времени теории возмуще-
ний*
№=^-|<Л^'|О|аР,	(4.1)
где оператор взаимодействия следующим образом выражается через
оператор ядерного тока j (г, /) и оператор электромагнитного потен-
циала А (г, /):
=-----— f j(r,/)-А(г, Z)tfr.	(4.2)
В формуле (4.1) р — плотность конечных состояний системы.
Возьмем для определенности начальную волновую функцию в ви-
де | г> = | а; кл>, где а описывает ядро в начальном состоянии,
а к и X — волновой вектор и поляризация фотона; в конечном со-
стоянии ядро находится в состоянии р с большей энергией возбужде-
ния, чем состояние а. Соответствующий матричный элемент в пред-
ставлении чисел заполнения фотонов в явном виде дается формулами
(3.1046) и (3.60):
<	01 А (г, 01 кЛ> = с I екХ e,k-r-i<B' .	(4.3)
Однако об операторе ядерного тока нам ничего не известно. В дан-
ный момент мы сделаем о нем лишь несколько предположений. Пер-
вым из них является то, что временная зависимость его матричных
элементов является обычной для квантовой механики:
<	₽ I j (г, t) | а) = <р | j (г) | а) е' (£₽~£ct) t/r\ (4.4)
где Еа и Ер — энергии ядерных состояний аир. Далее, мы пред-
полагаем, что j (г, /) удовлетворяет уравнению непрерывности
V	-<P|j(r, /)|а)=-А <р|р(г,0|а> =
ot
= i (-V-p)- <Р IР (г) | со е’~Еа) t/n, (4.5)
* Эта формула справедлива для гамильтониана 2f£', который, согласно
(3.121) и (3.123), определяется как интеграл по трехмерному пространству
от плотности энергии электромагнитного взаимодействия. Если пользоваться
ковариантным выражением V=j Jtl'dt из (3.124), то дополнительное интегри-
рование по времени приводит к дельта-функции Дирака, явно выражающей
закон сохранения полной энергии: V = 2л6 (Ej —	, где Е; и Ef —
соответственно начальная и конечная полная энергия системы. Таким обра-
зом, для расчета матричных элементов перехода можно использовать как ,
так и V.
88
где р (г, /) — оператор плотности заряда ядра, который, как пред-
полагается, также имеет обычную осцилляторную зависимость от
времени. Наконец, мы предполагаем, что при пространственных
вращениях j преобразуется как векторный оператор и что | а) и
| р> являются состояниями с определенными угловым моментом
и четностью.
Для процесса фотопоглощения, который мы сейчас рассматри-
ваем, конечное состояние системы является просто возбужденным
ядром. При этом будем считать, что соответствующий возбужденный
уровень является хорошо определенным и достаточно узким. Плот-
ность конечных состояний в этой энергетической области представ-
ляет собой одно состояние на интервал энергии, определяемый шири-
ной уровня (см., например, [246, стр. 4521). Таким образом, если
мы рассматриваем вероятность перехода, проинтегрированную по
всей ширине ядерного уровня, то
„I
(4.6)
В этой формуле мы предположили, что матричный элемент
очень мало изменяется на ширине уровня. Можно воспользоваться
формулой (4.6) для расчета сечения фотопоглощения, если разделить
ее на плотность потока налетающих фотонов, который, согласно
нашей прежней нормировке, равен c/L3 фотонов на единицу площа-
ди поверхности в единицу времени. Тогда сечение поглощения, про-
интегрированное по ширине линий, будет иметь вид
(4.7)
J	Нс
line
или с учетом (4.2) и (4.3)
f adEp=^
J	ОЭС
line
J<P| j (r)|a>.EM.elk r dr
(4-8)
Если первоначальный пучок фотонов неполяризован, то следует
усреднить по двум возможным состояниям поляризации. Как и
в (3.65), получим
=	j(r)la> eik-rdr|2 —
line
—11<-5 <Р| J (0 l«> eik r Дг|2}.	(4.9)
♦
Если рассмотреть процесс, обратный реакции поглощения, т. е.
процесс излучения, для которого |i> в формуле (4.1) описывает
ядро в возбужденном состоянии а, а конечное состояние \fy —
89
= | [3; kX) описывает ядро в состоянии [3 и фотон с волновым векто-
ром к и поляризацией X, то формула (4.3) заменится формулой
<U|A(r,0|0> = c 1/ -^-Ckle-ik(4.10)
Конечное состояние теперь содержит фотон, плотность состояний
которого, согласно (1.61), имеет вид
Г.3 л-л tn dk
р=--------afik k2 —
Г (2л)3 dE
Ls k*
(2л)3 he
(4.H)

где dQh — телесный угол, в который испускается фотон. Тогда
вероятность перехода с излучением фотона дается соотношением
W-—— — I (f | Ж' I i> I2 JQk
(2л)2 №с 1	11
или
w== ТТТI I j (О I «> -8kie-ik-r
2л/гс2 J
(4-12)
9
dQk.
(4-13)
Суммируя по конечным состояниям поляризации, получаем для
случая, когда поляризация конечного состояния не наблюдается,
i(r) la> e-ik‘rdr|2—
2лЛс2 1 1	1
—| к <|3 |j (г) | a) e~ik r dr |2}.	(4.14)
§ 4.1. Разложение по мультиполям и теорема Зигерта
Формулы (4.9) и (4.14) дают решение довольно простых задач
усреднения или суммирования по состояниям поляризации фото-
на. Мы еще не умеем решать другие вопросы проблемы, имеющие в ос-
новном геометрический характер, как, например, усреднение и
суммирование по подсостояниям спина ядра или интегрирование по
направлению фотона для процессов излучения. Выполним теперь
эти операции, чтобы более отчетливо выделить основные свойства
динамики ядра. Для этого нам потребуется метод разложения по
мультиполям, описанный в гл. 2.
В формулы (4.8) и (4.13) входят величины вида*
Л4ра (кХ) — |j (г)| «>-®kx ei k-r dr, Х= 1,2.	(4.15)
Свойства электромагнитного потенциала, связанные с угловым мо-
ментом, лучше всего видны, если выполнить разложение по муль-
* Оператор в формуле (4.13), соответствующий излучению фотона, эр-
митово сопряжен оператору в формуле (4.8) для случая поглощения, и, сле-
довательно, матричные элементы перехода для этих взаимно обратных про-
цессов комплексно сопряжены друг другу.
90
типолям (2.105) для плоской волны. С этой целью определим систему
сферических базисных векторов (2.39) так, чтобы вектор |0 был па-
раллелен вектору k, gj был направлен вдоль ек1, а g_j — вдоль
ек2. Это можно всегда сделать, так как векторы ek?. (X = 1,2) пер-
пендикулярны вектору к и друг другу. Введение сферического ба-
зиса в дальнейшем нам потребуется, чтобы рассматривать векторы
поляризации как комплексные величины и воспользоваться соот-
ношениями ортогональности (2.41). Эти комплексные векторы по-
ляризации физически соответствуют круговой поляризации фотонов
(см. §2.4). Таким образом, формула (4.15) заменяется формулой
Л1₽а (кц)= $ I j(r)|a>-1ц eik r dr, |л=±1.	(4.16)
Используя (2.105), получаем
Л4₽а (kjx)=|x}/2n	[ j (г) | <х> •
•И/ц(г; 1п) + 1цАц(г; е)]dr.	(4.17)
Ограничимся далее рассмотрением переходов электрического
мультиполя. Как следует из обсуждения в § 2.3, такие переходы
осуществлялись бы всегда, если бы мы рассматривали переходы
из состояния ядра со спином и четностью 7я — 0+ в состояние со
спином J' и четностью л' = (—I)7'. Это может быть также хорошим
приближением для многих случаев, где эффекты ядерной структуры
приводят к преобладающей роли электрических составляющих.
Для конкретного электрического перехода Е1 имеем
Мра (к ц; £’/)=] 2л 1 iz+1 <р | j (г) | а> • А/н (г; е) dr, (4.18)
где в соответствии с (2.80)
А/ц(П е)=	(^)Т«-1; ц(г)~
\ J- 1
- Ый) 1/2 ii+1 (М т"ь i: ц (4’19)
Для многих интересных с физической точки зрения излучающих
систем длина волны испускаемого излучения намного больше про-
странственных размеров изучаемой системы. В частности, это верно
для тех ядер, для которых характерными энергиями фотона являют-
ся энергии около 10 Мэв, а ядерный радиус составляет около 7 ферма
или меньше, так что kR = /?/Х	0,36. Учитывая поведение функ-
ций Бесселя при малых аргументах [см. (2.98)1, получаем, что вто-
рой член в (4.19) намного меньше первого, так как
/г +! (kr)/]! _! (kr) -> (kr)2/ [(21 + 1) (2/ + 3)].	(4.20)
Поскольку, кроме малости величины kr для фотонных переходов
также имеем /	1, то правая часть Соотношения (4.20) очень мала;
Для указанных выше чисел она фактически меньше 0,01.
91
Продольный мультиполь также имеет структуру, похожую на
структуру выражения (4.19). Согласно (2.65) и (2.68),
Ащ(г; I) = ±V/l(MV/M(?) =
К
= ( 91 м1 )	и (г) + ( „. . . ) Л+1(^г)^П4-1;ц(г), (4.21)
и поэтому в длинноволновом пределе
л / м , / Z+1V/2.	, п
J Агм(г;1) =
= (—) ’/2у Wz (М Ylfl (г).	(4.22)
Подставляя это в (4.18), находим
а) -> я.2^_[еалд±Д1"'гх
1	/г [	I
xj<₽| j(r)|a>-V/z(fer)rZli(r)dr.	(4.23)
Выполняя затем интегрирование по частям, используя уравнение
(4.5) и замечая, что для фотонного перехода | Еа — £р | = like, по-
лучаем для матричного элемента фотопоглощения

х J I Р (Г) I а> /г (kr) Ytll (г) dr.
(4.24)
Разумеется, при использованных для получения формулы (4.24)
предположениях функция Бесселя в подынтегральном выражении
может быть заменена, согласно (2.98), ее пределом при малых зна-
чениях аргумента.
Возможность замены оператора плотности тока в формуле (4.18)
оператором плотности заряда в (4.24) выражает суть теоремы Зи-
герта [318; 296; 53; 138; 297, стр. 232—245; 287, стр. 74—77].
Очевидная полезность этого результата заключается в том, что он
позволяет исключить технические сложности, связанные с опера-
тором тока, при вычислении вероятностей электромагнитных пере-
ходов, выполняемых в рамках ядерных моделей*. Она также дает
некоторое облегчение намного более значительных затруднений,
* При использовании теоремы Зигерта в ядерных моделях необходима
известная осторожность: непоследовательности, которые могут быть довольно
безобидными в других случаях, могут здесь привести к плотностям ядерного
тока и заряда, нарушающим уравнение непрерывности и, следовательно,
также и теорему Зигерта. Такая ситуация возможна, например, когда вы-
полняются расчеты смешивания конфигураций по модели оболочек. В этом
случае невозмущеиные волновые функции соответствуют энергии возбуждения,-
отличной от той, которая получается при учете остаточного взаимодействия,
так что величина | Еа —	| может быть не равна tike.
92
которые возникают при рассмотрении электромагнитных взаимо-
действий в ядрах. Эти затруднения связаны с тем, что при изуче-
нии структуры данного ядра может оказаться недостаточным рассма-
тривать только А нуклонов, которые оно содержит. Нуклоны свя-
заны вместе силами, которые, как обычно предполагается, обус-
ловлены обменом мезонами. Отнюдь не очевидно, что мезонными сте-
пенями свободы можно пренебречь при рассмотрении ядерной си-
стемы. Конечно, было бы желательно рассмотреть следствия обмена
мезонами существенно феноменологическим способом так, чтобы
этот обмен был бы в основном исключен из задачи. Например, счи-
тают, что мезоны ответственны за хорошо известные зарядовооб-
менные свойства ядерного взаимодействия. Этот эффект может быть
учтен с помощью соответствующей модификации двухнуклонного
потенциала, который, как предполагается, действует при рассея-
нии нуклонов на протоне. Далее обычно действуют, описывая ядро
только с помощью степеней свободы нуклонов, которые взаимо-
действуют через этот модифицированный потенциал.
Однако такая простая картина нарушается, когда рассматри-
вают ядро, взаимодействующее с электромагнитным полем. В этом
случае, даже если в выражение для плотности ядерного заряда
входят только сами нуклоны, плотность тока определяется не одни-
ми нуклонами. Дело в том, что обменное взаимодействие может из-
менять зарядовое состояние нейтрон-протонной пары, и тогда
в силу уравнения непрерывности должен возникать некоторый ток,
обусловленный мезонами. Таким образом, даже если предположить,
что заряд локализуется на нуклонах, оператор тока должен содер-
жать вклад, возникающий от мезонов. Этот вклад может быть вы-
числен только на основе довольно неопределенных предположений
о роли мезонов в ядрах. Следовательно, очень полезно знать, что
по крайней мере для электрических переходов при малых передан-
ных импульсах (kR 1) теорема Зигерта дает возможность огра-
ничиться в нашем рассмотрении плотностью заряда, для которой
нет необходимости явно учитывать заряды мезонов. Конечно, все-
таки нет гарантии в том, что мезонные степени свободы не будут
влиять на плотность заряда даже в указанном случае, но можно по
крайней мере надеяться, что это окажется случайностью. Мы
примем такую точку зрения, пока не появится достаточно доказа-
тельств противоположного утверждения. Поэтому будем пред-
полагать, что оператор плотности заряда может быть следующим
образом записан с помощью ядерных координат гх, г2, ..., гд для А
нуклонов:
р(г)= гг),	(4-25)
;=1
где е( — в для индексов i = 1, 2, ..., Z, которые относятся к про-
тонам, и et = 0 для нейтронов, i = Z -j- 1, Z + 2, ..., А. Для за-
дач, в которых существенны большие переданные импульсы, когда
становятся важны изменения плотности*на очень малых расстояниях,
93
протоны больше не могут считаться точечными зарядами как в фор-
муле (4.25). Тогда следует рассматривать распределение заряда
в протоне, найденное из экспериментов по рассеянию электронов
на протонах, и модифицировать дельта-функцию в формуле (4.25),
так, чтобы описать конечное пространственное распределение про-
тонного заряда. В этом случае, разумеется, модуль волнового век-
тора к будет одного порядка с обратной величиной зарядового про-
тонного радиуса, который намного меньше радиуса распределения
заряда ядра. Поэтому kR 1, теорема Зигерта больше не дейст-
вительна и следует учитывать мезонные эффекты.
Для магнитных переходов даже при малых переданных импуль-
сах фотон чувствителен как к распределению заряда, так и к распре-
делению тока. Эффекты обменного взаимодействия появляются
в этом случае не только в силу изменения зависимости волновой
функции ядра от координат нуклонов, но, вообще говоря, также
ввиду необходимости введения в оператор ядерного тока поправок
от мезонных степеней свободы. К сожалению, хотя прошло более
трех десятилетий с тех пор, как Кондон и Брейт [68] впервые указа-
ли на трудности, которые обменные силы представляют для изучения
ядерного фотопоглощения и излучения, все еще не имеется надеж-
ного способа рассмотрения мезонного тока, и при изучении струк-
туры ядра этими эффектами обычно вынуждены пренебрегать.
§ 4.2. Эффективные заряды для электрических переходов
Если в формуле (4.24) учесть, что аргумент функции Бесселя
мал, и воспользоваться формулой (4.25) для плотности заряда, то
матричный элемент для электрических переходов примет вид
xJ'FKrj, г2,...,гл)^^б(г—гг)Х
X (г) Та (гь г2.....гл) dti dr2... drA dr, (4.26)
где Ya и Tp — волновые функции начального и конечного состоя-
ний ядра, а функции
^/и(г) = г'У%(?)	(4.27)
суть пространственные 'сферические гармоники [см. сноску к фор-
муле (ПА.65)]. Выполнив интегрирование по г, получим
X f Т|(Г1, г2,..., гл) у ег^/ц(г,)Мп, г2,..., гл)б/Г1б/г2...б/гл. (4.28)
94
Выражение (4.28) для матричного элемента электрического пе-
рехода требует дальнейшего уточнения. Это связано с тем, что ядер-
ная волновая функция записана как функция ЗА нуклонных коор-
динат г1( г2, ..., гЛ, измеренных в произвольной системе отсчета.
Однако на практике бывает необходимо отделить взаимодействие
фотона с ядром как целым, которое посредством томсоновского рас-
сеяния приводит к изменению центра масс всей системы А частиц,
от взаимодействия, которое возбуждает внутренние степени свободы
ядра. Для этого явно введем координаты центра масс
R^-Lvr.	(4.29)
А
и координаты нуклонов, отсчитанные относительно центра масс*:
Р>=г,—4srb /=1,2,...,Д, (4.30а)
которые удовлетворяют соотношению
1₽7 = 0.	(4.306)
7=1
В общем случае ядерные расчеты выполняются с использованием ко-
ординат гъ г2, ..., Гл, так как обычно начинают с рассмотрения А
нуклонов в потенциале оболочечной модели ядра и строят решения
для частиц в этом потенциале. Эти решения нетрудно затем антисим-
метризовать, если пользоваться координатами гъ г2, ..., Гд, кото-
рые описывают каждый нуклон эквивалентным образом. Потенциал
в оболочечной модели определяется, разумеется, относительно вы-
деленной точки пространства, что нарушает требование трансля-
ционной инвариантности ядерного гамильтониана и нарушает закон
сохранения полного импульса в аппарате теории**. Можно далее
спросить, имеются ли какие-либо простые способы привязки расче-
тов вероятностей электромагнитных переходов, выполненных
в этой несовершенной системе координат, к расчетам, выпол-
ненным с более правильными координатами (4.30). Это может быть
сделано с помощью использования эффективных зарядов. Они за-
меняют обычный нуклонный заряд е для протонов и 0 для нейтронов
* В этой связи см. [151].
** Использование такого потенциала приводит также к проблеме «духо-
вых» состояний, которая отчасти связана с использованием эффективных
зарядов. Эти состояния возникают при рассмотрении А нуклонов, которые
считаются связанными в фиктивном внешнем потенциале. При этом можно
получить такие колебания, когда все нуклоны будут двигаться вместе в этом
потенциале, который они, по предположению, сами создают друг для друга.
Подобные колебания не соответствуют возбуждению внутренних степеней
Щ1°м°ДЫ ядРа 11 Должны быть исключены из аппарата теории (см., например,

95
зарядом, который эффективно учитывает вклад в мультипольный
момент отдачи остаточного ядра, когда частица ядра изменяет со-
стояние в процессе электромагнитного перехода. Такая модифика-
ция особенно важна для Е1 -переходов, для которых ее можно рас-
смотреть в совершенно общем виде. Можно также получить соот-
ветствующую модификацию и для других электрических мультипо-
лей, но в этих случаях следует ограничиться одночастичными пере-
ходами.
Начнем с рассмотрения оператора перехода (4.28) для El-муль-
типолей. Он пропорционален дипольному оператору
л	.— а	.--
(«О
где
(4.32)
В системе координат (4.30), которые соответствуют возбуждению
внутренних степеней свободы, последняя величина имела бы вид
(4.33)
(4.34)
В этом выражении первое суммирование проводится по Z протонам,
а второе — по N = А — Z нейтронам. Получаем
D'=_^Vr----?£ V г	(4.35)
А X< ’ А
i=I	i=Z+l
Если сравнить выражение (4.35) с выражением (4.32), то видно,
что использование координат (г^ г2, ..., гл} будет вполне допусти-
мым при условии, что каждому протону приписывается заряд
eNIA, а каждому нейтрону — отрицательный эффективный заряд
—eZIA. Оператор (4.32) без эффективных зарядов отличается от
оператора (4.33) на величину, в которую входят координаты центра
масс
D=D' + eZR.
(4.36)
Дополнительный член в D описывает томсоновское рассеяние для
ядра как целого, при этом все протоны дают вклад в полный заряд
eZ.
96
Результат, содержащийся в формуле (4.35), не зависит от ка-
ких-либо предположений, кроме использованных при получении
теоремы Зигерта и связанной с ней гипотезы о том, что заряд ядра
локализуется на нуклонах [см. формулу (4.25)]. Понятие эффек-
тивных зарядов (или эффективных магнитных моментов) может быть
обобщено и для магнитных переходов (мы столкнемся с примером
этого в § 4.3). Однако, поскольку теорема Зигерта не применима
для магнитных мультиполей, результаты для Л4/-переходов сильно
зависят от предположений, касающихся ядерного тока, и введение
эффективного заряда не является в этом случае особенно полезным.
Подобная концепция до некоторой степени также помогает при
рассмотрении электрических переходов более высокого порядка,
хотя необходимы специальные предположения помимо тех, которые
были использованы при получении формулы (4.35).
Рассмотрим общий вид оператора ^/-переходов в формуле (4.28)
(4-37)
«=1
Снова вводя координаты (4.30) для описания возбуждения внутрен-
них степеней свободы, получаем
^=2?» 3%(г4- R).
i=i
(4.38)
Применим теперь теорему сложения пространственных сфериче-
ских гармоник, которую мы докажем в конце данного параграфа.
Если а и b — два вектора, то
3%(а-Ь) = ]/4л 2 S (-1)ЬГ
L=0M = — L	L
(2/+ 1)!
(2L-P1)! (21—2L-H)!
1/2 X
X(/-LZJ1 Ц-ММИ) tyLM (b) ^,_щ_м(а).	(4.39>
Использование этой теоремы в выражении (4.38) дает

X (l—LLl I ц—ММц) Vlm (R)	(rf).	(4.40)
Здесь имеются два вида одночастичных членов, а именно, с L = 0
и L — I; для каждого из них
^оо (г) = 1/1 4л-	(4.41)
97
Однако для всех других членов входят координаты более чем одной
частицы. Выделяя член с L — I, получаем
= (-1)'Ze^M(R) +
А ____I — 1 L
2 (-dl
1 = 1	L=0M=—L
2(/+1)!
(2L+1)!(2/—26-^1)!
1/2
X
X (l—LLl | ц-ММр) tyLM (R)	(гг).	(4.42)
Снова используя формулу (4.39) для пространственных сферичес-
ких гармоник от аргумента R, можно написать
^;M=(-iyze
(2/^1)! j -11/2
(2L4> 1)! (2/—2L+1)!
X
X (l-LLl I |i—Л4Л1р) %lm ( 4~ r0	(4 У rj
Mi
A	l — IL L	L'
+v>(4^)v 2 2 2 (-nLx
r=l	L=OM=—L L'=0
--------------------------]1/2(/-Ш|И-ММИ)х
(2/ —2£4-l)!.(2L'4-l)l(2L—2£'4-l)!j	v
X(L—L'L'L\M—M'M'M)^l.m.( — гД X .
\ A )
1-ьц-м(гг).
(4.43)
В последней сумме члены с L' = L согласно (4.41), также приво-
дят к одночастичным членам для i-й частицы. Эта сумма переписы-
вается в виде
21 / J	\ /1	/
1—1 L L— 1	£.'	И
_p4nV V V V (_МГ---------------------------(?£±1Я____________
7|L(2/-2L+1)!(2L'+1)!(2L-2L'+1)!
X (l—LLl | |т—ЛШр,) (L—L'L'L | М—М'М'М) X
Х^ым'(4	I 4	^-М1-м(гг-)1. (4.44)
' А	I
где второй член был введен в процессе использования тождества
(4.39), чтобы вновь выделить первый член из суммы. Подставляя
98
(4.44) в (4.43) в используя (4.27), получаем
^=2
+ уе(1^у у Г„.
£-ом^_Д(2/-2£*1)Н
X J[(2L + 1)!Г1/2	( -L г Л	(4 S гЛ +
I	к /1	/	\ /1	/
I	'	/+»
+1 У* У (—1)L[(2£' + 1)!(2£ -2L' + 1)Ц-1/2Х
L'=0 M'=—L'
X(L—L'L'L\M—гЛ X
\ A )
X (4 2 r>)	(П)1	(4.45)1
M<	J
Коэффициент при yZ[i (r;) в (4.45) является эффективным заря-
дом для EZ-перехода. Для протонов он имеет вид
еР =е 4 (И- П' + (-0z {Z- 1)],	(4.46а)
а для нейтронов
en=eZ(— 1/Д)'.	(4.466)
Для £1-переходов формулы (4.46) приводят к полученному ранее
результату (4.35). В этом случае двухчастичные члены в формуле
(4.45) не дают вклада. Однако в формулы для мультиполей более
высокого порядка эти сложные члены входят. При этом нет причин
пренебрегать их вкладом [ 151]. Не существует простых не зависящих
от модели способов оценки указанных членов, так что концепция
эффективного заряда полезна для мультиполей более высокого
порядка только постольку, поскольку хотят сохранить одноча-
стичное описание перехода без какого-либо хорошего оправдания
этого приближения. Ситуация отчасти облегчается тем, что в эф-
фективный заряд мультиполей более высокого порядка, чем £1,
входит поправочный член порядка НА или еще меньше по сравнению
с обычным зарядом. Следовательно, такая поправка для тяжелых
ядер очень мала. Во всяком случае эта погрешность не больше той,
которая возникает во многих расчетах электромагнитных перехо-
дов, выполняемых в рамках ядерных моделей, так как в них часто
входит обрезание набора базисных функций ядра, которое дает
типичную ошибку порядка 1/Д или больше.
Во многих случаях пытаются обойти влияние указанного обре-
зания введением совершенно другого понятия эффективного заряда.
Новый «эффективный заряд» учитывает скорее конкретные эффекты
99
ядерной структуры, но не приводит к изменению характерных
черт механизма возбуждения. Иными словами, его введение дает
поправки к ядерным волновым функциям в матричном элементе
перехода, но не поправки к оператору перехода. Эти эффективные за-
ряды полуфеноменологическим путем учитывают поляризуемость
остова ядра. Их введение связано с тем фактом, что частица, движу-
щаяся вне остова ядра и претерпевающая при этом электромагнитный
переход, поляризует остов с помощью нуклон-нуклонных сил.
При изменении состояния частицы может измениться степень по-
ляризуемости остова, что приведет к эффективному движению заря-
да, отличающемуся от того, которое имел бы невзаимодействующий
нуклон вне остова. Эти эффекты могут быть учтены с помощью чле-
нов более высокого порядка в расчетах в рамках ядерных моделей,
но они обычно весьма громоздки и поэтому не могут быть рассмотре-
ны достаточно надежно.
Вернемся теперь к доказательству формулы (4.39). Свойства
неприводимых тензоров при пространственных перемещениях об-
суждались многими авторами [60, 289, 81]. Все они дают доказа-
тельства формул, подобных (4.39). Простой подход заключается в
использовании обычного разложения плоской волны. Напишем
еИа-Ь)-г = 4л 2 j, (| a—b | г) Ytil (a^b) Ш?) =
= eia.r e-ib.r = (4л)г V iL'~L jL, (ar) jL (br) X
LM L'M'
X Yl'M' (a) Ylm (b) Y*l-m- (?) YlM (?) =
= (4л)г2 2 ZJ Г (2L^1} (2L' + 1) 11/2(L'Lff|000)x
V ’ lmum‘^m( 4л(2£?+1) J
X (L'LSS | 44'AU/) iL’~L jL. (ar) jL (br) YL’m- (a) Ylm (b) Y*^ (?). (4.47)
где мы воспользовались формулой (ПА.26а). Рассматривая случай
малых г, когда приближение (2.98) справедливо для всех функций
Бесселя в (4.47), и пользуясь ортогональностью функций Y(г),
получаем
| а—b |г г1
(21^1)11
(a— b) = 4л У У Г(2^1)(2^<1)1
!	4л(2/-М)	]
LM L’M'
, nL'hLrL+L'
X(L'Ll | ООО) (L'Ll | M'Mjx) iL ~L	Yl-w(а)Уыи(Ь).
A). ![ZL, -J-1)1!
(4.48)
Левая часть содержит члены порядка г1 и члены более высокого
порядка, которые подавляются. Правая часть содержит члены,
включающие разные степени г, начиная с г1, так как правило тре-
100
угольника в коэффициентах Клебша—Гордана требует, чтобы
./ L + L'. Коэффициенты при г1 должны быть одинаковы в обеих
частях этого равенства. Поэтому, учитывая главные члены, получаем
для L' = I — Г
—X?» L (2/Ч>1)1!	Г(2Г+1)(2«—2Г + 1)11/2
Ь)=1/4л^(—1) (2L+l)!!(2i—2L+l)liL	2/ + 1	] Х
LM
х (l-LLl I 000) (l-LLl I р-ЛШр) %LM (b)	(a), (4.49)
Используя далее соотношения [288, стр. 47]
(l—LLl | ООО) =-----—-----Г (2f 2L)!(2L)ljl/2	(4 эд
v 1	' (/—£)!£! |_	(2/)l J
(2/+1)!1 Z!
[(2/4-i)!]1^
±[(2/4-1)!]1/2,
(4.51)
получаем формулу (4.39).
§ 4 J. Правила отбора по изоспину
Электрический дипольный оператор возбуждения внутренних
степеней свободы ядра выражается через эффективные заряды с по-
мощью формулы (4.35). Он может быть получен в виде, который бо-
лее отчетливо выражает некоторые из его свойств симметрии, если
ввести протонный и нейтронный проекционные операторы в изо-
спиновом пространстве. Для этого определим протон как состояние
со спином «вверх», а нейтрон — как состояние со спином «вниз»
в пространстве состояний со спином 1/2, которое и является изо-
спиновым пространством. Третья изоспиновая матрица Паули при
действии на протонное или нейтронное состояние | р> или | п> тогда
дает
гз1Р> = |Р>. тз1«>= —1«>-	(4-52)
Проекционный оператор для протонов имеет вид
Р+=1(1+т3)	(4.53а)
ч удовлетворяет соотношениям
Р+\р> = \р>, Р*\п> = 0.	(4.536)
Аналогично для нейтронов
р_ = 1(1-т3),	(4.53в)
Р_|р> = 0, Р_|и> = |п>.	(4.53г)
101
Формула (4.35) может быть переписана через эти величины следую-
щим образом:
tv _ v Г eN / 1+тз A	eZ ( 1 ~тз \ ]
aL а 2 л	а ( 2 W-
= \А з ri + у у (гг3)р	(4.54)
Для ядер с одинаковым числом протонов и нейтронов она принимает
простой вид
е ГА
D'=f 2(гтз)л	(4-55)
т. е. эффективные заряды для протонов и нейтронов равны j е и
±е(7\ lTf | Ml ОМ}) /рТ
2(гт);||аТг\.	(4.57)
Если теперь рассмотреть электрический дипольный переход меж-
ду двумя состояниями ядра аир, волновые функции которых ха-
рактеризуются хорошими изоспиновыми квантовыми числами Tt
и Tf, то соответствующий матричный элемент (4.28) будет пропор-
ционален величине
11	(4-5б>
2 X 1 J=J I /
В изоспиновом пространстве дипольный оператор является третьей
компонентой вектора. Поэтому, согласно теореме Вигнера—Эккарта
(ПА.54), имеем
II
Правило треугольника для коэффициента Клебша—Гордана требу-
ет, чтобы Tf = Tt — 1, Tt или Ti + 1. Однако поскольку мы огра-
ничили наше рассмотрение ядрами с N = Z, то проекции квантовых
чисел изоспина ядра равны
Л4)=ЛД=у(Х—Л/) = 0.
Поэтому выражение (4.57) содержит коэффициенты Клебша—Гор-
дана, для которых Tt + Tf + 1 четно, т. е. Tf = Tt ± 1. Таким
образом, правило отбора по изоспину [337, 278, 223, 156, 353, 256„
257] для El-переходов в ядрах с N = Z требует, чтобы изоспин
изменялся на единицу.
В действительности это правило отбора по изоспину частично
нарушается по нескольким причинам. Поскольку оно основано на
теореме Зигерта, небольшое отклонение от него может быть обус-
ловлено членами более высокого порядка по kR. Кроме того, ме-
102
зонные вклады, которые могут привести к ситуации, когда не все
заряды локализуются на нуклонах, будут нарушать формулу (4.25),
а также изоспиновое правило отбора. Наконец, кулоновские силы
и нейтрон-протонная разность масс нарушают эквивалентность
протонов и нейтронов в ядрах и приводят к смешиванию по изо-
спину различных состояний ядра. «Запрещенные по изоспину»
переходы могут иметь место из-за этих нарушений, так что рассма-
Рис. 4.1. Распределение силы El-переходов в единицах
Вайскопфа для ядер с Д^40.
Незаштрихованная гистограмма показывает переходы, разрешенные
правилом отбора по изоспину, заштрихованная — переходы, запре-
щенные этим правилом [319].
триваемый переход может быть заторможен, а не полностью запре-
щен. Некоторые типичные экспериментальные случаи показаны на
рис. 4.1, из которого можно видеть, что фактор задержки составляет
около 10-1.
Для электрических переходов более высокого порядка эффек-
тивные заряды (4.46) не приводят к правилам отбора по изоспину.
В то же время, поскольку магнитные переходы чувствительны к рас-
пределению тока и, следовательно, к мезонным эффектам, не сле-
дует также надеяться на какое-либо простое правило отбора по
изоспину для 7И/-переходов. Некоторое исключение составляют
результаты для М1 -переходов [255, 257], если постулировать опре-
103
деленную форму для ядерного тока, которая не учитывает вклад
мезонов кроме их возможного влияния на свойства отдельных ну-
клонов. С этой целью возьмем ток, который состоит из обычной кон
векционной части и части, обусловленной намагниченностью, в ко-
торую входят измеренные магнитные моменты протона или нейтро-
на:
<Р I j (г) I “> = 2 .[ |Х [ТР V'	+
+ ~ Kj X [та Та1| 6 (г-Гу) dr, dr2... drA.	(4.58)
Волновые функции ядра Та и Тр являются здесь функциями коор-
динат гъ га, ..., гА и зависят от квантовых чисел спина и изоспина
ядра. Операторы V; и ai относятся к /-му нуклону, ej равно е
для протонов и нулю для нейтронов и величины
/</=^=2,79 для протонов, |	g
Kj = Kn = —1,91 для нейтронов J
являются соответствующими эмпирическими значениями магнит-
ных моментов для нуклонов. Масса нуклона обозначается Л4.
Согласно (4.17), матричный элемент Ml-перехода имеет вид
М₽а (кр; М1) = pi ]/бл У [ Ш [Та V/Fa-(Vy Т₽*) Ta] +
+ |^Лу¥уХ[ТаоуТа]}.А1ц(гу: m)dr1dr2...drA. (4.60)
Проинтегрируем по частям второе слагаемое подынтегрального
выражения (в которое входит распределение тока намагничива
ния), перенося действие оператора rot на Л41-потенциал. Тогда,
учитывая уравнение (2.95а)
VyXi4,g(ry; tn) = Hiu(ry; ш) = £'цх(гу; е) = (гу; е),	(4.61)
получаем из (3.80) и (3.98) для случая kR 1
VyXA.^ry; m)-j i^l/4TIo:|i(i:y)=ifel/ V (4.62)
L у 3	|Z bn
Рассмотрим первое слагаемое, которое содержит распределение
конвекционного тока. Воспользуемся выражением (2.84а) для I = 1:
АцДгу; т)=-Хь/А(^у)^Цх(г/) = — Xr'xA1’x(l>
— - ^г>хТ'°^) = -;7=г№-	(4-63)
16	У 24л
104
f=i L
Подставляя это в формулу (4.60), интегрируя результат по частям
и учитывая, что магнитный потенциал поперечен, получаем для кон-
векционной части
-^2 J {^Г	dr.dr, ...drA.	(4.64)
Переставим местами множители в смешанном произведении, доба-
вим из (4.62) часть, соответствующую току намагничивания, и по-
лучим
Л1₽а (кр; м 1)(<б) Д аdr,dr2 ... drA,
/=1
(4.65)
где L= —irx V.
Если снова воспользоваться проекционными операторами (4.53),
то оператор перехода в этом выражении можно записать в виде
* 2 [ч -МрМ	+«п < -При Ч. (4.66)
/=1L \	1	\ * 'j	\ 2 'j Ju
Оператор полного углового момента ядра
L; + -Ojl , р,= —1, 0, 1,	(4.67)
2 Ju
весьма похож на ту часть выражения (4.66), которая не содержит
изоспиновых операторов. При этом как а, так и Р являются соб-
ственными векторами квадрата оператора J, так что из (ПЛ.55)
следует
<р | Ju | «> VMJi + V) (Jt \Jf | Mt vMf) <p | a>= 0, (4.68)
где (ДЛД) и — квантовые числа спина и его проекции. Мы
использовали тот факт, что переход происходит между двумя орто-
гональными состояниями ядра. Если теперь подставить (4.67)
и (4 68) в выражение (4 66), то оператор перехода примет вид
А	А
~\КР+Кп—21ь>+^р-^п)°>Ь(ь)/=
/=1	/=1
- 0,38 * V (О>)к + А 4 [Lj + 4,70<т7]и (т3);.	(4.69)
/=1	/=1
Для второго члена этого выражения применимо то же самое рас-
смотрение, которое было проведено для формулы (4.57) Именно
Для переходов в ядрах с N = Z, изоспины начального и конеч-
ного состояний которых удовлетворяют равенству Tf = Тг, в фор-
мулу (4.69) дает вклад только первый член. Если же Tf = Т, ± 1,
105
то первый член, являясь скаляром в изоспиновом пространст-
ве, не дает вклада, а второй дает. Мерой их относительного вклада
в вероятность перехода является квадрат отношения числовых
параметров в формуле (4.69). Таким образом, переходы с Tf = Tt
заторможены по сравнению с переходами с Tf = Tt ± 1 в отноше-
нии (0,38/4,70)а = 6.5-10-3.
Рис. 4.2. Распределение силы Л11-переходов в еди-
ницах Вайскопфа для легких ядер (4^40).
Заштрихованная гистограмма показывает переходы, за-
прещенные правилом отбора по изоспину [319].
Хотя правило отбора по изоспину для Ml-переходов возникает
как результат случайной частичной компенсации нуклонных маг-
нитных моментов, оно приводит приблизительно к той же самой за-
держке, которая найдена экспериментально (см. рис. 4.1) для более
обоснованного правила отбора по изоспину для Е1-переходов.
Рис. 4.2 показывает, что этот результат подтверждается экспери-
106
ментально. Как и для £1-переходов, фактор задержки для Л41-пере-
ходов составляет около 10-1.
Результаты, касающиеся правил отбора по изоспину как для
£1-, так и для 7И1-переходов, основывались на длинноволновом
приближении kR <£ 1. Это означает, что и другие электромагнит-
ные процессы в длинноволновом пределе будут также подчиняться
указанным правилам. Мы приходим к выводу, что для рассеяния
электронов, когда переданный ядру импульс может изменяться,
а энергия возбуждения ядра оставаться фиксированной, правило
отбора по изоспину действует [113] для малых углов рассеяния,
но не является обязательным* для больших углов, для которых
АТ? 1.
Правила отбора по изоспину дают довольно хороший пример
взаимосвязи между конкретным механизмом возбуждения и кон-
кретными свойствами структуры ядра. Существование этих правил
тесно связано с нашими предположениями о мезонных эффектах
в ядрах и даже о некоторых более детальных аспектах наших ги-
потез о ядерном токе, как, например, формула (4.58). Кроме того,
они требуют зарядовой независимости** ядерных сил и пренебреже-
ния кулоновскими поправками. Как только сделаны эти основные
предположения, правила отбора получаются как следствие приро-
ды оператора перехода без обращения к ядерным моделям или дета-
лям динамики ядра. С другой стороны, существуют другие специфи-
ческие эффекты структуры ядра, которые затормаживают конкрет-
ные £1- или ЛП-переходы. Эти эффекты относительно мало связаны
со свойствами операторов перехода. Они могут возникнуть из-за раз-
личия природы возбуждений ядра в начальном и конечном состоя-
ниях и быть следствием слабого перекрывания ядерных волновых
функций. При правильном рассмотрении эти эффекты, конечно,
должны быть разделены и классифицированы.
§ 4.4. Общие свойства электромагнитных переходов
в длинноволновом приближении
Установим теперь некоторые общие свойства электромагнитных
переходов данного порядка мультипольности, используя выражение
(4.17) и метод, сходный с тем, который мы уже применяли при
упрощении выражения для матричного элемента перехода в длинно-
волновом пределе. Дтя этого предположим, что существует какой-то
механизм, который действует так, что в задачу входит только один
мультиполь. Это ограничение может осуществляться строго, если
действуют правила отбора по угловому моменту и четности, или
оно может быть следствием специфических свойств динамики ядер,
приводящих к преобладающей роли одного мультиполя.
* Пример того, как учет эффектов ядерной структуры может опровергнуть
эти довольно простые аргументы, приведен в работе [314].
** Эти правила можно также получить, используя только гипотезу за-
Р ядовой симметрии сил [337, 223, 256].
107
Вероятность излучения фотона с волновым вектором к и поля-
ризацией р при переходе ядра из начального состояния а в конеч-
ное состояние р в процессе мульти пол ьного перехода типа а
(а = и или tn) получается из формул (4.13) и (4.17):
Т₽а (Zp; а) =-4v | Л4₽а (kp; al) |2 dQk,	(4.70)
2лпсл
где
Л4р„(кр; й/) = т] К2л/Р [ (|3| j (г) | а) • А/ц (г; a) dr (4.71a)
и
f if П - е,	/ Л У 1
Т]=|	(4.716)
|р, а= tn.
Таким образом,
^Ра(/р; 0)=(2/tP-| [<₽|j(r)|a>-A^r;D)dr|W (4.72)
псл I J	I
Предположим теперь, что оператор ядерного тока выражается
формулой (4.58). Рассмотрим сначала £7-переходы. Пользуясь
теоремой Зигерта* (4.24) и предполагаемым выражением (4.25)
для плотности заряда, получим для главного члена ^/-мультиполя
(л1)'” к‘ 24	...Л,. (4.73)
(21-f-1)11 \ I )	J
Вклад тока намагничивания в формуле (4.58) дает дополнительное
слагаемое вида
J	(т. e)drx... *л =
/=1
X гг v; (Гр4ц (б)Мп - drA-	(4.74)
Здесь выполнено интегрирование по частям и использованы соот-
ношения (2.846) и (2.70). Для Л4/-переходов те же самые операции,,
которые приводят к формуле (4.65), дают
С /о I • / хI \ »	/	\ j  h Id I I-p 1 \1/2
I <P J (r) a>-Azu(r; tn)t/r = i--------——	X
j i j \ / I z	,	2M (2/+1)!I z )
X 2 [Yd^L7. + eA;Oj-yvj.(r'rZlx(r>))l^rfr1... drA. (4.75)
/=i" L +	J
* Заметим, что из-за множителя (£а — E^/hkc знак в формуле (4.24>
для испускания фотонов должен быть заменен на противоположный по срав-
нению со случаем поглощения.
108
Подставляя (4.73)—(4.75) в (4.72), получаем
(/и; й) 1 <Р 1 Qz,i (й) 1 а> ‘2 dfik’ (4’76)
где
о.» (е) =	[vj Y,„ (r',)-.i £К,	(«,Х г,) V , (,}У,„ (?,))] (4.77)
И
£2/n(m)=i У17—---------—	(г.))1. (4.78)
2Л1с /+1	7 1 2Мс Ч JJ f 1ц\ 7//J- V /
В этих результатах для QZg (а) можно использовать эффективные
заряды для б/, как обсуждалось в § 4.2.
Формула (4.76) справедлива в системе координат с осью 2,
направленной вдоль вектора к. Можно перейти к произвольной
системе, как это сделано в формуле (2.106); интегрирование по на-
правлениям фотона может быть выполнено, если воспользоваться
соотношением
f v' (<Pk, 0k, 0)	(<Pk, ek, 0) dQk =	6tfV..	(4.79)
•j	z/-p 1
Сумма по индексам поляризации фотона v = ± 1 дает множитель 2.
Таким образом, вероятность фотоизлучения выражается форму-
лой
Г|М<'; ” вП<"41‘|!1‘I<₽l I«> !’	(4-80)
где П((1 (а) определяется формулами (4.77) и (4.78). Оставшийся
индекс р в действительности не является свободным индексом, так
как теорема Вигнера-—Эккарта требует*
<₽ |	(а) | а> = (Jf lJf | Mt pMf) <₽ || Ц || a>,	(4.81)
где (JiMi) и JfMj) — квантовые числа спина и его проекции в на-
чальном и конечном состояниях ядра и р = Л4, — Л4г. Восполь-
зуемся формулой (4.81), чтобы выполнить усреднение и суммирова-
ние по магнитным квантовым числам ядра. Это соответствует тому, что
в начальном состоянии ядро не поляризовано и в конечном состоя-
нии его поляризация не наблюдается. Введем вначале приведенную
вероятность перехода
|<P|Q/Ja>|a.	(4.82)
" 7 • 1 М-М.
Тогда
В(”'; <483>
См. примечание на стр. 323 в приложении А
109
Из формулы (4.81) получаем для случая, когда поляризация ядра
не учитывается:
В(а/;	=	V (J. lJf | М^-М'М^
1 MjMj
= S^I<mil“>la-	(4-84)
xs«/ i 1
Попытаемся теперь оценить относительные вклады различных
мультипольных операторов (4.77) и (4.78). Для этого мы сначала
не будем учитывать действие правил отбора, которые обычно для
данного случая приводят к исчезновению определенных а/-перехо-
дов. Иначе говоря, рассмотрим два перехода, которые приблизи-
тельно эквивалентны с точки зрения структуры ядра, но каждый
из которых разрешен для разной мультипольности. Сравним вероят-
ности этих переходов. Можно ожидать, что результаты такого при-
ближенного рассмотрения применимы в некотором статистическом
смысле, когда изучается много ядерных переходов. Большое замед-
ление или ускорение (по сравнению с этими оценками) будет нуж-
даться в каком-либо объяснении с помощью специфических свойств
ядра, которые могут играть роль в данной задаче.
Рассмотрим сначала роль двух членов, которые входят в опера-
тор Е/-перехода (4.77). Второй из них по отношению к первому
дает вклад порядка
—£-----^_=.—1-------(4.85)
2(/4И) Me 2(Z4>1) Мс2 ‘
Поскольку для ядерных переходов обычно порядка 10 Мэв,
в то время как Мс2 = 939 Мэв, то ясно, что в процессах излуче-
ния фотона вторым членом всегда можно пренебречь. С другой сто-
роны, для магнитных переходов оба члена в формуле (4.78) сравни-
мы. Спиновой член обычно немного больше члена, соответствующего
орбитальному угловому моменту, поскольку |К;|>1, особенно
для переходов с AT' = 1, в формулу для которых входит магнитный
момент, равный Кр — Кп — 4,70 [см. формулу (4.69)1.
Отношение вероятности М/-перехода к вероятности ^/-перехода
по порядку величины равно
(m)
2
~ 10
(4.86)
Здесь приблизительно учтено усиление, даваемое множителем Kj,
и использован тот факт, что оператор градиента в (4.78) уменьшает
на единицу степень ядерного радиуса /?. Таким образом, вероят-
ность Л4/-перехода имеет тенденцию быть несколько меньше, чем
вероятность соотвествуюшего ^/-перехода.
Можно сделать несколько более точные количественные оценки
вероятностей переходов, предполагая, что переход обусловлен изме-
нением орбиты одной ядерной частицы, и приписывая этой частице
110
схематическую радиальную волновую функцию, которая является
константой внутри ядра и равна нулю вне ядра. Нормировка
волновой функции такова, что она имеет вид
ф(г) = ]/37ЖГ/,м(г)Х,	(4.87)
где L — орбитальный момент, х— спиновая функция. Если пред-
положить, что переход определяют начальное состояние с орбиталь-
ным моментом L = I и конечное состояние с L = 0 и что оба уров-
ня имеют одинаковое спиновое состояние, то волновая функция
(4.87) дает
и
Т(1-,Е)
Т (l\ М)
2(/-Н)
/[(2/4-1)П]2
(4.88)
<о
!20(/-р1)
I [(2/4> 1)1’]2
(4.89)
где для магнитного случая использованы оценки по формуле (4.86).
Эти величины часто берутся в качестве удобных единиц как при
обработке экспериментальных данных, так и в теории. Они назы-
ваются единицами Вайскопфа*.
Из оценок (4.88) и (4.89) ясно, что как для электрических, так
и для магнитных мультиполей переходы порядка I + 1 заторможе-
ны по сравнению с переходами порядка I в отношении
I (Z + 2) [------------------Г (kR)2.
L (2/+3)(/ + 1)(/ + 4) J
(4.90)
Учитывая (4.86), получаем
7 (/-P1; £)
Т (/; /И)
— (Л7?)2(—М 2 = 1,2-10-М4/3
10 v \ McR /
1Мэв )
2. (4.91)
Поэтому при отсутствии специальных эффектов ядерной структуры
следует ожидать, что /Ш-компонента перехода будет весьма замет-
но преобладать над Е (Z + 1)-компонентой, если правила отбора
допускают смешивание этих компонент.
Оценки, приведенные в данном параграфе, строго говоря, спра-
ведливы лишь для малых переданных импульсов в электромагнит-
ных процессах, т. е. при kR 1. В частности, они применимы к пере-
ходам с энергией возбуждения в несколько мегаэлектронвольт,
* Эти единицы были введены Вайскопфом в работе [344]. Они также об-
суждаются в книге [43, стр. 623—629]. Другие единицы для Л4/-переходов
были предложены Мошковским [252, 254]. Они равны произведению единицы
Вайскопфа (4.89) на коэффициент
11L
в которых участвуют уровни, лежащие ниже порогов испускания
частиц. Мы увидим, что многие из описанных здесь свойств до не
которой степени верны и для более высоких энергий фотовозбуж-
денпя, кулоновского возбуждения и для неупругого рассеяния
электронов. Таким образом, полученные результаты будут также
служить руководящей нитью при рассмотрении указанных процессов
§ 4.5. Рассеяние фотонов; эффект Рамана
До сих пор при изучении взаимодействия электромагнитного
поля с ядрами мы обсуждали только одну сторону рассматриваемого
процесса. Мы рассматривали, как налетающий фотон может возбуж-
дать уровень ядра, не заботясь о том, как будет происходить вы
свечивание уровня, или предполагали, что возбужденное состояние
достигается в результате какого-то процесса, и затем рассчитывали
вероятность фотоизлучения с этого уровня. Теперь мы обратимся
к реакциям, в которых происходят возбуждение и разрядка уров-
ня. Для этого, вообще говоря, необходимо обсудить роль частиц
в реакциях, приводящих к возбужденным состояниям, а также
фотоядерные процессы, в которых частица испускается в ре-
зультате высвечивания с уровня, лежащего выше порога испус-
кания соответствующей частицы. Однако сейчас мы ограничимся
случаем электромагнитных взаимодействий и рассмотрим процессы,
в которых как возбуждение, так и разрядка происходят через по-
средство электромагнитного поля. В этой связи можно было бы ис
следовать реакции, в которых в начальном или конечном состояниях
участвуют электроны, но мы ограничимся упругим и неупругим
(эффект Рамана) рассеянием фотонов, т. е. реакциями вида
Y + ^a->7Vp+Y'.
В этом процессе в начальном состоянии системы мы имеем покоящее-
ся ядро в его основном состоянии а и фотон с волновым вектором к,
частотой со и поляризацией екх. В конечном состоянии остается
ядро в возбужденном состоянии [3 (или в основном состоянии a
для упругого рассеяния) и фотон с волновым вектором к', ча-
стотой го' и поляризацией tk-x'. Конечное ядро получит некоторую
энергию отдачи, но для рассматриваемой нами энергии фотона
(< 50 Мэв) — достаточно высокой, чтобы достичь обертонов гигант-
ского резонанса, но значительно меньшей порога рождения мезо-
нов — энергией отдачи ядра можно пренебречь.
Информация о структуре ядра, получаемая из анализа рассея-
ния фотонов, является более обширной, а предсказания ядерных
моделей — соответственно более строго проверяемыми, если при
этом используются поляризованные фотоны и ориентированные
ядра. По этой причине мы рассмотрим весьма общую теорию рассея-
112
ния фотонов*, хотя для того, чтобы понять характер результатов,
получаемых этим методом, мы в конечном счете будем учитывать
лишь электрические дипольные переходы в неориентированных
ядрах в отсутствие поляризации фотонов.
Поскольку при рассмотрении рассеяния фотонов мы должны
обсудить как поглощение, так и последующее испускание фотона,
то необходимо применять теорию возмущений во втором порядке.
Вероятность перехода в единицу времени, как обычно, дается
выражением
^ = #-|<f|^"|C|2P,	(492)
П/
где плотность конечных состояний р определяется формулой (4.11),
в которой волновой вектор заменяется на к'. Будем считать ну-
клоны нерелятивистскими, тогда оператор перехода во втором по-
рядке теории возмущений можно получить из формул (3.24) и (3.25;.
Для этого следует выделить в фотонном рассеянии вклад, обуслов-
ленный томсоновским рассеянием. Последнее описывает взаимо-
действие фотона с ядром как целым, что приводит не к возбуждению
внутренних степеней свободы, а к движению центра масс всего
ядра. Оставшаяся часть взаимодействия относится к релеевскому
рассеянию, в котором возбуждаются внутренние степени свободы
ядра. Напишем**
(4.93)
где Ж" ст описывает томсоновское рассеяние, а 5^"int — возбуж-
дение внутренних степеней свободы. Как и в (4.2), имеем в первом
порядке по взаимодействию
3€’ст=----— р(г, /)-А (г, f)dr,	(4 94а)
=----l-Jj(r,/)-A(r,/)dr,	(4.946)
где J — оператор тока центра масс. Операторы во втором порядке
выражаются обычной формулой, которую необходимо исправить,
чтобы учесть члены в (3.24), квадратичные по операторам фотонного
поля:
Жст = Z ^'ст р |Ях<Л|с ^ст +	А2>	(4’95а)
п	Еа-^-1ми —Е п	2,М с2
* Рассеяние фотонов с учетом лишь электрических дипольных переходов
рассмотрено в работах [271, 127] Обобщение на мультиполи более высоких
порядков сделано в [16, 317].
** Детальное обсуждение разделения координат центра масс и внутрен-
них координат дано в работе [316]. Разделение в этой форме возможно только
в длинноволновом пределе.
5 Зак. 1193	ИЗ
где Л—масса ядра (Л AM) и
А
м Р	Sе>А2о (4-95б>
£а4-/И1) — Еп	2Мс2
Сумма по промежуточным состояниям в этих выражениях включает
состояния п, описывающие различные внутренние возбуждения
ядра и движение центра масс; Еп — полная энергия системы, со-
стоящей из ядра и электромагнитного поля. Поскольку операторы А
в формулах (4.94) могут уничтожать и рождать один фотон, то
состояния п или не будут содержать ни одного фотона, или будут
Рис. 4.3. Три слагаемых, дающие вклад в формулы (4.95).
Диаграмма а включает оператор Л2. В этом случае фотон уничтожается и
снова рождается в одной и той же точке. Диаграмма б описывает промежу-
точные состояния п, в которых нет фотонов, так что в Еп входит лишь
энергия промежуточного состояния ядра ЕуВ случае в имеется два фотона
и Еп=Еу -f-ftco-f-ftco'.
содержать два фотона (рис. 4.3) Кроме того, в формулах (4.93)
и (4.95) пренебрегается связью внутреннего движения и движения
центра масс, осуществляемой через электромагнитное поле. Это
возможно при условии, что потенциал заметно не меняется в объеме
ядра, т. е. если kR 1. Если бы это условие не выполнялось, то
член с А2 давал бы форм-фактор, создающий внутренние возбужде-
ния вследствие мультипольных переходов. Отделение движения
центра масс больше не было бы полезным, и индентификация томсо-
новского рассеяния была бы значительно более трудной. Мы не
будем рассматривать этих усложнений, ограничиваясь случаем
kR 1.
Формулу (4.95) можно упростить, если учесть, что оператор
тока центра масс в (4.94а) дается формулой
J= —Р,	(4.96)
Л
где Р — импульс центра масс. Поскольку мы считаем, что ядро
находится в покое в начальном и конечном состояниях, то этот
член не дает вклада. Кроме того, слагаемое с А2 в формуле (4.956)
114
вообще мало, так как по отношению к первому слагаемому оно дает
вклад порядка
р2/М
А /
(4.97)
где р — средний импульс нуклона, а А — оценка для знаменателя
в (4.956). Вблизи интересующих нас резонансов в рассеянии фото-
нов последняя величина намного меньше, чем средняя энергия
нуклона, поэтому параметр (4.97) очень мал и слагаемое с А2 в фор-
муле (4.956) дает вклад, которым можно пренебречь. Тогда из (4.93)
и (4.95) получаем для Ж"
п
I И> <п I
Еа + ^ч>—Еп
&vint
+ -^А2
2.Мс*
(4.98)
Матричные элементы А2 между однофотонными
легко получаются из формул § 3.2:
</1 A2|t>— (Р; k'V | А2 |а; кХ> =
= 2{-^е^х--екх6ар6ша..
состояниями
(4.99)
Здесь использованы формулы (3.60), (3.81) и (3.93) и тот факт, что
конечное -состояние центра масс близко к начальному состоянию,
но не совпадает с ним. В формуле (4.99) также учтена возможность
использования комплексных векторов поляризации для описания
фотонов с круговой поляризацией.
Первое слагаемое в формуле (4.98) можно лучше всего для наших
целей рассмотреть, пользуясь для электромагнитного потенциала
в Sf'int из (4.946) разложением по мультиполям (2.106) и переходя
к пределу малых переданных импульсов, т. е. kR 1. С учетом
формул (3.104) это дает для матричных элементов, соответствующих
рождению или уничтожению одного фотона:
<Г, 0кХ|Ж'п’|а; кХ> =
= | V/2 2 DLMK (<рк, 6к, 0) Луа (/г;LM) (4.100а)
\ ы£3 / LM
и
<Р: V"k'\X'int\y, 0k-X'> =
= (^УУ/2 2 D^.(<pk.,0ks0)J/p+v(A!';L'M').(4.1006)
\ coL3 ' l-М-
Здесь величина
(k\ LM) = --— Л4Та (kM\ eL)--— Myo. (kM\ mL) =
c	c
r<2L+1)(L+l)y» <T! (e)+Wui (m)! O>
(4.101)
5*
115
является суммой двух слагаемых (для поперечных мультиполей),
даваемых формулами (4.71), (4.73)—(4.75), (4.77) и (4.78). С помо-
щью выражений (4.98)—(4.100) получаем
1	| Z>	е *	. SkX б бии +
М ©L3
 2лйс2 'V1 'V1 J Mfyy(k'\L' М') ^/ltya(k\LM)
L3 Vwco7	I p , t ,p 1 r4)
r V LML'M' Ea-\-ha — I Ey— — 1Г ]
•Jllfty (k‘, LM) ’/Ilya (k j L
Ea—ha' — I Ey— — ir
\	2
(4.102)
где с помощью введения ширины Г учтено затухание промежуточных
состояний у. Пользуясь свойством
“I ^м'Л'Сфк', Ок-, 0)£>л11((рк, 0ь, 0),
гД'* / t\M'—Г!1’*
(4.103)
и соотношением [получаемым из (4.77) и (4.78)]
<^(/г'; L’ М') = (— 1)L'+"' Jlya(k'-, L'—M'),	(4.104)
находим
<f t> =	/ (_ 1)хД' DL^. (R1)8 6QQ. +
. 2nhc2 Vi ,	i\L'~V [ ₽V » L' M’} Mya (k\ LM) (
(	~ 1 Г
v LML'M'	I Ea + fao —*Г I
dl-(4 ,05>
Ea — ha' —	I
Здесь 2? — поворот, описываемый углами Эйлера (срк, Ок, 0), ко-
торый располагает ось квантования вдоль направления налетаю-
щего фотона, R' — соответствующий поворот для испущенного
фотона и Rr = R^R' (рис. 4.4). При получении формулы (4.105)
мы использовали соотношение
ек*-х"8кх=(-1)х-х'^-л (Rr),	(4-106)
которое может быть легко получено из (2.106) для г = 0.
Дифференциальное сечение рассеяния фотонов получается из
формул (4.11) и (4.92) после деления вероятности перехода w на
116
плотность потока налетающих фотонов c/L3:
(4.107)
где
у LML’M'
— Л' I	(Й *	М')	(k’, LM.) [_
| fa —йо— ( Ey— — ir)
VZpv (fe; LMM/-ya(fe';£.' M')
Dti'-v(R')DLM}.(R). (4.108)
. Кс1
Ea—Aco'
Повороты /?(фк.
я' Opk',ek., о),
Рис. 4.4.
ек, о) и
которые располагают ось
квантования вдоль векто-
ров к и к', соответствен-
но, и поворот Rr=R~lR'.
который переводит ось
вдоль вектора к в ось
вдоль вектора к'.
V —


Формула (4.108) отчетливо демонстрирует
разделение амплитуды перехода на дина-
мическую и кинематическую части. Пер-
вая заключена в фигурные скобки и зави-
сит от специфических динамических свойств
изучаемых ядерных переходов. Эта зависи-
мость проявляется благодаря появлению
электрических и магнитных мультиполь-
ных моментов заряда и спина и через
энергии возбуждения и распадные ширины
ядерных состояний. Кинематическая часть
определяется матрицами конечных враще-
ний и описывает чисто геометрические
свойства задачи рассеяния.
Чтобы рассмотреть поляризацию фото-
нов и ориентацию ядер, введем матрицы
плотности o', т‘ для подсостояний фотона
и ядра в начальном состоянии и матрицы
of, xf для конечных подсостояний. Они
будут, конечно, обладать обычными свой-
ствами матрицы плотности (см., напри-
мер, (246, стр. 280—283] и Приложение В
рица плотности для фотона имеет вид
Op.v — ( — ] )W Г— ц
где с ! — компоненты вектора поперечной поляризации,
гю.= -(с_1|1+с1|_1),	(4.1096)
к этому тому). Мат-
(4.109а)
(4.110а)
причем с0 = 0. Можно записать матрицу плотности также в виде
о--L(l+p.s),
117
где о — матрицы Паули, Р — вектор Пуанкаре в декартовых ко-
ординатах:
р= {(01-1+0-11), i (Oi-!—O_u), (ou—o.i.j)}. (4.1106^
Если состояния фотона являются полностью поляризованными, то
Р — единичный вектор; если же имеется частичная поляризация,
то величина s = |Р| описывает степень поляризации, а формула
(4.109а) заменяется выражением
oUv = -^-(l—s)6nv+s ( — l)uС-—Ucv-	(4.111)
В формуле (4.110) Ps — разность вероятностей обнаружения фото-
на с правой и левой круговой поляризацией. Таким образом, ве-
личина |Р3| является степенью круговой поляризации, а (Р/+
+ Р22)1/2 — степенью линейной поляризации. При этом величина
Рг равна разности вероятностей обнаружения фотонов, линейно
поляризованных вдоль осей х и у. Вектор Пуанкаре имеет следую-
щие компоненты в сферическом базисе:
Р-ы =	Р0=Оц o~i-i, Р_х = V^Gi-i, (4.112)
которые с помощью разложения о на неприводимые части
2
<Vv=(— l)v 2 (1П| — p/vv— р)о(г_ц	(4.113а)
1 = 0
связываются с неприводимыми компонентами ранга I
О/Р=2(—1)V(I1Z|—nvp)c^v.	(4.1136)
uv
В явном виде неисчезающие компоненты имеют вид
'-0:	V5 •	
/-Ь	
, о - —1 / — 2. о^о — /— ’ °	/6	(4. НЗв)
-р 1	
°-2-2= 	 22 V2 ’	
Р+1	
°2'2	1/2	
Матрица плотности для рассеянных фотонов имеет вид, анало-
гичный формуле (4.111). Однако это выражение необходимо норми-
118
ровать так, чтобы Sp of равнялся не единице, а максимальному
отклику детектора. Таким образом,
2
ofnv
(1 --Sf) 6[TV + Sf (	1)W c— u cv
(4.114)
Где — компоненты вектора поляризации рассеянного фотона
в сферическом базисе, связанном с направлением к', и Sf = |Pf|.
Матрица плотности т; начального состояния ядра, вообще говоря,
не диагональна. Однако всегда можно выбрать не определенное
заранее направление оси квантования таким способом, чтобы ма-
трица т1 стала диагональной. (Это направление в действительности
может определиться внешним магнитным полем или осью симметрии
электрического поля кристалла.) Тогда
Тад М; = Ом- $м;	
It	lit
(4.115)
Условие нормировки имеет вид
SpV =	” 1-
1
(4.116)
Используя (4.115) и (4.116) можно построить 27г + 1 обычных
параметров ориентации [331]
Ао = g(Jt, G)-1 2 G-1 (-1)'*-^ (7f Ц G | Mi-Mi 0) aM , (4.117a)
где
g(h, G)=I?^ ((2Ц-СУ./(2Ц + G +1)!P/2. (4.1176)
Обратное соотношение имеет вид
aMi = ( - l)7«-"f У G (li li G | Л4г-7Иг 0) g (Ц, G) f‘co. (4. 117b)
г	G
Для выстроенных ядер aM.^a^Mi по определению и /оо=0для
нечетных G. Для неориентированных ядер ам.= 1/(2/г + 1) и
Zgo= 6go-
Матрица плотности т4 конечного состояния ядра может быть
рассмотрена таким же способом, за исключением того, что мы боль-
ше не имеем свободы выбора оси квантования, поскольку ее на-
правление выбрано так, чтобы il была диагональной. Поэтому т?
не может быть, вообще говоря, диагональной и мы должны ввести
более общие параметры ориентации для конечного состояния:
ffFF- = g(JftF)~l V (_!//+"/| -MfMfF'jxLfM'f
MjM'f
(4.117г)
119
Обычно в эксперименте не производится анализ ориентации ядра
после рассеяния фотона. Поэтому можно ограничиться лишь слу-
чаем
TAfyAff = f ИЛИ fpp- = (21 f + 1) о бр-о-
С учетом матриц плотности фотона и ядра в начальном и конеч-
ном состояниях сечение (4.107) для случая поляризованных фотонов
или ориентированных ядер принимает вид
do __ k'
dQ — k
V	Кмm.	Valm' Км^м' Оц-х' tM’Mf-
Ш	1 1	1 I f 1	J J
M-'U' M.M'iMfMf
(4.118)
Чтобы эффективно использовать формулу (4.108) при анализе гео-
метрического фактора этого сечения, разложим динамическую
компоненту Д'4, 4 на неприводимые части, являющиеся обобщен-
ными поляризуемостями:
</ I I К - 2 2 (- 1)L' (LL’j | ММ'tri) X
v ММ*
l £а + Йй—[ Ev — —	Ea—h(£i' — ( Ev——-
-1
ЛЛ,(г
(4.119)
Обобщенные поляризуемости представляют собой матричные эле-
менты неприводимых тензоров ранга /. Они содержат всю динамиче-
скую информацию о рассеянии фотонов, и матричный элемент пере-
хода выражается через них следующим образом:
Kf?- (-1)*' 2 2|(ЬЬ' /1 ММ'т)<[ | Р%' | i> X
LML’M' j
xD^(R)D^K.(R').	(4.120)
Поскольку Pjm’ являются неприводимыми тензорами, можно
применить теорему Вигнера—Эккарта и ввести приведенные обоб-
щенные поляризуемости, которые не содержат зависимости от маг-
нитных квантовых чисел:
<7У Mf | Р%' | 7г Ali>=(7i jlf | Mt m Mf) <7 ^Pf || 7г>.	(4.121)
120
Приведенный матричный элемент имеет вид
<ЛИ/ь'11Л>=2(-1)£'/ In\w(LL'IJf, //n)x
(fc')h> <тМ^(£)Ца> . .
x----------------—------h(
£а4-й(о —^£v—— ilj
<₽II^L (*)h> <TlU«L'(*')l|a>
x-------------
£a—Яш'
1
— iT
2
W(L'L It It- jln) x
Jllc*
(4.122)
где промежуточное состояние ядра у характеризуется спином 1п.
В приведенных обобщенных поляризуемостях можно далее выде-
лить различные вклады чисто электрических, чисто магнитных и сме-
шанных поляризуемостей. Они возникают от соответствующего
разделения величин .7Zva(A £Л4) в формуле (4.101). Мы можем
написать
<if\\PjL' II Л>= pi(EL> EL’> +М'piML') +
+ ХР,- (ML, EL') + X Р} (EL, ML').	(4.123)
Для чисто электрической и чисто магнитной поляризуемостей
Pj (EL, EL’) и Pj (ML, ML') четность меняется по закону (—1)L+L',
а для смешанных поляризуемостей £.• (ML, EL') и Pj (EL, ML') —
по закону (—1)L+L'+1. Поэтому чистые и смешанные поляризуе-
мости одного и того же типа (L, L’) не интерферируют.
Подставляя (4.121) в (4.120), окончательно получаем для матрич-
ного элемента, который входит в формулу (4.118),
K^=(-1)V S ^'(LL' j\MM' т)(1^ If\MimMf)X
LML’M' j	1
x <7/||PfL'||/i>JDMx(^)r>^-v (/?'),	(4.124)
где теперь вся динамика ядерной структуры содержится в приве-
денных обобщенных поляризуемостях (4.122). В формуле (4.124)
явно выделены геометрические факторы, в то время как выражение
(4.118) содержит суммы по магнитным квантовым числам подсостоя-
ний системы. Используя эти два выражения, формулы (4.113) и
(4.117), ряды Клебша —Гордана для матриц вращения и обычную
технику пересвязки из Приложения А, получаем
к LL'jKK ]
Х<//||Р^'||Л>*	3 (-l)GMofk' а^оГ^х
GFF'LfiK'p’ll'
121
х 2 (— 1)J+E/j' JGF2X2/^(11/| — XppX)x
JeJ'e'X
X (11/' |—[x'X'X'—pi')(LKJ\7.—рЛ—p)(L'K'J' | —X'p'p'—X') X
X (XFG | F'—F'O) (XJJ' | —F'e—e')
1 Г X)
h h G
Л Л f.
[/ /' x
L К J
L'K'J'
X
X g(Jh G) g(/f, F)D^-x- (/?').
(4.125)
Способ, с помощью которого можно проанализировать экспери-
ментальные данные для извлечения приведенных обобщенных поля-
ризуемостей, содержащих сведения о динамике ядра, подробно
обсуждается в работах [13, 15]. Общее выражение (4.125) для сече-
ния рассеяния фотонов там конкретизируется для случаев отсутствия
ориентации ядра или поляризации излучения*. Мы приведем
здесь в качестве примера результат для самого простого возможного
случая, когда не определены ни поляризация фотонов, ни ориента-
ция ядра. Тогда для матриц плотности фотонов имеем из (4.111)
и (4.114)
и из (4.113)
Goo=w G20= W СТоо=уГ’ G20==W	}
Для неориентированных ядер формулы (4.117) дают
/go = 6go> Zff'= (27^-[-1)6fo6f'o).	(4.128)
Подставляя эти результаты в формулу (4.125), получаем
-^-=-^--4 2 <Л11^'|1ЛХЛРГ'|1Л>*х
2k It LL’KK.'i
X 2 (— 1)Г+Ь+/ (GKJ I 1 —10) (L' K' J I 1 —10) x
X [I +(-i)/<+L+J| [i +(_1)L'+K'+J W(LKL'K'-, j/)Pj(cose)],
(4.129)
где использованы соотношения
2 (~ D"DJ E0 (R) DJe0 (R1) = Pj (cos 0),	(4.130)
—MO) 4
(0—угол рассеяния).
* О результатах предсказаний ядерных моделей, относящихся к рассея-
нию или поглощению фотонов, см. гл. 10 и 11 в т. 1.
122
_^(Ц2|-М0)]=—(4.131)
Уз
Как видно из формулы (4.129), в отсутствие ориентации ядра
не имеется интерференционных членов для поляризуемостей с раз-
ными переданными угловыми моментами / и /'. Таким образом,
чтобы получить информацию об относительных фазах поляризуе-
мостей с разными /, необходимо проводить эксперименты по рассея-
нию фотонов на ориентированных ядрах [14].
Наконец, можно далее рассмотреть случай мультипольных пере-
ходов, в которых угловой момент меняется на единицу, т. е. £=£' =
= К = К' = 1. Тогда формула (4.129) принимает вид
2 <ЛР/1|1Л><Л||Р'1|1Л>*^-(е), (4.132а)
k 1 i /=0,1,2
где
So (6) = -у (1 + cos2 6), gl (6) = ± (2 + sin2 6),
£2(0)--^(I3+cos26).	(4.132a)
Этот результат справедлив для чистого £1- или чистого М 1-рас-
сеяния, а также для случая, когда смешиваются лишь £1- и АП-муль-
типоли. Он показывает, что для скалярного рассеяния (/ = 0) полу-
чается типичное дипольное угловое распределение, тогда как тен-
зорное рассеяние (/ = 2) почти изотропно. Поэтому эти члены мож-
но разделить, используя только угловое распределение, если
вклад скалярного рассеяния не является подавляющим. В послед-
нем случае может быть эффективно использовано поляризованное
излучение [16].
§ 4.6. Фотоядерный гигантский резонанс
и правила сумм
При возбуждении ядер фотонами главным свойством сечения
поглощения является фотоядерный гигантский резонанс. Этот
резонанс проявляется во всех ядрах. В средних и тяжелых ядрах
его энергия заключена в интервале между 13 и 18 Мэв, в то время
как в более легких ядрах он наблюдается в области 20 Мэв. Его
полная ширина колеблется от 3 до 10 Мэв. Гигантский резонанс
образуется в основном в результате поглощения электрической
дипольной компоненты поля налетающего фотона.
Распространенность фотоядерного гигантского резонанса и его
преобладание в реакциях, вызванных фотонами, свидетельствуют
о том, что систематическое изучение его свойств по всей периодиче-
ской таблице может дать много информации о структуре ядра. Это
действительно так, хотя детальный анализ мы здесь проводить не
будем, а обсудим лишь те аспекты явления, которые не зависят от
тонких деталей ядерной структуры.
123
Тот факт, что фотопоглощение обусловлено главным образом
Е1-мультиполем, не кажется, конечно, удивительным в свете заме-
чаний в конце § 4.4. Это неизбежное свойство реакций с фотона-
ми, и объясняется оно тем, что участвующий в процессе фотон имеет
достаточно низкую энергию, так что его длина волны намного боль-
ше ядерных размеров. Однако тот факт, что резонансы должны по-
являться между 13 и 20 Мэв, систематически изменяясь с числом
нуклонов, действительно имеет отношение к вопросам структуры
ядра. Его можно довольно легко понять [169] с помощью представ-
лений о гигантском резонансе как о колебаниях протонов ядра
относительно нейтронов. Переменное электрическое поле налетаю-
щего фотона заставляет протоны колебаться, в то время как ней-
троны, чтобы сохранить положение центра масс, движутся в проти-
воположном направлении, т. е. протоны и нейтроны колеблются
в противофазе и, как обсуждалось в § 4.2, приобретают эффектив-
ные заряды е) и (—е) соответственно. Поскольку в процессе
этих колебаний происходит частичное разделение всех протонов по
отношению ко всем нейтронам, они появляются при намного боль-
шей энергии, чем колебания поверхности ядра, которые затраги-
вают лишь несколько нуклонов на поверхности. Такому обсужде-
нию можно придать количественную основу, используя коллектив-
ные модели или оболочечную модель. При этом можно весьма успеш-
но рассмотреть систематику по числу нуклонов ширины гигантского
резонанса в различных ядрах и свойства соответствующих колебаний
в конкретных ядерных реакциях*.
Один из важных вопросов, которые должны возникнуть в по-
пытках описать гигантский резонанс, заключается в том, имеется
ли что-либо очень характерное в концентрации силы электрических
дипольных переходов в резонансе. Эксперимент показывает, что
ответ на этот вопрос является утвердительным и что гигантский
резонанас обычно имеет тенденцию исчерпывать все Е1-переходы,
которые может иметь ядро. Данное утверждение делает разумным
предположение, что имеется верхняя граница дипольной силы, ко-
торую может иметь ядро. Более того, оно предполагает, что этот
предел достаточно надежно известен. Подобные утверждения можно
выдвинуть потому, что удается установить в значительной степени
не зависящим от модели способом правила сумм для фотовозбужде-
ния. Они доказывают, что проинтегрированное по энергии сече-
ние фотопоглощения должно быть равно определенной величине,
которая зависит от изучаемого ядра. Мы обсудим здесь два хорошо
известных правила сумм — правило сумм Томаса—-Райха—Куна
(ТРК) Для силы электрических дипольных переходов и правило
сумм Гелл-Манна, Гольдбергера и Тирринга (ГГТ) для суммы вкла-
дов всех мультиполей, проинтегрированной до порога рождения
мезонов ('—135 Мэв).
* См. гл. 10 и 11 в т. I.
124
Начнем с обсуждения правила сумм ТРК. Это правило наибо-
лее легко формулируется с помощью дипольных сил осциллятора
для перехода из основного состояния ядра а в возбужденное со-
стояние р. Для одного нуклона эта сила определяется следующим
образом:
2М (Е„— EA I с	|2
f₽a=------Д2~---- IJ <₽ IР (г) I a> zdr|	(4.133)
Используя формулу (4.8), теорему Зигерта и теорему Вигнера —
Эккарта, сечение поглощения для неполяризованных фотонов можно
записать в виде
J GdE^
line
J<p|p|a)zdr 2 =	(4.134)
где интегрирование проводится по ширине уровня р, который, как
предполагается, значительно уже Др. Плотность заряда для одного
нуклона в формуле (4.133) равна эффективному заряду этого ну-
клона, умноженному на соответствующую нуклонную плотность.
Следовательно,
fPa =	(£₽-Еа) | <р | z | а> |2 =
= ^{<« И Р> (£р-Да) <Р | 2\<Х>} =
=	{<« И Р> Ср I [И, z] i a>—(a I [Н, z] | р> (р | z | а»,	(4.135)
где Н — ядерный гамильтониан, т. е.
Я|а> = Д|а\ <р|Н = <р|Др.	(4.136)
Суммируя в (4.135) по всем конечным состояниям р и пользуясь
свойством полноты этих состояний, получаем
S/pa=^-<a|[2',[//,z]]|a).	(4.137)
Предположим, что гамильтониан для системы А нуклонов может
быть разделен на части, соответствующие кинетической и потен-
циальной энергиям:
(4.138)
125
Тогда легко вычислить двойной коммутатор для кинетической части
если воспользоваться соотношением lpz, z] = —
	[Z, \Н, z]] -	(4.139) i <j
или	2fPa=^ff(l+l/),	(4.140) p
где	v-~<a\ 2(z, Wij,	(4.141) hz	i <j
Таким образом, для одного нуклона сечение поглощения, проинте-
грированное по всем Е\-переходам, имеет вид
SjodEp ^^ff(l + v).
Р J	Me
(4.142)
Если просуммировать все вклады Z протонов и N нейтронов,
пользуясь при этом эффективными зарядами (4.46), то в результате
получим
2л2 е1 И
Мс
2"2e2/i —d + Z’l^eO—(T+'^l (Мэв-мбарн), (4.143)
А	А
где
(4.144)
Z N
Z
Мс А
Правило сумм (4.143) первоначально было получено для атом-
ных систем, для которых в потенциальную энергию не входят обмен-
ные или зависящие от скорости силы. Для таких потенциалов z ком-
мутирует с Vij и 1а = 0. В этом случае формула (4.143) дает со-
вершенно строгий, не зависящий от модели результат. Однако для
ядра обменные силы дают важный вклад, который необходимо
оценить, чтобы пользоваться правилом сумм с достаточной степе-
нью надежности. Если природа обменных сил такова, что протоны
и нейтроны стремятся сблизиться, то энергия, необходимая для
возбуждения колебаний протонов относительно нейтронов в ги-
гантском резонансе, будет больше и правая часть формул (4.134)
и (4.143) увеличится. Это соответствует случаю притягивающих
126
сил Гейзенберга и Майорана. Например, для сил Майорана*
К, = V (гц) Рм, и формула (4.141) для i-ro нуклона имеет вид
v =	<сх | [2гг V (ri}) Рм zt-z} V (ri}) Рм- V(rtj)P^ г2] | а> =
= — I [2гг z} —z? —zf ] V (riS) Рм\а)
пл
Л4
= —£<а1&-21)2¥(г1})Рм1а>.	(4.145)
пл
Поэтому для притягивающих сил Майорана (V (ri;) < 0) v и '/7
положительны. Численные значения v были оценены с помощью
различных моделей (см. [228; 230, гл. 3]). Эти оценки свидетель-
ствуют о том, что для типичных примесей обменных сил значе-
ния с17 заключены между 0,4 и 0,5.
Прежде чем сравнивать результаты, полученные с помощью пра-
вил сумм ТРК, с данными эксперимента и оценивать область их
применимости, обсудим правило сумм Гелл-Манна, Гольдбергера
и Тирринга для интегрального сечения фотопоглощения. Правило
сумм ГГТ может быть получено несколько более строгим путем,
чем правило сумм ТРК. Во-первых, в нем нет ограничений, связан-
ных с учетом лишь Е1-мультиполей и с использованием теоремы
Зигерта, которая должна обязательно нарушаться для высоколежа-
щих уровней, входящих в сумму по конечным состояниям в формуле
(4.143). Во-вторых, оно может быть получено только с помощью
принципа причинности без применения теории возмущений [166,
79]. Гипотеза причинности позволяет записать для полного сече-
ния фотопоглощения ст (со') с частотой со' хорошо известное [210,
211, 173] дисперсионное соотношение Крамерса—Кронига, т. е.
соотношение между реальной частью f (со) амплитуды рассеяния
вперед фотонов с частотою со и полным сечением фотопоглощения:
ос
Re/(co)-Kef(O) = -^-P С^Цао', (4.146)
J со 2—о2
о
где Р означает интегрирование в смысле главного значения.
Можно привести следующее нестрогое доказательство исполь-
зования принципа причинности при получении формулы (4.146).
Рассмотрим амплитуду рассеяния вперед f(oo) действительной волны.
Эта амплитуда может быть записана как фурье-преобразование от
действительной зависящей от времени амплитуды g (/):
оо
f (со) = g(t)ei,aldt.
—оо
(4.147)
* Оператор Майорана меняет местами пространственные координаты
Двухчастичных функций, на которые он действует;
Р™ф(Г1, (й; г2. £2)--ф (г2. гъ £2). где и £2—спиновые координаты.
127
Предположим теперь, что в рассеянии участвует очень узкий волно-
вой пакет, который достигает области взаимодействия в момент
времени t = 0. Тогда весь процесс рассеяния совершается при
t > 0, чтак что g(t) = 0 для t < 0, и мы можем записать
f(co) = g (/) eiwf dt.
о
(4.148)
Выделяя в амплитуде рассеяния вперед действительную и мнимую
части, получаем
R е f (со) = (j g (f) cos со/ dt,
о
(4.149a)
Im f (co) = g (t) sin co/ dt.	(4.1496)
о
Отсюда следует, что
Ref(—co) = Ref(co),	(4.150a)
и
Imf(—co) =—Imf(co).	(4.1506)
Введем соотношение
cosco/=—P I cfe/ sin<0 для	/>0,	(4.151)
л J co'—co
—oo
которое легко получается с помощью теории вычетов. Тогда из
формулы (4.149а) имеем
Ref(co) = {dtg(t) — Р ( с/со' 51 ”м	.	(4.152)
J	Л J <0 —со
0	-—ОО
Если f (со) — достаточно хорошая функция, то можно изменить
порядок интегрирования и воспользоваться формулой (4.1496), в ре-
зультате чего получится
Ref(co) = J_P f dco' .1т2.(и').
л J со —со
— оо
(4.153)
Область интегрирования, содержащая нефизические отрицательные
частоты, может быть исключена с помощью (4.1506), так как
Ref (со) = —— Р
Л
С+ 7dco'
J со'—со J	—со'—со
о	о
2 п , < ,т / (<*>')
= — Р \ с/со' со — ’ *	.
л J со'2—со2
о
(4.154)
128
Сходимость интеграла для больших частот можно улучшить вычи-
танием соотношения (4.154) при со = 0, т. е.
00 _ ,
Re ) (со) - Re f (0) = — Р f do/ I m f (co') |	“--Ц =
JI 3	CO —GT CO
0	L	J
= — P f do/ - Im .	(4.155)
л J co'(co' —co2)
Наконец, воспользуемся оптической теоремой [302]
о(со)=Imf(co) = — Imf (со),	(4.156)
k	со
которая связывает полное сечение и (со) с мнимой частью амплитуды
рассеяния вперед и которая может быть доказана с использованием
только свойства унитарности матрицы рассеяния. Подстановка
формулы (4.156) в (4.155) дает дисперсионное соотношение Крамер-
са—Кронига (4.146).
Формулой (4.146) мы будем пользоваться для трех случаев:
а) для рассеяния фотона на ядерной системе из А нуклонов (для
обозначения используется индекс Л), б) для рассеяния фотона на
одном протоне (индекс р), в) для рассеяния фотона на одном нейтро-
не (индекс п). Рассмотрим комбинацию этих трех амплитуд в виде
Re [f д (<о)-Zfp (со) - Nfn (со) -(fA (0) -Zfp (0) - Nfn (0))] =
ОО
гл2 б*	I
- Р —2 -Т [(“')- Zgp -N°n («')] de/. (4.157)
2л2 С J СО — со2
о
При нулевой частоте (см. § 4.5) амплитуда рассеяния дается томсо-
новским выражением. Тогда
/л(0)= ~(Ze^ , fp (0) = -^-, fn(0) = 0.	(4.158)
.Же2 ’ ,pV ’ Me2 ln' '	v
Далее, сечение поглощения на одном нуклоне равно нулю при
энергиях ниже энергии порога рождения пиона, т. е.
ор (со) — оп (со) =0, со <; рс2/7г,	(4.159)
где р — масса пиона. Подставим (4.158) и (4.159) в (4.157) и рас-
смотрим случай со -> оо. Тогда
N7 р2
Re [fA (<x/) — Zfp (<*>)-Nfn (oo)]A-2 +
ос
+ f [ад(оУ)—Zo(co')—JVan(o/)]da/= —
2л2с J
рс2/Л
v-c2/h
----J— f Од (co') c/co',	(4.160)
2л2 c J
о
129
где вся область интегрирования по частоте разбита на области выше
и ниже порога рождения мезонов. Предположим теперь, что при
очень высоких энергиях рассеяние вперед на Z протонах и N ней-
тронах, связанных в ядре, такое же, как и для того же числа сво-
бодных нуклонов. Тогда
Ь(оо)—Zfp(oo)~Nfn (оо) = 0,	(4.161)
и интегральное сечение фотоядерного поглощения имеет вид
a/,(to')d(W)= 25^2^(1+^) =
J	Мс А
о
= 60-^-(1 -f-W7) (Мэв-мбарн),	(4.162)
где
со
W = J [Z^(“,)+7VGn(co')_^(“')ld(^')- (4Л63)
цс2
Используя экспериментальные данные, Гелл-Манн, Гольдбергер
и Тирринг оценили этот поправочный член:
W--= 0,1	— 0,4.	(4.164)
Следовательно, в правые части правил сумм ТРК (4.143) и
ГГТ (4.162) входят сходные поправочные факторы, равные при-
мерно 1,4.
Однако эти два правила сумм имеют важные различия. Во-пер-
вых, необходимо отметить, что в правило сумм ГГТ входит опреде-
ленный верхний предел интегрирования по энергии — энергия мас-
сы покоя пиона. В правило сумм ТРК не входит такого предела,
хотя, поскольку оно не учитывает мезонных эффектов, подразуме-
вается тот же самый предел. Оно нарушается, конечно, еще раньше
из-за использования теоремы Зигерта. Правило сумм ГГТ содержит
вклады всех мультиполей и не ограничено условием kR 1-
В то время как правило сумм ТРК содержит явные ссылки на
природу ядерных сил и требует предположений о волновых функци-
ях ядра для оценки поправочного члена 2^, в правило сумм ГГТ не
входят какие-либо зависящие от модели утверждения. Его попра-
вочный член зависит от непосредственно измеряемых величин
ор и ап. Главный вклад в эти величины при высоких энергиях да-
ют процессы, включающие фоторождение пионов. Таким образом,
мезонные эффекты, которые феноменологически входят в правило
сумм ТРК в виде поправочного члена (4.141), обусловленного об-
менными потенциалами, явно входят в поправочный член W, и фун-
даментальная теория обменных сил должна объяснить эту связь.
Правило сумм ГГТ очень полезно при анализе эксперимен-
тальных данных, так как оно не требует разделения вкладов раз-
130
пых мультиполей. Более того, его получение основывается исклю-
чительно на фундаментальных и вполне приемлемых предположе-
ниях. Кроме численных неопределенностей при оценке 417, един-
ственный принципиальный вопрос, который может возникнуть
при доказательстве правила сумм ГГТ, заключается в законности
формулы (4.161). Это может привести к ошибке, обусловленной нали-
чием энергии связи нуклона в ядре; поправка при этом будет поряд-
ка энергии связи на один нуклон, деленной на массу нуклона, т. е.
около 1 % [157]. Кроме того, поправка такого же порядка возникает
Рис. 4.5. Зависимость от А интегрального сечения фотопо-
глощения ядер (проинтегрированного до 30 Мэв) [149].
из-за ослабления пучка фотонов с большой энергией при прохожде-
нии через ядро [79]. Такие малые эффекты не были бы важны, если
бы не тот факт, что различия в поведении амплитуд рассеяния при
высокой энергии приведут к тому, что подынтегральное выражение
в (4.163) не будет стремиться к нулю при верхнем пределе интегри-
рования. Это, в свою очередь, приведет к расходимости интеграла
в формуле (4.163). Однако указанную трудность можно обойти и
получить [79] малые численные поправки к оценке (4.164).
На рис. 4.5 дано сравнение экспериментального сечения фото-
поглощения, проинтегрированного до 30 Мэв (т. е. по области гигант-
ского резонанса), с интегральным сечением 60 (NZ/A) Мэв-мбарн.
Видно, что гигантский резонанс исчерпывает подавляющую часть
силы переходов, хотя для легких ядер выше этой произвольной гра-
ницы обрезания при 30 Мэв существует заметная сила, имеющая,
по-видимому, характер Е1-переходов.
131
§ 4.7. Поглощение фотонов большой энергии
и квазидейтронный механизм
В данном параграфе речь идет о квазидейтронном механизме,
который все еще остается мало понятным процессом, но представля-
ет большой интерес для изучения структуры ядра. Если фотон с
большой энергией Aw (мы рассматриваем интервал 50—400 Мэв)
поглощается ядром, то при этом не происходит передачи всей энер-
гии и импульса одному нуклону. Дело в том, что если бы один нуклон
получил всю энергию фотона, то его импульс был бы порядка
[2MAw]*/ 2, что намного больше первоначального импульса фотона
Aw с. Тот факт, что нуклоны находятся в потенциальной яме ядра,
не может привести к компенсации такой большой разницы, и по-
этому фотоиспускание одного нуклона невозможно. Рассмотрим,
однако, два нуклона, сталкивающиеся в ядре. Оператор диполь-
ного перехода фотона может привести к вылету протона и нейтрона,
имеющих приблизительно противоположные направления, так что
пара имеет небольшой полный импульс, равный импульсу, внесен-
ному фотоном. Но относительный импульс двух нуклонов в паре
при этом будет большим, и, следовательно, можно ожидать, что
в квазидейтронных процессах зондируются малые расстояния между
нуклонами в парах, находящихся внутри ядра.
В качестве первого шага для рассмотрения этих процессов можно
представить поглощающую систему состоящей из протон-нейтрон-
ного кластера, на которую не оказывают заметного влияния другие
нуклоны в ядре. Волновая функция такой системы отличалась бы
от волновой функции дейтрона вследствие того, что дейтрон есть
очень слабо связанная система, и поэтому два нуклона проводят
большую часть времени далеко друг от друга, тогда как квазидей-
трон имеет намного меньший эффективный объем. Можно ожидать,
что в центре квазидейтронной системы двухнуклонная волновая
функция имеет ту же самую форму, что и в случае дейтрона, цо уве-
личена по амплитуде, так чтобы скомпенсировать уменьшение
объема. Такие простые аргументы, основанные на соотношении
объемов, приводят к тому, что квадрат квазидейтронной волновой
функции будет в 8 раз больше, чем квадрат дейтронной волновой
функции. Более детальный анализ [229, 86] показывает, что сечение
для квазидейтронного процесса при энергии Aw связано с сечением
расщепления дейтрона при этой же энергии следующим соотно-
шением:
о (Aw) = 6,4 ~Од (Aw) l,64o^(Aw).	(4.165)
Поскольку квазидейтронный процесс является двухчастичным
переходом, он не может описываться с помощью одночастичного
оператора фотопоглощения, если только он не действует во время
столкновения двух частиц в ядре. Такие столкновения появляются
внутри области, определяемой длиной залечивания [167], которая
132
обусловлена наличием твердого кора в нуклон-нуклонных взаимо-
действиях. Если в двухнуклонном взаимодействии имеется беско-
нечно сильное отталкивание на очень коротких расстояниях, назы-
ваемое твердым кором, то волновая функция двухнуклонной системы
должна равняться нулю на радиусе кора (рис. 4.6). На расстоя-
ниях, значительно больших этого радиуса, волновая функция
в основном не должна меняться под действием короткодействующей
отталкивающей силы. Расстояние, начиная с которого волновая
функция начинает приближаться по форме к немодифицированной.
Рис. 4.6. Волновая функция относительного движения
двух нуклонов, взаимодействующих с помощью твердо-
го кора радиусом 0;16а-1 (а — параметр гармонического
осциллятора, подобранного для использования в оболо-
чечной модели легких ядер).
Абсцисса дана в единицах а—1; для ,6О а-1 «1,7 ферми. Сплош-
ная линия представляет собой некоррелированную волновую
функцию, н длина залечивания составляет около 0,5 а-1 «
«0,85 ферми [84].
и называется длиной залечивания. Поскольку в ядерных процессах
при низкой энергии участвуют малые переданные импульсы, то эти
явления не очень чувствительны к эффектам твердого кора, влия-
ние которого сказывается только в пределах длины залечивания.
Однако по мере увеличения энергии фотонов появляется возмож-
ность исследовать эту область, где происходят наиболее интенсив-
ные нуклон-нуклонные столкновения. Таким образом, квазидей-
тронный механизм должен быть чувствительным к свойствам кора.
Однако анализ [220, 116] поглощения связанных пионов, для ко-
торых справедливо аналогичное рассмотрение, указывает, что кор-
реляционные эффекты, обусловленные твердым кором, могут быть
легко замаскированы эффектами рассеяния в конечном состоянии
испущенных нуклонов. Это связано с тем, что для зондирования об-
ласти, в которой существенно влияние твердого кора, требуется
относительный импульс протона и нейтрона | р7, — р7| | «
«400 Мэв! с, т. е. энергия больше 200 Мэв. Кроме того, поскольку
133
эффект рассеяния в конечном состоянии действует в области, кото-
рая намного больше длины залечивания, это рассеяние соответствен-
но и более эффективно влияет на удаление пар из ядра Подобные
расчеты [220, 282] квазидейтронного эффекта, в которых учитыва-
лись как корреляции, обусловленные твердым кором, так и взаимо-
действие в конечном состоянии, указывают, что по крайней мере
до энергии налетающего фотона порядка 200 Мэв влиянием этих кор-
реляций можно пренебречь. Такие расчеты поглощения фотонов
с большой энергией, так же как и соответствующие расчеты для
пионов, весьма сложны и до некоторой степени не завершены.
Кроме того, экспериментальные данные, с которыми их можно
сравнить, все еще очень малочисленны. Следовательно, вопрос о том,
какая информация может быть получена из анализа таких процес-
сов, связанных с влиянием твердого кора, должен все еще счи-
таться открытым.
§ 4.8. Пример: фотопоглощение в 4Не
Чтобы конкретизировать некоторые из идей, рассмотренных в
этой главе, применим их теперь, пользуясь какой-либо моделыа
структуры ядра. Поскольку детальное обсуждение ядерных моделей
не является целью данного тома, мы рассмотрим крайне упрощен-
ную ситуацию, а именно оболочечную модель чисто гармониче-
ского осциллятора для 4Не. Она достаточно хорошо описывает
истинные свойства 4Не для того, чтобы проиллюстрировать ос-
новные рассматриваемые физические свойства. Поэтому такая
модель будет также полезна для понимания других механизмов
возбуждения, которые мы будем рассматривать позже.
В оболочечной модели предполагается, что два протона и два ней-
трона, которые составляют ядро 4Не, заполняют одночастичные уров-
ни потенциальной ямы гармонического осциллятора. Такая яма по-
казана на рис. 4.7, на котором для сравнения изображен и более ре-
алистический потенциал Вудса—Саксона. Для наших иллюстра-
тивных целей можно не учитывать таких усложнений, как спин-ор-
битальные силы, которые расщепляют уровни с одинаковыми зна-
чениями орбитального углового момента I, но с различными значе-
ниями полного углового момента а также остаточное нуклон-нук-
лонное взаимодействие, которое представляет собой разность между
одночастичным гармоническим потенциалом и истинным двух-
частичным взаимодействием. В основном состоянии 4Не имеется
тогда два нейтрона и два протона, находящихся на ls-оболочке
осцил.тяторной ямы. Такая конфигурация дает полный орбитальный
угловой момент, равный нулю, а поскольку в силу принципа
Паули один протон должен иметь спин «вверх», а другой — спин
«вниз» (аналогично и для нейтронов), то и полный спиновый угловой
момент основного состояния также равен нулю. Это дает полный
спиновый угловой момент J, равный нулю. Все нуклоны имеют по-
ложительную относительную четность, поэтому четность ядра тс
134
положительна. Таким образом, основное состояние имеет четырех-
частичную конфигурацию
(1s)4, L О, S О, J«=0+,
я соответствующая нормированная волновая функция имеет вид
^о(Гь г2, г3, г4) =
= - е*р-------«2 (г 1 + Г2 + Гз + ri)] Хр (0) х'1 (0),
(4.166)
Рис. 4.7. Сравнение потенциальной ямы гармонического осцилля-
тора (сплошная кривая) и потенциала Вудса — Саксона (пунктир-
ная кривая) вида V(r) = Vo [1 +exp(r —
Использованные здесь параметры подобраны для 1€О [195]: а=0,59 ферми —1
для осцилляторного параметра и Vo= —53 Мэв, /?=3,15 ферми, С=0,65 ферми
.дня потенциала Вудса — Саксона. Для глубоких уровней, например 1s и
1р, осциллятор является вполне удовлетворительным приближением для
описания более реалистического потенциала, но для 2s—ld-оболочки важно
поведение потенциала на поверхности ядра. Для несвязанных уровней
потенциал гармонического осциллятора не является удовлетворительным.
где хр (5р) и X" (5П) — функции полного спина для протонных
и нейтронных пар соответственно, Sp и Sn — полные спины прото-
нов и нейтронов, а — параметр гармонического осциллятора. Он
связан с осцилляторной частотой &» соотношением
а = Д/И<о//г,	(4.167)
135
где М — масса ядра; для гелия а « 0,73 ферми~г = 144 Мэв/с;.
/ка^22 Мэв есть расстояние между главными оболочками осцилля-
торного потенциала [170]. Уровни отрицательной четности ядра 4Не
можно построить в этой модели, переводя частицы из 1s- в 1р-обо-
лочку. Такие состояния, спектроскопически обозначаемые как
(ls)3lp, имеют энергию Асо. Можно построить и другие состояния
отрицательной четности (рис. 4.8), но все они лежат при энергии
ЗАо> или выше и здесь не учитываются. Принцип Паули ограничивает
Рис. 4.8. Различные состояния ядра 4Не в модели чистого гармонического*
осциллятора:
а — основное состояние 4Не; б — уровни отрицательной четности с энергией /iw; в,
д — состояния отрицательной четности с энергией 3Дед которые в данном рассмот-
рении не учитываются.
возможные волновые функции для конфигурации (ls)3lp четырьмя
типами. Если обозначить протоны индексами 1, 2, а нейтроны индек-
сами 3, 4, то волновые функции будут иметь вид
Ч'и (П. гз. d) =
=	(«Г + г2)м ехр [---а2 (г? + rl + rl + rl)l хр (0) х" (0),	(4.168)
л3	L 2	J
Ч'ьОТ, «Т», Г3, г4) =
= ^(1*3-1 r4)Mexp Г-----i- о? (r2i +гз +rl)l Хр (0) X" (0). (4.169)
л?	L 2	J
для перехода протона или нейтрона из основного состояния
в конфигурацию
(Is)3 Ip, L=l, S=0, /я=1~.
В этих выражениях /14 — проекция квантового числа J = 1 и
гЛ1 — М-я сферическая компонента вектора г. Для антисиммет-
ричных волновых функций, соответствующих конфигурации
(ls)3lp, L=l, 5=1, J"=0“, Г, 2~,
имеем
Ч'сОТ, г2, Г3, г4) =
=	1(«Т ~ г2) ехр Г---а2 (л? + d + d + d)] Хр (1) X" (0)1
Л	|	2	J	j J Л4
(4.170)
136
И	^(П, г2, г3, г4) =
= -^f(r3 — П)ехР [--~а2(г2 +Г2 +Гз+Г4)]х₽(0)Х"(1)[
л3 (	L 2	J	)JM
(4-171)
Заметим, что для получения состояния с правильным полным угло-
вым моментом в выражениях (4.170) и (4.171) необходимо связать
спиновую функцию пары со спином 1 и пространственную функцию
cL = 1. Это можно сделать, записав, как в выражениях (4.168) и
(4.169), пространственный вектор в сферическом базисе и пользу-
ясь коэффициентами Клебша—-Гордана (см. Приложение А):
V(llJ||rM—HM)(r,—г2)цХ^_и(1)-
в
Здесь величины
х«(1)=
aicc2,	7И=1,
—= (°Ч Рз+Р1а2) Л1=0,
/ 2
(4.172)
(4.173а)
Р1
М= —1,
выражаются с помощью нуклонных спиноров а и Р для магнитных
квантовых чисел 1/2 и —1/2. Антисимметричная спиновая функция
имеет вид
Х^(0) = -Ь(К1р2-Р1а2).	(4.1736)
V2
При получении волновых функций возбужденного состояния
(4.168)—(4.171) мы различали протонные и нейтронные возбуждения.
Это удобно для антисимметризации функций, но приводит к тому,
что четыре нуклона ядра гелия должны рассматриваться на неэк-
вивалентной основе. Поэтому введем нормированные линейно не-
зависимые суперпозиции этих функций, которые будут связаны
с собственными функциями полного изотопического спина. По-
скольку все четыре функции в' выражениях (4.168)—(4.171) яв-
ляются собственными функциями нашего модельного ядерного
гамильтониана с собственными значениями Лео, то и новые функции
также будут иметь собственные значения $ со. Эти функции имеют
вид
=----= (п + Г2 +г3 + г4)м X
л3 у 2
X ехр |---7TaZ(r' +rl+rl+rl)]xp(0)X"(0).	(4.174а)
'Гг —---71(Г1+Гг —г3 —Um X
л3]/2
X ехр [—у «2 (Н + г! + г?)] Х₽ (0) X" (0). (4-1746)
Для L 1, 5 = 0, 7я = 1~.
137
Тз	Kn-r?) у/ (1) X" (0) + (r3-r4) у/ (0) х" (1)Ъм X
хехрГ—1-а2(г|+гЦ-г|4-г1) ,	(4.174в>
= ~^т= КП —r2) Х₽ (1) X" (0)—(г3-г4) хр (0) х" (1)Ьм X
л3г2
ХеХР[----^“2(Г> +'1-Ьгз+г4)1 ,	(4.174г>
для L = 1,S — !,</"= 0 ,1,2.
Первая из этих функций соответствует «духовому» состоянию дви-
жения центра масс (см. §4.2). Здесь она имеет структуру координаты
центра масс, умноженной на волновую функцию основного состои-
29,6 МэВ Г 5=0	Т=1
27,7	О' 5=1	Т-1
26,0	Г 5=1 •	Т=1
24,5	2~ 5=1	Т-1
22,0	(2~	Т-0)
20,11	0+ 5=0	Т-0
ния. После преобразования (4.30) она
сведется к функции с нулевой нормой.
Функции ’Т3 и Tj имеют спин 5=1.
Следовательно, соответствующие состо-
яния могут быть получены из основно-
го состояния с 5 = 0, только если опе-
ратор перехода включает векторный опе-
ратор в спиновом пространстве, напри-
мер матрицы Паули <т. Однако это не
верно для дипольного оператора (4.35),
полученного с помощью теоремы Зигер-
та. Он обладает свойством при действии
на основное состояние давать функцию
именно
0+ 5=0	Т=0
те
Рис. 4.9. Экспериментальный
спектр уровней для систе-
мы с Л =4 (по данным ра-
боты [97]).
Все указанные здесь уровни,
за исключением основного и пер-
вого возбужденного состояний,
расположены выше порога вы
лета нейтронов и имеют боль-
шую ширину.
DMV0 = —^-Т2,
а Д/2
где использован эффективный заряд, оп-
ределенный в § 4.2. Таким образом, в
рассматриваемой модели чистого гармо-
нического осциллятора вся сила ди-
польного поглощения концентрируется
в одном уровне с энергией Й<о « 22 Мэв.
Сечение поглощения, проинтегриро-
ванное по этой единственной линии с
учетом теоремы Зигерта и формул (4.8)
и (4.175), получается в следующем виде:
§ odE — 2л2<ое2/а2с.
line
(4.175)
(4.176>
Поскольку энергия поглощения Ао>
должна здесь быть такой же, как и
138
энергия осциллятора, то из (4.167) получаем
§ udE= 2n?e2ti/Mc = 60 Мэв-мбарн,
line
(4.177)
что в точности дает результат, требуемый правилом сумм ТРК (4.143)
для М = 2 = 2и4 = 4. Этого, конечно, следовало ожидать, по-
скольку модель чистого гармонического осциллятора не включает
Рис. 4.10. Полное сечение фотопоглощения для ядра
4Не как функция энергии (см. [168]).
обменных членов и, следовательно, не дает поправочных членов
т. е. ЧУ = 0 в формуле (4.144).
Экспериментальный спектр для 4Не показан на рис. 4.9. Видно,
что имеется группа уровней с L = 1, S = 0, Jn = 1~ и с L — 1,
S = 1, Jn = О-, 1“, 2_ в области, расположенной вблизи Aw «
« 22 Мэв. Уровни с Т 1 в этой группе, в том числе предполагае-
мый уровень гигантского резонанса при 29,6 Мэв, подняты по срав-
нению с tit» Чтобы учесть эффекты такой тонкой структуры, можно
весьма успешно использовать более тщательно разработанный ва-
риант модели оболочек [97, 224, 327]. Этот вопрос мы обсудим в дру-
гом месте.
Полное сечение фотопоглощения показано на рис. 4.10. Хотя
единственным наиболее характерным признаком сечения является
уровень в районе 30 Мэв, ясно, что значительная часть силы погло-
щения соответствует более высоким энергиям, и эта сила должна
139
быть включена в правила сумм, рассмотренные в § 4.6. И снова,
чтобы объяснить такие свойства, требуются усовершенствования
рассмотренной чисто методической модели. (В частности, при более
высоких энергиях важную роль играет квазидейтронный механизм,
см. [1681.) Оказывается, что полное сечение поглощения, проинтег-
рированное до 170 Л4эв [168, 1311, равно 89±6 Мэв-мбарн, что не-
много превосходит значение 84 Мэв-мбарн, даваемое правилом сумы
(4.162) с поправочным членом (4.164).
*
* *
Многие из вопросов, обсужденных здесь, рассмотрены в моногра-
фии Левинжера о фоторасщеплении ядра [230] и в лекциях Даноса
[79]. Общие обзоры даны Фуллером и Хэйвардом [148] и в более
позднее время — Хэйвардом [183], Даносом и Фуллером [80],
Шевченко и Юдиным [315] и Спайсером 13221. См. также гл. 10
и 11 вт. I*.
* Работы [230, J48] переведены на русский язык. См. также [368], сбор-
ник [388], в частности, обзор Осокиной; труды Дубненской конференции по
электромагнитным взаимодействиям [386], в частности прекрасный обзор Ба-
лашова; обзор Лушникова [381], доклад Горячева, Ишханова, Шевченко
на Втором проблемном симпозиуме по физике ядра [375]. — Прим, переев.
ЧАСТЬ II
ЭЛЕКТРОВОЗБУЖДЕНИЕ ЯДЕР
ГЛАВА 5
ОБЩИЕ СВОЙСТВА
РАССЕЯНИЯ ЭЛЕКТРОНОВ
Так же как и фотовозбуждение, электровозбуждение ядер обла
дает одним весьма важным свойством. А именно, для обоих процес-
сов механизм реакции в принципе понят почти полностью, и поэтому
все неизвест ное в задаче может быть выделено и отнесено к про-
блемам структуры ядра. Действительно, поскольку взаимодействие
электронов с ядрами имеет электромагнитную природу, рас-
сеяние электронов обладает многими из тех свойств, которые
обсуждались нами при рассмотрении фотовозбуждения ядер. Но
оно отличается от фотовозбуждения в одном очень важном аспекте.
В то время как фотон, который возбуждает уровень с энергией Aw
над основным состоянием ядра, должен передавать ядру импульс
Jim. с, электрон, возбуждая тот же самый уровень, может передавать
ядру переменный импульс, начиная с величины, близкой к tia/c.
Это открывает возможности количественного изучения поведения
матричного элемента перехода для данного уровня как функции
переданного импульса. Наряду с прочими достоинствами это может
привести к определению мультипольности уровней. Рассеяние
электронов имеет также некоторое качественное отлиЧие от фото-
возбуждения: уровни, которые могут фактически не проявляться
в фотовозбуждении, могут иметь очень большие вероятности
перехода при более высоких переданных импульсах и, таким
образом, быть наблюдаемыми в электронном рассеянии. Вообще,
возбуждение данного уровня при больших переданных импульсах
позволяет исследовать свойства плотности тока перехода на малых
расстояниях, что в свою очередь дает информацию о поведении
соответствующих волновых функций на малых пространственных
интервалах.
На рис. 5.1 схематически показано энергетическое поведение
дважды дифференциального сечения электронного рассеяния при
фиксированном значении переданного импульса. В области энергий,
отмеченной цифрой /, виден пик, производимый упругим рассеянием.
Изучение этого пика как функции переданного импульса дает ин-
141
формацию о распределении заряда в основном состоянии ядра [189,
193]. Область II является областью возбуждения дискретных уров-
ней ниже порога испускания частиц, а область III относится к энер-
гиям непрерывного спектра ядра, где преобладают эффекты ги-
гантского резонанса. В обеих этих областях электровозбуждение
обеспечивает довольно хорошую проверку теорий, которые пыта-
ются описать такие уровни, а также может помочь определить их
mj льтипольность. Квазиупругий пик обозначается цифрой IV.
Рис. 5.1. Схематическая кривая, описывающая поведение дважды
дифференциального сечения электронного рассеяния в зависимости
от переданной энергии при фиксированном переданном импульсе.
Различные области по оси абсцисс соответствуют упругому рассеянию (/), воз-
буждению дискретных уровней (//), возбуждению уровней гигантского резо-
нанса (III), квазиупругому пику (IV) и вкладу, обусловленному рождением
пионов (V) [244].
Рассеяние электронов здесь происходит так, как если бы оно проис-
ходило на отдельных свободных нуклонах. Если бы нуклоны дей-
ствительно были свободными, этот пик был бы резким и появлялся
при энергии q-/2M, где q — переданный импульс, М — масса
нуклона (энергия отдачи свободного нуклона). Взаимодействие
между частицами ядра проявляется в том, что положение этого
пика перемещается в точку q2/2M*, где М* — эффективная масса
нуклона. Оно также приводит к уширению пика распределения по
импульсам связанных нуклонов. Наконец, область V расположена
выше порога рождения пионов, поэтому в этой области должны
в явном виде учитываться мезонные эффекты.
Пример данных по рассеянию электронов, полученных в недав-
них экспериментах с высоким разрешением, показан на рис. 5.2.
В этом эксперименте [323] изучалось электровозбуждение ядра 12С.
Энергетическое разрешение составляло около 200 кэв при начальной
142
на одни налетающий заряд откладывалась в зависимости от энергии рассеянных электронов. Погрешность равна примерно 1%. Поправок на
постоянную дисперсию спектрометра и радиационные эффекты не делалось. Энергетическое разрешение (полная ширина на половине высоты)
составляет 240 кэв для лннни упругого рассеяния и около 190 кэв для пика прн 15,1 Мэв. Указаны энергии возбуждения в 12С (Мэв), спины и
четности хорошо известных уровней ниже 17 Мэв Показаны также три самых низких порога (Мэв) реакций.
форт
1931
ней
ГИЯ’
ган'
обе
юте
му.
энергии 55 Мэв. В наблюдаемом спектре отчетливо виден упругий
пик (область /), пики, соответствующие возбуждению отдельных
низколежащих уровней (область II), и гигантский резонанс (об-
ласть III).
Обратимся теперь к построению формального аппарата для
описания электровозбуждения. Нам потребуется оценка некоторых
сложных эффектов, которые возникают при интерпретации данных
электронного рассеяния. Эти сложности обусловлены тем, что
взаимодействие электрона с кулоновским полем ядра приводит
к рождению фотонов всякий раз, когда скорость электронов изме-
няется из-за его взаимодействия с другими заряженными частицами.
Поскольку все эти эффекты имеют электромагнитную природу, то
их можно весьма надежно рассчитать. Однако их учет предполагает
более сложный анализ, чем тот, который требовался для фотонов.
§ 5.1. Взаимодействие электрона с ядром
Сечение рассеяния электронов ядром, отдачей которого мы пре-
небрегаем, имеет вид
|(ШПО|2ре-,	(5.1)
где vjl? — плотность начального потока электронов со скоростью
ve для волн, нормированных в ящике объемом L3; ре, — плотность
конечных состояний электрона. Если обозначить начальный им-
пульс и энергию электрона через р и Е, а конечные импульс и энер-
гию — через р' и Е', то
ve=p(?IE	(5.2)
и
=	(5.3)
6	(2лЛ)3с2	V
где dQ' — элемент телесного угла для рассеянного электрона.
Таким образом, имеем
do
dQ'
—ЕЕ'
4л 2А4 с4
(5.4)
Матричный элемент в (5.1) и (5.4) является, вообще говоря, матрич-
ным элементом соответствующего оператора перехода, но в первом
борновском приближении, которым мы будем в основном ограничи-
144
i
ваться. он является просто соответствующей энергией взаимодейст-
вия. Она имеет вид*
! р	pi^o I г —г' ।	___
=------- /ц(г)------— J» (г’) dr dr',	(5.5)
с2 J	|г—г I
где величина
выражается через потерю энергии q0, a (г') — плотность 4-тока
перехода электрона. Как и в (4.2),	(г) — оператор ядерного
4-тока. Формулу (5.5) легко понять с помощью принципа соответ-
ствия и классического запаздывающего ток-токового взаимодейст-
вия. Электронный ток (г')е~!*°с< создает 4-потенциал Atl (r')e-ifc<>c<,
где, как и в (1.13),
(V'2	Лц (г') = - — (г')-	(5.7)
С
Как известно, решение уравнения (5.7) выражается через интеграл
от величины, характеризующей источник, умноженной на функцию
Грина уравнения Гельмгольца, а именно [212]
1 fe1*»1 г—г'1
(г) = -М ------— J(1 (г') dr'.	(5.8)
с J |г —г I
Тогда, согласно (3.123), оператор энергии взаимодействия этого
поля с током ядра имеет вид
^"=-AJ/(i(r)^(r)dr,	(5.9)
что и приводит к формуле (5.5).
Разумеется, было бы желательно получить формулу (5.5), осно-
вываясь только на квантовомеханическом подходе, а не на полуклас-
сическом доказательстве, которое мы только что привели. Кванто-
вомеханический подход** трактует рассеяние электрона в низ-
шем порядке как результат испускания фотона одним из заряженных
тел и его последующего поглощения другим телом: Поэтому он
содержит второй порядок теории возмущений по взаимодействию
* Здесь подразумевается суммирование по повторяющимся индексам р.
Используемая метрика такова, что для /ц=(], /a)=(j. icp) = (j. i/o) inJn—
=1-'+/4Л j-J—с2 рл ре, или для Рц = (р. р4) = (р i£/c) = (р, 1р0)
РцРц = Р2 I р2 = р2—£2/с2= —/п2 с2.
** Метод, используемый ниже, для сферических электромагнитных волн
изложен в [336]. См. также [197].
6 Зак. 1193	145
электромагнитного поля с заряженными частицами. Кроме того,
взаимодействие двух заряженных частиц может также осуществлять-
ся через продольную и скалярную компоненты электромагнитного
потенциала, поскольку условие поперечности (1.58) не является
обязательным для ненаблюдаемых (виртуальных) фотонов, которые
входят в ток-токовые взаимодействия. Примером являются обыч-
ные кулоновские силы, действующие между двумя зарядами.
На рис. 5.3 представлены две диаграммы, которые могут да-
вать вклад в энергию ток-токового взаимодействия. В обоих слу-
чаях в начальном состоянии имеется электрон с энергией Е и ядро
Рис. 5.3. Диаграммы, которые дают вклад во втором порядке теории
возмущений в энергию ток-токового взаимодействия. Энергия про-
межуточного состояния для случая а равна Е'+Е а + han, для слу-
чая б — Е+ E^Jr/tam.
в основном состоянии с энергией Еа, конечное состояние системы
содержит рассеянный электрон с энергией Е' и возбужденное со-
стояние ядра с энергией Ер. Так как мы не учитываем энергию от-
дачи ядра, то
Е—Е' = Ер—Ea=hckQ.	(5.10)
Промежуточное состояние на рис. 5.3, а включает электрон с энер-
гией Е', ядро в основном состоянии а и фотон с энергией Й<о, а
промежуточное состояние на рис. 5.3, б имеет электрон с энергией
Е, возбужденное ядро в состоянии f> и фотон с энергией Лсот. В ре-
зультате матричный элемент перехода во втором порядке теории
возмущений имеет вид [302, стр. 202]
<f I Ж," | Г> = У I I »>	| Же I t>
'	1 ’ Z£ + £a_(£'+£aH fcM„)
, у </ 1	| О | -gy/ | t>
^£+f«-(£+£p+K.)
2 <7 | 2£n I n> <n I -УО | t> _ у Q I Me | m> </n | .M-1 t> 5 J J}
—A<on
n	tn
146
где нижние индексы А или е в соответствующем матричном элементе
показывают, что претерпевают переход ядро или электрон. Из
(3.123) и (3.104) получаем следующие выражения для этих матрич-
ных элементов:
<п | Ж | /> = — 1f (J (r'Hl-cp* (г') бХз] e-ik"-r' dr',
(5.12а)
<ДЖ' И>= ~ I	f U(г')-«и—сре(г')б(хз]е,к'"'г' dr',
(5.126)
<Л M'N\n>= -1/-^ f KPI j (r)|a>-ev-
r con Ld J
—c <|31 pN (г) |a> 67.3] eikn rdr,	(5.12b)
-^f[<₽|j(r)l«><-
k b>m L3 J
—c <₽ | pN (r) | a> 6цз1 e~Ik™ r dr.	(5.12r)
Волновые векторы k„ и km здесь имеют вид
kn=k„«„/c, km=kmcom/c,	(5.13)
и суммирование по промежуточным состояниям включает интегри-
рование по направлению этих векторов. Плотность заряда электро-
на обозначается так:
ре(г')=-К^(г') = —J0(r'),
С	с
PN (г) — оператор плотности ядерного заряда. Коэффициенты при
плотностях тока и заряда возникают из соображений калибровоч-
ной инвариантности для энергии взаимодействия (см. обсужде-
ние этого вопроса в конце § 3.3). Действительно, если воспользо-
ваться калибровкой Лоренца (1.10), то осцилляторная зависимость
от времени рассматриваемых здесь величин позволяет написать
V-A+— — =±ik-A4=i — <р = 0	(5.14а)
с dt	с
или
Ф = к-А:-=е3-А = 6Хзс|/-^-е±’кг,	(5.146)
где X — поляризационный индекс фотона, при этом X = 3 соот-
ветствует продольному фотону. В формуле (5.11) суммирование
6*
147
проводится также и по поляризационным состояниям, обозначенным
в формулах (5.12) индексами X и р.
Подставляя (5.12) в (5.11), переходя к пределу очень большого
нормировочного объема и используя выражение (4.11) доя плотно-
сти состояний фотона, получаем
О	к
X § (<Р | j (г) | а> -8х—с <р | pN (г) | а> 6хз1 eik'r dr X
X 5 [J («')• Ex—сре (г') бхзI е-ik‘r' dr' —
--------f dQ f w dco V	x
4л2 c3 J J	ck0 ; со
О U
X § [j (!•') Etl—cpe (r') 6u3]eik r' dr' x
X I j (г) I a> • eh—c <₽ IPN (r) I «> б1хз1 e~ik‘r dr,
(5.15)
где dQ — элемент телесного угла для к и k = kco/c. В первом
слагаемом выражения (5.15) заменим переменную интегрирования
на —со, при этом векторный потенциал А заменится его эрмитово
сопряженной величиной и, следовательно, £х заменится е£. Такая
замена позволяет нам записать энергию взаимодействия в более
симметричной форме

------!— С dQ С со dco V —----------х
4л2 с3 J J	ck0 со
—ОО	X
X 5 [<₽ I j (r) I а> -Ex—С <₽1 pN (г) | а> бхз] e-ik r dr X
X 5 [J (r')-Ex—сре (г') 6ХЗ] eikr' dr’,
(5.16)
где немой индекс р заменен на Л. Суммирование по поляризацион-
ным состояниям можно выполнить, если воспользоваться соотноше-
нием
2еХгх=Т,
х
(5.17а)
где I—единичный аффинор или, что эквивалентно,
2(ех)й (ех)ь=6«ь-
X
(5.176)
148
Для перекрестных членов уравнения непрерывности дают
§ J (г')-е3 eikr' dr' = § J(r')-keikr' dr' =
= — f J(r') • V"eik r' dr' =
ico J
=------- f(V'-J(r'))eik r' dr' =
ico J
==—c2 — f pe (rz) eik-r' dr’.	(5.18)
® J
Аналогичное соотношение получится для ядерного пространства
если воспользоваться (4.5). Таким образом,

X j[<₽|j(r)|a>-J(r')4-c2 (^1+2^) <₽ | pN (г) | а> рс (г')] х
X eik(r'-r) dr dr'.	(5.19)
Интегрирование по углам дает
J dQeik- (г' -о =	e-“°«/f),	(5.20)
где R = | г—г'|. Тогда
оо
[* -^-f[<₽|j(r)|a>-J(r') +
2л i с2 J cfeo+co J [
--------------------ОС
, rh \--------------ie>R/c — i««/c
+ c2 1-p2 — । <p I pw (r) I a> pe (r') --------dr dr'. (5.21)
\ co J	J R
Интегрирование по co теперь может быть выполнено, если мы
укажем, как обойти особенность при о» = —ck0. Первоначально
этот расходящийся член не входил в формулу (5.11), так как формулы
теории возмущений во втором порядке не содержат слагаемых, про-
межуточные состояния которых имеют энергию, равную начальной
энергии. Но при переходе к бесконечному нормировочному объему
мы не учитывали этого факта. Мы устраним эту неопределенность,
введя соответствующие граничные условия. В данном случае вы-
ходящая фотонная волна eik«R/R [в выражении (5.8) или в ниже-
следующем выражении (5.22)1 в согласии с принципом причин-
ности должна соответствовать запаздывающему, а не опере-
жающему взаимодействию. Это требует замены ck0 на ck0 + iq, т. е.
сдвига полюса по переменной со в нижнюю полуплоскость. Заметим,
что не существует полюса при со = 0, возникающего от членов заря-
довой плотности, поскольку величина eib>R/c — e~iaR^c в этой
точке равна нулю.
149
Интеграл берется с помощью техники контурного интегрирова-
ния. Контур для члена е’“й/с замыкается в верхней полупло-
скости и поэтому не содержит полюса при w = —ck0 — пр Контур
для e~iaR/c должен замыкаться в направлении по часовой стрелке
в нижней полуплоскости и давать полный вклад, т. е.
<f | Ж" | i> = J [<Р | j (г) | а> • J (г') -
—с2 <₽ I pN (г) I а> • ре (г')]	[ dr dr',
(5.22)
что соответствует формуле (5.5). Итак, мы явным образом показа-
ли эквивалентность полуклассического и «более квантовомеханиче-
ского» подходов.
§ 5.2.	Разложение по мультиполям
для взаимодействующих зарядов
Как и в случае фотопоглощения, теперь необходимо выполнить
разложение по мультиполям для взаимодействия (5.5). Это поз-
волит выделять в ядерном пространстве матричные элементы опре-
деленной мультипольности. Для случая реальных фотонов мульти-
польное разложение было выполнено для плоской фотонной волны,
тогда как здесь нам необходимо разложить сферическую волну
е’^/Д. так как она является скалярной функцией Грина, то
это разложение хорошо известно [247, стр. 497]:
= 4ni/j0 2 jL (k0 r<) Ylm (r<) hL (k0 r>) YLM (r>),	(5.23)
LM
где hL — сферическая функция Ганкеля первого рода, г> обозна-
чает тот из векторов гиг', который имеет большую абсолютную
величину, а г< — аналогичный вектор с меньшей абсолютной ве-
личиной. Это разложение соответствует скалярным членам плотно-
стей, входящих в выражение (5.5). Для членов, соответствующих
3-векторам токов, необходимо иметь разложение функции Грина,
содержащее единичный аффинор:
G(r, г')=1-^----—-,	(5.24)
|г—г' I
где I — единичный аффинор, или идемфактор, из формулы (5.17).
Он выражается через сферические базисные векторы (2.39):
<7 = 21в1в=2(-1)Чи1-ю	(5-25)
ц	ц
150
и для любого вектора
I J= J-I = J.
(5.26)
Таким образом,
ife0 ] г —г' |
G(r, r')^-----------—2У •
|Г—Г I n
(5.27)
По аналогии с векторными мультиполями Alm (г, а) (а=е, I, ш)
из § 2.3 введем величины
Blm (г; е) = (	) * hL _, (Ао г) TLL - >: м (г) -
— ( оЛ lY* (kor) T/.L+1; m (r),
Blm
(r; I) =	hL—\(kor)TbL—i- м (r) +
+ (2£^1l)/2^f-+1 (^ог)тьь+1;Л1(г) =
= J_V [MV)*Wr)],
«0
Blm (r; m) = hL (k0 r)TLL. M (r).
(5.28a)
(5.286)
(5.28b)
Эти величины отличаются от соответствующих величин Alai (г; й)
только заменой сферической функции Бесселя на сферическую функ-
цию Ганкеля первого рода. Из (5.28), (2.68), (2.73), (2.80) и (2.48)
имеем
2 2 Blm (г; а) А1м (г'; о) =
ьм а
= 2	2 (L'lL|AI'p'7W)(L'lL|M"p"M)x
LM L'M'M"n'n"
X Al- (Ao r) /L- (k0 r') Yl-m. (?) Yl-M" (?')	& =
= 2 2 ^>M’M" бц-ц" Al- (Aor) /L- (Ao r')YL-M- (r)Y*L’M" (r')	=
L'M' ц'ц"
- 2 А£-(Аог)/ь-(Аог')У£-м-(г)У1-м-(г')2и-^-	(5-29)
L'M'	Ц'
Сравнение с формулами (5.23) и (5.29) дает следующий вид для
мультипольного разложения функции Грина, содержащей еди-
ничный аффинор:
G(r, r')=I
ei*o 1 г —г' |
]Г-Г'|
= 4niA02 В LAI (Г>; а)А£м(г<; о).
LMtt
(5.30)
151
С помощью формул (5.23) и (5.30) нетрудно получить разложе-
ние по мультиполям матричного элемента оператора энергии
взаимодействия (5.5) или (5.22):
<f I 3t" I /> =	2 Ь f <₽ I j (г) I «> • Мм (г; о) dr X
с lm а о
ОС
X (г')-Вдл! (г'; a)dr' +
Г
оо	г
+ 2§<₽| j (г) | а> • В/.Л( (Г; a) dr $ J (г')-А1Л( (г'; a) dr'—
«о	о
— с2 $ <Р | PN (г) I а> }L (k0 г) Ylm (Г) dr 5 рс (Г') hL (k0 г’) Ylm (?) dr'—
О	г
— с2 5 <Р I pN (г) | о0 hL (k0 г) Ylm (г) dr § ре (г') jL (k0 г') Ylm (?)	.
О	о	j
(5.31)
Этот результат показывает, что, поскольку электрон может прони-
кать в ядро, матричный элемент оператора взаимодействия для
данного мультиполя невозможно представить в виде произведения
интегралов по ядерному пространству и по электронному пространст-
ву. Необходимо определить электронный ток и выполнить интегри-
рование по координатам электрона, один предел которого входит
в качестве аргумента в ядерное подынтегральное выражение.
Единственное важное исключение появляется для случая kR <£ 1.
В этом случае очень просто получить [113], что объем ядра дает
весьма малый вклад [порядка (Хг/?)21 в матричный элемент операто-
ра взаимодействия и поэтому может не учитываться. Последнее
реализуется заменой предела интегрирования г в выражении (5.31)
нулем, так что два интеграла не дают вклада, а два других включают
интегрирование по всему пространству. Кроме того, в пределе
kR 1 можно воспользоваться теоремой Зигерта [см. (4.22)—
(4.24)], чтобы заменить кулоновские матричные элементы попереч-
ными электрическими матричными элементами. Тогда ядерные ма-
тричные элементы, которые появятся в выражении (5.31), будут
совпадать с теми, которые описывают процесс с реальными фотона-
ми [см. (4.70)—(4.72)]. Таким образом, в длинноволновом пределе
динамические свойства ядра входят в формулы, описывающие элек-
тровозбуждение ядра, так же, как они входят в формулы для фото-
возбуждения.
152
§ 5.3- Результаты борновского приближения
с плоскими волнами
Интегралы по электронному пространству в формуле (5.31)
в принципе известны с любой точностцо, которая может потребо-
ваться. Плотности электронного тока и заряда берутся в виде*
Рс (г') = еф+- (г') фр (rz), 1
J (г') = есф+- (г') афр (г') )	( • а)
или
Jp (г')= 1есфр< (г') Тр фр (г'),	(5.326)
где а, — «скоростная» матрица Дирака, ум (р, = 1, 2, 3, 4) —
обычные** матрицы Дирака. Величины ф являются четырехмерными
спинорами для релятивистского электрона и
фр, (г') = ф+. (г') у4 = фр+- (г') р.	(5.32b)
Обычно функции ф(г') берутся либо в виде решения уравнения
Дирака в статическом кулоновском поле ядра, либо в виде волно-
вых функций Зоммерфельда и Мауэ, либо они могут рассматри-
ваться в некотором высокоэнергетическом приближении (см. § 5.6).
Однако физические результаты рассеяния электронов проявляются
наиболее отчетливо, когда ф берутся в виде плоских волн. Это
грубое допущение справедливо даже количественно для легких
ядер, особенно при рассеянии вперед. Приближение можно улуч-
шить с помощью вычисления последующих членов более высокого
порядка в разложении по Ze2/(fic) « Z/137, которые описывают
кулоновское искажение волновой функции. Выбор плоских волн
для электронной части выражения (5.5) называют борновским при-
ближением с плоскими волнами (БППВ), в то время как исполь-
зование искаженных электронных волн, соответствующих взаимо-
действию с обменом одним фотоном, мы будем называть борновским
приближением с искаженными волнами*** (БПИВ).
*	При выборе электронных волновых функций для использования их
в формулах (5.32) существенно, что мы рассматриваем рассеяние электронов,
а не другие типы взаимодействия электронов с ядрами, такие, как внутрен-
няя конверсия или образование пар в поле ядра. В других аспектах наше рас-
смотрение является достаточно общим для описания любого из этих альтер-
нативных процессов. Так как для обоих из них обычно выполняется условие
kR 1, динамические свойства ядер, которые определяют процесс, могут
рассматриваться тем же способом, что и при высвечивании с испусканием ре-
альных фотонов.
*	Система записи и обозначения введены в Приложении Б, в котором
дан краткий обзор теории Дирака.
*** Существенно, что промежуточный фотон не только дает вклад в иска-
жение электронной волновой функции в статическом кулоновском поле ядра,
но также принимает участие в возбуждении или высвечивании ядра. Если рас-
сматривается взаимодействие более высокого порядка, чем описываемое фор-
мулой (5.5) (см. § 5.6), то бывает очень трудно каким-либо разумным спосо-
бом разделить эти эффекты.
153
Если в формулах (5.32) взять волновые функции электрона
в виде плоских волн, то крайняя простота выражения для электрон-
ного тока приводит в БППВ к виду матричного элемента, который
легко интерпретировать. Имеем
фр(г') = L~’/2е>р-г'/^ ц (р),	(5.33а)
фр- (r') = е‘Р' г'/^ и (р')	(5.336)
и
Jlt,(r')=iecL~3(u (р') и (р)) eik‘r'.	(5.33в)
Функции фр (г') нормированы на единицу в объеме L3 так, чтобы
можно было пользоваться «золотым» правилом (5.1) зависящей от
времени теории возмущений:
5 Фр' (г') % (r')dr' = 6рр' •	(5.33г)
Величины и (р) и и (р') являются дираковскими спинорами в им-
пульсном пространстве, удовлетворяющими уравнению (см. При-
ложение Б)
(р—imc)u(p)= —ip ^а-р—— + $тс^ п(р)=0.	(5.34а)
При этом
ц+ (р) и (р) = 1, и (р) и (р) = — .	(5.346)
Е
В формуле (5.33в) k = q'A = (р — р')/А — волновой вектор пере-
данного импульса. Если теперь разложить по мультиполям пло-
скую волну в выражении (5.33в), подставить разложение в формулу
(5.31) и результат проинтегрировать, то получится матричный
элемент взаимодействия в БППВ. Однако тот же результат можно
получить значительно проще, если выражение (5.33в) прямо под-
ставить в формулу (5.5). Тогда
<f|^"|i>=—43(<₽1Мг)|а>Х
cL3 J
X ~1~*1	&(Р') Vn “ (Р)) eik’r' dr dr'- (5-35)
|г-г |
После замены переменной г' на переменную R=r'—г это выра-
жение принимает вид
(м (PZ) V.. и (р))
<f I Ж" 11> = — 4 л ie	ц - X
4/1	1	kcL3
ОС
X \ СР | /ц (г) | сс> eik r dr eik°R sin kR dR =
о
=	(MP->W(P>) Г<p|(r)!a>e«.,dr.	(5.36)
cL3 k2—ko	J
154
Величина
=	(5.37)
L k —ko
которая входит в матричный элемент
<f IЗГIО =-------у J<₽ | /ц(г) | а> (г)dr, (5.38)
называется потенциалом Мёллера. Он представляет собой 4-потен-
циал, создаваемый током электрона, описываемого плоской волной.
Далее мы должны выполнить разложение по мультиполям для
плоской волны в выражении (5.36). Воспользуемся для этого ме-
тодом, изложенным в § 2.4, где было показано, что удобно отдельно
рассмотреть поперечные и продольные плоские волны. В данном
случае можно аналогичным способом выделить в операторе ядер-
ного тока поперечную и продольную части (см.также § 1.1). Вве-
дем операторы ядерного тока, поперечные и продольные по отноше-
нию к волновому вектору потенциала Мёллера:
Г = k X (j х к), jz = j  кк,	(5.39а)
где
j = jz + jz.	(5.396)
Тогда из уравнения непрерывности для ядерного тока (4.5) полу-
чаем
f <Р I/о I а> eik’r dr= (*-£- • <р| j|a>eik’rdr =
J	J «о
= C<P|/zla>eik rdr.	(5.40)
«0 J
Соответствующее разделение на поперечную и продольную части
может быть осуществлено и для самого потенциала Мёллера. Для
этого в выражении (5.37) запишем
а'=кх(ахк), az = akk,	(5.41а)
a=az4-az.	(5.416)
Уравнение непрерывности для электронного тока приводит тогда
к «условию Лоренца» для потенциала Мёллера. Получаем из (5.34)
kv. a» = I, 2П'в2х	(Р') (Р~ Р") и (Р)) = 0	(5.42а)
n(k—ko) L3
или
оо = ± . a=AGz.	(5.426)
«о «о
Формулы (5.36)—(5.38) принимают вид
<f ------------[<Р| jz (r)|a>-a‘ + <P| jz(r)|a>-az—
155
— <₽l/o (r) I «>«()] eikrdr =
j[<₽ I Г (r) I «>-a‘-c (1-<P I pA'(r) I a> a0 e’k'dr =
J[<₽|j4r)l“>-a'~c<0|pw(r)|a>6]eik-rdr, (5.43)
где
fc = 4ne (u (p')yiu(p))
£3 k2
(5.44)
Если бы с самого начала мы пользовались кулоновской калибров-
кой, то это выражение появилось бы непосредственно из мгновенного
кулоновского взаимодействия (см. § 3.3 и 5.6), что соответствовало
бы в формуле (5.5) частному случаю k0 = 0 для времениподоб-
ных членов и опусканию членов, в которые входит продольный
ток. Главное преимущество подхода, основанного на использова-
нии формулы (5.5) в рассмотренном нами виде, заключается в том,
что она годится для ковариантного описания процессов с участием
электронов и поэтому используется довольно часто. Наконец, по-
скольку вектор j* автоматически ортогонален вектору а1, можно
воспользоваться формулой (5.416), чтобы переписать матричный
элемент энергии взаимодействия в виде
</|Я’"|/> =----~	е <р |pN(r) | а> й] eib,r dr =
-	pre* -	<г> I + i	1 °> X (р))_
\ J I k —fen	“	)	/
= (и (Р') [V • у + И4 у4] и (р)) = (« (Р') Й и (р))-	(5.45)
Сечение рассеяния электрона выражается формулой (5.4), в ко-
торую входит матричный элемент (5.45). После усреднения по на-
чальным состояниям спина электрона и суммирования по конечным
спиновым состояниям появляется следующее выражение для слу-
чая рассеяния неполяризованных* частиц:
= -l-Sp ₽уир
с2
spin.
р'с-\-\тс2 pc-pi/nc2
2iE' Yv’ 2iE
_FF- [(рД Иц)* (pv Vv) +(рц Гц)* <p' Vv) —

- (pi Pb + m2c2) (V* • V - VS Vo)],	(5.46)
* Эффекты поляризации электрона и ориентации ядра при электронном
рассеянии анализировались в работах [130,28,203,347, 174, 358]. Если
использовать ориентированные ядра, то появляются интерференционные члены
между ядерными матричными элементами различной мультипольности,
и можно надеяться, таким образом, отделить их вклады.
156
где для вычисления этих спиновых сумм мы использовали обычную
технику суммирования и усреднения, которая рассмотрена в При-
ложении Б. Отделяя пространственные и временные компоненты
в формуле (5.46), можно записать сечение (5.4) для случая отсут-
ствия поляризации электрона в виде
= 2е2 / р' \	1
dQ’	р / 2Jt + l
X у < ££' + еар.р' W I С <Р !	(r), g> e,t„ ф,, +
I к4	I J
М- Mf
ЕЕ’-с*р.р'-tn* с* IГ । .t (р) | а> eik-г dr |2 +
С2 (k2-k№ IJ	1
1 (k2-k20)2
J р-<₽| j'(r)|a>eik rdr
2 (£+£')
fe2 (k2—ko)
X Re^<p |рЛ'(г) | а>eik'r dr [$p-<₽| j'(r) | a> elk’r dr ] } > (5-47)
где введены средние no 2Jt + 1 проекциям спина начального со-
стояния ядра Jt (соответствующие магнитные квантовые числа
обозначены через Л4,-) и сумма по магнитным квантовым числам
Mf, соответствующим спину конечного состояния Jf.
Теперь можно выполнить разложение по мультиполям для ядер-
ного матричного элемента в выражении (5.47). Пользуясь форму-
лами (2.104) и разложением поперечной плоской волны (2.106),
получаем
§ <₽ | pN (г) | а> elk,rdr =
V4n^ L(JiLJf\MiMMf)Dko(4>, 0, 0)^a(k; CL) (5.48)
LM
И
$<P| j'(r)|a>eik-rdr =
= У 2^ 2 L {Ji LJf I Mi MMf) Ц pDb (ф, 0, 0) X
LtU	± 1 и
X Ец [7V₽a (k; ML) +pNpa (k; EL)],	(5.49)
где 0 и <p — полярный и азимутальный углы, описывающие на-
правление переданного импульса Йк. В формуле (5.48) также ис-
пользовано выражение
Омо(<р. 6, 0)= —Пм(0, <р).	(5.50)
L
157
Приведенные матричные элементы в формулах (5.48) и (5.49) опре-
деляются следующим образом:
CL) =
= 'iL $ <Р I PN (r) | «> 1'l (M Ylm (r) dr, (5.51a)
EL) =
= iL+1 $<₽ IJ (r) | <x> - АЬЛ1 (r; e)dr,	(5.516)
(Ji LJf | MtMMf) WPa (k; ML) =
=	<₽ I j (r) I a>-Alm (r; m)dr,	(5.51b)
где мы опустили значок t у оператора р, поскольку мультиполи,
обозначаемые индексами е и пг, поперечны, и поэтому продольный
ток не дает вклада в (5.516) и (5.51в). Приведенные матричные эле-
менты в формулах (5.51) определены таким образом, что в силу
инвариантности по отношению к обращению времени они должны
быть действительными (см. § 5.5).
Усреднение и суммирование по начальным и конечным подсо-
стояниям ядра легко выполняется с использованием техники, опи-
санной в Приложении А:
V (JiLJf[MiMMf)(JiL'JfIMiM'Mf)x
11 MiMf
х£)Ьц(Ф, е, о)/)мщ'(ф, о, о)=
=	^+ti4JiLJf\MtMMi){JiL'Jf\MiM'Mf)x
МгМу X
Х(ЬЬ'Х\М-М'М-М')(ЬЬ'Х\^-^~^)О^_М,^_^, о, о)=
= 2^+7 Z 2 (~	(Л I АЛ Mf-Mi Mf) X
X (Ji L'Jf I Mi Mf—Mi Mf) (LL'X I Mf—Mi Mi — Mf 0) X
X(LL'^|p —р')П^_ц, (ф, 0, 0) =
2Л4-1	6,,,
= ^FZT <-1)p+!l'(WZ I p-p0) x
Zu j p 1	Z-x_< “i 1
SC(>
X(LLX |н—И'!1—P')D^_^ (q>, 0,0),	(5.52a)
где суммирование no Mf проводилось при фиксированном р = Mf —
— Mt. Далее
2(—Dp(LLX|p-pO) =
р
= 2(— 1)lL(LLX\p—pO)(LLO|p—р0)=(— 1)£А6Ж0, (5.53)
р
158

И выражение (5.52а) дает
i>LL' д
2ЛЧИ 2L4-1 цц''
Символ Кронекера, который требует равенства р и р', гарантирует,
что поперечный и кулоновский члены не могут интерферировать
в формуле (5.47), поскольку первый имеет | р | = 1, а второй р = 0.
Таким образом, последний член в формуле (5.47) не дает вклада, если
отсутствует как поляризация электрона, так и ориентация
ядра. Для других членов, содержащих поперечные матричные эле-
менты, имеем для случая только поперечного электрического или
только магнитного мультиполя
2	1(1‘1|1'6цц----- 2.
(1(1' = ±1
(5.54а)
Однако для случая смешанных е- и m-мультиполей интерференция
снова отсутствует, поскольку
2	= 0.	(5.546)
11,11'=±i
Наконец, мы имеем члены, которые содержат
х (p-iu)(p-ia')V=p2-(k-p)2=
(1.(1' =±1
= (Р—kk • р) • (р + kk • р) = (pz — kk • р') • (р + kk • р) =
= РР'~(k-p)(k-p')>	(5.54в)
2 Р(Р-1ц) (Р= 0.	(5.54г)
ц,ц'=±1
Подставляя их в формулу (5.47), получаем следующее выражение
для дифференциального сечения рассеяния неполяризованных элек-
тронов на неориентированных ядрах:
<кз
dQ’
вне2 / р' \
(key \ р J
2Д+1	(££'-рс2р-р'-|-/п2с4
2£г + 1
|2Vpa(k; CL) |2ф-
— с2\рк'р'~т2с*11<k; l2+1(k;l2C • <5-55)
с2(/г2—/го)2	J
В пределе ультрарелятивистских электронов с малой потерей
энергии (Е, Е' тс2, kck0) оно принимает вид
CI)F+
dQ	2Д + 1 (Ze)2 р	1
_L + tg2_Le)[|Arpa(k; EL) |2 + | 2VPa(k; ML) |2]) , (5.56a)
159
где 0 — угол рассеяния, а величина
(5.566)
является сечением моттовского рассеяния электронов очень боль-
шой энергии на кулоновском силовом центре с зарядом Ze.
Как видно из (4.70) и (4.71), приведенные матричные элементы
для поперечных мультиполей, входящие в формулы (5.55) и (5.56),
пропорциональны матричным элементам, которые входят в вероят-
ности фотопоглощения и фотоизлучения. (Разумеется, для реальных
фотонов волновой вектор к по абсолютной величине равен Ло.)
Кулоновская часть сечения электронного рассеяния также может
быть связана с величинами, описывающими процессы с реальными
фотонами, но только для малых переданных импульсов kR<£ I.
Для этого случая теорема Зигерта в форме (4.24) позволяет устано-
вить связь
J/ / EL^ (557>
Кулоновский матричный элемент дает вклад при тех же самых усло-
виях по спину и четности, которые разрешены для KL-перехода*.
Эти результаты показывают, что для малых переданных импульсов
процесс электронного рассеяния эквивалентен процессам с участием
фотонов; поэтому электровозбуждение не будет давать новой инфор-
мации, если не имеется поляризации. Можно считать, что рассея-
ние электронов дает то спектральное распределение фотонов, кото-
рое определяется коэффициентами перед приведенными ь^тричными
элементами в формулах (5.55) или (5.56). Для данного набора кине-
матических переменных электрона указанные коэффициенты опре-
деляют эквивалентный спектр фотонов, приводящий к тому же про-
цессу р ассея ни я.
Как видно из формулы (5.57), вблизи области, в которой про-
исходит рассеяние вперед, кулоновский мультиполь дает вклад
в рассеяние электронов, сравнимый с вкладом поперечного элек-
трического мультиполя. Однако это верно только в той области,
где электроны создают виртуальные фотоны, которые не сильно
отличаются от реальных фотонов. При рассеянии на большие углы
кулоновский мультиполь имеет тенденцию становиться значитель-
но больше электрического мультиполя. Как впервые было указано
* Переход без Гпередачи углового момента, т. е. £0-переход, может су-
ществовать для кулоновского члена, но не для поперечного электрического
мультиполя.
160
Шиффом* [301], это происходит отчасти из-за того, что для коллек-
тивных возбуждений ядра плотность тока не связана с вращением,,
и поэтому конвекционный ток не дает заметного вклада в попереч-
ные мультиполи. Ток намагничивания такой вклад дает, но опера-
тор rot, который входит в него, приводит к дополнительному
множителю k. Вклад от намагниченности, следовательно, подавлен
при малых переданных импульсах, но даже и при больших k он
по-настоящему не конкурирует с кулоновскими членами. Преобла-
дание кулоновского вклада подтверждается в эксперименте и в рас-
четах, выполненных в рамках ядерных моделей [348, 115, 308].
Одно существенное исключение из выводов предыдущего абза-
ца имеется для угла 0 = 180е. Для рассеяния точно назад борцов-
ское приближение в ультрарелятивистском пределе [см. формулы
(5.56)] дает только поперечный вклад. Этот результат становится
менее точным, когда наши жесткие предположения несколько ослаб-
ляются. Однако остается справедливым, что для рассеяния на 180°
основной вклад дают поперечные компоненты. Эксперимент может
быть выполнен для угла 180° с варьированием энергии налетающей
частицы, так чтобы переданный импульс мог меняться, но возбуж-
дался бы при этом только один определенный уровень. Это позволит
изучить поведение поперечных матричных элементов в зависимости
от переданного импульса — ситуация, в которой часто могут на-
блюдаться весьма характерные свойства. Кроме того, такое свойст-
во электронного рассеяния может быть использовано для отделения
электрических мультиполей от магнитных, поскольку первые имеют
связанный с ними кулоновский вклад, который резко обрезается
на 180е, а вторые не обладают подобным свойством.
Можно использовать другую схему разделения EL- и ML-nepe-
ходов, также основанную на формулах (5.56). Она сводится к изме-
рению сечения при разных углах и энергиях, выбранных так, чтобы
переданный импульс
q-= Ip2—2рр' cos 0 + р'г]‘4 — 2 — sin f—6^	(5.58)
c \ 2	)
оставался фиксированным. Тогда зависимость величины (daldQ.')lcM
от tg2 (0/2) будет изображаться прямой линией, если приближения,
использованные при выводе формулы (5.56а), являются правиль-
ными. Если отрезок такого графика по мере уменьшения tg2 (0/2)
согласуется с формулой
^^=Г—+ tg2f—-e'jlx,	(5.59)
оЛ( I 2	6 U /1
* Другие аргументы в этой статье, касающиеся относительного вклада
поперечных членов и кулоновского члена, являются частично ошибочными.
Они основываются на идее, что в поперечные члены входит ядерный ток, и по-
этому они имеют порядок (скорость нуклона)/с » 1/5 по сравнению с куло-
новскими мультиполями. Что это заключение не подтверждается, можно ви-
деть из того факта, что как продольные, так и поперечные электрические
мультиполи содержат ядерный ток, но имеют одинаковое значение с куло-
новским членом для случая kR 1.
161
то кулоновского вклада не будет и можно предполагать, что пере-
ход имеет магнитный характер. Если же существует заметный куло-
новский вклад, то это означает, что наблюдается электрический
мультиполь (рис. 5.4).
Еще один способ определения значения мультипольности с по-
мощью данных по неупругому рассеянию электронов можно полу-
Рис. 5.4. Пример экспериментальных данных [321] по электронному рассея-
нию, которые допускают идентификацию поперечного и кулоновского вкла-
дов.
Функции Vl = ^-cos2( — ojsin	ИГ= g (l+sin2( —0) j sin-4 пропорциональ-
ны кулоновскому и поперечным матричным элементам в формуле (5.56а), полученной
в ультрарелятивнстском пределе. Таким образом, наклон проведенной по точкам пря-
мой линнн на этих графиках является мерой квадрата кулоновского матричного эле-
мента, а отрезок на ординате измеряет поперечный вклад. Данные слева получены
для перехода 3/2——>-5/2- с энергией 4,46 Мэв в ИВ, этот переход является смесью
Afl+E2. Данные справа получены для перехода 3/2“—>-3/2- с энергией 5,04 Мэв, кото-
рый, по-видимому, является чистым Л1/-переходом. Значения углов и переданных
импульсов приведены на рисунках.
чить, используя зависимость от переданного импульса, свойственную
различным матричным элементам в формулах (5.55) и (5.56). Для
малых переданных импульсов (kR 1) эта зависимость опреде-
ляется функцией Бесселя при малых аргументах, а именно
CL)~kL,	(5.60а)
Wpa(k; EL)~kL~l,	(5.606)
2V₽a(k; ML}~kL.	(5.60b)
162
Поэтому, если с помощью вышеупомянутых способов удается уста-
новить, имеется или нет кулоновский вклад, можно сузить область
возможных значений L для данного перехода. Пример такой иден-
тификации показан на рис. 5.5, где быстрый рост сечения в зависи-
мости от переданного импульса для уровня 20,2 Мэв в 16О указы-
вает, что наиболее подходя-
щим является значение
L = 2 [93].
Ниже будут обсуждаться
различные поправки к ре-
зультатам анализа электрон-
ного рассеяния в рамках бор-
новского приближения с плос-
кими волнами. Они включают
использование искаженных
кулоновских волновых функ-
ций электрона (БППВ), дис-
персионные эффекты в рас-
сеянии электронов (члены
более высокого порядка, чем
борновское приближение) и
обсуждение задачи извлече-
ния матричных элементов в
случае, когда вводятся ради-
ационные поправки. Следует
также заметить, что при по-
лучении формулы (5.55) мы
предполагали, что центр масс
ядра фиксируется в простран-
стве и поэтому отдачи ядра
нет. Если это условие опу-
стить, то наибольшей кинематической поправкой будет коэффи-
циент для плотности конечных состояний [94], на который умно-
жаются правые части формул (5.55) и (5.56). Он имеет вид
Рис. 5.5. Поперечный формфактор для
уровня 20,2 Мэв в ядре 16О в зависимо-
сти от переданного импульса.
Поскольку по предположению в переход даюг
вклад только поперечные компоненты, зависи-
мость от q показывает, что угловой момент,
переданный при возбуждении уровня, равен
2 (L=2). Таким образом, соответствующий
мультиполь есть М2, что при переходе из ос-
новного состояния J л =0+ на уровень 20,2 Мэв
должно соответствовать /Л =2“. Сплошная
кривая — результат расчета по модели оболо-
чек [93].
(5.61)
где Мт — масса ядра-мишени. Когда рассматриваются поправки
к плотности тока в матричных элементах, то конвекционный ток
отдачи ядра как целого не может взаимодействовать с поперечной
частью потенциала Мёллера, так как это дало бы (р — p')-Az (к) =
= Лк-А* (к) = 0 (см. [111]). Кроме того, с точностью до величины
Ь1МТ эффект членов динамической отдачи сводится к повороту ам-
плитуды рассеяния в комплексной плоскости. Поэтому с указанной
точностью главное изменение, обусловленное учетом отдачи, про-
исходит от членов, описывающих кинематическую отдачу [140].
163
§ 5.4.	Сравнение процессов электрорасщепления
и фоторасщепления ядра
В предыдущем параграфе мы видели, что матричные элементы,
которые входят в сечение неупругого рассеяния электронов в БППВ,
являются теми же самыми элементами, которые определяют про-
цессы фотопоглощения, при условии, что они вычисляются при
k = k0. Эта тесная связь между процессами с участием фотонов
и электронов будет рассмотрена в данном параграфе на примере
реакции расщепления. Рассмотрим прежде всего фоторасщепление:
сначала имеется ядро в состоянии а, а после поглощения фотона
получается другое ядро в состоянии р и вылетает ядерная части-
ца х:
Т +	>-Л/р+х.	(5.62)
То же самое расщепление ядра может быть получено в процессе
неупругого рассеяния электрона
в —|—Л^сс, —> ЛЛр ——|—лг.	(5.63)
Соответствующие сечения в БППВ будут тесно связаны для малых
переданных импульсов.
Обозначим Р импульс вылетевшей частицы х, а элемент телес-
ного угла, в который она испустилась, dQp. Дважды дифферен-
циальное сечение для электрорасщепления дается выражением
2	(5.64)
uQp (fQ	2	2 J; ч]— 1
1	е spin 11
рде ре’ и рР — плотности состояний на единицу телесного угла для
гассеяния электрона и частицы х. В формуле (5.64) осуществляется
усреднение по всем начальным спинам и суммирование по конечным
спинам, в том числе по спинам испущенной частицы, обозначаемым
через т. Остальные обозначения соответствуют тем, которые мы
установили для электронного рассеяния в предыдущих параграфах;
состояние |/>, конечно, теперь включает испущенную частицу х.
Используя (5.36), (5.40) и (5.42), выразим кулоновские (скалярные)
члены через продольные, а не наоборот (как раньше). Это делается
для того, чтобы рассмотреть формулировку задачи электронного
рассеяния только с помощью пространственно-подобных компонент
ядерного тока, которые должны входить для поперечной калибров-
ки в выражения для реакций с фотонами. Тогда можно написать
</|ЗГ|О =-----La'.f<pp|j(r)|a>e>k-rdr, (5.65)
С J
где а' — выражается через величину а, определяемую формулой
(5.37):
а' = а—a-kk/^o-	(5.66)
164
Используем ту же технику суммирования по спинам, что и в выра-
жении (5.46). В результате получим
d2a
dfip dQ'
On I 3	3	3
^Pe'PP 2 J TghNgh,
,we	g=lh=l
(5.67)
где	величина
^=42a«*aA=
spin
(4ne)2_____1
2EE4J (k2-ko)2
2Pg Ph+-j- w2 ~ 9°)	+(7g qh—PgPh—Phqg^
x (i -4+M	<2 (p'4)2 “2?2 (p'q) +4(?2 <?2)
\	<70	<70 ! qo	z
(5.68)
является симметричным тензором, и
т&=Аг. 2 [S<₽pi/«(r)i“>e,k"‘)d’x
1 Mf Mf m
X IS <₽p I ih (r) | a> eik r dr] .	(5.69)
Сечение фоторасщепления для переданного импульса к и вектора
поляризации фотона е, как и в гл. 4, имеет вид
^ = ^РР 2 2 ТеМ-	(5.70)
сшР пс g=lft=1
Если мы рассматриваем £1-переходы в длинноволновом пределе
kR < 1, то плоские волны в формуле (5.69) заменяются едини-
цей и в ядерном пространстве остается лишь один вектор Р. Симме-
тричный тензор наиболее общего вида, который можно построить
в этом пространстве, имеет вид
Те,=А(Р)^В(Р)^
(5.71)
где А (Р) и В (Р)— произвольные скалярные функции, завися-
щие от ядерных состояний а и |3 и энергии испущенной частицы.
Подстановка выражения (5.71) в формулы (5.67) и (5.70) дает
для малых переданных импульсов следующее выражение для се-
чения неполяризованных фотонов в случае £1 -переходов:
^_ = ^!рР	Bsin2eV	(5.72)
dQp Ас \	2	)
где 0 — угол между направлением вылетевшей частицы и началь-
ным пучком. Полученное выражение для сечения содержит те же
165
самые ядерные параметры А и В, которые входят в соответствую-
щее сечение электрорасщепления
д2а£1	2л L3	(4ле)2 Л2
--------7~ ~ ~~л--Ре' Рр-------X
dftpdfi nve r 2EE'Le
____1 . E2-\-E’2	2qom2c2
I2 L 2	c2(q2-q20)	(92-^)2]
, B MP2-(qP)2  2 [(f'p—£p')-P]211
\2rn2c2 (q2— qo)'	mW(.q2-ql)2 Jj‘	1	'
Этот результат, конечно, не верен для рассеяния на большие углы.
Однако если мы не наблюдаем направления вылетающего электрона,
то можно быть вполне уверенным, что большинство электронов испы-
тывает рассеяние вперед [см. формулу (5.56)1, и, следовательно,
удовлетворяется соотношение kR 1, так что, например, для
£1-переходов в области гигантского резонанса формула (5.73) спра-
ведлива. Далее необходимо провести интегрирование по dQ' для
данного перехода. Результат принимает особенно простой вид в пре-
деле Е, Е' тс2, tickt]\
dcEl
dQp
27.
где
Х= In (2Е2/Йтс3&0).
— ) sin2 ©1,
2 /	)
(5.74а&
(5.746)
2л22?
ko I
Сравнение формул (5.72), (5.73) и (5.74) показывает, что те же
два параметра, которые определяют динамические свойства ядер
в Е1-расщеплении, определяют и соответствующее электрорасщеп-
ление для рассеяния на малые углы. Эти параметры можно опреде-
лить из эксперимента [1001. Рассмотренные выше теоретические
соображения впервые были высказаны Боско и Фубини [47]. Обоб-
щение результатов на случай мультиполей более высокого порядка
было сделано в рамках зависящего от модели формализма [1141.
и модельно-независимым способом для двухчастичной системы [491-
Наконец, следует указать, что так как полученные результаты при-
менимы для испускания любой частицы х, они могут быть исполь-
зованы, чтобы связать фотонное рассеяние с электровозбуждением,
после которого происходит испускание фотонов [201, 41 (в области
далекой от той, в которой может происходить интерференция с элек-
тронным тормозным излучением).
§ 5.5. Упругое рассеяние
Результаты §5.1—5.3 без существенной модификации можно
использовать для рассмотрения упругого рассеяния электронов-
В этом случае энергия возбуждения ядра nck0 должна быть взята
равной нулю, а конечное состояние ядра | р> является тем же самым,
166
(5.75)
что и начальное состояние |а>, поэтому, в частности, Jnff =
Мультиполь порядка L , который входит в полученные формулы»
должен тогда удовлетворять правилам отбора
О L С 2Jt для CL,
1 CLC2J, для EL и ML.
Кроме того, при переходе не может изменяться четность, поэтому
в зависимости от основного состояния ядра должны рассматриваться
только мультиполи типа EQ, М1, Е2, MS, Е4, ..., которые опреде-
ляются спином основного состояния ядра.
Если основное состояние имеет спин j, = 0, то возможен только
электрический монопольный (ЕО) переход. Тогда из формулы (5.56)
получаем сечение в виде
do о,,
— = 4л-^|Маа(к;С0)Р,	(5.76)
где, согласно (5.51а),
оо
Naa (к; СО) = —=— § р (г) sin (kr) г dr. (5.77)
Д/4л k о
Здесь р (г) — радиальная зависимость распределения заряда в ос-
новном состоянии ядра. При анализе экспериментов на ядрах с ну-
левым спином обычно предполагается, что в центральной сфериче-
ской области ядра плотность приблизительно постоянна, а поверх-
ностная область имеет почти постоянную радиальную протяжен-
ность, не зависящую от А. Радиальная плотность параметризуется
•с помощью радиуса С, т. е. расстояния, на котором плотность
падает до половины ее значения в начале координат, и толщины
поверхности t, которая представляет собой расстояния между точ-
ками с плотностью 90 и 10% от ее значения в начале координат.
Обычно предполагаемая для феноменологического анализа форма —
это распределение Ферми (рис 5.6)
Ро		(5.78) (5.79)
где	rv'“ 1+е('~С)/а • t = 4а 1п 3 « 4,40 а.	
Нормировка	оо	
	§ р (г) г2 dr — 1	(5.80)
о
требует* с точностью до е~с/а выполнения равенства
3 /. . л2 а2 \-1	/с яп
Ро=^(1+“^) ‘ ( °
* Этот интеграл часто встречается в статистической механике при рас-
смотрении систем фермионов. См. [199, стр. 224].
167
Соответствующие распределения заряда для отдельных нуклонов
показаны на рис. 5.7.
Данные по упругому рассеянию электронов на ядрах с нулевым
спином [189] показывают, что для 20 А ^208 центральная плот-
Рис. 5.6. Распределение Ферми, которое, как предполагает-
ся, аппроксимирует распределение заряда в ядрах со спи-
ном 0.
ность р0 действительно постоянна, а ядерные радиусы удовлетворяют
соотношению
С = 1,123 Л1/3 ферми.	(5.82)
При этом следует ожидать, что характер зависимости от А опреде-
ляется свойствами ядерного насыщения. Толщина поверхности по-
стоянна и равна
t — 2,5 ± 0,1 ферми.	(5.83)
Отдельные результаты для различных ядер приведены в табл. 5.1.
Результаты недавних экспериментов по электронному рассеянию
[31] показывают, что при очень больших переданных импульсах
распределение Ферми совершенно не годится, и для объяснения
поведения формфактора становится необходимым наложить своего
рода рябь на зарядовое распределение (рис. 5.8). Разумеется, при-
ближение плоских волн для более тяжелых ядер (Z 20) не-
удовлетворительно, и экспериментальные данные должны анализи-
роваться с помощью искаженных кулоновских волновых функций
(см. дальше, § 5.6).
Кроме общих правил отбора, которые приводят к появлению
лишь мультиполей Е0, ЛИ, Е2, Л43, Е4, ...., сечение упругого рас-
сеяния в борцовском приближении подчиняется другим строгим пра-
168
вилам отбора, которые возникают из соображений инвариантности
по отношению к обращению времени. Чтобы изучить это свойство,
рассмотрим мультипольные матричные элементы (5.51). Используя
Рис. 5.7. Схематический вид распределений заряда
протона и нейтрона для сравнения с ядерным рас-
пределением на рис. 5.6.
Каждое из этих зарядовых распределений также содержит
дельта-функцию с центром в начале координат, которая не
показана на рисунке [192].
(2.7), (2.52) и свойства коэффициентов Клебша—Гордана, входящих
в формулы (5.51), напишем в общем виде
W₽a (k; CL) = (-1/-+-'*-'/ А (к; CL),
Jf
(к; EL) = (- 1)L+1 + Ji-Jf	Nafi (к; EL),
Jf
7Vga(k; AfL) = (-l)L+1+y/-y/4^n₽(k; ML).
Jf
(5.84a)
(5.846)
(5.84b)
169
Таблица 5.1
Параметры зарядового распределения Ферми для
различных ядер
Нуклид	R	С	t	ДЛ~ */з	СЛ-'/з
4Не	2,07	1,10	1,4	1,30	0,70
6Li	3,41	1,56	2,3	1,92	0,86
sBe	2,92	1,80	2,0	1,39	0,87
ПВ	2,90	2,00	2,0	1,31	0,90
12С	3,11	2,30	1,85	1,42	1,00
14N	3,20	2,40	1,85	1,33	0,99
i60	3,42	2,60	1,8	1,35	1,03
24Mg	3,85	2,93	2,6	1,33	1,01
27А1	3,76	3,07	2,28	1,25	1,02
28S1	3,93	2,95	2,8	1,29	0,97
з1р	3,96	3,21	2,45	1,26	1,02
S2S	4,03	3,20	2,6	1,27	1,01
40Са	4,55	3,64	2,5	1,33	1,06
4“Са	4,51	3,74	2,30	1,24	1,03
61\Z	4,63	3,98	2,2	1,25	1,07
бвре	4,84	4,00	2,50	1,27	1,05
S8Ni	4,92	4,09	2,51	1,27	1,06
60Ni	4,96	4,14	2,50	1,27	1,06
69Co	4,94	4,09	2,5	1,27	1,05
8KSr	5,35	4,80	2,3	1,20	1,08
nr,In	5,81	5,24	2,3	1,19	1,08
116Sn	5,88	5,28	2,37	1,21	1,08
422Sb	5,97	5,32	2,5	1,20	1,07
181Ta	7,10	6,4	2,8	1,25	1,13
107Au	6,87	6,38	2,32	1,18	1,10
говрь	6,96	6,48	2,31	1,17	1,09
20SBi	6,87	6,47	2,1	1,16	1,09
Примечание		. Во второй	колонке (R) приведены значения радиуса		
эквивалентного однородного распределения заряда, ние для случая kR<^A, что и распределение Ферми.				которое дает то же рассея-	
Возьмем обычный [299] антиунитарный оператор обращения вре-
мени К, удовлетворяющий соотношению
КсК-1 = с*,
(5.85а)
где с — любая неоператорная величина и
<В|/<-1|Л> = <КВ|Л>*.	(5.856)
Выберем условие для фаз наших ядерных состояний таким образом,
что (см. § ПА.6)
Л|	iy+^| J—М>.
(5.86)
170
Рис. 5.8. Экспериментальное и теоретическое дифференциаль-
ное сечение для упругого рассеяния электронов с энергией
757,5 Мэв на ядрах 40Са и 48Са.
Теоретические (пунктирные) кривые получены подгонкой данных прн
энергии 250 Мэв, при этом использовалось зарядовое распределение
(5.78), умноженное на коэффициент 1 + о»г2/С2. Значения параметров
равны: С •= 3,6685, ферми а «= 0,5839 ферми, w = — 0,1017 для 40Са и С=
=3,7369 ферми, а=0,5245 ферми, w«= —0,0300 для 48Са. Сплошная кри-
вая получена с учетом дополнительного зарядового распределения
в виде
ZeApq^ , !
/ 1 \
Др(г) =------У- I--sin?„ Г-!---— cos q„ г I exp--p2r2
2лЗ/2 U„r	2q%	I \	4	)
co значениями параметров p=0,5 ферми— *, ?o>=3,O ферми-', Д(40Са) =
= 0,5-10“3, Л(48Са) = 0,8-10~3. Сечение для 40Са умножено на 10, а для
48Са—на 10-' [31].
171
Ядерные операторы удовлетворяют соотношениям
Лр (г) ТС1 = р (г), /(j (г) Л"1 = — j (г),	(5.87)
XiL Р (г) Jl (kr) Ylm (г) X"1 =
= (— !)' +W iL Р (г) Д (kr) Yl-m(t), (5.88а)
^iL+1 j (г) АЛЛ1 (г; е)Л"1 = ( — 1)*-+" iL+‘j (r)-AL_w(г; е), (5.886)
К iL j (r)-Aw (г; m) Л?1 = (—1)L+W iL j (r)-AL_w (r; tn). (5.88b)
Все приведенные матричные элементы в формулах (5.51) действи-
тельны. Например,
<J/Af/|iL + I j(r)-Azjn(r; е)| 7гЛ4г> =
= (Jt LJ, | Mi MMf) Nf>a (k; EL) =
= < Jf Mf | X~l X [^+1 j (r) • ALM (r; e)J X'1 K\JtMi) =
= (Л (Jf Mf) | JC [i^+1 j (r)• Alm (r; e)J X'11 tf (Jt Mt)>* =
= (_1)^+^+Л+^г+^+^<7/_М/1 jL+t j (r).AL_w (г; e)| Л-ЛД>*=
= (_	+ +J.+Mi + L + M	LJ^ _Mi__	(k; EL} =
= (Ji LJf I Mi MMf) N$a (к; EL).	(5.89)
Так как в соотношения (5.84) входят действительные величины, то
Л7Ра (k; CL) = (-l)i+-'i-'/AMlfj(k; CL), (5.90а)
Jf
N&a (к; EL) = (- 1)L+1Na$ (k; EL), (5.906)
Jf
tf₽a(k; ML) = (-l)L+1+<zi-z/#^₽(k; ML). (5.90b)
Jf
Для упругого рассеяния начальное и конечное состояния одинако-
вы, поэтому р = а и Jt = Jf. Таким образом, кулоновские переходы
существуют только для четных L, а поперечные мультиполи —
только для нечетных L. Поскольку закон сохранения четности уже
исключил EL-переходы с нечетным L, то могут давать вклад лишь
мультиполи СО, ЛИ, С2, Л43, ... В частности, для рассеяния на
180° при большой энергии в рамках борновского приближения с пло-
скими волнами формула (5.56) дает, что для упругого рассеяния
будут наблюдаться лишь ЛН-, Л43-, ... переходы.
Для ядер с наблюдаемыми статическими магнитными моментами
Jг 1/2 полученные результаты указывают способ измерения этих
моментов. Эксперименты такого типа выполнены [279] для несколь-
ких ядер. Были также выполнены оболочечные расчеты [274], чтобы
изучить зависимость сечения от переданных импульсов (рис. 5.9).
172
Рис. 5.9. Зависимость поперечных матричных элементов от
переданного импульса для упругого рассеяния электронов
на 180° на ядре ПВ [279].
Кривые дают результаты расчетов с использованием простейшей
одночастнчной оболочечной модели. Пунктирные кривые показывают
отдельно вклады от и ЖЗ-мультиполей, сплошная кривая дает
их сумму. Эти теоретические кривые никак не подгонялись к экс-
периментальным данным.
Вблизи области дифракционного минимума для 7И1-рассеяния
становится важным М3-мультиполь (для ядер с Jt 3/2); в этом
случае может быть измерен статический магнитный октупольный
момент.
Называя моменты статическими, мы имели в виду экстраполяцию
на очень малые переданные импульсы. При этом из (4.75), (ПА.54)
и (5.51) имеем, например, для ЛП-момента
Naa (k;	< J* Ь II A->.	(5.91)
c 1	У 6л
где величина
Xi Ге j h	eh
ц — \ — Lj- -|-------KjGj	(5.92)
L2yw J
является оператором статического магнитного дипольного момента
1использованы обозначения из формулы (4.75)1; М—масса нуклона.
Для рассеяния на 180” указанная величина непосредственно изме-
ряется, ибо в тех случаях, когда вклад от дипольного момента яв-
ляется преобладающим, выполняется соотношение
da
dfi'
2£
Зс2 (Ze)2
[4- + tg2 (^-е)1к All^ll А>12-
L	\	/ J
(5.93)
§ 5.6. Выход за рамки борновского приближения
с плоскими волнами
Представленные выше результаты борновского приближения
с плоскими волнами дают очень полезные способы анализа экспери-
ментальных данных. Они математически просты — достаточно
просты, чтобы во многих случаях были возможны вычисления в зам-
кнутой форме, — и имеют ясный физический смысл как фурье-пре-
образование распределения тока и заряда. Однако они не являются
количественно надежными для тех ядер, для которых параметр
ZMc = Z/137 перестает быть малой величиной. Они также не-
удовлетворительны в области дифракционных минимумов, так как
величины, полученные в рамках борновского приближения с пло-
скими волнами, стремятся к нулю вблизи минимума. Для больших
углов рассеяния БППВ обычно может дать погрешность в 50—100%
для Z между 28 и 90. Некоторые из этих неточностей можно частич-
но устранить довольно незначительными улучшениями БППВ, но
часто необходимо бывает обращаться к расчетам, в которых учиты-
вается сильное искажение электронных волновых функций статиче-
ским кулоновским полем ядра. Такие расчеты приводят к весьма
сложным вычислительным проблемам и могут выполняться только
на быстродействующих вычислительных машинах. Поэтому они
лишены прозрачности, свойственной результатам борновского при-
174
ближения, и в конечном счете тоже не дают полностью удовлетво-
рительного решения проблемы кулоновских поправок.
Основное приближение таких расчетов БППВ заключается
в предположении, что можно учитывать лишь поправки порядка
Z/137, обусловленные кулоновским полем ядра, и пренебрегать
в то же время членами более высокого порядка, возникающими от
обмена более чем одним фотоном в процессе рассеяния. Последние
члены, как предполагается, имеют величины близкие к ёЧ1ъс — 1/137,
так как, по-видимому, в процессе возбуждения принимают участие
лишь несколько нуклонов. Эти дополнительные поправки приведут
к включению дисперсионных эффектов в электронное рассеяние;
они особенно важны вблизи дифракционных минимумов. Мы кратко
обсудим эти эффекты в конце данного параграфа.
Для изучения кулоновского искажения электронных волновых
функций рассмотрим уравнение Дирака* в присутствии электро-
магнитного поля:
са  ( —i Й v —
— А ] + рте2 -ф еф
ф = 1Й—ф, (5.94)
dt
где е— заряд изучаемой дираковской частицы: е ~ —4,8-10—10 ед.
СГСЭ. Возьмем ядро фиксированным в нашей системе отсчета,
тогда А — 0, а ф — потенциал, связанный с распределением ста-
тистического ядерного заряда. Поскольку электрон проникает
в ядро (т. е. перекрытием электронных волновых функций с ядер-
ными нельзя пренебрегать для больших переданных импульсов),
то следует взять ф в виде потенциала, создаваемого какой-либо
разумной аппроксимацией плотности истинного заряда, например
плотностью заряда, описываемой формулой (5.78). Для тех случаев,
когда электрон заметно не проникает в ядро, имеем простую формулу
(5.95)
, , Ze
Ф (г) =---------
Всегда будем предполагать, что соответствующее зарядовое распре-
деление имеет сферическую симметрию, так что функция <[ (г)
будет сферически симметричной. В сферических координатах урав-
нение Дирака имеет вид (см. Приложение Б и [290, стр. 157—158])
Дф = Fi Асу. о- г f—+ -----—	ф- V (г)-[-тс2 fi I ф = i й — , (5.96)
L	\дг г	г	]	J	dt
где У(г) = еф(г) — потенциальная энергия. Здесь
Д = р(о-Ь4-1),	(5.97)
где L = —ir XV; Д — оператор, который коммутирует с [3
с оператором полного углового момента j = L 4- -у ст и с оператором
* Для ознакомления с принятыми здесь обозначениями см. Прил ожение
о. Соответствующие материалы изложены в [290, 302].
175
Гамильтона в уравнении (5.96). Собственные значения К обозна-
чаются —х и являются целыми числами; х = ± (/ + 1/2), где
/ (/ +0 — собственное значение j2. Операторы Н, К, j2 и /2 обра-
зуют набор коммутирующих операторов, и их собственные функции
могут быть записаны в виде
g(r)^ \
if (г) X±J’
=
(5.98)
где р, — собственное значение /z, a х£ выражается через спиноры
Паули хт;
Х£=2	(5.99)
т \	'
Здесь j = | и | —1/2,
х для
— х—1 для
х>0,
х<0.
(5.100)
Радиальные части в (5.98), соответствующие энергии Е, удовлетво-
ряют следующим уравнениям:
= —	(5.101а)
dr г he
^l==_^fi±lg + J-(E + mc2 — V(r))f(r)	(5.1016)
dr	г	he
я нормированы так, что
$ (f2+g2)r2dr = 8(E—Е').	(5.102)
о
Волновые функции начального и конечного состояний электрона
могут быть разложены по этим решениям:
ф™ = 4л
ЛЛ3 С2 \ 1 / 2
2pEL3 ,)
х2 ize+‘4z у /
и. ц
р,—ттц ) Yin-tn (р) фи.
(5.103а)
ЛЛ3С2 \1/2
2p'E'L3
ф™ = 4л
р,—тт\\.
*г_т(р'М (5.Ю36)
X
476
где индекс т характеризует поляризацию электрона. Здесь
6и = Ях---|-луи —агёГСуи + пО+у (/ + 1)л, (5.104а)
где	____________
у = Ze2 Е/Ърс2, уи = У><2—(Ze2/Л с)2	(5.1046)
У + i У
Для малых значений квантового числах, таких, что 1	| х |	10,
электронные волновые функции довольно сильно отличаются от
нуля в области пространства, занимаемой ядром, и уравнения
(5.101) для fug должны решаться численно с потенциалом, напри-
мер, в виде зарядового распределения Ферми (5.78). Для больших
значений х электроны не проникают в ядро и их волновые функции
могут считаться такими же, как и для точечного ядра, а именно
[290, стр. 194]
' ' ’	\ лДрс2
1/2 е4^ |Г(Ти + 1у)| (2^г)”и х
Г(2Ти+1)
X Im {(y-z + iy}^e~'krJ\ (1+yx-|- i у, 2уи + 1,2 ikr)}, (5.105a)
rg(r) =
E-\-mc2 У/2 JLW 1 Г(ти + 1 y) |
лйрс2 )	Г(2уи-р1)
(2kr)Vil X
xRe [(Tx + if/Je’^e-^qF^l+Yx + if/, 2уи +1, 2ikr)}. (5.1056)
Такой вид парциальных волн должен сохраняться вплоть до
|х| ~ 30 или даже при еще больших значениях |х| [308].
Радиальные волновые функции, полученные таким способом,
подставляются затем в формулы (5.103), которые в свою очередь
используются в выражении для электронного тока при вычислении
матричного элемента энергии взаимодействия в формуле (5.31). По-
скольку большинство таких расчетов следует выполнять на быстро-
действующих электронновычислительных машинах, то здесь неце-
лесообразно продолжать дальнейшие обсуждения. Подробное опи-
сание вычислительной методики как для кулоновской, так и для
поперечной частей сечения дано Зиглером [367].
Расчеты в БППВ для кулоновской части сечения электронного
рассеяния были выполнены авторами работ [177, 263, 264]. На
рис. 5.10 дано сравнение их результатов с результатами расчетов
в БППВ кулоновского квадрупольного матричного элемента для
ядра с Z = 90. Ясно, что борцовское приближение с плоскими вол-
нами совершенно неудовлетворительно при больших углах, особен-
но вблизи дифракционных минимумов. С другой стороны, при
меньших угчах результаты расчетов в БППВ и БППВ довольно
7
Зак. 1193
177
хорошо согласуются, при условии что используемый для расче-
тов в БППВ радиус ядра увеличивается приблизительно на 10%.
Этот эффект известен из упругого рассеяния электронов [363, 364,
189]. Он возникает потому, что под влиянием притягивающего
кулоновского потенциала кинетическая энергия электрона увели-
чивается и, следовательно, увеличивается его импульс и переданный
импульс. Соответствующее увеличение переданного импульса мо-
Рис. 5.10. Сечение кулоновского рассеяния на ядре
с Z—90 с однородным распределением заряда
в БПИВ (пунктирная кривая) для радиуса ядра
/?=4,6 ферми и в БПИВ (сплошная кривая) для
/?=5,2 ферми. Изучаемое возбуждение — электри-
ческий квадруполь [177].
жег быть искусственно введено в БППВ путем увеличения размеров
ядра, так как для рассеяния вперед процесс рассеяния определяет
безразмерная комбинация kR. Изменение переданного импульса,
обусловленного кулоновскими поправками, будет количественно
обсуждаться ниже [см. формулу (5.126)]. Соответствующее измене-
ние радиуса ядра приблизительно описывается кривой на рис. 5.11.
Хотя (см. [367]) в рамках БПИВ можно выполнить расчеты
в общем виде, получаются значительные численные упрощения,
если ограничиться кулоновскими мультиполями. Такие упрощения
возможны для многих £/.-переходов, хотя не очень легко сформу-
лировать общие критерии, определяющие малость вклада попереч-
ных электрических мультиполей. Чтобы убедиться, насколько
178
мал этот вклад, обычно необходимо выполнить оценки в рамках
БППВ. Разумеется, если поперечные электрические мультиполи
не учитываются, а вклад от кулоновских остается, расчеты перестают
быть формально калибровочно инвариантными; однако при этом
можно получить вполне удовлетворительные численные результаты
[177; 39, стр. 202—239]. Естественной исходной точкой для таких
расчетов является формулировка описания электронного рассея-
Рис. 5.11. Относительное изменение эффективного радиуса
ядра для случая, когда БППВ используется для квадру-
польных возбуждений. Кривая получена с зарядовым рас-
пределением Ферми [177].
ния с помощью кулоновской калибровки. До сих пор мы описывали
запаздывающее ток-токовое взаимодействие электрона с ядром,
используя электромагнитные потенциалы, которые удовлетворяли
условию Лоренца. Это привело к формуле (5.22)
I Р	„1 k„ I г —г' I
<f IW" |i> = - 4 <₽ | /ц (г) | а) 4-— (г') dr dr'. (5.22')
с2 J	|г—г I
Если бы с самого начала мы использовали для потенциалов куло-
новскую калибровку, то энергия взаимодействия включала бы
запаздывающее взаимодействие между поперечными частями токов
и мгновенное кулоновское взаимодействие между плотностями заря-
дов (см. § 3.4);
Д|^"|О= -4(‘—КРи^(г)|а>-У(г')е^«1—•'!-
С2 J |г — г' |
—с2 <р | pN (г) | a>pe(r')] dr dr'.	(5.106)
Здесь величина
j'(r') = J(r')—J'(r')	(5.107а)
7*
179
является соленоидальной величиной, а величина
J* (г') = —V'
^^dr'
(5.1076)
— безвихревой, точно так же, как и в формулах (1.20) и (1.21). Ана-
логичное утверждение справедливой для величины <P|j(r)|a>.
Действительно, используя уравнение непрерывности с обычной
временной зависимостью для получения выражения для Jz в виде
У (г') = — V' С ре (г"}- dr"	(5.108)
4л J |г'-г"|	'
и применяя далее разложение по статическим мультиполям |
р	—г'|	4
\----5-----------dr' =-----—-----(eift° । r-r"i_ и, (5Д09)
J I г—г' 11 г'— г" |	r"|'
из выражения (5.22) для матричного элемента оператора энергии
взаимодействия с лоренцевской калибровкой находим
<f | Ж" 11> = - 4 f , 1 ,, IГ («О I “ >  J' (г') &k°1 г-г' । -
с J 1г г I
—<₽ | j (г) | a>-(V'Pe(r')) (еи°1 r-r' •- 1)-
«0
—c2<P|p7V(r)|a>pe(r')e,ftoli’-r/1] dr dr'.	(5.110)
Здесь перекрестные продольно-поперечные члены исчезают в ре-
зультате интегрирования по частям, а переменная интегрирования
г" заменена на г'. Интегрируя по частям второе слагаемое и поль-
зуясь уравнением непрерывности для оператора ядерного тока,
получаем формулу (5.106).
В борцовском приближении с плоскими волнами два члена в
формуле (5.106) приводят в точности к тем двум слагаемым, кото-
рые обозначены в формуле (5.55) как поперечный и кулоновский
вклады. В случаях, когда важны коллективные формы движения, не
содержащие ядерного тока намагничивания, поперечными ча-
стями можно пренебречь (см., например, [3081). Если в формуле
(5.106) поперечные слагаемые не учитываются, то энергия взаимодей-
ствия формально не является калибровочно инвариантной. С дру-
гой стороны, можно использовать обычное разложение по статиче-
ским мультиполям для | г — г' | -1, что дает значительные упроще-
ния без заметного влияния на численную справедливость резуль-
татов. Такие расчеты широко проводились группой из Дьюк-
кского университета [177, 263, 264, 283, 357], Шеком [308] и груп-
пой во Франкфурте [103, 104, 105]. С помощью такого же метода
парциальных волн было рассмотрено и монопольное электровозбуж-
дение [10, 307]. Расчеты с учетом некоторых поперечных эффектов
проводились авторами работы [338].
Эффекты искажения кулоновским полем могут быть также рас-
смотрены в рамках различных приближенных схем, основанных по
180
существу на методе ВКБ*. Например, можно рассмотреть стацио-
нарное уравнение (5.94) со статическим кулоновским потенциалом
у (r) = etp (г) и А (г) = 0 в ультрарелятивистском пределе
(£ » тс2)
[ — 1Аса-У + У(г)]ф(г) = £ф(г).	(5.111)
Если взять решение в виде
ф (г) — и (г) е‘s <г>,	(5.112)
то получим уравнение
[Леа- VS (г) + Е (г)—E}u(r) = ifica-yu(r).	(5.113)
♦
Чтобы найти нулевое приближение для решения этого уравнения,
положим
[flea -VS (г) V (г)—£] и0 (г) = 0,	(5.114)
где «о (г) следует рассматривать как обычный дираковский спинор
для плоской волны. Уравнение (5.114) будет иметь решения только
в том случае, если
/l2c2(VS)2 = (£—V)2.	(5.115)
Приближения более высокого порядка определяются рядом
u(r) = uo(r) + ui(r) + //2(r)+ ...,	(5.116)
члены которого подчиняются итерационному уравнению
[Аса  VS (г) + V (г) — Е\ ип+1 (г) = i^ca  уип (г).	(5.117)
Но практически обычно ограничиваются лишь членом п0 (г) 1366].
Эйконал S (г) получается из (5.115) интегрированием вдоль
классических траекторий:
Г
S(r) = S(r0)+-L f(£-V)ds =
he .
ro
= S(ro)+M£=!j>_iJV(,s.	(5.118)
To
Здесь использован тот факт, что в пределе большой энергии £ = рс
и классическая траектория нулевого порядка является прямой ли-
нией вдоль направления движения частицы. Волновая функция
налетающего электрона в асимптотической области должна вести
* Авторы используют название WKBJ — метод Вентцеля, Крамерса,
Бриллюэна и Джеффриса. При переводе сохранено принятое в нашей литера-
туре название «метод ВКБ». — Прим, перев.
181
себя как плоская волна, «падающая» из асимптотической области
г = lim (—гр). Поэтому мы выбираем S (г0) так, чтобы получить
г->оо
S (г) в виде
ос
S(r)=	f V(r-ps)ds,	(5.119)
h he J
где интегрирование выполняется по траектории налетающего элек-
трона. Легко видеть,что
оо
VS(r)=—-------— f	VV (г—ps) ds	= —----^-V(r).	(5.120)
h	he J	h	he
о
Следовательно, S (г) удовлетворяет уравнению (5.115), a u0 (r)
можно считать удовлетворяющей уравнению Дирака в ультрареля-
тивистском пределе
са-ри0 = Еи0,	(5.121)
что согласуется с уравнением (5.114). Кроме того, нетрудно по-
нять, что в асимптотической области, где г = —гр и г велико,
выражение (5.119) дает правильное описание налетающего электро-
на, поскольку интеграл от потенциала мал и выражение (5.112)
в области, далекой от области рассеяния, сводится к неискажен-
ной налетающей плоской волне с импульсом р. Аналогично вели-
чина
—оо
S'(г) =	f V(r—p's)ds =
h he
0
oo
=	+— I V (r + p's)ds	(5.122)
h he J
о
является соответствующим эйконалом для электрона в конечном
состоянии, поскольку вблизи детектора г = гр', г велико, что
также отвечает неискаженной плоской волне с импульсом р'.
После подстановки (5.112), (5.119) и (5.122) в формулу (5.32)
мы получаем выражение для электронного тока перехода при на-
личии кулоновского искажения
(г') = i ес фр- (г') уц фр (г') =
= iec\u (р') уц и (р)] eikr' X
ОС	)
5 [V (г' —ps) + V (г' + p's)] dsk (5.123)
о	J
где к (р —	— волновой вектор переданного импульса. Фор-
мула (5.123) отличается от обычного выражения для электронного
182
тока в БППВ только наличием последнего множителя. Поскольку
фазы, которые входят в него, меняются медленно, то аргумент в экс-
поненте можно вычислить, раскладывая соответствующее подынте-
гральное выражение в ряд Тейлора в точке г = 0. Ограничиваясь
первыми двумя членами в этом разложении, получаем
(г') = i ес [и (р') и (р)] eik г' х
оо
\ V (s) ds ехр — V (0) (р- р') • г
L пс
2i
ЙС Q
Рис. 5.12. Дисперсионные поправки для рассеяния электрона на ядре
N (а) Диаграмма, дающая вклад в кулоновские поправки для рассея-
ния электрона (б).
Таким образом, кулоновское искажение приводит к введению эффек-
тивного волнового вектора переданного импульса
k' = k— — V(0)(p— р')	(5.125)
he
и к несущественному постоянному фазовому множителю. Если
переданная энергия мала, так что р ~ р', и если используется
потенциал ядерного заряда, равномерно распределенного внутри
объема радиусом R, то это выражение принимает вид
к’=к(^тй)-	<SJ26)
Например, для мишени из кальция (Z — 20, R = 4,1 ферма.) и элек-
тронов с энергией 200 Мэв переданный импульс изменяется при-
близительно на 5%, и более высокие члены в разложении выраже-
ния (5.123) дают пренебрежимый вклад. Простой способ расчета
кулоновских поправок, даваемый формулой (5.126), соответствует
только линейной части кривой на рис. 5.11, описывающей изменение
эффективного радиуса ядра в зависимости от Z.
183
Подход в рамках приближения эйконала был развит Шиффом
[303] и Саксоном и Шиффом [298]. Это приближение широко приме-
нялось к рассмотрению неупругого рассеяния электронов в работах
Рис, 5 13. Относительные поправки на дисперсионные эффекты как функ
цин энергии и переданного импульса (Z = 28) [334J.
Пенни, Бооса и Равенхолла [366]; простые результаты (5.125) и
(5.126) были получены Чейзом и Готфридом [77].
Мы закончим этот параграф кратким обсуждением поправок
более высокого порядка по взаимодействию электрона с ядром, чем
поправки, учитываемые в борновском приближении. Соответствую-
184
щие диаграммы показаны на рис. 5.12 вместе с диаграммами, кото-
рые имеют аналогичную структуру, но в действительности дают
поправки, обусловленные кулоновским искажением, для одного
и того же возбуждения ядра. Попытки расчета дисперсионных попра-
вок с использованием обычной техники фейнмановских диаграмм
и оболочечной модели ядра были сделаны в работах [37, 50] для
ядер 12С и 16О. Дисперсионные эффекты порядка 1/Z были найдены
для дифракционных минимумов в формфакторах и при высоких
энергиях и для больших углов. В расчетах дисперсионных эффек-
тов в 40Са был применен метод связанных каналов [280] и было полу-
чено, что вблизи первого дифракционного минимума они составляют
5%. Эти эффекты можно рассмотреть также и в рамках теории соб-
ственных каналов [333]. Найдено, что их вклад в основном не зави-
сит от энергии налетающего электрона и увеличивается с увеличе-
нием переданного импульса (рис. 5.13). Следует также заметить,
что дисперсионные эффекты существенны при возбуждении 0_-уров-
ня из основного состояния 0+, так как не существует мультиполь-
ного оператора, с помощью которого можно непосредственно осу-
ществить такой переход. Поэтому указанный переход должен совер-
шаться посредством возбуждения промежуточного состояния ядра.
§ 5.7. Радиационные поправки для рассеяния электронов
Существует еще один класс электромагнитных поправок, возни-
кающих при рассмотрении рассеяния электронов на ядрах. Ими явля-
ются радиационные поправки, которые учитывают излучение реаль-
ных фотонов электроном, или излучение и последующее поглощение
вирту зльных фотонов, или эффекты поляризации вакуума. Глав-
ное слагаемое сечения рассеяния электрона в борцовском прибли-
жении показано на рис. 5.14, а. Поправки порядка 1/137, которые
определяются виртуальными процессами, представлены диаграм-
мами 5.14,6 — 5.14,6; б — поправки к вершине, в и г — члены
собственной энергии и 6 — поляризации вакуума. Диаграммы 5.14, е
и 5.14, ж описывают процессы тормозного излучения, которые
всегда могут идти со значительной интенсивностью для достаточно
мягких фотонов. Можно считать, что во все диаграммы на рис. 5.14
входят электроны, описываемые плоскими волнами, или электроны,
описываемые искаженными волнами, которые обсуждались в пре-
дыдущем параграфе. Радиационные поправки могут относиться
также и к ядерным частицам, но обычно их учет не является необ-
ходимым из-за большой массы частиц и соответственно малой
отдачи.
Вычисление радиационных поправок, показанных на рис. 5.14,
может быть выполнено на основе стандартных методов квантовой
электродинамики (см. ссылки в конце гл. 3). Мы не будем здесь при-
водить подобные расчеты. Это увело бы нас довольно далеко от
главной цели — от рассмотрения тех аспектов механизмов реакций,
С помощью которых можно изучать структуру ядра. Но радиацион-
185
ные поправки играют очень важную роль при извлечении информа-
ции о ядре из экспериментальных данных по рассеянию электронов,
и точность, с которой можно получить указанные поправки, имеет
большое влияние на определение предельных возможностей таких
экспериментов. Поэтому здесь мы кратко опишем некоторые из
основных элементов этого анализа.
Расчеты матричных элементов, соответствующих диаграммам
Фейнмана 5.14, б—5.14, д, приводят к хорошо известной инфракрас-
Рис. 5.14. Диаграммы, учитывающие вклад борновского приближения и раз-
личных радиационных поправок:
а — борновское приближение; б — поправки к вершине; tt, г — поправки, обусловлен-
ные собственной энергией электрона; д — поляризация вакуума; диаграммы е и &с
описывают испускание реальных фотонов.
ной расходимости в сечении электронного рассеяния. Мы должны
записать фотонный пропагатор в виде 1/(/г2 + А,2), где X — фиктив-
ная масса фотона. Оказывается, что измеряемые параметры рассея-
ния зависят от X и, что еще хуже, сечение становится бесконечным
при стремлении X к нулю. Это затруднение было разрешено Швинге-
ром [300]. Дело в том, что в любых измерениях процессов рассеяния
электронов, описываемых диаграммами 5.14, а—5.14, д, различные
детекторы частиц имеют конечное энергетическое разрешение АЕ,
которое, вообще говоря, намного меньше энергии электрона Е. По-
этому никогда не удается отделить вклады диаграмм 5.14, а—д от
вкладов 5.14, е—5.14, ж, в которых фотон испускается с энергией
меньшей ДЕ. При вычислении матричных элементов, соответствую-
186
щих диаграммам рис. 5.14, диаграмма 5.14, а дает матричный эле-
мент перехода порядка е, а диаграммы 5.14, б—5.14, д — порядка
е3. Вместе они дают сечение с точностью до членов порядка е4. Но
мы должны также рассмотреть с такой же точностью вклады в се-
чение от диаграмм 5.14, е—5.14, ж для тех случаев, когда тормоз-
ное излучение изменяет энергию электрона на величину меньшую
ДЕ. В окончательном выражении фиктивная масса фотона Z. выпа-
дает; она заменяется разрешением детектора ДЕ. Оказывается,
что экспериментально измеренное сечение упругого рассеяния сле-
дующим образом связано с «основным» сечением упругого рассея-
ния, описываемым диаграммой 5.14, а [300, 365]:
^РЭКСП 4<7ОСН . dO0CH ,,
-----=	е—°	-	( 1   О),
dQ dQ---------------------dQ
(5.127)
где в ультрарелятивистском пределе
Некоторые частные значения функции (5.129) следующие: Ф (0) = 0,
ф л) = 0,292, Ф (л) = л2/24 = 0, 411.
Учет диаграмм 5.14, е—5.14, ж требует также рассмотрения
дополнительных поправок при анализе данных по неупругому рас-
сеянию электронов. Когда в процессе упругого рассеяния имеет
место тормозное излучение, например с испусканием фотона с до-
вольно большой энергией Асо, то может появиться вклад от ядер-
ного уровня с энергией возбуждения вблизи Асо. Таким образом,
прежде чем получать сечение для первого возбужденного состоя-
ния, необходимо рассчитать эффект тормозного излучения от пика
упругого рассеяния (рис. 5.15). При рассмотрении второго возбуж-
денного состояния как упругий пик, так и первый неупругий пик
будут давать вклад в радиационные хвосты, обусловленные их
тормозным излучением. Их можно рассчитать с использованием
сечений, определенных для этих уровней, и таким образом может
быть получено новое сечение возбуждения второго уровня. Итера-
ционная процедура продолжается таким же способом, причем для
изучения каждого уровня ядра требуется вычитание радиацион-
ных хвостов всех уровней с более низкой энергией возбуждения.
187
Кроме рассмотрения процессов тормозного излучения, описывае-
мых диаграммами 5.14, е—5.14, ж, вычитание радиационного хвоста
также требует учета других процессов, которые могут понизить
энергию электронов до или после рассеяния. Такими процессами
являются испускание реальных фотонов в кулоновском поле дру-
гого ядра в мишени и рассеяние налетающего электрона на атомных
электронах мишени. Оба эти эффекта пропорциональны квадрату
Рис. 5.15. Спектр электронов, неупруго рассеянных от водяной ми-
шени.
Энергия электронов £"=90 Мэв, угол рассеяния в=100°. Кривая описывает
рассчитанный радиационный хвост, который должен вычитаться из экспери-
ментальных значений, чтобы получить информацию о возбуждениях в кисло-
роде. Пик, обозначенный Н, соответствует упругому рассеянию на водороде,
а пик справа — упругому рассеянию на кислороде [204].
толщины мишени в отличие от тормозного излучения в полях ядер
мишени, линейно зависящего от толщины мишени.
Детальная обработка данных по электронному рассеянию с уче-
том указанных выше различных радиационных поправок требует
использования сложных вычислительных методов и феноменологиче-
ского описания рассматриваемых процессов. Методы, используемые
в практических случаях, описаны Изабеллом и Бишопом [204]. Для
учета тормозного излучения необходимо интегрировать формулы
Бете—Гайтлера [186, 187] по всем направлениям фотона [239]. Об-
суждалось также влияние на тормозное излучение структуры в рас-
пределении заряда и магнитного момента [162, 163], а проблема
радиационных поправок к сечению неупругого рассеяния электро-
нов рассматривалась в работах [204 , 248, 240].
188
Обзор по упругому рассеянию электронов дан Хофштадтером
[189, 193]; неупругое рассеяние электронов обсуждалось в основ-
ном Барбером [201, Сосетти и Молинари [66], Бишопом [36] и Де-Фо-
рестом и Валечкой [94]. Рассеяние, обусловленное распределением
магнитного момента, рассмотрено Гольдембергом и Праттом [175];
фазовому анализу особое внимание уделено в книге о кулоновском
возбуждении Биденхарна и Бриссарда [39]. Обзор радиационных
поправок представлен Максимоном [243]. В некоторых докладах
на конференциях даны краткие обзоры последних данных по рас-
сеянию электронов, а именно в докладах Готфрида [172], Валечки
[342] и Изабелла [205].
ГЛАВА 6
ИНФОРМАЦИЯ О СТРУКТУРЕ ЯДРА,
ПОЛУЧАЕМАЯ ИЗ АНАЛИЗА
ЭЛЕКТРОВОЗБУЖДЕНИЯ ЯДЕР
При обсуждении электронного рассеяния мы до сих пор не
делали каких-либо значительных предположений, касающихся тех
процессов, которые существенно зависят от динамических свойств
ядер. В настоящей главе мы попытаемся установить главные свойст-
ва операторов ядерного тока в рассеянии электронов, не конкретизи-
руя при этом детали ядерных волновых функций. Мы воспользуем-
ся этими результатами, чтобы в рамках метода, в значительной
степени не зависящего от модели, обсудить правила сумм для элек-
тровозбуждения. В заключение в §6.3 и 6.4 будут даны простые
иллюстрации использования ядерных моделей для извлечения ин-
формации о структуре ядра из данных по электронному рассеянию.
В первом из этих параграфов будет кратко рассмотрено феномено-
логическое описание ядра, называемое моделью Хелма, а во втором
будет применен к ядру 4Не очень простой вариант модели оболочек.
В указанных параграфах не будет рассматриваться реалистическое
описание электромагнитных свойств ядер; их цель — показать, как
разные варианты теории структуры ядра могут быть объединены
с расчетами электровозбуждения и в конце концов подвергнуты
строгой проверке путем сравнения с данными по рассеянию элек-
тронов.
§ 6.1. Оператор электровозбуждения в ядерном пространстве:
преобразование Фолди — Вутхайзена
Чтобы обсудить вид оператора в ядерном пространстве, описы-
вающего взаимодействие электрона с ядром, рассмотрим сначала
в наиболее общем виде электромагнитный ток, который можно,
связать с отдельным нуклоном. Мы воспользуемся им, чтобы опре-
делить вид взаимодействия между электроном и нуклоном, и затем
обобщим его на случай ядра путем суммирования вкладов от состав-
ляющих его нуклонов. Полученный таким образом ядерный опера-
тор будет обобщением операторов ядерного заряда и тока (4.25)
и (4 58) на область больших переданных импульсов, которые появ-
190
ляются в задаче рассеяния электронов. Это будет составлять основу
нашего обсуждения в остальной части данной главы.
Движение отдельного нуклона описывается уравнением Шредин-
гера	ат
_OT=i^x-,	(6.1)
dt
где Y — волновая функция нуклона. Гамильтониан	+ Ж"
состоит из части, описывающей движение нуклона в отсутствие
возмущения и являющейся оператором Дирака:
.З^о = (Шс2 + са • р,	(6.2 а)
и части, учитывающей взаимодействие с электронным током. Если
для последнего взаимодействия пользоваться борновским прибли-
жением с плоскими волнами, то согласно (5.36) оно должно иметь
вид
4л i е (и+ (р') Вт,, и (р))
,ЗГ =-----------— ц В/„(г)е1к'г—iflrf =
с£3	k2 — /?§	7
=------ац₽/ц(г)е1кг-1ш'
С
(6.26)
где Р/ц (г) — оператор тока для отдельного нуклона (взятый между
дираковскими спинорами U+ и U). Мы использовали осцилляторную
временную зависимость с угловой скоростью со = (Е — E')lh = ck0,
которая вводится электронным током. В конечном счете такая вре-
менная зависимость необходима, чтобы ввести общий закон сохра-
нения энергии для взаимодействующей системы.
При нашем выборе оператора нуклонного тока мы руководствуем-
ся требованием, чтобы (г) был 4-вектором и чтобы он сохранялся
при действии между однонуклонными состояниями. Наиболее общий
вид такого оператора дается выражением [137]
/и = i ес IX Тц — F2 cTjj.v /evl,	(6.3)
L	2/Ис	J
где kv — (k, i/e0) — переданный импульс для нуклонных состоя-
ний, между которыми стоит этот оператор, К — аномальный маг-
нитный момент нуклона в отличие от полного магнитного момента,
который входит в (4.59). Величину crgv мы определяем в виде
= — (Тц Tv Tv Тв) •
Матрицы Дирака в формуле (6.3) действуют на спиноры нуклонов,
а величины
оо
Л=ЛО = 1 епС",
п = 0
оо
р*=F8O= 2 МпП"
п = 0
(6-4)
191
являются скалярными операторами общего вида, действующими
в пространстве нуклона. Поскольку в БППВ оператор Даламбера
при действии на плоские волны нуклона заменяется просто величи-
ной k2 — kvkv = к3 — kg, то функции (6.4) можно считать функ-
циями k2: F} = Ft (/г2), F2 — F2 (k2). Эти функции называются
формфакторами и нормируются так, чтобы для реальных фотонов
(/г2 = 0) ток в выражении (6.3) включал бы обычные заряды прого-
на и нейтрона и их аномальные магнитные моменты, а именно
Fi (0) =F2 (0) = 1, /<=1,79 для протонов, (6.5а)
F1(0) = 0, F2(0) = 1, /< =— 1,91 для нейтронов, (6.56)
В формулу (6.3) для оператора тока можно дополнительно ввести
третий член в виде F3/?ц. Но он не будет удовлетворять требованию
сохранения тока при подстановке его между спинорами плоских
волн Uae'p^x^ и f/pe1^*^, описывающими начальное и конечное
состояния нуклона, так как
-3й- [(t/p+ ₽F3 ka Ua) е“ik»	= _j kc pF3 ko Ua) x
dxc
X e-i*u -Ц = _ip3 (k2-^) (l/p+ pf/D) e-‘^ ,
что не равно нулю для виртуальных фотонов (к2 — k02 ф 0). Оба
члена, которые входят в формулу (6.3), удовлетворяют закону со-
хранения тока, так как из уравнения Дирака следует, что
Д/р1 Р/.’ц'Уц^/а) — 0 И	= 0.
Формулы (6.2) и (6.3) определяют взаимодействие между элек-
троном и нуклоном с точностью до неизвестных формфакторов F,
и Е2, которые могут быть извлечены из экспериментов по рассеянию
электронов на нуклонах. Если просуммировать гамильтониан вза-
имодействия по всем нуклонам в ядре, то эта сумма будет описы-
вать электрон-ядерное взаимодействие без учета мезонных вкладов.
Однако методы, которые были развиты для описания ядерной систе-
мы, вообще говоря, не позволяют рассматривать нуклоны как реля-
тивистские частицы, и поэтому, прежде чем мы сможем эффективно
исследовать многонуклонную систему*, необходимо найти нереля-
тивистский предел формул (6.2) и (6.3). При получении низкоэнерге-
тического предела электрон-нуклонного взаимодействия мы должны
быть особенно внимательны, так как большие переданные импульсы,
которые могут появиться в процессе рассеяния, имеют тенденцию
увеличивать вклады членов, которыми в других случаях можно
пренебречь.
* Было замечено [57], что в силу трансформационных свойств волновой
функции, описывающей сложное состояние, которое включает несколько
нуклонов, предположение об аддитивности нерелятивистского взаимодейст-
вия нарушается, даже если первоначальное взаимодействие было аддитивным.
Однако численные изменения от этого эффекта не очень велики и обычно
не рассматриваются в задачах ядерной структуры. [См. также ниже сноску
перед формулой (6.30).]
192
Метод получения операторов Дирака в нерелятивистском пре-
деле включает построение ряда из последовательных унитарных
преобразований, произведение которых известно как преобразова-
ние Фолди — Вутхайзена (ФВ) [136]*. Эти преобразования строят-
ся так, что при действии на первоначальный гамильтониан они
дают новый гамильтониан, главные члены которого включают нере-
лятивистские операторы с определенной степенью обратной массы
частицы Л1-1, а поправочные члены к последним имеют степень
более высокую по М~г. Таким образом, преобразование ФВ дает
систематический метод получения эффективного гамильтониана,
разложенного в ряд по величине (импульс/ТИс). Нам будет нужно
это разложение до членов порядка М~2.
Рассмотрим гамильтониан общего вида
,+ = Rlc2 + 8 + 0,	(6.6)
где 8 — так называемая «четная» часть гамильтониана, которая
коммутирует с матрицей Дирака р, т. е.
[8, Р] = [8, р]_ = 8р—08=0,	(6.7
а 0 — «нечетная» часть, антикоммутирующая с 0:
[0, р]+ = 0р + р0 = О.	(6.8)
Четные операторы связывают большие компоненты дираковских
спиноров с другими большими компонентами и малые компоненты
с малыми. Они простым образом связаны с операторами в пространст-
ве двухкомпонентных спиноров Паули в пределе малой энергии.
Нечетные операторы связывают большие компоненты с малыми,
и поэтому получение их вида в пределе малой энергии требует спе-
циального обсуждения.
Рассмотрим теперь унитарное преобразование уравнения (6.1)
в виде
T' = e<sT,	(6.9)
<ЭЧ '
где S может зависеть от времени. Тогда
iS —=i/ieiS —+ iS-^-4f = eiSOT+iS —
dt	dt dt	dt
deiS
dt

= eiS 3(e~iS + iti	e-iS T' = 3f' 4",
где
a e,S
3t' = eis e-iS + i h e~iS
dt
(6.10)
(6.П)
На русском языке см. книги [7, 376]. — Прим, перев.
193
Заметим, что, поскольку dS/dt может не коммутировать с 5,
нельзя записать
deiS . 5S	.
—— = 1 — efi	(неверно).
Разложение Ж' по степеням S имеет вид
		dS 1 — dt s,	+ i 5, St	5, Ж- p	 3			
					2		j
					as- dt .		
	2!						
i®	5,	s,	s, Ж — —		asi	-	
3!				4	dt J		
(6.12)
Для первого унитарного преобразования из нашего ряда выберем
эрмитов генератор
S(i)=_j_₽_0.	(6.13)
2/Ис2	’
Тогда, сохраняя члены с 7И~2, напишем
= -О +	{₽ [О, 81 + 20Оа},	(6.14а)
i2 [SO, [5(0, ЭД] =	-О+ -^[О, #1+ -^021 =
2Л4с2 L	2Мс2	Me2 J
=	02-----1^ [0 [0 £]] _ -1^03,	(6.146)
Me2 4Л42с4 L	J М2с*	(
i3[S(‘), [S(D г$и>,	-1—Гб0, =Ё.021=_2_03	(6.14б)
L L	JJ 2Мс2 [r Me2 ] Л42с4
При подстановке этих выражений в формулу (6.12) нечетный опе-
ратор в (6.6) сокращается с главным членом в (6.14а) , так что не-
четные операторы фигурируют только с точностью до 7И-1 или бо-
лее высокой:
Ж^ = Шс2 + 8 + ~^—О2 + -^—[О, 81 —
г	2Мс2 2Мс2
-----— [о, [О, $]]-----!_0з + 1й-L ~—
8Л42с4 L	1	ЗЛ12с'’	2Мс2 dt
-----\о, —1-|-члены порядка Л4-3.	(6.15)
87И2с4 L dt J
Первые три члена, пятый и шестой члены в этом выражении являют-
ся четными (предполагается, что d&dt нечетно), в то время как
194
остальные члены нечетные. Чтобы исключить остальные нечетные
члены порядка М~2, возьмем
S(2)= __i__gj------------------1_0з+,й_₽_ <*L)	(6,i6>
2714c2 (2Л1с2	3.Vl2c4	2Л4с2 dt)
Тогда с точностью до M~2 получаем
р7Ис214-
67I43c®
[[©,	+ ₽Mc2 + ^ =
О3-----^—[О, $]— iS-£- — +
2Мс2	2Л4с2 dt
]----—
47142с4
1
ЗМ2с1
1
^47И2с4
(6.17>
На этот раз взаимно уничтожаются нечетные члены порядка 7И-1,
и мы имеем
я<2> = Шс2+^ + о2----------— [е, [о, $]1 —
Н	2714с2	87142с4 L	J
-----— \о, —1+—— \[О, ё'Ц-	,g]-П	(6.18>
8A42c4 L dt J 4TI42c4 [	dt J dt	'
где все члены являются четными, кроме последних двух. Ясно, что
можно продолжать эту схему, каждый раз беря
5("+*)=—i а X (остающиеся нечетные члены в (6.19)
и таким образом увеличивая на единицу степень при 7И-1 в нечет-
ных членах. В следующую итерацию последние два члена в форму-
ле (6.18) не входят и нечетные члены появляются только с точностью
М-3, поэтому можно записать
Ж р/Ис2+	О2 — - 1	[О, [О, £]] —
1	27Ис2	87142с4 1	J
— 87142^4 [^’ ЧЛеНЫ П0РЯДка	(6.20)
Во многих приложениях, в том числе для электромагнитного
взаимодействия нуклонов |см. формулу (6.21)], О имеет вид
О = сар + б'(6.21)
где О’ и ё описывают слабое возмущение, так что членами порядка
&2 или О'ё и более высокого порядка можно пренебречь. Тогда
195
мы можем написать выражение для Ж
^=₽/Ис2 + ^ + р^-+—[a-Р, О'1+—
Г	*2М 2Мс	+
Г г <zi l i Л Г д&'1
? а-p, [а-р,	—- а-р, — +
2	8Л12с3 L от J—
+члены порядка (Л4-3, О’2, О'&),
(6.22)
которое является основным результатом преобразования ФВ с точ-
ностью до членов Л4-2 включительно.
Рассмотрим теперь систему, состоящую из взаимодействующих
между собой нуклона и электрона, поведение которой определяется
формулами (6.1)—(6.3), и воспользуемся выражением (6.22), чтобы
получить низкоэнергетический предел гамильтониана, описываю-
щего эту систему. Сравнивая (6.1)—(6.3) с (6.6)—(6.8) и (6.21),
получаем
~^Fzam&mn Ainl е*—(6.23)
[	2Мс	J
И
О' = -\e\F1am^m + ^F^aikm + koam)yn\^-^t (6.24)
2Мс	J
где все явно указанные дираковские матрицы относятся к нуклонно-
му пространству, а латинские индексы пробегают значения 1, 2
и 3. Нерелятивистское выражение для гамильтониана, описываю-
щего взаимодействующие друг с другом нуклон и электрон, полу-
чается подстановкой (6.23) и (6.24) в выражение (6.22). При вычис-
лении антикоммутатора удобно воспользоваться тем, что если р
и f являются величинами, которые коммутируют су и Г, но не друг
с другом, то
[ур, Г[1+ = у [у, Г1+ [р, Д+ + у [у, Г]_ [р, /]_.	(6.25)
Здесь не предполагается, что у и Г коммутируют. При использо-
вании написанного выражения для вычислений в формуле (6.22)
р играет роль оператора импульса, / — плоская волна, а у и Г
196
обозначают различные матрицы Дирака. При этом появляются
выражения
[Tz> ?ml- = 2 i <rZm,
[To ₽Yml-= ~ 206Zm,
[Tz. Tm] + = 26Zm,
lYz. ₽Tm]+ = —2 i ₽azm.
(6.26)
и
[ph elk'r]_ = Sfczelk-r.
(6.27)
Гамильтониан взаимодействия, который получается из (6.22)
с помощью формул (6.23)—(6.27), может быть записан в виде [2441
= zsztT blx + {^i eik’r — ~ (a  p elk•r + eik•r a • p) —
L3(k2 — kl)	2Мс
— (Н+КГ2) j o ,^k x a) e,k.r _ (^ + 2^)	(k2_£2) eik-r
2Л1с	8Л12 c2
(Fl^KA) j G х	—ftfc) elk-r —
8ЛГ c2
— eik-r (hk0 a—iik) x pl} и e—i<B/,
(6.28)
где матрица 0 заменена единицей, поскольку она не изменяет боль-
шие компоненты спиноров, которыми мы ограничиваемся в нереля-
тивистском пределе. В формуле (6.28) а действует в пространстве
электронных спиноров, а р и о являются импульсом и спиновой
матрицей Паули для нуклона. Найдено, что в принятых нами при-
ближениях измеренные формфакторы нуклона имеют вид [191, 192,
106]
Fi (k2) = F2 (/?) = f (k2) для протонов, |
Fi (k2) = 0, F2 (k2) = f (k2) для нейтронов, j
Заметим далее, что в случае неполяризованных нуклонов последний
(спин-орбитальный) член в выражении (6.28) не дает вклада, и его
можно не учитывать. Однако четвертый член, или член Дарвина—
Фолди, дает вклад, поскольку рассматриваемые переданные импуль-
сы могут быть очень большими. Первые три члена, которые описы-
вают кулоновское взаимодействие и взаимодействие, связанное с кон-
векционным током и спиновым током, или током намагничивания,
имеют порядок величины не меньше чем /И-1 и дают главные вклады,
особенно при малых переданных импульсах.
При переходе к ядру выражение (6.28) следует просуммировать
по Л нуклонам. Мы воспользуемся тем фактом, что операторы
различных нуклонов коммутируют, поэтому преобразование Фол-
Ди—Вутхайзена может быть выполнено для каждого из них в от-
197
дельности*. Далее для нерелятивистской системы А нуклонов фено-
менологически вводится нуклон-нуклонное взаимодействие, описы-
ваемое потенциалом. При этом предполагается, что распределение
заряда и магнитного момента данного нуклона заметно не меняется
из-за присутствия других нуклонов, и, следовательно, можно поль-
зоваться формфакторами свободных нуклонов (6.29) и для нуклонов
внутри ядра. Тогда можно написать [см. (5.36)1
Дтт р2
<f	I i> =	,2. f {[«+ (р')и (р)] (?₽а (к) -
Ь	ко)
— [и+(р')а«(Р)1Д₽а(к)},	(6.30)
где величины
А U
<2р« (к) = $	(Г, г2, ..., Гл) У	(ej—2р,д] х
Хе1кг1Чга(г1, г2, rA}dr1dri ... drA	(6.31)
И
А
J₽a(k)= §Ч^(г1( г2, Гл) 2 L^(Pj’eilt'rj’ + eik'r-' pj) +
+ ^1с7-х(Йк)е,к’г/1та(г1, г2, ..., гл) drt dr2 ... drA (6.32)
* Из рассмотрения трансформационных свойств сложной волновой функ-
ции, описывающей многонуклонную систему [57], следует что изменяются
даже те члены эффективного взаимодействия, которые имеют порядок М~2.
Например, для системы, состоящей из двух невзаимодействующих точечных
нуклонов, фигурную скобку в выражении (6.28), следует просуммировать по
двум нуклонам (обозначаемым, скажем, индексами 1 и 2), а также необходимо
добавить член вида
с.,2 2 (°1~ °г)' е2е1к Г1!(йЛои —Йк) X ( рх--— ^(rx) ) —
8 Al2 с2	L	\ с )
— ех elk ri (llk0 а —Лк) X ( р2 —	(r2)^j,
где ^(г) — потенциал Мёллера (5.37). Для ядра члены порядка Л1~2 удер-
живаются только в тех расчетах электронного рассеяния, в которые входит
большой переданный импульс; в этом случае член с множителем й2к2/8М2с2
в формуле (6.28) дает наиболее значительный вклад [как и в формуле (6.31)].
Приведенный выше поправочный член почти никогда не учитывается; часть
его, которая относится к однофотонному взаимодействию, уменьшается за
счет множителя, имеющего вид среднего нуклонного импульса, деленного на
Мс. Этот поправочный член возникает из-за того, что произведение спиноров
для двухнуклонных состояний не сводится в нерелятивистском пределе
к простому выражению от матриц Паули. Это соответствует тому физиче-
скому факту, что триплетное спиновое состояние в одной системе отсчета
будет частично проявляться в другой системе как синглетное спиновое со-
стояние. Следует заметить, что указанная поправка обусловлена трансформа-
ционными свойствами волновой функции-, использование же преобразования
Фолди—Вутхайзена для исключения нечетных дираковских матриц из опе-
ратора Гамильтона вполне корректно.
198
выражаются через волновые функции начального и конечного состоя-
ний Та и Чгр и через проекцию магнитного момента
И;-- у(1+т3)Д1 + Л')-у(1—=
= у(1+ТзЬ + 'Г3;Л'.	(6.33)
Здесь, согласно (6.5), К' ~ 1,85. Заряд ej равен единице для про-
тонов и нулю для нейтронов. В слагаемом формулы (6.31), соответст-
вующем члену Дарвина—Фолди, величина к2 — k2 заменена на к3,
поскольку в интересующей нас кинематической области импульс,
переданный ядру, намного больше переданной энергии. Чтобы полу-
чить дифференциальное сечение неупругого рассеяния электронов
в борновском приближении, необходимо теперь подставить матрич-
ный элемент (6.30) в формулу (5.1) или (5.4).
§ 6.2. Правила сумм для рассеяния электронов
В § 4.6 было использовано свойство полноты набора ядерных
состояний, чтобы способом, в значительной степени не зависящим от
модели, получить правило сумм Томаса—Райха—Куна для фото-
возбуждения. Подобный же метод может быть применен и для элек-
тронного рассеяния [102, 244]; в этом случае интегральное сечение
не равно константе, а является функцией переданного импульса.
В зависимость сечения от переданного импульса входит фурье-пре-
образованиеотнуклон-нуклонной корреляционной функции для рас-
сматриваемого ядра, что (по крайней мере в принципе) дает воз-
можность получить весьма важную информацию о структуре ядра.
Основные результаты такого анализа можно наиболее отчетли-
во увидеть, если ограничиться сначала кулоновским слагаемым
в выражении (6.30). Для этого опустим второй член в формуле (6.31)
и пренебрежем вкладом токовых членов (6.32) в формуле (6.30);
эти члены имеют порядок 7И~2 и .И-1 соответственно. Сечение рас-
сеяния электронов при переходе ядра из начального состояния
(или подсостояния) а в конечное состояние [3 может быть тогда
записано с помощью (5.46) и (5.47) в следующем виде:
do ___ 2е4
dQ' й4 с4
ЕЕ' + с2 р • р' + т2 с4
(к2-^)2
<Р1 У ^е1к г/|а>
(6.34)
В ультрарелятивистском пределе (Е, Е’ тс2, tick^
oM]iC(k, k0),
(6.35а)
199
где величина
^Р=|н^2)|2(-^Г
cos2----6
2
sin1 -— 6
2
(6.356)
является моттовским сечением рассеяния электрона большой энер-
гии на свободном протоне [см. (5.56в)[ и
C(k, k0) =
<₽| f e,eikr>|a>
i = i
(6.35в)
Последняя величина зависит от А’о, так как конечное состояние
ядра, которое входит в С (k, k„), имеет энергию возбуждения
соответствующую потере энергии электрона:
£р = £а + ^0-—•	(6.36)
Чтобы получить правило сумм для электронного рассеяния, необ-
ходимо сложить вклады от различных возможных ядерных состоя-
ний. Мы сделаем это путем суммирования по k0, что подразумевает
суммирование по энергии Ер конечного состояния ядра. При выпол-
нении этого суммирования зафиксируем переданный импульс.
Тогда в эксперименте по рассеянию, который мы имеем в виду, не-
обходимо будет определить сечение для разных значений углов,
энергий и энергетических потерь. В заключение проведем суммиро-
вание по потерям энергии для каждого значения переданного им-
пульса и угла. Для очень малых переданных импульсов k -> О
в выражениях (6.34) и (6.35) следует учитывать только вклад от
упругого рассеяния. Выделим относительно неинтересную зависи-
мость сечения упругого рассеяния от переданного импульса, вводя
величину
которая содержит суммирование по достаточно большим потерям
энергии, так что вклад от упругого рассеяния исключается. Исполь-
зуя свойство полноты набора конечных ядерных состояний
2|₽><₽|=1,	(6-38)
₽
получаем
C(fe) = Z-1<a| 2 S eJ4Cik‘(r>~r')|a>— Z-1| F (Л) |г,	(6.39)
j=i i= i
200
где величина
F (k) = 'а |	ej е,к’ri | а)	(6.40)
1=1
является формфактором упругого рассеяния для ядра, который,
как мы предполагаем, известен*. Одночастичные члены (j = /)
в формуле (6.39) дают
<а | 2 е1 I “> =	(6.41)
/ = 1
Для двухнуклонных членов (/ у= /) введем протон-протонную кор-
реляционную функцию
Р(г', г") = [Z (Z—I)]-1 <а | 2 oez6(r'-r;)6(r"-rz)|a>, (6.42)
/ i
которая удовлетворяет условию
J Р(г', г") dr'dr" = 1.	(6.43)
Эта функция является мерой вероятности того, что один протон на-
ходится в точке г', а второй — в точке г". Тогда
C(k)^- 1+(Z— l)$eik(r'“r")P(r', r")dr'dr"~Z^\F(k)\\ (6.44)
т. e. правило сумм для кулоновского рассеяния в основном опреде-
ляется фурье-преобразованием от протон-протонной корреляцион-
ной функции.
Асимптотическое поведение С (k) легко получить из формулы
(6.44). Для больших k подынтегральные выражения в (6.40) и (6.44)
осциллируют и интегралы (6.40) и (6.41) равны нулю. Таким обра-
зом, С (оо) =1, что соответствует рассеянию на отдельных протонах
при больших переданных импульсах; при этом двухнуклонный, или
корреляционный, член не дает вклада. Кроме того, поскольку при
построении функции С (k) член, соответствующий упругому рассея-
нию, был исключен, то С (0) = 0.
Выражение (6.44) дает возможность использовать правила сумм
для электронного рассеяния при анализе протон-протонных корре-
ляций в ядрах. Можно надеяться, что такой анализ окажется чув-
ствительным не только к весьма тривиальным корреляциям, обус-
ловленным принципом Паули, но и к корреляциям, обсуждаемым
в § 4.7, которые обусловлены той частью нуклон-нуклонного взаимо-
действия, которое по предположению описывается твердым кором.
Прежде чем проверять эту возможность, необходимо рассмотреть
поперечные мультиполи, учитывая в формулах (6.30)—(6.32) члены
* Заметим, что учет отдачи в соответствии с (4.30а) не изменяет величины
(А), так как она зависит только от разности координат нуклонов. Однако
величина F (k) при этом меняется.
201
порядка М-1 и М~2. Это было сделано Мак-Воем и Ван Ховом [244],
которые нашли, что величину С (k) следует заменить величиной
Т (k, 0), зависящей как от угла рассеяния, так и от переданного им-
пульса. Эта величина может быть записана в виде
T(k, 0)= (1 —
х Г2 tg2-А-е -ь 1 -
h2 k2
4M2c2
(z-i(Z^ + ^ji2) x
I 3 M2c2
Мс2 ) “
^го2)аи1
~ с2 k2 ]
- —	+ Z-1 <а I У eik (г/~гг) х
4Л12с*

й2
___[/г2<гг<Г/_(к.<ту)(к-<т1)1х
~ c2k2
h2 k2	о \ г
+	_1_ х
c2k2 1 ЛРс2
+ е е ,^-Р^
1 1 М2 с2
X [PzfPzl — PxjPxl'i
t2k2 j | a)—Z-11F (k) |2,	(6.45)
где <о и <®2>ОР — средние от частоты энергии возбуждения ядра и
ее квадрата, которые, согласно оценкам Мак-Воя и Ван Хова, будут
давать главный вклад в пик квазиупругого рассеяния (см. рис. 5.1):
o>~----(ь?) ~1,5(Л
2Л1	°1’
Компоненты импульса нуклона определены так, что pzj = p,-k,
а рх] является компонентой вектора р, в направлении, нормальном
к вектору к.
Результаты оценок [244] правила сумм в рамках модели оболо-
чек для рассеяния электронов представлены на рис. 6.1 для ядра
16О. Видно, что вклады, обусловленные оператором тока, вообще
говоря, очень важны в рассматриваемой области переданных им-
пульсов. Кроме того, важную роль в уменьшении как кулоновской
части, так и части, обусловленной оператором тока, играют эффек-
ты антисимметризации. Корреляции, связанные с твердым кором,
изменяют кулоновскую часть не более чем на 5% для области пере-
данных импульсов, в которой мезонные эффекты не играют суще-
ственной роли (k S7 2,5 ферлиг'У Следовательно, нельзя надеяться
с помощью такого анализа правила сумм извлечь информацию
о корреляциях, связанных с твердым кором. Это, конечно, не оз-
начает полной бесполезности указанного правила сумм для рассея-
ния электронов. Оно может быть использовано для проверки моде-
лей структуры ядра. Более того, Чейзом, Лесняком и Малецки 1781
202
было отмечено, что вклад, даваемым оператором тока в интегральное
сечение, в основном определяется членом в выражении (6 45) вида
^(ад+Ж)16>( 1 е)
Рис. 6.1. Результаты расчета правила сумм в рамках
модели оболочек для рассеяния электронов на яд-
ре 16О.
В величинах Тс, Tsm, Tqe, которые содержат поперечные
вклады, угол рассеяния фиксирован: 0 --90е. Кривые, обозна-
чаемые нижним индексом С, получены без учета антисим-
метризации в модели оболочек. Кривые, обозначаемые бук-
вами SM, получены в рамках аитисимметризованной оболо-
чечной модели гармонического осциллятора. Величины Тс и
Tsm, согласно выражению (6.45), содержат как кулонов-
скую часть, так и часть, обусловленную оператором тока,
тогда как Сс и Csm описывают лишь кулоновскую часть
(6.39). Кривая, обозначенная Cees, описывает кулоновское
рассеяние, рассчитанное с волновыми функциями, в кото-
рых учтены нуклон-нуклонные корреляции, соответствую-
щие рис. 6.2 (радиус твердого кора взят равным 0,4 ферми).
Кривые, описывающие кулоновское рассеяние, асимптотиче-
ски стремятся к единице, а кривые Тс и Tsm — к кривой
Tqe, которая соответствует квазнупругому рассеянию, давае-
мому однонуклоииыми членами в выражении (6.45).
При больших переданных импульсах отклонение от этого выраже-
ния в членах, связанных с током, составляет лишь несколько про-
центов. Характерная зависимость от угла рассеяния в виде tg2 б]
может быть выделена в результатах экспериментов по рассеянию
электронов, что дает возможность определить природу изменений
магнитных моментов нуклонов внутри ядра. Чувствительность
203
к магнитным моментам в данном случае особенно велика, так как
они входят в напйсанное выражение в квадрате, т. е. изменение ве-
личины магнитных моментов на 10% вследствие присутствия дру-
Рис. 6.2. Двухпротонная корреляционная функция
для 16О, рассчитанная Иденом, Эмери и Сампант-
харом [ИО] с использованием потенциала Гамме-
ля— Теллера [152, 153] (радиус твердого кора при-
нят равным 0,4 ферми).
Кривая, отмеченная индексом SM, получена в модели
оболочек без учета корреляций. Точка, в которой эти
кривые начинают сходиться, соответствует «длине зале-
чивания», равной приблизительно 2 ферми.
гих нуклонов изменит этот член на 20%. Эксперименты на 16О [205]
показывают, что если такая перенормировка магнитных моментов,
имеется, то она меньше 10%.
§ 6.3.	Модель Хелма
Выражение (6.28) для гамильтониана взаимодействия является
основой для тех расчетов неупругого рассеяния электронов, в ко-
торых используется описание ядра с помощью волновых функций
ддя А нуклонов. Такое описание ядра является весьма фундамен-
тальным по своей природе (оно было бы более фундаментальным,
если бы рассматривались мезонные степени свободы!). В действи-
тельности эта модель для многих случаев требует детальных,
неоправданно сложных математических расчетов. Это характерно,
например, для описания общего поведения формфакторов элек-
тронного рассеяния в зависимости от порядка мультипольности,
переданного импульса, размера ядра и т. д. Для таких целей удоб-
но использовать феноменологические описания ядер, дающие пара-
метризацию коллективных свойств нуклонов. Так, для рассмотрения
электровозбуждения колебаний гигантского резонанса может быть
использована модель жидкой капли [340], а также модель Гольдха-
204
бера—Теллера [1711. Одним из примеров подобного описания яв-
ляется модель Хелма [1841, которая особенно полезна ввиду ее
большой простоты.
С целью получения указанного феноменологического описания
рассмотрим кулоновский вклад в рассеяние электронов. Сечение
в БППВ в ультрарелятивистском пределе дается формулами (5.51)
и (5.56):
~ = 4л	У 17V₽a (k; CL) |2,	(6.46)
dQ 2Jf + 1 (Ze)2
где
(JiLJflMiMMfjNfcfk-, CL)=
= iL$<₽|p(r)|a>/l(^)yto(f)dr.	(6.47)
При рассмотрении упругого рассеяния электронов в модели Хел-
ма зарядовое распределение Ферми (см. § 5.5) заменяется более про-
стым распределением, имеющим те же самые общие свойства, т. е.
постоянную плотность в центре и уменьшающуюся плотность на
поверхности ядра, которое в свою очередь характеризуется опре-
деленной толщиной поверхности. Зарядовое распределение для упру-
гого рассеяния записывается в виде интеграла от произведения двух
функций
<а | р (г) | а) = е § р0 (г') рх (г—г') dr'.	(6.48)
Это выражение особенно удобно при получении формфактора, когда
необходимо выполнить преобразование Фурье. Зарядовое распре-
деление должно быть нормировано так, чтобы
<а | р (г) | а> dr = Ze,	(6.49а)
что можно получить, если взять
^p1(r)dr^=l,	(6.496)
р0 (г) dr = Z.	(6.49в)
В ультрарелятивистском пределе кулоновская часть сечения упру-
гого рассеяния в БППВ получается с помощью (5.47) в виде
do ол, 1	___
----=—--------------V |F(k)|2,	(6.50)
dQ' (Ze)2	+
’	1 1 м.м,
1 J
где
и	F (к) = <а | р (г) | а> eik •г dr = eF0 (к) Fr (к)	(6.51а)
	^«(к)= ps (г) eikrdr, s = 0,1.	(6.516)
205
Если принять, что р0 характеризует постоянную плотность в цен-
тральной области ядра, то из условия нормировки (6.49в) вытекает
Ро(г)= V 3	'
О, r>R.
(6.52)
Поверхностный слой учитывается распределением
Р1 (r) = (2ng2)-3/2 e-^/2g’_	(6.53)
Тогда
F(k)=3Ze-il(kR} e~kI^.	(6.54)
В § 5.5 мы видели, что толщина поверхности, вообще говоря, одна
и та же для разных ядер. Это выражается в модели Хелма для не-
упругого рассеяния электронов постоянным значением величины
g, именно g « 1 ферми.
Для неупругого рассеяния в модели Хелма предполагается, что
зарядовая плотность перехода локализуется на ядерной поверхности
радиуса R:
<₽ IР (г) I «> = -§" 6	ФЛ Mi (?),	(6.55)
vfip ф/гм. и — функции, характеризующие начальное и ко-
нечное ядерные состояния. Возможно, что распределение (6.55)
«размывается» гауссовским множителем, как в выражениях (6.48)
л (6.53). Подставляя в (6.47), получаем
2VPa(k;CL)= Ze iL <Jf 11*7 (г) || 7г> jL (kR),	(6.56а)
или в случае, когда используется «размывающий» множитель,
7Vha(k; CL) = ZeiL<Jy|!rL(r)||J/>/L(fe/?)e 2 g. t(6.566)
Оправдание вида зарядовой плотности перехода (6.55) заключается
в том, что принцип исключения Паули подавляет нуклон-нуклонное
рассеяние внутри ядра. Это происходит потому, что рассеянный
нуклон пытается занять орбиту, которая уже занята другим нукло-
ном. Вследствие этого в низколежащих возбуждениях ядра участ-
вуют нуклоны, находящиеся вблизи поверхности, где имеются неза-
нятые орбиты, на которые могут рассеяться нуклоны. Движения
заряда, связанные с возбуждением таких уровней, локализуются,
конечно, вблизи поверхности ядра.
Выражения (6.56) дают в случае электровозбуждения зависи-
мость вида kL для формфактора мультипольности L. Они также
дают полуколичественное описание положения дифракционных
минимумов и затухания формфактора для больших переданных
импульсов.
206
Мы можем, наконец, использовать модель Хелма, чтобы
сравнить кулоновские вклады для упругого и неупругого рассеяния.
Например, как видно из (6.54) и (6.56), для ядра со спином Jt — О
сечение электровозбуждения гигантского резонанса (Jf = L = 1)
следующим образом связано с сечением упругого рассеяния:
1	= — tkR)2 — । .
dfi' |ь= 1	3 d£l'
(6.57)
Множитель -g- (kR)2 является приблизительной мерой той доли за-
ряда, которая участвует в неупругом рассеянии.
§ 6.4. Пример: рассеяние электронов на 4Не
Проиллюстрируем теперь различные свойства электронного
рассеяния, обсуждаемые в этой и предыдущей главах, используя
очень простую оболочечную модель для 4Не, которую мы ввели
в § 4.8. Упругое рассеяние нетрудно рассмотреть с помощью волно-
вой функции основного состояния Чг() (4.166). Формфактор упругого
рассеяния имеет вид [см. (5.47), (6.40) и (6.51а)]
F(k) = e-^-Jехр [—a2(ri+/i 4-ri+rI)] X
X (eIk r* +eik r’)dr1(/r2cfr3dr4 =
=	(в.58)
(индексы 1 и 2 относятся к протонам). Значение а для 4Не определяет-
ся подгонкой формулы (6.58) к экспериментальным данным, что
дает а та 0,73 ферма.-1 — 144 Мэв/с (см. [145]). Окончательно
получаем
F(k) = 2е ехр [—(/г-0,69 ферми)2].	(6.59)
Этот результат полезно сравнить с результатом, найденным в рам-
ках модели Хелма [см. (6.54)1, которая для g = 1 ферми и kR 1
дает
F (к)= 2е ехр [—(/г-0,71 ферми)2].	(6.60)
В модели Хелма дифракционный минимум получается в точке, в ко-
торой ф (kR) первый раз обращается в нуль, а именно при kR = 4,49.
Такой минимум экспериментально [1461 обнаружен при k = 3,16фер-
ми~г, что соответствует значению R = 1,42 ферми при анализе
в рамках модели Хелма. Это, конечно, сравнимо с толщиной поверх-
ности для ядра 4Не, которое состоит только из поверхности. На
рис. 6.3 показаны результаты подгонки данных по упругому рас-
сеянию при k2 10 ферми~2 для гауссиана (6.59). Как видно из
этой кривой, полученный параметр соответствует параметру гармо-
нического осциллятора.
207
Для рассмотрения электровозбуждения колебаний гигантского
Если резонанса воспользуемся волновыми функциями возбужденных со-
тралг стояний Tg, V3h Чг4, определяемыми формулами (4.1746)—(4.174г).
Функция Т, описывает состояние, возбуждаемое в фотоядерном
гигантском резонансе. Матричные элементы в БППВ для электро-
возбуждения этого колебания даются выражениями (5.51а) и (5.51в),
в которые входит .El-мультиполь. Операторы заряда и тока в этих
матричных элементах мы возьмем из формул (6.31) и (6.32), но огра
Тогд
В §Е
и та
упру
£, ил
Л
заря
ради
где
нечн
«раз
и (6
Рис. 6.3. Формфактор упругого рассеяния электронов,
измеренный для 4Не [145, 146].
Кривая получена для функции ехр[—&2/(4а2)], где а =•
=0,73 ферми -1. Прн /г2=10,0 ферми—2 появляется дифракцион-
ный минимум и простая оболочечная модель гармонического ос-
циллятора для ядра 4Не становится непригодной.
или
ничимся малыми переданными импульсами Мс = 939 Мэв!с)
Опр	и поэтому не будем учитывать в (6.31) члены порядка М~2. В выра-
в то	жении (6.32) выразим векторное произведение переданного импуль-
рас< са на намагниченность через оператор rot и проинтегрируем резуль-
нук тат по частям для того, чтобы получить ядерный ток в виде, анало-
ном гичном (4.58). Тогда*
(J. Uf I MMf) N20 (k; Cl)= ej T; (rb r2, r3, r4)’x
x [ V1M (Fj) ii (ErJ + Y1 м (Г2) A (kr2)] X
X VqOT, r2, r3, r4) dr4 dr, dr3 dr4	(6.61)
1	* В правых частях написанных выражений введен множитель (—i), что-
Д«1К бы согласовать (4.1746) с (5.86) и сделать, таким образом, приведенные матрич-
МИ1	ные элементы действительными.
ИМ1
208
206
(Ji\Jf\MiMMf)Nw(k-, El) =
= i V J № V,-  (Аш (r>; e) To) + T; A,m (r,-; e) • V, 4'0] +
+ Aim (Г,-; e) •	X (^2 °i ^o)] | dri dr2 dr3 dr I +
+ i V C Aim (r/, e) { —V X (T; G/ M dri dT2 dt3dri' (6’62)
/=3 J
Сразу же видно, что члены, соответствующие току намагничивания,
содержат матричные элементы в спиновом пространстве нуклонов,
например, в виде
%р+ (О^оДРф).
Все они должны исчезать, так как <т является векторным оператором
в спиновом пространстве и не может связывать два состояния с S = 0.
Что касается слагаемых, соответствующих конвекционному току,
то заметим, что V- А^м (г>; е) = 0 и
—i-a'r’	—5- а’ г*
V е 2	= —а2 г е 2	.	(6.63)
Тогда
/V20(k; Cl) =	j	j1(kr) г3 dr =
=-----L=- е —	(6.64)
2) 6л а
И
Nw (k; Е1) = -	V е-“*'* [/„ (kr) + /2 (Ml г* dr =
3 р <5 м л
=--------— а	(6.65)
2 /Зл Л1	х
Выражения (6.64) и (6.65), взятые при а =	согласуются
с теоремой Зигерта, выведенной из (4.22) или (4.24)*. Кроме того,
подставляя (6.64) в (6.46) и (6.59) в (6.50), получаем
doc I   1 / k \ 2 dac
dfi' |ь= i 8 \ а ) dQ'
(6.66)
el
т. е. результат, подобный формуле (6.57), полученной в модели Хел-
ма. Из формул (6.64) и (6.65) также следует, что кулоновский ма-
* Заметим, что из (4.18) следует
Л-Ipa (kp; Е1) = 2n/(Vpa(k; El).
8 Зак. поз	209
j
тричный элемент преобладает над поперечным матричным элемен-
том для всех переданных импульсов, кроме весьма малых.
Формфакторы в выражениях (6.64) и (6.65) можно несколько мо-
дифицировать двумя способами. Первый из них заключается во
введении нуклонного формфактора f (А’2) из (6.29). При получении
матричных элементов в (6.64) и (6.65) предполагалось, что заряд
в ядре сосредоточен в точке, соответствующей каждому протону.
В действительности сечение электронного рассеяния уменьшается
для ненулевых переданных импульсов за счет «размазывания»
заряда протона. Это может быть учтено [190] множителем из (6.29)
f (k2) = exp [—k2/(4a2p)\,	(6.67)
где ap = 1,74 фермит1. Второй способ улучшения полученных
результатов связан с учетом отдачи по формуле (4.30а). Появление
координаты центра масс в плотностях заряда и тока при преобразо-
вании Фурье приводит для оболочечной модели гармонического
осциллятора к поправочному множителю [328]
ехр [/г2/(4Ла2)].	(6.68>
Множители (6.67) и (6.68) имеют тенденцию компенсировать друг
друга и никогда не дают более чем 10%-ную поправку. Их можно
учесть, если переопределить параметр гармонического осциллятора
а и находить его из формфактора упругого рассеяния (6.58), в ко-
торый входят те же самые поправки. Таким образом, они уже вве-
дены в наши последние результаты.
При рассмотрении других видов возбуждения ядра 4Не исполь-
зование спиновых функций в Чг3 и из (4.174) приводит к ситуа-
ции, противоположной той, которая возникает при использовании
функции Чг2. Конвекционный ток теперь не дает вклада в возбужде-
ние из основного состояния, но намагничивающий ток перехода дает
неисчезающий вклад. Кулоновский матричный элемент равен нулю
по той же причине. Интегрируя по частям в слагаемых, соответст-
вующих току намагничивания в формуле (6.62), и используя (2.956),
можно написать
X Aim (п; ш) • (Чгр <т, ¥0) drr dr2 dr3 dri =
= 1/4- (Kp ± Kn)	~ $ c- “2 jr (kr) r* dr =
= —!=- (KD zb Kn) e-ft2/(4“2>,	(6.69/
4Кбл v 1 n aM
где верхний знак относится к случаю р = 3, а нижний — к слу-
чаю Р = 4. В соответствии с (4.59) множители, обусловленные маг-
нитными моментами, равны Кр + Кп = 0,88 и КР — Кп = 4,70,
210
и вклад от Tg меньше с вклада от в отношении близком к фаг
тору задержки, определяемому правилом отбора по изоспину дл
магнитного диполя. Для Чг3 вклады от протона и нейтрона фор
мально складываются, но приводят к меньшему эффективном
магнитному моменту из-за того, что магнитный момент нейтрон
отрицателен. Возбуждения, описываемые функцией Tg, имеют пол
ный изоспин Т = 0. Чг4 описывает состояние , в котором вклады о
протонов и нейтронов противоположны по фазам, что соответствуе
полному изоспину Т = 1, при этом эффективный магнитный момен
велик. Природа ядерных возбуждений, описываемых функцией Чг,
заключается в том, что протоны со спином «вниз» и нейтроны с
спином «вверх» осциллируют по отношению к протонам со спино
«вверх» и нейтронам со спином «вниз». Это спин-изоспиновое во;
буждение, которое во Введении иллюстрировалось на рис. ВЛД
Изоспиновое возбуждение на рис. ВЛ, а описывается функцией Ч1
и соответствует состоянию, в котором протоны и нейтроны колеС
лютея в противофазе. Возбуждения, соответствующие функци
Чг3, — это возбуждения, в которых нейтроны и протоны со спино
«вверх» колеблются относительно нуклонов со спином «вниз>
Эти возбуждения называются спиновой волной. Ясно, что оба вид
возбуждений, включающие спин, т. е. 4% и Чг4, важны в электронно:
рассеянии только при больших переданных импульсах, когда он
могут конкурировать с формфакторами, соответствующими возбуж-
дению гигантского резонанса (6.64) и (6.65). Функции (4.174е
и (4.174г) описывают также состояния с Д = 0" и 2_. 2_-уровн
могут возбуждаться в электронном рассеянии и в случае Т =
приводят к возбуждению гигантского магнитного квадрупольног
резонанса, который, вообще говоря, несколько удален по энерги
от положения гигантского Е1 -резонанса и может быть отделен о
него и экспериментально.
Хотя данный анализ для 4Не является в значительной степей
упрощенным, тот же самый подход образует основу и для боле
реалистического рассмотрения структуры ядер в связи с фоте
и электровозбуждением. Мы увидим, что те же элементы анализ
входят также и при рассмотрении захвата мюонов и радиационног
поглощения пионов.
* *
*
Материал этой главы, так же как и гл. 5, содержится в обзора
Сосетти и Молинари [66,1 Бишопа [36] и Де-Фореста и Валечк
194]. Статья Мак-Воя и Ван Хова [244] очень полезна при изучени
темы, обсуждаемой в § 6.1 и 6.2.
8*
ГЛАВА 7
КУЛОНОВСКОЕ
ВОЗБУЖДЕНИЕ
До сих пор при обсуждении электромагнитных взаимодействий
в ядрах мы рассматривали механизмы возбуждения с помощью фо-
тонов или электронов, которые могут взаимодействовать с ядром
только электромагнитным способом. Мы использовали известные
сведения из электромагнитной теории, чтобы описать эти механиз-
мы, и сравнительно редко обращались к детальным предположени-
ям о структуре ядра. Можно воспользоваться тем же подходом,
чтобы обсудить возбуждение ядер заряженными бомбардирующими
частицами (снарядами), которыми могут быть исами ядра (например,
протоны, дейтроны, а-частицы, ионы 16О и т. п.) при условии, что
энергия частицы меньше высоты отталкивающего кулоновского
барьера. Если это условие выполнено, то два ядра никогда не будут
приближаться друг к другу достаточно близко для того, чтобы на-
чало действовать сильное взаимодействие. Однако ядро-мишень
(или снаряд) может все-таки перейти в возбужденное состояние бла-
годаря кулоновским силам, которые действуют между ядрами.
Такой процесс называется кулоновским возбуждением.
Кулоновское возбуждение, несомненно, очень тесно связано
с неупругим рассеянием электронов, и сведения о ядре, получаемые
из анализа этих механизмов, могут даже в какой-то степени перекры-
ваться. Ввиду большой массы снарядов, используемых в кулонов-
ском возбуждении, анализ этого процесса довольно прост. Он осно-
ван на полуклассическом приближении, которое совершенно не-
применимо для рассеяния электронов. Кроме того, при кулоновском
возмущении уменьшаются трудности, связанные с радиационными
поправками в случае неупругого рассеяния электронов. Поскольку
скорость снаряда v обычно весьма мала, то магнитные переходы
в кулоновском возбуждении сильно ослаблены в отношении поряд-
ка (vic)*, что также упрощает рассмотрение. Наконец, использова-
ние тяжелых ионов в качестве снарядов с большим зарядом приво-
дит к очень важному свойству, которое по существу не свойственно
электронам: вероятность возбуждения ядра становится большой, так
что могут быть важны процессы второго и более высокого порядка.
Многократное кулоновское возбуждение позволяет получить высо-
212
колежащие ядерные уровни с помощью ряда последовательных пере-
ходов, а соответствующие реориентационные эффекты могут быть
использованы для определения статических электромагнитных мо-
ментов возбужденных состояний.
В отличие от кулоновского возбуждения главное достоинство воз-
буждения электронами заключается в том, что не следует беспо-
коиться о нарушении простого электромагнитного описания про-
цесса рассеяния в случае проникновения через кулоновский барь-
ер. Даже внутри ядра электроны продолжают взаимодействовать
только электромагнитным способом. Поэтому электроны могут быть
использованы, чтобы возбуждать уровни ядра, лежащие при зна-
чительно более высокой энергии, чем уровни, доступные в кулонов-
ском возбуждении. Электроны также могут быть использованы, чтобы
передать ядру значительно больший импульс, что необходимо для
изучения явлений на малых расстояниях. Поскольку электроны
могут проникать внутрь ядра, они могут возбуждать электрические
монопольные переходы, что невозможно в кулоновском возбужде-
нии.
В настоящей главе мы дадим очерк теоретических методов, ис-
пользуемых при описании кулоновского возбуждения. (Многие из
них, конечно, тесно связаны с методами, используемыми для анали-
за электронного рассеяния.) Затем мы кратко рассмотрим те свой-
ства, которые возникают при использовании тяжелых ионов и яв-
ляются наиболее характерными для кулоновского возбуждения.
§ 7.1.	Полуклассическое рассмотрение кулоновского
возбуждения
Величиной, характеризующей влияние кулоновского поля ядра
на изменение траектории заряженной частицы, является безразмер-
ное число Зоммерфельда
z, Z, е2
Л = —;-----
hv
где Zxe — заряд налетающей частицы, v — ее асимптотическая ско-
рость, Z2e— заряд мишени. Этот параметр можно рассматривать
как отношение половины расстояния наибольшего сближения а
при лобовом столкновении [см. формулу (7.10)1 к длине волны
Де-Бройля частицы на бесконечности. Иными словами, он дает от-
ношение потенциальной энергии в точке наибольшего сближения
к энергии hv/a, связанной с эффективным временем прохождения
области взаимодействия. Если число Зоммерфельда мало (i] <£ 1),
то кулоновское поле заметно не меняет волновую функцию налетаю-
щей частицы и можно пользоваться борновским приближением
С плоскими волнами. Этот случай почти никогда не реализуется для
кулоновского возбуждения. Обычно необходимо иметь достаточно
сильные отталкивающие кулоновские силы, чтобы держать налетаю-
щую частицу вне области действия ядерных сил, и, следовательно,
’L 1. При таком условии можно рассматривать налетающую
(7-1)
213
частицу движущейся по классической траектории. Электромагнит-
ное поле, которое создает частица на этой траектории, может быть
затем рассмотрено как малое возмущение, возбуждающее ядро
из его основного состояния.
Чтобы математически описать в указанном приближении куло-
новское возбуждение, следует сначала решить классическую зада-
чу Кеплера для отталкивающих кулоновских сил и затем восполь-
зоваться обычной квантовомеханической теорией возмущений, чтобы
рассмотреть ядерные переходы. Поэтому мы начнем с рассмотрения
классического гамильтониана для двух частиц, которые взаимодейст-
вуют посредством кулоновских сил:
/7=-^—F 71Za--(7.2)
2Л1 г
где р — относительный импульс, г — вектор расстояния между
частицами, М. — приведенная масса системы. Введем классиче-
ский угловой момент
L : ГХР,
(7-3)
абсолютная величина которого 1С1 является интегралом движения.
В качестве второго интеграла движения возьмем вектор Паули*
	A' = f	Lxp— 1	(7.4) Zx Z2 e2 M
для	которого —= —	—Lxr=0	(7.5) dt	dt	Mr2
и	A'2 = 1 + 2MH f	L — ) \	(7.6) V Zi Z2 e2 M J
Если ввести классический аналог числа Зоммерфельда
t\cl=Z1Z^MlY2MH	(7.7)
и перенормировать наш второй интеграл движения
А = г)сгА'.	(7-8)
то выражение (7.6) примет вид
т]?г = А2—L2.	(7.9)
Поскольку L и А — взаимно ортогональные постоянные векторы
(для данных начальных условий на траектории налетающей части-
цы), можно ввести систему координат такую, что величины А =
* Этот подход основан на методе Паули [266] для квантования атома
водорода в матричной механике, который недавно снова получил признание
в качестве примера использования динамической симметрии при рассмотрении
физических систем (см. например, [21]).
214
= AM, LX А и L = L/L определяют оси x, у, z (рис. 7.1). Тогда
координатами траектории являются х = г-А, у = r-L X А и z = 0.
Они удобно параметризуются, если ввести величину
„	_______Zi Z2 е2 Zt Z2 е2	]f.<
ZrZ2e2M 2H Mv2 ’	( '
Рис. 7.1. Система координат для описания орбит Резерфорда [см. фор-
мулу (7.13).].
Орбита слева— для притягивающих кулоновских сил, справа — для отталки-
вающих сил.
которая является половиной расстояния наибольшего сближения
для траектории, в которой вектор г везде параллелен вектору р,
и эксцентриситет (рис. 7.2)
е = (1 + /?,/ 1]?г) > /2 = 1 /Sin (i/2 6),	(7.11)
Рис. 7.2. Геометрические определения расстоя-
ния наибольшего сближения а, параметра
удара 6, эксцентриситета е и угла рассеяния 0.
Любой из последних двух параметров может быть ис-
пользован для характеристик орбиты Резерфорда; оии
связаны соотношением e-l/sin^e). Как и на рис. 7.1,
орбита слева—для сил притяжения, орбита справа —
для сил отталкивания.
где 6 — угол отклонения, <р — азимутальный угол радиус-век-
тора. С помощью этих величин можно определить переменную w
спг^ -------------.	(7.12)
1 — ecos <р
215
Тогда
x=tz(chu) -J-е),
«/=ai е2— Ishu),
r = a (ech uy-f-1),
и время параметризуется согласно соотношению
t— — (е shw-f-w).
v
Параметр удара имеет вид
(7.13а)
(7.136)
Рис. 7.3. К рассмотрению столкновения в классической механике.
Частицы с прицельными параметрами между b и b+db собраны в обла-
сти с поперечным сечением площадью 2nbdb и рассеиваются в область уг-
лов между 0 и 04-J0. Случай, показанный на рисунке, соответствует от-
талкивающим силам.
Сечение Резерфорда для рассеяния на угол 0 выражается через эти
величины; оно дается просто числом частиц в плоской волне с еди-
ничным потоком и с параметрами удара между Ь и b 4- db для соот-
ветствующего угла отклонения (рис. 7.3):
б/от? = 2п | bdb | =-dL—г— d£l.	(7.15)
Мы должны теперь рассмотреть, как движение налетающей ча-
стицы по этой классической траектории возбуждает ядро. Предпо-
ложим, что траектория заметно не изменяется при возбуждении.
Тогда дифференциальное сечение возбуждения ядра имеет вид
da= Pd(jr<,	(7.16)
где Р — вероятность того, что ядро возбуждается при столкно-
вении, в результате которого налетающая частица рассеивается
в элемент телесного угла dQ. Эту вероятность можно выразить через
216
амплитуду Лра возбуждения ядра из начального состояния а в конеч-
ное состояние р. Если мы не учитываем ориентации ядра, то
Р=
1
27/4-1
2 IM2.
где
величина
оо
<₽тО|<х>е*<£₽-£“)//йЛ
1 h J
(7.17а)
(7.176)
выражается через энергию взаимодействия Н' (/) и энергии ядерных
состояний Еа и Е₽.
Для электрических переходов, которые вызываются частицами
с малой скоростью v <£ с, энергия взаимодействия определяется
только кулоновской энергией
<₽|Д'(/)|а> = 5<Р|р^(г)|а>ф(г, t)dr, (7.18)
где pN (г) — оператор заряда ядра,
Ф(г, t) =-------------
|г-гР(0| Гр (О
(7-19)
и Гр (/) — вектор положения налетающей частицы. В выражении
(7.18) учтено только прямое мгновенное кулоновское взаимодейст-
вие [ср. с (5.106)1, так как при малой скорости частиц поперечным
вкладом можно пренебречь. Кроме того, в выражении (7.19) мы в яв-
ной форме вычли монопольное взаимодействие между центрами
масс; это взаимодействие вызывает лишь отклонение частицы, кото-
рое мы рассматривали классически, и не дает вклада в возбуждение
ядра.
Используя обычное разложение по статическим мультипольным
моментам, имеем
<₽ I Н' (01 а> = 4л21 е £ V 2/4т Г^~' Х
L=1
> Пл1(гр)<₽|Йтм(е)|а>*,	(7.20)
где в величину
<₽|^M(e)|a> = J<₽|p(r)|a>rLKLA/(?)dr	(7.21)
входит тот же оператор, что и для испускания фотонов в формуле
(4.77) для случая малых переданных импульсов. Далее из (7.176)
^=^S;^<fWM(e)|a>*S£L,M,	(7.22)
получаем
где
Sel,m= $	(7.23)
--ОС
217
Как и в (4.81), (4.82), (4.84), можно ввести величины
B(EL- ./,->/,) = —1— У|<₽|йЛЛ/(е)|а>|2=
Zv i Н- 1
11 М- Mf
= 474тКР11^(е)11«>12.	(7.24)
через которые выражается дифференциальное сечение возбужде-
ния отдельных электрических мультиполей
duE— ^i^doEL,	(7.25)
где
4n2Z?e2 а2 В (EL; Jt ->	__
-------i-----f™)
sin4 — 0	'	’ M
2
Формула (7.26) получена с использованием соотношения ортогональ-
ности для коэффициентов Клебша—Гордана (ПА. 17) и суммирова-
ния по Л4г при фиксированном М = Mf — Mt. В системе коорди-
нат (7.13а) полярный угол 0; , = л (см. рис. 7.1 и 7.2) и
i Фр (О = хР (0 + i уР (t) = chw-Pe + iVe2 —1 shw
гр (/)	е ch w + 1
Следовательно,
SEL, м = —YLM (1 л, 0 } ILM (6, g),	(7.28)
va \ 2	/
где
/26^1 УА [(£—М)! (L+AQifA ./1(г+М)
„ (1 л\_Л 4п '	(L-M)!f(L-pM)!l	’
LM [ 2 Л’ )	L-\-M—четное число,
0,	L-\-M—нечетное число,
Ilm (6, g) = С exp [i g (e sh w + u>)l w j"e~^	W~dw (7.30)
J	(e ch 1)*-+™
—oo
и
t = “ (£p~gq) = ztz2e2 (£p—£a)	(7 3 J)
hv	hv 2Ea
Безразмерная величина g называется параметром адиабатично-
сти, так как произведение ge представляет собой отношение вре-
мени столкновения a/v к периоду ядерного возбуждения. Большие
значения g поэтому соответствуют сильно адиабатическим столк-
новениям.
218
Дифференциальное сечение для электрического мультиполя по-
рядка L может быть теперь записано в виде
do el=
2a~2L+2В (EL- Jt->Jf)dfEL(e, g),
(7.32)
где
df el (®, £)
21 (j "•«) ГI0- 8 Is W
Интегрируя выражение (7.32) по всем направлениям рассеяния,
получаем полное сечение ££-перехода
2 a~2L+2 В (EL-, J^JfjfELil),
(7-34)
где
16л3
™ J dfi
oj|2 j | ILM(6,1),2
0
cos ( 4- 6 )
-----(7.35)
sin3 ( — 6 |
\ 2 )
Функции ILm (0, E) и fEL (£) (7.30) и (7.35) отражают многие
свойства процесса кулоновского возбуждения. К сожалению, их
непросто вычислять даже в нашем предельном случае классической
траектории. Однако имеются довольно обширные таблицы этих
функций (см. 18,9]). Указанные функции обладают одним важным
свойством: при больших £ они уменьшаются экспоненциально,
в частности
7ьм(0, Е)~е“2Ч
Таким образом, вероятность возбуждения становится весьма малой
для сильно адиабатических столкновений. Это свойство является
общим свойством отталкивающего кулоновского поля.
На рис. 7.4 представлены функции f (Е) как для электрических,
так и для магнитных мультиполей. Функции f (Е) для магнитных
мультиполей связаны с сечениями формулой
°MT = (47)2^2L+2j6(yWL;	<7-36)
где величины В (ML-, Jt -> Jf) даются выражениями (4.82), (4.84)
и (4.78). Как обычно для электромагнитных явлений при низкой
энергии, следовало бы ожидать преобладания электрических ди-
польных переходов. Однако мы уже видели в гл. 4, что сила £1-пе-
рехода сконцентрирована в фотоядерном гигантском резонансе
при энергии в районе 15 Мэв, которая не достигается в кулоновском
возбуждении. При энергиях, которые можно получить в этом про-
219
цессе, El-переходы значительно подавлены и поэтому обычно не
представляют интереса. Кроме того, магнитные дипольные пере-
ходы подавлены по сравнению с электрическими переходами в от-
Рис. 7.4. Функции f(g) для полного сечения воз-
буждения в классическом пределе, построенные
в зависимости от параметра адиабатично-
сти g [8].
ношении (с/с)2, что и отражено в формуле для сечения (7.36). Для
скоростей налетающих частиц, используемых в кулоновском воз-
буждении, это значительно уменьшает вклад магнитных мультипо-
лей. Однако матричные элементы Е2-переходов имеют тенденцию
к усилению в области энергий, доступных кулоновскому возбужде-
220
нию, и электрические квадрупольные переходы оказываются наи-
более важными в этом процессе.
Чтобы придать количественный смысл понятиям «усилен» или
«подавлен», применяемым к матричным элементам ядерного пере-
хода для кулоновского возбуждения, удобно рассмотреть одноча-
стичные оценки вероятностей радиоактивного распада (4.88) и
(4.89). Вместе с (4.83) они дают
z>2	/ Q \ 2 п т
B(EL; j ) = (2b4-l)-f-) R2L (7.37)
\ L -j- 3 /
И
В (ML-. J, - /,) = 10 (2L + 1) £	’. (7.38)
Мы воспользовались соотношением
В (aL;
= в (aL; Jt -> Jf)
(7.39)
и (в духе одночастичных оценок для процессов возбуждения, в ко-
торых спин ядра обычно увеличивается) ввели статистический мно-
житель, соответствующий случаю Ji = 0, Jf — L.
Сечения, полученные с помощью формул (7.37) и (7.38), для
протонов, рассеянных на средних ядрах с Z2 = 50 и А2 = 120,
показаны на рис. 7.5. Энергия возбуждения в рассматриваемом слу-
чае предполагалась равной 200 кэв, а радиус ядра рассчитывался
по формуле R — 1,2Д */з ферми « 5,9 ферми. Поскольку вероятности
El-переходов в этой области энергий обычно меньше в 103—106 раз
по сравнению с одночастичными оценками, то из рис. 7.5 легко
видеть, что будут преобладать в основном Е2-мультиполи. Более
того, вероятности электрических квадрупольных переходов вообще
усилены в 10—100 раз по сравнению с одночастичными значениями.
Рис. 7.5 также показывает, что в тех случаях, когда имеются сме-
шанные ЛИ- и £2-переходы, кулоновское возбуждение будет
осуществляться главным образом посредством возбуждения
Е2-мультиполей. Такая важная роль Е2-переходов в кулоновском
возбуждении делает его весьма полезным инструментом для изуче-
ния коллективных квадрупольных поверхностных колебаний в яд-
рах, а также для изучения вращения деформированных ядер.
В этом смысле рассматриваемый метод дополняет анализ фотовоз-
буждения, который особенно полезен для изучения возбуждения
коллективных колебаний Гольдхабера—Теллера, соответствующих
высокоэнергетическим осцилляциям протонов относительно ней-
£ Тронов.
На рис. 7.6 представлены угловые распределения налетающих
частиц в процессах кулоновского возбуждения. Измерение этих
угловых распределений может быть использовано для определения
мультипольности. Их качественное поведение нетрудно понять.
Видно, что по мере увеличения L максимум углового распределения
221

смещается в направлении 0 = 180°. Это происходит потому, что
большой переданный угловой момент соответствует выделению малых
значений г, что в свою очередь означает увеличение рассеяния
назад. Кроме того, с увеличением £ увеличивается и переданная энер-
гия, т. е. начинают играть роль меньшие прицельные параметры/
Последнее означает рассеяние на большие углы. Однако рассея-
Рис. 7.5. Сечения кулоновского возбуждения про-
тонами уровня 200 кэв в ядре с Z2=50, Д2= 120
п /?=5,9 ферма.
Матричные элементы ядерного перехода получены с по-
мощью одночастичных оценок (8].
ние назад также и подавляется, поскольку при рассеянии назад
угловые моменты начальной и конечной волн должны быть малы,
чтобы налетающая частица смогла приблизиться к мишени. Так
как сумма этих угловых моментов должна быть больше или равна
L, то они оба не могут одновременно быть произвольно малыми.
С помощью выражения (7.22) для амплитуд перехода можно так-
же рассчитать [8, 39] угловое распределение фотонов при высвечи-
вании ядра и электронов внутренней конверсии. В противополож-
ность анализу полных сечений полуклассическое рассмотрение
процессов, происходящих при высвечивании ядра, часто является
222
f)
Рис. 7.6. Угловые распределения рассеянных частиц в кулоновском возбуж-
дении.
Кривые получены с помощью полуклассической формулы (7.33) и аналогичного вы-
ражения для магнитных переходов. Оии изображают величины dfb(6, £)/d£2 как функ-
цию угла в при фиксированном Сечения для электрических мультиполей норми-
рованы на единицу при 180°, а для магнитных мультиполей нормированы так, чтобы
Дать единицу для полного сечения [8].
недостаточным и оказывается необходимым переход к последова-
тельному квантовомеханическому описанию.
Существенным недостатком полуклассического анализа куло-
новского возбуждения является пренебрежение потерей энергии
на траектории налетающей частицы. Если попытаться улучшить
это приближение способом, который будет учитывать различия меж-
ду начальными и конечными параметрами, следует использовать
теорему взаимности [43]
(2^ + 1)/г? o^f=(2Jf+\)k2to{^,
(7-40)
где Oi-rf и — сечения прямого и обратного процессов, k,
и kf — волновые числа налетающей частицы для каждого из этих
процессов. Тогда для должно выполняться соотношение
«г Л
(7-41)
где ,Т О’, /) — функция, симметричная по начальным и конечным
параметрам.
Простой способ симметризации полуклассических результатов
заключается в замене параметров а и £ выражениями
Z^e2
а = -	—
MvjVf
ZtZ2e2 / _1___IX
А \ Vf V( I
(7.42)
(7.43)
где Vi и vf — начальная и конечная скорости налетающей частицы
Поскольку f (t) — четная функция t, выражения
6fCT£L=/^-VG-2^+2B(£L; J.^J )dfEL(6, g),	(7.44)
\ hvt }
^-a~2L+2 В (ML- Ji-^Jt}dfML(Q, g) (7.45)
\ ЙС j Vi
являются симметричными. Кроме того, предположения (7.42) и
(7.43) согласуются с формулами (7.10) и (7.31) в наинизшем порядке
по (Ер — Еа)1Еа.
Полуклассический результат может быть еще улучшен 139,
стр. 37] с помощью дополнительной замены, которая вытекает из
принципа соответствия для частиц в кулоновском поле. Это улучше-
ние заключается в замене числа Зоммерфельда rj = Mvalti величиной
2(П? + 1)(^ + 1) l1/s
(4? + 1),/г+(т1Н1),/> _
(7.46)
224
что, если выразить сечение (7.34) только через т), приведет к сле-
дующему выражению для
oel = —
П/
(л! + 1)1/г+(п| + 1)1Л
2(4? + l)(Tlf+I)
(4L— 6)/3
Л2
ZiZ2e2M
В (EL\ J, -- Jf)
(?г е)2
(7.47)

Симметризация с помощью формул (7.42) и (7.43) дает выражения
для полных сечений, согласующиеся в пределах нескольких про-
центов с результатами квантовомеханического рассмотрения, кото-
рое будет проведено в следующем параграфе. Это справедливо для
значений г|^3 и вплоть до £ = 2. Однако отклонения от квантово-
механических результатов при использовании формул (7.42) и (7.43)
для расчета дифференциальных сечений могут быть велики, и в этом
случае замена по формуле (7.46) может дать значительное улучше-
ние.
§ 7.2.	Квантовомеханическое рассмотрение
кулоновского возбуждения
При обсуждении кулоновского.возбуждения с точки зрения кван-
товой теории удобно воспользоваться некоторыми из наших ре-
зультатов для электронного рассеяния. Будем рассматривать ядро-
мишень фиксированным в процессе рассеяния, т. е. не будем учи-
тывать его отдачу, и расположим начало нашей системы коорди-
нат в центре заряда ядра. Поскольку при кулоновском возбуждении
частица не проникает внутрь распределения заряда, то эффект элек-
трической монопольной компоненты в электромагнитном взаимо-
действии сводится только к изменению начальной и конечной вол-
новых функций частицы. Эти волновые функции мы будем брать
в виде нерелятивистских кулоновских волновых функций. Матрич-
ный элемент взаимодействия, которое приводит к возбуждению ядра,
в лоренцевской калибровке имеет вид [см. (5.22)1
„	.	1 Ге‘*о1г~r'l
<f %' I О =-----т --------— [<₽ I j (г) I а> • J (г')-
С2 J | Г — Г I
—IPN (r) I а> Рг (r')l dr dr',	(7.48)
где J (г') — ток перехода для налетающей частицы, ре (г') — соот-
ветствующая плотность заряда. Разложение функции Грина по
мультиполям приводит к выражению (5.31). Поскольку в процессе
кулоновского возбуждения заряд частицы не может проникать
внутрь распределения заряда мишени, то членами с г' < г в (5.31)
следует пренебречь, а нижний предел в оставшихся интегралах по
225
пространству налетающей частицы может быть с хорошей точностью
заменен точкой начала координат. Тогда
2 f <Р I j (г) |«>-А£м (г; a)drx
с LM^a=e. l.nio
X J J (r')- Bzjw (r'; a) dr'—c2 J <p | рЛ' (r) | a) jL (k0 r) Y*LM(r) drx
о	о
X J pe (г') hL (k0 r') Ylm (?) dr'j	(7.49)
о
Используя формулу (2.65) для продольного мультиполя, интегрируя
(7.49) по частям* и применяя уравнения непрерывности для токов
мишени и налетающей частицы, получаем, что продольные и скаляр-
ные мультиполи взаимно уничтожаются. Матричный элемент взаимо-
действия принимает вид
2 f<₽|j(r)|a>X
с lm a=e, m "
X Alm (r; a) dr J J (r') • BLA( (r'; a) dr’,	(7.50)
0
или
<f I I 0= -4.4 2 —-1— (-if {<k, 191 (EL, Л4) I kt> x
LM
X <p1да(EL,—M) I a>—<kjJI (ML, M) | kf> <|31 да (ML,-M)|a»,(7.51)
где
™lm = ;L+i+,?ln f j (r) •v X L (jL (k0 r) Ylm (r)) dr, (7.52а)
"О C (L -p 1) J
Wlm (m) = - y2L + l)" f j (Г) • L (jL (k0 r) Ylm (r)) dr. (7.526)
ftoc(L4-l) J
®LM = ", /97° nil f J •v' XL' (Al (k0 r') Ylm (?)) dr', (7.52b)
CL iZL — 1) 11 v
аЛ4-1	«
®LM <m) = n„ f J <*')• L' M	(П)dr'- <7-52r)
Мы воспользовались формулами (2.84). Вид выражений (7.52) вы-
бран так, чтобы в пределе малых потерь энергии, т. е. при k0R 1
* Для отрицательно заряженных дираковских частиц, движущихся
в поле точечного ядра, нолновые функции имеют особенности в начале коор-
динат, что приводит к конечным поверхностным вкладам вблизи начала коор-
динат. В этом случае удобно выбирать так называемую «условную калибров-
ку» [287, 113], для которой поверхностные вклады равны нулю.
226
(что всегда имеет место для кулоновского возбуждения), с помощью
(4.71), (4.77) и (4.78) можно было получить
№lm (е)=(2Д.11)!! i 1/ 7V7 f j (r) • Атм (г; е) dr (е) (7.53а)
и
^LM(m) &LM (’«)•	(7.536)
Таким образом, приведенные вероятности перехода
!—	|<Р1^г.м(а)|а>|2, а=е, >п, (7.54)
2Ji + l MtMf
совпадают в этом пределе с приведенными вероятностями перехода,
входящими в выражения (7.24) и (7.36).
Нерелятивистское дифференциальное сечение в случае, когда
не учитывается ориентация ядер мишени, может быть записано
в виде
do=-^-^--------— у |<f|^'|i>|2JQ=
(2лй2)2 vt 2Jt + l	11
2 'Д(т+п.',')21<к<1а!ьм(.)|1<,>|ЦВ. (7.55)
h v‘ l a=e,[in	м
где состояния после акта рассеяния нормированы так, чтобы асимп-
тотически получить волну, описывающую одну частицу в единице
объема.
Для нерелятивистских частиц при вычислении интегралов по
пространству частицы можно воспользоваться длинноволновым
пределом, поскольку
kr'= 1г'(7.56)
\ V ) с ~ с
(ибо для r'w'v > 1 взаимодействие становится почти адиабатиче-
ским и вероятность возбуждения весьма мала). Тогда
hL (М — i (2L~l2'!	(7.57)
'O,kQr>0 (V) +1
Полагая, что заряд Zxe налетающей частицы находится в точке
Гр, имеем из (7.52)
(е) = Уш (ip)	(7.58а)
гр
и
(,n)=“ST L' V' (7^ Ylm <r'J) 	(7-58б)
227
Здесь мы не учитывали вклады, обусловленные магнитным моментом
частицы. В случае электрических переходов эти поправочные члены
[как можно видеть из (4.77)] имеют порядок величины (ц/с)2. Для
М/.-мультиполей cq > 1 в рассеянии участвуют большие орбиталь-
ные угловые моменты и вклад от членов, оставленных в выражении
(7.586), преобладает над вкладом от магнитных моментов [см. (4.78)1.
С помощью выражений (7.55) и (7.58) можно теперь написать
da= + d<jML),	(7.59а)
Ь=1
где
doEL= (^Ya~2L+2B(EL; Ji-^dfEL^, Ль Ю (7.596)
\ hvt I
и
doML =	a~2L+2 В (ML; 'Jt -> Jf) dfML (0, Ль g). (7.59в)
\ he / vi
Здесь а дается формулой (7.42) и
dfEL (6, Ль g) =_^-й2^2 2 I <к/ I rp~L~ ' VLM (Гр) | kf> |2 dO.,
(7.60а)
dfML (6, Ль £) = ,24* пз- 2 I < к/1 ч • vp (г-ь-  ylm (F,))|кг> |2Ж.
м
(7.606)
Вид выражений (7.60) выбирается так, чтобы формулы (7.59) нахо-
дились в соответствии с полуклассическим результатом (7.32). Кро-
ме того, в пределе
оо
функции dfEL(®, £) стремятся к классическим функциям
dfEL (0, Ю (7.33); для магнитных мультиполей также получаются
соответствующие результаты. В этом пределе параметр адиабатич-
ности записывается в виде
£=Л/—Ль	(7-61>
что согласуется с формулой (7.43).
Полное сечение кулоновского возбуждения получается интегри-
рованием (7.59) по всем направлениям вектора kf:
vEL= (— Ya~2L+2B(EL; Jf) fEL^it g),	(7.62a)
\ flVi /
—a~2L+2B(ML; Jf)fML(r]h E), (7.626)
'Wb \ he ) Vi
где
d/(e,^b|)	(7.62b)
dQ
Г(ъЛ)= J
228
Матричные элементы в пространстве налетающей частицы мож-
но вычислить, раскладывая нерелятивистские кулоновские волно-
вые функции по парциальным волнам. При этом волновая функция
начального состояния берется в виде произведения падающей пло-
ской волны и выходящей сферической волны, в то время как волно-
вая функция конечного состояния в асимптотической области пред-
ставляет собой произведение плоской волны и входящей сфериче-
ской волны. Соответствующие разложения имеют вид [320]
| кг> = 2 4я (-	>' ei°z<’,{) Yi-m (кг) У1т(Гр) , (7.63а)
"	kirp
IM =24л(-1)“ И е~ io*(V Hz_m (ку) F,m (г )	r?;), (7.636)
lm	kfrP
где величина
oz (rj) = arg Г (/ + 1 + it])	(7.63b)
является кулоновским фазовым сдвигом, (krp) — регулярное
решение радиального волнового уравнения для орбитального угло-
вого момента /. Это решение имеет асимптотический вид
Fi (*rA^osin [krp ~ —Л In (2krrJ) + oz (л) j.	(7.63г)
Используя соотношение (ПА.26), получаем
<k/|r/-1FLM(rp)|ki> =2 2 (4л)3/2 i'-'/x
/jOTj Ijmj
х el(ai+af\— 1)л(	(/. Llf 1000) (/, Llf I	x
XYi._m. (k.)yZ/m/(kz) Mt.(7.64a)
где
M^~L ~ = 7Г J F‘f r7L~lF‘i drP <7-646)
' f о
и
Ог>/= O,z /(rii,,).
Таким образом,
(t \ *2 ' 2 2 '2
o..|.O/_az-Of) illicit 1)L	! 000)	! 000)x
x м1[1, (~L- 0 M‘i‘f (~L~ П2 (-1)‘ Vi I'd I ooo) (/z г, /|ooo) x
X’U7(/z///;/f'; Ll)Pl (cos 0),	(7.65a)
fEL^h g)=
(7.656)
229
Аналогично для магнитных мультиполей *
<к, I Lp. vp (r-L-' Ylm (?p)) I кг> = 2 2 (4л)3/2 (- i)'~'/x
‘imi lfmf
X^ai+at\-\)X+mi2l^L+\)[L (А+1)(/г+1)(2/г+3)(27/+1)-Ч1/2х
X (liLlf | (It + lLlf | 000) W (LLlt + \lt\ 1/y) X
хУ/._т. (k;) Ylflf(kf)	(7.66)
и
Гла(Пь ^ = ^^2 a2L~2 2(2/г)2(2/г+1)(/г + 1)Х
X^lf + ^^i+UfL^^W^LUi + Ue, \lfY	(7.67)
Радиальные интегралы (7.646) можно вычислить точно. Их матема-
тические свойства обсуждаются в работе [8].
Из полученных квантовомеханических результатов следует, что
возможность использования полуклассической формулировки при
анализе экспериментов по кулоновскому возбуждению является
большим упрощением задачи. Чтобы обсудить область применимо-
сти полуклассического подхода, удобно ввести в рассмотрение вол-
новые функции налетающей частицы, полученные методом ВКБ. Это
позволит получить квантовомеханические результаты в полуклас-
сическом пределе. Конечно, можно также воспользоваться результа-
тами метода ВКБ в качестве хорошего приближения для случаев,
когда т[ >• 1, но классический предел г] 1 при этом не дости-
гается .
Радиальные волновые функции (7.63) в приближении ВКБ имеют
вид [302, 247, 2531
Fi (krp) = If (TjJk2^'1' sin ср,	(7.68a)
где
f(rp)==^gfe4	(7.686)
rP	r p
и
<p — — л-|- J [f(r)]1,2dr.	(7.68b)
ro
Выражение (7.68a) справедливо всюду, кроме классической точки
поворота г0, определяемой из уравнения f (rn) = 0. Вкладом в ма-
тричный элемент при гр < г0 пренебрегаем. После подстановки
выражения для Fi (krp) в (7.646) получаем член, содержащий сумму
начальной и конечной фаз фг + фу, и член, содержащий разность
фг — фу. Подынтегральное выражение для первого из этих членов
230
быстро осциллирует и здесь не учитывается. Для второго члена
разность фаз записывается в виде
Фг~Ф/»(^г—f^[f(r)]~,/2dr~~
г0
Гр	1
-[//(/z + D-Z/^ + DlJ [Ur)]-х 12	dr. (7.69)
го
Введем
krp — [г12 + /(/ + l)J1/2ch и>Д г|	(7.70)
и возьмем интеграл в (7.69); в результате получим
ср/—tpf »^(eshm4-tt))4-u,arccos e+ch m ,	(7.71)
1+e ch t£)
где
8= [!+/(/+ 1)/V]1/2, M =	(7.72)
Радиальные матричные элементы в (7.646) принимают вид
ЛД./.+Л)(—L — 1)
kL~2
£i| (eshw-|-E>)
4т]‘
[ch ш-ре-р i Kf'2—j	jyjM
[e ch to 4- 1]L+W	“
(7.73)
что по форме совпадает с полу классическим результатом (7.30).
Выражение (7.72) есть прямое обобщение выражения для классиче-
ского эксцентриситета (7.11), а М является угловым моментом,
переданным в направлении, перпендикулярном плоскости орбиты.
Для угла отклонения классической орбиты, определяемого формулой
(7.11), получаем
hL- 2
Ж,.+Л1(-£-1) = 4-г-/£Л)(е, g).
1 i
(7.74)
Полуклассические результаты для дифференциального и полного
сечений можно получить [8], заменяя коэффициенты при угловом
моменте в выражениях для dfsL.ML и [el, ml их предельными выра-
жениями для параметров при большом угловом моменте и исполь-
зуя формулу / = т] cos у 0. Вообще для значений т] между 1 и 10
результаты, полученные методом ВКБ, вполне хорошо согласуют-
231
Рис. 7.7. Сравнение результатов
точного квантовомеханического
расчета (7) с результатами бор-
новского приближения с плоскими
волнами (2) и полуклассического
приближения (3).
Кривые относятся к электрическому
квадрупольному переходу для случая,
когда не учитываются потери энер-
гии [8].
ся с квантовомеханическими ре-
зультатами. Для Т] 10 во многих
случаях оказываются пригодными
полуклассические расчеты.
Наконец, заметим, что для ку-
лоновского возбуждения может
быть использовано приближение
Борна с плоскими волнами в том
же духе, как и в § 5.3 для элек-
тронного рассеяния. Однако ре-
зультаты БППВ не годятся для
кулоновского возбуждения, кроме
области очень малых значений т].
Сравнение квантовомеханических
расчетов, результатов БППВ и ре-
зультатов полуклассического при-
ближения показано на рис. 7.7.
Видно, что для больших значений
ц БППВ существенно завышает
величину сечения. Это происходит из-за нереалистически больших
вкладов малых прицельных параметров, которые в действитель-
ности подавлены кулоновским отталкиванием.
§ 7.3. Многократное кулоновское возбуждение
и реориентационные эффекты
При использовании для кулоновского возбуждения тяжелых
ионов в качестве налетающих частиц вероятность индуцированных
переходов может стать достаточно большой, так что в результате
ряда последовательных переходов будут возбуждены относительно
высоколежащие уровни. Например, если ядро-мишень деформиро-
вано и имеет ротационную полосу с последовательностью уровней
0+, 2+, 4+, 6+, ..., то можно возбудить 4+-уровень путем Е2-перехода
из основного состояния 0+ в 2+-состояние и последующего Е2-пере-
хода из 2+- на 4+-уровень. Вероятность такого процесса может
намного превосходить вероятность прямого Е4-перехода из основ-
ного состояния в состояние 4*. Цепочка переходов такого типа до-
пускает кулоновское возбуждение уровней со спинами вплоть до
14+ [324]. Это расширяет возможности использования кулонов-
ского возбуждения, поскольку увеличивается число ядерных уров-
ней, наблюдаемых в указанном процессе, и появляется возможность
наблюдения вероятностей Е2-переходов между возбужденными со-
стояниями.
Расчеты многократного кулоновского возбуждения могут быть
выполнены с использованием конкретных ядерных моделей. В част-
ности, главные свойства этого процесса могут быть получены [391
путем рассмотрения ядер как жестких ротаторов или с помощью
анализа поверхностных колебаний сферических ядер. Могут быть
232
введены также и более сложные способы описания структуры ядра
[101, 179]. Создание больших программ для вычислительных
машин [357] также делает возможным выполнение весьма общих
расчетов многократного возбуждения. Такие расчеты затрудняются
тем, что для высоколежащих уровней, вероятность возбуждения
которых нужна в расчетах многократных процессов, нельзя пользо-
ваться теорией возмущений в первом порядке. Необходимо исполь-
зовать теорию возмущений более высокого порядка или численно
решить зависящее от времени уравнение Шредингера. Тем не ме-
нее, с целью получения главных свойств многократного кулонов-
ского возбуждения мы рассмотрим описание процесса, основан-
ное на теории возмущений в наинизшем порядке и на использова-
нии полуклассического приближения для тяжелых налетающих
частиц. Самым низким порядком теории возмущений, который дает
возможность выйти за рамки однократного возбуждения, является
второй порядок, что позволяет рассмотреть процессы двукратного
возбуждения. При формулировке теории возмущений для двухсту-
пенчатого процесса проявляется одно из важных свойств многократ-
ного возбуждения, а именно его зависимость от статических свойств
(в частности, от квадрупольных моментов) возбужденного состоя-
ния*.
Во втором порядке теории возмущений амплитуды перехода
в формулах (7.17) должны быть заменены величиной
<’=^ + 2^	(7-75)
v
где
оо
f <РI(01 Y> ei(£₽-£v>z/Mx
<1Й) Л
t
X ^\Ж^')\а)е'(Еч~Е^1'1пМ',	(7.76)
и величина дается выражением (7.176). Суммирование в фор-
муле (7.57) выполняется по всем промежуточным состояниям |у>.
Вводя ступенчатую функцию
©(/-/') =

f 1, t>t',
[ 0, t < t',
(7.77)
* Следует заметить, что многократное кулоновское возбуждение тесно
связано с дисперсионными эффектами в рассеянии электронов, кратко рассмо-
тренными в конце § 5.6. Конечно, последние учитывают только малую поправ-
ку в рассеянии электронов, поскольку налетающая частица всегда имеет
заряд, равный единице. Многократное кулоновское возбуждение также тесно
связано с эффектом поляризуемости ядра в мюонных атомах (см. ниже § 8.2).
233
где 8 — действительное положительное число, стремящееся к нулю
можно выполнить интегрирование по времени в выражении (7.76)’
Тогда
сю
frpv« =	f FT- (£P-£v~E) b'"(Ev-Ea + E)dE =
2л i J E4-18
—oo
= A-fcU) (E^-Ey) (Ey-Ea)~
oo
E f Ь^(Е^-Еу-Е)Ь^(Еу-Еа + Е)-^-,	(7.78)
>ni J	E
—oo
где было использовано
1	? P
E-pie e-o £
i-чб (E).
(7.79)
Здесь P обозначает интеграл в смысле главного значения. Послед-
ний член в (7.78) дает вклады от двух амплитуд переходов перво-
го порядка, которые находятся вне энергетической поверхности.
Предположим теперь, что промежуточное состояние получается
из основного состояния в результате электрического перехода муль-
типольности Li, а конечное состояние — из промежуточного в ре-
зультате электрического перехода мультипольности Т2. Тогда
амплитуда перехода (7.75) во втором порядке теории возмущений
может быть записана в виде [см. (7.22) — (7.24)]
Ь$ = 2 I М^М,) -Ц <Р || й2 (е) || а> SEL, м +
LM	I 1 -р 1
X < 4^\2 V £J ----1-------1--uz (J£1 J L2; JnL)x
^2( Hi ) п 2Li + l 2L2 + 1	1 ' 1 1 п ’
х <₽ ||	(е) || TXT I) Ql. (е) ||	(taY, gvP, 0) р
+ iJ^M(EaY> ёуР, 0)1],	(7.80)
где введены действительные функции
?ур, 9) = 2(ii7-2b|Al17W-M1/W)X
xSellM, (Е у—Ea) Sel2,n—Mi(E[\—Еу),	( 81а)
(taV, gvP. 6) = 2 (.LiL.L | MiM-M^X
Ml
p
X--- I SeLi, Mi (Ey — Ea + E) S EL2, M — MtX
234
X(E$—Ey—E)dE/E,	(7.816)
и аргументы функции Sel.m определяются частотой в экспоненте
выражения (7.23)*.
Вероятность возбуждения и дифференциальное сечение во вто-
ром порядке теории возмущений могут быть рассчитаны по форму-
лам (7.16) и (7.17). Используя /?ра из выражения (7.80), получим
величину вида
Р = Рп + Л-2 + Р22 « Рп + Л2.	(7- 82)
где Рц — результат, полученный в первом порядке теории воз-
мущений, Р12 — интерференционный член и величина Р22 билиней-
на по амплитудам второго порядка. Поскольку мы не будем рас-
сматривать интерференцию между амплитудами в первом и третьем
порядках, которые имеют тот же самый порядок величины, что и
Р22, то последний член должен быть опущен. Чтобы увеличить
точность наших полу классических результатов, следует выполнить
симметризацию параметров в соответствии с формулами (7.42) и
(7.43).
Особенно интересное применение находят результаты, получен-
ные во втором порядке теории возмущений, если промежуточное
состояние |у> является одним из магнитных подсостояний на-
чального или конечного состояния | а> или |р>. Процесс, описы-
ваемый такими характеристиками, принято называть эффектом
реориентации. Пример этого процесса иллюстрируется рис. 7.8,
где показаны процессы первого, второго и третьего поряд-
ков, приводящие к подсостоянию Mf = 0 возбужденного 2+-сос-
тояния ядра. Развитый здесь формализм, конечно, неприменим
к процессам третьего порядка, но может быть использован для
вычисления интерференционного члена, связанного с вкладами
первого и второго порядков. Оказывается, что он содержит ин-
формацию о статическом квадрупольном моменте возбужденного
2+-состояния. Физический смысл этого можно понять следующим
образом: рассмотрим ситуацию, в которой деформированное ядро
возбуждается кулоновским способом из его основного состояния
в первое возбужденное 2+-состояние. Заряженная налетающая
частица может продолжать взаимодействовать со статическим квад-
* Эти функции связаны с величинами а и р, фигурирующими в работе
[8]. соотношением
(lay ?т₽. 9) ]
Li> (Uy- ёур- 0)J
= (__n4 + L,+M I -2 — L,—|LS (aL-M (Д1’ bay- bTp- 6)1
l₽L-M (Й- gyp. 6)1’
235
рупольным моментом такого возбужденного состояния, вызывая
реориентацию момента.
В рамках нашего формализма подобную ситуацию нетрудно
объяснить выбором квантовых чисел | у), которые являются магнит-
ными подсостояниями состояния | р>. Рассмотрим конкретный слу-
чай, описанный в предыдущем абзаце, взяв начальное состояние
со спином = О, а конечное состояние со спином Jf = 2. Чтобы
применить формализм второго порядка теории возмущений, пред-
=2
1
О
-1
-2
0+
Рис. 7.8. Кулоновское возбуждение первого, второго
и третьего порядков для перехода из основного со-
стояния 0+ в возбужденное подсостояние с Mf=0 со-
стояния 2+.
положим также, что вблизи интересующего нас состояния | р> не
имеется других 2+-состояний. Тогда главным эффектом второго
порядка будет эффект реориентации. Из выражения (7.80) получаем
Ь& =	| <Р, Jf = 21| Q2 (е) || a, Jt = 0> х
1П D
X К . +	<₽, Jf = 2II Q2 (е) II р, Jf = 2> х
(	7	10 vi
х i-c; <и, °.0)+^(2м2; (^р> о> 6)1} -	<7-83)
где второй приведенный матричный элемент связан со статическим
квадрупольным моментом Q состояния с | р> следующим образом:
<Р, J/=2||Q2(e)||p,	=	^Q.	(7-84)
236
С помощью (7.82) и (7.17а) получаем для вероятности кулоновского
возбуждения
Р « Pn +Р12	I <Р, Jf= 2IIQ2 (e) IIa, Jt = 0> |2
Zo \ fl j
yf г c i2 I 1	e \
| SE2, M. |2 + — —-±- X
“I ’	5\ k J
X <P, Jf= 21| Q2 (e) || 0, Jf = 2> SE2, (ga₽, 0, 0) j. (7.85)
где функция Л(22> вклада не дает, так как все функции ^<22), ®<22
и SE2 действительны*.
Выражения (7.83) и (7.85) показывают, что во втором порядке
теории возмущений кулоновское возбуждение 2+-состояния зави-
сит от двух ядерных величин, а именно от приведенного матричного
элемента перехода
<₽, У/ = 2||Й2(е)|| a, Jf=0>
и статического момента Q возбужденного 2+-состояния (разумеет-
ся, другие эффекты второго порядка могут вызывать интерферен-
цию; они могут дать поправку 10—15% 1101, 1791). Эти два пара-
метра можно получить, если проводить эксперименты по кулонов-
скому возбуждению при двух различных энергиях бомбардирую-
щих частиц, при двух различных углах рассеяния или с двумя
различными налетающими частицами, имеющими различные заря-
довые числа Zi. Таким образом, можно довольно просто исполь-
зовать кулоновское возбуждение для того, чтобы извлечь ин-
формацию о квадрупольных моментах** возбужденных состояний,
которая не так легко получается другими методами.
* *
*
Самый ранний общий обзор 181 по кулоновскому возбуждению
является работой, которую до сих пор можно считать одной из
наиболее полезных работ по этому вопросу. Другие обзоры даны
Брейтом и Глукстерном [54], Биденхарном и Бруссардом [391
и Ньютоном [260]. Основные статьи о кулоновском возбуждении
собраны в книге, изданной под редакцией Альдера и Винтера [11].
Обзор реориентационных эффектов в кулоновском возбуждении
Дан Де-Боером и Эйчлером [92].
* Таблицы функций для расчетов реориентационного эффекта во втором
порядке теории возмущений даны в работе [92].
** См. также гл. 3 в т. I.
ГЛАВА 8
МЮОННЫЕ
АТОМЫ
I
Из классической атомной спектроскопии хорошо известно,
что для получения информации о ядре атома могут быть использо-
ваны данные анализа эффектов сверхтонкой структуры*. В част-
ности, с их помощью можно получить сведения о спине основного
состояния ядра и о магнитном дипольном и электрическом квадру-
польном распределениях. Для изучения некоторых свойств ядер
могут быть использованы также данные о сдвигах уровней в атом-
ных спектрах различных изотопов. В легких ядрах эффекты при-
веденной массы вызывают изменение энергии связи атомов. Для
более тяжелых ядер эти эффекты играют маленькую роль. В таких
ядрах энергия связи может уменьшаться вследствие проникнове-
ния электрона внутрь ядра, в результате чего он становится чув-
ствительным к меньшему эффективному ядерному заряду. Для
деформированных ядер, в которых величина деформации может
изменяться от изотопа к изотопу, эффект проникновения электрона
в ядро можно использовать для измерения изменений деформации
ядер [51, 52, 219].
Спектроскопические исследования подобного рода могут быть
выполнены и для системы, которая имеет отрицательный мюон,
находящийся на атомной орбите. Поскольку масса мюона в 207 раз
больше массы электрона, радиус воровской орбиты для мюона
в 207 раз меньше радиуса электрона в водородподобном атоме
с тем же самым зарядовым числом Z. Вследствие этого мюон много
времени проводит вблизи ядра и является таким образом очень
эффективной «пробной частицей» для изучения ядерной структуры.
Например, мюон в 203РЬ имеет самую низкую боровскую орбиту
радиусом около 3,2 фгрми. тогда как радиус ядра составляет приб-
лизительно 7,1 фгрми. Оказывается, что мюон на атомной орбите
1s в Pb проводит около половины времени внутри ядра. Энергия
связи уменьшается от ее значения 21,3 Мэз для точечного ядра до
10,1 Мэз для ядра конечных размеров. Таким образом, эффекты
тонкой структуры и гроес-струкгуры в мюэннык атомах могут
* Краткий обзор информации о структуре ядра, поручаемой на основе
изучения электронных атомоз (а также мюэнных и пионных атомов), не-
давно был дан Сенсом [313] (см., кроме того, [218, 227, 335, 354]).
238
быть использованы для определения параметров плотности заряда
ядра в основном состоянии.
Оказывается, что сверхтонкая структура мюонных атомов осо-
бенно чувствительна к электрическому квадрупольному распреде-
лению в ядре. Об этом можно судить по величине (e2Q/v/r3) /(PuPw/r®),
характеризующей относительную роль Е2-и М1 -взаимодействия
частицы с ядром, где Qn — квадрупольный момент ядра, рл< — его
магнитный дипольный момент, ри— момент мюона, г—средний
радиус орбиты. Для электронов это отношение близко к единице,
поэтому при определении положения энергетических уровней
в атоме £2- и АП -моменты играют сравнимую роль. Для мюонов,
напротив, это отношение равно приблизительно 200 и, таким об-
разом, можно извлечь сведения о £2-эффектах с относительно
малой примесью АН-эффектов.
Помимо определения статических квадрупольных моментов
ядра, изучение сверхтонкой структуры мюонных атомов позволяет
получить сведения о квадрупольных моментах при переходе из
основного состояния. Это связано с те^, что низколежащие рота-
ционные состояния сильно деформированных ядер имеют энергии
возбуждения порядка 100 кэв, которая сравнима с эффектами тонкой
структуры в рентгеновском спектре мюонных атомов. Существует
также динамический £2-эффект, в котором мюон поляризует ядро,,
приводя к смешиванию основного состояния ядра с различными
возбужденными состояниями, а также к смешиванию и расщепле-
нию мюонных состояний. Таким образом, измерение параметров
сверхтонкой структуры позволяет определить знак и величину
квадрупольных моментов возбужденных состояний способом, кото-
рый имеет много общего со способом, импользуемым при изучении
многократного кулоновского возбуждения (см. § 7.3). Эксперимен-
тальное наблюдение таких эффектов сверхтонкой структуры полу-
чило большое развитие благодаря использованию германиево-
литиевых детекторов с очень высоким разрешением [362, 313].
При анализе этих данных необходимо учитывать эффекты поля-
ризации вакуума [249, 141, 142]. Из-за близости мюона к центру
кулоновских сил поляризация может приводить к энергетическому
сдвигу в несколько десятков килоэлектронвольт для атомных
уровней 1s в тяжелых ядрах и к сдвигу в несколько килоэлектрон-
вольт для 3d- и 4/-уровней в этих ядрах.
§ 8.1. Сферическое распределение статического заряда
Получение информации о распределении заряда в основном
состоянии ядра из рентгеновских спектров мюонных атомов требует
решения радиального уравнения Дирака для потенциала, созда-
ваемого предполагаемым распределением заряда. Это уравнение-
получено в § 3 приложения Б. Из (ПБ.64) имеем
[•ТоС-Н	+ - — -К1)— ^ф(г)+₽-^гПф(г) = £ф(г), (8.1)
L \ or г г ’ he	nJ
239
где ( — е) и — заряд и масса мюона, ip (г) — спинорная волно-
вая функция и величина
K=|3(<r-L + 1)	(8.2)
выражается через оператор орбитального углового момента
L = — ir X V. В уравнении (8.1) ф (г) — центральный электро-
магнитный потенциал, создаваемый предполагаемым распределе-
нием заряда р (г); ф (г) дается выражением
Ф (г) = 4л
(8.3)
Как и в (5.96) — (5.101), введем собственные состояния орбиталь-
ного и полного углового моментов I и /, взяв решения уравнения
(8.1) в виде
=

(8-4)
где х—величина, противоположная по знаку собственному зна-
чению оператора К, и
/=|х|-1,	(8.5а)
х для х >0,
—х—1 для х<0.
(8.56)
Собственная функция оператора К берется в виде
(8.6)
tn \ £	J
где х"1—спинор Паули, р—собственное значение оператора \г.
В результате получаем систему радиальных уравнений
4-= — f-^(£-/nuc2 + «p(r))g(r),	(8.7а)
аг г пс
_2S±lg + J_(£ + mgC2+e(p(r))f(r)	(8.76)
dr	г пс
с нормировкой, удобной для связанного состояния
J (Л+g2) r2dr= 1.
О
240
Решения системы уравнений (8.7) для точечного заряда, конечно,
хорошо известны, и соответствующие собственные значения даются
формулой [302 J
Г	(ге/йс)2 ]~1/2	1!	Г89)
где
Yx=[x2—(ZeW)z]'/2	(8-Ю)
и п — главное квантовое число. Для мюонных атомов анализ от-
клонения от приближения точечного ядра особенно важен. Анализ
данных по рентгеновским спектрам проводился во многих случаях
с помощью зарядового распределения Ферми [даваемого выражением
(5.78)1
= (8Л1)
ж -q— t
где толщина поверхности t определяется формулой
Z= 4а In 3^4,40 а,	(8.12)
С — радиус распределения плотности заряда. Нормировочное зна-
чение ро имеет вид [см. (5.81)1
так что
J р (г) dr = Ze.	(8.136)
При получении конкретных численных результатов [2, 31 выра-
жение (8.11) с различными предполагаемыми значениями С и а
подставляется в формулу (8.3) и выполняется численное интегри-
рование. Полученный потенциал ср (г) используется в уравнениях
(8.7) вместе с исходными предположениями для собственных зна-
чений Е, вычисленных из выражения (8.9) для точечного ядра.
Затем радиальные уравнения Дирака решаются численно. Найден-
ные таким образом функции сравниваются на больших расстояниях
с известными решениями для точечного ядра, и предполагаемые
собственные значения Е модифицируются до тех пор, пока не полу-
чается удовлетворительного согласия.
При конкретном применении этой процедуры наиболее важной
поправкой, которую следует учесть, является поправка, обусловлен-
ная поляризацией вакуума. Она возникает вследствие связи куло-
новского поля ядра с электронно-позитронным полем и приводит
к изменению эффективного заряда мюона, как показано на рис. 8.1.
Поправки, обусловленные поляризацией вакуума, для ядра конеч-
ных размеров получены в рамках теории возмущений Фордом и
Вилсом [141, 1421. Если боровский радиус мюона намного меньше
9 Зак. 1193
241
комптоновской длины волны электрона hlmc, то в низшем порядке по
ZeNnc энергия изменяется на величину
AEp = j(f2+g2)Vp(r)rMr,	(8,14)
где
<815>
<РДг) = 2л-^Ср(г')г'(|г-г'|[1п-^|г-г'|-11-
r j	(	[ й	]
Рис. 8.1 Диаграмма, описывающая наиболее существен-
ные эффекты изменения заряда мюона. Это изменение
обязано связи кулоновского поля (создаваемого заря-
дом ядра Ze) с электрон-позитроиным полем.
и £ = 1,781. Поправки от поляризации вакуума, обусловленные
членами более высокого порядка по Zezltic, были оценены в работе
13521. Они приводят к изменению энергии примерно на 0,01%, и,
следовательно, ими можно пренебречь.
В деформированных ядрах 198], где требуются более общие
формулы, чем (8.11), вышеописанная процедура применяется для
сферической части зарядового распределения и приводит к эф-
фектам гросс-структуры и тонкой структуры. Деформация зарядо-
вого распределения затем дает эффекты сверхтонкой структуры
(см. § 8.2).
В то время как для более тяжелых ядер почти всегда приходится
численно решать уравнение Дирака для предполагаемой феномено-
логической параметризации распределения ядерного заряда, в слу-
чае легких ядер можно анализировать рентгеновские спектры мюон-
ных атомов, относительно редко используя сложные расчеты на
электронно-вычислительных машинах. Для легких ядер отклонения
от спектра точечного ядра можно рассматривать по теории возму-
щений. Более того, соответствующие поправки пренебрежимо малы
242
для всех орбит, кроме орбиты 1s. Тогда, учитывая, что волновая
функция 1 s-электрона в водород подобном атоме для малых г имеет
вид [302]
WH ~	=	256 ФеРлш^ (8-17)
получаем для энергетического сдвига, обусловленного конечностью
ядра:
= ]4:s(r)(V(r)+^-^ls(r)ar= ^J(v(r)+^dr, (8.18)
где V (г) — потенциал, создаваемый зарядовым распределением
ядра конечных размеров (это распределение предполагается сфе-
рически симметричным). Так как V2rz - 6, имеем
A£“=AJ(^)+^)(iw)‘,r"
" J r’vT1/<г)+Т’) *= р 0 ** * (8-19)
Здесь мы дважды проинтегрировали по частям и воспользовались
уравнением Пуассона. Формула (8.19) показывает, что сдвиг в поло-
жении 1s-уровня зависит от единственного параметра — среднего
квадрата радиуса ядра. Для тяжелых ядер (когда необходимо про-
водить численное интегрирование уравнения Дирака) мюон более
глубоко внедряется в ядро и рентгеновские спектры становятся
более чувствительными также и к толщине поверхности ядра.
Поправки, обусловленные поляризацией вакуума, могут быть
рассмотрены для легких ядер также с помощью простого способа,
не требующего использования вычислительных машин. Для точеч-
ного ядра дополнительный потенциал, обусловленный поляриза-
цией вакуума, имеет вид [249, 281 I
(8-20а)
где
Д 2w2 ( 1 — — и2')
J ехР ^Z)^'dv (8,20б)
о
и
p—rtnclK.
Ту часть изменения энергии, которая обусловлена поляризацией
вакуума, можно вычислить, если воспользоваться теоремой вириала
<Vp1=^_^HpVC:=4_g.	(8.21)
<Е> лйс <1/г> япс
9*
243
Функция G может быть рассчитана, например, для круговых орбит
(/ = п— 1), если учесть, что для них
	ф(г) = ЛМе-'7а,	(8.22)
где N — нормировочная константа и
	—\=У— 	(8.23} т^е2Z ( m^Z 1\тс 1 J тс	v ’
Тогда	0
(8.24}
где в последнем выражении необходимо выполнить численные ин-
тегрирования. Это можно легко сделать, например, с помощью
формулы Симпсона, которая дает хорошую точность для значений
xt и w (хг), приведенных в табл. 8.1. Таким образом, необходимый
анализ по извлечению радиуса заряда ядра из рентгеновских спект-
ров мюонных атомов в легких элементах может быть сделан с хо-
рошей точностью без использования вычислительных машин.
(Величина эффектов, обусловленных поляризацией вакуума, при-
водится для некоторых тяжелых ядер в табл. 8.2.)
Таблица 8.1
Аргументы Xi и весовая функция w(Xj) для вычисления
интеграла в формуле (8.24) но правилу Симпсона
xi		xi	
0,05	1,7777	0,50	0,3464
0,10	0,4444	0,60	0,1399
0,15	0,5925	0,70	0,2258
0,20	0,3331	0,80	0,0880
0,30	0,5907	0,90	0,1210
0,40	0,2200		
Для более тяжелых ядер, когда мюон проводит заметную часть
времени внутри ядра, точность современных экспериментов с мюон-
ными атомами [362 , 313] позволяет получить информацию не только
о радиусе ядра, но также и о толщине поверхности зарядового рас-
пределения. Анализ, основанный на использовании распределения
Ферми (8.11) и подстановке полученного выражения для ф (г)
в уравнения (8.7), обсуждался весьма подробно [2, 3, 98]. Вообще,
измерение энергии перехода 2р — 1s в мюонных атомах позволяет
определить область возможных значений радиуса ядра С и пара-
244
Т а б л и ца 8.2
Примеры изменения энергии, обусловленного поляризацией
вакуума, кэв
Ядро	Уровень	Is	2Р.Д	2Р=/2	3ds/s	3d7.	4fs/l	4H/t
152Sm		46,5	17,0	15,6	4,1	3,9	0,9	0,9
190Os		60,0	27,0	24,8	7,6	7,1	2,1	2,0
238 (J		73,6	38,9	36,0	13,3	12,2	4,1	3,9
Примечание. Энергии рассчитаны по формулам (8. 14) —(8. 16)
(см.[270]).
метров толщины а или t. Чтобы зафиксировать эти величины,
можно воспользоваться в дальнейшем переходом 3d — 2р или
данными по упругому рассеянию электронов (см. §5.5). Допустимые
области значений С и t, которые получаются из спектров мюонных
атомов, приведены для трех довольно легких ядер на рис. 8.2
[2]. Для одного из них (ядра кальция) показаны также результаты
эксперимента по рассеянию электронов 1741. Общие результаты
экспериментов с мюонными атомами свидетельствуют, что в до-
вольно широкой области ядер (35^ Л ^209) опытные данные, по-
видимому, согласуются с зарядовым распределением Ферми, имею-
щим параметры 1362 , 313]
С » 1,1 ЗА113 ферми,	(8.25)
2,2 ферми.	(8.26)
Значения этих параметров находятся в разумном согласии со зна-
чениями, полученными из данных по рассеянию электронов
1см. (5.82) и (5.83)1.
Утверждение (8.25), согласно которому радиус ядра изменяется
как И1/3, требует некоторого обсуждения. Поскольку ядерное
вещество является весьма несжимаемым, то следует ожидать, что
распределение вещества в ядрах будет иметь радиус, который уве-
личивается с числом нуклонов как Л1/3. С другой стороны, ниот-
куда не следует, что зарядсеый радиус, который зависит только от
распределения протонов, должен изменяться по закону Л1/3. В дей-
ствительности можно даже качественно представить, что при добав-
лении нейтрона к данному ядру уменьшается зарядсеый радиус,
поскольку при этом увеличивается полная энергия связи, умень-
шая таким образом хвост протонного распределения.
Нарушение закона Л1/3 было получено [178] из анализа дан-
ных [56] о группе мюонных атомов, в которую входили различные
изотопы и изотоны. Нарушение зависимости Л1/3 для зарядового
радиуса также наблюдалось [41, 69] в спектрах рентгеновских
лучей для мюонных атомов 4°Са и 44Са. Эти эксперименты показали
245
Рис. 8.2. Допустимые области значений радиуса ядра С
и толщины поверхности t для 17CI, 2оСа, 2бРе, получен
ные из данных об энергии перехода 2р — 1s в соответ-
ствующих мюоиных атомах. Для soCa показаны также
результаты экспериментов по рассеянию электронов
[74, 12]:
4---электронное рассеяние для 20Са;
—-------—2eFe Е (2р 1s)	1256,4 ±2.4 кэв;
--------—о0Са± (2р > 1s) — 783,8 ± L5 К9б;
----17С1 Е (2р 1s) = 578,6 ± 1,5 кэв.
изменение в энергии перехода 2р — 1s для двух изотопов кальция
ЛЕ (40Са — 44Са)	0,9 ± 0,3 кэв или 0,65 ± 0,3 кэв. Эксперименты
по рассеянию электронов [1941 для этих изотопов дали ДЕ (40Са —
44Са) = 0,7 ± 0,3 кэв. Если бы зарядовый радиус ядра давался
формулой R 1,2 Л1/3 ферми, то эти энергии перехода 2р — 1s
должны отличаться на 2,8 кэв. Если зарядовый радиус фиксируется
и в качестве причины для изменения энергии перехода рассматри-
вается только эффект приведенной массы, то величина ДЕ должна
быть равна —0,2 кэв. Таким образом, эксперимент указывает на
относительно малое изменение зарядового радиуса ядра в зависи-
мости от А (см. [118, 3261).
§ 8.2. Эффекты сверхтонкой структуры
Кроме информации об общих свойствах зарядового распределе-
ния ядра, которое может быть изучено на основе анализа гросс-
структуры рентгеновских спектров мюонных атомов, можно полу-
чить более детальную информацию об этом распределении с помощью
изучения сверхтонкой структуры таких спектров. Близость атом-
ного мюона к ядру делает его достаточно чувствительным инстру-
ментом изучения электромагнитных моментов ядра более высокого
порядка, чем монопольный момент, который обусловливает эф-
фекты гросс-структуры и эффекты тонкой структуры. Кроме того,
магнитный момент мюона достаточно мал, поэтому ЛИ-вклад в эф-
фекты сверхтонкой структуры обычно* приблизительно на два
порядка меньше, чем Е2-вклад. Таким образом, квадрупольный
момент ядра может быть определен довольно однозначно.
Чтобы рассчитать эффекты сверхтонкой структуры, предпола-
гают какую-либо модель ядра и используют сбычное приближение
теории возмущений [302 J для вычисления энергетического сдвига,
обусловленного несферической частью зарядового распределения.
Этот сдвиг дается выражением
ЛЕ( = <i| Ж" 11> + V J I21	(8.27)
•“ E; — Eh
k^i	1 Л
где состояние, обозначаемое индексом t, описывает основное сос-
тояние ядра и состояние мюона, энергетический сдвиг которого мы
* Исключение составляет, например, переход 2р^2 -> ls[/2 в 2n9Bi. Это
ядро имеет один протон вне дважды замкнутой оболочки. Поэтому оно яв-
ляется почти сферическим, и для рассматриваемого перехода не имеется ква-
друпольного взаимодействия. Спин основного состояния 2MBi равен 9/2, и,
следовательно, магнитный момент велик (~ 4,08 ядерного магнетона). Анализ
сверхтонкой структуры в этом случае был проведен как для статического
[231], так и для динамического [306] эффектов (см. также [362, 313]).
Магнитное сверхтонкое расщепление наблюдалось также в ядрах 203Т1
и 2OST1 с помощью прямого измерения ядерного у излучения [26] (см. также
расчет этого эффекта в работе [120]). Расщепления в основном состоянии со-
ставляют величину порядка 2—3 кэв и могут быть объяснены распределением
намагниченности, описываемым оболочечной моделью с учетом смешивания
конфигураций.
247
хотим рассчитать. Индекс k относится к полному набору состояний
системы «ядро 4- мюон». Энергии £г и Eh соответствуют энергиям
этой системы. Оператор энергии взаимодействия Ж" в (8.27) опре-
деляется из разложения по мультиполям статического кулоновского
взаимодействия. Мы будем предполагать, что в таком разложении
преобладает вклад электрического квадруполя.
Член первого порядка в выражении (8.27) представляет собой
ту часть сверхтонкой структуры, которая возникает вследствие
статического взаимодействия ядерных моментов с мюоном. Член
второго порядка описывает динамическое Е2-взаимодействие ядра
и мюона 173, 207, 351 I. Динамическое взаимодействие возникает
потому, что квадрупольное взаимодействие может быть настолько
сильным, что мюон вызовет поляризацию ядра. Сильное ^-взаи-
модействие смешивает основное состояние ядра с возбужденными
состояниями и одновременно смешивает состояния мюона. При
этом особенно изменяются дублеты 2р)/2— 2р3/2 мюонных атомов.
Было найдено, что сдвиги уровней мюонных атомов, обусловленные
эффектами поляризации ядра, составляют в тяжелых ядрах
величины порядка 1—3 кэв [306, 268, 270]. В результате динами-
ческого /^-взаимодействия даже в ядрах, имеющих в основном
состоянии нулевой спин и не обладающих поэтому квадрупольным
моментом в основном состоянии, может проявляться квадруполь-
ная сверхтонкая структура. В этом случае она будет обусловлена
исключительно ядерным возбуждением. Из наблюдаемой сверхтон-
кой структуры спектра можно получить как знак, так и величину
квадрупольного момента первого возбужденного состояния ядра
(см. также § 7.3).
Конечно, в тех случаях, когда матричные элементы оператора
Ж" в (8.27) становятся сравнимыми с энергиями возбуждения ядра
(40—200 кэв для ротационных уровней в деформированных ядрах)
или с тонкой структурой мюонных рентгеновских спектров (150 —
200 кэв в тяжелых ядрах), необходимо заменить выражение (8.27)
приближением теории возмущений для уровней, близких к вырож-
дению. Необходимо далее диагонализовать секулярные матрицы
в подпространствах, определяемых интегралами движения, такими,
как полный угловой момент системы «ядро 4- мюон». Для тяжелых
сильно деформированных ядер энергия Е2-взаимодействия может
достигать 50—100 кэв, и эта процедура является действительно
необходимой.
Чтобы рассчитать матричные элементы взаимодействия, удобно
использовать базисный набор, в котором спин ядра I и спин
мюона j связаны в полный спин F. В несвязанном представлении
матричные элементы статического кулоновского взаимодействия
определяются из (5.22):
| Ж" | г > = j </' М’, 01 p'v (г) | IM, а> X
X -—1 (j'm'n'n' | р’Дг') I fmxn) dr dr',	(8.28)
I г_Г ' I
248
где pN (г) — оператор ядерной плотности заряда (перехода),
рв (г') — соответствующая величина для мюона. Квантовые числа I
и М обозначают спин ядра и его проекцию в состоянии г, остальные
квантовые числа обозначены через а. Для мюона имеем полный
спин j и проекцию т, собственное значение и для волновых функций
(8.6) и главное квантовое число п в состоянии i. В состоянии k все
эти индексы приобретают штрих, а дополнительные квантовые
числа а заменяются на р. В связанном представлении после разло-
жения по мультиполям получаем
(fe1 Ж" | i> = 4л V —— V 2 U' /'F' I W т'М'^> X
X (IjF \MmMF) [J </' М’, рI р" (г) IM, ах rLdrx
О
X 7 </' т’ V.' п' I рв (г') I /тхм> Y*Lml (?)  * , dr’ +
j	г L+1
+ f </' М’, р | р" (г) | IM, а> YLMl (г) —dr X
J	rL-f- I
О	Г
X f </' т' и'п’ I р^ (г') I /7ихи> Ylml (г') r'Ldr'].	(8.29)
о
Здесь F, MF kF' и Mf — полные спины и соответствующие маг-
нитные квантовые числа. Так как взаимодействие диагонально
в связанном представлении, то F = F' и = MF. Заметим,
что выражение (8.29) учитывает тот факт, что мюон может проникать
за границу распределения заряда ядра.
Используя волновые функции мюона такие же, как в (8.4) —
(8.8), введем радиальные матричные элементы
</'Р; х'/г'|| Qz.ll 7, а; хн> =
4л р .
. f l/x'n' (г ) /ип (г ) + gK’n' (г ) gxn (г')1 Г2 dr' X
ZL, 1
О
оо
xjr'L £</', р||р" (г) Yl||/, a>r-L+4r +
г'
г'
+ r'-L-11 </', РIIРЛ' (г) Yl || /, а> rL+ 2 dr j.	(8.30)
249
Далее, используя теорему Вигнера — Эккарта (ПА.54) и формулу
(ПА.26а), получаем
<k | Ж" | i> </' 0; /' х' п'\ FMf | Ж" | /а; /хи; FMf} =
-222 2 (Г Г Р\М'т' MF){IjF\MmMF)x
ЬМ^М'т’ Мт XX'
X p'y/'pv'm'—/|^п—Ftn^ (ILl^'k—
X (ILF1000) —(- 1)^</', 0; x' n' IIQJ I, a- wi> б^кт'-v X
(4n)’/zZz
Х(/А/'|МЛ1тЛ1')=(4л)~1/2^</', 0; x'n' ||QL|| I, a; xn>x
x(_l)i.+/_r+F_/<_I/2^/, / ..,L|l_l0\W/,r; fL)j (831)
Рис. 8.3. Плотности монопольной
и квадрупольиой симметрий и се-
чения постоянной плотности для
деформированного распределения
Ферми [33, 1]
где мы воспользовались стандарт-
ной техникой пересвязки (см. при-
ложение А) и формулой (ПА.40).
В обычных случаях, когда преоб-
ладает вклад от электрического
квадрупольного взаимодействия,
в (8.31) следует ограничиться сла-
гаемым с L = 2. Заметим, что
если не имеется значительного
проникновения мюона в распреде-
ление заряда ядра, то радиаль-
ный матричный элемент (8.30) для
L = 2 и k = i непосредственно
связан с квадрупольным моментом
ядра в состоянии i, который опре-
деляется выражением 1ср. (7.84),
где / = 21
eQ0 = 2 1 / ул ( </Л4=7, a|pw(r)|/Af=/, а>У20(г)гМг. (8.32)
В случае, когда мюон заметно проникает в ядро, выражение (8.30)
может быть связано с внутренним квадрупольным моментом только
если вводятся соответствующие предположения.
Вопрос определения статических квадрупольных моментов ядер
в основном состоянии из данных о сверхтонкой структуре рентге-
новских спектров мюонных атомов более детально обсуждался
Де-Витом с соавторами [981 и Анкером [3]. Главная часть анализа
выполняется с использованием феноменологического распределения
250
заряда ядра, которое возникает от деформирования распределения
Ферми (8.11) [1]:
р(г, 6) = р0{1 +ехр[{г(1-роУ2о(О))-С}/а]}-\	(8.33)
где [3 0 — параметр деформации. Форма плотности квадруполь-
ной симметрии и сечения постоянной плотности для распределения
(8.33) показаны на рис. 8.3. Сверхтонкая структура, связанная
ми, полученными другими методами измерения этих моментов [98]:
X — кулоновское возбуждение: V — измерение периодов полураспада; О — опти-
ческие методы; Л — гигантский резонанс; • — мюонное рентгеновское излучение.
со статическим квадрупольным моментом, рассчитывается с по-
мощью формул (8.31) и (8.33), после того как монопольная часть
в р (г, 0) выделяется и используется для получения гросс-струк-
туры и тонкой структуры. Как только подгонкой спектров удается
определить три параметра С, а и |30 в формуле (8.33), квадруполь-
ный момент рассчитывается в предположении равномерно заря-
женного сфероида по формуле
<?о = 3(5л)->/2/С2(з71 +|1/’Ар0).	(8.34)
Результаты такого анализа для ядер в деформированной области
показаны на рис. 8.4. Они хорошо согласуются со значениями Qn,
найденными другими методами.
251
Динамический £2-эффект, обсуждавшийся для ротационных
уровней Якобсоном [207] и Вилетсом [351 ], хорошо иллюстрирует-
ся примером перехода 2р — 1s в ядре ^2W. На рис. 8.5 показано
влияние недиагонального квадрупольного взаимодействия на поло-
жение уровней 2pt/2 и 2р3/а в мюонном атоме [207]. При этом
учитываются основное состояние ядра = 0+ и первое возбуж-
денное 2+-состояние. Если предполо-
(ДЛД)	жить, что внутренний квадрупольный
{2 3/2 з/г)___/ момент возбужденного 2+-состояния сов-
’ ’ J	падает по величине и знаку с динамиче-
(2,3/2,.1/2)
(0,3/2 3/2)
(2,1/2,3/2)
(0,1/2,1/2)
Рис. 8.5. Влияние динамиче-
ского квадрупольного мо-
мента и а положение уров-
ней 2р в мюонных ато-
мах.
Случай а соответствует отсут-
ствию недиагоналыюго квадру-
польиого взаимодействия. Уров-
ни характеризуются спином яд-
ра /, угловым моментом мюона
/ и полным угловым момен-
том F. Случай б соответствует
учету иедиагонального взаимо-
действия. Различные состояния
с данными значениями F сме-
шиваются друг с другом.
ским квадрупольным моментом для ядер-
ного перехода 0+ -> 2+, то получается
теоретический линейчатый спектр, пока-
занный в верхней части рис. 8.6 [207].
Наблюдаемый спектр [295, 188, 22, 362]
показан внизу. Сравнение спектров под-
тверждает, что статический квадруполь-
ный момент 2+-состояния совпадает с
динамическим в пределах около 10%, и
указывает, что оба эти момента имеют
одинаковый знак.
Можно также рассчитать поляриза-
ционные эффекты ядра для уровней,
имеющих неротационную природу. Это
было сделано Пайпером и Грайнером
[268, 270] для таких видов ядерных
возбуждений, как поверхностные [3- и
у-колебания и гигантские монопольные,
дипольные и квадрупольные колебания,
а также и для ядерных вращений. Ока-
зывается, что Р- и у-колебания дают
очень малый вклад. Интенсивность виб-
рационных линий в спектрах мюонных
атомов меньше в 103 раз по сравнению
с максимальной интенсивностью пере-
хода 2р — 1s. Однако виртуальное воз-
буждение гигантского резонанса может приводить к вкладам в
сдвиги мюонных уровней 2р и 1s порядка* 1 кэв для тяжелых ядер.
Поскольку динамическое квадрупольное взаимодействие сме-
шивает возбужденные состояния ядра с основным состоянием, то
существует возможность наблюдения у-квантов при высвечивании
ядра после атомного перехода. Для случая, показанного на рис. 8.6,
* Были также предложены методы оценки этого эффекта способом, отно-
сительно слабо зависящим от модели [72]. При отсутствии подробных данных
по рассеянию электронов такой подход дает только довольно грубую оценку
сдвигов мюонных уровней, обусловленных гигантским дипольным резонансом.
Эти оценки также дают приблизительно 1 кэв для сдвигов мюонных уровней
2р и 1s в тяжелых ядрах.
252
доля интенсивности линий, которые соответствуют переходу ядра
в первое возбужденное состояние, равна 0,408 [2071. Недавно сооб-
щалось о наблюдении фотонов при переходе ядра из первого возбуж-
денного состояния в основное* [32, 33, 34, 24]. Поскольку этот
переход происходит в то время, как мюон все еще находится на
своей атомной орбите 1s, то его присутствие оказывает влияние на
положение уровней ядра. Это может привести к наблюдению [33, 34]
сдвигов энергий величиной 500—700 эв при фотонном распаде пер-
вых возбужденных состояний таких ядер, как ^“Nd, Jo2Sm и
|®4Gd. Последний эффект указывает на то, что зарядовый радиус
ядра в его возбужденном состоянии больше, чем в основном состоя-
нии, на несколько десятых долей процента. Однако для ядер
4®6Er, 4|2W, 4®4W и ,®6W энергия перехода уменьшается на 300
400 эв (табл. 8.3).
Т а б л и ца 8.3
Измеренные значения сдвига энергии фотона в мюоииых
атомах и соответствующие изомерные сдвиги
Изотоп	ЕехР, эе	Д<г*> <г, '10,> Ы = 0
1S2Sm	+500±40	+0,48
1S2W	—290+90	—0,02
1MW	—350+50	—0,04
i«6W	—400 ±40	—0,06
188Os	—400 +40	—0,08
isoos	—470 ±40	—0,14
		(-0,13)
«Юб	—610±50	—0,20
		(-0,19)
Примечание	 ЕехР~энеРг11я перехода;	Д<г2> • 10s — изменение ра- <г2>
диуса ядра в возбужде	ИНОМ состоянии.	
Чтобы интерпретировать этот результат, необходимо внести
поправку на эффекты, возникающие от магнитного сверхтонкого
взаимодействия [27, 83, 155]. Два подуровня возбужденного ядра
расщепляются на несколько сотен электронвольт и не могут быть
разрешены. Эти уровни не заполняются в соответствии с их статис-
тическими весами 2/ + 1 и не сохраняют свою начальную заселен
ность. Последнее утверждение является определяющим и возни-
кает из-за сильных ЛИ-переходов между этими уровнями, осущест-
вляемых через механизм внутренней конверсии, что приводит
к значительному увеличению заселенности нижнего уровня и,
* Теоретическое рассмотрение этого эффекта проводилось в работах
[200, 268, 270].
254
следовательно, к уменьшению сдвига энергии перехода на несколько
сотен электронвольт.
Кроме измерений положения уровней в системе «мюон — ядро»,
можно также наблюдать относительные интенсивности спектральных
линий, соответствующих переходам между различными атомными
уровнями. Эти интенсивности зависят от относительной заселен-
ности начальных атомных уровней и от вероятностей дипольных
переходов между уровнями. В качестве исходной точки обычно
принимается предположение, что все уровни заселяются в соответ-
ствии с их статистическим весом 2/ 4- 1. Волновая функция мюона
в атомном состоянии с главным квантовым числом п, орбитальным
угловым моментом I, полным угловым моментом / и проекцией т
имеет вид
| nljm> = Rnl (г) Zj ( / 77 /1 Кт (f) Xm-x, (8.35)
где Rnl (г) радиальная волновая функция, a X — спинор Паули.
Вероятность перехода определяется матричными элементами ди-
польного перехода [см. (4.77), (4.82) и (4.83)]
KitnAx
Wf V 2
Xmf-xf)	Rn.i.(r) r3 drx
X^Yt^^r^Yi.K.^dr,	(8.36)
где t и / используются для] обозначения начального и конечного
атомных состояний, ар — индекс компоненты дипольного вектора
г в сферическом базисе. Используя (ПА.26), обычную технику пере-
связки и (ПАЛО), мы можем записать, что вероятность перехода
пропорциональна величине
2 I <nf h if ra/l ru I ni it h mi> I2=
= (2/i + i) ( A 1 if || o —1)2 [ J Rnf lfRn.t,r3drj2. (8.37)
Здесь мы не усреднили, а просуммировали по начальным магнит-
ным квантовым числам, чтобы учесть статистический весовой мно-
< житель 2/ ф-l, характеризующий заселенность уровня.
Формула (8.37) дает следующие соотношения для переходов
между уровнями с данными фиксированными (м;/,-) и (nflf):
f (2рз/г —*• Isiyz): I (lpi/2 —* 2si/2) = 2 : 1,	(8.38a)
/ (3dE/2-► 2p3/2): / (3d3/2-> 2рз/г) : / (З^з/г-► 2pi/2) =9:1:5, (8.386)
I (4/7/2 3d5/2): 7(4/E/2 -> 3dE/2): I(4/5/2 -► 3d3/2) = 20:1:14. (8.38b)
255
i
Эти результаты слегка изменяются, когда в функцию й3, входящую
в выражение для вероятности El-переходов, подставляются раз-
ности энергий с учетом тонкого расщепления уровней и когда в мат-
ричных элементах электрических дипольных переходов учитывают-
ся эффекты конечных размеров ядра. В табл. 8.4 и 8.5 приведены
Таблица 8.4
Отношения интенсивностей мультиплетов тонкой
структуры для средних ядер [2]
Изотоп	7(2 р,1г^. И2 Р^/2-	1 S1/.> > 1 Sl/s)	Л3 d42+3 ds/2-»-2 ₽’/,) /(3 </зу2->2 pi/2>	
	Эксперимент	Теория	Эксперимент	Теория
50$П	1,83±0,11	1,953	1,73±0,15	1,953
51Sb	1,90±0,10	1,952	2,57+0,30	1,952
6гТе	1,95+0,13	1,954	1,86+0,20	1,954
И1	1,06+0,08	1,952	3,00+0,50	1,952
5&Cs	1,68+0,11	1,951	2,08 ±0,30	1,951
56^3	2,05+0,23	1,952	1,74+0,50	1,952
5?La	1,95±0,10	1,951	2,00+0,25	1,951
58 Се	1,84±0,12	1,950	2,10+0,50	1,950
59Р1*	1,81 + 0,14	1,950	2,56+0,40	1,950
eoNd	1,59±0,08	1,949	1,71±0,20	1,949
Таблица 8.5
Отношения интенсивностей мультиплетов тонкой
структуры для тяжелых ядер [2,362]
Изотоп	1(2 Р3/2-> 1 S1/s) /(2 Р1/2-^ 1 si/2)		7<3db/g 7(3<7з/2-	>2Py2)
	Эксперимент	Теория	Эксперимент	Теория
78Аи	1,50+0,10	1,926	1,40+0,14	1,752
soHg	1,29+0,06	1,925	1,75+0,15	1,751
31Т1	1,09±0,10 [ 1,68±0,08а	1,923	1,39+0,20	1,750
sgepb	1,45±0,10ь 1 2,00±0,30е ( 1,73±0,15а	1,922	1,57+0,15	1,749
2“1РЬ	1,50т 0,15ь* 1. 1,80+ 0,30е* ( 1,49±0,10а	1,922	1,57+0,20 1,74+0,15а	1,749
8зВ1	1,31±0,20ь ( 1,38+0,10d	1,920	1,44 + 0,20ь l,50+0,10d	1,748
п р. 425. Ь	римечание. а См. [2].	Ehrlich R. D. е	a. Phys. Rev. Lett., 1966. v. 16,	
с Anderson Н. L. е.		a. Phys. Rev. Lett	1966. v. 16, p.	434.
11 Bardin Т. Т. е. а.		Phys. Rev. Lett.,	1966, v. 16, p. 429.	
* Результаты получены в изотопов свинца.		экспериментах с использованием естественной смеси		
256
результаты расчетов [2] с учетом указанных эффектов и соответ-
ствующие экспериментальные результаты. Для средних ядер в об-
щем имеется хорошее согласие с данными эксперимента, за исклю-
чением переходов 2р — 1s в 531 и e0Nd. Для более тяжелых ядер
согласие довольно плохое. Аномалии могут быть связаны с эф-
фектами резонанса на некоторых уровнях ядра [202]. В случае
иода это является особенно привлекательной гипотезой, так как
расщепление уровня 2р, обусловленное наличием тонкой структуры,
составляет 59,9^3,0 кэв, а разность энергии между первым воз-
бужденным и основным состояниями ядра равна 58,5± 1,0 кэв.
Для неодима и некоторых более тяжелых ядер интерпретация
результатов усложняется тем фактом, что в экспериментах были
использованы естественные элементы, и поэтому необходимое рас-
смотреть разностные эффекты в различных изотопах.
§ 8.3. Пионные атомы
Рассмотрение свойств мюонных атомов может быть проведено
весьма подробно и с хорошей точностью, поскольку единственным
взаимодействием, которое представляет интерес, пока мюон не
достиг орбиты 1s, является электромагнитное взаимодействие.
Обычные методы, развитые для рассмотрения электронных атомов,
должны быть обобщены для описания новой физической ситуации,
ибо мюон намного тяжелее электрона, однако при этом нет необ-
ходимости выходить за рамки электромагнитной теории. После
того как мюоны достигают атомного уровня 1s, они могут быть
поглощены ядром (см. гл. 9 и 10). Этот процесс, равно как и естест-
венный распад мюона на электрон и два нейтрино, обусловлен сла-
бым взаимодействием, так что при рассмотрении атомных задач
его влиянием в очень хорошем приближении можно пренебречь.
Совершенно иная ситуация создается при рассмотрении системы
из ядра и отрицательного л-мезона, находящегося на атомной ор-
бите*. Кроме электромагнитного взаимодействия, которое обус-
ловливает существование атомов, в пионных атомах также имеется
сильное взаимодействие. Оно дает сдвиги в положении атомных
уровней, кроме тех, которые обязаны эффектам поляризации ваку-
ума и конечного зарядового радиуса ядра. Эти сдвиги можно наблю-
дать [75, 214, 215, 23, 272]. С помощью аппарата многократного
* Следует заметить, что подобные эксперименты возможны также и для
каонов Так как эти частицы значительно более массивны, чем пион или мюон
^тК ~ 494 Мэе), их орбиты находятся очень близко к ядру. Например, орби-
та 1s для каона в 16О имеет радиус около 6,8 ферми, что сравнимо с радиу-
сом ядра ~ 3 ферми. Кроме того, каоны сильно поглощаются ядрами, по-
этому процесс поглощения происходит преимущественно на поверхности ядра
и дает информацию об этой области в ядрах. Поскольку странность каона
равна единице, то о его поглощении свидетельствует появление Л- или S-ги-
перона.
257
рассеяния пионов на ядрах может быть затем исследована их связь
с фундаментальным процессом низкоэнергетического рассеяния
пиона на нуклоне
л~ N -э- л- 4- N
1121, 122, 123, 312, 150].
Кроме сдвигов уровней наличие сильного взаимодействия при-
водит также к важным эффектам поглощения, в результате кото-
рого пион захватывается ядром. Эти эффекты настолько велики,
что пион может вообще поглотиться ядром с атомной орбиты,
которая находится значительно дальше от центра кулоновских
сил, чем орбита 1s [245]. Действительно, для всех ядер, кроме самых
легких (Z^3), ядерное поглощение из состояния 2р наступает
быстрее, чем атомный переход 2р—>ls, а для немного более тяже-
лых ядер (Z^IO) вероятность поглощения с уровня 3d превосходит
вероятность испускания рентгеновских квантов при переходе
3d->-2p и т. д.
Элементарный процесс поглощения на несвязанном протоне
л- 4- р -> п
играет весьма малую роль в механизме поглощения пионов на
ядрах [235]. Разумеется, эта реакция вообще не может иметь места
для свободного нуклона, поскольку в ней не сохраняется энергия
и импульс. Когда нуклон связан в ядре, подобные кинематические
соображения больше не являются строгими. Однако и в этом случае,
находясь в потенциальной яме ядра, нуклон не обладает достаточ-
но большими значениями импульса, чтобы компенсировать боль-
шую величину импульса, приобретаемого нуклоном в конечном
состоянии после того, как он поглотит энергию, соответствующую
массе покоя пиона. В результате поглощение атомного пиона одним
некоррелированным нуклоном вносит лишь малую долю процента
в полную вероятность поглощения. Радиационное поглощение
пионов вида
л-4-р->п4-'у
может иметь место (см. § 10.3), но, являясь частично электромагнит-
ным процессом, оно составляет лишь несколько процентов от пол-
ного поглощения [87, 12]. Основной механизм поглощения —
захват пиона двумя взаимодействующими нуклонами:
3T- + p4-7V-^-n4-7V,
в котором существен процесс, обратный процессу околопорогового
рождения пионов в нуклон-нуклонных столкновениях. С точки
зрения структуры ядра этот механизм тесно связан с квазидейт-
ронным процессом, описанным в §4.7. Поглощение атомных пионов
двумя нуклонами может наблюдаться непосредственно [2621,
258
а также путем наблюдения ширин линий перехода 2р—>1$ для
пионных атомов [214, 215, 23, 2721. Однако такая реакция является
слишком сложной для того, чтобы получить отчетливую теорети-
ческую интерпретацию данных [123, 116, 1801.
*
* *
Обзорные работы о мюонных атомах были недавно опублико-
ваны By [362], Сенсом [313], Энгфером [119] и Даумом [83]. Имеют-
ся также полезные статьи Келли, Лаукайна, Таунса и Вилетса
[218, 227, 335, 354], касающиеся получения информации о ядре из
атомных спектров. По-прежнему остаются ценными и более старые
обзоры Рейнвотера [2811, Де-Бенедетти 189] и Форда и Хилла
[139], а также статья Фича и Рейнвотера [1341. Подробная статья
Аккера с соавторами [221 дает особенно полезное рассмотрение
теоретических методов, используемых для описания эксперимен-
тов в этой области. Наконец, мюонным атомам посвящен недавний
обзор Девонса и Дьюердота [88].
ЧАСТЬ III
СЛАБОЕ ВЗАИМОДЕЙСТВИЕ В ЯДРАХ
ГЛАВА 9
УНИВЕРСАЛЬНОЕ ВЗАИМОДЕЙСТВИЕ
ФЕРМИ И БЕТА-РАСПАД ЯДЕР
При обсуждении механизмов возбуждения ядер до сих пор
рассматривались процессы, в которых ядро совершало переход,
обусловленный электромагнитным взаимодействием. В этой и сле-
дующих главах будут рассмотрены переходы, которые обусловлены
слабым взаимодействием в ядрах. Речь идет о переходах, совер-
шающихся в результате p-распада ядер и захвата мюонов ядрами.
Последний процесс является особенно интересным, так как в нем
освобождается довольно большое количество энергии. Поэтому
увеличивается роль некоторых свойств слабых взаимодействий,
которыми пренебрегают в других процессах. Кроме того, ядро
получает возможность перейти в сильно возбужденное состояние.
Подобные возбужденные состояния тесно связаны по своей природе
с состояниями, играющими важную роль в процессах фото-и элект-
ровозбуждения.
Поскольку наше понимание слабых взаимодействий является
далеко не таким полным, как понимание электромагнитных явлений,
то, как мы увидим, необходимо одновременно развивать два направ-
ления. С одной стороны, следует рассматривать слабые взаимодей-
ствия как источник информации о структуре ядра. С другой сто-
роны, мы хотим использовать изучение слабых взаимодействий
в ядрах в качестве метода пополнения наших знаний о самых слабых
процессах. В частности, мы хотим знать, определяются ли в ко-
нечном счете процессы слабого взаимодействия в ядрах теми же
самыми законами, которые справедливы для слабых взаимодейст-
вий элементарных частиц.
§ 9.1. Гамильтониан слабого взаимодействия
Фундаментальные явления, которые мы будем обсуждать при
рассмотрении слабых взаимодействий в ядрах, суть такие процес-
сы, как распад свободного нейтрона на протон, электрон и антиней-
трино электронного типа
n-^p+e~ + ve
(9.1)
260
н соответствующий распад протона
p->n + e++ve.	(9.2)
Последний процесс может иметь место только внутри ядра, которое
дает необходимую энергию. Он конкурирует с захватом электрона
e~ + p-^ti + ve,	(9.3)
который для остановившегося электрона может происходить тоже
только внутри ядра. С этой реакцией захвата близко связан захват
отрицательного мюона, находящегося на атомной орбите:
+ (9-4)
Как известно из эксперимента*, нейтрино vM, связанное с мюоном,
отличается от нейтрино ve, которое связано с поглощением элект-
рона. Реакция (9.4) может, конечно, иметь место и для протонов
внутри ядра.
Взаимодействие, которое, как предполагают, ответственно за
эти слабые процессы, первоначально было предложено Ферми
[129] по аналогии со взаимодействием в электромагнитной теории.
Этот подход с некоторыми обобщениями и модификациями остается
справедливым и в настоящее время. Поэтому мы начнем с постули-
рования гамильтониана слабого взаимодействия в виде
Н' = ~{ Jx+(r)^(r, r')JK(r')drdr',	(9 5)
г Z v
где G — константа связи слабого взаимодействия, А(г) — полный
слабый ток, который будет определен ниже, и 2? (г, г') описывает
распространение той частицы, через которую осуществляется взаи-
модействие между слабыми токами. Введем удобные обозначения
/+ = (Д)+, Л= 1,2,3,
^+ = -(^)+,
и аналогично для других операторов 4-тока, так что Л-+ будет
характеризоваться теми же трансформационными свойствами отно-
сительно преобразования Лоренца, что и J-,..
Выражение (9.5) имеет очевидную аналогию с выражением
(5.5), которое описывает взаимодействие между различными чле-
нами полного электромагнитного тока. В электромагнитном случае
взаимодействие осуществляется посредством обмена фотонами,
которые не имеют массы, что приводит к выражению для 2?
(9.6)
* Общие свойства слабых взаимодействий обсуждаются в работах,
указанных в конце настоящей главы. В них имеются также ссылки на ориги-
нальные теоретические и экспериментальные работы в этой области.
261
Для слабых взаимодействий была предложена подобная модель,,
в которой взаимодействие обусловлено обменом массивным бозо-
ном, обозначаемым через W. В настоящее время мы знаем, что
если такая частица и существует, то она должна иметь массу 2 Гэв
или больше*. При рассмотрении |3-распада и захвата мюонов, в ко-
торых переданные энергии намного меньше 2 Гэв, масса любой
такой промежуточной частицы может быть взята бесконечной. Ина-
че, поскольку область действия сил определяется комптоновской
длиной волны промежуточной частицы, то можно сказать, что ком-
поненты слабого тока должны взаимодействовать в одной и той же
точке, или
$(г, г') = 6 (г—г')
и
(9-7)
J JK+(r)J}.(r)dr.
(9.8)
Гипотеза, выражаемая формулой (9.8), позволяет установить
природу слабого взаимодействия при условии, что известен вид
полного слабого тока J}. (г). Фактически большая часть исследо-
ваний по теории слабых взаимодействий (суммированных в работах,
которые указаны в конце этой главы) посвящена установлению
вида J-,. (г). В настоящее время считают, что Д. (г) содержит вкла-
ды многих пар фермионных полей. В частности, в отсутствие силь-
ных взаимодействий постулируется**
A(r)=i [фц(г)Гх,фуи(г)+фДг)Гх^е(г)+фп(г)Гхфр (г)],	(9.9)
*	Обзор имеющейся информации о 1Г-частице дан в работе [234].
*	* Мы опускаем здесь те члены в слабом токе, которые непосредственно
не дают вклада в слабые процессы в ядрах. Эти члены ответственны, например,
за распады странных частиц: Л -> р + л~, Л -» п + л°, Л -> р ~Г е~ +ve,
Е + -> р + л°, 2 + -+ Л + е+ + ve, К+ — р+ + у К+ ->• л+ + л° и т. д.
Включение таких процессов потребовало бы введения в выражение для тока
слагаемых типа	1фп1\ф2+ и т. д. Свойство странности эмпирически
приписывается некоторым сильно взаимодействующим частицам, чтобы объяс-
нить наблюдаемые правила отбора в процессах сильного взаимодействия. Если
частицам приписываются числа, указанные в таблице (см. также [293]), то
оказывается, что странность сохраняется и ведет себя как дополнительное
квантовое число в сильных взаимодействиях:
Частица	Странность	Барионное число	Частица	Странность	Барионное число
Л*. л°	0	0	Л°	—1	1
к-.	—1	0	2±. 2°	—1	1
К+. №	1	0	S-, Е°	—2	1
п, р	0	1			
262
где величины ф обозначают спинорные поля* * частиц указанных
нижним индексом, а Г?. —• соответствующие комбинации дираков-
ских операторов. Предполагается, что вид всех трех величин 1\, ко-
торые входят в выражение (9.9), один и тот же для всех процессов,
обусловленных только слабым взаимодействием. Это необычно силь-
ное ограничение, поскольку оно подразумевает, что константы
слабого взаимодействия G, которые входят в гамильтониан взаимо-
действия, описывающий p-распад нейтрона
Яр = £= f [фп Гх %]+ [фе I\ dr,	(9.10)
захват мюона
/7'ap=-^J	+ dr (9.11)
и распады мюонов р_ -> е~ + ve + Уц или р+ -> е+ + ve -ф т. е.
Яц~= J [фц	[фе фчд. | dr	(9.12а)
или
//4+=-^ [ l^r4vJ + ferxtpvJ dr, (9.126)
I Z V
все являются одинаковыми**. В этом заключается предположение
универсального взаимодействия Ферми (УВФ). Для процессов (9.10)
и (9.11) слабые взаимодействия сопровождаются эффектами силь-
ного взаимодействия, что до некоторой степени нарушает простое
описание с помощью УВФ. Мы увидим, однако, что многие из этих
эффектов могут быть учтены.
Матрицы Дирака Г\, которые входят в выражение (9.9), выби-
раются так, чтобы слабое взаимодействие было инвариантным
относительно собственных преобразований Лоренца. Хорошо из-
вестно, что в слабых процессах четность не сохраняется, и вследст-
вие этого гамильтониан взаимодействия может содержать смесь
скалярного и псевдоскалярного членов. Токи в выражении (9.9)
Кроме того, указанное барионное число сохраняется во всех известных про-
цессах, как сильных, так и слабых Поэтому, например, реакция л- + р -»•
-- S- + К+ может идти за счет сильного взаимодействия, а реакция л- +
+ р -> S+ + К~ — не может. Слабые процессы могут, конечно, изменить
полную странность всей системы, как, например, в слабом распаде Л -> р +
Ч- л-.
* Поляф должны раскладываться по операторам рождения и уничтоже-
ния соответствующего полного набора одночастичных состояний. Эти опера-
торы подчиняются коммутационным соотношениям (3.106). Мы не будем
здесь касаться свойств операторов этих полей и большинство наших результа-
тов будем выражать через спинорные коэффициенты, которые появляются
в разложении полей.
** Укажем, что полеф описывает уничтожение соответствующей частицы
в начальном состоянии или рождение античастицы в начальном состоянии,
тогда как ф описывает рождение частицы и уничтожение античастицы.
263
могут, таким образом, включать как векторную, так и аксиально
векторную части. В явном виде слабые взаимодействия, по-види-
мому, должны правильно описываться, если предположить, что
1\=ух(1+т5).	(9.13)
Ток можно представить в виде суммы векторной и аксиально-
векторной частей
Л(г)^ Л(г) + ЛЛ(г),	(9.14а)
Jk (г) = * I'l’u (г) Ya. 'Н (г) - (г) П ^ve (г) +^п (г) ух фр (г) |, (9.146)
jft?) = i [фц (г) ухУзФгц (Г) + фе (г) Yx Уз Ф\е (г) +ФП (г) Та Y= Ф,, (г).
(9.14в)
Результирующее взаимодействие называется V — А-взаимодей-
ствием* в соответствии с ранними обозначениями, в которых за-
пись в виде (9.13) означает, что векторная и аксиально-вектор-
ная константы имеют одинаковые абсолютные величины, но проти-
воположные знаки.
Однако для процессов с участием сильно взаимодействующих
частиц простые предположения универсального взаимодействия
Ферми и V — Л-взаимодействия непосредственно неприменимы.
В этом случае ввиду наличия сильного взаимодействия матричные
элементы тока нуклонов всегда содержат более общий оператор
Дирака, чем оператор (9.13). Мы используем матричные элементы
этого тока, имеющие наиболее общую структуру в соответствии с ос-
новными принципами симметрии, и в конечном счете получим такую
информацию, которая связана с различными имеющимися в нашем
распоряжении компонентами. Можно получить следующий общий
вид для матричного элемента тока нуклонов по состояниям протона
и нейтрона, взятым в виде плоских волн:
<« I (г) | р> - шп [/j ух +f2 пхр kp + if3 kK + (gy ух + ig2 kK '
+ ёз Ф-р kp) y5] up exp ^-<Р~П)~Г exp	(9.15)
Здесь pp = (p, iEp/c) и np = (n, iEn/c) — протонные и нейтронные
4-импульсы, ир и ип — спиноры этих частиц. Волновой вектор
переданного импульса обозначается как
kP= (Рр—Пр)/Г1^=рр/П.
Функции f и g являются инвариантными формфакторами**, кото-
рые зависят только от /г2 kpkp. В формуле (9.15) Охр " (1/2 i) y
X (ТхУр — УрУх)-
* Читается «V-минус Л-взаимодействие»
** Конкретный выбор нижних индексов, используемый для этих формфак-
торов, связан с тем, что в дальнейшем мы упростим выражение (9.15) путем
исключения членов, которые содержат f3 и g3.
264
При построении выражения (9 15) для тока можно также рас-
смотреть члены, сконструированные из вектора Кр= (Рр +
Такие члены не добавят ничего нового по сравнению с выражением
(9.15), что можно увидеть, используя уравнение Дирака:
ипК = ип [iy?. (Мр + Л1,,)- юхр^р] ир, (9 16а)
ип^рКрир ип[ук(Мр—Мп)- ikK]up, (9 166)
ип Тб	иР = чп [ — i (Л4Р—Мп) у>. Уб —	kp Тб111Р,	(9- 16в)
«п Охр Кр Уб ир - ип [ — у р у5 (Мр + М„) + iy5 А-p] ир,	(9.16г)
где Мр и Мп—массы протона и нейтрона. Кроме того,
i
№ Д-2(М^ + М=)^-~А:2,Ки^!=0,	(9.17)
гак что fug могут рассматриваться как функции только /г2.
В выражении (9.15) члены, содержащие ft и gt, дают векторный
и аксиально-векторный вклады. Если бы имелось только УВФ
с К — Д-взаимодействием, то эти формфакторы были бы равны
единице, а все остальные — равны нулю. Однако из-за наличия
сильного взаимодействия f± и gt отличаются от единицы, и должны
быть введены дополнительные члены*. Дополнительные слагаемые
включают член с f2, который содержит тензорный оператор в про-
странстве нуклонов. Этот член похож на слагаемое с аномальным
магнитным моментом в формуле (6.3), и поэтому вклад от него на-
зывается слабым магнетизмом Формфактор g2 входит множителем
в слагаемое, которое называется индуцированной псевдоскалярной
частью, и в основном обусловлен нуклонами, окруженными облаком
псевдоскалярных пионов, которые могут распадаться «слабым обра-
зом»; л->р или (со значительной меньшей вероятностью)
л -> е + те. Наконец, формфакторы fs и g3 входят в индуцирован-
ные скалярные и тензорные члены соответственно.
Если инвариантность относительно обращения времени сохра-
няется как для сильного, так и для слабого взаимодействий, то
все шесть формфакторов, входящие в выражение (9.15), будут
действительными. Однако в слабых процессах с изменением стран-
ности наблюдалось** нарушение инвариантности относительно ком-
бинированной операции зарядового сопряжения (С) и пространст-
венной четности (Р). Это означает, что инвариантность относитель-
но обращения времени нарушается при условии, что выполняется
* Это можно рассматривать по аналогии с влиянием сильных взаимодей-
ствий на электромагнитные токи нуклонов. Наличие мезонного облака при-
водит к изменению магнитного момента нуклона. (См. также §9.5 и 10.2.)
** Результаты о наблюдениях нарушения CP-инвариантности приведены
е работах [135, 91, 25] (см. также [293]).
265
СРТ-теорема*. Для слабых взаимодействий, в которых стран-
ность не меняется, ситуация еще не совсем ясна. Следствия инва-
риантности относительно обращения времени можно легко рас-
смотреть.
Соответствующий антиунитарный оператор для описания обра-
щенных по времени состояний в случае нерелятивистских частиц
имеет вид (см. § 6 Приложения А).
K=—i(JyK0,	(9.18)
где Ко — оператор комплексного сопряжения (предполагается
обычное представление для спиновых матриц Паули). В случае
релятивистских частиц нетрудно видеть, что выражение (9.18)
можно обобщить и получить оператор обращения времени в виде
[247, 299]
*^2^0 = ^is^o= Ti Ys^o	(9.19)
для представления у-матриц, рассмотренного в Приложении Б.
Обращенная по времени спинорная волновая функция имеет вид
ф'(г, /)=/<ф(г, — /)= Ш13ф*(г, — O=YiY3t*(r. —О- (9.20)
Для операторов Дирака в выражении (9.15) для матричного эле-
мента от тока нуклонов получаем в представлении, описанном
в Приложении Б:
АухА^=Т1У3у*у3У1 = ух.	(9-21а)
АахрЛ+ = /<И(ТхТр-ТрУх)]/<+- -п?.р,	(9.216)
L 21
KYxT5^+=TxY6-	(9.21b)
Лхц,рТ5/(+= — <JxpT5.	(9.21г)
Члены в гамильтониане взаимодействия, описывающие слабые
процессы в ядре, будут иметь вид
Я' = -^ f [ (г) YZ (1 + Ye)	(г)]+ 'h (r) dr - | -
px+ (r) [i^(r) n (1	(r)1 Jr> (922>
* СРТ-теорема (теорема Людерса—Паули) применима для того класса
полевых теорий, которые обладают свойством инвариантности относительно
собственных ортохронных преобразований Лоренца и содержат локальные
взаимодействия и обычную связь спина со статистикой. Она утверждает, что
такие теории инвариантны относительно СРТ-преобразования.
266
где индекс I относится к лептону (/ = е или р), и типичный спинор-
ный инвариант в этом выражении имеет следующую структуру:
[Щ / (1 + Т5) “vzl* [мп {fi Тх+f2 пхР kp + if3 kK +
+ (£1 Тх + >£2 + g3 рхр kP) To} “P] + комплексно сопряженные
члены.	(9.23)
Обращенное по времени выражение (9.23) имеет вид
[(№,)+ Ру1 (1 +т5) (K«v,)F t(^n)+ Р {fl Тх-А o?.p^-if3 ft +
4 (£1 Тх—i£2 ^х—£3 °Хр ft) у5} (KUp)] + комплексно сопряженные
члены = [и, К+ / (1 + Тб)	[wn К+ {Д Тх~f2 <ПР kp—if3 ft +
+ (£1 Тх—i£2 ft—g3 oip ft) y5} Kup]* + комплексно сопряженные
члены = [и, Д- (1 4- y5) uV[] К {Д ух + fl oXp ft + if*3 ft +
+ (£1 Tx + i£2 £x + £3 tfxp kp) y5} Up]* 4- комплесно сопряженные
члены.	(9.24)
Здесь мы использовали тот факт, что при действии оператора обра-
щения времени пространственные компоненты 3-векторов, которые
входят в (9.24), меняют знак, так что fex -> — ft. Записанный
в явной форме член в (9.24) похож на комплексно сопряженное
выражение для явно записанного члена в (9.23). Поскольку в вы-
ражения (9.23) и (9.24) входят слагаемые, комплексно сопряжен-
ные выписанным слагаемым, то оба выражения будут совпадать
при условии, что формфакторы /у, gj (j 1,2,3) действительны.
Это указывает на инвариантность относительно обращения времени.
Чтобы исключить скалярный и тензорный члены в выражении
(9.15), можно рассмотреть дополнительную симметрию. Для этого
необходимо ввести понятие G-четности. Оператор G-преобразования
представляет собой произведение операторов зарядового сопряже-
ния и поворота в изоспиновом пространстве. Этот поворот выби-
рается, в частности, в виде поворота на угол 180° вокруг второй
изоспиновой оси. Тогда
G = CeiItr«.	(9.25)
Поскольку предполагается, что сильное взаимодействие инвариант-
но относительно зарядового сопряжения и вращений в изоспи-
новом пространстве, то оно также инвариантно и относительно
G-преобразования.
Действие оператора поворота в изоспиновом пространстве в вы-
ражении (9.25) на нуклонные состояния легко устанавливается,
поскольку
е!лг2=е-/г<лт2_ iTa)	(9.26)
267
и для протонных и нейтронных состояний получаем
iT2|p>^= —|n>, ir2|n> |р>.	(9.27)
Чтобы определить действие оператора зарядового сопряжения
в пространстве спиноров, заметим, что уравнение Дирака
М ТЕ— j дт А) +	(*)=о <9-28)
L \ илИ 'LC	'l J
для зарядовосопряженного спинора яр' принимает вид
(9.29)
L V охи Яс	я J
Операция зарядового сопряжения заменяет частицу на античасти-
цу или меняет ролями решения с положительной и отрицательной
энергиями. Выразим зарядовосопряженную волновую функцию
через комплексно сопряженную функцию. Для этого напишем
ф' (х) = Сф* (х).	(9.30)
Тогда из (9.29) получаем уравнение
!Ьч А++Ac**wr(cr)_1“
= (A W к I -4" + i ) + ^1 (СО-1 = о ,	(9.31)
L и \ ох\х he 1 п |
которое в точности соответствует уравнению для ф+
о (9-32)
I \ охц Ъс	Ь .1
при условии, что
J м: 4‘-2’3} V».	(9.33)
Для представления, используемого в Приложении Б, это свойство
удовлетворяется, если выбрать
С=у2, откуда СТ=С=С~1.	(9.34)
Билинейное ковариантное спинорное выражение (иьйгио) при
операции зарядового сопряжения преобразуется следующим об-
разом*:
[1(Рт2 u*by Ц у2 u*] = [(₽Y2 uiy Qt Тз	=
|Цз ру2 Рт2«ь] -	(суммы нет) (9.35)
* Заметим, что величина в квадратных скобках является числом и, еле
довательно, равна своей транспонированной величине.
268
где т)'» = — 1 для скалярного, псевдоскалярного и аксиально-
векторного членов и г)', = 4-1 для векторного и тензорного
членов. Когда исследуется поведение выражения билинейного по
операторам поля по отношению к преобразованию зарядового соп-
ряжения, то перестановка операторов рождения и уничтожения в со-
ответствии с антикоммутационными соотношениями (3.106) при-
водит к появлению знака минус. Таким образом, поведение вели-
чин относительно зарядового сопряжения удобно характеризовать
с помощью фазы тц = —т)'ь такой, что тц ф- 1 для скалярного,
псевдоскалярного и аксиально-векторного членов и т]. = — 1 для
векторов и тензоров.
Теперь можно воспользоваться соотношениями (9.27) и (9.35),
чтобы установить действие оператора G-преобразования (9.25) на
билинейные выражения от нуклонных операторов. Имеем
[(«+ G+) ₽Пг Gup] = —Ц₽у2 у2 и*] =
= —'п/	11. [«„ «₽]•	(9.36)
Таким образом, выражение для векторного тока \uny^up является
четным по отношению к операции G-преобразования (тц — — 1),
а аксиально-векторное выражение i («пТхТ5ир) нечетно по отно-
шению к G-преобразованию (тц = 4-1). Поскольку сильное
взаимодействие инвариантно относительно G-преобразования, разум-
но постулировать, что оно не будет менять G-четность полного век-
торного и аксиально-векторного токов. Значит, те слагаемые в вы-
ражении (9.15), поведение которых не согласуется с этим предпо-
ложением, должны отсутствовать 1345]. В частности, соотношения
(9.35) и (9.36) указывают, что скалярные и тензорные слагаемые,
содержащие /3 и g3 соответственно, не должны входить. Исполь-
зуем этот результат и выражение (9.22), чтобы записать эффектив-
ный гамильтониан слабого взаимодействия для ядра с помощью
спинорных функций фп и фр:
<п | Н' | р> = —V С [1 44 (г)	(1| Тг,) 3pv (r)|+х
X [iiMO {ЛТх+^<Ър&р+(£1ТХ'Я£3Мт5}%И)] ^г. (9.37)
Для процессов, в которых в начальном состоянии имеются нейтро-
ны, в выражение (9.37) будут входить эрмитово сопряженные
операторы. Величина kp берется равной соответствующему вол-
новому вектору переданного импульса для рассматриваемого случая.
Она может считаться формально симметризованным оператором
Лр= —— д р - — i (др ф- др),
где операторы производных действуют в указанном направлении и
только в пространстве нуклонов.
269
§ 9.2.	Нерелятивистский предел пространстве нуклонов
Для применений в ядерной физике обычно необходим гамиль-
тониан (9.37), в котором состояния нуклонов описываются нере-
лятивистскими волновыми функциями. Задача здесь в значитель-
ной степени та же самая, что и при рассмотрении электромагнитных
процессов, где мы нашли общее выражение для нуклонного тока
при наличии взаимодействия с электромагнитным полем и перешли
в этом выражении к нерелятивистскому пределу. Полученный
результат можно использовать с обычными волновыми функциями
ядерных моделей.
Мы можем выполнить такую же программу, используя преобра-
ование Фолди — Вутхайзена (ФВ), которое рассматривалось
§ 6.1. Как следует из выражения (9.37), оператор Гамильтона
пространстве нуклонов имеет вид
h'(Г’ = 1 V 7?'+ (Г> п	°7-1' k(> +
+ (giTx + ig2^)T5}]-	(9-38)
Здесь /\(г, t) — лептонный ток, выражающийся через соответст-
вующие спинорные волновые функции лептонов:
Л+(г, t)= [1ф;(г)тх(1 + у5)^ (г)]+ехр (^(Ev — £2)Л (9.39)
где величины Е обозначают энергию соответствующих частиц
или отрицательную энергию для античастиц. Введем для удобства
величину io = (Ev — Ег) так, чтобы временная зависимость
лептонного тока имела простой вид ei0,/.
Прежде чем воспользоваться преобразованием ФВ в прост-
ранстве нуклонов, оператор (9.38) следует разбить на четную и
нечетную части, определяемые соотношениями (6.6) — (6.8) и
(6.21). Имеем
+	(9.40)
где
<s = i —%- [—fl ft + f2imkn+g! fa yj =
— 1	[ — fl jt + f 2 Pemn( fa^n CTj + i gi jm °m]	(9-41)
F
{мы воспользовались соотношениями (ПБ.28)] и
0=1 J г— [f 1 jm PYm fl G A fa &o) Tm
—gi it T5 + i g2 (h ktf ₽TSL	(9.42)
Поскольку рассматриваемое нами взаимодействие является сла-
бым, выражение (6.22) остается справедливым. Кроме того, пере-
370
данные импульсы в бета-распаде и мюонном захвате не очень велики,
и поэтому достаточно ограничиться в выражении (6.22) слагаемыми
порядка где Л4 — масса нуклона. Таким образом, необходимо
вычислить антикоммутатор величины ар с О'\
[а р, е']+=—^{f1[p-j+-4-j+-p-|-ia- (рХ j+)] —
V 2
—₽f2(i<r • {Р X (i /4 к—ГЛ)—(i f? k—Г*о) XP} +
+ {Р-(’/4 k—f	(P/4 +ji Pl— &₽[«Р(йЭД1}- (9-43)
Здесь использованы соотношения (6.25) и (6.26). Оказывается
(см. ниже § 9.5), что величина f2 сама имеет порядок Л1-1, и, по-
скольку выражение (9.43) входит в нерелятивистский гамильтониан
с множителем Л4-1, можно опустить член с /3 в антикоммутаторе.
Тогда преобразованный гамильтониан взаимодействия примет вид
h' =	—i fi 14+ + if2₽«• (ГXk)—gj' • о +
+-^-ИЛ1р-Г + Г-р+1о- (pxj+)i +
+ igi«-(p/4 +/4 Р)—g2₽o-P(/zA)+Jl},	(9-44)
где в пределе нерелятивистских нуклонов о является спиновой
матрицей Паули, а р может быть заменено единицей.
Чтобы получить окончательный вид гамильтониана слабого
взаимодействия в нуклонном пространстве, необходимо определить
вид лептонных спинорных волновых функций, которые входят в вы-
ражение (9.39). Нейтрино, как известно, описывается плоской вол-
ной, соответствующей импульсу v. Поскольку перед спинором ней-
трино всегда стоит множитель (1 -ф у5), удобно ввести величину
wv = (l+T5)uv,	(9.45)
которая выражается через обычный спинор нейтрино. В представ-
лении, используемом в Приложении Б, она имеет простой вид
=	J a-v)x±1/2,	(9.46)
где х±|/2 соответствует спину нейтрино «вверх» или «вниз».
Спинор (9.45) имеет отрицательную спиральность. Это можно
видеть, действуя оператором спиральности <м на wv:
О- vwv = —т5а -v(l + T5)«v=----T5(l+T5)«-Vuv =
= — (1 +y5)uv== — Wv.	(9 47)
Таким образом, в V — Д-теории все нейтрино имеют спины, на-
правленные антипараллельно их импульсу, тогда как антинейтрино,
описываемые величиной wv = uv (1 — у5), имеют спины, парал-
лельные импульсу.
271
Для многих целей можно также брать волновые функции заря-
женных лептонов в выражении (9.39) в виде плоских волн с им-
пульсом 1. Ток лептонов (9.39) будет тогда иметь вид
/х+(г, /) = L~sbK+e-ik rel<Ev-Ei)t/1i,	(9.48)
где величина k = v — 1 — волновой вектор импульса, передан-
ного лептонами, L3 — нормировочный объем и
b?.= i(wz у?.<ъу).	(9.49)
Учитывая, что
(рЛ+(г, /)) = —&к/*+ (г, t),	(9.50)
получаем
h' = yFP e~lk'r{—+if2g- (b+Xk)—gjЬ+-<т +
+ -J— [fi [—Йк  Ь+ + 2Ь+ • р—i Й<т • (к X Ь+)] +
2Л4с
+igi<T-(—Йк(Д +2bi p)4-frg2(o-k)(bKfej.)+]\.	(9.51)
Это выражение может быть использовано в качестве отправной
точки для рассмотрения ядерных операторов в p-распаде и захвате
мюонов. Его следует просуммировать по нуклонам, которые могут
дать вклад в изучаемый процесс. Для p-распада с испусканием
электрона дают вклад только нейтроны, которые в результате ре-
акции превращаются в протоны. Это может быть учтено введением
нормированного повышающего оператора 1см. также (ПА.9)]
T+==-^(Ti + iT2)= —^=- т+1,
(9.52а)
для которого выполняются соотношения
т+|р> = 0, т+|п> = |р>.	(9.526)
Для захвата мюонов и для Р-распада с испусканием позитронов
необходимо ввести величину, эрмитово сопряженную величине
(9.52а):
т-=~_(т1 —iT2)=y^T_j,	(9.52в)
которая удовлетворяет уравнениям
т_|п> = 0, т_|р>=|п>.	(9.52г)
Для последних двух процессов можно пользоваться оператором
(9.51), а для Р-распада необходима его эрмитово сопряженная ве-
272
личина. В результате получаем оператор Гамильтона для слабого
взаимодействия в ядре
h' = y^ 2 e~ik rHT-b{—i/iW +i/2<r- (b+xk)—
/ =1
—gib+-<H---— [/\ [—Ak b+-|-2b+ p—i/z<r- (к X b+)] +
2Mc
4- i gj <r • (— tl k/4 + 2bt p) +	(<r • k) (bK *z)+] | 6 (r—iy) +
+ эрмитово сопряженные члены.	(9.53)
§ 9.3. Разложение по мультиполям
Оператор, который входит в гамильтониан (9.53), в ядерном
пространстве имеет следующую структуру:
е—ik-|r х И, а _Р_ или ° ' Р 1	(9.54)
( Me	Me I
Для первого и последнего из этих операторов достаточно рассмот-
реть обычное разложение по плоским волнам
e-ik - г = 4зх j-гf (kr) Y*m (k) Ylm (?),	(9.55)
Im
имея в виду, что р не коммутирует с этим выражением. Для двух
других операторов напишем
е-'х-г й = 4л £ i-' /z (kr) Ylm (k) Ylm (i) & Йц=
= 4л 3 i-4l(kr)Ytm(k)(HJ\mnm+^^ TJZ;m+ll(r',fi), (9.56)
ImfiJ
где — сферические базисные векторы [см. (2.40) — (2.43)], а ве-
личины
Тл;м(г, fi) = S(/lJ|Al —рцЛ4)Угл1_ц(г)йц	(9.57а)
и
являются неприводимыми тензорами. С помощью соотношения
(2.48) эти величины можно также выразить через векторные сфери-
ческие гармоники, введенные при рассмотрении полей со спином
единица:
Ул;м(г', Я) = Тл, Л1(г) • й.	(9.576)
В табл. 9.1 приведены тензоры, которые входят в выражения
(9.54) — (9.57), а также указаны ранги J, изменения четностей
л и порядки величин вкладов, которые дают эти тензоры. При
Ю Зак. Н93
273
Таблица 9.1
Неприводимые тензоры, входящие в гамильтониан слабого
взаимодействия в ядрах
Тензор	Ранг J	Четность л	Порядок величины
Y/(r')	1	(-1)'	(kr)1
TJZ(r, о)	J	(-1)'	(kr)1
Р)	J	(-1)'+*	— (kr? с
i Гг(?)5-₽	1	(-1)'+*	— (kr)1 с
Примечание.	Некоторые и	з этих тензоров мог	ут иметь множитель
п1гЦМс), который будет уменьшать их вклад в 0-распад,			
переходе ядра из состояния со спином и четностью J"* в состояние
со спином и четностью Jnff должны выполняться правила отбора
A(JfJJy), я{ялу=1,
(9.58)
где символ А обозначает, что три аргумента должны удовлетворять
правилу треугольника.
Из табл. 9.1 ясно, что наиболее быстрые переходы для (3-рас-
пада (в котором выполняется условие kR 1) будут получаться
из первых двух типов тензоров для случая I = 0. Они называются
разрешенными переходами и имеют правила отбора
A (Jt GJf), т. е. Jt = Jf, щ = nf (переходы Ферми),
A(J£lJy), т. е. Ji=Jf, Jf± 1 (7г = Jy=/=O), я; = Яу
(переходы Гамова-Теллера).
(9.59)
Переходы Ферми обусловлены векторными членами в ядерном про-
странстве, а переходы Гамова — Теллера — аксиально векторными
членами.
Члены более высокого порядка в разложении по мультиполям
дают вклад в запрещенные переходы, в которых степень запрета
связана с порядком мультипольности. Однократно запрещенные
переходы имеют наименьший ранг тензора, согласующийся с из-
менением четности вида яг = — Пу. Поэтому в них входят ве-
личины
Л (г); Т01 (г, о), Тп(г, о), Т21(г, о);
-^—Ло(пр);	Y0(r)<r p-	(9 6°)
274
В процессах (3-распада переходы, содержащие эти члены, будут
иметь матричные элементы, которые уменьшены в соответствии
с множителями kR или v/c по сравнению с матричными элементами
разрешенных переходов.
Для n-кратно запрещенных переходов с 2 соответствующие
данные приведены в табл. 9.2. Кроме тех тензоров, которые ука-
заны там, разрешены правилами отбора некоторые другие тензоры,
но они (например, Уп+1 (г) в-р/Мс) дают лишь малые поправки
к указанным членам.
Таблица 9.2
п-Кратно запрещенные переходы
A J—1J • — J у|		Соответствующие тензоры
п	(-1)"	Уп(г). тпп (г. о), Тпп_[(г. р)
«+1	(-1)"	Лг-Щл Сг- °)
Пр	и м е ч а н и е.	Члены, не указанные здесь, но разрешенные правилами
отбора, дают малые поправки к приведенным в таблице членам. Для однократно		
запрещенных переходов		среди данных, приводимых в таблице, должны быть
переходы	с Д/=0 и л=	-1.
Наиболее интересными в процессах p-распада являются разре-
шенные переходы. В этом случае для AJ = 1 дают вклад только
переходы Гамова — Геллера, а для = Jf = 0 — только пере-
ходы Ферми. Для переходов Ферми правила отбора по изоспину
имеют вид АТ = 0, при этом возможность Tt = Тf — 0 исклю-
чается.
§ 9.4. Бета-распад
Хотя результаты предыдущего параграфа могут быть исполь-
зованы при рассмотрении переходов ядра, которые происходят
в результате захвата мюонов, но такой путь не является особенно
полезным. Дело в том, что для процесса захвата условие kR 1
не выполняется, и поэтому некоторые из специальных упрощений,
которые можно использовать для (3-распада, в данном случае от-
сутствуют. В настоящем параграфе мы рассмотрим те аспекты тео-
рии слабого взаимодействия, которые связаны с [3-распадом. Об-
судим только разрешенные переходы и покажем, как общие свойства
современной теории слабых взаимодействий подтверждаются в экс-
периментах по (3-распаду.
Начнем с рассмотрения общего случая, когда ориентированное
ядро претерпевает (3-распад. В эксперименте измеряется импульс
и поляризация вылетающей (3-частицы и определяется импульс
нейтрино путем измерения импульса отдачи ядра (см. например,
10*
275
где аир обозначают
(е, i£e/c) и (V, iEv!c —
рис. 9.1). Соответствующая вероятность перехода в единицу вре-
мени выражается «золотым правилом» теории возмущений
w== “т 2 SIS । <r> । “>dr |2 х
mv
X 6(£а-£р-£е—£v) X L-^ ,
е	(2лА)«
начальные и конечные состояния ядра,
iv) — 4-импульсы электрона и нейтрино;
суммирование выполняется по спинам
нейтрино и магнитным квантовым чис-
лам конечного состояния ядра. В ядер-
ный матричный элемент мы включим
только разрешенные переходы, отбра-
сывая все члены порядка hk> Мс, р!Мс
и kR. Тогда из выражения (9.53) полу-
чим для Р--распада
J<₽ | h’ (r)|a>dr =
—у1 b • <₽|от+|а>1,	(9.61)
ii	J
где в дальнейшем с целью упрощения
обозначений будем опускать изоспино-
вый повышающий оператор. Удобно
также ввести величины
G₽=Gfb * = gi/A, (9.62)
из которых первая является констан-
той слабого взаимодействия при пере-
данных импульсах, соответствующих
Р-распаду, а вторая представляет собой
отношение аксиально-векторного и векторного формфакторов.
Тогда
w= (XwS A/^6(£a-£₽-£e--£v)dedv,	(9.63)
2(2п)а пл J Mf
где в соответствии с (9.49)
Bw = 3 (ие уц (1 +у5) uv) (ие ур (1 + у5) uv)+ (9 64)
И
дг __ | —^<₽lanla>> Р = 1, 2, 3,	(9.65)
'* I i<₽|l|a>,	р=4.
е V
Электрон
Рис. 9.1. Бета-распад поля-
ризованного ядра 60Со (ука-
зано направление спинов
лептонов). Для определения
импульса нейтрино v необ-
ходимо наблюдать импульс
ядра отдачи.
276
Чтобы рассмотреть спины лептонов, введем единичный 4-век-
тор и'ц ~ О- В системе покоя электрона = (0, imc), и
этот вектор имеет вид = (п, 0), где п — единичный вектор вдоль
спина электрона, а в общем случае = 0. Далее можно опреде-
лить соответствующий релятивистский оператор для спиновой
проекции, который в системе покоя электрона переходит в обычный
спиновый проекционный оператор*
-^-(1—iwy5)->-^-(1-Ь₽о-п).	(9.66)
2	е->0 2
Здесь мы воспользовались соотношениями (ПБ.28). Тогда для
случая измерения спина электрона в направлении вектора п в сис-
теме покоя электрона имеем следующую величину в лептонном про-
странстве:
Вцр = 4-	[(«еТц(1+T5)“v)(«v (1 + ?5)Тр₽(1 — ‘^Т5)“е)] =
Z mvme
= — 4-Sp Гтр,(1 + т5)—Те) тр(1—iwy5) et.-* i mc- =
= ь/e Sp huU + T5)vyp(l—iwy5)(e + imc)], (9.67)
v e
где мы воспользовались выражением (ПБ.43) и тем, что (1 + у5)2 =
= 2(1 +у5). Учитывая (ПБ.51д) и соотношение
SP (Vv Уц Tv У я Ts) = 4еХцгл»
(9.68)
где e^uvn— полностью антисимметричный тензор четвертого ранга,
получаем
Вцр=тА- {^ер—6^(v;eT)+euvp—ep£tlvE etl —
Evre
—тс [л’цШр—6ц(тгшт) + ШцТр—e^vgayj}. (9.69
* В системе покоя электрона этот оператор «проектирует на» направ-
ления спинора, соответствующего спину электрона вдоль вектора п Напри-
мер, если ось г взята параллельной п, то
1 \	/ 1 \
0 /	\ 0 '
1 ,
т(1^а-п)и
=	(1 щ)
1	I ° \ г.
и — (I Ф oz) 1=0.
2	'	\ 1 )
Оператор (9.66) является, очевидно, проекционным оператором, так как
Г 1	~ Г 1	~
(1 — iw*yb) I =	(1 — iWs). При использовании этого оператора
в (9.67) он оставляет вклад от членов (в системе покоя электрона) со спином
вдоль п, но уничтожает состояния со спином, антипараллельным вектору п.
277
Таким образом,
BilpNlLN*p = -£^{2Ite[fa>- <0 | о | а> +v <Р | 11 <х>] X
се
х [Хе- <0 I а I сс> + (Ее/с) <0| 1 | а>]*—(v-e—vEe/c) X
X [ | X <01 о | а> |2—| <0 | 1 | сс> |2J—2 Im [<0 | 11 а> (v X e) •
• (X <0 | <r | a»*,—i | X|2(ve—Ee v/c) • <0 | о | a> X <0 | <r(a>*—
—me [[2Re [Xv  <01 о | a> +v(0| 1 |a>]X
X [Xw-<0 |o|a> +(w-ec/Ee) <0 11 |a>]* —
—(v-w—vw-ec/Ee) [|<0|о|a> |2 —| (01 l’| a> |2] —
—21m [<0 | 1 |a> (vXw)-(X<0|o|a»*[—J
— i | X |2 [vw— (w • ec/Ee) v] • <0| a | a> x <01 в | «>*][},	(9.70)
где учтено соотношение
wt = i}w • eclEe.	(9-71)
Для рассмотрения спинов ядра введем матрицу плотности
ориентированных начальных состояний. Она имеет вид [см. (4.115)1
[ Тм. м/ = Cai. ^мгм-	(9.72)
и нормирована условием
SpT'=2iaM.i= 1-	(9.73)
Рассмотрим ядерные матричные элементы, используя теорему
Вигнера — Эккарта:
<0 | 1 | a> = . jf 8М. Mf <01| 111<х> =	Mf, (9.74)
<0 l°mla> = (^i l-GI Mi mA1/)<0 llolla> —
= (J f\MimMj)Mgt, m=— 1, 0, +1,	(9.75)
Ь
где MF, Mot — приведенные матричные элементы Ферми и
Гамова — Теллера соответственно. Соответствующие суммы по
магнитным квантовым числам ядерных состояний тогда легко вы-
278
числяются:
£ aM.|<₽|H«>l2=4^l^l2.	(9-76)
M.Mf	1
S ам. <₽ I 1 I a>* <P I о I a> = 6, j f-АЗ	?M*FMGT, (9.77)
1	1 ' Vi + l J
2 ам, | <P | о | a> |2 = | Alcr |2,	(9.78)
2	Re 2 aw.[A-<P|ff|a>B-<p|ff|a>*] =
= (A-B—A-jB-j)|MG7-|2 +
+ (3A.jB. f-A- B)3aM Cj J (7WJ|AlCT |2,	(9.79)
m. 1 ‘ 1
i J]	C.[<₽|a|a> x <₽|<r|a>*] = C-PXjИ{|/Иот|2,	(9.80)
MiMf
где j—«единичный вектор вдоль оси поляризации ядра, величина
P=J^aw .(Mil Jt)	(9.81)
Mi 1
является вектором поляризации ядра и
4-м?
1) ’
Jf — J i — 1,
Cji =Iftt (A14 i
Zjy 4“ 1
M?
-----l----, Jf=Ji, (9.82)
Ji (.Ji +1)	1 V
(Ji + I)2 —M?
J-22—’-----L j = j + it
(Jt 4.1) (2Ji + 3)	1
1
Krf Jt=  7j|+ 1 ’
-Ji
U+ 1 ’
Jf= Jt— 1,
Jy= Jj,
(9.83)
Используя соотношения (9.76) — (9.80) в формулах (9.70) и (9.63),
получаем следующее выражение для парциальной вероятности
распада поляризованного ядра, в результате которого вылетает
электрон с импульсом е и спином (в системе покоя), направленным
279
1
вдоль вектора w, а нейтрино испускается в направлении 12v:
<te- -	F(Z, £,) I е IЕ,(Е,-Е,у dE,XI,d9.,x
Xlh+a^+C
I £v£e
v Jj(Ji+l)-3<(J;-j)2>
1 v • ec2
3~EVE
v e
ec
ё;
l-p- A
I-в
j ) (e j ) c2
EE
v e J
vc। p e X vc2
£v	£v £e.
me2
~Ё^
1 V • wc
3 Ev
j)2>
Ev
JiVJi-l)
w 
Ji (2Ji - 1)
4-P -[Aw + В+ D
L	£v \ Ee )
w X vc
(9.84)
Здесь Eo —- максимальная энергия электрона, приобретаемая
при переходе, и
?=|Л4г|2 + |1|2|Л4ог|2,	(9.85а)
а% = | MF |2--- 12i|21 Morl2,	(9.856)
c'g=-|X|2|A4Gr|2AJyJ.,	(9.85b)
Л? = -1 X |2 IMgt I2 k,f j. + 5j. . ('12 2Re [Mf X* MSrl, (9,85г)
+|X|2|MGr|2%J/J. + 6J.Jy(7-^-ry/22Re[AlFX*/WSr], (9.85д)
где
1 /2
2lm[AlFX*AlST],
(9.85e)
Ji
j i + 1
1 ,	
2/г— 1	Jf = J j,
Ji -h 1 Ji CJJi -1)	
	Jf - Л4-1
(Ji > 1) (2Ji + 3)	
(9.86)

Ллл =
и
<(Jrj)2>^5«M(9.87)
Для неполяризовапных ядер P = 0 и ам. = (2Ji + I)-1, поэтому
«J* •J)2> = ^гтг 2^ = 4^	<9-88>
‘ Мг
280
(Обозначения в формулах (9.85) — (9.87) выбраны такими же,
как и в работе Джексона, Трэймана и Вайлда 1208]).
При получении выражения (9.84) мы вычислили плотности
состояний в фазовом пространстве с помощью соотношения
vc—E0— тс*
е2-^	[ 6(E0-Ee-Ev)vMv = C-b|e|Ee(£0-Ee)2. (9.89)
о
Множитель F (Z, Ee) называется функцией Ферми и вводится для
того, чтобы приближенно учесть влияние кулоновского поля
на вылетающий электрон. Эта функция определяется как сумма
плотностей электронов в состояниях s1/2 и р^2 на поверхности ядра
и для точечного ядра дается выражением [см. (5.104) и (5.105)]
F (Z, Ее)= 2 (1 +уг) (2 |е| Д/Й)2 <*-'> е"*	(9.90)
где = [1 •— (Ze2/^)2]1^2. Функция Ферми приводит к эффекту
увеличения вероятности p-распада за счет увеличения значения
волновой функции электрона у ядра, обусловленного притягиваю-
щими ядерпыми силами. Кулоновское поле может также привести
к изменениям в различного рода корреляционных членах, содер-
жащихся в выражении (9.84). Эти эффекты были рассчитаны [209,
107], и, как оказалось, они приводят к дополнительным членам
с коэффициентами порядка Z/137.
Энергетический спектр электронов или позитронов, испускае-
мых в разрешенном p-распаде, может быть получен из выражения
(9.84), если его проинтегрировать по направлениям электрона и
нейтрино, положить Р 0, воспользоваться соотношением (9.88)
(поскольку ядро считается неполяризованным) и результат про-
суммировать по двум направлениям ±w спина электрона. Тогда
получим	,
I cGr I2
dw ii^?F(±z’£e)|e|£e(£-^£e)2£i£e’ (9-91)
где верхний знак относится к испусканию электрона, а нижний —
к испусканию позитрона*. Форму спектра обычно проверяют,
откладывая на графике величину
C(E₽)={-^- [F(±Z,£e)|e|Ee]-i)’/2,	(9.92)
которая, как следует из формулы (9.91), должна изображаться пря-
мой линией. Такой график называется графиком Кюри или графи-
* Энергетические спектры электронного и позитронного распадов раз-
личаются только электромагнитным взаимодействием. Однако в более общем
случае, описываемом выражением (9.84), эти распады различаются также
знаками в членах, содержащих корреляционные коэффициенты [208].
281
ком Ферми-, пример его приведен на рис. 9.2. Такие графики можно
использовать в качестве весьма чувствительного инструмента для
установления верхнего предела массы электронного нейтрино.
Это можно сделать, если исследовать форму спектра в выражении
(9.91) вблизи конечной точки. Если нейтрино имеет массу покоя,
отличную от нуля, то множитель (Е 0 — Ее)^ в плотности конечных
состояний заменяется на с\Еу, и тогда в окрестности верхней гра-
Рис. 9.2. График Кюри для разрешенного f-распада
n-+p+e~+ve [286].
ницы энергетического спектра электрона Ее « Ео, Ev « mV(,c2 и
v « [2mv (Ео — Ее)11/2- Таким образом, спектр имеет форму па-
раболы, которая пересекает абсциссу в точке Ее — Е 0 и имеет
в этой точке касательную, перпендикулярную оси. Таким способом
было получено, что масса электронного нейтрино должна удовлет-
ворять соотношению	0,2 кэв [2251.
Чтобы найти полную вероятность распада, необходимо проин-
тегрировать выражение (9.91) по энергиям электрона:
2л3 (Ас)’
gp(±Z, Ее)|е|Ее(Е0-Ее)МЕе=
lcGp|2
2л3(Ас)’
gf(±Z, Ео\
(9.93)
Полученное обратное время жизни связано с периодом полураспада
соотношением
6/2 = т In 2= 0,693т,	(9.94)
282
и поэтому удобно ввести величину
/ZU2 = -fSWln2‘ <9-95>
II S
Следовательно, величина £/^17 2 является универсальной констан-
той для разрешенного fi-распада. Если Е можно надежно рассчитать
для данного перехода, то соотношение (9.95) может быть исполь-
зовано для нахождения Gp. Таким случаем является позитронный
распад ядра 14О из основного состояния Jn = 0+, Т = 1 на воз-
бужденный уровень Jn = 0+, Т — 1 с энергией 2,311 Мэв ядра
14N. Рассматриваемые уровни, как предполагается, имеют изоспи-
новые проекции Tz — 1 и Tz — 0, принадлежащие одному и тому
же ядерному состоянию, поэтому ядерный матричный элемент
записывается в виде
Л4г=<а; Т= 1, Тг=0|Т_|а; T=l, 7'z 1> = )/Т,	(9.96)
где а обозначает все квантовые числа ядерного уровня, кроме изос-
пина, и использовано выражение (ПА.55). При этом предполагает-
ся, что оператор полного изоспина ядра является суммой однонук-
лонных изоспиновых операторов (9.52)
А
^±= S (т±)г
/=1
Поскольку переход 0+	0+ не имеет гамов-теллеровского вклада,
то из формулы (9.95) получаем
|cGp|2=^^^ln2.	(9.97)
/4/2
Этот результат должен измениться за счет радиационных поправок.
Возможны также поправки [441 в пределах нескольких процентов,
обусловленные нарушением чистоты изоспина для ядерных уровней,
что делает недействительной формулу (9.96). После рассмотрения
нескольких переходов*, имеющих простые ядерные матричные
элементы типа (9.96), и усреднения соответствующих результатов
измерений величины Gp получают [144]
Gg= (1,4029 +0,0022)-Ю-49 эрг-см3,	(9.98а)
или
Gp = 8,7566» 10-5 Мэв  ферми3,	(9.986)
1,0034
--------10"Б.
(Мр с2)2
Чтобы определить значение |%|, можно также воспользоваться
выражением (9.91). Например, для распада свободного нейтрона
* Такие переходы называются сверхразрешенными из-за полного пере-
крывания ядерных волновых функций в формуле (9 96) и соответственно боль-
ших вероятностей перехода.
(Ас)
283
|Л4г|2 — 1, | Мот |2 — 3 и = 10, 80 ±0,16 мин [641, откуда
получаем
| Л|= 1,23 ±0,01.	(9.99)
Рассмотрим теперь угловое распределение электронов, испус-
каемых поляризованными ядрами. Оно получается из выражения
(9.84) интегрированием по направлениям нейтрино и суммиро-
ванием по двум направлениям спина электрона ± w:
I cGr |2
X Г14-Л^-^]с1£ес1Йе.	(9.100)
L Ее J
Наличие анизотропного члена, содержащего величину Р-е, ука-
зывает на несохранение четности в слабых взаимодействиях. Это
следует из того, что поскольку величина е является вектором,
а Р — аксиальным вектором, то комбинация Р-е преобразуется
как псевдоскаляр, указывая таким образом на существование псев-
доскалярного члена в гамильтониане слабого взаимодействия.
Далее, как видно из (9.85а), если не имеется аксиально-векторного
слагаемого, т. е. Л. = 0, то этот член должен отсутствовать.
В 1965 г. Ли и Янгам было высказано предположение, что в сла-
бых взаимодействиях четность может не сохраняться [232]. Они
указали, что их гипотеза может быть проверена обнаружением
члена Р-е в формуле (9.100). Первый эксперимент, в котором про-
верялось это утверждение, был выполнен By с сотрудниками [359].
Они использовали в качестве источника электронов поляризован-
ные ядра 60Со, испытывающие чистый гамов-теллеровский пере-
ход 5+-> 4+, для которого, согласно (9.85), А = — 1. Экспери-
мент дал А —0,7. Для распада свободного нейтрона формула
(9.85) дает
2 .КеХ-1х12 .	(9.101)
l-f-3|X|2	v
Измерения этой величины [65] привели к значению А = — 0,115 ±
±0,008, что вместе со значением |Х| = 1,26±0,02, полученным
в том же эксперименте, дает
Re К= 1,26 + 0,02	(9.102)
или*
Х=|к|е;ч), ф=0°+11°.	(9.103)
Таким образом, в пределах указанных погрешностей X является
действительной величиной. Это необходимое условие того, что
fi-распад нейтрона удовлетворяет инвариантности относительно
обращения времени [см. замечания после формулы (9.24)].
* Усреднение данных по Р-распаду других ядер дает значение [2341
Ф = 0° ± 8°.
284
Продольную поляризацию электрона, испускаемого в [3-рас-
паде, можно вычислить, если положить вектор w параллельным
вектору е в выражении
^> =	dw (w)/dEe — dw (— w)/dEe
dw (w)/dEe -p dw (— w) ldEe
Тогда из выражения (9.84) для случая, когда отсутствует поляри-
зация ядра и не наблюдается направление нейтрино, получаем
—.	me2 ve
9' =---------w.	(9.105)
Eg с
Учитывая, что величина w удовлетворяет соотношению — 0
и, кроме того, является единичным 4-вектором = 1), имеем
р
w = ~^	(9.106)
и
— ve/c,	(9.107)
что находится в хорошем согласии с экспериментом [95] и подтверж-
дает правильность выбора одинаковых амплитуд для вектора и ак-
сиального вектора в V — Л-теории.
В заключение нашего рассмотрения V — Л-теории кратко об-
судим корреляции между электроном и нейтрино. В отсутствие
поляризации формула (9.84) дает
dw	I cGr|2
tZ' £*>1'1E- (£«-£')г X
X [1 +a eJ^- cos 0 J ,	(9.108)
L Ee J
где 6eV — угол между импульсом электрона и направлением ней-
трино, который определяется из измерений отдачи ядра. И снова
вид величины а, даваемый выражением (9.856) для V — Л-теории,
подтверждается экспериментально. В частности, можно исключить
возможность скалярного и тензорного взаимодействия. Измерен-
ное значение величины а [221] для нейтрона равно —0,08±0,01,
тогда как из (9.856) и (9.99) получаем а = —0,102±0,006.
Более интересный результат получается при исследовании кор-
реляции электрон — нейтрино для fi-распада в поляризованных
ядрах. Слагаемое в выражении (9.84) вида
OP-(exv)	(9.109)
нечетно по отношению к обращению времени, и наблюдение такого
члена после того, как электромагнитное рассеяние в конечном
состоянии правильно учтено, означало бы, что ядерный гамильто-
ниан слабого взаимодействия не инвариантен относительно этой
операции. В частности, поскольку для распада нейтрона величина D
285
пропорциональна Im (к), наличие этого члена приводит к формфак-
торам, которые не являются действительными. Полученные экс-
периментальные данные [59J
D = —0,04 ±0,05	(9.110а)
согласуются с инвариантностью теории относительно обращения
времени.
Кроме результатов (9.110а) для распада нейтрона, недавно было
измерено значение величины!) 161] для fi-распада ядра 1BNe. При
этом было получено
D = 0,002±0,014,	(9.1106)
что также согласуется с инвариантностью относительно обращения
времени*. Из анализа экспериментальных данных можно также
получить лучшую точность для фазового угла в формуле (9.103):
<Р = 0,2°±1,6°.	(9.110в)
§ 9.5. Гипотеза сохранения векторного тока
Как видно из (9.98), константа связи для [i-распада определяется
величиной
Ср=С/х(0)==( 1,4029+ 0,0022)-К)-49 эрг-см3	(9.111а)
в соответствии с формулой (9.62) и с учетом того, что переданный
импульс в |3-распаде близок к нулю. С помощью слагаемого (9.12а)
в гамильтониане слабого взаимодействия можно вычислить вероят-
ность распада мюона р" —> е~ ± ve ± vM, а сравнив результат
с данными эксперимента, получить значение константы, ответст-
венной за р-распад [2341:
G—(1,4350+0,0011)-10-49 эрг-см3. (9.1116)
Она отличается от Gp примерно на 2%. Поскольку неопределен-
ности анализа, используемого для извлечения этих значений
(радиационные поправки, эффекты нарушения чистоты изоспина),
имеют такой же порядок величины, экспериментальные значения
обеих констант G в (9.111 а) и (9.1116) могут считаться одинаковыми.
Это соответствует нашей исходной гипотезе об универсальности
описания слабых взаимодействий [см. (9.9)] и означает, что форм-
фактор, введенный для учета эффектов сильного взаимодействия
в векторную часть нуклонного тока, должен удовлетворять соотно-
шению
А(0) = 1.	(9.111В)
* Заметим, что неинвариантные по отношению к обращению времени
члены как в распаде нейтрона, так и в распаде ядра 19Ne искажают изоспи-
новые трансформационные свойства, приписываемые обычно аксиальному
току. Следовательно, эти частные виды распада не могут служить достаточно
хорошей проверкой инвариантности относительно обращения времени [276].
286
Такой результат является довольно неожиданным. Из него
следует, что эффекты различных полей, с которыми нуклон взаимо-
действует сильно при переданном импульсе, равном нулю, не из-
меняют константу связи слабого взаимодействия. Слово «не изме-
няет» означает, что константа является такой же, как и для мюона,
который не участвует в сильных взаимодействиях. Мы можем по-
лучить некоторые наводящие соображения о возможных причинах
такой ситуации, если обратимся снова к электромагнитной теории.
Сильные взаимодействия, очевидно, не меняют электромагнитную
константу связи, или заряд е, который имеет одну и ту же величину
для протона, электрона и мюона. Действительно, из (6.3) —
(6.5) вытекает, что электромагнитный зарядовый формфактор об-
ладает тем же свойством, что и (9.111в), т. е.
Ft(0) = 1.
(9.112)
Причины этого довольно хорошо понятны. Сильное взаимодейст-
вие в действительности вызывает изменения в распределении заряда,
но поскольку электромагнитный ток сохраняется, то полный
заряд в области взаимодействия является константой, хотя и
существуют эффекты сильной связи. Размеры области взаимодей-
ствия определяются комптоновской длиной волны различных
частиц, участвующих в сильном взаимодействии. Поскольку самая
легкая из этих частиц (пион) имеет конечную массу, то область
взаимодействия имеет конечные размеры (« Ас/140 Мэв =
= 1,41 ферма), так что фотон с очень большой длиной волны,
соответствующей нулевому переданному импульсу, будет «чув-
ствовать» полный заряд в этой области. Таким образом, электро-
магнитная константа связи при низких переданных импульсах
не перенормируется сильным взаимодействием вследствие сохране-
ния тока. Подобная же ситуация будет наблюдаться и для слабого
взаимодействия, если потребовать, чтобы векторный ток, входящий
в гамильтониан слабого взаимодействия, сохранялся.
В случае электромагнитных взаимодействий формальное выра-
жение для закона сохранения тока имеет вид
— = 0,	(9.113)
дхк
где
— / 1 4-т-, \	/ дФ+	дф 1 \
Д (х)= 1 ес фух ф + i ес —— Ф+ —Ф+ —t- Ц-...
\ 2 )	\ дх}	дх} I
...= 1есфу?.	ф—ес (фХ	.	(9.114)
\ 2	/	\ охк )з
В этом выражении Ф+ = 2-1^2 (Ф4	г‘Ф2) — поле, создающее по-
ложительные и уничтожающее отрицательные пионы, Ф — век-
торы в пространстве изотопического спина. Учет пионного тока
требуется потому, что благодаря сильной связи нуклоны интен-
287
сивно взаимодействуют с пионами, так что сохраняется лишь общий
ток, например в процессах, подобных процессам р^п л+.
Указание на опущенные члены в выражении (9.114) относится
к дополнительным возможным видам сильной связи нуклонов
с другими мезонами и т. д.
Изоспиновый проекционный оператор у (1 ф-т3) в выражении
(9.114) учитывает тот факт, что протон имеет заряд, а нейтрон его
не имеет. Член в нуклонном токе вида
/|0) — i ес фух ф	(9.115)
является изоскал ярным членом и автоматически сохраняется
вследствие сохранения барионного числа [см. сноску к выражению
(9.9)]. Оставшиеся члены в выражении (9.114) мы рассматриваем
как третью компоненту изовекторного тока
jx= ~ i есфу^тф —ес [ Ф X .	(9.116)
Мы постулируем, что векторный ток в слабом взаимодействии
сохраняется [158, 132], и в дальнейшем принимаем значительно
более сильную гипотезу, что этот сохраняющийся векторный
ток связан с сохраняющимся электромагнитным током с по-
мощью операции поворота в изоспиновом пространстве:
для данного нуклонного тока (9.146). Это, очевидно, включает
и нашу первую гипотезу, поскольку из инвариантности сильных
взаимодействий относительно вращений в изоспиновом пространстве
следует, что если третья компонента в изоспиновом пространстве
сохраняется, то сохраняются и другие изоспиновые компоненты.
Мы уже установили общий вид оператора электромагнитного
тока (jz)3, действующего между одночастичными состояниями
[см. (6.3) — (6.5)1, и вид соответствующих матричных элементов
оператора слабого тока JVK в выражении (9.15). Поскольку мы по-
стулируем, что оба эти тока имеют одинаковые свойства за исклю-
чением свойств вращений в изоспиновом пространстве, то можно
связать между собой формфакторы обоих токов*
fi(fe* 2)=F1(fe2), ^(0)=1.	(9.118а)
f2 (k2) =	= H(KP-Kn) ,9 j 186)
2Mc	2 Me
* Заметим, что в формуле (6.3) обозначает 4-импульс, переданный
ядру, тогда как в выражении (9.15)	—импульс, переданный от ядра.
2 88
где К'р и Кп — аномальные магнитные моменты протона и нейтрона,
Кр —	— 3,70. Более того, член в выражении (9.15), содержа-
щий величину if3ki, который исчезает в соответствии с гипотезой
сохранения G-четности [см. формулу (9.36)], также должен исчез-
нуть в силу гипотезы сохранения векторного тока (см. § 6.1). За-
метим, что так как Ху=1, то аксиальный ток в выражении (9.15)
не сохраняется (см. ниже, § 10.2).
Чтобы проверить справедливость гипотезы сохраняющегося
векторного тока (СВТ), соотношения (9.118) можно подвергнуть
экспериментальной проверке. Современная техника позволяет это
Рис. 9.3. Схема уровней в ядрах с Д = 12 для проверки гипотезы СВТ.
сделать в основном при k2 = 0, когда соотношение (9.118а) сводится
к (9.111b). Экспериментальное подтверждение последнего и послу-
жило сначала поводом введения гипотезы СВТ. Таким образом,
главным соотношением, которое следует установить, остается
f2 (0) — ti (Кр — КпУ^Мс. Этот вопрос изучался эксперименталь-
но [233, 360, 234] на основе анализа распадов основных состояний
ядер 12В, 12N с Jn — 1+, Т 1 в основное состояние ядра 12С и
фотонного распада аналогового состояния Jn = 1+, Т = 1 при
энергии 15,11 Мэв в 12С (рис. 9.3). Рассматриваемые Р-распады
являются разрешенными гамов-теллеровскими переходами с малы-
ми примесями запрещенного вклада от векторного тока. Используя
для рассмотрения распада 12N	12С + е+ -|- ve выражение (9.53),
получаем
/г'=-А_ V (T_)Ji (/2+^-'jo-(b+xk) — gib+.o] =
^2Z.S	I \ ZMc'	IJ
= - -° У (T-hb+-{i p2 + kxo-fto). (9.119)
V 2L3 y—	I \ 2Mc/	Jj
289
Имеется также поправка к аксиальной части, обусловленная запре-
щенными переходами, но, как оказалось, она несущественна для
быстрых частиц, и мы ее не учитываем. Из (9.119), (9.63), (9.69)
и (9.78) получаем для р -распада
dw= (dw0) [1 + — — (Е
°	~ 3 Пс \	2
/п2 с4
2£
(9.120)
где dw0 — вероятность разрешенного перехода, даваемая выраже-
нием (9.91) для гамов-теллеровских переходов и
а_ рчСА(0) + (2Л1сГ1 ДЛ(0)
8, (0)

(9.121а)
В (9.121а) мы учли, что в соответствии с требованием инвариантно-
сти относительно обращения времени константа связи является
действительной величиной, и воспользовались соотношением (9.118)
и тем, что Ер = Ер + 1 = 2,79 есть полный магнитный момент
протона. Если для вычисления (9.121а) пользоваться значениями
моментов свободных нуклонов, то получим
а = 0,20% !Мэв,
(9.1216)
тогда как в эксперименте [360, 2341 для распада 12В получено
а =0,21±0,04%Шзе, а для 12N а = 0,20±0,02 %/Л1эв.
Справедливость использования магнитных моментов, величины
которых не перенормируются ядерными силами, может быть про-
верена для этих переходов в ядрах с А = 12 путем исследования
вероятности перехода с испусканием фотона с уровня 15,11 Мэв
в основное состояние в ядре 12С. Используя выражения (4 78) и
(4.83) с J; = 1 и Jf = 0, получаем
1 k3 feh(Kp—Kn)
9 П ( 2Мс
2
= 0,80(Кр-К„)2| <₽И«>|2 эв/ti,
(9.122)
где, как показали расчеты [346, 3491, вкладом орбитальных токов
можно пренебречь. Если взять [360] экспериментальное значение
приведенного матричного элемента | <р || oj|a> | « 2,0, то из на-
блюдаемой [182] вероятности перехода Т = 53^11 эв/h получится
значение | Ер — Еп | ~ 4, что довольно хорошо согласуется с ве-
личиной Ер — Еп = 4,70, вычисленной с использованием магнит-
ных моментов свободных нуклонов.
Дополнительное доказательство справедливости гипотезы СВТ
может быть получено из рассмотрения угловых р — у-корреляций
в распадах 8Li и 8Ве и угловых р — ^-распределений в распадах
24Na и 24А1. Эта гипотеза подтверждается также наблюдением пред-
сказанных ею свойств распада л+ -* л° ~р е+ ve, в котором
пионное поле может быть теперь непосредственно связано с лепто-
нами, поскольку оно явно входит в векторный ток (9.117).
290
Для общей информации очень полезны книга Нильссона и
Пичмана [261] и обзорные статьи Джексона [2131, Ли и By [234],
Роуза и Нильссона [292] и Мартина [242]. Много глав, специально
посвященных ядерной физике, имеется в книгах Липкина [236],
Конопинского [222], Шоппера [3091 и By и Мошковского [361].
Обзоры теории Р-распада сделали Морита 12581, Копопинский и
Роуз [221], Блин-Стойл и Наир [45]*.
* Обсуждение отдельных вопросов, рассмотренных или упомянутых
в этой главе, можно найти в книгах [154, 371, 373, 380, 382, 383, 387,
389]. — Прим, персе.
ГЛАВА 10
ЗАХВАТ
МЮОНОВ
Когда мюон рождается при распаде медленно движущегося
пиона, он обычно теряет свою весьма малую кинетическую энергию
в процессе столкновений, приводящих к ионизации атомов окружаю-
щей среды. Положительно заряженные мюоны распадаются со вре-
менем жизни
т = (2,1983±0,0008) 10-е сек.	(10.1)
Но отрицательно заряженные мюоны, энергия которых уменьши-
лась до нескольких килоэлектронвольт, могут быть захвачены на
атомные орбиты с большим главным квантовым числом (п«14).
Затем могут осуществиться каскадные переходы сначала с испуска-
нием оже-электронов и с последующим излучением рентгеновских
у-квантов 1112]. Большинство отрицательных мюонов в конце
концов достигает атомной орбиты 1s, поскольку общее время, не-
обходимое для перехода на 1 s-орбиту, заключено в интервале
между 10-8 и 10-12 сек, что намного меньше времени жизни
(10.1). На ls-орбите мюон может распадаться на электрон и два
нейтрино или он может быть захвачен ядром. Захват происходит
по схеме
+	+	(Ю.2)
Вероятность перехода для реакции (10.2) зависит от Z прибли-
зительно как Z4. Эго объясняется тем, что вероятность нахождения
мюона в ядре в силу нормировки водородподобной волновой функ-
ции связанного мюона пропорциональна Z3, а число протонов, ко-
торые могут участвовать в реакции (10.2), равно Z. Для ядер
с Z > 9 вероятность ядерного поглощения превосходит вероятность
естественного распада*.
Процессы мюонного захвата представляют интерес по несколь-
ким причинам. Во-первых, вопрос, правильно или нет описываются
* Вероятность распада |х~ -> е~ + ve + уменьшается в тяжелых
ядрах, так как атомная связь уменьшает объем фазового пространства для
продуктов распада, но этот эффект мал для ядер с Z 12 (см. [108]).
292
они взаимодействием (9.11), связан с вопросом об универсальности
нашего описания слабых взаимодействий. Во-вторых, в отличие от
p-распада в захвате мюонов участвуют довольно большие передан-
ные импульсы, так что можно наблюдать вклад индуцированного
псевдоскалярного взаимодействия [содержащего формфактор g2
в выражении (9 37)1. Захват можно изучать на простейших ядер-
ных системах, например на протоне, однако в этом случае наблю-
дения усложняются химическим эффектом, а именно, способностью
мюона образовывать молекулярный ион со структурой (ррр). Ве-
роятность нахождения мюона в пространстве, занимаемом протоном,
для этой молекулы значительно отличается от аналогичной вели-
чины для мюонного атома водорода. Чтобы получить полезную
информацию о слабых взаимодействиях, надо знать указанную
вероятность, но она может быть найдена только в результате боль-
шой вычислительной работы*.
Получение сведений о слабом взаимодействии из данных о за-
хвате мюонов сложными ядрами затрудняется неопределенностью
в описании уровней ядер. Однако можно получить ценную ин-
формацию, которая дополняет то, что известно из изучения других
явлений. Можно осуществить много различных экспериментов,
в которых выполняются измерения вероятностей распада на опре-
деленные уровни дочернего ядра, радиационного захвата мюонов,
углового распределения ядер отдачи по отношению к направлению
остаточной поляризации мюона (равной 15—20%), изучаются свой-
ства продуктов распада после захвата мюона дочерним ядром,
находящимся в различных возбужденных состояниях. Кроме того,
для ядер с отличным от нуля спином наблюдается влияние сверх-
тонкой структуры на вероятность мюонного захвата, и этот эффект
может быть использован для подтверждения справедливости
V — Д-тсории в захвате мюонов при сравнении с предсказаниями
V 4- Д-теории [29, 76, 356]. Наконец, изучение захвата мюонов
ядрами приводит к некоторым интересным следствиям в теории
структуры ядра и, в частности, связывается с теми же самыми ос-
новными процессами, которые определяют фото и электровозбуж-
дение ядер.
§ 10.1.	Вероятность захвата
Вероятность захвата мюона дается обычной формулой, выра-
жающей «золотое правило» теории возмущений:
V f |	( <₽ | h' (r) | a) dr	(W.3)
he J J	(2nhy
* Недавно сообщались результаты эксперимента, в котором мюон за-
хватывается атомным водородом [277] Экспериментальное значение вероят-
ности захвата для синглетного состояния равно 651	57 сек-1, что хорошо
согласуется с теоретическим значением 626 ± 26 сек-1.
293
где v — импульс нейтрино, Qv — телесный угол в направлении
его вылета. Поскольку нейтрино обычно не наблюдается, то это
выражение должно быть проинтегрировано по dQv. Символ сум-
мирования означает усреднение по параметрам начальной ориен-
тации ядра и направлению спина мюона и суммирование по пара-
метрам конечной ориентации и спиновым состояниям нейтрино.
Оператор Гамильтона дается выражением (9.53), а множитель
Л3/2 в формуле (10.3) возникает из-за того, что заряженный лептон
первоначально находится в связанном состоянии и, следовательно,
не нормируется на объем L3. Мы берем мюонный спинор, который
в нерелятивистском приближении дается выражением
^=-7=-1 \%±1/2,	(Ю.4а)
/4л	\0 J
где R (г)— нерелятивистская радиальная волновая функция ls-
состояния в водородподобном атоме. Для легких ядер функцию
R (г) можно аппроксимировать константой, что мы здесь и будем
делать. С учетом нормировки
/ Z2 \i/2	п
Д(0)=21—j-j ,	-----=256 ферми. (10.46)
\ ац /	трfi2
Для более тяжелых ядер радиальную волновую функцию обычно
заменяют константой, полученной из условия совпадения со сред-
ней по объему ядра для мюонной волновой функции [237, 311].
Импульс tik в выражении (9.53) тогда всегда есть импульс ней-
трино.
Необходимые суммирования по проекциям спина в пространстве
лептонов могут быть выполнены по аналогии с (9.63), (9.64), (9.67)
и (9.69):
вро= — V («hYp(!+T5)«v)+(«цТо(1 by5)uv) =
Sp. Sv
1	Г	l+₽	v
=-----Sp yp(l + Y5) — Yo(l + Y6)— =
2	2	2iv
= ~~ Sp [yp (1 + ₽) Yo (1 -|-To) •v] =
4iv
=------ [64	+ 6<J4 vp — iv6g — Eiapk Vft] ,	(10.5)
iv
где ~ (1 4- P) — проекционный оператор для покоящегося мюона.
Используя формулу (9.53), получаем
V |b3/2$<₽|ft'(r)|a>dr|2 =
2 Sp sv
294
+ Ы2 [|(₽|tf|a)|2 + i^(P|tf|a>x (P|tf |а>*] +
+ 2Re [/jg! <p| 1 |a>v(P|tf|a>*] ( 1 + —'j +
-|-2Re(g1 /2/А) iv-(P | tf | а> x (P|tf|a>* +
+ 2Re(vg1f2/A) [( (P I ст j а > |2 — |v<P|tf|a)|2] —
—^lfi|2Re(₽| 1 |a>v-(0|p|a>* —
~M^cRelflS* <₽l 11 «> С₽к-Р|а>*1-
~~ «Р ।CTI a> ’<₽ I PI «>* — iv-(P I<r| «> X <₽ |p] «>*)] +
+ ^Refe/\) fiv-(p I tf I ct> x <p|tf|a>* +
+ |(P|tf |а> I2—I v - <p j cr [ <x>]2] H-
+ ^Ы2| v-(P|tf|a>|2—|£i |2 Re [v - <P|tf|a>(P|tf-p |a>*] —
—^7₽е[(Л^/^) <P| 11 a) v-(P| tf |a>*+(vgj,g.’/A)lv- (P|tf |a>|2] } ,
M	J
(10.6)
где в соответствии с точностью преобразования Фолди — Вутхай-
зена, используемого при получении выражения (9.53), мы исклю-
чили члены порядка М~2 и учли, что согласно (9.118) величина
/2 имеет порядок М-1. Далее, при наших предположениях о вол-
новой функции мюона ky, = (v, iv — imuc), где mu — масса мюона.
В выражении (10.6) мы определили
(Р | Q | а> = $¥£ (гъ г2,. .... гл)	е—ivr (т_). Q. х
X 'Fa (гъ г2, .... ГЛ) dr± dr2... drA,	(10.7)
где Q = 1, tf, р или tf-p. Выражение (10.6) можно несколько упро-
стить при суммировании по параметрам ориентации ядра в на-
чальном и конечном состояниях. С помощью разложения по муль-
типолям, описанном в § 9.3, теоремы Вигнера — Эккарта (ПА.54)
и рассмотрения законов сохранения четности можно получить
	(₽|tf |a> X (P|tf|a)*= 0,	(10.8а)
1 -I мг Mf
—----- V Re (Р | 11 a> v-(Р| tf ] a>*= 0.	(10.86)
2Ji + 1 M^if
295
9 , . , У Re <р | 11 а> <р | o p | а>*= 0,	(Ю.8в)
1 + лг Му
~ 1 У Re <₽ I о I а> • <Р I р I а>* = 0.	(10.8г)
। Л4 Л4-
Докажем, например, последнее из этих соотношений. Используя
(9.56) и то, что операторы о и р при инверсии четности ведут себя
противоположным образом, имеем
* ~7 21 <Р! ° I «> - <Р | Р | «>*
‘ ' М; Л1у
V V V i<-.F,.„.(v)r;„W х
2J; +1
lmJ[X I'm'J'y,' M- Mj
x (/1J | тцт + p) (I'U' | m'p'm' + p') x
X (Jt JJf | Mjtn -|- p7Wy) (J tJ' Jf | Mt m' + p' Mf) X
X lu-V <Pllh(vr)TJZ(r, o)||a> <pi|/> (vr) Tj-/-(r, p)[a>* =
= (4эт)2-|т^7 У Re<₽||//(vr)TJ/(r,o)i;a>x
i+ и
X <P||h(vr)TjZ(r, p)||a>*= o.	(10.9)
С помощью соотношений (10.8) получаем
Mi Щ sv
z: (O<0|1|«>I!(1 +£) +ls>liKPI«l«>P-
\ mc
-4lfi |2 Re <p | 1 | «> v.<₽|p|a>* +
Mc
+ 2Re
I2 — I v-<₽ H a> |2)
\ 2Mc fi 1
v
4---Re
Me
gi (gi—v-6P|(T|a>|2
\	ft /
+ y^-Re KgiK) iv-<P|tf|«> X <₽ | p | a>*] —
Me
|gil2Re[v-<PI<T|a><₽|a-p|a>*ll-
Me	1
(10.10)
296
В этом выражении матричные элементы, в которые входит ско-
рость нуклона р, М, обычно дают довольно малые поправки порядка
(vn/c). Они являются членами, учитывающими отдачу, и мы их
здесь опускаем. Оставшиеся в выражении (10.10) члены после под-
становки в формулу (10.3) приводят к вероятности перехода из ос-
новного состояния ядра а в возбужденное состояние 0, которая
выражается формулой
V2 i . l2	1
W-------— U'„ Г --------
2лй4с 1	2Ji+ 1
X {|Gy|2| <01 l|a>P + |G„ |2|<0|a| a) |2 +
H-2Re(G^ Gp) | v-(01 <r | a> |2}-
(10.11)
Мы ввели величину |i|yi|ai,e — среднее от волновой функции мюона
по объему ядра. Константы связи в формуле (10.11) определены
следующим образом:
(10.12а)
(10.126)
(10.12в)
Ga = Gg1(
— Л-v А
2Мс Н
(10.12г)
Теперь можно выполнить разложение по мультиполям в матрич-
ных элементах в выражении (10.11), используя определение (10.7)
и технику разложения, рассмотренную в § 9.3. Например, для
ядер с замкнутыми оболочками разрешенные переходы, которые
возникают после замены плоской волны в выражении (10.7) едини-
цей, не дают заметного вклада. Причина этого заключается в том,
что спиновый и изоспиновый операторы в выражении (10.11) изме-
няют ориентацию спина и изменяют зарядовые состояния нукло-
нов, но не влияют существенно на пространственные волновые функ-
ции нуклона. Таким образом, эти операторы усиливают роль конеч-
ных состояний, имеющих более чем один нуклон на одночастичном
уровне, но последнее запрещено принципом Паули. Для векторных
матричных элементов <0 |1| а> главный вклад дают дипольные
или запрещенные в первом порядке переходы. Действительно, если
рассматриваемые ядерные состояния имеют изоспин в качестве хо-
рошего главного квантового числа, то соответствующая комбинация
в выражении (10.11) легко может быть связана с сечением диполь-
297
ного фотопоглощения:
1	’V’ 1 / ®2 \ —1	v2 Г
2Д^1	2л2 UJ £₽'-£а J ₽'‘
M-Mj	line
(10.13)
Согласно (4.8), величина
( Р' | 2 (ГТз)> | ° )
j = i
(10.14)
является сечением дипольного фотопоглощения для переходов из
основного состояния а в возбужденное состояние Р'. Здесь р' —
изобарический аналог уровня р. Уровень Р' существует в том же
самом ядре, которому принадлежит и основное состояние а, тогда
как уровень р получается в результате мюонного захвата, в про-
цессе которого один протон заменяется нейтроном.
Для ядер с замкнутыми оболочками матричные элементы в вы-
ражении (10.11), содержащие спиновые операторы, также опреде-
ляются главным образом однократно запрещенными переходами.
Соответствующие конечные состояния совпадают с теми, которые
сильно возбуждаются намагничивающей частью ядерного тока при
больших переданных импульсах в процессе рассеяния электронов
[см. § 6.4, формула (6.69) и ниже]. Эти уровни лежат в той же обла-
сти энергий, что и фотоядерный гигантский резонанс для которого
сечение поглощения (10.14) велико. Таким образом, в легких ядрах
с замкнутыми оболочками в результате мюонного захвата возбуж-
даются уровни с энергией в интервале между 20 и 25 Мэв. Дина-
мические свойства такого процесса обычно аналогичны основным
свойствам механизмов электромагнитного возбуждения в ядрах.
Поскольку энергия возбуждения ядра при захвате мюонов близ-
ка к энергии гигантского резонанса, то обычно вычисляют кон-
станты связи (10 12) при v = 85 Мэв!с. Аргумент формфактора
тогда равен
Их) (П~ рх) =
1	(т
= —[2(mMc)-v —(mM.c)2]= 0,61	(10.15)
и в соответствии с гипотезой сохранения векторного тока [см. (9.118)1
при использовании параметризации (6.29) и (6.67) для электро-
2 98
Рис 10 1 Вероятность захвата мюона ядром 16О в еди-
ницах 103 сект1.
Теоретические значения отложены как функции от индуцирован-
ной псевдоскалярной константы взятой в интервале
предполагаемых значений. Кривая, отмеченная буквами GJ, яв-
ляется результатом расчета в рамках модели оболочек [164],
а кривая, отмеченная буквой М, рассчитана [284] в рамках ме-
тода Мигдала [250, 251]. Случай а относится к переходам, при-
водящим в первое возбужденное состояние (7л=0~) ядра leN.
Верхняя штрихованная полоса дает вероятность перехода, изме-
ренную авторами работы [70], нижняя заштрихованная область —
это данные измерений, приведенные в работе [17]. Случай б
соответствует захвату мюона с образованием ядра ,6N в основ-
ном состоянии J31 =2~. Экспериментальный результат заимство-
ван нз работы [70] (см. [284]).
магнитных формфакторов нуклона имеем fi 0,986 и f2k-
3,65/2Л1с. Далее мы предполагаем, что
gi
Тогда
0,61
«^(0)=1,23.
Gv 1,03 G, GA = 1,44G, G^ = 1,23 G,
GP— — (0,154-1-0,0453G,
(10.16)
где G дается формулой (9.98).
Как следует из (10.11), (10.12) и (10.16), точность измерений ве-
роятностей захвата мюона будет до некоторой степени зависеть
сдг/ьх
Рис. 10.2. Область возможных значений
индуцированной псевдоскалярной кон-
станты m^cgt/fr'k, полученной из данных
о захвате мюона в водороде. Заштри
хованная область дает эксперименталь-
ный результат, приведенный в работе
[291] (см. [234]).
Дополнительную информацию о
из экспериментов несколько другого типа
смотреть радиационный захват мюона
от величины и знака индуци-
рованной псевдоскалярной
константы связи* g2. Она мо-
жет быть определена в ука-
занных измерениях при ус-
ловии, что ядерные матрич-
ные элементы в выражении
(10,11) известны с достаточно
хорошей точностью, обеспе-
чивающей надежное значение
GP. Однако обычно это не
так. Даже результаты наибо-
лее тщательных вычислений
эффектов структуры ядра в
выражении (10.11) являются
весьма неопределенными, и
после того, как учтены экс-
периментальные погрешности
в измеряемых значениях ве-
роятностей переходов (см.
рис. 10.1 и 10.2), можно полу-
чить лишь очень широкие
пределы величины g.2.
величине g2 можно извлечь
Например, можно рас-
р.“+р->п + ^ + у.
(10.17)
В этом процессе энергия массы покоя мюона делится главным обра-
зом между нейтрино и фотоном. Поскольку в процессе участвует
фотон, то при взаимодействии с протоном мюон может иметь доволь-
но большие значения импульса, что усиливает вклад индуцирован-
* Следуя терминологии авторов, формфактор g2 мы в дальнейшем везде
называем константой g2. — Прим, перев.
300
ного псевдоскалярного члена. Поскольку коэффициент ветвления
для радиационного захвата мюонов равен примерно 10~4, экспе-
рименты желательно выполнять на довольно тяжелых ядрах, так
чтобы получить достаточно большую скорость счета фотонов во
время измерений. Руд и Толхук [294] рассчитали фотонный спектр
Рис. 10.3. Теоретические спектры фотонов для радиацион-
ного захвата мюонов ядром 40Са при различных предпола-
гаемых значениях индуцированной псевдоскалярной кон-
станты связи
Спектры даются в зависимости от величины х=со/сомакс — энергии
фотонов в единицах максимально возможной энергии фотонов — н
нормируются на вероятность нерадиационного мюонного захвата
в ядре 4ССа (см. [294, 332]).
для ядра 40Са, используя различные предполагаемые значения
g2 (рис. 10.3). Эксперименты [74] на 40Са дают величину mllcg^lhX =
= 13 + 3.
Наконец, для измерения величины g2 можно использовать [198]
угловое распределение нейтронов, испускаемых при захвате мюонов.
Угловое распределение обусловлено остаточной поляризацией
15—-20%, которой может обладать мюон после серии каскадных
301
Рис. 10 4. Диаграмма процесса одно-
пионного обмена, который по предпо-
ложению в основном ответствен за
индуцированное псевдоскалярное
взаимодействие в мюонном захвате.
Большая заштрихованная область отно-
сится к сильному взаимодействию, в ре-
зультате которого в нуклонном облаке рож-
дается пиои; вершина справа описывает
слабый процесс, соответствующий обычно-
му распаду пиона.
переходов, в конечном счете приводящих его на 1 s-орбиту. Однако
анализ экспериментов по угловому распределению нейтронов при
захвате мюонов более сложными ядрами, чем протоны, сильно ус-
ложняется ядерными эффектами, так что полезная информация об
индуцированной псевдоскаляр-
ной константе является, по-
видимому, недосягаемой.
Индуцированное псевдоска-
лярное взаимодействие в акси-
альном токе для слабого взаимо-
действия, как предполагается,
обусловлено в основном процес-
сом, показанным на рис. 10.4:
сильно взаимодействующая псев-
доскалярная частица(пион)рож-
дается из мезонного облака, ок-
ружающего протон, и затем сла-
бым образом взаимодействует с
мюоном. Изменение константы
индуцированного псевдоскаляр-
ного взаимодействия весьма важ-
но, поскольку можно использо-
вать указанную модель индуци-
рованного псевдоскалярного
взаимодействия для вычисле-
ния значения g2; это очень по-
лезно для установления связей
между сильным и слабым взаимодействиями [169]. Особенно удоб-
ный способ для вычисления величины g2 основан на использовании
гипотезы частично сохраняющегося аксиально-векторного тока.
§ 10.2. Гипотеза частично сохраняющегося
аксиально-векторного тока
Гипотеза о том, что векторный ток в слабом взаимодействии
сохраняется, была введена в § 9.5 для объяснения соотношения
ft (0) — 1, т. е. того факта, что векторная константа связи не пере-
нормируется сильным взаимодействием. Естественно спросить,
может ли сохраняться также и аксиально-векторный ток. Поскольку
gt (0) = 1,23, то ясно, что сильные взаимодействия частично из-
меняют аксиально-векторную константу, а это, видимо, исключает
возможность сохранения аксиально-векторного тока. Значительно
более убедительное доказательство последнего утверждения заклю-
чается в том, что если бы аксиально-векторный ток сохранялся,
то распад пиона был бы запрещен.
Слабый распад пиона

(10.18)
302
определяется гамильтонианом взаимодействия (9.8), в котором
один член в полном слабом токе (г) должен быть приписан пиону.
Матричный элемент взаимодействия имеет вид
<pv | Н' | л> = i -Д— f (01 JAK+ (г) | л> e~ik r dr х
F 2Ld J
X 1«цТл(1 + y6)wvb	(10.19)
где k = (v 4- jx)/A, и для определенности выбран случай распада
отрицательного пиона. Матричный элемент пионного тока должен
преобразовываться как 4-вектор, а единственный 4-вектор в нашем
распоряжении — это вектор импульса пиона л^, который в силу
закона сохранения равен hk% = (v + р)х. Используя волновую
функцию пиона, нормированную* на величину (2 £л/й2с2)£3, что
соответствует решениям уравнения Клейна — Гордона, получаем
j <0 | JAK+ (г)| л>е~ ik'rdr=
= — i (2лА)3б (л—v— ц)	А/я (£2 = — mh c2/h2) kK,
(10.20)
где f„ (k2) — произвольная скалярная функция, которая берется
при соответствующем значении аргумента пионного 4-импульса.
В системе покоя пиона вероятность распада дается «золотым пра-
вилом» теории возмущений**
Щ sv
u> = —	(2лЛ)3 ~ | A/л |2 X
h 2L6	2mn
Д(1 +T6M|26(v + fi)-^-
Н \ I Г5/ v/l \	f*/ (2лй)3	(2лй)3</£
2	р	f->	_
тЬ	2 1‘М(1 + ъ)фй'
16л2	44 J
SJX sv
lv, (10.21
* Эта нормировка аналогична нормировке в формуле (3.105) для фотон-
ного поля, где соответствующий множитель имеет вид (2Ey/4nh2c2)L3. Раз-
ница в 4л связана с использованием в (3 105) нерационализированных гаус-
совых единиц для электромагнитного поля. Поэтому члены, описывающие
источники в уравнениях Максвелла (1.1), умножались на 4л, тогда как здесь
для описания пион нуклонного взаимодействия мы используем рационализи-
рованные единицы [см также уравнение (10.29)].
** При нормировке в объеме L3 трехмерная дельт а-функция Дирака при
значении аргумента, равном нулю, заменяется согласно формуле (2лй)3б (0) -
= У dr = Р.
303
где Л= 1тлсР/А. Суммирование по спиновым состояниям дает
2 I О + Тв) г/т 12 =
spi sv
2 2 Г	~	~ । •	21
№	2iv	21ЕЦ
2 2	2 tri tn
= -^7£7TSp[P(1 + YsWC^ + i/^c2)] =	(10.22)
2v E.. fr	hz E„
|Л	p,
где мы ввели
P= v =	£u= 2^(^л + /Пц). -	(10.23)
Тогда
w = |£.(fe/n/mn) I2 _Sl ZnL(m2_m2)2.	(10.24)
8л hl тл
Экспериментальное значение времени жизни пиона равно [293]
тл= (2,604 ±0,007)-IO-8 сек,	(10.25)
откуда с помощью (9.98) и (9.111) получаем
|/л| = 0,93тл(Ас)1/2/А3.	(10.26
Если аксиально-векторный ток сохраняется, то для матрич-
ного элемента в формуле (10.19) мы будем иметь
!<°1^/ЛХ+(г>
л\ e~Ikrdr = i/fy ( <01 JA>-+ (г) | л> е—ikrdr =
= -ЙгУ <2лА)3 6 (v + н) \./2	с2/^) = 0.
\ й /	(2mnL )
(10.27)
Отсюда следует, что fn = 0 и время жизни пиона бесконечно. Такой
результат 1329] вынуждает нас отказаться от понятия сохраняю-
щегося аксиально-векторного тока. Однако это наводит на мысль
о другой гипотезе. Дивергенция от аксиально-векторного тока
должна преобразовываться как псевдоскаляр, а пионное поле яв-
ляется вполне подходящим псевдоскаляром. Целесообразно, таким
образом, ввести гипотезу [259, 159] частично сохраняющегося ак-
сиально-векторного тока (ЧСАТ), которая гласит, что дивергенция
от оператора аксиально-векторного тока пропорциональна опера-
тору пионного ПОЛЯ Ф
А/"+ = »Ф+.	(10.28
Оператор Ф+, так же как и в выражении (9.114), уничтожает
отрицательно заряженные пионы и рождает положительные пионы.
Поскольку имеет место только сильное взаимодействие, то Ф удов-
304
летворяет уравнению Клейна — Гордона с псевдоскалярным источ-
ником нуклонов
[□— (-£-) ]ф(*)=	(10.29)
где величины, обозначенные жирным шрифтом, относятся к изоспи-
новому пространству, а константа связи равна [2171
—^—=15,9 + 0,2.	(10.30)
4 л Нс
Подставляя (10.28) в (10.27), можно непосредственно определить
величину а из вероятности распада пиона. В системе покоя пиона
имеем
а С (0|Ф+|л) e~ik rt/r= (2rcA)36(v-|-p,)
h
(2тя£®)*'2
а,
(10.31)
где снова использована обычная нормировка пионной волновой
функции. Таким образом,
А/лФ.
(10.32а)
(10.326)
Значение последнего результата становится ясным, если мы
возьмем матричный элемент от этого операторного соотношения
между состояниями нуклона, описываемыми плоскими волнами.
Для левой части с помощью (9.15) получаем
< п | Jx I Р> = — и (n) [gi (k2)	+ ig2 (k2) kK kK y5] и (p) e1^
= li (n) Г i f MpC^Mn c. i gl (£2) Ys __ i £2 g2 (£2) Ys
\ n J
и (p) eift^ 4
(10.33)
а правая часть может быть вычислена с помощью (10.29):
-(-^ГА/л<п|Ф_ |р> =
\ Fl J
=	----ДД----/2Г^я(^)н(п)у5н(Р)е^Ч (10-34)
\ й / (тл С^Й)2 k2
где Fnn„ (k2) — формфактор поглощения или испускания пиона
нуклоном. При нормировке (10.30) эта величина нормируется так,
что
Лу№г( — /ПлС2/А2)= 1.	(10.35)
и
1 1 Зак. 1193
305
Если теперь сравнить (10.33) и (10.34) при k2 = 0 и предположить,
что FNNji (0) не сильно отличается от единицы, то мы получим
(Мр « Мп = М)
I -1Л9	‘ ~	Ма<°> ' „г>чт
У	5? ~ ► 2 ~Т~	<1036)
Этот результат называется соотношением Гольдбергера — Трей-
мана [169]. Подставляя численные значения (9.99) и (10.30), по-
лучаем
т„ F Нс
/л = 0,83-^------,	(10.37)
и2
что находится в разумном согласии с (10.26) и служит подтвержде-
нием гипотезы ЧСАТ. Далее мы можем сравнить (10.33) и (10.34)
при k2 = — т^ с2/И2, учитывая, что g2 (k2) должна иметь в этой
точке полюс, обусловленный вкладом диаграмм, подобных изобра-
женной на рис. 10.4, a gi (k2) в этой области должна изменяться
регулярно. Тогда с помощью (10.36) находим
2(Mc/H)gl(0)
(тяс/й)2^	(
Подставляя величину переданного импульса, дающую главный
вклад в процессе захвата мюонов [см. (10.15)], получаем для комби-
нации, содержащей константу связи индуцированного псевдоска-
лярного взаимодействия,
т с8г (£2)	2т., Мс2
—м- „	=--------------= 7,5,	(10.39)
ЯХ (тлс)2^И2И2	'
что весьма хорошо согласуется с экспериментальными результата-
ми*, приведенными на рис. 10.1 и 10.2. Константа, определяемая
соотношением (10.16), равна
Gp= — 0,57 G.	(10.40)
Гипотеза ЧСАТ может быть также использована вместе с ос-
новной гипотезой алгебры токов [160, 161] для того, чтобы выра-
зить значение gt (0) [5, 350] через сечение рассеяния пионов с ну-
левой массой на протонах. Использование эмпирических данных
о рассеянии реальных пионов дает [5]
|£Х (0)|= 1,24 ±0,03,	(10.41)
что находится в очень хорошем согласии с результатом (9.99).
* Для захвата мюона протоном [277] наблюдаемый результат для этого
числа есть 6,2 ±3,1.
306
§ 10.3. Связь радиационного поглощения пионов
с захватом мюонов
Как указывалось в § 10.1, после захвата мюона в ядре могут
возбуждаться изоспиновые или спин-изоспиновые колебания. Пе-
реходы, обусловленные векторной частью ядерного тока и приводя-
щие к возбуждению изоспиновых колебаний, связаны с возбужде-
нием уровней гигантского фотоядерного резонанса, тогда как ак-
сиально-векторная часть тока приводит к возбуждению спин-
изоспиновых колебаний, что соответствует большим передаваемым
импульсам в электровозбуждении ядер. Гипотеза ЧСАТ, рассмот-
ренная в предыдущем параграфе, позволит нам установить, что
в реакции радиационного поглощения пионов
л- 4- р п + у	(10.42)
также возбуждаются спин-изоспиновые уровни. При этом в отличие
от нейтрино, появляющегося в конечном состоянии в процессе
мюонного захвата, фотон в реакции (10.42) можно наблюдать
экспериментально [821 в случае, когда отрицательный пион вначале
связан на атомной орбите, а затем захватывается протоном в ядре.
Измерение фотонного спектра дает возможность определить рас-
пределение силы аксиально-векторных переходов в ядре. Информа-
ция, получаемая таким образом, дополняет информацию, извлекае-
мую из данных о фото- и электровозбуждении.
Чтобы определить вид матричного элемента взаимодействия,
который описывает реакцию (10.42), необходимо рассмотреть гипо-
тезу ЧСАТ с учетом электромагнитного поля. Естественно предполо-
жить, что для заряженных частиц наличие электромагнитного поля
приведет к обычной замене производной в выражении (10.326),
т. е. д/дхк -> д/дхк — i (е/Яс)Ак (х), где е — заряд частицы. Тогда
гипотеза ЧСАТ при наличии поля запишется в виде
(^- + 1^Л(х)Ъ^+=-(-^У^яФ+	(Ю.43)
1 дх^ he I	\ h ]
(для случая рождения положительного пиона). Законность такого
обобщения уравнения (10.28) можно доказать [6] для всех теорий,
в которых система взаимодействующих частиц может описываться
лагранжианом*. Вероятность перехода для процесса (10.42) опре-
деляется перекрытием волновой функции начального состояния,
содержащего ядро в основном состоянии а, и волновой функции
* Так же как и при получении (10.41), предположения, связанные с су-
ществованием лагранжиана, могут быть заменены [269] предположением о
справедливости гипотезы алгебры токов [269].
ПВ Зак. 1193
307
конечного состояния, в котором ядро находится в возбужденном
состоянии р, т. е.
<Ру | ал-> = <ру ] ф_ । «> =
= ~{тяс )	(10-44>
Член в правой части, содержащий производную, даст полный 4-им-
пульс пиона
= (л, i '/л* 2 4-	с2).
Для связанного пиона можно взять л 0, так же как и при рас
смотрении в § 10.1 захвата мюона с атомной орбиты. Кроме того,
мы введем гипотезу «мягких пионов», которая использовалась при
получении (10.41) и которая гласит, что с хорошим приближением
можно осуществить экстраполяцию на нефизический случай, в кото-
ром л 0 ( = тлс) исчезает. Тогда в выражение (10.44) дает вклад
только член, содержащий электромагнитный потенциал. Для
поперечной калибровки имеем [см. (3.105а)]
,о .	.	. ( h \2	1
(₽у[ая > = ш(—
X 1/2 [ <Р | Jt (г) | а> ez е~ikr dr,
\ J J
(10.45)
где e£ — l-я компонента вектора поляризации фотона, к — волно-
вой вектор фотона. Вклад от ядерного матричного элемента, входя-
щего в (10.45), идентичен аксиально-векторному вкладу в слабых
взаимодействиях (в частности, в мюонном захвате), даваемому вы-
ражением (9.22) для лептонов, описываемых плоскими волнами.
Разумеется, волновой вектор к здесь соответствует энергии массы
покоя пиона, освобождающейся в процессе поглощения, тогда
как вектор к в выражениях (9.48) и (9.53) отвечает несколько мень-
шим энергиям в мюонном захвате. Это различие может быть учтено
введением ядерного формфактора, который содержит зависимость
от к.
Поправки, обусловленные слагаемым с производной в выраже-
нии (10.44), можно вычислить [124], например, для 3Не, рассмат-
ривая это ядро как «элементарную» дираковскую частицу. Такой
расчет дает поправку к результату, полученному с помощью (10.45).
равную примерно 15%. Отношение Панофского для 3Не, предска-
занное 1124] с помощью выражения (10.45), находится в хорошем
согласии с экспериментом*, так же хорошо согласуются экс-
* Отношением Панофского называется отношение вероятностей процес
сов перезарядки и радиационного захвата пионов каким-либо ядром Для
л- -J- 3Не —> зт® —|—
3Не теоретическое значение этой величины Р = Зце	= 2,70
[124], экспериментальное значение Р= 2,28 ± 0,18 (Займидорога О. А.,
Кулюкин М. М. «Ж. эксперим. и теор. физ.», 1965, т. 48, с. 1267). — Прим,
перев.
308
периментальные значения вероятности захвата мюонов и ра-
диационного захвата пионов ядром «Ы, в результате которого
образуется «Не в основном состоянии [96].
Возбуждение спин-изоспиновых колебаний при радиационном
поглощении пионов можно непосредственно описать с помощью
выражения (10.45), если перейти к нерелятивистскому пределу
для слабого аксиально-векторного тока совершенно так же, как
это было сделано в § 9.2. Как видно из сравнения выражений (9.38)
и (9.44), доминирующий член содержит величину
<Р | J? (г) | а> ez е—lk'rdr-> — § <01 ат_ | a>«8e-ikr dr, (10.46)
где оператор в ядерном пространстве приводит к переходу из ос-
новного состояния с S ~ Т 0 в возбужденное состояние с S =
= Т = 1, и для ядра с замкнутыми оболочками вклад низшего
порядка дает член с линейной зависимостью от г в разложении
плоской волны. В действительности матричный элемент в выраже-
нии (10.46) представляет собой проекцию на вектор £ аксиально-
векторного матричного элемента в выражении (10.11) для вероят-
ности мюонного захвата. Тот факт, что радиационное поглощение
пионов приводит к возбуждению уровней вблизи гигантского фото-
ядерного резонанса, в котором возбуждаются спин-изоспиновые
колебания, подтверждается в изменениях фотонного спектра,
выполненных с низким разрешением для нескольких ядер [82].
Поправки к основному члену в выражении (10.45) или (10.46)
для вероятности радиационного поглощения пионов могут быть
также вычислены с помощью импульсного приближения [87, 12].
Импульсное приближение 1173] является систематическим мето-
дом для задач рассеяния на связанной системе. Оно позволяет
заменить амплитуду рассеяния на частице, находящейся в поле
потенциала, амплитудой рассеяния на свободной частице, при усло-
вии что является малой величина
Здесь f — амплитуда рассеяния, В — энергия связи частицы в ми-
шени, А — длина волны Де-Бройля рассеянной частицы, Е — энер-
гия этой частицы. Для радиационного поглощения пионов величина
£ равна приблизительно нескольким процентам. С физической точки
зрения это совершенно понятно [62]. Процесс поглощения включает
неопределенность в энергии порядка массы пиона, и, следовательно,
в задаче существенны временные интервалы порядка hlm^c1. Эти
интервалы намного меньше, чем характерное время, соответствую-
щее энергии связи и имеющее порядок величины h/B. Поэтому
реакцию можно рассматривать как импульс, во время действия
которого силы связи не играют существенной роли. Частицу мишени
можно рассматривать как свободную, а силы связи нужны лишь
для того, чтобы определить, какие компоненты импульса присут-
ствуют в ее волновой функции.
11В*
309
Термин «импульсное приближение» часто означает также,
что эффектами многократного рассеяния пренебрегают. Эти эф-
фекты несущественны при условии, что средняя длина свободного
пробега рассеянной частицы в мишени значительно больше разме-
ров мишени, что амплитуда рассеяния намного меньше среднего
расстояния между нуклонами и что эффекты, связанные с выходом
за массовую поверхность, малы. Для пионов с низкой энергией
(значительно меньшей энергии 3,3-резонанса*) первые два условия
выполняются, так как амплитуда пион-нуклонного рассеяния равна
лишь ~0,1 ферми; получить же определенное подтверждение для
третьего условия нелегко. Конечный результат импульсного приб-
лижения при условии пренебрежения эффектами многократного
рассеяния сводится к тому, чтобы заменить оператор Т, описываю-
щий взаимодействие с ядром, суммой амплитуд рассеяния tj для
А свободных нуклонов:
А
Т= 2 tj.	(10.47)
7=1
В дальнейшем этот оператор должен действовать между волновыми
функциями ядерных состояний для рассматриваемого перехода.
Амплитуда поглощения пионов на свободных нуклонах с рож-
дением фотонов высокой энергии хорошо известна 163]. Ее главный
член имеет вид
t = i V 2 eg о • Ат_ Ф.
2Л1с2
(10.48)
где А — векторный потенциал для фотонов и
Ф+ = (Фх + 1Ф2),	= (Ti—ir2).
Выражение (10.48) имеет ту же форму, что и выражение (10.46).
Можно написать и оценить поправочные члены к амплитуде. Для
поглощения связанных пионов на легких ядрах они составляют
от 5 до 10%. Используя выражение (10.48), получаем для вероятно-
сти радиационного поглощения пионов
И3 k ft
A
S aee~ikr
.2
г2
2
,	(10.49)
где ф (r) — нормированная на единицу волновая функция пиона
в водородподобном атоме, a g дается выражением (10.30).
* Так часто называют наиболее сильный и ранее других установленный
резонанс в сечении пион-нуклонного рассеяния. Его характеристики следую-
щие: энергия 1236 ТИэв в системе центра масс, изотопический спин 3/2, спин
3/2, четность положительна. — Прим, перев.
310
Дополнительным достоинством импульсного приближения явля-
ется возможность изучения радиационного поглощения пионов для
мезонов, находящихся на любой атомной орбите. Поэтому оно
позволяет выйти за рамки сравнения с мюонным захватом по фор-
муле (10.45), которая справедлива только для поглощения пионов
с 1 s-орбиты. Это свойство особенно ценно, так как для ядер, более
тяжелых, чем 4Не или 6Li, полная вероятность поглощения пиона
с 2р-уровня значительно превосходит вероятность перехода 2р-> 1s
с испусканием рентгеновских -р-квантов [245]. Таким образом, для
12С и 16О поглощение пионов происходит преимущественно из
2р-состояния, а для ядер, которые тяжелее 20Ne, вступает в действие
поглощение с Зй-уровня. Учет поглощения с 2р-уровня, т. е. ис-
пользование волновой функции пиона, находящегося на 2р-уровне
около ядра,
<Р(г)« т|=- Лм (г) (гУ'Г72'', ая = —193 ферл»и, (10.50)
может привести (помимо других возможностей) к возбуждению
состояний с Jn = 0“ в 12С и 16О. Этот гигантский 0_-резонанс,
который соответствует возбуждению спин-изоспиновых колебаний,
не может возбуждаться из основного состояния электромагнитным
способом. Следовательно, процесс радиационного поглощения пио-
нов играет очень важную роль в объяснении распределения и свой-
ств таких уровней. Этот гигантский монопольный резонанс завер-
шает формирование группы резонансов, которая включает гигант-
ский электрический дипольный (1“) резонанс и гигантский магнит-
ный квадрупольный (2~) резонанс. Совокупность возбужденных
состояний, соответствующих указанным резонансам, играет глав-
ную роль в явлениях, обусловленных электромагнитным и слабым
взаимодействиями в ядрах при энергиях 15—30 Мэв.
*
* 4=
Обсуждению свойств захвата мюонов посвящены книги Коно-
пинского [222], Шоппера [309], By и Мошковского [361], обзор-
ные статьи Ли и By [234], Роуза и Нильссона [292] и опубликован-
ные записи лекций Джексона [213], Толхука [332], Вайденмюл-
лера [349] и Примакова [275]. История расчетов мюонного захвата
с помощью ядерных моделей рассмотрена в важных статьях При-
макова [273], Фуджи и Примакова [147], Луайтена, Руда и Тол-
хука [237], Фолди и Валенки [143] и Ро [284, 285]. Эффекты ги-
гантского и спинового гигантского резонансов в захвате мюонов
и соответствующая связь с электромагнитными процессами воз-
буждения обсуждаются в обзорах Юбералля [339] и Валецки
[342]*.
* Работы [361, 234] переведены на русский язык. См также книгу
[383]. — Прим, перев.
ПРИЛОЖЕНИЕ А
КВАНТОВАЯ ТЕОРИЯ
УГЛОВОГО МОМЕНТА
В этом Приложении мы кратко обсудим те вопросы квантовомеханиче-
ской теории углового момента, на которые мы часто ссылались в тексте. Наша
цель — дать очерк традиционной теории и точно определить систему обозна-
чений; более подробные обсуждения имеются в книгах, указанных в конце
гл. 3.
§ ПА. 1. ОПЕРАТОРЫ УГЛОВОГО МОМЕНТА
В гл. 3 мы обсуждали влияние вращения системы координат на поле ф.
Если вращение /? характеризуется осью п, вокруг которой оно выполняется,
и углом поворота 6, то преобразованное поле имеет вид [см. (2.13), (2.20),
(2.24) и (2.30)]
[7(Л(п, ©))ф](г) = ехр (i©n-j)ip(r),	(ПА.1)
Оператор J в общем случае имеет следующую структуру:
J = L-$-S,	(ПА.2)
где Ь = —ir XV — оператор орбитального углового момента. Спиновый
оператор S вводится для того, чтобы учесть, что для полей общего вида ф
может быть вектором в виде столбца из п компонент*. Для частиц со спи-
ном s поле ф имеет 2s + 1 компонент и S является набором трех матриц
(2s + 1) X (2s + 1). В формуле (ПА.2) подразумевается, что L умножается
на единичную матрицу (2s + 1) X (2s + 1).
Чтобы более полно понять природу оператора J, который порождает
вращения, рассмотрим следующую ситуацию. Предположим, что осуществлен
бесконечно малый поворот вокруг оси х на угол е и после этого — второй
такой же поворот вокруг оси у на угол т). Далее предположим, что мы вы-
полнили эти же повороты в обратном порядке. Поскольку вращения не яв-
ляются коммутирующими операциями, результаты двух таких противополож-
ных последовательных действий не являются одинаковыми. Фактически можно
обнаружить «экспериментально» или с помощью соотношения (2.9), рассма-
тривая его для бесконечно малого поворота, что разность указанных последо-
вательных операций отличается от тождественного преобразования операцией
вращения вокруг оси г на угол ет). Таким образом, имеем из соотношения (ПА.1)
eiT)J2 е1еЛ_е1еЛ е1Ц^_ е1ецЧ_ j,	(ПА.З)
* В гл. 3 мы рассматривали скалярное поле и (г), для которого S исче-
зает, и векторное поле А (г), для которого S было некоторой комбинацией
матриц 3X3.
312
или в низшем порядке по е и т]
J \ J2-^2 *1 — ^З-
Аналогичное рассмотрение для других таких же пар поворотов приводит к за-
ключению, что некоммутируемость вращений означает, что порождающий их
оператор J удовлетворяет обычным коммутационным соотношениям для
углового момента
JxJ=iJ	(ПА.4а)
или
^/1= Jm-	(ПА.46)
Здесь — полностью антисимметричный тензор третьего ранга (см. снос-
ку в § 1.2), а индекс т может считаться индексом суммирования или не счи-
таться таковым, так как в любом случае вклад в правую часть дает только
один член. Эти коммутационные соотношения могут быть непосредственно
проверены, если для каждого конкретного случая воспользоваться явным
выражением для L = —ir X V и S.
Имея оператор углового момента J, мы можем построить оператор квад-
рата полного углового момента
J2=j24. j2^ j2f	(ПА.5)
который коммутирует с каждой компонентой J, так как
з
[J-. JZ]= 2	-МА} =
k = i
3
= •	^hlm {Jh	Jд} = О,	(ПА.6)
А=1 т— 1
где последнее равенство следует из того факта, что свертывание симметричной
двухиндексной величины с антисимметричной дает нуль. Как следствие соот-
ношений (ПАЛ) и (ПА.6) можно диагонализовать J2 одновременно с одним
и только одним оператором углового момента, скажем J3. Результирующие
собственные функции записываются какф^т. Как хорошо известно из кванто-
вой механики, можно с использованием соотношений (ПЛ.4) и (ПА.6) пока-
зать, что удовлетворяются уравнения
J2 Ф;т = 1 (/ф" 1) Фут	(ПА.7а)
и
•^3 Фут = ^Фут»	(ПА./б)
где j может быть любым целым или полуцелым числом 0, 1,/2, 1, 3/2, .... а
т — —j, —j + 1, ..., j. В этом месте удобно ввести повышающие и пони-
жающие операторы
J± = Ji ± i^2-	(ПА.8)
Изсравнения (ПА.8) с (2.39) видно, что это определение отличается от обыч-
ного выражения для векторов, разложенных по сферическому базису. Имеем
из (2.42) и (2.43)
•/j. 1 =	-- Т JJв= J3.	(ПА.9)
Еще раз используя коммутационные соотношения для операторов углового
момента, получаем
J± tyjm = К j Т m) (/ ± т 1)1 ‘/2 Ф/m ± 1	<ПА-10)
(с учетом обычного условия для фазовых множителей).
313
§ ПА. 2. СЛОЖЕНИЕ УГЛОВЫХ МОМЕНТОВ.
КОЭФФИЦИЕНТЫ КЛЕБША — ГОРДАНА И 3/-СИМВОЛЫ
Рассмотрим случай, когда система описывается двумя операторами угло-
вого момента Ja и Jb, действующими в двух различных пространствах.
Такая ситуация встречается при изучении двух разных частиц или рассмо-
трении орбитального углового момента и спина одной частицы. Тогда можно
говорить о двух разных собственных функциях ф,- _ (а) иф,- „ (6), для ко-
‘а а 'Ь Ъ
торых справедливы уравнения
J s (s) = is (is-f-1) Фта ms (s)-	(ПА. 11 a)
(Js)s Фу3 (s) = ms фу3 (s), s=a,b	(ПА.116)
Можно построить несвязанное представление, рассматривая в пространстве,
являющемся произведением пространств а и Ь, функции
’Ь’а та (°) тЪ
Поскольку Ja и Jb действуют в разных пространствах и, следовательно, ком-
мутируют, эти функции являются одновременно собственными функциями
операторов J2, (Jo)3, J|, (Jb)3 [см. уравнения (ПА.11)].
Оператор, о котором мы говорим как об операторе полного углового
момента системы, строится в виде
J = Jo-bJb,	(ПА.12)
где для того, чтобы обеспечить соответствующую размерность, подразуме-
вается прямое произведение на единичные матрицы. Так как Jo и Jb комму-
тируют, имеем, как обычно,
J X J = iJ.
Значит, оператор полного углового момента обладает теми же самыми свой-
ствами, что и оператор J в выражениях (ПА.4) и (ПА.6). Следовательно, можно
попытаться построить в новом пространстве функции, являющиеся общими
собственными функциями операторов J2 и J3:
Л2Ф/т=/(/->1)Ф/т.’|	(ПА, 13)
G Ф>т=,пФ/т- J
Чтобы дополнить до полного набора коммутирующих операторов, эти функ-
ции можно рассматривать также как собственные функции операторов J2
и Jg. Представление, осуществляемое функциями, которые удовлетворяют
уравнениям (ПА.13), называется связанным представлением. Унитарное
преобразование от несвязанного к связанному представлению записывается
следующим образом:
Ф7т = S (/« ib i[ma'nbm)4>jama(a)^jbmb(t>)- (ПА.14)
mamb
Матричные элементы этого унитарного преобразования называются коэффи-
циентами Клебша—Гордана. Для них существует много различных обозна-
чений. В работах [287, 288] они записываются как С (ja, jbj; татьт). В ра-
боте [109] диагональные операторы в каждом представлении связываются
через коэффициенты Клебша—Гордана, которые записываются в виде
(jama]bmb\ jajbim). Авторы работы [247] используют обозначение
</о/ьто/пь |/т> так же, как и в работе [55]. Однако фактически все авторы
выбирают фазы в этих преобразованиях тем же способом, что и Кондон и
Шортли [67], поэтому численные значения коэффициентов Клебша—Гордана
почти всегда одинаковы.
314
Свойства коэффициентов Клебша—Гордана получаются непосредственно
из их определения как унитарного преобразования, осуществляющего пере-
ход из представления {Jq, (Jo)s, Jfc, (Ль)з) к представлению {J2, Jg, J2, J3).
Например, действуя оператором j3 = (Jo + Ль)з на обе части выражения
{ПА. 14) можно установить, что
Ua ib iI tnambm) = 0, если та-^ть ф т.	(ПА.15)
Это свойство часто вводится в обозначения и используется запись
Ua 1ь Цт—тьтьт),
гле уже взято та = т — ть; можно вообще отбросить последний индекс
и записывать
Ua ib Цт—тьть).
Очевидно, что свойство (ПА. 15) сводит суммирование в формуле (ПА. 14)
к одной сумме.
Учитывая размерности связанного и несвязанного представлений, можно
далее показать, что
Ua ib i I m—mb mb m) =£ 0, только если | ja—jb | < j < ja-&jb. (ПА. 16)
Это условие на область изменения /, которое может быть также записано
в виде
11—jb I < ia < i-lrib или | j—ja | < jb < j+ja,
называют условием треугольника. Такое название выбирается по аналогии
с классическим представлением об ограничениях модулей векторов в равенст-
ве (ПА. 12). Иногда условие треугольника кратко обозначается в виде A (iajbj )
Поскольку коэффициенты в формуле (ПА. 14) являются элементами уни-
тарной матрицы, такой, что (ф;-а m(j (а) ф,- т& ( 6)) и ф7т нормированы, то
существует соотношение ортогональности
2 Ua ib i I ma ть m) (ja jb j' | ma mb tri)	(ПА.17)
mamb
Преобразование, обратное преобразованию (ПА. 14), имеет вид
та (а) %-ь ть (b) = 2 0‘« ib i I та ть та-$- ть) qjma+mb, [(ПА. 18)
где коэффициенты Клебша—Гордана выбраны действительными (доказано,
что это возможно). Соответствующее соотношение ортогональности имеет вид
2 Ua ib i | ma mb mamb) (ja jb j | m'a ть m’a mb) =	. (ПА. 19)
Для явного вычисления коэффициентов Клебша—Гордана необходимо
предварительно изучить действия понижающих и повышающих операторов
(Ja + Ль)± на выражение (ПА. 14). Общие формулы для коэффициентов вместе
с их другими свойствами имеются в книгах по теории углового момента, спи-
сок которых приведен в конце гл. 2. Здесь мы приведем некоторые наиболее
полезные результаты. Первый из них — это свойства симметрии, возникающие
11*
315
при произвольном изменении порядка сложения любых двух угловых мо-
ментов и при рассмотрении обращения времени. Они имеют вид
Uaib i\mambm)^[(— 1)'а+,ь 1 (jb ja j | mb ma tn) =
= ( — [)’a~'r‘a-L ^ja jjfc| ,Па—щь) =
/*
= ( —	-L (jjbjal—mmb—ma) =
ja
= ( — l)'a~m° ~ (jja jb\m—mamb) =
ib
= (—l)Jb+mb (jb jja |—tnb mma),	(ПЛ.20а)
ja
где j =	4-1- Кроме того, получаем симметрию из условия обращения
времени:
Ua ib j\mambm)= (—l)Ia+lb ' (ja jb /1 — ma— mb—m).	(ПА.206)
Из (ПЛ.206) следует, что
Ua ib j | ООО) #= о, только если (ia + ib-ri) четно. (ПА.21)
Коэффициенты, в которых все магнитные квантовые числа равны нулю, назы-
ваются четными коэффициентами Клебша—Гордана. Другой частный слу-
чай относится к сложению двух моментов по формуле (ПА. 12), один из которых
равен нулю. Тогда
Ua0j\mn0mb)=6ja j.
(ПА .22)
Значения коэффициентов Клебша—Гордана для jb= и /ь = 1 приведены
в табл. ПЛ.1.
Свойства симметрии, выражаемые соотношениями (ПА.20), более просто
записываются для некоторой модификации коэффициентов Клебша—Гордана.
В результате такой модификации получается величина, называемая 3)-сим-
волом. Она определяется так:
1а 1Ь ]=(___\\'а~!Ъ~т
та mb rn J
1
— (ia ib i I ma mb— m),
i
(ПА.23)
где, как видно из сравнения с (ПА.15) и (ПА. 16), jajb и j удовлетворяют пра-
вилу треугольника, а та + ть + т = 0 для неисчезающих 3/-символов.
Свойства симметрии, соответствующие соотношениям (ПА.20) для коэффи-
циентов Клебша—Гордана, выглядят совсем просто:
/ ib'll'a	_[Ja+lb + i / / ib ia
\ mb та mJ	\ т ть та
'( i 1ь ) = ( — i)'a+ib+jib i
\ та т ть )	\ —та — ть —т
316
Т а б л и ц а ПА. 1
Коэффициенты Клебша—Гордана для /г> = 1/2 и /ь = 1
12 Зак. 1193
317
С другой стороны, соотношения ортогональности немного усложняются,
а именно
V
тат
И
т'ь
ib /'
гад гп
(ПА.25а)
la
1Ь
ma mb
mb
la jb
mamb ~ma
(ПА.256)
ъ
1
i
I
1
Р

Одним из полезных применений коэффициентов Клебша—Гордана или
ЗУ-символов являются формулы для произведения сферических гармоник от
одного и того же аргумента
Yiama^Ylbmb ~ 2
1т
la 1Ь I
У 4л
la lb I \
та tnbm)Ylm^ =
V Zg ib
lm I "К4я
(la lb 11 ООО) (la 1Ь 11 та tnb m) yZm (г).
(ПА.26а)
и обратная формула
или
(ПА.266)
la h> I \ /
о о о/ \
(Z„ Zz, Z | ООО) KZm(r) = lV* V (la lb 11 mambm) Y, m (г)У,	(r).
la lb mamb	a a b °
(ПА.26в)
Их можно проверить, воспользовавшись свойствами матрицы конечных вра-
щений, построенной из операторов в формуле (ПА.1), взятых между состоя-
ниями с хорошим квантовым числом углового момента:
Dm’m(R (п- ©)) = </>«' I exp(i©n. j)| /т>.
Заметим, что, например, в формуле (ПА.26а) левая часть имеет четность
(—l)Z“+Zb, в то время как четность правой части есть (—l)z [см. (2.72)J.
Это не приводит к противоречию в силу свойства (ПА.21) 3/-символов или
коэффициентов Клебша—Гордана, которое дает (—1)г = (—l)Z“^b.
С помощью доказательства, аналогичному тому, которое необходимо при
установлении соотношений (ПА.26), получают также теорему сложения сфе-
рических гармоник
Рг(г'-г)= -~~l ^Ybnir^Yimir).
гп
(ПА.27)
318
§ ПА.З. СЛОЖЕНИЕ ТРЕХ УГЛОВЫХ МОМЕНТОВ,
КОЭФФИЦИЕНТЫ РАКА И 6/-СИМВОЛЫ
Пусть надо связать три угловых момента Ja, Jf,, Jc в полный момент J
J =	(ПА.28)
Для этого необходимо осуществить преобразование от представления, в ко-
тором операторы
= ia (ia‘ 1). (^а)з- =lna, J b = jb (jb~\- 1) .
(•lb)s — mb. J c = jc (jc “I- !)• (*^с)з = /r^c
являются диагональными, к представлению, в котором диагональны операторы
Ja=ja(ja+ 1). Jt = /b(jb+D.
Jc=7c(/c+l)> J2=j(/+1). /з= rn.
В последнем представлении нужен один дополнительный диагональный
оператор, чтобы иметь полный набор коммутирующих операторов. Им являет-
ся угловой момент, возникающий при промежуточном сложении двух момен-
тов при двукратном применении формулы (ПА. 14). Это значит, что можно
рассмотреть
метод 1: Ja-|-Jb = J', тогда J'-|-JC = J, что дает	или эквива-
лентный
метод 2: Jb + Jc = J", тогда Ja 1 J"=J.4TO дает f/m)/")-
Если использовать коэффициенты Клебша—Гордана, чтобы построить
в методе 1, то оператор J'2 =(Ja + Jb)2 = j' (/' + 1) будет диагональным; если
же использовать эти коэффициенты в методе 2, то результирующая ф;-т
будет собственной функцией оператора J'2= (Ль +Jc)2 с собственным зна-
чением /"(/" >1).
Существует унитарное преобразование, связывающее функции Фьп(/')
и	Запишем его в виде
= J " W (la ib Ис, j	(ПА.29
Коэффициенты W в этом разложении называются коэффициентами Рака. Как
легко показать, они не завсят от т. Кроме того, условия треугольника, воз-
никающие в наших двух методах, требуют выполнения условия
№ (iaib Ис, Г /")=0, если все (ja/bj'l. {j/сГ). (Me /"I > {ja И"} не Удовлетво-
ряют условию треугольника.	(ПА.30)
Используя соотношение (ПА. 14) для получения явного вида функций
и	можно показать, что имеет место соотношение
Ua jb i I та тЬ та ф- ть) (jj с id I та ф- тъ тс та ф- тъ ф- тс) —
= S it (ib ic 11 tnb mc mb ф- mc) X
t
X (iatid I тать-[-тс ma+mb-,-mc) W (ja jbjd jc, it) (ПА.31)
Отсюда и из соотношения (ПА. 17) можно найти явное выражение для коэффи-
циентов Рака в виде суммы по магнитным квантовым числам от четырех
коэффициентов Клебша—Гордана. Это приводит к тому, что если для коэффи-
12*	319
J
циентов Клебша—Гордана выбрано обычное условие для фаз, так что они
являются действительными, то и коэффициенты Рака также действительны.
Поскольку коэффициенты Рака непосредственно связаны с элементами
матрицы унитарного преобразования (ПА.29), нетрудно получить соотноше-
ния ортогональности, которым они должны удовлетворять
У & Р W (abed; ef) W (abed; eg} = f>fg.	(ПА.32)
e
Из других полезных соотношений отметим правило сумм Рака
V (—l)°+6-e W (abed; ef) W (bacd; eg) = W (afgb; cd)	(ПА.ЗЗ)
e
и тождество Эллиота-Биденхарна
^PW(Atdc; aC)W(bteC; Bc)W (Atfb; aB) =
= W (adbe; cf)W (AdBe; Cf).	(ПА.34)
Коэффициенты W (abed; ef) обладают высокой степенью симметрии, поскольку
существует 24 возможных набора параметров, удовлетворяющих правилам
треугольника. Если {ABCDEF] есть перестановка указанных шести пара-
метров, таких, что W (ABCD; EF) сохраняет все условия треугольников,
имеющиеся в W (abed; ef), то
W (ABCD; EF) = (— 1)Е+Р~е~1 W (abed; ef). (ПА.35)
Например,
W (abed; ef) = W (badc; ef) = W (aebd; fe) =
= ( —l)b+c~e-f W (aefd; bc) = ( — l)a+d~e~f W (ebef; ad). (ПА.36)
Эти условия симметрии более просто выражаются с помощью 6/-символов,
определяемых выражением
L J = (— i)“+6+c+d W (abed; ef).	(ПА.37)
\dc f)
Как следует из (ПА.35), 6/-символ остается инвариантным при любой четной
и нечетной перестановке его столбцов и при любой перестановке верхних и
нижних элементов в каждом из двух столбцов.
Наконец, укажем выражения для некоторых особенно часто встречаю-
щихся коэффициентов Рака:
W (abed; 0f)= ( — l)i~b~d~^—^,	(ПА.38)
bd
W(aabb; 1с)=(-1)“+^-'-----(ПА
2[а(а+1)(2а-ф1)6(6-Н)(26+1)]1/2
И
G l2(hl2J\000)W	^J1j2^|-y--yoY	(ПА.40)
где подразумевается, что /1т /2, J в правой части удовлетворяют условию
треугольника, а сумма Zj + Z2 + J должна быть четной
320
§ ПА. 4. СЛОЖЕНИЕ ЧЕТЫРЕХ УГЛОВЫХ МОМЕНТОВ. 9/-СИМВОЛЫ
Конструкции, которые мы рассматривали как коэффициенты унитарного
преобразования между разными представлениями для суммы трех угловых
моментов, могут быть также обобщены на четыре и более угловых момента.
Случай четырех угловых моментов имеет то достоинство, что получается уни-
кальный результат для изучаемого преобразования, который не имеет места
для пяти угловых моментов. Кроме того, это преобразование является чрез-
вычайно полезным, так как если рассматривается двухчастичное взаимодейст-
вие для частиц со спином и орбитальным угловым моментом, то в задаче фи-
гурирует как раз четыре угловых момента. Пусть требуется, например, полу-
чить преобразование между хорошо известными схемами связи LS и jf. Обо-
значим операторы углового момента через 1, соответствующие собствен-
ные значения отметим индексом I и введем также s и «для спина. Две части-
цы будем различать с помощью индексов 1 и 2. Тогда можно указать две
схемы связи (см. § ПА.З):
LS-связь: L = l14-lz, S = Si-)-s2. J = L-^S
с диагональными операторами
it it s?. st L2 = L(£4-1), S2 = S(S + 1).
J2 = J(J4-1). J3=M;
//-связь: ji=li4-Si, j2=l2+s2. J=ji4-j2
с диагональными операторами
it it st st j?=Jl(/l+l). ji = /2(j2 + l).
J2=J(J4-1), J3 = M,
Используя трижды формулу (ПА. 14) для каждой из схем связи, можно по-
строить соответствующие собственные функции	И ^imdd.y УНИТЭР-
ное преобразование между ними имеет вид
'P/m(LS) "= il А £ 3
it si ii
l2 s2 j2
L S J
'I’/m (/i id-
(ПА.41)
Эти коэффициенты называются Qj-символами. Они не зависят от т и обладают
тем свойством, что элементы любой строки или любого столбца удовлетворяют
условию треугольника, если 9/-символ неравен нулю; 9/-символы можнотакже
определить для любых четырех угловых моментов lx, 12, s1( s2, и их полезность
не ограничивается частным случаем орбитального и спинового угловых мо-
ментов двух частиц.
Поскольку при построении каждой из функцийф;т^^ и ф/т триж-
ды использовалась формула (ПА. 14), 9/'-символ может быть записан как
сумма по магнитным квантовым числам шести коэффициентов Клебша—
Гордана. Из этой записи можно сразу же заключить, что 9/ символ — действи-
тельная величина. С помощью (ПА.31) можно показать, что
Д si ii
/2 $2 /2
LSJ

X % PW (Sl l2 h £; tlj) W (l2 S1 j2 S; ts2) W (L^ Sj2; tJ). (ПА.42)
t
321
9/-символы- удовлетворяют условию ортогональности
V J2 /2 ££' SS'
/1 Ь
Z1 S1 /1
/1 s2 /2
L S J
) । h si ii\
, > Z2 S2 j2 | =6LL. ^SS'-
) U'S'J'J
(ПА.43)
и обладают такими свойствами симметрии, что перестановка любой строки
или столбца с любой другой строкой или столбцом приводит к умножению на
величину
/ pG+si + ii + Is+s2 + is+z—S -|-J
Отражение 9/-символа относительно любой из его диагоналей оставляет его
инвариантным. 9£символ, определяемый соотношением (ПА,42), иногда на-
зывается Х-коэффициентом и записывается в виде X l2s2j2‘, LSJ).
Укажем некоторые часто встречающиеся 9/-символы:
k si ii	j
Z2s2j2, = (-l),,+X-/l~s’V^-W,(Z1s1Z2s2; jjL) (ПА-44)
L L О	11 L
| 2 Zj /2 £§ (lt Z2L/OOO)
Zi 2 h
1
Z2 2 Zs
LSJ
1^ + 11+-^	. I 1
— ( '0 (ii is J 1 2	2 0) fiztLSJ)
(ПА 45a)
Здесь подразумевается, что в правой части сумма [1Г -|>Z2-ф-L должна быть
четной и
f12 (L0J) = -б„, f12 (JIJ) =	^T/s
1 / 2J—1 \ 1/2
fis (J —~j )	(э<1-4s-Xs — -Z).
, ,	1 Z2J + 3V/2
fis (-Z+ 1 1 •/) — -2 j + +	1);
Xi = (2/i+l)(Zi-ji). Z = l. 2.
(ПА.456)
(ПА.45в)
§ ПА. 5. ТЕНЗОРНЫЕ ОПЕРАТОРЫ И ТЕОРЕМА ВИГНЕРА — ЭККАРТА
Из закона преобразования (2.23) и (2.54) можно вывести соответствующий
закон для неприводимого тензорного оператора Tim (т = —I, —Z-f- 1, ..., Z)
ранга /. Этот закон имеет вид
I
Т (R) TlmT (R)~1 =	2	02.63)^.	(ПА.46)
m'= —I
Совокупность компонент неприводимого тензора Tim (m = —-Z, —Z + 1, .... Z)
иногда обозначают как Частным случаем такого оператора является
322
векторный оператор, который преобразуется как тензор первого ранга Если
Ух. Уз суть компоненты этого оператора в декартовом базисе, то величины
V±1 = Т—U (Vi±iV2). E0=V3 (ПА.47)
±	/2
являются тензорными компонентами [ср. (2.39)]. Скалярные операторы, ко-
нечно, соответствуют тензору нулевого ранга.
Если Sim и Тут’ — два неприводимых тензорных оператора, то их про-
изведение	также представляет собой тензорный оператор, но, вооб-
ще говоря, приводимый. Неприводимый оператор ULM может быть построен
следующим образом:
VLM = Ъ (If L\mm'M)SlmTt, m,t	(ПА.48)
mm'
что иногда записывается в виде
UtL][s[Z]® Т[/,]][Ч.	(ПА.49)
Рассмотрим специальный случай, когда I = Тогда в выражении (ПА.48)
L можно взять равным нулю и определить скалярное произведение
(S[']. TU]) = (-!)'/ [St'] ®	(-irS/mT’z-m. (ПА.50)
т= — I
При некотором частном выборе индексов скалярное произведение двух век-
торных операторов и приобретает вид (V^-W^ ^) = V-W =
= VxWj + V2W2 + V3W3.
Из закона преобразования (ПА.46) можно получить преобразование ве-
личины, эрмитово сопряженной Tjm:
Т	(Ох, 02, е3)* (7/m,)+] =
т' 1	J
= 2 (- i)m'-mD'_„/_m(e1. е2> е3) (?»+,	(ПА.51)
т'
где мы использовали свойство симметрии матриц конечных вращений. От-
сюда видно, что (—1)"' (Tit _m)+ преобразуется по тому же правилу, что и
Тimt Поэтому оператор ’ , эрмитово сопряженный тензорному оператору
мы определим в виде
(7’-)zm = (-Dm(7’/_m)+.	(ПА.52)
Коммутационные соотношения тензорных операторов с операторами угло-
вого момента (ПА.8) и (ПА.9) имеют вид
[J±t T’/m] = [(/Ч=т)[^±пг'Ф'1)]1^2 Tim ± I > (ПА.53)
[Лз- Tim]= mTim.	(ПА.536)
Отсюда можно получить доказательство теоремы Вигнера—Эккарта, которая
утверждает, что матричные элементы неприводимого тензорного оператора,
взятые между собственными состояниями операторов J2 и J3, могут быть за-
писаны в виде*
</' т' I Т1М I /т> = ULi' I тМт') </' || Т[/] || j>,	(ПА.54)
* Следует помнить, что теорема Вигнера—Эккарта сформулирована
несколько непривычно для русского читателя: приведенный матричный эле-
мент включаетв себя множитель (—1)2L (2/' 4 1)-1^2. Поэтому соответствую-
щие формулы имеют другой вид [см., например, (4.84) и (7 24)].—Прим, перев.
323
где дважды отчеркнутая величина называется приведенным матричным эле-
ментом и не зависит от всех магнитных проекций квантовых чисел. Иногда
мы пользуемся для него другим обозначением </' || TL || />. Зависимость от
т и т' полностью входит в коэффициент Клебша—Гордана. В этом коэффи-
циенте также учтены правила отбора, которые подразумеваются в изучаемом
матричном элементе, а именно: /, I, j' должны удовлетворять правилу тре-
угольника и должно выполняться соотношение т' — т + М.
Тривиальным частным случаем формулы (ПЛ.54) является равенство
<f m’\jm> = b/r Ьтт,
и до некоторой степени менее очевидный и очень полезный результат
<Г т' I Ju I jnv> = (jlj I тцт') [j (j -> 1)]1 /2,	(ПА.55)
где определяется формулами (ПА.9).
§ ПА. 6. ОБРАЩЕНИЕ ВРЕМЕНИ В ТЕОРИИ УГЛОВЫХ МОМЕНТОВ
Операция обращения времени играет важную роль во многих областях
ядерной физики, поскольку, как обычно предполагается, ядерные гамиль-
тонианы, инвариантны, относительно этой операции. Следовательно, необ-
ходимо рассмотреть введение обращения времени в формализм угловых
моментов. Это тем более полезно, так как дает возможность определить,
являются ли данные приведенные матричные элементы чисто действитель-
ными или чисто мнимыми.
Поскольку обращение времени означает изменение знака временной ко-
ординаты, т. е. t ->• —t. оператор обращения времени удовлетворяет соотноше-
ниям
КгК+ = г. КрК+ = —р	(ПА.56)
и таким образом изменяет знак в коммутационном соотношении [pi, гт] =
=	Значит, оператор К является антиунитарным (см., например,
[247]). Он может быть записан в виде
К = £/Ко,	(ПА.57)
где Ко — оператор комплексного сопряжения, a U — унитарный оператор.
Например, для одной частицы со спином 1/2 оператор U имеет вид U = —,
в котором предполагается обычный выбор [247] спиновых матриц. Этот выбо р
U учитывает тот факт, что, согласно (ПА.56), для оператора орбитального
углового момента KLK+ = —L, и, следовательно, в общем виде
KJK+= — J.	(ПА.58)
Если обозначить собственную функцию операторов J2 и J 3 через ф;т, ко-
торая удовлетворяет уравнениям (ПА.7) и (ПА. 10), то обращенная во времени
функция Ktyjm будет удовлетворять уравнениям
J2 (АФ/т) = / (/-> 1) (Аф;т).	[(ПА.59а)
Ja(Ktyjm) — KJ atyjm — т (АФ^т).	(ПА.596)
J± (АФтт) = — KJ^ Фтт=;— [(/ ± rn) (j Т т -> I)]1/2 (Аф/тТ j), (ПА.59в )
где для получения последнего результата использован тот факт, что К —
антилинейный оператор и, следовательно, преобразует число в его комплексно
324
сопряженное. Уравнения (ПА.59) означают, что преобразуются контра-
градиентно по отношению к ф;т. Если мы возьмем
Фут— (	1)у—т Д’!1/»»)'
(ПА.60)
то эта функция преобразуется обычным’ образом с помощью матрицы конеч-
ных вращений D,m,m (0j, 02, 03). Хотя любой фазовый множитель, содержащий
т, осуществлял бы желаемый закон преобразования для фут, данный выбор
в формуле (ПА.60) имеет то дополнительное преимущество, что если ф. (а)
‘а а
и	преобразуются по формуле (ПА.60), то этим же свойством обла-
дает и функция
Ф;тп= 2. (iaibi\mambm)^} т (а)ф,	(6).
тат^	*а а ‘Ъ о
поскольку из (ПА.206) следует
t,-m = (-iy-raW-m =
= У, Uaibi\ тать — m)( — ly + 'a + ib-m~ma~mb X
татЬ
= Г(/а ib j | та ть т) ф/а та (a)^jb ть (Ь).	(ПА.61)
татЬ
Аналогично (ПА.60) определим обращение по времени тензорного оператора
следующим образом:
Ггт= (-1)'-тКТг_тя + .	(ПА.62)
Значит, 1 имеет обычные трансформационные свойства (ПА.46) и удовлет-
воряет теореме Вигнера—Эккарта.
В случае целых квантовых чисел углового момента 1 оператор U в фор-
муле (ПА.57), как следует из формул (ПА.56) для орбитального углового
момента, берется в виде единичной матрицы. Тогда из (ПА.60) получаем
ф/т = (-1)'-тКофг_т = (-1)г-тф/*-т.
(ПА. 63)
Для сферических гармоник (2.7) это дает
F/m(F)= (-1)'У/т(г)-
(ПА. 64)
Ясно, что можно упростить рассмотрение обращения времени для собствен-
ных функций оператора орбитального углового момента, если определить
функции

(ПА. 65)
Они являются собственными[функциями операторов L2 и L3, и, как следует
из (ПА.60) или (ПА.64),

(ПА .66)
325
ПРИЛОЖЕНИЕ Б
ТЕОРИЯ ДИРАКА
В предыдущем Приложении мы рассмотрели главные элементы одного из
двух основных теоретических методов, необходимых для рассмотрения меха-
низмов возбуждения ядра Вторым методом является метод, используемый
в теории Дирака. В данном Приложении мы дадим очерк той его части, кото-
рая нужна в этой книге. Обзор будет служить целям установления исполь-
зуемых обозначений. Теория Дирака более подробно обсуждается в боль-
шинстве книг, указанных в конце гл. 4, и в книге Роуза [290].
§ ПБ. 1. УРАВНЕНИЕ ДИРАКА И ЕГО ТРАНСФОРМАЦИОННЫЕ СВОЙСТВА
Уравнение Дирака является релятивистским обобщением уравнения
Шредингера на случай частиц со спином 1/2. Оно представляет собой диф-
ференциальное уравнение первого порядка как по временным, так и по
пространственным производным и в отсутствие вн ешнего поля может быть
записано в виде
дф (г, t)
№p(r,/)=ife	(ПБ.1а)
где величина
H = ca-p-f-f}mc2	(ПБ.16)
выражается через оператор импульса р = ^~ j у и массу частицы т. Волно-
вая функцияф имеет несколько компонент в пространстве векторов-столбцов,
называемых спинорами. Эрмитовы матрицы а и₽ действуют в пространстве
спиноров.
Тот факт, что уравнение (ПБ.1) правильно описывает релятивистскую
кинематику частицы, будет установлен в конце данного параграфа Будет
показано, что два спинора, соответствующих решению уравнения (ПБ.1)
в двух различных лоренцевских системах отсчета, могут быть приведены во
взаимно однозначное соответствие и могут считаться описывающими одно
и то же физическое состояние. Сейчас мы только отметим, что уравнение (ПБ. 1)
действительно дает ожидаемое релятивистское соотношение между энергией
и импульсом, так как
। з з
№ = —с2	PjPh-^r
2	/=iд=1
3
фтс3 У, (а ур + ра;)р;-ТР2 (тс2)2 = с2р2-ф (тс2)2	(ПБ.2)
7=1
при условии, что выполняются коммутационные соотношения
asak^ah aj = 2&jh, ay Р-Р Рау = 0,	(ПБ.За)
и условия нормировки
₽»==1.	(ПБ.Зб)
Таким образом, а и Р образуют набор четырех эрмитовых и унитарных анти-
коммутирующих матриц; они должны быть, по крайней мере, матрицами
326
4x4. Частное выражение для этих матриц, удовлетворяющее условиям
(ПБ.З), имеет вид
I0 сХ	/ I 0\
-(.«) ’-(о.,)-	<ПБ4>
где о—матрицы Паули 2x2, т. е.
, О П , 0 — IX	, 1 ОХ	„ _
O1=G o’’ °2=G о)’ °3=1о-1)’	<пб5)
а / — единичная матрица 2X2.
Можно переписать уравнение Дирака в другой форме, в которой времен-
ные и пространственные производные входят более симметрично. Умножив
уравнение (ПБ.1) слева на (J/Йс, получим
или*
где
„ „ I д тс\
— iP«-V4-₽ — —-Ь — ф(г, /) = 0
ic dt Й )
I д тс \
(г» т)
Т= — i₽K, « = !₽?. ?4 = ₽.
(ПБ.6)
(ПБ.7)
(ПБ.8)
и х4 = ict. Согласно (ПБ.З), ^-матрицы должны удовлетворять соотношениям
YuYv + Vv ?n = 26uv
(ПБ.9)
Они являются эрмитовыми и унитарными, и рассмотренное частное представ-
ление (ПБ.4) дает
I 0 —io
v=G= о
(ПБ.10)
Обратимся теперь к установлению лоренцевской инвариантности урав-
нения (ПБ.7). В преобразованной системе отсчета это уравнение будет иметь
вид
I д тс \
(ПБ1,)
где преобразованные координаты х' связаны с исходными координатами хц
соотношением
xli=anvxv.	(ПБ 12)
Матрица преобразования должна быть ортогональной, т. е.
°nvaup &vp' avu apu ~ ®vp-	(ПБ.13)
Поэтому
det(a)=±l.	(ПБ.14)
* Греческие нижние индексы здесь пробегают значения 1, 2, 3, 4, в то
время как латинские индексы пробегают значения 1, 2, 3. По повторяющим-
ся индексам проводится суммирование. Для некоторых целей удобно ввести
нулевую компоненту 4-вектора Г4 = iV0.
327
Для преобразований, непрерывно переходящих от тождественного, матрица а
в действительности является унимодулярной, т. е.
det(a) = l.	(ПБ.15)
Эти преобразования называются собственными и не включают отражения
нечетного числа осей. Кроме того, преобразования, имеющие положительное
значение величин а44, называются ортохронными. Они сохраняют направле-
ние временной оси. Мы будем рассматривать здесь только ортохронные пре-
образования.
Мы должны показать, что решение уравнения (ПБ.11) связано с решением
уравнения (ПБ.7) с помощью преобразования Л, которое зависит от матрицы
а. Эго будет так, если существует такое Л (а), что
ф' (х') = Лф (х),
где Л должна быть матрицей 4X4. Так как
д dxv д д
дх^ =	^~д^’
то из уравнений (ПБ.7) и (ПБ.11) мы должны иметь
Л-1 Тц A = ap.v Tv
(ПБ.16)
(ПБ.17)
(ПБ.18)
С помощью теоремы, доказанной Паули (см. [290]), можно установить, что Л
должна существовать и должна быть неособенной. Действительно, если рассмо-
треть собственные бесконечно малые преобразования вида
a!.w	+ eiw,	(ПБ.19)
где в соответствии с (ПБ.13) ецх,= —evjr |то	
1Л=1ф —	(ПБ.20)
При этом S|iv=—Svp.. Из (ПБ.18) имеем [Тц, “^Avl ~ Tv ^u.7.	(ПБ.21)
Для собственных ортохронных преобразований можно НИЯ Q	1	-А Sirv = T^Tv’	найти из этого уравне- (ПБ.22)
последовательность бесконечно малых преобразова-
Тогда, рассматривая
ний, получаем
Л= ехр
env Ту, Tv I •
(ПБ.23)
4
Существование этой неособенной матрицы преобразования (ПБ.16) означает
ковариантность уравнения Дирака при собственных ортохронных преобра-
зованиях.
Матрица (ПБ.23) может быть использована для проверки трансформа-
ционных свойств различных комбинаций матриц Дирака, умноженных слева
328
на яр (х) - яр1 (х) Р яр+ (х) у4, а справа — на яр (х). Можно получить пять
полезных комбинаций:
S (х) = яр (х) яр (х) (скаляр),	(ПБ.24а)
(*) = ,Ф (*) Тц Ф (х) (вектор).	(ПБ.246)
Tnv (х) = Ф W °nv Ф W (тензор)	(ПБ 24в)
(*) =1яр(х) яр (х) (аксиальный вектор).	(ПБ.24г)
Р (х) = яр (х) у5 яр (х) (псевдоскаляр).	(ПБ.24д)
Здесь
1
aliv~ 2j (tyi Yv Vv V|<),	(ПБ 25)
и
Т5=?1?2?зТ4	(ПБ.26)
Можно показать,используя свойства матрицы Л, что пять комбинаций (ПБ.24)
трансформируются при преобразовании (ПБ.12) по правилам, которые соот-
ветствуют их обозначениям, а именно*
S'(x')=S(x),	(ПБ.27а)
^<x')=auv^vW-	(ПБ.276)
Kv <*') = “до ava ТРа (*),	(ПБ.27в)
^i(*') = det(a)%v (*)•	(ПБ.27г)
Р' (x') = det(a)P(x).	(ПБ.27д)
Матрицы, использованные для построения тензорного выражения Т^, обла-
дают полезным свойством
clm = — iy? Tm= i₽T5Tft=— Ysafe.	(ПБ.28)
где k, I, m образуют циклическую перестановку. В представлении (ПБ.24)
эта матрица 4X4 выражается через спиновые матрицы Паули 2X2
aft= я , fe = I, 2, 3.	(ПБ.29)
\ 0 OhJ
Матрица в псевдоскалярном выражении обладает свойством
Т6уц + уцу5=о. у|=1.	(ПБ.ЗО)
имеет представление
/ 0 —1\
о)	<ПБ’31
и является эрмитовой.
* Заметим, что для выбранной ниже нормировки (ПБ.40), которая зави-
сит от системы отсчета, величинами с простыми трансформационными свой-
ствами являются произведения E/tru? на величины, определенные формулами
(ПБ.24).
329
§ ПБ. 2. РЕШЕНИЕ УРАВНЕНИЯ ДИРАКА В ВИДЕ ПЛОСКИХ ВОЛН
Решение уравнения Дирака для свободной частицы может быть записа-
но в виде
гр (х) — и (р) е^к'х
(ПБ.32а)
где и (р) удовлетворяет спинорному уравнению
(cap рте2—£)ы(р) = 0	(ПБ.326)
или
[Yu Рц— <тс] и (Р) = °-	(ПБ,32в)
где р = Йк— импульс свободной частицы, £ = й<о =	—ее энергия и
т2 с4
£2 = р2 с2-|- т2 ci, со2 = к2с2^--.	(ПБ.32г)
й2
В соответствии с (ПБ.32г) четыре корня секулярного детерминанта, даваемого
спинорным уравнением (ПБ.32в), приводят к решениям £	[р'Д2 + т2с4]*/2,
встречающимся два раза, и к решениям £ —[р2с2 + /п2^]1 2, также встре-
чающимся два раза. Последний случай является решением с отрицательной
энергией и физически соответствует наличию позитрона. В теории, описываю-
щей одну частицу, позитрон интерпретируется как дырка в заполненном бес-
конечном наборе электронных состояний с отрицательной энергией. Введение
вторичного квантования электронного поля допускает, конечно, более про-
стое рассмотрение этих решений; они считаются относящимися к положитель-
ной энергии но для позитронных компонент поля, которые затем рассматри-
ваются на той же основе, что и электронные компоненты. Когда уравнение
Дирака используется для описания частиц со спином 1/2, отличных от элек-
трона, решения с отрицательной энергией дают соответствующую античас-
тицу, т. е. мюон—антимюон, нейтрино—антинейтрино, протон — антипро-
тон и т. д.
Решения, отвечающие двум положительным энергиям, могут быть
записаны в виде
Здесь
ф± W = U± (р)е‘(к’х “°.
(ПБ.ЗЗа)
(ПБ.ЗЗб)
2
где х — двухкомпонентный спинор Паули, удовлетворяющий уравнению
1 1
±	=*= ~2~
ОзХ 2=±Х	’	(ПБ.34)
Решения (ПБ.ЗЗб) удовлетворяют уравнению
(р — imc) и± (р) = О	(ПБ.35)
где Р=РцТц. В пределе р . тс это решение принимает вид
(±4^
“±(Р)~ X 2 ,	(ПБ.36)
\ О J
330
поэтому верхние две компоненты дираковского спинора называются боль-
шими компонентами.
Напишем решение для отрицательной энергии
чр(х) = п±(р)е-,(к’х-“° ,	(ПБ.37а)
соответствующее физическому позитрону с наблюдаемым импульсом р = йк
и положительной энергией —Е = й<о; здесь
(сс • р ±
I р | _ь_ тг2	%	|
lhl+mc .	(ПБ.37а)
4-1	I
2	/
X /
Это решение удовлетворяет уравнению
( —р- Г+~ ₽ — 1 тс) »± (Р) =
= I — р-у — —— Р—imclo±(p) = 0.	(ПБ.38)
в то время как v± (—р) удовлетворяет уравнению (ПБ.35) с р4= \Е/с —
= — XtiM/c. В низкоэнергетическом пределе р тс
( °
У±(Р)~| ±_L 	(ПБ.39)
Кх 2 J
Поэтому большими компонентами в нерелятивистском пределе для позитрон
ных состояний являются нижние компоненты.
Заметим, что нормировка в (ПБ.ЗЗ] и (ПБ.37) выбрана такой, что
u+(p)u(p)=l.	(ПБ.40)
Это соответствует нормировке плоских волн функции (ПБ.32а), принятой
в нерелятивистской квантовой механике. Такой выбор удобен для наших це-
лей, так как во многих приложениях нам понадобится волновая функция ну-
клона в нерелятивистском пределе в качестве первого шага для построения
волновых функций, описывающих многонуклонную систему при низких энер-
ниях. Мы можем затем получить все результаты обычного квантовомеханиче-
ского рассмотрения, в том числе хорошо известное выражение для плотности
состояний в случае плоских волн, нормированных в соответствии с (ПБ.32а)
и (ПБ.40):
1	. dp _	1 рЕ
-------р2 — dQ„ =-----------------—- dQ
(2л/г)3 dE р (2лй)3 с2 ₽’
(ПБ.41)
где Пр — элемент телесного угла для частицы с импульсом р. В приложениях,
требующих учета свойств инвариантности, удобно использовать нормировку
и' (р)ы (р) = и'+ (р)₽п'(р) = 1, что не выполняется в нашем случае Вместо
этого мы имеем
—	тс2
и(р) и (р) = и+ (р) ₽и (р) = —,
Е
(ПБ.42)
что можно легко проверить с помощью уравнения Дирака или используя яв-
ный вид решений (ПБ.ЗЗб) или (ПБ.376). Заметим, что в (ПБ.42) величина Е
331
положительна для решений с положительной энергией и отрицательна для
решений с отрицательной энергией.
Для рассматриваемых здесь решений уравнений Дирака для свободных
частиц можно ввести проекционный оператор для состояний частиц с положи-
тельной энергией
Р+= V uz(p)^(p) = £P±±^₽ =
1=4-	2i£
1 — 2 который удовлетворяет уравн Р+и± (р) Проекционный оператор для который дополняет оператор	(	ca-pJ-Pmc2 \ 0+ |£| )’	<ПБ43> ениям = «±(Р), Р+Р±( —р) = 0.	(ПБ.44) состояний частиц с отрицательной энергией, Р+, имеет вид
р-= 2 vk(—v)v Л— ± 1 = 2 Он обладает свойствами	,	ср-y-|-(i £/с) ft-Н znc2 *( Р)~	“	2i£
«± (Р) =	0, Р_ р± ( — р) = о± ( — р).	(ПБ.46)
Проекционные операторы особенно полезны для вычисления средних и
сумм по спиновым состояниям. Если для произвольной спиновой матрицы тре-
буется вычислить
б=2 2 I иц (₽') ЙМХ (Р) |2 =
X — zb Ц — zb
= 2 2 [<(р')₽й«?.(р)«^ (Р)п+1Ч(р')’	<ПБ-47>
X = zb Ц — zb
то определение (ПБ.43) дает
@ = 2 [< (P')PP-P+(P)«+₽UH(P')].	(ПБ.48}
Ц= ±
Сумму по оставшимся спинорам можно распространить также и на состоя-
ния с отрицательной энергией, если учесть, что проекционный оператор Р\-
аннулирует эти дополнительные слагаемые.
В силу (ПБ.44) можно написать
2 {«+ (₽') ₽йр+ <р) й+₽₽+ (р') «и (р')+
и= ± и
+*>£ (—р') ₽йр+ (р)й+ ₽^+ (р') t’n (—р')) =
= Sp{₽QP+ (р) Q+ ₽Р+ (р')}_
(ПБ.49)
Здесь мы воспользовались тем, что (р') и v t (—р') образуют пространство
решений уравнения Дирака (ПБ.32) с импульсом р', так что сумма четырех
диагональных матричных элементов оператора, которые можно построить
из этого набора состояний, дает шпур оператора.
332
Введение операции Sp в формулу (ПБ.49) значительно упрощает вычис-
ление сумм по спинам, так как при расчете величины © теперь можно приме-
нять различные теоремы, касающиеся шпуров Например, если мы хотим поль-
зоваться выражением (ПБ.43) для ©, в которое входят инвариантные обоз-
начения дираковских матриц, то можно применить свойство инвариантности
шпура при циклической перестановке матриц под знаком шпура и написать*
! ср-rime2________ ср' + i тс2 ]
й ~	----₽й+ ₽	---} •
2i£ н н 2i Е j
(ПБ.50)
Эту величину можно вычислить, если вспомнить, что шпур нечетного числа
у-матриц равен нулю:
	SP (?М П2 П, • • •	=°. если k нечетно,	(ПБ.51а)
тогда как	Sp(l) = 4,	(ПБ.516) S₽ (Тх?ц)=46Хц	(ПБ.51В)
или	SpC4 В) = 4(ЛцВд	(ПБ.51Г) Sp (Л В C 5)= 4 [(Лц Вц) (CvDv)-0w C»)(BVDV) + ♦AWW	(ПБ.51Д)
Sp (Ts) = Sp (у5 Yjl)=Sp (y5	уц) = Sp (v5 yA vv) = О,	(ПБ.5le)
	SP (V5 Vi Yu Yv ?л) = 4елцгл	<ПБ -51ж)
и т. д. Здесь я — полностью антисимметричный тензор четвертого ранга.
Из коммутационных соотношений (ПБ.9) получаем
ПП = 4,	(ПБ.52а)
ПЛП = -2Л,	(ПБ.526)
Ъ. Вта = 4(ЛцВц),	(ПБ 52в)
Л В С ya= —2С В А,	(ПБ.52г)
где подразумевается суммирование по X.
§ ПБ. 3. УРАВНЕНИЕ ДИРАКА ДЛЯ ЦЕНТРАЛЬНОГО ПОТЕНЦИАЛА
В дополнение к релятивистскому описанию свободной частицы со спи-
ном 1/2 в приложениях теории ядра часто бывает полезно рассмотреть урав-
нение Дирака при наличии электромагнитного поля. В этом случае его форма
может быть получена из уравнений (ПБ.1) или (ПБ.7) с помощью обычной
замены оператора 4-импульса:
е
---(ПБ.53)
333
где е — заряд рассматриваемой частицы со спином 1/2,	= (A, i<p)—4-по-
тенииал. Уравнение Дирака тогда примет вид
[/ д i е \ тс 1
Ц^-^ли)+тГ(х)=0-	(ПБ-54)
Если мы рассматриваем электрон или мюон, движущийся в статиче-
ском центральном кулоновском поле ядра, то 71^ = (А = 0, i<p (г)). В этом
случае мы получаем уравнение Дирака для стационарных состояний
тс
Можно переписать уравнение (ПБ.55) с учетом свойств симметрии централь-
ного потенциала. Для этого воспользуемся векторным тождеством
V= г (г • V)— г х(г X V)= г (г-V)—i г-1 г XL, (ПБ.56)
где L=— irXV. Тогда
а • V = а - г - — i г 1 а • г X L.	(ПБ.57)
or
е
i а - V -ф- -г—
Нс
ф (г) = £,ф (г).	(ПБ.55)
Применяя хорошо известные результаты для матриц Паули, можно устано-
вить, для матрицы	4X4 (ПБ.29), что	
	о • Ас • В = А • В 4н с (А X В).	(ПБ.58)
Подставив А ~ г ,	B = L, получим	
	з • г с • L = is •( г X L).	(ПБ.59)
Замечая далее, что	в соответствии с (ПБ.28)	
	“= — =,	(ПБ.60)
имеем	а • г а • L = ia - ( г X L).	(ПБ.61)
Таким образом, соотношение (ПБ.57) принимает вид		
	-id	\	
	a-V = «-г 	— г-1 с - L . \ дг	/	(ПБ.62)
Введем оператор	K=₽(O.L + 1),	(ПБ.63)
который коммутирует с Р, а-V, J = L 4—а и центральным потенциалом
<р (г). Тогда уравнение Дирака можно записать в виде
	д	1	₽	\	е
Я ф(г) = [ 1 у6а • г f		1	К 1		 сс\ (r\ 1
	. дг	Г	А Т 4 ФИТ г	г J Ис
ф(г)=£ф(г).
„ тс
'-’г
(ПБ .64)
Поскольку J2, J3 и К коммутируют с Н и друг с другом, то удобно использо-
вать представление, в котором эти три оператора диагональны. Радиальные
функции, получающиеся из решения уравнения (ПБ.64), кратко обсужда-
ются в § 5.6 для несвязанного электрона и в § 8.1 для связанного мюона.
334
ПРИЛОЖЕНИЕ В ।
МАТРИЦЫ ПЛОТНОСТИ
Здесь мы очень кратко рассмотрим формализм матрицы плотности, кото-
рый особенно полезен при обсуждении систем, описываемых некогерентными
суперпозициями различных состояний. Этот формализм очень широко ис-
пользуется при рассмотрении проблем, касающихся поляризованных пучков
или мишеней. Более подробные обсуждения можно найти в обзорных статьях
Фано [125|, Тер Хаара [330] н в книге Хуанга [199].
§ ПВ. 1. ОПРЕДЕЛЕНИЕ И ОБЩИЕ СВОЙСТВА
Для системы, описываемой некогерентной суперпозицией квантовых со-
стояний 1ф,>, оператор плотности определяется соотношением
р =31 Ci 1’ i	(ПВ.1а)
где действительные С, — статистические веса состояний	|ф,> системы, и
£С;=1. 1	(ПВ.16)
Для «чистого» случая, в котором система представлена	определенным кван-
товым состоянием |ф^>. С, =	Непосредственно можно установить, что	из формул (ПВ.1)
р — эрмитова матрица, т. е. р = р+,	(ПВ.2)
Spp=l,	(ПВ.З)
Pii > о,	(ПВ.4)
Sp р2 1.	(ПВ.5)
Среднее значение оператора Q дается формулой	
<Q>=Sp (Qp) = Sp (pQ).	(ПВ.6)
Последнее свойство может быть взято вместо формул (ПВ.1) для определения
матрицы плотности. Оно иллюстрирует полезность концепции матрицы плот-
ности, так как шпур оператора не зависит от представления, и, таким обра-
зом, все необходимые физические величины могут быть вычислены в любом
удобном представлении. В частности, представление (ПВ.1), в котором р
диагональна, не является обязательным.
Изменение р во времени описывается уравнением движения
Эр i
1Г = Т[Р’Я1’	(пв-7)
где Н — гамильтониан системы. Уравнение (ПВ.7) является аналогом урав-
нения непрерывности для плотности в фазовом пространстве в классической
статистической механике.
§ ПВ. 2. ПОЛЯРИЗАЦИОННАЯ МАТРИЦА ПЛОТНОСТИ
В § 4.5 мы рассматривали поляризационные эффекты при рассеянии фото-
нов на ядрах. Чтобы получить матрицу плотности поляризационных состоя
ний фотона, введенную в формулах (4.109)—(4.114), заметим, что ввиду попе-
речного характера электромагнитного поля излучения существуют два по-
ляризационных состояния. Ими могут быть состояния левой и правой круговой
335
поляризации или два ортогональных состояния линейной поляризации и т. д.
В любом случае чистое состояние может быть описано комплексным единич-
ным вектором
е==с1 С2 е24-Сз ед.	(ПВ.8)
Если выбрать систему координат, в которой ось z направлена вдоль направле-
ния распространения волны к, то с3 0, и в системе сферического базиса
(2.39)
• = —(С-1 £1 + с2 5-1)-
Матрицей плотности является матрица 2x2
°HV=(»u ’ 6)(6* ' £v) = (	О’* сцсу
ИЛИ
(ПВ.9)
(ПВ.Юа)
(ПВ.106)
Она определяется двумя действительными параметрами, а именно отноше-
нием абсолютных значений сх и с_х и относительными фазами величин су
и C_j.
Удобно ввести действительный трехмерный единичный вектор, компонен-
ты которого имеют вид
=	^>2 = i(CFi-i—°-u)> ?з=аи—(ПВ 11)
Этот вектор называется вектором Пуанкаре, и с его помощью матрица плот-
ности может быть записана в виде
a=-i-(l+P.s),	(ПВ.12)
где s обозначает три матрицы Паули. Формула (ПВ.12) сохраняется также
и для частично поляризованных фотонов, но в этом случае Р больше не яв-
ляется единичным вектором. Его модуль s = |Р| есть степень поляризации.
Формула (ПВ.10) заменяется следующей:
°nv = -у (1 ~ s) + S < “ 1 )Uc-u cv	<ПВ 13>
Разложение матрицы плотности на неприводимые части может быть теперь
выполнено так же, как и в (4.113).
ЛИТЕРАТУРА
1.	Acker Н. L., Marchall H. Phys. Lett., 1965, v. 19, p. 127.
2.	Acker H. L., Backenstoss G., Baum C., Sens J. C., de Wit S. A. Nucl. Phys.,
1966, v. 87, p. 1.
3.	Acker H L. Nucl. Phys., 1966, v- 87, p. 153.
4.	Acker H. L., Rose M. E. Ann. Phys. (New York), 1967, v. 44, p. 336.
5.	Adler S. L. Phys. Rev. Lett., 1965, v. 14, p. 1051.
6.	Adler S. L. Phys. Rev., 1965, v. 139, p. B1638.
7.	Akhiezer A., Berestetski V. B. Quantum Electrodynamics. Second Edition,
New York, Wiley, 1963. (См. на русском языке: Ахиезер А. И., Берестец-
кий В. Б. Квантовая электродинамика. Изд. 3. М., «Наука», 1969.)
8.	Alder К., Bohr A., Huus Т., Mottelson В., Winther A. Rev. Mod. Phys.,
1956, v. 28, р. 432; 1958, v. 30, р. 353.
9.	Alder К., Winther A. Kgl. Danske Videnskab. Selskab, Mat.-Fys. Medd.,
1956, v. 31, No. 1.
10.	Alder K-, Schucan T. H. Nucl. Phys., 1963, v. 42, p. 498.
11.	Alder K., Winther A. Coulomb Excitation. New York, Academic Press, 1966.
12.	Anderson D. K-, Eisenberg J. M. Phys. Lett., 1966, v. 22, p. 164.
13.	Arenhovel H., Danos M., Greiner W Phys. Rev., 1967, v. 157, p. 1109.
14.	Arenhovel H., Hayward E. Phys. Rev., 1968, v. 165, p. 1170.
15.	Arenhovel H. Phys. Rev. 1968, v. 171, p. 1212.
16.	Arenhovel H., Greiner W. Progr. Nucl. Phys., 1969, v. 10, p. 167.
17.	Astbury A. e. a. Nuovo Cimento, 1964, v. 33, p. 1020.
18.	Baldwin G. C., Klaiber G. S. Phys. Rev., 1947, v. 71, p. 3.
19.	Baldwin G. C., Klaiber G. S. Phys. Rev., 1948, v. 73, p. 1156.
20.	Barber W. C. Ann. Rev. Nucl. Sci., 1962, v. 12, p. 1.
21.	Bander M , Itzykson C. Rev. Mod. Phys., 1966, v. 38, p. 330, 346.
22.	Bardin T T. e. a. Phys. Rev. Lett., 1966, v. 16, p. 718.
23.	Backenstoss G. e. a. Phys. Lett., 1967, v. 25B, p. 365.
24.	Васке H. e. a. In «Hyperfine Structure and Nuclear Radiations». Amster-
dam, North-Holland, 1968, p. 65.
25.	Banner M., Cronin J. W., Liu J. K-, Pilcher J. E. Phys. Rev. Lett., 1968,
v. 21, p. 1107.
26.	Baader R. e. a. Phys. Lett., 1968, v. 27B, p. 425.
27.	Baader R. e. a. Phys. Lett., 1968, v. 27B, 428.
28.	Bernardini M., Brovetto P., Ferroni S. Nuovo Cimento, 1957, v. 5, p. 1292.
29.	Bernstein J., Lee T.D., Yang C. N., Primakoff H. Phys. Rev., 1958, v. Ill,
p. 313.
30.	Bethe H. A. Intermediate Quantum Mechanics. New York, Benjamin,
1964. (См. на русском языке: Бете Г. Квантовая механика. М., «Мир»,
1965.)
31.	Bellicard J. В., Bounin Р., Frosch R. F., Hofstadter R., McCarthy J. S.,
Uhrhane F. J., Yearian M. R., Clark В. C., Herman R., Ravenhall D. G.
Phys. Rev. Lett., 1967, v. 19, p. 527.
337
32.	Bernow S. e. a. Phys. Rev. Lett., 1967, v. 18, p. 787.
33.	Bernow S. e. a. Bull. Amer. Phys. Soc., 1968, v. 13, p. 678.
34.	Bernow S., Devons S., Duerdoth I., Hitlin D., Kast J. W., Lee W. Y..
Macagno E. R., Rainwater J., Wu C. S. Phys. Rev. Lett., 1968, v. 21, p. 457.
35.	Bishop G. R., Isabelle D. B. Phys. Lett., 1962, v. 1, p. 323.
36.	Bishop G. R. In: «Nuclear Structure and Electromagnetic Interactions»,
New York, Plenum Press, 1965, p. 211.
37.	BishopG., Bottino A., CiocchettiG., Molinari A.Phys. Lett., 1965, v. 14, p. 140.
38.	Biedenharn L. C., Van Dam H. Quantum Theory of Angular Momentum.
New York, Academic Press, 1965.
39.	Biedenharn L. C., Brussaard P. J. Coulomb Excitation. Oxford, Oxford
Univ. Press, 1965.
40.	Bjorken J. D., Drell S. D. Relativistic Quantum Mechanics. New York,
McGraw-Hill, 1964.
41.	Bjorkland J. A., Raboy S., Trail С. C., Ehrlich R. D., Powers R. J. Phys.
Rev., 1964, v. 136, p. B341.
42.	Bjorken J. D., Drell S. D. Relativistic Quantum Fields. New York,
McGraw-Hill, 1965.
43.	Blatt J. M., Weisskopf V. F. Theoretical Nuclear Physics. New York, Wiley,
1952. (См. на русском языке: Блатт Дж., Вайскопф В. Теоретическая
ядерная физика. М., Изд-во иностр, лит., 1954.)
44.	Blin-Stoyle R. J., LeTourneux J. Ann. Phys. (New Yerk), 1962, v. 18, р. 12.
45.	Blin-Stoyle R. J., Nair S. С. K- Advan. Phys., 1966, v. 15, p. 493.
46.	Bohr N., Rosenfeld L. Kgl. Danske Vidensk. Selskab, Mat.-Fys. Medd.,
1933, v. 12, No. 8.
47.	Bosco B., Fubini S. Nuovo Cimento, 1958, v. 9, p. 350.
48.	Bogoliubov N. N., Shirkov D. V. Introduction to the Theory of Quantized
Fields. (New York, Interscience, 1959). (См. на русском языке: Боголю-
бов Н. Н., Ширков Д. В. Введение в теорию квантовых полей. М., Гос-
техиздат, 1957.)
49.	Bosco В., Quarati Р. Nuovo Cimento, 1964, v. 33, р. 527.
50.	Bottino A., Ciocchetti G., Molinari A. NucL Phys., 1966, v. 89, p. 192.
51.	Brix P., Kopfermann H. Nach. Akad. Wiss. Cottingen, Math. Phys. KL,
1947. p. 31.
52.	Brix P., Kopfermann H. Z. Physik, 1949, v. 126, p. 344.
53.	Brennan J. G., Sachs R. G. Phys. Rev., 1952, v. 88, p. 824.
54.	Breit G., Gluckstern R. L. Handbuch der Physik, 1959, v. 41/1, p. 496.
55.	Brink D. M., Satchler G. R. Angular Momentum. Oxford, Clarendon Press,
1962.
56.	Brix P. e. a. Phys. Lett., 1962, v. 1, p. 56.
57.	Brodsky S. J., Primack J. R. Phys. Rev., 1968, v. 174, p. 2071.
58.	Burgy M. T., Krohn V. E., Novey T. B., Ringo G. R., Telegdi V. L. Phys.
Rev., 1958, v. 110, p. 1214.
59.	Burgy M. T., Krohn V. E., Novey T. B., Ringo G. R., Telegdi V. L. Phys.
Rev., 1960, v. 120, p. 1829.
60.	Carlson В. C., Rushbrooke G. S. Proc. Cambridge Phil. Soc., 1950, v. 46,
p. 626.
61.	Calaprice F. P., Commins E. D., Gibbs H. M., Wick G. L. Phys. Rev.,
Lett., 1967, v. 18, p. 918.
62.	Chew G. F„ Wick G. C. Phys. Rev., 1952, v. 85, p. 636.
63.	Chew G. E., Goldberger M. L., Low F. E., Nambu Y. Phys. Rev., 1957,
v. 106, p. 1345.
64.	Christensen C. J. e. a. Phys. Lett., 1967, v. 26B, p. 11.
65.	Christensen C. J. e. a Phys. Lett., 1969, v. 28B p. 411.
66.	Ciocchetti G., Molinari A. Suppl. Nuovo Cimento, 1964, v. 2, p. 57.
67.	Condon E. U., Shortley G. H. The Theory of Atomic Spectra. Cambridge
Univ. Press, 1935. (См. на русском языке: Кондои Е., Шортли Г. Тео-
рия атомных спектров. М., Изд-во иностр, лит., 1949.)
68.	Condon Е. U., Breit G. Phys. Rev., 1936, v. 49, p. 904.
338
69.	Cohen R. C., Devons S., Kanaris A. D., Nissim-Sabat C. Phys. Lett., 1964,
v. 11, p. 70.
70.	Cohen R. C., Devons S., Kanaris A. D. Phys. Rev. Lett., 1963, v. 11, p. 134;
Nucl. Phys., 1964, v. 57, p. 255.
71.	Conversi M., Diebold R., diLeila L. Phys. Rev., 1964, v. 136, p. B1077
72.	Cole R. K. Jr. Phys. Lett., 1967, v. 25B, p. 178.
73.	Cooper L. N„ Henley E M. Phys. Rev., 1953, v. 92, p. 801.
74.	Croissiaux M. e. a. Phys. Rev., 1965, v. 137, p. В 865.
75.	Crowe К- M. In: «Proceedings of the Williamsburg Conference on Interme-
diate Energy Physics». Williamsburg, Virginia, The College of William
and Mary, 1966, p. 145.
76.	Culligan G., Lathrop J. E., Telegdi V. L., Winston R. Phys. Rev. Lett.,
1961, v. 7, p. 458.
77.	Czyz W., Gottfried K. Ann. Phys. (New York), 1963, v. 21, p. 47.
78.	Czyz W., Lesniak L., Malecki A. Ann. Phys. (N. Y.), 1967, v. 42, p. 119.
79.	Danos M. Photonuclear Physics. Univ. Maryland, Dept, of Physics, Techni-
cal Report, 221, July, 1961.
80.	Danos M., Fuller E. G. Ann. Rev. Nucl. Sci., 1965, v. 15, p. 29.
81.	Danos M., Maximon L. C. J. Math. Phys., 1965, v. 6, p. 766.
82.	Davies H., Muirhead H., Woulds J. N. Nucl. Phys., 1966, v. 78, p. 673.
83.	Daniel H. Naturwiss., 1968, v. 55, p. 339.
84.	da Providencia J., Shakin С. M. Ann. Phys. (N. Y.), 1964, v. 30, p. 95.
85.	Daum C. In: «Proceedings of the International School of Physics «Enrico
Fermi». Course 38. Interaction of High-Energy Particles with Nuclei,
Ericson T. E. O., ed. New York, Academic Press, 1967, p. 166.
86.	Dedrick K- G. Phys. Rev., 1955, v. 100, p. 58.
87.	Delorme J., Ericson T. E. O. Phys. Lett., 1966, v. 21, p. 98.
88.	Devons S., Duerdoth. 1., Advan. Nucl. Phys., 1969, v. 2, 295.
89.	de Benedetti S. Suppl. Nuovo Cimento, 1956, v. 4, p. 1209.
90.	de Benedetti S. Nuclear Interactions. New York, Wiley, 1964. (См. на
русском языке: Де Беиедетти С. Ядерные взаимодействия. М., Атомиз-
дат, 1968.)
91.	de Bouard X. е. a. Nuovo Cimento, 1967, v. 52, р. 662.
92.	de Boer J., Eichler J. Advan. Nucl. Phys., 1968, v. 1, p. 1.
93.	de Forest T. Jr., Walecka J. D., Vanpraet G., Barber W. C. Phys. Lett.,
1965, v. 16, p. 311.
94.	de Forest T., Walecka J. D. Advan. Phys., 1966, v. 15, p. 1.
95.	Deutsch M., Gittelman B., Baner R. W., Grodzins L., Sunyar A. W. Phys.
Rev., 1957, v. 107, p. 1733.
96.	Deutsch J. P., Grenacs L., Igo - Kemenes P., Lipnik P., Macq P. C. Phys.
Lett., 1968, v. 28B, p. 315.
97.	de-Shalit A., Walecka J. D. Phys. Rev., 1966, v. 147, p. 763.
98.	de Wit S. A., BackenstossG., Daum C., Sens J. C., Acker H. L. Nucl. Phys.,
1966, v. 87, p. 657.
99.	Dirac P. A. M. The Principles of Quantum Mechanics. Fourth Edition.
Oxford, Oxford Univ. Press, 1958. (См. на русском языке: Дирак П. А. М.
Принципы квантовой механики. М., Физматгиз, 1960.)
100.	Dodge W. R., Barber W. С. Phys. Rev., 1962, v. 127, р. 1746.
101.	Douglas А. С., McDonald N. Phys. Lett., 1967, v. 24B, p. 447.
102.	Drell S. D., Schwartz C. L. Phys. Rev., 1958, v. 112, p. 568.
103.	Drechsel D. Nucl. Phys., 1966, v. 78, p. 65.
104.	Drechsel D. Z. Physik, 1966, v. 192, p. 81.
105.	Drechsel D., Toepffer C. NucL Phys., 1967, v. A100, p. 161.
106.	Durand III L. Phys. Rev. Lett., 1961, v. p. 631.
107.	Ebel M. E„ Feldman G. Nucl. Phys., 1957, v. 4, p. 213.
108.	Eckhause M., Siegel R. T., Welsh R. E. Nucl. Phys., 1966, v. 81, p. 575.
109.	Edmonds A. R. Angular Momentum in Quantum Mechanics. Princeton,
Princeton Univ. Press, 1957. (См. на русском языке: Эдмондс А. Угло-
вые моменты в квантовой механике. В кн.: «Деформация атомных ядер».
Под ред. Л. А. Слива. М., Изд-во иностр, лит., 1968, с. 305.)
339
110.	Eden R. J., Emery V. J., Sampanthar S. Proc. Roy. Soc. (London)
1959, v. A253, p. 186.
111.	Ehrenberg H. F., Hofstadter R., Meyer-Berkhout U., Ravenhall D. C.
Sobottka S. E. Phys. Rev., 1959, v. 113, p. 666.
112.	Eisenberg Y., Kessler D. Phys. Rev., 1961, v. 123, p. 1472; Nuovo
Cimento, 1965, v. 19, p. 1195.
113.	Eisenberg J. M., Rose M. E. Phys. Rev., 1963, v. 131, p. 848.
114.	Eisenberg J. M. Phys. Rev., 1963, v. 132, p. 2243.
115.	Eisenberg J. M., Spicer В. M., Rose M. E. Nucl. Phys., 1965, v. 71, p. 273.
116.	Eisenberg J. M., Le Tourneux J. Nucl. Phys., 1967, v. B3, p. 47.
117.	Elton L. R. Nuclear Sizes. Oxford, Oxford Univ. Press, 1961. (См. на
русском языке: Элтон Л. Размеры ядер. М., Изд-во иностр, лит., 1962.)
118.	Elton L. R. В., Swift A. In «Proceedings of the Williamsburg Conference
on Intermediate Energy Physics». Williamsburg, Virginia, The College
of William and Mary, 1966, p. 731.
119.	Engfer R. In: «Proceedings of the International School of Physics «Enrico
Fermi». Course 38. Interaction of High-Energy Particles with Nuclei.
(T. E. O. Ericson, ed.), New York, Academic Press, 1967, p. 64.
120.	Engfer R., Scheck F. Z. Physik, 1968, v. 216, p. 274.
121.	Ericson T E. O. In: «Proceedings of the Williamsburg Conference on Inter-
mediate Energy Physics Williamsburg, Virginia, The College of William
and Mary, 1966, p. 187.
122.	Ericson T. E. O. In: «Proceedings of the International School of Physics
«Enrico Fermi». Course 38. Interaction of High-Energy Particles with
Nuclei (T. E. O. Ericson, ed.), New York, Academic Press, 1967, p. 253.
123.	Ericson T. E. O. In: «International Nuclear Physics Conference», Gatlin-
burg, 1966, (R. L. Becker, ed.), New York, Academic Press, 1967, p. 437
124.	Ericson M., Figureau A. Nucl. Phys., 1967, v. 133, p. 609.
125.	Fano U. Rev. Mod. Phys., 1957, v. 29, p. 74.
126.	Fano U., Racah G. Irreducible Tensorial Sets. New York, Academic Press,
New York, 1959.
127.	Fano U. NBS Technical Note, 1960, No. 83.
128.	Fermi E. Rev. Mod. Phys., 1932, v. 4, p. 87.
129.	Fermi E. Z. Physik, 1934, v. 88, p. 161.
130.	Ferroni S., Fubini S. Nuovo Cimento, 1955, v. 1, p. 263.
131.	Ferrero F., Manfredotti C., Pasqualini L., Piragino G., Rama P. G. Nuovo
Cimento, 1966, v. 45B, p. 273.
132.	Feynman R. P., Gell-Mann M. Phys. Rev., 1958, v. 109, p. 193.
133.	Feynman R. P. Quantum Electrodynamics, New York, Benjamin, 1962.
(См. на русском языке: Фейнман Р. Квантовая электродинамика. М.,
«Мир», 1964.)
134.	Fitch V. L., Rainwater J. Phys. Rev., 1953, v. 92, p. 789.
135.	Fitch V. L., Roth R. F., Russ J., Vernon W. Phys Rev., 1967, v. 164,
p. 1711.
136.	Foldy L. L., Wouthuysen S. A. Phys. Rev., 1950, v. 78, p. 29.
137.	Foldy L. L. Phys. Rev., 1952, v. 87, p. 688.
138.	Foldy L. L. Phys. Rev., 1953, v. 92, p. 178.
139.	Ford K. W., Hill D. L. Ann. Rev. Nucl. Sci., 1955, v. 5, p. 25.
140.	Foldy	L.	L., Ford K- W., Yennie D. R. Phys.	Rev., 1959, v. 113, p.	1147.
141.	Ford	K.	W., Wills J. G. Los Alamos Scientific Laboratory Report
LAMS-2387, 1960.
142.	Ford	K.	W., Wills J. G. Nucl. Phys., 1962,	v. 35, p. 295.
143.	Foldy	L.	L., Walecka J. D. Nuovo Cimento,	1964, v. 34, p. 1026.
144.	Freeman J. M., Murray G., Montague J. H., White R. E., Burcham W. E
Phys. Lett., 1964, v. 8, p. 115.
145.	Frosch R. E., Rand R. E., Van Oestrum K- J , Yearian M. R. Phys. Lett.,
1966, v. 21, p. 598.
146.	Frosch R. F., McCarthy J. S., Rand R. E., Yearian M. R. Phys. Rev.,
1967, v. 160, p. 874.
147.	Fujii A., Primakoff H. Nuovo Cimento, 1959, v. 12, p. 327.
34 0
148.	Fuller E. G., Hayward E. In: «Nuclear Reactions II». Endt P. M., Smith
P. В , ed. Amsterdam, North-Holland, 1962, p. ИЗ. (См. па русском
языке Фуллер Э. Дж., Хейвард Э. В кн.. Ядерные реакции. Под ред.
Эндта П. М., Смита П. Б., т. II. М., Атомиздат, 1964.)
149.	Fultz S. С., Bramblett R. L., Berman В. L., Caldwell J. Т., Kelly М. А.
In: «International Nuclear Physics Conference». Gatlinburg, 1966. (Becker
R L., ed.) New York, Academic Press, 1967.
150.	Fulcher L. P., Eisenberg J. M., Le Tourneux J Can. J. Phys., 1967, v. 45
p. 3313.
151.	Gartenhaus S., Schwartz C. Phys. Rev., 1957, v. 108, p. 482.
152.	Gammel J. L., Thaler R. H. Phys. Rev., 1957, v. 107, p. 1337.
153.	Gammel J. L., Thaler R. H. In: «Progress in Elementary Particle and Cosmic
Ray Physics», v. V (Wilson J G , Wouthuysen S. A., ed.). Amsterdam,
North-Holland, 1960, p. 97.
154.	Gasiorowicz S. Elementary Particle Physics. New York, Wiley, 1966.
(См. на русском языке: Газнорович С. Физика элементарных частиц. М.,
«Наука», 1969.)
155.	Grodzins L., Gal A., Hiltner J. Phys. Rev. Lett., 1968, v. 21, p. 453.
156.	Gell-Mann M., Teiegdi V. L. Phys. Rev., 1953, v. 91, p. 169.
157.	Gell-Mann M., Goldberger M. L , Thirring W. E. Phys. Rev., 1954, v 95,
p. 1612.
158.	Gershtein S. S., Zeldovich I. B. Zh. Eksperim. i Teor. Fiz., 1955.
v. 29, p. 698. (См. на русском языке: Герштейн С. С., Зельдович Я. Б.
«Ж. эксперим. и теор. физ.», 1956, т. 2, с. 576.)
159.	Cell-Mann М., Levy М. Nuovo Cimento, 1960, v. 16, р 705
160.	Gell-Mann М. Phys. Rev., 1962, v. 125, p. 1067.
161.	Gell-Mann M. Physics, 1964, v. 1, p. 63.
162.	Ginsburg E. S-, Pratt R. H. Phys. Rev., 1964, v. 134, p. B773.
163.	Ginsburg E. S., Pratt R. H. Phys. Rev, 1965, v. 137, p. В 1500.
164.	Giilet V., Jenkins D. A. Phys. Rev., 1965, v. 140, p. B32.
165.	Goldhaber M., Teller E. Phys. Rev., 1948, v. 74, p. 1046.
166.	Goldberger M. L Phys. Rev., 1955, v, 97, p. 508.
167.	Gomes L. C., Walecka J. D., Weisskopf V. F. Ann. Phys. (New York), 1958,
v. 3, p. 241.
168.	Gorbunov A. N., Spiridonov V. M. Zh. Eksperim. i Teor. Fiz., 1958, v. 34,
p. 866. (См. на русском языке: Горбунов А. Н., Спиридонов В. М. «Ж.
эксперим. и теор физ.», 1958, т 7, с. 600).
169.	Goldberger М. L., Treiman S. В. Phys. Rev , 1958, v. Ill, p. 354.
170.	Goldhatnmer P. Rev. Mod. Phys., 1963, v. 35, p. 40.
171.	Goldemberg J., Torizuka Y., Barber W. C., Walecka J. D. Nucl. Phys.,
1963, v. 43, p. 242.
172.	Gottfried K- In: «Direct Interactions and Nuclear Reaction Mechanisms».
Clementel E., Villi C , ed. New York, Gordon and Breach, 1962, p. 720.
173.	Goldberger M. L., Watson К- M. Collision Theory. New York, Wiley,
1964. (См. на русском языке: Гольдберг М., Ватсон К. Теория столк-
новении. М., «Мир», 1967.)
174.	Gourdin М., Piketty С. A. Nuovo Cimento, 1964, v. 32, р. 1137.
175.	Goldemberg J., Pratt R. H. Rev. Mod. Phys., 1966, v. 38, p. 311.
176.	Goertzel G Phys. Rev., 1946, v 70, p. 897
177.	Gritty T. A., Onley D S., Reynolds J. T., Biedenharn L C Phys. Rev.,
1962, v. 128, p. 833.
178.	Greiner W., Scheck F. Nucl. Phys., 1963, v. 41, p. 424.
179.	Greiner B., Arenhovel H. Nucl. Phys., 1968, v. A107, p. 225.
180.	Guy R., Eisenberg J. M., LeTourneux J. Nucl. Phys., 1968, v. Al 12, p. 689.
181.	Hamilton J. The Theory of Elementary Particles- Oxford, Oxford Univ.
Press, 1959.
182.	Hayward E., Fuller E. G. Phys. Rev., 1957, v. 106, p 991.
183.	Hayward E. In: «Nuclear Structure and Electromagnetic Interactions».
MacDonald, N., ed. New York, Plenum Press, 1965, p. 141.
184.	Heim R. H. Phys. Rev., 1956, v. 104, p. 1466
341
185.	Heisenberg W., Pauli W. Z. Physik, 1929, v. 56, p. 1.
186.	Heitler W. The Quantum Theory of Radiation. Second Edition. Oxford,
Oxford Univ. Press, 1944.
187.	Heitler W. The Quantum Theory of Radiation. Third Edition. Oxford,
Oxford Univ. Press, 1954. (См. на русском языке: Гайтлер В. Квантовая
теория излучения. Изд. 3. М., Изд-во иностр, лит., 1956.)
188.	Hitlin D. е. a. Bull Amer Phys. Soc., 1966, v. 11, p. 130.
189.	Hofstadter R Rev. Mod Phys., 1956, v. 28, p 214.
190.	Hofstadter R., Bumiller F., Yearian M. R. Rev. Mod. Phys., 1958, v. 30,
p. 482.
191.	Hofstadter R., Bumiller F., Croissiaux. M. Phys. Rev. Lett., 1960, v. 5, p. 263.
192.	Hofstadter R., Herman R. Phys. Rev. Lett., 1961, v. 6, p. 293.
193.	Hofstadter R. Nuclear and Nucleon Structure New York, Benjamin, 1963.
194.	Hofstadter	R. e. a. Phys. Rev.	Lett., 1965, v.	15,	p. 758.
195.	Holder	F.	D., Eisenberg J. M.	Nucl. Phys., 1967,	v. A106,	p.	261.
196.	Hofstadter R., Collard H. R., Landolt-Bornstein. Group I, v. 2, p. 21.
197.	Hulme	H.	R. Proc. Roy. Soc.	(London), 1936,	v.	Л154, p.	487.
198.	Huang	K., Yang C. N., Lee T.	D. Phys. Rev.,	1957, v. 108,	p.	1340.
199.	Huang K. Statistical Mechanics. New York, Willey, 1963. (См. на
русском языке: Хуанг К- Статистическая механика. М., «Мир», 1966.)
200.	Hiifner J. Nucl. Phys., 1964, v. 60, p. 427.
201.	Hubbard D. F., Rose M. E. Nucl. Phys., 1966, v. 84, p. 337
202.	Hiifner J. Z. Physik, 1966, v 190, p. 81.
203.	Inopin E. V , Tishchenko В. 1 Zh. Eksperim. i Teor. Fiz., 1959, v. 37,
p. 1308. (См. на русском языке: Инопин Е В., Тищенко Б. И. «Ж.
эксперим. и теор. физ.», 1960, т. 10, с. 932).
204.	Isabelle D. В., Bishop G. R. Nucl. Phys., 1963, v. 45, p. 209.
205.	Isabelle D. B. In: «Proceedings of the International School of Physics
«Enrico Fermi». Course 38. Interaction of High-Energy Particles with
Nuclei. Ericson T. E. O., ed. New York, Academic Press, 1967, p. 302.
206.	Isabelle D B. In: «High-Energy Physics and Nuclear Structure» Alexan-
der G., ed. Amsterdam, North-Holland, 1967, p. 126.
207.	Jacobsohn B. A. Phys Rev., 1954, v. 96, p. 1637.
208.	Jackson J. D., Treiman S. B., Wyld H. W. Jr. Phys. Rev., 1957, v. 106.
p. 517.
209.	Jackson J. D., Treiman S. B., Wyld H. W. Jr. Nucl. Phys., 1957, v. 4,
p. 206.
210.	Jackson J. D. The Physics of Elementary Particles. Princeton, Princeton
Univ. Press, 1958.
211.	Jackson J. D. In: «Dispersion Relations. Screaton G. R., ed. Edinburg,
Oliver and Boyd, 1961, p 1
212.	Jackson J D. Classical Electrodynamics. New York, Wiley, 1962 (См. на
русском языке: Джексон Дж. Классическая электродинамика. М., «Мир»,
1965.)
213.	Jackson J. D. In «Elementary Particle Physics and Field Theory». New
York, Benjamin, 1963, p. 263.
214.	Jenkins D. A. e. a. Phys. Rev. Lett., 1966, v. 17, p. 1.
215.	Jenkins D. A., Kunselman R Phys. Rev. Lett., 1966, v. 17, p. 1148.
216.	Jost R. In «Theoretical Physics in the Twentieth Century» Fierz M..
Weisskopf V F., ed. New York, Interscience, 1960. (См. на русском язы-
ке: Пост Р. В кн.: Теоретическая физика двадцатого века. М., Изд-во
иностр, лит., 1962, с. 128.)
217.	Kallen G. Elementary Particle Physisc. Reading, Massachusetts Addison-
Wesley, 1964.
218.	Kelly F. M. Handbuch der Physik, 1958, v. 38/1, p. 59.
219.	Kopfermann H. Nuclear Moments. New York, Academic Press, 1958.
(См. на русском языке: Копферман Г. Ядерные моменты. М., Изд-во
иностр, лит., 1960.)
220.	Kopaleishvili Т. 1. J. Nucl. Phys. (U.S.S.R.), 1965, v. 1, р. 961; Soviet J.
Nucl. Phys., 1965, v. 1, p. 686.
342
221.	Konopinski E. T., Rose M. E. In «Alpha-, Beta-, and Gamma-Ray Spectro-
scopy». Siegbahn K., ed. Amsterdam, North Holland, 1965.
222.	Konopinski E. J. The Theory of Beta Radiactivity, Oxford, Oxford Univ.
Press, 1966.
223.	Kroll’ N., Foldy L. L. Phys. Rev., v. 88, p. 1177.
224.	Kramer P., Moshinsky M. Pnys. Lett., 1966, v. 23, p. 574.
225.	Langer L. M., Moffat R. J. D. Phys. Rev., 1952, v. 88, p. 689.
226.	Landau L. D., Lifshitz E. M. The Classical Theory of Fields. Reading,
Massachusetts, Addison-Wesley, 1962. (См. на русском языке:
Ландау Л. Д., Лифшиц Е. М. Классическая теория поля. Изд. 4. М.,
Физматгиз, 1962.
227.	Laukien G. Handbuch der Physik, 1958, v. 38/1, p. 120.
228.	Levinger J. S., Bethe H. A. Phys. Rev., 1950, v. 78, p. 115.
229.	Levinger J. S. Phys. Rev., 1951, v. 84, p. 43.
230.	Levinger J. S. Nuclear Photo-Disintegration. Oxford, Oxford Univ.
Press, 1960. (См. на русском языке: Левинжер Дж. Фотоядерные реак-
ции. М., Изд-во иностр, лит., 1962).
231.	Le Bellac М. Nucl. Phys., 1963, v. 40, p. 645.
232.	Lee T. D., Yang C. N. Phys. Rev., 1956, v. 104, p. 254.
233.	Lee Y. K-, Mo L. W., Wu C. S. Phys. Rev. Lett., 1963, v. 10, p. 253.
234.	Lee T. D., Wu C. S. Ann. Rev. NucL Sci., 1965, v. 15, p. 381. (См. на
русском языке: В кн.: Ли Т., By Ц. Слабые взаимодействия. М., «Мир»,
1968).
235.	LeTourneux J. Nucl. Phys., 1966, v. 81, p. 665.
236.	Lipkin H. J. Beta Decay for Pedestrians. Amsterdam, North-Holland,
1962.
237.	Luyten J. R., Rood H. P. C., Tolhoek H. A. Nucl. Phys., v. 41, p. 236.
238.	Mandi F. Introduction to Quantum Field Theory. New York, Interscien-
ce, 1959.
239.	Maximon L. C., Isabelle D. B. Phys. Rev., 1964, v. 133, p. B1344.
240.	Maximon L. C., Isabelle D. B. Phys. Rev., 1964, v. 136, p. B674.
241.	Marion J. B. Classical Electromagnetic Radiation. New York, Academic
Press 1965
242.	Martin B. R. Fortschr. Physik, 1967, v. 15, p. 357.
243.	Maximon L. C. Rev. Mod. Phys., 1969, v. 41, p. 193.
244.	McVoy K. W., Van Hove L. Phys. Rev., 1962, v. 125, p. 1034.
245.	Messiah A. M. L., Marshak R. E. Phys. Rev., 1952, v. 88, p. 678.
246.	Merzbacher E. Quantum Mechanics. New York, Wiley, 1961.
247.	Messiah A. Quantum Mechanics. Amsterdam, North-Holland, 1962.
248.	Meister N. T., Griffy T. A. Phys. Rev., 1964, v. 133, p. B1032.
249.	Mickelwait A. B., Corben H. C. Phys. Rev., 1954, v. 96, p. 1145.
250.	Migdal A. B. Nucl. Phys., 1964, v. 57, p. 29. (См. на русском языке:
Мигдал А. Б. Теория конечных ферми-систем и свойства ядер. М.,
«Наука», 1965.)
251.	Migdal А. В. In «Proceedings of the International Summer School of
Physics «Enrico Fermi». Course 36. Many-Body Description of Nuclear
Structure and Reaction. Bloch C., ed. New York, Academic Press, 1966.
(См. на русском языке: Мигдал А. Б. Метод квазичастиц в теории ядра.
М., «Наука», 1967.)
252.	Moszkowski S. A. Phys. Rev., 1951, v. 83, р. 1071.
253.	Morse Р. М., Teshbach Н. Methods of Theoretical Physics. New York,
McGraw-Hill, 1952. (См. на русском языке: Морс Р. М., Фешбах Н.
Методы теоретической физики. Т. 1, 2. М., Изд-во иностр, лит., 1958.)
254.	Moszkowski S A. In «Beta- and Gamma-Ray Spectroscopy». Siegbahn K-,
ed. Amsterdam, North-Holland, 1955, p. 373. (См. на русском языке:
Мошковский С. В кн.: Бета- и гамма-спектроскопия. Под ред. К. Зиг-
бана. М., Физматгиз, 1959, с. 353. См. также в кн.: Альфа-,бета- и гамма-
спектроскопия. Под ред. К. Зигбана. Вып. 3. М., Атомиздат, 1969, с. 5.)
255.	Morpurgo G. Phys. Rev., 1958, v. ПО, p. 721.
256.	Morpurgo G. Phys. Rev., 1959, v. 114, p. 1075.
343
257.	Morpurgo G. In «Proceedings of the International Summer School «Enrico
Fermi». Course 15. Nuclear Spectroscopy (Racah G., ed.). New York,
Academic Press, 1962, p. 164.
258.	Morita M. Suppl. Progr. Theor. Phys., 1963, v. 26, p. 1.
259.	Nambu Y. Phys. Rev. Lett., 1960, v. 4, p. 380.
260.	Newton J. O. In «Nuclear Structure and Electromagnetic Interactions».
MacDonald N., ed. New York, Plenum Press, 1965, p. 287.
261	Nilsson J., Pietschmann H. An Introduction to Weak Interaction Physics.
New York, McGraw-Hill (in preparation).
262.	Nordberg M. E., Jr..Kinsey K. F., Burman R. L. Phys. Rev., 1968, v. 165,
p. 1096
263.	Onley D. S., Griff у T A., Reynolds?. T. Phys. Rev., 1963, v. 129, p. 1689.
264.	Onley D. S., Reynolds J. T., Wright L. E. Phys. Rev., 1964, v. 134, p. B945.
265.	Panofsky W. К- H., Phillips M. Classical Electricity and Magnetism.
Reading, Massachusetts. Addison-Wesley, 1962.
266.	Pauli W. Z. Physik, 1926, v. 36, p. 336.
267.	Pauli W. Phys. Rev., 1940, v. 58, p. 716.
268.	Pieper W., Greiner W. Phys Lett., 1967, v. 24B, p. 377.
269.	Pietschmann H., Fulcher L. P , Eisenberg J. M. Phys. Rev. Lett., 1967,
v. 19, p. 1259.
270	Pieper W , Greiner W Nucl Phys., 1968, v. Л109, p. 539.
271.	Placzek G. Marx Handuch der Radiologie, 1934, v 6/2, p. 205.
272.	Poelz G. e. a. Phys. Lett., 1968, v. 26B, p. 331.
273.	Primakoff H. Rev. Mod. Phys., 1959, v. 31, p. 802.
274.	Pratt R. H., Walecka J. D., Griffy T. A. Nucl. Phys., 1965, v. 64, p. 677.
275.	Primakoff H. In «Proceedings of the Internationa] School of Physics
«Enrico Fermi». Course 32. Weak Interactions and High-Energy Neutrino
Physics. Lee T. D., ed. New York, Academic Press, 1966.
276.	Primakoff H. Private communication.
277.	Quaranta A. A. e. a. Phys. Rev., 1969, v. 177, p. 2118.
278.	Radicati L. A. Phys. Rev., 1952, v. 87, p. 521.
279.	Rand R. E., Frosch R., Yearian M. R. Phys. Rev. Lett , 1965, v. 14, p. 234
280.	Rawitscher G. H. Phys. Rev., 1966, v. 151, p. 846.
281.	Rainwater J. Ann. Rev Nucl. Sci., 1957, v. 7, p. 1.
282.	Reitan A. Nucl. Phys., 1962, v. 36, p. 56.
283.	Reynold J. T., Onley D. S. Nucl. Phys., 1965, v. 66, p. I.
284.	Rho M. Phys. Rev., 1967, v. 161, p. 955.
285.	Rho M. Phys. Rev. Lett., 1967, v. 19, p. 248.
286.	Robson T. M. Phys. Rev., 1951, v. 83, p. 349.
287.	Rose M. E. Multipole Fields. New York, Wiley, 1955. (См. на русском
языке: Роуз М. Поля мультиполей. М., Изд-во иностр, лит., 1957.)
288.	Rose М. Е. Elementary Theory of Angular Momentum New York, Wiley,
1957
289.	Rose	M.	E. J. Math,	and Phys ,	1958, v. 37, p. 215.
290.	Rose	M.	E. Relativistic Electron	Theory. New York, Wiley,	1961.
291.	Rothberg J. E. e. a.	Phys. Rev.,	1964, v. 132, p. 2664.
292.	Rose	M.	E.. Nilsson	J. In Handbook of Physics. Condon	E.	U.. Odis-
haw H., ed., New York, McGraw-Hill, 1967, p. 9.
293.	Rosenfeld A. H. e. a. Rev. Mod. Phys., 1968, v. 40, p. 77.
294.	Rood H. P. C., Tolhoek H.A. Phys. Lett., 1963, v. 6, p. 121.
295.	Runge K. e. a. Proceedings of the Williamsburg Conference on Intermediate
Energy Physics. Williamsburg, Virginia, The College of William and
Mary, 1966.
296.	Sachs R. G., Austern N. Phys Rev., 1951, v 81, p 705
297.	Sachs R. G. Nuclear Theory. Reading, Mass., Addison-Wesley, 1953.
298.	Saxon D. S., Schiff L. 1. Nuovo Cimento, 1957, v. 6, p 614.
299.	Sakurai J. J. Invariance Principles and Elementary Particles. Princeton,
New Jersey, Princeton Univ. Press, 1964.
300.	Schwinger J. Phys. Rev., 1949, v. 75, p. 898.
301.	Schiff L. I. Phys. Rev., 1954, v. 96, p. 765.
344
302.	Schiff L. I. Quantum Mehcanics. Second Edition. New York, McGraw-
Hill, 1955. (См. на русском языке: Шифф Л. Квантовая механика. М.,
Изд-во иностр, лит., 1959.)
303.	Schiff L. I. Phys. Rev., 1956, v. 103, p. 443.
304.	Schwinger J. Quantum Electrodynamics. New York, Dover Publ., 1958.
305.	Schweber S. S. An Introduction to Relatiwistic Quantum Field Theory.
Evanston. Row, Peterson and Co., 1961. (См. на русском языке: Шве-
бер С. Введение в релятивистскую квантовую теорию поля. М., Изд-во
иностр, лит., 1963.)
306.	Scheck F. Z. Physik, 1963, v. 172, р. 239.
307.	Schucan Т. Н. Nucl. Phys., 1965, v. 61, p. 417.
308.	Scheck F. Nucl. Phys., 1966, v. 77, p. 577.
309.	Schopper H. P. Weak Interactions and Nuclear Beta Decay. Amsterdam,
North-Holland, 1966.
310.	Scheid W., Greiner W. Ann. Phys. (New York), 1968, v. 48, p. 493.
311.	Sens J. C. Phys. Rev., 1958, v. 113, p. 679.
312.	Seki R., Cromer A. H. Phys. Rev., 1967, v. 156, p. 93.
313.	Sens J. C. In: «High-Energy Physics and Nuclear Structure». (Alexan-
der G., ed.). Amsterdam, North-Holland, 1967.
314.	Seaborn J. B., Eisenberg J. M. Nucl. Phys., 1965, v. 70, p. 264.
315.	Shevchenko V. G., Yudin N. P. Atomic Energy Rev., 1965, v. 3, p. 3.
316.	Silbar R„ Werntz C., ijberall H. Nucl. Phys., 1968, v. AI07, p. 655.
317.	Silbar R., Uberall H. Nucl. Phys., 1968, v. A109, p. 146.
318.	Siegert A. J. F. Phys. Rev., 1937, v. 52, p. 787.
319.	Skorka S. J., Hertel J., Retz-Schmidt T. W. Nucl. Data, 1966, v. 2, p. 347.
320.	Sommerfeld A. Atombau und Spektrallinien. Braunschweig, Vieweg, 1939.
(См. на русском языке: Зоммерфельд А., Строение атома и спектры. М.,
Гостехиздат, 1956.)
321.	Spamer Е., Artus Н. Z. Physik, 1967, v. 198, р. 445.
322.	Spicer В. М. Advan. Nucl. Phys., v. 2, p. 1.
323.	Spamer E., Goldmann, Titze. Private communication. Darmstadt, 1969.
324.	Stephens S. S. Jr., Diamond R. M., Perlman I. Phys. Rev. Lett., 1959, v.
3, p. 435.
325.	Streater R. E., Wightman A. S. PCT, Spin and Statistics, and All That.
New York, Benjamin, 1964. (См. на русском языке: Стритер Р. Ф., Вайт-
ман А. С. РСТ, спин, статистика и все такое. М., «Наука», 1966.)
326.	Swift A., Elton L. R. В. Phys. Rev. Lett., 1966, v. 17, p. 484.
327.	Szvdlik P. P., Philpott R. T. Bull. Amer. Phys. Sos., 1967, v. 12, p. 47.
328.	Tassie L. J., Barker F. C. Phys. Rev., 1958, v. Ill, p. 940.
329.	Taylor J. C. Phys. Rev., 1958, v. 110, p. 1216.
330.	Ter Haar D. Rept. Progr. Phys., 1961, v. 24, p. 304.
331.	Tolhoek H. A., Cox J. A. M. Physica, 1953, v. 19, p. 101.
332.	Tolhoek H. A. Ii: «Selected Topics in Nuclear Spectroscopy». (Verhaar B. J.r
ed.). Amsterdam, North Holland, 1964.
333.	Toepffer C., Greiner W. Ann. Phys. (New York), 1968, v. 47, p. 285.
334.	Toepffer C., Greiner W. Phys. Rev. (to be published).
335.	Townes С. H. Handbuch der Physik, 1958, v. 38/1, p. 377.
336.	Tralli N., Goertzel G. Phys. Rev., 1951, v. 83, p. 399.
337.	Trainor L. E. H. Phys. Rev., 1952, v. 85, p. 962.
338.	Tuan S. T., Weber H. J., Wright L. E. Phys. Rev., 1968, v. 167, p. 939.
339.	Uberall H. Suppl. Nuovo Cimento, 1966, v. 4, p. 781.
340.	Walecka J. D. Phys. Rev., 1962, v. 126, p. 653.
341.	Walecka J. D. In: «International Nuclear Physics Conference». Catlinburg,
1966. (Becker R. :L., ed.). New York, Academic Press, 1967.
342.	Walecka J. D. In «Proceedings of the International School of Physics
Enrico Fermi». Course 38. Interaction of High-Energy Particles with Nuclei.
(Ericson T. E. O., ed.). New York, Academic Press, 1967, p. 17.
343.	Wentzel G. Quantum Theory of Fields. New York, Interscience, 1949.
344.	Weisskopf V. F. Phys. Rev., 1951, v. 83, p. 1073.
345
345.	Weinberg S. Phys. Rev., 1958, v. 112, p. 1375.
346.	Weidenmiiller H. Phys. Rev. Lett., 1960, v. 4, p. 299.
347.	Weigert L. J., Rose M. E. Nucl. Phys., 1964, v. 51, p. 529.
348.	Weigert L. J., Eisenberg J. M. Nucl. Phys., 1964, v. 53, p. 508.
349.	Weidenmiiller H. In: «Selected Topics in Nuclear Spectroscopy». (Ver-
haar B. J., ed.). Amsterdam, North-Holland, 1964.
350.	Weisberger W. I. Phys. Rev. Lett., 1964, v. 14, p. 1047.
351.	Wilets L. KgL Danske Videnskab. Selskab, Mat.-Fys. Medd., 1954, v. 29,
No. 3.
352.	Wichmann E. H., Kroll N M. Phys. Rev., 1956, v. 101, p. 843.
353.	Wilkinson D. H. In «Proceedings of the Rehovoth Conference on Nuclear
Structure». (Lipkin H J., ed.). Amsterdam, North-Holland, 1958, p. 175.
354.	Wilets L. Handbuch oer Physik, 1958, v. 38/1, p. 96.
355.	Wigner E. P. Group Theory and its Applications to the Quantum Mehcanics
of Atomic Spectra New York, Academic Press, 1959. (См на русском
языке: Вигнер Е. Теория групп и ее применение к квантовомеханиче-
ской теории атомных спектров. М., Изд-во иностр, лит., 1961.)
356.	Winston R., Telegdi V. L. Phys. Rev. Lett., 1961, v. 7, p. 104.
357.	Winther A., de Boer J. California Institute of Technology Report, 1965.
358.	Wright L. E.. Onley D. S. Nucl. Phys., 1965, v. 64, p. 231.
359.	Wu C. S., Ambler E., Hayward R. W., Hoppes D. D., Hudson R. P. Phys.
Rev., 1957, v. 105, p. 1413.
360.	Wu C. S. Rev. Mod. Phys., 1964, v. 36, p. 618.
361.	Wu C. S., Moszkowski S. A. Beta Decay. New York, Interscience, 1966.
(См. на русском языке: By Ц. С., Мошковский С. А. Бета-распад.
М., Атомиздат, 1970.)
362.	Wu С. S. In: «International Nuclear Physics Conference». Gatlinburg, 1966.
(Becker R. L., ed.). New York, Academic Press, 1967, p. 409.
363.	Yennie D. R , Wilson R N„ Ravenhali D. G. Phys. Rev., 1953, v. 92,
p. 1953.
364.	Yennie D R , Ravenhali D. G., Wilson R. N. Phys. Rev., 1954, v. 95,
p. 500.
365	Yennie D. R., Frautschi S C., Suura H. Ann. Phys. (New York), 1961, v. 13,
p. 379.
366.	Yennie D. R., Boos F. L., Ravenhall D.G. Phys. Rev., 1965, v. 137, p. B882.
367.	Ziegler J. F. The Calculation of Inelastic Electron Scattering by Nuclei.
Yale-2726E-49/TID-4500, May, 1967.
Дополнительная литература
368.	Балдин A. M., Гольданский В. И., Максименко В. М., Розенталь И. Л.
Кинематика ядерных реакций. М., Атомиздат, 1968.
369.	Бейман Б. Ф. Лекции по применению теории групп в ядерной спектро-
скопии. Перев. с англ. М., Физматгиз, 1961.
370.	Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Релятивистская
квантовая теория поля. Ч. 1. М., «Наука», 1968.
371.	Бернстейн Дж. Элементарные частицы и их токи. Перев. с англ. М.,
«Мир», 1970
372.	Блохинцев Д. И. Основы квантовой механики. М., «Высшая школа», 1961.
373.	Бор О., Моттельсон Б. Структура атомного ядра. Перев. с англ. Под
ред. Л. А. Слива Т 1 М., «Мир», 1971.
374.	Вайнштейн А. И., Захаров В. И. «Усп. физ. наук», 1970. т 100, с. 225.
375.	Горячев Б. И., Ишханов Б. С., Шевченко В. Г. В кн : Проблемы совре-
менной ядерной физики. М., «Наука», 1971, с. 362.
376.	Давыдов А. С. Квантовая механика. М., Физматгиз, 1963.
377.	Давыдов А. С. Теория атомного ядра. М., Физматгиз, 1958.
378.	Ландау Л. Д., Лифшиц Е. М. Квантовая механика. М., Физматгиз, 1963.
Составлено переводчиком.
346
379.	Левич В. Г. Курс теоретической физики. Т. 1. М., «Наука», 1969.
380.	Лифшиц Е. М., Питаевский Л. П. Релятивистская квантовая теория.
Ч. II. М., «Наука», 1971.
381.	Лушников А. А. В кн.: Мигдал А. Б. Теория конечных ферми-систем
и свойства атомных ядер. М., «Наука», 1965, с. 451.
382.	Новожилов Ю. В. Введение в теорию элементарных частиц. М., «Нау-
ка», 1972.
383.	Окунь Л. Б. Слабое взаимодействие элементарных частиц. М., Физмат-
гиз, 1963.
384	Соколов А. Введение в квантовую электродинамику. М.—Л., Физ-
матгиз. 1958.
385.	Тамм И. Е. Основы теории электричества М , «Наука», 1966.
386 Труды Международной конференции по электромагнитным взаимодей-
ствиям при низких и средних энергиях Дубна, февраль, 1967. Т. 3. М.,
1967.
387.	Фелд Б. Модели элементарных частиц Перев. с англ. М., «Мир», 1971.
388.	Фоторасщепление в области гигантского резонанса. Труды ФИАН, Т 36,
М., 1966.
389.	Челлен Г. Физика элементарных частиц. Перев. с англ. М., «Наука»,
1966.
390.	Швебер С., Бете Г., Гофман Ф. Мезоны и поля. Перев. с англ. Под ред.
И. Е. Тамма. Т. 1. Перев. с англ. М., Изд-во иностр, лит., 1957.
391.	Юцис А. П., Бандзайтис А. А. Теория момента количества движения
в квантовой механике. Вильнюс, 1965.
345.	W
346.	W
347.	W
348.	W
349.	V
h
350.	V
351.	'
Г
352.	1
353.	'
354.
355.
356.
357.
358.
359.
360
361
361
36
36
3(
3
3
И. Айзенберг, В. Грайнер
МЕХАНИЗМЫ ВОЗБУЖДЕНИЯ ЯДРА
Электромагнитное и слабое взаимодействия
Перев. с англ. С. П. Камерджиева
Редактор В. А. Кузьмичева
Художественный редактор Л Т. Кирьянов
Переплет художника А. И. Шаварда
Технический редактор Н. А. Власова
Корректоры JI. С. Тимохова, Н. А. Смирнова
Сдано в набор 13.Х 1972 г.
Подписано к печати 28.IV 1973 г.
Формат 60X90*/ie Бумага типографская № 2.
Усл. печ. л. 21,75.	Уч.-изд. л. 22,04.
Тираж 2050 экз. Зак. изд. 70296. Зак. тип 1193.
Цена 2 р. 41 к.
Атомиздат, 10303L Москва, К-31, Ул. Жданова, 5/7.
Московская типография № 4 Союзполиграфпрома
при Государственном комитете Совета Министров
СССР по делам издательств, полиграфии
и книжной торговли
Москва, И-41, Б. Переяславская, 46.