Графическая теория представлений ортогональных и унитарных групп - Кузнецов Г.И., Москалюк С.С., Смирнов Ю.Ф., Шелест В.П.

Глава 1. Графическая реализация представлений ортогональных и унитарных групп
1.2. Неприводимые представления класса 1 ортогональных групп
1.3. Неприводимые представления класса 2 унитарных групп
1.4. Гиперсферические координаты и их графы. Теоретико-групповая интерпретация
1.5. Число различных деревьев и число классов эквивалентных деревьев
1.6. Разделение переменных в операторе Лапласа. Угловые функции
1.9. Некоторые свойства гиперсферических гармоник
1.10. Коэффициенты Клебша — Гордана ортогональных и унитарных групп
Глава 2. Унитарное преобразование между базисами, соответствующими деревьям разной топологической структуры
2.3. Аналитическое продолжение $T$-коэффициентов и $6j$-, $3j$-символы
Глава 3. Графическая теория $3nj$-коэффициентов
4.2. Теорема о фундаментальности 5-циклов
Глава 5. Матрицы конечных вращений в пространстве деревьев
Глава 6. Обобщение метода деревьев Виленкина — Кузнецова — Смородинского
6.2. Осцилляторные функции в гиперсферических координатах
Глава 7. Функции на трехмерном гиперболоиде
7.4. Разложение функций, заданных в пространственно-подобной области
Глава 9. Построение базисов инвариантов из динамических переменных, преобразующихся по заданному представлению компактной группы Ли
9.2. Производящие функции Молина для непрерывных групп
9.3. Обобщение производящих функций Молина
9.4. Комбинирование производящих функций Молина
Глава 11. Анализ совместности теоретико-групповых моделей
11.2. Краткое описание алгоритма вычислений
Глава 12. Фактор-системы теоретико-групповых моделей. Фактор-уравнения поля в анизотропном пространстве-времени
12.2. Фактор-уравнения для безмассового спинорного поля
12.3. Фактор-уравнения для векторного безмассового поля
12.4. Фактор-уравнения для массивного спинорного поля
12.5. Фактор-уравнения для векторного массивного поля
Глава 13. Двухмерные разложения релятивистских амплитуд
13.2. Связь между лоренц- и редже-амплитудами
$Глава 14. Парциальный анализ амплитуд $\mathcal{NN}$ и $\mathcal{N\bar N}$-рассеяния при высоких энергиях$
14.2. Разложение амплитуд по парциальным волнам и переход из канала в канал
14.3. Разложение спиральных амплитуд $s$-канала и связь между релятивистскими парциальными амплитудами $s$- и $t$-каналов
Глава 15. Исследование аналитических свойств фейнмановских амплитуд гомологическим методом
15.2. Нерелятивистские однопетлевые 5, 4, 3-хвостки
15.4. Собственные сингулярности однопетлевых $n$-угольных диаграмм Фейнмана
$Глава 14. Парциальный анализ амплитуд $\mathcal{NN}$ и $\mathcal{N\bar N}$-рассеяния при высоких энергиях$
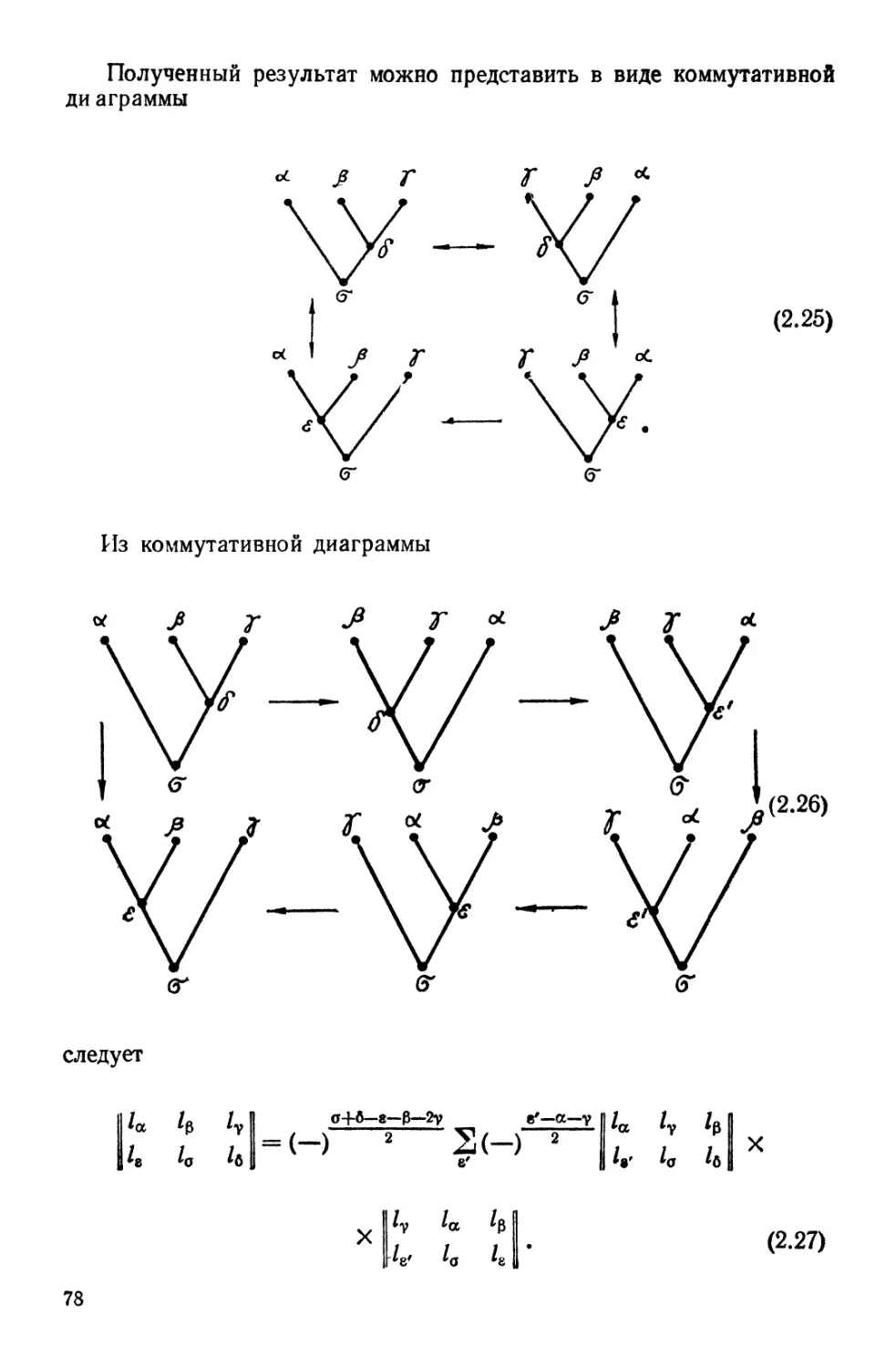
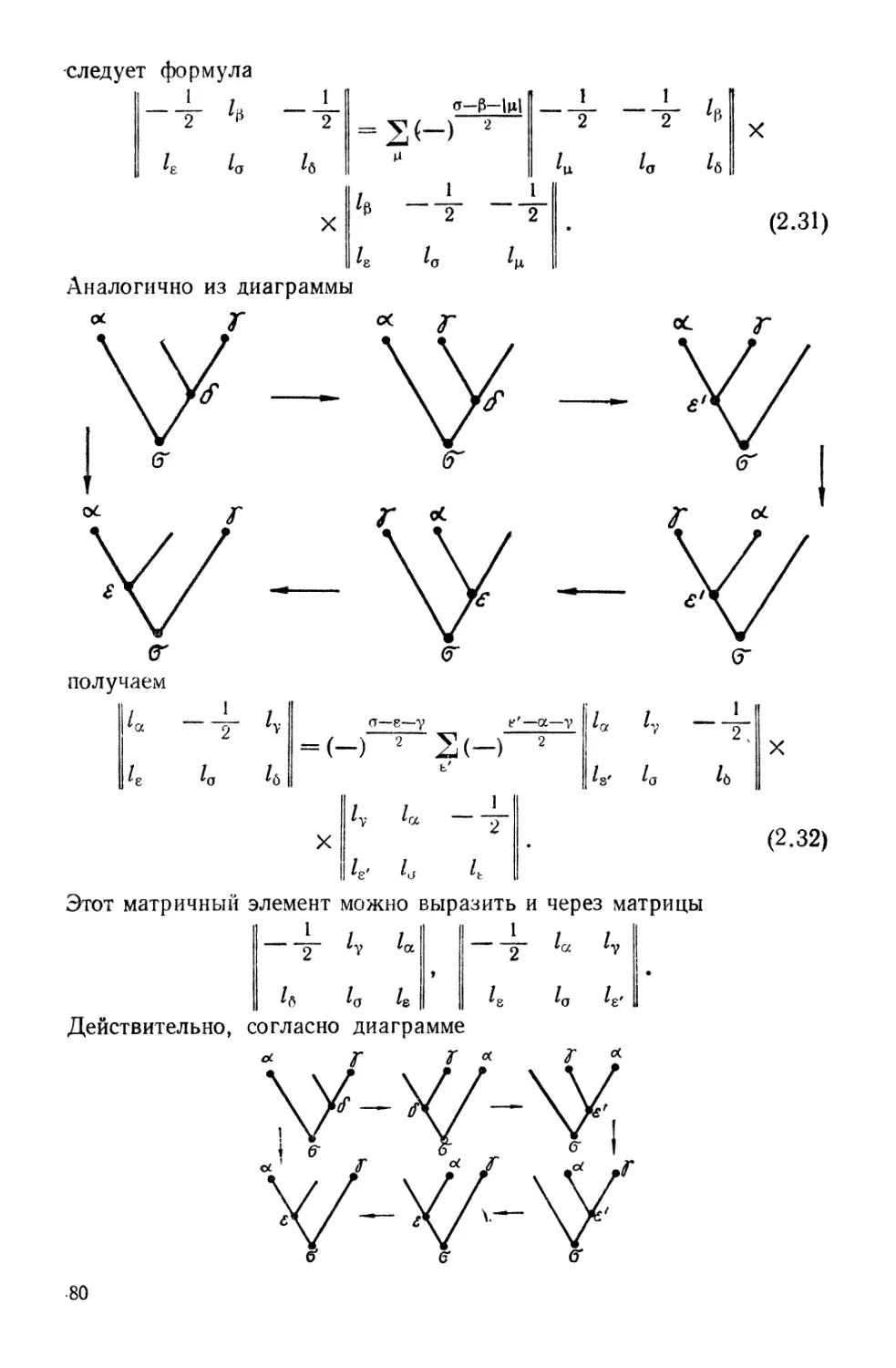
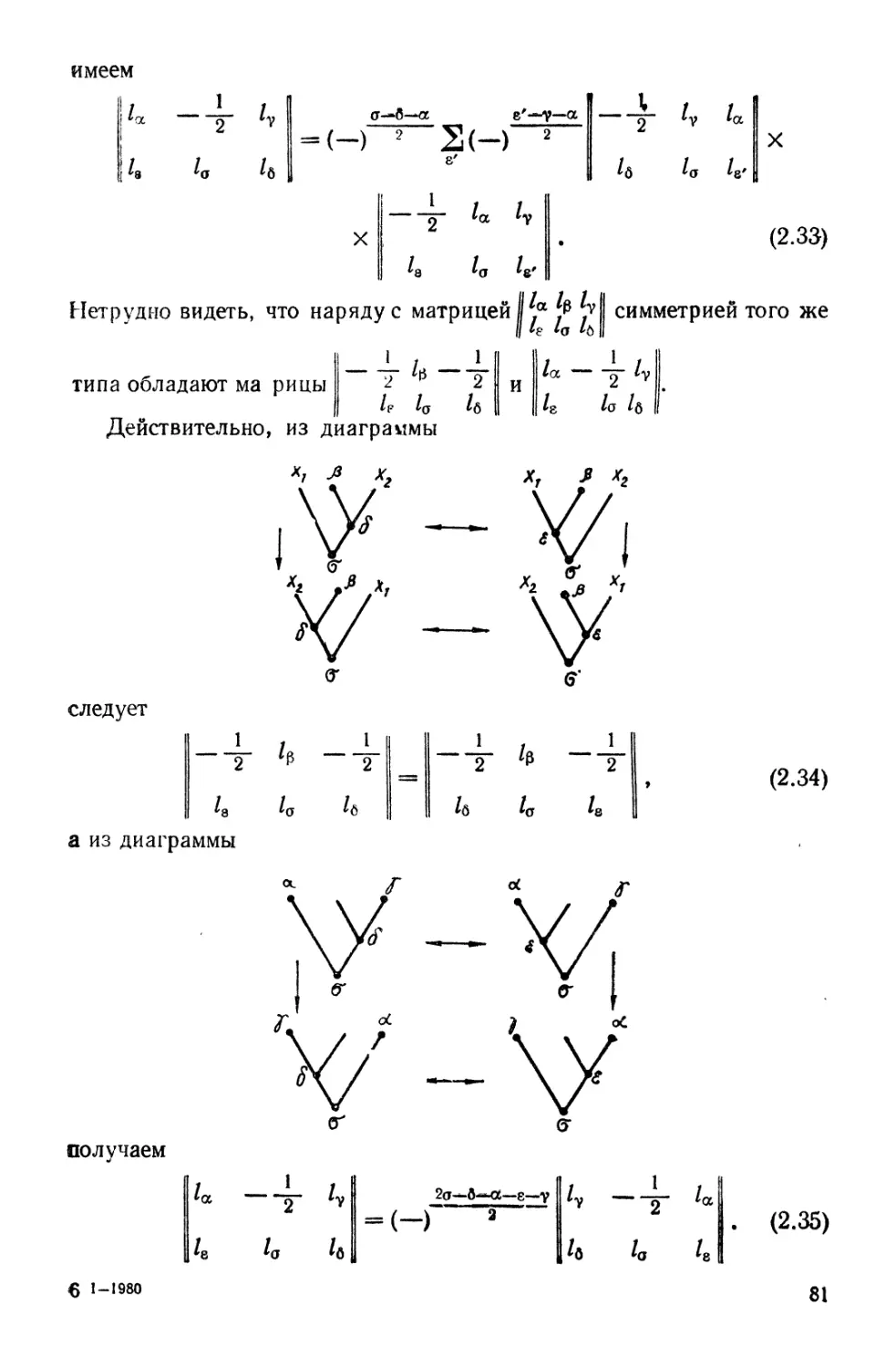
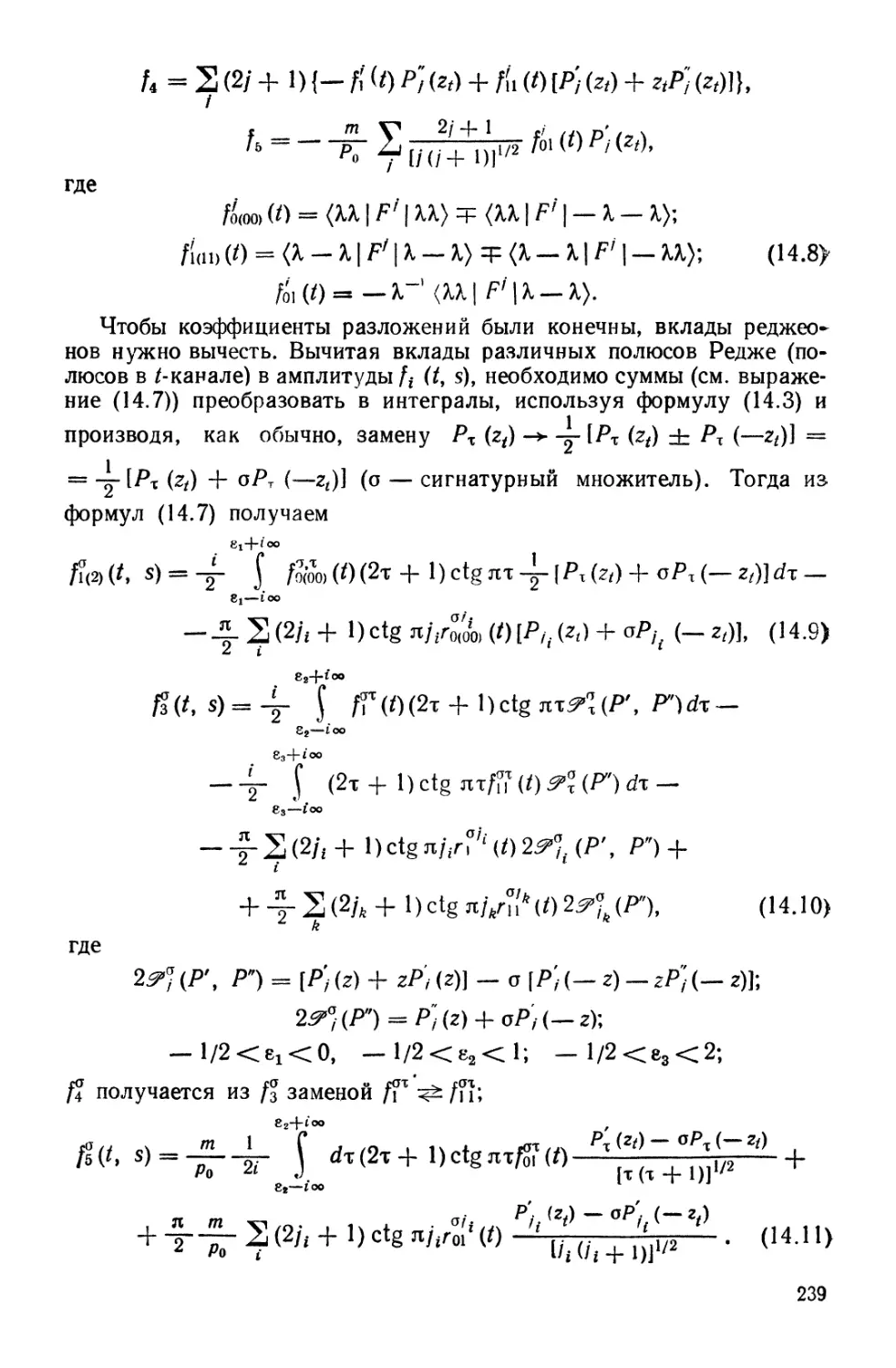Автор: Кузнецов Г.И. Москалюк С.С. Смирнов Ю.Ф. Шелест В.П.
Теги: физика математическая физика монография теоретическая физика квантовая физика издательство наукова думка теория ядра
ISBN: 5-12-002352-5
Год: 1992
Похожие
Спектры графов. Теория и применение
Теория представлений симметрических групп
Введение в теорию групп и ее применение в физике твердого тела
Теория групп и квантовая механика
Текст
                    АКАДЕМИЯ НАУК УКРАИНЫ
ИНСТИТУТ ТЕОРЕТИЧЕСКОЙ ФИЗИКИ
Ш.Кузнецов
С.С.Москалюк
Ю.Ф.Смирнов
ВПШелест
ГРАФИЧЕСКАЯ
ТЕОРИЯ
ПРЕДСТАВЛЕНИЙ
ОРТОГОНАЛЬНЫХ
И УНИТАРНЫХ
ГРУПП И ЕЕ
ФИЗИЧЕСКИЕ
ПРИЛОЖЕНИЯ
КИЕВ НАУКОВА ДУМКА 1992

УДК 530.1 : 51-72
Графическая теория представлений ортогональных и унитарных групп и ее фи-*
зические приложения / Кузнецов Г. И., Москалюк С. С, Смирнов Ю. Ф., Шелест В. П.;
Отв. ред. Зиновьев Г.М.; АН Украины. Ин-т теорет. физики.— Киев : Наук,
думка, 1992.— 288 с,— ISBN 5-12-002352-5
Монография знакомит читателя с нетрадиционными подходами современной
математической и теоретической физики: методом деревьев в теории представлений групп,
методами теории инвариантов в моделировании и гомологическим методом вычисления
интегралов Фейнмана. Графический метод деревьев с помощью простых и наглядных
алгоритмов и операций позволяет строить полный набор решений волнового
уравнения для произвольного числа частиц и суммировать сложные ряды от
гипергеометрических функций. Адекватный рассматриваемым физическим задачам, он
значительно упрощает их решения, заменяя громоздкие вычисления элементарными
геометрическими построениями. С помощью методов теории инвариантов можно
построить дифференциальные модели, допускающие заданную группу симметрии, найти
их факт р-уравнения и точные решения. Гомологический метод вычисления
интегралов Фейнманд сводит вычисление интегралов от многих комплексных переменных
к изучению топологических характеристик тех многообразий, по которым берутся
интегралы.
Для научных работников — физиков-теоретиков и математиков,
интересующихся теорией представлений групп и ее приложениями в теории ядра, атома, в физике
элементарных частиц и других разделах квантовой физики,— а также аспирантов и
студентов соответствующих специальностей.
Ил. 63. Табл. 6. Библиогр.: с. 267—283 (450 назв.)
Ответственный редактор Г. М. Зиновьев
Утверждено к печати ученым советом
Института теоретической физики АН Украины
Редакция физики и кибернетики
Редактор Я. М. Трут
„ 2202090000-116
221-92
БЗ-16-7-92
© Г. И. Кузнецов, С. С. Москалюк,
ISBN 5-12-002352-5 Ю. Ф. Смирнов, В. П. Шелест, 1992

ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
Математическое моделирование динамических систем является одной из главных
областей современной теоретической деятельности ученого. Предлагаемая вниманию
читателей книга — первый том из серии научных монографий «Методы
математического моделирования» (МММ). Тома настоящей серии будут содержать сводное из
ложение основных математических методов исследования моделей динамических
систем и будут вполне доступны не только математикам и физикам, но и другим научным
работникам, профессионально использующим методы математического моделирования
в своей работе.
Настоящее издание задумано как единое целое и в содержании каждого тома
будет учитываться содержание других томов, Один и тот же вопрос может
повторяться, если он освещается с различных точек зрения.
Тома будут нумероваться сквозной нумерацией по мере выхода в свет, однако
по своему содержанию они объединяются в крупные разделы методов
математического моделирования. Настоящий и последующие тома серии являются первыми в
разделе, посвященном систематическому изложению различных методов изучения
симметрии физических систем, которые были разработаны еще Софусом Ли (1842—
1899 гг.). На протяжении последующих десятилетий эти методы развивались,
подвергались модификациям, уточнениям и обобщениям. Вместе с тем нужно
подчеркнуть, что работы С. Ли содержат множество еще до сих пор не понятых идей.
В 1992 г. вся мировая научная общественность отмечает 150-летие со дня рож-
дения С. Ли. Изданием настоящей серии мы хотим засвидетельствовать
глубочайшее уважение к научной деятельности выдающегося норвежского математика —
Софуса Ли и его последователей,

Посвящается
Геннадию Ивановичу
Кузнецову
ПРЕДИСЛОВИЕ
Эта книга была задумана авторами как одна из серии монографий» в которых
предполагалось отразить и суммировать результаты исследований в области
математических методов современной теоретической и математической физики, полученные
физиками-теоретиками и математиками различных научных центров (Московский
государственный университет им. М. В. Ломоносова, Институт атомной энергии
им. И. В. Курчатова, Институт теоретической физики АН Украины, Физический
институт Российской АН, Объединенный институт ядерных исследований и др.)·
Предполагалось осветить ряд вопросов теории представлений групп, актуальных для
физических приложений, опираясь на графическую технику .деревьев Виленки-
иа — Кузнецова — Смородинского, разработанную в 60—70-е годы. Начало этому
методу положено в работах Виленкина — Кузнецова — Смородинского [1—151, где
были сформулированы основы метода деревьев, который позволил вскрыть структуру,
а в дальнейшем построить полную теорию сферических функций для групп
многомерных вращений SO (N). Значение работы [2), ставшей к настоящему времен^клас·
сической по теории гиперсферических функций, трудно переоценить, поскольку она
послужила математической основой одного из интересных современных методов
теории ядра — метода /(-гармоник.
Монография состоит из 15 глав. Глава 1 содержит детальное исследование
гиперсферических деревьев. Развиты алгоритмы для построения гиперсферических
гармоник в произвольной полисферической системе координат. Получены общие формулы
для коэффициентов Клебша — Гордана (ККГ), в которые входят представления
класса 1 группы SO (N) и класса 2 группы SU (N), позволяющие разложить
произведения гиперсферических гармоник в сумму таких же гармоник более высокого порядка.
Здесь использовалась аналогия между структурой групп U (N) и О {2Ν), которая
позволила получить большую серию результатов для представлений класса 2 группы
U (Ν), непосредственным обобщением того, что уже сделано для ортогональных групп*
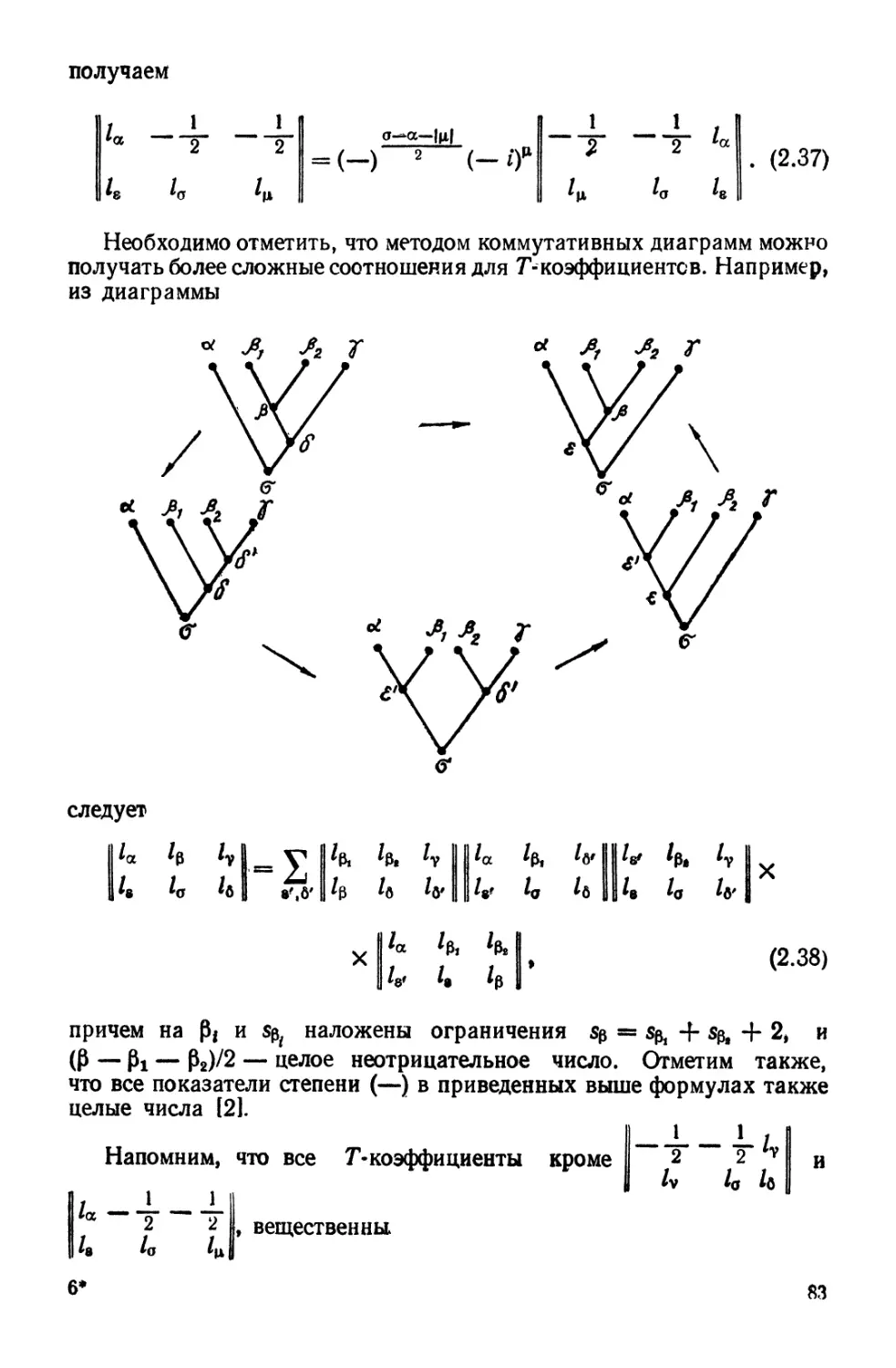
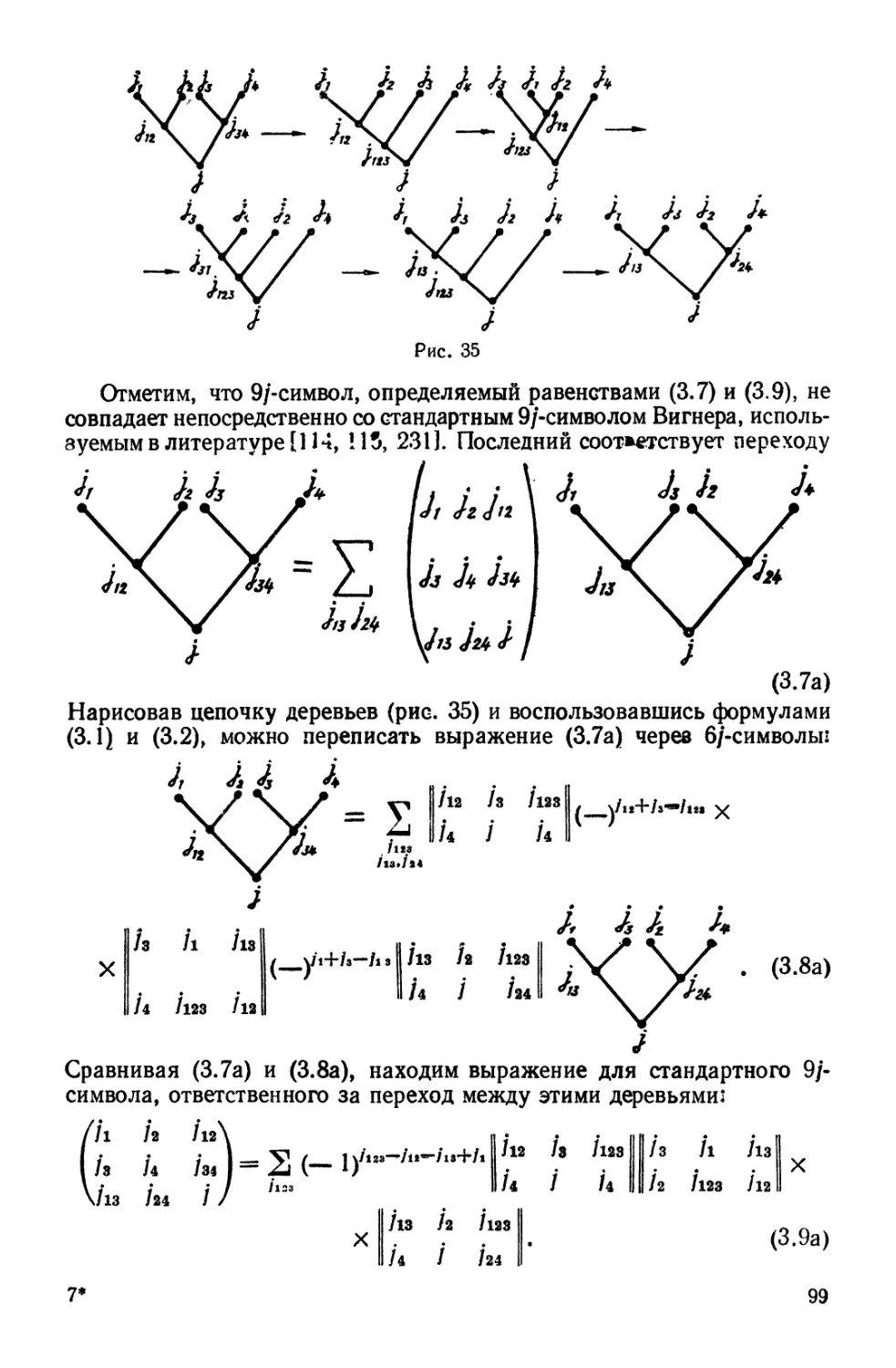
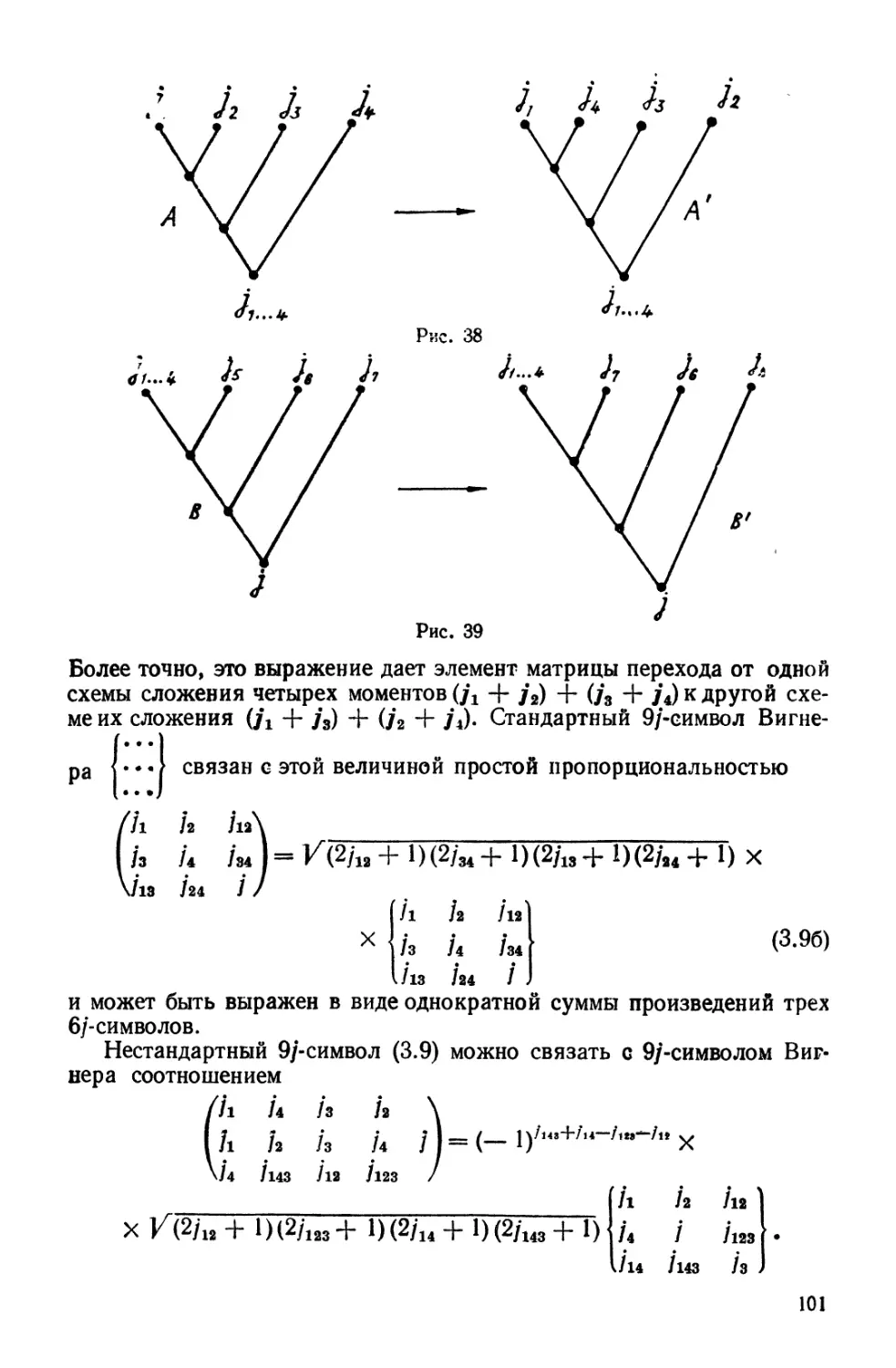
Глава 2 в основном посвящена коэффициентам перехода от одного дерева к
другому (Г-коэффициентам). В ней даны различные представления этих коэффициентов,
изучены их свойства симметрии и установлена связь Г-коэффициентов с 6/-снмвола-
ми. Рассмотрены вопросы, связанные с выражением Г-коэффициентов и их связью с
3/-символами и D-функцией Вигнера.
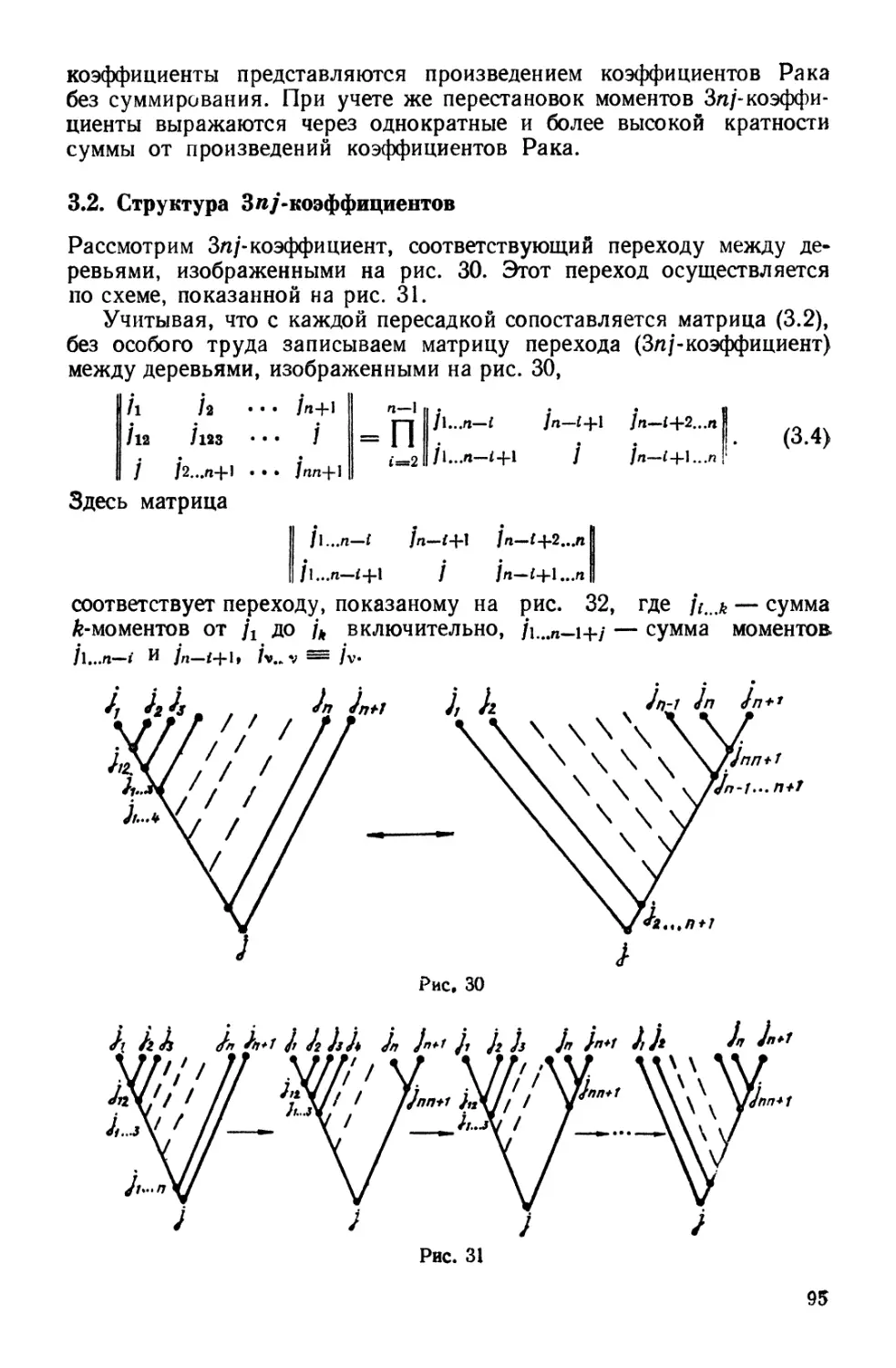
В главе 3 развит графический метод сложения моментов количества движения.
Он, конечно, эквивалентен известному графическому методу Ванагаса — Л ев и
неона — Юциса, но представляет собой оригинальную альтернативу, полностью
разработанную и доведенную до практических приемов вычисления. Два графических
метода легко сводятся один к другому. Чем пользоваться лучше? — разрезанием диа-
4

грамм или пересадкой ветвей — это дело вкуса. Во всяком случае, техникой
деревьев Виленкина — Кузнецова — Смородинского получен ряд новых соотношений
для сумм 6/-СИМВОЛОВ, которые приведены в главе 4, чем доказаны ее эффективность
и полезность. Одним из существенных результатов этой главы является теорема о
фундаментальности 5-циклов.
Глава 5 посвящена построению матрицы конечных вращений в пространстве
деревьев. Следует отметить, что в литературе предложены и другие методы вычисления
многомерных D-функций (работы Маекавы [16], А. У. Климыка, А. М. Гавр ил и ка
117-24) и др.).
В главе 6 отражено дальнейшее развитие метода деревьев Виленкина —
Кузнецова — Смородинского на основе концепции дополнительности групп (в смысле Мо·
шинского [25]), имеющейся между группами О (N) и Sp (2, R). В частности, решена
задача вычисления матричных элементов операторов в методе /(-гармоник, что, в
конечном итоге, и определило практическую важность этих результатов.
В главе 7 развита техника разложения функций от четырех переменных неевкли-
дового пространства по сферическим функциям на гиперболоиде. Рассмотрены пять
различных систем координат на гиперболоиде и получены формулы обращения,
которые исчерпывающим образом решают вопрос о разложении амплитуд по
сферическим гармоникам во времениподобной области; в пространственноподобной области
представлена только сферическая система координат на гиперболоиде. Приведено
обобщение этих формул на случай частиц со спином.
В главе 8 обсуждались системы функций на конусе и с их помощью
систематическим образом вычислены матрицы перехода между различными базисами унитарных
неприводимых представлений группы Лоренца.
Для некомпактной группы 0(3,1) решаются те же вопросы, что и для компакт*
ных групп О (N) с помощью техники деревьев, разработанной в главе 2.
В главе 9 рассмотрено построение базисов инвариантов из динамических
переменных, преобразующихся по заданному представлению компактной группы Ли.
Изложены методы вычисления и свойства производящих функций Моли на,
позволяющие установить число независимых инвариантов и их структуру в случав любой
конечной или непрерывной компактной группы G. Обсуждались вопросы
применения результатов классической теории инвариантов к задаче построения из
генераторов группы G феноменологических эффективных гамильтонианов для ядерных,
молекулярных и других квантовых систем, обладающих симметрией относительно
указанной группы. С учетом результатов главы 9 в главе 10 изложены вопросы
построения базисов дифференциальных инвариантов. В главе 11 рассмотрен алгоритм
анализа на совместность систем дифференциальных уравнений в частных производных
первого порядка, в основу которого положен подход Рикье — Жане — Кураниши.
Описана REDUCE-программа реализации этого алгоритма. Приведены примеры, на
которых тестировалась работа программы.
В главе 12 представлен теоретико-групповой аспект метода размерной редукции,
затем на основе анализа симметрии анизотропного пространства дано
геометрическое описание размерной редукции скалярного, векторного и спинорного полей.
Построена формула расчета компонент тензора энергии — импульса на значениях
переменных фактор-уравнений поля.
Глава 13 посвящена следствиям, вытекающим из существования релятивистски
инвариантных разложений, а именно — интегральным представлениям
релятивистских амплитуд и асимптотическим теоремам, связи между лоренц- и редже-амплиту-
дами и связи между лоренц- н редже-полюсами.
1

В главе 14 рассмотрена спиновая структура амплитуд )fjf~ я Jfjjf-рассеяния,
дана классификация редже-полюсов, исследован их вклад в различные парциальные
амплитуды s- и /-каналов. Приведено разложение амплитуд s- и /-каналов по пред·
ставлениям группы Лоренца, и установлены интегральные соотношения между
релятивистскими парциальными амплитудами s- и /-каналов.
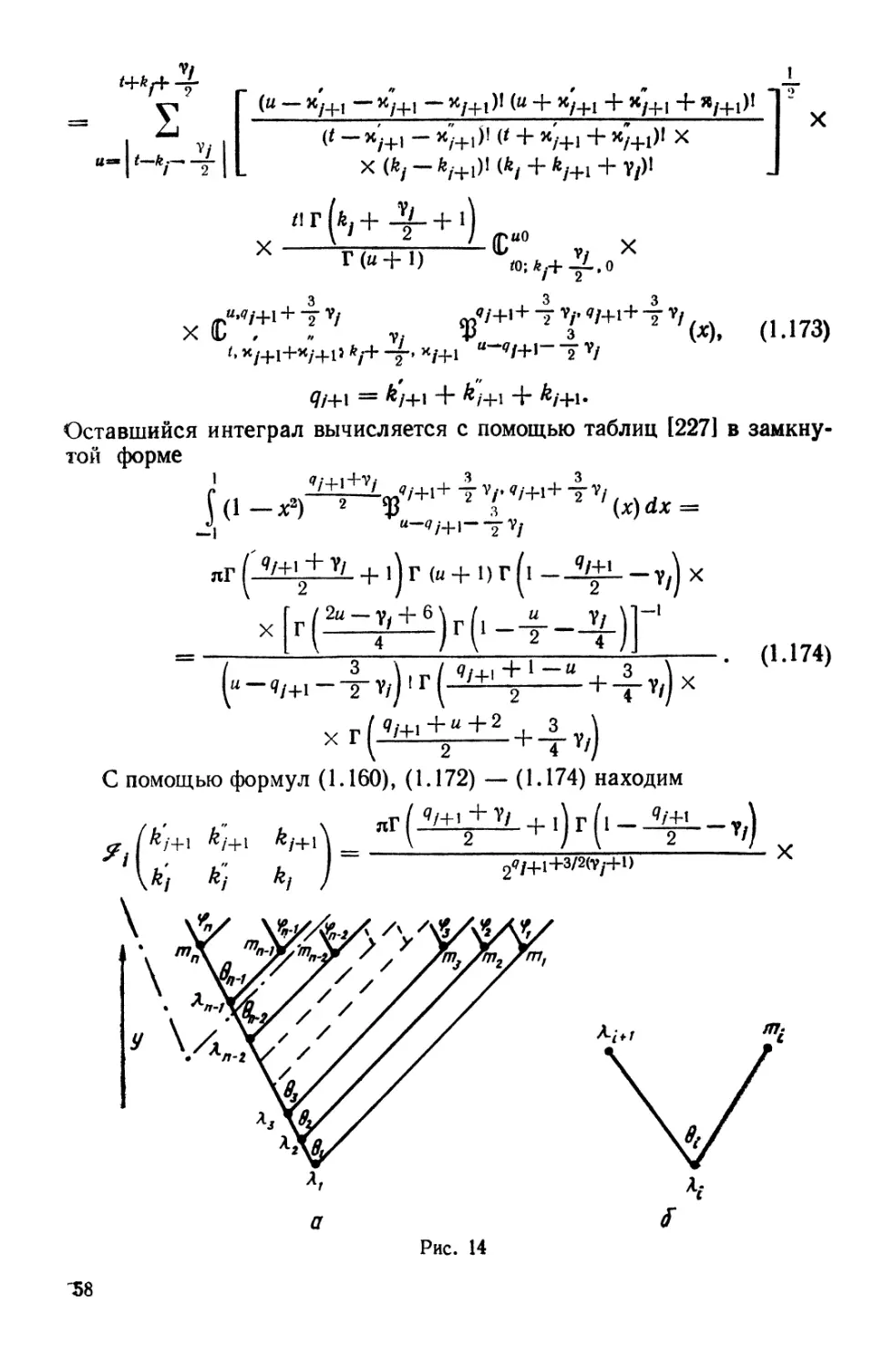
В главе 15 изучена аналитическая структура некоторых однопетлевых
нерелятивистских диаграмм методами теории гомологии. Построены группы гомологии»
установлен характер сингулярностей поверхностей Ландау и найдены соотношения
между абсорптивными частями диаграмм. Показано, что однопетлевые я-угольные
диаграммы определяются производными от 5-угольных редуцированных диаграмм и»
следовательно, имеют собственно им присущие сингулярности, помимо
сингулярностей, свойственных 5-угольнику [26].
'аким образом, развитие теории представлений ортогональных и унитарных
групп служит содержательным и ценным для практических приложений к
физическим задачам предметом исследования. Систематическому изложению ряда вопросов
теории представлений таких групп посвящена данная книга. Причем особое внимание
уделено тому, чтобы не только ознакомить читателя с техникой вычислений, но и
научить его активно пользоваться ею.
Предполагается, что читатель знаком со стандартным курсом квантовой
механики и имеет начальные сведения по теории групп.
Авторы выражают искреннюю признательность академику Η. Η. Боголюбову,
академику Л. Мишелю (Франция), профессору Б. Вайборну (Новая Зеландия),
профессору Н. Я. Виленкину, профессору К. Б. Вольфу (Мексика), профессору Г. М.
Зиновьеву, профессору Я. А. Смородинскому за полезные обсуждения и ценные советы
в процессе работы над книгой. Особенно признательны соавторам по научным
статьям: В, И. Авраменко, Р. М. Ашеровой, А. Ф, Верланю, В. Г. Ганже, И. С. Гусевой»
Ю. А, Данилову, М. С. Кильдюшову, И. В. Курдюмову, М. А. Либерману, А. А.
Макарову, С В. Мелешко, В. А, Миранскому, В. Г. Неудачину, Д. Т. Свиридову,
Е. Л. Суркову, В. Н. Толстому, Г. Ф. Филиппову, Ю. И. Харитонову, В. П. Шапее-
ву, К. В, Шитиковой, А, В. Нестеруку и С. А. Притоманову.
С. С. Москалюк, Ю* Ф. Смирнов, В. П, Шелест
Москва — Киев — Рахов, июнь 1990 г.

ВВЕДЕНИЕ
Красота никогда не оставляла никого равнодушным. Эмоциональные
люди испытывали при встрече с ней чувство глубокого восхищения,
люди же, склонные к анализу, стремились увидеть в красоте некую
логику. Понятие красоты неразрывно связано с такими понятиями,
как симметрия, гармония* соразмерность и т. п.
Древние философы, уделявшие много внимания симметрии,
усматривали в ней божественное совершенство. Особенно ярко симметрия
выражена в творениях зодчих, скульпторов, художников. Поиски
симметрии мира («гармоний мира») привели Иоганна Кеплера к
открытию законов движения планет, которые впоследствии легли в основу
механики Ньютона. Поэтому вполне разумно предположить, что
симметрия имеет не только эстетическое значение, но и позволяет априори
предсказывать некоторые свойства изучаемых систем. Математическим
описанием симметрии служит понятие группы.
Исключительно важны методы теории групп в современной
физике — в теории элементарных частиц, атомного ядра, атомов, молекул
и физике твердого тела. Применение теории групп в квантовой физике
связано в первую очередь с именами Вигнера [27], Вейля [28] и Ван-
дер-Вардена [29].
В названных работах показано, что теория групп дает в руки
физиков мощный инструмент, который позволяет, исходя из самых
общих свойств симметрии квантовомеханических систем, вывести
широкий круг следствий и получить весьма детальную информацию о
свойствах этих систем. В частности, в физике вопросы теории представлений
групп интересуют нас с двух точек зрения. Во-первых, всякий
физический процесс происходит в пространстве и во времени. Поэтому
необходимо учитывать при рассмотрении физических явлений
симметрию пространства (трехмерного в нерелятивистской квантовой
механике и четырехмерного в теории относительности). Во-вторых,
физические объекты (частицы, атомы, молекулы, кристаллы) часто
обладают некоторой симметрией, что, несомненно, должно учитываться
физической теорией. Следует отметить, что еще Платон связывал
правильную пирамиду, октаэдр, куб и икосаэдр с четырьмя основными
элементами — огнем, воздухом, землей и водой, а додекаэдр рассмат-
7

ривал как форму Вселенной в целом, т. е. и основным элементам и
пространству еще в глубокой древности приписывалась симметрия.
Обычно при описании физических явлений используется какая-
либо система координат, иными словами, в пространстве выделяются
некоторые направления, что противоречит изотропности пространства.
Поэтому в теории, инвариантной относительно вращений, физический
смысл имеют лишь те соотношения и величины, которые не изменяются
при повороте координатной системы. Одной из таких величин является,
как известно, скалярный квадрат вектора, равный сумме квадратов
его координат! г2 = т\ + г2у + г\. Кроме того, известно, что при
вращении координатных осей частные производные д/дх, д/ду, д/dz
некоторой функции φ (#, у, ζ) преобразуются так же, как и координаты
некоторого вектора гх, гуу г», а вторые производные д21дх2,д21ду2>д21дг2
преобразуются как квадраты координат. Именно это и определяет в
физике ведущую роль оператора Лапласа
Δ = д21дх2 + д2/ду2 + д21дг2. (0.1)
В этой связи простейшие физические законы, удовлетворяющие
условиям симметрии, которые накладываются свойствами изотропности
и однородности пространства, можно записать в виде
дифференциальных инвариантов групп 0(3), 0(5,2), 0(3,1)* уравнений Лапласа,
Гамильтона — Якоби и волнового уравнения.
Гелл-Манн и Нееман [30, 31} предложили кварковую модель
элементарных частиц (группа SU (3)), включающую дробные электрические
заряды кварков. Такой подход настолько шокировал физиков, что
сначала его даже не желали серьезно обсуждать. Однако следствия,
вытекающие из этой модели, совпадали с экспериментом с погрешностью
до 6—10 %, что побудило коренным образом изменить отношение к
данной систематике. Теория SU (3) оставляла без внимания спиновую
зависимость взаимодействий элементарных частиц. Объединение
группы унитарного спина (SU (3)) с группой обычного спина (SU (2))
привело к группе SU (6) [32—38], подобно тому как объединение группы
изотопического спина и группы обычного спина привело к группе
SU (4) [39]. В результате релятивистского расширения группы SU (6)
получались уже группы более высокой симметрии, например,
некомпактная группа U (12) [40].
Хотя релятивистские обобщения статической группы SU (6) не
оправдали возлагаемых на них надежд, тем не менее необходимость
применения и исследования высших унитарных групп до сих пор
остается актуальной проблемой. Это ввязано с тем, что при изучении
систем из нескольких частиц оператор кинетической энергии системы
можно рассматривать как оператор, действующий в многомерном
пространстве. При таком подходе появляется возможность описывать
системы частиц в рамках групп, обладающих более высокой
симметрией по сравнению с группой вращений. Для такого описания
используются уже не обычные сферические функции, а гиперсферические,
являющиеся собственными функциями многомерного лапласиана.
Графическая теория таких функций была сформулирована Н. Я. Ви-
ленкиным^ Г. И. Кузнецовым и Я. А. Смородинским в работах И, 2J.
8

Дальнейшее развитие графический метод (метод деревьев) получил в
цикле работ 13—15]. При использовании гиперсферических функций
физические состояния кроме обычного момента характеризуются еще
и высшими моментами. Для построения физических состояний систем
из нескольких частиц можно оперировать в качестве гиперсферических
функций функциями деревьев (см., например, [41—47]). Вопрос о
применении гиперсферических функций в задаче многих тел обсуждался
в работах 148—53]. Наиболее интенсивно гиперсферическое разложение
стало применяться после исследований Ю. А. Симонова и его
сотрудников [54—57]. В этих исследованиях использовался простейший класс
/f/f-сил (центральные силы без отталкивающего кора), позволяющий
ограничиваться только низшими гармониками. Такие JVW-силы
упрощают задачу в математическом отношении, однако расчеты согласно
полученной модели плохо согласуются с экспериментальными данными.
Для рассмотрения реальных yYVV-сил потребовалось развивать как
новый аппарат, так и новый метод [58—74J. Если в работах [42—46,
61, 75—79] метод гиперсферического разложения применялся в
основном к трехнуклонным системам, то в серии работ [80—84] на основе ги-
персфзрического разложения исследовался вопрос уже о стабильности
ядерной материи. Сегодня метод гиперсферического разложения
прочно вошел в теоретическую ядерную физику. Он позволяет гораздо
быстрее (по сравнению с другими) отвечать на вопрос, в какой мере можно
объяснять свойства ядер, исходя из модели нерелятивистских нуклонов,
взаимодействующих посредством универсальных двухчастичных сил.
Функции гиперсферического разложения можно рассматривать
также как функции, реализующие неприводимые представления (НП)
компактных ортогональных и унитарных групп.
Применение теории групп к описанию квантовомеханических систем
основано на том, что имеется однозначное соответствие между
собственными состояниями ψία системы и неприводимыми представлениями
D1 ее группы симметрии G. Кроме того, если известна группа
симметрии G, т. е. группа преобразований, которая оставляет гамильтониан
системы Η инвариантным, то методами теории групп можно:
провести классификацию состояний системы, т. е. определить общее
число различных типов ее собственных состояний и кратности их
вырождения;
найти правила отбора для переходов между различными
состояниями квантовомеханических систем;
вычислить (полностью или частично) матричные элементы
операторов физических величин и тем самым рассчитать средние значения этих
наблюдаемых, а также вероятности электромагнитных переходов или
процессов, обусловленных слабым взаимодействием и т. п., в физике
частиц, атомных ядер, атомов, молекул и твердого тела.
Собственные функции ψια(α= 1, 2, ..., т) вырожденного терма с
энергией Ех (т — кратность вырождения) являются базисными
векторами m-мерного неприводимого представления D1 группы G [85].
Как правило, состояния, отвечающие разным НП, невырождены.
В известных случаях нарушения этого правила, когда имеет, место .так
называемое «случайное вырождение» (атом водорода [86, 87], гармони-
9

ческий осциллятор [88—91], ион Щ [92] и т. п.), совпадение энергий
уровней, отвечающих разным НП группы геометрической симметрии
гамильтониана Gr, связано с тем, что полная группа симметрии
гамильтониана Gu в действительности более широкая, чем группа
геометрической симметрии (т. е. Gr является подгруппой группы Gn * Gn => Gr).
При этом вся совокупность вырожденных НП группы Gr образует одно
НП полной группы симметрии Gn- Так, в случае трехмерной кулоновой
задачи (или задачи Кеплера) группой геометрической симметрии
является группа трехмерных вращений Gr = SO (3), а полная группа
симметрии совпадает с ортогональной группой SO (4) (дискретный спектр) или
псевдоортогональной группой SO (3,1) (непрерывный спектр) [93].
В случае Af-мерного гармонического осциллятора с гамильтонианом
Яосц = ^ Я*.осц, (0.2)
Я,,осц = -г (Р? + *<) β 4~ (tfb + 4") Йсо' (°·3>
очевидной группой геометрической симметрии является группа Ν-
мерных вращений SO(N). Однако ее можно расширить до Gn =
= SU (Ν) — группы унитарных преобразований в Л/-мерном
пространстве операторов bt (bt) рождения (уничтожения) осцилляторных
квантов (бозонов). Группа Gn включает в себя не только повороты SO (N)
в координатном пространстве xt (ι = 1, 2, ..., Ν), но и определенные
преобразования в фазовом пространстве системы (xi9 pt).
Итак, рассмотренные выше примеры «случайного вырождения»
являются по существу не исключением из правила о том, что уровни,
отвечающие разным НП группы симметрии гамильтониана G,
невырождены, а служат его подтверждением, если под G иметь в виду Gn,
а не Gr. Впрочем, в последнее время в литературе обсуждался ряд
ситуаций, получивших название «вырождение без симметрии» 194—97],
когда вырождение уровней не связано с наличием у гамильтониана
группы симметрии Gn, более широкой, чем Gr (такой группы Gn не
существует). Этот вопрос требует дополнительного изучения, и мы его
касаться не будем.
Продолжим обсуждение основных принципов применения методов
теории групп в квантовой физике. Замечательным свойством теории
групп является то, чго она предлагает единый подход ко всем кванто-
вомеханическим системам, невзирая на различие их конкретных
физических свойств. А именно, вначале нужно выделить полную группу
симметрии гамильтониана G, далее следует проанализировать ее НП
Dk и выяснить, какие из них могут реализоваться при заданных
физических условиях. Построение точных (или приближенных) волновых
функций системы сводится к построению базисных функций (векторов)
этих НП. Правила отбора формулируются на основе теоремы Вигне-
ра — Эккарта, а вычисление матричных элементов операторов
выполняется с помощью алгебры неприводимых (тензорных) операторов.
Указанная выше универсальность методов теории групп принесла
им широкую популярность, и они стали интенсивно применяться прак-
10

тически во всех областях квантовой теории. Важный этап в развитии
теоретико-групповых методов квантовой механики составили работы
Рака 198—1021 по теории спектров многоэлектронных атомов. Они
определили основные пути использования теории групп в задаче
многих тел. Рака ввел в физический обиход, кроме обычных
геометрических групп симметрии (группы вращений, трансляций, перестановок,
точечные группы), полу простые группы Ли Si/ (N), SO (N), Sp (2 Ν)
и даже особую группу Ли G2, а также алгебры Ли указанных групп.
Он сформулировал метод описания многочастичных систем, известный
под названием алгебры Вигнера — Рака, который был быстро
адаптирован для теории ядра, спектроскопии примесных ионов в кристаллах,
теории мультикварковых систем и т. п. Указанный метод позволил
унифицировать расчеты спектров многочастичных систем разной
природы и использовать для их выполнения мощный аппарат теории
представлений простых групп Ли.
Общая схема метода Рака сводится к следующему. Пусть имеется
η тождественных частиц (электроны в атоме, молекуле или твердом
теле, нуклоны в ядре, кварки в барионе или какой-либо другой муль-
тикварковой системе, бозоны в ядерной модели взаимодействующих
бозонов 1103—107] и т. п.). Обычный метод описания таких систем
состоит во введении самосогласованного (или среднего) поля V% =
= V (г*), т. е. предполагается, что в низшем приближении частицы
движутся независимо и их состояние описывается гамильтонианом
я. =2 ft», <°-4>
где hi = U + Vfi U = p2il2m — кинетическая энергия.
В следующих. приближениях учитывается взаимодействие частиц
(обычно парное остаточное взаимодействие Wi/)t так что полный
гамильтониан системы имеет вид
я = 2 а,+ 2ψ"- (0·5)
t=t К/
Ясно, что к гамильтониану такого же вида приходим, если
описываем, систему многих тел как систему квазичастиц, которые в низшем
приближении считаются невзаимодействующими. Такая ситуация
имеет место, например, в модели сверхтекучести ядерного вещества [108],
где парные корреляции в ядре учитываются путем перехода к бого-
любовским квазичастицам. Поэтому данная схема применима и к
методу квазичастиц (только η равно числу не частиц, а квазичастиц),
и в дальнейшем не будет различия между частицами и квазичастицами.
Пусть также одночастичный гамильтониан h обладает симметрией
относительно группы преобразований G. Тогда собственные функции
Ψ>ΐα этого гамильтониана (называемые одночастичными орбиталями
или для краткости орбитами), соответствующие собственному значению
одночастичной энергии гд
hypAa (г) = εψΛα, (0.6)
принадлежат к НП DA группы G.
11

В случае атома G = SO (3). Если рассматривать задачу
примесного иона в кристалле [109], то О — группа симметрии того
электростатического поля, которое действует на примесный ион. Она зависит οι
расположения ионов кристалла, окружающих примесный ион, и
совпадает с какой-либо точечной группой Oft, Td, Czv и т. д. (кубическое,
тригональное и другие поля). В методе молекулярных орбит группа
G — точечная группа симметрии молекулы. В теории зонной
структуры кристаллов G — одна из пространственных кристаллографических
групп. В ядерной модели оболочек [90, 91J (и в кварковой оболочечнсй
модели нуклона [110, 111J) с осцилляторным оболочечным потенциалом
Vi группа симметрии G = SU (3). В случае среднего поля более
общего вида (например, для потенциала Вудса — Саксона) симметрия
задачи понижается до G = SO (3). Понижение симметрии имеет место
и при описании внутреннего состояния деформированных ядер, когда
среднее поле 1/г· аппроксимируется анизотропным трехмерным
осциллятором [1121 и т. п.
В системе ферми-частиц на каждом из одночастичных уровней гА
может находиться число частиц, не превышающее максимальною
значения п0А. Если размерность НП DA равна пА и каждая частица
характеризуется внутренними переменными ξ (спин у электронов,
спин и изобарический спин у нуклонов, спин, цвет и аромат у
кварков), которые могут принимать п% дискретных значений, то
пол = пА Χ щ. (0.7)
(Для бозонов это ограничение отсутствует.) Например, число мест на
атомной орбите с моментом I равно 2 (2/ + 1), поскольку щ = 2 (две
проекции спина s = 1/2). Для нуклона на подобной орбите нужно
взять П| = 4 (спин s = 1/2, изоспин t = 1/2). Для нестранных
кварков и, d, s имеем щ = 18 (спин s = 1/2, три аромата и три цвета) и
т. д. Основное состояние системы η фермионов отвечает заполнению
низших возможных энергетических уровней ег, e2, ..., ед. Каждая
орбита, на которой находится максимально возможное для нее число
частиц, образует заполненную оболочку. В основном состоянии только
одна оболочка, отвечающая самому верхнему занятому состоянию
%а, мо-кет быть незаполненной. Если в ней находятся k частиц, то в
результате заполнения k нуклонами состояний ι^α всеми возможными
способами получим набор из т = (п°А 1 антисимметричных вырожден-
ныэу^стояний с энергией ε0 + kzA (ε0 — энергия частиц в
заполненных оболочках).
Обозначим эти состояния символами Ф2, Ф2, ..., Фш. Тогда учет
остаточного взаимодействия между квазичастицами сводится к диаго-
нализации матрицы гамильтониана (0.5), построенной на базе этих
функций:
det|tfp,-£6p<7|=0, (0.8)
где HPQ = J ίίτψρ#ι|ν
12

Соответствующие собственные функции Ψ* = 2 Ck% находят
утем решения системы линейных уравнений
2 CQ (HPQ - ЕА«) = О, ρ = 1, 2, ..., m. (0.9)
Q
Мы рассмотрели только смешивание низших состояний системы ферми-
онов под влиянием взаимодействия между ними. Можно включить в
задачу и возбужденные состояния, полученные переходом одной или
нескольких частиц с низших уровней на более высокие, что увеличит
порядок матриц и степень алгебраического уравнения (0.8). Однако
сама процедура вычислений принципиально не изменится. Не будем
останавливаться на этих усложнениях, для уяснения схемы Рака
достаточно ограничиться только рассмотрением смешивания
состояний k частиц сверх заполненных оболочек, ибо последние играют
роль инертного остова, ими можно пренебречь. Выше при обсуждении
антисимметричных функций % мы не учитывали симметрию G одно-
частичного гамильтониана Лг. Рака показал, что целесообразно
использовать не антисимметричные функции % (детерминанты Слетера),
а такие их линейные комбинации, которые отвечают определенным НП
Dv группы G. Дело в том, что использование волновых функций с
определенной симметрией вместо ψρ существенно понижает порядок
матрицы и степень секулярного уравнения (0.8), а эта возможность
небезразлична даже для современных компьютеров. Очевидно, что
в системе двух частиц на орбитах ε^, и ед8 имеем дело с прямым
произведением НП группы G
DA'x D^=2£>r. (°10)
г
Соответственно двухчастичные волновые функции строятся с помощью
ККГ или 3/-символов для группы G
Ι Αχ** :ГЦ> - Σ (^M2<*a Ι Γμ) ψΛια< (г,) ψW2). (0.11)
α,α,
В случае системы фермионов ее надо антисимметризовать относи-
тельно перестановки Рп с помощью оператора Л = 1 — Р12, а для
системы бозонов — симметризовать с помощью оператора S = 1 +
+ Р1а. В трехчастичной системе встречаемся с тензорным
произведением представлений группы О : DAx X DA* X DA\ При ее
антисимметризации (симметризации) необходимо вычислить коэффициенты Рака
(или 6/-символы) для группы G. Четырехчастичная задача приводит
к 9/-символам для этой группы и т. д. В методе Рака многочастичные
волновые функции строятся с помощью генеалогических
коэффициентов, которые совпадают с ККГ для высших групп U (N), где N =
= дол (или Λξ), точнее говоря, с так называемыми изофакторами этих
ККГ, скалярными относительно подгруппы G группы U (N). Итак,
при рассмотрении многочастичных атомных, ядерных, кварковых
систем естественным образом возникает потребность в использовании
унитарных групп U (N) высоких порядков (найример, U (18) в моде-
13

ли кварков), а также их подгрупп SO (N), Sp (N) и т. п. Очевидна
актуальность разработки алгебры Вигнера — Рака для таких групп
(т. е. теория всевозможных Зл/-символов). Сложность подлежащих
изучению структур чрезвычайно быстро возрастает с увеличением
порядков N унитарных, ортогональных и симплектических групп, а
также с увеличением числа частиц η в системе. Поэтому большую
роль в решении этих вопросов могут сыграть графические методы.
Графическая техника, блестящим примером которой является
диаграммный подход Фейнмана в квантовой электродинамике, а затем и в не-
абелевых калибровочных теориях поля [113], всегда занимала в
задаче многих тел важное место. Ценность графиков и диаграмм состоит
не только в том, что они дают наглядное представление о структуре
того или иного объекта, изображаемого графиком, или о характере
того или иного преобразования, записанного графически, т. е. дают
информацию качественного характера, но и позволяют выписывать
точные выражения, формулы и соотношения, зашифрованные в
графических образах. Например, современные ЭВМ и системы
компьютерной алгебры типа REDUCE позволяют добиться автоматизации
вычислений соответствующих поправок или вероятностей каких-то
процессов, изображаемых диаграммами.
Что касается вопросов, обсуждавшихся выше, то в литературе
было предложено несколько вариантов графической техники,
позволяющих на диаграммном языке выполнять операции, строго
эквивалентные соответствующим алгебраическим преобразованиям. Для группы
G = SU (2) такими являются графический метод Ванагаса — Левин-
сона — Юциса [114] и его варианты [115, 116] и другие, а также
техника деревьев Виленкина — Кузнецова — Смородинского [1—151.
В настоящей книге мы остановились главным образом на технике
деревьев Виленкина — Кузнецова — Смородинского, которую можно
обобщить и на более высокие группы симметрии, например SU (3),
что актуально для теории ядра и элементарных частиц. Кроме того,
деревья с подобной топологической структурой обслуживают не
только теорию Зя/'-символов для разных групп, но и совершенно другие
области: теорию сферических функций для групп SO (N), SU (N),
SO (ρ, q), SU (ρ, q), а также теорию представлений квантовых алгебр
и др.
В настоящей книге ограничиваемся рассмотрением только
Некомпактных групп О (3, 1), О (4, 2) и О (5, 2) Вторичное открытие
бесконечномерных унитарных представлений группы Лоренца и ковариант-
ных уравнений для частиц с произвольным спином [117—125] дало
толчок применению в теории элементарных частиц нового
математического аппарата — гармонического анализа на поверхностях
транзитивности группы Лоренца. (Впервые бесконечномерные представлений'
группы Лоренца открыты Майорана [1261 Им найдены и ковариан-
тные уравнения для частиц с произвольным спином.
Познакомиться с результатами Майорана можно в статьях [127, 1281)
Гармонический анализ — это теория разложения функций,
заданных на определенном пространстве, по НП группы преобразований
этого пространства. Классическим примером такого преобразования
14

является преобразование Фурье квадратично-интегрируемой функции
(заданной на прямой), осуществляющее разложение этой функции по
НП группы трансляций. Преобразование фурье-функций, заданных
на двухполостном (пространстве Лобачевского) и на однополостном
(мнимом пространстве Лобачевского) гиперболоидах, является
обобщением известного преобразования Фурье, действующим в трехмерном
евклидовом пространстве.
В 1956 г. И. С. Шапиро [129], воспользовавшись резульгатами
исследований И. М. Гельфанда и М. А, Наймарка [120] по
преобразованиям Фурье на группе Лоренца, т. е. на пространстве, точками
которого являются элементы группы Лоренца, получил разложение
Фурье скалярной функции, заданной на двухполостном гиперболоиде.
Это разложение называется интегральным преобразованием Шапиро.
Впоследствии Чжоу Гуан Чжао, а также П. Г. Заставенко ИЗО] и
В. С. Попов [131] обобщили разложение Шапиро на случай
произвольного поля функций. Представленное в интегральной форме ядро этого
преобразования затем было проинтегрировано в работе [132]. Тем
самым была решена задача о разложении представлений группы
Пуанкаре по представлениям группы Лоренца. С группой Пуанкаре и ее
алгеброй можно познакомиться в работах Ю М. Широкова [133—137].
Преобразование Фурье на однополостном гиперболоиде сложнее,
нежели на двухполостном. Дело в том, что пространство точек,
формирующее однополостной гиперболоид, гораздо сложнее пространства
точек, образующего двухполостной гиперболоид. Известно, что
однородные пространства классифицируются по стационарной, подгруппе
(группа преобразований, оставляющая на месте фиксированную точку
пространства). Поскольку стационарная подгруппа «вершины» одно-
полостного гиперболоида некомпактна (0(2,1)) (стационарная
подгруппа вершины двухполостного гиперболоида О (3) компактна),
то это не позволяет сопоставить функцию, заданную на однополостном
гиперболоиде, и квадратично интегрируемую функцию на группе,
а также использовать результаты работы [120]. Эту трудность
преодолели И. М. Гельфанд и М. И. Граев с помощью интегральной
геометрии [138, 139]. Метод интегральной геометрии состоит в переходе от
функций, заданных на множестве одних геометрических объектов
(например, гиперболоидов), к функциям, заданным на множестве других
геометрических объектов (например, конусов), что позволяет свести
гармонический анализ на гиперболоиде к гармоническому анализу
на конусе. И. М. Гельфанд и Μ И. Граев показали, что разложение
скалярной функции в мнимом пространстве Лобачевского
представляется в форме интеграла по непрерывной переменной и суммы по
дискретной.
Полные системы функций в мнимом пространстве Лобачевского,
получены интегральным методом в работе [140] и инфинитезималь-
ным в работе [141]. Разложение Фурье на гиперболоиде сводится к
разложению по полной системе функций, заданной на этой
поверхности.
Физическое обоснование разложений ковариантных волновых
функций и релятивистских амплитуд рассеяния по базисным функци-
15

ям неприводимых унитарных представлений группы Лоренца дано
Н. Я. Виленкиным и Я. А. Смородинским [142]. Ими показано, что
интегральное преобразование Шапиро сводится к разложению
скалярной функции по унитарным собственным функциям оператора
Лапласа, заданного на двухполостном гиперболоиде. Прекрасной физической
реализацией бесконечномерных унитарных представлений группы
Лоренца является атом водорода [86, 143—146J. Вопросы, связанные
с разложением полей по представлениям группы Лоренца,
исследовались в работах [132, 140—142, 147—156]. Вычислению матричных
элементов группы Лоренца и выяснению их структур в основном были
посвящены работы [132, 154, 157—163]. Наиболее эффективным
методом при вычислении матричных элементов, на наш взгляд, является
интегральный. Применяя теорию бесконечномерных унитарных
представлений группы Лоренца к амплитудам реакций, можно изучать
проблемы, связанные о асимптотиками амплитуд, с дочерними
траекториями Редже и с дуальностью [164—171]. Естественно, что подход
к амплитудам как к аналитическим функциям с точки зрения
представлений группы Лоренца требует изучения аналитического продолжения
представлений [170, 172—174].
Кроме полей и амплитуд бесконечномерные унитарные
представления применялись для инвариантного разложения решений
релятивистских уравнений типа Гельфанда — Яглома [175, 176], при
анализе вопроса о разделении переменных в уравнении Бете — Солпитера
[177], при изучении интегральных преобразований, связанных с
уравнением Клейна — Гордона [178], а также для решения интегрального
уравнения в квазипотенциальном подходе 1179—182]. Как и в любой
теории представлений, в теории представлений группы Лоренца
приходится иметь дело о произведением представлений, что, в свою
очередь, приводит к необходимости вычислять ККГ. Этой проблеме был
посвящен большой цикл работ [148, 183—19Э]. Следует отметить, что
при вычислении ККГ весьма существенно использование
результатов М. А. Наймарка [191].
Еще одной привлекательной чертой применения бесконечномерных
унитарных представлений группы Лоренца является то, что
пороговые особенности амплитуд реакции (по своей природе они
принадлежат к кинематическим особенностям) явно содержатся в функциях,
реализующих эти представления.
С рассмотренными выше вопросами более подробно можно
познакомиться в работах [169, 192—194].
Что касается некомпактной группы О (5, 2) и ее подгрупп, то на
языке их дифференциальных инвариантов можно сформулировать все
богатство физических законов релятивистской и нерелятивистской
физики. Можем задаться встречным вопросом: каков наиболее общий
тип дифференциального уравнения, допускающего группу О (5,2) (или
ее подгруппу) в качестве своей группы симметрии? Ответ на этот
вопрос не только предоставит нам список больших наборов
дифференциальных уравнений, но и поставит задачу их классификации, для
решения этой проблемы необходимо привлечь аппарат математической
теории инвариантов [195]. Под классификацией традиционно подразу-
16

мевается проблема выделения «одинаковых» (в некотором смысле)
систем, разбиения всей совокупности систем на классы, соответствующие
определенным признакам, а также указание канонического способа
представления систем, так называемая проблема канонических форм.
Следует подчеркнуть, что частный случай актуальной проблемы о
взаимосвязи теории представлений групп и теории инвариантов с
изучением непрерывных семейств модулей объектов есть отношение
между вопросами задачи классификации, инвариантного описания и
математического моделирования.
При решении задач математического моделирования одной из
основных является проблема идентификации моделей, состоящих из
систем многомерных уравнений. Первым, естественно, решается
вопрос о совместности этих систем и их размерной редукции, т. е. задача
интерпретации многомерной теории в терминах объектов, заданных
в 4-мерном пространстве-времени или в пространстве меньшей
размерности, например в двухмерном пространстве энергии и угла
рассеяния.
Представляет известный интерес также обращение к эффективным
методам теории группы гомологии.
2 1-1980

Глава 1
ГРАФИЧЕСКАЯ РЕАЛИЗАЦИЯ ПРЕДСТАВЛЕНИЙ
ОРТОГОНАЛЬНЫХ И УНИТАРНЫХ ГРУПП
1.1. Метод гиперсферических гармоник в атомной
и ядерной физике
Данная глава посвящена применению метода деревьев,
разработанного Н. Я. Виленкиным, Г. И. Кузнецовым и Я. А. Смородинским [1,2,
15], к построению многомерных гиперсферических гармоник (ГГ)
или сферических функций в «-мерном евклидовом пространстве Еп.
Интерес к этим вопросам связан с широким использованием ГГ в
конкретных квантовомеханических расчетах энергий и волновых функций
различных состояний атомов или атомных ядер. Рассмотрим сущность
гиперсферического подхода, известного так же, как метод /(-гармоник
[54—57], на примере атома (или иона) с числом электронов Ζ и зарядом
ядра Zяд. Его гамильтониан имеет вид
H"-t4r+v^ ••••r*)· <u>
где т — масса электрона;
У(гг. •••.'*>--^Σ-Τ+Σ-ϊϊ^7Τ (,2)
t=l * i<j l '
— оператор потенциальной энергии.
Волновая функция системы ψ (rlt ..., rz) зависит от 3Z координат
электронов хь yif zt (i = 1, 2, ..., Ζ) и подчиняется уравнению Шре-
дингера
#8Τψ = £<ψ. (1.3)
Заметим, что оператор кинетической энергии в гамильтониане
(1.1) можно выразить через оператор Лапласа Д3л в SZ-мерном
пространстве:
ΣρΙ h2 А А й2 А ,, ,ч
ж^--шьА^--шА^ (Ι·4>
A V^ &
ГДеДзг= £ -щ-.
1Я

В методе ГГ в SZ-мерном пространстве одночастичных
переменных г ι вводят гиперсферические координаты , т. е. многомерный
радиус-вектор или гиперрадиус р;
ζ
рг= S /-L, (1.5)
а также 3Ζ — 1 сферических углов 9lf θ2, ..., θ3ζ~ι, совокупность
которых обозначим символом Ω. Не останавливаясь на конкретном
выборе этих угловых переменных, который подробно будет обсуждаться
в последующих параграфах, заметим, что радиальная и угловые
переменные в n-мерном (η = 3Ζ) лапласиане (1.4) разделяются:
Λη=-^-^(ρ"-'^) + -^ΔΩ, (1.6)
Ρ
где ΔΩ — угловая часть лапласиана, структура и свойства которой
также детально будут рассматриваться ниже.
В данный момент существенно лишь то, что на сфере в п-мерном
пространстве можно поставить задачу на собственные значения
ΔΩΚ (9lf ..., θ«_ι) = λΚ (θχ, ..., θ„_,), (1.7)
причем регулярными решениями этого уравнения являются так
называемые гиперсферические гармоники Υχν (Ω), которые отвечают
собственным значениям
λ = -Κ(Κ + η — 2), /( = 0,1,2,... (1.8)
Индекс ν заменяет совокупность всех остальных квантовых чисел
(помимо К), характеризующих ГГ. Не конкретизируя эти числа,
будем предполагать ортогональность ГГ по всем квантовым числам!
J dQYkv (Ω) Υκ>* (Ω) = бкк'буг. (1.9)
Суть метода ГГ состоит в том, что решение уравнения Шредингера
(1.3) ищут в виде разложения в ряд по ГГ
*(Г! rz) - 2 φ*'ν (Ρ)Υκ>ν(Ώ). (110)
Подставляя это выражение в уравнение Шредингера (1.3) и умножая
скалярно обе части на Υ*ν (Ω) с учетом свойстьа (1.9), получаем
уравнение на коэффициенты разложения ψκν (ρ)ι
— -^г^т^ (р"""1 -gj-) Φ*ν (Ρ) + Σ, Wkvxy (Ρ) Φκ'ν (Ρ) = ΕψΚν (ρ),
(1.11)
где
Ww* (Ρ) = J dQY^ (Ω) V (ρ, Ω) ΥΚ.Ψ (Ω). (1.12)
Придавая числам /С, ν всевозможные значения, приходим, вообще
говоря, к бесконечной системе зацепляющихся обыкновенных
дифференциальных уравнений на гиперрадиальные функции φχν (ρ). Ее
решают численно, обрывая разложение (1.10) на конечном числе
2* 19

членов, достаточно высоком, чтобы обеспечить сходимость метода и
получение достоверных результатов. Иногда систему (1.11) решают
в адиабатическом приближении [196]. Из изложенного выше ясно, что
для практической реализации метода ГГ необходимо иметь явные
аналитические выражения для ГГ в «-мерных пространствах Υχν (Ω) и
уметь вычислять «матричные элементы/) (1.12) от потенциальной
энергии (1.2): V {г19 ..,, г ζ) за V (ρ, Ω) (интегрирование в (1.12) проводится
только по гиперсферическим углам θχ, θ2,..., θ«-.ι). Этим
обстоятельством и диктуется необходимость детального изучения структуры и
свойств многомерных сферических гармоник, которое проводится в
настоящей книге, а также определяется практическая ценность
получаемых при этом результатов. Прежде чем перейти к изложению этого
материала, сделаем три замечания. Первое состоит в том, что выше мы
отвлекались от спиновых переменных электронов в атоме. С их учетом
разложение антисимметричных многоэлектронных волновых
функций (1.10) следует вести не по чистым ГГ, а по соответствующим
антисимметричным комбинациям сферических гармоник Υκν (Ω) и
соответствующих спиновых функций <3>sm$ (1, 2, ..., Ζ). Техника учета
принципа Паули в методе ГГ описана в обзорах [73, 197—1991.
Заметим, что, хотя при этом уравнение (1.11) несколько модифицируется,
основная трудность задачи снова состоит в вычислении матричных
элементов потенциальной энергии по ГГ типа (1.12).
Второе замечание касается использования метода ГГ в теории
ядра. Гамильтониан системы А нуклонов, взаимодействующих
посредством сил V (rt/), имеет вид
<=1 К/
1 А
Полезно выделить переменную центра масс ядра R = -χ 2 ri и
перейти к внутреннему гамильтониану ядра
#»7Tp=#^--2^/>2, (1.14)
А
где Ρ = 2 Pi — импульс ядра как целого.
Взаимное движение нуклонов внутри ядра удобно описывать с
помощью координат Якоби Х19 Х2, ..., Xa-i (относительно
конкретного выбора этих переменных см. ниже п. 6.1.2). Здесь важно лишь
то, что гамильтониан
H!F'--Ts!r&n + V(X1, X2, ..., Хл-г) (1.15)
выражается через лапласиан Δη в η = 3 (А — 1)-мерном
пространстве координат Якоби. В связи с этим можно снова ввести
гиперсферические координаты в данном пространстве и искать внутреннюю
волновую функцию ядра в виде разложения по соответствующим ГП
ЧС*Р (Χι, Χ* Хл-ύ = Σ Χ«ν (Ρ) Υκν Φ). (1.16)
κν
20

После подстановки этого разложения в уравнение Шредингера по
аналогии с (1.11) получаем уравнение на функции χχν (ρ)
(—Ы-з£г+ Τ - Е) χ«ν (Ρ) + Σ ^Wv (Ρ) %κ'ν (Ρ) = 0.
(1.17)
Отличие этого уравнения от (1.11) заключается в том, что здесь
использовано другое определение гиперрадиальной функции
^ν(ρ)=Ρ(^1)φκν(ρ). (1.18)
«Глобальный» момент L = К -\ у— .
Как видим, техника расчетов по методу ГГ в теории ядра полностью
аналогична атомному случаю, за исключением того, что здесь р2 =
= 2 X* — гиперрадиус в пространстве координат Якоби, а не
в пространстве одночастичных переменных, как было в атоме. В
уравнении (1.17) для простоты опускаем спиновые и изоспиновые
переменные нуклонов. Для последних справедливо то, что выше говорилось о
спиновых переменных электронов. В последующих главах
остановимся более подробно на вопросах построения волновых функций ядер
при рассмотрении осцилляторной модели оболочек. Теперь сделаем
последнее замечание, касающееся теоретико-групповой интерпретации
ГГ. Очевидно, что л-мерный оператор Лапласа Δη и его угловая часть
ΔΩ инвариантны относительно произвольных поворотов в я-мерном
евклидовом пространстве Еп. Более того, угловая часть ΔΩ совпадает
(с точностью до знака) с оператором Казимира второго порядка С2 для
группы О (п). Гиперсферические гармоники ΥΚν(Ω) являются
собственными функциями этого оператора и принадлежат к одному и тому
же его собственному значению К (К + п — 2). Это означает, что
набор ГГ с фиксированным К и всевозможными значениями квантовых
чисел ν образует базис некоторого неприводимого представления DK
группы SO (n). В общем случае неприводимое представление группы
SO (п) характеризуется набором чисел (сигнатурой) (Alf Λ2, ..., As),
каждое из которых независимо принимает целочисленные значения
At = 0, 1, ... Здесь s = [/г/2] — целая часть числа л/2. Представления
DK, реализующиеся в пространстве ГГ, полностью характеризуются
одним целым числом Аг = К = 0, 1, 2, ... Остальная часть сигнатуры
тривиальна (вырождена): Л2 = Л3 = ... = As = 0. Следовательно, при
обсуждении ГГ речь идет о частном типе НП, так называемых
максимально вырожденных неприводимых представлениях группы О (п) или
представлениях класса 1. Спинорные представления группы О (п) в
этих пространствах не содержатся.
Закончив предварительные замечания, перейдем к
систематическому рассмотрению ГГ в многомерных пространствах.
21

1.2. Неприводимые представления класса 1 ортогональных
групп
Рассмотрим группу О (п) ортогональных преобразований
действительного л-мерного евклидова пространства Еп. Обозначим векторы
этого пространства через χ = (хъ ...,хп), а скалярное произведение —
через (а? · у) а= 2 хгу^ Построим представление группы О (п) во
множестве RnK однородных полиномов степени К от одного л-мерного
вектора ж, определяя действие операторов Tg(g^O {n)) следующим
образом: Тярк (х) = рк (g~l x). Легко видеть, что под действием Tg
однородный полином степени К снова перейдет в однородный полином
степени /С. Однако это представление приводимо. Действительно,
пространство многочленов вида р2/?"'*"""2 инвариантно относительно
группы О (п). При этом представление Tg индуцирует в
фактор-пространстве Rn'K/p2Rn'K~~2 некоторое представление {/С}. Скалярный
квадрат (х · х) = р2 (р — гиперрадиус в Еп) является единственным
инвариантом относительно группы О (п), который можно построить из
одного вектора, что свидетельствует о неприводимости представления
{К}. Строгое доказательство неприводимости этого представления
можно найти, например, в [14], где показано, что оно эквивалентно
представлению класса \DK группы О (п) и реализуется в пространстве НпЛ
гармонических полиномов рк (х) степени К от вектора х. Эти полиномы
удовлетворяют уравнению Лапласа
ΔηΜ*) = 0, (1.19)
где Ап = 2 dVdxi
Размерность этого НП задается формулой [14]
dim DK = dim Η*·* = (2К + П^;%К-Щ ■ (1 -20)
Другую реализацию представления {К} можно получить, рассмотрев
скалярные функции на единичной сфере Sn~~l в Еп. При этом каждому
однородному гармоническому полиному рк £ НпЛ соответствует
функция на S"""1
«,(Ω) = ρ-%(4 (1.21)
являющаяся собственной функцией оператора Лапласа
ΔΩΗΚ (Ω) = - К (К + η - 2) ик (Ω), (1.22)
где
Назовем функции ик (Ω) гиперсферическими гармониками.
Представления высших классов реализуются в пространстве
тензорных полей на единичной сфере. В дальнейшем нас будут
интересовать лишь приведенные выше реализации представлений класса 1 груп-
22

пы О (η). Обозначив через $βη'κ пространство угловых функций,
получаемых из Нп'к, сформулируем основную теорему гармонического
анализа на Sn~l. Любую непрерывную функцию / (ξ) на Sn~] можно
с любой степенью точности равномерно приблизить суммой функций,
принадлежащих пространствам $βη,κ.
Таким образом, а?\п-\ = 2 ^пЛ>
Подробное изложение приведенного выше материала можно
найти в монографии Н. Я. Виленкина [14]. К теории ГГдля групп О (2п)
тесно примыкает теория представления класса 2 для группы U (п).
1.3. Неприводимые представления класса 2 унитарных групп
Известно, что группа U (я) (SU (η)) есть группа унитарных (унимо-
дулярных) преобразований в £п (комплексное л-мерное
пространство), оставляющих инвариантной квадратичную форму
2 |*//2 = const. (1.24)
/-ι
Если представить zk как zk = xk + iykt то инвариантную форму
(1.24) можно записать в виде уравнения для (2п — 1)-мерной
вещественной сферы
2*? + 2^ = P2=const> (1.25)
которое инвариантно относительно поворотов группы О (2/г) в
пространстве с координатами {xk, yk, k = 1, 2, ..., η). Отсюда видно, что
группу U (п) можно рассматривать как подгруппу группы О (2/г).
Гиперсферические гармоники и порядка /С, зависящие от переменных
(xi> ί/ί)> удовлетворяют уравнению
A2rt_itt + К (К + 2п — 2) и = 0 (1.26)
и осуществляют представление класса 1 DK, неприводимое по
отношению к группе О (2п). Однако оно будет приводимым по отношению
к подгруппе U (я). Для сужения представления DK на подгруппу
U (п) нужно потребовать, чтобы ГГ были собственными функциями
η
второго оператора Казимира Η = — I 2 д/д(ръ гДе Ф* — Фаза комплекс-
ного числа zk. Пространством НП группы SU (п) будут ГГ для группы
О (2л), удовлетворяющие помимо (1.26) уравнению
#и=/тш, (1.27)
где т = /С, К — 2, ..., — /С.
Это НП задается двумя числами /Сити называется
представлением класса 2 для группы SU (п). В общем случае НП группы SU (п)
задается сигнатурой (А1э Л2,..., Д«-л), где каждое Л^ независимо
принимает целочисленные значения 0, 1, 2, ... Представления класса 2,
23

рассматриваемые нами, имеют вырожденную сигнатуру Аг =-j (К+
+ т)9 Лл-1 = γ (К — /я), Л2 = Л3 == ... = Лл_2 « 0. Таким
образом, разложение представления класса 1 DK группы О (2п) на
неприводимые представления D(Al,0,0A't~1) подгруппы SU (п) имеет вид
β* β ^ D(pA Λ~ρ) (1.28)
(исключение составляет случай О (4) о £/ (2) (см. параграф 1.8)).
Следует отметить, что для группы SU (3) решения системы (1.26),
(1.27) реализуют всевозможные НП, поскольку группа SU (3)
является группой 2-го ранга и ее оператор Казимира третьего порядка
С3 выражается через оператор Лапласа на сфере Δ5 и оператор Н.
Соотношения (1.27), (1.28) становятся особенно ясными, если
представления класса 2 унитарных групп реализовать в пространстве
однородных полиномов рк от комплексных переменных ги zl [2]j
*>« = Σ fciVlVf ... (ζηγz\zL2 ... aff. (1.29)
s-Ь/Н \-m*=q
Здесь ρ (#) — степень контравариантных (ковариантных) векторов
Выразим 2л-мерный оператор Лапласа Δ и оператор Η через
комплексные переменные
δ-4Σι$γ· <'·30»
Η = 2 (2,д/дг, - z'dldz1). (1.31)
Предполагается, что дифференцирование будет производиться так,
как если бы zi и zt были независимыми переменными. Из (1.31) следует,
что полиномы рк, удовлетворяющие уравнениям (1.26) и (1.27),
должны отвечать собственным значениям
/п = p — q при ρ + q = К, ρ = О, 1, ..., /С, (1.32)
т.е.т = К —2<7, ^ == О, I, ..., К, или m =/С, /С — 2, ...,— /С, как было
указано выше. Отсюда следует и редукция (1.28). Одночлены Μ (/?,
<7) = (ζ1)1 (ζ2ψ ... (ζ")νζίζ2 ... 2^, входящие в полиномы (1.29), можно
рассматривать как компоненты смешанного тензора ранга ρ по
контравариантным и ранга q по ковариантным переменным (общий
ранг К = ρ + q). Очевидно, что мономы с фиксированными
значениями ρ и q преобразуются друг через друга под действием
преобразований группы U (л), так как ковариантные векторы преобразуются
через ковариантные, а контравариантные — через контравариантные.
Уравнение Лапласа для рк также инвариантно по отношению к U (п).
Это означает, что базис неприводимого представления D^'0 м)
класса 2 группы U (п) можйо построить из полиномов рк (1.29), удов·
24

летворяющих уравнению Лапласа
Арк (z<, zt) = 0. (1.33)
Определим число линейно независимых полиномов рк или размерность
неприводимого представления D^'0 0,<7) группы U (п). Учтем, что
полином рк симметричен по ρ переменным t и q переменным гг в
отдельности.
Целая однородная функция степени К имеет
Nt = | ? ~ ш ι ΐ -Γη ι коэффициентов. Уравнение Лапласа (1.32)
налагает
М = (р + п-2)\(д + п-2)\
2 (р —1)1(п —1)1 (9—1)1(п— 1)!
условий, поскольку понижает степень полинома до К — 2. Отсюда
следует, что общее число линейно независимых однородных гармони·
ческих полиномов степени К = ρ + q определяется Ν = Νχ — Ν2+
Например, для η = 2 и η = 3 соответственно
N(2) = p+q+lf N(3) = {p+\)(q+l)(p+q + 2)/2. (1.34)
Эти результаты совпадают с известными выражениями для
размерности соответственно N (2) = 2/ + 1 неприводимого представления
DJ с / = К/2 группы SU (2) и размерности dim (/?, q) = Ν (3)
неприводимого представления DiP'Q) группы SU (3). Уравнение Лапласа
(1.33) в пространстве гармонических полиномов соответствует
обращению в нуль следа тензоров Μ (/?, q). Однородные гармонические
полиномы на многомерных сферах сводятся к гиперсферическим функциям
или полиномам Якоби.
1.4. Гиперсферические координаты и их графы.
Теоретико-групповая интерпретация
Как мы уже отмечали, представление {К} = DK можно получать»
рассматривая скалярные функции на единичной сфере Sn—{ вЕп. В
связи с этим необходимо ввести сферические координаты. Поскольку
пространство многомерно, то в дальнейшем такие координаты назовем
гиперсферическими. Оказывается, их можно выбирать различными
способами. С каждым выбором будем сопоставлять некий граф, точнее,
дерево [2]. Поясним это. Пусть хи ..., хп — декартовы координаты
точки на сфере. Изобразим их в виде некоторых отрезков (рис. 1, а).
Объединим отрезки так, чтобы в узел попало на первом этапе не более
двух координат, на втором — не более двух предшествующих
объединений и т. д. При построении координатной системы для U (п) на
первом этапе обязательны попарные объединения как следствие того, что
2х = г + ζ*. В результате построения получим такую конструкцию,
которая в комбинаторике называется деревом (рис. 1, б).
Как видно из рис. 1, существуют два типа линий: линии с узлами
на обоих концах и линии с одним узлом. Первые назовем внутренними,
вторые — свободными концами. Число свободных концов равно раз-
2S

xf x2 xs xn
xf xz xs xu xsx6 #7.·· xn.t *,
% · · ·
a
мерности пространства, цисло узлов — числу параметров, задающих
положение точки на сфере. Каждому узлу припишем угол θ^
условимся линию, идущую налево от узла 0if сопоставлять с множителем
cos Qif идущую направо — с множителем sin θ*. Узел θ — вершина
графа. Тогда путь от узла, например, θ до узла φ2 (см. рис. 1, б)
представится как последовательность внутренних линий, которую нужно
сопоставить с произведением косинусов и синусов, соответствующих
узлам, встречающимся на этом пути:
5
А„=/7 =
2 9Γ-Θ
0;
9,
4*1
(1.35)
Запишем графическое выражение (1.35) в явном аналитическом виде
/ΐφ, = cos θ cos β cos α sin γ. Аналогичные выражения можно
написать для любого узла дерева. Декартовы координаты определяются
через узлы по формуле
χΨ*Ηψ •г
(1.36)
т. е. коэффициент /ц нужно «умножить» на свободный конец,
примыкающий к углу ф£. В явном виде это выглядит, например, для
координат л;3, #4 следующим образом:
xs = ρ cos θ cos β cos α sin γ cos φ2,
*4 = Ρ cos 9 cos β cos α sin V sin Φ2·
Среди всевозможных деревьев выделим одно, так называемое
каноническое дерево, которое изображено на рис. 1, в. Связь между
декартовыми и гиперсферическими координатами имеет вид
хх = ρ sin 0n_t ... sin θ2 sine! 0<p<oo,
jc2 = ρ sin 9n_t ... sin62cosG1, 0<θχ<2π, (1.37)
26

%n-\ = Ρ sin θ„_! cos θ„-_2, Ο^θ^π, i = 2, 3, ..., η — 1,
Χη =рСО5 0л_Ь
Элемент объема dV в n-мерном пространстве записывается так:
dV = dxxdx2 ... dxn = p^dpdQ, (1.38)
где элемент телесного угла
dQ = sin"~29„_i sin^^n^ ... sin θ2άθη-\άθη-2 ... dBv (1.39)
Полный телесный угол легко подсчитать, интегрируя это выражение
по всем углам Θ* в пределах, указанных в (1.37). В результате
Ω = J dQ = 2π"'2/Γ (η/2). (j 40)
В частности, в случае η = 3 для стандартной системы сферических
координат
х3 = /· cos θ,
х2 = /· sin θ cos φ,
хг = /*sin6sinq),
которой соответствует дерево, изображенное на рис. 2, а, получаем
известные результаты: dV = r2drdii, dQ = sin 6*Шф, Ω = 4π.
Вернемся к каноническому набору гиперсферических^углов,
задаваемому соотношениями (1.37). Совокупность всех поворотов в
пространстве Еп с координатами хи я2,..., хп образует группу n-мерных
вращений О (/г). Если ограничимся поворотами.в подпространстве Ε^ι
с координатами хъ ..., хп-\> то перейдем к подгруппе О (п — 1).
Переход от Еп к Еп-\ производится обращением в нуль угла дп-\ в наборе
(1.37). Вектор, направленный вдоль n-й оси, имеет координату θ«_ι =
= 0 и инвариантен по отношению к группе О (п — 1). В связи с этим
каноническому гиперсферическому дереву (см. рис. 1, в) можно
придать определенный теоретико-групповой смысл: указанное дерево
отвечает редукции группы О (п) на цепочку вложенных друг в друга
подгрупп:
0(л)=>0(я— 1)=> ··· zdO(3)zdO(2), (1.41)
X
Рис. 2
27

которая называется канонической редукцией Гельфанда — Цетлина
[200, 201]. В цепочке (1.41) каждая группа О (i) действует в
подпространстве Et с координатами xlf x2,...,xt. Переход от Еп к
/^осуществляется последовательным обращением в нуль углов 0Ь θι+ь ...
..., θη—ι.
Точно так же некоторую цепочку подгрупп можно поставить в
соответствие гиперсферическому дереву общего вида. Для выделения
этой цепочки нужно учесть, что обращение в нуль угла Qk,
отвечающего вершине, образованной двумя внутренними линиями, из которых
«произрастает» соответственно тип свободных ветвей, означает
переход от пространства £т+л размерности (т + п) к прямой сумме
подпространств Ет θ Εη. Следовательно, обращение в нуль такого угла
Qk ведет к редукции О (т + п) zd О (т) х О (л). Это соображение
позволяет записать полную цепочку подгрупп, отвечающую любому
гиперсферическому дереву. Например, дереву, изображенному на
рис. 2, б, отвечает редукция
0(6) =з 0(3) χ 0(3)
и и
0(2) 0(2),
где первая группа О (3) действует в подпространстве с координатами
*ΐι *2» *з, а вторая — в подпространстве с координатами х4> Хы хв-
Угол θ3 связывает радиус-векторы plf p2 в этих подпространствах с
общим гиперрадиусом р: рг = ρ cos θ3, р2 = ρ sin θ3, 0 <! θ3 <! π/2,
остальные углы 6lf θ2, θ4, θδ — обычные сферические углы в указанных
трехмерных подпространствах. Вообще говоря, редукцию,
отвечающую развилке, помеченной углом θ2 (или θ5), необходимо записывать
следующим образом: О (3) =э О (2) χ О (1), подразумевая под О (1)
группу, действующую в одномерном пространстве с координатой х3 (х6)
и состоящую из единичного элемента и операции инверсии *3-> —х3
(хв -> — х9). В силу тривиальности таких групп в дальнейшем их не
выписываем. Аналогично фиксируем и редукцию О (2) -> О (П X
X О (1), отвечающую узлам, помеченным углами θ2 и θ4.
При построении дерева, естественно, возникает вопрос: сколько же
различных деревьев можем построить в л-мерном пространстве? Ответ
на этот вопрос дадим в следующем параграфе.
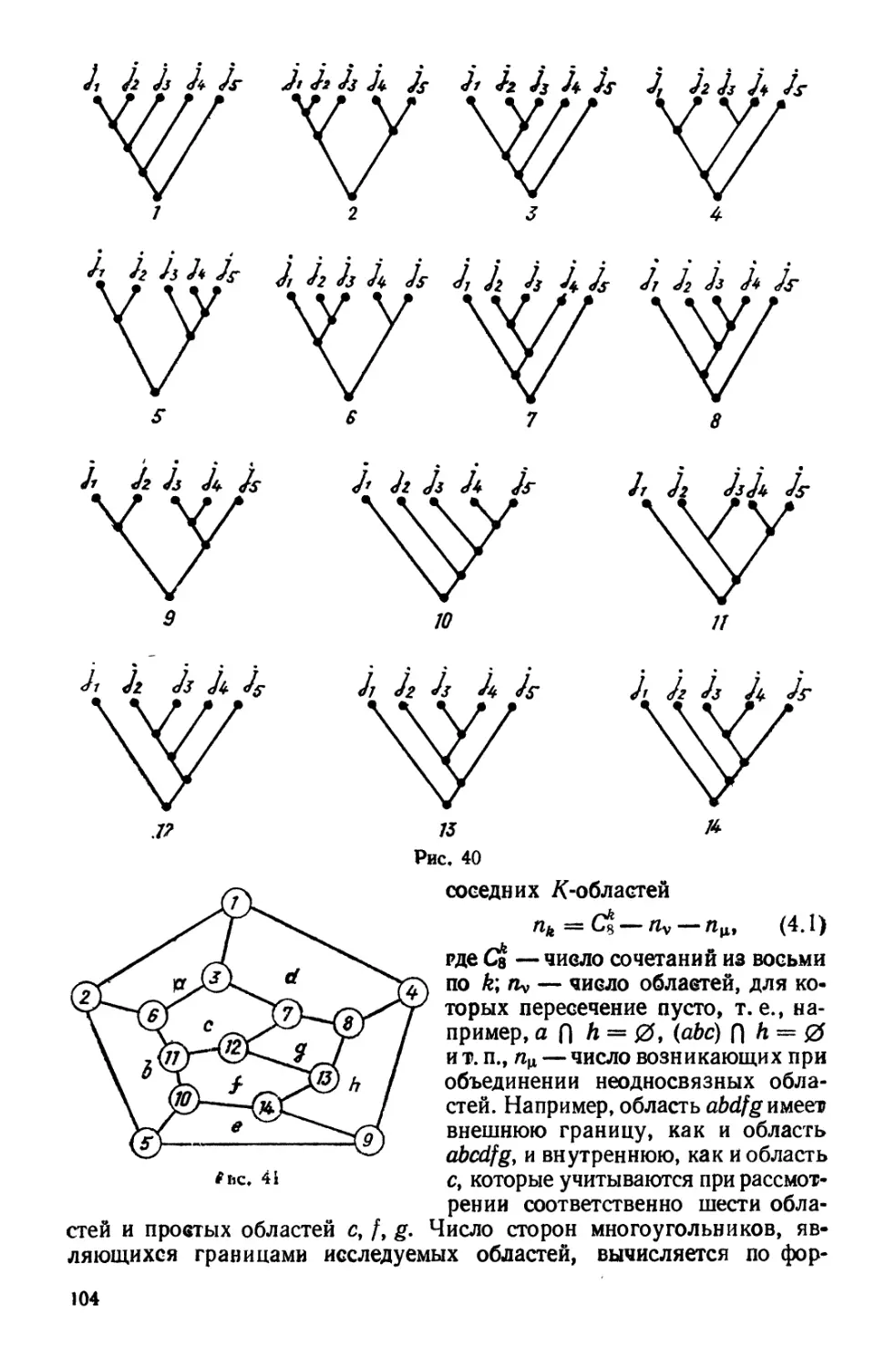
1.5. Число различных деревьев и число классов
эквивалентных деревьев
Выше мы ввели метод деревьев в связи с проблемой выбора
гиперсферических координат. Однако подобные графы будут встречаться и в
других задачах. Поэтому рассмотрим общий вопрос о числе различных
деревьев с η свободными ветвями.
Согласно методу построения дерева задача о нахождении полного
числа деревьев в я-мерном пространстве сводится к задаче об
отыскании числа способов g (n) образования бинарного, но неассоциативного
произведения η сомножителей, взятых в порядке хъ хъ ..., хп, т. е.
28

π-r п-г
С,
2 τ
т
σ
Рис. 3
числа способов расстановок скобок в произведении η сомножителей
таких, что в каждой скобке присутствуют только два фактора. Для η =
= 2 g (2) = 1, а для трех сомножителей имеются возможности {хгх2)хз
и *ι (*2*з)» т. е. g (3) = 2. Положим формально, что g (1) = 1. Если
бинарное произведение является соединением первых г букв,
умноженным на некоторое соединение оставшихся η — г букв (xlt ..., хг) X
X (jtr+i, .-., хп)* т0 первые г букв можно скомбинировать g (r)
способами, а остальные η — г букв— g (п — г) способами. Отсюда для
η > 2 получаем рекуррентную формулу
g(n) = %g(i)g{n-i). (1.42)
t=rl
Положим [2021
Тогда из рекуррентного соотношения (1.42) имеем функциональное
уравнение
/"(*) + * = /(*)- (1.44)
Решая его как квадратное уравнение и ограничиваясь только одним
корнем, поскольку / (0) = 0, получаем
2f(x)= 1 — ΚΠΓ4Ϊ. (1.45)
Учн1ывая формулы (1.43) и (1.45), находим1
Отметим, что формула (1.46) рассматривает деревья, аналогичные
изображенным на рис. 3, как различные.
Здесь блоки Сг и С2 символизируют разные виды конструкций
деревьев, образующих полное дерево при одних и тех же размерностях
пространств г и η — г.
Однако, как видно из рис. 3, повернув, например, левое дерево
вокруг вертикальной оси, проходящей через вершину σ (без
изменения структуры блоков Сх и С2), получим правое дерево. Поэтому бу-
1 Числа g (л), удовлетворяющие рекуррентному соотношению (1.42),
называются числами Каталана (см. например, [203])·
29

Υ
Л-2
n=S
л=4
Рис. 4
/7=5
дем говорить, что два дерева имеют одну и ту же природу
(принадлежат к одному классу), если с помощью операций вращения вокрур
вертикальной оси (либо осей), проходящей через вершину (либо
вершины), одно из них переходит в другое. Таким образом, приходим к
разбиению полного числа деревьев на классы. Элементы,
принадлежащие к различным классам, являются истинно различными
структурами, иначе говоря, истинно топологическими неэквивалентными
конструкциями. В этой связи формулу (1.42) следует модифицировать,
чтобы уметь считать число классов. А именно, вместо суммирования до
л— 1 вести суммирование до —· , причем в случае η = 2т вместо
g (m) g (m) писать g (m) g (m) — (g (m) g(m)—g (m))/2. Последняя
модификация связана с тем, что матрица gCl (m) g r (т) симметрична
относительно замены Сх ^ С2. Принимая во внимание сказанное
выше, записываем для g (n) (число классов деревьев) рекуррентное соот·
30

ношение
:(«)
И. _ 1 + ( ,-ϊίτ-Η'-ϊί-τ))
'•=1
которое можно записать также в виде
(1.47)
(1.48)
ί=1
С помощью этого соотношения легко подсчитать число классов
деревьев. Учитывая формулы (1.43) и (1.47), для функций / (х) и Φ (χ) =*
= 1 — / (χ) имеем функциональные уравнения
2/(*)=/2U) + f(*2) + 2x, (1.49)
Φ (α:2)— Ф2(х)=2л;. (1.50)
Приведем зависимость численных значений g (ή) и g (ή) от размерности
пространства η = 2 — 6.
Л
SW
g(/i)
2
1
1
3
2
1
4
5
2
5
14
3
6
42
6
Явный вид различных древовидных графов показан на рис. 4, а для
η = 2 -τ- 5, а топологически неэквивалентных деревьев — на рис. 4, б.
1.6. Разделение переменных в операторе Лапласа.
Угловые функции
Представим в терминах гиперсферических координат оператор Лап-
η
ласа Δ = 2 д2/дх2. Известно, что если в ортогональной системе
криволинейных координат Еп дифференциал длины дуги имеет вид
dl* = 2 hWh
ί=1
(1.51)
то оператор Лапласа в этой системе координат выражается формулой
Δ =
= * у д Lr~U д
(1.52)
где qt — углы.
Коэффициенты ht называются коэффициентами Ламе. Можно пока·
зать, что они выражаются формулой (1.35). Как отмечалось в
параграфе 1.1 (см. 1.6)), оператор Δ связан с лапласианом ΔΩ, заданным на
31

c+1
Рис, 5
сфере, соотношением
Лапласиан ΔΩ имеет собственные значения λ = —К (К + η — 2)ι
AQYK(Q) + K(K + n-2)YK(G) = Q, /C= 0, 1, 2, ..., (1.54)
где Υ κ (Ω) — функция, заданная на (п — 1)-мерной сфере в Еп.
Изучая топологически различные деревья с помощью метода
математической индукции, можно сформулировать алгоритм записи
оператора ΔΩ, τ. е. уравнение (1.54) в гиперсферических координатах,
соответствующих дереву (см. рис. 1, б), имеет вид
\ l д д Δ" (Ρ)
1 *.Cos<esin*e-|r+ —£_- +
L cosc θ sin* θ Μ Μ ^ cos* θ
+ 4^1Τ + Κ(Κ+ η - 2)] Υκ (Ω) = 0. (1.55)
Здесь с — число последующих узлов налево от вершины Θ; s — число
последующих узлов направо от вершины Θ, с 4- s = η — 2;
лапласианы Δω и Aq заданы соответственно на с- и s-мерных сферах. Для них
деревьями будут левая (от вершины Θ) и правая части большого
дерева (см. рис. 1, б) с вершинами β и θχ соответственно (рис. 5).
Напомним, что узлу дерева (см. рис. 1, б), помеченному углом Θ,
соответствует редукция О (п) id О (р) X О (q), где ρ = с + 1 —
число свободных ветвей, произрастающих из левой ветви данной
развилки; q = s + 1 — число свободных ветвей, стягиваемых линией, ры-
ходящей из этого узла направо. Лапласианы Δ» и Δβ$ — операторы
Казимира — Лапласа для указанных выше подгрупп О (р) и О (q) (ρ +
+ q = η). Их собственные значения и собственные функции задаются
формулами, подобными (1.54), в которых нужно только η заменить
ρ и q соответственно, а вместо глобального момента К в n-мерном
пространстве подставить соответствующие моменты KL и /С2 в
подпространствах Ер и Eg. Для них допустимы, вообще говоря, те же
значения Κι = 0, 1, 2, ... Вопрос о том, какие значения К\ и Кг
совместимы с данным полным глобальным моментом К (или наоборот, какие
значения К возможны при фиксированных значениях К\ и Кг)%
будет рассмотрен в следующем параграфе при прямом решении
уравнения (1.55). Однако, чтобы записать это уравнение в явном виде, нужно
32

выразить лапласиан ΔΩ через sin β, cos β и д/д$, а также через
лапласианы на сферах меньших размерностей; так же следует расписать
лапласиан Δω и т. д.
Алгоритм записи этих лапласианов в гиперсферических
координатах остается тем же, что и для Дд. «Разворачивая» таким образом
лапласиан Δα согласно ветвлениям данного дерева, получаем его
явный вид в гиперсферических координатах. Образно говоря, при таком
подходе видим (как на киноленте) последовательное разделение
переменных в лапласиане.
1.7. Уравнения для ячеек и их решения
Уравнение (1.55) будем решать методом разделения переменных. В
результате в каждом узле появится постоянная разделения
переменных (аналогичная К в вершине на рис. 1. б), которая вместе с углом
дополнительно характеризует узел. Итак, для решения уравнения
(1.55) нужно рассмотреть каждый узел отдельно, написать
соответствующее ему уравнение, найти его решение и представить полное
решение как произведение отдельных решений. При таком подходе ветре·
тятся три типа узлов (три типа ячеек), показанных на рис. 6.
Условие однозначного покрытия сферы налагает следующие
ограничения на область изменения узлов:
0<φα<2π, 0<φ,<π, ?L<q>6,<JL, 0<(p6<-f-. (1.56)
Рассмотрим элементарную ячейку графа, изображенную на рис. 6, в.
Здесь т, τ, xs, тс, σ — постоянные разделения переменных.
Уравнение по переменной θ = φ6 имеет вид
[ ' * 05<θ8ίη»θ * ^Д-1» -
cos'esinse 0Θ д® cos2 θ
ts(ts + s — 1)
+ σ (σ + c+ s)] ψ(θ) = 0. (1.57)
sin2 θ
Обозначим sin2 θ = ζ н решение будем искать в виде 2μ (1 — ζ)ν χ
Χ F (α, b\ c'\ ζ). Тогда для функции F (α, b\ c'\ z) получим
гипергеометрическое уравнение
2(1 -z) r + \±t^ + xs _|-i^i- + T0 + ts + l] г} F'-
(tc + Ъ) (тс + τ5 + с + s) — о (а + с ■+■ s) ρ _ 0 Π 58>
V V V
т
δ1
Р«с. 6
33

при условии, что 2v = хс и 2μ = xs. Сравнивая уравнение (1.58) с
канонической записью гипергеометрического уравнения
2(1 _z)F' + [с' - (а + b + l)z] F'—abF = 0, (1.59)
записываем
2a = Tc+Ts + c + s; 26 = τ, + τ8-σ, c'=xs + -±±L. (1.60)
Отсюда решение уравнения (1.57) имеет вид
ψ(θ) = cos^Qs\r\^QF(at b\ c'\ sin2 θ). (1.61)
Требование регулярности налагает на тс и т8 ограничения
V, τ8>0. (1.62)
Вместо F (a, 6; с'; sin θ) по известным формулам решение (1.61) можно
записать через многочлены Якоби:
ψ (θ) = cos1* θ sin'O^ (cos 2Θ), (1.63)
где 2/г = σ — хс — xs; a = xs + -^— ; β = τ, + c~ ; гг = 0, 1,2
3, ..., причем тогда и только тогда, когда л ]> 0 (см. теорему 4.22
[204]).
Полиномы Якоби ортогональны с весом (1 — х)а (1 + *)β, т. е.
l{\-xf(l+x)*№{x)№(x)dx =
= 2^^Γ(^+α+1)Γ(η- + β+1)6^ _ β
(2Λ' + α + β + 1)Γ(Λ/ + 1)Γ(η/ + α + β+1) ~~/Vn' °nn'· Ι1'0*'
Так как элемент объема dQ =X\hidqu то оказывается, что множитель
i
cosc θ sins6, стоящий перед дифференциалом d cos 2Θ вместе с
квадратом множителя cos1* θ sinx* θ, находящимся перед полиномом в (1.63),
дает нужный вес
cos* θ sins θ cos21* θ sin21* OdO =
s—1
(_) (i — cos 2Θ) *' 2 (1 + cos 2Θ)
^V^VFOHrtOTFi d C0S 2Θ·
Итак, ортонормированное решение уравнения (1.57),
соответствующее ячейке, изображенное на рис. 6, в, имеет вид
tflis (χ) = 2 4 {Λ#β} 2 (1 _ χ) * (1 + χ) 2 $f 3 (*), (1.65)
где
x = cos20; 0<θ<-£; 2η =σ- τ, — τ8;
α = ** + -Цг— — τ, + -^-; β = τ, + -i=i- α τ, + -Χ;
34

с (s) — число левых (правых) узлов, лежащих выше вершины σ;
Sx, 5τ — числа узлов, лежащих выше соответственно узлов ts
и ν
Используя связь полиномов Якоби ф/с13 (х) с функциями &1т,п (х)
ю»и-»^г-/Шет(,_„-?-„ +
+ *f 2^«Ve-a W. (166)
2 ' 2
записываем решение (1.65) в виде
У 12(-т + —-1) + 1 J
х ^ Ξ±4^ΐ , v^ + ^.W· (L67)
(1_*) 4 (1+*) 4 2^4 f 2 + 4
Здесь n' = c + s + 2 — размерность пространства, имеющего в
графическом представлении вершину σ.
Функция ^ί,,ν (χ) в (1.67) является матрицей конечных вращений
группы SU (2) с моментом / ^ γ + f — '» который, как видно из
формулы, в случае пространств нечетной размерности принимает
четвертьцелые значения [3, 6, 13]. Закономерность появления в этой
задаче четвертьцелых моментов можно понять, обратившись к симп-
лектической группе Sp (2, R) [197, 205] (см. ниже п. 6.2.2).
Поясним теоретико-групповой смысл полученного решения (1.67).
Как отмечалось в параграфе 1.4, узел типа (1.67), помеченный углом
Θ, отвечает редукции О (п) zdO (р) X О (q) (ρ = с + 1, q = s + 1).
Постоянная разделения σ совпадает с глобальным моментом К в п-
мерном пространстве σ = /С, а постоянные τ0 и τ8 задают глобальные
моменты в подпространствах Ер и Ед ι %с = Къ Ts = ^Сг- Из (1.63)
следует
К1 + Кш=К — 2т, /п = 0, 1,2 [tf/2], (1.66а)
т. е. разложение неприводимого представления DK группы О (п) по
неприводимым представлениям DKi X DKs подгруппы О (ρ) X О (q)
(ρ + q = η) имеет вид
DK= 2 D*'X D*% (1.67a)
где суммирование проводится по любым значениям Къ Къ = 0, 1, 2, ...
при условии /d -Ь Аг2 ^ /С» ΛΓ — 2, ..., 1 или 0. Этот результат можно
прокомментировать еще следующим образом. Сделаем в уравнении
3* 35

(1.57) замену W (θ) = cos*'2 θ sirW2 θψ (θ). Тогда оно приводится к
виду уравнения Шредингера
- W (Θ) + (VPT — ε) W (θ) = 0 (1.68)
с так называемым потенциалом Пешля — Теллера [2061
VpT = м** + ц , *»<*■« +υ (1 69)
VpT cos2 θ + sin2 θ · lKW'
Здесь Lx = ^ + -γ(ρ - 3); L2 - /ί2 + -I- (<7 ~ 3)·
Собственное значение «энергии» ε связано с собственным
значением λ в (1.54) и глобальным моментом К следующим образом:
β = -λ + \(n-2f = [/С + -J-(Ρ + 9-2)]2. (1.70)
Очевидно, что спектр собственных значений ε является дискретным,
он неограничен сверху, и допустимые значения К определяются
формулой (см., например, [206])
ε - (L, + L2 + 2m + 2)2, m = 0, 1,2, ... (1.71)
В результате этого снова приходим к соотношению (1.66а) /С = /Ci +
+ /С2 + 2/л. Поскольку выражение (1.65) войдет как множитель в
состав полной гиперсферической гармоники Υκν (Ω), то перепишем его
в обозначениях К> Κι, К2> Р> Я* характеризующих эту ГГ:
УкКгкЛЪ = NKK%K,{cosQf (sin9)K^8+ ^~l* K,+ ^-1 (cos29), (1.72)
где
ΝκκιΚ2 =
(2K + p + q
К! + К2+К + р + д — 2\ (к — Кг-К^
_2)Г 1Кг + К2+К + р + д-2\/
t(k+«*-k*+<\t(«+«*i;k*+'u
-)γ(« + «*7«» + ').
1/2
Допустимые значения Къ ΛΓ2 = 0, 1, 2, ... при фиксированном К
определяются соотношением (1.66а).
Функции (1.72) нормированы при элементе объема ί/Ω = cos^O x
χ sin?-1 Qdd. Обратимся к другим типам ячеек, приведенным на рис. 6.
Символы, показанные на рис. 6, б, удобно рассматривать отдельно.
Заметим, что ячейка на рис. 6, б' соответствует ячейке на рис. 6, б,
в которой произведена замена cos q>6 -*■ sin φ6. Согласно
сформулированному выше правилу уравнение по переменной θ = q>6
записывается следующим образом!
[Tik "Я- Si"S θ -«Г- %$ {%SstSB~ !) + τ (τ + s)] Φ (8) - 0. (1.73)
Обозначая cos θ через ζ и делая подстановку Φ (θ) = (1 — ζ2)*1 Ρ (ζ),
для Ρ (ζ) получаем уравнение
(1 _*·)/>■ ~(2т>ь + s + l)zP' + (τ -τ8)(τ + τ$ + s)P = 0 (1.74)
36

при условии 2μ = τ$. Его
решением являются ультрасферические
функции или полиномы Гегенбауэра
[204] %>а (ζ), где η = τ — τ5, α =
ι s— 1
Следовательно, решение уравнения
(1.73) можно записать так:
*рЪ
τ
а
РиоЛ
0(e) = sinxs0^a(cos0).
(1.75)
Ячейки α и б на рис. 7 имеют одинаковые решения, что видно из
формул (1.63) и (1.75).
Поскольку полиномы Гегенбауэра ортогональны с весом (1 —
— г2)06, т. е.
\(\-z^Tna(*)%}a{*)dz
—ι
22α+1Γ2(Λ' + α+1)δ/
tin*
(2л' + 2а + 1) Г (п' + 1) Г (п1 + 2а + 1)
= ΝΤδη
(1.76)
то ортонормированное решение уравнения (1.73), соответствующее
ячейке на рис. 6, б, имеет вид
ψΧ(ζ) = {Λ#α} 2(1
•г2) 2Тп*{г)>
s — 1
(1.77)
где ζ = cos θ; 0 < θ ^ π; λ = τ — τ3; α = τ3 + 2' , η > 0, 1, 2, ...
Узел, изображенный на рис. 7, α, отвечает редукции группы
О (q) zd О (q — 1), q = s + 2. Отождествляя τ с глобальным
моментом /С в Ед (τ = /С), а τ8 с глобальным моментом Кг в подпространстве
f^-i (τ8 = Κι) и вводя для полиномов Гегенбауэра стандартные
обозначения [14, 207, 208]
C%/Z) = аза-1/2,а-1/2 /z\ Г (2а + Ό Γ (а + 1/2)
(1.78)
Г (2а) Г (а+1/2 +л) '
можно записать блок Υκκχ (θ), входящий в полную ГГ и отвечающий
узлу рис. 7, а, в виде
где
Νκκ, =
^к«, (Θ) = #KKl sin* 9CKLKl2 (cos θ),
22Κ+ν_4 {Κ _ Κι)] (2Κ + q _ 2) ρ, /^ + q — 2\
(1.79)
1/2
πΓ (Κ Η- /Cx + 9 - 2)
Переход от ячейки на рис. 6, б к ячейке на 6, б' совершается путем
замены θ -»·-^— Θ. В результате с ячейкой на рис. 6, б' можно
сопоставить следующий множитель, включаемый в состав полной ΓΓι
*.+ -S--I
ΥκΚι (θ) = NKKl cos* θ (- lf-K,C«_K,2 (sin θ),
(1.80)
37

В формулах (1.79) и (1.80) допустимые значения Κι при фиксированном
К задаются условием
/СЛ =—/С, /С—1 0. (1.81)
Элемент объема, с которым нормированы функции (1.79) и (1.80),
имеет вид соответственно sin *-2 QdQ и cfos*-2 Ы%.
Для полноты изложения напишем очевидные тождества
\*/=eimlVbi> 0<φ<2π, т = 0, ± 1, ±2, ... (1.82)
т
Запишем в явном виде ГГ для любого гиперсферического дерева.
В частности, для η = 3
\j)K
fYm = Ylm (θ, φ) = NcHm2 (cos θ) sin™ Qeim\ m > 0, (1.83)
m_ (/ — m)l (2/ + 1) |(2m — 1)!P
~~ 4n(l + m)\ *
где Yim (θ, φ) — обычная нормированная сферическая функция.
Сферические гармоники с т < 0, как обычно, получаем из
соотношения
Yim (θ, φ) = (- 1 )m Yi-m (θ, φ). (1.84)
Отметим, что на рис. 6, β в случае с, s = 1 τβ, τ5 могут принимать как
положительные, так и отрицательные значения. Их связь с квантовым
числом σ задается следующим образом: 2т = σ — J ic | — | ts L
т = 0, 1, ..., [σ/2], при этом в формуле (1.65) α = | %$ |, β = | τ€ |.
1.8. Примеры представлений групп U(2), SU(2)^
SO (3), U (3), SU (3), SO (4), SO (5), 50 (6)
Проиллюстрируем сказанное выше на примерах пространств
представлений групп, наиболее часто применяемых в физике.
Группы U (2), SU (2), SO (3). Начнем с группы U (2).
Инвариантная квадратичная форма в С2 для U (2) есть
Ы2 + Ы2 = 1 (1-85)
или при ζχ = Χι + ixf z2 = x3 + ί*4
х? + х22 + *з + *4=1. (1.85а)
Уравнение (1.85а) есть уравнение сферы единичного радиуса в
4-мерном вещественном пространстве £4- Зададим в Я4 биполярную
систему координат, изображейную на рис. 8s
38

*τ
xt = cos θχ cos Φι \ ^ У
x2 = cos Qt sin φχ yfa
xs = sin θχ cos φ2 = \
*4 = sin θχ sin φ2
^ */
ι
Рис. Ρ
\J
(1.86)
Метрика для (1.86) определяется так:
dP = dtf\ + cos2 θ^φ? + sin2 θ^φΙ. (1.87)
Инвариантный лапласиан, соответствующий метрике (1.87),
Δ<ι (2) = Л л -3— COS θ. Sin θ, -3s— + «a -r-5- +
u v ' cos θχ sin θι dQt l l OTj cos* θ! dq,* '
+ Sin* θ! 0$ '
(1.88)
Еще одним инвариантом представления будет оператор,
соответствующий общему изменению фазы вектора г = (zlt z2) как целого [209]:
1 / д ι д \
m= — [d<fl + а<р,/·
Регулярные решения системы уравнений
(1.89)
[Δα(2) + 1(1 + 2)]ψ = 0, (m —/π)ψ = 0 (1.90)
дадут НП группы U (2). Решение уравнений (1.90) ищем в виде
Ψ (Φι. θι. <Рг) = б'т,ф*Ф (θι) eim,<pS
где функция Φ (θχ) удовлетворяет уравнению
(1.91)
COS
Έ—^-q 35— COS 9t Sin Θ* -3ir
m,
^2
m2
+ /(/+2)
COSa0!
Φ (θχ) = 0.
(1.92)
(1.93)
sin2 θχ,
Из второго уравнения (1.90) следует
Щ + Щ = я*·
Согласно (1.65) ортонормированное решение уравнения (1.92)
можно записать так:
<tfi? (*χ) - 2 [ЫГ\ * (1 - ^х)а/2 (1 + XlfV (*). (1.94)
где
x1 = cos201; 0<6j<-^-; а = |т2|; β = 1«ι|: О·95)
2п = / — | тх | — | тг |.
38

Используя равенство (1.66), записываем (1.91) в явном виде
<*. (Φι. 6lf φ2) = exp {i mi + m2 (Φι + φ2)} Χ
X &l^+m2 mx-m% (COS 2θχ) exp U Щ ~ "*2 (фх — ψ2)} , (1.96)
где 0 < φχ + φ2 ^ 4π; — 2π ^ φ, — φ2 ^ 2π.
Умножим (1.96) на exp \i {m1 — m2) π} и введем привычное
обозначение Вигнера
&£к. (ЧЧ. β. Ь) = eiK^^Kl (cos β) eiK'\
Тогда получаем связь 4-мерных сферических гармоник, отвечающих
дереву (1.86), cD-функциями Вигнера или матрицами конечных
поворотов группы SO (3):
С (Φι» θι> Φ.) = №. (Ψι, β, ψ2). (1.97)
Здесь ψ! = φχ + φ2; ψ2 = 2π + ψ! — φ2; 2/Ci = /λχ + m2; 2Κ2 =
= /ηχ — m2; β = 2θχ.
Из (1.95) следует
п = |//2-|/С1|, \Кг\>\К,\, (l98)
\U2-\K,\. \Κ,\>\Κι\.
т. е. —112 ^ Къ К2 ^ //2 и размерность представления равна / + 1.
С числами ρ и q числа I, m связаны простым соотношением
l = p + q, m=:p~-q. (1.99)
Последнее равенство тривиально следует из (1.32) и (1.90). Функции
(1.97) реализуют представления U (2), которые задаются числами /,
т или /?, q. При переходе к подгруппе SU (2) возникает отличие от
результата (1.28), которое связано с тем, что группа SU (2) имеет
ранг 1 и представлений класса 2 у нее не существует, или более
точно — ее представления (/?, q) класса 2 эквивалентны представлениям
[р + q = /} класса 1. В результате по отношению к подгруппе SU (2)
все представления группы U (2) с различными т становятся
эквивалентными друг другу. Тем самым все представления D1 группы SU (2),
входящие в представление D1 группы О (4), характеризуются одним
числом / = 112 — весом представления. Таким образом, для
группы SU (2) мы получили все ее неприводимые представления: целый
вес / при четных I и полуцелый — при нечетных.
Основываясь на известном гомоморфизме SU (2) и SO (3),
рассмотрим полученные представления с точки зрения группы SO (3).
Решение (1.97) есть матрица, отвечающая при неприводимом представлении
веса 1/2 произвольному вращению g с углами Эйлера я|)1э β, ψ2. Правда,
i|)lf ·ψ2 изменяются пока от нуля до 4π, τ. е. при таком вращении дважды
покрываем двухмерную сферу и получаем однозначные представления
SO (3) и при полуцелом весе.
В итоге при таком подходе мы получили D-функцию (решение
(1.97)), поскольку известно, что на группу 50 (3) можно отобразить
.40

трехмерную сферу с отождествленными диаметрально
противоположными точками 1210], т. е. трехмерная сфера в £4 является областью
задания континуума функций g, которые суть элементы группы SO (3).
Иначе говоря, мы задавали оператор Лапласа непосредственно на
группе вращений. В случае отождествления диаметрально
противоположных точек азимутальные углы φ1 и φ2 изменяются в пределах
0<<Ρι, φ2<π, (1.100)
а тъ т2 = ±0, 2, 4, 6, ..., и / — четные числа. В результате (1.97)
становится матрицей представления целого веса (однозначное
представление), а ψχ, β, *ψ2 изменяются как обычные углы Эйлера. При
т1 = ± т2 = т (1.97) превращается в обычные сферические функции,
что видно из рис. 7, а также из уравнения (1.92), которое превращается
в уравнение для дерева (1.83):
β-θ. (1.101)
Получим двузначные представления, наличие которых связано
с топологической структурой группы, а именно, с ее двусвязностью,
т. е. существуют замкнутые кривые, не переходящие одна в другую
при гомеоморфизме. Поэтому налагаем дополнительное условие
0<Φι+ φ2<2π, (1.102)
хотя φ! и φ2 могут изменяться от нуля до 2π, τ. е. осуществляем
некоторую «синхронизацию» вращений в плоскостях (ΧιΧ2) и (л:3^4): если
(Рх = 2π, то φ2 = 0 и наоборот. При этом тът2 = ± 0, 1, 2, 3, ... и
/ = 0, 1, 2, 3, ... при нечетных I получаем двузначные представления
SO (3).
Отметим, что если положить в (1.88) φχ = φ2 = φ, то первое
уравнение (1.90) превращается в уравнение вида
[wisinpi+w^+4-(4-+ 1)]Φ»·»>==°·
(1.103)
которое допускает в качестве своего решения присоединенные
функции Лежандра полуцелого порядка при нечетных I. Уравнение (1.85а)
превращается в уравнение некоторой двухмерной поверхности при
Φι = Ф2» причем при θχ = л/4х1 (х2) становится тождественным xs (*4),
а уравнение (1.85а) формально распадается на два уравнения
окружностей
*? + *i=4-. 4 + 4 = 4"· О·104)
Вследствие тождественности хг и xSi х2 и хА эти окружности
тождественны и их нужно склеить. Итак, требованием φχ = φ2 из
трехмерной сферы в £4 делаем некоторую двухмерную двусвязную
поверхность. Если осуществлять представление группы SU (2) линейными
операторами в пространстве функций (1.97), то 1/2 можно
отождествить со спином (изоспином), а (т1 — /л2)/2 — с его проекцией.
41

Группы U (3), SU (3). Вектор в (С3 можно параметризовать тЕй
2 = (cos θ£ίφι; sin θ cos вге1**; sin θ sin вге***) или графически в ак
хг = cos θ cos ylf
*2 = cos θ sin φΐ9
x3 = sin θ cos θχ cos φ2ι
л:4 = sin θ cos θλ sin φ2,
хъ = sin θ sin θχ cos φ3,
я6 =s sin θ sin θχ sin φ8.
(1.105)
Рис. 9
Согласно общему правилу (1.55) легко записать инвариантный
лапласиан
Δ«(3>- coseL^e ircos9sin39ir +
+ 1ΙΡΤΔ«(2)·
Существует еще один инвариантный оператор
L - ' / а , « , а \
1
cos* θ
а*
0φ?
+
(1.106)
(1.107)
d<p2 d<p.
Отсюда представление U (3) реализуется решением уравнений
[Δ„(3) + σ(σ-Μ)]ψ=0, (m — т)г|)=0. (1.108)
Используя результаты (1.65), (1.82), записываем решение уравнений
(1.108) для графа, изображенного на рис. 9:
♦5^(9. θ1§ φ,) = 'ФЖГ11 W Л·/:^1 (ί/) exp (t Si т/Ф/) , (1.109)
где χ = cos 2Θ; у = cos гэ^, 2η! = σ — Ζ — | mx |; 2η2 = / — | m21 —
— |m3|; αζι,2^0. Из nlf л2]>0 следует
<* — \*П\\> 1>\щ\ + \т*\>\т — Щ\. (1.110)
Второе уравнение (1.108) дает условие
Щ + Щ +mz = mt (l.lll)
и из (1.32) и (1.107) вытекает
m = p — q. (1.112)
Учитывая (1.34), (1.32) и (1.112), получаем, что число линейно
независимых решений (мультиплетность) (1.69), выраженное через
квантовые числа σ и т, задающие представление, имеет вид
σ + 2 Г (σ + 2)а
#* =
rjo-
m*
(1.113)
Этот результат можно получить из условия (1.110) с помощью
диаграммы на плоскости (/, mx) [209].
42

Решение (1.109) для группы SU (3) реализует все ее неприводимые
представления (р, q), а для группы U (3) — лишь некоторые. Чтобы
получить все представления U (3), нужно рассмотреть все
представления подгруппы общего изменения фазы, которые задаются
положительными целыми степенями детерминантов (скаляров SU (3))
**fiyZ?\A)Zlh f^zfzf. Как и в случае SU (2), в SU (3) удобно
отсчитывать фазы от центра [2]:
1 3 3 т 3
tS mt 2 ф* = ~з~2 φ*.
ί=1 fe=l fc=l
тогда
exp U g ладЛ = exp [i **ι-ρ-*» (Φι - q>2)] Χ
X exp [i mi + m32 - 2m* (φ2 - φ3)] exp (f -S- g φ,), (1.114)
Обсудим связь полученных выше результатов с ароматической
симметрией SUf (3) в теории элементарных частиц. Легко видеть, что
дереву, изображенному на рис. 9, можно поставить в соответствие
редукцию
SUf(3)zzSUt(2)xUy{1), (1.115)
где подгруппа изоспина SUt (2) действует в пространстве z2, z3 ана"
логично тому, как было описано выше. Ясно, что гармоники (1.109)
преобразуются по неприводимому представлению D этой группы с
изоспином Τ = 1/2. Они являются также собственными функциями
оператора гиперзаряда
Ϋ = ~(2тх — т2 — щ) (1.116
о собственным значением Υ = j- (2т1 —тт2 — т3). Границы
изменения значений квантовых чисел тъ т2, т3, I (или Г, Т)
сформулированы в (1.109) — (1.112). Их удобно записать в виде правила
параллелограмма [2111, в котором под каждым из допустимых в
неприводимом представлении (мультиплете) (pq) значений гиперзаряда Υ
указаны совместные с ним значения изоспина Т\
(Р, Я)« * min * min + 1
т -τ я 4-(ί? + Ι)
4-07-О
5СЬ Кшш = j-(2/> 4" Я)',
* min ~г ^ · · · * min -J- P * max
^-(q + 2) ... 4-0*+?)
1
2 9
-r(?-2)
0 ... -γ{ρ)
Уш* = -ъ-(р+2я)·
(1.117)
&

Если учесть, что каждому значению изоспина Τ соответствует 27 +
+ 1 значений проекции изоспина Мт = -у (пг2 — /л3) (—Τ ^ Мт ^
^ Т), то полное число частиц, входящих в SU (З)-мультиплет (р, q) и
соответствующих клеткам этого параллелограмма, будет равно
размерности данного представления (см. (1.34), (1.113))
dim(p9q)=-L(p+l)(q+l)(p + q + 2). (1.118)
Рассмотрим знаменитый октет барионов (pq) = (11), для которого
параллелограмм (1.117) принимает вид
(И) -1 0 1
Τ 1/2 1
О 1
Это означает, что в указанный мультиплет входят следующие частицы:
Барионы
Барионы
Ρ
η
Λ°
Σ+
Σ°
Σ~
Ε°

ΕΥ
1
1
0
0
0
0
— 1
— 1
τ
~ί/2~
1/2
0
1
1
1
1/2
1/2
Μτ
ί/2~
-1/2
0
+ 1
0
— 1
1/2
— 122
Электрический заряд частиц задается формулой
Q = \ + Мт =4-(2m*-mi — пгд).
Для декуплета барионов (3 0) параллелограмм (1.117) вырождается в
одну строчку
(3 0) — 2 — 1 0 1
Τ 0 1/2 13/2
В него входят частицы Δ++, Δ+, Δ·, Δ" (Κ - 1, Τ = 3/2), Σ+*, Σ°*,
Σ—(Г = 0, Г = 1), Ξ0*, Ξ"·(Κ = — 1, Γ= 1/2), Ω~(7 = —2, Γ =
= 0). Здесь Σ*, S* — барионы, обладающие теми же квантовыми
числами Υ у 7\ Мт% что и Σ-, Ξ-гипероны со спином 1/2, входящие в
состав октета, но в отличие от последних они имеют спин 3/2 и более
высокую массу.
Мультиплет кварков (10) состоит из трех частиц: и (Υ = 1/3,
Τ = 1/2, Мт = 1/2), d (Υ = 1/3, Τ = 1/2, Мт = —1/2), s {Y = —1/2,
Τ = 0, Mr = 0). Электрические заряды u-, d- и s- кварков равны
соответственно +2/3, —1/3 и —1/3. Диаграммы, показывающие структуру
(1.119)
(1.120)
44

Рис. 1С
этих мультиплетов, в плоскости (Г, Мт) изображены на рис. 10.
Точке (0, 0) на диаграмме мультиплета (11) отвечают две разные частицы
Λ°ηΣ°.
Группы SO (4), SO (5), SO (6). Для этих групп, как следует из
рекуррентной формулы (1.47) и рис. 4, имеем g (4) = 2, g (5) = 3 и
g (6) = 6 соответственно при η == 4, 5 и 6. Таким образом, можно
нарисовать соответственно два (рис. 11), три (рис. 12) и шесть (см. рис. 9)
топологически неэквивалентных деревьев. Декартовы координаты на
45

рис. 11, а записываются в виде
*1==cos0, xs = sin Θ sin Ό cos φ, ,. «οη
χ2 == sin θ cos θ, я4 = sin θ sin ϋ sin φ,
а метрика определяется так!
dl2 = d62 + sin2 6d02 + sin2 θ sin2 Ыу2. (1.122)
Лапласиан Δ (4), соответствующий этой метрике, имеет вид
A(4)=ii^4-sin28^+-ihW(wwsin^ +
т sin* θ dip» /'
а сферические гармоники являются решениями уравнения
[Δ(4)+σ(σ+2)]φ = 0, σ = 0, 1,2, ... (1.123)
Используя сформулированный выше алгоритм (1.77), записываем орто-
нормированное решение уравнения (1.123)
ψσ/m (θ, Α, φ) = {No-,2 * } (1 - COS2 θ) 2 %J ' 2 (COS θ) Χ
хК,т(«,ф). (1.124)
Рис. 12, б (для 50 (4)) фактически совпадает с рис. 8 (для U (2)).
Поэтому все уравнения и формулы для 50 (4), за исключением уравнения
(m — т) ψ = 0 и условия тг + т2 = /л, те же, что и для (/ (2).
Случай η = 5 не будем обсуждать подробно, а сразу напишем
решения согласно алгоритмам (1.65) и (1.77), относящиеся к деревьям а—в
(см. рис. 12). Для дерева а
Ψασ/„(β, θ, Ο, φ) = {Λ^σ+1} 2 (1 ~COS2p)2 X
Χ ΐ£±1σσ+'(cos β) %lm (θ, Ο, φ), (1.125)
где ψσ/m (θ, Ο, φ) — ортонормированное решение (1.124).
Для дерева б находим
L j_
ψχ/π,,π,, (β, θ, φι, φ2) = {N'+liw} 2 (1 - cos2 β)2 χ
Χ ^//+1(cos β) <ft|m>> (cos 2Θ) ^ ^ . (1.126)
Здесь O%u{rn,\cos 2Θ) — ортонормированное решение (1.94), θχ = θ.
В случае дерева в
Wm(9> d, φ, φχ) - 24 [NgJl^Z) 2 (* - cosG)2 χ
2
χ (1 + cos 2Θ) 2 j)J,N (cos 2Θ) У/да (Ο, φ) -1—r-. (1.127)
——= у 2л
46

Как мы уже отмечали, для группы SO (6) можно нарисовать шесть
топологически неэквивалентных деревьев, одно из которых
изображено на рис. 9. Решения (1.109) (без условия тх + т2 + m3 = m)
реализуют одно из представлений класса 1 группы SO (6). Другие типы
деревьев для SO (6) здесь рассматривать не будем.
1.9. Некоторые свойства гиперсферических гармоник
Рассмотрим некоторые общие свойства ГГ при произвольном значе
нии п. Для определенности используем систему координат, отвечаю·
щую каноническому гиперсферическому дереву (см. рис. 1, в). В этом
случае оператор Лапласа на η — 1-мерной сфере задается
рекуррентным соотношением
^=ii^^(sin"-4-'^)+i^<4-,· (ищ
Гиперсферические гармоники — собственные функции данного
оператора, регулярные на (п — 1)-мерной сфере и относящиеся к
собственным значениям — 1п (1п + η — 2), где 1п — целые неотрицательные
числа. Указанные собственные значения имеют большую кратность
вырождения, определяемую формулой (1.20), в которой гипермомент
1п обозначен буквой /(. Для того чтобы отличать разные ГГ,
отвечающие этому вырожденному собственному значению, нужно снабдить их
дополнительными квантовыми числами. Для этого, например, можно
потребовать, чтобы ГГ были собственными функциями всех
лапласианов Δω^ (i = 2, ..., η — 1) в пространствах меньшей размерности Et
с координатами хи х2, ..., хи Тогда ГГ будет характеризоваться не
только л-мерным гипермоментом /п, но и гипермоментами /2,13, ..., Ζη-ι
в пространствах меньшей размерности. Обозначим такую ГГ символом
Ylm (Э1э θ2, ..., θ„_ι), где L = /n, a M заменяет всю совокупность
гипермоментов 1п-*\, ..., 12:
^Ylm (θ,) = - lf (/, + / - 2) YbM (θ,),
-i^YLM(Qg) = l2YLM(QQ), ι = ~n. (1.129)
Набор гипермоментов М достаточен для полной и однозначной нуме-
рации вырожденных ГГ. Допустимы следующие значения
гипермоментов:
ln>ln~i>ln-2> ··· >h>\k\, (1.130)
12 может быть отрицательным и может принимать целочисленные
значения, удовлетворяющие условию
-'з<'а<'з. (1.131)
Соответствующая ГГ имеет аналитический вид!
r«(W-JVn\*^ £>£ (1-132)
4?

2ί„_Μ+η-/-4(/η__ _ ^^^, (2/^ + я _ . _ 2) χ
«■--tff _-'('--±^
/Jo πΓ (/»-/ + '«-/-Ι + я - / - 2)
UW-W(rt i^1) (m-2*)!4*« *
В случае п = 3 формула (1.132) переходит в известное выражение длз
обычных сферических функций
У, ίθ п^ - l/ (/-m)l(2/+7T v , ns (3 ~2s~ 1)11 (cose)'-"-28
*!»(<>. φ) - У (/ + т)!4я 2/~ *' 2ssl (2 _m-&)! X
X sinmQexp(im<p), m>0. (1.133)
Гармоники (1.132) ортонормированы:
f dQrLA1 (θ«) K^ (Θ,) = Oll-oaim'. бмлг = Ъ . .. Λ л (1.134)
(Элемент объема dQ приведен в (1.39)). Из соотношений (1.129) следует,
что гипермомент 1п характеризует неприводимое представление Din
группы О (л), по которому преобразуется ГГ Υlm (θ?). Гипермоменты
U задают неприводимые представления подгрупп О (/) из цепочки
(1.41), к которым принадлежат соответствующие ГГ.
Гиперсферические гармоники Υш Фд) образуют канонический базис Гельфанда —
Цетлина для неприводимого представления Dln класса 1 группы О (п).
Поэтому матричные элементы операторов бесконечно малых
поворотов в л-мерном пространстве (генераторов группы О (п)) по функциям
(1.132) можно находить по формулам Гельфанда — Цетлина [200,
2011.
Остановимся на некоторых свойствах ГГ, аналогичных свойствам
обычных сферических функций. Положим в (1.132) θΛ_ι = 0. Тогда
ГГ Ylm (θ/ι-i = 0) отлична от нуля только в случае Ζη_ι = 0. При
этом согласно (1.130) имеем 1п-г = 1п-з = ... = /2 = 0 и Ylm (On-ι =
= 0) не зависит от углов θη_2, О^з, ..., 02, 9Ь которые также можно
считать равными нулю. В итоге имеем соотношение
-^ ш
:-2)(2/ч + л-2)
■1)1
Smo = δ/ί1_1οδ/„_2ο.. А8о» (1.135)
являющееся аналогом известного свойства трехмерных сферических
функций
Yim(0t 0) = 6^Y*L±L. (изб)
Обращение ln-\, ln-2> ...9 1% в нуль при θ„-ι = 0 вполне естественно,
ибо, переходя к θη_ι = 0, получаем функцию, которая зависит
только от декартовой переменной хп и является инвариантом по отношению
48

4
к подгруппам О (η — 1), О (η — 2), ..., О (2) из цепочки (1.41), т. е.
соответствует нулевым гипермоментам в пространствах ££ с
координатами хъ х2, ..., х% (i = 1, 2, ..., η — 1).
Можно также доказать соотношение
Уьхмг (%) Yb,\it (%) =■
- *%' (L1M1L2M2\LM)(L10L20\L0)YLM(%)X
г(-^-)г(л + ^--2)Г(/2 + £2-.2)(2^+п--2)(212 + д--2)/:!
2πη/^!ί La* Γ (η — 1) (2L + η — 2) Γ (η + L - 2) '
(1.137)
которое является «-мерным аналогом известного свойства трехмерных
сферических гармоник
УцтЛЬ <P)*We,q>) =
= JS / {/ (2\ΐ(2/(+2ΐΓ·11 (/1тЛт2 ' /Ш) (/l0/2°l Ю) Ym (θ' Φ)·
'~,/l~'2' (1.138)
Соотношение (1.137) позволяет разложить произведение двух ГГ от
одних и тех же аргументов по ГГ от того же аргумента. Величины
(LxMxL2tA2 | LM) — коэффициенты Клебша — Гордана для группы
О (п), осуществляющие разложение прямого произведения двух НП
Eh xi^^J^ (1.139)
л
группы О {η) на неприводимые компоненты. Отметим, что в
разложение этого прямого произведения входят не только представления DL
класса 1, но и более общие представления DA класса 2. Однако наличие
в правой части формулы (1.137) ККГ (Lx0L2§ \ L0) обеспечивает то,
что в сумму по L входят фактически только неприводимые
представления DL класса 1. Неприводимое представление D группы G
называется представлением класса 1 по отношению к подгруппе Н> если
в пространстве представления D имеется вектор, инвариантный
относительно подгруппы Н. Согласно определению ККГ (LXQL2 (0) | L0)
неприводимое представление DL, которое может входить в разложение
(1.137), должно быть таким, чтобы в нем был вектор сМ = 0,
инвариантный относительно подгруппы О (п — 1). Поэтому данный ККГ
отличен от нуля только для представлений DL класса 1 по отношению
к подгруппе О (п — 1). Заметим также, что в (1.137) так же, как и для
обычных сферических гармоник (т. е. в формулу (1.138)), должны
входить только ГГ, удовлетворяющие условию Lx + L2 + L = четное
число. Это легко понять, сравнивая четности левой и правой частей
соотношения (1.137). Четность ГГ Ylm (θ*) определяется значением
(—1)L. Последнее становится очевидным, если вместо ГГ рассмотреть
гармонические полиномы степени L ι рш (xl9 χΖί .„t xn) = pL χ
4 1-1980
49

X Уьм (θ*), которые в силу их однородности в результате инверсии
(*ι -*· —Χι) приобретают фазу (—l)L. Схема вывода соотношения
(1.137) та же, что и в случае группы SO (3). Сначала устанавливаем
связь сферических гармоник с матрицами конечного поворота, для чего
действуем на функцию F/m (θ, φ) оператором поворота R (α, β, у)
на углы Эйлера α, β, γι
Yim{Q\ φ') = R(afiy)Ylm(Q, φ) = %&„*{*№) Υik{b φ)· (1.140)
k
Положим θ = φ = 0, τ. е. выберем направление единичного вектора
/ι, от которого зависит сферическая гармоника Ytk (n), вдоль оси г,
т. е. положим θ = φ = 0 (η \\ οζ). После поворота R (α, β, γ) этот
вектор η займет новое положение п\ которое характеризуется полярными
углами θ' = β, φ' = α. С учетом свойства (1.136) соотношение (1.140)
при θ = φ = 0 превращается в равенство
Κ/Λ(β,α)= j/"-^i-Zym0(af β, ...) (1.141)
(при k = 0 элементы матрицы конечного поворота Dlmo не зависят от
третьего угла Эйлера γ, и в правой части равенства (1.141) его
опустили). Для D-функций справедливо соотношение
0^1(αβν)ϋ^8(αβγ) =
= Σ 0>\ЩкЩ I Щ Dlmk (αβγ) {lxkxl2k2 \ Ik), ^ j 42)
m = m1Jr m2, k = kx + k2t
которое по существу является определением ККГ (l1m1l2m2 \ lm) как
величин, осуществляющих разложение прямого произведения дв^с
НП группы 50 (3)
/У'хо'^ *Σ °ι (1Л43>
на неприводимые компоненты D1.
В случае kx = k2 = k = 0 при учете (1.141) формула (1.142)
превращается в свойство сферических гармоник (1.138). Аналогом
формулы (1.141) в n-мерном пространстве является соотношение
Ylm(V<,)=Y ИГ(я—1) uM0(Qq, ···)· (1.144)
Аргументами D-функции для группы О (п) в общем случае являются
η (η — 1)/2 углов Эйлера Ω, но функция частного вида Dm (Ω) (так
называемый матричный элемент нулевого столбца [14]) зависит только
от η — 1 углов QQ, поэтому остальные углы Эйлера в правой части
(1.144) заменены многоточием. Аналогом соотношения (1.142) для
разложения (1.139) является формула
Ζ^ιΚι(Ω)ί>Μ8κ8(Ω) =
- Σ (L1MlL2M21 Λμ) £#κ (Ω) {L^L^ | Λκ), (1.145)
Λμχ
50

в правой части которой суммирование проводится по представлениям
DA классов 1 и 2. Однако в случае Κι = К2 = К = 0 в ней
«выживают» только неприводимые представления DL класса 1 (L = Lx + L2,
Li + L2 — 2, ..., 1 или 0). Заменяя в (1.145) D-функции на ГГ в
соответствии с (1.144), приходим к свойству (1.137) для «-мерных ГГ.
Если умножить обе части равенства (1.142) на Dmk (αβγ) и
проинтегрировать по углам Эйлера (dQ = sin §d$dady), то, учитывая
свойство ортогональности D-функций
J dQDlZk (Ω) D^.k. (Ω) = -^rfr Ьи-*™-***, (Ы46)
получаем соотношение
(lxmxl2m2 J lm) (lxkxl2k2 | Ik) - -^±Л J dQD1^ (Ω) 0&Λ (Ω) D&,*, (Ω),
(1.147)
которое позволяет найти произвольные ККГ (1гтх12т2 \ 1т) путем
вычисления интеграла, входящего в правую часть данного равенства.
Для этого надо зафиксировать значения kx, k2 и k, вычислить
указанный интеграл при различных значениях ти т2, т и разделить его на
нормировочный коэффициент (lxkxl2k21 Ik), который можно найти по
той же формуле (1.147), полагая тх = ku т2 = k2, т = ki
(lxkxl2k21 Ik? = -^i- J dQQfc (Ω) 1%ъ (Ω) D^, (Ω). (1.148)
Значения kx> k2> k следует выбирать так, чтобы нормировочный
коэффициент (1.148) был отличен от нуля (например, можно положить
kx = lx, k2 = —l2f k = lx — l2 или kx =s /lf k = I, k2 = I — /j, в
обоих случаях ККГ (1.148) отличны от нуля при любых допустимых
значениях \ 1х — /21 ^ / ^ 1Х + /2). Рассмотрим приведенный выше
алгоритм при kx = k2 = k = 0. Тогда с учетом (1.141) из формулы
(1.147) получаем
(1хтх12т211т) = (/х0/20\Ίθ)~] χ
х V (2//+(ι2/(2"Λΐ) ί Y*m (θ' φ) Υι^ (θ» φ) Yl>m>(θ» Φ) sin ΜθΛρ·
(1.149)
Отсюда видно, что вычисление интеграла от трех сферических
функций позволяет найти ККГ для группы SO (3), но не в общем случае,
а при условии
l = li + k, h + U — 2* ...» 1 или 0, (1.150)
ибо ККГ с нулевыми проекциями
(/х0/а0110)* = —-Ш±^ J sin 640^0(6)^0(0)1^0(0) (1.151)
будет отличен от нуля только для значений /, перечисленных в (1.150).
Ниже используем и-мерный аналог формулы (1.149)
{L1MlLtM% | LM) = (L^O | L0)-1 χ
4* 51

χ / 2nn^L1\L2\T(n^l)(2L + n^2)T(n + L-2) χ
Ι/ Γ Ι -γ\ Γ (л + Lt — 2) Γ (η + L2 — 2) (2LX + η - 2) (2La + η — 2) L!
Χ J ЯНЪи (θ,) rfilMl (θ,) rLfMt (θ,) (1.152)
(или точнее — ее упрощенный вариант) для того, чтобы найти ККГ для
группы О (п). Однако заметим, что при этом будут получены ККГ не
для всех представлений DA, входящих в разложение прямого
произведения (1.139), а для представлений DL класса 1, ибо только для
последних отличен от нуля нормировочный ККГ (LiOL20 \ L0). Это
замечание относится также к ККГ для неприводимых представлений
класса 2 группы U (п) (в частности, для группы SU (3)).
1.10. Коэффициенты Клебша--Гордана ортогональных
и унитарных групп
Коэффициенты Клебша — Гордана играют, как известно, важную
роль в теоретической физике. С их помощью вычисляются атомные и
ядерные спектры, а ККГ для высших групп широко применяются в
физике элементарных частиц. Однако эти величины хорошо изучены в
литературе лишь для групп SU (2) и 50 (3) (см., например, обзор
[212]). Для групп высших симметрии, таких как SU (3), SU (4),
SU (6), несмотря на определенный прогресс [213—226] работа по
исследованию ККГ еще далека от завершения. В данном параграфе,
пользуясь графической техникой, изложенной выше, вычислим ККГ
дл,я представлений класса 1 группы 50 (п) и представлений класса 2
группы SU (ή) при канонической редукции пространства 50 (η) ζ>
zd SO (η — 1) r> SO (n — 2)z=> ... гэ 50 (2) и SU (η) zd SU (n —1) zd
zd ... id SU (2) соответственно [9, 10]. Будут рассмотрены только
такие ККГ для групп 50 (п) и SU (я), у которых три входящих в них
представления являются представлениями классов 1 и 2
соответственно. Определения представлений класса 1 для 50 (ή) и класса 2 для
SU (п) были даны в параграфах 1.2 и 1.3.
1.10.1. Коэффициенты Клебша — Гордана представлений класса 1
группы SO (n). В разложении прямого (кронекеровского) произведе-
52

ния {k'} X \k") неприводимых представлений класса 1 группы SO (ή)
(п>3) на неприводимые содержатся как представления класса 1,
так и представления класса 2 (т. е. такие, которые определяются
двумя числами). При этом представления {к} класса 1 содержатся
однократно и лишь те, для которых k + k' + k" — четное число и
выполняется соотношение | k' — k" | <; k ^ k' + k".
ККГ, выделяющие из кронекеровского произведения представле·
ния класса 1, можно найти из следующей формулы (другая запись соот·
ношения (1.152) с несколько измененным обозначением ΚΚΓ)ι
SO(n) l l
При параметризации группы SO {η) с помощью углов Эйлера
[14) Θ/1 (1 ^ т <Ξ η — 1, 1 ^ / ^ т) дифференциал нормированной
инвариантной меры имеет вид
я—1 гп .
^ = 4ПП sm'^QfdQf. (1.153)
Здесь
А _ А Г(~И 0<θΓ<2π,
Li 2π*/2 ; °<θ7<π· Ζ^1·
В наших обозначениях {Λ|} = {klt k2, ..., &п_з, mn~2}9 {0} =»
= {0, 0, ..., 0}, причем (см. (1.130)) k s== kQ ^ &x ;> &2> ... > &„_3 >
^ | /η«-21. Полагая для краткости kn-<i = | тп-ъ | и γ/ = η — / —
— 3 (с числами S/ работы [2] числа γ/ связаны соотношением γ/ = s; —
— 1), записываем явный вид матричных элементов нулевого
столбца [His
<ft<о>(8) = A\ki) V{2k + nk^-k2»n_~ ехрЦт.ЛГ*) Χ
V/ V/
χ Π (sin θ^ζί.,)^1 Φ^1^Τ# "/+l4"~ (cos 9^/«ι), (Ы54)
/-ο
*/-*/+*
где
2 η—3
γ(-) '=» '
#*ж = (*; - W (2k/ + V/ + ')Γ (fe/ + */+ι + V/+ i)
*/ 22*/+'+v/+,r»(*/+-J_+l)
$f* (χ) — полином Якоби [204].
(1.155)
БЗ

Однако согласно параграфу 1.7 этой главы (см. также [2, 5])
решению (1.154) соответствует каноническое дерево, приведенное на рис. 13,
на котором помимо гиперсферических углов Θ,- указаны также для
каждого узла значения kj (/ = 1, 2, ..., η — 2), задающие величину
гипермомента в пространстве En—j (очевидно, что kj совпадает с 4-/,
использованным в параграфе 1.9). Подобный график однозначно
задает структуру соответствующей ГГ.
Согласно (1.137) ККГ определяют разложение произведения двух
деревьев по самим же деревьям. Для удобства в выражении (1.154)
используем полиномы Якоби с равными индексами вместо полиномов
Гегенбауэра, встречавшихся в (1.132). Полагая в (1.152а) {k\) =
= {ki) =a {kt} = {0}, имеем
__ (2k + n — 2)(k + n — 3)1
~" k\(n — 2)!
h\
Используя
«Mm (β)--} wzrn^
J ^0} {0} (g) $>} {0}
Ό(η)
(1.156)
SO(n)
n—3 n—3
2 ' 2
a«—I
(cosen), (1.157)
а также значение интеграла D {I, m, n, p) [14, c. 485], находим явное
выражение правой части (1.156). Проведем калибровку ККГ, выбирая
fk' {0}\
k" {0} I действительным и неотрицательным. Тогда после несложных
вычислений можно записать
2"~4 (2k + η — 2) Г ίγ (k')\ (k")\ Γ (Ι + η — 2)
VHΓ Ι "Ι ) (k' + η— 3)! (k" + η — 3)! Γ (/ — k' + 1)
„/ « — 2 \ / η —2 \ / η—2 \
TU~k' + —s—JT[l-k' + —s—JT^-k+—T—J
Γ(ί-*·+1)Γ(/-*+1)Γ^+-5-)
где 2/ - ft' + k" + k.
Отсюда искомый ККГ
fk' {k'i}
k" {k() ) = 6(mn-.2 + /Пп-2, m„,2) X
X
(1.158)
54

χ
(ft _j_ η _ 3)1 Γ (^i1—) Г (/ — fe' + 1) Г (/ — ft'-f 1)Х
χ Γ (Ζ — k+l) r(l + -%-\{n—2)\
2«-4fe! Г 1^^- \ Γ (ί + η - 2) Γ // - k< + ^—-) χ
χΓ(/-*. + ^)γ(/-* + ^)
η—1
г 2
Χ
(2k· + η — 2) (2*· + η — 2) Γ (-3-1
\k'j k) kt ) "l "l '
k, у
(1.159)
*'
х j(i-*8)
—ι
2 337+1; */+·
Mx
Ъ+^(Х)№+^\x)dx.
κ}+1=^·+1 + -^-. (1.160)
Таким образом, задача вычисления ККГ группы 50 (л) свелась к
вычислению интеграла (1.160). Отметим частный случай этого интеграла
при j — η — 3
Ч'г_2 k"n-2 kn-2\ Г(2*1-а+»)(2б;_ч+1) 1т у
*„-з+0 ]
ra-3
^kn—3 kn—3 kn—Э)
(2*„-з +
2(2*
*п-Зи
У (Γ "~ό~ /ρ*η—3·*η—2
*η—3°·*η—3° *«—3*η—2· *π_3*η—2
(1.161)
который совпадает с формулой (1.149), где использовано другое
обозначение для ККГ
Из теории представлений группы SU (2) известна формула
разложения произведения модифицированных функций Якоби с помощью
ККГ [14, с. 192]:
&Ъ (х) **£.* (х) = Σ' $ЯШ*№*1+*.г+* (*)· (1162)
/«|/ι-/8|
Принимая во внимание, что [14, с. 133]
*1Пв0(х) = 2ГМР* У(1-т)Ц1 + т)\ {χ _ ^ 2 эд^т, {χ)$ (1 Л63)
55

получаем формулу
<ημ..μ. (r\ <??"»* — 'V? Γ (λ-μι —μ>)1(λ + μ1 + μ2)! ΥΤ
-Ρλ,-μ, W ^λ2-μ, - 2j Ι (λ, - μι)Ι (λ, + μι)! (λ, - μ,)Ι (λ2 + μ2)! Ι Χ
λ«|λ,-λ2| L J
χ -^- <Cj^&1&^^ (1.164)
λ,+λ? ]
Из теоретико-групповых соображений следует, что разложение
(1.164) справедливо лишь для целочисленных значений всех
параметров. В качестве первого шага на пути вычисления интеграла (1.160)
докажем следующую лемму.
Лемма. Пусть kt^0 и μί ^ 0 — целые или полуцелые числа,
такие, что μ, ^ λ^ и kt — μ^ — целые числа, тогда справедливо раз-
ложение
λ+λ, -Ϊ-
Ж«·* (г\Ш*>»> (г\ - V Г (λ~μ!-μ2)Ι(λ + μι + μ2)1 Ι2 ν
,-μ, (X) Vb-bW - 2j (λ, - μι)! (λ! + μι)Ι (λ, - μ,)! (λ, + μ2)!J X
Χ ΡΥ5Γ+Τ) ^λ10λ$00/λίμ1λίμ2-Ρλ—μ,—μ, W» (1.100;
где суммирование распространяется на целые или полуцелые значения
λ в зависимости от целостности λχ + λ2, α (ϋλ?ολ2ο — аномальный
ККГ, который определяется формулой
С" λο
λ,0λ20 =
nrpnsfl^+λ,-λι/ (2λ + 0 (λ + λα — λ2)! (λ — Xt + λ8)? (Xt + λ2 — λ)ϊ
2 Г (λι + λ2+λ+1)! *
χΓ/λ1+λ2 + λ + ΛΓΓ/λι-λ8 + λ + λ
χΓ/λ,-λ,+λ + Λρ/λ, + λ,^λ + Λγι^ (1Лб6)
(Очевидно, что при целочисленных значениях параметров аномальный
коэффициент (Смдо переходит в обычный.)
Доказательство· Запишем разложение (1.165),
предполагая коэффициенты разложения неизвестными:
юн.». /r\ W·*· (у\ - V Г (λ-μι — μ«)'(λ + μι + μ«)1 р ν
Λ. -И. W *W, W - 2j [ (λ, - μχ)! (λ, + μι)! (λ2 - μ,)! (λ, + μ,)! J X
Χ Α^μ,; λ2μ2; λ)^^+»*(χ). (1.167)
Продифференцировав (1.167) по х и воспользовавшись
аналогичными разложениями для слагаемых, возникающих в левой части,
получим рекуррентное соотношение для коэффициентов А
Κίλ,-μιΗλχ+μχ+Ι) Α (λιμι + 1; λ,μ^ λ) +
+ Κ^-μ^ + μ,+ Ι) Л (λιμι; λ2μ2 + 1; λ) =
- ν(λ-μι-μ2)(λ + μι + μ2) Α (λιμι; λ,μ,; λ). (1.168)
56

Равенство (1.168) совпадает с рекуррентным соотношением для ККГ
группы SU (2). Отсюда
Α (λιμι; λ2μ2; λ) = В (λΛλ) (С&Й,· (1 · 169)
Для определения множителя В (λ^λ) положим в (1.167) μχ = λ1 и,
воспользовавшись ортогональностью многочленов Якоби, найдем
Г (1 - дс^+'ЧдеЗ. (χ) ϊ&^+μ· (*) d^: =
j_
_ Γ (λ-λ^-μ^Κλ + λ^μ,)! Ι 2
-[ (^ΟΙίλ,-μ^Ιίλ, + μ,)! J A
V 22Μ-2»,+1Γ»(λ+1) β fU +μί π 170
Χ (2λ + 1) (λ + λχ + μ,)1 (λ - λχ - μ,)Ι ΰ (λιλ*λ) ^λ,λ,λ,μ,· (1.1 ™>
Интеграл в левой части (1.170) вычисляется с помощью соотношения
J(1 _jfif да*WfWd* = -I- J (l _ ду**^1 Ac.
ККГ в (1.170) не содержит суммы и имеет простое одночленное
выражение. После несложных вычислений можно записать
*<МЛ =Γ(λϊπλΧιλ)'+>)^,ο, (1.171)
где (Сх5>м определяется формулой (1.166). Лемма доказана.
Воспользуемся формулой (1.165) для вычисления интеграла
(1.160). Представим произведение первых двух многочленов Якоби в
виде
$*/+i;*/+i (Х) $>r *ж {х) β
= $*Ж' κ/-Η (χ) Βκί+Γ */+ι (jc) β
(* - к]+1 — Х/+1)1 (< + Х;+1 + Х;+1)1
*;+*
/+v/
/-!*,—*,·|
г
Χ
r(fe;.+4-+')r(fe'/+4-+1)
Χ γ. —(С / γ/ „ γ.·
χ £'*/+ΐ+*/+ι β φ/+)+*Η·1·*ί+ι+*Ι+*(χ). (1.172)
Аналогично записываем
ус/+1+к/+1. κ/+1+*/+1 до срхщ, κ/+1 до
«7

V/
α« ί—*ί- ■
(Ц — x)+1 - Χ/+ι - Χ/+1)1 (Ц + Х/-Ц + Χ/+ι + Я/+|)1
(* -χ)+ι - χ}+ιίΐ Ρ + χ)+ι + xj+i)! χ
Χ (fy — */+ι)! (fey + */+1 + V/)!
Γ*
χ
"Γ(»/+-%- + »)
Γ(β+1)
С
uO
V/
Χ
»;*/+-g£-.o
Χ С
WH + TV/
??+,+ 4?:H,+ 4t,W. (1.173)
ί. κ'/+1+*/+1> Ar;.+ i, χ/+ι*'α"-^/+1— Τ ν/
<7/+ι = */+ι + */+ι + */+ι·
Оставшийся интеграл вычисляется с помощью таблиц [227] в замкну
той форме
—1
~33
«-"ж—г?/
'(*)<** =
πΓ (J/±J_t*L + l) Г «ι + 1) Г (l -Jj+L - V/) X
Γ / 9п — «. J- fi\ / /j v. \1—1
X
r(^±i)r(,-j-4)]
(.-,<+,-iv,).r(^t'""+i'-)x
хг(лн^±1+4Т/)
С помощью формул (1.160), (1.172) — (1.174) находим
„r(^i-tlL+i)r(i-ifL
(1.174)
■*)
^/4-1+3/2^+1)
Λέ4/
Рис. 14
^58

Χ 1(2*1 + 7/ + 1) W'i + Υ/ + Ο (2*/ + Υ/ + 012 Χ
(" + <//-Η + — Υ/) ι
*/+*/+*/
·—·*/—*y< «-
<-*.—
[("-<?/+!-—Υ/)'
©»
с<*Ж + к/+,
, ν/ » V/
tOk,
У/
V/
Τ/
y+—0 fty-l- _ ,χ/+, ;*,+ ._ ; K/+1
' [(<?/+I + I - «)/2 + "Τ Υ,] Γ [(<//+1 + « + 2)/2 + -j- Y/]
».H/+,+x/+i:ft/+-r.H/+,
^-i)r(,-^-A)·
(1.175)
(1.176)
*„_з, — fth^}, имеем
(1.177)
Отметим некоторые свойства симметрии вычисленных коэффициентов.
Очевидно, что
k {kt} J \k {ki)
Далее, вводя обозначение {k^ = {k^ k2,
k'{k'i)\ /k'{k'(\
Наконец, из формулы (1.159) нетрудно получить
J,Г\ 1 - Г *»<У + "-3)1(2*' + я-2) 1 2 / .
'?'Г (*')!(Л + л —3)!(2fc-f-n —2) I Ι* \**}
ft' {k\)J \fr{ftf}
Эти симметрии являются обобщением соответствующих симметрии
ККГ группы SO (3) при условии, что V + Г + I — четное число.
(О вычислении ККГ для группы О (п) см. также [2281.)
1.10.2. Коэффициенты Клебша — Гордана представлений класса 2
группы SU (п). Согласно параграфу 1.7, а также работам [2,5] с
канонической редукцией SU (п) =э SU (п — 1) z> ... id SU (2)
сопоставляется дерево, изображенное на рис. 14, а. (Можно также
рассматривать дерево, зеркально отраженное в плоскости листа относительно
вертикальной оси у. Вопросы симметрии при таком отражении будут
рассмотрены в следующей главе.)
Воспользовавшись алгоритмом, сформулированным в параграфе
, напишем ортонормированное решение, относящееся к дереву
59
(1.178)
1.7

(см. рис. 14, я), в виде
ψΓΓ.Χΐι Φι» · · ·» θ#|-*ι; 4>ι· · · · t Фл) =»
= idp" Л ^Ш/Ф/ Д *Vw*i (в,) X
Χ [2((λ^2+1 )] V-X (cos 2Θ«·,), (1.179)
2 * 2
где ^μ,ν (cos 2Θ) — матрица конечных вращений группы SU (2)
(на рис. 14, а выделенный штрихпунктирной линией блок, экспоненты
выделены в общее произведение). Функция, соответствующая ячейке
(рис. 14. б), имеет вид
п\ 2. Imtl
*!*+,«, (ft) =2* [A^f *(1-сов2в,) 2 (1 +
ii±L
+ cos20O 2 $^(008 29,), (1.180)
где 0<θ^π/2; 0.^φΛ^2π; ηΊ == 2nj — размерность вещественного
подпространства; α = | mf | -J- -^— ! β — Wi + -^— ! 0* = 2/г —
— (2/+1); 2* = Яг — λί+ι — I ml |, *>0; Ci(s*) — число узлов,
лежащих налево (направо) от вершины /.
Для дерева (см. рис. 14, a) sf = KB дальнейшем нам понадобится
другой вид решений (1.180), а именно их выражение через матрицы
конечных вращений группы SU (2). Учитывая связь полиномов Яко-
би и матриц конечных вращений группы SU (2) [14, 2101, получаем
выражение для решений (1.180)
п. JL
IVi+i-i <*i> = 2~ Г*** [^f1] ' Црг <*, С*Л С1.1в0«>
(1 + *,) 4
где
*=}/—1; A:i=cos20/; п\ = 2п — 2(1 — 1);
;-А.1 ι. „ - *4+i + lm|l . n'i ь
vi== - +—— 1.
Вид проекций μ^ ν^ обусловлен соотношением с% — $ι~ η] — 4,
вытекающим из условий сг + si = п\ — 2 и st = 1.
ККГ для представлений класса 2 группы ί/ (η) (ненормированные]
определяем по формуле
C:;;sK^ ъ* ?»....*) χ
«О

mi ••••«тя»'п ,л
Х*Г ι' <θι· ••·»θ»-ι; φι φ»)
ft И
Ή. т„
ι η
«.+· ··+*» ■■я»*
//г = 2 "**» m\* ..., mn, λχ, ..., λ«—ι
t=
m =
— 2 ^*' ^1* · · · · mn* *Ί· · · · » \i—l
i=l
(1.181)
Χ 4^Ι#·" m*nim*$i> . · .i *n~u Φι. ..., Φη).
Умножая левую и правую части равенства (1.181) на ^Ι'"""1/1'"1" χ
Χ (θ^..., θιι_ι9 ψι,..., φβ) и интегрируя по всем углам, имеем
η
т ~ Σ m** mi» · · ·» mn' **» · · ·» ^л""1
ί«1
m
' = 2 friit m\9 · · · § fwrt> λι, ... t λΛ_ι
m* == 2 mI» mi> · · ·» m«» ^i» · · ·» ^—ι
i«l
Ъ*,....С-\ (Qi> · · · ♦ θ"-'« Φι Φ™) Χ
Ω
Χ утУ""У-т' (Qlf..., θ„_,, φ! φ„) ψ"? "Ι"·"1 Χ
&Ι*···ιλη—1 λ^ λη_ι
Χ (8lf ..., θ„_ι, φΧ9 ..., φη) dQ, (1.182)
dQ я Π cosc' θί sin θ^θ, Π dq>k - Π :^ <**ι Π dtp*. (1.183)
η-1
ί=1
Λ=!
i=t
Ί+3
6=1
Учитывая формулы (1.179) и (1.183), получаем для ККГ
выражение
1ΐί% tfl^9 · · · t fTljif ^ί* · · · ι Α*ι—ρ
< «i «* λί ^ |= Πί^;/[5ί/(2)]χ
\m"f n%u ... ι //in» λι* ...» λ/ι_ι,
«~2 J
*#-!
x Д j V^***^;^ <**%;+,,.; <*'> 4k dx"
2 2
(1.184)
61

в котором выражение для / [SU (2)] имеет стандартную форму
интеграла от произведения трех матриц конечных вращений:
λ,
η—Ι
*9> } . * * (Xn-tidxn-u (1.185)
2 * 2
Интегрируя (1.185), имеем
,,»«, . 2 (i=^±if (U-tlf (.%iif x
V-l mn+mn—\
x(C 2 ' 2 , , , χ
λη—1 rnfl-\-mn_l ^ Xn_\ mn+mn__x
2 ' 2 : 2 * 2
X (C 2 * 2 , , , . (1Л86)
2 * 2 2 ' 2
Здесь (С/^,/2р,2 — ККГ для группы SU (2).
Чтобы получить явное выражение для ККГ группы SU (л),
необходимо вычислить интеграл
2 2
(1.187)
Подставляя (1.180а) в выражение (1.187), записываем
χ $ *ί,,4 <*,> ^; w ^ —Vr · (1 ·188)
-1 (ΐ+ν 4
62

От произведения трех матриц 5*μ,ν (χ) перейдем к одной матрице по
формулам
pit (х) &\ Ах) - "£ £JiMl, , (Π''"' - ?ι. . (х), (1 · 189)
h
P[ . (χ) = (_)V-V'i ,.(*), (1-190)
μ.,ν, μΓν.
&h {x)9>l, ,(x)l?'t , (x) = (—)V'_tli У (J ", I ", , X
Ji
■,J,M, ^J,N
Jl i'ri i i'i i
причем Aif = Μ; + μ'ί = μι + μ] + μ£, Nt = #ί + ν] = vf + νί + vt:.
С учетом формул (1.189) — (1.191) выражение (1.188) можно
переписать в виде
χ <-)ν'"μ' у (р^ <rJ'iN'1 <rJiM* <rJ'Ni χ
Χ { (1 + x,)"1"^^. (*ι) d*i- (1 · 192)
-ji *' *
Если в последнем интеграле перейти от Фм^ (х) к полиному Якоби
по формуле [14]
^MvNt (X) - 2 ι [ (7,-Λφ! (/, + *,)
1/2
Χ
Mt—Νι Mt+Nt
χ{1-χ)-^Γ- (1 +x)—— Щг^^Нх),
то получим стандартный интеграл [227, с. 201].
Отметим, что фазовые множители перед интегралом
компенсируются. Так как Mt — Nt - | m, | + | ml \ + | mi J, то Г|т'|Чт',+|т'1 X
χ f«r-wi = (-)~"Ч Вместе с тем (-)ν'"μ' = (-)"""'', следова-
тельно, (—)ν'~μ' (—)""'' = Ι-
Вычисляя интеграл с помощью таблиц [227], получаем

χ
п(ьж + х;_(.1ч- λ;+1)/2-Μ-π
χ/
Γ И | m{ | + \ηϊ( | + | m" | )/2 + 1J Γ[(λί+1 + λ'ι+ι + λ^ +1 я», | +
Γ (./,-Λ^, + ΛΙ,)! μ
Χ 2j [ (Jt-Mt)\Ut+Nt)l J
— Jt + Mit Ji + Mi + l, s 1-1;
|«il + |«i| + |«i| + lt Mr
n — i —I
+ 2
4.
(1.193)
Здесь s^a \Pl' p2' ^3M — значение гипергеометрической функции
Wi» Яг I
ρ /Л. Л, Λί ζ\
при ζ = 1 [229];
κ=ί 1 η — |m,.|— |mi| — \пЦ\\ /, = λ, + n~g~' ;
/ί = λ/ +
/; = λ; +
η — ί— 1
n — i —I
2 ; 2μ{ = λί+, +1 m, | + η — ι — 1;
2ν, — λί+ι — |/Π|| + η — Ι — 1;
/Л'Л 'Л'Л WX Wzvi
2Μ',(Μ) = λί+1 + λί+ι _±|т,| ±|m'i| + 2(η-ί- 1); (1.194)
2Λί4(Λ^ι) = λί+ι + λί+ι +λ"ι+ι ±\m,\±\m'l\±\m"l\ + 3(n — i— l);
Λί, + ΛΛ, = λί+ι + λί+ι + λί+ι + 3 (π — Ι — 1).
При записи окончательного вида для ? (t) мы учли формулу
удвоения для Г-функции.
Таким образом, формула для ККГ представлений класса 2 группы
SU (я) имеет вид
/Я, /Hj, . · . , ttljit Aj, . · · a An—1\
m', mi m;, λ', С, ) = /[Si/(2)] ft «,^χΠ *(fc
(1.195)
Рассмотрим группу SU (3). Для нее произведение ? (i)
вырождается в один сомножитель ? (1) (так называемый изоскалярный фактор).
€4

Поэтому формула для ККГ упрощается:
т, ml9 т2, т3, λΐ9 λΛ
т\ т'и тъ тъ, λί, λ2 Ι —
кт\ т'и т2, щ, λϊ, λ2/
= I[SU(2)\f(l)Tl6a
ί=1
%+m
ν k
(1.196)
Выражение ? (1) есть значение
интеграла (1.193) в случае η = 3.
Редукции группы Si/ (3) =э S£/ (2) теперь соответствует более простое
дерево (рис. 15), левый блок которого представляет собой группу
изоспина SUt (2). Представление группы SU (3) задается числами
λί и т = тх + т2 + т3. С числами ρ и q, характеризующими
степени контрвариантных либо ковариантных векторов, λχ и т связаны
соотношениями [2]
p + q=Xl9 p — q^m. (1.197)
Для более полной характеристики ККГ группы SU (3) напомним
соотношения между введенными нами квантовыми числами и
собственными значениями операторов изоспина 7\ его проекции Т2*
гиперзаряда Υ и заряда Q (см. формулы (1.116) — (1.120)):
27 = λ2, 2Г3 = щ - /na, Q = Т3 + К/2,
ЗУ = гпг + т2 — 2ml9 3Q = 2m3 — m2 — mlf
(1.198)
^ + 2p
<V<
P + 2<7
Ρ + 1Я
<Q<
Ър + Я
Учитывая соотношения (1.197) и (1.198), нетрудно переписать
формулу для ККГ группы SU (3) через р, q, Г, Т3, Y. Отметим, что
формула (1.196) дает ненормированные ККГ и, кроме того, не все ККГ для
разложения прямого произведения [k'} X \k"} на неприводимые
компоненты могут быть получены с ее помощью, как явствует из
замечаний, сделанных согласно формуле (1.152). В частности, в разложении
прямого произведения представлений
(PiQi) X (РгЧг) = Σ &' Ч) vpq О·1")
'Ρ,Φ
она охватывает только те слагаемые {pq)y у которых ρ + q = рх + qx +
+ Р2 + 72, Ρι + 4ι + Ρ2+42 — 2, ..., 1 илиО, ρ —9 = ρ1 + 9ι + ρ2—92,
т. е. (/?, 9) = (рг + pt9 qx + qt), (Pl + p2 — 1, qx + q2 — 1), ..., (α, ft),
где
(я, ft) = (0, qlJrq2 — Pl — p2), если /?t + p2 < ^ + ^2;
(1.200)
(a, ft) =» (/>, + p2 — qx — ft, 0), если jt>i + /?2 > <7i +
Причем если представление (р, q) из набора (1.200) встречается в
разложении (1.199) с кратностью vpq > 1, то описанная выше
процедура позволяет получить только один комплект ККГ типа
5 1-1980
65

((piQi) X (Р2Я2) I (Pi Я)) Для группы SU (3), т. е. не решает проблемы
кратности представлений в разложении (1.199). В частности, в
известном разлол елии произведения «октета» на «октет»
(11) X (11) = (00) + (30) + (03) + 2 (И) + (22) (1.201)
таким путем можно получить только ККГ для (pq) = (00), (22) и для
одного из двух представлений (11), а именно, для представления (1 l)s,
входящего в симметричный квадрат представления (11). Процедура
получения ККГ для произвольных представлений группы SU (3)
в каноническом базисе SU (3) =э SU (2) с полным решением проблемы
кратности предложена в [223—227]. На ее основе составлены и
функционируют программы расчета ККГ для группы SU (3) в случае как
канонической редукции, так и неканонической редукции SU (3) =э
о SO (n\
В случае как группы 50 (ή), так и группы SU (п) находились ККГ,
соответствующие канонической редукции групп, а именно, функции,
относящиеся к деревьям, изображенным на рис. 13 и 14, а. Для того
чтобы знать ККГ при других редукциях групп, необходимо уметь
переходить от дерева, соответствующего фундаментальной редукции
пространства, к произвольному дереву. Этим вопросам в основном
и посвящена гл. 2.

Глава 2
УНИТАРНОЕ ПРЕОБРАЗОВАНИЕ
МЕЖДУ БАЗИСАМИ, СООТВЕТСТВУЮЩИМИ
ДЕРЕВЬЯМ РАЗНОЙ ТОПОЛОГИЧЕСКОЙ
СТРУКТУРЫ
В ряде задач ядерной физики возникает вопрос о построении волновых
функций определенной симметрии относительно перестановок частиц
(нуклонов). Именно перестановка приводит к тому, что мы должны
уметь преобразовывать дерево одной структуры в дерево другой
структуры. Действительно, в качестве ГГ для системы частиц выберем
функции, графический образ которых получим, объединив при построении
дерева координаты, принадлежащие каждой из частиц. Тогда,
например, для трех частиц находим дерево, изображенное на рис. 16, а.
Как видно из рис. 16, а, перестановка частиц приводит либо к функции,
соответствующей этому дереву, но с другими квантовыми числами,
либо к функции, построенной в соответствии с деревом, приведенным
на рис. 16, б. Аналогичные графы можно построить для любого числа
частиц.
Коэффициенты, переводящие угловую функцию одного дерева в
угловую функцию другого, называются Г-коэффициентами [3,6] (tree
coefficients).
Угловая функция, умноженная на ρ в соответствующей степени
(р — многомерный радиус), является однородным гармоническим
многочленом и может быть разложена по многочленам, соответствующим
другому дереву.
Для того чтобы разложить угловую функцию, заданную на сфере
Snmm] и относящуюся к дереву 77?, по угловым функциям, построенным
в соответствии с деревом 77?', введем графы 77?lf..., TRn-\ (TR0 a
ев TR, TRn = TR'). При этом дерево 77?/ отличается от 77?/-.ι (/ =
= 1, ..., η) лишь пересадкой одного «сучка» с левой ветки
относительно некоторого узла σ на правую или наоборот. Причем при пересадке
ближайший «сучок» слева (справа) становится ближайшим справа
(слева) относительно узла σ. Очевидно, что матрица (77? | TR'} при
этом факторизуется:
(ТР | TR') шш (TR01 ΤRn) - (TR0 \ TRX) (TRX \ TR2)...
...(TRn^\TRn).
В дальнейшем матрицы (77?/_ι | 77?/) назовем Т-коэффициентами.
Поэтому необходимо найти лишь матрицы, соответствующие пересад-
5*
67

l'f Χ* X3 у' ϊ* Χ3]Χ1 У* Υ·*
*7 АГ ЛГ λ2 At 2 AJ AJ Aj
Рис. 16
<* β Τ
\ \ }
\ V
\ Yr
V
IF
6Г
ОС β
ν
ν
ν
.-тис.
Рис. i8
ке одного сучка с правой ветки на левую либо наоборот. Ввиду
унитарности матрицы перехода одни и те же коэффициенты выполняют
прямое и обратное преобразования. Приведем на рис. 17 основной
конструктивный элемент деревьев. Из рисунка видно, что каждая
из трех внешних линий либо имеет узел на конце, либо нет. Отсюда
получаем число типов пересадок, равное 23. Детальный вывод
выражений дадим для двух коэффициентов и краткий — для остальных.
2.1. Различные представления для Т-коаффициентов
2.1.1. Рассмотрим выражение для Г-коэффициента в общем случае.
Согласно правилам, изложенным в гл. 1 (см., также [230]), связь
между функциями, относящимися к основным элементам деревьев
(рис. 18), можно представить так:
2 * {Λ^/αΓι/2(ΐ -*f\\ + *)a/%6;/a(*)2 * \Νιί*Τχβ
χ
Χ (1 - *i)V/2 (1 + *ιΓ V^ (Χύ Πφ,ρν » Σ J)
'α 'β 'ν
'ε 'σ *ο
%+s3+4
e+sv+4
χ
-1/2
Χ
χ {tf#Tl/2 (ΐ -yf2 0 + yf2^t(у) 2 4 К*!*)
X (1 -У1>е/?0 + Уг)а,2%^(Уг)Ща^ (2.1)
Здесь1 Πψαβν — произведение функций, относящихся к веткам,
лежащим выше узлов α, β, Yi /а //ν — Г-коэффициент в
«/-представлении»;
χ = cos 2Θ, хх — cos 2φ, ί/ = cos 2Φ, ί/χ = cos 2·ψ,
68

ία
/.
#1
= α +
= 8 +
σ —
2
S8
2
η2 =
δ-
2
—
α
/ι.
Ί».
ε —
- =
/δ = δ +
δ-
α —β
2 ~"
SP
2
2
-Ρ-
2
'.-
'σ-'ό-'α-·
2
Ό-4-
'ν*
— /2, /γ —
== *23>
-γ _ *a~
'«-'β-*
2
-; л^2 =
1
7 +
2
"" »
σ —
2
ΐίϊ.
8 —
2
— 1
JL
/
4
4
Χ2
*β
4
4
9
*2.
+ 4 +
2
+4
+ 4-
+ 4 +
-4
9
4
4
4
Введя вместо косинусов их выражения через декартовы координаты
ха = ρ cos θ, Cos 2Θ - *?~$?^-
x$ = ρ sin θ cos φ,
xy = ρ sin θ sin φ, cos 2φ =
для левого дерева и
Ха = Ρ COS Φ COS ψ, C0S 2ϋ =
*β = ρ cos Φ cos ψ,
a;v = ρ sin Φ, cos 2ψ =
для правого (ρ2 — ха + х$ + Ху) (см. рис. 18), можно сократить
левую и правую части соотношения (2.1) на одинаковые множители и,
естественно, на Пг|>ару, которое мы ввели лишь для полноты. В
результате такого сокращения
2^/2 (sin2 θ)"1 ψ*;1* (cos 2Θ) ψ*** (cos 2φ) =
= ΣΙ !α /β ί712'ε/2 <cos2 *)"2 Щ*г (cos 2*) f£/a (c°s 2ψ), (2.2)
где ffi;v (χ) = $£ν (χ)/[Νην}{/2 — нормированный полином Якоби·
Это соотношение можно рассматривать как тождество.
Положим χν = О, т. е. Φ = φ = О, Θ = г|> и cos 2Θ = cos 2ψ =- χ.
Тогда формула (2.2) примет вид
2-г-п·(i-xrWg*(x)W,z'4i) -
_ у суГ I la h ly
h ^|^в(1)ЧЩ.'«(х). (2.2а)
69

Г Умножая (2.2а) на $£'а (х) и
интегрируя полученное выражение
от —1 до 1, записываем
la. h l\
<δ-Ί
Рис. 19
(пг + 1ЛШъ + 1г\^ (!
/. Ιο Ц
Χ [Ν***)*1" (Ν'/*}-1'2 χ
χ C\tly) (%ΐ Τ \(ΐ - x)*tlH3 (*+x)ta %*la ix) v'*la (x) dx-
(2.3)
Учитывая значение интеграла [227], для Г-коэффициента находим
выражение
Ι/α h *т! Г^^л^/р+^Г^/^п^/р)
|/t lo h\ Т1Ь+1)Т<*1 + *а+Ь + Ы* + 2>
N%\ l6lBT fa + /p + /γ + 1) Γ (JVX + /fl + /tt + 1) Г (пг + /β+ 1)
^1!ιι1Ιπ1!Γ(ΑΤ1 + ίό + 1)Γ(Λ1 + /, + 1)Γ0ν, + /τ + Ι, + 1) Χ
Χ
Γ (ηχ + /γ + 1) Γ (η, + *« + /β + Ο Γ (Ν% + /g + 1)
1/2
Χ г(^+/7 + 1)1Г(Л/1 + /а+1)Г(Л1 + /3+1)Г1 J X
χ F \— η*> 'α + /β + /4+ 1, лх + /э+ Ί, /t& + '& — 'λ + 1;1 f24)
4 9[h+U ηι + Ια + Η + Νχ + 29 m + lfi-lb-^+l J
2.1.2. Воспользуемся рис. 19 для представления коэффициента
перехода между деревьями.
Согласно работе [13], свободный конец можно считать линией,
содержащей узел (a, sa), с а = 0, Sa = — 1. Поэтому здесь будем
пользоваться более удобными обозначениями для Г-коэффициентов,
чем в работах [6, 7]. Поступая так же, как и в п. 2.1.1, находим
2" h lvL· [jyy*r|/2 ιΚ*!&~ιβ [Kttrl/2 №ιι/2 ^^ χ
Κ la h I
χ/η1 + /ν\/^Ζν\^ ([(^^«.^^(^^(^^ (2.5)
Здесь обозначения те же, что и в п. 2.1.1. В случае (σ — δ) Φ (ε — δ) χ
Χ (mod 2) интеграл в (2.5) обращается в нуль. Поэтому рассмотрим
два случая.
При σ — δ ~ 2ρ, ε — β = 2q, используя формулу из § 7 [61, находим
/α—ιν
-χ h h\ <-)«ф + 9+—)2~
/. /, /J rtk + OitrL + ij + i + ^JiB!-
X
?)i
70

Рис. 20
Рис. 21
X
пг! Nt\ Г (lit + /ρ + 1) Г (пх + 1у + 1) Г <Λι + /ft + 1у + 1) Χ ~| 1/*
XT(2p+2l6 + \)l{sle(2q)\
(2р)1 Г (29 + 2/р + 1) Г (N2 + ly + 1) Г (N2 + ly + 1г + 1) X
ΧΐΤ(Ν% + 1Β + \)Γι
X
хЛ
— Л Ρ+'β+'-o-t ^ + ^+1,^+1;
k + 1, nx + Za + i + ^t πχ — ί+i
. (2.6)
При σ —- δ = 2/? + 1, е — β = 2<7 + 1 с помощью формулы из
§ 8 [6] получаем
• "2" *β *ν ι
/p.
la U
Χ
(-).г(,е+<+4)^·"·""
Γ (l6 + l)q\T /я, + ίβ + </+ -§-) («!-</)'
«ι» #,! Γ (щ + Ζβ + 1) Γ (щ + ί? + 1) Γ (Я1 + /β + ί? + 1) χ
хГ(2/> + 2<а + 2)<а'е(^+')'
(2р + 1)1 Γ (2q + 2/β + 2) Γ (tf, + *ν + 1) Γ (Nt + ly + /e + 1) χ
Х|Г(Л/а + /8 + 1)Г'
Χ
1/2
Χ
Χ 4^1
—ρ, ρ + ι* + -γ, «ι + /β + ι. "ι+ΐ;
*δ + 1, ti + *e + <7+-s-, «ι—^+Ι
(2.7)
2.1.3. Рассматривая рис. 20 и следуя развитому выше методу,
находим
/ L /
I? In U
= [Ν'^Γ1'2 [Νι$'«Γι/2 [<«'«Γ1/2 ]tfV.]'/?2v'-v' χ
Χ
+ /v\/iV2 + /ν\ > J ι(Ι _χ1),β^«.(1 _2jti)!pWaW4
где v2 =» ε — α; νχ == δ — γ.
(2.8)
71

χt хг ι/, х- хг у3
V-V
сг
Рис, 22
Рис. 23
Интеграл в (2.8) отличен от нуля лишь при пг = п2 (mod 2).
Учитывая это условие, а также формулу из § 10 [6], получаем
/ L
/,
^-2-Ό-ν-ν·
Vi + Va -f 3
)(^)
Χ
Γ (Νχ + 16 + 1) Γ (ЛГ, + /β + 1) Γ (Λ/χ + /α + /6 + 1) χ
Χ Λ^Ιν^Ι /a/sr (V! + 2/γ + 1)
Γ (Νι + Ια + U Γ (Ν2 + /ν + 1) Γ (Ν2 + /ν + /ε + 1) χ
Χ
Χ Α7!ΐν2![Γ(ν2 + 2/α+1)Γ
ϊ
1/2
X
χΛ
— tflf ЛГг + /а + /0 + 1,
/ ι 1 νι — ν2 + 2
νι+ 1
νι + ν2 + 3
Vi + *
+ /α
(2.9)
2.1.4. На рис. 21 удобнее разлагать угловые функции правого
дерева по функциям, соответствующим левому дереву. Коэффи-
I/ / LII
циент α 3 2 отличен от вычисленного в п. 2.1.2 коэффициента
(I t$ Lq Lq [J
1
только заменой /ν -> /α, Ιε -> k и множителем (■
\ε—Ρ-σ+β
—jhh\
*ε ^σ *ό (ι
2 1.5. На деревьях, изображенных на рис. 22, в вершине вилки
(ххх^ мы поставили постоянную ν вместо ε в связи с тем, что ε ;> 0,
а у вилки со свободными концами постоянная может быть как
отрицательной, так и положительной. Используя подход, предложенный в
п. 2.1.1, находим
£- /.
/ν
Ιο
Χ [<^]
'δ 1-1/2
_ι 2π
f sin6-^' φ ^_ΐ'6Λ (cos φ) erl*tdy.
(2.10)
72

Интегрируя выражение (2.10) с помощью формулы из § 4 [6],
приходим к следующему виду для Г-коэффициента:
2 2 'ν
L
/λ
(-)' r (Ό>
ikn (k —1)\
T(2l6-k)
T(N + \v\+\)N\2lbk\
X
In + /δ + 4" -*)я1 г (
r|/v + /6 +
X з'г
'ν + lb + ^Γ
1/2
Χ
— η.
k + ~;
-'ν+1. -Z + ft + l
(2.11)
где
k = /ό — ly —2" ; η== la — k —2~
_ σ —γ —jv| __ /0 - ly - \ly 1 - !
iV "" 2 ~~ 2
л σ — у — ν ^σ — ^γ ^ν *
' ~~ 2 2
; h = г + -%- ; г = γ»ν> <*» δ·
2.1.6. Рассматривая рис. 23 и производя операции, аналогичные
проведенным в п. 2.1.1, получаем
1 / х
h —о"
2
= [Νν*Γιβ ιν1Άγ]/2 [№\l'2i№r1'2 χ
χ
(-Γ~δ г (/σ + 4")Γ ('ε + * + i) s\ 2m>~m
/·!Γ(/β+/· + 1)Γ(/η2+/ε + 1)
1
χ J<i-*),p+r¥££(*)$S(*)d*,
χ
(2.12>
где
/η^δ-β; г = [-^-]; /β=β +
т2 = о — ε; s =
"-1-I; ίδ = δ + 4-; 4=e + 4-i
[г] — целая часть г.
Интеграл (2.12) отличен от нуля лишь при условии σ — δ = (ε —
— β) (mod 2). Поэтому приходим к двум выражениям для
Г-коэффициента в зависимости от четности σ — δ и ε — β: а) σ — δ = 2р, ε —
— β = 2q\ 6) σ — δ = 2ρ + 1, ε — β - 2q + 1.
уа

В первом случае, воспользовавшись формулой из § 7 [6], получим
I 1 / >
[-~т 1» —г
"Г
(_ !)»·+»+» 2m'~2/en1/2s' Г (1г + s + 1)
Г (/в + 1) Г (? + /р + 1) qi Г (г + i„ + q + -γ\ (/■-«)!
mt! (2q)\ Γ (m1 + 2/p + 1) Γ (2p + 2/6 + 1) Γ (2<? + 2/p + ») "j"2
m2! (2p)l Г (m, + 2/, + 1) [(2/^ + 2/p + 1) (4<? + 2/p + l))"1 J
χ Λ
— Ρ, P + 'e + -2-, г-Ни-И, г+1;
/в + 1, г-Ь/а+^Ч-·^-, г — д+ 1
(2.13)
Во втором случае, учитывая формулу из § 8 [6], имеем
I—2" '»
ι
/. la h
(_)'+«+' qmt-2tW2s\ Г (/в + t + 1)
Г (/δ + 1)Г (<?+ /р + 1)?! Г [г + /р +? + -|-) (' -ί)«
Wl! (2q+l)l Γ (mx + 2/p + 1)Γ (2ρ + 2/6 + 2) Г (2g + 2/p +2) ]i/2
m,! (2p + 1)! Г (m, + 2/, + 1) [(2^ + 2fp + 1) (4, + Щ + 3)]
— Ρ, P + h+ -γ ,
JL]1,
,-l J
X 4' 3
r+k + h r+i;
k + h Γ + Ια + ς + -ψ-, r — q+l
(2.14)
2.1.7. Для деревьев, изображенных на рис. 24, удобнее разлагать
угловые функции, соответствующие правому дереву, по функциям,
относящимся к левому. Несложные вычисления показывают, что коэф-
11 1 Hi и ι ι "
2 2
/ / /
*g mj *μ
отличается от I 2 2 ν| лишь заменой
*ν ^σ ^6
1
_(α+|μΗσ)
ν ->■ μ (Ζν -*■ /μ), /ν ->■ 'α, /б -> /е и множителем (—ί)μ (—1) 2
Очевидно, что
.JL L ι
2 2 ^
/λ,
/Λ
/ι
2
/α
-L ι и
2 *ν|
2.1.8. Каждому из деревьев, изображенных на рис. 25,
соответствуют обычные сферические функции (см. гл. 1), и переход от одной
U

Рис. 24
Рис. 25
сферической функции к другой осуществляется £>-функциями Вигне-
ра (матрицы конечных вращений группы SU (2)). Тогда
Г-коэффициент, ответственный за переход между деревьями (рис. 25), есть D-
функция Вигнера. Рассмотрим это более подробно.
Запишем разложение функции левого дерева по функциям правого
дерева!
№ {Ν™*}-1'2(sin θχ)μ $?4 (cos 9t) =
1 1_ 1_ II
«- VI 2 Ieiy*9 №-*Г1/2 (cos ea)v^v (sin e2).
ν ι ν σ + -τρ μ J
(2.15)
Выражая сферические координаты через декартовы и полагая
х9 =з 0, находим для Г-коэффициента интегральное представление
I 2 2 2
ν σ + -γ μ Ι 1 *ν /σ /μ
(-) 2 2«
>σ—μ,
pf^Hzr^i')
Γ(σ+1)
Χ
[14]
Χ / glg'UtS ΐί <sin ΦΓ «&(«*,>)«-"·*,. (2.16)
Используя связь функций Якоби с матрицами конечных вращений
ЗП(*) = 2Т»Д}/17-
μ)!(/ + μ), О-*2) 2<oW,(2.17)
а также связь присоединенных полиномов Лежандра с матрицами
*ifl 1141
Г (2.18)
получаем
/?(*) = ;" /Ji±g^>o(JC)>
sin» φ^Λ(COSφ) - {~}ΙζΙΙ Pf (х).
(2.19)
75

Итак, можем записать
ι 2"
1 = ~έγ\ sintl ч>ЭД-» (cos φ) β~'νφ d(f =
о
Функция Ρα (cos φ) имеет интегральное представление [14]
Р%(cosφ) = /μ^ + μ)ί J (el«cos2jc/2 + e~ie sin2x/2)°е***йх. (2.21)
π о
Подставляем (2.21) в (2.20), изменяем порядок интегрирования,
интегрируем и учитываем интегральное представление матриц
конечных вращений. В результате этих операций
/_2μ_σ.^σ Г (σ + 1) |/ (σ + ν)»(σ-ν)1 ^σ Q)
r№ + 1)r(-^ + i) V <° + »Ч-М ^ν(0)·
(2.22)
Отсюда для искомого коэффициента
_1_ i_ _1_
2 2 2
in
lv ίσ /μ ||
= (-ΓσΟ«ν(θ,-f, —f). (2.23)
Итак, мы вычислили восемь типов 7-коэффициентов. Теперь
изучим их свойства симметрии.
2.2. Симметрии Г-коэффициентов
Свойства симметрии Г-коэффициентов можно находить либо из их
интегральных представлений, либо из их представлений через
гипергеометрические функции. В этом параграфе будем исследовать
свойства симметрии, пользуясь графическими представлениями и
операциями отражения дерева и пересадки веток [7, 81.
РассмотрИхМ ячейки на рис. 26. Здесь xt обозначает одну
координату (свободный конец), а ух (у2) — набор координат (х\, ..., х*\)%
(х{2, ..., л:?), с которыми связан узел α (β). Посмотрим, как преобразу-
У ются указанные ячейки при отраже-
f^ нии относительно вертикальной оси,
проходящей через узел σ:
* +
*ι
Vj + 4 τ Vj + 4
76

Лг х,
\/= ( ** + г-7=^=-\ =
= i°
Ж.
VJ+4
*- + *■
К?
Ч-г*2 г *, + *;
Из вида функций Якоби для ячеек бив (см. [2, 204] следуют
равенства
Уг
у, у2 у* у,
σ
Переход от одного дерева к другому с помощью операций отражения
и пересадок можно произвести различными путями, что и позволяет
исследовать симметрии Г-коэффициентов, работая только с графами.
Переход
<* β
β Τ
V —
осуществляется с помощью матрицы
&
Ια /β /γ
'ε ^σ *δ
. (Далее в этом
параграфе работаем везде в /-представлении lg = g 4- -у-, g = α, β, γ, ...
Для свободного конца в верхней строке будем ставить (—1/2).)
Тройной переход
* β Г ϊ β * Τ fi ы * β Г
& & <r
снова приводит к тому же дереву. Отсюда
&
lg Lq Ifi
ly I ft la
h la Is
(2.24)
77

Полученный результат можно представить в виде коммутативной
ди аграммы
+ β Г
ν -
<?
Г β «
J Г Г β *
f
(2.25)
Из коммутативной диаграммы
« β Г J Г ос J γ ее
(2.26)
следует
la 1$ ly Ι
0-f6—Е~-Р»^2у
(-) 2
e' II *·' *σ *61
ly la h
(2.27)
78

Другая коммутативная диаграмма
J Τ «
β Г «t
I
\y, _ χ/ _ \y
<* β Τ
γ ol β
Г ее J\
(2.23>
уу^ ν -V
(Г
приводит к равенству
|/0 /β 1Л 2σ1«-ε-«-ν
^8 Aj 'δ
= (-)
в-
σ-ε'—β II /, / /η
ε' 1*6 1>α *ε'
Χ
1 ^ν 'α ^
(2.29)
которое, однако, вследствие (2.24) и формулы
/ α-6-6-β + ε-«-3γ| ^ | За -6 -е -,' - « - β - у j (mod 2)
совпадает с предыдущим. Окончательно перепишем формулы (2.27) »
(2.29) в виде
Ι 'α ίβ ^ν
IК lo h
=(-)"
σ-τ-β—ε—б
Σ(-)
g'-a~1' II/й /α £,||ία Ύ 'β Ι
[ 'ε ^σ ^ε'ΙΙ || ^ε' ^σ ^δ II
(2.30).
Мы учли, что δ — γ — β = 2η', η' — 0, 1, 2, 3, ... (см. [2] и параграф·
1.7). Далее из диаграммы
х, β X,
σ
J
X, Хг
79·

следует формула
-"2" h
ιε ια /β
1 1 ι
σ-β-Μ
Χ
= Σ<-> 2
Μ
; L L
Ιρ. *Ή
2" '»
In le,
(2.31)
Аналогично из диаграммы
вг
ос
г *
получаем
h L ι
/ε /σ /^
a—E—y k-'—oi—y
= (-) 2 Σ(-) 2
/ ι __!_
Ζ Ζ ——
Л ^8' ^σ
Χ
Этот матричный элемент можно выразить и через матрицы
(2.32)
— / I
2 Ly lol
■ — ι ι
Действительно, согласно диаграмме
* ι γ *
Lq Iq l&'
Τ Α
80

имеем
L In /л
^{~)~Ύ~ Σ(-) 2
Ι L / / f
II — ο ν α "
'ό /σ /β
Χ
χ
L / ι
'a 'α 1&*
(2.33)
Нетрудно видеть, что наряду с матрицей На л / симметрией того же
_i_ t Lll
типа обладают ма рицы || 2 ·* 2 | и
Действительно, из диаграммы
'а 9~ ^V
/ε Ιο 1ь
χ. β χ?
χ, β χ2
V - \У'
ι
следует
а из диаграммы
Ι 1
2
и
h
Ιο
1 Ι
2
h
1
2
h
k
la
1
2
/.
'-V
получаем
/α -
1
ί.
2 'ν
la Ц
= (-)
2о^а-«-е-т |μν s- /α
Ι *β la ls
(2.34)
• (2-35)
€ 1-1980
81

Равенство (2.35) можно переписать в виде
ι
1 /а сг 'ν
IU la h
δ—ν—ε-fa
= (-) 2
/δ ^σ 'e
(2.35а)
Пользуясь графической техникой, без труда получаем установленную
в п. 2.1.4 и 2.1.7 связь между коэффициентами
L L /
2 2 1а
а также
/а
h
1
2
Ιο
pet /β
Ц/е /σ
1 Ι!
2
4
1
2
/б
-1
! I
-"Η
/σ /δ
ΣΤ Η ^α
Из диаграммы
οί β
Τ '3
^
находим
<r
*α *β ο"
= (_)—Г
i[Z±=!±Pl όΓ *β *α!
14 la 16
Аналогично из диаграммы
ее / 2
h la l\
б *σ *ε
oC J 2
/V-Уч
f 2 ос 2 1 οι 2 1 К
>
f Z Of. Δ I w- Ζ / **
(2.36
82

получаем
'«2 2
L U
L
= (-) 2 (-'Г
2 2 la
L
L 4
(2.37)
Необходимо отметить, что методом коммутативных диаграмм можно
получать более сложные соотношения для Т-коэффициентов. Например,
из диаграммы
* А Л Г
* Л Л Г
следует
/„
/.
k 1У
la k
Σ
j la hi l&
h* ly
Ι ^ 'ββ ly
\k Ιο
l8t l9 /ρ
&
(2.38)
причем на β| и s^ наложены ограничения δβ « s^ + s& + 2, и
(β — βι — β2)/2 — целое неотрицательное число. Отметим также,
что все показатели степени (—) в приведенных выше формулах также
целые числа 121.
Напомним, что все Г-коэффициенты кроме
2 2 I вещественны
1 ^8 KF 'ц |
4--U
2
/ν
2 *»
1о k\
S3

Преобразования с помощью невещественных коэффициентов
имеют вид
/ 2
причем
.1.1 z
h Is IS
-1.1,
2 2 LT
h V Iff
£« 2 2 '
, 1 1
i£ ^ lju
1 г г
/ 2 Г
(2.39)
'$ f (2.40)
<* 2 J
V
* 2 J
(2.41)
(2.42)
σ—tt—|μ|
= (-) 2 (-0P
1 /
2.3. Аналитическое продолжение Г-коэффициентов
и 6/-, 3/-символы
В параграфе 2.1 мы получили различные представления для
Г-коэффициентов. В данном параграфе рассмотрим вопросы их
аналитического продолжения. В основном будем работать с первым и пятым
коэффициентами из параграфа 2.1, поскольку остальные также
выражаются либо через 4F3(..., ..., 1), либо через 9F2 (...,..., 1).
2.3.1. В формуле (2.4) 1г заменим /Ί \ lt = 2/£ + 1. В результате
этого получаем выражение для Г-коэффициента в /-представлении!
/1
11/12
h
/
/з
/(2/12+ 1) (2/23+ 1) Г (/ + /8 -/!-/■)
~ Г(2/а + 2)Г(/ + /1 + /2-./з + 2)
X
X
Г (/ - /23 + /1 + 1) Г (/ + h + /23 + 2) Г (/23 + /2 - /3 + 1) X
ХГ(/28 + /2 + /з+2)Г(/ + /1а-/з + 1)Г(/-/,-/1а)Х
ХГ(/12-/1 + /2+1)Г(/1а + /1+/2 + 2)
Ρ(/+/23-/ι+1)Γ(/---/ι-/23)Γ(/28--/2 + /8+1)Χ
ХР(/'28~/2-/8)Г(/-/11 + /з+1)Г(/ + /, + /1а + /а)Х
X Г (/12 - k - /2) Г (/12 + /ι - /а + 1)
1/2
X
84

/—/ι· + /ι + /ι+1. /i + /a + /i2 + 2, /*23 + /а —/з + Ь
Χ Л I /2 — /s — /и;
\2/, + 2, Л + /2 + / - /3 + 2, h + /, -/ - /8 + 1; 1
(2.43)
Принимая во внимание связь «моментов» jt между собой, легко
показать, что ни множитель перед 4F8 (..., ..., 1), ни гипергеометрическая
функция 4F3 ( 1) не обращаются в бесконечность, т. е. Г-коэф
фициент — конечная величина. Известно, что коэффициент Рака (6/-
символ) тоже выражается через ^з ( , 1) (см. [212]);
W (abed; ef) = A (abc) Δ (cde) Δ (acf) Δ (bdf) [Γ (e + f + 1 — b — с)]-' х
/a + b + c + d + 2 \
χΓ| a + b + i—e, c + d+l—e, α + β+\— /, Ι χ
\b + d+l-f, e + f+i-a-d J
Ff e — a — b, e — c — d,f — c — a, f — b — d; \
4 *[—a — b—c — d-l,e + f+ 1— a — d, e + f+l—b — c; \)'
(2.44)
где
A(^) = fr^ + ^ + 1-2· * + *+i~y> * + *+ι-*\Γ
t\ х + У + г + 2 )\
J a, b, ...\ _
= Г (а) Г (ft).
T(p)V(q).'
a =
с =
/12
/ —
£ =
— /23 — /a
2
/2З 'l2 "—
2
= /l>
-/
•/2
-1,
-1.
b
d =
=
/
/12·
/23 -
=s —
-/2 +/аз
2
" / — /12 -
2
■/β —1.
+/
-/a
Это означает, что Т-коэффициент и коэффициент Рака связаны
между собой. Для установления данной связи необходимо одни
параметры (набор /) выразить через другие (набор а, Ь, ..., /). Из формул
(2.43) и (2.44) находим
1, (2.45)
Итак, мы связали Т- и 6/-символы между собой. Однако у нас
получились б/'-символы от сложных комбинаций моментов. Представляет
несомненный интерес попытка упростить эти комбинации. Если учесть
формулы (22.22) и (22.19) из монографии [231]
(а Ь е) . ία b e)
\d с /Г'4-* (а ъ ?|· *-« + * + «-/»+/ι-/·-ι.
Id с f\ \d с f)
85

где α= — а — 1; d = — d— 1; c= —с— 1; / = —f— 1» то
можно написать выражение
d of] \d l J,
Если же еще учесть формулы (22.11) и (22.10) из [231]
(2.46)
[а Ь е
\d с /)
ss —a, s^—e, e
(ss — a, s3 — b, f\
, 2s3 = a + b -f с + d,
Ui h У l/i h У'
то 6/-СИМВОЛ, стоящий в правой части формулы (2.46), легко
приводится к нормальному виду
ί/ι /ι /з1 ί/ι /ι /з) I
К /. У U, Ί У I
/i + /i + /m —/it
2
/ + /i + /u —/t»
2
/Ц + /28 + / — h
2
/ι + /ι« + /μ—/
2
= (S —/12 β—/, /Ί)
~\s — its s —/ /·/
ί/β / /ι
l/ia /а /з
где 2s = / + /j + /a8 + /u.
Таким образом,
ί/u /ι /t) = (/x Λ /ui (2.47)
l/аз / /а) 1/з / /гз)
6
Г (аЫ; в/) = (_)-<·+*+·*-« J*
= {(_)/»+/·+/(/х /г Μ
l/з / /»)
;|-(-)'"+"+'+!{a
b e
Ό I
(2.48)
При написании этой формулы мы приняли во внимание (2.46) и
соотношение а + b + с + d = — 2/2 — 3.
Подставляя (2.44) и (2.48) в (2.43) и учитывая формулу для Г-функ-
ций Г (х) Г (1 — х) = π/sin шс и то, что /^ — /г — ]\ — целое число,
находим
Ι!1 Ϊ !3|1 = (-)Л+/*+/'+,К(2/12+1)(2/м+1)х
11/12 / /23 11
X {I '■ £} <*, - КШ /У I /ι (/Уз) /) <*„. (2.49)
где f(/i/2) /У Ι /ι (/г/з) /1 — матрица перехода от одной схемы связи
моментов к другой, а множитель Φ записываем так!
<иМ· — / ν/«+/·-/ ί (—),"h"it sin π (— / + я + iu) sin 2π/ 11/2 (ζ) ςΠ.
ф//м/«-(—) [ 8ίη2π/125ίη2π/§ ] ' ^όΌ)
86

Следует ометить, что вследствие симметрии Т- и
6/-коэффициентов (ей (2.24) и [8]) относительно замены ]\ ^> /3 и /12 <^ /23 в формуле
(2.49) вместо функции Ф/}///м необходимо поставить
Итак, мы установили связь между Г-коэффициентами и 6/-символа-
ми. Однако если в методе деревьев «суммарный» момент задается в
области jik > ji + Jk (чт° следует из (1.66)), а в теории угловых
моментов — в области | ji — jk J ^ jck ^ Η + /*, то функции слева и
справа в соотношении (2.49) заданы: одна в «физической» области,
другая — в «нефизической». И выход в эту «нефизическую» область мы
совершили с помощью операции замены /-*- — / — 1.
Таким образом, Г-коэффициент есть аналитически продолженный
6/-СИМВОЛ.
Попробуем разобраться с множителем Φ//{;,·28. Напомним, что
ji = аг/2 + (S| — 2)/4, аь st — целые числа, т. е. в случае нечетных
значений Sj моменты и становятся четвертьцелыми. Из формулы (2.50)
видно, что при целых и полуцелых значениях / множитель Φ имеет
конечное значение. Рассматривая вместо отношений синусов
отношения вычетов Г-функций, из которых возникли эти синусы
[Г (х) Г (1 —х) = π/sin πχ] (см., например, [232]), в случае целых
и полуцелых значений / имеем
1/2
= I.
β случае же четвертьцелых значений моментов (например, /12, /з
и /23» /ι —четвертьцелые, а/ — целое или полуцелое число) фактор Φ
обращается в нуль (бесконечности он никогда не равен), a U1 h ί12} —
из / Ьз;
в бесконечность, тем самым обеспечивается конечное значение Г-
коэффициента.
Исходя из сказанного выше, заключаем, что для целых и
полуцелых значений моментов / Г-коэффициент есть аналитически
продолженная матрица пересвязывания моментов, не содержащая никакого
множителя. Для четвертьцелых значений / Г-коэффициент конечен, а
б/'-символ (в формуле (2.44)) бесконечен. Поэтому для четвертьцелых
значений вместо общепринятого представления для 6/-символов (2.44)
следует использовать выражение Г-коэффициентов через
гипергеометрическую функцию 4F3 (·.., ..., 1) в форме (2.43) [230]. Совпадение
Г-коэффициентов с некоторыми нестандартными 6/-символами не
случайно. В гл. 6 будет показано, что Г-коэффициенты действительно
являются 6/-символами, но не для группы SU (2), а для некомпактной
группы SU (1, 1).
2.3.2. Матричные элементы, вычисленные в п. 2.1.5 и 2.1.7,
приводят к гипергеометрическому ряду 3^2 (..·> .·> 1). Кроме того, ККГ
группы SU (2) также выражается через BF2 от единичного аргумента.
Поэтому интересно устанорцть связь между полученными коэффици*
87

ентами и ККГ. Вернемся к формуле (2.11). Введем следующие
обозначения:
i—T + 4"· '-« + -?-· М = 1у = у + -%-,
m, =
*ν
Заметим, что для дерева (рис. 22) Sv = 0, s0 = Sy + 2, S6 = Sy + 1.
В новых обозначениях
I—L
2
= (-)
Ь
2ί—У-f-fWj—m2
2
ΐ! 2/+1 /+1/2Ι
Γ(%+1)
(ί — m2)! (J -— ί — /ηχ)!
Χ
[ Γ(/-
I Γ(ί
~т1Ч-1)Г(/ — т2+ 1)(27+ 1) (У — ΛΙ)! (У + ΛΙ)! ]ΐ/2
χ^
31 2
: + 1Ш + 1) Γ (/ + тя + 1) (2ί - /)! (21 + J + 1)!
— 2/, У — / — т1 + 1
Воспользовавшись тождеством [233]
Г—2ί + 7, -i + m2, У+1;
2i J — / — тх -\- 1
_2ί + /, ,/—Λί+1, —i—т^
ijrj — m1+\f — ΛΙ — 2ί
приведем выражение (2.51) к виду
X
(2.51)
л["
- Г (—2/)Г(—J —Αί)
Г(—/)Г(—Λί — 2ί)
X я/7-
з* 2
Μ
2t—y-fmi—m2
= (-)
im2 — mx 2i'+l У+1/2|
/I (2f + M)\ Ц1 - яц)! (J - Al)l (2У + 1)11/2 χ
(J — i — тг)\ [(« + mx)! (1 - от,)I (i + m2)!|1/2
X [(J + Λί)! (2i — У)! (2г + У + 1)!Г'/2 Χ
— 2t +У У —Λί+1, — г —тх;
У — t — mx -f- 1, —M — 2i
Вместе с тем для З/'-символа Вигнера имеем выражение [231]
X Λ
(2.52)
У
Μ
т«
„ j-mi+m, J\ (2С + Μ) Ι
88

*[■
(J- Μ) ! (i- mx)! Ι1/2 χ
(2i — J) \ (2/ + J -f 1)! (/ + M) \ (i + ma)»(i - m2) 1 (/ -f mx) I
Γ —. 2/ + У, У — Μ + 1, —i—m.
[—i+J — щ + 1, —M — 2i
X 3^2
Следовательно,
ι-
(2.53)
2t—3J-|-m2—mt
2
1/2
= (_) (2У + 1Г X
—Γ —2" M
\m2 — m1 2t+l У + 1/2
J=(—1) 2 (2У + 1) , .,
(2.54)
Принимая во внимание связь ККГ и 3/-символов Вигнера 185]
ей..— (-y^-<w + D-(^ ':г _JM).
имеем
ι ι
2" —2" Λί
2f-3J+mg-m1 „ _м (2.55)
]m2 —mx 2*+l У + 1/2)
Таким образом, Г-коэффициент, вычисленный в п. 2.1.5, есть
просто ККГ (g точностью до фазы). Причем его не нужно аналитически
продолжать, поскольку условие 0 ^ J ^ 2ί для ККГ в переменных
σ, δ есть 0 ^ δ ^ σ, которое определяет область изменения парамет ров
Τ коэффициента, ответственного за переход между деревьями,
изображенными на рис. 22.
2.4. Вырожденные Г-коэффициенты
Как известно, существует восемь типов Г-коэффициентов. Однако
при некоторых значениях параметров для более сложных переходов
они вырождаются в Г-коэффициенты для более простых переходов.
Кроме того, свободные концы дерева можно рассматривать как линии
с узлами, если характеристики узлов записываются так! α, β = 0;
Say s$ = —1 (параграф 2.1 и [13]). Это обстоятельство позволяет
связать вырожденные 7-коэффициенты (а тем самым — и вырожденные
6/-символы) с 3/-символами и D-функцией Вигнера от угла π/2. Будем
исходить из интегрального вида Г-коэффициентов и так же, как в
предыдущем параграфе, будем работать только с двумя из них [234].
Формулы для Г-коэффициентов в /-представлении имеют вид
ΙΙ/Ί к /з 1 _ г W2/.+I.2M-1 1-1/2 (Λτ2/2,+1,?/1+1ι~1/2ίΛ/2/ί+1^1+1ΐ--1/2
11 /12 / /23II
х!|^Щ/;!+1|1'?2/^'-^+,(./23 + /з~/а .)(. / + /з~/1а,Гх
\/гз — h — h — * / \/ — li2 "~" /з — ν

+1
Χ {(1-х)'
-ι
/„-/»-/.
(1 + х?*1&&$ (х) tf^ffi, (х) dx, (2.56>
4 4 ,s
/l2 / /23
= ^gS1 даЛйГ ί^:.+Λ»]-1/2 χ
"423 + "ψ
2/„+1.2/23-fl !-1/2
Χ [Л/2/—2/23—1/2 J
2/23-2/;
/—/ιι+/ι
Ι Ι V/ — /12 /3 1
—1
23 *ЧЗ 2
2π 9/ -2/--L
x(sin,M /3 2 φ^ιΙΛ^Ι(οοβφ)β-,«»·+*ιΙφι (2.57)
_з_ _ _з_ з_
4 4 4
/ι
/ /23
(_)-/+/«+1/4
^2
3 3
тг —τ /·
/ll / /23 Β/·=—3/4
(2.58)
Принимая во внимание соотношение между полиномами Якоби
ft-^-O- ^^/^Γίη^ *»*(«), (2·59>
V π Γ (α + 2/1+ 1)
а также связь $„
Vn
J_ 1^
2 ' 2
J 1_
2 ' 2
(*) с полиномами Чебышева
ι
22η (л!)а 2^ (я!)2
ω- (21Γ1? -^SrCQS^> Φ = arc cos χ, (2.60)
получаем
• η 2π Ι
/l /а /з Я Л f . 2Ьз-2/8 ~ cr>2* . ι 2/-.4.I y ч w
• I/ ,· 3 = -?=■ \ sin ΦΡΛ Τ ν (cos Φ) Χ
/12 / /23 Ь'^-— V2j ^2/-2/„--J~V ψ'
χ cos(2/12 + 1)фйф.
(2.61)
Коэффициент А в (2.61) равен деленному на два множителю,
стоящему перед интегралом (2.57). Учитывая (см. формулу (2.54))
з_ з_ .
4 4 h
/12
/ /23
= (-) 4 У2(2/28 + 1),/2Х
/ 2/м + 4-
Ч/« — /и /з + /и + 1 — 2/'з — 1у
(2.62)
90

и формулы (2.57) и (2.61), находим
з_ з_ .
4 4 iz
/12
/
/23
= (-) 4[i +
м·—--
2/*23 + 2
+(_1)2/88_2/^/18_1/2](2/23+1)1/2 / J
\/з — /i2 /з + /12 + 1 — 2/з — 1,
(2.63)
С учетом формулы (2.23) для простейших Г-коэффициентов
получим
3
4
/12
3
4
/
з 1
4
/гз 1
(-)
/12-/+ ■
п
_з_
" 4
/м
h
/23
'—4 =
-(./+4-) ./+4- (0 я «\
(2.64)
На основании (2.62) и (2.64)
(-)2;+/"-3/-(2/2S+l)l/2
2/м +
—4 ?а ^X2 ~^~ 7"
^/,,+ι^/,,+ι [θ. -γ» °) ·
(2.65)
например,
1
4
3
4
1
4
1
4
1
2
1
2
— Ои (θ. -ξ-· θ). (2.65а)
Учитывая формулу (106.17) из [85], а также выражение D\\ (0,
θ, 0) = cos2 θ/2, убеждаемся в справедливости равенства (2.65а). Итак*
мы установили связь вырожденных Г-коэффициентов (6/-символов) с
3/-символами и D-функциями. Если учесть выражение всех этих
символов через гипергеометрические функции (см. параграф 2.1 и [3, 61),
то можно установить связь 4^з(···» ···» ') с 3^2 (···» ···» 1) и %Р\ (···> •••»~2j
в тех случаях, когда между ними нет тривиального перехода типа
Λ (αβγδ, αεκ, 1) -* 3^2 (βγδ, εκ, 1).
91

Глава 3
ГРАФИЧЕСКАЯ ТЕОРИЯ
Зл/КОЭФФИЦИЕНТОВ
Задача сложения моментов количества движения в квантовой механике
не принадлежит к числу трудных: полный результирующий момент
получаем, складывая последовательно моменты по правилу сложения
векторов. Аналитические выражения для коэффициентов векторного
сложения (3/, 6/, ..., Зл/-символов) очень громоздки, хотя переход от
одной схемы сложения моментов к другой не сложен (всякий переход —
не что иное, как некоторая перегруппировка моментов). Естественно
поэтому ожидать, что различные выражения для Зл/-символов и их
различные свойства удастся получить столь же просто. Опыт работы
с кинематикой л-тел показал эффективность графического метода
деревьев, поэтому в данной главе также будем использовать указанный
метод. Однако в отличие от работ 12, 5—10, 46], в которых деревья
использовались как символы координатных систем в многомерных
пространствах и решений уравнений Лапласа, соответствующих этим
системам и реализующих НП класса 1 ортогональных групп, в
настоящей главе те же деревья будем рассматривать как схемы сложения
моментов. При полном изоморфизме деревьев последние различаются
только обозначениями (если раньше каждому узлу мы приписывали
собственное значение соответствующего оператора Лапласа и угол»
а линиям—либо косинус, либо синус соответствующего угла, то
теперь узлам приписаны моменты, а линии указывают, какие моменты
складываем).
Переход от одной схемы сложения моментов к другой, как
известно, осуществляется с помощью Зл/-символов. На языке деревьев
такой переход производится с помощью операций последовательных
пересадок веток и вращений веток вокруг узлов.
Графические схемы в теории моментов количества движения не
новы (см., например, монографии [114, 115, 231] и приведенную в
них библиографию). В отличие от этих работ ниже изображаем
графически не Зл/-символы, а схемы сложения моментов. Матрицы перехода
от одного дерева к другому определяют представление Зл/-символов.
По нашему мнению, изображение схемы сложения моментов деревом
является более естественным, поскольку дерево повторяет весь
процесс сложения моментов. Кроме того, поскольку с каждой пересадкой
92

сопоставляется коэффициент Рака (или 6/-символ), а с каждым
поворотом — фазовый множитель, то, пользуясь такими операциями, очень
легко можно получить различные представления Зя/-символов.
Отметим, что, осуществляя переход от одного дерева к другому различными
путями, можно получить не только соотношения между
коэффициентами Рака типа тождества Эллиотта — Биденхарна 1231, 235—2371,
но и гораздо более сложные соотношения. Вопрос о многократных
суммах произведений коэффициентов Рака будет рассмотрен в
следующей главе.
3.1. Деревья как символы сложения моментов
Независимо от числа складываемых моментов количества движения
процесс сложения всегда осуществляется последовательно, т. t.
сначала складываются любые пары (или пара), затем к
результирующему моменту добавляется либо какой-нибудь момент из первоначаль
но взятого набора, либо какой-нибудь другой результирующий
момент и т. д. Таким образом, на каждом этапе всегда складываем два
момента. Это означает, что с любой схемой сложения всегда можно
сопоставить дерево типа дерева, изображенного на рис. 27. (Мы взяли
η + 1 момент для того, чтобы писать, как это принято, 3/г/-, а не
3 (п — 1) /-коэффициент.) Назовем такое дерево деревом Вигнера.
При заданном порядке расположения моментов (всего их η + 1)
согласно (1.46) можно нарисовать 2п\1п\ (п + 1)! различных деревьев
[2, 202]. Если учесть перестановки (п + 1)-го момента, число которых
равно (п + 1)1, то число деревьев возрастает до (2п)\/п\. Если же
операции вращения веток вокруг узлов считать тривиальными и относить
деревья, которые можно получать друг от друга·с помощью операций
поворота, к одному классу, то число классов равно (2п)\/п\Т (число
узлов в дереве п). Поскольку фазовые множители различимы, то
будем работать с (2п)\/п\ разными деревьями. При таком подходе 3nj-
л.л. (2л) * ч. (2Ό!
коэффициенты суть элементы *—у- χ ——--матрицы всевозможных
переходов между деревьями. Так как матрица переходов
симметрична, то число различных типов Зп/-символов равно (2п)1 [(2п)\ — nl]/2 X
X (я!)2.
Основным структурным элементом дерева является ячейка,
приведенная на рис. 28.
Рис. 28
Λ А
*1К
93

Из свойств ККГ (см. [153], а также [7]) следует
(-)'
к
(3.1)
ш Л/
Как и в гл. 2, чтобы перейти от дерева TR к дереву 77?', вдесь
также необходимо рассмотреть последовательность деревьев TRl9 TR2, ...
..., TRk (TR = TR0, TRk a TR'). Очевидно, что матрица перехода
(TR I TRr) при этом факторизуется! (TR | 77?') = (77?01 Г#Л) =
= (TR01 77?д) ... (TRk-i | 77?Λ). Поэтому необходимо найти
матрицу, соответствующую пересадке одного сучка с левой (правой) ветки
на правую (левую), т. е. можно рассмотреть лишь переход,
показанный на рис. 29.
Как известно, матрица такого перехода Ijijklikjij \ \ JtlkJiibifl
с точностью до нормировки есть 6/-коэффициент Вигнера или
коэффициент Рака [196, 231]
[IiJkJikiii\iiJkiiJkij] =
I in* ι ]ы Ι
Х[(2^+1)(2/Л+1)Г/»^ '* £),
где Lci — 6/-коэффициент Вигнера, который связан с
циентом Рака формулой
в] = (_)*+*+<+* W (abed; ef).
с
η
(3.2)
коэффи-
(3.3)
Если речь идет о переходах от одного дерева к другому с
одним и тем же порядком расположения η + 1 суммируемых моментов,
то число пересадок не больше η — 1 (крайние левый и правый
моменты не пересаживаются), число же промежуточных моментов, по
которым производится суммирование, также не больше η — 1 (всего
узлов у дерева п> а корневой узел общий), причем число пересадок
совпадает с кратностью суммы. Следовательно, в этом случае 3nj-
Рис. 29
94

коэффициенты представляются произведением коэффициентов Рака
без суммирования. При учете же перестановок моментов Зя/-коэффи-
циенты выражаются через однократные и более высокой кратности
суммы от произведений коэффициентов Рака.
3.2. Структура Зя/-коэффициентов
Рассмотрим З/i/-коэффициент, соответствующий переходу между
деревьями, изображенными на рис. 30. Этот переход осуществляется
по схеме, показанной на рис. 31.
Учитывая, что с каждой пересадкой сопоставляется матрица (3.2),
без особого труда записываем матрицу перехода (Зя/-коэффициент)
между деревьями, изображенными на рис. 30,
| /ι /а · · · /«-Η
/l2 /l23 · · · /
I / /2...П+1 · · ' Jnn+\ I
Здесь матрица
n-l ι
-П '
j\...n—i /rt-i+1 /η—ί+2...ι
i-.2ih~n-i+l
1 /„-ί+l...n?
(3.4)
/l.../ι—f /n-i+I /η-ί+2...η Η
II /l ...n-i+l / /tt-i+1..л 1
соответствует переходу, показаному на рис. 32, где /У..* — сумма
^-моментов от /Ί до jk включительно, /ι...Λ ι^./ — сумма моментов
/l.../ι—ι И jn—i+\t /v.* v = /ν·
4 «U
Л"/ 4 П in*1
Рис. 30
y«V/// // AtV// / У/.-.. iV/// \7Ля*/ \\ХЛ
95

A../I-/ Jn-i+t Jn~M..tff Л.*Ы Jn-i't Jn-hi.
Jti-i+t"*n
J«- h, Λ, h
Для более наглядного прослеживания графических операций
подробно исследуем случай сложения четырех моментов количества
движения. При одинаковом порядке расположения моментов можно
нарисовать коммутативную диаграмму из пяти различных деревьев
(рис. 33).
От дерева А к дереву В можно перейти с помощью одной пересадки
ветки или с помощью четырех пересадок (движение против часовой
стрелки на коммутативной диаграмме). Отсюда между
коэффициентами перехода получается соотношение
Ι /α /β /ν
Ι/β /σ /б I
L £ I*, k /ν
'в'/в- i /β /в /в'
1 /в /ι
II /а
Ι/ν
5. /β.
Ь, ΜΙ'8' Λ» /ν
/σ /в 111 /в /σ /б'
Χ
*l/, /. fcl· <3·5>
Осуществляя переход, например, от дерева А к дереву С по
часовой стрелке и против нее, получаем еще одно соотношение между
96

коэффициентами перехода»
1/ /σ /«II/·
/β. /ν J J/α
k /в· II/.'
/β« /β.
/ε /β
/β. /в'Щ/е·
h
h
U
/β, /ν
U h·
(3.6)
Если учесть формулу (3.2), то соотношение (3.6) можно переписать
через 6/-символы2
2(2*+п(-)*{;
χ
β
b
с\\а'
χ
α
β
b'
br
о
it; a-
(3.6a)
Для фазы φ справедливо q>~x + a + $ + y + a + b + c +
+ α' + 6' + с'. При получении этой формулы мы воспользовались
свойством симметрии 6/-символов
Ua h U\\h U ΙΑ [la h W
\la h У ft la I.} \la lb К
и ввели обозначения? /α = α, /β = β, /8 = γ, /ν = α, /σ ~ Ьь /в = с,
/V· = α'> /·' = Ь\ /λ — с'> /V = *·
Выражение (3.6а) представляет собой тождество Эллиотта — Би-
денхарна [114, 231, 235—237]. Коммутативная диаграмма наряду g
тождеством (3/6) позволила получить тождество (3.5). Нетрудно
проверить, что структура тождеств не вависит от обозначения деревьев
Л, В, ..., Е.
Таким образом, методом деревьев можно без вычислений находить
сложные соотношения между 6/-символами, т. е. суммировать
громоздкие выражения. Из коммутативной диаграммы (ем. рив. 33) также
видно, что в случае сложения четырех моментов о заданным порядком
их расположения 9/-символы, осуществляющие переход от одного
дерева к другому, выражаются через произведение двух 6/-символов
или просто вырождаются в 6/-символы.
Рассмотрим переход между деревьями с разным порядком склады-
ваемых моментов (по-прежнему рассматриваем случай сложения
четырех моментов). Такой переход символически, например, можно
записать следующим образом!
J;4 hto }fZ Jns
\ Jr Α Λ л
/
(3.7)
7 1-1980
97

// Л Л Л *г J' h Л /» Ji h Л «ι Ji h /s
Нарисовав цепочку деревьев (рис. 34) и воспользовавшись
формулами (3.1) и (3.2), можно переписать выражение (3.7) через 6/-символы:
Jt Λ h h
/l2»/l23»/48
/123 / hi
(->
/•+/4—/·4
X
X
/2 /l
/21 7
/43
/l43 I
|/l /4 /δ
II /l4 /l43 /43
(->
/.+/»«»—/
(3.8)
Сравнивая формулы (3.7) и (3.8), находим выражение для 9/-сим-
вола, ответственного за переход между этими деревьями:
'h U /з /г\
h /2 /З /4 )=(_У'+Ь+/»+^»+/.+/».-/х
V/l4 /l43 /l2 /l23/
χς<-ιΗ·μ u HI7'2 7l HI'1 '* '· 1· (з-9>
/48 II/i23 / /43IIII/21 / /143111/14 /143 /43!
Из этой формулы видно, что представление для 9/-символа при
учете перестановок складываемых моментов становится более сложным,
а именно, оно выражается не произведением 6/-символов, а суммой от
произведений 6/-символов Причем, как мы уже отмечали выше, Зя/-
символы при учете перестановок будут выражаться не только через
однократные суммы, но и через суммы более высокой кратности.
98

Рис. 35
Отметим, что 9/-символ, определяемый равенствами (3.7) и (3.9), не
совпадает непосредственно со стандартным 9/-символом Вигнера,
используемым в литературе [114, 115, 231]. Последний соответствует переходу
Jt h h J* j j
v ku ^.a;/
(3.7a)
Нарисовав цепочку деревьев (рис. 35) и воспользовавшись формулами
(3.1) и (3.2), можно переписать выражение (3.7а) черев 6/-снмволы:
/12 /з /l23|L_yr18+Wm χ
X
/з /i /is
/4 /l23 /l2
Λ -4 4 Λ
/ ч/1-Ь/з—/ι s 1 Jl3 /2 /ΐ23
1/4 / /μ Ι ^
(3.8а)
Сравнивая (3.7а) и (3.8а), находим выражение для стандартного 9/'-
символа, ответственного за переход между этими деревьями:
Ίι Ь /ΐ2^
/з /4
v/lS /24 /
Ун.-/м-/и+/1р'" /» ^'123
/13 /2 /l23
/3ί| = Σ(-ΐ)'
/tea It/4 / /4
/з /ι /i3
/l23 /
12 1
X
1/4 / /24
X
(3.9a)
99

\n+1
Ji..,H+f
l к λ λ λ. ι л ;, ι
λ <fs
100

Ji Js «4
], h h h
Рис. 38
<f/...4
is Js J?
А..* Л Ji &
Рис. 39
Более точно, это выражение дает элемент матрицы перехода от одной
схемы сложения четырех моментов (jx + j2) + (j3 + у4) к другой
схеме их сложения (j\ + /3) + (/2 + /4). Стандартный 9/-еимвол Вигне-
ра
связан с этой величиной простой пропорциональностью
Πι /a /la^
/з U /ы )= №'Ы + 1)(2/з4+ 1)(2/„+ 1)(2/м + 1) X
Ч/is hi l
f/i /2 /12)
х /3 и Ц <3·96>
l/м /24 / J
и может быть выражен в виде однократной сумма произведений трех
6/-СИМВ0Л0В.
Нестандартный 9/-символ (3.9) можно связать с 9/-символом Виг-
нера соотношением
fli U /з
(-1)
/l48+/l4—i\tb~-Jti
Χ
/ι h /s h 1
W4 /l43 /l2 /l23
f/i /2 /12
X VWn + 1) (2/123 + 1) (2/14 + 1) (2/ш + 1) /4 / /123
W14 /l43 /з J
101

Отметим, что в случае, если переход осуществляется между
деревьями, у которых имеется какой-либо общий промежуточный момент,
Зп/-символ может распадаться на 3kj X 3 (η — 3) /-символы (например*
переход между деревьями, изображенными на рис. 36).
Матрица этого перехода равна произведению матрицы,
ответственной за переход между блоками Л и Л', на матрицу, осуществляющую
переход между деревьями В и В' (рис. 36, /// и IV), которые являются
частями деревьев / и //, т. е.
3/г/(1->П) = 3/г/(Л->Л') χ 3(п — k)j(B-+B'). (ЗЛО)
Поясним это на простом примере, показанном на рис. 37. Матрица
такого перехода равна произведению матрицы, осуществляющей
переход между деревьями, изображенными на рис. 38, на матрицу перехода
между деревьями, показанными на рис. 39, т. е.
I8j(l-+Il) = 9j(A+ Α') χ 9ЦВ-+ В'), (3.11)
где нестандартные 9/-символы — 9/(А -> Л') и 9/ (В — В') —
определяются формулой (3.9).
Итак, ценность графической теории 3/г/-символов заключается не
только в наглядности, но и в простоте получения различных
представлений Зя/-символов и всевозможных соотношений между ними.

Глава 4
ПРАВИЛА СУММ
ДЛЯ 6/-СИМВ0Л0В
При изучении угловых корреляций γ-излучений в каскадных
переходах в ядрах, а также при исследовании угловых распределений
(дифференциальных сечений) реакций важная роль принадлежит 6/-символам.
Поэтому вывод различных соотношений и правил сумм для 6/-симво-
лов представляет несомненный интерес. В предыдущей главе на основе
варианта графической теории 3nj-коэффициентов [11] мы
автоматически получили тождество Эллиотта — Биденхарна. Действуя
аналогично, в этой главе получаем более сложные правила сумм и
доказываем затем теорему об их приводимости.
4.1. Сложение пяти моментов
В случае сложения пяти моментов с заданной нумерацией существует
14 схем сложения моментов, с каждой из которых сопоставляем
дерево (рис. 40). Число деревьев при сложении (п + 1)-го момента
определяется формулой (1.46) и равно (2п)1/(п + 1)М.
Переход от одного дерева к другому осуществляется с помощью
одной либо нескольких пересадок веток (см. гл. 3).
Располагая рядом деревья, отличающиеся друг от друга лишь
пересадкой одной ветки, можно *чарисовать коммутативную диаграмму
(рис. 41). Она представляет собой граф, в каждой вершине которого
помещено дерево, обозначенное его номером. Линии, соединяющие
вершины графа, соответствуют 6/-коэффициентам, осуществляющим
переход между деревьями. Полная область, занимаемая графом,
состоит из восьми областей а, 6, с, ..., ft, границы которых суть 4- и 5-уголь-
ники, называемые, по терминологии Харари, простыми соответственно
4- и 5-циклами [238].
Для установления правила сумм для 6/-коэффициентов
необходимо рассмотреть все замкнутые пути (границы областей), изображенные
на рис. 41, и дать их классификацию. Из этого рисунка видно, что
существует восемь замкнутых путей, представляющих собой границы
областей а, 6, с, ..., ft. Однако можно рассматривать границы и более
сложных областей, составленных из 2, 3, ..., 7 и 8 областей а, Ь, с, ...
..., ft. Нетрудно видеть, что число замкнутых путей при объединении
103

</, A А A A J^ Л А Л Js Л h Jj A A Jr J2 Js A Js
V
/ 2 S 4
A i i }:l· л л л ь ь л л л л л л л л л Js
J Jz Jj Л Js J Ji js Л Js Jr j2 ЛЛ Js
" ν
* w η
Л A Js A JS Jr J2 Js J4 Js· Л J2 Js Л Jf
J?
15
Рис, 40
я
соседних /(-областей
Пь—С^ — Пу — Пц, (4.1)
рде Се — число сочетаний из восьми
по k; /iv — число областей, для
которых пересечение пусто, т.е.,
например, α Π Λ = 0, (abc) f) h = 0
и т. п., ημ — число возникающих при
объединении неодносвязных
областей. Например, область abdfgHMeev
внешнюю границу, как и область
abcdfgy и внутреннюю, как й область
с, которые учитываются при
рассмотрении соответственно шести
областей и провтых областей с, /, g. Число сторон многоугольников,
являющихся границами исследуемых областей, вычисляется по фор-
f пс, 4i
104

m=2lmk — 2ml, (4.2)
к
где tnk —> число сторон объединяемых областей; mt —число внутренних
линий в полученной сложной области.
С помощью формул (4.1) и (4.2) находим
^=8 = 4(4 уг) + 4(5 уг), (4.3)
п2 = 16 = 6(8 уг) + 10(7 уг), (4.4)
/1з=32 = 6(П уг) + 12(10 уг) + 6(9 уг) + 8(8 уг), (4.5)
л4 = 53 = 2(14 уг) + 12(13 уг) + 14(12 уг)+6(11 уг) +
+ 8(10 уг) + 9(9 уг)+2(8 уг), (4.6},
л5=46=4(14 уг) + 12(13 уг) + 10(12 уг) +
+ 6(11 уг)+4(10уг) + 9(9 уг)+1(8 уг), (4.7)
лв== 18=6(11 уг) +6(10 уг) + 2(9 уг) + 4(8 уг), (4.8>
ηΊ = 5 = 3 (8 уг) + 2 (7 уг), (4.9)
«8= 1 = 1(5 уг). (4.10)
Отсюда следует, что полное число замкнутых путей
/г = 2 "*= 179 = 6(14 уг) + 24(13 уг) + 24(12 уг) +
+ 24(11 уг) + 30(10 уг) + 26(9 уг)+24(8 уг) +
+ 12(7 уг) + 5(5 уг) + 4(4 уг). (4.11)
Необходимо отметить, что 5-цикл п8 является простым, а не
составным циклом. Действительно, граф, изображенный на рис. 41, можно
представить как сетку, натянутую на сферу. Отсюда видно, что цикл
(12594) простой и не отличается от остальных восьми простых циклов.
Рассмотрение графа на сфере не противоречит теореме Эйлера
[239]
V— £+F=2, (4.12)
где V — число вершин; Ε — число ребер; F — число граней.
В нашем случае V = 14, Ε = V « 3/2 = 21 (из каждой вершины
выходят три ребра, и каждое принадлежит двум вершинам), F = 9.
Может показаться, что мы неправильно сосчитали число путей.
Однако это не так. Действительно, мы должны учитывать границы при
объединении цикла (12594) с одним (а, 6, с, ..., h) либо с совокупностью
циклов ((ab)y (abc), ...). Но получаемая при этом поверхность имела
бы гуже границу, что и поверхность, дополняющая исходную до сферы
(все дополняющие поверхности мы уже рассмотрели). Нетрудно
видеть, что при изображении графа на плоскости роль цикла (12594)
мэг бы играть любой из циклов а, &, с, ..., Н.
Для примера напишем ряд циклов (в качестве обозначения циклов,
используем буквенное обозначение областей):
bfhd — 14-угольник, bfgd — 13-угольник,
10S

behg — 12-угольник, bfhg — 11-угольник,
abce— 10-угольник, acg— 9-угольник,
cfg — 8-угольник, ab — 7-угольник.
Располагая по кругу 14-, 13-, 12-, ..., 7-угольцики (6-угольников нет,
а 4- и 5-угольники опишем ниже) деревьев и приравнивая
последовательность операций при движении по малой и большой дугам
окружности, получаем соотношения между((2 и 12, 3 и 11, ..., 6 и 8), (2 и
11, 3 и 10, ..., 6 и 7), ..., (2 и 5, 3 и 4)) 6/-коэффициентами (при условии,
конечно, что выбираем лишь деревья (между которыми
осуществляется переход), лежащие в различных подобластях, формирующих одну
сложную область). Однако все эти соотношения приводимы, что легко
понять, если рассмотреть структуру циклов. Возьмем 14-цикл adefg
(рис. 42).
Вследствие связи между деревьями, изображенной на рис. 41,
в 14-цикле появились хорды. Поскольку путь по дуге длиннее пути
по хорде (длина линии, соединяющей две точки, принимается равной
единице), то структура соотношений между 6/-коэффициентами в 14-
цикле упрощается. Кроме того, видно, что хорда отсекает как минимум
4-цикл, т. е. 14-цикл редуцируется как максимум к 12-щжлу.
Нет смысла рассматривать редукцию 13-, 12-, 11-циклов, поскольку
длина дуги конкурентна g длиной хорды лишь в 10-циклах.
Действительно, если нарисовать внутренние точки вдоль диаметра (рис. 43),
то длина полуокружности будет равна длине диаметра (для циклов,
длина окружности которых меньше 10, путь по внутренним линиям
длиннее пути по внешним дугам). Поскольку в каждой точке должны
пересекаться три линии, то даже в самых «неблагоприятных» случаях,
когда, например, линии 1—3 идут направо и отрезают лишь 4-циклы
(3-циклов у нас нет!), остальные линии, исходящие из точек диаметра,
должны идти налево, например, налево идет одна линия 4. Она, как
минимум, отсекает 4-цикл, поэтому слева уже остается не 10-цикл, а
8-цикл. Соотношения между 6/-символами для 8- и 7-циклов й их
редукции к более простым структурам получим, рассматривая переходы
(пересадки веток) между деревьями. Из такого рассмотрения
непосредственно виден путь получения соотношений для 6/-символов и их
}редукции для любых циклов.
Рис. 42 Рис, 43
106

ι к ιι }s ι h л hh Jr μ л Us
\ к h h 4 л h h л Js i h л л Л
/f Л <TJ <4 Jjr Jf J2 <TS Jb <& J7 <T2 J J J4 <ff
В качестве примера выбираем 8-цикл (6—3—7—5—13—14—10—
11—6)t являющийся границей трех объединенных областей с, /, g
(рис. 44).
Приравнивая последовательности операций, например, по путям
6—3—7—8 и 6—11—10—14—13—5, получаем соотношение
у |/а /з U ЦП /1 /23 /4 11Λ-..з U /δ
/Wi...3/«||/23 /2···4 /34IIII/1...3 /1...4 /2...4II/1...4 / /45II
у Ι /1 /2...4 /5 II /2 /34 /5 |||/з /*4 /5 Ι χ
β /2...5/3...5/«|/l...4 / /2...5II/2...4 /*2...5 /з...5|| ||/з4 /*3...5 /451|
/ia/l···3
|{2 /з Ζ4·!!/1 ;'23 /4βL (4.i3)
II/23 /2...5 /3...5Ц/1...З / /2...5I
X
107

которое, очевидно, можно записать так!
/2
1/23
- Σ
/2...5/3..
/з
/2...4
1 к
Ι/Ί...4
и
/34!
1/-1
1/Ί...3 j
J2...4 /б ||
/
/2...5II
X
/23
/1.4
/2
/2...4
/45
/4
/2...4II
/34
/2...5
/Ί
/1...3
/1...4
/δ |
/з...5||
/23
/4
/
I/з
1/з4
/5
/45 ||
/4
/3...5
/δ
/45
X
(4.13а)
/5
/3...5
X
/2 /з /45 /l /23 /45
Ι /Μ /2...5 /3...5||Ι/ΐ...3 / /2...δ|
(располагаем 6/-символы справа налево). Таким образом, мы
выразили двукратную сумму произведений пяти 6/-символов через
произведение трех 6/-СИМВОЛОВ. Однако формула (4.13а) приводима (ее можно
упростить). Действительно, от дерева 11 к дереву 13 можно пройти по
пути как 11—10—14—13, так и И—12—13. Отсюда немедленно следует
соотношение (тождество Эллиотта — Биденхарна)
|/2 /з п || /23 и /б IL· 2 II /а /з*
В/23 /2...4 /з4|11/2...4 /2...5 /*451 '3...51|/*2...4 /2...S
х|/з h h\h /з /45 II
Я/34 /3...5 /4δΊ/23 /2...5 /З...б|
Подставляя (4.14) в (4.13а), получаем правило сумм для 6/-коэф-
фициентов, образующих 7-цикл (6—3—7—8—13—12—11—6):
1/2 /з и ΑΙ /1 /23 /4 Н/1...3 /4 /δ Ι
1/23 /2...4 /34ΙΙ/1...3 /1...4 /2...4ΙΙ/1...4 / /45||
-Σ Ι/1
/2...5|/l...4
(4.15)
Приводимость этого соотношения очевидна. Действительно* выно-
h /з /4
(4.14)
/2...4
/
/»
/2·..5
ill7'2
1 /23
/3
/2...4
Ч
/J
II ^2з
II/2...4
/4
/2...5
/· 1
/45 II
| it /28 /45 |
1/Ί...3 / /2...5Ι
и сокращая на
неся из-под знака суммы коэффициент
В /аз /2...4 /s41.
го левую и правую части выражения (4.15), получаем правило сумм
для 6|'-символов, образующих 5-цикл (6—3—7—12—11—6), которое
β <*' J*
W,
αϊ'
Λ'
w9
w,
Рис, 45
108

уже неприводимо (в 5-цикле нет диагоналей) и по своей структуре
аналогично формуле (4.14).
Несколько слов следует сказать о 4-циклах. Они возникают при
пересадках веток по схеме, изображенной на рис. 45. (Блоки а и
α', β и β' отличаются друг от друга лишь одной пересадкой).
Получаемые таким образом 4-циклы не несут никакой информации (из них
лишь следует WtWk = WkWit Wt = Wu ψ\ = 1). Однако эти циклы
важны для связи 5-циклов. Других простых циклов при сложении
пяти моментов не существует.
4.2. Теорема о фундаментальности 5-циклов
Теорема. При сложении, произвольного числа моментов с одинаковым
расположением складываемых моментов максимально неприводимым
соотношением между коэффициентами Рака, получаемым путем
перехода между различными схемами, будет тождество Эллиотта —
Биденхарна.
Доказательство. В основу наших рассуждений положим
метод индукции. Выше довольно подробно мы изучили случай
сложения пяти моментов.
Теперь рассмотрим сложение шести моментов, для которого можно
нарисовать 42 дерева (рис. 46). Если их представить в виде точек в
пространстве, то получится тело, построенное из «брусков», грани и
сечения которых суть 4- и 5-угольники (рис. 47).
f f f f f f
4 Ч Ч Ч Ч Ч
Ч Ч Ч Ч Ч Ч
Ч Ч Ч Ч Ч Ч
ч ч ж ч ч ч
ч ч ж ч ч ч
Рис. 46
ч
ч
ч
ч
ч
ч

/
/7
/
'-**.
_ Л#Жя tt&rX- - - -~ ---Ж-^. - .у
- - rife: зСиш*:ϊ > _4^
L4/
J%r-w L· нк*
$*£
*■
W
η + 1-κ
Рис, 47
п + 1-к
Рис. 48
Рис, 49
Рис. 50
Если представить эту картину на плоскости, то получится карта
пересекающихся «дорог». В пространстве же удалось нарисовать
граф без единого пересечения ребер, содержащий 58 простых циклов:
20 5-угольников и 38 4-угольников. Его уже нельзя натянуть на
сферу, поскольку из формулы Эйлера V — Ε + F = 2 следовало бы,
что F = 44 (V = 42, Ε = 4V72 = 84), так как из каждой вершины
выходит по четыре ребра (при сложении (п + 1)-го момента из
вершины выходит η — 1 ребро).
Этот граф нельзя натянуть на сферу с ручками и дырами,
поскольку из формулы Эйлера для такой поверхности
V — E + F=2 — 2p— q (4.16)
(ρ — число ручек; q — число дыр [239]) число граней F было бы
меньше 44 (в действительности их 58). Из рис. 47 видно, что циклы более
чем с пятью сторонами являются составными.
ПО

Допустим, что при сложении η моментов получается граф (тело),
грани и сечения которого суть 4- и 5-циклы. Перейдем к сложению
(п + 1)-го момента. В этом случае можем нарисовать деревья типа,
изображенного на рис. 48, где k — число складываемых моментов,
(k = 1, 2,..., η— 1, η). Однако нетрудно видеть, что, считая какую-
либо пару одним объектом, сразу же возвращаемся к схемам сложения
η моментов, диаграммы связи деревьев которых в качестве простых
циклов содержат лишь 4- и 5-циклы.
Таким образом, и при сложении (п + 1)-го момента структура
простых циклов остается неизменной. А поскольку с каждой стороной
сопоставляется 6/-символ, то максимально неприводимым
соотношением будет тождество Эллиотта — Биденхарна. Теорема
доказана [12].
Постараемся ответить на вопрос: «Почему так происходит?».
Действительно, любое дерево всегда можно свести к блочной схеме одного
из типов деревьев, показанных на рис. 49, например к типу,
приведенному на рис. 50. Но с помощью пересадок блоков можем получить
остальные четыре дерева и нарисовать 5-угольный цикл, в вершины
которого помещены деревья. В каждом из блоков может быть
несколько моментов (от одного до л — 2 при сложении (п + 1)-го момента).
О связывающей роли 4-циклов, появляющихся при сложении 4 + k
(k = 1, ..., η — 3) моментов, мы говорили ранее. Итак, мы не только
показали, из каких простейших структур состоит граф, но и
выяснили причины их появления.
В заключение отметим, что графический метод обладает не только
эстетической привлекательностью, но и позволяет с минимальной за*
тратой сил суммировать сложные ряды.

Глава 5
МАТРИЦЫ КОНЕЧНЫХ ВРАЩЕНИЙ
В ПРОСТРАНСТВЕ ДЕРЕВЬЕВ
Известно, что матрица вращения трехмерного пространства
индуцирует D-функцию Вигнера, которая осуществляет преобразование
сферических функций, определенных на двухмерной сфере. Нашей
задачей является построение функции, порождаемой вращением п-мерного
пространства и преобразующей функции деревьев (высшие
сферические функции, определенные на (п — 1)-мерной сфере).
В группе вращения л-мерного пространства можно выбрать η (η —
— 1)/2 различных однопараметрических подгрупп, осуществляющих,
например, только преобразование переменных х% и х% (i Φ k) и не
меняющих остальные переменные [2001:
#*<0«
1
0
0
0
0
0
0
0 .
1 .
0 ..
0 .
0 .
0 ..
0 ..
.. 0
.. 0
. 1
.. 0
. 0
. 0
(0
0 .
0 .
0 .
COS* .
— sin ί .
. о .
0 .
0 .
(k)
.. 0
.. sin t
.. cos t
.. 0
... 0
... 0
... 0
... 0
... 0
... 1
... 0
0
0
0
0
0
0
1
(0
(5.1)
Из соображений удобства построим матрицу конечных вращений
в пространстве деревьев, соответствующих канонической редукции
пространства [21. Поскольку переход к другим типам деревьев
известен (см. гл. 2), то тем самым будет построена матрица вращения в
любом пространстве деревьев.
Согласно гл. 1 с канонической редукцией пространства Rn z>
zd Rn-\ =э ... zd Ri сопоставляется дерево (рис. 51) и соответствую-
112

щее ему решение ур^в^ния Лапласа
12 3 п_2 п-1 П
г
= Π {Λ^+ιΛ+ΐ} (1-^) 2 χ
f-1 '
χ fl4*"+> (ί/ί) ±__ - Π ♦,(*> -2-ps-. (5.2)
ί—ι
где η£ = щ — obf+i; */* «- cosθ*, lt = af + (η — i — l)/2 = 2/, 4- 1.
Нормированное решение ехр (/αη_ιθ«-.ι)/Κ2π соответствует
вилке, образованной координатами хп-и *п>
V/ Х"
у - exp(ian^en^)/V2a. (5.3)
Очевидно, что при вращении в плоскости (хп-\хп) вилка (5.3)
будет умножаться на экспоненту. Отсюда для построения матрицы
преобразований функций деревьев, возникающей при вращении координат,
необходимо построить вилку из координат, в плоскости которых
совершается вращение (иначе говоря, перейти к другому дереву с
помощью пересадок веток (гл. 2)), осуществить поворот на угол φ и
затем с помощью обратной пересадки вернуться к исходному дереву.
Допустим, что в плоскости (XkX*) (k' = k + т) производится
вращение на угол φ. Осуществляя последовательную пересадку fe-й
ветки с &-го места до (k + m)-ro, приходим к формуле
(5.4)
g 1-1980
113

где ф&5Г/п""1 (у1У ..., уп-ι) определяется формулой (5.2), а ψ£Ηη ({у}} —
выражением
/ 2 н-1 ,н+2
k-\
Рис. 52
2т-3 - — ах+/
π ιν'*+/·'*+/ } 2 (1 — 0'1 ) * $!*+>''*+' (
/«■3,5,..·
n—fe—т-}-2 |_ ak+m+\ ах+2т~2
Х2 4 {Л^'«} * (1-*/х+2т_3) 2 (1+*/х+2т-з) 2 X
. rt-"2 *'αη—1θη—1 *'ах+2т—2Ф'
X $Ус(^+2т-3) Π ψ, (у,)' ^ —17Г · (55)
i^k+m+t У2л У2л
Здесь у' = cos θ'; /κ+ί = ακ+< + (η —- & — ί — 1)/2; #: = cos θ,;
OQ ; Ι ^ & — /Я — 2 « · ι
Ун4-2т~3 = COS Z«x-j-2m—3i *s = α^+ζη+Ι Τ g » ^Ι ακ+2/η—2 \\
η' = (ак+2гп—3 — ακ-ί-2/η—2 — afe+m-hi)/2.
Из формул (5.2) и (5.5) видно, что функции, соответствующие
этим деревьям, отличаются друг от друга с &-й по (k + т)-ю ветку
для дерева, изображенного на рис. 51, и с (k + 1)-й по (k + т)-ю
ветку для дерева, изображенного на рис. 52, т. е. для вычисления
матрицы перехода из формулы (5.4) достаточно лишь вычислить интеграл
перекрытия между этими участками.
На основе правил, изложенных в гл. 2—4, для матрицы перехода
к формуле (5.4) имеем выражение в /-представлении
Ikf /&Н-Ь ··· » lk+rn+l
ι . i Ы+2т-~2
/κ-j-l» /κ4-3» ··· » /x+2m—3
2 |"3/4 ~3/4 >к+т+1\х (5.6)
/х./х+2—·♦/x+2m—4 ||/κ+2»ι—2 /x+2m—3 /^+т |
m
χΠ
t«2
114
m—1
_3/4 -3/4 /ft+I | 2/*+2r4+1
— 3/4 -3/4 /*+<
/κ+21—4 /κ+2ι—5 /*-f2i — 3

при т = 2, 3, ..., η — 2; при т = 1 в случае, когда соседние χ* и
#/ц-1 не образуют вилки,
//*. 1ш . \ 1-3/4 -3/4 /,+2|
, М+2 = . . . (5.6а)
\/κ-1» /κ / И /κ /κ-l /*-fl ||
и в случае, когда хк и Xk+i образуют вилку,
(/*. /*+u /*f2)—1. (5.66)
Величины Ι Ζ1 . '3 в формулах (5.6) — (5.66) суть Г-коэффи-
II /*12 / /23 1
циенты, которые в данном частном случае являются (с точностью до
фазы) ККГ, т. е.
)Т "Г ^{-у",а+,"'2,'~5Ч1^^№-+и (5·7)
В общем случае они оказываются 6/-символами, аналитически
продолженными в нефизическую (с точки зрения теории моментов)
область /[13, 230].
Действуя оператором Rk,k+m (φ) (оператор поворота в плоскости
(k, k + m) на угол φ) на функцию ψ<5"η""η'*"1 (Уь ..., Уп-ι) и учитывая
ее связь с функцией
находим выражение для матрицы поворота
Ас-НАи-3-/х+2т-
2 //*, ...,/*+«+! /х+2тЛх
Κ3···/κ+2/η—3 \/κ+1> /κ4-3 f ··· · /κ+ί&η—з /
х^х+2тв.2Ф/ /*· /Vi t .· ι A+m» /*+*+ι /κ+2/ηΛ# (5i8)
\/κ-|-It /κ+3 ι . · . ι /x+2m—3 /
Величины ( .] в (5.8) определяются формулами (5.6) —
(5.66) и представляют собой один из типов Зя/-символов
(относительно Зл/-символов см., например, [116]).
Произведение η (η — 1)/2 таких матриц с коэффициентами
/ .1, определенными (5.6) — (5.66), дает функцию «симметрич-
(2αχ + η — 2) (η + οι — 3)!
ного волчка» в пространстве ——"-—( J^L· L\
измерений, т. е. матрицу конечных вращений в пространстве деревьев. На-
8* 115

пример, в 4-мерном пространстве при т = 1 из (5.8) записываем
«;4+1(ф>==2
/%
— 3/4 —3/4 /*+2
/κ /к~1 /*+1
ί(2/κ+1>φ
е χ
X
х|~3/4 ~3/4 {^Γ-ί-ϊ^^^χ
/κ
/>/Η2-/κ·νν*Η2+/χ+1 ·
Эта матрица с точностью до фазы совпадает с полученным выше
выражением [240].

Глава 6
ОБОБЩЕНИЕ МЕТОДА ДЕРЕВЬЕВ
ВИЛЕНКИНА - КУЗНЕЦОВА - СМОРОДИНСКОГО
6.1. Структура волновых функций трансляционно-
инвариантного осцилляторного базиса
в модели ядерных оболочек. Деревья Якоби
6.1.1. Обол очечная модель ядра. В модели оболочек в качестве
нулевого приближения к полному гамильтониану ядра, состоящего из А
нуклонов,
я = ^4+21/Ы (6-0
используется оболочечный гамильтониан
^-Σ^ + ν-ίΓ,)). (6.2)
Таким образом, предполагается, что в результате взаимодействия
(rt/·) каждого нуклона i с остальными нуклонами ядра (/ Φ Ϊ)
формируется определенный средний одночастичный (или оболочечный)
потенциал, в котором нуклоны движутся независимо. Чаще всего в
качестве такого среднего потенциала используется потенциал
трехмерного гармонического осциллятора
rV^-i-mcoV2. (6.3)
Состояния нуклона с массой т в этом потенциале описываются
волновыми функциями
Wnlmi (г) к | nlml (г) > = Rnl (r) Ylmi (θ, φ), (6.4)
отвечающими собственному значению энергии εηι = (2п + / + 3/2)йсо.
Здесь радиальная волновая функция имеет вид
Xndr/r0)=V^nln!+3/2)(r/r0)!Lln+l/2(rVrbe *° . (6.5)
Масштабный параметр г0 («радиус осциллятора») записывается так;
r0 = (ft/mo). Присоединенные полиномы Лагерра определяем обычным
образом:
С (X) - S (- D* (,.£+%« **> (6·6>
117

а стандартные трехмерные сферические гармоники обозначим
Уш1 (θ, φ). Функции (6.5) нормированы условием
-χ { r2drRm (r/rQ) Rn>i (г/Го) = 6W*. (6.7)
В модели оболочек нуклоны ядра некоторым образом распределяются
по одночастичным состояниям (6.4) (т. е. заполняют орбитали \nlmi)c
главным квантовым числом /г, орбитальным моментом I и его проекцией
mi), и полная волновая функция ядра Ψ конструируется в виде
произведения указанных одночастичных волновых функций:
Ψ06 = Μ Π | nilimh (η) >χ5σΛ. (6.8)
Здесь мы добавили еще спин-изоспиновые волновые функции нуклонов
(σ — проекция спина s = 1/2 нуклона; τ — проекция изоспина t =
= 1/2 нуклона: τ = +1/2 соответствует протону, τ = —1/2 —
нейтрону). Для учета требований статистики Ферми — Дирака (принципа
Паули) введен также оператор антисимметризации
^=Σ(-1)ΡΛ
ρ
в котором суммирование проводится по всем А! перестановкам Ρ всех
переменных (пространственных, спиновых и изоспиновых) в системе
А нуклонов, (-— 1)р — четность соответствующей перестановки Р.
Практические расчеты в осцилляторной модели оболочек подробно
описаны, например, в работе [241]. Следует подчеркнуть, что точный
гамильтониан ядра (6.1) трансляционно-инвариантен, т. е. не
изменяется при общем сдвиге г ι -*· rt + a (i = 1, 2, ..., Л), в то время как
оболочечный гамильтониан (6.2) таким свойством не обладает. В
модели оболочек центр масс ядра не неподвижен, а совершает колебания
относительно некоторой фиксированной точки пространства —
начала координат.
Наиболее отчетливо это видно в случае потенциала (6.3), поскольку
гамильтониан осцилляторной модели оболочек можно разделить на
две части: гамильтониан центра масс Яц.м и гамильтониан
внутреннего движения нуклонов ядра Нвнутр:
^ Л- т(°ГП _ £7 , I/ /ft Q4
"2^ I 2 / — "и·* » "внутр» \Р'*Р
«-■K+V (*Чг?'«'-?*)· (610>
= 4 s[JiLiril!-+J!r- <-—.)*]· <«-">
Таким образом, в гамильтониане (6.9) внутренние переменные и
координата центра масс нуклонов ядра R разделяются и собственную
г°б __
2Ат
А
•Σ
+
pa
2Лт
118

функцию можно записать в виде
ΨνΛμ(Λ//?ο)ΨηΗΥΤΡ(^^ ·.., *л-1), /?*=(п/Лта>), (6.12)
где Х±, Х2, ..., Χα-ι — некоторые координаты, описывающие
внутреннее движение нуклонов в ядре; η — число осцилляторных квантов,
приходящееся на внутренние степени свободы.
В качестве последних обычно используются координаты Якоби
(см. ниже). Из (6.9) и (6.12) видно, что в обычной модели оболочек
центр масс нуклонов ядра не находится в покое или в равномерном
прямолинейном движении, а совершает гармонические колебания
около начала координат. Поскольку эти движения ядра как целого
являются нефизическими, ими следует пренебречь. В связи с этим более
адекватным приближением к точному гамильтониану ядра (6.1) будет
не гамильтониан (6.2), а гамильтониан трансляционно-инвариантной
модели оболочек (ТИМО)
А Г η2 Ί
Ятимо *= -2^- + Явнутр = S ["2^- + ^Т~ (гг — Д)2] =
-a-^+s-^-ci-^. (6.13)
который так же, как и (6.1), обладает свойством трансляционной
инвариантности. Из записи этого гамильтониана, приведенной во
второй строке, видно, что он формально имеет вид оболочечного
гамильтониана с осцилляторным потенциалом, описывающим колебания
нуклонов относительно не начала координат, а центра масс нуклонов
ядра R. Из записи, приведенной в третьей строке (6.13), видно, что
его можно также трактовать как гамильтониан системы А нуклонов,
взаимодействующих друг с другом посредством двухчастичных
упругих сил
^упР(^/) = -^(г,-г,)2. (6.14)
Эта задача имеет точное решение, и ее волновые функции
Ψτημο = ехр (ίΚΗ)ΨΤγΎ[>(Χ1, Xt, ..., ΧΑ_Χ) (6.15)
можно использовать для аппроксимации собственных функций Ψ
точного гамильтониана (6.1) Ψ = ехр (iKR) ΨΒΗγτρ (Хъ- Х2, ..., ХА-Х).
Например, можно искать внутреннюю часть точной волновой функции
в виде разложения по осцилляторным функциям Ψη (Xl9 Х2, ..., Χη-ι):
ΨΒΗγτρ (Xl9 Χ2, ... , ΧΑ_Χ) = Σ «нутр (Χν Χ2, ... , Χα-χ\ (6.16)
η
Все свойства ядра (энергии возбуждения уровней, статические
моменты ядерных состояний, вероятности электромагнитных переходов
и т. п.) определяются волновой функцией ψΒΗγτρ (Хъ Х2, „., ЛГЛ—ι) и
не зависят от множителя ехр (iKR)t описывающего движение ядра
как целого с импульсом Ρ = ЬК. Вследствие этого нас будут
интересовать только внутренние волновые функции ТИМО ψ°Ηγτρ (Хь ЛС2> ...
119

\., Xa-\), входящие в разложение (6.16) и являющиеся собственными
функциями гамильтониана (6. L). Последний разделяется в
координатах Якоби и, как будет показано ниже, имеет вид
Л2уп>= Σ[--^4+4-*^ω. (6.17)
В общем случае оболочечная функция типа (6.8) с полным числом
А
осцилляторных квантов N = 2 ni является линейной комбинацией
состояний (6.12) с различными значениями чисел квантов ν и η (Ν =
= ν -f- η). Однако в случае низшей оболочечной конфигурации, когда
заполнены (без пропусков) только низшие по энергии осцилляторные
состояния |ftf/f/nj)v связь между функциями (6.8) и (6.12) имеет более
простой вид. Если N = Nm\n (Nmm — минимальное допустимое
принципом Паули число осцилляторных квантов в системе А нуклонов),
ТО П = Nmiv И V = 0;
Ψ06 (Nmin) - Ψ™, (Да) ΨΕ£Ιη (Χι, Χ» ·.. , Χ»-ι). (6.18)
Для ядер с 4 ^ А ^ 16 низшая оболочечная конфигурация имеет
вид sV4-4 и Nmin = А — 4, для ядер с 16 < А < 40 с
конфигурацией S4/?12 (2s — 2d)A~{6 N™ = 2Л — 20 и т. д.
6.1.2. Координаты и деревья Якоби. Волновая функция Ψ ядра,
состоящего из А нуклонов, должна быть трансляционно-инвариант-
ной, поэтому в качестве ее аргументов обычно выбирают координаты
Якоби Хъ Х2, ..., Ха-\- Каждая из этих координат Xt представляет
собой расстояние между центрами масс двух групп нуклонов, одна из
которых содержит р% нуклонов, другая — qt нуклонов (pif qt ^ 1).
Координате Xt можно поставить в соответствие приведенную массу μ* =
= Piqifn/(pi + qi), где т — масса нуклона. Удобно ввести
«нормированные» координаты Якоби xt = Xt Ϋ'μί/ηι. Выделим стандартный
набор координат Якоби:
*1= (1/^2) (гх-г2),
х2 = \/Щ [(1/2) (гг +r2)-r3],
*3 == VW4l(l/S)(rx + г2 + r3)-r,]t (6.19)
,/тггг ι ν ι
**-■ - у —ΊΓ [Т^Т & г* -ГА\ ·
Здесь гг — координаты ί-го нуклона; каждая координата xt
стандартного набора определяет расстояние между (i + 1)-м нуклоном и
центром масс группы нуклонов с номерами 1, 2, ..., i.
Прочие наборы координат Якоби назовем нестандартными.
В частности, если в наборе (6.19) произвести некоторую перестановку
координат нуклонов г,·, то получится нестандартный набор координат
Якоби. Выбор координат Якоби показан на рис. 53 в виде дерева Яко-
J20

Рис. 53
2 S
би. Свободные концы этого графа отвечают
координатам нуклонов гь каждая
внутренняя линия означает координаты центров
масс той группы ρ нуклонов, номера
которых обозначены на свободных концах,
«произрастающих» из этой внутренней линии.
С внутренней линией сопоставляется масса
рт, а со свободным концом — масса т.
Каждому узлу отвечает определенная
координата Якоби, составленная из координат
центров масс двух группировок ρ и q
нуклонов, соответствующих линиям, идущим
вверх из этого узла. Если линия уходит
влево, то соответствующая ей координата
берется со знаком плюс, а если вправо —
со знаком минус. Разность координат двух
центров масс надо умножить на \pql\p +
+q)\l/2. Стандартному набору координат
Якоби (6.19) отвечает приведенное выше
дерево Якоби. Нестандартное дерево
Якоби, показанное на рис. 54, описывает
следующий набор координат Якоби:
*2=(1/К2)(г3-г4), (6.20)
ж3 = (1/2) (гг +г2 — г3 — г4).
6.1.3. Операции над деревьями.
Рассмотрим переходы от одного дерева к
другому. Совокупность всех преобразований от одного дерева к
другому называется группоидом перестройки [242]. Это множество
отличается от группы тем, что не для всех его элементов определено
произведение и не для всех произведений умножение ассоциативно.
Подробности о структуре группоидов перестройки для различных величин А и
их представлениях изложены в работе [242]. Отметим, что количество
элементов группоида также чрезвычайно быстро растет с увеличением
значения А. Однако любое сколь угодно сложное преобразование
деревьев можно свести к последовательности некоторого числа
элементарных преобразований. Этими элементарными операциями, как ив
случае гиперсферических деревьев и деревьев Вигнера, являются
следующие: 1) отражение РаЬ в развилке дерева aby из которой выходит
ветви а и Ъ\ структура кроны, основанием которой является ветвь av
и структура кроны над ветвью Ь не изменяются и перемещаются в
новое положение; 2) пересадка Са{ь)С одной ветви b в развилке abc с
левого сучка на правый или наоборот. При этом, как и в случае
отражения, структуры крон, расположенных над ветвями а, Ь и с, не
изменяются. В дальнейшем рассмотрим только такие случаи, когда матрицы
преобразования Саф)с будут унитарными и вещественными, т. е.
обе пересадки, изображенные на графе, будут характеризоваться од-
121

ними и теми же коэффициентами
преобразования. Поэтому оба таких
взаимообратных перехода
обозначим СИМВОЛОМ Саф)С.
Итак, любую перестройку
деревьев можно свести к
последовательности элементарных операций
Р, С, производя на каждом этапе
пересадку только одной ветви с одного сучка на другой, выходящий
из того же узла. Разбиение перехода между двумя деревьями
с четырьмя свободными концами на элементарные операции
показано на рис. 35. В соответствии с ним результирующий переход G можно
записать в виде
G = ^3(2)4^13,2^2(1)3^12^12(3)4· (6.21)
Это представление G через операции С и Ρ не единственное, например,
G = С\ (3)24^24,3^2(4)3^34^1 (2)34 (6.22)
и т. д. Однако запись (6.21), (6.22) минимальна в том смысле, что
нельзя свести преобразование G к меньшему числу операций Р, С.
6.1.4. Переход от одного дерева Якоби к другому в базисе
гармонического осциллятора. Коэффициенты Тальми — Мошинского.
В результате непосредственной проверки можно убедиться в том, что
гамильтониан (6.11) разделяется в любом наборе координат Якоби и
принимает вид (6.17). Поэтому рассмотрим произведения осцилля-
А—1
торных функций от координат Якоби Ψ = Π Ψν,/,™, (χί)> гАе ν* —
= 2ttj + li — число квантов; lt — орбитальный момент; mt — его
проекция для соответствующего осцилляторного состояния. Полезно
сложить каким-нибудь способом моменты 11у ..., Ia—\ в полный момент
L, полученную в результате волновую функцию обозначим
\1г12 ... lA-X:LMDwDj), (6.23)
где Dj — дерево Якоби, которое определяет структуру используемых
координат Якоби х1у х2у ..., ха-\\ Dw — дерево Вигнера, задающее
схему сложения моментов количества движения по отдельным
координатам Якоби /lf 12У ..., /л_1 в полный момент L. В дальнейшем при
антисимметризации волновой функции Ψ по отношению к перестановкам
нуклонов преобразуем функции (6.23) к другим наборам координат
Якоби. Поэтому получим матрицы элементарных преобразований Р9
С в базисе (6.23). Операция отражения Ρ в некотором узле дерева
Якоби означает изменение знака координаты Якоби xiy которая
соответствует этому узлу. В итоге функция (6.23) умножается на фазу (—1)'.
Операция пересадки ветки Срт изображена на рис. 55, где
свободные концы означают координаты центров масс Rpy Bq, R, трех
нуклонных группировок с массами соответственно /?, q% л Узлы
отвечают двум парам координат Якоби:
Ρ Ι τ Р 1
ср(ч)гхря.
*г
Рис. 55
122

bPW
V(p + q + r)(P + q) 1Р*Р+ЯВ,-{Р+Ч)ЯЛ. (6.24)
Xqr=Y'
ЯГ
Я + r
{Rq-Rr\
*p* = V(p + q+Pr){q + r) № + ')rp~яЪ-rRrl
Эти два набора координат Якоби связаны ортогональным
преобразованием
/рг , ι f q (ρ -)- q -f- г)
(Ρ + Я) (Я + r) X">r + V (р + я)(я + г) Χ™> {625)
т ._ \ί Я (Ρ + Я + г) |/ рг
Xqr-V (Р + Я)(Я + г) Xp«'r-V (p + q){q + r) Х™>
рассматриваемым как кинематический поворот на угол
φ - arctgVpr/[q(p+q + r)]. (6.26)
Выделим ту часть функции (6.23), которая связана с координатами
Якоби xpqy xPgtP. Тогда согласно [243, 244]
I ЯЛ (*рдЛ п212 (Воя) : ΛΛί) =
= Σ, , (ηΑη^ζ ι Л | prlq {ρ + q + ή \ п[1[п212: Λ) Χ
«1/1"2/2
Χ I n[l[ (xPtgr) n& (xqr): ΛΛί), (6.27)
где {п^п^ъ: Л \ μ!/μ2 \ nUlihk: Л) — обобщенные коэффициенты Таль-
ми — Мошинского [245]. Таким образом,
Wl (Xpq) Щ12 (Xpq,r) ·* ΛΛί \ Cp(q)r / tl\l[ (Xpq) TlJl (Xpq,r) ·* AM) ==
= {п212пх1г ι Λ/prlq(p + q + r)\n^Wih : A). (6.28)
Отметим, что если осцилляторные состояния | n1lim1)>,\ n^m^
в (6.27) не только векторно сложены, но и из них образована
комбинация с определенной симметрией (λμ) относительно SU (3), т. е.
| лл : (λμ) LM > = 2 <'(Γι0) 1?'0) | ί/λμ)> | п^п^ : LM) (6.29)
((/?ι0#'°1 Ζ,(λμ)> — ККГ для группы SU (3) в редукции SU (3) zd
zd SO (3) [246], то матричный элемент пересадки СШг выражается
проще [247, 248]:
(ял : (λμ) LM \ СрШ \ п\п2: (λμ) LM) = d*& (φ). (6.30)
Здесь в правой части стоит обычная D-функция Вигнера [249]
(функция симметричного волчка с т = (пг — л2)/2, т = (щ — щ)12)\
φ — угол кинематического поворота.
С помощью формул (6.27), (6.28) можно выразить матрицу любого
перехода от одного дерева Якоби к другому в осцилляторном базисе
(6.23) в виде суммы произведений нескольких обобщенных коэффи-
123

циентов Тальми — Мошинского. Прежде чем вычислять матричный
элемент от операции С, следует перегруппировать моменты таким
образом, чтобы моменты, относящиеся к координатам Якоби,
охватываемым преобразованием С, складывались так, как в (6.28). Поэтому
общее выражение будет содержать кроме коэффициентов Тальми —
Мошинского и фазовых множителей также необходимое число Зл/-сим-
волов.
Итак, мы рассмотрели, как преобразуются при перестройке
деревьев Якоби осцилляторные функции (6.23). Такие операции
производятся при построении волновой функции с заданной
перестановочной симметрией. Перейдем к описанию структуры волновых функций
в методе К-гармони к.
6.2. Осцилляторные функции в гиперсферических координатах
6.2.1. Решение уравнения Шредингера для /г-мерного
гармонического осциллятора в гиперсферических координатах. В (3Λ-—3)-
мерном пространстве координат Якобиxt (i = 1, 2, ..., Α — 1) можно
ввести гиперсферические координаты : гиперрадиус
ρ2=Σ· *? = ]£(г*-я)2
(rt — координата отдельных нуклонов; R — центр масс нуклонов
ядра) и гиперсферические углы 9У (/ = 1, ..., ЗА — 4). Тогда
гамильтониан (6.17) переписывается следующим образом!
" = -ш [i=r ir (ρ""' -w) + ίγΑ] + τ*"ν. (6·31>
где я= ЗА — 3; Δθ, — угловая часть оператора Лапласа.
При этом собственные значения энергии задаются формулой
ΕΝ = (2κ + К + η/2) Йа). (6.32)
Здесь 2κ + К = N — полное число квантов, а собственные функции
имеют вид
ψ„Κν = R„K (ρ) ΥΚν (θ,) Dr, (6.33)
где Υκν (θί) — некоторая ГГ с общим гипермоментом /(, отвечающая
выбранному гиперсферическому дереву Dr; v — набор остальных
гипермоментов, характеризующих состояние
*** <Р) - /г(*Л'+п/2) е-^У^'2»"-* (р>), (6.34)
где ρ дано в единицах г0 = (Й//гш)1/2. Формула для присоединенных
полиномов Лагерра дана в (6.6). Здесь и ниже размерность
пространства η может рассматриваться произвольной, а не обязательно
кратной трем, как это имеет место в ТИМО.
Известно [243], что набор осцилляторных функций с
фиксированным числом квантов TV образует базис симметричного НП со схемой
Юнга [N] группы U (п) = U (ЗА — 3), генераторами которой явля-
124

ются операторы
Aia.n ** а&а/ь ϊ, /= 1, 2, ... , Л — 1, α, β = *, уу г, (6.35)
где аЙс, Λία — операторы рождения и уничтожения квантов по а-й
декартовой компоненте координаты Якоби xt.
Действительно, и^ известных коммутационных соотношений для
операторов рождения и уничтожения квантов as ξ= ща и at = ati
[at, at] = 0, \as, aA = 0, [aS9 at] - 6SS, (s - 1, 2, ... , n)(6.36)
следуют стандартные коммутационные соотношения для генераторов
алгебры U (п)
[APQ, Ars] = bqrAps — bp,ArQ (ρ, q, /·, s= 1, 2, ... , я). (6.37
Ясно также, что волновые функции вида (6.33) с фиксированным
ΝΚ и всевозможными значениями ν принадлежат к НП группы
SO (η) = 50 (ЗЛ—3) с гипермоментом /С.
Поэтому набор функций (6.33) отвечает редукции SU (ЗА— 3) гэ
zd SO (ЗА — 3). Нас будет интересовать вопрос: как связаны между
собой функции (6.33) и осцилляторные функции в координатах Якоби
(6.20). Чтобы ответить на него, решим следующую вспомогательную
задачу. Пространство с базисом хг, х2, ..., хп разобьем на два
подпространства размерности пх и п2 (пг + п2 = п) с базисами хи хъ ..., хП1
и Xnt+u ···» *п соответственно. Введем гиперсферические координаты
Ρι» Φ и р2, Θ/ в этих подпространствах и построим осцилляторные
функции Ψλ^/Civ,» ^NtKtVt типа (6.33) в каждом из этих
подпространств. Выразим функции (6.33) от ρ, θ через функции от рь
θίί р2» Θ/J
Ψ**ν= Σ (ΝιΚ1Ν2Κ2\ΝΚ)ΨΝικιν^Νΐκ^. (6.38)
Здесь предполагается, что сферическая функция Υκν в левой части
выбрана в соответствии с редукцией SO (η) zd SO (rii) X SO (η — пг)
(см. формулу (1.72)). Поэтому коэффициенты перехода (6.38) не
зависят от квантовых чисел v, vlf v2 и справедливо равенство
Σ (NiWtK* IN К) RNtKi (Pl) RNtKi (P2) - i6 39)
- R*k (P) N2KKiK, sin«< θ cos*' θφ»^^^2-'» (cos 2Θ),
где ρ2 = ρ cos θ; pi = ρ sin θ.
Оказывается, коэффициенты разложения в (6.38) можно связать
с ККГ для группы Sp (2, R) или локально-изоморфной ей группы
Si/(1,1) [13, 205]. В результате Г-коэффициенты пропорциональны
Зд/-символам для этой группы, которые содержат моменты, кратные
1/4. Указанная связь между соответствующими величинами для двух
разных групп SO (η) и Sp (2, R) основана на том, что эти группы
дополнительны в смысле определения, предложенного Мошинским с
сотрудниками [25].
125

6.2.2. Дополнительные группы. Пусть имеется прямое
произведение Нх X Н2 двух групп Hi и Н2 и дано некоторое линейное
пространство &, в котором реализуется D-представление (вообще говоря,
приводимое) группы Нх X #2. Назовем группы Нг и Я2 дополнительными
внутри ^-пространства, если существует взаимно однозначное
соответствие между всеми НП групп Нг и H2t содержащимися в D-пред-
ставлении, т. е. в прямой сумме
0 = 2ϋ/Λ (6.40)
i
каждое неприводимое D '-представление группы Нх встречается в
комбинации только с одним определенным неприводимым D
'-представлением группы #2 (и наоборот), причем каждая такая комбинация
D', D ' встречается в разложении D-представления не более одного
раза.
Известно, что группой инвариантности системы ρ частиц в
(7-мерном осцилляторе является группа Sp (2pq; R) канонических
преобразований, генераторами которой служат операторы α£α/β, (1/2) χ
X (OiaCift + d^afa), atadft (/ = 1, 2, ... , p\ a = 1, 2, ...tq).
Совокупность всех состояний с четным числом квантов N = 0,
2, ..., сообразует базис бесконечномерного представления с младшим
весом [1/4· 1/4...1/4] = [1/4W] этой некомпактной группы. Все
нечетные состояния осциллятора входят в другое представление с
весом [3/4· 1/4... 1/4] гз [3/4 · 1/4рд~~1]. Мошинским с
сотрудниками показано [25], что внутри пространств этих представлений
группы Sp (2q\ R) и О (ρ) являются дополнительными. В дальнейшем нас
будет интересовать случай Sp (2л, R) -> Sp (2, R) X О (л). Тогда
имеем, что Ок-представление класса 1 группы О (п) с глобальным
моментом К комбинирует с одним определенным О'-представлением
группы Sp (2, R), которая локально-изоморфна группе SU (1, 1).
Если К дано, то «момент» J в обозначениях, принятых для группы SU
(1,1), связан с глобальным моментом /О
•/=4+JLr1 <6·4Ι>
(именно такой «момент» появился в формуле (1.67) для
гиперсферических гармоник, аналогичные моменты jt фигурируют в /-представлении
для Г-коэффициентов (см. параграф 2.4)).
Это означает, что осцилляторная функция (6.33) для состояния с
числом квантов N и глобальным моментом К принадлежит к НП
группы Sp (2, R) с моментом J = (1/2) (К — 2) + я/4 и характеризуется
его проекцией Μ =* (1/2) Ν + η/4. Тем самым имеем двузначные
унитарные НП группы Si/(1,1) из положительной дискретной серии
[14]. Отметим, что с каждой функцией ортогональной схемы, а
следовательно и соответствующей ГТ, можно естественным образом
сопоставить момент, кратный 1/4. Это обстоятельство в конечном счете и
приводит к тому, что Г-коэффициенты пропорциональны п/-символам
с четвертьцелыми моментами.
126

Обсудим вопрос о дополнительности групп О (п) и Sp (2, R) более
подробно. Для этого сначала рассмотрим группу Sp (2,7?). Возьмем
одномерный осциллятор с гамильтонианом
Η0 » 4" <α+α + αα+>йо)· <6·42>
Его динамической группой является группа Sp (2, R)
(локально-изоморфная группе Si/(1,1)), поскольку гамильтониан Я0 совпадает с
одним из трех генераторов алгебры Ли этой группы
J+ = ±a+a+y J- = -\-aa, J0 = ±-{а+а + аа+) = ±H0i (6A3)
удовлетворяющих коммутационным соотношением
[J09 J±) = ± yt; [J+9 J_] = 2У0, (6.44)
но с другими свойствами по отношению к эрмитову сопряжению
(JoY=Jo> (Ль)*--/*. (6.45>
Собственные векторы | η) — /— (аГ) |0) гамильтониана (6.42>
Н0\п) = (я + 1/2)|я) характеризуются «проекцией» момента т =
= -γ-(η+1/2): У0|я) = — (я + 1/2) |л). Повышающий генератор У_^
переводит л-квантовое состояние в состояние с η + 2 квантами
У+1 л> = К(л+1)(л + 2) | я + 2), (6.46)
а понижающий генератор У- уменьшает число квантов на две
единицы:
/_ | π) β _ |Λι (п.— 1) / л — 2>. (6.47>
Таким образом, полное пространство состояний | п) одномерного
осциллятора распадается на два подпространства с четными η = О, 2,
4, ... и нечетными η = 1, 3, 5, ..., в каждом из которых реализуется
бесконечномерное НП алгебры (и группы) Sp (2, /?). Неприводимые
представления этой некомпактной группы можно характеризовать
вещественным числом / (некомпактным угловым моментом), которое
задает собственное значение / (/ + 1) оператора Казимира группы
S/>(2, R) (или SU (1,1))
Ρ = J+J- +J20-J0~j (/ + 1). (6.48)
Набор векторов | п) ограничен снизу значением η = О или л = 1, а
сверху не ограничен. Поэтому в пространстве волновых функций
гармонического осциллятора реализуются унитарные неприводимые £>/+-
представления группы Sp (2, R) (Si/(1,1)), принадлежащие к так
называемым положительным дискретным сериям. Базисные векторы
Ψ/m D'-представления нумеруются проекциями т момента /,
причем т = / + 1, / + 2, .., Младший вектор с минимальной проекцией
удовлетворяет условию
7_Ψ//+Ι - 0, (6.49)
^//+ι«/</ + 1)Ψ//+ι· (6.50)
127

Поскольку минимальное значение «проекции» т для четных
состояний одномерного осциллятора равно 1/4, то / = —3/4; для нечетных
состояний ттт = 3/4 и / = —1/4. Впрочем, имея в виду зеркальную
симметрию / -+ —- / — 1 [1141, можно считать, что четные состояния
также характеризуются моментом / = —1/4'. Мы снабдили его
штрихом, чтобы отличать от неэквивалентного представления, имеющего
в качестве базиса нечетные состояния.
Возьмем произведения осцилляторных функций, зависящих от
переменных хг и х2, и произведем векторное сложение
соответствующих моментов /\ и /2, равных —3/4 или —1/4?
l/i/*: /12^12) =
= Σ (/ι"*ι/2"*21 /umu) I i1m1 (xt)) j%m2 (xt)). (6.51)
Следует иметь в виду, что правило векторного сложения для
«некомпактны»» моментов дает допустимые значения для суммарного
момента
/it-/i+/t + l, /1 + /2+2... (6.52)
Генераторы группы Sp (2, /?), которая действует в пространстве
состояний (6,51), имеют вид
'±0. 2) = /±(1) + ^±(2),
Л(1, 2) = У0(1)+У0(2) =4-(^о(1)+//0(2)), (6.53)
где оператор Js (i) (i =» 1, 2) действует только на функцию от
переменной х%.
Таким образом, функции (6.51) являются собственными функциями
гамильтониана двухмерного осциллятора с полным числом квантов
2т12 — 1, т. е. каждую функцию (6.51) можно сопоставить с волновой
функцией двухмерного осциллятора в цилиндрических координатах!
р2 = х2) + xl; tg φ = xjxt;
l f cos Λφ,
I /1/2: /ΐ2^12> Zt Ι "ιΛ>± = y=- RniA (P) j sin A (6.54)
При этом rti = 2m12 — 1. Минимальное значение /п12, допустимое при
фиксированном значении проекции орбитального момента Λ (Α »
= 0,1, 2, .*.) и равное (Λ + 1)/2, реализуется в состояниях | ΛΛ)+.
Очевидно, что понижающий генератор /_ (1, 2) ~ αχαγ + а2<ц
обращает каждую из этих функций в нуль:
У—(1, 2)|ΛΛ)± = 0, (6.55)
2
а повышающие генераторы ./+(1, 2) = 2 atdt переводят эти
функции в состояние с большим числом квантов;
(./+ (1, 2))* | ΛΛ)± ~ | Λ + 2k, Λ>±. (6.56)
128

Так как генераторы /±(1, 2), /0(1, 2) = -«-Σ (^tat + а(аТ) являют-
ся скалярными по отношению к группе О (2) (повороты в плоскости
хи х2)у то они не изменяют значений проекции орбитального момента
Л и тип симметрии соответствующей волновой функции. Действуя
оператором Ρ (1, 2) = J+ (1, 2) У_ (1, 2) + 4 (1, 2) — J0 (1, 2) на
векторы (6.56), легко убедиться в том, что они являются собственными
векторами этого оператора:
У2(1>2)|Л + 2£, Л>±==/12(/12 + 1)|Л + 2*, Л>±, k = О, 1, 2, ...,
(6.57)
при /12 = -у(А — 1), поскольку оператор Казимира /2(1, 2)
коммутирует с J+ (1, 2). Это означает, что в пространстве волновых
функций двухмерного осциллятора | Л + 2А, Л)± реализуется
неприводимое унитарное 0/1?+-представление группы Sp (2, R) (SU (I, 1)) из
положительной дискретной серии. Если заметить, что квантовое число
Λ задает НП группы О (£) (повороты в плоскости хъ х2), то видно, что
волновая функция двухмерного осциллятора (6.54) принадлежит
одновременно к неприводимому Ол-представлению компактной группы
О (2) и неприводимому D ^-представлению некомпактной группы
Sp (2, R). Причем индексы представлений этих двух групп
однозначно связаны друг с другом /12 = -у- (Λ — 1), т. е. Ол-представление
группы О (2) встречается только в комбинации с 0(Л~"1)/2+-представ-
лением группы Sp (2, R). Это и есть содержание понятия
дополнительности групп О (2) и Sp (2, R) в пространстве состояний двухмерного
осциллятора. Точнее, одному значению Λ отвечают два D 12-
представления с /12 = -о- (Λ — 1). Однако они построены на состояниях
| ΛΛ)± разной структуры и отличаются друг от друга значениями
«моментов» /Ί и /2, из которых они скомбинированы. Именно Λ =
= 2/12 + Ι; /Ί = —3/4, /2 = —3/4 соответствуют четным значениям
Λ и угловой функции типа cos Λφ (нижний индекс +); /Ί = —3/4 и
/2 = —1/4 соответствуют нечетным Λ и угловой функций типа sin Λφ.
При /Ί = —1/4 и /2 = —3/4 имеем нечетное Λ и зависимость от угла
φ типа cos Λφ. Наконец, случай /Ί = —1/4, /2 = —1/4 приводит к
четному Λ и угловой функции типа sin Λφ. Поэтому соответствие между
функциями в левой и правой частях равенства (6.54) имеет взаимно
однозначный характер. В силу этого соответствия можно
рассматривать (6.51) как разложение волновой функции двухмерного
осциллятора в цилиндрических координатах через функции в декартовых
координатах:
|ΐιΛ>± = 2 (ηιΑ\ηχη2) \ηι(χ1))\η2(χ2)). (6.58)
9 1-1980
129

Если использовать для радиальной функции осциллятора
стандартное выражение
Rn±а(Р) = V 2 (лχ/2 + Л/2)! (пх/2 - Л/2)! X
Σ (
Ь=|Л|,|Л|+2 nL
-1 (6_|Л|)
Χ Σ (-1) ехр(-р2/2)Х
х £
(6/2 — Л/2)! (6/2 + Л/2)! (л±/2 — 6/2)! '
то для матрицы перехода от цилиндрических координат к декартовым
получаем выражение
(п1А\п1п2) =
(•—1) , если η ι четное,
η /2-1/2 (6,59)
(— 1) х , если п± нечетное.
Связь между параметрами в левой и правой частях этого равенства
была указана выше.
Складывая момент /12 с моментом /3 = —3/4 или —1/4,
отвечающим координате х3> получаем волновую функцию | j\j2 (/12), /3 *
: /12зт12з)» которая соответствует решению уравнения Шредингера
для трехмерного осциллятора в сферических координатах: {п1А)± =
= Rm (г) У/л (θ, φ). При- этом число квантов η = 2 (m123 — 3/4), а
значение компактного момента / (символ НП группы SO (3)) можно
однозначно связать с величиной некомпактного момента /123 : / =
= 2/ι23 + 1/2. (Действительно, минимальная «проекция» т123 = /ι23 +
+ 1 принимает при фиксированном значении трехмерного
орбитального момента / значение -у- (I + 3/2).) Это соотношение снова является
выражением (или следствием) дополнительности групп SO (3) и
Sp (2, R), проявляющейся в том, что функции | п1А)± с
фиксированным трехмерным моментом (и любыми допустимыми η и Л),
принадлежат одновременно к неприводимым D1- и 0/т+-представле-
ниям групп соответственно SO (3) и Sp (2, R). Заметим, что здесь и
далее используются вещественные сферические гармоники
γ± ί (i/VmYiMb ф)(- ΐ)Λ + У/.-а (θ, Ф)])β
/Α( ' Φ) 1 (1/Κ2)[Κ/ιΛ(θ, φ)(- 1)Α-ΧΚ-Αφ, <p)j (
ι ί cos Λφ;
= -^-θ/λ(Θ) Ι.ηΛ (6.60)
Κ π I sin Λφ,
где Κ/,±μ — обычные сферические гармоники.
Продолжая эту процедуру, добавляем к /123 последовательно /4>
/е. —. U- Тогда получаем функцию | jj2 (j12), /3 (/128), ..., /«-ι (/ΐ2...«-ι);
yn : /Μ), которая соответствует решению осцилляторного гамиль-
тониана в n-мерных сферических координатах:
l/i/t (/it). · · · , In -J Μ) = Ψ,νκν = /?ivK (Ρ) y*v(elf θ2, ... , θ^). (6.61)
130

Здесь ρ2 = х\ + Х2 + ... + Хп\ Υκν —
гиперсферическая гармоника» соответствующая
каноническому дереву, изображенному на
рис. 13; ν —совокупность гипермоментов /(\,
К2, ···> Кп-2 в пространствах размерности
η — 1, ..., 3, 2 (эти гипермоменты указаны
около узлов дерева); К— глобальный момент _
в л-мерном пространстве. >4,8^ ~— sinAw
Каждому такому гипермоменту Ks соответ- л у. У#- *
ствует (в смысле дополнительности групп
0(п — s) и Sp(2, R)) «некомпактный» момент Рис· ^
/l2...„-s = 4" К* + ^Р4 · (6*62)
В отличие от гл. 1 здесь используем вещественные сферические
гармоники. Поэтому в развилке дерева с двумя свободными концами,
приведенными на рис. 56, нужно указать знак «+» или «—».
Дерево, приведенное на рис. 13, можно рассматривать в двух
аспектах: с одной стороны, оно характеризует выбор гиперсферических
углов, а с другой — задает схему сложения моментов типа —3/4, —1/4.
Если использовать не последовательное сложение, а какую-то
другую схему сложения, то она будет соответствовать другому выбору
гиперсферических углов. Отсюда ясно, что скалярное произведение
двух л-мерных осцилляторных функций Ψ^κν и Ψ^κν с
фиксированными Λ/, К для двух вариантов ν и ν' выбора гиперсферических
координат совпадает с некоторым /-символом для группы Sp (2, R),
отвечающим переходу от схемы связи ν моментов /i/a.../n к схеме связи v'j
<Ψ*κν I Vnkv) — (Υκν Ι Υκν) « <(/ι/, ... /Λ)ν Ι (/ι/3 ... /nV>. (6.63)
6.2.3. Т-коэффициенты и З/г/'-символы. Рассмотрим с этой точки
зрения Г-коэффициент для операции пересадки, показанной на рис. 18.
Согласно изложенному выше ее можно рассматривать как переход
между деревьями Вигнера, образованными следующими
«некомпактными» моментами:
/р = -f + -^=^- , ρ - α, β, γ, δ, ε, σ. (6.64)
Здесь ηρ — размерность пространства, в котором задан
гипермомент р.
В соответствии с рис. 29 такая пересадка выполняется с помощью
6/-символа для группы Sp (2, R) (SU (1,1)):
'; * '■. (6.66)
Сравним этот результат с формулами (2.43), (2.49). В последних
фигурируют моменты fa = -γ- (lp — 1). Поскольку lp = ρ + Sp/2 (см.
пояснения к формуле (2.1)), a sp = пр — 2 (как следует из обсуждения
формулы (1.65)), то /ρ = -γ lp + *^γΛ> что согласуется с (6.64). Таким
9*
131

образом, Г-коэффициенты и 6/-символы, обсуждавшиеся в гл. 2,
идентичны коэффициентам Рака для «некомпактной» группы SU (1,1)
(Sp (2, R)), рассмотренным выше. Следствием соотношения
дополнительности между группой Sp (2, /?), а также группой О (п) и ее
подгруппам является то, что Т-коэффициенты играют двоякую роль.
По отношению к группе О (п) они образуют матрицу перехода от
одного способа редукции группы О (п) на ее подгруппы к другому типу
редукции, а по отношению к группе SU (1, 1) (Sp (2, R)) являются
коэффициентами перехода от одной схемы связи η «некомпактных»
моментов типа —3/4 (—1/4) к другой схеме их сложения (3 (лг — 1) /-
символ). В частности, Г-коэффициенты для пересадки (см. рис. 18)
образуют матрицу перехода от редукции
О (п0) ZDO(na) X 0(пь)
(6.66)
-+0(nz)xO(ny)
к другой редукционной цепочке
0(na)zDO(nB)x 0(пу)
(6.66а)
-0(/ι«)χ0(ηβ)
(Па + Щ + Пу = Па, Па + Щ = Яе» Щ + Щ = Нь)
и одновременно играют роль коэффициентов Рака типа (6.65) для
группы SU (1.1).
Таким образом, мы убедились, что Г-коэффициент {Υκν \ Υκν),
характеризующий унитарное преобразование ГГ при переходе от
одного дерева к другому, совпадает с 3 (п — 1) /-символом для группы
Sp (2, R), содержащим моменты, кратные 1/4.
В гл. 2 отмечалось, что эти /-символы являются аналитическим
продолжением обычных /-символов, известных в квантовой теории
углового момента. В частности, ККГ вычисляются по формуле [2491
(hm^m^JM)^
__ , nAf-y-i \f (2У + 1) Г (Д +mt + 1) Г (/, + та+1) Г </-/!-/,)'
~~К Ч У Г(У + М+1)Г(М —У)Г(/И! —/Ί) А
χ Υ ,Л(у + /2~Лг^?Лт2Т/2\ о χ
х L
Г (У + /ι ~ /2 + 1) Г (У + η + /2 + 2)
(-1)гГ(г+1)Г(М + У-г)
Г(г + у-А« + 2)Г(г + /1-т1 + 2)Г(/1-/1 + А1-г)х '
X Г (Λί — г — /ж — /я — 1)
(6.67)
Если сравнить полученное выражение с формулой для ККГ группы
SU (2), приведенной в работе [250], то (6.67) получается из последней
формулы путем замены каждого / на —/ —1 и т на —т:
{кЩНЩ I JM)su<2) -> UimJtm% \ JM)Sp(2tRh (6.68)
если /, -> —jl — 1; /2 -* —/2 — 1; J -* — J — 1; щ -*- —тг\ т2 ->
-*- —т2; Μ -*- — Μ. Переход от ККГ группы SU (2) к соответствую-
132

щим величинам для группы Sp (2, R) подобен операции зеркального
отражения в теории обычного углового момента [251].
Для ККГ группы Sp (2, R) справедливо соотношение симметрии
</1m1/2m2 / J Μ) = (- i/h-/·-'-1 (km^m, \JM). (6.69)
Имеется компьютерная программа для расчета ККГ для группы
SU (1, 1), основанная на формуле (6.67) [252].
Что касается коэффициентов Рака для некомпактной группы
Sp (2, /?), то для них был получен ряд соотношений в гл. 2. Их можно
также вычислить по формуле, приведенной в работе [205]:
Ihh (Jn)y h:J Ι /ι, /г/з (Лз): «flsi/U.D s
- ί/ (/ι/У/з; A.^.) = (- i)y^/eW+J- χ
X Vr(Ju-U + /ι+ 1)Γ(Λ2 +1\ + h + 2)Г(У23 + /2- '"""*
■/s + 1)Г(У23+/2+/з+2)Х
2 +
- χ
/ (2/lf + 1) (2У23 + 1) Г (У -Уа3 - /Ί) Г (/ι + 7 -У23 + 1) Г (/.
νΈ/ Ч- -/ц — /ι + О Г (У1а — Ь — /а)
I/ Г(У + У11-/,+ 1)Г(У + У11 + /, + 2)Г(У + ^»-
f -/1+1)Г(У + У23 + /1 + 2)
X КГ(/8 + ^-У12+1)Г(У-Аа-/в)Г(У88-/а-/8)Х """
Ч"'" X ГОз —/а + Лз+ 1) X
х V (—1)^Г(2У —г + 1) 6 0
А £0 Г(г+1)Г(/1 + У-У23+1-г)Г(/з + У-У12+1-г)Г X ' ^'U'
X Г (У —/8 -У12 - г) χ Г (У23 -У + /t + 2 + У1а + г) χ
хГ(7-7ад-/1-г)Г(У18-/1--./ + 711+1 + г)
которую снова можно получить из общего выражения для
коэффициентов Рака группы SU (2), если в последнем / заменить —/ — 1.
Хотя формулы для ККГ и Рака групп SU (2) и Sp (2, R) и сходны
друг с другом, но в эти коэффициенты входят совершенно различные
моменты jl9 /2, У12, поскольку такие тройки моментов в случае групп
SU (2) и 5/? (2, R) подчиняются абсолютно различным правилам
векторного сложения (см. (6.50)). Впрочем, можно показать, что ККГ
для группы SU (2), содержащие только целые и полуцелые моменты,
совпадают численно с некоторыми коэффициентами группы SU (2).
Явные соотношения такого рода получены в работе [25].
6.2.4. Преобразование осцилляторных функций в
гиперсферических координатах при переходе от одного набора координат Якоби
к другому. Выше мы рассматривали преобразование осцилляторных
функций при переходе от одного набора координат Якоби к другому.
Аналогичная задача возникает и в методе /С-гармоник. Для ее решения
необходимо оперировать с осцилляторными функциями в
многомерных сферических координатах. Используем полисферические
координаты, выбранные таким образом, что общая гиперсферическая функ-
133

%
Рис. 57
ция ^/см!!(./л-1 конструируется из сферических функций с
моментами /ь /2, ..., /л—ι для отдельных координат Якоби хъ хъ ..., ха-\
по правилам, сформулированным в гл. 1. Символ Ьг указывает
на вид гиперсферического дерева, задающего конструкцию ГГ; щ —
промежуточные гипермоменты данного дерева. Целесообразно
сложить каким-то способом моменты 1Ъ /2, ..., /л—ι в полный момент L.
В связи с этим укажем дерево Вигнера Dw, которое задает схему
сложения моментов и промежуточные моменты Xt. Полученную в итоге
гиперсферическую функцию обозначим Укш'м^а—х · Осциллятор-
ная функция с числом квантов N в выбранных гиперсферических
координатах имеет вид
IV, ... /ϋ-ι, ft*i, DwKr.NKLM) = Rm(p)YDK[X^A_r (6.71)
В предыдущем параграфе мы отмечали, что конструирование осцилля-
торной функции в многомерных сферических координатах по
заданному гиперсферическому дереву Dp можно рассматривать как
сложение А — 1 моментов вида /\ = (/f — \ 12)12 с помощью ККГ для
группы Sp (2, /?) или SU (1,1) в полный момент [К + (ЗЛ — 7)/2]/2
с промежуточными моментами ji9 значения которых определяются
промежуточными гипермоментами щ. Для краткости назовем эту
процедуру просто сложением моментов 1Ъ /2 , ..., 1а-\ в полный
момент К в смысле группы Sp (2, R) с промежуточными моментами щ.
Далее для определенности примем, что схема сложения моментов
1и в смысле группы Sp (2, /?), такая же, как и по отношению к обычной
группе вращений, т. е. структура деревьев Dr и Dw одинакова.
Функцию (6.71) такого типа обозначим
IV, ... /4-i; *ltiNKLM).
(6.72)
Такую функцию нетрудно выразить через волновые функции
трехмерного осциллятора для каждой из координат Якоби. Например, для
А = 4 при выборе деревьев Dw, Dr, изображенных на рис. 57,
функция (6.72) имеет вид
M12W12
X (1пЩ21гЩ I ^M} I «i^i (*i)> I ^'2^2 (*a)> / "з^М^з))· (6.73)
134

Аналогично устроены и функции для более сложных систем: имеет
место параллелизм в сложении моментов 1Ъ /2, ..., /л—ι по группе
вращений и по группе Sp (2, R).
Обсудим переход от одних координат Якоби хъ хъ ..., ха-\ к
другим х{, ..., ха-\ в функциях (6.72). Операция отражения Ρ
какой-то координаты xt производится тривиальным образом:
Р = (^1)^. (6.74)
Рассмотрим элементарный кинематический поворот (6.25) на угол φ,
связывающий две координаты Якоби,
\1г12; NKLM(xpg, %,г)) =
- Σ <*А I Щ*А Ι ίЙ: NKLM {хяп *„,)>. (6.75)
Коэффициенты преобразования (6.75) были введены в работе [2531 и
называются коэффициентами Рейнала — Реваи. Поскольку при
преобразовании (6.25) радиус-вектор ρ = [xpq + хрд.г]1/2 не изменяется,
то по существу преобразование (6.75) относится только к угловым
частям осцилляторных функций — гиперсферическим гармоникам:
YlJtKAM {Xpq, Xpq,r) = 2 (lll2 | Щ™ Y/,'« к м (*V.* p.gr). (6.76)
Ί'ί
С помощью соотношений (6.75) и (6.27) нетрудно найти связь
коэффициентов Рейнала — Реваи с коэффициентами Тальми — Мошинского
(6.28):
(V. Ι Ί%>£Λ = Σ <% W2 / ΚΑ) {n\l\n2(21 ΚΑ) Χ
n,-f-n8=K
X {пАп212: ΛI prlq (p + q + r) \ n\lu riiU : Λ) =
= Σ (iimj*m% I I'm) (/imi/imi | jm) (ηχΙγη%12 : Λ | prlq (p + q + r) X
mt-f-m2=m
fn\-\-m2=tn'
Χ Ι /ιί/ι> л&'.Л), (6.77)
где /ι = (lt — l/2)/2; /«=(/( + l)/2. Впрочем, в сумме по пъ п2 и
п\, я2 можно взять ограничение пх + п2 = fti + ni = К, или
положить /гх + п2 = Л1 + п2 = N с любым N = К, К + 2, ...
Соотношения типа (6.77) были получены Я. А. Смородинским и В. Д. Эфросом
146]. Матрицы преобразования гиперсферических функций при
переходе от одного набора координат Якоби к другому представляют собой
в общем случае суммы произведений нескольких коэффициентов
Рейнала — Реваи. Эти матрицы также можно связать с коэффициентами
Тальми [254, 255].
Отсюда становится ясным способ получения матриц
преобразования ГГ при переходе от одного набора координат Якоби к другому,
если известно выражение для матрицы преобразования осцилляторных
133

функций, зависящих от таких же координат Якоби. Способ состоит
в том, что нужно в этом выражении заменить все коэффициенты Таль-
ми соответствующими коэффициентами Рейнала — Реваи и каждые
коэффициент Рака или более высокий символ для моментов 1и /2, ...
..., /л-i следует продублировать соответствующим ш-символом для
группы Sp (2, R), а к каждой фазе (—\у1ч+1&4 добавить фазу
(—\y~JЧ+ΐc+i&1 % Ниже используем это правило для получения
генеалогических коэффициентов в методе /С-гармоник, следуя работе
[197].
6.2.5. Генеалогические коэффициенты в методе /ί-гармоник. В
предыдущих параграфах рассматривался вопрос о том, как построить
ГГ с заданным орбитальным моментом L и гипермоментом К для того
или иного набора координат Якоби. Теперь нужно выяснить, как
скомбинировать эти гармоники со спин-изоспиновыми волновыми
функциями в полную антисимметричную волновую функцию. Для
этого нужно прежде всего построить ГГ К/амлсь которые
обладают определенной перестановочной симметрией, т. е. преобразуются
по неприводимому представлению DU] со схемой Юнга [/] группы
перестановок А частиц Sa и по строке (г) этого представления ((г) —
символ Яманочи, см., например , [256]). Затем полная
антисимметричная функция Ψ строится из Yklmukh и спин-изоспиновых функций
% ~~ с сопряженной схемой Юнга и символом Яманочи по из-
ST[f](r) r
вестной формуле
Ψ = —;L- E YklmumdX ~ -, (6.78)
V ^ r Ui ST[f](r)y V '
где rif — размерность неприводимого D^1-группы представления Sa.
В свою очередь, гармоники с определенной перестановочной симмет-
риеи можно построить из гармоник типа Yij^ja^klm с помощью
операторов Юнга
с[Лп = -Зг Σ «Я м Iр Ι [/ι (''» р< <6-79>
Ρ
где сумма берется по всем перестановкам Ρ группы Sa;
(If] (г') | Ρ Ι [/] (г')) — элемент матрицы перестановки Ρ в стандартном
ортогональном неприводимом представлении Юнга — Яманочи [256].
Оператор Юнга обладает тем свойством, что, действуя на
произвольную функцию Ф, он превращает ее в функцию с перестановочной
симметрией [/] (г'):
Чт^^-^с^Ф, (6.80)
где нормировочный коэффициент задается формулой
№=(Ф\С\1\{П\Ф). (6·»1)
Переписывая эту формулу применительно к ГГ, получаем
YkLMUW* = Ύ Clr)ir')Yhh.^A-xKLM- (6.82)
136

Здесь индекс ε различает разные гармоники с одинаковыми наборам»
квантовых чисел KLM if] (г). Конкретный вид гармоники (6.82)
зависит от выбора вспомогательного символа Яманочи (г') и
характеристик 1Ъ /2, ..., lA-xDvKiDw^i «затравочной» гармоники, стоящей в
правой части (6.82). Если разложить гармоники (6.82) по гармоникам
l\l2.. l'A__]KLM'
Yklww = 4е , . Σ , , <ί6 ... Ά-ικίλ]: KL \ (%Ί | Χ (6.83)
/|/2...·./>|-ΐ.κί.λί
χ |/, ... /л-.хЛ:^)^^^.
Коэффициенты разложения в (6.83) сводятся к матричным
элементам от перестановок частиц, т. е. к матричным элементам операций
перехода от одного набора координат Якоби к другому.
Такие величины были вычислены в предыдущем параграфе.
Поэтому формула (6.83) в принципе решает задачу построения ГГ с
определенной симметрией. Однако с практической точки зрения эти
вычисления довольно громоздки для больших значений А и К» Более
удобна рекуррентная процедура построения гармоник с заданной
перестановочной симметрией. При этом задача формулируется так:
пусть известны ГГ с перестановочной симметрией Yk'L'M'ww)*'
для А — 1 частиц и их нужно объединить со сферическими гармони·
ками YiA_lmA^l для степени свободы
*л-1 = К (Л- \)/А (гА - -,-L·- Д? п)
в полную ГГ с фиксированной перестановочной симметрией.
Образуем произведения осцилляторной функции | N'K'L'M' X
Χ [/Ί (г')г') для А — 1 частиц на осцилляторную функцию для
последней координаты Якоби xA—\ и подействуем на нее оператором
Юнга. В результате получим некоторую осцилляторную функцию А час·
тиц с заданной перестановочной симметрией
\ANKLM[f](r)e) =
= 4г С^<"> Σ {N'K'nl IN К) I N'K'L'%' [/'] (r')f Ш :LM). (6.84V
Для того чтобы общая функция соответствовала гипермоменту /С, мы
сложили моменты по отношению к группе Sp (2R).
Отметим, что функции (6.84) с одним и теми же квантовыми
числами NKLM [/], полученные путем симметризации состояний с
различными значениями [/'], (г'), ε', не обязательно ортогональны друг другу
и даже не все из них линейно независимы. Поэтому для нахождения
полного набора состояний необходимо из общего количества функций
(6.84) сконструировать нужное число линейно независимых и орто-
нормированных состояний. Указанная перестройка функции (6.84>
13?

приведет к соответствующему изменению формул для генеалогических
коэффициентов, приведенных ниже (см. соотношения (6.86) — (6.89)).
Разложим функцию (6.84) по произведениям функций А — 1
частиц на функцию движения последней частицы относительно центра
масс группировки А — 1 частиц:
| ANKLM [/] (г) е> = Σ (АК \f\U\A-l К' Щ LV, V) χ
N"K"n'l'z"L"
X {N"K"n'l' IΝ Κ) I N"K'L\ ε" [/'] (г'), n'V : LM). (6.85)
Коэффициенты разложения в правой части (6.85) называются
генеалогическими коэффициентами отделения одной частицы в
ортогональной схеме [256]. Если они известны, то задача построения симмет-
ризованных функций для А частиц из симметризованных функций
А — 1 частиц решается полностью. Для вычисления этих
коэффициентов можно воспользоваться формулами, полученными в ТИЛЮ, слегка
.видоизменив их в соответствии со способом, изложенным в
предыдущем параграфе. Формулы (7.23) — (7.25), приведенные в работе [243],
в которых генеалогические коэффициенты (А | А — 1) выражаются
'через (А — \\ А — 2), переписывают следующим образом:
(АКЩ Le\(A -1)^1/] LA, k) = -±- j/~-^
i-x
η ,
/1
Χ «ΙΜΓ А.АкЛл +(Λ-1) t Σ, , -jf ([/I] [/J | Ρϋ-м Χ
Ι Κι№ιει
Χ |[/ί]1/'))[η(- 1)''+''(- l)/|_"+/W2i/(L;a/i; LXL.) χ
Χ U(L\llLlt; L'L0) ((A _ 1)Κχ[/»] L&\(Λ-2)К\ [/,'] L,'ei; d) Χ
Χ ((Α - 1) Κ' [Π LV | (Л — 2) /(,' [/,'] Цг[1\) U [J\hJh\ Vel X
Xl/[W/i; ·/'·/„] <у2|У,>£
Ч L0/(o
(6.86)
= 1+(Л-1) Σ ^<[/ί]1/Ί|^~Μ|[/ί][Π>[ηΧ
'Τ
χ ((Л - 1) К' [/'] LV I (Л - 2) Κί ifi) L'iei, 4> <(Л - 1) /С' [/'] LV X
χ |(4-2)/Ci[/i]L,'e,\ /;>(- l)',+''(- l)/,_/2i/(L,'iiLV, L'Lo) χ
xU(L[l[Ll2; L'L0)V[J\uJh; J'J0]U [j[j\jj2; J'J0](l2i2\l2l\)^K\ (6.87)
*-arc*e/=5=i; /,--f(/,-4-W--r^+-2iT:I);
138

/' * 1st9 t ЗЛ —13 \ г 1 /„ , ЗЛ — 10 \
у = 4. (/С + -^^-); Л = -f (*° + 1); <688)
щ — размерность неприводимого представления [/] группы Sa\
([/ι] lft) | Рд-1,л | l/ίΐ [/'])[f] — элемент матрицы стандартного
неприводимого представления той же группы.
Заметим, что коэффициенты типа (А = 2 | (А — 1) = 1) = 1.
Поэтому с помощью рекуррентных формул (6.86), (6.87) можно
последовательно вычислить все необходимые генеалогические
коэффициенты. Символом U [...] обозначены коэффициенты Рака для группы
Sp (2, /?); U (...) — обычные коэффициенты Рака. Если выделить в
(6.85) только угловые части функций, то при использовании (6.39)
можно написать разложение ГГ для А частиц с перестановочной
симметрией по таким же гармоникам для А — 1 частиц:
Yklmuws = Σ (АК [f]Le\A-l КГ [Л LV, V) {JL'MTVm! \ LM) χ
/C"L"/'8"
M"m'
X YK'L-*>j-vvrYrm'NrKK*r sin*" θ cos'' θ ffi^g^fl-U'+W (cos 2Θ);
(6.89)
генеалогические коэффициенты для метода /(-гармоник были введены
в работах [257, 258].
Аналогично можно ввести генеалогические коэффициенты
отделения двух и более частиц. В частности, двухчастичные генеалогические
коэффициенты определяются следующим образом:
Укьмщпш = г Σ (№(г)|U*](г.), [М> (АК[Я 1л\А-
L'^('ΛL0лί'л^oμΛ^2
-WtlfJLfy, A{LX}; L0)(L'M'L0M0\LM)(L2M^\L'M') χ
Χ ^Κ^,^υ/ίΚτ^β,^Αμ (#Α-2 — R2) YL0Mn (Га~1 — ^) Χ
X NKK.L,NK,KtAsinKX cosL% sin*' ^cos^^^i^-A^2-1·^172 X
χ (cos 2Θ2) $»lTf/2-u°+l/2 (cos 2Θ0. (6.90)
Предполагается следующая схема сложения моментов по группе
вращений и группе Sp (2, /?):
L. + A.-L'; L' + L0 = L, J2 + JA = J'; J' + J0 = Ji
^л = 4-(А-1/2); /0 = -i-(L0—f); /=:-l-(/( + ^L);(6.91)
/' = 4_(/С+31г^): y.^^+idpli).
Здесь L0 — момент количества относительного движения пары
нуклонов А — 1 и Л (степень свободы хА-\ = (гА — r^-i)/]/^); Λ —
момент этой пары относительно остальных А — 2 частиц (степень свободы
139

х\-ч =[(1/2) (rA-i + га) -(А- 2)-1 2ψ2 (А - 2)1 А.
Двухчастичные генеалогические коэффициенты выражаются
через одночастичные следующим образом:
(АКЩ Lz\A- 2K2[/2] L2e2, Л [UK'); L,) =
= <ГЯ (г)11/.]Ы [/о! (/-о))"' 2 И*[/] U\A- 1Кг[h] Ιλ, /х) χ
χ (Л - 1/d[/J LA\A-2K2[/,] L2e2, Z2>(- l)^-/? χ
x <'Λ I AL0)f t/ (L2ALL0; Ζ/λ) ί/ [J2JAJJ0\ J'J*l (6.92)
Здесь φ = arctg V {A—2)12, схема [/J и соответствующие символы
Яманочи (г2) и (г) выбираются произвольным, но фиксированным
образом (см. формулу (2.43) в книге [243]).
Генеалогические разложения (6.89), (6.90) удобны для вычисления
матричных элементов операторов в методе /(-гармоник.
6.2.6. Вычисление матричных элементов операторов в методе К-гар-
моник. Рассмотрим вопрос о вычислении матричных элементов
гамильтониана в методе /(-гармоник. Обозначим антисимметричные
комбинации ГГ со спин-изоспиновыми функциями У>Щг$тмТ символом
| АК [/] eLSTMlMsMt) = -7=- У УитП1г)£1Щтмг (6.93)
V nf г
Здесь [/] (г) — схема Юнга и символ Яманочи, сопряженные с [/] (г);
щ — размерность неприводимого представления Dif] группы
перестановок Sa.
Введем полные двухчастичные генеалогические коэффициенты для
/(-гармоник (6.93):
\AKlf]ELSTMLMsMT) =
Σ (АК If] eLST I Л— 2 [/2] e2L252T2, Л (UK'): L0S»J0) χ
K' L'LqSoTq
M'M0
ms0mTo
X (L'M'L0M01 LM) (S2MSa50AiSo | SMS) (T2MTJ0MTo \ TMT) X
χ NKK>, sin*' Θ, cosL° Θ^'+J^^-1 (cos 2Θ,) χ
χ I A - 2 [/2] e252r2L2/(2, Λ (I7C) M'MStMTt) I L0M0S0MSoT0MTo).
(6.94)
Здесь последний множитель зависит от угловых переменных
взаимного движения частиц А — 1 и Л, а предпоследний множитель включает
в себя угловые переменные взаимного движения А — 2 частиц, угол,
задающий длину радиус-вектора, соединяющего центры масс А — 2
частиц и отдельной пары нуклонов, а также полярные углы этого
вектора; га-\,а = ρ cos θ^
140

Полный генеалогический коэффициент конструируется из
орбитальных и спин-изоспиновых генеалогических коэффициентов:
(АК [/] zLST \А — 2КШ I/iJ ε2/^2Γ2, Л (L7T); L0S0TQ) =
= Vni7nt(AK[f]*L\A-2K[ft]B%L%9 A(L'K'); L0) χ
χ ((st)A[}]ST№A-*[nS'T'9 (stYSQT0). (6.95)
В силу антисимметрии функций (6.93) матричный элемент
потенциальной энергии взаимодействия между нуклонами
А
ν=Σ V(r4) И V(m) - /(Γί/ϊ^σχ (6.96)
i<i
можно записать в виде
(АК [f] eLSTMLMsMT \V\AR [J)VLSTMLMSMT) =
- ^f^(AKin*LST\V(rA-\.A)\AK =
= A{A~X) Σ {AK[fULST\A-2K2\h\X
1 /C2L/8]e2L2
Sj/ zLqSqTо
Λί/Κ'
Xe2LaS2T2, A(L'K'); L0 Vo><^ Я [/]eLS 71 Λ -2 *,[/,! X
X e2L2S2r2, Λ (L'/C'). *><>№ <50T01 ^στ | SJ0) R$L, (p). (6.97)
Здесь
Я$, (Ρ) = J A (sin θ^"7 (cos θχ)2 1/kk.l.N^J (ρ cos θχ) χ
χ ίΡ»1ΐ06)/2-|χ»+,/2 (cos 2θι); (6.98)
(S0T0 Ι №στ | S0T0) — спин-изоспиновая часть матричного
элемента взаимодействия. Для простоты мы взяли только центральные силы.
Формулу (6.97) несложно обобщить на случай тензорных и векторных
сил, а также сил, зависящих от скорости.
Поскольку при N = Nm\n волновая функция ТИМО, с одной
стороны, очень простым образом связана с /(-гармониками (К = Nm\n)
(см. формулу (6.18))
| ANmine [/] LST) = RNminK=Nmin (Ρ) I АК [/] eLST); (6.99)
*** = УтЩТЩ=Ш]рК^{-р%/^ (г0Г(1/2)(2/с+3^3), (6.100)
а с другой — ее можно просто связать с оболочечной волновой
функцией, то можно существенно упростить вычисление матричных
элементов (6.97). Действительно, например, для ядер р-оболочки имеем, что
оболочечная функция | s4/?^""4 I/l LST) выражается через функцию
141

ТИМО следующим образом:
| sy4-4 [/] LST) = ψοοο (ЯА) | ANmln [f] eLST), (6.101)
где ψ000 (На) — волновая функция нулевых колебаний центра масс.
Очевидно, что
(s*pA-4 [f] eLST I VI s·/-4 [/] eST) =
- <^mln [/'] eLST I V> | /Wmin [/] ILST). (6.102)
Матричный элемент по оболочечным волновым функциям
обычными методами [243, 259, 260] можно свести к двухчастичным матричным
элементам типа (nl | V (гa—ua) | ril') и в конечном счете к
интегралам Тальми Ik\
< ANmin [/'[ eLST I V I ANmin [f] UST) = 2 Ά. (6.103)
где /, = Jexp(r2/^)r"+2F(r)dr.
Если левую часть этого равенства интегрировать не по всем
переменным, а по гиперсферическим углам, то, учитывая (6.100), получаем
(АК [Л *LST | ί> Ι Μ [Л eLST) = 2 /* (p)Q*, (6.104)
где
/* (Ρ) = Nk J (1 - 2)K-*+"y+3/V (p VI) dz; (6.105)
0
Nk = Г (К + 3/2) Г (3/2)/Г (Я — Λ + 3/2) Г (k + 3/2);
Рл—2 = Ρ sin θ; га-\.а = Ρ cos θ; ζ = cos2 θ; 1 — г = sin2 θ.
Таким образом, при вычислении матричных элементов
потенциальной энергии по /(-гармоникам с низшим допустимым для данного А
гипермоментом /Cmin можно воспользоваться оболочечными
результатами, в которых следует заменить обычные интегралы Тальми Ik
функциями Ik (p) (6.105). Этот результат был получен в [258]. Подобным
способом можно получать матричные элементы не только
потенциальной энергии, но и других операторов. Результат (6.104) можно также
найти из формулы (6.97), расписывая в явном виде полином Якоби в
(6.98) через тригонометрические функции от Θ. Можно указать еще
одну интересную возможность получения точных выражений для
потенциалов W$v (р)9 описанную в работах [261, 262]. С помощью
обратного преобразования Лапласа авторы сводят вычисление этих
потенциалов к нахождению интегралов типа Тальми
j r2"+2(p«_ ^(χ+κ·+ι»/2-τа/27} dr
О
от двухчастичного нуклон-нуклонного взаимодействия V (К 2/*).
Выше мы рассмотрели расчет матричных элементов потенциальной
энергии нуклонов. Добавим несколько слов о том, какую роль они
142

играют в методе /С-гармоник. В этом методе волновая функция ядра»
А задается в виде разложения по /С-гармоникам IАК. IfhLST}
(ср. с (1.16)):
Ψ= Σ v[n*LST(p)\AK[j)eLST), (6.106)
ше J φκ (Ρ) Рзл~4 dp = 1.
Гамильтониан ядра имеет вид (см. (1.15))
// = —
-)-^А' + *· (6-»07>
2т рЗ^-4 dp \f dp
Если подставить функцию (6.106) в уравнение Шредингера и
результат умножить слева на (АК If] ε LST |, то получим систему
уравнений вида (1.17)
(-"2^"-ф^+ W +Ь\*К Ф) +
+ _Σ ^йВ]Вг(р)Хз? = о- (6108>
Здесь LK = /( + (ЗЛ — 6)/2; Х* = р<зл-4>/2 φ* (ρ); число
уравнений в этой системе и число членов в сумме (6.108) равны числу
слагаемых, включенных в разложение (6.106).
Потенциалы Wk (p) как раз и есть те матричные элементы,
которые обсуждались выше (см. также (1.11), (1.17)):
И®]Ж(Р) = (АК If) eLST \V\AK [Я 237). (6.109)
Обратим внимание на чрезвычайно сильный «центробежный»
потенциал Lk (Lk + 1)/р2, который входит в эти уравнения и является
следствием принципа Паули, поскольку высокие значения L/< связаны с
тем, что большими являются уже значения /(mm, совместимые с
принципом Паули.
Выше мы показали, что методы, развитые в модели оболочек,
довольно легко переносятся и обобщаются на случай метода /С-гармоник.
Оболочечный подход особенно эффективен для приближенных
вычислений потенциалов W* (р) по методу Базя — Жукова — Суркова
[263], который является асимптотическим и может давать достоверные
результаты лишь при достаточно больших массовых числах А. Суть
его сводится к следующему. Используя равенства (6.99), (6.100),
(6.102), (6.109), приходим к результату
(s*pA~4 [f] eLST IVΙ *У-4 [/] ^Sf). V$fM <r0) -
- const { dpp3A-4+2K exp(- p*/Tl) W$#M(p). (6.110>
Представим интеграл в правой части этой формулы в виде
J dpWSggg (Ρ) ехр {ЗА - 4 + Щ (in p/r0 - -^-g—Λ
43-

и вычислим его методом Лапласа [2641. Ограничиваясь низшим
членом по степеням (ЗЛ — 4 + 2К)~], получаем
vligl? (г0) = <$ίΙ (г, ΥΤΤ^ΞΙ.). (б.н ι)
Таким образом, чтобы найти приближенные значения потенциала
W в точке р, достаточно вычислить оболочечный матричный элемент
(6.110) при значении оболочечного параметра
0 К* + (М-4)/2 *
Физические приложения метода /С-гармоник к теории легких ядер
описаны в монографии [73] и обзоре [197]. Вопросы использования
метода /(-гармоник в атомной физике изложены в работах [196, 199J.
Другие методы получения волновых функций с необходимой
перестановочной симметрией в методе /(-гармоник описаны в работе [265].

Глава 7
ФУНКЦИИ НА ТРЕХМЕРНОМ
ГИПЕРБОЛОИДЕ
7.1. Системы координат и собственные функции
оператора Лапласа на гиперболоиде
Из принципа релятивистской инвариантности и унитарности
вытекает, что амплитуду рассеяния следует разлагать по функциям,
реализующим унитарные бесконечномерные представления группы
Лоренца. Эти функции являются решениями уравнений 1210, 266]
Δ/ = (-1-ρ2+ν*)/, (7.1)
Δ'/«-νρ/, (7.2)
где Δ и Δ' — инвариантные операторы Казимира группы Лоренца,
построенные из инфинитезиа^ьных операторов пространственных и
гиперболических поворотов Μ и Ν:
Δ = Σ(Μ}-Νί), (7.3)
Δ'= 2 ΑΙ,ΛΤ,. (7.4)
i=*l
Подробно рассмотрим разложение скалярной функции / (и),
заданной на гиперболоиде u2 = p%lrr? = 1. В этом случае оператор Δ
равен лапласиану на гиперболоиде, а оператор Δ', связанный со спином,
тождественно равен нулю. Далее укажем модификацию разложений
для случая спина, отличного от нуля.
На гиперболоиде можно ввести различные системы координат, к:
описанию которых сейчас и переходим.
Сферическая система координатSj
и0 а» сН а\ и2 = sh a sin θ cos φ;
и3 = sh a cos Θ; ux = sh a sin θ sin φ; (7.5)
0<α<οο; 0<θ<π; 0<φ<2π.
В переменных α, θ, φ оператор Лапласа примет вид
Λ 1 д ьа д , 1/1 д . А д t 1 д* \
(7.6)
Ю 1-1980
145

(7.8)
Собственные функции, соответствующие этому оператору g
собственным значением -- (1 + р2), записываются так:
(plm | αθφ) = (sh а)~ Т/>~ Τ~* (ch a) Ylm (θ, φ). (7.7)
Система координат Лобачевского Ls
w0 = ch я ch 6 ch с; н2 = ch α sh 6;
u3 = chachb sh c; ax = sh a;
— oo <a, 6, c<oo.
Лапласиан в переменных a, b, с определяется формулой
д __ 1 д Ь2 д . 1 / 1 ?> hf>jLj * d2 \
L~"~ ch2a да СП а да ~r ch*a \ sh Ъ дЬ δΠ " дЬ + sh*6 дса / '
(7.9)
а его собственные функции
<р?т|ate> = (chаУсЪЬГхР*± ζ (thα)Я^ /m(th6)eim<. (7.10)
Гиперболическая система координат И:
и0 = ch a ch b\ u2 = ch a sh b sin φ;
w3 = ch ash ft cos φ; w1 = sha; (7.11)
— oo<a<oo; 0<fc<oo; 0<φ<2π.
В этой системе оператор Лапласа и соответствующие ему собственные
функции имеют вид
Λ _ 1 д Ь2 _д_ 1/1 д_ . hJi_ , 1 а2 \
L ~~ ch*a да СП а да + ch2a \sh& # d* "·" sh2 6 dq>2 / ;
(7.12)
(pqm | abq>) = (ch аГУ р ι (th a) Pm ι . (ch 6) eim<p. (7.13)
Цилиндрическая система координат Ci
u0 = chb ch a\ u2 = sh b sin φ;
w8 =ч sh b cos φ; wx = ch b sh a; (7.14)
0<6<oo; — oo<a<oo; 0<φ<2π.
Лапласиан и собственные функции в С-системе записываются в форме
Al== ch&sh* 'Wchbshb~W + 4^^da^ + lh^'l^'9 (7Л5>
(pxm I aby) = е'(та+тф) (sh ft)m (ch Ь)'т^^ χ
Χ2^({1±1+Ι£±ίΕ, Wt^+»-^;W+l; th"*). (7.16)
146

Орисфери<*еская система координат Οι
щ = 1 /2 [е- + (Л- 1) еа]\ и2 » reacos φ;
«3=1/2[г-с + (г^1)А ut=reasm<p; (7.17)
0<α, г<оо; 0<φ<2π.
В переменных α, г, φ лапласиан дается выражением
Л 2а Г д ±.2а д 1 д д . \ д% λ /71Qv
а его собственн >ie функции
<p£m I ftrq>> = (*ft) /CiP (Aft) Jm (kr) Л (7.19)
Здесь Ktp (kb) и Jm (kr) — соответственно функции Макдональда и
Бесселя; ег° = Ь,
7.2. Метод орисфер
Итак, мы построили различные собственные функции. Теперь
необходимо эти функции ортонормировать или найти формулы обратного
преобразования. Это можно легко сделать β помощью формул Гельфан-
да — Граева [138, 1391. Пусть f (и) и h (k) — скалярные функции,
заданные соответственно на гиперболоиде и конусе k2 » 0. Если
h (k) = { / (и) δ [(«и) _ 1 ] -£iL, (7.20)
то
^ - -5&Г- ί «*->««*)- 1]Α(*)^- (7.21)
при η = 2/n + If
η
/(«)- (-£^(,,) J Κ"*>- >Γ*(*)·^- (7.22)
при η = 2m. Здесь η — размерность многообразия; сГи/и0 и dnk/k0 —
инвариантные меры на гиперболоиде и конусе.
Разложим h (к) на однородные компоненты 2з
Α<*>=-ά- ί ф<*» σ>ώσ' <7·23>
6-β·ίθΟ
причем
оо
Φ (fc, σ) = J A (kt) r°-]dt. (7.24)
θ
Из формул (7.20) и (7.24) следует
ф(Ь а) = J / (и) (uk)adnu/u0. (7.25)
9 Величина δ выбирается такой, что полюсы Φ (&, σ) лежат вне полосы 0 ^ Re σ <
<δ,
Ю* 147

Используя выражения (7.21) — (7.23), получаем *
x <Woo Γ
(7.26)
для п = 2m + 1 и
JL -1 δ+ίοο
f/ ч (—)2 С Г(о + я —1) *
/(Ы) = 1ткг-ЛЗг Πα) >ctg"gX
0—loo
X J Φ (ft', aHuftT^+^ft'da (7.27)
r
для η = 2m.
Контур интегрирования Г — произвольный контур на конусе,
пересекающий все образующие конуса; (F~xk' —- элемент объема этого
контура, определяемый равенством
d(tk') « f^dtdV (0<t<oo).
В унитарном случае σ = γ h ίρ.
7.3. Вывод формул обращения
Получим формулы обращения, связанные с собственными функциями
лапласиана.
5-система. Контур интегрирования Г в S-системе является
сферой (ft0 = 1). Функция Φ (ft, σ) задана на сфере. Разложим ее в ряд
по сферическим гармоникам
Φ (*, σ) - Σ аш (ο) Yim (*/| к |). (7.28)
1т
Подставляя (7.28) в (7.26) и интегрируя по d*ft = d£if получаем
/(α)-—ί L ГУ(-)1 Γ°~σ) Χ
tW (2я)^ * Χ%( >Γ(-σ-Ι-»Χ
„-ΤΓ- Ρ » (cha)F/m(6, φ) da. (7.29)
Κ sha — ~ —σ
Учитывая формулы (7.28) и (7.25), для коэффициента щт (σ)
находим выражение
«*<*> = (^-ι?ΐ)+ '} J/Wah-Tep-T-(che) x
Χ ΚΓ« (θ, φ) -ζ- . (7.30)
* Впервые формула (7,26) бала получена И, С, Шапиро [129] для л = 3,
148

Здесь
сРи/и0 = sh2 ada sin QdQdy.
Формулы (7.29) и (7.30) написаны для обычного 4-мерного
пространства (п = 3). Функции на многомерных гиперболоидах исследованы
в работах [1, 146].
//-система. Разложение в гиперболической системе координат
выполняется тем же способом, что и в сферической. Контур
интегрирования Г состоит из двух частей Г+ и Г-, соответствующих двум
сечениям конуса плоскостями kz = ± 1. Вычисления приводят к
следующим результатам:
Ни)-- <chc>~' Τ 'Τ уТ(а + т + 2)Г(о-т + 1) t
'<"' 8(2π)« J J 2j Γ(σ)Γ(/η-σ) TCigJiTX
6—ioo e-J-ioo m
К />*,_, (ch b) eim» [at (τ, σ) Р=?Г| (- th α) +
+ aTm (τ, σ) ΡΖ"Ζ' (th α)} dtdo, (7.31)
где
^(τ,σ)- Γ<^-°.7.7γ',-!.Γ°' Ι/«*"№«■* x
χ Ρ? (ch 6) <Г1Шф dsa/i/0. (7.32)
Унитарный случай соответствует величинам σ = — 1 + ip и
O-CHGTeMa. В орисферической системе координат в качестве
контура интегрирования Г выбираем сечение конуса плоскостью
к0 — £3 == *·
К = ' + μ2» *2 = 2μ cos α;
£3 = _ 1 + μ2; kx » 2μ sin α. (7'33)
Представляя функцию Ф (&, σ) в виде
2π οο
φ (k9 σ) « J J ψ (κ, θ, σ) *ίκμ cos (θ-α) <ίθκ<ίκ (7.34)
ο ο
и подставляя это выражение в (7.26), после вычисления получаем
><M)=W ί Γ"'(σ)ί ί*(χ.θ,α)χ
ν ' δ—too 0 0
Χ (-f )σ+2 ^'κμίθ~φ) /C-σ-ι (6κ) dxdQda. (7.35)
Коэффициенты ψ (κ, θ, σ) определяются по формуле
* <*«"> " ЙГР^7 (4)°+1 ί / W «""" C°S (Θ~Φ> **Η (6x) -jr **/«..
(7.36)
В выражениях (7.35), (7.36) Км (х) — функция МакдоналЬда;
е-а = b\ cPu/u0 =± rdrdbdO.
149

С-ои1тема. Рассмотрим цилиндрическую систему координат»
контур интегрирования Г в которой есть сечение гиперболоида
цилиндром kl — &i = 1. Параметризуем Г следующим образом!
kQ = ch с; k2 = sin α;
Ηγ = ch c\ kz = cos α.
Используя фурье-разложение
(7.37)
Φ (*. σ) - 2 [ ат (τ, σ) βΗιη«+Χ0)άτ, (7.38)
т*в—o©__ ^
после вычисления для / (и) получаем представление
б—too
X (-дГб-)"+2 «Л И. 5i m + 1; th2 й) dtdo. (7.39)
Здесь 2Л = m + σ + ίτ + 2; 25 = m 4- σ — ίτ + 2.
Коэффициенты am (τ, σ) в этой системе имеют вид
a<nV>°>- 4πΓ(/η+1)Γ(-σ) 3Ш °\ chft / Х
X 2F, (Л\ β'; m + 1; th8 b) е1{-пФ+ха) f (и) -^- , (7.40)
где d*u/u0 = sh2 adadbdQ); 2A' = m — σ + ίτ; 2Β' =* m — σ — ίτ.
Таким образом, мы записали разложение амплитуды рассеяния
в четырех системах координат по функциям, реализующим
бесконечномерные унитарные представления группы Лоренца класса 1. В
системе координат Лобачевского мы не выводили формулы обращения,
потому что, во-первых, для описания амплитуд рассеяния достаточно
лишь два параметра (например, α и ft, если положить с = 0), при
которых L-система переходит в //-систему для φ = 0, и, во-вторых,
имеется подробный вывод формул обращения в работе [1421.
7.4. Разложение функций, заданных
в пространственноподобной области
Для разложения функции, заданной в пространственной области,
следует воспользоваться формулой Гельфанда — Граева в виде [1391
б-f-ioo
Ка>в-зйг Ι σ(σ + ,)ίF(*>σ)|("·k)ra~~2d*kd° +
Здесь / (и) — четная квадратично-интегрируемая функция; и
,2
2
= ыо — u% =* 1; k2 = 0; Г —- контур интегрирования на конусе (сфера
150

при k0 = 1); Числа σ и η — веса представлений группы Лоренца
основной и дискретной серий, причем, как и прежде, в унитарном
случае σ = — I + ip. Чтобы написать разложение для нечетной
функции / (и) = — / (—и) (и0 -»· — и0, и -> — и), нужно в формуле
(7.41) | (uk) |"~σ~2 заменить sign (uk) X | (uk) |~σ~2 и во втором
слагаемом 2п заменить 2п — 1 (cto. работу [140]). Если разложить функции
F (k, σ) и F (&, и\ η) по функциям Υι,η (к/ \ к |) и Dlmn (к/\ к\)и ввести,
например, сферическую систему координат
a0 = sha, &0 = 1,
и* = ch a cos θ, L· = cos θ',
(7 42)
ы2 = ch α sin θ cos φ, k2 = sin θ' cos Φ, ν
иг = ch a sin θ sin φ, kx = sin Θ' sin Φ,
tro, выполнив интегрирование по (Pk = d cos Θ' d<D, получим
(£2>) -tSf j>+"г(-"- ■> § κ»Μ·χ
X a/m (σ) ch"1 a [P?+1 (th a) ± (-)' P?+1 (- th a)) do +
+ -It Σ {Jl ,) Σ-2ΪΤΓ *- <">"Wr {(ρ^ζΐ) )} Г-(θφ)'
(7.43)
где P?+1 (th а) и Ρ? (th a) — присоединенные функции Лежандра;
f4 (и) и /H.w (w) — соответственно четная и нечетная функции. Первое
слагаемое в этом выражении аналогично разложению функций на
двухполостном гиперболоиде, полученному в работе [142], второе
слагаемое представляет собой разложение функций по дискретным
представлениям группы Лоренца, данное В. Л. Гинзбургом и И. Е. Там-
мом [121]. Полную же систему функций в пространственноподобной
области относительно нормы образует пространство пар функций
ch~laP?+1 (th a) Ylm (θ, φ) и ch~~la Ρ? (th a) Ylm (θ; φ). С вопросами,
связанными с аналитическим продолжением амплитуд в пространст-
венноподобную область, познакомимся в гл. 13 и 14. С этой темой
также можно ознакомиться в работах [172, 173, 1761.
7.5. Разложение полей
Мы рассмотрели разложение скалярной функции по собственным
функциям оператора Лапласа на двух- и однололостном
гиперболоидах. Чтобы разложить функцию со спином s и проекцией σ·4 на
направление импульса ρ (спиральное состояние см. в [267, 268]), необходимо
модифицировать ядро интегрального преобразования (7.26), т. е.
вместо ядра ukTx~~lp следует писать kvr^i{i Ds (/?), где R — не-
4 В этом параграфе σ — проекция спина, а не число, характеризующее
представление группы Лоренца.
151

который поворот, учитывающий
переквантование спина; Ds (R) —функция Вигнера.
Поясним, зачем нужно производить
переквантование спина. Для невырожденных
представлений группы Лоренца (случай
ν Φ 0) необходимо получать спиральные
функции на гиперболоиде с помощью
интегрального преобразования спиральных
функций на конусе. Так как для спиральных
функций на гиперболоиде спин закванто-
ван по фиксированному направлению и =
= р/т, а для безмассовых частиц, т. е. ча-
Рис. 58 стиц, описываемых функциями на конусе,
спин направлен по к (но по к ведется
интегрирование), то ядро интегрального преобразования должно
учитывать переквантование спина. Поворот R от направления, задаваемого
вектором &, на направление и можно представить как произведение
двух вращений: одного — /?е, поворачивающего спин от направления А?
на направление оси г системы координат (1, 0, 0, 0) (заметим, что в этой
системе выбираем ось г, параллельную оси ζ координатной системы
конуса), и другого — /?а, возникающего при переходе от координатной
системы (1, 0, 0, 0) к системе (и0, и).
Для нахождения углов поворота R = ReRa можно вычислить углы
поворота репера от к на иу используя формулы лоренц-преобразова-
нйя [130, 1311. Однако проще вычислить сразу суммарный поворот
методом геометрии Лобачевского на модели Бельтрами. Действительно,
рассмотрим треугольник АВО (рис. 58). Точка О (центр окружности
единичного радиуса) соответствует сис?еме покоя частицы (1, 0, 0, 0),
точка А — системе координат, в которой частица имеет скорость и =
= (и9) и), точка В (точка абсолюта) описывает частицу с массой нуль,
причем
thO^=JiLL, th05=|«|=J^L , (7.44)
Опустим перпендикуляр из В на АО. Так как В — бесконечно
удаленная точка» то прямые В А, ВС, ВО параллельны и угол А ВО = 0,
а углы ОАВ = Θ' и АОВ = θ суть углы параллельности Лобачевского.
Следовательно,
cos θ = th ОС, cos θ' = th AC. (7.45)
Угол α, обусловленный прецессией спина при переносе его по
контуру А ВО, равен площади треугольника АОВ [2691:
α = π — θ — θ'. (7.46)
Этот результат можно получить еще короче, если рассмотреть поворот
спина β точки зрения наблюдателя в Л. Он считает, что надо
переквантовать спин от направления на В (направление квантования спина
на абсолюте одинаково для всех наблюдателей) на направление от
начала координат (т. е. на направление скорости частицы). Из рис. 58
видно, что угол поворота осей равен π — θ'.
152

Из формул (7.44) — (7.46) находим угол поворота R
cos (α + θ) = — cos θ' = th (АО — ОС) = "°™^{~1?] , (7.47)
где η = к/1 k | = (cos Θ, sin θ cos φ, sin θ sin φ).
Таким образом, разложение функции ψ5σ (и) с заданным спином на
гиперболоиде по собственным функциям Φρν (k), преобразующимся
по неприводимым относительно собственной группы Лоренца
представлениям, определяется следующим выражением [130—132J:
S СО
** <"> = T75HF Σ ί Φ (Ρ' + ν2> ί («*Γ1_ίΡ "Οαν (Я) Φνρ (*) (Ρ k,
V ' v=—s — oo Γ
(7.48)
где Г — контур интегрирования (сфера при сечении конуса k2 = О
плоскостью k0 = 1); s — спин; ν — спиральность на конусе; σ —
проекция спина на гиперболоиде; d?k = άΩ\ поворот R в плоскости
(к, и) определен формулой (7.47).
Пусть функция Φρν (k) представлена в виде ряда
Φρν (k) = Σ am (Ρ) (2 J + 1) DJMv (к/\ к |). (7.49)
JM
Тогда, подставив выражение (7.49) в формулу (7.48) и выполнив
интегрирование по ^Ω, получим [132]
S оо
^ (") = ~ШЖ Σ J Φ (Ρ2 + ν2) Σ α™ (Ρ) Ο* (")· ί7·50)
V=—s—oo J Μ
Здесь
Is£jm (и) = Ο (a) DJMa (Φ, θ, _ Φ); (7.51>
Iqvjm (α) == 2π 2 (—ί ' Gjovfisovr Χ
r J
Xexp((a-v-l-ip+2r-2s)e Γ <У + Sr7/++S^+ ° X
X Λ О +ip +s, J + s— μ+ 1; У + s — r; 1 —β""20),
μβσ_ν + Γ + /; (7.52)
(7.53)
.σ-ν l(J — σ)1 (У + σ)! (J - v)l (J + v)l >/1/? .
ίΙ(/_σ-/)Ι(/ + σ-/)!<σ-ν + /)Ι ·
^Μσ (Φ» *K —Φ) — матрица конечного поворота группы вращений
[270]; и = (и0, и) = (ch a, sh a cos Φ, sh a sin * cos Φ, sh a sin1* sin Φ).
Функция (7.52) представляет собой матрицу конечного
гиперболического поворота группы Лоренца и совпадает с выражениями, полу-
153

ченными для нее другими методами в работах [154, 157, 158]. Эта
функция описывает состояние с «главными квантовыми числами» —
собственными значениями операторов Казимира ρ, ν, полным
моментом J и его проекцией Μ на полярную ось, спином s и его проекцией
σ на скорость частицы; при s, v = 0 она переходит в функцию (7.7).
Отметим, что спин, входящий в (7.48) — (7 52), играет роль vmax.
Выражение f*Q%j (а) можно также представить через ряд по
функциям Лежандра ΡΖί/Ι-ί-ίρ (ch a) [132, 151].
В заключение отметим, что для построения функций,
реализующих представления группы Лоренца (ρ, ν), мы использовали
интегральный метод. Другие способы построения релятивистских сферических
функций изложены в работах [147—149, 151, 1831.

Глава 8
ФУНКЦИИ
НА ТРЕХМЕРНОМ КОНУСЕ
8.1. Системы координат, полные наборы квантовых чисел
и базисные функции на трехмерном конусе
Рассмотрим реализацию представлений группы Лоренца на функциях,
заданных на конусе (£2 = 0), и вычислим матрицы преобразования
между представлениями, отвечающими редукции на различные
подгруппы [132]. Матрицы преобразования для вырожденных
представлений (ν = 0) получены в работе [271]. Очевидно, что указанные
коэффициенты перехода не зависят от способа реализации
представлений, и поэтому с их помощью из функций (7.51) можно получить
базисные функции группы Лоренца, отвечающие редукции на
подгруппы О (2, 1), Ε (2) и т. д. Вычислению коэффициентов преобразования
для группы Лоренца посвящены также работы [272—274].
Выберем инфинитезимальные операторы Μ и N в виде [275]
где k = (&o, fc) — 4-мерный вектор, лежащий на конусе, т. е. импульс
частицы с нулевой массой покоя.
Базисные функции группы Лоренца являются собственными
функциями операторов Казимира Δ и Δ', определяемых выражениями
(7.3) и (7.4), и двух других коммутирующих операторов,
определяемых выбором подгруппы. (Эти операторы — оператор Казимира
подгруппы и оператор ее простой абелевой подгруппы (здесь везде О (2)).)
Введем на конусе системы координат и выпишем соответствующие
диагональные операторы и их собственные функции.
8.1.1. S-система. Для подгруппы О (3) :=> О (2)
k0 = ел9 k2 = еа sin θ cos φ,
kx = ea sin θ sin φ, k3 = ea cos Θ,
где — oo < a < со; 0 < θ ^ π; 0 < φ < 2π.
155

Диагональными операторами являются
+ Γ+^(ι·-4-+λ). ",-ί^ + λ (8.3)
g собственными значениями J (J + 1) и М соответственно. Отсюда
следует, что угловая зависимость базисных функций определяется
D-функцией Вигнера Dm (φ, 9, —φ) [270]. Напомним, что Μ —
проекция J на неподвижную ось, а λ — проекция на подвижную ось (на
скорость или волновой вектор).
Таким образом, полные нормированные базисные функции на
конусе имеют вид
Α (α, θ, φ) = γ HI е(-жр)сД(а (φ, θ, - φ), (8.4)
причем
2π
J e2ada j sin Odd J ψ}%> (α, θ, φ) tfiSl (α, θ, φ) dip =
~oo 0 0
= Syy^M'S(p-p'). (85)
Итак, нами построены волновые функции частиц с нулевой массой
покоя, обладающие заданной спиральностью λ = ν (это докажем в
п. 8.1.4), моментом J и его проекцией Μ на неподвижную ось:
4>V/L (А) - (^г)~ЖР V ^^ Dl* «Р. θ· - Φ)· (8·6)
Мы выбрали третий угол Эйлера φ, отличный от нуля, чтобы не
возникло недоразумений при дифференцировании, т. е. при действии
генераторов.
Здесь мы ввели некоторую постоянную частоту ω, чтобы сделать
формулу безразмерной. Если вернуться к экспоненциальной форме
и положить 1η ω = £>, то множитель перед D-функцией примет вид
ехр (—1 + ф) (а — &), т. е. фурье-разложения поля с частотой Ь.
Функции (8.6) по определению преобразуются при любых
преобразованиях Лоренца друг через друга, так что остаются неизменными
лишь ρ и λ. Последнее обстоятельство следует особо подчеркнуть. При
преобразованиях Лоренца (а тем более при вращениях) спираль-
ность частицы остается неизменной. Если преобразуем, например,
потенциал электромагнитного поля обычными формулами
преобразования Лоренца для вектора, то для возвращения к спиральным или
просто поперечным амплитудам надо дополнить это преобразование
еще и градиентным преобразованием5. Функция (8.6) преобразуется
так, что автоматически включает в себя градиентное преобразование.
Для записи обычного разложения электромагнитного поля по
спиральным амплитудам (ср., например, с [277]) надо построить из функ-
6 Комбинация градиентного преобразования с лоренцевым для фотона рассмот·
рена в работе [276],
156

ций (8.6) вектор, опуская временно множители перед D-функцией и
задавая орты D-функцией Ομλ. В этих функциях λ — проекция орта
на волновой вектор; μ — проекция на неподвижные оси.
Используя эти орты, получаем «шаровые» векторы [132]
{Yjm)»=%D]ixD'mx. (8.7)
λ
Если разложить произведение двух D-функций по D-функциям, то
получим разложение «шаровых» векторов, рассмотренное В. Б. Бе-
рестецким [278]. (С этими вопросами также можно познакомиться по
работе В. Б. Берестецкого, А. 3. Долгинова и К. А. Тер-Мартиросяна
1279] и монографиям [277, 280]). Например, для «электрического
шарового» вектора
(->— <Ю*~Vj{Jm\\ _l_ >«,«.+
- (J — 1 1 J \
+ *Λ/ + >+μ -μ -М)У"»*» <8·8>
Шаровая функция возникла в результате того, что один из
индексов у D-функций в (8.7) повторяется. Разложение (8.8) можно
описать как разложение компонент вектора по НП со спиральностью,
равной нулю.
Подчеркнем, что функции (8.7) и (8.8) при преобразовании
Лоренца приобретают лишние компоненты, от которых нужно избавляться
градиентным преобразованием. Только неприводимые амплитуды
перестраиваются нужным образом.
После подробного изложения вопроса о функции в 5-системе (на
конусе) функции в остальных системах координат (на конусе) опишем
фрагментарно.
8.1.2. Я-система. Для подгруппы О (2,1) ^ О (2)
k0 =r ea ch β, k2 я еа sh β cos φ,
kx = ea sh β sin φ, kz = геау
где —οο<α<;οο; —οο<β<οο; 0^φ^2π;
+ 1 для k3>0,
(8.9)
' — 1 для fe8<0.
Диагональными операторами являются
2ελ
с собственными значениями ф + 1/4 и Μ соответственно (здесь q —
вещественное число для унитарных представлений). Собственные
функции операторов Н2 и Мд суть
71л(Φ, β, -Ф) = <ΓίΑ14ίΙ(<±β) e'\ (8.11)
157

где dm (ch β) следующим образом выражаются через функции Якоби
[14] %д (ch β):
<$λ(Λβ) = ?&Λ((Λβ), ε-1,
<fi?x (ch β) - $LMд (ch β), ε = - 1.
8.1.3. 0-система. Для подгруппы £ (2) г> О (2)
» α 1 + Г2 * а
k0 = е —^— , k2 — e rcos φ,
(8.12)
^βΛ8ΐπφ, k3 = ta -1 + г3
(8.13)
2
где — оо < α < оо; 0 < г < оо; 0 < φ < 2π.
Диагональные операторы представлены в виде
+ -£-('-£+*·)·· Αί»-'-4-+λ· <8Л4>
Собственные значения О2 и Мъ соответственно равны κ2 и М, где
κ вещественно, а собственные функции
/т (<Р, '. - ф) = e-tMVM+x (нг) *,λφ. (8.15)
Здесь /м-ья (хг) — функция Бесселя.
8.1.4. С-система. Для подгруппы О (2,1) id О (1,1)
k0 = / ch β, L· = e* cos φ,
(8.16)
Λχ = ea sin φ, £3 =а еа sh β,
где —- оо < α < оо; — οο<β<οο;0^φ^2π.
Диагональными операторами являются М3 и Ν3 с собственными
значениями Λ1 и τ. Их собственные функции записываются таю
1W(Φ, β, - Φ) - e-lme"%ibf. (8.17)
Вычисляя операторы Казимира Δ и Δ' во всех системах координат
на конусе, находим, что все они имеют одинаковый вид [132, 1691:
Δ—£г+2-аг + х*· <8J8>
Δ'-,λ (» + тег) · <8Л9>
Решая уравнения (7.1) и (7.2) с учетом (8.18) и (8.19), получаем,
что для унитарных представлений λ = ν, а часть базисных функций*
зависящая от а, равна ехр (—1 + /р) а.
8.2. Матричные элементы
В различных физических задачах требуется знать матричные
элементы преобразования от базисных функций, соответствующих редукции
группы Лоренца на одну цепочку подгрупп, к базисным функциям,
158

отвечающим другой редукции. Ввиду того что такие матричные
элементы не зависят от способа реализации представлений , их проще
всего вычислять с помощью функций на конусе [169].
Матричные элементы перехода S — С. Пусть
базисные функции в 5-системе (αθφ | pvJM), а в С-системе
(&ξφ | ρντΛί). Тогда матричные элементы перехода из S-системы в
С-систему определяются интегралом
(ρντΜ | pvJM') = J -££- (ρντΜ | 6ξφ) (αθφ | pvJM). (8.20)
Выразив переменные в С-системе через переменные в 5-системе
ё* = е° sin θ, th ξ = cos θ и подставив явный вид базисных функций,
получим
оо η 2л
(ρντΜ | pvJM') = NsNc $ e2ada J sin θ<ίθ J dy X
—oo 0 0
χ β-'^β«-Ι-"»ν-1+"*,β-'<*-Μ')φβί<*-Λ1)νί,.ν(α)8θ) =
= NsNc $ sin № (sin ΘΓ1+ι (tg -|T <?JMtV (cos Θ), (8.21)
о * '
где Ns и Νχ — нормировочные множители функций (#θφ | pvJM) и
(6ξφ Ι ρντΛί) соответственно.
После вычисления интеграла (8.21) и подстановки значений Ν&
и Nc окончательно находим
(ρντΜ Ιρν7Λ1 > = олш-2 ι ]/ ?(j + ν)\ {J-Μ>ι Χ
Γ / 1 + Μ + ν + <τ + ф \ Γ / 1 + Μ + ν — /τ + ф \
Χ Γ(Λ4 —v-f 1) Γ (1 +Λί + φ) Χ
p + *f + i. *-Λ !(. + «-, + (, + »],
\Λ1—ν + 1, l+M+ip J
Как и в п. 2.1.5, здесь матрица перехода выражается через функцию
9F2 от единичного аргумента. Однако некоторые параметры теперь
стали комплексными, поскольку переход между S — С-системами
можно представить как переход между деревьями (рис. 59) с той лишь
модификацией по сравнению с п. 2.1.5, что некоторые углы стали
гиперболическими (а, а\ b), a постоянные разделения переменных —
комплексными. Таким образом, матрицу (ρντΛί | pvJM') можно вы-
Рис. 59
15*

разить через аналитически продолженные к комплексным моментам
ККГ группы SU (2).
Матричные элементы перехода в остальных случаях вычисляются
аналогично. Используя таблицы интегралов из справочников [227,
2811, находим для них следующие выражения.
Матричные элементы перехода S — О:
у-м (_)" (/ + Μ + н)1 (-L) iCv^,p^n (κ)
Х 2j (Λί — ν + η)\ (J — Μ — η)! α! Γ (Μ + я + φ + 1)1 ' (8·23)
Здесь Kv-io-n (κ) — функция Макдональда 114].
Матричные элементы перехода S — Я:
(pvJM | ρν^Λί') = ««м- У (ν) + (-fJ-M~*> J (_ V)b (8.24)
где через У (± ν) обозначено выражение
J(±v) = n4M^2J+iq~Tx
1
χ
(-J--H
г ί-^ + Μ — i<Ar (-γ — Μ + ίη\τ (у + уи + i) г μτν+ΐ)
\ί (/τν)ΐ(/ + .
" (J±v)l(/-M)l у .__.„ Π-Ζ + Μ + η+Ι)
/1 \ /1 \ i( ' Γ(Λ1^ν + η+1)η!η'Ι
г (т +iq ± η' (Τ +*» +ίρ) "-"'
r(JTv + n+l) Γ(4- — M + lq + n'\r (-Y + ig±v + n'\
Г (1 — Μ ± ν + n') Г (/И ч= ν + η + η') Г-1 /-g- + Μ + «9 + <ρ =F v + л -f- η'J
/ з 1
Χ ι^ι ("J" + J + Μ + iq Τ ν + « + π', -γ + iq + /ρ;
4- + Αί+*? + ίρ + η + ι'; _ι). (8.25)
Матричные элементы перехода О—Ci
2_t+itr / Μ + ν Η- Φ + ft + > \
(ρνκΛί | ρντΜ') = β**. — ' — . (8.26)
κΤ +ίχΓ| уи + т-ip-ft + l \
Матричные элементы перехода Я — Ci
2-'РГ ( ' + ν + <?) Г (-L - iq + φ)
(ρντΜ \pvqM') - бщ. ^ ^-ff f- X
(2π)' Γ (ν - ΛΙ + 1) Γ LL. + ΛΙ + iq]
160

χ
Γ f 1 + ν — Μ — φ + iτ \
(1 ,. . 1 , . 1+ν — Μ — ί'ρ+ίτ
- M—iq, -2~ + v— iq, —x _ £Ζ—
|. (8.27)
ν-Μ + 1, 1-^ + ν-Α1 + φ-(τ. χ
Матричные элементы перехода О — Hi
(ρνκΜ Ι pvqM') = 6MM>2n V% [Jx (κ) + У2 (κ)], (8.28)
где Jt (κ) и У2 (κ) выражаются через G-функции Мейера [281]
г (4" ~ ν + <"<?) г (4—iq ~ *)
1 / 2\^+v
am-4-(4-)
χΣ
Γ(4-+Α|+|')Γ(4-+Λ,-<»)Γ(4-
Γ (4"+Λ1~ι<?+")Γ ("Γ+ν~"?+η)
Γ(Μ + ν + η+1)ηΙ
+ ν·
Χ
■"?]
Χ
., ~ιι / κ2
Μ + ν
■^ μ-4-(4-)'
0, —4-+ί9+φ —«· —"/'
м+v τ(4—<*+*)r(4-+v+<*)
(8.29)
γ.Γ^
г (-J-+«+<?)г (4—м-"?)г (4-+ν~,'</)
XGSI4
Γ (ν — Λί + Λ+ 1) η!
2 ^ V . (8.30)
\Μ + ν + n — iq, 0, Μ+ν/
Эти коэффициенты при ν = 0 переходят в соответствующие выражения
для матриц перехода вырожденных представлений, полученные в
работе [2711 Отметим, что для унитарных представлений матричный
элемент обратного преобразования определяется, очевидно, эрмитово-
сопряженной матрицей. Таким образом, например, из матричных
элементов (5 | С) и (О | С) можно получить матричный элемент (S | 0)ι
t (S j О) = (S I С) {C | О) и аналогично другие матрицы.
И 1-1980

Глава 9
ПОСТРОЕНИЕ БАЗИСОВ ИНВАРИАНТОВ
ИЗ ДИНАМИЧЕСКИХ ПЕРЕМЕННЫХ,
ПРЕОБРАЗУЮЩИХСЯ ПО ЗАДАННОМУ
ПРЕДСТАВЛЕНИЮ КОМПАКТНОЙ ГРУППЫ ЛИ
9.1. Производящие функции Молина для конечных групп
В данном параграфе без доказательства приведем результаты
классической теории инвариантов, необходимые для дальнейшего изложения.
Доказательства можно найти в [282—286].
Пусть дана некоторая совокупность операторов {$}, α = 1, 2, ...
..., [γ], образующих базис представления γ группы G ([γ] — размерность;
α — индекс строки представления γ). Для простоты будем считать,
что операторы # коммутируют друг с другом, но результаты легко
обобщаются и на случай некоммутирующих операторов.
Основная задача, решаемая теорией инвариантов, заключается в
нахождении общих выражений для всех независимых инвариантов и
ковариантов группы G, которые можно построить из степеней
операторов Ра.
Утверждение 9.1. Исходя из операторов {/J}, всегда можно
построить совокупность однородных полиномиальных инвариантов /1э /2, ...
..., ΙΝ+Κ группы G, называемую целым рациональным базисом (ЦРБ)
инвариантов (integrity basis) и обладающую следующими свойствами:
а) первые N инвариантов, называемые основными, являются
алгебраически независимыми; б) произвольный полиномиальный инвариант
У можно представить в виде
/ = Р0 + /лч-Л + · · · + Ιν+κΡκ, (9.1)
где {Pt} — полиномы только от основных инвариантов N = [γ]; К^О.
Инварианты lN+u .., Ιν+κ, называемые вспомогательными, входят
в выражение (9.1) линейно (т. е. не выше чем в первой степени).
Степень полинома It по операторам $ назовем порядком инварианта /£.
Очевидно, что совокупность всех однородных полиномиальных
операторов степени Ω, построенных из $, образует базис некоторого,
вообще говоря, приводимого представления DQ группы G. Его можно
разложить на НП Dr этой группы 6;
£>й = 2я(Г, γ, Ω)ϋΓ. (9.2)
г
β Очевидно, что η (Γ, γ, Ω) — коэффициенты разложения симметричной степени
Vs' (или симметричного плетизма у X [QJ) в ряд по НП группы G,
162

Функция Молина Φ (Γ, γ, λ) является производящей функцией (ПФ)
для кратностей η (Γ, γ, Ω) в разложении (9.2), т. е. коэффициенты ее
разложения в ряд Тейлора по вспомогательному параметру λ
Φ(Γ,γ,λ) = Ση(Γ,γ,Ω)λΩ (9.3)
Ω
задают число линейно независимых ковариантов типа Г и степени Ω,
которые можно построить из операторов i%9 Хотя в ядерной физике
нас интересуют, как правило, непрерывные группы SU (я), SO (я),
Sp (2л), процедуру построения ПФ для числа ковариантов легче всего
пояснить на примере конечных точечных групп. Для них эта задача
была решена русским математиком Т. Э. Молиным [287].
Теорема Молина. Производящая функция для числа линейно
независимых ковариантов типа Г и степени Ω конечной группы G
определяется формулой
где %г (g) — характер элемента группы g в Η Π Γ; Dy (g) — матрица
элемента g в представлении у; \ G | — порядок группы G; Ε —
единичная матрица.
Доказательство. Как отмечалось выше, нас интересует
представление DQ группы в пространстве однородных полиномов,
построенных из базисных векторов {/£} представления у группы G.
Базис пространства образуют мономы
(ИГ (й)"1 ... (<?νΐ)\ν1. пг + п2+ ··. +ηΓγ] = Ω, (9.5)
представляющие собой компоненты симметричного тензора п-го ранга
в векторном пространстве размерности Ιγ]. Таким образом,
представление DQ — Ω-я симметризованная степень yQ (или плетизм у Χ [Ω]),
и речь идет о разложении ее на неприводимые компоненты Dr в
соответствии с (9.2). Кратности η (Г, γ, Ω) можно найти с помощью теории
Групповых характеров [27, 85, 283, 288J
η (Г, γ, Ω) - -^ 2 Х? (g) χΩ (g), (9.6)
если известны характеры представления DQ. Последние можно найти
следующим образом 1283, 287]. Векторы /« преобразуются под
действием элемента g по формуле
D(g)tl = %DUg)tl
Можно выбрать базис представления γ так, чтобы матрица Dv (g)
элемента g в этом базисе была диагональназ
D (£) й - μα$, D£3 (g) = μαδα3, (9.7)
где μα — собственные значения матрицы Dv (g).
11* 163

Компоненты симметричного тензора ранга Ω преобразуются по закону
ОШИГ · ■ ■ Ш = μ?'μ? ... wtfKtff ··· «ЬЛ
Тогда матрица элемента g в представлении Dy также будет диагональна
и ее след (характер) имеет вид
Ы£)= 2 μϊ'μ? . . . μβ?. (9.8)
Поскольку характер представления не зависит от выбора базиса
представления, то, подставляя этот результат в формулу (9.6) и
полученное при этом выражение для η (Γ, γ, Ω) в соотношение (9.3),
записываем последнее в виде
<D(I\V)X)=-L-2x?te) 2 λη,+-+η[ν -..μ^]· (9-9)
Далее воспользуемся тем, что суммирование по каждому пь можно
проводить независимо от 0 до оо и применим формулу для суммы
членов бесконечной убывающей геометрической прогрессии
(полагаем, что все λμι < 1). Произведение (1 — λμχ)... (1 — λμ[Υ]) —
детерминант матрицы | Ε — KDy (g) |:
Π (1 - λμ,) = det I Ε - KDy (g) |. (9.10)
i
С учетом этого обстоятельства выражение (9.9) дает формулу Молина
(9.4).
Заметим, что наборы собственных значений матриц Dy (g) и Dy (/)
для сопряженных элементов / = hgh~] одинаковы. Действительно,
если матрица Dy (g) приведена к диагональному виду (9.7), то матрица
Dy if) — к точно такому же виду преобразованием U = Dy (/f~l):
UDy (/) ί/""1 = Dy {g). Поэтому произведение (9.10) для всех
элементов одного класса одинаково. В результате в формуле Молина (9.4)
сумму по всем элементам группы можно заменить на сумму по классам
■»<Γ·τ·4-τλΣ*«.ι«'ΐ"Ηΐ· <9">
где пс — число элементов класса С; Dy (С) — матрица какого-либо
(одного) элемента из этого класса в представлении Dy (удобнее выбрать
такой элемент, у которого эта матрица диагональна).
Инварианты — это коварианты типа Г = Аъ и формула Молина
в случае инвариантов
Φ (Α, γ, λ) = -rlj- У —τ . (9.12)
|GI вей det|£—λΖ)λ(^)| ν '
Характеристические полиномы в (9.4) и (9.12) можно вычислить по
формуле (9.10), а также с помощью соотношения
[vl
det\E-lDy(g)\= 1 +Σ 4<*)λ· (9ЛЗ>
!64

где %Ak (g) — характер элемента g в k-и антисимметризованной
степени представления у.
Если исходное представление у приводимо: γ = yt φ...© γΛ, то
характеристический полином факторизуется:
det | Ε — XDy (g)\=U det | £ — XDyi (g) |. (9.14)
Важность ПФ Молина определяется тем, что они содержат
информацию не только о числе линейно независимых инвариантов (ковари-
антов) той или иной степени, но и об алгебраической структуре ЦРБ
для инвариантов (и ковариантов) группы G. Связь функции Молина
со структурой ЦРБ инвариантов устанавливается посредством
следующего утверждения [287].
Утверждение 9.2. Если ЦРБ включает в себя N основных и К
вспомогательных инвариантов, имеющих порядки соответственно п{ (1 ^
^Ξ ι ^ Щ* и/ О ^ / ^ Я), т° ПФ Молина имеет вид
Φ(Γ,ΐ|λ)- ,+ί~;+-+1';„ . (9.15)
где числа щ и xj могут повторяться.
Утверждение, обратное данному, вообще говоря, неверно в силу
того, что при вычислении функции Молина можем получить вместо
точной функции (9.15) выражение, в котором частично (или
полностью) сокращены общие множители в числителе и знаменателе (или,
наоборот, присутствуют лишние общие множители). При этом информация
о степенях некоторых основных и вспомогательных инвариантов, а
также об их общем числе может оказаться искаженной. Поэтому,
получив функцию Молина в виде (9.15) (или приведя ее к такому виду,
чтобы коэффициенты при всех λκ/ в числителе были положительными
и целыми, а знаменатель состоял из скобок (1 — λ"*)), мы должны
интерпретировать степени щ и Xj как порядки базисных инвариантов с
определенной осторожностью. Если отвлечься от этого осложнения,
то можно сказать, что ПФ Молина позволяет определить (или, по
крайней мере, высказать вполне обоснованную гипотезу), сколько
основных и вспомогательных инвариантов входит в ЦРБ и каковы их
порядки. Таким образом, функция Молина содержит очень полезную
информацию о количестве основных и вспомогательных инвариантов,
образующих ЦРБ, и их порядках. Правда, окончательное суждение о
структуре ЦРБ, за исключением простых случаев, можно сделать
только после построения набора базисных инвариантов в явном виде и
доказательства его полноты. Однако ПФ Молина является
исключительно ценным руководством при отборе кандидатов на роль базисных
инвариантов.
Если исходное представление γ разлагается в сумму НП у = уг ©
© γ2, то полезно обобщить определение ПФ, введя для каждого НП
вспомогательные переменные λ и μ. Тогда ПФ для числа линейно
165

независимых ковариантов имеет вид
Φ (Г, V' Φ γ", λ, μ) = J Ci*V' Π 1ΊτΊίΓ , (9.16)
i k (1 — λ *μ *)
и комбинация λ s * μ s означает, что ЦРБ содержит ковариант
(инвариант), который имеет порядок κ5 по операторам /ν' и порядок xs по
операторам ty". Такие обобщенные ПФ позволяют получить более
детальное представление о структуре ЦРБ инвариантов. Если известны
отдельно ПФ Молина Φ (Γ', γ', λ) и Φ (Γ\ γ", μ) для числа
ковариантов, порождаемых операторами ty' и ty соответственно, то легко
получить ПФ для числа независимых инвариантов, которые можно
построить из операторов f' и ty\ Известно, что из ковариантов νζ< типа
Г' (сконструированных из операторов f) и ковариантов W%» типа Г"
(построенных из tr) можно построить инвариант Од, только при
условии, что Г" = (Г')* (Г* — комплексно сопряженное представление),
и притом единственным образом»
(ΐΑ^ΣνΧΊ. (9.17)
α
Это означает, что если число ковариантов типа Г' порядка Ω' равно
η (Γ", γ', Ω'), а число ковариантов типа Г * порядка Ω" равно η (Г",
γ", Ω), то общее число инвариантов порядка Ω, которое из них можно
построить,
п(АъУ'®у\&) = Σ η(^γ\Ω>(Γ'*,γ",Ω'').
Ω'+Ω"=Ω
Домножая эту величину на λΩ и суммируя по всем значениям Ω и
всевозможным Г', получаем согласно (9.3) ПФ для инвариантов
Φ(Λι.Υ'Θϊ\λ)= Σ Αζ(Γ\γ\Ω>(Γ*,γ\Ω--Ω')λΩ==
Ω,Ω',Γ'
= Σ η (Γ', γ', Ω') η (Γ'*, γ", Ω") λΩ'+Ω" -
Ω',Ω",Γ'
= ΣΦ(Γ',Υ', λ)Φ(Γ'*,γ\λ). (9.18)
Γ'
Для сохранения информации о том, какой порядок по операторам f\
t7" в отдельности имеют интересующие нас инварианты, следует
использовать двухпараметрическую ПФ
Φ И1Э γ' Θ γ"; λ, μ) = 2 Φ (Γ, γ'; λ) Φ (Γ*, γ"; μ). (9.18а)
Γ'
Формулы (9.18) и (9.18а) являются примером построения ПФ в случае
приводимых представлений путем комбинирования более простых ПФ
для неприводимых составляющих. Такой метод комбинирования
используется очень часто (см. параграф 9.4) и является эффективным
приемом построения ПФ для сложных случаев.
166

Произвольный полиномиальный ковариант Аг типа Г
относительно группы G можно представить в виде
Ат = V\PX + ViP2 + ·. · + VtmPm. (9.19)
где Pi — полиномы от основных инвариантов, входящих в ЦРБ
инвариантов, описанный выше; Ι/f — вспомогательные однородные
полиномиальные коварианты типа Г относительно группы G.
Совокупность операторов 1Ъ ..., IN, VT\, ..., 1/м называется ЦРБ ко-
вариантов. Заметим, что число Μ вспомогательных ковариантов типа
Г связано с числом К + 1 вспомогательных инвариантов (с учетом и
единицы) соотношением Μ = [Г] (К + 1).
Если ЦРБ состоит из N основных инвариантов и Μ
вспомогательных ковариантов типа Г, степени которых равны щ (\ ^.i^N) и
ml{\ ^,Ι^,Μ) соответственно, то ПФ для числа ковариантов типа
Г можно привести к виду
Φ (Γ, γ,λ) = λ"' + λ™*+ ... +λ"Μ (920
Обратное утверждение в общем случае снова несправедливо. Тем не
менее ПФ (9.20) является мощным эвристическим инструментом для
нахождения ЦРБ ковариантов. Сформулированные выше общие
положения верны как для конечных, так и для непрерывных групп.
Обратимся к построению функции Молина для непрерывных групп. Здесь
решающую роль играет теория характеров для групп Ли, построенная
Г. Вейлем [283].
9.2. Производящие функции Молина для непрерывных групп
Поясним процедуру получения ПФ Молина для группы SO (3) на
ряде примеров. В частности, рассмотрим задачу построения инвариантов
и ковариантов из генераторов этой группы Lx, Ly, Lz. Поскольку
генераторы группы SO (3) являются компонентами вектора, т. е.
преобразуются по НП DL группы SO (3) с весом (моментом) L = 1, то речь
идет о построении ПФ Φ (Γ, γ, λ), где γ = D1, а Г = £)°, в случае
инвариантов, Г =DL (L = 1, 2, 3, ...) в случае ковариантов.
Коварианты Vm — неприводимые тензорные операторы ранга L, построенные из
степеней генераторов^, Ly, Lz (или L0 = L2, L± = Lx± iLy),
поэтому ниже часто будем писать «L-тензор» вместо термина «ковариант».
Заметим, что совокупность (пространство) мономов L\ l% Ll с
произвольными неотрицательными степенями а, 6, с образует так
называемую универсальную обертывающую алгебру USO (3) для группы
50(3). Поэтому фактически рассматриваем задачу о построении ПФ
Молина для числа линейно независимых L-тензоров (неприводимых
тензоров ранга L) на обертывающей алгебре группы SO (3).
9.2.1. Функция Молина для инвариантов на обертывающей
алгебре 50(3). Формула (9.11) для функций Молина непосредственно
обобщается на непрерывные группы, только суммирование по классам за-
167

меняется соответствующим интегралом, а число элементов группы
| G | — ее объемом Vg — f dC:
ф(Г, γ, λ) «-i- f dC Ui£L . (9.21)
v r ^c J det | Ε — KDr (С) \ *
В группе вращений SO (3) класс определяется величиной угла
поворота 0 ^ θ ^ 2π вокруг некоторой оси, поэтому характер НП Dh
зависит от этого угла θ и задается известной формулой
Χ» (Θ) = Σ eimQ = **+{-fl # ζ = е*\ (9.22)
Элемент объема берем в виде dC = sin2 -у d6, тогда
2л
VG = ~ J sin2 -L d0 = 1. (9.23)
о
В качестве представителя класса С удобно выбрать поворот на угол θ
вокруг оси Ζ (оси квантования). В этом случае матрица D1 имеет
диагональную форму с собственными значениями μ1 = eie = ζ, μ2 =
= 1, μ3 = e~ie = ζ-1. В результате формула (9.21) для данной задачи
приобретает вид
(DL (/?) = —[ sin2 4- dQ -Μ? дг-. (9.24)
Интеграл по θ от Одо 2π представляет собой интеграл по окружности
единичного радиуса с центром в точке (0, 0) в плоскости
комплексного ζ
φ, fnV- l f *0-*>f г^(г) r9 25>
^lW- π J 4г* (1«р)(г-р)(1-рг) · (У'Л)
Он сводится к сумме вычетов в точках ζ = 0 и ζ = /?, лежащих (при
/? < 1) внутри единичного круга и являющихся простыми полюсами.
Поэтому в случае L = 0 окончательно получаем
Фо(Р) = 7Г^Г = 2(^. (9-26)
Следовательно, весь ЦРБ инвариантов сводится к одному
инварианту второго порядка, которым является оператор Казимира L2.
Поскольку N (k, 0) = 1 для четного k = 2п и N (k, 0) = 0 для нечетного
k = 2п + 1, то SO (3) — инвариант, построенный из генераторов этой
группы,— может иметь только четный порядок k = 2п и в этом случае
он равен (с точностью до постоянного множителя) L2n. Других
инвариантов в обертывающей алгебре SO (3) нет (т. е. нет других операторов
Казимира, не сводящихся к степеням оператора Казимира второго
порядка L2). Это простая и очень ценная информация, которую можно
получить при построении инвариантов путем перебора комбинаций
L%LoLL ca + b-\-c = 2n после громоздких выкладок, в то время как
168

использование ПФ Моли на сводит этот утомительный анализ к
простому и изящному вычислению.
9.2.2. Функция Молина для L-тензоров на обертывающей алгебре
SO(S). ПФ Ol (ρ) = Φ (L, / = 1; ρ) для произвольных L-тензоров с
L = 1, 2, ... можно получить, если в формулу (9.24) подставить явное
выражение (9.22) для характера %l (θ)· После простых
преобразований получаем ПФ для числа линейно независимых L-тензоров,
составленных из компонент какого-либо вектора г (или векторного
оператора L) в виде
Φι(Ρ) = ΣΝ(k, L)pk = -J^-r = ΣPL+2a. (9.27)
k l —Ρ η
Это означает, что любой L-тензор имеет вид произведения
простейшего L-тензора YLm (г) = rLYLM (θ, φ) (в операторном виде YLM Щ) на
инвариант (г2)п (или (L2)") и эта конструкция единственна. В
частности, тензор Tll (с максимальной проекцией Μ = L) можно записать так:
TLL~{L+)L(L*)n. (9.28)
9.2.3. Функция Молина для инвариантов, построенных из квадру-
польных операторов. В предыдущих пунктах речь шла об
инвариантах и L-тензорах, сконструированных из векторных величин (γ = D1).
Аналогично можно рассчитать ПФ Ф0 (d) для числа инвариантов,
составленных из компонент тензора второго ранга (Qm, m = ±2, ±1,
0), т. е. у = D2. В этом случае матрица D2 имеет диагональную форму
с собственными значениями: μχ = #сд = ζ2, μ2 = eie = г, μ3 = 1,
μ4 = eiB == z-\ μ5 = e~m = z~2 и ПФ Ф0 (d), подобно (9.25),
определяется интегралом по группе (по Θ, 0 ^ θ ^ 2π):
*№ --Н -**£* '
(l-d)(\-dz)(i 1|(1_ώ«)|ΐ—^-J
(9.29)
который при d <C 1 равен сумме вычетов внутри единичного круга в
полюсах ζ = d и г = ± К5:
Ф0«О = У Res | -» О-«)'/» J =
(l—d)*d
-м-
2 (1 — d) [ (1 — d2) (1 — d*) (cia — d)
(\—Vd)*Vd
(\—dV~d) (1 — d?) (Vd—d) 2V'd
■ +
+
t (i+i^)2e^) 1 j ,q ш
^ {\ + dVlt)(\-d*)(Vd + d)2\fd | (i—d*) (l—rf») · ^·ου>
Аналогично получается ПФ для числа L-тензоров, которые можно
построить из компонент квадрупольного оператора (£п (и вообще из
любых величин, преобразующихся по НП D2 группы трехмерных
вращений, например, из координат квадрупольных колебаний αμ или опе-
16$

раторов рождения квадрупольных фононов b%i в модели Бора — Мот-
тельсона и т. д.). Мы не случайно в обозначениях ПФ (9.27) и (9.30)
использовали в качестве параметров буквы pud. Коэффициенты при
рп в разложении ПФ Φ (L, / = 1, ρ) показывают число состояний с
моментом L, которые можно построить из η частиц, каждая частица
имеет момент / = 1. Эти состояния симметричны относительно
перестановок частиц, т. е. имеет место схема Юнга In]. Итак, ПФ Φ (L, / = 1, ρ)
решает задачу классификации состояний частиц, образующих «обо-
лочечную» конфигурацию рп, т. е. в ПФ содержится информация о
числе линейно независимых волновых функций вида | рп In] L). Из
формулы (9.27) следует, что при каждом L допустимы только значения
η = L, L + 2, L 4- 4, ... и каждое из них встречается один раз.
Конечно, этот результат хорошо известен, например, из решения
уравнения Шредингера для трехмерного гармонического осциллятора.
{Дело в том, что перечень состояний Wmm трехмерного осциллятора
эквивалентен набору состояний /?-бозонов | рп [п] 1т), а для
осциллятора известно, что число квантов η = / + 2fe, k = 0, 1,2, ...). Однако
информация, получаемая из ПФ Φ (L, /, λ), уже не столь тривиальна.
Ценность ПФ Φ (L, Ι, λ) заключается в том, что в ней в свернутой форме
содержится информация о классификации состояний | ln In] L),
которую обычно приводят в виде сложных и объемистых таблиц,
особенно громоздких при I = 3,4 и т. п.
9.3. Обобщение производящих функций Молина
Метод производящих функций нашел широкое применение при
решении ряда задач атомной и ядерной спектроскопии, а также получил
дальнейшее математическое развитие. Это было сделано в основном в
работах монреальской группы [289—298], в которых было
предпринято обобщение функций Молина по нескольким направлениям для того,
чтобы с их помощью исследовать более разнообразный круг
спектроскопических и теоретико-групповых задач. Одно из этих обобщений
состоит в следующем. Выражение (9.27) — это ПФ для числа L-тензо-
ров на обертывающей алгебре SO (3) при фиксированном L и
всевозможных значениях суммарной степени η по генераторам. Возникает
вопрос о получении ПФ, которая давала бы не только классификацию
тензоров на обертывающей алгебре при данном L, но и позволяла
перечислить все допустимые значения L, встречающиеся на обертывающей
алгебре, т. е. в пространстве мономов L+ LoLL. Соответствующая ПФ
должна зависеть не только от параметра р, степень которого рп
фиксирует порядок коварианта я, но и от параметра У, степень которого
JL (L = 0, 1, 2, ...) фиксирует ранг L соответствующего коварианта.
Очевидно, что искомая ПФ имеет вид
со ос
= |οΦ(Ι,/=1;ρ)/=Στ^==-(Γ^ν(,-^Γ· (9·31)
170

В литературе [293] встречается несколько иная форма записи этой ПФ:
Ее можно рассматривать как ПФ для L-тензоров на обертывающей
алгебре. Она означает, что из генераторов L+, L0, L~ (их символом
является буква J) можно построить только один L-тензор п-и
степени (п = 2k + L) вида (L2)k L+, если учитывать компоненту старшего
веса (максимальной проекции) Μ = L. Этот вывод согласуется с
нашим обсуждением в п. 9.2.2. Аналогично можно получить ПФ для
L-тензоров, построенных из компонент квадрупольного момента [291]:
G(d, J) = 2^Ф(£,1 = 2; d) J = (1 _d2) (1 _d») (l — ^Уа) (l — da72) =
= l+dJ2+d*(l+J2+J*) + d*(l+J2 + P + P + J*) + ... (9.32)
В этом разложении член Cd?JL означает, что симметричный тензор
ранга а, построенный в 5-мерном пространстве компонент
квадрупольного оператора, содержит С неприводимых SO (З)-тензоров с моментом
L (т. е. преобразующихся по НП DL). Эти результаты можно
использовать для классификации состояний системы d-бозонов (или квадру-
польных фононов). В частности, из (9.32) для конфигурации d1
получаем L = 2, для d2 — L = 0, 2, 4, в случае d3 [284] L = О, 2, 3, 4, 6
и т. д. Такие результаты неоднократно получались разными способами
[299—305]. ПФ (9.32) содержит их в наиболее концентрированной
форме. Удобство формулы (9.32) по сравнению с результатами в [299—
305] состоит в том, что она позволяет как анализировать состояния с
разными η при фиксированном L, так и находить спектр допустимых
значений L при данном числе частиц п. Последнее более интересно для
конкретных расчетов. Ценность формулы (9.32) не ограничена
классификационными возможностями, она дает также информацию о
структуре ЦРБ, с помощью которой можно построить волновые функции
системы d-бозонов. Она показывает, в частности, что в состав ЦРБ
входят инварианты второго и третьего порядков Х00 = [Ь+ X 6+]о,
Хоо = [&+ X Ь+ X Ь+]о (6+ — операторы bfm, объединенные в
скаляры), символом этих инвариантов являются величины d2, d? в
знаменателе формулы (9.32). Скобка в знаменателе, содержащая dJ2>
означает оператор первой степени по Ь+ с моментом 2, т. е. символу dP
соответствует оператор Хчт = btm- Аналогично символу d2P отвечает
квадруполь второго порядка Х%т = [Ь+ X b^Ym. Наконец,
конструкция d3,/3, стоящая в числителе, символизирует тензор Хзт = [6+ X
χ 6"1" X b^fm, который может встречаться в волновой функции не
более одного раза 7. В итоге это означает, что полный (но не ортонорми-
рованный) набор состояний с данными L и η образуют функции вида
7 Согласно [299—305], в конфигурации dz состояние L = 3 встречается один раз,
т, е. в силу симметрии тензора по отношению к перестановкам операторов 6**" его кон·
171

\cfLM = L) = X00X00X22X22X33 [ 0), где показатели степеней а, Ь9
с, d принимают любые неотрицательные целочисленные значения при
условии
2а + ЗЬ + с + 2d -f Зе = п, 2c+2d + 3e = L,
е = 0 для четного L, е = 1 для нечетного L.
Именно такова структура неортогонального базиса модели Бора —
Моттельсона [300] (/(5) zd 50 (5) zd SO(3), использованного в работе
[299]. Оператор Х0о описывает пары d-бозонов, объединенных в момент
L = 0, тем самым величина υ = η — 2а — это значение числа сеньо-
рити [306]. В результате ПФ (9.32) позволяет установить вид ЦРБ для
многофононных функций и выразить их в виде произведения
необходимого числа элементарных факторов, которыми и являются элементы
ЦРБ Х00, Хоо, Х2» Хг, Хз· (О методе элементарных факторов при
построении базисов НП групп Ли, отвечающих неканоническим редукциям
на подгруппы, см. [297].)
9.4. Комбинирование производящих функций Молина
Рассмотренный нами прямой способ построения ПФ для инвариантов
и L-тензоров на обертывающей алгебре SO (3) (формально) можно
обобщить на случай непрерывных групп большего ранга. ПФ
представляется в виде /-кратного интеграла по группе (/ — ранг группы) от
характеров соответствующих представлений и сводится к некоторой
сумме вычетов в полюсах, отвечающих отдельным скобкам в знаменателе.
Однако для групп достаточно большого ранга (/ ;> 3) выполнение
суммирования и приведение ПФ к виду (9.20) весьма трудоемкая
процедура. Такой способ непосредственного вычисления ПФ (9.21) для SO (3)-
инвариантов на обертывающей алгебре 50(3) дает [289]
Φ (/>,<*) =
i С dz(\—z)* ^
д J 4г» (1 — р) (1 — d) (1 — pz) (l —-7") (l — Τ") (1 —Λ») (l — -ρ-)
1 ^ Res *<&-2»-l> __
— 2(1—ρ) (1 — d) L· ν (1—ρ2)(ρ —ζ)(1—£fe)(2-d)(l-dza)(22-d)
z—p,d
z-=±V~d
l+P3d* (q 00ч
— (1 —/?*) (1—d2) (1—d3) (\ — p4) (\ — p*d2) * KU }
Покажем, как можно более просто получить этот результат путем
комбинирования ПФ (9.21) и (9.31). Дело в том, что восемь
генераторов группы SO (3) преобразуются по приводимому представлению под-
струкция единственна и, например, может быть записана в виде
ЦЬ+ X 6+]2 X b+fm = 2 (2ro'2m"|2m' + го") (2т' + m"2m"|3m) χ
т' ,т",тт
172

группы SO (3) D = D1 + D2, а именно, операторы орбитального
момента L образуют тензор 1-го ранга, а квадрупольные операторы Qm
составляют тензор 2-го ранга. Поэтому соответствующие производящие
функции (9.31) для L-тензоров с γ' = V = 1 и ПФ (9.32) для L-тензо-
ров с у" = Г = 2 можно использовать при нахождении ПФ для числа
SO (З)-инвариантов на обертывающей алгебре SU(3) в виде
Φ(ρ,ί=Σ«(«.'=1; J)n(t9l= 2; У)/?sd'. (9.34)
Явное выражение для такой ПФ в виде дробно-рациональной функции
(9.33) можно получить, если взять произведения ПФ (9.31) и ПФ (9.32),
положить Jx = У, У2 = У""1, разложить обе ПФ в ряд и оставить в нем
только члены с У в нулевой степени G (/?, У) G (d, У~1) = [G (/?, У) X
X G (d, У~1)]0 + члены, пропорциональные Уа (а Ф 0).
Итак, Φ (ρ, d) = [G (p, У) G (d, У"1)^. Поскольку
Φ (ρ, d) = G{p,J)G(dtJ~l) =
ι
(1—ρ«) (1 —rf») (1
=2x+2y
\ Σ PnJndx
n,x,y
Ln=2x+2y
-\-2yj-2x-2ff ,
+ Σ p*j*tf+w*j-*x-*i,-f\ 9
nyxyq
п=2х+2у+Ъ
то, отбирая члены, не зависящие от У, получаем два вида слагаемых:
= Σ (P2d2)x (p2d2)y =
ι
V 2^-{-2^-|-3^х-К2г/Ч-3 __ '
Объединение этих сумм дает искомую ПФ Молина Φ (/?, d) для числа
SO (З)-инвариантов в обертывающей алгебре SU(3) в виде
дробно-рациональной функции (9.33), позволяющей установить структуру ЦРБ
инвариантов в случае SU(3) zd 50(3) редукции.
Выше мы комбинировали ПФ для тензоров ранга Lx с другой ПФ
для тензора ранга L2 с тем, чтобы получить ПФ для числа инвариантов,
т. е. для суммарного момента L = 0 (в этом случае требуется Lx = L2).
Однако можно скомбинировать их так, чтобы получить ПФ для L-тен-
зора с произвольным моментом L. Для этого нужно воспользоваться
ПФ Фкг (Л, S; С) для ряда Клебша — Гор дана
ФКГ(Л, β; С) - Σ Φι(Ιι, 4)Φ2(ί,2, β) Фкг (LT\ IT1; С).
173

Штрих у знака суммы означает, что нужно разложить функции <Dlf Ф2,
ФКг в ряды, удержать только члены, не содержащие Ll9 L2, и
произвести суммирование [292].
Пример 1. Построим ПФ для ряда Клебша — Гордана группы SU (2). ПФ
F (р, q; J) в случае сложения целых моментов 1г + 12 = 2 fyf1 Ci» ^2» ^ — Целые)
λ
можно вычислить по формуле
Ιι+/·
F (/>, <?; У) _ 2 "V2 Σ ^λ· <9·36>
Смысл ее таков: коэффициент при члене pliqlzJl — это кратность момента h при
векторном сложении 1г + h, которая, как известно, равна единице при | 1г — /2 | ^ 1Ί -Ь
+ 1% и равна нулю в остальных случаях. Выражение (9.36) можно записать в виде
двух слагаемых с 1г > /2 и 1г < /2:
f (р. <?;/)= J А'г- г£т L +
—J 1—у
Вычислим каждое слагаемое. Первое слагаемое имеет вид
ι °° U
Т=Т Σ P'ijU Σ (я'гГ-'>-д1Ф+1)
/,=0 /2«0
1 У
1_
1 —./
W)
[(l_-f)(l_„y) (I—f)(l
(l-pj)(l- qj) + (1 _ «μ) (1 _ рдЛ) J
Для второго слагаемого запишем
1 ОО ОО 1 00 00
-n-^jT Σ "''·>''' Σ 4ι^--7Γ=ΊτΣρ1φ*λ Σ я1Ф-
1
(1 -J)
2 Λ/-'*-2*A//rH
/,=0 /,=0
qj (\ - pqj* - J + pqj)
2 tf'^5!
/f-/,+l
- (1—У) (I — 9У)(1 —/wy) {\-pqJ*i ·
Складывая оба слагаемых, получаем ПФ ряда Клебша — Гордана:
1 + pJq
F iP* q; J) *" l\-pJ)(l-pq)(l-qJ) ·
Знаменатель формулы (9.37) дает члены типа pliql*Jk с
λ=/, + /2, /i + /,-2f ... , \1г-1%\.
т. е. с шагом, равным двум. Член pqJ в числителе добавляет в ряд пропущенные чле*
ны, так что в (9.38) шаг становится равным единице*
(9.37)
(9.38)
174

Результат (9.37) можно получить непосредственно из общего выражения для ПФ
ряда Клебша — Гордана группы Si/(2) [291, 292]:
F(AU Аг; А) = {i ^ AlA) (I ~ АгА) (I - А^ =
= 2 АЧ^A\+tAa+b = 2 ^^'^Л^+^-2е, (9.39)
λι As,с
если отдельно рассмотреть четные и нечетные значения с= О, 1, 2, ..., min (λχ, λ2) »
ввести обозначения Л^ = /?, Р^— q, A2~ J.
Пример 2. ПФ для ряда Клебша — Гордана группы SU (3) имеет вид
F(AxBlt A2B2: Л£) =
I
- (1— А1А)(\—В1В)(\-А2А)'Л-В2В)(\-АХВ2)(\ — В1А2) Х
Г ι #ι#2λ 1
х [ ι-ли,* + i-w] · (9·40>
Здесь степени параметров Л^^и А2В2 задают вид первого и второго из
перемножаемых НП, а степени А и В — вид результирующего НП, т. е.
F (АХВЪ А2В2, АВ) = 2 Γ(λμ) KVi) ® (λ2μ2)] Χ
(λ1μ,).(λϊϋ«).(λ,μ)
Χ Л^'Л^М*^,
где Γ^ [(λχμι) ® (λ2μ2)] — кратность НП (λμ) во внешнем произведении (λ1μ1) ®
® (λ2μ2).
Формула (9.40) позволяет систематически находить кратности Γ(λμ), которые
ранее обычно табулировались другими методами (путем проведения на ЭВМ расчетов;
по теореме Литтлвуда) [289, 307]. Заметим, что при Вх = В2 = 0 выражение (9.40)
переходит в формулу (9.39) для ПФ F (Al9 Л2; Л) для группы SU (2), если положить
В= 1, λ= 2/.
9.5. Эффективные гамильтонианы
Эффективные гамильтонианы (ЭГ) широко используются при
теоретическом изучении ядерных, атомных, молекулярных и твердотельных
систем. Смысл их введения заключается в том, что они позволяют
выделять и отдельно изучать свойства системы, обусловленные лишь
частью из имеющихся у нее степеней свободы. Известны два подхода
к построению ЭГ. Первый основан на переходе от полного истинного
гамильтониана к ЭГ с помощью одной из форм теории возмущений,
второй — на феноменологическом построении ЭГ путем включения в
него всех допустимых из физических соображений членов.
Наиболее часто встречаются при феноменологическом построении
ограничения, связанные со следующими свойствами ЭГз 1) эрмито-
востью; 2) инвариантностью по отношению к обращению времени;
3) свойствами его симметрии; 4) характером выделяемых степеней
свободы.
При феноменологическом построении ЭГ обычно представляют его
в виде степенного ряда по соответствующим динамическим
переменным или операторам. Методы теории групп эффективны в том случае,
175

когда рассматриваемая система обладает какой-либо симметрией,
характеризуемой группой G. Поэтому предположим, что наши
динамические переменные преобразуются по некоторому (возможно
приводимому) представлению γ группы G.
В задачах атомной, ядерной физики и теории поля группа
симметрии G является непрерывной — одной из групп Ли ((5i/(3), Sp (6, R))t
какой-либо неабелевой калибровочной группой). В молекулярной
физике и физике твердого тела группа G — одна из точечных или
пространственных групп.
Чтобы ЭГ удовлетворял условиям 3, 4, необходимо из
динамических переменных {$} построить степенное выражение наиболее общего
вида, инвариантное относительно группы G. Полезно рассмотреть более
широкую задачу, а именно, вопрос о построении из динамических
переменных {й} не только инвариантов, но и степенных ковариантов
Μβ} группы G, характеризующихся произвольной симметрией Г, т. е.
преобразующихся по определенному неприводимому \ представлению
Г группы G. Инварианты можно получить, в частности, путем
прямого перемножения ковариантов, отвечающих различным степеням
свободы.
Из утверждения 9.1 следует, что феноменологический ЭГ для
системы с группой симметрии G можно искать в виде
Ν+Κ
Н= Σ Cnt ηΝ+κ Π (It)\ (9.41)
где щ = О, 1,2,... для I ^ Ν, nj = 0 или 1 для Ν + \ ^] ^.N + К.
Коэффициенты СПи...,Пм+к, являющиеся подгоночными параметрами,
находятся путем сравнения результатов теории с экспериментальными
спектрами. Обычно в выражении (9.41) ограничиваются конечным
числом слагаемых, например членами, у которых суммарная степень Ω
операторов f*a не превышает определенного числа Ω0. Отсюда для
построения ЭГ необходимо знать: 1) полное число линейно независимых
инвариантов η (Г = Alt γ, Ω) степени Ω, которые можно построить из
операторов {^}; 2) количество основных и вспомогательных
инвариантов Ii9 образующих ЦРБ, и их порядки; 3) нужно сконструировать
набор базисных инвариантов U в явном виде и доказать его полноту.
Ответы на вопросы 1 и 2 дает функция Молина.
Рассмотрим структуру ЭГ, построенного из генераторов группы
SU (3) (модель Эллиотта в теории ядра).
Напомним, что параметрам ρ и d в формуле (9.35) соответствуют
генераторы L и Q. Тогда можно воспользоваться соответствием,
определяющим число и структуру основных р2 ->■ L2, (Ρ ~ (Q · Q), d3-r
~(Q* Q- Q), P2d ~ {[L X L){2) . Q), p2cP ~ ([L X Q] . [Q X D) β
= Ωο и вспомогательного p*d? ~ (\L χ L χ L] · [Q X Q χ Q]) «
» [Ω, QD] инвариантов. Если ограничиться членами не выше
четвертого порядка по генераторам, то ЭГ с симметрией SU (3) можно
записать в виде
Язфф = AL2 + ΒΩ + CQD + · · * (9.42)
176

В такой форме он был использован в работах [308, 309] для
расчета спектра вращательных состояний ядер редкоземельной и
актинидной областей.
Если перейти от модели Эллиотта к рассмотрению симплектиче-
ской коллективной модели ядра [63, 211], то значительный интерес
представляет построение ЭГ модели с симметрией Sp (6, R).
Совокупность из 21 генератора этой группы разбивается на семь неприводимых
тензоров по отношению к подгруппе трехмерных вращений 50(3), а
именно: три скаляра N = 2 b%b%. (/ = 1,2,..., А — 1, α = *, у, ζ) —
/.α
полное число осцилляторных квантов, р+ = 2 Ь/аЬ/а, Р~~ = 2 b}abjai
/,α Λα
вектор Ly = —/2 Saiybjabfa — орбитальный момент системы Л-нукло-
нов, три квадрупольных тензора
Здесь £>/£ (fe/a) — обычные операторы рождения и уничтожения
осцилляторных квантов, отвечающих колебание вдоль α-й декартовой
компоненты с номером /; операторы N, Lv, Q<£p—генераторы подгруппы
i/(3); Ly—генераторы подгруппы 50(3). Искомый эффективный
гамильтониан симплектической коллективной модели Sp (6, R) должен
быть полиномиальным 50 (З)-инвариантом, составленным из
генераторов L, Q+, Q°, Q~~, к каждому члену которого можно добавить в
виде множителей произвольные степени скаляров N, р+, р~\ Таким
образом, в данном случае γ — приводимое представление группы 50(3),
которое разлагается на НП D1 + D\ + D\ + Dl.
Используя формулы (9.21) — (9.25) по аналогии с (9.27), (9*29),
(9.30), получаем для ПФ Молина, задающей число 50 (З)-инвариантов
на обертывающей алгебре Sp (6, R):
Ф(Р> d> S' '> β 2(1 — p)(l —^)(1—S)(l—Ζ) Χ
χ
V πΜ / (2z-*-l)g»
^^ 1(1 —/72) ί/7 — ζ) (1 — dz) (г —d) (1 — ds
\ 1(1 - рг) {ρ - ζ) (1 — dz) (г - d) (1 -dz*) (г« _ </) (i - «) Χ
χ (г — s) (1 - sz*) (г2 — s) (1 - /г) (2 — 0(1- ka) (г2 — f)J
Вычеты необходимо вычислить в полюсах ζ = /?, d, ± Kd, s, db V^s, /,
± V~t. В этом выражении параметры /?, d, s, *< 1 контролируют
степени генераторов соответственно L, Q+, Q°, Q"~. К сожалению, эта
сумма весьма громоздка и в общей форме привести ее к стандартному виду
для функции Молина (9.15) трудно. Поэтому расчеты на ЭВМ
проводились только для однопараметрического случая t = p = d = s = a*
Имеем
$22
Ф № β (1-β«)'(1-α«)·(1-αψ · ί9·43)
12 1-1980
177

где S322 = β22 + 10α19 + 19α18 + 32α17 + 83α16 + 142α15 + 196α14 +
+ 276α13 + 317α12 + 312α11 + 317α10 + 276α9 + 196α8 + 142α7 +
+ 83α6 + 32α5 + 19α4 + 10α3 -Ь 1.
Из полученного выражения ясно, что число базисных инвариантов в
этой задаче велико и построение ЭГ является сложной задачей,
поэтому необходимо отобрать более узкий набор инвариантов для
включения в ЭГ исходя из конкретных физических соображений. Видимо,
в этом случае следует воспользоваться процедурой комбинирования
ПФ, используя тот факт, что ПФ для L-тензоров, которые можно
построить из операторов L, Q+, Q° и Q~ по отдельности, известны (это
ПФ для классификации р- и d-бозонов (9.27) и (9.31)). Теперь нужно
воспользоваться ПФ для ряда Клебша — Гордана и объединить
тензоры YLi (L)f Yu (Q+), Yu (Q°), Yu (СГ) в общий SO (З)-инвариант
на обертывающей алгебре Sp (6, R).
Подведем некоторые итоги. Теория инвариантов дает основу для
построения ЦРБ инвариантов или ковариантов и тем самым для
конструирования ЭГ для систем, обладающих теми или иными
свойствами симметрии. ПФ Молина и ее обобщения дают возможность найти
полное число инвариантов (или ковариантов) данного порядка и
установить состав и структуру ЦРБ. Поэтому знание этих функций
существенно облегчает задачу фактического построения ЦРБ и ЭГ. Были
продемонстрированы типичные приемы построения ПФ и показано,
что ПФ позволяют решать помимо практических задач моделестрое-
ния также многие вопросы самой теории представлений групп. Так, в
литературе [289—2981 построены ПФ:
1) для весов всех НП данной полупростой группы Ли G;
2) для размерностей всех НП группы G;
3) для коэффициентов ветвления при редукции всех НП группы
Ли G на ее подгруппы Ли Н;
4) то же для конечной подгруппы Н;
5) для разложения тензорных произведений двух любых НП
группы Ли в прямую сумму ее НП;
6) для числа полиномиальных L-тензоров любых степеней.
С помощью ПФ производится:
7) вычисление всех плетизмов данного представления непрерывной
или конечной группы G;
8) исследуется структура обертывающей алгебры полупростой
группы G;
9) осуществляется построение ЦРБ для задач 3—8.
Мы уделили внимание в основном вопросам 6, <?, 9 и частично 3, 5,
7 [310]. Дальнейшие подробности можно найти в обзорах и
оригинальных работах [291—293]. Следует иметь в виду, что непосредственным
образом ПФ легко вычисляются только для групп Ли не очень
высокого ранга (/ = 2, 3) или же для отдельных типов представлений
(вырожденных). С увеличением порядка группы явные выражения для
ПФ быстро усложняются. Для их получения целесообразно
использовать ЭВМ. Здесь могут оказаться полезными алгебраические
языки REFAL, REDUCE, MAPLE и т. п., позволяющие производить
аналитические вычисления.
178

В заключение мы хотели бы также отметить, что описанная выше
техника необходима не только в теории ядра или теории молекул для
построения ЭГ, но и в теории фазовых переходов в физике твердого
тела [307, 311] (здесь речь идет о построении термодинамического
потенциала Φ (Χ) в виде инвариантного полинома от параметров порядка
Ха, преобразующихся по НП у группы С), а также в теории поля при
рассмотрении спонтанного нарушения симметрии (задача о
построении С-инвариантного лагранжиана хиггсовского поля L (φ) в виде
полинома от компонент φ« этого поля, преобразующихся по НП группы
G) [312, 313].
12*

Глава 10
ТЕОРЕТИКО-ГРУППОВЫЕ
МОДЕЛИ
Существование аналогии между математическими моделями, которые
сильно различаются физическим содержанием,— хорошо известный
факт. Случается, что построение новой модели и выбор
математического аппарата более или менее сознательно определяются из опыта
других моделей. Например, в теоретической физике модели часто
повторяются вплоть до мельчайших деталей, что проявляется в
одинаковой форме уравнений двух моделей, в одинаковых математических
свойствах сравниваемых уравнений, в одинаковой строгости
используемого математического аппарата и т. д.
Возникают следующие вопросы. Что лежит в основе аналогии
между разными математическими моделями? Как сформулировать
задачу при математическом моделировании динамической системы? Как
разработать новые математические модели и распространить их на
новые области приложения?
Классический взгляд физики на моделирование — это
дескриптивный подход: модели, описывающие природные явления, устойчиво
подчинены некоторым универсальным законам, и задача заключается.
в их открытии. Часто модели и законы постулируются на основе
математической логики и эстетического подхода (божественного
совершенства, симметрии и т. д.), и только позднее выясняется, 4to они
также могли быть до некоторой степени выведены из уже имеющихся
знаний и наблюдаемых фактов. В этом смысле модели появляется не на
базе дедукции или индукции, а в результате вдохновения.
Однако возможен и другой подход* вначале имеются семейства
измерений и база данных классов моделей, затем процесс моделирования
состоит в решении задач теории идентификации, т. е. в выборе на
основе результатов измерений подходящего элемента из данного класса
моделей, в предположении наиболее сильной неопровергнутой модели,
которая точно объясняет исходные данные. В этом подходе
ключевыми понятиями будут сложность модели и несогласованность между
моделью и измерениями. Иными словами, искомая оптимальная
модель является самой точной в пределах допустимого уровня сложности
или наименее сложной моделью, которая аппроксимирует наблюдае
мые данные с точностью до заданного допустимого несогласования.
180

Если предположить, что в основе аналогии между разными
моделями лежит симметрия динамических систем, то естественно ввести
понятие динамической системы как действие группы Ли на некотором
дифференцируемом многообразии, именуемом фазовым пространством.
Класс моделей строится на уровне качественного описания
динамической системы с п-ривлечением математической теории
инвариантов, поскольку методы инвариантного описания тесно связаны с
задачами классификации.
Под классификацией традиционно подразумевают следующие
проблемы: выделение «одинаковых» (в некотором смысле) моделей, т. е.
моделей, инвариантных относительно заданной группы G; разбиение
всей совокупности моделей на классы, т. е. построение базисов
инвариантов группы G и ее подгрупп; канонический способ представления
моделей (так называемая проблема канонических форм), т. е.
представление моделей в терминах инвариантов их групп симметрии.
Определение 10.1. Модели, построенные в терминах элементов
базиса инвариантов группы G, называются теоретико-групповыми.
В дальнейшем ограничимся рассмотрением только математических
моделей, построенных в терминах функциональных и
дифференциальных инвариантов.
Следует подчеркнуть, что отношение между вопросами
математического моделирования инвариантного описания и задачами
классификации есть частный случай актуальной проблемы о взаимосвязи
теории представлений групп и теории инвариантов с изучением
непрерывных семейств модулей объектов.
10.1. Алгебра инвариантности релятивистских
и нерелятивистских моделей
В гл. 7 и 8 рассмотрены вопросы, связанные с представлениями
группы Лоренца О (3.1). Лоренц-инвариантность означает равноправие
всех инерциальных систем отсчета и однородность пространства Мин-
ковского. Если потребовать еще инвариантность относительно
параллельных переносов во времени и пространстве, то придем к группе
Пуанкаре. Таким образом, группой Пуанкаре Ρ (3.1) называется
совокупность преобразований пространства Минковского, оставляющих
инвариантным интервал между любой парой точек этого пространства.
И наконец, представляет интерес группа всех преобразований
пространства Минковского (метрический тензор пространства при этих
преобразованиях умножается в каждой точке на число), которая локально
изоморфна группе конформных преобразований 0(4.2) [314—321J.
Запишем алгебру Ли группы 0(4.2) [322, 323]:
Шаь, Mcd) = gadMbc + gbcMa(i — eacMbd — gbdMac, (ЮЛ)
[Λίον, Λίσρ] - go0Mvo + gvoM0() — gtoMVp — £νρΜοσ, (10.2)
[Λίμν, Ρο] Ρ= gvoK ~ ё*оК [Яц, К] = 0, (10.3)
[ΑΛΐ] = -Ρμ, [Λίμν,Ο]=0, (10.4)
181

[*μ.Κν]«0, [Α*μ]=*μ.
(Ю.5)
[Λίμν, Κα] = gvoK» — ^μσ^ν, [/(μ, Ρ ν] = ~ 2 (Λίμν + £μν£>),
где подалгебра (ЮЛ) называется алгеброй Ли ортогональной группы
О (3); подалгебра (ЮЛ), (10.2) — алгеброй Ли группы О (ЗЛ);
подалгебра (10.1) — (10.3) — алгеброй Ли группы Ρ (3.1); подалгебра (10.1) —
(10.4) — алгеброй Ли группы P(3A)+)D\ подалгебра (10.1)—
(10.5) — алгеброй Ли группы 0(4.2).
В этом параграфе латинские строчные индексы пробегают
значения 1, 2,'ίί, прописные — 0, 1, 2, 3, 4, греческие строчные индексы
принимают значения 0, 1, 2, 3. В дальнейшем под повторяющимися
индексами подразумевается суммирование.
Изучение всевозможных унитарных представлений группы Gr
сводится к классификации ее НП, так как любое унитарное представление
этой группы можно разложить в прямую сумму (или интеграл) НП.
Например, для группы Пуанкаре Ρ (ЗЛ) из ее генераторов можно
составить два (и только два) независимых оператора Казимира (т. е. два
полинома от генераторов, коммутирующие со всеми генераторами)
ρ· —ρμρμ и w^w^w» (^λ = 4"ε^μΛίνΡ)»
кратных единичному оператору в пространстве, в котором
реализуется любое неприводимое унитарное представление группы Ρ (ЗЛ), и их
значения в этом пространстве используются для классификации НП
[313—322]. Основная невырожденная серия НП группы конформных
преобразований параметризуется одним дискретным и двумя
непрерывными действительными параметрами. Основная вырожденная серия
соответствует тому, что один из параметров принимает дискретные
значения вне действительной прямой [323—326].
Рассмотрим галилеево пространство — предельный случай
пространства Минковского, в котором изотропный конус вырождается в*
плоскость. Требование равноправия всех инерциальных систем отсчета
(принцип относительности Галилея) в сочетании с предположением об
однородности и изотропности галилеева пространства математически
описывается группой Галилея С (1.3) [327—329]. Группой
всевозможных преобразований галилеева пространства является группа Шре-
дингера [328—331].
Запишем алгебру Ли группы Шредингера [329, 331 ]\
[Mob, Mcd) = gadMbo + gbcMad — gaMbd — gbdMM\ (10.6)
[Mab, Pc] = gbcPa - gacPb, [Λρ К] = 0*, (10.7)
lh Mat] - [Pt, Pa] = 0; (10.8)
ШаЬ, 2g = gbc&a — gac&b* i&a> Ρ Λ = ~ К* /jg 9)
l*а, Рь] = gabA, [9Fh sk\ - [Ph Λ] = [Pa9 Λ] = [ЗГЬ Λ] = [Mat, Λ] - 0;
182

[ϋ> Ρή* - Pi9 [Я, »,] = »,, [Λ, Ρ,] = - 2Λ, (10 ,0)
[Я, Маь] = [0, Λ] - 0;
ι*,Α] = --0, [j/. pj —— srlf [j/, ^] = —2лг, 1011
[^, ^,] = [j/, Ma*] = [jrf, Λ] = 0,
где подалгебра (10.6) называется алгеброй Ли ортогональной группы
0(3), подалгебра (10.6), (10.7) — алгеброй Ли группы Евклида Ε (3),
подалгебра (10.6) — (10.8) — алгеброй Ли группы Аристотеля А (1.3),
подалгебра (10.6) — (10.9) — алгеброй Ли группы Галилея G (1.3) при
Λ = 0 и алгеброй Ли расширенной группы Галилея G (1.3) при Λ Φ
Φ 0, подалгебра (10.6) — (10.10) — алгеброй Ли группы G (1.3) +) D
при Λ = 0 и алгеброй Ли расширенной группы С (l .3) +) D при Λ Φ
Φ 0, алгебра (10.6) — (10.11) — алгеброй Ли группы Шредингера
Sch (1.3) при Л = 0 и алгеброй Ли расширенной группы Шредингера
Sch(l.3) при Λ Φ 0. Индекс ί обозначает абсолютное время.
Унитарные неприводимые представления группы Галилея
найдены в работах [332—334], группы Шредингера — в работах [329, 3311.
Определение 10.2. Математические модели, обладающие свойством
сохранять свой вид при преобразованиях группы Пуанкаре (группы
Галилея), будем называть релятивистскими (нерелятивистскими).
В работе [335] найдена группа О (5.2) как максимальная группа
симметрии, допускаемая уравнением Гамильтона — Якоби. Ее алгебра
Ли имеет вид
[Man, MBr\ = gARMNB + gNuMAR — gABMNR — gNftMAB,
Λ /4 /S
[MAN> PB] = gNBPA — gABPN,
[Pa, Pn\ = [KA, Kn] = [Ma*, D] = 0, J2)
ID, Pa] =—Pa, [D,Ka\=Ka,
[MAN, Kb] = gNBKA — gABKN, [KA, PN]= — 2 (MAN + gAND),
goo = — git = — £44 =* 1» Mab = — Mba*
Сопоставим с генераторами группы 0(5.2) Р4, Мц9 Λί40, /С4 соот-
ветственно генераторы группы Sch(l.3): Pt, Эи Я, si по формулам
А = % (А + Ь0Х»), Э% - а, (Ми + ЬгХ\)9 ,0 13)
® = а*(М*о + Ь2Х% J* = as(K* + bzX*).
Подставив (10.13) в соотношения (10.6) — (10.11) с учетом (10.12),
получим систему алгебраических уравнений для αν, 6μ, Χσ. Решая эту
систему, имеем
η _ 1 - 1 _ 1 - 1
0"" W' αι pf · а* ' а* ТрТ'
183

Таблица 10.1
Pt
Л
&l
m
4
К
0
0
1 -
у~й l
*—Л
-VWt
1
V~23
Mi0 j
1 ρ·
~К2Г'
- ' P. 1
K"5 '
-ρ=-[β|/(0-β) +
-2(|Г§Д|/0 + у/)
I ' /г
2^2Л/
Ко
^"2®
j/1> (2D — а>)
L-K
V2 Л<
2|^2J
0
К/
2 (/"2М/0+ :?,·)
— 2S>,
ЧцЛ
*/
0
D
Ρ/
Λ
0
0
-Л
(10.14)
Таким образом, из (10.13) следует
Положив (10.14) в (10.12), представим коммутационные
соотношения генераторов подгруппы 0(4.2) и подгруппы Sch (1.3) в виде
табл. 10.1.
Таким образом, коммутационные соотношения табл. 10.1 вместе
с соотношениями (10.1) — (10.5) и (10.6) — (10.11) образуют алгебру
Ли группы О (5.2).
10.2. Дифференциальные инварианты
Помимо попыток отыскать все неприводимые унитарные
представления групп О (5.2), Sch (1.3), О (4.2), Sch (1.3) и их подгрупп, можем
задаться вопросом: каков наиболее общий тип дифференциальных
уравнений, допускающих эти группы в качестве групп симметрии?
Эта задача решается посредством дифференциальных инвариантов
упомянутых выше групп, с их помощью конструируются и
классифицируются уравнения, допускающие группы 0(5.2), Sch (1.3), О (4.2),
Sch (1.3) или их подгруппы.
Ниже приводятся основные определения и положения,
необходимые для решения такого рода задач.
184

Рассмотрим базисные инфинитезимальные операторы
/--параметрической группы Gr в пространстве Rn (χ1, ..., χ") χ Ym (и1, ..., ит):
дх · '«ν *~· ~' аИ '
χ~(χ\ ..., A ы = (и\ ..., am)f (10.15)
ν = 1, ... , η я, b, ι, /, / = 1, ... , η\ Л, β, L, Ν = 1, ... , т.
Находим s-e продолжение инфинитезимальных операторов группы
G, согласно формулам продолжения векторного поля (ξ*, ην) [336—
3411
ΥΑ д , УА __
xv = xv + ivb —χ + ζν*ί -—τ + · · · ι (ίο.ΐ6>
где
Ui =——г- , Uij —
ξ^ » Z>t (ηί) — itf Ζ>, (ξί);
дх1 диг диу диуа
Порядок продолжения s выбираем из условия [336]
rang [ξι, ηί,ζί,,ζί/ι, ...] = r. (10.17)
Определение 10.3. Функция η независимых и т зависимых
переменных, а также производных от и1, ..., ит по х1, х2, ..., хппорядка не вы-
те s, равная той же функции от х\ х2 ..., хп, и'1, ..., ит, и тех же
производных и4,..., ит по х\ х2у ..., х>п для всех преобразований
продолжения порядка s называется дифференциальным инвариантом
порядка s данной группы Gr.
Теорема 10.1. Для того чтобы функция F (х1, х2, ..., хп\ и1, ..., ит\
и1, ..., ит\ ...; и1,..., ит) была дифференциальным инвариантом порядка
\ \ S S
s группы Gr, необходимо и достаточно, чтобы
XvF = 0, (10.18)
где Xv — s-e продолжение инфинитезимальных операторов алгеб-
S
ры Ли группы Gr,
ux—\dxi ' дх* ' " ' дхп j' * * * ' &+, dxM '
Ι κ I = κι + · · · + κ* < s + 1; κ = (хг, ... , κ„) — мультииндексы.
Доказательство этой теоремы приведено в работе [342].
Определение 10.4. Операторы λ1 (я, и, и, ..., u)Dlt..., λη (χ, и, u,...
1 s 1
..., и) Dn называются операторами инвариантного дифференцирования
185.

группы Gr, если для любого дифференциального инварианта F
группы Gr отображения kkDkF (k = 1, ..., η) также являются
дифференциальными инвариантами этой группы.
Коэффициенты λ = (λ1, ..., λη) определяются из следующей
системы уравнений [336]:
Χνλ'= λ'ϋ,ξί. (10.19)
Сформулируем еще несколько утверждений, доказательства которых
приведены в работах [336—342].
Теорема 10.2. Для любой группы Gr преобразований пространства
Ζ = R (x1, ...,хп) X Ym {и1, ..., ит) существуют η = dim R
операторов инвариантного дифференцирования, линейно независимых над
полем инвариантов этой группы.
Теорема 10.3. Для любой группы Gr существует конечный базис
дифференциальных инвариантов порядка s, где число s определяется из
соотношения (10.17), т. е. такой конечный набор скалярных
дифференциальных инвариантов, что любой дифференциальный инвариант этой
группы получается из инвариантов базиса с помощью конечного числа
функциональных операций и операций инвариантного
дифференцирования.
Теорема 10.4. Базис дифференциальных инвариантов группы Gr
однозначно определяет эту группу.
Теорема 10.5. Пусть Gr — локальная группа преобразований,
действующая на Ζ = Rn X Ym. Совокупность Σ1 (jc, и, u, ..., u), ..., ΣΓ (χ,
I s
и, и, ..., и) образует базис дифференциальных инвариантов s-го поряд-
ι $
ка группы Gr. Тогда любое дифференциальное уравнение, допускающее
группу Gr в качестве своей группы симметрии, можно представить в
эквивалентном виде, содержащем только дифференциальные
инварианты группы Gr.
В работах [329,343—346] построены инварианты и базисы
дифференциальных инвариантов групп С (1.3) (G(1.3)),G~(1.3) +)D (0(1.3) +)D),
Sch (1.3) (Sch (1.3)) и их подгрупп. (Базисы дифференциальных
инвариантов группы Пуанкаре см. в [347].) В работе [348] найдены базисы
дифференциальных инвариантов группы О (5.2) (включающей О (4.2)
и Sch (1.3)) и ее подгрупп, из которых конструируются
релятивистские и нерелятивистские теоретико-групповые модели.

Глава 11
АНАЛИЗ СОВМЕСТНОСТИ
ТЕОРЕТИКО-ГРУППОВЫХ МОДЕЛЕЙ
Теоретико-групповые модели, рассмотренные в гл. 10, представлены
системами дифференциальных уравнений в частных производных.
Первая проблема, которая возникает еще до решения таких систем,
состоит в том, чтобы узнать априори, существует ли их решение.
Одной из характерных черт исследования этого вопроса является
проведение большого объема аналитических выкладок. При этом анализ
совместности системы дифференциальных уравнений сводная к
последовательному выполнению алгебраических операций с помощью
символьной обработки на ЭВМ. Это позволяет значительно уменьшить
затраты в аналитическом исследовании систем дифференциальных
уравнений [349—353].
Теория совместности систем дифференциальных уравнений с
частными производными отвечает на вопрос: имеет ли заданная система
дифференциальных уравнений решение, и каков его произвол. Под
произволом решения подразумевается произвол в выборе начальных
данных в общей задаче Коши.
Задача исследования на совместность систем дифференциальных
уравнений ставится в различных методах построения математических
моделей и их точных решений: метод дифференциальных связей,
построение инвариантных и частично инвариантных решений
относительно групп Ли и Ли — Беклунда и т. д.
Эта задача ставится следующим образом. Пусть дана система
дифференциальных уравнений с частными производными
5, (х, и, д]%/дха) = 0 (i = 1, 2, ... , ρ),
χ = (#ь x2i . . . , χη)9 и = (иъ и%<> · · · » ur)>
где α = (alt α2, ..., αη) — мультииндекс, | α | = at + α2 + ...+ αη <
^ m.
Принято говорить, что система (11.1) недоопределена, если г > р%
переопределена, если ρ > г, и определена, если ρ = г. Решением
системы (11.1) называется такой набор функций щ (х) (i — 1, 2, ..., г),
который обращает ее в тождество. При этом предполагается, что у
решения существуют все Необходимые производные. В дальнейшем
также будем требовать необходимую гладкость рассматриваемых функций.
187

В общем случае система дифференциальных уравнений с частными
производными имеет бесконечное множество решений. Идеальным
является единое аналитическое представление всех решений данной
системы (нахождение общего интеграла), например представление
д'Аламбера для волнового уравнения. Однако такое представление
возможно только для узкого круга систем. Для многих же систем
дифференциальных уравнений, возникающих в механике и физике, нет
единого и эффективного способа построения общего интеграла,
Характерной чертой применяемых методов построения общих
решений частного вида систем дифференциальных уравнений является
прежде всего представление общего решения через частные.
Отдельные решения и классы решений можно выделять различными
способами. В методе дифференциальных связей выделение частных решений
системы дифференциальных уравнений (11.1) осуществляется путем
присоединения к ней дополнительных дифференциальных
соотношений [354]
Ф* (*, и, $%/дха) = О (ί =» 1, 2, ... , q). (11.2)
Полученная таким образом переопределенная система (11.1), (11.2)
в общем случае нуждается в исследовании на совместность. При этом
наличие того или иного произвола в общем решении задачи Коши
системы (11.1), (11.2), который также определяется из теории
совместности, позволяет разбивать множества всех решений системы (11.1)
на классы. При групповом анализе [355] нахождение решения
системы (ИЛ) также сводится к интегрированию переопределенной
системы (11.1), (11.2) с определенного вида системой (И.2) [356].
Если рассматривать пространство /?*, в котором координатами
являются величины х,ии все производные от и по χ до порядка т
включительно, то в нем уравнения (11.1) представляют собой конечные
функциональные соотношения* Будем говорить, что система (11.1)
алгебраически зависима, если какое-либо уравнение в (11.1) обращается в
тождество вследствие других уравнений системы (11.1), т. е. в результате,
исключения переменных указанного пространства Rk из этого
уравнения с помощью других уравнений без применения операции
дифференцирования. Такое уравнение назовем алгебраическим следствием
других уравнений. Если у системы уравнений есть алгебраическое
следствие, не содержащее неизвестные функции и (х) и их
производные, то такая система называется противоречивой или несовместной,
поскольку она не имеет решения. Соотношения, которые получаются
дифференцированием системы уравнений (11.1) по переменным χ с
учетом зависимости переменных и от х, называются дифференциальными
следствиями. Совокупность системы (11.1) и всех ее дифференциальных
следствий после однократного дифференцирования назовем
продолженной системой. Пусть система разрешима относительно части
старших производных (их называют главными, все остальные
производные — параметрическими). Если продолженная система в качестве
алгебраического следствия имеет уравнение, из которого одна из
параметрических производных исходной системы (11.1) выражается через
другие ее параметрические производные, то такое следствие (его назыж
1ЯЯ

вают новым уравнением) необходимо присоединить к системе (11.1)
и учитывать при исследовании ее свойств и при построении любого
ее решения.
Продолжение продолженной системы называется вторым
продолжением и т. д. В общем случае новые уравнения, а также
противоречивые соотношения могут появиться и при последующих
продолжениях. В системе в инволюции при последующих продолжениях не
появляются ни новые уравнения, ни противоречивые соотношения [357, 358].
Согласно теореме Картана из теории совместности [357, 358]
можно утверждать, что после конечного числа продолжений любую
систему дифференциальных уравнений можно привести в инволюцию или
прийти к противоречию. Наряду с ответом на вопрос о совместности
системы дифференциальных уравнений в этой теореме указывается и
произвол в постановке условий задачи Коши для системы в
инволюции. Он называется произволом общего решения и зависит от
характеров Картана, которые определенным образом связаны со старшими
параметрическими производными.
В настоящее время имеются два алгоритма анализа на совместность
систем дифференциальных уравнений. Один из них является
алгоритмом Картана, подробное описание которого можно найти в [358]. Этот
подход основан на использовании исчисления внешних форм. Картан
указал на некоторые формальные алгебраические свойства систем
внешних форм: для их описания он ввел специальные целочисленные
величины, называемые характерами, которые упорядочены с помощью
системы неравенств. Когда эти характеры удовлетворяют
определенным соотношениям, система называется инволютивной. Однако
применение этого подхода связано со значительными трудностями.
Другой подход берет начало от работ Рикье [359]. Методы Рикье,
примененные Жане [360] к системам дифференциальных уравнений в
частных производных, имеют совершенно иной характер. Современное
изложение этого метода наиболее полно можно найти в работах Ку-
раниши [361] и Поммаре [362].
Кураниши [361] использовал классические методы, а также
совместил исследования Жане по условиям интегрируемости и работы
Картана, касающиеся инволютивности. Изложение основ теории
совместности или формальной интегрируемости общих систем нелинейных
дифференциальных уравнений в частных производных можно найти
в работе [362].
Далее алгоритм Рикье — Жане — Кураниши назовем RJK-алго-
ритмом.
При анализе на совместность конкретных систем
дифференциальных уравнений, как было отмечено, необходим большой объем
аналитических выкладок, связанных: с продолжением системы
дифференциальных уравнений, подстановкой сложных выражений, переходом
на многообразие, нахождением рангов матриц. Трудоемкость
выполнения этих операций вызывает необходимость применения для этой
цели ЭВМ.
Появление языков типа ЛИСП [352], РЕФАЛ [353] и других
способствовало развитию области автоматизации аналитических выкла-
189

док на ЭВМ. С повышением уровня компьютеризации, с появлением
ЭВМ для персонального использования применение вычислительных
машин для аналитических преобразований становится все более и
более важным аппаратом в эффективном решении задач в различных
областях математики и физики [363—369].
К настоящему времени существует много различных систем
аналитических вычислений на ЭВМ как отечественных, так и зарубежных.
Краткий обзор по ним можно найти, например, в [370, 371].
Цель данной главы — представить /?.//(-алгоритм и
соответствующую RED U СЕ-программу исследования на совместность систем
дифференциальных уравнений первого порядка с произвольным числом
зависимых и независимых переменных.
11.1. Математическое описание метода исследования
на совместность
В этом параграфе излагается алгоритм исследования на совместность
систем дифференциальных уравнений в частных производных,
основополагающая формулировка которого дана в работах Рикье [359],
Жане [376], Томаса [379], Ритта [377]. Дальнейшее обоснование и
современное изложение алгоритма на языке расслоенных многообразий
получили в работах Спенсера [378], Гольдсмидта [375], Кураниши
[361] и Поммаре [362]. Среди работ советских авторов отметим
работы В. П. Паламодова [372], С. Н. Самборского [373], Б. Д. Чеботарев-
ского [374].
Здесь будем придерживаться конкретных объектов, по
возможности обходясь минимальными средствами для того, чтобы показать, к
каким вычислениям сводится вопрос о совместности системы
уравнений в частных производных. Подход, используемый при этом, изложен
в работах [349, 354, 361, 362].
Напомним^ что здесь используется локальный подход. Под
открытой областью подразумевается малая окрестность рассматриваемой-
точки. Все многообразия и функции предполагаются необходимое
число раз непрерывно дифференцируемыми.
Пусть Ε — многообразие размерности η + г, N — многообразие
размерности η, ρ — отображение Ε на Ν, ρ : Ε -> Ν, имеющее в
каждой точке w ζ Ε ранг п. И пусть U — открытая область в £, V —
открытая область в Ν, в которых введены системы координат (х9 и) и (х)
соответственно.
Определение 11.1. Тройка (Е> Ν, р) называется расслоенным
многообразием, если диаграмма
коммутативна.
190

Здесь р (U) = V, π обозначает каноническую проекцию пространства
Rn X Rr на /Л
Определение 11.2. Отображение f : V -> Ε называется локальным
сечением расслоения (£, Ν, р), если композиция р/ есть тождественное
отображение в V. Множество V называется областью сечения.
Во введенных системах координат сечение / задается с помощью г
функций / (х) = (х, f1 (x), f2 (χ), ..., f (χ)). Обозначим
№ ( da' \ / да»
дх« \ дх? J \ дх
λ Л λ №? a 1 О
PO = / , Pa = Л ' , λ = 1, A . . . , Г.
Возьмем два сечения fug, чьи области содержат точку х0, и пусть
т — целое число (т ;> 0).
Определение 11.3. Дш локальных сечения f и g— т эквивалентны в
х0, если для любой системы координат (х, и): U -> Rn X Rm такой,
что xQ(zP (U), и для любой частной производной —-— порядка a (| a | ^
дх
^ т) в точке х0 выполнены равенства
^f'^-^TSHxo), λ= 1, 2, ..., г. (11.3)
Условие (11.3) есть отношение эквивалентности, которое
разбивает множество всех сечений на эквивалентные классы. Если / —
сечение, область которого содержит jc0, то класс эквивалентности,
содержащий /, называется /л-джетом в точке х0 и обозначается через /™0 (/)♦
Для т = —1 положим по определению /?0 (/) = х0. Множество всех
/л-джетов в точке х0 обозначаем через Jm (Е)х., а Jm (Ε) = [) Jm (E)x*
Любой элемент в Jm (Ε) будет определяться координатами х, и, р. Для
краткости Jm (Ε) обозначим просто Jm, а У0 и У""1 будут обозначать
Ε и N соответственно.
Если через pf, т !> k !>—1, обозначить отображение из Jm на
/\ действующее по формуле р™ (/™ (/)) = /* (/j, то каждая из троек (Jm>
J у Р/Г) будет расслоенным многообразием.
Для дифференцируемого многообразия Ε обозначим через TWE
касательное в точке wkE пространство (w ζ E)t через Τ (Ε) — множество
всех касательных векторов во всех точках Ε (Τ (Ε) = U TJE). На
Τ (Ε) также можно ввести систему координат и определить структуру
многообразия. Тройка Τ (£), Ε и проекция φ : Τ (Ε) -> £, которая
каждому касательному вектору ставит в соответствие w, есть
векторное расслоение над £, называемое касательным векторным
расслоением над £. Обозначим через Тх пространство, двойственное к ΤΧΝ, а
через Т* — кокасательное векторное расслоение над /V.
191

Пусть Х0 — точка в /", Τ (Jm) — касательное расслоение над Jm.
В дальнейшем пишем ТХо (Jk) для k^m вместо 7>0 (Jk), где Y0 =
= Pk (Хо).
Через Qx0 (Jm) обозначим ядро отображения фт-ι * ΤΧο (Ут) -*
-> Γχ0 (Ут_1). Согласно этому Qv (Ут) порождается элементами (—г)
<| а I = /п) при m > 1, |—г-) при /л = 0.
\ dir /х6
Определение 11.4. Отображение
<"Qxo(Jm)-»Qxo(Jm~l)®TmXo (1<т) (11.4)
называется функциональным отождествлением.
В координатах (х, и, р) это отображение выглядит так: элемент
принадлежащий Qxe (/"), отождествляется с
где α' в α,ΐ связано с α по формулам ak = α* при k Φ iy и при & = ί
имеем at- = af — 1, тогда если о^ > 1, то α,ί = at·. При этом /—j-\ и
\ "α /Χβ
(d*i)*0 — базисы соответственно в Qxt (Jm) и Τχ0, связанные с данной
системой координат.
Здесь можно дать следующее определение системы
дифференциальных уравнений (S) [349, 354, 3621.
Определение 11.5. Системой дифференциальных уравнений (S)
порядка т на расслоении (£, Ν, р) называется подмногообразие S в Jm (E)
такое, что (5, Ν, pl\) есть расслоенное многообразие. Решением
системы (S) называется локальное сечение f \ V -+ Ε такое, что j™ (J) ζ. S
для всех χ £ V.
Расслоение /μ (S) вложим в Ут+Д (Е).
Определение 11.6. Продолжением μ-го порядка системы (S)
называется подмножество Ρμ (S) = J* (S) f) Ζ"*"*"*1 (£)·
Пусть (S) в некоторой системе координат (х, и, р) задается
системой соотношений (S) 5μ (χ, иу ρ) = 0, μ = 1, 2, ..., s. Подмножество
Ρ (S) будет определяться уравнениями (5) и уравнениями
DtS1(х9 и, р) = 0, i — 1, 2 η; /" = 1, 2, ... , s. (11.5)
Здесь Dt —оператор полного дифференцирования по переменной xt\
где α ι
192
* 1α|=0 σ^α
= (ab α2, *.., af -f 1, ...а αη).

Матрицу/—~), | а | = т, назовем матрицей системы (11.5). Она
является основной матрицей, если систему (11.5) рассматривать как
бистему линейных алгебраических уравнений относительно
производных ра, | α | = т + 1, в точке Х0.
Пусть элемент Х0£ (5), где (5) — система порядка т. Обозначим
через СХо (S) подпространство Всех ξ £ QXo (Jm~~{) ® Tl0 таких, что
частная производная по направлению ξ в Х0 от любой функции 5μ (*,
и, ρ) (μ = I, 2, ..., s) равна нулю. Из сказанного следует, что в
системе координат (х, и, р) элемент
5= Σ Μ-ττ) еЯхлП (П.6)
принадлежит Сх0 (S) в том, и только в том, случае, если
Σ ξα^¥^=0, μ-1, 2, ...,s. (11.7)
|a|=m °Pa
Прежде чем дать определение системы в инволюции в терминах
расслоенных пространств, введем понятие инволютивных
подпространств. Пусть W и Τ — конечномерные векторные пространства, Г* —
пространство, двойственное к Г, Sm (Г*) — подпространство
симметричных тензоров в ® Г* = 7*(g)... ® Т* —тензорном произведении
m
m пространств Г*, А — подпространство W ® Т*.
Определение 11.7. Продолжением подпространства А называется
подпространство
ρ (А) = (Л ® Г*) П (ИГ ® 52(Г*)). (П.8)
Пусть /\ ..., /" — базис в Г*. Положим
Ак = А () (W ® Гп-к), Tk = dimAk9 0<Λ</ι—1, (11.9)
где T*n-k обозначено подпространство 7*, порожденное векторами
АН /*
Можно показать [361], что для любого базиса Р, ..., tn
dimP(i4)<2xlf τί+ι<τ,, i = 0, 1, 2, ...,л — 1. (11.10)
ι—Ο
Определение 11.8. Если существует базис t1, ..., f в 7* такой, что
сНтР(Л) = т0 + т1+ ... +τ„_ι, (11.11)
то А называется инволютшным подпространством тензорного
произведения W ® Г*, а упорядоченный базис t1, t2t ..., tne Т* — квазире~
гулярным базисом для инволютивного подпространства А.
Определение 11.9. Упорядоченная система t\ ..., f линейно
независимых элементов Т* называется слабоквазирегулярной системой для
А, если dim ((W ® T*„k) ft A) - min dim ((№ ® 7*«Λ) П Л), где
7Х_Л — подпространство Т*л порожденное векторами ί**1, ..., /·; лш-
13 1-1980 193

нимум берется по всем (п — к)-мерным подпространствам Tn-.k
пространства Г*, k = i — 1, i, ..., η — 1.
Для приложений может быть полезным следующее утверждение
[380, 381].
Утверждение 11.1. Пусть А— инволютивное подпространство
W ® Т* и /\ ..., С ζΤ* —слабоквазирегулярная система для А. Тогда
эту систему можно расширить до квазирегулярного базиса для А.
Определение 11.10. Система дифференциальных уравнений порядка
т находится в инволюции в точке Χ0ζ (5), если выполнены следующие
условия: существует окрестность G a Jm точки Х0 такая, что (Р (S) f|
Π (Pm4"1)"""1 (G),(S) Π G, pm+1) есть расслоенное многообразие; Сх0(5) —
инволютивное подпространство в Qx0 (Jm~l) ® Τχ0.
Для системы в инволюции (5) аналитичность многообразия S обео
печивает существование аналитического решения независимо от
применяемого алгоритма анализа на совместность. Но аналитичность S
не является необходимым условием существования решения системы
в инволюции (5).
Покажем, к каким операциям сводится проверка каждого условия.
Первое условие, во-первых, требует, чтобы Ρ (S) было
подмногообразием на Jm+X в окрестности G точки Х0. Во-вторых, на этом
подмногообразии часть переменных (главных) можно выразить
функционально через остальные переменные (параметрические). При этом
параметрические переменные, которые были на подмногообразии 5, должны
оставаться параметрическими и на подмногообразии Ρ (S). Это
означает, что следствием 0|5μ (χ, и, ρ) = 0 (i = 1, 2, ...> п\ μ = 1, 2, ..., s)
не должно быть соотношение φ (χ, иу ρ) = 0, которое не содержит
старших производных порядка т + 1 и не зависит от системы
уравнений 5μ (χ, и, ρ) = 0. Последнее проверяется в общем случае
подсчетом рангов соответствующих якобианов с учетом всех соотношений,
определяющих Ρ (S).
Для проверки второго условия пользуемся формулами (11.8) —
(П. 11) и соответствующими определениями. В них вместо А берем
подпространство Сх0 (5), вместо W — Qx0 (Jm~~l), вместо Г* — Τχ0. При
выбранном базисе (dxi)Xo в ТХо (связанном с системой координат (х) на
N) в качестве T£_* берем подпространства, порожденные векторами
(dxk+i)x9, (d**+2)*.. ···> (dxn)x. и
Ak = СХо (S) П Qx0 (Г"1) ® ТО*-*.
В последнем тензорном произведении отсутствуют компоненты
Ι-ΛΑ ®(dXt)Xo (ί = 1, 2, ...,&, |a|=m-l),
так что Ak в Сх0 (S) кроме соотношений (11.7) определяют
дополнительные соотношения
ξλ=:0, λ- 1,2 η £= 1, 2 Л; ja| = m—1. (11.12)
194

Так как
л\гг,п ит\ г(п+т—\\ _(п + т—\)\
a\mQxt(J)=r\^ m j=r (п_|)!от, ,
то из (11.12) имеем
<roSdimCX,(S)= r^+^-1\_rank^V |<x|=m, (11.13)
где —г-1 —матрица системы (11.7), линейной относительно ξα,
\ дЪ Mo
| ос | = т. Величины τΛ вычисляются как разности dim Qx0(Jm) и
ранга матрицы системы (11.7), (11.12).
Размерность Ρ (Сх9 (5)) подсчитывается просто [361], если знать,
что С~ (Р (5)) = Ρ (СХо (5)), где Х0 — слой над Х0 в Ρ (S), т. е. Х0 ζ
ζ Ρ (S) и р£+1 (Х0) = Х0. Отсюда
dimP(cxjs)) = r(^+7)-rank(li^:1)· 1«Ь« + ».
и в терминах алгоритма Картана [358] она равна числу всех
произвольных элементов на наиболее общем л-мерном интегральном много-
образии. Число Картана Q =^^, и условие (11.11)
dim Ρ (CX.(S))=Q (H.14)
— не что иное, как критерий Картана. Характеры Картана подсчи-
тываются по формулам σί+ι = τ* — ъ+\, τη = О» i = О, 1, ..., η — 1.
Если (11.14) выполнено, то второе условие инволютивности системы
(5) также выполнено. Если в данном базисе (dxt)Xo (в системе координат
dim Я (С*Л5))< 24, (11.15)
то нужно найти такой базис (dXi)X(i (такую систему координат (*)), в
п—1
котором Q = 2 τί минимальна из всех возможных. Если в последней
выполнено (11.14), то второе условие выполнено для (S); если
выполнено (11.15), то система (S) не в инволюции. В последнем случае при
выяснении совместности системы ее надо продолжить и все повторить
для Ρ (S) и т. д. При дальнейших продолжениях через конечное
число шагов получится либо противоречие, либо система в инволюции
[358, 361, 362].
Несомненным достоинством сформулированного алгоритма
анализа на совместность систем уравнений в частных производных
является то, что здесь нет необходимости переходить к внешним
дифференциальным формам, а также делать внешнее дифференцирование и в
общем случае выкладки в отличие от анализа по Картану могут быть
короче.
13* 195

По данному алгоритму можно рлпать и обратную задачу теории
совместности, когда вид функций 5; (х, и, /?), / = 1, 2, ..., s, частично
или полностью не определен. Ее формулировка такова: каким
должен быть вид функций S1 (а:, и, /?), / = 1, 2, ..., s, чтобы система (11.3)
имела заданный произвол в решении.
Пусть вид уравнений в системе (5) полностью или частично не
определен за счет того, что в выражения 5μ (χ, и, ρ) входят
неопределенные (параметрические) функции ψ* (χ, и, /?), k = 1, 2, ..., /.
Формально можно выделить три типа обратных задач.
К первому отнесем случай, когда для системы (S) выполнено первое
условие инволютивности, но не выполнено второе условие. Равенства
(11.14) можно добиться за счет увеличения dim Ρ (С*,. (5)), что, в свою
рчередь, достигается уменьшением ранга матрицы системы (11.5). Для
этого нужно положить равными нулю все определители
соответствующего порядка, составленные из элементов этой матрицы.
Ко второму типу отнесем случай, когда для системы (S)
выполнено второе условие, но не выполнено первое условие инволютивности.
Необходимо потребовать равенство рангов основной и расширенной
матриц системы (11.5), для чего следует приравнять нулю
соответствующие определители, составленные из элементов расширенной
матрицы системы (11.5).
В третьем случае не выполнены ни первое, ни второе условия
инволютивности. Достигается выполнение этих условий за счет
приравнивания нулю соответствующих определителей, составленных из
элементов расширенной матрицы системы (11.5).
11.2. Краткое описание алгоритма вычислений
Рассмотрим алгоритм исследования на совместность. Пусть дана
система уравнений в частных производных
(S): S,(x, и, /7)=0, / = 1, 2, ,.., s, (11.16)
с г неизвестными функциями и = (и1э ..., и,) от η независимых
переменных χ = (хъ ..., хп), где ρ обозначает производные ра и а =
== (аь ..., ап), | а | = 1, ..., т. Присоединим к системе уравнения
DiS,^, и, р) = 09 ί=»1,2 я, / = 1, 2, ... , s, (11.17)
где Di — оператор полного дифференцирования по переменной,
Di = -gj- + 2 Pat -£г ■ α·< = (αι> ... , α* + 1, .. . , αη).
* |α|=0 °Ρα
Объединенную систему (11.16), (11.17) назовем продолженной и
обозначим Ρ (S). Рассмотрим векторное пространство Ε с координатами
ξα в количестве, равном числу всех производных | α | = /п. В нем
подпространство Е0 определим соотношениями
£о: Σ £*»/<*;?» »>, о, /-1,2, ...... λ = 1, 2, ...,,
(11.18)
196

где 2 обозначает суммирование по всем последовательностям из це-
лых положительных чисел с | α | = т.
Подпространства Ek определим соотношениями
_, ,α дФ,- (χο> "о» Ро)
Л1а—ъ ' (1119)
Ιξα = 0, |α| = m, аг= a2 = ··· = afe^0, k= 1, .. . , η— 1,
так что £„-.1 с= £п_2с ... cz E0cz Ε. Обозначим буквой Ak матрицу
системы (11.19) Ak = dOyd/?£, /= 1, Д ...,δ;λ= 1, 2, ..., г, | α | = т.
Пусть точка (х, и, р) такая, что ранг матрицы А в малой окрестности
не изменяется. Для того чтобы выяснить, находится ли система (5) в
инволюции, необходимо проверить два условия. Сначала
проверяется, есть ли у системы Ρ (S) в качестве следствия соотношения вида
ψ(χ, и, р)=0, (11.20)
которые не содержат производных /?α, | α | = т + 1, λ = 1, ..., г, и
не зависят от системы (S). Для этого надо подсчитать ранг матрицы
P{A)^d{DiQ>j (χ, и, p))/dpl i = 1, 2 я;|оь| = т, λ = 1,2,..., г,
и ранг расширенной матрицы системы (11.17). Подсчет ведется в
точке (х0, и0, р0) на многообразии, определяемом всеми соотношениями
(11.16) в пространстве (*, и, р). Если эти ранги не равны
тождественно, то возникает новое соотношение (11.20) из требования их
равенства. Такие соотношения назовем новыми уравнениями. Их надо
присоединить к системе и снова начать анализ, взяв в качестве
исходной систему (11.16), (11.20).
Если ранги матрицы Ρ (А) и расширенной матрицы системы (11.17)
равны, то проверяется второе условие инволютивности. Для этого
подсчитываем число т0 = d m £ — rank Л0, %k = dim Ε — rank Aky k =
==: 1, 2| ..., /ι — 1. Пусть Ρ (Ε) — векторное пространство с
координатами в количестве, равном числу всех производных /?«, | α | = m + 1,
. = 1, 2, ..., г. Подсчитаем число
%=dimP(S)-vank { г ' \ Р>> , |α| = т + 1, λ = 1, ... , г,
дРа
/= 1, ... , я; /= 1, ... , s.
Если
£=2τ'· <и-21>
n-1
то система (5) находится в инволюции. Если τ<^ τ* при любом вы-
ι=0
боре системы координат в пространстве независимых переменных χ· =
= (хъ ..., хп), то систему (S) надо продолжить. В качестве исходной
на следующем шаге алгоритма берется система Ρ (S). Через конечное
число шагов продолженная система будет в инволюции либо
получится противоречивое соотношение вида ψ (χ) — 0. Во втором случае
система будет несовместна, т. е. противоречива.
197

Если система (S) в инволюции, то характеры подсчитываются по
формулам σ/+ι=τ|—Τί-μ, t = 0, 1, ..., η — 1 (xj^Tj+it τη = 0) и
решение системы (S) зависит от ση-функций от η аргументов, аЛ_1-функ-
ций от η— 1 аргументов, ..., агфункций от одного аргумента.
С точки зрения символьных вычислений на ЭВМ алгоритм сводится
к следующим операциям: дифференцирование сложных функций,
подстановки, приведение подобных, различные группировки отдельных
членов выражений, подсчет рангов матриц, решение систем линейных
алгебраических уравнений с прямоугольными матрицами и пр. [382].
11.3. Описание REDUCE -программы
В процессе реализации описанного выше алгоритма на ЭВМ создана
RED UС'/^-программа с подпрограммами верхнего и нижнего уровней.
Подпрограммы верхнего уровня выполнены в системе REDUCE [251]
в алгебраической моде, а подпрограммы нижнего уровня — в
символьной моде ЛИСП [252]. Перечислим подпрограммы верхнего уровня по
их назначению: алгебра рациональных функций от многих переменных
(сложение, вычитание, умножение, подстановка, приведение
подобных, дифференцирование); формирование различных матриц; подсчет
рангов матриц методом Гаусса.
Среди программ нижнего уровня можно назвать следующие:
подпрограммы различных перекодировок из одного представления в
другое; различные подпрограммы обработки символьных выражений
(например, построение выражения Ρ (3, 0, 1, 1) из символов 3,2,2);
дифференцирование сложных функций.
RED(/Сопрограмма состоит из файлов RJK и RJKE. Первый
файл содержит основные программы, во втором находятся входные
данные.
Переменные и их значения видны из табл. 10.2. Их имена не
должны использоваться для обозначения других математических объектов.
Рассмотрим работу программы на примере исследования
совместности системы, описывающей двойную волну в изоэнтропийном
течении политропного газа [354, 381]
ди. 2 dU. fit)
~3ί7~ ~д*Г ~ Φί = dxt ·
С идентификаторами хг = χ (1), х2 = χ (2), t = χ (3), иг = u(l), u2 =
= w(2), θ = tet (w(l), «(2)), в соответствии с обозначениями,
приведенными выше, уравнения (11.22) на REDUCE запишутся следующим
образом:
for i i= 1 j 2 do
deq(i)i=df(u(i)f x(3)) +
198

Таблица 10.2
Текст
Программа
Значение
N
Μ
S
οι
Xi
Uk
S/
duk
dxi
P(k9 0,
1
N
Μ
NDEQ
SIGMA(i)
x(i)
u(k)
DEQ(j)
... , 0, 1, 0
Число независимых переменных
Число зависимых переменных
Число уравнений
Характеры Картана
Независимые переменные
Зависимые переменные
Дифференциальные уравнения
0) Частные производные
+ for k : = 1 : 2 sum (и (k) * df (и (i), χ (k)) + df (tet,
u(k)) * df(u(k), x(i)));
deq (3): =for k : = 1 : 2 sum
{df (tet, u(k)) **2 — kap* tet) * df (u (k), χ (k)) + 2 * df (tet,
и (1)) * df (tet, и (2)) * df (u (2), x(l));
deq (4) : = df(u(\)y χ (2)) - df (u (2), χ (I)).
He вдаваясь в детали, опишем основные шаги работы программы
по представленному выше 7?У/С-алгоритму. Работа программы
выполняется по шагам (работают функции STEPI ( ); STEP2( ) и т. д.).
Сначала выполняется функция STEPI ( ), которая делает замену
производных df (и (/), χ (k)) оператором ρ (i, 0, ..., 0, 1, 0, ..., 0) в
уравнениях DEQ(l). Например, в данном примере df(u(i), χ (Ι))
заменяется ρ (/, 1, 0, 0), df (и (ί), χ (2)) — ρ (/, 0, 1, 0) и т. д. Не
расписывая подробно остальные действия программы, рассматриваем
по шагам, что она выполняет. После первого шага STEPI ( )
дифференцированием уравнений DEQ(l) по всем операторам ρ (i, l, 0, 0), ...
составляется матрица * А * (матрица А системы (11.19)). На следующем
шаге по алгоритму Гаусса находятся ранги матриц Л, после чего
составляется сумма * TAU * (см. τ в (11.21)). Следующим шагом
программа получает продолженную систему уравнений (DS) путем
полного дифференцирования с помощью L/SP-процедуры (Idifp (deq (k),
(χ, /))). Затем находится ранг матрицы Ρ (Л), который в программе
представлен идентификатором * ТА UРА *. Для системы (11.22)
* TAU * = * TAUPA *, поэтому для пользователя идет сообщение
THE SYSTEM IS IN INVOLUTIVE AND THE CHARAKTERS
OF CARTAN ARE:
SIGMA (1) := 2
SIGMA (2) :=0
THE END OF WORK OF PROGRAM!
В случае, когда *TAU* Φ *TAUPA*t программа сообщает
THE SYSTEM OF COORDINATE IS NOT CVAZYREGULAR
OR THE SYSTEM (S) IS NOT INVOLUTIVE.
Последнее сообщение означает, что выбранный базис независимых
координат является неквазирегулярным и необходимо сделать соответ-
199

ствующее преобразование независимых переменных. Обычно в
задачах, встречающихся в приложениях, видно, как надо выбрать
систему координат, чтобы базис был квазирегулярным. Если же базис
квазирегулярен, то последнее сообщение означает, что система не
находится в инволюции и ее необходимо продолжить, а затем
продолженную систему исследовать на совместность. В следующих версиях
программы этот шаг также будет автоматизирован.
Приведем еще несколько примеров, на которых тестировалась
работа программы.
1. Уравнение безвихревого изоэнтропийного течения политроп-
ного газа в трехмерном пространстве запишем в виде 1354]
-|r + (i>ve) + (v_l)edivf>=Of
dt
dvs dv,
L = 0 (t</), (ί, /-1, 2, 3).
ox? dx(
В результате вычисления на компьютере получено σχ = 4, σ2 = 3,
J,
σ3 = 2, σ4 = 0, τ = 16, 2л i°i — τ· Как видим, новых соотношений нет,
£=1
значит, система находится в инволюции с характерами Картана
σ, (1 = 1-=- 4).
2. Рассмотрим систему уравнений одномерной неупругой сплошной
среды [354J
ut — ox = 0f Et — vx = 0t σ/ —ε4 —(σ — jqri ε*+1) β °· (11'23)
Дифференциальные связи выбирались из следующих уравнений:
ох — гкгх = 0, (11.24)
σ, — &k/2vx = 0, (11.25)
ох + гкЪ>х = 09 (11.26)
οχ+υχ = 0. (11.27)
Результаты исследования этих систем на ЭВМ для случая k = 2
приведены в табл. 10.3.
3. Исследуем уравнения вида (354J
CGo — GCo = 0, CF0-FC0 — C8 = 0, FGG -GF0 + Се = 0.
После исследования на ЭВМ находим ог = 2, σ2 = 1, и = 4, 2л i°i =
= <с. Поскольку новых соотношений нет, то система находится в
инволюции.
Подпрограмма дифференцирования LDIFP(u, x). Так как в
продолжающихся уравнениях присутствуют сложные функции, их
степени или производные от них, то следует подготовить операцию диф-
200

Таблица 10.3
Номера уравнений
Характеры Картана
°л
σ2
τ
Наличие

соотношений
Ин вол кэ-
ти вность
(11.23)
(11.23), (11.24)
(11.23) — (11.25)
(11.23) — (11.26)
(11.23), (11.25), (11.26)
(11.23), (11.27)
(11.23), (11.24), (11.27)
3
2
1
0
1
2
1
0
0
0
0
0
0
0
3
2
1
0
1
1
0
Нет
Да
Нет
ференцировакия сложной функции и полинома от нее или от ее про-
ивводной. Например, в случае двойной волны, описанной выше, это
θ (иъ и2) или дв/дик. Дифференцирование полинома выполняется на
ЛИСПе в ^(^-представлении с использованием подпрограммы DIF (и, я),
которая написана в алгоритмической моде. При этсм подпрограмма
DIF осуществляет дифференцирование сложной функции и
производной от нее. Она также использует часть подпрограмм,
написанных на языке ЛИСП.
Подпрограммы работы с полиномами на языке ЛИСП. При
продолжении уравнений необходима работа с полиномами в символьной
моде. Поэтому были также подготовлены подпрограммы работы с
ними в этой моде. Например, для перемножения полиномов
использовалась подпрограмма
algebraic procedure RUMNP (и, ν); и * υ;
symbolic procedure LUMNP (u, υ);
reval RUMNP (u, υ).
Здесь на входе LUMNP полиномы имеют SQ-представление, а на
выходе представлены в виде префиксного выражения.

Глава 12
ФАКТОР-СИСТЕМЫ ТЕОРЕТИКО-ГРУППОВЫХ
МОДЕЛЕЙ. ФАКТОР-УРАВНЕНИЯ ПОЛЯ
В АНИЗОТРОПНОМ ПРОСТРАНСТВЕ-ВРЕМЕНИ
Интерпретация многомерной теоретико-групповой модели в
пространстве меньшего числа измерений получила название размерной
редукции или факторизации. В этой главе выделены два аспекта метода
размерной редукции — теоретико-групповой и геометрический.
Введем пространство Jk (n, m), точки которого определяются
координатами {хъ ..., хп, и1, ..., ит, д^иЧдх?, ..., д^ит1дх?), и пусть задано в этом
пространстве замкнутое подмногообразие Ε — система нелинейных
дифференциальных уравнений в частных производных &-го порядка!
FaUu .... Хп, "Η*), ···. Um{X)'l^)=0 (12Л)
относительно вектор-функции и (х) = (и1 (х), ..., ит (x))f χ = (xl9 ...
..., χη)9 которая допускает /--параметрическую группу Gr. Здесь 1 ^ α ^
^ р\ σ = (al9 ..., ση) — мультииндексы; | σ | = σχ +...+ οη ^ k. Все
функции предполагаются гладкими (класса С°°) в некоторой области.
С. Ли [383] разработал метод построения фактор-системы E/Grt
которая обладает следующими свойствами: проекция любого неособого
инвариантного β,,-решения и есть решение фактор-системы E/G,, и
обратно, каждое восстанавливаемое решение фактор-системы EIGr
является проекцией некоторого инвариантного Сг-решения системы. В
работах [329, 336—342, 384, 385] изложено современное развитие
классического алгоритма нахождения фактор-системы, а также его
компьютерные реализации в системах аналитических вычислений MACSYMA,
REDUCE и др. Ниже предложено обобщение лиевского метода
построения фактор-системы.
Рассмотрим базисные инфинитезимальные операторы
/--параметрической группы Gr в пространстве Rn (χ) Χ Ym (и)
Xv^lU*, u)-£- + i$(x, и)-£л> (I2·2)
ν = 1, ... > /·, i, /, / = 1, ... , η, Α, β, C= 1, ... , m
{по повторяющимся индексам подразумевается суммирование).
Находим s-e продолжение инфинитезимальных операторов группы Gr co-
,202

гласно формулам продолжения векторного поля (ξ,{ν; Ήν) 1336]
Χν ==Χν +ζνι —χ +ζνί/--Τ^4~ + *·*» (12.3)
s aui aui/
где
А диА а д*и*
ui — "~лТ"~ > иИ =
дх. ' ч — дх.дх,- '
ζνΐ = Dt (η?) - i^D, (ξ7ν); ζ£„ = Ο/ (ζί<) - 4ΰ/ (ξί);
Л1 дил dw? duffl
Выберем порядок продолжения s из соотношения Тресса [3861
rang[gt, ηί, ζ£·, ζ£7, ...] = r (12.4)
и запишем наиболее общий вид линейного дифференциального
оператора Ζ,μ, построенного из базисных элементов s-ro продолжения
алгебры Ли группы Gr
Ιμ = βμΧν> (12.5)
где μ = (μχ, ..., μτ) — мультииндексы; | μ | = μχ + μ2 +...+ μτ <
^ Γ, βμ = COnst.
Интегрируя систему дифференциальных уравнений первого
порядка
L^U nf-^LJ=Of (12.6)
κ = (κυ ..., κη) — мультииндексы; | κ | = κχ + ...+ κη <Ι s,
находим наборы Πμ инвариантов ω^ (jt), Φμ (jc, и) и дифференциальных
инвариантов Σμ [χ, uf —£-) группы Gr или ее подгрупп. Каждому най-
\ дх I
денному набору Πμ соответствуют анзатцы инвариантных решений
u(x)=U(x, φ (ω)), 4т" =Ω(χ, и, ψ (ω, Φ, Σ)), (12.7)
дх°
после подстановки которых в систему £ (12.1) находим фактор-систему
£/0μ.
Для нелинейных уравнений Шредингера, Гамильтона — Якоби и
Навье — Стокса, допускающих группу Шредингера и ее подгруппы,
получены фактор-системы в работе [329].
В случае искривленного пространства-времени, в частности
анизотропного, геометрический аспект метода размерной редукции
состоит в нахождении набора полей редуцированной теории, ее
псевдогруппы Ли и действия [387, 388]. Наличие ряда симметрии
пространства, таких как трансляционная инвариантность по времени и
пространственным координатам, инвариантность относительно
пространственных вращений, приводит к набору известных сохраняющихся
величин — интегралов движения (теорема Нетер), таких как энергия,
импульс и момент импульса, собственный спиновый момент поля.
203

Именно наличие таких инвариантов обусловливает специфику
решений полевых уравнений: например, факт сохранения энергии и
импульса поля позволяет сразу же сделать вывод, что решения полевых
уравнений можно искать в виде плоской волны. Действительно, если
выписать вид преобразований оператора поля под действием общего
Л Л А.
элемента группы трансляций φ (/, χ) = exp (+tP0 + хгРг + x2P2 +
+ x3/^) φ (Ο, 0), где Ρμ — генераторы группы трансляций, то они
соответствуют обычной плоской волне. Но такое представление
соответствует обычной в теории обыкновенных дифференциальных уравнений
процедуре разделения переменных. Поэтому подобная процедура
перестает с очевидностью работать, если симметрия
пространства-времени такова, что какие-либо из Ρμ не являются интегралами движения.
Первый простой случай, иллюстрирующий эту ситуацию,
соответствует снятию трансляционной инвариантности по времени. Это
легко достигается следующим изменением метрики плоского
пространства:
ds2 = dt2 — a2 (t) [(dx1)2 + (dx2)2 + (dx3f]. (12.8)
Это общий вид метрики, описывающей однородное и изотропное
пространства, в каждой точке которых одинаково изменяется масштаб со
временем (такие метрики описывают расширяющиеся пространства
моделей Вселенной Фридмана — Робертсона — Уокера).
Поскольку метрика (12.8) переопределением времени dt = α (η)^
приводится к конформно-плоскому виду
ds2 = α2 (η) (drf — dx\ (12.9)
то для всех видов полей, удовлетворяющих конформно-инвариантным
уравнениям, решение можно записать в виде φ (η, χ) = exp (ί'ωη —
— ikx), где ω — энергия поля, к — импульс, которые в этом случае
постоянны.
Если же конформная инвариантность нарушена, то энергия не
сохраняется и часть решения, зависящая от времени, удовлетворяет
более сложному уравнению φ (η, χ) = φ (η, к) exp (ikx), причем
содержательная задача сводится к нахождению функций φ (η, к) и
расчету на их значениях плотности энергии поля, а в более общем
случае — компонент тензора энергии-импульса (ТЭИ) Τμν (η). В силу
симметрии метрики (12.8) постоянными являются компоненты плотности
импульса поля Pt =? Гог. Величины же 700 (плотность энергии) и Тц
(давление) зависят от времени. Физически несохранение энергии
означает рождение из вакуума частиц и его поляризацию. При этом
модификацией закона сохранения служит условие консервативности ТЭИ
νμΓμν = 0, где νμ — ковариантная производная в метрике (12.9).
Следующим по сложности является случай обобщения метрики
(12.9) на однородное анизотропное пространство
ds2 - л2-2 А*(0(d*)2> (,2·10)
ί = 1
904

или, что эквивалентно,
ds* = α2 (η)
^η2-2α2(η)(^')2
(12.10a)
В этом случае кроме отсутствия трансляционной инвариантности по
времени отсутствует и симметрия относительно пространственных
вращений. Здесь даже для уравнений конформно-инвариантных за счет
отличия метрики от конформно-плоской энергия поля не сохраняется,
а решение уравнения не представимо в виде ехр (ί'ωη). Отсутствие
инвариантности относительно вращений приводит к изменению во
времени величин момента импульса поля и его спина. Задача опять
сводится к решению уравнений для временной части решения общего
уравнения поля и вычислению компонент ТЭИ на них.
Спецификой рассматриваемых задач является то, что не всегда
можно найти явную, непосредственную связь величин, относительно
которых записаны уравнения, и собственно степеней свободы поля,
имеющих физический смысл. Если подобная связь очевидна для
скалярного поля, то для уравнений спинорного и векторного полей она
требует более подробного анализа. В случае векторного поля ситуация
усугубляется еще и тем, что для нахождения решений для временной
части функций поля необходимо принимать во внимание чисто
геометрическую — векторную структуру поля. При этом в общем случае
получается сложная система уравнений второго порядка
относительно переменных, которые непосредственно физического смысла не
имеют. Ниже рассмотрен ряд фактор-систем для скалярного, векторного
и спинорного полей в анализируемом пространстве-времени [387, 388].
12.1. Фактор-уравнения для скалярного поля
Квантованию скалярного поля в различных анизотропных моделях
посвящено большое число известных работ [389, 390]. Здесь, следуя
работе [390], кратко изложим результаты этих работ применительно
к нашим целям.
Ковариантное уравнение для массивного скалярного конформно-
инвариантного поля в метрике (12.10) имеет вид
νμνμφ + (m2 + /?/6) φ = 0, (12.11)
где νμ — ковариантная производная R — скалярная кривизна.
Запишем решение этого уравнения [391, 392] φ* (л;) = (16π)~3/2 χ
Χ α (η)-1 gk (η) ехр (—ikx). Временная функция gk (η) удовлетворяет
уравнению осцилляторного типа
Λ+ΙμΜηί^οίτΰ + ΟίηΜΛ-Ο. (12.12)
Здесь и далее в этой главе будем использовать следующие обозначения!
&=(/ео, к), k=:(ku k2y k3) = & (sin (θ) cos (φ), sin (θ) sin (φ), cos (θ)),
/Co(η, *) = *2 + тУ(Л. θ, φ), £ = α(η)/μ(η, θ, φ), С, = ά,/α„
(12.13)
205

c2.
2> fl sin* (Θ) cos* (φ) . sin» (6) sin» (Φ) , cos ?
α\ (η) α* (η) <*3 (η)
Q = [(Сг - Q2 + <Са - С3)2 + (Сх - С3)2].
Используя метод Лагранжа, ищем решения уравнения (12.12) в виде
gk (η) = (μ# οΓ1 [«** f + β**-1. г (η) = — ίμ^ο 1*#+ — β^-1»
e± = exp^±ij/T0(V)dvV
В результате вместо одного дифференциального уравнения второго
порядка для gk (η) получается система двух линейных уравнений
первого порядка для комплексных функций ak (η) и β* (η), связанных
дополнительным условием | ak (η) |2 — | βΑ (η) |2 =ls
\ 2 2 / 1 (12.14)
Pfe = I — + * —J «**- + ι — Pfc»
где Ж = μ/μ + /(0/#0; ίΤ = $/(μ/Γ0).
На практике удобнее перейти от двух комплексных функций ак (η)
и β* (η) к трем действительным функциям
5*(η) = |β*Ι2> Uk(4) = 2Re(aSkei.), Κ,(η) = 21т(аД^1), (12.15)
для которых можно получить систему трех линейных уравнений
S^-^-Ub+^-V» Uk = ^{2Sk+l)-& + 2K0)Vk,
Vk-??(2Sk + \)-(W + 2K0)Uk
с начальными условиями Sk = Uk = Vk = О при η = η0.
Используя введенные функции и обозначения, записываем
вакуумные средние нормально упорядоченного оператора тензора энергии-
импульса Γμν (η) = (0,·„ Ι ΛΓηΓμν (η, χ) 10i„) для скалярного поля [390]:
Г» <Ч> = (2π)Λ«(η) J ^ ^ ^ θ· ^ Κ* (4> *) (5* (η) -
- о»/ «^"iVf μ [S* <Ч> + 4" ^* (П)1) ·
2μ2(η, θ, <ρ)Κ'0(ΐ), k)L <= J/
Γ':(τι) = (2η)»α«(η) J** ι*(η. θ· «?)^»(η» *)χ
(12.17)
206

к (η) + 4"^* Η
Χ ■ ^
my (η, Ο, φ)
4 (η, Λ)
Таким образом, решив систему уравнений (12.16) и исследовав-
свойства функций Sk> Uk и Vky получим информацию о тензоре
энергии-импульса скалярного поля.
12.2. Фактор-уравнения для безмассового спннорного поля
Рассмотрим безмассовое спинорное поле в метрике (12.10). Для этого
используем тетрадный формализм и представим метрику в виде
ds2 = g^vax^dx* = tjab (hffdx*) (h^dx*), где fu = diag (1, — 1, — 1,
—1) —метрический тензор в касательном пространстве Минковского;
/ι(μ} — реперные векторы (а, 6 = 0, 1, 2, 3). При этом Λ(%Λ(&)μ = ήα&,
Λμ%α)ν = £μν. Реперные векторы в данной метрике удобно выбрать в
виде Λμ* = 6{μ9 h(k} = j^6*. Запишем общековариантное уравнение
Дирака
/γμ(*)νμψ(χ)= 0. (12.18)
Здесь γμ (χ) = Ка)уа — 4-вектор относительно общих преобразований
координат; V^ = дц + -j- CW/i(ucVva — спинорная ковариантная п^
изводная; Саьс — коэффициенты вращения Риччи.
Для постоянных γ-матриц используется представление
где о* — матрицы Паули.
Единственно отличны от нуля символы Кристоффеля и
коэффициенты вращения Риччи Г** = л/к^к> Г*0 = ^/^л, CW = ^J^k (нет
суммирования по k). Спинорные ковариантные производные имеют
вид V0 = dldt, Vk = dldxk + л/ку°ук/2. Тогда уравнение (12.18)
преобразуется в вид
_ _ j£
dt Г2^АТ Jtk dxk
^+iE4-+T^r)*w=0·»'-^
От второго слагаемого легко избавиться, представив ψ (χ) так: ψ (jc) =
- (А^^зГ^ (х). Тогда
д , ak д
^ + ^-^>ψ^ = 0· П2Л9>
207

Поскольку νμγν (я) = 0 (по определению Vu), то функции Ψ (χ)
должны удовлетворять дополнительным условиям, аналогичным
плоскому пространству, т. е. Ρ+Ψ (х) = 0 для частиц с положительной спи-
ральностью и Ρ-Ψ (х) = 0 для частиц с отрицательной, где Р± =
= (1 ± Y5)/2 — проекционные операторы. Следовательно, как и в
плоском пространстве-времени, биспиноры Ψ, (х) (г = ±1) (в
зависимости от спинового состояния) будем искать в виде
Ψ* (*) = ***** (О. Xkr(t) = (V*rit)). (12.20)
\rVkr(t)l
Подставляя (12.20) в (12.19), получаем уравнения Вейля для
спиноров
iJ^L = rqaVkr, (12.21)
где qk = kkIAk — компоненты физического импульса частиц.
Представив спинор Vkr в виде
получим систему линейных уравнений первого порядка
at
dZkr
— r[iqzfkr + i (qx — iq2) gkrl
(12.22)
di = —t [iqzgkr + i (qi + iq2) fkA.
В сферической системе координат (12.13)
—. ^i — ^sm W cos(9) __ k2 __ fesin (Θ) sin (φ)
fc, k cos (Θ)
^3 αα3 αα32 '
о 2.2,2 &2 9 fc2 о A;2
Решение системы (12.22) ищем в виде
fkr (t) - 4" ω-^β-'^ίΚω —rfo«^+ + г V^TW3 β**.],
iAr(0 = 4"ω-ι>2*-ΠΦ/2[_г KV+7^akFe+ + V<»-rq3β^_],
где tg(<D)= -2Mg(q>).
Отсюда
et*r (0 = ω-1^-. [VlT^T^fkreW -rV^ + rq, g^er1**], (12 24)
β*Γ (0 = ω·'/26+ [г КЙ^ /^ίΦ/2 + V^^Tqs gbe-W].
208
(12.23)

Непосредственной подстановкой с учетом условий нормировки можно
получить дополнительное условие на функции а*, (/) и β^ (t): | akr |2 +
4- \$kr |2 = 1. Дифференцируя(12.24) по времени, приходим к системе
линейных дифференциальных уравнений первогр порядка
непосредственно для а& (t) и β&- (t)\
κ J \ О2·25)
где q\ - «? + £ ш=9^-^; w, -г£-Ф; ш, = г-£-Ф.
На практике удобнее перейти от двух комплексных функций а^ (О
и β*„ (/) к трем действительным функциям Skr (t) = | β*Γ |2, i/*r (/) =
= — 2Re (akrbkre2-), V^ (t) = —2 Im (α^β^Ι), для которых можно
получить систему трех линейных уравнений
Sb^-Z-Uk, φ-ν*, Ukr = w(-.2Skr+l) + (-w3+2Ko)Vk*9
2 νΛΓ 2
(12.26)
(^ = —wL (-2S*r + l)-(— щ + 2*β)1/*
С НаЧаЛЬНЫМИ УСЛОВИЯМИ Skr = ί/fcr = Vkr = 0 ПрИ / α /0.
Структура системы уравнений, как видим, аналогична системе
уравнений (12.16) для скалярного поля.
Используя введенные функции и обозначения, находим вакуумные
средние нормально упорядоченного оператора тензора
энергии-импульса Γμν (t) = (0in Ι ΛΓ,Γμν (ί, χ) \ 0in> для спинорного поля [391 h
^W- (2πΛ'(η) gi^^
Г' О - (2*)»* (η) S ί <*Vi (Хкг + X* cos (2Ф) - Ζ* sin (2Φ)),
Γ* W - (2π)»ί(η) S ί **Й <**r - *Ar COS (2Ф) + Zfc Sin (2Ф)),
7l(0=W7¥2i«f^ (12.27)
Г? (i) = 0, 2-1, 2, 3.
В отличие от скалярного поля у спинорного поля отличны от нуля
гакже недиагональные компоненты тензора энергии-импульса}
Т> О - (2π)»α'(η) ? ί Λ<^ Sin (2Φ)·
T* (0 - (2π)»α«(η) 2 ί d>kqxq9 [(X*, + Υ*) cos (Φ) - Ζ& sin (Φ)],
(12.28)
Τ*®= 12H^W?i^^l(78l(X*' + y*')sin((I>)""ZAreOS((I))1·
14 1-1980 209

В предыдущих выражениях введены обозначения
Следовательно, нам опять удалось свести анализ тензора энергии-
импульса квантованного безмассового спинорного поля к анализу
системы уравнений для функций S*r, Ukr и Vkn
12.3. Фактор-уравнения для векторного безмассового поля
Ковариантные уравнения безмассового векторного поля без
источников имеют вид
Vu^v = 0, νμ(*/0μν = 0, (12.29)
где F^ — тензор векторного поля; (*^)μν — сопряженная g ним
величина, определяемая равенством (*F) р = —т= Mtynl-^W
[αβγη] — полностью антисимметричный тензор, причем [0123] = 1.
Поскольку метрический тензор (#μν) не зависит от
пространственных координат, имеет место инвариантность теории при
пространственных трансляциях, и, следовательно, можно провести
пространственное преобразование фурье-компонент тензора:
F»V(U *)= i£Wfcexp(ite)rv('. *0.
J (12.30)
(*F)»v(t, x) = \(Ркехр(1кх)(*^^9 к).
Подставив (12.30) в (12.29), придем к уравнениям для /μν (/, к):
ik
/'-о, -[^з.(/-*Л+'*/']-о. (12.31)
Поскольку f/l = — Ijri) si; (*f)r°/V—g, последнее уравнение
приобретает вид
4- (У~е F) = -' Μ *ι·^ w (· Я"- ν 2·32>
Аналогично для сопряженной величины
М*Л/0 = 0, ^(/^(•/)/0)«i[/m/JiMJ.Wr. (12.33)
Для упрощения системы (12.31) — (12.33) введем новые
переменные
Sf =>^[/0/±/(*/)/Θ]. (12.34)
Тогда уравнения (12.31) — (12.33) разделяются для Sf и SJi
kjSf = 0, tsf^^^Lk^ist (12.35)
ш γ _ g
210

Дальнейшее упрощение состоит во введении в импульсном
пространстве сферических координат по формуле
(*ι. К К) = k (sin (δ) cos (ξ), sin (δ) sin (ξ), cos (δ)). (12.36)
Тогда равенство (12.35) можно автоматически удовлетворить, перейдя
от (12.34) к величинам
S? = cos (δ) cos (ξ) S? + cos (δ) sin (I) Si - sin (δ) S3*. (1237)
Sf = -sin(g)Si + cos(g)S2*.
Из равенства (12.35), которое записываем в виде sin (δ) (cos (ξ) 5* +
+ sin (ξ) Si) + cos (δ) Si = 0, и определения S? выводим
соотношения 5б* = -^щ- (cos (ξ) Si* + sin (ξ) S2*), Si = - 5δ* sin (δ).
Рассматривая последнюю формулу и определение S% как систему
уравнений, для S* и S? получаем соотношения связи
Si* - S* cos (ξ) cos (β)-Sf sin (ξ), ,^
S2* = S?sin(g)cos(e)+Sfcos(g)f S3* = — S? sin (δ).
Чтобы получить уравнения для S* и S*, продифференцируем по /
величины (12.37)2
S? . cos (δ) cos (I) S* + cos (δ) sin (I) Si - sin (δ) S3*,
. . . . . . ( 1-С.оУ)
Sf = - sin (ξ) Si* + cos (ξ) S2*.
Далее используем уравнения (12.35)
± Si* - — -4= (cos (δ) j4S2* - sin (δ) sin (ξ) j/lS3*),
± S2* = + l7J= (cos (δ) j^Si* - sin (δ) cos (I) j*20Si),
V — g
± S3* = -t4= (sin (δ) sin (ξ) jrfSf - sin (6) cos (ξ) j/fo*),
а потом формулы (12.38). В результате для S* и Sf получаем
уравнения
± S? = — fcaS* — ftftSf, ± Sf = + *£?S? + *aSf. (12.40)
Величины a, b и с представим в виде
аят cos (6)0030) sin (ξ) {j4{t)_^m (12 41)
K— g
b = -7=1= (j^ (t) cos2 (ξ) + jrf (t) sin2 (Q)f
с = p== (Л (i) cos2 (δ) cos2 (ξ) + j*i (/) cos2 (δ) sin2 (I) + j*i (/) sin2 (δ)).
Для дальнейшего анализа необходимо обсудить вопрос о временной
зависимости базисных векторов пространства. Метрика #μν определяет
И* 2П

естественный ковариантный «единичный» вектор е^ с ковариантны-
ми компонентами е* = 6" и естественный контравариантный вектор
βμ с контравариантными компонентами ва = δ£. При этом (βμβν) = £μν.
Отсутствие недиагональных членов в метрике означает, что
построенный из векторов βμ базис ортогональный, но длины пространственных
базисных векторов изменяются со временем согласно равенству
(ez·^) = jfi (О· Отсюда следует, что компоненты различных тензоров,
вычисленных в этом базисе, не несут полной информации о
соответствующих полях. Указанная трудность легко устраняется в данном
случае введением тетрадных базисных векторов по формулам έφ} = e0f
ей) = et/jfi (t). При этом оказывается, что (β(μ)β(ν)) = ημν·
В нашем случае, поскольку £μν не зависит от пространственных
координат, тетрадный базис можно ввести для всех точек
пространства в каждый данный момент времени.
В тетрадном базисе векторы электрической и магнитной напряжен-
ностей можно записать в виде
β (U x)=\d*k exp (ikx) 2 J*t (t) /* V, к) e(i),
J <=! (12.42)
91 (t9 *) = ΓέΡ*βχρ(ι**)2 ·** (0 (· fl'° ('» *)«<*>·
Спектральные компоненты (£ и 9i, вычисленные в тетрадном базисе,
ортогональны изменяющемуся во времени направлению,
определяемому вектором k{t) = kjjii (t). В связи с этим удобно ввести
изменяющиеся во времени единичные векторы
ek = sin'(6) cos (φ) β(ΐ) + sin (θ) sin (φ) e(2) + cos (θ)) e(3h
eQ = cos (θ) cos (φ) e{{) + cos (Θ) sin (φ) e(2) — sin (θ) β(3), (12.43)
βφ = — sin (φ) e{i) + cos (φ) e(2),
где углы θ и φ определяются равенством
(sin (θ) cos (φ), sin (θ) sin (φ), cos(0)) =
= ц-1 (sin №) cos (ξ) sin (6) sin (ξ) cos (6)\
_ / sin8 (6) cosa (I) sin2 (6) sin2 (ξ) cos2 (6) \ I/»
"I 4 + ^ + 4 j ·
(12.44)
Преобразуем выражения (12.42), используя введенные ранее
функции 5*, Sf. Сделаем это для магнитного поля 9£. Используя (12.44),
представляем 9? в виде
Я <<, х) = j d*k exp (ft*) J L_ <S,+ - 5Г) a/, (0 Ч» -
= —4= 2 f ** exp (ifc*)r 2 ST^iWeco.
212

В последней формуле мы перешли от обозначения S? к обозначению
5/, где г = ±1. Рассмотрим внутреннюю сумму. Замена Sf-^S't и Sg
По формулам (12.38) приводит ее к виду
2 S'tJtt (t) e(l) = Srt I- sin (ξ) α/Λΐ) + cos (ξ) j/2e(2)] +
+ Se [cos (ξ) cos (6) j^d + sin (ξ) cos (6) j*2e(2) — sin (δ) j*3em].
Перейдем от углов ξ, δ к углам φ, θ. Для этого используем следующие
формулы перехода, которые можно получить из (12.44):
sin(φ) β (_«$»■* sin (ξ)' cos(φ) β <-tf*bW C0S(ξ)' (12·45)
sin (θ)» f*4* sin (δ), cos (θ) = J cos (δ),
μ (—Я)1' μ Λ
В результате с учетом определения еф получим
2 STiJii (0 «</> = J=|^- [«μ (-^- * cos (φ) cos (θ) е{1) +
+ -^jj^- ft sin (φ) cos (θ) eg» — sin (θ) β(3)] + Sfc&e«p>l .
Далее легко проверить выполнение равенства
("^Г" * - ΐ) «β (φ) cos (θ) β(1) +
+ JJ^L ft _ ή sin (φ) cos (θ) *(2) = JL *φ>
используя соотношение
(J3L_,),izl!in,(i), (_^_Л=^СМ.(|)
и формулы связи (12.45), Тогда окончательно
S S'^*(0·ω = (^*Γ Ι5β(μ«β + аеф) + Sfre,] =
Напряженность магнитного поля записывается теперь таю
* = 2/(lg)^ Л ι ί ^* 6ХР (Яи° Г^1/2 [5*μβθ ~ Τ ^Н ' (12'46)
Для вектора напряженности электрического поля вычисления
проводятся аналогично и результат следующий!
β " 2i(-g)4* Μι ^ ** eXP {ШХ) ώ~1β [^ ~ Τ ^4 * (12·47)
213

Формулы (12.46) и (12.47) показывают, что электрическое и
магнитное поля полностью описываются функцией 5б. Поэтому удобно
перейти от (12.40) к уравнению второго порядка для Si. Для этого
продифференцируем по t первое из уравнений (12.40), подСтавим туда второе
уравнение, а оставшиеся члены с S% исключим опять с помощью
первого уравнения. В результате
-A. Sr6« ± Sr6 + Sr6 (- km + fc* (α2 - be) + \ ka).
Используя равенство α2 — be = —μ2, получаем
$ _ -*- Sr6 + (ft V + *ЛГ) Si - 0, (12.48)
где Лг = г ίά g- a) .
Выясним, какие ограничения возникают на функции S£, из того
факта, что поля (£ и 91 вещественные. Из условий Fae (/, χ) — F*p (t, x)f
(*F)a& (t, χ) = (*£)αβ (/, ж) сразу же вытекает требование f* (/, ft) =
= /*β (/, -ft), (*/)αβ(ί, Λ)= (*/)αβ (ί, —*). Тогда из определения (12.34)
сразу же следует
Sf (t, ft) - ST (t, - к), Syr (/, ft) = S~r ft- к). (12.49)
Поскольку отражение в импульсном пространстве соответствует
замене
δ' = π — δ, ξ' = π + ξ, cos (δ') = — cos (δ), sin (δ') = sin (δ),
cos (ξ') = — cos (ξ), sin (ξ')--sin (ξ), το Sr6(t, k) = S^r(tf -к)
(векторы ее и еф при замене к на — к преобразуются таким образом!
eQ (_ft) = eQ (ft), еФ (—к) = —е9 (к)).
Представим функции Si в виде
S£= C\{k)3r'(t. *)+ С5(Л)^Г(^ Л). (12.50)
Такое представление соответствует тому, что St удовлетворяет
уравнению второго порядка (12.48). Величины С[,? (к) являются
коэффициентами, зависящими от импульса ft, а функции &' (/, ft) невут
информацию о зависимости от времени t.
Установим свойства С\$ (ft) и &' (/, ft). Найдем сначала связь
между С\ и С£. Для этого рассмотрим изотропный случай jtfx == j/2 =
= j/8 = /?. При этом легко установить, что а = 0, b = 1//?, μ =
= 1//?. Подстановка этих величин в (12.48) преобразует уравнение к
виду
Sb + -jjjT ^6 + ~βϊ~ ^ = 0.
214

Легко проверить, что общее решение последнего имеет вид SJ =
= С\ (ft) exp (—ikr\) + Cr2 (ft) exp (ikr\)t где η = [dtIR (t).
Тогда равенство (12.49) можно записать так:
Sf (— ft) = Ct (— к) exp (ikr\) + Ct (— ft) exp (— ί*η),
SJ (ft) = CT (ft) exp (— ikx\) + CT (ft) exp (*£η),
откуда следует Ct (—ft) = CT (ft), ft (—ft) = СГ (к).
В общем случае анизотропной метрики равенство (12,49) имеет вид
Ct (- ft) &+ (- ft) + Ct (- ft) &+ (- ft) = CT (к) &~ (ft) +
+ СП*)У~(*).
или
C7 (ft) &+ (— ft) + СГ (fc) У+ (— ft) = CT (ft) ^~ (ft) 4- CT (ft) ^~ (ft).
Последнему равенству легко удовлетворить» положив &+ (—ft) =
= З'"" (ft). В изотропном случае У* (ft) == С0 ехр (Игц), τ. е.
последнее равенство выполняется тривиально.
Подставим в (12.47) выражение (12.50). Легко проверить, что
справедливо равенство
Σ [sfo*e--T-$6e<pl= Σ [Ci(*)Uf(<. k) + a(k)Vir(tt ft)],
где UJ (£, ft) = μ^Οθ £- ^Γβφ.
Тогда <£ приобретает вид
<£ =
2 { &к exp (ifc.r) b~l/2 [C\ (ft) Uo (f, ft) +
2(-£)1/4 ri±i
+ C5(*)US(/, ft)].
Выражение для (£ представлено двумя интегралами. Поменяем во
втором из них переменную интегрирования ft на —ft и рассмотрим
выражение
Σ Cr2(-k)K(t, -ft) =
r=±l
- Σ СП-^М-*)-^, -ft)ee(-ft)-
- rS t СГ (u) (μ (к) 3S~r (t, к) е, (к) + -J- У"' (*, к) βΨ (к)) -
= Σ Ci(*)US(<, fc).
215

После этого выражение для <£ принимает вид
е = о, \ш 2 ЫЬ-хп[Ci(к)Щ(/, к)ехр(ifce) +
+ Ci(ft)US(*, к) ехр (—**)!. (12.51)
Представим <£ в виде разложения по полной системе собственных
функций соответствующего уравнения с амплитудами Ci (к), у
которых впоследствии будем опускать индекс «Ь.
Векторы Uo (t, к), участвующие в разложении (12.51), являются
в случае анизотропного пространства аналогом векторов, задающих
определенное состояние круговой поляризации (на квантовом языке
задающих состояния частиц с определенной проекцией спина на
направление движения).
Разложение для магнитного поля % аналогичное (12.51),
имеет вид
% = 2.(Jg)1/4 Σ±χ d*krb~42[С(к) %(ty к)ехр(ikx) +
+ Сг (к)tto(/f fc)exp(— ikx)]. (12.52)
В дальнейшем изменим вид (12.51) и (12.52), внеся все функции
времени в определение векторов Uq(f, k)i
Окончательно разложение для электрического и магнитного полей
(ЭМП) имеет вид
« = 4- Σ \dPk[C(k)Vir(ty k)exp(ikx) + C+ir)(k)Ur{t, к) χ
xexp(-ite)], (1253)
SI-4- Σ f d*kr[C(k)Vt(t9 k)exp(ikx) +
+ С+(г) (к) Ur (/, к) ехр (— ikx)].
Основной характеристикой квантовых эффектов ЭМП в
анизотропном пространстве являются вакуумные средние операторы симметри-
зованного тензора энергии-импульса ЭМП
' αμ (t) = (0\NtTavi(t, ж)10>, NtT <<ΜΓ«μ|0,>.
Ταμ = - -£- {^μο, Fav) + Τ^Μ l>BV. ^Ρν'}, Μ, Β} = ЛВ + ΒΑ
В частности, Τ0 (0 = -rr (0 [ Λ^^// (/) 10>. Аналогично тому, как
общее решение уравнений Максвелла можно представить в виде
суперпозиции плоских волн с волновым вектором fr, ТЭИ можно разложить
£16

следующим образом:
П- $άξάδ sin (δ) $ dK0(t, k, δ, ξ)Π(/, Κ δ, ξ), (12.54)
где /Со (*> &, δ, ξ) β £μ (ί, δ, ξ) — физическая частота фотона.
Отличные от нуля спектральные компоненты выражения (12.54)
имеют вид
/■=1
Я - 4" Σ [-cos <2*) *' +sin <*р> уг - JisrSL <2S' + "'>] ·
7* = 4" S [cos (2φ) Xr - sin (2φ) Г - ™ψ- (2Sr + Ur)] ,
Ίί - -γ- 2 [- cos2 (θ) 2S' + sin» (θ) Щ,
(12.55)
fu=w Σ isin <2<p)*r +cos (2(p) γΓ]>
fl3 β "таг Σ [cos (Φ)j!^ (25r + i/r) + sin (φ) tg (Θ) Y%
Ϊ™ = ~аЖ Σ [sin (Φ) iiT2§L <2S' + ^ ~ cos (Φ) *δ <θ>Г] ·
Величины Toi = 0 в силу пространственной однородности
метрики. След выражения (12.55) Т» = 0, так как поле безмассовое.
Выполняется условие консервативности νμΓμν = 0, которое в выбранной
метрике является содержательным только для диагональных
компонент тензора энергии-импульса.
В отличие от случая изотропного пространства, где ТЭИ для всех
видов полей диагоналей, в анизотропном пространстве ТЭИ
оказывается недиагональным по пространственным индексам. Это связано с
неортогональностью поляризационных векторов U(+,) (t, к) и U*""1* (t, h)i
(U(+1)(/, fe), U'-'V, *)) = ^1(0(-^(0r1/V(^ *)У+Ч к) χ
x &-\t% к) —-^г &+{ (t, k)&-](t, к)).
(При t = t0 согласно начальным условиям (U(+1), lr !)) = 0.)
Поэтому оказывается невозможным повернуть ортогональные оси, в
которых вычисляется данная компонента ТЭИ, при фиксированном к
так, чтобы они совпадали с направлением векторов ttr (t, к).
В формулах (12.55) для спектральных компонент ТЭИ введены
обозначения
X' = 2Sr-(2Sr+Ur) cos*f + l , y = wcos(8)r.
217

Введение функций S% Ur и Vw осуществляется в два этапа. Сначала
введем функции Фг и ΨΓ по формулам
з,г _ ^_γ {фГе+ + Те_)г Фг _ .Кй ^ь_у (фге+ _ ψβ)
Функции Фг и ΨΓ удовлетворяют системе уравнений
где W и W определяются равенствами W = μ/μ — 6/b, W = Δ///μ#
//£ s Mt^iu АН = Я8 — Я1в
Определим функции S', ί/Γ и Κι
5Г = | ΨΓ Ρ, [/г = 2 Re (Ψ'ΦΓ4)> У = 2 Im (ΨΓΦ'4).
Дифференцируя эти выражения по t и учитывая (12.56), получаем
систему уравнений, которым удовлетворяют функции Sr, (/, Vr:
Sr = ^~ t/r + r~ Vrf Ur = W (2Sr + 1) - (rW + 2K0) V\
(12.57)
Vr = r# (2S' + 1) + (rW + 2K0) Ur
с начальными условиями SF = Ur = Vr = 0 при / = /0. Кроме того,
справедлива формула связи (i/r)2 + (Vr)2 = 4S' (Sr + 1).
Сравнивая результаты для всех трех типов полей, приходим к
выводу, что систему уравнений для функций Sr, t/r, Vr можно записать
в общем виде:
W W
Τ" т~
О -(rW+2K0)
2rW rW + 2K0 0
12.4. Фактор-уравнения для массивного спинорного поля
Рассмотрим массивное спинорное поле в метрике (12.10). Для этого
используем тетрадный формализм и представим метрику в виде ds2 =
= ё^Ых* = Ъаь (hfdx») (h^dx*), где ξ* = diag (1, —1, —1,
—1) — метрический тензор в касательном пространстве
Минковского; Л{? — реперные векторы (а, Ъ = 0, 1, 2, 3). При этом ή(%Λ<6>μ =»
— fyabf h{f?h{a)v = g»v. Реперные векторы в данной метрике удобно
выбрать в виде/ι^ » δμ, ftjf = j4kb%. Запишем общековариантное урав-
218

нение Дирака
<*Υ(*)νμ-/η)ψ(*)~0. (12.59)
Здесь * у» (χ) = ή(%Ύα — 4-вектор относительно общих преобразова-
ний координат; Vu = дй + -j- Сд/,^'yV — спинорная ковариантная
производная; Саьс — коэффициенты вращения Риччи.
Для постоянных γ-матриц используется представление
где σ** — матрицы Паули.
Символы Кристоффеля и коэффициенты вращения Риччи Г» =
= sikjik, Г*о = J?kljtb Cm = ^*/^ (нет суммирования по k) отлич-
ны от нуля. Спинорные ковариантные производные V0 = dldt, Vk =
= dldxk + j/ky°yk/2. Тогда уравнение (12.59) преобразуется в вид
От второго слагаемого легко избавиться, представив ψ (χ) в виде
ψ (*) = (j^^)-1'2 Ψ (д:). Получим
('
a , . α*
^+1Ж-^Г-Рт)¥<*> = °· (12.60)
Биспицор Ψ^ (я) (/" =» ±1) вследствие однородности метрики можна
представить в виде
Ψ^(χ) « ^ΧΛΓ(/), Х„ (Ζ) = (ΐ* Μ). (12.61)
Здесь спиноры f*, (t)t Qkr (t) зависят только от времени; индекс г
определяет проекцию спина на направление движения.
Подставляя (12.61) в (12.60), получаем систему уравнений для
спиноров \kr (t) и Qkr (/):
--±- = — i (mUr + rqsasQkr), -^ = — i (— mg^ + r?sa$W)
(5=1, 2, 3), (12.62)
где qk = fc*/jtf* — компоненты физического импульса частиц.
В сферической системе координат (12.10)
-= kl — & sin (θ) cos (φ) __ k2 __ k sin (Θ) sin (φ)
kt *COS(6) 2 2,2,2 k* 2 ** 2 **
Для нахождения решения системы (12.62) поступим следующим
образом. Выберем ортогональные спиноры Ru и for, описывающие
219

независимые спиральные состояния в безмассовом случае в виде
'Ι/ д — гдг ^ΐφβ \ / lfq + rq9c-»i<i>j2)
ГТ/Г^ + rq* top J I ]/? — /gtgM>.
/?2^ = — io2R\n R\9 = ta2R2n
где tg(<D) = -^Mg(<p).
Из этих спиноров составим новые спиноры
Р4, = - ι'σ,Ρι,, P^Pir = 2, Р^Рзг == - PtPir = 4т<7/шг. (12.63)
В безмассовой теории Р\, и Р2г будут описывать независимые спираль*
ные состояния. Если т φ О, то происходят переходы fv *♦ д*г,
причем амплитуда перехода пропорциональна tn/ω [393].
Решение системы (12.62) ищем в виде
fto (0 = -Lffl-i/2[|/iiir^ Р1гаье+ + г V^Tm ОД*-1,
fl*, (0 = 4" ω"'/21Γ ^«Й7^ ргг ά**+ + V^^in P4,pVJ, (12.64)
в± = ехр^±1|К0(П^].
Отсюда
άν (0 = 4- ">_1/2б- [Κω —m Pt W — r V^+m Ptqtr],
(12.65)
pV (0 = 4" ω-1/2β+ VV«> + tn Pt\kr + V& — m Pig*,].
Непосредственной подстановкой с учетом условий нормировки можно
проверить выполнение соотношения | а*Г Is + | β*τ |2 = 1.
Дифференцируя (12.65) по времени, приходим к системе линейных
дифференциальных уравнений первого порядка непосредственно для а», (/]
и β* (t)i
а*, = l-^- + i -^-) β*^1 — i -ψ- ά*„
v^ ^ ' ^ (12.66)
220

где
ωο. Ι ω* ω* J · ω8 ' -1 ω
(12.67)
8 ω V ω8 ω2 / ' ω8
На практике удобнее перейти от двух комплексных функций akr (t)
и $kr (ί) к трем действительным функциям ©^ (*) = | β^Γ |2, Щг (t) =
» о * л
= —2 Re (α*ΓβΛΓ£_), 93^ (t) = —2 Im (α*Γβ^-), для которых можно
получить систему трех линейных уравнений
©*г = -^-U*. ?g±- »*, 11*, = ОД(— 2©^ -f 1) + (- ад3 + 2А:о) »Аг,
(12.68)
&*г - - «ι (— 2S*r + 1) — (— αι3 + 2К0) Пы
е начальными условиями <S*r = 11*,= SS^. =» 0 при t = /0.
Структура системы уравнений, как видим, аналогична системе
уравнений, полученных для безмассовых полей в параграфах 12.3 и
12.4. Изменения претерпели только величины сц, α\χ и сц3} в которых
появились слагаемые, зависящие от массы.
Используя введенные функции и обозначения, рассчитываем
вакуумные средние нормально упорядоченного оператора тензора энер-
рии-импульса Τμν (t) = (0*п | ΝίΤβν (t, χ) \ 0in) спинорного поля:
^й" (2я)»1«(т,) Σί^ω@^,
Т! (/) = (2π)4'(η) 2 J <*Vi <** + Ζ»cos(2Ф) - Qkr sin (2Ф)),
71Ю" W^fipSi dVi(3E*r--&rC0s(2O)+ 3*^ΐη(2Φ)),
^(^ (2κ)»*(η) 2Ц**?зЭ*г, Τ? (Ζ)-0, ί= Ι, 2, 3, (12.69)
Т> О = (2π)'ά«(η) ? J ^х<7з [<**■ + ?V) cos (Φ) - Skr sin (Φ)],
Г'(/) = (2π)»α«(η) ? ί ***' *» № + ^ $Ш (Ф) ~~ ^ C°S (Φ)1"
В предыдущих выражениях введены обозначения:
Vu (is. ■ 1t \ ®*r , 1 ■?*% / ?2 m« \ , m» „
*ftr(©ftr, И*) = -^ + -γ -^— {—r - -^J + -^- Щг,
IMS*,·, U*,) = — 2—^Γ"1"^ - -Ί*)+ -W Ukr>
8*r(**r> =
1 «to
2 *1
22!

Следовательно, нам опять удалось свести анализ тензора энергии*
импульса квантованного безмассового спинорного поля к анализу
системы уравнений для функций ©&-, Ukr, ®лг.
12.5. Фактор-уравнения для векторного массивного поля
Рассмотрим векторное массивное поле, удовлетворяющее уравнению
Прока в метрике (12.10):
V^v+"*Mv==0, (1270)
где компоненты тензора Fuv связаны с компонентами
вектор-потенциала соотношением
ίμν = ^Λ-Μμ (12.71)
и выполняется дополнительное условие
νμΛμ = 0, (12.72)
являющееся следствием уравнения (12.70),
Легко проверить, что если ввести сопряженную величину ^)μν,
определяемую равенством ί*/7)060 = —j=r [αβγη] F^y где [αβγη] —
2 Κ— g
полностью антисимметричный тензор, [0123] = 1, то в силу (12.71)
будет выполняться тождество
νμ(*/Τν = 0. (12.73)
Поскольку метрический тензор (#μν) не зависит от
пространственных координат, имеет место инвариантность теории при
пространственных трансляциях и, следовательно, можно провести
пространственное преобразование фурье-компонент тензора и вектор-потенциала!
Я" (/> χ) e j cPkехр (ikx) fμν (f, ft),
(* Ffv (t, x) = j d3ft exp (ikx) (* \fv (it ft), (12.74)
Лд(/, #) = [d^kexp(ikx)afl(t9 ft).
Подстановка (12.74) в (12.70), (12.72), (12.73) дает две группы
уравнений:
содержащие массу
/*/' _ т*а° e о, * д0 (V~g f°) + ikjf - mV - 0, (12.75)
V — g
не содержащие массу
к j (* f)0/ - 0, yL·, д0 (V~g (* f)/0) + Λ, (* f)" - 0 (12.76)
и дополнительное условие
1
-μ= д0 (V- g if) + ikfli - 0. (12.77)
V — g
222

Используя связь fl = —[/ri] jfr (*\ffV—g, преобразовываем
уравнения, содержащие первые производные по времени!
д0 (V~g F) - - / [jml] ktjSm (t) (· ίΓ + ηϊά V~g, щ
до 0/^S (· f)/9) - / [/«fl *!·*£ (О Г.
Вводя новые переменные
©f-K=i[fvd=i(*f)/0l, (12.79)
преобразовываем уравнения поляз
k&f - mV K=i = 0, 4" ©/* = m2fl/ l^ =F j{S *ι·*ί.©£·
(12.80)
Дальнейшее упрощение состоит во введении в импульсном
пространстве сферических координат по формуле (kv k2, ks) = k (sin (δ) χ
X cos (ξ), sin (δ) sin (ξ), cos (δ)). Легко проверить, что единичные
базисные векторы в импульсном пространстве связаны с базисными
векторами, построенными в сферической системе координат,
соотношениями
Ч\ /еь\ /cos (ξ) cos (δ) — sin (ξ) cos (ξ) sin(6)\/*a
4 I = ΩΙ *ξ Ι = Ι sin (ξ) cos (δ) cos (ξ) sin (ξ) sin (δ) 11 e
KeJ \ -sin(δ) 0 cos(6)/W
так что связь между ©*, ©ξ, ©β, @Λ дается соотношениями
f@t\ /@?\ /@βλ /@*
@±j-Q @± , @f =ωτ©±
Аналогичные соотношения выполняются для производных функций'
и вектор-потенциала
K*J W W V,
Уравнения (12.80) преобразовываются в два этапа!
*@* = k (©f cos (ξ) sin (δ) + @2* sin (ξ) sin (δ) + ©3* cos (δ)) =
©ι* - mW 1/Hi ± -7^=; (cos (δ) A!®? - sin (δ) sin (ξ) ^©з*),
V~8 (12.81>
©* = m2a2 y—g± *L· (sin (6) cos (ξ) i4l@f - cos (б) Л?@?),
©з* « m2a3 V~g ± ^A= (sin (δ) sin (ξ) Λ?@ί - sin (δ) cos (ξ) Λ|@?),
@ί - m2a* V^g ± * (я©** + 6Sf + Α® *λ
22*

©f = m2a, V— g±k(— c<5fj-a©f + p@f),
ek =~m2akV—g.
Для получения последнего уравнения использовано дополнительное
условие (12.77). В (12.81) введены обозначения
д_ cos (δ) cosj^sin (ξ) ι* ji. h __ sin (δ) cos (ξ) sin (ξ) 2 _ a
/-g 2 l' V11!
b - -= (A cos2 Ш + jt\ sin2 (ξ)),
У-* (12.82)
q = 7=1= (^2 sin2 (I) + jrf? cos2 (ξ)),
V —g
С - ? COS2 (6) + ^L· Sin2 (δ), ρ = (p^= - (7 J Sin (6) COS (6).
Преобразуем физические характеристики векторного поля,
аналогичные электрическому полю, магнитному полю и векторному
потенциалу. Для этого перейдем к базису в импульсном пространстве,
зависящему от времени, используя простое соотношение ещ = e^jit (f).
Соответствующие сферическим координатам орты, изменяющиеся во
времени, имеют вид
^θ\ /е<п\
βφ) = Ω~1(θ, φ) β(2)),
где углы θ и φ связаны с δ и ξ соотношением
(sin (θ) cos (φ), sin (θ) sin (φ), cos(0)) =
_ -ι /sin (δ) cos (ξ) sin (δ) sin (ξ) cos (δ) \
/sin2 (δ) cos2 (ξ) , sin2 (δ) sin2 (ξ) f cos2 (δ) \
μβ1 Ί\ +—Ί\ + Α )
Начнем с вектор-потенциала A (t, к) = Σ^ί (0 β' (*» Щ Ш) (0· Вы·
ражая αί через αδ, ας и α*, а также используя связь между в(/> и ев, βφ,
<е*, получаем
А & к) = ^//Ι 1αδ (μ^θ + αβφ) + αφβφ + ак (Uek + Ve% + Ле,) J,
(12.83)
где к уже введенным величинам (12.82) добавляются новые?
i^^P^V' V (=*)μ sm(6)cos(6).
Поперечная часть вектора-потенциала имеет вид
А J- Ct к)β //2 fa<> (I** + αβφ) + αδ*βφ + ah (VeQ + he*)],
224

продольная —
Исходя из общего выражения для магнитного поля и используя
те же, что и для A (t, к), преобразования, получаем
Μ
(*, *) - i J d*fc exp (ikx) | J] j/f (0 p== [Oimn] «„^e^K, (*, *)J t
+ ^((-1)(α4ν + αΛμ))ϊ, (12.84)
откуда, как и следовало ожидать, видно, что вектор магнитного поля
поперечен. Сравнивая (12.84) и (12.83), получаем естественное усло-
виесвязи, вытекающее из (12.71)ι 9Ϊ(/, к) = i [A (t, к) X fcj. Посколь.
ку 9Ϊ (t, к) выражается через функции ©i, ©^ @* в виде
+ M@fa + ©^ + ©ft)],
можно осуществить вывод уравнения связи между аа, α*, α* и функци.
ями @а, ©ξ, ©*ι
f= Σ '©β = k (a*h + α6α + αφ),
2V-g r-±i (,2β86)
οι/? fg Σ '©6 + b Σ ^'λ^/ίμ^ν +aw).
Аналогично приступаем к получению выражения для вектора
электрического поля
β « — m0fe+ 2 (2j/«fll + ·*!*') *«>·
Нас интересует представление его в форме
k \ ί θ
<£(*) = —too* + е<*)
IH...IH.*.!·
Используя аналогичные предыдущему преобразования, после
длительных вычислений можно показать, что
{k 1= (Т'^'/4 {α"υ+2υ ια*№ cos2 (ξ)+% sina (ξ)) sin2 (δ)+
+ % cos2 (δ) -f α6 (% cos2 (ξ) + Я, sin2 (ξ) — %) sin (δ) cos (δ) +
+ αξ (% — Slj sin (δ) sin (ξ) cos (£)]};
15 '-"««о 225

α-
°ш>
akV + αβμ + ak I -^ I ^ cos2 (ξ) + 9?2 sin2 (|) -
_ Jyfj sin (6) cos (δ)] + a6 \ -L·- (% cos2 (ξ) + % sin2 (|)) cos2 (δ) +
V — g J 1 l Из
+ 2
^:Sin2(6)
μΚ-g
Φ
+ Я| J sin (|) cos (|) cos (δ) -U- (%2 — 5№x)
; (12.86)
(-«>
1/4
l1/2
{α»/ι + αδα + αφ + ak(h + hd0 In ]/— g) +
+ a6(a + ad0 In V— g) + as (6 + bd0 In K^g)}.
Исходя из того, что G можно выразить в терминах @а, <S| и @£ :
«с *>= 2(. ,;.«»■* {(д^^д^+кд; @*Ь+
+ (α Σ б* + Ь Σ @ί + Л 2 ©ή «φ) ,
\ r=-tl «=-tl r=±l / J
записываем набор уравнений связи
-^+{.!.)-("Л.*)«,-^>»·
-Μ.*·*·1^.*)'^»"· (12·87)
|ф) = (<" 2 βί + 6 Σ βΊ + ft Σ βί
(...) \ '=±1 r=±l r=±l
1
2(_^)ΐ/4 61/2 '
Легко проверить, что найденные уравнения связи обращают в
тождество группу уравнений поля, полученных из (12.73):
Σ r&b^-kla Σ ©δ + b Σ ©ι + h Σ ©ί) .
г=±1 \ r=±l r=*±l r=±\ Ι
Σ r&i=k[c Σ @6 + α Σ @ϊ-Ρ 2 ©ή, 2 r©r* = 0.
г=±1 \ r=±l г=±1 г=±1 / г=±1
(12.88)
Теперь задача состоит в нахождении решения другой группы
уравнений, содержащих массу:
Σ±χ ©β - - 2m*a0 К^ - * (а (Д r@SJ + Ь (Σ±{ гЩ ,
Д ®* β - 2m*a* Ϋ~ g + k [c (Д r®*) + a (Лι ГЩ
(12.89)
Для этого немного упростим задачу и рассмотрим случай аксиально-
симметричного пространства-времени jjx = л/2 . В данном случае а =
226

В первую очередь можно существенно упростить выражения
®(к) = (-^»"« (®ftt/e* + "SET ^θβθ + Μ * (12.90)
Л <*> = (_g)'l/4fe {Ж ®*** + "fe- Ubej + ^} '
im- V — g
где ί/θ= 2 r@s; ί/φ^Κ^Κ-
r=±l
В такой форме представления оказывается легко провести
квантование векторного поля, представив оператор поля (например, 6) в
виде
« = jd»fc(_g)J46l/2[^ {©*i/e*Cft+ + -4- ί/eeeCt + 0*еЩ +
+ *-'** {@»i/«*C* + -^ 0β«Α + 0ФеД}]
и наложив стандартные коммутационные соотношения [Cr (&),
С+ (Л')] = δ„<δ3 (к - *'), г = Л, θ, φ.
Теперь можно вывести уравнения для функций ©Л> ί/β, ίΛρ.
Начнем с уравнения для ί/φ. Воспользовавшись вторым уравнением (12.89)
и первой связью (12.85), легко показать
Дифференцируя по / третье из условий связи (12.87), разрешенное
относительно Σ©|, получаем
2 ©ξ = 2^3^φ»
r=±l
r2
■2^«2^ф + А[/ф)в.^ (12.91)
Учитывая ft = 1/Л3, записываем уравнение для {/фз
#Φ+-Φ-ίΛρ + #οίΛρ==0. (12.92)
Теперь получим уравнение для ί/ο, для чего продифференцируем
по t второе уравнение в системе (12.88) и исключим из того же
уравнения Σ@ξ!
tfе = ·§- #θ - *Vfe - 2/η2αό K=g te - 2йр[®4 + \± L) @,| #
15* 22?

Исключив аь из второго условия связи (12.85), выразив его через Qk
и использовав последнее уравнение системы (12.81), окончательно
получим
0в-4#е + К2£/в = -2*о(-2г-гг)@*. <Ι2·93>
Аналогичными методами можно найти уравнение для @ftj
ikc (12.94)
F (Η, АН) = 5Я + АН I -|- (2 cos2 (б) - sin2 (6)) - /U£|*>\2 χ
*з — Jt\
~^С08«(б)+^81п»(в)
X ,2^,f , fL,^] · #* = ^'^, Δ// = ^3- ΗΙΨ
в изотропном случае F (Я, 0) = 5Я, Я ss (Я! + Я2 + Я3)/3.
Видим, что ура нения для функций t/e и @Л расщепляются
только при АЯ = 0 или т = 0, когда @* si 0.
Основной характеристикой квантовых эффектов векторного поля
в анизотропном пространстве являются вакуумные средние оператора
симметризованного тензора энергии-импульса векторного массивного
поля
A gVP А , Л CLJ- Л
* αμ = g— Π** μρ» '"αν} "Γ {« αν» ^μρ/Ι 4"
+ "1 ι\λ+, Αα) + {Л+, Αμ}] - (12.95)
Ταμ (0 = (ο Ι /ν,:Γαμ (ί, *) ι ο), Ν(ται1 = ταιχ - <ο, ι ταμ \ ο,>,
α
τ
2
"Γ
-*»[--rift. ^v) + 4-H- *U
В частности,
4 (0 = -γ (ο | #,я (010), ν = K^i δ3 (θ),
где Η (ί) — гамильтониан векторного поля,
tf--Ljcp*K=i[({e+, е}) + ({й+. Щ) + т*[{А£, Α.) +
Подстановка Н в (12.90) дает выражение
1%(ί) = р== J d»*/(, [s* + se + δ,].
228

где функции ski se, s* определяются следующим образом: sr = | ψ, |2,
а ψΛ связаны с @Л о t/fe, t/y и ί/φ стандартными соотношениями
ί/Γ = fr (Фге+ + ψΓ*_), ί/, = iK0fr (Фге+ — г|>ге_)>
1Фг|а-|Ф,|2=1. e+ = expli$dt'K0(t')\
fr = ^Γ172^1, ft = u*/bm*K0, ge = μ2/4^ν/(0, £φ - W0.
Функции Фг и ψΛ удовлетворяют следующей системе уравнений:
ψφ = ^3ΚφΦΨ4, ^ф^^-Х' Фф = т-!
Ψθ
ϊφψφ^-.;
ψ* =
Р(Я, Δ#)
1 Κ0 , /ft
2 К» ^ /*
t* +
_Κο
Ко
■F(tf, АЯ)
Ф*е* +
+
^1-
ф* =
F(W, ДЯ)
1 Ко
h
2 Кл ^ f„ \
Ф* +
+ ■
Ко
+^"^ШШ «■*» + **->·
От системы с ·ψφ и Фф можно сделать стандартный переход к
системе уравнений непосредственно для функций ©, U и 1Л ©^ = | ψ4 Ι2,
ί/φ = 2 Re (ψΦΦφ^+), Ι/Φ = 2 Im (ψφΦ^+),
©φ = J&L υφ, ϋφ = 28φ (2S* + 1) - 2K0KU, Уф = 2Κουφ
с начальными условиями @ф = ί/φ = Уф = 0 при ί = t0. Для
компонент θ и k переход к аналогичной системе функций и уравнений
нецелесообразен, поскольку получается система зацепляющихся
уравнений первого порядка ранга 9x9 [394].

Глава 13
ДВУХМЕРНЫЕ РАЗЛОЖЕНИЯ
РЕЛЯТИВИСТСКИХ АМПЛИТУД
Исходным представлением исследований по аналитическим свойствам
релятивистских амплитуд служат выражения, в которых в качестве
переменных выбраны переменные s, t, и. Естественным первым шагом
оказывается разложение амплитуд на парциальные волны.
Рассмотрим разложения амплитуд рассеяния для случая равных
масс. Зависимость амплитуды рассеяния двух частиц от двух
переменных (энергии и угла рассеяния) позволяет нам определить эти
переменные через координаты точки на трехмерном гиперболоиде при
учете равенств pi = mi, рх + р2 = р3 + /?4 [142], т. е. для амплитуды
4-хвостки достаточно использовать координаты только одного из
свободных концов. Отсюда следует, что амплитуду рассеяния можно
рассматривать как функцию, заданную для определенности на верхнем
поле двухполостного гиперболоида. Тогда операторы сдвига на этой
поверхности (которые, очевидно, реализуют собственную группу
Лоренца) можно использовать для преобразования амплитуды рассеяния
от одного значения переменных к другому. Назовем расширенным
условием релятивистской инвариантности такого перехода от одного
значения амплитуды рассеяния к другому с помощью операторов сдвига
на гиперболоиде (или конусе). Заметим, что амплитуда зависит от
инвариантных переменных 5, t. Такое расширение определения
инвариантности, необходимое для введения разложений, приводит,
естественно, к условиям поведения функций при больших значениях аргумента.
13.1. Интегральные представления релятивистских амплитуд
и асимптотические теоремы
Для получения асимптотических разложений [165] исходим из
записи амплитуды в виде
f{E, θ, φ) = Ц-, ( V(_)'a,m(p) Ρ'Π-Φ) χ
XP ] . (cha)K/m(0, q>)dp, (13.1)
-t-«p
230

где Е = ch a\ θ, φ — углы рассеяния; ρ характеризует унитарное
представление группы Лоренца;
2 (ch a)
-*>-'13%-ro'wf/<'· θ· »> "V^ κ»<θ· *)χ
χ sh2odadQ. (13.2)
Функция, для которой справедливы прямое и обратное
преобразования (13.1) и (13.2), удовлетворяет следующим условиям:
квадратично-интегрируема:
{|/(x)|2dx<oo, (13.3)
где χ — совокупность переменных α, θ, φ; dx = ch2adadQ —- элемент
объема;
реализует регулярное представление Tg группы движений на
гиперболоиде, изоморфной группе Лоренца [14]:
TJ(x) = f(g'ix). (13.4)
Пусть Ε -> оо при фиксированном Θ. Если интеграл и
подынтегральная функция суть равномерно сходящиеся функции, то символ
предела можно перенести под знак интеграла [395, 396J. Воспользовавшись
асимптотическим выражением для присоединенной функции Лежанд-
ра Ρϊ (ζ)
p-j~l (z) 1 /г(-/р)«-*1д* . Г(»)^1дЬ \ (135)
^±_,.р(2)"--у^-1г(-ф + /+1) + Г(ф+/+1))\(13-5)
получим
fm(E. *)*>-?= consi С Л (θ, ρ).ιο,η2Εφ, (13.6)
где
Л (θ, p)= ^(-) Г(^,р^/)Г(фг+/+1) Pz(cos9), (13.7)
причем Α (θ, —ρ) φ Л* (θ, ρ).
Следует отметить, что в других системах координат тоже
находится фурье-разложение типа (13.6). Поскольку In 2E ->- оо при
фиксированном Θ, то из-за осцилляции в экспоненте интегрирование по ρ в
(13.6) должно фактически ограничиваться областью малых
значений р. Учитывая это, а также условие кросс-симметрии в форме [397J
f(E + iO, θ) = /(_£-Я), θ) = /*(-£+Λ), θ), (13.8)
нетрудно получить соотношения между амплитудами рассеяния / (£, Θ)
и / (£, Θ) частицы и античастицы соответственно на одной и той же
мишени [165]
асимп (£,9)=Im/ асимп (Ε, Θ), (13.9)
Re /«««π (Ε, Θ) = - Re /асиМп (Ε, Θ), (13.10)
231

т. е.
!/аоимл(£, в)| = |/авимп(£, θ)|, (13.11)
что представляет собой содержание теоремы Померанчука [395] в
случае 9=0, доказанной на основе дисперсионных соотношений и
требования постоянства полного сечения.
Для ненулевого угла рассеяния равенство (13.11) получено в
работе [396] при использовании принципа причинности и локальности,
а также в работах [398, 399] с помощью теоремы Фрагмена — Лин-
делефа. Квадратичная интегрируемость / (£, Θ) требует, чтобы на
бесконечности | / (Еу Θ) | убывал быстрее, чем 1/Е. Если отказаться от
квадратичной интегрируемости амплитуды / (Ε, Θ), то парциальные
амплитуды Л (ρ, Θ) станут обобщенными функциями, например δ-функ-
циями и их производными [165].
13.2. Связь между лоренц- и редже-амплитудами
Следуя работам [152, 153, 159, 166, 167, 173, 400], рассмотрим
разложение амплитуды по представлениям группы Лоренца, отвечающим
редукции на подгруппу О (2, 1). Наиболее просто это можно сделать,
если использовать указанные разложения, реализованные на базисных
функциях группы Лоренца, определенных на конусе [401]. Для
получения параметризации, соответствующей этим разложениям, удобно
построить изотропный вектор
кш=Рг-р0е-А(\ (13.12)
rjxesh A (t) = (pip0)/m2; pt = m (ch ach β, cha sh β, 0, sha) — импульо
одной из частиц, участвующих в реакции (i = 1, 2, 3, 4); р0 = т (0,
0, 0, 1) — импульс начала координат системы Брейта.
Положив ch a = еа, получим kw = me7· (ch β, sh β, 0, 1).
Соответствующая формула разложения амплитуды по НП группы Лоренца
имеет вид8
6-И*оо L-H'oo
/(α, β)= J άσ(σ + 1) J Α (α, /)<Γσα(2/ -f l)ctgji//>z(ch^d/.
ft—too L—<oo
(13.13)
Напомним, что унитарный случай соответствует σ = —1 -f- ip и
I =z — -f iqu Переменные Мандельстама s и t следующим образом
связаны с α и βι
Можно показать, что реджевское представление амплитуды в /-канале
есть аналитическое продолжение части разложения (13.13), соответ-
8 Так как амплитуда — скаляр, то разложение идет лишь по вырожденным
представлениям с ν = 0.
232

ствующей разложению по подгруппе 0(2.1) из s-канала в /-канал.
Учитывая это, получаем, что парциальная амплитуда в /-канале а (/, /)
связана с лоренц-амплитудой Α (σ, /) преобразованием Лапласа
(преобразованием Фурье в унитарном случае):
6+too
a(l9 t) = 2icosnl [ аа(о + 1)е~шА(о, I). (13.14)
б—too
Переходя в (13.14) к унитарному случаю (δ = —1, σ = —1 -f- Φ)
и интегрируя от нуля до бесконечности по р, находим вид лоренц-амп-
литуды, порождающей полюс у функции a (Z, t):
Л (ρ, /)== «pf± »/(/)} t (13Л5>
где f (I) — произвольная функция с Im/ (Ζ) ^ 0; А (р, /) следует
понимать в смысле обобщенной функции.
13.3. Лоренц- и редже-полюсы
В работе И. С. Шапиро [164] показано, что реджевское
асимптотическое поведение амплитуды Sl(t) отвечает полюсу парциальной лоренц-
амплитуды в р-плоскости.
Д. В. Волков и В. Н. Грибов [402] нашли целые семейства
траекторий Редже. Затем Толлер и другие [152, 153, 159,166] в случае / = 0
доказали, что полюс в лоренц-амплитуде генерирует целую серию
эквидистантных редже-полюсов (дочерние траектории). Случай
бесконечно малого переданного импульса рассмотрен Саламом и
другими [167].
Исследованию дочерних траекторий посвящены также работы
[403—411], в которых на определенных моделях дана классификация
редже-полюсов по лоренц-полюеам. Самый простой епособ показать,
возникновение дочерних траекторий состоит в следующем [169].
Рассмотрим амплитуду рассеяния / (s, /) двух скалярных частиц с
одинаковыми массами т. Определим переменные s, /:
s = (Pi + Ρ*? - 2m2 (1 + ch α12), t = (Pl - ps)* = 2m2 (1 - ch α18),
(13.16)
где dik— расстояние между точками ί, k, лежащими на гиперболоиде
радиуса т, т. е. р] = т? = т2. В дальнейшем рассматривается
случай / = 0.
Пусть Pi ζ {^4 :pl — pl — pl — p\ = m2}. Поскольку /(s, 0) есть
лоренц-инвариантная амплитуда (в смысле Tgf (s, 0) = / (g~ls, 0) =
= / (s, 0)), то будем ее разлагать по лоренц-инвариантным функциям»
а именно, по элементарным сферическим функциям, которые
удовлетворяют соотношению
νΊτ^-Σ-Μΐ-Μΐ)· (1317)
где ψρ/m (р^Щ) — функция (7.7); индекс / означает номер частицы.
23&

Поэтому можно написать следующее разложение:
оо оо
f(s, 0)= ^(pj/Z^-pVp-jaO,)^-^. (13.18)
о и
Здесь а12 = а.
Кроме того, известно, что при рассеянии бесспиновых частиц
пространственная часть импульса полностью определяется двумя
компонентами, иначе говоря, можно считать, что pt £ {^3 : pi — pt — р2\ =
= т2}. Это означает, что / (s, 0) следует разлагать по скалярному
произведению функций, реализующих представление веса /группы О (2.1),
т. е. по функциям Лежандра:
Λ (ch а) = У Фи [-%-) Фш (-g-) , (13.19)
т ϊίΐΐΦ -
где φίηΊ(ρι//Πί)=^ Pi (ch aj)e l; I—комплексное число.
Таким образом,
f(s, 0) = -^ J dte(/)P_/-i(cha)/ctgjW, (13.20)
причем
a(/) = J/(s, 0)Pz(cha)shada (13.21)
для унитарного случая / = ψ+iq. Подставляя выражение
(13.18) в (13.21) и выполняя интегрирование по а, получаем
оо
α(ί) = -^Γ^Ρα(Ρ)^(1,ρ), (13.22)
где
р = -
sin π/
2π
Γ(/+2+<Ρ)ΠΓ(-±^Β·)
(13.23)
Если допустить существование полюсов у функции а (р), то,
сдвинув контур, найдем
а(/) = V ϋ-ι_ г(-Щ^-) Г (1±^BL) X
χ Г (- ±3^-) Г (- -Ц^) + J Ф« (Ρ) β (/, Ρ). (13.24)
Из формулы (13.24) видно, что каждый р-полюс порождает серию
эквидистантных полюсов в /-плоскости как полюсов Г-функций.

Глава 14
ПАРЦИАЛЬНЫЙ АНАЛИЗ АМПЛИТУД
ЛГЛГ - И ЛГ'ЛГ-РАССЕЯНИЯ
ПРИ ВЫСОКИХ ЭНЕРГИЯХ
К настоящему времени имеется большое количество теоретических
работ, посвященных JTJ*- и JOf-рассеянию. В основном в этих
работах проводится нерелятивистский парциальный анализ амплитуд при
использовании подхода Гольдбергера и других [412] (разложение по
представлениям группы 0(3) с последующим привлечением модели
Редже (см., например, [402]) либо модели Венециано [413]).
Наша цель_—- дать релятивистский парциальный анализ
амплитуд jrjr- и ЛОГ-рассеяния [170], т. е. дать разложение амплитуд по
представлениям группы 0(3.1).
Сначала рассмотрим скалярную амплитуду. Ее разложение по
представлениям группы 0(3.1), соответствующим сферической системе
координат (S-система), аналитически продолжим из /-канала в s-канал.
При этом окажется, что аналитически продолженная амплитуда в s-
канале будет разложена по представлениям группы 0(3.1),
соответствующим гиперболической системе координат (Я-система).
Затем аналогичную процедуру проведем для спиральных
амплитуд JfJT- и jrjr-рассеяния. В свою очередь, амплитуды s-канала
(собственно s-канала, а не аналитически продолженные из / в s) можем
разложить по представлениям группы 0(3.1), соответствующим S-си-
стеме функций. Сопоставляя эти разложения (г. е. разложения по S-
и Я-системам функций), получаем интегральные соотношения можду
релятивистскими парциальными амплитудами ь- и /-каналов
14.1. Аналитическое продолжение скалярной амплитуды
из t -канала в s- и и-каналы
При разложении амплитуды рассеяния по группе Лоренца возникает
вопрос о связи этих разложений в разных каналах. Если во всех
каналах выделить полюсные части (которые определяютреджевские
асимптотики), то для оставшейся части амплитуды разумно предположить,
что выполняются условия сходимости. Изложение задачи удобно
начать с выбора параметров. Если ограничиться случаем равных масс
и начать разложение с /-канала, в котором выбрана сферическая
система координат, то переход в s- и w-каналы будет сопровождаться
переходом в гиперболические системы координат.
235

Известно, что разложение скалярной амплитуды в сферической
системе координат в /-канале в системе центра масс имеет вид
' ι (ch at)
fit, s, M)=jV(2/+l)at(P)r(!:(-^) ~V+^ X
υ / r t
X Pz(cos6,)p2dp, (14.1)
где
' = (/>i + />i)2=4m2ch2a,; s =, - 2p2(l + *); и = -2/>2(l -ζ);
2 = cos Θ, = cos θη ; ch α* = -~— ; 2 =
Ръ Pi'» />2» № — 4-импульсы частиц и античастиц соответственно в
начальном и конечном состояниях; т — масса.
Переходя из /-канала в s-канал, из области изменения ζ ι — 1 ^
^ ζ = 5~/ ^ 1» приходим в область 1 ^г = * Т"ц < оо, где
4/л2 ^ s < оо; —оо < и ^ 0, т. е. величину (5 — u)/(s + и) можем
обозначить ch βδ.
Так как Ρν (ζ) имеет разрез от —оо до 1, то в w-канал необходимо
продолжить величину (и — s)/(u + s) и обозначить ее для области
4т2 ^ и < оо, —оо < s ^ 0 как ch βΒ. Чтобы оказаться в физической
области s-, w-каналов, нужно аналитически продолжить амплитуду по
/, а именно из области 4/л2 ^ / <; оо (]/7/2т = ch at) перейти в область
—оо < / ^ 0. Тогда величину V—//2т можно обозначить sh α (что
эквивалентно замене at на —α + /π/2). Поскольку продолжаем
функцию по / от / + /ε до —/ — /ε, то знак перед корнем У —tl2m = sha
однозначен. Следовательно, a > 0. Для дальнейшей работы удобнее
представить
Ψρ/W = n-»(-i)} sh"T«P='i^p(cha)
в виде
^ <"> - г (Ι+ΐο) rd+/ - φ) У τ- -Яг-1 · <14·2>
Для получения этого выражения используем свойства Г-функций
Г (1 — х) Г (х) = π/sin пх, связь между Р- и Q-функциями
—1—Р"!"1 (cha)=/e^>Pbl/A ! Qr"(ctha)
и учтем, что / — целое.
Прежде чем осуществить аналитическое продолжение, например,
из /-канала в 5-канал, необходимо в формуле (14.1) от суммирования по
/ перейти к интегрированию по τ (комплексное /), воспользовавшись
в несколько модифицированном виде представлением Зоммерфельда —
236

Ватсона
/<*, *)=Ц(2/ + 1)«/(0Яг(^) =~Jr f <2т + l)^(OctgjtxPc(^)rfx.
/ с
(14.3)
Развернув контур интегрирования, получим интеграл вдоль
вертикальной прямой в виде разложения функции / (/, s) по
представлениям группы 0(2,1)· Чтобы перейти из /-канала в s-канал, нужно
сделать замену переменных cos θ/ ch β, и α, (—α + /π/2) («правило
подстановки»).
Тогда, учитывая формулу
(£*' (-*)--£■ ctg π (τ - φ) Ρ?» (_ х) —ξ- 3ίηπ('τ_/ρ) P7ip (Χ),
получаем
, β Γ(1+τ + φ)Γ(φ-τ) (- -1 +'р),я χ
Tpm Γ(1+/ρ)^2π
[Р~1° (*) - cos π (φ - τ) Ρ?* (- *)]
χ ап% » (Α4.4)
где * = th α. Здесь Г""1 (1 + τ — φ) мы заменили τΓ] sin (ф — τ) χ
Χ Γ (ф — τ). Однако если бы мы сделали эту замену в формуле (14.2)
(при целых /), то не смогли бы развернуть контур интегрирования до
Rex = —1/2 из-за наличия полюсов Г (ίρ — τ).
Учитывая формулы (14.3) и (14.4), можно написать для
аналитически продолженной из ^-канала в s-канал амплитуды следующего
вида разложение:
0 pt—ieo
χ τ ctg ητΡχ (ch β) ch~'a [a+ (ρ, τ) ΡΓίρ (— th a) + α-1 (ρ, τ) P\l(> (th a)],
(14.5)
где
fl+(p, T) = -(2n)7/2eH+i0bjl±i_coS„(tp_T)a(p, χ);
a-(p, ,)-(2«Ге(-Г Ч'-^±1в(р, τ).
Выражение (14.5) представляет собой разложение функции / (s, ί)
в гиперболической системе координат в s-канале в системе Брейта
[142]. В формуле (14.5) переменная α положительна, т. е. мы получили
функцию, заданную только на одной половине гиперболоида. В
дальнейшем же при нахождении связи между коэффициентами разложений
в различных каналах нужно интегрировать по всему гиперболоиду.
Поэтому необходимо задать функцию f (α, β) и для отрицательных а.
237

Это можно сделать, аналитически продолжив выражение (14.5) в
область отрицательных значений а. После этого f (α, β) можно
рассматривать как комбинацию ее симметричной и антисимметричной по а
частей:
О Si—loo
χ τ ctg πτ/\ (ch β) ch~la {Л+ (ρ, τ) [Ρ7ίρ (— th a) +>Γίρ (th a)] +
+ Α~(ρ, T)lP7l4)(^tha)-P7ip(tha)]}, (Ι4·6>
В формулах (14.5) и (14.6) переменные s, tu и связаны с
переменными α, β следующим образом! s = 2m2 ch2 a (1 + ch β), и = 2m2 ch2 a (1 —
-Λβ), / = -4m2sh2a, т. е. tha = V 1=Ш^ · ch^ = 7τίτ·
Аналогично мы могли бы осуществить аналитическое
продолжение амплитуды из a-канала в s-канал и получить выражение типа (14.6),
в котором были бы свои коэффициенты Аи (ρ, τ), а переменные α (и),
β (и) были бы связаны с s, t, и:
*α(«)-/1Γ^Γ.<Αβ(ιι)—i=f.
Функцию симметричную (антисимметричную) в s-канале
относительно замены и <± / можно написать как полусумму (полуразность)
аналитически продолженных из /- и ^-каналов в s-канал амплитуд.
Если амплитуду s-канала / (s, t) разложить по представлениям
группы 0(3,1), соответствующим сферической системе координат
(разложение типа (14.1) только с переменными s, t, определенными как
s = 4m2ch2as, / = —2m2ch2as (1 — zs)), то между коэффициентами
а/ (р) и Α (ρ, τ) (релятивистские парциальные амплитуды) можно
установить соотношение аг (р) = J Κι (ρ, τ) Α (ρ, τ) άτ. Ядро Κι (ρ, τ) и
τ
ядра того же типа будут вычислены в последней части данного пара·
графа (см. формулы (14.48) и (14.49)).
14.2. Разложение амплитуд по парциальным волнам
и переход из канала в канал
Известно [412], что пять амплитуд ΛΟ^-рассеяния можно представить
в виде
/ι-Σ(2/+ΐ)/£(0Ρ,(ζ<), /.-Σ <2/ + ΐ)/&><<)/м%).
/з =2(2/+ 1)^(01^/(2/)+ ztP)(Zt)]-fii{t)P](zt))t (14.7)
/
238

/ι -ΣW+ 1>(-КВД<г() + /!|(0|Р;<г,) + г,Р;(г,Ш.
где
&оо> (0 = <λλ | F' Ι λλ> τ (λλ | F1 | - λ - λ);
/ίαι> (Ο = <λ — λ | Fy | λ — λ> =F <λ — λ | Ζ771 — λλ); (14.8>
/ί,(/)β_ λ"1 <λλ| F'> —λ).
Чтобы коэффициенты разложений были конечны, вклады реджео-
нов нужно вычесть. Вычитая вклады различных полюсов Редже
(полюсов в /-канале) в амплитуды ft (Ϊ, s), необходимо суммы (см.
выражение (14.7)) преобразовать в интегралы, используя формулу (14.3) и
производя, как обычно, замену Ρτ (zt) -> -у [Ρτ (zt) ± Ρτ (—zt)] =
= -γΙΡχ fe) + οΡτ (—zt)] (σ — сигнатурный множитель). Тогда из
формул (14.7) получаем
ει-Η'οο
/?<2) (/, s) = -f J /55» (0 (2τ + 1) ctg πτ -1 [Л (ζ,) + σΡχ (- 2,)] dx -
-4-2 (2/, + 1) ctg π/Λ (О [Л, (г.) + σΡ/ (- ζ,)], (14.9)
/? (/, s) = -f J /Γ (0 (2τ + 1) ctg πτ^ (Ρ', Ρ") Λ -
ε2—ΐοο
ε3+ίοο
-4- J (2τ+1)οί§πτ^ι(0^?(ηίίτ-
- τγ Σ <2/« + 1} ct§ *''r·"'(/) 2^ί (Ρ'> ρ"> +
+ 4-2 (2/* + 1) ctg π/Л* (0 2^/, (Ρ'), (14.10)
где
2*7 (Ρ', Ρ") = [Ρ) (ζ) + ζΡ) (ζ)} - σ [Я)(- ζ) - ζΡ", (- ζ)];
2<?αι(Ρ') = Ρ"/(ζ) + σΡ'/(-ζ);
-1/2<ει<0, — 1/2<ε2<1; -1/2<ε3<2;
/J получается из /з заменой /Г ^ /и;
fin <л m· f j /о ι 1ч + ίστ/Λ Ρτ (г<) — σ/>τ (—ζ,)
U (t, s) = — -g- J dx(2τ + 1)ctg πτ/S, (/) [τ(τ + 1)]Ι/2 +
+ -r^- ? (2/i + 1} °tg π/ίΓ01 <*> I/, </, + !)]'/* ' <14Л1>
239

Нетрудно показать [402], что в амплитуду fx дают вклад при σ = 1
траектории η, π; при σ = —1 — траектории η', Β\ в амплитуду f9 при
0=1 — траектории Р, Р', Л2, а при σ = —1 — траектории ω, ρ; в
/3, f4 при σ = +1 — траектории D', А[, Р, Р', Аъ а при σ = —1 —
траектории D, Аи ω, ρ, /; в }ъ при σ = 1 —траектории Ρ, Ρ', Л2, а
при σ = —1 —траектории ω, р. В формулах (14.9) — (14.11) r{ (t) —
вычет парциальной амплитуды fi (t) в полюсе.
Итак, выражения для амплитуд ft (/, s) сводятся к интегралу вдоль
вертикальной прямой и сумме вычетов в полюсах, лежащих справа от
этой прямой:
ft(t, s) = ft(t9 s) + ZRes (...). (14.12)
Для получения разложения по представлениям группы О (3.1)
амплитуд/,· (t, s) нужно парциальные амплитуды f{ (t) разложить по
функциям ch~!aP7ip (±th α). Воспользовавшись результатами параграфа
14.1, можно написать двойные интегральные разложения в
//-системе для функций fi (/, s), аналитически продолженных из ^-канала в
$- канал:
/ГЛ(/, .)- ]dp±XdrC(P, τ) P^ + f^ x
0 βι—/οο
X [4м.(Р, ч)^г(а) + Айоо)%гШ (14.13)
оо 82-f~io°
lm(t, s)= j*-g" [ dxC^' τ^°(ρ'> Н[^Ш1)(Р, τ) χ
θ ε4—too
Χ ψ£ (α) - ^ΓΤίί) (Ρ, τ) С (α)] - j Φ -f J άτ€ (P. τ> *
X ^(ОИЛ<»(Р. *)Ч&«) + ЛПЬ(р, τ)ι|£(α)], (14.14)
*Λ«-55ττί+ ί *c<>. * Tfr+У χ
Χ [ Λ0Ϋ (ρ, τ) ψ+ (α) + Λ^ (ρ, τ) ψ~ (α)], (14.15)
где
Ч&<«)" '^(Т^^сьГ^ [^(-tha)±Prgp(tha)];
С (ρ, τ) = (2πΓ4ρ2τ^πτ, p0(t)=Vt/2.
Поскольку аналитически продолженные из /-канала в s-канал
/г (s, ί) определяют при больших s асимптотику амплитуды рассеяния,
то приведем асимптотические выражения функций Лежандра и
присоединенных функций Лежандра для написания асимптотического вида
240

^ (2t) - 2 = \—2—) ~γ^-τ
выражений (14.9) — (14.11) и (14.13) — (14.15)!
n—ip/iu ч V"n chipa . „ι |л
Р% (thefts ~ 2<p г|1+(» + т)/2]П1/2 + «р-.т)/2)' (14Jb)
ib+ithai -· 2'~'Γ[(1 + Φ + τ)/2]Γ(φ-τ) ,h-t+tP
tfc, (tn a)«^o fii Γ[(1+φ-τ)/21Γ(1 + φ) Ctl a ~
= Я(р, τ) ch-1+ip a, ψ£ (th a)a-„ ~ 0; (14.17)
~ — ζ =
= η(σ, τ)β(τ)ζτ; (14.18)
3*{Ρ, Ρ")=η(σ, т)р(т)Аы; (14.19)
^(Ρ')βΔί!ΐΖ^ίίΐ^βη(σ| τ).τ.β(τ)./-ι; (14.20)
<^ (/>") = 2~] [ρ; (ζ) + οΡτ (- ζ)] = η (σ, τ) · β (τ) · τ · (τ - 1) · ζτ~2.
(14.21)
Из представлений амплитуд (14.9) и (14.10), а также из
асимптотических выражений (14.17) — (14.21) видно, что при s-> oo (zt -+ оо)
амплитуда /3 (/, s) определяется парциальной амплитудой f[ (/), а
/4 (£, s) — парциальной амплитудой f[\ (t). Принимая во внимание
сказанное выше, легко написать асимптотические выражения при s-^oo
и / -> 0 (в //-системе s и / связаны с параметрами α, β следующим
образом! s = 2/л2 ch2 a (1 + ch β), / = —4m2 sh2 a, ц = ch β > 1) для
амплитуд ft (tf s):
оо Βι+ίοο
77(2 (t, s) = jdp-^- j dxC(p, τ)η(σ, τ) β (τ) Я (ρ, τ) χ
0 8ι—ίοο
Χ Λίο«(ρ, τ) , .+{„ ■ , (14.22)
[ch ι^φα] ι
?S,4>(*. s) = Jrfp-^- j dxC(p, τ)η(σ, τ)β(τ)τ2//(ρ, τ)χ
0 ε,—ίοο
Χ Λ#Β (Ρ, τ) ch5_tPa , (14.23)
1
"МО"
χ / ^|7 я <ρ» τ> Λί° (Ρ» τ> ch"'+iP агГ'· (14·24)
16 1-1980 241
оо бг-М00
}s0, s) = ^- 4- J Φ J dxC (ρ, τ) η (σ, τ) β (τ) χ
0 ε2— ίο

Спиральные амплитуды s-канала
связаны со спиральными
амплитудами /-канала формулой [170]
φ(μί, μ2'> μι. μ2) =
= Σ(-)^λ41(θ2)^,(*;)χ
{λ> ' 2М<2
xC(*i)<'2'(#!) Φ (Κ, λί; λ,, λί).
(14.25)
Вопросы, связанные с
переходом из одного канала в другой,
рассматривались в работах [268, 414—4171. При выводе формулы (14.25)
мы пользовались результатами работы [268] и рассматривали частицы
2 и 2' в s-канале как частицы 2.
Пользуясь рис. 60, легко записать выражения для углов поворота
$1 через переменные s, /. Заметим, чтоО) = π — О, ϋτ = ϋ2 = ΰ\ θί =
= #2, ch sV = ch si ch 11' — sh si sh 11' cos*, ch 11' = 1 — //2m2,
ch si = ch si' = j/"s/2m, откуда
Рис. 60
cos
•—Y-phscV-έ
4m2
(14.26)
Направление углов 2 и 2' учтено в формуле (14.25). Не
представляет труда написть явный вид матрицы поворота спинов при переходе
из /-канала в 5-канал1
л»2
%l
xs4
_xi.
= ΊΓΧ
sin2 θ1
sin2 ϋ
sin2 θ
1 + cos2#
— sin 20
sin2 ϋ
— (l-+-cos20)
sin2 θ
— sin2 О
_ sin 20
(1 + cos2i
sin2 ϋ
sin2 0
— sin2*
— sin 2*
t '
φι
/
фЗ
/
φ4
/
1_ф5
sin2 θ
— sin2 ϋ
1 + cos2 θ
sin2tf
sin 2*
sin 20
sin 2*
sin 20
— sin 20
—2 cos 2*
X
(14.27)
242

Здесь X? = Χ (++; ++); П = Χ (++; }; Xs3 = Χ (-+; -+);
Χ\ - Χ (-+; +—); XI = Χ (—+; ++).
Согласно Гольдбергеру и другим 1412] (см. также [402]), при /-> 0
φ5 -► 0, а из выражения для cos θ и структуры матрицы (14.27) видно,
что при t -► 0 достаточно ограничиться только матрицей 4 X 4, т. е.
рассматривать лишь первые четыре спиральные амплитуды, при этом
элементы матрицы (14.27) будут равны ±1+0 (t).
14.3. Разложение спиральных амплитуд s -канала
и связь между релятивистскими парциальными амплитудами
s- и /-каналов
Вместо спиральных амплитуд XI рассмотрим спиральные
амплитуды Х\> определенные как реджевские члены
Х\ = Х\. (14.28)
Эти амплитуды уже будут квадратично интегрируемы, что позволит
пользоваться формулами разложения (прямыми и обратными) амплитуд
по представлениям группы Лоренца, установленными в работе [142].
Как известно, для спиральных амплитуд можно написать
следующее представление [412]ι
Χ' (μιμ2; μ#2) = Σ (2/ + 1) (μίμ2 | Ff | μ^) <ν2 (*s), (H.29)
/
где Vi = μ1 — № va = μί — μ2, а для амплитуд <μίμ2 | F! \ μ^) —
выражение вида
ι
(μίμ* I Fl I μιμ;> - -J- J &$<„ (zs). (14.30)
—1
Для матриц ^(cosO) справедливы соотношения d^(cosu)«
β ^£.λ_μ (cos Φ) a (—)λ"~μ d^v (cos θ). Удобно ввести функции
(14.31)
Используя (14.30) и (14.31), можем выразить парциальные
амплитуды f{ (s) через полиномы Лежандра!
ι
и,-4- ί ~^2 <s·')р' <*«) dz°> <14·32)
, /i'(ii)(s) =
"" Τ J I'"<3><s·')ρι<ζ·) Η ^/+1 ^ /3<« (s· 0Jdzs, (14.33)
1
/&1<в>--^| /,(s. o[-^±i2.(^iW-/,/+1(«.))] <fe„ (14.34)
16* 243

где /о (s) — синглетная амплитуда, /оо (s) — триплетная амплитуда с
/' = / ± 1; /{ (s) — триплетная амплитуда с / = Z; /п (s), /01 (s) —
триплетные амплитуды с / = / ± 1.
Чтобы получить представление для релятивистских парциальных
амплитуд а{ (р), воспользуемся разложениями [142]
ι ' (сНа)
-Ир
/Ш-|р2ф1^(Р)ге(ф^/) 71Гг К/т(9' φ)· (14·35)
-/
(cha)
fli«(p)-f/(6)
ί'
г (Φ)
Г (/ρ-/)
И sha
Ι2=ξΙ-Ι2=1·
4 _,„ *- -' <Ρξ
W Π«(θ, Ф)1Г. (Ι4·36>
Это так навываемое разложение скалярной функции по
представлениям группы Лоренца в сферической системе координат (S-система).
С помощью формул (14.35) и (14.36) можно записать
оо
- Т +iQ
(cha)
sh a
(14.37)
(cha)
a'(p)=j/i!
(s)
Γ (Φ)
Г(Ф-/)
W—d^(fl).
/sha
(14.38)
где ί/μ (α) = sh2oda.
Более удобно пользоваться нормированными функциями
Ψρ/W- | г (ф — ,) |
- т +и>
(cha)
Klhl
(14.39)
Принимая во внимание сказанное выше, для парциальных ампли
туд di (p) получаем выражения
я6(Р, s = 0, / = /) | j_ г г I Ms, О
floo(P, s = 1, / = / ± 1) I ~ 2 J i I /2(s, 0
+
a{(p, s= 1, / = /)
a'„(p, s= 1, j = l± 1)
/8 (s, 0
oo ι
^(zs)tp/(a)dzs^(a).
(14.40)
Us, t)
Ρ}&) +
Μ*. 0
(/ + l)P/-1(25)+/P/+lfe)
2/+1
^ρ/(«)<Μμ(α), (14.41)
244

οβ 1
<&», >ai, i = i± i)= -^ff-j'j' /.(«, О ЗД+1* χ
0 —1
X [/>,_, (zs) - Ρ,·+1 (z,)J ψΡ/ (α) ώ,έίμ (α). (14.42)
Чтобы получить связь между амплитудами а{ (р) и Л^ (τ, ρ),
необходимо в формулы (14.40) — (14.42) вместо β (s, t) подставить их
выражения через Д· (s, /)> аналитически продолженные из ί-канала в s-ка-
нал и представленные в виде (14.13) — (14.15), и выполнить
интегрирование по dzs и άμ (а).
Ввиду громоздкости выражений будем подставлять в интегралы
асимптотические формулы для f\ (s, 0 (s -> оо, t -> 0) и производить
асимптотическое интегрирование.
Учитывая формулы (14.31), а также матрицу (14.27) при / -> 0,
получаем
Ласимп (S, Г) ^ -g- {/2аеимп — /1 асимп — 2/ [/3 асимп + /4 асимп]}» (14.43)
/2асимп (5, ?) ^ —g- {/2асимп ~г /11асимп — Z* [/Ласимп — /4асимп]}» (14.44)
^jps /0 а >^ * I '2асимп "Г 2^/Засимп _. Μ асимп г;'4а«имп
/3,4асимп (S, 1)£Ζ -ψ] r-j— +
2 1 1+г5 ^ 1_г5
1 J /2асимп ι ZVЗасимп _ ' 1а«шп 2#4авимп V /1 л лх.\
- "г 1 2 + г=^ j · (14·45)
Как уже отмечалось ранее, при t -* 0 и s-> оо амплитудой /5 (s, /)
можно пренебречь.
В формулы (14.43) — (14.45) подставляем выражения (14.22),
(14.23). Полученное представление для $аСимп ($> 0» в свою очередь,
следует подставить в (14.40), (14.41) и проинтегрировать по dzs и άμ (а).
Для вычисления интеграла нам понадобится асимптотическое
выражение функции
*,<«) ~ 1^*1* 2
*'w«;; ιγ(φ-/)ι
1 г 1 . 1
2 2 Г(ф)сЬ 2 а .
Г(1+ф+/)/в
. 2 2 Г(—tp)ch 2 а
+ Γ(ΐ—ίρ + /) VU
(14.46)
и связь параметров α, θ5, α, β:
(14.47)
г, = cos 0S, zt — ch β,
245

которая получается из выражений для s и / в сферической системе
координат s = 4/л2 ch2 a, t = —2/л2 sh2 а (1 — г8) и гиперболической
системе координат s = 2m2 ch2 а (1 + ch β), / = —4т2 sh2 α при а -> оо
(s-> оо).
Выполнив интегрирование в учетом формул (14.46) и (14.47),
получим интегральные соотношения между релятивистскими
парциальными амплитудами а\ (р) и At (ρ, τ)ι
<(р; s = 0, /-0
αοο(Ρ, s= 1, / = /± 1)
g,-fio°
= #(p, /)-f
8i-H'°°
ί,
8ι—too
=F At (ρ, τ)) - j τ*ίίτΛί°τ/ (4f (ρ, τ) ± Atf (ρ, τ))
j dxM°0v(At(p, τ)Τ
, (14.48)
ε«—too
α{°(ρ, s=l, /-/)
aft
3ί (ρ, s=l, / = 0 · Γι
ζ<ί(ρ, s=l, / = /±1) 2 еД те 2
x[Af^ + -|^Af^_1+irLrAl"t/+I]i4^(p, τ) +
ε2+ί<»
+ ^ν (ρ, /·) 4- j ^τ -|- [лс,- + -^- м^_, + -^Lj. M°m+i I x
ε8—ίοο
{ε,+ίοο
Ει—ίοο
]а^°Ф, τ)- Γ ύίτ-^χ
τ+1 Ρ/-1 '
2/ + 1 ^τ+1ρ/+1
ε2—ίοο
χ [μ?+Ιρ/· - -Ш- Λί?+, ρ/_, - 1Γ^Τ Μ?+1 ρ/_, ] ЛЙ° (ρ, τ)} , (14.49
где
N(p,i):
Κπ|Γ(ίΡ)|Γ(-(·ρ)
|r(ip-/)|r(-ip + /+l)2,/2+*·
Л1?р/ = С(р, τ)η(σ, τ) β (τ) Η (ρ, τ) Ι (ρ, /, т) = Я(р, τ, <χ)/(ρ, /, τ);
Λί?Ρ/ = /?(Ρ, τ, σ)/[(τ+ 1), /, ρ]; С = ^f™ ;
ϊΐ(σ, τ)==—Χ, ί
(2я)«
246

2,-,Л| + /р + .\Г(,р_т| 2>г(,+ ')
(-+-^)Г
(-)/ 2τ+'
/(Ρ, /,τ) =
(-τ + 2φ£Ρ+/+ι
2 / \ 2
При выводе формул (14.48), (14.49) мы использовали значение
интеграла
Г (I 4-х)"Ρ (x)dx У+11Г(а + 1)]«
]_ν+χ) ^vWa*- Γ(σ + ν + 2)Γ(1+σ-ν) ·
Итак, применяя формализм спиральных амплитуд и представлений
группы Лоренца, получаем разложения амплитуд jrjr- и ЛО^'-рас-
сеяния в 5- и Я-системах и устанавливаем связь между релятивистскими
парциальными амплитудами s- и /-каналов.

Глава 15
ИССЛЕДОВАНИЕ АНАЛИТИЧЕСКИХ
СВОЙСТВ ФЕЙНМАНОВСКИХ АМПЛИТУД
ГОМОЛОГИЧЕСКИМ МЕТОДОМ
Фам, Фруассар, Ласку и Фотиади предложили исследовать
аналитические свойства фейнмановских интегралов методом теории гомологии
[418—42U. Возможности традиционного подхода, т. е. практического
осуществления аналитического продолжения, прослеживания
движущихся особенностей, построения пересечений многообразий,
содержащих особенности, и т. д., быстро иссякают с ростом числа переменных.
В новом методе громоздкие аналитические выкладки заменяются
изучением топологических характеристик дополнения к многообразиям
особенностей. Он нечувствителен к увеличению числа переменных и
обладает, помимо этого, многими другими преимуществами. Сначала
сформулируем основные определения и перечислим факты,
необходимые для понимания дальнейшего. При этом, разумеется,
пренебрежем строгостью, необходимой для математических работ, и
ограничимся! по возможности, наглядными представлениями [419, 421, 422}.
Рассмотрим выпуклый л-мерный полиэдр Δ", снабдим его
ориентацией ε, τ. е. упорядочим определенным образом множество его
вершин. Ориентацию любой из его (п — 1)-мерных граней выбираем так,
чтобы она была согласована с ε. Для этого вычеркнем из
упорядоченного (в соответствии с ε) полного набора вершин Δ" ту, которая не
принадлежит рассматриваемой грани. Оставшиеся вершины зададут
в ней ориентацию, индуцированную ε (согласованную с ε). Переход от
ориентированного полиэдра Ап к сумме всех его (п — 1)-мерных
граней, снабженных индуцированными ориентациями, назовем взятием
границы и обозначим символом д.
Элемент л-мерной цепи σ определим как «-мерный выпуклый
ориентированный полиэдр Δ". Сумма конечного числа таких элементов,
взятых е целыми коэффициентами, называется л-мерной цепью yi
к
<у = 2 яга.·. Граница цепи д (у) определяется по формуле ду =
k
= 2^д (σ,·). Доказывается, что д2о=0 для любой цепи σ. Цепь с
нулевой границей называется циклом С\ дС =0. Может случиться так,
что некоторая /ι-мерная цепь А может служить границей (п + 1)-
мерной цепи Βι А == дБ. В этом случае цепь А называется точной.
248

Точная цепь всегда имеет нулевую границу: дА = д (дБ) = д2В = О
и, следовательно, является циклом.
Циклы размерности η (сокращенно «-циклы) можно умножать на
целые числа и складывать. Они образуют абелеву группу Ln (группу
«-циклов). Множество точных цепей образует в Ln подгруппу Вп,
называемую подгруппой границ.
Фактор-группа Нп = LJBn называется «-мерной группой
гомологии (рассматриваемого пространства). Если пространство fe-мерно^
то η = О, k.
Нас будут интересовать группы относительных гомологии. Это
означает, что, разбивая циклы на классы, считаем эквивалентными
(гомологичными) не только такие циклы, разность которых служит
границей цепи, на единицу большей размерности, но и циклы с
разностью, принадлежащей выделенным многообразиям (в нашем
случае — поверхности Ландау).
Помимо граничного оператора д, понижающего размерность цепи
на единицу, нам понадобится так называемый кограничный оператор
δ, повышающий размерность цепи на единицу. Наглядно действие δ
можно представить следующим образом. Если σ — одномерная цепь
(ориентированная прямая), то δ сопоставляет с ней поверхность
кругового цилиндра, ось которого совпадает с σ, а ориентация в любом
поперечном сечении (направление обхода) образует с ориентацией σ
правый винт. Оператор δ позволяет значительно упростить вычисление
групп гомологии (теорема Фруассара).
Введенные выше понятия оказываются весьма естественными для
качественного описания свойств интегралов функций многих
переменных, в частности для классификации интегралов Фейнмана.
Вообще говоря, интегралы Фейнмана образуют широкий класс
специальных функций нескольких переменных, теория которых пока еще
не развита. Топологические методы позволяют выяснить общие
свойства этих функций.
В этой главе нас будет интересовать вопрос об особенностях
интеграла, т. е. о том, какие из особенностей подынтегральной функции
могут стать особенностями интеграла.
Чтобы ответить на этот вопрос, многообразия особенностей
должны зажать цепь, по которой производится интегрирование («пинч»),
а другие циклы (они называются исчезающими) должны стянуться в
точку. Информацию о возможных сингулярностях интеграла получим*
изучив пересечения цепи интегрирования с исчезающими циклами в
терминах так называемых индексов Кронекера, или индексов пересечения.
Пусть Мх и М2 — дра ориентированных многообразия
размерностей k и / в W-мерном (для простоты евклидовом) пространстве,
пересекающихся лишь в конечном числе точек. Размерности k и /
удовлетворяют' равенству k + I = N. В каждой из точек пересечения Мг иЖг
находятся в общем положении, т. е. касательные гиперплоскости,,
проведенные к ним в точке пересечения, нигде не пересекаются. Если
Λ1] и М2 — одномерные кривые на плоскости, то общее положение
для них означает, что в точке пересечения касательные (а
следовательно, и нормали) не коллинеарны.
24Й

Будем говорить, что во всех точках пространства заданы
стандартные согласованные реперы, если от одного из них к другому можно
перейти с помощью параллельного переноса и однородного линейного
преобразования с положительным определителем.
Рассмотрим подокрестности Ux и U2 точки пересечения О, лежащие
в Мх и М2. Пусть {vlt v2, ..., vk) — набор из k линейно независимых
векторов (касательных к Λί, в точке О), определяющий в ί/χ
ориентацию, согласующуюся с заданной (многообразия Мг и М2
ориентированы). Пусть, далее, {vk+u ^+2; ..., vN\ — набор из I линейно
независимых векторов, касательных к М2 в точке О, также определяющий в
U2 ориентацию, согласованную с заданной. Поскольку Μλ и М2 в
точке О находятся в общем положении, объединение наборов {vlf v2f ..., vk,
vk+u .·., vn] задает репер во всем пространстве. Если этот репер
согласуется со стандартным в точке О, то индекс Кронекера KI в точке
О равен +1; в противном случае К1 =—1 Если Λίι и М2 в данной
точке не пересекаются, то /С/, по определению, полагается равным нулю.
Индекс Кронекера полного пересечения (состоящего, по предпо·
лржению, из конечного числа точек) равен сумме индексов в отдель»
ных точках. Зная индексы Кронекера KI для пересечения цепи
интегрирования с исчезающими циклами, с помощью теоремы Пикара —
Лефшею сможем ответить на вопрос о том, что происходит с цепью
интегрирования при обходе того или иного особого многообразия.
Такова общая схема излагаемого ниже материала. Разумеется,
нарисованная нами картина сильно упрощена и не претендует на роль
сколько-нибудь серьезного введения в теорию гомологии. Наша цель
состояла лишь в том, чтобы облегчить труд читателя, соверешенно
незнакомого с применяемым нами методом.
15.1. Стандартная форма интегралов и сингулярные поверхности
(поверхности Ландау)
Говорят, что
/(0-f πω(χ·° (15.1)
f Π 5. (χ, t)
i
— интеграл стандартного вида, если V t 6 Τ (Τ — пространство
параметров) уравнения St (х, f) = О задают в я-мерном комплексном
многообразии компактные аналитические подмножества, аналитически
зависящие от /; ω (*, f) — регулярная внешняя η-форма на Х>
голоморфная при / £ Т\ Г с: X — U Si (x, t) — компактный л-мерный
i
цикл; X компактно, а многообразия St (x, t) = О находятся в общем
положении при / ζ Т.
В фейнмановских интегралах в /-мерном пространстве (/ = п)
_ _ _ 1+2 _ _
St (χ, I) есть р^ = {q I ptq = 0}, ptq = 2 (Pt)k4k, x — замыкание Σ'
пространства Σ' (комплексная /-мерная сфера 2 Qi + ?/+ι β 1)> а
1=1
250

ω (χ) и Г переходя! соответственно в ω (q) и Re Σ . Более подробно
это покажем в следующем параграфе.
Поверхности Ландау (на которых функция, задаваемая
интегралом (15.1), имеет особенности) определяются уравнениями [419—423]
Σ** **£0 -0» *=»L 2, .... / + 2, 5,(^,0 = 0,(15.2)
ι= 1, 2, 3, ... , т.
Здесь m — число пропагаторов в интеграле (15.1).
Учитывая замену St (x, t) -> pt (qt ρ), эти уравнения
переписываем в другой форме;
det(pi -ρΛ) = 0, (15.3)
где (pi*Pk) — скалярное произведение (I + 2)-мерных векторов.
Поскольку определитель (15.3) может обратиться в нуль вследствие
равенства нулю миноров, то особенности Ландау (в дальнейшем L (/))
можно представить в виде
L(t)= U ί*ν(0. (15.4)
β.ν
где Ц (t) — миноры определителя (15.3); у — коразмерность, т. е.
число уравнений, определяющих многообразие в некотором я-мерном
пространстве.
Рассмотрим случаи с γ = 1.
Основная цель исследования фейнмановских интегралов —
установить характер особенностей Ц (/). Для этого предварительно нужно
установить число функций, которые можно определить с помощью
данного фейнмановского интеграла. Ответы на эти вопросы дают
теоремы Фруассара и Пикара — Лефшеца.
Число различных функций, которые определяет данный фейнма-
новский интеграл, равно числу независимых циклов
(соответствующей размерности) группы гомологии дополнения X — U /?/. Эти
циклы легко сосчитать из теоремы о разложении (теорема Фруассара)!
Н* {Т ~ М, ?<) " н* (Σ' ~ Д1 Pj) = ®в/И//в*-«м ?р η Σΐ)> <15·5)
β€={1, ..., т—\).
Здесь Hcq — компактная ^-мерная гомологическая группа; δ — ко-
граничный оператор; *р = ρ(ι Π Π Ρί3; Ι — β — размерность
пересечения β/7 Π Σ'; рт — I — размерность бесконечно удаленной
плоскости.
Известно [419], что если q = ρ, 0, то Hcq (Σρ) = Ζ, Щ (Σ°) = Ζ Χ
Χ Ζ. Здесь Σρ является р-сферой, а Ζ — свободная абелева группа
целых чисел по сложению. Циклы, соответствующие разложению груп-
пы HU Σ — (J pfj9 обозначим через е$ (базис группы), β с: {I, ...
251

..., m — 1}. В случае β = / согласно Hi (Σ°) = Ζ Χ Ζ имеются два
цикла е£9 е'р', причем е$ = ef — ejT. Следует также отметить, что
е* = δβ(9νβ, (15.6)
где е3 — исчезающие циклы группы Hcq (Σ*, β/?); ^p = pix U ... U Λβί
д — граничный оператор.
Введем е0 = (—/Г, Г = Re Σ1, 0 — пустое множество.
Вопрос о характере сингулярностей фейнмановского интеграла на
различных римановых поверхностях можно изучать с помощью
теоремы Пикара — Лефшеца:
Λρ^Σ'-£ρ^Αρ(Σ'- U^^j, рф1% p = l = m-l,(l5.7)
hi^hi + ne^ p = l>m— 1,
которая показывает, как варьируется элемент hp \Σι — (j ~ρλ
группы Нр γΣζ — U ρ λ при обходе в положительном направлении
сингулярного многообразия Ζ,β. В формуле (15.7)
4 </-ΙβΙ+ΐ)</-|βΙ+2>
п = (—)2 KI(h, e&). (15.8)
Таким образом, структура сингулярностей интеграла полностью
определяется таблицей индексов ΚΙ {Κ £β)» т. е. индексов Кронекера,
которые легко вычисляются с помощью формул Картана [424, 425]
ΚΙ (Γ, *β) = (-)2
О, γ с£ β,
4 (/-|βΐχ/-|βΐ+ΐ) 4 <Μβΐ> c-iPl-1)
/(/(*ν, *β) = { (—) +(-) . Υ=·β, (15.9)
4 tf-IVlH'—hrt-H>
(-) . Ydp.
Поскольку используем теорему Пикара — Лефшеца в форме (15.7)
и изучаем случаи простого пинча, то для нас существенно ограничение
/>т — 1.
Поэтому рассматриваем гомологическим методом лишь
5,4,3-угольные диаграммы для / = 3 и 5-угольные для / = 4.
Если ввести базис {^}, дуальный к базису ев в смысле ΚΙ (ββ, уе) =
= δβν для β с {1, ..., т— 1},
R 4 <«-1Э'н'-/й-ь
** = (-) (*.β-«.β*) (15.10)
для βcz {1, ..., т— 1}, 0<| β|< /,
0«в(_)'/ад+1> _f, = ^ (-)i/HvVv.m, i* = «.,,.-*,
252

для β cz (1, 2, ..., m — 1}, Ι β Ι = /, то, используя формулы (15.9),
можно получить соотношения между циклами, или соотношения
между абсорптивными частями фейнмановской амплитуды [425]
в^в{(_1)'-/*_1}е,_ 2 (~)2 ββ.
YC3C{1.2 т—\)
(15.11)
Замечательной особенностью этого соотношения является то (в
случае, если / нечетно, а γ = 0), что цикл интегрирования Г можно
представить в виде линейной комбинации циклов
_, 413Κ2/-Ι3Ι-1)
2Г = ет+ 2 (-)2 *. (15.12)
ЗС{1.2 т-1>
Первоначальный интеграл можно записать как линейную
комбинацию его абсорптивных частей. Отметим, что элементы базиса еь etj,...
соответствуют диаграммам, в которых t-пропагатор, i, /-пропагаторы
и т. д. заменены на 6-функции.
15.2. Нерелятивистские однопетлевые 5, 4, 3-хвостки
И. С. Шапиро 1426] предложил описывать амплитуду прямых ядерных
реакций с помощью так называемых нерелятивистских диаграмм,
уравнения особенностей которых (уравнения Ландау [423]) получены
ватем Л. Д. Блохинцевым, Э. И. Долинским и В. С. Поповым [427].
В этом параграфе, используя методы теории гомологии, находим
характер сингулярностей амплитуд, определяемых
нерелятивистскими диаграммами, строим группы гомологии и определяем различные
линейные соотношения между скачками амплитуды [428]. Хотя
детально будем исследовать лишь 5- и 3-угольные диаграммы, вопрос о
приведении интеграла к стандартной форме изучим на примере п-уголь-
ной диаграммы.
Приведение интеграла к стандартной форме. Интеграл,
соответствующий однопетлевой диаграмме, показанной на рис. 61,
записывается в виде 1427]
Fn = lim f dz f dlq\\\ (tf- 2/щв, _ ιδΓι\
(15.13)
Здесь qit mit ef — импульсы, массы и кинетическая энергия
виртуальных частиц.
В каждой вершине выполняются следующие законы сохранения!
4% + Р*+1 = ?Ч-ь £f+i + ^i == ^ί+it
Et « pb2Mt + Af „ «г, = 9?/2m, + mu
pit Mt — внешние импульсы и массы.
Рассматриваем вместо 3-мерного /-мерное пространство.
Деформируя контур интегрирования и используя теорему о вычетах.
253

представляем выражение (15.13) в форме
4»
где
Рис. 61
(15.14)
(15.15)
(15.16)
вЪ - (ι
Q7-{2q-Αϊ+ ?+&);
Λ-('-ΐΓ(·'-^4
α? - "5" **) ~^ C4 £* ~%Ej+mv)+2тФ
(15.17)
t ζ Τ — пространство всех внешних параметров; индексы /, v
нумеруют пропагаторы и вычеты соответственно; 2п > I + 2 — условие ехо-
димоети интеграла; ak (I) = 2 ρμ (/).
Таким образом, /г-хвостка превращается в сумму «-приведенных
т = (/г — О-хвосток с пропагаторами типа (15.15).
Для применения методов алгебраической топологии к изучению
аналитических свойств интеграла его требуется привести к
стандартному виду (см. параграф 15.1). Осуществим последовательность
операций. Сначала погрузим R1 -> /?/+1 — {0} е помощью отображения
χ £ R1 -+ ЗГ Έ3* (х, 1) ζ Rl+\ Сопоставляя с V χ 6 R* его прообраз при
стереографической проекции
2(*, 1)
аг ·.
I)2
>w
1 в R "*" . При таком пре-
переходим на сферу 2 */ + (*ι+ι
г==1
образовании область интегрирования становится сферой. Дополним
R1 — {0} началом координат и осуществим вложение #/+1 -> (D/4"! ->
-> СРЖ (7?/+|, (С/+\ CP/+1 — соответственно вещественное,
комплексное и комплексное проективное пространства размерности
1+ 1).
В CPi+l уравнение сферы в однородных координатах имеет вид
2 Μ + Я/-и = */+2·
Объемлющее пространство X становится замыканием Σ; простран-
ства!' (комплексная /-мерная афера 2 *? + *?+ι = 1). Поверхности
Q/ переходят в S? = X (] р* (/), где р) (/) — аффинная /-плоскость в
254

(Сж, а ρί (Ι) — соответствующая проективная /-плоскость в СР/+3.
Интеграл (15.14) в результате преобразований принимает вид
/>(0-V<-2*0 f JLbtL±lLt£^-.t (15.18)
где
2?-{,:|«-ο}·.
*! = -^
*Ж
*/+?
Σ'
(15.19)
(15.20)
(15.21)
=(|,^^^)^1Л ■··Adx/+2· (ΐ5·22>
* = (*ΐι ···» *ι> */+ь **+г)— однородные координаты в C^/+I;
q = (x» ..., xи Χι+u — ^/+2)е(СЯ/+|;
й= [2(7 · ЛГ, β?ν- ie- 1; ί(β?ν —ίε+ 1)]. (15.23)
Поверхности Ландау. /Многообразия особенностей Ландау
задаются уравнениями det (ρ), ρ]) (см. (15.2), (15.3)).
Используя выражения (15.16), (15.17), (15.23), получаем
(at — α,·)2 —2(mi— т}) χ
l-^U(l- m>
|(аг — αν)2 —
-2(m,--mv)(2 £*— Σ £a) + 2(m,-mv)2 —
\*=1 a=l / J
■ -J- (a,— avf — 2{т3 — т)Ы £β-Σ E0) + 2(mj — mvf
mv L \e=i o-\ J
«v/\ mv)\
2(mi — m})2 — Rii +
+ -5-[^v-2(mi-mv)2] + ^i.[/?/v-2(m/-mv)2]], (15.24)
OTv mv J
(pV)2 = _4^_^LJ ^.[^^г^-лкП (15.25>
255-

Ввиду большого числа параметров вычисление определителей
приводит к громоздким формулам. Поэтому запишем явный вид только
простейшей поверхности Ландау
а и а и
исэ*-
П {Riv — 2 (mi
ΐφν
■ mv)2} = 0. (15.26)
Это так называемые пороговые особенности. Выражение L{f$t-*
-> det'Mi = 0 для фиксированной энергии дает, например, в случае
3-, 4-хвосток квадратное уравнение для переданного импульса.
5- и 4-угольная диаграммы в случае I = 3. Рассмотрим 5-угольную
диаграмму, т. е. η = 5, т = 4, ν = 1, 2, 3, 4, 5. Из теоремы Фруасса-
ра (15.5) следует
/ΤΗΣ»- U Р] =Яз Σ3
/¥-ν
U р7 -
ίΦηι
ζ + ζ
(15.27)
Таким образом, восемь элементов из дезяти: Г, et (v), eif (ν), ец%
(пара et'jk (ν) формирует лишь один цикл интегрирования eijk (ν) =
= efjk (ν) — β^ (ν)) образуют базис группы Н\ (Σ3 — |J "pv\ для
каждого ν, ν Φ ί, /, &; i φ /', &; / Φ k. Заметим, что число восемь
следует также из формулы для образующих группы я0бР = 2т"~1 при
т = 4. Однако если через т обозначаем бесконечно удаленную
поверхность, то т также не равно v.
Приведем в табл. 15.1 индексы Кронекера для 5-хвостки.
Используя теорему Пикара — Лефшеца (15.7) и табл. 15.1,
находим, что поверхности Ландау Ц> Ρβ соответствуют особенности типа
квадратного корня, а поверхности Lv{j и L^z отвечают соответственно
логарифмической и полюсной особенностям. Действительно, после
двукратного обхода поверхности Ц
r-+r — ei-+r — ei — ei + 2ei^r (15.28)
снова возвращаемся к исходному контуру Г, а при обходе k раз
поверхности Uq получаем контур
Γ-»Γ + β£/-*Γ + β,/ + *ί/-* ... ^r+kec/. (15.29)
Аналогичная процедура легко проводится и для поверхностей Lifk и
г V
Таблица 15.1
/V
κι
г
ei
е{/
eifk
etjki
e,i
—1
—2
0
0
0
'.*/
1
—1
0
0
0
e*ifk
— 1
—1
— 1
2
0
eilfkt
—I
—1
—1
1
0
256

Наконец, воспользовавшись формулой (15.11), выпишем
соотношения между абсорптивными частями фейнмановского интеграла:
eim (ν) = 2 etj (v) + еци (ν), eijm (ν) = — 2еч (ν) — ei/k (v), (15.30)
/cp
2Γ = ет (ν) +Σει(ν)-Σ еи (ν) - eifk (ν).
Под β подразумеваем множество {1, 2, ..., 5}, из которого исключе ы
элементы ν и т.
Для квадратной диаграммы (случай η = 4, т = 3, ν = 1, 2, 3, 4)
базис группы Hi ΙΣ3 — U /?v) состоит из четырех элементов· Г, et (ν),
V ΐΦν j I
etj (v).
Значения индексов Кронекера для 4-угольной диаграммы легко
получить из табл. 15. 1j для этого в ней нужно вычеркнуть последнюю
строку и последний столбец. С помощью теоремы Пикара —Лефшеца
нетрудно установить, что, как и прежде, Ρ и Lvijk — корневые
особенности, a Vti — логарифмическая.
Формула (15.11) дает следующие соотношения между
абсорптивными частями 4-хвостки;
eim (v) =a etf (ν), ецт (ν) = — 2βί/ (ν), (15.31)
2r=em(v) + 2ef(v)-ei,(v)f
«'cp
где
β с ({1,2, 3,4} -ν, -m) —
|{1.
1{ΐ.
{1.
2},
3},
2},
V
V
V
-з,
= 2,
= 4,
m
m
т.
= 4.
= 4,
= 3,
Треугольная диаграмма. Из выражения (15.18) в случае I = 3,
л = 3 видим, что в знаменателе появляется дополнительный
множитель Pq_== *4 + Ч- Сингулярности, возникающие при необщем
положении р0 и pty называются сингулярностями второго рода или нелан-
даувскими сингулярностями.
Рассмотрим сингулярности треугольной диаграммы обоих типов.
Для особенностей такой диаграммы Lv = \J Ц, β с {0, 1, 2, 3 — ν} —-
β
— {0} имеем уравнение
1+={ίζΤ\ϋύ(ρΤρΤ)-0}9 ί,/ζβ.
Пусть
(ρ {1,2}, ν-3,
Λ-{β|{0}2β}-ρ({1,2,3,-ν})- ρ {2,3), ν= 1,
1ρ{1,3}, ν = 2,
Α = {β| {0} ζβ} =ρ({0, 1, 2, 3, - ν})-ρ({1, 2, 3, -ν}) U {0}.
17 1-1980 257

Тогда Lv = Lv U Λν, Lv = U Ц, Л = U H = ti U tf/. Здесь Л —
А А
обычные особенности (особенности Ландау), уравнения для которых
легко найти, либо приравнивая нулю диагональные элементы матрицы
\PiPl {ΡΪΥΙυζΑ
либо вычисляя ее определитель.
Поверхность р„ = xt + х% можно записать в виде р0 = (р0 · q), где
р0 = (0, 0, 0, 1, t)._
Учитывая, что р\ = 0, /)0 · р) = —2, выписываем уравнение для
неландаувской особенности Ц1} [419]:
/О —2 —2 \
del ( - 2 0 pi Q>) ~ р!) ) = 0. (15.33)
V-2 pKpJ-p)) о /
Используя (15.23) (либо (15.24), (15.25)) и вычисляя определитель,
получаем
i2,i = {/er|(i4?-i4S)»=so}f Lj23 = {/eт\(А\-л^=о},
^13 = {^^|(Л?-4)2 = 0}, (15.34)
Lo, Lot — пустые многообразия. Поскольку 3-мерное импульсное
пространство евклидово, то из (15.34) следует
Л? = Л32, Al=Al Al=Al (15.35)
Принимая во внимание (15.16), имеем, например, для ν = 3
р2 (т3 — тг) = рх (щ — /п2), ръ (т3 — тг) = рх (т2 — /п3), (15.36)
т. е. неландаувские особенности возникают в случае линейной
зависимости внешних импульсов. Следует отметить, что в отличие от
релятивистской 3-хвостки [419] в нерелятивистском случае мы получили
[428] неландаувские особенности, зависящие от внутренних масс.
Рассматривая в качестве бесконечно удаленной поверхности р0, как и в
случае 4-хвостки (р0 играет роль дополнительного пропагатора),
получаем четыре независимых цикла: Г, е,- (ν), ец (ν) и тот же характер
особенностей для поверхностей Ljj> (L/, Lot*/ — корневые, Zj;· —
логарифмическая).
Естественно, что и соотношения между циклами будут типа (15.31):
ею (ν) = еч (ν), еы/ (ν) = — 2eij (ν), 2Γ = е0 (ν) + 2 *t (ν) — еч (ν).
(15.37)
15.3. Релятивистская 5-хвостка
Методами теории гомологии исследуем аналитические свойства 5-
угольной диаграммы, показанной на рис. 62 [429].
Используем следующие обозначения: pt — внешние импульсы (р =
258

β (Ρ* Ρ)> Ρ = (Φο> Ρ)); <7 = (<7ο> ?) — внут-
ренний импульс; mf — внутренние массы;
ι
Щ = Σ Л, ί = 1» 2, ..., 5; аъ = Ο, α, =
s=l
= bh Qj = (β/ + q)2 + my — пропагаторы
Qi> = Q/ + ie.
Совокупность параметров (aif ra;) = /
образует некоторое подмножество в
25-мерном комплексном пространстве (С25 = 7\
Как известно, интеграл Фейнмана,
соответствующий этой диаграмме, можно
представить в виде
Рис, 62
/i=$d*<7 $ dq{
1
О 5
Σ<?/8
/-1
(15.38)
Повернув контур интегрирования обычным образом, получим
7a=af d4q-~ . (15.39)
* Π Q/e
/»ι
Здесь интегрирование ведется по вещественному 4-мерному евклидову
пространству. Форма (15.39) не имеет еще стандартного вида,
необходимого для применения нужных нам теорем. Проведя
последовательные операции (см. параграф 15.1), осуществляющие
стандартизацию интеграла, находим
ω4 (*б + *е)
где
МО- $
Σ4={<7|<72 = 0}; p^-folprf-0};
(15.40)
ί=1 5
ж = (χ, х6, хл) — однородные координаты в (DP8; q = (χ, xit — ιχβ) f
jt?/e = [2α;, c/ + m2+ /ε + 1, ι(a? + m) + te + 1)]. (15.41)
17* 259

Из уравнения det (/?/ » pk) (см. (15.3)), где (pi · рк) — скалярное
произведение 6-векторов (15.41),
Т~ (Pi · Pk) = - И/ + ml + (α, - akf] (15.42)
находим выражения для поверхностей Ландау
МО = U WO, β с: {1,2, 3,4, 5}, γ = 1.
Нетрудно указать явный вид некоторых миноров определителя
(15.3), если учесть формулу (15.42):
^i U U U L3 U L4U Le9<-*det'Al=0-*nm? = 0f (15.43)
«=ι
Li;Э ^-> detl/M ^O^^ — a^+im^rfcmi)2^ 0, (15.44)
Li* Ъ t-* det''''* M = 0, detp Μ = | ^7· · Λ |, /, * 6 β, (15.45)
^1234 Э <-* Shsl* - 4m2S23S34 (SM + S34) + 2m2S23S34S16 -
— 3m45?5 + 10m4S23S34 + 6m6S15 — 3m8 = 0. (15.46)
Если 515 = m2, то уравнение (15.46) переходит в уравнение
гиперболы (особенность квадратной диаграммы)
5 .2
М2345 3
t -+ 4mxo - 5/л8 ^ St ί+, + me 2 S? «+, +
+ 7m6 2 Si i+iSi+i i+2 + 2me ^ 5/ i+1Si+2 *+4 —
5,
— 2m* ^j (Si i+i5i+i i+2 + Si-j-i i+25i i+i) —
5 5
— 2m4 2j St i-f-iSi+i i-f.2Si-}_3 i-f4 — w4 ^j St· i+i5i-fi i-f2Si-f2 t-j-з +
i=l i=l
5 5
i i-f-l5i-j_l i+2— *n22j Si i+\Si+\ i+2Si+2i-f-3 +
i=l i=al
5
+ 2m2 2j Si i-f iSi+i i+2Si_p i+3Si+3i+4 — S12S23S34S45S51. (15.47)
t = l
Если индекс больше пяти, то его значение понимается по mod 5. Как
обычно, Sik = — fa + pk)2. Ввиду громоздкости общего выражения
явный вид уравнений гиперповерхностей L1234 и L12345 приведен для
случая равных внешних и внутренних масс. Итак, мы нашли
многообразия Lp (/), на которых интеграл (15.40) имеет особенности. Для
изучения этих особенностей необходимо вычислить группы гомологии
260

дополнения X — U pj, т. е. перечислить независимые циклы соответ-
/=' .
ствующих размерностей и указать соотношения между ними.
Для этого воспользуемся теоремой Фруассара (теорема о
разложении) (15.5). В качестве бесконечно удаленной 4-плоскости выбираем
р6; I = 4, {<7}тах = 4. Зная это, получаем
Щ (ς* - JJ, ~p)j = Щ (ς* - Дι ρ}) = W (Σ4) +
+ 6а)Щ (Ρι Π Σ*) + δ®Hi {ρ, П Σ4) + δ& Щ (ρ3 Π Σ4) +
+ Ь14}Щ(рл П Σ«)+ б(1,б(2)//с2(12/> П Σ*) + δ(1)δ(3)Η'2(ιαρ Л Σ*) +
+ б(1)б(4>ЯН14Р П Σ4) + δ^Ή^ρ Π Σ4) +б(2)б(4,Яс2(24/? Л Σ4) +
+ 6*(Ρΐη<?ρ Π Σ4) + δ^δ^Ηΐ^ρ П Σ4) +
+ δ4®δ(4)ΗΪ(™Ρ П Σ*) + δ(4%^Ηί(19*ρ П Σ4) +
+ e®ewow//i ί234/? П Σ4) + 8(¥б¥^0 Π Σ*) =
= φ Ζ + Ζ ® Ζ, (15.48)
Щ (ς* - U t Pj) = #з (Σ*) + 6(i)#£ ('ρ Л Σ4) +
+ δ(< Dm С Ρ Π Σ4) + #с'к)Щ (ikp П Σ4) = φ Ζ, (15.49)
Η% (ς* - £ ρΛ = //<2(Σ4) + δ(1)Η\(ρ Л Σ*) + δ^Η^'ρ Л Σ4) = φ Ζ,
'*' (15.50)
Ηΐ(Σ*-^Ρ}) = ΗΗΣ*) + δ(1)Η'0(ιρ(\ Σ4) = ® Ζ, (15.51)
#ο (ς4 - U ( ρ,) = HI (Σ*) = Ζ, (15.52)
τ. е.
1С /ν4
#< (Σβ - U Pi - (Ο1, 1«, 2β, 3*. 41·) (15.53)
/=ι /
соответственно для q = 0-~4. (Мы написали 16 4-мерных циклов (416)
вместо 17 по той причине, что пара образующих формирует лишь один
цикл интегрирования.)
В формулах (15.48) — (15.52) мы принимали во внимание
размерность β/? Π Σ4, равную 4 — β.
Пустьва — образующие группы Н\ ί Σ4 — [) рХ а с: {1, 2,3, 4}.
Нас будут также интересовать исчезающие циклы £а. (Метод их
построения подробно изложен в работе [425].) С образующими группы
гомологии они связаны формулой (15.6).
261

Таблица 15.2
κι
Г
*ι
eq
4(fk
e12S4
eJ
1
0
0
0
0
«.«/
1
1
—2
0
0
e,ijk
1
1
—1
0
0
e»iu4
1
1
—1
—1
2
6flfeS4«
—i
—1
В дальнейшем нам понадобятся лишь 16 4-мерных циклов: Г =
= ReZ4 (1), ег (4), е*;(6), ецк (4), e122i(l). (Цифры в скобках обозначают
число циклов.)
Как известно, для выяснения характера сингулярностей каждой
из поверхностей Ландау L$ (t) необходимо знать индексы Кронекера,
которые легко вычисляются с помощью формулы (15.9). Их вначения
для 5-угольной диаграммы приведены в табл. 15.2.
Используя теорему Пикара — Лефшеца (15.7) и табл. 15.2,
находим, что при /^-кратном обходе многообразия Lt (t) контур Г
превращается в контур Г + ket\
Г-^Г + в*-*Г+2е^ .*. -*Г+йв„ (15.54)
а при двойном обходе Ьц (ί) контур Г снова превращается сам в себя:
Г-> Г + еи-+ Г + еи + еи - 2еи = Г. (15.55)
Следовательно, многообразие Lt (t) соответствует логарифмической
особенности, а многообразие Ьц (t) имеет особенность типа
квадратного корня. Поверхности Ландау Ьф (0 и L1234 (t) имеют
соответственно логарифмическую и корневую особенности.
Поскольку размерность цикла интегрирования (четыре) на
единицу меньше числа пропагаторов (пять), а вариация контура при обходе
^12345 (О равна нулю при отличном от нуля индексе Кронекера,
можно заключить [419], что поверхность L12Sib (0 имеет полюсную
особенность. Если KI = 0, то этот полюс не находится на
рассматриваемом листе. Напомним, что при I < т — 1 не может быть простого пин-
ча. Простой пинч, более точно — квадратичный нулевой пинч, имеет
место в точке хх = хг = ...= хг = 0 при k (t) = 0, когда
пересечения {m)S = Sx Π··· Π Sm поверхностей сингулярностей slt s%i ..., smf
определяемых уравнениями
Sl:s1^x1 = О,
«^2 : $2 ==: "^2 == "»
S^-i · Sm-1 = Хт-\ = 0, (15.56)
-*(0 = о,
262

Таблица 15.3
<*βΓ'>
г.
«.
'/.
*/*,
1234g
e0 0 1 1 —1 —1
eoi 0—2—1 1 1
eoik 0 0 0 1 1
ев*/* ° 0 0—2-1
e012s4 0 0 0 0 0
описывают локальным (в многообразии St f) 52 Π··· Π Sm-i)
квадратичным уравнением
X2m+Xm+l+ ··· +*/— £(/)=0. (15.57)
Закончим исследования аналитических свойств 5-хвостки выводом
соотношений между ее абсорптивными частями. Хстя есть общие
формулы (15.11) для нахождения таких соотношений, тем не менее, на
примере релятивистской 5-хвостки приведем их детальный вывод, что, по
нашему мнению, позволит глубже понять гомологический метод.
Ранее поверхность рь была выделена (считалась бесконечно
удаленной), поэтому мы не рассматривали относительные циклы,
замыкающиеся на рь. Их можно учесть, если от α cz {l, 2, 3, 4} перейти к
β с: {0, 1,2, 3, 4}. Далее вместо индекса «5» запишем индекс «0»,
т. е. переходим от еа к ββ. Для этого введем дуальный базис
г t
1 е = et0ik — e,ik, 1 е = е%цк — £ о*/*» е = е.хы — £.01234. (15.58)
Тогда
*β = 2 Ыа *>*<*. (15.59)
α
Матрица перехода (ββ \ ае) легко вычисляется g помощью формул
(15.58) и табл. 15.3.
Табл. 15.3 содержит все сведения о соотношениях между
абсорптивными частями. Как и в нерелятивистском случае, с элементами
базиса еь eik, ... сопоставляются диаграммы, в которых t-пропагатор,
i- и Л-пропагаторы и т. д. заменены δ-функциями. Тогда каждому из
разложений
4
€0 = 2 «I + ^12 + в13 + e2Z + eU + еЫ — в123 — *124 — *234 _
в134 ^1234»
eoi = — 2et — 2 eik + 2 eikm + e1234, eoik = 2 еЩ + βι234> (15.60)
например
e012 = еш + еш -|- e1234, eoijk = — 2ei/fe — e1234,
263

- -ζ
Рис. 63
будет соответствовать определенное соотношение между диаграммами
т. е. соотношение между абсорптивными частями. Например,
последнее разложение можно представить в виде, изображенном на рис. 63.
Волнистая линия отвечает частице, находящейся на массовой
поверхности, т. е. б-функции.
15.4. Собственные сингулярности однопетлевых /г-угольных
диаграмм Фейнмана
Как известно, ς однопетлевой я-угольной диаграммой обычно
сопоставляется интеграл
1П = \-Р-, (15.61)
J Π Μ
где [i] = k2 — 2ptk — Δ|·, Af =m2. — p\\ p%— линейная комбинация
внешних импульсов; mt — внутренние массы; k — 4-импульс
интегрирования.
В 4-мерном пространстве для η > 5 всегда можно написать
η η
2 βιΛ = 0, Σ аг=0. (15.62)
(Впрочем, это иногда может быть верным и для η ^ 5.) Тогда
2 fl|[fl--2 ^Δ~Δ, (15.63)
т. е. в случае Δ Φ О выражение (15.61) можно переписать в виде*
i==I
Коэффициенты at можно найти, вводя 5-вектор гг = (рь 1) с
евклидовой пятой компонентой [4301
г? = р?+1. (15.65)
После этого условия (15.62) можно записать в ферме
2¥/=0. (15.66)
ί«1
264

Если рассмотреть вектор, например, для л = 6 в виде
Iri ■■· rt I
\plx ··· Рбх
Я= det , (15.67)
\Ρΐχ · ·
\Ри ..
1 ··
• Рбх\
. Pet
. ι
то из его структуры видно, что он равен нулю» Отсюда разложение по
первой строке даст условие (15.66), миноры этого опеделителя дадут?
выражение для at. Коэффициенты at/A (аналогично а^/а,·)
представляют собой рациональную дробь и, следовательно, не вносят никаких
новых точек ветвлений для 1п [430].
Таким образом, для Δ Φ 0 я-угольную диаграмму с помощью
последовательной редукции можно привести к сумме 5-угольных
диаграмм, особенности которых определяются уравнениями Ландау (см.
предыдущий параграф), обусловленными простым пинчем. Однако,
как указано в работе [419], для η > 5 в 4-мерном пространстве
простого линча быть не может. Поэтому утверждение о том, что в я-уголь-
ной диаграмме нет никаких других особенностей, кроме особенностей^
присущих 5-угольной диаграмме, представляется нам ошибочным.
В связи с этим необходимо рассмотреть и вариант Δ = 0. В этом
случае одно из щ не равно нулю, например аг. Тогда аг можем выразить
через остальные аи ιφ 1, по формуле
αι[1]=-Σβ|[Π, (15.68>
откуда
7 у αι с щук __ у Д| -i-f м**
п~~ iS at J ΠΙ*И ...In) fij, ai dm2 j ||J|2] рлл1п] ·
(15.69)
Осуществляя последовательную редукцию типа (15.69), можно
представить η-угольную диаграмму через сумму производных
(п — 5)-го порядка по квадратам внутренних масс от 5-угольных
диаграмм, полученных стягиванием в точку (п — 5) внутренних линий
я-угольной диаграммы.
Пятиугольная диаграмма имеет логарифмические особенности на
поверхности Ландау Lb Ц^, корневые — на L*/, Ьцы и полюс — на
Ltjkim {Lu Lih Lijk, Lijki, Lijklm — детерминанты первого — пятого
порядков). Об этих особенностях мы уже говорили в предыдущем
параграфе. В результате дифференцирования интегралов, определяющих
5-угольные диаграммы, появляются кратные полюсы вплоть до
(п — 4)-го порядка, соответствующие поверхности ЬцЫт, кратные
полюсы до (п — 5)-го включительно, соответствующие поверхностям Lt и
Ltfkt и кратные полюсы вплоть до (п — 5)-го или (п — 4)-го порядков,
соответствующие поверхностям Lf/, U #/. (Корневые особенности
бывают либо (L,y)1/2, (Цт)Х12, либо (^Гт, (£*/*/)"" т.) Редукцию
265

η-угольной диаграммы к сумме 5-угольных диаграмм можно произвести
различными способами, причем каждый из этих способов можно
изобразить графически, сопоставляя с ним свое дерево, совершенно
аналогичное по структуре деревьям, рассмотренным в гл. 1—6.
Естественно, что характер сингулярностей η-угольной диаграммы от
типа редукции не зависит.
Итак, помимо особенностей 5-угольной диаграммы, л-угольная
диаграмма имеет кратные полюсы [26], которые являются
собственными особенностями я-угольника. Однако положение этих полюсов по-
прежнему определяется уравнениями Ландау для 5-угольника с η
свободными концами. Отметим, что эти выводы были подтверждены на
примере статических η-угольных диаграмм в статистике в работе 1431].
Анализ особенностей в комплексной плоскости по диаграммам теории
возмущений составил основное содержание рабст [432—443].
Гомологическим методом исследованы собственно-энергетические,
вершинные, лестничные до шестого порядка включительно диаграммы, а
также однопетлевые диаграммы любого порядка как в квантовой теории
поля, так и в фивике атомного ядра [428, 429, 444—450].

СПИСОК ЛИТЕРАТУРЫ
\. Виленкин Η. Я. Полисферические и орисферические функции//Мат. со.—
1965.-68(110), № 3.—С. 432—443.
2. Виленкин Н.Я., Кузнецов Г.И„ Смородинский Я-А. Собственные функции
оператора Лапласа, реализующие представления групп U (2), SU (2), SO(3), U (3),
SU (3) и символический метод//Ядер, физика.— 1965.—2, № 5.—С. 906—917.
3. Кильдюшов Μ. С. Гиперсферические функции типа «деревьев» в задаче л тел //
Там же.— 1972.— 15, № ι._ С. 197—208.
4. Кильдюшов Λί. С. Задача η тел. Матричные элементы перестановок // Там
же.— 1972,— 16, № 1.— С. 217—221.
5. Кильдюшов М. С, Кузнецов Г. И. Графическая реализация представлений
класса 1 ортогональных групп.— М., 1973.— 20 с.— (Препр./ Ин-т атом, энергии;
№ 2257).
6· Кильдюшов М.С., Кузнецов Г. И. Унитарное преобразование между
базисами, соответствующими деревьям разной топологической структуры.— Μ., Ι973β—
20 с.— (Препр./ Ин-т атом, энергии; № 2263).
7. Кильдюшов М. С, Кузнецов Г. И. Симметрии Г-коэффициентов и матричные
элементы представлений класса I группы SO (η).— Μ., 1973.— 15 с— (Препр./ Ин-т
атом, энергии; №|2258).
8. Кильдюшов М.С., Кузнецов Г. И. Некоторые свойства симметрии Г-коэффи-
циентов // Ядер, физика.— 1973.— 17, № 6.—С. 1330—1336.
9. Кильдюшо^М.С, Кузнецов Г. И. Коэффициенты Клебша — Гор дана
непрерывных представлений класса I группы SO (n) и непрерывных представлений класса
II группы SU (л).— М., 1973.— 15 с— (Препр.// Ин-т атом, энергии; № 2317).
10. Кузнецов Г. И. Коэффициенты векторного сложения представлений
класса II группы Si/(л) //Теорет. мат. физика. — 1974. —18, №3.-0.367—373.
11. Кузнецов Г. И., Смородинский Я- А. К теории Зя/-коэффициентов // Ядер,
физика.—1975.—21, №5.-0. 1135—1143.
12. Кузнецов Г. И. К вопросу о правилах сумм для 6/-символов//Там же.—
1976.—24, № 1.—С. 235—240.
13. Кузнецов Г. И., Смородинский Я· А. Гиперсферические деревья и Зл/-коэф-
фициенты // Письма в журн. эксперим. и теорет. физики.— 1975.— 22, № 7.—
С. 378—380.
14. Виленкин Н. Я* Специальные функции и теория представлений групп.— М. :
Наука, 1965.— 665 с.
15. Кузнецов Г. Я. Групповой анализ амплитуд и состояний в теории ядра и
квантовой теории поля: Дис. ... д-ра физ.— мат. наук.— М., 1976.— 220 с—
Машинопись.
16. Maekawa Т. Formula for the computation of the representation matrix elements
of the group SO (n) II J. Math. Phys.— 1975.— 1β, Ν 2,— P. 334—340.
17. Klimyk A. U., Gavrilik A. M. Matrix elements and Clebsch — Gordan
coefficients of representations of semisimple Lie groups // Ibid.— 1979.— 20, № 8, —
P. 1624—1642.
18. Klimyk Л. С/. Representations for matrix elements of compact Lie groups/
Lett. Math. Phys,— 1980,- 4, N 5.- P. 399-404.
267

19. Gruber В., Kllmyk A. U. Representations of the groupsGL\(nt R) and SU (n) in
an SO (n) basis //J. Math. Phys.— 1981.— 22, N 12.— P. 2762—2769.
20. Klimyk A. U. Representations of the groups Sp (n, R) and Sp (n) in a U (n)
basis // Ibid.— 1983.— 24, № 2.— P. 224—231.
21. Klimyk A. U., Gruber B. Structure and matrix elements οί the degenerate
series representations of U (p + a) and U (p, a) in а и (ρ) Xu (q) basis // Ibid.— 1982.—
23, N 8.— P. 1399—1408.
22. Климык А. У. Матричные элементы и коэффициенты Клебша — Горда на
представлений групп.— Киев : Наук, думка, 1979.— 304 с.
23. Kachurik I. /., Klimyk A. U. Matrix elements for the representations of SO (n)
and S0(n, L)//Rept. Math. Phys.— 1984.—20, N 3.—P. 49—62.
24. Klimyk A. U., Vilenkin N. L. Relations between spherical functions of
compact groups//J. Math. Phys.—1989.—30, N 6.—P. 1219—1225.
25. Moshinsky M., Quesne С Noninvariance groups in the second quantization
picture and their applications//Ibid.—1970.—11, N 5.—P. 1631—1639.
26. Кузнецов Λ И. Собственные сингулярности однопетлевых я-угольных
диаграмм Фейнмана//Ядер, физика»—1972.— 15, №4.— С. 846—848.
27. Вагнер Е. Теория групп и ее приложение к квантовомеханической теории
атомных спектров.— Μ. : Изд-во иностр. лит., 1961»—443 с.
28. Вейль Г. Теория групп и квантовая механика.— М. : Наука, 1986.— 495 с·
29. Вандер-Варден Б. JI. Метод теории групп в квантовой механике.—
Харьков : ГНТИ Украины, 1938.— 199 с.
30. Гелл-Манн М. Восьмеричный формализм: теория симметрии в сильных
взаимодействиях // Элементарные частицы и компенсирующие поля.— М, : Мир, 1964.—
С. 117—146.
31· Ne'eman Υ и. Derivation of strong interactions from a gauge invariance // Nuch
Phys.— 1961.— 25, N2.—P. 222—229.
32. Gursey F., Radicati L. A. Spin and unitary spin independence of strong
interactions // Phys. Rev. Lett.— 1964.— 13, N 5.— P. 173—175.
33. Pais A. Implications of spin-unitary spin independence // Ibid,— P. 175—177.
34. Sakita B. Supermultiplets of elementary particles// Phys. Rev. В.— 1964.—
136, N 6.— P. 1756—1760.
35. Боголюбов Η. Η., Струминский Б. В., Тавхелидзе А. Н. К вопросу о
составных моделях в теории элементарных частиц.— Дубна, 1965.— 15 с.— (Препр./Объед,
ин-т ядер, исслед.; Д-1968).
36. Боголюбов* Η. Я. Теория симметрии элементарных частиц//Физика
высоких энергий и теории элементарных частиц (Ялта, 1966).— Киев : Наук, думка,
1967.—С. 5—112.
37. Bogolyubov Ν. Ν., Matveev V.A., Tavkhelidze A. N. Colour quarks//
Gravitation and Elementary Particle Physics,— Moskva: Mir, 1983.— P. 220—285.
38. Боголюбов Η. Η. Избранные труды.— Киев : Наук, думка, 1969 — 1971.—
Т. 1.— 1969.— 647 с; Т. 2.— 1970.—522 с; Т. 3.— 1971.—487 с.
39. Wigner Ε. P. On the consequences of the symmetry of the nuclear Hamiltonian
on the spectroscopy of nuclei // Phys. Rev.— 1937.— 51, N 2.— P. 106—119.
40. Salam Α., Delbourgo R., Strathdee I. The covariant theory of strong
interaction symmetries // Proc. Roy. Soc. London. Α.— 1965.— 284, N 1397.— P. 146—
158.
41. Кильдюшов Μ. С, Сурков Е. Л. О представлениях группы 04, возникающей
в задаче пяти тел // Ядер, физика.— 1971.— 13, № 4.— С. 904—912.
42. Кильдюшов М. С, Сурков Е. Л. Гиперсферические функции в задаче пяти
тел // Там же.— 14, N 3,— С. 551—566.
43. Кильдюшов М. С, Сурков Е. Л. Полная система гиперсферических функций
для задачи четырех тел // Там же#— 1975.— 22, № 3.— С. 648—658.
44. Эфрос В. Д. Гиперсферические функции для трех частиц // Там же.— 1971.—
13, N° 6.— С. 1318—1332.
45. Эфрос В. Д. К методу /С-гармоник в задаче нескольких нуклонов // Там же.—
1972.— 15, № 2.—С. 226—241.
46. Смородинский #. Α., Эфрос В. Д. Ортогональные преобразования
многомерных угловых гармоник//Там же.— 1973.— 17, № 1.— С. 210—224.
47. Эфрос В. Д. Замечания о методе /С-гармоник в ядерной задаче трех тел //
Там же.—№ 5.—С. 988—1000,
268

48. Smith F. Т. Generalized Angular momentum in many-body collisions // Phys.
Rev.— I960.— 120, N 3.— P. 1058—1069.
49. Delves L. M. Tertiary and general oFdef collisions. I // Nucl. Phys.— 1958.—
9, N 3.— P. 391—403.
50. Delves L. M. Tertiary and general order collisions. II // Ibid.— I960.—20,
N 2.— P. 275—308.
51. Grynberg M., Koba Z. Symmetry properties of я-pion wave functions// Ann.
Phys.— 1964.—26, N 3.— P. 418—441.
52. Zickendraht W. Coordinates for the' quantum -mechanical three-body problem//
Proc. Nat. Acad. Sci. USA.—1964.—52, N 6.—P. 1565—1567.
53. Горелик P. Б., Клепиков Η. #., Юдин В. А. Унитарное описание реакций
с образованием нескольких нерелятивистских частиц//Ядер. физика.— 1965.— 1,
N° 1.-T-G. 152—159.
54. Симонов Ю. А. Задача трех тел. Полная система угловых функций // Там
же.— 1966.— 3, N° 4.— С. 630—638.
55. Вадалян А. М., Симонов Ю. А, Задача трех тел. Уравнение для
парциальных волн//Там же.— N° 6.—С. 1032—1047.
56. Симонов Ю.А., Бадалян А. М. Энергия связи и волновая функция Н3 и Не3//
Там же.— 1967.—5, № 1.—С. 88—100.
57. Бадалян А. М., Гальперин £. С, Ляховицкий В. Н. и др. Уровни в системе
четырех нуклонов // Там же.— 6, N° 3.— С. 473—487.
58. Пустовалов В. В., Симонов Ю. А. Полная система угловых функций в
задаче трех тел для произвольного орбитального момента // Журн. эксперим. и теорет.
физики.—1966.—51, N° ι (7).—С. 345—360.
59. Богословский Г. Ю., Клепиков Н. П. Параметризация S-матрицы в
неортогональном базисе// Ядер, физика.— 1968.—7, № 3.—С. 644—653.
60. Базь А. И., Демин В. Ф., Жуков М. В. Расчет ядра Не10// Там же.— 1969.—
9, N° 6.—С. 1184—1191.
61. Пустовалов В. В., Смородинский fl. А. Задача трех тел. Полная система
ортогональных угловых функций // Там же.— 10, № 6.— С. 1287—1295.
62. Нири Ю., Смородинский Я. А. Собственные функции в задаче трех тел//
Там же.— 1970.— 12, N° 1.—С. 202—216.
63. Wybourne B.%G., Symmetry principles and atomic spectroscopy.— New York :
Wiley Interscience, 1970.— 194 p.
64. Жуков Μ. В., Эфрос В. Д. Реакции в системе нескольких нуклонов // Ядер,
физика.— 1971.— 14, N° 3.—С. 577—589.
65. Пермяков В. П.,ι Пустовалов В. В., Фенин Ю. И., Эфрос В. Д. Система
четырех нуклонов. Рассеяние нейтрона на тритии // Там же.— С. 567—576.
66. Дзюблик А. Я-, Овчаренко В. И., Стешко А. И., Филиппов Г. Ф. Вывод
уравнении коллективной модели Бора — Моттельсона на основе гамильтониана
многочастичной задачи // Там же.— 1972.— 15, N° 5.— С. 869—879.
67. Фенин Ю. И., Эфрос В. Д. Коррелированный базис в задаче нескольких
нуклонов // Там же.— С. 887—897.
68. Базь А. И., Жуков М. В. Модель уравнений ядерной физики// Там же.—
16, N° 1.-С. 60-73.
69. Базь А, И., Жуков М. В. Модель уравнений ядерной физики. Один канал
распада // Там же, N° 5.— С. 958—973.
70. Демин В. Ф., Эфрос В. Д. Решение ядерной задачи трех тел с
реалистическими потенциалами // Письма в журн. эксперим. и теорет. физики.— 1972. — 16,
Ко 8.— С. 504—508.
71. Demin V. F.t Pokrovsky Yu. E.P Efros V. D. Bound-state properties of three and
four nucleons with realistic forces // Phys. Lett. В.— 1973.— 44, N 3.— P. 227—230.
72. Demin V. F.t Pokrovsky Yu. E. Calculation of SH, 3He properties with realistic
J/Jf-potentials in the hyperspherical basis // Ibid.— 47, N° 5.— P. 394—396.
73. Джибути P. И., Крупенникова Η. Б. Метод гиперсферических функций в
квантовой механике нескольких тел.— Тбилиси : Мецниереба, 1984.— 183 с.
74. Горбатов A.M. Метод угловых потенциальных функций. Общие формулы //
Ядер, физика.— 1974.— 20, N° 2.— С. 326—333.
75. Gallina К., Nata P.f Bianchi L. On the three-body Green's functions iov
S-states // Nuovo Cim.— 1962.— 24, N° 5.— P. 835—847,
269

76. Kramer P. Symmetrieangepasste Funktionen fur ein System aus drei Teijchen
verschiedener Masse// Zeits. fur Naturforschung. Α.— 1963.— 18, № 2.— S. 260—
261.
77. Dragt A. I. Classification of three-particle states according to SUZ II J. Math,
Phys.— 1965.— 6, № 4.— P. 533—553.
78. Zickendraht W. Construction of a complete orthogonal system for the quantum-
mechanical three-body problem//Ann. Phys.—1965.—35, JSfe l,— p. 18—41.
79. Levy-Leblond 1. M., Levy-Nonas M. Three-particle nonrelativistic kinematics
and phase space//J. Math. Phys.— 1965.—6, № 10.—P. 1571—1575.
80. Calogero F., Simonov Yu. A. The hyperspherical expansion approach to nuclear
bound states. I // Nuovo Cim. Α.— 1970.— 67, N 4.— P. 641—657.
81. Badalyan A. M., Calogero F., Simonov Yu. A. The hyperspherical expansion
approach to nuclear bound states. II // Ibid.— 68, N 4.— P. 572—590.
82. Calogero F., Simonov Yu. Α., Surkov E. h. The hyperspherical expansion
approach to nuclear bound states. Ill // Ibid.— 1971.— 1, N 4.— P. 739—758.
83. Calogero F., Andrea A. D., OlivieH E. et al. The hyperspherical expansion
approach to nuclear bound states. IV // Ibid.— 1973.— 14, N 3.— P. 445—476.
84. Calogero F., Olivieri E., Scalia M. et al. The hypetfspherieal expansion appro*
ach to nuclear bound states. V // Ibid.— P. 477—500.
85. Ландау Л. Д., Лифшиц Е. Μ. Квантовая механика. Нерелятивистская тео- .
рия.— М. : Наука, 1974.— 752 с.
86. Fock V. A. Zur Theorie der WasseFstoffatoms // Zeits. fur Phys.— 1935.— 98,
N* 1.—S. 145—147.
87. Bargmann V. Zur Theorie der Wasserstoffatoms // Ibid.— 1936.— 99, N 5.—
S. 576—582.
88. Hill F. L.t J audi I. M. On the problem of degeneracy in quantum mechanics //
Phys. Rev.— 1940.— 57, N 7.— P. 641—653.
89. Демков Ю. Η. Определение группы симметрии квантовой системы.
Анизотропный осциллятор // Журн. эхсперим. и теорет. физики.— 1963.— 44, № 6.—
С. 2007—2010.
90. Elliot J. P. Collective motion чп the nuclear shell model. 1. Classifications scne?
mes for states of mixed configurations // Proc. Roy, Soc, London. A.— 1958,— 245f
N 1240.—P. 128—145.
91. Elliot J. P., Harvey M. Collective motion in the nuclear shell model. 3. The
calculation of spectra// Ibid.— 19β3.— 272, N 1351.— P. 557—577.
92. Аллилуев С. П., Матвиенко А. В. Группа симметрии молекулярного иона
водорода (системы с разделяющимися переменными) // Журн. эксперим. и теорет.
физики.— 1966.— 51, Но 6 (12).—С. 1873—1879.
93. Базь А. И., Зельдович Я■ Б., Переломов А. М. Рассеяние, реакции й распады
в нерелятивистской квантовой механике.— М. : Наука, 1971.— 544 с.
94. Berry Μ. V., Wilkinson M. Diabolic points in the spectra of triangle // Proc
Roy. Soc. London. Α.— 1984.— 392, N 1.— P. 15—43.
95. Did R., Moshinsky M. Accidental degeneracy and symmetry Lie algebra //
J. Phys. Α.- 1985.— 18, N 13.— P. 2423—2428.
96. Siddal Τ. Η., Sullivan I. I. Substitutional symmetries and extra degeneracies
of real symmetric matrices // J. Math. Phys.—1988.—29, N 5.—P. 1091—1096.
97. Lea K. R., Leask M. I. M., Wolf W. P. The raising of angular momentum
degeneracy of /-electron terms by cubie crystal fields//J. Phys. Chem. Solids— 1962.—
23, N 10.— P. 1381—1405.
98. Racah G. Theory of complex spectra. I // Phys. Rev.— 1941.— 61, N 2.—
P. 186—197.
99. Racah G. Theory of complex spectra. II // Ibid.— 1942.— 62, N 3.— P, 438—
462.
100. Racah G. Theory of complex spectra. Ill//Ibid.— 1943.—63, N'3,—
P. 367—382.
101. Racah G. Theory of complex spectra. IV // Ibid.— 1949.—76, N S,—
P. 13г.2—1365.
102. Racah G. Group theory and spectroscopy. Lecture notes.— Princeton: Inst.
Adv. Study, 1958.— 102 p.
103. Janssen D., Jolos R. V., Donau F. An algebraic treatment oi the nuclear
quadrupole degree of freedom // Nucl. Phys. Α.— 1974.— 224, N К— Р. 93—116.
270

104. Arima Α., Iachello F. Interacting boson model of collective nuclear states. L
The vibrational limit // Ann. Phys.- 1976.— 99, N 2.— P. 253—317.
105. Arima Α., Iachello F. interacting boson model of collective nuclear states»
II. The rotational limit // Ibid.— 1978.— Ill, N 1.—P. 201—238.
106. Arima Α., Iachello F. Interacting boson model of collective nuclear states*
III. The transition fFom SU (5) to SU (3) // Ibid.— 115, N 2.— P. 325—366
107. Anma Α., Iachello F. Interacting boson model of collective nuclear stales,
IV. The О (6) limit // Ibid.— 1979.— 123, N 2.— P. 325—366.
108. Соловьев В. Г. Теория атомного ядра : Квазичастицы и φ )ноны.— М. : Энер·
гоатомиздат, 1989.— 304 с.
109. Свиридов Д. Г., Смирнов Ю. Ф. Теория оптических спектров ионов
переходных металлов.— М. : Наука, 1977.—328 с.
ПО. Фелд Б. Модели элементарных частиц.— М. : Мир, 1971.— 486 с.
111. Шелест В. П., Зиновьев Г. М., Миранский В. А. Модели сильновзаимодей-
ствующих элементарных частиц.— М. : Атомиздат, 1975—1976.— Т. 1.— 1975.—
232 с; Т. 2.— 1976.— 248 с.
112. Нильсон С. Связанные состояния индивидуальных нуклонов в сильнодефор-
мируемых ядрах//Деформация атомных ядер.— М# : Изд-во иностр. лит., 1958.—
С, 233—304.
ЦЗ. Славное Α. Α., Фаддеев Л. Д. Введение в теорию калибровочных полей.—
М. : Наука, 1988,— 268 с.
114. Юцис А. #., Левинсон И. Б., Ванагас В, В. Математический аппарат теории
момента количества движения.— Вильнюс : Госполитнаучиздат, 1960.— 243 с.
115. Эль-Баз, Кастель Б. Графические методы алгебры спинов в физике атома,,
ядра и элементарных частиц.— М. : Мир, 1974.— 353 с.
116. Варшалович Д. Α., Москалев А. Н., Херсонский В, /С. Квантовая теорий
углового момента.— Л. : Наука, 1975.— 439 с.
117. Dirac Р. Α. Μ. Unitary representations of the Lorentz group // Proc. Roy·
Soc. London. Α.— 1945.— 183, N 2.— P. 284—301.
118. Bhabha H. I. On relativistic wave equations for elementary particles // Rev»
Mod. Phys.— 1945.— 17, N 2.— P. 200—215.
119. Harish-Chandra. On relativistic wave equations // Phys. Rev,— 1947.— 71,
N 11.—P. 793—805.
120. Гельфанд И. Μ., Наймарк Μ. А. Унитарные представления группы
Лоренца//Изв. АН СССР. Сер. математики.— 1947.— 11, № 5.-6. 411—504.
121. Гинзбург В. Л., Тамм И. Е. К теории спина // Журн» эксперим. и теорет.
физ.— 1947.— 17, № 3.—С. 227—237.
122. Harish-Chandta. Infinite irreducible representations of the LoFentz group //
Proc. Roy. Soc. London. Α.— 1947.— 183, N 3.— P. 372—388.
123. Wild E. On first order wave equations for elementary particles without sub*
sidiary conditions // Ibid.— 191, N 2.— P. 253—267.
124. Bargmann V., W-igner E. Group theoretical discussion of relativistiG equa*
tions//Proc. Nat. Acad. USA.— 1948.—34, N 2.—P. 211—225.
125. Гельфанд И, М., Яглом А. Μ. Общие реглятивистеки инвариантные урав-
нения и бесконечномерные представления группы Лоренца // Журн. эксперим. и те*
орет, физики.— 1948.— 18, № 8.—С. 703—733.
126. Majoranr E. Teoria relativistica di particelle con momento intriseco
arbitrary // Nuovo Cim.— 1932.— 9, N 3.— P. 335—350.
127. Гюрши Ф. Введение в теорию групп / Теория групп и элементарные
частицы.—М. : Мир, 1967.—С. 25—113.
128. Мишель Л., Шааф М, Симметрия в квантовой физике.— М. : Мир, 1974.—
250 с.
129. Шапиро И. С. Разложение волновой функции по неприводимым
представлениям группы Лоренца // Докл. АН СССР.— 1956.— 106, № 4.— С. 647—649.
130. Чжоу Гуан-Чжао, Заставенко Л. Г. Интегральное преобразование И. С.
Шапиро // Журн. эксперим. и теорет. физики.— 1958.—35, №6 (12).—С. 1417—1425.
131. Попов В. С. К теории релятивистских преобразований волновых функций и
матрицы плотности частиц со спином // Там же.— 1959.— 37, № 4 (10).—С. 1116—1126,
132. Кузнецов Г. И., Либерман М. А., Макаров Α. Α., Смородинский Я. А. Спи-
ральность и унитарное представление группы Лоренца // Ядер, физика,— 1969.—
10, № 3.— С. 644—656.
271

133. Широков Ю. Μ. Теоретико-групповое рассмотрение основ релятивистской
квантовой механики. I. Общие ввойства неоднородной группы Лоренца // Журн. экс-
оерим. и теорет. физики.— 1957.—33, № 4 (10).— С. 861—872.
134. Широков Ю. М. Теоретико-групповое рассмотрение основ релятивистской
квантовой механики. И. Классификация неприводимых представлений неоднородной
группы Лоренца//Там же.—№ 5 (11).—С. 1196—1207.
135. Широков Ю. М. Теоретико-групповое рассмотрение основ релятивистской
квантовой механики. 1Л. Неприводимые представления классов Р0 и 00 и не вполне
приводимые представления неоднородной группы Лоренца // Там же.— р. 1208—
1214.
136. Широков Ю. М. Теоретико-групповое рассмотрение основ релятивистской
квантовой механики. IV. Пространственные отражения в квантовой теории // Там
же.— 1958.—34, № 3.—С. 717—724.
137. Широков Ю. М. Релятивистская теория поляризационных эффектов // Там
же.— 1958.— 35, № 4 (10).— С. 1005—1012.
138. Гельфанд И. М., Граев М. И. Применение метода орисфер к спектральному
анализу функций^в вещественном и мнимом пространствах Лобачевского // Тр. Моск.
мат. о-ва.— 1962.—№ П.—С. 243—308.
139. Гельфанд И. М., Граев М. И., Виленкин И. Я· Интегральная геометрия и
связанные с ней вопросы теории представлений.— М. : Физматгиз, 1962.— 652 с.
140. Кузнецов Г. Я. К вопросу о построении полной системы функций в прост-
ранственноподобной области // Журн. эксперим, и теорет. физики.— 1968.— 54,
№ 6.—С. 1756—1763.
141. Вердиев И. А. Полная система функций на однополостном гиперболоиде- //
Ядер, физика.— 1969.— 10, JSfe 6.— С. 1282—1286.
142. Виленкин Η Я-, Смородинский Я- А. Инвариантные разложения
релятивистских амплитуд // Журн, эксперим. и теорет. физики.— 1964.— 46, № 5*—
С. 1793—1808.
143. Климык А. У., Качурик И. И. Вычислительные методы в теории
представлений групп.— Киев : В ища шк., 1986.— 224 с.
144. Малкин И. А,, Манько В. И. Симметрия атома водорода V Письма β журн.
эксперим и теорет. физики.— 1965.— 2, № 5.— G. 230—234.
145. Переломов A.M., Попов В. С. Группа Лоренца как группа динамической
симметрии атома водорода // Журн. эксперим. и теорет. физики.— 1966.— 50, № 1.—
С. 179—198.
146. Кузнецов Г. И. Замечание о многомерной кулоновской задаче // Там же·—
61. № 1.—С. 216—221.
147. Долгинов А. 3. Релятивистские сферические функции. I // Там же,— 1956»—
30, № 4.— С. 746—755.
148. Долгинов А. 3., Топтыгин И. Н. Релятивистские сферические функции. II И
Там же.— 1959.—37, № 5 (И).—С 1441—1451.
149. Долгинов А. 3., Москалев А. Н. Релятивистские сферические функции. III //
Там же.— 1959.—37, № 6 v12).—С. 1697—1707.
150. Вингпернитц П., Смородинский Я. Α., Углирж М. К теории
четырехмерного момента количества движения // Ядер, физика.— 1965.— 1, № I.— С. 163—172.
151. Либерман Μ. Α., Смородинский Я- Α., Шефтель М. Б. Унитарные
представления группы Лоренца и функции со спином//Там же.— 1968.— 7, № 1.—
С. 202—214.
152. Sertorio L·., Toller M, Complex angular momentum and three-dimensional
Lorentz group // Nuovo Cim — 1964.— 33, N 2.— P. 413—433.
153. Toller M. Three-dimensional Lorentz group and harmonic analysis of the
scattering amplitude // Ibid.— 1965.— 37, N 2.— P. 631—657.
154. Вердиев Й. Α., Дадашев Л. А. Матричные элементы унитарного
представления группы Лоренца // Ядер, физика.— 1967.— в, № 5.— С. 1094—1099.
155. Смородинский Я. Α., Хусар М. Представления группы Лоренца и
обобщение спиральных состояний // Теорет. мат. физика.— 1970.— 4, № 3.— С. 328—340.
156. Huszar Μ. Angular momentum and unitary spinor bases of the Lorentz group.—
Dubna, 1970.- 20 d,- (Prepr. / JINR; E2-5429).
157. Strom S. On the matrix elements of a unitary representation of the
homogeneous Lorentz group // Ark. Fys.— 1965.— 29, N 39.— P. 467—483.
158. Дао Вонг Дык, Нгуен Ван Хьеу. Матричные элементы преобразования Ло-
272

ренца для унитарного представления // Докл. АН СПЕР.— 1967.— 173, № 6.—
С. 1281—1283.
159. Sciarrino Α., Toilet M. Decomposition of the unitary irreducible
Representations of the group SL (2C) restricted to the subgroup SU (l.i) // J. Math. Phys,—
1967.— 8, N6.-P. 1252—1265.
160. Riihl W. Complete sets of solutions of linear Lorentz covariant field
equations with an infinite number of field components // Comm. Math. Phys.— 1967.— G,
N 4.—P. 312—342.
161. Mukmda M. Unitary Fepresentations of th. homogeneous Lorentz group in
an О (2.1) basis//J. Math. Phys.— 1968.—9, N 1.—P. 50—61.
162. Смородинский Я- Α., Шепелев Г. И. Матричные элементы буста в О (3, 1) и
продолжение к 0(4)// Ядер, физика.— 1971.— 13, № 2.—С. 441—453.
163. Смородинский Я. Α., Шепелев Г. И, Матричные элементы буста для
редукции О (3, \)ZDO (2, 1) 3 О (2) // Там же.— 1973.— 18, № 47.— С. 934—943.
164. Шапиро И. С. Разложение амплитуды рассеяния по релятивистским
шаровым функциям//Журн. эксперим. и теорет. физики.— 1962.— 43, № 5(11).—
С. 1727—1730.
165. Кузнецов Г. И., Смородинский Я А. Интегральные представления
релятивистских амплитуд и асимптотические теоремы // Ядер, физика.— 1967.— 6, № 6.—
С. 1308—1312.
166. Toller Μ. An expansion of the scattering amplitude at vanishing
four-momentum transfer using the representations of the Lorentz group // Nuovo Cim. A.— 1968.—
53, N 3.— P. 671—716.
167. Delbourgo R., Salarn Α., Strath dee J. Harmonic analysis in terms of the
homogeneous Lorentz group // Phys. Lett. В.— 1967.— 25, N 3.— P. 230—232.
16S. Винтернитц П., Смородинский Я- Α., Шефтель Μ. Б. Двумерные
разложения релятивистских амплитуд, траектории Редже и дочерние полюса // Ядер,
физика.— 1968.— 8, № 4.— С. 833—846.
169. Кузнецов Г. //., Либерман Μ. Α., Смородинский Я. А. Двумерные
разложения релятивистских амплитуд// Физика элементар. частиц и атом. ядра.— 1971.—
2, № 1.— С. 105—128. _
170. Кузнецов Г. И. Парциальный анализ амплитуд JTJT- и jfjf -рассеяния при
высоких энергиях//Ядер, физика.— 1972.— 15, № 5.— С. 1035—1046.
171. Вердиев И. А. Группа О (2, 1) и дуальность // Там же.— 1974.— 20, № 4.—
С. 819—826.
172. Кузнецов Т. И., Смородинский Я А. Интегральные представления
релятивистских амплитуд в нефизической области // Там же.— 1966.— 3, № 2.—
С. 383—395.
173. Воусе J. 1. Relation of the О (2, 1) partial-wave expansioa to the Regge
representation I! J. Math. Phys.—1967.—8, N 4.—P. 675—684.
174. Olive D. The connection between Toller and Froissart-Gribow signatured
amplitudes//Nucl. Phys. В.— 1970.- 15, N 2.—P. 617—627.
175. Агамалиев А. К., Атакишиев Η. Μ., Вердиев Й. А. Инвариантное
разложение решений релятивистских уравнений//Ядер, физика.— 1969.— 9, № 1.—
С 201—211.
176. Агамалиев А. К.. Атакишиев Η. Μ., Вердиев Й. А. Инвариантное
разложение решения уравнения Дирака // Там же.— 10, № 1.— С. 187—192.
177. Вердиев Й. А. Разделение переменных в уравнении Бете-Солпитера в
пространстве Минковского // Там же.— 1973.— 17, № 3.— С. 643—659.
178., Смородинский Я Α., Сурков Е. Л. Об интегральных преобразованиях,
связанных с уравнениями Клейна — Гордона.— Дубна, 1967.— 8 с.— (Препр./ Объед.
ин-т ядер, исслед.; Р2—3323).
179. Kadyshevsky V. G., Mir-Kasimov R. M., Skachkoo N. /J. Quasi -potential
approach and the expansion in relativistic spherical functions // Nuovo Cim.— 1968.—
55, N 2.- P. 233—257,
180. Кадышевский В. Г., Мир-Касимов Р. Μ., Скачков Η. Б. Релятивистская
проблема двух тел и исчисление конечных разностей// Ядер, физика.—1969,— 9,
№ 1.—С. 212—223.
181. Кадышевский В. Г., Мир-Касимов Р. М., Скачков И. Б. Разностное
уравнение Шредингера для двух релятивистских частиц в простейших случаях // Там
же.— № 2.—С. 462—471,
18 1-1980
273

182. Кадышевский В. Г„ Мир-Касимов Р. М,9 Фриман М. Разностные гяпергео-
метрические уравнения и релятивистская кулонова проблема // Там же.— № 4.—
С. 646—652.
183. Долгинов А. 3., Топтыгин И. А. Разложение Клебша — Жордана для
бесконечномерных представлений группы Лоренца // Журн. эксперим. и теорет.
физики.— 1958.— 35, No 3 (9).— С. 794—796.
184. Bisiachi G., Fronsdal С. Unitari representations and relativistic coupling
coefficients for 5L2C//Nuovo Cim.— 1966.— 41, N 1.—P. 35—47.
185. Bamberg?. G. Clebsch-Gordan coefficients for SL (ny C) II Proc. Roy. Soc.
London. Α.— 1967.— 300, N 1462.— P. 337—355.
186. Anderson R. L., Raczka R., Rashid M.A., Winternitz P. Clebsch-Gordan
coefficients for the coupling of SL (2,C) principal — series representations//J. Math.
Phys.— 1970.— 11, N 3.— P. 1050—1058.
187. Гаврилик Α. Μ. Коэффициенты Клебша — Гордана группы SL (2, С) II
Теорет. мат. физика.— 1972.— 11, № 1.—С. 56—68.
188. Вердиев Й. А. Коэффициенты Клебша — Гордана группы Лоренца//Там
же.- 1973.- 16, № 3.— С. 360—367.
189. Вердиев Й. Α., Керимов Г. Α., Смородинский Я. А. Коэффициенты
Клебша — Гордана группы О (2, 1) // Ядер, физика.— 1974,— 20, № 4.— С. 827—838.
190. Вердиев Й. Α., Керимов Г. Α., Смородинский Я. А. Коэффициенты
Клебша — Гордана группы Лоренца // Там же.— 1975.— 21, № 6.— С. 1351—1361.
191. Наймарк М. А. Разложение тензорного произведения неприводимых
представлений собственной группы Лоренца на неприводимые представления. I,Случай
тензорного произведения представлений основной серии//Тр. Моск. мат. о-ва.—
1959.— 8.— С. 121 — 153.— П. Случай тензорного произведения представлений
основной и дополнительных серий // Там же.— 1960.— 9.— С. 237—282.
192. Винтернитц П., Фриш И. Инвариантные разложения амплитуд и
подгруппы собственной группы «Лоренца//Ядер, физика.— 1965.— 1, № 5.— С.889—
901.
193. Verdiyev Y. A. Expansion of the helicity amplitude in terms of unitary
representations of the Lorentz group// Ann. Phys.— 1972.— 72, N 1.— P. 139—170.
194. Биденхарн Jl., Лаук Дж. Угловой момент в квантовой физике.— М. : Мир,
1984.— Т. 1.- 302 с; Т. 2.-648 с.
195. Вейль Г. Классические группы, их инварианты и представления.— М. :
Изд-во иностр. лит., 1947.— 408 с.
196. Fano U. Correlation of two excited electrons // Rept. Progr. Phys.— 1982.—
46, N 2.- P. 97—165.
197. Смирное Ю. Ф., Шитикоеа /О В. Метод /(-гармоник и модель оболочек /
Физика элем^нтар. частиц и атом. ядра.— 1977.— 8, № 4.— С. 847—910.
198. Джибути Р. #., Шитикоеа К. В. Метод гиперсферических функций в
атомной и ядерной физике,— М. : Энергоатомиздат, 1991.— 300 с.
199. Lin CD. Doubly excited states, including new classification schemes // Adv.
At. Mol. Phys.— 1986.— 22.— P. 77—142.
200. Гельфанд И. M.t Цетлин М. Л. Конечномерные представления группы
ортогональных Матриц//Докл. АН СССР.— 1950.-71, № 6.—С. 1017—1020.
201. Барут Α., Рончка Р. Теория представлений групп.—М. : Мир, 1980.—
Т. 1.-455 с; Т. 2.—395 с.
202. Холл М. Комбинаторика.—М. : Мир, 1970.—424 с.
203. Shorey Т. N., Tijdeman R. Exponential Diophantine equations.—
Cambridge : Cambridge Univ. Press, 1968.— 240 p.
204. Сеге Г. Ортогональные многочлены.— Μ. : Физматгиз, 1962.— 500 с.
205. Кныр В. Α., Пипирайте П. П., Смирнов Ю. Ф. Канонические
преобразования, «деревья» и моменты, кратные 1/4 // Ядер, физика.— 1975.— 22, № 5.—
С. 1063—1072.
206. ФлюегеЗ. Задачи по квантовой механике.— М. : Мир, 1974.— Т. 1.— 341 с;
Т. 2.- 315 с.
207. Справочник по специальным функциям / Под ред. М. Амбрамовича, И. Сти-
гана.— М. : Наука, 1979.— 830 с.
208. Никифоров А. Ф., Уваров В. Б. Основы теории специальных функций.—
М. : Наука, 1974.— 303 с.
274

209. Судаков В. В. Сферические функци и трехмерной унитарной группы и
классификация супер мул ьтиплетов // Вопросы физики элементарных частиц,— Ереван :
Изд-во АН АрмССР, 1964.—С. 117—124.
210. Гельфанд И. М., Минлос Р. Α., Шапиро3. Я- Представления группы
вращений и группы Лоренца, их применения,— М. : Физматгиз, 1958.— 368 с.
211. Филиппов Л. Ф., Овчаренко В. //., Смирнов Ю. Ф. Микроскопическая
теория коллективных возбуждений атомных ядер.— Киев : Наук, думка, 1981.— 368 с.
212. Смородинский Я- Л., Шеле пин Л. А. Коэффициенты Клебша — Горда на о
разных сторон//Успехи физ. наук.— 1972.— 106, № 1.— G. 1—45.
213. De Swart I. 1. The octet model and its Clebsch-Gordan coefficients// Rev.
Mod. Phys.— 1963.— 35, N 4.— P. 916—939.
214. Pursey D. L. Irreducible representations of the «unitary symmetry» group //
Proc. Roy. Soc. London. Α.— 1963.— 275, N 1361.— P. 284—294.
215. Moshinsky At. M. Wigner coefficients for the SU3 group and some
applications // Rev. Mod. Phys.— 1962.— 34, N 4.— P. 813—828.
216. Hecht /(. T. SU (3) recoupling and fractional parentage in 2s—Id shell // Nucl.
Phys.—1965.—62, N 1.—P. 1—36.
217. Kuriyan I. K., Lurie D., Macfarlane A. J. Algebraic tabulation of Clebsch-
Gordan coefficients of SU3 for the product (λ, μ) ® (1.1) of representations of SUSII
3. Math. Phys.— 1965.—6, N 5.—P. 722—733.
218. Carter /. C, Coyne /. /. SU (6) Clebsch-Gordan coefficients for the product
35 X 70 // Ibid.— 1969.— 10, N 7.— P. 1204—1210.
219. Carter /, C, Coyne I. /., Meshkov S.SU (6) Clebsch-Gordan coefficients for
the product 35 X 56 // Phys. Rev. Lett.- 1965.— 14, N 13.— P. 523—526.
220. Mc Namee P., Chilton S. /., Chilton F. Tables of Clebsch-Gordan coefficients
of SU3/I Rev. Mod. Phys.— 1964.— 36, N 4.— P. 1005—1024.
221. Hecht К. Т., Sing Chin Pang. On the Wigner supermultiplet scheme // J. Math.
Phys.— 1969.— 10, N 8.— P. 1571—1616.
222. Asherova R. Α., Smirnov Yu. F. Projection operators and Clebsch-Gordan
coefficients for the group SU (3) // Nucl. Phys. В.— 1968.— 4, N 4.— P. 399—412.
223. Гусева И. С, Смирнов Ю. Φ., Толстой В. Н., Харитонов Ю. И.
Коэффициенты Клебша—Гордана группы SU (3). 1. Маркировка базисных состояний и явный
вид коэффициентов Клебша—Гордана в каноническом базисе.— Л., 1981.— 42 с,—
(Препр./ АН СССР. Ленингр. ин-т ядер, физики; № 678).
224. Гусева И. С, Смирнов Ю. Ф., Толстой В. Н., Харитонов Ю. И.
Коэффициенты Клебша—Гордана группы SU (3). 2. Ортогонализация и свойства
симметрии.— Л., 1983.— 33 с— (Препр./ АН СССР. Ленингр. ин-т ядер, физики; № 837).
225. Гусева И. С, Смирнов Ю. Ф., Толстой В. Н., Харитонов Ю. И.
Коэффициенты Клебша — Гордана группы SU (3). 3. Неканоническая редукция SU (3) :э
=э 50(3).— Л., 1984.—35 с—(Препр./АН СССР. Ленингр. ин-т ядер, физики;
Nb 999).
226. Смородинский Я. А. Унитарная симметрия элементарных частиц // Успехи
физ. наук.— 1964.—84, № 1.—С. 3—36.
227. Бейтман Г., Эрдейи А. Таблицы интегральных преобразований.— М. :
Наука, 1970.— Т. 2.— 384 с.
228. Норвайшас Э. 3., Алишаускас СИ. Изоскалярные множители для
связывания симметричных представлений ортогональных групп // Литов. физ. сб.— 1974.—
14, № 5.—С. 715—725.
229. Бейтман Г., Эрдейи А. Высшие трансцендентные функции.— М. : Наука,
1973.- Т. 1.-294 с.
230. Кузнецоь Г. И., Смородинский Я. А. Г-коэффициенты и 6/-символы.— М.,
1976.— 10 с— (Препр./ Ин-т атом, энергии; № 2659).
231. Юцис А П., Бандзайтис А. А. Теория момента количества движения в
квантовой механике.— Вильнюс: Минтис, 1965.— 463 с.
232. Морс Ф. М., Фешбах Г. Методы теоретической физики.— М,: Изд-во иностр.,
лит.,— 1958—1960.— Т. 1.- 1958.— 930 с; Т. 2.— I960.— 886 с.
233. Baily W. W. Generalized hypergeometric series,— Cambridge: Univ. Press,
1965.- 220 p.
234. Кузнецов Г. И., Смородинский Я- А. Вырожденные Г-коэффициенты и их
связь с 3/-символами и D-функцией Вигнера// Ядер, физика,— 1977,—- 25, № 2.—
С 447-449.
1Я*
275

235. Biedenharn L. С, Blatt L M., Rose Μ. Ε. Some properties of Racah
coefficients // Rev. Mod. Phys.— 1952.— 24, N 2.— P. 249—263.
236. Biedenharn L. С identity which satisfied by Racah coefficients//J. Math.
Phys.- 1953.— 31, N 2.- P. 287—290.
237. Elliot J. P. Theoretical studies in nuclear structure. V // Proc. Roy. Soc.
London. Α.— 1953.— 218, N 3.— P. 345—357.
238. Харари Ф. Теория графов.— М. : Мир, 1973.— 304 с.
239. Болтянский В. Г., Ефремович В. А. Очерк основных идей топологии // Мат.
проев.— 1957.— 2.— С. 3—34.
240. Freedman D. Z., Wang 1. Μ. Ο (4) symmetry and Regge-pole theory // Phys.
Rev.— 1967.—160, N 5.—P. 1560—1571.
241. Немец О. Φ., Неудачин В. Г., Рудчик А. Т. и др. Нуклонные ассоциации в
ядрах и реакции многону клон ной передачи.— Киев : Наук, думка, 1988.— 488 с.
242. Клепиков Н. Я. Перестройки в системе трех частиц // Ядер, физика.—
1974.— 19, № 2.—С 462—471.
243. Неудачин В. Г., Смирнов Ю. Ф. Нуклонные ассоциации в легких ядрах,—
М. : Наука, 1969.—414 с.
244. Kurdyumov /. V., Smirnov Yu. F., Shitikova /С. V. et. Translationally
invariant shell model //Nucl. Phys.— 1970.—145, N 2.—P. 593—612.
245. Smirnov Yu. F. Talmi transformation for particles with different masses //
ibid.—1961,—27, N 1.—P. 177—184.
246. Horie H. Representations of the symmetry group and the fractional parentage
coefficients//J. Phys. Sol. Japan.—1964.—19, N 10.—P. 1783—1799.
247. Verhaar B. F. Transformation brackets for harmonic oscillator states // Phy-
sica Α.— I960.— 2β, Ν 12.— P. 1045—1046.
248. Ванагас В. В. Алгебраические методы в теории ядра.— Вильнюс : Минтис»
1971.—378 с.
249. Эдмондс А. Угловые моменты в квантовой механике // Деформация атомных
ядер.— М. : Изд-во иностр. лит., 1958.— С. 305—352.
250. Shapiro J. Matrix representation of the angular momentum projection opera-
top//J. Math. Phys.— 1965.—6, N 11.—P. 1680—1691.
251. Кампе Ж. Φ., Кемпбелл Р., Петьо Г.$ Фогель Т. Функции математической
физики.— М. : Физматгиз, 1963.— 102 с.
252. Михелашвили Т. #. Расчет обобщенных коэффициентов Тальми — Мошин-
ского — Смирнова.—Тбилиси, 1985.—24 с—(Препр./АН ГССР. Ин-т физики;
ЯФ-1).
253. Raynal /., Revai I. Transformation coefficients in the hyperspnrical
approach to the three-body problem // Nuovo Cim.— 1970.—68, № 4.— P. 612—622.
254. Джибути P. Я., Томчинский В. Ю.м Шубитидзе Я. Я. Коэффициенты
преобразования в гиперсферическом подходе к проблеме четырех тел с неравными
массами // Ядер, физика.— 1973.— 18, № 6.—С. 1164—1172.
255. Олевский М. Я. Триортогональные системы в пространствах постоянной
кривизны, в которых уравнение А2и + Хи = 0 допускает полное разделение
переменных // Мат. сб.— 1950.— 27 (69), № 2.— С. 379—426.
256. Каплан Я. Г. Симметрия многоэлектронных систем.— М. : Наука, 1969.—
407 с.
257. Курдюмов И. В., Смирнов Ю. Ф., Шитикова К- В. О связи трансляционно-
инвариантной модели оболочек с методом /(-гармоник // Теорет. мат. физики.—
1971.— 7, № I.—С. 45—55.
258. Ванагас В. В., Петраускас А. К., Янкаускас /С. Я. Связь между
матричными элементами метода /(-гармоник и модели схемы U (3(Л—1)) // Ядер, физика.—
1971.— 14, JSIb 4.—С. 724—733.
259. Лейн Л. Теория ядра.— М. : Атомиздат, 1967.— 253 с.
260. Мошинский Μ. Μ. Гармонический осциллятор в современной физике: от
атомов до кварков.— М. : Мир, 1972.— 149 с.
261. Chacon Ε., Moshinsky M. Representations of finite C/3 transformations // Phys,
Lett.— 1966.— 23, N 10.— P. 567—569.
262. Levi D.t Moshinsky M. Relations between hyperspherical and harmonic-
oscillator many-body matrix elements//Nuovo Cim.—J974,— 20, N 1.—
P. 107—114,
276

263. Базь А, И., Гринь Ю Г., Демин В. Ф., Жуков Μ. В. Некоторые
приложения метода К-гармоник к расчету свойств атомных ядер // Физика элементар.
частиц и атом, ядра.— 1974.—3, вып. 2.—С. 275—317.
264. Лаврентьев Μ. Α., Шабат Б. В. Методы теории функций комплексного
переменного.—М. : Наука, 1987.—688 с.
265. Крупенникова Н. Б., Саркисян Л. Л. Методика расчета коэффициентов
преобразований и симметризации гиперсферического базиса для четырех и пяти тел.—
Тбилиси, 1989.— 52 с— (Препр./ АН ГССР. Ин-т физики; Кя ЯФ-21).
266. Наймарк М. А. Линейные представления группы Лоренца.— М. : Физмат-
гиз, 1958.— 376 с.
267. Wick G. С. Angular momentum states for three relativistic particles // Ann.
Phys.— 1962.— 18, N 1.—P. 65—80.
268. Trueman T. L., Wick G. С Crossing relations for helicity amplitudes //Ibid.—
1964.— 26, N 3.— P. 322—335.
269. Смородинский Я- А. Кинематика и геометрия Лобачевского // Атом,
энергия.— 1963— 14, № 1.—С. 110—121.
270. Ванагас В. В. Алгебраические основы микроскопической теории ядра—
М. : Наука, 1988.—264 с.
271. Либерман Μ. Α., Макаров А. А. Инвариантные разложения на конусе и
унитарные преобразования амплитуд // Ядер, физика.— 1969.—9, №6.— С. 1314—1325.
272. Strom S. Some remarks on the decomposition of a unitary representation of
the Lorentz group with respect to representations of non-compact subgroups // Ark.
Fys.— 1967.— 34, N 19.— P. 215—225.
273. Delburgo R.0 Koller K-> Mahanta P. On transformations between baesis vc-
tors of unitary SL2C representations//Nuovo Cim. Α.— 1967.—52, N 4.—P. 1254.
274. Akyeampong D. Α., Boyce /. F., Rushid M. A. On the transformations from
03 to 02 , bases in SL2C II Ibid.— 1968.— 53, N 3.— P. 737—744.
275. Lomont I. S., Moses Μ. Ε. Simple realizations of the infinitesimal generators
of the proper orthochronous inhomogeneous Lorentz group for mass zero //J. Math.
Phys.— 1962.— 3, N 3.— P. 405—418.
276. Любошиц В. Л., Смородинский Я· А. Ковариантное разложение
электромагнитного поля // Журн. эксперим. и теорет. физики.— 1962.— 42, № 3.—
С. 846—856.
277. Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. Я. Релятивистская
квантовая теория.— М. : Наука, 1968.— 480 с.
278. Берестецкий В. Б. Электромагнитные поля мультиполей // Журн.
эксперим. и теорет. физики.— 1947.— 17, № 1.—С. 12—18.
279. Берестецкий В. Б., Долеинов А. 3., Τ ер-Мартиросян К- А. Угловые
волновые функции частиц со спином // Там же.— 1950.— 20, № 6.— С. 527—537.
280. Ахиезер А. И., Берестецкий В. Б. Квантовая электродинамика.— М. :
Наука, 1981.—432 с.
281. Градштейн И. С, Рыжик И. М. Таблица интегралов, сумм, рядов и
произведений.—М. : Физматгиз, 1963.— 1100 с.
282. Burnside W. Theory of groups of finite order.-Cambridge, 1911.—210 p.
283. Спенсер Э. Теория инвариантов.— Μ. : Мир, 1974.— 156 с.
284. Спрингер Т. Теория инвариантов.—М. : Мир, 1981.— 191 с.
285. Мак Вильяме Ф., Слоан Н. Теория кодов, исправляющих ошибки.— М. :
Связь, 1979*— 744 с.
286. Stanley R. P. Invariants of finite groups and their applications to
combinatorics// Bull. Amer..Math. Soc— 1979.— 1, N 3.—P. 475—511.
287. Molein T. Ober die Invarianten der linear Substitutions gruppe // Berliner
Sitzungsberichte— 1898— 11.— S. 1152—1156.
288. Бейман Б. Ф. Лекции по применению теории групп в ядерной
электронике.— М. : Изд-во иностр. лит., 1961.— 227 с.
289. Judd В., Miller W., Patera J., Winternitz P. Complete sets of commuting
operators and О (3) scalars in the enveloping algebra of SU (3) // J. Math. Phys.— 1974.—
15, N 1.—P. 1787—1799.
290. Gaskel R., Peccia Α., Sharp R. T. Generating functions for polinomial
irreducible tensors//Ibid.—1978—19, N 4—P. 727—733.
291. Patera Js, Sharp R. T. Degenerating functions for characters of group
representation and their applications//Lect. Notes in Phys,— 1979.—94,—P. 175—183.
277

292. Couture MH Sharp R. Т. Reduction of enveloping algebras of low-rank
groups// J. Phys. Α.— 1980— 13, N П.—Р. 1925—1945.
293. Gilmore R., Draayer J. P. Dynamical group chain and integrity basis //
J. Math. Phys— 1985.—26, N 12.—P. 3053—3067.
294. Giro k Υ., Couture M.$ Sharp R. T. Degenerate enveloping algebras of SU (3),
50(5), G2 and SU (4) //J. Phys. Α.— 1984.— 17, N 6.—P. 715—725.
295. Gaskell R., Sharp R. T. Generating functions for G2 characters and subgroup
branching rules // J. Math. Phys.—1981.—22, N 12.—P. 2736—2741.
296. Gaskell R., Rosensteel G.t Sharp R. 7\ Sp (6) states in an SU (3) X U (1) basis //
Ibid—P. 2732—2735.
297. Bargmann V., Moshinsky M. Group theory of harmonic oscillator. I. The
collective modes //Nucl. Phys.—1%0.—18, N 4.— P. 697—712.
298. Sharp Я. 7\, LamC.S. Internal babelling problem//J. Math. Phys—
1969.—10, N 11.—P. 2033—2038.
299. Chacon £., Moshinsky M.M Sharp R. T. U (5) =э О (5) r> О (3) and the exact
solution for the problem of quadrupole vibrations of the nucleus // Ibid.— 1976.— 17,
N 5.— P. 668—676.
300. Бор О., Моттельсон Z>. Структура атомного ядра.—М. : Мир, 1971 —
1977.— Т. 1— 1971.— 456 £.; Т. 2— 1977.— 664 с.
301. Айзенберг М., Грайнер В. Модели ядер. Коллективные явления.— М. :
Атомиздат, 1975.— 454 с.
302. Kemmer N., Pursey D. L·, Williams S. Л. Irreducible representations of the
fifth-dimensional rotation group. I//J. Math. Phys.— 1968.—9, N 8.—P. 1224—
1229.
303. Γαιϊ Ε. В. Матрицы операторов коллективной модели ядра и физический
базис группы О (5) //Ядер, физика.—1974.—19, N 1.—С. 83—92.
304. Ашерова Р. Λί., Смирнов Ю. Ф., Толстой В. Н. Проектированный базис
для многофононных систем в коллективной модели ядра.— Обнинск, 1973.— 18 с.—
(Препр./ Физ. эксперим. ин-т: № 424).
305. Asherova R. Μ., Smirnov Yu. F.t Tolstoy V. N. Projected basis for many-pho-
non system//J. Phys. G.; Nucl. Phys.— 1978.—4. N 2.—P. 205—217.
306. Racavy G. The classification of states of surface vibrations // Nucl. Phys.—
1957.— 4, N 3.—P. ,289—294.
307. Изюмов Ю. Α., Сыромятников В, Н. Фазовые переходы и симметрия
кристаллов.— М. : Наука, 1984.— 246 с.
308. Draayer J. P., Weeks К- J- Shell model description on low-energy structure
of strongly deformed nuclei//Phys. Rev. Lett.— 1983.—51, N 16.—P. 1422—1426.
309. Авраменко В. И., Ашерова P.M., Смирнов Ю. Φ., Филиппов Г. Φ.
Феноменологический гамильтониан модели SU (3) и спектр ядра 164Ег // Изв. АН СССР.
Физика.— 1986.—50, N 1.—С. 100—105.
310. Ашерова Р. М., Жилинский Б. И., Павлов-Beревкин В. Б., Смирнов Ю. Ф.
Эффективные гамильтонианы и теория инвариантов.— Киев, 1988.— 29 с.—
(Препр./ АН УССР. Ин-т теорет. физики; № 88-70 Р).
311. Гуфан Ю. М. Структурные фазовые переходы.— М. : Наука, 1982.— 304 с.
312. Michel L. Invariants polynomiaux des groups de symmetric moleculaire et
crystallographique // Proc. 5th Intern. Coloq. Group theoretical Methods in Physics.—
New York: Acad. Press, 1977.—P. 75—91.
313. Michel L. Symmetric en physique//Comptes rendus.— 1985.—2, N 1.—
P. 27—36.
314. Basu D., Wolf /С. В. The unitary irreducible representations of SL (2, R) in all
subgroup reductions//J. Math. Phys.—1982.—23, N 2.—P. 189—205.
315. Basu D.> Wolf /(. B. The Ciebsch — Gordan coefficients of SL (2, R) in the
parabolic basis//Ibid.—1983—24, N 1—P. 55—65.
316. Basu D., Wolf K- B. The Ciebsch — Gordan coefficients of the
three-dimensional Lorentz algebra in the parabolic basis // Ibid.— N 3.— P. 478—500.
317. Frank Α.ι Wolf /C. B. Lie algebras for potential scattering//Phys. Rev.
Lett.— 1984.— 52, N 12.— P. 1737—1740.
318. Frank Α., Wolf К- В. Lie algebras for system with mixed spectra. I. The
scattering Poshel Teller potential II 3. Math. Phys.— 1985.—26, N 6.—P. 973—985.
319. Alhassid 7.t Gursey F.p I ache Ι ίο F. Group theory Approach to scattering. I //
Ann. Phys,—1983,—148, N 2.—P. 346—350.
278

320. Alhassid Υ., Gursey F., Iachello F. Group Theory Approach to Scattering. II //
Ibid.—1986—167, N 1.—P. 181—195.
321. Wu J., Iachello F., Alhassid Y. Group theory approach to scattering. HI.
Realistic Models // Ibid— 1987— 173, N 1— P. 68—87.
322. Боголкбэв //. //., Логунов Α. Α., Оксак А. //., Тодоров И. Т. Общие
принципы квантовой теории поля.— М. : Наука, 1987.— 616 с,
323. Менский М. Б. Метод индуцированных представлений: пространство—
время и концепция частиц.— М. : Наука, 1976.— 228 с.
324. Kihlberg Α., Muller V., Halbwacks F. Unitary Irreducible Representations
of SU (2, 2) // Commun. Math. Phys— 1966— 3, N 3— Ρ 194—217.
325. Macfadyen N. W- Conformal group in a Poincare ba is. I. Principal
continuous series//J. Math. Phys— 1971— 12, N 8—P. 1436—1450.
326. Macfadyen Ν. ψ. On the nondegenerate complementary series of representa^
tions of the group SU22 II Nuovo Cim. A— 1972— 10, N 2— P. 268—276.
327. Москалюк С. С. Системы уравнений ньютоновской механики, инвариантные
относительно основных групп симметрии // Теоретико-алгебраические исследования
в математической физике.— Киев : Ин-т математики АН УССР, 1981.— С. 74—76.
328. Москалюк С. С, Шелест В. П. Теоретико-групповые модели
нерелятивистских динамических систем // Тр. III Междунар. семинара «Теоретико-групповые
методы в физике».— М. : Наука, 1986.— Т. 2.— С. 222—229.
329. Верлань Α. Φ.β Москалюк С. С. Математическое моделирование непрерывных
динамических систем.— Киев : Наук, думка, 1988.— 288 с.
330. Lie S. Uber die Integration durch bestimmte Integrate von einer Klasser li-
neare partiellen Differentialgleichungen//Arch. Math.—1981.—6, N 3.—S. 328—
368.
331. Niederer U. The maximal kinematical invariance group of the free SchrOdinger ·
equation // Helv. phys. acta.— 1972.— 45, N 5.— P. 802—810.
332. Bargmann V. On unitary ray representations of continuous groups // Ann.
Math — 1954— 69, N 1—P. 1—46.
333. Voisin I. On some unitary representations of* the Galilei group. Irreducible
representations//J. Math. Phys.—1965.—6, N 10—P. 1519—1529.
334. Кемпфер Ф. Основные положения квантовой механики.— М. : Мир, 1967.—
391 с.
335. Воуег С. P. Conformal symmetry of the Hamilton—Jacobi equation and
quantization // Nuovo Cim. В.— 1976— 31, N 2.— P. 195—210.
336. Овсянников Л. В. Групповой анализ дифференциальных уравнений.— М. :
Наука, 1978.—400 с.
337. Ибрагимов Н. X. Группы преобразований в математической физике.— М. :
Наука, 1983.— 280 с.
338. Bluman G. W-, Cole J. D. Similarity methods for differential equations-
New York etc.: Springer — Verl, 1974.— 332 p.
339. Виноградов А. М., Красильщик И. С., Лычагин В. В. Введение в геометрию
нелинейных дифференциальных уравнений.— М. : Наука, 1986.— 336 с.
340. Symmetries of partial differential equations: conservation laws —
applications — algorithms // Ed. by A. M. Vinogradov.— Dordrecht etc.: Kluwer Acad. Publ.,
1989—449 p.
341. Олвер П. Приложения групп Ли к дифференциальным уравнениям.—М. :
Мир, 1989—639 с.
342. Эйзенхарт Л. Я. Непрерывные группы преобразований.— Μ : Изд-во
иностр. лит., 1947.— 359 с.
343. Москалюк С. С. Базисы дифференциальных инвариантов группы Галилея
и ее подгруппы // Тез. докл. Всесоюз. науч.-техн. конф. «Моделирование-85»:
Теория, средства, применение.— Киев : ИПМЭ АН УССР, 1985.— Ч. 1.—С. 54—56.
344. Москалюк С. С. О некоторых точных оешениях нелинейного уравнения
Шредингера//Укр. физ. журн— 1981— 26, Ν*6— С. 1045—1046.
345. Москалюк С. С. О некоторых точных решениях уравнений Гамильтона —
Якоби // Тр. III Междунар. семинара «Теоретико-групповые методы^в физике».— М. :
Наука, 1986—Т. 2—С. 329—337.
346. Москалюк С. С. О некоторых точных решениях системы нелинейных
уравнений Шредингера в трехмерном пространстве // Теорет. и мат. физ%— 1987.— 72,
N 2.—С. 172—182.
279

347. Фущич В. И., Штелень В. М., Серов Н. И. Симметричный анализ и точные
решения нелинейных уравнений математической физики.— Киев : Наук, думка,
1989 — 336 с.
348. Moskaliuk S. S. Group-theoretical models of nonrelativistic and relativis-
tic'dynamical systems.— Kiev, 1992.— 28 p.— (Prepr./ AS Ukraine, Int. Ther. Phys.;
Mb 92).
349. Ганжа В. Г., Мелешко 0. В., Москалюк С. С. и др. Применение системы
I.EDUCE для анализа совместности систем дифференциальных уравнений.— Киев,
1990—26 с— (Препр./ АН УССР. Ин-т теорет. физики; № 90-84Р).
350. Ganzha V. G.t Melcshko S. V., Shelest V. P. Application of REDUCE system
for analysing consistency of systems of PDE'S // Proc. of ISSAC90— New York:
Addison — Wesley Publ. Сотр. 1990— P. 301—348.
351. Hearn A. C. REDUCE users manual: ver. 3.3.CP 78.— Santa Monica: The
Rond Corporation, 1987.— 230 p.
352. Marti У. В., Griss M.> Griss С Standart Lisp report // ACMSIGPLAN
Notices.— 1979.— 14, N 10— P. 48—68.
353. Базисный РЕФАЛ и его реализация на вычислительных машинах.— М. :
ЦНИПИАСС, 1977— Вып. У-40— 258 с.
354. Сидоров А. Ф., Шапеев В. П., Яненко Η. Н. Метод дифференциальных
связей и его приложения в газовой динамике.— Новосибирск : Наука, 1984.— 272 с.
355. Hill J. Μ. Solution of differential equations by means of one-parameter
groups.— Boston ect.: Pitman Advanced Publ. Program, 1982.— 161 p.
356. Мелешко С. В. Дифференциальные связи и одно параметрические группы
преобразований Ли — Беклунда//Докл. АН СССР.—1983.—271, N 1.—С. 42—46.
357. Картан Э. Внешние дифференциальные формы и их геометрические
приложения.— М. : Изд-во Моск. ун-та, 1962.— 231 с.
358. Фиников С. Я. Метод внешних форм Картана в дифференциальной
геометрии.— М. ; Л. : Гостехиздат, 1948.—348 с.
359. Riquer С. Н. Les systemes d'equations aux derivees partielles.— Paris: Ga-
uthier — Villars, 1910— 390 p.
360. Janet M. Legons sur les systemes d'equations aux derivees partielles.—
Carriers scientifiques, fax IV.—Paris : Gauthier—Villars, 1929.— 190 p.
361. Kuranishi M. Lectures on involutive systems of partial differential equations.—
Sao Paulo: Publ. Soc. Math., 1967—Vol. 77— 121 p.
362. Поммаре Ж. Системы уравнений с частными производными и псевдогруппы
Ли— М. : Мир, 1983— 400 с.
363. Шурыгин В. Α., Яненко Н. Н. О реализации на
электронных,вычислительных машинах алгебраическо-дифференциальных алгоритмов // Пробл.
кибернетики.— 1961.—Вып. 6.—С. 33—43.
364. Арайс Е. A.t Сибиряков Г. В. Авто-Аналитик.— Новосибирск : Изд-во
Новосиб. ун-та, 1973.— 285 с.
365. Арайс Ε. Α., Шапеев В. П., Яненко Η. Η. Реализация метода внешних форм
Картана на ЭВМ//Докл. АН СССР—1974—214, N 4—С. 737—738.
366. ТопуновВ. Л. Применение ЭВМ к исследованию пфаффовых систем // Числ,-
методы механики сплошной среды.— 1983.—14, N 3.— С. 150—158.
367. Ганжа В. Г., Мелешко С. В., Мурзин Ф. А. и др. Реализация на ЭВМ
алгоритма исследования на совместность систем уравнений в частных производных //
Докл. АН СССР— 1981—261, № 5—С. 1044—1046.
368. Schwarz F. Symmetries and involution systems: some experiments in
computer algebra // Proc. Oberwolfach Meeting on Nonlinear Evolution Equations, Summer,
1986 /Ed. by M. Ablowitz et al— Singapore : World Sci. Press, 1987— P. 290—299.
369. Ганжа В. Г., Мелешко С. В., Шапеев В. П. Промежуточные выкладки в
аналитических исследованиях дифференциальных vpaBHeHHn на ЭВМ //
Моделирование в механике.— 1989.— 3 (20), № 4.—С. 49—58.
370. Грошева М. В., Ефимов Г. Б., Брумберг В. А. и др. Системы аналитических
вычислений на ЭВМ (аналитические пакеты прикладных программ).— М., 1983.—
65 с— (Препр./ АН СССР. Ин-т прикл. математики, № 1).
371. Пакеты прикладных программ. Аналитические преобразования.— М. :
Наука, 1988.— 156 с.— (Сер. «Алгоритмы и алгоритм, языки»).
372. ПаламоОов В, П. Линейные дифференциальные операторы с постоянными
коэффициентами— М, ; Наука, 1967,— 487 с.
280

373. Самборский С. Η. О задаче Коши для инволютивных систем уравнений с
частными производными // Дифференц. уравнения.— 1980.— 16, № 3.— С. 516—521.
374. Чеботаревский Б. Д. Категория дифференциальных уравнений на
многообразиях //Дифференц. геометрия многообразий фигур.— 1979.— № 10.— С. 148—
153.
375. Goldschmidt Η. Integrability criteria for systems of non-linear partial
differential equations// J. Differ. Geom.— 1969.— 1, N 5.—P. 269—307.
376. Janet H. Sur les systemes d'equations aux derivees partielles // J. Math,
pnres et appl.— 1920 — 3, N 1.— P. 65—151.
377. Riit J. F. Differential algebra.— Dover, 1966.— 70 p.
378. Spencer D. С Overdetermined systems of linear partial differential
equations//Bull. Amer. Math. Soc— 1965— 75, N 1.—P. 1—114.
379. Tomas J. M. Riquier's theory//Annals of Math.— 1929.—30, N 1,—
P. 120—163; 1934.— 35, N 5.— P. 730-820.
380. Guillemin V., Kuranishi M. Some algebraic results concerning involutive
subspaces//Amer. J. Math.—1968.—40, N 4.—P. 1307—1320.
381. Мелешко С. В. К классификации плоских изэнтропических течений газа
типа двойной волны // Прикл. математика и механика.— 1985.— 49, № 3.—
с. 406—410.
382. Akritas A. G. Elements of computer algebra with applications.— New York :
Wiley Intersci. publ., 1989.—425 p.
383. Lie S., Scheffers G. Vorlesungen uber-Differentialgleichungen mit bekann-
ten infinitesimalen Transformationen.— Leipzig : Teubner, 1891.— 568 s.
384. Schwarz F. Symmetries of differential equations: from Sophus Lie to
computer algebra // SIAM Rev.— 1988.—30, N 3.—P. 450—481.
385. Schwarz F. Programming with abstract data types: the symmetry packages
SODE -and SPDE in Scratchpad // Lect. Notes in Comput. Sci.— 1988.— 296.—
P. 167—176.
386. Tresse A. Sur les invariants differentiels des groupes continus de
transformations // Acta math.— 1894.— 18, N 3.— P. 1—88.
387. Москалюк С. С, Нестерук А. В., Притоманов С. А. Редуцированные
уравнения поля и интегралы движения в анизотропном пространстве.— Киев,
1990.— 20 с— (Препр./ АН УССР. Ин-т теорет. физики; № 90-40Р).
388. Москалюк С. С, Нестерук А. В., Притоманов С. А. Решение уравнений
поля и интегралы движения массивных спинорных и векторных полей в
анизотропном пространстве.— Киев, 1990.— 17 с— (Препр./ АН УССР. Ин-т теорет.
физики; № 90-79Р).
389. Гриб Α. Α., Мамаев С. Г.» Мостепаненко В. М. Вакуумные квантовые
эффекты в сильных полях.— М. : Энергоатомиздат, 1988.— 288 с.
390. Зельдович Я· В., Старобинский А. А. Рождения частиц и поляризация
вакуума в анизотропном гравитационном поле // Журн. эксперим. и теорет. физики.—
1971.—61, № 6.—С. 2161—2175.
391. Притоманов С. А. Рождение безмассовых фермионов в космологической
модели первого типа по Бианки // Изв. вузов. Физика.— 1984.— 1, № 1.— С. 35—40.
392. Гриб Α. Α., Нестерук А. В. Рождение частиц и тензор энергии —
импульса в анизотропном пространстве-времени // Ядер, физика.— 1983.— 38, №5(11).—
С. 1357—1366.
393. Зельдович Я- В., Хлопов М. Ю. Масса нейтрино в физике элементарных
частиц и космологии ранней Вселенной // Успехи физ. наук.— 1981.— 135, № 1.—
С. 45—77.
394. Притоманов С. А. Квантовые эффекты в анизотропных космологических
моделях // Исследования по классической и квантовой теории гравитации.—
Днепропетровск : ДГУ, 1985.—С. 75—81.
395. Померанчук И. Я· Равенство полных сечений взаимодействия нуклонов
и антинуклонов при больших энергиях // Журн. эксперим. и теорет. физики.—
1958.—34, № 3.— С. 7^5—736.
396. Мейман И. И. Причинность и асимптотические амплитуды рассеяния
мезона на нуклоне//Вопр. физики элементар. частиц.— 1964.— 4.—С. 258—281.
397. Берестецкий В. Б. Динамические свойства элементарных частиц и теория
матрицы рассеяния//Успехи физ. наук.— 1962.—26, № 1,—С, 25—77,
281

398. Логунов Α. Α., Нгуен Ван Хьёу, Тодоров И. Т., Хрусталев О. А.
Асимптотические соотношения между сечениями в локальной теории поля // Журн. экспе-
рим. и теорет. физики.-- 1964.— 46, № 3.—С. 1079—1089.
399. Логунов Α. Α., Нгуен Ван Хьеу, Тодоров И. Т. Асимптотические
соотношения между амплитудами рассеяния в локальной теории поля // Успехи физ. наук.—
1966.—88, № 1 —С. 51—91.
400. Винтернитц П., Смородинский Я- Α., Шефтель М. Б. Пуанкаре-лоренц-
инвариантные разложения релятивистских амплитуд // Ядер, физика.— 1968.—
7, № 6.—С. 1325—1338.
401. Либерман М. А. 0(3, 1)-разложение амплитуды рассеяния и полюса
Редже//Там же.— 1969.— 10, № 4.—С. 881—882.
402. Волков Д. В., Грибов В. И. Полюса Редже в амплитудах нуклон-нуклон-
нош и нуклон-антинуклонного рассеяния // Журн. эксперим. и теорет. физики.—
1963 — 44, № 3.—С. 1068—1077.
413 Goldberger Μ. L., Jones С. Ε. Analyticity constraints on unequal-mass
Regge formulas 7/Phys. Rev.— 1966.— 150, N 4.—P. 1269—1275.
404. Freed!, a> D., Wang I. Regge poles and unequal-mass scattering processes//
Ibid — 1967.— 153, N 5.—P. 1596—1609.
405. Freedman D., Jones С Ε., Wang I. Daughter trajectories and unequal-
mass scattering // Ibid.— 155, N 5.— P. 1645—1647.
406. Domocos G. Four-dimensional symmetry // Ibid.— 159, N 5.— P. 1387—
1403.
407. Freedman D., Wang /.0(4) symmetry and Regge-pole theory//Phys. Rev.
Lett.— 1967.— 18, N 20.— P. 863—867.
408. Domocos G. Approximate four-dimensional symmetry and hadron
spectroscopy//Phys. Lett. В.— 1967.— 24, N 6.—P. 293—296.
409. Durand L. Regge poles in the scattering of particles of unequal-mass.
Remark on a paper of Freedman and Wang // Phys. Rev.— 1967.— 154, N 5.— P. 1537—
1539.
410. Regge T. Introduction to complex orbital momenta // Nuovo Cirn.— 1959.—
14, N 5.—P. 951—976.
411. Либерман Μ. А. О полюсах Редже при рассеянии в кулоновском поле//
Ядер, физика.—1969.—9, № 3.—С. 655—667.
412. Goldberger Μ. L·., Grisary M. Т., MacDowell S. Μ.β Wang D. Theory of
low-energy nucleon-nucleon scattering// Phys. Rev.— 1960.— 120, N 6.— P. 2250—
2276.
413. Mutter Κ- Η. Veneziano model for nucleon-nucleon and nucleon-antinuc-
leon scattering. Ϊ//Z. Phys.— 1970.—239, N 1.—P. 30—41.
414. Смородинский Я- А. К теории спиральных амплитуд // Журн. эксперим.
и теорет. физики.—1963.—45, №3(9).-С. 604—609.
415 Marinov Μ. S.> Roginsky V. I. Crossing-relations for helicity scattering
amplitudes// Nucl. Phys.—1963.—49, N 2.—P. 251—256.
416. Atkinson O. A. Crossing Symmetry for Helicity Amplitudes.— CERN,
1964.-. 30 p.
417. Сурков Ε. Л. К теории кросс-симметрии и спиральных амплитуд// Ядер,
физика — 1965.— 1, № 6.—С. 1113—1120.
418. Fotiadi D.$ Froissart M., Lascoux I., Pham F. Applications of an isotopy
theorem // Topology.— 1965.—4, N 2.— P. 159—191.
419. Хуа Р., Теплиц В. Гомология и фейнмановские интегралы.—Μ. : Мир,
1969—223 с.
420. Pham F. Formules de Picard-Lefschetz generalisees et ramification des inte-
grales//Buil. Soc. Math. France.—1965—93, N 4—P. 333—367.
421. Pham F. Introduction a I'Etude topologique des singularites de Landau.—
Paris : Gauthier—Villar,1967— 120 p.
422. Хилтон П., Уайдли С. Теория гомологии. Введение в алгебраическую
топологию.— М. : Мир, 1966.— 452 с.
423. Ландау Л. Д. Об аналитических свойствах вершинных частей в
квантовой теории поля // Журн. эксперим. и теорет. физики.— 1959.— 37, № 1 (7).—
С. 62—70.
424. Cartan Ε. Oeuvres completes.— Paris : Gauthier—Villar, 1952.— Vol. 1,
pt 1.—P. 569—1356.
282

425. Boy ling I. В. Construction of vanishing cycles for integrals over hypersphe-
res//J. Math. Phys.— 1966.— 7, N 10.—P. 1749—1763.
426. Шапиро И. С. К дисперсионной теории прямых ядерных реакций // Журн.
эксперим. и теорет. физики.— 1961.— 41, №5(11).— С. 1616—1627.
427. Блохинцев JI. Д., Долинский Э. И., Попов В. С. Аналитические свойства
нерелятивистских диаграмм//Там же.— 1962.— 42, № 6.— С. 1636—1646.
428. Кузнецов Г. И. О характере сингулярностей некоторых однопетлевых
нерелятивистских диаграмм // Ядер, физика.— 1971.— 13, № 1.— С. 212—215.
429. Danilov Υ и. Α., Kuznetsov G. /., Smorodinsky Ya. A. Study of analytical
properties of pentagon Feynman graphs by homological method.— Dubna, 1969.—
22 p.- (Prepr. /J1NR; E2-4717).
430. Brown L. M. Analytic properties of η-point loops in perturbation theory //
Nuovo Cim.— 1961.—22, N 1.— P. 178—182.
431. Бровман Ε. Г., Каган Ю. Об особенностях многохвостных кольцевых
диаграмм для ферми-систем//Журн. эксперим. и теорет. физики.— 1972.— 63,
№5 (11).— С. 1937—1949.
432. Колкунов В. Α., Окунь Л. Б., Рудык А. П. Особые точки некоторых фейн-
мановских диаграмм // Там же.— 1960.— 38, № 3.— С. 877—881.
433. Taylor I. С. Analytic properties of perturbation expansions. // Phys. Rev.—
I960.— 117, N 1.—P. 261—275.
434. Eden R. I. Analytic structure of collision amplitudes in perturbation
theory // Ibid.— 119, N 5.— P. 1763—1783.
435. Tanki I. Analyticity of fourth order scattering amplitude with two complex
invariants//J. Math. Phys.— I960.— 1, N 2.— P. 149—163.
436. Cutcoski R. E. Singularities and discontinuities of Feynman amplitudes //
Ibid.— N 5.— P. 429—433.
437. Грибов В. Н., Данилов Г. С, Дятлов И. Т. Аналитические свойства
квадратной диаграммы с нераспадными массами // Журн. эксперим. и теорет.
физики.— 1961.-41, № 3(9).— С. 924—936.
438. EdenR. I., Landshoff P. V., Polkinghorne J. С, Taylor I. C. Acnodes and
cusps on Landau curves//J. Math. Phys.— 1961.— 2, N 5.— P. 656—670.
439. Симонов Ю, А. Многократные дисперсионные соотношения // Журн.
эксперим. и теорет. физики.— 1962.—43, № 6 (12).—С. 2263—2272.
440. Fairlie D. В., Landshoff P. V.> Nuttal /., Polkinghorne I. С.
Singularities of the second type //J. Math. Phys.— 1962.— 3, N 3.— P. 594—605.
441. Fairlie D. В., Landshoff P. V.t Nuttal J., Polkinghorne J. C.
Physical sheet properties of second type singularities // Phys. Lett.— 1962.— 3, N 1.—
P. 55—56.
442. Симонов Ю. А. Интегральное представление квадратной диаграммы с
аномальным соотношением масс//Журн. эксперим. и теорет. физики.— 1963.— 44,
№ 5.—С. 1622—1627.
443. Eden R. /., Landshoff P. V., Olive D. /., Polkinghorne J. С The
analytic S-matrix.— Cambridge : Univ. Press, 1966.—210 p.
444. Federbush P. Calculation of some homology groups relevant to six-order
Feynman diagrams//J. Math. Phys.— 1965.—6, N 6.—P. 941—954.
445. Federbush P. Note on non-Landau singularities // Ibid.— N 5.— P. 825—
826.
446. Regge T. The fundamental group of Poincare and analytic properties of
Feynman relativistic amplitudes. Oslo, 1968.— 20 p.— Nobel Symp. Series. Ser 7.
447. Ponzano G., Regge Т., Speer E. R., Wesiwater M.J. the monodromy rings
of a class of self-energy graths // Commun. Math. Phys.— 1969.— 15, N 1.— P. 82—
90.
448. Ponzano G., Regge T. The monodromy group of one-loop relativistic
Feynman integrals.— Princeton, 1968.— 25 p.— (Prepr./ Inst, for Advanced Study;
N 2295).
449. Lascoux I. Perturbation theory in quantum field theory and nomology //
Lectures in Mathematics and Physics (Battele Rencontres, 1967) // Ed. by С. М. De
Witt et al. New York, 1967.— P. 50—125.
450. Москалюк С. С, Смирнов Ю. Φ., Шелест В. П. Теоретико-групповые
и компьютерно-алгебраические методы в физике.— Киев, 1992.—16 с— (Препр./ АН
Украины. Ин-т теорет. физики; № 92).
283

ОГЛАВЛЕНИЕ
Предисловие редактора серии ♦·* , 3
Предисловие 4
Введение * 7
Глава 1. Графическая реализация представлений ортогональных и
унитарных групп 18
1.1. Метод гиперсферических гармоник в атомной и ядерной физике ... 18
1.2. Неприводимые представления класса 1 ортогональных групп .... 22
1.3. Неприводимые представления класса 2 унитарных групп 23
1.4. Гиперсферические координаты и их графы. Теоретико-групповая
интерпретация 25
1.5. Число различных деревьев и число классов эквивалентных деревьев 28
1.6. Разделение переменных в операторе Лапласа. Угловые функции ... 31
1.7. Уравнения для ячеек и их решения 33
1.8. Примеры представлений .групп U (2), SU (2), SO (3), U (3), SU (3),
SO (4), 50(5), 50(6) 38
1.9. Некоторые свойства гиперсферических гармоник 47
1.10. Коэффициенты Клебша — Гордана ортогональных и унитарных групп 52
Глава 2. Унитарное преобразование между базисами,
соответствующими деревьям разной топологической структуры 67
2.1. Различные представления для Τ-коэффициентов 68
2.2. Симметрии Т-коэффициентов 76
2.3. Аналитическое продолжение Т-коэффициентов и 6/-, 3/-символы ... 84
2.4. Вырожденные Т-коэффициенты 89
Глава 3. Графическая теория 3/г/-коэффициентов 92
3.1. Деревья как символы сложения моментов 93
3.2. Структура 3/г/-коэффициентов 95
Глава 4. Правила сумм для бу-символов 103
4.1. Сложение пяти моментов 103
4.2. Теорема о фундаментальности 5-циклов 109
Глава 5. Матрицы конечных вращений в пространстве деревьев .... 112
Глава 6. Обобщение метода деревьев Виленкина — Кузнецова — Смородин-
ского 117
6.1. Структура волновых функций трансляционно-инвариантного осцил-
ляторного базиса в модели ядерных оболочек. Деревья Якоби .... 117
6.2. Осцилляторные функции в гиперсферических координатах 124
284

Глава 7. Функции на трехмерном гиперболоиде 145
7.1. Системы координат и собственные функции оператора Лапласа на
гиперболоиде 145
7.2. Метод орисфер , 147
7.3. Вывод формул обращения 148
7.4. Разложение функций, заданных в пространственно-подобной области 150
7.5. Разложение полей 151
Глава 8. Функции на трехмерном конусе . 155
8.1. Системы координат, полные наборы квантовых чисел и базисные
функции на трехмерном конусе 155
8.2. Матричные элементы 158
Глава 9. Построение базисов инвариантов из динамических переменных,
преобразующихся по заданному представлению компактной группы Ли . . 162
9.1. Производящие функции Молина для конечных групп 162
9.2. Производящие функции Молина для непрерывных групп 167
9.3. Обобщение производящих функций Молина 170
9.4. Комбинирование производящих функций Молина 172
9.5. Эффективные гамильтонианы 175
Глава 10. Теоретике-групповые модели 180
10.1. Алгебра инвариантности релятивистских и нерелятивистских моделей 181
10.2. Дифференциальные инварианты 184
Глава 11. Анализ совместности теоретико-групповых моделей 187
ИЛ. Математическое описание метода исследования на совместность . . . 190
11.2. Краткое описание алгоритма вычислений 196
11.3. Описание REDUCE-программы 198
Глава 12. Φ актор-системы теоретико-групповых моделей.
Фактор-уравнения поля в анизотропном пространстве-времени 202
12.1. Фактор-уравнения для скалярного поля 205
ч 12.2. Фактор-уравнения для безмассового спинорного поля 207
12.3. Фактор-уравнения для векторного безмассового поля 210
12.4. Фактор-уравнения для массивного спинорного поля 218
12.5. Фактор-уравнения для векторного массивного поля 222
Глава 13. Двухмерные разложения релятивистских амплитуд . ♦ . . . 230
13.1. Интегральные представления релятивистских амплитуд и
асимптотические теоремы 230
13.2. Связь между лоренц- и редже-амплитудами 232
13.3. Лоренц- и редже-полюсы 233
Глава 14. Парциальный анализ амплитуд JTJf~ и JTJT-рассеяния при
высоких энергиях 235
14.1. Аналитическое продолжение скалярной амплитуды из /-канала в s- и
м'-каналы 235
14.2. Разложение амплитуд по парциальным волнам и переход из канала в
канал 238
14.3. Разложение спиральных амплитуд s-канала и связь между
релятивистскими парциальными амплитудами s- и /-каналов 243
?85

Глава 15. Исследование аналитических свойств фейнмановских
амплитуд гомологическим методом 248
15.1. Стандартная форма интегралов и сингулярные поверхности
(поверхности Ландау) 250
15.2. Нерелятивистские однопетлевые 5, 4, 3-хвостки . * . 253
15.3. Релятивистская 5-хвостка 258
15.4. Собственные сингулярности однопетлевых «-угольных диаграмм Фейн-
мана 264
Список литературы
267

Научное издание
|Кузнецов Геннадий Иванович|
Москалюк Степан Степанович
Смирнов Юрий Федорович
Шелест Виталий Петрович
ГРАФИЧЕСКАЯ
ТЕОРИЯ
ПРЕДСТАВЛЕНИЙ
ОРТОГОНАЛЬНЫХ
И УНИТАРНЫХ
ГРУПП И ЕЕ ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
Художественный редактор Я. Я. Антонюк
Технический редактор Я. Я. Лукашенко
Корректоры Л. Я. Лембак, 3. А. Ерохина
Сдано в набор 10.06.91. Подп. в печ 25.05.92. Формат 60X90/16. Бум. тип. № 2. Лит. гари.
Вые. печ. Усл. печ. л. 18,0. Уел кр.-отт. 18,0. Уч. изд. л. 19,12. Тираж 1500 экз.
Зак. Ns 1—1980.
Издательство «Наукова думка». 252601 Киев 4. ул. Репина, 3.
Отпечатано с матриц Головного предприятия республиканского производственного объедг
нения «Полиграфкнига» 252057, Киев, ул. Довженко, 3 в Жовковской книжной типографии.
292310 Жовква Львовской обл.. ул. Василианская 8. Зак. 1653.

ИЗДАТЕЛЬСТВО «НАУКОВА ДУМКА»
В 1992 г.
ВЫПУСТИТ В СВЕТ КНИГУ:
Волкович В. Л., Волошин А. Ф., Заславский В. Α., Ушаков И. А. Модели и
методы оптимизации надежности сложных систем.— 20 л.— 12 р.
Авторский коллектив известных ученых Института кибернетики АН Украины,
Вычислительного центра Российской АН, Киевского университета им. Тараса
Шевченко, в течение многих лет работающих в области создания
алгоритмического и программного обеспечения для исследования и проектирования сложных
систем и преподавания, в новой книге обобщает опыт решения прикладных задач
и разработки учебных курсов. Впервые в систематизированном виде на основе
отечественной и зарубежной литературы приводятся известные,
зарекомендовавшие себя на практике модели и новые постановки задач, методы и алгоритмы
выбора структуры сложных систем по критерию надежности с учетом различных
способов резервирования и ограничений на ресурсы проектирования. Модели
последовательных систем и систем сложной структуры рассматриваются в классах
однокритериальных и многокритериальных задач дискретного и комбинаторного
программирования. Предлагаются новые методы оптимизации систем большой
размерности, многоуровневого проектирования и резервирования планирования
технического обслуживания и оптимизации состава информационных сетей,
базирующиеся на методологии последовательного анализа вариантов.
Многочисленные числовые примеры и фрагменты описания программного обеспечения носят
иллюстративный и учебный характер.
Для научных и инженерных работников в области проектирования систем,
а также преподавателей, аспирантов и студентов вузов физико-математических и
технических специальностей.
Приобретение этой книги Вам гарантирует при получении предварительного
заказа магазин издательства «Наукова думка» (252001, Киев 1, ул.
Грушевского, 4) — для киевлян, для иногородних читателей — местные книжные магазины.